Автор: Черепанов Г.П.
Теги: общая механика механика твердых и жидких тел механика физика твердого тела твердое тело
Год: 1983
Текст
Г.П. ЧЕРЕПАНОВ
МЕХАНИКА
РАЗРУШЕНИЯ
КОМПОЗИЦИОННЫХ
МАТЕРИАЛОВ
МОСКВА "НАУКА"
ГЛА&НАЯ РЕДАКЦИЯ
ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ
19 8 3
22.25
446
УДК 531
Черепанов Г. П. Механика разрушения композиционных материалов. -
М.: Наука, Главная редакция физико-математической литературы, 1983. —
296 с.
Разрушение конструкций из составных материалов с различными физичес-
физическими свойствами обладает многими специфическими особенностями, весьма
затрудняющими адекватное теоретическое описание основных механизмов их
деформирования и разрушения.
В книге излагаются на современном уровне теоретической строгости наибо-
наиболее принципиальные вопросы механики разрушения композитов: закономер-
закономерности развития и торможения трещин, армирование упругих тел сингулярны-
сингулярными элементами, оптимальное проектирование композиционных материалов.
Рассмотрены волокнистые и многослойные материалы, а также сингулярно-
армированные элементы конструкций.
Предназначена для научных работников, занимающихся механикой разру-
разрушения, а также разработкой и применением композиционных материалов.
Будет полезна также инженерам, преподавателям, аспирантам и студентам, за-
занимающимся механикой твердого тела, а также проблемами прочности и раз-
разрушения.
Табл. 60, илл. 120, библ. 203.
Геннадий Петрович Черепанов
МЕХАНИКА
РАЗРУШЕНИЯ
КОМПОЗИЦИОННЫХ
МАТЕРИАЛОВ
Редактор А.Б. Елагин
Тех. редакторы В.В. Лебедева, СВ. Геворкян
Корректоры Т.В. Обод, Т.А. Печко
ИБ№ 12152
Сдано в набор 01.02.83. Подписано к печати 30.6.83
Т-15611. Формат 60 X 90/16. Бумага тип №1
Печать офсетная. Усл.печл. 18,50. Уч.-издл. 21,01
Тираж 4 250 ЭКЗ. Тип. зак.699Цена 3 р. 50 к.
Издательство "Наука"
Главная редакция физко-математической литературы
Москва, В—71, Ленинский проспект, 15
4—я типография издательства "Наука"
630077, Новосибирск, 77, ул. Станиславского, 25
1703040000 112 ©Издательство "Наука".
1703040000-112 101^3 Главная редакция физико-
05 3 @2) -83 математической литературы, 1983
ОГЛАВЛЕНИЕ
Предисловие 4
Глава 1. Механизмы и закономерности разрушения композитов 7
§ 1. Основы механики разрушения 7
§ 2. Теория адгезии «... 28
§ ,3. Вязкость скольжения. Энергия адгезии % 41
§ 4. Торможение трещины границей раздела различных упругих сред .... 55
§ 5. Растяжение однонаправленных волокнистых композитов 66
§ 6. Развитие поперечной трещины в композите (стохастический процесс) 76
§ 7. Вязкость и энергия разрушения 83
§ 8. Сжатие однонаправленных волокнистых композитов 90
§ 9. Усталостное и коррозионное разрушение композитов 94
§ 10. Композиты с дисперсными включениями 111
Глава 2. Асимптотическая теория армирования упругих тел 129
§ 1. Общий метод. . . - ; 129
§ 2. Инвариантные Г-интегралы в особых точках и на особых линиях
поля (теория Г-вычетов) 135
§ 3. Точечные соединения пластин, оболочек и трехмерных тел 145
§ 4. Передача усилий в стержни, армирующие оболочку или пластину . . . 159
§ 5. Расчет клепаных панелей 178
§ 6. Один аналог задачи Койтера. . . . 183
§ 7. Армирование трехмерных тел стержнями . . . 190
Глава 3. Оптимальное проектирование некоторых композиционных материа-
материалов на основе механики разрушения 206
§ 1. Введение 206
§ 2. Однородные пластины максимальной долговечности 217
§ 3. Оптимальное проектирование многослойных пластин (непрерывная
задача) 228
§ 4. Оптимальное проектирование многослойных пластин (дискретная
задача) 247
§ 5. Многослойные пластины и оболочки переменной толщины 258
§ 6. Общая теория трещины расслаивания в многослойных оболочках. • • 266
§ 7. Некоторые задачи о трещинах расслаивания . 279
Приложение. Алгоритм конструирования оптимальной многослой-
многослойной пластины 286
Лнтерп/ра 289
ПРЕДИСЛОВИЕ
Хотя слово "композит" сравнительно новое, к композитам, т.е. состав-
составным материалам, можно отнести почти все искусственные материалы, при-
применяемые в инженерной практике. Однако, если в прошлом находка ново-
нового материала иногда приводила к новой эпохе в истории человечества, то в
наше время новые материалы, обладающие замечательными свойствами,
создаются целенаправленно и довольно часто, а в будущем, несомненно, ма-
материалы с заданными свойствами будут проектироваться подобно кон-
конструкциям. Тем не менее структура и свойства некоторых природных ком-
поз.итных материалов, без сомнения, достойна изучения и подражания (к та-
таким материалам можно отнести, например, нефрит, материал зубов, крове-
кровеносных сосудов и многие другие). Несомненно, например, что механизм
разрушения древесины во многом схож с механизмом разрушения таких
современных однонаправленных композитов, как углепластик, стеклоплас-
стеклопластик, боралюминий и некоторые другие, уже нашедших широкое приме-
применение.
Опыт показьюает, что уже на стадии изготовления композитов
или же на очень ранней стадии их эксплуатации в композитах появляются
трещины.
Теория разрушения твердых тел основана на представлении о том, что
работоспособность и долговечность материалов в конструкции определяет-
определяется закономерностями развития трещин и трещиноподобных дефектов.
Механика разрушения, занимающаяся изучением развития трещин в твер-
твердых телах, как самостоятельный раздел физики сложилась за последние
двадцать лет, когда были открыты некоторые основные закономерности
процесса разрушения. Она является основным научным звеном, связываю-
связывающим инженерное конструирование и материаловедение с фундаментальны-
фундаментальными дисциплинами: физикой и механикой твердого тела. От состояния этого
звена в значительной степени зависит решение проблемы качества современ-
современных конструкций и материалов, позволяющее оптимальным образом увя-
увязать противоречивые требования надежности и экономичности.
Конструирование новых композиционных материалов, обладающих вы-
высокой удельной прочностью, жесткостью и вязкостью разрушения, обычно
достигается путем армирования матрицы высокопрочным и жестким
составляющим. Этот прием с давних пор известен строителям и конструк-
конструкторам, которые для увеличения жесткости, прочности и несущей способ-
способности конструкции применяют всевозможные накладки, стрингеры, пере-
перекрытия и т.п. элементы.
4
Теория деформирования и разрушения таких составных систем наталки-
наталкивается на существенные трудности в тех случаях, когда армирующий эле-
элемент является сингулярным, т.е. приводит к теоретически бесконечным
перемещениям в точках прикрепления его к матрице. Таковы, например,
все клепаные конструкции, в которых армирование или соединение различ-
различных элементов происходит в точках, т.е. на площадках очень малых разме-
размеров. Таковы материалы, армированные весьма тонкими и жесткими нитя-
нитями, и многое другое.
Хотя в этой области было опубликовано огромное число работ, теории
армирования не было создана, так как не была преодолена основная труд-
трудность: как записать условие совместной работы упругих элементов в син-
сингулярных точках? Исследователи обычно уходили от ответа на этот вопрос,
отказываясь от таких полезных абстракций, как точка, идеально тонкий
стержень и т.п. Получающиеся в результате простые, но трудоемкие задачи
приходилось решать или грубо, приближенно, или на ЭВМ. Таким образом,
создание рациональной и строгой теории армирования является одной из
стержневых проблем механики разрушения композиционных ма-
материалов.
Настоящая книга состоит из трех глав. В первой главе дается математи-
математическое описание некоторых основных эффектов, ответственных за разви-
развитие и торможение трещин в композиционных материалах и тем самым опре-
определяющих механизмы их разрушения. Излагаемая здесь теория основана на
инвариантных Г-интегралах и постулате подобия.
Во второй главе развивается строгая (асимптотическая) теория армиро-
армирования упругих тел сингулярными элементами. Условие разрушения таких
систем оказывается возможным записать при помощи инвариантных
Г-интегралов.
В третьей главе предлагается теория оптимального проектирования неко-
некоторых многослойных материалов на основе механики разрушения.
Теория армирования, исследование механизмов разрушения и оптималь-
оптимальное управление ими в практических целях — таковы наиболее принципи-
принципиальные вопросы механики разрушения композитов, поскольку они оказы-
оказывают наиболее существенное влияние на технологию и производртво ма-
материалов.
Математический аппарат, используемый в книге, включает в себя метод
Винера-Хопфа, краевые задачи Римана - Гильберта, методы теории случай-
случайных функций, методы теории операций.
Монография основана на публикациях автора и его учеников. Часть ре-
результатов публикуется впервые.
Для чтения книги весьма подезно (но не обязательно) предварительное
ознакомление с методами механики разрушения и с экспериментальными
Данными по современным композиционным материалам. Наиболее полнбе
изложение указанных вопросов имеется в следующих изданиях:
1. Fracture (Ed. by H.Liebowitz),vol. 1—7, Academic Press, New York and
London, 1968-1974.
2. Composite Materials (Ed. by LJ. Broutman and R.H. Krock), vol. 1-8,
Academic Press, New York and London, 1973-1976.
3. Treatise on Materials Science and Technology (Ed. by H. Herman), vol. 1-
11, Academic Press, New York and London, 1976-1978.
5
4. С h e r e p a n o v G.P. Mechanics of Brittle Fracture. - Me Graw Hill,
New York, 1979, pp. 950.
Для первоначального ознакомления с основными видами структур ком-
композиционных материалов, основными типами их разрушений в различных
условиях и с некоторыми теоретическими моделями можно рекомендовать
том 5 из упомянутой энциклопедической серии "Composite Materials",
переведенный на русский язык: Композиционные материалы. Разрушение
и усталость. - М.: Мир, 1978,483 с.
Перечислим наиболее часто встречающиеся в монографии обозначения.
Величина Г — инвариантный контурный интеграл или Г-интеграл. Нижний
индекс у Г обычно совпадает с обозначением контура интегрирования.
Безындексное обозначение Г применяется для величин Г-вычета, т.е. для
значения Г-интеграла по произвольному замкнутому контуру, охватываю-
охватывающему особую точку физического поля и стягивающемуся в нее. Если из
предыдущего изложения ясно, что речь идет о Г-вычете для конид трещины,
то нижний индекс применяется для обозначения величины Г-вычета, харак-
характеризующей ту или иную стадию развития трещины, механизм локального
разрушения или внешние условия. Например, индекс sec (stress corrosion
cracking) для Tscc означает пороговую величину Г-вычета в конце трещины,
ниже которой не происходит докритического роста трещины в образце, на-
находящемся в химически активной среде под постоянной нагрузкой: индекс
с (critical) для Гс означает величину Г-вычета в конце трещины в начале
быстрого критического роста трещины в хрупком образце, подвергаемом
монотонному нагружению в химически инертной среде, так что при Г < Гс
роста трещины не происходит; индексу (yielding) для Ту означает величину
Г-вычета в конце трещины, ниже которого не происходит роста усталостной
трещины в упруго-пластическом материале при циклическом нагружении.
При наличии докритического роста трещины вследствие химической актив-
нос ги внешней среды, усталости материала и т.п. величина Гс характеризует
начало быстрого, критического ускорения роста трещины.
Вычисление расходящихся Г-интегралов называется Г-интегрированием;
оно основано на строго выводимом правиле "конечная часть расходящегося
интеграла", обоснованном лишь для Г-интегралов.
Величины К\ , Кц ,Кщ — коэффициенты интенсивности напряжений, ха-
характеризующие поле напряжений и деформаций вблизи конца трещины в
упругом теле; нижние индексы I, II и III (римские цифры) означают нор-
нормальный разрыв или отрыв, поперечный и продольный сдвиг соответствен-
соответственно (в английской литературе эти типы разрушения называются opening,
sliding and tearing modes соответственно). Дополнительные нижние индек-
индексы обозначают то же, что и для Г, однако имеют смысл только в случае
квазихрупкого разрушения или, точнее, при наличии тонкой структуры в
конце трещины.
Аналогично к\, кц, кш — коэффициенты интенсивности напряжений, ха-
характеризующие поле напряжений и деформаций в сверхтонкой структуре
вблизи конца трещины в упругом теле.
Остальные обозначения относятся к более традиционным понятиям ме-
механики. Они объясняются в основном тексте и не требуют дополнительных
пояснений.
ГЛАВА I
МЕХАНИЗМЫ И ЗАКОНОМЕРНОСТИ РАЗРУШЕНИЯ
КОМПОЗИТОВ
§ 1. Основы механики разрушения
В механике разрушения исходят из того, что во всех твердых телах всег-
всегда имеются разнообразные дефекты структуры, которые служат источника-
источниками трещин. Разрушение твердых тел представляет собой процесс развития
трещин. В дальнейшем будем различать трещины двух типов: а) трещины
отрыва (нормального разрьюа), б) трещины скольжения. Трещина первого
типа представляет собой полость, одно из измерений которой весьма мало
по сравнению с Двумя другими. Когда такая трещина перерезает тело, оно
разделяется на две части. Трещины скольжения не образуют пустот в твер-
твердом теле; противоположные берега трещин скольжения сомкнуты, так что
при тангенциальном взаимном смещении этах берегов возникают касатель-
касательные силы трения. Последние трещины часто реализуются в композитах на
границе различных сред в виде расслоений; в металлах они реализуются
обычно в форме пачек скольжения Людерса.
Распространение фронта трещины определяется в функции некоторых
основных параметров, описывающих распределение напряжений, деформа-
деформаций, температуры, электрического потенциала и тд. вблизи фронта. Основ-
Основные усилия исследователей в области теории разрушения направлены имен-
именно на поиски таких параметров, контролирующих этот сложный процесс
и — как во всякой физической теории — на поиски соответствующих физи-
физических постоянных. За последние 20 лет на этом пути были достигнуты зна-
значительные успехи.
Сформулируем два наиболее общих постулата, позволяющих построить
общую теорию разрушения твердых тел.
Постулат инвариантности. Пусть тело представляет собой деформируе-
деформируемую сплошную материю, находящуюся в электромагнитном поле, в самом
общем случае взаимодействия поля с материей (так что электромагнитное
поле вызывает деформацию среды и, наоборот, деформирование материи
генерирует электромагнитное поле).
Таким образом, общая теория рассматривает также пьезоэлектрические
и ферромагнитные материалы, разрушение которых может существенно
зависеть от внешних электромагнитных полей (и, наоборот, их разрушение
должно сопровождаться существенным электромагнитным излучением).
Указанные эффекты могут оказаться значительными и для обычных мате-
материалов при весьма большой плотности (и малой длительности) электромаг-
электромагнитных импульсов; последнее, по-видимому, имеет место, например, при
разрушении кристаллов рубина гигантским импульсом лазера. Эти эффек-
эффекты могут оказаться существенными также при некоторых электрохими-
7
ческих процессах разрушения, при разрушениях, вызываемых интенсивны-
интенсивными пучками протонов, электронов, нейтронов. Воздействие сильных токов
на рост трещин в металлах также охватывается этой теорией.
Состояние электромагнитной деформируемой материи характеризуется
векторами электромагнитного поля Е, В, D, Н, вектором смещения и и
тензорами напряжения и деформации oikieik. Имеют место следующие
уравнения:
уравнения Максвелла
ЪВг _ bDt _
*цъЩ,ъ + — - 0, eifkHftk — -/,,
О/,|-8. в(,,-о,л.!+—= о;
уравнения Ньютона
кинематические условия для малых деформаций
2eif = Н|,/ + uUi\ A.3)
локальный закон сохранения энергии
bi + Oijeij (/,/=1,2,3). A.4)
Здесь / — вектор плотности тока, р — плотность материи, 5 — плотность
заряда, t — время, q — вектор некомпенсированного теплового потока, U—
скорость изменения внутренней энергии материи в единице объема; точка
над буквой означает полную (материальную) производную соответствую-
соответствующей величины по времени; eijk - тензор Леви-Чивита*.
Деформации среды для простоты считаются малыми всюду, за исключе-
исключением некоторой области вблизи трещины, размер которой имеет порядок
раскрытия трещины в ее конце. В теории малых деформаций последним
размером можно пренебречь, а трещину можно считать математическим
разрезом. (Последующее легко обобщить также на случай конечных дефор-
деформаций, что, впрочем, вряд ли может иметь существенное значение для прак-
практики.)
Все функции, участвующие в уравнениях A.1)—A.4), предполагайся
непрерьюно дифференцируемыми всюду, за исключением фронта трещины,
который представляет собой движущуюся особую линию, где эти уравнения
не имеют смысла. Целью теории является изучение законов движения этой
линии.
Рассмотрим некоторую окрестность точки О на фронте трещины. Осъх2
декартовой прямоугольной системы координат OxiX2x3 направим по нор-
нормали к поверхности трещины, а ось х3 — вдоль фронта (см. рис. 1, а)..
Всюду в дальнейшем в малой окрестности любого фиксированного мо-
момента времени t = 0 будем различать следующие две системы координат в
Компоненты этого тензора принимают следующие значения: е12Э = е гг\ =6з12 =
-1,е13а =€3ai =€2i3 =~1; остальные е,у^ равны нулю. Здесь и всюду в дальней-
дальнейшем приняты обычные правила индексных обозначений суммирования и дифферен-
дифференцирования (например,?щ = и* + и] + й\ ,Ujk = Э Uj/Ъхки т.д.).
Рис. 1.
рассматриваемой точке О фронта трещины: подвижную Ох\х2х'3 и непод-
неподвижную OxiX2x3i так что
x'i = *i - Vt, ъ =х2, хъ=хъ. A.5)
Здесь V — скорость распространения фронта трещины * в данный момент
t = 0 в рассматриваемой точке О. Система Ох\х\хъ связана с фронтом тре-
трещины, а система Ох\Х2х3 — с телом. При t = О эти системы координат сов-
совпадают.
Вследствие сингулярности поля на фронте трещины градиенты поля
вдоль фронта будут малы по сравнению с градиентами поперек фронта, т.е.
для любой переменной поля А
ЪА ЬА ЪА ЪА
« , « . A.6)
Эх3 Ъх2 Ъхъ Ъхх
Отсюда вытекает, что вблизи точки О в плоскости Охгх2 асимптотически
реализуются условия плоской задачи, если линейный размер рассматривае-
рассматриваемой окрестности точки О мал по сравнению с радиусом кривизны фронта
трещин в этой точке или по сравнению с каким-то другим характерным ли-
линейным размером тела и трещины. Рассмотрим именно такую окрестность
точки О; при этом все переменные поля будут зависеть лишь от хх и х2
(соответственно от х\ и х2),а зависимостью их от х3 (и от х$ можно прене-
пренебречь* *. Процесс локального развития трещины в точке О можно рассмот-
рассмотреть в переменных х\ и х2 на плоском чертеже рис. 1, б; при этом трещина
изобразится bv виде полубесконечного математического разреза вдоль
х2 = 0, х[ < 0 (— °° < х'з < + °°); фронт трещийы изобразится одной точ-
точкой О, которую далее будем называть концом трещины.
Обозначим через 2 замкнутый контур в плоскости Ох\х'2, составленный
отрезками верхнего B+) и нижнего B_) берегов трещины, а также мало-
малого BГ) и большого B#) контуров, охватывающих точку О (см. рис. 1,6,
Предполагается, что окрестность фронта трещины вблизи точки О является глад-
гладкой кривой, что точка О не является неподвижной или граничной точкой этой
кривой, а также, что фронт трещины в этом пдложении не образует излома на ее
поверхности (это обнаруживается в последующие моменты времени t > 0).
То есть поле имеет вид произведения "слабоизменяющейся функции хъ на
"бысгроизменяющуюся" функцию х\ и х\.
где стрелкой указано также направление обхода контура). Контур 2; пред-
представляет собой след на плоскости Ох\х2 от соответствующей тороидальной
поверхности с разрезом, соосиой фронту трещины. Контур 2 движется в
системе координат Охххгхъ.
Рассмотрим следующий контурный интеграл (Г-интеграл):
1
Г2= / [я1(Э + Ф+-рй,й,) + (О/Я1+1?,Я1 -оции1)щ]йЪ A.7)
(л — единичный вектор нормали к контуру 2; /, / = 1,2). Здесь введены
следующие обозначения:
W^U-EtDi-HfBi, . A.8)
Э
grad Ф = (BxD)- dE-Jx В.
Ы
Можно показать при помощи уравнений Максвелла, что при 6 = const
(что и предполагается здесь) потенциал Ф существует, т.е. ротор правой час-
части последнего уравнения A.8) равен нулю (rot grad Ф= 0).
Примем следующую гипотезу квазистационарности: существует такая
малая окрестность точки О на фронте трещинъг, что поле в этой окрестности
можно считать стационарным*.
Для произвольного замкнутого контура S в стационарном поле имеют
место следующие уравнения:
уравнение закона сохранения энергии
/ [пх(Э + Ф+—рй§ + —pti|) + — рпх (пх -КJ +
2 L 2. 2
+ щ (PiEt + BtHx)-jj ,
-a3/if/ii3,i]dS = 0 (i,/=l,2), A.9)
уравнение закона сохранения количества движения
0 (/,/=1,2). A.10)
При этом предполагается, что внутри замкнутого контура 2 нет каких-
либо сингулярностей (особенностей) поля, по которым Может происходить
сток (или приток) энергии или импульса в рассматриваемую физическую
систему внутри койтура ?. Это условие весьма существенно; в частности,
для анализа роста трещин выбор контура X в виде, изображенном на
рис. 1, б, накладывает определенные ограничения на скорость роста трещи-
трещины и на структуру физического доля вблизи конца трещины. Например, для
такого контура нельзя рассматривать сверхзвуковое движение трещины в
упругом теле, так как при этом от конца трещины будут отходить ударные
волны (представляющие собой особые линии, на которых имеет место сток
энергии). Аналогично такой контур не позволяет рассмотреть разрывные
* Иначе говоря, поле имеет вид произведения "слабоизменяющейся" функции t на
"быстроизменяющуюся " функцию х\ и У2.
10
Рйс.2.
Рис.3.
поля в упруго-пластическом теле вблизи конца трещины. Однако этот недо-
недостаток легко преодолеть, если разрывы неподвижны в системе координат
Ох\х\.
На рис. 2 для иллюстрации показано, как нужно выбирать контур 2 в
случае сверхзвукового распространения трещины в однородном линей-
линейном теле:
2 = 2lR + ... + Б? + 2J + ... + 2? + 25 + ... + 2* + 2 + + 2_ + Ц + 2*.
Величины ар и ots определяют углы "конусов" Маха:
sin ots = cs/V, sin olp = cp/F,
где CpHCj- скорость распространения продольной и поперечной волн соот-
соответственно*.
На рис. 3 приведен контур 2 при наличии разрыва (например, вследствие
неоднородности материала) на продолжении трещины вблизи ее конца:
Можно привести и другие примеры правильного выбора контура 2 (не-
(некоторые из них можно найти далее в § § 3 и 8 этой главы).
Вычитаем из A.9) уравнение A.10), используем, кроме того, равенство
frii d 2 = 0. Вспоминая выражение A.7), получаем следующий результат.
Интеграл Г? равен нулю для любого замкнутого контура 2, не содержа-
содержащего внутри себя каких-либо сингулярностей поля и неподвижного в систе-
системе координат, в которой все физические величины не зависят от времени.
Это свойство Г-интеграла совершенно аналогично свойству инвариантнос-
инвариантности относительно контура интегрирования интеграла от аналитической функ-
функции по замкнутому контуру. Поэтому такие интегралы будем называть ин-
инвариантными Г-интегралами. Существует бесконечно много других инва-
инвариантных интегралов; способы их построения были разработаны авто-
автором [1].
Индексы р и s обычно применяют в сейсмологии и динамической теории упругости
для обозначения продольной и поперечной волн.
11
Рис.4.
Свойство инвариантности позволяет произ-
произвольно деформировать контур интегрирования
Г-интеграла по незамкнутому контуру, не из-
изменяя величины интеграла, если концы конту-
контура неподвижны и контур при деформировании
не пересекает особых точек и особых линий
поля. Величина Г-интеграда по замкнутому кон-
контуру (любой связности), содержащему внутри
себя особые точки и особые линии поля, не
изменяется при любой деформации контура,
если при деформировании- контур не пересе-
пересекает особых точек и особых линий поля. По-
Поэтому величину Г-интеграла по замкнутому
контуру, содержащему внутри себя одну особую точку поля, можно считать
основным физическим параметром, характеризующим состояние поля в этой
точке. Точно так же величину Г-интеграла по контуру
2+ +2_+2е1 +2е2 , где e<KL,
2iL — характерный линейный масштаб) вблизи особой линии поля можно
считать основным физическим параметром, характеризующим состояние
поля в рассматриваемой точке О особой линии (рис«4).
Инвариантный Г-интеграл Г? для электромагнитного поля в пустоте
(т.е. при м = 0, ?/ = 0,^ = 0, р = 0,/ = 0) представляет собой поток энергии-
импульса поля, введенного Максвеллом. В теории упругости (при щ = 0,
q = 09Е = 0,2? = 0) интеграл Г2 впервые появился в работе Эшелби 1951 г.
[2], который применил его для вычисления конфигурационных сил, дейст-
действующих на неоднородность в упругом поле. В 1967 г. Черепанов получил
интеграл Г? для произвольной сплошной среды при малых деформациях
с учетом лишь термомеханических процессов [3] (т.е. при2Г = 0,1? = 0);
он же применил его впервые для изучения роста трещин* в твердых телах
[3,4]. В 1968 г. появилась знаменитая работа Раиса [5], в которой он при-
применил интеграл Эшелби для анализа концентрации напряжений и де-
деформаций в окрестности вырезов и щелей** в нелинейно-упругих
телах.
Из уравнений A.9) и A.10) ясен физический смысл Г-интеграла: он
представляет собой поток энергии через контур интегрирования. В особых
точках и особых линиях поля происходит сток энергии из системы
по механизмам, не описываемым принятыми уравнениями физического
поля.
С течением времени значение Г, вообще говоря, изменяется; поэтому
величина Г является в общем случае некоторым функционалом по време-
времени от длины трещины, внешних нагрузок, конфигурации тела.
В гидродинамических системах были построены также инвариантные
Г-интегралы, описывающие поток импульса [1] и имеющие основное зна-
* В работах [3,4] Г-интеграл по контуру Хг обозначался через 27-
*¦ Райе назвал этот интеграл независящим от пути /-интегралом. Интеграл Раиса
совпадает с инвариантным Г-интегралом (при щ == 0, q = 0, Е = 0).
12
чение для определения взаимодействия тел между собой и с потоком жид-
жидкости или газа * .
Аппарат инвариантных Г-интегралов представляет собой мощное сред-
средство построения физических теорий движения сингулярных точек поля
(зарядов, материальных точек, фронта трещины, дислокаций, вихрей,
источников и т.п. [1 ]).
Рассмотрим контурный интеграл Гг согласно A.7) по замкнутому
контуру 2, проходящему в малой области квазистационарности вблизи
конца трещины (рис. 1,6):
/ +/ * / +... = 0. A.11)
2r ZR ?* + 2_
Для трещин отрыва можно считать, что о21 = о22 = 0 на 2+ + 2_. Вели-
Величина/^ Е\ +В2 #i, интеграл от которой равен потоку энергии-импульса
электромагнитного поля через соответствующую площадь, может быть
отличной от нуля только при наличии весьма большой плотности электро-
электромагнитного излучения в полости трещины отрыва. Это излучение сущест-
существенно в тех случаях, когда механизм роста трещины связан с непосредст-
непосредственным "разрезанием" тела мощным потоком элементарных частиц (элек-
(электронов, фотонов, протонов, электронной плазмы и т.п.).
Для закрытых трещин скольжения можно считать, что на берегах трещи-
трещины потоки энергии-импульса электромагнитного поля равны нулю, а скачки
величин и2, о22 иа21 на трещине также равны нулю, т.е. [и2] = 0, [ ]
= [а21]=0.
Обозначим
Дг=1ш1 f (D2EX +B2H1)n2dxl,
Qr=lim / о21иг г n2dxl9
r+0 E + ?
Здесь в последнем интеграле (и ниже) точками обозначены те же члены, что
и в подынтегральном выражении A.7).
Учитывая обозначения A.12) и то, что fix = 0 на 2+ + 2_, уравнение
A.11) можно записать в таком виде:
открытые трещины отрыва
Г = -Яг-/ [...]<ffl, A.13)
закрытые трещины скольжения
г=ег-/ [...]&. A.14)
Естественно принять следующий постулат: величина Г является единст-
единственным параметром, контролирующим прямолинейный рост трещины. Это
предложение будем называть постулатом инвариантности.
* См. также работу [200] по упомянутым вопросам. В этой работе дается, кроме
того, теория Г-вычетов, основанная на доказанном правиле Г-интегрирования "ко-
"конечная часть расходящегося интеграла'*.
13
Формулы A.13) и A.14) показывают, что величина Г инвариантна отно-
относительно деформации замкнутого контура, охватывающего конец трещины,
с точностью до слагаемого Rr или Qr.
Величина Г зависит от времени, от положения точки О (например, от
длины или радиуса трещины), от внешних нагрузок и конфигурации тела.
Эта зависимость в общем случае необратимых (диссипативных) процес-
процессов, как правило, является нелинейно-функциональной по времени. В слу-
случае недиссипативных (вне фронта трещины) процессов величина Г будет
обычной функцией времени, параметров внешней нагрузки, геометрии тела
и трещины.
Согласно постулату инвариантности скорость роста трещины V представ-
представляется в общем случае в виде некоторого функционала Got Г (t):
]. A.15)
Вид функционала G определяется при помощи экспериментальных дан-
данных или же при помощи структурной теории конкретного механизма разру-
разрушения, раскрывающей природу и внутреннюю структуру конца трещины*.
Коль скоро функционал G известен, закономерность A.15) представля-
представляет собой интегродифференциальное уравнение относительно размера трещи-
трещины (длины, радауса и т. п.). Решение этого уравнения позволяет опреде-
определить движение фронта трещины во времени, т.е. полностью решить проб-
проблему разрушения.
Функционал G вырождается в обычную функцию, если свойства мате-
материи и состав внешней среды в полости трещины вблизи ее конца не изме-
изменяются в процессе развития трещины (или же изменяются несуществен-
несущественно). В этом случае пренебрегается, в частности, транспортными процес-
процессами в полости трещины. При этом общая закономерность развития тре-
трещины имеет вид
К=К(Г) A.16)
и может быть представлена на плоскости КГ в виде некоторой кривой,
которую будем называть диаграммой V — Г.
Зависимость A.16), строго говоря, справедлива лишь в условиях ста-
стационарного нагружения, т.е.'при Г = 0.
Диаграмма V — Г является основной характеристикой стационарно-
стационарного процесса разрушения в данной системе "материал — среда". Характер-
Характерные точки на этой диаграмме будут некоторыми постоянными данной
системы. Наиболее важными являются постоянные Гс и rscc. Величина
Гс отвечает началу быстрого, динамического (критического) роста трещи-
трещины, а величина Г5СС — началу медленного докритического роста трещины
(рис.5).
В ряде случаев можно пренебречь влиянием внешней среды и, вообще,
временными процессами как в самом материале, так и в окружающей
среде**. В этих случаях роль времени будет играть единственный пара-
параметр нагружения, величина Г. При этом общая закономерность развития
* По мнению автора, наилучшей является формула "опыт -^теория первого прибли-
приближения -*опыт -+теория второго приближения и т.д."
** Этот случай представляется, например, для большинства конструкционных ма-
материалов, когда натружение происходит с достаточно высокой скоростью.
14
ML
ctr'
fscc
Га Г
Pkc.5.
Гп Г
Рнс.6.
трещины имеет вид
Л
A.17)
(/ — длина трещины), и может быть представлена кривой, которую будем
называть диаграммой dl/dT - Г (см. рис, 6). Диаграммаdl/dT -Г являет-
является основной характеристикой разрушения материала в отсутствие времен-
временных эффектов, пригодной для любых путей нагружения. Характерные
точки на этой диаграмме будут некоторыми постоянными данного ма-
материала. Наиболее важными являются Ту (начало докритического роста
трещин) и Гс (началокритического роста трещины).
При помощи диаграммы dljdT — Г можно вычислить приращение длины
(радиуса и т. п.) трещины для любого циклического, случайного или про-
программированного пути нагружения. Таким образом, эта диаграмма лежит
в основе теории роста усталостных трещин, если в этом процессе влияние
частоты нагружения пренебрежимо мало.
При монотонном нагружении вплоть до разрушения роль основной
характеристики материала может играть диаграмма А/—Г зависимости
приращения трещины А/ от Г, получающаяся интегрированием дифферен-
дифференциального уравнения A.17) (см. рис. 7). Однако при использовании послед-
последней диаграммы следует иметь в виду, что асимптотическая ветвь этой диа-
диаграммы не реализуется в опытах на тех образцах, для которых соответ-
соответствующая хрупкая трещина неустойчива.
В случае, если существенны как временной эффект, так и мгновенная
упруго-цластическая реакция на увеличение нагрузки, естественно взять
общую закономерность развития трещин в виде
К=К0(Г)+Г/(Г), A.18)
обобщающем уравнения A.16) и A.17). Эту закономерность, пригодную
как при быстрых изменениях внешних нагрузок, так и при значительных
временных эффектах, уже нельзя представить в виде какой-либо одной
диаграммы. Однако при помощи уравнения A.18) можно вычислить
приращение длины трещины для любого переменного пути нагружения.
Поэтому теорию роста усталостных трещин, учитывающую частоту нагру-
нагружения, форму циклов и т. п. факторы, легко построить на основе уравне-
уравнения A.18).
Квазихрупкое разрушение. Вычисление величины Г, определенной
формулами A.12)—A.14), значительно упрощается в случае квазихруп-
15
кого разрушения, когда характерный раз-
размер пластической области вблизи фронта
трещины мал по сравнению с характерным
размером тела и трещины*. В качестве
примера можно рассмотреть сквозную тре-
трещину нормального разрыва длины / в
пластине ширины Lo при изотермическом
и монотонном процессе увеличения внеш-
внешней нагрузки р, приложенной симметрично
Рйс-7- относительно плоскости трещины (см.
рис. 8). Толщина пластины считается
достаточно большой, так что можно принять условия плоской де-
деформации. Фронт трещины перпендикулярен плоскости пластины
(точка О на рис. 8). С ростом р вблизи точки О растет область пласти-
пластических деформаций, характерный размер этой области обозначим через d.
Кроме того, с ростом р и со временем t длина / увеличивается, т.е.
точка О движется вправо. Функция / (г) зависит от физико-механических
свойств материала, размеров образца, внешней среды, скорости нагруже-
ния, температуры и т.п. Для всех материалов и внешних условий существу-
существует некоторая критическая область, в которой происходит резкое увеличе-
увеличение скорости /.
Квазихрупкое разрушение реализуется, если выполняется ограничение
d < /, d < Lo, 0-19)
так что существует область
d<r<Q9L0), A.20)
в которой поля напряжений oik и деформаций eik даются следующими
формулами:
oik = *iBirr)-1/2//*(*,vuv2,...), A.21)
€ik = K^lnr)-!*2 gik(fi, *i,I*,...) (I, * = 1, 2, 3).
Здесь г, в — полярные координаты с центром в точке О; i/j. i>2> • • . —
упругие постоянные; fik и gik - некоторые определенные функции, вы-
вычисленные практически для всех возможных случаев [1]; К\ — коэф-
коэффициент интенсивности напряжений, который является некоторой функ-
функцией внешних нагрузок, длины трещины, формы тела и трещины. Кз ус-
условия нормировки принято, что/22 = 1 при 0 = 0. Формулы A.21) явля-
являются следствием физически очевидного факта, что все твердые тела при
достаточно малых нагрузках и достаточно малых временах нагружения
линейно-упруги.
Формулы A.21) справедливы для произвольной анизотропии, а также
для кусочно-однородного тела, когда поверхность раздела совпадает с
плоскостью трещины. Определение К\ в функции внешних параметров
является задачей математической теории упругости и вязкоупругости,
решенной до конца во многих случаях.
В общем случае для вычисления Г приходится с самого начала применять числен-
численные методы (наиболее эффективен и прост метод конечных элементов).
16
Асимптотические разложения типа A.21) вбли-
вблизи конца трещины были выделены в работах
Вильямса [6], Снеддона [7] и др. Роль коэффициен-
коэффициента Ki как управляющего параметра разрушения
впервые была понята Ирвином [8]. Доказатель-
Доказательство общности таких разложений для трещин и
тел любой формы дано в работе [9].
Сводку формул для вычисленных коэффициен-
коэффициентов интенсивности напряжений в образцах с трещи-
трещинами различной конфигурации и нагрузок можно
найти в книгах, руководствах и монографиях по
механике разрушения (см. [1]). Описание экспе-
экспериментальных процедур механики разрушения
(изготовление образцов, регистрация трещин, изме-
измерения и т.п.) имеется в изданиях [1,10 - 14].
Структура поля A.21) говорит о том, что любой процесс локального
разрушения в точке О контролируется внешними параметрами только
через посредство одного промежуточного параметра — коэффициента
К\. В частности, скорость роста трещины V представляет собой некото-
некоторый функционал F от К\ (t) :
V=F[Kl(t)9r]. A.22)
Здесь в функционал входят также величины, характеризующие свойства
материала и внешней среды вблизи точки О и ответственные за локаль-
локальное разрушение в этой точке [15].
Если свойства материи и состав внешней среды вблизи точки О не
изменяются в процессе развития трещины (или же изменяются в пределах,
не влияющих на скорость локального разрушения в точке О), то скорость
роста трещины будет представлять собой некоторую функцию коэффи-
коэффициента интенсивности напряжений
F=K*i)- A.23)
Однако закономерность A.23) выполняется даже при стационарном
нагружении далеко не всегда. Например, при существенном адсорбцион-
адсорбционном эффекте (в системах "жидкий металл - твердый металл" и др.), при
кислородной деполяризации и некоторых других случаях локальная ско-
скорость разрушения лимитируется скоростью доставки активного реагента
в устье трещины, т.е. нелокальными транспортными процессами. В этом
случае нужно использовать общую зависимость A.22).
Графическое изображение зависимости A.23)вкоординатах VиК\ на-
называется диаграммой V — К\. Диаграмма V — К\ является характеристи-
характеристикой данной системы "материал — среда" (за упомянутыми исключения-
исключениями) , которая может быть определена непосредственно из опыта.
Теоретическое и экспериментальное установление этого факта для
многих встречающихся на практике систем явилось основным совместным
Достижением механики разрушения и коррозии металлов под напряже-
напряжением. Это достижение позволило поставить основную общую задачу этих
дисциплин как проблему изучения зависимости диаграмм V— A'i для
различных систем от состава материала, состава внешней среды, темпера-
температуры и других внешних условий.
17
Различные характерные точки на этой диаграмме можно описать при
помощи соответствующих критических значений коэффициента К\. Од-
Однако существует одно критическое значение этого коэффициента, называе-
называемое вязкостью разрушения АГ1с, которое характеризует резкое увеличение
скорости трещины до околозвуковых скоростей и которое не зависит
от внешней среды, так как скорость всех параллельно протекающих про-
процессов локального разрушения в точке О оказывается малой по сравнению
со скоростью локального механического разрушения в вакууме или в
инертной среде. Таким образом, величина К\с является константой ма-
материала, характеризующей его предельное сопротивление развитию
трещины.
Концепция Kic, впервые сформулированная Дж. Ирвином [8, 16],
имеет универсальный характер для всех материалов (при достаточно боль-
больших размерах образца и достаточно быстром нагружении). Эта концепция
обычно выводится из энергетических представлений Гриффитса [17]
о поверхностной энергии твердых тел, однако следует заметить, что с
тем же успехом ее можно получить из совершенно других (и даже абсурд-
абсурдных) физических допущений, лишь бы они относились к области A.20)
и не зависели от времени. Имеется около 10 построений разных авторов,
основанных на различных допущениях о структуре области A.19) и при-
приводящих к концепции К\с. В некоторых случаях (например, в системах
"стекло — вода", для некоторых высокохрупких сталей в органических
спиртах и некоторых других) скорость миграции среды и скорость локаль-
локального адсорбционного воздействия среды столь велики, что можно практи-
практически говорить о снижении вязкости разрушения под действием среды.
Из этих соображений вытекает, в частности, влияние скорости нагруже-
ния: чем она больше, тем меньше роль более медленно протекающих про-
процессов локального разрушения, под воздействием внешней среды. Напри-
Например, при достаточно большой скорости нагружения в коррозионных си-
системах с ветвящимися трещинами ветвление можно не наблюдать, а раз-
разрушение будет "преждевременным" (так как К\с < К\р, где К\р — вяз-
вязкость разрушения при весьма медленном нагружении).
Другим, наиболее существенным, критическим значением коэф-
коэффициента интенсивности напряжений К\ является так называемое порого-
пороговое значение коэффициента интенсивности напряжений K\scc, ниже ко-
которого трещины не растут в данной системе "металл — среда". Наличие
К is ее ПРИ статических нагрузках, не изменяющихся или слабо изменяю-
изменяющихся во времени, было установлено почта для всех исследованных кор-
коррозионных систем (впрочем, результаты некоторых экспериментов были
подвергнуты сомнению из-за недостаточной базы испытания).
В случае нагружения с достаточно высокой скоростью (когда нельзя
уже считать Кг равным нулю) часто можно пренебречь влиянием внешней
среды и, вообще, временнь'ши процессами как в самом материале, так
и в окружающей среде. В этом случае роль времени играет параметр на-
нагружения К\, а общая закономерность докритического роста трещины
имеет вид (рис. 9)
^Г =fo(Ki). A.24)
18
Диаграмма dljdK\ - К\ является основ- dl
ной характеристикой квазихрупкого раз- dHT
рушения материала в отсутствие времен-
временных эффектов, пригодной для любых пу-
путей и скорости нагружения. Характерные
точки на этой диаграмме являются неко-
некоторыми постоянными материала. Наиболее
важны вязкость разрушения Кгс ивеличи- q. #~ J^
на Ку, характеризующая начало докрити-
ческого роста трещины. При помощи ди- ftic# 9*
аграммы dljdK\ - K\ можно вычислить
приращение трещины для любого переменного пути нагружения и
тем самым построить теорию роста усталостных трещин в условиях
квазихрупкого разрушения, если влияние частоты пренебрежимо мало.
Величины Ку весьма малы; так, было установлено существование
порогового коэффициента Ку для алюминиевого сплава 2024-ТЗ
(см. [18]). Испытания проводились в диапазоне скоростей роста
трещин A0Г10 -г 10) см/цикл. Соответствующее пороговое значение
оказалось примерно в 20 раз меньше величины Кс.
По-видимому, при циклических и, вообще, быстропеременных нагруз-
нагрузках концепция порогового коэффициента интенсивности напряжений
Ку оправдывается лишь для очень небольшого числа систем "металл —
среда". Целесообразно всегда указывать базу испытания, на которой было
получено пороговое значение. Кроме того, в некоторых случаях регистри-
регистрируемая скорость до критического роста трещины оказывается столь малой,
что за время службы конструкции подросшая трещина не является опас-
опасной. Очевидно, что такой материал вполне может быть признан годным
к эксплуатации. Все это говорит о том, что несмотря на важность концеп-
концепции Ку и Kiscc необходима полная информация о всей диаграмме разру-
разрушения для окончательной оценки материала.
Следует отметить, что зарождение трещины принципиально возможно
и при Ki < Kiscc, так как механизм распространения трещины может
быть отличен от механизма ее зарождения. Аналогичное объяснение можно
дать наблюдаемым на практике случаям, когда гладкие образцы не рас-
растрескиваются, а заранее созданные трещины прекрасно растут в данной
среде (эта ситуация, в известной мере, типична, если удается избежать
питинговой коррозии на гладком образце, материал которого, однако,
подвержен локальному водородному охрупчиванию в конце трещины).
Катастрофическая чувствительность некоторых высокопрочных сплавов
к воде была почти одновременно замечена многими исследователями
(Ирвин, Кайс и Бернштейн [19, 20], Штайгервальд [21] и др.). Они же
дали правильное объяснение этому явлению, связав его с докритическим
ростом трещин. Штайгервальд [21] первым показал, что это явление не
связано с концепцией К\ с и его надо изучать отдельно. Механика кор-
коррозионного разрушения, основанная на изучении диаграмм V — К\ и кри-
критических коэффициентов интенсивности напряжений на образцах с трещина-
трещинами, обязана своим формированием работам Джонсона и Вильнера [22],
Брауна и Бичема [23], Ханна, Трояно и Штайгервальда [24], Хэнкока
и Джонсона [25], Видерхорна [26], Ирвина [27], Мулерина [28], Петер-
19
сона с сотр. [29], Ван дер Слайса [30], Джонсона и Пэриса [18], Смита,
Пайпера и Дауни [31 ] и др.
При монотонном нагружении до разрушения в отсутствие временных
эффектов роль основной характеристики квазихрупкого разрушения
материала может играть диаграмма Д/ — К\9 которая получается интегри-
интегрированием дифференциального уравнения A.24). Наиболее существенное
значение она имеет для сквозных трещин в пластинах. Асимптотическая
ветвь этой диаграммы не реализуется в неустойчивых ситуациях (когда
bKi/Ы > 0).
В том случае, если существенны как временной эффект, так и мгновен-
мгновенная упруго-пластическая реакция на увеличение нагрузки, общую законо-
закономерность докритического роСта трещины при квазихрупком разрушении
естественно взять в следующем виде:
A.25)
являющемся обобщением уравнений A.23) и A.24) .Теория роста усталост-
усталостных трещин квазихрупкого разрушения с учетом частотных эффектов
строится при помощи уравнения A.25).
Подход механики разрушения, основанный на коэффициентах
К\ (т.е. на существовании линейно-упругой асимптотики A.21)), реа-
реализуется лишь при выполнении ограничений A.19), т.е. практически для
высокопрочных и хрупких материалов. Впрочем, при циклическом или
быстропеременном нагружении пороговый коэффициент весьма мал (или
вообще равен нулю), поэтому даже для малопрочных и весьма пластичных
металлов при определении долговечности часто можно ограничиться указан-
указанным подходом, поскольку основной вклад в долговечность делает область
малых интенсивностей напряжений К\.
Механика усталостного разрушения зародилась в работах Пэриса, Го-
меса, Андерсона [32], Доналдсона и Андерсона [33], Пэриса [34] и др.
Теория докритического роста усталостных и коррозионных трещин
была развита в работах автора [35-42]. В этих работах были предложены
также приведенные здесь общие представления.
В случае квазихрупкого разрушения инвариантный Г4штеграл выра-
выражается через коэффициенты интенсивности напряжений К\ и Кц. Приве-
Приведем некоторые относящиеся сюда результаты [1] в отсутствие электро-
электромагнитного поля:
трещина нормального разрыва {отрыва), однородное изотропное тело
Г = —— К\, A.26)
трещина скольжения, однородное изотропное тело
1 -V2
Г = — К\г A.27)
(v — коэффициент Пуассона, Е — модуль Юнга).
Были изучены также различные анизотропные, неоднородные, нелиней-
нелинейно-упругие тела (см. [ 1 ]).
Формулы A.26) и A.27) получаются деформированием контура в
A.12) в область действия асимптотики A.21) (или аналогичной асимпто-
20
тики в случае трещин скольжения). Это преоб-
преобразование существенно использует постулат инва-
инвариантности.
При стационарном нагружении величина Kiscc
довольно близка к^с для большинства сплавов
низкой и средней прочности, а размеры элементов
конструкций таковы, что условие A.19) в этой
области не выполняется; для таких материалов
указанный подход не годится и нужно применять
более общий подход, основанный на асимптотиках
низшего порядка [1]. Например, можно использо-
использовать следующий метод [1]. Металл считается не-
несжимаемым вплоть до разрушения при всесто-
всестороннем растяжении, а при одноосном растяжении его поведение аппрокси-
аппроксимируем следующим нелинейно-упругим телом (диаграмма а-е, см.
рис. 10):
Рис. Ю.
г Ее при е < е0,
. а0 + Ек(е - бо)к при е > е0.
A.28)
Здесь Еу Ек, Од, е0, к - некоторые постоянные. Эти допущения позволяют
найти полную систему уравнений, описывающих поведение однородного
и изотропного металла любой формы и при любых нагрузках (с некото-
некоторой ошибкой, проистекающей от приближенности этих допущений). Точ-
Точный анализ показывает, в частности, что в этом случае вблизи конца трещи-
трещины, т.е. в области (см. рис. 8)
г < d, г < /, г < Lo, A.29)
поле напряжений и деформаций имеет следующий вид [1]:
, к ч
Х= —- .
A.30)
Здесь обозначения аналогичны принятым в формулах A.21), через d обо-
обозначен характерный размер "пластической" области, в которой е > е0.
Величина к\ определяется в зависимости от параметров внешней нагрузки
и размеров тела из решения конкретной краевой задачи нелинейной теории
упругости (это решение, конечно, сложнее, чем в случае соответствующей
линейной задачи, имеющей место для определения Къ однако вполне
достижимо современными вычислительными средствами).
При таком подходе управляющим параметром будет коэффициент
&ь а основной задачей механики разрушения является определение диа-
диаграмм V —kin dl\dk\ — k\. Аналогично можно сформулировать кон-
концепцию к\с * (характеризующую начало нестабильного роста трещины)
и концепцию k\scc (характеризующую минимально возможное значе-
значение &ь при котором имеет место докритический рост трещин в данной
среде при стационарном нагружении).
Величины Г, к\ и К\ связаны определенными соотношениями [1],
поэтому из экспериментов на малых образцах можно прогнозировать
21
а)
Ptoc. 11.
результаты испытаний на больших образцах (когда выполняются условия
A.19)),и наоборот.
В общем случае правило масштабного переноса закономерностей раз-
разрушения устанавливается постулатом подобия.
Постулат подобия. Будем сравнивать явление разрушения для двух
масштабов, В и Т (рис. 11). Масштаб Т — это конкретно реализуемая
ситуация вязкого разрушения под действием некоторой внешней нагруз-
нагрузки р (t); именно этот масштаб обычно интересует конструктора и инже-
инженера (рис. 11,6). Масштаб В —локальная ситуация квазихрупкого разру-
разрушения; эта ситуация может быть реализована лишь при достаточно больших
геометрических размерах тела и трещины (рис.11,д). На рис. 11 заштрихо-
заштрихованы области пластических деформаций.
Ограничимся рассмотрением трещин скольжения и трещин отрыва.
И в том, и в другом случае процесс деформирования и разрушения в мас-
масштабе В полностью описывается при помощи одного коэффициента ин-
интенсивности Напряжений, который обозначим через Кв (t). Согласно посту-
постулату инвариантности процесс деформирования и разрушения в масштабе
Т полностью описывается при помощи инвариантного интеграла Г = Гт (t).
Так как этот параметр пригоден также для описания масштаба В (обозна-
(обозначим его через Г = Гв (О), естественно сформулировать следующий
постулат.
Пусть для одного и того же материала в некоторый момент времени
t выполняются условия
Гт@ = Гв@, tT(t) = rB(t). ... A.31)
Тогда в тот же момент времени скорость трещины для обоих масштабов
будет одной и той же:
VT{t)=VB{i). A.32)
Этот постулат (постулат подобия) позволяет пересчитать закономер-
закономерности разрушения, полученные на лабораторных образцах определенной
формы, на образцы и элементы конструкций произвольной конфигурации
другого (большего или меньшего) масштаба, сделанные из одного и того
же материала. Понятие "один и тот же материал" включает в себя одинако-
одинаковую технологию. Последнее требование наиболее трудно соблюсти для
изделий различных масштабов. Поэтому для правильного использования
постулата подобия необходимо проводить дополнительное исследование
22
В
dl-0
6)
Рис. 12.
по влиянию основных технологических факторов на процесс разрушения.
Соотношения A.31) и A.32) дают правило, по которому закономер-
закономерности докритического роста усталостных и коррозионных трещин в услови-
условиях квазихрупкого разрушения переформулируются на произвольный случай
вязкого разрушения, Например, в случае трещин отрыва в однородном
изотропном теле нужно в соответствующем уравнении типа A.23)—A.25)
величину коэффициента интенсивности напряжений К\ заменить на
\/ЕГ1A — v2) согласно формуле A.26). Получающееся уравнение отно-
относительно V и Г согласно постулатам инвариантности и подобия будет
справедливо для любых вязких разрушений.
Функция Г т (/) как функционал от нагрузки, и длины трещины опре-
определяется численными методами. При некоторых дополнительных допу-
допущениях величину Гт можно считать функцией длины трещины и нагруз-
нагрузки, и в этих случаях эту функцию можно определить экспериментально
по диаграмме податливости "нагрузка — смещение" для образца с трещиной.
Изложим этот метод на примере образца, изображенного на рис. 12,а.
Образец представляет собой прямоугольную пластину из исследуемого
материала, содержащую сквозное отверстие, к которому приложены раз-
разрывающие силы Р. От отверстая вдоль линии симметрии отходит сквоз-
сквозная трещина длины /. Смещение в точке приложения силы обозначим через
v (точнее говоря, v — это смещение абсолютно жесткой шайбы, к ко-
которой приложена сила Ри которая давит на тело).
Будем снимать зависимость смещения v от силы Р в процессе увеличе-
увеличения силы при некоторой фиксированной начальной длине трещины (диа-
(диаграмма Р - v, см. рис. 12,6). На начальном участке О А трещина не растет,
в точке А начинается докритический рост трещины (т.е. на участке АВ
приращение трещины будет отлично от нуля). Предположим, что точка
В находится бесконечно близко к точке А, Сделаем следующее важное
допущение*: поведение тела на участке нагружения ОАВ эквивалентно
некоторому нелинейно-упругому телу.
На основании этого допущения необратимая- работа, затраченная на
увеличение длины трещины на величину dl (на участке АВ) в рассматри-
Это допущение оправдано для упруго-пластических тел (т.е. практически для
любого материала при достаточно высокой скорости нагружения).
23
ваемом материале и равная TAdl, может быть вычислена по следующей
формуле:
ИГАШ= f Pdv. A.33)
ОАВ
Здесь h — толщина образца; контурный интеграл равен бесконечно малой
площади гистерезисной петли, образовавшейся в процессе "нагружение —
разгрузка" воображаемого эквивалентного нелинейно-упругого тела (на
рис. 12 — площадь заштрихованного криволинейного треугольника ОАВ).
Свойства реального материала при разгрузке существенно отличны
от воображаемого нелинейно-упругого тела (в частности, может быть
dl Ф 0). К счастью, сформулированного выше допущения и вытекающей
из него формулы A.33) достаточно для вычисления инвариантного ин-
интеграла ГА в точке А (т.е. в начале роста трещины). Поэтому участок
разгрузки реального материала на диаграмме Р - v нигде далее не ис-
используется.
На рис. 12,6 штрихами обозначен участок разгрузки ОВвоображаемого
эквивалентного нелинейного упругого тела; для этого тела на участке
разгрузки приращение длины трещины, очевидно, будет равно нулю.
Рассечем равномерно весь диапазон длин трещин /, представляющий
физический интерес, и для каждой начальной длины / = /0, /i, h, • • • из
этого диапазона снимем диаграмму Р - v при монотонном увеличении
силы Ру фиксируя на каждой диаграмме точку начала роста трещины.
Начальная трещина каждый раз должна создаваться искусственно (напри-
(например, при помощи усталостного вибратора).
Аппроксимируем всю совокупность полученных экспериментальных
диаграмм Р - v (до точки начала роста трещины) при помощи следующего-
аналитического выражения:
()ХП A-34)
Здесь X/ (/) и/,- (Р) — любые непрерывные функции (например, полиномы),
N — некоторое число. Сложность этого выражения зависит от требуемой
точности аппроксимации, которая, очевидно, может быть выбрана сколь
угодно высокой.
Вычисляем, используя формулу A.34) и рис. 12,5,
§ Pdv = - f vdP = - § Z \i(l)fi(P)dP =
ОАВ ОАВ ОАВ /=1
= - f Z Xi(l)dFi(P)= Z ф Fi(P)d\i(l) =
OABi=l *=1 OAB
N dXs
/=i dl
dl A.35)
при l=lA
Здесь Ft(p)= fft(P)dP
о
24
Сравнивая это выражение с A.33), находим инвариантами Г-интеграл
в точке А (т.е. при / =lA Р- Р^ :
lA)UA) A.36)
Л 1=1
Аналогично можно вычислить значение Г в точках В, С, .. . диаграммы
Р - v; при этом нужно лишь в A.36) заменить индекс А на В, С, ... В ре-
результате для любой точки диаграммы Р - v получаем
Г = l- Z /v(i>)\;(/). A.37)
h /=i
В частности, для квазихрупкого разрушения имеем N = 1, //(/*) = Р,
A.38)
Это известная формула Ирвина.
При помощи зависимости A.37) легко определить диаграмму Д/ — Г
(см. рис. 7). Для этого нужно в формулу A.37) подставить функцию
Р = Р{1), полученную простым пересчетом из экспериментальных диаграмм
Р - v для различных начальных длин трещин (величина Р отвечает мо-
моменту страгивания трещины).
Из полученной таким образом диаграммы Д./ — Г при помощи диф-
дифференцирования легко получить диаграмму dl/dF — Г, которая имеет
более общее и ценное значение, так как позволяет прогнозировать рост
трещины при циклическом и вообще любом программированном пути
нагружения.
При помощи зависимости A,37) легко определить также диаграммы
V — Г, характеризующие скорость роста трещины в данном материале
в присутствии какой-либо коррозионно-активной или водородо-содер-
жащей среды. Для этого нужно нагруженные образцы из данного материала
(для которых получена зависимость A.37), см. рис. 12,а) поместить в
изучаемую среду и снять кривую зависимости длины трещины / от време-
времени t. Затем при помощи дифференцирования следует найти график зави-
зависимости скорости трещины V от длины / при данной нагрузке Р. Сравни-
Сравнивая этот график с кривой A.37), получаем искомую диаграмму V — Г.
Изложенный метод легко обобщить на случай образцов произвольной
формы при наличии креплений в точках приложения нагрузки.
Образцы специальной формы. Другим удобным методом экспери-
экспериментального определения диаграмм разрушения (и, в частности, констант
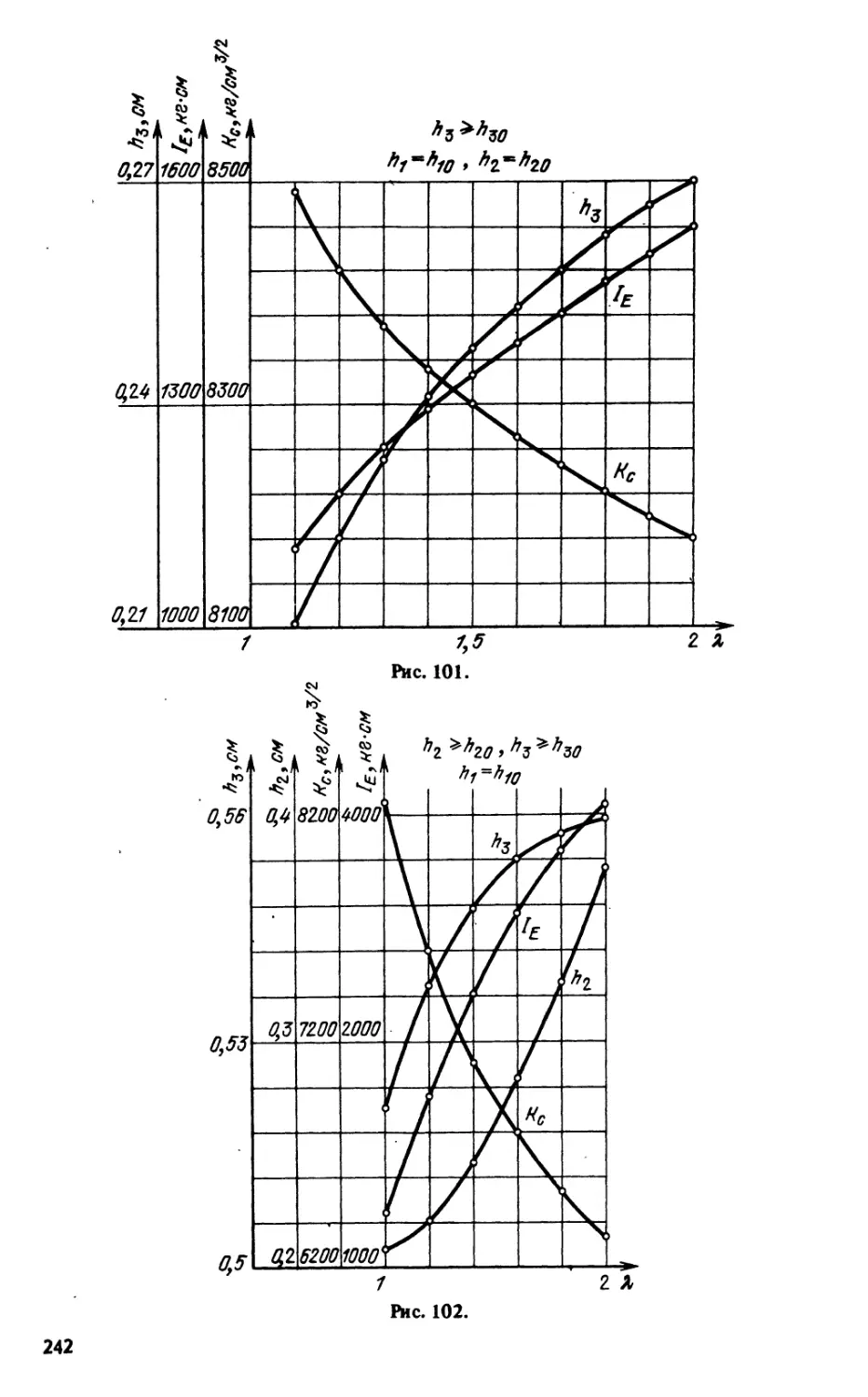
Гс> Гу, Г5СС) являются опыты на образцах специальной формы, для ко-
которых величина Г вычисляется теоретически. Остановимся на одном типе
таких образцов, для которых величина потока Г к тому же оказывается
не зависящей от длины трещины (рис. 13).
Возьмем пластину из исследуемого материала толщины h0 и сделаем в
ней краевой сквозной острый прямолинейный разрез длины /0, перпен-
перпендикулярный плоскости пластины и ее краю. Существует много технологи-
технологических способов совершения последней операции. Для металлов обычно
25
Рйс. 13.
используют вибратор и выращивание усталостной трещины при как можно
юлее низких напряжениях из предварительного механического надреза
в малом отверстии. Длина разреза должна быть гораздо больше толщины
пластины, т.е. lo>ho. Далее возьмем целую пластину толщины hi из друго-
другого (или того же) материала и жестко соединим эти две пластины вдоль
смежных боковых плоскостей, оставив свободной полосу ширины h9
симметричную относительно следа разреза на боковой плоскости первой
пластины (рис. 13,г). Для осуществления соединения пластин можно
применить диффузионную сварку, электросварку, склеивание и др. тех-
технологические операции. На рис. 13, а, в, г изображены три сечения биметал-
биметаллической пластаны с трещиной, на рис. 13, б — та же пластина без трещин
(/ = /0 в начальный момент роста трещины).
Полученную таким образом биметаллическую пластину растянем усили-
усилием Р в направлении, перпендикулярном плоскости начального разреза:
P=(E0h0+E1h1)eoo, A.39)
где б» - заданная деформация биметалла на больших расстояниях от
трещины, Ео и Ех —модули Юнга основного и вспомогательного материалов.
Вычислим величину интеграла Г на фронте развивающейся трещины.
Выберем начало декартовой системы координат в середине трещины на
свободной плоскости биметалла, так что ось хг совпадает с направлением
роста трещины, ось х2 лежит в. плоскости ххх2 начальной 1рещины пер-
перпендикулярно плоскости пластины, ось х3 перпендикулярна плоскости
начальной трещины. Фронт трещины в процессе ее развитая, вообще говоря,
26
искривляется и может, кроме того, хотя бы частично выйти из начальной
плоскости (сдвиг по площадкам, расположенным под углом 45° к свобод-
свободной границе и начальной плоскости). Край биметалла хх = 0 свободен от
внешних нагрузок.
Рассмотрим замкнутую поверхность 2, которую образуют при пере-
пересечении следующие поверхности: плоскость хх = 0, берега трещины и
свободного от нагрузок разреза в форме полосы в плоскости х2 = h0;
плоскости х2 = 0 и Х2 = h0 + hx; тороидальная поверхность 2f малого
радиуса, охватывающая фронт трещины; плоскости хъ = ±А и хх = +5, где
А > /, В > /, / > h0 A.40)
(/ — характерная длина развивающейся трещины).
Можно показать [1], что интеграл по замкнутой поверхности ^опреде-
^определяемый выражением A.7) (в котором нужно считать /,/ = 1, 2, 3, а через
щ обозначать компоненты нормали к поверхности 2), равен нулю в сле-
следующих двух случаях:
а) процесс стационарен, т.е. все физические переменные зависят лишь
от Xi — Vt, x2, х3, где V — окорость распространения фронта трещины
(одинаковая во всех точках фронта);
б) процесс недиссипативен, т.е. qt = 0, щ = 0 (диссипация энергии на
фронте трещины, конечно, всегда отлична от нуля).
Последний случай реализуется также при нагружении, если считать,
что в процессе увеличения деформации €« реакция тела с трещиной
(вплоть до страгивания трещины) эквивалентна поведению некоторого
нелинейно-упругого тела.
Интегралы по отдельным участкам поверхности 2 (кроме 2Г, хх = 0
и хх = В) равны нулю вследствие того, что на них либо пх = 0 и а/;- щ = 0,
либо uifl =0.
Будем считать, что фронт трещины распространяется вдоль оси хх ста-
стационарно, т.е. не изменяя своей формы со временем, причем всюду на
фронте величина Г одна и та же. Это допущение "равнопрочности" конту-
контура трещины по существу вытекает из общего энергетического подхода,
согласно которому локальный рост трещины определяется параметром Г.
Поэтому в начальный, переходный период своего развития фронт трещи-
трещины перестраивается таким образом, чтобы всюду на фронте величина Г
была одной и той же. При Xi = 0 и хх = В материал можно считать линейно-
упругим.
Таким образом, получаем
r = AUI(nho)(AU=U6-Ua). A.41)
Здесь AU — разность упругой энергии пластинок, конфигурация которых
в плане изображена на рис. 13,6 и а соответственно (пластинки имеют
единичную толщину в направлении оси хх и находятся в плоском напря-
напряженном состоянии), 77/*о — длина фронта трещины (не путать с /!).
Высвобождающаяся вследствие образования сквозной щели энергия
AU находится из решения стандартных плоских задач теории упругости,
изображенных на рис. 13,а и & Ее можно записать в следующем виде:
AU=W2/Eo, A-42)
где безразмерный коэффициент X зависит от ExlE0, hx/hOi vOi vx. Величи-
27
Рис. 14.
ну AU легко найти из прямого
эксперимента по измерению по-
податливости соответствующих
плоских образцов без разреза
и с разрезом (см. рис. 14 со схе-
схематической диаграммой Р - и,
на которой площадь Д?/заштри-
хована).
Как видно, величина Г не
зависит от длины трещины и
может легко регулироваться
заданием усилия Р.
Для изучения роста внут-
внутренних трещин со стеснен-
стесненной деформацией на фронте
описанный образец нужно изменить так, чтобы исключить образо-
образование "губ среза". Этого можно достигнуть, если пластину исследуемо-
исследуемого материала со сквозной начальной трещиной с обеих сторон соединить
с двумя пластинами из более прочного и жесткого материала. Для вели-
величины Г в таком образце по-прежнему имеет место формула A.41).
Диаграмма А/ — Г этим методом определяется непосредственно при
помощи формул A.41) и A.42) по измеряемым в опыте кривым P(t)
и / (г). Из этой диаграммы нетрудно получить также диаграмму dljdY - Г.
Сняв, кроме того, кривую / (г) в присутствии данной коррозионно-
активной среды, простым пересчетом легко определить диаграмму V — Г
для изучаемой пары "материал — среда".
Для образцов рассматриваемого типа одновременно можно использо-
использовать описанный выше метод диаграмм Р — v (см. рис. 12). Это важно
для проверки надежности получаемых результатов.
§ 2. Теория адгезии
Вопросы адгезионной прочности контактного слоя на границе различных
сред являются едва ли не важнейшими при определении возможности
конструирования оптимальной композиционной пары из двух материалов.
Не случайно этим вопросам посвящены два тома упомянутого выше изда-
издания [И].
Сцепление различных материалов имеет разную физико-химическую
природу, однако математическое описание процесса разрушения адгезион-
адгезионных связей разной природы оказывается одинаковым. Теория адгезии
при сдвиге аналогична теории Гриффитса — Ирвина; согласно теории
адгезии адгезионная прочность описывается одной новой константой (вяз-
(вязкостью скольжения контактного слоя), а также размером дефекта или
слабого места на контакте различных материалов. Константа является
объективной характеристикой прочности адгезии, а размер дефекта —
чисто технологической или эксплуатационной характеристикой.
Постановка и решение краевой задачи. Основным механизмом тормо-
торможения поперечных трещин в однонаправленных волокнистых композитах
является развитие цилиндрических микротрещин сдвига, расположенных
28
X
на границе волокна с матрицей и пер-
перпендикулярных трещине. Первые иссле-
исследователи этого явления Келли и Кот-
трелл [43—45] описывали адгезию во-
волокна с матрицей при помощи одной по-
постоянной Ту, равной касательному напря-
напряжению взаимодействия противополож-
противоположных берегов микротрещины при сдвиге
(shear), при этом концентрацией напря-
напряжений на краю микротрещин пренебрега-
лось. Таким образом, величина rs оказалась единственной характеристикой
прочности адгезии волокна с матрицей. Этот подход совершенно недостато-
недостаточен в случае хрупких материалов нитей и матрицы, когда локальной концен-
концентрацией напряжений пренебрегать нельзя. Такими являются, например,
стеклопластики, углепластики, боропластики и др. Вопрос о прочности ад-
адгезии различных материалов при сдвиге представляет интерес не только для
материаловедения, но и для многих других инженерных дисциплин.
Рассмотрим теорию адгезионной прочности разных хрупких материалов
на плоской модели, аналогичной модели Гриффитса.
Пусть одна однородная и изотропная упруго-хрупкая среда занимает
верхнее полупространство у > О, а другая — нижнее полупространство
у < О (рис. 15). Границы полупространств жестко сцеплены всюду, одна-
однако прочность адгезии на промежутке (-/, +/) контакта меньше, чем на
остальной границе; поэтому при определенной величине напряжения сдвига
г вдоль этого промежутка возникает трещина сдвига или скольжения.
Следуя Келли, будем считать, что противоположные берега трещины нале-
налегают друг на друга с напряжением трения тху
й
= т5
При дальнейшем уве-
увеличении нагрузки концентрация напряжений на краю трещины возраста-
возрастает, достигая в конце концов предельной величины.
Таким образом, имеем следующую задачу математической теории
упругости:
при у = О
при у = О, I jc I </
^ху ~ Ts>
при 7 = 0, Ix I >/
B.1)
B.2)
B.3)
при х2 +у2
°х = °у = 0
ГХу = Г.
Здесь и и v — компоненты смещения по осям х и у; ох,оу, тху — напряже-
напряжения; скобка означает скачок величины, заключенной в скобки.
На основании формул Колосова— Мусхелишвили имеем
ах + оу =
(z = х +1»,
fa()
oy + irxy =. <p'k(z) + <p'k(z
2цк(и + iv) = Kkipk(z) - z<p'k(z) - фк(г)
B.4)
(к = 1, 2).
29
Здесь \рх (z) и 0i (z) — аналитаческие функции при>> > 0, у2 (z) и 02 (z) -
аналитаческие функции при у < О, ц — модуль сдвига, к равно Ъ — Av
для плоской деформации и C — v)\(\ + v) для пластинки, *> - коэффи-
коэффициент Пуассона; индексы 1 и 2 относятся к верхней и нижней полуплоско-
полуплоскости соответственно.
Краевые условия B.1) при помощи B.4) можно преобразовать так:
при у = О
<pi + <Pi + W\ + 0i = <?;> + Ж + ^2 + 02, B.5)
при >> = О
(I +kO7i +0i ^_0i +Vi'-Vi'] = Mi[(l +к2)^2 -
02-02 + z^-z^]. B.6)
На бесконечности искомые функции согласно B.3) и B.4) ведут себя
так:
при z -> °о
^=/Q+o(l), 0^= /г+ оA) (*=1,2), B.7)
где действительные постоянные Q определяют вращение на бесконечно-
бесконечности. Одну из них без ограничения общности можно положить равной нулю,
а другая определяется из условия сцепления на бесконечности при помощи
третьего соотношения B.4). Получаем
Сх = г М М С2=0. B.8)
(l +)
Согласно краевому условию B.5) функция у (z), равная
+ 0l(z) при у >0,
B.9)
02(z) при у < О,
аналитична во всей плоскости z и по теореме Лиувилля на основании B.7)
есть следующая константа:
ф) = Цт + Сх). B.10)
При помощи B.9) и B.10) исключаем 0^(z) из краевого условия B.6),
получаем
при у = О
\М2 Ml/ \Ml M2/
Ц2
B.11)
Согласно B.11) функщгя 0 (z), равная
- ) </?i(z) + ( — + — ) ^2(z) + 2/I
\Ml М2
при ^ > О,
при>'<0, B.12)
Mi/
аналитична во всей плоскости z и по теореме Лиувилля из условий на
30
бесконечности есть следующая константа:
-- -)(r + d). B.13)
Ml M2/
При помощи B.12) и B.13) получаем
к2 1\ , ¦ /Hi 1 \_, /1 1 \
+)i()+( + — Wi(z) = / (— - -)(r + d). B.14)
Ml M2 / \Ml JLt2/
Исключаем фк(г) из соотношений B.4) при помощи B.9) и B.10),
находим следующие формулы:
при у-0
р
I- +-
\М2 Ml
о у + irxy = y[ (z) + v'2{z) +1 (r
„ / Эм Эу \
2/i* ( — + i — ) =
\Ъх Ъх)
л а ч B-15)
Эм Эуч v j
Введем функцию cj(z) следующим образом:
( KiM2^i(^)-Mi^2^2(z)+/C при>'>0,
Ф) = r # B.16)
где С = (д2
Согласно второму соотношению B.14) и условию непрерывности сме-
смещений вне трещины скольжения функция cj(z) будет аналитической всюду
во внешности разреза (-/, +/) комплексной плоскости.
На бесконечности согласно B.7) и B.8) функция co(z) ведет себя так:
при z -> °°
Mi M2 —Mi
co(z)=&\ Я = 7~ — . B.17)
М2 1 + К !
При помощи B.14) и B.16) выражаем функции $\ (z) и ^2 (z) через
to(z) и подставляем в первое соотношение B.15). В результате получаем
B.18)
(Mi +)()C
—~———¦
(M2 +K2/x1)d;(z)-(/c1//2 +]Lt1)co(z)-irD
5 ; , B.19)
пои v ~~ 0
2 2 / ч
где/) = k^J -к2д! +(/i2 -Mi)
M2
^1/ l+^2\
— IM2 +Mi 1;
M2 \ 1 +^i/
Эм 2*lAt2(l KtiC2)Mi _ . .
при z=x + iO — = Re со(z),
Эх 2д1(к1/х1 -к2м0
Эм 2k2Mi +A+KiK2)m2
при z = x - iO — = ; Re со (z).
Э 2(! k2Mi)
31
ФормулыB.19) и B.20) выражают напряжения и смещения на границе
раздела через аналитическую функцию co(z).
При помощи B.17) граничное условие B.2) сводится к следующей
задаче Дирихле во внешности математического разреза (—/, +/) плоско-
плоскости z:
прих=х±Ю, Ijc К/ lmoj(z)=A, B.21)
tD
где А =
O
Решение этой задачи должно иметь интегрируемую особенность в концах
интервала (-/,+/).
При этом условии решение краевой задачи B.21), B.17) будет един-
единственным; оно имеет вид
i(B-A)z
' B.22)
Развитый метод можно применить также для решения задач с любым
числом трещин скольжения вдоль действительной оси.
Распространение трещины скольжения. Представляет интерес опреде-
определение критической величины напряжения т, при котором трещина сколь-
скольжения начнет двигаться. Для этого определим вначале поле напряжений
в окрестности конца трещины.При помощи B.22), B.18), B.9), B.10)
и B.1) щходимпри;>>0,г <^ /
4Ки в
°х + Оу = ~~ —7—7 sin ~, А = 1 +
А\/2пг 2
Ки /в 36 Mi+KiM2 0\
ov = — —т—п sin— — sin в cos — — sin —I, B.23)
y A>/2w\ 2 2 M2+K2MJ 2/
Ku ( в в
;\ c°s — — sin у sin
\ 2
36 М1+К1Д2 в\
sin — + cos —I,
2 /i2+*2/ii 2/
ы ки ( 6 36 Mi +/C!M2 . e\
2iX\ — = — ¦ . ,1 Ki sin— + sin в cos -— + sin —I,
Э ДДЛ 2 2 /I+/CM 2/
ы ки ( 6 36
— = — ¦ . ,1 Ki sin— + sin в cos -—
Эх ДлДтгЛ 2 2
B.24)
При Kt =к2, Д! =/i2 A^n =(г — Ту) VttT! B.25)
Здесь г,6 — локальные полярные координаты с центром в конце трещины
(см. рис. 15), Кц — единственный внешний параметр, от которого зави-
зависит упругое поле вблизи конца трещины скольжения. Будем называть
его коэффициентом интенсивности напряжений. (Согласно B.25) в част-
частном случае однородного тела он совпадает с аналогичйым коэффициентом
в [1], поэтому формулы B.23)—B.24) дают обобщение этого понятия
на общий неоднородный случай.) При у < 0 поле напряжений получает-
32
ся из B.23) заменой индексов в упругих постоянных и изменением знака
перед 0.
Поле B.23) можю получить также непосредственно, применяя метод
сингулярных решений. Этот метод позволяет показать, что распределение
B.23) характеризует малую окрестность конца трещины скольжения
при любых конфигурациях границы тела,формах и числе трещин, изменя-
изменяется лишь параметр Кц. В случае локального хрупкого разрушения су-
существует критическое значение коэффициента КПс такое, что при Ки <
< Кцс развитие конца трещины скольжения не происходит, а случай.
Кц > Кцс невозможен. Таким образом, условие локального скольжения
в конце трещины определяется дополнительным соотношением
Кц^Кцс- B.26)
Здесь Кцс — некоторая постоянная адгезии двух материалов, которую
мы будем называть вязкостью скольжения. Эта новая константа в теории
адгезии играет такую же роль, какую вязкость разрушения К\с играет
в теории хрупких трещин отрыва. Эта константа является объективной
физической характеристикой прочности адгезии (наряду с постоянной
трения г5).
Таким образом, рассматриваемый феноменологический подход позволя-
позволяет охарактеризовать прочность адгезии различной и сложной природы
при помощи постоянной Кцс, которая должна определяться в специаль-
специально поставленных экспериментах на образцах с заранее созданными трещи-
трещинами скольжения вдоль изучаемого контакта двух материалов.
Следует подчеркнуть, что согласно B.23) трещина скольжения суще-
существенно отлична от похожего и хорошо изученного случая трещины по-
поперечного сдвига со свободными от нагрузок берегами [1]; в частности,
у трещин скольжения сохраняется особенность, присущая однородному
телу, в отличие от трещин поперечного сдвига. Применение одинаковых
обозначений Кцс для разных постоянных не может привести к путанице,
так как в случае адгезии необходимо указывать как упругое постоянные
материалов, так и технологию их адгезии.
Вернемся к нашей конкретной задаче. Согласно условию B.26) и
формуле B.24) критическая нагрузка ть в зависимости от размера де-
дефекта дается следующим соотношением:
(l+Ki)/l2+(l+K2)Ml К\\с „
Ч = *s + 7 ТТ?' B*
Согласно B.27) процесс будет происходить следующим образом
(см. схематичную диаграмму, изображенную стрелками на рис. 16). Вна-
Вначале, при увеличении нагрузки от нуля до rs
трещины нет, затем при г = т$ в месте располо-
расположения дефекта мгновенно образуется трещина
скольжения длины /0. При дальнейшем увели-
увеличении нагрузки длина трещины не изменяется,
пока не будет достигнуто критическое значе-
значение нагрузки ть, после чего начинается дина-
динамический процесс, так как кривая B.27), оче-
очевидно, неустойчива. Величину ть нельзя считать h
хорошей характеристикой прочности адгезии, Flic. 16.
33
ч
N
, ^
так как она зависит от размера дефекта lQf определяемого тонкостями
технологических операций и процессом эксплуатации.
Диаграмма на рис. 16 является наиболее типичной для развития трещин
скольжения. Рассмотрим ее аналог на следующей простой модели, когда
два плоских образца соединены внахлестку и растягиваются силой Р
(рис. 17,а). Соответствующая диаграмма "сила Р — смещение и" изобра-
изображена на рис. 17, б. При Ps > Р> О адгезионное соединение ведет себя как
бездефектное; при Р = Р5 в наиболее слабом месте мгновенно образует-
образуется трещина скольжения, которая изменяет податливость соединения при
Рь> Р> Ps (в этом интервале трещина скольжения не растет). При Р = Рь
и в последующем процессе трещина скольжения захватывает всю площадь
сцепления образцов. Дальнейший (неустойчивый) процесс может быть
реализован при идеально жестких захватах, к которым приложена сила
Р (т.е. мы имеем возможность задавать смещение и, а силу Р замерять,
какой она получится). Как только трещина захватит весь контакт, кон-
концентрация напряжений исчезнет, процесс стабилизируется и изменение
силы с ростом будет связано лишь с уменьшением площади контакта
(рис. 17, б). Последовательные участки диаграммы рис. 11,6 физически
можно охарактеризовать как "упругость — упрочнение — разупрочнение —
течение".
Такой характер процесса можно считать общим для всех адгезионных
соединений. Например, кривые, подобные изображенным на рис. 17,5,
наблюдал Келли в своих знаменитых опытах по вытяжке нити из матрицы
[43, 45]. Теория Келли, в которой пренебрегается участком диаграммы
вплоть до точки А (т.е. считается, что Кцс = 0), соответствует жестко-
пластической модели явления, когда учитывается лишь участок течения.
В опытах с хрупкими матрицами Келли наблюдал весьма значительные
горбы на диаграмме Р — и, предшествующие точке А, однако не дал им
объяснения. (Точка А расположена на нисходящей ветви диаграммы,
она соответствует самому началу течения, когда трещина скольжения
только что захватила всю площадь контакта S, т.е. РА - tsS) .
Поток энергии в конец трещины скольжения. Выведем формулу, связы-
связывающую поток энергии в конец трещины скольжения с коэффициентом
интенсивности напряжений. Чтобы разобраться в том, куда деваетЪя энер-
энергия, поступающая в конец трещины из внешнего упругого поля, обратим-
обратимся вновь к диаграмме рис. 17, б. Представим себе, что из точки Л диаграм-
диаграммы произведена разгрузка; разгрузка, очевидно, будет происходить вдоль
прямой и приводить обратно в начало координат, если пренебречь необ-
необратимыми деформациями (при этом все напряжения в теле исчезнут).
Pi
Рйс.17.
34
Площадь образующейся петли заштрихована на рис. 17,6; она равна необ-
необратимой работе, затраченной на продвижение трещины скольжения вдоль
всей площади контакта S. Энергия упругого поля, поступившая в конец
трещины, равна этой работе диссипации.
Рассмотрим малую окрестность конца трещины, в которой справедливы
асимптотические формулы B.23) > и применим инвариантный Г-интеграл
по замкнутому контуру L в форме узкого прямоугольника ABCD с раз-
2R
Рйс. 18.
резом (рис. 18). Поток энергии в конец трещины скольжения согласно
формулам A.7) и A.12) равен
R-+0 L
8/R-+0
AB
7
Kli тг/ в зв\( в зе\
/ [а - 2 sin — sin — I ( b + 2 cos - cos — )dB + ..., B.28)
327TMi о \ 2 2 / \ 2 2 /
где
Ml
M2 +*2Ml
Здесь точками обозначено аналогичное слагаемое, получающееся из перво-
первого перестановкой индексов в упругих постоянных м и к. В преобразовании
B.28) учтено, что вклад в общую сумму от интегралов по отрезкам ВС,
DA и берегам трещины будет пренебрежимо мал, так как д <R иЯ -*0,
а вдоль отрезков CDnAB будет 5 = г sin В и sin2 Odx = — 8d$.
Простое вычисление интеграла B.28) приводит к следующему резуль-
результату:
f , . Mi +*iM2 ,,
— ( 1 + II *i +¦
Г =
M2
M2 +«2Ml
+ - 1 +
М2
Mi
M2
Ml
•)]¦
B.29)
В частном случае однородного тела при кх = к2 = к и цх = Мг " М отсюда
получается уже известный результат [ 1 ].
Другой интересный частный случай отвечает условию Mi ^M2> когда
один из материалов гораздо жестче другого. Этот случай часто реализует-
реализуется в композиционных материалах (модуль Юнга нитей гораздо больше
35
модуля Юнга связующего). Формула B.29) в этом случае упрощается:
к3
г = —г—; ки .0*1 >*г). B.зо)
4A +)
Теорию трещин скольжения можно построить по аналогии с теорией
Гриффитса из чисто энергетических соображений. Будем считать, что дня
увеличения единицы площади поверхности трещины скольжения требует-
требуется затратить необратимую работу 7/т> которая является физической по-
постоянной, характеризующей прочность адгезии двух материалов. Будем
называть ее энергией адгезии двух материалов / и т. Величина ?/т связа-
связана с вязкостью скольжения Кцс формулой B.29), в которой нужно за-
заменить Г на 27/т> а Кц — на Кцс. Таким образом, согласно B.29) энерге-
энергетический подход Гриффитса к трещинам скольжения приводит к резуль-
результату, идентично совпадающему с полученным выше силовым методом.
Формула B.29) позволяет определять вязкость скольжения экспери-
экспериментальным путем по измеряемой необратимой работе, расходуемой
та развитие трещины скольжения. Например, при соединении внахлестку,
как показано на рис. 17, а, нужно снять диаграмму Р - v и найти величину
площади, заштрихованной на pic. 17, б; разделив эту величину на площадь
поверхности контакта, найдем значение 7/т» а затем —по формуле B.29) -
величину Кцс.
В настоящей теории не учтены различные усложняющие факторы, которые
при определенных условиях могут иметь первостепенное значение. Это тер-
термохимическая неустойчивость адгезионного слоя, влияние внешних сред,
влияние циклических или переменных нагрузок и тд. Поэтому ее (как и
теорию Гриффитса - Ирвина) следует рассматривать как теорию первого
приближения. Некоторые из указанных факторов будут рассмотрены далее.
Открытые трещины на границе раздела двух различных сред [46].
Рассмотрим находящееся в условиях плоской Деформации упругое тело,
состоящее из двух полупространств с различными упругими постоянными;
границу полупространств берем за плоскость у = 0. В плоскости у = 0
тело имеет полости, проекцией которых ни плоскость комплексного
переменного z = jc + iy являются п разрезов ?,- = я,&/ (/ = 1,2,..., п)
оси х; совокупность этих разрезов обозначим через L.
Компоненты вектора смещения и и v и компоненты тензора напряже-
напряжения оХУ оуу тху выражаются формулами B.4), где постоянную кк выразим
здесь через постоянные Ляме Хк и iik:
Рассмотрим тот случай, когда функции ipk(z) и фк(г) при больших z име-
имеют вид / t
X Y
B.32)
Щ
Го = 7(tft +tf2), Г' = -\(NX -N2)e-2i« (i, * = 1,2; i Фк).
4 2
Здесь N\ и N2 — величины главных напряжений в бесконечно удаленной
точке; а — угол, составленный направлением оси Nt с осью х; X, Y — ком-
компоненты главного вектора усилий, приложенных к разрезам L.
Введем аналитические во всей плоскости z, кроме, может быть, оси
х, функции
Mi
[*i(z) + z*i'(z) + 0f,(z)]
при Im z < О,
при Im z > О,
B.33)
2 О)
при Im z > 0,
при Im z < 0.
Легко показать, что для того чтобы граничные условия сцепления вы-
выполнялись в бесконечно удаленной точке раздела упругах сред, необходи-
необходимо и достаточно удовлетворить соотношению ( Райс| Грилицкий и другие
аторы, не знакомые со статьей [46], позже также изучали эту задачу)
B.34)
Из B.32) и B.33) видно, что'функции Ф(г) и п(г) при больших z
ведут себя следующим образом:
Hi X + iY
<*>(z)=r0-
Mi
ST
B.35)
ft(z)=ro+r' +
X + iY
Из формул B.31) и B.33) получаем необходимые в дальнейшем основ-
основные соотношения, выражающие производные по х от компонентов вектора
смещения и компоненты тензора напряжения через функции Ф(г) и S2(z):
В верхней1 полуплоскости (Im z > 0)
B.36)
- hxy = Ф B) + ft (z) + (z -
a э
37
в нижней полуплоскости (Im z < 0)
Г All -Д2 Л/ ч
Re ФB)+ S2(z)
L Mi +7X2K1
Ф B) + ft B) +
O+K)
-
U(z)
1—)
Эх/
М1-Д2
* jf
¦]
Выражения для смещений получаются простым интегрированием. При-
Примем, что lim .уф' (х + iy) = 0, lim yti (x + iy) = 0 при ^ -* 0 для всех х
На основании формул B.36) и B.37) легко найти, что граничные условия
на участках сцепления
(и + w)zssx+i0 = (и + /u)z= х-,ч>
приводят к соотношениям
Ф+ = Ф", ^+ = П", B.38)
т.е. функции Ф(г) и ^(z) аналитически продолжимы через промежутки
оси х, на которых имеет место сцепление упругих сред.
Пусть на разрезах L заданы напряжения
(оу -iTxy)z=x±iQ =p± (х), B39)
где р~(х) — заданные комплексные функции, знаки плюс и минус соот-
соответствуют верхнему и нижнему берегам разрезов.
Принимая во внимание соотношения B.36) и B.37), граничные условия
B.39) можно написать в виде
Ф+ + ?Г = р*на L,
B.40)
Умножая второе условие B.40) на — 1/[mi A +^2)] и на 1/[мг A +*i)]
и складывая с первым, получаем две решаемые порознь краевые задачи
38
йшана - Гильберта для одной функции:
Р1-Гг=р*-р\ Fl + mFl =/. B.41)
Здесь
Ml
/=
M2
В классе функций, имеющих в концах разрезов х=ак,х=Ьк интегри-
интегрируемую бесконечность, общее решение краевой задачи B.41) примет
вид [47]
1 р* - р"
Fi B) = f — dx + С (С = const),
2ni LX~Z B.42)
1 г f(x)X(x)
2mX(z) l.L x - z
Здесь
X(z)=U (z -акГ>+ * (z - ЬьУ'-'Р, 0= ±-In m,
k=l 27Г
Pn (z) = СЛz" + /.. + Co (Co, Cx,..., Cn = const).
При этом выбирается ветвь ^f(z) такая, что при больших значениях z фун-
функция X(z)=zn +o(zw). Из условия на бесконечности B.35) следует, что
Mi (l+«c2)
B.43)
СЛ=2тг/BГ0 + Г').
Остальные п неизвестных коэффициентов полинома Рп (z) определяются
из условий однозначности смещений аналогично случаю однородного
пространства [48].
В частном случае изолированного симметрично нагруженного
(р+=р" = р) разреза (-/,+/) выражения для функций <I>(z)h?2(z) прини-
принимают вид
ф (Z) =
Ml +M2 +Ml*2 +M2«1 ,- лл.
B.44)
п Суд A + k2)-(mi +№i)F2\z)
Ml +М2 +Ml*2
39
Здесь
j
* 1
J
j
Ц2 +K2Ml -I X - Z
Постоянная С дается формулой B.43). Если разрез не нагружен (р+
=р~=0), предыдущие соотношения дают
B.45)
В качестве другого примера рассмотрим периодическую систему раз-
разрезов с периодом 2L. Используя отображение на плоскость комплексно-
комплексного переменного ? =sinGrz/2L) при решении краевой задачи B.41) или не-
непосредственный предельный переход в решении B.42) при и-*^° для пе-
периодических граничных условий задачи, можно найти
+M2
B.46)
Ml
где
fe (H-«i)t)l. (!+«»)«> p [x @1 (<tX)"""'(t-
M2+Ml^2 -X f-f
X = sinGr//2I), f = sin
Если предположить, что р±(х) ограничена при стремлении х к концам
разрезов, то анализ полученного точного решения показывает, что в малой
окрестности любого конца щелей напряжения и потенциалы выражаются
формулами C.124) и C.114) книги [1], полученными методом сингуляр-
40
ных решений. Коэффициенты К\ и Кц легко находятся из полученного
решения для различйых частных случаев. Некоторые результаты таких
расчетов имеются в §1 Приложения к книге [1].Рассмотрим малую ок-
окрестность конца трещины, в которой справедливы эти формулы, и вычис-
вычислим инвариантный интеграл Г по замкнутому контуру С в форме узкого
прямоугольника с разрезом (см. рис. 18 и формулы A.7), A.12)). В
результате получаем
Условие локального хрупкого разрушения (и продвижения конца тре-
трещины) записывается в форме некоторого соотношения между К\ и Кц.
Бели трещина развивается вдоль границы раздела, то естественно принять
концепцию Гс (см. § 1): величина Г равна постоянной контактного слоя
2jfm на границе раздела сред в момент продвижения конца трещины,
при Г < 2jfm роста трещины нет (jfm — энергия адгезии). Таким обра-
образом, на плоскости (Ki, Кц)условие предельного равновесия представля-
представляется некоторой окружностью.
Хотя и для открытых трещин, и для трещин скольжения предельное
значение Г было обозначено одной и той же буквой jfm, нужно ясно пред-
представить себе, что численные значения энергии адгезии ту™ в этих случаях
могут существенно различаться в зависимости от физико-химической
природы адгезии. Опытных данных по этому вопросу пока совершенно
недостаточно.
§ 3. Вязкость скольжения. Энергия адгезии
Одной из наиболее простых схем прямого экспериментального опре-
определения вязкости скольжения Кис является опыт на плоской модели,
схематично изображенной на рис. 19. Пусть один материал (матрица)
занимает нижнюю полуплоскость, а другой (например, материал нити)
заполняет полосу постоянной толщины, жестко сцепленную с матрицей
по той же технологии, что и в композите. Предварительно в полосе пер-
перпендикулярно к ее границе можно сделать глубокий и тонкий надрез,
который при одноосном растяжении инициирует трещину нормального
разрыва, перерезающую полосу целиком (вдоль оси .у) и приводящую
к образованию трещины поперечного сдвига на границе раздела сред (вдоль
оси я). Представляет интерес зависимость длины трещины сдвига 2/ от
взаимного смещения берегов трещины нормального разрыва 2м0 вследст-
вследствие растяжения.
Найдем точное аналитическое решение
этой задачи в предположении, что мате- '>//////////////
риал полосы во много раз жестче материа- ^ .
ла полуплоскости. Для большинства наи-
наиболее интересных композиционных пар ^^^KKftfli I тммшммм*
это условие выполняется. При растяжении [* ZL *\
рассматриваемой упругой системы вдоль 2
оси х можно считать, что взаимное сме- Рйс. 19.
41
щение двух полуполос одинаково во всех точках и равно раскрытию трс
щины нормального разрыва 2 и0, т.е.
=0, х>1 u=u0i y = 0,
C.1)
при v = 0, х <- I и = —и0, v = 0.
На трещине скольжения должны выполняться следующие условия:
при у = 0, \х\ </
и = 0, Txy = -Tsd0 (х), C.2)
где 50 (*) = 1 при х >0и 50 (х) = — 1 при х <0;т5 — постоянная трения,и
и v — компоненты вектора смещения по осям х и у соответственно.
Требуется найти длину трещины поперечного сдвига 2/ в зависимости
от раскрытия трещины отрыва 2и0.
Напряжения и смещения в плоской задаче можно представить по фор-
формулам Колосова при помощи аналитических функций у (z) и ф (z) следую-
следующим образом:
ох +оу =4 Rey?'(z) (z=x+z>),
оу - ох + Птху = 2 [сУ (z) - ^ (z) - (z -7)*" (z)], C.3)
2ц (и +/и) = к\р (z) - co(z) - (z - z)<p' (z),
где w(z) = z^'@+ *W (к
Сквозное граничное условие у = 0 при .у = 0 согласно C.3) имеет вид
Ьп [к\р (z) + со (z)J = 0 при у = 0. C.4)
Согласно условию C.4) для всех z будет справедливо следующее тож-
тождество:
co(z) = -k^(z). - C.5)
При помощи этого уравнения из представлений C3) вытекают следую-
следующие формулы:
при у = 0
/iw = к Re i (z), ¦
C.6)
а^ - ах + 21тху = - 2 (/с + 1)<р' (z) .
При помощи этих формул оставшиеся граничные условия C.1) и C.2)
можно записать в виде следующей смешанной краевой задачи теории ана-
аналитических функций:
при у = 0, | х\ < I Im \р' (z) =—— 50 (х),
1+к C.7)
при 7=0,'|jc|>/ R/() 0
42
Функция ${z) имеет интегрируемую особенность в конце трещины
при z -*±/,а при z->°° она ведет себя, очевидно, как потенциал дис-
дислокации с постоянным вектором Бюргерса, равным 2и0 и направлен-
направленным вдоль оси х. Следовательно, при z-><» имеем
C.8)
TTKZ
Решение краевой задачи C.7) - C.8) имеет следующий вид:
,,ч_ т* V до(х)у/х2 -I2' ш 2/ш0/
{к + i)y/z" -г -г х - z
.2 /2* =
(Vz -I2 =z+ O(l/z) при z->oo). C.9)
Корень под интегралом берется на нижнем берегу разреза (-/, +/) вдоль
действительной оси (этот разрез выделяет однозначную ветвь y/z2 - /*)
Вычисляя интеграл в C.9), получаем
, __ 2/rj / 2/
7Г(к+1)аГ 8 \JZ2 - I2'
По потенциалу^' (z) можно определить все интересующие нас величины.
Вблизи правого конца трещины имеем:
при z->/
C.11)
Таким образом, согласно B.23) разрыв смещения представляет собой
трещину скольжения со следующим коэффициентом интенсивности напря-
напряжений:
/ ли. ^
CJ2)
В предельном состоянии величина Кп равна вязкости скольжения ^ц с;
из этого условия по формуле C.12) находим зависимость длины трещины
2/ от перемещения и0:
2
1 Г Гп Цк +1) VF I
U/Ab+iK\ C.13)
2 L 4fs kts s
Как видно, длина трещины монотонно увеличивается с ростом пара-
параметра нагружения и0; следовательно, рассматриваемая трещина сдвига
всегда устойчива. В частности, имеем следующие интересные предельные
случаи:
к + 1 /1
при Кцг = О I = — м0 >
кг," C.14)
при
Я\ К/ Аи/.
43
Формула C.12) может служить для определения константы Кис по за-
замеряемым в опыте величинам /, м0 > М> ?$ и к в момент начала движения тре-
трещины скольжения. На одном и том же образце можно получить несколь-
несколько точек, отвечающих разным величинам / и и0.
Проверка показывает, что на трещине скольжения при у = О, \х\ <1
напряжение оу — сжимающее (оу < 0), а напряжение ах — растягивающее
0>0)
Рйс.20.
До сих пор всюду предполагалось, что оба составляющих композита
линейно-упруги вплоть до разрушения (такими можно считать, например,
стеклопластики, углепластики, боропластики и т.д.). Теперь рассмотрим
случай, когда по крайней мере один из материалов перед разрушением
испытывает существенные пластические деформации, так что в предель-
предельном состоянии, предшествующем локальному разрушению на фронте
трещины, упругие асимптотики с коэффициентами интенсивности напря-
напряжений Ki и Кц не реализуются вследствие значительных пластических
зон. Этот случай соответствует условиям нелинейной механики разруше-
разрушения для однородных материалов. Для таких композитов в качестве па-
параметра, контролирующего развитие конца трещины вдоль границы раз-
раздела, естественно выбрать инвариантный Г-интеграл первого рода Тх,
где ось х совпадает с направлением развития трещины. Он равен дисси-
диссипации энергии в конце трещины при ее движении, приходящейся на еди-
единицу площади (удвоенная энергия адгезии). Критическими значениями
этой величины, отвечающими, например, началу движения трещины
(Г5СС)или началу нестабильного роста (Гс), можно характеризовать проч-
прочность адгезии рассматриваемой композиционной пары.
Наиболее надежным методом изучения энергии адгезии является при-
применение в опыте образцов специальной формы с искусственными трещина-
трещинами, для которых величину Гх можно теоретически определить для твер-
твердого тела с любыми реологическими свойствами. Этот метод является
естественным обобщением подхода § 1 на неоднородные тела.
Рассмотрим несколько примеров.
Сдвиг и сжатие неоднородной полосы с продольной трещиной. Пусть
полоса с основаниями у = +Лх иу = — h2 содержит полубесконечный раз-
разрез у = 0, х < 0 (рис. 20). Верхняя ее часть при ^>0 заполнена одним
материалом, а при у<0— другим (при у = 0,х>0— неразрушенный
адгезионный слой, обеспечивающий при деформации условия сцепления,
т.е. непрерывности смещений). Основания полосы защемлены, так что
вектор смещения постоянен вдоль каждого основания (но различен для
у = + hi и для у = - h2 ). Противоположные берега разреза налегают друг
на друга, так что имеют место условия
при у'= О, х < О
Ы=0> г*,=*, - C.15)
где постоянная к предельного состояния определяется из отдельного эк-
эксперимента (без неразрушенного адгезионного слоя). Она зависит от
сжатия оснований полосы.
Напомним, что на основании теории инвариантных Г-интегралов в ква-
квазистатических процессах для любого замкнутого контура 2 в однород-
однородном нелинейно-упругом теле имеют место равенства [1 ]
ф (Unk - OijUitknj) <*2 = О C.16)
В случае стационарных процессов для любых * твердых тел имеет место
уравнение
h]2=°- C л7)
Здесь обозначения аналогичны принятым в формуле A.7) с учетом
того, что направление роста трещины в рассматриваемых ниже случаях
совпадает с направлением оси х.
Величина Г равна интегралу от такого же выражения по замкнутому
контуру, охватывающему конец разреза (например, по окружности ма-
малого радиуса). В качестве контура 2возьмем контур АВСС'В'-А'О, сос-
составленный берегами разреза, основаниями полосы, малой окружностью
с центром в конце разреза и отрезками линии х = ±N (где N — некоторое
большое число). Этот контур изображен на рис. 20 стрелками.
Нетрудно показать, что равенство C.17) справедливо для выбранного
контура 2 вследствие условий пх = 0, [by nj\ = 0 и [щгХ\- 0 на границе
раздела сред при у = 0, х > 0. Следовательно, уравнение C.17) справедливо
также для неоднородных сред, если границы раздела различных сред парал-
параллельны оси х. Это обобщение будет применяться в дальнейшем без напо-
напоминаний.
Интеграл по основаниям полосы обращается в нуль вследствие того, что
пх = 0, а также вследствие того, что на основаниях удовлетворяется одна из
следующих комбинаций: a) uifX = 0; б)оу = тху = 0; в) тху = 0, иух = 0,
г) оу = 0,ихх = 0. Интеграл по берегам разреза вследствие C.15) сво-
сводится к следующему выражению:
а'оа \ дх у Ьх
C.18)
где Дм — скачок смещения их на противоположных берегах разреза при
X -* - оо.
* Неоднородных вдоль оси >\
45
Будем считать для простоты, что при х -* ± °° материал полосы нахо-
находится в упругом квазистатическом состоянии, т.е.
при х
Э
C.19)
где U— упругий потенциал единицы объема.
В качестве условий нагружения примем на бесконечности условия
чистого сдвига:
при х -> + °° ох = оу = О,
Tim Пл Т IIл П .
C.20)
гху s
"о
при*-*-*
5 0,
Txv s^
Здесь w0 - заданная разность смещения их на основаниях полосы. Эпюра
смещения их по у на краях полосы показана на рис. 21. Величина скачка
смещения Аи на берегах разреза, очевидно, равна
ио-к(— +— .
\М2 Ml /
C.21)
Так как при чистом сдвиге U = т1у/Bц), то согласно C.19) имеем
/
CC'
'- av
Ъх
— ty
s =-
A'B'
buy
k2
сС
ul
А'В'
А:2
C.22)
/ =- / Udy*-— h2
АВ АВ 2Ц2
Собирая вместе полученные выражения, на основании C.17) получаем
следующую формулу для Г в данной задаче:
Г= \А , Д=—L + -i. C.23)
2 A Mi М2
При м0 < А: А трещины скольжения нет, она возникает при и0 = к А, а
при м0 > ?А вблизи ее вершины формируется поле, характеризующее
адгезионное сопротивление данной па-
пары. При некотором критическом зна-
значении Г начинается движение трещины;
при некотором, вообще говоря, дру-
другом значении Г движение трещины
становится нестабильным (т.е. движе-
движение происходит при постоянном и,
возможно, даже уменьшающемся зна-
значении и0). Какое из этих критических
Рис. 21. значений принять за удвоенную энер-
а? -•>+оо
46
гию адгезии в качестве характеристики
прочности адгезионной пары, в значитель-
значительной мере зависит от соглашения.
Для стационарного процесса заданием
эпюры Э при х -* —°° можно учесть также
любое распределение остаточных деформа-
деформаций и вычислить величину Г (в общем слу-
случае, когда размер пластической области
сравним с/^иЛг). Формула C.23)
для Г справедлива также в случае неста- ft|C 22
ционарного процесса для нелинейно-упру-
нелинейно-упругих тел (линейных при х -* ± <*>).
В этой задаче вычисления были проведены подробно, в нижеследу-
нижеследующих — аналогичные вычисления будут опущены.
Скалывание выступа. Пусть к полуплоскости у < 0 из материала 2
припаян длинный узкий брусок из другого материала 1 при 0 < у < h,
- Кх <L, где / и L гораздо больше h (рис. 22). На границе раздела
при7 = 0, - I <х <0 имеется трещина скольжения, на которой касатель-
касательное напряжение равно нулю. На границу бруска при х = - / давит плоский
абсолютно жесткий гладкий штамп силой Р в направлении оси х. Остальные
границы бруска и полуплоскости свободны от внешних нагрузок.
Контур ? показан на рис. 22 стрелками. Г — интегралы по отрезку
х = L,0<y <h и по полуокружности х2 + у2 = L2, у < 0 пренебрежимо
малы, так как напряжения на них имеют порядок 1/г* ( как от сосредо-
сосредоточенной силы на границе полуплоскости). При х = - / материал бруска
считаем упругим. В результате вычислений, аналогичных предыдущим, при
помощи C.17) получаем
C-24>
Все, сказанное в предыдущей задаче относительно энергии адгезии и
вязкости скольжения, справедливо также в данном случае. Если энер-
энергия адгезии или вязкость скольжения данной пары уже известны, то фор-
формула C.24) позволяет определить предельное значение силы, скалываю-
скалывающей выступ.
Трещины в тонких слоях инородного материала. Пусть на границе двух
бесконечных полос из различного материала, спаянных друг с другом,
имеется полубесконечная трещина скольжения или открытая трещина со
свободными берегами (рис. 23). Обе эти полосы впаяны в бесконечную
плоскость из третьего материала. На трещине скольжения предполагаются
условия
[uy] = 0, [оу]
0.
Контур 2, показанный стрелками на рис. 23, составлен окружностью
радиуса L (где L весьма велико), берегами трещины и малой окружностью
с центром в конце трещины. Г-йнтеграл по окружности большого радиуса
обозначим через Г«>. При помощи C.17) получаем
Г = Гоо. C.25)
47
а)
Величину Г» достаточно легко найти из решения конкретной внеш-
внешней задачи, если предположить, что материал 3 находится в упругом
состоянии.
Действительно, возьмем любое тело или образец (например, конфигу-
конфигураций, приведенных в Приложении к книге [1]) из какого-либо достаточ-
достаточно хрупкого материала 3 с тем отличием, что в нем трещина с обеих сторон
заключена в тонкие слои из двух материалов 1 и 2, составляющих испыту-
испытуемую адгезионную пару. Длина трещины и вообще любой характерный
размер образца гораздо больше толщины инородных слоев. При таких
условиях коэффициенты интенсивности»характеризующие упругое поле на
расстояниях от вершины трещины, больших по сравнению с толщиной поло-
полосы (но малых.по сравнению с длиной трещины), на основании принципа
микроскопа равны коэффициентам интенсивности в соответствующем
всюду однородном теле. Величина П» определяется по известным коэф-
коэффициентам интенсивности при помойш обобщенных формул Ирвина (см.,
например, формулы A.26), A.27), B.29), B.47) и др. [1]).
Таким же образом можно определять энергию и вязкость резрушения
однородного материала 2 на тонких слоях, впаянных в другой, более хруп-
хрупкий, материал 3 (см. рис. 23, б и в, на последнем изображена одна из воз-
возможных схем испытания). Для обеспечения прямолинейного роста трещины
на образцах можно делать боковые просечки и фиксировать при этом лишь
момент начального продвижения фронта в центральной части (например,
по скачку на диаграммах Р - и или при помощи акустической техники).
Например, в частном случае хрупкого материала 2 (см. рис. 23, б) и
симметричной ситуации коэффициент^, соответствующий Г, выражает-
48
Рис. 24.
ся согласно C.25) через коэффициент К\, соответствующий Г», следующим
образом:
/ A — *>з) ^2 A О/С\
Соотношение C.25) справедливо также для случая другой типичной си-
ситуации в композитах, когда трещина на границе двух сред отходит в одну
из сред и распространяется в однородном материале параллельно границе
раздела на некотором малом расстоянии от нее (см., например, обзор
By в пятом томе издания [11]). В этом случае величина Г» соответствует
хрупкой трещине на границе сред.
Модифицированная задача Келли. Пусть полоса толщины h из материа-
материала 1 погружена в бесконечное пространство из материала 2 (рис. 24, а).
На границе сред при х < О имеется две одинаковых полубесконечных от-
открытых трещины или трещины скольжения, на которых касательное напря-
напряжение равно нулю. Полоса между трещинами растягивается продольной
силой Р в направлении, противоположном оси х.
Контур 2 составлен окружностью большого радиуса с центром в начале
координат, берегами разрезов и двумя малыми окружностями с центром
в вершинах трещин. Г-интеграл по большой окружности равен нулю, так
как напряжения на ней убывают, как \\г (сосредоточенная сила в беско-
бесконечной плоскости). Считаем, что материалы 1 и 2 находятся в упру-
упругом состоянии. На основании C.17) находим
. C.27)
Изучим теперь осесимметричный аналог этой задачи, который получает-
получается, если линию- симметрии — ось х — на рис. 24, а превратить в ось сим-
симметрии (рис. 24, б). Это задача о вытягивании силой Р инородного цилинд-
цилиндра из бесконечного пространства*. Рассмотрим поверхность 2, составлен-
составленную сферой весьма большого радиуса с центром в начале координат, бере-
берегами цилиндрической трещины и тороидальной поверхностью, охватываю-
охватывающей круговой фронт трещины. В этом случае напряжения на сфере убьюают
с радиусом, как 1/г 2, и поэтому соответствующий Г-интеграл равен нулю.
Материал цилиндра и матрицы считаем по-прежнему упругим. В силу
осевой симметрии величина Г во всех точках фронта трещины одна и та
же. Отсюда при помощи C.17) получаем
где d — диаметр цилиндра. Напомним, что величина Р в формуле C.27)
имеет размерность погонной силы, т.е. силы, деленной на длину.
Условия последней задачи реализуются в условиях опытов Келли ([45],
см. также [49—52]) по вытягиванию волокна из матрицы, если в процессе
* При другом знаке эта задача может быть интерпретирована также как задача об уда-
ударе цилиндра о полупространство с образованием цилиндрической трещины сдвига.
49
1
1
Рис. 25.
адгезии волокна с матрицей — полупространством некоторый участок
волокна вблизи свободной границы остался свободным (рис. 24, б). При
этом длина участка должна быть в несколько раз больше диаметра нити.
Из соотношения C.28), в частности, получается следующая формула
для критической силыР*, при которой начинается движение трещины:
Р*=
vT
C.29)
Эта сила, как видно, не зависит от длины трещины (в указанных преде-
пределах), поэтому ее движение, начавшись, будет продолжаться; некоторое
увеличение силы потребуется лишь на преодоление бокового трения. Пос-
Последнюю легко оценить, если в том же опыте снять диаграмму "смещение —
сила" (см. рис. 24, в, где схематично изображена характерная кривая
Р - v). Участок плато соответствует той стадии процесса, когда трещина
охватила всю боковую поверхность нити и сопротивление связано лишь
с боковым трением. Поэтому критическая сила Р* равна
Р*
Р - Р*
C.30)
где Рт — наибольшая величина вытягивающей силы, Pf — закритическое
значение силы.
Прочность покрытий и пленок. Различные виды покрытий в виде лаков,
пленок, красок, напыленных покрытий и т.п. широко используются в прак-
практике. Покрытие должно удовлетворять следующим трем основным требо-
требованиям:
а) покрытие не должно растрескиваться раньше разрушения основного
материала;
б) при наличии случайной сквозной царапины покрытие не должно отста-
отставать от основного материала под действием рабочих напряжений в детали;
в) размер зон нарушения адгезионной связи между покрытием и основ-
основным материалом не должен превышать некоторых критических размеров.
Аппарат инвариантных Г-интегралов позволяет развить математичес-
математическую теорию прочности пленок и покрытий. Рассмотрим некоторую окрест-
окрестность точки на свободной поверхности какой-либо детали с покрытием.
Основной материал можно представить в ввде бесконечного полупростран-
полупространства^ < 0, а покрытие— в виде полосы 0 <у < h (рис.25, а). Пусть рабо-
рабочая деформация ех детали в рассматриваемой точке равна е. Из условия
совместности "находим напряжения в покрытии и в основном материале:
°Х2 =
(а2 = v
C.31)
50
Теперь предположим, что в тонкой пленке произошел случайно сквоз-
сквозной разрью (при х-*-*» у > 0). Допустим также, что на границе раздела
при х < 0 имеется трещина технологического или эксплуатационного про-
происхождения (рис. 25, а). Спрашивается, будет ли она расти под действием
рабочей деформации детали? Следует отметить, что допущение о полубеско-
полубесконечности трещины не является сколь-нибудь существенным ограничением:
такая ситуация на основании "принципа микроскопа" возникает каждый
раз, когда характерный размер произвольной трещины в плане значительно
больше толщины слоя.
При наличии разрьюа все напряжения в слое при х-*-°° будут равны
нулю. Рассмотрим контур 2, показанный стрелками на рис. 25, а. На основа-
основании C.17) получаем
he2El
Отсюда находим предельное значение деформации е*, при которой трещи-
трещина движется и происходит отставание пленки:
...у.
Это же явление отслаивания может произойти при нагревании или охлаж-
охлаждении детали вследствие разности коэффициентов теплового расширения
покрытия и основного материала (или же вследствие остаточных техноло-
технологических напряжений). С учетом этих явлений получаются следующие фор-
формулы:
C.34)
hEx
Здесь «i, а2 — коэффициенты теплового расширения, б0 — начальная дефор-
деформация детали при температуре AT, равной нулю и соответствующей нена-
ненапряженному состоянию в рассматриваемой окрестности детали.
Таким образом, термостойкое покрытие и условия работы детали долж-
должны удовлетворять требованию е < е*, где е* дается формулой C.34). Есте-
Естественно, должно также выполняться условие е < еь, где еь — предельная де-
деформация слоя, чтобы не было преждевременного растрескивания.
Выражение C.34) для €* годится, очевидно, как для сжимающих, так
и для растягивающих напряжений. При сжатии наличие технологических
или эксплуатационных трещин на границе раздела может привести к ло-
локальному выпучиванию слоя. Рассмотрим это явление при помощи плоской
модели рис.25, б. Считая слой упругой балкой, защемленной на концах, по
теории Эйлера находим величину деформации е+, при которой происходит
51
выпучивание:
тг2 A -px2)h2
е+ = —2
C.35)
где L — длина трещины.
Процесс разрушения покрытия может протекать различно в зависимости
от соотношения величин б*, еь и €+, характеризующих три его возможных
1'
i
7?!
¦X
Phc. 26.
механизма. На основании полученных уравнений нетрудно провести деталь-
детальный анализ различных вариантов этого процесса. Остановимся лишь на од-
одном аспекте этого процесса, не столь очевидном.
Пусть в условиях растяжения имеет место условие еь < €*. В этом слу-
случае при е = еь происходит растрескивание покрытия на отрезки длины по-
порядка 2/*, где величину/* легко оценить из следующей модели передачи
растягивающего усилия на припаянный стрингер (рис. 26). Касательное уси-
усилие т (jc) на стрингере от действия растяжения является нечетной функ-
функцией х (начало координат — в центре стрингера).
В предельном состоянии максимальный эффект передачи осуществля-
осуществляется следующей функцией:
t(x) = ts при jc>0, t(x)=-ts при х<0, C.36)
где Ту — предельное сопротивление сдвигу.
Растягивающее напряжение ох в стрингере определяется из уравнения
равновесия:
C.37)
При значении /, равном
/ h
C.38)
наибольшее напряжение в стрингере равно прочности на разрыв оъ. Стрин-
Стрингер длины 2/, меньшей 2/*, не разрушится при любой величине растяжения.
Если при сжатии е*<е+, то прие = €* происходит развитие начальной
трещины до предельной длины/,, определяемой из C.35) при е+ = е**при
которой происходит выпучивание (см. также ниже стр. 173).
Опыты на двуслойных образцах. Пусть два слоя толщины h1 и h2 из раз-
разных материалов соединены внахлестку, причем на границе раздела имеется
полубесконечная трещина скольжения х < 0, у = 0 с нулевым касатель-
52
р \
и
2
¦
Рйс. 27.
ным напряжением на ее берегах или же открытая трещина со свободными
берегами (рис. 27). Основания полос свободны от внешних нагрузок. Рас-
Рассмотрим два варианта нагружения: а) при х -> — °° один из слоев растяги-
растягивается силой Р, а другой - свободен; при х -+ + <*> на оба припаянных слоя
действует суммарная растягивающая силаР (рис. 27, а); б) прих->— ©о
оба слоя изгибаются двумя равными и противоположно направленными мо-
моментами М; при *-» + <» оба слоя свободны от напряжений (рис. 21,6).
Считаем, что материалы слоев находятся в упругом состоянии. Контур
2 выберем так, как показано стрелками на рис. 27. После вычислений
при помощи C.17) получаем следующие результаты.
Вариант а):
Г =
2A -v22)hxEx
C.39)
1 - vi 1-1
вариант б):
C.40)
Вариант а) можно использовать для определения энергии адгезии и вяз-
вязкости скольжения, вариант б) - для определения энергии и вязкости разру-
разрушения.
Неравновесная кинетика фазовых превращений твердых тел. Рассмотрим
безграничное пространство, заполненное твердым веществом, находя-
находящимся в двух состояниях: вещество в состоянии 2 заполняет внутренность
полубесконечного прямого кругового цилиндра радиуса г, движущегося со
скоростью V вдоль своей осих, а вещество в состоянии 1 заполняет внеш-
внешность этого цилиндра (рис. 28, а). На торце цилиндра х = Vt,y2 +z2 <r2 в
? Г
а)
н
Flic. 28.
53
любой фиксированный момент времени t происходит переход вещества из со-
состояния 1 в состояние 2. Этот переход сопровождают следующие процессы:
а) тепловой эффект Q фазового превращения (в расчете на единицу
объема);
б) образование границы раздела с некоторой межфазной поверхностной
энергией уг 2 (в расчете на единицу площади);
в) фазовое расширение, характеризуемое коэффициентом а (в расчете
на единицу длины);
г) увеличение энтропии и изменение внутренней энергии AU (в расчете
на единицу объема).
Приведенная модель характеризует некоторые реальные фазовые про-
процессы в твердых телах (например, образование игл мартенсита в некоторых
сталях, распространяющихся со скоростью порядка скорости звука в наи-
наиболее твердых компонентах).
Рассмотрим две замкнутые поверхности 2Х и 22 в фиксированный мо-
момент времени/. ПоверхностьХг образована боковой поверхностью и тор-
торцом цилиндра, заполненного веществом в состоянии 2, плюс боковая по-
поверхность соосного цилиндра весьма большого радиуса плюс поперечные
сечения х = L и х = - L (L > г), второе сечение находится между двумя
рассматриваемыми цилиндрами (см. рис. 28, б, на котором замкнутый
контур A i Вх Сх Dx H GFE представляет собой осевое сечение поверх-
поверхности Si). Поверхность 22 образована боковой поверхностью и торцом
цилиндра, заполненного веществом в состоянии 2, плюс поперечное сечение
этого цилиндра прих = - L (см. рис. 28, б, на котором замкнутый контур
A BCD представляет собой осевое сечение поверхности 22) •
Внутри каждой из этих поверхностей вещество однородно; поэтому
уравнение C.17) справедливо для любой из этих поверхностей. Напишем
уравнения C.17) для поверхностей Si и Б2, а затем сложим их. Г-интегра-
лы по боковым поверхностям АВ и Ах Bl9 CD и Сх Dx сократятся вслед-
вследствие условий [ог1 rij] =Q,nx= 0, [uix] = 0. Разность Г-интегралов по ВС и
Вх Сх даст величину яг2 Q + 2пгух2, представляющую собой диссипацию
энергии на фронте фазового перехода (при его передвижении на единицу
длины вдоль оси х). Г-интеграл по замкнутому контуруEHG Fравен
т2 AU - Ue, где Ue - упругий потенциал слоя единичной толщины между
jc = -Z,HJt = -L-h Действительно, на EF и HG напряжения убывают как
1 /г2 (или же быстрее), а наЕНи FG величины uix и щ имеют порядок
меньше 1 /г4, где г — расстояние от торца цилиндра; поэтому соответствую-
соответствующие члены не дают вклада в окончательный результат. Материал в обоих
состояниях считаем упругим.
В результате получим
ттг2 (AU-Q) = 2nryx2 +Ue. C.41)
Упругий потенциал Uei обусловленный фазовым расширением, легко рас-
рассчитать по теореме Клапейрона, считая, что круглая шайба радиуса A + а) г
из материала 2 вставлена в круглое отверстие радиуса г в упругой плоскос-
плоскости из материала 1. Находим
на2 г2
. C.42)
54
Подставляя это выражение в C.41) и решая это уравнение относительно
г, получаем
2712
/• =
C.43)
AU-Q
Из физических соображений знаменатель этой дроби всегда должен быть
положительным. Таким образом, радиус цилиндрической иглы превращен-
превращенного вещества есть строго определенная величина, зависящая от термо-
термодинамических характеристик процесса и некоторых физических посто-
постоянных.
Уравнение C.43) можно использовать также для определения значения
AU или 7i 2 .по экспериментально замеряемой величине г . Следует подчерк-
подчеркнуть, что величина межфазной поверхностной энергии для большинства
композиционных пар значительно меньше энергии адгезии и энергии разру-
разрушения (аналогично однородным материалам).
Из уравнения C.43), в частности, следует, что плоский фронт фазового
превращения возможен лишь в том случае, когда 712 гораздо больше зна-
знаменателя.
§4. Торможение трещины границей раздела
различных упругих сред
Основным механизмом торможения поперечных трещин в волокнистых
композитных материалах является образование трещин скольжения, возни-
возникающих на границе раздела различных упругих сред при пересечении ее ма-
магистральной трещиной нормального разрыва. Этот механизм проанализиро-
проанализирован ниже на основе точного решения [1,53] обобщенной задачи Зака — Виль-
ямса, найденного методом Винера — Хопфа. Предполагается, что длина
скольжения мала по сравнению с длиной магистральной трещины отрыва
и характерным размером тела. В этом случае решение Зака — Вильямса
представляет собой точную асимптотику полученного решения на расстояни-
расстояниях, больших по сравнению с длиной скольжения, но малых по сравнению с
длиной магистральной трещины отрыва. Получены точные замкнутые фор-
формулы для напряжений в конце трещины и для коэффициента интенсивности
напряжений в конце трещины скольжения.
Введение и постановка задачи. Рассмотрим
два однородных изотропных полупространства
из различных упругих материалов, жестко
сцепленных вдоль плоскости х = 0 (ряс. 29).
Фронт трещины совпадает с началом коорди-
координат О, задача считается плоской. Одно из полу-
полупространств х < О разделено на две части ма-
магистральной трещиной отрыва при .у =0, х < 0,
берега которой свободны от напряжений. На
линии раздела пространств имеется поперечная
трещина скольжения, длину / которой без огра-
ограничения общности можно взять равной едини-
единице (jc = 0, | у\ < 1). В случае, если длина трещины Рис. 29.
55
скольжения равна нулю, получается сингулярная задача, точно решенная
Заком и Вильямсом [54]. В рассматриваемой задаче решение Зака — Виль-
ямса должно реализоваться как заданная асимптотика искомого решения
при г -> °° (г, 0 - полярные координаты). Эту асимптотику можно записать
в следующем виде [1 ] :
ог = Кх (X + 1) BтгГ1/2^ [B - X) cos Х0 - В cos (X + 2) 0], D.1)
тгв = Кг (X + 1) Bя)Г1/2гх [X sin Хв + В sin (X + 2) в ]
(О<0<тг/2),
где
(ЗХ + 2)-А;2 A +2Х) + Х + 1
В =
Здесь Oq , ar, rr5 - напряжения, v и д - коэффициент Пуассона и модуль
сдвига соответственно (индексы 1 и 2 относятся к левому и правому полу-
полупространствам соответственно); К\ - коэффициент интенсивности напря-
напряжений, являющийся заданным параметром нагружения в рассматриваемой
сингулярной задаче класса TV [1]; X — единственный действительный корень
уравнения
+ Z>(X+1J D.2)
2k? -2kxk2 +2kx - k2 + 1
(-¦
лежащий в интервале (— 1,0).
Граничные условия нашей задачи имеют следующий вид:
При 0 = 7Г OQ = Тгв = 0, D.3)
при 0 = 0 тгв =0, ив = 0, D.4)
" " '0, D.5)
п @<г<1 тгв=т3ч
при0=- D.6)
Здесь ur, uq — перемещения; квадратные скобки означают скачок величины,
заключенной в них.
Из условия симметрии можно ограничиться верхней полуплоскостью.
Предполагается, что величина rs постоянна; она характеризует сопротивле-
сопротивление сдвигу адгезионного слоя в предельном состоянии.
Искомое решение уравнений теории упругости должно удовлетворять,
кроме граничных условий D.3) — D.6) и условия на бесконечности D.1),
также условию ограниченности решения в конце трещины отрыва при г -* 0.
56
Вблизи конца трещины скольжения при г -» + 1 на основании B.23) должна
реализоваться следующая асимптотика:
sm —
АлДтг? 2
ii *Р I Ф 3(^\
^—¦ sin—f2-A-2cos— cos—I, D.7)
ДУ217 2 \ 2 2/
(/? / 2 ip 3</> \
cos — 11 sin — sin — I.
2 \ A 2 2 /
Здесь кц — коэффициент интенсивности напряжений, подлежащий опреде-
определению; е,(/? - локальные полярные координаты с центром в конце трещины
скольжения (рис. 29).
Решение поставленной задачи в свою очередь является асимптотикой ре-
решения многих других задач, в которых длина трещины отрыва или размеры
тела конечны, однако длина трещины скольжения мала по сравнению с по-
последними. Следует подчеркнуть, что для перспективных волокнистых ком-
композитных материалов этот случай имеет наибольшее практическое значение,
так как отвечает наиболее благоприятному сочетанию хрупкости и вязкос-
вязкости материала. Для пластичных однородных материалов он соответствует
квазихрупкому разрушению. Заметам, что коэффициент К в данном случае
имеет размерность силы, деленной на длину в степени B + А).
Вывод уравнения Винера — Хопфа. Применим интегральное преобразова-
преобразование Меллина
f(p)=Jf(r)rpdr D.8)
0
к уравнениям равновесия
дог 1 ЭтГ0 ог - oq _ 1
дг г дв г г дб
D.9)
и к условию сплошности
/ 1 Э / Э \ 1 Э2 \
Д(сгг + ов) = 0 (А = [г — I +— г). D.10)
К ' \ г дг \ дг) г2 дб1)
В результате для функции о в (р> 6) получим обыкновенное дифференциаль-
дифференциальное уравнение четвертого порядка:
+ [(Р + 1J +О-0 ] — +(р2-1Jа0 = О. D.11)
Функции т ге у о г в ыражаются через о # так:
1 doe I d2oQ
Тгв р-1 d6 ' р-1 d62 в° D-12)
Общий интеграл уравнений D.11) имеет вид
при О<0<я/2
о в =Аг cos(p + 1) в +А2 cos(p — 1N +А3 sin (p + 1N +
+ АА sin (p- 1N, D.13)
57
При Я/2 <0 <Я
о в =ВХ cos О + 1H + Я2 cos(p- 1H +#3 sin О + 1H +
+ В4 sin СР - 1H« D.14)
Здесь Л /,/?/ (/ = 1,2,3,4) — неизвестные функции комплексного парамет-
параметра р. Любые семь из них выражаютсячерез одну неизвестную функциюпри по-
помощи "сквозных" граничных условий D.3) — D.6), преобразованных по г.
Применяя к закону Гука преобразование Меллина, получим
Ъиг 1 +i>/
— = —— К1 - vi) °г - Щ о$],
^ Ei D.15)
Ъщ 1 + v* Г do r doal
Ъг Ei(p + 1) L <» rffl J
(f/ - модуль Юнга, / = 1, 2).
Из преобразованных граничных условий D.3) — D.5) при помощи
D.12) - D.15) приходим к следующим уравнениям:
Л3 (Р + 1) +Л4 (р - 1) = О, А3 (р + IJ +Л4 (р - IJ = О,
B?! +/?2)cosptf+ (^з+^4)sinp7r= О,
[5j (р + 1) +Я2 (р - 1)] sinp тг - [В3 (р + 1) +Я4 (Р - О] cosp7r = 0,
ртт ртт рп
042 — ^41) sin + 043-^4)cos— =B?2-#i)sin +
L 2* **
pn
+ (S3-54)cos —,
ртт pn
(Bt -A^ip + 1)cos—- + (A2-B2)(p-l)cos— =
pn pn
= (A3 -B3)(p + l)cos (А*-В*)(р-I)sin—- ,
P /L 2
1-"а Г. , .ч, Рп . , ..„ P*
+ p(p-l)L"*4r '' 2 *4" ' 2
1 + "i U 2p _ 1 -v\
Ex l\p-l ""'" p
pn pn _ pn
,(P+ )COS— - 3(P+ 2 4 P- Sin 2
1 — v\ Г , ря , , pn
h (P + 1) cos — -52 (p - 1) cos— +
/ ч Ui (P I) cos ^ 2(pl)c
p(p- 1) L 2 2
Р7Г p^ll
53(p + lK sin-^— -j54(P-IK sin— . D.16)
58
Решение этой системы уравнений запишем в следующем виде:
At(p)= (p-l)D(p)A(p), A3=A4=0,
Аг (Р)=А (p)J2(р2 - sin2 у)[к2 -kt(p + I)] -p(p + cos ртг)} ,
[( рп Ърп \ рп
к2 I sin sin р 1 + sin2 +
\ 2 2 V 2
рп 1
+ 2кх sin2 (р - cos ртг) I,
[/ рп Ърп рп \ рп ( рп
*2|P-pcos—cos sin2—1-sin—fpsin
\ 22 2/ 2\2
Зртг\ . pn ' 1
+ sin J - 2kx (p + 1) sin2 (p + cos pn) ,
2 / 2 J
ртг Г Зртг рп
(p)sin—— ^2 cos + cos +
2 [ 2 2
pn I ~ pn \"|
+ 2kx cos I p + 2 sin2 I ,
2 V 2 /J
[Р7Г / Зр7Г РП \
k2 cos — ( p sin - sin —- I +
2 \ 2 2 /
I * pn \ Pn ( pn 3pn\l
+ .*i (p + 1) sin ртг 12 sin2 — - pj-sin— Ipcos + cos '11.
D.17)
Здесь
/)(р)ь 2 sin2— -p -2kx (p2 -sin2— ).
2 \ " 2 /
Введем следующие функции:
D.18)
4
8A -»?)(*a -*,)(*, +1)
Функция *+ ( p) аналитична в полуплоскости Rep > — 1, а функция Ф+ (р)
на основании D.1) аналитична в полуплоскости
Rep<_X_i (гдеО>Х>-1).
59
При помощи введенных функций "дуальные" условия D.6) запишутся в
виде
при в =я/2
D.20)
8 A_„|)(А:2- к,
О
Согласно формулам D.13) — D.17) эти условия можно записать в виде
следующих уравнений:
*
рп Г
1т[
рп
sin2
„ рп
*1 —
4(*2-*,)(!+*,)
D.21)
Исключая функцию/1 (р) из этих двух соотношений, приходим к следую-
следующему функциональному уравнению Винера — Хопфа:
Здесь
ctg
X)jt,
G(P) =
рп
—
D.22)
D.23)
2 4(к2 -кх){кх +1)
Решение краевой задачи. Функциональное уравнение D.22) имеет место
в полосе - 1 < Rep < - 1 - X, - °° < Im p < + °°.
ФункцияG(р)в полосе - 1 <Rep<- 1 -X, -<*><Imp<«> обладает
следующими свойствами:
Л"
-1
60
Рис. 30.
Ыр
9ър
а) при р -> °° вдоль прямой р = — 1 — X + if
функция G (р) стремится к единице;
б) всюду на контуре L функция G (р) не име-
имеет ни полюсов, ни нулей; контур L состоит из
прямой р = -1 - X + it (-ьо < f < +оо) и левой
полуокружности малого радиуса с центром в
точке р - -1 - X, направление обхода конту-
контура L совпадает с направлением мнимой оси
(рк~.ЗО);
в) функция 7 (р), равная
- sin
2 рп <к2 + 1
2 — +
2 4(*2 -
/ —* dt I - { D25)
L2irii: r-p J \сГ(р) (рбВ).
имеет нуль первого порядка в точке р = — X - 1; нуль этой функции явля-
является корнем характеристического уравнения D.2).
Области, находящиеся слева и справа от контура L, обозначим соот-
соответственно через Х>+ и D— Функцию G (р) можно представить в виде
G(p)=~ (ре*), D24)
где
ехр
Функции G+(/?)h С"(/7)аналигачны и не имеют нулей соответственно
в областях D* и Z)"; на бесконечности они стремятся к единице.
Используем следующее известное представление (см., например, [55],
стр.53):
К(р) = К+(р)К-(р). D.26)
Здесь
Г[1±(р + 1+Х)]
К* (р) = l V — D27)
Г[1/2±(р + 1+Х)] V ^
(Г (р) — гамма-функция).
Согласно свойствам гамма-функции функция К*(р) регулярна и не
имеет нулей при Rep < — (X + 1/2), а функция К~(р) регулярна и не имеет
нулей при Re р > — (X + 3/2). Кроме того, согласно формуле Стерлинга
имеем
при р -* оо к* (р) = (± рI/а + оA). D28)
С учетом факторизации D24) — D26) уравнение D22) можно за-
записать так:
,¦1] DЮ)
Используем теперь следующее представление:
р+Х+1 р+Х+1
С4-30)
61
Подставляя его в D.29), получаем
Ф+(р)+ 2f'" + > + n
K+(p)G+(p)
D.31)
Левая часть этого равенства аналитична в D*9 а правая - в D", На осно-
основании принципа непрерывного продолжения они равны одной и той же
функции, аналитической во всей плоскости. Чтобы найти эту единую анали-
аналитическую функцию, нужно изучить поведение искомых функций Ф*(р)
и^"(р)при р-*°°. Это поведение определяется из известной асимптоти-
асимптотики D.7) в конце трещины скольжения.
По теореме абелева типа [55] на основании D.7) находим
при р -> оо *+(р) = J|L, *цр) = - Jj!L . D.32)
На основании D32), D25) и D.28) единая аналитическая функция в
D.31) стремится к постоянной -кц/у/Тпрн р-+°°. Следовательно, по
теореме Лиувилля она тождественно равна этой постоянной во всей плос-
плоскости р. Таким образом, решение краевой задачи имеет вид
knK+(p)G+(p) rs Г \K+(p)G+(p)
Г \K+(p)G+(p) I
L (p + X+l)^(-l)G+(-l)JJ
Определяя отсюда при помощи D.21) функцию А (р), находим преоб-
преобразования Меллина напряжений, а после обращения преобразования и са-
сами напряжения.
Анализ решения. В решение D.33) входит неизвестный параметр ки,
который должен быть определен из условия на бесконечности D.1).
По теореме абелева типа, на основании D.1), находим
Х-В \п
(при р -> -X - 1). С другой стороны, при р -* -X - 1 по формуле D.33)
имеем
*+(-х-1)с*(-\-1)г.. ^УГ 1
62
(Х 1)(ХЯ) Хтг
,/ri(A:)=1r—— -sin — . D37)
Сравнивая D.34) с D35) и переходя к размерным переменным, нахо-
находим
где
Приравнивая локальный коэффициент интенсивности ки вязкости
скольжения кцС, находим уравнение, служащее для определения длины
трещины скольжения /:
% ^Ьг Fi (*) - *• (*>• D-38)
^j *
Как видно, длина трещины скольжения / монотонно растет с увеличе-
увеличением коэффициента интенсивности Къ если корень характеристического
уравнения D.2) лежит в интервале -1 <Х<-1/2.Если концентрация
напряжений на краю трещины скольжения пренебрежимо мала, т.е.
кцС<т5\/7, то формула D38) упрощается:
D 39)
• D39)
Если, наоборот, кцс>т3\/Г, то длина / будет равной
Г *ис 1 2'<1 + 2Х>
/= D.40)
Преобразуя формулу D.25), находим
/cos— 4Z>o(X +1) + 7rsin Хэт t ,XJ
^ . _ / 2 L J 1 - m(t) dt^
27rsin— cos ——дл(Л+1)
2L 2 'I
D.41)
1 « Г X t тЛ
1(-1) = exp — / ln(n2 + m2) + j arctg— Л,
ГA/2-Х)
63
Здесь
Ро (О=*о [(Х+1J -f2] -cos2 — ctf — + sin2 — sh2—,
2 2 2 2
Qq (f) = - 2aot (X + 1) sin Хтг sh r?r,
Pi (О = *о [(Х + 1J -Г2] -cos2 — ch2— + sin2— sh2— +C0,
1
^i (f) = - 2Z>0^ (X + 1) - —sin Хтг sh fir,
P @ =Pi (OPo @ + flfi @ ^o (Os
sh tn \p {f) sh tтг - q (f) sin Хтг ]
/ , Хтг _ fn\ -
Ichrni cos2 — + sh2 — 1 'ф\ + q\)
shfTT [q (f) shfTT fp (f) sin Хтг]
m (i) =
' -4 D.42)
12+^i)!cos2 — 4sh2 —
При вычислении интегралов D.41) на ЭВМ необходимо использовать
следующие соотношения:
г ! ¦ m{f)
lim —arctg =
йог n(t)
Г
тг д
о ^1 I *
) -cos2 — + sin Хтг 2до(Х+1)+ — sin Хтг
lim/
lim
64
sin Хтг 1
2^sin
i (t\ —
Хтг
cos —
2
w (f) = 0.
Хтг Г
2 [
[4Ь0
cos2
cos2
(X +
Хтг
2
Хтг
2
1)
- До (X +
- До (X +
+ Trsin Хя]
iJ
iJ
]
]
Графики функций Fo (к)9 Fx (к) и X (к) построены при помощи ЭВМ для
vx =p2 = 0,3 и приведены на рис.31.
Как видно, функция Fx (к) при к = 10 достигает максимального значе-
значения, равного 0,47.
Вычислим также величину напряжений в конце магистральной трещи-
трещины отрыва; приведем результат вычислений:
при г -> 0
о = —? {хC +cos20)
(-1)] -(I
^ 1
- — E - Ъкх - 4к2 cos20 + 3cos20 - 20 sin 20) |
2ts (
ar=—? XC-cos20)
Г ^'(-1) G+'(-l)
^С-1) G+(-l)
« v л,„ (-1) -(l+2XA:2)C-cos20) +
XV2 J
A + Ski - 4k2 cos20 + 3cos 20 - 20sin 20I ,
2rs
sin 20
X )
— D k2 sin 20 - 3sin 20 - 20cos 20I
Здесь
^_
2 m l
65
f
I
Г/к)
>
'k)
W
Начало развития магистральной трещины определяется некоторым кри-
критическим значением коэффициента интенсивности К\. Формулы D,38) —
— D.40) настоящего параграфа дают точную зависимость этого крити-
критического значения от длины поперечной трещины скольжения. Как видно,
чем больше эта длина, тем больше критическое значение Kj (и тем су-
существеннее граница раздела тормозит развитие магистральной трещины),
0,475
0,45
0,35
0,5
0,25
0,1
0,175
0 4 В 11 16 к
Рис. 31.
если трещина переходит из более жесткой среды в более мягкую, а точ-
точнее, при-К X <-1/2.
При переходе же из более мягкой среды в более жесткую качественная
картина будет более сложной.
§ 5. Растяжение однонаправленных волокнистых композитов
Однонаправленные волокнистые композиты являются важным кон-
конструктивным элементом многих современных композиционных матери-
материалов. Сопротивление их растяжению часто решает вопрос о применении
их в той или иной конструкции. При этом по разным технологическим
обстоятельствам совершенно неизбежен обрыв отдельных нитей задол-
задолго до разрушения всего образца. Например, в стеклопластиках обрывы
замечены уже при нагрузках, составляющих лишь 1/10 от предельных.
В настоящем параграфе вначале рассматривается растяжение бесконеч-
бесконечного упругого пространства с инородным упругим цилиндром, имеющим
сквозную щель (обрыв); вводится представление о зоне влияния обрыва
и определяется его радиус. Это представление позволяет дать простой
ответ на вопрос об оптимальной укладке нитей, а также дать простую
оценку нижней границы объемной доли волокон, для которой разрушение
композита будет идеально вязким, так что влиянием обрывов нитей мож-
можно пренебречь.
При помощи обобщенной модели Розена—Паррата определяется теоре-
теоретическая прочность идеально вязкого композита. Содержание §§ 5и7
этой главы в значительной мере основано на работе ЮЛ. Работнова и
ГЛ. Черепанова [56].
Зона влияния обрыва одной нити. Пусть в, однородном бесконечном
и изотропном упругом пространстве (Матрица-связующее) имеется бес-
66
конечный однородный и изотропный упругий цилиндр радиуса г0 из дру-
другого материала (нить). На границе нити со связующим имеют место усло-
условия жесткого сцепления. Пусть в некоторый момент времени вследствие
однородного растяжения всего тела вдоль оси цилиндра в нем образует-
образуется сквозная плоская щель, перпендикулярная оси цилиндра (рис. 32, а).
Требуется определить поле напряжений и деформаций вблизи трещины.
Эта задача является типичной и в некотором смысле ключевой для
волокнистых композитов. Действительно, все используемые в компози-
¦¦¦¦¦¦
ИНН
Рйс. 32.
тах волокна обычно обладают высокой среднестатистической прочностью,
но весьма малой вязкостью разрушения и вследствие этого чрезвычайно
чувствительны к малейшим трещинам, которые неизбежно возника-
возникают в процессе изготовления волокон. Поэтому некоторая часть воло-
волокон непременно разрушается при весьма низких растягивающих
нагрузках.
К сожалению, точного решения этой задачи пока не имеется. Приме-
Применим подход, неточность и ограниченность которого вполне окупается
простотой и эффективностью получающихся результатов.
Сформулируем граничные условия:
г<г0 а2=г,2=0, E.1)
при r<r0,
при r>r0 (ух =v2).
Здесь г, 6, z — цилиндрические координаты, оГУо2Уов, тГ2 — напряжения,
боо — однородная деформация растяжения вдали от щели, Е — модуль
Юнга, индексы 1 и 2 относятся к нити и матрице соответственно
(рис. 32, б).
Характерный размер зоны пластических деформаций вблизи края тре-
трещины будем считать пренебрежимо малым по сравнению с радиусом ци-
цилиндра.
В малой окрестности контура трещины нормального разрыва, выхо-
выходящей перпендикулярно на границу раздела двух сред, на основании D.1)
при г2 + z2
IB,
'¦"к
67
имеет место следующая асимптотика упругого поля:
при z = 0, r = ro+€ (e<r0)
az=KBn€)\ E2)
где
Здесь К\ — коэффициент интенсивности напряжений, число X является
единственным действительным корнем уравнения D2), лежащим в интер-
интервале (-1,0).
При больших k методом малых возмущений нетрудно найти следую-
следующее асимптотическое выражение для искомого корня уравнения D.2):
E3)
Pi
где
Практически этим выражением можно пользоваться при рх > 10/i2, что вы-
выполняется во многих волокнистых композиционныхматериалах. Пpи/tZl-
:=M2 и vx -v2 корень X естественно равен ^1/2, что отвечает однородно-
однородному телу.С увеличением Mi/j*2 величинах монотонно растет.
Введем представление о зоне влияния обрыва одной нити, аппрокси-
аппроксимировав напряжение oz на продолжении трещины следующим образом:
при z = 0
(Ki [2тг (г - г0)] (г0 < г <Гоо),
Oz = „ ¦ . . х E4>
Здесь гм — радиус зоны влияния обрыва, Кг — коэффициент интенсивнос-
интенсивности напряжений. Обе эти величины подлежат определению. Распределение
E.4) совпадает с точными при г -> °°и г -> г0.
Имеем два очевидных условия:
условие равновесия
2п 7 razdr # л?*2есо (ri -г\) + я^боог|; E5)
условие непрерывности
^[2я(/-« -/•о)]х=?>2боо. E.6)
№ этих условий, используя E.4), найдем г» й К:
5
г5т ( ^ +0 -*H + A)B+'A)i - 1 } , E.7)
E.8)
Здесь
^2 A
Ei (l
В наиболее важном для композитов случае малых 5, используя также
E.3), имеем
( E.9)
г0 2* 2 \ 1+> / V '
•10/ia). E.10)
При ixx >20/z2 вместо E.10) можно использовать следующую упрощен-
упрощенную формулу:
К-Е2еоо BяГоо)~~\ E.П)
Оценим ошибку данного метода в вычислении коэффициента интен-
интенсивности напряжений на примере однородной среды, когда согласно точ-
точному решению
К\ - 2Jb2 €оо \/г о/п. E.12)
При нашем методе согласно E.7) и E.8)
т.е. приближенное значение Кг на 49% больше точного. На рис. 33 приве-
приведена эпюра напряжения oz на продолжении трещины в этом случае (сплош-
(сплошная линия — согласно приближенному решению, штриховая линия — сог-
согласно точному решению).
Из физических соображений с увеличением Mi \\хг ошибка приближен-
приближенного решения убывает. Очевидно также, что полученное приближенное
значение коэффициента интенсивности напряжений представляет собой
оценку сверху точного значения.
Рассмотрим вопрос о величине предельной нагрузки (или растяжения
€оо), при которой начинается локальное разрушение на контуре трещины.
Согласно механике разрушения существует экспериментально определя-
определяемая константа К\са размерности "сила, деленная на длину в степени
B + X)", характеризующая свойства системы "нить - матрица - адгези-
адгезионный слой". Критерием локального разрушения является равенство
К^К1са E.14)
на контуре трещины (при К\ < Kica разрушения не происходит).
Отсюда, используя выражение E.8), находим величину растяжения
с,», при которой происходит локальное растрескивание в конце трещины:
Kit" *"~ ' E.15)
Е2 vo
Вопрос о том, в каком направлении будет происходить развитие тре-
трещины и каков характер этого развития (устойчив или неустойчив), бу-
будет рассмотрен ниже в § 7.
69
Рйс. 33.
Рйс. 34.
Оптимальная укладка волокон. Рассмотрим бесконечное упругое про-
пространство с набором одинаковых соосных круговых цилиндров из друго-
другого материала (волокна в связующем). Растяжение вдоль оси приводит
к образованию ряда сквозных трещин в нитях. Предположим, что тре-
трещины не распространяются в матрицу (развитие трещин рассматривает-
рассматривается ниже). В этом случае на основании результатов предыдущего пунк-
пункта можно утверждать: если радиус зоны влияния одного обрьюа л» мень-
меньше половины кратчайшего расстояния между осями цилиндров (нитей),
то любое число обрывов в нитях не окажут влияния друг на друга и, сле-
следовательно, на прочность композита в целом. В этом случае масштабный
эффект для композита в целом отсутствует: разрушение имеет идеально
вязкий характер, а его прочность оъ определяется по правилу смесей
оь = ofvf + от A - vf), E.16)
где Vf - объемная доля нитей (fiber), Of - среднестатистическая прочность
нитей, от — прочность связующего (matrix). Величина оу соответствует оп-
определенной неэффективной длине, а схема разрушения в данном случае от-
отвечает модели Розена — Паррата (см. ниже).
В рассматриваемом случае трещины в волокнах полностью тормозят-
тормозятся матрицей и композит является практически идеально вязким матери-
материалом. Разумеется, если в композите будут находиться большие начальные
трещины (с радиусом, гораздо большим радиуса нити), то и в этом слу-
случае правило смесей может нарушаться, а композит может вести себя как
хрупкое тело.
С увеличением Vf прочность композита продолжает возрастать; однако
появляется масштабный эффект и хрупкость материала. Поэтому при дос-
достаточно больших Vf происходит уменьшение прочности композита в целом
вследствие уменьшения вязкости разрушения, а также вследствие неиз-
неизбежных технологических отклонений, приводящих к образованию дефек-
дефектов структуры. На рис. 34 зависимость оь от Vf изображена схематично
в пренебрежении величиной от, так как обычно от < Of. В области прояв-
проявления масштабного эффекта при vo<Vf<l>где зависимость ob (iy) не-
нелинейна и где находится максимум среднестатистической прочности оь
(при tf/ = iO, величина оь зависит от геометрии микроструктуры и на-
начальных дефектов, т.е. от чисто технологических факторов. Прочность
оь становится поэтому случайной величиной, а характерная величина откло-
нений от среднего - мерой надежности материала. На рис. 34 вертикаль-
вертикальными отрезками схематично указан разброс величин оь . В области v0 <
< Vf < i>* торможение трещин производится в основном нитями (см. ни-
ниже § 6,7). Улучшение технологии приводит к уменьшению статистическо-
статистического разброса и к увеличению значений v0, и* и оь . Следует подчеркнуть,
что даже при идеальной технологии (т.е. при полном отсутствии дефек-
дефектов в исходном материале, что недостижимо) его вязкость разрушения
К\С является чрезвычайно важной характеристикой, так как она характери-
характеризует устойчивость материала к развитию в нем трещин в условиях эксплу-
эксплуатации.
Из условия отсутствия масштабного эффекта и формулы E.16) выте-
вытекает, что оптимальная укладка нитей в однонаправленном и волокнистом
композите дается решением следующей чисто геометрической задачи:
как разбросать в плоскости круги заданного радиуса г0, чтобы" величина
наименьшего расстояния между их центрами была максимальной при
заданной доле иу, т.е. при заданном отношении площади всех кругов к
площади той области, в которой они разбросаны. Очевидно, что когда
г0 гораздо меньше поперечных размеров образца, можно считать, что кру-
круги образуют в плоскости двояко-периодическую решетку с периодом
г/, и задача сводится к следующей: найти максимум по у наименьшей
из двух величин: d — 2г0 или dsin ^sec (<p/2) — 2r0, при условии, что iy =
=const (здесь dny — длина стороны и острый угол в равностороннем па-
параллелограмме периодов с центром в центре круга). Так как
ЯГо
d2 sin \p '
sin <p sec (#/2) > 1 при 90° > </? > 60°,
sin\p sec (ip/2) < 1 при 6°
то при 0 < \р < 60° нужно найти то значение <р, при котором максимальна
функция
\р I 7Г </? у/2тТГ0 (fi
d sin v? sec — =гоу — sin $ sec — = —=— tg -»- , /5 jg\
2 €f 2 y/€/ 2 \ • /
а при 90° >ip> 60° нужно найти то ^, при котором максимальна функция
. E.19)
В обоих случаях максимум будет при \р = 60°, т.е. центры любых трех
ближайших нитей при оптимальной укладке должны лежать в углах рав-
равностороннего треугольника.
Заранее заданное расположение нитей можно реализовать технологиче-
технологически в ламинатных композитах, образованных вследствие склейки ряда
плоских слоев; каждый слой составлен из упорядоченной однонаправлен-
однонаправленной совокупности нитей так, что оси всех нитей параллельны и лежат в'од-
в'одной плоскости.
71
Таблица 5.1
?Чггёкло
В
SiC,
В - А1
Fe-Al
vf 0,2 0,3 0,4 0,25
Et асгс/мм2 7,5 X 103 39X103 39 X 103 50 X 103
/•ooAo 3,3 5,2 5,2 2,5
\ - 0,79 -0,92 - 0,92 - 0,98
v0 0,083 0,034 0,034 0,145 0,036
0,045
Отметим, что при максимально плотной укладке (когда d = 2г0) вели-
величина Vf равна
Я Г% 2 7Г Го
Граница масштабного эффекта Vf = t>0 при оптимальной укладке со-
соответствует условию 2г'„ = d. Отсюда находим
Величина tJtq находится при помощи E.9) или E.13); она зависит
лишь от упругих прстоянных д,рг>и2. В таблице 5.1 приведены значения
у0 для некоторых композитов, вычисленные по формулам E.21) и E.7)
(в первой строке таблицы указан лишь материал волокон, связующее во
всех случаях — эпоксидная смола при Ег = 350 кгс/мм2, v2 = 035).
В случае металлических матриц вблизи обрыва нужно учитывать плас-
пластические деформации, которые могут образовывать сравнительно большую
область. В этом случае радиус зоны влияния г^ оценим при помощи сле-
следующей аппроксимации:
при z=0
E.22)
(г>г00),
где os - предел текучести матрицы при растяжении. Из уравнения равнове-
равновесия
2тг / rozdr=
+ ттЕ2 €„(ri -
E.23)
находим величину
''о
os-E2e0
E.24)
В таблице 5.1 приведены значения v0 для боралюминия (В — А1) и для
композита "стальная проволока — алюминий" (Fe — А1), подсчитанные
при помощи E.21) и E.24) при Еге00 < os, os = 10 кгс/мм2, of =
= 250 кгс/мм для бора и оу = 200 кгс/мм2 для стальной проволоки.
72
zz
Z2
22
Z
Z2
ZZ
ZZ
ZZ
22
:zz
zz
zz
zz
zz
z
2
22
Z
Z2
Z2
ZZ
SZ
ZZ
22
Рис.35.
Данные таблицы 5.1 показывают, что вза-
взаимным влиянием обрывов нитей можно пре-
пренебречь лишь при сравнительно малых объем-
объемных долях волокон. Именно в этой области
реализуется теоретическая прочность компо-
композита, а схема разрушения соответствует моде-
модели Розена — Паррата. В остальной области ма-
магистральная трещина успевает развиться рань-
раньше, чем реализуется эта схема.
Прочность однонаправленного композита.
Согласно теории Розена — Паррата (см. [57,
58]) разрушение однонаправленного волокнистого композита, при мо-
монотонном увеличении растягивающей нагрузки происходит постепенно,
путем накопления обрывов нитей, причем поперечные трещины в нитях
не распространяются в матрицу. Это объясняется масштабным эффек-
эффектом прочности волокон: более короткое волокно прочнее (среднеста-
(среднестатистически). Максимальной нагрузке отвечает обрыв всех волокон на
отдельные звенья критической длины (неэффективная длина) — если длина
волокна меньше критической, то такое волокно вытаскивается из матрицы,
не обрываясь (рис. 35). Поэтому прочность при таком механизме разруше-
разрушения определяется правилом смеси, в котором прочность волокна оу- со-
соответствует неэффективной длине.
Прочность волокна представляет собой случайную величину, плотность
вероятности которой р(оу) описывают обычно при помощи распределения
Вейбулла:
p(pf)=L ot&(Pf~x exp(- L а а/),
E.25)
где L — длина волокна, а и /J— два параметра, характеризующие распре-
распределение и определяемые экспериментально. Этой плотности вероятности
соответствует следующая функция распределения:
Of
f p(a)<ia=l-exp(-aZ,a/). .. E.26)
о
Модифицируем модель Розена — Паррата с учетом того обстоятельства,
что длина каждого звена волокна L в предельном состоянии является слу-
случайной величиной, представляющей собой некоторую функцию оу. Эта
функция определена далее для нескольких механизмов разрушения, когда
L равна неэффективной длине.
В качестве двумерной функции распределения двух случайных величин
L и Of примем выражение E.26). Заметим, что в данном случае функция
E.25) уже не будет плотностью вероятности.
Подставляя функцию L = L(pf) в E.26), получаем следующую одномер-
одномерную функцию распределения случайной величины оу:
F(Of) = 1 - ехр [- a of L(af)}. E.27)
Теоретическая прочность композита аь получится осреднением по боль-
большому числу волокон в поперечном сечении:
= A - vf) om+vf <.of) , (af) = / of(F) dF.
E.28)
73
Здесь Qf(F) — функция, обратная функции E.27).
Теоретическая прочность композита согласно модели Розена — Паррата
может быть реализована лишь на участке 0 < Vf < v0 диаграммы оь - Vf,
при дальнейшем увеличении объемной доли волокон появляется вероят-
вероятность хрупкого разрушения и масштабный эффект.
С точки зрения принципа равнопрочности [59] идеальные композицион-
композиционные пары должны были бы иметь одинаковую предельную деформацию.
Для большинства композитов это условие не выполняется: разрушаются
вначале волокна, затем отдельные обрывы объединяются, образуется тре-
трещина, развитие которой приводит к окончательному разрушению. Однако
равнопрочность осуществляется согласно механизму Розена — Паррата,
если не происходит хрупкого разрушения.
Рассмотрим теперь тот случай, когда армирующие волокна имеют неболь-
небольшую длину и распределены в матрице. Таким является, например, наиболее
перспективный жаропрочный композит "сапфир — молибден", в котором
нитевидные кристаллы ("усы") сапфира хаотически и однонаправленно
распределены в молибденовой матрице. Прочность на растяжение таких
материалов достигает 25 кгс/мм2 при 1300° С, а ползучесть начинается при
более высоких температурах. При рабочих температурах порядка 700 —
1300° С матрицу и адгезионный слой можно считать пластическим материа-
материалом (а нити сапфира остаются хрупкими), так что эффектами концентра-
концентрации напряжений вблизи концов цилиндрических трещин скольжения мож-
можно пренебречь [56]. Механизм разрушения таких композиционных материа-
материалов определяется теорией Келли — Коттрелла [43—45].
В частности, неэффективная длина /* равна
l* = rof/2Ts. E.29)
Здесь оу — прочность волокна длины /*, г — радиус цилиндрического
волокна, Ту — касательное напряжение текучести в адгезионном слое.
Если длина волокна L меньше /*, то оно вытягивается из матрицы, не
обрьюаясь; если же L > /*, то при вытягивании волокна оно обрывает-
обрывается. Соответственно, если длина всех волокон в однонаправленном компо-
композите меньше 2/*, то при пересечении композита поперечной трещиной
разрьюа все волокна целиком вытаскиваются из матрицы, не обрываясь;
в случае же, если в исходном композите имеются волокна с длиной, боль-
большей 21*, то при постепенном увеличении нагрузки такие волокна постепен-
постепенно оборвутся на волокна с длиной, равной или меньшей, чем 2/*, затем уже
произойдет вытягивание волокон из матрицы. Последний механизм соот-
соответствует идеально вязкому разрушению композита, без развития магис-
магистральной трещины.
С точки зрения принципа равнопрочности [59] оптимальная длина во-
волокон равна 2/*, если, реализуется идеально вязкое разрушение. Опреде-
Определим в этом случае предельное сопротивление композита оь растяжению.
При этом учтем один дополнительный случайный фактор, который не был
принят во внимание в теории Розена — Паррата.
Будем предполагать, что поверхность разрыва составлена плоскостью,
проходящей в матрице, и нитевидными волокнами, выходящими из плос-
плоскости перпендикулярно к ней на длину х (х — случайная величина). Нити
расположены в матрице хаотически с объемной плотностью iy, так что
74
Pii
a) 5)
Pkc. 36.
среднее число волокон на единицу площади поперечного сечения равно
я= vfl(irr2). E.30)
Для случайной величины х, изменяющейся от нуля до /*, на основе
гипотезы равновероятности имеем следующую плотность вероятности:
0 при *<0, х>1* ,
I//* при 0<*</*. E'31^
Отсюда находим
2
где от — прочность матрицы, < х > — среднее значение х. Как видно,
предлагаемая более точная теория дает значение оь, примерно в два
раза меньшее, чем по классической теории (правило смесей), не учитываю-
учитывающей случайного рельефа поверхности разрушения.
Определим теперь сопротивление рассматриваемого композита развитию
в нем поперечных магистральных трещин отрьюа. При достаточно больших
размерах поперечного сечения композитного образца его разрушение
будет неизбежно хрупким, а механизм разрушения — совершенно отличен
от идеально вязкого.
Оценим вначале работу А, затраченную на вытягивание из матрицы
нити длины х (рис. 36, а). В принятых допущениях зависимость силы
/\ приложенной к нити, от перемещения v нити относительно матрицы
будет линейной (рис. 36, б). Поэтому работа будет равна площади треу-
треугольника на этом рисунке:
A=«rrsx2 . E.33)
Поверхность магистральной трещины отрыва составлена плоскостью
в матрице и волокнами, выходящими из плоскости перпендикулярно к ней
на длину х (рис. 36, в). Поэтому эффективная поверхностная энергия
композита 7* (энергия разрушения) равна
7* = П (А) + ут A — Vf) = Л Г П Ts { X2 ) + 7m A — Vf) =
rvfo}
—щ ¦*¦<¦-•* <5-34>
гДе 7m ~ энергия разрушения матрицы.
Выведенные здесь формулы для оь и 7* остаются верными, очевидно,
также для произвольно упорядоченного расположения волокон в матрице.
75
§ 6. Развитие поперечной трещины в композите
(стохастический процесс)
Стремление к большой прочности заставляет конструктора работать на
участке (v0, у*) диаграммы оь - Vf (см. рис. 34), тем более что боль-
большинство используемых в настоящее время матриц обладает сравнительно
малой прочностью и модулем Юнга (это приводит к малому значению
о0). Очевидно, что масштабный эффект можно практически нивелировать
(здесь не рассматривается влияние случайных отклонений от упорядочен-
упорядоченной упаковки, что также приводит к масштабному эффекту и конструк-
конструкционной хрупкости [60]), если уменьшить до нуля статистический раз-
разброс прочности волокон Of.В таких композитах теоретические значения
v0 и и* близки к предельной величине 0,9.
Исследуем развитие поперечных трещин в однонаправленных волокнис-
волокнистых композитах с учетом статистических свойств отдельных волокон.
Рассмотрим вначале ленточную модель композита (рис. 37, а)9 когда
все нити — цилиндры радиуса г 0 — расположены соосно в одной плоскос-
плоскости в полосе связующего ширины h на одинаковом расстоянии d друг от
друга (одномерная решетка). Композит однородно растягивается в направ-
направлении волокон напряжением о = Ех €«>. Укладку нитей считаем достаточно
плотной. Обрывы волокон располагаются в области концентрации напря-
напряжений вблизи конца трещины; размер этой области вдоль оси нитей равен
неэффективной длине L (рис. 37, б). Величина L определяется ниже в §7.
В аналогичной постановке была рассмотрена проблема разрушения лен-
ленты, состоящей из конечного числа волокон, в работе Скопа и Аргона [61]
(см. также обзор Аргона в томе 5 издания [11]). В теории Скопа и Аргона
рассматривается лишь простейший вариант каскадного разрушения, стохас-
стохастический процесс ими не рассматривался.
Пусть в композите имеется начальная трещина длины 2/0, перпендику
лярная волокнам (рис. 37, в). Найдем напряжения в целых волокнах, на-
находящихся вблизи последнего разрушенного волокна. Для этого вначале
мысленно заменим композит эквивалентной ему по упругой реакции од-
однородной ортотропной пластиной (толщины И ) с осями упругой симмет-
симметрии вдоль и поперек волокон. Напряжение bz на продолжении сквозной
поперечной трещины в такой пластине равно Ki[\J2tix\ где К\ — коэф-
коэффициент интенсивности напряжений, определяемый из решения задачи
в целом, х — расстояние от конца трещины на ее продолжении^ — направ-
направление волокна (рис. 37, г). Отсюда, возвращаясь к нитям, из условия рав-
равновесия
о21тг20= h f . rdx F.1)
kd \/2т1Х
(предполагается, что всю нагрузку несет волокно) находим напряжение
в целых волокнах вблизи конца трещины:
(k =1,2,3,...), F.2)
где kd — расстояние центра рассматриваемого волокна от конца трещины.
76
щ
1
\
ч
I
%
1
1
|
1
i
\
/ 2 3
ftic. 37.
В частности, в наиболее напряженном ближайшем волокне (при к= 1) имеем
F.3)
В теории Скопа и Аргона [61] концентрация напряжений определяется
другим, более частным методом; получающееся выражение отлично от
полученного.
В дальнейшем предполагаем, что развитие трещины идет путем последо-
последовательного обрыва наиболее напряженных нитей в ее конце, а другими
возможными обрывами в глубине тела на пути основной магистральной
трещины пренебрегаем. В случае изолированной трещины имеем
Ki = oyJ~n7 F.4)
B/ — длина трещины). В других случаях К\ определяется методами теории
упругости для эквивалентного ортотропного тела (см. Приложение 1 в
книге [1]).
Спонтанное разрушение. Опыт показывает, что при повышении внешней
нагрузки трещина вначале почти не растет, а начиная с некоторого крити-
критического значения растет весьма быстро. (Влиянием внешней среды и вре-
временными процессами замедленного разрушения здесь пренебрегается).
Найдем вероятность спонтанного развития начальной трещины при постоян-
постоянной внешней нагрузке, пренебрегая ее подрастанием в процессе увеличения
нагрузки. Эту вероятность можно записать в виде следующего произведе-
произведения условных вероятностей:
F.5)
событие
Л= I
Здесь Ап - событие "длина трещины равна 2(/0 + nd)", An+X/An-
Ап+\ при условии, что произошло событие Ап. Очевидно, имеем
°п
)— с
г It J
о
F.6)
77
где в случае изолированной трещины
oh-
ап =
В случае других геометрических конфигураций тела и трещины величина
концентрации напряжения оп легко определяется при помощи форму-
формулы F.3).
Зададимся доверительной (fiducial) вероятностью Pf, т.е. будем считать
некоторое событие невозможным, если его вероятность меньше Pf. Вели-
Величина Pf должна задаваться нормативно в зависимости от назначения и важ-
важности конструкции. Видимо, в серийных и сравнительно малоценных из-
изделиях ее можно брать равной 0,01 -^0,05, а в уникальных и дорогостоящих
конструкциях 0,0001 -г 0,001, если разрушение данного элемента конструк-
конструкции чревато большими последствиями.
Формулы F.5), F.6) определяют вероятность разрушения тела с началь-
начальной трещиной под нагрузкой. Отсюда, полагая р(о, /0) <Р/, находим
безопасную область на плоскости параметров а и /0. В частности, если все
волокна имеют одинаковую прочность а/, т.е. р(а) представляет собой
дельта-функцию 5 (а - оу), то безопасная область определяется следующим
неравенством, вытекающим из F.3):
F.7)
а в случае изолированной трещины согласно F.4) отсюда имеем
ТГГо Of
о< *' . F.8)
Hy/2d /0
Правая часть неравенства F.7) равняется вязкости разрушения Kic рас-
рассматриваемой ленточной модели композита.
Из физических соображений очевидно, что задача об изолированной тре-
трещине относится также к случаю ленты конечной ширины, если начальная
трещина мала по сравнению с шириной полосы.
Вероятность спонтанного разрушения бездефектного ленточного компо-
композита при постоянной нагрузке о равна (в пренебрежении докритическими
разрывами нитей)
Р(о)=р0 П рп (/0=0), F.9)
где
Ро = / р (a)da = 1 - ехр (- a L о*),
о
Предлагаемый подход позволяет легко учесть также влияние границ тела,
других нагрузок и вообще более сложных граничных условий.
Начальные трещины образуются или вследствие внешних неучитываемых
в модели воздействий (и тогдз их следует считать заранее заданными), или
же могут образовываться случайно в процессе увеличения нагрузки от
нуля до величины а.
Докритический рост трещин. Рассмотрим дискретный случайный процесс
образования и развития краевой поперечной прямолинейной трещины в по-
полосе ширины Nd, где N — число нитей в полосе (рис. 38, а). Внешнюю наг-
78
ttt
Nd
О Г 2 3
б)
5А
дЛ
U
А
г
В)
Рйс. 38.
рузку а считаем монотонно возрастающей, а процесс нагружения - дис-
дискретным, так что нагрузка возрастает всегда на одну и ту же величину А,
рис. 38, б (см. также рис. 38, в на котором изображена, в частности, схема-
схематичная зависимость а от времени t).
Конец трещины движется вдоль прямой, перпендикулярной границам по-
полосы, вправо под действием случайных обрывов волокон, происходящих
при нагрузке 1Д, 2Д, ЗА,. . . , &Д, . . . , где к - переменное целое число.
Конец трещины может находиться в точках с координатами Id, Id, 3d, . . .
. . . , nd,. . . , Л/с/, где л — переменное целое число. В пренебрежении вре-
временными процессами деформирования и разрушения композитной ленты
нагрузка о играет роль времени в рассматриваемом случайном процессе.
При повышении нагрузки от к А до (к + 1)А конец трещины с вероятностью
&nks перемещается вправо из положения nd на расстояние sdB положение
(n + s)d, где nd - координата конца трещины под нагрузкой kA,s- число
оборвавшихся волокон при увеличении нагрузки на Д. С вероятностью
fink длина трещины остается равной nd под нагрузкой (А: + 1)Д, причем
s=\
F.10)
Считаем, что волокна рвутся только на фронте трещины; внутренними
обрывами пренебрегаем.
Обозначим через рпк вероятность того, что при нагрузке Л: А длина тре-
трещины равна nd (пик — дискретные переменные, п — "координата", к —
"время").
Поставленная задача математически идентична следующей проблеме,
возникающей в теории неоднородных марковских цепей. Пусть некоторая
частица движется вдоль прямой вправо под действием случайных толчков,
происходящих в моменты времени 1, 2, 3, . . . , к, ... Частица может нахо-
находиться в точках с координатами 0, 1, 2, 3, . . . , п, . . . , N. Каждый толчок
мгновенно перемещает частицу на расстояние s вправо с заданной вероят-
вероятностью otnks.C вероятностью f$nk частица остается на прежнем месте. В на-
начальный момент к = 0 частица с заданной вероятностью р00 находилась в
точке w = 0. Требуется найти вероятность рпк нахождения частицы в точке п
79
в момент времени к. Процесс заканчивается, как только частица попадает
в точку п = N.
Выведем функциональное уравнение для рассматриваемого случайного
процесса. Конец трещины может оказаться в точке ж/при нагрузке к А
лишь следующими (л + 1)несовместимыми способами: 0) при нагрузке
(к - 1) А он находился в точке га/и остался на месте при увеличении наг-
нагрузки, 1) при нагрузке (к - 1) А он находился в точке (я - 1) rf, 2) при наг-
нагрузке (к - 1) А он был в точке ((л - 2)df ... v it) при нагрузке (к - 1) А он
был в точке 0. Суммируя вероятность соответствующих способов, прихо-
приходим к следующему функциональному уравнению процесса:
Рпк -Рп, к- 1 0л, к-1 + Рл-1,/г-1 <*л-1,*-1,1 +
+ р„_2,*г-1 <*п-2,к-1,2 + Рл-3,*-1 <*л-3,*-1,3
F.11)
Требуется решить это функциональное уравнение в области п > 0, к > 0
при следующих граничных условиях:
Р00 =/710 =Р2О =РЗО = • • • = PN0 = 0>
F.12)
, ..., Pok =
[-aZ B*
Здесь первая строка представляет собой запись начальных условий:
вероятность разрушения любой нити при нулевой нагрузке равна нулю. Во
второй строке при помощи распределения Вейбулла E.26) записана вероят-
вероятность обрыва крайней нити при нагрузке А. Величина ро* представляет со-
собой вероятность того, что соседняя с ней нить не оборвется при нагрузке
а= к А; при этом для определения напряжения в этой нити принято допуще-
допущение, то вся пригрузка из-за обрыва крайней нити воспринимается одной со-
соседней нитью. Это допущение не вызывает сомнений в том случае, когда
модуль Юнга у нити гораздо больше, чем у матрицы. При I >2d для расчета
концентрации напряжений в наиболее напряженной нити на конце трещины
применим метод эффективного ортотропного тела и формулу F.3). Вели-
Величина коэффициента интенсивности К\
для краевой трещины длины nd в
ортотропной полосе ширины Nd при-
приближенно равна коэффициенту интен-
интенсивности К\ для периодической систе-
системы трещин длины 2 nd вдоль оси х с
периодом 2Nd (при том же растяже-
растяжении на бесконечности). Это равенство
выполняется тем точнее, чем больше
отношение модуля Юнга вдоль воло-
волокон к модулю Юнга поперек волокон.
Отсюда, используя известную форму-
формулу для коэффициента интенсивности
напряжений в задаче об однородном
растяжении плоскости с периодичес-
периодической системой щелей [1], по формуле
8 п
80
h h h l h m*in ^аж **ъ
а) б) в)
Рис, 40.
F.3) получаем напряжение в самой напряженной нитивблизиконцатрещины:
2А hd I Tin '
Теперь, используя распределение Вейбулла E.26) и формулу F.6),лег-
F.6),легко найти вероятности переходов ocnks:
*nki = [1 - exp (-alTn*)] exp [-a^/n + i,fc],
:)] exp [- (
X [1 -
exp [-
X
и т.д.
Функциональное уравнение F.11) при заданных коэффициентах anks и
заданных граничных условиях легко решается в квадранте и>0, fc>0,
если последовательно переходить от точки к = 2, п = 1 к точкам & = 3, л = 1
и к = 3, /2 = 2, затем к точкам * = 4, я = 1;? = 4, л = 2;? = 4, и = 3и т.д. В
частности, очевидно, что при п > к все вероятности рпк равны нулю.
Аналитическое решение этого уравнения, дающее выражение рпк для
любых значений п и к> слишком громоздко и неудобно для употребления;
поэтому лучше непосредственно использовать указанную процедуру вычис-
вычислений. Алгоритм вычислений указан стрелками на рис. 39 (крестиками от-
отмечены нулевые значения рпк).
Следует отметить, что функциональное уравнение, учитывающее внутрен-
внутренние обрывы волокон в процессе роста, столь сложно и необозримо, что ста-
становится бесполезным (к тому же невероятно усложняется задача вычисле-
вычисления коэффициентов этого уравнения).
При достаточно малом шаге нагружения А можно, очевидно, сколь угод-
угодно близко подойти к непрерывному нагружению о (/) (см. рис. 38, в).
Определим предельную нагрузку. Для этого, после того как функцио-
функциональное уравнение решено и поле рпк найдено, определим линии уровня
Рпк =Ро = const на плоскости пк (или на соответствующей плоскости /а, см.
рис. 40, а ). Максимум на линии уровня представляет собой, очевидно, пре-
предельную нагрузку obi отвечающую заданной вероятности ро\ величина lCt
соответствующая точке максимума, представляет собой "критическую"
длину трещины, отвечающей заданной вероятности р0 (см. рис. 40). Соеди-
Соединяя максимумы на различных линиях уровня, получаем некоторую кривую
81
на плоскости la. Uo этой кривой легко постро-
построить зависимость предельной нагрузки оь от
критической длины трещины 1С (рис. 40, б),
а также плотность вероятности р0 (аь) случай-
случайной величины оъ (рис. 40,в). После этого
искомая предельная нагрузка определяется
как математическое ожидание случайной вели-
величины оъ\
Изложенную теорию легко обобщить также на тот случай, когда компо-
композитная лента конечной ширины имеет начальную краевую трещину длины
/р = nod. В этом случае решение того же функционального уравнения
F.11) нужно найти в области п> п0, к > 0 при следующих граничных
условиях (вместо F.12)):
рпк= 0 при п<п0,
Рпо,о = 1, Рпо = 0 при пФщ,
PnOil= exp(-aZ/y?OfO),
Рпо,к=
где величина упк дается формулой F.13).
Данная краевая задача решается тем же методом, что и прежняя: поле
рпк строится последовательно в указанном выше порядке (в частности, при
п>п0 +к всегда будет рпк = 0).
При заданном о = к А величины рп к дают плотность вероятности дискрет-
дискретной случайной величины / = nd. Математическое ожидание длины трещины /
при заданной нагрузке о равно
п=к+п0
</> = М+ d 2=w прпк. F.17)
Построив дискретную зависимость </> от а по этой формуле, можно
обнаружить участки устойчивого и неустойчивого роста трещины; разделя-
разделяющий их максимум на кривой дает критическую длину 1С трещины и пре-
предельную нагрузку < оь) тела с начальной трещиной (рте. 41).
Полученный эффект роста трещин формально идентичен докритическо-
му подрастанию сквозных трещин в пластинах из упруго-пластического ма-
материала при повышении нагрузки, однако, как видно, имеет совсем другую
физическую природу. В частности, при повторном нагружении до прежнего
уровня нагрузок образования новых трещин (и подрастания старых) в дан-
данном случае не будет.
Развитая теория может быть почти без всяких изменений перенесена на
произвольные структуры однонаправленных волокнистых композитов дос-
достаточно плотной укладки.
82
§ 7. Вязкость и энергия разрушения
Хрупкий однонаправленный композит. Рассмотрим произвольную попе-
поперечную трещину в однонаправленном волокнистом композите. Найдем нап-
напряжения в целых волокнах, расположенных вблизи фронта поперечной
трещины. Обозначим через п число нитей, приходящихся на единицу площа-
площади поперечного сечения композита. Очевидно, объемная доля нитей равна
v/= ято п. На одну нить приходится площадь сечения, равная 1/л2. Фронт
трещины продвигается вглубь тела сразу на расстояние, равное d = 1/%//?,
вследствие почти одновременного разрыва нескольких нитей вдоль фронта
трещины (элементарный акт разрушения). Развитие трещины в композите
состоит в некоторой последовательности элементарных актов.
Основным механизмом торможения поперечных трещин в волокнистых
композитах является диссипация энергии на цилиндрических контактных
микротрещинах сдвига. Величина этой диссипации в конце концов контро-
контролируется одним параметром - вязкостью скольжения поверхности раздела
"нить — матрица" Кцс. Вязкость скольжения играет важную роль для дос-
достижения оптимальных свойств композита. Существенно, что она не должна
быть ни слишком большой (иначе обрью нити приведет к разрыву матри-
матрицы — такой композит будет весьма хрупок), ни слишком малой (иначе об-
обрью нити приведет к ее отслоению, и материал потеряет целостность). Вна-
Вначале рассмотрим случай весьма хрупкого композита,'когда Кцс очень вели-
велико, так что неэффективная длина вблизи края трещины имеет порядок d
(или же меньше d).
Используя соображения, аналогичные положенным в основу вывода фор-
формулы F.2), находим напряжения в целых волокнах на продолжении плос-
плоскости трещины вблизи ее фронта:
¦°*= Аз/4 а " (*=1,2,3,. . . ). G.1)
тгутгл ' Го
Здесь Ы - кратчайшее расстояние центра рассматриваемой нити от фронта
трещины, ось z совпадает с направлением нитей, К\ — коэффициент интен-
интенсивности напряжений для эквивалентного однородного анизотропного тела.
В частности, в наиболее напряженных ближайших к фронту волокнах (при
- 1) имеем
С7*2)
Развитие трещины идет путем последовательного обрыва наиболее напря-
напряженных нитей в ее конце. Приравнивая oz средней прочности волокон (Of),
отсюда находим вязкость разрушения однонаправленного композита (для
поперечных трещин)
j f4 G.3)
Таким образом, получаем следующий замечательный результат: вязкость
разрушения хрупкого композита прямо пропорциональна средней прочнос-
прочности нитей, корню квадратному из радиуса нити и объемной доле нитей в сте-
степени 3/4, причем коэффициент пропорциональности равен 7г3^4/2~ ^2. Следует
83
иметь в виду, что величина (о/) зависит от неэффективной длины, которой
определяется величина L в формуле Вейбулла E.26). Как будет видно из
дальнейшего, неэффективная длина является постоянной величиной для
каждого заданного композита, зависящей, в частности, от объемной доли
волокон Vf. Поэтому зависимость вязкости разрушения Kic композита от
v/будет более сложной, чем это вытекает из формулы G.3).
Прочность композита находится методами механики хрупкого разруше-
разрушения в зависимости от размеров и формы дефекта (и от внешних нагрузок)
при помощи условия Кг = Kie. Например, в случае Сквозной изолированной
прямолинейной трещины длины 27 в ортотропной пластине (листовой ком-
композит) имеем Ki = ау/пТ. Отсюда прочность композита равйа
*-. G.4)
Например j лмеем
1 L
при / =» d =— °ь=~1=Г < of>vft
\/п \]2
при 7 «= 2d оъ = — < Gf> Vf.
Остановимся еще на влиянии статистических свойств нитей на развитие
. .трещин. В принципе, это влияние можно рассчитать совершенно так же, как
в ленточнЬй модели, если допустить, что конфигурация трещины в процессе
ее развития известна (а также известен коэффициент интенсивности напря-
напряжений для любой ее формы). При этом роль плотности вероятности проч-
прочности одной нити будет играть плотность вероятности среднего арифмети-
арифметического йрочностей нескольких нитей, участвующих в одном элементарном
акте разрушения. Например, в случае плоской сквозной трещины в листо-
листовом композите будем считать, что фронт трещины всегда перпендикулярен
плоскости листа. Следовательно, в каждом элементарном акте разрушения
обрывается 2bs/n тлей, в результате чего фронт трещины продвигается на
расстояние гГ1^2 вглубь тела (Л — толщина пластины). Плотность вероятнос-
вероятности случайной величины
1 Ну/п
n /=i
определяется вероятностью элементарного акта разрушения. Ойа может
быть найдеца по функциям распределения случайных величин ot (прочность
>й нити) или же непосредственно из опыта. Очевидно, однако, что при
большом числе нитей дисперсия распределения случайной величины G.5)
стремится к нулю. Поэтому при достаточно большом ку/п(чго чаще всего
встречается на практике) статистический разброс прочности нитей не оказы-
оказывает влияния на вязкость разрушения и прочность композита в целом.
Таким образом, сопротивление развитию трещин композита с плохими
(с большим статистическим разбросом) и хорошими (с меньшим разбро-
разбросом) нитями одинаково, если число слоев в листе достаточно велико и если
величины/оу) одинаковы для обоих сортов нитей. Более того, нити плохо-
плохого сорта будут даже лучше работать в композите, если для них <оу> больше.
84
Преимущество хороших нитей сказывается лишь для небольшого числа
слоев в листе; кроме того, вероятность зарождения одинаковых начальных
трещин под нагрузкой в композитах с хорошими волокнами меньше, чем в
композитах с плохими волокнами. Вероятность зарождения начальной
дискообразной трещины радиуса md при нагрузке о можно оценить форму-
формулой вида
Qm (о) =Ро Рг Рг • . • Рт% G.6)
где Ро — вероятность обрыва одной нити под нагрузкой о,рх — вероятность
обрыва всех ближайших соседних нитей в условиях концентрации напряже-
напряжений, вызванной обрывом первой нити, и т.д. Более точное значение этой ве-
вероятности получается применением теории предыдущего параграфа. Напри-
Например, при оптимальной укладке нитей каждая нить имеет всего шесть бли-
ближайших соседей, поэтому Рх — это вероятность обрьюа всех 6 нитей (под
нагрузкой примерно G/6) о),р2 — это вероятность обрыва всех 12 нитей
( под нагрузкой примерно A9 /12) а) и т.д. Этот метод позволяет оценить
вероятность зарождения дискообразной трещины любого радиуса md под
нагрузкой о. При га > 2 концентрацию напряжений лучше считать методом
эквивалентного однородного ортотропного упругого тела, с тре-
трещиной.
По заданному уровню рабочих нагрузок методами механики разрушения
можно найти критический размер трещины. Вероятность зарождения такой
трещины в композите должна быть меньше доверительной вероятности;
в противном случае материал должен быть забракован.
Квазихрупкое разрушение. Неэффективная длина. Рассмотрим окрест-
окрестность конца трещины, выходящей из более жесткой среды на границу разде-
раздела перпендикулярно к границе (рис. 29). Такая ситуация типична в компо-
композитах, когда вследствие обрыва нити перерезающая ее трещина выходит на
поверхность раздела с матрицей. Критерий начала дальнейшего развития
трещины был рассмотрен в § 5, однако вопрос о том, в каком направлении
будет происходить это развитие, остался открытым. На этот вопрос можно
дать ответ, изучив окрестность конца трещины, малую по сравнению с ради-
радиусом нити; в этой окрестности будет иметь место локальная плоская де-
деформация.
Напряжения в матрице вблизи фронта трещины будут следующими:
ог =Кг (X + 1) Bтг)-1/2 Л [B - X) cos Хв-В cos (X + 2) 0] , G.7)
)~1/2 г* [XsinX0+?sin(X
Здесь г, 0 — полярные координаты с центром в конце трещины, остальные
обозначения те Же, что и в формулах E.2).
При достаточно большом отношении^ /ц2 будет? = 3 — 4р2 и,соглас-
и,согласно G.7), получаем следующую картину распределения напряжений в матри-
матрице: напряжения ог и ов монотонно убывают в промежутке @, тг/2), стре-
стремясь к нулю при 0 -> тг / 2, а напряжение тге монотонно возрастает от нуля
в этом же промежутке, причем максимумы oq и тг$ совпадают по величине.
Именно этот случай реализуется в большинстве композитов.
85
I
0
/
2
Таким образом, в этом случае возможны лишь
два варианта разрушения:
1) отрыв (или нормальный разрыв) матрицы
под углом 0 = 0, .
2) поперечный сдвиг вдоль поверхности разде-
ла при 0 = 7г/2.
Второй вариант предпочтительней, так как
при этом вдоль поверхности раздела образуется
поперечная трещина сдвига, которая препятству-
препятствует распространению основной трещины в матри-
матрицу. Развитие трещины сдвига контролируется
вязкостью скольжения Кцс. Следовательно, если
вязкость скольжения Кцс вдоль границы раздела
меньше вязкости разрушения матрицы Kic, то образуется трещина скольже-
скольжения. В большинстве перспективных композиционных материалов это имеет
место.
Рассмотрим развитие поперечной трещины вдоль цилиндрической грани-
границы раздела после обрыва нити, находящейся в безграничной упругой одно-
однородной среде ({«с. 42). Длину симметричной цилиндрической трещины
сдвига обозначим через 2L0. Аппроксимируем напряжение rrz на границе
цилиндра следующим выражением:
при r = r0 \z\<L0,
Рнс. 42.
Ту, =
при г-г0 \z\ >L0 .
G.8)
Здесь т5 — постоянная трения нити о матрицу, Ки — коэффициент интенсив-
интенсивности касательных напряжений.
Выражение G.8) правильно описывает асимптотику напряжения rrz на
концах интервала, т.е. при z -+L0 и при z -> °°. Заметим, что при удалении от
трехмерной полости напряжения убывают обратно пропорционально кубу
расстояния от центра полости, если главный вектор сил, приложенных к
стенкам полости, равен нулю.
Из условия равновесия половины цилиндра
г0Ег боо = 2tsL0 + 2 /° Trz dz G.9)
при помощи G.8) находим
?.-2т,10)
G.10)
где
dt
«0,705.
Удобно также считать т? некоторым постоянным числом, определяемым
экспериментально или из точного расчета.
86
В предельном состоянии величина Кц должна равняться вязкости сколь-
скольжения КПс контактного слоя "волокно — матрица". Из этого условия по
формуле G.10) находим длину цилиндрической трещины
(УЗт?2
2L0 -
. G-И)
27ГТ/
Как видно, величина Lo монотонно возрастает с увеличением внешней
нагрузки Ei боо; следовательно, рассматриваемая трещина скольжения
всегда устойчива.
Неэффективную длину/, (размер всей возмущенной области вдоль
ochz) на основании G.8) без большой ошибки можно взять равной 4L0.
Формула G.11) относится только к одиночному обрыву; в сложно-на-
сложно-напряженном состоянии длина цилиндрической трещины будет другой. Опре-
Определим длину цилиндрической трещины сдвига вокруг нити, когда она пере-
переходит из неразрушенного состояния в разрушенное на фронте поперечной
макротрещины.
Предположим, что характерный размер макротрещины (радиус, длина
и т.п.) велик по сравнению с искомой длиной 2L0 поперечных цилиндри-
цилиндрических трещин сдвига, образующихся при пересечении нитей макротрещи-
макротрещиной. Будем считать на основании этого допущения, что отличное от нуля
распределение касательного напряжения тГ2 на продолжении трещин сдвига
вдоль боковых поверхностей нитей целиком лежит в области действия
асимптотики фронта макротрещины. Следовательно, вытаскивающая сила,
действующая на образованную нить на фронте трещины, может быть найде-
найдена из усредненной асимптотики напряжения oz (для эквивалентного орто-
тропного тела) вблизи фронта трещины при х = 0 (см. рис. 37). Используя
известную асимптотику на фронте трещины в анизотропном теле, можно
найти [1]
при х = 0
'z s/Wz ' » 2 ~
G.12)
/ Ех ГТХ 7 Z7"\?
2G V E, \ 2G I
2G ?¦, V 2C
ЗдесьEx,Ez,vx,G — упругие постоянные эквивалентного орготропного те-
тела, определяемые законом Гука (для плоского напряженного состояния
по у)
°х - vx az az - vz ax
7. > e2 =
1 G.13)
7xz= — rXZl (vxEz=vzEx)
&
(x — направление развития макротрещины, у — фронт трещины, z — направ-
направление волокон).
87
Сразу после обрыва нити на фронте трещины должно выполняться урав-
уравнение равновесия половины нити
=rsL0+f Trzdz. G.14)
l0
Здесь принято, что на расстоянии 2L0 от фронта трещины вдоль поверхнос-
поверхности волокна напряжение тг2 пренебрежимо мало. В качестве аппроксима-
аппроксимации тГ2 на боковой поверхности нити примем, по-прежнему, выражевде
G.8). Подставляя его в G.14), получаем коэффициент интенсивности нап-
напряжений Кц для цилиндрической микротрещины сдвига, образующейся
вследствие вытяжки нити после ее обрыва макротрещиной, в зависимости
от коэффициента интенсивности напряжений Кг на фронте макротрещины:
кп "
э). G.15)
Отсюда, приравнивая Ки вязкости скольжения КцС9. находим длину
микротрещины Lo в зависимости от К\ как положительный корень куби-
кубического уравнения
° 1 =0. G.16)
KllcL0-
4\/7rTsVf
В простейшем случае т5 = 0 имеем
• G-17)
Неэффективную длину/, можно считать равной 4Z,0, т.е.
1= ^°К\ (г, = 0). G.18)
Таким образом, неэффективная длина для макротрещины в композите
прямо пропорциональна коэффициенту интенсивности напряжений на ее
кромке. Этот результат показывает, что при рассмотрении докритического
развития трещины как случайного процесса ( § 6) неэффективную длину L
следует считать зависящей от К\ согласно формуле G.16) или G.18).
В предельном состоянии поперечной макротрещины в композите величи-
величина убудет равна вязкости разрушения ?1с; следовательно, согласно
{7.17) имеем
\ (т,=0). G.19)
Lo = . к \ (т,=0).
4\/Зг)игК11с
В частности, отсюда вытекает важный результат: поверхность попереч-
поперечного излома композита покрыта цилиндрическими микротрешинами сколь-
скольжения постоянной длины вокруг каждой оборванной нити (рис. 43). Этот
результат по своему физическому смыслу аналогичен концепции квази-
квазихрупкого разрушения для металлов.
При помощи G.3) и G.19) находим для хрупкого композита
)
4V6t?i>//4 К
G.20)
При вычислении < оу > параметр Z, распределения E.26) надо брать рав-
равным неэффективной длине.
Отметим, что если KUc = 0, то согласно G.16)
G.21)
G.22)
/ $г0К1с \2/з
а для изолированного обрыва, согласно G.10),
¦ = г0Е1ев.
° 2т,
Энергия разрушения композита. Определим теперь удельную энергию
разрушения композита поперечной трещиной. Поверхность излома состав-
составлена матрицей, волокнами и поверхностями раздела вдоль цилиндричес-
цилиндрических микротрещин. Предположим, что удельная поверхностная энергия посто-
постоянна вдоль поверхности излома одного и того же материала (это может
быть справедливо, по существу, лишь для идеально хрупкого композита).
Тогда получим следующее выражение для энергии разрушения компо-
композита у:
у = yfvf + XiTw (I - и/) + 2 я r0L0 nyfm . ' G.23)
Здесь Xi — коэффициент, отражающий неровный ландшафт излома мат-
матрицы (xi > 1); 7/, Ут 9 У/т - поверхностная энергия материала нитей, связу-
связующего и контактного слоя соответственно; Lo — полудлина цилиндричес-
цилиндрической микротрещины,определяемая формулой G.16).
Так как величина Lo значительно больше радиуса нити г0 в наиболее ин-
интересном случае квазихрупкого композита, то в формуле G.23) можно
пренебречь первыми двумя слагаемыми, т.е.
7 = 2 7/w
-1
G.24)
Здесь 7/w > вообще говоря, зависит от иу и г0.
Постоянная у в общем случае связана с вязкостью разрушения компо-
композита^ следующим уравнением [1]:
4^7 = ^
G.25)
Полученные формулы, связывающие
основные микро- и макроконстанты раз-
разрушения и деформирования композита,
позволяют использовать их также для
оптимального конструирования волок-
волокнистых композиционных материалов.
1
I
1
I
х
1
1
1
\
1
1
\
1
I
I
I
\
X
1
1
1
1
|
I
\
1
I
Y.
1
1
I
I
!
1
I
\
\
1
Рис. 43.
89
Для сквозных поперечных трещин в однонаправленном ламинатном
композите разница между А"с и К\с, т.е. зависимость Кс от толщины плас-
пластины будет, очевидно, несущественной (в отличие от металлов).
В композитах с пластичной матрицей, хорошей адгезией и хрупким воло-
волокном (типа боралюминия) основной вклад в энергию разрушения компо-
композита 7 делает матрица. Поэтому удельная необратимая работа деформаций
в пластическом слое толщины Lo вблизи поверхности излома равна
где os и eb — предел текучести и предельная деформация матрицы. Отсюда,
принимая величину Lo равной неэффективной длине G.22), получаем
7 = r0Ef A - uf) e? .
В композитах с пластичной матрицей и хорошей адгезией развитие попереч-
поперечных трещин скольжения можно рассматривать в рамках предельного плас-
пластического анализа (при однократном нагружении до разрушения).
§ 8. Сжатие однонаправленных волокнистых композитов
Разрушение однонаправленных волокнистых композитов при сжатии
в направлении волокон объясняется обычно потерей устойчивости воло-
волокон при некоторой критической нагрузке (теория Дау — Грунфеста — Ро-
зена — Шурца, см. 157]). Следует отметить, что расхождение этой теории
с экспериментальными данными оказывается довольно существенным как
для стеклопластиков, так и для случая высоко модульных волокон.
8 этом параграфе рассматривается (как наиболее вероятный для ряда
случаев) другой механизм разрушения при сжатии, основанный на раз-
развитии цилиндрических микротрещин на границе между волокном и мат-
матрицей. Источниками таких микротрещин являются обрывы волокон, а так-
также места слабой адгезии технологического или эксплуатационного проис-
происхождения (начальные микротрещины). Развитие цилиндрических микро-
микротрещин приводит к локальному выпучиванию волокон на свободных боко-
боковых поверхностях образца. В зависимости от отношения длины выпучен-
выпученной зоны к длине всего образца это выпучивание может привести или непос-
непосредственно к расслаиванию всего образца, или же может служить источни-
источником распространения трещиноподобной области, наклоненной к оси образ-
образца и аналогичной трещинам скольжения {62] в сжатых горных породах.
На фронте такой трещины скольжения волокно подвергается (наименее
благоприятным для него) большим деформациям изгиба.
Невозмущенное поле напряжений вблизи волокна при растяжении - сжа-
сжатии. Рассмотрим осевое сжатие — растяжение силой Р упругого неоднород-
неоднородного цилиндра, составленного из двух материалов: материала /(fiber) при
г О0 и материала т (matrix) при r0 <r<rx (рис. 44). На границе различ-
различных сред г = г0 имеет место жесткое сцепление материалов, а граница г =гх
считается свободной от внешних нагрузок. Принимается, что при Р = О все
напряжения в цилиндре равны нулю, т.е. пренебрегается начальными на-
напряжениями. В условиях, близких к рассмотренным, находится волокно
вблизи свободной поверхности однонаправленного композита, подвергну-
подвергнутого осевому сжатию — растяжению и изгибу (если поперечный размер об-
90
разца значительно больше радиуса волокна). Величины гг и г0 связаны оче-
очевидно соотношением r02 = Vfrx 2.
Опуская несложные вычисления, приведем получающиеся выражения
для напряжений аг, ов,о2ъ цилиндрических координатах ry6,z (рис. 44):
при г<г0
2Р
f-1 - 1),
-1-!)];
при г0 <г<гг (rx2 =r02 vr~l
2
ов= -
\ r2vf I'
Wo \ I2 Vf
Vf-V,
2 \ rvf I
(8-1)
Здесь
2A
Как видно, в неоднородном цилиндре возникают напряжения огиов,
которые имеют при г < г0 тот же знак, что и сила Р, если vf>vm\ при vm >
> Vf, что обычно имеет место в композитах, знак напряжений огиое ( где
г < г о ) противоположен знаку Р.
91
При Ef>Em имеет место следующая оценка наибольших напряжений ог
гог (fm)9
Ef
где Of — напряжение oz в нити.
Следовательно, при сжатии композита растягивающее напряжение ог на
границе "матрица — волокно" примерно на три порядка меньше сжимающе-
сжимающего напряжения в нити для большинства композитов. Таким образом, при
хорошей и однородной адгезии разность коэффициентов Пуассона нитей и
матрицы сама по себе не имеет существенного значения и в большинстве
случаев вряд ли может объяснить наблюдаемую прочность однонаправлен-
однонаправленных композитов на осевое сжатие.
Развитее цилиндрических микротрещин. Рассмотрим задачу о развитии
цилиндрической трещины отрыва r = ro,\z\< L/2 на границе двух сред,
составляющих, как и выше, неоднородный цилиндр (рис. 45, а). Берега
трещины свободны ох внешних нагрузок, а на бесконечности действуют
сжимающие силы Р. При L >2r x трещину можно считать полубесконеч-
полубесконечной; именно этот случай рассматривается в дальнейшем.
Рассмотрим замкнутую поверхность 2, составленную берегами полубес-
полубесконечной трещины, тороидальной замкнутой поверхностью, охватывающей
круговой фронт трещины npnz = 0,r = ro> а также торцами и боковой по-
поверхностью цилиндра г = rx, \z | <?*«», где/,*»^^ (на рис. 45, б показано
стрелками радиальное сечение поверхности 2).
Принимая метод вычислений, изложенный в § 3, можно показать, что
?/-а2_ )nzdr9 (8.3)
Г= — / г
Го AB + CD
где интеграл берется по торцам цилиндра. Как и в § 3, при этом
достаточно потребовать упругого поведения материала. (Обозначение
Г то же, что ив § 1). При z -> — °°, очевидно, лишь напряжение oz
отлично от нуля:
— РЕгГо2Ь'х при r<r0, z-»-°o9
7Г
—PEm Tq2 5 при ro<r<rly z-»-<*>,
l 7Г
где 5 =Ef + Em(v~f- 1), а все остальные напряжения равны нулю. При
z ->+ °° напряженное состояние совпадает с (8.1).
Приведем результат вычислений по формулам (8.3) и (8.1) :
Г= — i-—- (8.4)
n2r03 6/0
При ?у > ?т отсюда получаем
92
В предельном состоянии Г = 2тут; отсюда получаем величину прочности
на сжатие композита, разрушающегося по данному механизму:
где Р* — значение силы, при которой начинается движение трещины.
Формула (8.6) дает реальные значения прочности лишь для низкомо-
низкомодульных композитов типа стеклопластиков. Отметим, что она годится так-
также, как легко проверить, для осевого растяжения, если разрушение при
растяжении начинается с движения цилиндрических микротрещин скольже-
скольжения. Для композитов, разрушающихся по данному механизму, величина
прочности на сжатие близка к прочности на растяжение. В то же время
формула (8.6) явно не годится для высокомодульных композитов типа
углепластиков и боропластиков *.
Вообще же, изученный механизм может иметь практическое значение
лишь тогда, когда начальные обрывы волокон заблокированы (например,
при сжатии, когда противоположные берега обрьюа упираются друг в дру-
друга) или же когда начальных обрывов волокон слишком мало для того, что-
чтобы выключение из работы соответствующих волокон оказало влияние на об-
общую прочность.
Таким образом, для волокнистых композитов при растяжении — сжатии
вдоль волокон наиболее существенным механизмом является развитие ци-
цилиндрических микротрещин расслаивания вдоль границы "волокно — мат-
матрица".
Локальное выпучивание волокон. Рост цилиндрической микротрещины
происходит лишь до тех пор, пока ее длина не достигнет эйлеровой длины
/,, при которой происходит выпучивание волокна вблизи свободной по-
поверхности образца.
Величина/, равна
L =7гго>/—- , (8.7)
°f
где Of—.осевое напряжение в волокне в момент выпучивания (of = o* v/1).
Как видно, величина/, имеет порядок A0 *г 50) г0 для основных компози-
композитов. Локальное выпучивание волокон имеет лавинный характер, так как
после выпучивания одного волокна в соседних волокнах вследствие кон-
концентрации напряжений возрастает осевое сжатие. Образующаяся область ло-
локального выпучивания имеет форму трещиноподобной полости, плоскость
которой наклонена к оси волокон под острым углом; полость распростра-
распространяется подобно трещине скольжения в горных породах при сжатии [62].
Для высокомодульных композитов типа углепластиков и боропласти-
боропластиков начало разрушения при сжатии можно объяснить наличием технологи-
технологических несовершенств: начального эксцентриситета волокон и начальных ци-
Ниже в § 9 будет показано, что для волокнистых композитов важнейшим крити-
критическим механизмом является развитие цилиндрических микротрещин расслаива-
расслаивания от обрывов волокон. Этот механизм разрушения начинает действовать при зна-
значительно меньших нагрузках.
93
линдрических микротрещин с длиной порядка нескольких десятков ради-
радиусов волокон. Соответствующая теория получается включением свободных
участков (трещин) в волокне, выпучивающемся с учетом бокового сопро-
сопротивления по теории Дау — Грунфеста — Розена — Шурца. Однако наиболее
существенны начальные обрывы волокон, служащие источниками цилин-
цилиндрических микротрещин.
§ 9. Усталостное и коррозионное разрушение композитов
Остановимся на некоторых механизмах развития усталостных и корро-
коррозионных трещин, специфических для композитов. Поверхность раздела
матрицы и волокна имеет наименьшую энергию разрушения и скольжения;
поэтому естественно, что при переменных нагрузках и при воздействии аг-
агрессивных сред новые качества композита, отличные от составляющих, зави-
зависят от возможности докритического развития цилиндрических микро-
микротрещин по поверхностям раздела.
Общая теория. Рассмотрим малую окрестность некоторой точки О на
фронте трещины, распространяющейся вдоль границы раздела двух сред.
При этом, как и ранее (см., например, рис. 3), можно считать, что:
а) граница раздела совпадает с плоскостью у = 0, б) фронт трещины совпа-
совпадает с осью z и распространяется в направлении оси х. Согласно § 1 в рас-
рассматриваемом случае справедливы все теоремы об инвариантности Г-ин-
теграла и производных от него по х Г-интегралов [1].
На основании общей теории в данном случае докритический рост трещин
контролируется величиной Г. При этом основной характеристикой данной
системы "материал — внешняя среда" будет диаграмма V — Г, снятая при
стационарных внешних нагрузках (V — скорость роста трещины). Нали-
Наличия такой единой диаграммы следует ожидать в тех случаях, когда адсорб-
адсорбционное воздействие внешней среды и нелокальные транспортные эффекты
в полости трещины пренебрежимо малы. Последнее всегда имеет место
для трещин скольжения, так как их фронт недоступен для внешней среды.
Поэтому для трещин скольжения диаграмма V — Г не зависит от внешней
среды и целиком определяется свойствами самого материала.
Характерные точки на диаграмме V — Г будут некоторыми постоянны-
постоянными системы. Важнейшими из них являются величины Гс и Tscc; первая
характеризует быстрое ускорение роста трещины до околозвуковых ско-
скоростей при небольшом увеличении Г, вторая характеризует начало роста
трещины в данных условиях (т.е. при Г < Г5СС трещина не растет). Вели-
Величина Гс равна удвоенной энергии адгезии.
Для идеально хрупких композитов, когда диссипативные зоны вблизи
фронта трещины имеют характерный размер, малый по сравнению с радиу-
радиусом нити, указанную теорию «легко переформулировать на язык коэффи-
коэффициентов интенсивности напряжений, так как в этом случае между величи-
величиной Г и коэффициентами интенсивности имеет смысл зависимость B.29)
для трещин скольжения или зависимость B.47) — для открытых трещин.
Однако, применяя общий подход § 1, можно обходиться лишь величиной Г
(без коэффициентов интенсивности напряжений) и переносить полученные
результаты также на тот случай, когда пластические зоны вблизи фронта
цилиндрических микротрещин сравнимы с радиусом нитей.
94
Для определения диаграммы V — Г можно использовать в опытах, на-
например, любую из схем, изученных в § 3 (или какую-либо другую
схему, для которой можно эффективно вычислить инвариантный Г-ин-
теграл).
Рассмотрим теперь случай, когда подрастание трещины при характерной
стационарной величине Г мало по сравнению с ее подрастанием вследствие
увеличения Г (система с мгновенной реакцией). В этом случае характерис-
характеристикой материала является диаграмма А/ - Г, где А/ — подрастание трещи-
трещины. Диаграмма А/ — Г определяется экспериментально в процессе моно-
монотонного увеличения Г от нуля до Гс. Характерные точки этой диаграммы
также будут некоторыми постоянными неоднородного материала.
В случае произвольно изменяющейся во времени величины Г подраста-
подрастание трещины за произвольный промежуток времени легко находится
интегрированием бесконечно малых приращений из диаграммы V — Г (в
системах с пренебрежимо малой мгновенной реакцией) или из диаграммы
dljdT - Г (в системах с определяющей мгновенной реакцией).
В случае произвольных систем, когда существенны и последействие
и мгновенная реакция, можно применить принцип аддитивности [1], сог-
согласно которому приращение трещины dl равно сумме двух слагаемых
дифференциалов dlt + dlp, первое из которых для заданной функции
Г(/) определяется при помощи диаграммы V — Г, а второе — при помощи
диаграммы dl/dT — Г. Таким образом, можно изучить случай пе-
периодических, случайных или любых программированных внешних
нагрузок.
На основании общих физических постулатов инвариантности и подобия,
а также на основании конкретных механизмов локального разрушения,
рассмотренных в книге [1], нетрудно получить следующие результаты:
диаграмма dl/dF — Г в каждой точке удовлетворяет уравнению
(9..)
диаграмма V — Г для наводораживаныя в композитах с металлической
матрицей {открытые трещины)
V = Afm(y/T-Bfm) (Г,СС<Г<ГС); (9.2)
диаграмма F — Г для коррозионных открытых трещин
V*const (Г,СС<Г< Гс); (9.3)
диаграмма V —Г для общего кинетического механизма
(9.4)
Здесь ^fm^fm,Afm,Bfm,\)fm - некоторые постоянные. Во временных
процессах разрушения композитов с полимерной матрицей наибольшую
роль играет, по-видимому, общий кинетический механизм.
Сжатие — растяжение однонаправленных волокнистых композитов.
В некоторых случаях величина инвариантного интеграла Г не зависит от
длины трещины (см., например, задачи § § 3 и 8). В этих случаях прира-
95
щение длины трещины /т за промежуток времени от 10 до Г равно
/т=/ f[nt)]dt, (9.5)
to
где функция / (Г) вполне определена диаграммами V - Г и dl/dT - Г. В
частности, если внешние нагрузки не зависят от времени, скорость роста
трещины постоянна.
Пусть однонаправленный волокнистый композит подвергается осевому
растяжению — сжатию некоторой однородной деформацией е = e{i). Сос-
Состояние волокон на свободной поверхности образца можно описать при по-
помощи модели предыдущего параграфа (см. рис. 45). Для цилиндрических
микротрещин (с длиной больше 2г0) на таких волокнах величина Г соглас-
согласно формуле (8.4) равна
Г = арб г0 б2 (ут - iy)(iy* - 1) . (9,6)
В частности, при Ef > Em имеем
г* е2 Em(Vr» — vMv'f— Y)
Г = — 2US //v * > . (9.7)
2(l+^w)(l-2^w+i;71)
Отсюда при помощи соответствующей диаграммы легко найти приращение
трещины за любой промежуток времени для любой функции е@ (см,
например, диаграммы (9.1) — (9.4)). Некоторое характерное время рас-
расслаивания можно принять за долговечность образца; например, естественно
в качестве долговечности принять тот период, за который микротрещина
подрастает на величину L, определяемую формулой (8.7) и соответствую-
соответствующую выпучиванию отслоившегося волокна.
Анализ уравнения (9.7) в зависимости от входящих в него параметров
позволяет сделать следующие общие выводы:
а) в углепластиках и боропластиках докритический и критический рост
цилиндрических микротрещия практически невозможен, так как в них
величина Г чрезвычайно мала вплоть до предельных деформаций;
б) в стеклопластиках докритический рост цилиндрических миХротре-
щин весьма существен, так как в них величина Г значительна уже при
деформациях, значительно меньших предельных;
в) докритический рост цилиндрических микротрещин становится менее
существенным с увеличением отношения Ef/Em.
Большую роль при усталостном разрушении композитов с металлической
матрицей играют начальные обрывы волокон, так как они чаще всего выс-
выступают инициаторами поперечных усталостных трещин в матрице. Этот
вопрос подробно изложен в обзорной статье Хэнкока (см. том 5 издания
[11]) .В случае хорошей адгезии долговечность композита с металлической
матрицей определяется скоростью роста поперечной трещины нормального
разрыва (как и в однородных материалах). При этом волокна могут
ускорять или замедлять рост усталостных трещин в зависимости от проч-
прочности адгезии (т.е. величин rs и 7/т)- С «ухудшением адгезии из-за цилинд-
цилиндрических микротрещин скольжения тормозящая роль волокон возрастает.
При достаточно плохой адгезии усталостная долговечность будет опреде-
определяться ростом цилиндрических микротрещин.
96
Рнс.46.
Рассмотрим развитие цилиндрической микротрещины вблизи обрыва
волокна (рис. 46). Пусть в бесконечной матрице имеется произвольное
число сборных бесконечных цилиндров из другого материала, жестко сцеп-
сцепленных с матрицей (рис. 46,а).Форма поперечного сечения цилиндров и
их взаимное расположение — совершенно произвольны (рис. 46,5). Все
составное тело подвергается осевому растяжению — сжатию однородной
деформацией е = e(f) (рис. 46,г). Пусть в некотором циллиндре А (рис.
4б,в) имеется сквозной поперечный обрыв, который приводит к образова-
образованию цилиндрической микротрещины на границе цилиндра и к перераспре-
перераспределению напряжений и деформаций в окрестности обрыва. Влиянием
соседних обрывов будем пренебрегать.
Будем предполагать, что коэффициент Пуассона материала матрицы
больше, чем у материала цилиндров . Это условие выполняется для боль-
большинства волокнистых комцозитов, применяемых на практике. В этом
случае дри осевом растяжении на границе раздела будет действовать сжи-
сжимающее нормальное напряжение, а при осевом сжатии — растягивающее
нормальное напряжение. Величина этого напряжения на несколько поряд-
порядков меньше, чем осевое напряжение в нитях, однако оно может существен-
существенно воздействовать на рост цилиндрической микротрещины вблизи обрыва;
при Ьсевом сжатии противоположные берега трещины расходятся и стано-
становятся свободными от нагрузок, а при осевом растяжении противоположные
берега микротрещины смыкаются и вызывают взаимное трение, предельная
величина которого равна т,. Вследствие этого осевое сжатие всегда будет
сопровождаться докритическим ростом цилиндрических трещин, длина
которых при сжатии может возрастать неограниченно (если величина е
достаточно велика); осевое растяжение не можех сопровождаться неогра-
неограниченным докритическим ростом трещин, при Одном осевом растяжении
длина трещины L всегда меньше неэффективной длины Lo -r0Ofl(jLT^)y
где Of— наибольшее осевое растягивающее напряжение в цилиндре А.
Если длина трещины больше Lo, то ее рост будет иметь место при осе-
осевом сжатии, а при осевом растяжении она будет неподвижна.
Вычислим инвариантный Г-интеграл на фронте цилиндрической микро-
микротрещины, считая ее полубесконечной. Фронт представляет собой некоторый
контур С в плоскости х = 0, где х — ось цилиндра А. Берега трещины
97
свободны от внешних нагрузок; цилиндр, окаймленный трещиной, свобо-
свободен от напряжений на бесконечности (при х -> — «>).
Такая постановка задачи достаточно близка к точной, если/, > 2г0 и
если имеет место осевое сжатие.
Применяя теорему об инвариантных Г-интегралах и деформируя поверх-
поверхность интегрирования, можно показать, что в данной задаче имеет место
уравнение
^ (9.8)
где S — площадь поперечного сечения цилиндра А. При этом мы пренебрег-
пренебрегли вкладом напряжений, нормальных к границе раздела, в потенциальную
энергию тела на бесконечности. Вклад этих напряжений имеет порядок
правой части в уравнении (9.6), т.е. мал по сравнению с правой частью
(9.8).
Можно показать также, что уравнение (9.8) справедливо для произволь-
произвольного замкнутого контура С на боковой поверхности цилиндра А.
Будем считать, что фронт трещины С в конце концов будет распрост-
распространяться вдоль оси х параллельно самому себе, не изменяя формы. Это
естественно вытекает из того обстоятельства, что изменение фронта трещи-
трещины со временем должно быть направлено в сторону выравнивания величи-
величины Г на контуре С, приводя в пределе к условию Г = const на всем контуре
("равнопрочный" контур трещины). Последнее объясняется монотонно
возрастающей зависимостью скорости роста трещины от Г (за исключе-
исключением коррозии и адсорбции, роль которых для внутренних обрывов, види-
видимо, мала).
Таким образом, для равнопрочного контура С получаем
^ , (9.9)
где Рс — периметр контура С. В частности, для круглого цилиндра и кру-
кругового фронта трещины имеем
Г= - e2r0Ef. (9.10)
Это простое выражение при помощи соответствующей диаграммы V — Г
позволяет легко определить длину трещины как функцию времени для
произвольной переменной функции e(t\ если в расчете учитывать лишь
периоды сжатия; растяжение вносит лишь постоянное слагаемое Lo.
Как только трещина дойдет до границы образца, соответствующее во-
волокно полностью выключится из работы. При достаточном количестве
начальных обрывов этот момент будет фиксировать расслоение образца,
т.е. его разрушение.
Очевидно, что оптимальной адгезией с точки зрения усталостной дол-
долговечности является такая адгезия при прочих равных обстоятельствах,
при которой скорость роста цилиндрических микротрещин находится
в определенном отношении к скорости роста поперечной трещины. Это
отношение может определяться, например, требованием, чтобы та и другая
98
трещины достигали границ тела одновременно. Таким образом, оптималь-
оптимальная структура композита и технология его изготовления тесно связаны с
назначением, условиями работы и, в частности, конфигурацией и размерами
элемента конструкции.
Докритический рост поперечных трещин в армированных материалах.
Армирование высокопрочными волокнами является наиболее эф-
эффективным и технологически доступным средством увеличения проч-
прочности и долговечности материала, подверженного растяжению в направле-
направлении армирования. Это объясняется, прежде всего, замедлением докритичес-
кого роста поперечных эксплуатационных трещин, которое может на поря-
порядок увеличить долговечность даже при малой объемной доле волокон.
Армируют металлические и полимерные матрицы волокнами стекла, бора,
углерода, высокопрочной стальной проволокой, "усами" кристаллов и т.д.
Рассмотрим закономерности докритического роста усталостных и кор-
коррозионных трещин, распространяющихся в направлении поперек волокон в
однонаправленном композите (на рис. 47 изображена окрестность края
макротрещины).
Ограничимся рассмотрением квазихрупкого разрушения, когда характер-
характерная длина оборванных волокон, вытянутых из матрицы, мала по срав-
сравнению с длиной макротрещины* но велика по сравнению с радиусом ци-
цилиндрического волокна, т.е.
1>1е>г0>10. (9.11)
Здесь /, 1С и /0 — характерная длина макротрещины, цилиндрических
микротрещин и субмикротрещйн в волокнах соответственно; г0 — радиус
волокна. Условия (9.11) представляются необходимыми для оптимального
сочетания вязкости и жесткости в композите.
Вследствие случайного расположения субмикротрещйн в нитях рас-
расположение обрывов в волокнах вблизи фронта трещины будет хаотичес-
хаотическим, а излом будет иметь весьма сложную иррегулярную форму. Однако
на расстояниях от фронта, больших по сравнению с длиной обрьюов, на ос-
основании принципа "микроскопа" можно пользоваться решениями теории
упругости для идеализированной гладкой трещины, не имеющей резких
выступов и ям в изломе.
Рассчитаем вначале поле напряжений в рассматриваемом композите с идеа-
идеализированной гладкой макротрещиной. Для этого заменим неоднородный
композит ортотропным однородным упругим телом, эквивалентным уп-
упругому композиту по усредненной упругой реакции, определяемой зако-
законом Гука
ох — vOy — vx oz Оу — vox — vx oz
6v = "¦™""""""^"~—¦——¦———¦——¦ ? = "————————————¦»
л С 'У г?
Уху = -Т— т*у . С9-12)
1 1
Ixz = — TX2, 7yz = — Tyz {VXEZ = VZE).
G G
99
Рис. 47.
Х7/77777777777777'
21
Рис. 48.
7777777X
z
lh
Рис. 49.
I I 1'
Здесь Е, Ez,vx,vz, v, G, Gxy —эффективные упругие постоянные компози-
композита, z — направление армирования, ху — "усредненная" плоскость трещины.
Считаем, что упругая реакция воображаемого ортотропного тела (9.12)
совпадает с упругой реакцией реального композиционного материала в сле-
следующих мысленных опытах: а) одноосное растяжение вдоль оси z, когда
только напряжение az Ф 0, а деформация ez одинакова в нитях и матрице;
б) двуосное растяжение в плоскости ху, когда только напряжения
°х = оу Ф 0 (и одинаковы в нитях и матрице); в) всестороннее сжатие,
когда ох = а у = oz; г) чистый сдвиг в плоскостях ху inxz; д) двуосное
сжатие в плоскости ху при неравных нулю напряжениях
Из этого допущения находим следующие соотношения:
-. v- 2vxvz
с
_
Эти уравнения позволяют определить эффективные упругие постоянные
композита по модулю Юнга, коэффициенту Пуассона и модулю сдвига его
составляющих (индекс / относится к волокнам, а индекс т— к матрице).
Они достаточно хорошо подтверждаются на опыте.
100
Таким образом, расчет усредненного поля напряжений в композите с
макротрещиной сводится к классической задаче теории упругости для ор-
тотрогаюго однородного упругого тела с математическим разрезом. Эта
задача может быть эффективно решена во многих случаях [1]. При этом
оказывается, в частности, что с точностью до некоторого множителя рас-
распределение напряжений и деформаций вблизи фронта трещины будет одним
и тем же для тел различной конфигурации и внешних нагрузок, а коэф-
коэффициент интенсивности напряжений К\ зависит лишь oi нагрузок и формы
тела. При этом на продолжении трещины вблизи ее конца имеет место то
же соотношение, что и в изотропном однородном теле:
приг=0 °г= -7Ш' (9Л4)
где х — расстояние до конца трещины.
Приведем результаты вычисления коэффициентов интенсивности К\ для
некоторых простейших частных случаев.
В случае однородного растяжения нагрузкой р безграничной ортотроп-
ной пластины с изолированной сквозной трещиной длины 2/ имеем
(рис. 48)
Кг=р\/пГ. (9.15)
В случае однородного растяжения нагрузкой р ортотропной полосы
ширины 2h с одной боковой сквозной щелью длины / имеем (рис. 49)
I ИГ
Кг = р V 2h tg —- при Е2 >Е . (9.16)
2h
Теперь вычислим растягивающее напряжение^ в волокне, ближайшем
к фронту трещины (см. рис. 47), используя прием, описанной ранее при
рассмотрении ленточной модели композита в § 6 (см. формулы F.1) —
F.3)). Этот прием оправдан при Ef> Emy когда нити несут практически
всюосевую нагрузку. Получаем
(9.17)
При рассмотрении докритического роста поперечных трещин в компози-
композите можно пренебречь влиянием матрицы, а развитие трещины можно пред-
представить скачкообразным процессом последовательного обрыва волокон
на фронте трещины. При этом среднюю скорость докритического роста
поперечной макротрещины dl/dt можно записать в $иде
dl d V7r0
-- = -= . (9.18)
dt t TVf
Здесь г '— время, необходимое для продвижения макротрещины на вели-
величину d. Это время равно
(9.19)
где Tf — время замедленного разрушения нити псщ напряжением oz,tc —
период развития цилиндрической микротрещины от магистральной тре-
101
щины в матрице к обрыву волокна, TfC — время совместного протекания
этих двух процессов.
В зависимости от материала нити наиболее существенными механизмами
замедленного разрушения волокна могут служить следующие процессы:
1. Общий кинетический механизм термоактивированного разрушения.
Этот механизм, по-видимому, доминирует для неметаллических волокон
типа стекла, бора, графита, кремния и т.п.
2. Накопление пластических деформаций и усталостное разрушение при
переменных нагрузках.
3. Охрупчивание и разрушение под действием диффундирующего ато-
атомарного водорода и коррозионные разрушения в химически активной
среде.
Последние два механизма наиболее типичны, по-видимому, для метал-
металлических волокон (причем третий механизм превалирует для высокопроч-
высокопрочных сталей во влажных средах).
Следует отметить также статистический эффект докритического роста
трещины, связанный с первоначальным обрывом наиболее слабых волокон
вблизи фронта трещины, перераспределением напряжений в близлежа-
близлежащих нитях вследствие развития цилиндрических микротрещин около об-
обрывов и последующим обрывом наиболее нагруженных и слабых нитей.
Статистический эффект докритического развития трещины пропадает, если
перед испытанием композита на длительную выносливость подвергнуть
материал без трещины кратковременному осевому растяжению достаточ-
достаточно высокой нагрузкой, близкой к предельной. Именно этот случай рас-
рассмотрим в дальнейшем.
Обозначим через ot среднее значение порогового (treshold) напряжения
в нити, ниже которого нить не разрушается за время работы конструкции.
Отсюда при помощи (9.17) находим пороговое значение коэффициента
интенсивности напряжений Kt > ниже которого докритический рост тре-
трещин не происходит:
(9.20)
Величины ot и Kti естественно, могут зависеть от вида внешней нагруз-
нагрузки (циклическая, стационарная, стационарная с циклической составляю-
составляющей и т.п.).
Оценим период развития цилиндрической микротрещины тс. Вначале
до обрыва волокна величина Г на контуре круговой цилиндрической
микротрещины согласно (9.6) имеет порядок
Г~ЕтЕ;2о22г0(Рт-1>г). (9.21)
После образования сквозного разрыва в волокне величина Г согласно
(9.10) будет иметь порядок
Г «Я/1 о22г0. (9.22)
Как видно/ после образования разрыва в волокне величина Г возрастает
примерно в Ef/[Em(vm - vf)] раз, т.е. на несколько порядков. Следова-
Следовательно, согласно закономерностям докритического роста трещин скольже-
102
ния (см. например, уравнения (9.1) - (9.4)), скорость развития микротрещи-
микротрещины после образования разрыва в волокне столь велика, что временем ее раз-
развития в данном случае можно пренебречь* по сравнению с ту- (см. форму-
формулу (9.19)). Следовательно,^ т^ и величину г можно считать равной
времени замедленного разрушения нити, близлежащей к фронту трещины
и подвергнутой одноосному растяжению напряжением oz (см. (9.17)).
Выведем вначале закон движения поперечной трещины в композите
при стационарных нагрузках. Время г*, за которое разорвется нить, доста-
достаточно хорошо описывается эмпирической формулой Александрова — Жур-
кова
o>ot (A=T0eu«RV). (9.23)
Здесь о — постоянное во времени напряжение растяжения нити, Т — абсо-
абсолютная температура,R — универсальная газовая постоянная, rOi U и у — не-
некоторые постоянные. Формула (9.23) выводится также из теоретических
представлений Журкова о термоактивационном характере разрушения
(U — энергия активации, у — структурная постоянная, т0 = 102 ¦=¦10"* 3 с).
При переменном во времени нагружении o(t) время до разрушения
т* определяется при помощи закона Бейли
Здесь интегрирование ведется лишь по тем участкам o(t) , где o(t)> ot.
Подынтегральное выражение в (9.24) по определению представляет собой
меру повреждаемости нити за время dt\ суммирование всех повреждае-
повреждаемостей за время т* дает предельную повреждаемость, равную единице
и отвечающую разрыву нити. Всякое нагружение нити при о> ot приводит
к некоторой повреждаемости; все они накапливаются и в конце концов
приводят к обрыву нити согласно (9.24). Цоэтому закон Бейли (9.24)
называют также правилом суммирования или накопления повреждаемости**
Он достаточно хорошо подтверждается опытными данными.Будем считать,
что при о < at повреждаемостей в нитях не возникает (за время работы
конструкции).
Вычислим растягивающее напряжение oz в волокне, расположенном в
полосе (к - 1) d <x <kd на продолжении макротрещины, где к =
= 1,2,3,... (см. рис.47). Используя известный прием (см. формулы
F.2) и (9.17)), получаем
а2 = — Кг V ( V*1- VT^T) . (9.25)
Vf nd
В частности, при к = 1 отсюда получается выражение (9.17).
Величину oz можно считать постоянной вдоль нити вплоть до расстояния
от оси х порядка неэффективной длины.
Однако им нельзя пренебречь при высоких динамических нагрузках, когда это
время становится доминирующим в протекании временного процесса разру-
разрушения.
Были предложены также более сложные зависимости, обобщающие правило
Бейли. Использование их в данной теории нисколько не усложняет теоретиче-
теоретический анализ, однако затрудняет возможности практического применения.
103
Если К\ > Kt у то в нитях с номером к = 1, 2, 3,..., D будет возникать
повреждаемость, которая будет накапливаться в каждой нити по мере
приближения к концу макротрещины в процессе ее развития. Согласно
(9.25) число D будет наибольшим целым числом, для которого выполняет-
выполняется следующее неравенство:
2
(9.26)
При достаточно больших D (практически при D > 3) отсюда вытекает,
что
L
(9.27)
2тг d v2f
где знак [...] означает целую часть числа, заключенного в скобки.
В соответствии с приближением квазихрупкого разрушения предпола-
предполагается, что величина Dd зоны накопления повреждаемостей в нитях мала по
сравнению с длиной макротрещины или каким-либо другим характерным
линейным размером тела.
Средняя скорость движения макротрещины мало изменяется на рас-
расстояниях порядка Dd, поэтому каждое волокно, вступая в зону накопле-
накопления повреждаемостей;подвергается кусочно-постоянной нагрузке o(t), мо-
монотонно возрастающей через равные промежутки времени ту (рис. 50).
Время пребывания волокна в зоне повреждаемостей, очевидно, равно
DTf. Величина нагрузки на каждом этапе определяется формулой (9.25).
Отсюда при помощи закона Бейли (9.24) находим время г (равное
ff), фигурирующее в (9.18):
1 1
1 d
- = — 2 ехр
г A * i
L RTvf nd J
(9.28)
Подставляя это выражение в (9.18), получаем искомый закон движения
поперечной макротрещины в композите при стационарных нагрузках:
dl_ _ rQs/lT D Г у Кг Г~Г
at AVf k = \ I RTvf it d
Так как величина К\ согласно теории ортотропной упругости представ-
представляет собой некоторую функцию длины трещины / и внешних нагрузок
р(г), то соотношение (9.29) является дифференциальным уравнением
первого порядка, решение которого определяет функцию l(t)9 время,
в течение которого макротрещина перережет тело, и другие характерис-
характеристики, необходимые для правильной оценки ра-
работы композита в конкретной конструкции.
Изложенные представления легко обоб-
к'В-1 щить на другие механизмы замедленного
разрушения нитей (например, вследствие
коррозии или водородногр охрупчивания
металлических волокон). Для этого вместо
Рис. 50. (9.23) нужно взять другую зависимость,
k-Л
104
лучше описывающую опытные данные по замедленному разрушению
нитей.
Выведем теперь закон движения поперечной усталостной трещины в ком-
композите при циклической нагрузке. В этом случае время удобно измерять чи-
числом циклов п (т.е. период нагружения принимается за единицу времени).
При достаточно большом числе циклов до разрушения с переменной п мож-
можно обращаться как с непрерывной.
Теория роста усталостных поперечных трещин в композитах строится
на основе тех же представлений, что были здесь развиты. Поэтому изложим
ее кратко.
Средняя скорость развития поперечной усталостной трещины равна (ана-
(аналог (9.18))
±.± = ^Ь-. (9.30)
dn N Nvf
Здесь N - среднее время в циклах, необходимое для продвижения макро-
макротрещины на величину d.
Пусть число циклов до разрушения нити N* описывается формулой
вида (аналог (9.23) )
^)- (931)
Здесь атах и amin - наибольшее и наименьшее значения напряжения в
нити за цикл, со— частота циклов (ffmax, amin и со не зависят от времени).
В функцию F в принципе можно включить и другие переменные, характе-
характеризующие форму цикла. Эмпирические кривые Велера описываются фор-
формулой (9.31) при фиксированных значениях amjn, когда влияние частоты
пренебрежимо мало.
Формула (9.31) имеет место лишь в некоторой области D* в пространст-
пространстве переменных amax, amin и со; эта область определяется следующим нера-
неравенством:
*(<7max,<7min,co)>0 (932)
(обобщение понятия предела усталости).
В области /)"*, определяемой неравенством
(9.33)
обрыва нити не происходит за время работы конструкции.
Это неравенство есть некоторое обобщение понятия предела усталости
оу (действительно, пренебрегая частотой, при amjn = 0 получаем Ф = отах—
-Оу).
Если величины amax, amin и со зависят от времени (в циклах), то чис-
число циклов до разрушения TV* определяется при помощи закона Майнера
(аналог закона Бейли)
N* dn
j ———————— =| (9.34)
Здесь интегрирование ведется лишь по области D*, определяемой
неравенством (9.32). Закон Майнера называют также правилом сумми-
105
рования или накопления усталостных повреждений; мерой повреждаемос-
повреждаемости за время dn в данном случае является подынтегральное выражение
в (9.34).
Величины отах и amin в волокнах на продолжении усталостной макро-
макротрещины определяются формулой (9.25), в которой К\ нужно заменить
на Kimax и Ajmin (наибольшее и наименьшее значения К\ за цикл).
Размер Dd зоны накопления усталостных повреждений в нитях вбли-
вблизи края макротрещины определяется при помощи неравенства (9.32).
Для этого нужно подставить в функцию Ф величины атах и amin согласно
(9.25) npak=D и решить неравенство (9.32) относительно/). Время пребы-
пребывания волокна в зоне накопления повреждений равно DN.
Величину N находим при помощи закона Майнера (9.34) :
1 _ D l
n \1 ^ЖТЖЗ ' (935)
Здесь
1 ГТ
^} - ^ImaxV —
Vf Ш
(fc)
ffmin
1 /21
= — *lmin V -
Подставляя это выражение в (9.30), находим закон аокритического
роста поперечной усталостной макротрещины в композите при цикли-
циклической нагрузке:
?> 1 т (936)
dn vf дг-i F(a&&& )
В частности, когда влияние частоты несущественно, а минимальное
значение внешней нагрузки в течение цикла равно нулю, эмпирическую
кривую Вёлера аппроксимируем зависимостью
l (amin=O,amax> ot). (9.37)
Здесь NAnjN— некоторые постоянные. В этом случае уравнение (9.36)
принимает следующий вид:
yL (9.38)
[2ndv}a2t
Полученные закономерности позволяют определить сопротивление
данного композита докритическому росту поперечных трещин в любой
конкретной конструкции.
Докритический рост продольных трещин в армированных материалах.
Рассмотрим циклическое растяжение - сжатие вдоль волокон однонаправ-
106
ленного композиционного материала типа стеклопластика. Разрушение
таких материалов происходит в следующем порядке:
I) образование разрывов волокон (в процессе отвердевания смолы,
а также на ранней стадии эксплуатации);
II) развитие цилиндрических микротрещин от обрывов волокон;
III) рост продольных усталостных трещин в полимерной матрице под
действием бокового давления свободных участков волокон (выпучив-
(выпучившихся или же изогнутых вследствие начального эксцентриситета);
IV) рост боковых цилиндрических микротрещин вокруг волокон вслед-
вследствие различия коэффициентов Пуассона.
Согласно формулам (9.6) и (9.10) имеем
- на этапе II,
г= ^ 4Efvf (9.39)
офд ——- (ут — Vf) A - Vf) на этапе IV.
Здесь о— одноосное напряжение растяжения — сжатия в композите.
В предельном состоянии величина Г равна 2jfm, поэтому критическое
значение напряжения а будет следующим:
Or =
fQ
на этапе II,
- »гУ1 С1 -"/Г1 на этапе IV.
(9>40)
Приведем ориентировочные результаты расчетов по этим формулам
для нескольких типовых материалов:
стеклопластик (матрица — эпоксидная смола)
ty = 0,5, г0 = К* см, yfm = l^2 кгс/см,
?> = 7,5 -10s кгс/см2, Ет =3,5 • 104 кгс/см2,
^=0,2, vm =0,32,
[ 40 кгс/мм2 на этапе II,
| 600 кгс/мм2 на этапе IV;
углепластик (матрица - эпоксидная смола)
1^ = 0,5, го = 1СГ3см, yfm =10Г2 кгс/см2,
Ef = 4,5 • 106 кгс/см2, Ет =3,5 • 104 кгс/см2,
^m=0,32, iy-0,42,
ос = 90кгс/мм2 на этапе II;
ос ~3000 кгс/мм2 на этапе IV;
107
бороалюминип
Vf = 0,5, r0 = 1(Г2 см, ут = 1 кгс/см,
• 106 кгс/см2, Em = 7,4 •105 кгс/см2,
y , *>m=0,32,
[300 кгс/мм2 (на этапе II),
ас = \
[3600 кгс/мм (растяжение, на этапе IV).
Как видно, этап IV вряд ли может быть реализован даже в стеклопласти-
стеклопластиках при сжатии.
Исходные данные взяты из источников [10,11]. Величина 7/т была
взята примерно равной эффективной поверхностной энергии матрицы,
что привело к завышенным значениям оС9 так как энергия адгезии, по-
видимому, может быть значительно меньше этой величины. К сожалению,
надежные данные по энергии адгезии пока отсутствуют. Напомним, что
докритический рост микротрещин возможен при значениях а, значитель-
значительно меньших предельных.
Рост продольных усталостных трещин в матрице подчиняется следую;
щей закономерности [1]:
к\с Klc~ AImin
где ршиА:1с- постоянные материала матрицы. Если #Imin <0,то в
этой формуле следует полагать Ajmin = 0.
Уравнение (9.41) справедливо при значениях/Г1тах, больших порогово-
порогового значения Kt;jnpn KimuX<Kt скорость роста трещины равна нулю. Это
уравнение хорошо подтверждается опытом для металлических, и поли-
полимерных материалов, если выполняются два основных условия: а) влияние
частоты нагружения пренебрежимо мало, б) справедливы условия квази-
квазихрупкого разрушения.
При не слишком высоких значениях коэффициента интенсивности
можно без большой ошибки пользоваться первым членом пазложения
правой части (9.41) в ряд Тейлора
В частности, при Aimin < 0 отсюда получаем следующую зависимость:
-=-%- Xtmax. (9.43)
dn 2K\C max
Это известная эмпирическая формула Пэриса, предложенная им в 1964 г.
[34] и выведенная автором теоретически в 1968 г. [35].
В работе [63] (см. также статью Хэнкока в пятом томе издания [11])
наблюдалось примернб 200-кратное увеличение скорости роста продоль-
продольной усталостной трещины в образцах из бороалюминия, помещенных в
108
Рйс.51.
воду. Уравнение (9.43), пригодное для усталостных трещин в алюминиевой
матрице, позволяет легко объяснить этот катастрофический эффект. Дейст-
Действительно, было доказано экспериментально, что под непосредственным
адсорбционным воздействием воды происходит весьма быстрое продоль-
продольное расщепление борных волокон. Поэтому при обычной объемной доле
волокна порядка 50% эффективный коэффициент Kimax в алюминиевой
матрице вследствие расщепления волокон примерно в два раза больше,
чем в отсутствие расщепления. Кроме того, постоянная j3m в водных сре-
средах для алюминиевых сплавов примерно в десять раз больше, чем в инерт-
инертной среде [1]. Отсюда согласно формуле (9.43) получаем увеличение
скорости роста усталостной трещины в 10* 24(~200)раз.
Оценим развитие продольных трещин в матрице (на этапе III) под дей-
действием боковых сил от изогнутых волокон (см. рис. 51). Обозначим
через 21 длину свободного участка волокна, образовавшегося, напри-
например, вследствие развития цилиндрической микротрещины расслаивания
(рис. 51, а). Величину эксцентриситета обозначим через е (очевидно,е<
<1). Волокно и матрицу будем считать упругими.
Смещение волокна ну в точке приложения боковой (lateral) силы со-
сопротивления Pi под действием осевой (axial) силы Рая силы Р/ равно
wf = kfaPa-kfiPi. (9<44)
Здесь kfa икр— коэффициенты упругой податливости криволинейного
круглого стержня (нити) в точке О под действием сил Ра и Рх соответст-
соответственно (рис.51).
Смещение матрицы wm в точке приложения силы Pi равно
wm= kmPx. (9.45)
Здесь кт — коэффициент податливости матрицы в точке О под действи-
действием силы Pi (рис. 51, б).
Согласно условию совместности деформаций ну = wm; отсюда на ос-
основании (9.44) и (9.45) имеем
Л = -^-. (9.46)
k/i + km
109
Так как величина е мала по сравнению с L, то коэффициент kfa бу-
будет зависеть лишь от е и йзгибной жесткости нити ?///, коэффициент
kfi будет зависеть от L и ?///, а коэффициент кт — от радиуса нити г0
и модуля Юнга матрицы Ет. Отсюда на основании анализа размернос-
размерностей находим
4 ^
Здесь ^1,^2,1з — некоторые безразмерные коэффициенты, которые мо-
могут зависеть от коэффициентов Пуассона, от формы криволинейного
стержня, от относительного размера площадки контакта и от других вто-
второстепенных параметров.
Так как Jf= j яг о* то на основании (9.46) и (9.47) имеем
Р
Первое слагаемое в знаменателе значительно больше второго, поэтому
находим
(9.49)
Под действием циклического осевого растяжения — сжатия развива-
развивается усталостная продольная трещина, которую приближенно можно пред-
представить себе плоской и круговой радиуса 2/; сила Рг поочередно прикла-
прикладывается к противоположным берегам трещины в ее центре. Согласно
(9.49) ее зависимость от времени в течение полуцикла имеет тот же харак-
характер, что и осевая нагрузка.
Развитие усталостной трещины во времени легко оценить при помощи
уравнения (9.43), положив
Величина Кц на контуре трещины играет сравнительно малую роль по
сравнению с Къ и ею можно пренебречь.
Предельно большое значение радиуса трещины U при достаточно боль-
большом числе циклов определяется из (9.50) посредством условия К\ = Kt;
находим
V2/3
Для оценки этой величины возьмем следующие типичные данные:
L -10 j; fi ~$2; г0 ~1СГ* см;
Vf —0,5; о — 100 кгс/мм2; а — г0;
Kt - 1СГ2 Klc - 10Г2 кгс/мм3/2.
110
По формулам (9.49) и (9.51) получаем
/оо ~ 0,1 см, т.е. /оо ~ Ю L.
При а-^Юкгс/мм2 и тех же остальных данных согласно (931) име-
имеем /оо ~~ 1СГ2 см, т.е /оо ~~ L.
Таким образом, наличие свободного участка волокна и незначитель-
незначительного эксцентриситета волокна на этом участке при циклическом нагру-
жении приводит к образованию продольных усталостных трещин в мат-
матрице, размер которых сравним или же значительно больше длины свобод-
свободного участка расслаивания.
§ 10. Композиты с дисперсными включениями *
Рассмотрим составное упругое тело, состоящее из сплошной упругой
среды (матрицы) и распределенных в ней включений из другого матери-
материала. Процесс разрушения таких материалов определяется концентрацион-
концентрационным взаимодействием включений с матрицей, осложненным наличием
начальных технологических напряжений из-за температурного натяга.
В этом параграфе наиболее существенные механизмы локального разру-
разрушения подобных материалов проанализированы на модели с одним сплю-
сплющенным эллипсовидным включением; остальные включения "размазы-
"размазываются", а тело вне выделенного включения представляется однородным
и изотропным, с соответствующими эффективными упругими констан-
константами (по правилу "смесей").
Поле напряжений в окрестности эллипсоидального включения. Пусть
безграничное тело находится в условиях плоской деформации или плоско-
плоского напряженного состояния. Положение каждой точки этого тела опре-
определяется декартовыми координатами х,ушм. одной комплексной ко-
координатой z = х + iy. Пусть это тело содержит упругое включение эллипти-
эллиптической формы, так что граница раздела различных упругих сред описыва-
описывается уравнением
х2 у2
Здесь а = R(l + m), b -R(l — m); R,m— параметры эллипса L\a и Ъ — по-
полуоси эллипса L; индексом 1 в дальнейшем отмечены все величины, от-
относящиеся к эллиптическому вкладышу, а индексом 2 — относящиеся к
основному материалу (рис. 52, я).
Напряжения ох, оу,тху и смещения и, у в плоской задаче теории упру-
упругости можно представить при помощи комплексных потенциалов Колосо-
Колосова — Мусхелишвили у (z) и ф (z):
оу-ох+ 2irxy = 2 [zV>0 + Ф'(?)], (ЮЛ)
2д (и + /у) = кф) - zlpjz) - J(z)
и к — упругие постоянные).
* Этот параграф написан на основе статей [64-69].
111
la
Рис. 52.
Считаем, что всюду на границе контакта L имеет место жесткое сцепле-
сцепление различных сред. Отсюда получаем
(z
- ift (z)) -
A03)
где a - коэффициент линейного температурного расширения; Го - на-
начальная температура; Т- температура тела после нагревания (или ох-
охлаждения).
Будем считать, что йри z-><» действуют постоянные напряжения Ох>Оу,
ху
,т.е.
1
4
1
"г
<е
A0.4)
Таким образом, требуется найти функции ^i,<р2» ^i > Ф 2 по краевым у*>
ловиям A0.2) - A0.4).
Следуя Хардиману [64], предположим, что напряжения во включении
постоянны:
Они должны быть определены в процессе решения.
Потенциалы <Pi (?) и ty\(z)\ соответствующие этим напряжениям,име-
напряжениям,имеют вид
-1 о+ о .
4 *, у
(С— неопределенная действительная постоянная, подлежащая определе-
определению).
112
Из формул A0.2), A0.3) и A0.6) получим следующее краевое ус-
условие:
F(z)=Az~ (zGL). A0.7)
Здесь
А fri
А -
k2L>2(z)-z\
L 4/Hi
Конформно отобразим внешность эллипса L плоскости z на внешность
единичного круга параметрической плоскости f при помощи функции
(рис. 52, б)
Краевая задача A0.7) с учетом A0.9) переходит в следующее условие:
= 1). A0.10)
Аналитически продолжая краевое условие A0.10) на всю плоскость f,
получаем искомое решение
A0.11)
При помощи A0.8) — A0.11), используя аналитическое продолже-
продолжение, находим
[+ 7) - 2м2 («1 - а2) (^ - То)
1+к2
* "
Mil
1+к2 L 4цх ' 4цх
A0.12)
_i_ о о -о Az AR(m2f-l)
2 у х ху 1 + к2
+ Л— [mi + -1,
2A+к2) V if
- r0), D = k2 - 1 - — (Kl - 1).
Mi
113
Из условий на бесконечности A0.4) и A0.12) получим
ffo ffo = (qT- О [2 + Mafri - 1)/Mi - ФяД - тДа
Mi
4m (^ -//2)г~у
Г (l+m2XMi-^2I 2Дт2
I Ml+Ka) J MiO
+k2) J
Л1 [4g + (l+x2)(g~+g;)] 2m fa-ъ)
+ CTv = — A
0) ()
A0.13)
B " M2 («1 -
_ 1 ™ -——
[ Mi A +*г) J Mi 0 + *г)
Формулы A0.12) и A0.13) дают полное решение поставленной за-
задачи, удовлетворяющее всем краевым условиям.
В полученном решении содержится много интересных частных случа-
случаев, часть которых была исследована ранее другими авторами (Колосо-
(Колосовым, Инглисом, Мусхелишвили, Шерманом, Хардиманом). Случай Хар-
димана (В = 0) был исследован им несколько другим способом.
Найдем поле напряжений в основном материале:
¦ ^+^^-i)(a.+oJ)_i5_ + -l_Rej
A0.14)
4Az(l - т2)$3 2А m2f4(?2 - Зт) + З?2 - т
K2)(f2-raK 1+к2 (?2-wK
114
Выделение промежуточной асимптотики. Особый интерес представля-
представляют включения в форме тонкого сплющенного эллипса, когда модуль
упругости включения мал по сравнению с модулем упругости основно-
основного материала, т.е.
3 = 1-т<\, 5=2~,— «1. A0.15)
а /х2
Включения такого типа приводят к значительным локальным концентра-
концентрациям напряжений вблизи краев и наиболее существенно влияют на проч-
прочность всего тела.
В случае A0.15) вблизи концов включения формируется промежуточ-
промежуточная асимптотика решения, имеющая место на расстояниях от конца вклю-
включения, больших по сравнению с радиусом кривизны конца, но малых
по сравнению с длиной включения, т.е. если выполняется условие
l>|w|>52, w = z/a-l.' A0.16)
После некоторых преобразований формулы A0.12) при условиях
A0.15) и A0.16) промежуточную асимптотику (сингулярную часть)
потенциала у\ (z) можно привести к такому виду:
A0.17)
dz a(l+K2)\/2w
Как видно, эта асимптотика определяется одним комплексным ко-
коэффициентом, который будем обозначать через Кх - НСц по аналогии
с обычными трещинами и называть коэффициентом интенсивности напря-
напряжений
2А5 у/т
m | y/2ir(z -а)— | = -
z-
Кг - iKu = 2 lim y/2n(z - а] — = -
L dz 1
к i — 1) — 2\хх В iTxy M2
1)+ 26m2 (kx - 1) Mi О + к2) + 2Ъ\хг
A0.18)
В предельном случае трещины со свободными берегами, когда Mi=0,
по этим формулам находим известные соотношения
Кх = Оу >ДШ, Ки = ТхУ у/Ш. A0.19)
Формулу A0.17) запишем так:
dz 2 у/2п (z - aj
A020)
Можно показать, используя принцип "микроскопа" и точное решение
для параболического включения [65], что при некоторых условиях фор-
формула A0.20) годится для тонких податливых включений совершенно
произвольной формы в плане.
Таким образом, выведенные формулы можно рассматривать как обоб-
обобщение классических представлений о коэффициентах интенсивности на-
115
пряжений для трещин на случай тонких податливых включений из друго-
другого материала. Отметим, что двойной предел при т -> 1, \к\ -* 0 существен-
существенно зависит от порядка перехода к пределу в формулах A0.18).
Сравним формулу A0.18) с выражением для коэффициента интенсив-
интенсивности напряжений, получейным для тонкого эллиптического включения
при т™у = 0 из приближенного решения задачи на основе гипотезы упру-
упругого основания [67]
(К2^1)^ A0:21)
Как видно, при иЛ(бцг)< * первые слагаемые в формулах A021) и A0.18)
одни и те же; вторые - близки по величине (для случая плоского напря-
напряженного состояния при Vi = 1/2). Третье слагаемое в A0.21) мало по срав-
сравнению с первыми двумя, только если дi /(бд2) < 1.
Проведенное сравнение точного решения для эллиптического включения
с приближенным решением, основанным на гипотезе упругого основания
типа гипотезы Винклера, показывает, что приближенный подход дает ре-
результаты, близкие к точным решениям, если
> 1/6 >1. ! A022)
Следует ожидать тот же результат в теории балок на винклеровском осно*
вании.
Если же выполняется условие
1<ц21их <-1/6, A0,23)
то упругое поле почти без изменений передается почти на все упругое
включение (ру = а~, т$у = т™у, о$Ф а~), за исключением малой области
размером порядка 2Ь вблизи конца включения, в которой упругое поле
будет существенно отличаться от невозмущенного.
Можно показать, что условие
M2/Mi>l/V^>l ,A0.24)
является необходимым и достаточным условием, при котором вблизи
края тонкого включения формируется локальная концентрация напря-
напряжений, описываемых формулой A0.20).
Если /Ltj/jLii ~6~1/2 или /i2/Mi ^б ,то локальная концентрация напря-
напряжений вблизи края тонкого упругого включения отсутствует.
Тонкие включения произвольной формы. Пусть однородное и изотроп-
изотропное упругое тело произвольной формы (и произвольным образом нагру-
нагруженное по своей поверхности) имеет упругие включения из другого ма-
материала произвольной формы (типа гладких замкнутых или незамкнутых
оболочек или пластин). Обозначим через h характерную толщину вклю-
включения (толщина может быть переменной, однако считается,что dh/ds<\9
где s — любое направление вдоль срединной поверхности оболочки), а
через / — характерный линейный размер срединной поверхности оболоч-
оболочки. Пусть Mi и ix2 -т модули сдвига включения и основного материала.
Предположим также, что выполняется условие
116
В этом случае на основании результатов предыдущего параграфа всю-
всюду в составном теле почти все напряжения будут точно такими же, как
для соответствующего однородного тела; исключение составляет напря-
напряжение os во включении, которое вычисляется по формуле
«1-3
Os = ~ — Оп ,
кг + 1
где п - нормаль к срединной поверхности оболочки в рассматриваемой
точке.
Вблизи краев оболочки (во включении и матрице) будет существо-
существовать местная зона концентрации напряжений; поле напряжений в этой
зоне зависит от формы включения в его конце (и от внешнего поля).
Локальное поле напряжений вблизи конца включения можно точно опре-
определить в том случае, когда конец включения имеет форму параболы или
клина [65].
В случае, когда М2/М1 >//* > 1,для определения напряжений в состав-
составном теле можно применить более сложные методы, основанные на замене
упругого включения моделью типа модели Винклера.
Если М2/М1 ^ l,h/K 1,то упругое включение можно рассматривать
по теории тонких упругих оболочек, а реакцию основной упругой сре-
среды моделировать винклеровским основанием.
Изгиб плоскости с эллиптическим включением. Как известно в теории
гармонического потенциала, однородное электрическое поле вызывает
также однородное поле в диэлектрике, если последний по форме представ-
представляет собой эллипсоид. Это обстоятельство было использовано в работе
[64] и здесь для решения аналогичной упругой проблемы, описываемой
бигармоническим потенциалом. Можно показать, что для плоского вклю-
включения эллиптической формы имеет место более сильный результат: если
на бесконечности напряжения представляют собой полиномы некоторой
степени, то внутри включения напряжения также являются полиномами
той же степени. Аналогичный результат справедлив в отношении электри-
электрических, магнитных, тепловых, фильтрационных и других полей, описывае-
описываемых теорией гармонического потенциала, а также для аналогичных прост-
пространственных задач в случае инородного эллипсоида как в теории потенци-
потенциала, так и в теории анизотропной упругости. Чтобы сделать доказательст-
доказательство более простым и наглядным, ограничимся конкретным случаем чистого
изгиба. Общий гармонический и бигармонический случаи рассматриваются
совершенно аналогично.
Предположим, что напряженное состояние плоскости с эллиптическим
включением представлено на бесконечности следующими функциями
(при z -> °°):
^2(z) = ez2 + o(?j, ф2(z) = cz2 + o(jj A025)
(еис — некоторые заданные комплексные постоянные).
В этом случае предположим, что потенциалы </>i (z) и фг (z) во вклю-
включении представляют собой аналогичные функции
*i(z)«*0*2, ^(z) = r0z2. A0.26)
117
Здесь еоисо— некоторые комплексные постоянные, подлежащие опре-
определению.
Краевые условия A0.2) и A0.3) приводят к выражению
F(zLl - —)BeozY +c0l2) (z EL), A0.27)
\ Mi/
где
F(z) = (l+K2)^(z)-(l+/c1-
\ Mi
Конформно отобразим внешность эллипса L плоскости z на внешность
единичного круга параметрической плоскости ?. Краевая задача A0.27)
с учетом A0.9) переходит в следующую краевую задачу на плоскости f:
cm =i).
A028)
Аналитически продолжив это краевое условие на всю плоскость f,
получим
1 / цЛ .
Y>2(z)= ——Il+Ki—Je0z2 +
1 + Ко ^ Ml/
Функцию ф2 (z) находим по краевому условию A0.2):
. A0.30)
Согласно условиям на бесконечности A0.25) получаем
Ml +М2*1 ^ Ml ~ М2 //Л _ 2Л /,AQ14
е0 + — Bте0 + cow2), A031)
MO+K)
2 _ 2 Ml
4MiM2 ^ Mi+M2*i о 2/. _ 4Mi-M2
+ с) 2те0 - 2т2 Bе0 + сот)
118
Соотношения A0.31) представляют собой систему четырех действи-
действительных линейных уравнений, служащую для определения четырех не-
неизвестных величин: Ree0, Ime0, lmc0, Rec0. Эта система однозначно раз-
разрешима, так как соответствующая однородная система при е = 0 и с = 0
имеет только тривиальное решение в силу теоремы единственности те-
теории упругости. Таким образом, линейное поле напряжений на бесконеч-
бесконечности вызывает также линейное поле напряжений внутри эллиптического
включения.
Прочность хрупких тел с включениями. Исходные положения. Сформи-
Сформируем исходные допущения и проанализируем основные возможные меха-
механизмы локального хрупкого разрушения, что позволит нам проследить
структурный метод построения диаграмм предельного состояния микро-
микронеоднородных хрупких тел. Примем следующие допущения:
а) характерный линейный размер начальных трещин и пор мал по срав-
сравнению с характерным линейным размером наиболее опасного инородно-
инородного включения;
б) все микронеоднородности (трещины, зерна, поры, включения и тд.),
кроме одного наиболее опасного включения, "размазываются", и тело
вне этого включения представляется бесконечным однородным и изотроп-
изотропным упругим телом;
в) нормальное сечение выделенного включения считается сплющенным
эллипсом, а включение — бесконечно протяженным в направлении норма-
нормали к этому сечению (включение в форме сплющенного эллиптического ци-
цилиндра) ;
г) модуль упругости включения мал по сравнению с модулем упругос-
упругости матрицы.
Все эти допущения аналогичны принятым в теории Гриффитса, кото-
которая, очевидно, должна получиться как предельный случай из излагаемой
теории при /ц/Мг ~* 0- Допущения а), б) иг), по существу, определяют тот
класс материалов, к которому может относиться теория. Допущение в)
носит чисто геометрический характер и связано с тем, что наиболее опас-
опасны именно сплющенные включения продолговатой формы, когда материал
включения или гораздо более податливый (по упругим свойствам), или
гораздо менее прочный (или то и другое, вместе взятое). Именно для
таких включений, как показал предыдущий анализ, наблюдается наибо-
наиболее значительная концентрация напряжений вблизи края включения в
основном материале. Включения такой формы часто встречаются в ком-
композиционных материалах с дисперсными включениями, в горных поро-
породах (прослойки, прожилки, тектонические трещины с заполнителем и
тд.), в металлах (окисленные слои, пластинки графита в чугуне и тд.).
В зависимости от отношения упругих постоянных и прочности состав-
составляющих, а также от характера внешних нагрузок разрушение может про-
протекать совершенно различно. Рассмотрим следующие два основных слу-
случая: трещина начинает развиваться во включении; трещина начинает раз-
развиваться в матрице.
Начальное развитие трещин во включении. Укажем сначала формулы
для напряжений во включении в рассматриваемом случае, когда
а-Ъ
^ 1 > I —т = д <19 где т = , а и Ъ — полуоси эллипса.
а + Ь
119
В этом случае формулы A0.13) можно привести к следующему прос-
простому виду:
' °У °*
С помощью A0.14) найдем напряжения в точке наибольшей концентра-
концентрации напряжений,т.е. в точке х = а, у = 0 в матрице:
и у — ох -
Txv = "
у М
Вблизи концов включения в матрице формируется промежуточная
асимптотика, которая определяется следующими коэффициентами ин-
интенсивности напряжений:
* ™" "~ .00:34)
Рассмотрим теперь разрушение включения. Поперечные f рещины, кото-
которые в нем могут возникнуть, неопасны, так как весьма малы. Начало раз-
развития продольных трещин будет определяться условием типа / (т?у, о* ) <
< 0 (знак неравенства соответствует отсутствию разрушения). Трещина во
включении находится в поле постоянных напряжений, равновесие ее неус-
неустойчиво, гщэтому она будет развиваться в динамическом режиме до тех
пор, пока ее длина 2/не станет равной длине включения 2а. Будем считать,
что рассматриваемое включение ориентировано по отношению к внешним
нагрузкам самым опасным образом. На плоскости главных напряжений
о i о2 теперь нетрудно определить область F (рх, о2, а) < 0, граница которой
отвечает условию разрушения включения (а — угол между направлением ох
и осью х вдоль трещины).
Проведем расчет до конца для конкретной зависимости типа сухого ку
лонова трения со сцеплением т%у < к0 - оу° tg p (рис. 53), которая удов
летворительно описывает разрушение многих в среднем структурно одно-
однородных материалов (к0 — коэффициент сцепления, р — угол внутреннего
трения).
120
Рйс. 53.
Phc.54.
Найдем функцию F (ох, а2, а):
F(ou о2,а)±тх°у -ко+ а/ tgp =
= — к0 +А2 о2 + (а2 — Ox)(Ai sina cosa - А2 sin2а),
Mi A+Ka).
A0.35)
Mi A +*2)
Mi (l+Ka)(l+^i)tgP
Точка a = a* является точкой максимума функции F (aj, a2, a), причем
sina,,
A0.36)
sin2a,
1Яё'2?1-й2?2 — константы составного тела, не зависящие от размера вклю-
ченця.
Область Вг ох +В2о2<к0, о2 <-ог качественно изображена и заштрихо-
заштрихована на рис. 54 (она, очевидно, зеркально симметрична относительно пря-
прямой tfi =02). Диаграмму, приведенную на этом рисунке, будем называть
диаграммой разрушения включения.
Далее, при той же нагрузке трещина может перейти в основной материал
и перерезать все тело или может остановиться, так что при дальнейшем уве-
увеличении нагрузки достигается новое критическое неустойчивое состояние.
В случае открытых трещин отрыва диаграмма разрушения будет следу-
следующей: „
тах(G1,а2)< -—; . A0.37)
7ГЯ
Однако при достаточно большой величине сжатия берега ее уже налегают
друг на друга. Сам момент перехода от открытой трещины к налегающей
подлежит определению в процессе решения. Пусть берега воздействуют
между собой по закону сухого кулонова трения гху = — к + оу tg р,где
коэффициенты к и р, вообще говоря, отличаются от соответствующих кон-
констант для неразрушенного включения. В этом случае' коэффициент интен-
121
сивности напряжений Кц равен [1]
г-4 1
Кц = -утга 2к - аг tgp - о2 tgp + — ах (sin2a +
+ tgp cos2a) + — o2 ( - sin2a - tgp cos2a) (A"i = 0). A0.38)
Отсюда найдем угол а = а*, при котором Кц максимально, и сам макси-
максимум:
( ) () A039)
\ 2к - tgp ( ог + о2 - 1 (а2 >ох).
L \ 2sinp /J
2sinp
Безопасная область для тела с трещинами скольжения определяется
условием
A0.40)
(Кис — вязкость скольжения).
Таким образом, согласно формуле A0.39) имеет место следующая диаг-
диаграмма разрушения:
Ол — (Ь \
2 sinp /
если характер нагрузки обеспечивает смыкание и сухое трение противопо-
противоположных берегов трещин (это, наверное, обеспечено при ох <0и о2 <0,
а также при о2 > 0, но достаточно больших по абсолютной величине отрица-
отрицательных ох).
На рис. 55 качественно изображена диаграмма разрушения тела с трещи-
трещинами, получающаяся наложением диаграмм A0.41) и A0.37) . Эта область
полностью определяется заданием величин p,kyKiCyK\\c,ay которые счита-
считаются константами данного тела (они могут быть определены из самостоя-
самостоятельных опытов). Если точка (аь а2)выходит на границу этой области,
происходит разрушение; механизм разрушения (отрью, сдвиг или проме-
промежуточный режим) также легко определяется по положению этой точки на
диаграмме.
Совсем другая диаграмма разрушения может получиться, если взаимная
ориентация внешних нагрузок и трещин не может варьироваться, так как
она определена расположением наиболее опасного включения, т.е. формулой
A0.36). В этом случае дальнейшее развитие трещины зависит от характера
внешних нагрузок. Если противоположные берега трещины смыкаются
и взаимодействуют по закону сухого трения, то диаграмма разрушения
определяется условием А'11<А'11с при помощи формул A0.38) и A0.36)
А\\ К\Лс
p+ — )<-7^ + 2* (о2>ох). A0.42)
А2 / \f-na
122
А
.«у
Рис.55.
Рис.56.
Если же берега трещины не взаимодействуют, то нужно применить тео-
теорию трещин обобщенного нормального разрьюа [1 ].
Наложение диаграммы A0.42) с последней дает полную диаграмму раз-
разрушения тела с трещиной. Она зависит от величин А х, А2, р, к,К\с, Кцс, а,
являющихся константами составного тела, определяемыми независимо
в других опытах. Термин "наложение диаграмм" обозначает общую часть
областей.
Для того чтобы отыскать требуемую диаграмму разрушения для исход-
исходного тела со включением, необходимо произвести наложение следующих
диаграмм: диаграммы В.х ох +В2 о2 <& (разрушение включения, см.
рис. 54), диаграммы A0.42) и диаграммы неустойчивого развития откры-
открытой трещины длиной 2а, образовавшейся на месте наиболее опасного вклю-
включения. Если последняя диаграмма целиком расположена внутри области
Вгох + В2 о2 <&, то устойчивой остановки трещины после разрушения
включения никогда не будет; если же область ^i^ +B2o2<kцеликом
расположена внутри области, определяемой другими диаграммами, то ус-
устойчивая остановка этой трещины перед полным разрушением тела будет
всегда. Сравнение этих диаграмм позволяет легко дать полный ответ и для
всех других возможных случаев.
Последовательное применение механики разрушения для построения
диаграмм предельного состояния проводится в книге [203].
Начальное развитие трещины в матрице. Рассмотрим теперь наиболее ин-
интересный случай, когда локальное разрушение и образование трещины впер-
впервые происходит в малой окрестности конца включения в основном матери-
материале. В одном случае упругое поле описывается двумя коэффициентами,
К\ и Кп, которые даются формулами A0.34).
Согласно общефункциональному методу механики разрушения локаль-
локальное разрушение определяется критериями вида
f(Kl9Ku) =
A0.43)
(f — некоторая функция, определяемая экспериментально).
Поскольку опытных данных по определению этой функции пока недоста-
недостаточно, оценим ее по двум предельным случаям, которые можно рассмот-
рассмотреть до конца аналитически: а) на продолжении включения образуется тре-
трещина отрыва, а коэффициент Кц равен нулю; б) на продолжении включе-
включения образуется трещина сдвига, а коэффициент К\ равен нулю.
123
Используя A0.34), находим диаграмму разрушения:
в первом случае sv ( П
/1а(к1-1)тах(а1>аа)-2/11Д< Ic^*' [цг A + *2) + 25д2]
A0.44)
во втором случае
и, I
(l+*i) • 00.45)
М2 J
Наложение этих диаграмм схематически показано на рис. 56. Получен-
Полученную сводную диаграмму примем в качестве диаграммы разрушения, опи-
описывающей начальное разрушение матрицы вблизи конца включения. Заме-
Заметим, что новые постоянные Ajc/ и Кцсг не совпадают с соответствующими
константами теории трещин (поэтому здесь был взят дополнительный ин-
индекс * , чтобы подчеркнуть их различие).
Сравнение диаграмм рис. 55 (разрушение включения) и рис. 56 (раз-
(разрушение матрицы вблизи конца включения) позволяет ответить также на
вопрос, какой из этих двух основных механизмов реализуется в том или
другом конкретном случае.
Дальнейший характер протекания разрушения зависит от того, устой-
устойчив или неустойчив образовавшийся разрыв вблизи края включения. Если
разрью устойчив, то он. будет развиваться до тех пор, пока нагрузка на
включение не достигнет предельной величины; после этого включение раз-
разрушится и трещина станет неустойчивой (критическое состояние).
Чтобы ответить на этот вопрос, нужно построить диаграмму разрушения
тела с трещиной, которая имеет в центре перемычку длиной 2а. Решим эту
задачу при следующих двух допущениях: а)плоскость разрьюа в критичес-
критическом состоянии совпадает с плоскостью включения; б) длина разрыва 2L в
критическом состоянии гораздо больше длины включения 2j (рис. 57).
Заметим, что йлина разрыва 2L неизвестна и должна быть определена в
ходе решения задачи. Используя допущение б), для вычисления коэффици-
коэффициентов интенсивности напряжений перемычку можно заменить двумя рав-
равными и противоположно направленными силами, приложенными к разным
берегам трещины в ее середине (составляющие силы по осям*и>> наверх-
нем берегу равны Р и Q соответственно).
В случае открытых трещин коэффициенты интенсивности получаются су-
суперпозицией известных решений
Q
К\ = -+у/пЕ(ох sin2a + a2 cos2a),
v7^ A0.46)
p
Кц = ¦ j—- + yfnL (pi — o2) sina cosa.
у/пТ
В данном случае наиболее опасное включение ориентировано перпенди-
перпендикулярно направлению наибольшего растяжения, поэтому
Q
^max(ol9o2), Ku=0. A0.47)
* Первая буква слова inhomogeneous.
124
Величина Q в критическом состоянии равна 2а оь, где оь — прочность на
разрыв включения или адгезии "матрица — включение". Отсюда по форму-
формуле A0.47) находим
2ааь Ки
ог< — + -рг {о2>аху A0.48)
Из физических соображений величина Kici должна быть больше вяз-
вязкости разрушения матрицыKic; так как/, >а, то из тех >ке физических со-
соображений правая часть в формуле A0.48) меньше, чем правая часть в
формуле A0.44). Тот же вывод из аналогичных соображений следует для
трещины скольжения. Вследствие концентрации напряжений это тем более
будет справедливо для случаев, когда длина разрыва сравнима с длиной
включения.
Таким образом, из физических соображений вытекает, что образовав-
образовавшийся разрыв вблизи края рассматриваемого включения будет всегда неус-
неустойчив и, следовательно, диаграмма разрушения композита по второму ме-
механизму совпадает с диаграммой локального разрыва вблизи края включе-
включения (оценка последней дается формулами A0.44), A0.45) и рис. 56).
Для того чтобы определить, как ой. из основных механизмов реализуется
» данном композите, нужно построить общую диаграмму разрушения ком-
композита. Последняя получается наложением соответствующих диаграмм, по-
строенных для этих механизмов в отдельности. Сводная диаграмма, которая
представляет собой общую часть всех этих диаграмм, может применяться в
непосредственной практике для расчета разрушения микронеоднородных
тел при любых комбинациях сжатия, сдвига, растяжения. Макроконстанты
разрушения на этой диаграмме выражаются описанным здесь способом че-
через микроконстанты неоднородного тела. Следует подчеркнуть, что какой-
либо однозначной зависимости между микро- и макроконстантами, пригод-
пригодной для всех тел, не существует (как видно из изложенного анализа): для
каждого материала или, по крайней мере, типа материалов такую зависи-
зависимость нужно ртроить отдельно.
Возможен еще случай развития начальной трещины на границе раздела
"матрица — включение" с последующим переходом трещины в матрицу.
Несколько таких задач в точной постановке было рассмотрено в статьях
[70,71] на основе замкнутого решения [46] для трещин, находящихся
на круговой границе раздела разных сред. Приведем это решение.
Разрезы вдоль дуги окружности на
границе двух упругих сред. Пусть упру-
упругое тело, находящееся в условиях плос-
плоской деформации, представляет собой в
комплексной плоскости z = х + iy внеш-
внешность разрезов Lk = akbk (к = 1,2,.. .,л)
одной и той же окружности радиу-
радиуса г =1, причем упругие постоянные
материал*, находящегося в круге
г < 1, отличны от упругих постоянных
Материалов вне круга {L = L х + L 2 + ...+
¦t Ln). Компоненты напряжения в Рйс.57.
125
полярных координатах ог,ое,Тгв и производные по в от компонентов
вектора смещения в декартовых координатах uhv выражаются формулами
=4Re Ф,G) (/=1,2),
(Эй Эи \
)
or+iTre = Фу (z) + Фу (z) -z Ф; (z) Фу (z),
(Эй Эи \
— +1 — ) =
= /Z куФу (Z) - Фу (Z) +Z Ф} (Z) + j- Фу (Z) I . A0.49)
Индекс/ = 1 относится к внутренности круга г < I, индекс/ = 2 - к внеш-
внешности круга.
При больших z функции Ф2 (z) и Ф2 (z) имеют вид
* + iT 1 / 1 \
Ф2 (z) = Г +0 — I, A0.50)
2тг A +к2) z \ z2 /
2тгA+к2) z \ z2 /
Здесь Г1 и Г— постоянные, определяемые напряжениями на бесконечности,
ХиУ- компоненты главного вектора сил, приложенных к разрезам/,.
Введем аналитические во всей плоскости z, кроме, может быть, окруж-
окружности г = 1, функции Ф (z) и п (z):
ФB)
2 Д2
приг>1,
7 *2(т) приг<1'
Mi +M2*i L W/ z \z/ z2 \, z>
Ф2 (z) прт r>\. A0.51)
126
Из формул A0.50) и A0.51) видно, что при больших z
Jf + iT 1 / 1 \
Ф() +0 — ),
( +к2) z \ z2 /
Ц2A + К
S2(z) =
2тгA +к2)
Ц2A + К ! ) Л ! - Г{]Л2К! -Ъ1ХК2)
+
Mi
ЛГ+/У
2тгA +к2) z
Здесь
(М2 + Ml К2 ) Ф (€) + (Р-2 — Ml ) ^ (е)
/li =lim .
е->о МгA+К1)
В окрестности точки z = 0 функции Ф (z) и П (z) имеют вид
М2+Mi^2 ь^тгО+Кг) z z2 J
A0.52)
В функциях Ф (z) и П (z) компоненты смещения и напряжения записыва-
записываются в виде:
при г> 1
о, + ов(),
аг -Итгв = Ф (г) + п ( —
аг гв () j ^
M2+Mi*2 M2-M1 A°-53)
+ M2Kl
I Ъи . Эу \ Г М2+Mi«i M2-M1
I — +г — =*z Ui Ф(г) + К! • S2
V Э0 Эв / L '^(I+kO W M2(|+«i)
M2^i+Mi / 1 \ MiK2~M2*i A/ ! \ -/- * \Т
121 — 1+ = Ф — J-Zl Z }^
MaO+^i) V ? / M2O+K1) \z/ \ zj
127
Здесь
Считаем, что
lim A - г) ^2 (О = 0 при г -* 1.
Представления A0.53) показывают, что на участках сцепления
Ф+=Ф-, ?2+ =12-.
Таким образом, функции Ф (z) и 12 (z) аналитичны во внешности разре-
разрезов плоскости 2, кроме точки z = 0, где они имеют полюс не выше второго
порядка с главной частью, определяемой формулами A0.52). При помощи
формул A0.53) основные задачи с заданием на разрезах напряжений, или
смещений, или их комбинации сводятся к краевой задаче Римана — Гиль-
Гильберта для системы функций Ф (z) и 12 (z) с постоянными коэффициентами,
разрешаемой в замкнутом виде [47]. Ввиду некоторой громоздкости, зак-
заключительные формулы, определяющие решение, здесь не приводятся.
При помощи представлений A0.53) могут быть решены также некото-
некоторые другие задачи, в частности контактная задача, если на площадке кон-
контакта справедливы условия сцепления.
Анализ процесса развития круглых трещин на основе этого решения
приводит к диаграммам разрушения, аналогичным диаграмме рис. 55 и со-
соответствующим рассмотренному выше случаю начального развития тре-
трещины во включении.
Исторические сведения
По-видимому, впервые инвариантные интегралы появились еще в работах Максвел-
Максвелла при определении тензора напряжений электромагнитного поля. В статической тео-
теории упругости аналогичные интегралы весьма искусственным методом ввел в 1951 го-
году Эшелби [2], который не обратил на них должного внимания и фактически исполь-
использовал лишь для вычисления конфигурационной силы, действующей на упругую
неоднородность в форме эллипсоида. В 1968 году Райе [5], не знакомый с работой Че-
Черепанова [3], чисто эвристически взял один из интегралов Эшелби (он назвал его /-ин-
/-интегралом) и непосредственно доказал его инвариантность при помощи теоремы
Гаусса — Остроградского. Все общие результаты Эшелби и Раиса являются некоторы-
некоторыми частными случаями результатов Черепанова [3], опубликованных раньше статьи
Раиса независимо от работ Эшелби и полученных совершенно другим, более общим
методом (см. продолжение на стр. 205).
ГЛАВА 2
АСИМПТОТИЧЕСКАЯ ТЕОРИЯ АРМИРОВАНИЯ
УПРУГИХ ТЕЛ
§ 1. Общий метод
Рассмотрим упругую систему, состоящую из набора упругих элементов
(континуумов) разных измерений и, вообще говоря, из различного материа-
материала. Пусть телоDx (измерения^) сцеплено с теломD2 (измерения^)
вдоль площадки контакта С с измерениемА^. Контакт может быть точеч-
точечным (Nc = 0), линейным (Nc = 1), двумерным (#с= 2) и трехмерным
(Nc = 3). (Последний как некоторая абстракция реализуется в так назы-
называемых двойных сплошных средах.) Разумеется, представление об изме-
измерении тела и площадки контакта является чисто асимптотическим и зависит
от характерного линейного масштаба рассматриваемой задачи. Например,
предположение о том, что контакт точечный, означает малость всех линей-
линейных размеров площадки контакта по сравнению с характерными линей-
линейными размерами тел/?1 и/J. Тело Dx может быть стержнем, балкой,
нитью (N% =1); пластиной, оболочкой (Nt = 2); массивным телом (Nt =
= 3). То же* относится к телу D2.
В случае, если
(l, A.1)
условие совместной работы тел Dj и D2 состоит в равенстве соответствую-
щих смещений этих тел в точках площадки контакта С. (Естественно,
необходимо соблюдать также условия равновесия.)
В случае же, если
-Nc, N2 -NC)>1, A.2)
вектор смещения в теле наибольшей размерности стремится к бесконеч-
бесконечности при стремлении точки к области С. (Исключение составляет попереч-
поперечный изгиб пластин и оболочек под действием сосредоточенных сил, отно-
относящийся1с предыдущему случаю A.1)). Поэтому в этом случае условие
совместности так же просто записать не удается и приходится применять
специальные асимптотические методы, которые подробно рассматривают-
рассматриваются ниже в § § 2—7 этой главы. Эти методы основаны на некоторых общих
асимптотических представлениях, которые излагаются далее в этом параг-
параграфе и которые называют методом внешних и внутренних разложений.
Этот метод широко применяется в аналитических исследованиях краевых
задач математической физики. Изложение этого параграфа основано на
работе [72].
Пусть в некоторой области D трехмерного пространства требуется найти
решение определенной краевой задачи для системы дифференциальных
129
уравнений в частных производных. Пусть область D обладает следующим
свойством: в ней можно ввести безразмерный (геометрический) малый
параметр е :
0<е<\ .
Этот Параметр представляет собой отношение
где / и L — некоторые характерные линейные размеры области D (/ будем
называть внутренним параметром, a L — внешним).
Метод внешних и внутренних разложений заключается в следующем.
Из области D образуются две более простые области (которые обозначим
через D/ и DL); они получаются при помощи следующих предельных пе-
переходов:
Di= lim D (/конечно), A.3)
DL = Вт D (L конечно). (L4)
/->o
Данную краевую задачу для рассматриваемой системы дифференциаль-
дифференциальных уравнений решаем отдельно для области D/ и области DL. Соответ-
Соответствующие решения обозначим через 5/(r, О и *$х (r, Z,), где г -* радиус-век-
радиус-вектор точки в области D (решение St будем называть внутренним, а решение
SL —внешним).
Будем исходить из того, что решение исходной краевой задачи для об-
области D (обозначаемое через SQ (r, е) существует и единственно. Найдем
следующие асимптотики полученных решений Sj(r, I) nSL(r, L):
5Г(г,/) = 5,(г,/) приг>/, A.5)
S°L(r,L) = SL(rfL) при r<L (r2 =x?+*!+*!). A.6)
Здесь предполагается, что начало декартовой системы координат хх х2 х3
выбрано в некоторой точке области />/. В случае плоских или локально-
плоских краевых задач координату х3 можно считать равной нулю.
Функции SJ(r, О И $l (r> ?) будем называть внутренним и внешним раз-
разложением соответственно. Из теоремы существования и единственности
корректной краевой задачи для области/)вытекает следующее:
1. Внутреннее и внешнее разложения совпадают:
ST(r,l) = S?(r,L) . A.7)
2. Внутреннее решение определяется с точностью до нескольких неопре-
неопределенных постоянных, определяющих его поведение на бесконечности
(при г/1 -> <»).
3. Общее число неопределенных постоянных и сами разложения 5* и
Sl с точностью до коэффициентов определяются из общего решения крае-
краевой задачи для области Ds:
Ds= lim D . A.8)
Краевая задача для области Ds называется сингулярной (singular), ее
решение — сингулярным решением. Теория сингулярных решений в ли-
130
нейной теории упругости и некоторые ее приложения развиты в работе авто-
автора [73].
Решение сингулярной задачи не единственно и определяется с точностью
до нескольких неопределенных коэффициентов; некоторые сингулярные
решения отбрасываются по физическим соображениям.
4. Внешнее решение единственно, если его асимптотика в нуле (при
r/L -> 0) совпадает с сингулярным решением, удовлетворяющим допол-
дополнительным физическим условиям.
Решение исходной задачи "сшивается" из внутреннего и внешнего реше-
решений вдоль некоторого слоя или "пояса" (охватывающего начало коорди-
координат) при помощи "условия сшивания" A.7). Геометрическая форма и раз-
размеры этого "пояса" зависят от конкретной задачи. Внутри "пояса" справед-
справедливо внутреннее решение, вне — внешнее решение.
Некоторые обобщения метода. Параметры / или L могут быть связаны
не с геометрией области Да с физическими процессами, отраженными
в коэффициентах решаемой системы дифференциальных уравнений и гра-
граничных условий. В этом случае величины / или L будут характеризовать
область действия того или иного физического эффекта. В этом случае дан-
данное выше описание метода полностью сохраняется с точностью до несущест-
несущественных и совершенно очевидных изменений.
При предельных переходах A.3), A.4) или A.8) упрощается не только
область, но также сами дифференциальные уравнения. Поэтому этот
метод представляет большие возможности для аналитических исследований.
В дальнейшем рассмотрены некоторые его приложения в теории упругости
и механике разрушения.
Предварительно выведем общие уравнения деформирования упругого
континуума, армированного несингулярными упругими элементами мень-
меньшего измерения (когда выполняется условие A.1)).
Континуум, армированный оболочкой. Рассмотрим областьD в трехмер-
трехмерном пространстве, заполненную двумя упругими материалами, одно из
которых занимает область D/ типа тонкого криволинейного слоя или обо-
оболочки, так что справедливо условие
h<R. A.9)
Здесь h — характерная толщина оболочки,/? — характерный радиус кривиз-
кривизны срединной поверхности оболочки. Вдоль границы контакта упругие
материалы жестко сцеплены.
В данном случае малым параметром е является отношение h/R. Об-
Область ?)/ при больших R и конечных h представляет собой классическую
оболочку, изучаемую в специальных курсах теории оболочек*. В данном
случае составляющие Х[,Х'2,Х'3 вектора интенсивности приведенной
* Строго говоря, при R/h -* °° получается бесконечный плоский слой постоянной тол-
толщины в бесконечном упругом пространстве. Внутренние разложения в напряже-
напряжениях будут представлять собой некоторые ограниченные величины, различные при
*з~*+о° и х'3-*—<*> и удовлетворяющие только условиям равновесия. Таким об-
образом, тонкая оболочка получается безмоментной и не влияющей на распределение
напряжений. Подход, излагаемый в тексте, позволяет учесть эффект самостоятель-
самостоятельной передачи упругой энергии вдоль оболочки; этот подход справедлив в том слу-
случае, когда модуль Юнга оболочки существенно больше модуля Юнга основного
материала.
131
поверхностной нагрузки по осям подвижной системы координат
равны
*ifs I**;*;!, *2 = [r*;*;], *3'=[<^]. A.10)
Здесь осьхз направлена по нормали к срединной поверхности оболочки,
осих[ пх2 лежат в касательной плоскости; тх>х»-9 тх;х;, ах*з - соответ-
соответствующие компоненты напряжения в основном материале; скобки [А] оз-
означают скачок величины А при пересечении оболочки в направлении по-
/ |*; = л/2 \
ложительной нормали [т.е. Л I I. Считаем, что координатыxt и
V u;=-/i/2/
х2 образуют криволинейную ортогональную систему координат на средин-
срединной поверхности оболочки.
Обозначим через иг, и2, v3 составляющие вектора смещения срединной
поверхности оболочки по осям х'ь х'ъ х'ъ. Общие уравнения теории оболо-
оболочек (уравнения равновесия в смещениях) можно записать в виде*
!„»,=*,' (/,/=1,2,3). A.11)
Здесь Ьц — определенные линейные дифференциальные опраторы по х[ и
х'2 (см., например, стр. 237—238 книги [74]); они зависят от геометрии
оболочки и от упругих постоянных. В случае линейной вязкоупругости
упругим постоянным соответствуют некоторые линейные операторы по
времени, характерные для материала оболочки.
По известному полю vl9 и2, из при помощи соотношений теории оболо-
оболочек можно полностью установить возмущающее поле деформаций и нап-
напряжений в оболочке .Наложение на него составляющих ?viJC^, тх'2Х 'з9ох'ъ
(равных соответствующим напряжениям, взятым из внешнего решения
при х*ъ = ± й/2 ) дает искомое поле напряжений в оболочке.
Пусть xlfx2,x3 образуют некоторую неподвижную прямоугольную
декартову систему координат. Тогда согласно A.11) компонеты Хг, Х2,
Хъ поверхностной нагрузки по этим осям координат будут следующими:
Xt = *qL,kvk (/,/,*« 1,2,3). A.12)
Здесь атп — косинус угйа между осями х& и хп, т.е. некоторая геометри-
геометрическая характеристика оболочки.
Область DLi которая получается при h -* 0 (R конечно), представляет
собой всю область Д разрезанную вдоль срединной поверхности оболочки
(математический разрез нулевой толщины). Противоположные берега раз-
разреза сцеплены в соответствующих точках, лежащих на одной и той же нор-
нормали; в точках] разреза к телу приложена внешняя сила интенсивности
(- Хх, - Х2, - ЛГ3) . Последнее вытекает из уравнений равновесия и яв-
является аналогом "условия сшивания" внутреннего и внешнего решения.
Уравнения теории упругости для области DL с объемной силой (уравне-
(уравнения Ляме) можно записать в виде
Мцц = -Х1и(хихг9хъ) (/,/-1,2,3), A.13)
где
/о = «[*i - *\(х[, х2\ х2 - v?2(х[ 9х2),х3 -
¦ По повторяющемуся индексу производится суммирование.
132
Здесь и х, и2, и 3— составляющие вектора смещения • по осям хг, х2, х3;
Мц — определенные линейные дифференциальные операторы второго по-
порядка похихг>хЪу зависящие от упругих постоянных. Эти операторы
можно найти в учебниках по теории упругости. В случае линейной вязко-
упругости упругим постоянным соответствуют некоторые линейные опера-
операторы по времени, характерные для основного материала.
Уравнения
' *i=W(*b*J) O'= 1,2,3) A.14)
представляют собой уравнения срединной поверхности оболочки. Функция
/о(*ь#2»*з) в правой части A.13) представляет собой дельта-функцию,
определяемую следующим образом:
/ F(xux2fx3)fo(x1>x2fx3)dxldx2dx3 =
A.15)
где F(xlf х2> х3)- произвольная непрерывная функция.
Решение уравнений A.13) дает внешнее решение исходной задачи. Сог-
Согласно условию жесткого сцепления смещение срединной поверхности обо-
оболочки, определяемое из решения внутренней задачи A.12), т.е. вектор
(Vi,v2,v3), должно равняться смещению соответствующей точки той же
поверхности, определяемому из решения внешней задачи A.13), т.е. векто-
вектору («ьм2,"з)' Следовательно, на поверхности A.14) должно выполняться
следующее условие совместности:
ик = ак1щ (*,/= 1,2,3). _ A.16)
При помощи этого соотношения уравнение A.12) запишем так:
Х^щ^как1щ (*,/,*,/=1,2,3). A.17)
Здесь использовано то обстоятельство, что дифференцирование в операто-
операторах Ljk производится только по переменным х[их2 (т.е. вдоль поверх-
поверхности A.14)).
Подставляя теперь величиныХг из A.17) в A.13), находим искомые
уравнения деформирования упругого или вязко-упругого континуума,
армированного оболочкой:
Mif Uj = - 5(xi- Ч>\,х2- 02,*з- te)aijLjkakiyr (/,/,к, /= 1, 2,3)..A.18)
В предельном случае, когда модуль Юнга основного материала стремится
к нулю, отсюда получаются обычные уравнения теории оболочек для арми-
армирующей компоненты.
Оболочка, армированная криволинейными стержнями. Совершенно
аналогичный метод позволяет вывести следующие общие уравнения теории
оболочек, армированных стержнями:
^/U/ = -5[x;-^(s),^-^2(s)]^/y/ (/,/=1,2,3). A.19)
Здесь уравнение главной оси растяжения криволинейного стержня (ко-
(которая по предположению расположена на срединной поверхности оболоч-
оболочки) дается уравнениями х{ = ^/(s), где i =1,2. Величины vt, v2yv3 пред-
представляют собой составляющие вектора смещения по осямх'1э x2t x3 со-
133
ответственно; Ny — известные линейные дифференциальные операторы
по s> зависящие также от геометрии стержня и его упругих постоянных.
Остальные обозначения уже пояснялись выше.
Уравнения
Xt (/,/, = 1,2,3) A.20)
являются уравнениями равновесия криволинейного стержня в смещениях.
Уравнения A.18) и A.19) содержат в качестве коэффициентов при не-
некоторых членах дельта-функции. Уравнения автоматически учитывают
структуру неоднородного континуума, поэтому граничные условия для не-
него, как и для однородного тела, ставятся только на границе области D. В
частности, армированной может быть граница области /)или некоторая
часть границы. Нетрудно написать также соответствующие динамические
уравнения, рассматривая силы инерции как некие массовые силы.
Развитая теория армированного континуума позволяет поставить в рам-
рамках строгого математического подхода многие интересные задачи оптималь-
оптимального проектирования и материаловедения. Теория годится, очевидно, для
тех случаев, когда модуль Юнга армирующей компоненты велик по сравне-
сравнению с модулем Юнга основного материала, а армирующий элемент не вно-
вносит сингулярность во внешнее поле смещений.
В том случае, когда модуль Юнга инородного включения существенно
меньше модуля Юнга основного материала, требуется дополнительное ис-
исследование. Предположим, что включение по-прежнему залегает в виде тон-
тонкого слоя или стержня в основном материале. В этом случае самостоятель-
самостоятельной передачей упругой энергии вдоль слоя (дальнодействием слоя) можно
пренебречь, нужно учитывать лишь локальную работу слоя на растяжение
(сжатие) и на сдвиг. Граничные условия при этом с границы сцепленного
контакта можно переносить на срединную поверхность оболочки (что
соответствует предельному переходу h -*0 к области DL для внешнего ре-
решения, где h — толщина слоя).
Внутреннее решение (для плоского слоя толщины h ) получается одно-
однородным, причем
[тх'1Х'3] =0,
hox'3 =?M, [ax'9] =0.
Внешнее решение представляет собой решение соответствующей краевой
задачи теории упругости для тела D с математическим разрезом вдоль сре-
срединной поверхности оболочки; на разрезе должны выполняться граничные
условия A.21). Нетрудно составить граничные условия также для того слу-
случая, когда слой находится в пластическом состоянии или же на границе кон-
контакта допускается проскальзывание с трением (или без трения). В частном
случае при Е -* 0 получается трещиноподобная полость со свободными от
нагрузок берегами (см. также более подробно § 10 главы 1 по этому воп-
вопросу).
В последующих параграфах 2—7 рассматривается принципиально более
трудный и малоисследованный случай сингулярных армирующих элементов.
134
§ 2. Инвариантные Г-интегралы в особых точках
и на особых линиях поля (теория Г-вычетов)
Условие совместной работы упругого континуума и сингулярного ар-
армирующего элемента в критическом состоянии записывается при помощи
инвариантных Г-интегралов вдоль замкнутой поверхности, охватывающей
сингулярность поля. Величину такого Г-интеграла будем называть Г-выче-
том поля в соответствующей сингулярности. Как известно [1], Г-вычетне
зависит от формы и размеров замкнутой поверхности, охватывающей рас-
рассматриваемую сингулярность поля.
Г-вычеты вычисляются по правилу "конечная часть расходящегося интег-
интеграла". Строгое математическое обоснование этого правила покоится на
существовании некоторой промежуточной зоны "сшивания", в которой
справедливо как внутреннее разложение решения, так и внешнее разложе-
разложение. Рассмотрим этот вопрос на примере типичных сингулярностей упруго-
упругого поля в однородном и изотропном теле.
Комплексное представление инвариантных Г-интегралов первого рода в
плоской теории упругости. Рассмотрим (плоское) упругое поле напряже-
напряжений и деформаций в случае сложного сдвига, плоской деформации или
плоского напряженного состояния в плоскости декартовых координат
хх х2. Инвариантные Г-интегралы первого рода для произвольной дуги
L на плоскости xt хг в данном случае будут следующими [1 ]:
rk = f(Unk-oifuiikn,)dL (/=1,2,3; /,*=1,2). B-1).
Здесь U — упругий потенциал единицы объема, Оц — напряжения, щ —
смещения, (ль п2) — составляющие внешней единичной нормали к дуге L.
Плоское поле в теории упругости описывается при помощи трех ком-
комплексных потенциалов Ф(г), ?(z)hF(z), являющихся аналитическими
функциями комплексного переменного z = xr + ix2 и связанных с напря-
напряжениями плоского поля следующими формулами:
2/1 (и, + ш2) = W(z)-zf(z)- ф(г\
ои + о22 =4Re<fc(z),
о22 - оп + 2 ial2 = 2 [IФ'(г) + ? (z)], B'2)
<>13 -^23
Здесь
Отметим также следующие представления [1]:
(к +1)Ф(г) = а22 +2мы1Д +/(-а12 +2ци2 2)= ап
к +1
+ /(а12 -2ци1у2) = Ц. (wlfl +w2>2) + /M(«2,i
К — 1
F(z)-u3tl -iu3<2.
Здесь д— модуль сдвига, v — коэффициент Пуассона, к - упругая постоян-
постоянная, равная 3—4р Для плоской деформации и C — *>)/A + v) — для плоского
напряженного состояния.
135
Из B.2) и B.3) можно вывести следующие формулы:
к 1
опи12 +ol2u2t2 = - Im [(an
к + 1
o22u21 +al2w14=—— Ъп [(о22 + iat2) Ф(z)],
к +1 1
a12 uX2 +o22u2t2 = --—Re [(a22 + го12)Ф(г)] - — (о1Хо22 -
к + 1 1
+ R[(+/а12)ФС0]
[(n12)С0]
B.4)
,1 = /iReF(z)Re [/zF(z)],
,2 =- /ibnF(z)Re [«F(z)].
Здесь через п обозначено комплексное число
п = «! + /я2- B.5)
При помощи B.2) - B.5) можно вывести следующую формулу для уп-
упругого потенциала [/плоского поля (не зависящего отдг3) :
11 . B.6)
[()] M()()
М 2 2/i
Используя соотношения B.2) — B.6), из B.1) найдем следующее выра-
выражение для комплексного Г-интеграла:
1 к +1 1
Tj + /Г2 = м/ п F(zJdL + /{— п [Ф2 (z)-<b(z?]+
2 L 2/i L l 2
+ а7Ф (z) [z Ф' (z) + * (z)]}di (я = Hi + i/i2). B.7)
Рассмотрим особую точку О плоского поля внутри тела. Г-вычет в точке
О удобно вычислять по окружности малого радиуса R с центром в точке О
(рис. 58). Приведем формулу для Г-вычета в точке. О, полученную при по-
помощи B.7):
Гг + /Г2 =- Я Г Г- ew (Ф2 -Ф2)+ е~(вФ (zi'+
2м о 1-2
-LtxRY e-ieT2de. B.8)
2 о
Вычислим Г-вычеты по этой формуле для фронта трещины и дислокации,
а также для линейных сосредоточенных сил и моментов.
Внутренняя сосредоточенная сила. Пусть в некоторой точке z = z0 плос-
плоского поля действует сосредоточенная линейная сила интенсивности (Хг, Х2,
Хэ) в расчете на единицу длины особой линии (перпендикулярной плоскос-
136
Рйс. 58.
Рис. 59.
та xt x2). В этом случае упругое поле вблизи точки z= z0 определяется сле-
дующими потенциалами:
*0Оф (** *)
2тгA +/c)(z-z0)
2тгд (z-z0)
B.9)
2тгA +k)(z-z0) 2тгA + к) (z-zof
Здесь ФОг *0» Fo - комплексные постоянные, определяющие внешнее не-
невозмущенное поле в точке z = z0 в отсутствие сосредоточенной силы, ос-
остальные слагаемые дают собственное поле сосредоточенной силы.
Подставляем потенциалы B.9) в (?.8) и вычисляем Г-вычет по правилу
"конечная часть расходящегося интеграла"; получаем
1\ + /Г2 = • [X (к Ф"о- Фо) - YT0] + Х3 Fo. B.10)
2д
При помощи B.2) и B.3) эту формулу можно записать через производ-
производные перемещений невозмущенного внешнего поля в особой точке следую-
следующим образом:
Г/ = Xku°ki (/=1,2; к =1,2,3).
Правило *'конечная часть расходящегося интеграла" заключено в сле-
следующем уравнении:
ffgdL=f(fsgo+gsfo)dL
L L
(/=Л+/<ъ *=^
B.11)
Здесь fs и gs — сингулярные составляющие поля (собственное поле сингу-
сингулярности),/^ и#о —регулярные составляющие поля (невозмущенное внеш-
внешнее поле в особой точке), контур L в B.11) охватьюает особую точку.
Докажем это правило, исходя из общих асимптотических представлений
предыдущего параграфа. Действительно, из них вытекает справедливость
следующих оценок:
гН> ffogodL=Ol —
B.12)
137
Здесь предполагается для определенности, что в особой точке функциями
gs имеют порядок г, а /0 и g0 — конечные величины. Напомним, что /0 —
это характерный линейный параметр особенности, зависящий от ее струк-
структуры (внутренний, параметр); Lo — характерный линейный параметр внеш-
внешнего поля (внешний параметр).
Предположим, что существует промежуточная зона поля, в которой
внешнее и внутреннее разложения совпадают (условие "сшивания" A.7)).
В этой зоне одновременно выполняются следующие два условия:
R>l0, R<L0. B.13)
Теперь воспользуемся инвариантностью Г-интеграла и деформируем
контур интегрирования в B.11) в указанную промежуточную зону "сшива-
"сшивания". В результате на основании B.12) и B.13) придем к уравнению
B.11).
Нетрудно сформулировать аналогичное уравнение для любого другого
порядка особенности функций Л и 8s (э*йм порядком определяется соответ-
соответствующая компонента разложения внешнего поля, представляющая инте-
интерес).
Например, если fs и gs имеют порядок О (г' ), то /0 и#0 будут иметь
порядок О (г) и т.д.
При наличии нескольких слагаемых различного порядка в сингулярном
поле fs и gs будет иметь место принцип суперпозиции, заключающийся в
том, что для каждого члена разложения fsngsB отдельности будет выпол-
выполняться уравнение B.11) с соответствующими составляющими/0 ng0 внеш-
внешнего поля.
Таким образом, при вычислении Г-вычетов соблюдается принцип супер-
суперпозиции (несмотря на квадратично-нелинейный характер подынтегрального
выражения).
Указанную асимптотическую процедуру вычисления Г-вычетов будем на-
называть Г-интегрированием, а соответствующий способ его вычисления —
правилом Г-интегрирования. Очевидно, приведенные соображения имеют
вполне общий характер, относясь к любым физическим полям и к любым
сингулярностям поля,
Внутренний сосредоточенный момент. Пусть в точке z = z0 действует со-,
средоточенный линейный момент интенсивности М в расчете на единицу дли-
длины особой линии (рис. 59). В этом случае упругое поле вблизи точки z = z0
определяется следующими потенциалами:
ФB) = Ф0+Ф! (z-z0) (F = 0),
т B14)
2n(z-z0J
Здесь Фо, Ф\, ^о> *i — комплексные постоянные, определенные из разло-
разложения внешнего поля в точке z = z0.
Вычисляем Г-вычет при помощи формулы B.7) по правилу Г-интегри-
Г-интегрирования; получаем
П+^ — ^Ф,, B.15)
2ц
138
'//////////Л У///////////////..
Рйс.60.
Сосредоточенная сила на границе полуплоскости. Пусть упругое тело за-
занимает полуплоскость х2 < 0, причем в начале координат приложена линей-
линейная сосредоточенная сила интенсивности (Хх , X2f Х3)в расчете на единицу
длины особой линии (рис.. 60, а). Остальная граница свободна от внешних
нагрузок. В этом случае упругое поле будет следующим:
B.16)
27TJJLZ
Здесь первое слагаемое —собственное поле сосредоточенной силы; Фо, ^о»
Fo - комплексные постоянные, определенные из разложения внешнего по-
поля в точке О в отсутствие сосредоточенной силы. Вследствие граничного ус-
условия (а22 + *'<*12 = 0» ^23 = 0 прих2 =0) согласно B.2) должно выпол-
выполняться следующее соотношение:
Фо +*Фо +^о=О, Im Fo = 0. B.17)
Используя это условие, нетрудно показать, что инвариантный интеграл
Fj, определенный формулой B.1) при к = 1,имеет одно и то же значение
для любого незамкнутого контура L, охватывающего точку О в нижней
полуплоскости и концы которого расположены на ее границе (рис. 60,6). Вы-
Выберем контур L в виде малой полуокружности радиуса R. При этом для F'i
будет справедлива формула B.8) с пределами интегрирования от п до 2тг.
При помощи B.16), используя правило Г-интегрирований, находим отсюда
Г-вычет
к +1 _
Fj = Re^o X ) + X3F0 (X = XX + iX2\ B.18)
т.е. \\ =Xi u\^
При Хх = Хъ = 0 на границе полуплоскости согласно B.6) и B.16) имеем
2=0 о12 = С722 = 0, F = 0, U = (Re ФоJ. Отсюда, используя
Г-интегрирование, нетрудно видеть, что в этом случае интеграл Г2, опреде-
определенный формулой B.1), также имеет одно и то же значение для любого не-
незамкнутого контура L, охватывающего точку О в нижней полуплоскости и
концы которого расположены на ее границе (рис. 60). Выберем контур L в
139
форме полуокружности радиуса R и воспользуемся формулой B.8) с пре-
пределами интегрирования от тг до 2тг. Находим Г-вычет:
Tl + / Г2 = - ^-/Фо Хг (X, = Хъ = 0), B.19)
Сосредоточенный момент на границе полуплоскости (рис. 61). В этом
случае упругое поле вблизи точки О определяется следующими потен-
потенциалами: жж%
Mi Mi
Ф 00 = Г + Ф1 *, Ф СО = о + *1 *
_27rz . *z B.20)
BФ, +Ф! + ^ =0, F=0).
Здесь удержаны лишь те члены разложения, которые дают конечный вклад
в Г-вычет. При помощи Г-интегрирования по нижней полуокружности в
формуле B.8) находим
Гг + / Г2 = - -^- Фх Mi, B.21)
2м
т.е. Г, =- И Л#(и§э1 -w?,2),r, Г2=ЙМ^ (м1э1 +iiM)fl .
к - 1
Формулы B.10), B.15), B.18),'B.19) и B.21) используются в асим-
асимптотической теории соединений пластин, оболочек и стержней.
Линейная дислокация. Пусть плоское упругое поле вблизи начала коор-
координат имеет вид
B.22)
7Г|A
Здесь (&!, Ь2, Ь3 ) — вектор Бюргерса дислокации; первое слагаемое - соб-
собственное поле дислокации, расположенной в начале координат, второе —
внешнее невозмущенное поле.
При помощи формулы B.8) находим Г-вычет
Тх + /Г2 = ib Wo- 2 ib Re Фо - /i ЬЪТО1 B.23)
Величины Fo, Фо и Фо согласно B.2) имеют следующий физический
смысл:
Re Фо = - (о202 - а,0,;), Im Фо = а?2, B.24)
Здесь a?i, а?2, а22, а?3, ^2°з— напряжения внешнего невозмущен-
140
м
РИс. 61.
ного поля в начале координат. При помощи B.24) формулу B.23) можно
записать так:
r, = ei/3c&** (/=1,2; л*=1,2,3), B.25)
где ew - символ Леви-Чйвита *
Это известная формула Пича - Келера для конфигурационной силы,
действующей на дислокацию. Она лежит в основе теории дислокаций.
Движение дислокации согласно общей теории движения сингулярностей
поля [1] происходит, как только вектор Гг + / Г2 достигнет предельной по-
поляры S (Г}, Г2 ) (которая находится из опыта). В случае изотропии поляра
представляет собой окружность и предельная величина вектора Ft + г Г2 не
зависит от направления движения дислокации. Если же из опыта известно
направление движения дислокации, то предельная величина Гс будет равна
диссипации энергии поля при продвижении дислокации в указанном направ-
направлении на единицу длины (эта величина определяется из опыта или из струк-
структурной теории).
Кинетика движения дислокаций во времени должна описываться в рам-
рамках зависимости ее скорости движения от вектора Гх + *Т2.
Трещина. Пусть плоское упругое поле вблизи начала координат описыва-
описывается следующими потенциалами:
B.26)
Здесь Кь Ku, Km - коэф4ициенты интенсивности напряжений в конце
открытой трещины, расположенном в начале координат.
При помощи формулы B.8) легко находим Г-вычет:
iK
ш
К + 1
Г, + гТ2 =—- [Kj
1
-~
2м
B,27)
Напомним, что et
равны нулю.
=е321 =€213=-1, все другие eifk
141
В случае закрытых трещин (трещин скольжения) сингулярное упругое
поле вблизи конца трещины описывается теми же потенциалами B.26) при
Кг = 0. Поэтому на основании B.27) для трещин скольжения в однородных
изотропных телах имеем
Г, + i Г2 = -~- АГ|, + -i- K\n . B.28)
o/i. z/i
Эти формулы лежат в основе теории развития трещин в однородных и
изотропных упругих материалах [1].
Внутренняя сосредоточенная сила в пространстве. Рассмотрим трехмер-
трехмерное статическое упругое поле напряжений и деформаций в однородном
изотропном теле. Инвариантные Г-интегралы первого рода для произволь-
произвольной поверхности 2 в пространстве хх x2 хъ будут следующими [1]:
Г* = / (Unk - о$п и^к - Оцп un%k - ann uHtk)d 2 B.29)
(*= 1,2,3).
Здесь %у\п — криволинейная ортогональная система координат (?,т? — гаус-
гауссовы координаты на поверхности 2, п — направление внешней нормали к
поверхности 2); о$п, оцп, апп — напряжения; м$, ип, ип - смещения;
{пип2,пъ) — единичный вектор внешней нормали к 2.
Пусть в некоторой точке О внутри тела приложена сосредоточенная сила
(Хи Х2,Х3). Величина Г* по любой замкнутой поверхности 2, охватываю-
охватывающей точку О (Г-вычет в точке О)9 будет инвариантна относительно фор-
формы 2.
Вычислим вначале Г\. Выберем в качестве поверхности 2 поверхность
тонкого прямоугольного параллелепипеда | хх | < R, \x2\<R, \х3\<д,гце
d<R (рис. 62). На основании B.29) имеем
Aц +ог23м2,1 +<*зз"з,1)лз<**1 dx2. B.30)
Упругое поле вблизи точки О запишем в следующем виде:
,oik = о?к + о?к, щ,к = щ*к + u°ik. B.31)
Здесь первое слагаемое (сингулярный член) — собственное поле сосредото-
сосредоточенной силы; второе слагаемое — внешнее поле в точке О в отсутствие
сосредоточенной силы.
Подставляем формулу B.31) в B.30) и используем правило Г-интегри-
рования, получаем
, +*ззиз,1)лз<&1<&2. B-32)
Согласно уравнениям равновесия
// of3 пъ dxx ix2 = - Xt (/ = 1,2,3). B.33)
142
Обозначим
и J =**«;* ft* =1,2,3). B.34)
Здесь и*к — /-я составляющая вектора смещения под действием единичной
ошы, направленной вдоль оси хк. Например, имеем (решение Кельвина, см.
[75])
B.35)
и1
и?»
16
16
1
7TJUA
1
1
-V)
-V)
—12
г3 '
Х2Х3
г3
1-,
(г2 =*?
Другие составляющие и3* получаются из B.35) простой перестановкой
индексов. Отметим следующие свойства симметрии этих сингулярных ре-
решений: а) функции и** - четные функции х3 при /, * = 1, 2; б) функции
3,i и мз3,1"~ нечетные функции хх; в) us$ti- нечетная функция х2. Кроме
того, простое вычисление показывает, что
// и\3г dxx dx2 =0, ffu'fi dx, dx2 =0. B.36)
Действительно, согласно B.35) левые части равенства B.36) с точнос-
точностью до множителя равны следующему интегралу:
+оо **, 02 +1 - 2а2 +оо с?0 +оо 1 - 2Г2
L L "'; ;
L L
Используя указанные свойства симметрии и уравнения B.33), B36),
находим по формуле B.32)
Г, =*,!#, A = 1,2,3). B.38)
Аналогично можно получить инвариантные интегралы Г2 и Г3. Приведем
итоговую формулу для Г-вычетов от сосредоточенной силы
Г* =*,!#* (/,*= 1,2,3). . B.39)
Сосредоточенная сила на границе полупространства. Пусть упругое тело
занимает пространство хъ < 0 (рис. 63); граница полупространства свобод-
свободна от внешних нагрузок, за исключением точки О, в которой действует со-
сосредоточенная сила(Хг, Х2,Х3). В этом случае величины Гх и Г2 будут ин-
инвариантны относительно любой незамкнутой поверхности 2 в полупростран-
полупространстве хъ <0, граничный контур которой лежит в плоскости хх х2 и охваты-
охватывает точку О (рис. 63, а). В качестве Б можно взять плоскость х3 = — 5 при
5 ->0 (рис. 63, б). В этом случае, по-прежнему, будут справедливы уравне-
143
//////////л
Рйс. 63.
О щ
в)
B.40)
ния B.31) - B.33), причем согласно граничным условиям
о\ъ=о\ъ = а3°3=0.
Аналогично получаем следующие Г-вычеты:
?к = Хги\к (/=1,2,3; * = 1,2). B.41)
Интеграл Г3 будет инвариантен относительно незамкнутой поверхности
Е, окружающей точку О в нижнем полупространстве (см. рис. 63,в), лишь
в том случае, когда
*i=*2=0, *>=1/2. B.42)
В этом случае сингулярная составляющая поля напряжений (при Хъ = 1)
выражается формулами
\ ^3 =
2тгг5 f
27ГГ5
B.43)
(остальные напряжения равны нулю). Поэтому на границе х3 = (У будет
I/ = 0 (за исключением точки О), а величина Г3 выражается формулой
2 B.44)
Г3 =-
B - плоскость х3 ~ - 8
0).
В данном случае упругий потенциал равен
j/s_ [азз и + (jJ3 (Й1 з +Мз i) + 02з(м2 з +мз гI • B.45)
2 . f ' " '
Подставляем его в B.44), применяем правило Г-интегрирования, гра-
граничные условия B.40) и уравнения равновесия; в результате получим
I
Г3 = — Хъи%^. B.46)
Полученные формулы B.39), B.41) и B.46) являются основой асимп-
асимптотической теории разрушения массивных упругих тел, армированных
инородными упругими связями с точечными контактами.
Линейная сосредоточенная сила в пространстве или полупространстве.
Рассмотрим кривую линию в пространстве, в точках которой действует со-
сосредоточенная сила с интенсивностью (Хг, Х2, А^) на единицу длины. Будем
считать, что в каждой точке О особой линии выбрана локальная система
144
декартовых координат О хх х2 хъ, причем о.сьх3 совпадает с касательной к
данной точке 0. На расстояниях, малых по сравнению с радиусом кривизны
этой линии, вблизи точки О имеет место локальная плоская деформация в
плоскости О xt хг\ поэтому справедливы формулы B.9) и B.10). Послед-
Последняя дает локальную интенсивность инвариантного Г-вычета в точке О осо-
особой линии; интегрируя iio всей линии, нетрудно найти Г-вычет для особой
линии в целом. При этом формула B.10) дает лишь составляющие Т\ и Г2
Г-вычета. Найдем теперь составляющую Г3 интенсивности Г-вычета,определя-
Г-вычета,определяемую следующей формулой [1] :
Г3=-/ oitu^nfdL (/=1,2,3; /=1,2) B.47)
(сравни с формулой B.1) ).
Контур L представляет собой поперечное сечение тороидальной поверх-
поверхности малого радиуса, охватывающей особую линию.
Особые линии асимптотически порождают армирующие жесткие стерж-
стержни, стрингеры, накладки и т.п. одномерные упругие элементы, жесткость
которых намного превышает жесткость армированной упругой среды.
Аналогично особые линии возникают на поверхности упругого тела при дей-
действии на него узких штампов (типа лезвия, ножа), а также при соединении
оболочек и пластин с поверхностью массивного упругого тела.
Упругое поле имеет вид
а(/ = а?/ + а^, и/,3=4з + usi3 B.48)
причем слагаемое м?3 имеет слабую (логарифмическую) особенность. При-
Применяя правила Г-интегрирования и уравнения равновесия, получаем
Гэ =-/ fill и?.э n,dL = Xful3 (/=1,2,3). B.49)
L
Теория Г-вычетов является основой строгой асимптотической теории
разрушения упругих тел.
§ 3. Точечные соединения пластан, оболочек
и трехмерных тел
Изложим асимптотическую теорию упругого деформирования несколь-
нескольких пластин или оболочек, соединенных между собой в точках. Эта теория
является бесструктурной, т.е. справедливой при любой геометрии контакт-
контактных площадок сцепления ("точек"). При анализе процесса разрушения она
использует инвариантные Г-интегралы и легко обобщается на другие анало-
аналогичные задачи математической физики.
Рассмотрим параллельно наиболее типичные конкретные задачи.
Приклепанные пластины. Пусть две бесконечные тонкие пластины из раз-
разных упругих материалов прикреплены одна к другой в двух точках А иВ,
расположенных на расстоянии / вдоль оси хх (рис. 64, а и б). "Точка"
представляет собой в меньшем масштабе плоскую площадку контакта
(сцепления) произвольной конфигурации (см. рис. 64, в); на этом рисун-
рисунке л (л 1, п2) представляет собой вектор единичной нормали к контуру L
площадки. Это соединение упругих тел будем для краткости называть за-
заклепкой, однако следует иметь в виду, что излагаемая теория относится к
любой технологической операции или способу прикрепления (сварка,
145
А В
д)
t t t«
Рис. 64.
склеивание, клепка и т.д.), лишь бы размер площадки сцепления был мал
по сравнению с характерными размерами тела (в данной задаче по сравне-
сравнению с /).
Вдали от заклепок пластина 1 (рис. 64, б) подвергается однородному
прлю напряжений в плоскости пластины:
при z->°°
On=oTi, O22 = 022, а12 =0 B=*! +/Х2). C.1)
Пластина 2 предполагается свободной от внешних нагрузок, напря-
напряжения в ней возникают лишь вследствие реакции заклепок. Напряженное
состояние в обеих пластинах будем считать плоско-напряженным, пре-
пренебрегая возможными эффектами продольного изгиба (А,- — толщина
1-й пластины).
Требуется найти усилия в заклепках А и В, обозначаемые через htPA и
hxPB соответственно. Из условий равновесия пластины 2 следует, что эти
силы имеют лишь составляющие вдоль оси хх, причем
Ра=-Рв- C.2)
Упругое поле вблизи каждой заклепки имеет структуру, качественно
изображенную на рис. 64, г, где через г обозначено расстояние от центра
заклепки, а через а — характерное напряжение. Асимптотический метод
основан на существовании некоторой промежуточной зоны rt<r<rei в ко-
которой близки по величине два решения: одно, внутреннее (inner), характе-
характеризующее ту или иную структуру заклепки (кривая ?,-), а другое внешнее
(exterior), независящее от строения заклепки (кривая Le). Первое всюду
146
ограничено и стремится к нулю при г -* °°; второе — сингулярно при г -* О
(сосредоточенная сила) и ограничено при г -* °° вследствие наличия внешне-
внешнего поля.
В данной задаче внешнее упругое поле в обеих пластинах легко найти в
замкнутом виде:
пластина 1
РА ( z I - z \ 1
2тгA + *i) \ Д //4
,/ч *i^4 Л z f /-z\ PAI f 1 1 \
i//(z)= — (in— -In 1- I + — 1 +
2A+)\ A / / 21ГО+1С!) \z-7 //
i C3)
2тгA+к1)
пластина 2
( z l~z\
2тг/г2A +к2)
C.4)
— (in—Д-ln—V ^-^— f—— +—V
2)\ / А/ 2тгЛ2A+/с2) \z-l l)
2nh2(l + к
Эти выражения справедливы всюду, за исключением некоторой ближней
зоны вблизи заклепки г < г/, имеющей порядок характерного линейного
размера площадки сцепления.
Величина А, фигурирующая в формулах C.3) и C.4), является основ-
основным физическим параметром асимптотической теории армирования упру-
упругих тел точечными связями. Она имеет размерность длины и по порядку ве-
величины равна характерному линейному размеру точечной связи ("радиус"
заклепки). Вообще говоря, она зависит от материала заклепки и ее конст-
конструкции. Всюду в дальнейшем величину А будем считать известной из допол-
дополнительно проведенного эксперимента. Зависимость усилия в заклепке от А
оказывается довольно слабой, поэтому ошибка в определении А несущест-
несущественно влияет на результат.
Согласно решению C.3) и C.4) перемещения в обеих пластинах на рас-
расстоянии А от начала координат (т.е. примерно в зоне сшивания на рис. 64, г)
имеют порядок А, а точнее
Здесь и — характерное перемещение, о — характерная внешняя нагрузка.
Таким образом, перемещения обеих пластин в заклепке А выбраны рав-
равными нулю с асимптотической точностью C.5).
Условием совместной работы двух пластин в нашей задаче является
асимптотическое равенство перемещений пластин в другой заклепке В, по-
поэтому потребуем, чтобы вблизи заклепки В выполнялось аналогичное
147
соотношение
при |z-/| = A — =о( — V C.6)
А \Е)
Это условие совместности служит для определения неизвестного параметра
Pji в приведенном решении C.3), C.4).
Воспользуемся вначале инвариантными Г-интегралами первого рода
пространственной теории упругости [1 ]
Гк = / {Unk-oifuitknf)d2 (/,/,* = 1,2,3) C.7)
(обозначения те же, что и в предыдущем параграфе).
Отметим основное свойство Г-интегралов (свойство инвариантности):
Интегралы Г* по замкнутой поверхности X равны нулю, если внутри
S упругое тело однородно и если внутри ? упругое поле не содержит осо-
особых точец или особых линий.
Нетрудно показать, что это свойство сохраняется для интегралов Гх и Г2,
если упругое тело неоднородно, однако упругие постоянные зависят лишь
от координаты хъ..
Рассмотрим замкнутую поверхность 2, составленную совокупностью
следующих поверхностей в- рассматриваемом упругом теле: свободные бо-
боковые плоскости пластин 1 и 2 плюс тороидальная поверхность Xt малого
радиуса, Охватывающая контур L площадки сцепления, плюс замкнутая
цилиндрическая поверхность Ъх + 22 в области действия асимптотики
C.5) и C.6),;образующие которой являются нормалями к пластинам
(Хх - в пластине 1,1^ - в пластине 2).
Инвариантные интегралы Тх и Г2 по поверхностям Si и Х2 образуют
Г-вычеты от внутренней сосредоточенной силы в пластине, вычисленные в
предыдущем § 2; обозначим через Гр* соответствующий Г-вычет Г/ в k-k
пластине, приходящийся на единицу толщины пластины (/, к = 1,2).
Вдоль свободных боковых плоскостей пластин интегралы ГЛ и Г2 обрат
щаются в нуль, так как на них пх = л2 =0, оц щ = 0.
Интегралы Тх и Г2 по тороидальной поверхности 2f можно записать в
следующем виде у
f (Unx - oifui>x nf)dX = / Гпх dL,
L C.8)
/ {Un2-otiui92nj)dL= J Vn2dL (/,/ = 1,2,3).
?f ( L
Здесь величина Г, как обычно, обозначает основной локальный параметр,
контролирующий движение особой линии (см., например>формулы( 1.12)—
A.14) первой главы), а именно, составляющую на нормаль к L в плоскости
ххх2 локальной интенсивности инвариантного Г-интеграла, приходящейся
на единицу длины особой линии L. (В правой части уравнений C.8) стоят
компоненты нормали к контуру L на плоскости ххх2, а в левой ^ компо-
компоненты нормали к поверхности 2Г.)
Для простоты ограничимся случаем контура L, симметричного относи-
относительно осей хх и х2 (см. рис. 64, в).
148
Пусть величины Xlt X2 и Л/ обозначают компоненты равнодействующей
и крутящий момент сил, действующих на площадке сцепления со стороны
заклепки на пластину 1 (и приходящихся на единицу толщины этой пласти-
пластины) . При Х\ - О, М = 0 значение Г в точках контура L , симметричных отно-
относительно оси х2, будет одним и тем же, а составляющая пх будет иметь одну
и ту же абсолютную величину, но противоположный знак. При Х2 = О, М = О
значение Г в точках контура L , симметричных относительно оси xlf будет
одним и тем же, а составляющая п2 будет иметь одну и ту же абсолютную
величину, но противоположный знак. При Хх -Х2 =0 контур L будем
считать круговым, так что величина Г будет постоянной вдоль всего конту-
контура L . Поэтому имеем
при Хх =0, Л/ = 0 / Гп^Ь=0,
L
при Х2 = 0, М = 0 / Vn2 dL = 0, C.9)
L
приХ1=Х2=0 fTnkdL=O (A: = 1,2).
L
В нашем примере для каждой из заклепок А и В выполняется следующее
соотношение:
кгГР +/*2Г1<2> = / Г«! dL. (ЗЛО)
L
Величина Г-вычетов определяется формулой B.10), в которой согласно
решению C.3), C.4) нужно положить:
пластина 1 (Х2 =Х> =0, М = 0)
Р 1
/
C.11)
C.12)
2тг/Л2
При помощи B.10), C.11) и C.12) соотношение (ЗЛО) запишется так:
C.13)
Ех
Напомним, что это уравнение выведено для произвольной формы пло-
площадки контакта и справедливо также для материалов, нелинейно-упругих
вблизи этой площадки. Распределение же плотности Г по контуру L можно
найти лишь из решения (весьма сложной) внутренней задачи. Именно это
распределение позволяет ответить на вопрос о несущей способности заклеп-
149
ки и об изменении этой способности со временем. При расчете по критичес-
критическому состоянию безопасной работе заклепки отвечает неравенство Г < Гс
всюду на контуре L. Отсюда при помощи C.13) легко получить достаточ-
достаточное условие безопасной работы заклепки
hiPA(p7i -ViO2i)<ElTcPL C.14)
(Pl — периметр контура L ). Здесь было для простоты принято следующее
допущение:
Ра<1\<Кх-*°п\, C.15)
которое выполняется при достаточно больших //Д.
Соотношение C.13) позволяет, например, дать оценку несущей способ-
способности заклепки на основе некоторых дополнительных предположений в сле-
следующем виде:
/TZC.16)
где SL — площадь поперечного сечения заклепки.
Вернемся к нашему примеру (рис. 64). В этом случае условие совмест-
совместности в начале координат определяется формулой C.6), в которой соглас-
согласно B.2), C.3) и C.4) нужно положить:
пластина 1 (z = / - А)
Рл
й; C.17)
;
1 +i>! ttA+Ki) А 2тгA +kO
пластина 2 (z = / -A)
2к2Ь1РА I PAhx
2/iaiii = In — . C.18)
7гЛ2A+к2) А 2тгЛ2A+/с2)
Приравнивая различные выражения для ul9 на основании C.17) и C.18)
получаем уравнение для определения величины РА; из него находим:
2nlE2h2 (afi -^1022 )
Р = 2 2V li LJli . C.19)
\n(l/A)[E2h2(l +^)C-^i)+^iAi(l +^) C>)]
Здесь мы пренебрегли величиной Dk) по сравнению с In (//А), так как
0,15 > Dk) > 0,083.
В частности, для одинаковых пластин, когда vx = v2 = v, Ex = 2Г2 = Е, ht =
= Л2 = Л, имеем
Ра= — — • C.20)
В двух других крайних случаях имеем:
при E2h2 >Ethi PA =
E2h2
при Exhx >E2h2 PA =——-
150
Нетрудно проверить, что общее условие совместности C.6) выполняет-
выполняется, если РА взять согласно C.19).
Аналогично можно рассмотреть любое число разлинных тонких упругих
оболочек и пластинок произвольной формы, приклепанных попарно в лю-
любом числе точек. Внешние усилия могут быть приложены к краям оболочки
или к ее граничным поверхностям.
Общий алгоритм решения таких задач следующий.
1. Для каждой из пластинок (оболочек) строится решение, являющееся
линейной функцией неизвестных усилий в заклепках и имеющее вблизи
каждой заклепки асимптотику вида
2кХг г л
= 1П — + и\ ,
1 /
/
C.22)
2кХ2 г _
In—+м$, иъ=и%.
7ГA
Здесь Mi, u2 и м3 — составляющие вектора смещения, лежащие в срединной
поверхности оболочки и вдоль нормали к последней соответственно; г, 0 —
полярные координаты в срединной поверхности оболочки с центром в рас-
рассматриваемой заклепке; Xif Х2 и М — усилия и крутящий момент, дейст-
действующие со стороны заклепки на данную оболочку и приходящиеся на еди-
единицу толщины оболочки; и\, и2 — постоянные разложения внешнего поля.
Формулы C.22) получены при помощи B.2), B.9) и B.14) в предположе-
предположении, что размеры заклепки весьма малы по сравнению с радиусом кривиз-
кривизны оболочки.
2. На основе построенных решений для каждой заклепки составляются
три условия совместности
Г *Xi
C.23)
[!!?]= О (/=1,2)
(квадратные скобки означают разность соответствующих величин для двух
различных оболочек в рассматриваемой заклепке). В результате получается
система, состоящая из Ъп линейных уравнений (где п — число заклепок).
Число неизвестных также равно Ъп (со стороны каждой заклепки на обо-
оболочку действуют три компоненты сосредоточенной силы). Решение этой
системы, очевидно, существует и единственно, так как в противном случае
будет существовать нетривиальное решение исходной однородной задачи,
что невозможно (в рассматриваемых здесь задачах класса 5).
В большинстве встречающихся на практике случаев моменты в заклеп-
заклепках сравнительно малы, так как на основании B.14) и C.23) очевидно, что
Х1>М при 1>А. C.24)
Здесь X и М — величина сосредоточенной продольной силы и крутящего мо-
момента в заклепке, / — характерный линейный размер срединной поверхнос-
поверхности оболочки (например, кратчайшее расстояние между заклепками). При
этом условии неизвестными моментами в решении можно пренебречь.
151
Точное равенство нулю крутящего момента в заклепке осуществляется
при наличии соответствующей симметрии задачи в целом (как в примере
рис. 64), или при наличии определенной "шарнирной" конструкции заклеп-
заклепки, исключающей появление в ней крутящего момента. Приведенные со*
ображения, основанные на условии C.24), показывают, что произвольные
конструкции заклепок можно считать "шарнирными".
Тот случай, когда три (или больше) оболочки скреплено в одной точке,
может быть изучен аналогично. В качестве иллюстраций метода рассмотрим
некоторые конкретные задачи.
Кручение и растяжение двух приклепанных пластин. Пусть две бесконеч-
бесконечные упругие тонкие пластинки приклепаны друг к другу в двух точках^
(О, 0) и (/, 0). На бесконечности к пластине 1 приложены заданная сила
{X?, X™ ) и крутящий момент М относительно начала координат (приходя-
(приходящиеся на единицу толщины пластинки). Со стороны заклепок на пластину 1
действуют сосредоточенные силы (hxAx, h2A2) n(hxBx, h2B2) соответст-
соответственно (моментами пренебрегаем). К пластине 2 приложены все те же внеш-
внешние нагрузки, но с противоположным знаком.
Неизвестные силы реакции Ах, A2, Вх, B2 связаны тремя уравнениями
равновесия
Ах + ВХ =ЛТ, А2 +В2 =Л7, 1В2=М. C.25)
Так как А2 иВ2 вполне определены этими уравнениями, осталось найти
A i и Вх (при этом М и Х2 можно положить равными нулю).
Упругое поле в пластине 1 определяется следующими потенциалами:
Ах z Вх l-z
kd(z) = Лп In
2A+кх) А 27ГО+КО /
C.26)
ф(г) = In — + ¦ In +
2(l+Kj) A 2ir(l +) /
кх) \ z-l
Упругое поле в пластине 2 определяется теми же потенциалами, взятыми
с обратным знаком и умноженными на hx/h2 (кроме того, кх заменяется
нак2).
Согласно C.26) при z = / - А имеем:
Ах кх(Вл -Ах) t /.
2MiWj = — + ———— In — ,
2тгA + кх) тгA +кх) А
C.27)
hx \ Ах ш кг{Вх -Ах) /]
+
h2 L 2тгA
г{Вх -Ах) f /]
In — I.
тгA+к2) A J
Приравниваем их согласно асимптотическому условию совместности и
решаем получившееся уравнение совместно с первым уравнением C.25),
152
результате получим
XT к
XT,
l+k
. . С3-28)
2к21п(//Д)/ М2 П U\ 2кх\пA/А)
В частности, при v x = v2 = v имеем
1 / 3-v\
k=l (к= -). C.29)
2к1п(//Д) \ l+i; /
Следовательно, к близко к единице и Ах « Вх. Например, при у = 0,3,
//Д = 30 будет к = 0,93 и Ах = 0,52X?, Вх = 0,48ХГ.
Рис. 65.
Любопытно, что если бы мы изменили направление координат на проти-
противоположное, то Ах и Вх в формулах C.28) поменялись бы местами. Как
легко видеть, этот парадокс проистекает вследствие того, что в формулах
C.27) — C.29) мы сохранили слагаемое Bк1п(//Д)), по условию малое
по сравнению с единицей. (Напомним, что аналогичный член в предыдущей
задаче был опущен.) Таким образом, указанное "уточнение" является ошиб-
ошибкой, хотя и несущественной; поэтому при последовательном применении
асимптотического метода второй член в C.29) следует опустить. Приведем
окончательный правильный ответ (рис. 65)
А^В^ЪХ?. C.30)
Растяжение полубесконечной пластины, приклепанной к бесконечной
пластине. Пусть полубесконечная пластина 1, расположенная вдоль х$ = 0,
х2 > 0, прикреплена своим торцом в двух точках» @, 0, 0) и A,0, 0), к
бесконечной пластине 2, расположенной в плоскости х2 =0 (рис. 66).
Пластина 1 растянута на бесконечности напряжением о™х, пластина 2 под-
подвержена лишь силам реакции заклепок: ( — Н2Р> 0, 0) в точке @, 0, 0) и
(h2P, 0,0) в точке (/,0,0).
Упругое поле будет следующим:
пластина 1 (z=xx + ix2 )
h2P z h2P l-z \
--i— In— +-1— In + — o?xz,
2nhx A 2irhx I 4
C.31)
h2P z h2P l-z h2P ' * ' '
2nhx A 2nhx I 2nhx
153
пластина 2 (z = Xi + ix3 )
(z)= P fin -L-ln—1
2тгA+к2) \ А П / /'
K2/> / l-z z \
- (in -In - ) +
) \ / A/
2тгA +к2) \ / А/ 2тгA+/с2)
Условие совместности можно записать так:
I
In — .
А
C.32)
L ( /а~ _ 4 -2— in — =
4 \ -nhi А/
Отсюда находим величину
C.33)
C.34)
Растяжение двух приклепанных полубесконечных пластин. Пусть пласти-
пластины 1 и2 занимают полуплоскости х2 > О и х2 < О соответственно (рис. 67, с).
Эти пластины прикреплены одна к другой в
трех точках свободаой границы (—/, 0), @, 0)
и (/, 0). На бесконечности пластина 1 подверг-
подвергнута однородному растяжению напряжением
I afiH нагружена сосредоточенной силой
@, Х2). Способы прикрепления пластин мо-
Г гут быть различными (например, встык или
внахлест) ; при Х% = 0 пластины могут состав-
составлять двугранный угол (см. рис. 67, б). На
пластину ) со стороны заклепок действуют
сосредоточенные силы реакции (P2i —Pi),
@, -Ро) и (-Р2, -Pi) соответственно,
приходящиеся на единицу толщины этой пластины, причем
/г» I ' х Q У\. 2 . I J,J J I
На пластину 2 действуют лишь силы реакции заклепок и сила @, — h x
на бесконечности.
Упругое поле будет следующим:
пластина 1
РИС. 66.
iP0 z
т— +¦
2тг А 2тг
In-
iKz) = — In — + — In
/2-z2
/2
+ z
In-
/ + z 1
27Г l-Z
C.36)
2тг А 2тг l-z n(z2 -I2)
—Y
2 - i2 )'
154
пластина 2
i
iPohi z iPihi /2 -z1 P2A, l + z
2nh2 П~А~ 2ith2 ~~T2 2th2 l-z
ф(г)
in
A 2nh2
C.37)
nh2 \z2-l2 2 l+z
Здесь при \z | = А перемещения выбраны имеющими порядок О(оХ\ Д/#),
т.е. равными нулю в асимптотическом приближении. Требуется определить
неизвестные параметрыPq,P\»P2.
Условия совместности можно записать следующим образом:
[K<p(z) - zJ{z) — ф(г) 1
—— — — = 0. C.38)
На основании C.36) и C.37) эти условия можно привести к следующе-
следующему виду:
1 1 -»\ оо 1 \ S+v2 Pohi
/а°° = д. In — —i
2 1+^ A L 1 + v2 2nh2
h 1 2^
4P2ht
+ v2) 2nh2(l
Решая систему C-35), C.39), находим
A
C.39)
1 +2*
C.40)
* =
Положительные направления всех сил указаны на рис. 67 стрелками.
Рис. 67.
155
I,
5
Рис. 68.
Армирование полупространства продольной пластиной. Пусть бесконеч-
бесконечная тонкая пластина толщины А, расположенная в плоскости ххх2, прикреп-
прикреплена в двух точках @, 0, 0) и (/, 0,0) к поверхности упругого полупрост-
полупространства х3 < 0 (рис. 68, а), Пластина растягивается на бесконечности в од-
однородном поле напряжений aj\ и а~2 (рис. 68, б). Со стороны заклепок на
пластину действуют сосредоточенные силы реакции: (Д 0, 0) в точке
@,0,0) и (-Р, 0,0) в точке (/, 0,0).
Упругое поле определяется следующими формулами:
пластина (z =хг + ix2)
2тгЛA +
2тгЛA+к,
фB) =
2
граница полупространства (х3 <0)
Р
Mi =
7)+7*(а"
Z-/
./. z z-l\
(In —-In ——
к,)\ Д 1 )
2тгЛA+к,)
/, f41)
Г 1
27TJU2
C.42)
Здесь приводится лишь одна компонента смещения на границе, полученная
из решения Буссинеска.
Условие совместности имеет вид
при*з = 0, х2 = О, хх = / - А [их ]'= 0. C.43)
Перемещение заклепки вдоль границы полупространства подчиняется
закономерности
C.44)
Здесь А — характерный радиус заклепки, rjR — постоянный коэффициент,
зависящий от конструкции заклепки (для круговой площадки сцепления
156
a)
it-
Рйс. 69.
I ^
ff)
радиуса А он имеет порядок 0,2). Так как смещения от сосредоточенной
силы убывают очень быстро при удалении от заклепки, то влиянием других
заклепок на зависимость C.44) при / > А можно пренебречь. Коэффициент
Vr будем считать заданной величиной, определяемой или эксперименталь-
экспериментально, или из решения внутренней задачи.
Перемещение их пластины в точке z = / - А согласно C.41) равно
щ =-— \l
2ц1 i
C_„ )in_
2nh A
C.45)
Отсюда при помощи C.44) получаем
Армирование полупространства поперечной пластиной (рис. 69). Пусть
полубесконечная тонкая пластина 1 толщины А, расположенная в полуплос-
полуплоскости х2 =0, х3> 0, лежит торцом на свободной границе полупространст-
полупространства хъ <0, прикрепленная к нему в двух точках, @, 0, 0) и (/, 0,0). Плас-
Пластина растянута на бесконечности напряжением а~1? полупространство 2
подвергается лишь сосредоточенным силам: (-Р, 0, 0) в точке @, 0, 0) и
(/>, 0,0) в точке (/,0,0).
В данной задаче упругое поле в пластине определено формулами C.31)
при z =Xi +/лг3, hx=h, /*2 = 1; в полупространстве — суперпозицией
решений Буссинеска, в частности, для их на границе — формулой C.42).
Аналогично предыдущей задаче находим
. C.47)
Два скрепленных полупространства. Пусть упругое полупространство
1\ (*з ^0) скреплено с упругим полупространством 2 (х3 < 0) в двух
точках границы @, 0, 0) и (/, 0, 0). Полупространство 1 растянуто на бес-
бесконечности напряжениями afx и а^°2, а полупространство 2 подвергается
лишь сосредоточенным силам: (—Р, 0, 0) в точке @,0,0) и (Р, 0,0) в точ-
точке (/,0,0).
В данной задаче условие совместности имеет вид
C.48)
157
Левая и правая части этого уравнения представляют собой взаимное сме-
смещение заклепок, вычисленное по деформациям полупространств 1 и 2 соот-
соответственно.
В результате получаем
2vE(lJ +M)
Растяжение и сдвиг двух полупространств. Пусть упругое полупростран-
полупространство 1 (х2 > 0) скреплено с упругим полупространством 2 (х2 < 0) вдоль
двух прямых линий границы х2 = 0: хг = 0 и xt = / (— °° <хъ < + °°). Полу-
Полупространство 1 подвергнуто на бесконечности однородному сдвигу напря-
напряжением а~! и однородному растяжению напряжениями aj°i и а~3, а полу-
полупространство 2 подвергается лишь воздействию сосредоточенных линейных
сил интенсивности: (—Р, 0,-7) вдоль линии х2 - 0, хх = 0 и (Р, 0, Т) вдоль
линии Х2 =0, х% =/.
Упругое поле в полупространстве 1 согласно B.2) описывается следую-
следующими формулами:
Р ( z z-l \ 1
= - —(^1п — -In-у- 1+ —
Р ( Z Z-1\ Р / I \
ф(г)= In In + 1
C.50)
\z\ U.-/I
Д ~ П /
В полупространстве 2 справедливы те же формулы с противоположным
знаком (при aj°i = а~з = <*Гз = 0).
Условия совместности имеют вид
^ 7Г^ Д 7Г?2 Д
аГз 2Г / • 27' /
2/Ui тг/ii Д пц2 Д
Отсюда определяем искомые силы реакции
тг/?2(дГ1 -^аГз)
41п(//Д)(?1+?2).'
Разумеется, рассмотренные задачи являются лишь простейшими иллюст-
иллюстрациями применяемого метода. Читатель легко обобщит их, произвольно
158
увеличивая, например, число заклепок, места их расположения, конфигу-
конфигурацию скрепляемых тел и их взаимное расположение.
Точечное соединение различных элементов конструкций является, как
правило, наиболее простым технологически и наиболее дешевым способом
соединения. Поэтому оно нашло широкое применение на практике. Доста-
Достаточно сказать, что в большинстве отечественных авиационных конструкций
до сих пор в основном используется заклепочный способ соединения.
§ 4. Передача усилий в стержни, армирующие
оболочку или пластину
Для подкрепления оболочечных и пластинчатых конструкций часто при-
применяют всевозможные стрингеры, стержни, накладки и т.п. В материа-
материалах также часто в качестве армирующего элемента применяют стержни и
нити (железобетон, стеклопластик, боралюминий и т.д.). Подкрепляющие
стержни в конструкциях обычно прикреплены в нескольких точках к
основной конструкции посредством заклепок, точечной сварки, шурупов
и т.д. В материалах при разрушении также возможны аналогичные проме-
промежуточные ситуации с точечными связями.
В настоящем параграфе излагается асимптотическая теория армирова-
армирования упругих конструкций стержнями с точечными связями. Эта теория
относится к любой геометрии контактных площадок сцепления ("точек").
Теория излагается параллельно с решением простейших типичных задач.
В дальнейшем будем предполагать, что: а) силы трения между пласти-
пластиной и стержневой системой отсутствуют, б) эффект эксцентричного изгиба
стержней относительно срединной плоскости пластины пренебрежимо мал,
в) в пластине реализуется плоское напряженное состояние.
Растяжение бесконечной пластины со стрингером. Пусть тонкий прямо-
прямолинейный призматический стержень 1 прикреплен в точках @,0) и @, /) к
бесконечной тонкой пластине 2, расположенной в плоскости хх х2 (рис.70, а).
Пластина растягивается на бесконечности напряжениями o^i и оГ2, в ре-
результате этого в заклепках появляются сосредоточенные силы Р, растяги-
растягивающие подкрепляющий стержень постоянного поперечного сечения с
площадью SF (рис. 70, б). При *i < 0 и xt >/ стержень в теории будем
считать бесконечным, однако это предположение не играет существенной
роли, так как при удалении от места приложения силы напряжения в этой
части стержня убывают очень быстро, так что уже на расстояниях порядка
одного-двух диаметров поперечного сечения стержня ими можно пренеб-
пренебречь (т.е. можно считать стержень коротко обрубленным с обоих концов).
Материал стержня и пластины, вообще говоря, разный.
р
\
t
t
р
•г
II
Рйс. 70.
б)
159
Рассмотрим вначале инвариантный интеграл Тх по замкнутой поверх-
поверхности 2, охватывающей точку @, 0, 0) (см. уравнение C.7) или B.29)).
Поверхность 2 равна 2/ + Хх + 22 + 2*, где 22 - сечение пластины 2 пря-
прямым круговым цилиндром х\ + х\ = R2, Zi — сечение стержня плоскостью
jcj =Л, 2/ - свободная (free) поверхность стержня и пластины, 2, - торо-
тороидальная (toroidal) поверхность радиуса г, охватывающая контур L пло-
площадки сцепления пластины со стержнем. Предполагается, что / >R> A>r ,
где А — характерный радиус койтура L; последний для простоты считается
симметричным относительно оси х2 (рис. 70, в).
Интеграл Г1 по поверхности 2/ равен нулю, так как пх = 0 и G//Л/ = 0 на
2/. Интеграл Тх по поверхности 22 согласно B.10) равен Л? ?1 (Г-вычет).
Интеграл П по Ъх и 2Г можно вычислить непосредственно:
Р2
-,
F D.1)
В симметричных относительно оси xt точках контура L интенсивность Г
имеет одно и то же значение, а величина п%, относящаяся к контуру L на
плоскости XiX2i меняет знак. Напомним, что в малой окрестности некото-
некоторой произвольной точки сингулярной* линии L поле будет локально-плос-
локально-плоским (в плоскости, перпендикулярной к L в этой точке); величина Г по оп-
определению равна составляющей Г-вычета B.27) на нормаль к L (см. фор-
формулы A.12) - A.14) первой главы).
На основании свойства инвариантности интеграл Тг по поверхности 2 ра-
равен нулю; отсюда имеем
/rML=A?fl+ 7ГТ"'
L lE\ op
Величина деформачции и^^ (в точке @, 0) пластины), возникающей 6т
действия сосредоточенной силы в точке (/, 0) и нагрузок aj*i, 6?2 , легко
находится при помощи C.3) :
•*»•» l-t Off '
Е2 8тпЦ
Подставляя это выражение в D.2), получаем
/ TnxdL = Р -^ -?- г- — Р2 ( —• + I. D.4)
L Е2 2 \4тг/Л2м2 EXSF )
Это уравнение аналогично соотношению C.13). Замечательно, что оно
является некоторым конечным интегралом решения (весьма сложной)
внутренней задачи и строго справедливо для произвольного контура L и
любого нелинейно-упругого вблизи контактной площадки материала.
Теория Г-вычетов позволяет аналогично выводить подобные соотношения
для любых сингулярных задач указанного типа. Эти соотношения дают
возможность получать простые оценки работоспособности сингулярных
связей в критическом и докритическом состоянии.
160
п п
a)
В рассматриваемом примере рис. 70 на основании C.6) и C.3) условие
совместности имеет вид
oti-Wii Ъ -v2 I _ PI
E2 ^Tfi±2h2 A EtSp
Отсюда получаем
D.5)
D.6)
Рассмотрим теперь общий случай одного или. нескольких различных
брусьев, прикрепленных к безграничной пластине любым конечным числом
заклепок. Брусья могут быть криволинейными. В малой окрестности неко-
некоторой произвольной заклепки О брус может быть прямолинейным (рис.71, а),
шарнирно-угловым с нулевым моментом в заклепке (рис. 71, б), жестким
угловым с отличным от нуля моментом в заклепке (рис. 71, в). Внешняя
нагрузка, приложенная к брусу и пластине, направлена параллельно плос-
плоскости пластины.
Перенумеруем все N заклепок индексом к (к = 0,1,2,.,., N— 1), zk —
координата к-й заклепки (z0 - 0).
Упругое поле в пластине описывается следующими потенциалами (за
исключением ближней зоны около заклецок):
XQ z n- i Xk z — zk
-*(*) = ¦ ' ~
2тгA +к) Д k=i 2тгA
-1 1Мк
2ТГ
D.7)
2тгA + к)
z
In— +
Д
- N-1
+ 2
2тгA + к)
In
Xkzl
2тгA
Здесь hXk и hMk — комплексный вектор усилия и момент в к-й заклепке
соответственно, <Po(z) и Фо(г) — известное упругое поле от внешних нагру-
нагрузок. Отсчет перемещений в пластине ведется от заклепки к = 0, в которой
согласно D.7) они равны нулю.
Расчет растяжения — сжатия и изгиба брусьев производится хорошо из-
известными методами; при этом перемещения, усилие и изгибающий момент
161
в брусьях также можно записать в виде некоторой линейной функции 3Nне-
3Nнеизвестных реакций Хк. иМк.
Для определения этих реакций необходимо сформулировать 3 (N— 1) не-
независимых условий совместности; вместе с тремя уравнениями равновесия
они составят замкнутую линейную систему уравнений.
Заметим вначале, что каждый элемент пластины в общем случае плоско-
плоского напряженного состояния испытывает, кроме собственно деформации
(измеряемой некоторым тензором), перенос как жесткое целое (измеряе-
(измеряемый комплексным вектором перемещения) и вращение (измеряемое не-
некоторым скаляром). То же самое относится к брусьям. Условия совмест-
совместности состоят в том, что в каждой жесткой заклепке перемещения и враще-
вращение, рассчитанные для пластины и бруса, должны совпадать.
Из уравнений равновесия в заклепке следует
Pk-Pk-i=Xk,Mk=[M\. D.8)
Здесь Рк — комплексный вектор усилия в брусе справа от (к — 1)-й заклеп-
заклепки, [М] — скачок изгибающего момента (рис. 71).
Напомним формулу для вращения е элемента пластины:
6 = 4jT Ы *'(Z) Bб = ,i - «1.2>- D-9)
Вращение заклепки происходит за счет вращения бруса (вычисляемого
по второй формуле D.9)) и локального вращения пластины от внешних
нагрузок, вычисляемого по первой формуле D.9) при у = <р0 (*) • Обозна-
Обозначим вычисленный таким образом скачок несовместного вращения в к-и
заклепке через [ек]; этот скачок должен уничтожаться моментом Мк. За-
Зависимость угла поворота заклепки от момента имеет вид
[**]=& -^7 (*=1>2> -.-,^-1). . D.10)
Здесь %R — упругий коэффициент, зависящий от конструкции заклепки.
Для осесимметричной заклепки на основании точного решения B.14) мож-
можно принять
Уравнение D.10) представляет собой одно из искомых условий совмест-
совместности.
Два других согласно асимптотическому условию C.6) в к-и заклепке на
основании D.7) приводят к следующему комплексному уравнению:
In
2м
(*=1,2, ...,ЛГ-1). D.12)
Здесь (мj, u2 ) — перемещение бруса при z =zki являющееся линейной функ-
функцией Хк иМк.
Решение 3(N — 1) линейных уравнений D.10) и D.12) позволяет найхи
искомые реакции в заклепках. Этот метод годится также для любых огра-
162
ничейных" пластин; при этом затрудняется лишь отыскание </?0 (z) и Фо (z).
Рассмотрим простейшие примеры.
Растяжение полубесконечной пластины со стрингером. Пусть тонкий
призматический стержень 1 прикреплен в точках @, 0) и @, /) к границе
полубесконечной тонкой пластины 2, расположенной в полуплоскости
х2 < 0 (рис. 72). Пластина растягивается напряжением о?г, в результате
чего в заклепках появляются сосредоточенные силы Р, растягивающие под-
Рис. 72.
крепляющий стержень. В этом случае из условия совместности
аП \-v2 I PI
I -Л _2 -Pin— = D.13)
Е2 ттЕ2Н2 A E\Sp
находим
Р= 2 1 F(Jl1 D.14)
Начальные напряжения в армированной пластине. В рамках изложенной
теории легко вычислить также начальные напряжения, возникающие вслед-
вследствие заданной предварительной деформации стержней до их прикрепления
к пластине или оболочке. Это один из широко распространенных приемов,
применяемых конструкторами для управления напряженным состоянием
рабочих панелей.
При помощи условия совместности нетрудно найти усилие в заклепке Ро,
возникающее вследствие начальной деформации стержня е0:
стержень 1 и бесконечная пластинка 2 (рис. 70)
Ро = 2,eoh2ElE2SF
A +и2) [4/й +ESC )l(l/A)]
стержень 1 и полубесконечная пластинка 2 (рис. 72)
ж «ow,fr
nlh2E2 + 2EXSF{\ - v2 ) In (I/A)
Бесконечная пластина, подкрепленная периодической системой прямоли-
прямолинейных стрингеров. Пусть бесконечная упругая пластинка 2 подкреплена
бесконечной периодической системой одинаковых стрингеров 1 длины /,
расположенных на расстоянии а один от другого (рис. 73, а). Пластинка
подвергается на бесконечности однородному растяжению вдоль стрингеров
напряжением о22 =ож. Кроме того, каждый из стрингеров имеетодинако-
163
t
t
JL*.
oo
a,
P P P
I I I'
P P
Рис. 73.
вую начальную деформацию €0. Требуется определить сосредоточенные си-
силы Р в заклепках (выбор знака см. рис. 73, б).
Напряженно-деформированное состояние пластины описывается следую-
следующими комплексными потенциалами:
iP +~ z-an-il 1
y(z) в 2 In
2тгЛ2A
z-an+il 4
z-an-il 1
In f + —
zm-an+il 2
D.17)
'__* +? (Л1± 221L).
2nh2(l+K2) п = -оо \ z - an - il z-an+il J
Эти формулы можно записать короче, используя известные соотношения
(см., например, стр. 50 и 60 справочника [77])
1
—
4
1
\p(z) = —
2
iP
2тгЛ2A+/с2)
In
iK2P
In
sm[n(il-z)la]
sin [it(iI-z)la]
D.18)
+ к2) sin [тгО*/ + z)/a]
rz n(z -2it) it(z
2+/2
z2+/
2j
IiJ_L ctg JL±lL_
2a a 1
Условие совместности в данной задаче согласно C.6) имеет вид
oj Ъ-уг J_ PI
Е2 ° Аъ\х2Н2 A EtSp
D.19)
164
/у/ууу,^ /уууууу.
Рис. 74.
УУУУУУУУу^
с га А
Отсюда находим искомую силу Р
l-nlh^xSpixj^-e^)
[4tt/m2/i2
D.20)
Как видно, усилие в заклепке не зависит от наличия других стрингеров,
если они непосредственно не соединены с рассматриваемым стрингером.
Этот результат справедлив и для произвольного расположения любого чис-
числа стрингеров. Разумеется, он верен лишь в том случае, когда расстояние
между Стрингерами гораздо больше величины А.
Две пластинки, скрепленные тонкими стержнями. Пусть две тонкие по-
полубесконечные пластинки с прямолинейными параллельными границами
расположены в плоскости xtx2 (рис. 74, а). Пластинки скреплены друг с
другом тремя тонкими прямолинейными стержнями, перпендикулярными
границе и отстоящими на одинаковом расстоянии а один от другого. Все
заклепки в одной и той же пластине расположены на расстоянии / от сво-
свободной границы (рис. 74, б). Материал крайних стержней 1 может отличать-
отличаться от материала пластинок "+" и "—", а также от материала Среднего
стержня ".
Пусть средний стержень перед скреплением был нагрет до температуры Т,
а Температура То остальных стержней и пластинок была одинаковой. Длина
всех стержней перед скреплением была одинаковой и равнялась L . После
соединения средний стержень остыл до температуры То, что привело к
возникновению в нем растягивающей силы\Р (в двух боковых стержнях,
очевидно, появилась сжимающая сила HP. Требуется определить силу Р,
определяющую начальные напряжения в данной упругой системе. В задачах
такого типа начальные напряжения вызываются неодинаковым начальным
удлинением стержней.
Найдем упругое поле в пластинах.
На основании B.2) аналитические функции F\ (z) и F2(z), равные
Fi(p) = ztf(z)+ *(*), F3(z) = 2^z)+Ft(z) (z=*i+ixa),' D.21)
D.22)
должны удовлетворять следующим граничным условиям:
при х2 = 6 Ле F2 = 0, Ьп Fx = 0.
165
Обозначим:
D.23)
2тгЛA+к)
2/z(a2 -/2)-/z2 -/(Зд2 -
[(z+/7J-*2]2
(h — толщина пластинки). Функции Ф5 и % представляют собой решение
соответствующей задачи о деформации бесконечной упругой плоскости под
действием указанных трех сил (сингулярная часть искомого решения).
Решение краевой задачи D.22) с заданными особенностями удобно
представить при помощи функций Ф5(г)и У5(г) следующим образом:
D.24)
F2(z) = 2Ф,(г) - 2Ф,(г) + *,(z) - %() [b'() Ф;()]
Согласно D.21)
F2(z)-F1(z), ^B) = ^(г)-2Ф'B). D.25)
Формулы D.23) - D.25) дают точное решение задачи. После некоторых
вычислений с их помощью найдем значения % и % этих функций в точке
z = — //, получающиеся после отбрасывания сингулярной части:
(д2+4/2J '
D.26)
Р [ + 3/с ка* +2/2(к+2)(д2 +4/2) 1
*° " 4тг/ЛA+к) L ~ (а2 +4/2J J *
Отсюда при помощи B.10) получаем величину Г-вычета в точке z = — //:
Р2 Г 7 + 3/с
2 8тт/дАA+к) L 4
-8)-8/4(к+2) ,
' D.27)
]
J •
Условие совместности в рассматриваемой задаче можно записать как
условие однозначности смещений при обходе замкнутого контура, прохо-
проходящего через об^пластины, два различных стержня и четыре заклепки. Из-
Изменением смещения внутри заклепки пренебрегаем. Используя D.23) и
D.24), получаем следующее условие совместности
PL 3 а C - р. 3 - v \ PL
+ Pin —( i- + =• )+ =P0L(T-T0). D.28)
E0SF 16тг Д \ д+Л+ n_h_ J 2ElSl
166
Отсюда находим силу Р
1 1_ 3 ±C~
EqSq 1E\S\ ISitL I
В частном елучае весьма жестких оснований, когда
xSx,
D.29)
L\i_h_>EqS0,
отсюда получается результат, известный из элементарного исследования.
Чистый изгиб балки, прикрепленной к пластинке в двух точках. Пусть
тонкая балка постоянного сечения прикреплена в двух точках (—а, 0) и
(а, 0) к границе пластинки, занимающей полуплоскость х2 < 0. Край балки
подвержен чистому изгибу моментом М (рис. 75, а). Вследствие чистого
изгиба в заклепках возникнут изгибающие моменты Мi иМ2, удовлетво-
удовлетворяющие условию равновесия балки
Мх +М2 =М. D.30)
Упругое поле полубесконечной пластинки согласно B.20) описывается
потенциалами (рис. 75, б)
Мх Ш2
2irh(z-a)
D.31)
так что величина Фг,равная регулярной части </?"(z) при z =-а, будет сле-
следующей:
iM2
Ф1=_.
D.32)
8тгАд3
Отсюда при помощи B.21) получаем Г-вычет в сингулярной точке (-я, 0) :
Рассмотрим Г-интеграл Fi пр замкнутой поверхности, охватывающей
заклепку в точке (— а, 0)* и образованной, кроме граничных поверхностей
составного тела, поперечным сечением Sp балки справа от заклепки и ци-
цилиндрическим поперечным сечением пластинки, интеграл по которому
{г)
1а
Рис. 75.
167
равен Г-вычету. Так как в поперечном сечении балки отлична от нуля лишь
составляющая ох х, причем
Мх2 Оц 1
ап= , щ ! = , [/=-.апмм D.34)
(х2 отсчитывается от нейтральной линии), то на основании теоремы инва-
инвариантности Г-интегралов имеем
/ {U-alxux x)dL = -. D.35)
sF ' 2EI
На основании D.33) и D.35) получаем следующее соотношение, анало-
аналогичное D.4):
_ М\ "Al
ь Пх " 2EI
Условие совместности получается из условия однозначности вращения е
при обходе замкнутого контура, проходящего через пластину, балку и две
заклепки. Вращение балки, равное 1Аи2 ?1, удовлетворяет уравнению упру-
упругой линии
- =~7 (I*!<*)• D-37)
dxi 2EI
Вращение заклепок ех и е2 прих = -аих =+а соответственно согласно
D.10) будет следующим:
Mt М2
«1 = $r —7 ' е2 = Sr -^ D38)
Решение уравнения D.37), удовлетворяющее граничным условиям D.38),
приводит к следующему условию совместности:
аМ j М2 - М!
Jf~=b \2 • D-39>
Решение системы D.30), D.39) дает следующие выражения для момен-
моментов в заклепках:
к 1 SREI
Мх = М, М2 = М, к = —^ . D.40)
1+А: 1+Jfc- aixA2+%REI
Поперечный изгиб и растяжение балки, прикрепленной в двух точках к
пластинке. Пусть упругая система имеет ту же конфигурацию, что и в пре-
предыдущей задаче, но внешняя нагрузка представляет собой силу (Р, Q),
приложенную к концу балки на расстоянии b от правой заклепки. В заклеп-
заклепках будут действовать сосредоточенные силы {Хг Jfi), (X2, Y2) и момен-
моменты Mt,M2, подлежащие определению (рис. 76,а).
Моменты М^1^ и М2, очевидно, находятся по формулам D.40), в кото-
которых нужно положить M = bQ(Mx =м?1'*+м?2^). Далее, силы Хх иХ2 оп-
определяются лишь продольной нагрузкой Р, а силы Yx и Y2 зависят лишь от
168
Ж -J /Tf X. la
a) 6)
Рис. 76.
поперечной нагрузки Q * Поэтому удобно использовать принцип суперпо-
суперпозиций.
Взаимное смещение двух заклепок в пластине в направлении оси хх на
основании уравнения, аналогичного уравнению D.12), равно
l-v\ 2а
i(XX1)ln — . D.41)
Д
.' (Постоянные Ех и vt будем относить к пластине, а Е2 — брусу.) Это смеще-
смещение должно равняться удлинению бруса между заклепками 2aXl/(E2SF).
Отсюда получаем следующее уравнение совместности:
l-Pt 2a 2aXt
_№-*,),„—.—. D.42)
Решение этого уравнения вместе с уравнением равновесия Хх + Х2 =
= - Р дает
. Р кР 2irahEl
X 1==_ , Х2 = , А:=1+ — . D.43)
1+Л 1+к E2SF(l-vx)\nBal&)
Взаимное смещение двух краевых заклепок в пластине в направлении
осилг2 равно
1 — Vt 2a
—-^ХГ.-УгУЫ—. D.44)
Д
Это смещ^ще должно равняться прогибу бруса между заклепками под
действием поперечной силы Q и момента -Q Ь (снимающего момент в за-
заклепке: *i = а) на правом конце бруса. Это нагружение равносильно прило-
приложению силы Q непосредственно в заклепке хх =а. Эпюра моментов будет
следующей:
M = -YtQc-a) (\x\<a), D.45)
причем
ЛГр> = 2дГ1. D.40)
Так как м2,11 = — М1(Е21), то упругая линия бруса согласно D.45) бу-
будет следующей:
) D.47)
и2 j
ЬЕ21
Здесь Со, Сх — некоторые постоянные. Без ограничения общности можно
считать, что щ = 0 при х = 0; отсюда Со = 0. Так как момент в заклепке
169
а)
4+L
Pfcc. 77.
хг=а равен нулю, то согласно D.10) равно нулю вращение е = 1Л u2t% =
= 0 в этой точке; отсюда С! = 0. Теперь на основании D.47) смещение за-
заклепки Xi = — a равно
2IL D.48,
D.49)
ЪЕ21
Согласно D.44) и D.48) условие совместности будет следующим:
1 - vt 2а _ 4а3 Yx
irhEt 2 1 А ЪЕ21
Используя D.40) в новых обозначениях, D.46) и D.49), получим окон-
окончательный результат
Ух =-
Mx =
kQ
2 1+*'
1+A:O
M2 =
kobQ
1+A:O
D.50)
Величины X! и Х2 выражаются формулами D.43).
Теория упругой заделки. При закреплении конца одномерной балки в
каком-либо двумерном или трехмерном теле все исследователи, начиная с
Бернулли, Эйлера, Лагранжа и др., принимали в рассматриваемом конце
балки условия жесткой заделки. Согласно этому условию положение и
направление упругой линии балки в этой точке было фиксированным и за-
заданным. На самом деле, в заделке имеется смещение и поворот, определяе-
определяемые упругими свойствами, нагрузками и формой всего тела в целом.
Прежде чем вывести граничное условие упругой заделки в общем случае,
рассмотрим следующую конкретную задачу (рис. 77, а). Пусть полоса 0 <
<х2 <h, —°° < Xi < +°° скреплена жестко вдоль площадки х2 = 0, ' | xt \ <
< Й / с полуплоскостью х2 < 0 из другого материала. При xt -* — о?" в поло-
полосе действуют напряжения, соответствующие продольной силе Р и изгибаю-
170
щему моменту М. При хх -> + <» в полосе, а т!акже*при х\ + х2 -> °° в полу-
полуплоскости, напряжения исчезают.
Кроме того, при xt < — Ы.1 в полосе действуют также напряжения, отве-
отвечающие перерезывающей силе Q. Таким образом, действующие на перешей-
перешейке напряжения статически эквивалентны силе(Р, Q) и моменту М. Факти-
Фактически указанные условия на бесконечности в полосе при хх -> ± °° реали-
реализуются уже при Xi « A -г 2I. Все границы свободкы от внешних нагрузок.
Для определенности рассматривается случай плоского напряженного со-
состояния.
Эта задача является внутренней, "структурной" задачей для конкретной
частной конструкции упругой заделки криволинейного стержня в про-
произвольном упругом теле (рис. 77, б), когда конец стержня имеет форму
весьма малой "хоккейной клюшки", т.е.
KRAip<L Q<r<L)
(здесь L — характерный линейный размер внешней задачи). При этом усло-
условии заделку (включающую в себя концевое искривление и площадку сцеп-
сцепления) можно считать точечной. Величины?, Q яМ будут соответствующи-
соответствующими усилиями и моментом в заделке.
Инвариантный интеграл Г\ по замкнутому контуру 2, определяемый
формулой B.1), равен нулю. Контур 2 состоит из свободных границ тела,
большой полуокружности радиуса г, гораздо большего /, отрезков xt = ± г,
О < х2 < h и двух окружностей радиусом, гораздо меньшим /, с центрами
в сингулярных точках хх = ± /, х2 = 0.
Аналогично предыдущему, используя формулы B.18) и B.21), находим
D.51)
Здесь. Г/1* и Г/2) —величина Г-вычетов в сингулярных точках*! =—Й/ и
хх = + &/ соответственно, м^ р Wj i> e°i ~ параметры решения внешней
задачи с точечной связью (при ifL -+ 0) ] Е - модуль Юнга полосы, Ъ - пле-
плечо силы Q. В уравнении D.51) мы пренебрегли членом
и Q2b
2b2 /х \2
так как по предположению Z> > х* > 1.
Величины Г/1^ и Г[2) контролируют прочность упругой заделки в рас-
рассматриваемом случае.
Сформулируем теперь граничные условия в общем случае упругой задел-
заделки криволинейной балки в точке хх =хо,х2 =Уо упругой пластины произ-
произвольной формы.
Пусть U=Ui +iU2 - комплексный вектор перемещения упругой линии
балки, а х — угол поворсга упругой линии балки. Обозначим также
1Ы*), D-52)
Здесь </>, ф,и, е — комплексные потенциалы, вектор перемещения и вра-
вращение упругого поля пластины, представляемые в виде суммы регуляр-
171
2L
21
a)
РИс. 78.
ной (во всей пластине) и сингулярной составляющих. Начало координат
поместим в некоторой регулярной точке пластины, перемещения и враще-
вращение в ней примем нулевыми.
Граничные условия при z = z0 (гд,его~хо +iy0) будут следующими:
AttEh
In
|Zo1
D.53)
Величины Et jjl, uf h относятся здесь к пластине, постоянная 5 = 4A'— v)
в случае расположения упругой заделки на свободной границе пластины и
6 = C — v) (I + v), если упругая заделка находится во внутренней точке
области, занимаемой пластиной.
Условия D.53) являются условиями совместной работы пластины и бал-
балки в упругой заделке. Они выводятся совершенно аналогично уравнениям
D.10) и D.12). Множители при X и М в уравнениях D.53) играют роль
коэффициентов "упругой постели".
Рассмотрим два простейших примера.
Отрыв балки от края пластины поперечной силой (рис. 78, а). Пластина
занимает полуплоскость х2 < 0. В этом случае требуется найти момент М в
упругой заделке (при хх =±L).
Из элементарного расчета упругой линии балки имеем
du2 LQ - AM
при Xi =L = L
dxx 4EJ
D.54)
Так как е0 = О,
получаем
_ 1
" 2
= ,ь из второго условия D.53) на основании D.54)
D.55)
Симметричный изгиб двух одинаковых балок, упруго заделанных свои-
своими концами в две пластины х2 > 0 и х2 < - 2L (рис. 78, б). В этом слу-
случае неизвестной является величина моментов М в заделке.
Обозначим через 2€ж взаимное вращение двух пластин на бесконечности.
Из второго условия D.53) при е0 = €» и значении х> определяемом форму-
172
лой D.54), находим
1 »A\QL 2е,Ех1)
М= —1 . D.56)
2 liiLtf+iEl
Здесь знаки /'+" и "—" отвечают различным балкам.
На бесконечности к каждой из пластин приложен момент, по абсолютной
величине равный
Рассмотрим некоторые задачи о стрингерах, армирующих пластину или
оболочку при жесткой заделке стрингера вдоль всего его контура. Такой
будет работа упругой системы и при заклепочном соединении в случае доста-
достаточно частого расположения заклепок. Эти задачи относятся уже к регуляр-
регулярному случаю A.1). Они приводят к смешанным краевым задачам матема-
математической физики. Имеющиеся в этой области результаты аналитически весь-
весьма громоздки й малоэффективны, несмотря на большое число исследований
в этом направлении. Асимптотические методы гораздо более эффективны,
если, в самом начале решения учесть наличие в таких задачах двух малых
параметров:, отношение жесткости матрицы к жесткости армирующего эле-
элемента и отношение характерного диаметра поперечного сечения ртрингера
к erb длине.
Изучим несколько примеров.
Прямолинейный стрингер в пластине. Пусть упругий стрингер 1 располо-
расположен вдоль отрезка х2 * 0, | xt | </ в пластине 2, растягиваемой на беско-
бесконечности напряжением оц = ато вдоль стрингера. В том случае, когда жест-
жесткость стрингера гораздо больше жесткости соответствующего элемента
Пластины, вблизи стрингера существует своеобразный пограничный слой,
в котором приемлемы следующие допущения:
Э Э
Щ>и2, — >—- . D.57)
ОХ2 ОХ\
При этих допущениях уравнения теории упругости сводятся к следую-
следующим соотношениям (уравнения погранслоя в пластине):
2 -v/, 4 2 Н2 >
Э*! 9х2
¦ " ¦ . : D.58)
1 dfcj ' 2 d^!
Здесь Who- перемещение и нормальное напряжение в стержне* г - напря-
напряжение т% 2 в пластине при х2 = О, I Xj |< /, h - толщина пластины, 5/? - пло-
площадь поперечного сечения стержня.
Как видно, в пограничном слое в пластине существенным является лишь
касательное напряжение т12, все остальные напряжения пренебрежи-
пренебрежимо малы.:
173
Общее решение первого уравнения D.58) имеет следующий вид:
При х2 = 5 это решение должно "сшиваться" с внешним, невозмущенным
решением их = xt o00/E2. Отсюда имеем
—
М2
Это уравнение вместе с двумя последними уравнениями D.58) состав-
составляет замкнутую систему относительно функций о,т nW. Запишем общее
решение этой системы для о:
(к2 = ~^Н D.61)
где Сх и С2 — произвольные постоянные.
Напряжение а на концах стержня пренебрежимо мало по сравнению с
максимальным его значением атах. Поэтому можно положить*
при хх =±/ о = 0. D.62)
Отсюда находим постоянные
Сг = С2 = —— D.63)
26№2A+)сЬИ
и нормальное напряжение в стержне
Ех
41) D.64)
Величины W, т, их и г12 легко определяются отсюда по формулам D.58)
и D.59).
Согласно D.64) максимальное напряжение достигается в середине
стержня, оно равно
¦*¦(¦-—).
Е2 \ chkl/
Отметим два предельных случая этой формулы:
весьма длинный стрингер
И>1, ^„=0.-7, D.66)
идеально жесткий стрингер
td<l9 amax= — . D.67)
тах 26f(l+^) ;
174
На основании D.65) длина изолированного стрингера не должна превы-
превышать /#,равной
1 ОооЕх
/, = - arch , D.68)
к OooEi - овЕ2
где ав — временное сопротивление материала стрингера. В противном слу-
случае он разорвется пополам.
Полученное решение содержит один неопределенный параметр — толщи-
толщину пограничного слоя 6. Наиболее общий способ его определения следую-
следующий. Исходная задача в строгой постановке решается на ЭВМ каким-либо
численным методом (например методом конечных элементов) лри опреде-
определенных значениях параметров //f, l/h, vu v2,Ei/E2. В результате решения
вычисляется функция, представляющая наибольший практический интерес
(например о(<зж в зависимости от хх II), Сравнение численного решения с
приближенным решением погранслоя позволяет найти 5 (и заодно оценить
точность приближенного решения). Разумеется, решение на ЭВМ всей за-
задачи невозможно из-за обилия параметров.
В данной задаче параметр 5 можно определить, используя точное решение
исходной задачи в предельном случае идеально жесткого стрингера, когда
выполняются следующие граничные условия:
при х2 = 0, \хх |</ их = и2 = О,
при xf+xJ-*<*> оц^о^, а12=а22=0.
При помощи представлений B.2) краевая задача D.69) формулируется
следующим образом:
при*2=0, \Xl[<l кФ(*)-2Фф-Фф-*ф = 0,
при <b{) 40(-2) *()& °(~2)
При помощи вспомогательной аналитической функции u(z) =
+ Щг) краевая задача D.69) запишется так:
при*2=0, |jctl</
^) 0,
1 • , 1 , DЛ1)
= — Ооо +O(z), П = -— aoo+0(z).
4 4
Решение задачи Дирихле D.71) будет следующим:
1
= — (к-I) о.. D.72)
4
(при z ->°° \Jz2 -12 = z + (^(z)). Отсюда по формулам B.2) можно
найти перемещения и напряжения в данной задаче. Найдем касательное на-
напряжение на стрингере:
+ lJ*i
175
Интегрируя уравнение равновесия для стрингера .(последнее уравнение
D.58)), получаем нормальное напряжение в стрингере
gc(« + lJ т г
а=—- ^-х\. D.74)
В частности, максимальное напряжение равно
D.75)
Приравниваем это точное значение величине атах> полученной в прибли-
приближении погранслоя (формула D.67) ); получаем толщину погранслоя
8 =—-2-7. D.76)
О
Таким образом, толщина погранслоя для изолированного стрингера в
пластине равняется примерно одной шестой длины стрингера.
Сравним приближенное решение с точным. Согласно D.64) при kl<\
имеем
(^) D-77)
Как видно, абсолютная ошибка приближенного решения постепенно на-
нарастает с удалением от середины стрингера, достигая максимального значе-
значения lU 0щах пРи *i = * V3?2. Ошибку можно уменьшить за счет уменьше-
уменьшения параметра б (примерно на20%), при этом атах увеличится тоже при-
примерно на 20%. Это обстоятельство целесообразно учесть при выборе коэф-
коэффициента запаса для атах; из этих же соображений для величины б следует
пользоваться формулой D.76).
Оптимальное армирование пластины. Согласно полученному решению
зона влияния изолированного стрингера длины 2/ представляет собой пря-
прямоугольник с размерами 2/ X 25. Этот простой результат позволяет эффек-
эффективно решать оптимальные задачи армирования пластин стрингерами.
Пусть, например, бесконечная пластина постоянной толщины растягива-
растягивается одноосно некоторым предельным напряжением о0. Спрашивается,
каково оптимальное расположение и длина стрингеров (при минимальной
массе), которыми нужно подкрепить пластину, чтобы она выдержала боль-
большее напряжение о>а0. Нетрудно видеть, что оптимальная структура стрин-
стрингеров образует на плоскости пластины шахматную решетку, причем стрин-
стрингеры длины 2/ располагаются лишь по полям одного цвета (вдоль направ-
направления растяжения в середине полей); каждое поле представляет собой пря-
прямоугольник размерами 2/ X 25. Величины / и 5 определяются по форму-
формулам D.68) и D.76). При этом величина а*», фигурирующая в формуле
D.68) ив других соотношениях, в данном случае неизвестна; она представ-
представляет собой напряжение ох х в "пустых" полях. Для ее определения служит
уравнение равновесия, записываемое для одного периода шахматной ре-
решетки.
176
Периодическая система стрингеров. Пусть стрингеры расположены в бес-
бесконечной пластине вдоль отрезков | хх | < /, х2 = 2па9 где 2а — шаг решетки
(и = 0, ±1, ±2, ... ). Пластина растягивается на бесконечности напряже-
напряжением ох i = <Ьо. Если величина а больше толщины погранслоя 5, то каждый
стрингер работает изолированно от других; этот случай уже изучен.
При а < 8 картина резко меняется. Упругое поле не проникает через
пластину между стрингерами; при удалении от концов полуполосы между
стрингерами краевой эффект затухает экспоненциально. Следовательно, в
этом случае вся нагрузка передается целиком через стрингеры, которые
играют роль проводников упругого поля. Поэтому максимальное напряже-
напряжение в стрингерах будет равно
lah
Ooo — . D.78)
При точном решении задачи этот переходный процесс, конечно, будет
протекать плавно.
Два близко расположенных стрингера. Пусть два параллельных стринге-
стрингера^ = 0идг2 =2дпри \хх |</в бесконечной пластине растягиваются на-
напряжением оц =ож на бесконечности. При а > д стрингеры не влияют друг
на друга. При а < д упругое поле не проникает в пластину между стринге-
стрингерами; они работают как один стрингер удвоенного поперечного сечения.
В Этом случае взаимодействие стрингеров с внешним упругим полем
осуществляется через две внешние боковые стороны. Напряжение о в каж-
каждом стрингере дается правой частью формулы D,64), деленной на два.
Зона влияния — прямоугольная область: \хх \ < /, -6 <х2 < 2а + 5.
Совершенно аналогично рассматривается случай трех, четырех и любого
числа параллельных стрингеров одинаковой длины.
Изолированный стрингер под действием продольной силы. Пусть к стрин-
стрингеру х2 = 0, 0 < хг < I в бесконечной пластине приложена внешняя силаР
в начале координат, а напряжения на бесконечности равны нулю. В этом
случае напряжение в стрингере, очевидно, определяется формулой D.61)
при ож = 0, а постоянные Сг и С2 находятся из следующих граничных ус-
условий:
при*! =0 а = а<ь при Xi =/ a = 0 (ao=P/SF). D.79)
В результате получаем
ch kl - ch kxi
1
ch kl - 1
D.80)
В предельном случае к! < 1 существует точное решение этой задачи, ко-
которое согласно D.70) и D.71) определяется следующими потенциалами:
2тгA + к) Vz(z ^7)
В этом случае напряжения ант будут следующими:
177
Стрингер в цилиндрической оболочке. Пусть бесконечная цилиндри-
цилиндрическая оболочка х\ + х\ =R2 растяптается вдоль оси хъ напряжением
^зз =ог<х, на бесконечности. Вдоль образующей цилиндра к оболочке 2
прикреплен жесткий стрингер 1 длины 2/.
В пограничном слое вблизи стрингера в оболочке наиболее существен-
существенными переменными будут и nS — перемещение вдоль образующей и каса-
касательное усилие в радиальном сечении оболочки. Производные вдоль обра-
образующей, по-прежнему, считаются малыми по сравнению с производными в
поперечном направлении.
Уравнения теории цилиндрических оболочек при этом сводятся к сле-
следующим уравнениям погранслоя:
д2и Ъи
— = 0, S = hn2—-,
Эг bs
D.83)
dW I do
о^Е, — r = --f— ($=SF/h).
dx3 2 dx3
Здесь 5 — длина дуги в поперечном сечении оболочки (на стрингере будет
T=S/h). Эти уравнения совпадают с соответствующими уравнениями D.58)
для пластины, если произвести замену s -+х2, х3 ->JCi, hTx 2 -*S.
Решение задачи совершенно аналогично задаче об изолированном стрин-
стрингере в пластине. В частности, напряжение о и толщина погранслоя 5 опре-
определяются формулами D.64) и D.76).
Метод эффективен также для оболочек другой формы.
§ 5. Расчет клепаных панелей
Подкрепление панелей широко применяется в технике и, прежде всего,
в авиастроении. Наибольшее распространение получили клепаные панели,
в которых подкрепляющие элементы взаимодействуют с тонкими пласти-
пластинами дискретным образом через заклепки. В практических расчетах обычно
пренебрегают дискретностью взаимодействия элементов панели, как бы
"размазывая" заклепки и считая взаимодействие распределенным вдоль
всей линии контакта. Тем самым исходная сингулярная проблема типа
A.2) сводится к регулярной проблеме типа A.1), постановка и решение
которой принципиально проще. Однако такой прием оправдан лишь при
весьма частом расположении заклепок. Ряд регулярных задач типа A.1) о
взаимодействии бесконечных и полубесконечных пластин с конечным,
полубесконечным и бесконечным стержнем, работающим на растяжение —
сжатие, впервые был рассмотрен в работах [78 — 82].
Будянский и By в работе [83] рассмотрели сингулярную задачу типа
A.2) о передаче силы от бесконечного стержня, работающего на растяже-
растяжение — сжатие, к бесконечной пластине через периодическую систему закле-
заклепок. При этом они предложили рациональную структурную теорию закле-
заклепочных соединений, основанную на определенных допущениях о конструк-
конструкции и работе заклепок. Эта теория используется ниже в § § 5 и 6 для реше-
решения некоторого класса задач, представляющих практический интерес. Срав-
Сравнение ее с бесструктурной теорией, изложенной выше, показывает сущест-
178
венные преимущества бесструктурной теории. Эти преимущества, прежде
всего, следующие: а) решение, полученное, при помощи структурной тео-
теории, содержит некоторые "сорные" структурные параметры, которые прак-
практически не влияют на силы, передаваемые через заклепки, на усилия в
стрингере, а также на упругое поле пластины, за исключением малой облас-
области вблизи заклепок; б) бесструктурная теория гораздо более красивд и
изящна. Однако представление о структурной теории также полезно иметь,
так как она более проста для понимания. В данном параграфе * излагается
(основанный на структурной теории Будянского — By) метод расчета поля
напряжений и смещений в плоских клепаных панелях, подкрепленных про-
произвольной конечной стержневой системой ферменного типа. Простейшим
примером ферменной подкрепляющей системы может быть стрингер,
работающий только на растяжение — сжатие.
Пусть к тонкой пластине прикреплена плоская стержневая система. Сле-
Следуя, статье [83], примем следующие допущения: 1) стержневая система —
ферменного типа, т.е. стержни работают только на растяжение — сжатие;
2) силы трения между пластиной и стержневой системой отсутствуют;
3) стержневая система взаимодействует с пластиной в ,ее срединной плос-
плоскости, т.е. не учитьщается эффект эксцентричного прикрепления стержне-
стержневой системы относительно срединной плоскости пластины; 4) ослабление
стержней подкрепляющей системы за счет постановки заклепок не рассмат-
рассматривается; 5) в пластине реализуется плоское напряженное состояние;
6) заклепки в пластине моделируются круглыми жесткими включениями.
Будем также предполагать, что нагрузка, действующая на панель, —
плоская и слагается из нагрузок, приложенных к пластине и центрально
действующих на заклепки сил Xj =Х*ц +iX\j (/=1,2, ... ,т;т —число за-
заклепок) .
Пусть, далее, xlf х2 - прямоугольные декартовы координаты, a z = xt +
+ ix2 — комплексная переменная. Отделим от пластины подкрепляющую
систему и приложим к центрам заклепок Zj пластины и подкрепляющей
системы неизвестные силы взаимодействия Xj = XXj + iX2/- и - Xj соответст-
соответственно.
Если между к-и и и-й заклепками {кФп\ к, п<т) имеется стержень,
то для их взаимного смещения в направлении этого стержня справедливо
следующее условие совместности:
Re {[*(**)-*(**)]«-''*»} = f*18^*18 . E.1)
Здесь w(z) = Mi +ш2 — комплексный вектор смещений пластины, рав-
равный [48]
zk -zn=Rknexp(ipkn),
Et=EhKl-»2)9 к =C-i
где h - толщина пластины, v, Е - коэффициент Пуассона и модуль упру-
* Этот параграф следует статье [84].
179
гости материала пластины, <p'(z), ф(г) — комплексные потенциалы, Nkn —
усилие в стержне, (E0FQ) kn —жесткость стержня на растяжение — сжатие.
Для нахождения функций <p(z)ni//(z) необходимо решить плоскую за-
задачу теории упругости для области, занятой пластиной, при наличии в ней
т круглых жестких включений, имитирующих заклепки. Однако в боль-
большинстве практически важных случаев радиусы заклепок малы по сравне-
сравнению с другими характерными геометрическими размерами панели. Это
позволяет ограничиться учетом асимптотического взаимодействия включе-
включений путем применения принципа суперпозиции в виде
т т
?>(*)= 2 ^(z), ф(г)= 2 ^.(z), E.3)
/=о ' /=о '
где <a>(z)h Фо(г) — потенциалы, определяемые внешней нагрузкой, дейст-
действующей на пластину при отсутствии жестких включений; <py(z) и ^/(z) при
/=1,2, ..., т - потенциалы, определяющие поле в пластине с одним
/-м круглым включением, к центру которого приложена сила Xf.
Из равновесия/-й заклепки, соединенной в панели стержнями с заклеп-
заклепками *ь к2, .. ., kt.9 следует:
Xf = JT/+ 2 Nksf еш«х*в~ */> =0 (/ = 1,2,..., т\ E.4)
S ~ X
Уравнения E.1) и E.4) представляют искомую систему линейных алгеб-
алгебраических уравнений относительно неизвестных сил Xf и усилий Л^„. Заме-
Заметим, что порядок этой системы всегда равен числу неизвестных. Поле на-
напряжений и смещений в пластине легко определяется по найденным силам
Xf с помощью формул Колосова — Мусхелишвили.
Конкретный вид системы уравнений существенно зависит от решаемой
задачи. Так, в случае бесконечной пластины, загруженной на бесконечности
постоянными усилиями, характеризуемыми тензором N%p(a, 0 = 1,2), име-
имеем [48]
КХ: XfГ If Г) 1
(z)= ' ln(z-z,) + '- т-i— + 1— . E.5)
K 2ir(l +к) J) 2тгA?+K)[zZf (zZff J ;
Здесь
Tf - радиус /-й заклеша!.
Учитывая, что (rnfRknJ < 1, после некоторых преобразований условие
совместности смещений E.1) с помощью соотношений E.2), E.3), E.5)
180
приводим к виду
ук„+ 2 (TkniPkni + Gkn,QknJ) =
где /=1 ^Г°>*»
Г 1 -v
Ti - Л^Г2) cos Щп + 2iVr2 sin 2pkn J,
Tfcn/ = - 2к In eknl + cos 2(^fc/ - |3Лл) - cos 2«3n/ - 0Л„) (/ # Л, и),
Gknk=Gknn=0, Gknj = sin2(pkf -pkn) -sin2(finf -рк„), (}Фк,п)
E.6)
В качестве примера рассмотрим случай, когда бесконечная пластина под-
подкреплена однородным конечным стрингером (с жесткостью на ]растяже-
ние — сжатие E0F0), расположенным под углом 0 к оси Охх и приклепа-
зным к пластине т заклепками одинакового радиуса г с постоянным шагом
R = 1/(т - 1), где / - длина стрингера (рис. 79). Вместо уравнений равно-
равновесия E.4) имеем уравнения
Pm=P*m-Nm-U
fffNH1 (/^l,m), G/ = G/ (/ = 1,2, ...,m),
с помощью которых условия совместности E.6) приводятся к виду
2 bk4Nj=N*k (*=1,2, ...,if!-l). E.8)
В формулах E.7) и E.8) обозначено:
b0 = 2(т? - 1 - 2к In e), fei = 6el = 1 + 2k In 2e,
^ = b_^ = 2/cln(l-^2) (кФ091)9
m
^•=7o-Д гк_,р;,
To = * A + к)Д Г y~ (ЛГП +iV2" ) + (Vfi -^V
-Го=Г_! =1+2к1пе, Гк = 2к1пA +А) (Аг^О.-l), e=—
1 У ?t^
l+v E0F0
181
В частности, при т = 2 (стрингер
приклепан двумя заклепками, R = /)
имеем
7о+О+2к1пе)(Л*-/У)
2(и-1-2к1пб)
и согласно уравнениям E.7)
Рйс. 79.
Рассмотрим некоторые численные
результаты. В зависимости от внешней
нагрузки, действующей на панель, мож-
можно выделить две характерные задачи
(см. рис. 79) : 1) задача включения в ра-
2,
боту панели от силы PJ = — 1 (/ = 1,
, т)\ 2) задача включения от внешнего поля пластины, задаваемого
тензором Л^. Описываемые ниже результаты вычислений получены при
R/r = 40 и т = 20. Коэффициент Пуассона материала пластины был принят
равным 1/3.
На рис. 80 и 81 показаны эпюры усилий в стрингере, вызванных изоли-
изолированно действующими силами Pi* = - 1 и Pi * = - 1, Для двух значений
относительного параметра жесткости пластины и стрингера: т? = 0,1 (внешние
эпюры, мощный стрингер) и т?= 10 (внутренние эпюры, слабый стрингер).
В силу уравнений E.7) скачки усилий над заклепками, свободными от
внешней нагрузки, равны передаваемым через них реактивным силам.
Как видно, для усилий в стрингере и сил, передаваемых через заклепки,
наблюдается своеобразный краевой эффект, зона затухания которого за-
зависит от значения параметра жесткости г?. Более полное представление о
влиянии этого параметра на усилия в стрингере в зоне действия внешних
нагрузок Р? = — 1 и Р\о = 1 дают кривые, приведенные на рис. 82 и 83.
Аналогичные кривые для усилий стрингера в зоне краевого эффекта,
обусловленного действием одного внешнего поля пластины, представлены
на рис. 84. Заметим, что на рис. 82—84 вдоль оси т?использован переменный
масштаб: слева и справа от точки т? = 1 отложены симметрично относитель-
относительно нее значения ци 1 \ц соответственно.
Большая часть результатов этой главы, публикуемая впервые, была по-
получена автором в 1976 году (см. Черепанов ГЛ. Асимптотическая теория
сопряжения упругих континуумов разных измерений. — Аннотации докла-
докладов. IV съезд по механике, Киев, 1976).
0,8
0,6
0,1
5 10
Рйс. 80.
0,4
0,1
О
-0,1
-0,4
Г0,1
182
0,8
0,4
„
0,4
0,2
-1
1—>2^"*
1Г
^^к^10
0,5 1,0 2,0
1,0
Ркс. 84.
Вычисления показьгоают, что изменение параметраR /г в области его ре-
реальных значений практически не влияет на величину усилий в стрингере
(а следовательно, и на величину сил, передаваемых через заклепки).
§ 6. Один аналог задачи Койтера*
Рассматривается плоская контактная задача о взаимодействии беско-
бесконечной пластины и полубесконечного стрингера через бесконечную систе-
систему жестких круглых включений (заклепок). Задача приводится к беско-
бесконечной системе линейных алгебраических уравнений с коэффициентами,
зависящими от разности индексов; точное решение этой системы строится
сведением ее к изученной проблеме Римана — Гильберта. Данную задачу
можно рассматривать как дискретный аналог задачи Койтера о кон-
континуальном взаимодействии пластины с полубесконечным стринге-
стрингером [81].
Постановка задачи. Пусть к бесконечной тонкой пластине приклепан
под углом/3 к осиОхх полубесконечный стрингер постоянного попереч-
поперечного сечения Fo (xt, x2 — прямоугольные декартовы координаты в сре-
срединной плоскости пластины,z =xx +/х2 — комплексная переменная).
Заклепки расположены с постоянным шагом R и имеют одинаковый ра-
радиус г (рис. 85).
Этот параграф следует работе [85].
183
Рис. 85.
Примем допущения теории Будян-
ского — By, приведенные в предыду-
предыдущем § 5.
Ограничимся рассмотрением случая,
когда пластина загружена на беско-
бесконечности постоянными усилиями, харак-
характеризуемыми тензором Nafi (а, 0 = 1,2),
а к центрам заклепок Zj приложены
сосредоточенные силы
j
Xf =
X*
j
Отделим мысленно стрингер от плас-
пластины и приложим к центрам заклепок
Zj пластины и стрингера неизвестные
j
силы взаимодействия Xj = XXj + iX
2j
j j j
и — Xj соответственно. Пусть Nj - уси-
усилие в стержне на участке между /-й и (j + 1)-й заклепками. Из равно-
равновесия части стрингера в окрестности/-й заклепки следует:
Xj = X* + (Nj-ej_lNj_l)eW (/ = 0,1,2,...), F.1)
' 10 при/ = -1,-2,.
С учетом обозначений
Р, +1<2; = Х;е-*Р, Pj*+iQf =X?e-i
соотношениям FЛ) можно придать вид
(/-0,1,2,...)
F.2)
Q, = Q*<J =0,1,2,...).
Отсюда, в частности, следует, что
Nk = ?(Pj-P?) (ft = 0,1, 2,...). F.3)
С целью определения передаваемых через заклепки неизвестных сил
Pj запишем условия совместности взаимных смещений смежных закле-
заклепок в пластине и стрингере. Пусть ук — взаимное смещение ft-й и (к + 1)-й
заклепок в пластине по направлению стрингера. Тогда
ук = Re {[w (zk+1)-w(zk) ] е-
0,1,2,...-),
F.4)
(B=Eh/(l-v>), K
F.5)
где соотношение F.5) для определения комплексного вектора переме-
перемещений w = Ui + ш2 записано согласно 148]; h — толщина пластины, vyE —
соответственно коэффициент Пуассона и модуль Юнга материала пласти-
184
ны,</>B)и ф (z)— комплексные потенциалы,/:^- модуль Юнга матери-
материала стрингера.
Для нахождения функций у (z) и ф (г) необходимо решить плоскую
задачу теории упругости для плоскости с бесконечным числом жестких
круглых включений, имитирующих заклепки. Однако в большинстве
практически важных случаев радиус заклепок мал по сравнению с их
шагом (r/R =0,02-0,1). Это позволяет ограничиться учетом асимптоти-
асимптотического взаимодействия включений и использовать принцип суперпозиции
в следующем виде:
Здесь
/=о
F.6)
2яA
Ц In {z-Zf) (/ = 0,1,2,...).
2ir A + к)
In (z-
xi
F.7)
где ^ B), i^ B) — потенциалы заданного однородного внешнего поля,
ty B), Ф1 B) - потенциалы для плоскости с одним/-м жестким круговым
включением, к центру которого приложена сила Xj.
Учитывая, что (r/RJ < 1, после некоторых преобразований условия
совместности F.4) при помощи соотношений F.5)-F.7) можно при-
привести к виду
Nk
/=0
Здесь
7o =
+ (Л
Г*г =
4тгД
1 + *>
-г_*_
A+*)?
8тгП -
1
S)cos
1 =
1
2
т
V
+
-1
к
+ 2Л^
2к1п
-2к
In A J
° +
1?
6
In
h 1
¦
sin 2/3
е
/*)
при
при
при
А:
* =
= - 1
0,
F.8)
F.9)
F.10)
185
Вычитая в системе F.8) из к-го уравнения (* - 1) -е уравнение (при
к = 1,2 ), с учетом F.2) найдем
/>0+со? Г./Р/^огуо+ЛЛ />*+со5 bk_jPj=Pk* (*=1,2,...),
/=0 /=0
F.11)
где
BГ0 при * = 0,
1+2к1п2е при 1 А: 1 = 1, F.12)
2к1пA -Г2) при |*|=2f3,...
Уравнения F.11) служат для определения передаваемых через заклеп-
заклепки сил/у, усилия в стрингере Nf- находятся затем из соотношения F.3).
Поле в пластине легко определяется по найденным Р; формулам F.1),
F.2), F.6) и F.7).
Решение бесконечной алгебраической системы. Следуя методу, предло-
предложенному ЯЛ.Фельдом [86], рассмотрим функции
F.13)
#(г)= 2
Так как
lim \bk
к - «>
i1
оо
=
lini
fc-»oo
+ ©о
Г(г)= S
[2к | In A
-
оо
г2
Г***.
) I]1
и ряд
? l) F.14)
Аг= 1
сходится, то функция В (z) регулярна на единичной окружности С. Можно
далее показать с помощью соотношений F.10), F.12), что
Я(г) = A -г) Г (г).
Предположим, что функции
fc = 0 * = 0
аналитичны в области D+ + C(D+hD_ - области внутри и вне единичной
окружности соответственно). В отношении функции Р* (z) это допущение
оправдывается после решения задачи. Аналитичность функции Р* (z)b об-
области /)¦ + С обеспечивается рассматриваемым характером распределения
внешних сил Рк*.
Из этих рассуждений следует:
1 (к)
Рк= —fp*WS~k' Xd$ = P @)/(*!) (*=0Л,2,...), F.15)
27Г/ С
причем
1 . \Рк при * = 0,1,2
T-.fP\t)S k -ldS = \ F F.16)
2т с @ при *= - 1, 2
186
Аналогичные соотношения имеют место для величин /\* и Р* (z).
С учетом этих выражений уравнения F.11) принимают вид
1 1+ыГШ +
— / Г—1- P*(S) di = сото + Л>*, F-17)
2т с f
P*(f)-^(i)
F^ dr"° t*-».2,...). F.18)
Здесь
G (?)' = 1 + сов (П = 1 + со A - f) Г (Г). F.19)
Введем в рассмотрение кусочно-аналитическую функцию
являющуюся решением краевой задачи Римана - Гильберта
P-U) = G(S)P\S)-P*(S) (Гее). F.20)
Тогда условия F.16) и F.18) будут выполняться в силу определения
функции/'(z), а уравнение F.17) с учетом F.19) и F.20) переходит в
соотношение
Z^G), F.21)
отражающее условие равновесия отдельного от пластины полубесконеч-
ного стрингера.
Согласно F.14) и F.19) функция G (f) (f € С) действительна и положи-
положительна, так что ее индекс по окружности С равен нулю. Поэтому решение
задачи F.20) имеет вид [47]
l inC(f) 1 р*ц) F22)
F±(z)=
/ rff, /4) /
Находя постоянную Р " (°°) из уравнения равновесия F.21)
p-(oo)= —^ LI -/A),
JTA)
запишем окончательно решение в следующем виде:
Отсюда согласно F.7) находим
<*)
г сото +РЧР r I ?jo) _L rrfrtjr *Ы1 w
(Л =0,1,2,...). F.23)
187
Отметим в заключение более удобную для вычислений форму записи
последнего уравнения. Для этого используем следующие рекуррентные
соотношения:
(&) (w) (к - т)
? (*»o
к ! А: т = о т ! (к-т)\
(к =1,2,...), F.24)
А: ! m = o m ! (/: - т)!
Обозначим
1 (*) 1
— / ln^(a) cos/tarfa (^(a) = G(e/o)). F.27)
7Г 0
ki UlxiW F<28)
Учитьтая, что
= exp[-F(l)],
F.29)
Xo
rff- —,
2
2я# с f - 1 2
при помощи F.23) - F.28) получим
Рл- = [ ШУ°\р,A) -f*O)]pk+h (* = 0,l,2,...), F-30)
где
Pit-_-Ls Ч^Х,, (*=1,2,...), F-31)
5* = 2 Pfc_m»?m (* = 0,l,2,...). F.32)
т = О
Численные результаты. В качестве иллюстрации полученного общего ре-
решения рассмотрим частный случай, когда внешнее поле отсутствует, т.е.
N™p = 0 и 7о = 0, а к крайней заклепке (к = 0) приложена силаХо* = е*$.
188
Тогда Ро* = Р* (z) = 1 ,f+ (z) = 0, щ = О, и согласно F.30), F.32)
Теперь требуется найти квадратуры F.27) и применить рекуррентную
формулу F.31).
На рис. 86 при v = 1 /3 представлены кривые зависимости усилий Ро и Рх в
двух крайних заклепках от относительного параметра жесткости со при
двух значениях параметра е, равных 0,02 (штрихи) и 0,1 (сплошные ли-
линии). Между этими значениями расположена область встречающихся на прак-
практике величин е. Вычисления проводились на М-222М; время счета составило
около двух минут, (при 17 точках на каждой кривой).
Отметим, что на рис. 86 вдоль оси со использован неременный масштаб:
левее 1 отложены значения самого параметра со, а правее 1 - значения
1 / со, так что при со < 1 точки со и 1 / со располагаются симметрично отно-
относительно точки <о = 1.
Зависимостьi\ ПРИ & = 2,3,... от параметра со качественно повторяет
кривые на рис. 86 Для Рх. О распределении сил Рк по заклепкам можно
судить по следующим данным (приведены значения 104Рк>к = 0,1,... ,5):
€
0,1
0,02
од
1,0
10
од
1,0
10
к = 0
6325
2617
871
5360
2089
689
1
1162
566
124
1397
537
112
2
526
376
91
651
369
84
3
294
280
74
355
277
69
4
185
222
63
216
219
59
5
126
182
55
142
179
51
Отметим, что при наличии одного внешнего поля, когда Л^ Ф 0, Хк* = 0,
имеем
что с точностью до множителя со совпадает с рассмотренным только что
случаем.
Следует отметить, что данная структурная теория приводит к числовым
результатам, вообще говоря, несколько отличающимся от числовых резуль-
результатов, полученных по бесструктурной теории. Это объясняется тем, что
в рассматриваемой конструкции заклепки с 1у0\
твердым вкладышем интеграл §[U]nx dL
по контуру жесткого включения отличен от
нуля. Аналогичный результат получается, если
включение предположить упругим, но с мо-
дулем Юнга и коэффициентом Пуассона, от-
отличными от основного материала.
При этом окончательные результаты оказы-
оказываются зависящими в некоторой степени от
размеров и конфигурации инородных, вклю-
чений, моделирующих заклепку.
—
о95 1>0
Рис. 86.
2,0
(О
189
Таким образом, бесструктурная теория позволяет четко указать те об-
общие требования, которым должна удовлетворять конструкция (структура)
заклепки, чтобы работа подкрепленной упругой системы в целом мало за-
зависела от структуры заклепок. Эти требования предполагаются выполнен-
выполненными всюду в §§ 3,4, 7 второй главы.
§ 7. Армирование трехмерных тел стержнями
В этом параграфе на ряде примеров иллюстрируется асимптотический
метод расчета трехмерных упругих тел, армированных нитями или стерж-
стержнями.
Растяжение полупространства со стрингером, прикрепленным в двух точ-
точках границы. Пусть упругое полупространство лг3 < 0 однородно растягива-
растягивается в двух направлениях напряжениями ох°1 и о2°2 • В двух точках гра-
границы полупространства @,0,0) и (/, 0, 0) к нему прикреплен прямолиней-
прямолинейный стержень, вообще говоря, из другого материала (рис. 87,а). Упругие
постоянные, относящиеся к трехмерному телу и к армирующему стержню,
здесь и в дальнейшем будем снабжать индексами 1 и 2 соответственно. На-
Начальную деформацию стержня (в момент, предшествующий началу нагруже-
ния) обозначим через бо .
Со стороны заклепок на полупространство действуют две равные и про-
противоположно направленные сосредоточенные силы Л которые требуется
определить из условия совместной работы стержня и полупространства
(рис. 87,б).
Приведем вначале необходимые решения из теории упругости. Пусть в
начале координат к свободной границе одномерного и изотропного полу-
полупространства х3 <0 приложена сосредоточенная сила (Xt, X2, Х3). Обо-
Обозначим через и* составляющую вектора перемещения вдоль оси xh вызван-
вызванную единичной сосредоточенной силой, приложенной в начале координат
и направленной вдоль оси**. Имеем следующие результаты (решение Бус-
синеска - Черутти [87,88]):
1 jc,2 1 - 2v xf (I - 2v)
+f + ^(/ = *=12)
r-x3 г(г-хъу
F2 Г-Х3
=--i -f + (/=1,2),
r \ r2 r-x3 I
= ^ [~ +2A-*)]
190
p *f
Рис. 87.
Здесь в упругих постоянных^ и v для краткости опущен индекс 1. Дефор-
Деформации и напряжения в упругом теле при произвольной силе легко опреде-
определяются при помощи формул G.1) на основании принципа суперпозиции,
закона Гука и кинематических соотношений.
Перейдем к нашей задаче (рис. 87). Рассмотрим замкнутую поверхность,
охватывающую заклепку в начале координат и состоящую из свободной
границы составного тела, поперечного стержня справа от заклепки и любого
сечения упругого полупространства, генерирующего Г-вычет. Предполо-
Предположим, что граница раздела различных материалов совпадает с плоскостью
х3 =0, а заклепка не имеет свободных границ, перпендикулярных этой
плоскости (т.е. стержень лежит на границе полупространства). Форма кон-
контактной площадки сцепления может быть произвольной; контур ее обозна-
обозначим через L. Рассмотрим инвариантный Г-интеграл B.29) по рассматрива-
рассматриваемой поверхности при к = 1 ; имеем
G.2)
Кроме того, согласно общим выражениям B.41) имеем в данной задаче
следующее значение Г-вычета:
Г$х)=Рщх G.3)
о
Здесьих у— в данном случае деформация полупространствам, , в начале
координат, возникающая под действием сосредоточенной силы в точке
(/, 0,0) и однородного растяжения. При помощи формул G.1) находим
Ех
G.4)
На основании выражений G.2) —G.4) получаем следующее соотношение
для внутренней задачи:
Г \ г О л i — V\ 04 2
FT -Ч- ~->—"л +р ;— • <7-5>
t2op I znnil Ei
Это соотношение позволяет оценить прочность точечной связи.
Работа заклепки характерного радиуса А описьюается закономерностью
Р> G.6)
д
1 /
^-Pl
2 V
Здесь ик — смещение заклепки в направлении оси хк под действием силы
\Р1<>Рг<>Ръ)* приложенной к заклепке, щк — известные из опыта коэффици-
191
-11
Phc. 88.
енты. В случае осесимметричной конструкции заклепки rjn = 1?2 г, Vi 2=r?-21 >
Vi з = 1?2 з, т?з l = *?з 2; по порядку величины 7]ik ~1 (кроме th 2 ~0).
Условие совместности в нашей задаче имеет вид
Р1
-/€о=/
Отсюда получаем
о1Х -
i e0
G.7)
G.8)
Используя начальную деформацию стержня, можно управлять напряжен-
напряженным состоянием полупространства (создавая, например, зоны разгрузки
или сжатия в области около середины стержня).
Тонкий стержень в бесконечном пространстве. Пусть конечный цилиндр
2 длины /произвольного поперечного сечения расположен вдоль ochXj в
бесконечном пространстве из другого упругого материала 1. Участки ши-
ширины А вблизи торцов цилиндра жестко сцеплены с материалом 7, а осталь-
остальная поверхность цилиндра свободна от нагрузок (боковая поверхность мо-
может также контактировать с материалом 1 в условиях свободного про-
проскальзывания, без трения). Предполагается, что длина цилиндра / гораздо
больше Д, а также характерного диаметра поперечного сечения. Другими
словами, две точки упругого пространства скреплены инородной упругой
связью (рис. 88,а).
Будем считать, что на бесконечности пространство подвергнуто однород-
однородному растяжению вдоль оси хх напряжением о{\. Кроме того, учтем на-
начальную деформацию стержня е0 в начале процесса растяжения. Эта величи-
величина имеет технологическое происхождение; она существенна, например, если
коэффициенты линейного температурного расширения материалов 1 и 2
различны, а началу растяжения предшествовал процесс охлаждения или наг-
нагревания составного тела. В точках @,0,0) и (/, 0,0) упругого пространства
1 действуют две равные и противоположно направленные сосредоточенные
силы Р (равные усилию в стержне), которые требуется определить из усло-
условия совместной работы только стержня 2 и пространства (рис. 88, б).
Упругое внешнее поле в данной задаче определяется суперпозицией реше-
решений B.35). Условие совместности совпадает с уравнением G.7); поэтому
сила Р определяется выражением G.8) при а2°2 = 0.
Следует отметить, что для внутренней заклепки одинаковые по обозна-
обозначению и смыслу коэффициенты щк будут отличны по величине от соответст-
192
\
•4»
1 z
Рис. 89.
вующих коэффициентов для заклепки, расположенной на свободной грани-
границе. Например, в случае сферически симметричной заклепки на основании
B.35), очевидно, имеем r\ik «0 при гФк^ц = щг = т?з з *** У*\ последние
коэф4»1циенты примерно в два раза меньше, чем для случая граничной
заклепки.
Расчет болтов крепления. Для укрепления бортов карьеров или кровли
подземных выработок в горном деле применяют болты специальной кон-
конструкции, служащие для создания сжимающих напряжений в заданной ос-
ослабленной области за счет легко управляемой деформации растяжения
болтов [89,90]. Встающие при этом проблемы и методы их решения проил-
проиллюстрируем на следующей характерной задаче.
Пусть упругое полупространство z>0 (горная порода) разбито на две не-
несвязанные между собой области (см. рис. 89, а, на котором волнистой линией
показана произвольная граница раздела этих областей). Для скрепления
этих областей бурится круглое отверстие, пронизывающее насквозь одну из
областей; в отверстие вставляется цилиндрический стержень (болт), внут-
внутренний конец которого жестко сцепляется с породой, а внешний — растяги-
растягивается при помощи резьбового соединения головкой болта, лежащей на гра-
границе полупространства*. Встает вопрос, каково напряженное состояшге по-
полупространства в зависимости от задаваемой деформации болта е0?
Нетрудно сообразить, что искомое напряженное состояние создается дву-
двумя равными и противоположно направленными сосредоточенными силами
величины?, одна из которых приложена к границе полупространства, а дру-
другая — в глубине тела (рис. 89, б). Сила Сравняется величине растягиваю-
растягивающего усилия в болте (в пренебрежении боковым трением). Деформацию
болта можно представить себе происходящей следующим образом (см. схе-
схематический рис. 89, в): вначале недеформированный тонкий стержень дли-
длины/закрепляется нижним концом в некоторой точке полупространства,
затем внешней силой стержень растягивается на величину еа / и скрепляется
верхним концом с граничной точкой полупространства; полученная упру-
упругая система представляется сама себе, в результате чего длина тонкого стер-
стержня уменьшается на некоторую величину ех /. Окончательная деформация
болта равна
Р
* Существуют различные технические способы скрепления концов болта с породой;
для дальнейшего расчета эти различия несущественны.
193
{Eb — модуль Юнга болта, Sp — площадь его поперечного сечения). Полный
путь закручивающей винтовой головки болта при затяжке, очевидно, равен
€0 /; его можно считать заданным. Требуется найти зависимость силы Р от
деформации е0 из условия совместной работы стержня с трехмерным упру-
упругим телом.
Условие совместности имеет следующий вид:
^йй^ G10)
Здесь индексы ей/ относятся к граничной и внутренней заклепкам соответ-
соответственно. Отсюда усилие, в болте равно
@bF
р= . G.11)
d AES(Sl4T)
Упругое поле в полупространстве описывается суперпозицией решения
Буссинеска (для нормальной краевой силы Р) с решением осесимметричной
задачи теории упругости о напряженном состоянии однородного полупрост-
полупространства z > О под действием сосредоточенной силы Р, приложенной в точке
г = 0, z = / и направленной вдоль оси z (r,z - цилиндрические координаты).
Приведем решение этой задачи, найденное Миндлином [91]:
_/) A-2*>H-0 3(z-/)
8тгA-*0 I R? R? RJ
30z/(z+/K 3C-4*/)z(z+/J -:
P(l-2v) \ z-l C-4i»)(z+/)-6/ 4A-1»)
°е - тт; т I "^т
— V)l Ki
-2v)Ri V
R2(R2+z+l)
G.12)
"r Sn (l-p) i
4 (i _ v) A - 2v)
R2(R2+z+l)
6/A -2v)(z+fJ
3r2
-6/2
R?
Az-
Rl
(Z +
/)
0
K2
30/r2z(z+/)
-3C-4*0r2 (z-l)
Ri
194
]¦
Рг Г \-2v \-lv 3 (z -1J 30/z(z-b/J
3C_4j;)Z(Z+/)_3/CZ+/)
]
Здесь v — коэффициент Пуассона полупространства.
Первое слагаемое *в знаменателе формулы G.11) представляет собой
"собственную упругость" полупространства в данной задаче. При]и/А>
>EbSF податливость полупространства пренебрежимо мала, упругое тело ве-
ведет себя как идеально жесткое. Если иметь в виду горную породу с обыч-
обычным отношениемЕь/Е = 2 + 10,то уже при/А/SF >50 собственной подат-
податливостью породы можно пренебречь и рассчитывать усилие в болте по гипо-
гипотезе идеально-жесткого основания
P=e0EbSF. G.13)
На рис. 90 приведена зависимость безразмерного усилия в болте Р от па-
параметра относительной податливости породы б
F4hr> 8
e0EbSF
Граничные условия при упругой заделке балки. Пусть произвольная кри-
криволинейная балка заделана своим концом в трехмерном теле любой фор-
формы, вообще говоря, из другого упругого материала. В асимптотической
постановке балка представляет собой пространственную упругую линию,
а заделка — точку в трехмерном теле.
Обозначим через Ut и X/ составляющие векторов перемещения и поворо-
поворота упругой линии балки, а через uf и ef — регулярные составляющие век-
векторов перемещения и вращения внешнего упругого поля в рассматриваемой
точке (заделке) трехмерного тела B?= rot м).
В асимптотическом приближении граничные условия в заделке будут
следующими:
ОД =1,2,3),
GЛ4)
Здесь Рк и Мк — составляющие векторов усилия и момента в заделке, А —
характерный структурный параметр ("радиус заделки"), fjt — модуль сдви-
сдвига материала в трехмерном теле, %ki и r}ki — эмпирические коэффициенты,
зависящие от конструкции и материала заделки. Наибольшие из этих коэф-
коэффициентов (при соответствующем выборе А) имеют порядок единицы для
внешней заделки и порядок 0,5 - для внутренней заделки.
195
Граничные условия G.14), так же
как и соответствующие условия
D.46) для двумерных задач, можно
вывести непосредственно при помощи
инвариантных Г-интегралов и теории
Г-вычетов. Уравнения G.14) представ-
представляют собой условия совместной ра-
работы балки и трехмерного тела в соот-
соответствующей заделке.
Большой интерес представляют так-
также сингулярные задачи об упругом
деформировании трехмерного тела,
армированного тонкими стержнями или нитями из другого материала, при
сплошной заделке стержня вдоль всей его боковой поверхности. Рассмот-
Рассмотрим некоторые характерные задачи.
Вдавливание жесткого узкого штампа в упругое полупространство.
Пусть основание жесткого параллелепипеда с размерами 2/ X 2 Л симмет-
симметрично давит на упругое полупространство х3 < О силой Р9 причем / > h
(рис. 91,а). При этом условии нормальное напряжение на площадке кон-
контакта в пренебрежении силами трения выражается следующей формулой:
N(Xl)
Gл5)
Здесь N(xi)— искомая функция (интенсивность сосредоточенной силы
на особой линии).
При помощи инвариантного интеграла Ту по контуру рис. 91,6 нетруд-
нетрудно найти следующую промежуточную асимптотику смещения м3:
1 — v г
при l>r>h м3=- ЛМп — (r2=xf+*!). G.16)
Г г 2 _ 2 2
ТГ/i Л
Вдали от штампа асимптотика соответствует сосредоточенной силе:
Р . . . .
при R
и3 =
G.17)
Покажем, что при / >h интенсивность N(xx) постоянна, за исключением
концевой области штампа, имеющей порядок нескольких h . Действитель-
ч
ч
Р
21
а)
Рис. 91.
196
но, скорость затухания краевого эффекта (т.е. влияния краев штампа при
хх =±0 определяется собственными числами следующей однородной крае-
краевой задачи:
irpHJC3<0 Ди3=0; при R^-<*> иъ -*0;
з^О, \x2\<h м3 2=0 (д = JL + JL +—V
V Элг| Ъх\ Ъх\Г
а=0 1*21>й w3,3=0. G.18)
Эта краевая задача допускает группу х[ = х1 + Сх, х'2 = х2>*з = *з; поэ-
поэтому ее решение имеет вид м3 = W(x2, x3) eXxi, где X - собственное
число краевой задачи.
Ранее [1] был доказан следующий общий результат (принцип Сен-Ве-
нана): для цилиндрических или призматических тел любого поперечного се-
сечения (с осью, параллельной оси xt в данном случае) собственные числа
X любой корректной однородной задачи статической теории упругости
удовлетворяют следующему строгому неравенству:
ReX<0. G.19)
Этот результат верен и в частном случае D.18). Следовательно, крае-
краевой эффект затухает экспоненциально, т.е. весьма быстро; поэтому в
асимптотическом приближении интенсивность Сбудет постоянной и равной
N=— . G.20)
Глубину внедрения узкого штампа др в упругое тело найдем, "сшивая"
промежуточную асимптотику G.16) с асимптотикой перемещения и3 при
х\ = х2 = 0, bc3 I > / под действием силы Р. Имеем
l_i/ r* lNC-2v)
8р= Nln — + — .
тгд h 2лцг*
Радиус "сшивания" г# выберем так:
h Xh
где а — некоторый параметр "сшивания" Отсюда получаем
1 - v I NC- 2v)
5Р= aNln— + —
пц h 2тг/1
При выборе естественного радиуса "сшивания " г* = / будет a = 1 и
формула упрощается:
^ . // г /з 1
5 = — ( 1 - v)ln — + v\. G.21)
тг/i L h 2 J
Армирование упругого пространства тонким прямолинейным стержнем
конечной длины. Пусть в бесконечном упругом пространстве имеется уп-
упругое включение из другого, более жесткого материала в форме прямого
кругового цилиндра радиуса г0 и длины 21, причем / > г0 (рис, 92, а). На
всей боковой поверхности цилиндра имеют место условия идеального сцеп-
сцепления. Пространство растягивается на бесконечности напряжением р вдоль
оси стержня Задача осесимметричная, поэтому удобно применять цилинд-
197
I
_Ч7_
21
Ю
m
(
\
\
\ (
J \
. r »
)
21
б)
Рис. 92.
рические координаты г = у/х\ + *| , z = jti. Касательное напряжение т на
^боковой поверхности цилиндра связано со средним нормальным напряже-
напряжением а в цилиндре следующим уравнением равновесия:
На расстояниях от стержня, гораздо больших г0, возмущенное упругое
поле совпадает с полем, порожденным сосредоточенными силами интенсив-
интенсивности Z(z), распределенными вдоль особой линии г = 0, \z К / и направ-
направленными параллельно оси z, причем очевидно, имеет место равенство
Z = 2я г0 т.
По условию в задаче имеется два малых параметра
x = i?^1> 6=?=<i. G.23)
/ ^
Обозначим: Ет, vm и ?у, iy~ модуль Юнга и коэффициент Пуассона
матрицы и стержня соответственно.
При X = 0 точное решение задачи при любых € будет следующим:
при г<г0
oz=- 2vfpA{ym -iy), oz=ge=-pA(ym-vf\
при r>rQ
G.24)
z ;
J 4
2 + 2 !/„
G.25)
1+^
198
ron
w
- 2vf)Yl).
Здесь и, w - перемещения по осям г hz соответственно, аг, а^, а2 — нап-
напряжения.
В дальнейшем для простоты положим vm = Vf. В этом случае точное ре-
решение будет следующим:
1
ах = — Р при r<r0, oz =р при г>г0,
ar""a<?" dz Em '
При сколь угодно малых X > 0 вблизи стержня возникнет возмущен-
возмущенное поле типа погранслоя, удовлетворяющее условиям
д Э
w>u, oz>or, oz>oe, — > — . G.27)
Ъг Ъг
При этом уравнения погранслоя будут следующими:
d2w I dw dw 3w
+ _ =0, az=?m — , rr2= Gm — ,
ЭГ Г дГ bZ ЪГ G.28)
dW 1 ?o_
Г Jz ' Г ~ 2 Г° dz
Здесь И^— перемещение стержня, Gm — модуль сдвига матрицы.
Решение уравнений G.28) имеет следующий вид:
w= — In — + W, Trz = г— ,
a2 »2A +^m)ror'(z)In — + W\z) G.29)
На границе погранслоя при г = г» решение G.29) должно "сшиваться'*
с невозмущенным решением dw/9z =p/Em ( r* - радиус "сшивания").
Отсюда получаем следующее уравнение:
й/'B)+ Jl ъИт'Мш JL . G.30)
Вместе с последним уравнением G.29) оно служит для определения
t(z) и W(z) в пограничном слое. Запишем решение этих уравнений, удов-
удовлетворяющее условиям симметрии ( при z = 0 г = 0, Н^ = 0). Находим
Р ~€gmax Jt?
Г h
T(Z) Л In— , G.31)
P ( P \ kz
a- - -^_ -amaxjch у . * -
\ kz
xjch у .
^ amaxjch у . * х2A+,тIп<Гф/Го)
Здесь атах — наибольшее значение а (при z = 0).
199
Напряжение о в концах стержня пренебрежимо мало; поэтому можно
положить при z = ± / а = 0.
Отсюда при помощи G.31) находим
<W =-(l- ~гА G.32)
€ \ chk I
Отметим следующие предельные случаи:
при к>\ атах= р/е, G.33)
при к < 1 атах = й Р*2/е. G.34)
Радиус "сшивания" г* выберем следующим образом:
где'а - некоторый параметр "сщивания" (порядка единицы).
Для точного определения этого параметра воспользуемся данными
численного расчета исходной задачи методом конечных элементов*. Рас-
Расчет был проведен при следующих значениях параметров: X = 0,01; vm*Q$\
е * 0,1,0,01,0,002; 10~3,1СГ4,1СГ5. В частности, при е = 10~5 было найдено
amax = ИЗО. Воспользуемся в этом случае формулой G.34); получаем
а = 0,738. G.36)
С учетом G.35) решение G.31) принимает следующий окончательный
вид:
1* / '
pip \ kz p / 1 \
о= l--0max)ch— , amax = —A-—— I, G.37)
6 \ e / / e \ chk J
P ro • ! л €
И/= z - ат —— in— k2 = —
Em Gm X aX2(l+^m)lnX-1
Сравнение этого решения с численными данными Г.П. Никишкова при
вышеуказанных значениях параметров показало следующее: функция
атах(е) совпадает с численными значениями.в соответствующих точках
с точностью 1%, функции t(z) и o(z) - с точностью 2% (за исключением
малой окрестности вблизи концов стержня порядка 2 г0).
На основании G.37) при е > 10 X2 In X наибольшее напряжение в
стержне практически равно р/е.
Основное в излагаемой теории уравнение G.30) можно получить также
строго при помощи инвариантных интегралов и теории Г- вычетов, исполь-
используя контуры, изображенные на рис. 92, б и в.
* Эти данные были получены Г.П. Никишковым.
200
На рис. 93 приведены графики функций t(z) и a(z) при к= 1,32 в без-
безразмерных переменных
ет
€0
z =—*
Как видно, с увеличением длины армирующего стержня максимальное
напряжение атах монотонно возрастает.
Из полученного решения вытекает следующее интересное следствие.
Обозначим прочность на разрыв стержня через оь- На основании G.37),
если
Х21пХ<;80,
где б0 =
6 I и P
- I arch
* »m) \ P ~
G.38)
V2
Г , то армирующий стержень раз-
рывается пополам.
Асимптотическое решение неравенства G.38) при малых X приводит
к следующему явному выражению:
G.39)
Величина в правой части G.39) играет роль неэффективной длины.
Это оптимальная длина армирующего волокна, при которой максимально
используются его прочностные свойства.
Настоящая задача была рассмотрена впервые автором в статье [200].
Однако в процессе решения были допущены вычислительные ошибки,
на которые обратил внимание Эшелби [201]. Эшелби предложил собст-
собственное приближенное решение этой задачи при е -*0, основанное на методе
Ландау и Лифшица решения задачи теории поля о проводящем цилиндре,
находящемся в однородном электростатическом поле диэлектрика. Вычисле-
Вычисления Эшелби привели, в частности, к следующему значению для максималь-
максимального напряжения в стержне (в наших обозначениях): amax = apk2fBe).
Сравнение с полученным решением G.34) и G.37) показывает, что при лю-
любых, сколь угодно малых, б результаты Эшелби дают весьма большую
погрешность (например, в десять раз при соответствующих X). Эшелби
указал, что его результаты по-
получаются также методами Ван- о,5
Дайка и Халлена.
Предложенный выше метод
прост, эффективен и достаточ-
достаточно точен. Его можно использо-
использовать для решения многих дру-
других аналогичных задач. Пусть, 0,2
например, к тонкому жесткому
прямолинейному стержню в уп-
упругом пространстве приложена
продольная сила Р в начале ко- 0 Q5 -
ординат (задача Келли); стер-
стержень расположен при г = 0,
1
¦У
У
\
Q5
Рйс 93.
201
0 <z < I. Напряжения на бесконечности — нулевые. Все остальные условия
и обозначения — те же, что и выше. Для напряжений в стержне опт полу-
получаются следующие выражения:
shit
-г)] (*¦¦?)
7 = Ch
shA:
Фактически матрица не может выдерживать касательных напряжений,
больших ts\ поэтому вблизи левого конца стержня на его боковой поверх-
поверхности образуется пластический слой, в котором т = ts. Длина этого слоя
равна / - /*, где /¦ согласно G.40) определяется как корень следующего
уравнения (локальная концентрация напряжений вблизи конца слоя не учи-
учитывается) :
/ а0 1 1 \
thfc*= \*kJ I, G.41)
\ 2т5 X X* /
где
Л* ¦— , К 4с _____
Предельная сила вытаскивания стержня из матрицы, очевидно, равна
Учет пластических слоев проскальзывания вблизи концов стержня
легко произвести и в предыдущей задаче.
Теории армирования упругих тел в регулярном случае A.1), а также
различным вариантам технической теории армирования, посвящено
очень много работ. Отметим из них лишь некоторые труды монографичес-
монографического или обзорного характера [92-112].
Задача о пучке волокон. Развитый выше асимптотический метод поз-
позволяет эффективно решать и более сложные задачи о взаимодействии лю-
любого числа волокон (стержней) в упругой матрице.
Пусть матрица представляет собой цилиндрическое или призматическое
тело произвольного поперечного сечения, содержащее в себе любое число
прямолинейных волокон различной конечной длины, параллельных обра-
образующей цилиндра и оси хъ. В каждом поперечном сечении цилиндра зада-
заданы усилие и момент, равные соответствующим усилию и моменту, при-
приложенным на бесконечности; боковая поверхность цилиндра считается
свободной от внешних нагрузок.
Рассмотрим некоторое поперечное сечение цилиндра Оху. Обозначим
через L контур зоны влияния волокон в этом сечении. По определению,
в области ZL внутри контура L * имеет место возмущенное упругое поле
и справедлива теория погранслоя; в остальной области D+ поперечного
сечения волокна отсутствуют, а упругое поле остается невозмущенным,
т.е. таким, каким оно было в теле без волокон. (Контур L для разных
сечений, вообще говоря, различен вследствие изменения числа и положе-
положения волокон.) Область D_ , вообще говоря, многосвязна.
202
Приведем основные уравнения теории погранслоя в области /)__:
дХ ' G.42)
bw I Ъ2 Ь2
(д— модуль сдвига матрицы).
На неизвестном заранее контуре L имеют место следующие граничные
условия:
dw dw
— = w0 + аох + boy, —- = Со (х3) G.43)
Ъхъ Ъп
Здесь п — нормаль к контуру L\ w0, a0, b0 — заданные постоянные, при-
причем и>0 = р/Е, где р - постоянное напряжение (в цилиндре без волокон);
PL — периметр контура L. Второе условие G.43) означает, что касательное
напряжение тпЪ не изменяется вдоль контура!».
В области Ь_ имеется 7V волок он в точках (xkf ук)9 где к = 1,2, 3,... JV.
В этих точках перемещение w имеет логарифмическую особенность
(не суммировать !) G.44)
npnz
причем
->z^ vv= In
М
+ W
1
do
dx3
r
, r
= E
+ Wk (не
= lz-Zfcl),
G.45)
Здесь Wki ak9 rk,Efk - перемещение, нормальное напряжение, радиус
и модуль Юнга соответственно, относящиеся к к-му волокну.
Требуется определить контур L и напряжение ок в каждой нити.
В случае однородного растяжения при достаточно редком расположении
волокон контур L представляет собой совокупность окружностей с радиу-
радиусами, определенными формулами G.35) и G.36). При пересечении окруж-
окружностей задача усложняется.
Укажем общий метод решения задачи для любого числа взаимодействую-
взаимодействующих нитей в случае односвязной области ZL.
Введем комплексный потенциал /(z) следующим образом:
~ = Ref(z), ~ (r, + /т„) = цШе'а. G.46)
Ъхъ охг
Здесь а — угол между осями х и t (t, n — произвольная декартова система
координат), индекс 3 у касательных напряжений опущен.
При помощи функции z = о)(?) конформно отобразим область D_ на
внутренность единичного круга If t < 1 плоскости f. Для двух ис-
искомых функций F(f) =/(a>(f)) и cu(?) согласно G.43)-G.46) получаем
203
следующую нелинейную краевую задачу:
2 Wq +flcj(f) ¦+
Ftf) = С la/(?) I;
при If И.
при
Здесь
C=2C0'
G.47)
G.48)
G.49)
—
G-50)
Краевое условие G.47) можно записать в виде
Подставляя отсюда
при If 1= 1 С la
в G.48), находим
где r*(f) и T~(f) аналитичны при If I > 1 и If l< 1 соответственно. Следо-
Следовательно, функции r*(f) и r~(f) составляют единую, аналитическую во
всей плоскости f функцию F(f),_имеющую заданные логарифмические
особенности в точках f = f k и f = Г/J. Получаем
= S Ak In j~\ . G.52)
7'53)
Далее рассмотрим лишь случай а = 0 (однородное растяжение — сжатие).
Введем новую функцию A(f j = In [Cco'(f )] .Так как при If I < 1 a/(f) =?0,
функция A(f) будет аналитической при If К 1. Согласно G.53) имеем
при If 1=1 ReA(f) = ln?(f). G.54)
Используя решение этой задачи Дирихле, получаем
^/0, arg co'@) = 0). G.55)
= ехр [ -i- У In g(i0)
L 2
При помощи G.49) и G.52) находим
Вк = a co(ffc) + 2 w0 - Ак In (Г*1 - Г*) • G.56)
Подставляя сюдаЛ^ и В к согласно G.50), получаем систему N нелиней-
нелинейных дифференциальных уравнений второго порядка относительно функций
204
ок(х3)> Решение этой системы позволит определить напряжение в каждом
волокне (на конце волокна напряжение равно нулю). После этого коэф-
коэффициенты Ак вычисляются по формулам G.50) и подставляются в форму-
формулы G.52) и G.55), определяющие напряжения в матрице и контур L.
Параметр Pi в рамкдх данной асимптотической теории остается неопреде-
неопределенным (параметр "сшивания").
При достаточно плотном расположении нитей во всем поперечном сече-
сечении цилиндра погранслой исчезает, за исключением концов нитей; невоз-
невозмущенное поле охватывает всю матрицу. В этом предельном случае напря-
напряжения в нитях и матрице определяются по "правилу смесей" (см. гл. 1).
Вырождение погранслоя может происходить и локально, в местах наиболее
плотного расположения волокон или вблизи свободной боковой поверх-
поверхности цилиндра.
Исторические сведения
В 1967 году Черепанов [3] предложил общий метод получения инвариантных ин-
интегралов, основанный на физических законах сохранения. Этим методом был полу-
получен [3] инвариантный энергетический интеграл для произвольного твердого тела:
/-интеграл Эшелби - Раиса [2,5] является его частным случаем. При таком подходе
инвариантность Г-интеграла оказывается тривиальным следствием закона сохранения
(на основании этой инвариантности в работах [3,4] были использованы различные
контуры для вычисления Г: в форме окружности и прямоугольника). В той же работе
[3] впервые было сформулировано условие ограниченности Г как необходимое усло-
условие корректности той или другой модели твердого тела. Далее, в [3] была предложена
общая теория разрушения твердых тел; соответствующая основная константа разру-
разрушения Тс обозначалась там через 27 (введенная позже константа Раиса Jc равна 2у в
частном случае нелинейно-упругих тел). В работах [1,15,123] дано развитие этого
метода.
ГЛАВА 3
ОПТИМАЛЬНОЕ ПРОЕКТИРОВАНИЕ НЕКОТОРЫХ
КОМПОЗИЦИОННЫХ МАТЕРИАЛОВ НА ОСНОВЕ
МЕХАНИКИ РАЗРУШЕНИЯ
§1. Введение*
Наиболее простыми по структуре композиционными материалами яв-
являются многослойные листовые материалы, состоящие из нескольких
однородных слоев. Вязкость разрушения и конструкционная прочность
однородной пластины зависят от ее толщины; максимум этих величин
достигается при некотором значении толщины, зависящем от материала и
технологии изготовления пластины [1]. Обычно эта толщина довольно
мала (например, для большинства конструкционных металлов она из-
изменяется в пределах 10~3^ 1(Г6м). Поэтому даже однородный листовой
материал, набранный из слоев одного и того же материала, обычно имеет
большую прочность на разрыв и более надежен при растяжении, чем моно-
монолитный лист из того же материала. Механика разрушения позволяет пос-
поставить и решить проблему оптимального проектирования многослойных
материалов; эти вопросы излагаются ниже в порядке нарастающей труд-
трудности.
Теорией оптимального проектирования конструкций с других позиций
занимались многие исследователи. В обзорных статьях [118, 119] подроб-
подробно изложено состояние вопроса вплоть до 1968 г. (в основном, по иност-
иностранным источникам). Хорошим обзором работ отечественных исследо-
исследователей является доклад [120]. Исследования последних лет отражены в
работах [121,122,59].
Применение многослойных материалов в авиации. Многослойные
конструкции широко используются в различных областях техники, преж-
прежде всего в авиационной и ракетной технике, а также в судостроении, жи-
жилищном и промышленном строительстве, энергомашиностроении и нефте-
нефтехимической промышленности [124, 125]. Рациональное проектирование
конструкций из многослойных материалов позволяет достигнуть высокой
хрупкой прочности, ударной вязкости и долговечности, требуемых звуко-
и теплоизоляционных свойств, демпфирующих и вибропоглощающих
характеристик. Применение слоистых конструкций началось с авиации.
Практические возможности использования слоистых материалов тесно
связаны с технологической операцией соединения слоев. В 1941 г. фирмой
Air Research (Англия) был зпервые разработан процесс "редукс" для
склеивания металлических панелей. При разработке этого метода оказалось
[126], что в отличие от деревянных склеивание металлических конструк-
* Параграфы 1-4 этой главы написаны совместно с В.М. Смольским. Они основаны
на работах [113-117].
206
ций технологически более сложно, однако по сравнению с клепкой этот
способ соединения дешевле и создает более прочные соединения. Так, при
испытаниях оказалось, что прочность клееной панели на 30% выше клепа-
клепаной. С тех пор процесс "редукс" находит широкое применение в граж-
гражданском самолетостроении Англии. В качестве примеров можно привести
самолет максимальной скорости "Хорнет" и военный морской самолет
"Москито". Склеивание многослойных конструкций в английском авиа-
авиастроении применяется и в настоящее время. Так, у штурмового и учебно-
тренировочного самолета "Ягуар" (Франция — Англия) в обшивке приме-
применены слоистые панели, в районе кабины - сотовые конструкции [127].
Заметим попутно, что метод "редукс" успешно применяется также для
крепления резины к металлам. Достигаемая прочность примерно равна
прочности сцепления при гальваническом покрытии металлов. Это имеет
важное значение при монтаже резиновых прокладок на металл для умень-
уменьшения вибраций.
Отмечается [128], что фрезерование алюминиевых панелей для фюзеля-
фюзеляжа американского реактивного самолета "Боинг-737" связано с целым
рядом трудностей. Значительного упрощения процесса производства пане-
панелей добились соединением листов промежуточным слоем адгезионной
пленки. Для строительства самолета "Боинг" требовались панели толщи-
толщиной 1,8 мм, отдельные участки которой фрезеровались бы на глубину
0,9 мм. Как показали испытания, такие панели имеют высокий предел
прочности на срез в широком диапазоне температур. Было решено исполь-
использовать систему панелей из двух спаренных листов по 0,9 мм из алюминие-
алюминиевого сплава 2024-ТЗ (более 50 панелей максимального размера от 152,4 мм
до 3902,2 мм - в каждом самолете для изготовления фюзеляжа, дверей и
люков). Адгезионная пленка йрименяется в качестве защитного средства
при химическом фрезеровании. К тому же двойные панели обладают от-
отличной характеристикой по гашению вибраций.
Фирма "Боинг" продолжала успешно применять слоистые панели и в
других самолетах. Весной 1963 г. были начаты первые разработки круп-
крупнейшего в то время пассажирского самолета "Боинг-747". За всю 50-лет-
50-летнюю историю авиакомпании программа создания этого самолета была са-
самой значительной. Достаточно заметить, что производство было начато в ан-
ангаре объемом 4,5 млн.м3 A мая 1967 г.). Склеенные металлы применены в
этом самолете в следующих узлах: горизонтальные и вертикальная по-
поверхности хвостовой части, нижняя и верхняя несущие панели крыльев
[129].
В 1990-х годах в США ожидается появление космического самолета
второго поколения [127]. Как известно, в 1963 — 71 гг. в США разрабаты-
разрабатывался сверхзвуковой транспортный самолет "Боинг-2707" [130].
Разработка прекращена в 1971 г., а в июне 1972 г. продолжена. Согласно
данным [131], для осуществления проекта необходимо снижение веса
конструкции на 15-20%, что можно достигнуть лишь благодаря примене-
применению композитных и слоистых материалов.
По пути создания крупногабаритных клееных панелей пошла другая
американская фирма "Локхид" [132]. Фюзеляж самолета "Тристар",
построенного этой фирмой, представляет оболочку полумонококовой
конструкции с диаметром до 5,97 м. Клеевое соединение используется по
207
всей длине герметизированной части D6 м) и для присоединения усиливаю-
усиливающих двойных и тройных накладок вокруг вырезов в обшивке. Обшивка
и стрингеры поддерживаются шпангоутами из листового металла, располо-
расположенными на расстоянии примерно 1,5 м друг от друга. Размеры склеивае-
склеиваемых панелей 11,6 х 4,6 м2, что вдвое больше любых ранее склеиваемых
панелей в самолете. Это позволило сократить количество соединительных
швов обшивки и увеличить усталостную долговечность. Для склейки при-
применялся самый крупный автоклав с размерами 6,7 х 20 м2.
Весьма интересное исследование конструкции крыла самолета-истреби-
самолета-истребителя Convair проведено фирмой "General Dynamics" [133 - 135]. В качест-
качестве исходного (базового) варианта для сравнительной оценки был выбран
кессон крыла самолета F-111, отвечающий с точки зрения веса, долговеч-
долговечности, стоимости и других проектных параметров современному уровню
техники. Элементы кессона крыла этого самолета, который является
одновременно и топливным отсеком, выполнены механической обработ-
обработкой из плит алюминиевого сплава 2024-Т851. Крепление нижней панели к
каркасу осуществляется с помощью механического крепежа.
Для проведения количественной оценки исследуемых вариантов кон-
конструкции была использована система весовых коэффициентов, разработан-
разработанная лабораторией динамики полета ВВС. Основные задачи при разработке
перспективных вариантов конструкции кессона крыла были следующие:
а) определение, по крайней мере, одного варианта, который дает сниже-
снижение веса на 15% по сравнению с исходным вариантом при одинаковой или
меньшей стоимости;
б) определение хотя бы одного варианта, который дает снижение стои-
стоимости на 15% при том же весе;
в) разработка промежуточного варианта с максимальной долговеч-
долговечностью.
На начальном этапе рассматривалось 119 вариантов конструкции при
весьма различных технологических процессах их изготовления. По резуль-
результатам аналитической оптимизации для дальнейшей проработки были выб-
выбраны девять вариантов; после их оценки по весу и стоимости выбраны
два наиболее эффективных.
На рис. 94 показан вариант кессона крыла, представляющий сотовую
конструкцию со специальным гофрированным заполнителем на всю тол-
толщину кессона (сечения А и В на рис. 94 показаны с установленными
верхними панелями). Титановый сотовый заполнитель имеет перфорацию
для прохода топлива B — перфорированные грани ячеек, 3 — стенка
переднего лонжерона). Для улучшения характеристик допустимой пов-
повреждаемости и обеспечения передачи нагрузки титановая нижняя обшивка
выполнена многослойной с накладками. Сборка верхней и нижней обши-
обшивок с сотовым заполнителем осуществляется пайкой мягкими припоями
для обеспечения максимальных прочностных свойств титановых сплавов
G— пайка мягкими припоями). Конструкция с уменьшенным числом кон-
концентраторов напряжений в сочетании с пониженной скоростью распростране-
распространения усталостных трещин в многослойной паяной нижней обшивке дает воз-
возможность выбрать необходимые толщины материала, исходя из действую-
действующих напряжений 64,5 кгс/мм2. Данный вариант конструкции является наибо-
наиболее легким из всех рассмотренных и вторым по максимальной стоимости.
208
Pfcc.94.
Многослойная панель
нижней оо~шивки (А)
Z
1
Рйс. 95.
Снижение веса по сравнению с исходным вариантом составляет 38,8%, а
увеличение стоимости — 31%.
На рис. 95 показан вариант кессона крыла, который был классифици-
классифицирован первым по сравнению с остальными и представляет собой много-
лонжеронную конструкцию с гофрированными стенками. Цифрами на этом
рисунке обозначены следующие элементы конструкции: 1 — слоистые
панели нижней обшивки, 2 — гофрированная стенка, 3 — нижняя полка
лонжерона, 4 — передний лонжерон, 5 — клеесварка, 6 — прессованная полка,
7 — химически отфрезерованная пластина, 8 — стенка заднего лонжерона,
9 — гофрированный лонжерон, 10 — верхняя полка лонжерона, 11 —
верхняя обшивка. Верхняя обшивка выполнена химическим фрезерова-
фрезерованием из плиты алюминиевого сплава 7050-Т73651, а нижняя — клееной
из листового алюминиевого сплава 7050-Т76, при этом в зонах, где
209
критическими являются циклические напряжения, механический крепеж
отсутствует. Крепление верхней панели к заднему и промежуточным
лонжеронам осуществляется через широкие полки, связанные с гоф-
гофрированными стенками. Такая конструкция является наиболее эконо-
экономичной по сравнению с механически обработанными лонжеронами и
позволяет повышать напряжения сжатия от изгиба верхней панели. Дан-
Данный вариант конструкции кессона дает снижение веса на 24,2% и умень-
уменьшение стоимости на 13,8% по сравнению с исходным.
В исследовании отмечается, что разработанные конструкции кессона
крыла имеют ряд преимуществ перед конструкцией крыла самолета
F-111, и они были достигнуты за счет следующих характерных изменений:
1) исключение механического крепежа и других концентраторов нап-
напряжений в нижних растянутых элементах, что позволяет нижней обшивке
работать безопасно при высоком уровне напряжений;
2) изготовление многослойной нижней обшивки с накладками при
помощи пайки или склейки; такие соединения обеспечивают безопасность
повреждения (остановку распространения поверхностного дефекта),
увеличивают критическую дайну трещин при плоском напряженном
состоянии в тонколистовых обшивках и уменьшают скорость развития
трещин за счет перераспределения нагрузки (поэтому в определенных
конфигурациях можно использовать сплавы, которые нельзя использовать
в монолитных конструкциях из-за низких характеристик вязкости раз-
разрушения) ;
3) повышение устойчивости обшивки как в сотовом варианте, так и в
варианте многолонжеронной конструкции.
В Японии применение клееных панелей находится в стадии разра-
разработки. Ожидается [136], что клееные панели фюзеляжа увеличат усталост-
усталостный срок службы соединений и улучшат характеристики безопасности
каркаса самолета по сравнению с заклепочными соединениями. Кроме того,
герметизация кабины упрощается, если она выполнена с помощью клеево-
клеевого соединения. Еще совсем недавно клеевые соединения не применялись в
авиационных силовых конструкциях, исключая поверхность рулей управ-
управления, лопастей роторов вертолетов и второстепенных элементов конструк-
конструкций, например полы кабин. Данный вид соединений является относительно
новым в самолетостроении этой страны. Склеивание элементов конструк-
конструкции фюзеляжа осуществляется при повышенной температуре в автоклавах;
основной проблемой является достижение однородности качества
склеивания.
Следует заметить, что многослойные конструкции используются и при
производстве транспортных средств, прежде всего, баков давления, кузовов,
цистерн и контейнеров, нефтяных танкеров. Именно в этих конструкциях
требуется уменьшение веса с сохранением прочности [137].
Наряду со склеиванием, успешно применяется и метод горячей прокат-
прокатки для соединения листов в многослойную панель. С этой целью филиал
Северо-Американской авиационной фирмы в Лос-Анжелесе сконструи-
сконструировал и установил на своем заводе одну из крупнейших в мире вакуум-
вакуумных печей с охлаждающимися стенками для твердой пайки многослойных
конструкций. Печь имеет размеры 0,914 X 1,524 X 2,438 м3, максимальная
температура нагрева 1158°С [138]. Для соединения слоев из алюминие-
210
вых сплавов применялась тонкая пленка коммерчески чистого алю-
алюминия.
В отличие от отечественного самолетостроения капиталистические стра-
страны не применяют заклепочные соединения как ведущие соединения лис-
листов или подкрепляющих элементов, а применяют или разрабатывают
соединения многослойных панелей склеиванием, горячей прокаткой с тон-
тонким слоем мягкого материала или порошка и т.д. Дальнейшее имеет
ввиду в первую очередь именно такие соединения листов в многослойную
панель; однако все выводы годятся и для заклепочного соединения мно-
многослойной панели, если пренебречь двумя факторами: а) весом заклепок по
сравнению с весом панели; б) уменьшением прочности панели из-за кон-
концентрации напряжений в заклепках.
Масштабный эффект. При проектировании слоистых конструкций
большие требования предъявляются к их прочности. Поскольку критерия-
критериями проектирования здесь будут выбраны хрупкая прочность и долговеч-
долговечность (время безопасного распространения трещины) листового материа-
материала, прежде чем проектировать материал, необходимо количественно оце-
оценить зависимость прочности отдельного листа от его толщины.
Оценка прочности элементов конструкций основана на концепции ста-
статической прочности, принадлежащей Галилею и заключающейся в том, что
предельное разрушающее растягивающее напряжение — предел прочности—
является постоянной материала и не зависит от геометрии конструкции.
Эта концепция позволяет оценивать статическую прочность конструкции,
если предварительно определить на малых образцах из этого материала пре-
предел прочности материала конструкции. Чтобы предел прочности материала
образца соответствовал пределу прочности материала конструкции, ста-
стараются сохранить геометрическое и механическое подобие образца и
конструкции. Под механическим подобием в частном случае статического
нагружения внешними силами и давлением понимается выполнение сле-
следующих требований [139]:
ЛГ2 = const, p = const, A-0
где Р — внешняя сила, р — давление, а - характерный линейный (соот-
(соответствующий) размер образца и конструкции.
Накопление практического опыта испытания материалов показало, что
имеется много существенных отклонений от этой концепции. Поскольку
эти отклонения означают влияние масштабов или размеров образца или
конструкции, все причины, вызывающие отклонения от закона подобия,
называют масштабным фактором, а само проявление его — масштабным
эффектом.
Для масштабного эффекта есть металлургические и технологические при-
причины. Металлургические причины заключаются в различии качества метал-
металла в крупных и мелких слитках, а также в различной термомеханической
обработке материала для создания из него образца или конструкции. Тех-
Технологическая причина масштабного эффекта заключается в том, что практи-
практически невозможно достаточно точно смоделировать эквивалентные техноло-
технологические процессы, что связано как с трудностью создания соответствую-
соответствующего оборудования, так и с трудностью создания одинаковых условий
нагрева для толстых конструкций и тонких листов при технологической
211
6)
б)
Ркс. 96.
обработке. Но даже при последовательном приближении металлургических
и технологических условий для образца и конструкции масштабный эф-
эффект будет весьма существенным при хрупком или квазихрупком разру-
разрушении, т.е. при существенном влиянии трещин на процесс и параметры раз-
разрушения. Действительно, в рассматриваемом случае сквозных трещин в
пластине постоянной будет вязкость разрушения/^ (а не предел прочности),
которая связана с характерным внешним давлением р и длиной трещины /
следующим образом:
Kc^otpy/HF. A.2)
Здесь безразмерный коэффициент а зависит от относительных размеров
конструкции и трещины (а также от безразмерного отношения различных па-
параметров нагрузки). Таким образом, условиями механического подобия
при квазихрупком разрушении вместо условий A.1) будут следующие:
Ра~У2 =const. A.3)
Вместе с условиями геометрического подобия эти соотношения состави-
составили бы необходимые и достаточные условия моделирования, если бы вели-
величина Кс не зависела от толщины пластины. Для большинства конструк-
конструкционных металлов значение Кс существенно зависит от толщины пластины.
Поэтому в большинстве случаев изучение хрупкого разрушения и роста
трещин на моделях ме'нылего масштаба практически невозможно.Следова-
невозможно.Следовательно, в рассматриваемом случае масштабный эффект нельзя описать прос-
простым законом A.3).
Физическую природу этого явления легко понять, если пронаблюдать
структуру фронта сквозной трещины в пластине из упруго-пластического
материала.
Вблизи свободных поверхностей пластины условия пластического де-
деформирования близки к плосконапряженному состоянию (когда скольже-
скольжение происходит по плоскостям, лежащим под углом 45° к плоскости плас-
пластины) , а в глубине пластины условия пластического деформирования близ-
близки к плоской деформации (когда скольжение происходит по плоскостям,
перпендикулярным плоскости пластины).
На рис. 96, а изображен фронт трещины в ее плоскости, а на рис. 96Д и
96,в — фронт трещины в сечении, перпендикулярном ее плоскости (б —
весьма тонкая пластина, отвечающая плоскому напряженному состоянию
и косому срезу под 45°, в — более толстая пластина, в средней части кото-
которой реализуется плоская деформация и прямолинейный фронт).
212
Полезно ввести следующую величину [140]:
Х= jc/Л, A.4)
где h — толщина образца, х — ширина прямолинейного в плане фронта тре-
трещины (рис. 96). Величина X характеризует долю состояния плоской дефор-
деформации в объемном напряженном состоянии в окрестности конца трещины.
Для тонких образцов X * 0 и разрыв происходит при плоском напряженном
состоянии; берег трещины имеет форму среза. Для толстых плит X ^ 1 и
разрыв происходит при плоской деформации; форма берега трещины в пла-
плане почти прямолинейна ("губы среза" у свободных поверхностей пластины
относительно незначительны). Промежуточному напряженному состоянию со-
соответствует некоторое промежуточное значение X, причем с возрастанием h
от некоторого начального значения h0 величина X сначала резко возрастает,
затем асимптотически приближается к единице. Аналогично происходит из-
изменение всех характеристик хрупкой прочности (вязкости разрушения Кс,
ударной вязкости, кривой усталости [140]), т.е. все они в области резкого из-
изменения X меняются резко, а в области медленного приближения X(/z) к
асимптоте изменяются мало (см. рис. 96, гид).
Статистическое описание масштабного эффекта. При построении статис-
статистической теории хрупкой прочности отвлекаются от описанной выше физи-
физической природы этого явления и оценивают опасность разрушения от де-
дефектов статистически.Тем самым природа масштабного эффекта объясняет-
объясняется лишь статистической закономерностью распределения дефектов в мате-
материале в зависимости от характерного размера (объема, площади или линей-
линейного размера) материала V. Вероятность P(V) отсутствия в теле размером
V неоднородности критических размеров легко получается из следующих
гипотез:
1) неоднородности равномерно распределены по объему;
2) неоднородности независимо распределены по объему;
3) вероятность отсутствия дефекта критических размеров в бесконеч-
бесконечном объеме равна 0.
Найдём эту вероятность. Рассмотрим два непересекающихся объема, Ки
Vx. В силу первых гипотез
P(V+Vl)=P(V)P(Vl). A.5)
Возьмем производную от обеих частей по V и разделим полученное ра-
равенство на соотношение A5); получаем
d d
— libP(K+Kj)= — lnP(K). A.6)
dV dV
Отсюда следует, что функция d[\n P(V)]/dV не зависит от своего аргу-
аргумента, т.е.
d
— \nP{V) = const = с. A.7)
dV
Интегрируя уравнение A.7) при начальном условии Р (°°) =0 (гипотеза 3),
получаем
<ГсК. A.8)
213
Бели считать, что попадание в объем V единственной неоднородности
критических размеров приводит к разрушению этого объема, то вероят-
вероятность разрушения (fracture) равна
Pf(V) = 1 -P(V) = l-e-*v. A.9)
Заметим, что уравнение A.9) имеет совершенно общий характер и не
зависит от допущений относительно физической природы неоднородностей,
поскольку оно вьюедено из чисто вероятностных гипотез 1 -3.
Формула A.9) легко обобщается на тот случай, когда для разрушения
необходимо не менее п неоднородностей критических размеров:
? ^. AЛ0)
1 к=П к\
Плотность вероятности разрушения получаем отсюда дифференцирова-
дифференцированием по V:
(cVY1
Ц± A.11)
что является плотностью гамма-распределения вероятностей. Из формул
A.9) и A.10) следует, что вероятность разрушения растет с ростом объема.
Таким образом, увеличение вероятности разрушения с ростом характер-
характерного объема (площади или длины) рассматриваемого образца вытекает из
вероятностных рассуждений, если считать, что разрушение обусловлено
критическим числом неоднородностей атомной структуры. Однако даже
статистический учет этих неоднородностей атомной структуры не позволяет
приблизить статистическую теоретическую прочность к экспериментальной.
В механике разрушения уменьшение прочности с увеличением объема
объясняется наличием макроповреждений в реальных телах. Введение пов-
повреждений типа трещин делает возможным анализ полей напряжений вокруг
них на основе линейной теории упругости. С помощью таких представлений
может быть количественно объяснено большое различие между теоретичес-
теоретической прочностью атомных связей и реальной макроскопической прочностью,
наблюдаемой на образцах конечных размеров, без необходимости рассмот-
рассмотрения неоднородностей атомного масштаба.
Расчетная модель статистической теории разрушения состоит в замене
однородной среды с теоретической однородной прочностью средой с извест-
известной неоднородной прочностью с помощью следующих допущений:
а) повреждения различной степени опасности распределены в среде так,
что каждое из них определяет прочность окружающего его объема;
б) взаимодействие повреждений исключается;
в) прочность элементов объема связана с размерами повреждения —
трещины по теории Гриффитса;
г) прочность любого макроскопического образца определяется проч-
прочностью того элемента объема, который содержит наиболее опасное повреж-
повреждение (концепция наислабейшего звена).
На базе этих допущений, используя формулу A.2), можно установить
связь между вероятностными распределениями прочности Fp(x) и длин тре-
трещин Fi(x):
( ^)(^ A.12)
214
Хотя распределение длин трещин по различным объемам определить
трудно, для распределения максимального размера дефекта по различным
объемам Фреше получил следующую формулу [141 ]:
-(х/и)-0]. A.13)
Тогда по предыдущей формуле получаем
Fp(x) = I -.exp [ -(*/«0а*Ь A.14)
где v = у/пКс/(а у/и) (и и 0 — постоянные материала).
Теперь необходимо предсказать прочность образца в целом. Используем
последнее допущение. Применяя аналогичные приведенным выше вероят-
вероятностные рассуждения, получаем аналог формулы Фреше для вероятности
того, что х есть прочность п К-объемов:
Ф„(*) = ехр[-л(х/и)-0], A.15)
откуда сразу следует выражение функции распределения общей прочности
от объема:
Здесь Vo — характерный объем однородных образований в материале.
Если посчитать моменты этого распределения, то нетрудно найти, что
средняя общая прочность и ее среднеквадратическое уклонение умень-
уменьшаются с ростом объема, а коэффициент изменчивости от объема не за-
зависит.
Параметр 0 является мерой дисперсии повреждений: чем больше 0, тем
ближе распределение размеров трещин к однородному и тем меньше влия-
влияние плотности повреждений, которое исчезает совсем при полностью одно-
однородном распределении их размеров. Это является результатом принятия
концепции наислабейшего звена.
Изложенный вариант статистической механики разрушения полезен и
конструктивен для изучения таких вопросов, как зависимость прочности
хрупких волокон и нитей от их длины, а также зависимость прочности
хрупких и квазихрупких пластин от площади их поверхности (при
одинаковых условиях работы различных точек вдоль волокна или плас-
пластины) .
Однако такой подход малоконструктивен для изучения влияния толщи-
толщины пластины на ее прочность и вязкость разрушения. Гораздо более эффек-
эффективным является подход, излагаемый ниже и основанный на непосредствен-
непосредственных экспериментальных данных.
Количественное описание масштабного эффекта в механике разрушения.
Для получения аналитической зависимости К\{К) аппроксимируем экспе-
экспериментальные данные зависимости от h эффективной энергии разрушения
7(h) для алюминиевого сплава 7075-Т6 и титанового сплава ВТ-14 (табли-
(таблица 1.1).
215
2h0
Экспериментальные данные ло сплаву 7075-Т6 [ 142 ]
Таблица 1.1
6,75
3,5
2,5
2,15
1,85
Аналитические зависимости
1
2
3
6,75
6,75
6,75
3,68
3,45
3,48
2,76
2,3
2,39
2,15
2
2,03
1,85
1,9
1,85
Экспериментальные данные по сплаву ВТ-14 [143]
3,9
2,2
1,7
1,6
1,5
Аналитические зависимости
1
2
3
3,9
3,9
3,9
2,4
2,2
2,3
1,9
1,68
1,77
1,65
1,53
1,59
1,5
1,48
1,5
Для аналитической аппроксимации можно использовать следующие вы-
выражения:
2h)=K2lc+(K2c0-Kl)^ (h>h0),
со
1+21
(Kc0 -i
Лс)' 3 ' ° \п^ /to)
), К1с = lim Kc(h))-
A.17)
Из табл. 1.1 видно, что экспериментальные данные по сплаву 7075-Т6
лучше приближаются третьей аналитической зависимостью, в то время как
данные по сплаву ВТ-14 лучше приближаются второй зависимостью. На-
Наибольший интерес представляет область малых толщин (h0 < Л < 4Л0)> где
можно практически пользоваться любой из указанных аппроксимаций.
В дальнейшем будем пользоваться второй зависимбстью, поскольку она
имеет точку перегиба, как и экспериментальная кривая.
К аналогичным результатам приводят аналитические аппроксимации
экспериментальных данных других авторов. Отметим по данному вопросу
следующие экспериментальные работы: по сталям [144 - 147], по титано-
титановым сплавам [148,149], по алюминиевым сплавам [150 — 152]. Например,
для алюминиевого сплава 7075-Т6 максимальное значение Кс равно ЪК\С и
достигается дпя пластины толщиной h0 = 1,2 мм. Излагаемые ниже мето-
методы представляют интерес также для оптимального проектирования безопас-
безопасно повреждаемых элементов конструкций [15.3].
216
§ 2. Однородные» пластаны максимальной долговечности*
В данном параграфе на основе теории роста усталостных трещин [1] оп-
определяется оптимальная толщина однородной пластины, работающей при за-
заданной циклической нагрузке (нагрузка может быть напряжением или уси-
усилием) . В некоторый момент времени пластина может подвергнуться задан-
заданному однократному усилию-перегрузке. Для выбора оптимальной толщины
пластины используется критерий максимального времени роста в ней уста-
усталостной трещины.
Эта задача является весьма важной для оптимального проектирования
простейших композиционных материалов — многослойных пластин и обо-
оболочек, когда все слои — из одного и того же материала. Наиболее дешевая
и простая технология соединения металлических слоев — холодная прокат-
прокатка с использованием специальных плакировочных адгезионных пленок.
Можно ожидать, что в ближацшем будущем будут изготовляться таким спо-
способом все важнейшие,несущие толстостенные элементы металлических
конструкций (атомные и химические реакторы, сосуды давления, трубо-
трубопроводы, броня танков, корпуса судов и подводных лодок и т.д. [1]).
Эта технология позволит также освоить более прочные марки сталей, ко-
которые при старой технологии были малонадежны.
Считается, что пластина имеет небольшую сквозную начальную трещину
длины 2/0, которая медленно подрастает под действием циклических экс-
эксплуатационных нагрузок до некоторого критического значения 2/с, начи-
начиная с которого распространяется неустойчиво, так что происходит разру-
разрушение пластины.
Согласно теории роста усталостных трещин, из всех моментов времени,
когда перегрузка может произойти, наибольший рост трещины перегрузка
вызовет в завершающий момент разрушения. Поэтому естественно считать,
что величина 1С определяется однократной аварийной перегрузкой, а уста-
усталостный рост трещины происходит под действием лишь циклической нагруз-
нагрузки. При этом за счет смещения однократной перегрузки в конец процесса
нагружения получается оценка долговечности пластины снизу.
В качестве примеров определена оптимальная толщина панелей из сле-
следующих материалов: алюминиевые сплавы Д16Т и В95, титановый сплав
ВТ-14; мартенситно-стареющая никелевая сталь HI8 (американская марка).
Излагаемый подход может быть использован также для выбора оптималь-
оптимального материала на основе какого-либо дополнительного критерия (удель-
(удельной прочности, стоимости и т.д.).
Оптимизация долговечности пластины, работающей при заданном цикли-
циклическом напряжении. Пусть на плоскую пластину толщины h с внутренней
сквозной трещиной длины 2/ действует одноосная циклическая нагрузка
Р (t), где 0<pmin<p(t)< Ртах • На участках возрастания напряжения p (t)
трещина будет необратимо подрастать. Скорость роста усталостной трещи-
трещины определяется по формуле [1]
dn [К2 \ К1-ж1р2тЫ /J
* Этот параграф основан на работе [117].
217
Здесь Кс - вязкость разрушения пластины (зависящая от ее толщины),
п — число циклов, а — постоянная материала (на зависящая от толщины
пластины).
Из формулы B.1) получаем следующее выражение для долговечности
пластины (числа циклов до разрушейия л#):
1 ic dl
5 '
a i. ДО
Ы
/
1-
Кс -
Здесь 1С — критический размер трещины, равный
B3)
В силу B2) и B.3) долговечность «¦ зависит от толщины пластины толь-
только через Кс.
Дифференцируем интеграл B.2) по переменной К%; получаем следую-
следующее выражение:
_Ли__»в( Ы . , /. Ы
d{K\)~ |,
1 11 dl ^ dlc /dn\
которое с помощью равенства
К2С
(K2C - nlp2max) (A* -
и интегрирования по частям приводится к виду
1
in) J
rf(^c) к2 Xdi /| /, rf(^)\a/ /"¦'с
Отсюда при помощи B.3) получаем окончательную формулу
с/и. /0 I
B4)
Из формулы B.4) следует, что долговечность пластины при действии
циклического напряжения монотонно растет с увеличением вязкости
218
разрушения. Известно [1], что вязкость разрушения металлических плас-
пластин имеет хорошо выраженный максимум при определенной толщине
пластины/t0 (различной для разных материалов). Следовательно, пласти-
пластина толщины Ио обладает наибольшей долговечностью при заданном цикли-
циклическом напряжении.
Относительное изменение долговечности с толщиной панели для алю-
алюминиевого сплава Д16Т приведено в таблице 2.2.
Таблица 2.2
Л/Ло
It a \*t /
1,2
0,95
1,5
0,77
2
0,55
3
0,41
4
0,37
Определение оптимальной толщины пластаны, работающей при цикли-
циклическом нагружении и одноразовой перегрузке. Допустим, что, кроме
циклического нагружения, панель должна выдержать также некоторое
одноразовое (например, аварийное) усилие величины N, большее значения
hpmax. В этом случае критическая длина трещины 1С равна
h2K2c
а долговечность п* зависит от А- через посредство двух переменных К\ и /с.
Для определения оптимального значения h приравняем нулю полную
производную п. по h и используем B.4)
эл
/о
dh
2hK2c
= 0.
dn.. = Jln^ d{Kf) dn
dh ~ d(K2) dh Ыс
B.6)
Из этого уравнения определяется оптимальное значение h при заданной
функции Kc(h).
Безразмерная величина Ыо/К2. в большинстве случаев, представляющих
практический интерес, значительно меньше единицы; разложением в ряд
по этой величине получаем следующее соотношение:
и формулу B.6) преобразуем к виду
dh
N2
B.7)
где
bh2
219
На рис. 97 последовательно построены качественные графики функций
bh2 bh2
n(N2 -h2p2min) irN2
h dKl
у dh
Функция g(h) монотонно возрастает на [09N/pmax], g(h)-+ — °° при
A ~* 0>8(М/ртлх) = °> кривая х (Л) пересекает # (h) в одной точке, отку-
откуда следует единственность решения уравнения B.7). Кроме того, из гра-
графика ясно, что корень уравнения B.7) находится в области d (K2)/dh < 0
или h>h0. Таким образом, единственный максимум долговечности име-
имеется и при наличии перегрузок. Представляет интерес вопрос, насколько
корень уравнения B.7) отклоняется от h0 в зависимости от /0. Рассмот-
Рассмотрим случай, когда эксплуатационная нагрузка мала по сравнению с перегруз-
перегрузкой, т.е
bh2 h2p2
Разлагая функцию g(h) по этим двум малым параметрам, получаем со-
соотношение
2ЛГ4 Г / N2 N2
2ЛГ Г Iff1 N2 Х\
= -7Т74 ГТ+ ° тах(т7'ГТ~ '
и условие B.7) приводится к виду
d(K2) _ 2nl0N2
Заметим, что формулу B.8) можно получить также из формулы Пэ-
риса [1]
dl a
— ~ -— (К — К - ^ Г2 9^
dn К\ шах шш
Действительно, на основании формулы B.9) имеем
А
п»=—г
Pminf v/o Iс 9 h dh hic
Формула B.8) с учетом B.5) идентична последнему равенству.
Зависимость вязкости разрушения пластины #c от ее толщины h ап-
аппроксимируем вторым аналитическим выражением A.17)
2(й/Л0 - IJ
B.10)
220
1,2-
1,1
Рис. 97.
оуг о,4 о,б
Рйс. 98.
Используя это выражение, решение уравнения B.8) можно записать
в виде
, 2Х(Х-1)
где
|2 '
/о Кс0
B.11)
Л **" ттшт, о —
На рис. 98 изображен график зависимости безразмерной оптимальной
толщины пластины X от безразмерной аварийной нагрузки 5.
Следует заметить, что при расчете реальных пластин необходимо про-
проверять выполнение обычных для механики разрушения предположений:
характерный размер пластины (длина или ширина) велик по сравнению
с 1С и N/h<098ob.
Примеры, Рассчитаем оптимальную толщину пластины, находящейся
под действием циклической нагрузки, когда
кгс _ кгс
Ртах - Ю 2> Р™»1 "" * 2 *
ММ ММ
Исходные данные для расчета взяты из работ [142,143,1, i54,155].
А. Алюминиевый сплав Д16Т:
h0 = 2,5 мм, Кс0 = 240 кгс/мм3/2,
Kic = 120 кг/мм3/2, оъ = 45 кгс/мм2, N = 50 кгс/мм,
/с = 45,8 мм, /0 =7 мм при Х=1,1.
Оптимальная толщина пластины равна hQ =2,5 мм, если длина началь-
начальной трешины 21 о меньше 14 мм. Если же 2/0 >14мм, то оптимальная
221
толщина пластины для данного усилия будет больше 2,5 мм (точное ее
значение в зависимости от /0 определяется формулой B.11), см. рис. 98).
В. Алюминиевый сплав В95:
h0 = 2 мм, Кс0 = 240 кгс/мм3/2, АГХс = 118 кгс/мм3/2,
оь = 583 кгс/мм2, Л" = 40 кгс/мм,
/с = 46 мм, /0 = 7,3 мм при X = 1,1.
Оптимальная толщина пластины равна h0 = 2 мм, если длина начальной
толщины меньше 14,6 мм.
В.Мартенситно-стареющая никелевая сталь Н18:
h0 = 1 мм, А:с0 = 700 кгс/мм3/2 , КХс = 300 кгс/мм3/2,
оь = 120 кгс/мм2, W= 100 кгс/мм,
/с .= 15,6 мм, /о = 2,7 мм при X = 1,1.
Оптимальная толщина пластины равна hQ = 1 мм, если начальная дли-
длина трещины меньше 5,4 мм.
Г. Титановый сплав ВТ-14:
h0 = 0,8 мм> Кс0 = 300 кгс/мм3/2, К1с = 175 кгс/мм3/2,
оь = 120 кгс/мм2, N = 50 кгс/мм;
/с = 7,2 мм^ /0 = 1 мм при X = 1,1.
При длине начальной трещины менее 2 мм оптимальная толщина пласти-
пластины равна 0,8 мм.
Долговечность пластины, работающей при заданном циклическом уси-
усилии и одноразовой перегрузке. Пусть на пластину с трещиной начальной
длины 21 о действует усилие, циклически меняющееся от 0 до Nx, где Nx —
некоторая заданная величина, не зависящая от толщины панели h. Как
и ранее, будем считать, что пластина должна выдержать одноразовую пере-
перегрузку N. Долговечность пластины оценивается по формулам B.2), B5),
где следует взять
nN\
*=ТГ > Pmin=0. B.12)
п
Соотношения B.12) позволяют упростить формулу B.2), рассматри-
рассматривая ее правую часть как интеграл, зависящий от параметра h. Дифферен-
Дифференцируя п* по h , используя соотношение
ЪЬ~Ь Э/
и интегрирование по частям, получаем
*..2b_Js_f»aS)t
dh h аАД/о) [ К* dh
222
Считая, как и ранее, что blo/Kl < 1, приходам к следующему диффе-
дифференциальному уравнению для определения nm{h):
+*^ +2Л:Л B.14)
Поскольку для металлических материалов hKc(h)— обычно монотонно
возрастающая функция, второе слагаемое положительно, и поэтому дол-
долговечность панели — возрастающая функция ее толщины.
Решая уравнение B.14) при начальном условии и* = 0 при 1С = /0 или
h2K2(h) = nl0N2, получаем следующую формулу:
Легко видеть, что формула B.15) справедлива не только для циклов с
Pmin = 0, но также в том случае, когдарт{П < 0. В последнем случае нуж-
нужно формально считать, что рт1П = 0 (это равносильно физическому допу-
допущению: трещина не подрастает за тот промежуток цикла, на котором дей-
действует напряжение сжатия [ 1 ]).
Таким образом, при заданном циклическом усилии оптимальная тол-
толщина пластины определяется из какого-либо дополнительного ограниче-
ограничения на толщину пластины. Например, если из ограничения на вес пласти-
пластины следует, что И <Л«, то настоящее рассмотрение показывает, что опти-
оптимальной толщиной с точки зрения долговечности при заданном цикличес-
циклическом усилии будет h *.
Применение полученных результатов к проектированию. Рассмотрим
вопрос оптимального проектирования как однородных пластин, так и
многослойных пластин из одного и того же материала. Прежде всего сле-
следует различать случаи заданного напряжения или усилия (результаты оп-
определения оптимальной толщины панели в этих случаях различны даже
качественно). Это особенно существенно для легких равнопрочных кон-
конструкций.
Так при проектировании летательных аппаратов (ЛА) большей грузо-
грузоподъемности на базе некоторой модели ЛА, стараются сохранить действу-
действующие напряжения, увеличив толщину стенки конструкции (возможно,
при этом требуется увеличить и размеры несущих элементов конструк-
конструкции) . В связи с проявлением масштабного фактора, у более толстостенной
конструкции уменьшается хрупкая прочность, что является причиной
уменьшения ее долговечности. Чтобы увеличить нагрузку, выдержива-
выдерживаемую однородной пластиной, без уменьшения долговечности пластины,
надо настолько изменить ее толщину, чтобы оставить неизменным не дей-
действующее растяжение, а размерное отношение o(h)/Kc(h) (при этом счи-
считается, что остальные размеры пластины остаются примерно теми же).
Если при таком изменении толщины пластины окажется, что она близка
к удвоенной начальной толщине, то значительно более выгодно, с точки
зрения хрупкой прочности и долговечности, создать двухслойную панель
(клееную или соединенную горячей прокаткой с промежуточным вязким
слоем [1,150,152]). Хрупкая прочность двухслойной панели, составлен-
составленной из тонких слоев, примерно в полтора раза выше хрупкой прочности
223
монолита той же толщины, а долговечность ее будет выше примерно в 5
раз (или, при той же долговечности, можно в полтора раза поднять эксплуа-
эксплуатационные циклические нагрузки!). Именно поэтому фирмой "Локхид"
фюзеляж самолета 'Тристар" сконструирован двухслойным [132].
Особенно значительно можно поднять хрупкую прочность и долговеч-
долговечность толстых плит, создавая их конструкцию многослойной. Для толстой
многослойной плиты вязкость разрушения близка к Кс0 (при соответству-
соответствующем подборе слоев), в то время как для однородной плиты эта вели-
величина близка к Kic, т.е. примерно втрое меньше; долговечность при одина-
одинаковых нагрузках для многослойной плиты становится больше, чем у моно-
монолита, примерно в 80 раз.
При начальном проектировании конструкции ЛА (а не доработке из-
известной модели) исходят из усилия, которое должна выдержать пласти-
пластина; таким образом, в этом случае долговечность пластаны растет с ее
толщиной (при этом напряжения в ней падают и конструкция в целом
может оказаться неравнопрочной).
Как показано в этом параграфе, хотя одноразовая перегрузка и из-
изменяет долговечность однородной пластаны (или многослойной пласта-
пластаны, составленной из одинаковых слоев), на оптимальную толщину плас-
пластины одноразовая перегрузка влияет только при сравнительно больших на-
начальных размерах дефекта. Если одноразовой перегрузки нет, то оптималь-
оптимальная толщина пластаны при заданных напряжениях равна толщине пластаны
с максимальной вязкостью разрушения независимо от размера начально- *
го дефекта (трещины).
Результаты настоящего параграфа можно применить к проектированию
пластаны и в более общем случае, когда действующие на нее кратковремен-
кратковременные перегрузки являются случайными. Действительно, пусть на пластину
с внутренней сквозной трещиной помимо циклической нагрузки действу-
действует перегрузка со случайно меняющейся амплитудой и одной и той же дли-
длительностью интервалов нагружения (такая ситуация характерна, например,
для панелей ЛА). Мысленно перенесем перегрузки большой амплитуды в
конец процесса нагружения; вычисленная при таких нагрузках долговеч-
долговечность панели будет хорошей оценкой снизу истинной долговечности. Бели
известно распределение вероятности амплитуд перегрузок (которое вклю-
включает и эксплуатационные циклические нагрузки), то долговечность пане-
панели можно оценить следующим образом:
л= /3 n(s)dsf B.16)
°i
1
n(S) =
a ls
Здесь концы отрезков интегрирования Ls определяются следующим об-
образом: /0 считается заданным, 1С определяется максимальной перегруз-
перегрузкой ог по формуле B.3), а остальные Ls определяются из соотношений *
~= const, ULs=[l0,lc]. B.17)
* ULS - сумма отрезков Ls iio всем s в смысле теории множеств.
s
224
Плотность распределения вероятности амплитуд нагрузок обозначена
через <р(х), причем ох <х<а2,а функция /(/,«) определяется формулой
B.2) при s=pmuX. Задача определения толщины пластины, имеющей
максимальную долговечность B.16) при ограничениях B.17), определя-
определяющих значения величин LS9 является довольно сложной при произвольной
функции <^(х),цо при малом времени действия перегрузок ее решение
легко предсказать: оптимальной толщиной пластины будет величина h0,
независимо от величин LS9 если величина /0 достаточно мала.
Таким образом, оптимальное решение оказывается устойчивым по отно-
отношению к мгновенным перегрузкам, если время действия перегрузок не-
незначительно по сравнению с временем действия эксплуатационных цикли-
циклических нагрузок.
Долговечность однородной пластаны с трещиной, подверженной слу-
случайной нагрузке * . Будем считать, что плоская пластина равномерно
нагружена в одном направлении напряжением ? @, являющимся диффе-
дифференцируемым случайным процессом. В момент времени t0 в пластине
имеется сквозная внутренняя трещина длины 2/0, ориентированная пер-
перпендикулярно направлению нагрузки. Считая величину /0 много меньшей
длины и ширины пластины, коэффициент интенсивности напряжений и
малое приращение длины трещины в момент t можно выразить в виде
[1] *•
Кг = |@\/лГ, Л = 20 -J dKx при Кг > О, <ЙГ, > 0. B.18)
Предположим, что в области устойчивого подрастания трещины выпол-
выполнено одно из неравенств
(fill) {KilKef <l, | ? @dl\ < | /rf$(r)|.
Тогда из соотношений B.18) получим зависимость
207Г2 , .
— $3$ при ?>0и|>0,
B.19)
0 при ?<0 или |<0.
Усредним обе части равенства B.19) по реализациям процесса ?@
и изменим в левой части порядок дифференцирования и усреднения. Про-
Проинтегрировав полученное дифференциальное уравнение от t0 до среднего
момента разрушения панели **, получим соотношение
1 1 . 20тг2 и
<->=—Г f A(")du, B.20)
где
^@= 7 7 x*yp(x,y,t)dxdy.
о о
Здесь скобки О — усреднение по реализациям % (t)\p (xr, yy t) — совместная
плотность вероятности процесса %(f)n его производной, зависящая от t
неявно через характеристики {•(*);/¦— критический размер трещины.
* Этот раздел основан на работе [156].
225
Уравнение B.20) является функциональным уравнением для опреде-
определения среднего времени до разрушения t*. Вычислим эту величину в слу-
случае, когда ? (г) нормальный, дважды дифференцируемый, стационарный
случайный процесс с математическим ожиданием т, дисперсией а2и ко-
коэффициентом корреляции к (г)# В этом случае [157]
1 f I \{x-mf у2 11
р(х,у, t)=p(pc,y) = - ехр - - v-—i + — , B.21)
Inooi [ 2 I о2 о\ J J
величины A(t)n A/U) не зависят от t и соответственно равны
А= / дгехр — \dx =
2па \ Ч 2а2 J
2
max
1
/*
2 /^
7T<^max>
К2
2
ol
о2 -t
.2 i
) к
IV
, @)
-
о1
a?+4(
'o\
4 _2
2
B.23)
Формула B.23) получена усреднением распределения относительных
максимумов [157] дважды дифференцируемого стационарного случай-
случайного процесса ? @ . Поэтому с вероятностью 1 оценка среднего времени
до разрушения t*9 когда /«оценивается по формуле E), мало отлича-
отличается от среднего значения времени разрушения панели.
Подставляя B.23) в B.20), получим
,.-,..-$- [1-^4 B.4,
2/Зя2Л L/ К2 У V '
где А определяется формулой B.22). Попутно получается оценка сверху
К* /1 jtw2\
t, - t0 < —с— ( — . B.25)
2рп2А \/0 К2С I
В случае, когда зависимость коэффициента интенсивности напряжений
от характерного размера трещины более сложная по сравнению с трещиной
226
Гриффитса
*i = $(') П(О, B26)
получим следующую формулу, аналогичную B.19):
20 ...
1 dl
7@ А"
^4 « * ИР"
О при ?<0 или ?<0,
B27)
и для определения среднего времени до разрушения получим функци-
функциональное уравнение, обобщающее B.20):
I* dl 2/3 U
'~47?в7Г f A(u)du> B28)
/о г (О *$ *.
где величины IqJ*J* и функция Л(г) имеют прежний смысл.
В качестве примера рассмотрим усталостный рост поверхностной полу-
полуэллиптической трещины с равнопрочным контуром в пластине под действи-
действием стационарной случайной нагрузки ?(t).B [1] приводится следующее
выражение функции ц (/) для этого случая:
П\Ъ) = 0,0105 (KbJ \ 5~(*/*}ч 1 , B.29)
L 2 - (b/h) J
где Ъ - глубина растущей по всему фронту трещины, h - ширина пластины.
Из формул B.28) и B.22) для t* получим выражение
К\с ь, \2-(v/h)Y dv
• 0,0105 {
или в безразмерном виде
/^с 0,021 тг2 х;
-./2-х\*Л
(xo=bo/h, x*=b*/h<0A).
Для последнего интеграла в [1] дано приближенное аналитическое вы-
выражение, используя которое приходим к окончательной формуле
8QAh(t*-t0) 1 1 6 х* 3
-? = _ _ - _ -in — + - (х. -Хо)9 B.32)
Ajc JCo X* 5 Хо 10
где х* определяется из равенств B.23), B.26), B.29):
0,1024юс*И <е2тах >(^1J= К21с . B.33)
\ 2 —х*/
Формулы B.24) и B.32) для долговечности однородной пластины
позволяют определить оптимальную толщину пластины максимальной
долговечности в случае сквозной и поверхностной трещины соответствен-
227
но. Например, в случае сквозной трещины согласно B.24) для заданных
случайных нагрузок и заданного материала долговечность прямо про-
пропорциональна Кс и, следовательно, оптимальная толщина будет совпадать
с толщиной пластины максимальной вязкости разрушения. В случае не-
несквозной трещины оптимальная толщина пластины согласно B.32) за-
зависит от глубины начальной трещины.
§ 3. Оптимальное проектирование многослойных пластин (непрерыв-
(непрерывная задача)*
В этом параграфе предлагается подход, позволяющий оптимально про-
проектировать некоторые неоднородные соединения. К таким соединениям от-
относятся клеевые соединения, соединения горячей прокаткой с химически
чистым металлом или порошком и др.
Вначале формулируется принцип равнопрочности, составляющий идей-
идейную основу оптимального проектирования конструкций и инженерных
материалов. Рассматривается вопрос об алгоритмизации процесса вы-
выбора оптимального материала. Затем анализируется прямая задача о плос-
плоском напряженном состоянии многослойной пластины из различных мате-
материалов со сквозными трещинами. Рассматривается постановка основных
обратных задач оптимального проектирования многослойной пластаны.
Выделяются безаварийный и аварийный режимы работы пластины, при-
приводящие к некоторым математическим проблемам дробно-линейного
программирования. Каждая из сформулированных проблем разбивается
на дискретную (являющуюся частным случаем общей задачи оптимального
конструирования и решенную в следующем параграфе) и непрерывную
задачи; для решения последней применяется метод множителей Лагран-
жа. Рассмотрены конкретные примеры оптимального проектирования
шестислойных пластан.
Предложенный подход годится также для оптимального проектирова-
проектирования многослойных безмоментных оболочек.
Принцип равнопрочности. Работоспособность конструкции зависит
от следующих основных факторов, тесно связанных между собой: ге-
геометрия конструкции, материал, внешние нагрузки, температура и агрес-
агрессивность среды и тд. Пусть параметры хх, х2,...,хп описывают эти фак-
факторы для некоторого проекта конструкции. Для определения возможных
проектов необходимо в пространстве параметров {хх ,х2,... ,хп) найти
область безопасной работы конструкции. Если такая область существует,
то нужно найти оптимальный проект, т.е. определить такие значения пара-
параметров, для которых выполнялось бы определенное условие экстремума
(например, условие минимального веса или максимальной прочности
конструкции). Прямой и очевидный метод решения задачи оптимального
проектирования заключается в решении весьма большого числа прямых
задач для различных комбинаций параметров и в последующем сравнении
полученных решений по требуемому критерию с целью выделения един-
единственного решения. Задача конструктора заключается в том, чтобы ра-
разумно сузить круг конкурирующих проектов, подвергаемых точному
расчету и испытаниям.
* Этот параграф основан на работах [ 113,114 ].
228
В рамках примерно заданной геометрии конструкции весьма полезен
эвристический принцип равнопрочности, сразу приводящий к некоторой
прямой математической проблеме относительно оставшихся неопреде-
неопределенными параметров искомого решения (например, толщины оболочки).
Примем следующие допущения А, Б и В.
А.Конструкция сделана из достаточно надежного материала, т.е. не
содержит опасных трещиноподобных дефектов металлургического или
технологического происхождения, не обнаруженных методами неразру-
шающего контроля.
Б. Конструкция работает в условиях, исключающих опасное развитие
в ней эксплуатационных трещин за требуемый промежуток времени (к
эксплуатационным относятся усталостные, коррозионные и другие тре-
трещины) .
Эти допущения позволяют считать конструкцию "бездефектной" и
для определения условия локального разрушения пользоваться фено-
феноменологическими теориями,-3/которых отсутствуют структурные пара-
параметры, характеризующие несовершенства материала (размер трещины,
величину зерен или пор и т.д.). При этом критерий разрушения опреде-
определяется опытным путем на гладких образцах; размеры образца, состо-
состояние материала, из которого он изготовлен, вид нагружения и условия
внешней среды должны имитировать соответствующие условия для рас-
рассматриваемого элемента конструкции.
Существенным недостатком теорий прочности является то, что в слу-
случае сложного напряженного состояния локальное разрушение часто не
приводит к разрушению всей конструкции. Фактически в окрестности
опасной точки появляется либо пластическая зона, либо образуется тре-
трещина, которая развивается с увеличением нагрузок. Поэтому расчеты
по феноменологическим теориям дают неудовлетворительные результаты
для концентраторов напряжений — надрезов, выточек и т.п.
В. Локальное разрушение приводит к разрушению или потере работо-
работоспособности конструкции в целом.
Согласно этому допущению можно пренебречь развитием пластичес-
пластических зон и трещин от момента их возникновения до потери несущей спо-
способности всей конструкции. Очевидно, это допущение идет в запас проч-
прочности.
Конструкцию, удовлетворяющую допущениям А, Б, В, будем называть
равнопрочной, если она спроектирована так, что разрушение в ней начи-
начинается одновременно во всех точках конструкции (или же, если послед-
последнее невозможно, в максимально большой части конструкции). В такой
конструкции весь материал "работает" равномерно, и для заданного
материала равнопрочность является также достаточным условием ми-
минимального веса конструкции. Указанное требование, предъявляемое
к конструкции при ее проектировании, будем называть принципом равно-
равнопрочности. Этот принцип сводится к известному принципу равнонапря-
женности лишь в простейших частных случаях.
Для многих важных случаев соображения принципа равнопрочности
позволили сформулировать и решить прямые нелинейные математические
проблемы для отыскания оптимальной переменной толщины оболочки
(пластины), а также ее формы [158—164].
229
Заметим, что экстремум, получаемый на основании принципа равно-
прочности, вообще говоря, будет локальным, так как геометрия конструк-
конструкции считается примерно заданной. Поэтому необходимо стремиться к
использованию принципа равнопрочности на как можно более ранней
стадии проектирования. Следует подчеркнуть, что при использовании
различных материалов максимум удельной прочности может быть дос-
достигнут на неравнопрочных конструкциях или материалах (один такой
случай рассматривается ниже).
Выбор материалов. Выбор оптимального материала зависит от назна-
назначения конструкции. При этом определяющими являются конструктивные,
технологические и экономические соображения. Следует подчеркнуть,
что конструкционный анализ (например, с помощью принципа равнопроч-
равнопрочности) , основанный на каких-либо идеализированных и практически труд-
трудно реализуемых предположениях, представляет интерес, вне зависимости от
экономических и технологических соображений, поскольку последние
обычно носят преходящий характер.
Процесс выбора оптимальных материалов, в идеале, может быть алго-
алгоритмизирован следующим образом. Все имеющиеся материалы, удовлетво-
удовлетворяющие технологическим соображениям, нужно разбить на конкурирую-
конкурирующие сочетания. Каждому сочетанию соответствует свой проект равно-
равнопрочной конструкции, размеры которой определяются при помощи прин-
принципа равнопрочности. Затем проекты сравниваются по нескольким приз-
признакам. Перечислим основные из них: технические возможности (напри-
(например, прочность, вес, скорость, управляемость и т.п.); экономические
(стоимость конструкции, окупаемость и т.п.); эстетические и т.д.
Волевым решением один из конкретных признаков берется в качестве
основного признака сравнения, а для всех остальных должны быть установ-
установлены приемлемые границы. Те проекты, которые не удовлетворяют пос-
последним, исключают из рассмотрения. В тех случаях, когда основной приз-
признак имеет меру, этот алгоритм приводит к простому перебору равнопроч-
равнопрочных проектов, допущенных к сравнению по этому критерию. Если крите-
критерий одинаков для нескольких конкурирующих проектов, то среди остав-
оставшихся признаков надо выделить основной и повторить по нему процесс
перебора. В тех случаях, когда основной признак неизмерим (удобство
управления, качество, комфортабельность и т.п.), можно воспользоваться
системой оценки его по баллам группой экспертов или по двоичной сис-
системе ("хорошо"или "плохо").
Этот процесс выбора можно проиллюстрировать на простейшей задаче
о выборе оптимального клея. Пусть задано два материала, 1 и 2, которые
можно склеить, применяя клеи марок Ах ,А2, ... ,Ап с соответствующей
стоимостью #i, q2,..., qn на единицу площади склеиваемой поверхности
(включая технологические затраты, связанные с подготовкой поверхности).
Технические возможности клеев оцениваем по двум признакам: а) сопро-
сопротивление нормальному отрыву; б) сопротивление переходу трещин из од-
одного склеиваемого материала в другой.
Возможно сравнение также и по другим признакам (сопротивление
сдвигу, длительная или антикоррозионная прочность, теплостойкость
и т.д.). Будем считать, что свойства конкурирующих клеев находятся в
приемлемых границах по этим признакам.
230
Какой из выбранных двух признаков считать основным? Это зависит
от назначения склеиваемого элемента конструкции. В изгибаемых мно-
многослойных пластинах, балках и оболочках основным признаком будет
сопротивление переходу трещин из одного слоя в другой. Действитель-
Действительно, если металлический слой подвергается переменному (циклическому,
случайному и т.п.) нагружению, то с его поверхности вглубь обычно раз-
развивается усталостная трещина. Скорость ее роста зависит от коэффициен-
коэффициента интенсивности напряжений у края трещины. При выходе трещины на
границу слоев дальнейшее ее развитие может происходить двояко в зави-
зависимости от свойств клея и тормозящего материала. Если клей недостаточ-
недостаточно прочен, то трещина пойдет по границе слоев и раздвоится; при этом
коэффициент интенсивности напряжений в конце трещины уменьшается
в несколько раз, что существенно задержит время перехода трещины
из одного слоя в другой. Если клей весьма прочен, то трещина сразу пе-
перейдет из одного слоя в другой, не раздваиваясь. Очевидно, клеи, вызы-
вызывающие раздваивание трещины, лучше; поэтому клеи, не обладающие
этим свойством, следует исключить из рассмотрения. Оставшиеся клеи
наиболее целесообразно сравнивать по сопротивлению сдвигу (наиболее
опасным при раздвоении трещин является расслаивание клееной конструк-
конструкции от сдвиговой нагрузки). Клеи, для которых сопротивление сдвигу доста-
достаточно высоко, следует сравнивать по стоимости и выбрать наиболее дешевый.
В случае нормального растяжения основным признаком будет сопро-
сопротивление отрыву или усталостная прочность. Условию равнопрочности
будет удовлетворять тот клей, прочность которого равна прочности сла-
слабейшей из склеиваемых компонент. Дальнейшее сравнение проводится
по стоимости, хотя экономический критерий может и заранее ограничить
применение слишком дорогих клеев, в особенности для маловажных узлов.
Аналогичный процесс алгоритмизации можно использовать для выбора
оптимального метода сварки или какого-либо другого технологического
способа сцепления двух материалов.
Прямая задача расчета многослойной пластины со сквозными трещина-
трещинами. Для постановки обратной задачи оптимального проектирования кон-
конструкции необходимо найти решение прямой задачи об определении коэф-
коэффициента интенсивности напряжений в окрестности конца трещины, на-
наиболее опасной для данной конструкции. Для многослойной пластины
такой трещиной является поперечная сквозная трещина, пересекающая
все слои пластины; поверхностные трещины являются менее опасными,
так как при переходе из одного слоя в другой трещину удерживает поверх-
поверхность раздела.
Расчет многослойной пластины с поперечной сквозной трещиной при
наиболее общих предположениях относительно распределения напряжений
по толщине выполнен Бадальянсом и Си [165]. Вычисленный ими коэф-
коэффициент интенсивности напряжений можно использовать в рамках механи-
механики разрушения [1]. Однако этот прямой расчет трудно применить для
оптимального проектирования многослойных пластин по следующим
причинам:
а) в момент начала неустойчивого развития фронт трещины является
криволинейным, в то время как в указанном расчете решается задача
для прямолинейного фронта трещины;
231
б) результаты расчета для трехслойной симметричной пластины пред-
представлены в виде графических зависимостей коэффициента интенсивности
напряжений от упругих постоянных и толщин отдельных слоев пластины,
и эти зависимости практически невозможно использовать при оптимальном
проектировании;
в) для многослойной пластаны коэффициент интенсивности напряжений
выражается через толщину и упругие постоянные отдельных слоев пласти-
пластины с помощью решения интегральных уравнений Фредгольма, поэтому
затруднительно осуществить пересчет коэффициента интенсивности на-
напряжений с одного набора слоев на другой или выразить его через коэф-
коэффициенты интенсивности напряжений отдельных слоев пластаны.
В связи с указанными трудностями рассмотрим обобщенное стати-
статическое плоское напряженное состояние многослойной пластаны с некото-
некоторыми дополнительными допущениями.
Пусть пластина постоянной толщины h составлена из к различных
упругих слоев толщины hg (/ = 1,2 А:), соединенных друг с другом.
Будем считать, что срединная плоскость панели является плоскостью
симметрии задачи (включая внешние нагрузки и геометрию панели).
Введем следующее основное допущение: средние смещения и, v и сред-
средние деформации еХ9 еу и уху всех слоев не изменяются вдоль нормали
к срединной плоскости (х, у — прямоугольные декартовы координаты
в этой плоскости). Это допущение справедливо в том случае, когда взаим-
взаимное проскальзывание слоев невозможно, а величина h гораздо меньше
размеров пластаны в плане.
Определяющие уравнения в рассматриваемом приближении будут иметь
следующий вид:
уравнения равновесия
Л 0,
Ьх Ъу Ьх Ьу
закон Гука
= 0, —& + —К- + УA) = 0, C.1)
Ьх Ь
_ Eghg Ibu bv\
= -М-№+иМ C.2)
l-tf\ty , ax/
^y " 2(i+n)W + ax/
Здесь ?*,-, v/ — модуль Юнга и коэффициент Пуассонаi-го слоя, Л^1*, N$l\
,N$ — соответствующие компоненты усилий, приложенных к /-<му спою
в его плоскости, Х^\ Y^1^ — компоненты реакции соседних слоев на
/-й слой плюс объемная внешняя сила, отнесенные к единице площади
срединной поверхности слоя.
232
Отметим также следующие очевидные зависимости:
к
Б
к
S
i=l
А,=
щ
h,
1
. °у *
ЛГ C.3)
1 1
-гЫУ т*у = ТМ*у
ft П
Здесь величины без верхнего индекса относятся к панели в целом, а о^,
а? * >г^^ ~ компоненты напряжений в i-м слое.
Напомним, что для большинства металлов коэффициенты Пуассона
весьма близки по величине, поэтому будем считать их одинаковыми для
всех слоев, т.е.
Vl = #2 = . . . = Vk = V. C.4)
В этом случае, суммируя по / уравнения C.1) и C.2), легко найти
обычные уравнения теории плоского напряженного состояния:
dNx bNxy dNxy bNy
Eh (Ъи bv\ \
-NX= Г!— +^— ), ^у= -I— + V — J,
l-v2\bx by y 12W Э/
+ —¦=* + х=о, —^ + —* +у=о,
Эх Э.у Эх Ъу
Eh /Ъи Ъи\
ЪуУ "у 1 -р2\Ъу Эх/
Eh /Ъи bv\
N^^Z7-\\T + r) ' C-5)
2A +v)\by Ъх)
1 к
Е = — 2 /*,?/. C.6)
Л/=1
Здесь ДГ; Y - компоненты объемной силы, отнесенные к единице площади
срединной поверхности панели.
Таким образом, получилась хорошо изученная плоская задача теории
упругости; напряжения в слоях согласно C.3), C.2) и C.5) равны
ТГ IT 17
\О — /т * /тС'/ — п W — . /''^ П\
Е Е Е
Предположим теперь, что в пластине образовалась сквозная трещина
длины 2/ перпендикулярно действующему растягивающему напряжению а
Тогда коэффициент интенсивности напряжений в окрестности края
трещины для пластины в целом будет равен
Кг = arj(l\ C.8)
а в каждом слое
где функция т?(/) определяется геометрией панели в плане и расположением
233
в ней трещины. Из формул C.7) -C.9) получаем соотношение
*i@=*A (ЗЛО)
ь
умножение которого на hf и последующее суммирование по / приводит
к выражению коэффициента интенсивности напряжений для всей панели
через коэффициенты интенсивности напряжений в отдельных слоях:
Формула C.11) остается верной, если в ней коэффициенты интенсив-
интенсивности нормального отрыва заменить коэффициентами интенсивности
сдвига Кц.
Величины К\ и Кц вычислены в зависимости от геометрии пластины
в плане и расположения трещины в ней в весьма многих случаях; наиболее
полная сводка этих результатов имеется в книгах [1,166,167].
Можно показать, что формулы C.7) и C.11) справедливы также в
том случае, когда многослойная конструкция образует произвольную
криволинейную оболочку, находящуюся в безмоментном состоянии.
Некоторые задачи оптимального проектирования. Определим теперь
прочность растягиваемой многослойной пластины. Дня этого примем
следующее основное допущение: каждый слой пластины работает на раз-
разрушение так, как если бы его боковые поверхности были свободны от
напряжений. Это допущение справедливо только для хорошо подобран-
подобранных клеев, соединяющих слои, когда клей сравнительно слабо сопротивля-
сопротивляется скалывающим напряжениям, так что при разрушении одного из слоев
в соседних неразрушенных слоях можно пренебречь концентрацией напря-
напряжений на продолжении разрыва вследствие образования поперечной трещи-
трещины вдоль клея. Справедливость этого допущения именно для клеевого
соединения листов в панель доказана опытами Кауфмана [150] по опре-
определению вязкости разрушения многослойных клееных образцов из алю-
алюминиевых сплавов. В случае жестких соединений это, допущение не вы-
выполняется.
Будем различать два основных режима работы многослойной пластины:
а) безаварийный, когда пластину можно считать бездефектной и нужно
применять обычную теорию прочности; б) аварийный, когда пластина
имеет сквозной дефект (например, усталостную трещину, брешь от метео-
метеорита или снаряда и т. п.). Сквозной дефект можно моделировать разрезом-
трещиной даже в тех случаях, когда его фактическая форма довольно
далека от математического разреза [1], причем различие в форме идет
в запас прочности.
В зависимости от назначения конструкции тот или иной режим ее ра-
работы будет определяющим при оптимальном проектировании.
Безаварийный режим. Пусть сплошная плоская панель подвергнута
однородному растяжению напряжением а. При принятом допущении слои
панели воспринимают нагрузку независимо, и диаграмма о—е для много-
многослойной панели будет кусочно-линейной, если пренебречь пластичностью.
Точки разрыва на диаграмме соответствуют последовательному разруше-
234
кию слоев. Величины б1? е2, . . . суть предельные деформации отдельных
слоев в момент разрушения, перенумерованных в порядке убывания
их жесткости (отметим, что условие равнопрочности выполняется только
в том случае, когда ег = е2 = ... = €*).
Определим последовательно напряжения в слоях ах, <h, . . . в момент
соответствующего разрыва:
Пусть наибольшее напряжение оь, выдерживаемое панелью, достигает-
достигается при разрьше ги-го слоя, т.е.
оь = — I A,a<<>(em), ?||| ^ h _ V *,« | Л/. C.12)
Отсюда получаем выражение для удельной прочности, пртходящейся на
единицу веса панели:
Z А*а@(€«) Ь,
^=^ — (р4
р к к \ А /=
S А,-р/ S А/
i=l i=m
где д.— плотность матертала /-го слоя, a(l^ (e) — зависимость а от е ма-
материала /-го слоя.
В случае линейно-упругого поведения всех слоев будет
C.14)
Удельная прочность является одной из важнейших характеристик ма-
материала, определяющей перспективы его применения в космической и
авиационной технике [127,168,169].
Аварийный режим. Пусть по каким-либо непредвиденным причинам
в пластине образовалась сквозная трещина; требуется так спроектиро-
спроектировать пластину, чтобы работоспособность (живучесть) конструкции с трещи-
трещиной была максимальной.
Развитие трещины, образовавшейся в пластине, подвергнутой некоторо-
некоторому растяжению, зависит от коэффициента интенсивности напряжений
на краю трещины. Согласно условию локального хрупкого разрушения
развитие трещины начнется в том оюе, в котором впервые будет достиг-
достигнуто равенство К^ = К^, где К}1^ — вязкость разрушения i-то слоя.
Это локальное продвижение фронта трещины вызовет перераспределение
напряжений в окрестности ее края и локальное торможение; дальнейшее
поэтапное развитие фронта трещины проследить трудно. Однако ясно,
что предельный стационарный режим роста трещины, когда локальное
разрушение на фронте трещины во всех слоях происходит одновременно,
235
отвечает условию равнопрочности, так как каждый из слоев предельно
сопротивляется разрушению на фронте трещины.
Аналогичная ситуация возникает и в однородном материале на краю
криволинейной трещины. Так, например, если в растягиваемом упругом
теле есть внутренняя эллиптическая трещина в плоскости, перпендику-
перпендикулярной растяжению, то с увеличением нагрузки она устойчиво распростра-
распространяется до круговой (равнопрочной) формы, затем неустойчиво растет
Рйс.99.
"кругами" до разрушения. При расчете разрушающей нагрузки надо сразу
исходить из круговой (равнопрочной) формы трещины, радиус которой
равен большей полуоси эллипса. Применение принципа равнопрочности
позволяет указать разрушающую нагрузку и при действии момента на
внутреннюю [170] и поверхностную [1] эллиптические трещины в упругом
теле, а также при действии комбинированных нагрузок.
Распространению равнопрочной трещины длины 2/ в многослойной
пластине отвечает напряжение
У/Ш
где согласно принципу равнопрочности и формуле C.11)
h i=i
а X - некоторый безразмерный множитель, зависящий от формы пластины
в плане и расположения трещины в ней. Величина А^1' характеризует
сопротивление 1мгс> слоя развитию трещины. Она зависит от материала
и толщины слоя hii аналитическое описание зависимости К^ от ht дано
во введении, так как согласно основному допущению указанная зависи-
зависимость может быть определена в опытах на одном свободном слое.
Заметим, что асимптотика упругих напряжений и смещений в окрест-
окрестности конца трещины, характерная для тонкой структуры, в данном случае
реализуется на расстоянии гот конца сквозной трещины, таком, что г > А,
г > h, r </, где А - характерный линейный размер "языка" фронта трещи-
трещины, / - длина трещины (рис. 99).
Таким образом, если действующее в панели напряжение меньше а,
определяемого формулой C.15), то образование щели длины 2/ не при-
приведет к мгновенному хрупкому разрушению.
Удельная прочность панели со сквозной трещиной, равная, как и в
безаварийном случае, о/р, при одинаковой геометрии пластины и трещины
согласно C.15) прямо пропорциональна множителю
2М*Й/?*,А. C.17)
236
Поэтому при расчете и прогнозе аварийных ситуаций для обеспечения
максимума живучести конструкции естественно проектировать панель
так, чтобы величина C.17) была максимальной.
Постановка многокритериальной задачи оптимального проектирования
в аварийном и безаварийном случаях. Пусть имеется п листовых материа-
материалов, перенумерованных в порядке убывания их жесткости. Каждый из
этих материалов, в частности z-й материал, характеризуется следующими
величинами: р,- — плотность, ht — толщина листа, е,- — деформационный
предел упругости, Е\ — модуль упругости, oei — предел пропорциональ-
пропорциональности {aei = Е(€ёд, °^ (€т) — снимаемое с диаграммы о—е для /-го
материала значение напряжения для деформации em(i > m), к?1^ — вяз-
вязкость разрушения.
Пусть кроме того, задана матрица взаимного склеивания материалов
icif) (/,/=1,2,...,«):
(lj если лист /склеиваетсй с листом/,
C.18)
О, если склеивание листов / и/ невозможно.
Введем п двоичных независимых переменных х,-, которые характеризу-
характеризуют присутствие /-го материала в пластине:
II i если лист из /-го материала имеется в пластине,
C.19)
О, если 1-го листа нет в пластине.
В этих обозначениях основными характеристиками многослойной панели
являются:
1) изгибающая жесткость пластины, пропорциональная величине
- - . 1 п з з '
3 /=i /=o
2) предел пропо^ящональности, характеризующий условие работы
пластины в упругой области
С2\Х, П)— I L /2/Х/ I L /5/Л/Х/€ (€ —
\|=1 /1=1 {
3) вязкость разрушения пластины
4). вес пластины, пропорциональный величине
— — л
С^(х, /i) ==/> = 2 hjPiXji
5) толщина пластины (объем пластины пропорционален толщине)
С$\Х9hj = 2 Xjhg*9
237
6) удельная прочность пластины, пропорциональная величинам:
для безаварийного режима
C6(jc,A)=-=
2 hiPiXj 2 А,*,
/= 1 i=m
для аварийного режима
С6(х,А) =
? *,*,*<'>
I А/ДС/р,-
При выборе переменных^,^, х,- стараются добиться возможно больших
значений характеристик^xjx, А), С2 (х, А), С3 (х, А), С6 (х, А) и возможно
меньших значений С4 (х, А), С5 (х, А). Поэтому общую многокритериаль-
многокритериальную задачу оптимального проектирования многослойной пластины
можно сформулировать следующим образом (критерий Парето [171-
173]):
6 б
max I X;C,(x,A), 2 IX; I = 1,
*/. Л/ /=1 /=1
кки C.20)
х (>0 при /= 1,2,3,6,
; [<0 при/ = 4, 5.
Величины Ху характеризуют важность отдельного критерия в много-
многокритериальной задаче и выбираются при постановке задачи либо по уже
известным решениям однокритериальных задач [171, 172], либо волевым
решением группы экспертов.
Разбиение многокритериальной задачи на вспомогательные. Другим
подходом сведения многокритериальной задачи к задаче с одним критери-
критерием является выбор одного критерия в качестве главного (на остальные ха-
характеристики пластины накладываются ограничения в форме неравенств).
Если при этом в задаче есть один параметр, по которому критерии
меняются монотонно, удается дать наглядную интерпретацию множителям
Ху. В нашей задаче в качестве характерного параметра можно взять пара-
параметр t пропорционального изменения толщины пластины А/ = А*г. По
этому параметру критерии можно разбить на две группы: одни улучша-
улучшаются с увеличением t (увеличение изгибной жесткости пластины), другие
ухудшаются (увеличение вязкости разрушения, уменьшение веса и толщи-
толщины пластины); предел пропорциональности и удельная прочность в без-
безаварийном режиме не меняются с изменением t.
Многокритериальные задачи возникают тогда, когда есть критерии из
различных групп (противоречивые критерии), иначе решение оптимальной
238
задачи тривиально. Например, решение задачи
max (\3КС - \4Р), Х/>0, / = 3,4,
Л/. */
сводится к определению такого /1, при котором достигается
max [ЛзЛ
1 <1<Л
и решением задачи является набор переменных xt ^ = 1,
Л/ =h] о, Xi=hj = Q для остальных /.
После разбиения критериев на группы по характерному параметру
удобно сначала оценить критерии по их сложности и наиболее сложный
взять в качестве основного (в наших условиях это, по-видимому, первый
критерий).
Рассмотрим следующую задачу:
maxCi(jc,A) C.21)
при ограничениях
^l'2^- 022)
Cj0 при / = 3,6.
Поскольку критерий C.21) монотонно растет с увеличением толщины
любого слоя, решение задачи C.21)—C.22) находится на границе ограни-
ограничений C.22). Поэтому решение этой задачи распадается на решение не-
нескольких задач с ограничениями типа равенства и проверкой выполне-
выполнения для этих решений оставшихся ограничений. Решение общей Задачи
оптимального проектирования многослойной пластины получается вы-
выбором наилучшего решения из конечного числа решений этих вспомо-
вспомогательных задач. Полученные вспомогательные задачи методом множи-
множителей Лагранжа сводятся к решению задачи с критерием C.20) и условием
нормировки \х = 1, однако параметры X/ определяются в ходе решения
задачи; таким образом, устанавливается связь между множителями Ху-
и константами С/0 в ограничениях C.22). Впервые этот метод был ис-
использован В.М. Смольским при оптимизации одного глобального метода
поиска экстремума [174].
Поставленная задача C.21)—C.22) содержит непрерывные (/%) и дво-
двоичные (х/) переменные. В этом параграфе будет решена задача оптимиза-
оптимизации только по непрерывным переменным; оптимизация по двоичным
переменным осуществлена частичным перебором в следующем параграфе.
Поэтому считается, что количество материалов фиксированно и все они
используются при построении оптимальной пластины (jc/ = 1).
Оптимизация изгибной жесткости при заданной вязкости разрушения
многослойной пластины. Из вспомогательных задач рассмотрим как наи-
наиболее сложную следующую задачу:
1 и i
max— 2 Ei(af - <z?_i) (д, = Б hh h0 =0), C.23)
hj 3 /=1 /=0
I [*?'>(*,)-*o] A/= 0. C.24)
/=i
239
Остальные ограничения C.22) не выписываем; их учет производится
в конце решения задачи.
Составим функцию Лагранжа
и необходимые условия для определения оптимальных значений А/ и X:
bF n
ЗА,- "*=/****"**"' ^ C25)
/, (А,) = KP(hi) -Ко + А, —^-^ (/. = 1,2,*.. - п).
Вместо системы уравнений C.25) рассмотрим эквивалентную систему,
полученную из последнего уравнения системы C.25) и последовательных
разностей /-го и (/ + 1)-го уравнения этой системы
2Ъ A,)
/=o 7
,) Xfn (Ан) = 0, C.26)
o 7
4) [})/(/)] (/= 1,2, я — 1). C.27)
Соотношение C.24) дополняет условия C.26) и C.27) для определе-
определения оптимальных А/ иХ.
Примечательно, что система уравнений C.27) не содержит Ко, поэто-
поэтому можно, задавая X, рекуррентно по / выразить все А/ через X и h\. Под-
Подставив Ко из C.24) в C.26), получаем еще одну связь hn и h\. Затем
решаем полученные уравнения и получаем для заданного X оптималь-
оптимальные толщины всех слоев и величины А'0(Х), С/0(Х) (/ = 2, 4, 5, 6). По
графикам этих функций от X определяем то значение X, при котором все
ограничения выполнены (одно из них является равенством).
Таким образом, при решении задачи считается заданной не величина
Ко, а значение X, по которому потом определяется #0 (X); поэтому важ-
важно указать границы изменения величин X и А,-. Для этого нужно провести
конкретное исследование функции /,- (А).
Как показано в § 1 (см. формулы A.17)), удобна и реалистична сле-
следующая аппроксимация:
с,- = (tf?>J, d, = [КР(Н1О)J - с,, xt = h,/h,0 - 1 > 0.
В этом случае
Отсюда следует, что при А„ > 1,5 А„о функция /И(АЯ) отрицательна
и для выполнения равенства C.26) необходимо неравенство X > 0. Тогда
240
во всех соогаошениях C.27) будет
•0 niZ
Рис. 100.
причем эта разность монотонно убывает
с ростом / (считается, что Ег растет
с ростом /)• Это соответствует посте-
постепенному приближении) hf к й/0 с умень-
уменьшением /.
Примерный график функции //(й,) +
+ Ко показан на рис. 100; при Ко >
> max K$ ^ существуют отрицатель-
отрицательный относительный минимум //(й,),
и поэтому, вообще говоря, две точки, hix и hi2, которые удовлет-
удовлетворяют /-му необходимому условию в системе условий C.27). Ясно,
что для получения большей жесткости надо брать точки hi2 для слоев с
ббльщим номером, однако при этом ограничения C.22) могут не удовлет-
удовлетворяться. Кроме того, в решении надо учитывать и граничную точку ht =
= й/о, так как на границе выполнение необходимых условий необязатель-
необязательно. Таким образом, непрерывная задача C.21) -C.22) сводится к выбору
оптимальной точки среди Ъп точек вида
{*
i/. , h2j2
з/3,
0 = 1,2,..., п; jt = 0,1,2).
Из проведенного исследования вытекает, что для многослойных пластин
из материалов, у которых существенно различны модули упругости, оп-
оптимальными будут следующие величины толщин слоев: для всех слоев,
кроме последнего, надо брать й/ = й,0, а для последнего слоя й„ = йя2.
ДОя материалов с близкими характеристиками надо проводить расчет
по формулам C,24), C.26) и C.27).
В качестве первого примера проведем расчет оптимальной трехслойной
пластины для следующего набора листовых материалов:
алюминиевый сплав 7075-Т6
й0 = 0,26 см, Kic = 4200 кгс/см k,
Kc(h0) = 9165 кгс/см3/2, Е = 7,1 • 105 кгс/см2;
титановый сплав ВТ-14
й0 = ОД см, К1с = 5500 кгс/см
*с(йо) = 9420кгс/см3/2, Е = 1,15 • 10б кгс/см2
сталь ВКС-1
й0 = ОД см, КХс = 6300 кгс/см 1г,
Kc(h0) = 9030 кгс/см3/2, Е = 2,05 • 106 кгс/см*.
Графики зависимостей С/0(Х) приведены* на рис. 101. Расчетом под-
подтверждается решение для материалов с существенно различными модуля-
модулями упругости, изложенное выше.
h
2;
¦ Напомним, что Со з = Кс, Со х = a I& где /?¦ - изгибная жесткость, а -
несущественный множитель.
241
s
* 11
427
1600
8500
0,24
13008500
\
к
Vh
0,11 1000 8100 t
1,5
Рис. 101.
2 Я
0,56
0,53
0,5
0,4
I $
8100 mo
0,3
7ZO02OO0
0,16200 WOOY
- у
2 A
Phc. 102.
242
0,7
7500
7000
6500
xm
1500
1500
<
к
\
Л
f
'a
к
N
A
A
f
1*10 9
X
/
A
/
N
ho
/
И
/
I
Й
f
\
A
N
0,6
2 X
Рйс. 103.
В качестве второго примера спроектируем шестислойную симметричную
пластину из следующих алюминиевых сплавов с близкими характерис-
характеристиками:
сплав 7075-Т6 (его характеристики даны в первом примере); сплав
Д16 (йо = 0,2 см, К1с = 4000 кгс/см72, Kc(h0) = 9000 кгс/см /2, Е =
= 7,2 • 105 кгс/см2): сплав АК-8 (h0 = 0,22 см,^1с =4000 кгс/см^э
Kc(h0) = 8200 кгс/смЭ/2,? = 7,3 • 105 кгс/см2).
Графики зависимостей С/0(Х) приведены на рис. 102, 103. Толщина
отдельных слоев отличается от величины Л,о при больших значениях вяз-
вязкости разрушения и монотонно изменяется с увеличением X. Решения,
представленные на рис. 102 и 103, отвечают внутреннему и граничному
экстремумам соответственно.
Если полученное оптимальное решение не удовлетворяет другим огра-
ограничениям C.22), необходимо заменить ограничение на вязкость разруше-
разрушения другим ограничением из той же группы по введенному характерному
параметру. Тем самым вспомогательная задача оптимального проектиро-
проектирования сводится к частным задачам на условный экстремум с ограничения-
ограничениями-равенствами. Аналогично решаются задачи, содержащие и другой кри-
критерий из той же группы в качестве основного.
Оптимизация вязкости разрушения при заданной толщине многослой-
многослойной пластины. Рассмотрим теперь случай, когда критерий выбран из другой
243
группы. Выберем в качестве основного критерия вязкость разрушения
многослойной панели и будем искать максимум этой величины по пере-
переменным А/ (А/ > А/о). При этом считаем, как уже ранее отмечалось для
вспомогательных задач, что материалы уже выбраны. Очевидным реше-
решением этой задачи будет набор А/ = А,о 0' = 1, 2, . . . , п), так как для этих
значений вязкости разрушения отдельных слоев являются максимальны-
максимальными. Задача оптимального проектирования получается закреплением одно-
одного параметра из противоположной группы критериев. Наиболее простым
представляется ограничение типа равенства на толщину панели. В результа-
результате приходам к следующей задаче:
max 2 K^(hi)hh А= 2 А/= const > ? А/о. C.28)
Как в предыдущей вспомогательной задаче, составим функцию Ла-
гранжа
F(hh\)'-
и, переходя к новым безразмерным переменным
запишем систему необходимых условий для определения х,- и X:
„.^bM.X.JSLb.,^ „), (з„,
A+2*?J \ 1*2х?7
Исследуем уравнение относительно х при постоянных с, d, X:
A+2х2J \ 1+2х2/
Поскольку производная левой части при х = 0 отрицательна, а правой -
равна нулю, то для существования близкого к нулю положительного корня
левая часть уравнения C.30) должна быть больше правой при х = 0, т.е. X <
< \Jc + d] При х = 1 правая часть уравнения C.30) больше левой, если вы-
выполняется следующее неравенство:
Применяя эти рассуждения к системе C.29), получаем границы изме-
изменения параметра X:
1
4
X < min у с,- + di = Хх.
244
^
i
9200
8900
8400
i
1,25
1
ы
0,61
0,55
0,45
i у 5
\
S
^^
4850 5780 6700 7620 9000 MO'1*
Flic. 104.
Заметим, что при X, приближающемся к Хо, в оптимальной пластине
начинает резко расти толщина того слоя, у которого величина А^ наи-
наибольшая, а толщина остальных слоев примерно не меняется. По-
Поэтому оптимальное решение для X < Хо можно построить по решению
для Х = Х0.
Все Xj и h являются монотонными функциями X, поэтому поиск набора
неизвестных X/, соответствующих заданному X, можно проводить ите-
итерациями, начиная с оптимального набора х{, полученного по предыдуще-
предыдущему X.
Общая схема получения зависимостей х,- (X), h (X), Кс (X) такова:
1) уменьшаем X на выбранную постоянную величину АХ, начиная со
значения X = \х;
2) для всех г, начиная со значения xi9 соответствующего предыдущему
значению X (перед началом расчета все xt = 0), определяем такое значение
X/, при котором меняет знак следующее выражение:
определяем/! иЛс для заданного X;
4) повторяем всю процедуру, пока величина X не станет равной Хо.
На рис. 104 представлены графики расчета оптимальных размеров сим-
симметричной шестислойной пластины (по два одинаковых слоя одного и того
245
3) по формуле C.28) и видоизмененной формуле (ЗЛ6)
же материала, все величины приводятся для половины пластины) из следую-
следующих материалов:
алюминиевый сплав 7075-Т6
Ло =0,26 см, К1с = 4200 кгс/см3'2,
*с0=9165кгс/см3/2;
титановый сплав ВТ-14
h0 = 0,1 см, К1с = 5495 кгс/см3/2, Кс0 = 9420 кгс/см3'2;
сталь ВКС-1
h0 = 0,1 см, Kic = 6300 кгс/см3/2, Кс0 = 9030 кгс/см3'2.
Из графиков видно, что при \ < Хо действительно растет только толщина
слоя из третьего материала.
Чтобы определить оптимальную толщину каждого слоя при заданной
общей толщине, по графику h (X) определяем соответствующее X, затем
толщину каждого слоя и величину #с.
Полученное решение является хорошим приближением к решению за-
задачи проектирования многослойной пластины заданного веса и максималь-
максимальной вязкости разрушения. Для этого в перечисленные характеристики
надо включить функцию
/>(Х) = 2 А*,оО+*/)
/=1
и определять X по заданному Р.
В заключение отметим ограниченность применения решения вспомо-
вспомогательной задачи оптимального проектирования многослойной пластины
по критерию вязкости разрушения. Действительно, если иметь возмож-
возможность многократно использовать один и тот же материал с максимальной
вязкостью разрушения при h = Ло, то, набирая слои толщиной h0 из этого
материала до тех пор, пока не будут выполнены ограничения, получаем
глобальный экстремум задачи оптимального проектирования. Найденное
ранее решение является относительным экстремумом, так как было введе-
введено условие обязательного однократного использования всех материалов.
Поэтому при постановке задачи естественно считать, что А,о ^Л/ < 2/*/0>
/ = 1, 2, . . ., п, и именно при этом изменении переменных строить решение.
Отсюда следует, что найденное решение является локальным дополнени-
дополнением общего решения задачи оптимального проектирования. Действительно,
если при проектировании многослойной пластины в аварийном режиме
толщина листов и их число могут быть любыми, то из количественного
описания масштабного эффекта следует, чтб для большинства листов
оптимальная толщина равна величине hi0, соответствующей максимуму
вязкости разрушения слоя. Бели по технологическим или экономическим
причинам этого достичь невозможно, т.е. для некоторых заготовок
hf > hf о, то оптимальная толщина листов равна минимально возможному
значению толщины ht г. Таким образом, при решении задачи оптимального
проектирования многослойной пластины в аварийном случае можно
считать, что толщина слоя /-го материала представлена в виде Л,- = kt hi i +
+ hi2 у где hii < hi2 < 2hix и kt - целое число. Задача оптимального про-
246
ектирования разбивается на целочисленную задачу определения величин
к( и непрерывную задачу определения величин hi2- Особенностью послед-
последней является необходимость удовлетворения лишь некоторых ограниче-
ограничений, так как ограничения типа неравенств, в основном, удовлетворяются
решением дискретной задачи. Поэтому во всех рассмотренных вспомо-
вспомогательных задачах при решении учитывалось только одно ограничение.
В дискретной задаче оптимального проектирования, наоборот,, будут ис-
использованы методы, в которых скорость решения задачи практически
не зависит от числа ограничений.
§ 4. Оптимальное проектирование многослойных пластан
(дискретная задача)*
Сведение к задаче исследования операций. В предыдущем параграфе
была решена непрерывная задача оптимального проектирования много-
многослойной пластины, т.е. задача оптимизации многослойной пластины по
непрерывно изменяющимся толщинам отдельных слоев. Для случая аварий-
аварийного режима, когда основным критерием оптимизации является вязкость
разрушения, указанная непрерывная задача разбивается на локальную
непрерывную и дискретную задачи.
Дискретная задача оптимального проектирования возникает и непосред-
непосредственно при наличии заготовок-листов заранее заданной толщины, из ко-
которых надо набрать многослойную пластину. Каждую заготовку можно
считать материалом (даже если они и одинаковы) и ввести двоичные пере-
переменные для характеристики присутствия этой заготовки в оптимальной
пластине. С помощью этих переменных задача оптимального проектиро-
проектирования многослойной панели сводится к дискретной задаче дробно-линейно-
дробно-линейного программирования, которая решена одной из разновидностей методов
частичного перебора — гибкой процедурой преребора с правилом Балаша
[175-181].
Кроме уже примененных в непрерывной задаче оптимального проекти-
проектирования линейных ограничений на указанные двоичные переменные, воз-
возможны ограничения на взаимное расположение заготовок-листов в опти-
оптимальной пластине. К таким ограничениям относится, например, ограниче-
ограничение на склеиваемость уже выбранных листов или ограничение на стоимость
этого склеивания.
С учетом всех этих положений дискретная задача оптимального проекти-
проектирования многослойной пластины ставится следующим образам.
Пусть имеется п заготовок (листов), каждая из которых, в частности,
/-я заготовка, характеризуется следующими величинами: р,- — плотность,
hi - толщина заготовки, et - деформационный предел упругости, Et -
модуль упругости, а(/) (ет) - снимаемое с диаграммы о-е для /-й за-
заготовки значение напряжения для деформации епик?1^ -вязкость раз-
разрушения /-й заготовки; задана матрица взаимного склеивания {с/;}
( 1, если лист / склеивается с листом/,
си =
10, если склеивание листов i и/ невозможно
(в случае ограничения на стоимость склеивания величины с/;- равны стои-
* Этот параграф основан на работе [115].
247
мости склеивания листов i и/; при этом Сц = °°, если склеивание листов
i и/ невозможно).
Введем п двоичных независимых переменных xt, которые характеризу-
характеризуют присутствие /-и заготовки в панели:
II, если i'-я заготовка имеется в панели,
О, если /-й заготовки в панели нет.
Требуется найти величины xi$ чтобы удельная прочность была мак-
максимальной, т.е. требуется максимизировать функцию F или Ф:
Б
F — t DЛ)
р п
2
S
s
D2)
при следующих ограничениях:
Д D.3)
2 hixia^{el)>N0. D.4)
Кроме указанных линейных ограничений, необходимо выполнение условия
склеивания листов в панель.
Условия D.3) и D.4) требуют, чтобы вязкость разрушения и несущее
усилие многослойной панели были не меньше величин Ко и No, задавае-
задаваемых из конструктивных соображений; в эти ограничения можно внести
и ограничения на вес или толщину панели.
Условие склеивания листов в панель не имеет смысла записывать ана-
аналитически. Для этого следовало бы ввести п2 + п новых переменных и
записать линейные соотношения между ними [173]', что лишь усложнило
бы постановку задачи и не помогло бы ее решению, так как последнее
осуществлено методами исследования операций, а не линейного дискрет-
дискретного программирования.
Следует отметить, что для разрушения хорошо спроектированного
клеевого соединения пластины с весьма жесткими слоями должна быть
справедлива концепция критической длины, аналогичная соответствующей
концепции неэффективной длины для композитов с волокнами (см.,
например, [1, 49, 60, 182]). А именно, при достаточно высоком напряже-
напряжении растяжения жесткие слои разделяются поперечными трещинами на
отдельные участки, длина которых в направлении растяжения меньше
248
величины
2г,
где ts — прочность клея на сдвиг.
Получающиеся задачи дробно-линейного программирования решаются
в дальнейшем методами исследования операций [173, 183, 184]. При
малом числе заготовок задачу легко решить полным перебором всех ва-
вариантов, задавая порядок перебора от п = 1 к п = 2, п - 3 и т. д. Нетрудно
заметить, что из п заготовок без учета ограничений-можно создать
1
2
п
Б С
*=i
1
"* Лт' = •—
2
я!
п
2 -
к-\ <
1
[п — к}\
1
=« —еп\
2
различных пластин. Ясно, что уже при п = 6 решать задачу полным пере-
перебором нерационально. Поэтому для решения задачи применяется метод
частичного перебора - аддитивный алгоритм [173,175].
Для выбранных листов проверка условия склеивания является доста-
достаточно сложной задачей. Поэтому вычислительный алгоритм, решающий
поставленную задачу, для выбранного набора листов сначала должен про-
проверить выполнение ограничений D.3)—D.4), затем увеличение функции
D.1) или D.2) и, наконец, как самое трудоемкое, выполнение условия
склеивания.
При решении задачи линейного программирования в двоичных пере-
переменных аддитивным алгоритмом [175] сначала инверсной заменой не-
некоторых переменных приводят задачу к канонической:
min 2 сгщ (ct > 0), D.5)
Х( 1=1
Д*|/*/>*/ A = 1,2,...,!»), D.6)
х; = 0,1 (/=1,2,...,я). D.7)
Набор переменных видоизменяют так, чтобы по возможшсти лучше
удовлетворить ограничениям. Как только обнаруживается набор пере-
переменных, удовлетворяющий ограничениям D.6) - такой набор переменных
называется допустимым решением, — не имеет смысла, согласно D.5),
рассматривать наборы переменных, которые получаются из допустимого
решения заменой одного или нескольких его нулей единицами; при этом,
очевидно, лучшего допустимого решения получить нельзя. Игнорирова-
Игнорирование таких наборов переменных и создает частичность перебора (правило
Балаша [175,184]).
Итак, аддитивный алгоритм ориентирован на скорейшее выполнение
ограничений (с помощью правила Балаша) и отсеивание тех наборов пере-
переменных (в том числе и допустимых решений), которые заведомо дадут
худший критерий.
Алгоритмы отсечения менее пригодны для данной задачи по следующим
причинам: 1) задача записана в двоичном виде и приспособлена для аддитив-
аддитивного алгоритма; 2) в общую схему аддитивного алгоритма легче вста-
249
вить проверку ограничения на склеиваемость; 3) хотя частичный пере-
перебор требует большего числа итераций по сравнению с другими алгорит-
алгоритмами (например, эвристическим или алгоритмом отсечения), он всегда
приводит к оптимальному решению, если оно существует.
Преимущество алгоритма Балаша заключается также в том, что он
аддитивный, т.е. использует только операции сложения и вычитания. Кроме
того, время счета задачи (число итераций) определяется лишь числом
переменных и почти не зависит от числа ограничений [176, 184].
Алгоритм Балаша помимо экспоненциального роста с числом пере-
переменных времени счета задачи имеет и тот недостаток, что он ориентирован
на скорейшее выполнение ограничений без учета: оптимизируемой функции
[176], т.е. переход от одного набора переменных к другому не зависит
от величин Cf в формуле D.5). Чтобы избежать этого недостатка, Фримен
[177] предложил в задачах линейного программирования ввести некоторое
ограничение на оптимизируемую функцию и скорейшее выполнение этого
ограничения значительно сократило время счета.
Следует заметить, что улучшение Фримэна производится автомати-
автоматически при преобразовании задачи дробно-линейно го программирования
в задачу линейного программирования (точнее, в задачу скорейше-
скорейшего удовлетворения линейных неравенств), так как критерий D.1)
заменяется следующим простейшим критерием с линейным неравенством
на переменные дс,-, где / = 1,2,..., п:
S
max Г, S (р,?-*<'>)*,*, <0. D.8)
Ограничение D.8) является прямым применением идеи Фримена для
задачи дробно-линейного программирования (аналогично нетрудно пре-
преобразовать критерий D.2)). После такого преобразования задачи D.1),
D.3), D.4) в задачу D.8), D.3), D.4) к ней можно применять аддитив-
аддитивный алгоритм, хотя она записана и не в канонической форме D.5) -D.7),
так как ограничение в D.8) обеспечивает частичность перебора. Заметим
также, что аддитивность алгоритма для внутриалгоритмических операций
сохраняется; она теряется только при вычислении критерия ? для до-
допустимого решения. Кроме того, дополнительной работой, вносимой дроб-
но-линейностью задачи, является пересчет коэффициентов в ограничении
D.8) в связи с изменением ? для очередного лучшего допустимого
решения.
Аддитивный алгоритм в форме, предложенной Балашем, по логике
похож на метод возможных направлений. Выделяются три множества
наборов переменных:
1) множество уже просмотренных наборов;
2) множество наборов, для которых ограничения не могут быть вы-
выполнены;
3) множество наборов переменных, для которых критерий не может
быть лучше, чем для текущего допустимого решения (сюда включена
частичность перебора).
Текущий набор переменных выбирается по правилу Балаша из пере-
пересечения дополнений этих множеств. Однако указанные множества можно
построить лишь с помощью весьма сложной логики [175, 184].
250
Более удобная форма реализации аддитивного алгоритма предложена
Джоффрионом [178, 179]. Однако за последнее время получило призна-
признание обобщение этой процедуры — гибкая процедура перебора, которая
впервые предложена Туаном [180]. Сетевая трактовка гибкой процедуры
перебора и некоторое ее усовершенствование даны Элвейном [181]. При-
Применяемый здесь алгоритм основан на этих статьях.
При реализации процедуры перебора каждой переменной приписывает-
приписывается наименование: свободная, выбранная или помеченная. В случае нашей
задачи свободные и помеченные переменные имеют значение 0, а выбран-
выбранные переменные — значение 1.
Состояние поиска характеризуется списком и ранее определенным до-
допустимым решением. Список содержит номера выбранных и помеченных
переменных, причем помеченную переменную отличает знак минус перед
номером; свободные переменные в список не вносятся. Например, список
{2,4, 6, -в, -7,10, И, И, -3, -5, -1} D.9)
определяет переменные х2 = х* = х6 = хх 0 - Хц = хх 4 = 1 как выбранные,
*8 = *7 = *з = *5 = *i = 0 — как помеченные, х9 = х12 = *i з = 0 — как
свободные переменные; тем самым, списком определяются значения
всех переменных. Состояние поиска список характеризует еще и потому,
что в нем переменные стоят в определенном порядке (иначе список мог
бы содержать только «-мерный вектор троичных чисел). Процедура пере-
перебора осуществляет переход от одного списка к другому с выделением
допустимых решений, не упуская лучших из них - именно эта алгорит-
алгоритмизация предложена Джоффрионом [178].
По значениям переменных можно составить величину невыполнения
ограничений d
d = id/9 D.10)
где
(Si - 10Г7 при st <0 n
10 при Sj >0 /=1
Малая постоянная 1СГ7 обеспечивает неравенство dx< 0 при невыполне-
невыполнении строгого неравенства D.8), что соответствует ограничению D.8),
остальные dj строятся аналогично, а именно, если ограничение записано
в виде Sj > 0, то
[ Sj при Sj < 0
4= ./ = 2,3.
{ 0 при Sj >0
Для допустимого решения величина d = 0. Цель процедуры — перебрать
допустимые решения с большими значениями максимизируемой функции.
Перед начальным шагом процедуры список пуст (все переменные свобод-
свободны), и ? = О. Затем последовательно осуществляются шаги процедуры.
Шаг процедуры состоит из анализа списка, его изменения и проверки до-
допустимого решения, если оно встретится.
251
При анализе списка определяется возможность выполнения ограниче-
ограничений, если некоторым или всем свободным переменным придать значение 1.
Так, если для нашей задачи для списка не выполнено условие D.8)
(d{ < 0), то, придав значение 1 только тем свободным переменным, для
которых К^ — p,f > 0, подсчитаем снова d\. Если dx < 0, то выполнить
ограничения, в частности первое, свободными переменными нельзя. Ана-
Аналогично проверяются другие ограничения.
Бели ограничения можно выполнить свободными переменными, то
определяется та свободная переменная, перевод которой в выбранные
и внесение в список сделает для нового списка максимальной величину
d (такой прием выбора переменной называется правилом Балаша). Эта
переменная вносится в список справа как выбранная. Так, например,
если список D.9) допускает выполнение ограничений и в выбранную
переменную надо обратить ху 2, то новый список будет
{2,4,6,-8,-7,10,11,14,-3,-5,-1,12} .
Возможно для нового списка будет d = 0, тогда список определяет до-
допустимое решение; для этого решения вычисляется максимизируемая
функция и сравнением с текущим значением f определяется, фиксиро-
фиксировать ли новое допустимое решение (и менять f) или нет.
Если ограничения выполнить свободными переменными нельзя, то
определяется, есть лив списке выбранные переменные. При отсутствии их
поиск заканчивается и текущее допустимое решение является оптималь-
оптимальным. Если выбранные переменные в» списке есть, то из последней группы
(крайней справа) выбранных переменных переводится в фиксированные
та, которая для нового списка сделает максимальной величину d. Новая
фиксированная переменная ставится в списке в конце группы (справа)
выбранных переменных, к которой она принадлежала; все фиксированные
переменные справа от нее переименовываются в свободные (исключа-
(исключаются из списка). Так, если для списка D.9) в фиксированную надо пере-
перевести переменную JCi x, то новый список будет
{2,4,6,-8,-7,10,14,-11} .
Следует заметить, что отличие гибкой процедуры перебора от аддитив-
аддитивного алгоритма в форме Джоффриона заключается в том, что при замене
выбранной переменной на фиксированную выбор этой переменной про-
производится по правилу Балаша. В алгоритме Балаша для этой цели в списке
выбиралась крайняя правая выбранная переменная. Число итераций при
этом нововведении сокращается примерно на 40% [181] при незначитель-
незначительном увеличении времени счета одной итерации.
Итак, на шаге гибкой процедуры перебора либо в список вносится
одна переменная и возможно допустимое решение, либо список не увели-
увеличивается и возможен конец поиска. Поиск осуществляет частичный про-
просмотр допустимых решений.
Блок-схема и алгольный текст программы, составленной по описанно-
описанному выше алгоритму, приводятся в Приложении в конце книги.
Поскольку процедура перебора обеспечивает скорейшее выполнение
ограничений D.3), D:4) и вязкость разрушения у заготовок большей
толщины меньше, первое допустимое решение имеет сравнительно малое
252
значение критерия среди всех допустимых решений. Затем алгоритм осу-
осуществляет перебор части допустимых решений и для лучших из них про-
проверяется условие склеивания.
Целевой алгоритм перебора. В гибкой процедуре от одного набора
переменных к другому используется правило равномерного выполнения
ограничений и критерия (правило Балаша). При этом в процессе работы
алгоритма многие допустимые решения "подозреваются в оптимальности",
и для них проверяется условие склеивания. Чтобы быстрее получить близ-
близкое к оптимальному допустимое решение, можно применять правило
перебора, учитывающее только критерий. Это рационально делать, когда
число ограничений невелико B—3 ограничения). При таком поиске удобно
расположить переменные в порядке убывания критерия.
Правило перебора сводится к следующему. Если для текущего набора
переменных ограничения можно удовлетворить свободными переменными,
то в список вводится и становится выбранной переменная с наименьшим
порядковым номером. Если ограничения для этого набора переменных
выполнены или свободными переменными их удовлетворить нельзя, то
из списка исключаются справа все помеченные переменные до ближайшей
выбранной, которая переводится в помеченные.
Таким образом, порядок переменных в списке всегда определяется
их номером, а свободные переменные всегда имеют большие номера, и
потому список полностью определяется знаками на местах соответствую-
соответствующих переменных. Например, список {+, +, —,—,+} определяет перемен-
переменные хх = х2 =х5 = 1 как выбранные, х3 =*4 = 0 — как помеченные; осталь-
остальные переменные х6, х7 > • • • свободные. Весь список можно задать числом
в двоичной системе и количеством переменных в списке, что удобно при
применении вычислительной техники, так как преобразование списка
можно записать в логических операциях.
Поиск с; таким правилом выгодно применять, когда допустимых реше-
решений много (много одинаковых заготовок или ограничения не обремени-
обременительны) . Оптимальное решение определяется быстрее, и потому проверка
условия склеивания, когда ограничения необременительны, производится
реже, однако проверка оптимальности решения требует ббльшего перебора,
чем при решении с правилом равномерного выполнения ограничений и
критерия.
Проверка возможности склеивания листов. Составим матрицу из тех
элементов q7-, для номеров i и / которых выполняются равенства xt =
= Xj = 1. В случае, если задана стоимость склеивания, то выделенную по
полученному набору переменных матрицу требуется дополнить нулевыми
строкой и столбцом, а так же бесконечным диагональным элементом. В
п
этой матрице порядка щ= 2 х,- + 1 требуется отыскать щ элементов,
i
которые удовлетворяют ограничению на стоимость и из которых можно
составить замкнутый маршрут, т.е. так упорядочить, чтобы номер столбца
предыдущего элемента совпадал с номером строки последующего и номер
столбца последнего элемента совпадал с номером строки первого. Эта
задача сводится к хорошо известной задаче коммивояжера — определе-
определение замкнутого маршрута наименьшей стоимости. Решив задачу коммиво-
коммивояжера для нашей матрицы, проверяем выполнение ограничений для ре-
253
шения задачи коммивояжера; таким образом, проверяем выполнение
ограничения на стоимость склеивания.
Для решения задачи коммивояжера в настоящее время разработаны
как точные, так и приближенные методы. Приближенные методы разра-
разрабатываются для задач с большой размерностью (когда порядок матрицы
в задаче коммивояжера примерно 40—100). К подобным методам отно-
относятся метод движения в ближайший городи метод оптимизации; существу-
существуют и другие приближенные методы [185-190]. Метод движения в ближай-
ближайший город подменяет полный перебор пх! маршрутов частичным пере-
перебором щ маршрутов; а именно, начиная с каждого из щ номеров, осу-
осуществляется выбор (/?! - 1) наименьших по стоимости чисел сц после-
последовательно в маршруте, а последнее число замыкает маршрут. В результа-
результате получается локально-оптимальный маршрут, близкий по стоимости к
оптимальному [191]. Методом г-оптимизации тоже можно получить лишь
локальный экстремум: сущность метода заключается в совершении все-
всевозможных замен г коммуникаций С/7 в уже имеющемся маршруте.
Практически используется оптимизация при г = 3 ч- 4 [192].
Для задачи коммивояжера средней размерности (порядок матрицы
до 25) не имеет конкуренции сравнительно давно разработанный метод
Литтла [173, 183, 184, 193]. Этот метод — точный и потому трудоемкий;
время решения задачи экспоненциально растет с ростом ее размерности.
Однако, учитывая такой же порядок скорости счета аддитивным алго-
алгоритмом и то, что проверку ограничения на стоимость склеивания нужно
проводить не более чем до 15 листов, разумно применять точный метод
Литтла. (Здесь метод Литтла для решения задачи коммивояжера описы-
описываться не будет: похожим методом решена задача проверки склеивае-
мости листов.) Если для допустимого решения надо проверять условие
склеивания листов в панель, то выделенную по набору переменных допусти-
допустимого решения 0 — 1 матрицу дополняют единичными строкой и столбцом
и нулевым диагональным элементом. В этой матрице порядка щ = Ъх( + 1
/=1
требуется отыскать nt элементов, которые равны 1 и составляют замкну-
замкнутый маршрут. Для решения этой задачи создан алгоритм ветвления, по
логике сходный с алгоритмом Литтла.
Объектом ветвления является набор элементов исходной матрицы
и матрица, порядок которой равен разности щ и числа элементов в наборе
(в начальный момент набор элементов объекта пуст, а матрица объекта
совпадает с исходной). Для объекта определяется возможность ветвления:
если матрица объекта содержит нулевую строку или столбец, то ветвление
объекта заканчивается. Для ветвления объекта в матрице объекта опре-
определяются элементы ветвления и замыкания. Элемент ветвления с/у- = 1
является единственной единицей в строке / или столбце /, а если такого
элемента в матрице объекта нет, то для него сумма элементов в строке
и столбце наименьшая. Элемент замыкания с некоторыми или всеми эле-
элементами набора и элементом ветвления составляет замкнутый маршрут.
Ветвление объекта А сводится к получению вместо него двух объектов.
Один объект содержит тот же набор элементов, что и Л, а матрица его
отличается лишь элементом С/у, равным нулю. Набор другого объекта
содержит набор А и элемент ctj. Матрица другого объекта получается
254
из матрицы объекта А исключением строки / и столбца / и обращением
в нуль элемента замыкания.
Алгоритм заключается в ветвлении того объекта, набор которого со-
содержит наибольшее число элементов. Если закончено ветвление всех объ-
объектов, то выбранные листы не могут образовать клееную пластину. Если
матрица одного из объектов имеет вид{1}, то листы склеиваются; порядок
склеивания листов в пластине предписывается набором объекта и послед-
последним элементом его матрицы.
Физический смысл алгоритма проверки условия склеивания листов
заключается в том, что к уже отобранным элементам в набор объекта
всегда выбирается такой элемент сц, чтобы матрица объекта содержала
как можно больше склеиваемых комбинаций. Это способствует скорейше-
скорейшему получению хотя бы одного замкнутого маршрута из единиц при наимень-
наименьшем ветвлении, т.е. оптимально решает задачу проверки условия склеива-
склеивания (выбранных допустимым решением) листов в многослойную пластину.
Блок-схема и программа описанного выше алгоритма помещены в
Приложении в конце книги.
Компромиссный критерий. Кроме указанного однокритериального под-
подхода (по безаварийному или аварийному режимам), можно применять
также подход, основанный на компромиссном критерии, представляющем
собой некоторую комбинацию критериев D.1) и D.2). При этом подходе
целесообразно сначала найти величину Fmax в аварийном режиме, затем
величину Фтах в безаварийном режиме; окончательным решением будем
считать такое решение, которое минимизирует следующую функцию:
D.11)
Здесь X — некоторое число, определяющее относительную важность аварий-
аварийного или безаварийного режима.
В качестве компромиссного критерия можно взять также критерий
минимальной вероятности разрушения. Выведем его.
Пусть в каждом режиме для значения относительного уклонения кри-
критерия от оптимального известны вероятности разрушения конструкции:
Р° if) - ДЛЯ аварийного режима и р° (<р) — для безаварийного режима.
Если еще известны вероятности того, что в момент разрушения конструк-
конструкция работала в аварийном или безаварийном режиме (рс ир0 соответствен-
соответственно) , то по формуле полной вероятности, вероятность разрушения конст-
конструкции равна
где величины/ и у определяются формулой D.11). В качестве критерия
естественно взять минимум функции D.12).
Функции рс if) и р° (</>) можно определить экспериментально на об-
образцах, находящихся в условиях работы реальной конструкции, а величи-
величины рс и ро определяются режимом разрушения реальной конструкции.
Вероятностный критерий является разумным компромиссным критери-
критерием в промежуточной области изменения рс (когда величины рс и р0 срав-
сравнимы). Возможны и другие варианты компромиссного критерия [194].
255
I
1
g «Л
< с-
Н 0Q
U
А
U
•о I о
с Ч. м
N -ч.и
со •* *-<
< со о
о о 12 о©
UHow
•ч о
Й >
«о со*4
*^ о
U2S
g
S
2
СО
о
2
о
«о оо
о о\
S S
г- сч »-« -н* г- о ~*
°1 г-
О «О
о
5 I 2 2
О 00
о оо
о
ЧО
О
so ?
•ч СО
О v>
7 330
о
О
^ о
со vo О
Х
О.
О1
Таблица 4.2
1
2
2
0
3 1
4. 0
5 0
6 1
7 0
9 0
10 1
11 0
12 0
Ограничения
2 см < h < 4 см
4 см < h < 6 см
Аварийный режим
Безаварийный
режим
* В первых пяти
3 4
1 0
0 1
1 0
1 0
0 0
0 1
1 1
0 0
0 1
0 0
Проводи-
Проводи5
0
1
0
0
1
0
0
1
0
0
лась провер-
проверка условий
склеивания
нет
да
нет
да
1,2,3,5,9,
1,5,6,7,8,
строках —
Номера
6
1
0
0
1
0
0
1
0
0
1
7
0
0
1
0
0
0
0
0
1
0
заготовок
мальную панель
2,9,10,
4,9,10,
3,9,10,
5,3,2,6
10,11,12,
8,7,6,5,1
удельная
ней строке - удельная прочность в см
И,
И,
И,
,9,
12,
11
11,
12,
ю,
И,
10
ю,
12,
И,
ю,
вязкость
9
0
1
1
0
1
0
0
1
0
0
, входящих в
9,2
9,4
11,10,9,3
11,10,9,6,2
9,5,3,2,1
разрушения
10
1
0
0
1
0
0
1
0
1
1
опта-
,3,5
11
0
0
1-
0
0
1
0
1
1
0
В СМ /2,
12
0
0
0
0
1
0
0
1
0
0
Таблица 4.3
Критерий*
3,001 • 106
2,48 • 106
2,743- 106
2,56 Ю6
2,53 106
25200
в послед-
Численный пример. На ЭЦВМ М-20 с помощью комбинированного ал-
алгоритма, состоящего из модификаций гибкой процедуры перебора и агь
горитма проверки условия склеивания, численно сконструированы 4 па-
панели из 10 наборов листовых заготовок из трех материалов (алюминиевые
и титановый сплавы, характеристики которых даны в табл. 4.1). В каждом
наборе имелось по две заготовки. Требовалось создать две пластины с
максимальной удельной вязкостью разрушения при ограничениях на их
толщины 2см<Л<4сми4см<Л<6см соответственно; для одной
из этих панелей возможность склеивания не проверялась, а для другой
условия склеивания предписывались фиктивной матрицей (она помеще-
помещена в табл. 4.2). Результаты проектирования (удельная вязкость разрушения
оптимальных пластин и номера входящих в них заготовок) представлены
в табл. 4.3. Проверка на склеиваемость значительно увеличивает время
счета задачи. Так, определение оптимальных пластин без проверки условия
склеивания потребовало 0,4 и 3 мин, а при проверке условий склеивания —
8 и 34 мин соответственно.
257
Применение целевого алгоритма перебора вместо гибкой процедуры
перебора для указанной задачи сокращает время счета примерно вдвое:
0,2 и 1,4 мин без проверки условия склеивания.
В двух других примерах из материалов, характеристики которых по-
помещены в табл. 4.1, сконструированы две пластины для работы в аварий-
аварийном (Ко =6000кгс/см ^) и безаварийном GV0 = 1500 кгс/мм) режимах.
Условие склеивания не проверялось. Как видно из табл. 4.3, две послед-
последние пластины состоят в основном из различных листов. При малом числе
ограничений изложенный выше алгоритм следует применять при "дефици-
"дефиците" заготовок в наборе. Если допустить произвольное число заготовок
в наборе, то во всех примерах оптимальной по критерию вязкости раз-
разрушения будет пластина из однотипных заготовок №9 табл. 4.1, а при
учете склеивания - пластина из заготовок № 9 и 10, склеенных поочередно:
9—10—9—10—9 для ограничения на толщину 2 см </* <4 см.
§ 5. Многослойные пластины и оболочки
переменной толщины
Проектирование оптимального многослойного материала (т.е. структу-
структуры оболочки по толщине) приводит, вообще говоря, к многослойным
оболочечным конструкциям переменной толщины, так как передаваемые
усилия и другие характеристики конструкции, как правило, различны
в разных точках пространства. Срок службы такой слоистой конструкции
обычно определяется скоростью развития трещин расслаивания. В этом па-
параграфе излагается новый подход к общей теории многослойных оболочек
переменной толщины, необходимой для изучения механики расслаивания
оболочек.
Многослойные оболочки переменной толщины из одного и того же
материала. Уравнения теории тонких упругих оболочек переменной толщи-
толщины с непроскальзывающими слоями из одного и того же материала имеют
следующий вид:
уравнения равновесия
Э ЪВ Ъ ЪА
— (BNa)-N& — + — {ASfi)+Sa — + ABKaQa + АВ (ра + Ката) = 0,
да да д/3 Эр
Э ЪА Ъ ЪВ
— (ANв) -Na — + — (BSa) +S» — + ABKpQp + АВ (р& + К$т&) = 0,
Э0 да да да
da
Э
эр ^a
258
'.¦*Л>
а
—(Вта)
da
дя
ada
дЛ
да
д
эр
д
dp ^
+
0
ЪА
гэр
д
д^
да
«?,> +
= 0,
= 0; E.1)
уравнения закона Гука
Eh | h2
12
Na =
12A -V
м 24A +*>)
геометрические соотношения
1 bit 1 ЬА
E.2)
1
ЪВ \ bv
Л За Л^ 30 ЛЯ За В Ър Р
В Э0
В
_ ЪКа и ЬКр v г2 1 3 /1 3w\ 1 ЗЛ 3w
Ка За Л 30 ^ а А За \Л За / ЛЯ2 30 30
ЗА'д // ЪКв v , 1 3 / t 3w\ 1 ЗЯ bw
Кр = —- — + 2. __^2W I \ ^
За Л 30 В В 30 \ В 30 / Л2Я За За
1 |Л Ъ . v\ В Ъ I v\] 2
2 * [В дР \А j А За \В/1 АВ
\ ЪА bw I 3Z? bw \
2 /32w
\3а30
E.3)
Здесь а, Р - гауссовы ортогональные координаты средней поверхности обо-
оболочки, выбранные так, что координатные линии являются линиями главных
кривизн этой поверхности; z - нормаль к этой поверхности (a,0,z образу-
образуют правую систему); м, u, w — составляющие смещения точек средней по-
поверхности по осям a, P, г; еа, ер, со, ка, к$, т — характеристики деформаций
оболочек; Na, N$% Sa, S@ — нормальные и касательные усилия; Ма, Мр,
259
Mpa — изгибающие и крутящие моменты; Qa, Qp - перерезывающие
силы; А, В — коэффициенты первой квадратичной формы средней поверх-
поверхности в координатах а, 0; Ка, Кр — главные кривизны координатных линий;
Et v - модуль Юнга и коэффициент Пуассона; ра> ppt pz - компоненты век-
вектора интенсивности заданной внешней распределенной нагрузки: таьтр —
компоненты вектора интенсивности заданного внешнего изгибающего рас-
распределенного момента (т2 = 0); h — толщина оболочки,являющаяся задан-
заданной функцией а и 0.
Толщину оболочки можно представить в следующем виде:
И (а, 0) = h0 + еЛ1 (а, ff) (е < 1). E.4)
Здесь Ао - постоянная; hx - известная функция а и /J; е - некоторое ма-
малое число.
Уравнения E.1) - E.3) справедливы лишь при условиях малости произ-
производных dh /да и ЭЛ/ Э/3; в местах резкого изменения толщины оболочки
(например, на границе оболочки) возникает краевой эффект, для изуче-
изучения которого обычное приближение теории оболочек не годится и нужно
так или иначе привлекать трехмерные уравнения теории упругости. Условие
малости указанных производных, очевидно, эквивалентно уравнению E.4),
т.е. существованию некоторого малого числа.
Уравнения E.1) - E.3) совпадают с уравнениями A1.4) - A1.6), рас-
рассмотренными и описанными в книге В. 3. Власова [195], добавлены лишь
члены с распределенной моментной нагрузкой, а толщина считается перемен-
переменной согласно уравнению E.4) (в целях удобства некоторые обозначения из-
изменены по сравнению с книгой.[195] ).
Систему уравнений E.1) - E.3) можно записать в следующем виде:
I(A, (/) = F, E.5)
U = (iVa, Sa, М^ Мар, Мр, Nq, Sp, Mpa, Qa> Qp, ea, e$, cj, ка, к#, r, w, и, w).
Здесь L (A, U) - матрица линейных относительно ?/дифференциальных опе-
операторов с переменными коэффициентами, зависящими от h (размерность
матрицы 19JK 19);
U - искомая функция-строка; F - строка заданных функций, в которой
первые пять элементов равны соответственно
-АВ(ра +Ката\ -АВ(рр+ Кртр),
-ЛВрг~— (Вта) - — (Атр\ -АВта, E.6)
да Э/3
- АВ nip,
а остальные 14 элементов равны нулю.
Как видим, точное решение системы уравнений E.1) - E.4) отличается
от точного решения соответствующей трехмерной задачи теории упругости
вдали от краев оболочки на величину порядка О (е2).
Ошибка именно такого порядка возникает при выводе уравнений закона
Гука для оболочки переменной толщины (см. уравнения A1.2) в книге
[195], содержащие в себе такую погрешность в случае переменной толщины
и служащие основой для уравнений A1.4), совпадающих с точностью до
обозначений с приведенными уравнениями E.2)). В этом можем убедиться
260
также, непосредственно анализируя имеющиеся точные решения теории
упругости (например, для случаев растяжения и изгиба тонкой клиновидной
пластинки [75]). Следовательно, решение системы уравнений E.1) — E.4)
приближенно описывает состояние физической системы (оболочки) с пог-
погрешностью порядка О (е2 ).
Возникает вопрос о необходимости нахождения новой, более простой
системы уравнений, эквивалентной исходной системе E.1) — E.4) при ус-
условии, что решение новой системы отличается от искомого решения лишь
на величину порядка О(е2). Очевидно, что в таком случае решение новой
системы можно назвать "точным" решением исходной системы; его точ-
точность соответствует точности исходной системы.
В данном случае такую эквивалентную систему уравнений легко пост-
построить методом малого параметра. Используем далее общую матричную за-
запись E5) . Итак, пусть требуется найти решение какой-либо характерной
краевой задачи для уравнений E.5). В дальнейшем предполагается, что ре-
решение этой краевой задачи существует и оно единственно. Ищем решение
этой задачи в следующем виде:
U=Uo+eUl9 E.7)
где Uo и Ux — новые неизвестные функции, не зависящие от в .
Подставляем функции h и Uсогласно формулам E.4) и E.6) в уравне-
уравнение E.5) и приравниваем коэффициенты при одинаковых степенях малого
параметра (при с0 и б1), пренебрегая более высокими степенями разложе-
разложения, выходящими за рамки точности исходных уравнений. В результате по-
получим
L(hOfUo) = F, E.8)
Здесь 1}ъ и Fx - функции-строки, в которых первые элементы будут:
для?/3
- e^+ve*- —
*8 ,„
Ehx Г
= W77) Г
и
Eh% hi
Eh%
М
8A
261
/•'/г, Г hi
~^) И+ »"<2+*«(«? +"«&)!•. E.Ю)
da
Э/3 9C да да
d ^ dB d ^ ^ dA
AB(KaN°a+K(, Nf), -— {ВМ°ар)-Ща — +— (АЩ)-М°а — .
da da Эр op
1 (Д<)-л^ ~ . E.П)
ofi da
Остальные элементы A1—в ?/3h14-bFj) равны нулю.
Таким образом, система уравнений, эквивалентная исходной системе
E.1) - E.4), состоит из двух однотипных систем E.8) и E.9), различаю-
различающихся своими правыми частями . Первая из них полностью совпадает с
уравнениями E.1) - E.3) при h = h0 = const,. вторая отличается от первой
лишь своей правой частью, которая согласно E.9) - E.11) определяется
решением первой системы. Для систем E.8) и E.9) нетрудно сформули-
сформулировать однотипные корректные краевые задачи, эквивалентные краевой за-
задаче для исходной системы E.1) - E.4), хотя эта формулировка неодноз-
неоднозначна. Решение краевых задач для системы уравнений E.8) - E.9) можно
получить в квадратурах, если известна функция Грина соответствующей
краевой задачи для системы E.8), т.е. известно решение этой задачи для
сосредоточенного внешнего воздействия в произвольной точке ot-ot0yp-
= K0 оболочки постоянной толщины:
Pz =Pz 5 (ос - Оо. Р - Pol та = ТО1д(а- a0, P - A,), E. 12)
Здесь 6 (a - a0, P - j30) - дельта-функция Дирака; Pa> Pp, Pz, Tay Tp - сос-
сосредоточенные силы и моменты.
Функция Грина может быть найдена аналитически для многих случаев
(цилиндрическая, сферическая, пологая оболочки; плоские пластины раз-
различной формы в плане и др.). В этих случаях при помощи принципа супер-
суперпозиции решение исходной краевой задачи для оболочки переменной тол-
толщины записывается в форм*е четырехкратных (в более простых случаях
двухкратных) интегралов.
* Этот подход опубликован в статье [ 196].
262
Пластины кусочно-постоянной толщины. В случае плосконапряженного
состояния плоской пластины переменной толщины уравнения E.1) - E.4)
в декартовых координатах .х, у имеют следующий вид:
ЪNX dNxy __ ЪМху dNy
Ъх Ъу ' Э.х Ъу
Eh ( Ъи Ъv \ Eh t Эу дм \
^v = ; I + v— ь ^v = ; — + v — , E.13)
\-v2 \Ъх bv У У \-v2 \Эг Эх/ 1 '
Nxy =
Eh [ Ъи Ъv
/ 014 OV \
— + —
\ bv dx /
2A
Система E.8) для данного случая идентична E.13) при h=h0; система
E.9) совпадает с E.13), где h = h0, а правая часть получается заменой
;'о Рхг = - hx рх +№х —^ + Nxy ——,
Э^х Ъу E.14)
У У ху Ъх у Ъу
Таким образом, рассматриваемый случай приводится к двум связанным
и последовательно решаемым задачам классической плоской теории упру-
упругости однородного изотропного поля. Поэтому многие краевые задачи для
системы уравнений E.13) при помощи предложенного подхода можно
решить в квадратурах. Рассмотрим плосконапряженное состояние пластин
кусочно-постоянной толщины.
Применим теперь к рассматриваемому случаю общий подход предыду-
предыдущего пункта, предполагая вначале, что толщина пластины переменна в уз-
узкой полосе ширины 2 An, симметрично охватывающей контур L; вне этой
узкой полосы функция h (x, у) постоянна. Предполагается, что производная
dh/dn (где п - нормаль к контуру L) является дельтаобразной функцией,
что можно записать так:
lim dh/dn = Ah 5 (п).
Здесь 5 (п) - функция Дирака, Afi — скачок толщины.
В результате получаем, используя предельный переходи свойства дельта-
функции,
^oC*>.V)=- IfO(xtyfx0i у0) [px(xOfyo)+ iPy(xOtyo)] dxodyo,
1 / Aj
U2 (x,
1 / Ah \
-- / 1 +— )G(x,y,x0 (t\y0 (t)) [JT(r)+ /У@1 dt
2 l ^ h0 }
h0
Ah
+ / — G(x.y. x0 (t\y0 (r)) [X°n @ + / Y°n(t)} dt.
L h0
X°n = N° cos (w, x) + Nxy cos (я, у)у
Y°n=Nxy cos (n,x) + №ycos(n,y\ E.15)
где X, Y — интенсивность внешних сосредоточенных (линейных) сил,при-
263
ложенных к контуру L; G (х, у, xOt у0) - функция Грина, соответствующая
решению данной краевой задачи для пластины постоянной толщины h 0 от
сосредоточенной силы величины A + /), приложенной в точке (xOt у0);
х =*о (*)>У ~Уо (О— уравнение контура L. Скачок АЛ может принимать
разные постоянные значения на различных участках контура L.
Решение E.15) получено формально в том случае, когда величина
е ~~ АЛ/Ло мала. Однако это решение отличается от точного решения соот-
соответствующей пространственной задачи и от приближенного решения теории
плосконапряженного состояния лишь вблизи контура L (на величину по-
порядка самоуравновешенного краевого эффекта).
Тонкие упругие оболочки сложной структуры. Рассмотрим теперь тон-
тонкие оболочки из линейно-упругих материалов любой, сколь угодно слож-
сложной, структуры. Заметим, что в технике применяются часто оболочки
довольно сложного строения (например, многослойные, гофрированные,
сотовой конструкции и др.). Поиск новых оптимальных моделей структу-
структуры оболочки является одним из перспективных направлений инженерного
искусства.
Сделаем одно предварительное замечание. Пусть имеется произвольное
неоднородное тело А, состоящее из любого набора линейно-упругих мате-
материалов без каких-либо трещин или расслоений. Тело подвержено внешним
нагрузкам, которые описываются/и параметрами рь р2,.. Л рт> а дефор-
деформация этого тела описывается п параметрами бь е2,.. ., е„. В самом общем
случае имеет место следующая линейная связь:
0'=1,2, п\ к = 1,2,... ,/я). E.16)
Здесь тп постоянных A ik характеризуют реакцию упругого телаЛ. Эти пос-
постоянные можно определить или точным расчетом, или экспериментально
(например, на моделях). Представим теперь себе, что какое-то другое тело
В состоит из конечного или бесконечного набора тел (блоков) АХ,А2, ...,
каждое из которых геометрически подобно рассмотренному телу А. Тогда
упругое поле внутри каждого из блоков естественно считать известным с
точностью до параметров е^, pfk (где 7 - номер блока), связанных между
собой соотношениями E.16); при этом величины^/* будут уже заданы.
Теперь следует записать уравнения равновесия и условия совместной* рабо-
работы блоков в теле Я Решение получившейся системы уравнений позволит
определить искомые параметры ef и/7^ и тем самым найти упругое поле те-
теВ
ла В в целом.
Применим указанный подход к оболочкам сложной структуры. Будем
считать ее составленной из бесконечного числа элементарных геометрически
подобных блоков; каждый из блоков расположен внутри параллелепипеда
с измерениями h X Да X А/3, причем ни одно из этих измерений нельзя
уменьшить, не отсекая какую-либо часть блока. Предполагается, что
L>Aa>h, L>Ap>h. E.17)
Здесь L - характерный линейный размер оболочки в плане, h — "толщина"
оболочки, а,0 - гауссовы ортогональные координаты на некоторой средней
поверхности оболочки, выбранные так, что координатные линии совпадают
с линиями главных кривизн этой поверхности.
264
Переходя к дифференциалам, сделаем следующие основные допущения.
1. Упругое поле внутри каждого из элементарных блоков определяется
восемью независимыми параметрами нагрузки
Pi,Pi,.-.,Ps, где
Pi =^а,р2 =Sa, Ръ = Щ, Р* =Sfi, E.18)
Ps =Ма, р6 =Мр,р7 = Мар, р8 =Мра9
и шестью независимыми параметрами деформации еь е^,. .. , е6, где
ei =ea, €2 = €р, 63 -со,
E.19)
U = *<*, 6§ = Кр, €6 = Г,
причем параметры нагрузки удовлетворяют уравнениям равновесия E.1),
я параметры деформации - геометрическим соотношениям E.3), где под
и, v, w надо понимать составляющие некоторого среднего смещения
элементарного блока по осям а, 0, z (условия совместной работы блоков,
выраженные только через параметры деформации, можно получить, исклю-
исключив из шести соотношений E.3) три переменных м, v и w).
2. Параметры нагрузки и, деформации элементарного блока связаны
между собой восемью линейными соотношениями
Pi = Eik ek (/= 1,2,.. ., 8; *= 1, 2,. . . ,6). E.20)
Здесь 48 постоянных Eik характеризуют упругую реакцию элементарного
блокд.
Таким образом, предложенный подход позволяет разбить общую проб-
проблему деформирования оболочки сложной структуры на две последователь-
последовательно решаемые и более простые задачи: "локальную" задачу деформирования
элементарного блока и "глобальную" задачу совместного деформирования
бесконечной системы элементарных блоков согласно сформулированным
уравнениям. Целью решения первой задачи является определение постоян-
постоянных Eik> причем все размеры элементарного блока при расчете можно
произвольно (геометрически подобно) увеличить, так как в данном случае
при помощи принципа подобия легко произвести затем пересчет для любых
сколь угодно малых, блоков. Грани параллелепипеда (элементарного бло-
блока) при а = ± Уг Да и 0 = ± у2 А/3 считаются жесткими плоскостями, каждая
из которых как жесткое целое может перемещаться поступательно, повора-
поворачиваться и вращаться. Соответствующее задание таких перемещений жест-
жестких плоскостей позволит задать параметры деформации еа, е^, со, ка, к р, г
элементарного блока, отвечающие их геометрическому смыслу согласно
уравнениям E.3). При этом параметры А^Л^,^,^, Ма, Мр,Мар,Мра най-
найдутся из решения сформулированной трехмерной задачи линейной теории
упругости как некоторые интегральные характеристики решения, вполне
определяемые их механическим смыслом.
Предложенное разбиение общей задачи весьма удобно при реализации
и анализе расчета на современных вычислительных машинах.
Сформулированные выше допущения для построения решения глобаль-
глобальной задачи удобно было бы представлять себе как мысленную замену исход-
* Переменные Qa и Qp можно исключить из E.1) при помощи двух последних уравне-
уравнений; поэтому можно считать, что имеется всего три уравнения равновесия относи-
относительно указанных параметров нагрузки.
265
ной оболочки сложной структуры некоторой однородной анизотропной
оболочкой, эквивалентной первой по упругой реакции. Однако это не сов-
совсем верно, так как в самом общем случае анизотропии независимых посто-
постоянных Eik будет всего лишь 21 и, следовательно, должно было бы сущест-
существовать 27 соотношений между постоянными Eik. Поэтому предложенные
уравнения глобальной задачи более общие по сравнению с моделью "конст-
"конструктивной анизотропии".
Следует отметить, что для обобщения в качестве основы были взяты
уравнения Власова E.1) — E.3); однако предложенный подход также
легко применить, если взять в качестве основных другие варианты теории
оболочек (например, уравнения Кирхгоффа - Лява, Рейсснера и др.).
Отметим еще одно почти очевидное обобщение изложенной теории на ма-
материалы, являющиеся линейно-вязкоупругими. Для этого нужно упругие
постоянные Eik в E.20) заменить соответствующими линейными операция-
операциями по времени, например в достаточно общем виде операторами Вольтерра
Pi @ = Щ°к ек (г) + / Eik (г - г) ек (т) dr. E.2I)
о
Здесь E°ik - некоторые постоянные, определяющие мгновенную реакцию,
Eik @ - некоторые функции, определяющие последействие (ползучесть).
§ 6. Общая теория трещин расслаивания
в многослойных оболочках
В этом параграфе рассматриваются трещины, развивающиеся вдоль гра-
границы различных слоев в многослойной тонкой оболочке. Характерный ли-
линейный размер трещины в плане предполагается большим по сравнению с
толщиной оболочки.
Вьюод граничных условий на контуре трещины расслаивания. Обозначим
через S криволинейную поверхность трещины расслаивания на границе раз-
раздела слоев в многослойной оболочке, а через/, — контур этой поверхности
(рис. 105, а). Трещина разделяет исходную целую оболочку в области S на
две отдельные оболочки, которые будем обозначать индексами " + " и " —"
(так же, как и все относящиеся к этим оболочкам величины, (рис. 105, б).
Требуется установить, как изменяется во времени и в зависимости от внеш-
внешних нагрузок контур L. Это нелинейная проблема теории оболочек; ее не-
нелинейность заключается в том, что контур L заранее неизвестен и его тре-
требуется определить в ходе решения.
Установим все относящиеся к этой проблеме граничные условия. Вдоль
контура L сопряжены три оболочки: " + ", " — " (в области S) и основная,
исходная, с индексом " (вне области S). Каждая из них удовлетворяет
соответствующим дифференциальным уравнениям теории тонких оболочек
(см. предыдущий параграф). На контуре сопряжения L должны выполнять-
выполняться следующие граничные условия:
условия неразрывности
и* = и~=и°, и+ = и~=и°, w+ = w"=w°; F.1)
* Все буквенные обозначения, относящиеся к оболочкам, те же, что и в предыдущем
параграфе.
266
уравнения равновесия
S°n=st + S~, F.2)
F.3)
Q°n =Qt + G«. M°nt=MZt+ M~t. F.4)
Здесь tun — касательная и нормаль к контуру L.
Трещина расслаивания может быть открытой и закрытой. В последнем
случае в каждой точке области S должны выполняться следующие условия
совместной работы оболочек " + " и " — ":
условие нормального смыкания
w+= иГ, F.5)
уравнение предельного равновесия (в состоянии проскальзывания)
(АраJ + (АррJ =f(APz), F.6)
уравнение ассоциированного закона пластичности (см. рис. 105, в)
Au/Av = ApJApp ,r уч
Здесь через Ара, Ар@, Apz обозначены соответствующие компоненты век-
вектора интенсивности дополнительной распределенной нагрузки, воз-
возникающей из-за взаимного налегания оболочек "+" и"—", функция / в
простейшем случае удовлетворяет закону сухого кулонова трения / =
= \До + APz tgp (ко и р — коэффициент сцепления и угол трения),
Аи и Ai) — составляющие скорости взаимного проскальзывания оболочек
Аи -и+ — и~
Av -
— \Г
Таким образом, в случае налегающих оболочек в области S появляются
три новые неизвестные функции, Ара, Ар@ и Ар2, зависящие от а и /3 и
участвующие в уравнениях равновесия каждой оболочки; три уравнения
F.5)-F.7) вместе с уравнениями теории тонких упругих оболочек (см.
§ 5) составляют замкнутую систему. Эта система оказывается, естественно,
нелинейной вследствие нелинейности уравнений F.6) и F.7). На контуре
L функции Ара и Арр должны обращаться в нуль. Заметим, что если пре-
небречьсилами контактного трения и положить Ара = Ар$ = 0, то уравне-
уравнения F.6) и F.7) исчезнут; задача снова станет линейной, а одной но-
новой функции Ар2 будет соответствовать одно новое уравнение F.5).
0^
б)
Рйс. 105.
267
Рис. 106.
При наличии частичного контакта оболочек "+" и "—" сама область кон-
контакта должна быть определена в ходе решения задачи. На границе, разде-
разделяющей открытую и закрытую области расслаивания, для каждой из оболо-
оболочек должны выполняться очевидные условия сопряжения.
Все сформулированные до сих пор уравнения позволяют ставить и ре-
решать задачи в том случае, когда положение фронта трещины известно.
Для вывода дополнительных граничных условий на фронте трещины рас-
расслаивания привлечем инвариантные Г-интегралы и общую теорию, изложен-
изложенную в § 1 первой главы книги.
Рассмотрим зону пограничного слоя в окрестности некоторой точки
О контура/, трещины расслаивания (рис. 106,а). Ширина этой зоны (вдоль
нормали п к контуру) считается малой по сравнению с характерным линей-
линейным размером трещины в плане (в частности, с радиусом кривизны конту-
контура L и радиусом кривизны оболочки), но велика по сранению с толщиной
оболочки (практически, на основании точных решений, в два-три раза
больше толщины оболочки). В погранслое приближение теории оболочек
не годится, и нужно привлекать точную, трехмерную теорию. В обычном при-
приближении тонких оболочек упругое поле в погранслое можно считать плос-
плоским в окрестности точки О, т.е. не зависящим от координаты t вдоль
контура трещины, а саму оболочку - плоской многослойной пластиной
с фронтом трещины вдоль оси t прямоугольных декартовых координат
Otnz.
Введем следующее допущение *
Развитие трещины расслоения в точке О определяется следующими
величинами в этой точке: Nn,N~nfN%\Sn,Sn>S%\Mn,M~n,Mnfu не зависит
от других изгибающих и крутящих моментов и перерезывающих сил в
этой точке. Развитие трещины в точке О не зависит также от наличия рас-
распределенных касательных и нормальных нагрузок на берегах трещины
и боковых поверхностях оболочки вблизи точки О.
Это допущение выполняется тем точнее, чем меньше отношения h/l и
h/R (где И - толщина оболочки, R - радиус кривизны оболочки, / -
характерный линейный размер трещины в плане).
На основании предложенного допущения процесс развития трещины
в точке О может быть изучен на плоском чертеже погранслоя рис. 106,5 с
учетом лишь указанных нагрузок и в пренебрежении внешними нагруз-
Это, довольно парадоксальное, допущение имеет эвристический характер. Оно
вытекает из интуитивных физико-механических представлений и подтверждается
известными точными решениями.
268
ками на берегах трещины. Отсюда имеем следующую краевую задачу в
плоскости nz для многослойной полосы с трещиной:
при z =h+ и 2 =— h_
n ozT2nrzt , F.8)
при z = 0 и п < О
при п -+ + оо е„ = €„° + к°п z , ynt = 7°, ,
при л->- oo(z>0) €„ = €++к^ z, 7иг = 7+А!г; F.9)
при fl-»-°°(z<0) €„ = б~+к^ z,'ynt = ynt .
Здесь бм и ynt - нормальная и тангенциальная деформации. * Вдоль гра-
границ раздела слоев при z = const имеют место условия жесткого сцеп-
сцепления.
В случае линейно-упругих тел имеют место следующие соотношения:
Л#=*?ея, K=kte+, N- = k-ee-n; F.10)
'S°=k*y*t, s;=ktytti s; = k-synt; F.11)
М°п=к?к<>, M^kUL M- = klK-n. F.12)
Здесь ke, ks и kb — жесткости многослойной полосы на растяжение, сдвиг
и изгиб соответственно; они получаются суммированием соответствующих
жесткостей всех слоев в полосе
^ F.13)
/ 1 - v{ i / 1 - v\
Здесь hif Ef, G/, vu It — соответствующие параметры /-го слоя: толщина,
модуль Юнга, модуль сдвига, коэффициент Пуассона, момент инерции
относительно нейтральной оси полосы.
Рассмотрим замкнутый контур 2 в плоскости Onz, образованный проти-
противоположными берегами трещины, окружностью весьма малого радиуса, ох-
охватывающей точку О, боковыми плоскостями полосы и ее поперечными
сечениями при п -> ± °° (см. рис. 106, б). Согласно теории инвариантных
Г-интегралов имеет место слудующее уравнение [1]:
/ {Unr-oijnjtit^dZ^O (/=1,2,3; /=1,2). F.14)
Здесь ¦«; — единичная нормаль к контуру 2, о^ - напряжения, щ — пере-
перемещения, U — упругий потенциал единицы объема. Уравнение F.14) спра-
справедливо также для любых неупругих тел (упруго-пластических, вязкоупру-
гих и др.) при квазистационарном движении точки О вдоль оси п со ско-
скоростью, значительно меньшей скорости звука в полосе; при этом под Uпо-
Uпонимается удельная энергия деформаций.
Обозначим через Г величину интеграла в F.14) по окружности, охваты-
охватывающей точку О(Т-вычет в точке О). Из F.14) на основании граничных
269
условий F.8) и F.9) имеем
Г = / (U- of ,uitl) dz= f (U- onen - rn z uzn - rntynt)dz =
/. l
= / Udz- en f ondz- Kflf z ondz - uz>n f rnz dz - ynt f rntdz =
L L L L L
= IUdz-(€nNn+KnMn+yntSn)\L =[!/,], F.15)
L
где
(M->_co)
(«-
Us=-Ud+N,,en+MnKn+Snynt, [Ud]=f Udz,
L
Ud = fNn den +MndK,,+Sndynt.
F.15')
Здесь Ud - энергия деформации, приходящаяся на единицу площади
многослойной пластины в плане, Us — дополнительная энергия деформации
(физический смысл Ud и Us ясен из одномерной схемы растяжения
рис. 107, полученной следующим образом: растягиваем образец заданной
во времени t деформацией еп - en(t) и снимаем соответствующее усилие
Nn = Nn(t), затем, исключая t, строим кривую Nn = Nn(en) для данного
пути нагружения). Скобки [... ] означают скачок величины, заключенной
в скобки, при пересечении фронта трещины.
Уравнение на фронте трещины
Г =[!/,] F.16)
является основным результатом теории трещин расслаивания в многослой-
многослойных оболочках из любых материалов.
Из него вытекает, например, что, если скорость роста трещины V гораздо
больше h/т:
V>h/r, F.17)
где г - характерное время протекания реакции последействия многослой-
многослойного материала, то развитие трещины будет определяться лишь мгновен-
мгновенной реакцией материала в целом (т.е. его упруго-пластическими свойства-
свойствами) и не будет зависеть от реакции последействия материала (т.е. от его
свойств ползучести и вязкости). Действи-
Действительно, ширина погранслоя An практически
равняется B + 3)h (асимптотическая бес-
бесконечность рис. 106, б), поэтому при условии
F.17) правая часть уравнения F.16) —вели-
—величина [6(у] (определяемая реологическими
свойствами многослойного материала в це-
целом) — зависит лишь от его мгновенной
реакции.
Левая часть уравнения F.16), величина
Рис.107. Г, определяется свойствами материала в
270
весьма малой окрестности фронта трещины (малой по сравнению с тол-
толщиной отдельного слоя Л/), т.е., по существу, химическими и физико-
механическими свойствами поверхности раздела слоев на продолжении
трещины. Именно эти последние свойства объясняют наблюдаемые эф-
эффекты докритического роста трещин расслаивания и аварий многослой-
многослойных конструкций при относительно низких нагрузках.
Три типа трещин расслаивания. Как и в общем случае [1], в зависимос-
зависимости от напряженного состояния многослойной оболочки вблизи фронта тре-
трещины будем различать следующие частные случаи (см. рис. 106).
1. Нормальный разрыв или отрыв:
N° = К = N~ = 0, 5л° = 5„+ = S- = 0. F.18)
2.Поперечный сдвиг:
<=М„+=Л/„" = 0, Sn°=Sn+=S,; = 0. F.19)
3.Продольный сдвиг:
Мп°=М;=Мп- = 0, Nn°=Nn+=N»- = 0. F.20)
Содержание этого и следующего параграфов основано на работе автора
[202].
Распределение напряжений и деформаций вблизи фронта трещины нахо-
находится из решения краевой задачи F.8), F.9) для погранслоя (см. рис.
106, б). В случае линейно-упругого тела эта задача может быть решена
методом Винера — Хопфа при помощи преобразования Фурье по п. К
счастью, закономерности развития трещин расслаивания могут исследовать-
исследоваться непосредственно при помощи общего уравнения F.16), минуя анализ
напряжений и деформаций в самом погранслое.
Исследование законов развития трещин расслаивания опытным путем.
Уравнение F.16) позволяет изучать скрытые и сложные процессы разру-
разрушения в конце трещины (левая часть этого уравнения) на макрообразцах
с трещинами путем измерения изменения во времени t двух макровеличин:
длины трещины / и величина [Us] (правая часть уравнения). Принципиаль-
Принципиальная схема исследования легко может быть понята на простейшем примере
нормального разрыва двухслойного образца концевыми силами (рис 108).
Пусть требуется изучить развитие трещины расслаивания нормального
разрыва в многослойной оболочке, распространяющейся вдоль границы
раздела двух слоев. Для этого нужно приготовить двухслойные балки из
материала этих слоев 7 и 2, в точности воспроизводя способ и технологию
соединения их поверхностей, а также внешние условия. Размеры балки-
образца (толщина и длина в плоскости От, см. рис. 108) могут быть прак-
практически любыми (их нужно подобрдть, исходя из мощности наличных ис-
испытательных машин). Затем балка с искусственно созданной начальной
трещиной расслоения длины / растягивается двумя силами Q согласно
схеме* рис. 108 по задаваемой программе Q{t). В данном случае в конце
Можно использовать и многие другие схемы образцов, например, аналогичные
тем, которые рассматриваются ниже в примерах.
271
трещины имеем согласно F.15)
<=0, к„0=0, Мп+=-Мп-= Q(t)l(tl
F.21)
Ш =QI(k: - к'п) - f Qld{K+n - к»)
(с учетом знака кривизны).
Величины к„ (г) и к„(t) в конце трещины могут измеряться непосред-
непосредственно; однако удобнее и точнее рассчитывать их по реологической моде-
модели материалов / и 2, определяемой из независимых экспериментов на
однородных материалах без трещин. Таким образом, по измеряемой функ-
функции I(t) при помощи F.21) находится функция [Us(t)]. Последняя соглас-
согласно F.16) равна Г (г) , а определение этой функции является целью исследо-
исследования.
Результаты этого изучения следует изобразить в инвариантных перемен-
переменных в виде кривой зависимости скорости роста трещины / = dljdt от вели-
величины Г (диаграмма / — Г); эта диаграмма в общем случае, естественно,
будет зависеть от "пути нагружения", описываемого функцией [Us(t)].
Согласно постулату подобия (см. § 1 первой главы) полученную диаг-
диаграмму можно использовать для расчета развития трещины расслоения
нормального разрыва между материалами 7 и 2 в любой произвольно
нагруженной многослойной оболочке при той же функции [Us(t) ]. Для
этого нужно функцию Г(/) из диаграммы подставить в левую часть урав-
уравнения F.16) и решить получающееся дифференциальное уравнение отно-
относительно l(t).
Достаточно большим набором диаграмм / — Г и соответствующих
им "путей нагружения" [Us(t)] можно описать развитие трещин расслое-
расслоения для любой пары материалов с любыми свойствами. При этом в рас-
расчетах удобнее определить вначале набор l(t) и [Us(fj] по известным диаг-
диаграммам, а реализуемую функцию I(t) выбирать по наибольшей близости
расчетной и "паспортной" функции [Us(t)].
Расчет по критическому состоянию. Скорость трещины / с увеличением
Г обычно плавно возрастает (и, по крайней мере, не убывает), но сущест-
существует критическое значение Г = 2jfm, при приближении к которому наблю-
наблюдается резкое увеличение / (рис. 109). Величину yfm будем называть
удельной энергией адгезии [1] пары материалов,/ и т. Из предыдущего
ясно, что в общем случае она зависит от функции [Us(t)], т.е. от предысто-
предыстории. Однако для многих материалов и внешних условий такой зависи-
зависимостью, так же, как и докритическим ростом трещин, часто можно (или
1 ^\
<
1 n
Рис. 108.
Рис. 109.
272
Рис. 110.
нужно) пренебречь. При этом общее уравнение F.16) приобретает следую-
следующий простой вид:
Ws) = 27/m • F-22)
Приведем несколько простых примеров расчета по критическому состоя-
состоянию F.22).
Разрушение двухслойной балки из упруго-пластических материалов.
Рассмотрим схему разрушения балки двумя консольными силами, как
показана на рис. 108. Каждый из материалов является идеальным упруго-
пластическим (рис. ПО, а). Сила Q считается неубывающей (простое наг-
ружение).
По диаграмме оп - еп легко рассчитать диаграмму Мп -ккп чистого
изгиба балки (рис. 110, #). Находим
Л Ellnh3
при 0<Kn<2os/(hE),
при — <кп <°° .
Отсюда по формулам F.15) вычисляем величину Г (рис 110, в) :
F.23)
о
— ЕНЪ
24
2 Е
при 0 < кп <
2а,
не'
2 а?
ЗЕ2кп
при
НЕ
F.24)
273
' 1
Рис. 111.
Рйс. 112.
Теперь определяем Г =
= и
=
= 0) в конце трещины, где Мп =
= QI (рис. ПО, г). В зависимости от соотношения постоянных и величи-
величины нагрузки возможны следующие варианты:
при 6QKosl h\ <os2h2 (упругий слой 1 плюс упругий слой 2)
->2/2
1
1
Exh\
F.25)
при oslhi < 6QI < os2h\ (упруго-пластический слой 1 плюс упругий
слой 2)
Г =
4QI 6
+
G2/2;
F.26)
1 1
при 01 - — os\h{ <z — os2h\ (упругий слой 2 плюс упруго-пластический
4 6
слой i в предельном состоянии, с "пластическим шарниром" в конце тре-
трещины, рис. 111)
F.27)
2А,
при osXhi < os2h\ <6QK—osjh\ (упруго-пластический слой 1 плюс
упруго-пластический слой 2, рис. 112)
2 L 4Ql'
^ г,- А2 - — -
Формулы F.25) - F.28) позволяют на основе критерия роста трещины
F.22) без труда проанализировать развитие процесса разрушения в упру-
упруго-пластической двуслойной балке с трещиной. В зависимости от соотно-
соотношения постоянных возможны следующие варианты (Qb — предельная на-
нагрузка) :
при 6QbI < osth\ < os2 h\ рост трещины начинается до возникновения
пластических зон в слоях 1 и 2 (квазихрупкое разрушение)
пь-
Wv
F.29)
274
при osi h i < 6Qbl < os2h\ рост трещины начинается после возникнове-
возникновения пластических зон в слое 1 (хрупко-пластичный слой 2 плюс квази-
квазихрупкий слой 1), a Qb является корнем уравнения
l 2EX
при osl h\ < os2h\ < 6?2&/< — os\ hi рост трещины начинается после
развития пластических зон в слоях 1 и 2 (хрупко-пластичные слои 1 и 2),
а ??/, является корнем уравнения
os\
osl \f3t2 os2
Если выполняются условия
2
2Ь\
или
За,? At ., .2 . 2
zrM Z?2 V3?2 ^52
— a,, A? > cs2h\ >osl h\,
то трещина не развивается, а разрушение происходит вследствие исчерпа-
исчерпания несущей, способности балки 1 при упругом или упруго-пластическом
состоянии слоя 2
Рост трещины в рассматриваемой задаче всегда является быстроускоря-
ющимся, неустойчивым, так как Qb ~ 1/д.
В случае жестко-пластических материалов обоих слоев, когда
7fmE2
трещина не развивается, а разрушение происходит вследствие образования
"пластического шарнира" в балке / в конце трещины (см. формулу
F.32)), Можно показать, что этот результат справедлив для самого произ-
произвольного случая нагружения многослойных оболочек с трещинами расслаи-
расслаивания.
275
ип
Рис.113.
Рис. 114.
Трещина поперечного сдвига в двуслойной балке (рис. 113). В этом
случае имеем
Мп° =Mt =М- = 0, Sn° = S * = 5" = О,
Лг° = п л/+=_л/ л/-=л/- F.33)
при
при
1е„1>е,;
F.34)
-hEe*
при 1ел1<€
при I е„ I > е^
F.35)
Отсюда при помощи уравнения F.22) находим предельные нагрузки iVft
в случае монотонного возрастания N:
при Nb<hx osl <h2 os2 (квазихрупкое разрушение)
Nb =
при hx osl < 2
F36)
(пластическое разрушение слоя 1
h2E2/
с нера!звивающейся трещиной)
Nb=h, osl. F.37)
Докритический рост трещин расслаивания в многослойных оболочках из
упруго-пластических материалов. Рассмотрим простой пример докритачес-
кого развития трещины расслаивания нормального разрыва в двуслойной
балке (рис. 114). В этом случае величина Г в докритическом состоянии при
простом нагружении определяется формулами F.25), F.26) и F.28), в
которых нужно положить Ql = M. Она не зависит от длины трещины /; как
легко проверить, эта независимость от / сохранится для любых, сколь угод-
угодно сложных, путей нагружения M(t)9 хотя соответствующие выражения
F.26) и F.28) будут уже другими (они будут зависеть от предшествую-
предшествующего пути нагружения).
Нетрудно проверить непосредственным подсчетом,что для сложного пути
нагружения величина Г будет меньше (или, по крайней мере, не больше),
чем для простого пути нагружения. Это обстоятельство справедливо не
только для данного примера, но и в общем случае трещин расслаивания в
многослойных оболочках из упруго-пластических материалов. Все законо-
276
мерности докритического роста трещин имеют следующий общий характер:
развитие трещины начинается, как только будет превзойдено некоторое по-
пороговое значение Г, зависящее от конкретного физико-химического меха-
механизма процесса разрушения непосредственно на фронте трещины [1]. От-
Отсюда вытекает следующий общий вывод: если действующие на оболочку
внешние нагрузки быстро увеличить, а затем уменьшить до нормальных, ра-
рабочих значений, то это приведет, вообще говоря, к увеличению порогового
значения Г. Этот физический эффект пластичности "в большом" может ока-
оказаться полезным во многих практических приложениях.
Легко видеть, что эффект Баушингера приводит к еще большему умень-
уменьшению величины [Us]. Поэтому предварительным наложением на оболочку
нескольких циклов "нагружение — разгрузка" можно добиться существен-
существенного увеличения уровня пороговых нагрузок, при котором начинается до-
критический рост трещин.
Найдём для некоторых случаев скорость'докритического роста трещи-
трещины расслаивания / в рассматриваемом примере рис. 114, основываясь
на уравнении F.16) и закономерностях (9.1) —(9.4) первой главы книги:
подрастание трещины, мгновенно следующее за нагружением
, Pfm[Us][Us] .
/=="т—т; гтгттпРи Ws]>0\ F-38)
27fmByfm-[Us])
развитие трещины вследствие водородного охрупчивания (в метал-
металлах)
Vj F.39)
рост трещины вследствие кинетического механизма локального ста-
старения
I = vfm exp -^—- ; F.40)
RT
рост трещины вследствие коррозии
/ = const. F.41)
Формулы F.38) — F.41),очевидно, пригодны и в общем случае трещин
расслаивания в многослойных оболочках, причем уравнение F.38) нуж-
нужно дополнить условием необратимости трещины при разгрузке (/ = 0 при
[Us] <0). Уравнения F.39) — F.41) получены, строго говоря, для квази-
квазистационарных процессов. При одновременном действии нескольких ме-
механизмов докритического роста трещин нужно сложить соответствующие
приращения длины трещины для каждого механизма, если отсутствует
их взаимное влияние друг на друга [ 1 ].
В случае трещины поперечного сдвига, изображенном на рис. 113, ве-
величина [Us] не зависит от / и пути нагружения. Схемы рис. 113 и 114
наиболее удобны для экспериментального изучения трещин расслаивания.
В случае консольного нагружения силами (см. рис. 108) трещина будет
ускоряться; точная зависимость / (г) может быть найдена из соответству-
соответствующего дифференциального уравнения, полученного после подстановки
[Us] согласно F.25) - F.28) в уравнения типа F.38) - F.41).
277
Зависимость предельных нагрузок от пути нагружения. Рассмотрим
простейший случай чистого изгиба балки на жесткой подложке (когда
слой 2 в схеме рис! 114 - абсолютно жесткий). На рис. 115 изображена
зависимость изгибающего момента Мп от кривизны кп в основании балки
(в конце трещины). Пользуясь этой диаграммой, легко вычислить значе-
значение [Us] для любых путей нагружения. Например, имеем
в точке А по пути О A [Us] = S(OAE),
в точке С по пути ОАВС [Us] = - S(OABC),
в точке А по пути OABCD [Us] = S(OAE) - SB
и т.д. Здесь S обозначает площадь соответствующей криволинейной фи-
фигуры на рис. 115; SB — площадь гистерезисной петли Баушингера {ABCD).
Обобщая эти построения, можно прийти к следующим общим выводам:
А. Предельные нагрузки для многослойных упруго-пластических обо-
оболочек с трещинами расслаивания не зависят от пути нагружения, если
можно пренебречь вторичными эффектами типа эффекта Баушингера.
Б. Гистерезисный эффект Баушингера (изображенный на рис. 115)
приводит к увеличению предельных нагрузок для многослойных оболо-
оболочек с трещинами расслаивания.
Эти выводы справедливы вообще для любых нагрузок "инициирова-
"инициирования", при которых начинается рост трещин.
Таким образом, при отсутствии эффекта Баушингера величина [Us]
представляет собой функцию Mn,NnnSn, не зависящую явно от времени
и вычисляемую по простому пути нагружения (это равнозначно допуще-
допущению, что оболочка с трещиной является нелинейно-упругой). Следователь-
Следовательно, в этом случае нагрузки, при которых начинается рост трещин расслаи-
расслаивания в многослойных оболочках, можно вычислять в предположении
соответствующего нелинейно-упругого поведения материала.
Усталостные трещины расслаивания. Пусть внешние нагрузки пред-
представляют собой некоторые периодические функции времени. Тогда ве-
величина [Us] будет также некоторой периодической функцией времени
со слабо изменяющимися коэффициентами. Используя закономерности
докритического развития трещин типа F.38) — F.41), можно найти при-
приращения трещины для любого программированного или случайного нагру-
нагружения [1].Ограничимся здесь лишь учетом пластических эффектов мгно-
мгновенной реакции, описываемых уравнением F.38).
Интегрируя это уравнение, при помощи известного подхода [1] можно
прийти к следующей закономерности:
J# _ / [tffaxl - [^min] SB
dn m v 2тл„
-In
L). F.42)
27/m ~[US ] + AS
Здесь n — число циклов нагрузки (играет роль времени), dl/dn — скорость
трещины, [*/Гах] и [Usmin] — соответствующие наибольшее и наименьшее
278
Ftoc. 115.
значения [Us] в течение цикла, вы-
вычисленные по простому пути нагру-
жения, Sв — площадь соответству-
соответствующей гистерезисной петли Баушин-
гера, AS - слагаемое, отражающее
влияние предыстории в начале цик-
цикла (в большинстве случаев его
можно положить равным нулю, см.
рис.115).
Упругая многослойная оболоч-
оболочка с квазихрупкими трещинами рас-
расслаивания. В этом случае величи-
величина Г выражается через коэффици-
коэффициенты интенсивности напряжений при помощи формулы B.29) для за-
закрытых трещин скольжения и при помощи формулы B.47)— для от-
открытых трещин. Поэтому уравнение F.16) можно использовать для вы-
вычисления коэффициентов интенсивности по усилиям и изгибающим мо-
моментам, определяемым из расчета упругой оболочки.
Оптимальное проектирование многослойных оболочек с трещинами
расслаивания. Опыт показывает, что образование трещин расслаивания
в многослойных конструкциях неизбежно, в особенности в процессе ее
эксплуатации. Поэтому важно, чтобы образующиеся повреждения были
безопасными и не мешали выполнить целевое назначение конструкции.
Анализ, проведенный в этом и предыдущем параграфе, позволяет выделить
важнейший конструкционный параметр многослойной оболочки, который
управляет этим процессом. Этим параметром является величина Г; кон-
конструкция должна быть спроектирована так, чтобы эта величина была наи-
наибольшей в зонах, наиболее опасных с точки зрения расслаивания. Техно-
Технология создания конструкции должна обеспечить максимально возможное
торможение трещин расслаивания; важнейшими физико-химическими ха-
характеристиками прочности соединения слоев являются параметры 7/т>
fifm > Vfm > a/w > Afm, ^scc и др. В зависимости от условий работы конструк-
конструкции какой-либо из этих параметров может играть главную роль при
выборе оптимальной технологии и оптимального многослойного
материала.
§ 7. Некоторые задачи о трещинах расслаивания
Рассмотрим некоторые примеры, иллюстрирующие общую теорию.
Эллиптическая трещина в пластине. Пусть плоская пластина склеена
из двух одинаковых слоев толщины h (рис. 116, а). На границе слоев име-
имеется трещина эллиптической формы L в плане
хл у*
7V-
G.1)
где 2а и 2Ъ — диаметры эллипса (рис. 116, б). К берегам трещины прило-
приложено постоянное давление р. Вследствие симметрии достаточно рассмотреть
деформацию верхнего слоя.
279
Рис.116.
Для нормального смещения w слоя имеем следующую краевую
задачу:
Э4и> 34w
G.2)
где
0 12A -v2) '
на контуре L :
dw
Эх Эу
Решение этой задачи имеет следующий вид:
= 0.
w = .
где
8 \а4
G.3)
G.4)
Пусть л и Г - направление внешней нормали и касательной соответственно
к контуру L. Вторые производные в системе координат nt выражаются
на контуре L так:
d2w d2w d2w
Ъп2 ~ d? lHnbt
2w d*w d2w \
дх2 Ъу2' 1ЪхЪу Г
G.5)
где а — угол между осями хип.
Так как на контуре Ld2w/dt2 = 0 и d2w/dndt = 0, при помощи G.4) и
G.5) сразу находим кривизну кп на контуре/,:
d2w
p
2, 2
4х2у
2у2
280
Величина Г, определяющая развитие трещины расслаивания, в данном
случае равна (с учетом второго слоя)
оР2 Г/ х2 у2 \2 4х2у2 1
r.tbd-M''- [G -F) + -rf-]. fc,Nt G.7)
Найдем также коэффициент интенсивности напряжений
А )+ !$г ¦ G-8)
Величина ^монотонно убывает вдоль контура эллипса L от макси-
максимального значения при х = 0, у = ±Ь, равного
ЪЪ2 2 3 V1
G-9)
до минимального значения при х - ± а, у = 0, равного
3 2 За2\ -1
)
Для сплющенного эллипса, т.е. при малых ?/#, вблизи точки х = ±д,
.у = 0 появляются два абсолютных минимума, меньших величины G.10)
примерно на 10%.
Таким образом, эллиптическая трещина расслаивания всегда начинает
развиваться вдоль малой оси; контур трещины изменяется до тех пор,
пока не станет круговым с диаметром, равным большому диаметру Та
начального эллипса. После этого трещина растет вдоль всего контура,
оставаясь круговой. Оценим рост трещины в процессе увеличения давле-
давления на основе следующего приближенного допущения: контур трещины
все время остается эллиптическим с малым диаметром, равным 2Ь = 2Ь(р),
и неизменным большим диаметром 1а . Ограничимся лишь рассмотрением
предельных состояний, когда A^imax =^ic в точке Jc = O,.y = ±Z?; докри-
тическое развитие трещины легко изучить при помощи этого же допущения.
На основании G.9) получаем
(^ ^) GЛ1)
График зависимости р=р(р) изображен на рис. 117. Как видно, по
достижении предельного давления рС9 соответствующего начальной вели-
величине bo, трещина развивается неустойчиво, переходя при Ь= 1 на круго-
круговую форму. При этом а = Ь - г; в случае дискообразной трещины имеем
8 / r \
Р=— г=->1,
г \ а '
G.12)
281
21
РИс. 417.
Рис. 118.
Отметим предельный случай b/а -> 0 (полоса \у \ <Z>,-00<*<00). В
этом слз^чае согласно G.9) имеем
^ 2pb2 3
К 'Т- G13)
В отличие от случая эллиптической трещины в трехмерном теле эл-
эллиптическая трещина расслаивания в пластине не имеет участка устойчи-
устойчивого подрастания (впрочем, при наличии других слоев из более жесткого
материала такие участки, очевидно, должны появиться).
Параболическая трещина в пластине. Пусть в условиях предыдущей
задачи трещина расслаивания занимает в плане область
У
~ Х Г0 >
G.14)
где г о — радиус кривизны параболы в ее вершине.
Решение краевой задачи G.2), G.3) для этой области будет следую-
следующим:
РГ% ( X2 ч 2
вкь \ 2r0 I
Ъп2
9к„
2 -г20J+4х2],
G.15)
hy/bh
Функция К\(х) имеет один локальный максимум при л* = 0, равный
и два абсолютных минимума при х = ± го/у/Т, равных
282
Гиперболическая трещина в пластине. Пусть в условиях предыдущих
задач трещина занимает в плане область
^2 „2
х2
где а кЬ — параметры гиперболы.
Решение краевой задачи G.2), G.3) для этой области будет следующим:
w
kb\a2 b2 I
, p2 г/ х2 у2 \2 4x2v2 1
2— -г- -V +-3-3-K Gi7)
A:ft IV ft4 / а*Ь* У V '
Трещина расслаивания в двухслойной цилиндрической оболочке. Пусть
в круговой цилиндрической оболочке радиуса R толщины 2/г имеется
осесимметричная трещина расслаивания, которая разделяет исходную
оболочку на две цилиндрические оболочки толщины hx иЛ2> сделанные
из различных материалов Bh = hi +Л2). К берегам трещины приложено
постоянное давление р (рис. 118).
Радиальное смещение w цилиндрической оболочки толщины И удовлет-
удовлетворяет следующему уравнению [195]:
cfw Eh I
—т-+ —г- w = р, G.18)
dx4 R2kb kbP* K
kb 12A -v2)
Изгибающий момент Мх и перерезывающая сила Qx выражаются через
w так: ,, .
d2w d3w
М^-къ—т, Gy=^__. G.19)
dx dx*
Граничные условия для внутренней трещины длины 2L будут следую-
следующими (рис. Ц8) :
при x = ±L G.20)
dw
w=0, —- = 0.
Эх
Решение краевой задачи G.18), G.20) запишем так:
pR2 / sinXLchXx + sh\L cos \x \
[1 ), G.21)
\ sinXLchXL + shXLcosXL /
где
Eh N1'4
283
w =
Eh
Кривизна кп оболочки на фронте трещины согласно G.21) равна
-V2) tgXZ, - thXZ
d2w\
^ = --гт
dx1 \X=±L
Eh2
tgXZ, + thXL
G.22)
Отсюда определяем величину Г (с учетом обоих цилиндрических обо-
оболочек) :
р = к, „з . ? -2
2* 2,
1 2n2' 1 M
= —p2R2 , ——
2 L^i^i V
tgA2Z,-thA2Z,
2Z,\
2Z /
G.23)
где
= (l2 о !
Эта формула позволяет исследовать критическое и докритическое
развитие трещины расслаивания. Изучим лишь критическое состояние,
в котором выполняется критерий Г = 2jfm; ограничимся случаем двух
одинаковых слоев толщины ht = h2 = А.
Р Согласно G.23) в этом случае имеем
tg/T+thZ"
\
1
4
\
ft
V
1
\
\
9
Ж
\
It
\
ш
\
ft
\дяг
г
tgL-thL
G.24)
где
Рис.119.
l/4
График функции p (Z) изображен на
рис. 119. Он состоит из бесконечного
числа "почти" периодических неустойчи-
неустойчивых ветвей, имеющих своими асимптота-
асимптотами следующие прямые:
5 9 13 17
*Lb= 0, -тг - 4 . ЮЛ-тг — 7Г— я,...
4 4 4 4
G25)
Поведение трещин расслаивания в ци-
цилиндрической оболочке оказывается весь*
ма своеобразным. При любой начальной
284
трещине Lo она всегда подрастает к ближайшему справа значению Lh и бу-
будет оставаться в этом положении L-Lb сколь угодно долго и при любых
нагрузках (так как при L -Lb величина Г равна нулю). Подрастание тре-
трещины в критическом состоянии будет неустойчивым, быстрым, а в докри-
тическом состоянии может быть достаточно медленным.
Наличие бесконечного числа возможных "барьерных" состояний, в
которых трещина "стационарна" и не подвержена какому-либо росту
в критическом или докритическом режиме, роднит рассмотренную систему
с квантовомеханическими системами, для которых такое поведение явля-
является типичным.
Эллиптическая трещина в мембране. В рассмотренных выше примерах
считалось, что изгибные напряжения велики по сравнению с напряжения-
напряжениями растяжения срединной поверхности. Рассмотрим другой крайний слу-
случай, когда изгибные напряжения малы по сравнению с предварительным
натяжением пластины напряжениями ох и оу .
Вначале отметим простую общую формулу для [Us] в случае трещи-
трещины расслаивания в произвольной многослойной безмоментной оболочке
(мембране)
[Us] = %д*(Эм>7Эл)а + y2if(dw-/bn)\ ju* = Zht a*/. G.26)
Таким образом, согласно F,16) и G.26) развитие трещины расслаива-
расслаивания в безмоментной оболочке определяется углами поворота соответству-
соответствующих оболочек в рассматриваемой точке контура трещины.
Пусть плоская упругая мембрана толщины 2h склеена из двух одинако-
одинаковых слоев; на границе раздела имеется эллиптическая трещина расслаива-
расслаивания L, к берегам которой приложено постоянное давление р. Для нормаль-
нормального смещения н>верхнего слоя имеем (см. рис. 116)
p
= 0пи (x,y)eL. G.27)
Ьх2 ' by2
Решение этой краевой задачи имеет вид
у2
; I, D= — I — + -И ,
G.28)
Как видно, цри а2 о у >Ь2ох трещина начинает развиваться вдоль оси .у,
а при а2 о у <Ь2ох — вдоль оси х. В процессе развития при заданных ах и
Оу форма трещины изменяется, стремясь к эллипсу х2/ох +у2/оу = X,
описывающему начальный; в дальнейшем развитие трещины сводится к
автомодельному расширению последнего эллипса за счет монотонного воз-
возрастания параметра X (на этом эллипсе Г = const вдоль всего контура).
При фиксированных ох и оу рост трещины всегда неустойчив с увеличе-
увеличением р. Параметры ох и оу являются стабилизирующими факторами,
поэтому в зависимости от пути нагружения в трехмерном пространстве
(р,ох,оу) можно получить картины любого изменения эллиптических
трещин (безразличное равновесие, устойчивость, неустойчивость, "хлоп-
"хлопки" и т.д.).
285
ПРИЛОЖЕНИЕ
АЛГОРИТМ КОНСТРУИРОВАНИЯ ОПТИМАЛЬНОЙ
МНОГОСЛОЙНОЙ ПЛАСТИНЫ
1. Блок-схема гибкой процедуры
перебора с обращением к алгорит-
алгоритму проверки условия склеивания.
2. Блок-схема алгоритма проверки
условия склеивания листов в па-
панель.
Создание начальной задачи
и начального плана.
2 л Вычисление оптимизируемой
функции.
Ограничения выполнены?
Можно выполнить ограничения
свободными переменными?
* а Можно повысить значение
' 5) функции свободными
переменными?
Все несвободные переменные
фиксированы?
Вычисление функции.
функция больше критерия?
Проверка на склеиваемость
по предыдущему алгоритму.
Запоминание значения функции
как критерия и соответствую-
соответствующего набора переменных.
[ff) Печать результата. Стоп.
мет
Начальное формирование матрицы
объекта и ее запоминание. Размер-
Размерность набора объекта равна 0.
Есть ли нулевая строка
или столбец?
Если размерность набора равна 1,
то конец - склеивание.
Определение элемента ветвления
и замыкания. Увеличение размер-
размерности набора на 1.
5 J Было ответвление?
нет
6) Восстановление матрицы.
Если размерность набора равна 0,
го конец - склеивание невозможно.
Восстановление последнего состоя-
состояния ветвления, занесение нуля
в элемент ветвления, уменьшение
размерности набора на 1.
3. Реализация на языке алгол-60 гибкой процедуры
перебора с обращением к алгоритму проверки
возможности склеивания.
1. begin integer t, m, n;
2. input (Г, т, л); output (Г, т, л);
3. begin integer n 1,/. ii,/2,i3,/,/l,/2,/3;
4. integer array x, xq, у [ 1: n ];
5. real u, v, v\,z, zq,h\^H2\
6. real arrayd[\ :m\,k, h, r, c[l:nl,
l.a[\\mt l:/i], f[l:n, 1 :n];
8. input (Al, A2, k, h, r); output (A 1, A2, k,
286
9. A, r)\ if t > 0.5 then begin
10. input (/); output (f) end;
11. for /': = 1 step 1 until n do begin
12.я [1, /]:=?['] X A[i'l; c[i] :=*[/]/
14. -h[i] end; </[l]:=0; tf[2]: = -Al;
15. d [3]: = A2; for /: = 1 step 1 until n do
16.x[i]: =y[i]: = 0;zq: = 0; /1: = 0; /2: = 1;
17.1Л :и: - -106;for /: = 1 step 1 until n
18. do begin for /1: = 1 step 1 until/1 do
19. i(abs(y [/1 ]) = / then go to 12;
20. u: = 0; for/: = 1 step 1 until m do
21. if d[j] + <г [/, i) < 0 then v: = u +
22. d [/] + a [/, /); if v > и then begin
23. if u = w Ac[i2] >c[i] then go to 13;
24. u: = u; /2: = /;/,3: end;?2: end;
25.*[/2]: = l;/l:=/l + l;v[/l]:=/2;
26. for /: = 1 step 1 until // do
27. d[i]: = d[i) +a\Uil\\
28. for /: = 1 step 1 until m do \id\i] < 0
29. then go to /,4;go to L5;
30.14: for /: = 1 step 1 until m do begin
31. u: = 0; for/: = 1 step 1 until n do begin
32. for/1: = 1 step 1 until/ldo if abs{y[i\]')
33. = /then go to L6; if <?[/,/] >0
34. them/: = u +a[/,/]; 16: end;
35. if i/ +</[/] < 0 then go to Z8 end;
36. u: = - ! 06; for/: = 1 step 1 until n do
37. begin for/1: = 1 step 1 until/1 do
38. if abs (y[i\ ]) =/ then go to 17;
39. if c\j] > и then begin u: =c[j];
4O./2:=/end;Z,7:end;jc[/2]: = 1;
41. u: = u: = 0; for /: = 1 step 1 until n do
42. begin*/: =w + *[/] X h[i\ Xjc[/];
43. i>: = u + r[/] X h[i] X x[j] end;
44. jc [/2]: =0;if u = 0thenz: =0
45. else z: = u/u; if z < zqthen
46. go to 18; go to 111;
47.18: for /: = 1 step 1 until/1 do
48. ify[i] > 0 then goto L9;go to 111;
49. L9: for /: =/1 step - 1 until 1 do
5O.ify [/J >0 then /3: =/; /2: = 1;
51, for i: = /3 step - 1 until 1 do
52. if у [/] < 0 then begin/2: = / + 1;
53.gotoZ,21end;121:w: = - 106;
54. for /: = 1 step 1 until n do for /1:
55. step 1 until/3 do ify[i\] = 1 then
56. begin, v: = 0; for/: = 1 step 1 until m
57. do if d[j] -a[j, i] < 0 then
/2
M Лс[/|
60. then begin u: = u; /2: = i;
61./3:= /lend end;
63.y[/3]: = - /2; for /: =/3 + 1 step 1
64.unta/l do>>[/]: = 0;/l: =/3;
65. for /: = 1 step 1 until m do
66.d[i):=d[i] -a[i, /2] ;go toZ,4;
67. L5:u: = v: =0;for/: = 1 step 1 until я do
68. beginm: =u+k[i] X h[i) Xx[i];
69. v: = и + /•[/] X h[i] X jc[i] end;
70. if v = 0 then 2: = 0 else z: = w/u;
71. if z > zq then go to Ml;
72. go to Z,4; 1,10: z?: = z;
73. for 1: = 1 step 1 until n do begin
14.xq[i]:=x[i];a[\,i]: = h[i) X
75.(fc[/J -r[i] Xzq) end;
76.</[lJ: = 0;gotoZ,4;
77.Z11: output (zq, xq),go to L\2;
78. Л/1: if t < 0.5 then go to 110;
79. n\: = 0; for /: = 1 step 1 until n
80.dowl: -n\ +jc[/];
81. begin integer array p, p\,p2,
S2.q,ql[l:nl],aq, bq[l:nl, l:/il];
83. /2: = 0; for/: = 1 step 1 until л do
84. if*[/J =1 then begin/2: = 0;
85. /2: = /2 + 1; for/: = 1 step 1 until n do
86. itx[f] = 1 then begin/2: =/2 + 1;
87.<7?[/2,/2] :=/[/,/] end end;
88. for /: = 1 step 1 until wl - 1 do
89.aq[nl9i]:=aq[i, /il]: = 1;
9Q.aq[nl9nl]: =/1: =0;
91. for 1: = 1 step 1 until «1 do for/: = 1
92. step 1 until n 1 do bq [/, /]: = aq [/, /];
93. for 1: = 1 step 1 until л 1 do p[i]: =
= ^7[/]: = 0;
94. M2: for /: = 1 step 1 until n 1 do begin
95. for/2: = 1 step 1 until/1 do ifp[/2] =
96./thengotoM3;u: = 0;
97. for/: = 1 step 1 until n\ do begin
98. for/2: = 1 step 1 unttt/1 do if q\j2) =/
99. then go to Л/4; u: = v + 0?[/, /];
100. Л/4: end; if v = 0 then go to M13;
101.Л/3: end;for/: = 1 step 1 until«1 do
102. begin for /2: = 1 step 1 until /1 do if
103. ^[i] =/thengotoAf5;u: = 0;
104. for/: = 1 step 1 until л 1 do begin
105. for/2: = 1 step 1 until /1 do if
106. pf/2] =/ then go toM6\
107. v: = v + aq[j, i];M6: end;
108.ifu = 0thengotoM13;
109. MS: end; if /1 = n 1 then begin
110. t: = l;gotoZ,10end;
111.!*: = 2 X nl;fori: = 1 step 1 untilwl
112. do begin for /2: = 1 step 1 until /1 do
113.ifp[/2] =/thengotoM7;
114. for/: = 1 step 1 until nl do begin
115. for/2: = 1 step 1 until/1 do if
116. q[j2) =j then go to MS;
117. if 04 [i/] =1 thenbfcgin
118. v: = 0; for /2: = 1 step 1 until nl do
119. if/2 Ф i then begin for/2: = 1
120. step 1 until/1 do if p[;2] = /2
121. then go toM9; v: = v+aq[il9j];
122.Af9:end;ifu = 0 then go toM17;
123. wl: *»u;for/2: = 1 step 1 until/il
287
124. do if/2 Ф] then begin for/2: = I
125. step 1 until /1 do if? [/2] =/2
126. then goto M10; v: = v + aq[i, /2];
127. M10: end; if и = ul then go to Ml 7;
128. if и <u then begin u: = u;/3: =/;
129./3: =/end end;MS: end;Ml: end;
130.gotoA/18;M17:/3:=/;/3:=/;Afl8:
132.Mil: for/2: = 1 step 1 until/1 - 1 do
133. if p[j2] =/3 then begm/3: =?[/2];
134.go toMll end;M12: for/2: = 1
135. step 1 until il - 1 do if q[f 2] =/3
136. then begin /3: =p[/2J ;go toM12
137. end; if/1 = n\ - 1 then begin
138. if aq\j'3,i3] = 1 then begin t: = 1;
139. go to Z,10 end; t: = 0;go toM16 end;
142. M13: if Г = 0 then go to Л/16;
143. for /: = 1 step 1 until «1 do begin
144. for Hi = 1 step 1 until/1 do
145. if p [il] =/then go to Л/14;
146. for/: = 1 step 1 until «1 do begin
147. for/2: = 1 step 1 until/1 do
148.if?[/2] =/thengotoA/15;
149.047[/,/]: = bq[i,j] \M 15: end;
150. Л/14: end; for /: = 1 step 1 unttt /1
152. if/1 =0thengotoZ,4;
153.Ш6:/3:=
154. aq[i3j'3]:
141.р2[/1]:=ДG[/3,/3];
0;/l:=/l -1;
157. go to Ml end; 112: end end
4. Соответствие между пунктами блок-схем
и строками алгольной программы.
Место в блок-схеме
(пункты блок-схемы)
Описание и ввод исход-
исходных данных
Блок-схема гибкой
процедуры перебора
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
И.
Место в '
программе
(номера
ctdok)
1 -10
11 -16
17-27
28-29
30-35
36-46
47 -48
49-66
67-70
71
72 -76
77
Место в блок-схеме
(пункты блок-схемы)
Блок-схема алгоритма
проверки возможности
склеивания
1.
2.
3.
4.
5^
6.
7.
8.
Место в
программе
(номера
строк)
78-93
94 - 108
109 -ПО
111 -141
142
143-151
152
153-156
ЛИТЕРАТУРА
1. Cherepanov G.P. Mechanics of Brittle
Fracture. - New York: Me Graw-
Hili, 1979, p. 950.
2. Eshelby J.D. The force on an elastic
singularity. - Phil. Trans. Roy. Soc,
1951, ser. A, vol. 244, p. 87.
3. Черепанов Г. П. Распространение тре-
трещин в сплошной среде. — ПММ,
1967, т. 31, вып. 3, с. 476 - 488.
4. Cherepanov G.P. Cracks in solids. -
Int. J. of Solids and Structures, 1968,
vol.4, p. 811-831.
5. Rice J.R. A path independent integral
and the approximate analysis of strain
concentration by notches and cracks.-
J. Appl. Mech., 1968, vol. 35, № 2,
p. 379.
6. William* M.L. Stress singularities resul-
resulting from various boundary conditions
in angular corners of plates in exten-
extension. - J. Appl. Mech., 1952, vol. 19,
№ 4, pp.526-528.
7. Sneddon I.N. The distribution of stress
in the neighborhood of a crack in an
elastic solid. - Proc. Roy. Soc, 1946,
ser. A, vol. 187, p. 229.
8. Irwin G.R. Fracture. - In: Handbuch
der physik, Bd. 6. - Berlin: Springer-
Verlag, 1958, S. 551.
9. Черепанов Г. П. О сингулярных ре-
решениях в теории упругости.—В кн.:
Механика твердого деформирован-
деформированного тела. Л., Судостроение, 1970.
10. Fracture. An Advanced Treatise in 7
volumes/Ed, by H.Liebowitz. - New
York and London: Academic Press,
1968 - 1972. Русский перевод: Раз-
Разрушение, тома 1 - 7. - М: Мир,
1972 - 1978.
11. Composite Materials. Volumes 1 -8/Ed.
by L.J. Broutman and R.H. Krock. -
New York and London: Academic
Press, 1973 - 1976.
12. Treatise on Materials Science and Tech-
Technology. Volumes 1 - 11/Ed. by Her-
Herman. - New York and London: Aca-
Academic Press, 1976-1978.
13. Fracture Toughness. - Special Tech-
Technical Publication №514, ASTM, 1972.
14. Cracks and Fracture. - Special Tech-
Technical Publication, №601, ASTM, 1976.
15. Черепанов Г.П. Инвариантные Г-ин-
тегралы и некоторые их приложе-
приложения в механике. - ПММ, 1977, т.41,
вып. 3, с. 399 -412.
16. Irwin G.R. Analysis of stresses and
strains near the end of a crack traver-
traversing a plate. - J. Appl. Mech., 1957,
vol. 24, №3, p. 361.
17. Griffith A. A. The phenomenon of
rupture and flow in solids. - Phil.
Trans. Roy. Soc, London, 1920,
ser. A, vol. 221, p. 163.
IS. Johnson Н.Я., Paris PC Sub-critical
flaw growth. — Engng Fract. Mech.
1968, vol. 1, p. 3.
19. Irwin G.R., Kies J.A. Fracture theory
applied to high strength steels. - Metals
Progr., 1960, vol. 78, p. 73.
20. Bernstein #, Kies J.A. Crack growth
during static tests of rocket motor
cases. - Metals Progr., 1960, vol. 78,
p. 79.
21. Steigerwald E.A. Delayed failure of
high-strength steel in liquid environ-
environments. - Proc. ASTM, 1960, vol. 60,
p. 750.
22. Johnson H.H., Willner A.M. Moisture
and stable crack growth in a high
strength steel. — Appl. Mater. Res.,
1965, vol. 4, p. 34.
23. Brown B.F., Beachem CD. A study
of the stress factor in corrosion crac-
cracking. - Corrosion Sci., 1965, vol. 5,
p. 745.
24. Hanna G.L., Troiano A.R., Steiger-
Steigerwald E.A. A mechanism for the embritt-
lement of high strength steels by aque-
aqueous environments. — ASM Trans. Q.
1964, vol. 57, p. 658.
289
25. Hancock G.G., Johnson H.H. Hydrogen,
oxygen and subcritical crack growth in
a high-strength steel. - Trans. Metal.
Soc, AIME 1966, vol. 236, p. 513.
26. Wiederhorn S. The influence of water
vapor on crack propagation in soda-
Lime glass. - Natl. Bur. Stand., 1966,
Rep. №9442.
27. Irwin G.R. Moisture assisted slow
crack extension in glass plates. - Naval
Res. Lab. Memo., 1966, Rep. № 1678.
28. Mulherin J.H. Stress corrosion suscep-
susceptibility of high strength steel, in rela-
relation to fracture toughness. — Trans.
ASME, 1966, Ser. D, vol. 88, p. 777.
29. Peterson M.H., Brown B.F., Newbe-
gin R.L., Groover R.E. Stress corrosion
cracking of high strength steels and
titanium alloys in chloride solutions
at ambient temperature. - Corrosion,
1967, vol. 23, p. 142.
30. Van der Sluys W.A. Effects of repeated
loading and moisture on the fracture
toughness of SAE4340 steel. - Trans.
ASME, 1965, ser. D, vol. 87, p. 363.
31. Smith H.R., Piper D.E, Downey F.K.
A study of stress-corrosion cracking by
wedge-force loading. - Engng Fract.
Mech., 1968, vol. 1, p. 123.
32. Paris P.C, Gomez M.P., Anderson W.E.
A rational analytic theory of fatigue. -
The Trend in Engineering, 1961, (Janu-
(January), vol. 13.
33. Donaldson DR., Anderson W.E. Crack
propagation behavior of some airframe
materials. - Proc. Crack Propagation
Symp., Cranfield (England), Cranfield
College Aeronaut, 1962, vol. 2,
p. 375.
34.Paris P.C. The fracture mechanics ap-
approach to fatigue. — В кн.: Fatigue.—
Proc. 10 th Sagamore Army Mater. Res.
Conf., 1963, Syracuse Univ. Press,
1964.
35. Черепанов. Г.П. О росте трещин при
циклическом нагружении. - ПМТФ,
1968, №6. с. 64-75.
36. Cherepanov G.P., Halmanov H. On the
theory of fatigue crack growth. - Engng
Fract. Mech., 1972, vol. 4, p. 219.
37. Cherepanov G.P. On the theory of
electrochemical stress corrosion crack-
cracking. - Proc. of the third Congress on
Fracture, Munich, 1973.
38. Cherepanov G.P:, Ershov L. V., Kuz-
min G.G. On the growth of corrosion
cracks. - Corrosion, 1972, vol. 27,
№12, pp. 100-104.
39. Cherepanov G.P. On the theory of crack
growth due to hydrogen embrittle-
290
ment. -Corrosion, 1973, vol. 28, №8,
p. 305.
40. Cherepanov G.P., Halmanov H. On the
crack growth below Kjscc. - Engng
Fract. Mech., 1974, vol. 6, №3, p. 551.
4L Черепанов Г.П., Кулиев В.Д Влияние
частоты нагружения и неактивных
внешних сред на рост усталостных
трещин. - Проблемы прочности,
1972, № 1, с. 31 -37.
42. Cherepanov G.P Stress corrosion crac-
cracking. Chapter 8 in Encyclopedical
Treatise "Electrochemistry "/Ed. by
J.O.M. Bockris, - New York: Plenum
Press, 1983.
43. Kelly A. The strengthening of metals
by dispersed particles. - Proc. Roy.
Soc, 1964, ser. A, vol. 282, p. 63.
44. Cornell A.H.. Strong solids. - Proc.
Roy. Soc, 1964, ser. A, vol. 282, p. 1.
45. Kelly A. Interface effects and the work
of fracture of a fibrous composite. -
Proc. Roy. Soc, 1970, ser. A, vol. 319.
p. 95.
46. Черепанов Г.П. О напряженном со-
состоянии в неоднородной пластинке
с разрезами. - Изв. АН СССР, ОТН,
механика и машиностроение, 1962,
№1,с. 131.
Al.Faxoe Ф.Д. Краевые задачи. - М.:
Физматгиз, 1958.
48. Мусхелишвили Н.И. Некоторые ос-
основные задачи математической
теории упругости. — М.: Наука,
1966.
49. Kelly A., Davies G.I The principles of
the fibre reinforcement of metals. -
Metallurgical Reviews, 1965, vol. 10,
№37, pp. 1-78.
50. Cooper G.A., Kelly A. Strain energy of
matrix in fibre composite materials. -
J. Mech. Phys. SoUds, 1967, vol. 15,
p. 279.
51. Whisker Technology/Ed, by A.P.Le-
A.P.Levitt. - New York - London: Wiley-
Interscience, 1970. Русский перевод:
Упрочнение металлов волокна-
волокнами/Под ред. А.Т. Туманова. - М.:
Наука, 1973.
52. GargS.K., Svalbonas V., Gurtman G.A.
Analysis of Structural Composite Ma-
Materials. - New York: M. Dekker Inc.,
1973, p. 473.
53. Кулиев В.Д., Работное Ю.Н., Черепа-
Черепанов Г.П! Торможение трещины на
границе раздела различных упругих
сред. - Изв. АН СССР, МТТ, 1978,
№4, с. 315.
54. Zak A.R., Williams M.L. Crack point
stress singularities at bimaterial inter-
face. - Trans. ASME, ser. E, J. Appl.
Mech., 1963, vol. 30, № 1, p. 142.
55. Нобл Б. Применение метода Вине-
Винера - Хопфа для решения дифферен-
дифференциальных уравнений в частных про-
производных. - М.: ИЛ, 1962.
56. Rabotnov Yu.N., Cherepanov G.P.
Fracture Mechanics of aligned fibrous
composites. — Proc. of the Conference
on Fracture and Technology of Mate-
Materials (Hong Kong, 1977). - Noordhoff
Intern. Publishing, 1977.
SI. Розен Б.В., Дау Н.Ф. Механика раз-
разрушения волокнистых компози-
композитов. - В кн.: Разрушение, т. 7. М.,
. Мир, 1977.
58.КортёнМ.Т. Механика разрушения
композитов. - В кн.: Разрушение,
т. 7, М., Мир, 1977.
59. Черепанов Г.П., Ершов Л.В* Механи-
Механика разрушения. - М.: Машинострое-
Машиностроение, 1977, с. 224.
60. Мипейко СТ., Сорокин Н.М.,Цир-
лин A.M. Прочность бороалюми-
ния - композита с хрупким волок-
*ном. - Механика полимеров, 1973,
№5, с. 840-846.
61. Scdp P.M., Argon A.S. - The fractu-
fracture growth in laminated composites. -
J. Compos. Mater., 1969, vol. 3, p.30.
62. Черепанов ГЛ. Равновесие откоса
с тектонической трещиной. -
ПММ, 1976, т. 40, вып. 1,
с. 136-151.
63. Smith КН., Shahinian P. Fatigue
cracking rate of boron-aluminium
composite in water vapour environ-
environment. - Presented at Int. Conf.
Corrosion Fatigue, 14 - 18 June
1971, Storrs, Connecticut, 1971.
64. Hardiman NJ. Elliptic elastic inclu-
inclusion in an infinite elastic plate. -
Quart. J. Mech. and Appl. Math.,
1954, vol. 7, p. 2, pp. 25-43.
65. Черепанов ГЛ., Кочаров Р.С., Сот-
килава О.В. Параболическое вклю-
включение в упругой плоскости. —
Труды Моск. горн, ин-та, 1975,
с. 36-46.
66. Черепанов Г.П., Кочаров Р.С., Сот-
килава О.В. Об одном трещино-
видном дефекте в упругой плос-
плоскости. - Прикладная механика,
1977, т. 13, №2, с. 48-55.
67. Соткилава О.В., Черепанов ГЛ.
Некоторые задачи неоднородной
теории упругости. — ПММ, 1974,
т. 38, вып. 3, с. 539-550.
68. Черепанов ГЛ., Кочаров Р.С., Сот-
Соткилава О.В. К теории прочности
микронеоднородных хрупких
тел. -Прикладная механика, 1977,
т. 13, №3, с. 3-10.
69. Черепанов Г.П. О прочности ком-
композитов. - ПЩФ, 1967, № 3,
с. 271.
70.Бережницкий Л.Т., Панасюк В.В.,
Черепанов ГЛ. О прочности состав-
составных тел, ослабленных трещина-
трещинами. - В кн.: Концентрация напря-
напряжений, вып. 3, Киев, Наукова
Думка^ 1971.
ll.Perlman A.B., Sih G.C Elastostatic
problems of curvilinear cracks in
bonded dissimilar materials. - Int. J.
Engng. Sci., 1967, vol. 5, p. 11.
72. Черепанов ГЛ. Метод внешних и
внутренних разложений в теории
упругости. - В кн.: Механика де-
деформируемых тел и конструкций.
М., Машиностроение, 1975.
73. Черепанов ГЛ. О развитии трещин
в вязких телах. - МТТ, 1969, № 1,
с. 65-72.
74. Reports of the Research Institute
for Strength and Fracture of Ma-
Materials. - Tohoku University (Ja-
(Japan), 1980, vol. 15, № 2, p. 55.
75. Тимошенко ГЛ., Гудьер Дж. Тео-
Теория упругости. - М.: Наука, 1975.
76. Тимошенко СП., Гере Дж. Меха-
Механика материалов. - М.: Мир, 1976.
П.Градштейн И.С, Рыжик ИМ. Таб-
Таблицы интегралов, сумм, рядов и
произведений. — М.: Физматгиз,
i962.
78. Melan Е. Ein Beitrag zur Theorie
geschweisster Verbindungen. - Ing.
Archiv, 1932, Bd. 3, S. 123 -
129.
79. Buell E.L. On the distribution of
plane stress in semi-infinite plate
with partially stiffened edge. - J.
Math, and Phys., 1948, vol. 26,
pp. 223 - 233.
80. Benscoter S.U. Analysis of a single
stiffener on an infinite sheet. - Trans.
ASME, ser. E, J. Appl. Mech., 1949,
vol. 16, №3, pp. 242-246.
Sl.Koiter W.T. On the diffusion of load
from a stiffener into a sheet.- Quart.
J. Mech. and Appl. Math., 1955,
vol. 8, №2, pp. 164- 178.
82. Brown ЕЛ. The diffusion of load
from a sjiffener into an infinite elas-
elastic sheet. - Proc. Roy. Soc, Math,
and Phys. Sci., 1957, ser. A, vol. 239,
№1218, pp. 296-310.
S3.Budiansky В., Wu T.T. Transfer of
load to a sheet from a rivet-attached
291
stiffener. - J. Math, and Phys., 1961,
vol. 40, pp. 142 - 162.
84. Черепанов ГЛ., Рыбаков Л.М.
К расчету клепаных панелей. —
Прикладная механика, 1977, т. 13,
№ 8, с. 3 - 7.
85. Рыбаков Л.С., Черепанов ГЛ. Дис-
Дискретное взаимодействие пластины
с полубесконечным стрингером. -
ПММ, 1977, т. 41, вып. 2,
с. .322 - 328.
86. Фельд ЯЛ. О бесконечных систе-
системах линейных алгебраических
уравнений, связанных с задачами о
полубесконечных периодических
структурах. - Докл. АН СССР,
1955, т. 102, №2,.с. 283.
87. Лурье А.И. Теория упругости. -
М.: Наука, 1970, с. 939.
88. Новацкш В. Теория упругости. -*-
М.:Мир, 1975, с. 872.
89. Wijk G. A theoretical remark on the
stress field around prestressed rock
bolts. - Int. J. Rock Mech. Min. Sci.,
1978, vol. 15, p. 289-294.
90. Me Niven H.D., Ewoldsen H.M. Rock
bolting of tunnels for structural sup-
support. - Int. J.. Rock Mech. Min. Sci.,
1969, vol. 6, p. 465 - 497.
91. Mindlin R.D. Force at a point in the
interior of a semi-infinite solid. -
Physics, 1936, vol. 7, p. 195 - 202.
92. Ван фо фы ГА. Теория армиро-
армированных материалов. — Киев: Hay-
кова Думка, 1971, с. 232.
93. Скудра А.М., Булаве Ф.Я., Ро-
ценс К А. Ползучесть и статисти-
статистическая усталость армированных
пластиков. - Рига: Зинатне, 1971.
94. Композиционные материалы во-
волокнистого строения. - Киев:
Hay кова Думка, 1970.
95. Немец Я., Серенсен СВ., Стреля-
ев B.C. Прочность пластмасс. — М.:
Машиностроение, 1970.
96. Огибалов П.М., Малинин Н.И.,
Нетребко В.П., Кишкин БЛ. Кон-
Конструкционные полимеры. - М.:
Изд-воМГУ, 19/2.
97. Алюминиевые и магниевые спла-
сплавы, армированные волокнами
(сборник). - М.: Наука, 1974.
98. Рабинович А.Л. Введение в меха-
механику армированных пластиков. -
М.: Наука, 1973.
99. Упрочнение металлов волокна-
волокнами. -М.: Наука, 1973.
100. Армированные материалы и конст-
конструкции из них. - Киев: Наукова
Думка, 1970.
292
101. Конструкционные свойства пласт-
пластмасс. - М.: Машиностроение, 1968.
102. Ашкенази Е.К. Анизотропия ма-
машиностроительных материалов. —
Л.: Машиностроение, 1969.
103. Механика композиционных мате-
материалов. - М.: Мир, 1978, с. 556.
104. Handbook of Fiberglass and Advan-
Advanced Plastics Composites.- New York:
Me Graw Hill, 1969, p. 894.
105. Composite Materials: Testing and De-
Design. - ASTM STP № 460, Philadel-
Philadelphia, Pa., 1969.
106. Шермергор Т.Д Теория упругости
микронеоднородных тел. - М.:
Наука, 1977, с. 399.
107. Неупругие свойства композитных
материалов. - М.: Мир, 1978.
108. Работное ЮЛ. Элементы наследст-
наследственной механики твердых тел. -
М.: Наука, 1977, с. 383.
109. Ильюшин А.А., Победря Б.Е. Ос-
Основы математической теории тер-
мо-вязкоупругости. - М.: Наука,
1970, с. 280.
110. Малмейстер А.К., Тамуж В.П.,
Тетере ГА. Сопротивление жест-
жестких полимерных материалов. -
Рига: Зинатне, 1972, с. 498.
111. Бажанов В.Л. Пластины и оболоч-
оболочки из стеклопластиков. — М.: Ма-
Машиностроение, 1970, с. 304.
112. Москвитин В.В. Сопротивление
вязко-упругих материалов. - М.:
Машиностроение, 1972, с. 328.
113. Черепанов ГЛ., Смольский В.М.
К оптимальному проектированию
многослойных панелей. — Изв.
АН Армянской ССР. Механика,
1978, т. 31, №3, с. 43-48.
114. Черепанов ГЛ., Смольский В.М.
К решению многокритериаль-
многокритериальной задачи оптимального проек-
проектирования многослойных пане-
панелей. - Изв. АН Армянской ССР.
Механика, 1979, т. 32, №1,
с. 73 - 80.
115. Черепанов ГЛ., Смольский В.М.,
Таги-заде А.Г. Об оптимальном
проектировании некоторых инже-
инженерных материалов. — Изв,. АН
Армянской ССР. Механика, 1976,
т. 29, №3, с. 51 -62.
116. Cherepanov G.P., Smolsky V.M. Ap-
Applications of Research Operations to
Materials Optimum Designing: Prog-
Program for Second National Symposium
on Computerized'Structural Analysis
and Design. - School of Engineering
and Applied Science, George Washing-
ton University, Washington, 29 — 31
March, 1976. '
117. Черепанов ГЛ., Смольский B.M.
К расчету толщины панели мак-
максимальной долговечности. —
Машиноведение, 1979, № 4,
с. 62 - 65.
118. Wasiutynski Z., Brandt A. The pre-
present state of knowledge in the field
of optimum design of structures.-
Appl. Mech. Reviews, 1963, vol. 10,
№•5, p. 341 - 350.
119. Sheu C.Y., Prager W. Recent deve-
developments in optimal structural de-
design. - Appl. Mech. Reviews, 1968,
vol. 21, №10, p. 985 -992.
120. Васильев В.В. Оптимальное проек-
проектирование пластинок и оболо-
оболочек. - Тр. VII Всесоюзной конфе-
конференции по теории оболочек и плас-
пластинок (Днепропетровск). — М.:
Наука, 1970.
121. Second National Symposium on
Computerized Structural Analysis
and Design. - Washington: G. Wa-
Washington Univ., 1976.
122. Рейтман М.И., Шапиро ГС. Методы
оптимального проектирования де-
деформируемых тел. — М.: Наука,
1976, с. 267.
123. Черепанов ГЛ. Механика хруп-
хрупкого разрушения. — М.: Наука,
1974, с. 640.
124. Образцов И.Ф. Развитие теории
пластин и оболочек при создании
конструкций современных лета-
летательных аппаратов: Теория и прак-
практика проектирования пассажирс-
пассажирских самолетов. - М.: Наука, 1976,
с. 61 -73.
125. Григолюк Э.И., Коган Ф.А. Совре-
Современное состояние теории много-
многослойных оболочек. — Приклад-
Прикладная механика, 1972, т. 8, № 6,
с. 3 -17.
126. Bruyne N.A. Applications of the
"Reducs" Method to Airplane De-
Design. - British Science News, 1949,
vol. 2, №20, p. 232-235.
127. Современные самолеты США и
стран Западной Европы, ч. 2. -
В кн.: Авиастроение, т. 2, М.:
ВИНИТИ, Итоги науки и техники,
1976, с. 192.
128. News Products and People. Adhesive
Bonding Solves Aircraft Panel Pro-
Production Problems. - Modern Metals,
1968, vol. 24, №6, p. 86.
129. Heitz E. Verbundwerkstoffe. Ver-
fahrenstechnikcn in der Flugzeugin-
dustrie. - Kunststofftechnik, 1972,
Bd. 11, №4 s. 94-99.
130. Fitz Simmons R.D., Roensch R.L.
Advanced supersonic transport. -
Society of Automotive Engineers,
Preprint, 1976, №750617, pp. 1-6.
131. Yaffee M. USAF pushes composite
structure work. — Aviation Week and
space Technology, 1975, vol. 102,
№2, p. 38 -39.
132. Толстобров ЕЛ. Изготовление
крупногабаритных клееных пане-
панелей обшивки фюзеляжа самоле-
самолета. - Экспресс-информация
ВИНИТИ. Авиастроение, 1972,
№ 3, с. 5 - 8.
133. Me Anally R. W. Air Superiority Figh-
Fighter Wing Design for Cost and Weight
Reduction. - AIAA Paper, 1974,
№338, p. 1 - 10.
134. Pitman W.A., Bigham CR. Advanced
Structural Concepts for Transport
Aircraft Wings. - AIAA Paper, 1974,
№339, p. 1 -6.
135. Струков ЮЛ. Программы иссле-
исследования перспективных конструк-
конструкций крыла. — Экспресс-информа-
Экспресс-информация ВИНИТИ. Авиастроение, 1976,
№ 44, с. 1 - 48.
136. Kumakura Ikuo, Iwazaki Kazuo. —
Fatigue strength of adhesive-bonded
joints in a simplified model of a
fuselage structure under repeated
cabin pressure. — Technical Report
of the National Aerospace Labora-
Laboratory, 1976, №445, pp. 1 -37.
137. Heitz E. Einsatzbeispiele der Ver-
bundtechnik. - Kunststofftechnik,
1973, Bd. 12, № 7, S. 180- 184.
138. Fair P. Frazing of Sandwich Structu-
Structures in High Temperature Vacuum
Furnace. - Industrial Heating, 1957,
vol. 24, №10, p. 1980- 1986.
139. Давиденков H.H. Некоторые проб-
проблемы механики материалов. — М.:
Газетно-журнальное издательство,
1943.
140. Иванова B.C., Ботвина Л.Р. Об-
Общие закономерности изменения
механических свойств металлов и
сплавов при различных условиях
нагружения. — Физика и химия об-
обработки материалов, 1971, № 3,
с. 43 - 47.
141. Frechet M. Defect's Distribution in
the Elastic Body. - Ann. Soc. Polon.
Math.(Cracow), 1927, vol. 6, p. 93.
142. Прикладные вопросы вязкости
разрушения. - М.: Мир, 1968,
с. 552.
293
143. Черепанов ГЛ., Каплун А.Б., Пуч-
Пучков Ю.И. О влиянии масштабного
фактора на хрупкую прочность. -
Проблемы прочности, 1970, № 7,
с. 14 - 17.
144. Cook /., Gordon J.E. A Mechanism
for the Control of Crack Propagation
in All-Brittle Systems. - Proc. Roy.
Soc, 1964, ser. A, vol. 282, p. 508.
145. Me Cartney R.F., RichardR.C, Troz-
zoP.S. Fracture Benavior of Ultrahigh-
Strength-Steel Laminar Composites.—
Transaction ASM, 1967, vol. 60,
p. 384.
146. Floreen S., Hay den H W., Pilliar RM
Fracture Behavior of an Fe-Cu
Microduplex Alloy and Fe—Cu Com-
Composites. - Transactions of Metals,
AIME, 1969, vol. 245, p. 2529.
147.Floreen S., Hayden H.W., Steigel-
man J.Q. Fracture Modes in Lamina-
Laminated Steel — Nickel Composites. —
Transactions of ASM, 1969, vol. 62,
p. 812.
148. Baird R.B., Forbes F. W., Lipsitt HA.
Tensile and Fatigue Properties of La-
Laminate Sheet Structures. - Proc. of
the Amer. Soc. of Testing and Mate-
Materials, 1959, vol. 59, p. 755.
149. Forsyth PJ.E. et al. Some Prelimi-
Preliminary Experiments on Improving the
Mechanical Properties of Metals bv
Reinforcement. — Royal Aircraft
Establishment Technical Note,
Met. - Phys., Farnborough, 1962,
p. 353.
150. Kaufman J.G. Fracture Toughness of
7075-T6 and T651 Sheet, Plate, and
Multilayered Adhesive-Bonded Pa-
Panels. - J. Basic Engng, Trans. ASME,
1967, ser. D, vol. 89, № 3. Русский
перевод: Кауфман Д.Г. Вязкость
разрушения листов, плит много-
многослойных клееных панелей из алю-
алюминия. - Труды Американского
общества инженеров -механиков,
1967, серия D,t. 89, № 3, с. 57-62.
151. Plumbridge W.J., Ryder DЛ. A Preli-
Preliminary Study of the Tensile and Fa-
Fatigue Properties of Autogeneous Alu-
Aluminium and Aluminium-Copper Al-
Alloy Laminates. - J. Inst. Met., 1971,
vol. 99, p. 233.
152. Taylor L.G., Ryder D. A. The Fatigue
and Fracture Toughness of Lamina-
Laminated Composites Based on 7075-T6
Aluminium Alloy. - Composite,
1976, vol. 7, №7, 27-33.
153. Weiss W.L., Zola J.C The Applica-
Application of Fracture Mechanics to the
294
Design of Damage-Tolerant Compo-
Components for the UTTAS helicopter. -
J. Amer. Helicopt. Soc, 1975, vol.20,
№3, p. 28 - 38. Русский перевод:
Виленский М.А. Применение меха-
механики разрушения при создании бе-
безопасно повреждаемых элементов
конструкций вертолета UTTAS. -
Экспресс-информация ВИНИТИ.
Авиастроение, 1976, № 6, с. 5 - 15.
154. Forman R.G., Kearney V.К, Eng-
le R.M. Numerical Analysis of Crack
Propagation on Cycle Loaded Structu-
Structures. - Trans. ASME, 1967, ser. D,
vol. 89, № 3.
155. Браун У., Сроули Дж. Испытания
высокопрочных металлических
материалов на вязкость разруше-
разрушения при плоской деформации. -
М.: Мир, 1972.
156. Черепанов Г.П., Смольский ВЖ
К расчету среднего времени до
разрушения панели с трещиной от
случайной нагрузки. - Машино-
Машиноведение, 1978, № 6, с. 58 - 60.
157. Тихонов В.И. Выбросы случайных
процессов. - М.: Наука, 1970.
158. Новожилов В.В. Тонкие упругие
оболочки. - Л.: Судпромгиз,
1962, с. 431.
159. Cherepanov G.P. Optimal Design of
Some Filamentary Cylindrical
Shells. - Abstracts of International
Astronautical Congress, Amsterdam,
1974, p. 168.
160. Cherepanov G.P, Taghi-Zade A.G.
Extention of Plates and Shells of
Uniform Strength. - Letters in Ap-
Applied and Engineering Sciences, 1975,
№2, p. 112-123.
161. Cherepanov G.P, Taghi-Zade A.G.
Bending of Plates and Shells of Uni-
Uniform Strength. - Letters in Applied
and Engineering Sciences, 1975, № 3,
p. 167 - 176.
162. Черепанов ГЛ., Таги-заде А.Г. Из-
Изгиб равнопрочных балок. - Труды
Куйбышевского гос. ун-та, Куйбы-
Куйбышев, 1975, с. 118-134.
163- Черепанов ГЛ. Обратные задачи
плоской теории упругости. — ПММ,
1974, вып. 6, с. 963 -979.
164. Черепанов ГЛ., Таги-заде А.Г. Од-
Одна новая обратная задача теории
упругости. - В кн.: Механика де-
деформируемого твердого тела, Изд.
Куйбышев, гос. ун-та, 1976, № 2.
165. Badaliance R., Sih G.C An Approxi-
Approximate Three-Dimensional Theory of
Layered Plates Containing Through
Thickness Cracks. - Engineering
Fracture Mechanics, 1975, vol. 7,
№l,p. 1 -22.
166. Sih G.C., Handbook of Stress-Inten-
Stress-Intensity Factors, vol. 2, — Bethlehem:
Lehigh Univ. Press, 1974, p. 406.
167. Tada H., Paris., P.C, Irwin G.R. The
Stress Analysis of Cracks Hand-
Handbook. — DEL Research Corporation,
1973, p. 488.
168. Hoffman G.A. The Effect of Fila-
Filamentary Materials on Pressure Vessel
Design. — Proceedings of Internatio-
International Astronautical Congress. — New
York.: Pergamon Press, 1960.
169. Schuerch H.U., Burggraf O.R. Analy-
Analytical Design for Optimum Filamentary
Pressure Vessels. - ARSJ, vol. 34,
№ 5, p. 1964.
170. Черепанов Г.П., Смольский ВМ
Напряжения в окрестности эл-
эллипсоидальной выработки в гор-
горном массиве. - В кн.: Проблем-
Проблемные вопросы механики горных
пород. - Алма-Ата: Наука, 1969.
171. Trofanowski St. Wielokrijteriowa opti-
malizacja w sensie Pareto niewspo-
limierych funkcji celu. - Przeglad
Statystyczny, 1975, vol., 22, № 3,
427 -433.
т.Бартель Д.Л., Маркс ЕВ. Опти-
Оптимальное проектирование механи-
механических систем при противоречи-
противоречивых критериях. - Труды Амери-
Американского общества инженеров-
механиков, 1974, сер Б., № 1,
с. 72 - 80.
173. Вагнер Г. Основы исследования
операций. -М.: Мир, т. 1 - 3, 1972.
174. Смольский В.М. Апостериорная
оценка промежуточного параметра
в комбинированном методе поис-
поиска экстремума. - Автоматизация
управления нефтеперерабатываю-
нефтеперерабатывающей и нефтехимической промыш-
промышленности, 1972, вып. 2, с. 77 - 8.1.
175. Balas Е. An Additive Algorithm for
Solving Linear Programs with Zero -
One Variables. - Operations Research,"
1965, vol. 13,№4, p. 517 - 546. Рус-
Русский перевод: Балаш Э. Аддитив-
Аддитивный алгоритм для решения задач
линейного программирования в
Двоичных переменных. - М.: ВЦП,
1965.
176. Гришухин В.П. О среднем числе
итераций алгоритма Балаша. -
В кн.: Исследования по дискрет-
дискретной математике. - М.: Наука,
1973, с. 58-68.
177. Freeman R.I. Computational Expe-
Experience with a "Balasian" Integer
Programming Algorithm. - Opera-
Operations Research, 1966, vol. 14, № 15,
p. 935 -941.
178. Geoffrion AM. Integer Programming
by Implicit Enumeration and Balas'
Method. - SIAM Review, 1967,
vol. 9, №2, p. 178-190.
179. Trottler L.E, Shetty G.M. An Inte-
Integer Programming Algorithm for Ze-
Zero - One Variables. - J. of the Asso-
Association for Computing Machinery,
1974, vol. 21, №3, p. 505-513.
180. Tuan Nghiem Ph. A Flexible Three-
Search Method for Integer Program-
Programming Problems. - Operations
Research, 1971, vol. 19, № 1,
p. 115-122.
181. Ellwein Leon B. A Flexible Enumera-
Enumeration Scheme for Zero - One Prog-
Programming. - Operations Research,
1974, vol. 22, № 1, p. 144 - 150.
182.Кортен Х.Т. Разрушение армиро-
армированных пластиков. — M.: Химия,
1967, с. 165.
183. Акдф Р., Сасиени М. Основы ис-
исследования операций. - М.: Мир,
1971, с. 533.
184. Корбут А.А., Финкелыитейн Ю.Ю.
Дискретное программирование. -
М.: Наука, 1969.
185. Евенко Л.И. Экономико-матема-
Экономико-математическое моделирование в пище-
пищевой промышленности. - М.: Пище-
Пищевая промышленность, 1970.
186. Телемтаев ММ. К вопросу о реше-
решении задачи о коммивояжере. -
Изв. АН СССР. Техническая кибер-
кибернетика, 1972, № 6, с. 94 - 100.
187. Любкин А.А. О задаче коммивоя-
коммивояжера. — В кн.: Вопросы эконо-
экономико-математического модели-
моделирования. - МГУ, 1973, с. 402-
406.
188. Hansen K.H., Krarup J. Held - Garp's
Algorithm for the Solution of Sim-
metrical Salesman Problem. - Mat-
hem. Program., 1974, vol. 7, № 1,
p. 87 -96.
189. Гимади З.Х.. Перепелица В.А.
Асимптотический подход к реше-
решению задачи коммивояжера. - В се-
серии: Управляемые системы, Ново-
Новосибирск: Наука, 1974, вып. 12,
с. 35 -45.
190. Бурдюк В.Я., Трофимов В.Н.
Обобщение результатов Гилмора и
Гомори по решению задачи ком-
коммивояжера. - Изв. АН СССР. Тех-
295
ническая кибернетика, 1976, № 3,
с. 16 - 22.
191. Леонтьев В.К. Исследование одно-
одного алгоритма решения задачи ком-
коммивояжера. - ЖВММФ, 1973, т. 15,
№5, с. 1228-1236.
192. Hristofldes N., Eilon S. Algorithms
for the Solution of Salesman Prob-
Problem. — Operations Research Quar-
Quarterly, 1972, vol.23, №4, p. 511-518.
193. Little J.D.S., Murty K.G, Swe-
Sweeny D. W., Karel G An Algorithm for
the Travelling Salesman Problem. -
Operations Research, 1963, № 11,
p. 972 - 989. Русский перевод:
Литтл Дж„ Мурти Л., Суини Д.,
Кэрел К. Алгоритм для решения
задачи коммивояжера. — Эконо-
Экономика и математические методы,
1965, т. 1,вып. 1, с. 94-98.
194. Волкович В.Л., Даргейко Л.Ф. Об
одном алгоритме выбора компро-
компромиссного решения для линейных
критериев. - Кибернетика, Киев,
1972, №5, с. 133-136.
195. Власов В.З. Общая теория оболо-
оболочек. -М.: Гостехиздат, 1949, с. 784.
196. Черепанов Г.П., Кулиев С.А. Плас-
Пластины и оболочки переменной
толщины. - Прикладная механика,
1979, т. 15, №10, с. 70-74.
197. Гузь А.Н. Устойчивость трехмер-
трехмерных деформируемых тел. - Киев:
Hay кова думка, 1971.
198. Гузь AM. Устойчивость упругих
тел при конечных деформациях.-
Киев: Hay кова думка, 1973.
199. Каминский А.А. Механика разру-
разрушения вязко-упругих тел. - Киев:
Наукова думка, 1980.
200. Cherepanov G.P. Invariant Г-integ-
rals. - Eng. Fracture Mechanics, 1981,
vol. 14, №1, p. 39-58.
201. Eshelby J.D. The stresses on and in
a thin inextensible fibre in a stret-
stretched elastic medium. - End. Frac-
Fracture Mechanic, 1982, vol. 16, № 3,
p. 453.
202. Черепанов ГЛ. Механика разру-
разрушения многослойных оболочек.
Теория трещин расслаивания. -
ПММ, 1983, т. 47, вып. 5.
203. Панасюк В.В. Предельное равно-
равновесие хрупких тел с трещина-
трещинами. — Киев: Наукова думка,
1968, с. 245.