Текст
R&C
ТЭуиамаы.
Instabilities and Catastrophes in Science and Engineering
J. M. T. Thompson
Professor of Structural Mechanics University College London
A Wiley-Interscience Publication
John Wiley & Sons
Chichester • New York • Brisbane . Toronto • Singapore 1982
Дж. М. Т. Томпсон
НЕУСТОЙЧИВОСТИ И КАТАСТРОФЫ
В НАУКЕ И ТЕХНИКЕ
Перевод с английского
В. Л. Бердичевского
Москва «Мир» 1985
ББК 22.17
Т56
УДК 517: (53+ 57/59)
Томпсон Дж. М. Т.
Т56 Неустойчивости и катастрофы в науке и технике: Пер. с англ.—М.: Мир, 1985.— 254 с., ил.
Книга известного английского специалиста в области механики охватывает широкий круг явлений из различных областей науки и техники, в которых важную роль играют неустойчивости, бифуркации, резкие переходы из одного состояния в другое. Изложение отличается краткостью, наглядностью и простотой; книга богато иллюстрирована и содержит обширную библиографию.
Для всех, кто интересуется современными достижениями в науке и технике.
„ 1702070000-118 л
Т 041 (01)-85 42'85’ ч’1
ББК 22.17
517.8
Редакция литературы по математическим наукам
© 1982 by John Wiley & Sons Ltd. All Rights Reserved. Authorized translation from English Language edition published by John Wiley & Sons, Ltd.
© Перевод на русский язык, «Мир», 1985
ОТ ПЕРЕВОДЧИКА
Многие выдающиеся события в науке связаны с изменением ее языка и возникновением новых терминов и понятий. Именно такими изменениями сопровождалось рождение теории катастроф. Теория катастроф обнаружила общие закономерности во многих, на первый взгляд совершенно различных явлениях механики и физики и предложила универсальный способ их описания.
В последние годы на русском языке появилось несколько прекрасных книг по теории катастроф: Арнольд В. И. Теория катастроф.— М.: Изд-во МГУ, 1983; Постон Т., Стюарт Я. Теория катастроф и ее приложения.— М.: Мир, 1980; Арнольд В. И., Варченко А. Н., Гусейн-Заде С. М. Особенности дифференцируемых отображений. В 2-х томах. Т. 1.— М.: Наука, 1982; Т. 2.— 1984; Брёкер Т., Ландер Л. Дифференцируемые ростки и катастрофы.— М.: Мир, 1977; Голубицкий М., Гийемин В. Устойчивые отображения и их особенности.— М.: Мир, 1977; Гилмор Р. Прикладная теория катастроф. В 2-х томах.— М.: Мир, 1984. Отметим также тесно примыкающий к этой тематике сборник переводов «Странные аттракторы».— М.: Мир, 1981. Предлагаемая вниманию советских читателей книга известного английского ученого Дж. Томпсона займет среди них достойное место. Она почти не пересекается с упомянутыми изданиями и написана в совсем другом стиле. Это не монография и не учебник, а скорее своего рода путеводитель по литературе, содержащий популярное изложение основных идей, часто апеллирующее к физической интуиции (и определенным знаниям) читателя. При этом автор иллюстрирует излагаемые идеи на большом числе хорошо подобранных примеров.
в От переводчика
Наиболее поучительный итог от прочтения этой книги — ощущение единства и простоты причин, лежащих в основе потери устойчивости в самых разнообразных явлениях механики, физики, химии и биологии. Можно ожидать, что книга Дж. Томпсона будет способствовать формированию нового языка, стиля и облика прикладных исследований по устойчивости.
В текст перевода без специальных оговорок внесены некоторые пояснения. В заключение мне -хочется выразить благодарность проф. Дж. М. Т. Томпсону за внимание к русскому изданию его книги.
В. Бердичевский
ПРЕДИСЛОВИЕ
Имеется одна особенность, которая привносит большие трудности в механику, физику, химию, технику, астрономию и биологию. Эта особенность заключается в том, что устойчивое равновесие при непрерывном изменении параметров системы может стать неустойчивым, а непрерывный процесс с течением времени может стать разрывным.
В последние годы активное сотрудничество между прикладными математиками и учеными, работающими в перечисленных выше областях, привело к созданию удивительной теории, благодаря которой возникла общая и весьма плодотворная точка зрения на указанные выше трудности. Эта теория часто излагается так, что многочисленные технические детали мешают ее восприятию неспециалистами.
Вряд ли кто-нибудь мог бы подготовить современное и очень ясное изложение существа предмета более квалифицированно, чем проф. Дж. М Т. Томпсон. Написанную им книгу можно горячо рекомендовать каждому читателю, интересующемуся современными достижениями в науке и технике.
Дж. Лайтхилл
Моей семье
ПРЕДИСЛОВИЕ АВТОРА
Явления устойчивости представляют огромный интерес для всех научных работников и инженеров, и в настоящей книге дается неформальный обзор некоторых современных интересных и важных примеров из самых разных областей науки и техники, иллюстрирующих эти явления. Среди примеров — потеря устойчивости и галопирование тонкостенных конструкций под действием веса и ветровой нагрузки, экзотическая астрофизика коллапсирующих звезд, внезапное разрушение кристаллической решетки, термодинамическая самоорганизация биохимических систем, взрывное развитие популяций конкурирующих экологических видов, возникновение турбулентности в быстро движущейся жидкости, открытое в последнее время хаотическое движение в простых детерминистических моделях, флаттер самолетов, управление положением космического корабля и нейродинамика мозга.
Общая точка зрения на все эти различные проблемы устойчивости достигается при помощи новых идеи теории бифуркации и катастроф. Однако изложение этих идеи ведется, насколько это возможно, на уровне популярных журналов, таких, как Scientific American ° или New Scientist, и рассчитано на столь же широкую аудиторию. Одна очень важная особенность книги — доведенный до сегодняшнего дня большой список оригинальных работ, содержащий 337 наименований, который может ввести интересующегося читателя непосредственно в специальную литературу по любой теме.
Чтобы понять предмет достаточно глубоко, требуется некоторое знание математики, и на протяжении всей книги читатель систематически и ненавязчиво вводится во многие математические аспекты проблемы, однако мы всегда остаемся в рамках обычных понятий, известных большинству инженеров и научных работников. Студенты первого курса университета, специализирующиеся в любой об-
11 С 1983 г. переводится на русский язык в издательстве «Мир» под названием «В мире науки».
Предисловие автора
9
ласти науки и техники, должны легко воспринимать изложенное. Все, что требуется от читателя,— это элементарное знание алгебры, анализа и простых дифференциальных уравнений.
Математическая теория бифуркации и неустойчивости, своими историческими корнями глубоко уходящая в механику и астрофизику, в последние годы получила дальнейшее существенное развитие в основном в результате усилий топологов. Два особенно важных достижения — это глубокая классификация теории катастроф Тома и Зимана, основанная на топологическом понятии структурной устойчивости, и непреходящий подъем, вызванный открытием странных аттракторов, порождающих движение, которое воспринимается нами как хаотическое.
Основное содержание этой современной теории часто излагается в обозначениях и понятиях абстрактной топологии и недостаточно доступно многим научным работникам, знакомым с обычной прикладной математикой. Можно надеяться, что эта небольшая книга поможет им войти в круг общих идей, а ссылки на литературу укажут путь к овладению специальными вопросами.
В книге описываются как статические неустойчивости, которые представляют основной предмет теории катастроф, так и динамические неустойчивости, которые возникают, например, при ветровом флаттере самолета и подвесных мостов,— реакция этих конструкций не связана только с потенциальной энергией. Описаны некоторые игры и эксперименты с тем, чтобы побудить читателя сделать их самому; кроме того, книга содержит около 150 подробных диаграмм и фотографий. .
Многое из излагаемой теории будет вскоре напечатано в книге «Elastic Instability Phenomena» (издательство «Уайли»), написанной мной совместно с Г. У. Хантом п, и я глубоко признателен Гилсу Ханту за продолжительные совместные исследования многих вопросов.
Глава 1 — общее введение в эту книгу — основана на моей ина-угуральной лекции «Неустойчивости и катастрофы в естественных науках» в Лондонском университетском колледже 3 мая 1979 г. Она воспроизведена с любезного согласия университетского колледжа и журнала Journal of Engineering Science (University of Riyadh), где была напечатана под названием «Статическая и динамическая неустойчивости в естественных науках» [274].
Раздел 10.2 был набросан вчерне проф. Томом Кейном из Стэнфордского университета и основан на его недавней статье, написанной совместно с Д. А. Левинсоном [327], и я в высшей степени благодарен этим двум ученым за их вклад в книгу.
Дж. М. Т. Томпсон
4 Эта книга уже вышла в свет и включена в список литературы (см. [37]).— Прим, перев,
Тонкая упругая сферическая оболочка под равномерным внешним давлением. Полученные на ЭВМ графики здесь и далее выполнены Ричардом Томпсоном.
Глава
ВВЕДЕНИЕ
В этой главе дается краткий обзор некоторых концепций теории устойчивости и тех приложений теории, которые более подробно будут рассмотрены в дальнейшем.
1.1. Исторический обзор от Ньютона до Андронова
Основы механики были заложены сэром Исааком Ньютоном в его «Началах» в 1686 г. [1]. Интересно обнаружить в этой работе подробное экспериментальное исследование движений простого маятника в воздухе и воде. Затухающие колебания такого маятника представляют наиболее типичный пример асимптотически устойчивой системы, и его результаты напоминают нам, что воздух отнюдь не является линейным вязким демпфером.
Примерно 50 лет спустя, в 1744 г., Леонард Эйлер использовал только что созданное им вариационное исчисление для определения равновесных конфигураций сжатой упругой колонны [2]. В его честь эту проблему бифуркаций в инженерной механике называют проблемой Эйлера.
Лагранж, молодой друг Эйлера, развил аналитический энергетический метод в механике, приводящий к важным обобщениям, которые трудно сделать в рамках ньютоновского подхода [3]. Метод Лагранжа привел к фундаментальной теореме о том, что минимум полной потенциальной энергии системы является достаточным для устойчивости,
Дальнейший существенный вклад в аналитическую механику принадлежит Гамильтону, который понял, как описать векторное поле фазовых траекторий системой дифференциальных уравнений первого порядка.
Основоположником теории бифуркаций, как мы понимаем ее сегодня, был выдающийся французский математик Анри Пуанкаре. Он, как и Леонард Эйлер, обладал феноменальной памятью и способностью обдумывать сложнейшие проблемы анализа в самой шум
12 Гл. 1. Введение
ной обстановке. В его наследии, содержащем около 500 статей и свыше 30 книг и охватывающем всю современную ему математику, Пуанкаре дал набросок общей теории бифуркаций [4—6] и создал общую качественную теорию динамических систем, многое из которой взяла современная теория устойчивости.
Краткие биографии Эйлера, Лагранжа и Пуанкаре даны в приложении к этой книге.
Математическую точность основному определению устойчивости придал Ляпунов. В своей основополагающей работе 1892 г. [7] он ввел обобщенные энергетические функции, носящие теперь его имя.
Следуя по пути, предложенному Пуанкаре, Андронов и Понтрягин [8] ввели в 1937 г. важное топологическое понятие структурной устойчивости, которое лежит в основе последующих классификаций Тома, Зимана, Смейла и Арнольда [9—15]. В настоящее время эти достижения качественной теории динамических систем Пуанкаре представляют большую топологическую главу основ механики
УСТОЙЧИВОСТЬ состояний Ньютон Уравнения движения 1642—1727 маятника Лагранж Аналитическая механика 1736—1813 Энергетическое условие устойчивости Гамильтон Система обыкновенных 1805—1865 дифференциальных уравнений механики (первого порядка) Ляпунов Квазиэнергетические 1857—1918 функции Андропов Смейл Арнольд Том Зиман Рис. 1. История развития основ теории УСТОЙЧИВОСТЬ ТРАЕКТОРИЙ Эйлер Эластика 1707—1783 Пуанкаре Теория бифуркаций 1854—1912 Качественная теория динамических систем Структурная устойчивость Классификация структурно устойчивых особенностей устойчивости.
1.1. Исторический обзор от Ньютона до Андронова 13
вообще и теории устойчивости в частности, как видно, например, из второго издания недавно вышедшей монографии Абрахама и Марсдена 116].
Приведенный краткий исторический обзор теории устойчивости в рамках классической механики схематически представлен на рис. 1.
Очень быстрый рост науки и, в частности, прикладной механики привел к специализации и возникновению разнообразных версий первоначальных классических результатов, однако здесь мы охарактеризуем кратко специальный раздел — теорию упругой устойчивости. Она связана с реакцией упругих тел и конструкций на некоторые виды механической нагрузки и имеет важные технические приложения для оценки критической силы, вызывающей потерю устойчивости инженерных сооружений. Следует отметить, что существуют два различных типа механических систем — консервативные системы (в эту категорию включаются также системы с малой диссипацией энергии, которые являются при отсутствии диссипации консервативными) и неконсервативные системы, обычно имеющие неограниченный источник энергии.
Говоря о консервативных системах, прежде всего необходимо упомянуть о классическом исследовании бифуркаций Койтера [17], проведенном в его основополагающей диссертации (Дельфт, 1945 г.). Исследование Койтера основано на континуальной формулировке, однако после исключения пассивных деформаций энергия оказывается алгебраической функцией от амплитуд мод, по которым происходит потеря устойчивости. Этот прием лежит в основе нашего дальнейшего рассмотрения дискретных систем. Современное объяснение нелинейного ветвления континуальных упругих систем под действием консервативной нагрузки предложено Будянским [181, и в том же томе Advances in Applied Mechanics можно найти важное обобщение Хатчинсона, относящееся к неустойчивости конструкций, нагружаемых в пластической области [19].
Для неконсервативных систем важные линейные классификации были даны Циглером [20] в 1956 и 1968 гг.; необходимо также упомянуть прекрасные обобщающие работы Херрманна [21], Лейпгольца [22—25] и их коллег. Эти исследования неконсервативных упругих систем ограничены в основном областью малых линейных перемещений.
Исследования, проводившиеся по изучению теории устойчивости в Университетском колледже в Лондоне, были связаны главным образом с нелинейным ветвлением дискретных или дискретизованных консервативных систем; некоторые наиболее важные публикации приведены в списке литературы (см. [26—35]). Эта группа была образована в 60-х годах сэром Генри Чилвером, теперь вице-канцлером Крэнфилдского технологического института; его работа тесно связана с исследованием инженерных конструкций методом
14 Гл1 1. Введение
конечных элементов. Многие из его результатов представлены в монографии Томпсона и Ханта [36], вышедшей в 1973 г., а более поздние работы, включающие теорию катастроф и неконсервативные задачи, отражены в монографии этих же авторов [37]. Последнюю монографию можно рассматривать также как совместный вклад в настоящую книгу, поскольку она содержит математические основы для многих последующих обсуждений.
Основная связь современных исследований с исследованиями Эйлера и Лагранжа осуществляется теорией катастроф Ренэ Тома и Кристофера Зимана [9—11]. Глубокие и стимулирующие параллели, которые возникли между инженерными и топологическими подходами, описаны в ряде работ [34, 38] и, по-видимому, имеют большое значение для создания единой статической теории бифуркаций [39].
1.2. Неустойчивости линейного осциллятора
После этого краткого исторического обзора, прежде чем перейти к рассмотрению современных идей, лежащих в основе этой книги, изложим сначала в общих чертах некоторые из основных идей теории устойчивости.
Типичные статические и динамические неустойчивости видны на примере линейного осциллятора с затуханием, изображенного на рис. 2. Здесь масса т удерживается упругой пружиной с жесткостью s и амортизирующим демпфером, который создает вязкую силу, противоположную скорости. Изображая график зависимости перемещения х от времени /, получаем знакомую картину затухающих
Рис. 2. Поведение линейного осциллятора с затуханием.
неустойчивого фокусов.
Рис, 3. Траектории в случае устойчивого н
pri'+ri+-sa: = 0 ic+bi+ca:=O
®=ext
|л2+ЬЛ+ѫР|
D=bZ-4c
Д>0
U<0
A-Kj, Rg A = R±Ii
Рис. 4. Уравнение движения и корни характеристического уравнения линейного осциллятора,
16 Гл. I. Введение
Рис, 5. Фазовый портрет и структура корней для линейного осциллятора.
колебаний, характерных для движения маятника в воздухе. В фазовом пространстве переменных х и x=dx/dt имеется устойчивый фокус, переходящий в окружности или эллипсы для незатухающей системы. Трехмерный график такого асимптотически устойчивого поведения показан на рис. 3 в пространстве переменных х, х и t.
Уравнение движения осциллятора приведено на рис. 4. Там же выписано уравнение движения, отнесенное к массе и имеющее удобную стандартную форму. Отыскивая экспоненциальное решение, получаем характеристическое уравнение — оно обведено рамкой на рис. 4. В рассматриваемом случае характеристическое уравнение квадратично по X.
Решение зависит от корней характеристического уравнения, которые будут действительными или комплексными в зависимости от знака дискриминанта D. Если дискриминант D положителен, имеются два действительных корня (темные кружки), и, как и предполагалось, решение ведет себя экспоненциально; если же дискриминант D отрицателен, уравнение имеет два комплексно сопряженных корня (светлые кружки) и дает решение вида eRt sin It. Таким образом, осциллятор с демпфером становится неустойчивым, если хотя бы один из корней имеет положительную действительную часть.
Возможные типы поведения осциллятора изображены на рис. 5. Есди жесткость велика и затухание мало, то корни комплексные и
1.3. Нелинейные статические и динамические бифуркации 17
имеется устойчивый фокус. Если уменьшать жесткость в направлении горизонтальной стрелки, то, как только пересекается парабола критического затухания 0=0, корни становятся действительными и фазовый портрет превращается в устойчивый узел.
Нагрузка на упругую конструкцию может вызвать статическую потерю устойчивости, при которой эффективная жесткость системы меняется с положительной на отрицательную. Эта статическая неустойчивость, характеризуемая появлением смежного положения равновесия, изображается горизонтальной стрелкой. Если же гибкая упругая конструкция подвергается силовому воздействию, скажем, ветра, то порыв ветра может вызвать галопирование конструкции, при котором эффективное затухание становится отрицательным, как показано вертикальной стрелкой. При этой динамической неустойчивости устойчивый фокус переходит в неустойчивый, которому соответствует растущее колебательное движение. При движении вдоль каждой из стрелок перемещения линейной системы становятся бесконечными в точке перехода к неустойчивому режиму, однако на поведение реальной системы обычно оказывают влияние нелинейные эффекты. Этот вопрос мы будем обсуждать в следующем разделе.
Прежде чем закончить обсуждение, связанное с рис. 5, следует, однако, отметить, что консервативная система без демпфирования с центром эллиптических траекторий в действительности представляет критический промежуточный случай между устойчивой и неустойчивой областями, и рассмотрение упругой устойчивости без демпфирования приводит к патологическим корням, изображенным на рис. 6. Об этом часто забывают, и пренебрежение демпфированием, которое несущественно для некоторых консервативных систем, может привести к парадоксальным результатам для гироскопических и вращательных систем, как показано Херрманном [40] и Циглером [41]. Позже мы обсудим этот вопрос подробнее.
1.3. Нелинейные статические и динамические бифуркации
Возвращаясь к роли нелинейности, рассмотрим три типичные статические бифуркации, показанные на рис. 7. Они моделируют механическую систему типа шарика, катающегося по поверхности энергии, которая деформируется, если приложена нагрузка Л. В первой асимметричной точке бифуркации [36], наблюдаемой при потере устойчивости рам, минимум и максимум сливаются и затем снова расходятся. Во второй устойчиво симметричной точке бифуркации, известной конструкторам по поведению эйлерова стержня, исходный минимум переходит в широкую яму с маленьким пиком в центре. Третья картина демонстрирует неустойчиво симметричную точку бифуркации, которая является обращением
• Статическая неустойчивость о Динамическая неустойчивость © Упругая неустойчивость
Рис. 6. Механизмы неустойчивости.
Любое положительнее R приводит к неустойчивости
1.3. Нелинейные статические и динамические бифуркации 1&
предыдущего случая и наблюдается при потере устойчивост арок и оболочек.
В каждой из этих бифуркаций, как мы видим, тривиальное равновесное состояние с нулевым перемещением q становится неустойчивым при пересечении со вторичной равновесной траекторией. Это наблюдение находится в соответствии с недавно установленной теоремой [36, 42, 43], которая утверждает, что для консервативной системы нелинейная бифуркация, в которой нет предельной точки, всегда свидетельствует о неустойчивости.
Динамические точки бифуркации, вероятно, несколько менее известны; простой пример динамической бифуркации нелинейного осциллятора изображен на рис. 8. Здесь вместо симметричной за-критической равновесной траектории имеется семейство растущих предельных циклов, которые рассматриваются в фазовом пространстве переменных х, х при различных значениях параметра нагруже; ния Л.
Случай положительных D представляет динамический аналог устойчиво симметричной точки бифуркации. Тривиальное состояние
aS +Ы+сх + D (х2+хг) х = О
а-с ш = 1 а = A cos t DAz=-b
Рис. 8. Динамическая бифуркация нелинейного осциллятора.
20 Гл. 1. Введение
х=0 является устойчивым для Л, меньших Ас, и представляет притягивающий фокус. Для Л, больших Лс, это состояние соответствует неустойчивому отталкивающему фокусу, и все локальные движения системы стремятся к устойчивому притягивающему предельному циклу, представляющему устойчивое конечное колебание. Амплитуда предельного цикла увеличивается с ростом Л от значения, равного нулю в критическом равновесном состоянии.
Динамический аналог неустойчиво симметричной точки бифуркации соответствует случаю, когда коэффициент нелинейности D отрицателен. Тривиальное равновесное решение опять теряет свою устойчивость при Л=ЛС. При этом значении Л притягивающий фокус переходит в отталкивающий. Устойчивое докритическое равновесное состояние имеет, однако, лишь конечную область притяжения, ограниченную неустойчивым предельным циклом. Если в результате конечного возмущения система оказалась вне
Рис, 9, Сравнение двух статических и двух динамических бифуркаций.
1.4. Статические бифуркации и теория катастроф 21
этого цикла, то возникнут возрастающие колебания, даже если управляющий параметр Л меньше своего критического значения. Устойчивое тривиальное решение при этом называют метаустой-чивым, как в соответствующей статической неустойчиво симметричной бифуркации. Наиболее типичные динамические бифуркации такого типа называют бифуркациями Хопфа 11 после появления знаменитой теоремы [44, 45].
По-видимому, поучительно изобразить перестройки в фазовом пространстве для четырех симметричных бифуркаций на одной диаграмме, как сделано на рис. 9. Здесь фазовые портреты воспроизведены для до- и закритической нагрузок и хорошо видны аналогии между двумя статическими и динамическими бифуркациями. Отметим, однако, что для двух статических бифуркаций фокус всегда переходит в узел в окрестности бифуркации — это не во всех случаях специально оговаривается.
В гидродинамике устойчиво (неустойчиво) симметричные бифуркации называются за(до)критическими бифуркациями, и топологи по очевидным соображениям называют симметричную бифуркацию камертоном. Асимметричную точку бифуркации называют транскритической бифуркацией.
Мы вернемся к динамическим бифуркациям позже при обсуждении гидростатических нагрузок на сооружения, а теперь обратимся к более тщательному рассмотрению статических бифуркаций, типичных для поведения консервативных систем.
1.4. Статические бифуркации и теория катастроф
Существенную роль в классификации статических неустойчивостей играет теория катастроф. Сводка основных результатов теории катастроф дана в табл. На рис. 10.
Чтобы установить эти результаты для дискретных консервативных систем, поведение которых определяется потенциальной функцией, Ренэ Том привлек топологическую концепцию структурной устойчивости. Теория катастроф объяснила зависимость экспериментально наблюдаемых форм неустойчивости от числа управляющих параметров. В связи с этим, если имеется только один управляющий параметр X, в случае общего положения можно наблюдать лишь катастрофу складки, которая имеет локально потенциальную функцию, указанную в таблице.
Если имеется независимое управление двумя параметрами X1 и X2, которые могут быть, например, поперечной нагрузкой и осевой нагрузкой на стержень, можно дополнительно наблюдать сборку. В случае независимого управления тремя параметрами X1, X*
1) В литературе на русском языке принято также название «бифуркация рож-
дения цикла»,— Прим. pedt
22 Гл. 1. Введение
Складка Предельная точка Асимметричная
Сборка Устойчиво симметричная Неустойчиво симметричная
Ласточкин хвост 9®+xv+^V+^<?
Бабочка £+X V+ X3<?3+XV+
Г иперболическая омбилика <?a+ <?i + М?2<71 — — №qi Моноклинная Гомоклинная
Эллиптическая омбилика gz—dq^qi + X1 (9г + <?i) — —xv—xv Антиклинная
Параболическая омбилика <?2?i-b(7i~b^1?2+XV—X3<?2—Wq i
Рис, 10. Список семи элементарных катастроф.
и I3 можно дополнительно наблюдать ласточкин хвост и гиперболические и эллиптические омбилические катастрофы. При четырех управляющих параметрах может наблюдаться любая катастрофа из нашей таблицы.
Приведенный перечень включает все структурно устойчивые особенности, которые могут наблюдаться в окружающем нас мире при воздействии от одного до четырех управляющих параметров. В частности, он имеет непосредственное отношение к биологии развития, где пространство и время являются, как правило, первичными управляющими параметрами при дифференцировке клеток,— это мы увидим позже. Следует отметить, что первые четыре катастрофы из списка катастроф имеют только одну активную обобщенную координату q, как при простой потере устойчивости, в то время как последние три катастрофы имеют активные координаты qY и qt, как в случае одновременной потери устойчивости по двум формам.
В правой стороне таблицы помещены инженерные наименования некоторых из особенностей, и мы увидим позже, что более подробная подклассификация, не претендующая на завершенность, возникает из рассмотрения бифуркаций с одним управляющим параметром.
1.5. Складка или предельная точка 23
Существенно высказывание Тома, что патологические ситуации можно наблюдать только при достаточно высоком уровне управления, и мы продемонстрируем это сейчас для катастрофы складки, следуя работе [46L
1.5. Складка или предельная точка
Как мы видели, в случае катастрофы складки имеется только одна активная координата, и соображения Тома можно проиллюстрировать на рис. И. На нем прописными буквами Q и Л обозначены общие переменные, заменяющие локальные переменные, которые обозначались строчными буквами q и Л, V — полная потенциальная энергия.
Если ребенок небрежно начертит на доске вид V как функции от Q, его каракули, как правило, будут иметь максимум и минимум, в которых dV/dQ обращается в нуль, однако мы не можем ожидать наличия точки перегиба, в которой в нуль обращаются одновременно первая и вторая производные. Появление такой критической точки следовало бы рассматривать как патологию, и мы могли бы приписать ей вероятность, равную нулю. В полном соответствии с рисунком на доске при построении модели конструкции в лаборатории и приложении фиксированной нагрузки мы не можем ожидать, что конструкция окажется в точности в критическом равновесном состоянии.
Единственный способ наблюдать точку перегиба заключается в том, чтобы нарисовать семейство кривых, параметризованных переменной Л, как это и сделано на рисунке. Поэтому для того, чтобы наблюдать критическое равновесное состояние, в котором две первые производные обращаются в нуль одновременно, мы долж-
Рис, Ц. Изменение энергии в случае катастрофы складки.
24 Гл. I. Введение
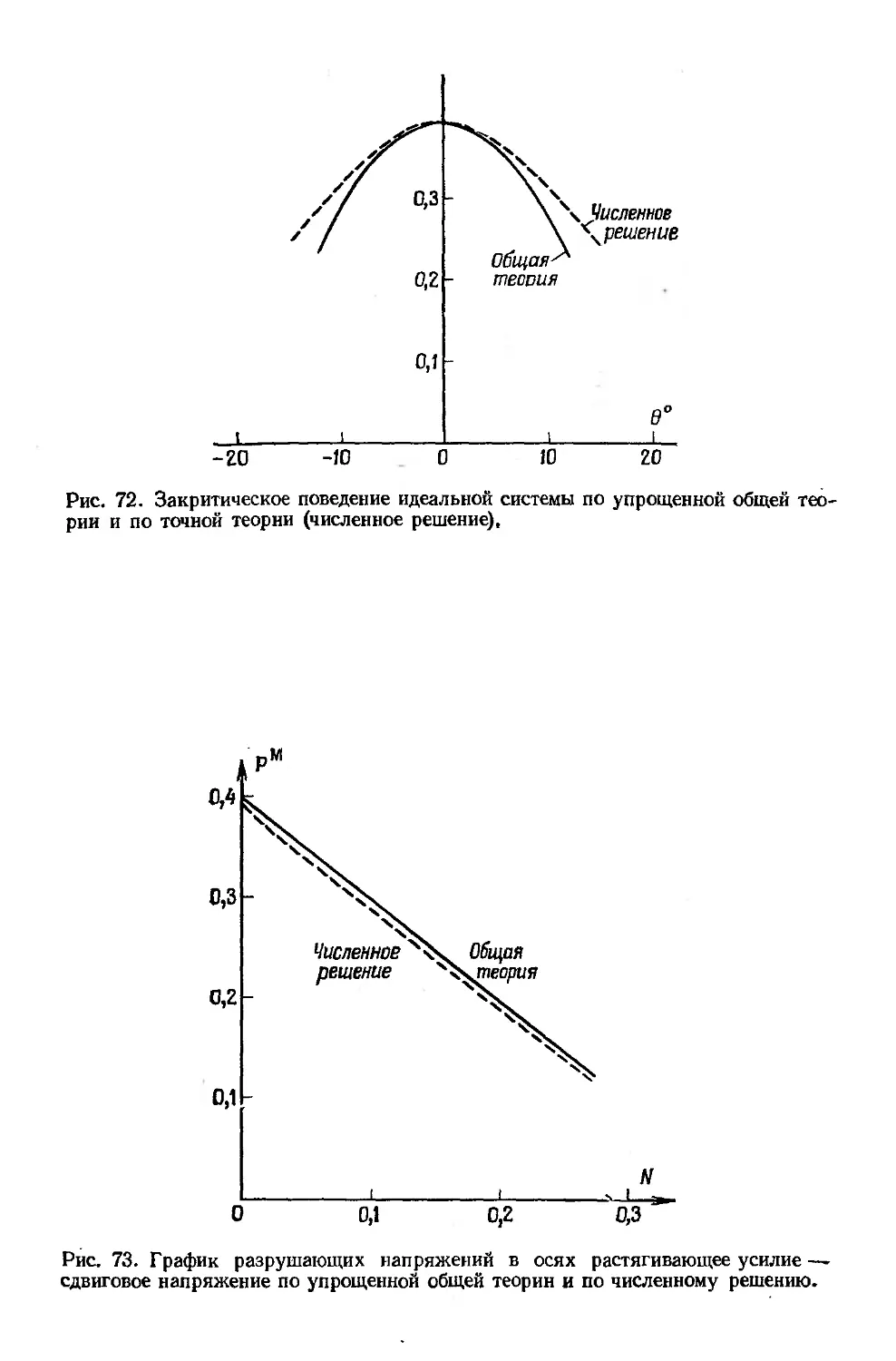
Рис. 12. График зависимости нагрузки от перемещения в центре для пологой арки, концы которой стянуты пружиной.
ны изменять параметр Л, и это в точности то, что мы делаем, когда нагружаем конструкцию до потери устойчивости.
Рассмотренная сейчас наиболее простая трансформация энергий, заключающаяся в слиянии и исчезновении минимума и максимума под действием единственного управляющего параметра, называется катастрофой складки. Ей соответствует траектория равновесия XCY, которая загибается в критической точке С, меняя при этом характер устойчивости.
Катастрофы складки встречаются во многих вопросах науки и техники. По-видимому, наиболее простая механическая модель — это арка, изображенная на рис. 12. Здесь первоначально прямая упругая полоска из стали удерживается в форме пологой арки горизонтальной упругой пружиной. Под действием груза, прочно прикрепленного в вершине, арка может перескочить в положение равновесия, зеркально отраженное относительно начального положения равновесия, как показано на рисунке. Причем при медленном циклическом нагружении арка проходит замкнутую петлю гистерезиса.
На рис. 13 показано более сложное явление типа катастрофы складки, которое может возникать при больших перемещениях пологих арок и куполов. Это явление как при мертвом, так и жестком нагружении недавно исследовалось [471 при помощи новой теоремы сопряжения, которая позволяет сделать неочевидные заключения об устойчивости при помощи представления о последовательности складок. На траектории, изображенные на рис. 13, весьма похожи траектории складок для равновесия массивной холодной звезды с двумя устойчивыми режимами, соответствующими белому карлику и нейтронным звездам. Они также изучены (см. [47]) и будут обсуждаться в следующей главе. Это очень красивая задача механики, возникающая в общей теории относительности,
Рис. 13. Последовательные складки на траекториях равновесия пологой арки и сферического купола.
Рис. 14. Асимметричная бифуркация как катастрофа складки,.
26 Гл. 1. Введение
Асимметричная или транскритическая бифуркация, которую мы обсуждали раньше, представляет по существу взгляд на складку под необычным углом в расширенном пространстве управлений (рис. 14). Более точная классификация бифуркаций будет рассмотрена в связи с обсуждением катастрофы гиперболической ом-бил и ки.
Интересно отметить, что грозы возникают в связи с неустойчивостями заряженных водяных капель в электрическом поле, которые, как было показано исследованиями Рэлея и Тэйлора [48], порождаются как раз такой транскритической бифуркацией. Это изящный пример теории ветвления, в котором электрическое поле играет роль начального несовершенства, разрушающего основную симметрию.
1.6. Сборка или симметричная бифуркация
Мы уже рассмотрели неустойчиво симметричную точку ветвления (см. рис. 7). Если ввести дополнительно параметр несовершенства е, то получится картина, изображенная на рис. 15 [36], которая эквивалентна картине траекторий равновесия, приведенной на рис. 49 гл. 2. Траектория равновесия идеализированной, не содержащей несовершенств системы окружена траекториями равновесия системы с несовершенствами. В правой части рис. 15 приведен график зависимости критической нагрузки от параметра несовершенства е. Зависимость содержит точку возврата при е=0.
Ясно, что при нагружении реальной и потому всегда содержащей несовершенства конструкции траектория равновесия не пройдет
Рис. 15. Чувствительность к несовершенствам в неустойчиво симметричной точке ветвления.
1.6. Сборка или симметричная бифуркация 27
Рис. 16. Эксперименты Роорды по потере устойчивости пологой арки [27].
непосредственно через точку ветвления и будет представлять одну из траекторий, близких к траектории равновесия идеальной системы. Это означает, что при однопараметрическом нагружении неустойчивость будет восприниматься так же, как в случае катастрофы складки. Саму точку ветвления можно наблюдать экспериментально только в том случае, когда одновременно меняется как параметр нагружения, так и параметр несовершенства. В действительности же эта точка ветвления — проявление катастрофы сборки, а необходимость в двухпараметрической развертке подтверждает предсказание Тома.
Эта статическая бифуркация хорошо видна на примере неустойчивости упругой арки, при которой нагрузка приложена не обязательно в центре арки (рис. 16). Одновременно измеряя как нагрузку Р, так и эксцентриситет силы f, Роорда [27] при проведении своих классических экспериментов в Университетском колледже смог экспериментально определить чувствительность к несовершенству по степенному закону двух третей. Мы видим, что, как и предсказывает Том, двухпараметрическая неустойчивость приводит к появлению сборки, напоминая — это не очевидно a priori,—
28 Гл. 1. Введение
Рис. 17. Эквивалентность неустойчивой сборки и неустойчиво симметричной точки ветвления.
что единственный управляющий параметр несовершенства адекватен балансу всех технологических дефектов в испытываемой арке, как это и происходит при f=f0. Как и предполагалось, экспериментально найденная сборка смещена от центра, но, кроме того, по теории Тома она также наклонена: в окрестности сборки имеется небольшая асимметрия, которая представляет проявление значительного общего наклона. Конечно, Том не говорит, насколько она будет наклонена!
Топологи обычно рисуют трехмерные равновесные поверхности, и на рис. 17 показана эквивалентность симметричной точки ветвления и общепринятого изображения сборки Зимана [10, 49]. Здесь траекториям на бифуркационной диаграмме соответствуют постоянные е. Можно отметить, что граница устойчивости, след складок, проектируется на горизонтальную плоскость управляющих параметров как точка возврата со степенным законом двух третей.
Устойчиво симметричная точка ветвления, которая возникает, например, в задаче об устойчивости эйлерового стержня, также классифицируется Томом как сборка вследствие их полного топологического подобия. Сборка при эйлеровой потере устойчивости будет рассмотрена в следующей главе.
1.6. Сборка или симметричная бифуркация 29
Рис. 1S. Катастрофа сборки, иллюстрирующая поведение животного, которое испытывает одновременно ярость и страх.
Примером устойчивой сборки (сейчас мы переходим от консервативных механических систем к механике жидкости) является классическая гидродинамическая неустойчивость течения Куэтта между вращающимися цилиндрами (см. рис. 94 гл. 7). Если цилиндры длинные, так что краевыми эффектами можно пренебречь, то при увеличении угловой скорости основное циркуляционное течение становится неустойчивым в устойчиво симметричной закритиче-ской точке ветвления. Как показано в верхней части графика на рис. 94, эта статическая бифуркация вызывает образование устойчивых вихрей, названных в честь Тэйлора (G. I. Taylor).
Совсем недавно Бенджамин [50] исследовал это явление экспериментально, используя, однако, цилиндр ограниченной длины (это показано на нижней части рисунка). Здесь краевые условия изменяют простой основной поток; Бенджамин рассматривает угловую скорость и переменную длину как независимые параметры, управляющие фазовым переходом между двух- и четырехячеечными течениями. Таким образом он получил наклонную сборку, показанную на графике зависимости длины L от числа Рейнольдса Re. Результаты Бенджамина изображены схематически в трехмерном пространстве на рис. 95. Сборка, регулирующая морфогенез течения Куэтта, аналогична сборке теории клеточной дифференцировки, построенной Зиманом в его статье по биологии развития, которую мы представим в гл. 5,
30 Гл, I. Введение
Фото 1. Точка возврата, наблюдаемая в стакане молока, стоящего на солнце,— пример катастрофы сборки, возникающей как каустика при отражении лучей от цилиндрического зеркала. Эта фотография получена непосредственно на чувствительной фотобумаге, положенной под кружок алюминиевой фольги; изготовлена при помощи моих детей Элен и Ричарда.
Сборка, будучи простой катастрофой с интересной и поддающейся изображению в трехмерном пространстве структурой, вызвала большой интерес, но, к сожалению, для многих она представляет синоним самой теории катастроф. Зиман [10, 49, 51] предложил много интересных применений катастрофы сборки в общественных и описательных науках. Его примеры, являясь крайне стимулирующими, вызывают некоторую полемику [52—55]. Так, в частности, Зиман применяет катастрофу сборки в психологии, описывая противоречивые стимулы ярости и страха (рис. 18).
Сборка в виде симметричных бифуркаций возникает, конечно, во всех математических науках, и теория катастроф накопила важный багаж и может, в частности, продемонстрировать структурную устойчивость сборки при наличии только двух управляющих параметров.
Одна из областей, в которой складки и сборки возникают в ситуации, когда определена общая потенциальная энергия,— это исследование гидростатической неустойчивости мениска. В этой связи следует упомянуть работы Микаэля и его соавторов по электрогидростатике [56—59], которые важны при изучении пробоя электроизоляции, и работу Тэйлора по образованию полостей в слое жидкости [60]. Микаэль [61] дает обзор результатов о неустойчи-
1.6. Сборка или симметричная бифуркация 31
Рис, 19. Изображение каустики, полученной при помощи компьютера.
востях мениска и, в частности, отмечает аналогию с мертвым и жестким нагружением инженерных конструкций [47].
Прежде чем закончить рассмотрение катастрофы сборки, следует отметить, что она часто встречается в оптике. Действительно, ее можно наблюдать в стакане молока, стоящем на солнце. Это показано на фото 1 и рис. 19, полученном при помощи расчета на компьютере. Здесь имеются глубокие связи с теорией, поскольку свет распространяется по траектории с минимальным (или, точнее, стационарным) временем. Действительно, луч, проходя от точки А в точку В через искривленное зеркало С, принимает форму, которую приняла бы упругая лента, если бы ее закрепили в точках А а В и позволили бы свободно двигаться через бусину, находящуюся в точке С.
32 Гл. 1. Введение
Фото 2. Каустика, образовавшаяся при рефракции лазерного луча на водяных капельках, случайно разбросанных по плоской стеклянной пластине. Каустика сос. тоит из гладких кривых, содержащих складки, которые пересекаются в точках, образующих точки возврата, в полном соответствии с теоремой Тома, согласно которой на плоскости возможны только такие устойчивые конфигурации. Воспроизведено с разрешения Берри (М. V. Berry),
В широко Известных работах Берри, Ная и др. [62—67] световые каустики интерпретируются как простые катастрофы сборки (фото 2) и как многие из катастроф высшего порядка (фото 7 в гл. 4), в то время как Най использует теорию катастроф для описания особенностей трехмерных векторных полей [68, 69L
1.7. Гиперболическая омбилика и ветвление в вершине 33
1.7. Гиперболическая омбилика и ветвление в вершине
Обратимся теперь к гиперболической омбилике, которая является одной из катастроф более высокого порядка в списке Тома, включающем семь катастроф. Эта катастрофа имеет три управляющих параметра и две активные координаты, поэтому равновесные поверхности лежат в пятимерном пространстве и их обычное изображение неосуществимо. Рассмотрим вместо пятимерного трехмерное пространство управляющих параметров (рис. 20).
Здесь на правом графике показаны границы устойчивости в пространстве управляющих параметров, соответствующие графику чувствительности к несовершенствам для сборки. При изменении параметров меняются и равновесные решения, их форма претерпевает топологическое изменение при пересечении одной из критических поверхностей. Сплошной кружок на схеме обозначает устойчивый минимум энергии, незаштрихованный кружок — неустойчивый максимум энергии и полузаштрихованный кружок — неустойчивую седловую точку. Четыре области пространства управляющих параметров соответствуют указанным равновесным реше-
Рис. 20. Характерные траектории для катастрофы гиперболической омбилики.
2 £528
34 Гл, 1. Введение
Рис. 21. Две моды деформации при потере устойчивости подкрепленных пластин.
ниям. Например, перед поверхностями вообще нет равновесных решений, позади них имеется четыре равновесных решения и в промежуточных областях — два равновесных решения.
Поэтому система будет претерпевать изменения устойчивости каждый раз, когда пересекается одна из критических поверхностей в пространстве управляющих параметров. При движении по разным траекториям А, В и С, проходящим через центр гиперболической омбилики, возникают явления, показанные слева [70], и именно эти явления, связанные с траекториями в пространстве параметров, приводят нас к подклассификации катастроф Тома. Необходимые подклассификации, возникающие вследствие введения предпочтительных управляющих параметров, были сделаны топологами, особенно Вассерманном [71—73] и, совсем недавно, в глубокой работе Голубицкого и Шэффера [74—76].
Привлекательным примером гиперболической омбилики является потеря устойчивости подкрепленных пластин. На рис. 21 показаны две моды деформации пластины, спроектированной так, что при сжатии вдоль оси она теряет устойчивость по обеим модам
Рис. 22. Катастрофа гиперболической омбилики в задаче о чувствительности к несовершенствам подкрепленных пластин, показывающая структурную устойчивость границы катастрофы: вид спереди согласно Ханту 178].
Рис, 23, Вид сзади катастрофы гиперболической омбилики согласно Ханту [78].
2*
36 Гл. 1. Введение
‘’’и
Рис. 24. Гиперболическая омбилика в задаче о неустойчивости атомной решетки.
одновременно в соответствии с простой теорией оптимизации [77]. Здесь нагрузку Л и геометрические несовершенства в двух модах деформации следует рассматривать как управляющие параметры. На рис. 22 показаны расчетные трехмерные графики чувствительности к несовершенствам, полученные Хантом [78].
На графике слева показаны критические поверхности при одновременной потере устойчивости, а справа — те же критические поверхности, когда критические нагрузки, вызывающие потерю устойчивости, расщеплены четвертым управляющим параметром. Топологическое подобие этих двух форм является результатом структурной устойчивости катастрофы гиперболической омбилики; это гарантирует невозможность разрушения формы критических поверхностей, если число управляющих активных параметров больше трех, необходимых для универсальной развертки особой точки.
На рис. 23 показан вид этих привлекательных поверхностей сзади. Эти результаты в последнее время дополнены Хантом в ряде
1.8. Катастрофы высокого порядка и оптимизация конструкций 37 статей (79—81], опубликованных Королевским обществом (Royal Society). Новые работы Ханта расширяют диапазон применения асимптотического анализа путем включения гиперболической омбилики в управляемую катастрофу параболической омбилики.
Вторым примером гиперболической омбилики в хорошо поставленной задаче может служить бифуркационная неустойчивость атомной решетки под действием внешних нагрузок, которая исследована Томпсоном и Шорроком [82, 83] и будет обсуждаться в гл. 4. Она возникает в кристалле, когда при одноосном растяжении может развиться относительный сдвиг, нарушающий симметрию задачи, а наложение поперечного сжатия может вызвать неустойчивость типа точки ветвления в вершине (рис. 20). Граница устойчивости в трехмерном пространстве управляющих параметров представляет поверхность разрушающих напряжений, изображенную на рис. 24.
Новый пример катастрофы эллиптической омбилики дали Берри и Мэкли (84, 85] при описании раскручивания неустойчивого потока жидкости с образованием кольцевого вихря.
На фото 6 гл. 4 изображена изготовленная в домашних условиях картонная модель границ устойчивости катастрофы гиперболической омбилики. Она показывает замысловатые детали этой поверхности, в том числе и заостренный край: обычно в картйнах катастроф высокого порядка можно найти катастрофы низкого порядка.
1.8. Катастрофы высокого порядка и оптимизация конструкций
Бифуркации высокого порядка, выпадающие из перечня семи элементарных катастроф и включающие множественность мод потери устойчивости, часто возникают в задачах оптимизации конструкций в сочетании со свойственной этим задачам симметрией [77]. Множественность мод порождает сложные вторичные бифуркации [86—89], которые играют важную роль в эволюции планет и химической термодинамике.
Сложная неустойчивость упругой пластинки, теряющей устойчивость одновременно по двум модам, обсуждается Постоном и Стюартом в их замечательной книге [11], где они определяют физические параметры, необходимые для построения соответствующей катастрофы двойной сборки.
Пример конструкции с чрезвычайно сложным бифуркационным поведением дает замкнутая сферическая оболочка, подверженная действию постоянного внешнего давления. Эта задача была исследована Койтером [90, 91]. На рис. 25 представлен характер поведения такой оболочки согласно теории. Здесь при жестком нагружении [47] появляется динамический скачок при постоянном объеме.
38 Гл. 1. Введение
Рис. 25. Скачок при постоянном объеме, возникающий при коллапсе замкнутой сферической оболочки.
Этот эффект наблюдался экспериментально для оболочки с несовершенствами [92 , 93].
Классификация элементарных катастроф коразмерности, меньшей или равной пяти, дана Зиманом [94] в 1976 г.
1.9. Галопирование и флаттер подвесных мостов
Перейдем теперь от рассмотрения статических бифуркаций к рассмотрению динамических бифуркаций. Они характеризуются не статической траекторией равновесия, а траекторией предельных циклов.
Рассмотрим ровный ветер, обдувающий гибкую упругую конструкцию. Он может вызывать и поддерживать колебания с большой амплитудой, похожие на те, которые разрушили подвесной мост Такома Нэрроуз (Tacoma Narrows), показанный непосредственно перед разрушением на фото 11 гл. 9.
Имеются три различных механизма аэроупругой неустойчивости: галопирование по одной моде, вихревой резонанс и бимодальный флаттер. Предполагают, что мост Такома был разрушен вследствие сочетания более чем одного из этих явлений. Однако остановимся на простом галопировании, которое в чистом виде наблюдается при опасных колебаниях покрытого льдом кабеля.
1.9. Галопирование и флаттер подвесных мостов 39
ту+гу+ку = у pV2 аС(а)
Рис. 26. Галопирование квадратной (в сеченин) призмы, помещенной в поток ровного ветра: модель и аэродинамические характеристики получены Паркинсоном и Бруксом 195]. Воспроизводится с разрешения Amer. Soc. of Meeh. Engrs.
Рассмотрим, например, квадратную (в сечении) призму (рис. 26), которая вынуждена благодаря пружине и амортизатору двигаться в вертикальной плоскости. Пусть призма обдувается ветром со скоростью V. Когда призма движется вниз со скоростью у, скорость ветра относительно призмы имеет значение VR, как показано в треугольнике скоростей. Этот относительный ветер создаст вертикальную компоненту силы. В квазистатическом приближении коэффициент силы С просто зависит от угла а, который в свою очередь зависит от у. На нижней диаграмме показаны две типичные зависимости С от а. Эти зависимости были получены Паркинсоном и Бруксом [95, 96] на основании аэродинамических испытаний стационарно наклоненных профилей.
Мы видим, что ветер приводит по существу к отрицательному демпфированию, вызывая неустойчивость типа динамической бифуркации Хопфа при скорости ветра, пропорциональной постоянной амортизатора г. Отметим, что при отсутствии демпфера система
40 Г л. 1. Введение
дестабилизируется под действием сколь угодно слабого ветра — это указывает на структурную неустойчивость полностью консервативной системы.
Различные поперечные сечения дают различные функции С(а) и, следовательно, различные явления галопирования; некоторые формы поперечных сечений, рассмотренные Новаком [97], детально обсуждаются в гл. 9. Возможны как устойчивые, так и неустойчивые бифуркации вместе с гистерезисным скачком динамических складок при слиянии устойчивых и неустойчивых предельных циклов.
Полезный современный обзор работ по колебаниям, вызываемым потоком жидкости, содержится в книге Блевинса [98].
1.10. Возникновение порядка в биохимических реакциях
Бифуркации являются ключевыми факторами при спонтанном появлении упорядоченных структур в химических и биохимических системах; это освещалось в работах брюссельской группы Пригожина [99, 100]. Исследование вопроса о пространственной и временной самоорганизации необходимо для понимания морфогенеза-в биологии развития. Этот вопрос обсуждается в гл. 5.
Появление порядка в силу второго начала термодинамики может происходить только в открытой системе, которая, кроме того, должна иметь нелинейное поведение. В такой системе процесс самоорганизации сопровождается неустойчивостью траектории стационарных состояний, а затем эта неустойчивая первоначально гомогенная система может прийти к упорядоченному состоянию или диссипативной структуре.
Физическим примером этого явления может служить хорошо известная реакция Жаботинского, а фотография Уинфри [101] спиральных химических волн, которые могут появиться во взболтанной однородной химической смеси, приведена на рис. 74 гл. 5. Спиральные химические волны можно сравнить с драматическими формами живых организмов, которые воспроизводятся в классической книге Дарси У. Томпсона «Оп Growth and Form» [102].
Кинетика реакции Жаботинского довольно сложна, поэтому большой теоретический интерес вызвала тримолекулярная модельная система, так называемый брюсселятор [100]. При отсутствии пространственного распределения эта система в фазовом пространстве концентраций двух химических веществ х и у обнаруживает динамическую бифуркацию, и на рис. 78 гл. 5 показаны растущие предельные циклы. Здесь в качестве управляющего параметра рассматривается заданная концентрация третьего химического вещества В, а устойчивые предельные циклы для концентрации В, большие ее критического значения, представляют собой поддержи-Ьаемые колебания химических компонент смеси. Кажется вполне
1.11. Неконсервативные задачи 41
оправданным ощущение, что колебания такого типа могут объяснить действие таинственных пока биологических часов.
Если эту модельную реакцию рассматривать распределенной в пространстве, то появление диффузии вызовет самопроизвольное образование пространственных структур, как это имеет место в реакции Жаботинского. Это позволяет думать, что самоорганизация такого типа может объяснить появление жизни из первичного бульона.
Аналогично этому, хотя и не полностью, для динамики популяций и экологии типа хищник — жертва в гл. 6 строятся модельные уравнения эволюции Лотки — Вольтерры, которые предсказывают возникновение колебаний [103]. Были предприняты попытки использовать теорию катастроф в эволюции [104, 105], а роль бифуркаций и сложное динамическое поведение в экологических системах рассмотрены в работе Мэя [106].
1.11. Неконсервативные задачи лри гидродинамических воздействиях
В какой-то степени мы уже обсуждали галопирование, теперь же кратко остановимся на вихревом резонансе, отметив просто, что модели жидкого осциллятора, рассматриваемые Айвеном и Блевинсом [107] и Хартленом и Кюрри [108], образуют уравнения двух связанных нелинейных осцилляторов с, возможно, несимметричной матрицей инерции, как показано на рис. 27. Пур и Аль-Рави [109] -обсуждают бифуркации Хопфа при колебаниях, вызванных ветром.
Чтобы понять, какие типы обобщенных сил возникают при взаимодействии с жидкостью, рассмотрим три хорошо поставленные
Скрытый „ внутренний /параметр
Вихревой резонанс
cyl(y Q Q
ЦИЛИНДР
ЖИДКОСТЬ
y+w + j/+w + j/+w = О ~ .. ГТ . I Гз" t/+W4-y+W+t/+W « W
Рис. 27. Уравнения колебания жидкости пря вихревом резонансе. Слагаемые, подчеркнутые верхней линией,— слагаемые Айвена и Блевинса; слагаемые, под-черкнутые нижней линией,— слагаемые Хартлена и Кюрри,
42 Гл. 1. Введение
задачи о поведении систем под действием гидродинамических натру» зок, после чего дадим некоторую предварительную классификацию сил с точки зрения механики.
Начнем с работы Доуэла [ПО, 1111 по классическому аэродинамическому флаттеру [112], который обсуждается в гл. 9. Рассмотрим сначала сверхзвуковой поток ветра, который обдувает упругую панель, образуя устойчивую динамическую бифуркацию, возможно бифуркацию типа Хопфа с растущим устойчивым предельным циклом. Суммируя матрицы и нелинейные члены в рамках двухмодового гармонического анализа, можно заметить, что поток газа дает положительно определенное демпфирование, пропорциональное скорости U, и антисимметричную циркуляционную матрицу, пропорциональную U2.
Вторая задача — это задача о шарнирно опертой трубе, по которой транспортируется жидкость,— она проанализирована Холмсом [113]. В гл. 9 приведены соответствующие матрицы и нелинейные члены в рамках двухмодового гармонического анализа. Оказывается, что сила со стороны жидкости описывается антисимметричной
2—3/2«« — 1
3/2и2_1-| ^Cij =
1 J Ча= ч _Г2—3/2п3 3/4иа—И ~[з/4И2_ 1 J J
Г 0 3/4««1
“ L-?/4«S О J
.—положительная полуопределенная диссипация
Рис. 28. Л1И1рицы сил в задаче Бенджамина о двух сочлененных трубах, по ко» торым течет жидкость,
1.11. Неконсервативные задачи 43
гироскопической матрицей, связанной с силами Кориолиса, которые пропорциональны скорости жидкости U, и симметричной матрицей, связанной с центробежными силами, пропорциональными U2. Последняя матрица идентична по форме матрице сжатия с приложенной осевой сжимающей нагрузкой. Поскольку силы Кориолиса, будучи антисимметричными, не совершают работы и поскольку предполагается, что конструкция содержит демпфер, в этой системе не может появиться предельный цикл и, следовательно, не может образоваться бифуркация Хопфа. Действительно, эта система обнаруживает неустойчивость типа разбегания, совершенно аналогичную первой и последующей потерям устойчивости сжатого стержня Эйлера. Следует отметить, что при нагрузке выше второй нагрузки Эйлера, движение, отличное от тривиального неустойчивого состояния, вследствие действия сил Кориолиса представляет собой растущее колебательное движение, похожее на флаттер. Когда система начинает съезжать с энергетического холма, сила Кориолиса направлена под прямым углом к направлению движения и поворачивает траекторию системы, это и вызывает колебания.
Рис. 29. Движение корней характеристического уравнения в комплексной плоскости в задаче Бенджамина о сочлененных трубах.
44 Гл. 1. Введение
И наконец, третья задача — это задача о линейном флаттере сочлененных труб с одним заделанным концом, рассмотренная Бенджамином [1141. Матрицы, приведенные на рис. 28, показывают, что силы со стороны жидкости можно разложить на силы с положительно определенной диссипацией и не совершающие работу гироскопические силы (и те и другие пропорциональны U) и симметричные консервативные и антисимметричные циркуляционные силы (и те и другие пропорциональны (72). Центробежные силы с!}, действующие со стороны жидкости, пропорциональны Ц2 и фактически статически эквивалентны следящей силе на конце трубы, из которого вытекает жидкость.
На комплексной плоскости рис. 29 показано движение корней характеристического уравнения. Поскольку Бенджамин не включает в рассмотрение демпфирование конструкции, корни для нулевой скорости жидкости лежат на мнимой оси в точках Л. Небольшой поток жидкости приводит к появлению отрицательных действительных частей, а в точках С, где два комплексно сопряженных корня пересекают мнимую ось, возникает динамическая неустойчивость. При отсутствии полной нелинейной формулировки о воздействий на конструкцию со стороны жидкости и о поведении конструкции можно предположить, что динамическая неустойчивость в точке С является бифуркацией Хопфа устойчивого или неустойчивого
Силы, действующие со стороны жидкости Зависящие от скоростей Зависящие от перемещений cifj
симметричные диссипативные антисимметричные гироскопические симметричные упругие антисимметричные вращательные
Бенджамин "[!.'] положительная полуопреде-ленная неопределенная
Холмс "[° “Я "[-U] отрицательно определенная
Доуэлл 4J5] положительно определенная
Рис. 30. Сводка предположений о силах, действующих со стороны жидкости, по трем .работам.
1.11. Неконсервативные задачи 45
типа. Здесь, возможно, уместно упомянуть исследования некоторых нелинейных задач [115—117].
Аналогичное исследование цельной трубы с одним заделанным концом (например, шланга) было выполнено Пайдусисом в ряде его работ и обсуждается в гл. 9. Кроме того, Бишоп и Фаузи [1181 также рассматривают задачу о цельной трубе с одним заделанным концом и обсуждают вопрос о вынужденных колебаниях трубы; на один удивительный парадокс обратили внимание Пайдуссис и Декснис [119].
В каждой из трех задач силы, действующие со стороны жидкости, линеаризуются, а получающиеся в результате матрицы приведены на рис. 30. Видно, что исследования Доуэлла и Холмса используют дополняющие друг друга вклады, в то время как в исследованиях Бенджамина на консольную балку с опертыми концами действуют силы всех типов.
Эти примеры реальной нагрузки со стороны жидкости приводят нас к следующей классификации сил (рис. 31). Термин «приложенные» предлагается для сил, зависящих от скорости, которые совершают над системой положительную работу, как это имеет место для аэродинамических сил при галопировании. На рис. 32 пред-
КЛАССИФИКАЦИЯ СИЛ
• Инерциальные (0) симметричная положительно определенная
• Дисснпатииные ' ^/(0) симметричная положительно определенная "Г Siflj -4-
Г ироскопические Gij антисимметричная
Приложенные
• Упругие Uи (0) симметричная положительно, определенная >Vf7(0) I ciflj -4-
Консервативные W ij (0) симметричная
Вращательные С.7
1—» Нелинейности i ^, (<7/, q'k. Qi)
ф Предполагаются всегда присутствующими 0
Рис. 31. Предлагаемая классификация механических сил.
46 Гл. I. Введение
лакается окончательная классификация систем. Отметим, что все системы считаются имеющими инерциальные, упругие и положительно определенные диссипативные силы. Последние необходимы для построения хороших моделей реальных явлений, на чем мы остановимся в следующем разделе. Как указывалось в [120], при сделанном выше допущении относительно диссипации минимум общей потенциальной энергии дискретной системы становится и не-
КЛАССИФИКАЦИЯ СИСТЕМ
\ Силы Системы \ Зависящие от скоростей Зависящие от перемещений Примеры Энергетическая теорема Vmin^ устойчивость
гироскопические (не совершают работу) приложенные (совершают работу) консервативные (получаемые как производные функции V) вращательные (не получаемые как производные функции V)
Консервативные • Потеря устойчивости эйлерова стержня Да
Гироскопические • • Раскачка шарнирно закрепленной трубы Да
Приложенные • • Г алопиро-вание тел плохообтекаемой формы Нет
Вращательные • • Флаттер крыла самолета Her
Г ироскопи-ческие и вращательные • • • Флаттер консольной трубы Нет
Считается, что инерциальные, диссипативные и упругие силы присутствуют всегда
Рис. 32. Предлагаемая классификация систем с примерами для каждого типа сил; бтмечено, для каких сил имеет место энергетическая теорема.
1.12. Теория динамических систем 47
обходимым, и достаточным условием устойчивости консервативных и гироскопических систем.
Тематически и технически очень важными проблемами неустойчивости, вызываемой жидкостью, как предсказал Рейни [121—123J, являются неустойчивости Матье, которые присущи моделям привязанных нефтяных платформ (платформ на опоре, плавучих привязанных платформ, секционных вышек и др.) и возникают под действием установившегося движения цепочки поверхностных волн.
1.12. Теория динамических систем и топологическая устойчивость
Мы считаем, что программа дальнейших инженерных исследований должна иметь целью приложение относительно новых понятий и идей теории динамических систем к исследованию устойчивостей, связанных с движением жидкости, как подчеркивалось в ряде статей Холмса, Марсдена, Рэнда и Чиллингуорта (113, 124—134].
Многие результаты теории, изложенной в введении, могут быть найдены в трудах Нью-Йоркской конференции по теории бифуркаций [135], в книге Абрахама и Марсдена [16] и в родственных работах [136—142]. Теория динамических систем играет ключевую роль в понимании структурной устойчивости и объясняет, почему наши модели должны быть нелинейными (в точке бифуркации) и должны
Рис. 33. Стержень, нагруженный следящей силой,— пример структурно неустойчивой модели, в которой бесконечно малое демпфирование вызывает конечную дестабилизацию.
48 Гл. 1. Введение
обязательно включать затухание. Учет затухания служит для устранения таких хорошо известных инженерных парадоксов, как конечная дестабилизация при бесконечно малом демпфировании [143, 144] (см. рис. 33).
В теории динамических систем еще отсутствует полная классификация, соответствующая классификации элементарной теории катастроф, но уже установлено, что бифуркация Хопфа и бифуркация седло — узел (или катастрофа складки) являются единственными структурно устойчивыми локальными бифуркациями, наблюдаемыми при изменении одного управляющего параметра. Существенное значение вывода о наличии бифуркации Хопфа при колебаниях шланга состоит в том, что гарантируется его структурная устойчивость и тем самым возможность экспериментального наблюдения бифуркации при изменении одного управляющего параметра.
Важная концепция теории динамических систем, на которую обратили внимание Чиллингуорт и Холмс, состоит в том, что многообразие, на котором имеется простая бифуркация Хопфа для двумерного фазового пространства, может быть погружено в фазное пространство более высокой размерности [45]. '
1.13. Хаос, турбулентность и странные аттракторы
Одним из наиболее волнующих результатов последних исследований по динамике является понятие странного аттрактора. Это понятие появилось в связи с работой «Лоренца по атмосферным явлениям [1451, а возникновение хаоса при решении простого детерминистического дифференциального уравнения было привлечено Рюэлем и Такенсом [146) для объяснения гидродинамической турбулентности. В этой области по-прежнему имеется целый ряд нерешенных вопросов, о которых будет сказано в гл. 7.
Хаотические фазовые портреты странных аттракторов наблюдались для чрезвычайно простых нелинейных динамических систем в трехмерном фазовом пространстве. Действительно, Роеслер [147, 148) сказал: «Если колебание является типичным поведением двумерных динамических систем, то хаос точно так же характерен для трехмерных динамических систем». Здесь хаос представляет собой «бесконечное число неустойчивых периодических траекторий и несчетное количество непериодических повторяющихся траекторий»,
Такое хаотическое поведение наблюдалось Холмсом с соавторами в совершенно простых механических системах [149—156], в частности при колебаниях слегка выпученного стержня, на который действует боковая сила. Наличие хаоса может оказывать значительное влияние на интерпретацию и понимание результатов численного интегрирования и методы усреднения Следует отметить книгу [157] по этой быстро развивающейся области исследований.
1.14. Заключительные замечания 49
В качестве краткого введения в эту область в гл. 8 излагается принадлежащее Хенону [158] простое численное исследование странного аттрактора, который связан с разностным уравнением, моделирующим отображение Пуанкаре для непрерывной системы. Аналогичные разностные динамические системы изучались численно Хсу с соавторами [156—161).
1.14. Заключительные замечания
Я надеюсь, что в этой книге мне удастся отразить некоторые источники неустойчивостей, бифуркаций и катастроф как в аналитической механике, так и в других науках. Возможно, этот вводный обзор следует закончить цитатой из Корнелиуса Ланцоша [162):
«Аналитическая механика представляет собой много больше, чем эффективный инструмент для решения динамических проблем, встречающихся в физике и технике. Вряд ли существует другая такая математическая наука, в которой строгая абстрактная модель и экспериментальные данные столь хорошо согласуются и поддерживают друг друга.
Имеется огромная сокровищница философского смысла, который открывается в великих теориях Эйлера и «Лагранжа, Гамильтона и Якоби... источник величайшего интеллектуального наслаждения для каждого математически мыслящего человека.»
Глава
ПОТЕРЯ УСТОЙЧИВОСТИ КОНСТРУКЦИЙ
Исторически и логически исследование потери устойчивости упругих конструкций представляет центральную главу теории устойчивости. Рассмотрение простых физических моделей упругих конструкций является прекрасным введением к дальнейшим более специальным вопросам. По этой причине мы начнем изложение с простейшего анализа некоторых задач теории устойчивости упругих конструкций и закончим обзором современных исследований в этой области.
2.1. Простые эксперименты с изгибаемым стержнем п
Предположим, что мы заострили концы гибкой полоски длиной L изготовленной из упругого металла или дерева, и сжимаем ее вдоль оси; используя нагружающее устройство, показанное на рис. 34. Увеличивая медленно мертвую нагрузку Р, можно измерить отклонение центральной точки Q и изобразить зависимость Р от Q в виде графика. Вместо такого нагружения можно, конечно, использовать червячную передачу 147], чтобы фиксировать уменьшение длины стержня; равновесные состояния тогда будут теми же самыми, однако область устойчивости изменится.
Нагружая стержень мертвой нагрузкой, мы найдем, что очень малые значения Q будут регистрироваться до тех пор, пока Р не приблизится к некоторому критическому значению Рс. Как показывают наблюдения, вблизи этой нагрузки боковые отклонения быстро растут с ростом нагрузки. Соответствующая зависимость Р от Q изображена кривой OKN на рис. 34. Возрастание Q, связанное с потерей устойчивости, в дальнейшем замедляется в связи с увеличением жесткости системы в закритическом состоянии. В точке N стержень находится в сильно изогнутом положении, подобном
** В книге термин «стержень» употребляется для перевода нескольких различных английских слов: column, strut, beam, rod, поскольку им соответствует одна и та же математическая модель.— Прим, перев.
2.1. Простые эксперименты с изгибаемым стержнем 51
Рис. 34. Поведение сжатого эйлерова стержня (теория и эксперимент).
положению, в котором оказывается человек, опершийся на тростник. Несмотря на быстрый рост перемещения около точки Рс, естественная траектория равновесия OK.N везде устойчива, и движение вдоль нее гладко и обратимо (что отмечено стрелками на рисунке). Говоря это, мы подразумевали, что разрушения материала не происходит и необратимых деформаций не возникает, так что поведение материала является упругим и стержень всегда восстанавливает исходную прямую форму при снятии нагрузки.
Как известно, тростник может быть сильно изогнут в любом направлении, как с положительным, так и отрицательным Q, и при высокой сжимающей нагрузке его можно привести во второе устойчивое состояние М, подталкивая в случае необходимости рукой. Если затем разгружать стержень, то окажется, что в точке минимума J стержень перепрыгнет обратно в состояние К на естественной траектории нагрузки, при этом во время быстрого динамического Хлопка не возникает изменения мертвой нагрузки. Последующие йагружение и разгрузка приведут к первоначально наблюдавшему
52 Гл. 2. Потеря устойчивости конструкций
ся гладкому естественному поведению. Скачок в предельной точке J представляет собой пример катастрофы складки.
Допустим, что мы хотим теперь смоделировать это поведение математически. Прежде всего можно попытаться использовать простую инженерную теорию изгиба, в которой кривизна малого элемента стержня аппроксимируется величиной d2w/dx2, где w(x, t) — перемещение поперечного сечения, находящегося на расстоянии х от нижней опоры в момент времени t. Полагая, что кривизна пропорциональна изгибающему моменту, вычисленному в недеформиро-ванном состоянии (соответствующему нулевым перемещениям)» найдем решение w=Q. Это, конечно, правильный ответ для состояния равновесия идеально прямого стержня, однако он ничего не говорит нам об ожидаемой потере устойчивости.
Дело в том, что так же как натяжение гитарной струны повышает собственную частоту колебаний, так и сжатие прямого упругого стержня понижает собственную частоту до тех пор, пока она наконец не станет равной нулю. Это происходит при значении нагрузки, равной критическому значению Рс. Действительно, анализ линейных колебаний, в котором сохраняются только квадратичные члены энергии, показывает, что корень из основной собственной частоты для первой гармоники w=Q sin nx/L уменьшается до нуля по линейному закону при увеличении нагрузки до эйлеровой нагрузки потери устойчивости Pc=n2EHL2. Здесь £7 — изгибная жесткость, которая представляет собой произведение модуля Юнга упругости материала Е на момент инерции поперечного сечения /.
Эта критическая нагрузка, которая имеет фундаментальное значение в строительной механике, может быть получена при помощи анализа потери устойчивости в рамках статики, если аппроксимировать кривизну по-прежнему выражением d^w/dx2, но изгибающий момент в деформированном состоянии определить как Pw. Результат такого линейного анализа соответствующей задачи на собственные значения предсказывает, что перемещение будет стремиться к бесконечности на некотором множестве критических нагрузок, соответствующих гармоническим перемещениям w— —Qnsm(rmx/L), где п=1, 2, 3, . . ., причем наименьшая критическая нагрузка Рс соответствует п=1.
Полный нелинейный статический анализ закритического поведения, использующий более сложное точное выражение для кривизны, дает всю картину равновесия идеального стержня, которая была впервые найдена Эйлером в его классической работе [2]. Фрагмент этой картины для значений нагрузки, близких к Р=РС, показан жирными линиями на рис. 34; сплошными кривыми обозначаются устойчивые траектории деформации, а штрихами неустойчивые.
Чтобы добиться согласования с экспериментом, надо ввести в математическую модель начальные несовершенства, всегда имеющиеся в стержне, такие, как, скажем, начальные отклонения его
2.1. Простые эксперименты с изгибаемым стержнем 5S
Рис, 35. Трехмерная картина траекторий равновесия эйлерова стержня. Показана зависимость перемещения Q от нагрузки Р и параметра несовершенства е.
от прямолинейной формы. Эти несовершенства измеряют основное тривиальное решение, и траектория равновесия уже не проходит через точку бифуркации Рс, как показано на полной бифуркационной диаграмме. Здесь светлыми линиями представлены траектории равновесия двух систем, содержащих несовершенства, одна с положительным значением параметра несовершенства е, другая с отрицательным значением е. По-прежнему сплошными и штриховыми кривыми показаны устойчивые и неустойчивые траектории соответственно. Изображенное здесь симметричное ветвление состояния равновесия исследовалось в общем виде Томпсоном ц Хантом [36].
Теперь мы подготовлены к тому, чтобы изобразить поверхность-равновесия в трехмерном пространстве обобщенных координат — переменной состояния Q и двух управляющих параметров Р и е (рис. 35). Видно, что устойчиво симметричная точка бифуркации эйлерова стержня является катастрофой сборки. Обсуждение эйлеровой потери устойчивости в терминах теории катастроф было дано Чиллингуортом [163] и Зиманом [164].
Прежде чем приступить к анализу стержня, представляющего систему с бесконечным числом степеней свободы, для иллюстрации.
54 Гл. 2. Потеря устойчивости конструкций
некоторых основных идей рассмотрим модель шарнира, содержащую одну степень свободы. Шарнир, связанный с упругой пружиной, можно рассматривать как простейшую модель стержня, закрепленного на одном конце (качественно он ведет себя как нижняя часть шарнирно опертого стержня).
2.2. Исследование модели консольного шарнира
Рассмотрим невесомый недеформируемый стержень длиной L, соединенный с упругой пружиной жесткости k (рис. 36). Пружина сопротивляется вращению стержня. Стержень несет точечную массу т на конце и находится в постоянном гравитационном поле с ускорением g, что означает, что консоль находится под действием силы величиной P=mg. Мы будем рассматривать Р как управляющий параметр нагружения и будем исследовать потерю устойчивости системы по мере того, как Р постепенно увеличивается от нулевого значения.
Выберем в качестве обобщенной координаты угол поворота от вертикали Qt и проведем сначала статический анализ. Энергия деформации, накопленная в пружине, есть U—YzkQl, а расстояние, на которое опустилась масса т, вычисляется по формуле
S = L(1— cosQj).
Общая потенциальная энергия системы дается равенством
V = U—Р£ = l/2 kQ'i —PL (1 —cos Qt).
Уравнение равновесия
V^-g^Qi-PLsin Q’ = 0
имеет тривиальное решение Q=0 для всех Р и решение, определяемое из уравнения
',=ЕжтЕ-т('+т«+-)-
Следовательно, имеются две траектории равновесия. Они обозначены на рис. 36 жирными линиями. Устойчивость равновесных состояний определяется выражением
V^^^k-PLcosQi.
Вдоль основной «тривиальной» траектории равновесия коэффициент устойчивости равен —PL, и устойчивость имеет место при
Р, меньшем Рс, а неустойчивость — при Р, большем Рс, где Рс= ^k/L.
Аналогичным образом находятся устойчивые траектории равновесия в закрнтическом состоянии, и ясно, что общая потенци-
2.2. Исследование модели консольного шарнира 55
Рис. 36. Статическое и динамическое поведение шарнирно опертого стержня а круговой пружиной.
альная энергия V (Qi) имеет единственный минимум для заданного Р<.РС и два минимума, разделенных максимумом, для каждого Р>РС- Это схематически показано на рис. 36.
Динамику системы в рамках нелинейной теории легко найти качественно при помощи графиков общей потенциальной энергии системы. Если пренебречь демпфированием, то центр, соответствующий тривиальному состоянию для P<ZPC, будет трансформироваться в два центра, разделенных седлом, для Р>РС, как показано на рисунке. Если имеется некоторая положительная вязкость, то устойчивый фокус в тривиальном состоянии для Р<.РС будет переходить в два устойчивых фокуса, разделенных седлом, как показано на рисунке для Р>РС.
Мы не будем исследовать эти нелинейные движения и вместо этого рассмотрим линейные колебания около состояния равновесия Qi=0. Будем считать, что стержень невесом. Тогда кинетическая энергия системы сводится к кинетической энергии точечной массы т и дается формулой Т= % mLPQl. Сравнивая ее с общим выражением для кинетической энергии Т= ¥2 TuQl, имеем Ти~тЬй. Угловая частота малых колебаний ю тогда дается теорией линейного осциллятора 137] в виде
,ч2 _
Ти~ mL* ’
Эта частота уменьшается до нуля, когда Р возрастает до Рс. Мы видим, что имеются три различных пути для определения критической нагрузки РС1
56 Гл. 2. Потеря устойчивости конструкций
(1) ветвление тривиальной траектории равновесия;
(2) исчезновение минимума потенциальной энергии;
(3) обращение в нуль частоты колебаний.
Эквивалентность (1) и (2) гарантируется основной теоремой те ории упругой устойчивости [42, 43], которая была упомянута в гл. 1. Эквивалентность (2) и (3) установлена для общих консервативных механических систем, в которых дополнительно учитывается малая вязкость [37]. Эквивалентные линейные критерии для широкого класса механических систем подробно рассмотрены Циглером [20].
В заключение этого раздела рассмотрим влияние начальных геометрических неосовершенств на изменение траектории статического равновесия системы. Предположим, что в силу небольшой технологической ошибки пружина находится в недеформированном состоянии не тогда, когда стержень вертикален, а когда он наклонен по отношению к вертикали на малый начальный угол Q?=e. Общая потенциальная энергия системы с точностью до произвольной постоянной имеет теперь вид
V=k (Qi-zy-PL (1 -cos Qi), поэтому для равновесия получим
Vt = k(Q—е)—PL sin Qf = 0, что приводит к равенству
р , е)
L sin Qi
Видно, что траектория тривиального равновесия переходит в семейство равновесных кривых P(Qi), соответствующих различным значениям е и окружающих бифуркационные кривые идеальной -системы, как показано на рис. 36.
Более полный статический анализ этой задачи можно найти в монографии [36].
2.3. Конечные перемещения стержня
.Для того чтобы исследовать поведение сплошного стержня, нам потребуется нелинейная теория конечных перемещений, которую мы приведем здесь в энергетических терминах [36]. Это позволит использовать метод Рэлея — Ритца, чтобы перейти к системе с одной •степенью свободы, а затем уже рассмотреть большое число гармонических мод. Дадим точное выражение для энергии деформации упругого стержня или колонны при конечных перемещениях.
Рассмотрим стержень длиной L, изображенный на рис. 37, для определенности шарнирно опертый и нагруженный осевой силой
2.3. Конечные перемещения стержня 57
Рис. 37. Схема перемещений стержня.
Р, которая сохраняет величину и направление при деформации стержня. Стержень предполагается нерастяжимым, а соответствующая изгибная жесткость обозначается через EI. Точка А стержня, находившаяся на расстоянии х от левой опоры, перемещается в точку В, и это перемещение, как показано на рисунке, можно представить в виде суммы горизонтального и вертикального перемещений. Поскольку центральная линия остается нерастяжимой, длина дуги SB равна х, и деформированное положение стержня определяется в целом одной функцией w (х), где х изменяется в пределах от 0 до L. Отметим, что график функции w(x) не имеет такую же форму, как изогнутый стержень, благодаря тому, что точки стержня получают некоторые горизонтальные перемещения.
Кривизна х по определению есть скорость изменения угла наклона касательной к оси, так что (см. рис. 37)
X = = т" arcsin w' = w" (1 —u>'2)~1/2,
где штрихом обозначается дифференцирование по х. Энергия деформации, накопленная в элементе стержня длиной 6х, есть 8U= — iiM'/fix, где М— изгибающий момент, даваемый равенством М=Е1%, так что
W^EItfbx.
58 Гл. 2. Потеря устойчивости конструкций
Полная энергия деформации поэтому дается равенством L
U- — EI §x2dx = О
L
= 1Е/J (1 —tw'2)-1 о
L
= ^EI^ (w”2 + w"2w’2 + и/'2©'4 + ...) dx. 0
Единственно, что необходимо оставить в этом выражении для линейной теории бесконечно малых перемещений,— это уже известный нам подчеркнутый член. Из рисунка видно, что
6е = (бх2—to2)1'- = 6х(1 — и/2)1'2,
так что укорочение стержня равно
и/2)1'2 dx =
L
Ч(4“',+4ю'‘+и о
Здесь главный подчеркнутый член — снова единственный, который необходимо оставить для линейного анализа устойчивости или теории колебаний.
Для применения точной нелинейной формулировки только в статике при написании выражения для кинетической энергии введем некоторые аппроксимации. Если т — масса единицы длины стержня, то кинетическая энергия элемента стержня приблизительно равна 67”=/гтбхпу 2, где точка обозначает дифференцирование по времени t.
Отсюда, поскольку общая потенциальная энергия V есть разность U—PS, в рамках линейного анализа имеем известное выражение для энергии
L L
V- ^EI J w"2dx—w'2dx, о о
I.
Т = у т § w2dx. о
2.4. Потеря устойчивости и закритическое поведение 59
2.4. Потеря устойчивости и закритическое поведение по первой гармонике
Начнем с анализа линейных колебаний и потери устойчивости шарнирно опертого стержня или колонны, подверженных осевому сжатию Р. Энергии задаются выписанными выше выражениями, и в соответствии с методом Рэлея — Ритца для получения системы с одной степенью свободы надо принять, что имеется некоторая изгибная мода с произвольной амплитудой Q. Форма моды должна удовлетворять геометрическому краевому условию задачи, и мы выберем в качестве ее полуволну синусоиды, так что
w — Q (/) sin (six/L).
Дифференцируя, имеем
w = Q sin (nx/L), w' = Q (л/L) cos (nx/L), w" — — Q (n/L)2 sin (nx/L).
Используя соотношение
L L
C . „six , P „six 1 ,
\ sin2 -j-dx= \ cos2— = y L,
о о
после подстановки в выражения для потенциальной и кинетической энергии по линейной теории получим
Как известно, по линейной теории [37] имеем
V=VaVuQ2. 7'=1/2Tn(0)Qs,
и сравнение с полученными выше выражениями для энергии приводит к следующим значениям коэффициентов:
Ta^)=m(L/2).
Угловая частота дается равенством
<o2 = VIi/7’1I(O),
так что окончательно имеем
ю8 (л/£)Ч£/(л/ра-Р} т
60 Гл. 2. Потеря устойчивости конструкций
Рис. 38. Зависимость частоты от нагрузки для шарнирно опертого стержня: приближенный и точный результаты.
Видно, что квадрат угловой частоты уменьшается по линейному закону при увеличении сжимающего усилия Р, пока не обратится в нуль при достижении Р критической нагрузки Рс, определяемой по формуле
Рс — (л/Л)2Е/.
Эти выражения для со2 и Рс фактически являются точными потому, что выбранная в качестве моды полуволна синусоиды в действительности является собственной модой колебаний и модой, по которой происходит потеря устойчивости.
Если бы мы предположили, что мода имеет параболическую форму, и провели бы все проделанные выше выкладки, то получили бы следующий результат:
0)2 = (10//,°) {£/ (12/1°) - Р} т
Он представляет некоторое приближенное решение и изображен на рис. 38.
Отметим, что приближенные значения частоты и соответствующей критической нагрузки больше истинных, как это и должно быть в соответствии с процедурой Рэлея — Ритца. Видно также, что приближенный подход дает правильную форму решения и что даже весьма грубая аппроксимация для w (x) приводит к достаточно точному ответу для угловой частоты и критической нагрузки.
Мы смогли так далеко продвинуться в предсказании потери устойчивости только за счет того, что задача на собственные значения была линейной. Чтобы разобраться в закритическом поведении после прохождения нагрузкой критического значения, линейного
2.4. Потеря устойчивости и аакритическое поведение 61
-анализа недостаточно, и в выражении для общей потенциальной энергии необходимо сохранить нелинейные члены высшего порядка.
Приведем здесь анализ начальной стадии закритического поведения для статического равновесия сжатого шарнирно опертого эйлерова стержня, используя ту же форму деформированного состояния, что и раньше: w=Q sin (лх/L). Общая потенциальная энергия будет равна V=U—PS, где в соответствии с приведенными выше формулами
L
(/ = у £/ J (of2 + w"2w'2 + w'^w'* + ...) dx, О
L
о '
Здесь первые члены рядов дают энергию по линейной теории Уг KnQ8, в то время как вторые члены дают вклад в нелинейную энергию вида (1/24) VnllQ*.
Подстановка выражения для перемещения w по х приводит к следующей формуле для энергии:
V = ±£7 (2L)‘|q2+|e/ (£)*-g-Q4+...
-РШт)2Т<22+4(г)4Й<24+—
Сравнение ее с разложением в ряд Тейлора позволяет определить коэффициенты в выражениях для энергии
IZoC |С_ /луь
v 11 ~ 6Q2 дР I — \ L } 2 ’
^ini-dQ4| - s \ L) ’
где значком С отмечается значение в точке ветвления, в которой, как было установлено,
Теперь можно использовать результат общей теории ветвления 137]
1 1 Vim 2
Здесь X — отклонение управляющего параметра от критического значения: Х=Р—Рс, a q — отклонение кинематической характеристики системы Q от значения в точке ветвления: q=Q—Qc. Поскольку Qc=0, величины q и Q совпадают.
62 Гл. 2. Потеря устойчивости конструкций
Закритическое решение первого порядка малости можно получить и прямым вычислением из уравнения равновесия системы
' £7 (тГ<22-о \ L /
Итак, имеется устойчиво симметричная точка ветвления, и, поскольку в рассматриваемой задаче энергия не содержит кубических членов, анализ методом Рэлея — Ритца в рамках модели с одной степенью свободы дает правильную начальную кривизну траектории закритического равновесия.
2.5. Модель стержня с двумя степенями свободы
Прежде чем приступить к многомодовому анализу стержня, рассмотрим модель трехзвенного шарнирно опертого стержня, который имеет две степени свободы. Этот стержень в деформированном соо» тоянии изображен на рис. 39.
Он состоит из трех стержней длиной L, соединенных шарнирами и образующих цепь длиной 3L. Краевое звено цепи вращается вокруг фиксированной точки, а второе звено может свободно вращаться вокруг краевого звена. При относительном вращении стержней в точках соединений возникает сопротивление со стороны двух круговых пружин, каждая из них имеет жесткость k. Пружины
Рис, 39, Перемещения и моды в модели стержня с двумя шарнирами,
2.5. Модель стержня с двумя степенями свободы 63
находятся в недеформированном состоянии, когда стержни лежат на прямой линии, так что при отсутствии нагрузки стержни находятся на прямой горизонтальной линии между опорами. Система нагружается мертвой сжимающей нагрузкой Р, которая по предположению сохраняет свое первоначальное значение и направление при деформировании шарниров.
Система имеет две степени свободы. Вертикальные смещения точек соединения обозначаются через QiL и Q2L, как показано на рисунке, так что общее деформированное состояние системы может быть полностью описано безразмерными обобщенными координатами Qi и Q2. Обе они равны нулю в недеформированном состоянии системы.
Энергия деформации, накапливаемая в двух круговых пружинах, дается формулой
которая может быть переписана в виде
(7 = 1/2^{arcsin Qf—arcsin(Q2—Qi)}2+ l/2 Marcsin Qs + + arcsin(Q2 —QJ}2.
Раскладывая каждый из тригонометрических членов в ряд по Qi, Q2, имеем
L/ = 1/2^(5Q?—8QXQ24-5Q2-f-члены высшего порядка малости).
Укорочение стержня, вызванное поперечным перемещением точек сопряжения, дается равенством
^ = £[3-(l-QI)V2 _(i_Q2)i/a
Раскладывая снова в степенной ряд, имеем
S — L(Ql — QtQ2 + QI + члены высшего порядка малости).
Итак, общая потенциальная энергия системы есть
V(Q/) = £7(Qz)-P<!?(Qi);
последний член представляет потенциальную энергию приложенной нагрузки. Вторая вариация потенциальной энергии V равна
W = >/2 k (5Q2-8QiQ2 + 5Q|)-PL (QI- QXQ2 + Q2).
Это та самая квадратичная форма, которую нужно исследовать для изучения устойчивости прямой конфигурации. Прямая конфигурация является равновесным состоянием, поскольку в разложении потенциальной энергии отсутствуют линейные члены и первая вариация 6V равна нулю.
Если имеются две квадратичные формы и одна из них положительно определена (в рассматриваемой задаче квадратичная форма Энергии деформации пружин положительно определена, так как она
64 Гл. 2. Потеря устойчивости конструкций
выведена из выражения, состоящего из суммы двух квадратов), всегда можно найти линейную замену переменных, которая одновременно приводит две формы к диагональному виду. В нашей задаче это достигается невырожденным преобразованием
Ы1== (Qi 4" Сг)/2» иа= (Qi Qa)/2,
которое имеет следующее обращение:
Ql 4“ ^2» Qa” ^1 ^2*
Чтобы понять, как расположены новые оси ut в {фД-пространстве, заметим, что Qj=—Qa при Wj=0 и Q1=Q2 при ы2=0. Поэтому оси координат щ ортогональны и повернуты на угол 45° по отношению к осям координат Qj, как показано на рисунке.
Рис. 40. Трехмерная диаграмма нагрузка—перемещение в линейной теории шарнирно опертого стержня, Показаны энергетические поверхности для различных значений нагрузки»
2.5. Модель стержня с двумя степенями свободы 65
В терминах главных координат и±, и2 прямой подстановкой находим
6V = V2 k (2й‘ + 18м|)—PL (и} + 3«1).
Сравнивая это выражение с суммой квадратов в стандартной форме б2У=1/2ад+1/2ад,
получаем коэффициенты устойчивости
С, = 2k—2PL, С2 = 18k—6PL.
Если приложенная нагрузка равна нулю, то прямая конфигурация устойчива, поскольку
Ci = 2k>0, С2=18£>О, и энергия имеет локальный минимум, как показано внизу справа на рис. 40.
По мере увеличения осевой сжимающей нагрузки Р два коэффициента устойчивости уменьшаются по линейному закону до тех пор, пока Ci не достигнет значения, равного нулю, которое соответствует первой критической нагрузке Р1, даваемой равенством P1—klL. При этой нагрузке кривизна поверхности энергии в направлении Ut уменьшается до нуля, так что вторая вариация имеет цилиндрическую форму, показанную справа на рис. 40. Говорят, что стержень теряет устойчивость по моде при этой критической нагрузке.
Если нагрузка превысила значение Р1, коэффициент Cf становится отрицательным, в то время как коэффициент С2 остается пока положительным. Поверхность второй вариации энергии V имеет теперь форму седловой точки, загибающейся вверх в направлении координаты и2 и вниз в направлении координаты ult как показано на рисунке. Основная прямая конфигурация системы теперь является неустойчивой. Можно сообщить больше информации, если сказать, что прямая конфигурация неустойчива по отношению к ut, но устойчива по отношению к и2.
Если мы продолжаем увеличивать приложенную нагрузку Р, второй коэффициент устойчивости С2 достигнет, наконец, нулевого значения, когда нагрузка становится равной второму критическому значению Р2, даваемому формулой P2—3k!L.
При этой второй потере устойчивости вторая вариация энергии б2Е снова изображается цилиндрической поверхностью, как показано на рис. 40, а для достаточно больших значений нагрузки она имеет локальный максимум. Можно сказать, что в модели стержня происходит потеря устойчивости по моде и2 при второй критической нагрузке Р2, хотя это условие не может быть достигнуто экспериментально без наложения дополнительных ограничений, исключающих более раннюю потерю устойчивости по моде и^.
3 Mi ,528
66 Гл. 2. Потеря устойчивости конструкций
Модель стержня
Сплошной стержень
Рис. 41. Моды потери устойчивости в модельной задаче и задаче о реальном сплошном стержне.
Подчеркнем, что каждая поверхность энергии, изображенная в правой части рис. 40, соответствует заданному фиксированному значению приложенной нагрузки Р.
Легко охарактеризовать деформации системы в терминах ui, и2. Когда речь идет о моде и^, то подразумевается деформация, которая происходит при ы2==0. Равенство м2=0 означает, согласно формулам перехода к старым переменным, что Qi=Q2, так что мода соответствует симметричной деформации, аппроксимирующей первую гармонику сплошного стержня, как показано на рис. 41. Аналогично равенство щ=0 означает, что Q,=—Q2, так что мода м2 соответствует антисимметричной деформации, аппроксимирующей вторую гармонику сплошного стержня, как показано на рисунке.
Отметим в заключение, что две критические нагрузки Р1 и Р2 могли бы быть определены без диагонализации второй вариации энергии, а из уравнения, получающегося приравниванием нулю детерминанта устойчивости:
I d2V I I (5&—2PL) (—4k + PL)
4k + PL) (5k—2PL) ”
Из этого уравнения имеем 9k2—12APL-|-3P2L2=0. Последнее соотношение является квадратичным по PLIk и может быть представлено в виде произведения двух сомножителей:
Это дает PLIk—\ или 3.
Исследование, подобное проведенному и имеющее целью определить критические нагрузки при помощи изучения второй вариации потенциальной энергии V, называют линейным анализом собственных значений. Оно не добавляет новой информации о поведении системы после начального момента потери устойчивости, которое управляется слагаемыми энергии, имеющими в состоянии критического равновесия более высокий порядок малости.
2.6. Полный гармонический анализ стержня 67
2.6. Полный гармонический анализ стержня на упругом основании
Дополним этот короткий аналитический экскурс в теорию устойчивости многомодовым линейным гармоническим анализом шарнирно опертого стержня, который взаимодействует (или не взаимодействует) с упругим основанием. Упругое основание действует поперек оси стержня [36, 37] и может быть реализовано как пружинящая подложка, на которой горизонтально лежит стержень. Упругое основание можно представлять себе как большое число упругих пружин, сопротивляющихся поперечным перемещениям w.
Линеаризованное выражение для энергии, которое требуется в теории колебаний с малой амплитудой и для анализа устойчивости упругого стержня, следует из приведенных выше формул. Энергия деформации изгиба есть
L ив=^Е1 { uf2dx, о
потенциальная энергия мертвой осевой сжимающей нагрузки Р есть
L иР = — § w'?dx,
о
а энергию деформации простого упругого основания, на котором находится стержень, можно записать в виде
L
w2dx, о
где К—жесткость основания. Итак, общая потенциальная энергия V может быть записана в форме
V — uB+uF + ир.
Кинетическая энергия дается равенством
L
Т —-^m^^dx.
о
В этом разделе мы рассмотрим дискретную модель сплошного упругого стержня, задаваясь следующим разложением и> по модам!
ш(х, = Mi(x).
i
Здесь амплитуды qt— некоторые функции времени, а каждая из мод Mi предполагается удовлетворяющей геометрическим граничным
3*
68 Гл. 2. Потеря устойчивости конструкций
условиям задачи. Каждая мода не обязательно удовлетворяет ес-тественным или динамическим граничным условиям, которые будут выполнены автоматически (насколько это возможно) в силу последующей энергетической процедуры.
Для конечного множества мод Mt (х) мы применим хорошо известный метод Рэлея —Ритца. Если же моды образуют полное (и, следовательно, бесконечное) множество функций, то наш анализ будет точным классическим при условии сходимости соответствующих бесконечных рядов.
Используя правило суммирования Эйнштейна по повторяющимся индексам [36], имеем
да=^(.Л1(., ш' = 9;Л4-, w" = ^.A4'i, w = qtMh поэтому можно написать
да'2 = q-fl/M '(М’Ь w'z =
Энергия деформации изгиба примет вид
L uB=±-EI q flJ М'-М'- dx. о
Сравнивая это выражение со стандартной записью квадратичной формы
«в=1/8 ufafy
находим коэффи ци енты
L ufj=EI ^M-M-dx. - и
Аналогично потенциал нагрузки имеет коэффициенты
Uq ==- — Р у MIM] dx, о
а энергия деформации основания — коэффициенты
L
Uq = К У MiMj-dx.
о
Коэффициенты потенциальной энергии представляют сумму
2 6. Полный гармонический анализ стержня 69
Кинетическая энергия есть
L
Т = mq^j § MfMy dx, о
и сравнение с выражением Т— Уг T^q^j дает L
TtJ — MfMj dx.
о
Уравнения Лагранжа для малых колебаний имеют вид [37] Л/9/+^7<7/ = 0-
Эти уравнения дают решение задачи о поведении стержня в дискретном представлении.
В качестве примера возьмем для шарнирно опертого стержня разложение в ряд Фурье, полагая A4j=sin(inx/L), где i изменяется от 1 до оо. Это сильно упрощает исследование благодаря условиям ортогональности
L
С . inx . inx , п
I sin-j- sin ip dx — 0
0
L
C inx inx , n
I cos -f- cos'-j-dx — 0
J
0
ДЛЯ I ~f— I,
которые показывают, что все коэффициенты в энергии диагональные. Это позволяет утверждать, что для шарнирно опертого стержня фурье-гармонивд фактически представляют одновременно моды потери устойчивости и собственные формы колебаний: обобщенные координаты q, являются также главными координатами и уравнения движения распадаются на цепочку независимых уравнений.
Поскольку
L L
р . „ inx , р „ inx , 1 ,
\ sin2-pax= \ cos2— dx = -gL, о о
для диагональных коэффициентов энергии имеем
Поэтому угловая частота для i-й моды дается равенством , Vu El (tn/L)4+К — Р (in/L)2
4 Ту т '
70 Гл. 2. Потеря устойчивости конструкций
Рис. 42. Критические нагрузки для стержня на упругом основании в зависимости, от меры жесткости основания.
Величины cof суть собственные частоты колебаний шарнирно опертого упругого стержня с массой на единицу длины т и изгибной жесткостью EI, покоящегося на упругом основании жесткости К и несущего осевую сжимающую нагрузку Р.
Если положить сог равными нулю (или, что эквивалентно, Уц равными нулю), то получатся критические нагрузки потери устойчивости системы
pi __ EI (in/L)i~\- К
~~ (in/L)2
Критические нагрузки для шарнирно опертого стержня, не взаимодействующего с основанием, соответствуют нулевому значению К'.
Р‘ = EI (in/L)*.
Наименьшая из этих критических нагрузок есть
Р1 ——-jj ДЛЯ МОДЫ
Видно, что для стержня на основании с жесткостью К первая гармоника (t=l) не всегда соответствует наименьшей нагрузке потери устойчивости, как показано на рис. 42.
Если положить жесткость основания, и изгибную жесткость равными нулю (К=£/=0) и написать Р——S, то получим формулу для собственной частоты колебаний струны, растягиваемой усилием <$;
2.7. Симметричное и несимметричное прощелкавшие арок 71
Потери устойчивости и закритическое поведение стержня на упругом основании со свободным и заделанным концами рассматривались Эль-Наши [1651, который также разъяснил механизм потери устойчивости кольца [1661.
2.7. Симметричное и несимметричное прощелкивание арок
Рассмотрим теперь несколько иные эксперименты. Если изогнуть прямой упругий стержень и связать его концы сильно растянутой пружиной, то получится лук или пологая арка. Будем считать, что арка в состоянии проходить «сквозь» пружину, и одно возможное практическое устройство, использующее две симметрично расположенные пружины и обладающее этим свойством, показано на рис. 43.
Прежде всего заметим, что при отсутствии вертикальной поперечной нагрузки эта предварительно напряженная механическая система имеет три возможных равновесных состояния. Во-первых, стержень может быть расположен так, что он изогнут либо вверх, либо вниз,— это дает два устойчивых состояния равновесия А и С на рис. 44. Кроме того, осторожно подталкивая стержень, мы можем привести его в равновесное состояние, которое является неустойчивым и в котором стержень прямой, а пружина сильно растянута; при этом стержень сжат нагрузкой, гораздо большей, чем эйлерова критическая нагрузка.
Если теперь приложить мертвую поперечную нагрузку Р, то будут наблюдаться равновесные состояния, которым соответствует петля гистерезиса, изображенная на рис. 44. Здесь два динамических перескока возвращают арку обратно в состояние А после того, как приложенная нагрузка проходит полный замкнутый цикл, включающий отрицательные значения Р.
Перескоки происходят в двух складках или предельных точках D и Е. Отметим, что при прохождении мертвой приложенной нагрузкой замкнутого цикла область траектории неустойчивого равновесия, изображенная штрихами между этими двумя критическими
Рис, 43, Физическая модель арки, концы которой связаны пружиной.
72 Гл. 2. Потеря устойчивости конструкций
состояниями, экспериментально не наблюдается. Эта область может фактически стать устойчивой и наблюдаться при жестком нагружении, в котором значения перемещения задаются при помощи червячной передачи.
В рассмотренном простом явлении траектория деформации арки ADBECF всегда симметрична относительно центральной оси О—О. Если, однако, сделать арку не очень пологой, она будет терять устойчивость по второй гармонике прежде, чем нагрузка достигнет точки максимума D, как изображено на рис. 45. Поэтому возникнет несимметричная деформация, измеряемая величиной Q2, и арка последует по траектории равновесия, показанной на рис. 45 в трех измерениях.
Для нагрузки, при которой непологая арка должна совершить динамический скачок из состояния G в состояние Н, основная траектория с Q2—0 теряет устойчивость в точке ветвления G. Во время скачка арка будет проходить из симметричного состояния G через несимметричные состояния в симметричное состояние И.
Три равновесных состояния арки ори Р=0
А устойчивое В неустойчивое С устойчивое
Рис. 44. Симметричные деформации пологой арки с концами, соединенными пружиной,
Рис. 45. Несимметричные деформации непологой арки с концами, соединенными пружиной. Показаны равновесные траектории в трех измерениях.
Рис. 46. График зависимости нагрузки от перемещений и график чувствительности к несовершенствам критической нагрузки для непологой арки с закрепленными концами.
74 Гл. 2. Потеря устойчивости конструкций
Эта нарушающая симметрию неустойчивость связана с неустойчиво симметричной точкой бифуркации G, которая представляет пример неустойчивой сборки. Нарушение симметрии может, конечно, быть вызвано малым несимметричным возмущением или дефектом, которые определят, будет ли Q2 при движении стержня положительным или отрицательным.
Рассматриваемое неустойчиво симметричное ветвление обладает сильной чувствительностью к несимметричным дефектам, как показано на рис. 49. На этом рисунке Л соответствует нагрузке Р, ut— амплитуде второй гармоники Q2, е — начальному дефекту по моде Q2. Аналогичное поведение арки с заделанными концами (которая может рассматриваться как арка с бесконечно жесткой пружиной) показано на рис. 46, где отклонение нагрузки f моделирует начальный дефект. Справа внизу на рисунке показана чувствительность к несовершенствам на графике зависимости несущей способности Р!Л от величины f. Эксперименты с такими арками, проделанные Роордой 127], были описаны выше (см. рис. 16, иллюстрирующий обсуждение катастрофы сборки).
2.8. Некоторые'изолированные и слившиеся точки ветвления
Три типа точек ветвления, вкратце рассмотренные в гл. 1, более подробно показаны на рис. 47—49, изображающих графики зависимостей нагрузки от перемещений и графики чувствительности к несовершенствам. Впервые они были проанализированы Койтером [17] в 1945 г. и в дальнейшем исследовались в Университетском колледже в Лондоне при помощи теории возмущений [36, 167, 168]; последние работы повторены в Японии [169].
Асимметричная точка бифуркации, показанная на рис. 47, представляет некоторую проекцию складки [33, 39] и возникает в задаче о потере устойчивости ферм [36, 170, 171].
Устойчиво симметричная точка бифуркации, показанная на рис. 48, это устойчивая сборка, встречавшаяся при рассмотрении упругого стержня. Она возникает также в различных задачах о потере устойчивости и закритическом поведении упругих пластин, которые в закритической области гораздо жестче и в связи с этим более удобны для применения в упругих конструкциях по сравнению со значительно более гибкими стержнями.
Неустойчиво симметричная точка бифуркации, показанная на рис. 49, представляет собой неустойчивую Оборку и также уже встречалась при рассмотрении устойчивости непологой арки. Она часто возникает в задачах о потере устойчивости упругих оболочек, очень чувствительных к несовершенствам, в противоположность к более слабой чувствительности, наблюдаемой у ферм и арок. Именно эта слабая чувствительность к несовершенствам позво-
Рис. 47. Каноническая диаграмма асимметричной точки ветвления, показывающая кривые нагрузка — перемещение и кривую чувствительности к несовершенствам.
Рис. 48. Каноническая диаграмма устойчиво симметричной точки ветвления, показывающая кривые нагрузка — перемещение и кривую чувствительности к несовершенствам.
Рис. 49. Каноническая диаграмма неустойчиво симметричной точки ветвления, показывающая кривые нагрузка—перемещения и кривую чувствительности к несовершенствам.
Рис. 50. Шесть обычных точек ветвления теории упругой устойчивости. В верхнем ряду — три изолированные точки: асимметричная, устойчиво симметричная и неустойчиво симметричная. В нижнем ряду — три полусимметричиые точки: моноклинная, гомоклинная и антиклииная.
$.8. Некоторые изолированные и слившиеся точки ветвления 71
лила Роорде проделать свои знаменитые опыты по ветвлению и чувствительности к несовершенствам для этих трех различных точек бифуркации [27].
Переходя к сложному ветвлению, включающему одновременно две или более различные критические нагрузки, сравним три общие полусимметричные двускладчатые точки ветвления с тремя различными точками ветвления на рис. 50. Здесь показаны траектории равновесия в трех измерениях на графике зависимости нагрузки А от двух амплитуд и q2 для мод, по которым происходит потеря устойчивости. Их можно назвать моноклинными (с одной закритической траекторией), гомоклинными (с тремя траекториями, выходящими в одном и том же направлении) и антиклинными (с тремя траекториями, выходящими в противоположных направлениях) [39]; они возникают при выборе различных траекторий на омбилической катастрофе [70]. Варианты двух из этих случаев имеются на рис. 20 гл. 1.
Томпсон и Гаспар [172] предложили модель потери устойчивости, которая точно соответствует этим полусимметричным формам, и связали ее с омбилическим браслетом Зимана [173]. Слияние высшего порядка двух симметричных точек ветвления также было предметом моделирования [87] в связи с оптимизацией конструкций; соответствующие трехмерные траектории равновесия показаны на рис. 51. Видно, что слияние двух устойчиво симметричных точек ветвления порождает неустойчивое сложное поведение, которое приводит к неожиданному появлению чувствительности к несовершенствам. Мы должны здесь отметить, что при идентифи-
Рис. 51. Слияние двух устойчиво симметричных точек ветвления. Видно, как происходит «втягивание» неустойчивых траекторий,
78 Гл. 2. Потеря устойчивости конструкций
кации наиболее грубых типов дефектов при сложной потере устойчивости оказываются полезными теоремы Дьен Хо [174—176].
Изящное исследование Ханта по гиперболической омбилике в задаче о потере устойчивости подкрепленных пластин было отмечено в введении, и связь между теорией устойчивости консервативных конструкций и теорией катастроф в последнее время используется многими авторами [34, 39, 177—182].
Постон и Стюарт в своей фундаментальной монографии по теории катастроф [11] подробно рассмотрели траектории расщепления двукратной критической нагрузки и нашли соответствующие физические расщепляющие параметры; Шэффер и Голубицкий [183] рассмотрели влияние граничных условий на моды в закритическом поведении прямоугольных пластин. В последнее время значительный вклад в исследование общих проблем теории устойчивости в механике твердого тела был сделан Чиллингуортом [184].
Основы теории устойчивости упругих тел могут быть найдены в основополагающей статье Кнопса и Уилкса в Handbuch der Physik [185].
2.9. Практические задачи оценки нагрузок
Мы не будем пытаться дать здесь подробный обзор обширной технической литературы по потере устойчивости и закритическому поведению встречающихся на практике инженерных конструкций, однако приведем некоторые важные ссылки на современную литературу для того, чтобы ориентировать интересующегося читателя.
После классических работ Кармана и Цзяня [186] и Койтера [17] сложная проблема потери устойчивости тонких упругих оболочек в основном исследовалась специалистами по аэрокосмическим проблемам. Такие оболочки очень чувствительны к несовершенствам, что часто связано с кратностью или близостью значений критических нагрузок. На рис. 52 приведен построенный Койтером график, который иллюстрирует чувствительность к несовершенствам при закритическом поведении цилиндрической оболочки. График изображает зависимость отношения несущей нагрузки к критической нагрузке идеальной оболочки от амплитуды геометрических дефектов формы срединной поверхности замкнутой цилиндрической оболочки, подверженной постоянному осевому сжатию.
После стимулирующей работы Ван-дер-Нойта [187] многие современные исследования были нацелены на изучение потери устойчивости подкрепленных пластин и оболочек [188—195]. В связи с инженерными задачами для большого разнообразия подкрепленных и неподкрепленных тонкостенных конструкций были выполнены обширные работы Кролла с соавторами [196—199]. Рядом авторов [200—203] были разработаны численные методы исследования,
2.9. Практические задачи оценки нагрузок 79
Рис. 52. Чувствительность к несовершенствам сжимаемой вдоль оси цилиндриче. ской оболочки по Койтеру.
основанные на общей теории устойчивости; отметим работу [204], в которой дается анализ конструирования ферм. Обзор явлений, связанных с потерей устойчивости при ползучести, был дан Хоффом [205], а влияние ползучести на закритическое поведение конструкций в последнее время изучалось Хейманом [206]. Прекрасный обзор работ по теоретическим вопросам потери устойчивости и за-критическому поведению был сделан Койтером, Будянским и Хатчинсоном [207—210], а современные работы по приложениям теории устойчивости указаны в обзорах [211—214].
Глава
АСТРОФИЗИКА
И ГРАВИТАЦИОННЫЙ КОЛЛАПС
Многие понятия и идеи теории устойчивости исторически возникли при изучении проблем астрофизики звезд и планет. Моделирование последних жидкими или твердыми сплошными средами приводит к краевым задачам, аналогичным по форме другим задачам механики; наличие богатых групп симметрии открывает широкие возможности для поиска аналитических решений.
Эта глава начинается с рассмотрения одной замечательной механической проблемы общей теории относительности Эйнштейна — гравитационного коллапса массивной холодной звезды. Причиной использования в этой задаче теории относительности являются не высокие скорости [215], а большие значения скалярной кривизны пространства-времени [216].
Далее мы рассмотрим термодинамическую неустойчивость горячей сферической звездной системы, которая «страдает» тем, что Линден-Белл назвал гравотермической катастрофой.
В конце мы кратко остановимся на развитии неустойчивости вращающейся жидкой самогравитирующей массы. Эта задача исторически связана с теорией бифуркаций [4, 217] и относится к проблеме образования и эволюции планет.
3.1. Коллапс массивной холодной звезды в общей теории относительности
Чтобы изучить реальный гравитационный коллапс массивной горячей звезды с учетом углового момента количества движения, магнитных полей, турбулентности и ударных волн, Гаррисон, Торн, Вакано и Уилер [218] рассмотрели основные состояния системы из А барионов (нейтронов и протонов), которые дошли до последней стадии термоядерной эволюции и достигли температуры, близкой к абсолютному нулю.
Для Л = 1 основное состояние соответствует атому водорода, для А—4—атому гелия, для А =56 — атому железа. При по-
3.1. Коллапс массивной холодной звезды в теории относительности 81
М
L Мо
1,5
Релятивистская теория с уравнением состояния Гаррисона-Уилера
А
105 10'° 10'5 10го
А »«/«"*
Рис. 53. Решение уравнения равновесия для холодной звездной массы. График зависимости массы-энергии от плотности в центре р0.
вышении значения А до 56- 10е основное состояние получаемого вещества будет соответствовать 10е атомов железа Fe6-6, расположенных в узлах объемноцентрированной кубической решетки. Когда число барионов достигнет значения порядка 10s-6—10s-7, самограви-тация становится столь большой, что электроны достигают релятивистских энергий и преобразуют протоны в нейтроны. Ядерный состав меняется от Fe5-6 до более тяжелых и более богатых нейтронами ядер.
Используя универсальное уравнение состояния, соответствующее холодной материи, можно исследовать сферически симметричные конфигурации равновесия самогравитирующей звездной массы. Необходимое общее релятивистское уравнение гидростатического равновесия получается из условия экстремума «ощущаемой» массы. Устойчивость конфигураций равновесия относительно радиальных сферически симметричных возмущений определяется изучением собственных акустических мод колебаний и исследованием второй вариации массы-энергии при фиксированном числе барионов.
На рис. 53 приводятся результаты исследования равновесия и устойчивости, в которых масса-энергия представлена как функция плотности в центре звезды. Здесь видно, что возможны только две области устойчивости, соответствующие белым карликам и нейтронным звездам. С увеличением числа барионов и массы-энергии каждая из этих областей достигает критического положения равновесия, или катастрофы складки, при которой доминируют гравитационные силы и может начаться коллапс. Ниже этих критиче
82 Гл. 3. Астрофизика и гравитационный коллапс
ских точек коллапс можно предотвратить только посредством потенциального барьера, который стремится к нулю по мере приближения к критическому состоянию. При этом, конечно, все более вероятным становится квантовомеханический туннельный переход через уменьшающийся потенциальный барьер.
Следует отметить, что критические массы имеют порядок массы Солнца и что состояние критического равновесия за пределами точки С представляет собой дальнейшую дестабилизацию звездной системы.
Дальнейший анализ, не связанный с уравнением состояния холодного вещества, показывает [218], что «никакое уравнение состояния, совместимое с причинностью и отсутствием в веществе микроскопического коллапса, не может спасти систему от принятия ею неустойчивой конфигурации относительно макроскопического гравитационного коллапса». Гаррисон и др. рассматривают идеализированную динамику коллапса, во время которого общая масса-энергия, включающая релятивистские эквиваленты потенциальной и кинетической энергий, остается постоянной. Поскольку не существует подходящих устойчивых состояний равновесия, потеря устойчивости при критических состояниях равновесия А и С представляет собой начало коллапса в направлении черной дыры, коллапса, который может быть приведен в действие равномерным гравитационным захватом вещества холодным белым карликом или нейтронной звездой.
Информацию о существовании первых двух максимумов, ограничивающих устойчивые области, можно найти в пионерской работе Л. Д. Ландау [219], опубликованной в 1932 г. Первый максимум, при котором преодолевается электронное давление, был частично исследован в работах Чандрасекхара [220, 221] в 1935 г. При помощи уравнения гидростатического равновесия Ньютона он получил асимптотику при подходе к критическому значению массы. Второй максимум был исследован в работах Оппенгеймера и Волкова [222] в 1939 г. при помощи общего релятивистского уравнения равновесия для идеального нейтронного газа.
Полная кривая, содержащая оба максимума, была впервые получена Гаррисоном и др. [218], при этом использовалось уравнение состояния Гаррисона — Уилера для холодного вещества, в котором при любом данном давлении доминируют ядра своего вида. Система уравнений состояла из уравнения состояния и общего релятивистского уравнения гидростатического равновесия Тол-мена — Оппенгеймера — Волкова и интегрировалась численно, начиная с выбранного значения плотности в центре. Кроме того, в отдельном исследовании было показано, что имеется бесконечное число критических точек (складок), поскольку масса становится затухающей периодической функцией log р0 для высоких значений плотности в центре
3.1. Коллапс массивной холодной звезды в теории относительности 83
Начальный участок траектории равновесия соответствует атомам водорода, затем железным ядрам, скоплениям планетарной массы и, наконец, холодным белым карликам. Первая неустойчивость у складки А, которую можно предсказать, используя только уравнение равновесия Ньютона, соответствует преодолению электронного давления при числе барионов 1,4- 1087. В точке минимума В звездное вещество измельчается и достигает плотности атомного ядра, а увеличение жесткости приводит к образованию устойчивых нейтронных звезд. Во втором максимуме С гравитационные силы в конце концов преодолевают даже эту ядерную жесткость. Следует отметить, что число барионов в точке С ниже, чем в точке А, и равно 0,84-105.7. Поэтому если при идеализированном динамическом коллапсе холодного белого карлика нет изменений в числе барионов (количество вещества остается неизменным), то звезда не может прийти в стационарное состояние как нейтронная звезда.
Следует отметить, что число 1057 атомов на звезду является довольно типичным (предполагается, что в обычной галактике 1011 звезд и 1010 галактик во Вселенной, так что число атомов во Вселенной равно Ю78). Следовательно, нет ничего необычного в том, что звезда, охлаждаясь после исчерпания ядерного топлива, коллапсирует по крайней мере в нейтронную звезду.
Впервые устойчивость последовательности положений равновесия была исследована Мизнером и Запольским [223] в 1964 г. при помощи гармонического анализа, основанного на вариационном принципе Чандрасекхара. Они показали, что устойчивость первой собственной моды колебаний пропадает, когда траектория проходит через второй максимум С, а в зоне Е траектория везде неустойчива по отношению к первой моде. Таким образом, зона ВС устойчива, а устойчивость по первой моде не восстанавливается в точке минимума D, что в свою очередь означает дальнейшую потерю устойчивости.
На самом деле, как мы увидим, каждый последующий максимум и минимум представляют собой дальнейшие потери устойчивости, которые объясняются Гаррисоном и др. следующим образом:
«Для любой заданной большой плотности в центре имеется внутренняя область звезды, которая балансирует на грани коллапса. Акустическая мода собственных колебаний высокого порядка имеет много чередующихся зон с увеличивающейся и уменьшающейся плотностью внутри критической области. Следовательно, она не имеет эффективных связей при наличии значительной степени свободы. Чтобы возбудить эту моду, следует возбудить такое колебание, которое не провоцирует возникновение коллапса. С другой стороны, чтобы возбудить акустическую моду низкого порядка, надо создать увеличение плотности по всей критической области и вызвать коллапс, т. е. неустойчивость мод низкого по
84 Гл. 3. Астрофизика и гравитационный коллапс
рядка. Таким образом, граница между неустойчивыми и устойчивыми модами проходит по состоянию, в котором положение наиболее близких к центру узлов колебаний проникает в критическую сферу, радиус которой меняется как р7/г.»
Полный анализ устойчивости относительно сферически симметричных возмущений был дан Гаррисоном и др. [218]. Они ввели массу-энергию М как определяющий потенциал, связывающий равновесие и устойчивость с числом барионов А (или, что эквивалентно, с массой системы барионов МА, пропорциональной Л), которое играет роль управляющего параметра, и с плотностью в центре р0, которая в данном случае является обобщенной координатой. Была Построена трехмерная картина энергетических переходов в пространстве М—А—р0, которая соответствует катастрофе складки при дМ/дА = У=£0 в критической точке. Оказалось, что при этом условии как потенциал М, так и параметр А принимают экстремальные значения в критической точке траектории равновесия. Авторы установили степенной закон — закон двух третей — в точке возврата, появляющейся при проектировании в простран-
Рис. 54. Проекция решения уравнения равновесия в пространство энергия — управляющий параметр, показывающая точки возврата вскладках; Др5= барионное число х барионная масса. Степень неустойчивости: •, нуль-устойчивость;
•, один-устойчивость; О, два-устойчивость.
3.1. Коллапс массивной холодной звезды в теории относительности 85
Рис. 55. Качественная картина изменения коэффициентов устойчивости в зависимости от плотности в центре.
ство энергия — управляющий параметр [47], что и показано далее на рис. 56.
Начальная масса системы МА равна числу барионов А, умноженному на стандартную массу барионов ps, и представляет собой управляющий параметр. Однако значения этого параметра мало отличаются от значения равновесной массы-энергии М, и по этой причине проекция траектории равновесия на плоскость энергия — управляющий параметр лежит очень близко к линии 45°. Чтобы наблюдать за поведением точек возврата, более удобно построить кривую М—МА (которая является также потенциальной функцией) в зависимости от параметра МА, что сделано на рис. 54. На основании этого графика при рассмотрении уровней энергии, близких к складкам, можно сделать вывод о последовательности смены устойчивых и неустойчивых состояний (см. рис. 55).
В положении А первоначально устойчивая траектория теряет свою устойчивость по отношению к первой моде колебаний при про
86 Гл. 3. Астрофизика и гравитационный коллапс
хождении через нуль первого коэффициента устойчивости Гц. Устойчивость восстанавливается в точке В при прохождении обратно через нуль У1Ъ но в конце концов теряется в точке С, когда этот коэффициент устойчивости снова становится отрицательным. Каждая складка после точки С соответствует потере устойчивости: V22 становится отрицательным в точке D, V33 — отрицательным в точке Е, Г44— отрицательным в точке F.
При внимательном рассмотрении рис. 54 мы, к нашему удивлению, видим, что некоторые из конфигураций равновесия имеют положительные значения М—МА, так что их масса-энергия больше начальной.
Таким образом, существуют решения общего релятивистского уравнения гидростатического равновесия, которые обладают избыточной энергией по отношению к диспергированным атомам FeS6 в состоянии покоя при бесконечном взаимном удалении [218]. Следовательно, эти состояния будут метастабильными по отношению к полной дисперсии атомов. Гаррисон и др., следуя Я. Б. Зельдовичу, описывают, как посредством гипотетической откачки, включающей добавление и удаление барионов, можно достичь этих состояний избыточной энергии, чтобы вызвать непрерывное движение вдоль траектории равновесия.
Кроме того, заметим, что величина М—МА принимает свое самое низкое абсолютное значение в критической точке С, так что в соответствии с вышесказанным имеет место теорема 14 из [218]: «Связанное состояние в критической точке С является наиболее плотным, которое только можно достичь для любой конфигурации равновесия холодного вещества, удерживаемого самогравитацией и подчиняющегося уравнению состояния Гаррисона—Уилера».
Статические расчеты и соответствующий анализ линейных колебаний дают прекрасную иллюстрацию последовательности катастроф складок, а медленный гравитационный захват массы белым карликом или нейтронной звездой дает пример процесса, соответствующего медленному эволюционному изменению управляющего параметра. Однако если коллапс начинается в точках А или С по направлению к состояниям с большей плотностью, то часть принятых допущений оказывается неприемлемой. Барионы могут покидать систему; кроме того, может возникнуть излучение, уносящее часть энергии, поэтому значение А как управляющего параметра теряется. Таким образом, вопросы, связанные с возможным образованием черной дыры путем коллапса звезды, находятся за пределами этого исследования.
Численные значения МА и М на траектории равновесия оказываются очень близкими, и это вызвало некоторое непонимание в прошлом. Принципиальное отличие ясно и существенно, как было подчеркнуто Зиманом в частной переписке с автором: начальная масса МА представляет собой управляющий параметр теории ката-
3.2. Сверхновые взрывы холодных звезд 87
Таблица 1. Таблица, показывающая экстремумы отношения массы-энергии М к начальной массе Мд в критических состояниях равновесия
Управляющий параметр — начальная масса МА
Потенциальная функция- -масса-энергия м
М/МА
Первый максимум А 0, 9999
Первый минимум В 1,0041
Второй максимум С 0, 9701
Второй минимум D 1,0980
Третий максимум Е 1, 0603
МА-= барионное число Лхбарионная масса р,$.
строф, в то время как конечная масса является потенциалом теории катастроф. Однако, когда уравнения равновесия решены и графики зависимости значений равновесия М и МА от обобщенной координаты р0 построены, обнаруживается идентичность этих двух графиков для всех практических задач. Для иллюстрации этого утверждения в табл. 1 приводится отношение М к МА в критических точках, где оно все дальше отходит от единицы, и видно, что графики равновесия трудно отличимы друг от друга [47].
Дальнейшие подробности «танталовой» теоретической проблемы гравитационного коллапса можно найти в известных работах Уилера [224, 225], Вайнберга [226], Хокинга и Эллиса [227], Миз-нера, Торна, Уилера [228] и Риса, Руффини и Уилера [229].
3.2. Сверхновые взрывы холодных звезд
Коллапс растущей нейтронной звезды в черную дыру является все же событием умозрительным. В противоположность этому коллапс массивного белого холодного карлика в нейтронную звезду с образованием сверхновой звезды понимается сравнительно хорошо.
Когда массивная изолированная звезда начинает охлаждаться в конце установившейся термоядерной эволюции, внутренняя температура и давление падают, а сердцевина начинает коллапсировать под действием собственной силы тяжести. Возникающий в результате взрыв создает большие перемещения в наружных слоях звезды, которые затем выбрасываются со скоростью тысяч километров в секунду. При взрыве ядро сильно коллапсирует, уменьшая за доли секунды свои размеры от тысяч до десятков километров. В результате образуется сильно сжатая и чрезвычайно плотная нейтронная звезда. На поверхности такой звезды яблоко будет весить около 30 млн. т, а предмет, упавший со стола, пробьет пол со скоростью 2 млн. миль в 1 час,
88 Гл. 3, Астрофизика и гравитационный коллапс
Любое небольшое вращение звезды до взрыва сильно возрастет после взрыва из-за значительного уменьшения момента инерции, поэтому быстрое ее вращение позволит обнаружить звезду как пульсар, излучающий регулярные радиоимпульсы.
Во время образования сверхновой звезды светимость в течение короткого периода времени будет равна яркости миллиона обычных звезд, и в течение следующих десятилетий расширяющаяся оболочка превращается в светящийся остаток сверхновой, иногда не совсем точно называемый туманностью. Первоначально этот термин применялся для описания всех туманных объектов во Вселенной, включая галактики, звездные скопления и газообразные облака.
Классическим примером сверхновой является Крабовидная туманность в созвездии Тельца, которая со своим центральным вращающимся пульсаром является ключевым объектом в современной астрофизике. Это первый объект, который приводится в каталоге Мессье, поэтому он обозначается Ml.
Сейчас считается, что Крабовидная туманность представляет результат коллапса сверхновой звезды, который наблюдался китайскими астрономами в 1054 г. и был назван ими «гостевой звездой». Она была настолько яркой, что ее можно было видеть днем в течение 23 дней, а ночью в общей сложности в течение 653 дней. Сейчас невооруженным глазом она не видна, но может быть обнаружена при помощи небольшого любительского телескопа или даже бинокля, а с помощью большого телескопа видна ее структура (см. фото 3(a)), представляющая собой переплетение светящихся волокон. Это, несомненно, сверхновая, а не новая звезда. Она является наиболее сильным источником радиоволн на небе, не считая Солнца, и представляет сегодня огромный интерес для радиоастрономов.
Центральная вращающаяся относительно собственной оси нейтронная звезда — пульсар — была обнаружена в Крабовидной туманности 9 ноября 1968 г. Ее период в 33 мс означает, что нейтронная звезда вращается со скоростью 30 об/с — феноменальная скорость для такого массивного объекта. Излучение импульсов нейтронной звездой Крабовидной туманности происходит исключительно регулярно, и их можно наблюдать во всем спектре электромагнитных волн, начиная от 100 МГц, по всему оптическому диапазону частот вплоть до рентгеновских лучей. Что касается скорости вращения других пульсаров, она оказывается несколько меньшей. Масса Крабовидной туманности оценивается как две-три солнечные массы, а масса нейтронной звезды — как одна солнечная масса.
На протяжении ряда лет наблюдалось движение деталей этой туманности по радиусу наружу от центра. Экстраполяция движения назад во времени дает хорошую корреляцию с данными китай-
Фото 3. Остатки сверхновых звезд, (а) Крабовидная туманность, ослепительный взрыв которой был зарегистрирован китайскими астрономами в 1054 г. Центральная вращающаяся нейтронная звезда — пульсар — была открыта в 1968 г. Фотография любезно предоставлена обсерваториями Хейла. (Ь) Остатки сверхновой, наблюдавшейся Тихо Браге. Эта новая радиофотография, сделанная в 1980 г. на волнах длиной 11 см и опубликованная в New Scientist от 25 сентября 1980 г., показывает сколлапсировавшую нейтронную звезду около центра туманности, Воспроизводится с разрешения С, Галла и Г, Пули,
90 Гл. 3. Астрофизика и гравитационный коллапс
ских астрономов. Расширение туманности хорошо показано, например, на комбинированном снимке, выполненном Вирджинией Тримбл, которая наложила позитивный фотоснимок 1950 г. на негативный отпечаток 1964 г. При таком монтаже быстро движущиеся волокна имеют черную переднюю кромку.
Каждый год в галактиках (кроме Млечного пути) наблюдается около 10 сверхновых звезд, а внегалактических сверхновых в каталог занесено около 400. Сверхновые звезды крабовидного типа очень важны для образования тяжелых элементов в галактиках.
Интересно, что, несмотря на изобретение телескопа, ни одной сверхновой не было обнаружено на Млечном пути, хотя статистически такое открытие ожидалось давно. Некоторые значительные сверхновые звезды в нашей галактике были обнаружены в 1006 г., как сообщают восточные и арабские источники, Краб— в 1054 г., звезда, открытая Тихо Браге,— в 1572 г., сверхновая, которую наблюдал Кеплер,— в 1604 г. Недавно в New Scientist от 25 сентября 1980 г. сообщалось о сколлапсировавшем ядре внутри сверхновой Тихо. Новые наблюдения с высокой разрешающей способностью, проведенные при помощи Кембриджского пятикилометрового радиотелескопа Стивом Галлом и Гаем Пули, обнаружили ряд интересных деталей. На фотографии 3(b), полученной в результате их радионаблюдений, можно видеть остатки сверхновой звезды Тихо с минутным, но интенсивным радиоисточником, расположенным недалеко от центра туманности. Предполагается, что это нейтронная звезда, образовавшаяся в результате взрыва сверхновой, хотя никаких пульсаций до сих пор отмечено не было, в отличие от нейтронной звезды в Крабовидной туманности.
3.3. Гравотермическая катастрофа горячих звездных систем
Термодинамическая устойчивость самогравитирующих звездных систем является хорошей иллюстрацией катастрофы складки. В этой проблеме имеется хорошо определенный термодинамический потенциал — энтропия изолированной системы (взятая с обратным знаком), а также физические и геометрические характеристики, такие, как энергия Е или радиус R, которые можно рассматривать как управляющие параметры.
При изучении изотермических сфер, состоящих из одинаковых частиц, начало так называемой гравотермической катастрофы предсказывается при помощи теоремы сопряжения. Эта термодинамическая гравитационная неустойчивость связана с появлением структур типа красного гиганта или ядра-гало1’, и, как показано Лин-
1( Ядро-гало — структура с ярко светящимся центром и слабо излучающей оболочкой.— Прим, перев,
3.3. Гравотермическая катастрофа горячих звездных систем 91 ден-Беллом и Вудом [230], это проливает свет на эволюцию и конечную судьбу галактик, звездных скоплений и, возможно, отдельных звезд.
Линден-Белл и Вуд в своей статье дают тщательный термодинамический анализ равновесия и устойчивости таких ограниченных самогравитирующих изотермических сфер. Они отметили необычность используемой термодинамики, так как самогравитирую-щие системы обладают отрицательной удельной теплоемкостью'. если между двумя элементами системы передается тепло, то более горячий теряет тепло и становится горячее, в то время как более холодный приобретает тепло и становится даже холоднее. Ниже будет показано, что эволюция таких систем может быть далека от равновесного состояния. Работа [230] проливает свет на результаты численных экспериментов, полученных Арсетом [231], а также на задачу Антонова [232]. Кроме того, в ней показано, что применение термодинамики концентрированных систем позволяет объяснить появление в конце эволюции структур типа ядра-гало. В частности, обсуждается вопрос о потере устойчивости равновесной траектории в предельной точке.
Предположим, что рассматриваемая звездная система имеет постоянную массу М и занимает сосуд с объемом V, в котором находится под давлением Р. Если сосуд не деформируется, то объем является заданной величиной, в то время как давление Р — величина определяемая, пассивная. Если сосуд можно деформировать и он находится в среде с заданным мертвым давлением Р, то объем сосуда устанавливается сам, так что управляющим параметром становится уже давление. Здесь имеется прямая аналогия с мертвой и жесткой нагрузками в инженерных конструкциях [47].
Стенка сосуда может состоять как из хорошего термоизолятора, так и из хорошего проводника тепла, связывающего систему с окружающим термостатом с постоянной температурой. Результат классификации образующихся четырех складок суммирован в табл. 2. Для каждого случая указывается соответствующая потенциальная функция. Эта классификация совпадает с классификацией Глансдорффа и Пригожина [233, стр. 46] негравитирующих систем.
Сосредоточивая внимание на случае теплоизолированного жесткого сосуда, Линден-Белл и Вуд берут выражение Больцмана для энтропии и максимизируют его, используя метод множителей Лагранжа для снятия ограничений на М и Е. При этом получается дифференциальное уравнение равновесия. Они повторяют доказательство Антонова, в котором утверждается, что только сферически симметричные состояния могут доставлять локальный максимум энтропии, поэтому следует рассматривать только сферически симметричные решения, и дифференциальное уравнение сводится к хорошо известному выражению для изотермической газовой сферы. Наконец, они устанавливают критерий экстремальности энергии.
92 Гл. 3. Астрофизика и гравитационный коллапс
Таблица 2. Термодинамические потенциалы для равновесия и устойчивости системы с постоянной массой М по Глансдорффу и Пригожину [233] и Линден-Беллу и Вуду [230]
Система Управляющие параметры Потенциальная функция
Адиабатическая Кинематическая связь Энергия Е Объем V Энтропия с противоположным знаком,—S
Мертвое давление Энтропия S Давление Р Энтальпия Н
В термостате Кинематическая связь Температура Т Объем V Свободная энергия Гельмгольца F
Мертвое давление Температура Т Давление Р Свободная энергия Гиббса G
Используя эти формулировки, можно определить момент потери устойчивости изотермических сфер для всех четырех случаев табл. 2. В каждом из них потеря устойчивости связана со складкой, или предельной точкой на равновесной траектории.
На рис. 56 [47] изображена складка для случая жесткого теплоизолированного сосуда вместе с траекторией изменения энтропии. Однако следует отметить, что на чертеже Линден-Белла и Вуда [230, стр. 509, рис. 2] максимальные значения S при фиксированном значении управляющего параметра соответствуют линии уровня минимума в этой точке. Это связано с тем, что вычерчены уровни постоянной энтропии, а не зависимость S от управляющего параметра. Кроме того, Линден-Белл и Вуд схематически изобразили поверхности равновесия и обсудили возможность потери устойчивости в точке ветвления.
Кац [234—236] проводит на этих поверхностях расчетные кривые с тем, чтобы показать, как можно использовать теорему сопряжения для установления переходов устойчивости в последовательности складок вдоль равновесной траектории. Эта теорема детально изучена в [47] для структурно устойчивой складки; следует заметить, что Кац доказал ее с некоторым ослаблением требований непрерывности.
Для предсказания устойчивости Кац рассматривает зависимость обратной температуры Т-1 от энергии Е (рис. 57) и сосредоточивает внимание на случае системы с неизменным объемом. На рис. 57 кривая равновесия параметризована при помощи величины »
Рис. 56. Трехмерные картины катастрофы складки, показывающие потенциальную энергию V как функцию обобщенной координаты Q при разных значениях управляющего параметра Л. На рисунке справа показан наклон точки возврата кривой энергия — управляющий параметр, когда дК/дЛ|с=К'с#0,
Потеря устойчивости —-при заданной Т (потенциал-сеободная энергия Гельмгольца)
Потеря устойчивости^, при заданной Е (потенциал-энтропия С отрицательным знаком)
Т"’
й=32,1
4,5-10’
5,2-103
<5 709
5,4 • 10
Е
Рис. 57. Траектория равновесия звездной системы, параметризированная при помощи параметра h — контрастности плотности. Кривая получена для изотермических сфер, содержащих одинаковые частицы. Масса и объем постоянны. На рисунке отмечены точки, в которых происходит изменение характера устойчивости: О — изменение характера устойчивости теплоизолированной звездной системы; ф изменение характера устойчивости звездной системы в термостате,
94 Гл. 3. Астрофизика и графитационный коллапс
контрастности плотности, т. е. отношения плотности в центре к плотности на границе. Видно, что этот параметр увеличивается при закручивании спирали.
Для высоких температур, при которых Т~г стремится к нулю, звездная система ведет себя как устойчивый бесстолкновительный газ, так что часть кривой справа оказывается устойчивой. Таким образом, имеется известная область устойчивости, которая помогает проследить за развитием потерь устойчивости.
Для термически изолированной звездной системы с постоянным объемом изменения устойчивости происходят в окрестности точек с вертикальной касательной, где управляемый параметр — энергия Е — постоянен. Кац использует теорему сопряжения, чтобы показать, что, как только кривая загибается внутрь, устойчивость утрачивается и в дальнейшем не появляется вновь. Аналогично этому для системы с неизменным объемом, находящейся в термостате, изменения устойчивости происходят в окрестности точек с горизонтальной касательной, где управляемый параметр — температура Т — постоянен. Здесь Кац снова использует теорему сопряжения для доказательства того, что, как только кривая загибается внутрь,-, снова отсутствует рестабилизация.
Мы видим, что при низких значениях Т и Е состояний равновесия не существует. Поэтому в случае изотермической сферы, находящейся внутри нетеплопроводящего сосуда, не существует состояния равновесия энергии Е (<0) и массы М, если радиус сосуда больше, чем 0,335 СМ*Ц—£), где G — гравитационная постоянная.
3.4. Ядро-гало в шаровых звездных скоплениях
Термодинамические исследования свидетельствуют об эволюции системы к структуре с ядром-гало, с сиянием в окрестности ядра системы, обнаруженной у шаровых звездных скоплений. Интересный пример такой структуры показан на фото 4. Термодинамические исследования подтверждаются численным моделированием звездных скоплений, которое обнаруживает некоторые особенности околоядерного нимба. В этой связи следует упомянуть пионерскую работу Арсета, в которой используется «точный» подход задачи N тел. Численный анализ может ближе подвести к реальным условиям звездных скоплений за счет включения дополнительных деталей: потери массы, различия звездных масс, (а не идентичности частиц, как раньше), а также, внешних возмущений, таких, как приливное поле.
Пример подобного моделирования, выполненного Терлевич совместно с Арсетом, изображен на фото 5. На ней тысяча звезд с разными массами запущена с произвольными скоростями внутрь сферы; площадь нарисованных кругов пропорциональна массе изображаемой звезды. Виды (а) и (Ь) показывают скопление в возрасте 463
2,4< fldpo-гало в шаровых звездных скоплениях 95
Фото 4. Шаровое скопление в созвездии Геркулеса (номер М13 по каталогу Мес-сье), представляющее структуру типа ядра-гало, Гравотермический коллапс ядра шарового скопления обсуждается Линден-Беллом и Эгглтоном (Mon. Not. R. Astr. Soc., 1980, 191, р. 483), которые касались возможного образования центральных черных дыр в звездных системах. Фотография публикуется с разрешения обсерваторий Хейла.
млн. лет с двух различных направлений с тем, чтобы проиллюстрировать сжатие, вызванное галактическим приливным полем. Вид (с) показывает то же самое звездное скопление через 703 млн. лет, когда осталось только 200 звезд, Помимо простых внутренних гравитационных взаимодействий моделирование при помощи задачи W тел включает действие галактического приливного поля, потерю массы при образовании в звездных скоплениях сверхновой звезды и межзвездные облака. Эффектный фильм, созданный на основе
96
Гл. 3, Астрофизика и гравитационный коллапо
Фоте S. Три кадра численной модели звездного скопления и фотография реального скопления: (а) и (Ь) показывают скопления в возрасте 463 млн. лет с двух различных направлений для иллюстрации галактического приливного сжатия; (с) показывает это же звездное скопление через 703 млн. лет, когда исчезло большое количество звезд. Эти картинки были получены на основе динамического моделирования галактического звездного скопления, в котором орбиты индивидуальных звезд вычисляются при помощи прямого метода N тел. Расчеты были выполнены г-жой Э. Терлевич в Кембриджском институте астрономии и были любезно предоставлены С. Арсетом. Аналогичные модели N тел Арсета (Astrophys. and Space Sci., 1971, 13, p. 324) показывают типичную эволюцию высокоэнергетической центральной двойной звезды. Фотография реальной звезды (d) показывает открытое или галактическое звездное скопление М67. Публикуется с разрешения г-жи Э. Терлевич.
этой модели, показывает звезды, которые двигаются возвратно-поступательно в звездном скоплении, как молекулы в горячем газе (время отсчитывается миллионами лет).
3.5. Эволюция вращающихся планетарных масс 97
На фото 5(d) показано для сравнения реальное открытое звездное скопление. Для моделирования шарового звездного скопления необходимо большое количество звезд. Одной из важных особенностей моделирования может быть появление центральных двойных звезд, с которыми связана большая часть общей энергии.
3.5. Эволюция вращающихся планетарных масс
Относительное равновесие и устойчивость вращающейся массы гомогенной самогравитирующей жидкости является классической проблемой в астрофизике, корни которой восходят к Пуанкаре [4—6] и даже к Ньютону. Эта проблема широко обсуждалась в трудах Дарвина [237], Джинса [238, 239], Литтлтона [240], Леду [241] и Чандрасекхара [242]. Здесь мы рассмотрим систему в условиях свободного вращения, наш анализ может относиться и к простой планетарной массе.
Поскольку главным вопросом является относительное равновесие и устойчивость, логично изучать вращающиеся объекты во вращающейся с угловой скоростью IF системе координат, жестко связанной с объектом. В условиях свободного вращения мы можем, например, выбрать систему отсчета, такую, что угловой момент количества движения относительно этой системы остается равным нулю; W будет меняться вместе с изменением момента инерций /.
Для определенности, следуя Кацу [235], остановимся сначала на эллипсоидальных состояниях относительного равновесия вращающейся жидкой массы. Предположим, что плотность эллипсоида р равномерна по объему, а полуоси а, b и с вращаются вокруг оси с с угловой скоростью IF. Масса М=4/злаЬср и угловой момент L— — 4bM(a2+b2)W~lW сохраняются. В сопутствующих координатах, направленных вдоль а, b и с, энергия системы, согласно Леду, дается формулой
V = у J рф dv L2l21, где ф — потенциал притяжения.
Условия элементарной теории катастроф выполнены, так как конфигурации равновесия представляют стационарные значения V и вековая устойчивость имеет место, если стационарное значение V является локальным минимумом. Здесь под вековой устойчивостью подразумевается устойчивость при наличии полной внутренней диссипации, действие которой заключается в аннулировании любой гироскопической стабилизации, вызываемой силой Кориолиса. Можно сослаться на теорему Циглера [20]: «Диссипативные силы, приложенные к системам, отличным от негироскопических консервативных систем, могут оказывать дестабилизирующий эффект. Если они прикладываются к гироскопической консервативной сис
4 № 528
98 Гл. 3. Астрофизика и гравитационный коллапо
теме и если диссипация полная, они аннулируют стабилизирующий эффект гироскопических сил».
Ограничивая рассмотрение эллипсоидами, можно считать а, Ь, с и W переменными, на которые наложены два ограничения: М и L постоянны. Плотность р тогда можно рассматривать как единственный управляющий параметр. В приложении к физике можно, например, считать, что речь идет об изолированной платерной массе, плотность которой медленно увеличивается вследствие охлаждения.
От ограничений можно освободиться путем уменьшения числа координат до двух. Запишем их в виде
д, = (а/с)8, <72 = (Ь/с)2.
Кроме того, можно ввести комбинированный управляющий параметр
А —25 /±5£.У/3 £2
1 \ЗМ J 3GM3’
где G — гравитационная постоянная. Тогда энергия V принимает
вид
V = — GM2?—У/3
V 10 \ ЗМ)
GP
о
+ М (91 + £) (9г + ^)}~Х/2 dX-f-
+ Л-^-1/3 91 +?г
Уравнения равновесия
dV/dq^dV/dq^O
имеют два множества решений — сфероиды Маклорена с alc—blc и эллипсоиды Якоби с а=^Ь. Последние ответвляются от сфероидов Маклорена с а!с=Ыс в точке а/с=Ь/с=Г,716, Л=0,769. Для этих решений Кац при помощи метода Томпсона [47] доказал устойчивость эллипсоидов Якоби везде и сфероидов Маклорена для Л, меньших 0,769.
Более сложные расчеты, допускающие отклонения от эллипсоидальных состояний, показывают, что со временем эллипсоиды Якоби становятся неустойчивыми относительно грушевидных изменений формы, и соответствующие вторичные точки ветвления показаны на рис. 58. Здесь параметр момента количества движения является функцией двух параметров, характеризующих деформацию: (а—Ь)/с.и р. Через р обозначено смещение в третьей неэллипсоидальной моде колебаний, имеющей грушевидную форму. Параметр р для эллипсоидов Маклорена и Якоби равен нулю. График, приведенный на рис. 58, был составлен на основе численных результатов, полученных Литтлтоном для деформаций эллипсоидальных мод колебаний, однако зависимость от р дана схематично, так как
3.5. Эволюция вращающихся планетарных масс 99
расчеты на этой стадии становятся настолько сложными, что допускают лишь качественные прогйозы.
Когда момент количества движения невелик, имеется лишь одна траектория равновесия, лежащая на оси а=Ь, р=0. Это сплющенные сфероиды Маклорена. Видно, что сплющенные сфероиды суть состояния равновесия вплоть до бесконечного значения момента количества движения, которому соответствует бесконечно тонкий неограниченный диск. Однако эта траектория равновесия становится неустойчивой в устойчиво симметричной точке бифуркации В, пример устойчивой сборки, где она пересекает траекторию равновесия, соответствующую эллипсоидам Якоби с а^=Ь.
Рис. 58. Неустойчивость простой планеты. На этом графике показано развитие потери устойчивости и симметрии самогравитирующей вращающейся жидкой массы. Аналогичные неустойчивости могут играть основную роль в эволюции планет.
4*
100 Гл. 3. Астрофизика и гравитационный коллапс
Эта траектория также продолжается до бесконечно больших значений углового момента, когда жидкая масса имеет форму бесконечно длинной линии с а=оо и Ь=с=О. Однако траектория равновесия Якоби теряет устойчивость в состоянии С, где имеется вторичная неустойчиво симметричная бифуркация, или неустойчивая сборка, в которой она пересекается с неустойчивой траекторией равновесия, соответствующей планетам грушевидной формы.
Возможная связь этих неустойчивостей с эволюцией планет и происхождением спутников обсуждается подробно в цитированной литературе.
Глава
БИФУРКАЦИОННАЯ НЕУСТОЙЧИВОСТЬ АТОМНОЙ РЕШЕТКИ
Если идеальный кристалл растягивать вдоль оси симметрии решетки, то можно ожидать, что кристалл будет удлиняться в направлении приложенной силы, и это приведет в конце концов к разрушению. Однако при некоторых условиях может неожиданно возникнуть деформация сдвига, которая нарушает симметрию и приводит к преждевременному сдвиговому разрушению, напоминающему образование полос сдвига [243].
Ниже будет изложено недавнее исследование этого явления, принадлежащее Томпсону и Шорроку [82]. Оно дает повод обсудить много фундаментальных идей теории ветвления в очень интересной и весьма специфичной области.
4.1. Нарушение симметрии
Рассмотрим слой плотноупакованных атомов, показанный на рис. 59. Пусть этот слой растягивается в одном направлении уси-лиём оц, и пусть при растяжении напряжение сдвига о12 отсутствует. Тогда можно было бы ожидать, что кристалл удлинится в направлении усилия ои и приобретет деформацию еи. Это будет происходить до тех пор, пока кривая напряжение — деформация , не достигнет максимума — состояния, при котором преодолеваются силы атомного притяжения. Соответствующая основная траектория равновесия в плоскости сгп, еи показана на верхней диаграмме рис. 59.
Основная симметричная траектория равновесия идеального кристалла может стать неустойчивой в точке ветвления А, что показано при помощи линейного анализа собственных значений Макмилланом и Келли [244]. Исследование в рамках нелинейной теории [82] показало, что точка ветвления представляет неустойчиво симметричную точку ветвления и связана с катастрофой сборки. Вторичная траектория неустойчивого равновесия с ненулевыми деформациями сдвига е12 выходит из точки ветвления, как показано
102 Гл. 4. Бифуркационная неустойчивость атомной решетки
Рис. 59. На верхнем рисунке показаны траектории равновесия атомной решетки при и22=0, на нижнем левом рисунке — проекции этих траекторий на плоскость _(оц, Cis)- Здесь видна уже хорошо нам знакомая неустойчиво симметричная точка бифуркации, или катастрофа сборки. Устойчивые участки траекторий равновесия изображены сплошными линиями, а неустойчивые — штрихами. На нижнем правом рисунке построена соответствующая граница устойчивости, или граница катастрофы, которая представляет кривую разрушающих напряжений с предсказываемой теорией точкой возврата с законом двух третей.
на рисунке. Нагрузка, при которой происходит бифуркация, является разрушающей нагрузкой для идеального кристалла. При этом критическом значении нагрузки даже бесконечно малые возмущения будут инициировать быстрое разрушение механически нагруженного кристалла.
Ясно, что небольшие сдвиговые напряжения Oi2 будут действовать так же, как начальные несовершенства. При этом вместо основной траектории равновесия возникнут близкие траектории, как
4.1. Нарушение симметрии 103
Рис. 60. Этот рисунок показывает, как изменяется картина, представленная на рис. 59, если подвергнуть кристалл боковому сжатию с напряжением о22=а22> которое сдвигает точку бифуркации в точку максимума кривой деформация — напряжение. Кривая разрушающих напряжений состоит из двух лучей.
показано на рисунке светлыми линиями. Проекция в плоскость (°ii, е12) изображена слева внизу на рис. 59. Видно, что имеется неустойчивая сборка, причем чувствительность к несовершенствам описывается законом двух третей и показана на диаграмме внизу справа. Здесь сборка в двумерном пространстве управлений (olif о12) порождает кривую разрушающих напряжений. Конечно, следует ожидать аналогичной сильной чувствительности к геометрическим несовершенствам, которые нарушают симметрию.
Если ввести теперь дополнительно растягивающее усилие о22 (см. рис. 24 гл. 1), то получится задача с тремя управляющими напряжениями. Положительное значение <т22 приводит к подавлению бифуркационной неустойчивости и сдвигает точку ветвления А
104 Гл. 4. Бифуркационная неустойчивость атомной решетки
Рис. 61. Граница устойчивости в пространстве разрушающих напряжений, соответствующая границе катастрофы для катастрофы гиперболической омбилики.
ближе к состоянию максимального растяжения. Можно вычислить критическое значение of2, для которого точка ветвления А совпадает с точкой максимума (рис. 60). Было показано [82], что при условии o22=of2 исходный закон двух третей в двумерном пространстве управлений оц и Oi2 переходит в кривую разрушения, состоящую из двух лучей, как показано на рис. 60. Из рис. 20 гл. 1 видно, что точка ветвления в верхней точке рельефа потенциальной функции неустойчива и состоит из слившихся точек ветвления. Она представляет пример катастрофы гиперболической омбилики [83] и позволяет сделать набросок полной трехмерной поверхности разрушения в пространстве переменных сг12 и о22, приведенный на рис. 61. Его можно сравнить со сделанной из картона моделью границы устойчивости полной гиперболической омбилики на фото бис гиперболической омбилической каустикой на фото 7.
Здесь видно, что на гребне Oi2—0 при значении напряжения точка возврата вырождается в две прямые линии, а затем переходит в кривую, имеющую параболическую форму. Гребень изгибается между точками Л и С, в которых он соответствует разрушению в точке ветвления. Между точками С и В гребень приблизительно прямой и параллелен оси сг22; на этом участке разрушение связано просто с достижением максимума основной траектории равновесия, а бифуркация движется вслед за максимумом и поэтому
4.1. Нарушение симметрии 105
Фото 6. Фотография модели границы устойчивости для катастрофы гиперболической омбилики в трехмерном пространстве управляющих параметров. Модель изготовлена из картона. Ясно видна линия пересечения двух отдельных листов, причем у каждого листа на ней происходит переход от сборки к гладкой границе,
не инициирует более разрушения кристаллов. Поверхность разрушения имеет форму, характерную для границы устойчивости катастрофы гиперболической омбилики, которую часто сравнивают с волной разрушения.
Этот конкретный привлекательный пример катастрофы гиперболической омбилики дополняет пример Ханта потери устойчивости подкрепленной пластины (см. гл. 1), который является другой иллюстрацией этой катастрофы в нелинейной теории упругости.
Макмиллан и Келли показали, что бифуркация в точке А может быть на 20% меньше, чем в основном максимуме. Часто, однако, она располагается гораздо ближе, и необходимо рассмотреть случай, когда бифуркация в точке А близка, но не точно совпадает с основным максимумом. Здесь теория изолированных сборок 136], хотя и справедлива для точек, близких к А, может давать неверные результаты. В этом случае можно сохранить простоту и компактность анализа при помощи предположения, что критические точки полностью совпадают, и дальше в этой главе будет приведен пример подобной процедуры.
106 Гл. 4. Бифуркационная неустойчивость атомной решетки
Фото 7. Часть световой каустики, возникшей при рефракции лазерного луча на сильно неоднородном стедле «для ванных комнат». Виутренияя кривая с заострением и гладкая внешняя кривая образуют сечение катастрофы гиперболической омбилики. В силу волновой природы света каустика украшена характерной картиной интерференционных полос. Воспроизводится с разрешения Берри (М. V. Berry).
4.2. Квантовомеханическая и ньютоновская постановки
Прежде чем приступить к исследованию устойчивости кристалла, необходимо сделать несколько замечаний о предположениях, в рамках которых оно будет рассматриваться. Наиболее общая и удовлетворительная точка зрения для изучения механических свойств многих твердых тел основана на представлении о стационарных состояниях квантовомеханической системы. При этом для того, чтобы получить уравнения Шредингера только для одних атомных ядер, электроны можно исключить из рассмотрения при помощи
4.2. Квантовомеханическая и ньютоновская постановки 107
адиабатической аппроксимации Борна — Оппенгеймера [245]. Если мы хотим изучить влияние внешних консервативных сил на механическое поведение кристалла, то следует просто добавить потенциал сил к эффективной энергии межатомных взаимодействий.
Решения квантовомеханической задачи теснейшим образом связаны с решениями соответствующей задачи в рамках ньютоновской постановки. Например, в гармоническом приближении квантовомеханические уровни энергии связаны весьма просто с частотами классических колебаний, так что для многих ньютоновских результатов можно легко указать квантовомеханический аналог, как это видно, например, в работе Дина [246]. В частности, ясно, что стационарные квантовомеханические состояния могут наблюдаться только в окрестности устойчивого ньютоновского состояния равновесия. Поэтому первый логический шаг для квантовомеханического решения задачи заключается в проведении статического анализа устойчивости в рамках ньютоновской механики, и действительно, этот шаг часто дает всю необходимую информацию для описания макроскопических механических свойств твердого тела. В качестве типичной работы этого направления можно упомянуть работу Макмиллана и Келли, в которой для описания взаимодействия атомов в рамках ньютоновского приближения используются полуэмпири-ческие потенциалы типа потенциалов Леннард-Джонса и Борна — Майера.
Необходимый аппарат для исследования кристаллической решетки в рамках ньютоновской механики — это общая теория упругой устойчивости дискретных консервативных систем [36]. В соответствии с этим будем считать эффективный потенциал V однозначной функцией п обобщенных координат Qlt определяющих допустимые положения атомов, и параметра нагрузки А, задающего, например, амплитуду внешней нагрузки. Задача заключается в нахождении положений равновесия консервативной механической системы с конечным числом степеней свободы, которая определяется заданием общей потенциальной энергии системы V(Qf, А), и в исследовании устойчивости этих положений равновесия. В работе [36] был развит метод возмущений для изучения нелинейного поведения системы в окрестности любой точки ветвления.
Если идеальная кристаллическая решетка, к которой приложены внешние силы, имеет две существенно различные критические точки, для их исследования можно применить результаты для неустойчиво симметричной точки ветвления, полученные в явном виде в замкнутой форме; качественно мы уже обрисовали их структуры в разд. 4.1. Однако в кристаллах, как уже отмечалось, критические точки, как правило, довольно близки (и могут быть вообще сделаны совпадающими за счет введения усилий во втором направлении), и, как было объяснено, в этом случае следует привлечь об: щую теорию неустойчивости для слившихся точек ветвления
108 Гл.4. Бифуркационная неустойчивость атомной решетки
Такая теория не была развита в предыдущей монографии автора, и, поскольку мы собираемся применить ее к исследованию разрушения кристалла, дадим сейчас краткий ее набросок.
4.3. Теория возмущений в верхушечной точке ветвления
Излагаемая дальше теория имеет в основном аппаратный характер, и по этой причине читатель, если он этого пожелает, может пропустить весь разд. 4.3 — необходимые качественные результаты уже были описаны. При этом у читателя, не прочитавшего этот раздел, в дальнейшем не должно возникнуть трудностей.
Рассмотрим консервативную систему с конечным числом степеней свободы с энергией V(Qi, Л). Для наших целей достаточно предположить, что имеются только две (активные) координаты Qi и Qa. В предположении, что функция V — четная функция Qi, будем считать, что уравнения равновесия У>=0 определяют траектории равновесия, вид которых изображен на рис. 62. Чтобы исследовать точку ветвления в верхушке траектории равновесия, введем локаль-
Рис. 62. Ветвление в вершине основной траектории напряжение — деформация кристалла.
4.3. Теория возмещений в верхушечной точке ветвления 109
ные координаты
Uf=Qi, и2~— Q2 Qf. (1)
Энергия в терминах локальных координат запишется в форме
D(ut, Л) s= V(ut, Q? + «2, Л). (2)
Чтобы найти локальную форму второй траектории равновесия, запишем ее в параметрической форме
ы2 = ы2 («1), Л — Л («J. (3)
Подстановка этих соотношений в уравнения равновесия £)г=0 приводит к тождествам
01 = {«ъ u2(«i), Л («!>} = О, 02{ыь u2(ut), A(«j)} = 0. (4)
Для определения производных функций ыг(«1) и A(«i) в соответствии с общей схемой метода возмущений продифференцируем эти тождества повторно по иг.
D1J4-Di2«?’4-DlA‘« = 0, (5)
£>214-ад”4-О2Л«’ = 0, (6)
(Ош + Dii2up + РцЛ<«) -J- (D121 + П122м<1) + %Л«’) up +
+d^p+(£>,,+ D\2up 4- d;a‘«) л‘» -I- о;л’2' = о, (7) (D21I+DMx>+d2ja‘u)+(D221+D222up 4- D2'2A‘«) up 4-
4- D22up 4- (%4- D22up 4- р;л‘«) A‘« 4- ^A‘2) = 0 (8)
и т. д. Здесь верхним индексом в скобках обозначается порядок производной по «1, а штрихом — дифференцирование по Л.
Преобразуем несколько эти уравнения, замечая, что производные вычисляются в точке ветвления С и что в силу сделанного выше предположения о свойствах симметрии энергии имеют место равенства
Df2 = D;c = 0, Df22 = £>;c = £>£=О, Dfu = 0. (9)
В частности, из равенств (9) видно, что матрица Dfi диагональна, и, следовательно, координаты щ являются главными координатами. Поскольку в критическом состоянии равновесия, как мы предположили, сливаются две точки ветвления, два коэффициента устойчивости' обращаются в нуль:
рс=о. (10)
При нулевых значениях указанных коэффициентов равенство (5) не содержит новой информации. В случае предельной точки в плоскости (Л, Qz), согласно общей теории, имеем [36]
j%c=£0. (И)
110 Гл. 4. Бифуркационная неустойчивость атомной решетки
При этом предположении равенство (6) позволяет найти первую представляющую интерес производную
Л<1,с = 0. (12)
В рассматриваемом случае
(13) поэтому из равенства (7) находим вторую представляющую интерес производную
«?’с = 0, (14)
Наконец, из равенства (8) следует формула
£>2114-£>;Л‘«|с = 0, (15)
так что справедливо соотношение
л‘^=-(пй2/п;)|с, (16)
которое позволяет определить начальную кривизну второй траектории равновесия в точке ветвления, соответствующей первому ненулевому чйену. разложения функции Л (ut) в ряд Тейлора в окрестности ТОЧКИ Ui— 0.
Столь далеко мы сумели продвинуться лишь потому, что предположили, что система идеальна и не содержит несовершенств. Обсудим теперь, какие изменения внесет в наше исследование учет несовершенств. Будем считать, что соответствующая неидеальная система имеет энергию D (uit Л, е), где е — параметр несовершенства, обращение которого в нуль соответствует переходу к рассмотренной выше идеальной системе. Равновесные траектории такой системы с е=/=0 изображены на рис. 63 светлыми линиями. Прежде всего нас будут интересовать максимумы этих траекторий. Для значений параметров в точке максимума будем использовать следую
Л
Рис, 63. Ветвление в вершине для идеальной и неидеальной систем.
4.3. Теория возмущений в верхушечной точке ветвления 111
щие обозначения:
Л = ЛЛ1, ut = u^, е = ем. (17)
Попытаемся построить функцию Л^е41) вдоль траектории максимумов (ММ на рис. 63). Чтобы это сделать, запишем уравнение траектории максимумов в параметрической форме
Л = ЛЛ1(м(и), «г = «г1 (и?1), е = еЛ1(п,Л1). (18)
Максимумы, во-первых, являются положениями равновесия системы и, во-вторых, критическими положениями равновесия, поэтому ясно, что они должны удовлетворять системе уравнений Ог=0, A=|Dw|=0, где А —определитель, составленный из производных Da функций Dt. Эту систему уравнений можно записать в виде
Ам(и?), ем(и1м)}^0, (19)
D2 {u^. Лм(пЛ, в" («")}= °, (20)
А{щм, «2м(«П, Лм(и"), e«(U^^DuD22-Dt2^0. (21)
Повторное дифференцирование этих равенств по и™ и вычисление производных в критической точке идеальной системы
щЛ’=0, Лм = Лс, ем = 0 (22)
дает после простых вычислений значения требуемых производных:
ем tn с = 0> (23)
Лма>с = о> (24)
ем<а>с = :р2/£и2\/£^у/г1с> (25)
дм (2) с = Iе (26)
D2 I
При выводе этих равенств предполагалось, что
= (27)
где точкой над буквой обозначается дифференцирование по е. Поучительно отметить, что
дм <2>с==2Л'г’с. (28)
Если теперь рассмотреть разложение в ряд Тейлора функций Лм(и^) и еЛ1(п(и) в окрестности точки w^=0 и оставить только первые существенные члены, то придем к выражениям
Лм = Лс 4- 1/8 Ам ,2) с (п?1)2, (29)
8Л1 = 1/28Л1<2)С(ЩЛ1)2, (30)
где первые ненулевые производные Л7*1*2’0 и eMla)C были определены выше при помощи метода возмущений. Исключение «f1 из равенств
112 Гл. 4. Бифуркационная неустойчивость атомной решетки
(29) и (30) приводит к искомой локальной зависимости Л7*1 от ем, которая характеризует чувствительность к несовершенствам:
(31)
\Г>2 / \Utl2/
Особенности составной критической точки теперь ясны и показаны на рис. 60 и 63. Основное отличие от изолированной критической точки заключается в том, что функция ЛЛ1(е7И), характеризующая чувствительность к несовершенствам, меняется не так быстро, поскольку закон двух третей в точке возврата локально переходит в линейную зависимость.
В теории кристаллов обычно встречается точка ветвления, которая является строго изолированной, но тем не менее очень близкой к максимуму кривой деформация — напряжение. В этом случае общий результат о законе двух третей применим в очень малой окрестности точки ветвления, и в ней действительно имеется точка возврата. Однако, как только мы отойдем на некоторое расстояние от этих двух критических точек, будет казаться, что они совпадают, и можно ожидать, что будет более справедлива линейная зависимость.
В дальнейшем мы действительно убедимся, что, хотя критические точки являются строго изолированными, приближенное рассмотрение, в котором они считаются совпадающими, дает очень хорошее согласие с численным решением для весьма широкой области значений параметров, представляющей практический интерес.
Можно, наконец, отметить, что применение теории слившихся точек ветвления гораздо проще, чем теории изолированных точек ветвления, поскольку в нее входят производные от энергии меньшего порядка. Например, в теории слившихся точек ветвления требуется знать частные производные третьего порядка и в то время как в теории изолированных точек ветвления — производную четвертого порядка D\1U.
4.4. Чувствительность к несовершенствам при разрушении кристалла
Если представить кристалл как систему N плотноупакованных идентичных атомов, то получится система с 3N степенями свободы, соответствующими координатам Xt атомов. Рассмотрим сначала более простую систему — плотноупакованный кристаллический -слой атомов, который растягивается усилием ои в направлении, перпендикулярном плотной упаковке. Считается, что в кристалле могут реализоваться только плоские кинематически допустимые поля перемещений с однородными деформациями и только двумя степенями свободы. При этом точка бифуркации располагается на основной траектории равновесия гораздо ниже точки максимума.
4.5. Потенциал Леннард-Джонса ИЗ
Собственный вектор, соответствующий деформации сдвига е12, и малое напряжение сдвига о12 вводятся в качестве малых «несовершенств». Затем находится равновесие системы в рамках нелинейной постановки и исследуется задача об устойчивости, во-первых, на основе численного решения и, во-вторых, с использованием общей теории ветвления в верхушечной точке ветвления. Прекрасное совпадение обоих решений подтверждает значение использованного нами упрощенного анализа.
В дальнейшем мы укажем, как плоское поле перемещений одного плотноупакованного слоя атомов, связанное с однородными деформациями, может быть использовано для построения допустимого поля перемещений гранецентрированной кубической решетки с однородными деформациями или допустимого поля перемещений плотноупакованного гексагонального кристалла с неоднородными деформациями.
4.5. Потенциал Леннард-Джонса для межатомных взаимодействий
Примем, что потенциальная энергия взаимодействия между любыми двумя атомами есть некоторая функция v (s), где s — расстояние между центрами; v (s) — сферически симметричный потенциал взаимодействия двух тел, для которого сила взаимодействия направлена по прямой, соединяющей их центры. В дальнейшем ограничимся рассмотрением взаимодействия только ближайших соседей. Поскольку суммарная сила, действующая на каждый атом, равна нулю для ненагруженного кристалла, кристалл можно рассматривать как плотноупакованную решетку сфер диаметром d, где
<to/ds|s==d = 0. (32)
В частности, в качестве v можно взять потенциал Леннард-Джонса, который применялся Макмилланом и Келли [244] для описания взаимодействия атомов аргона:
n(s) = X(Bs-12—s"6). (33)
Здесь А и В — некоторые физические постоянные. Из равенства (32) находится связь между Bud:
B = ^d*. (34)
Полагая s=yd, можно написать
v (?) = Ad~* СМ*-12-?-6). (35)
Потенциал v изображен на рис. 64. Максимальная сила взаимодействия Т дается равенством
Т = J ) (1 —у’6), (36)
ds \у7^7/ v 1
0,2
pdE A
Td7„ 10
6A 8
0,5 —1—
-0,2
-0,4
Рис. 64. Потенциал межатомного взаимодействия И и сила притяжения Т соседних атомов.
Рис. 65. Потенциал взаимодействия двух атомов в плоскости, построенной при помощи компьютера,
4.6. Плотноупакованный слой атомов 115
которое (см. рис. 64) достигает максимума
когда у принимает значение
у = (13/7)1/в. (38)
Производные от функции v по у, которые потребуются в дальнейшем, записываются в форме
t»v = 64t/-e(— у-13+у-’), uVv = 64d-e(13y-M—7у-«) (39) и т. д.
На рис. 65 приведен график потенциала в плоском случае, построенного при помощи компьютера Ричардом Томпсоном; потенциал инвариантен относительно вращений.
4.6. Плотноупакованный слой атомов
Отнесем плотноупакованный кристалл к декартовой системе координат 0xit ориентированной так, что оси Ох^ и 0х3 лежат в плоскости плотноупакованных атомов, при этом ось 0хг направлена вдоль плотноупакованной цепочки атомов, как показано ца рис. 66. Начало координат лежит посредине между центрами атомов.
Рассмотрим теперь поле перемещений с компонентами ut(Xj), так что атом с начальными координатами хг после деформации имеет координаты
Х^х.Ч-нДХу). (40)
Здесь, как и раньше, используются обычные соглашения относительно индексов. Если ограничиться однородными деформациями
Рис. 66. Плотноупакованный слой атомов в ненапряженном состоянии; р= = Кз/2, 6=0, Р=0.
116 Гл. 4. Бифуркационная неустойчивость атомной решетки
кристалла, то можно написать
= (41)
где Су — некоторые постоянные, при этом
Xf^Xi + CijX;-. (42)
В качестве меры конечных деформаций можно взять те же величины, которые использовались в работе Макмиллана и Келли 1244]:
i ~ Кч’ j "К cj i 4" (43)
однако, как было отмечено в этой работе, для вычислений удобно в качестве мер деформаций оставить постоянные с^.
В связи с тем что мы считаем деформацию однородной, кристалл имеет только девять степеней свободы, которые соответствуют постоянным сц. Из этих девяти степеней свободы три связаны с движением кристалла как твердого тела и будут исключены при помощи некоторых ограничений.
Мы собираемся растягивать кристалл вдоль оси хг усилием о11т при этом будем считать, что атомы в плоскости х3= 0 при деформации остаются в этой плоскости, так что имеют место равенства £з1~с32 = 0. (44)
Кроме того, будем считать, что атомы, лежащие на оси хи также остаются при деформации на этой оси, т. е.
с21- = 0. (45)
Таким образом, осталось шесть степеней свободы, соответствующих шести ненулевым постоянным ci}.
Рассмотрим плоскость ч плотноупакованных атомов х3=0. Приложенное к ней напряжение аи стремится раздвинуть плотноупа-
Рис. 67. Плотноупакованный слой атомов в основном деформированном состоянии; р—1,0, 0=0, Р=0,40.
4.7. Четырехатомная ячейка 117
Рис. 68. Плотноупакованный слой атомов в закритическом состоянии; р=1,0 6=9°, Р=0,325.
кованные цепочки атомов, как показано на рис. 67. Кажется правдоподобным, что при достаточно большом значении удлинения elt эти цепочки становятся неустойчивыми по отношению к вращению, так что может возникнуть сдвиговое напряжение, как показано на рис. 68.
Для исследования этой возможности сначала для одного слоя атомов в нашем распоряжении имеются три ненулевых коэффициента Си, Cis и с22, однако мы будем считать допустимыми деформации плоскости только с двумя степенями свободы, предполагая (возможно, это предположение и не соответствует действительности), <что плотноупакованные цепочки атомов при вращении не изменяют своей длины. При этом деформацию удобно описывать расстоянием между цепочками, которое мы обозначим через pd, и углом вращения цепочек 6, как показано на рис. 68. Коэффициенты Сц, С12 и с22 записываются в терминах обобщенных координат 0 и р в виде
cu = (2/|/"3) р — 1, Cj2 = sin6, c22=cos6—1, (46>
причем, как уже отмечалось, c2i=0, если атомные цепочки не поворачиваются.
Слой растягивается приложенным первоначально усилием ои, и в качестве «несовершенства» введем дополнительно малое сдвиговое усилие О12.
4.7. Четырехатомная ячейка
Легко видеть, что при выполнении наших предположений общая потенциальная энергия бесконечного слоя пропорциональна энергии элементарной ячейки, состоящей из четырех атомов (рис. 69),
118 Гл. 4. Бифуркационная неустойчивость атомной решетки
Итак, важно изучить подробно поведение элементарной ячейки, так как оно полностью определяет поведение всей системы.
При сделанном выше предположении о взаимодействии только ближайших соседей ненагруженная ячейка находится в равновесии при нулевых силах взаимодействия, как показано в верхней части рис. 69. При деформации расстояние d между центральными атомами в соответствии со сделанным выше предположением не изменяется, и две независимые обобщенные координаты 0 и р позволяют определить деформацию элементарной ячейки. Удобно ввести две зависимые переменные аир, смысл которых ясен из рис. 69. Переменные а и Р выражаются через 6 и р по формулам
а2=1/4 + ра —psin6, ₽2 = 1/4 + p2 + psin0. (47)
Рассмотрим деформацию элементарной ячейки под действием сил F и L, которые связаны простым образом с усилиями ои и о12. Потенциал этой системы имеет вид
—2Fpd — Ld sin 6. (48)
Функцию (48) можно аппроксимировать функцией
—2Fpd — LdQ, (49)
так что суммарная потенциальная энергия элементарной ячейки записывается в виде
V (6, р, F, М) = 2v {а (6, р)} 4- 2v {₽ (6, р)} - 2Fpd - Мб. (50)
Здесь мы написали Af вместо величины Ld для того, чтобы подчеркнуть, что выражение для энергии будет точным, если представить •себе, что на центральные атомы действует момент М, а не силы L.
Рис. 69. Четырехатомная элементарная ячейка в недеформированном и деформированном состояниях.
4.7. Четырехатомная ячейка 119
Производные функции V записываются в виде
Ve-=2t»aae + 2t)pPe —М, Ур = 2пасхр4-2прРр — 2Fd, (51> где да 2р—sin 6 да —pcosO /СО.
aD = -ч- = —н-----, «е -дл- = —---------• (52)
р др 2а ’ ° дО 2а ' '
Для «идеальной» системы с /И=0 из уравнений равновесия У6 = 0, Ур = 0 (53>
можно найти основное решение с 6=0. Оно определяется из уравнения
4wvTp = 2^. (54}
где через у обозначается либо а, либо р, и
/5^S = V-8(,-V’6W-,),/2- (55>
В терминах р уравнение (55) принимает вид
р=2Р {(р2+vj-4 - (р2+г)-’}. (5б>
Зависимость силы от деформации (56) изображена на рис. 70.
На этой основной траектории равновесия в силу симметрии системы производная У0р равна нулю, поэтому устойчивость траектории равновесия определяется двумя коэффициентами устойчивости Уве и Урр, где индексом F отмечаются значения величин на траектории равновесия. Обращение в нуль коэффициента Урр соответствует максимальной точке траектории равновесия. Точка, в которой обращается в нуль коэффициент У£0, является точкой
Рис. 70. Численные решения для бесконечного слоя атомов, иллюстрирующие-поведение идеальной системы и одной неидеальной системы.
320 Гл. 4. Бифуркационная неустойчивость атомной решетки
Рис. 71. Неустойчиво симметричная точка ветвления на графике зависимости параметра нагрузкй Р от параметра сдвиговой деформации
«бифуркации, в которой могут начать развиваться деформации сдвига с ненулевыми значениями 0. Полагая
Vef0 = O, (57)
находим соответствующее критическое значение у:
ус= (7/4)1/®. (58)
Видно, что эта бифуркация появляется прежде, чем основная траектория равновесия достигнет максимальной точки (см. рис. 70).
Решая уравнения равновесия численно для «идеальной» системы с ненулевыми сдвиговыми напряжениями и для «неидеальной» системы с М=Мс!?/6А^0, получим кривые, показанные на рис. 70 и 71. Соответствующие им деформации слоя атомов оказываются именно такими, какими мы и предполагали их ранее,— за-критическими равновесными состояниями, изображенными на рис. <68.
4.8. Применение общей теории
Отождествляя Л с Р, с 6 и е с N, запишем асимптотические результаты общей теории бифуркации в случае задачи об устойчивости кристалла:
d2P с_ %оР
rf62 Vp
рм рс— I f W ^ррр Г (60)
WLAVeBp/ г
(59)
Рис. 72. Закритическое поведение идеальной системы по упрощенной общей теории и по точной теории (численное решение).
Рис. 73. График разрушающих напряжений в осях растягивающее усилие— сдвиговое напряжение по упрощенной общей теории и по численному решению.
122 Гл. 4. Бифуркационная неустойчивость атомной решетки
Уравнение (59) дает выражения для начальной кривизны вторичной траектории равновесия, а уравнение (60) определяет значения разрушающих нагрузок. Эти уравнения справедливы строго в составной критической точке, в которой и вычисляются производные от энергии. Однако, желая сделать исследование достаточно простым, будем применять эти общие выражения для точек ветвления, похожих на составные. Для этого можно просто вычислять производные или в точке ветвления, или в предельной точке.
Найдем производные в действительной точке ветвления, которая обозначается С. Выпишем нужные нам производные:
д2У да2 Ф d2V d0dW
87,78А
~ d®
6А d®’
d2V
дрдР д3У др®
c==V-c______
— р — d® ’ c_vc _ 351,1A
— 'ppp je
(61)
c-vgep
Используя равенства (61), мы сразу же получаем искомые решения. Сравнение этих решений с результатами численного счета приведено на рис. 72 и 73. Видно, что они совпадают исключительно хорошо.
4.9. Трехмерная решетка
Если сделать довольно сильное предположение, что при деформации плотноупакованных плоскостей x3=const расстояние между ними не меняется и остается равным d, то можно так расположить деформированные слои, чтобы получилось кинематически допустимое поле перемещений трехмерной решетки. В случае гранецентрированной кубической решетки поле деформаций будет однородным, в случае плотноупакованного гексагонального кристалла поле деформаций будет существенно неоднородным.
Для гранецентрированного кубического кристалла коэффициенты сц имеют значения
Поэтому на основной траектории равновесия имеем
4.10. Дальнейшие исследования 123
При этом собственный дается формулой
гО
дси С __ Л 60
_0
вектор изолированной критической точки
(64)
4.10. Дальнейшие исследования
В качестве продолжения приведенного выше анализа был рассмотрен вопрос о характере огрубления, вносимого переходом от уравнения (48) к (49), и ослаблено ограничение о недеформируе-мости вертикальных цепочек, позволяющее учесть эффект Пуассона; была изучена также задача, в которой коэффициенту c2i разрешается быть отличным от нуля. Во всех этих случаях численные результаты очень близки к результатам, изложенным выше.
В работе [831 было включено в рассмотрение влияние боковой нагрузки о22 и вычислено критическое значение этой нагрузки, при которой возникает реальная верхушечная точка ветвления. Метод возмущений для этой точки приводит, как мы уже обсуждали, к поверхности гиперболической омбилики (рис. 61).
Прекрасное исследование устойчивости идеальных кристаллов дано Хиллом [2471 и Хиллом и Милстейном [2481. В первой из этих работ Хилл подчеркнул, что при проведении вычислений приведенного здесь типа необходимо тщательно рассмотреть воздействия на однородный элемент кристалла, поскольку неустойчивость под действием нагрузки, естественно, зависит от ее точного описания. Выше мы считали нагружение мертвым и, для того чтобы исключить бифуркации в нагруженном состоянии, добавили, что кажется вполне разумным, ограничение на поворот. В качестве альтернативного к мертвому нагружению можно рассматривать различные типы следящих нагрузок, хотя не вполне ясно, как можно реализовать их в эксперименте. Ясно, что стратегическая цель исследования заключается в том, чтобы использовать вычисленные критические значения усилий для предсказания разрушения в местах концентрации напряжений в нагруженном теле, однако, поскольку состояние в окрестности областей концентрации напряжений меняется от задачи к задаче, далеко не ясно, какой процесс нагружения является наиболее подходящим при использовании для расчета однородного элемента.
Результаты проведенного исследования имеют непосредственное отношение к механике разрушения, поскольку неустойчивая бифуркация в области больших напряжений в вершине трещины может представлять механизм нарушения симметрии в плоскости распространяющейся трещины. Так как мы ограничились здесь
124 Гл. 4. Бифуркационная неустойчивость атомной решетки
рассмотрением однородных деформаций, мы интерпретировали малые нарушающие симметрию сдвиговые напряжения как «несовершенства». Ясно, однако, что дислокация должна была бы вести себя как источник чувствительности к несовершенствам — это можно рассматривать как асимптотическое утверждение о слабом влиянии дислокации.
Аналогичное исследование устойчивости молекул в химии выполнено в прекрасно написанной работе Коулсона [249]; атомистические основы механики сплошной среды обсуждались Миндлином [250]. К этим , работам примыкают исследования бифуркаций при растяжении в плоскости [251] и образовании полос сдвига [243].
Глава
СПОНТАННЫЙ ПОРЯДОК
В БИОХИМИЧЕСКИХ РЕАКЦИЯХ
И БИОЛОГИЯ РАЗВИТИЯ
Бифуркация уменьшает энтропию
Элен Петард
В химических и биохимических системах, как лаконично сформулировала Элен Петард, бифуркации являются ключевыми факторами самопроизвольного появления структур с пространственно-временной организацией. Действительно, a priori ясно, что наличие пространственной или временной самоорганизации в первоначально однородной среде является проявлением неустойчивости, которая нарушает симметрию. Явления самоорганизации являются основополагающими для понимания морфогенеза в биологических системах, таких, как развитие и дифференциация костей и мышечных тканей в растущем организме.
Возникновение порядка, согласно второму закону термодинамики, может иметь место только в открытой системе. Поведение системы, кроме того, должно быть существенно нелинейным. Процесс самоорганизации в такой системе сопровождается неустойчивостью траектории стационарного состояния, термодинамической ветви, соответствующей поведению типа термодинамического равновесия. Помимо этой неустойчивости первоначально однородная система имеет возможность прийти в некоторое упорядоченное состояние — диссипативную структуру [252]. Как для химических, так и биохимических реакций имеются экспериментальные данные об образовании диссипативных структур.
Классическим примером самоорганизующейся химической реакции является реакция Белоусова — Жаботинского. Оказывается, что во взболтанной однородной химической смеси, оставленной в неглубокой кювете, может возникнуть спиральная структура типа структуры, изображенной на рис^74. Поскольку кювета является по существу замкнутой системой, такая самоорганизация является только временной, и в конце концов система возвращается к однородному хаотическому состоянию: химический «организм» умирает! Однако можно поддерживать постоянно организованное состояние, если непрерывно подавать и выводить из такой системы соответствующее количество химических веществ. На фото 8 показан пример аналогичной самоорганизации в пробирке.
Рис. 74. Спиральные волны в реакции Белоусова — Жаботинского. Это интересная картина пространственного порядка в первоначально однородной химической смеси построена Уинфри, и мы отсылаем читателей к его прекрасной работе по реакциям [101]. Рисунок заимствован из работы Уинфри (Winfree А. Т. Spatial and temporal organization in the Zhabotinski reaction.— Advances in Biological and Medical Physics, 1977, 16, p. 115; с разрешения Academic Press).
Фото 8. Самопроизвольное появление пространственных структур в реакции Жаботинского [233]. Равные объемы Се2 (SO4)3, КВгО3, СН2(СООН)2 и H2SO4 тщательно перемешаны вместе с небольшим количеством окислительно-восстановительного индикатора. Некоторое количество однородной смеси налито в пробирку и поддерживается при постоянной температуре 21°С. Сразу же возникают временные колебания, при которых цвет периодически меняется, переходяЧ из красного, соответствующего избытку Се3+, в синий, свидетельствующий об избытке Се4+, с периодом в 4 мин. Через некоторое количество таких колебаний появляется небольшая неоднородность концентрации, из которой попеременно образовывались слои то красного, то синего цвета. Вследствие того что пробирка является замкнутой системой, такая пространственная структура может сохраняться в течение только ограниченного периода времени, около 30 мин, после чего система приближается к состоянию равновесия и возвращается к однородному распределению вещества. Фотография публикуется с любезного разрешения Гершкович-Кауфмана (М. Herschkowitz-Kaufman).
5.1. Брюсселяторная модель химической реакции 127
5.1. Брюсселяторная модель химической реакции
Большой теоретический интерес вызвала тримолекулярная модельная система, так называемый брюсселятор, который является одной из самых простых моделей, обнаруживающих явление самоорганизации [100, 233]. Реакция Белоусова — Жаботинского в противоположность этому является сложной реакцией, которая даже сейчас понятна не в полной мере.
Брюсселятор учитывает следующие гипотетические реакции:
А-^Х, B + X-^Y + D, 2X + Y—>ЗХ, Х—^Е,
причем тримолекулярная стадия видна в третьей реакции. Здесь А, В, D и Е являются начальными и конечными продуктами, концентрации которых предполагаются постоянными. Кроме того, предполагается, что все стадии реакции необратимы, а скорости реакции постоянны и равны единице.
На рис. 75 показана схема реакции. Видно, что система действительно открытая: химические вещества А и В непрерывно поступают в систему, а химические вещества D и Е постоянно из нее выходят.
Обозначая концентрации химических веществ теми же буквами, что и сами вещества, получим, что скорость образования вещества X в первой реакции будет просто А, а скорость исчезновения X во второй реакции равна произведению ВХ. Суммарная скорость образования вещества X в третьей тримолекулярной стадии равна №У, и, наконец, скорость исчезновения в четвертой
Рис. 75. Тримолекулярная брюсселяторная модель химической реакции с двумя переменными промежуточными стадиями X и Y и конечным и начальным продуктами А, В, D и Е. Каждый замкнутый контур, содержащий одно промежуточное вещество, свидетельствует о наличии одной моли этого промежуточного вещества в соответствующей фазе реакции,
128 Гл. 5. Спонтанный порядок в биохимических реакциях
реакции равна X. Таким образом, можно записать
^ = Л-(В+1)Х4-№У
и аналогично
~ = BX — XSY. dt
Эти уравнения образуют систему двух нелинейных уравнений кинетики реакции, решая которую можно найти эволюцию X и Y во времени при заданных постоянных А и В. Приравнивая скорости реакции к нулю, получим основное решение для термодинамической ветви
Х = А, Y = B/A.
Представим теперь X и Y в виде
Х = А + х, Y = B/A+y, где х и у — отклонения концентрации от равновесных значений. Система уравнений приобретает следующий вид:
х = х(В — 1)4-г/ (И2) 4- х2 (В/Л) 4-2хуА 4-хгу,
у — х (—В) 4- у (—Л2) — х2 (В/Л) — 2хуА — хгу.
Для анализа линейной устойчивости нужно сохранить только подчеркнутые члены. Запишем линейные уравнения в стандартной форме
х = сих4-с12у, г/ = с21х4-с22у, где
cu = B—1, с12 = Л2,
с21 = —В, с22 = —Л2.
Характеристическое уравнение при этом принимает вид
X X (си 4" Г22) 4* ^12^21 = О-
Коэффициенты в характеристическом уравнении имеют значения
сис22 ^12^21 > (Гц 4“ г22) — 14“ В.
Поскольку величина Л действительна (и положительна), не возникает статической неустойчивости, при которой первый коэффициент стремится к нулю, но, как легко видеть, обращение в нуль второго коэффициента обусловливает динамическую неустойчивость при Вс=1+А\
Принимая Л = 1 и рассматривая концентрацию В как управляющий параметр, найдем, что устойчивый фокус имеет место при В<ВС и неустойчивый фокус — при В>ВС, где Вс=2. Действи-
5.1. Брюсселяторная модель химической реакции 129
Рис. 76. Затухающие колебания в . направлении устойчивого ' фокуса при докритическом значении В.
телыю, при В=ВС возникает динамическая бифуркация Хопфа, при которой образуется устойчивый} закритический предельный цикл. Некоторые полученные численно фазовые портреты полных нелинейных уравнений кинетики показаны на следующих трех рисунках.
На рис. 76 показаны затухающие устойчивые химические колебания для В=1,5. При В=3 образуется устойчивый предельный
Рис. 77. Притяжение к устойчивому предельному циклу незатухающих химических колебаний при еакритическом значении В.
5 № 528
130 Гл. 5. Спонтанный порядок в биохимических реакциях
Рис. 78. Совокупность растущих предельных циклов, образованных по мере того, как В увеличивается от своего критического значения, равного двум.
цикл. При докритическом значении В=1,5 возмущения затухают, а химические концентрации всегда возвращаются к значениям, которые имеются на термодинамической ветви х=у=0.
На рис. 77 показана система, движущаяся к устойчивому за-критическому предельному циклу при В=3. При этом устанавливаются постоянные химические колебания с хорошо определяемым периодом цикла.
На рис. 78 приведена совокупность предельных циклов для ряда закритических значений В.
5.2. Образование пространственного порядка в термодинамике
Выше рассмотрена временная организация самопроизвольных колебаний химических реакций. Рассмотрим теперь пространственную самоорганизацию. Предположим, что химическая система размазана вдоль линии с продольной координатой г, изменяющейся на отрезке от 0 до 1. Если допустить, что диффузия химических веществ X и У происходит вдоль этой линии с коэффициентами диффузии Di и D2, то уравнения кинетики примут следующий вид1 ^ = Л-(В+1)Х + №У + П1^,
д¥ DV V2AZ . П dt=BX~XY + D^'
При постоянных Л и В опять получаем основное решение, постоян-
5.2. Образование пространственного порядка в термодинамике 131
ное по п
Х-А, Y = B/A,
которое совместимо с краевыми условиями
Х(0, 0 = X (1, 0 = А У (О, 0 = У(1, t) = B/A.
Анализ устойчивости по-прежнему можно провести в переменных х и у, являющихся отклонениями от равновесных значений концентраций X и Y. При этом получим следующие линейные уравнения:
^=(В-1)х+Л-,+Р1^, У-----Вк-А’у+О,^.
Решения этих дифференциальных уравнений в частных производных имеют вид
х(г, 0 — xuewt sin nnr, у (г, t) = уf)e'a,t sin nnr.
Они дают нам как установившиеся состояния, так и периодические по времени собственные функции.
Видно, что система может иметь синусоидально изменяющуюся пространственную структуру. На рис. 79 изображены результаты нелинейного исследования возмущений, проведенного Аух-мути и Николисом (253]. Если волновое число п — четное, то имеется устойчиво симметричная статическая бифуркация, приводящая к образованию устойчивых закритических диссипативных структур. Если число п — нечетное, то имеется асимметричная статическая бифуркация, ведущая к образованию транскритических диссипативных структур с устойчивыми областями, обозначенными на графике сплошной линией. Таким образом, если химические вещества распределены в пространстве вдоль линии, то как пространственные, так и временные структуры могут спонтанно образовываться из-за неустойчивости основной термодинамической ветви.
Отметим, что были проведены также двумерные исследования этой модели химической реакции (254]. Обобщение Проведенного выше одномерного анализа дано в недавней работе Махара и Мат-ковского (Нью-Йорк) и Гершкович-Кауфмана (Брюссель). При этом было обнаружено существование вторичных бифуркаций [100].
Вторичные бифуркации могут быть связаны либо с близостью устойчиво симметричной и асимметричной точек ветвления, и в этом случае они обусловлены омбилической катастрофой, либо q близостью двух устойчиво симметричных точек ветвления, в этом
5*
Рис. 79. Самопроизвольное появление пространственного порядка в брюсселяторе при распределении вещества вдоль линии. Бифуркации включают стационарные решения, показывающие появление устойчивых диссипативных структур после потери устойчивости основного термодинамического решения.
«4
Рис. 80. Рестабилизация во вторичной точке ветвления. Это явление
представляет интерес для специалистов в области термодинамики, поскольку может вызвать образование возможных диссипативных
структур, далеких от термодинамического равновесия.
5.3. Дифференцировка клеток в биологии развития 133
случае они обусловлены катастрофой двойной сборки. Значение вторичных бифуркаций заключается в том, что они могут означать стабилизацию траектории, выходящей из второго термодинамического собственного значения, что дает новую устойчивую диссипативную структуру, показанную на рис. 80.
Дополнительные комментарии к этим последним данным можно найти в известной монографии Николиса и Пригожина (100]. Чувствуется, что неустойчивость и колебания химической и биохимической систем тесно связаны с первоначальным появлением жизни из «первичного бульона» и с действием таинственных биологических часов [255].
5.3. Дифференцировка клеток в биологии развития
Наконец остановимся кратко на анализе Зимана дифференцировки клеток, в котором на новом уровне моделируется морфогенез в биологии. В качестве упрощенной биологической модели рассмотрим дифференцировку существенно идентичных клеток на, скажем, костные и мышечные во время развития эмбриона. Предположим, что клетки образуют множество идентичных систем, регулируемых локальной концентрацией ряда химических веществ.
Рассмотрим одномерную область организма, в которой клетки распределены вдоль оси Ох. Концентрации химических веществ изменяются вдоль координаты х, которую наряду со временем можно считать основным управляющим параметром, так что мы имеем два управления А1 и А2.
Исследуя эту задачу, Зиман [10] построил модель процесса дифференцировки, показанную на рис. 81. Здесь единственная переменная Q, описывающая внутреннее состояние, характеризует меру дифференцировки клетки. На ранней стадии Q непрерывно меняется по х от значения т, соответствующего клеткам-предшественницам мышечной ткани, до значения Ь, соответствующего предшественницам костных клеток. В конце рассматриваемого временного интервала, когда дифференцировка клеток окончилась, имеется скачок величины Q между значениями М и В (М соответствует мышце, В — костной клетке). Осуществляя развертку по времени, Зиман рисует катастрофу сборки, которая наклонена таким образом, чтобы не быть строго параллельной оси времени. Зиман рассматривает эту особенность сборки как существенное обстоятельство, обеспечивающее структурную устойчивость и, следовательно, повторяемость. Отметим, что сборка, параллельная оси времени, дает более простую схему и при определенных обстоятельствах может быть также приемлемой аппроксимацией.
Клетки со значениями х, меньшими хс, развиваются непрерывным гладким образом и образуют мышечную ткань в точке М. Клетки со значениями х между лгс и хА испытывают динамический
134 Гл. 5. Спонтанный порядок в биохимических реакциях
Рис. 81. Дифференцировка клеток в биологии развития. Предполагается, что клетки эмбриона расположены вдоль линии с координатой х. При малых значениях х клетки должны развиться в мышечную ткань, а в области больших значений х — в кость. Единственный внутренний параметр Q характеризует степень «костности» клетки. На рисунке показано представление этого процесса Зиманом как катастрофы наклонной складки. Воспроизводится с разрешения American Mathematical Society из работы Зимана (Zeeman Е. С. Primary and secondary waves in developmental biology.— Lectures on Maths in the Life Sciences, 1974, 7, p. 69).
скачок, связанный, возможно, с «внезапным включением генных программ», во время которых имеется ступенчатое изменение Q (по направлению образования мышцы). Время скачка изменяется вместе с х, так что через тело проходит волна развития, скачки становятся все более сильными до тех пор, пока волна не остановится в точке А. Здесь мы имеем асимметричную точку ветвления, разделяющую докритические клетки с х, меньшим хА, которые скачкообразно развиваются в мышцу, и закритические клетки с х, большим хА, которые не испытывают неустойчивость и плавно развиваются в костную ткань.
Теория предсказывает, что волна развития зарождается с конечной скоростью и затем постепенно замедляется по параболическому закону. Конечным результатом является образование резкой пространственной границы между мускулом и костью в точке
5.3. Дифференцировка клеток в биологии развития 135
хА. Бифуркация в точке А имеет характер существенного роста, хотя заметное действие основной волны может в течение некоторого времени не проявиться. Эта возможная задержка приводит к понятию вторичных волн, тормозящих появление основной волны. Именно вторичная волна обладает физическим свойством, позволяющим ей подать сигнал о высвобождении химической энергии и образовании физической энергии для морфогенеза, создания пространственных форм. Интересно отметить близкое сходство между явлениями, представленными на рис. 81, и исследованием Бенджамином потока жидкости между вращающимися цилиндрами, которое обсуждается в главе по гидродинамике.
Эти же идеи применяются Зиманом для описания эмбрионного развития лягушек и развития слизистых грибов. Еще одно применение теории катастроф в биологии также принадлежит Зиману и может быть найдено в работе о сокращениях сердца.
В большой и развивающейся области биологического морфогенеза модель Зимана является примером попытки решения фундаментальной проблемы на высоком и абстрактном уровне моделирования. Более последовательное и детальное изучение, основанное на некоторых представлениях биохимии, принадлежит, как уже отмечалось, брюссельской школе И. Пригожина и Г. Николиса, и в заключение мы кратко упомянем о прекрасной работе Эрнё и Хирно.
В своей последней статье [256] они подчеркивают, что «образование структур является сложным процессом, при котором клетки, обладающие одними и теми же генетическими потенциями, приобретают различные состояния молекулярной дифференцировки, ведущей к образованию типичной пространственной структуры. Образование таких дифференцированных структур связано с существованием неоднородного распределения химических веществ, так называемых морфогенов, для всех морфогенетических полей» [257]. Показана особая роль вторичных бифуркаций в термодинамике этих процессов.
Кроме того, дан [258] численный анализ и анализ точек ветвления в классической теории морфогенеза Тьюринга [259]. Николис и Малек-Мансор [260] показали, что при неравновесных фазовых переходах и химических реакциях основные уравнения дают ответы, отличные от конструкции Максвелла, которую использовал Том.
Аналогичные проблемы самоорганизации будут рассмотрены при изучении нейродинамики мозга в последней главе книги.
Глава
ДИНАМИКА ПОПУЛЯЦИЙ и эволюция ЭКОЛОГИИ ТИПА ХИЩНИК—ЖЕРТВА
В последние годы, как можно увидеть, например, из последних глав книги Николиса и Пригожина [100], интенсивно изучаются динамика, эволюция и организация экологических систем. Здесь мы обсудим одну из последних работ [103] с любезного разрешения Institute of Mathematics and Its Applications.
Интересное и поучительное введение в динамику популяции экосистемы хищник — жертва представляют классические уравнения Лотки — Вольтерры. Фазовые траектории этих уравнений можно легко проследить при помощи карманного электронного калькулятора, а настольная игра в лису и кролика, описываемая здесь, представляет прекрасную иллюстрацию уравнений, в которые вводится элемент случайности. Интерес игрока связан с возможностью вымирания или взрывного роста популяции кроликов.
Дифференциальные уравнения, определяющие рост, упадок и общую эволюцию взаимодействующих биологических видов, аналогичны по структуре и форме уравнениям, которые встречались в химической кинетике, и мы увидим, как в динамике популяций простой экосистемы типа хищник — жертва могут возникнуть колебания, похожие на устойчивые колебания маятника без затухания.
6.1. Уравнения Лотки — Вольтерры
Следуя Николису и Пригожину [100], предположим, что при наличии пищи А члены биологической популяции X воспроизводятся со скоростью, пропорциональной произведению АХ, так что dXldt=klAX. Здесь k3— постоянная. Символы X и А используются как для обозначения популяции и пищи, так и для обозначения соответствующих мер этих величин. Аналогичным образом можно предположить, что скорость смертности пропорциональна численности популяции X и двум постоянным k3 и В, так что dXldt=—k3BX. Объединяя эти уравнения, для скорости изменения численности
6.1. Уравнения Лотки — Вольтерры 137
популяции получаем
dXfdt = (kiA-k3B)X.
Если бы в систему постоянно подавалась пища, т. е. Л=сопз(, то это уравнение предсказало бы экспоненциальный рост популяции X при kiA^kaB, известный как мальтузианский рост. С другой стороны, при l^A^kaB получим экспоненциальный спад численности популяции до нуля.
Эти неудовлетворительные результаты приводят к выводу, что в популяциях животных экологическая система стабилизируется посредством ограничения пищи, скорость потребления которой должна быть учтена при математическом моделировании. Проиллюстрируем это на простой экологической модели, включающей единственную жертву, скажем кролика, численностью X, в присутствии единственного хищника, скажем лисицы, численностью Y. Предположим, что кролики имеют неограниченный запас пищи в виде овощей, так что их воспроизводство подчиняется ранее упомянутому закону dX/dt=klAX, где и А — теперь постоянные, а смертность возникает только в результате взаимодействия с лисами. Это последнее условие предполагает, что всегда имеется достаточное количество лисиц, которое гарантирует, что кролики в среднем не доживают до старости. В отношении хищников предполагается, что они умирают естественной смертью в соответствии с ранее установленным законом dY!dt=—k3BY, где k3 и В — постоянные.
Взаимодействие между популяциями происходит за счет захвата жертвы хищником, который является причиной уменьшения популяции кроликов и увеличения популяции лис, так как воспроизведение популяции лис пропорционально запасам пищи. Вероятность поимки лисой кролика и, следовательно, общая скорость захвата пропорциональны произведению численностей популяций лис и кроликов XY, поэтому в уравнения следует добавить скорости их взаимодействия:
S=-W 5-+W
где k2 — постоянная. Объединяя вклады рождения и смерти, получим нелинейную систему уравнений эволюции популяций
Х = МХ-Л2ХУ,
(1)
Y = k2XY — k3BY, * 7
где точка обозначает дифференцирование по времени t. Это классические уравнения Лотки — Вольтерры^/ описывающие динамику простой экологии типа хищник — жертйа. Их использовали в течение многих лет для моделирования основных биологических яв-
138 Гл. б. Динамика популяций и эволюция экологии
лений, таких, как биологические часы и нестационарные нейронные сети.
Можно заметить, что уравнения Лотки — Вольтерры в точности эквивалентны уравнениям кинетики трех химических реакций со скоростями kx, k2 и ks:
Л + Х-Х2Х,
Х + кЛ2У, y+b^e+b, если концентрации химических веществ А и В поддерживаются постоянными и равномерными внутри реактора.
6.2. Устойчивость стационарного состояния
Приравнивая правые части уравнений (1) нулю, получим единственное, не считая тривиального и неинтересного решения Х=0, У=0, нетривиальное стационарное решение
Xs = k3B/k2, Ys = kxAlkz. (2)
Если с самого начала численность популяций будет иметь значения (2), то количество жертв и хищников останется постоянным во времени в соответствии рассматриваемой детерминистской моделью. В более реальной стохастической модели вводятся случайные флуктуации.
Чтобы исследовать устойчивость стационарного состояния, представим X и Y в виде суммы
Х = Х.+х, Y = Y3+y.
Подставляя эти выражения в уравнение (1), допустим, что приращения х и у — малые величины, так что их произведениями можно пренебречь. Таким образом, получим линеаризованные уравнения
x = —ksBy, y=+kxAx, (3)
которые описывают поведение малых отклонений численности популяции от стационарного состояния. Исключая у, получим хорошо известное уравнение
х4-^3ЛВх = 0 (4)
— уравнение простого гармонического осциллятора с круговой частотой
(5)
и периодом T=2nlv),
6.2. Устойчивость стационарного состояния 139
Фазовые траектории в пространстве X, Y являются концентрическими эллипсами, расположенными в малой окрестности точки Xs, У8, и, следовательно, стационарное состояние устойчиво. Для конечной амплитуды колебаний около точки Xs, Ys фазовые траектории уже не будут эллиптическими, однако останутся замкнутыми кривыми с непрерывно изменяющимся периодом; таким образом, колебания с большой и малой амплитудами полностью аналогичны колебаниям маятника без затухания. Соотношения, связывающие уравнения Лотки — Вольтерры и уравнения Гамильтона классической механики, подробно освещены Николисом и Пригожином в их последней монографии. Они показали, что постоянная движения в уравнениях Лотки — Вольтерры тесно связана с избытком энтропии 62S в окрестности состояния равновесия.
Здесь следует заметить, что предсказание существования эллиптических центров по линейному приближению не гарантирует, вообще говоря, наличие эллиптических центров у исходной нелинейной системы. Например, асимптотически устойчивые фокусы может дать только нелинейное затухание в механической системе, даже если линеаризованная теория (без затухания) предсказывает центры.
Движение вдоль фазовых траекторий вследствие постоянного изменения периода будет лишь орбитально устойчивым, а случайные флуктуации вызовут постоянное упорядоченное движение между орбитами в противоположность стремлению к предельному циклу в химической модели брюсселятора.
На рис. 82 показаны три фазовые траектории, для которых постоянные полагаются равными единице:
k1A = ksB = ki=\,
Рис. 82. Замкнутые фазовые траектории для модели хищник — жертва. Видна аналогия с маятником без затухания.
140 Гл. 6. Динамика популяций и эволюция экологии
что дает стационарное состояние Х«=У«=1; в этом случае эллипсы линейного приближения становятся кругами.
В действительности пространство X, Y заполнено бесконечной совокупностью таких фазовых траекторий, каждая со своим периодом. Траектория, проходящая через любую начальную точку, представляет полную динамическую эволюцию экосистемы. Таким образом, если система отклонена от стационарного состояния S, то появляются незатухающие колебания около точки Xs, У8, амплитуда которых зависит от первоначального отклонения от S.
6.3. Численные решения, полученные при помощи метода конечных разностей
Дифференциальные уравнения (1) можно приближенно решать численно при помощи конечно-разностных уравнений
ДХ = (М^-МЛЛ#. lXY^(k2XY-ksBY)M, (6) так что если в какой-то момент времени траектория проходит через точку X~Xit Y—Yi, то через время Д/ она пройдет через точку •х/+1=х,+дх, у/+1=у,+ду.
Подставляя в выражение (6) значения для ДХ и ДУ в состоянии i+1 и делая следующий шаг по времени, получим
Х/+1 = Х/+1+ДХ, Y^-Y^+bY
и т. д. Последовательности такого типа легко могут быть запрограммированы на карманном электронном калькуляторе. Программа для калькулятора Commodore SR4148R приводится в табл. 3. Отметим, что последовательность, примененная в этой программе, немного отличается от приведенной выше за счет более удобного использования величины XJ+1 при вычислении У/+1.
На рис. 83 показаны результаты двух таких расчетов с константами (как и ранее), равными единице, и шагом по времени Д<=1/4. Внешняя траектория начинается в точке Х=1, У=2,6, имеющей номер 1=0, до точки с t=28, так что фазовая траектория является практически замкнутой. Двадцать восемь шагов по времени показывают, что период колебания с выбранной амплитудой приблизительно равен 7=28/4=7. Внутренняя траектория начинается в точке Х = 1, У =1,75 с номером t=0 и прослеживается до приблизительного замыкания при 1=25. Таким образом, период равен примерно 6,5. Он несколько отличается от периода внешней траектории 7 и периода 2л, вычисленного в приближении малых амплитуд по линейной теории.
На рисунке хорошо видно изменение фазовой скорости, причем она увеличивается с расстоянием от начала координат. Эта особенность будет более ярко выражена в последующем рассмотрении.
6.3. Численные решения при помощи метода конечных разностей 141
Таблица 3. Программа вычисления фазовых траекторий иа карманном электронном калькуляторе
Параметры: L = klA)ki, M=k3B/k2, N=k2M
ХСП _YVS2 заслать Хо в ячейку памяти 1 заслать Ко в ячейку памяти 2
L считать L
— вычесть
R2 вызвать Yj из ячейки памяти 2
X умножить
R1 вызвать Х[ из ячейки памяти 1
X умножить
N считать N
XX присвоить ДХ
21 добавить ДХ в ячейку памяти 1
R1 вызвать Х;+, из ячейки памяти 1
— вычесть
м считать М
X умножить
R2 вызвать Y{ из ячейки памяти 2
X умножить
N считать N
+ сложить
R2 вызвать Yt из ячейки памяти 2
XX присвоить У,--|-ДУ
S2 переслать содержимое У;-|-ДУ в ячейку памяти 2
R1 вызвать н напечатать Х{+^ из ячейки памяти 1
R2 вызвать и напечатать из ячейки памяти 2
Уравнения: (L—Y)XN = &X, (X—M\YN — tYY Калькулятор: Commodore SR4148R
Точность численных решений, которые сравниваются здесь с точными кривыми, взятыми из рис. 82, допустима для качественного анализа, и ее, конечно, можно увеличить путем уменьшения шага по времени А/.
Для моделирования эволюционной игры, которая в общих чертах будет обрисована в следующем разделе, приведем несколько численных расчетов, показанных на рис. 84 для случая, когда постоянные в уравнениях имеют следующие значения: ktA=2, k3B=l, &2=1/10. Им соответствует стационарное состояние в точке с координатами Х8=10, У8=20, а период малых колебаний Т=* =2л/И2. При вычислениях шаг по времени А/ снова выбран постоянным и равным 1/4.
Значительные изменения фазовой скорости более всего заметны на внешней орбите. Это означает, что шаг по времени слишком ве-
Рис. 83. Простая оценка траектории при помощи карманного электронного калькулятора. Используемые постоянные шаги по времени проясняют характер изменений фазовой скорости.
Риш, 84. Грубые численные расчеты, моделирующие эволюционную игру лиса — кролик. 1 — медленная независимая эвсмйоция: хищники исчезают, жертвы размножаются.
6.4. Эволюционная игра 143
лик для получения точных результатов при больших X и Y. Постоянное приращение времени Д/=1/4 использовалось только для того, чтобы показать, какие интересные качественные результаты могут быть получены за несколько минут на карманном электронном калькуляторе, а кроме того, чтобы смоделировать нашу эволюционную игру, в которой относительно большое значение Д/= = 1/4 необходимо для того, чтобы сделать игру быстрой и интересной.
Ход внешних орбит может быть легко проиллюстрирован при помощи асимптотического анализа исходных уравнений Лотки — Вольтерры (1). При больших значениях X и Y линейными членами в правой части уравнений (1) можно пренебречь. В результате получим
Х = — k^XY, У = +А2ХУ.
Следовательно, Х=—Y. Фазовая скорость велика, и кривые двигаются назад под углом 45°.
Если X и У малы, то можно пренебречь нелинейными членами правой части уравнений (1); тогда получим
Х = МХ, У = — kJ3Y.
Система уравнений распалась на два независимых уравнения, которые описывают экспоненциальный рост популяции кроликов и экспоненциальное уменьшение популяции лис.
Физические механизмы, лежащие в основе этого процесса, очевидны. Если начинать с малых значений численности каждого вида, небольшое число лис приводит к взрыву популяции кроликов, подчиняющемуся приблизительно экспоненциальному мальтузианскому закону роста. Когда пища лис становится обильной, это приводит к взрыву численности их популяции, и они быстро опустошают популяцию кроликов. Как только жертва достигает низкой плотности популяции, у лис не хватает пищи и их количество уменьшается, и мы возвращаемся к исходной точке. Этот цикл может повторяться до бесконечности.
6.4. Эволюционная игра
Сейчас мы опишем эволюционную игру, в которой в уравнения в конечных разностях вводится интересный и реалистичный элемент случайности.
Игра осуществляется при помощи уравнений в конечных разностях (6) с теми же значениями констант, что и раньше:
М = 2, k9B=\, fe2=Vio. Ы = Х,= 10, У,=20,
так что
ДХ = 7аХ-7«ЛУ, ДУ = 1/*оХУ-1/4У-
144 Гл. 6. Динамика популяций и эволюция экологии
Рис. 85. Модифицированная шахматная доска, иа которой играют в игру лиса — кролик.
Кролики X представляются X белых фишек, а лисы У представляются У черных фишек.
Фишки бросают произвольно на доску, похожую на шахматную (рис. 85). Одна половина общей площади доски — белая, четверть— серая и'четверть — черная. Кроме того, толстыми линиями доска поделена на 16 больших квадратов.
Любая лиса, попадающая на черный квадрат, считается убитой и снимается с доски. Поскольку черное поле составляет четвертую часть площади всей доски, то при этом точно моделируется член — /4 У, описывающий вымирание лисиц, но, конечно, уже с элементом случайности.
Любой кролик, попадающий на белую клетку, считается воспроизведенным, и новый кролик ставится на доску рядом с первым. Поскольку белый цвет занимает половину доски, то это правило точно моделирует член, описывающий размножение кроликов, + УгХ.
И наконец, лисам разрешается съесть кроликов внутри одного из больших квадратов, ограниченных толстыми линиями. Отождествляется как можно больше пар лиса — кролик, причем каждый большой квадрат рассматривается в порядке очереди. Затем кролик в каждой паре заменяется лисой. При этом в равных количествах уменьшается популяция кроликов и возрастает популяция лис. Поскольку образование пар, несомненно, зависит от произведения популяций лис и кроликов, в настоящий момент мы точно смоделировали члены взаимодействия.
Действительно, при экспериментальной калибровке было установлено, что при неоднократном бросании 20 фишек (лис) и 20 фишек (кроликов) в среднем получается 10 взаимодействий на бросок, значит, ДУ=10 для Х=20, У=20, и, следовательно, постоянная равна 1/40 — вот почему в первую очередь было выбрано именно это значение!
6.4. Эволюционная игра 145
Рис. 86. Результаты типичного броска, показывающие мертвых лис, воспроизведенных кроликов и кроликов, которые попадаются на обед лисам.
Перечеркнутый темный кружок означает следующее: мертвые лисы, которые убираются из черных квадратов;
оо результат воспроизводства кроликов на белых квадратах;
Q превращение кролика в лису при парном взаимодействии внутри больших квадратов, ограниченных толстыми линиями.
Лисы: 43-»-56.
Кролики: 37->27.
После этого подсчитываются новые значения X и У, фишки повторно бросаются на доску и процесс повторяется снова. На рис. 86 показан пример образования пар лиса — кролик внутри больших квадратов, ограниченных толстыми линиями.
Следует обратить внимание на важное обстоятельство: доску нужно установить на внутренней стороне крышки коробки так, чтобы кромка мешала фишкам упасть с доски (фото 9). Это существенно, поскольку фишки должны падать свободно на доску, чтобы их распределение по доске происходило равномерно. Если же фишкам дать возможность собраться в центре доски, то вероятность столкновения лиса — кролик заметно возрастет.
На рис. 87 показаны результаты нескольких игр, и автор надеется, что заинтересовавшиеся читатели попытаются сыграть в эту игру сами. Можно получить разные результаты, но одно ключевое решение оставляется игроку — это выбор начальной точки.
Новая реалистичная особенность, проявляющаяся в игре, это возможность вымирания вида — обычно кроликов! Эта возможность увеличивается, когда популяция небольшая, а случайная
146 Гл. 6. Динамика популяций и эволюция экологии
Фото 9. Элен изучает судьбу кроликов во время игры иа модицифированной шахматной доске. Черные фишки представляют лис, белые — кроликов. После того как фишки произвольно бросают на доску, каждый кролик, оказавшийся рядом с лисой, считается съеденным. Живой хищник с пренебрежением смотрит иа игру.
флуктуация неблагоприятна, как показано в одной из игр, изображенных на графике.
Очень интересная начальная точка расположена близко или несколько выше стационарного состояния (10, 20). Здесь игра начинается медленно с небольших неустойчивых шагов до тех пор, пока большая флуктуация не образует более интенсивное фазовое
6.4. Эволюционная игра 147
Рис. 87. Некоторые типичные результаты игры, демонстрирующие возможность вымирания кроликов или взрыв их популяции.
движение. Из положения, которое находится несколько выше стационарного состояния, количество кроликов обычно уменьшается, и наиболее интересным становится вопрос, выживет ли популяция. Если кролики выживают, в то время как популяция лис уменьшается, то может возникнуть типичный взрыв популяции, который часто исчерпывает количество фишек и решимость игрока. Иногда полный цикл возникает во второй игре «в саЛки».
К сожалению, лисы вымирают редко, и игроки могут экспериментировать с правилами так, чтобы борьба ослабевала на каждом цикле. Мне бы хотелось узнать о любых таких усовершенствованиях! Например, можно ввести дополнительный элемент эволюции в виде мутанта детеныша суперкролика с более длинными ногами, чем у его соплеменников. При встрече с лисой этот суперкролик
148 Гл. 6. Динамика популяций и эволюция экологии
имеет 50 : 50 шансов уйти от лисы, и это можно решить путем бросания монеты. Суперкролики воспроизводят супер кроли ков, когда они падают на белые квадраты,’ и интерес сосредоточивается на успехе или неудаче этой благоприятной мутации.
6.5. Структурная устойчивость
Уравнения Лотки — Вольтерры имеют один недостаток, отмеченный Николисом и Пригожином [100] и Мэем [261], который заключается в том, что они имеют такую же структурную неустойчивость, как консервативная механическая система без затухания, фазовые траектории которой можно топологически изменить путем введения бесконечно малого вязкого трения.
Можно ожидать, что при введении малого трения получится более реалистичная система уравнений: не с бесконечным количеством нейтрально устойчивых траекторий, а со структурно устойчивыми фокусами и предельными циклами, как это имеет место в химической кинетике брюсселятора. Например, притягивающий предельный цикл будет приводить к проявлению более когерентного циклического поведения с отчетливо выраженным периодом Т. Несмотря на этот недостаток; полезность уравнений Лотки — Вольтерры при моделировании колебаний системы хищник — жертва в силу исключительной простоты очевидна.
6.6. Экологические исследования
Колеблющиеся экологические системы, конечно, наблюдаются в природе. Это подтверждает табл. 4, взятая из статьи Мэя [261]. Здесь К является мерой местного ресурса пищи для жертвы, а г Is— истинные скорости роста жертвы/хищника. Отметим, что система заяц —рысь является единственной экосистемой, в которой существуют большое К и немалые значения r/s. Это — теоретическое условие Мэя для существования колебаний; и действительно, мы видим, что система заяц — рысь представляет собой единственную систему, в которой проявляется циклическое поведение. Таблица 4 составлена на основе некоторых фактов из истории жизни восьми природных систем жертва—хищник, описанной Тэннером [262] и изложенной Мэем. Возможно, нам следовало назвать ее игрой в зайца и рысь!
Конечно, для хорошего экологического планирования и контроля необходимо точное знание динамики популяции в настоящий момент времени. Если, например, в нашей игре мы хотели бы помочь кроликам, то можно предложить удалить несколько лис. Если бы это было сделано из состояния А на рис. 88, то это дало бы маленький цикл с приблизительно тем же средним числом кроликов. Если предположить, что кроликам могло помочь крупномасштаб-
6.6. Экологические исследования 149
Таблица 4. Из истории жизни восьми природных систем хищник—жертва, описанной Тэннером [262] и изложенной Мэем [261]. Воспроизводится с разрешения Ecological Society of America (©, 1975)
Жертва Хищник Географическое положение К большое? Отношение r/s Поведение
Воробей Ястреб Европа Нет 2 Установившееся
Ондатра Норка Сев. Америка В 3 В
Заяц Рысь Сев. Америка Да 1 Циклы
Чернохвостый олень Горный лев Скалистые горы Да 0,5 Установившееся
Белохвостый олень Волк Онтарио » 0,6 »
Карибу » Аляска в 0,4. »
Американский лось Королевский остров в 0,4 »
Белая овца Аляска в 0,2 в
ное уничтожение лис, и уменьшить популяцию лис до значения, соответствующего состоянию В, то результатом был бы взрыв популяции кроликов, за которым следует взрыв популяции лис с последующим почти несомненным вымиранием кроликов.
Такие экологические исследования играют действительно важную роль при регулировании вредителей, таких, как саранча, и касаются нас даже в большей степени, чем если жертвой является человек, а хищником — оспа.
Рис. 88. Возможное неправильное управление экологией на основе стратегии, которая на первый взгляд кажется правдоподобной.
Вымирание
150 Гл. 6. Динамика популяций и эволюция экологии
6.7. Последние работы
Мы уже обращались к известной работе Мэя [106, 261, 2631 и, наконец, должны упомянуть его исследование о бифуркациях и динамике экологических систем.
На приложимость теории катастроф к исследованию эволюции экосистем указывали еще Том [9], Вэддингтон [104] и Додсон [105], а Зиман [10] и Постон и Стюарт [И] исследовали как бегущие волны, так и стабилизацию пространственных границ между, например, лугом и лесом. Постон и Стюарт обсуждают также экономику колоний пчел.
Николис и Пригожин в своей прекрасной книге по самоорганизации [100] изучают термодинамику и устойчивость эволюционных процессов, включая анализ пребиотического образования полимера и эволюционную обратную связь. Обсуждается также организация в сообществах насекомых и разделение труда.
Глава
ГИДРОДИНАМИЧЕСКАЯ НЕУСТОЙЧИВОСТЬ И ВОЗНИКНОВЕНИЕ ТУРБУЛЕНТНОСТИ
В этой главе рассматриваются бифуркационные неустойчивости, возникающие при течении вязких несжимаемых жидкостей. В частности, обсуждаются хорошо известное течение Пуазейля в длинной трубе и течение Куэтта между вращающимися цилиндрами. Это типичные примеры неустойчивости, возникающей при течении жидкости или газа, аналогичные потере устойчивости упругих конструкций. Постепенное увеличение числа Рейнольдса приводит к потере устойчивости исходного и сначала устойчивого потока. В течении Куэтта эта потеря устойчивости — первая в каскаде бифуркаций, который приводит к развитию полностью турбулентного потока с высокими скоростями.
На основании открытия Лоренцем 1145] странного аттрактора Рюэль и Таккенс [146] предположили, что такие аттракторы могут играть ведущую роль в развитии турбулентности, и многочисленные современные исследования направлены на изучение этого вопроса. В следующей главе приводится простой пример странного аттрактора, построенный Хеноном [158].
В двух случаях — течения Пуазейля и течения Куэтта при малых числах Рейнольдса — может быть построено простое теоретическое решение, которое становится неустойчивым в симметричной точке ветвления. В течении Пуазейля в кольцевом зазоре мода неустойчивости периодическая по времени и нелинейно неустойчивая. В течении Куэтта между коаксиальными цилиндрами она установившаяся и нелинейно устойчивая. В случае течения Куэтта мы увидим, как в реальном эксперименте краевые эффекты разрушают симметричную бифуркацию и приводят к наклонной сборке, определяющей структурную устойчивость ячеистого течения.
Прекрасный общий обзор по теории турбулентности, в котором перечислены многие классические работы, включая первую работу Рейнольдса [264], дал сэр Джеймс Лайтхилл в докладе на состоявшемся в Манчестере симпозиуме Osborne Reynolds Centenary [265].
152 Гл. 7. Гидродинамическая неустойчивость
7.1. Течение в трубе круглого сечения
При течении вязкой несжимаемой жидкости (например, воды по трубе) или при обтекании неплоского тела можно наблюдать два различных типа потоков. Если скорость потока достаточно низкая, то наблюдается устойчивое ламинарное течение: жидкость течет гладко вдоль фиксированных линий тока. Если, однако, скорость достаточно велика, то развивается неустойчивый турбулентный поток, в котором мгновенные локальные скорости и давления хаотически меняются во времени.
Вода, медленно бегущая из крана, движется в ламинарном режиме, пока поверхностное натяжение не разрушит ускоряющуюся и, следовательно, утоньшающуюся струю. Быстрый поток воды из крана турбулентный.
Простое экспериментальное исследование этого явления может быть легче всего проведено, если вода нагнетается вниз по тонкой трубе круглого сечения длиной L с высотой напора Н, как показано на рис. 89. Если расход Q измерять при различных значениях высоты напора Н, замеряя, например, объем воды, вытекающий
Рис. 89. Возникновение турбулентности при течении воды в трубе.
7.1. Течение в трубе круглого сечения 153
Рис. 90. Результаты простого домашнего эксперимента по исследованию турбулентного течения в трубе.
из трубы за единицу времени, обнаружится, что зависимость Н от Q вначале линейная, но затем она испытывает скачок, когда Н и Q достигают критического значения. Разрыв на графике (его можно оценить визуально) соответствует началу турбулентности. Будет показано, что точные критические значения заметно зависят от того, какие будут предприняты меры для устранения колебательных возмущений, обеспечения условий гладкого входа потока в трубу и т. д. Результаты, полученные из простого эксперимента, выполненного в домашних условиях с помощью моих детей Элен и Ричарда, приводятся на рис. 90 и в табл. 5.
Эксперимент был осуществлен при помощи сифона, откачивающего воду из ведра, которое наполнялось водой из шланга. Сифон представлял собой пластиковую трубку длиной 583 см и внутренним радиусом 0,32 см, которая была растянута за концы так, чтобы образовалась кривая с небольшим гладким прогибом. Расход воды за 50 с измерялся при помощи мерной колбы при различных
154 Гл. 7. Гидродинамическая неустойчивость
Таблица 5. Результаты домашнего эксперимента по возникновению турбулентности в пластиковой трубе
Напор Я, см Q. см’/50 с tg Q lgH/Q’
5 ПО 2,041 —3,383
10 220 2,342 —3,684
15 325 2,511 —3,847
20 450 2,653 —4,005
20 420 2,623 —3,945
22,5 460 2,662 —3,973
25 500 2,698 —4,000
27,5 540 2,732 —4,025
30 580 2,763 —4,049
35 650 2,812 —4,081
40 700 2,845 —4,088
45 740 2,869 —4,085
50 760 2,880 —4,062
Длина трубы 583 см; радиус трубы 0,32 см; кинематическая вязкость воды принята равной 0,01 см2/с. Температура не измерялась, как это следует всегда делать в лабораторной работе вследствие сильной зависимости вязкости от температуры.
значениях высоты столба жидкости — расстояния от поверхности ведра до горизонтального выпускного отверстия.
При всех значениях высоты столба жидкости, кроме 20 см — области с отчетливо выраженной неустойчивостью,— результаты измерений могут быть повторены с большой точностью, однако в окрестности этого значения результаты могут меняться от опыта к опыту, и в потоке отмечаются колебания с частотой, приблизительно 4 Гц, указывающие на то, что поток флуктуирует между ламинарным и турбулентным режимами. Высокое значение скорости при //=20 см было получено лишь в первом опыте, проведенном при этом напоре, и более не повторилось, причем пульсаций не наблюдалось, так что, по-видимому, это была удачная реализация высокоскоростного ламинарного течения. Впоследствии при этом напоре многократно повторялись низкие значения скорости потока.
Полученные показания нанесены на верхнем графике рис. 90, а обычный график в логарифмических осях построен на нижнем рисунке. Число Рейнольдса, при котором произошла потеря устойчивости течения, составило 1790, но это значение следует рассматривать скорее как приближенное, так как внутренний диаметр трубы измерялся весьма неточно.
Возникновение турбулентности, наблюдавшееся в этом домашнем эксперименте, и есть то явление, которое обсуждалось Рейнольдсом [264] и Лайтхиллом [265].
7.1. Течение в трубе круглого сечения 155
Как можно заметить из результатов эксперимента, приведенных на рис. 89, напор Н является управляющим параметром, под действием которого жидкость приобретает доступную для нее скорость. Эта ситуация, однако, легко может быть обращена, как, например, при мертвой и жесткой нагрузках на инженерные конструкции в лаборатории, нагнетанием жидкости при помощи поршня или плунжера с регулируемым расходом Q. Получающийся при этом перепад давления может быть измерен водяным манометром.
Более того, график Q—Н на рис. 89 очень напоминает зависимость прогиба от нагрузки при потере устойчивости цилиндрической или сферической оболочки. Эта аналогия, как будет видно, определяется глубоким сходством неустойчивостей, лежащих в основе этих явлений.
Мы видели, что турбулентность приносит с собой увеличенное сопротивление потоку; значение скорости Q для заданного напора Н оказывается меньшим, чем если бы течение оставалось ламинарным. Поэтому, если нас интересует прокачивание воды по трубе, с практической точки зрения турбулентность следует рассматривать как нежелательное явление.
Легко вывести хорошо известную теоретическую формулу Хагена — Пуазейля для ламинарного потока вязкой жидкости в круглой трубе радиусом Ь. Скорость жидкости или газа в точке с радиальной координатой г, меньшей Ь, обозначим через U(r), а касательное напряжение в направлении оси трубы в этой точке — через т: x=pdU/dr, где р — коэффициент вязкости. Пусть градиент давления, вызывающий течение, равен Р, тогда для цилиндра жидкости радиусом г единичной длины можно записать
лг2Р + 2nrydU /dr = О, и, следовательно,
dU/dr = — (/’/2р.) г.
Интегрируя, получаем
U = — (Р/4р)г2 + К,
и, поскольку частицы жидкости или газа, касающиеся стенки трубы, будут всегда покоиться, краевое условие U (Ь)=0 дает постоянную интегрирования К: К=(Р/4р)Ь2. Таким образом, распределение скорости по поперечному сечению трубы подчиняется параболическому закону
U(г) = (Р/4р) (Ь2 - г2) = Um [1 - (г2/Ь2)].
Скорость жидкости достигает максимального значения на оси трубы:
^т = ^(0) = ^2/(4р).
156 Гл. 7. Гидродинамическая неустойчивость
Интегрируя, легко найти среднюю скорость. Она оказывается равной половине максимального значения Um, так что расход составляет
Q = пЬ2РЬ3/(8ц) =jtP6V(8p).
Это соответствует экспериментально найденному линейному закону между Q и Н, который осуществляется в условиях ламинарного течения.
В случае турбулентных течений в жидкости появляются ускорения, так что в игру вступают инерционные силы, и уравнения возмущенного движения включают плотность жидкости р, в которой до сих пор необходимости не было. Эти уравнения и простые соображения о размерностях наводят на мысль, что для других жидкостей и аналогичных экспериментов, отличающихся лишь масштабами, турбулентность начнется при критическом значении безразмерного числа Рейнольдса, определяемого в виде
Р Характерная скоростьX Характерный размер Кинематическая вязкость ’
где кинематическая вязкость v является просто отношением р/р.
Этот вывод подтверждается экспериментами, и, определяя число Рейнольдса Re в опытах с трубой по формуле Re=t/ra6/v, находим, что его критическое значение имеет порядок 2200 (см. график Джозефа на стр. 121 в [266]). Через объемный расход условие перехода в турбулентный режим записывается в виде Re=2Q/(jcvb)« «2200.
Отсюда видно, что при течении в трубе тяжелое моторное масло будет иметь более высокую крйтическую скорость, чем вода. Так что при данной скорости вода имеет большую тенденцию к переходу в турбулентный режим, как мы обычно себе это и представляем.
Для исследования возникновения турбулентности в течении Хагена — Пуазейля в трубе удобнее рассматривать более общий случай течения Пуазейля в кольцевом зазоре, которое включает течение по трубе с сечением в форме круга как частный случай.
7.2. Поток в кольцевом зазоре
Рассмотрим вязкую жидкость, текущую по кольцевому зазору между внутренним твердым цилиндром радиусом а и полым коаксиальным наружным цилиндром радиусом Ь. Эта задача сводится к обсуждавшейся в предыдущем разделе, если радиус а приравнять нулю.
Линейный анализ устойчивости уравнений Навье — Стокса движения жидкости показывает, что ламинарное течение в кольце
7.2. Поток в кольцевое зазоре 157
вом зазоре теряет устойчивость из-за бесконечно малых возмущений при некотором критическом значении числа Рейнольдса, определяемом по формуле Re—Um(b—a)/v. Потеря устойчивости соответствует неустойчиво симметричной точке ветвления, которая в механике жидкостей и газов называется обычно докритической точкой ветвления.
Режим неустойчивости является периодическим по времени, как и в бифуркации Хопфа. Такая зависящая от времени неустойчивость не может, конечно, возникнуть в консервативной системе и не описывается элементарной теорией катастроф, но это явление знакомо инженерам, сталкивающимся с флаттером аэродинамически нагруженных крыльев и подвесных мостов.
Нелинейный анализ позволяет исследовать эту зарождающуюся неустойчивость и показывает, что она является крайне неустойчивой. На графике рис. 91 изображена’ штриховая кривая, которая выходит из критической точки ветвления С, за пределами которой ламинарное течение неустойчиво. Эта схематическая диаграмма основана на данных Джозефа [266, стр. 91 и 93]. Коэффициент трения представляет собой выбранную подходящим образом меру сопротивления потоку.
Итак, если бы в идеализированном эксперименте можно было медленно увеличивать число Рейнольдса от низкого значения при условии, что имеются только бесконечно малые возмущения, а тру-
Рис. 91. График в логарифмических координатах, схематически показывающий скачкообразное появление турбулентности в трубе, имеющей вид кольцевого зазора. А — скачок, связанный с бесконечно малыми возмущениями; В — скачок, связанный с конечными возмущениями; Rer->oo при a'b-t-Q,
158 Гл. 7. Гидродинамическая неустойчивость
ба идеально изготовлена и идеально прямая, то ламинарное решение будет сохраняться вплоть до точки С. В предположении, что управляющим параметром является числа Рейнольдса, состояние системы в этой точке резко изменится до устойчивого, но хаотического режима, как показано стрелкой А. Этот скачок обусловлен бифуркационным решением, периодическим по времени, однако конечным результатом является турбулентное течение, не связанное, по-видимому, с этим зарождающимся неустойчивым движением. Поэтому считают, что полный переход к турбулентности есть либо повторное ветвление, при котором имеется цепочка последовательных потерь устойчивости течений с менее сложной структурой, переходящих в течения с более сложной структурой [266], либо скачкообразный переход к странному аттрактору.
Хотя первоначально ламинарное течение устойчиво относительно малых возмущений, устойчивость становится все более ненадежной по мере приближения числа Рейнольдса к Rec. Небольшие, но конечные возмущения могут легко вызвать преждевременный переход в турбулентность, как показано стрелкой В на рис. 91. Экспериментальные наблюдения подтверждают, что на практике можно достичь очень высоких чисел Рейнольдса, если принять меры предосторожности, исключающие, насколько это возможно, возмущения исходного ламинарного течения.
Общий разброс большинства экспериментально найденных значений критического числа Рейнольдса лежит в диапазоне 2000< Re<2300, который свидетельствует о том, что даже в лабораторных условиях имеются достаточно большие возмущения, которые снижают критическое число Рейнольдса до этого уровня. Результаты одного экспериментального исследования показаны на рисунке темными кружками.
Мы видим, что здесь имеется ситуация, аналогичная во многих отношениях потере устойчивости сферических и цилиндрических оболочек в теории упругой устойчивости. В каждой области имеется нелинейная крайне неустойчивая бифуркация в триггерную моду, которая существенно отличается от достигаемого в результате динамического процесса конечного состояния и обнаруживает значительную чувствительность к несовершенствам и динамическим возмущениям; имеющееся на графиках отчетливо выраженное плато свидетельствует лишь о недостаточном уровне современного эксперимента. Действительно, единственная качественная разница между рис. 91 и приведенным выше рис. 25 гл. 1, иллюстрирующем потерю устойчивости сферической оболочки, заключается в том, что из уважения к принятым в механике жидкости и газов (и в остальных науках ) обычаям мы нарисовали управляющий параметр по горизонтальной оси, а не по вертикальной, как это неудачно принято делать при исследовании устойчивости оболочек.
Завершим этот пункт следующим замечанием: критическое число
7.2. Поток в кольцевом зазоре 159
Рис. 92. Бесконечная чувствительность к несовершенствам при ламинарном течении в трубе. Видно экспериментальное плато при Re=2000.
Рейнольдса, найденное по линейной теории, стремится к бесконечности, когда отношение а/b стремится к нулю. Поэтому в круглой трубе без внутреннего цилиндра ламинарное течение можно наблюдать при сколь угодно высоких значениях числа Рейнольдса, если при этом, конечно, соблюдаются соответствующие меры предосторожности при проведении эксперимента. Попадание большинства экспериментально найденных критических чисел Рейнольдса в диапазон 2000<Re<2300 свидетельствует о том, что течение Хагена — Пуазейля обладает сильной чувствительностью к несовершенствам, которая возвращает критическую точку из бесконечности и дает отчетливо выраженное плато. Это схематически иллюстрируется на рис. 92.
7.3. Общая гидродинамическая неустойчивость
Как мы только что видели на примере течения Пуазейля в трубе, проблемы нелинейных бифуркаций в механике жидкости имеют очень точные аналоги и в механике твердого тела.
Общий теоретический анализ основных уравнений движения Навье — Стокса для хорошо определенного течения, например течения Пуазейля или Куэтта, показывает, что при низких значениях числа Рейнольдса имеется единственное решение, соответствующее единственному устойчивому установившемуся ламинарному течению, которое мы называем основным. Этот факт тесно связан, хотя
160 Гл. 7. Гидродинамическая неустойчивость
и не непосредственно вследствие своей общей природы, с теоремой единственности Кирхгофа для малых перемещений в линейной теории упругости.
Поскольку основное течение не наблюдается экспериментально при больших числах Рейнольдса, следует предположить, что оно становится неустойчивым относительно по крайней мере малых, но конечных возмущений при медленном увеличении Re. Исследование этой потери устойчивости является центральной и фундаментальной проблемой теоретической гидродинамики, привлекающей в последние годы пристальное внимание, и происходит параллельно активному изучению проблем упругой потери устойчивости.
Теоретическая неустойчивость колебаний жидкости, предсказываемая анализом ветвления решений, обычно не соответствует неустойчивости в жидкости с полностью развитой турбулентностью и со случайными флуктуациями скорости и давления, а представляют собой либо установившиеся, либо периодические по времени вторичные течения, которые можно рассматривать как простейшую из возможных турбулентностей, представляющую первый шаг на пути к полностью турбулентному режиму. Существование периодических бифуркаций подчеркивает отсутствие в этих проблемах потенциала типа энергии.
Остановимся вкратце на установившихся течениях и обрисуем в общих чертах последнюю работу Бенджамина (50]. На рис. 93
Рис. 93. Возможные-теоретические бифуркационные диаграммы для идеализированных установившихся течений жидкости; ±1 — индексы Лере — Шаудера.
7.4. Вихри Тэйлора между вращающимися цилиндрами 161
из работы [50] воспроизведена серия возможных бифуркационных диаграмм для идеализированных теоретических течений. На рисунке указаны значения индекса Лере — Шаудера (±1). Отрицательное значение индекса Лере — Шаудера обеспечивает неустойчивость соответствующего решения, однако, так же как и детерминант устойчивости консервативной системы, положительное значение устойчивости не гарантирует. Бенджамин показал, как симметричные точки ветвления на этих графиках, соответствующие решениям идеализированных теоретических моделей, разрушаются в реальных экспериментальных условиях. Это будет рассмотрено ниже на примере течения Куэтта между вращающимися цилиндрами.
7.4. Вихри Тэйлора между вращающимися цилиндрами
Рассмотрим несжимаемую вязкую жидкость, заполняющую цилиндрический кольцевой зазор между двумя длинными твердыми коаксиальными цилиндрами, как показано на рис. 94. Если закрепить наружный ' цилиндр и вращать внутренний с угловой скоростью со, то жидкость будет двигаться по окружности. Жидкость, находящаяся в непосредственном контакте с внутренним цилиндром, будет увлекаться им во вращение, в то время как жидкость, контактирующая с наружным цилиндром, всегда покоится.
В случае малых чисел Рейнольдса, предполагая временно, что длина цилиндров велика по сравнению с их радиусами, так что краевыми эффектами можно пренебречь, получим крайне простую картину течения: все частицы жидкости будут двигаться вдоль замкнутых линий тока с постоянной скоростью, которая будет гладко меняться от curt на внутренней границе до нуля на внешней границе.
В цилиндрической системе координат (г, 6, г), где г — координата вдоль оси, соответствующие компоненты скорости (vr, ve, vz) как функции координат и времени
иг = иг(г, 9, г, 0. vo = ve(r, 9, г, t), vz = vz(r, 9, г, t)
будут такими: vr=0, v0=v0(r), п2=0. В частности, тангенциальная составляющая скорости имеет вид [267, стр. 8]
пе = Аг + В/г,
где константы А и В определяются из краевых условий
Це (г1) = сог1, пе(г2) = 0.
При увеличении угловой скорости основное течение может стать неустойчивым при некотором критическом значении числа Рейнольдса, которое определяется формулой Re=ri(o/v. При значениях числа Рейнольдса, превосходящих критическое значение, может появиться установившееся вторичное течение, в котором скорости будут периодическими функциями продольной координаты г. Это связано с ячеистыми спиральными вихревыми потоками, которые
6 As 528
162 Гл. 7. Гидродинамическая неустойчивость
Рис. 94. Тэйлеровские вихри между цилиндрами, поясняющие, как появляется в идеализированной ситуации устойчиво симметричная точка ветвления и наблюдаемая в эксперименте структурно устойчивая наклонная сборка. Экспериментальные результаты Бенджамина [501 воспроизводятся с разрешения Royal Society of London.
показаны на рис. 94, а их скорости можно записать следующим образом:
vr = vr(r, z), ve = ve(r, г), vz = vz(r,z}.
Отметим, что вторичное течение является установившимся и осесимметричным, так как поле скорости не зависит от времени t и угловой координаты 0. Это установившееся вторичное течение Куэт-та впервые наблюдалось Тэйлором [268] в 1923 г. Прекрасные снимки такого течения, выполненные Фенстермахером и Суинни, представлены на фото 10.
Теоретический анализ идеализированной ситуации, соответствующей бесконечно длинному цилиндрическому кольцу, показы-
7.4. Вихри Тэйлора между вращающимися цилиндрами 163
Фото 10. Переход к турбулентности в жидкости, заключенной между концентрическими цилиндрами; внутренний цилиндр вращается, (a) Re/Rec= 1,1, стационарное тэйлоровское вихревое течение с 18 вихрями. Течение на верхней и нижней поверхностях жидкости направлено внутрь жидкости. Вертикальные метки разделены углами в 10°. (b) Re/Ref=6,0. (с) Re/Re<,=16,0. (d) Re/Rec=23,5. На фотографиях (b) и (с) — волновые вихревые течения с 4 волнами вокруг зазора, на фотографии (d) волны отсутствуют. На фотографиях (Ь), (с) и (d) имеется по 17 вихрей, и течение направлено наружу на верхней и внутрь на нижней поверхностях жидкости. Воспроизводится с разрешения Cambridge University Press из работы Fenstermacher Р. R., Swinney Н. L., Gollub J. Р. Dynamical instabilities and the transition to chaotic Taylor vortex flow.— J. Fluid Meeh., 1979, 94, p. 103.
вает, что потеря устойчивости имеет вид устойчиво симметричной точки ветвления (рис. 94), или, по терминологии гидродинамиков, соответствует закритцческой бифуркации. Для такой устойчивой
б«
164 Гл. 7. Гидродинамическая неустойчивость бифуркации вряд ли имеется сильная чувствительность к динамическим возмущениям или влиянию удаленных концов, которые в принципе в состоянии заметно изменить основное течение. И действительно, имеется прекрасное соответствие между экспериментальным значением критической величины угловой скорости со для длинных зазоров и найденным значением при помощи линеаризованной теории устойчивости. Подробные сравнительные данные теоретических и экспериментальных результатов можно найти в гл.7 монографии Чандрасекхара [269].
Однако эта идеализированная ситуация по существу является искусственной, и для более коротких кольцевых зазоров краевые эффекты начинают доминировать при формировании структуры течения. Для того чтобы разобраться с возникающей картиной, Бенджамин [50] привлекает понятие структурной устойчивости или ситуации общего положения. Он показал, что симметричная бифуркация сменяется наклонной сборкой, которая будет наблюдаться, если систематически изменять два управляющих параметра. При этом сборка содержит асимметричную (транскритическую) точку ветвления.
Для подтверждения этого теоретического вывода Бенджамин представил результаты экспериментального исследования структуры потока, используя в качестве двух управляющих параметров угловую скорость внутреннего цилиндра и длину зазора L. Его экспериментальная установка в основном аналогична использованной Тэйлором и схематически показана в нижней части рис. 94. Длина кольца, заполненного жидкостью, относительно невелика, и ее можно непрерывно регулировать. Наружный цилиндр изготовлен из плексигласа, что дает возможность наблюдать за течением. Водный раствор глицерина становится видимым при добавлении небольшого количества гранулированного вещества. Наружный цилиндр закреплен неподвижно по всей длине, а внутренний цилиндр вращается с регулируемой скоростью со. Отношение радиусов цилиндров rjr2 равно 0,615, а ширина зазора D=r2—гг равна 23 мм. В таком устройстве краевые эффекты хорошо ощущаются во всем объеме жидкости, и можно наблюдать устойчивый рост основных потоков с двумя или четырьмя циркуляционными ячейками.
Переходы между этими двух- и четырехячеечными режимами подробно изучены как функции двух независимых параметров со и L, а точка возврата на рис. 94 изображена в соответствии с кризисами течения, видными на рис. 95. Эта точка представляет собой устойчивую сборку; верхняя- ветвь соответствует устойчивым че-тырехячеечным потокам, а нижняя — устойчивым двухячеечным течениям. При увеличении числа Re в окрестности точки В можно наблюдать асимметричную транскритическую бифуркацию.
Сообщалось, что при проведении эксперимента трудно проанализировать мелкие детали сборки в окрестности точки С (как почти
7.4. Вихри Тэйлора между вращаюшчмчся цилиндрами 165
Рис. 95. Схематический рисунок наклонной устойчивой сборки, показывающий морфогенез двух- и четырехячеечиых форм.
всегда бывает при экспериментальных исследованиях), но при увеличении, а затем уменьшении угловой скорости неоднократно наблюдался четко выраженный гистерезис для значений L/D между точками В и С. Эта полученная в эксперименте наклонная сборка полностью аналогична тон, которую предлагает Зиман [101 в биологии развития (гл. 5), и представляет собой значительный шаг вперед в экспериментальных наблюдениях структурно устойчивого морфогенеза.
Дальнейшие современные исследования турбулентности содержатся в Proceedings of the Berkeley Turbulence Seminar [2701; кроме того, нам хотелось бы отметить работу Каплана и Йорка [271]. Берри и Мэкли [84 , 851 продемонстрировали применение теории катастроф для объяснения развития неустойчивых инерционных расходящихся потоков, включая образование вихря. Лэчер, МакАртур и Бузина в American Scientist в 1977 г. обсудили в рамках теории катастроф внезапные изменения режима циркуляции атмосферы. Имеется экспериментальная модель таких явлений при помощи течения жидкости в кольцевом зазоре с регулируемым перепадом температур и скоростью вращения внутреннего цилиндра.
Глава
ХАОТИЧЕСКАЯ ДИНАМИКА СТРАННОГО АТТРАКТОРА
Для того чтобы дать представление о странных аттракторах, используем конечно-разностное отображение, следуя статье [272], написанной в соавторстве с моим сыном Ричардом, которая воспроизводится здесь с разрешения Institute of Mathematics and Its Applications.
Открытие Лоренцем странных аттракторов при изучении чрезвычайно простых автономных динамических систем вызвало большой интерес, поскольку эти аттракторы порождают хаотическое и по существу случайное поведение хорошо определенной детерминистической модели. Как уже говорилось в гл. 7, имеется надежда, что аттракторы могут моделировать гидродинамическую турбулентность. В последней работе Холмса указан странный аттрактор для нелинейных колебаний, вызванных синусоидальной силой при потере устойчивости конструкций, имеющих лишь одну степень свободы. Исследование Холмса [151] основано на решениях обыкновенного дифференциального уравнения на аналоговой вычислительной машине и на анализе и исследованиях отображения Пуанкаре Р и аппроксимации Ра к Р на цифровой машине.
Действительно, такие аттракторы имеют много общего, и Роеслер [147, 148] утверждает, что, подобно тому, как колебание является типичным поведением динамических систем с двумерным фазовым пространством, так хаос может быть типичным поведением систем с трехмерным фазовым пространством или с фазовым пространством большей размерности. Он определяет хаос как «бесконечное число неустойчивых периодических траекторий и несчетное число непериодических повторяющихся траекторий».
Таким образом, странные аттракторы могут оказывать значительное влияние на моделирование случайного поведения, поскольку сейчас видно, что нет необходимости в стохастических моделях во всех случаях, когда поведение системы носит случайный характер. Для простых детерминистических механических систем наличие странных аттракторов означает, что результаты, полученные на
8.1. Конечно-разностное отображение Хенона 167
вычислительной машине, должны быть тщательно изучены (как должны быть изучены любые результаты, полученные обычным методом усреднения Крылова — Боголюбова), поскольку одной из особенностей странного аттрактора является то, что система может совершить внезапный скачок после длительного периода кажущегося состояния покоя. Кроме того, следует тщательно следить за известной чувствительностью странного аттрактора к вариациям начальных условий, и требуется переосмысливание понятий устойчивости и повторяемости.
В настоящей главе мы исследуем отображение плоскости на себя, которое было изучено Хеноном [158]. Отображение выбирается так, чтобы смоделировать отображение Пуанкаре странного аттрактора Лоренца [145], при этом мы рассмотрим различные участки картины, впервые полученной Хеноном, используя 10е итераций на цифровой вычислительной машине. Это простое отображение можно исследовать более быстро и обстоятельно, чем трехмерную непрерывную систему Лоренца, и она обладает по- существу теми же основными иерархическими свойствами, что и система Лоренца. Мы расширим работу Хенона исследованием разбегания решений, выходящих из двух близко расположенных начальных точек, что можно рассматривать как моделирование ошибок, возникающих из-за ошибок округления.
8.1. Конечно-разностное отображение Хенона
На основе численных экспериментов Хенон наглядно показал, что простое отображение плоскости на себя, по-видимому, содержит странный аттрактор, аналогичный тому, который обнаружил и исследовал Лоренц для системы трех дифференциальных уравнений первого порядка. Этот странный аттрактор, по-видимому, является произведением одномерного многообразия на канторово множество.
Для уравнений Лоренца трехмерный фазовый поток имеет постоянную отрицательную дивергенцию. Это означает, что любой объем сжимается экспоненциально со временем. Все траектории стремятся к множеству меры нуль, называемому аттрактором. В некоторых случаях аттрактор — это просто точка, которая тогда является устойчивым состоянием равновесия, или замкнутая кривая, называемая предельным циклом. Но бывает, что аттрактор имеет гораздо более сложную структуру. Тогда его называют странным аттрактором. Внутри такого странного аттрактора траектории блуждают явно нерегулярным образом и чрезвычайно чувствительны к вариации начальных условий. Такое поведение стимулировало большой интерес к теории динамических систем и рассматривалось как возможная модель гидродинамической турбулентности.
Хенон выбрал итерационную схему для быстрого и точного исследования поведения этого типа. По существу он рассматривает не
168 Гл. 8. Хаотическая динамика странного аттрактора
Рис. 96. Отображение Пуанкаре траектории в фазовом-пространстве.
целые траектории в трехмерном пространстве, а только их последовательные пересечения с двумерной секущей поверхностью S. Таким образом, когда траектория выходит из данной точки А секущей поверхности S, мы будем следить за траекторией до тех пор, пока она снова не пересечет поверхность S в новой точке Т (Л); это определяет отображение Т поверхности S в себя. Соответствующее отображение иногда называют отображением Пуанкаре; оно иллюстрируется рис. 96. Траектория, таким образом, заменяется бесконечным множеством точек на S, получаемых при последовательных применениях отображения Т. Поскольку существенные свойства траектории сохраняются как соответствующие свойства этого множества, трехмерная непрерывная задача формально сводится к исследованию двумерного отображения.
Конечно, мы не можем найти отображения данного трехмерного потока без интегрирования дифференциальных уравнений, но один из методов заключается в том, чтобы угадать подходящее отображение и посмотреть, как оно себя ведет.
В этом смысле Хенон поставил задачу определить простое отображение, которое может реально быть связано с трехмерным странным аттрактором. Его отображение Т таково:
xi+i = У. + 1 ~ ах о yi+i = bxt.
Здесь а и Ь — постоянные. Отметим, что якобиан этого отображения равен —Ь:
d(xi+i, yi+1) _ .
d(xh уд
Так как якобиан постоянен, то соответствующее уменьшение площади меньше, чем для системы Лоренца.
Заметим, что Т — взаимно однозначное отображение плоскости на себя, так как может быть легко построено обратное отображение. Это естественный аналог того, что в системе Лоренца через каждую точку проходит только одна траектория. Построенное эмпирически.
8.2. Численные результаты и увеличение последовательностей 169
на основе постулирования естественных свойств отображение, как показано Хеноном, является наиболее общим квадратичным отображением с постоянным якобианом.
Отображение Т имеет две инвариантные точки, которые можно получить, если положить хг+1=хг, Уг+1=^, откуда
.. -(I-*) ±К(1-*)24-4а
2а
У = Ьх.
Эти точки действительные, если
а > au = (1 — Ь)2/4.
При выполнении этого условия одна из точек всегда неустойчива, в то время как другая неустойчива только при
а > ах = 3 (1 — Ь)2/4.
Подходящие значения для управляющих параметров а и Ъ (а=1,4; А =0,3) Хенону удалось найти только после некоторого экспериментирования.
8.2. Численные результаты и увеличение последовательностей
Установлено, что независимо от (локальной) начальной точки итерации Т приводят к картинам, изображенным на рис. 97 и 98, которые, возможно, представляют сам аттрактор. Например, начиная с произвольно выбранной точки хо=О, уо—О, последовательность итераций А, В, С, D на рис. 97 показывает, что точка потерялась внутри аттрактора после всего лишь четырех итераций (при исходном масштабе рисунка).
Продвигаясь дальше, внимательно наблюдали за поведением аттрактора на протяжении 100 шагов. Следующие двенадцать точек пронумерованы для того, чтобы показать случайные скачки, которые являются типичными для всех движений на аттракторе.
Хенон заметил, что одна из двух инвариантных точек с координатами х=0,63135448..., у=0,18940634... принадлежит аттрактору, и, для того чтобы исключить переходные состояния, мы последуем методу Хенона и возьмем эту точку в качестве начальной (при указанной точности). Эта точка, обозначенная буквами Не, помечена на рис. 97 крестиком.
Последовательность из 600 точек, начинающаяся в точке Не, показана на рис. 98, а аналогичная последовательность из 2000 точек — на рис. 99.
Рассмотрим сейчас более подробно маленький квадрат С на рис. 99, который увеличен до нормального размера на рис. 100. Здесь компьютер совершил 10* итераций, причем на график наносились лишь те точки, которые попадают в интересующий нас квад-
У
о,4
112 шсгоь
-.10 ° л’ • 12 -G
А*
Неустойчивая инвариантная „ точна Не О /
i*D 11
•’з
г
Ё
4
В
9
’ .1
-0,4
1,5 Нумерации точек начинается после 100 шагов 1,5 х
Рис. 97. Странный аттрактор после 112 шагов. Последовательность начинается в точке А.
дУ
600 mazes
0,4
хН1=у,+1-1,4а:? УМ=О>3^
А
-0,4 д
-1,5 1,5 X
Рис. 98. Увеличение последовательности; все серии начинаются в точке Не. Используется не очень экономная программа, и построение графиков занимает 5, 18, 20 и 202 мии соответственно.
8.2. Численные результаты и увеличение последовательностей 171
Рис. 99. Увеличение последовательности; все серии начинаются в точке Не. Используется не очень экономная программа, и построение графиков занимает 5, 18, 20 и 202 мин соответственно.
рат. Аналогичное увеличение было проделано с квадратом D, который увеличен до нормальных размеров на рис. 101 при 10? итерациях. Здесь мы видим, что множество, казавшееся на предыдущих рисунках единой кривой, распалось на 6 параллельных кривых.
Аналогичное увеличение последовательности, начинающейся, как всегда, в точке Не, показано на рис. 102—104. Последний график соответствует 106 итерациям, и только небольшая часть точек попадает в квадрат и откладывается на графике. Здесь снова первоначально единая кривая распадается на шесть параллельных кривых, и мы ясно видим из толщины этих шести кривых, что дальнейшее увеличение приведет к еще более мелкому расщеплению. Эти 10е итераций заняли 12,5 ч на настольном компьютере Hewlett Packard 9815А, соединенном с графопостроителем 7225А, работающим с точностью 12 знаков.
На рис. 105 показана зависимость.^ от номера шага у последовательности, начинающейся в инвариантной точке Не. Мы видим, что после медленного начала график быстро развивается в функцию, имеющую вид белого шума. В пространстве (х, у) аттрактор состоит из ряда приближенно параллельных кривых, а точки последовательных итераций в конце концов всюду плотно распределятся на этих кривых в почти случайном порядке.
Рис. 100. Увеличение последовательности; все серии начинаются в точке Не. Используется не очень экономная программа, и построение графиков занимает 5* 18, 20 и 202 мин соответственно.
0,06667
0,024
1,28 x
Рис. 101. Увеличение последовательности; все серии начинаются в точке Не. Используется не очень экономная программа, и построение графиков занимает 5* 18, 20 и 202 мин соответственно,
Рис. 102. Второе увеличение последовательности, использующее экономящую время программу. Все серии начинаются в точке Не и занимают приблизительно 8 мин, 9 мин и 12,5 ч соответственно.
У
-0,07493
•0,1176
1,035
1,195 X
Рис. 103. Второе увеличение последовательности, использующее экономящую время программу. Все серии начинаются в точке Не и занимают приблизительно 8 мин, 9 мин и 12,5 ч соответственно.
Рис. 104. Второе увеличение последовательности, использующее экономящую время программу. Все серии начинаются в точке Не и занимают приблизительно 8 мин, 9 мин и 12,5 ч соответственно.
Рис. 105. График зависимости у от числа шагов, начинающийся в инвариантной точке Не,
8.3. Чувствительность к начальным условиям 175
Рис. 106. Начальное разбегание из двух стартовых точек, расположенных вблизи начала координат.
Как мы видели, в поперечном направлении происходит неограниченное размножение кривых, так что каждая видимая кривая на самом деле состоит из бесконечного числа квазипараллельных кривых. На основе этих наблюдений Хенон заключает, что поперечной структурой является канторово множество.
Тот факт, что даже после наших 106 итераций решение не расходится, свидетельствует о том, что на плоскости есть область, из которой точки не могут выйти. Этот результат Хеноном доказан: он нашел область R вокруг аттрактора, которая отображается внутрь себя.
8.3. Чувствительность к начальным условиям
Особенностью странного аттрактора, которую Хенон отдельно не исследовал, является его чрезвычайная чувствительность к начальным условиям, и здесь мы проведем предварительное исследование этого явления.
На рис. 106 показано разбегание двух траекторий, выпущенных из близких точек, во время нескольких первых итераций, а соответствующая зависимость расстояния г между двумя решениями от количества шагов итерации показана на рис. 107. Точки быстро расходятся и образуют аналог белого шума, когда их положения становятся по существу некоррелированными.
-3 ?
Стартовые точки (0, о) и (О,О<, 0,01)
Рис. 107. График зависимости расстояния г от числа шагов в случае начала счета из двух точек, близких к началу координат.
из двух точек, близких к началу координат точек.
8.4. Чувствительность к ошибкам вычислений 177
Рис. 109. Графики зависимости расстояния г от числа шагов, построенные в логарифмических осях, для нескольких пар начальных точек, расположенных вблизи начала координат.
Аналогичный график для очень близких начальных точек (0, 0) и (10-8, 10-8) показан на рис. 108, где отчетливо виден начальный экспоненциальный рост расщепления г.
Очевидно, что для отчетливого наблюдения этого явления график необходимо строить в логарифмических осях, как показано на рис. 109, где, как и можно было ожидать, для близких начальных точек получается практически прямая линия. Здесь показаны начальные точки с координатами (0, 0) и (Ю-*, Ю-^) для значений К, изменяющихся от 3 до 9. Легко видеть, что графики хорошо скоррелированы до тех пор, пока расщепление не становится относительно большим и —1g г стремится к нулю.
8.4. Чувствительность к ошибкам вычислений, получаемым в результате округлений
Только что обсуждавшиеся близкие начальные точки можно рассматривать как условные ошибки, полученные в результате округления. На рис. 109 мы видим, что при начальной ошибке порядка 10-3 соответствующую точность можно гарантировать только на протяжении 10 шагов, в то время как при начальной ошибке порядка 10-8 можно сделать 40 шагов. Очевидно, что компьютер любого размера и-точности быстро начинает давать ошибки при таком силь
178 Гл. 8. Хаотическая динамика странного аттрактора
ном разбегании. Шестнадцатизначная точность, которую использовал Хенон на IBM 7040, действительно несколько лучше, чем наша двенадцатизначная.
Какой смысл в таком случае можно придать численным решениям, при наличии столь сильного разбегания траекторий? По-видимому, ответ будет таким: в то время как правильное положение точки решения быстро теряется внутри притягивающих кривых, положение самих кривых точно определяется при помощи вычислений. Это объясняется тем, что наряду с сильным разбеганием точек внутри кривых имеет место также сильная сходимость к самим кривым аттрактора. Вот почему наши кривые по форме очень похожи на кривые, вычисленные Хеноном.
Некоторые авторы сомневались, действительно ли Хенон генерировал странный аттрактор, однако Холмс в своей статье [151] подтверждает, что Хенон действительно был прав. То, что такое безобидное отображение может вызвать очень сложное и квазислу-чайное поведение, представляет большой интерес для всех, кто пользуется вычислительными машинами; если решение представляет собой периодическое движение с очень большим периодом, то значение сказанного уменьшается ненамного.
8.5. Хаотические движения стержня
за пределом устойчивости. Некоторые современные работы
Странное поведение простой детерминистической динамической системы впервые наблюдал Лоренц и описал это явление в своей работе по атмосферной динамике [145], Рюэль и Такенс [146] предложили использовать странное поведение системы в теории гидродинамической турбулентности.
Большое количество современных статей по этому вопросу опубликовано в Annals of the New York Academy of Science под редакцией Гурела и Роеслера [135]. В книге Гумовского и Миры [157] имеется большое число рисунков типа рисунков Хенона. Устойчивость конечно-разностных систем исследуется Хсу и др. [159— 161].
Глубокое исследование странного хаотического поведения в механике имеется в работах Холмса [149—156]. Он исследовал физический и вычислительный смысл такого случайного поведения и провел специальное исследование магнитоупругой системы.
В частности, важным является его подробное исследование хаотических движений слегка выпученного,- подвергающегося боковому синусоидальному возмущению стержня [151]. Этот стержень можно моделировать системой с одной степенью свободы и с сильно нелинейной потенциальной энергией, определяющей две близкие конфигурации потери устойчивости. Представляющиеся случайными колебания стержня вызваны попеременным захватом траек-
8.5. Хаотические движения стержня 179
Рис. НО. Экспериментальная зависимость поперечного перемещения стержня, потерявшего устойчивость под действием синусоидальной силы, от времени.
тории двумя закритическими равновесными состояниями. На рис. ПО показан один предварительный результат, полученный на основе экспериментального исследования в University Colledge.
Прекрасное и хорошо написанное введение в теорию странных аттрактов с рисунками отображения Хенона, рассмотрением турбулентности жидкости и описанием частот спектра, наблюдаемых в течении Куэтта, дано Рюэлем [273]. В [273] определяется странный аттрактор и обсуждается множество физических проблем.
Глава
САМОВОЗБУЖДАЮЩИЕСЯ КОЛЕБАНИЯ ПРИ НЕКОНСЕРВАТИВНОЙ ГИДРОДИНАМИЧЕСКОЙ НАГРУЗКЕ
Ровный ветер, обдувающий инженерное сооружение, или вода, быстро текущая через трубу, могут непрерывно перекачивать энергию в систему, вызывая при этом большие и опасные вибрации и, возможно, разрушение. Гидродинамическая нагрузка не имеет потенциала и называется неконсервативной в противоположность, например, силе тяжести, которая для тела массы т, находящегося на высоте h в гравитационном поле напряженности g, имеет потенциал tngh. Изменение энергии системы, взаимодействующей с потоком жидкости, объясняется не диссипацией, присутствующей всегда за счет внутреннего трения, а наличием источника энергии.
В том случае, когда нагрузка на упругое тело или конструкцию является неконсервативной в указанном выше смысле, т. е. приложенные силы не могут быть представлены как градиент некоторой потенциальной функции, не имеет больше места простой энергетический статический критерий устойчивости [35, 37] и появляется возможность динамических бифуркаций устойчивости.
По проблемам этого типа в строительстве, машиностроении и авиационной промышленности было проведено много исследований; краткий обзор представлен в гл. 1 и публикации [274]. Здесь уместно сослаться также на другие работы по колебаниям и устойчивости механических систем [275—288], начиная от классической работы Крылова и Боголюбова 1947 г. и кончая современной монографией Найфе и Мука, в которой имеется обширная библиография. Кроме того, следует упомянуть работы по проблеме динамической потери устойчивости [289—291].
В работах Плаута [292, 293] рассматриваются общие неконсервативные системы; важное продвижение в анализе нелинейной устойчивости таких систем принадлежит Хусейну [294, 295], использовавшему метод возмущений. Для изучения бифуркаций, соответствующих раскачке и флаттеру автономных систем общего вида, Хусейн применяет непрерывное преобразование к каноническому якобиану, похожее на наши ранние схемы непрерывной диагонализации [36]. Преобразование позволяет провести полный анализ
9.1. Аэроупругое галопирование плохообтекаемых конструкций 181' устойчивости всех рассматриваемых траекторий равновесия. Кроме того, Хусейн в полной мере использует наличие многих управляющих параметров, следуя своей более ранней работе [33,351. Динамические бифуркации типа Хопфа также поддаются изучению в терминах теории катастроф; это кратко описано Стюартом в имеющем, большое значение обзоре [296].
На недавней конференции Торнтон [297] дал общий обзор современных и пока нерешенных проблем неустойчивости, с которыми сталкиваются в нефтяной промышленности при проектировании конструкций для открытого моря. Сюда относятся вибрации, вызванные водоворотами у места швартовки, вибрации в напорных трубах, а также возможная динамическая неустойчивость плавучих платформ.
9.1. Аэроупругое галопирование плохообтекаемых конструкций
Имеются три различных вида аэроупругой неустойчивости: галопирование по одной моде, вихревой резонанс и бимодальный флаттер; последний будет рассмотрен в следующем разделе.
Эффектные колебания и разрушение подвесного моста Такома, вызванные ровным ветром [298, 299], запечатлены на фото 11; можно думать, что они стали возможными-вследствие сочетания более чем одного из этих явлений. Участки Н-образной формы сечений в некоторых более ранних конструкциях подвесных мостов действительно легко вовлекались в крутильные колебания, вызываемые вихрями. Новый мост Хамбер (Humber) на фото 12 в настоящее время имеет самый длинный в мире пролет, который в полтора раза длиннее подвесного моста Такома, что свидетельствует о том, что инженеры-строители тщательно изучили проблему аэроупругости и полностью в ней разобрались.
Рассмотрим математическую теорию чистого галопирования, например, когда ветер со скоростью V обдувает квадратную призму (рис. 26 гл. 1). Призма массы tn, высоты Н и длины L может перемещаться только в вертикальном направлении под прямым углом по отношению к ветру и имеет одну обобщенную координату у, представляющую смещение вниз от положения равновесия. Призма опирается на упругую пружину жесткости k и соединена с вязкостным демпфером, который создает тормозящую силу гу, всегда противоположную скорости у.
Когда призма движется вниз со скоростью у, скорость воздуха относительно тела будет равна Vд (см. треугольник скоростей на рис. 26). Эта. относительная скорость ветра VR при угле а создаст вертикальную составляющую силы
182 Гл. 9. Самовозбуждающиеся колебания
где р — плотность воздуха, V — заданная горизонтальная скорость ветра, а а — площадь фронтальной поверхности HL. В предположении квазистатичности коэффициент С просто зависит от угла: a=arg tg(y/V), и, считая, что сила направлена вниз, действительно можно ожидать, что коэффициент будет отрицательным, как это всегда имеет место при больших значениях а. Однако при малых вертикальных скоростях коэффициент а может быть положительным для некоторых плохообтекаемых профилей, таких, например, как квадратная призма; на нижнем графике показаны две типичные зависимости С от а. Эти графики были построены Паркинсоном и Бруксом [95] на основании аэродинамических испытаний стационарно наклоненных профилей, следуя квазистатической гипотезе. Когда коэффициент С имеет тот же знак, что и у, аэродинамическая
Фото 11. Мост Такома Нэрроуз (Tacoma Narrows), Вашингтон, совершающий сильные крутильные колебания под действием ровного ветра. Этот подвесной мост с длиной пролета 2800 футов разрушился из-за аэроупругих вибраций в 1940 г. всего лишь через четыре месяца после введения в строй. Повороты составляли около 45° относительно горизонтали в обоих направлениях, а скорость ветра в момент разрушения моста была около 42 миль в час. Фотография приводится с разрешения Эллиота (В. D. Elliot),
Фото 12. Новый подвесной мост Хамбер (Humber), на сегодняшний день имеющий самый длинный в мире единственный пролет. Длина пролета (4626 футов) более чем в полтора раза больше злополучного моста Такома. Это показывает, что инженёры разобрались в аэродинамике конструкции и сумели подавить ранние формы неустойчивости. Консультирующей фирмой являлась фирма Freeman Fox and Partners. Фотография воспроизводится с разрешения Иннеса (I. Innes).
184 Гл. 9. Самовозбуждающиеся колебания
сила способствует любому начальному движению, и ветер можно рассматривать как отрицательный демпфер.
Уравнение движения аэроупругого осциллятора будет иметь следующий вид:
tny + г у + ky = 1i2pViaC (а),
а на основании графика экспериментальной зависимости С (а) коэффициент С можно представить в виде степенного ряда по ylV=* =tg а, откуда получаем уравнение
1 I 7 ’ \ 7 ' \3 7 • \& 7 • \71
my + ry + ky = трУ2а—+ ~
Здесь выписаны только нечетные степени в силу симметрии поперечного сечения призмы. Положительные и отрицательные знаки перед коэффициентами являются вопросом соглашения, и приведенная запись гарантирует, что для квадратной призмы все коэффициенты будут положительными.
При линеаризации этого уравнения следует сохранить только первый член ряда С, тогда результирующий коэффициент при у станет равным г—%рУ2а(Л1/Р). При положительном Аг для нашей квадратной призмы это результирующее демпфирование исчезает при критической скорости ветра, равной Ус=2г/(раЛ1).
Таким образом, для малых начальных отклонений любое начальное возмущение будет затухать при значениях V, меньших Vе, но при значениях V, больших Vе, малые возмущения будут расти вследствие отрицательности значения суммарного демпфирования, которое вызывает экспоненциальный рост колебаний. Следовательно, тривиальное равновесное решение у=0, справедливое при любых V, становится неустойчивым при критической скорости ветра Vе.
Выше этой критической скорости линейная теория предсказывает неограниченный экспоненциальный рост колебаний, в действительности же высшие члены в разложении С приводят к появлению предельного цикла конечной амплитуды. Размер этого предельного цикла растет от нуля, когда V проходит значение Vе, таким же образом, как мы уже видели в случае динамической точки бифуркации.
Некоторые типичные зависимости коэффициента аэродинамического сопротивления С (а) и образующиеся в результате динамические неустойчивости, полученные Новаком [97], показаны на рис. 111. Здесь, поскольку а очень близко к tg а во всем диапазоне указанных углов, вид функции С (а) идентичен виду функции C(y/V).
В первом случае, представляющем прямоугольное поперечное сечение в слегка турбулентном потоке, наклон кривой С (а) моно-
9.1. Аэроупругое галопирование плохообтекаемых конструкций 185
Рис. 111. Четыре характерные формы поведения коэффициента сопротивления, данные Новаком [97}, и результирующий динамический отклик системы на графике зависимости амплитуды предельного цикла у от скорости ветра V. Динамические бифуркации показаны в точке с критической скоростью Vе, устойчивые предельные циклы обозначены непрерывной кривой, неустойчивые предельные циклы — штриховой кривой. Скачок амплитуды колебаний, который будет наблюдаться при медленном увеличении скорости ветра, обозначается вертикальной стрелкой. Воспроизводится с разрешения Science Council of Japan.
тонно убывает от некоторого начального положительного значения. Это приводит к устойчивой динамической бифуркации, показанной на плоскости «амплитуда колебаний у — скорость ветра V». Устойчивый предельный цикл амплитуды у растет гладко от нуля по мере того, как скорость ветра увеличивается, превысив значение Vе.
Второй случай представляет собой рассмотренную ранее квадратную призму при ровном ветре. Сначала наклон С (а) убывает от своего начального положительного значения, вызывая опять устойчивую динамическую бифуркацию. Однако после этого начального уменьшения наклон на время увеличивается до тех пор, пока в конце концов не станет отрицательным. Это временное увеличение оказывает дестабилизирующее действие, вызывая образование складки на траектории предельного цикла. Таким образом, при медленном увеличении V система будет испытывать скачкообразное увеличение амплитуды колебаний, как показано стрелкой, а при последующем уменьшении скорости ветра наблюдается явление гистерезиса. Ниже в этом разделе дано экспериментальное, и теоретическое исследование этого случая.
186 Гл. 9. Самовозбуждающиеся колебания
А, 2,69
Аз 168
AS 6270
А7 59 900
Рис. 112. Полиномиальная аппроксимация экспериментально полученной зависимости коэффициента сопротивления Сфс) в случае квадратного поперечного сечения и соответствующие теоретические и экспериментальные результаты Паркинсона и Смита [96] на графике зависимости амплитуды колебаний от скорости ветра. Как видно, экспериментальные точки подтверждают теоретически предсказанный гистерезис и асимптоту. Экспериментальные значения скорости ветра существенно выше отмеченной области вихревого резонанса. Воспроизводится с разрешения Oxford University Press.
В третьем случае прямоугольный блок обдувается в продольном направлении ровным ветром. Функция С (а) при увеличении а сначала растет, а затем резко падает, что приводит к неустойчивой динамической бифуркации с последующей стабилизацией предельных циклов. Здесь снова при гладком изменении скорости V наблюдаются два динамических скачка.
В последнем случае рассматривается прямоугольный блок, стоящий поперек потока ветра. Угловой коэффициент функции С (а) вначале отрицателен. Это означает, что динамической бифуркации нет, но из-за того, что впоследствии он становится положительным, появляются, как показано, предельные циклы с большими отклонениями; их можно инициировать с помощью конечного динамического возмущения системы.
Следуя Паркинсону и Смиту [96], проанализируем нелинейное поведение с большими отклонениями квадратной призмы, принимая следующие значения коэффициентов:
Аг = 2,69, А, = 168, Дб = 6270, Д7 = 59900.
9.1. Аэроупругое галопирование плохообтекаемых конструкций 187
Как показано на рис. 112, эти значения хорошо согласуются с экспериментом.
При введении новых переменных
У = у/Н, x=~-wt, w2 = klm, U = V/(wH), п = p№L/(2m), Р = r/(2mw)
уравнение движения принимает вид
У + 2рУ + У = иП2С, где точка теперь обозначает дифференцирование по т. Более подробно это уравнение можно 'записать в следующем виде:
Здесь видно, что критические значения параметра U равны Uc=t
Уравнение равновесия имеет вид
Y + Y = F(Y).
Его можно решить с использованием первого приближения Крылова — Боголюбова
Y= Л cos (т + р).
Здесь амплитуда А и фаза р—медленно меняющиеся функции временного параметра т. В предположении медленного изменения амплитуды и фазы имеем приближенное равенство
Y = — A sin (т-J-p).
Умножая уравнение движения на Y, получим ^{Y* + Y*) = YF(Y), что дает
-j- Л2 = — Д sin (т + р) F (—A sin (т + р)).
Предполагая, что период цикла будет небольшим по сравнению с интервалами времени, за которые происходят заметные изменения амплитуды, можно усреднить правую часть уравнения по периоду цикла:
2л
4- 4г- = — о— ? A sin vF (—A sin v) dv.
2 dx 2n J ' '
о
188 Гл. 9. Самовозбуждающиеся колебания
Подставляя выражение для F и интегрируя, получим
-J-.L ( л5 \ до_35 f д7 \ д81
8 \AXU2) 64 к AtU6 J f *
Легко видеть, что полученное соотношение имеет характер баланса работ, в котором увеличение энергии приравнивается к работе сил, зависящих от скорости. Заметим, что величина р, которая не фигурировала в этом анализе, в первом приближении может быть положена равной нулю.
Для предельного цикла с постоянной амплитудой скорость изменения А2 можно положить равной нулю; тогда получим /у/ 2Р А2 3 ( Лз ) Д4-4-— (_А_^ А6 — — f Л8 = 0
[U nAjA ~ 4\ AiU + 8 k /htH 64 кД,^
Сокращая на Л2 и подставляя выражение для Uc, получим
,, Z7C ( ЗЛ3 \ а2 / 5ДБ \ Д'* ./ 35Д7 \ Д’
U ~ \ 4Аг ) U \8At) Us + \ 64 Д7 ) U2 ’
откуда следует, что при U—Uc имеет место динамическая бифуркация. Для закритического поведения в первом приближении имеем
U-Uc= .
к 4Аг) jjc
Ясно, что динамическая бифуркация является бифуркацией устойчивого типа с устойчивым предельным циклом, растущим по мере того, как U увеличивается, превзойдя значение Uc.
Разделив на U, получим
(ЫьД fAV_ /5Д5А / Д_у / 35Д7 \ / ду U ~\4A1J \ U ) к 8Д J \ U ) к 64Д1 U ) •
Отсюда видно, что, когда U стремится к бесконечности, левая часть уравнения стремится к единице, так что A!U должно стремиться к некоторому постоянному значению. Это означает, что график зависимости А от U будет стремиться к асимптоте, проходящей через начало координат. Кроме того, заметим, что если построить зависимость A/Uc от UIUC, то будет существовать единственная кривая, не зависящая от п и р.
Результаты расчета показаны на рис. 112, где видно, что они находятся в отличном согласии с экспериментальными данными, опубликованными Паркинсоном и Смитом [961. Устойчивость предельных циклов можно оценить, изучая знак производной dA2/dt, а гистерезис экспериментальных данных ясно виден на рисунке.
Фазовый портрет, показывающий совокупность из трех предельных циклов при Й/С/с=1,6, приведен на рис. 113, а график универ-
9.2. Флаттер крыла самолета при сверхзвуковых скоростях 189
Рис. 113. Два устойчивых предельных цикла, разделенных неустойчивым предельным циклом.
сальной кривой описан Новаком [300], который рассматривал скачкообразное поведение непрерывных систем. Полезный обзор литературы имеется в последней работе Блевинса [98].
9.2. Флаттер крыла самолета при высоких сверхзвуковых скоростях
Флаттерная неустойчивость пластин и оболочек представляет важную техническую проблему, изучение которой стимулировалось выходом из строя самолетных конструкций, деталей космических и реактивных двигателей [111]. Современные исследования много сделали для преодоления первоначальных расхождений между теорией и экспериментом, однако важные нелинейные задачи остаются нерешенными до сих пор. Они связаны. главным образом со структурной нелинейностью пластин, которая стабилизирует зарождающийся флаттер на конечном предельном цикле. Эта стабилизация обычно предотвращает немедленный выход из строя деталей конструкций, который часто возникает у несущих поверхностей, но открывает дорогу продолжительному усталостному разрушению.
Проводились обширные экспериментальные исследования в сверхзвуковых аэродинамических трубах, в испытательных поле-
190 Гл. 9. Самовозбуждающиеся колебания
тах гиперзвукового исследовательского самолета Х-15 и пусковых ракет S-IVB для программы исследования Луны «Аполло». Эти испытания, а также теоретический анализ Доуэлла [НО] показывают, что сверхзвуковой флаттер соответствует устойчивой динамической бифуркации Хопфа, как показано схематически на рис. 114. Здесь, как и во всех работах по теории флаттера, в качестве управляющего параметра выбран скоростной напор A=pt72/2 — половина произведения плотности на квадрат скорости потока. Считается, что число Маха значительно больше единицы и поддерживается постоянным.
mtfij+gijq j+Qjq j+Ni(qj)=O
mij—инерция
glj — поток U
I поток
C/y < упругость
I сжатие
Нелинейная упругость
Л/i = 4^i -f-169192
N2—169192+6492
Эти формулы следуют из выражения для энергии
1/л-=9?+&№ + 16?!
Рис. 114. Флаттер длинной панели, вызываемый сверхзвуковым потоком газа с большим числом Маха. Основной управляющий параметр — динамическое давление А, число Маха поддерживается постоянным. Второй управляющий параметр — предварительное напряжение Р,
9.2. Флаттер крыла самолета при сверхзвуковых скоростях 191
Рассмотрим, в частности, существенно сверхзвуковой поток, обтекающий панель (рис. 114) [1101. Она шарнирно оперта по краям и имеет на конце пружину, которую можно использовать для предварительного напряжения. Длина панели равна а.
Доуэлл использует уравнения теории упругости, соответствующие уравнениям Кармана для пластин с большим прогибом, так что нелинейность системы объясняется в основном действием в плоскости мембранных усилий, а не влиянием кривизны. Используется квазистационарная и линейная аэродинамическая теория, согласно которой нормальные силы пропорциональны угловому коэффициенту dwldx и скорости dwldt. Отметим, что нелинейные аэродинамические силы рассматривались Болотиным [2801.
Отклонения w(x) представляются в виде ряда Фурье, причем мы рассмотрим здесь только первые два члена ряда. Чтобы получить точные количественные результаты, Доуэлл вводит в рассмотрение шесть мод, при этом он показывает, что две моды дают правильную качественную картину.
Для получения системы уравнений движения, которая обведена на рис. 114 в рамку, используется метод Галеркина. Ниже под рамкой вычислены коэффициенты уравнений. Система уравнений решается численно. Инерционные члены связаны с обычными колебаниями панели. Демпфирование конструкции исключено из рассмотрения, однако течение газа порождает эффективную положительно определенную вязкую диссипацию, пропорциональную скорости U, как видно из выражений для коэффициентов gtj. Кроме того, поток газа вызывает силы ci}qj, линейно зависящие от смещения. Вклад в коэффициенты с1}, связанный с потоком газа, антисимметричен и, следовательно, порождает вращательное движение. Он пропорционален квадрату скорости.
Другие два вклада в коэффициенты ci7- связаны с упругостью панели и предварительным напряжением Р. Наконец, нелинейные упругие силы и N2 порождаются нелинейным потенциалом 1^; их можно получить из теории пластин с большим прогибом [36], учитывающей квадрат удлинения.
Поскольку силы со стороны газа, зависящие от скорости, соответствуют положительно определенной вязкой диссипации, мы видим, что непосредственной причиной, вызывающей флаттерную неустойчивость, является антисимметричная часть матрицы ci}. Сравнение с другими причинами флаттера показано на рис. 30 гл. 1. Кроме того, следует отметить, что линейная неустойчивость заметно стабилизируется нелинейным действием упругих мембранных сил.
Наконец, Доуэлл дает диаграмму .взаимодействия флаттера и дивергенции в пространстве управляющих параметров А и Р и описывает некоторые нелинейные взаимодействия между этими явлениями. Этот аспект исследуется Холмсом [1131, который связывает его с классификацией Такенса [301, 302]. Доуэлл вводит
192 Гл. 9. Самовозбуждающиеся колебания
в рассмотрение эффект, связанный с перепадом статического давления, который здесь игнорируется.
В заключение следует упомянуть исследования флаттера, проведенные Доуном [303, 304] и опубликованные Aeronautical Research Council.
9.3. Динамическая и статическая неустойчивость трубы, по которой перекачивается жидкость
Рассмотрим быстрый поток воды в гибкой упругой трубе под действием на нее по всей длине некоторой силы. Если труба изогнута и неподвижна, то жидкость испытывает центростремительное ускорение U2!R, где U — скорость потока, a R — локальный радиус кривизны трубы. Таким образом, появляется поперечная центробежная сила величины MU2&x'R, действующая на элемент трубы длиной 6х, где М. — масса жидкости на единицу длины. Массу М можно записать в виде рА, где р— плотность жидкости, а А — площадь попер.ечного сечения трубы.
Как ни странно, эти поперечные центробежные силы, распределенные по всей длине трубы, механически эквивалентны сжимающей торцевой нагрузке величины ЛШ2, приложенной у выпускного отверстия [305]. Однако следует помнить, что физически при отсутствии сопла такой торцевой нагрузки не существует.
Для шарнирно опертой трубы, у которой нет поперечных перемещений на концах и один конец служит для выпуска жидкости в атмосферу, сила со стороны жидкости MU2 будет по существу консервативной. Она может изогнуть первоначально прямую упругую трубу при критической продольной нагрузке Эйлера, равной MU2==n2EllL2. Выражение в правой части уравнения было получено в гл. 2 в случае механического нагружения. Здесь EI — жесткость трубы на изгиб, a L -— длина трубы между шарнирными опорами. Такую статическую потерю устойчивости называют дивергенцией для того, чтобы отличить ее от колебательного динамического флаттера. Она идентична статической потере устойчивости, которая наблюдается у механически нагруженного стержня и соответствует нелинейной устойчиво симметричной точке ветвления, в которой основная траектория безызгибного равновесия пересекает траекторию устойчивого закритического равновесия [305].
Для трубы-консоли, один конец которой закреплен, а из другого конца вытекает жидкость, сила со стороны жидкости, равная по величине MU2, будет касательна к свободному концу трубы. Такая следящая сила является неконсервативной и не может быть выведена из энергии. В соответствии с терминологией гл. 1 она классифицируется как циркуляционная и может перекачивать энергию во время любого замкнутого цикла колебаний.
9.3. Динамическая и статическая неустойчивость трубы 193
Рассматривая первоначально прямую упругую трубу-консоль, можно сделать вывод, что «эффективная» торцевая сила не может удержать трубу в статическом изогнутом состоянии. Это становится очевидным, если рассмотреть знак кривизны и изгибающий момент в окрестности конца. Попытка представить трубу, кривизна и момент которой имеют противоположные значения, несовместима с упругими свойствами трубы. Поэтому для трубы-консоли вообще не существует решений уравнений равновесия как с большими, так и с малыми прогибами, отличными от тривиального прямого состояния.
Следовательно, у трубы-консоли не бывает статических бифуркаций. Однако общеизвестно, что при определенной скорости потока неизогнутая форма трубы становится неустойчивой и в трубе развиваются динамические колебания большой амплитуды. Отрезок гибкой резиновой трубы, прикрепленный к выпускному отверстию, будет испытывать динамический флаттер. Такая неустойчивость соответствует динамической бифуркации Хопфа, при которой линейный анализ предсказывает экспоненциальный рост колебаний. Исследование Бенджамином модели трубы, составленной из звеньев, обсуждалось в гл. 1.
При движении шарнирно опертой или консольно заделанной трубы начинает играть роль вторая распределенная поперечная сила, вызванная кориолисовым ускорением жидкости, текущей Через вращающийся элемент трубы. Это происходит вследствие ускорения полярной координаты 2г 0, где г — скорость жидкости, а 0 — скорость вращения элемента трубы. Роль этого ускорения, возникающего при лабораторных испытаниях в центрифуге, описывается в небольшой статье [3061.
При малых изгибах шарнирно опертой трубы кориолисовы силы являются по своей природе гироскопическими и не совершают работы на действительных перемещениях. Однако они совершают работу на некоторых виртуальных перемещениях, и их необходимо включить в любой динамический анализ. При малых изгибаниях трубы-консоли эти силы совершают отрицательную работу и, таким образом, диссипируют энергию, как видно на рис. 28—30 гл. 1.
Третья сила, действующая на трубу со стороны жидкости,— это осевое сопротивление, но оно обычно исключается из анализа [305], поскольку, как показал Бенджамин [114], оно обычно не играет роли при больших и малых (статических или динамических) изгибаниях трубы.
Дифференциальное уравнение для поля малых поперечных перемещений w(x, t) упругой трубы выражает условие равенства нулю суммы поперечных сил, действующих на элемент трубы. Эти силы перечислены в таблице рис. 115. Здесь w — поперечное перемещение
7 № 523
5^=0 Шарнирно заделанная труба, по которой транспортируется жидкость
Инерция от,7 У2Ь (т + М) 1 0 0 1
dw c dt Демпфирование со стороны воздуха Sif YiLc 1 0 0 1
d*w dx* dt Демпфирование в материале стенок трубы Е*1 (л/L)*Y2L 1 0 0 16.
WM-^r dx dt Кориолисова сила, действующая на жидкость 4 2UM.-O О 0 -1 1 0
El9^ dx* Упругая сила ciJ El(n!L)*ytL 1 0 0 16
p 9*w P°d? Предварительное сжатие P^nlL^ У2Ь -1 0 0 —4
Kw Реакция основания У2ЬК 1 0 0 1
N=E1^+E*l^ дх2 1 дх2 dt
дх
dQ , n d2w
Рис. 115. Схема и коэффициенты в задаче о колебаниях шарнирно опертой трубы, по которой перекачивается жидкость. Сумма поперечных сил на элемент длины дает дифференциальное уравнение движения, которое дискретизируется методом Галеркина для двух гармоник.
П р одолжение
mu2^-dx2 Центробежная сила, действующая иа жидкость ch- MU2(n/L)2V2L -1 0 0 -4
у dx2 X 0 2 dx Осевая упругая сила Ni i/skL2 (л/L)4 <?i + 4<7i<?2 4?i<?2 + 16<7з
у dx2 X L ч a i e/dw' *dt 2a\\dx, 0 2 | dx Осевая вязкость l/«aL2 (л/L)4 9191 + 4<71<72<72 4919192+ 169292
196 Гл. 9. Самовозбуждающиеся колебания
в момент времени t точки, находящейся в начальный момент времени на расстоянии х от левой опоры. Дифференциальное уравнение применимо как для шарнирно опертых, так и для консольно заделанных труб, поскольку эти случаи отличаются лишь краевыми условиями.
Первый член представляет собой силу инерции единицы длины трубы и жидкости с массами т и М соответственно. Они умножаются на поперечное ускорение d^wldt2.
Второй член представляет собой вязкое демпфирование со стороны воздуха, окружающего трубу, и равен произведению коэффициента трения с на поперечную скорость dwldt.
Третий член — это демпфирование, вызванное вязкоупругими свойствами материала трубы. Здесь Е*1— параметр трубы, аналогичный жесткости трубы на изгиб EI.
Четвертый член — это вышеупомянутая сила Кориолиса; смешанная производная d2wldxdt является скоростью вращения элемента трубы. Отметим, что этот член линейный относительно скорости потока U.
Пятый член является обычным в теории упругости; он вызывается сдвигающей силой, действующей внутри трубы.
Шестой член представляет собой дестабилизирующее действие предварительного сжатия Ро. Он возникает как результат взаимодействия мембранного усилия сжатия и кривизны д2ы'дх2.
Седьмой член возникает, если труба опирается на сплошное упругое основание жесткости К- Предполагается, что такое основание может действовать на единицу длины трубы поперечной силой Kw.
Восьмой член является вкладом уже обсуждавшихся центробежных сил и равняется величине MU2, умноженной на линейную аппроксимацию кривизны d2w/dx2. Мы видим, что этот член имеет вид, полностью эквивалентный действию предварительного сжатия Рй.
Девятый и десятый нелинейные члены возникают при учете влияния продольных перемещений и здесь рассматриваться не будут.
Приравняв сумму первых восьми членов нулю, получим линейное дифференциальное уравнение движения трубы, испытывающей малые поперечные колебания. Вывод этого уравнения без подробного обоснования можно найти в работе Пайдуссиса и Иссида [307].
Запишем дифференциальное уравнение движения трубы в форме D{u>(x)}=0. Будем решать его приближенно для шарнирно опертой трубы, применяя метод Галер кина. Для этого аппроксимируем w(x, t) двумя членами ряда Фурье:
w(x, 0 = ?i(0sin-2-+?2sin —.
Каждое слагаемое в. этом выражении удовлетворяет краевым условиям для шарнирно опертого стержня или трубы.
9.3. Динамическая и статическая неустойчивость трубы 197
Подставляя это выражение в D, получим, что D (w) не равно нулю, но, приравнивая нулю два средних значения с некоторым весом и выбирая сами моды как весовые функции, придем к уравнениям
L L
J D {&> (х)} sin dx = О, J D {w (х)} sin dx = 0. 0 О
Интегрируя и используя хорошо известные свойства ортогональности тригонометрических функций, после некоторых алгебраиче-, ских вычислений получим систему обыкновенных дифференциальных уравнений
т.уЪ + ЁцЧ} + cl}q} = О, где суммирование производится по повторяющимся индексам, индексы принимают значения 1 и 2, точка обозначает дифференцирование по времени t. В последних столбцах таблицы рис. 115 приводятся вклады, которые дают различные члены уравнения в коэффициенты tTlij, gtj и с1}.
Отметим, что для энергетических членов результаты применения метода Галеркина в точности совпадают с результатами расчета по методу Рэлея — Ритца. Воздушное демпфирование и демпфирование трубы описываются симметричными положительно определенными матрицами: первая имеет такой же вид, как матрица инерции, а вторая — как матрица упругости. Уже известные нам симметричные матрицы упругости и предварительного сжатия приводят к двум самым низким критическим эйлеровым нагрузкам для стержня. Предварительное сжатие увеличивается за счет центробежных сил ЛП72. Упругое основание описывается простой диагональной матрицей, что позволяет, как было отмечено в гл. 2, легко найти эйлеровы нагрузки для стержня на упругом основании.
Силы Кориолиса дают антисимметричную матрицу, поэтому эти силы не совершают работу и их можно классифицировать как гироскопические. Два дифференциальных уравнения движения оказываются связанными только благодаря силам Кориолиса. Поскольку в рассматриваемой гироскопической системе имеется положительно определенное демпфирование, минимум общей потенциальной энергии будет как необходимым, так и достаточным условием устойчивости, а значит, неустойчивость можно будет легко предсказать. Из-за непрерывной диссипации энергии образование предельных циклов будет невозможно, и, следовательно, появится динамическая бифуркация Хопфа. Однако, как мы увидим, в основном неустойчивом состоянии равновесия при нагрузках выше второй эйлеровой критической нагрузки под действием сил Кориолиса может происходить увеличение амплитуды колебаний. Другими словами, хотя кориолисовы силы могут влиять на детали динамики, эти не совер
198 Гл. 9. Самовозбуждающиеся колебания
шающие работы силы не меняют зон устойчивости демпфированной системы.
Исследуем сначала линейное приближение без учета гироскопических сил. Это даст информацию об устойчивости трубы, по которой течет жидкость. Заметим, что при приравнивании U и М нулю получатся уравнения, описывающие динамику демпфированного эйлерова стержня с учетом или без учета упругого основания. При исключении из рассмотрения членов, связанных с силой Кориолиса, уравнения движения расщепляются, при этом получаются уравнения двух независимых затухающих линейных осцилляторов. Демпфирование всегда положительно, поэтому, когда жесткость принимает нулевое значение, имеет место статическая потеря устойчивости (дивергенция). Таким образом, приравнивание сг1 нулю дает потерю устойчивости по первой моде, когда
Рс + MU* = El (n/L)2 4- К (Ь/л)2,
а приравнивание с22 нулю дает потерю устойчивости по второй моде, когда
’Р9 + MU* = ЬЕ1 (n/LY + >/4К (L/ny.
Здесь за счет потока жидкости происходит увеличение эффективного-сжатия на ЛП72; кроме того, можно проследить за влиянием на колебания упругого основания. При M=K=U—Q получается обычная формула Эйлера для критической нагрузки.
Рассмотрим теперь линейное поведение гироскопической системы, учитывая влияние жидкости и отбрасывая члены, вызывающие демпфирование. Как будет видно дальше, это приведет к патологической системе, в которой при введении бесконечно малого затухания гироскопическая стабилизация не сохраняется. Линейные уравнения движения такой системы имеют вид
tntjqjA-gijqj-PCijqj =0.
Положим qj—Ajeu. Условие существования нетривиального решения есть равенство нулю характеристического определителя:
I + §,-/ + са\ = °-
Матрицы тц и Сц теперь являются диагональными, a g^ в отсутствие демпфирования — антисимметричная матрица, так что характеристическое уравнение имеет вид
(/т?! Д2 4- С(1) (/7?22>-2 + С22) + gl№ = 0.
Полагая Х2=М, получим квадратное уравнение относительно N:
N* (тит22) 4- N (тис22 4- m22cn 4- glA 4- сис22 = 0.
Чтобы записать коэффициенты в более удобном безразмерном виде, разделим уравнение на эффективную массу и введем вспомо
9.3. Динамическая и статическая неустойчивость трубы 199
гательную временную переменную x=zt, подбирая при этом пара' метр z так, чтобы модуль упругости равнялся единице. Тогда систе' му дифференциальных уравнений можно записать в форме
[1 01.. ГО —11. Г1 0 1 Г—1 01
[0 1]9/ + И«л | i о]9у + [о 16]‘7у + Л 0 — 4у/ = °’ где точкой обозначается дифференцирование по т, параметр а имеет значение
а= (16/Зп)2 (М)(т-\- М)),
а в качестве параметра нагрузки взята величина
Л = ЛШ2/(л2Е//£2).
Здесь мы положили P«g=K=0, сосредоточивая основное внимание на влиянии нагрузки на трубу со стороны жидкости при отсутствии упругого основания.
После подстановки коэффициентов из нормированной системы уравнений характеристическое уравнение принимает вид
№ + # (17-5Л+аЛ) + (1 - Л) (16-4Л) = 0.
Отметим, что оно удовлетворяется при N=0, когда нагрузка соответствует эйлеровой критической нагрузке при Л, равном единице или четырем. В этом уравнении а представляет собой относительную интенсивность кориолисовых сил, которая равна нулю, когда 7И//и=0, и принимает максимальное значение, равное (16/3л)2=« =2,882, когда М/т стремится к бесконечности.
Для исследования устойчивости основного состояния равновесия трубы необходимо для заданного значения а изучить движение корней характеристического уравнения при возрастании параметра нагрузки Л от нулевого значения. Запишем X=/?4~t7, где I — мнимая единица. На рис. 116 построены траектории движения' корней характеристического уравнения в трехмерном пространстве (Л, R, I). При а=0 получаем картину, соответствующую стержню Эйлера; она показана на первой диаграмме. Здесь имеются две статические неустойчивости, когда корни последовательно меняются от мнимых до действительных, соответствующих значениям Л=1 и 4.
При а=0,03 единственная заметная разница заключается в развитии двух замкнутых контуров, где относительно небольшие силы Кориолиса могут привести к колебаниям в небольшой зоне с приблизительно равными действительными частями.
При а=0,2882 и Л4/(Л4+/тг)=0,1 эти замкнутые контуры выросли. Более ясно они показаны на рис. 117 при малых значениях Л, где выделены некоторые характерные особенности их геометрии. В точке F можно ясно увидеть начало роста колебаний типа флаттера. Эти флаттерные точки F движутся внутрь с увеличением а до
200 Гл. 9. Самовозбуждающиеся колебания
Рис. 116. Движение корней в комплексной скорости (R, 1) показано в пространстве трех измерений с нагрузкой Л по вертикальной оси. Рисунки построены для шарнирно опертой трубы без демпфирования.
тех пор, пока при а=0,75 не произойдет их слияние со статической бифуркацией Л=4, как показано на рис. 116.
График для большего значения а=1,441 (это соответствует значению М/(М-\-т)—0,5) показан на рис. 116, а увеличенное его изображение— на рис. 117. Здесь вторая статическая бифуркация при Л=4 соответствует не переходу вторых корней I-+R, а обратному переходу первых корней Это означает, что имеется область устойчивости, находящаяся выше второй эйлеровой нагрузки и возникающая перед началом флаттера в точке F. Однако эту гироскопическую стабилизацию следует классифицировать как временную, поскольку она полностью разрушается даже при бесконечно малом демпфировании. Это непосредственно вытекает иа
Рис. 117. Несколько увеличенные детали двух картин из рис, 116 более ясно показывают переходы устойчивости.
£02 Гл. 9. Самовозбуждающиеся колебания
энергетического рассмотрения, поскольку прогнозируемые замкнутые колебания невозможны даже при наличии небольшого демпфирования. Так как общая потенциальная энергия (включая вклад от MUZ) достигает максимума в основном состоянии равновесия выше второй эйлеровой критической нагрузки, незначительное демпфирование уведет систему от верхушки горба потенциала по колебательному закону. График при экстремальном значении а=2,882 не содержит новых особенностей.
На рис. 118, который взят из статьи Томпсона и Лунна [308], показано, как вследствие небольшого демпфирования разрушается временная гироскопическая устойчивость.
В табл. 6 дана сводка работ, в которых рассматривалась задача о шарнирно опертой трубе. Следуя Ниордсону [3091, Бенджамин [114] проводит некоторые теоретические и экспериментальные наблюдения по поведению шарнирно опертых труб, полученные при исследовании сочлененных труб-консолей. В 1969 г. Турман и Моут [310] провели исследование больших нелинейных колебаний труб
9.3. Динамическая и статическая неустойчивость трубы 203
Таблица 6. Список исследований по колебаниям шарнирно опертой трубы, по которой перекачивается жидкость
Цельная или составная труба Включает эксперимент Линейная или нелинейная Включает демпфирование
1954 Ниордсон Цельная Hei Линейная Нет
1961 Бенджамин Составная Да » в
1969 Турман и Моут Цельная Нет Нелинейные колебания в
1974 Пайдуссис и Иссид В » Линейная Да
1975 Хусейн и Плаут » в В Нет
1975 Плаут и Хусейн » » в В
1977 Холмс » Нелинейная . проблема Эйлера Да
1981 Холмс » » То же В
Отметим также обсуждение источников энергии Уивером (1974) и исследование труб с защемленными концами Пайдуссиса (1975).
с шарнирно заделанным концом, но при этом не рассмотрели статическое закритическое поведение.
В 1974 г. Пайдуссис и Иссид [307] провели глубокий теоретический анализ наряду с обширным обзором более ранней литературы. Они изучили линейное поведение опертых труб как с учетом, так и без учета демпфирования. Кроме того, они наблюдали за флаттером после начальной дивергенции, а также за тем, как демпфирование разрушает любую временную гироскопическую устойчивость. Хусейн и Плаут [311, 312] проанализировали линейное недемпфированное поведение шарнирно опертых труб, используя метод Галер-кина.
И наконец, Холмс в двух важных статьях по нелинейным колебаниям [113, 313] рассмотрел закритическое поведение таких труб. Во второй статье он отметил, что при наличии демпфирования трубы не попадают в режим незатухающего флаттера в предельном цикле из-за отсутствия неконсервативного источника энергии. Действительно, флаттер с увеличивающейся амплитудой, который можно наблюдать при нагрузке выше второй эйлеровой критической нагрузки, возникает в системе, проходящей через максимум энергии. Холмс отмечает, что в данном случае за колебательную природу переходов через максимум ответственны не совершающие работу силы Кориолиса. Следует обратить внимание на этот аргумент,
204 Гл. 9. Самовозбуждающиеся колебания поскольку было много путаницы относительно источника энергии [314] флаттера при больших нагрузках.
Прежде чем перейти к анализу трубы-консоли, следует отметить, что труба, заделанная на двух концах, которая ведет себя так же, как и свободно опертая труба [305], являлась предметом обсуждения в работе Пайдуссиса [315] в 1975 г.
В табл. 7 представлена история, изучения флаттера трубы-консоли, начиная с классической работы Бенджамина [114], написанной, в 1961 г. Он изучил как теоретически, так и экспериментально трубы, составленные из шарнирно соединенных звеньев, и рассмотрел предельный переход к цельной трубе, когда число звеньев становится большим. В линейной постановке Бенджамин получает уравнения движения, используя метод Лагранжа и Гамильтона, и отмечает, что демпфирование консольных труб обусловлено силами Кориолиса, и поэтому отпадает необходимость введения демпфирования конструкции. Не применяя линеаризацию системы, он доказывает ненужность учета сопротивления жидкости и рассматривает эквивалентные концевые сжимающие нагрузки как для консольных, так и для свободно опертых труб. Выражение для энергии колебания цикла было выведено аналогично дифференциальному уравнению для цельной трубы.
Следующие три работы Херрманна и его соавторов посвящены теории, линейного флаттера двухзвенной модели со следящей силой на торце. Поскольку члены, связанные с кориолисовыми силами, не учитывались, эти работы (а также другие, рядом с которыми в таблице написано «следящая сила») не касаются непосредственно труб с движущейся жидкостью, поскольку в них моделируется лишь эквивалентное торцевое сжатие, вызванное центробежными силами. В 1964 г. Херрманн и Бангей [316] исследовали эффект изменения соотношения между консервативной и неконсервативной нагрузками, вводя коэффициент запаздывания а;, демпфированием в модели пренебрегал ось. Херрманн и Джонг [143] в 1965 г. исследовали конечную дестабилизацию бесконечна малого демпфирования при а=0 (см. рис. 33 гл. 1). Через год они рассмотрели эту проблему для случая В 1966 г. Херрманн и Немат-Нассер [317] рассмотрели ту же самую модель с демпфированием для а=0 при помощи энергетического метода.
Важное исследование двухзвенной модели со следящей силой было выполнено в рамках нелинейной теории Роордой и Немат-Нассером [116] в 1967 г. с привлечением энергетического подхода. Они показали, что при устойчивом зафлаттерном поведении в нормальном случае положительная закритическая кривизна зависит от скорости затухания.
Пайдуссис и соавторы в ряде работ [119, 307, 318, 319], написанных за период с 1966 по 1974 г., рассмотрели теоретически и экспериментально поведение цельных консольных труб, по которым.
9.3. Динамическая и статическая неустойчивость трубы 205
Таблица 7. Обзор исследований по флаттеру труб-консолей, по которым течет ж идкость
Течение в цельной или составной трубе; или двухзвенной со следящей силой Включает эксперимент Линейный или нелинейный Учитывает демпфир ова н ие
1961 Бенджамин Составная с цельной в качестве предела Да Линейный Да, из-за кориолисовых сил
1964 Херрманн и Бангей Следящая сила Нет » Нет
1965 Херрманн и Джонг » » » » Да
1966 Херрманн и Немат-Нассер » » » » »
1966 Грегори и Пайдуссис Цельная Да » Да плюс кориолисовы силы
1967 Poopда и Немат-Нассер Следящая сила Нет Нелинейный +, демпфирование Да
1970 Пайдуссис Цельная Да Линейный »
1970 Пайдуссис и Декснис Составная и цельная » Да, из-за кориолисовых сил
1972 Бургесс и Левинсон Следящая сила Нет Нелинейный +/—, жесткость Нет
1974 Пайдуссис и Иссид Цельная Нет. стр. 281 экспериментальные предельные циклы Линейный »
1974 Бон и Херрманн Составная Да, с обсуждением нелинейных эффектов Линейный Да
1976 Бишоп и Фаузи Цельная в случае классических мод Да » »
1977 Руссле и Херрманн Составная Короткие корреляции Нелинейный +/—, масса Да, плюс кориолисовы силы
Плюс или минус в нелинейном анализе обозначает знак закритической кривизны, зависящей от системы параметров следящей силы.
транспортируется жидкость. В одной из этих статей [119] Пайдус-сис и Декснис обращают внимание на тот факт, что теория для сочлененных труб не очень хорошо согласуется с теорией для цельных труб, даже когда число звеньев становится большим. Теоретическая часть этих четырех работ была выполнена в рамках линейной
206 Гл. 9. Самовозбуждающиеся колебания
теории, но в работе Пайдуссиса и Иссида [307] кратко обсуждаются экспериментальные данные для нелинейных предельных циклов.
Нелинейный анализ системы со следящей силой, проведенный Бюргессом и Левинсоном [320] в 1972 г., недостаточен в связи с тем, что авторы не включают в рассмотрение демпфирование, которое, будучи даже бесконечно малым, может, как мы видели, явиться причиной конечных изменений при критической флаттерной нагрузке. Они нашли положительную и отрицательную закритиче-скую кривизну, зависящую от используемых коэффициентов нелинейной жесткости.
Бон и Херрманн [321] в 1974 г. провели теоретическое и экспериментальное исследования трубы, составленной из двух звеньев, по которой течет жидкость. Демпфирование было включено в линейную теорию, обсуждаются также некоторые нелинейные экспериментальные данные. Вслед за этой работой в 1976 г. Бишоп и Фаузи [118] провели большое теоретическое и экспериментальное исследование, в котором рассмотрели линейные колебания и устойчивость подвешенной трубы с соплом как с учетом, так и без учета гармонической вынуждающей силы.
В последней в этом списке статье Руссле и Херрманна [117], опубликованной в 1977 г., дается нелинейный теоретический анализ шарнирно сочлененной трубы из двух звеньев, по которой течет жидкость. В рассмотрение включено демпфирование. Наблюдаются устойчивые и неустойчивые точки динамической бифуркации, получена зависимость знака закритической кривизны от отношения масс, хорошо коррелирующая с экспериментом. Заданной величиной здесь является высота гидростатического напора, а не скорость течения. Эта работа является существенным вкладом в проблему течения в трубах, предсказывая как за-, так и докритические динамические бифуркации, зависящие от точного отношения масс в модели шарнирно сочлененных труб.
Многообещающий энергетический подход, который позволяет исследовать закритическое поведение неконсервативных автономных и неавтономных систем, разработан Лейпхольцем [322].
9.4. Резонансная чувствительность динамической бифуркации Хопфа
В этом заключительном разделе главы о неконсервативных задачах рассмотрим одну неавтономную задачу, включающую в качестве частного случая задачу о нелинейном осцилляторе, возбуждаемом периодической силой. На протяжении многих лет, начиная с первых работ Ван дер Поля [323, 324], вынужденные колебания нелинейной системы являются важной проблемой в теории электрических цепей. Недавно Холмс и Рэнд [124, 131] исследовали некоторые из рассматриваемых ниже бифуркаций.
9.4. Резонансная чувствительность бифуркации Хопфа 207
Речь пойдет о чрезвычайно простом нелинейном осцилляторе, который, если линейное демпфирование становится отрицательным, при отсутствии вынуждающей силы проявляет динамическую бифуркацию типа Хопфа. В этом отношении его поведение аналогично галопированию упругой конструкции. Резонанс в такой конструкции может быть вызван периодическим срывом вихрей, что и служит некоторым наводящим соображением для излагаемого дальше исследования вынужденных колебаний осциллятора. Изложение основано на недавней статье Томпсона и Лунна [325].
Галопирование плохообтекаемого упруго опертого тела в стационарном потоке жидкости может носить неустойчивый динамический характер, а значит, можно ожидать некоторой чувствительности к несовершенствам, как это имело место в статическом случае. Однако известно, что при изменении единственного управляющего параметра такая динамическая бифуркация Хопфа остается топологически устойчивой; это означает, что изменением второго управляющего параметра нельзя скруглить или разрушить топологическую форму бифуркации Хопфа.
Однако, поскольку динамические неустойчивости связаны с хорошо определенной ненулевой циклической частотой, можно ожидать, что разрушающие «нагрузки» будут чувствительны к резонансному периодическому воздействию. Такое периодическое воздействие не следует обычно рассматривать при оценке топологической устойчивости, но оно может естественно возникнуть в ре-1 альной физической проблеме.
Фактически мы покажем, что периодическое вынуждающее воздействие изображается траекториями, окружающими бифуркацию Хопфа, и приводит к закону чувствительности двух третей аналогично точке возврата для катастрофы сборки в статике. Для рассматриваемого частного нелинейного уравнения движения аналогия со статической бифуркацией в действительности очень точна и дает возможность использовать стандартные статические диаграммы и формулы для динамической бифуркации.
Рассмотрим нелинейный осциллятор с одной степенью свободы, который описывается уравнением
x+bx + cx + N (х, x) = fsinco/, где х—отклонение, b — коэффициент затухания, с— коэффициент жесткости, а через N обозначены нелинейные члены; точкой отмечается дифференцирование по времени t. Вынуждающая сила в правой части уравнения имеет амплитуду f и циклическую частоту со2=с, ту же самую, что и в случае соответствующего линейного осциллятора без демпфирования.
Предположим, что, так же как и в задаче о галопировании по одной моде, коэффициент затухания Ъ уменьшается в зависимости от скорости жидкости. Меру этого уменьшения мы и будем рассма-
208 Гл. 9. Самовозбуждающиеся колебания
Рис. 119. Эвристическая схема чувствительности динамической бифуркации Хопфа к периодическому воздействию.
тривать в качестве основного управляющего параметра Л. Предположим, кроме того, что динамическая неустойчивость появляется в связи с изменением коэффициента Ь, который включает как положительное демпфирование конструкции, так и отрицательное демпфирование, вызванное течением жидкости, и проходит через нуль при Л=ЛС, что можно моделировать равенством 6=ЛС—Л.
При подходящем выборе нелинейного члена N(x, х) и при f=0 получаем неустойчивую бифуркацию Хопфа, в которой амплитуда предельного цикла А равна положительной постоянной, умноженной на корень квадратный из декремента нагрузки Ь:
A — kbll\ A* = k*b,
как показано на рис. 119. Наложение некоторого вынуждающего воздействия /=И=0, очевидно, вызовет появление неустойчивости при значении Л, меньшем Лс. Мы сможем это установить, рассматривая случаи, когда вынужденные колебания линейного резонанса будут иметь амплитуду неустойчивого предельного цикла.
Полагая М=0, при малом затухании для амплитуды линейного резонанса получим хорошо известный результат A=f/(ab), так что при постоянном значении f имеем асимптотически растущую кривую, показанную на рис. 119. Она пересекает траекторию предельных циклов при kbl,^=f/(ab), откуда получаем искомый результат нашего эвристического рассмотрения:
b = [f/(^W)]2/3#
9.4. Резонансная чувствительность бифуркации Хопфа 209
Поскольку k и со — постоянные, а Ь=ЛС—Л, получаем зависимость Уменьшение нагрузки се (вынуждающая сила)1/з,
показывающую, что справедлив степенной закон двух третей для резонансной чувствительности. Отсюда следует, что мы имеем чувствительность типа сборки. Сейчас мы проведем анализ специального нелинейного осциллятора, для которого удается найти решение в замкнутой форме для установившихся колебаний.
Предположим, что в исходном уравнении нелинейные члены имеют вид
/V = D (х2 + х2) х,
где G — постоянная. Решение будем искать в виде установившегося периодического движения х—А cos at: Подставляя это выражение в уравнение движения, получим, что коэффициент при cos at обращается в нуль, так как а2=с. Очевидно, нелинейное уравнение допускает простое решение с замкнутыми фазовыми траекториями, если а>=1, так что х2+х2=А2. Будем предполагать сейчас, что мы имеем дело именно с этим случаем. Уравнение движения содержит только члены с sin at и тождественно удовлетворяется, если А является решением кубического уравнения
DA:i + bA + f--=O.
При /=0 мы имеем динамическую бифуркацию Д=0 или А2= =k2b, где k2=—D"1; величина D считается отрицательной, чтобы обеспечить неустойчивую бифуркацию, как показано на рис. 8 гл. 1.
Решения при ненулевых значениях f окружают бифуркацию точно так же, как и в случае статической неустойчиво симметричной бифуркации, соответствующей энергии
V = */4Рх» _ i/2. (Д - Лс) х2 -J- ех,
для которой уравнение равновесия есть
dV/дх = Dx2 — (Л — Л6) х+8 ==0.
Это уравнение идентично полученному выше кубическому уравнению, причем имеет место соответствие А=х, Ь——(Л—Лс). Параметр Л был определен выше при помощи последнего соотношения. Видно, что амплитуда вынуждающей силы f равна параметру несовершенства е статической теории.
Таким образом, сейчас мы можем построить хорошо известную диаграмму бифуркации рис. 17 гл. 1 теперь уже с динамической бифуркацией Хопфа в точке С и динамической складкой для «неидеальной» системы. Динамическая складка включает слияние и исчезновение устойчивого предельного цикла с неустойчивым, и в
210 Гл. 9. Самовозбуждающиеся колебания
Рис. 120. Некоторые вычисленные кривые зависимости амплитуды А от управляющего параметра Л (или Ь).
этом смысле динамическая складка является динамическим аналогом статической складки, или предельной точки. Используя общий результат статической теории бифуркаций (уравнение 8.3 на стр. 187 нашей монографии [36]), получим, что резонансная чувствительность равна
A-Ac = 3Dl/8 (//2)2/3.
Сравнение с результатом эвристического рассмотрения показывает, что при таком подходе мы получили правильный вид решения, но неправильный числовой коэффициент, в чем, конечно, нет ничего удивительного.
На рис. 120 показаны некоторые численные результаты для стационарных решений. Здесь для амплитуды вынуждающей силы /=0,1 имеются три установившихся колебания: Р, S и С при Ь=0,5. Из них Р является устойчивым решением, в то время как два других неустойчивые. Сохраняя постоянную несовершенства f равной 0,1 и уменьшая Ь, мы видим,- что Р и S сливаются и исчезают при критическом значении Ь, оставляя только неустойчивое колебание, соответствующее точке С. Коэффициент D берется равным —1.
9.4. Резонансная чувствительность бифупкации Хопфа 211
Рис. 121. Двумерные фазовые траектории для сглаженного уравнения в вариациях.
Чтобы более ясно увидеть переходы между установившимися состояниями, необходимо изучить переходный процесс. Это лучше всего сделать, считая, что амплитуды меняются медленно, и строя график сглаженных траекторий автономного уравнения в вариациях в плоскости Ван дер Поля. Это приводит к фазовому портрету, изображенному на рис. 121. Здесь показана зависимость фазы от амплитуды. Подробности можно найти в уже цитировавшейся статье [325].
На рисунке три установившихся состояния выступают как точки равновесия, причем центральный сток является устойчивым решением Р. Если уменьшать b при постоянном значении f=0,l, то сток будет двигаться по направлению к левому седлу S, и при критическом значении b произойдет слияние седла с узлом. После этого правый источник С будет единственным оставшимся стационарным состоянием.
Мы видим, что при этой бифуркации седло — узел конечная область стока Р мгновенно исчезает, и, следовательно, все траектории, выходящие из С, уйдут в бесконечность.
Глава
ОРБИТАЛЬНАЯ УСТОЙЧИВОСТЬ И УПРАВЛЕНИЕ ОРИЕНТАЦИЕЙ КОСМИЧЕСКОГО КОРАБЛЯ
В этой главе будут введены некоторые концепции теории устойчивости движения [326), включая понятие орбитальной устойчивости, отличающееся от понятия устойчивости по Ляпунову, Понятие орбитальной устойчивости используется при изучении устойчивости орбиты малого спутника, находящегося в поле силы тяжести массивного тела, такого, как, например. Земля или Солнце.
Будет рассмотрена пассивная нутация вращающегося относительно собственной оси космического корабля, имеющего на борту демпфер колебаний. Изложение основано на недавней работе Кейна и Левинсона 1327]. В более ранней работе [328] Кейн и Барба изучили эффекты, связанные с диссипацией энергии у вращающегося спутника, состоящего из двух упруго соединенных твердых тел. Эта работа относится к одной из основных задач небесной механики — задаче вращения симметричного спутника по круговой орбите. Год спустя, в 1967 г., Роуб и Кейн [329] провели исчерпывающий анализ устойчивости такого упругого спутника. Они показали, что некоторые формы спутников, которые считались устойчивыми при их анализе как твердого тела, с учетом деформируемости оказываются неустойчивыми.
10.1. Устойчивость движения орбитального тела
В качестве первого примера устойчивости движения рассмотрим свободное вращение тела массы т вокруг неподвижной точки С, с которой оно связанно легкой нерастяжимой нитью длиной R (рис. 122). Движение тела происходит в одной плоскости. Оно имеет только одну степень свободы 0, поэтому соответствующее фазовое пространство (0, 0) оказывается двумерным. Поскольку 0 является циклической переменной, фазовое пространство лучше всего изображать на поверхности цилиндра.
При отсутствии затухания сила натяжения нити является един-
10.1. Устойчивость движения орбитального тела 213'
Рис. 122. Двумерное цилиндрическое фазовое пространство (0, 0) для тела, вращающегося на невесомой нитн.
ственной силой, действующей на частицу, поэтому все движения тела происходят с постоянной угловой скоростью 6. Таким образом, фазовые траектории являются окружностями, причем фазовая скорость окружностей увеличивается вместе с 6 из-за уменьшения периода.
Рассмотрим устойчивость основного движения F по отношению к возмущенному движению Р, которое начинается в точке 6=0 с несколько большим значением 6. Из-за небольшого различия фазовых скоростей изображающие точки Р и F через некоторое время разойдутся достаточно далеко друг от друга, и на очень большом интервале времени они часто будут полностью не в фазе. Изучая движение точек на фазовой плоскости и проведя сравнение в различные времена, можно сделать вывод о неустойчивости по Ляпунову основного движения F.
Тем не менее с геометрической точки зрения, не принимая невнимание время, можно видеть, что полная фазовая траектория Р равномерно близка к траектории F. Поэтому мы говорим, что движение F орбитально устойчиво.
В качестве второго примера устойчивости движения рассмотрим вращение спутника массы т вокруг неподвижного тела массы М, к которому он притягивается гравитационной силой, обратно пропорциональной квадрату расстояния (рис. 123). В полярных координатах (г, 6) уравнения движения спутника принимают вид.
214 Гл. 10. Орбитальная устойчивость и управление ориентацией
т
Рис. 123. Спутник иа орбите вокруг неподвижного тела массы М и фазовый портрет эквивалентного осциллятора.
(после деления на массу спутника zn)
;_Г02 + £^ = О, . ’ ГЛ
гё 4-2/0=о.
Эти уравнения могут быть выведены непосредственно из законов Ньютона или легко получены из уравнений Лагранжа. Здесь точка обозначает производную по времени, a G — гравитационная постоянная.
Интегрируя второе уравнение, придем к соотношению г20= =р=const, которое выражает закон сохранения момента количества движения. Исключая 0, получаем единственное уравнение для определения л
г —р2/г3 4-СЛ1/г2 = О, которое представляет собой уравнение движения нелинейного осциллятора с одной степенью свободы. Интегрирование этого уравнения приводит, к закону сохранения полной энергии Е:
г2 , р2 GM v . т+ъ*--------— = £ = const.
Здесь г2/2— кинетическая энергия осциллятора Ге, а оставшиеся члены в левой части уравнения представляют собой потенциальную энергию осциллятора УЕ.
Для заданного значения р вид функции УЕ показан на рис. 123, а линии постоянной энергии Е на фазовой плоскости дают нам фа-
10.1. Устойчивость движения орбитального тела 215
Рис. 124. Схематическое представление четырехмерного фазового пространства спутника на основной круговой орбите.
Z=r,6-W
зовые траектории. Здесь изображены одна круговая орбита (для фиксированного значения р) — орбита с постоянным радиусом г, семейство замкнутых орбит с радиусом г, меняющимся между двумя конечными значениями, и неограниченные движения с большими значениями Е. Представляя г как функцию 6, можно показать, что в реальном пространстве замкнутые орбиты являются эллипсами.
Рассмотрим устойчивость круговой орбиты радиусом R, для которой
r = R, г = О, бос?, О = W = const.
Для тщательного изучения ее устойчивости следует рассмотреть все близкие траектории в четырехмерном фазовом пространстве (г, г, 6, 0). Схематическое представление будем строить в пространстве (г, 0), откладывая г и 0 на оси г, перпендикулярной плоскости (г, 0) (рис. 124).
Основное круговое движение F изображено жирной линией. Слегка возмущенное движение Р будет в общем случае иметь нем» ного отличное значение р и, следовательно, несколько иную кривую Ре и немного другое значение Е. Как следует из приведенного анализа, Р может быть небольшой замкнутой траекторией на плоскости (г, г). Отсюда следует, что в любой момент времени слабо возмущенное движение имеет значения т, близкие к R, при этом радиальная скорость г близка к нулю, а угловая скорость ft=plr2 близка к W, так что траектория Р будет всегда геометрически близка к траектории F. Назовем такое основное круговое движение орбитально устойчивым.
Тем не менее основное движение неустойчиво по Ляпунову, поскольку близкие траектории в общем случае будут иметь другие периоды. Например, уравнение круговой орбиты имеет вид
tm?r — GmM/r2t
216 Гл. 10. Орбитальная устойчивость и управление ориентацией
а ее период
Т = 2л/<о = 2 л r'-'lGM
является функцией г. Таким образом, неустойчивость по Ляпунову может быть проиллюстрирована, если в качестве возмущенной траектории взять круговую, близкую к основному движению.
10.2. Затухание пассивной нутации вращающегося спутника
Этот раздел, посвященный физическому смыслу неустойчивости космических аппаратов, был вчерне написан проф. Томом Р. Кейном из Станфордского университета, основан на его и Левинсона недавней работе [327] и приводится с разрешения American Institute of Aeronautics and Astronautics.
Некоторые искусственные спутники Земли состоят из единственного твердого тела, движущегося таким образом, что одна из его главных осей инерции все время остается перпендикулярной плоскости орбиты, описываемой центром масс тела. Для сохранения такого движения спутник следует привести во вращение таким образом, чтобы его угловая скорость была перпендикулярна плоскости орбиты. Кроме того, его следует оснастить гасителем нутации, т. е. устройством, диссипирующим энергию при отклонениях в движении спутника, что способствует возвращению спутника на заданную траекторию. Однако вращение и демпфирование могут оказывать также и неблагоприятное воздействие. Если некоторые параметры •системы подобраны неправильно, то может случиться так, что даже небольшое возмущение вызовет падение спутника. Математическая теория устойчивости позволяет определить опасные значения этих параметров, а решения дифференциальных уравнений, описывающих движение спутника, проясняют физический смысл возникающих неустойчивостей. Эти соображения проиллюстрированы ниже на одном примере.
На рис. 125 буквой В обозначено твердое тело, внутри которого расположена частица Р, соединенная с пружиной S и амортизатором D; Ki, Y2 У3— главные оси инерции тела В относительно центра масс В *, которые далее будут называться главными осями. Частица Р может двигаться лишь, вдоль оси У^ пружина S находится в недеформированном состоянии, когда частица Р лежит на линии У 2. В отсутствие внешних сил система может совершать простое вращение. Другими словами, она может двигаться таким образом, что Р остается на линии У2, а ориентация оси У1 сохраняется неизменной по отношению к астрономической системе координат А, в то время как угловая скорость тела В в системе А имеет постоянную величину Q и направлена вдоль оси Уъ Если такое движение испытывает возмущение в момент времени t=0, то ориентация У1 относительно системы А и отклонение q частицы Р от линии
10.2. Затухание пассивной нутации вращающегося спутника 217
Рис. 125. Схематическое представление космического корабля.
У 2 меняются со временем при />0. Такое простое вращение называется неустойчивым, если не удается удержать q и отклонение оси У1 от ее первоначальной ориентации сколь угодно малыми за счет уменьшения амплитуды возмущений.
Можно сформулировать три условия, нарушение любого из которых гарантирует неустойчивость. Они содержат скорость вращения Q, параметры, характеризующие тело В, и элементы гасителя нутаций Р и S. Пусть В — однородный прямоугольный блок плотности р со сторонами длиной Llt L2, L3, как изображено на рисунке, и пусть масса частицы Р — v-я часть массы тела В, а пружина S — линейная с постоянной жесткостью о, тогда решение, изложенное в статье [330], приводит к заключению, что рассматриваемое простое вращение неустойчиво, когда отрицателен по крайней мере один из параметров uls и2, и3, которые задаются равенствами
^1 = ^3 ^1>
и2=(Ц-Ц)(1 + х)+ \2vb*. o(14-v) 12vt2
Us = vpZ.jZ.2Z.3Q2 ’
Два условия Uj<0, w2<0 могут быть названы критериями «не-максимальности инерции», поскольку удовлетворение любого из них гарантирует, что вектор угловой скорости параллелен линии, не совпадающей с осью максимального момента инерции системы, образованной телом В и частицей Р. Условие tz3<0 называется критерием «податливости», так как оно может быть выполнено только тогда, когда жесткость пружины о достаточно мала.
218 Гл. 10. Орбитальная устойчивость и управление ориентацией
Рис. 126. Условия нарушения устойчивости ориентации космического корабля.
Все три условия неустойчивости могут нарушаться одновременно только одним способом, обозначенным на рис. 126 буквой N, обозначающей «не неустойчивость». Удовлетворение одного или нескольких условий может осуществляться пятью способами, которые обозначаются буквами Ult U2, U3, Ui, U&- Поскольку параметр iis зависит от параметра и2 таким образом, что условие и2<0 приводит к неравенству п3^0, две комбинации щ>0, н2<0, и3<0 и щ<0, п2<0, «3<0 оказываются невозможными и' потому отсутствуют на рисунке. В случае И, мы имеем дело с космическим кораблем, для которого рассматриваемое простое вращение не является неустойчивым, если частица Р жестко крепится к телу В. При условии «!>0 и п2>0 ось вращения параллельна оси максимального момента инерции (когда Р лежит на линии У 2), и для твердого тела это гарантирует маргинальную устойчивость. Следовательно, U\ представляет дестабилизацию, вызываемую гасителем нутаций. Возможность такой неустойчивости была отмечена Принглом [331] и обсуждалась также Кейном и Тейксейрой [332]. Символы U2, U8 и Ut соответствуют движениям, которые были бы неустойчивыми, даже если бы частица Р была зафиксирована относительно тела В, поскольку ось вращения параллельна главной оси, являющейся ни осью максимума, ни осью минимума центрального момента инерции. Для твердого тела неустойчивость проявляется в виде больших отклонений Уп так что мы не сумеем проследить за U2, и3 и С/4 далее. В противоположность этому неустойчивость U6 снова связана со структурой космического корабля, при этом подвижность Р является фактором решающей важности. В воз-
10.2. Затухание пассивной нутации вращающегося'спутника 219 пикающем движении ось вращения будет параллельна оси минимального момента инерции, так что если частица Р будет неподвижна относительно тела В, то будет наблюдаться маргинальная устойчивость. Более того, неустойчивость сейчас нельзя относить за счет избыточной податливости, поскольку «3>0. Однако можно считать, что она возникает из-за диссипации энергии.
После присвоения всем параметрам системы численных значений можно проделать следующие процедуры: записать динамические дифференциальные уравнения, описывающие поведение q, осей У1, Y2, У в и компонент toj, от2, <о3 вектора угловой скорости от тела В в системе координат А; написать кинематические дифференциальные уравнения, включающие со,, ы2, от3 и элементы матрицы направляющих косинусов [Сг,1, которая связывает оси Уъ У2, У3 с осями Xlt Х2, Х3, неподвижными в системе координат А и совпадающими в начальный момент времени с Уъ У2, У3 соответственно; проинтегрировать все уравнения, используя следующие начальные значения: q=q=O, от^П, от2=еП, <о3=О и [Сг;|=/, I — единичная матрица размера 3x3; вычислить для дискретных моментов времени значение угла а (рис. 125) между Ух и вектором Н момента количества движения системы, который остается неподвижным в А, и построить график зависимости а от t. Здесь <о2=еП представляет собой возмущение простого вращения.
Для последующего изучения условий Ui и Ub рассмотрим сначала ситуацию N на рис. 126, принимая р=2760 кг/м3 (плотность массы алюминия), Li=l,2 м, L2=l,225 м, L3=l,3 м — описание тела В заключается в задании этих параметров. Положим v= =0,01, так что масса частицы Р составит 1 % от массы тела В, и закончим определение гасителя нутаций, полагая о=52,744 Н/м и 6=105,487 Н-с/м, где 6 — постоянная, характеризующая гаситель нутаций D; сила, действующая на частицу Р со стороны демпфера D, задается выражением 6|г/|. Числовые значения величин о и 6 подобраны так, что осциллятор, образованный/3, S и D, имеет собственную круговую частоту 1 рад/с и быстро затухает. Наконец, положим 6=1 м и П=1 рад/с; замечая, что, как следует из уравнений «1=0,1 м, «2=0,181 м2, ц3=0,348, мы видим, что действительно имеем дело с движением, нарушающим все три критерия неустойчивости рис. 126. Численное интегрирование выполнялось для е=0,1. Вычисления приводят к кривой, обозначенной на рис. 127 через /7(0,1), которая показывает, что со временем а затухает. Таким образом, гаситель нутации действительно выполняет предназначенную ему роль. Интересно отметить, что такое удовлетворительное поведение проявляется и тогда, когда собственная частота осциллятора равна скорости вращения космического аппарата.
Увеличим теперь податливость пружины 5, уменьшая о до значения 26,372 Н/м — половины от первоначального, но сохраним все остальные значения параметров неизменными. При этом «3
220 Гл. 10. Орбитальная устойчивость и управление ориентацией
Рис. 127. Устойчивые и неустойчивые отклонения осей вращения.
станет равным — 0,157, в то время как иг и и2 сохранят свои прежние положительные значения. Следовательно, мы имеем дело со случаем Л71 на рис. 126. Возмущение, аналогичное использованному ранее с е=0,1, приводит теперь к возрастающей кривой, обозначаемой на рис. 127 через 77, (0,1). Из рисунка очевидно, что гаситель нутаций фактически действует как генератор нутаций. Можно было бы предположить, что такая реакция связана с избыточно большим начальным возмущением. Для того чтобы убедиться, что причина заключается не в этом, изменим е от 0,1 до 0,05. Проводя повторно вычисления для случаев N я Uh построим соответствующие кривые 7V (0,05) и 771(0,05). Четыре кривые на рис. 127 иллюстрируют высказанное утверждение. Когда движение устойчиво, уменьшение возмущения приводит к уменьшению отклонения от основного движения; но, когда движение неустойчиво, уменьшение возмущения просто приводит к некоторой задержке таких отклонений. Таким образом, кривая 7V(0,05) лежит ниже кривой Л? (0,1) в течение всего времени, в то время как кривая 771(0,05) достигает значений, сравнимых с самыми большими значениями кривой 771(0,1), хотя и более медленно.
Неустойчивость не всегда проявляется так явно, как в рассмотренном примере. Для того чтобы проиллюстрировать это, изменим размеры тела В и жесткость пружины S и положим 7.1=0,5 м, Т.2= 1,2 м, 7.3=3,185 м, о=0,527 Н/м, а параметры р, v, 6, b оставим неизменными (тело В имеет ту же массу, что и раньше, а пружина з 100 раз более податлива, чем в предыдущем случае). Тогда «1=2,685 м, ц2=1,322 м2, «3=—0,081, так что снова имеет место
10.2. Затухание пассивной нутации вращающегося спутника 221
Рис. 128. Неожиданное отклонение оси вращения.
случай на рис. 126. Но при том же возмущении, что и раньше с е=0,1, получаем более сложную реакцию системы; она изображена на рис. 128. Одной из интересных особенностей поведения системы является сохранение малых значений а в течение первых двух минут движения, имеющее видимость по крайней мере маргинальной устойчивости, но затем появляется очень быстрый рост возмущений. Этот график иллюстрирует второй основной факт. Если движение представляет практический интерес только в течение ограниченного отрезка времени, неустойчивость может оказаться несущественной, так как нежелательно большие возмущения основного движения могут появиться только после интересующего времени.
Неустойчивость, связанная со случаем U& на рис. 126, возникает, например, если Lx=2 м, L2=0,948 м, L3= 1,008 м, в то время как р, v, о, 6, b и £2 имеют значения, использующиеся ранее для случая N. При этих значениях параметров системы тело В имеет ту же массу, что и раньше; эллипсоид инерции системы, образованной телом В и частицей Р, имеет форму вытянутого сфероида, когда частица Р находится на оси У2 (главные моменты инерции имеют значения 894 и 2205 кг-м2), и ось вращения этого сфероида параллельна Yi, так что во время рассматриваемого невозмущенного движения вектор угловой скорости тела В параллелен оси минимального момента инерции; при этом Wi=—0,992 м, w2=—3,012 м2, w8= 1,050. При е=0,1 получается кривая, обозначенная на рис. 129 через 175(0,1), которая показывает, что диссипация энергии служит теперь причиной того, что тело В переходит в «плоское вращение», т. е. ось становится перпендикулярной вектору момента коли-
222 Гл. 10. Орбитальная устойчивость и управление ориентацией
. t.c
Рис. 129. Неустойчивое движение оси вращения и движение как твердого тела.
чества движения. Утверждение, что диссипация энергии играет основную роль в этом случае особенно существенно, так как если частица Р закреплена на оси У2, что исключает диссипацию энергии, то твердое тело, образованное из В и Р, будет совершать хорошо известное движение — вращение, сопровождаемое прецессией, и оно будет происходить таким образом, что угол а в течение всего времени будет сохранять начальное значение; этому движению на рисунке соответствует горизонтальная линия.
Обсуждение орбитальной и структурной устойчивости и устойчивости по Ляпунову, включающее обзор типов и размеров предполагаемых возмущений (детерминистических и стохастических), проведено Маззилли [333]. Эта работа содержит также изучение параметрической неустойчивости вынужденных колебаний маятника с переменной длиной, аналогичной неустойчивости Матье нефтяной платформы с растяжимой опорой.
Глава
ПОЛЕВЫЕ ТЕОРИИ НЕЙРОННОЙ АКТИВНОСТИ МОЗГА
Мы закончим настоящий обзор по неустойчивостям и катастрофам рассмотрением важного и волнующего вопроса о моделировании человеческого мозга. Связи между поведением отдельных нейронов, представляющимся весьма простым, и высоким уровнем организации, который ассоциируется с нашим мышлением и сознанием, начинают исследоваться только в последнее время. Приводимый ниже обзор может рассматриваться как естественное продолжение гл. 5 по самоорганизации химических и биохимических систем.
Для моделирования нервной ткани мозга Уилсон и Коуен i334] построили динамические уравнения популяций тормозящих и возбуждающих нейронов. Для пространственно распределенных популяций получена система нелинейных дифференциальных уравнений, которые исследуются численными методами и методом фазовой плоскости. Обнаружено, что складки в стационарных решениях вызывают явление многократного гистерезиса; в то же время наблюдаются предельные циклы (моделирующие ритмы мозга), в которых частота колебаний является монотонной функцией интенсивности раздражителя. Обобщение этой работы, учитывающее пространственное распределение нервной ткани, имеется в работе Уилсона 1335].
11.1. Мозг и центральная нервная система
Мозг можно представлять себе как сеть нейронов, соединенных случайным образом при помощи синапсов. Когда нейрон «загорается», раздражение передается через синапсы к смежным нейронам. «Зажигание» в смежных нейронах может произойти после синаптического запаздывания.
Нейронная популяция может быть разделена на возбуждающие нейроны, которые во время «горения» испускают положительный раздражитель, и тормозящие нейроны, которые испускают отрицательный раздражитель. Нейрон зажжется тогда, когда сумма полу
224 Гл. 11. Полевые теории нейронной активности мозга
ченных раздражений превысит некоторое пороговое значение; после загорания он находится в неактивном состоянии в течение некоторого периода невосприимчивости, даже если сумма полученных раздражений превысит пороговое значение.
Такая дискретная нейронная сеть легко может быть смоделирована на ЭЦВМ. Волны нейронной активности, наблюдавшиеся при моделировании на ЭЦВМ, обсуждаются Анниносом [336].
Для построения моделей высших функций мозга и центральной нервной системы представляется более удобным изучать поведение не дискретной системы случайно соединенных нейронов, а континуум нейронных популяций, в которых случайность «смазывается» и возникает детерминистическое поведение. Это точный аналог континуальных теорий поля в механике твердого тела и механике жидкости. В теории упругости, например, случайные колебания атомов роли не играют, но приводят к появлению объемных макроскопических модулей. Совершенно аналогично жидкость на молекулярном уровне находится в тепловом броуновском движении, а при макроскопическом рассмотрении той же жидкости может наблюдаться гладкое ламинарное течение. Континуальный детерминистический подход подтверждается при исследованиях мозга методом локальной избыточности нейронов в малых объемах корковой ткани.
Работа Уилсона и Коуена [334] отличается от аналогичных работ включением в рассмотрение как тормозящих нейронов, так и возбуждающих.
11.2. Механика возбуждения и торможения
В модели Уилсона и Коуена в качестве двух основных переменных вводятся в рассмотрение доля возбуждающих клеток, загорающихся за единицу времени Е (/), и доля тормозящих клеток, загорающихся за единицу времени / (/). Отметим, что обе эти величины являются скоростями загорания нейронов; для исключения некоторых кратковременных эффектов необходимо усреднить эти величины по некоторому короткому промежутку времени.
Предполагается, что Е и / в момент времени 1+т после запаздывания т будут равны доле клеток, которые являются чувствительными и которые, кроме того, получают по крайней мере пороговое возбуждение.
Нечувствительными клетками являются те, которые загорелись недавно и не могут загореться опять в течение периода невосприимчивости. Если период абсолютной невосприимчивости равен г, то долю чувствительных возбуждающих клеток можно выразить в виде Еа=1—геЕ. Для Is получается аналогичное выражение. Отметим, что период невосприимчивости для возбуждающих клеток, обозначенный здесь через ге, может отличаться от периода невосприимчивости для тормозящих клеток гг.
11.2. Механика возбуждения и торможения 225
Ожидаемые доли подпопуляций, получающих за единицу времен ни по крайней мере пороговое возбуждение, будут функциями Е и /. Доля популяции для возбуждающих клеток записывается в форме
^(х) = ^[Се£-^/ + Р(0] и аналогично для тормозящих клеток
^/(x) = ^I.[Cl.£-grIJ + Q(n].
Коэффициенты здесь постоянные, представляющие среднее'число синапсов, приходящихся на одну клетку, a P(t) и Q(t)— внешние возбуждения.
Функции отклика & (х) будут зависеть от распределения вероятностей нейронных порогов. Это показывает, что они будут иметь S-образную форму, похожую на знак интеграла, возрастая монотонно с ростом х от 0 до 1 и приближаясь асимптотически к значению, равному или близкому к единице при х, стремящемся к бесконечности. В аналитических работах они берутся в виде
1 4-ехр [— а(х—6)] 1 +ехр (с0)
с различными значениями постоянных а и 6 для двух типов нейронов.
Если вероятность того, что клетка является чувствительной, не зависит от вероятности того, что она временно возбуждена выше своего порога, то можно перемножить вероятности и, привлекая несколько грубых предположений, получить [334]
Е (t + те) = (ke-ГеЕ) zf е\сеЕ — geI + Р (/)], / (t 4-т() = (k/— rj) ^/[CfE—gil + Q (0].
Здесь постоянные ke и kt заменили единицу в предыдущих выражениях для Es и Ig, в действительности эти постоянные очень близки к единице и определяются равенством k—<I7(oo). Они используются в качестве небольшой коррекции параметров, позволяющей сделать решение Е=0=1 устойчивым состоянием покоя при нулевых внешних возбуждениях.
Если воспользоваться теперь приближением Тейлора
Е (t 4- те) = Е (0 4- (dE/dt) хе
и аналогичным приближением для I, то можно получить следующую систему уравнений:
= ~Е + - ГеЕ) [сеЕ -geI + P (/)],
ZT = -1 + <ki - tci£ - Sii + Q (OJ.
8 № 523
226 Гл. 11. Полевые теории нейронной активности мозге
Рис. 130. Типичные множественные складки и гистерезис в состоянии стационарного загорания со скоростью Е как функция от управляющего параметра Р (внешнего возбуждения) прн Q=0.
Рассмотрим частный случай, когда внешнее возбуждение тормозящих нейронов равно нулю (Q(/)=0), a P(t) есть постоянная величина Р, которая будет рассматриваться дальше как управляющий параметр.
11.3. Складки и множественный гистерезис в стационарных состояниях
При Q=0 и управляющем параметре Р, не зависящем от времени, стационарное состояние dE/dt—dlldt=Q обнаруживает множественные складки и гистерезис при некоторых значениях коэффициентов, как показано на рис. 130. Появление здесь гистерезиса является наиболее важным фактором, так как гистерезис предполагается как физиологическая основа кратковременной . памяти: таким образом, имеется по крайней мере одно экспериментальное подтверждение гистерезиса в центральной нервной системе.
11.4. Временные колебания, соответствующие предельному циклу
Уилсон и Коуен [334] показали, что рассмотренная модель может обнаруживать затухающие колебания в ответ на импульсное внешнее воздействие, как действительно и следовало бы потребовать от удовлетворительной модели. Более того, при Q, равном нулю, и Р, равном некоторому постоянному значению, модель может при соответствующем выборе коэффициентов обнаружить устойчивый предельный цикл, как показано в двумерном фазовом пространстве (Е, /) на рис. 131. Эти предельные циклы, возникающие в нашей довольно реалистической нейронной модели, обеспечивают конкпет-
11.5. Структурообраэование в пространстве нейронного поля 227
Рис. 131. Устойчивый предельный цикл в фазовом пространстве (Е, /). (Е — скорость загорания возбуждающих нейронов, / — скорость загорания тормозящих нейронов.) Значения коэффициентов указаны в таблице. Предельный цикл представляет устойчивые колебания двух скоростей загорания.
dE
£ + т ~dT= (k~rE} &{сЕ ~ е1+Р) Ь
/ + т = (ft- Н) & (сЕ - gl+Q
гдет — синаптическое запаздывание, k примерно равно 1, г — период невосприимчивости, Р — внешнее возбуждение.
ную физиологическую основу для изучения ритмов на электроэнцефалограмме (ЭЭГ), таких, как имеющие большое значение альфа-ритмы.
11.5. Структурообраэование в пространстве нейронного поля
Следующий важный шаг в изучении нервной ткани состоит в исследовании поведения модели, учитывающей распределение нейронов в пространстве,— нейронном поле. Мы уже видели, как это может быть сделано для модели брюсселятора в гл. 5, где исследовалось спонтанное появление порядка в химических и биологических полях. Работа по построению уравнений нейронного поля опубликована Уилсоном [3351 в серии лекций под редакцией Хаке-на, создателя новой дисциплины — синергетики. Аналогичная работа принадлежит Амари [337J.
8»
228 Гл. И. Полевые теории нейронной активности мозга
Уравнения поля позволяют исследовать пространственные взаимодействия внутри слоев нейронной ткани, которые характерны для коры мозга; важные детали все еще продолжают исследоваться, к ним относятся геометрия, размеры и краевые условия для нейронных полей. Уже исследованы многие особенности структурообразо-вания в группах и полях нейронов. Расположенные в пространстве предельные циклы получил Уилсон [335], а появление катастрофы сборки обсуждается Амари [337].
Приложение
НЕКОТОРЫЕ БИОГРАФИИ ТВОРЦОВ ТЕОРИИ УСТОЙЧИВОСТИ
ЛЕОНАРД ЭЙЛЕР, 1707—1783 гг.
Историю теории устойчивости, по-видимому, следует начать с гениального математика Леонарда Эйлера, определившего в приложении к своей основной работе по вариационному исчислению, опубликованной в 1744 г., формы равновесия сжатого упругого стержня. Эйлер был одним из наиболее продуктивных исследователей во всей истории математики; современники называли его «воплощением анализа». Он начал свою карьеру в год смерти Ньютона, а полную силу своего аналитического подхода к задачам механики проявил в трактате 1736 г.
Эйлер обладал завидным умением работать где угодно и при любых условиях, наброски своих статей он, как правило, делал в течение получаса перед ужином. Ему помогала удивительная память и способность к устному счету, которые сослужили ему хорошую службу, когда его поразила полная слепота: его продуктивность на самом деле возросла, и он в уме выполнил полный анализ задачи трех тел. Его ум сохранил ясность и силу до самой смерти в 1783 г. ».
Эйлер родился в 1707 г. в семье небогатого швейцарского пастора, получил степень магистра искусств в Базельском университете (1724 г.), начал изучать богословие, но затем целиком отдался математике и ее приложениям. В 1727 г. девятнадцатилетний Эйлер приехал в Петербург, где занял вакантное место по спе. циальности физиологии в недавно созданной там Академии наук. Но работать он стал в области математики. В свой первый четырнадцатилетний петербургский период он опубликовал свыше 50 трудов, активно занимаясь в то же время преподаванием и разнообразными практическими задачами.
В 1741 г. Эйлер переехал в Берлин, где работал до 1766 г., не прерывая своих связей с Петербургской академией, в изданиях которой он за это время опубликовал свыше 100 книг и статей. Затем он снова вернулся в Петербург, оставаясь там до конца своих дней. Несмотря на постигшую его почти полную слепоту, в свой второй семнадцатилетиий петербургский период Эйлер подготовил около 400 работ.— Прим. ред.
230 Приложение
ЖОЗЕФ-ЛУИ ЛАГРАНЖ, 1736—1813 гг.
Молодым другом Эйлера был великий французский математик Жозеф-Луи Лагранж, к которому Наполеон обращался как к «вершине пирамиды математических наук». Богатый отец Лагранжа промотал большую часть состояния в безрассудных спекуляциях, но Лагранж, понимая жизнь, философски замечал: «Если бы я получил богатое наследство, то, возможно, и не связал бы свою судьбу с математикой». Сложилось так, что Лагранж был назначен преподавателем математики в возрасте 16 лет, и ему пришлось обучать студентов старше себя. Продолжение его карьеры было исключительно ярким.
Лагранж развивал скорее аналитический, чем геометрический подход к механике, и в предисловии к своей основной работе «Аналитическая механика» [3] написал: «В этой работе не будет ни одного графика». Тем не менее он обнаружил, что механика основана на аналитической геометрии четырехмерного пространства-времени — точка зрения, нашедшая завершение в работах Альберта Эйнштейна.
Уравнения Лагранжа продолжают играть в механике фундаментальную роль благодаря тому, что основанный на них подход является более общим, чем векторный подход Ньютона: они естественным образом привели Лагранжа к представлению о минимуме общей потенциальной энергии системы в состоянии устойчивого равновесия консервативной системы.
Книга Лагранжа вышла в свет с некоторым запозданием в 1788 г., за год до падения Бастилии. Появление книги застало его в состоянии хронической депрессии. Говорят, что она пролежала на его столе два года нераскрытой.
Во время Французской революции Лагранж был ведущим создателем метрической системы мер и весов — это он спас нас от бедствий предлагавшейся тогда двенадцатеричной системы! В последние годы жизни его возродившийся математический энтузиазм был направлен на переиздание «Аналитической механики».
АНРИ ПУАНКАРЕ, 1854—1912 гг.
Анри Пуанкаре был одним из гигантов математической мысли и, возможно, последним, кто охватывал в своей деятельности всю современную ему математику. Общеизвестный экспоненциальный рост математических знаний делает такой охват невозможным в наши дни. Он опубликовал около пятисот научных статей по различным математическим проблемам и более тридцати книг.
Пуанкаре был чрезвычайно одарен интеллектуально, но физически неуклюж, со слабой мускульной координацией и из-за этого однажды получил нулевую оценку на экзамене по рисованию. В юно
Биографии творцов теории устойчивости 231
сти он случайно подстрелил птицу, и тяжелое ощущение этого события преследовало его долгие годы.
Подобно Эйлеру, он обладал поразительной способностью мысленно «видеть» огромный материал, и свои работы по комплексному анализу он обычно делал в уме во время любых шумных мероприятий. Несмотря на это, а быть может именно из-за этого, в повседневной жизни он был очень рассеян.
Он заложил основы современной теории бифуркаций, ясно намеченные в статье о вращающихся массах жидкости [4], и разработал долговременную программу исследований по качественной теории динамических систем.
Пуанкаре был одним из первых, кто признал революционную важность работы Эйнштейна. Он провел психологическое исследование природы математического творчества, заключив: «Математические открытия, малые или великие, . . . никогда не рождаются спонтанно. Они всегда предполагают почву, засеянную предварительными знаниями и хорошо вспаханную трудом, как сознательным, так и подсознательным».
ЛИТЕРАТУРА
1. Newton I. Mathematical Principles of Natural Philosophy, 1686. Reprinted by the University California of Press, Berkeley, 1974. [Имеется перевод: Ньютон И. Математические начала натуральной философии (пер. А. Н. Крылова).— Изв. Никол, морск. акад., 1915, вып. IV; 1916, вып. V; см. также: КрыловА. Н. Собрание трудов. Т. 7.— М.— Л., 1936.]
2. Euler L. Methodus Inveniendi Lineas Curvas Maximi Minirhive Proprietate Gaudentes (Appendix, De curvis elasticis).— Lausanne and Geneva: Marcum Michaelem Bousquet, 1744. [Имеется перевод: Эйлер Л. Метод нахождения кривых линий, обладающих свойством максимума или минимума.— М.: ГТТИ, 1934.]
3. Lagrange J. L. Mechanique Analytique.— Paris: Courcier, 1788. [Имеется перевод: Лагранж Ж- Аналитическая механика. Т. I, II.— М.— Л.: Гос-техиздат, 1950.]
4. Poincare. Н. Sur I’equilibre d’une masse fluide animee d’un mouvement de rotation.— Acta math., 1885, 7, 259.
5. Poincare H. Les Methodes Nouvelles de la Mecanique Celeste. Vols 1—3.— Paris: Gauthier-Villars, 1892—1899. [Имеется перевод: Пуанкаре А. Новые методы небесной механики.— Избранные тр. А. Пуанкаре, т. 1, 2.— М.: Наука, 1972.]
6. Poincare Н. Oeuvres.— Paris: Gauthier-Villars, 1951.
7. Ляпунов А. А. Общая задача об устойчивости движения.— Харьков, 1892.
8. АндроновА. А., Понтрягин Л. С. Теория «грубых систем».— ДАН СССР, 1937, т. 14, с. 247; см. также: Андронов А. А. Собрание трудов.— М.: Изд-во АН СССР, 1956, с. 181.
9. Thom R. Structural Stability and Morphogenesis.— Reading: Benjamin, 1975.
10. Zeeman E. C. Catastrophe Theory: Selected Papers 1972—1977.— London: Addison Wesley, 1977.
11. Poston T., Stewart I. Catastrophe Theory and its Applications.— London: Pitman, 1978. [Имеется перевод: Постои T., Стюарт И. Теория катастроф и ее приложения.— М.: Мир, 1980.]
12. Smale S. On dynamical systems.— Bol. Soc. Mat. Mexicana, 1960, I960* p. 195—198.
13. Smale S. Differentiable dynamical systems.— Bull. Am. Math. Soc., 1967, 73, p. 747.
14. Арнольд В. И. Малые знаменатели и проблемы устойчивости движения в классической и небесной механике.— УМН, 1963, т. 18, вып. 6, с. 91.
15. Ариольд В. И. Лекции о бифуркациях и версальных семействах.— УМН, 1972, вып. 5, с. 119.
16. Abraham R., Marsden J.E. Foundations of Mechanics. 2nd ed.— Reading: Benjamin, 1978.
Литература 233
17. Koiter W. T. On the Stability of Elastic Equilibrium. Dissertation. Delft, 1945 (см. также: Tech. Trans. NASA, 1967, F10, p. 833).
18. Budiansky B. Theory of buckling and post-buckling behaviour of elastic structures.— In: Advances in Applied Mechanics. Vol. 14.— New York: Academic Press, 1974.
19. Hutchinson J. W. Plastic buckling.— In: Advances in Applied Mechanics. Vol. 14.— New York: Academic Press, 1974.
20. Ziegler H. Principles of Structural Stability. 2nd ed.— Basel: Birkhauser Verlag, 1977. (Имеется перевод: Циглер Г. Основы теории устойчивости конструкций.— М.: Мир, 1975-1
21. Herrmann G. Stability of equilibrium of elastic systems subjected to nonconservative forces.— Appl. Meeh. Rev., 1967, 20, p. 103.
22. Leipholz H. H. E. Stability Theory: An Introduction to the Stability of Dynamic Systems and Rigid Bodies.— New York: Academic Press, 1970.
23. Leipholz H. H. E. Six Lectures on Stability of Elastic Systems, 2nd ed. (revised and enlarged).— Waterloo: Solid Meeh. Div., University of Waterloo, 1974.
24. Leipholz H. H. E. Direct Variational Methods and Eigenvalue Problems in Engineering.— Leyden: Noordhoff, 1977.
25. Leipholz H. H. E. Stability of Elastic Systems.— Alphen: Sijthoff and Noordhoff, 1980.
26. Thompson J. M. T. Basic principles in the general theory of elastic stability.— J. Meeh. Phys. Solids, 1963, 11, p. 13.
27. Roorda J. Stability of structures with small imperfections.— J, Engng Meeh. Div. Am. Soc. Civ. Engrs, 1965, 91, p. 87. См. также: Roorda J. Buckling of Elastic Structures.— Waterloo: Special Publications Series, Solid Meeh. Div., University of Waterloo, 1980.
28. Roorda J. The buckling behaviour of imperfect structural systems.— J. Meeh. Phys. Solids, 1965, 13, p. 267.
29. Roorda J. On the buckling of symmetric structural systems with first and second order imperfections.— Int. J. Solids Structures, 1968, 4, p. 1137.
30. Thompson J. M. T. A general theory for the equilibrium and stability of discrete conservative systems.— Z. angew. Math. Phys., 1969, 20, p. 797.
31. Croll J. G. A., Walker A. C. Elements of Structural Stability.— London: Macmillan, 1972.
32. Supple W. J- (ed.). Structural Instability.— Guildford: IPC Science and Technology Press, 1973.
33. Huseyin K. Non-linear Theory of Elastic Stability — Leyden: Noordhoff, 1974.
34. Thompson J. M. T., Hunt G. W. The instability of evolving systems.— Interdisciplinary Science Reviews, 1977, 2, p. 240.
35. Huseyin K. Vibrations and Stability of Multiple Parameter Systems.— Alphen: Noordhoff, 1978.
36. Thompson J. M T., Hunt G. W. A General Theory of Elastic Stability.— London: Wiley, 1973.
37. Thompson J. M T., Hunt G. W. Elastic Instability Phenomena.— London: Wiley, 1984.
38. Thompson J. M. T. Experiments in catastrophe.— Nature, 1975, 254, p. 392.
39. Thompson J. M. T., Hunt G. W. Towards a unified bifurcation theory.— J. Appl. Math. Phys. (ZAMP), 1975, 26, p. 581.
40. Herrmann G. Determinism and uncertainty in stability.— In: Instability of Continuous Systems (Ed. H. Leipholz) — Berlin: Springer, 1971.
41. Ziegler H. Trace effects in stability.— In: Instability of Continuous Systems (ed. H- Leipholz).— Berlin: Springer, 1971.
42. Thompson J. M. T. Basic theorems of elastic stability.— Int. J. Engng Sci., 1970, 8, p. 307.
43. Chillingworth D. R. J. A Problem from Singularity Theory in Engineering.—
234 Литература
Lecture to Symposium on Non-linear Mathematical Modelling, University of Southampton, August, 1976.
44. Hopf E. Abzweigung einer periodischen Losung von einer stationaren Losung eines Differentialsystems.— Berichten der Math.-Phys. Klass der Sachlischeft Akademie der Wissenschaften zu Leipzig, 1942, 94, p. 3.
45. Marsden J., McCracken M. The Hopf Bifurcation and Its Applications.— Berlin: Springer Appl. Math. Series, No. 19, Springer, 1976. [Имеется перевод: Марсден Дж., Мак-Кракен М. Бифуркация рождения цикла и ее приложения.— М-: Мир, 1980.]
46. Thompson J. М. Т. Catastrophe theory and its role in applied mechanics.— Proc. 14th IUTAM Congress, Delft, August, 1976.— Amsterdam: North Holland, 1976—1977.
47. Thompson J. M. T. Stability predictions through a succession of folds.— Phil. Trans. Roy. Soc. London, Ser. A, 1979, 292, p. 1—23.
48. Taylor G. I. Disintegration of water drops in an electric field.— Proc. Roy. Soc. London, Ser. A, 1964, 280, p. 383.
49. Zeeman E. C. Catastrophe theory.— Scientific American, 1976, 234, No. 4, p. 65.'
50. Benjamin T. B. Bifurcation phenomena in steady flows of a viscous fluid. I. Theory, II. Experiment.— Proc. Roy. Soc. London, Ser. A, 1978, 359, p. 1—26, 27—43.
51. Postle D. Catastrophe Theory.— London: Fontana, 1980.
52. Croll J. G. A. Is catastrophe theory dangerous? — New Scientist, 1976, 70, p. 630.
53. Zahler R. S., Sussmann H. J. Claims and accomplishments of applied catastrophe theory.— Nature, 1977, 269, p. 759 (см. также: 1977, 270, p. 381 x 1978, 271, p. 401).
54. Sussmann H. J., Zahler R. S. Catastrophe theory as applied to the social and biological sciences: a critique.— Synthese, 1978, 37, p. 117.
55. Woodcock A., Davis M. Catastrophe Theory.— New York: Dutton, 1978.
56. Michael D. H., O’Neill M. E., ZuercherJ.C. The breakdown of electrical insulation in a plane layer of insulting fluid by electrocapillary instability.— J. Fluid Meeh., 1971, 47, p. 609.
57. Michael D. H., O’Neill M. E. Two-dimensional problems of electrohydrostatic stability.— Phil. Trans. Roy. Soc., Ser. A, 1972, 272 (1224), p. 331.
58. Michael D. H., O’Neill M. E. The bursting of a charged cylindrical film.— Proc. Roy. Soc. London, Ser. A, 1972, 328, p. 529.
59. Michael D. H., Norbury J., O’Neill M-E. Electrohydrostatic instability in electrically stressed dielectric fluids.— J. Fluid Meeh., 1974, 66, p. 289.
60. Taylor G. I. On making holes in a sheet of fluid.— J. Fluid Meeh., 1973, 58, p. 625.
61. Michael D. H. Meniscus stability.— Ann. Rev. Fluid Meeh., 1981, 13, p. 189.
62. Berry M. V. Cusped rainbows and incoherence effects in the rippling-mirror model for particle scattering from surfaces.— J. Phys., Ser. A, 1975, 8, p. 566.
63. Berry M. V. Waves and Thom’s theorem.— Adv. Phys., 1976, 25, p. 1.
64. NyeJ.F. Optical caustics in the near field from liquid drops.— Proc. Roy. Soc. London, Ser. A, 1978, 361, p. 21.
65. Berry M. V., Nye J. F., Wright F. J. The elliptic umbilic diffraction catastrophe.— Phil. Trans. Roy. Soc., 1979, 291 (1382), p. 453.
66. NyeJ.F. Optical caustics from liquid drops under gravity: observations of the parabolic and symbolic umbilics.— Phil. Trans. Roy. Soc., Ser. A, 1979, 292 (1387), p. 25.
67. Berry M. V. Focusing and twinkling: critical exponents from catastrophes in non-gaussian random short waves.— J. Phys., Ser. A, 1977, 10, p. 2061.
68. Thorndike A. S., Cooley C. R., Nye J. F. The structure and evolution of flow fields and other vector fields.— J. Phys., Ser. A, 11, 1978, p. 1455.
Литература 233
69. NyeJ.F., Throndike A. S. Events in evolving three-dimensional vector fields.— J. Phys., Ser. A, 1980, 13, p. 1.
70. Thompson J. M. T., Tan J. K- Y., Lim К. C. On the topological classification of post-buckling phenomena.— J. Struc. Meeh., 1978, 6, p. 383.
71. Wassermann G. Stability of unfoldings in space and time.— Acta Mathema-tica, 1975, 135, p. 57.
72. Wassermann G. Stability of Unfoldings.— Springer Lecture Notes in Mathematics No. 393.— Berlin: Springer, 1975.
73. Wassermann G. (r, s)-stable unfoldings and catastrophe theory.— Structural Stability. The Theory of Catastrophes, and Applications in the Sciences (ed. P. Hilton).— Lecture Notes in Mathematics No. 525.— Berlin: Springer, 1976.
74. Golubitsky M., Schaeffer D. An analysis of imperfect bifurcation.— Annals, New York Academy of Sciences, 1979, 316, p. 127.
75. Golubitsky M., Schaeffer D. A theory for imperfect bifurcation via singularity theory.— Comm. Pure Appl. Math., 1979, 32, p. 21.
76. Golubitsky M., Schaeffer D. Imperfect bifurcation in the presence of symmetry.— Comm. Math. Phys., 1979, 67, p. 205.
77. Thompson J. M. T., Hunt G. W. A bifurcation theory for the instabilities of optimization and design.— Synthese, 1977, 36, p. 315.
78- Hunt G. W. Imperfections and near-coincidence for semi-symmetric bifurcations.— Proc. Conf, on Bifurcation Theory and Applications in Scientific Disciplines, New York, October, 1977.— In: Annals, New York Acad. Sci., 1979, 316, p. 572.
79. Hunt G. W. Imperfection-sensitivity of semi-symmetric branching.— Proc. Roy. Soc. London, Ser. A, 1977, 357, p. 193.
80 Hunt G. W., ReayN. A., YoshimuraT. Local diffeomorphisms in the bifur-cational manifestations of the umbilic catastrophes.— Proc. Roy. Soc. London, Ser. A, 1979, 369, p. 47.
81. Hunt G. W. An algorithm for the nonlinear analysis of compound bifurcation.— Phil. Trans. Roy. Soc., Ser. A, 1981, 300 (1455), p. 443.
82. Thompson J. M. T., Shorrock P. A, Bifurcational instability of an atomic lattice.— J. Meeh. Phys. Solids, 1975, 23, p. 21.
83. Thompson J. M. T., Shorrock P. A. Hyperbolic umbilic catastrophe in crystal fracture.— Letter to Nature, 1976, 260, p. 598.
84. Berry M. V., Mackley M. R. The six roll mill: unfolding an unstable persistently extensional flow.— Phil. Trans. Roy. Soc. London, Ser. A, 1977, 287, p. 1.
85. Mackley M. R. Flow singularities, polymer chain extension and hydrodynamic instabilities.— J. Non-Newtonian Fluid Meeh., 1978, 4, p. 111.
86. Chilver A. H. Coupled modes of elastic buckling.— J. Meeh. Phys. Solids, 1967, 15, p. 15.
87. Thompson J. M. T., Supple W. J. Erosion of optimum designs by compound branching phenomena.— J. Meeh. Phys. Solids, 1973, 21, p. 135.
88. Bauer L., Keller H., Reiss E. Multiple eigenvalues lead to secondary bifurcation.— SIAM J. Appl. Math., 1975, 17, p. 101.
89. Keener J. P. Perturbed bifurcation theory at multiple eigenvalues.— Arch. Rational Meeh. Anal., 1974, 56, p. 348.
90. Thompson J. M. T. The rotationally-symmetric branching behaviour of a complete spherical shell.— Proc. K- ned. Akad. Wet., Ser. B, 1964, 67, p. 295.
91. Koiter W. T. The non-linear buckling problem of a complete spherical shell under uniform external pressure.— Proc. K- ned. Akad. Wet., Ser. B, 1969, 72, p. 40.
92. Thompson J. M. T. The elastic instability of a complete spherical shell.— Aero. Quart., 1962, 13, p. 189.
93. Thompson J. M. T. The post-buckling of a spherical shell by computer analysis.— In: World Conference on Shell Structures (eds. S. J. Medwadowski et al.).— Washington: National Academy of Sciences, 1964.
236 Литература
94. Zeeman Е. С. The classification of elementary catastrophes of codimension less than or equal to five.— In: Structural Stability. The Theory of Catastrophes, and Applications in the Sciences (ed. P. Hilton). Lecture Notes in Mathematics No. 525.— Berlin: Springer, 1976.
95. Parkinson G. V., Brooks N. P. H. On the aeroelastic instability of bluff cylinders.— J. Appl. Meeh., 1961, 28, p. 252.
96. Parkinson G. V., Smith J. D. The square prism as an aeroelastic non-linear oscillator.— Quart. J. Meeh, and Appl. Math., 1964, 17, p. 225.
97. Novak M. Galloping and vortex induced oscillations of structures.— Proc. 3rd Int. Conf, on Wind Effects on Buildings and Structures.— Tokyo: Science Council of Japan, 1971.
98. Blevins R. D. Flow-induced Vibration.— New York: Van Nostrand, 1977.
99. Nicolis G. Patterns of spatio-temporal organization in chemical and biochemical kinetics.— SIAM — AMS Proc., 1974, 8, p. 33. .
100. Nicolis G., Prigogine I. Self-Organization in Non-Equilibrium Systems. From Dissipative Structures to Order through Fluctuations.— New York: Wiley, 1977. [Имеется перевод: Николис Г., Пригожин И. Самоорганизация в неравновесных. системах,— М.: Мир, 1979.]
101. Winfree А. Т. Rotating chemical reactions.— Sci. Am., June 1974, 230, p. 82.
102. Thompson D’Arcy W. On Growth and Form.— Cambridge: The University Press, 1971.
103. Thompson J. M. T. An evolution game for a prey — predator ecology.— Bull. Inst. Math, and Its Appl., 1979, 15, p. 162.
104. Waddington С. H, A catastrophe theory of evolution.— Annals, New York Academy of Science, 1974, 231, p. 32.
105. Dodson M. M. Quantum evolution and the fold catastrophe.— Evolutionary Theory, 1975, 1, p. 107.
106. May R. M. Bifurcations and dynamic complexity in ecological systems.— Annals, New York Academy of Sciences, 1979, 316, p. 517.
107. Iwan W. D., Blevins R. D. A model for vortex-induced oscillation of structures.—J. Appl. Meeh., 1974, 41, p. 581.
108. Hartlen R. T., Currie I. G. Lift oscillation model for vortex-induced vibration.— J. Eng. Meeh. Div. Am. Soc. Civ. Engrs, 1970, 96, p. 577.
109. Poore A. B., ALRawi A. Some applicable Hopf bifurcation formulas and an application in wind engineering.— Annals, New York Academy of Sciences, 1979, 316, p. 590.
110. Dowell E. H. Non-linear oscillations of a fluttering plate.— AIAA J., 1966, 4, p. 1267. [Имеется-перевод: Ракетная техн, и космои.— М.: Мир, 1966, №7,-с. 149.]
111. Dowell Е. Н. Aeroelasticity of Plates and Shells.— Leyden: Noordhoff, 1975.
112. Fung'Y. C. An Introduction to the Theory of Aeroelasticity.—New York: Wiley, 1955.
113. Holmes P. Bifurcations to divergence and flutter in flow induced oscillations: a finite dimensional analysis.— J. Sound Vibr., 1977, 53, p. 471.
114. Benjamin T. B. Dynamics of a system of articulated pipes conveying fluid.,I. Theory, II. Experiments.— Proc. Roy. Soc. London, Ser. A, 1961,261, p. 45/— 486, 487—499.
115. Lunn T.S. Flow-induced Instabilities of Fluid-conveying Pipes.—Ph. D. Thesis, University College of London, 1981.
116. Roorda J., Nemat-Nasser S. An energy method for stability analysis of non-linear, non-conservative systems.— AIAA J., 1967, 5, p. 1262. [Имеется перевод: Ракетная техн, и космон.— М.: Мир, 1967, № 7, с. 58.]
117. Rousselet J., Herrmann G. Flutter of articulated pipes at finite amplitude.— J. Appl. Meeh., 1977, 44, p. 154.
118. Bishop R. E. D., Fawzy I. Free and forced oscillation of a vertical tube containing a flowing fluid.— Phil. Trans. Roy. Soc. London, Ser. A, 1976, 284 (1316), p. 1.
Литература 2ST
119. Paidoussis М. Р., Deksnis Е. В. Articulated models of cantilevers conveying fluid: the study of a paradox.— J. Meeh. Engng Sci., 1970, 12, p. 288.
120. Koiter W. T. On the instability of equilibrium in the absence of a minimum of the potential energy.— Proc. K. ned. Akad. Wet., Ser. B, 1965, 68, p. 107.
121. Rainey R. С. T. The dynamics of tethered platforms.— Trans. Roy. Inst. Naval Architects, 1978, 120, p. 59.
122. Rainey R. С. T. Parasitic motions of offshore structures.— Trans. Roy. Inst. Naval Architects (in press).
123. Richardson J. R. Mathieu Instabilities and Response of Compliant Offshore Structures.— National Marine Institute, NMIR 49 (OT-R-7913), February 1979.
124. Holmes P. J., Rand D. A. The bifurcations of Duffing’s equations: an application of catastrophe theory.— J. Sound Vib., 1976, 44, p. 237.
125. Marsden J. E. Qualitative methods in bifurcation theory.— Bull. Am. Math. Soc., 1978, 84, p. 1125..
126. Holmes P. J., Marsden J. Bifurcations to divergence and flutter in flow-induced oscillations: an infinite dimensional analysis.— Automatica, 1978, 14, p. 367.
127. Holmes P., Marsden J. E. Qualitative techniques for bifurcation analysis of complex systems.— Annals, New York Academy of Sciences, 1979, 316, p. 608.
128. Holmes P. J., Lin Y. K. Deterministic stability analysis of a wind loaded structure.— J. Appl. Meeh., 1978, 45, p. 165.
129. Lin Y. K-, Holmes P. J. Stochastic analysis of a wind loaded structure.— J. Eng. Meeh. Div. Am. Soc. Civ. Engrs, 1978, 104, p. 421.
130. Chillingworth D. R. J., Holmes P. J. Dynamical systems and models for reversals of the earth *s magnetic field.— J. Math. Geology, 1980, 12, p. 41.
131. Holmes P. J., Rand D. A. Bifurcations of the forced Van der Pol oscillator.— Quart. Appl. Math., 1978, 35, p. 495.
132. Holmes P., Rand D. Identification of vibrating systems by generic modelling.— Proc. Int. Symp. on Shipboard Acoustics, Delft (ed. J. H. Janssen), Elsevier, 1977.
133. Holmes P. J., Marsden J. E. Bifurcations of dynamical systems and nonlinear oscillators in engineering systems.— In: Nonlinear Partial Differential Equations and Applications. Lecture Notes in Mathematics No. 648.— Benin: Springer, 1978, p. 163.
134. Holmes P. J. (ed.) New Approaches to Nonlinear Problems in Dynamics.— Proc. Conf. Pacific Grove, 1979.— Philadelphia: SIAM, 1980.
135. Gurel O., Rossler О. E. (eds). Bifurcation theory and applications in scientific disciplines.— Annals, New York Academy of Sciences, 1979, 316.
136. ChowS. N., Hale J. K., Mallet-Paret J. Applications of generic bifurcation, I and П.— Arch. Rat. Meeh. Anal., 1975, 59, p. 159; 1976, 62, p. 209.
137. Hale J. K- Generic Bifurcation with Applications, Heriot-Watt Lecture. Vol. I.— London: Pitman, 1977.
138. Potier-Ferry M. Bifurcation et stability pour des systemes derivant d’un po-tentiel.— Journal de Mecanique, 1978, 17, p. 38.
139. Potier-Ferry M. Perturbed bifurcation theory.— J. Diff. Equations, 1979, 33, p. 112.
140. El NaschieM. S., Al Athel S. On the morphology of controlled systems.— In: Proc. IUTAM Symp. on Structural Control.— Amsterdam: North Holland Publ. Co., 1980.
141. Guttinger W., Eikemeier H. (eds.) Structural Stability in Physics.— Berlin: Springer-Verlag, 1979.
142. Chillingworth D. R. J. Differential Topology with a View to Applications.— Research Notes in Mathematics No. 9.— London: Pitman, 1976.
143. Herrmann G., Jong I. On the destabilizing effect of damping in non-conserva-tive elastic systems.— J. Appl. Meeh., 1965, 32, p. 592. [Имеется перевод: Прикл. механ.— М.: Мир, 1965, № 3, с. 128.1
238 Литература
144. Nemat-Nasser S., Prasad S. N., Herrmann G. Destabilizing effect of velocitydependent forces in nonconservative continuous systems.— AIAA J., 1966, 4, p. 1276. [Имеется перевод: Ракетная техн, и космон.— М.: Мир, 1966, №7, с. 160.1
145. Lorenz Е. N. Deterministic non-periodic flow.— J. Atmos. Sciences, 1963, 20, p. 130. [Имеется перевод в сборнике статей: Странные аттракторы (ред. Я. Г. Синай и Л. П. Шильников).— М.: Мир, 1981-1
146. Ruelle D., TakensF. On the nature of turbulence.— Comm. Math. Phys., 1971, 20, p. 167. [Имеется перевод в сборнике статей: Странные аттракторы (ред. Я-Г. Синай и Л. П. Шильников).— М.: Мир, 1981.1
147. Rossler О. Е. Continuous chaos — four prototype equations.— Annals, New York Academy of Sciences, 1979, 316, p. 376.
148. Rossler О. E. Chaos.— In: Structural Stability in Physics (eds W. Guttinger, H. Eikemeier).— Berlin: Springer, 1978, p. 290.
149. Holmes P. J. Strange phenomena in dynamical systems and their physical implications.— Appl. Math. Modelling, 1977, 1, p. 362.
150. Moon F., Holmes P. J. A magneto-elastic strange attractor.— J. Sound Vibr., 1979, 65, p. 275.
151. Holmes P. J. A nonlinear oscillator with a strange attractor.— Phil. Trans. Roy. Soc. London, Ser. A, 1979, 292, p. 419.
152. Holmes P. J. Averaging and chaotic motions in forces oscillations.— SIAM J. Appl. Math., 1980, 38, p. 65.
153. Holmes P. J. Global bifurcations and chaos in the forced oscillations of buckled structures.— Proc. IEEE Conf, on Decision and Control, San Diego, 10—12 January, 1979.’— New York: Inst. Elec. Electronics Engrs.
154. Marsden J. E., Holmes P. J. A horseshoe in the dynamics of a forced beam.— Proc. Int. Conf, on Nonlinear Dynamics, New York, 1979 (New York Academy of Sciences, 1980).
155. Holmes P. J., MoonF. Addendum: a magnetoelastic strange attractor.— J. Sound and Vibr., 1980, 69, p. 339.
156. Holmes P. J. Periodic, nonperiodic and irregular motions in a Hamiltonian system (to appear).
157. Gumowski L, Mira C. Dynamique Chaotique,— Toulouse: Cepadues Editions, 1980.
158. Henon M. A two-dimensional mapping with a strange attractor.— Comm. Math. Phys., 1976, 50, p. 69. [Имеется перевод в сборнике статей: Странные аттракторы (ред. Я-Г. Сииай и Л. П. Шильников).— М.: Мир, 1981.]
159. Hsu С. S., Yee Н. С. Behaviour of dynamical systems governed by a simple nonlinear difference equation.— J. Appl. Meeh., 1975, 42, p. 870.
160. Hsu C. S., Cheng W. H. Steady-state response of a nonlinear system under impulsive periodic parametric excitation.— J. Sound and Vibr., 1977, 50, p. 95.
161. Hsu C. S., Yee H. C., Cheng W. H. Determination of global regions of asymptotic stability for difference dynamical systems.— J. Appl. Meeh., 1977, 44, p. 147.
162. Lanczos C. The Variational Principles of Mechanics. 2nd ed.— Toronto: The University Press, 1962. [Имеется перевод: Ланцош К. Вариационные принципы механики.— М.: Мир, 1965.]
163. Chillingworth D. The catastrophe of a buckling beam.— In: Dynamical Systems, Warwich, 1974 (ed.- A. Manning). Lecture Notes in Mathematics No. 468.— Berlin: Springer, 1975. -
164. Zeeman E. C. Euler buckling.— In: Structural Stability. The Theory of Catastrophes, and Applications in the Sciences (ed. P. Hilton). Lecture Notes in Mathematics No. 525.— Berlin: Springer, 1976.
165. El Naschie M. S. Exact asymptotic solution for the initial post-buckling of a strut on a linear elastic foundation.— ZAMM, 1971, 54, p. 677.
166. El Naschie M. S. Zutn knickmechanismus des idealen kreisringes.— Der Stahl-bau, 1976, 1, p. 23.
Литература 239
167. Thompson J. М. Т. Discrete branching points in the general theory of elastic stability.— J. Meeh. Phys. Solids, 1965, 13, p. 295.
168. Thompson J. M. T. The branching analysis of perfect and imperfect discrete structural systems.— J. Meeh. Phys. Solids, 1969, 17, p. 1.
169. Hangai Y., Kawamata S. Analysis of geometrically nonlinear and stability problems by static perturbation method.— Rept. Inst. Indust. Sci. Univ. Tokyo, 1973, 22, No. 5.
170. Britvec S. J., Chilver A. H. Elastic buckling of rigidly-jointed braced frames.— J. Eng. Meeh. Div., Am. Soc. Civ. Engrs, 1963, 89, p. 217.
171. Britvec S. J. The Stability of Elastic Systems.— New York: Pergamon, 1973.
172. Thompson J. M. T., Gaspar Z. A buckling model for the set of umbilic catastrophes.— Math. Proc. Camb. Phil. Soc., 1977, 82, p. 497.
173. Zeeman E. C. The umbilic bracelet and the double-cusp catastrophe.— In: Structural Stability. The Theory of Catastrophes, and Applications in the Sciences (ed. P. Hilton). Lecture Notes in Mathematics No. 525.— Berlin: Springer, 1976.
174. Ho D. Higher order approximations in the calculation of elastic buckling loads of imperfect systems.— Int. J. Non-linear Meeh., 1971, 6, p. 649.
175. Ho D. The influence of imperfections on systems with coincident buckling loads.— Int. J. Non-linear Meeh., 1972, 7, p. 311.
176. Ho D. Buckling load of nonlinear systems with multiple eigenvalues.— Int. J. Solids Struct., 1974, 10, p. 1315.
177. Thompson J. M. T. Bifurcation aspects of catastrophe theory.— Proc. Conf, on Bifurcation Theory and Applications in Scientific Disciplines, New York, October 1977.— Annals, New York Academy of Science, 1979, 316, p. 553.
178. Huseyin K- The multiple-parameter stability theory and its relation to catastrophe theory.— In: Problem Analysis in Science and Engineering.— New York: Academic Press, 1977.
179. Hansen J. S. Some two-mode buckling problems and their relation to catastrophe theory,— AIAA J., 1977, 15, p. 1638. [Имеется перевод: Ракетная техн, и космон.— М.: Мир, 1977, № 11, с. 123.]
180. Hui D., Hansen J. S. The swallowtail and butterfly cuspoids and their application in the initial post-buckling of single-mode structural systems.— Q. Appl. Math., 1980, 38, p. 17.
181. Samuels P. The relationship between postbuckling behaviour at coincident branching points and the geometry of an umbilic point of the energy surface.— J. Struct. Meeh., 1979, 7, p. 297.
182. Samuels P. Bifurcation and limit point instability of dual eigenvalue third-order systems.— Int. J. Solids Struct., 1980, 16, p. 743.
183. Schaeffer D., Golubitsky M. Boundary conditions and mode jumping in the buckling of a rectangular plate.— Commun. Math. Phys., 1979, 69, p. 209.
184. Chillingworth D. R. J. Universal bifurcation problems in mechanics of solids.— In: The Rodney Hill Sixtieth Anniversary Volume (eds. H. G. Hopkins, M. J. Sewell).— Oxford: Pergamon, 1981.
185. Knops R. J., Wilkes E. W. Theory of elastic stability.— In: Handbuch der Physik (ed. S. Fliigge). Vol. VIa/3.— Berlin: Springer, 1973.
186. von Karman T., Tsien H. S. The buckling of spherical shells by external pressure.— J. Aeronaut. Sci., 1939, 7, p. 43.
187. Van der Neut A. The interaction of local buckling and column failure of thinwalled compression members.— Proc. 12th Int. Congr. Appl. Meeh., Stanford, 1968.— Berlin: Springer-Verlag, 1968.
188. Thompson J. M. T., Lewis G. M. On the optimum design of thin-walled compression members.— J. Meeh. Phys. Solids, 1972, 20, p. 101.
189. Gilbert R. B., Calladine C. R. Interaction between the effects of local and overall imperfections on the buckling of elastic columns.— J. Meeh. Phys. Solids, 1974, 22, p. 519.
240 Литература
.190. SvenssonS. Е., Groll J. G. A. Interaction between local and overall bucklin_
Int. J. Meeh. Sci., 1975, 17, p. 307.
191. Walker A. C. Interactive buckling of structural components.— Sci. Prog. Oxf., 1975, 62, p. 579.
192. Thompson J. M. T., Tulk J. D., Walker A. C. An experimental study of imperfection-sensitivity in the interactive buckling of stiffened plates.— In: Buckling of Structures (ed. B. Budiansky).— Berlin: Springer-Verlag, 1976.
193. Maquoi R., Massonnet Ch. Interaction between local plate buckling and overall buckling in thin-walled compression members — theories and experiments.— In: Buckling of Structures (ed B. Budiansky).— Berlin: Springer-Verlag, 1976.
194. Byskov E., Hutchinson J. W. Mode interaction in axially stiffened cylindrical shells.— AIAAJ., 1977, 15, p. 941. [Имеется перевод: Ракетная техн, и кос-мон.— М.: Мир, 1977, № 7, с. 57.]
195. Koiter W. Т., Van der Neut A. Interaction between local and overall buckling of stiffened compression panels.— In: Thin-Walled Structures(eds. J. Rhodes, A. C. Walker).— London: Granada, 1980.
196. Croll J. G. A. Towards simple estimates of shell buckling loads.— Der Stahl-bau, 1975, 8, p. 243. 9, p. 283.
197. Batista R. C., Croll J. G. A. A design approach for axially compressed unstiffened cylinders.— In: Stabiliy Problems in Engineering Structures and Components (eds T. H. Richards, P. Stanley).— London: Applied Sci. Publ., 1979.
198. Ellinas С. P., Croll J. G. A. The basis of a design approach for stiffened plates.— In: Stability Problems in Engineering Structures and Components (eds T. H. Richards, P. Stanley).— London: Applied Sci. Publishers, 1979.
199. Batista R. C., Croll J. G. A. A design approach for unstiffened cylindrical shells under external pressure.— In: Thin-Walled Structures (eds. J. Rhodes, A. C. Walker).— London: Granada, 1980.
200. Thompson J. M. T., Hunt G. W. A theory for the numerical analysis of compound branching.— Z. angew. Math. Phys., 1971, 22, p. 1001.
201. Riks E. The Incremental Solution of Some Basic Problems in Elastic Stability.— National Aerospace Lab., NLR, TR 74005 U, 1973.
202. Besseling J. F. Post-buckling and non-linear analysis by the finite element method as a supplement to a linear analysis.— ZAMM, 1975, 55, p. 3.
203. Fujii H., Yamaguti M. Structure of Singularities and its Numerical Realization in Nonlinear Elasticity.— Inst. Computer Sic, Kyoto Sangyo University, Res. Rept., KSU/ICS 79-09, Semptember 1979.
204. Rosen A., Schmit L. A. Design oriented analysis of imperfect truss structures. Part I: Accurate analysis. Part II. Approximate analysis.— Int. J. Num. Meth. Engng, 1979, 14, p. 1309; 1980, 15, p. 483.
205. Hoff N. J., Theory and experiment in the creep buckling of plates and shells.— In: Buckling of Structures (ed. B. Budiansky).— Berlin: Springer-Verlag, 1976.
206. Hayman B. Aspects of creep buckling. I. The-influence of post-buckling characteristics. II. The effects of small deflexion approximations on predicted behaviour.— Proc. Roy. Soc. London, Ser. A, 1978, 364, p. 393—414, 415—433.
207. Hutchinson J. W., Koiter W. T. Post-buckling theory.— Appl. Meeh. Rev., 1970, 23, p. 1353.
208. Koiter W- T. Current trends in the theory of buckling.— In: Buckling of Structures (ed. B. Budiansky).— Berlin: Springer-Verlag, 1976.
209. Budiansky B., Hutchinson J. W. Buckling: progress and challenge.— In: Trends in Solid Mechanics (eds J. F. Besseling, A. M. A. Van der Heijden). Proc, of the Symp. dedicated to the sixty-fifth birthday of W. T. Koiter.— Delft: The University Press, 1979.
210. Koiter W. T. Forty years in retrospect, the bitter and the sweet.— In: Trends in Solid Mechanics (eds. J. F. Besseling, A. M. A. Van der Heijden). Proc, of the Symp. dedicated to the sixty-fifth birthday of W, T, Koiter.— Delft: The University Press, 1979,
Литература 241
211. GioncuV., Ivan M. Buckling of Shell Structures (на румынском яз;)—Bu-curesti: Editura Academiei Republicii Socialiste Romania, 1978.
212. Gioncu V. Thin Reinforced Concrete Shells.— Chichester: Wiley, 1979.
213. Rhodes J., Walker A. C. (eds). Thin-Walled Structures.— London: Granada* 1980.
214. Allen H. G., Bulson P. S. Background to Buckling.— London: McGraw-Hill* 1980.
215. Einstein A. Zur Elektrodynamik bewegter Korper.— Ann. Phys., 1905, 17* p. 891. [Имеется перевод: Эйнштейн А. Собрание научных трудов. Т. I.— М.: Наука, 1965, с. 7.]
216. Einstein A. DieGrundlagen der allgemeinen Relativitaetstheorie.— Ann. Phys., 1916, 49, p. 769. [Имеется перевод: Эйнштейн А. Собрание трудов. Т. I.— М.: Наука, 1965, с. 452.]
217. Ляпунов А. М. Sur les figures d’equilibre peu differentes des ellipsoides d’une masse liquide homogene douee d’un mouvement de rotation.— Записки Академии наук Санкт-Петербурга, 1906, 1, с. 1.
218. Harrison В. К-, Thorne К-S., WakanoM., Wheeler J. A. Gravitation Theory and Gravitational Collapse.— Chicago: The University Press, 1965. [Имеется перевод: Гаррисон Б., ВаканоМ., Торн К., Уилер Дж. А. Теория гравитации и гравитационный коллапс.— М.: Мир, 1967.]
219. Ландау Л. Д. О теории звезд.— Физический журнал АН СССР, 1932, т. 1, с. 285.
220. Chandrasekhar S. The highly collapsed configurations of a stellar mass.— Mon. Not. Roy. Astr. Soc., 1935, 95, p. 207.
221. Chandrasekhar S. An Introduction to the Study of Stellar Structure.— New York: Dover, 1958.
222. Oppenheimer J. R., Volkoff G. M. On massive neutron cores.— Phys. Rev., 1939, 55, p. 374. [Имеется перевод: Оппенгеймер ГО., Волков Г. О массив ных нейтронных сердцевинах.— В сб. статей: А. Эйнштейн и теория гравитации (к 100-летию со дня рождения).— М.: Мир, 1979, с. 337—352.]
223. Misner С. W., Zapolsky Н- S. High-density behaviour and dynamical stability of neutron star models.— Phys. Rev. Letters, 1964, 12, p. 635.
224. Wheeler J. A. Geometrodynamics.— New York: Acad. Press, 1962.
225. Wheeler J. A. Geometrodynamics and the issue of the final state.— In: Relativity Theory, Groups and Topology (ed. B. De Witt).— London: Gordon and Breach, 1964.
226. WeinbergS. Gravitation and Cosmology: Principles and Applications of the General Theory of Relativity.— New York: Wiley, 1972. [Имеется перевод: Вейнберг С. Гравитация и космология. Принципы и приложения общей теории относительности.— М.: Мир, 1975.]
227. HawkingS. W., Ellis G. F. R. The Large Scale Structure of Space-Time.__
Cambridge, University Press, 1973. [Имеется перевод: Хокинг С., Эллис Дж. Крупномасштабные структуры пространства-времени.— М.: Мир, 1977.]
228. Misner С. W., Thorne К-S., Wheeler J. A. Gravitation.— San Francisco: Freeman, 1973. [Имеется перевод: Мизиер Ч., Торн К., Уилер Дж. Гравитация.—М.: Мнр, 1977.]
229. ReesM., Ruffini R., Wheeler J. A., Black Holes, Gravitational Waves and Cosmology: An Introduction to Current Research.— Topics in Astrophysics and Space Physics No. 10.— New York: Gordon and Breach, 1974. [Имеется перевод: Рнс M., Руффини Р., Уилер Дж. Черные дыры, гравитационные волны и космология.— М.: Мир, 1977.]
230. Lynden-Bell D., Wood R. The gfavo-thermal catastrophe in isothermal spheres and the onset of red-giant structure for stellar systems.— Mon. Not. Roy. Astr. Soc., 1968, 138, p. 495.
231. AarsethS. J. Dynamical evolution of clusters of galaxies.— Mon. Not. Roy. Astr. Soc., 1963, 126, p. 223.
232. Антонов В. А. Наиболее вероятное распределение фаз в сферических звезд
242 Литература
ных системах и условия их существования.— Вестиик ЛГУ, сер. матем., мехаи и астр., 1962, т. 17, № 7, с. 135.
233. Glansdorff Р., Prigogine I. Thermodynamic Theory of Structure, Stability and Fluctuations.— London: Wiley, 1971.
234. Katz J. On the number of unstable modes of an equilibrium.— Mon. Not. Roy. Astr. Soc., 1978, 183, p. 765.
235. Katz J. On the number of unstable modes of an equilibrium. II.— Mon Not. Roy. Astr. Soc., 1979, 189, p. 817.
236. Katz J. Stability limits for isothermal cores in globular clusters.— Mon. Not. Roy. Astr. Soc., 1980, 190, p. 497.
237. Darwin G. H- Scientific Papers. Vol. III. Figures of Equilibrium of Rotating Liquid and Geophysical Investigations.— Cambridge: Cambridge University Press, 1910.
238. Jeans J. H. Problems of Cosmogony and Stellar Dynamics.— Cambridge: Cambridge University Press, 1919.
239. Jeans J. H. Astronomy and Cosmogony.— Cambridge: Cambridge University Press, 1928.
240. Lyttleton R. A. The Stability of Rotating Liquid Masses.— Cambridge: Cambridge University Press, 1953.
241. Ledoux P. Stellar stability.— In: Handbuch der Physik (ed. S. Fliigge). Vol. LI.— Berlin: Springer-Verlag, 1958.
242. Chandrasekhar S. Ellipsoidal Figures of Equilibrium.— New Haven: Yale University Press, 1969. [Имеется перевод: Чандрасекхар С. Эллипсоидальные фигуры равновесия.— М.: Мир, 1973.]
243. Hutchinson J-. W., Tvergaard V. Shear band formation in plane strain.— Int. J. Solids Structures, 1981, 17, p. 451.
244. Macmillan N. H., Kelly A. The mechanical properties of perfect crystals.— Proc. Roy. Soc., Ser. A, 1972, 330, p. 291.
245. Born M., Huang K. Dynamical Theory of Crystal Lattices.— Oxford: University Press, 1954. [Имеется перевод: Борн M., Кунь X. Динамическая теория кристаллических решеток.— М.: ИЛ, 1958.]
246. Dean Р. Atomic vibrations in solids.— J. Inst. Maths. Applies., 1967, 3, p. 98.
247. Hill R. On the elasticity and stability of perfect crystals at finite strain.— Math. Proc. Camb. Phil. Soc., 1975, 77, p. 225.
248. Hill R., Milstein F. Principles of stability analysis of ideal crystals.— Phys. Rev., Ser. B, 1977, 15, p. 3087.
249. Coulson C. A. The role of mathematics in chemistry.— IMA Bull., 1973, 9, p. 206.
250. Mindlin R. D. Elasticity, piezoelectricity and crystal lattice dynamics.— J. Elasticity, 1972, 2, p. 217.
251. Hill R., Hutchinson J. W, Bifurcation phenomena in the plane tension test.— J. Meeh. Phys. Solids, 1975, 23, p. 239.
252. Nicolis G. Irreversible thermodynamics.— Reports on Progress in Physics, 1979, 42, p. 225.
253. Auchmuty J. F. G., Nicolis G. Bifurcation analysis of nonlinear reaction-diffusion equations. I. Evolution equations and the steady state solutions.— Bull. Math. Biol., 1975, 37, p. 323.
254. Erneux T., Herschkowitz-Kaufman M. Dissipative structures in two dimensions.— Biophys. Chem., 1975, 3, p. 345.
255. Goodwin В. C. The analysis of rythmic behaviour in organisms: a phenomenological approach.— IMA Bull., 1976, 12, p. 2.
256. Erneux T., Hiernaux J. Transition from polar to duplicate patterns.— J. Math. Biology, 1980, 9, p. 193.
257. Woipert L. Positional information and the spatial pattern of cellular differentiation.— J. Theor. Biology, 1969, 25, p. 1.
258. Erneux T., Hiernaux J., Nicolis G. Turing’s theory of morphogenesis.— Bull. Math. Biology, 1978, 40, p. 771.
Литература 243
259. Turing А. М. The chemical basis of morphogenesis.— Phil. Trans. Roy Soc. London, Ser. B, 1952, 237, p. 37.
260. Nicolis G., Malek-Mansour M. Non-equilibrium pha^e transitions and chemical reactions.— Progress of Theoretical Physics, Suppl. No. 64, 1978, p. 249.
261. May R. M. (ed.). Theoretical Ecology: Principles and Applications.— Oxford: Blackwell, 1976.
262. Tanner J. T. The stability and the intrinsic growth rates of prey and predator populations.— Ecology, 1975, 56, p. 855.
263. May R. M. Thresholds and breaking points in ecosystems with a multiplicity of stable states.— Nature, 1977, 269, p. 471.
264. Reynolds O. Papers on Mechanical and Physical Subjects (reprinted from various Transactions and Journals, in three volumes).— Cambridge: Cambridge University Press, 1900—1903.
265. Lighthill M. J. Turbulence. Chapter 2.— In: Osborne Reynolds and Engineering Science Today (eds. D. M. McDowell, J. D. Jackson).— Manchester: Manchester University Press, 1970.
266. Joseph D. D. Stability of Fluid Motions. Vols 1, II. Springer Tracts in Natural Philosophy Volumes 27 and 28.— Berlin: Springer-Verlag, 1976. [Джозеф Д. Устойчивость движения жидкости.— М.: Мир, 1980.]
267. Lin С. С. The theory of Hydrodynamic Stability.— Cambridge: University Press, 1967. [Имеется перевод: Линь Цзя-цзяо. Теория гидродинамической устойчивости.— М.: ИЛ, 1958.]
268. Taylor G. I. Stability of viscous liquid contained between two rotating cylinders.— Phil. Trans. Roy. Soc. London, Ser. A, 1923, 223, p. 289—343.
269. ChandrasekharS. Hydrodynamic and Hydromagnetic Stability.— Oxford: The University Press, 1968.
270. Bernard P., Ratiu T. (eds.) Turbulence Seminar, Berkeley 1976/1977. Springer Lecture Notes in Mathematics No. 615.— Berlin: Springer, 1977.
271. Kaplan J. L., Yorke J. A. The onset of chaos in a fluid flow model of Lorenz.— Annals, New York Academy of Sciences, 1979 , 316, p. 400.
272. Thompson J. M. T., Thompson R. J., Numerical experiments with a strange attractor.— Bull. Inst. Maths and Its Applies, 1980, 16, p. 150.
273. Ruelle D. Strange attractors.— The Mathematical Intelligencer, 1980, 2, p. 129.
274. Thompson J. M. T. Static and dynamic instabilities in the physical sciences: an inaugular lecture.— J. Eng. Sci., Univ. Riyadh, 1980, 6, p. 71.
275. Крылов H. M., Боголюбов H. H. Новые методы нелинейной механики.— М—Л.: ОНТИ, 1934.
276. Андронов А. А., Хайкии С. Э., Теория колебаний.— М.— Л:. ОНТИ, 1937.
277. Андронов А. А., ВиттА. А., Хайкин С. Э. Теория колебаний.— М.: Наука, 1981.
278. Андронов А. А., Леонтович Е. А., Майер А. Г., Гордон И. И. Качественная теория динамических систем.— М.: Наука, 1966.
279. La Salle J., Lefschetz S. Stability by Liapunov's Direct Method with Applications.— New York: Academic Press, 1961. [Имеется перевод: Ла-Салль Ж-, Лефшец С. Исследование устойчивости прямым методом Ляпунова.— М.: Мир, 1964.]
280. Болотин В. В. Неконсервативиые задачи теории упругой устойчивости.— М.: Физматгиз, 1961.
281. Болотин В. В. Динамическая устойчивость упругих систем.— М.: Гостех-издат, 1956.
282. Hayashi С. Nonlinear Oscillations in Physical Systems.— New York: McGraw Hill, 1964. [Хаяси T. Нелинейные колебания в физических системах — М.: Мир, 1968.]
283. Pars L. A. A Treatise on Analytical Dynamics.— London: Heinemann, 1965.
284. Rosenberg R. M. On nonlinear vibration of systems with many degrees of freedom.— Adv. Appl. Meeh., 1966, 9, p. 159.
285. Blaquiere A. Nonlinear System Analysis,— New York: Academic Press, 1966.
244 Литература
286. Jordan D. W., Smith P. Nonlinear Ordinary Differential Equations.—Oxford: Clarendon Press, 1977.
287. Pippard A. B. The Physics of Vibration. Vol. I.— Cambridge: The University Press, 1978.
288. Nayfeh A. H.,Modk D. T. Nonlinear Oscillations.— New York: Wiley, 1979.
289. Mettler E. Dynamic buckling.— In: Handbook of Engineering Mechanics (ed. S. Fliigge), Ch. 62.— New York: McGraw-Hill, 1962.
290. Hutchinson J. W., Budiansky B. Dynamic buckling estimates.— A1AA J., 1966, 4, p. 525. [Имеется перевод: Ракета, техи. и космон.— М.: Мир, 1966.J
291. Thompson J. М. Т. Dynamic buckling under step loading.— In: Dynamic Stability of Structures (ed. G. Herrmann).— Oxford: Pergamon Press, 1966.
292. Plaut R. H. Postbuckling analysis of nonconservative elastic systems.— J. Struct. Meeh., 1976, 4, p. 395.
293. Plaut R. H. Branching analysis at coincident buckling loads of nonconservative elastic systems.— J. Appl. Meeh., 1977, 44, p. 317.
294. Huseyin K- On the stability of equilibrium paths associated with autonomous systems.— J. Appl. Meeh., Paper No. 81-APM-9.
295. Huseyin K-, Mandadi V. On the instability of multiple-parameter systems. Sectional Lecture.— Proc. 15th Int. Congr. Theor. and Appl. Meeh., Toronto, 1980.— North-Holland PubL Co., 1980.
296. Stewart I. Applications of catastrophe theory to the physical sciences.— Phy-sica (D: Nonlinear Phenomena), 1981, 2, p. 245.
297. Thprnton D. A general review of future problems and their solution.— In: Proc. 2nd Int. Conf, on Behaviour of Off-Shore Structures, BOSS’79, Imperial College, London, August, 1979.— Cranfield: BHRA Fluid Engng, 1979.
298. Pugsley A. The Safety of Structures.— London: Arnold, 1966.
299. Bishop R. E. D. Vibration.— Cambridge: Cambridge University Press, 1979.
300. Novak M. Aeroelastic galloping of prismatic bodies.— J. Eng. Meeh. Div. Am.
Soc. Civ. Engs, 1969, 95, p. 115. /
301. TakensF. Singularities of vector field.— Publ. IHES, 1974, 43, p. 47.
302. Takens F. Forced Oscillations and Bifurcations. Communication No. 3.— Utrecht: Mathematical Institute of Rijksuniversiteit, 1974.
303. Done G. T. S. The Effect of Linear Damping on Flutter Speed.— ARC Reports and Memoranda No. 3396, March 1963.
304. Done G. T. S. The Flutter and Stability of Undamped Systems.— ARC Reports and Memoranda No. 3553, November 1966.
305. Thompson J. M. T., Lunn T. S. Static elastica formulations of a pipe conveying fluid.— J. Sound and Vibr., 1981, 77, p. 127.
306. Thompson J. M. T. On the simulation of a gravitational field by a centrifugal field— Int. J. Meeh. Sci., 1971, 13, p.. 979.
307. Paidoussis M. P., Issid N. T. Dynamic stability of pipes conveying fluid.— J. Sound and Vibr., 1974, 33, p. 267.
308. Thompson J. M. T., Lunn T. S. The non-linear dynamics of a simply-supported pipe conveyieg fluid (to appear).
309. Niordson F. Vibrations of a cylindrical tube containing flowing fluid.— Acta Polytechnica, Mechanical Engineering Series, 1954, 3, No. 2.
310. Thurman A. L., MoteC. D. Nonlinear oscillation of a cylinder containing a flowing fluid.— J. Engng for Industry, 1969, 91, p. 1147.
311. Huseyin K., Plaut R. H. Transverse vibrations and stability of systems with gyroscopic forces.— J. Struct. Meeh., 1975, 3, p. 163.
312. Plaut R. H., Huseyin K. Instability of fluid-conveying pipes under axial load.— J. Appl. Meeh., 1975, 42, p. 889.
313. Holmes P. J. Pipes supported at both ends cannot flutter (to appear).
314. Weaver D. S. On the non-conservative nature of gyroscopic conservative systems.— J. Sound and Vibr., 1974, 36, p. 435.
315. Paidoussis M. P. Flutter of conservative systems of pipes conveying incompressible fluid.— J. Meeh. Engng Sci., 1975, 17, p. 19.
Литература 245-
316. Herrmann G., Bungay R. W. On the stability of elastic systems subjected to non-conservative forces.— J. Appl. Meeh., 1965, 31, p. 435.
317. Herrmann G., Nemat-Nasser S. Energy considerations in the analysis of stability of nonconservative structural systems.— In: Dynamic Stability of Structures (ed. G. Herrmann).— Oxford: Pergamon Press, 1966.
318. Gregory R. W., Paidoussis M. P. Unstable oscillation of tubular cantilevers conveying fluid. I. Theory, II. Experiments.— Proc. Roy. Soc. London, Ser. A, 1966, 293, p. 512—527, 528—542.
319. Paidoussis M. P. Dynamics of tabular cantilevers conveying fluid.— J. Meeh. Engng Sci., 1970, 12, p. 85.
320. Burgess I. W., Levinson M. The post-flutter oscillations of discrete symmetric structural systems with circulatory loading.— Int. J. Meeh. Sci., 1972, 14, p. 471.
321. Bohn M. P., Herrmann G. Instabilities of a spatial system of articulated pipes conveying fluid.— J. Fluids Engng, 1974, 96, p. 289.
322. Leipholz H. H. E-. On the application of the energy method to the stability problem of nonconservative autonomous and nonautonomous systems.— Acta. Mechanica, 1977, 28, p. 113.
323. Van der Pol B. Forced oscillations in a circuit with nonlinear resistance.— Phil. Mag., 1927, 3, p. 65.
324. Van der Pol B. The nonlinear theory of electric oscillations.— Proc. Inst. Radio Engrs., 1934, 22, p. 1051.
325. Thompson J. M. T., Lunn T. S. Resonance-sensitivity in dynamic Hopf bifurcations under fluid loading.— Appl. Math. Model ng, 1981, 5, p, 143.
326. Четаев H. Г. Устойчивость движения.— M.: Гостехиздат, 1955.
327. KaneT. R., Levinson D. A. Stability, instability, and terminal attitude motion of a spinning, dissipative spacecraft.— AIAA J., 1976, 14, p. 39.
328. Kane T. R., Barba P. M. Effects of energy dissipation on a spinning satelite.— AIAA J., 1966, 4, p. 1391. [Имеется перевод: Ракетная техн, и космои.— М.: Мир, 1966.1
329. Robe Т. R., Капе Т. R. Dynamics of an elastic satellite. I, II and III.— Int. J. Solids Structures, 1967, 3, p. 333—352, 691—703, 1031—1051.
330. Teixeira D. R., KaneT. R. Spin stability of torque-free systems.— AIAA J., 1973, 11, p. 862. [Имеется перевод: Ракетная техн, и космон.— М.: Мир, 1973.]
331. Pringle R., Jr. On the stability of a body with connected moving parts.— AIAA J., 1966, 4, p. 1395. [Имеется перевод: Ракетная техн, и космон.— М.: Мир, 1966.]
332. Капе Т. R., Teixeira D. R. Instability of rotation about a centroidal axis of maximum moment of inertia.— AIAA J., 1972, 10, p. 1356. [Имеется перевод: Ракетная техн, и космон.— М.: Мир, 1972.]
333. Mazzilli С. Е. N. A Class of Non-linear Vibrations and Their Stability.— Ph. D-Thesis, University College of London, 1981.
334. Wilson H. R., Cowan J. D. Excitatory and inhibitory interactions in localized: populations of model neurons.— Biophysical J., 1972, 12, p. 1.
335. Wilson H. R. Mathematical models of neural tissue.— In: Cooperative Effects, Progress in Synergetics (ed. H. Haken).— Amsterdam: North-Holland; Publ. Co., 1974.
336. Anninos P. A. The usefulness of artificial neural nets as models for the normal and abnormal functioning of the mammalian CNS.— Progress in Neurobiology, 1975, 4, p. 57.
337. Amari S. A mathematical approach to neural systems.— In: Systems Neuroscience (ed. J. Metzler).— New York. Academic Press, 1977.
ИМЕННОЙ УКАЗАТЕЛЬ
Абрахам (Abracham R.) 13, 47
Айвэн (Iwan W. D.) 41, 236, 241
Аллен (Allen Н. G.) 241
Аль-Ател (Al Athel S.) 237
Аль-Рави (Al-Rawi А.) 41, 236
Амари (Amari S.) 227, 228, 245
Андронов А. А. 11, 12, 243
Аннинос (Anninos Р. А.) 224, 245
Антонов В. А. 91, 92, 241
Арнольд В. И. 5, 12
Арсет (Aarseth S. J.) 91, 94, 96, 241
Ахмути (Auchmuty) 131, 242
.Балсои (Bulson Р. S.) 241
Бангей (Bungay R. W.) 204, 245
Барба (Barba Р. М.) 212, 245
Батиста (Batista R. С.) 240
Бауер (Bauer L.) 235
Белоусов 125, 125, 127
Бенджамин (Benjamin Т. В.) 29, 42, 44, 45, 135, 161, 162, 164, 193, 202—205, 234, 236, 240, 244
Весселинг (Besseling J. F.) 240
Бернард (Bernard Р.) 243
Берри (Berry М. V.) 32, 34, 37, 106, 165, 235
Биеков (Byskov Е.) 240
Бишоп (Bishop R. Е. D.) 45, 205, 236, 044 245
Блевинс (Blevins R. D.) 40, 41, 189, 236
Блэквайер (Blaquire А.) 243
Боголюбов Н. Н. 167, 180, 187, 243
Болотин В. В. 191, 243
Больцмаи Л. (Boltzman L.) 92
Бон (Bohn М. Р.) 205
Брекер (Broker Т.) 5
Бритвек (Britvec S. J.) 239
Брукс (Brooks Р. Р. Н.) 39, 182, 236
Будянский (Budiansky В.) 13, 79, 233
Бузина (Buzyna) 165
Бургесс (Burgess I. W.) 205, 245
Варченко А. Н. 5
Вайнберг (Weinberg S.) 87, 241
Вакано (Wakano М.) 80, 241
Ван-дер-Нойт (Van der Neut А.) 78, 239, 240
Ван дер Поль (Van der Pol В.) 206, 245
Вассерман (Wassermann G.) 34, 235
Витт А. А. 243
Волков (Volkoff G. М.) 81, 241
Вольперт (Wolpert L.) 242
Вольтерра (Volterra) 41, 136
Вуд (Wood R.) 91—93, 241
Вэддингтон (Vaddington С. Н.) 150, 236
Галеркин 191, 195—197
Галл (Gull S.) 89, 90
Гамильтон (Hamilton) II, 12, 139, 204
Гаррисон (Harrison В. К.) 80—82, 84,
241
Гаспар (Gaspar Z.) 239
Гаттингер (Gattinger W.) 237
Гершкович-Кауфман (Herschkowitz-
Kaufman М.) 126, 242
Гийемин (Gijemin W.) 5
Гильберт (Gilbert R. В.) 239
Глансдорф (Glansdorf Р.) 91, 92, 242
Голлаб (Gollbub J. Р.) 163
Голубицкий (Golubitski М.) 5, 34, 78,
239
Грегори (Gregory R. W.) 205, 245
Гудвии (Goodwin В. С.) 242
Именной указатель 247
Гумовский (Gumowski 1.) 178, 238
Гурел (Gurel О.) 178, 237
Гусейн-Заде С. М. 5
Дарвин (Darwin G. Н.) 97, 242
Дьен Хо (Но D.) 78, 239
Декснис (Deksnis Е. В.) 45, 205, 237
Дин (Dean Р.) 107, 242
Джилмор (Jilmor Р.) 5
Джинс (Jeans J. Н.) 97, 242
Джиоиси (Gioncu V.) 241
Джозеф (Joseph D.) 156, 157, 243
Джонг (Jong I.) 204, 237
Джордан (Jordan D. W.) 244
Додсон (Dodson М. М.) 150, 236
Доуэлл (Dowell Е. Н.) 42, 44, 45, 236
Доун (Done G. Т. S.) 191, 244
Жаботинский 40, 41, 125—127
Запольский (Zapolsky) 83, 241
Зельдович Я. Б. 86
Зиман (Zeman Е. С.) 12, 14, 30, 38, 53, 77, 86, 133—136, 150, 165, 232, 234, 236, 238, 239
Иннес (Innes I.) 183
Иссид (Issid N. Т.) 196, 203, 205, 244
Йорк (Yorke J. А.) 165, 263
Кавамата (Kawamata S.) 239
Каладайн (Kalladine С. R.) 240
Каплан (Kaplan J, L.) 165, 243
Карман (Karman Т.) 78, 239
Кац (Katz J.) 93, 94, 97, 98, 234
Кейн (Kane Т. R.) 10, 212, 216, 218,
245
Келлер (Keller Н.) 235
Келли (Kelly А.) 101, 105, 113, 116,
242
Кеплер И. (Kepler J.) 90
Кинер (Keener J. Р.) 235
Кнопс (Knops R. J.) 78, 239
Койтер (Koiter W. Т.) 13, 37, 74, 78,
79, 233, 235, 237, 240
Коуен (Cowan J. D.) 223, 224, 226, 245
Коулсон (Coulson С. А.) 124, 242
Крылов Н. М. 166, 180, 187, 243
Кролл (Croll J. G. А.) 78, 240
Кули (Cooley С. R.) 234
Куэтт (Couette) 29, 151, 161
Кюрри (Currie I, G.) 41, 236
Лагранж (Lagrange J.) 12, 204, 230 232
Лайтхилл (Lighthill J.) 5, 151, 154 243 *"
Ландау Л. Д. 81, 241
Ландер (Lander L.) 5
Ланцош (Lanczos С.) 49, 238
Ла Салл (La Salle J.) 243
Левинсон (Levinson D. A.) 10, 205
212, 245
Леду (Ledoux P.) 97, 242
Лейпхольц (Leiphoiz H. H.) 206, 245-
Лере (Leray) 160, 161
Лефшец (Lefschetz S.) 243
Лнм (Lim К. C.) 235
Лин (Lin Y. K.) 237
Линден-Белл (Linden-Bell D.) 80, 90, 92, 93, 95, 241
Лин Цзя-цзяо (Lin С. C.) 243
Литтлтон (Littleton R.) 97, 98, 242
Лоренц (Lorenz E. N.) 48, 151, 166— 168, 238
Лотка (Lotka) 41, 136
Лунн (Lunn T. S.) 202, 207, 236, 244, 245
Льюнс (Lewis G. M.) 239
Лэчер (Lacher) 165
Ляпунов A. A. 12, 232, 241
Маззили (Mazzilli С. E. P.) 222, 245
Мак-Артур (McArthur) 165
Маклорен (Maclaurin) 98, 99
Макмиллан (Macmillan L. H.) 101,
105, 113, 116, 242
Макуа (Maquei R.) 240
Малек-Мансор (Malek-Mansour M.) 135, 243
Малле-Парэ (Mallet-Paret J.) 237
Мандади (Mandadi V.) 244
Марсден (Marsden J. E.) 13, 47, 232,
237, 238
Матковский (Matkowsky) 133
Махар (Mahar) 133
Меттлер (Mettler E.) 244
Мизнер (Misner C. W.) 83, 87, 241
Микаэль (Michael D. H.) 30, 234
Милстейн (Milstein F.) 123, 242
Миндлин (Mindlin R. D.) 124, 242
Мира (Mira C.) 178, 238
Mot (Mote C. D.) 202, 203, 244
Мук (Mook G. T.) 180, 244
Мун (Moon F.) 238
Мэй (May R. M.) 41, 148, 150, 236, 243
Мэкли (Mackley M. R.) 37, 165, 235-
Массоне (Massonnet Ch.) 240
248 Именной указатель
Най (Nye J. F.) 32, 234, 235
Найфэ (Nayfeh А. Н.) 180, 244
Немат-Нассер (Nemat-Nasser S.) 204, 205, 236, 238, 245
Николае (Nikolis G.) 40, 131, 133, 135, 136, 148, 150, 236, 242
Ниордсон (Niordson F.) 202, 203, 244
Новак (Novak М.) 40, 184, 185, 189, 236, 244
Пайдуссис (Paidoussis М. Р.) 45, 196, 203
Паркинсон (Parkinson G. V.) 186, 188
Постон (Poston Т.) 150
Пригожин (Prigogine I.) 133, 135, 150
Руффини (Ruffini R.) 87, 241
Рэлей (Rayleigh) 26, 56, 59, 62, 68
Рэнд (Rand D. А.) 47, 206, 237
Рюэль (Ruelle D.) 48, 151, 178, 179, 238, 243
Самуэльс (Samuels Р.) 239
Саппл (Supple W. J.) 235
Свенсон (Svensson S. Е.) 239
Смейл (Smale S.) 12, 232
Смит (Smith J. D.) 236
Смит (Smith Р.) 186, 188, 244
Стюарт Я. (Stewart I.) 6, 37, 78, 150, 232, 244
Суиини (Swinney Н. L.) 163
Такенс (Takens F.) 48, 151, 178, 191, 239 244
Талк (Tulk J. D.) 240
Твергард (Tvergaard V.) 94, 96
Тейксейра (Teixeira D. R.) 218, 245
Терлевич (Terlevich Е.) 94, 96
Толмен (Tolman) 82
Том (Thom R.) 12, 21, 23, 27, 28, 32, 34, 135, 150, 232
Томпсон (Thompson D’Arey W.) 40, 236
Томпсон (Thompson J. M. T.) 7, 14, 37, 53, 77, 98, 101, 166, 202, 207, 239, 240, 243—245
Томпсон (Thompson R.) 9, 115, 166, 243
Торн (Thorne К. S.) 80, 87, 241
Торндайк (Thorndike A. S.) 234, 235
Торнтон (Thornton D.) 181, 244
Тримбл В. (Trimble V.) 90
Турман (Thurman A. L.) 202, 203, 244
Тэйлор (Taylor G. I.) 26, 28, 162, 164, 243
Тэи (Tan J. K. Y.) 235
Тьюринг (Turing A. M.) 135, 243
Уивер (Weaver D. C.) 203, 244
Уилер (Wheeler J. A.) 80, 81, 87, 241
Уилкс (Wilkes E. W.) 78, 239
Уилсон (Wilson H. R.) 223, 224, 226—*
228 245
Уинфри (Winfree A. T.) 40, 236
Уолкер (Walker A. C.) 240, 241
Фанг (Fung V. C.) 236
Фаузи (Fawzy I.) 45, 205, 236
Феистермахер (Fenstermacher P. R.) 163
Фудзии (Fujii H.) 240
Хаген (Hagen) 155
Хайкин С. Э. 243
Хансен (Hansen J. S.) 239
Хангай (Hangai Y.) 239
Хант (Hunt G. W.) 10, 14, 35—37, 53,
78, 105, 233, 235
Хартлеи (Hartlen R. T.) 41, 236
Хатчинсон (Hutchinson J. W.) 13, 79,
233, 240, 242, 244
Хаяси (Hayashi C.) 243
Хейл (Hale J. K.) 237
Хейман (Hayman B.) 79, 240
Хенон (Нёпоп M.) 49, 151, 167—169,
178, 179, 238
Херрманн (Herrmann G.) 13, 17, 117, 204, 205, 233, 237, 238, 245
Xcy (Hsu C. S.) 49, 178, 238
Хилл (Hill R.) 123, 242
Хирно (Hiernaux J.) 135, 242
Xo (Ho D.) 78, 239
Хокинг (Hawking S. W.) 87, 241
Холмс (Holmes P.) 42, 45, 47, 48, 166,-
178, 191, 203, 206, 237, 238, 244
Хопф (Hopf E.) 21, 41, 157, 234
Хофф (Hoff N. J.) 79, 240
Xy (Hui D.) 239
Хуан (Huang K.) 242
Хусейи (Huseyin K.) 180, 181, 203, 239, 244
Цёрхер (Zuercher J. C.) 234
Цзяиь (Tsien H. S.) 78, 239
Циглер (Ziegler H.) 13, 17, 56, 233
Чандрасекхар (Chandrasekhar S.) 81,
83, 97, 164, 241, 242
Именной указатель 249
Чеиг (Cheng W. Н.) 238
Цр*гярн Г ОЛ.Ц
Чилвер (Chilver А. Н.) 13, 235, 239
Чилингуорт (Chillingworth D. R. J.)
47, 48, 53, 78, 237—239
Чоу (Chow S. N.) 237
Шаудер (Schauder) 160, 161
Шмит (Schmit L. А.) 240
Шоррок (Shorrock Р. А.) 37, 101, 235
Шэффер (Schaefer D.) 34, 235, 239
Эгглтон (Eggieton) 95
Эйкмайер (Eikemeier Н.) 237
Эйлер (Euler L.) 11, 12, 52, 229, 232
Эйнштейн А. 68, 80, 231, 241
Эллинас (Ellinas С. Р.) 240
Эллиот (Elliot В. D.) 182
Эллис (Ellis F. G. R.) 87, 241
Эль-Наши (El Naschie М. S.) 237
Эрнё (Erneux Т.) 135, 242
Ямагути (Yamaguti М.) 240
Якоби (Jacobi) 98, 99
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Арка 23, 24, 27
Аттрактор 19, 167
— странный 48, 167
Бифуркации асимметричные 25
— вторичные 133
— динамически устойчивые 20
— закритическйе 164
— нелинейные динамические 17
--- статические 17
— статически устойчивые 20
— транскритические 21
— Хопфа 21, 42, 44, 206
Ветвление в вершине 33
Галопирование 17, 38, 39, 181
Границы устойчивости 33
Демпфирование отрицательное 39
Деформация пассивная 13
Дифференцировка клеток 133
Закон «двух третей» 27, 84, 112
Звезды нейтронные 24, 81
Карлик белый 24, 81
Катастрофа бабочки 22
— высокого порядка 37
— гиперболической омбилики 22
— ласточкин хвост 22
— параболической омбилики 22
— сборки 21, 22, 29, 53, 99, 101
— складки 21,— 23, 71, 81, 82, 90, 93
— эллиптической омбилики 22
Коллапс 80
Коэффициенты устойчивости 65, 85
Купол сферический 25
Неустойчивость атомной решетки 36
— динамическая 14, 16
— Матье 47, 222
— статическая 14, 16
— структурная 40
— упругая 18
Оптимизация конструкций 37
Осциллятор линейный 14
Параметр несовершенства 26, 53
— управляющий 21
Петля гистерезиса 24
Поверхность разрушающих напряжений 37
Потеря устойчивости по первой гармонике 59, 65
Развертка универсальная 36
Резонанс вихревой 38, 41, 181
Репеллер 19
Сборка 21, 22, 29, 53, 99, 101
— неустойчивая 28, 74, 100
— устойчивая 164
Седло 16
Система консервативная 13, 17
— неконсервативная 13
Скачок динамический 37, 38
Складка 21—23, 71, 81, 82, 90, 93
Структура диссипативная 40
Теорема сопряжения 24, 93
Точка возврата 30
— критическая 23
--- изолированная 112
Предметный указатель 251
----составная 112
— предельная 19
Точка бифуркации
---- антиклинная 76
----асимметричная 17, 75, 76, 164
гомоклинная 76
----динамическая 19, 185
— — докрнтическая 157
— — изолированная 74
— — моноклинная 76
----неустойчиво симметричная 17,
21, 28, 76, 101, 157
----слившаяся 74
----устойчиво симметричная 17, 19,
28
Траектория вторичная равновесная 19
— равновесная 19
Узел вырожденный 16
Устойчивость орбитальная 213
— по Ляпунову 213
— структурная 12, 164
— топологическая 47
Флаттер 38, 42, 181, 189
Фокус неустойчивый 15
— отталкивающий 20
— притягивающий 20
— устойчивый 15
Цикл отталкивающий 19
— предельный 19
— притягивающий 19
Чувствительность к несовершенствам 75, 112
ОГЛАВЛЕНИЕ
От переводчика...................................................... 5
Предисловие.......................................................... 7
Предисловие автора .................................................. 8
Глава 1. ВВЕДЕНИЕ................................................. 11
1.1. Исторический обзор от Ньютона до Андронова . ........ 11
1.2. Неустойчивости линейного осциллятора...................... 14
1.3. Нелинейные статические и динамические бифуркации.......... 17
1.4. Статические бифуркации и теория катастроф................. 21
1.5. Складка или предельная точка.............................. 23
1.6. Сборка или симметричная бифуркация........................ 26
1.7. Гиперболическая омбилика н ветвление в вершине........ 33
1.8. Катастрофы высокого порядка и оптимизация конструкций . . 37
1.9. Галопирование и флаттер подвесных мостов ................. 38
1.10. Возникновение порядка в биохимических реакциях........ 40
1.11. Неконсервативные задачи при гидродинамических воздействиях 41
1.12. Теория динамических систем и топологическая устойчивость . 47
1.13. Хаос, турбулентность и странные аттракторы............... 48
1.14. Заключительные замечания.................................. 49
Глава 2. ПОТЕРЯ УСТОЙЧИВОСТИ КОНСТРУКЦИЙ............................ 50
2.1. Простые эксперименты с изгибаемым стержнем............ 50
2.2. Исследование модели консольного шарнира............... 54
2.3. Конечные перемещения стержня'......................... 56
2.4. Потеря устойчивости и закритическое поведение по первой гармонике ........................................................ 59
2.5. Модель стержня с двумя степенями свободы.............. 62
2.6. Полный гармонический анализ стержня на упругом основании . 67
2.7. Симметричное и несимметричное прощелкивание арок...... 71
2.8. Некоторые изолированные и слившиеся точки ветвления .... 74
2.9. Практические задачи оценки нагрузок................... 78
Глава 3. АСТРОФИЗИКА И ГРАВИТАЦИОННЫЙ КОЛЛАПС.................... 80
3.1. Коллапс массивной холодной звезды в общей теории относительности ..................................................... 80
3.2. Сверкновые взрывы холодных звезд........................... 87
3.3. Гр геотермическая катастрофа горячих звездных систем .... 90
3.4. Ядро-гало в шаровых звездных скоплениях ................... 94
3.5. Эволюция вращающихся планетарных масс...................... 97
Оглавление 253
Глава 4. БИФУР КАЦИОННАЯ НЕУСТОЙЧИВОСТЬ АТОМНОЙ РЕШЕТКИ 101
4.1. Нарушение симметрии................................. 101
4.2. Квантовомеханическая и ньютоновская постановки...... 106
4.3. Теория возмущений в верхушечной точке ветвления....... 108
4.4. Чувствительность к несовершенствам при разрушении кристалла 112
4.5. Потенциал Леннард-Джонса для межатомных взаимодействий 113
4.6. Плотноупакованный слой атомов....................... 115
4.7. Четырехатомная ячейка . . ................... ... 117
4.8. Применение общей теория............................ . 120
4.9. Трехмерная решетка.................................. 122
4.10. Дальнейшие исследования............................. 123
Глава 5. СПОНТАННЫЙ ПОРЯДОК В БИОХИМИЧЕСКИХ РЕАКЦИЯХ И БИОЛОГИЯ РАЗВИТИЯ....................................... 125
5.1. Брюсселяторная модель химической реакции.............. 127
5.2. Образование пространственного порядка в термодинамике . . . 130
5.3. Дифференцировка клеток в биологии развития............ 133
Глава 6. ДИНАМИКА ПОПУЛЯЦИЙ И ЭВОЛЮЦИЯ ЭКОЛОГИИ ТИПА ХИЩНИК-ЖЕРТВА ............................. 136
6.1. Уравнения Лотки — Вольтерры............................ 136
6.2. Устойчивость стационарного состояния................... 138
6.3. Численные решения, полученные при помощи метода конечных разностей................................................... 140
6.4. Эволюционная игра.....................................
6.5. Структурная устойчивость............................... 148
6.6. Экологические исследования.............................. 148
6.7. Последние работы........................................ 150
Глава 7. ГИДРОДИНАМИЧЕСКАЯ НЕУСТОЙЧИВОСТЬ И ВОЗНИКНОВЕНИЕ ТУРБУЛЕНТНОСТИ ........................................... 151
7.1. Течение в трубе круглого сечения . ................. 152
7.2. Поток в кольцевом зазоре............................... 156
7.3. Общая гидродинамическая неустойчивость.................. 159
7.4. Вихри Тэйлора между вращающимися цилиндрами............. 161
Глава 8. ХАОТИЧЕСКАЯ ДИНАМИКА СТРАННОГО АТТРАКТОРА . . 166
8.1. Конечно-разностиое отображение Хенона................... 167
8.2. Численные результаты и увеличение последовательностей . . . 169
8.3. Чувствительность к начальным условиям................... 175
8.4. Чувствительность к ошибкам вычислений, получаемым в результате округлений............................................. 177
8.5. Хаотические движения стержня за пределом устойчивости. Некоторые современные работы.................................... 178
Глава 9. САМ0В03БУЖДАЮЩИЕСЯ КОЛЕБАНИЯ ПРИ НЕКОНСЕРВАТИВНОЙ ГИДРОДИНАМИЧЕСКОЙ НАГРУЗКЕ............................... 180
9.1. Аэроупругое галопирование плохообтекаемых конструкций . . 181
9.2. Флаттер крыла самолета при высоких сверхзвуковых скоростях 189
9.3. Динамическая н статическая неустойчивость трубы, по которой перекачивается жидкость..................................... 192
9.4, Резонансная чувствительность динамической бифуркации Хопфа 206
254 Оглавление
Глава 10. ОРБИТАЛЬНАЯ УСТОЙЧИВОСТЬ И УПРАВЛЕНИЕ ОРИЕНТАЦИЕЙ КОСМИЧЕСКОГО КОРАБЛЯ.................................... 212
10.1. Устойчивость движения орбитального тела............... 212
10.2. Затухание пассивной нутации вращающегося спутника .... 216
Глава 11. ПОЛЕВЫЕ ТЕОРИИ НЕЙРОННОЙ АКТИВНОСТИ МОЗГА . . 223
11.1. Мозг и центральная нервная система.................... 223
11.2. Механика возбуждения и торможения..................... 224
11.3. Складки и множественный гистерезис в стационарных состояниях .................................................... 226
11.4. Временные колебания, соответствующие предельному циклу 226
11.5. Структурообразование в пространстве нейронного поля .... 227
Приложение. НЕКОТОРЫЕ БИОГРАФИИ ТВОРЦОВ ТЕОРИИ УСТОЙЧИВОСТИ . 229
ЛИТЕРАТУРА. . ........... ... .232
Именной указатель............................................. 246
Предметный указатель ........................................... 250