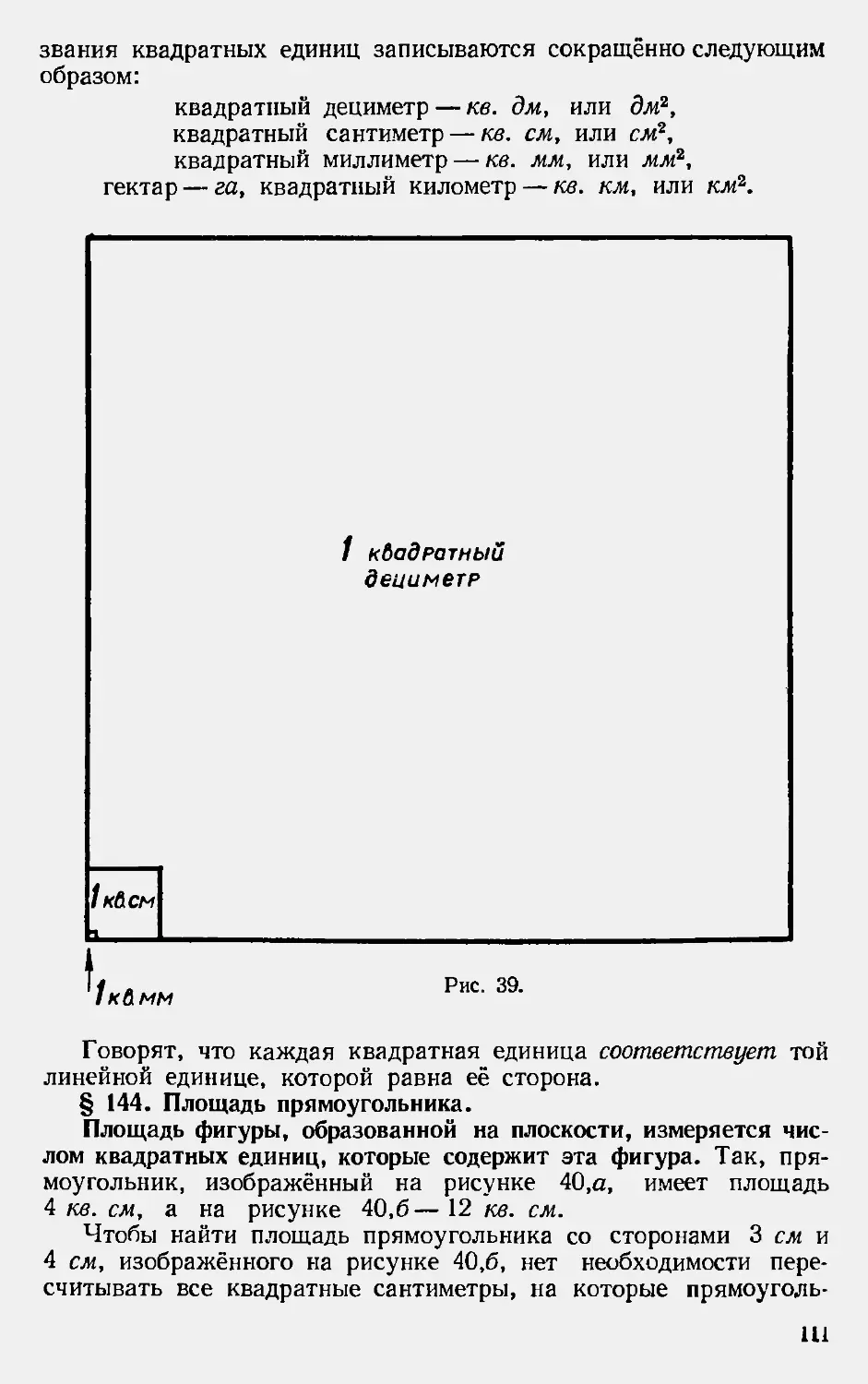
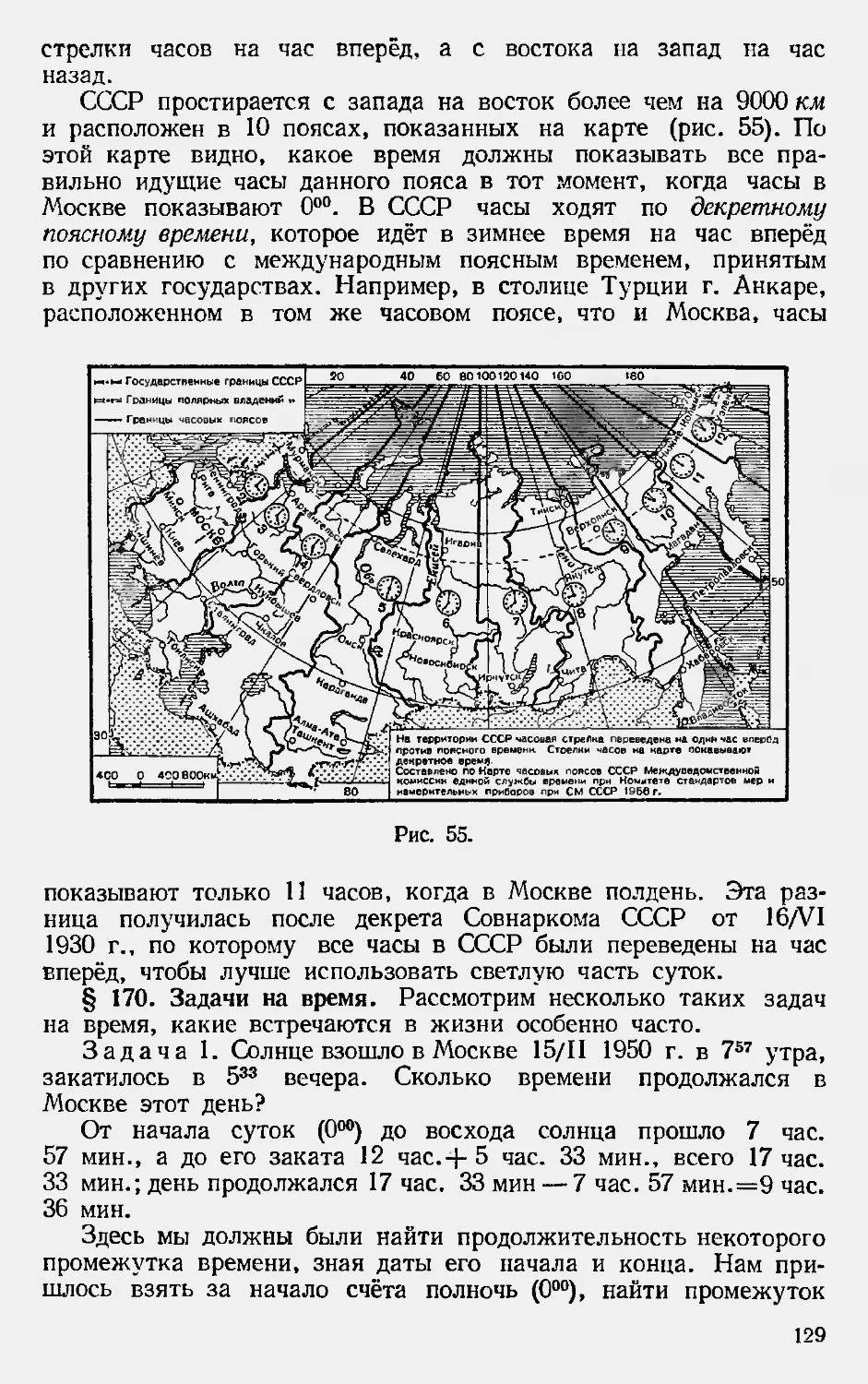
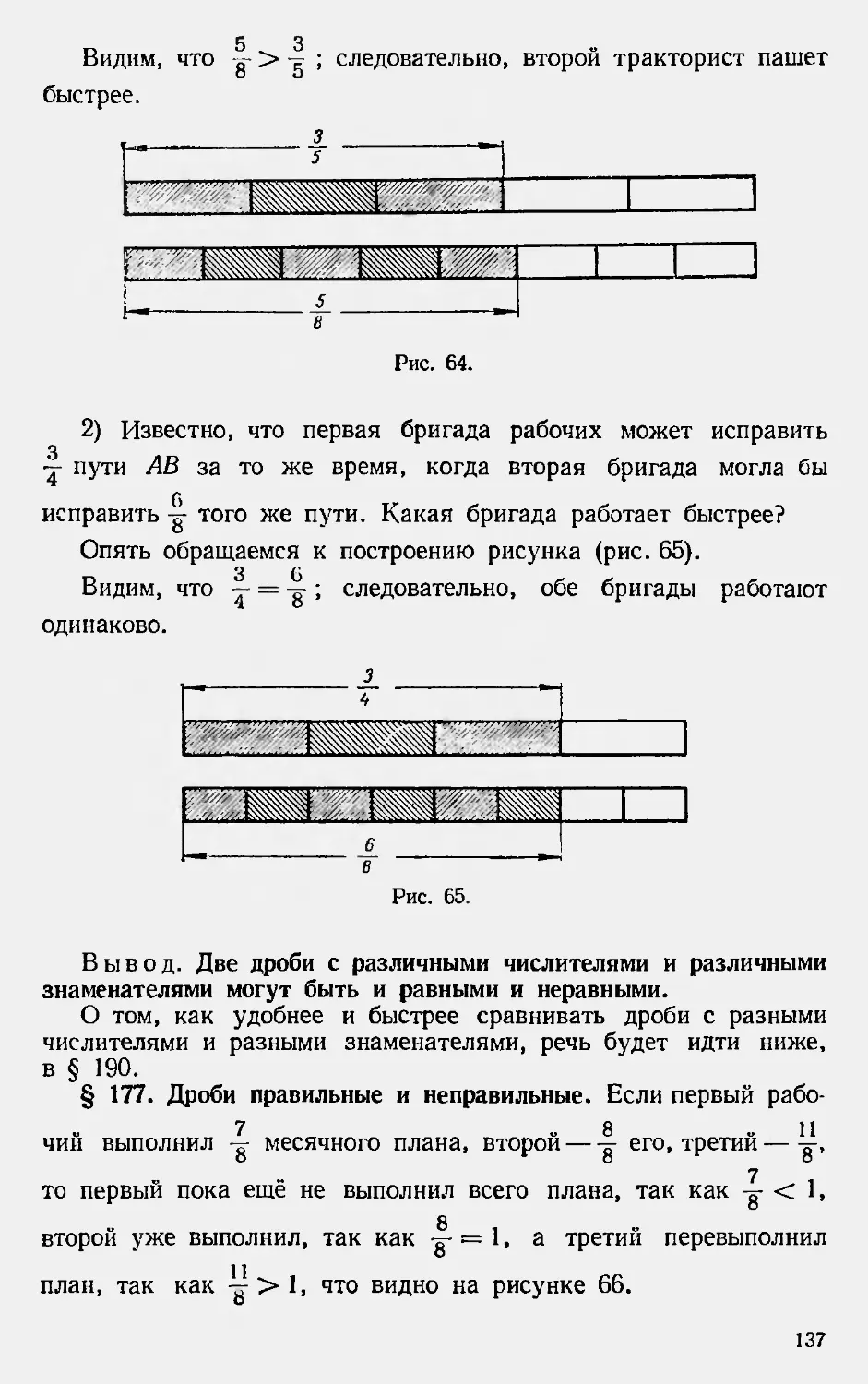
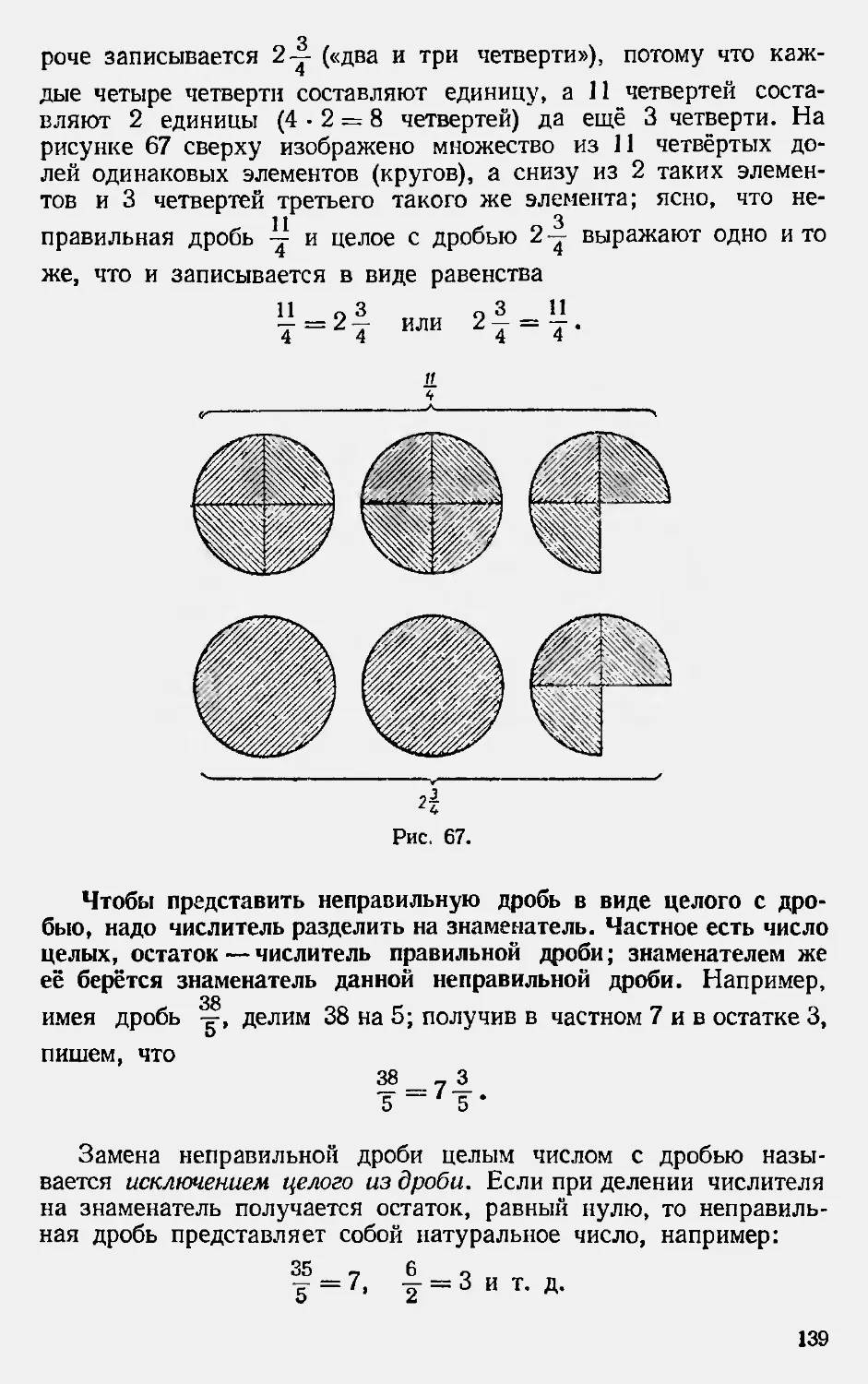
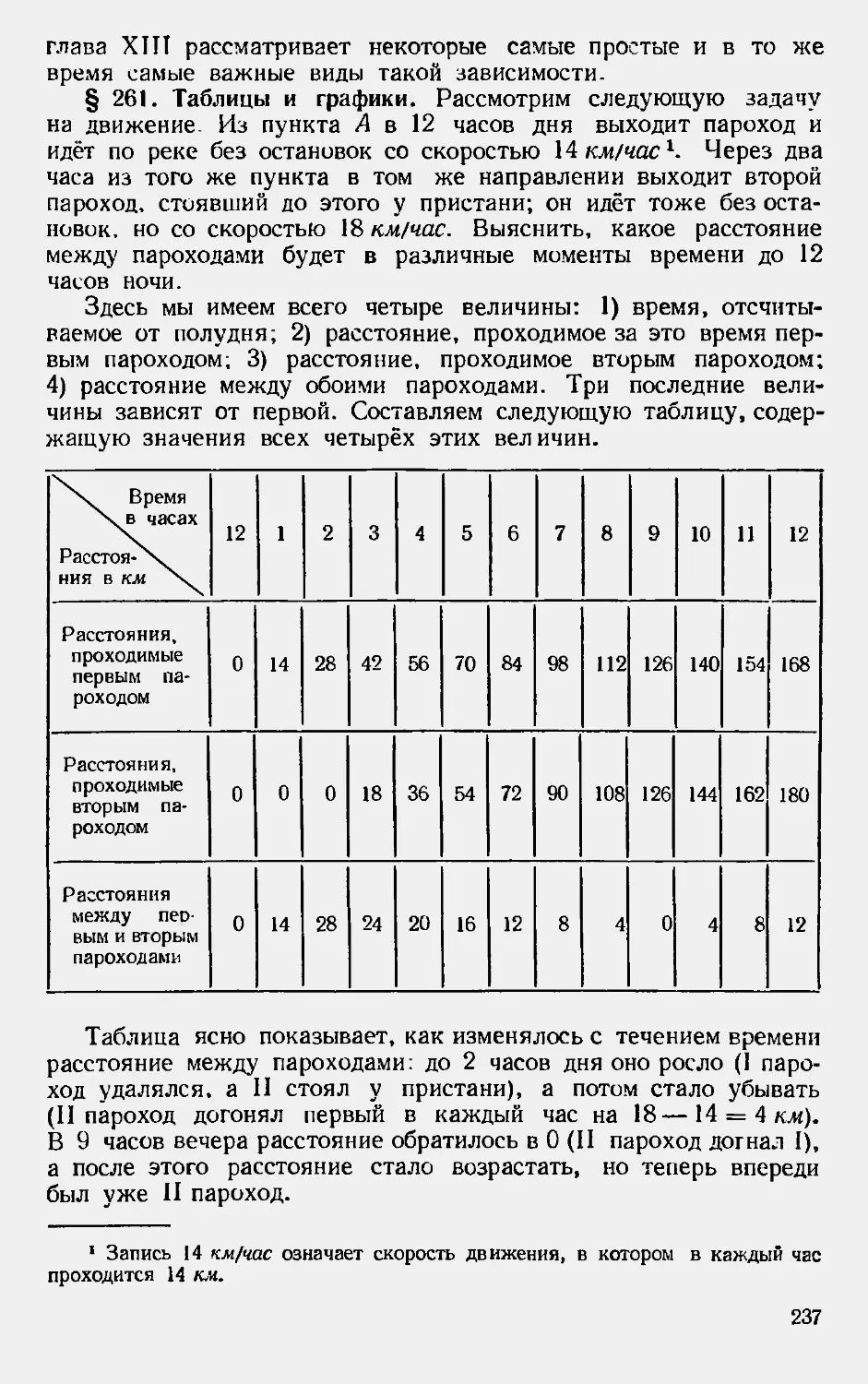
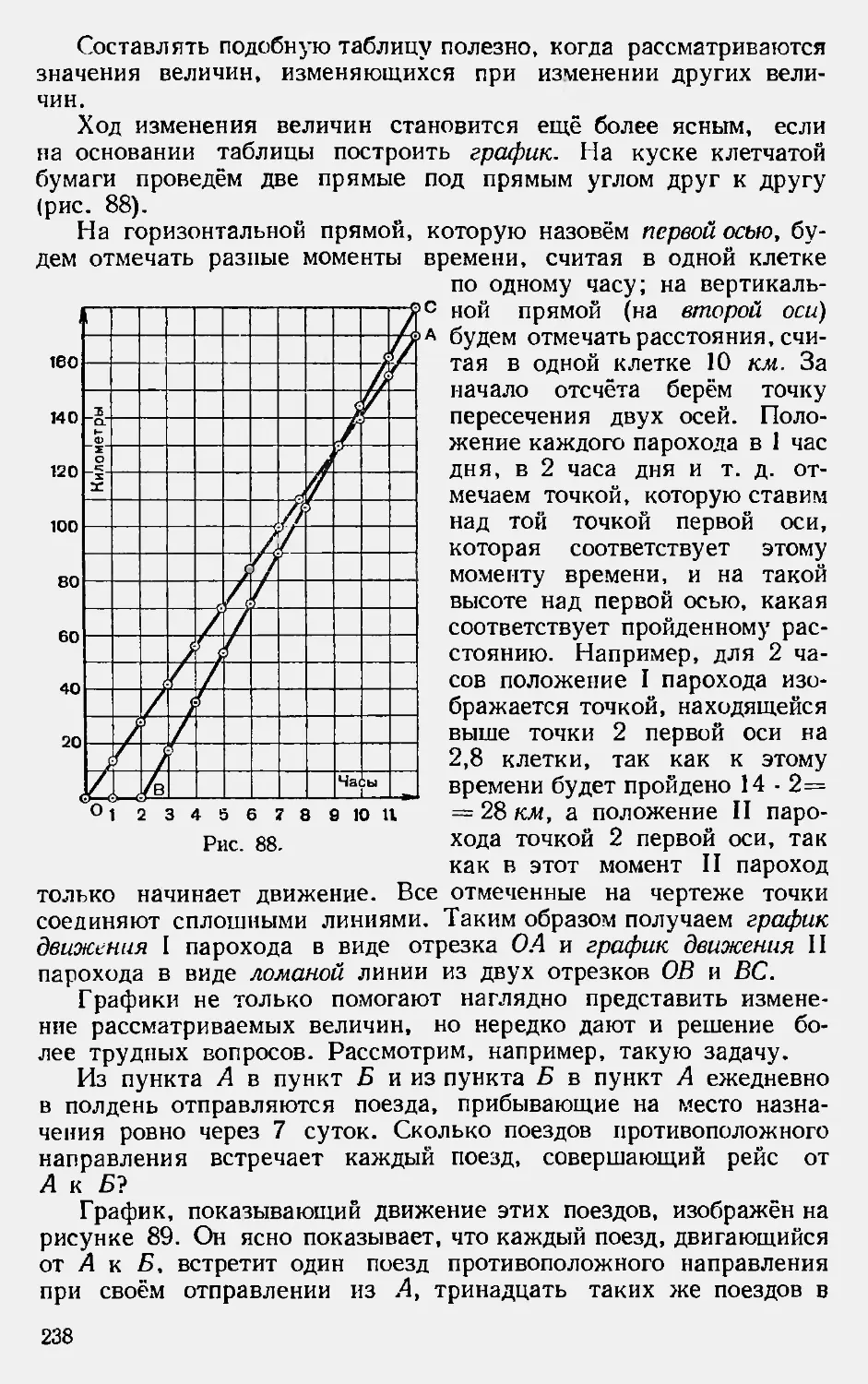
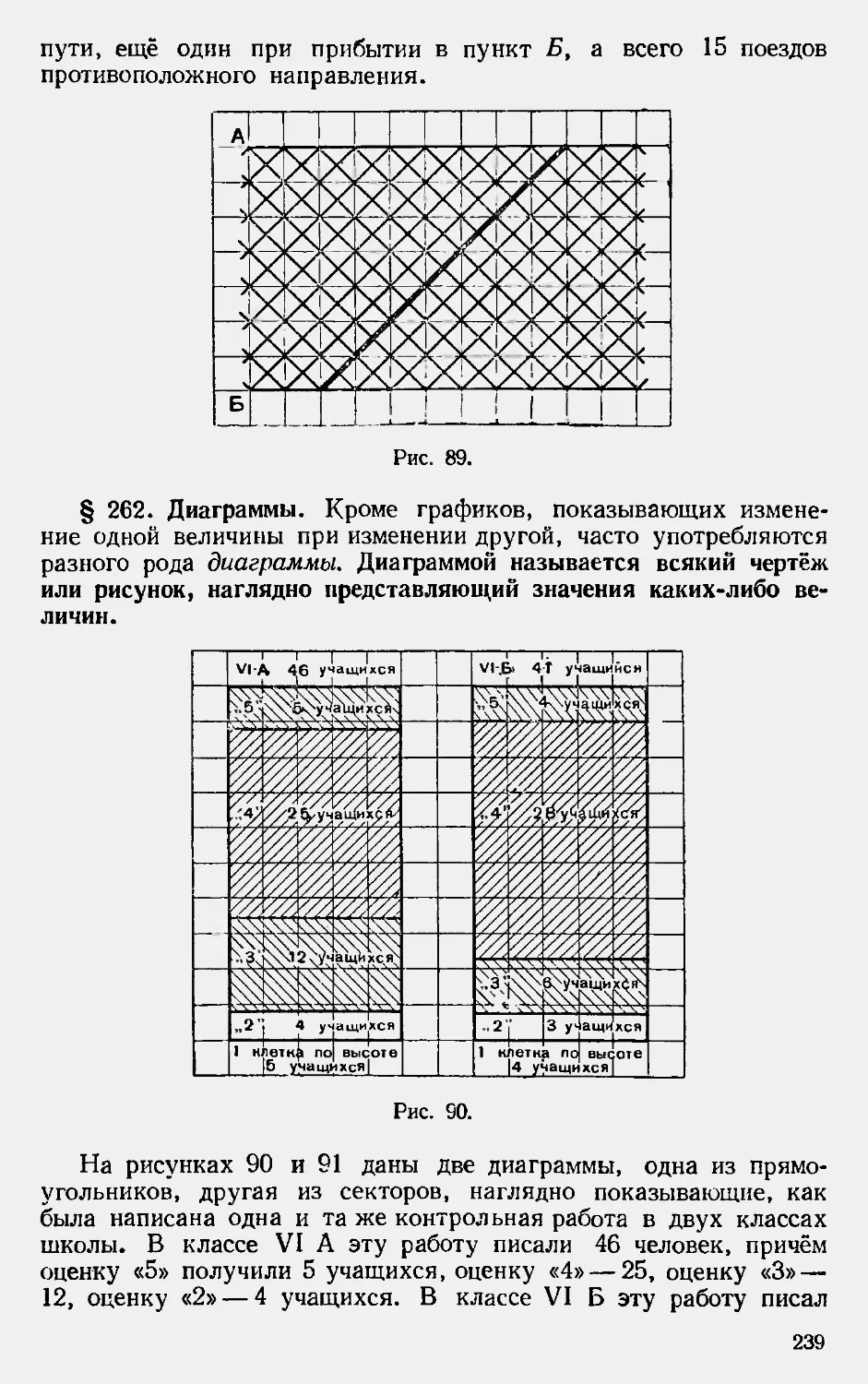
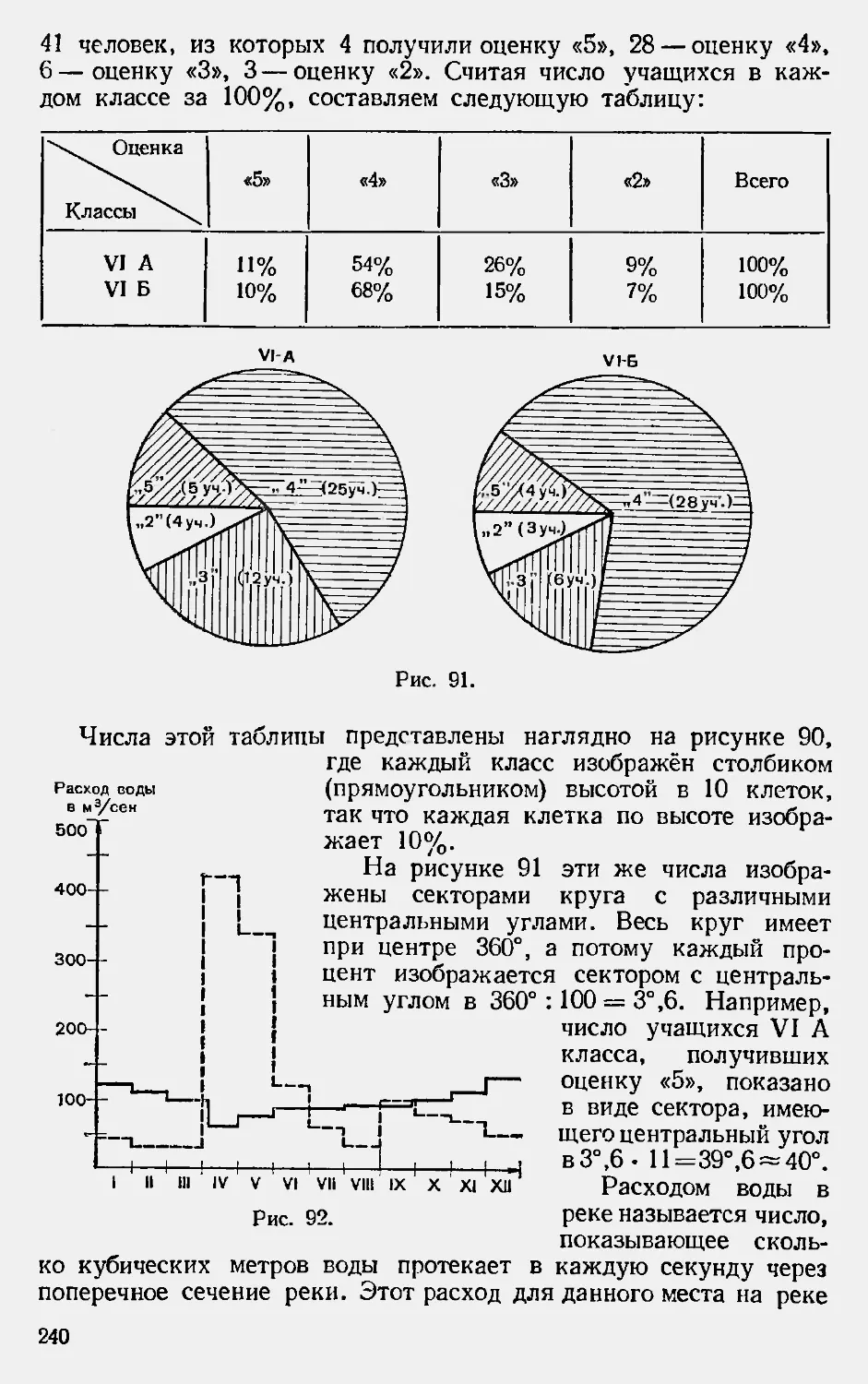
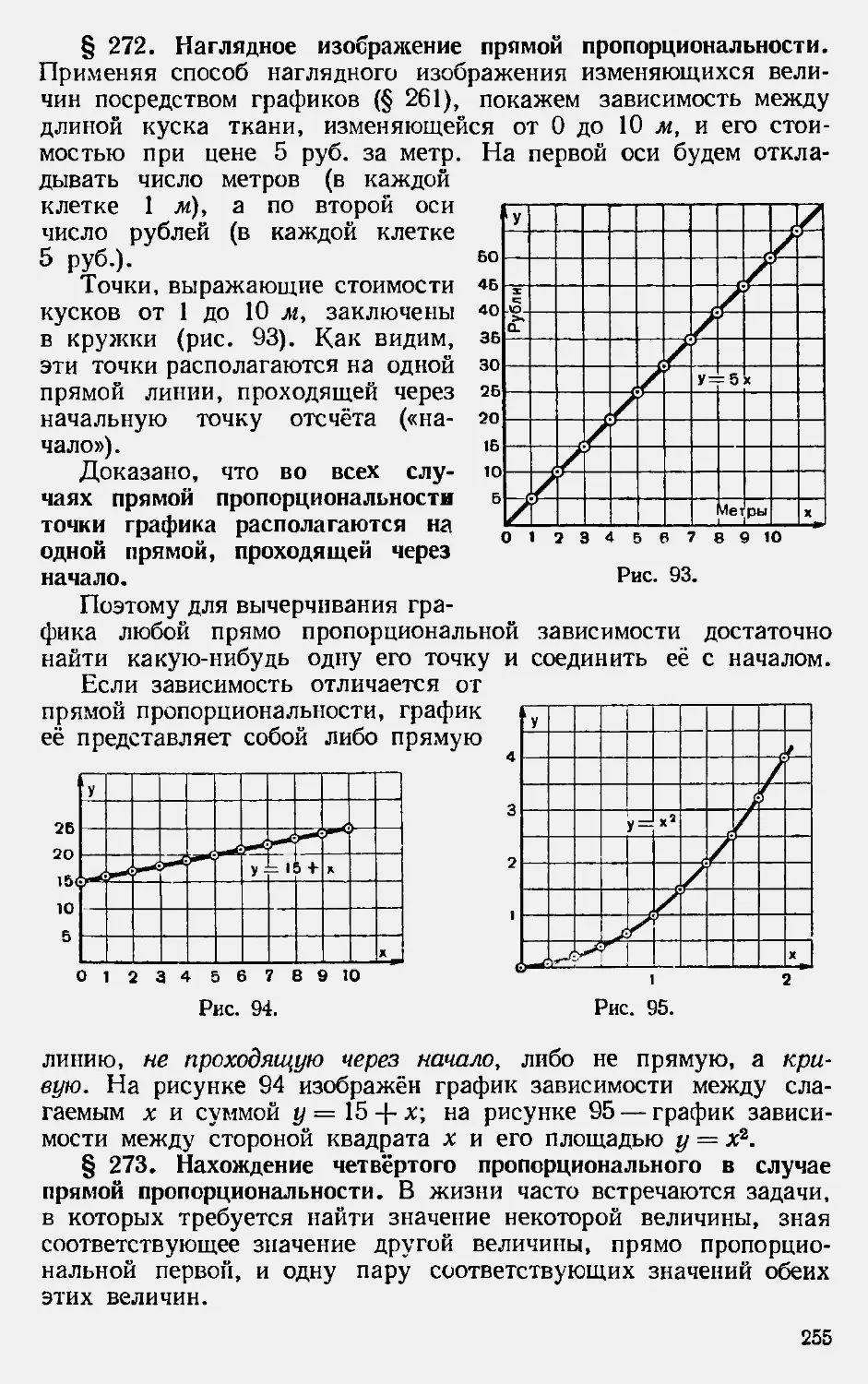
Текст
И. К. АНДРОНОВ и В.М.БРАДИС
АРИФМЕТИКА
УЧПЕДГИЗ -1957
И. к. АНДРОНОВ и В. М. БРАДИС
АРИФМЕТИКА
ПОСОБИЕ
ДЛЯ СРЕДНЕЙ ШКОЛЫ
ГОСУДАРСТВЕННОЕ
УЧЕБНО-ПЕДАГОГИЧЕСКОЕ ИЗДАТЕЛЬСТВО
МИНИСТЕРСТВА ПРОСВЕЩЕНИЯ РСФСР
Москв а—1957
ПРЕДИСЛОВИЕ
Данное пособие было задумано как учебник для уча-
щихся V и VI классов средней школы.
Будучи напечатано в 1955 г. небольшим тиражом (в ви-
де макета) с целью обсуждения, это пособие получило боль-
шое количество самых разнообразных отзывов, содержавших
часто противоречивые пожелания об изменениях, какие в
нём надо выполнить. Учитывая всё то, что нам представля-
лось в замечаниях ценного, мы публикуем это учебное по-
собие со значительными изменениями по сравнению с маке-
том. Надеемся, что как пособие она будет не бесполезна и
что более широкое её обсуждение позволит с полной опре-
делённостью установить её слабые и сильные стороны. Книга
является результатом совместной работы обоих авторов, но
окончательная редакция всего текста пренадлежит первому
из них. Все замечания и пожелания просим направлять авто-
рам через издательство (Москва, Чистые пруды, 6, Учпедгиз,
редакция математики).
И. К. Андронов
В. М. Б радио
22 августа 1956 г.
К УЧАЩИМСЯ
В 5 и 6 классах средней школы изучается курс арифметики,
содержащий основы науки о числах. Это название происходит от
греческих слов арифмос — число и техне — искусство. Точный его
перевод — числовое искусство.
Изучение арифметики в 5 классе начинают с более глубокого
изучения целых чисел 0, 1, 2, 3, 4 и т. д., с которыми учащиеся
имели дело в 1—4 классах, а затем рассматривают дробные числа
(дроби). Дальнейшее изучение чисел ведётся в курсе алгебры.
Помните, что от сознательного и прочного усвоения арифме-
тики целиком зависит успешность усвоения многих других пред-
метов и особенно алгебры, геометрии, тригонометрии, физики,
химии, астрономии, черчения.
Знайте, что хорошо усвоить предмет арифметики — это значит:
во-первых, ясно понять всё то, о чём в ней говорится;
во-вторых, запомнить определения, разъясняющие смысл вво-
димых в ней понятий, и предложения, в которых говорится о свой-
ствах этих понятий, а также вытекающие из них правила',
в-третьих, научиться размышлять и доказывать эти свойства;
в-четвёртых, уметь хорошо решать примеры и задачи и при-
менять полученные знания к практической жизни;
и, наконец, в-пятых, приучиться говорить точно и кратко,
чтобы в речи не было ничего лишнего и ничего недостающего.
Как же надо учиться, чтобы этого достигнуть?
1. На уроке надо быть настолько внимательным, чтобы не
пропустить ни одной мысли учителя, и быть настолько дисцип-
линированным, чтобы выполнять всё то. что укажет учитель.
2. Дома, после уроков, надо вдумчиво прочитать заданные
места книги, причём читать с карандашом в руке и с тетрадью,
выполняя в ней все расчёты, указанные в книге.
3. Поняв прочитанное, надо постараться всё основное запо-
мнить; для этого полезно устно (может быть, несколько раз) вос-
произвести изложенное с таким расчётом, чтобы в конце концов,
не заглядывая в книгу, уметь свободно изложить своими словами
прочитанное.
4. После усвоения по учебнику теории следует приступить к
решению указанных задач.
3
5. Если, несмотря на все усилия, разобраться в чём-нибудь
самостоятельно не удаётся или не вполне удаётся, непонятные
места надо отмечать в тетради и не позже следующего урока обра-
щаться за разъяснением к учителю. Здесь не надо стесняться или
бояться сказать о своём непонимании. Знайте, что и специалистам
не всё бывает сразу понятно в новых открытиях науки.
6. Помните, что все основные определения, предложения, пра-
вила, напечатанные в этой книге более жирным шрифтом, пред-
назначены для запоминания, хотя дословного заучивания не тре-
буется. Их можно излагать несколько иначе, своими словами,
но непременно правильно.
7. Знайте, что в арифметике каждый шаг вперёд основан на
том, что было усвоено ранее. Изучая новое, надо всё время воз-
вращаться к старому, либо вспоминая пройденное, либо наводя
справки по книге. Чтобы облегчить такие справки, в книге дано
подробное оглавление и сделаны ссылки (в скобках) на те пара-
графы, которые рекомендуется вспомнить.
8. Желательно завести небольшую тетрадь-словарик для за-
писи новых терминов (слов), которые будут встречаться при чте-
нии книги, указывая, где эти термины объяснены — в книге или
в тетради.
9. «Арифметика» должна быть настольной книгой ученика на
протяжении всех годов обучения в средней школе, так как она
необходима при дальнейшем изучении математики и других пред-
метов. К ней часто придётся обращаться за различными справ-
ками.
Часть 1
НАТУРАЛЬНЫЕ ЧИСЛА И НУЛЬ
Глава I. НУМЕРАЦИЯ
§ 1. Множество и его элементы. Людям всё время приходится
иметь дело с различными собраниями вещей, или, как говорят,
с их множествами. Вещи, составляющие множество, называются
его элементами. Можно говорить, например, о множестве людей,
находящихся в этой комнате, о множестве тетрадей на столе, о
множестве букв в слове «Москва» и т. д.
В арифметике термин «множество» применяется и тогда, когда
элементов мало. Так, хотя в обыденной жизни не говорят, что
у человека множество рук, однако рука левая и рука правая также
образуют множество. Если из комнаты уйдут все, кроме одного,
всё же и тогда говорят о множестве людей, которые в ней находятся;
в этом множестве — единственный человек. Есть немало слов,
означающих различные множества. Например, множество летящих
вместе птиц называется стаей, множество пасущихся вместе жи-
вотных— стадом, множество беспорядочно сваленных вещей —
кучей и т. д.
§ 2. Численность множества. Натуральные числа. О каждом
множестве можно спросить, сколько в нём элементов, или, дру-
гими словами, какова его численность. Только этим свойством
численности множеств и занимается арифметика, не обращая
внимания на другие их свойства. Численность множества узнают
посредством счёта его элементов и выражают числом. Так, уже
маленький ребёнок может сосчитать, что у него две руки, что
на каждой руке пять пальцев, что на обеих руках десять паль-
цев и т. д.
Каждое из чисел: один (единица), два, три, четыре, пять ...
... — называется натуральным числом. Все натуральные числа,
взятые по порядку, образуют натуральный ряд.
В натуральном ряду каждое число больше любого, ему пред-
шествующего, и меньше любого, за ним следующего. Чтобы срав-
нить численность двух множеств, надо пересчитать элементы каж-
дого. Если получится одно и то же число, численности множеств
5
равны-, если разные — не равны, численность одного множества
меньше, другого больше.
Для сокращения записи применяются знаки = (равно), 4= (не
равно), < (меньше), > (больше). В знаке равенства (=) расстоя-
ние между левыми концами двух чёрточек равно расстоянию меж-
ду правыми их концами. В знаке «больше» (>) расстояние меж-
ду чёрточками уменьшается от большего числа к меньшему; в
знаке «меньше» (<) расстояние между чёрточками увеличива-
ется от меньшего числа к большему.
§ 3. Порядок при подсчёте элементов множества. Натуральное
число, выражая численность множества, не зависит от того по-
рядка, в каком пересчитывались его элементы. Например, считая
буквы слова «Москва» слева направо, или справа налево, или
в каком угодно ином порядке, мы каждый раз получим число
шесть. Надо только следить за тем, чтобы ни один элемент пере-
считываемого множества не был пропущен и ни один не сосчитан
дважды.
§ 4. Натуральный ряд бесконечен. Объясняя выше (§ 2), что
такое натуральный ряд, мы поставили после слова «пять» много-
точие, чтобы показать, что запись не закончена: после пяти идёт
шесть, после шести — семь и т. д. Натуральный ряд имеет начало —
число один (единица), но не имеет конца. Действительно, какое
бы натуральное число мы ни взяли, оно выражает численность
некоторого множества. Добавляя в это множество еще один эле-
мент, получим новое множество, численность которого выража-
ется новым натуральным числом, а именно числом, на единицу
большим, занимающим в натуральном ряду следующее по порядку
место. Таким образом, последнего числа в натуральном ряду
нет, т. е. натуральный ряд бесконечен.
§ 5. Число нуль. Если все, кроме дежурного, из классной
комнаты уйдут, то множество людей, в ней находящихся, будет
состоять из одного человека. А если уйдёт и дежурный? Тогда
в этом множестве не будет ни одного человека; в арифметике гово-
рят, что здесь пустое множество. Сказать, что множество пустое,
всё равно, что сказать: во множестве нет ни одного элемента.
Численность пустого множества выражается числом нуль.
Присоединяя нуль к натуральному ряду чисел, его помещают
перед числом один: нуль, один, два, три, четыре, пять, ..., де-
сять, ..., сто, .... тысяча, ..., миллион... Нуль — число целое,
но натуральным числом его не называют.
§ 6. Что такое словесная нумерация? Как в практической
жизни, так и в науке приходится иметь дело с огромным мно-
жеством натуральных чисел, и чтобы различать их, надо дать
каждому особое название.
Способ, при помощи которого можно назвать каждое из мно-
гих натуральных чисел, пользуясь немногими словами, именуется
словесной нумерацией. Общепринятая словесная нумерация на-
зывается десятичной по причине, которая будет выяснена ниже.
6
Наши далёкие предки пришли к тому, как немногими сло-
вами можно назвать все натуральные числа от единицы до са-
мых больших, которые могут встретиться в практике. Большин-
ство народов, и в том числе наш народ, решили этот вопрос в
основном одинаково: пятнадцати основных слов оказалось доста-
точно, чтобы назвать все натуральные числа, которые необхо-
димы в жизненной практике. В нашем языке установились сле-
дующие основные названия: один (единица), два, три, четыре,
пять, шесть, семь, восемь, девять, десять (десяток), сто (сотня),
тысяча, миллион, миллиард, триллион. Остальные названия стро-
ятся из этих пятнадцати на следующих двух основаниях:
первое — разложение множества на десятки, что ведёт к по-
нятию разряда в десятичной нумерации;
второе — составление множества из единиц, десятков и сотен,
что ведёт к понятию класса в десятичной нумерации.
Можно разлагать множества по пяткам, по дюжинам (по двенадцати;
или по иным группам. Однако большинство народов, в том числе и наш народ,
остановились на десятичном разложении множеств. Почему же народы оста-
новились на счёте десятками, а не другими группами? На это великий учё-
ный Фридрих Энгельс отвечает, что счёт десятками определили десять пальцев
на руках человека. Можно предполагать, что если бы человек имел по четыре
пальца на руке, то люди вели бы счёт восьмёрками, а не десятками.
§ 7. Разложение множества на десятки и образование разря-
дов в десятичной нумерации. Счёт десятками. Чтобы пересчитать
большое число элементов, применяют счёт десятками. Пусть, на-
пример, изготовлена куча пуговиц и надо узнать, сколько их.
Будем отсчитывать по десяти пуговиц и пришивать каждый от-
считанный десяток на особый кусочек картона; каждый десяток
таких картонок сложим стопкой и свяжем ниткой, каждые десять
стопок поместим в отдельную коробку, каждые десять коробок
свяжем в один пакет, каждый десяток пакетов положим в от-
дельный ящик. В конце концов пусть у нас получилось семь ящи-
ков, два пакета, четыре коробки, восемь стопок, шесть картонок,
пять пуговиц.
На каждой картонке у нас десять пуговиц, в каждой стопке
десять десятков, или сотня их, в каждой коробке десять сотен,
или тысяча, в каждом пакете десять тысяч, в каждом ящике
сто тысяч. Всего в куче оказалось семь сотен тысяч и два де-
сятка тысяч да четыре тысячи и ещё восемь сотен да шесть де-
сятков и пять пуговиц.
Таким образом, счёт десятками состоит в том, что каждые
десять элементов пересчитываемого множества рассматриваются
как один элемент нового множества. Каждые десять элементов
нового множества опять рассматриваются как один элемент сле-
дующего нового множества и т. д.
Счёт десятками приводит к общепринятой десятичной нумера-
ции. Числа один, десять (десяток), сто (сотня) в десятичной ну-
мерации получили название единиц первого, второго и третьего
7
разряда. Каждые десять единиц любого разряда образуют еди-
ницу следующего высшего разряда; например, десять сотен — еди-
ницу четвёртого разряда — тысячу; десять тысяч — единицу пя-
того разряда — десяток тысяч; десять единиц пятого разряда —
единицу шестого разряда — сотню тысяч; десять единиц шестого
разряда — единицу седьмого — миллион и т. д. Числа один, де-
сять, сто, тысяча, десять тысяч и т. д. называются разрядными
единицами.
§ 8. Составление множества из единиц, десятков и сотен. Об-
разование классов в десятичной нумерации. Путём разложения
множества на десятки можно его численность выражать немно-
гими словами. Но люди заметили, что названия чисел становятся
ещё более краткими, если каждые три последовательных разряда
объединять в один класс.
Все числа, меньшие тысячи, образуют первый класс, или класс
простых единиц. Число тысяча называется единицей второго клас-
са, число миллион (тысяча тысяч) — единицей третьего класса,
миллиард (тысяча миллионов) — единицей четвёртого класса, трил-
лион (тысяча миллиардов) — единицей пятого класса и т. д.
В каждом классе три разряда. Так, в классе тысяч первый
разряд образуют единицы тысяч, второй — десятки тысяч, тре-
тий — сотни тысяч.
Чтобы назвать любое натуральное число, надо выделить в
нём разрядные единицы первого, второго, третьего разряда каж-
дого класса, а затем назвать число единиц каждого класса. За-
мечательно, что любое из огромного множества чисел первых пя-
ти классов можно назвать при помощи всего лишь пятнадцати
основных названий.
Кроме основных названий, в десятичной нумерации употреб-
ляются названия составные, получаемые соединением двух основ-
ных в одно слово. Например, один и десять — один на десять,
или одиннадцать; два и десять — два на десять, или двенадцать;
два десятка (сокращённо) — двадцать, две сотни (сокращённо) —
двести и т. д. Вместо трудного для произношения слова «четыре-
дцать» говорят сорок, вместо «девятьдесят» — девяносто.
Прочтём указанное выше (§ 7) число путём называния каж-
дого его разряда, а также пользуясь понятием класса, как без
сокращений, так и с принятыми сокращениями.
1. Подробное чтение с названием каждого разряда 11. Краткое чтение с названием каждого класса II1. Краткое чтение с сокращённым назва- нием каждого класса
Семь сотен тысяч и два десятка тысяч да четыре тысячи и ещё восемь сотен да шесть десятков и пять единиц Семь сотен два де- сятка четыре тысячи и восемь сотен шесть десятков пять единиц Семьсот двадцать четыре тысячи во- семьсот шестьдесят пять единиц
8
§ 9. Что такое письменная нумерация? Все народы давно на-
учились изображать натуральные числа особыми знаками. Способ
обозначать (записывать) каждое из многих натуральных чисел
при помощи немногих знаков называется письменной нумерацией.
В десятичной системе счисления существует всего десять зна-
ков, называемых цифрами-, для обозначения каждого из девяти
первых натуральных чисел—цифры 1, 2, 3, 4, 5, 6, 7, 8, 9, а
для обозначения нуля — цифра 0.
Систему счисления, основанную на обозначении всех натуральных чисел
десятью знаками-цифрами, впервые развил в IX в. в одной из рукописей
гениальный сын узбекского народа Мухаммед Аль-Хорезми’. В этой рукописи,
написанной на арабском языке, научном языке народов Ближнего Востока
того времени, было отмечено, что в основу труда положена практика некото-
рых вычислителей Индии. Вот почему, когда впервые в Европе (XII в.) по-
знакомились с этим трудом, знаки-цифры стали называть арабскими, или
индусскими, но их можно называть и хорезмскими.
§ 10. Цифры и поместное значение цифр. Казалось бы, что,
кроме этих десяти цифр, нужны ещё особые знаки для обозна-
чения десятка, сотни, тысячи и других разрядных единиц. Од-
нако уже много веков назад люди догадались, что наименование
разрядных единиц можно и не указывать, если считать, что цифра,
записанная на первом (крайнем справа) месте, означает единицы,
на втором — десятки, на третьем — сотни, на четвёртом — тысячи
и т. д.
Этот закон поместного значения цифр позволяет коротко
записывать сколь угодно большие числа, используя только ука-
занные выше десять цифр. Так, число пуговиц, которое мы полу-
чили выше в § 7, записывается в виде 724865. Запись 308 озна-
чает число, состоящее из трёх сотен и восьми единиц; в нём нет
десятков, входящих во второй разряд. Запись 3080 выражает
число из трёх тысяч и восьми десятков: в нём нет сотен, вхо-
дящих в третий разряд, нет простых единиц, входящих в пер-
вый разряд.
Устная десятичная нумерация чисел до пятого класса вклю-
чительно требует всего лишь 15 слов. Письменная нумерация еще
совершеннее: десяти цифр достаточно для записи любого нату-
рального числа.
Изобретение письменной системы счисления на основе поместного значения
цифр является одним из важнейших исторических событий. Известный фран-
цузский учёный П. Лаплас (1749—1827) сказал: «Мысль выражать все числа
десятью знаками, придавая им, кроме значения по форме, ещё значение по
месту, настолько проста, что именно из-за этой простоты трудно понять,
насколько она удивительна».
§ 11. Виды чисел. Число, которое в десятичной системе изобра-
жается одной цифрой (двумя цифрами), называется однозначным
1 По другому написанию Магомет ибн Муса (т. е. сын Мусы) аль-Хова'
резми (т. е. из Хорезма).
9
(двузначным) числом. Однозначных чисел 10, а именно: 0, 1,2,
3, 4, 5, 6, 7, 8, 9. Двузначных 90, а именно: все от 10 до 99.
Натуральные числа, которые в десятичной системе изобра-
жаются более чем двумя цифрами, называются многозначными
числами. Среди многозначных чисел имеются: 1) трёхзначные,
их 900 — от 100 до 999; 2) четырёхзначные, их 9000 — от 1000
до 9999 и т. д.
Из двузначных и многозначных чисел выделяются так назы-
ваемые круглые числа. Например: 20, 90, 700, 2000, 4000000 и т. д.
Натуральное число, у которого все цифры, кроме цифры стар-
шего разряда, нули, называется круглым числом.
Двузначных круглых чисел девять, а именно: 10, 20, 30, 40,
50, 60, 70, 80, 90. Трёхзначных круглых чисел девять, а имен-
но: 100, 200, 300, 400, 500, 600, 700, 800, 900. Четырёхзначных
круглых чисел тоже девять и т. д.
Круглое число можно записать как однозначное, если указы-
вать наименование единиц его старшего разряда. Так указанные
круглые числа можно записать так: 20 = 2 десятка, 90 = 9 десят-
ков, 700 = 7 сотен, 2000 = 2 тысячи, 4 000000 = 4 миллиона.
§ 12. Как прочитать число, записанное цифрами? 1. Чтобы
прочитать число, имеющее не более трёх цифр, называют после-
довательно каждую цифру начиная со старшего разряда, давая
название разряда каждой цифры.
2. Чтобы прочитать число, имеющее более трёх цифр, его раз-
деляют начиная от низших разрядов на классы по три цифры
в каждом; в последнем классе может оказаться цифр и меньше.
Потом читают числа каждого класса, как указано в первом
правиле, начиная со старшего, давая названия каждого класса.
Многозначные числа пишутся и печатаются с небольшими
промежутками (интервалами) между классами; это облегчает
чтение. Например, число 5738070409 читается так: пять миллиар-
дов семьсот тридцать восемь миллионов семьдесят тысяч четы-
реста девять.
§ 13. Как записать число цифрами? 1. Чтобы записать циф-
рами число, меньшее 1000, надо изображать цифрой каждый раз-
ряд начиная со старшего, а если в числе нет единиц соответ-
ствующего разряда, то в этом разряде надо ставить нуль. Напри-
мер, число триста пять запишется так: 305.
2. Чтобы записать цифрами число, большее 1000, надо выде-
лить в нём классы (триллионов, миллиардов, миллионов, тысяч,
единиц) и выписывать последовательно числа каждого класса
начиная с высшего. При этом надо помнить, что в каждом
классе, кроме, быть может, высшего, должно быть три цифры;
поэтому недостающие значащие цифры надо замещать нулями,
а если нет целого класса, то на его место ставятся три нуля.
Например, двадцать миллиардов (20) сорок два миллиона
(042) семьдесят восемь единиц (078) изображаются так:
20042000078.
10
Ошибки в записи чисел чаще всего бывают из-за пропуска
нулей; например, вместо 92074 пишут 9274. Таких ошибок не
будет, если помнить места различных разрядных единиц каждого
класса и оставлять промежутки между классами. Чтобы не оши-
баться при записи и чтении больших чисел, надо твёрдо знать
название и место единицы каждого разряда.
Названия разрядов Сотни триллионов Десятки триллионов Единицы триллионов Сотни миллиардов Десятки миллиардов Единицы миллиардов Сотии миллионов Десятки миллионов , Единицы миллионов Сотни тысяч Десятки тысяч Единицы тысяч Сотни Десятки | Единицы
Номера разрядов 15 14 13 12 11 10 9 8 7 6 5 4 3 2 1
Номера классов ПЯТЫЙ четвёртый третий второй первый
Названия классов трил- лионы милли- арды миллио- ны тысячи простые единицы
Номера разрядов в классах III II I III II I III II I III II I III 11 I
§ 14. Количественные и порядковые натуральные числа. Соз-
дав натуральный ряд чисел, люди тем самым нашли средства
находить численность множества вещей и, следовательно, отве-
чать на вопрос: сколько?
Одновременно с этим было найдено и средство отвечать на
вопрос: который из элементов множества в натуральном ряду
чисел расположился раньше и который позже?
Рис. 1.
Так, на рисунке 1 указаны перенумерованные телеграфные
столбы, идущие вдоль железной дороги. Когда понадобится сме-
нить телеграфный столб, то будет указан его номер. Заменён-
ный столб будет находиться между двумя смежными.
Народ в своём языке образовал два рода имён числительных,
передающих натуральный ряд чисел:
11
1) к оличественные числительные: один, два, три...
2) п орядковые числительные: первый, второй, третий...
Количественное числительное выражает численность множе-
ства предметов и отвечает на вопрос: сколько предметов содер-
жит данное множество?
Порядковое числительное указывает, какое место при счёте
занимает тот или иной предмет, и отвечает на вопрос: которым
по счёту будет данный элемент?
§ 15. Римская нумерация. Наряду с десятичной нумерацией,
но гораздо реже, применяется нумерация римская, широко упо-
треблявшаяся у римлян, или латинян, — народа, занимавшего
территорию современной Италии. В этой нумерации числа изоб-
ражались при помощи следующих семи знаков:
Римские знаки IV X L С D М
Их значение 1 5 10 50 100 500 1000
Цифры С и М произошли от сокращенной записи латинских
слов центум (centum) и милле (mille), означающих сто и тысячу.
В римской нумерации принято, что знак I, поставленный слева
от другого (старшего) знака, уменьшает на единицу его значение,
а справа — увеличивает на столько же его значение; поэтому чис-
ла 4, 6, 9, 11 изображаются знаками IV, VI, IX, XI. Подобным
же образом знаки XL, LX, ХС, СХ, СМ, МС означают числа
40, 60, 90, ПО, 900, 1100. Для обозначения других чисел при-
меняется повторение знаков.
Ниже приведены числа от 1 до 50 в римской нумерации:
I XI XXI XXXI XLI
II XII XXII XXXII XLII
III XIII XXIII XXXIII XLIII
IV XIV XXIV XXXIV XLIV
V XV XXV XXXV XLV
VI XVI XXVI XXXVI XLVI
VII XVII XXVII XXXVII XLVII
VIII XVIII XXVIII XXXVIII XLVIII
IX XIX XXIX XXXIX XLIX
X XX XXX XL L
Если число содержит несколько (немного) тысяч, то для записи его в
римской нумерации пользуются повторением знака М. Вообще же числа вто-
рого класса записываются при помощи буквы m (от слова mille — тысяча),
слева от которой записываются тысячи, а справа — сотни, десятки, единицы.
Так, запись CXXXIIImDCCCXLII означает число 133 842, MCMXVII — 1917.
Римская нумерация менее удобна, чем современная десятичная. Отсут-
ствие поместного значения цифр вызывает необходимость громоздкой и мало-
наглядной записи сколько-нибудь больших чисел. Так, для записи числа
133 842 в римской нумерации нужны 16 знаков. Часто смешивают числа IV
и VI, IX и XI и др.
12
Рис 2.
Римские знаки иногда употребляют для записи порядковых натуральных
чисел: I—первый, II — второй, III—третий и т. д. Нередко римские цифры
помещают на зданиях и памятниках. Например, на рисунке 2 видим памятник
Петру Первому (в Ленинграде). На одной стороне скалы высечена дата его
постановки в римской нумерации — MDCCLXXXII, а на другой в десятич-
ной— 1782.
Глава II. СЛОЖЕНИЕ И ВЫЧИТАНИЕ
Раздел I. ТЕОРИЯ СЛОЖЕНИЯ
§ 16. Объединение множеств. Из птичника вышло несколько
белых гусей, а затем несколько серых гусей, и оба стада стали
пастись вместе. Произошло объединение двух множеств в одно
новое множество. Ещё пример: если первое множество состоит из
деда, его сына и его внука, а второе из того же деда, его дочери
и его внучки, то объединённое множество состоит из деда, сына,
дочери, внука и внучки. Здесь дед — общий элемент объединя-
емых множеств. В дальнейшем, говоря об объединении множеств,
всегда будем предполагать, что объединяемые множества общих
элементов не имеют, как это было в первом примере (с гусями).
13
§ 17. Сумма натуральных чисел. Очень часто, зная числен-
ность каждого из данных объединяемых множеств, находят чис-
ленность множества, которое получается после объединения. На-
пример, если известно, что в одном стаде 12 белых гусей, в
другом 7 серых гусей, можно спросить, сколько гусей в обоих
стадах. Пересчитав объединённое множество, находим, что здесь
всего 19 гусей. Пользуясь знаком сложения + (плюс), это запи-
сывают в виде равенства 12 + 7 = 19.
Слагаемыми называются числа, которые выражают числен-
ности объединяемых множеств (здесь 12 и 7).
Суммой данных слагаемых называется число, которое выра-
жает численность объединённого множества (здесь 19).
Сложением называется действие нахождения суммы по данным
слагаемым (12 -f- 7 = 19).
Когда находят сумму чисел, то говорят, что эти числа скла-
дываются или что к одному из них прибавляется другое. Вместо
того чтобы говорить: сложим числа 12 и 7, можно сказать: уве-
личим число 12 на 7 единиц.
Понятно, что слагаемых может быть не только два, а и три,
четыре, сколько угодно; найдя сумму двух слагаемых, надо при-
бавить к ней третье, затем четвёртое и т. д., пока не будут
прибавлены все слагаемые.
Сумму можно найти простым пересчитыванием элементов
объединённого множества, но это не всегда удобно, а иногда и
невозможно.
Положим, например, что в школе учится 386 детей и ожи-
дается поступление ещё 79 человек. Пересчитать объединённое
множество здесь нельзя, так как новых учащихся ещё нет. Ко-
нечно, можно взять 386 каких-нибудь элементов (например, спи-
чек), присоединить к ним ещё 79 элементов и пересчитать,
сколько будет всего. Убедившись, что всего получается 465 эле-
ментов, заключаем, что в школе будет столько же учащихся.
Но человек, знающий арифметику, найдёт сумму 386 + 79
гораздо скорее. Этому учат ещё в начальной школе. Выясним,
на каких свойствах действия сложения основаны соответствую-
щие вычисления.
§ 18. Обозначение суммы. Будем обозначать объединяемые мно-
жества латинскими буквами А и В (а большое, бэ большое), а
натуральные числа, выражающие их численности, — соответству-
ющими строчными буквами а и Ь (а малое, бэ малое). Запись
А + В означает объединённое множество, запись а + b — его чис-
ленность, т. е. сумму чисел а и Ь. Если рассматривается более
двух множеств, употребляются другие буквы: С и с (цэ большое
и цэ малое), D и d (дэ большое и дэ малое) и т. д.
Знак сложения ( + ) возник в XV в. и стал распространяться с XVI в.
Этот знак потому закрепился, что он хорошо напоминает о процессе сложения:
один предмет (вертикальная палочка) кладётся на другой (горизонтальную
палочку). Название знак получил от латинского слова plus (плюс), что зна-
чит «больше».
14
§ 19. Переместительный закон сложения. Легко видеть, что
суммы 12 + 7 и 7+12 равны: каждая из них равна 19. Этим
переместительным свойством обладает сумма любых двух сла-
гаемых: каковы бы ни были два числа, сумма первого со вторым
и второго с первым — всегда одно и то же число.
Обозначая данные числа буквами а и Ь, переместительное
свойство можно кратко записать равенством а + b = b + а. Это
одно из основных свойств чисел. Оно называется переместитель-
ным законом сложения и выражается так:
Сумма не изменяется от перемены мест слагаемых:
17+ 125= 125+ 17 | а+ 6 = 6 +а.
Иначе, конечно, и быть не может: Д + В и В + .4— не два
разных множества, а одно и то же множество, содержащее все
элементы множеств А и В и не содержащее никаких других
элементов. Численность этого множества можно выразить в виде
а + b и в виде b + а, а потому а + b = b + а.
§ 20. Сочетательный закон сложения. Положим, что кроме
тех 12 белых и 7 серых гусей, о которых была речь выше (§ 16),
из птичника вышли ещё 9 уток. Сколько птиц вышло всего из
птичника? Узнать это можно двумя способами.
Во-первых, можно к 12 прибавить числа 7 и 9 последова-
тельно: гусей вышло всего 12 + 7 = 19, гусей и уток вместе
19 + 9 = 28;
Во-вторых, можно к 12 прибавить сразу сумму 7 + 9: к пер-
вому стаду из 12 белых гусей присоединилось всего 7 + 9 = 16
птиц; всего из птичника вышло 12 + 16 = 28 птиц.
Прибавляя к 12 числа 7 и 9 последовательно, получаем то
же, что и прибавлением сразу суммы 7 + 9.
Чтобы указать (при письменном обозначении) порядок образо-
вания суммы из слагаемых, со времени XVII в. установились
особые знаки вида ( ), называемые скобками.
Скобки показывают, что заключённое в них есть одно число,
которое предварительно надо найти, чтобы продолжить вычисле-
ния с числами вне скобок.
Вот почему начатое рассуждение можно кратко передать так:
(12 + 7) + 9 = 12 + (7 + 9) | (а + Ь) + с = а + (6+с)
Запись (а + Ь) + с означает, что сперва надо образовать сумму
из а и b и лишь потом приложить слагаемое с, а запись а +
+ (Ь + с) означает, что сперва надо образовать сумму из Ь и с,
а потом к а приложить эту сумму. Этим свойством обладает
сумма любых трёх чисел. Оно называется сочетательным законом
сложения: вместо того чтобы к числу прибавлять последовательно
два слагаемых, достаточно к нему прибавить сразу их сумму.
Иначе, разумеется, не может и быть: множества
(Л + В) + С и А + (В + С)
15
это не два разных, а одно и то же множество, содержащее все
элементы трёх данных множеств Л, В и С и не содержащее ни-
каких других элементов. Численность этого множества можно
выразить с одинаковым правом суммой (а + Ь) + с и суммой
с+(& + с)- Во второй сумме произведено предварительное сое-
динение или сочетание, второго и третьего слагаемых, отсюда
название этого закона — сочетательный.
Сочетательным законом обладает сумма не только трёх, а и
любого числа слагаемых: сумма остаётся неизменной, если после-
довательное прибавление каких-нибудь слагаемых заменить при-
бавлением суммы этих слагаемых. Например,
1 + 2 + 3 + 4 = 1 + (2 + 3 + 4) = 1+9=10.
Отсюда вывод:
1 ) Чтобы прибавить сумму, достаточно прибавить каждое сла-
гаемое последовательно.
Например: 2 + (3 + 4) = (2 + 3) + 4.
2 ) Чтобы к сумме прибавить число, достаточно его прибавить
к какому-нибудь одному из её слагаемых, оставляя остальные без
изменения.
Например: (2 + 3) + 4 = 2 + (3 + 4) = (2 + 4) + 3;
(2+7 + 8)+ 11 =2+ 7+(8+ 11) = 2 +(7 + 8)+ 11 =
= (2+ Н) + 7 + 8.
§ 21. Сложение с числом нуль. Присоединяя к какому угодно
множеству А пустое множество, мы ничего в этом множестве А
не изменяем. Численность пустого множества выражается числом
нуль, а потому принимаем, что сложение любого числа а с ну-
лём даёт то же самое число а. Это можно записать так:
а + 0 = а; 0 + а = а, а также 0 + 0 = 0.
Раздел 2. ТЕХНИКА УСТНОГО И ПИСЬМЕННОГО СЛОЖЕНИЯ
Хорошо усвоив определение и свойства суммы, т. е. теоре-
тическую сторону действия сложения, надо дать себе полный
отчёт о тех практических приёмах выполнения этого действия,
какие были усвоены ещё в начальной школе. Оказывается, что
сложение любых чисел можно свести к сложению однозначных
и круглых чисел.
§ 22. Сложение однозначных чисел, или табличное сложение.
Результаты сложения любых двух однозначных чисел показаны
в следующей табличке, где в каждой клетке помещена сумма
числа, записанного на этой же строчке слева, и числа, находя-
щегося в этом же столбце сверху. Все эти результаты запоми-
наются ещё в начальной школе. Если выучены те из них, кото-
рые обведены толстой ломаной линией (их всего 45), то осталь-
16
ные получаются сразу на основании переместительного свойства
суммы. Например, помня, что 8 -f- 6 = 14, можно сказать, что
6-|-8=14.
1 2 3 4
1 2
2 3 4
3 4 5 6
4 5 6 7 8
5 6 7 8 9
6 7 8 9 10
7 8 9 10 11
8 9 10 11 12
9 10 11 12 13
5 6 7 8 9
10
11 12
12 13 14
13 14 15 16
14 15 16 17 18
Если какой-нибудь из этих результатов табличного сложения
позабыт, его легко получить. Так, например, чтобы найти сумму
3-]-5, представляем себе множество из каких-нибудь пяти эле-
ментов, присоединяем к нему ещё одно множество из трёх эле-
ментов, и пересчитываем все элементы объединённого множества.
Первые 5 элементов уже сосчитаны; пересчитывая остальные
элементы, которые будут шестым, седьмым, восьмым, получаем
в результате сумму 8. Надо помнить, что суммы 3 4-5 и 5 4-3
равны и что выгоднее всегда начинать считать с большего сла-
гаемого.
Иногда целесообразно бывает применить и сочетательное свой-
ство суммы. Так, чтобы найти 8 4- 6, замечаем, что 8 4-2=10,
а 6 = 2 4- 4, и действуем так: 84-6 = 84-(2 4-4) = (8 4-2) 4-4 =
= 10 4-4= 14.
Чтобы уверенно выполнять это прибавление по частям, надо
твёрдо помнить те пары чисел, какие дают в сумме 10, а именно:
14-9; 2 4-8; 3 4-7; 4 -J- 6; 5 4- 5; но ещё лучше твёрдо помнить
все 45 табличных результатов.
§ 23. Сложение круглых чисел. Сложение круглых чисел, со-
держащих единицы одного и того же разряда, сводится к сло-
жению однозначных чисел. Действительно, имея, например, сумму
8000 4-7000, можем записать её в виде 8 тыс. 4-7 тыс. и, скла-
2 Арифметика
17
дывая однозначные числа 8 и 7, получаем в сумме 15 тыс.,
или 15000. Если же складываются круглые числа разных раз-
рядов, то производится простое соединение их как в записи, так
и в речи. Например, сумма 5000 и 70 равна пяти тысячам семи-
десяти (5070).
§ 24. Сложение многозначных чисел. Рассмотренные выше
свойства суммы позволяют сводить сложение любых многознач-
ных чисел к сложению однозначных и круглых чисел. Действи-
тельно, пусть надо найти, например, сумму чисел 324 и 572. Вы-
полним это сложение со всеми подробностями.
324 4- 572 = (300 -f- 20 -f- 4) + (500 4- 70 4- 2) = (1)
= 300 + 20 + 4 + 500 + 70 + 2 = (2)
= 300 + 500 + 20 + 70 + 4 + 2 = (3)
«= (300 -I- 500) + (20 + 70) + (4 -J- 2) = (4)
= 800 + SO 4- 6 = (5)
= 896. (6)
Легко объяснить каждую строку этой подробной записи, осно-
вываясь на том, что было сказано выше о свойствах суммы и о
нумерации: на строке (1) сделана замена каждого слагаемого
суммой круглых чисел и единиц, на строке (2) прибавление
суммы заменено последовательным прибавлением слагаемых, на
строке (3) использован переместительный закон, на строке (4) —
сочетательный закон, на строке (5) найдены суммы круглых и
однозначных чисел, на строке (6) использован закон поместного
значения цифр.
Если в каком-нибудь разряде получается сумма 10 или более
единиц этого разряда, производится замена десятка единиц одной
единицей следующего высшего разряда; осуществляется так на-
зываемый «перенос десятков».
Приведённая выше подробная запись сделана только с целью
объяснения. На практике же постоянно применяется краткая за-
пись «столбиком», при которой удобно складывать единицы каж-
дого разряда всех слагаемых, так как они оказываются в одном
вертикальном столбце и тем самым трудно их перепутать, напри-
мер:
.324 Д_ 324 12111
“ 572 ' 59 738 , 58 307
896 60 062 + 138 451
8743 295
8952164
Сложение по разрядам ведётся обычно справа налево, т. е. от
младших разрядов к старшим. При переносе десятков полезно
записывать их число над цифрой соответствующего разряда пер-
вого слагаемого. Записывать числа переносимых десятков на
стороне не рекомендуется.
18
Сумму двух многозначных слагаемых можно находить и слева
направо, т. е. начиная с высших разрядов, что при небольшом
навыке даёт заметное ускорение работы.
§ 25. Устное сложение. Результаты сложения однозначных
чисел надо твёрдо помнить. Результаты сложения любых дву-
значных чисел надо уметь правильно и быстро находить устно
без записи. При этом применяются разные способы, использую-
щие свойства суммы. Так, чтобы найти сумму
63 4- 28 4- 18,
лучше сперва сложить десятки и единицы в отдельности, что
даёт 90 и 19, или всего 109, или так:
63 4- 28 = 63 4- (27 4- 1) = (63 4- 27) 4- 1 = 90 4- 1 = 91;
91 4- 18 = 91 4- (9 4- 9) = 100 4- 9 = 109.
Применение переместительного и сочетательного свойств суммы
позволяет ускорять и облегчать (проводить почти устно) вычис-
ления. Например, сложение чисел
7117 4- 2397 4- 2883
целесообразнее провести так:
7117 4- 2883 4- 2397 = 10 000 4- 2397 = 12 397.
Сложение чисел
15879 4-2452 4- 121 4-4000
целесообразнее провести так:
(15879 4- 121) 4- 4000 4- 2452 =
= 16000 4- 4000 4- 2452 =
= 20000 4-2452=
= 22 452.
§ 26. Проверка сложения. При сложении, как и при всяком
другом арифметическом действии, малейшее невнимание приводит
к ошибке. Поэтому следует всегда проверять правильность по-
лученного результата.
Для проверки устного сложения проверяют, выполняя его
вторично, причём лучше иным способом. При письменном сложе-
нии сумму также находят вторично, ведя сложение по разрядам,
не сверху вниз, как обычно, а снизу вверх или в каком-нибудь дру-
гом порядке, сочетая слагаемые наиболее удобным образом.
Раздел 3. ТЕОРИЯ ВЫЧИТАНИЯ
§ 27. Удаление части множества. Несколько детей отправи-
лись на прогулку. Заморосил дождь, и те из них, кто был
без пальто, вернулись домой, остальные продолжали путь.
Можно сказать, что здесь из множества детей «удалена» его
часть, тоже представляющая собой некоторое множество. Полу-
2*
19
чилось новое множество, которое можно назвать остатком. Воз-
никает задача: зная численность множества и численность уда-
лённой его части, найти численность множества-остатка. Конечно,
его можно просто пересчитать: если на прогулке было 13 детей,
а ушли 5 из них, то легко пересчитать оставшихся и убедиться,
что их 8. Однако пересчитать остаток множества не всегда удобно.
Арифметика учит, как находить его численность, не прибегая
к счёту.
§ 28. Разность натуральных чисел. Пусть имеется какое-
нибудь множество, содержащее сколько-то элементов. Из этого
множества удаляется некоторая его часть, и в результате полу-
чается остаток.
Натуральное число, выражающее численность множества-остат-
ка, называется разностью данных натуральных чисел; действие
нахождения разности называется вычитанием и обозначается
знаком — (минус).
В приведённом выше примере мы имели разность чисел 13 и
5, а именно: 13 — 5 = 8.
Число, из которого вычитают, называется уменьшаемым
(в примере 13), а то, которое вычитается, называется вычи-
таемым (в примере 5).
Когда находят разность а — Ь, то говорят, что из числа а
вычитают или отнимают число 6; говорят также, что а умень-
шают на b единиц.
Рассматривая, кроме натуральных чисел, ещё число нуль,
имеем следующие особые три случая вычитания:
1) К огда из натурального числа вычитается равное ему число,
то получается нуль, так как здесь разность есть численность
пустого множества:
а — а — 0.
2) К огда из натурального числа вычитается нуль, то полу-
чается данное натуральное число, так как удаление из любого
данного множества пустого множества ничего в этом данном
множестве не меняет:
а — 0 = а.
3) К огда из нуля вычитается нуль, то получается нуль, так
как при удалении пустого множества из данного пустого мно-
жества остаётся так же пустое множество:
0 — 0 = 0.
Легко видеть, что вычитание натуральных чисел возможно,
если уменьшаемое больше вычитаемого или равно ему, и невоз-
можно, если уменьшаемое меньше вычитаемого.
§ 29. Связь вычитания со сложением. Если разность 13 — 5,
равную 8, сложить с вычитаемым 5, получим уменьшаемое 13,
т. е. 8 5 = 13. Так бывает всегда.
20
Действительно, удаляя из множества А его часть В, а затем
соединяя остаток (Л — В) с множеством В, мы вернёмся к мно-
жеству А, а потому сумма чисел (а—Ь) и Ь, выражающих их
численности, равна числу а, показывающему численность множе-
ства А, т. е.
(а— Ь) + Ь — а.
Таким образом, действие сложения обратно действию вычи-
тания: сложение (а — Ь) и Ь как бы уничтожает вычитание Ь,
восстанавливая первоначально взятое число а.
В свою очередь вычитание обратно сложению: если к числу
а прибавить какое-нибудь число Ь, а затем от суммы a -f- b от-
нять Ь, получим опять а, т. е.
(a -f- Ь) — b — а.
Поэтому действия сложения и вычитания называются взаимно
обратными.
Вычитанием называется действие, состоящее в нахождении
одного из слагаемых по данным значениям суммы и другого сла-
гаемого; при этом сумма получает название уменьшаемого, из-
вестное слагаемое — вычитаемого, искомое слагаемое — разности.
Короче: вычитанием называется действие, где по сумме двух сла-
гаемых и одному из них находят другое.
Знак вычитания (—) возник в XV в. и стал распространяться с XVI в.
Этот знак потому закрепился, что он хорошо напоминает процесс вычитания:
в знаке сложения было два предмета: один (вертикальная палочка) снят,
а другой (горизонтальная палочка) остался. Название знак(—) получил от ла-
тинского слова minus (минус), что значит «меньше» (уменьшить).
§ 30. Вычитание суммы. Если из 13 человек уйдут 5, а затем
ещё 2, сколько человек останется? Эту задачу можно решить
двумя способами: можно узнать, сколько останется после ухода
пятерых (13 — 5 = 8), затем после ухода двоих (8 — 2 = 6), а
можно сперва узнать, сколько человек ушло всего (54-2 = 7),
затем сразу число оставшихся после второго ухода (13 — 7 = 6).
Вообще если от а надо отнять как Ь, так и с (при условии,
что b 4- с меньше или равно а), применимы оба эти способа:
первый даёт (а—Ь) — с, второй а—(Ь 4- с).
Оба способа ведут к удалению одних и тех же элементов из
данного множества. Множества (Л—В) — С и А — (В 4-С) не
два различных, а одно и то же множество, содержащее элементы
множества А без элементов множеств В и С и не содержащее
никаких других элементов (если численность (В 4- С) не больше
численности Л).
Получаем такое свойство разности: вместо того чтобы из дан-
ного числа вычитать сумму, достаточно вычесть последовательно
каждое слагаемое в отдельности, и обратно: вместо того чтобы
21
последовательно вычитать несколько чисел, достаточно вычесть
сумму всех вычитаемых чисел: от а надо отнять как Ь, так и с,
применимы оба эти способа: первый даёт (а — Ь) — с, второй
а— (&_]_ с).
13—(5 4-2) = 13—5—2; a— (b 4-с) = а — Ь — с;
13—5 — 2=13—(5-f-2); а — Ь — с = а — (&4*с)-
По переместительному закону сложения получаем:
13 —(54-2)= 13 —(2 4-5) | а—(&4-с) =а—(с4-&).
Зная свойство вычитания суммы, имеем:
13 — 5—2 = 13 — 2 — 5 | а — b — с — а — с — Ь.
Следовательно, когда имеется несколько вычитаемых, то их
можно переставлять.
§ 31. Вычитание из суммы. Разберём задачу. У меня было
5 руб., я получил ещё 4 руб., а затем уплатил 3 руб. Сколько
денег у меня осталось? Здесь мы имеем вычитание числа 3 из
суммы 5-f-4 = 9. Ясно, что уплатить эти 3 руб. я могу безраз-
лично или из тех 5 руб., что были первоначально, или из тех
4 руб., что были получены: результат будет один и тот же.
Наблюдения привели к открытию следующего свойства разности:
чтобы вычесть число из суммы, достаточно его вычесть из ка-
кого-нибудь одного слагаемого, оставив другие без изменения
(предполагается, что это слагаемое больше вычитаемого).
Коротко записываем это так:
(5 4- 4) — 3 = (5 — 3) 4- 4 = 5 4- (4 — 3);
(а 4- Ь) — с — (а — с) 4- & = а 4- (Р — с).
Это следует из того, что множества (Д 4- В) — С, (Д — С) 4- В
и Д 4- (В — С) — одно и то же множество, содержащее все эле-
менты А и В без элементов С и не содержащее никаких других
элементов (если С есть часть множества как Д, так и В).
§ 32. Прибавление разности. Разберём задачу. На экскурсию
ушли 13 учащихся; к ним решили присоединиться ещё 8 человек,
но по дороге 3 раздумали и вернулись обратно. Сколько всего
человек отправилось на экскурсию? Эта задача решается двумя
способами: можно сначала узнать, сколько же человек действи-
тельно прибавилось (8 — 3 = 5), а затем сколько всего отправи-
лось (13 4- 5 — 18); но можно сперва узнать, сколько человек
пошло бы, если бы никто не раздумал идти (13 4- 8 = 21), а затем
вычесть число учащихся, которые раздумали идти на экскурсию
(21 — 3 = 18). Оба способа привели к одному и тому же оконча-
тельному результату. На основании наблюдений можно заключить,
22
что для прибавления разности достаточно прибавить уменьшаемое
и вычесть вычитаемое. Это свойство разности записывается так:
13 4-(8 — 3) = (13 4- 8) — 3; | а 4- (6 — с) — (а 4- Ь) — с.
Это следует из того, что множества
Л 4-(В — С) и (Л + В) — С
являются одним и тем же множеством, содержащим все элемен-
ты Л и В без элементов С и не содержащим никаких других
элементов (предполагается, что С есть часть множества В).
§ 33. Вычитание разности. Иногда приходится не прибавлять,
а вычитать разность. Например, если я имею 25 руб., образо-
ванных из денежных знаков 10, 10 и 5 руб., и надо отдать за
покупку 8 руб., то имеется затруднение, так как у меня нет
денежного знака в 8 руб. Тогда соображаю, что 8=10 — 2;
значит, надо из 25 отнять 10 — 2, т. е. разность, что осущест-
вляется так: из 25 руб. я беру 10 руб. и передаю кассиру,
который возвращает мне в виде сдачи 2 руб. Короче: когда
надо найти 25 — (10 — 2), берут (25—10)4-2; результат будет
тот же, т. е.
25 — (10 — 2) = (25 — 10) 4- 2 = 17.
Получаем новое свойство разности: чтобы вычесть разность,
достаточно вычесть уменьшаемое, а затем прибавить вычитаемое
(предполагается, что первое уменьшаемое больше второго).
Вот краткая запись этого свойства:
25 —(10 —2) = (25— 10) 4-2;
а — (Ь — с) = (а — Ь) 4- с, где а > Ь > с.
Запись Л—(В — С) означает, что из множества Л требуется
удалить множество В без его некоторой части С. Если из Л
удалить всё множество В, то вместе с В удаляется и его часть С,
чего не требовалось; поэтому надо в оставшееся множество Л — В
вернуть обратно удалённое множество С, т. е. к Л — В при-
бавить С. Следовательно, множества
Л—(В —С) и (Л —В) 4-С
не являются различными, а совпадают (при этом, конечно, пред-
полагается, что С есть часть множества В, а В есть часть мно-
жества Л).
Раздел 4. ТЕХНИКА УСТНОГО И ПИСЬМЕННОГО ВЫЧИТАНИЯ
§ 34. Табличное вычитание. Каждый помнит все 45 таблич-
ных результатов сложения однозначных чисел (стр. 17). Немного
надо труда, чтобы применить эту таблицу для вычитания, когда
по сумме, которая не более 18 единиц, и одному однозначному
слагаемому по памяти быстро называется другое слагаемое.
23
Например, чтобы найти 9 — 6, надо вспомнить, что 9 есть
6 + 3, и тогда получаем 9 — 6 = 3. Чтобы из 15 вычесть 8, надо
вспомнить, что 8 + 7=15, и узнаем, что 15 — 8 равно 7. Но
можно заменить вычитание числа 8 вычитанием суммы: 5 + 3
15 —8 = 15 —(5 + 3) = 15 —5 — 3= 10-3 = 7.
Вычитание, основанное на применении таблицы сложения,
называется табличным вычитанием. К табличному вычитанию
сводится и вычитание круглых чисел, содержащих единицы
одного и того же разряда, как например:
70000 — 40000 =
= 7 десятков тыс. — 4 десятка тыс. =
= 3 десятка тыс. = 30000.
Знание таблицы сложения помогает выполнять и такое вычита-
ние, как, например,
1400 — 800 = 14 сотен — 8 сотен = 6 сотен = 600.
§ 35. Вычитание многозначных чисел. Умея выполнять таб-
личное вычитание, мы можем выполнить вычитание любых мно-
гозначных чисел, основываясь на рассмотренных выше свойствах.
Поясним это подробно на примере:
895 — 352 = 800 + 90 + 5 — (300 + 50 + 2) =
= (800 — 300) + (90 — 50) + (5 — 2) =
= 500 + 40 + 3 =
= 543.
Переходя от первой строки ко второй, мы использовали два
свойства: вычитание суммы и вычитание от суммы. Разумеется,
что подробная запись сделана только для объяснения. Обычно
применяется всем известная запись «столбиком», при которой
цифры одинаковых разрядов уменьшаемого и вычитаемого ока-
зываются записанными друг под другом, что облегчает получе-
ние разности, например:
895
— 352
543
Если в каком-нибудь разряде уменьшаемого меньше единиц,
чем в том же разряде вычитаемого, как, например, при вычита-
нии 352 от 841, то приходится применять «раздробление», заме-
няя одну единицу следующего высшего разряда уменьшаемого
десятью единицами низшего разряда. Чтобы не забывать об этой
замене, полезно иногда ставить точку над цифрой этого высшего
разряда
841
“352
489
24
Как и сложение, вычитание многозначных чисел ведётся от
младших разрядов к старшим, т. е справа налево, хотя можно
и наоборот — слева направо, что труднее, но быстрее.
§ 36. Устное вычитание. Вычитание однозначного числа вы-
полняется всегда в уме, каково бы ни было уменьшаемое. Устно
же выполняется вычитание и в том случае, когда уменьшаемое
и вычитаемое—числа двузначные. На практике применяют раз-
личные способы устного вычитания. Вот несколько примеров:
1) 90 —28 = 90—.(20 + 8) = (90—20) —8 = 70 —8 = 62 (вы-
читание суммы);
2) 90 — 28 = (60 + 30) — 28 = 60 + (30 — 28) = 60 + 2=62 (вы-
читание из суммы);
3) 90 — 28 = 90 — (30 — 2) = (90 — 30) + 2 = 60 + 2 = 62 (вы-
читание разности);
4) 41—25= (30+ 11) —(20 + 5) = (30 — 20)+ (11—5) =10 +
+ 6=16 (вычитание суммы и вычитание из суммы);
5) 41 — (21 +4) = (41 — 21) — 4 = 20 — 4 — 16 (вычитание
суммы);
6) 87 — 29 = 87— (30— 1) = (87 — 30) + 1 = 57 + 1 = 58 (вы-
читание разности);
7) 87 — 29 = 87 —(27 + 2) = (87 — 27)— 2 = 60 — 2 = 58 (вы-
читание суммы).
Установленные свойства вычитания позволяют часто ускорять,
облегчать, проводить почти устно вычисления и с многозначными
числами. Например:
1) вычитание чисел 1258 — (158 + 79) целесообразнее провести
так: (1258 —158) —79= 1100 — 79 = 1021;
2) вычитание чисел (983 + 748) — 883 целесообразнее провести
так: (983 — 883) + 748 = 100 + 748 = 848;
3) прибавление разности 587 + (1413—887) целесообразнее
провести так: (587 + 1413) — 887 = 2000 — 887 = 1113;
4) вычитание чисел 1083 — (1596 — 917) целесообразнее про-
вести так: (1083 + 917) —1596 = 2000—1596 = 404.
§ 37. Вычитание по способу дополнения. Продавцам и кас-
сирам часто приходится давать сдачу, а для этого им надо нахо-
дить разность между суммой денег, получаемой от покупателя,
и стоимостью покупки. Они это делают по «способу дополнения»,
который легко уяснить на следующем примере. Покупатель же-
лает купить товар стоимостью 27 руб. 85 коп. и подаёт в кассу
100 руб.; кассир даёт ему чек и говорит: «27 руб. 85 коп.», затем
даёт 15 коп. и говорит: «28 руб.», затем — 2 руб., говоря: «30 руб.»,
затем добавляет 10 руб., ещё раз 10 руб., наконец, 50 руб.,
говоря при этом: «40 руб., 50 руб., 100 руб.».
Широкое применение этого способа показывает, что он имеет
преимущества по сравнению с другими; к нему следует привы-
кать при устном счёте. Чтобы вычесть, например, из 154 число
86, добавляем к 86 сперва 14, получая 100, затем добавляем 54,
25
получая 154. Замечая, что всего добавлено 14 4-54 = 68, нахо-
дим тем самым искомую разность.
§ 38. Проверка вычитания и сложения. Выполнив вычитание,
следует сделать проверку, основываясь на том, что уменьшае-
мое равно разности плюс вычитаемое, или на том, что вычитае-
мое равно уменьшаемому без разности.
Проверка вычитания проводится так:
1. Складывается полученная разность с данным вычитае-
мым—должно получиться уменьшаемое; если не получилось, то
сделана где-то ошибка.
2. Или полученная разность вычитается из данного умень-
шаемого— должно получиться вычитаемое; если не получилось,
то где-то сделана ошибка.
Пример. Проверка.
37812 , 27825 37812
— 9987 + 9987 ИЛИ “27825
27825 37812 9987
При устном вычитании рекомендуется выполнить вычитание
вторично, применяя какой-нибудь другой способ.
Зная взаимную связь вычитания со сложением, можно указать
второй способ проверки сложения: от полученной суммы вычи-
таем данное слагаемое (или сумму остальных слагаемых) — должно
получиться другое слагаемое; если не получилось, то где-то сде-
лана ошибка.
Пример. Проверка.
, 1734 2301 2301
"* 567 1734 или 567
2301 567 1734
Раздел 5. СЛОЖЕНИЕ И ВЫЧИТАНИЕ НА ПРИБОРАХ
§ 39. Русские счёты1. Как бывают народные сказки, народные
песни, так бывают и народные приёмы вычисления. Наиболее от-
личились в изобретении удачных вычислительных приборов на-
роды китайский и русский.
В Китае с древних времён был изобретён и сохранился по на-
стоящее время в вычислительной практике национальный прибор,
называемый «сван-пан», показанный на рисунке 3.
На Руси был изобретён более совершенный вычислительный
прибор, который стал известен на нашей родине с XV—XVI вв.
и который называют «русскими счётами» (рис. 4). Другие назва-
ния того же прибора: «конторские счёты», «торговые счёты».
Народы исторически шли от вычислительных приёмов на при-
борах к письменным вычислениям; вот почему и письменная ну-
1 Читая этот параграф, необходимо иметь под руками счёты.
26
мерация и письменные приёмы сложения и вычитания похожи на
приёмы вычислений на счётах.
Нумерация на счётах. На счётах также представлена пози-
ционная десятичная система: косточки, находящиеся на первой
снизу проволоке, означают первый разряд, на второй — второй раз-
ряд и т. д. Иногда на
счётах отмечают цветом
первой косточки переход
к классам: второму, треть-
ему и четвёртому. Вместо
цифр от 0 до 9 на каж-
дой проволоке отклады-
вается справа налево столь-
ко же косточек; каждая
пятая и шестая косточки
на одной и той же прово-
локе счётов окрашиваются
в чёрный цвет, чтобы не
пересчитывать косточки,
а схватывать зрением,
сколько их отложено.
2 7 0 9 1
Рис. 3.
2
7
О
9
1
Рис. 4.
МШ1
На «сван-пане» по одну сторону средней планки только пять
косточек, а по другую две. Первые означают единицы, а вторые
пятёрки. Однозначные числа откла-
дываются на первой справа прово-
локе, круглые — на соответствующей
следующей проволоке, а многознач-
ные путём разбиения на круглые и
однозначные. На рисунках 3 и 4 пе-
редано число 27091 на китайском
«сван-пане» и на русских счётах.
Сложение и вычитание на счётах.
В случаях, когда приходится скла-
дывать и вычитать много чисел, хо-
тя бы и небольших, рекомендуется
пользоваться русскими счётами. При-
менять их выгодно и тогда, когда
данных немного, но эти данные
выражаются многозначными числами.
Овладеть приёмами сложения и вы-
читания на счётах совсем нетрудно,
так как они основаны на тех же
свойствах сумм и разностей, что и
Им!
правила устного и письменного выполнения этих действий; только
на счётах ведутся вычисления, начиная со старших разрядов.
Так, чтобы сложить числа 563 и 231, кладём на счётах пер-
вое слагаемое, а затем прибавляем на третьей проволоке, где
уже есть слева пять косточек, ещё две, на второй проволоке к
27
шести косточкам прибавляем ещё три, на первой проволоке к трём
прибавляем ещё одну и читаем полученную сумму.
Если на какой-нибудь проволоке надо добавлять больше кос-
точек, чем их осталось на ней справа, добавляется одна косточка
на следующей верхней проволоке, а на данной проволоке «сбра-
сывается», т. е. переносится слева направо, надлежащее число
косточек (применяется прибавление разности).
Например, чтобы к 563 прибавить 279, приходится вместо семи
косточек на второй проволоке добавить одну косточку на третьей
проволоке, а на второй сбросить три, так как 70= 100 — 30,
а затем вместо добавления девяти косточек на первой проволоке
добавить ещё одну на второй и сбросить одну на первой, так
как 9 = 10 — 1. Ещё лучше принять во внимание, что 279 =
= 300 — 21, и добавить сразу три косточки на третьей проволоке,
сбрасывая затем две на второй и одну на первой.
Подобным же образом выполняется и вычитание. Желая, на-
пример, вычесть из 563 число 231, кладём на счётах уменьшаемое
и сбрасываем, т. е. переносим слева направо, две косточки на
третьей проволоке, три на второй, одну на первой.
Если на какой-нибудь проволоке приходится сбрасывать боль-
ше косточек, чем их имеется на ней слева, сбрасывают одну ко-
сточку на следующей верхней проволоке и добавляют надлежащее
число косточек на данной проволоке.
Например, при вычитании числа 279 из 563 вместо невоз-
можного здесь сбрасывания семи косточек на второй проволоке
сбрасывают ещё одну косточку на третьей проволоке и добав-
ляют три косточки на второй, а вместо невозможного здесь сбра-
сывания девяти косточек на первой проволоке сбрасывают ещё
одну на второй и добавляют одну на первой. Ещё лучше сразу
сбросить три косточки на третьей проволоке и добавить две на
второй и одну на первой.
При письменном сложении и вычитании идут от младших раз-
рядов к старшим (справа налево), а при сложении и вычитании
на счётах — от старших к младшим (сверху вниз). Таким обра-
зом, работа на счётах идёт вполне согласованно с нашей устной
нумерацией. Складывая письменно несколько чисел, мы находим
сперва сумму всех простых единиц, потом сумму всех десятков,
всех сотен, всех тысяч и т. д.,ана счётах сперва находят сумму
старших разрядов, потом следующих низших разрядов и т. д.
и, наконец, простых единиц.
§ 40. Арифмометр «Феликс». Ещё больше выгод чем счёты
доставляют вычислительные машины, над созданием которых ра-
ботали многие учёные, в том числе и знаменитый русский мате-
матик Пафнутий Львович Чебышев, живший с 1821 по 1894 г.
У нас самое широкое распространение получила вычислительная
машина, называемая арифмометром. Его изобрёл ещё в 1874 г. ин-
женер экспедиции заготовления государственных бумаг В. Т. Однер,
работавший в Петербурге, нынешнем Ленинграде. До Великой
28
Октябрьской революции арифмометры изготовляли только за гра-
ницей. Теперь массовым изготовлением их занимаются наши
механические заводы, причём марка «Феликс» в честь Феликса
Эдмундовича Дзержинского, знаменитого соратника Владимира
Ильича Ленина, присвоена усовершенствованным арифмометрам
системы Однера (рис. 5).
Нашей родине принадлежит, таким образом, первенство (при-
оритет) в создании счётной машины, получившей всемирное при-
знание и массовое распространение.
Рис. 5.
Нумерация на арифмометре. В верхней части арифмометра
виден ряд прорезов, из которых торчат концы рычажков, допу-
скающих движение по этим прорезам. Вдоль каждого прореза
нанесены цифры от 0 до 9. Крайний справа рычажок предназ-
начен для единиц, следующие — для десятков, сотен, тысяч и
т. д. Чтобы установить на арифмометре какое-нибудь число,
надо каждый рычажок установить против цифры, показывающей
число единиц соответствующего разряда. На рисунке 5 показана
установка рычажков для числа 418 509. Поворот рукоятки к себе
вызывает появление этого числа в «ответных окошечках», распо-
ложенных в нижней части машины, а именно в так называемой
«каретке» справа.
Сложение и вычитание на арифмометре. Чтобы сложить два
числа на арифмометре «Феликс», устанавливают на нём первое
слагаемое и поворотом рукоятки по направлению к себе пере-
носят его вниз, где оно появляется в ответных окошечках. Затем
устанавливают вверху второе слагаемое и новым поворотом ру-
коятки к себе переносят его тоже вниз, причём оно автоматически
складывается с первым, так что в ответных окошечках появляется
сразу сумма. Для вычитания достаточно повернуть рукоятку не
к себе, а от себя.
29
Работая с арифмометром, надо следить за тем, чтобы перед
первым поворотом рукоятки в ответных окошечках были нули.
Это обеспечивается вращением особого «барашка», находящегося
внизу справа. Рукоятка начинает вращаться только после того,
как её слегка потянут направо, и ей всегда надо давать полный
оборот. Если она не доведена до своего исходного (начального)
положения, переставлять рычажки нельзя. Оба барашка внизу,
слева и справа, тоже должны быть доведены до своего началь-
ного положения, иначе рукоятка не будет вращаться. Вообще
при работе с арифмометром нельзя применять усилий: если ры-
чажки не перемещаются или не вращается рукоятка, что-то уста-
новлено неправильно. Пытаясь что-либо двигать с усилием, рис-
куем сломать машину.
Как и на счётах, сложение и вычитание на арифмометре вы-
полняется последовательно в любом порядке: имея несколько
данных чисел, часть которых надо сложить, а остальные вычесть
из суммы первых, берут одно за другим все эти числа и пово-
ротом рукоятки в ту или другую сторону прибавляют или от-
нимают каждое из них.
Пользуясь арифмометром, человек может вычислить столько,
сколько сделают за то же время 10—12 человек, вычисляющие
письменно. Кроме того, и это не менее важно, ошибки при работе
на исправном арифмометре, как показывает опыт, очень редки.
Русские счёты позволяют выполнять сложение и вычитание
почти так же быстро и точно, как арифмометр, но отстают от
арифмометра при выполнении других действий, о которых речь
будет дальше.
В настоящее время в СССР создана быстродействующая элек-
тронная счётная машина — БЭСМ. Она похожа на щит управления
большой электростанции. На ней имеются сотни кнопок управ-
ления и штепселей.
Машина работает автоматически, делая в 1 секунду до 8000
вычислительных операций (действий сложений, вычитаний, ум-
ножений, делений). Она ведёт вычисления почти в 100000 раз
быстрее человека. За несколько часов на ней можно произвести
столько вычислений, сколько хороший вычислитель не может
сделать за всю свою жизнь.
Глава III. УМНОЖЕНИЕ И ДЕЛЕНИЕ
Раздел 1. ТЕОРИЯ УМНОЖЕНИЯ
§ 41. Объединение множеств одинаковой численности. Объ-
единение двух или более множеств одинаковой численности встре-
чается так часто, что заслуживает особого рассмотрения. Вот при-
мер: завод выпускает ежедневно по 9 машин; сколько он выпустит
за неделю, т. е. за 6 рабочих дней? Здесь мы имеем шесть мно-
жеств, каждое из которых содержит девять элементов, и ставится
30
вопрос о численности множества, получающегося при их объеди-
нении. На него можно ответить, находя сумму 94-94-94-94-94-
4- 9 = 54, но при более значительном числе объединяемых мно-
жеств это потребует длинной записи и значительного вычислитель-
ного труда; упростим запись и вычисление на основе нового дей-
ствия — умножения.
§ 42. Произведение натуральных чисел. Только что найденная
сумма шести слагаемых, каждое из которых равно девяти едини-
цам, называется произведением 9 на 6. Вообще произведением
называется сумма равных слагаемых, повторяющееся при этом
слагаемое называется множимым, а число слагаемых — мно-
жителем. Для множимого и множителя вместе существует об-
щее название — сомножители. Умножением называется действие
нахождения произведения по данным сомножителям.
Вместо того чтобы говорить: находим произведение 9 на 6,
говорят: умножим 9 на 6 или повторим 9 шесть раз, или уве-
личим число 9 в шесть раз.
Умножение принято обозначать так: сперва, записав множимое, ставят
знак умножения — точку (•) или косой крест (х), затем множитель. Знак
умножения (•) возник в XVII в. и закрепился не сразу.
Таким образом, имеем:
9-|-9-|-9-|-9-|-9-|-9 = 9 • 6 а 4- а 4- а 4- ... 4- а = а • Ь
6 слагаемых
Ъ слагаемых
Вернёмся к примеру с машинами. Как мы видели, за неделю,
т. е. за 6 рабочих дней, завод выпускает 9 • 6 = 54 машины. Если
надо узнать, сколько будет их выпущено за две недели, надо вы-
полнить ещё одно умножение, а именно:
54 4- 54 = 54 • 2 = 108.
Можно сказать, что мы здесь нашли произведение трёх со-
множителей:
9 • 6 - 2 = 108.
Запись а • Ь • с означает, что сперва берётся произведение
а • Ь, затем это произведение умножается на с.
Можно находить произведение любого числа сомножителей,
как, например:
2 • 3 • 4-5 = 6.4 - 5 = 24 - 5 = 120.
§ 43. Переместительный закон умножения. Рассмотрим рису-
нок 6, на котором изображены вырытые для посадки ямки на
опытном участке. Сколько вырыто ямок? Ответ можно найти
двояко:
31
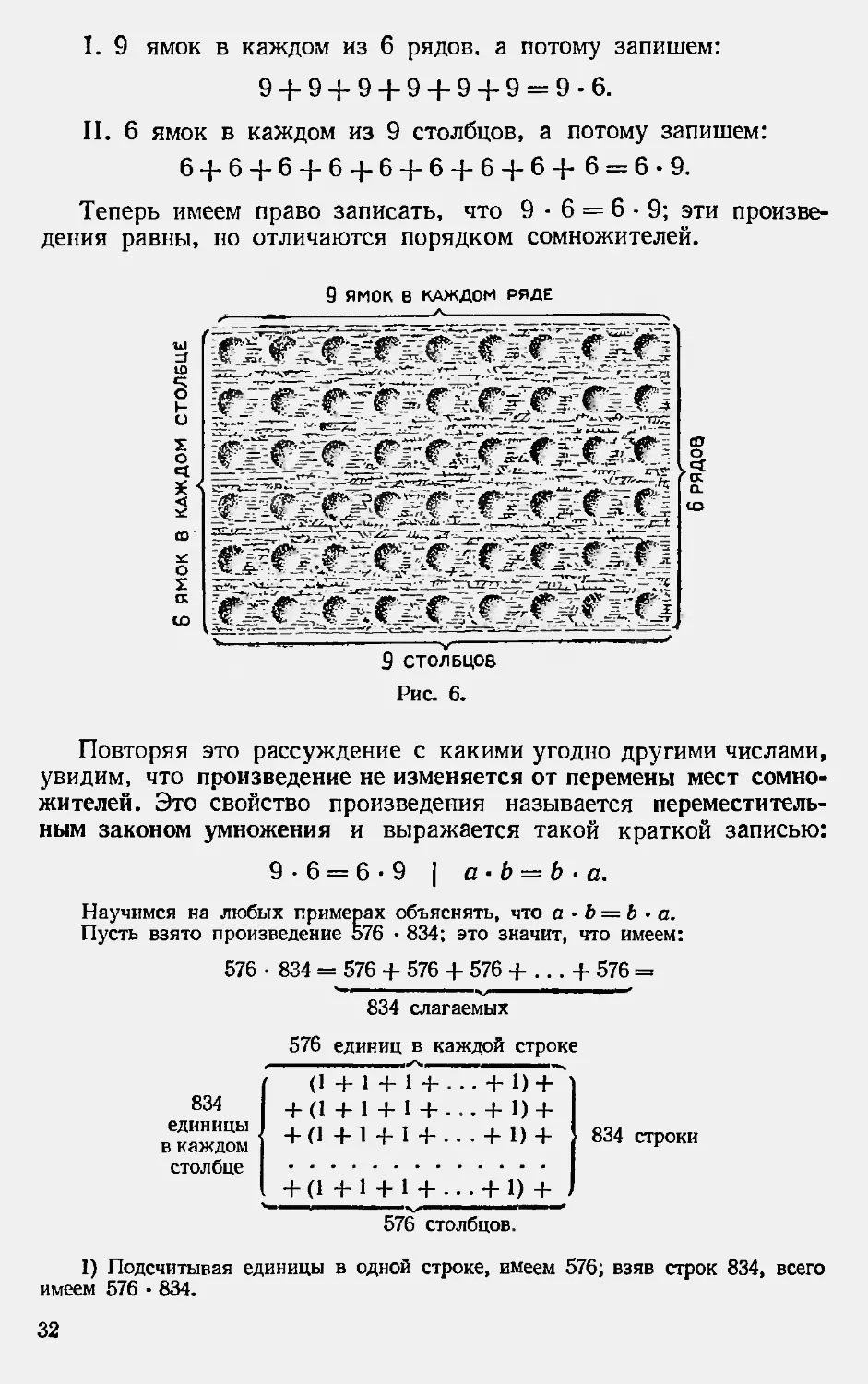
I. 9 ямок в каждом из 6 рядов, а потому запишем:
9 + 94-9 + 9 + 94-9 = 9-6.
II. 6 ямок в каждом из 9 столбцов, а потому запишем:
6 + 6 + 6 + 6 + 6 + 6 + 6 + 6+ 6 = 6-9.
Теперь имеем право записать, что 9 - 6 = 6 • 9; эти произве-
дения равны, но отличаются порядком сомножителей.
9 ЯМОК В КАЖДОМ РЯДЕ
9 СТОЛБЦОВ
Рис. 6.
Повторяя это рассуждение с какими угодно другими числами,
увидим, что произведение не изменяется от перемены мест сомно-
жителей. Это свойство произведения называется переместитель-
ным законом умножения и выражается такой краткой записью:
9 • 6 = 6 • 9 | а - b — Ь • а.
Научимся на любых примерах объяснять, что а • b = b • а.
Пусть взято произведение 576 • 834; это значит, что имеем:
576 • 834 = 576 + 576 + 576 + .. . -f- 576 =
834 слагаемых
834
единицы
в каждом
столбце
576 единиц в каждой строке
(1 4-1 4-~4-. .. 4-D 4-"
+ (1 4-1 4- 1 4- - • -4-1) 4-
4-(14-14-14-...4-1) 4-
4-(1 4-1 4- 1 4-•••4-1) 4- .
576 столбцов.
834 строки
1) Подсчитывая единицы в одной строке, имеем 576; взяв строк 834, всего
имеем 576 • 834.
32
2) Подсчитывая единицы в одном столбце, имеем 834; взяв столбцов 576,
всего имеем 834 • 576.
3) В итоге подсчитаны одни и те же единицы двумя различными приёмами,
а потому 576 • 834 = 834 576.
Знание переместительного закона позволяет иногда значи-
тельно ускорить получение произведения. Например, чтобы найти
произведение 2-37, можно взять равное ему произведение
37 • 2 = 37 + 37 = 74, что гораздо легче, чем искать сумму 37
слагаемых, каждое из которых равно 2.
§ 44. Сочетательный закон умножения. Положим, что в каж-
дую ямку, изображённую на рисунке 6, кладётся по 4 жёлудя.
Сколько надо иметь желудей, чтобы провести такую «гнездовую»
посадку на опытном участке?
Расчёт можно выполнить двумя способами:
1) в каждую ямку верхнего ряда кладут 4 жёлудя, всего в
этот ряд положат:
4 + 4 + 4 + 4 + 44-4 + 4 + 4 + 4 = 4 -9,
9 слагаемых
но таких рядов 6, а потому надо иметь всего желудей для по-
садки:
4.9 + 4.9 + 4.9 + 4.9 + 4.9 + 4.9 = (4.9).6;
6 слагаемых
2) в каждую ямку кладётся по 4 жёлудя, а всего ямок 9 • 6;
следовательно, имеем:
4 + 4 + 4+ . .- + 4 =4 -(9-6).
9 • 6 слагаемых
Понятно, что каковы бы ни были взятые числа, оба способа
всегда дадут одно и то же число. Умножение, какое пришлось вы-
полнить при первом способе, коротко выражается записью 4 • 9 • 6,
говорящей, что здесь производится последовательное умножение
числа 4 на 9 и 6. Второй же способ выражается записью 4 • (9 6),
говорящей, что 4 умножается сразу на произведение 9 • 6, кото-
рое должно быть найдено в первую очередь.
Итак, вместо того чтобы умножить 4 последовательно на 9
и на 6, можно умножить 4 сразу на произведение 9 6. Это
свойство произведения называется сочетательным законом умно-
жения и коротко записывается так:
(4-9). 6 = 4. (9-6) | (а. 6). с = а-(6-с).
33
Научимся объяснять на любых примерах, что (а - 6) • с = а - (Ь • с).
Пусть взято (2345 • 793) • 5843; имеем:
793 слагаемых в каждой строке
(2345-793) -5843 = (2345 + 2345 + 2345 + . .. + 2345? +
4- (2345 4- 2345 4- 2345 4- •. • 4- 2345) 4- 5843 строки
4- (2345 + 2345 4- 2345 + + 2345) 4-,
2345 повторено слагаемым
793 • 5843 раза
1) Подсчитываем 2345 по одной строке: надо 2345 повторить слагаемым
793 раза; затем полученное повторим слагаемым 5843 раза, т. е. столько,
сколько было строк; будем иметь: (2345 • 793) - 5843.
2) Предварительно подсчитаем, сколько всего раз число 2345 записано
слагаемым; для этого число 793, показывающее, сколько слагаемых в одной
строке, умножим на число всех строк, т. е. на 5843; будем иметь 793 • 5843.
После этого легко подсчитать всю сумму, где слагаемое 2345 повторено
793 • 5843 раз; имеем 2345 • (793 5843).
3) В итоге одно и то же произведение подсчитано двумя различными спо-
собами, а потому
(2345 • 793) • 5843 = 2345 • (793 - 5843).
Сочетательным законом обладает не только произведение
трёх, но и любого числа сомножителей. Таким образом, чтобы
умножить число последовательно на два или более множителей,
достаточно умножить его сразу на их произведение, и обратно:
чтобы умножить число на произведение, достаточно умножить
его последовательно на все сомножители этого произведения.
Знание сочетательного закона помогает при вычислениях.
Так, желая найти 396 -5-2, можно взять сперва произведение
5-2=10, а затем 396 • 10 = 3960, что легче, чем находить
396 • 5 = 1845 и 1845 • 2 = 3690.
§ 45. Распределительный закон умножения. Рассмотрим задачу.
В саду посажены деревья в 8 рядов, в каждом ряду по 5 яблонь
и по 4 груши. Сколько всего деревьев посажено?
Здесь тоже два способа решения: 1) Можно узнать, сколько по-
сажено яблонь и груш в отдельности (5 • 8 = 40; 4-8 — 32), а за-
тем сложить эти два числа (40 4- 32 = 72). 2) Можно сперва узнать
число деревьев в каждом ряду (5 4-4 = 9), а потом найти искомое
общее число деревьев (9 • 8 = 72). Оба способа дадут одно и то же:
5 - 8 4 • 8 = (5 4) - 8.
Таким образом, мы имеем новое свойство чисел, называемое
распределительным законом умножения относительно сложения:
Чтобы умножить сумму чисел, достаточно умножить каждое
слагаемое и полученные произведения сложить. Вот краткая
запись этого свойства:
(5 4- 4)- 8 = 5- 84-4-8 | (а^Ь) с = а с + Ь • с.
34
Научимся на любых примерах объяснять, что
(а 4- 6) • с = а • с + Ъ • с.
Например:
(5394 + 4372) • 725 =
= (5394 + 4372) + (5394 + 4372) + ... + (5394 + 4372) =
725 слагаемых
(по определению умножения)
= (5394 + 5394 + ... + 5394) + (4372 + 4372 + ... + 4372)=
725 слагаемых 725 слагаемых
(по сочетательному и переместительному законам сложения)
= 5394 • 725 + 4372 • 725 (по определению умножения).
На практике это свойство часто используют в обратном по-
рядке; вместо того чтобы находить сумму произведений двух
каких-либо чисел на одно и то же третье число, находят сперва
сумму двух данных чисел, а затем умножают её на третье число.
Например:
237 • 9 + 763 • 9 = (237 + 763) • 9 = 1000 • 9 = 9000.
Можно видеть, что распределительным законом обладает и
произведение разности на число. Например:
(25 —6) • 4 = 19 4 = 76, 25 - 4 — 6 • 4 = 100 — 24 = 76,
вообще
{а — Ь) • с = а • с — b • с.
Научимся на любых примерах объяснять, что
(а — 6) • с = а • с — b • с.
(1534 — 789) • 936 =
= (1534 — 789) + (1534 — 789) + ... + (1534 — 789) =
936 слагаемых
= (1534 4- 1534 + .. . + 1534) — (789 + 789 + .. . + 789) =
936 слагаемых 936 слагаемых
=1534 • 936 — 789 • 936.
В результате получаем распределительный закон умножения
относительно вычитания:
Чтобы умножить на данное число разность, достаточно умно-
жить на него уменьшаемое и вычитаемое в отдельности и из
первого произведения вычесть второе.
§ 46. Умножение на единицу. Определение произведения, дан-
ное в § 42. не годится для случая, когда множитель равен еди-
нице, так как невозможно повторить число слагаемым один раз
(слагаемых не бывает меньше двух).
Определяем, что умножить число на I—значит оставить его
без изменения, т. е.
5725 • 1 = 5725 | а 1 = а.
35
При таком дополнительном определении действия умножения
его законы (переместительный, сочетательный и распределитель-
ный) сохраняются и для случая, когда множитель равен единице.
В самом деле:
1) 1 • 275 = 275 • 1 = 275;
2) 575 • (429 1) = (575 • 429) • 1 = 575 429;
3) (623 + 74) • 1 = 623 • 1 + 74 • 1 = 623 -J- 74.
§ 47. Умножение нуля и умножение на нуль. Указанное выше
определение произведения применимо и тогда, когда множимое
есть нуль, т. е. когда объединяется пустое множество. В самом
деле:
О . 5 = 0 + 0 4- 0 + 0 + 0 = 0 0 • о = 0 + 0 +... 4-0 = 0, а>1.
0-1=0 а слагаемых
Вывод: произведение нуля на любое натуральное число
есть нуль. В случае, когда множитель равен нулю, указанное
выше определение произведения неприменимо: в сумме не может
быть нуль слагаемых. Поэтому принято ещё одно дополнительное
определение произведения: произведение любого числа на нуль
равно нулю:
5-0 = 0 |а-0 = 0.
Такое определение сохраняет переместительный, сочетательный
и распределительный законы умножения и для случая, когда
множитель равен нулю. В самом деле:
0-315 = 315-0 = 0
417 • (563 • 0) = (417 - 563) -0 = 0
(748 4- 211) • 0 = 748 - 0 4- 211 - 0 = 0
0 • а = а • 0 = 0
а • (6 • 0) = (а • Ь) • 0 = 0
(Ь 4- с) • 0 = b 0 4-
4-с-0 = 04-0 = 0.
Из нового дополнительного определения следует, что
0-0 = 0.
Раздел 2. ТЕХНИКА УСТНОГО И ПИСЬМЕННОГО
УМНОЖЕНИЯ
§ 48. Табличное умножение. Умножение любых многозначных
чисел выполняется без особого труда, если научиться умножать
однозначные числа, а также круглые числа.
В приведённой ниже таблице даны произведения любых двух
однозначных чисел. Сомножители указаны в верхней строке и ле-
вом столбце, а произведения поставлены на пересечении соответ-
ствующих строк и столбцов.
Необходимо запомнить 45 произведений, находящихся в той
части этой таблицы, которая обведена жирной линией. Осталь-
36
ные 36 произведений получаются сами собой в силу перемести-
тельного свойства. Например, помня, что 9 • 8 = 72, можем сразу
сказать, что 8 • 9 = 72. Эта таблица умножения составляется и
изучается ещё в начальной школе.
Если какое-нибудь содержащееся в ней произведение позабы-
то, его всегда можно найти. Например,
7.8 = 8- 7 = 8 + 8-}-8-|-8-|-8 + 8-}-8 = 56.
Или, короче, зная, что
7-10 = 70 и 7 - 2 = 14,
имеем:
7 - 8 = 7-(10 — 2) =7- 10 — 7 - 2 = 70— 14 = 56.
1 2 3 4 5 6 7 8 9
1 1
2 2 4
3 3 6 9
4 4 8 12 16
5 5 10 15 20 25
6 6 12 18 24 30 36
7 7 14 21 28 35 42 49
8 8 16 24 32 40 48 56 64
9 9 18 27 36 45 54 63 72 81
§ 49. Умножение круглых чисел. Приписывая к числу справа
нуль, мы увеличиваем это число в 10 раз (это следует из поме-
стного значения цифр). Легко найти и запомнить следующие
произведения разрядных единиц: 10 • 10 = 100; 100 - 10 =
= 10 - 100 = 1000; 100 • 100 = 10000; 10000 • 100 = 100 • 10000 =
= 1 000 000 и т. д.
Таким образом, в произведении двух разрядных единиц всегда
получается разрядная единица, в записи которой имеется столько
нулей, сколько их во множимом и множителе вместе.
Умножение любых двух круглых чисел сводится в силу
свойств произведения (§ 43, 44, 45) к умножению однозначных
37
чисел и разрядных единиц. Выполним такое умножение для слу-
чая 6000 300:
6000 • 300 = (6 • 1000) . (3 • 100) =
= 6 • 1000.3 • 100 =
= 6 • 3 • 1000 100 =
= (6 . 3) (1000 . 100) =
= 18 • 100 000 =
= 1 800 000
(на основании поместного значения
цифр)
(по свойству умножения иа произве-
дение)
(по переместительному закону)
(по сочетательному закону)
(по таблице умножения)
(на основании поместного значения цифр).
Полученный окончательный результат можно написать сразу,
если следовать правилу: чтобы перемножить круглые числа, надо
написать произведение первых цифр этих чисел и приписать спра-
ва столько нулей, сколько их в обоих сомножителях вместе.
§ 50. Умножение многозначного числа на однозначное. Если
надо найти произведение, например 452 • 7, представляют множи-
мое в виде суммы круглых чисел и, пользуясь распределительным
свойством произведения, сводят вопрос к умножению круглых
чисел на однозначные. Действительно:
452 • 7 = (400 4- 50 4- 2) • 7 = (на основании поместного значения цифр)
= 400 • 7 4- 50 7 4- 2 • 7 = (по распределительному закону)
= (4 - 7) • 100 4- (5 - 7) - 10 4- 2 7 = (по сочетательному и переместитель-
ному законам)
= 28 • 100 4- 35 • 10 4- 14 = (по таблице умножения)
= 2800 4- 350 4- 14 = (на основании поместного значения
цифр)
= 3164 (сложение частичных произведений).
Здесь приведена подробная запись с объяснением каждого
шага, а ниже даны два вида обычпой краткой записи, при кото-
рой умножение круглых чисел и сложение их произведений де-
лаются одновременно.
Не рекомендуется писать на стороне число десятков двузнач-
ного числа, получаемого от умножения множителя на однознач-
ные числа, находящиеся в каждом разряде множимого; лучше
привыкнуть запоминать эти числа.
§ 51. Умножение многозначных чисел. Положим, требуется
найти произведение 452 • 367. Заменяя множитель суммой
300 -}- 60 -|- 7 и пользуясь распределительным свойством произведе-
ния, сводим дело к умножению числа 452 на круглые числа 300,
60 и однозначное число 7, что мы уже умеем делать. Приведём
подробную запись для полного объяснения:
452 • 367 = 452 - (300 4- 60 4- 7) =
= 452 • 300 4- 452 • 60 4- 452 • 7 =
= 452 • (3 100) 4- 452 • (6 • 10) 4- 452 7 =
= (452 - 3) • 100 4- (452 - 6) • 10 4- 452 • 7 =
= 1356 - 100 4- 2712 • 10 4- 3164 =
= 135 600 4- 27 120 4- 3164 =
= 165 884.
38
Краткая запись этого примера:
452 или 452 • 367
Х 367 1356
3164 4- 2712
+ 2712 3164
1356 165884
165884
При письменном умножении двух многозначных чисел лучше
взять множителем то число, в котором цифр меньше: умножить,
например, 8354 на 129 легче, чем 129 на 8354 (меньше частичных
произведений!); результат в силу переместительного свойства
произведения получается один и тот же.
Если сомножители имеют справа нули, их мысленно отбрасы-
вают, умножая обычным порядком числа, выражаемые оставши-
мися цифрами, а затем приписывают к полученному произведению
справа все отброшенные нули.
Если множитель имеет нули в середине, то на них умножения
не делают, но в этом случае надо очень внимательно относиться
к записи частичных произведений на следующие за нулями цифры
множителя. Приводим примеры:
1) 493 или 493 504
504 .2465
, 1972 1972
+ 2465 248472
248472
2) 4937 или 4937 • 5004
5004 , 24685
, 19748 19748
+ 24685 24704748
24704748
§ 52. Число цифр в произведении. В табличном произведении можно за-
метить два случая: 1) произведение есть двузначное число, например: 7-8 =
= 56; 2) произведение есть однозначное число, например: 2-3 = 6. Из 45
табличных произведений первый случай встречается 32 раза, а второй 13 раз.
В каждом первом случае оказалось в произведении столько цифр, сколько
их было в обоих сомножителях вместе, а в каждом втором случае —на одну
цифру меньше.
Можно убедиться, что этот вывод остаётся верным и для произведения
любых двух натуральных чисел: произведение двух натуральных чисел имеет
или столько цифр, сколько их в обоих сомножителях вместе, или на одну цифру
меньше. Например, в произведении 345 на 67, равном 23 115, имеется 3 4-2 =
= 5 цифр, а в произведении 345 на 12, равном 4140, только 5— 1=4 цифры.
§ 53. Устное умножение. Умножение однозначных чисел де-
лается всегда в уме: таблицу умножения надо знать наизусть.
Вот что говорит об этом один из первых русских учителей
математики Леонтий Филиппович Магницкий в своём замечатель-
ном учебнике «Арифметика», напечатанном в 1703 г.:
«Аще ю не твердит
Да умом гордит,
То не свободь от муки
Во всей науки».
Здесь старинным языком выражена та мысль, что всякий, кто,
гордясь своим умом, не учит её, т. е. таблицу, наизусть, тот будет
мучиться при всём дальнейшем изучении науки.
39
Знание таблицы умножения позволяет устно находить и про-
изведения круглых чисел. Умножение любого двузначного числа
на всякое однозначное тоже следует делать в уме; оно требует
двух умножений и одного сложения, например:
78 • 9 = 70 • 9 + 8 - 9 = 630 + 72 = 702.
Зная свойства произведения, часто удаётся существенно упро-
стить и облегчить вычислительный труд. При этом используются
свойства суммы и разности и особые свойства некоторых чисел,
как, например, то обстоятельство, что 37 • 3 = 111. Вот несколько
примеров, в которых все вычисления можно сделать устно (по-
дробная запись приведена только для объяснения).
1) 63 • 49 = 63 - 50 — 63 = 3150 — 63 = 3087 (распределительный закон);
2) 729 • 25 • 4 = 729 • (25 • 4) = 729 • 100 = 72 900 (сочетательный закон);
3) 37 • 24 = 37 • (3 • 8) = 37 • 3 • 8 = 111 • 8 = 888 (сочетательный закон);
4) 37 • 297 = 37 - (300 — 3) = 37 300 — 37 - 3 = 11 100 — 111 = 10 989
(распределительный закон);
5) 357 • 125 • 25 • 8 • 4 = 357 • (25 - 4) - (125 • 8) = 357 • 100 • 1000 =
= 35 700 000 (переместительный и сочетательный законы);
6) 42 • 11 = 4 сотни + (4 + 2) десятка + 2 • 1 = 462 (распределительный
закон и сочетательный закон сложения);
7) 58 • 11=5 сотен + (5 + 8) десятков + 8-1=5 сотен -|- 13 десятков-f-
+ 8 = 638 (распределительный закон и сочетательный закон сложения);
8) 64 • 35 = (32 • 2) • 35 = 32 • (2 • 35) = 32 • 70 = 2240 (переместительный
и сочетательный законы умножения);
9) 73 • 24 + 24 - 17 = (73 + 17) • 24 = 90 • 24 = 2400 — 240 = 2160 (распре-
делительный закон).
§ 54. Проверка умножения. Простейший способ проверки
письменного умножения — вторичное выполнение этого действия
при изменённом порядке сомножителей. При устном умножении
результат для проверки находят ещё раз, применяя какой-нибудь
иной способ вычисления.
Примеры:
1) 8507 • 246
17014
, 34028
+ 51042
2092722
2) 58 - 15 = (29 • 2) • 15 =
= 29 • (2 • 15) =
= 29 • 30 =
= 870
Проверка:
246 - 8507
1968
, 1230
+ 1722
2092722
58- 15 = 58 • (10 + 5) =
= 58-10 + 58 - 5 =
= 580 + 290 =
= 870
Действие умножения значительно труднее сложения и вычи-
тания, и опыт показывает, что при его выполнении чаще появ-
ляются ошибки. Поэтому следует делать проверку каждого по-
лученного произведения.
40
Раздел 3. ТЕОРИЯ ДЕЛЕНИЯ
§ 55. Разложение данного множества на новые множества
одинаковой численности. Задачу объединения нескольких мно-
жеств одинаковой численности мы рассмотрели в § 41, а потому
сумеем решить следующую задачу:
Сколько надо принести в класс тетрадей, чтобы каждый из
20 учеников получил по три тетради?
З4-З4-З4- ...4-3 = 3 - 20 = 60 (тетрадей).
20 слагаемых
К этой задаче возможно подобрать две обратные задачи.
I. В класс принесено 60 тетрадей для выдачи ученикам по
3 тетради. Сколько учеников получат тетради?
Расчёт поведём так:
60 = 34-34-34-...4-3
неизвестно, сколько
слагаемых
Склады- ваем по три 6 9 12 15 18 21 24 27 30 33 36 39 42 45 48 51 54 57 60
Отме- чаем чис- ло сла- гаемых 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
Итак, оказалось 20 слагаемых.
II. В класс принесено 60 тетрадей для того, чтобы их раз-
дать поровну 20 учащимся. Сколько тетрадей получит каждый
учащийся?
Расчёт поведём так:
60 тетрадей надо разложить на 20 множеств одинаковой числен-
ности, т. е.
60 = ?4-?4-?4- ...4? = x4-x4-x4-...4-x
20 слагаемых 20 слагаемых
Сперва раздаём каждому из 20 учащихся по одной тетради
(20 тетрадей), потом по другой (40 тетрадей), по третьей (60 тет-
радей), роздали все 60 тетрадей. Следовательно, х = 3.
В обеих рассмотренных задачах мы занимались разложением
данного множества на новые множества одинаковой численности.
Если элементов много, простое раскладывание затруднительно
или практически невозможно. Надо найти такой способ решения
подобных задач, какой не требовал бы этого раскладывания.
41
§ 56. Частное натуральных чисел. В практике часто прихо-
дится данное множество, в котором имеется сколько-то элемен-
тов, разлагать (разделять) на несколько новых множеств одина-
ковой численности.
В связи с этим приходится данное число делить на равные
слагаемые; здесь обнаруживается два случая:
1) когда данное число (например, 60) разделяется на известные
равные слагаемые (по 3) и находят число образовавшихся сла-
гаемых (например, 20);
2) когда данное число (например, 60) разделяется на известное
число слагаемых (например, 20), а находят каждое образовавшееся
слагаемое (3).
Эти задачи называют задачами деления, точнее — полного де-
ления.
Разделить первое данное число (например, 60) на второе дан-
ное число (например, 20)—значит найти третье число (3), ко-
торое, будучи умножено на второе данное число, даёт первое
(3 • 20 = 60).
Первое из данных чисел называется делимым, второе дели-
телем, искомое же третье число — частным. Делением называется
действие нахождения частного.
§ 57. Связь деления с умножением. Если частное 60:20, рав-
ное 3, умножить на делитель 20, получим делимое 60. Так бы-
вает всегда:
(а :Ь) • b = а.
В самом деле: пусть а, делённое на Ь, даёт частное с, т. е.
а : b = с.
По смыслу деления найдено третье число (с), которое, будучи
умножено на второе (число Ь), должно дать первое (число а),
т. е. с • b = а, или, подставив вместо с равное ему а: Ь, имеем
(а : Ь) • b = а.
Таким образом, действие умножения обратно действию деле-
ния: умножение чисел (а : Ь) и 6 как бы уничтожает деление на Ь,
восстанавливает первоначально взятое число а.
В свою очередь деление обратно умножению: если число а
умножить на число Ь, а затем произведение а • b разделить на Ь,
то получим опять а, так как а, умноженное на Ь, даёт произве-
дение а • Ь. Поэтому действия умножения и деления называются
взаимно обратными.
Делением называется действие, где по произведению двух
сомножителей и одному из них находят другой, при этом произ-
ведение называется делимым, известный сомножитель — делителем,
а искомый сомножитель — частным.
Делимым называется то число, которое делят, а делителем
то число, на которое делят; частным называется то число, кото-
рое получается при делении.
42
Знак деления (:) возник одновременно со знаком умножения (•) в XVII в.;
впервые их предложил Лейбниц, в частности знак (:) в 1684 году. Этот знак
напоминает, что данное число надо разложить по крайней мере на два равных
слагаемых.
Вместо того чтобы говорить: «разделить 24 на 3», вообще
«разделить а на Ь», можно сказать: «уменьшить 24 в 3 раза»,
«уменьшить а в b раз».
Необходимо заметить, что имеется два вида деления:
1) когда по произведению и множимому находят множитель
(смотри I случай § 55);
2) когда по произведению и множителю находят множимое
(смотри II случай § 55);
Так как умножение обладает законом переместительности, то
оба случая сливаются в одно понятие деления, где по произве-
дению двух сомножителей и одному из них находят другой.
Деление натуральных чисел, о котором шла до сих пор речь,
выполнимо далеко не всегда. Например, разделить 10 на 3 нельзя,
так как 3-3 = 9 меньше 10; 3 • 4 = 12 уже больше 10; частного
от деления 10 на 3 среди натуральных чисел нет; множество из
10 элементов нельзя представить в виде трёх множеств одинако-
вой численности.
§ 58. Особые случаи деления.
1) Любое число делится на 1, и частное равно этому же числу,
например:
7:1=7, так как 7-1=7;
вообще
а : 1 = а, так как а • 1 = а.
2) Любое натуральное число делится само на себя, и частное
равно единице, например:
7:7=1, так как 7-1=7;
вообще
а : а = 1, так как а • 1 = а.
3) Добавляя к множеству натуральных чисел ещё число 0,
убеждаемся, что нуль делится на любое натуральное число и
частное равно нулю, например:
0:7 = 0, потому что 0-7 = 0;
вообще
0 : а = 0, так как 0 • а = 0.
4) Но делить число на 0 нельзя. Например, частное 7:0 не
существует, так как умножение любого числа на 0 даёт 0, а не 7.
Деление же 0 на 0 ничего определённого не даёт, так как любое
число, умноженное на нуль, даёт нуль. Ввиду этого деление на
нуль невозможно или неопределённо.
§ 59. Деление суммы и разности. Задача. Звено из 5 кол-
хозников выработало за неделю 20 трудодней на уборке зерно-
43
вых и 30 трудодней на уборке овощей. Сколько трудодней вы-
работал каждый член этого звена?
Эту задачу можно решить двумя способами: во-первых, можно
узнать, сколько трудодней выработали все колхозники (20 -|-
-}-30 = 50), а затем сколько выработал каждый (50:5=10);
во-вторых, можно узнать, сколько выработал каждый на уборке
зерновых и овощей в отдельности (20:5 = 4; 30:5 = 6), а затем
сколько всего (4 6 = 10). Понятно, что оба способа дают один
и тот же ответ.
Наблюдения приводят к выводу: чтобы разделить сумму,
достаточно разделить каждое слагаемое в отдельности и резуль-
таты сложить. Это свойство суммы сохраняется и в случае лю-
бого числа слагаемых. Вот краткая запись этого свойства:
(20 + 30): 5 = (20 : 5) -f- (30 : 5); | (а + Ь): с = (а : с) + (Ь : с),
так как по определению деления и свойству умножения имеем:
[(а-J-b) : с] • с = а + b и {a: c-j-b :с)-с= (а: с) -с + (Ь:с)-с = а-]-Ь.
Рассмотрим ещё задачу. Звено выработало за неделю 50 тру-
додней, в том числе 20 на уборке зерновых, остальные—на
уборке овощей. Сколько выработал каждый член звена на уборке
овощей, если всего было 5 человек и если все работали одина-
ково?
Здесь опять два способа решения: первый, требующий одного
вычитания и одного деления (50 — 20 = 30; 30:5 = 6), и второй,
требующий двух делений и одного вычитания (50:5 = 10;
20:5 = 4; 10 — 4 = 6). Оба способа дают один и тот же ответ:
6 трудодней. Подобные рассуждения можно провести на любых
числах. Приходим к выводу: чтобы разделить разность, достаточно
разделить уменьшаемое и вычитаемое в отдельности и из первого
частного вычесть второе. Вот краткая запись этого свойства:
(50 —20) :5 = (50:5) —(20:5); | (а— Ь): с = (а :с) — (Ь :с),
так как [(а—Ь) : с]-с—а—b и (а : с—Ь:с)-с=(а: с)-с—(Ь : с)-с—а—Ь.
§ 60. Деление произведения и деление на произведение.
1) Чтобы разделить сумму, достаточно разделить каждое сла-
гаемое в отдельности, но, чтобы разделить произведение, доста-
точно разделить только один из сомножителей. Действительно,
найти, например, частное от деления произведения 6 9 = 54 на
3 можно двумя способами: разделив первый сомножитель или
разделив второй сомножитель на 3. Если же разделить на 3
каждый сомножитель этого произведения, оно разделится уже
не на 3, а на 9, так как (6 :3) • (9 :3) = 2 • 3 = 6, а не 18.
Вот краткая запись этого свойства:
(6 • 9) :3 = (6:3) 9 = 6 • (9:3); | (а • 6) :с = (а:с) • Ь=а-(Ь:с),
так как [(а • Ь): с] • с=а • Ь и [а • (Ь ; с)] • с=а • [(& : с) • с]=а Ь.
44
Чтобы разделить число на произведение, достаточно разделить
его последовательно на каждый сомножитель этого произведения
в отдельности. Так, чтобы получить частное от деления числа 30 на
произведение 2-3 = 6, можно сначала разделить 30 на 2, а затем
полученное частное 15 разделить на 3, что даст 5.
Вот краткая запись этого свойства:
30 : (2 - 3) = (30 : 2) : 3 = (30 : 3): 2;
а: (Ь • с) = (а:Ь)-.с — (а:с):Ь,
так как [а: (be)] • be = а и [(а: с) : Ь] • Ьс = (а: с) • с — а.
§ 61. Число цифр в частном. Зная делимое и делитель, можно предвидеть
число цифр в частном, не вычисляя последнего. Так как деление есть дей-
ствие, обратное умножению, то надо обратиться к установленной связи между
числом цифр сомножителей и произведения (§ 52).
Известен первый случай, когда в произведении двух сомножителей число
цифр равно сумме числа цифр множимого и множителя; в этом случае при-
ходим к выводу: число цифр в частном равно разности числа цифр делимого
и делителя. Например:
373 945 : 523 = 715
(6 цифр) (3 цифры) (3 цифры), 6 — 3 = 3.
Но известен и второй случай, когда в произведении двух сомножителей
число цифр равно сумме числа цифр множимого и множителя, уменьшённой
на единицу; в этом случае приходим к выводу: в частном число цифр на
единицу больше разности числа цифр делимого и делителя. Например:
736 776 : 324 = 2274
(6 цифр) (3 цифры) (4 цифры), 6 — 3 + 1 = 4.
Кроме этих двух случаев, никаких иных не встречается. Число цифр
частного или равно разности числа цифр делимого и делителя или на еди-
ницу больше.
§ 62. Деление с остатком. Если надо делить поровну между
20 учащимися не 60 тетрадей, как это было выше, а например,
62, то сделать это полностью не удаётся: отложив для каждого
ученика по 3 тетради, мы получим две тетради в остатке, а дать
каждому ученику по 4 тетради нельзя, так как не хватит 18
тетрадей. Хотя 62 не делится на 20 в том смысле, в каком это
действие рассматривалось выше, всё же можно выполнить непол-
ное деление или деление с остатком, получая неполное частное 3
и остаток 2.
Неполным частным называется самое большое число, которое
при умножении на делитель даёт произведение, меньшее дели-
мого, а остаток — разность делимого и этого произведения.
Ясно, что 1) остаток всегда меньше делителя и 2) сумма ос-
татка и произведения неполного частного на делитель равна де-
лимому.
Так, если делить 100 на 13, получаем неполное частное 7
и остаток 9,
9< 13, 9-}-7 • 13= 100.
Краткая запись:
100 :13 — 1 (остаток 9).
45
Говорят, что одно данное число не делится или делится на
второе данное число, смотря по тому, получается ли при делении
остаток, или оно выполняется полностью. Например: 10 не де-
лится на 3, но делится на 5.
§ 63. Деление в широком смысле. Оба рассмотренных вида деления,
а именно полное деление и деление с остатком, объединяются в одном общем
понятии деления в широком смысле.
Делением в широком смысле называют действие, состоящее в том, что по
двум данным числам, делимому и делителю, находят два других числа, частное
и остаток, удовлетворяющие следующим двум условиям: 1) если частное умно-
жить на делитель и прибавить остаток, получается делимое; 2) остаток меньше
делителя.
Если остаток нуль, мы имеем полное деление, если не нуль — деление
с остатком. Например, при делении 30 на 5 получается частное 6 и остаток О,
так как 6 • 5 + 0 = 30, а при делении 30 на 7 частное 4 и остаток 2, так как
4 - 7 + 2 = 30, 2 < 7.
Если делить какое-нибудь натуральное число а на какое-нибудь натураль-
ное число Ь, то, обозначая частное буквой q и остаток буквой г, будем иметь
bq + г = а, остаток г меньше делителя Ь1.
Если делимое меньше делителя, частное есть нуль, остаток равен дели-
мому. Возможно и деление нуля на любое натуральное число: частное нуль,
остаток нуль. Имея какое-нибудь делимое а и делитель Ь, отличный от нуля,
можно взять произведения этого делителя на последовательные числа 0, 1,
2.....останавливаясь на таком произведении b • q, которое меньше а или рав-
но а, причём b (q + 1) уже больше а. Тогда число q и будет искомым частным,
число же а — bq = r — остатком. Остаток не может быть больше, чем (Ь—1).
Таким образом, деление в широком смысле выполнимо всегда, каковы бы ни
были делимое и делитель, если делитель отличен от нуля.
Раздел 4. ТЕХНИКА УСТНОГО И ПИСЬМЕННОГО ДЕЛЕНИЯ
§ 64. Табличное деление. Нам известны 45 табличных произ-
ведений, где по любым двум однозначным сомножителям находится
однозначное (например, 2-3 = 6) или двузначное (например,
3 • 8 = 24) произведения. Зная их, легко выполнять деление на лю-
бой однозначный делитель всех однозначных делимых и тех дву-
значных, у которых частное однозначно. Так, желая разделить 9 на
3 или 35 на 7, вспоминаем по таблице умножения, что 3-3 = 9
или 7 • 5 = 35; следовательно, 9:3 = 3 или 35 : 7 = 5. Но если
таблица сразу не вспоминается, то частное находим последова-
тельными пробами, а именно: 3-1 = 3; 3-2 = 6; 3-3 = 9, так
что 9:3 = 3, или: 7-1=7; 7-2=14; 7-3 = 21; 7-4 = 28;
7 -5 = 35, так что 35:7 = 5. Так обстоит дело, когда деление
осуществляется без остатка. Такими же пробами выполняется
деление с остатком, например, 39 на 7, а именно: 7 • 4=28 —
мало, 7 • 5 = 35 — тоже мало, 7 • 6 = 42 — уже много: видим,
что 39— 35 = 4, окончательно 39 :7 = 5 (остаток 4).
§ 65. Деление на 10, 100, 1000 и т. д. Деление любого числа
на 10 выполняется очень просто: взяв делимое без последней
1 Здесь впервые встречаемся с двумя новыми латинскими буквами q и г,
которые читаются, как «ку малое» и «эр малое», и обычно употребляются для
обозначения частного и остатка. Напоминаем, что знак < заменяет слово
«меньше», знак > слово «больше».
46
цифры, получаем частное, а эта последняя цифра представляет
собой остаток. Например, 2873: 10 = 287 (остаток 3), так как
287 • 10 = 2870; 2870 + 3 = 2873, а остаток 3 меньше делителя 10,
и, следовательно, оба требования, предъявляемые к частному и
остатку, выполнены. Подобным же образом деление на 100 сво-
дится к отбрасыванию двух последних цифр делимого, деление
на 1000 — трёх последних его цифр, деление на любую разрядную
единицу — стольких последних его цифр, сколько нулей в записи
этой разрядной единицы. Так, 8147: 100 = 81 (остаток 47);
8147 :1000 = 8 (остаток 147), 42 164073 :100000 = 421 (остаток
64 073).
§ 66. Деление круглых чисел. Чтобы найти частное 8000 :2, за-
мечаем, что 8000 есть произведение 8 • 1000, и вспоминаем, что для
деления произведения достаточно разделить один из сомножи-
телей. Разделив 8 на 2, получаем 4 и находим, что
8000 : 2 = (8 - 1000): 2 = (8 : 2) - 1000 = 4 - 1000 = 4000.
Конечно, ответ можно получить сразу:
8000 :2 — 8 тыс.: 2 = 4 тыс. = 4000.
Таким образом, имея какое-нибудь однозначное или двузнач-
ное число, делящееся без остатка на однозначный делитель и
сопровождаемое нулями, находят частное, выполняя деление этого
числа и приписывая к полученному частному все нули, какие это
число сопровождают.
§ 67. Деление на однозначное число. Чтобы разделить сумму,
достаточно разделить каждое слагаемое в отдельности и сложить
полученные частные (§ 59). Этим свойством частного и пользуются
при делении любого числа на однозначное, если это деление не
сводится к табличному.
Данное делимое заменяют суммой двух или более слагаемых,
выбираемых так, чтобы все они, кроме, быть может, одного,
делились на делитель без остатка и давали числа единиц каждого
разряда частного. Такие слагаемые будем называть «удобными».
Так, чтобы разделить 84 на 3, заменяем 84 суммой
84 = 60 + 24
и выполняем деление каждого из этих «удобных» слагаемых в
отдельности
60 : 3 = 20; 24:3 = 8,
а затем берём сумму полученных частных (20 -ф 8 = 28) и имеем
окончательно 84 :3 = 28 (проверка 28 • 3 = 84).
Чтобы разделить 19852 на 7, представляем делимое в виде
суммы
19852 = 14000 + 5600 -J- 210 -|- 42
и получаем частное (14 000 : 7) + (5600 : 7) + (210 ; 7) -j- (42 :7) =
= 2000 + 800 + 30 4- 6 = 2836.
Проверка: 2836 • 7 = 19852.
47
Для деления 847 на 5 надо взять (500 4- 300 4- 45 4- 2): 5 =
= 100 4- 60 4- 9 (остаток 2) = 169 (остаток 2); проверка 169 • 5 4-
4- 2 = 845 4- 2 = 847 показывает, что деление сделано верно.
«Удобные» слагаемые, суммой которых представляется делимое,
получаются постепенно. Взяв цифру старшего разряда делимого,
делят выражаемое ею число на делитель (табличное деление) и
получают цифру первого слева (старшего) разряда частного: в
последнем примере приходится делить 8 (сотен) на 5, что даёт 1
(одну сотню) в частном и 3 (сотни) в остатке. Произведение
1-5 = 5 (сотен) или 500 и есть первое удобное слагаемое, которое
здесь нужно. Вычитая его из 8 (сотен) и присоединяя к разности
8 — 5 = 3 (сотни), именуемой первым остатком, те 4 десятка, ка-
кие имеются в делимом, получаем всего 34 десятка. Разделив
34 десятка на 5 (опять табличное деление), находим частное 6
(десятков), а затем произведение 6 • 5 = 30 (десятков), что и есть
второе удобное слагаемое. Вычитая его из 34 (десятков), полу-
чаем второй остаток 34 — 30 = 4 (десятка); присоединяем к нему
те 7 единиц, какие имеются в разряде единиц делимого, и делим
47 на 5. Это третье табличное деление даёт в частном 9 и в остат-
ке 2. Этот третий остаток есть в то же время остаток всего деления,
частное же равно сумме 1 сотня 4- 6 десятков 4- 9 единиц, или 169.
Всё, что мы сделали при делении 847 на 5, можно записать
в следующем кратком виде:
847
5
34
30
47
45
2
5
169
Проверка: 169-5 Остаток 2
845 меньше делителя 5
+ 2
847
Присоединяя к полученному очередному остатку соответствую-
щую цифру делимого, можно отмечать её сверху знаком, похожим
на запятую.
Особого внимания требуют случаи, когда после такого при-
соединения получается число, меньшее делителя, а потому цифрой
соответствующего разряда частного является нуль, как, например,
при делении 1442 на 7 (частное 206, остаток 0) или 28038 на 4
(частное 7009, остаток 2).
Вполне возможно и очень полезно выработать навык сокра-
щённой записи деления многозначного числа на однозначное, а
именно записывать в этих случаях только данные (делимое и де-
литель) и искомое частное, выполняя все операции в уме. Тогда
запись деления 847 на 5 сведётся к такой: 847 : 5 = 169 (остаток 2).
§ 68. Деление многозначного числа в случае однозначного
частного. Если делимое меньше произведения делителя на 10,
частное выражается однозначным числом, которое находят посред-
ством немногих проб. Положим, требуется разделить 882 на 212.
48
Берём произведения: 212-1=212; 212-2 = 424; 212-3 =636;
212 • 4 = 848; 212 • 5 = 1060 и заключаем, что искомое неполное ча-
стное равно 4, а остаток равен 882 — 848 = 34,
Проб требуется меньше, если в данном делителе отбросить
все цифры, кроме первой слева, и столько же цифр, считая справа,
отбросить в делимом, и выполнить деление тех чисел, которые
получаются после такого отбрасывания.
Так, в нашем примере, заменяя делитель 212 числом 2, де-
лимое 882 числом 8, делим 8 на 2, получаем в частном 4 и убеж-
даемся, найдя 212 - 4 = 848, что искомое частное есть 4, так
как 848 < 882; 882 — 848 = 34 < 212.
Ещё пример: желая разделить 2148 на 245, находим сперва
частное от деления 21 на 2 и, получив 10, сразу убеждаемся,
что число слишком велико: 245 • 10 = 2450 > 2148. Пробуя вместо
10 число 9, обнаруживаем, что оно тоже слишком велико:
245 • 9 = 2205 > 2148; пробуя после этого число 8, выясняем, что
оно годится: 245 • 8 = 1960 < 2148; 2148— 1960 = 188 < 245.
Приведём запись того, что приходится записывать (всё осталь-
ное делается в уме):
882 212
848
34
2148
1960
188
I 245
I 8
§ 69. Деление произвольных многозначных чисел. Умея нахо-
дить однозначное частное, легко найти и любое многозначное ча-
стное. Желая, например, разделить 854 927 на 365, берут в дели-
мом (слева) столько цифр, сколько их в делителе, и выполняют
деление 854 на 365, что даёт 2 в частном и 124 в остатке. Записав
2 как цифру разряда тысяч искомого частного, присоединяем к.
остатку 124 (тысячи) 9 сотен, имеющихся в делимом, и получаем
число 1249 (сотен). Разделив это число на 365, получаем частное
3 и остаток 154. Цифру 3 записываем как цифру разряда сотен
частного, а к остатку 154 присоединяем 2 десятка, имеющихся в
делимом: 154 сотни-f-2 десятка составляют 1542 десятка. Новое
деление (1542:365) даёт 4 (это цифра разряда десятков частного)
и остаток 82 (десятка). Присоединив к нему 7 единиц, имеющихся
в делимом, получаем число 827, и новое деление (827 :365) даёт
цифру 2 для разряда единиц частного и остаток всего деления
97. Всё, что здесь пришлось сделать, удобно записать так:
854927
730
1249
1095
1542
1460
827
730
97
I 365
I 2342
Проверка: 2342 • 365
7026
,14052
+ 11710
854830
4-97
854927
Остаток 97
меньше делителя 365
3 Арифметика
49
Всё рассмотренное деление сводится к представлению делимого
в виде суммы 730 000 4- 109 500 4- 14 600 4- 730 4- 97, в которой
каждое слагаемое, кроме последнего, делится без остатка и даёт
цифру одного разряда частного, а последнее слагаемое не делится
и, будучи меньше делителя, полностью идёт в остаток.
Очень рекомендуется, приступая к делению, сейчас же после
записи делимого и делителя выяснить, сколько цифр будет иметь
частное, и отметить точками места для всех его цифр. В рассмот-
ренном примере, заметив, что начинать надо с деления 854 тысячи
на 365, видим, что старшим разрядом частного будет разряд
тысяч, а потому ставим для частного четыре точки, отмечая тем
самым места для записи цифр разрядов тысяч, сотен, десятков,
единиц.
854’927 | 365
Если бы делить надо было число 254 927 на 365, отделять в
делимом пришлось бы не столько цифр, сколько их в делителе,
а одной больше, и в частном мы имели бы не 4, а только 3 цифры,
так как начинать здесь приходится с деления 2549 (сотен) на 365.
2549’27 | 365
§ 70. Устное деление.
Деление однозначных и двузначных чисел делается всегда устно,
так как в этих случаях либо имеем табличное деление, либо
делимое легко представить в виде суммы удобных слагаемых. Вот
примеры, записанные для объяснения подробно:
96 :8 = (80 4- 16) : 8 = 10 4- 2 = 12, проверка 12 • 8 = 96;
89 : 12 = (84 4- 5) : 12 = 7 (остаток 5), проверка 7 • 12 = 84,
84 4- 5 = 89;
87:3 = (90 — 3): 3 == 30 — 1 = 29, проверка 29 • 3 = 87.
В последнем примере делимое удобнее представить не в виде
суммы, а в виде разности.
Деление многозначного числа на однозначное, как уже от-
мечалось, легко выполнять с неполной записью. Так же делают
и деление на такие числа, как 11, 12, 15, 20, 25 и др., произ-
ведения которых на однозначные числа легко получать в уме.
Вместо того чтобы делить на круглое число, выгоднее бывает
делить последовательно на два числа, произведение которых даёт
это круглое. Так, например, 84 600 :200=84 600 : 100 :2=846:2=423.
Надо, однако, иметь в виду, что при неполном делении этот
способ не даёт правильного остатка.
Многие особые приёмы, упрощающие умножение, упрощают
и деление. Например, зная, что 37 -3 = 111, легко выполнить в
уме деление:
7881 :37 = 7881 : (111 :3) = (7881 :111) -3 = 71 -3 = 213.
50
§ 71. Проверка деления и умножения. Производить деление
ещё труднее, чем умножение; поэтому всякое деление следует
сопровождать проверкой, умножая частное на делитель и при-
бавляя к произведению остаток, если он есть. Когда всё сделано
правильно, полученная сумма равна делимому. Кроме того, сле-
дует смотреть, чтобы остаток всегда был меньше делителя.
Ошибки в делении чаще всего бывают из-за недостаточного
внимания к нулям, которые могут получиться среди цифр част-
ного, как, например, при делении 260543 на 849, когда вместо
правильного ответа 307 пишут 37, или при делении 41 254 974 на
5806, когда вместо частного 7009 получают 709 или даже 79.
Таких ошибок не будет, если, находя цифру старшего раз-
ряда частного, подумать о том, какой это разряд, и отметить
точками места цифр всех остальных разрядов частного.
Нередко также не замечают, что получается остаток, больший
делителя, т. е. что взятая цифра частного слишком мала. Это
приводит иногда к грубому искажению частного, как, например,
в следующем делении:
Неправильно Правильно 546 | 67
546 67
469 71 536 | 8
77 10 1
67
Вовремя сделанная проверка сразу обнаруживает подобные
ошибки: 1) 71 -67 = 4757, 4757 4- 10 = 4767, а не 546; 2) 67-8=
= 536, 536 4- 10 = 546.
При проверке деления без остатка делимое можно разделить
на найденное частное. Если всё сделано правильно, в качестве
нового частного должен появиться прежний делитель.
Зная взаимную связь умножения и деления, можно указать
второй способ проверки умножения: полученное произведение де-
лится на один из данных сомножителей — должен получиться дру-
гой сомножитель; если он не получился, то где-то сделана ошибка.
Раздел 5. УМНОЖЕНИЕ И ДЕЛЕНИЕ С ПОМОЩЬЮ ТАБЛИЦ,
И ВЫЧИСЛИТЕЛЬНЫХ ПРИБОРОВ
§ 72. Таблицы произведений. Умножение многозначного числа
на многозначное становится гораздо более лёгким, если предва-
рительно составить табличку произведений одного из сомножи-
телей на все однозначные числа. Приводим такую табличку для
числа 31 416. Она составляется одними сложениями:
1 2 3 4 5 6 7 8 9
31 416 62 832 94 248 125664 157 080 188 496 219912 251 328 282 744
3
51
Чтобы умножить это число на любое многозначное число, бе-
рём из таблицы готовые частичные произведения и, подписывая
надлежащим образом друг под другом, сложим их.
Если приходится делить любое число на тот же делитель
31 416, эта табличка тоже существенно облегчит работу: цифры
частного получаются с одного взгляда на неё, частичные произ-
ведения берутся готовыми, остаётся только вычитать их для по-
лучения остатков. Например:
31416 • 57892 13254847 | 31416
157080 125664 | 421
219912 68844
, 251328 62832
+ 282744 ' 60127
62832 —31416
1818735072 287И < 31416
Существуют печатные таблицы, которые содержат произведе-
ния всех натуральных чисел, имеющих две, три, четыре цифры,
на все однозначные и двузначные числа. Таблица очень облег-
чает труд, связанный с умножением и делением многозначных
чисел. Таких таблиц имеется несколько, например «Таблицы
умножения» О’ Рурка, М. В. Яковкинаи др. В предисловии
к ним рассказывается, как с ними обращаться.
§ 73. Русские счёты. I. Произведение на однозначный множи-
тель можно получать, взяв множимое слагаемым столько раз,
сколько единиц содержит множитель; поэтому русские счёты
можно использовать и для умножения. Для ускорения можно
поступать так:
1) если множитель 4, то а • 4 = а • (2 • 2) = (а • 2) 2, т. е.
удвоить удвоенное;
2) если множитель 5, то а • 5 = а • (10 :2) = (а : 2) • 10 =
= (а • 10): 2;
3) если множитель 6, то а • 6 = а (2 • 3) = (а • 2) • 3, или
а • 6 = а • (10 — 4) = (а • 10) — (а 4);
4) если множитель 7, то а • 7 = а - (10 — 3) = (а • 10) — (а • 3);
5) если множитель 8, то а • 8 = а • (2 • 2 • 2) = (а • 2) • 2 • 2;
6) если множитель 9, то а • 9 = а • (10— 1) = а 10 — а.
II. Умножение на 10, 100, 1000 и т. д. на счётах произво-
дится путем откладывания множимого на счётах так, что каждый
разряд его передвигается вверх на одну проволоку, на две, на
три и т. д.
III. Умножение на круглое число производится путём пред-
варительного умножения на разрядную единицу, а результата на
однозначное число, например: а • 300 = а • (3 • 100) = (а • 100) • 3.
IV. Умножение на многозначное число производится на основе
распределительного свойства путем умножения на разрядные еди-
ницы (круглые числа) и сложения частичных произведений, на-
пример: 238 • 243 = 238 • (200 + 40 + 3) = (238 • 200) + (238 • 40) ф-
4- (238 • 3). Вычисление ведётся без всякой записи.
52
На счётах можно делать и деление путём последовательного
вычитания. Чтобы разделить, например, 164 на 47, где частное
однозначное, кладут на счётах делимое и вычитают из него де-
литель столько раз, сколько это возможно: 164 — 47= 117; 117—
— 47 = 70; 70 — 47 = 23 и своевременно на верхней незанятой
проволоке отмечают косточкой каждое вычитание; в результате
на счётах прочтут: на верхней проволоке частное 3, а на основ-
ных— остаток 23. Здесь возможны упрощения, подобные тем,
какие указаны при умножении.
Люди, постоянно имеющие дело со счётами, как, например, сче-
товоды, кассиры, вырабатывают навыки быстрого умножения и де-
ления многозначных чисел на счётах, применяя различные приёмы.
§ 74. Арифмометр «Феликс». Умножение и деление много-
значных чисел выполняется на арифмометре «Феликс» в 10—12 раз
быстрее, чем обычным письменным способом, причём овладеть на-
чальной техникой этого дела можно за какие-нибудь 20—30 минут.
Умножение любого числа на однозначное делается как по-
вторное сложение: установив множимое рычажками, вращают ру-
коятку к себе столько раз, сколько единиц имеет множитель,
причём число сделанных оборотов появляется в окошечках счёт-
чика оборотов (внизу слева).
Если сдвинуть каретку вправо на 1, 2, 3 и т. д. мест, то
каждый оборот рукоятки заменяет 10, 100, 1000 и т. д. её
оборотов при начальном положении каретки, так что при умно-
жении на любое многозначное число приходится делать столько
оборотов рукоятки, сколько единиц содержит сумма цифр мно-
жителя.
Например, для умножения на 8276 надо сделать всего 84-24*
4- 7 4- 6 = 23 оборота рукоятки. Многозначный множитель появ-
ляется в окошечках счётчика оборотов. Замечая, что 8276 =
= 10 300 — 2024, и вращая рукоятку то к себе, то от себя, по-
лучаем то же самое произведение после (1 4- 3) + (2 + 2 4*
4- 4) = 12 оборотов.
Чтобы выполнить на арифмометре деление, устанавливают
делимое в ответных окошечках, а затем вычитают из него де-
литель, установленный рычажками, до тех пор, пока в остатке
не получится число, меньшее делителя. Частное при этом полу-
чается в окошечках счётчика оборотов, где появляются красные
цифры.
Так, чтобы разделить 357 на 83, приходится вычитать из 357
делитель 83 четыре раза. В счётчике оборотов получается при
этом красная цифра 4 (частное), в ответных окошечках 25 (оста-
ток). Чтобы разделить 3870 на 83, приходится вычитать, пред-
варительно сдвинув каретку на одно место вправо. После четы-
рёх оборотов получается остаток 550. Вернув каретку в начальное
положение, вычитаем из 550 делитель последовательно шесть раз
и получаем остаток от всего деления 52. Частное 46 читаем в
окошечках счётчика оборотов.
63
Глава IV. СОВМЕСТНЫЕ ДЕЙСТВИЯ
Раздел 1. ВЗАИМНАЯ СВЯЗЬ ДАННЫХ И РЕЗУЛЬТАТОВ
ДЕЙСТВИЙ
§ 75. Сложение и вычитание. Рассмотрим теперь несколько
новых задач, связанных с действиями сложения и вычитания,
причём ради краткости записи будем для обозначения неизвестно-
го числа употреблять латинскую букву х (читается «икс»).
I. Зная, что 5 4-х = 13, найти х.
Эта краткая запись означает, что по данному первому слагае-
мому (5) и данной сумме (13) надо найти второе слагаемое (х).
Другими словами, к множеству, численность которого известна (5),
присоединено множество с неизвестным числом элементов (х), и
получилось множество из 13 элементов; найти х. Например: библио-
текарь помнит, что у него на столе было 5 книг, а теперь их 13;
следовательно, какое-то число книг принесено. Сколько книг
принесено?
Хотя здесь идёт речь об объединении двух множеств, но для
получения х надо применять вычитание, так как вопрос сводится
к разысканию неизвестного слагаемого по сумме и другому сла-
гаемому (§ 29). Итак, если 5 4-*= 13, то х= 13— 5.
II. Зная, что х 4-15 = 29, найти х.
Вспоминая переместительный закон сложения (§ 19), убеж-
даемся, что эта вторая задача сводится к первой и решается
тоже вычитанием: х = 29— 15 = 14.
Решение задач I и II показывает, что слагаемое равно сумме
без другого слагаемого. Иными словами: чтобы найти слагаемое,
надо из суммы вычесть другое слагаемое.
Это свойство сложения можно записать так:
если а4-Ь = с, то а = с—Ъ, Ъ = с — а.
Так выражается взаимная связь данных и результата при
сложении (в случае суммы двух слагаемых).
III. Зная, что х— 12 = 9, найти х.
Здесь из множества, численность которого неизвестна (х), уда-
ляется часть, представляющая собой множество из 12 элементов,
причём оставшееся множество содержит 9 элементов. Хотя речь
идёт об удалении части множества, но для получения неизвест-
ного надо сделать сложение чисел 12 и 9, так как разность 9
есть число, которое, будучи сложено с вычитаемым 12, даёт умень-
шаемое х (§ 29). Итак, если х—12 = 9, то х= 12 4-9.
Отсюда вывод: уменьшаемое равно вычитаемому плюс раз-
ность. Другими словами, чтобы найти уменьшаемое, надо вычи-
таемое сложить с разностью.
IV. Зная, что 24 — х = 6, найти х.
Здесь из множества, содержащего 24 элемента, удаляется ка-
кая-то его часть (х), после чего остаётся множество из шести
54
элементов. Замечая, что 6-}-х = 24, возвращаемся к задаче I и
видим, что х - 24 — 6 = 18.
Таким образом, вычитаемое равно уменьшаемому без разности.
Другими словами, чтобы найти вычитаемое, надо из уменьшав*
мого вычесть разность.
Последние два свойства разности можно записать при помо-
щи букв следующим образом:
если а — Ь = с, то a = b -J- с, Ь = а — с.
Так выражается взаимная связь данных и результата при
вычитании.
§ 76. Умножение и деление. При умножении, зная множимое
и множитель, находят их произведение; при делении, зная дели-
мое и делитель, находят частное (остаток предполагаем равным 0).
Разберём следующие задачи.
I. Зная, что 8 х = 40, найти х.
Здесь множимое (8) и произведение (40) известны, надо найти
множитель (х). Вспоминая определение частного (§ 56), видим,
что эта задача решается делением: х = 40:8 = 5.
II. Зная, что х • 9 = 54, найти х.
В силу переместительного закона умножения эта задача сво-
дится к предшествующей и тоже решается делением: х=54:9=6.
Итак, каждый сомножитель равен произведению, разделён-
ному на другой сомножитель. Иначе: чтобы найти один сомно-
житель, надо произведение разделить на другой сомножитель.
Это свойство умножения записывается так:
если а • b = с, то а — с: b, b = с :а.
Так выражается взаимная связь данных и результата при
умножении в случае двух сомножителей.
III. Зная, чтох:5 = 7, найти х.
По определению частного (§ 56) имеем 7 • 5 = х, х = 35.
Итак, делимое равно делителю, умноженному на частное. Дру-
гими словами, чтобы найти делимое, надо умножить делитель на
частное.
IV. Зная, что 28:х = 4, найти х.
Пользуясь снова определением частного, имеем 4 • х = 28, а
потому х = 28 :4. Следовательно, делитель равен делимому, раз-
делённому на частное. Другими словами, чтобы найти делитель,
надо делимое разделить на частное.
Последние два свойства деления кратко записываются так:
если а : b = с, то а = b • с, b = а:с.
Так выражается взаимная связь данных и результата при
делении без остатка.
На основе установленного легко решается такая задача:
Задумано число х, к нему прибавлено 3, сумму умножили
55
на 4, из полученного произведения вычли 2 и в результате полу-
чили 38. Как найти х?
Запишем условие короче:
(х + 3) • 4 — 2 = 38.
Будем решать с конца.
1) Когда вычли 2, то получили 38; следовательно, до вычи-
тания было 38 + 2 = 40, так как уменьшаемое равно разности
(38) плюс вычитаемое (2). Имеем: (х-|-3) • 4 = 40.
2) Когда умножили на 4, то получили 40; следовательно, до
умножения было 40 :4 = 10, так как сомножитель равен произ-
ведению, делённому на другой сомножитель. Имеем: х -J- 3 — 10.
3) Когда прибавили 3, получили 10. Следовательно, до при-
бавления было 10—3=7, так как слагаемое равно сумме без дру-
гого слагаемого. Имеем: х = 7.
Проверка: (7 4* 3) • 4 — 2= 10-4 — 2 = 40 — 2 = 38.
§ 77. Деление с остатком. Положим, выполнено такое деле-
ние: 30:8= 3 (остаток 6). Здесь всего четыре числа, а именно:
делимое (30), делитель (8), частное (3), остаток (6).
Проверяя оба условия, каким должны удовлетворять частное
и остаток (§ 62), убеждаемся, что они здесь выполнены:
3-8 4-6 = 30; 6 <8.
Любое из этих четырёх чисел (делимое, делитель, частное и
остаток) можно найти, зная остальные три.
I. Зная, что х:8 = 3 (остаток 6), найти х.
II. Зная, что 30:х = 3 (остаток 6), найти х.
III. Зная, что 30:8 =х (остаток 6), найти х.
IV. Зная, что 30:8 = 3 (остаток х), найти х.
Задача I решается сразу, если вспомнить смысл деления с ос-
татком (§ 62); произведение делителя на частное плюс остаток
даёт делимое: х = 8 • 3 4- 6 = 30.
Задача II сводится к нахождению х из равенства 3-х4-6 =
— 30; здесь неизвестно первое слагаемое 3-х, но известны сум-
ма (30) и второе слагаемое (6), а потому 3 • х = 30 — 6 = 24;
остаётся найти неизвестный сомножитель по данному другому
сомножителю (3) и произведению (24), что мы уже умеем делать:
х = 24 :3 = 8.
Подобным же образом задача III сводится к нахождению х
из равенства 8 • х 4- 6 = 30, откуда 8 • х = 30 — 6 = 24, х =
= 24 : 8 = 3.
Задача IV сводится к нахождению х из равенства 3-8 4-
4- х = 30, откуда х = 30 — 3 • 8 = 30 — 24 = 6.
56
Это рассуждение остаётся в силе для любых чисел.
30 : 8 = 3 (остаток 6) а : b = q (остаток г)
Делимое равно делителю, умно-
30 = 8 • 3 + 6 женному на частное, плюс ос- таток. Делитель равен делимому без а = b • q + г
8 = (30 — 6) :3 остатка, разделённому на част- ное. Частное равно делимому без b = (a — r)-.q
3 = (30 — 6) : 8 остатка, разделённому на дели- тель. Остаток равен делимому без q = (a — r):b
6 = 30 — 8 • 3 произведения делителя на част- ное. II Й 1 О’ <5
Когда г — 0, то из этих общих свойств получаются выше-
установленные частные свойства:
1) а = b • q — делимое равно делителю, умноженному на част-
ное;
2) b=a:q — делитель равен делимому, разделённому на
частное.
Раздел 2. ИЗМЕНЕНИЕ РЕЗУЛЬТАТОВ ДЕЙСТВИЙ
В ЗАВИСИМОСТИ ОТ ИЗМЕНЕНИЯ ДАННЫХ
Если при выполнении какого-либо арифметического действия
мы изменим данные числа и выполним действие вторично, то по-
лучим уже не тот результат, какой был получен в первый раз.
Как говорят, результат зависит от данных. Этот новый резуль-
тат можно найти, не выполняя действия вторично. Рассмотрим,
как это сделать, для каждого действия отдельно.
§ 78. Изменение суммы. Задача. На птицеферме было
850 кур и 267 уток, добавили ещё 135 кур. Сколько всего
птиц было на птицеферме раньше и сколько стало потом?
Найдя, что раньше на птицеферме было всего 850-]-267= 1117
птиц, можно узнать, сколько кур стало на ней потом (8504-135=
=985), и наконец найти новое число всех птиц (9854-267=1252).
Но этот окончательный результат можно получить короче: от
прибавления 135 кур общее число птиц, бывших раньше (1117),
увеличилось тоже на 135, а потому новое число всех птиц можно
узнать сразу, произведя сложение 1117 и 135, что даёт 1252.
Легко сообразить, как обстоит дело при уменьшении одного из
слагаемых.
Итак, увеличение (уменьшение) одного из слагаемых на
сколько-нибудь единиц вызывает увеличение (уменьшение) их
суммы на столько же единиц Ч
1 Здесь записаны для краткости сразу два заключения. Первое читают,
пропуская слова в скобках, а второе — пропуская слово перед скобками.
Б7
Зная, как изменяется сумма при изменении одного из сла-
гаемых, можно рассчитать, как она меняется при совместном из-
менении двух и более слагаемых. Так, если в сумме
128 4-212+ 147 = 487
первое слагаемое увеличить на 7, второе уменьшить на 10, а
третье увеличить на 15, то сумма увеличится на 7 + 15 = 22 и
уменьшится на 10, т. е. в итоге увеличится на 22 — 10=12 и ста-
нет равной 487+12=499. Для проверки находим
(128 + 7)+(212—10)+ (147+ 15) = 135 + 202+ 162 = 499
и убеждаемся, что расчёт сделан верно.
Правило изменения суммы выгодно применять при устном
счёте. Например, чтобы найти 97+48, берём 100+50=150 и за-
мечаем, что замена 97 через 100 вызвала увеличение суммы на 3,
а замена 48 через 50 — её увеличение на 2; следовательно, най-
денная сумма 150 больше, чем надо, на 3 + 2=5, и искомая сум-
ма равна 150 — 5 = 145.
§ 79. Изменение разности. Положим, у меня имеется 250 руб.
и я плачу за покупку 134 руб., после чего у меня остаётся
250— 134= 116 руб.
Если бы у меня было не 250 руб,, а на 50 руб. больше, то
после той же покупки у меня осталось бы не 116 руб., а на
50 руб. больше, т. е. 116 + 50 = 166 руб.
Если бы, имея те же 250 руб., я уплатил за покупку на
50 руб. больше, то у меня осталось бы не 116 руб., а на 50 руб.
меньше, т. е. 116 — 50 = 66 руб. Эти расчёты легко проверить:
250 + 50 = 300; 300 — 134 = 166; 134 + 50 = 184; 250 — 184 = 66.
Понятно, что будет, если не увеличивать, а уменьшать умень-
шаемое или вычитаемое.
Этот пример показывает правильность следующего заключе-
ния: увеличение (уменьшение) уменьшаемого на несколько единиц
вызывает увеличение (уменьшение) разности на столько же еди-
ниц, а увеличение (уменьшение) вычитаемого на несколько единиц
вызывает уменьшение (увеличение) разности на столько же единиц.
Отсюда следует, что совместное увеличение (или уменьшение)
уменьшаемого и вычитаемого на одно и то же число не вызывает
никакого изменения разности.
Рассмотренные правила изменения разности с выгодой приме-
няются при устном счёте. Например, чтобы найти 358 — 99, берём
358—100 = 258 и, замечая, что вместо вычитаемого 99 мы взяли
на 1 больше, заключаем, что получена разность, на 1 меньшая,
чем надо, и что искомая разность равна 258 + 1 = 259.
§ 80. Изменение произведения. Если в каждом из 15 рядов
посадить по 12 кустов, то всего будет посажено 12-15=180 кус-
тов. Увеличивая вдвое число кустов в каждом ряду, мы посадим
в тех же 15 рядах уже не 180, а 180 • 2 = 360 кустов, так как
всего теперь будет (12 • 2) • 15 = (12 • 15) • 2 = 180 • 2 (исполь-
зуем сочетательное и переместительное свойства умножения).
58
Точно так же уменьшение вдвое числа кустов в каждом ряду
вызывает уменьшение вдвое числа всех кустов, которые будут
посажены в тех же 15 рядах: (12 :2) • 15 = (12 • 15) : 2 — 180 : 2,
так как для деления произведения надо делить только один из
сомножителей.
Принимая во внимание переместительный закон умножения,
приходим к такому заключению: увеличение (уменьшение) одного
из сомножителей во сколько-нибудь раз вызывает увеличение
(уменьшение) произведения во столько же раз.
Изменять сомножители полезно при многих случаях устного
умножения. Так, чтобы найти произведение 25-884, можно уве-
личить в 4 раза множимое, взять произведение 100 • 884 = 88400,
а затем уменьшить его в 4 раза, что даст 88400 :4 = 22 100. Ра-
зумеется, можно, увеличив множимое в 4 раза, уменьшить мно-
житель в 4 раза и сразу получить искомое произведение 25-884=
= 100 - 221 = 22 100.
§ 81. Изменение частного.
Если деление выполняется без остатка, увеличение (умень-
шение) делимого во сколько-нибудь раз вызывает увеличение
(уменьшение) частного во столько же раз, а увеличение (умень-
шение) делителя во сколько-нибудь раз вызывает, наоборот, умень-
шение (увеличение) частного во столько же раз. Так, например,
24 делим на 6 и получаем 4. Увеличение делимого вдвое вызы-
вает увеличение частного тоже вдвое (48:6 = 8), а увеличение
вдвое делителя вызывает уменьшение вдвое частного (24 : 12 = 2).
Если надо разделить 3690 на 15, можно увеличить вдвое дели-
тель и найти 3690 : 30 = 123; это частное вдвое меньше искомого,
а поэтому остаётся только увеличить его вдвое; окончательно
3690 : 15 = 246.
Совместное увеличение или уменьшение делимого и делителя
в одно и то же число раз не меняет частного.
Например, частное 2400: 1200 одинаково с частным 24:12,
равным 2, а частное 375:5 с частным 750:10, равным 75.
Но если при делении получается остаток, то при совместном
увеличении (или уменьшении) делимого и делителя во сколько-
нибудь раз этот остаток увеличивается (или уменьшается) во
столько же раз. Действительно, взяв, например, 540 :70 = 7 (оста-
ток 50), имеем после уменьшения делимого и делителя в 10 раз
уже 54:7 = 7 (остаток 5), а взяв 34:5 = 6 (остаток 4), имеем
после умножения делимого и делителя на 2 уже 68 :10 = 6 (оста-
ток 8).
Легко убедиться, что так будет всегда:
если а : b = q (остаток г), то а = Ь • q -J- г; а • k = (b • k) • q
+ г • k", (а • k) :(b • k) = q (остаток г • k).
Действительно, г < b, а потому г • k < b k. Подобным же
образом обстоит дело и при уменьшении делимого и делителя в
одно и то же число раз.
59
Раздел 3. ЗАДАЧИ И ЗАПИСЬ ИХ РЕШЕНИЙ ПОСРЕДСТВОМ
ФОРМУЛ
§ 82. Задачи простые и составные. Все арифметические задачи
можно подразделить на простые и составные.
Задача называется простой, если для её решения достаточно
выполнить лишь одно из арифметических действий (сложение,
вычитание, умножение, деление).
Задача называется составной, если для её решения нужно
выполнить два или более арифметических действий. Можно ска-
зать, что решение каждой составной задачи сводится к решению
двух или более простых задач.
Рассматривая отдельные действия, мы решали много простых
арифметических задач, требующих выполнения какого-нибудь
одного из этих действий. Мы видели, что:
1) все задачи, в которых дана численность двух или более
множеств без общих элементов, а требуется найти численность
множества, получаемого от объединения этих множеств, решаются
сложением.',
2) если известна численность какого-нибудь множества и чис-
ленность некоторой его части, удаляемой из него, то посредством
вычитания находят численность остающейся части этого мно-
жества;
3) если дано несколько равночисленных множеств и требуется
найти численность их объединения, то надо применять умножение;
4) если данное множество надо разделить на равные части,
то для нахождения численности каждой из них требуется дей-
ствие деления-, оно применяется и тогда, когда известна числен-
ность каждой из этих частей, а нужно найти число этих частей.
Теперь надо рассмотреть некоторые вопросы, связанные с ре-
шением составных арифметических задач.
§ 83. План решения составной задачи. Задача. От каждой
из 16 коров получили по 5996 л молока за год с содержанием
219 л молочного жира. Сколько детей можно обеспечить в тече-
ние всего года молоком этих коров, если считать, что 1 л мо-
лока достаточно на день двоим детям и что удой от всех коров
за каждый день одинаков (в году было 366 дней)?
Решение этой, как и всякой составной задачи, надо начинать
с составления плана. Обычно план записывается в виде ряда
последовательных вопросов, указывающих те простые задачи, к
решению которых сводится решение данной составной задачи. В
нашей задаче можно поставить такие вопросы:
1) Сколько получили молока от всех 16 коров за год, если
каждая давала 5996 л?
2) Сколько молока получали от всех 16 коров за день?
3) На сколько человек хватит дневного удоя, если 1 л моло-
ка хватает на двоих?
60
Ставя вопрос, надо выяснить, каким действием получается
ответ на него. Так, для ответа на первый вопрос надо найти про-
изведение 5996 • 16, так как здесь идёт речь об общей числен-
ности 16 множеств, каждое из которых содержит 5996 элементов;
для ответа на второй вопрос надо разделить полученное число
на 366; на третий — умножить полученное частное на 2.
§ 84. Вычисления согласно плану. Когда план составлен, при-
ступают к выполнению действий, им предусмотренных. Подробно
записывают только те действия, какие трудно сделать в уме.
При решении задачи, поставленной в § 83, вся запись сводится
к следующему:
1) 5996 л • 16 = 95936 л
2) _ 95936 366
732 262 (л)
2273
“ 2196
776
732
44 < 366
Проверка:
59960 (произведение на 10)
4-29980 (произведение на 5)
5996 (произведение на 1)
95936
Проверка:
366 • 262
732
4-2196
732
,95892
4- 44
95936
3) 2 • 262 = 524 человека. Проверка в уме.
Ответ. Молоком от 16 коров можно обеспечить 524 человека,
причём получится остаток в 44 л.
Отметим, что для ответа на вопрос задачи не понадобилось
данное о жире (219 л); про такие задачи говорят, чтоб их усло-
вии имеется лишнее данное.
§ 85. Числовая формула. Решение сложной задачи можно
выразить не словами, а короче, записывая только числа и знаки
действий. Решение рассмотренной выше (§ 84) задачи запишется
так:
(5996 • 16 :366) - 2.
Это есть числовая формула решения задачи.
Числовой формулой называется всякая запись чисел, соеди-
нённых знаками действий. Например, выражения:
(3 4- 7) • 6 4- 4; | (а + Ь) с+ d
представляют собой числовые формулы: первая в частном виде,
а вторая в общем виде.
Решения задач записываются короче числовыми формулами,
и через них отчётливее становится план решения задачи. Так,
числовая формула (5996 • 16 :366) • 2 указывает, что сначала
61
число 5996 умножили на 16, результат разделили на 366, а но-
вый результат умножили на 2.
В формулах широко применяются различные скобки, указы-
вающие порядок действий. Рассмотрим правила, по которым
ведутся вычисления по формулам.
§ 86. Порядок действий в числовых формулах. Чтобы не за-
громождать формулы излишним числом скобок, которые указы-
вают порядок действий, постепенно в истории арифметики уста-
новилось четыре правила.
Предварительно отметим, что сложение и вычитание, являясь
действиями взаимно обратными и имея в силу этого многие сходные
свойства, носят общее название действий первой ступени, а умно-
жение и деление (по той же причине) — действий второй ступени.
Рассмотренная выше формула имеет только действия второй
ступени; также, например, числовая формула 12 — 5 ф- 14 27 — 9
имеет только действия первой ступени, формула 150:5-6 —
только действия второй ступени.
Как же вести вычисления по ним?
Первое правило. В формуле без скобок, где имеются
действия только первой ступени (сложение и вычитание), вычис-
ления ведутся в порядке их записи (слева направо).
Пример: 12 — 5-|-14-|-27 — 9 = 7 ф- 14 ф- 27 — 9 = 21 ф-
ф-27— 9 = 48—9 = 39. Понятно, что можно было не записы-
вать промежуточные результаты.
Второе правило. В формуле без скобок, где имеются
действия только второй ступени (умножение и деление), разли-
чают два случая: 1) если имеются действия только умножения
или только деления, вычисления ведутся в порядке их записи;
2) если имеются как действия деления, так и умножения, то
сперва выполняется умножение, а потом делениег.
1 Замечание. По этому поводу следует отметить, что в нашей стране
принято иное правило во 2-м случае.
Порядок действий в соответствующих формулах является исторически сло-
жившимся соглашением. К сожалению, стихийное развитие арифметики привело
к тому, что порядок действий в формуле вида а : Ь • с понимается различно;
1) в принятых курсах арифметики в этом случае вычисления ведутся в
порядке записи, например:
150 :5 - 3 = 30 - 3 = 90;
2) во всех принятых курсах алгебры, высшей математики, в физике, тех-
нике (у нас и за рубежом), а также в арифметике зарубежных стран в этом
случае вычисления ведутся в ином порядке, а именно: а : b • с, сначала умно-
жают Ь на с, а потом число а делят на произведение. Поэтому при подстанов-
ке в формулу а : b • с чисел вместо а = 150; 6 = 5; с = 3 получим:
150 : 5-3= 150 : 15 = 10.
Мы считаем, что надо иметь единое соглашение именно то, которое при-
нято в алгебре и в других учебных предметах.
62
1-й случай:
1) 25 • 4 • 15 • 2 = 100 • 15 - 2 = 1500 • 2 = 3000,
2) 20000 : 4 : 125 :5 = 5000 : 125 : 5 = 40 :5 = 8.
2-й случай:
1) 150:5-6 = 150:30 = 5,
2) 200 20 : 4 • 50 = 4000 : 200 = 20.
Но бывают формулы, где имеются действия и первой и вто-
рой ступени, например:
1) 2.5 4-7.3,
2) 2 + 5 -8:4,
3) 2 + 500 :4 • 5.
Как вести вычисления по ним?
Третье правило. В формуле без скобок, где имеются
действия и первой и второй ступени, сперва выполняются действия
второй ступени (с учётом двух различных случаев по второму
правилу), а потом — первой ступени (по первому правилу).
Вышезаписанные формулы вычисляются так:
1) 2 • 5 + 7 • 3= 10 + 21 =31,
2) 2 + 5 • 8 : 4 = 2 + 40 :4 = 2 + 10 = 12,
3) 2 + 500 : 4 • 5 = 2 + 500 :20 = 2 + 25 = 27.
Если надо написать формулу с порядком действий, отличаю-
щимся от указанных, то пользуются скобками, а именно: скоб-
ками первого рода (а + 6), которые называются круглыми-, скоб-
ками второго рода [а + Ь], получившими название прямоуголь-
ных: скобками третьего рода {а + 6), или фигурными. Иногда
встречаются скобки четвёртого, пятого, шестого рода, которым
дают большие размеры, но ту же форму, что и скобкам пер-
вого, второго и третьего рода.
Так, бывают формулы вида:
1) (5 + 7) - 3,
2) [(20 • 3 + 4): 8 + 2] -3 — 4,
3) {[96 —(16 + 2)-2] :6 + 18}:4.
Как вести вычисления по ним?
Четвёртое правило. В формулах со скобками сперва
находят результаты действий над числами, записанными внутри
скобок первого рода, потом внутри скобок второго рода, далее
третьего рода и т. д.
Вышеуказанные примеры решаются так:
1) (5 + 7) • 3 = 12 • 3 = 36,
2) [(20-3+4) : 8+2]. 3 — 4=[64 :8+2] • 3—4=10 • 3 — 4=26,
3) {[96—(16 + 2) • 2] : 6 + 18}: 4 = {[96—18 • 2]: 6 + 18}:4 =
= {60:6 + 18}: 4 = 28 :4 = 7.
63
Составляя формулы, надо избегать лишних скобок. Напри-
мер, в записи 50 — (3 -8) скобки не нужны, так как и без них
в формуле 50 — 3-8 порядок действий в силу второго правила
о порядке действий будет тот же. Но в формуле (50 — 3) • 8
скобки необходимы.
Горизонтальная черта в связи с порядком действий. Чтобы
сделать запись менее громоздкой, в формулах часто применяется
горизонтальная черта, которая служит одновременно и знаком
деления и заменой скобок: прежде находят результат, записан-
ный над чертой, затем под чертой, и делят первое полученное
из этих чисел на второе. Например, чтобы найти
20 + 15
20— 15 ’
производят прежде сложение 20+ 15 = 35, затем вычитание
20—15 = 5, наконец деление 35:5 = 7 (ответ х = 7). Эту фор-
мулу можно написать и без черты, вводя две пары скобок:
х = (20 + 15): (20 — 15).
На странице 65 (рис. 7) воспроизведена картина «Устный
счёт», написанная замечательным русским художником Н. П. Бог-
дановым-Бельским в конце XIX в. и хранящаяся в Третьяков-
ской галерее в Москве. Одиннадцать бедных крестьянских уче-
ников старой досоветской школы с напряжением ищут в уме
решения числовой формулы, написанной на доске учителем
С. А. Рачинским. Там, на доске, видите формулу
102 + II2 + 122+ 132 + 142
365
что в подробной записи означает:
10 - Ю-р 11 • 11 4- 12 • 12-f- 13 • 13 + 14 • 14
365
Как лучше сгруппировать слагаемые? Как скорее вычислить?
Способные ученики сообразили: на основе сочетательного
свойства и правила деления суммы получается:
100 + 121 + 144 , 169 + 196 365 , 365 , , , о
----365----+ ~365~’ или Збб + збВ- или 1 + 1=2‘
Эта догадка требует и хорошего навыка в устном счёте и
большого творческого напряжения, что так ярко выражено на
лицах и в позах всех учеников.
64
Рис. 7.
§ 87. Запись наименований. Выполняя действия над числами,
необходимо давать себе отчёт в том, что выражает каждое число,
т. е. в том, о каком множестве идёт речь. Такой сознательности
в работе содействует постановка надлежащих наименований, при-
водимых полностью или сокращённо после записи чисел. Вот
примеры записи.
Задача 1. В уплату за покупку стоимостью 9 руб. дано
25 руб. Сколько причитается сдачи?
25 руб. —9 руб. = 16 руб.
Задача 2. Какое расстояние пролетит за 4 часа самолёт,
имеющий скорость 300 км в час?
300 км • 4 = 1200 км.
4 Арифметика
65
Особенно важно, чтобы было указано наименование резуль-
тата каждого действия. Это мы и будем постоянно делать, опус-
кая иногда (ради сокращения письма) наименования данных.
§ 88. Поиски плана решения задачи. Составить план решения
не всегда так просто, как это было во всех рассмотренных до сих
пор задачах, так как условия задачи часто не подсказывают, как
разбить эту составную задачу на простые. Рассмотрим для при-
мера две такие более трудные задачи.
Задача 1. В трёх ящиках лежит всего 107 тетрадей, при-
чём в первом ящике на 8 больше, чем во втором, и на 10 меньше,
чем в третьем. Сколько тетрадей в каждом ящике?
I. Поиски Плана решения. Изобразим условия задачи
наглядным рисунком (рис. 8).
Здесь три прямоугольника I, II, 1П с равными основаниями
и разными высотами показывают число тетрадей в ящиках I, II, III.
Легко видеть, что добавление
8 тетрадей во II ящике и умень-
шение на 10 числа тетрадей
в III ящике сделают число тет-
радей и во II ив III ящиках
одинаковым с числом тетрадей в
I ящике.
II. План решения. ^Сколь-
ко тетрадей будет во всех трёх
ящиках, если добавить во II ящик
8 тетрадей?
2) Сколько тетрадей будет во
всех трёх ящиках, если вынуть из III ящика 10 тетрадей?
3) Сколько тетрадей было в I ящике?
4) Сколько тетрадей было во II ящике?
5) Сколько тетрадей было в III ящике?
III. Вычисления. Руководствуясь этим планом произво-
дим вычисления.
1) 107 -|- 8 = 115 (тетрадей);
2) 115— 10 = 105 (тетрадей);
3) 105 : 3 = 35 (тетрадей);
4) 35— 8 = 27 (тетрадей);
5) 35 + 10 = 45 (тетрадей).
Ответ. В I ящике 35 тетрадей, во II — 27, в III — 45.
IV. Проверка: 35 -|- 27 -j- 45 = 107 (тетрадей); 35 — 27 =
= 8 (тетрадей); 45 — 35= 10 (тетрадей).
Мы решили задачу, уравнивая число тетрадей во втором и в
третьем ящиках с числом тетрадей в первом. Желательно решить
её двумя другими способами, уравнивая число тетрадей первого
и третьего ящиков со вторым, а также число тетрадей первого
и второго ящиков с третьим. Оба эти способа приведут к тому же
ответу, что и первый.
66
Задача 2. Груз в 86 тонн перевезён двумя машинами, из
которых одна брала каждый раз по 3 тонны, а другая по 5 тонн.
Зная, что обе машины сделали всего 22 поездки, найти, сколько
поездок сделала каждая.
I. Поиски плана решения. Для решения этой задачи
предположим, что все 22 поездки сделала трёхтонка. Тогда она
перевезла бы только 3-22 = 66 тонн, а 20 тонн (т. е. 86 — 66)
остались бы неперевезёнными. Пусть один раз вместо трёхтонки
шла пятитонка; мы перевезём больше на 5 — 3 = 2 тонны, не-
перевезёнными останутся уже только 20 — 2 = 18 тонн. Для про-
верки находим, сколько тогда перевезла бы трёхтонка (3-21 =
= 63 тонны) и сколько обе машины (63 -|- 5 = 68 тонн); останется
действительно 86 — 68= 18 тонн.
Если вместо трёхтонки пустить пятитонку не один, а два
раза, останется 18 — 2 = 16 тонн (проверка: 3 • 20 = 60, 5 • 2 =
= 10, 60-|- 10 = 70, 86 — 70= 16 тонн); если три раза, остаток
будет только 16 — 2=14; если четыре раза, то 14 — 2=12
и т. д. Сколько же раз надо заменить трёхтонку пятитонкой, чтобы
остатка вовсе не было? Очевидно, столько раз, сколько раз
2 тонны содержится в 20 тоннах, т. е. 20:2 = 10.
Итак, было 10 поездок пятитонки, остальные 22—10=12
поездок сделала трёхтонка. Для проверки узнаем, сколько груза
перевезла трёхтонка (3 • 12 = 36), сколько пятитонка (5 • 10 =
= 50), сколько перевезено всего (36 50 = 86), и убеждаемся,
что задача решена правильно.
Мы начали решение с предположения, что ездила только трёх-
тонка, но можно было предположить, что ездила только пяти-
тонка. Тогда перевезено было бы не 86, а 5 • 22 = НО тонн, т. е.
на ПО — 86 = 24 больше, чем в действительности, и мы видим,
что для устранения этого излишка надо заменить пятитонку
трёхтонкой 24 :2 = 12 (раз). Таким образом, этот второй способ
решения приводит к тому же результату, что и первый.
II. План решения и вычисления. 1) Сколько груза
было бы перевезено, если бы все 22 поездки совершила трёх-
тонка? 3 • 22 = 66 тонн.
2) Сколько груза осталось бы тогда неперевезённым? 86 —
— 66 = 20 тонн.
3) На сколько уменьшается остаток груза при замене трёх-
тонки пятитонкой в одной поездке? 5 — 3 = 2 тонны.
4) Сколько раз надо сделать такую замену, чтобы остатка не
было вовсе? 20 :2 = 10 (раз).
5) Сколько поездок сделала трёхтонка, если пятитонка сде-
лала 10 поездок? 22—10=12 (поездок).
Ответ. Трёхтонка сделала 12 поездок, пятитонка сделала
10 поездок.
III. Проверка: 1) 1210 = 22 (поездки); 2) 3 • 12-f-
-|-5 • 10 = 36 + 50 = 86 тонн.
4*
67
Глава V. ДЕЛИМОСТЬ НАТУРАЛЬНЫХ ЧИСЕЛ
Раздел 1. ДЕЛИТЕЛИ И КРАТНЫЕ
§ 89. Делители данного натурального числа. Для решения
многих задач арифметики надо уметь находить все числа, на ко-
торые данное натуральное число делится без остатка. Например,
можно убедиться, что 21 864 делится без остатка только на сле-
дующие натуральные числа: 1, 2, 3, 4, 6, 8, 12, 24, 911, 1822,
2733, 3644, 5466, 7288, 10 932, 21864. Говорят, что каждое из
этих 16 чисел является делителем числа 21 864.
Итак, делителем данного натурального числа называется каж-
дое натуральное число, на которое данное число делится без
остатка.
Учение о делителях натуральных чисел даёт возможность узна-
вать некоторые особенности тех множеств, численность которых
характеризуется этими натуральными числами.
Так, зная, что число 36 имеет только следующие делители:
1, 2, 3, 4, 6, 9, 12, 18, 36, можно утверждать, что число 36 можно
набрать равными слагаемыми: единицами, двойками, тройками,
четвёрками, шестёрками, девятками, дюжинами, а также слагае-
мыми по 18, или взять сразу все 36 единиц, и нельзя набрать
никакими другими равными слагаемыми. Иначе: множество, чис-
ленность которого 36, можно набрать равными слагаемыми
девятью способами. Например, если в классе 36 учеников, то
имеется только девять возможностей построения в колонны с
равным числом учащихся в каждом ряду: 1) по одному в ряду
(гуськом); 2) по паре в ряду; 3) по три в ряду; 4) по четыре;
5) по шесть; 6) по девять; 7) по 12; 8) по 18 и 9) одной шерен-
гой, когда в ней 36 учащихся.
Но стоит взять другой класс, где 37 учеников, и будет уже
иная картина, так как число 37 имеет только два делителя: еди-
ницу и 37. Здесь имеются только две возможности построения
в колонну с равным числом учащихся в каждом ряду: 1) по од-
ному (гуськом) и 2) одной шеренгой, когда в ней 37 учеников.
Необходимо отметить, что слово «делитель» в арифметике
употребляется в двух смыслах: 1) делителем называют то число,
на которое делят, независимо от того, получается остаток
или нет, и 2) делителем данного числа называется нату-
ральное число, на которое данное делится без остатка. Так, если
делят 15 на 6, то число 6 является делителем, но 6 не есть
делитель числа 15.
Это различие выражается в языке так: в первом случае го-
ворят делитель действия, а во втором — делитель числа.
§ 90. Кратные данного натурального числа. В предшествую-
щем параграфе был рассмотрен вопрос о натуральных числах,
на которые данное натуральное число делится без остатка. Есте-
ственно, возникает обратный вопрос — установить, для каких на-
туральных чисел заданное натуральное число является делите-
68
лем. Например, 4 есть делитель следующих натуральных чисел:
4, 8, 12, 16, 20, ... Говорят, что каждое из этих чисел кратно 4,
числа же 1, 2, 3, 5, 6, 7, 9, ... не кратны 4. Слово «крат»
старинное русское слово, означающее «раз». Слово «многократно»
означает «много раз».
Итак, кратным данного натурального числа называется каж-
дое натуральное число, которое делится без остатка на данное.
Всякое натуральное число, кратное двум, называется чётным
числом, а не кратное двум — нечётным.
§ 91. Сравнительные свойства делителей и кратных данного
натурального числа.
1. Каждое натуральное чис-
ло имеет наименьший делитель:
это — единица.
2. Каждое натуральное чис-
ло имеет наибольший делитель:
это — само данное натуральное
число.
3. Каждое натуральное чис-
ло а имеет не более чем а дели-
телей, так как все делители не
больше, чем а.
4. Существует натуральное
число, имеющее только один
делитель; это число — единица,
которая делится без остатка
только на единицу.
5. Существуют натуральные
числа, имеющие только два де-
лителя, например, 37, делители
которого только 1 и 37, или 311,
у которого делителями являют-
ся только 1 и 311.
6. Нуль — единственное це-
лое число, имеющее бесконеч-
ное множество делителей, так
как нуль делится без остатка
на каждое натуральное число.
1. Каждое натуральное чис-
ло имеет наименьшее кратное:
это само натуральное число.
2. Каждое натуральное чис-
ло не имеет наибольшего крат-
ного; в самом деле, если возь-
мём любое кратное и удвоим
его, получим новое кратное,
большее взятого.
3. Каждое натуральное чис-
ло а имеет бесконечно много
кратных: а, 2а, За, 4а, 5а, ...
4. Не существует натураль-
ного числа, имеющего только
одно кратное, так как у каж-
дого натурального числа беско-
нечное множество кратных.
5. Не существует натураль-
ного числа, имеющего только
два кратных числа.
6. Нуль — единственное це-
лое число, которое не имеет на-
туральных кратных, так как ни-
какое число нельзя делить на
пуль.
§ 92. Нахождение всех делителей данного натурального числа.
Если данное число, например 28, есть произведение двух раз-
личных множителей, как, например, 28 = 4 • 7, то каждый из
сомножителей 4 и 7 является делителем 28. Отсюда следует, что
если найден один из делителей, например 3, числа 36, то част-
ное 36; 3 = 12 даёт другой делитель 36, так как 36 = 3 • 12.
69
Такие два различных делителя числа 36, как 3 и 12, 4 и 9,
1 и 36, 2 и 18, называются взаимно дополнительными делите-
лями. Итак, взаимно дополнительными делителями данного нату-
рального числа называются такие два различных его делителя,
которые в произведении дают данное натуральное число. Каждое
натуральное число, большее единицы, имеет такую пару дели-
телей, для разыскания которых не требуется никаких приёмов:
это единица и само данное натуральное число.
Пусть надо найти все делители числа 36.
1. Укажем его два взаимно дополнительных делителя: 1 и 36.
2. Найдём все пары взаимно дополнительных делителей путём
последовательного деления 36 на 2, 3 и т. д., причём если данное
число делится на испытываемое число, то записываем и делитель
и частное:
1) 36:2= 18.
2) 36 : 3 = 12.
3) 36:4 = 9.
4) 36 не делится на 5.
5) 36 : 6 = 6.
Замечаем, что делители уве-
личиваются:
2 < 3 < 4 < 6,
а частные уменьшаются:
18 > 12>9>6.
Дальше пробы прекращаются, так как делитель и частное
стали равными, а потому начнётся повторение, только поменяются
местами делители и частные, т. е.
36 :9 = 4; 36 : 12 = 3; 36 : 18 = 2.
Таким образом, мы выделили все пары взаимно дополнитель-
ных делителей: 1 и 36, 2 и 18, 3 и 12, 4 и 9 и ещё делитель
6 без взаимно дополнительного ему.
В результате получается следующая краткая запись:
Делители 36: 1 2 3 4 6
36 18 12 9
Если надо найти все делители числа 84, применяем тот же
способ проб, прекращая их, как только получим частное, мень-
шее, чем делитель. Получается запись:
Делители 84: 1 23467
84 42 28 21 14 12
Пробы деления на 5, 8, 9, 10 не записывают, так как 84 на
эти числа не делится; дальше 10 пробы не ведутся, так как 84 : 10
даёт частное меньше 10.
Раздел 2. ПРИЗНАКИ ДЕЛИМОСТИ
§ 93. Что называется признаком делимости? Чтобы узнать,
делится ли одно данное число на другое данное число, надо вы-
полнить деление и посмотреть, каков остаток. Но во многих
случаях удаётся, и не выполняя деления, заранее сказать, будет
70
ли остаток равен нулю или нет. Свойства чисел, позволяющие
делать такие предсказания, дают возможность установить при-
знаки делимости.
Признаками делимости называются предложения, в которых
указывается, как можно предсказать делимость одного числа на
другое, не выполняя самого деления этих чисел.
§ 94. Признаки делимости суммы. I. Зная, что 21 и 35 де-
лятся на 7, можно утверждать, что и их сумма 21 + 35 = 56
тоже делится на 7. Действительно, числа 21 и 35 можно набрать
семёрками, а потому семёрками можно набрать и их сумму: 21 +
+ 35 = (7 + 7 + 7) + (7-f-7-f-7-f-7-|-7) = 7 • 8. Это рассуждение
применимо к любым двум числам, имеющим один и тот же дели-
тель. Получаем следующий первый признак делимости суммы:
Если каждое слагаемое делится на какое-нибудь число, то и
их сумма разделится на то же число.
Научимся объяснять этот признак делимости суммы следую-
щим образом.
Пусть подобраны числа так, что каждое из них делится на
данное, например:
1) 216 999 делится на 513 I а делится на с
и 409374 делится на 513. | и b делится на с.
2) Это по смыслу деления значит, что
216999 = 513 + 513 4- ... +513; а = с-\-с-\- ... + с;
409 374 = 513 + 513 + ... + 513; b = с + с + ... + с.
3) Сложив данные числа, будем иметь:
216999 + 409 374 = (513 + 513+ ...+ |а + 6 = (с + с+...+
+ 513) + (513 + 513 + ... + 513). | +с)+(с+с+ ... +<?).
4) Видим, что сумма состоит из равных слагаемых:
по 513 единиц;
следовательно, сумма
216999 + 409 374 делится на 513,
по с единиц;
следовательно, сумма
а + b делится на с,
т. е. на то число, на которое делится каждое слагаемое.
Легко понять, что этот признак делимости суммы верен не
только для двух, но и для любого числа слагаемых.
II. А что можно сказать о делимости суммы двух слагаемых,
если одно из них делится, а другое не делится на некоторое
данное число? Возьмём, например, числа 21 и 38, из которых
первое делится на 7, а второе при делении на 7 даёт остаток 3.
Ясно, что сумму 21 + 38 нельзя набрать одними семёрками, в
неё войдёт, кроме семёрок, ещё и этот остаток 3:
21 + 38 = (7 + 7 + 7)+(7 + 7 + 7 + 7 + 7 + 3) = (7 +
+ 7 + ... + 7) + 3.
71
Деление суммы 21 -J- 38 на 7 даёт остаток 3; эта сумма на 7
не делится. Подобное рассуждение применимо к сумме не только
двух, но и любого числа слагаемых, из которых все, кроме од-
ного, делятся на некоторое данное число, а это одно на него не
делится. Отсюда получаем следующий второй признак делимости
суммы:
Если каждое слагаемое, кроме одного, делится на какое-ни-
будь число, а это одно на него не делится, то и сумма всех этих
слагаемых на него не разделится.
Убедившись, что 216999 делится на 513, а 409 395 на 513 не
делится (получается остаток 21), предсказываем, что при деле-
нии суммы 216999 4-409 395 на 513 получится этот же остаток
21. Это легко проверить, выполняя деление.
Если натуральное число а делится на с, а b не делится на
с, давая остаток г < с, тоа = с4-с4-">'4~с; b = с + с -р
4- ... 4- с 4- г; а 4- b = (с4-с 4* ••• 4" с) 4- (с4~с4~- • • 4-с4-/')==
= (с 4- с 4- ... 4- с) 4- г. При делении а-\-Ь на с получается
остаток г.
Возникает ещё вопрос: что можно сказать о сумме, когда
установлено, что ни одно из слагаемых не делится на данное
число?
Рассмотрим примеры. Вначале возьмём слагаемые 17 и 12;
каждое из них не делится на 5; их сумма 17 4- 12 = 29 также
не делится на 5. Далее возьмём слагаемые 17 и 13, каждое из
которых не делится на 5; их сумма 17 -|- 13 = 30 делится на 5.
Следовательно, могут быть оба случая:
При неделимости каждого слагаемого на одно и то же число
сумма, в зависимости от выбранных слагаемых, может как де-
литься, так и не делиться на то же число.
Вот почему на поставленный вопрос: что можно сказать о
сумме, когда установлено, что ни одно из слагаемых не делится
на данное число? — надо ответить, что ничего заранее сказать
нельзя.
§ 95. Признак делимости разности. Вычитание есть действие,
связанное со сложением так, что уменьшаемое есть сумма, вы-
читаемое— одно из слагаемых, а разность—другое слагаемое.
Поэтому, чтобы установить признак делимости разности, надо
вернуться к вопросу о делимости суммы.
Если сумма двух слагаемых и одно из них делится на ка-
кое-либо число, то будет ли на это число делиться и второе
слагаемое.
Но ведь установлено, что если одно слагаемое не делится,
а другое делится, то и сумма не должна делиться, — вот почему
ответ должен быть утвердительным, т. е. если сумма двух сла-
гаемых и одно из этих слагаемых делятся на какое-либо число,
то и другое слагаемое обязательно делится на то же число. Это
значит что если уменьшаемое и вычитаемое делятся на какое-
нибудь число, то на это число делится и их разность.
72
Так, зная, что 2247 и 826 порознь делятся па 7, можно пред-
сказать, что их разность 2247 — 826 также делится на 7.
§ 96. Признак делимости произведения. Легко убедиться, что
для делимости произведения на какое-нибудь число нет необхо-
димости в том, чтобы на него делился каждый сомножитель.
Произведение делится на данное число, если хотя бы один из
сомножителей на него делится. Например, произведение 12-10=
= 120 делится на 4, так как на 4 делится сомножитель 12,
хотя другой сомножитель (10) не делится на 4.
1) В самом деле, пусть взято число:
4301, делящееся на 17, а, делящееся на с,
где частное 253; следовательно, где частное q;
4301 = 17 • 253. следовательно, а = cq.
2) Возьмём произвольное число, например:
221. | Ь
3) Рассмотрим произведения:
4301 • 221. | а • Ь
4) Эти произведения можно выразить иначе так:
4301 - 221 = (17 • 253) - 221. | а • b = (с • q) • Ь.
5) По сочетательному закону умножения записываем:
(17 253) • 221 = 17 • (253 - 221). | (с- q) • b = с • (q • 6).
6) Следовательно, эти произведения делятся:
на 17, | на с,
т. е. на то число, на которое делится один из сомножителей.
Итак, для делимости произведения достаточно, чтобы де-
лился на это число по крайней мере один из сомножителей; од-
нако это условие не является необходимым. Так, например, про-
изведение 12 • 10 = 120 делится на 8 и даёт частное 15, хотя ни
один из сомножителей, ни 12 ни 10, не делится на 8.
Из этого признака делимости произведения вытекают два след-
ствия.
I. Если одно число делится на другое, а это другое делится
на третье, то первое делится на третье. Заметив, например, что
120 делится на 24 и что 24 делится на 8, можем утверждать,
что 120 делится на 8.
1) В самом деле, подберём такие
6250 делится на 50, где частное 125;
6250 = 50 - 125.
50 делится на 5, где частное 10;
50 = 5 • 10.
числа:
а делится на Ь, где частное q\
а = b • q.
b делится на с, где частное d;
b = c-d.
2) Первое произведение запишем иначе:
6250 = (5 • 10) • 125. | а = (с • d) • q.
3) По сочетательному закону умножения запишем:
6250 = 5 • (10 • 125). | а = с - (d • q).
4) Видим, что произведение делится на третье число, т. е.
на 5. | на с.
73
II. Если одно число не делится на другое, то оно не может
делиться и ни на какое, кратное этому другому.
Например, зная, что 600 не делится на 7, можем предсказать,
что 600 не разделится ни на одно число, кратное семи, т. е. на
14, 21, 28, 35 и т. д.
Доказывается это весьма просто: если бы нашли кратное 7,
такое, что 600 разделилось бы на него, то по первому следствию
600 разделилось бы и на 7, что невозможно.
Основываясь на этих следствиях, можно делать упрощения
при нахождении всех делителей данного натурального числа
(§ 92). Так, при нахождении делителей 84, убедившись, что 84
не делится на 5. не надо было пробовать делить на 10.
§ 97. Признаки делимости на 2, 5, 10.
Если написать какое угодно натуральное число и закрыть его
так, чтобы видна была только последняя его цифра, а именно
цифра единиц (на рисунке 9 цифра 8), то можно с полной уве-
ренностью сказать, делится или не делится написанное число на 2,
5, 10, хотя мы и не знаем закрытых его цифр.
Рис. 9.
Действительно, всякое натуральное число можно представить
в виде суммы двух слагаемых:
1) полного числа его десятков и
2) числа простых его единиц.
Десяток делится на 2, на 5 и на 10, а потому всё закрытое
число полных десятков всегда делится и на 2, и на 5, и на 10.
Теперь всё будет зависеть от числа простых единиц (в данном
примере 8), т. е. от второго слагаемого в разложении числа:
если оно делится на 2, или на 5, или на 10, то и всё данное
число будет делиться на 2, или на 5, или на 10 (по признаку
делимости суммы). Если цифра единиц, как в нашем примере,
есть 8, то данное число делится на 2, но не делится ни на 5, ни
на 10. Итак, на 2, на 5, на 10 делятся те и только те числа, у
которых в разряде единиц стоит число, делящееся соответственно
на 2, на 5 или на 10.
Уточняя этот общий признак делимости на 2, 5 и 10 для
каждого из них в отдельности, получим:
1) Так как из однозначных чисел на 2 делятся только числа: 0,
74
2, 4, 6, 8, то отсюда следует вывод: на 2 делятся те и только
те числа, у которых в разряде единиц — число чётное.
2) Так как из всех однозначных чисел на 5 делятся только
О и 5, то отсюда следует, что на 5 делятся те и только те числа,
у которых цифра единиц — нуль или пять.
3) Так как на 10 делится из однозначных чисел только нуль,
то, следовательно, на 10 делятся те и только те числа, у которых
цифра единиц есть нуль.
§ 98. Признаки делимости на 4, 25, 50, 100. Если в написан-
ном на классной доске или на бумаге числе закрыть все цифры,
кроме двух последних, т. е. кроме цифры единиц и цифры де-
сятков, то можно с уверенностью сказать о делимости этого числа
не только на 2, 5, 10, но и на 4, 25, 50 и 100.
Действительно, это число можно считать суммой числа (за-
крытого), состоящего из одних сотен, и числа (открытого), со-
стоящего из десятков и единиц. Так как сотня делится и на 4,
и на 25, и на 50, и на 100, то и закрытая часть числа, выра-
жающая столько-то сотен, будет делиться на эти числа; следо-
вательно, всё будет зависеть от второго (открытого) слагаемого:
если оно делится на 4, или 25, или 50, или 100, то и всё число
разделится на то же число (§ 94), а если не делится, то и всё
число не разделится. Если, например, открыто число 50, то, за-
мечая, что 50 делится на 25 и 50, но не делится на 4 и 100,
утверждаем, что всё данное число делится на 25 и на 50, но не
делится на 4 и на 100.
Итак, на 4, или 25, или 50, или 100 делятся те и только
те числа, у которых разряды десятков и единиц образуют дву-
значное число, делящееся на 4, или 25, или 50, или 100.
Уточняя этот общий признак делимости для каждого из чисел
4, 25, 50 и 100 в отдельности, получим:
на 4 делятся те и только те числа, у которых последние две
цифры образуют число, кратное 4;
на 25 делятся те и только те числа, у которых две последние
цифры 00, или 25, или 50, или 75;
на 50 делятся те и только те числа, у которых две последние
цифры 00 или 50;
на 100 делятся те и только те числа, у которых последние две
цифры нули.
§ 99. Признаки делимости на 8, 125, 250, 500, 1000. Если открыть три по-
следние цифры числа, то по ним можно судить о делимости всего данного числа
на числа 8, 125, 250, 500 и 1000. Рассуждая почти как в § 97—98, придём к
такому заключению:
на 8, 125, 250, 500, 1000 делятся те и только те числа, у которых разряды
сотен, десятков и единиц образуют трёхзначное число, делящееся на 8, 125,
250, 500 и 1000. Отметим, что для 125 и 1000 последнее можно выразить
иначе:
на 125 делятся те и только те числа, у которых последние три цифры
есть: 000, 125, 250, 375, 500, 625, 750, 875;
на 1000 делятся те и только те числа, у которых последние три цифры
нули.
75
§ 100. Признаки делимости на 3 и на 9. Сначала установим,
какие остатки получаются от деления на 9 различных разрядных
единиц, т. е. чисел 10, 100, 1000 и т. д. Легко видеть, что все разряд-
ные единицы при делении на 9 дают один и тот же остаток 1.
Отсюда следует, что каждую разрядную единицу можно предста-
вить в виде суммы числа, кратного 9, и единицы: 10 = 9 4-1;
100 = 99 -}- 1; 1000 = 999 4- 1 и т. д.
Какой остаток даёт при делении на 9 любое круглое число
(§ 11)? Взяв, например, круглое число 300, имеем 300= 100 • 3 =
= (99 4- 1) • 3 = 99 • 3 4- 3. Первое слагаемое делится на 9, второе
равно цифре старшего разряда данного круглого числа. Так дело
обстоит с любым круглым числом: любое круглое число можно
представить в виде суммы двух слагаемых, одно из которых де-
лится на 9, а второе есть цифра старшего разряда данного круг-
лого числа. Например:
600000 = 99999-6 4-6.
Каково бы ни было данное число, его всегда можно представить
в виде суммы круглых чисел и однозначного числа, как, напри-
мер:
52 418 = 50 000 4- 2000 4- 400 4- 10 8.
Заменяя каждое круглое число такой суммой, о какой была
речь, и применяя переместительный и сочетательный законы сло-
жения, приходим к выводу, что любое натуральное число можно
представить в виде суммы числа, кратного 9, и числа, равного
сумме цифр данного числа. Например,
52418 = (9999 - 5 4- 999 • 2 99 • 4 4- 9 • 1) 4- (5 4- 2 4- 4 4- 1 4- 8).
Здесь в первой скобке записана сумма чисел, кратных 9, т. е.
число, кратное 9 (§ 94), а во второй сумма цифр данного числа.
Основываясь на этом, легко получить такой признак дели-
мости на 9: всякое число, у которого сумма чисел, выраженных
его цифрами, кратна 9, делится на 9; всякое число, у которого
сумма чисел, выраженных его цифрами, не кратна 9, не делится
на 9.
Короче: на 9 делятся те и только те числа, у которых сумма
цифр кратна 9.
Полезно заметить, что важна не сама сумма цифр, а лишь
тот остаток, который получается при её делении на 9: остаток
от деления на 9 любого числа равен остатку от деления на 9
суммы его цифр. Поэтому, складывая цифры числа, можно сбра-
сывать каждую накопившуюся девятку. Например, чтобы узнать,
делится ли на 9 число 27 824, нет надобности находить полностью
сумму цифр 24-74-84-24-4 = 23; достаточно взять 2 4-7 = 9;
9 — 9 = 0; 0 4-84-2 — 9 = 1; 14-4 = 5. Остаток от деления чис-
ла 27824 на 9 есть 5, это число на 9 не делится.
76
Число 9 делится на 3, а потому всякое число, делящееся на
9, делится и на 3. То же самое представление числа в виде сум-
мы двух слагаемых, из которых одно кратно 3, а другое есть
сумма его цифр, показывает, что на 3 делятся те и только те чис-
ла, у которых сумма цифр кратна 3.
Например, число 4872, имея сумму цифр 4-|-84-7-]-2 = 21,
делится на 3, но не делится на 9; число 53 181 с суммой цифр
18 делится и на 3, и на 9; число 53182 с суммой цифр 19 не
делится ни на 3, ни на 9.
§ 101. Признаки делимости на 6, 12, 15. Если число не делится на 2, то
оно не делится и на 6, так как любое число, кратное 6, делится на каждый
делитель 6, в том числе и на 2. Точно так же обстоит дело и с делимостью
на 3: если число не делится на 3, оно ие может делиться и на 6.
Можно сказать, что для делимости на 6 необходима делимость на каждое
из чисел 2 и 3 в отдельности.
Число 789 не делится на 6 потому, что оно не делится на 2, хотя делится
на 3; число 788 тоже не делится на 6, но по другой причине — оно не делит-
ся на 3, хотя делится на 2.
Возникает вопрос: если оба эти необходимые условия выполнены, т. е. если
данное число кратно как 2, так и 3, можно ли быть уверенным, что оно крат-
но 6? Другими словами, достаточна ли делимость на 2 и на 3 для дели-
мости на 6?
Чтобы ответить на этот вопрос, рассуждаем так: если данное число кратно
3, его можно представить как сумму нескольких слагаемых, каждое из кото-
рых есть 3:
34-3 + 34-...4-3.
Может ли эта сумма содержать нечётное число слагаемых? Нет, так как
тогда, заменяя сумму каждых двух троек одной шестёркой, мы получили бы
сумму из нескольких шестёрок и одной тройки, а эта сумма не делится на 2.
Значит, данное число есть сумма чётного числа троек, а потому есть сумма
нескольких шестёрок и, следовательно, делится на 6.
Итак, на 6 делится каждое число, которое делится как на 2, так и на 3 в
отдельности; не делится на 6, если оно не делится хотя бы иа одно из чисел
2 и 3. Короче: на 6 делятся те и только те числа, которые делятся иа каждое
из чисел 2 и 3 в отдельности.
Говорят, что делимость на 2 и на 3 не только необходима, но и доста-
точна для делимости на 6.
Рассуждая подобным же образом, приходим к следующим двум призна-
кам делимости:
на 12 делятся те и только те числа, которые делятся на каждое из чисел
3 и 4 в отдельности;
на 15 делятся те и только те числа, которые делятся на каждое из чисел
3 и 5 в отдельности.
Раздел 3. ЧИСЛА ПРОСТЫЕ И СОСТАВНЫЕ
§ 102. Три вида натуральных чисел. У каждого натурального
числа имеется по крайней мере один делитель — единица. Суще-
ствует единственное число, имеющее только один делитель —
единицу; это число — сама единица. У каждого числа, большего
единицы, имеются по крайней мере два различных делителя: еди-
ница и само это число. Существуют числа, имеющие только два
делителя, например 7 или 13; первое имеет делители 1 и 7, а
77
второе 1 и 13. Существуют числа, имеющие только три дели-
теля, например у 4 или 9 соответственно делители 1, 2, 4 и 1,
3, 9. Существуют числа, имеющие более трёх делителей, напри-
мер число 21 864 имеет 16 делителей (см. § 89).
По числу делителей можно различать три вида натуральных
чисел: числа только с одним делителем, числа только с двумя
делителями, числа более чем с двумя делителями.
Чисел первого вида только одно, а именно единица.
Числа второго вида называются простыми; к ним принадле-
жат, например, числа 2, 3, 5, 7.
Числа третьего вида называются составными; к ним принад-
лежат, например, числа 4,6,8, 9, 10. Натуральное число называется
простым, если оно имеет два и только два различных делителя,
и составным, если у него более двух различных делителей.
Число 1 не принадлежит ни к простым, ни к составным, а
всякое число, большее единицы, является либо простым, либо
составным.
Взяв первые 30 натуральных чисел, нетрудно убедиться, что
в их числе имеется 10 простых:
2, 3, 5, 7, 11, 13, 17, 19, 23, 29
и 19 составных:
4, 6, 8, 9, 10, 12, 14, 15, 16, 18, 20, 21, 22, 24, 25, 26, 27,
28, 30.
§ 103. Простые делители составного числа.
Всякое составное число имеет по крайней мере один простой
делитель. Например, у составного числа 4 есть один простой де-
литель 2, у 6 два простых делителя (2 и 3), у 8 один (2), у 9
тоже один (3), у 10 — снова два (2 и 5) и т. д.
Следующее рассуждение доказывает, что всякое составное
число имеет по крайней мере один простой делитель. Какое бы
составное число а мы ни взяли, у него есть делители (по край-
ней мере один), отличные от единицы и самого числа а, иначе
оно было бы простым, а не составным; наименьший из этих де-
лителей (назовём его Ь) всегда число простое, так как если бы
он был составным, то он имел бы в свою очередь делитель с,
меньший Ь, отличный от единицы, и число а, делясь на Ь, дели-
лось бы на с, что невозможно, так как по условию b — наимень-
ший делитель, отличный от единицы.
§ 104. Распознавание простых и составных чисел. Чтобы уз-
нать, является ли данное число простым или составным, надо
искать его делители, что мы делать уже умеем. Надо пробовать
делить данное число только на последовательные простые числа:
2, 3, 5, 7, 11, ..., а на составные делить не надо. Действительно,
если данное число не делится ни на какое простое, то оно не мо-
жет делиться и на составное, так как всякое составное имеет де-
литель— простое число. Например, если установлено, что число
78
не делится на 2, то незачем пробовать делить его на числа со-
ставные: 4, 6, 8 и т. д.
Делимость на последовательные простые числа испытывается
до тех пор, пока не встретится делитель данного числа: если же
данное число не разделится ни на одно из испытуемых простых
чисел и в частном (при этом делении с остатком) образовалось
число, меньшее делителя, то данное число простое.
Почему? Потому что, если бы а разделилось на какое-то чис-
ло р, т. е.
a-.p = q, (1)
причём
<7<Р.
то из (1) следовало бы, что а = pq, а потому а делится и на q,
а этого быть не может, так как при последовательном делении
мы уже испробовали все числа, меньшие р (в том числе и q), и
деления у нас не получалось.
Мы пришли к противоречию, следовательно, а не может де-
литься на р. Поэтому пробы надо прекращать, как только в част-
ном получается число, меньшее делителя.
Покажем, как можно распознать вид числа 221.
1) Взяв признаки делимости, замечаем, что число 221 не де-
лится на 2, на 3, на 5.
2) Непосредственным делением убеждаемся, что 221 не де-
лится на 7 и на 11, но на 13 делится: 221 : 13= 17, а поэтому
221 —число составное, так как 221 имеет не менее трёх различ-
ных делителей: 1, 13, 17, 221.
Установим вид числа 449.
1) По признакам делимости устанавливаем, что 449 не делится
на 2, на 3, на 5.
2) Непосредственным делением убеждаемся, что 449 не де-
лится ни на одно из последующих простых чисел 7, 11, 13, 17,
19, 23.
3) При делении на 23 частное равно 19, т. е. числу меньшему
делителя; значит, пробы надо прекратить.
Следовательно, 449 — число простое.
Установим вид числа 899.
1) По признакам делимости убеждаемся, что 899 не делится
на 2, на 3, на 5.
2) Пробуя делить 899 на 7, 11, 13, 17, 19, 23, 29, обнаружи-
ваем, что 899 :29 = 31.
Следовательно, 899 — число составное.
Так как распознавание вида числа представляет значительный
труд, в особенности если данное число велико, то возникает во-
прос, нельзя ли составить полную таблицу всех простых чисел
или таблицу всех составных чисел. Оказывается, сделать ни то
ни другое невозможно, так как множество простых чисел и мно-
жество составных — бесконечные множества. Но возможно соста-
79
вить таблицу всех простых чисел первой сотни или первой ты-
сячи и т. д. Способ, каким можно без особого труда составить
эту таблицу, рассмотрен в § 106.
§ 105. Бесконечность множества составных и множества про-
стых чисел. Рассмотрим сперва множество составных чисел. Если
бы составных было конечное множество, то, располагая их по
возрастанию, мы имели бы самое большое составное х, но 2-х
больше х и 2 • х также составное. Значит, не может быть послед-
него составного, а потому составных бесконечное множество.
Труднее показать, что множество всех простых чисел беско-
нечно. Однако ещё в древней Греции гениальный математик
Евклид (III век до н. э.) в своём знаменитом труде «Начала» на-
шёл доказательство этого положения.
Приведём его доказательство с некоторыми изменениями. Относительно
множества простых чисел можно сделать два предположения, из которых
истинно только одно. Первое предположение: множество простых чисел есть
множество конечное, т. е. существует последнее самое большое простое число,
которое обозначим через р.
Второе предположение: множество простых чисел есть множество беско-
нечное.
Покажем, что первое предположение ошибочное.
1. Перемножим все простые числа, что можно сделать, так как их по пер-
вому предположению — конечное множество;
2 • 3 • 5 • 7 • 11 • 13 • 17 • 19 • 23 • 29 • 31 ... р = п.
Пусть получится в результате умножения число п.
2. Рассмотрим новое число, а именно п -f- 1:
а) оно больше п, а п больше р\ следовательно, больше последнего просто-
го р; тем самым п -f- 1 не может быть простым; значит, оно составное;
б) по § 103 всякое составное число имеет по крайней мере один простой
делитель а, поэтому п + 1 делится на а.
3. Но п образовалось из произведения всех простых чисел, следовательно,
а входит в это произведение 2 • 3 • 5 7 • 11 • 13 • 17 • 19 • 23 • 29 31 ... р = п,
а поэтому п также делится на а.
4. По признаку делимости разности имеем, что разность (п -f- 1)— 1 = п
целится на а, т. е 1 делится иа число а, большее единицы, что невозможно.
Итак, первое предположение ложное, а поэтому истинным будет второе пред-
положение.
§ 106. Составление таблицы простых чисел в промежутке от
1 до п. Так как простых чисел бесконечное множество, то воз-
можно составить таблицу не всех простых, а только их части,
например таблицу всех простых первой сотни или первой тысячи
и т. д. Для составления таблицы простых чисел был найден
приём также в древней Греции немного позже Евклида, учёным
того времени Эратосфеном. Этот приём называется «решетом Эра-
тосфена».
Рассуждения Эратосфена были следующие:
1) Пусть надо выделить из первой сотни натуральных чисел
все простые; для этого возьмём сто пустых клеточек (как ука-
зано на рисунке 10).
2) Вычеркнем точкой первую клеточку, так как в ней еди-
ница, а единица — число не простое.
80
3) Вычеркнем все составные, кратные 2, кроме 2, общий вид
таких чисел будет: 2 -)- 2 • и, так как 2 + 2 п имеет по край-
ней мере три делителя: 1, 2 и 2 -]-2 • п. Само вычёркивание осу-
ществляется просто: каждая вторая клетка через одну, начиная
от второй (как показано на рисунке), отмечается точкой.
• • • - □ • © в • • в
© • • □ • — © Е • — • 0 • — □
© • в • • о □ - • • □ © — • в
• © • □ • • - • • Б • о • □
— • © □ • — • Е о • — • □ • © - □
Рис. 10.
4) Вычеркнем все составные, кратные 3, кроме 3, общий вид
таковых будет 3 -]- 3 • п.
Само вычёркивание осуществляется так: каждая пустая кле-
точка через две, начиная от третьей, отмечается чёрточкой.
Правда, здесь некоторые клеточки будут вычёркиваться дважды,
например клетка шестая, так как 6 кратно и 2, и 3. Это явление
не должно смущать составителя таблиц (см. тот же рисунок).
5) Вычеркнем все составные, кратные 5, кроме 5 (их общий
вид 5 -]- 5 • п), через четыре на пятую, начиная с пятой клеточки
(вычёркиваем, ставя квадратики). Совпадение двух или трёх зна-
ков вычёркивания в одной клеточке также не должно смущать
составителя таблиц.
2 3 • 5 • 7 — □ 11 • 13 © в • 17 • 19 □
© • 23 • □ • - © 29 Б 31 • - • 0 • 37 • - □
41 © 43 • В • 47 • О □ - • 53 • □ © — • 59 Е
61 • © □ • 67 • — 71 • 73 • в • о • 79 □
— • 83 © □ • — • 89 в О • — • □ • 97 © — □
Рис. 11.
6) Наконец, вычеркнем все составные, кратные 7, кроме 7
(их общий вид 7 -]- 7 • п), через шесть на седьмой клеточке ста-
вим кружочек как новый знак вычёркивания. Для данного про-
межутка далее прекращаются вычёркивания, так как при делении
100 на 11 частное 9 меньше делителя (§ 104).
7) Все оставшиеся невычеркнутые клеточки есть те, которые
по счёту их местоположения будут давать номера только простых
чисел. Вставим последние путём простого счёта клеточек. Оказа-
лось 25 простых чисел в первой сотне натуральных чисел (рис. 11).
5 Арифметика
81
Остаётся только выписать все найденные простые числа подряд.
Если взять не сотню, а тысячу первых натуральных чисел,
то, применяя такие «отсеивания», придём к следующей таблице
всех простых чисел первой тысячи.
ТАБЛИЦА ПРОСТЫХ ЧИСЕЛ ПЕРВОЙ ТЫСЯЧИ
2 47 109 191 269 353 439 523 617 709 811 907
3 53 ИЗ 193 271 359 443 541 619 719 821 911
5 59 127 197 277 367 449 547 631 727 823 919
7 61 131 199 281 373 457 557 641 733 827 929
11 67 137 211 283 379 461 563 643 739 829 937
13 71 139 223 293 383 463 569 647 743 839 941
17 73 149 227 307 389 467 571 653 751 853 947
19 79 151 229 311 397 479 577 659 757 857 953
23 83 157 233 313 401 487 587 661 761 859 967
29 89 163 239 317 409 491 593 673 769 863 971
31 97 167 241 331 419 499 599 677 773 877 977
37 101 173 251 337 421 503 601 683 787 881 983
41 103 179 257 347 431 509 607 691 797 883 991
43 107 181 263 349 433 521 613 701 809 887 997
Пользуясь этой таблицей, мы можем простой справкой в ней узнать, яв-
ляется ли любое данное число первой тысячи простым или составным, а при-
меняя надлежащие деления, можем это узнать относительно любого числа пер-
вого миллиона.
Так. чтобы установить вид числа 875 053, надо пробовать делить его на
все простые числа этой таблицы до 883 (оказывается, что 875 053 делится
только на 883 и 991).
§ 107. П. Л. Чебышев и И. М. Виноградов. Распознавание простых и
составных чисел — одна из арифметиче-
ских задач, которой люди стали зани-
маться очень давно, но которая не реше-
на полностью до нашего времени. На-
ряду с ней существует много других
труднейших арифметических задач, свя-
занных с простыми числами, частью уже
решённых, частью нет. Ими занимается
наука, называемая теорией чисел; многие
из них решены русскими учёными. Осо-
бенно велико значение работ академика
Пафнутия Львовича Чебышева, жившего
ещё в дореволюционное время (с 1821 по
1894 г.), и советского академика, лауреата
Сталинской премии, Героя Социалисти-
ческого Труда Ивана Матвеевича Вино-
градова (родился в 1891 г.).
Из ряда труднейших задач, решён-
ных П. Л. Чебышевым, укажем только
одну. Он доказал, что между любым на-
туральным числом, большим 1, и числом,
вдвое большим, всегда имеется по край-
ней мере одно простое число. Легко ви-
деть, что для небольших чисел это так:
П. Л. Чебышев.
между 2 и 4 есть простое число 3,
между 3 и 6 простое число 5, между 4
и 8 два простых числа, а именно
82
5 и 7; между 5 и 10 простое число 7 и т. д.
Но будет ли так для всех остальных на-
туральных чисел? Простая проверка здесь
невозможна, так как натуральных чисел
бесконечно много. Давно предполагали,
что этим свойством обладают все нату-
ральные числа начиная с 2, но оконча-
тельно решить вопрос не мог никто,
хотя занимались этим вопросом многие
виднейшие учёные всего мира, и только
П. Л. Чебышев сделал это в 1850 г.
В 1742 г. член Петербургской Ака-
демии наук Гольдбах высказал догадку,
что любое число, большее 5, представ-
ляет собой сумму трёх простых чисел.
Действительно, эта догадка проверяется
на всех числах, к каким её пробовали
применить: 6 = 24-2 + 2, 7 = 2+ 2 + 3,
8 = 2 + 3 +3, 9 = 3 + 3 +3, 10 = 2 +
+ 3 + 5 и т. д. Но выяснить, верна ли
она для всех натуральных чисел, оказа-
лось очень трудным. Возникла проблема
Гольдбаха, над которой крупнейшие ма-
тематики мира безуспешно работали в
течение почти 200 лет. Лишь в 1937 г.
И. М. Виноградов.
эту проблему почти полностью решил
академик И. М. Виноградов, доказавший, что всякое достаточно большое не-
чётное число есть сумма трёх простых чисел.
Раздел 4. РАЗЛОЖЕНИЕ ЧИСЕЛ НА ПРОСТЫЕ
МНОЖИТЕЛИ
§ 108. Как выразить составное число в виде произведения
простых чисел? В дальнейшем часто будет необходимо уметь
представить данное составное число в виде произведения простых
чисел. Оказывается, что любое составное число есть произведение
двух или более простых чисел. Для небольших чисел это легко
проверить:
4 = 2-2, 6 = 2-3, 8 = 2-2-2, 9 = 3-3, 12 = 2 - 2 - 3 и т. д.
В том, что это утверждение верно для любого составного
числа, убеждает следующее рассуждение.
Как было показано в § 103, любое данное составное число
имеет по крайней мере один простой делитель. Разделив на него
данное число, получаем в частном или простое число (I случай),
или составное (II случай).
Например, разделив 35 на 5, получаем в частном простое
число 7, а разделив 30 на 2, получаем составное число 15.
В I случае данное составное число есть произведение двух про-
стых (в примере 35 = 5 • 7). Во II случае данное составное число
есть произведение простого на составное (в примере 30 = 2 • 15).
У этого составного имеется по крайней мере один простой дели-
тель, и деление на него опять-таки даёт один из тех же двух
случаев. В примере составное число 15 есть произведение про-
5*
83
стых чисел 3 и 5, а потому число 30 = 2 15 есть произведение
трёх простых чисел: 30 = 2 • 3 5.
Взяв число 36, последовательно получаем
36 = 2 - 18 = 2 • (2 • 9) = 2 2 • (3 • 3) = 2 • 2 • 3 • 3.
Как видим, это число есть произведение четырёх простых мно-
жителей.
Когда делят на число, большее единицы, получается частное,
меньшее, чем делимое, а потому, действуя указанным способом,
мы будем искать делители для всё меньших и меньших чисел и
тем самым дойдём до частного — простого числа.
Поэтому любое составное число, как бы велико оно ни было,
можно представить в виде произведения простых чисел или, как
говорят, разложить на простые множители.
Записывая простые множители данного составного числа,
обычно их располагают в порядке возрастания. Например:
30 = 2-3-5, 385 = 5- 7 -11.
Если какой-нибудь множитель повторяется, его пишут только
один раз, а несколько выше и правее пишут число, называемое
показателем, показывающее, сколько таких множителей надо
взять. Например, вместо произведения 3 • 3 пишут З2, что чи-
тается: «три с показателем два» или «три в квадрате», вместо
3 • 3 • 3 = З3 («три с показателем три» или «три в кубе»), вместо
3 • 3 • 3 • 3 = З4 («три с показателем 4») и т. д. х. Разложение
числа 8 записывается как 23; числа 24 как 23 • 3; числа 420 как
22 • 3 • 5 • 7; числа 4680как 23 • З2 5 • 13; числа 1668как22 • 3 • 139;
числа 11 412 как 22 • З2 • 317 и т. д.
Представить составное число в виде произведения можно не-
редко разными способами. Например,
420 = 42 • 10 = 21 -20 = 14 • 30.
Но разложение каждого составного числа на простые мно-
жители возможно только одним способом, т. е. это разложение
единственное.
Так, если будет предложено разным ученикам разложить
число 420000000 на простые множители, то все ученики получат
один и тот же результат, а именно:
420000000 = 28 3 • 57 - 7.
В том, что это так для заданных небольших чисел убеждаемся
пробами, а что это справедливо и для любых чисел, как угодно
больших, доказывается в высшей арифметике (теории чисел),
изучаемой в высших учебных заведениях. Итак, всякое составное
число можно представить в виде произведения простых чисел
и притом единственным образом.
1 Говорят также: «три во второй степени» (З2), «три в третьей степени»
(З3) и т. д.
84
§ 109. Техника разложения составных чисел на простые мно-
жители. Небольшие числа легко разложить на простые множители
в уме, с записью сразу окончательного результата. Например,
44 = 22-11, так как 44 =4-11, а 4=22; 45=32-5, так как 45 — 5 • 9;
9 = З2; 48 = 24 • 3, так как 48 = 6 • 8 = (2 - 3) • (2 - 2 - 2) = 2« • 3.
Иногда удаётся указать сразу разложение и для большего числа,
как, например, 1000 — 23 • 53, так как 1000 = 10-10-10; 10=2-5.
Каково бы ни было данное составное число, его всегда можно
разложить на множители начиная с выделения наименьшего
простого его делителя.
Так, чтобы разложить 1274, замечаем, что число делится на 2,
и находим дополнительный делитель (1274 : 2 = 637). Это число
637, как показывают признаки делимости, не кратно ни 2, ни 3,
ни 5, но, пробуя делить на 7, убеждаемся, что оно кратно 7.
Замечая, что 637 = 7-91, ищем дальше наименьший делитель
числа 91. Оказывается, что 91 делится на 7, причём в частном
получается простое число 13. Итак,
1274 = 2 637 = 2 - 7 • 91 = 2 - 7 • 7 • 13 = 2 • 72 • 13.
Выяснять делимость надо только на последовательные простые
числа 2, 3, 5, 7, ..., применяя, когда можно, признаки дели-
мости. Вот удобная краткая запись всего разложения («стол-
биком») :
1274 2
637
91
13
1
7
7
13
Ответ: 1274 = 2 • 72 • 13.
Здесь все деления легко сделать устно. Но если приходится
иметь дело с большими числами, некоторые деления выполняются
письменно (полностью или частично).
Вот пример. Разложить на простые множители число 114 885.
114885 3 851 : 7 = 121 (ост. 4)
38295 3 851 : 11 = 77 (ост. 4)
12765 3 851 : 13 = 65 (ост. 6)
4255 5 851 : 17 = 50 (ост. 1)
851 23 851 : 19 = 44 (ост. 15)
37 37 851 : 23 = 37
1
Ответ: 114885 = З3 • 5 • 23 - 37.
Дойдя здесь до числа 851, следовало бы навести справку в таб-
лице простых чисел (§ 106), так как если бы это число оказалось
простым, никаких проб делением не понадобилось бы.
Используя признаки делимости, можно значительно ускорить
работу разложения на простые множители. Вот запись, которую
85
следует рекомендовать для разложения на простые множители,
например чисел 39600, 16800:
39600 100 = 4 • 25 = 22 - 52
396 4 = 2-2 = 22
99 9 = 3-3 = З2
11 11
39 600 = 24 • З2 • 52 • 11
100 = 4 • 25=22 • 52
8 = 2 • 2 • 2 = 23
3 • 7
16800
168
21
16 800 = 25 • 3 • 52 • 7
§ 110. Общий признак делимости. Имея разложение двух чи-
сел на простые множители, можно решить вопрос о том, делится
ли одно из них на другое. Одно число делится на другое тогда
и только тогда, когда выполнены два условия: во-первых, если
делимое содержит все простые множители делителя, и, во-вторых,
если, кроме того, каждый простой множитель в делимом имеет
показатель, больший, чем показатель того же множителя в дели-
теле, или по крайней мере равный ему. Если хотя бы одно из этих
условий не выполнено, делимости быть не может; например,
320 = 2® • 5 не делится на 24 = 23 • 3, так как, делясь на 24, число
320 делилось бы и на делитель 24, равный 3, а этого нет; то же
число 320 не делится на 50 = 2 • 52, так как, делясь на 50, число
320 делилось бы и на делитель 50, равный 25 = 52, а этого нет. Де-
лимость обеспечена, если оба условия выполнены; например,
51 480 = 23 З2 • 5 - 11 • 13 делится на 156 = 22-3-13, так как первое
число можно представить в виде произведения (22 • 3 • 13) • (2 х
X 3-5 - 11) = 156-(2-3-5 - 11).
Этот общий признак делимости очень упрощает разыскание всех дели-
телей данного числа, чем мы уже занимались в § 92. Пусть, например, надо
найти все делители числа 1170 = 2-32-5- 13. Перебирая все последовательные
натуральные числа начиная с 2 и принимая во внимание их разложения,
сразу видно, что делители здесь таковы:
1 2 3 5 6 9 10 13 15 18 26 30
1170 385 390 234 195 130 117 90 78 65 45 39
Под каждым найденным делителем здесь записан делитель дополнительный.
Дойдя до делителя 30, перебираем дальше последовательные числа: 31; 32 = 2®;
33 = 3 - 11; 34 = 2 • 17; 35 = 5 • 7; 36 = 22 • З2; 37; 38 = 2 • 19; 39 = 3 • 13,
и убеждаемся, пользуясь общим признаком делимости, что ни одно из них,
кроме последнего, не является делителем для 1170 (так как в каждое входит
такой простой делитель, который не входит в разложение данного числа или
входит с большим показателем). Но этот делитель (39) уже записан как до-
полнительный для 30, поэтому список делителей исчерпан.
Глава VI. НАИБОЛЬШИЙ ОБЩИЙ ДЕЛИТЕЛЬ
И НАИМЕНЬШЕЕ ОБЩЕЕ КРАТНОЕ ДАННЫХ ЧИСЕЛ
Раздел 1. ОБЩИЕ ДЕЛИТЕЛИ И НАИБОЛЬШИЙ ОБЩИЙ ДЕЛИТЕЛЬ
§ 111. Что называется общим делителем данных натуральных
чисел? Если имеются в одной школе 36, а в другой 40 физкуль-
турников, то каждая школа может построить колонны с равным
числом учащихся в каждом ряду следующим образом. Первая
86
школа имеет 9 возможностей — поставить в один ряд по 1, по 2,
по 3, по 4, по 6, по 9, по 12, по 18, по 36. Вторая школа имеет
8 возможностей — поставить в один ряд по 1, по 2, по 4, по 5, по 8,
по 10, по 20, по 40. Если надо, чтобы первая и вторая школы шли
одинаковыми колоннами, то имеются только три возможности:
идти по одному в колонне, по 2 или по 4.
Здесь надо из делителей данных чисел 36 и 40 отобрать та-
кие, которые являются общими для них.
Делители 36: 1, 2, 3, 4, 6, 9, 12, 18, 36.
Делители 40: 1, 2, 4, 5, 8, 10, 20, 40.
Общие делители 36 и 40 будут: 1, 2, 4.
Общим делителем данных натуральных чисел называется вся-
кое натуральное число, на которое делится каждое из данных.
Найти все общие делители данных чисел можно посредством
отбора; для этого надо:
1) выписать все делители каждого из данных чисел;
2) отобрать из них те, которые одновременно служат делите-
лями для всех данных чисел.
Другой, более удобный способ получения всех общих делите-
лей указан в § 116.
§ 112. Что называется наибольшим общим делителем данных
натуральных чисел? Делителей у данного натурального числа ко-
нечное множество, потому и подавно общих делителей у несколь-
ких данных чисел будет также конечное множество. Эти общие
делители можно расположить в порядке возрастания: во всех
случаях будет вначале самый малый общий делитель—единица,
а в конце самый большой, который нельзя указать заранее, так
как он изменяется при переходе от одних данных чисел к другим.
Например: общие делители чисел 36 и 40 будут 1, 2, 4, наи-
больший общий делитель их 4; общие делители 40 и 80 будут
1, 2, 4, 5, 8, 10, 20, 40, наибольший общий делитель 40.
Наибольшим общим делителем данных чисел называется са-
мый большой из их общих делителей, или иначе: наибольшим об-
щим делителем данных чисел называется самое большое число,
на которое делится каждое из данных чисел.
Покажем, как находить НОД1 данных чисел способом нахо-
ждения их общих делителей.
1) Найти НОД (18 и 24).
Делители 18: 1, 2, 3, 6, 9, 18.
Делители 24: 1, 2, 3, 4, 6, 8, 12, 24.
Общие делители 18 и 24: 1, 2, 3, 6.
НОД (18 и 24) = 6.
2) Найти НОД (120, 420, 500).
Делители 120: 1, 2, 3, 4, 5,6, 8, 10, 12, 15, 20, 24, 30, 40, 60, 120.
1 НОД — сокращённая запись термина «наибольший общий делитель».
87
Делители 420: 1, 2, 3, 4, 5, 6,7, 10, 15, 20, 21, 28, 42,60,70,
84, 105, 140, 210, 420.
Делители 500: 1, 2, 4, 5, 10, 20, 25, 50, 100, 125, 250, 500.
Общие делители чисел 120, 420, 500: 1, 2, 4, 5, 10, 20.
НОД (120, 420, 500) = 20.
§ ИЗ. Взаимно простые числа. Всякая пара натуральных
чисел имеет единицу в качестве общего делителя. Существуют
пары чисел, у которых наибольший общий делитель есть еди-
ница; такова, например, пара 9 и 16; такие числа называются
взаимно простыми. Есть пары чисел, у которых наибольший
общий делитель не равен единице; например, пара 10 и 2 имеет
наибольший общий делитель 2; такие числа не являются взаимно
простыми.
Взаимно простыми числами называются два или несколько
натуральных чисел, наибольший общий делитель которых равен
единице.
Во многих машинах (например, в токарных станках) имеются
зубчатые передачи, при помощи которых изменяют скорость или
направление вращения. На рисунке 12 изображены две такие
Рис. 12.
передачи: одна из колёс с 12 и 25 зубцами, другая из колёс
с 10 и 20 зубцами. Числа зубцов первой пары колёс — взаимно
простые, второй — нет. В работе этих двух передач можно заме-
тить существенную разницу: в то время как во второй один
и тот же зубец большого колеса часто попадает в одну и ту же
впадину малого колеса, а именно через каждые два оборота ма-
лого колеса, в первой передаче это будет происходить гораздо
реже — только через каждые 25 оборотов малого колеса. Подбор
числа зубцов имеет большое практическое значение; не следует
88
брать передачу, подобную второй, так как чем чаще будет вхо-
дить один и тот же зубец в ту же впадину, тем скорее произой-
дёт износ шестерни, а работа станка при этом не будет плавной.
§ 114. Некоторые свойства НОД. Сравним разложения на
простые множители каждого из данных чисел, например:
120 = 23 • 3 • 5; 420 = 22.3 • 5 - 7; 500 = 22 • 58,
с разложением их наибольшего общего делителя, равным в дан-
ном примере 20 = 22 • 5. Легко видеть, что наибольший общий
делитель любых чисел имеет следующие свойства.
I. Если НОД данных чисел выразить через произведение
простых чисел, то легко видеть, что множители этого произведе-
ния входят в каждое данное число и нет в этом произведении
такого множителя, который бы не входил в каждое из данных
чисел.
В нашем примере НОД содержит простые множители 2 и 5,
которые входят в разложение каждого из трёх данных чисел, и
не содержит ни множителя 3, так как его нет в разложении 500,
ни множителя 7, так как его нет в разложениях 120 и 500, ни
каких-либо других простых множителей.
Если НОД содержит какой-нибудь простой множитель р,
каждое из данных чисел, делясь на НОД, должно делиться и
на р, а потому должно иметь р в своём разложении (§ ПО).
II. Каждый простой множитель входит в разложение НОД с
показателем, наименьшим из всех, с каким он входит в разложе-
ния данных чисел.
В нашем примере данные числа содержат соответственно мно-
жители 23, 22, 22, а наибольший общий делитель—множитель 22;
они содержат множители 5, 5, 53, а наибольший общий делитель—
множитель 5.
Любой простой множитель р, входящий в разложение наи-
большего общего делителя, не может иметь показатель, больший,
чем тот, с каким р входит в разложения данных чисел, так как
иначе какое-нибудь из данных чисел на него не делилось бы (§ 110).
III. Каждый делитель НОД данных чисёл есть общий дели-
тель этих чисел. Например, наибольший общий делитель чисел
18 и 24 есть 6; у числа 6 имеются делители 1, 2, 3, 6; все они яв-
ляются общими делителями чисел 18, 24. Иначе, конечно, и быть
не может: каждое из данных чисел делится на их наибольший
общий делитель, а потому делится и на любой делитель НОД.
IV. Всякий общий делитель данных чисел есть делитель их
наибольшего общего делителя. Например, у чисел 18 и 24 нет
других общих делителей, кроме тех четырёх чисел 1, 2, 3, 6,
которые являются делителями наибольшего общего делителя чи-
сел 18 и 24, равного 6.
Сравнение разложений данных чисел с разложением их наи-
большего общего делителя показывает, если принять во внимание
общий признак делимости (§ ПО), что так бывает всегда.
89
Раздел 2. ТЕХНИКА НАХОЖДЕНИЯ НАИБОЛЬШЕГО
ОБЩЕГО ДЕЛИТЕЛЯ
§ 115. Нахождение НОД посредством разложения на множи-
тели. Знание свойств наибольшего общего делителя позволяет на-
ходить наибольший общий делитель гораздо быстрее, чем посред-
ством отбора общих делителей.
Для получения наибольшего общего делителя достаточно раз-
ложить каждое из данных чисел на простые множители и взять
произведение общих простых множителей с наименьшими пока-
зателями, с какими они входят в эти разложения.
Если данные числа невелики, всё делается без записи, как,
например, при разыскании наибольшего общего делителя чисел
45 и 75, равного 15. Если же данные числа велики, находят
письменно их разложения на простые множители, после чего
сразу записывают наибольший общий делитель.
Например, желая найти наибольший общий делитель чисел
39600 и 16 800, находят сначала их разложения на простые мно-
жители:
39600 = 24 З2 • 52 • 11; 16 800 = 25 • 3 • 52 • 7,
а потом сразу заключают, что искомый наибольший общий де-
литель есть 24 - 3 • 52 = 1200.
Ещё пример: найти наибольший общий делитель чисел 4181
и 4847. Здесь труднее разложить на множители. После ряда
пробных делений находим, что у числа 4181 есть делитель 37,
и получаем разложение:
4181 =37 • 113.
Пробуя делить 4847 на 37, убеждаемся, что
4847 = 37 • 131.
Числа 113 и 131 — простые (см. таблицу в § 106), а потому наи-
больший общий делитель чисел 4181 и 4847 равен 37.
Если требуется найти наибольший общий делитель чисел 1600
и 1800, можно рекомендовать следующую запись:
1600 100 = 22 • 52 1800 100 = 22 • 52
16 8 = 23 18 9 = З2
2 2 2 2
1600 = 26 • 52 1800 = 23 - З2 • 52
НОД (1600; 1800) = 23 • 52 = 8 • 25 = 200.
§ 116. Нахождение всех общих делителей при помощи наи-
большего общего делителя. В § 111 мы видели, что найти все
общие делители данных чисел можно посредством отбора. Но
S0
свойства III и IV, установленные для наибольшего общего дели-
теля в § 114, позволяют решать эту задачу гораздо проще: надо
найти наибольший общий делитель данных чисел, а затем найти
все делители этого наибольшего общего делителя; это и будут
все общие делители данных чисел. Например, желая найти все
общие делители чисел 120, 420, 500, находим их наибольший
общий делитель, равный 20, а потом все делители этого числа 20,
а именно делители 1, 2, 4, 5, 10, 20; это и есть все общие де-
лители чисел 120, 420 и 500.
§ 117. Способ нахождения наибольшего общего делителя, основанный на
последовательном делении. Как видим, вся трудность разыскания наибольшего
общего делителя заключается в разложении данных чисел на простые множи-
тели. Эту трудность преодолел в III в. до нашей эры гениальный Евклид, ко-
торый в своих «Началах» указал приём последовательного деления. Этот приём
основан на следующих двух свойствах наибольшего общего делителя.
I. Если большее из двух данных чисел делится на меньшее, то меньшее
число есть наибольший общий делитель этих двух данных чисел.
В самом деле:
1) Пусть взяты числа 3060 и 60, где
3060 : 60 = 51.
2) 60 есть общий делитель чисел 60
и 3060, так как каждое из этих
чисел делится на 60.
3) Число 60 не разделится ни на ка-
кое число, большее 60; значит, 60
есть самый большой общий дели-
тель чисел 60 и 3060, т. е. их НОД.
1) Пусть взяты числа а и Ь, где
а :Ь = с.
2) b есть общий делитель чисел а и Ь,
так как a :b = c; b : b = 1.
3) Число b не разделится ни на какое
число, большее 6; значит, Ь есть
самый большой общий делитель чи-
сел а и Ь, т. е. их НОД.
II. Если большее из двух данных чисел не делится на меньшее, то наи-
больший общий делитель этих двух данных чисел равен наибольшему общему
делителю меньшего из иих и остатка от деления большего на меньшее.
В самом деле:
1) Возьмем числа 3075 и 60; имеем
3075 = 60 • 51 + 15,
где 51 есть частное от деления 3075
на 60, 15 — остаток.
2) Пусть взят какой-нибудь об-
щий делитель чисел 60 и 3075, напри-
мер 5.
3) По определению общего дели-
теля числа 3075 и 60 должны делить-
ся на 5 и на любой другой общий де-
литель данных чисел.
4) По признаку делимости про-
изведение (§ 96) 60 • 51 также должно
делиться на 5 и на любой общий де-
литель чисел 3075 и 60.
5) По признаку делимости разно-
сти (§ 95) 15, т. е. остаток, должен
делиться на 5 н на любой другой
общий делитель данных чисел.
1) Возьмем числа а и Ь < а; имеем
а = Ь • q + г,
где q есть частное от деления а на Ь,
г — остаток.
2) Пусть взят какой-нибудь об-
щий делитель чисел а и Ь, равный с.
3) По определению общего дели-
теля числа а и Ь должны делиться
на с.
4) По признаку делимости про-
изведения число b • q также должно
делиться на с и на любой общий де-
литель чисел а и Ь.
5) По признаку делимости раз-
ности г должно делиться на с н на
любой другой общий делитель дан-
ных чисел.
91
Следовательно, всякий общий делитель данных двух чисел есть общий де*
литель меньшего числа и остатка от деления большего числа на меньшее.
6) Пусть взят какой-нибудь об-
щий делитель чисел 60 и 15, напри-
мер 5. Числа 60 и 15 делятся на 5 и
на любой другой общий делитель
этих чисел.
7) По признакам делимости про-
изведения и суммы число
3075 = 60 -51 -1- 15
делится на 5 и на любой другой об-
щий делитель чисел 60 и 15.
6) Пусть взят какой-нибудь об-
щий делитель чисел b и г, равный d.
Числа b и г делятся иа d, делятся и
на любой другой общий делитель этих
чисел.
7) По признакам делимости про-
изведения и суммы число
а = b q + г
делится на d и на любой другой об-
щий делитель чисел bur.
Следовательно, кроме того, что всякий общий делитель двух данных чисел
есть общий делитель меньшего из них и остатка (от деления большего из них
иа меньшее), можно утверждать, что и обратно: всякий общий делитель мень-
шего из данных чисел и остатка (от деления большего из них на меньшее)
есть общий делитель двух данных чисел. Таким образом, эти две пары чисел
имеют одни и те же общие делители, в том числе и один и тот же наибольший
общий делитель.
Покажем на примерах, как с помощью свойств I и II можно иайти наи-
больший общий делитель любых двух чисел, не разлагая их на простые мно-
жители.
Пример 1. Найти наибольший общий делитель чисел 3075 и 60.
Разделив 3075 на 60, получаем частное 51 и в остатке 15, и по свойству II
заключаем, что наибольший общий делитель чисел 3075 и 60 есть в то же
время наибольший общий делитель чисел 60 и 15.
Разделив 60 на 15, получаем частное 4 и остаток 0; по свойству I заклю-
чаем, что НОД (60; 15) = 15.
Итак, НОД (3075; 60) = 15.
Пример 2. Найти НОД (4847; 4181).
Разделив 4847 на 4181, получаем частное 1 и остаток 666,
НОД (4847; 4181) = НОД (4181; 666).
Разделив 4181 на 666, получаем частное 6 и остаток 185,
НОД (4181, 666) = НОД (666; 185).
Разделив 666 иа 185, получаем частное 3 и остаток 111,
НОД (666; 185) = НОД (185; 111),
Разделив 185 на 111, получаем частное 1 и остаток 74,
НОД (185; 111) = НОД (111; 74).
Разделив 111 на 74, получаем частное 1, остаток 37,
НОД (111; 74) = НОД (74; 37).
Разделив 74 на 37, получаем частное 2 и остаток 0,
НОД (74; 37) = 37.
Итак, НОД (4847; 4181) = 37.
Понятно, что найти этот результат посредством разложения на простые
множители было бы значительно труднее.
Вывод. Для получения наибольшего общего делителя двух натуральных
чисел достаточно: 1) разделить большее число на меньшее; 2) меньшее на пер-
вый остаток; 3) первый остаток на второй остаток и т. д. до тех пор, пока
ие получится частное без остатка; 4) первый делитель, при котором осуще-
ствится деление без остатка, и будет наибольший общий делитель данных
чисел.
S2
Понятно, что техника нахождения НОД последовательным делением должна
быть краткой. Она имеет следующий вид:
1) Найти НОД (3075; 60)
3075 60
75 51
60 15
4;
Следовательно, 15 = НОД (3075; 60).
2) Найти НОД (15456; 14041).
1415
1306 I 109
216 |11
15456
14041 | 1415
1306 | 9
1
I 14041
| 1
Следовательно, 1 = НОД (15 456; 14 041), т. е. эти числа взаимно про-
стые.
Понятно, что найти НОД этих чисел посредством разложения на простые
множители было бы гораздо труднее.
Чтобы получить этим способом последовательного деления наибольший
общий делитель трёх, четырёх и большего числа данных чисел, находят сперва
наибольший общий делитель первых двух, потом наибольший общий делитель
полученного числа и третьего из данных чисел, затем наибольший общий де-
литель полученного числа и четвёртого из данных чисел и т. д., пока не пере-
берут все данные числа. Например, чтобы найти наибольший общий делитель
чисел 748, 561, 493, находят сперва НОД (748; 561)= 187, затем НОД (187;
493)= 17. Это последнее число и есть искомое.
Раздел 3. ОБЩИЕ КРАТНЫЕ И НАИМЕНЬШЕЕ ОБЩЕЕ КРАТНОЕ
ДАННЫХ ЧИСЕЛ
§ 118. Что называется общим кратным данных натуральных
чисел? На рисунке 13 представлено полотно железной дороги,
где по одну сторону идут телеграфные столбы на расстоянии 40 м
друг от друга, а по другую сторону на расстоянии 50 м. На стан-
ции оба столба находились друг против друга по разные стороны
полотна, а дальше стали расходиться, так как между ними разные
промежутки. Через сколько метров от станции будут происходить
Рис. 13.
вновь совпадения, т. е. столбы левой и правой сторон полотна
окажутся друг против друга (будут находиться на одном и том же
расстоянии от станции)? Чтобы ответить на этот вопрос, надо
93
найти такие числа, которые одновременно делились бы и на 40
и на 50. Таковыми будут: 200, 400, 600, 800, 1000 и т. д. Каждое из
этих чисел называется общим кратным чисел 40 и 50.
Общим кратным данных чисел называется всякое натуральное
число, которое делится на каждое из данных чисел без остатка.
Отметим, что произведение данных чисел является их общим
кратным, так как оно делится на каждое из них. Умножив полу-
ченное общее кратное на любое натуральное число, найдём ещё
общее кратное, большее, чем полученное ранее. Так как нату-
ральных чисел бесконечное множество, то и общих кратных для
данных чисел будет бесконечное множество. Этим объясняется,
что приведённая выше последовательность чисел 200, 400, 600,
800, 1000 и т. д. оборвана словами «и т. д.».
Если взять для зубчатой передачи колёса в 36 и 40 зубцов, то
каждый зуб одного колеса будет попадать в ту же впадину дру-
гого через поворот на числа зубцов: 360, 720, 1080, 1440 и т. д.,
являющиеся общими кратными чисел 36 и 40, или через число
оборотов первого: 10, 20, 30, 40 и т. д., второго: 9, 18, 27, 36 и т. д.
§ 119. Что называется наименьшим общим кратным данных
натуральных чисел?
Наименьшим общим кратным данных чисел называется самое
малое натуральное число, которое делится на каждое из данных
чисел.
Каковы бы ни были данные числа, их наименьшее общее крат-
ное можно получить, выписывая все последовательные кратные
каждого из них, не превосходящие их произведения. Например,
чтобы найти наименьшее общее кратное чисел 6 и 9, находим
6 • 9 = 54 и выписываем все кратные числа 6, не превосходящие 54;
6 • 1 = 6; 6 2 = 12; 6 3 = 18; 6 4 = 24; 6 • 5 = 30; 6 • 6 = 36;
6 • 7 = 42; 6 • 8 = 48; 6 • 9 = 54,
и все кратные числа 9, тоже не превосходящие 54:
9 • 1 = 9; 9 • 2 = 18; 9 • 3 = 27; 9 • 4 = 36; 9 • 5 = 45; 9 • 6 = 54.
Сравнивая эти два ряда кратных, замечаем, что общими крат-
ными для 6 и 9 являются числа
18, 36, 54, так что НОК 1 (6; 9) = 18.
Способ этот весьма громоздок; на практике применяется дру-
гой способ нахождения наименьшего общего кратного, основанный
на следующих его свойствах.
§ 120. Некоторые свойства НОК. Предполагая, что и данные
числа и их наименьшие общие кратные разложены на простые
множители, легко установить, основываясь на общем признаке
делимости чисел, что наименьшее общее кратное любых чисел
имеет такие свойства:
1 НОК — сокращённая запись термина «наименьшее общее кратное».
94
I. Каждый простой множитель входит в НОК с показателем,
самым большим из тех, с каким он входит в разложение данных
чисел, и не входит в НОК никакой простой множитель, которого
нет в разложении данных чисел.
Разберёмся в этом на примере наименьшего общего кратного
чисел 6 и 9, равного, как мы видели, 18. Здесь
6 = 2-3,
9 = З2
НОК (6; 9) = 18 = 2 • З2.
Разложение наименьшего общего кратного содержит те и
только те простые множители 2 и 3, какие входят в разложение
данных чисел 6 и 9. Без множителей 2 и 3 не было бы дели-
мости на 6. Множитель 2 достаточно взять в наимень-
шем общем кратном один раз, но множитель 3 — два раза,
так как иначе не было бы делимости на 9. Никаких множителей,
которых нет в разложении данных чисел, нет и в наименьшем
общем кратном; добавление какого-нибудь такого множителя,
например 5, дало бы (18-5 = 90) опять-таки общее кратное, но
не наименьшее общее кратное. Эти соображения объясняют пер-
вое указанное выше свойство наименьшего общего кратного.
II. Наименьшее общее кратное двух взаимно простых чисел
равно их произведению.
Если два числа взаимно просты, у них нет ни одного общего
делителя, большего, чем 1, их разложения не содержат ни одного
общего множителя; их наименьшее общее кратное получается,
если к разложению одного добавить полностью разложение дру-
гого, т. е. их наименьшее общее кратное равно их произведению.
Например:
8 = 23,
9 = З2,
НОК (8; 9) = 23 • З2 = 72.
III. Произведение наименьшего общего кратного двух данных
чисел на их наибольший общий делитель равно произведению
данных чисел.
Пусть даны два числа, например 60 и 36. Разложим их на
простые множители и найдём их наибольший общий делитель:
60 = 22 3 • 5, 36 = 22 • З2,
НОД (60; 36) = 22 • 3.
Отсюда видим:
60 = 22 3 • 5 = 5 • (22 3) = 5 • НОД(60; 36),
36 = 22 • З2 = 3 (22 • 3) = 3 • НОД (60; 36);
Короче:
60 = 5 • НОД (60; 36),
36 = 3-НОД(60; 36).
95
Перемножим:
60 • 36 = [5 • НОД (60; 36)] [3 • НОД (60; 36)],
или:
60 - 36 = [5 - НОД (60; 36) • 3] • НОД (60; 36).
Из последней формулы видим, что в квадратных скобках
стоит первое данное число, умноженное на 3, т. е. на тот мно-
житель второго числа, которого нет в первом. Следовательно,
в квадратных скобках находится НОК (60; 36).
Итак, имеем:
60 • 36 = НОК (60; 36) • НОД (60; 36).
Раздел 4. ТЕХНИКА НАХОЖДЕНИЯ НАИМЕНЬШЕГО ОБЩЕГО
КРАТНОГО
§ 121. Нахождение наименьшего общего кратного посредством
разложения на простые множители. Для небольших чисел наи-
меньшее общее кратное отыскивают в уме, разлагая каждое из
данных чисел на простые множители и руководствуясь I и II
свойствами наименьшего общего кратного (§ 120). Так, чтобы
найти НОК (30; 36), замечают, что разложение числа 30 содержит
три простых множителя — 2, 3, 5, каждый по одному разу, а раз-
ложение числа 36 — два простых множителя 2 и 3, каждый по
два раза.
В разложение НОК (30; 36) должны войти все эти три простых
множителя 2, 3, 5, причём первые два по два раза, а потому
искомое наименьшее общее кратное равно:
22 • З2 • 5 = 36 • 5 = 180.
Можно сказать, что мы взяли второе из данных чисел 36, убе-
дились, что для делимости на 30 в его разложении недостаёт
одного простого множителя, а именно 5, и нашли произведение
36-5 = 180.
Чтобы найти наименьшее общее кратное трёх чисел, напри-
мер НОК (30; 36; 42), надо, найдя НОК (30; 36) = 180, сообра-
зить, чего недостаёт в этом числе
180 = 22 - З2 • 5
для делимости на 42 = 2 • 3 7, и добавить этот недостающий
множитель 7, что и даёт:
НОК (30; 36; 42) = 180 • 7 = 1260.
Если данные числа велики, разыскание их наименьшего общего
кратного ведут письменно, действуя по следующему правилу:
чтобы найти наименьшее общее кратное любого числа данных чи-
сел, разлагают каждое на простые множители и берут произведе-
ние всех полученных простых множителей с наибольшими пока-
зателями, с какими они входят в эти разложения.
96
Пусть, например, надо найти НОК (60; 105; 150). Замечая, что
60 = 22 - 3 • 5; 105 = 3 - 5 - 7; 150 = 2 - 3 - 52, имеем НОК (60; 105;
150) = 22 • 3 - 52 • 7 = 100 • 21 = 2100.
Рекомендуется следующая краткая запись решения этой за-
дачи:
Найти НОК (60; 105; 150)
60 I 10 = 2 • 5 105 I 15 = 3 • 5 150 10 = 2-5
6 | 6 = 2 - 3 7 I 7 15 15 = 3-5
60 = 22 - 3 - 5 105 = 3- 5-7 150 = 2-3-52
НОК (60; 105; 150) = 22 3 - 52 - 7 = 2100.
Для получения наименьшего общего кратного надо: 1) разло-
жить каждое из данных чисел на простые множители, 2) из обра-
зовавшихся разложений выделить все общие простые множители,
взяв их с наибольшими показателями, и 3) перемножить выделен-
ные числа.
§ 122. Нахождение наименьшего общего кратного посредством наиболь-
шего общего делителя. Как было показано в § 120, произведение наименьшего
общего кратного двух данных чисел на их наибольший общий делитель равно
произведению этих данных чисел. Это позволяет находить наименьшее общее
кратное без разложения данных чисел на простые множители. Найдя наиболь-
ший общий делитель двух данных чисел способом последовательного деления
(§ П7), делят на него произведение данных чисел и получают в частном ис-
комое наименьшее общее кратное. Например, чтобы найти НОК (4847; 4181).
последовательным делением получаем
НОД (4847; 4181) = 37,
как это сделано в § 117, а затем делим 4847 • 4181 на 37.
Чтобы разделить произведение, достаточно разделить какой-либо один из
его сомножителей, а потому искомое НОК получаем, разделив на 37 первый
сомножитель
(4847 :37) • 4181 = 131 • 4181 = 547 711.
Для проверки вычисляем это НОК вторично, разделив на 37 второй сомно-
житель:
4847 • 4181 : 37 = 4847 • 113 = 547 711.
6 Арифметика
Часть II
ДРОБНЫЕ ЧИСЛА
Глава VII. ВЕЛИЧИНЫ И ИХ ЗНАЧЕНИЯ
§ 123. Счёт и измерение. До сих пор мы имели дело только с
натуральными числами и нулём, которые служат для выражения
численности различных множеств. Но есть ещё и другое приме-
нение чисел: они служат для выражения значений таких величин,
как длина предмета, как вес различных предметов, как время и
многие другие.
Арифметика изучает не только натуральные числа, которые
применяются при счёте элементов множества, но и дробные
числа, какими пользуются, кроме натуральных чисел, при изме-
рении величин. Этими дробными числами мы и будем заниматься
в настоящей второй части книги. Предварительно рассмотрим
некоторые величины и способы их измерения.
Раздел 1. ОТРЕЗОК И ЕГО ДЛИНА
§ 124. Прямая линия. Если аккуратно сложить вдвое лист
бумаги, получим в сгибе прямую линию АВ (рис. 14).
Рис. 14.
Для проведения прямых линий на бумаге пользуются линейкой
(рис. 15), предварительно убедившись, что её ребро действительно
прямолинейно. Для проверки этого линейку кладут на бумагу и
проводят по ребру прямую, на которой отмечают какие-нибудь
две точки А н В (рис. 16), а затем переворачивают её и по тому
98
же ребру снова проводят прямую через те же точки А и В.
Если проверяемое ребро правильно, вторая прямая сольётся с
первой; если они не слились, это ребро не прямое, а кривое;
линейку надо заменить или исправить.
Рис. 15.
Рис. 16.
Иногда приходится проводить более длинные отрезки прямых,
например на длинной доске. Тогда вместо линейки берут тонкую
бечёвку, натирают её ме-
лом, прижимают к доске уЛ _ . , ,
в двух данных точках А
и В, туго натянув её, а за- ~ _ Jr
тем оттягивают в какой- г
нибудь внутренней точке Рис. 17.
и резко отпускают. Уда-
рившись о доску, бечёвка даёт на ней отпечаток в виде прямой
линии (рис. 17).
Когда требуется провести ещё более длинный отрезок на мест-
ности, применяется провешивание: поставив в двух данных точках
А и В вехи, устанавливают третью веху Стак, чтобы она закрывала
веху В, если смотреть от вехи А (рис. 18).
Рис. 18.
6*
99
Затем то же делают с вехами В и С и устанавливают четвёр-
тую веху D и т. д.
§ 125. Отрезок и единицы длины.
Отрезком называется часть прямой линии, заключённая
между какими-нибудь двумя её точками. На рисунке 19 изобра-
жены три отрезка, называемые единицами длины, или мерами
длины, а именно: миллиметр, сокращённо обозначаемый буквами
мм, сантиметр (сокращённо см), содержащий 10 мм, и дециметр
(сокращённо дм), содержащий 10 см, или 10 • 10 = 100 мм.
tHH ч
/ cn •
I вн » ---------------------------------------------—<
Рис. 19.
Кроме миллиметров, сантиметров и дециметров, употребляются
также более крупные единицы длины, а именно метр (сокращён-
но м), содержащий 10 дм, или 100 см, или 1000 мм, и километр
(км), содержащий 1000 м. Существуют ещё единицы длины: дека-
метр (дкм), содержащий 10 м, и гектометр (гм), содержащий
100 м, но эти меры на практике редко применяются.
Для измерения очень малых отрезков употребляется единица
длины микрон (сокращённо |х). В 1 мм содержится 1000 микронов.
Лист бумаги, на которой напечатана эта книга, имеет толщину
около 100 у., тончайшая паутинка — около 10 |х.
Единицы длины называются линейными единицами.
§ 126. Измерение длины.
Измерить длину отрезка — значит узнать, сколько раз в нём
укладывается какая-нибудь единица длины. Для измерения не-
больших отрезков пользуются масштабной линейкой, вдоль ребра
которой нанесены миллиметровые и сантиметровые деления, как
на рисунке 20.
Рис. 20.
Чтобы измерить длину отрезка при помощи масштабной ли-
нейки, её прикладывают к измеряемому отрезку так, чтобы началь-
ная точка, обозначенная цифрой 0, совпала с одним концом от-
резка, и смотрят, против какого деления линейки оказался другой
его конец. На рисунке 20 изображено измерение длины спички,
показывающее, что её длина 48 мм.
Более длинные отрезки измеряются при помощи рулетки
(рис. 21); в ней имеется лента, обычно 10 или20л« длиной, с де-
лениями на метры и дециметры.
100
Длина отрезка АВ иначе называется расстоянием между его
концами А и В.
§ 127. Метрические меры длины. У нас в СССР и почти во
всех других странах мира употребляются указанные выше меры
длины, именуемые метрическими. Основной мерой является метр-,
длина этого отрезка была взята не произвольно, а при измерении
земного меридиана, о чём речь будет дальше (в § 135). Названия
других единиц длины получились с помощью латинских слов деци
(одна десятая), санти (одна сотая), милли (одна тысячная) и гре-
ческих слов дека (десять), гекто (сто), кило (тысяча).
Каждая метрическая единица длины содержит 10, или 100,
или 1000 и т. д. более мелких единиц. Так, например,
1 км = 10 гм = 100 дкм = 1000 м - 10000 дм = 100000 см =
= 1 000 000 мм.
Так как умножение и деление
на 10, 100, 1000 и т. д. производится
в нашей десятичной нумерации осо-
бенно просто, то переход от одних
метрических мер к другим выпол-
няется всегда устно. Такой переход
от более крупных мер к более мел-
ким называется раздроблением и
выполняется с помощью умножения Рис. 21.
на 10, 100, 1000 и т. д., а обратный
переход от более мелких к более крупным называется превра-
щением и требует деления на 10, 100, 1000 и т. д.
Примеры. Раздробление: 35 м = 350 дм = 3500 см —
= 35000 мм.
Превращение: 8000 см = 800 дм = 80 м.
§ 128. Старые русские и некоторые зарубежные меры длины. До Великой
Октябрьской социалистической революции в России употреблялись другие меры
длины, несравненно менее удобные, чем общепринятые в настоящее время
метрические: аршин, равный приближённо 71 см (точнее 71 см 1 мм 200 р);
сажень, содержащая три аршина; верста, содержащая 500 сажен; аршин под-
разделялся на 16 вершков. Мера аршин имела то удобство, что выражала
приближённо длину шага взрослого человека среднего роста. Наряду с этими
старыми русскими мерами в России применялись также столь же неудобные
старые английские меры, до сих пор употребляемые в Англии и Соединённых
Штатах, а раньше употреблявшиеся в некоторых других странах, в том числе
в Голландии, откуда они попали и в Россию. Важнейшие старые английские
меры длины: дюйм, равный приближённо 25 мм (точнее 25 мм 400 р), и фут
равный 12 дм. Старая русская сажень содержала ровно 7 футов. Для изме-
рения более длинных отрезков в Англии пользуются милей (английской),
содержащей 1609 м, и морской милей, содержащей 1852 м.
§ 129. Простые и составные именованные числа. Раздробление
и превращение. Значение величины иногда выражается при помощи
какой-нибудь одной единицы, а иногда при помощи двух и более
единиц. Например, измерение длины спички (рис. 20) дало число
48 мм, или, что то же, 4 см 8 мм. Говорят, чтоб первом случае
101
мы имеем простое именованное число, во втором составное име-
нованное число.
Всякое составное именованное число можно заменить простым
именованным числом, выражающим то же значение величины.
Для этого применяют раздробление более крупных единиц в бо-
лее мелкие. Составные именованные числа, выраженные в метри-
ческих мерах, заменяются простыми именованными числами осо-
бенно легко: весь расчёт делается в уме, сразу пишется окон-
чательный результат; например,
6 м 8 дм 7 см = 687 см\ 4 дм 5 мм = 405 мм\
2 км 453 м = 2453 2 км 72 м = 2072 м.
Обратно: простое именованное число можно во многих случаях
выразить составным именованным числом, применяя превращение
мелких мер в более крупные. В метрических мерах эта замена
простого именованного числа составным требует только деления на
10, 100, 1 000 и т. д. и выполняется в уме. Например, 3018734 мм
составляют 3 км 18 м 734 мм, или 3 км 18 м 7 дм 3 см 4 мм.
§ 130. Измерения по плану и карте. Масштаб. На плане
комнаты, здания, города, а также на всякой карте, изображающей
более или менее значительную часть поверхности земли, все
отрезки представляют собой уменьшённые изображения соответ-
ствующих отрезков на местности, причём мера этого уменьшения
называется масштабом плана или карты. Масштаб указывают
двумя способами: либо делают (на плане и карте) пометку, вроде
следующей: «в 1 см 200 му>, либо пишут, например, «масштаб
1 :20 000». В первом случае мы имеем указание, что каждый
отрезок длиной 1 см на карте соответствует отрезку длиной
200 м на местности. Во втором случае число, записанное после
цифры 1 и двоеточия, показывает, во сколько раз каждый отре-
зок на местности больше своего изображения на плане. При
масштабе 1 :20 000 отрезок длиной в 1 см на плане изображает
отрезок в 20000 см = 200 м на местности. Возьмём, например,
карту Европейской части СССР с пометкой «масштаб 1 : 5 000 000»
и измерим по ней расстояние от Москвы до Ленинграда. Получив
130 мм, легко находим действительное расстояние между этими
двумя городами, равное
130 мм • 5000000 = 650000000 мм = 650 000 м = 650 км.
Раздел 2. ОКРУЖНОСТЬ
§ 131. Определение окружности. Все предметы, среди которых
мы живём и которые постоянно приходится видеть, ограничены
поверхностями. Различают плоские поверхности, или плоскости,
и кривые поверхности. Например, вода, налитая в стакан, огра-
ничена сверху и снизу плоскостью, а с боков — кривой поверх-
ностью.
102
Плоскую поверхность имеет гладко оструганная доска, ровно
уложенный на столе лист бумаги, классная доска, оштукатурен-
ная стена и т. д. Кривые поверхности бывают различные. Особый
вид кривой поверхности, а именно цилиндрическую поверхность,
образует боковая стенка стакана. Другой особый вид кривой
поверхности представляет собой поверхность мяча, которая назы-
вается шаровой поверхностью, или сферой.
Возьмём на плоскости какую-нибудь точку О и какой-нибудь
отрезок АО (рис. 22). На этой плоскости имеется бесконечное
множество точек, отстоящих от точки О на такое же расстояние,
как и точка А, например точки В, С, D, Е и т. д. Все эти точки
Рис. 22. Рис. 23.
образуют линию, которая называется окружностью. Точка О
называется её центром, равные друг другу отрезки АО, ВО, СО,
DO, ЕО и т. д.— её радиусами.
Итак, окружностью называется такая проведённая на плоскости
замкнутая линия, все точки которой одинаково отстоят от неко-
торой точки этой плоскости.
Два радиуса, расположенные на одной прямой, как, например,
радиусы ОА и OF на рисунке 22, составляют диаметр, или по-
перечник, окружности.
Хордой окружности называется отрезок, соединяющий две
какие-нибудь её точки. Например, на рисунке 23 показаны хорды
АВ и CD. Можно сказать, что диаметром окружности называется
всякая её хорда, проходящая через центр.
Часть плоскости, находящаяся внутри окружности, назы-
вается кругом.
§ 132. Циркуль. Для проведения прямых употребляется ли-
нейка, а для проведения окружностей — особый инструмент, на-
зываемый циркулем и изображённый на рисунке 24,о. Рядом
показаны некоторые замены чертёжного циркуля: циркульная
ножка, надеваемая на карандаш (рис. 24,6); полоска плотной
бумаги с отверстиями, в одно из которых вставляется булавка,
103
а в другое карандаш (рис. 24,в); бечёвка с двумя колышками,
которой пользуются для проведения окружностей большого ра-
диуса на земле (рис. 24,г).
Рис. 24.
§ 133. Дуга и дуговой градус.
Дугой окружности называется любая часть окружности, за-
ключённая между двумя её точками. Два конца одного диаметра
AD определяют на окружности две равные дуги, называемые
полуокружностями (рис. 25); они совпадают, если перегнуть чер-
тёж по этому диаметру. Две точки А и В, лежащие на одной
окружности, но не на одном её диаметре, делят окружность на
две дуги, из которых одна меньше, другая больше полуокруж-
ности. Говоря о дуге АВ, обычно имеют в виду дугу, меньшую
полуокружности.
Окружность принято делить на 360 равных частей; каждую
такую часть называют дуговым градусом, или просто градусом.
104
Итак, дуговым градусом называется такая дуга окружности, кото-
рая укладывается на ней ровно 360 раз.
Дуговые градусы обозначают маленьким кружком, поставлен-
ным справа и выше числа: вся окружность содержит 360°, полу-
окружность 180°. Число, показывающее, сколько дуговых гра-
дусов содержит дуга, называют градусной её мерой.
Существуют более мелкие единицы, чем градус, а именно:
минута, равная одной шестидесятой части градуса, и секунда,
равная одной шестидесятой части минуты.
Дуги измеряют при помощи инструмента, называемого транс-
портиром и изображённого на рисунке 36 (стр. 109). Об
его применении сказано
в § 141. ---------------------Хг
§ 134. Длина окруж-
ности и длина дуги окруж- Рис. 26.
ности. Если хорда мала
по сравнению с радиусом, то она почти сливается с дугой. Отло-
жив такую малую хорду последовательно несколько раз на
дуге окружности, мы получаем ломаную линию, имеющую почти
ту же длину, что и соответствующая дуга.
На рисунке 26 изображена дуга АС окружности.
Откладывая хорду длиной 1 см по этой дуге, придём после
пяти откладываний в точку В, а проводя хорду ВС, убеждаемся,
что ВС — 2 лл. Итак, вся дуга АС имеет длину почти 52 мм.
Откладывая такие малые (по сравнению с радиусом) хорды,
можно измерить длину всякой дуги окружности и всей окружно-
сти. В главе XII мы рассмотрим другой, более удобный и
более точный способ измерения длины окружности.
Рис. 27.
Бающийся в меридиане 40 млн. раз.
и изготовили точный её образец, или
§ 135. Происхождение метра.
Раньше каждое государство имело
свои меры, и это создавало большие
неудобства, да и сами по себе эти
меры были во многом неудобны. В кон-
це XVIII в. передовые учёные рево-
люционной Франции провели большую
работу по созданию новой, весьма
совершенной системы мер, предна-
значенной «для всех времён, для всех
народов».
Единицу длины было решено взять
из природы. Планета Земля, на кото-
рой мы живём, представляет собой
почти шар, вращающийся около оси.
Если через эту ось мысленно провести
плоскость, она пересечёт поверхность
Земли почти по окружности, называ-
емой меридианом. Учёные сумели из-
мерить длину меридиана в старинных
французских мерах и приняли за но-
вую единицу длины отрезок, уклады-
Эту новую единицу назвали метром
эталон метра. В дальнейшем более
105
точные измерения показали, что этот эта-
лон укладывается в земном меридиане не
40 млн. раз, а несколько больше (по но-
вейшим измерениям 40 009 153 раза).
Однако изготовленный эталон решили не
менять, отступив от первоначального
замысла Таким образом, метром в насто-
ящее время считается точная длина эта-
лона, хранящегося в Международном бюро
мер и весов (в Севре близ Парижа), а
копия — во Всесоюзном научно-исследо-
вательском институте метрологии имени
Д. И. Менделеева в Ленинграде. Однако
полезно помнить, что дуга, составляю-
щая одну четверть земного меридиана,
содержит приблизительно 10 млн. м, или
10000 км, а весь меридиан 40 млн. м,
или 40 000 км (рис. 27).
Метрические меры оказались настоль-
ко удобными, что их постепенно при-
няли все государства мира, кроме Англии
и Соединённых Штатов Америки. В Рос-
сии ещё давно была проведена большая
Д. И. Менделеев. работа по введению метрической системы
в научные измерения и по подготовке её
введения в торговле, в быту, в промышленности.
Особенно большую работу по разработке и введению метрической системы
провёл знаменитый русский химик Дмитрий Иванович Менделеев, живший с
1834 по 1907 г.
Но царское правительство противилось переходу к метрической системе,
боясь нового, прогрессивного. Только после Великой Октябрьской социалисти-
ческой революции метрическая система была введена у нас во всеобщее упот-
ребление. Закон о ней был издан за подписью Владимира Ильича Ленина
14 сентября 1918 г.
Раздел 3. УГОЛ И ЕГО ИЗМЕРЕНИЕ
§ 136. Луч. Часть прямой, идущей только в одну сторону от
какой-нибудь её точки, называется лучом, а эта точка—начальной
точкой, или началом, луча.
На рисунке 28 изображены прямая АВ, луч CD, отрезок EF\
возможность неограничен-
ного продолжения обозна- —........................... —
чена пунктиром. D
§ 137. Угол. Всякие два ---------------—
луча, проведённые из одной
и той же начальной точки, fi — \г
образуют угол. Эти лучи на- Рис. 28.
зываются сторонами угла,
а их общая начальная точка — вершиной угла. Угол обозна-
чают тремя буквами, из которых первая указывает какую-
нибудь точку на одной стороне угла, вторая — его вершину, тре-
тья — какую-нибудь точку на другой его стороне. На рисунке 29
изображены четыре угла, и именно: АОВ, А1О1В1, А2ОгВ2, А303В3.
Всякий угол разделяет плоскость, в которой он лежит, на две
10G
части. Об одной из них говорят, что она находится внутри
угла, о другой — вне его. На рисунке 29 часть плоскости, на-
ходящаяся внутри каждого из изображенных на нем углов, от-
мечена штриховкой. Вырезав её,
модель угла (стороны мысленно
Если один угол можно на-
ложить на другой так, чтобы
совпали их вершины и сторо-
ны, то эти два угла равны.
Если при совмещении вершин
и одной пары сторон две дру-
гие стороны совместить нельзя,
углы неравны, причём меньше
тот угол, у которого вторая
сторона оказывается располо-
женной внутри другого угла.
На рисунке 30 показано
сравнение углов АОВ и AiO^i
например из бумаги, получаем
продолжаются неограниченно).
Рис. 29.
и установлено, что первый из них меньше второго.
Для сравнения углов у мастеров (столяров, слесарей и др.) име-
ется инструмент под названием малка, показанный на рисунке 31.
луча расположены
вершину, то они
Рис. 31.
§ 138. Развёрнутый и прямой угол. Если два
на одной и той же прямой и имеют общую
образуют угол особого рода, называемый развёрнутым. Развёрну-
тый угол есть не что иное, как
прямая линия, продолженная без
конца в обе стороны, с одной
отмеченной на ней точкой — вер-
шиной угла. На рисунке 29 раз-
вёрнутый угол изображён слева
внизу; он делит плоскость на две
полуплоскости.
Сложив вдвое кусок бумаги,
получаем модель полуплоскости.
Сложив его вдвое ещё раз, как
показано на рисунке 32, получим угол, составляющий половину
развёрнутого и называемый прямым. Всякий угол, меньший
прямого, называется острым, больший прямого — тупым. На ри-
107
сунке 29 изображены, кроме развёрнутого, ещё прямой угол
(справа внизу), острый (слева наверху), тупой (справа наверху).
§ 139. Угольник. Прямой угол строится на бумаге и на клас-
сной доске при помощи угольника. Угольники разного вида изо-
бражены на рисунке 33: первые три из них употребляются чер-
тёжниками и называются чертёжными треугольниками, четвёр-
тый — в столярном и слесарном деле.
Рис. 32.
Отрезки АО и ВО, расположенные на сторонах прямого угла,
называются катетами угольника, отрезок АВ — его гипотенузой
(рис. 34).
Прежде чем применять купленный или самодельный угольник,
его надо проверить. Для этого угольник кладут на бумагу, рас-
полагая один из его катетов, например АО, по ребру линейки,
как показано на рисунке 34,а, и проводят луч ОВг по другому
катету ОВ. Затем переворачивают угольник другой стороной,
опять-таки помещая вершину в точку О и располагая катет АО
Рис. 33.
б)
Рис. 34.
б)
по ребру линейки, и проводят луч ОВ2 по катету ОВ вторично.
Если эти два луча ОВг и ОВ2 совпадут, то угольник правилен.
Если же они не совпадут, то угольник неправилен, так как угол
АОВ меньше половины развёрнутого (рис, 34,6) или больше её
(рис. 34,в).
108
§ 140. Эккер. Если прямой угол приходится строить не на
бумаге, а на земле, пользоваться угольником неудобно. Вместо
угольника тогда применяют особый инструмент, называемый
эккером. Эккер простейшей конструкции изображён на рисунке 35.
Булавки А, В, С, D расположены так, что прямые АВ и CD об-
разуют четыре прямых угла.
Чтобы через данную на земле точку О провести луч, обра-
зующий прямой угол с проведённым на земле лучом ОЕ, вты-
кают колышек, на котором укреплён эккер, в
направляют прямую АВ по лучу ОЕ. Тогда
прямая CD определяет два луча, образующих
прямые углы с лучом ОЕ, и остаётся только от-
метить на местности какую-нибудь точку одного
из этих лучей.
Исправность эккера тоже следует проверять.
Для этого достаточно направить по данному лучу
ОЕ вместо прямой АВ другую прямую CD и
определить искомый луч при помощи булавок
Л и В (вместо С и D). Если получится тот же
луч, что и в первый раз, эккер правилен.
Получение другого луча показывает, что эккер
нуждается в исправлении.
§ 141. Измерение углов в градусах. Если,
приняв за центр вершину угла, провести ок-
ружность, то некоторая её дуга окажется вну-
этой точке О и
три угла. В случае развёрнутого угла внутри Рис. 35.
него окажется полуокружность, т. е. дуга в
180°, в случае прямого—в 90°, в случае острого дуга меньше,
чем в 90°, в случае тупого — дуга больше 90°, но меньше 180°.
Если внутри угла окажется дуга в один дуговой градус (1°), то
Рис. 36.
говорят, что угол этотесть угловой градус, его обозначают тем же
знаком, что и дуговой градус. Таким образом, измерение углов и
угловых градусов сводится к измерению дуг дуговыми градусами
и производится при помощи транспортира. На рисунке 36 пока-
зано, как надо уложить транспортир, чтобы измерить данный
угол АОВ-. в нём оказалось 55°.
100
Раздел 4. ПЛОЩАДИ
§ 142. Прямоугольник и квадрат. Прямоугольником назы-
вается фигура, которая строится следующим образом. Взяв какой-
нибудь отрезок АВ, проводят под прямыми углами к нему в одну
и ту же сторону два равных отрезка AD и ВС (рис. 37), затем
соединяют точки С и D. Оказывается, что углы ADC и BCD при
этом получаются прямыми, а отрезок DC равным отрезку АВ.
Четыре точки А, В, С, D называются вершинами прямоуголь-
ника, отрезки АВ, ВС, CD, DA — его сторонами. Таким образом,
в прямоугольнике имеются две пары соответственно равных сто-
рон (одна пара — АВ и CD, другая пара — AD и ВС) и четыре
прямых угла.
Рис. 38.
Длины двух сторон, сходящихся в одну вершину, называются
измерениями прямоугольника. Часто большее из них называют
длиной прямоугольника, а меньшее — его шириной или высотой.
Прямоугольник с равными сторонами называется квадратом
(рис. 38). Всякий квадрат, следовательно, есть в то же время
прямоугольник, но не всякий прямоугольник — квадрат.
§ 143. Квадратные единицы. Квадратной единицей, или еди-
ницей площади, называют всякий такой квадрат, стороны кото-
рого равны единице длины. На рисунке 39 мы видим квадрат-
ный дециметр, т. е. квадрат со стороной в 1 дм, или 10 см.
В левом нижнем его углу изображён квадратный сантиметр, а
в левом нижнем углу квадратного сантиметра — квадратный мил-
лиметр.
На классной доске или на полу комнаты нетрудно изобра-
зить квадратный метр, т. е. квадрат, каждая сторона которого
равна 1 м, а на дворе—квадратный декаметр, т. е. квадрат, каж-
дая сторона которого равна 1 декаметру (или 10 м).
Для квадратного декаметра существует удобное краткое на-
звание— ар1. Квадратный гектометр, т. е. квадрат со стороной
в 1 гм (или 100 м), иначе называется гектар. Квадратный ки-
лометр есть квадрат, сторона которого равна 1 км. Все эти на-
1 В повседневной жизни ар называют соткой, так как он равен одной
сотой части гектара.
НО
звания квадратных единиц записываются сокращённо следующим
образом:
квадратный дециметр — кв. дм, или дм2,
квадратный сантиметр — кв. см, или см2,
квадратный миллиметр — кв. мм, или мм2,
гектар — га, квадратный километр — кв. км, или км2.
1 квадратный
дециметр
1 кв см
1к&мм
Рис. 39.
Говорят, что каждая квадратная единица соответствует той
линейной единице, которой равна её сторона.
§ 144. Площадь прямоугольника.
Площадь фигуры, образованной на плоскости, измеряется чис-
лом квадратных единиц, которые содержит эта фигура. Так, пря-
моугольник, изображённый на рисунке 40,а, имеет площадь
4 кв. см, а на рисунке 40,6— 12 кв. см.
Чтобы найти площадь прямоугольника со сторонами 3 см и
4 см, изображённого на рисунке 40,6, нет необходимости пере-
считывать все квадратные сантиметры, на которые прямоуголь-
111
Нйк разделён. Достаточно заметить, что его можно разделить на 3
одинаковые полоски, каждая длиной 4 см и шириной 1 см, и
что каждая полоска разрезается на 4 кв. см\ следовательно,
весь прямоугольник можно разрезать на 4-3=12 кв. см.
Если прямоугольник имеет в длину а каких-нибудь единиц,
а в ширину b таких же единиц, его можно мысленно разрезать
на Ь одинаковых полосок, каждая из которых имеет в длину
а единиц и в ширину одну единицу и разрезается, следовательно,
на а квадратных единиц, соответствующих этим линейным еди-
ницам. Весь же прямоугольник разрезается на а-b квадратных
единиц. Отсюда правило: чтобы найти площадь прямоугольника,
Рис. 40.
измерения которого выражены чи-
слами в каких-нибудь одинаковых
единицах, надо перемножить эти
числа; полученное произведение
показывает, сколько соответству-
ющих квадратных единиц имеет
площадь прямоугольника.
Обозначая длины сторон пря-
моугольника буквами а и Ь, а
его площадь буквой S, выражаем
это правило формулой
S = а • Ь.
Например, классная комната,
длина которой 9 м, ширина 6 м,
имеет площадь 54 кв. м.
Это правило применяется только тогда, когда стороны прямо-
угольника выражены в одинаковых линейных единицах. Если же
они выражены в разных единицах, надо предварительно перейти
к одинаковым единицам. Например, желая узнать площадь, ка-
кую занимает дорога шириной 12 м и длиной 50 км, мы должны
сперва выразить длину в тех же мерах, что и ширину (50 км =
= 50000 м), а затем умножением 12 на 50 000 найти, что дорога
занимает всего 600000 кв. м.
Измерение длины отрезка производится непосредственным
сравнением его с теми отрезками, длины которых указаны на
масштабной линейке. Измерение же площади прямоугольника
производится согласно только что рассмотренному правилу кос-
венным путём-, непосредственно измеряются только стороны пря-
моугольника, а площадь его находится по расчёту.
§ 145. Площадь квадрата. Всякий квадрат есть прямоуголь-
ник с одинаковыми сторонами. Только что установленное пра-
вило измерения площади прямоугольника применимо поэтому
и к квадрату. Вспоминая, что произведение двух равных чисел,
например 135-135, читается как «135 с показателем 2» и записы-
вается в виде 1352, приходим к правилу: чтобы найти площадь
квадрата, надо взять длину его стороны с показателем 2.
112
Итак, для площади квадрата имеем формулу:
Х = а2,
где а выражает длину стороны квадрата, a S — его площадь в со-
ответствующих единицах.
Теперь становится понятным, почему вместо выражения «а с
показателем 2» употребляется выражение «а в квадрате».
Легко убедиться в правильности следующей таблички, пока-
зывающей, сколько более мелких квадратных единиц содержит
каждая более крупная квадратная единица
1 кв. км = 1000-1000 кв. м = 1000000 кв. м, или 100 га.
1 га = 100-100 кв. м= 10000 кв. м.
1 ар — 10-10 кв. м = 100 кв. м.
1 кв. м = 10-10 кв. дм = 100 кв. дм.
1 кв. см= 10-10 кв. мм = 100 кв. мм.
Найдя в § 144, что дорога занимает 600000 кв. м, делением
на 10000 устанавливаем, что дорога занимает 60 га.
§ 146. Задачи на площадь прямоугольника. Чаще всего при-
ходится решать следующие две задачи на площадь прямоугольника:
1) зная стороны прямоугольника, найти его площадь; 2) зная
площадь прямоугольника и одну из его сторон, найти другую его
сторону. Первая задача решается умножением, вторая, ей обрат-
ная,— делением. Приводим примеры:
Задача 1. Школе дали участок, имеющий форму прямо-
угольника со сторонами 45 м и 62 м. Какова его площадь?
Ответ. 45-62 = 2790 (кв. м), или почти 28 соток (точнее—
28 соток без 10 кв. м).
Задача 2. Имеется поле в виде длинного прямоугольника
шириной 32 м; надо отделить от него участок площадью 2 га
тоже прямоугольной формы и той же ширины. Какой длины
должен быть этот участок?
Здесь одна сторона прямоугольника известна (32 м), другая
нет, но зато известна площадь — 2 га, или 20 000 кв. м. Искомая
длина участка составляет 20000 : 32 = 625 м.
Первая задача всегда решается без всяких затруднений, вто-
рая же не вызывает затруднений только тогда, когда деление не
даёт остатка. Иногда помогает переход к более мелким единицам.
Например, желая найти сторону прямоугольника площадью
1200 кв. см, другая сторона которого имеет длину 125 см, мы по-
лучаем при делении 1200 на 125 в частном 9 и в остатке 75; пря-
моугольник со сторонами 125 см и 9 см имеет площадь только
1125 кв. см, т. е. меньше, чем надо, на 75 кв. см, а прямоугольник
со сторонами 125 см и 10 см — уже 1250 кв. см, т. е. больше, чем
надо, на 50 кв. см. Переход от сантиметров к миллиметрам позво-
ляет решить эту задачу точно: 1200 кв. см= 120 000 кв. мм,
125 см = 1250 мм, 120000:1250 = 96 (мм). Искомая сторона
прямоугольника имеет длину 96 мм.
7 Арифметика
113
Проверка. 1250-96= 120000 (кв. мм) = 1200 (кв. см).
Изучив дроби, мы будем в состоянии решать вторую задачу
при любых данных.
§ 147. Задачи на площадь квадрата. Задача 1. Зная сторону
квадрата, например а = 14 см, найти его площадь.
Эта задача, как мы уже знаем, решается одним умножением:
14-14 = 196 кв. см.
Задача 2. Зная площадь квадрата, например S = 676 кв. м,
найти его сторону а.
Эта задача, обратная задаче 1, представляет значительно
большую трудность. Однако мы всё же можем решить её, поль-
зуясь подбором (систематическими пробами). Надо подобрать
число а, которое при умножении на себя давало бы 676. Взяв
а = 10, находим, что это число слишком мало: 10-10 = 100. Далее
берём а = 20, 5 =20-20 =400, а=30, 5=30-30 = 900, и убеждаем-
ся, что искомое значение а заключено между 20 и 30. Пробуя
а = 25, имеем 5 = 625, а потому искомое значение больше 25, но
меньше 30. Взяв а = 26, находим S = 26-26 = 676. Задача, следо-
вательно, решена: данную площадь 676 кв. м имеет квадрат со
стороной 26 м (и никакой другой).
Такой подбор не всегда приводит к цели так хорошо, как в
рассмотренной задаче. Пусть, например, надо найти сторону
квадрата с площадью в 12 кв. км, или 12 млн. кв. м. Систематиче-
скими пробами находим, что она больше 3464 м и меньше 3465 м,
так как 34642 = 11 999 296, что меньше 12 млн. на 704, а 34652=
= 12006225, что больше, чем надо, на 6225. Мы нашли прибли-
жённые значения искомой стороны с точностью до метра по недо-
статку (3464) и по избытку (3465), причём оказалось, что первое
число значительно ближе к искомому, чем второе. Продолжая
пробы, можно получить точность до дециметров, сантиметров
и т. д.
§ 148. Старые русские меры площади. Старым русским мерам длины
(§ 128) соответствовали свои меры площади. Отметим из них квадратный ар-
шин, т. е. квадрат со стороной в 1 аршин, и квадратную сажень, т. е. квад-
рат со стороной в 1 сажень. Для измерения земельных участков до Великой
Октябрьской социалистической революции пользовались десятиной, содержащей
2400 кв. сажен. Нетрудно подсчитать, что десятина
немного больше, чем гектар: она содержит 1 га 9 а
25 кв. м, или 109 соток 25 кв. м.
§ 149. Площади параллелограмма и тре-
угольника. На рисунке 41 изображён прямо-
угольник Д1В1С£), от которого справа от-
резан кусок ВВ^, приставленный затем
слева в положении AAtD. Получилась фи-
гура ABCD, имеющая название параллело-
и DC называются основаниями параллело-
Рис. 41.
АВ
грамм. Отрезки
грамма, отрезки AtD и ВГС — его высотами, отрезки AD и ВС —
его боковыми сторонами.
114
Разрезая прямоугольник и превращая его перекладыванием
в параллелограмм, мы не меняем его площади.
Отсюда правило: чтобы узнать площадь параллелограмма, надо
измерить в одинаковых мерах его основание и высоту и пере-
множить полученные числа.
Отрезок, соединяющий две противоположные вершины прямо-
угольника, как, например, отрезок АС на рисунке 42, называется
диагональю прямоугольника. Диагональ делит прямоугольник
на две одинаковые части, каждая из которых является прямо-
угольным треугольником. В прямоугольном треугольнике имеются
три стороны; две из них {АВ и ВС), образуют прямой угол, они
называются катетами, третья сторона (ЛС) — гипотенузой. Чтобы
узнать площадь прямоугольного треугольника, достаточно измерить
в одинаковых мерах его катеты и взять произведение получен-
ных чисел, делённое на 2. Действительно, произведение катетов
даёт площадь прямоугольника ABCD, т. е. площадь двух одина-
ковых прямоугольных треугольников, а потому площадь каждого
из них равна половине этого произведения.
Чтобы найти площадь остроугольного треугольника АВС, изо-
бражённого на рисунке 43, а, его надо разрезать на два прямо-
угольных треугольника ACD и BCD отрезком CD, который про-
водится под прямым углом к стороне АВ и называется высотой
треугольника. Площадь треугольника АВС получим как сумму
площадей прямоугольных треугольников ACD и BCD, а для этого
надо взять половину произведения длины AD на CD и половину
произведения длины BD на CD, а затем сложить результаты.
Вспоминая распределительное свойство произведения и частного
(§ 45, 59), убеждаемся, что можно сперва сложить длины отрез-
ков AD и DB, что даёт основание АВ, а затем умножать на CD
и делить на 2.
Отсюда правило: чтобы найти площадь треугольника, доста-
точно измерить в одинаковых мерах его основание и высоту, а
затем взять произведение полученных чисел, разделённое на 2.
Это правило справедливо не только для остроугольного тре-
угольника, но и для тупоугольного, изображённого на рисун-
ке 43, б. Здесь высота CD берётся до продолжения основания АВ.
Найдя площадь большого прямоугольного треугольника ACD,
7* 115
равную произведению длин отрезков AD и CD, делённому на 2,
вычитаем из неё площадь малого прямоугольного треугольника
BCD, равную произведению длин отрезков BD и CD, тоже де-
лённому на 2. Распределительное свойство произведения и част-
ного имеет место не только для суммы, но и для разности
(§ 45 и 59), а потому можно сперва сделать вычитание отрезка
BD из AD, получая отрезок АВ, а потом уже умножить АВ на
CD и делить произведение па 2. Тем самым приходим к тому
же правилу, что и выше.
Раздел 5. БРУС И КУБ
§ 150. Брус. Такие предметы, как спичечная коробка, обыкно-
венный кирпич, сундук, комната и многие другие предметы (или
Рис. 44.
тела) имеют форму бруса. Его науч-
ное название — прямоугольный парал-
лелепипед. Брус ограничен шестью плос-
кими гранями, каждая из которых пред-
ставляет собой прямоугольник. Пред-
ставляя себе брус, поставленный на
стол перед нами, как на рисунке 44,
будем различать в нём грани: ниж-
нюю (ABCD) (обычно называемую осно-
ванием), верхнюю (ДхВхС^х), переднюю
(ABBi.41), заднюю (DCCiP^), правую боковую (BCCYB^, левую
боковую (ADD^A^. Грани нижняя и верхняя, противоположные
друг другу, равны. Точно так же равны противоположные грани
передняя и задняя, а также левая и правая боковые. Итак,
брус есть тело, ограниченное шестью попарно равными прямо-
угольниками.
Каждые две грани бруса, пересекаясь, образуют ребро. Всего
брус имеет 12 рёбер: четыре нижних (АВ, ВС, CD, DA), четыре
верхних (ABb В^, CjDx, D^), четыре боковых (ДД, ВВ1г CClt
DI\). Рёбра АВ, AjBj^, CD, CJJl имеют одну и ту же длину;
рёбра ВС, В^!, DA, тоже равны друг другу; равны между
собой и боковые рёбра.
Длины трёх рёбер, сходящихся в одну вершину, называются
измерениями бруса. Самое большое из них обычно называют
длиной бруса, два других — его шириной и высотой.
§ 151. Изготовление модели бруса. Изготовить модель бруса
проще всего при помощи его развёртки (или выкройки). На ри-
сунке 45 показана развёртка бруса.
Вычертив на плотной бумаге, её вырезают по сплошным
линиям, слегка надрезают по пунктирам, надлежащим образом
сгибают и склеивают, причём надрезанные края желательно
приклеить изнутри. Чтобы получить хорошую модель, надо очень
аккуратно начертить развёртку и столь же аккуратно вырезать
её и склеить.
116
Другой способ изготовления модели бруса требует предвари-
тельной заготовки 12 палочек, по четыре одной длины, например
кусочков жёсткой проволоки, и восьми шариков из пробки или
мягкого дерева. Заострив концы палочек, втыкают их по три раз-
ной длины в один шарик так, чтобы каждые две палочки были
сторонами прямого угла. Получается модель бруса, изображён-
ная на рисунке 46.
Третий способ изготовления модели бруса — вырезание его из
сплошного куска какого-нибудь материала, например дерева,
металла, большой картофелины или брюквы. Этим способом
можно изготовить хорошую модель, если для проверки правиль-
ности взаимного расположения граней пользоваться столярным
угольником.
1ку5.см 1 квбмм
Рис. 47.
§ 152. Куб. Если у бруса два измерения равны, а третье
больше или меньше, то говорят, что это брус с квадратным сече-
нием или квадратным основанием. Таковы, например, брусы с из-
мерениями 4 см, 1 см, 1 см и 4 см, 4 см, 1 см. Если же равны все
три измерения, брус называют кубом. Итак, кубом называется
такой брус, у которого все три измерения равны. У куба все
шесть граней представляют собой равные квадраты.
§ 153. Кубические единицы. Кубической единицей, или едини-
цей объёма, называется всякий куб, ребром которого является
единица длины. На рисунке 47 изображены кубический санти-
117
метр и кубический миллиметр. Понятно, что такое кубический
дециметр, кубический метр, кубический километр. Употреби-
тельны следующие сокращённые обозначения этих кубических
единиц: куб. мм, куб. см, куб. дм, куб. м, куб. км или мм3,
см3, дм3, м3, км3.
Говорят, что всякая кубическая единица соответствует той
линейной единице, которой равно её ребро, и той квадратной
единице, которую представляет собой её грань.
154. Объём бруса.
Объём какого-нибудь
кубических еди-
это тело. Возь-
с измерениями
Рис. 48.
тела измеряется числом
ниц, которые содержит
мём, например, брус
5 см, 4 см, 3 см (на рисунке 48 брус
уменыпён). Его можно мысленно разре-
зать на три бруса размерами 5 см, 4 см,
1 см (один из них изображён отдельно
ниже), а каждый из них в свою очередь
на четыре бруса размерами 5 см, 1 см,
1 см (один из них показан ещё ниже).
Но каждый такой брус можно разре-
зать на 5 куб. см, и легко видеть, что
данный брус содержит всего 5-4-3—
= 60 куб. см.
Имея брус с рёбрами в а см, b см,
с см, можем разрезать его на с брусов
с рёбрами а см, b см, 1 см, а каждый
из них на Ь брусов с рёбрами а см,
1 см, 1 см-, в каждом из них а куб. см\
всего таким образом получим а • b • с
куб. см.
Итак, чтобы найти объём бруса,
измерения которого выражены числами
в каких-нибудь одинаковых линейных единицах, надо перемножить
эти числа; полученное произведение показывает, сколько соответ-
ствующих кубических единиц имеет объём бруса.
Обозначая длины рёбер буквами а, Ь, с, а объём бруса бук-
вой V, запишем это правило формулой:
V = а • Ь • с.
Произведение длин двух рёбер бруса, например а и Ь, вы-
ражает площадь S той грани бруса, сторонами которой служат
эти рёбра. Если эту грань считать основанием бруса, то третье
ребро с будет его высотой, получается правило:
Чтобы найти объём бруса, берут площадь его основания, вы-
раженную в каких-нибудь квадратных единицах, и умножают её
на его высоту, выраженную в соответствующих линейных еди-
ницах.
118
Вот краткая запись этого правила:
V = S • с.
Если измерения бруса выражены в разных единицах, их пред-
варительно надо выразить в одинаковых, а затем уже перемно-
жить.
Измерение объёма бруса, как и измерение площади прямо-
угольника, производится, таким образом, не непосредственно,
а косвенно. Непосредственно измеряются рёбра, а объём на-
ходят расчётом.
§ 155. Объём куба. Всякий куб есть в то же время брус
с тремя равными измерениями. Только что установленное пра-
вило измерения объёма бруса применимо поэтому и к кубу.
Вспоминая, что произведение трёх равных сомножителей, напри-
мер 5-5-5, читается как «5 с показателем 3» и записывается
как 53 (§ 108), приходим к правилу:
Чтобы найти объём куба, надо взять с показателем 3 число,
выражающее длину его ребра в каких-нибудь линейных еди-
ницах.
В результате получится число, выражающее объём куба в
соответствующих кубических единицах.
Объём V куба с ребром а выражается формулой:
Теперь становится понятным, почему вместо «а с показате-
лем 3» говорят: «а в кубе».
Легко убедиться в правильности следующей таблицы, пока-
зывающей, сколько более мелких кубических единиц содержит
каждая из более крупных кубических единиц.
1 куб. км = 1 000 000 000 куб. м.
1 куб. м = 1000 куб. дм = 1 000000 куб. см =
= 1 000 000 000 куб. мм.
1 куб. дм = 1000 куб. см = 1 000000 куб. мм.
1 куб. см = 1000 куб. мм.
§ 156. Задачи на объём бруса. Чаще всего приходится ре-
шать три следующие задачи на объём бруса.
Задача 1. Зная три измерения бруса, например а = 12 см,
Ь = 5 см, с = 4 см, найти его объём V.
Эта задача решается умножением чисел а, Ь, с; в данном
случае V = 12 • 5 • 4 = 240 куб. см.
Напоминаем, что измерения бруса должны быть выражены
в одинаковых единицах длины.
Задача 2. Зная объём бруса (V) и площадь одной из его
граней (S), например V = 600 куб. м и S = 120 кв. м, найти
длину (с) того ребра бруса, которое не лежит в этой грани.
119
Здесь вопрос сводится к разысканию одного из сомножите-
лей (с) по данному произведению V = 600 и другому сомножи-
телю S = 120 и решается, следовательно, делением:
600:120 = 5, с = 5 м.
Числа V и S должны быть выражены в кубических и квад-
ратных единицах, соответствующих одной и той же единице
длины. Например, желая узнать глубину слоя воды, какой по-
лучится, если налить 45 куб. дм воды в аквариум, имеющий
форму бруса с площадью дна в 30 • 50 = 1500 (кв. см) мы должны
сперва выразить данный объём в кубических сантиметрах, а за-
тем уже произвести деление: 45000 : 1500 = 30 (ши).
Задача 3. Зная объём бруса V и длину одного из его рё-
бер с, например V = 175 куб. м и с = 5 м, найти площадь грани,
в которой не лежит с.
Здесь опять-таки дело сводится к получению сомножителя
по данному произведению и другому сомножителю, т. е. к деле-
нию: 175: 5 = 35 (кв. м). И тут нельзя забывать о необходимости
выражения данных в соответствующих мерах.
Задачи 2 и 3 разрешимы при помощи натуральных чисел да-
леко не всегда. Иногда помогает переход к более мелким еди-
ницам, как, например, в случае, когда ищут с по данным V =
= 20 куб. см и S = 8 кв. см. Здесь с можно найти, перейдя
к миллиметрам: 20000 куб. мм: 800 кв. мм = 25 мм. Чтобы ре-
шать эти задачи при любых данных, приходится иметь дело
с дробями.
§ 157. Задачи на объём бруса с квадратным основанием и на
объём куба. Задача 1. Брус с квадратным основанием имеет
объём V = 5120 куб. см, а ребро, не лежащее в квадратной
грани, имеет длину с = 20 см. Найти сторону квадратной грани.
Найдя площадь квадратной грани 5120:20 = 256 (кв. см),
пробуем разные значения для длины стороны этой грани: 10 • 10 =
= 100 (мало), 20 - 20 = 400 (много), 15 • 15 = 225 (мало), 16 • 16 =
= 256 (как раз). Итак, мы нашли пробами, что искомая сторона
квадратной грани равна 16 см.
Задача 2. Объём куба равен 13824 куб. см. Какова длина
его ребра?
Эта задача решается тоже пробами: 103= 1000 (мало), 203 =
= 8000 (мало), 303 = 27 000 (много), 253= 15625 (много), 243 =
= 13824 (как раз). Итак, длина ребра данного куба равна
24 см.
Задачи 1 и 2 далеко не всегда удаётся решить точно, даже
применяя дроби. Часто приходится довольствоваться приближён-
ным решением этих задач, находя два числа, мало отличающихся
одно от другого, одно из которых меньше искомого, другое
больше его. Так, чтобы найти ребро куба объёмом 100 куб. см,
пробуем числа 103 = 1000 (много), 53 = 125 (много) и убеждаемся,
120
1Л
что искомый куб имеет ребро больше 4, но меньше 5 см, ближе
к 5 см, так как 125 отличается от 100 меньше, чем 64.
Переходя к миллиметрам, можно решить задачу точнее, а
именно установить, что искомое ребро больше 46 мм и меньше
47 мм, ближе к 46.
Раздел 6. ОБЪЁМ ЖИДКИХ И СЫПУЧИХ ТЕЛ
§ 158. Литр. Наряду с кубическими единицами употреб-
ляются другие меры объёма, называемые «мерами жидких и сы-
пучих тел», а также «мерами ёмкости», или «мерами вмести-
мости». У нас основная мера ёмкости — литр, равная (с доста-
точной для практических целей точностью) 1 куб. дм, т. е.
1000 куб. см\ сокращённое её обозначение — л. Об
очень незначительной разнице между литром и
кубическим дециметром сказано ниже (§ 160).
Образец литра изготовляется в виде кружки
(рис. 49). Подсчитано, что если поперечник дна
этой кружки равен 100 мм, то высота её равна
почти 127 мм.
Более крупные меры ёмкости — декалитр, т. е.
Юл (сокращённое обозначение дл}, и гектолитр,
т. е. 100 л (сокращённое обозначение гл). В тор-
говле часто применяется мера в 20 л. Каждый
литр содержит 1000 миллилитров (мл)-, 1 мл практически ра-
вен 1 куб. см.
§ 159. Старые русские меры ёмкости. До Великой Октябрьской социали-
стической революции в России применялись старинные меры ёмкости: для
сыпучих тел, как, например, зерна,— четверик, или мера, содержавшая не-
много больше 26 л (точнее 26 240 куб. см), для жидкостей — ведро, содержав-
шее немного больше 12 л (точнее 12 300 куб. см). Каждые 8 четвериков со-
ставляли четверть, в каждом четверике содержалось 8 гарнцев. Ведро разде-
лялось на 20 бутылок, вмещавших каждая 615 куб. см. В употреблении были
также более крупные бутылки, которых в ведре было только 16. В настоящее
время бутылки у нас изготовляются ёмкостью в 1 л, 750 куб. см, 500 куб. см,
250 куб. см и др.
Литр как мера ёмкости применяется во всём мире, за исключением Англии
и Соединённых Штатов Америки, до сих пор упорно сохраняющих свои ста-
ринные неудобные меры ёмкости.
Раздел 7. ВЕС
§ 160. Грамм, килограмм, тонна. Грамм есть вес 1 куб. см
чистой холодной воды. На письме слово «грамм» заменяется бук-
вой г или Г1. В 1 куб. дм содержится 1000 куб. см, а потому
1 куб. дм воды весит 1000 Г, или килограмм (сокращённо кГ).
В 1 куб. м содержится 1000 куб. дм, а потому 1 куб. м воды
весит 1000 кГ, или тонну (сокращённо Т). Итак:
1 куб. сантиметр воды весит 1 грамм (1 Г).
1 Чтобы не было расхождения с обозначениями, принятыми в физике для
единиц веса, будем обозначать их так: грамм — Г, килограмм — кГ, тонна — Т.
121
1 куб. дециметр воды весит 1000 граммов, или 1 килограмм (1 кГ).
1 куб. метр воды весит 1000 килограммов, или 1 тонну (1 Т).
Эги определения были установлены в конце XVIII в., когда
создавалась метрическая система мер. Была изготовлена с наи-
большей возможной тогда точностью гиря, имевшая вес 1 кГ
(«эталон килограмма»). Как показали дальнейшие более точные
измерения, эта гиря не вполне соответствует своему определе-
нию. Чтобы не заменять её другой, решили считать её вес за
килограмм, отклонившись от первоначального определения кило-
грамма.
Вес I куб. дм воды в силу этого оказывается чуть меньше
1 кГ, вес 1 куб. м воды чуть меньше 1 Т: 1 куб. м воды
весит не 1000000 Г, а 999972 Г. Литр определяется, как объём
1 кГ воды и чуть-чуть превосходит 1 куб. дм-. 1 Т воды —
1 000 028 куб. см.
Это расхождение между первоначальными определениями
грамма, литра и других мер и точными современными их опре-
делениями столь незначительно, что его принимают во внимание
только при таких научных расчётах, когда требуется наивысшая
точность. При обычных расчётах пользуются указанными выше
данными о весе воды.
Вес предмета есть та сила, с какой этот предмет притяги-
вается Землёй. Но эта сила меняется в зависимости от того,
где предмет находится; например, чем ближе к полюсу, тем она
больше; чем выше над поверхностью Земли, тем она меньше.
Поэтому наряду с весом предмета, рассматривают его массу,
которая остаётся одной и той же, куда бы мы этот предмет ни
перенесли, и выражается в единицах, имеющих те же названия
(грамм, килограмм, тонна), что и вес, но обозначается малень-
кими буквами (г, кг, т).
§ 161. Другие метрические меры веса. Наряду с тремя ука-
занными выше единицами веса (Г, кГ, Т) употребляются также
следующие единицы: центнер (сокращённое обозначение — русская
буква ц), содержащий 100 кГ; миллиграмм (мГ), выражающий
вес 1 куб. мм воды; сантиграмм (сГ), равный 10 (мГ). Для изме-
рения веса драгоценных камней применяется особая единица —
карат, равный 200 мГ. При самых точных измерениях веса
пользуются мельчайшей единицей—микрограммом-, в 1 Г
1000000 микрограммов; в 1 мГ — 1000 микрограммов.
§ 162. Старые русские меры веса. В дореволюционной России основными
мерами веса были пуд и фунт, изредка применяемые и теперь. Пуд содержит
40 фунтов, фунт — 32 лота, лот — 3 золотника, золотник — 96 долей. Фунт
равен приблизительно 400 Г, точнее 409 Г 512 мГ 410 микрограммов, а пуд
несколько больше 16 кГ (точнее 16 кГ 380 Г).
Наименование «фунт» за границей носят много различных мер веса.
Английский торговый фунт, применяемый также и в Америке, содержит около
450 Г и подразделяется на 16 унций, так что 1 унция — 28 Г 35 сГ. Меры
«центнер» и «тонна» в Англии означают также не то, что во всех остальных
странах: английский центнер равен 50 кГ 800 Г; английская тонна — 1016 кГ.
122
Раздел 8. ВРЕМЯ
§ 163. Сутки и части суток. Промежуток времени от восхода
солнца до его заката образует день, а от заката до восхода —
ночь. Продолжительность дня (и ночи) в разных местах земного
шара и в разное время года различна, да и в одном и том же
месте не остаётся неизменной, а потому для измерения времени
день и ночь не пригодны. Более пригоден промежуток времени
от одного восхода солнца до следующего его восхода в том же
месте, мало отличающийся от суток.
Сутки — продолжительность одного оборота земного шара
около своей оси Ч В обыденной жизни вместо слова «сутки»
часто говорят «день»; вместо того чтобы сказать «прошло трое
суток», говорят: «прошло три дня».
Сутки принято делить на 24 равные части, каждая из кото-
рых составляет час, час делят на 60 минут, минуту — на 60 се-
кунд.
Часовая стрелка правильно идущих часов делает за сутки
два полных оборота, а минутная — 24 полных оборота.
За начало суток принимают некоторый момент, называемый
полночью и обозначаемый 0 часов 00 минут, или, что то же са-
мое, 24 часа 00 минут. В этот момент обе стрелки часов схо-
дятся на метке, обозначенной на циферблате числом 12 (или XII).
Время суток определяется по показаниям часовой и минутной
стрелок. Например, говоря, что сейчас «одиннадцать двадцать
пять», имеют в виду, что от полуночи прошло 11 часов 25 минут.
Часовая стрелка находится в этот момент почти посередине
между метками с числами 11 и 12 (или XI и XII), а минутная
на метке с числом 5 (или V). Употребительна сокращённая
запись показаний часов 11—25 или II25 (без приведения слов
«часов», «минут»).
В обыденной жизни счёт часов ведут от полуночи до 12—00;
этот момент называют полднем-, к показаниям часов при этом
добавляют слова: «ночи», «утра», «после полуночи» или «попо-
луночи». После 12—00 счёт часов начинают снова и ведут его
от 0—01 до 12—00, добавляя теперь уже слова «дня», «вечера»,
«после полудня», «пополудни».
На железных дорогах и предприятиях связи (почта, телеграф,
телефон, радио), а также в некоторых других учреждениях
пользуются более удобным 24-часовым счётом времени, прибав-
ляя во второй половине суток, т. е. в промежуток времени от
полудня до полуночи, к показанию часовой стрелки ещё 12 ча-
сов: вместо «1 час дня» говорят «13 часов», вместо «6 часов ве-
чера»— «18 часов», вместо «12 часов ночи» — «24 часа». При
этом 24-часовом счёте надобность в добавлении слов «пополу-
ночи», «пополудни», «утра», «дня», «вечера», «ночи» отпадает.
1 В науке различают «звёздные сутки» и «солнечные сутки»; здесь и в
дальнейшем речь идёт о солнечных сутках.
123
Правильность хода часов надо постоянно проверять, поль-
зуясь особыми сигналами времени, какие передаются из Москвы
по радио ежедневно в I00, 700, 1200, 1900 московского времени, или
по бою часов Спасской башни Московского кремля в 600 и 2400
(рис. 50).
За правильностью хода этих часов следит Московская астро-
номическая обсерватория имени учёного — революционера
П. К. Штернберга; она же даёт и сиг-
налы времени.
§ 164. Неделя. Каждые 7 суток со-
ставляют неделю.
Происхождение недели восходит к
далёкой древности. Наблюдая за дви-
жением Луны, легко установить сле-
дующие четыре фазы её. I — от «заро-
ждения серпа» до формы Луны в виде
полукруга; II — от полукруга до пол-
ного круга; III — от него вновь к
форме полукруга; IV — от полукруга
вновь к форме «серпа». Каждая фаза
проходит приблизительно 7 дней. От-
сюда зародилось понятие о «седмице»,
или о неделе.
Каждый день недели имеет своё
название. Один день недели является
у нас в СССР днём отдыха; его назы-
вают по-русски «воскресеньем», по-ук-
раински просто «неделей» («недиля»),
т. е. днём, когда не работают, не
делают. Первый день, следующий за
этим «днём недели», называют «поне-
Рис. 50. дельником»; второй — «вторником»; тре-
тий, занимающий в неделе среднее
место, называют «средой»; четвёртый — «четвергом»; пятый —
«пятницей»; для шестого дня принято особое (нерусское) назва-
ние «суббота».
Имея вполне определённую продолжительность (7 суток), не-
деля пригодна для измерения более значительных промежутков
времени. Например, в неделях выражают срок карантина, в те-
чение которого заболевший ученик не может посещать школу.
§ 165. Год и век. Смена дня и ночи вызывается вращением
Земли вокруг своей оси, смена времен года — её движением во-
круг Солнца. Полный оборот вокруг Солнца Земля совершает
в промежуток времени, называемый годом. Год равен приблизи-
тельно 365 суткам 6 часам (с точностью до секунды год содер-
жит 365 суток 5 часов 48 минут 46 секунд).
Чтобы начало каждого нового года не приходилось на раз-
ные часы, принято считать три года подряд по 365 суток (эти
J 24
годы называются «простыми»), четвёртый же год, называемый
«високосным», за 366 суток. Таким образом в високосный год
почти исправляется ошибка, накопившаяся за три предшествую-
щих простых года.
Високосными годами считаются те, номера которых делятся
на 4, как, например, 1940, 1944, 1948, 1952 и т. д. Применяя
признак делимости на 4 (§ 98), замечаем, что високосными яв-
ляются все годы, у которых число из последних двух цифр
номера кратно 4. Для большей точности установлено особое
правило для вековых годов: 1800, 1900, 2000, 2100 и т. д.; они
считаются високосными только тогда, когда первые две цифры
образуют число, кратное 4.
Началом года условно считается момент 0—00 1 января
(«Новый год»). Каждому году присвоен некоторый порядковый
номер. Великая Октябрьская социалистическая революция про-
изошла в год, имевший номер 1917. В СССР иногда считают но-
мера лет от этого года. 7 ноября 1956 г. советские люди празд-
новали 39-ю годовщину Великой Октябрьской социалистической
революции; в этот день начался новый, 40-й год существования
первого в мире социалистического государства.
Каждые 100 лет составляют один век. Века условно обозна-
чаются порядковыми номерами. Чтобы получить номер века, ко-
торому принадлежит какой-нибудь год, надо отбросить последние
две цифры в порядковом номере этого года и прибавить 1 к по-
лученному числу. Так, 1950 г. принадлежит к XX веку, 1812 г.—•
к XIX веку, 1789 г.— к XVIII веку и т. д.
§ 166. Месяц и квартал. Во многих случаях сутки и недели
оказываются слишком малыми мерами времени, год же слишком
большой. Поэтому люди издавна стали пользоваться ещё одной
единицей времени — месяцем, первоначально связанным с изме-
нением вида Луны. Теперь считают, что год имеет 12 месяцев,
но так как числа 365 и 366 на 12 не делятся, то разные месяцы
имеют разную продолжительность. На русском языке до сих пор
употребляются старинные латинские названия месяцев, данные
им ещё около 2000 лет назад. Надо знать эти названия, а также
номера месяцев и число суток в каждом. Всё это указано в
следующей табличке, содержащей также и украинские названия;
эти названия указывают на те явления природы, какие в этом
месяце происходят (см. табл, на стр. 126.).
Февраль простого года содержит 28 суток, високосного — 29.
Четыре месяца, а именно апрель, июнь, сентябрь, ноябрь содер-
жат по 30 суток. Остальные 7 месяцев имеют по 31 суткам.
Каждые три месяца составляют квартал. Первый квартал
охватывает январь, февраль, март и имеет 90 (если год простой)
или 91 сутки (если високосный); второй квартал — апрель, май,
июнь (91 сутки); третий квартал — июль, август, сентябрь
(92 суток); четвёртый квартал — октябрь, ноябрь, декабрь (92 су-
ток).
125
МЕСЯЦЫ ГОДА
Поряд- ковый номер Число суток Название на русском языке Название на украинском языке и его объяснение
1 31 Январь Сичень Мелкий снег сечёт лицо; производится рубка (сеча) леса
II 28 или 29 Февраль Лютый Суровые, «лютые» мо- розы
III 31 Март Березень Оживает берёза
IV 30 Апрель Цветень, или Квитень Появляются цветы
V 31 Май Травень Появляются травы
VI 30 Июнь Червень Появляются красные (по-украински «черво- вые») ягоды
VII 31 Июль Лыпень Цветёт липа
VIII 31 Август Серпень Идёт жатва серпами
IX 30 Сентябрь Вересень Идёт молотьба (от сло- ва «врещи» — моло- тить)
X 31 Октябрь Жовтень Растения желтеют (жёл- тый — «жовтый»)
XI 30 Ноябрь Листопад Опадают листья с де- ревьев
XII 31 Декабрь Грудень На дорогах мёрзлые ко- леи (от «грудка» — ку- сок, комок)
§ 167. Датирование. Сутки каждого месяца нумеруются, полу-
чая номера от 1 до 30 или 31 (в феврале от 1 до 28 или 29),
именуемые «числами месяца». Обозначение числа месяца, назва-
ния месяца (или номера месяца) и номера
года образует дату. Иногда в дату входит
также указание часов и минут. Указание
даты называется датированием. Так, дата
дня рождениям. В. Ломоносова записывается
как 19 ноября 1711 г., или короче как
19/XI 1711.
Датирование применяется очень часто.
Так, например, на каждом письме, отпра-
вляемом по почте, ставятся штемпели, со-
Рис. 51. держащие даты поступления письма в по-
чтовое отделение места отправления и места
назначения. На рисунке 51 изображён почтовый штемпель на
письме, поступившем в Б-3 почтовое отделение г. Москвы
28 ноября 1956 г. в 19 часов.
Дату имеет и всякий железнодорожный билет; она выбивается
на билете при помощи компостера и состоит из цифр, хорошо
126
видных на обратной стороне билета и означающих номер поезда,
число месяца, порядковый номер месяца, последнюю цифру по-
рядкового номера года. Например, на рисунке 52 изображён
билет, на котором компостер выбил цифры 82 10 XII 5, озна-
чающие, что этот билет годен для проезда в поезде № 82 10 де-
кабря 1955 г.
Несколько иначе производится датирование на телеграммах.
Каждая вручаемая адресату телеграмма имеет ниже адреса, но
выше текста служебную пометку вроде той,
Рис. 52.
что изображена на рисунке 53. Она говорит,
что телеграмма отправлена из Киева за № 4009,
содержит 17 слов, подана 26 числа в 22 часа
21 минуту. Ни месяц, ни год на телеграмме не
указываются.
§ 168. Календарь. Старый и новый стиль.
Правила счёта дней, недель, месяцев, годов
составляют так называемый календарь. В до-
революционное время принятый в России ка-
лендарь несколько отличался от того, каким
мы пользуемся теперь. Тогда применялся так
называемый «старый стиль», отстававший от
общепринятого международного «нового стиля»
в XX в. на 13 суток, в XIX в.— на 12, в
XVIII в.— на 11. Так, когда 1 мая 1890 г. впервые был про-
ведён международный праздник трудящихся, в России считалось
ещё 19 апреля; начиная с 1900 г. 1 мая нового стиля прихо-
дилось на 18 апреля старого
стиля.
Только при советской власти
это различие было уничтожено:
по постановлению Совета Народ-
ных Комиссаров день, следую-
щий за 31 января 1918 г. был
объявлен днём 14 февраля. Таким
образом, события, происходившие
до этого числа имели две даты.
Например Великая Октябрьская
произошла 25 октября по старому
она произошла 7 ноября. Дата по
старому стилю (25 октября) переводится на дату по новому стилю
(7 ноября) путём прибавления 13 суток: 25+ 13 = 38; в октябре
31 сутки, поэтому вместо «38 октября» имеем, отнимая от
38 число 31, дату по новому стилю — 7 ноября.
Великий русский поэт Александр Сергеевич Пушкин родился
26 мая 1799 г. по старому стилю, что даёт по новому стилю
6 июня, так как в XVIII в. разница составляет 11 суток, а в
мае 31 сутки. Поэтому 150-летие со дня рождения Пушкина мы
праздновали 6/V1 1949 г.
Г Е Л £ Г Р
Прими Пг|
| ^КИЕВД «009 17 26 2 2211
| I
Рис. 53.
2 2211
социалистическая революция
стилю; по новому же стилю
127
Для перехода от нового стиля к старому разницу приходится
вычитать, предварительно добавляя к числу месяца, если оно
меньше этой разницы, число суток в предшествующем месяце.
Например, зная, что Алексей Максимович Горький родился по
новому стилю 28 марта 1868 г., легко установить, что по ста-
рому стилю это было 16 марта. Годовщину дня смерти Софьи
Васильевны Ковалевской, первой среди женщин всего мира по-
лучившей учёную степень доктора наук, мы отмечаем 10 фев-
раля каждого года; она умерла в 1891 г., и дата дня её смерти
по старому стилю 10 + 31 — 12 = 29 января.
Рис. 54.
§ 169. Поясное время. Видимое движение Солнца, обуслов-
ленное вращением Земли, происходит с востока на запад. В раз-
ных точках земного шара Солнце восходит не одновременно,
а чем западнее, тем позже, чем восточнее, тем раньше. Поэтому
когда в Москве, например, полночь, то на мысе Дежнёва (край-
няя восточная точка территории СССР) уже больше 10 часов
утра. Если бы часы показывали время точно по Солнцу, то во
всяком пункте земного шара было бы своё «местное» время.
Одинаковое время показывали бы только часы в пунктах, рас-
положенных к северу или югу друг от друга (на одном мери-
диане); переход на каждую дуговую минуту (на широте Москвы
это соответствует расстоянию около километра) к востоку вызы-
вает увеличение местного времени на 4 секунды.
Чтобы не переводить часы при каждом перемещении на вос-
ток или на запад, введено так называемое поясное время: весь
земной шар разделён на 24 пояса (рис. 54). В пределах одного
пояса все часы показывают одно и то же время. При путешест-
вии с запада на восток, пересекая границу пояса, переводят
128
стрелки часов на час вперёд, а с востока на запад на час
назад.
СССР простирается с запада на восток более чем на 9000 км
и расположен в 10 поясах, показанных на карте (рис. 55). По
этой карте видно, какое время должны показывать все пра-
вильно идущие часы данного пояса в тот момент, когда часы в
ЛАоскве показывают О00. В СССР часы ходят по декретному
поясному времени, которое идёт в зимнее время на час вперёд
по сравнению с международным поясным временем, принятым
в других государствах. Например, в столице Турции г. Анкаре,
расположенном в том же часовом поясе, что и Москва, часы
Рис. 55.
показывают только 11 часов, когда в Москве полдень. Эта раз-
ница получилась после декрета Совнаркома СССР от 16/VI
1930 г., по которому все часы в СССР были переведены на час
вперёд, чтобы лучше использовать светлую часть суток.
§ 170. Задачи на время. Рассмотрим несколько таких задач
на время, какие встречаются в жизни особенно часто.
Задача 1. Солнце взошло в Москве 15/11 1950 г. в 757 утра,
закатилось в 533 вечера. Сколько времени продолжался в
Москве этот день?
От начала суток (0°°) до восхода солнца прошло 7 час.
57 мин., а до его заката 12 час.+ 5 час. 33 мин., всего 17 час.
33 мин.; день продолжался 17 час. 33 мин — 7 час. 57 мин.=9 час.
36 мин.
Здесь мы должны были найти продолжительность некоторого
промежутка времени, зная даты его начала и конца. Нам при-
шлось взять за начало счёта полночь (0°°), найти промежуток
129
времени от полуночи до начала искомого промежутка (до восхо-
да солнца), затем промежуток времени от той же полуночи до
конца искомого промежутка (до заката солнца) и от второго
числа отнять первое.
Задача 2. Солнце зашло в 533, на следующий день взошло
в 754. Сколько времени продолжалась ночь? Здесь за начало
счёта удобнее взять полдень первых суток. От этого полудня до
заката прошло 5 час. 33 мин., от этого же полудня до восхода
12 час.+ 7 час. 54 мин.— 19 час. 54 мин.; ночь длилась 14 час.
21 мин. (19 час. 54 мин.—5 час. 33 мин).
Задача 3. Ученик уехал из города в деревню вечером
28 мая, вернулся утром 24 августа. Сколько дней он был вне города?
За начало счёта примем 1/V, точнее — начало этих суток,
т. е. О00. До отъезда прошло в мае 28 дней (28/V он провёл
в городе), а до возвращения за май, июнь, июль и август
прошло 31 + 30 + 31 + 23 — 115 дней (23/VIII прошло тоже вне
города). Вне города ученик провёл 115 — 28 = 87 дней.
Здесь в искомый промежуток не вошли ни день отъезда
(28/V), ни день приезда (24/VIII). Если бы отъезд был утром
28/V, а приезд вечером 24/VIII, эти дни пришлось бы тоже до-
бавить, и ответ был бы 89 дней.
В подобных задачах надо всегда точно указывать, включаются
ли в искомый промежуток дни его начала и конца, или нет.
Задача 4. Путёвка в санаторий действительна с 16 июня
в течение 48 дней. Надо узнать дату последнего дня.
Считая с 1/VI, имеем до первого дня действия путёвки 15
дней, а до последнего дня 15 4-48 = 63 дня, из которых 30
пройдут в июне, 31 в июле, остальные 63 — 30 — 31 = 2 в ав-
густе. Следовательно, последний день действия путёвки — 2 ав-
густа.
Задача 5. Служащий вернулся из командировки 17/1II
1948 г., пробыв в ней 89 дней. Указать дату начала команди-
ровки, считая 17/1II последним её днём.
Командировка продолжалась в марте 17 дней, в феврале
29 дней (год високосный!), в январе 31 день, всего в 1948 г.
было 17 4- 29 4- 31 = 77 дней командировки. Следовательно,
первые 89 — 77 = 12 дней командировки были в 1947 г. В де-
кабре до начала командировки прошло 31 —12 = 19 дней, она
началась 20/XII 1947 г.
Глава VIII. МНОЖЕСТВО ДОЛЕЙ И ДРОБИ
Раздел 1. ДЕЛЕНИЕ МНОЖЕСТВА НА РАВНЫЕ ЧАСТИ (ДОЛИ)
§ 171. Доли элементов (предметов). В природе можно наблю-
дать, как некоторые элементы множеств (некоторые предметы)
распадаются на несколько новых элементов. Так, горошина, про-
растая, распадается на две части — семядоли. Если апельсин
130
очистить от кожуры, он легко разделяется на Юдолей. В своей
трудовой деятельности люди часто разрезают предметы на рав-
ные части — доли. Так, столяру нередко приходится распили-
вать длинную доску на несколько одинаковых коротких, ого-
родный участок часто разбивают иа одинаковые грядки, каждая
из которых является долей всего участка.
В § 62 мы занимались делением данного множества на равные
части и видели, что это часто оказывается невозможным. Так,
множество из 5 элементов нельзя разделить ни на 2, ни на 3,
ни на 4 равные части, но можно разделить на 5 равных частей.
Множество из одного элемента нельзя разделить ни на 2, ни
на какое большее число равных частей.
Однако это становится возможным, если данный элемент
каким-нибудь способом разложить (разрезать, разбить, раздро-
бить, разломать, разъединить, разделить) на равные части или
доли и тем самым вместо каждого данного элемента получить
два или более одинаковых новых. Так, уже маленькие дети
хорошо понимают, что если дано одно яблоко на двоих, надо
разрезать его пополам и дать каждому по одной из полученных
долей («половинок»). Вместо множества из одного данного эле-
мента (яблока) у нас теперь множество из двух новых элемен-
тов (половинок яблока), и деление на 2 становится возможным.
Конечно, такое разложение элемента на доли не всегда вы-
полнимо. Если этот элемент, например живое существо, разде-
лить его поровну между двумя или более лицами нельзя. Дальше
у нас будет идти речь только о таких элементах, которые до-
пускают разложение на равные части (доли). Таковы, например,
отрезки, окружности, дуги, прямоугольники, брусы и вообще
элементы, представляющие собой значения тех величин, о кото-
рых шла речь в главе VII.
Если данный элемент (предмет) можно разделить на равные
части, то каждая из них называется долей элемента. Различают
половины, или вторые доли (если деление произведено на две
равные части), трети или третьи доли (если — на три), чет-
верти, или четвёртые доли (если — на четыре), пятые, шестые,
седьмые и т. д. доли (если — на 5, 6, 7 и т. д. равных частей).
Разделив элемент на п равных частей, где п — любое натураль-
ное число, получим энные доли этого элемента.
Для обозначения доли на письме пользуются горизонтальной
чёрточкой, над которой пишется 1 и под которой пишется на-
туральное число, показывающее, на сколько равных частей раз-
делён предмет.
Половина обозначается в виде i, треть — 4-, четверть—4
X «J т
и т. д.
§ 172. Деление отрезка и прямоугольника на равные части.
Посмотрим, как получить доли отрезка и прямоугольника. Взяв
бумажную полоску, можно сложить её пополам и получить две
131
её половины, или вторые доли. Складывая каждую половину
ещё пополам, получим четверти всей полоски, так как 2-2 = 4.
Новое складывание даст восьмые доли (2 • 4 = 8), затем шест-
надцатые доли (2 • 8 = 16), трид-
цать вторые доли (2 • 16 = 32)
и т. д. На рисунке 56 показаны
результаты такого последова-
тельного деления пополам взя-
той полоски.
Чтобы показать деление от-
резка и прямоугольника на
любое число п равных частей,
проще всего взять полоску клет-
чатой бумаги, содержащую п
клеточек (или число, кратное п).
На рисунке 57 изображена по-
лоска, которую удобно разде-
лить на 11 долей; применяя
дальнейшее деление пополам,
получим 22-е и 44-е доли.
Если требуется разделить на дан-
ное число равных частей заданный
отрезок, применяют способ последо-
вательных исправлений. Пусть, напри-
мер, надо получить пятые доли отрез-
ка АВ, показанного на рисунке 58. Берём на глаз немного меньше четверти
этого отрезка, а именно отрезок ААЪ и откладываем циркулем 4 отрезка
AjA2, А2А3, А3А4, А4А5, равных АА4. Если точка А5 окажется левее точки
7
2
4
8
1
16
32
Рис. 56.
В, как на рисунке 58 слева, взятый отрезок ААХ слишком мал. Его
надо исправить, увеличивая его (на глаз) на пятую часть отрезка — раз-
ницы АЪВ, и отложить исправленные отрезки А4А2 и др.; они отмечены чёр-
точками на рисунке 58 снизу. Точка As теперь совпала с точкой В, деление
закончено. Если бы совпадения не получилось, пришлось бы выполнить второе.
132
третье и т. д. исправления. На рисунке 58 справа показано, как поступают
в случае, когда взятый отрезок АА, оказался слишком большим.
При делении на шесть долей делят отрезок сперва пополам, потом каж-
дую половину на три доли; при делении на 10 долей — пополам, потом каж-
дую половину на пять долей; при делении на 12 долей — пополам, ещё раз
пополам, каждую четверть на три доли и т. д.
Рис. 58.
§ 173. Деление окружности и круга на равные части. Разделить
окружность на 2, 4, 8, 16 и т. д. долей так же легко, как и
отрезок: применяется последовательное складывание круга по-
полам. Делить окружность на 6 долей ещё легче, чем прямо-
угольник: откладывая последовательно хорду, равную радиусу,
6 раз, мы всегда вернёмся в исходную точку. Деление на 3,
12, 24 доли делается при помощи деления на 6 долей. Если
Рис. 59.
окружность разделена на требуемое число долей, для деления
круга надо только соединить все точки деления с центром. Все
эти случаи деления окружности и круга показаны на рисунке 59.
Деление на 5, 7, 11, 13 и т. д. долей выполняется по способу последова-
тельных исправлений. На рисунке 60 показано деление окружности на пять
долей, которое приходится делать для построения пятиконечной звезды —
эмблемы Советской Армии. Для деления на девять долей сперва делят окруж-
ность на три доли, затем каждую треть ещё на три равные части; для деления
на 10 — сперва на пять, потом каждую пятую долю пополам и т. д.
133
§ 174. Деление множества на равные части. Умея находить
доли какого-нибудь элемента, мы можем разделить на любое
число равных частей
и всякое множество, состоящее из таких
элементов. Так, если четверым детям даны
3 яблока и надо разделить их поровну,
можно разрезать каждое яблоко на 4 доли,
а затем, имея всего 4-3=12 долей, дать
каждому по 12 : 4 = 3 доли. Другой спо-
соб решения той же задачи: разделить
на 4 части сперва только 2 яблока, раз-
резая каждое пополам, затем разделить
третье яблоко, разрезав его на 4 доли;
каждый получит по половине и по чет-
верти яблока. Оба способа дележа по-
казаны на рисунке 61.
Ещё пример: надо разделить поровну
между 5 лицами 17 одинаковых листов бу-
маги; сколько получит каждый? Раздав
всем по 3 целых листа, мы получим в
остатке ещё 2 листа и разрежем каждый
из них на 5 долей, а затем разделим
поровну эти 5 • 2 = 10 долей. Каждый
получит таким образом по 3 целых листа
и по 2 пятых доли листа.
Рис. 61.
Мы пришли к следующему важному выводу: если множество
состоит из одинаковых элементов, допускающих деление на рав-
ные части (доли), то возможно деление этого множества на любое
число равных частей (долей).
Раздел 2. ДРОБИ, ИХ РАВЕНСТВО И НЕРАВЕНСТВО
§ 175. Определение дроби. Если дано, например, множество
яблок, то, пересчитав их, узнают численность этого множества
(например, 7). Численность множества элементов указывают од-
ним натуральним числом.
Если дано, например, множество четвёртых долей яблок, то,
пересчитав их, узнают численность этого множества четвертей
(например, 28). Имея дело с множествами одинаковых долей эле-
ментов, надо указывать два натуральных числа: во-первых,
число, которое показывает, сколько долей входит в множество,
134
и, во-вторых, число, которое показывает, каковы эти доли, т. е.
на сколько частей разделён каждый элемент.
Такая пара натуральных чисел получила название дробного
числа, или дроби. Первое из них называют её числителем, вто-
рое — знаменателем.
Не обращая внимания на то, что представляет собой взятый
элемент, будем говорить о нём как о «единице».
Итак, дробным числом, или дробью, называется пара нату-
ральних чисел, выражающих одну или несколько долей единицы;
числителем дроби называют натуральное число, показывающее,
сколько долей входит в это множество, знаменателем—нату-
ральное число, показывающее, на сколько долей разделена каж-
дая единица. Дробь записывается посредством горизонтальной
черты, выше которой пишут числитель, ниже — знаменатель.
Например, запись (пять восьмых) означает, что каждая еди-
ница разделена на 8 равных долей и таких долей взято 5.
Запись ~, где буквы а и п означают любые натуральные
числа, может выражать какую угодно дробь («а энных долей»).
При п = 1 эта запись выражает под видом дроби натуральное
5 е
число а; например, у есть не что иное, как натуральное число 5.
Можно сказать, что дробь является обобщением натурального
числа: всякое натуральное число а можно считать дробью со
1 о
знаменателем 1, а именно у.
§ 176. Равенство и неравенство дробей. 1. Если, например,
7 5
кукурузой засеяно у га земли, а пшеницей у- га, то легко
усмотреть, что кукурузой засеяно больше, чем пшеницей, так
как 7 восьмых имеет 7 долей, а 5 восьмых имеет тех же до-
лей 5.
Рис. 62.
12
Возьмём дроби J2и У2' Легко видеть, что вторая дробь
больше первой, так как доли у них одинаковые, а число их у
второй дроби больше, что видно на рисунке 62.
Рассуждая так, будем всегда приходить к выводу:
135
Две дроби с одним и тем же знаменателем, но разными числи-
телями всегда различные, а именно больше та, у которой числи-
тель больше, так как доли, выражаемые обеими дробями, оди-
наковы, но взято их не поровну.
11 5 I а Ь ,
12>12 I ->й, если а>й.
7 7
2. Если, например, выделить -g- или арбуза, то легко до-
гадаться, что первая часть арбуза, больше второй, так как в 7
восьмых взято столько же (7) долей, что и в 7 двенадцатых,
но доли, выражаемые первой дробью, крупнее, чем второй.
3 3 3
Возьмём дроби -g- и 2б • Легко установить, что у больше,
з
чем эд, так как число долей у них одинаковое, но доли, выра-
жаемые первой дробью, крупнее, чем второй. Это же видно и
на рисунке 63.
2 2
8 > 20
Рассуждая так, придём к выводу:
Если у дробей одинаковые числители, а знаменатели различны,
то дроби всегда различны, причём больше та дробь, у которой
знаменатель меньше:
а а
— > — , если п < т.
пт
3. А как сравнивать дроби с различными числителями и одно-
временно с различными знаменателями?
Рассмотрим две задачи.
1) Известно, что за одно и то же время один тракторист
3 5
может вспахать земли у га, а другой -g га. Какой из тракто-
3 5
ристов пашет быстрее? Иначе: какая дробь больше, g- или -g?
Заметьте, что у этих дробей различные числители (3 =£ 5) и
различные знаменатели (5 8). Как сравнивать такие дроби?
Обратимся к построению рисунка (рис. 64).
Возьмём полоску, как указано на рисунке, разделим её сперва
на 5 равных частей и выделим из них 3, а потом разделим на
8 частей и выделим 5 частей.
136
5 3
Видим, что д- > -f ; следовательно, второй тракторист пашет
о О
быстрее.
2) Известно, что первая бригада рабочих может исправить
з
Y пути АВ за то же время, когда вторая бригада могла бы
исправить -g- того же пути. Какая бригада работает быстрее?
Опять обращаемся к построению рисунка (рис. 65).
Видим, что ; следовательно, обе бригады работают
одинаково.
Рис. 65.
Вывод. Две дроби с различными числителями и различными
знаменателями могут быть и равными и неравными.
О том, как удобнее и быстрее сравнивать дроби с разными
числителями и разными знаменателями, речь будет идти ниже,
в § 190.
§ 177. Дроби правильные и неправильные. Если первый рабо-
7 8 11
чий выполнил -g месячного плана, второй — -g- его, третий — g-,
7 .
то первый пока еще не выполнил всего плана, так как -g- < 1,
g
второй уже выполнил, так как -g- = 1, а третий перевыполнил
план, так как > 1, что видно на рисунке 66.
137
Правильной, дробью называется дробь, у которой числитель
меньше знаменателя, а неправильной дробью называется дробь,
у которой числитель равен или больше знаменателя.
Например:
Дроби вида:
7 1 99 100
8 ’ 10 ’ 20 ’ 100 ’ 1001 И Т‘ Д‘
правильные, а дроби вида:
И _8 !£° 1000 1001
8 ’ 8 ’ 2 ’ 99’ 1000 ’ 1000 И Т’ Д’
неправильные.
Рис. 66.
Легко видеть, что правильная дробь выражает множество до-
лей, в которых их взято меньше, чем было при разбиении одного
элемента на доли, а в неправильной дроби долей берётся столько,
сколько их получилось из одного или более элементов, а потому
всякая правильная дробь меньше единицы, а всякая неправиль-
ная дробь равна или больше единицы.
. 7 . 1 , 3 . 99 . 1000 „
Например. 8 < ; 10 < ; 20 < 1; 100 < 1, 1001 <1 и т. д.
8 . 10 , 20 , 100 , 1001 .
8 — ’ 10— ’ 20 ~ ’ 100 ~ ’ 1001 “* 1 и т- д-
11 - 1 3 „ 1- 100 >> .. 1001
К" 2" > 1 ’ 99 > *’ 1000" > 1 и т. д.
вообще < 1, если а < п,
о 1
— = 1, если а = п,
п
— > 1, если а > п.
п
Если числитель правильной дроби равен её знаменателю, вме-
сто нее можно написать 1; так, = 1; = 1. Если числитель
дроби больше её знаменателя, вместо неё можно написать нату-
ральное число с правильной дробью или, как говорят короче,
целое с дробью. Так, j можно записать в виде 2 + -|-, что ко-
138
о
роче записывается 2— («два и три четверти»), потому что каж-
дые четыре четверти составляют единицу, а 11 четвертей соста-
вляют 2 единицы (4-2 = 8 четвертей) да ещё 3 четверти. На
рисунке 67 сверху изображено множество из 11 четвёртых до-
лей одинаковых элементов (кругов), а снизу из 2 таких элемен-
тов и 3 четвертей третьего такого же элемента; ясно, что не-
11 3
правильная дробь и целое с дробью 2 — выражают одно и то
же, что и записывается в виде равенства
я
‘t
Рис. 67.
Чтобы представить неправильную дробь в виде целого с дро-
бью, надо числитель разделить на знаменатель. Частное есть число
целых, остаток — числитель правильной дроби; знаменателем же
её берётся знаменатель данной неправильной дроби. Например,
38
имея дробь делим 38 на 5; получив в частном 7 и в остатке 3,
□
пишем, что
38 _ _ 3
5 ~ ' 5 *
Замена неправильной дроби целым числом с дробью назы-
вается исключением целого из дроби. Если при делении числителя
на знаменатель получается остаток, равный нулю, то неправиль-
ная дробь представляет собой натуральное число, например:
139
Иногда приходится заменять целое с дробью равной непра-
вильной дробью. Если имеются, например, два каких-нибудь
одинаковых элемента и три пятых доли такого же элемента, то
легко видеть, что пятых долей этих элементов будет всего
5-2 + 3=13:
9_3 _ 13
5 5 ‘
Чтобы целое с дробью представить в виде неправильной дроби,
надо умножить знаменатель на целое и прибавить к произведе-
нию числитель. Полученная сумма записывается числителем,
а знаменатель берётся прежний.
U о 2 3-8 + 2 26
Например, 8 у =-----g---= у.
§ 178. Деление натуральных чисел. Введя дроби, мы получаем
возможность выполнять полное деление натуральных чисел во
всех случаях без исключения, так как всегда выполнимо деление
множеств, если их элементы допускают деление на равные части.
Например, чтобы разделить 6 на 7, достаточно представить каж-
дую единицу делимого в виде 7 седьмых долей, что даст нам
всего 6 • 7 = 42 седьмые доли. Так как 42 :7 — 6, то деление 6
на 7 даст в частном шесть седьмых долей, т. е. у. Итак,
6:7 = у.
Например, если надо разделить 6 яблок поровну между 7 ли-
цами, надо дать каждому у яблока.
Каковы бы ни были два данных натуральных числа, всегда
возможно первое из них разделить на второе; в частном получается
дробь, числителем которой является делимое, знаменателем — де-
литель. Например,
24 : 35 = = , 15:8 = ^, и вообще а:Ь — ^-.
оа о и
Если делимое больше делителя, в частном получается непра-
вильная дробь, из которой можно исключить целое число; на-
пример,
23:4 = у = 5-.
4 4
Это деление надо сделать, например, для решения такой
задачи: 23 яблока разделены поровну между 4 лицами; сколько
получил каждый?
з
К ответу 5 у можно, разумеется, прийти иначе, рассуждая
так: чтобы разделить 23 яблока поровну между 4 лицами, дадим
140
каждому по 5 яблок, а оставшиеся 3 яблока режем на четвёртые
3 ,
доли и даем каждому еще по яблока.
Всякое дробное число можно рассматривать как частное от
7
деления числителя на знаменатель: дробь есть частное от деле-
ния 7 на 12; дробь — есть частное от деления а на п. Обратно:
частное от деления одного натурального числа (произвольного)
па другое натуральное число (тоже произвольное) есть дробь,
в которой делимое является числителем, делитель — знаменателем.
§ 179. Представление натурального числа в виде дроби.
Разделив единицу на 2, 3, 4, 5, ... равных частей, можем
написать, что
1 _ 2^_ А — А — А -
1—2— 3“ 4“ 5 ’
а потому
2 —± —А —А —12— А —А_12 —12 —
Z~2 — 3~4~ 5—•••’ ~ 2 3 ~ 4“ 5 ~ •
и т. д.
Например, число 13 можно представить в виде дроби со зна-
менателем 8:
13 —121
13 8 .
Это равенство полезно представить себе наглядно, например
так: имеется 13 яблок, затем каждое разрезано на 8 долей,
получилось всего 8 • 13 = 104 такие доли, а потому дробь 221 вы-
ражает тоже 13 яблок, только в ином виде.
Любое натуральное число равно дроби с произвольным знаме-
нателем, у которой числитель равен произведению этого знамена-
теля на данное натуральное число.
Кратко это свойство чисел записывается в виде равенства
ап о
а — —. Здесь а и п — произвольные натуральные числа.
§ 180. Проценты. В жизни особенно часто встречаются дроби
со знаменателем 100, а потому сотая доля получила особое назва-
ние— процент и особое обозначение — знак %. Например, дробь
10Q, т. е. тридцать семь сотых, можно прочесть как «тридцать
семь процентов» и записать без знаменателя в виде 37%. Запись
123% читается как «сто двадцать три процента» и означает то
123
же самое, что запись . Если сказано «предприятие выполнило
за неделю 27% месячного плана», то это означает, что за неделю
27
сделали того, что надо сделать за месяц.
141
Раздел 3. ТРИ ОСНОВНЫЕ ЗАДАЧИ НА ДРОБИ
§ 181. Нахождение дроби от числа. Рассмотрим задачу:
От дощечки длиной 16 см надо отпилить часть, равную -g её
длины. Как сделать разметку, чтобы отпилить требуемую часть?
Для решения этой задачи достаточно подумать о том, что вы-
5
ражает дробь -g-: данный отрезок разделён на 8 равных частей
(долей), взято 5 таких долей. Следовательно, для решения задачи
надо ответить на два следующих вопроса: 1) Какова длина
5
отрезка? 16:8 = 2 см. 2) Какова длина g- отрезка? 2 • 5 = 10 см
(рис. 68).
Теперь можно на расстоянии 10 см от начала дощечки по-
ставить необходимую метку, как указано на рисунке 68.
Здесь мы имеем одну из самых важных основных задач па
дроби — нахождение дроби от числа.
Если дано какое-нибудь число и требуется найти некоторую
его дробь, делят это число на знаменатель дроби, а затем полу-
ченный результат умножают на её числитель.
Иначе: чтобы найти дробь — от числа Ь, надо найти сперва
частное Ь : п, потом произведение (Ь : п) - а.
Если b : п не натуральное число, а дробь, для решения задачи
надо уметь умножать дробь на натуральное число, чему мы
научимся дальше.
Решим ещё задачу: Пальто стоило 600 руб. Сколько при-
дётся уплатить за него после снижения цены на 21%?
21 1
Как мы знаем, 21% есть не что иное, как Но от 600
21
(один процент от 600) равна 600:100 = 6, а от 600 (двадцать
один процент от 600) равна 6 • 21 = 126, а потому новая цена
пальто 600— 126 = 474 руб.
§ 182. Нахождение числа по его дроби. Рассмотрим теперь
обратную задачу. Известно, что отпиленная часть дощечки имеет
5
длину 10 см, причём она составляет -g- всей дощечки. Какова
была первоначальная длина всей дощечки?
142
Зная, что пять восьмых долей отрезка имеют длину 10 см,
находим, какова длина одной восьмой его доли, а для этого
делим 10 на 5 и получаем 2 см. Далее, зная длину одной вось-
мой отрезка, находим длину всего отрезка, умножая 2 см на 8;
получаем 16 см (рис. 69).
Выше мы имели одну из основных задач на дроби — нахожде-
ние дроби от числа. Теперь мы встретились со второй основной
задачей на дроби — с нахождением числа по данной его дроби-,
эта вторая задача, как и первая, решается двумя действиями.
- /б см
Рис. 69
Если надо найти неизвестное число, зная, чему равна некото-
рая его дробь, делят известное число на числитель дроби, а затем
полученный результат умножают на её знаменатель.
Иначе: чтобы найти число, зная, что дробь от него равна Ь,
надо найти сначала частное b : а, а потом произведение (Ь : а) • п.
Если Ь: а не натуральное число, а дробь, для решения задачи
требуется умение умножать дробь на натуральное число.
Решим для примера ещё такую задачу. Рабочий собрал 72 ма-
шины, что составляет 24% его недельного плана; сколько машин
24
должен он собрать по этому плану за неделю? Если 24%, или
недельного плана, составляет 72, то 1% составляет 72:24 = 3,
а весь план, имея всего 100%, или 100 сотых долей, составляет
3 • 100 = 300 машин.
§ 183. Нахождение отношения двух чисел. Если длина класса
12 м, а ширина 6 м, то частное 12:6 = 2 показывает, что длина
больше ширины вдвое, или что отношение длины к ширине
равно 2.
Если длина класса 8 м, а ширина 6 м, то частное 8:6 = 4
О
4
показывает, что, взяв от ширины класса, т. е. от 6 м, получим
(6 :3) • 4 = 8 м, т. е. длину класса. Говорят, что здесь отношение
длины класса к его ширине равно 4:3, или 4, но нельзя ска-
О
4 .
зать, что длина класса в -д- раза больше его ширины, так как в
арифметике слово «раз» соединяется только с натуральными
числами: один раз, два раза, три раза и т. д.
143
Итак, отношением одного данного числа к другому называется
дробь, которую надо взять от второго данного числа, чтобы полу-
7
чить первое данное число. Например, отношение 70 к 40 равно у,
7 4
так как у от 40 составляют 70; отношение 40 к 70 равно у, так
4
как у от 70 составляют 40.
Чтобы найти отношение двух чисел, надо первое разделить на
второе: отношение числа а к числу b равно частному от деле-
ния а на Ь, т. е. дроби у .
Нахождение отношения двух чисел является третьей основной
задачей на дроби.
Три основные задачи на дроби тесно связаны друг с другом.
В первой из них мы ищем первое из двух чисел, зная второе
и отношение первого ко второму. Во второй ищем второе из
двух чисел, зная первое и отношение первого ко второму. В третьей
мы ищем отношение первого числа ко второму, зная и первое
и второе.
§ 184. Некоторые более сложные задачи на дроби, сводящиеся
5
к основным. I. Человек проехал всего пути и узнал, что ему
осталось ехать ещё 42 км. Какова длина всего пути.
Рис. 70.
Решение задачи становится совершенно ясным, если изобра-
зить её условие чертежом (рис. 70). Весь путь содержит 12 две-
надцатых долей. Когда человек проехал 5 из них, осталось
у
проехать ещё 12 — 5 = 7 таких же долей, т. е. всего пути, а
эта дробь всего пути составляет согласно условию 42 км.
Остаётся найти число, которого равны 42, т. е. решить вто-
рую основную задачу на дроби. Приводим примерную запись
всего решения (с проверкой).
1) Какую дробь всего пути осталось проехать, когда проехали
5 □
всего пути?
/ 7\
12 — 5 = 7 двенадцатых долей, или =1.
144
2) Сколько километров составляет ~ пути, если его равны
42 км?
42 км : 7 — 6 км.
3) Каков весь путь, если ~ его равна 6 км?
6 км • 12 = 72 км.
Проверка.
5
1) Чему равны всего пути, равного 72 км?
72 км : 12 = 6 км; 6 км • 5 = 30 км.
2) Сколько пути осталось, когда проехали 30 км?
72 км — 30 км = 42 км.
II. Рабочий взялся изготовить некоторое количество деталей.
Когда он изготовил 69% от этого количества, то подсчитал, что
ему остаётся сделать на 874
штуки меньше, чем он сделал.---------------------------------
Сколько деталей он взялся из- -------------------------------
готовить? -----------------------------
Изобразим всё множество-----------------------------------
деталей, какие рабочий взялся--------------------------------
Сселанс 69%
изготовить, в виде квадрата----------------------------------
из 100 клеток (рис. 71). Тогда-------------------------------
каждая клетка будет выражать
одну сотую долю всего мно-___________________________________
жества, или 1%. Изготовлен-__________________________________
ные им69% изобразятся 69клет-________________________________
ками, а неизготовленные — ос-________________________________
тальными 100 — 69 = 31 клет- ________________________________
ками, выражающими остальные П I
31 сотых (31%). Изготовлено Рис 71
больше, чем не изготовлено,
на 69 — 31 =38 (38%), что составляет по условию задачи
38
874 штуки. Теперь остаётся найти число, которого, или 38%,
составляет 874, что мы уже умеем делать:
874 : 38 = 23; 23 - 100 = 2300.
Итак, рабочий взялся изготовить 2300 деталей.
Для проверки находим число изготовленных деталей (2300:100=
= 23; 23 • 69 = 1587), остаток (2300 — 1587 = 713), разницу между
числом изготовленных деталей и остатком (1587 — 713 = 874) и
убеждаемся, что задача решена верно.
III. Надо было засеять поле в 180 га. В первый день засеяли
2 3
-д- его, во второй остатка, а в третий день работа была закон-
чена. Сколько гектаров засеяли в третий день?
69:
Ос
no.-mca сс'епсть
31%
Рис. 71
8 Арифметика
145
160 га
/
де по
2
ь- поля
П де н о
Ш-день
Рис. 72.
Вот примерная запись решения этой задачи.
1. Сколько гектаров было засеяно в первый день?
180:9 = 20 (га), 20 • 2 = 40 (га).
2. Сколько гектаров осталось на второй и третий дни?
180 — 40 = 140 (га).
3. Сколько гектаров было
засеяно во второй день?
140 : 5 = 28 (га),
28 • 3 = 84 (га).
4. Сколько гектаров было
_ засеяно в третий день?
Достатка 140 — 84 = 56 (га).
_5 поля
£ Решение задачи полезно ил-
люстрировать чертежом (рис.
72), представив поле в виде
- прямоугольника со сторонами
в 9 клеток и 5 клеток. Легко
сообразить, что каждая клетка
изображает 180 : 45 = 4 (га).
2
IV. Найти площадь поля, зная, что за первый день засеяли
3 у
его, за второй остатка, а за третий остальные 56 га.
з
Когда во второй день засеяли у остатка, то на третий день
5 3 2 сс г
осталось -g — -g- = y остатка, что составило 56 га. Следовательно,
остаток был равен (56: 2) 5 = 140 (га). Таким образом, когда в
первый день засеяли всего поля, то осталось 140 га, составляв-
9 2 7
ших -д-—g — g всего поля. Поле имело всего (140 :7)-9=180 га.
Решение задачи IV представляет собой проверку решения
задачи III, а решение задачи III — проверку решения задачи IV.
Задачи III и IV взаимно обратны.
Раздел 4. СВОЙСТВА ДРОБНЫХ ЧИСЕЛ
§ 185. Кратное изменение числителя. Возьмём какую-нибудь
дробь, например -g-, и увеличим ее числитель во сколько-нибудь
раз, например в 5 раз, оставляя без изменения её знаменатель.
Сравнивая полученную дробь
3 • 5 _ 15
8 — 8
146
з
с первоначально взятой дробью -g-, видим, что она больше перво-
начально взятой дроби в 5 раз: там было множество из 3 восьмых
долей единицы, здесь имеем множество из 3*5—15 таких же
долей.
Это рассуждение применимо ко всякой дроби и ко всякому
увеличению её числителя в несколько раз. Отсюда вывод: уве-
личивая во сколько-нибудь раз числитель дроби и оставляя без
изменения её знаменатель, мы увеличиваем во столько же раз
саму дробь.
Если замена числителя числом, в несколько раз большим, при
сохранении неизменным знаменателя приводит к увеличению
дроби во столько же раз, то
замена числителя числом,
в несколько раз меньшим
(опять-таки при сохранении
неизменным знаменателя),
приводит к уменьшению дро-
би во столько же раз. Так,
например, уменьшив чнсли-
тель дроби -g- в 5 раз, мы
получим дробь -g-, меньшую,
15 к
чем g-, в 5 раз.
Увеличение и уменьше-
ние числа в несколько раз
называют общим термином
«кратное изменение». Таким
образом, можно сказать, что
мы выяснили, как меняется дробь при кратном изменении её
числителя.
§ 186. Раздробление (размельчение) и укрупнение долей. Раз-
делив какую-нибудь долю, например , на 2, 3, 4, 5, 6 и т. д.
равных частей, мы получим новые, более мелкие доли той же
единицы, а именно четверти, шестые, восьмые, десятые, двенадца-
тые и т. д. доли. Действительно, разделив каждую половину по-
полам, мы получим доли, которых во всей единице будет 2*2 = 4;
разделив половину на три равные части, получим доли, которых
во всей единице будет 3*2 = 6 и т. д. (рис. 73). Разделив одну
четвёртую долю, например, на 2, 3, 6 равных частей, получим
соответственно восьмые, двенадцатые, двадцать четвёртые доли
единицы.
Такое «раздробление» («размельчение») долей, по крайней мере
мысленное, возможно для любой доли единицы, причём раз-
дроблять её можно на любое число равных частей. Например,
имея сороковые доли, можем разделить каждую на 12 равных
8*
147
частей и получим новые более мелкие доли, которых во всей
единице будет 12 • 40 = 480; следовательно, каждая такая мелкая
доля представляет собой четырёхсот восьмидесятую часть еди-
ницы.
Раздробив — долю на k равных частей, получим во всей еди-
нице п k новых более мелких долей, каждая из которых есть
1
часть единицы.
Итак, когда переходим от долей четвёртых к восьмым, два-
дцатым, сотым и т. д., то доли размельчаем; обратно, когда пе-
реходим от долей восьмых, двадцатых, сотых и т. д. к четвёр-
тым, то доли укрупняем. Соединив вместе несколько одинаковых
долей, нередко получаем возможность рассматривать их как одну
более крупную долю той же единицы. Так, если единица раздроб-
лена на двадцать четвёртые доли, то каждые две такие доли
составляют двенадцатую долю, каждые три — одну восьмую,
каждые четыре — одну шестую, каждые шесть — одну четверть,
каждые восемь — одну треть, каждые двенадцать — одну вторую,
т. е. половину. Это наглядно показано на рисунке 74.
Укрупнение долей возможно столькими способами, сколько де-
лителей имеет знаменатель дроби, если не считать 1 и самого
знаменателя. Так, двадцать четвёртые доли можно укрупнить
шестью указанными выше способами, потому что число 24 имеет
шесть таких делителей, а именно: 2, 3, 4, 6, 8, 12. Сотые доли
можно укрупнить семью способами, а именно: в пятидесятые,
двадцать пятые, двадцатые, десятые, пятые, четвёртые, вторые
148
доли, так как число 100 имеет, кроме 1 и 100, ещё семь делителей
(2, 4, 5, 10, 20, 25, 50). Доли, выражаемые дробями с простыми
знаменателями (2, 3, 5, 7, 11, 13...), укрупнения не допускают.
§ 187. Кратное изменение знаменателя. Если взять какую-
й е 3
нибудь дробь, например , и увеличить ее знаменатель во сколь-
ко-нибудь раз, например в 5 раз, сохраняя числитель без изме-
3 3
нения, то новая дробь ^5 = будет состоять из долей более
« з
мелких, чем первоначально взятая дробь -у.
Единица раньше была разделена на 4 доли, теперь на
4 • 5 = 20 долей. В каждой четверти 5 двадцатых долей, каждая
из которых в 5 раз меньше, чем четверть, и этих более мелких
долей взято 3, т. е. столько же, сколько раньше было взято
з
более крупных долей. Очевидно, новая дробь в 5 раз меньше,
Л 3
чем первоначально взятая дробь
Подобное рассуждение применимо к любой дроби и ко всякому
увеличению её знаменателя в несколько раз, а потому, увеличи-
вая во сколько-нибудь раз знаменатель дроби и оставляя без
изменения её числитель, мы уменьшаем во столько же раз саму
дробь.
Если же, сохраняя неизменным числитель дроби, уменьшить
её знаменатель во сколько-нибудь раз, т. е. разделить его на
какое-нибудь число, которое является его делителем, то мы заме-
ним мелкие доли таким же числом более крупных долей. Напри-
3 3
мер, уменьшение в 5 раз знаменателя дроби даёт дробь ,
содержащую вместо трёх мелких долей (двадцатых) столько же
более крупных долей (четвёртых), каждая из которых в 5 раз
больше, чем одна двадцатая.
Таким образом, уменьшая знаменатель дроби во сколько-ни-
будь раз и сохраняя неизменным числитель, мы получаем новую
дробь, во столько же раз большую, чем первоначально взятая.
§ 188. Основное свойство дроби. Производя размельчение до-
лей, можно любую дробь выразить в более мелких долях.
Например, в виде X. Имеем:
D 1U
3 6 . „ '
у меньше у вдвое (числитель второй дроби вдвое
больше числителя первой).
Уд меньше у вдвое (знаменатель второй дроби вдвое
меньше знаменателя первой).
3 6
Отсюда видим, что -5 и равны одному и тому же третьему
з 6
числу, а потому у = jq •
149
3 6 9 12 15
Рассуждая так же, получим: — те = ™ = ее и т. д.
‘ О 1U 10 ZU zo
Если увеличить во сколько-нибудь раз числитель дроби и во
столько же раз увеличить её знаменатель, дробь увеличится и
вместе с тем уменьшится в одно и то же число раз, т. е. оста-
нется без изменения.
Мы пришли к основному свойству дроби: дробь не меняет
своего значения, если её числитель и знаменатель увеличить (или
уменьшить) в одно и то же число раз.
Краткую запись основного свойства дроби даёт формула
а _а • k
п n-h'
где буквы а, п, k означают какие угодно натуральные числа.
Это свойство дроби имеет много применений. Например,
3 г
если надо разделить кусок в м на 5 равных частей, пред-
3 3 • 5 15
ставляют в виде ^5= 20 и замечают» чт0 каждая из
искомых частей будет содержать 15:5 = 3 двадцатых доли.
Таким образом, деление даст кусочки по м. Для проверки
3
решим ту же задачу, переходя к миллиметрам: м составляют
(1000 : 4) • 3 = 250 • 3 = 750 миллиметров;
750 мм: 5 = 150 мм. Но м равны как раз (1000 : 20)-3 =
= 50 • 3 = 150 мм.
§ 189. Сокращение дробей. Если дробь состоит из долей,
допускающих укрупнение, её в некоторых случаях можно выра-
зить в более крупных долях. Так, дробь Ц можно представить
9 6 3
в виде уз- 8 ’ Т-
Замена данной дроби равной ей дробью, выраженной в более
крупных долях, называется сокращением данной дроби. Сокра-
тить дробь возможно тогда, когда её числитель и знаменатель
имеют общий делитель, отличный от единицы. Таким образом,
сокращение дроби производится посредством деления её числи-
теля и знаменателя на какой-либо их общий делитель, отличный
от единицы. Сокращение не меняет значения дроби.
Это свойство дроби вытекает из основного её свойства, выра-
жаемого формулой . Действительно, переписав эту фор-
а-6 а ..
мулу в виде —= — , убеждаемся, что деление числителя и зна-
менателя дроби на какой-нибудь общий их делитель даёт новую
дробь, равную прежней, но имеющую меньший знаменатель, т. е.
выраженную в более крупных долях.
150
Дробь, выраженная в более крупных долях, удобнее дроби,
выраженной в мелких долях, а потому сокращение дроби при-
меняют всегда, когда оно возможно, если только нет каких-либо
особых причин предпочитать более мелкие доли. Например, по-
2
лучив при решении задачи в ответе число у, его следует запи-
73 1
число gig в виде у.
сать в виде у
Если дана дробь, например jqqq , то её можно выразить проще:
зоо _ зо
1000 ~ 100
(уменьшили числитель и знаменатель в одно и то же число раз).
Полученная дробь вновь сократима:
зо _ з
100 — ю •
Дальнейшее сокращение невозможно, так как 3 и 10—вза-
имно простые числа.
Дробь сократима, если НОД числителя и знаменателя не равен
единице [как имели выше: НОД (300; 1000) — 100], и несокра-
тима, если НОД числителя и знаменателя равен единице [как
имели выше: НОД (3; 10) = 1].
Всякая дробь либо является несократимой (например,
- „ / 16 4 \
либо ее можно привести к несократимой [например, gg = -g-l.
Сокращение дроби ведут: 1) либо постепенно, записывая по-
следовательно получаемые дроби «цепочкой»; 2) либо сразу, деля
числитель и знаменатель на их НОД. Вот пример:
Сократим дробь
, , 60 30 15 5
1 способ. м — 42 — 21 — 7 .
II способ: НОД (60; 84) = 12; § = |.
Сокращая дроби ц-; получаем несократимые дроби:
3 _ 2.. 169 = 13
9 — 3 ’ 1300 ~ 100'
Иногда бывает нелегко решить вопрос о том, сократима ли
данная дробь, и если сократима, то на сколько. Так, если даны
дроби
195
221
195
И 289’
то сразу не видно, сократимы ли они.
Разлагаем числитель 195 на простые множители и получаем:
195 = 3 5 13.
151
Замечая по признакам делимости, что оба знаменателя не де-
лятся ни на 3, ни на 5, убеждаемся, что если сокращение воз-
можно, то только на 13.
Пробуя делить знаменатели на 13, замечаем, что первая дробь
15
сократима и равна , вторая же несократима.
и А , 34967 29341
Чтобы узнать, сократимы ли дроби 39923 и 39923» пР°ВДе всего
найти НОД числителя и знаменателя для каждой дроби способом
последовательного деления (§ 117). Оказывается, что первая из
них несократима, так как НОД (34967; 39923) = 1, вторая же
сократима, так как НОД (29341; 39923) = 481, и равна
Если числитель или знаменатель дроби записан в виде произ-
ведения, лучше сперва выполнить сокращение, когда оно воз-
можно, а потом уже умножать. Например, имея дробь gygo,
к 3
лучше сперва сделать сокращение на о и получить 8 10, а по-
з
том уже умножать, что даст
Надо уяснить и твёрдо запомнить, что
2%. или 2- 100’ равны 1 50’
4%> или 4 Too ’ равны 1 25’
5%, или 5 100’ равны 1 20*
ю%, или 10 100’ равны 1 10 ’
20%, или 20 100 ’ равны 1 . 5 ’
25%, или 25 100’ равны 1 . 4 ’
40%, или 40 100 ’ равны _2 . 5 ’
50%, или 50 100’ равны _1_. 2 ’
75%, или 75 100’ равны 3. 4 ’
100%, или 100 100’ равны 1;
150%, или 150 100’ равны 3 . 2 ’
200%, или 200 100 ’ равны 2 и т. д.
§ 190. Приведение дробей к одному знаменателю. Имея две
дроби и желая сравнить их, надо представить их в виде дробей
152
с одним и тем же знаменателем. Пусть, например, имеются дроби
и и надо узнать, какая из них больше. Как нам уже из-
5
вестно, дробь -jg можно представить в виде дроби с любым зна-
менателем, кратным 12, а именно:
12 - 2 = 24; 12 - 3 = 36; 12 • 4 = 48; 12 • 5 = 60 и т. д.;
7
дробь же в виде дроби с любым знаменателем, кратным 16,
именно:
16 • 2 = 32; 16 • 3 = 48; 16 • 4 = 64 и т. д.
Как видим, обе дроби можно выразить в сорок восьмых долях:
5 _ 5 4 _ 20 . 7 _ 7 • 3 _ 21
12 — 12 • 4 “ 48 ’ 16 — 16 • 3 ~ 48 *
7 21
Теперь становится ясным, что дробь jg = немного больше
А 5 20 21 . 20
дроби 12 = ^8, так как 4g>4g.
Число 48, которое помогло нам решить задачу, есть не что иное,
как наименьшее общее кратное (НОК) знаменателей данных дро-
бей 12 и 16 (§ 119). Теперь легко формулировать правило при-
ведения дробей к одному знаменателю, относящееся не только
к двум, а к любому числу данных дробей: чтобы привести данные
дроби к наименьшему общему знаменателю, надо найти НОК всех
знаменателей, разделить его на знаменатель каждой из этих дро-
бей и умножить оба члена каждой из них на полученные частные.
Пример: привести к одному знаменателю дроби
7 11 11
20 ’ 54 ’ 30'
Имеем:
20 = 22 • 5; 54 = 2 • З3; 30 = 2 • 3 • 5;
НОК (20; 54; 30) = 22 . З3 • 5 = 540;
540 :20 = 27; 540 : 54 = 10; 540 : 30 = 18;
7 _ 7-27 _ 189.
20 — 20 - 27 — 540 ’
11 _ 11-10 ПО. 13 _ 13 - 18 _ 234
54 ~ 54 • 10 540 ’ 30 — 30 • 18 — 540 *
Умея приводить дроби к одному знаменателю, можно сравни-
вать любые дроби, а не только дроби с одинаковыми числителями
или одинаковыми знаменателями (§ 176). Так, из трёх только что
рассмотренных дробей самой большой является , самой
„ 11 ПО 234 . 189. ПО
малой нт = нтп > так как езн > > ета •
54 540 ’ 540 540 540
153
Il 12
Если надо установить, что больше, или у^, находим
наименьшее общее кратное знаменателей, равное 156, и заме-
чаем, что:
. 11 _ 11 • 13 _ 143 .
а> 12 — 12 • 13 — 156’
. 12 _ 12 • 12 _ 144 .
13 — 13 • 12 ~ 156 ’
. 143 144
В> 156 < 156 ’
Следовательно,
1
ставляет .
15о
-И ,, 12
дробь 12 меньше дроби у^, причем разница со-
Глава IX. СЛОЖЕНИЕ И ВЫЧИТАНИЕ ДРОБЕЙ
Раздел 1. СЛОЖЕНИЕ ДРОБЕЙ
Рис. 75.
§ 191. Сумма дробей с равными знаменателями. Если даны
два или более множества без общих элементов и даны натураль-
ные числа, выражающие численность каждого из этих множеств,
то суммой этих натуральных чисел
называется, как мы знаем (§ 17), на-
туральное число, выражающее числен-
ность множества, которое получается
от объединения всех данных множеств.
Если элементы данных множеств пред-
ставляют собой одинаковые доли каких-
нибудь других элементов (единиц), то
объединение этих множеств приводит
к понятию суммы дробей с равными
знаменателями.
Пусть, например, имеется древес-
ный питомник, разделённый на 20
одинаковых частей (долей), изображённых на рисунке 75
3 7 9
клетками; засеяно семенами ясеня, —клёна, gg — дуба.
Требуется узнать, какая часть площади всего питомника занята
этими тремя культурами. Ясно, что вопрос здесь сводится к разы-
сканию численности множества, которое получается от соедине-
ния трёх множеств, содержащих одно 3, другое 7, третье 9 оди-
наковых элементов, т. е. к разысканию суммы 3-}-7-(-9=19. Здесь
элементами соединяемых множеств являются двадцатые доли всей
площади, а потому выполненное действие можно записать в та-
ком виде: 3 двадцатые доли 7 двадцатых долей + 9 двадцатых
долей = 19 двадцатых долей. Применяется более удобная запись:
А д- — д_ 2 —
20 + 20 + 20 ~ 20 •
154
Если известно, что площадь питомника равна 480 кв. м, то
задачу можно решить иначе, не прибегая к сложению дробей:
Q 7 Q
= от 480 есть 72; ™ от 480 есть 168; от 480 есть 216; всего
£xJ
72 4- 168 + 216 = 456, что составляет тик = всей площади. Это
4oU Zu
второе решение можно рассматривать как проверку первого.
Итак, суммой дробей с одним и тем же знаменателем назы-
вается дробь с тем же знаменателем, а числителем, равным сумме
числителей всех данных дробей. Краткая запись:
10 . 6 = 16.
17 17 — 17 ’
10 6^ 2__ 18.
17 “г 17 + 17 — 17 ’
а , ft ________а + b .
1г ' п п ’
а b . с а + Ь + с
п + п + п п
Сложение натуральных чисел можно считать частным случаем
сложения дробей, а именно дробей, у каждой из которых знаме-
натель 1, например
4 + 7 = ± + 1 = = И.
Другим частным случаем сложения дробей с одним и тем же
знаменателем является сложение процентов от одного и того же
числа. Например, если рабочий до перерыва выполнил 67% днев-
ного плана, а после перерыва ещё 49% его, то всего за смену
он дал 116% дневного плана, т. е. выполнил план с превыше-
нием на 16%.
§ 192. Сумма дробей с разными знаменателями. Может слу-
читься, что объединяемые множества долей состоят из разных
долей одних и тех же элементов. Пусть, например, человек был
. - 1
в дороге 4 часа, причем двигался он в течение -% первого часа,
2 3 5
второго, — третьего, -g- четвёртого часа, а остальное время
отдыхал. Сколько всего часов он двигался? Ясно, что здесь надо
наити сумму у + -3 + , чт0 легко сделать, если все дан-
ные доли раздробить в одинаковые более мелкие.
Вспоминая приведения дробей к одному знаменателю (§ 190),
находим НОК (2, 3, 4, 6) = 12 и заменяем данные слагаемые рав-
ными им дробями со знаменателем 12, после чего остаётся только
сложить дроби с равными знаменателями:
1,2,3, 5 _ 1 • 6 + 2 • 4 + 3 • 3 + 5 • 2
2 ’ 3 "г 4 + 6 12 ~
6 + 8 + 9+ 10 33 11 о3
=------12-----= 12 = Т = 2 * часа.
155
Получив здесь после сложения числителей дробь , мы
должны были сократить её (на 3), а затем исключить целое.
Эту задачу можно решить и не пользуясь сложением дробей,
если перейти от часов к минутам. Действительно, замечая, что
-% часа содержит 60 :2 = 30 минут, часа — 40 минут, часа—
5
45 минут, g- часа — 50 минут, находим сумму 30 4- 40 4- 45 4- 50 =
45 3
= 165 (минут), или 2 часа 45 минут = 2 часа = 2-^- часа.
Итак, каковы бы ни были данные дроби, всегда можно найти
их сумму; до упрощения она имеет знаменатель, равный наи-
меньшему общему кратному знаменателей всех данных дробей,
и числитель, равный сумме числителей дробей, которыми заме-
няются числители данных дробей после приведения этих дробей
к одному знаменателю.
Может случиться, что сумма дробей имеет числитель, кратный
знаменателю, и представляет собой натуральное число. Например,
1 , 1 , 1 _ 3 * * + 2 4-1 _ 6 _ 1
2 + 3 + 6 — 6 — б — к
§ 193. Свойства сложения дробей. Действие сложения дробей
обладает следующими двумя свойствами, которыми обладает
и сложение натуральных чисел.
1. Сумма дробей не изменяется при изменении порядка сла-
гаемых (переместительный закон сложения). Чтобы в этом убе-
диться, достаточно подумать о том, что сложение любых дробей
сводится к сложению дробей с равными знаменателями, а сло-
жение дробей с равными знаменателями сводится к сложению
натуральных чисел (их числителей), при сложении же натураль-
ных чисел выполняется переместительный закон. Например:
3 5 _ 3 + 5 _ 5 4- 3
11+ 11 ~ 11 — 11
5,3
11 + 11 ’
Следовательно,
з 5 _ 5 з
11 + 11 ~ н + и •
а . b а + b Ь + а
п ‘ п п п
b , а
п ‘ п ’
Следовательно,
с , 6 6 , а
п ‘ п п * п ’
II. Вместо того чтобы прибавлять каждое слагаемое последо-
вательно, можно прибавить сразу их сумму и, обратно, вместо
того чтобы прибавлять сумму, можно прибавить каждое из её
слагаемых последовательно (сочетательный закон сложения).
Чтобы в этом убедиться, достаточно подумать о том, что
сложение любых дробей сводится в конце концов к сложению
натуральных чисел, а сложение натуральных чисел обладает со-
четательным законом. Например:
156
/5 ,11) , 7 _ (5 + И) + 7 _
\12 + 12/ + 12 12
5+ (11 +7)
“ 12 ~
-5J1M
“12т \12 12/ *
Следовательно,
/А . 1П + А_А + р1 . X)
\12 12/ * 12 12^112^12/
(!L _L £ — (а + ь'> + с
\п ' п) ' п п
_ а + (6 + с) __
““ п
Следовательно,
§ 194. Техника сложения дробей. Целое число с дробью можно
рассматривать как сумму натурального числа и правильной дроби,
3 3
например 15-^- = 15 4--^-. Основываясь на переместительном и со-
четательном законах сложения легко убедиться, что при сложе-
нии таких слагаемых, каждое из которых представляет собой
целое с дробью, надо отдельно складывать целые, отдельно
дроби.
Например, если от одной коровы надоили 15у л, от другой
Ну л, от третьей 10-|- л, то всего надоено
15|+114 + 101 = (15-Ь11 + 10) + (|+1 + 1) =
= 36 + (1 + -1) = 371 (л).
При решении подобных задач учащиеся иногда обращают
данные в неправильные дроби. Легко видеть, что это приводит
к большому и совершенно ненужному усложнению выкладок
/ 1кЗ . 1 , 1П1 63 , 23 , 41 63+46+41
(в нашем примере + 11 2 + I04 = Т + Т + 4 =-----------4----=
150 75 1 \
= — = у = 37у); так никогда не следует делать.
Если среди данных встречаются столь большие числа, что
вычисление в уме становится затруднительным, можно приме-
нять следующую примерную запись:
Найти сумму чисел 253А, 1035^, 507-^
Предварительно найдём:
32 = 2®
24 = 23 • 3
15 = 3-5
НОК (32; 24; 15) = 25 • 3 • 5 = 480
11 - 15 + 23 - 20 + 7 - 32
253
+ 1035
507
1795
253g + 1035g + 507 1 = 1795-----------w
, 849 . 369 . 123
= 1795 480= 1796 480= 1796160-
11 • 15= 165
23 • 20 = 460
7 • 32 = 224
сумма = 849
157
Вычисления выполнены здесь в таком порядке:
1) найдена сумма (1795) натуральных чисел, входящих в сла-
гаемые (столбик слева);
2) найдено наименьшее общее кратное данных знаменателей,
а для этого все они разложены на простые множители;
3) найдены (в уме) частные от деления общего знаменателя
32 • 3 - 5 = 480 на знаменатели всех данных слагаемых, т. е. так
называемые дополнительные множители: (32 • 3 - 5): 32 = 3 • 5 =
= 15; (32-3-5):24 = 32 - 3 • 5 : (23-3)= 4 - 5 = 20; (32 • 3 - 5): 15 =
= (32 - 3 - 5): (3 - 5) = 32;
4) найдена сумма произведений числителей данных дробей на
соответствующие дополнительные множители (столбик справа);
1-701:849
5) получив сумму l'95jgQ, выполняем исключение целого
числа и сокращение дроби.
Обе строки, начинающаяся с 253^ и оканчивающаяся отве-
(123\
1796 убд1, заполняются постепенно по мере того, как произ-
водятся вспомогательные действия, которые записываются ниже
или сбоку (на полях). Разумеется, всё, что можно сделать устно,
записывать не следует. Никогда не следует забывать о необхо-
димости сокращения: ответ должен быть выражен в виде несо-
кратимой дроби.
Нередко сложение дробей существенно упрощается благодаря
применению переместительного и сочетательного законов сложе-
ния. Например, для вычисления суммы
Ц+4+1Ц+Н
нет надобности приводить все слагаемые к общему знаменателю:
заметив, что
1+1+1=1
сразу в уме находим, что сумма равна 29 1 + = 30.
Следует особо заметить два следующих частных случая сло-
жения дробей:
1) если знаменатели данных дробей взаимно просты, их наи-
меньшее общее кратное равно их произведению. Например:
5 4 _ 5 - 35 + 12 - 4 _ 175 + 48 _ 223 .
12 + 35— 12 -35 ~ 420 — 420 ’
1 3 , 7 _1-8 -15 J-3-7 -15+ 7- 7-8
7 ' 8 15— 7-8-15
_ 120 + 315 + 392 _ 827 .
~ 840 “ 840 ’
158
2) если знаменатель одной из данных дробей делится на зна-
менатели всех остальных, то он и будет общим знаменателем.
Например:
17 2 , 5 _17 + 2- 2 + 5- 3_36_„
18”*” 9 ”*” 6 — 18 — 18 —
§ 195. Проверка сложения дробей. Чтобы проверить, пра-
вильно ли сделано сложение дробей, рекомендуется выполнить
его ещё раз, в чём-либо изменяя способ решения. Например,
17 . 2 . 5
найдя сумму yg + g + g > как показано выше, можно предста-
вить ее в виде jg + I'g + "gj и вычислить еще раз, получая
17 2 • 2 + 5 • 3 _ 17 , 19 _ 17 + 19 _ 36 _ 2
18”*” 18 — 18+18~ 18 — 18“
Нередко для проверки сложения дробей можно перейти к бо-
лее мелким мерам и либо вовсе устранить сложение дробей,
либо складывать дроби с меньшими знаменателями. Например,
3 1 1
найдя у м + у м = Ijg м, можно для проверки перейти к сан-
тиметрам, что даст
60 см -J- 50 см = 110 см — 1 м 10 см = 1 м — 1 м.
Раздел 2. ВЫЧИТАНИЕ ДРОБЕЙ
§ 196. Разность дробей. Зная сумму двух натуральных чисел
и одно из них, находят другое посредством вычитания. Но та-
кие же задачи встречаются
и на дробные числа.
Например, если надо уз-
нать, на сколько сантимет-
ров выйдет из доски толщи-
ной в 1^- см забитый в неё
3
гвоздь длиной 2-^ см (рис.
76), следует узнать, сколько
надо прибавить к см.
Рис. 76.
3
чтобы получить см. Эта задача решается вычитанием и тре-
бует получения разности.
Разностью двух дробных чисел называется такое третье число,
которое, будучи сложено со вторым из них, даёт первое. Так,
разность чисел 2-|- и 1-1- равна 1-1 , так как 1-1- -J- 1-1- = 2-|-.
3 11
Здесь 2-^- — уменьшаемое, 1 — вычитаемое, 1 — разность. При-
нята запись: оЗ . 1 _ . 1
4 12 — *4 •
159
Действие нахождения разности называется вычитанием.
Если уменьшаемое и вычитаемое выражены в одинаковых долях,
то разность показывает, сколько долей останется, если из
множества долей, указываемых уменьшаемым, удалить столько
13
долей, сколько указывает вычитаемое. Например, разность —
7 6 3 / 3 . 7 13\ , о
— 16 ~ 16 = ’8'\так КаК 1Г •'16 = 16/ пока3ь1вает> что, если из
шестнадцатых долей удалить 7 этих долей, то останется 6 шест-
з
надцатых долей, или (после сокращения на 2)-^-.
Разность двух дробей с одним и тем же знаменателем равна
дроби с тем же знаменателем и с числителем, равным разности
числителей уменьшаемого и вычитаемого. Например:
= В = 42% — 17% = 25%;
- а Ь а—Ь
вообще-------=-----.
п п п
Чтобы найти разность двух дробей с разными знаменателями,
их предварительно приводят к одному знаменателю. Например:
7 5 7-3 5-2 21 10 21 —10 11
8 12 “ 24 24 ~ 24 24 “ 24 ~ 24'
§ 197. Свойства вычитания дробей. Как видим, разность дро-
бей и действие вычитание определяется так же, как для нату-
ральных чисел (§ 28—29). В силу этого и свойства вычитания
дробей те же, что у натуральных чисел (§ 30—33).
1. Из одного числа вычесть другое можно тогда и только тогда,
когда уменьшаемое больше вычитаемого или по крайней мере
равно ему. Например, от ~ отнять -1- можно, но от отнять
у нельзя. Разность равных чисел равна 0.
2. Вместо того чтобы вычитать сумму дробей, можно вычесть
каждое слагаемое последовательно, и обратно: вместо того чтобы
вычесть каждое слагаемое последовательно, можно вычесть сразу
их сумму. Например:
1—— fA _ hi _ _ 1 _ JL _ 53
17 \17 40/ \ 17 17/ 40 — 1 40 — 40 *
,_3___1_____39 _ .2 _ М . 39\ _ 3^
1 4 40 40 — 1 4 \40 40/ 4
3. Чтобы вычесть дробь из суммы, достаточно вычесть её из
какого-нибудь одного слагаемого. Например:
/и , Ц _ и _ /и _ и)
\37 "1" 4/ 37 (37 37/ 4 “ 4 ’
160
4. Чтобы прибавить разность дробей, можно прибавить умень-
шаемое и вычесть вычитаемое. Например:
10+Uo 11/~ bo + 10/ 11“ 11 •
5. Чтобы вычесть разность дробей, можно вычесть уменьшае-
мое и прибавить вычитаемое. Например:
15 \ 15 10/ “ \15 15/ + 10 ~ 10 •
Может случиться, что вычитать уменьшаемое нельзя, так как
оно слишком велико. Тогда можно сперва прибавить вычитаемое,
а потом от суммы вычесть уменьшаемое. Например:
§ 198. Техника вычитания дробей. Рассмотренные ниже при-
меры ясно показывают, что техника вычитания дробей в основ-
ном та же, что и техника их сложения, за одним исключением
(о котором скажем немного позже). Рассмотрим примеры:
п 13 7 _ 13 — 7 _ 6 _ 2
15 15“ 15 ~ 15“ 5 *
™ 3 _ 5 _3-9—5-2_27—10_ 17
' 4 18 “ 36 “ 36 “ 36 *
Здесь НОК чисел 4 и 18 найдено в уме.
3) Ц-2в = (5 + т)-(2+й=
= (б + 1) — 2 — -А = (по свойству 2);
= (5 — 2) -{- — А) — (по свойству 3);
_ о . 8 — 3 _ q5
“ Л + 16 “ П6 *
Здесь подробная запись дана только для объяснения. На прак-
тике применяется такая запись:
г J____о 2_2_____9 2__? А
°2 16 “° 16 2 16 16*
51 __9А ___5—___2 —___4 —__2 —__2 15
z 16 “ ° 16 z 16 16 16 “ 2 16 ‘
Здесь из дробной части уменьшаемого дробную часть
/9\
вычитаемого Ijgl вычесть нельзя; поэтому берём одну единицу
161
из целой части уменьшаемого, раздробляем её в шестнадцатые
доли и присоединяем их к дробной части. В этом и заключается
то отличие техники вычитания дробей от техники их сложения,
о котором было упомянуто выше.
5) 51?25 — 147зо — 517 jgQ — 147 jgg — 516 —
Конечно, лёгкие действия надо всегда выполнять в уме. Так,
в примерах 1 и 2 вполне возможно сразу писать ответ.
Иногда при вычитании целого с дробью применяют обращение
в неправильные дроби, которые затем приводят к одному знаме-
нателю. Это представляет собой ненужное осложнение, вызываю-
щее много лишней работы и увеличивающее возможность ошибки.
Например, производя этим способом вычитание в последнем рас-
смотренном примере, имеем:
С1, 8 , л-7 19 12933 4429 12933-6 — 4429-5
01 '25 1 'ЗО~ 25 30 ~ 150 ~
77598 — 22145 55453 ссп 103
~ 150 — 150 “ ^150*
Этим способом никогда не следует пользоваться.
§ 199. Проверка вычитания дробей. Проверка правильности
вычитания производится посредством сложения: сумма разности
и вычитаемого должна давать уменьшаемое. Например, найдя
разность дробей
514-147ё=36С’
вычисляем для проверки сумму
369|g+ 147^ = 516^ = 517^ = 517^
150 30 150 150 25
и убеждаемся, что всё сделано правильно.
§ 200. Совместное сложение и вычитание дробей. Нередко
требуется выполнить несколько сложений и вычитаний, чтобы по-
лучить один окончательный результат. Тогда можно либо произво-
дить каждое действие последовательно в том порядке, в каком
они указаны, либо найти сперва сумму всех слагаемых, потом
сумму всех вычитаемых, а затем из первой суммы вычесть вторую.
Для примера найдём обоими способами результат нескольких
действий:
534Й-72й+19Г2-8^-
I способ:
1) 534 - 72 g = 462 68 ~39 = 4621? ;
162
2) 462§+ igl = 481^^ = 481^;
3) 481 g - 8 1 = 473™^ = 4722-Ц=®1 = 472^ .
II способ:
1) 534 " + 19± = 553*+? = 553g = 5541 ;
2)72я + 8г6 = 80т = 80я = 81«:
3) 5541 - 81 1 = 473 4-^ = 472 ~ = 472
' 36 48 144 144 144
Совпадение результатов, полученных обоими способами, яв-
ляется хорошей проверкой правильности вычисления.
При решении задач во многих случаях возможно также
применять различные особые приёмы, упрощающие и сокращаю-
щие вычисление. Например, желая найти сумму нескольких
слагаемых:
1 । 1 [ ! I J [ ? [ ! г ! । ! г I
1-2 + 2-3 + 3-4 + 4-5 + 5-6 + 6-7 + 7-8 + 8-9 + 9-10 ’
замечаем, что
i . i , _L__!_____1 • J_ — 1 _ 1. J________!_____1.
1-2 ~ 1 2 ’ 2-3 — 2 3 ’ 3-4 ~ 3 4 ’ ' ’ ' 8-9 ~ 8 9 ’
gTjo = 4 ~ 1Т ’ и легко УбежДаемся> что х = 1 — 4 = Б) ‘
То же самое даёт и приведение всех дробей к одному знамена-
телю, требующее во много раз большей вычислительной работы.
Глава X. УМНОЖЕНИЕ И ДЕЛЕНИЕ ДРОБЕЙ
Раздел 1. УМНОЖЕНИЕ ДРОБИ НА НАТУРАЛЬНОЕ ЧИСЛО
И НА НУЛЬ И ДЕЛЕНИЕ НА НА ТУРАЛЬНОЕ ЧИСЛО
§ 201. Определение умножения дроби на натуральное число и на
нуль. Произведением двух натуральных чисел (§ 42) называется
сумма, образованная повторением одного из этих чисел (множи-
мого) слагаемым столько раз, сколько единиц в другом данном
числе (множителе):
5-3 = 54-5-}-5 = 15, ] а b = а-\- а-\- а -{-а
Ь слагаемых
Вместо того чтобы говорить: «возьмём данное число слагаемым
столько-то раз», можно сказать: «увеличим данное число во
столько-то раз» или «умножим данное число на столько-то».
163
Особого упоминания требует умножение на 1, когда произ-
ведение равно множимому (5-1=5, а • 1 = а), и умножение на О,
когда произведение равно нулю (5-0 = 0, а • 0 = 0).
Это определение произведения сохраняет силу и для того
случая, когда множимое — любое дробное число, но множитель
по-прежнему натуральное число.
Умножить дробь на данное натуральное число, большее 1, —
значит повторить эту дробь слагаемым столько раз, сколько
имеется единиц в данном натуральном числе. Например:
L ? — А т 5 г 5 — 15 — 1 7 •
8 ‘ J “ 8 + 8 + 8 — 8 — 1 8 ’
2-1 - 5 = 2 |-I-2 | + 2± + 2 | +2 J = 10^ = 14 ;
вообще
k слагаемых
Находить эти произведения приходится, например, при реше-
нии таких задач. Какова общая толщина трёх железных листов,
5
если каждый имеет толщину дюйма? Сколько тонн перевезёт
грузовик за 5 рейсов, если будет каждый раз брать 2-^-7'?
§ 202. Правило умножения дроби на натуральное число. Умно-
жение дроби на натуральное число, большее 1, сводится к сложе-
нию равных дробей, а это сложение — к умножению числителя.
_5 „ _ 5 . 5 . 5 _ 5 4-5 + 5 _ 5-3 5 о _ 5-3 _ 15.
17 ’ d — 17 + 17 + 17 ~ 17 — 17 ’ Т‘ е‘ 17 ’ d — 17 “ 17 ’
вообще
а , а , а . а , , а а 4- а 4- а 4- . .. 4- a a-k
7Г-*=п + « + п+---+ п =----------------п-------- = V’T-e-
° -/г = ^.
п п
Отсюда получаем вывод: для умножения дроби на натуральное
число достаточно умножить на это число её числитель, сохранив
без изменения знаменатель.
Если знаменатель множимого имеет общий делитель (отлич-
ный от 1) с множителем, необходимо сначала выполнить сокра-
щение. Например:
5 . _5-4__ 5 _q 1
8 8 ~ 2“ 2 ’
17 сс 17-56 17-7 119 1П 5
48 48 6 6 6
164
Если знаменатель множимого кратен множителю, умножение
числителя можно заменить делением знаменателя (§ 188); напри-
мер:
1.4-J__ I
8 8:4 — 2 2*
Умножение целого с дробью на натуральное число можно де-
лать двумя способами: либо умножить отдельно целое, отдельно
правильную дробь, либо предварительно обратить множимое в
неправильную дробь. Первый способ даёт результат быстрее, чем
второй, и его следует предпочитать, но вторым способом выгодно
пользоваться для проверки. Вот пример.
I способ: 314 12 = 314-12+ -!-• 12 = 3768 4-8 = 3776.
О о
тт л 2 ю 944 944-12 944-4 0-7-7/;
II способ: 314 = • 12 = — • 12 =—=— = —— = 3776.
О О о 1
Решим задачи: 1) 100 человек отправляются в экскурсию на
четыре дня. Сколько надо взять с собой хлеба, если каждому тре-
7
буется -g кГ в день?
U • Юо) • 4 = • 4 = 7 • 50 = 350 (кГ).
\ о / о ' z
2
2) Заметили по часам, что 1 км проходили за 9g- мин. За
сколько времени пройдут с той же скоростью расстояние в 5 км?
п2 с 2 • 5 .,-10 .Q 1 ,
9= • 5 = 45 -=—= 45 = = 48 = (минут).
О О О и
§ 203. Деление дроби на натуральное число. Планку длиной в
з
— м надо аккуратно (пилочкой) разделить на 6 равных частей.
Как это сделать? Для этого выполняют деление: : 6.
Неизвестный пока результат деления обозначим буквой х:
3 с
=: 6 = х.
4
Как найти этот результат?
Так как деление — действие, обратное умножению, где надо
было умножать числитель, то попробуем, не достаточно ли для
деления умножить знаменатель на 6. Имеем:
_3__ 1 _ 1 _
4-6 — 4-2 “ 8 ~ Х'
Как проверить правильность этого?
3 3
Из формулы : 6 = х следует, что х • 6 — — .
165
и про-
изнести
по ним
Подставив сюда вместо х полученный результат )
ведя вычисления, видим, что
1 с 6 3
8 ’6= 8 =Т’
т. е. догадка оказалась верной. Итак, надо на планке
1 100 1000 ,ое
метки через каждые м = -к- см — —^-мм = 125 мм и
О О о
разрезать пилкой.
Делением дробного числа на натуральное число называется
действие, где по произведению (дробному числу) и множителю
(натуральному числу) находят множимое.
Проведём рассуждения, связанные с делением дроби на нату-
ральное число, на любых примерах:
3.33 3.3-5 3
4 ' 5 — 4-5 — 20 ’ ТаК КЭК 20 ’ 5 ~ 20 - 4 ’
а . а а . a- k а
вообще — : k ~ —г , так как —г k = —- = — .
п n*k n-k n-k п
Приходим к выводу:
Чтобы разделить дробь на любое натуральное число, достаточ-
но умножить на это число знаменатель, сохраняя без изменения
её числитель.
Если числитель данного делимого имеет общий делитель (от-
личный от 1) с данным делителем, надо сперва выполнить сокра-
щение, а потом уже умножать. Например:
15. 12 = 15 _ 5 = 5
16' 16-12 16 - 4 64 ’
Если числитель делимого кратен делителю, можно умножение
знаменателя сразу заменить делением числителя, как, например,
в случае
15. с _ 15 :5 _ 3
1616 ~ 16"
Деление целого с дробью на натуральное число делается после
предварительного обращения делимого в неправильную дробь.
Например:
. ое__40 • 25 — 40____—____—
10 3 0 — 3 3 • 25 ~ 3 - 5 “15‘
Если же, однако, целая часть делимого кратна делителю, то в
этом обращении надобности нет: проще разделить целую часть и
дробную часть порознь. Сравним оба способа:
т „ .„„11 _ 5135 _ 5135 5135 11
I спосоо: 427^:7 =: 7 = — = — = 61^. II
II способ: 427^:7 = 427:7 + ^:7 = 61+^ = 61^.
л. £ О* О*ж
166
Если целая часть делимого значительно больше делителя, де-
лить её отдельно выгодно даже тогда, когда она не кратна дели-
телю. Например, деление 430на 7 выгодно выполнить в два
приёма, разбив делимое на два слагаемых и найдя порознь част-
ные:
427 : 7 = 61 и 3: 7 = , а всего 61^.
Раздел 2. УМНОЖЕНИЕ НА ДРОБЬ
§ 204. Недостаточность прежнего определения умножения.
Умея умножать любое дробное число на натуральное, мы ещё
не в состоянии выполнять умножение в том случае, когда множи-
тель — дробь, так как определение произведения как суммы рав-
ных слагаемых теряет тогда смысл: нельзя число взять слагаемым,
например, 2 у раза. Возникает вопрос: нужно ли заниматься умно-
жением на дробь? Рассмотрим следующие четыре задачи, отли-
чающиеся одна от другой лишь числовым значением одного из
данных, но решаемых по-разному.
I. Один килограмм товара стоит 12 руб. Что стоят 5 кГ? Эта
задача решается одним действием — умножением 12 на 5;
12 руб. • 5 = 60 руб.
II. Один килограмм товара стоит 12 руб. Что стоит -^-кГ?
Эта задача решается тоже одним действием: делением 12 па 4:
12 руб. : 4 = 3 руб.
О
III. Один килограмм товара стоит 12 руб. Что стоит -^кГ?
Эта задача решается уже двумя действиями: сперва находят де-
лением стоимость -^к1, затем умножением стоимость кГ:
1) 12 руб. :4 = 3 руб.; 2) 3 руб. -3 = 9 руб.
IV. Один килограмм товара стоит 12 руб. Что стоит 5 -^кГ?
Эта задача решается четырьмя действиями : сперва находят стой-
1 3
мость 5 кГ, потом стоимость кГ, затем стоимость кГ, наконец
з
стоимость 5 -г кГ:
4
1) 12 руб.-5 = 60 руб.; 2) 12 руб. : 4 = 3 руб.; 3) 3 руб. -3 = 9 руб.;
4) 60 руб. -J- 9 руб. = 69 руб.
167
з
Заметим, что в задаче IV замена целого с дробью 5— пепра-
23
вильной дробью делает эту задачу подобной задаче III и
позволяет обойтись вместо четырёх только двумя действиями:
1) 12 руб. : 4 = 3 руб.; 2) 3 руб. • 23 = 69 руб.
Строго говоря, рассмотрена одна задача, в которой одно из
данных принимает четыре различных значения: один килограмм
13 3
товара стоит 12 руб. Что стоит х кГ, если х — 5; ; 5-j ?
Естественно, возникает вопрос: нельзя ли все четыре рассмотрен-
ные задачи, столь похожие друг на друга, решать подобно первой
из них одним действием умножения? Это станет возможным, если
мы научимся умножать на дробь. Но что значит умножить на дробь?
§ 205. Новое определение действия умножения. Умножить ка-
кое угодно данное число, целое или дробное, на дробь — значит
найти эту дробь от данного числа. Например, найти произведе-
ние 8 на - значит найти от 8, что равно 4. Найти произ-
4 4
ведение 20 на •=—значит найти -= от 20, т. е.
О о
(20 :5) • 4 = 16.
2 3 3 2
Найти произведение 6 у на — значит найти от 6 , а
именно:
(6у:4) -3 = (5 :4)-3 = у .3 = т=43.
Умножение на дробь есть нахождение этой дроби от данного
числа. Приняв это новое определение произведения, можем утверж-
дать, что рассмотренная выше задача нахождения стоимости
разных количеств товара решается одним действием умножения
во всех четырёх случаях:
1) За 5 кГ надо уплатить:
12 • 5 = 12 4- 12 4- 12 4- 12 + 12 = 60 (руб.)
2) За ~ кГ — уплатить:
12 • = 3 (руб.) (у взять от 12
3) За кГ — уплатить:
12 •-|-=(12 : 4)-3 = 9 (руб.) взять от 12^
168
з
4) За 5 у кГ — уплатить:
12 - б|= 12 у,
4 4
23
т. е. -г найти от 12:
4
(12 :4) • 23 = 69 (руб.).
За х кГ надо уплатить 12-х. Задача решается во всех слу-
чаях умножением.
Но имеем ли мы право новому действию, а именно, отыска-
нию дроби от числа, давать старое название — умножение? Не
произойдёт ли от этого противоречия или путаницы?
Как мы уже знаем, всякое натуральное число можно считать
дробью, числитель которой кратен знаменателю, например 4 есть
4 8 12 л
—, или у , или -д и т. д., а поэтому произведение любого числа
на 4 можно найти и на основании старого определения (произве-
дение— сумма равных слагаемых) и на основании нового опре-
деления (произведение на дробь — дробь от данного числа), при-
чём оба раза получается одно и то же:
6.4 = 6-|-6-|-6-|-6 = 24;
6 - у = (6 : 1) • 4 = 24; 6 • =(6 : 2) • 8 = 24 и т. д.
Так же обстоит дело при умножении на любое натуральное
число. Старое определение умножения входит в новое его опре-
деление как частный случай этого нового определения, новое
определение оказывается обобщением старого. Никакого проти-
воречия между старым и новым определением умножения, таким
образом, нет.
§ 206. Правило умножения дробей. Умножение на дробь соглас-
но новому определению есть нахождение дроби от данного числа,
7 3 3 7
а потому умножить, например, у на у — значит найти у от у .
Сделать это можно двумя действиями: сперва находим у
7 7.7
от , а для этого делим на 4 и получаем ; затем на-
D D 0-4
3 7 7
ходим у от -у, а для этого умножаем уу на 3 и получаем
7-3 21 . 1
уу, ИЛИ уу , ИЛИ 1 2У .
Ведя подобные рассуждения на любых примерах, получаем
вывод: чтобы умножить дробь на дробь, достаточно произведение
их числителей разделить на произведение их знаменателей.
Вот краткая запись этого правила:
а b а-Ь
п k n-k ’
169
Рассуждение, проведённое для получения произведения -g- • ,
проводится точно так же и для любых двух дробей: найти
a b „ Ь а
произведение------г — значит наити — от —, а для этого сперва
ПИ к fl
находят, чему равна ~ от деля на k:
а 1 о
— =
п n-k ’
ba a i
затем находят, чему равны рот умножая—. на о:
/V П fl’ ft
a t a-b
n-k n-k
3
Возьмём задачу: найти стоимость м шнура при цене 1 руб.
40 коп. за метр.
а) Её можно решить без умножения на дробь двумя действиями:
1) 1 руб. 40 коп. : 4 = 140 коп. : 4 = 35 коп.;
2) 35 коп. • 3 — 105 коп. = 1 руб. 05 коп.
7
б) Замечая, что 1 руб. 40 коп. составляют -g-руб., можем ре-
7 3
шить ту же задачу одним действием, умножив руб. на -т-:
"0т
4 ру6- руб- = §руб-= 1 iруб-= 1 руб-05 коп-
Ещё задача: скорый поезд прошёл за 1 минуту 1300 м, или
з
1-jy км‘, какое расстояние он пройдёт при той же скорости за
л 1 з
ми нуты ?
Её можно решить тремя следующими способами.
I способ (вовсе без действий над дробями).
За 1 минуту поезд прошёл 1300 м.
За минуты он пройдёт 1300 м : 2 = 650 м.
За 4-^ минуты он пройдёт:
650 м -f- 5200 м — 5850 м, или 5 км 850 м.
II способ (без умножения на дробь).
За 4 минуты поезд пройдёт:
1 з . .12 С1
Itt; КМ • 4 = 4 км = 5-=- км.
1U 10 о
За 4 минуты он пройдёт:
,3 о 13 13
км : 2 = км = 20 км-
170
За 4 у минуты он пройдёт:
к1 । 13 с 4 .13 с 17 к осп
5-с км + он км — 5 ™ км + км = 5 ™ км, или 5 км 850 м.
О ZU ZU ZU ZU
III способ (с умножением на дробь).
За 4 у минуты поезд пройдёт:
3 1 13*9 117 17
1 тт) км • 4-^- = км = -57г км = 5 хг. км, или 5 км 850 м.
1U Z 1U * Z ZU ZU
Как видим, умножение на дробь позволило получить результат
значительно быстрее.
§ 207. Свойства умножения дробей. I. Переместительный за-
кон: произведение не изменяется от перемены мест сомножителей.
В самом деле:
3 5 3-5 правило умножения а b а • b
4 8 4-8 дробей; п ' k п•k~
5-3 переместительный за- Ь а
8 • 4 кон умножения нату- ральных чисел; ’ k • п —
5 3 правило умножения b а
“ 8 ' 4 дробей. k ' п ’
Краткая запись переместительного закона:
а Ь Ь а
п k k n
II. Сочетательный закон: чтобы умножить число на произве-
дение, достаточно его умножить последовательно на все сомно-
жители этого произведения, и обратно: чтобы умножить число
последовательно на два или более множителей, достаточно его
умножить сразу на их произведение.
В самом деле:
1 (Л. кЦ -
4 * \ 8 " 10/ —
3 5 • 11 _
“ 4 ‘8-10 —
_ 3 • (5 - 11) _
— 4 • (8 • 10)
_ (3 - 5) • 11 _
— (4 • 8) • 10 —
3-5 11 _
— 4 • 8 ‘ 10 ~
правило умножения
дробей;
оно же;
сочетательный закон
умножения натураль-
ных чисел;
правило умножения
дробей;
оно же.
а /6 с )
п \k т)
_ а Ь • с
п k • tn
__ а (b с)
п <k • т)
(а • Ь) с
(и • k) • т
а • Ь с
п • k т
171
Часто применение переместительного и сочетательного зако-
нов умножения ведёт к ускорению и упрощению вычислений,
например:
.. 17 /8 125\ 8
1) J25 • Ijjj • Tf) = пр так как на основе переместительного
и сочетательного законов вместо данного произведения взято
(в уме) такое:
17 /125 _8_\ _ /17
125 ’ \ 17 111/ “ \125 '
125)
17/
8 _ 1 8 __8_
’ 111 ~ 1 ’ 111 — 111 ’
/34
ЦП ’ 23/
46 34
50 = > тоже в уме проведено:
/3£ 25\
\111 ’ 23/
46 _ 34 /25 46 \ _ 34 /25 4б\ 34
50 — 111 ’ \23 ‘ 50/ — 111 ’ V50 ’ 23/ — 111
Краткая запись сочетательного закона:
1 _ 34
2 / ~ 111'
III. Распределительный закон: чтобы умножить сумму (раз-
ность) чисел, достаточно умножить каждое слагаемое (уменьшае-
мое и вычитаемое) и полученные произведения сложить (вычесть).
В самом деле:
/2 4- —1 2. =
(3 — з/’ 8 —
_ 5+2 5 _
~ 3 ' 8 ~
(5 + 2). 5
~ 3-8 “
_5-5 + 2-5_
3-8 ~
правило сложения (вы-
читания) дробей;
а + Ь с
п k
(а± Ь) • с
п • k
a-c+b-c
п • k
5-5 , 2-5_
' 3-8 —3-8~
__5 2 J- £ 5.
~ 3 ‘ 8 — 3 * 8
правило умножения
дробей;
распределительный за-
кон умножения нату-
ральных чисел;
правило сложения (вы-
читания) дробей;
правило умножения
дробей.
' п • k — п k
а с . Ь с
п k — п k '
Распределительный закон умножения дробей сохраняется и
тогда, когда складываются (вычитаются) дроби с разными знаме-
нателями, так как их всегда можно привести к одному знамена-
телю, а потому возможна и следующая его запись:
с, 6] с ___ а с . fr с
п т] ' k п ' k tn k ‘
172
Часто применение распределительного закона умножения уско-
ряет и упрощает вычисления, например:
') Н + 4МН = 1оГо+144 =24и:
2) ц1’= (ю+11). 1=24-1 = 24.
' 45 \ 4/5 '4 4
Итак, умножение дробей имеет те же три свойства (переме-
стительности, сочетательности, распределительности), что и умно-
жение натуральных чисел.
Следует отметить и одну особенность умножения на дробь:
если множитель — правильная дробь, то произведение меньше мно-
2
жимого. Например, 100 • д- = 40. Иначе, конечно, не может и
2
быть, так как умножение 100 на есть не что иное, как на-
2
хождение от 100. Но и при умножении на целое число не
всегда происходит увеличение: так, умножая натуральное число
на 1 или 0, получаем число, равное множимому, или меньше
его — нуль [п • 1 = п; п • 0 = 0].
§ 208. Техника умножения дробей. Умножая дроби, надо всегда
выполнять сокращение, если оно возможно, притом прежде, чем
делать умножения в числителе и в знаменателе произведения,
например:
12 10 4 • 2 8
25 ‘ 21 “ 5 • 7 ~ 35 •
Отметим, что правило умножения дроби на дробь (§ 205)
применимо во всех случаях. В самом деле:
1) 15 • 4 = у • 1 = __ 6Q (рекОмендуется единичный знаме-
натель не писать, а подразумевать).
15 д — 15 4 _ 15 ’ 4 _ 60 _ о 4
7 7‘1— 7-1~ 7“В7‘
о, о 100 _ 6 100 _ 6 • 100 _ 600 _ 45
° ill — 1 III “ ГЛТГ — ПТ ~ ° 111 •
4) 2-1-15 = 1. * 1115 = 11 = 414.
7 4 41 4-1 4 4
о 3 л 5 27 29 9 • 29 261 w 5
5) 38- ’Ч = 8” 6 = У?2 = Тб~ = 16Гб'
Легко в уме находить произведения вида:
15 16 _
16 ’ 15 —
или
100 111
111 * 100
= 1 и т. п.
Два числа, произведение которых равно единице, называются
взаимно обратными числами.
173
§ 209. Вычисление площади прямоугольника и объёма бруса.
В § 144 мы видели, что для получения площади прямоугольника
в каких-нибудь квадратных единицах надо перемножить два чис-
ла, выражающие длины сторон этого прямоугольника в соответ-
ствующих линейных единицах, причём предполагалось, что эти
числа натуральные. Возникает вопрос: сохраняет ли силу это
правило, записываемое формулой S = а • Ь, в том случае, когда
числа а и b дробные?
Пусть имеется какой-нибудь прямоугольник, длины сторон
которого выражаются в сантиметрах дробями с одним и тем же
знаменателем, например изображённый на рисунке 77 прямоуголь-
1 13 3 11
ник со сторонами 3-^см = ~^см и 2см = см. Примем за
Рис. 77.
единицы
площади, или -=- кв.
новую единицу длины отрезок в
1
-^см; соответствующая единица
площади — квадратик со сторо-
1
нои в см; старая единица
площади (кв. см) содержит
4-4=16 таких новых квадрат-
ных единиц. Стороны данного
прямоугольника содержат со-
ответственно 13 и 11 новых
единиц длины. Они выражены
натуральными числами, а по-
тому площадь прямоугольника
содержит 13 • 11 = 143 новые
о 15
см, т. е. 8-f^ кв. см.
Правильность этого результата можно проверить и непосред-
ственно по чертежу. На рисунке 77 видим 6 кв. см; к ним надо
присоединить ещё 8 маленьких квадратиков справа, 12 • 3 = 36
таких же квадратиков снизу, 3 квадратика в правом нижнем
углу, а всего 8 + 36 -}- 3 квадратиков, каждый из которых со-
ставляет кв. см. Вся площадь, таким образом, равна:
6 + й = С + 2ГЙ=8й
Но тот же самый результат получается гораздо проще, если
перемножить дробные числа, выражающие длины сторон данного
о 1 о 3 13-11 143 о 15
прямоугольника в сантиметрах: 3 — • 2 — = 4 4 = — = 8 — .
Правило вычисления площади прямоугольника, выраженное
формулой S = а • Ь, сохраняет силу и в тех случаях, когда длины
сторон прямоугольника — дробные числа.
Легко убедиться, что это действительно всегда так, следующим рассуж-
дением. Какими бы дробными числами ни выражались длины сторон данного
прямоугольника, их всегда можно представить в виде дробей с одним и тем
174
же знаменателем — и — ; ту единицу длины, в какой они выражены, будем
называть «старой» единицей длины; ей соответствует «старая» единица пло-
щади. В «новых» единицах длины сторон данного прямоугольника выража-
ются уже не дробными, а натуральными числами а и Ь, а потому его площадь
равна а • b новых единиц площади. Но старая единица площади содержит
п • п = л2 новых квадратных единиц, площадь же прямоугольника в старых
. , , а • Ь
единицах выразится частным ао : п1, т. е. дробью —j- , которую можно рас-
а Ь _
сматривать как произведение — • — . Итак, для получения площади S прямо»
a b а Ь . _
угольника со сторонами — и — достаточно перемножить числа — и —, причем 5
получается в квадратных единицах, соответствующих тем линейным, в кото-
рых выражены длины сторон.
Задача. Найти площадь побелки стен и потолка класса,
31 19 17
если его длина 8у^л1, ширина и высота 3 м\ в нём
7 97
имеются 4 окна равных размеров: 1 высотой и шири-
13 17
ной, и 1 дверь высотой 2^л< и шириной 1
1) Сначала найдём площадь стен:
(g—-3—-*-5—• 3—) • 2 (кв. м).
\° 100 100 1 100 100/ ' 7
2) Потом найдём площадь потолка:
о 31 к 19 ,
8100 ’ 5 100 (Кв'
3) Теперь найдём площадь всех окон и двери:
/, 7 97\ , о 13 1 17 /.о\
I1 io ’ Тоб/ ’ 4 2loo ’ ioo^
4) Наконец найдём площадь побелки:
/о 31 чЛ_1_Ц_Ч l/Tl —
Iе 100 ' ° 100 “* ° 100 100/ 100 100
_ Л 7 97 ,,9_13 1_!7\_/я 31, е_19\
\ 10 ‘ 100 100 ’ юо/ V 100 100'
о_17 9 , 831 519_ /17 97 . , 213 117\ _
х 6 юо ‘ 2 "* юо' юо \ ю ' юо ' 4 “* 100 * 100/
, q 1 о 17 , 431 289 /6596 . 24 821\ _
— 1-э 2 • Z • d 10() -f- 1000() ^1000 -j- 10С00/
27 • 317 431 289 90 781 _ 855 900 + 431 289 — 90 781 _
~ 100 *" 10 000 10 000 ~ 10 000
_ 1 196 408 _ . <q 6408 ~ J20
— 10000 ~ 11У 10000 1/и
175
Подобным же образом можно убедиться, что правило вычисле-
ния объёма бруса, установленное в § 154 для случая, когда дли-
ны его рёбер выражены натуральными числами, сохраняет силу и
тогда, когда эти длины—дроби. Например, чтобы найти объём
бруса с рёбрами в 3-^-см, 2 у см, 1 ^-см, достаточно взять произ-
7 5 3 105 1О 1 „ л
ведение • тг • -к — = 13 . Проверить это можно либо
Z Z Z о о г
переходом от сантиметров к миллиметрам (взятый брус имеет
рёбра длиной 35 мм, 25 мм, 15 мм, а потому его объём равен
35 • 25 • 15 = 13 125 куб. мм, или
35 мм
Рис. 78.
13 125 :1000 = 13 = 131 куб.
см), либо рассматривая чертёж
(рис. 78), где ясно видно, что
данный брус содержит 6 кубиков
с рёбрами по 1 см, т. е. 6 куб. см,
затем 6-}-24-3=11 брусов с рёб-
рами 1 см, 1 см, см (6 сверху,
2 справа, 3 сзади), каждый из
которых есть половина кубиче-
ского сантиметра; далее 6 брусов
ill
с ребрами в 1 см, % см, -% см
(2 справа сверху, 3 сзади сверху,
1 справа сзади), каждый из кото-
рых есть одна четверть кубиче-
ского сантиметра; наконец,
1 кубик с ребром в у см (справа
сверху сзади), составляющий одну восьмую долю кубического
сантиметра. Всего в нашем брусе содержится:
6 + 4 -11+ + |-6 + 5j + ly+|=131(<^.
Задача. Сколько поездок должна сделать машина грузо-
подъёмностью 3 тонны, чтобы перевезти 1000 досок длиной 7~м,
1 4 1
шириной — м и толщиной 40 мм = 4 см — м = м, если
4
1 м3 этой древесины весит Т?
1) Сперва найдём объём одной доски:
1 1 15/ , ч
-.-.^(куб. м).
2) Потом найдём объём 1000 досок:
±•1.^.1000 (куб. м).
176
3) Теперь найдём вес 1000 досок:
„4 • 4- • • Ю00.4 = 1.1.3.10.2 = 60 (Г).
ZO 4 Л О
4) Наконец найдём число поездок, необходимых для пере-
возки досок;
60 : 3 = 20 (поездок).
Раздел 3. ДЕЛЕНИЕ НА ДРОБЬ
§ 210. Определение частного. При переходе от умножения
на натуральное число к умножению на дробь понадобилось но-
вое определение умножения. При переходе же от деления на
натуральное число к делению на дробь в новом определении
деления надобности нет, так как деление есть действие, обратное
умножению, или: деление есть действие, где по данному произве-
дению двух сомножителей и одному из них находят другой сомно-
житель.
Частным от деления одного числа, целого или дробного, на
другое число, целое или дробное, называется такое третье число,
целое или дробное, которое, будучи умножено на второе (дели-
тель), даёт первое (делимое).
Как решить следующую задачу? Имеется 7-1- м красной тка-
ни. Сколько из неё выйдет праздничных флагов, если на каждый
- з _
идет м ткани?
1) Обозначим неизвестное пока число флагов буквой х.
з
2) Так как на каждый флаг идёт м, то всего пойдёт
-j- • х (м) ткани.
3) На это должна быть израсходована вся ткань 7-1- м, а по-
тому имеем:
Здесь по произведению ^7 -2) и одному
надо найти другой сомножитель — х. Это
— 7.L 2 — 15-2
Х~ ‘ 2 : 4 — 2 • 4*
- / з\
из сомножителей I I
находится делением:
Теперь возникла новая трудность: как разделить дробь на
дробь?
§ 211. Правило деления дробей. Нельзя ли действие деления
свести к действию умножения дробей (§ 206), помня, что деле-
ние обратно умножению
9 Арифметика
177
Попробуем вместо деления -% на уможить на обратное
4
число, т. е. на -у; имеем:
15 . _ 15 ±
2 • 4 — 2 * 3'
15 4
Проверим догадку: полученное частное -% • -д- умножим на де-
литель 4-. Имеем:
4
/15 4\ 3 15/4 3\ 15 . 15
\2 ‘ З/ ’ 4 — 2 \ 3 " 4 / — 2 ‘ 1 — 2 ’
т. е. получим делимое. Это рассуждение верно для любых дробей.
Вывод. Чтобы разделить первое число на второе, достаточно
первое число умножить на число, обратное делителю. 3
Задача 1. Сколько стоит 1 кГ товара, если за кГ упла-
тили 15 руб. 60 коп.? Задачу можно решить двумя способами:
1) Сначала находим, сколько стоит кГ товара, производя
деление 15 руб. 60 коп. на 3 и получая 5 руб. 20 коп.; затем
находим, сколько стоит кГ, или 1 кГ, производя умножение
5 руб. 20 коп. на 8 и получая 41 руб. 60 коп.
з
2) Замечая, что 15 руб. 60 коп. составляют 15-д- руб., зада-
чу можно решить одним действием:
1С3 3 78 3 78-8 26-8 208 .. 3 ... , „„ .
15Т : 8=-5 = 573 = 5ТТ=-5- = 41-5 <41 РУ6* 60 К0П-Ь
7
Задача 2. Сколько кусков бечёвки по м каждый можно
1
получить из бечёвки длиной 10 у м?
1) При решении этой задачи можно обойтись без деления на
7 1
дробь, если перейти к сантиметрам: м — 70 см-, 10-g.M =
= 1050 см-, 1050 : 70 = 15 (кусков).
2) При помощи деления дробей получим ответ скорее:
1 7 21 • 10 3-5 1С
10 -2 : П) = ТТГ =гп = 15-
Если же длина бечёвки равна, например, 12 у м, то из неё
1О 1 7 25 - 10 25 - 5 125 6
можно нарезать 12 „ 7 = —у — -=- — 17 -у таких кус-
1-7 - 6
ков, т. е. 17 таких кусков и еще у частей такого куска.
§ 212. Техника деления дробей. Производя деление дробей,
надо всегда выполнять предварительно сокращение, если оно
возможно. Например:
12 . 4 _ 12 • 7 _ 3
35 : 7 ~ 35 • 4 — 5 •
178
Отметим, что правило деления дроби на дробь применимо во
всех случаях. В самом деле:
1) 15:4=15--^- = -р'4==Т = 3'^ (рекомендуется единич-
ный знаменатель не писать, а подразумевать).
9. 15.4 _ |5 2_____15 _ 15
7 : 4 — 7 4 — 7.4 — 28"
„ п.100 „ 111 3-111 333 „33
b: 111 — ь • 100“ 50 — 50 ~ о0’
.. „ 3 1,- 11 1 И
4) 2 Г : 15 = — — =
' 4 4 15 00
~ „ 3 . 5 27 29 27 • 3 81 . .
5) ^“8:4-g=-g:-g- = 472g = jjg (при делении целого с дробью
достаточно предварительно обратить его в неправильную дробь).
Но бывает целесообразнее иногда отступить от общего пра-
вила и выполнить действие короче. Например:
1) 60| :3 = 2о|; 2) 84~ : 4 = 21 3) 801: 20 у = 4.
§ 213. Что выражает частное? Если частное есть натураль-
ное число, большее 1, оно показывает, во сколько раз первое
число больше второго; если это частное равно 1, оно показывает,
что числа равны; если частное равно какому-нибудь дробному
числу, оно показывает, сколько и каких долей второго числа
составляет первое.
Примеры:
1) число 12 больше числа 6 в 2 раза, так как 12:6 = 2
2
2) число 12 составляет две трети числа 18, так как 12 :18=-=-;
3) число 12 составляет три вторых числа 8, так как 12 :8 =у.
Говорят также, что 12 в полтора раза больше 8, так как
Л=1±
2 2'
Вспоминая § 183, можно сказать, что частное от деления
одного числа, натурального или дробного, на другое число, на-
туральное или дробное, выражает отношение первого из них
ко второму.
Вот почему не удивительно, что отношение малых чисел
может быть числом большим:
1 . 1 _ юоооооооо .„„„
1000000 : ЮОООООООО “ 1 000 000 — 1иии’
т. е. в одном малом числе второе, ещё меньшее, содержится
1000 раз.
§ 214. Свойства деления дробей. Как мы видели, деление
дробей определяется точно так же, как деление натуральных
чисел (§ 57). Сравним теперь свойства деления дробей со свой-
ствами деления натуральных чисел.
9*
179
1. Деление натурального чи-
сла на натуральное число не
всегда выполнимо, если ограни-
чиваться одними натуральными
числами; оно выполнимо тогда
и только тогда, когда делимое
кратно делителю 80 : 10 = 8,
так как 80 кратно 10; 81 не де-
лится на 10, т. е. 81 некрат-
но 10.
2. Если деление натурально-
го числа на натуральное выпол-
нимо в натуральных числах, то
получается частное, меньшее или
равное делимому
80: 10 = 8, где 8 < 80
80 : 1 = 80, где 80 = 80
0 ; 10 = 0, где 0 — 0.
1. Деление дробного числа
на дробное возможно всегда
(если только делитель не есть
нуль), так как всегда возможно
делимое умножить на число,
обратное делителю.
2. Частное от деления дроби
на дробь может быть меньше,
равно и больше делимого: мень-
ше и равно при делении на не-
правильную дробь, больше при
делении на правильную дробь:
£ _ £ 4-7 _ 28 £
5 : 7 — 5 - 9 — 45 < 5 ’
Д-1=± = ±
5 • 5 5’
9 -.1 _ ^>9
7 : Т “ 28 > 7
Следующие ниже свойства верны для любых чисел:
3. Чтобы разделить сумму (или разность) чисел, достаточно
разделить каждое из данных чисел, а затем взять сумму (или
разность) полученных частных.
В самом деле:
£
3
. £
: 8 —
£ £ , 4 £ _
10 • 3 ± 10 • 3 -
2 .£ . £ .£
10 : 8 - 10 • 8 ’
правило деле-
ния дробей;
/ а . Ъ \ £
-*- л/ с
а £ 1 £ £
7Г ‘ с п ' с
распредели-
тельное свой-
ство умноже-
ния;
правило деле-
ния дробей.
а • с
п ' k — п ' k
Пользуясь этим свойством, иногда возможно ускорять вычис-
ления. Например:
/53 2_\ . 53 _ . , 409 _ . 409 .
а' \409 + 100/ : 409 — 1 + 5300 — 1 5306’
..347 .3 147 . 3 /347 147\ . 3 _ . .37
°' 200 : 7 200 ‘ 7 ~ \200 200/ '7 1 * 7 3 ’
180
4. Чтобы разделить произведение, достаточно разделить только один из его сомножителей. В самом деле:
II z^ Г-К со Z* ( а \ п ь \ с k/'m
II ю |« со |ч< Z II правило деления дробей; =а b\ т k) с
II со II сочетательное свойство умножения; а п (Ъ т\ \ k с /
2 |ю 5~_1~ СО II правило деления дробей. _ а п / b . с \ k 'т)
Пользуясь этим свойством, можно ускор ить вычисления.
/120 Пк 120 _ 17
аЦ 23 ’ 42/ : 23 ~ 42'
/120 17\ 60 _ „ 17 _ 17
°' \ 23 ' 42/ ' 23 — ‘ 42 — 2Г
в) Что больше, 30% от 40 руб. или 40% от 30 руб.?
Легко видеть, что результаты равны, так как
40
— — — 30 — 30 • —
100 — 100 0U “ 100*
5. Чтобы разделить число на произведение, достаточно выпол-
нить деление последовательно на все его сомножители.
В самом деле:
3 Л7 5\ _
4 : \13 ' 26/
_ 3 . 7-5
— 4 : 13 • 26 —
_ 3 13 • 26 _
— 4 ' 7-5 —
правило умножения дро-
бей;
правило деления дробей;
правило умножения дро-
бей;
сочетательное свойство
умножения;
а . / Ь с 1
п '\т k)
___ а Ь с
п ' т • k
а т • k
п Ъ - с
правило деления дробей.
Покажем на примере, как помогает это свойство ускорять
вычисления:
.43/37 43\ _ . . 37 _ 70 _ . 33.
а) 50 470 ’ 50/ “ 1 ' 70 “ 37 — 1 37’
60 /37 30\ „ . 37 _ 140 _ „ 29
°) 37 : \70 ' 37/ — : 70 — 37 ~ d 37'
181
6. Если делимое и делитель умножить или разделить на одно
и то же число, частное не изменится.
1) 10:29
2) (10."):(29.£) =
10 - 17 29.17
“ -ПТ- : “ПТ- “
ю-17 ш
_ Ill ‘29-17-
= g = 10 :29.
1) т : п
n. / а\ ( а\
2) (ni--rl:n--r-l =
\ о / \ о /
т • а , п • а
~ '~b~Z
tn а Ъ
b п • а
- т:п.
т
п
При устном делении иногда выгодно бывает умножить дели-
мое и делитель на одно и то же число так, чтобы свести деле-
ние дробей к делению целых чисел. Например:
5:| = (5.7):(| -7) = 35:2 = 17^;
1б1;4 = (1б4- ю) = 165 : 6 = 55 : 2 = 271
ZO\Z/\O/ Z
Выполнив деление, следует умножить полученное частное на
делитель с целью проверки.
§ 215. Задачи на площадь прямоугольника и объём бруса.
Умея делить дроби, мы можем при любых данных решать обрат-
ную задачу на площадь прямоугольника, т. е. находить одну из
сторон прямоугольника по данной его площади и другой сто-
роне (§ 146). Например, пусть требуется найти ширину прямо-
, 4
угольного поля площадью 1-=-га, зная, что его длина равна
2561 м.
Вспоминая, что 1 га (гектар) есть квадрат со стороной в 100 м
и содержит, следовательно, 100 • 100= 10 000 кв. м, находим, что
4
площадь поля равна 10000кв. м • 1-=-= 18000кв. м, а искомая
о
ширина выражается частным от деления 18 000 кв. м на 256уЛ1,
равным
18 000 - 2 4000 „п10 _п .„31
---==--М = м = 70 == м — 70м \Л~см
olo----о/ О/ о/
31
Таково точное значение этой ширины. На практике дробью g? см,
немного превышающей у см, можно пренебречь и сказать, что
искомая сторона поля больше 70 м 17 см, но меньше 70 м 18 см
(второе число немного ближе к точному значению, чем первое).
182
Для проверки находим площадь поля со сторонами 256Ь м и
70^. jw, равную 17998^ кв. м, что меньше 18 га на 1 кв. м,
и площадь поля со сторонами 25бЬ м и 70^ м, равную
17 17
18 001 Эду кв. м, что больше 18 га на l^ кв- м-
Точно так же теперь разрешимы при любых данных и об-
ратные задачи на объём бруса (§ 156). Например, зная, что
площадь основания бруса равна 45 кв. см, а его объём 112 —куб. см,
можно найти его высоту, равную
1121:45 = ^ = 2-1 («0.
Тот же результат получается и без деления дробей, если
перейти к более мелким единицам:
112у куб. см = 112 500куб. мм\ 45 кв. см = 4500 кв. alw;
112 500 : 4500 = 25 ли; = 2 Ь см.
§ 216. Совместные действия с дробями. Вычисления по число-
вым формулам с дробями производятся по тем же правилам, как
и с натуральными числами (§ 84—86). Особое внимание необхо-
димо обратить на строгое соблюдение правил порядка действий.
Для примера выполним полностью вычисление по числовой формуле
К 5 3) 2 2] 3
10 6 ~~8 4 / * 8 5 + 3 * 5 3 J * 17
47 7~1 2\ 5
10 60 ~ (8 5 ~ 5 3 / ' 8
Последовательно производим следующие действия:
п 1Г)_5_чА_______10 —___3—_7—•
Ч 1U6 6 7 4 ~ 1U12 б12 — '12’
9. 7 1 о 2 _ 85 • 42 17-7_119_f.q 1
Ч ' 12 ’ ° 5 ~ 12 • 5 “ 2 • 1 “ 2 2 ’
3) 59^- 4-5| = 59-|--р 5-| = 64-^- = 65-Ь
’ 2'3 6'6 6 6 ’
1 3 391 . 3 23 - 1 23 .. 1
4) 65 6 '17= 6П7 = 2ТГ= 2-=11Т:
5) 8Ь-5| = 8А_5}| = 2А;
RA 9 8 5 _ 38 • 5 _ 19 • 1 _ 19 _ . 7
™ Z 15 ’ 8 ~ 15 • 8 — 3 - 4 — 12 “ 1 12’
7) 10 — 1 — — 10 — 1 — = 9—= 9 —•
60 1 12 60 60 60 5 ’
„ . .. 1 . Q 1 23 - 5 1-5 5 .1
8) 11 T •9‘5'-= 2^46 = ^72 = T = 1 T’
Ответ: 1Д-.
4
183
Глава XI. ДЕСЯТИЧНЫЕ ДРОБИ
Раздел 1. ОПРЕДЕЛЕНИЕ И СВОЙСТВА ДЕСЯТИЧНЫХ ДРОБЕЙ
§ 217. Почему действия с дробными числами проводятся зна-
чительно сложнее, чем те же действия с натуральными числами?
Действия сложение и вычитание с натуральными числами
проходят несравненно легче, чем с дробями. Почему? Потому что
натуральные числа записывают (передают) в одной десятичной
системе, а дробные числа в различных системах. В самом деле,
возьмём два числа в различных системах (десятичной и двена-
дцатеричной):
ТЫСЯЧИ 5 сотни 4 десятки 3 единицы 6 или 5
гроссы 4 дюжины 3 единицы 2 или 4
103 + 4 • 1023 • 104-6
122 4-3. 12 4-2
Как их складывать или вычитать? Понятно, что с такими
натуральными числами придётся поступать так же, как и с дро-
бями, т. е. приводить к одной системе, например к десятичной.
Имеем: 4 122 4- 3 - 12 4- 2 = 4 144 4- 36 4- 2 = 576 4- 38 = 614.
Теперь числа 5436 и 614 можно складывать и вычитать.
Возьмём две дроби с различными знаменателями, например
90 и 100’ иначе — 41 девяностых и 17 сотых; они также заданы
в различных системах долей: первая в девяностых, вторая в
сотых; поэтому при сложении и вычитании этих дробей прихо-
дится их также приводить к одной системе долей, например к
41 410 17 153 ~
девятисотым долям; имеем пп — ййй и тт — опп- Теперь их можем
wUU хии
складывать и вычитать.
§ 218. Открытие десятичных дробей. В XIV—XV вв. жившие
на территории Узбекской республики передовые для того времени
учёные-узбеки уделяли большое внимание различным наукам и в
особенности науке о звёздах — астрономии; поэтому им прихо-
дилось производить много вычислений с натуральными и дроб-
ными числами. Основателю астрономической обсерватории в Са-
марканде Аль Каши удалось открыть новую форму записи дроб-
ных чисел, значительно упрощающую все преобразования и вы-
числения,— так называемые десятичные дроби. Своё открытие он
изложил в книге «Ключ к искусству счёта» в 1427 г.
Такое же открытие было сделано позднее (более чем на пол-
тораста лет) в Европе бельгийским учёным Симоном Стевином
и опубликовано в 1585 г. в книге «О десятичном счёте».
В основу этого способа был положен известный принцип
поместного значения цифр, позволяющий записывать любое иа-
184
туральное число при помощи только десяти знаков — цифр. При
такой записи значение каждой цифры числа зависит от того места
(позиции), на котором цифра находится; значение цифры увели-
чивается в 10 раз при переходе на одно место справа налево и,
наоборот, уменьшается в 10 раз при переходе на одно место
слева направо.
Так, например, при помощи одной цифры 4 записано число
4444, содержащее:
ТЫСЯЧ сотен десятков единиц
4 4 4 4
Распространив позиционное значение цифр правее единиц,
нашли форму для выражения дробей в десятичной системе:
ТЫСЯЧИ сотни десятки единицы десятые сотые тысячные
1) 4 5 9 2
2) 1 0 3 0 7
3) 0 3 5 1
что можно прочитать так:
1) сорок пять целых, 9 десятых и 2 сотые доли;
2) сто три целые, 0 десятых и 7 сотых, короче: сто три це-
лые и 7 сотых;
3) 0 целых, 3 десятых, 5 сотых и 1 тысячная доля.
Понятно, что, приняв принцип поместного значения цифр,
нет необходимости в наименовании каждого разряда; достаточно
отметить только один разряд, лучше разряд единиц, и тогда
каждому будет видно, что слева от этого разряда идут по порядку
десятки, сотни, тысячи и т. д., а справа от этого разряда идут
по порядку десятые, сотые, тысячные и т. д. доли.
Встаёт вопрос: каким знаком делать отметку единиц?
История знает много попыток введения знака дробности, ука-
зывающего место разряда единиц. Одни предлагали ставить меж-
ду разрядом единиц и разрядом десятых долей вертикальную
черту, другие точку и т. д. Наиболее удачным знаком, предло-
женным астрономом Иоганом Кеплером (1571—1630, Австрия),
оказалась запятая, принятая у нас и во многих других странах,
кроме Англии и США, где знаком дробности является точка,
что нельзя считать удачным, так как точка уже принята в ка-
честве знака умножения.
185
Итак, вышеназванные числа записывают таким образом:
45,92 — сорок пять целых, 9 десятых, 2 сотых;
103,07 — сто три целых, 7 сотых;
0,351—нуль целых, 3 десятых, 5 сотых, 1 тысячная.
§ 219. Определение десятичных дробей.
Дробь, например, вида: 1) можно записать иначе:
9876 _ 0000 + 800 + 70 + 6 _ 9000 800 70 , 6
1000 — 1000 — 1000 + 1000 + 1000 + 1000 ~
— q 4- ® 4- 7 4- 6 Q R7R
1 10 1 100 1 1000 — J,KZb‘
2) 452 10 — 450 ~Ь 2 _ 450 . 2 __ 2 _ ис 2 10 ~ 10 + 10 ~ + 10 ~
3) 1358 _ 102 " _ 1300 . 50 . 8 । о । 5 । 8 . „ -п ю2 "г ю2 "г ю2 ~ * 10 102 —
4) 4569 _ 103 “ . 4ввв i §2- + _2_ — 4 + Л + .2 4 'SRQ 103 ~ 103 ~ 103 ~ 103 10 102 Ю3 ~
Дробью в десятичной системе, или десятичной дробью, назы-
вается дробь, у которой знаменателем служит число 10 с каким-
нибудь показателем (101 = 10; 102 — 100; 103 = 1000; 104 = 10 000;
105= 100000 и т. д.) и которая записана в позиционной деся-
тичной системе так, что знаменатель только подразумевается.
В противоположность ей дробь, записанная обычным спосо-
бом (над чертой числитель, под чертой знаменатель), называется
обыкновенной. Таким образом, дроби || — обыкновенные;
дроби 0,3 (нуль целых, три десятых), 1,23 (одна целая, две деся-
тых, три сотых), 0,876 (нуль целых, восемь десятых, семь сотых,
5
шесть тысячных) и т. д. — десятичные. Дробь согласно это-
му определению обыкновенная, но она допускает запись в виде
десятичной (0,05).
Различают целую часть десятичной дроби, т. е. то, что запи-
сывается левее знака дробности (запятой), и дробную её часть,
которая записывается правее его. Первая цифра справа от знака
дробности, т. е. цифра десятых, называется первым десятичным
знаком-, вторая, т. е. цифра сотых, — вторым десятичным зна-
ком и т. д. Полезно твёрдо усвоить следующую табличку:
первый дес ятичный знак выражает десятые доли,
второй » » » сотые доли,
третий » » » тысячные доли,
четвёртый » десятитысячные доли,
пятый » » » стотысячные доли,
шестой И т. д. » » » миллионные доли.
186
§ 220. Чтение и запись десятичных дробей. Десятичную дробь
можно прочесть поразрядно, указав сперва, сколько в ней целых,
а затем называя по очереди каждый десятичный знак и указы-
вая его значение; например, дробь 6,789 этим способом читается,
как шесть целых, семь десятых, восемь сотых, девять тысячных.
Более употребителен другой способ, основанный на сложении
дробей, выражаемых каждым десятичным знаком в отдельности;
7 . 8 . 9 789 й
замечая, что jg + jgg + jggg = iggg . читают десятичную дробь
6,789, как шесть целых, семьсот восемьдесят девять тысячных.
Таким образом, указав целую часть десятичной дроби, надо про-
честь в качестве числителя всю дробную её часть, а знамена-
телем назвать доли, выражаемые последним десятичным её зна-
ком. Например:
7,82 читается, как семь целых, восемьдесят две сотых;
26,032 — двадцать шесть целых, тридцать две тысячных;
0,3001 — нуль целых, три тысячи одна десятитысячная.
В отступление от общего правила, иногда читают десятичную
дробь «телефонным» способом: дробь, имеющую четыре десятич-
ных знака, читают без указания знаменателя, произнося два
двузначных числа, называемых одно за другим после целых.
Так, число 0,4317 читается, как нуль целых, сорок три семнад-
цать; число 27,1902 — как двадцать семь целых, девятнадцать,
нуль два; число 6,0785 — как шесть целых, нуль семь, восемьдесят
пять. Точно так же десятичную дробь, имеющую пять знаков,
например 0,30103, можно читать, как нуль целых, тридцать, сто
три, и т. д.
Записывать десятичную дробь удобнее всего, если она дик-
туется поразрядно. Если же дробная часть названа сразу, надо
сперва сообразить, основываясь на приведённой выше табличке,
сколько десятичных знаков она имеет, записывая в надлежащих
случаях необходимое число нулей непосредственно вслед за зна-
ком дробности. Так, дроби: восемь целых, тридцать две сотых,
восемь целых, тридцать две тысячных; восемь целых, тридцать
две миллионных надо писать в виде: 8,32; 8,032; 8,000032. В
последнем случае замечаем, что миллионные доли изображаются
шестым знаком, а потому, кроме двух цифр, изображающих чис-
литель тридцать два, нужно ещё 6 — 2 = 4 нуля, записываемых
непосредственно после знака дробности.
§ 221. Свойства десятичных дробей. Возможность удобной
записи без знаменателей представляет собой одно из важных
свойств дробей со знаменателями 10; 100; 1000 и т. д. Отметим
ещё следующие существенные их свойства.
1. Легко обыкновенную дробь со знаменателем 10, 100= 102;
1000= 103; 10000= 104 и т. д. представить в виде десятичной
дроби.
187
Например: 1 = 0,3; ® _ 3 + ’ = 3,5;
354 _ 350 + 4 _ 35 1 А — 35 4-
Ю — 10 — + ю — й0’4’
41 _ 40 + 1 40 1 _ 4 1 _
100 100 100 ^100 10^100“и’ ’
417 _ 400+Ю + 7 _4.1,2_-4 17-
100 100 т 10^100 ’ ’
353 _ 300 + 50 + 3 _ 3 , 5 , 3 п „„
1000 — 1000 ~ 10 100 + 1000 — и,гЮб’
35 30 + 5 3 । 5 q
1000 “ 1000 Too+ 1000 = и,Ш0;
1723 _ 1700 + 20 + 3 2 3 „„
100 ~ 100 ~ 1 т" 10 + 100 ~
Вывод. Чтобы выразить обыкновенную дробь, у которой зна-
менатель 10 с каким-либо показателем, в виде десятичной, доста-
точно записать только числитель, поставив в нём знак дробности
(запятую) так, чтобы справа оказалось столько цифр, сколько
нулей в знаменателе.
Например:
345__о де-
то ~
204781 _
10 000 —
20,4781
два две цифры
нуля после запя-
той
4 нуля
четыре
цифры
после
запятой
31
1000
0,031;
42
1000 000
= 0,000042
3 нуля | 3 цифры
6 нулей | 6 цифр
представить в виде обыкновенной
2. Легко десятичную дробь
дроби.
Например: 0,3 = ^; 3,5 = 34-1 = ^;
35,4 = 35 + А = ^;
0,41 = io 1 Too = то’ 4,17 = 4 + То + то= то*
0,353 = jo 4* [ой + Гобо = Тооо • 0,°3^ = Too 1 Тобб ~ Тббб :
17 23________________ 17 4- — 4_3 __ 1723
1/.Z6 — 1/ 4- 10 4- 100 — 100 .
Вывод. Чтобы выразить десятичную дробь в виде обыкно-
венной дроби, достаточно отбросить знак дробности и взять по-
лученное натуральное число числителем, а знаменателем взять
знаменатель последнего десятичного знака.
188
257
Например: 2,57 = ^д, так как последний десятичный знак 7
имеет знаменатель 100.
1 л лат 14 007
14,007 = •, так как последний десятичный
знак 7 имеет знаменатель 1000.
3. Если надо десятичную дробь представить в более мелких
десятичных долях, то это выполняется легко следующим образом:
0,8 = 0,80 = 0,800 = 0,8000 и т. д., так как
°’8 = Тб = ТОО = 1000 = Тбббб [главное свойство дробей]
8 8-10 8-100 8-1000
10 — 10-10 “ 10-100 “ 10-1000 •
Вывод, Чтобы выразить десятичную дробь в более мелких
десятичных долях, достаточно приписать соответствующее число
нулей после последнего десятичного знака.
Например, 17,83 = 17,830 = 17,8300 = 17,83000...
4. Возникает задача, обратная вышерассмотренной. Как выра-
зить в более крупных десятичных долях десятичную дробь, у ко-
торой имеется в конце хотя бы один нуль? Это делается легко:
например, 17,8300000 = 17,8300 = 17,830 =17,83, так как 17 целых,
8 десятых, 3 сотых, 0 тысячных, 0 десятитысячных и т. д. есть то
же, что 17 целых, 8 десятых, 3 сотых, так как нули долей указы-
вают, что этих долей нет.
Вывод. Чтобы выразить десятичную дробь, имеющую на кон-
це хотя бы один нуль, в более крупных десятичных долях, доста-
точно зачеркнуть (отбросить) эти нули.
Например, 0,8000 = 0,8, что следует из того, что
(сократили и числитель и знаменатель на 1000).
5. Десятичные дроби легко привести к одному общему наи-
меньшему знаменателю; так, если даны дроби 10,3; 1,24; 0,1708,
запишем их в виде 10,3000; 1,2400; 0,1708, где число десятичных
знаков в каждом 4, т. е. столько, сколько имелось в данном с
наибольшим числом десятичных знаков.
Вывод. Чтобы привести данные десятичные дроби к общему
наименьшему знаменателю, надо выделить то данное, где имеет-
ся наибольшее число десятичных знаков, а потом в остальных
данных приписать справа нули так, чтобы во всех оказалось по-
ровну десятичных знаков.
Из этого свойства сразу видно, что дробь 0,3 больше, чем
0,299 или 0,0005 > 0,000483, так как 0,3 = 0,300, а 0,0005 —
= 0,0005000.
Итак имеем: из двух десятичных дробей больше та, у кото-
рой больше целая часть; при равенстве целых — та, у которой
десятых долей больше; при равенстве целых и десятых — та, у
которой сотых долей больше, и т. д.
189
Как видим, десятичные дроби имеют ряд преимуществ перед
обыкновенными. На основании этого можно ожидать, что и дей-
ствия над десятичными дробями выполняются проще, чем над
обыкновенными. Как мы убедимся дальше, действия над десятич-
ными дробями выполняются почти так же просто, как над нату-
ральными числами.
§ 222. Проценты и промилли. Как мы уже отмечали (§ 180),
из всех дробей чаше всего в жизни употребляются дроби со зна-
менателем 100, получившие особое название проценты (от латин-
ских слов «про центум»—на сто) и особое обозначение при помощи
знака %. Можно сказать, что знак % употребляется для сокра-
щённой записи десятичных дробей со знаменателем 100: вместо
0,57 пишут 57%, вместо 3,15 пишут 315% и т. д.
Так как каждая десятая доля содержит десять сотых долей,
то десятичные дроби с одним десятичным знаком тоже можно
выражать в процентах: вместо 0,1 =0,10 пишут 10%; 0,2 = 0,20,
т. е. 20%, и т. д.
Каждая тысячная доля представляет собой одну десятую
часть от одной сотой, поэтому 0,001 =0,1%. Всякую десятичную
дробь с тремя десятичными знаками можно выразить в виде числа
процентов с одним десятичным знаком, например: 0,328 = 32,8%;
1,854 = 185,4% и т. д. Но существует и особое наименование и
обозначение для тысячных: их называют промиллями (от латин-
ских слов «про милле» — на тысячу) и обозначают знаком °/0().
Таким образом, 0,328 = 328%0, 1,854 = 1854°/00.
Раздел 2. СЛОЖЕНИЕ, ВЫЧИТАНИЕ, УМНОЖЕНИЕ И ДЕЛЕНИЕ
ДЕСЯТИЧНЫХ ДРОБЕЙ
§ 223. Сложение десятичных дробей. Здесь, так же как и при
сложении дробных чисел, имеются два случая: 1) когда даны
дроби с одним и тем же числом десятичных знаков (то есть с рав-
ными знаменателями) и 2) когда даны дроби не с одним и тем же
числом десятичных знаков (то есть с неравными знаменателями).
Установленные выше свойства суммы дробей позволяют сво-
дить сложение десятичных дробей к сложению натуральных чисел.
Действительно, пусть надо найти, например, сумму 12,213 и 6,465.
Выполним это сложение с подробным объяснением:
12213 6465
1) 12,213 4- 6,465 = 'юоо + Jqqq (определение десятичных дробей);
2) , 12213 (сложение числителей дробей при равных знаменателях);
6465
18678
18678
3) 12,213 + 6,465 = = 18,678 (представление дробного числа в деся-
тичной системе).
190
Как короче получить эту сумму? Достаточно данные числа
записать в «столбик» и складывать так же, как складывают на-
туральные числа, что показано ниже:
12,213
6,465
18,678
Если слагаемые имеют разное число десятичных знаков, их
предварительно можно привести к одному знаменателю, добав-
ляя надлежащее число нулей, но на практике этого добавления
не делают (эти нули можно просто подразумевать). Например,
если надо сложить числа 24,82; 0,3573; 1,992, то применяется пер-
вая из двух следующих записей, хотя возможна и вторая:
24,82
+ 0,3573
1,992
27,1693
24,8200
+ 0,3573
1,9920
27,1693
Таким образом, сложение десятичных дробей производится,
как сложение натуральных чисел, с записью их столбиком, при-
чём все знаки дробности должны располагаться друг под другом:
цифры десятых под цифрой десятых, сотых — под сотыми и т. д.
Сложение по разрядам производится справа налево, т. е. от са-
мых мелких долей, хотя возможно при некотором навыке и дви-
жение слева направо.
Как и при сложении натуральных чисел, при сложении деся-
тичных дробей широко применяются русские счёты и арифмометр
(см. § 39—40), причём на арифмометре знаком дробности служит
металлическая «запятая», перемещаемая на планке, расположен-
ной выше установочных рычажков. Такая же «запятая» имеется
над ответными окошечками.
Всё, что было сказано в § 22—26 о технике устного и письмен-
ного сложения натуральных чисел, сохраняет силу и для сложе-
ния десятичных дробей.
§ 224. Вычитание десятичных дробей. Здесь так же, как и
при сложении, рассмотрим два случая: 1) когда даны дроби с
одинаковым числом десятичных знаков (т. е. с равными знаме-
нателями) и 2) когда даны дроби с неодинаковым числом деся-
тичных знаков (т. е. с неравными знаменателями).
Установленные свойства разности дробей позволяют сводить
вычитание десятичных дробей к вычитанию натуральных чисел.
Действительно, пусть надо найти, например, разность между
числами 3,27 и 1,43.
Выполним это вычитание с подробным объяснением:
1327 143
1) 13,27 — 1,43 — — т™ (определение десятичных дробей);
1UU 1UU
191
2) 1327 (нахождение разности числителей при равных знаменателях);
~ 143
1184
1184 (представление дробного числа в деся-
3) 13,27 - 1,43 = = 11,84 тичной системе).
Как получить эту разность короче?
Записав данные в «столбик», надо вычитать так же, как вы-
читают натуральные числа:
13,27
~ 1,43
11,84
Если уменьшаемое и вычитаемое имеют разное число деся-
тичных знаков, их легко уравнять приписыванием нулей справа,
а затем произвести вычитание по только что указанному прави-
лу. И здесь, как и при сложении, эти приписываемые нули мож-
но только подразумевать. Если из числа 4,3 надо вычесть чис-
ло 1,2687, применяется запись, приведённая ниже (лучше справа):
4,3000 4,3
— 1,2687 — 1,2687
3,0313 3,0313
Таким образом, вычитание десятичных дробей производится
так же, как вычитание натуральных чисел, причём вычитаемое
записывается под уменьшаемым так, чтобы знак дробности ока-
зался под знаком дробности, цифра десятых под цифрой деся-
тых, и т. д.
Вот несколько примеров:
3,27 ~ 1,43 0,8497 0,5200 0,8497 0,52 4,3000 ~ 1,1686 4,3 — 1,1686
1,84 0,3297 0,3297 3,1314 3,1314
В последнем примере пришлось взять одну десятую долю,
раздробить её в сотые доли, из полученных десяти сотых взять
одну и раздробить в тысячные доли; из полученных десяти ты-
сячных взять одну и раздробить в десятитысячные, а затем вы-
читать из полученных 10 десятитысячных долей те 6 десятиты-
сячных долей, какие имеются в вычитаемом, что даёт 4; из 9
тысячных вычитать 8 тысячных, что даёт 1; из 9 сотых вычитать
6 сотых, что даёт 3; из 2 десятых вычитать 1 десятую, что даёт
1, и, наконец, из 4 целых вычитать 1 целую, что даёт 3. Эти
случаи раздробления можно отмечать точками.
Для проверки достаточно сложить полученную разность с
вычитаемым и убедиться, что получается уменьшаемое; это де-
лается без новой записи.
К вычитанию десятичных дробей относится всё то, что было
сказано в § 34—36 о технике устного и письменного вычитания
натуральных чисел, а также то, что было сказано в § 39—40 о
вычитании с помощью русских счётов и арифмометра.
192
§ 225. Умножение и деление на 10, 100, 1000 и т. д. Умно-
жение десятичных дробей на числа 10, 102= 100, 103 = 1000,
104 = 10000 и т. д., т. е. на разрядные единицы десятичной ну-
мерации, производится особенно просто. Например, чтобы умно-
жить 3,849 на 10, действуем по правилу умножения дроби на
натуральное число (§ 202) и получаем:
3,849 • 10 ~ 381вд010 = W = 38,49‘
Как видим, при умножении десятичной дроби на 10 происхо-
дит только перемещение знака дробности на одно место вправо.
Умножение на 100 = 10 • 10 можно заменить двукратным последо-
вательным умножением на 10; умножение на 1000 = 10-10-10 —
трёхкратным умножением на 10; умножение на любую раз-
рядную единицу — умножением на 10, произведённым столько
раз, сколько нулей в записи этой разрядной единицы. Следова-
тельно, чтобы умножить десятичную дробь на 10, 100, 1000, во-
обще на какую-нибудь разрядную единицу, достаточно перенести
во множимом знак дробности вправо соответственно на одно, два,
три места, вообще на столько мест, сколько нулей в записи
этой разрядной единицы.
В случае, когда этих нулей больше, чем десятичных знаков,
приходится добавлять недостающее число нулей. Например, что-
бы умножить 3,84 на 100000, добавляем справа ещё три нуля
и получаем произведение 384000. Можно сказать, что здесь ум-
ножение сделано в два приёма согласно более подробной записи:
3,84 - 100000 = (3,84 - 100) • 1000 = 384 • 1000 = 384000.
Если перенесение знака дробности на одно место вправо рав-
носильно умножению на 10, то перенесение его на одно место
влево равносильно делению на 10.
Отсюда правило: чтобы разделить десятичную дробь на 10,
100, 1000, вообще на какую-нибудь разрядную единицу, достаточ-
но перенести в делимом знак дробности влево соответственно на
одно, два, три места, вообще на столько мест, сколько нулей
в записи этой разрядной единицы.
Если цифр в целой части делимого не хватает, добавляются
нули. Например:
816,3:10 = 81,63; 816,3:100 = 8,163;
816,3 :1000 = 0,8163; 816,3 :10 000 = 0,08163.
§ 226. Умножение десятичных дробей. Установленные выше
свойства позволяют сводить умножение десятичных дробей к ум-
ножению натуральных чисел. Действительно, пусть надо найти,
например, произведение 5,12 на 0,129. Выполним умножение с
подробным объяснением:
В 5 12 0 129 — 512 129 _512 • 129 (определение десятичной дроби);
' , -и,1/э—100 • 1000— iqoooo (умножение двух дробных чисел);
193
2) 512- 129 = 66048 (умножение числителей);
3) Имеем; 5,12 0,129 = = 0,66048 (определение десятичной дроби).
lUuUvU
Как короче получить это произведение?
Видим, что всё сводится к умножению натуральных чисел,
которые получаются, если в данных сомножителях отбросить
знаки дробности, и к делению на произведение знаменателей дан-
ных дробей. Но произведение знаменателей есть разрядная еди-
ница со столькими нулями, сколько десятичных знаков во мно-
жимом и множителе вместе.
Отсюда правило: чтобы перемножить две десятичные дроби,
достаточно перемножить два натуральных числа, получаемых пу-
тём отбрасывания в данных сомножителях знаков дробности, а за-
тем в полученном произведении отделить столько десятичных зна-
ков, сколько их в обоих сомножителях вместе.
Записав данные в «столбик», надо умножить так же, как ум-
ножают натуральные числа. Например:
5,12 0,0234 62,5
‘0,129 ‘0,15 ’ 0,16
4608 ,1170 , 3750
+ 1024 + 234 + 625
512 0,003510 10,000
0,66048 0,00351
При умножении десятичных дробей следует использовать всё
то, что было сказано в § 51—54 об умножении натуральных
чисел.
§ 227. Умножение десятичных дробей при помощи таблиц и
вычислительных приборов. Проверка умножения. В § 72 было
показано, какие выгоды доставляют при умножении натуральных
чисел таблицы произведений, как составляемые самим вычисляю-
щим, так и готовые печатные. Понятно, что такие таблицы по-
лезны и для умножения десятичных дробей.
Пусть, например, требуется узнать, сколько стоят разные
количества товара, именно: 4,4 кГ; 2,8 кГ; 432,4 кГ; 96,2 кГ;
при цене 4,35 руб. за 1 кГ. Если под руками имеется «таблица
умножения» О’Рурка, содержащая произведения натуральных
чисел до 999 на 99, то достаточно раскрыть её на той странице,
которая содержит произведение числа 435 на все двузначные чис-
ла, и мы можем сразу записать два первых результата. Для по-
лучения двух следующих результатов пользуемся распредели-
тельностью умножения и имеем:
4,35 • 432,4 = 4,35 • 430 + 4,35 - 2,4 = 1870,5 + 10,44 = 1880,94;
4,35 96,2 = 4,35 • 96 + 4,35 • 0,2 = 417,6 + 0,87 = 418,47.
Здесь произведения числа 4,35 берутся готовыми из таблиц,
надо лишь надлежащим образом поставить запятую, а сложение
194
делается на счётах или письменно с записью «столбиком». Окон-
чательно получаем следующее:
Количество (кГ) 4,4 2,8 432,4 96,2
Стоимость (руб.) 19,14 12,18 1880,94 418,47
Умножение натуральных чисел на русских счётах было рас-
смотрено в § 73, а на арифмометре «Феликс» в § 74. Понятно,
что всё, там сказанное, сохраняет силу и для умножения деся-
тичных дробей: не обращая внимания на знаки дробности, на-
ходят при помощи счётов или арифмометра произведение соот-
ветствующих натуральных чисел, а после этого остаётся только
поставить, где следует, запятую.
Как и при умножении натуральных чисел, при умножении
десятичных дробей применяется проверка повторным умножением
с перестановкой мест множимого и множителя. Например, вы-
полнив умножение, показанное ниже слева, выполняют для про-
верки умножение, показанное справа:
43,4
* 7,83
1302
+ 3472
3038
339,822
7,83
' 43,4
3132
4- 2349
3132
339,822
Другой способ проверки произведения — повторное его выпол-
нение каким-либо иным способом, чем первый раз. Например,
найдя произведение на счётах, находят его вторично письменно.
Рекомендуется всякое умножение начинать с «прикидки», т. е.
с грубо приближённого подсчёта, когда в уме устанавливают
значение цифры первого (старшего) разряда. Например, прежде
чем находить точное произведение 43,4 • 7,83, замечают, что оно
близко к произведению 40 • 8 = 320, и в дальнейшем убеждаются,
что найденное произведение 339,822 грубой ошибки не содержит.
§ 228. Деление натуральных чисел. Как мы видели в § 178,
введение дробей позволяет выполнять деление натуральных чи-
сел во всех случаях без исключения: в частном получается
дробь, числителем которой является делимое, знаменателем де-
литель. Преимущества десятичных дробей наводят на мысль
представить частное двух натуральных чисел в виде десятич-
ной дроби. Выясним, как это делается и всегда ли это возможно.
Положим, отрезок длиной 63 см надо разделить на 48 равных
частей и требуется выразить десятичной дробью длину одной
такой части. Здесь можно упростить дело, перейдя к более мел-
ким мерам:
195
63 см = 630 мм = 630 000 [i,
630000 : 48= 13 125,
13125 р.= 13,125 мм = 1,3125 см.
Но этот ответ можно получить иначе, производя деление
63 см на 48: получив в частном 1 и в остатке 15 см, раздроб-
ляем этот остаток в десятые доли, что даёт 150 (десятых долей
сантиметра); разделив 150 на 48, имеем в частном 3 (десятые
доли сантиметра) и в остатке 150— 144 = 6 (десятых долей сан-
тиметра); раздробив этот второй остаток в сотые доли санти-
метра, делим 60 (сотых долей сантиметра) на 48, получаем в
частном 1 и в остатке 60 — 48= 12 (сотых долей сантиметра);
раздробив этот третий остаток в тысячные доли сантиметра, де-
лим 120 на 48 и получаем в частном 2 и в остатке 120 — 96 = 24
(тысячных долей сантиметра); раздробление этого четвёртого ос-
татка в десятитысячные доли сантиметра и новое деление (240
на 48) даёт частное 5 и остаток 0. Тем самым деление закон-
чено, получено частное 1 4- 0,3 4- 0,01 4- 0,002 4- 0,0005 = 1,3125 см.
Здесь мы произвели то самое разбиение делимого на «удоб-
ные» слагаемые, о котором была речь в § 67: делимое 63 мы
представили в виде суммы пяти «удобных» слагаемых:
48 4- 14,4 4- 0,48 4- 0,096 4- 0,0240
(«удобных» в том смысле, что каждое из них легко делится на
48), а затем заменили деление суммы делением каждого слагае-
мого в отдельности, т. е. использовали распределительное свой-
ство деления. Получив:
48 : 48 4- 14,4 ; 48 4- 0,48 : 48 4- 0,096 : 48 4- 0,0240 : 48 =
= 1 4- 0,3 4- 0,01 4- 0,002 4- 0,0005,
имеем частное 1,3125. Проверка умножением (1,3125 - 48 = 63)
показывает, что деление сделано правильно.
Вся запись, применяемая для получения этого частного, сво-
дится к одной из двух следующих (более короткая вторая заслу-
живает предпочтения):
63 ] 48 63 | 48
48 11,3125 150 11,3125
__ 150 60
120
__50 240
48_
120
~ 96
_240
240
0
В рассмотренном примере мы получили остаток 0 после того,
как нашли 4 десятичных знака частного. Но очень важно заме-
196
тить, что весьма часты случаи, когда остаток 0 не получается ни-
когда (например, при делении 1 на 3). О таком «бесконечном»
делении речь будет идти дальше.
Ограничиваясь пока случаями, когда такого бесконечного де-
ления нет, можем формулировать следующее правило: производя
деление одного натурального числа на другое по обычному пра-
вилу и получив остаток в целых единицах, ставим в частном знак
дробности, а деление продолжаем, снося к последовательно полу-
чаемым остаткам цифру 0 (нуль десятых, нуль сотых, нуль ты-
сячных и т. д.), пока не получится остаток нуль.
§ 229. Деление десятичной дроби на натуральное число. По-
ложим, требуется узнать, какую площадь имеет каждый из 12
равных участков, на которые разделено поле площадью в 382,53 га.
Нужное здесь деление десятичной дроби 382,53 на натуральное
число 12 выполняется точно так же, как только что рассмот-
ренное деление одного натурального числа на другое: получив
остаток в целых единицах, раздробляем его в десятые доли и
прибавляем к нему число десятых делимого (5); остаток в деся-
тых раздробляем в сотые и прибавляем к нему число сотых де-
лимого (3); остаток в сотых раздробляем в тысячные и прибав-
ляем к нему число тысячных делимого (0) и т. д. Вот два спо-
соба той записи всего деления,
второй):
как здесь требуется (лучше
1 12 382,531 12
131,8775 22 |31,8775 105 93 90 60
382,53
“36_
22
~~ 12
105
96
93
— 84
90
~84_
60
0
Ответ. 31,8775 га, или 31 га 87 а 75 кв. м — 31,88 га;
Проверка. 31,8775 - 12
, 637550
+ 318775
382,5300
382,53
Заметим, что при таком небольшом делителе, как 12, можно
вообще не записывать ничего, кроме данных и результата, вы-
полняя все операции в уме.
§ 230. Деление дроби на дробь. Как мы уже видели в § 214,
частное от деления одной дроби на другую не изменится,
если умножить делимое и делитель на одно и то же число. Это
197
свойство частного позволяет заменять деление на десятичную
дробь делением на то натуральное число, которое получится,
если в данном делителе отбросить знак дробности.
Пусть, например, требуется узнать, сколько куплено учебни-
ков по 1 руб. 35 коп., или по 1,35 руб. за экземпляр, если всего
уплачено 113 руб. 40 коп., или 113,4 руб.
Надо разделить 113,4 на 1,35. Заменяя дробный делитель 1,35
натуральным числом 135, т. е. перенося в нём знак дробности
на два места вправо, мы увеличиваем делитель в 100 раз, а по-
тому, чтобы получить искомое частное, должны увеличить во
столько же раз и делимое.
Таким образом, деление 113,4 на 1,35 заменяется делением
11340 на 135, дающим частное 84. Для проверки умножаем 84
на 1,35 и получаем произведение 113,4, как и должно быть.
Ещё пример: 4,0651 :0,265= 15,34.
_ 4065,1 1265
265 115,34
1415
~ 1325
901
795
1060
1060
0
Проверка.
15,34 • 265
3068
, 9204
+ 7670
4065,10
4065,1
Итак, приходим к правилу: чтобы разделить на десятичную
дробь, надо перенести знак дробности в делимом и делителе на
одно и то же число мест так, чтобы делитель стал натуральным
числом, а затем выполнить деление на это натуральное число.
Иногда при делении одной десятичной дроби на другую пере-
носят знак дробности так, чтобы не только делитель, но и дели-
мое заменились натуральными числами. Это тоже даёт правиль-
ный результат, но требует лишней записи, а потому так делать
не следует.
§ 231. Случай бесконечного деления. Пусть имеется гряда
длиной 5 м и требуется разделить её на три равные части. Деле-
ние 5 на 3, если выражать частное в виде десятичной дроби,
оказывается бесконечным: без конца повторяется остаток 2, а в
частном цифра 6. Это частное записывают в виде 1,666..., ука-
зывая многоточием на бесконечное повторение цифры 6, или в
виде 1, (6), заключая повторяющуюся цифру в скобки.
—5 I 3
3_ 11,666...
20
— 18
20
— 18_
20
“ 18_
2
193
Такое частное называют бесконечной периодической десятичной
дробью (с периодом 6), но это не соответствует общепринятому
определению дроби как пары натуральных чисел, показывающих,
сколько и каких долей единицы взято. Мы будем называть такое
частное периодическим десятичным рядом и займёмся в дальней-
шем его изучением.
Что касается практической задачи деления 5 м на 3 равные
части, то приходится признать, что выразить точную длину одной
части в виде десятичной дроби здесь невозможно. Её надо выра-
5 2
зить в виде обыкновенной дроби или 1-^- м, или же ограни-
О о
читься приближённым значением частного, о котором будет речь
в главе XII.
Раздел 3. ПРЕДСТАВЛЕНИЕ ОБЫКНОВЕННЫХ ДРОБЕЙ
В ВИДЕ ДЕСЯТИЧНЫХ И ОБРАТНАЯ ЗАДАЧА
Десятичные дроби имеют такие преимущества, что естественно
возникает вопрос: нельзя ли любую обыкновенную дробь пред-
ставить в виде десятичной? Как мы сейчас увидим, это возможно
во многих случаях, но далеко не всегда.
§ 232. Представление обыкновенных дробей в виде десятичных
способом умножения. Заметим, что 10 = 2 - 5, 100 = 22 52,
1000 = 23 • 53 и т. д.; знаменатель любой десятичной дроби
представляет собой произведение равного числа простых множи-
телей 2 и 5.
Отсюда заключаем, что всякую дробь, знаменатель которой
содержит только простые множители 2 и 5, можно представить в
виде десятичной, добавляя в её числитель и знаменатель столько
множителей 2 и 5, чтобы число тех и других стало в знамена-
теле одинаковым. Вот примеры на применение этого «способа
умножения»:
3 _ 3 _ 3-2-2 _ 12 _ п ,9.
25 ~ 5 5 — 5 • 5 • 2 - 2 — 100 — U,1Z’
7 _ 7 _ 7-5-5-5 _ 875 _ „ „ _
80“ 2-2-2-2-5“ 2-2-2-2-5-5-5-Б “ 10000 “ ,
123 _ 123 _ 123-5-5 _ 3075 п ЧП7С-_
400 _ 100 • 2 - 2 — 100 • 2 • 2 - 5 5 “ 10 000 ~
1877 _ -277 г 277 _ к 277 • 55 _ 865 625 _ _ огггог
320 “ °320 — °10 - 26 “ ° 10 - 25 • 5s “ °1 000 000 —
2947 2947 2947 - 2е 188 608 п юоспо
15625 “ 56 “ 56 • 26 ~ 106 “ 0,1ооо08.
§ 233. Представление обыкновенных дробей в виде десятичных
способом деления. Во всех случаях, когда применим способ умно-
жения, т. е. когда знаменатель не содержит других простых
множителей, кроме 2 и 5, применим также способ деления.
199
Рассматривая данную дробь как частное от деления числителя
на знаменатель, выполняют это деление так, как это делалось
в § 228, т. е. представляя частное в виде десятичной дроби.
При этом всегда получается, конечно, тот же результат, что и
по способу умножения, но при больших знаменателях общее
количество необходимых выкладок при способе деления несколько
меньше, чем при способе умножения. Вот примеры (записывается
только то, что трудно выполнить в уме):
1 = 3 :25 = 0,12; = 7 : 80 = 0,7 : 8 = 0,0875;
= 123 : 400 = 1,23 : 4 = 0,3075;
400 ’
= 187,7 : 32 = 5,865625
= 2947 :15625 = 0,188608
15625
187,7 I 32
277 | 5,865625
210
180
200
80_
160
2947 I 15625
29470 0,188608
—15625
138450
— 125000
134500
— 125000
95000
93750
125000
""125000
0
§ 234. Обыкновенные дроби, не допускающие представления
в виде десятичных. Итак, всякую дробь, знаменатель которой
не содержит других простых множителей, кроме 2 и 5, можно
представить в виде десятичной, притом двумя способами — умно-
жением и делением.
Теперь надо рассмотреть такие дроби, у которых знаменатель
содержит хотя бы один простой множитель, отличный от 2 и 5
(3, или 7, или Пит. д.), причём будем предполагать, что дробь
несократима.
Ясно, что способ умножения к ним не применим: если в зна-
менателе дроби имеется, например, сомножитель 3, то он сохра-
нится и после умножения числителя и знаменателя на любое
число, а потому получить знаменатель 10 = 2-5 или 100 =
= 22 • 5а и т. д. нельзя.
Пробуя применить способ деления, мы легко убедимся, что
деление каждый раз оказывается бесконечным, в частном полу-
200
чается не десятичная дробь, а бесконечный десятичный ряд,
например:
4 = 5:3= 1,666 ... = 1,(6);
О
1 = 5 : 6 = 0,8333 ... =0,8(3);
= 0,272727 ... = 0,(27);
у = 0,142857 142857 ... = 0,(142857).
Никакая несократимая дробь не допускает представления в
виде десятичной дроби, если она имеет хотя бы один простой
делитель, отличный от 2 или 5.
,т _ . , а
Чтобы доказать это утверждение, возьмем несократимую дробь , где
р — какое-нибудь простое число, отличное от 2 и 5, а и b — какие угодно на-
туральные числа, причём в силу несократимости а не делится на р. Допустим,
что существует десятичная дробь , равная данной дроби. Из равенства
10*
а _ с
Pb ~ iofc
после умножения обеих его частей на р • Ь и 10й получится равенство
а • 10й = с • р • Ь,
где справа находится натуральное число, кратное р, а слева — натураль-
ное число, не кратное р (а и 10й не делятся на р), и, следовательно, это равен-
ство неверно. Поэтому сделанное допущение о существовании десятичной дроби,
равной данной обыкновенной дроби
-—, неправильно. Ни способом умноже-
ния, ни способом деления, ни каким бы то ни было другим способом пред-
ставить эту обыкновенную дробь в виде десятичной нельзя. Здесь мы опираемся
на ту единственность разложения натурального числа на простые множители,
о которой речь была в § 108.
Сопоставляя оба полученных выше заключения, можно утвер-
ждать, что обыкновенная несократимая дробь допускает представ-
ление в виде десятичной дроби тогда и только тогда, когда её
знаменатель не содержит ни одного простого множителя, отлич-
ного от 2 и 5.
Иными словами, для обращения обыкновенной несократимой
дроби в десятичную необходимо и достаточно, чтобы знаменатель
был числом вида 2", или вида 5й, или вида 2” • 5й.
Это условие необходимо, т. е. без его соблюдения обращение
невозможно; оно в то же время достаточно, т. е. при его со-
блюдении обращение выполнимо.
§ 235. Представление десятичной дроби в виде обыкновенной.
Выяснив, при каком условии возможно представить данную обык-
новенную несократимую дробь в виде десятичной, рассмотрим
201
обратную задачу: дана какая-нибудь десятичная дробь, требуется
представить её в виде обыкновенной.
Ясно, что достаточно написать эту дробь со знаменателем и,
если возможно, сделать сокращение. Задача эта всегда разре-
шима и всегда имеет единственное решение.
Примеры: 0,575 = ; 0,64 = ;
°’07 = ТО>
0,78125 = ШЖ = II: 1,207163 =
Задача представления данной десятичной дроби в виде обык-
новенной названа обратной по отношению к задаче представле-
ния данной обыкновенной дроби в виде десятичной, так как в ней
искомым является то, что было там дано, а- данным то, что там
было искомым.
Раздел 4. ПЕРИОДИЧЕСКИЕ ДЕСЯТИЧНЫЕ РЯДЫ
§ 236. Периодичность частного при бесконечном делении. Здесь мы будем
рассматривать только такие несократимые дроби, знаменатели которых содер-
жат хотя бы по одному простому множителю, отличному от 2 и 5, т. е. дроби
со знаменателями 3, 5, 7, 9, 11, 12, 13, 14, 15, 17, 18, 19, 21 и т. д.
Как было доказано в предшествующем параграфе, такие дроби не до-
пускают представления в виде десятичных: деление числителя на знаменатель
оказывается бесконечным, в частном получается не десятичная дробь, а беско-
нечный десятичный ряд. При этом во всех рассмотренных нами примерах эти
десятичные ряды оказывались периодическими-, каждый раз без конца повто-
рялась какая-нибудь цифра или группа из двух или более цифр; эта повто-
ряющаяся группа цифр называется периодом. Вот несколько примеров:
1) у = 0,333... =0,(3); здесь период из одной цифры (3), начинающийся
сразу после запятой; такой десятичный ряд называется чистым периодиче-
ским;
2) -g- = 0,1666... = 0,1(6); здесь период тоже из одной цифры (6), но
начинается он не сразу после запятой; такой десятичный ряд называется сме-
шанным периодическим;
3) у = 0,142857 142857... = 0,(142857); здесь чистый периодический де-
сятичный ряд с периодом 142857 из 6 цифр;
15
4) 22 = 0,6818181... = 0,6 (81); получился смешанный периодический ряд
с одной цифрой до периода и с периодом из двух цифр (81);
5) — = 0,270270...; получился чистый периодический ряд с периодом из
трёх цифр (270).
Возникает вопрос: всегда ли получается такое повторение одной или не-
скольких цифр, какое мы наблюдаем в этих примерах? Всегда ли получаемый
в частном десятичный ряд оказывается периодическим?
202
Производя деление, мы получаем последовательные остатки. Например,
при делении 1 на 7 получаются остатки, идущие в таком порядке: 3 (от де-
ления 10 на 7), 2 (от деления 30 на 7), 6 (от деления 20 на 7) и т. д.
212____________
10 | 0,142857...
“' 7
30
“28
20
“14
60
“К
40
~35
50
“49
1
Но остаток всегда меньше делителя; поэтому при делении на 7 не может быть
Других остатков, кроме 0, 1, 2, 3, 4, 5, 6. Остатка нуль получиться не может,
так как тогда дробь 2 была бы представлена в виде десятичной, что, как мы
знаем, невозможно.
Таким образом, при делении на 7 возможны только шесть различных
остатков (от 1 до 6), а так как деление бесконечно, то остатки должны по-
вторяться. Но как только какой-нибудь остаток повторится, начнут повто-
ряться и последующие, повторяться будут и цифры частного, получится пе-
риод. При делении 1 на 7 получаются последовательно остатки 3, 2, 6, 4,
5, 1. Появление остатка 1, равного делимому, вызывает повторение всех по-
следующих остатков и всех соответствующих цифр частного.
Положим, имеется несократимая дробь — , и деление а на п оказывается
бесконечным. Возможны только остатки от 1 до п — 1, а потому неизбежно
повторение их. Различных остатков самое большее п — 1, а потому здесь по-
лучится период, причём в нём будет либо п — 1 цифр, либо меньше.
В рассмотренном примере и = 7, п — 1 — 6 получился период из шести
цифр, т. е. наиболее длинный, какой возможен.
5
У дроби — число п— 11, возможных различных остатков 11 — 1 — 10,
5
но повторение начинается гораздо раньше;’ — = о, (45).
15
У дроби gg возможен 21 различный остаток, но повторение начинается
тоже гораздо раньше, причём не с первого, а со второго остатка; получается
смешанный десятичный периодический ряд 0,6 (81).
Итак, мы пришли к такому заключению: если деление числителя на зна-
менатель оказывается бесконечным, то в частном получается периодический
десятичный ряд, чистый или смешанный, с периодом, имеющим не больше
цифр, чем знаменатель без единицы.
§ 237. Получение чистого периодического десятичного ряда. Будем брать
только такие несократимые дроби, у которых знаменатель взаимно прост с 10,
т. е. не содержит простых множителей 2 и 5. Таковы знаменатели:
3, 7, 9, 11, 13, 17, 19, 21, 23, 27, 29, 31 и т. д.
203
Производя деление каждой из таких дробей на её знаменатель, получаем
всякий раз чистый периодический ряд:
4 = 0, (3); 1=0, (142857); 1 = 0, (1); 1 = 0, (18); 1 = 0, (076923);
О I zJ 11 ю
1 = 0, (0588235294117647) и т. д.
Докажем, что так будет всегда.
Положим, даиа несократимая дробь , где п > 1 и п не делится ни
на 2, ни на 5. По доказанному в § 236 эта дробь при делении числителя на
знаменатель даст периодический десятичный ряд. Надо выяснить, будет ли этот
ряд чистым или смешанным.
Обозначим неполное частное и остаток от деления а на п буквами q и
а — nq = и.
Этот первый остаток раздробляем в десятые доли и делим на и, полу-
чая десятичный знак частного qt и второй остаток:
= 10rt — nq^.
Повторяя эту операцию, получим бесконечный ряд последовательных цифр
частного:
9г, 9з. Qit • • •
и ряд остатков:
r3- rit rs....
причём
10rs — nq2 = r8, 10r3 — nqs = r4, 10r4 — nqt = rc и т. д. без конца.
Обозначая последний неповторяющийся остаток буквой Гк, будем иметь
первый повторяющийся остаток:
Wrh-nqk = rb+1-
Такой первый повторяющийся остаток непременно встретится (в силу до-
казанного в § 236) после того, как пройдёт самое большее п — 1 остатков.
Может ли rft+1 равняться г2? Если rk+l=r2, то qk+l = qi, так как по-
вторение остатка влечёт за собой повторение соответствующей цифры частного.
Из равенств
гя = Юг! - nqi и гй+1 = 10rft - nqh
получаем равенство:
10Г1 — nqt = Юг* — nqh-
Если /-J > гь, то после прибавления к этим равным разностям числа
и вычитания от них числа Юг* приходим (используя распределительный закон
натуральных чисел; см. § 45) к равенству:
Ю (fl - rk) = п (qi - qh)- (А)
Если же Г! < гк, то вместо равенства (А) мы получим:
Ю (rh - Г1) = п (qk - 91)- (В)
Каждый из остатков и гь равен одному из натуральных чисел от 1 до
п — 1, их разность меньше п (наибольшее возможное её значение есть
(п — 1) — 1 = п — 2); ни разность гг — Гк (при гА > гд), ни разность гь —
(при г, < делиться на п не может, так как гй — п < п. Не может делиться
на п и произведение 10 • (rt — гь) или 10 • (гк — п), так как по условию
числа п и 10 взаимно просты; добавление множителя 10 = 2-5 не поможет
делимости на п.
204
Итак, левая часть равенства (А) не делится на п, правая же его часть
делится на п. Такого равенства быть не может, как не может быть и ра-
венства (В).
Предположение, что rh+l = rz, привело, таким образом, к противоречию,
его необходимо отбросить как неверное.
Точно так же убедимся, что неверны предположения:
rh+l ~ гз> гЛ+1 = г*> • • rk+l — rk-
Первым повторяющимся остатком rft+t не может быть никакой из преды-
дущих остатков, кроме первого (fi), а потому получающийся в частном пе-
риодический десятичный ряд не может иметь допериодической части.
Итак, доказано, что всякая несократимая дробь, знаменатель которой
взаимно прост с 10, даёт при делении числителя на знаменатель чистый пе-
риодический десятичный ряд.
§ 238. Получение дроби, соответствующей данному чистому периодическому
десятичному ряду. Выяснив, как получить чистый периодический десятичный
ряд, займёмся обратной задачей: имея какой-нибудь чистый периодический
десятичный ряд, найдём соответствующую обыкновенную дробь, т. е. дробь,
дающую этот ряд при делении числителя на знаменатель.
Доказано1: 1) что каждый десятичный ряд выражает некоторое число,
и 2) что при перенесении в десятичном ряду знака дробности (запятой) на
одно место слева направо выражаемое этим рядом число увеличивается
в 10 раз. Отсюда следует, что перенесение запятой на 2, 3, 4... мест слева
направо вызывает увеличение выражаемого этим рядом числа в 100, 1000,
10 000... раз.
Пусть дан какой-нибудь чистый периодический десятичный ряд с периодом
из одной цифры, например 0,(5). Допустив, что искомая обыкновенная дробь
существует, обозначим её буквой х. Тогда
откуда
Но если
х = 0,5555...,
10г = 5,555... = 5 + 0,555... = 5 4- х.
10г = 5 + х, то 10х — х = 5,
так как каждое слагаемое равно сумме без остальных слагаемых. Выполняя
вычитание, имеем Эх = 5, откуда х = -д . Для проверки делим 5 на 9 и убе-
ждаемся, что задача решена правильно.
Если период содержит не одну, а две цифры, то умножать надо не на 10,
а на 10® = 100. Например, полагая
получаем:
а потому
х = 0,141414...,
100х = 14,141414... = 14 + 0,141414... = 14 + х.
100х — х = 14;
14
14^ = 99-
Проверка делением и здесь показывает, что этот результат правилен.
Имея период из 3 или 4 цифр, умножаем соответственно на 10s = 1000
или 104 = 10 000. Например, имея х = 0,243 243 243..., находим:
ЮООх = 243 + х.
откуда
999х — 243 х= = — = —
yyyx_24d, 999 ш 37.
1 В курсе алгебры.
205
а в случае
х= 0,(2105)
получаем:
10 000 х= 2105 4-Х, х = Х
Из рассмотрения частных примеров вытекает следующее общее правило:
чтобы получить обыкновенную дробь, дающую при делении числителя на зна-
менатель данный чистый периодический десятичный ряд (с нулём целых), надо
написать период числителем, а знаменателем число, изображаемое столькими
девятками, сколько цифр в периоде.
Это правило даёт в результате дробь, меньшую единицы, во всех случаях,
кроме того, когда период состоит из одной цифры 9: ряд 0,999... нельзя по-
лучить делением числителя на знаменатель какой бы то ни было обыкновенной
дроби.
Если дан чистый периодический десятичный ряд 0, (аь а2, ..., as), то,
обозначая одной буквой Р натуральное число, составляющее период, произво-
дим умножение на 10h и получаем:
ЮМ = Р 4- л; (10* - 1).Х = Р, X =
k цифр
Если число Р имеет хотя бы одну цифру, отличную от 9, х есть правиль-
ная дробь, деление её числителя на знаменатель даёт данный чистый перио-
дический десятичный ряд.
Итак, поставленная обратная задача имеет решение во всех случаях,
кроме того, когда период состоит из одной цифры 9.
§ 239. Получение смешанного периодического десятичного ряда. Будем
рассматривать дроби (несократимые), знаменатели которых, имея хотя бы один
простой множитель, отличный от 2 и 5, уже не взаимно просты с 10, а со-
держат хотя бы один простой миожитель 2 или 5; таковы числа 6, 12, 14,
15,18, 22, 24, 26, 28, 30, 34 и т. д.
Всякая такая дробь при делении числителя иа знаменатель даёт, как мы
уже знаем, периодический десятичный ряд. Он не может быть чистым пери-
одическим, так как по только что доказанному всякий чистый периодический
десятичный ряд получается при делении числителя на знаменатель такой
дроби, у которой знаменатель есть 9, или 99, или 999 и т. д., а ни одно из
таких чисел не делится ни на 2, ни на 5; следовательно, получаемый в част-
ном периодический десятичный ряд всегда смешанный.
Правильность этого заключения видим на примерах:
= 0,1 (6); = 0,41 (6); = 0,2 (142857);
4 7 9
15 = 0,2 (6); = 0,3 (8); g = 0,4 (09);
А = 0,208 (3); ^=0,4(3); ~ = 0,28 (3) и т. д.
OU ои
Внимательное их рассмотрение обнаруживает, что число цифр между за-
пятой и периодом равно каждый раз большему из чисел, показывающих,
сколько двоек или сколько пятёрок входит в разложение знаменателя, иапри-
17
мер: 60 = 22«3-5; здесь две двойки и одна пятёрка, в ряду для gg между за-
пятой и периодом — две цифры. Число 24 = 23 • 3 содержит три двойки и не
5
содержит пятерок, в ряду для — между запятой и периодом — три цифры.
Ряд для несократимой дроби со знаменателем 75 = 3-52 должен иметь, если
эта догадка справедлива, две цифры между запятой и периодом; действительно,
~ = 0,01 (3). Можно доказать, что эта догадка оправдывается всегда.
206
Итак, всякая несократимая дробь, знаменатель которой содержит хотя бы
один простой множитель, отличный от 2 и 5, и хотя бы один из множителей 2 или
5, даёт при делении числителя на знаменатель смешанный периодический де-
сятичный ряд. В самом деле:
где 7 — простое
7-28-5’ число, причём
7#=2 и 7 =# 5, и где 3>1;
17 17-5®
7-23-5 ~7-23- (5‘-53) ~
425
7- (23-53) =
425
~ 7-Ю3 -
= (425 : 7): 103 =
= 60, (714285): 10s =
= 0,060 (714285)
3 цифры до периода,
т. е. столько, каков наи-
больший показатель у 23
или 51, т. е. 3.
а где р — простое число, причём р э4 2 и
р.2п-5й’ Р=#5, и где пусть п>А:
а а-5п~ь (основное свойство
р.2п.5k ~ р.2п. (5Л.5П-Л) “ дробей).
Ъ
р- (2п-5п)
b
р 10"
(найдено произведение);
= (свойства произведения);
— (б : р): 10п = (деление на произведение)
= стст—1 ... cn+icncn—1 ... QCi, (^1^2 де) Ю” “
— стст—1 •- сп+1> спсп—I сгс1 (^1^2 ••• &s)
п цифр до периода, т. е.
столько, каков наиболь-
ший показатель у 2П или
5А, т. е. п, так как пред-
положили, что п А;
если бы А > п, то тогда
имелось бы в допериоди-
ческой части А цифр
(рассуждения ведутся ана-
логичные проведённым).
Вопрос о том, что получается при делении числителя несократимой дроби
на её знаменатель, разрешён теперь полностью.
В случае, когда знаменатель не содержит других простых множителей,
кроме 2 и 5, в частном получается десятичная дробь.
В случае, когда знаменатель взаимно прост с 10, частное оказывается
чистым периодическим десятичным рядом.
В случае, когда наряду с простыни множителями, отличными от 2 и 5,
есть хотя бы один множитель 2 или 5, частное — смешанный периодический де-
сятичный ряд.
§ 240. Получение дроби, соответствующей данному смешанному периоди-
ческому десятичному ряду. Нам остаётся решить ещё один вопрос: дан какой-
нибудь смешанный периодический десятичный ряд; требуется найти обыкно-
венную дробь, которая даёт этот ряд при делении числителя на зна-
менатель.
Пусть, например, дан ряд 0,405 (63). Полагаем:
х — 0,405 (63)
и замечаем, что
lOOQx = 405, (63) - 405 + 0, (63) = 405 + = 405 ~
откуда
х =
4JL2;1ooo=^ = ^
11 11000 5500
Проверка делением показывает, что эта дробь действительно даёт дан-
ный ряд.
207
Подобным образом задача решается для любого смешанного периодиче-
ского десятичного ряда с периодом, отличным от 9; в случае периода 9 она не
имеет решения (например, не существует обыкновенной дроби, которая давала
бы при делении числителя на знаменатель ряд 0,1329999...).
Возвращаясь к ряду х = 0,405 (63), найдём х из равенства
1000х = 405 + Ц,
63
несколько иначе, а именно: не сокращая дробь gg. представим правую часть
в виде:
405-994-63 405-(100— 1) 4- 63 405-100 — 405 4-63 _ 40 563 — 405
99 “ 99 - 99 99
а искомую дробь х в виде:
40 563 — 405
99 000 ‘
Как видим, для получения дроби, дающей при делении числителя на
знаменатель данный смешанный периодический десятичный ряд, надо написать
числителем число, находящееся между запятой и вторым периодом, минус
число, находящееся между запятой и первым периодом, знаменателем же на-
писать число, изображаемое столькими девятками, сколько цифр в периоде,
в сопровождении стольких нулей, сколько цифр между запятой и периодом.
Чтобы показать справедливость этого правила для всех случаев, берём
смешанный периодический десятичный ряд в общем виде и поступаем с ним
точно так же, как поступали выше при рассмотрении примера. Если
то
х — 0, ... ап (6162^3
х-10” = Q 4- 0,(Р),
где Q и Р означают натуральные числа, образованные цифрами от запятой до
р
периода и цифрами в периоде. Далее имеем: x-10n = Q 4- —у =
Q.lOft —Q4-P _ (Q-lOfe 4- P) — Q
— IQfe — 1 10* — 1
и окончательно:
Q-10* 4* P — Q _ OjGg ••• 4- ^1^2 —a„ __
X = (10*—i)-10" — 99 ... 900 ... 0 ~
k цифр n цифр
k цифр
•—•>—» _____________ _______ _________________ ___________
01^2 ... 0^00 ... 0 4" ^1^2 ••• - ^1^2 On ^1^2 On ^1^2 O^Qg ••• On
99 ... 900 ... 0 = 99... 900... 0
k цифр n цифр k цифр n цифр
что и представляет собой краткую запись приведённого выше данного
правила.
208
Раздел 5. О СОВМЕСТНЫХ ДЕЙСТВИЯХ С ОБЫКНОВЕННЫМИ
И ДЕСЯТИЧНЫМИ ДРОБЯМИ
§ 241. Вычисления с обыкновенными дробями и целесообраз-
ность их замены десятичными дробями. Так как действия над
десятичными дробями вести проще и легче, то встаёт вопрос:
не целесообразно ли всегда переходить к соответствующим де-
сятичным дробям? Например, надо найти результат
г84-7и+84:4 х 1 1 17 25 4:ТГ5-2944 21 57 73 44 . _5 4161 88 2 ’ 10 + 5 : 2 20 + 25 101 . _L-2944 17 l2^-5-2944 17 4 ' 125 25 4 25
2Ц $2 211 — 100 100
1 17 3156 4- — 2944 '4 4 25 211 125-6^- 211 — 100 11100
Перейдём к соответствующим десятичным дробям:
28,5-7,3 + 8,8 : 2,5 208,05 + 3,52 211,57
Х ~ 25,25 ; 0,008 — 2944,68 “ 3156,25 — 2944,68 “211,57
Видно, что переход к десятичным дробям ускорил и упростил
вычисления.
Но так как известно, что не всякую обыкновенную дробь
можно представить в виде десятичной, то не всегда надо пытаться
делать этот переход. В рассмотренном примере все несократи-
мые дроби имели в составе знаменателей только простые мно-
жители 2 и 5, а потому в этих случаях часто целесообразен
будет переход от обыкновенных дробей к десятичным.
Найти:
4.11.4 16 । 1 64 + 125 189
125 ’’ 4 + 7 : 7 125 + 4 500 500 1000
Х~ 1 937 “ 8 + 937 “ 945 “ 189 “ 500 ~ 2‘
625+ 5000 5000 5000 1000
0,032 : 0,25 + 0,25 _ 0,128 + 0,25 _ 0,378 _ 378
Х~ 0,0016 + 0,1874 “ 0,1890 “ 0,189 “ 189 “ Z
Хотя в этом примере и были обыкновенные дроби со знаме-
нателем, отличным от 2 и 5, но они взаимно исключались.
§ 242. Вычисления, когда в числовую формулу входят и обык-
новенные и десятичные дроби.
Как лучше вести вычисления: в обыкновенных или в деся-
тичных дробях? Рассмотрим примеры:
1) х= 121 + 0,125 + 4 +6,25.
Z о
10 Арифметика
209
«=124+4+1+6т-,8т+4-14-
х= 12,5
0,125
+ 0,625
6,25
19,500 = 19,5
Одинаково просто получаются результаты.
2) x = 2i+(121- 10,875) = 2±+ (121-10^ = 21+(121-
— 10
32-21 1 11 _ч6+11 _ 17
Здесь перейти к десятичным дробям невозможно, так как
имеется знаменатель 3.
3)Л-<8''4:Й
/407 2301
\ 50 U 50
— /14749 50 _
\ 1000 ‘ 301 1
-46,02-0,03) : 4 + 0,2109- 1
О
f о 7_ . 1 _ 4fi 1 JLV 4 4- 2109
‘ й 50 10 50 ‘ 100/ ’ + 10000 ‘
749 „1 . М
\ 1000 • 650 1 4)
- -3J.4 +
100/ 20000
1Ь51 + 12-1
4 / 50 Ф 125
(81 । 19034 703_
= \81 5 1 5000J ’ 4 + 20000
~ (49_ j 1) . 51 12JL
\20 4 ) 50 Ф 125
20 _97_ + 703
20000 20000
jl.51 + 12-1
5 50 125
69ОЗ\ 703
’ 5000/ ‘ 4 4*20000
_ , 1| Л + 12Л -
4 I 50 125
6
• 1 — + 12 —
’ 50+ 125
(f-
/ 14749
\20-301
gn 97 703
5000 ‘ "Г 20000
1 IV 51. + 12J7 “
4) 50 + 125
501 501
25 _ 25
“ ЗОЁ+12-1 1—+12 —
250+ 125 125 + 125
(21
\ 20
“в
1 51
5 ’50
501
25
+ 12 —
+ 125
501
25
_ 501 _ 167 _ 1
— 9 “334 - 334 - 1 334 ~ 1 2 •
13 25 25
(8,14 : 0,1 — 46,02 • 0,03) : 4 + 0,0703 - 0,5
Х~ (14,749-6,02— 1,25)- 1,02 + 12,136 “
_ (81,4 — 1,3806): 4 + 0,03515 _(80,0194) : 4 + 0,03515 _20,00485 + 0,03515
~ (2,45 — 1,25) • 1,02 + 12,136 — 1,2 - 1,02 + 12,136 — 1,224+ 12,136
_ 20,04 _
- 13,36 ~ *’5,
Понятно, что, где возможно, надо всегда переходить от обык-
новенных дробей к десятичным, так как результат находится
значительно проще с десятичными дробями.
210
Открытие метрической десятичной системы и десятичных дро-
бей даёт возможность на практике пользоваться преимуществен-
но десятичными дробями.
Что же касается того случая, когда невозможно обратить
обыкновенную дробь в десятичную, то в следующей главе будет
рассмотрено учение о приближённых вычислениях, что даёт
возможность и в этом случае переходить к десятичным дробям
с необходимой точностью.
Глава XII. ПРИБЛИЖЁННЫЕ ЗНАЧЕНИЯ ВЕЛИЧИН
И ДЕЙСТВИЯ НАД НИМИ
Раздел 1. ПРИБЛИЖЁННЫЕ РЕЗУЛЬТАТЫ СЧЁТА
И ИЗМЕРЕНИЯ
§ 243. Счёт элементов множества большой численности. Пере-
считать элементы множества тем труднее, чем их больше. Легко
узнать, сколько человек в этой комнате, но точно подсчитать,
сколько, например, зёрен в мешке пшеницы, очень трудно.
Нужды государства нередко требуют счёта элементов множеств
большой численности, как, например, множества всех людей,
живущих в области. Здесь приходится тратить много усилий,
чтобы обеспечить получение точных результатов, обычно же до-
вольствуются получением не вполне точных, приближённых
результатов.
Например, если несколько человек возьмутся считать, сколько
учащихся пришло на школьный праздник, у каждого обычно
получается иной результат, чем у других: один, например, на-
считает 489 человек, другой 508, третий 514, четвёртый 498.
В таких случаях рекомендуется находить среднее арифмети-
ческое всех полученных результатов: найдя сумму всех получен-
ных чисел, делят её на число их и берут полученное частное в
качестве окончательного результата. В нашем примере имеем:
489 + 508 + 514 + 498 = 2009 ; 2009 :4 = 502,25.
Можно принять, что в школу явилось 502 человека; надо
помнить, что результат этот только приближённый, но заслужи-
вает большего доверия, чем результаты отдельных подсчётов.
Средним арифметическим двух или более чисел (или короче,
их средним) называется частное от деления их суммы на их число.
Среднее чисел 100 и 120 равно:
(100 4- 120) : 2 - ПО;
среднее чисел 15, 17, 20 равно:
(15 4- 17 4-20): 3 = 17у.
10*
211
Среднее чисел alt а2, а3,..., ап равно:
(°1 + °2 + аз + • - - + Gn) : п-
Вычисление среднего арифметического применяется всегда,
если повторный счёт даёт новое число, причём каждый раз при-
ходится выяснять, какие цифры среднего стоит сохранить.
Рассмотрим такую задачу: сколько зёрен ржи в 1 кг её, если,
отвесив пять раз по 10 г и сосчитав число зёрен в каждой из
этих «навесок», получили числа 308; 332; 328 ; 342; 307.
Здесь среднее равно:
1617:5 = 323,4.
Цифра сотен (3) получалась при каждом подсчёте, она безу-
словно надёжна. Цифра десятков в среднем (2) уже не вполне
надёжна, так как в результатах отдельных подсчётов мы
имели разные цифры десятков (0, 3, 2, 4, 0). Цифра единиц
среднего результата (3) уже вовсе не надёжна, и в окончатель-
ном результате её, как и цифру десятых, следует отбросить.
Итак, на вопрос о том, сколько зёрен содержится в каждых
10 г имеющейся у нас ржи, даём ответ: в среднем 320 зёрен, а
потому в 1 кг её 320 • 100 = 32000 зёрен.
За первую цифру этого числа (3), выражающую число десят-
ков тысяч зёрен, мы ручаемся. Относительно второй цифры (2),
выражающей число тысяч, говорим, что в ней возможна неболь-
шая неточность. Об остальных цифрах мы уже ничего сказать
не можем.
Во избежание недоразумений ответ лучше записать в таком
виде: 1 кг нашей ржи содержит приближённо 32 тыс. зёрен.
Итак, найдя среднее из результатов всех произведённых под-
счётов, сравнивают его с этими результатами и сохраняют в нём
все надёжные цифры и одну не вполне надёжную, остальные же
отбрасывают.
Применяя только что указанное правило на практике, мы
встречаемся иногда со случаями, когда трудно решить, является
ли некоторая цифра среднего не вполне надёжной или вовсе не
надёжной. В таких случаях рекомендуется находить разности
между результатами отдельных подсчётов и найденным средним,
называемые уклонениями от среднего, а затем среднее значение
всех этих уклонений, или так называемое среднее уклонение.
(При подсчёте разности каждый раз из большего числа вычи-
тается меньшее.)
В рассмотренном выше примере со счётом зёрен ржи имеем
уклонения:
323,4 — 308 = 15,4; 332 — 323,4 = 8,6; 328 — 323,4 = 4,6;
342 — 323,4 = 18,6; 323,4 — 307 = 16,4
и среднее уклонение
(15,4 + 8,6 + 4,6 + 18,6 + 16,4): 5 = 12,72.
212
Не вполне надёжной цифрой среднего результата можно счи-
тать цифру того его разряда, какой выражен старшей, т. е.
первой слева, цифрой среднего уклонения (нуль целых и другие
нули слева, если они имеются, в счёт не идут). В рассматрива-
емой задаче старшая цифра среднего уклонения выражает де-
сятки, а потому в найденном среднем результате 323,4 цифру
десятков, как первую не вполне надёжную, сохраняем, а все
цифры справа от неё отбрасываем, заменяя цифру единиц нулём.
Получим 320 (пе надёжную цифру подчёркиваем).
Рекомендуется следующая запись решения рассмотренной за-
дачи:
Навески по 10 г Число зёрен Уклонение от среднего
№ 1 308 15,4 Среднее число зё-
№ 2 332 8,6 рен в навеске в 10 г—
№ 3 328 4,6 320, в 1 кг — 320-100 =
№ 4 342 18,6 =32 тыс.
№ 5 307 16,4 Ответ. В 1 кг 32 тыс. зёрен.
Сумма 1617 63,6
Среднее 323,4 12,72
§ 244. Точность измерения длины и других величин. Наблю-
дая, как производится измерение длины в различных областях
практической деятельности человека, легко убедиться, что вся-
кий раз применяются только некоторые определённые единицы
длины, а также более крупные единицы; более мелкие же еди-
ницы и их доли вовсе не принимаются во внимание.
Измерения длины производится всегда с определённой точно-
стью, различной в различных случаях. Вот несколько примеров.
Длины железных дорог и других значительных расстояний
на земле и по морю указываются в километрах: от Москвы до
Ленинграда по железной дороге 651 км, от Москвы до Сверд-
ловска 1818 км, длина газопровода Саратов — Москва 843 км.
Здесь мы имеем результаты измерений, произведённых с точ-
ностью до километра', долями километра пренебрегают.
Измеряя поля, принимают во внимание только целые метры,
их долями пренебрегают; например, говорят, что поле имеет
длину 284 м, ширину 195 м, хотя бы на самом деле эти отрезки
были на какие-то части метра больше или меньше.
213
Все измерения, какие приходится делать при пошивке белья,
платья, обуви, производятся с точностью до сантиметра', мил-
лиметры во внимание не принимаются.
Ученические чертежи в тетрадях делаются с точностью до
миллиметра, доли миллиметра в расчёт не берутся; но мно-
гие чертежи, какие выполняются инженерами, дают размеры с
точностью до десятых долей миллиметра. На часовых заводах
интересуются не только сотыми, но и тысячными долями мил-
лиметра— работают с «микронной точностью», но пренебрегают
долями микрона.
Производя измерение длины, надо подумать о том, с какой точ-
ностью следует его выполнять, т. е. о том, какие единицы длины
надо при этом принять во внимание, а какими пренебречь.
То же самое относится и к откладыванию отрезков заданной
длины. При черчении на бумаге обычно принимают во внимание
целые миллиметры, но пренебрегают их долями. Раскраивая ма-
терию, чтобы сшить платье, принимают во внимание сантиметры,
миллиметрами же пренебрегают. Производя разбивку огородной
грядки или цветочной клумбы, откладывают отрезки в дециметрах,
вовсе не считаясь с сантиметрами и миллиметрами.
Как и результаты измерения длины, результаты измерения
всевозможных других величин не бывают совершенно точными:
при всяком измерении пользуются только некоторыми определён-
ными единицами, вовсе не обращая внимания на их доли.
Так, например, при отвешивании товара в магазине прини-
мают во внимание только целые граммы, вовсе не обращая вни-
мания на дециграммы, но в аптеке, приготовляя лекарства, по-
стоянно применяют разновески в десятые и даже сотые доли
грамма (дециграммы и сантиграммы).
С другой стороны, когда врач взвешивает человека, то при-
нимает во внимание только килограммы и десятые их доли,
т. е. сотни граммов, пренебрегая десятками граммов; например,
устанавливают, что пионер до приезда в лагерь весил 29,8 кг,
а при отъезде из него 31,2 кг, и находят, что он прибавил в
весе на 1,4 кг.
Если речь идёт о продолжительности какого-нибудь проме-
жутка времени в пределах дня, например о том, сколько вре-
мени продолжается урок или прогулка, указывают часы и ми-
нуты, пренебрегая секундами, а если говорят о более значи-
тельных промежутках, например о том, каков возраст ребёнка,
то принимают во внимание только годы и месяцы, пренебрегая
днями. На спортивных состязаниях часто указывают не только
секунды, но и десятые их доли.
Итак, всякое измерение даёт только приближённое значение
измеряемой величины, всякое измерение производится с некото-
рой определённой точностью. Встречаясь с каким-нибудь резуль-
татом измерения, надо подумать о том, какие единицы и их доли
приняли во внимание при его получении и какими пренебрегли.
214
Число, представляющее собой приближённое значение какой-
нибудь величины, называют приближённым числом. Числа, полу-
ченные в результате измерений, всегда приближённые, в то
время как в результате счёта получаются иногда точные, иногда
приближённые числа.
§ 245. Запись результатов счёта и измерения. Повторные из-
мерения. Запись чисел, выражающих результаты счёта и измере-
ния должна ясно указывать на точность этих результатов.
Положим, производится измерение миллиметровой линей-
кой длины диагонали квадрата со стороной в 40 мм. Пользуясь
знаком <с (меньше) и знаком ~ (приближённо равно), записываем
результат этого измерения в следующих видах:
1) 5 см < х < 6 см\ 3) 5,6 см < х < 5,7 см\
2) х ~ 6 см', 4) х~ 5,65 см.
Первая запись говорит, что искомая длина х заключается ме-
жду 5 см и 6 см-, измерение произведено с точностью до целых
сантиметров. Вторая запись указывает, что при измерении до це-
( П II| НН | IIН |!1 li 11 III ] НП [111! р III ) 1 2 3 lllipill 1 iiiqiiii|iiiipin j б то г
Рис. 79.
лых сантиметров х оказывается ближе всего к отрезку в 6 см
(это хорошо видно на рис. 79). Ведя измерение с точностью до
миллиметров, убеждаемся, что х заключается между 5,6 см и
5,7 см (третья запись).
По рисунку 79 нельзя решить, к которому из этих двух зна-
чений х ближе, а потому считаем, что х приближённо равен
56у мм, или 5,65 см, что и говорит четвёртая запись. В ней
мы имеем две верные (безусловно надёжные) цифры, а именно,
цифры целых (5) и десятых (6), третья же цифра (цифра сотых 5)
не вполне надёжна: наше измерение не позволяет ручаться за то,
что длина х содержит, кроме 56 мм, ещё ровно 0,5 мм. Действи-
тельно, производя это измерение более точным прибором, мы
нашли бы, что длина х равна с точностью до микронов 56,569 мм,
а потому при измерении до десятых долей миллиметра мы должны
взять х ~ 56,6 мм, или х~5,66 см.
Приближённый результат следует записывать так, чтобы
последняя его цифра указывала на его точность; все цифры, кроме
последней, должны быть верными, и лишь в последней допустима
небольшая неточность. Так, запись температуры /~37° говорит,
что измерение было сделано с точностью до целого градуса
(обыкновенным стенным термометром), а запись t = 37°,0 означает
215
К. Н. Крылов.
В таких случаях, как
уже несколько иное, а именно, что
измерение сделано с точностью до
десятых долей градуса (например,
медицинским термометром).
Это правило записи приближён-
ных чисел называют правилом
академика Крылова. Его впервые
указал знаменитый русский мате-
матик и инженер-кораблестроитель,
Герой Социалистического Труда, ака-
демик Алексей Николаевич Крылов
(1863—1945).
Нередко бывает, что повторные
измерения той же величины дают
уже результаты, несколько отлича-
ющиеся от первого, хотя все изме-
рения делались одним и тем же при-
бором с одинаковой тщательностью.
Так бывает, например, если изме-
ряют метровой линейкой длину от-
резка в несколько десятков метров,
и при повторных подсчётах численности
множества (§ 243), находят среднее арифметическое всех резуль-
татов повторных измерений и округляют его, сохраняя все без-
условно надёжные цифры и одну не вполне надёжную.
Очень рекомендуется вычисление среднего уклонения, ясно
показывающего, какие цифры среднего результата следует со-
хранить. Рассмотрим пример.
Произведено 6 раз измерение длины х фасада здания посред-
ством метровой линейки с сантиметровыми делениями, и полу-
чены результаты, показанные ниже; найдена их сумма и их
среднее, затем уклонение от среднего и среднее уклонение.
Измерения длины X Результат в м Уклонение от среднего
№ 1 51,63 0,352
№ 2 52,12 0,138
№ 3 52,20 0,218
№ 4 51,87 0,112
№ 5 51,91 0,072
№ 6 52,16 0,178
Сумма 311,89 1,070
Среднее 51,982 0,178
51,9 м < х < 52,0 м\
х «52,0 м.
216
Убедившись, что старшим разрядом среднего уклонения явля-
ются десятые доли метра, заключаем, что цифра десятых в числе
51,282 не вполне надёжна, а потому цифры сотых и тысячных надо
отбросить. Число 51,9 меньше искомого значения х, число 52,0
больше его. Из этих двух чисел второе ближе к найденному сред-
нему, его и берём как окончательный результат.
Раздел 2. ОКРУГЛЕНИЕ
§ 246. Округление по недостатку и по избытку. Пусть дано
какое-нибудь число (натуральное число, или десятичная дробь,
или десятичный ряд). Нередко приходится заменять его другим,
более или менее близким к нему, которое записывается короче,
т. е. при помощи меньшего числа цифр. Такая замена называется
округлением.
Округлением по недостатку jw некоторого разряда назы-
вается отбрасывание всех цифр числа, записанных правее цифры
этого разряда, и замена их нулями; прибавляя к полученному
числу одну единицу этого разряда, производим округление по
избытку (до этого разряда).
Например, число 217,5073 округляем до разряда сотен, де-
сятков, единиц, десятых долей, сотых долей, тысячных долей и
получаем:
до разряда сотен по недостатку 200 по избытку 300
» » десятков » 210 » 220
» » единиц » 217 » 218
» » десятых долей » 217,5 » 217,6
» » сотых долей » 217,50 » 217,51
» » тысячных долей » 217,507 » 217,508
В некоторых случаях годится округление только по недо-
статку, в некоторых — только по избытку. Вот примеры.
1) Требуется разделить 50 руб. на 6 человек поровну. По
скольку денег получит каждый?
Деление 50 на 6 даёт десятичный ряд 8,3333... Округляя
это частное по недостатку до единицы, получаем 8, до сотых
долей 8,33. Если каждому дано по 8 руб., то останется 2 руб.,
а если по 8,33 руб. = 8 руб. 33 коп., то останется 2 коп. Округ-
ление по избытку здесь не годится, так как если давать по
8,34 руб., то денег не хватит.
2) 14 учащихся взялись собрать центнер желудей; сколько
должен собрать каждый? (Один центнер равен 100 кГ.)
Частное от деления 100 на 14 равно 7,142857... Округляя по
избытку до целых, получаем 8; если каждый принесёт по 8кГ,
всего соберётся 8-14=112 кГ. Если же округлить по избытку до
десятых долей, получаем 7,2 на каждого, а всего соберём 7,2 • 14 =
= 100,8 кГ. При округлении по избытку до сотых долей будем
иметь на каждого 7,15кГ, а всего 7,15 • 14 = 100,ЮкГ. Округление
по недостатку здесь не годится — будет собрано меньше, чем
требуется.
217
§ 247. Основное правило округления. Во многих задачах го-
дится округление и по недостатку и по избытку. Какое предпо-
честь?
Округление по недостатку заменяет данное число другим чис-
лом, меньшим данного, а по избытку — большим данного. Лучше
применять такое округление, при котором получается число, отли-
чающееся от данного по возможности меньше. Например, при ок-
руглении числа 17,384 до единиц по недостатку получаем 17, что
меньше данного числа на 17,384 —17 = 0,384, а по избытку 18, что
больше его на 18— 17,384 = 0,616. Как видим, здесь лучше приме-
нить округление по недостатку. Но округляя это же число до де-
сятых долей по недостатку, получаем 17,3, что меньше данного
числа на 17,384— 17,3 = 0,084, а по избытку 17,4, что больше его
на 17,4— 17,384 = 0,016. Таким образом, округлять число 17,384
до десятых лучше по избытку. Если допустимо округление как по
недостатку, так и по избытку, лучше применять округление по
недостатку в тех случаях, когда первая отбрасываемая цифра
есть 0, 1, 2, 3, 4, и по избытку, если эта цифра есть 5, 6,7, 8, 9.
Например, при округлении числа 0,2504 до десятых лучше взять
значение по избытку, а именно 0,3, так как оно отличается от дан-
ного числа на 0,3 — 0,2504 = 0,0496, в то время как округление
по недостатку даёт 0,2, т. е. меньше данного числа на 0,2504—
— 0,2 = 0,0504. Если же округлять это число до сотых, лучше
применить округление по недостатку, так как 0,2504 — 0,25 =
= 0,0004, 0,26 — 0,2504 = 0,0096.
Указанное выше правило называют основным правилом округ-
ления и применяют всегда, если нет особых причин округлять по
недостатку или по избытку.
Особого правила требует случай, когда отбрасывается одна
единственная цифра 5, как, например, при округлении числа 17,5
до единицы, когда оба округлённых числа 17 и 18 отличаются от
данного числа 17,5 поровну. Чтобы обеспечить один определённый
результат, здесь применяют правило чётной цифры: если отбрасы-
вается одна единственная цифра 5, применяют округление по не-
достатку, когда предыдущая цифра чётная, и по избытку, когда
она нечётная. При округлении числа 17,5 надо взять 18, а числа
18,5 — тоже 18.
В результате округления всегда получается число, представ-
ляющее собой приближённое значение данного числа, или, короче,
приближённое число. При округлении по недостатку и по избытку
разница между этим приближённым числом и данным числом мо-
жет доходить до одной единицы последнего сохранённого разряда.
При округлении по основному правилу — только до половины
единицы этого разряда. При округлении по правилу чётной цифры
эта разница составляет ровно половину единицы последнего со-
хранённого разряда.
При вычислении приближённых чисел по этим правилам ок-
ругления сохраняется также правило академика Крылова (§ 245).
218
Раздел 3. ПРИБЛИЖЁННЫЕ ЧИСЛА И ИХ ТОЧНОСТЬ
§ 248. Четыре источника получения приближённых чисел.
Как мы видели выше, приближённые числа получаются в
результате счёта, измерения, округления, причём счёт иногда
даёт и точные значения, а измерение и округление — всегда только
приближённые. Но есть ещё один (четвёртый) источник получе-
ния приближённых чисел — вычисление.
Если среди чисел, входящих в вычисление, есть хотя бы одно
приближённое, то результат вычисления представляет собой только
приближённое значение искомой величины, т. е. тоже является
приближённым числом.
Например, если измерение показало, что стороны прямо-
угольного поля равны 254 м и 194 м, то число 254 194 = 49276
представляет собой лишь приближённое значение его площади
в квадратных метрах.
Возникает вопрос, какие цифры этого произведения заслу-
живают доверия и как записать это число в согласии с прави-
лом академика Крылова. Дальше мы установим правила, позво-
ляющие отвечать на эти вопросы.
§ 249. Десятичные знаки и значащие цифры. Употребляются
два способа указывать, какова точность данного приближённого
числа; в некоторых случаях удобнее один из них, в некоторых дру-
гой, а потому надо уметь пользоваться обоими.
Десятичными знаками числа называются все его цифры, запи-
санные справа от знака дробности. Например, числа 3,1; 8,04;
0,142 имеют соответственно 1, 2, 3 десятичных знака.
Значащими цифрами числа называются все его цифры, кроме
нулей, записанных левее первой отличной от нуля его цифры, и
нулей, записанных справа, если эти нули заменяют неизвестные
цифры.
Так, числа 3,1; 8,04; 0,1420; 0,017 имеют соответственно 2,
3, 4, 2 значащие цифры. Число 12,4 см, полученное при измерении
отрезка с точностью до миллиметра, имеет три значащие цифры.
Если округлить до десятков значение 124 мм, то получим прибли-
жённое число 120, в котором только две значащие цифры, так так
цифра 0 здесь не является значащей.
Чтобы дать понятие о точности приближённого числа, запи-
санного согласно правилу академика Крылова, указывают число
его десятичных знаков или число значащих его цифр.
Подсчитывать число десятичных знаков следует тогда, когда
сравниваются приближённые значения одной и той же величины,
притом выраженные в одних и тех же единицах. Например, если
одно взвешивание показало, что предмет весит 14,7 Г, а другое,
выполненное на более точных весах, что он весит 14,684 Г, то
можно сказать, что второе приближённое значение точнее пер-
вого, так как первое имеет только один десятичный знак, второе
же — три десятичных знака.
219
С переходом к другим единицам число десятичных знаков
меняется, но число значащих цифр остаётся неизменным, а по-
тому точность различных приближённых чисел следует сравни-
вать, подсчитывая число их значащих цифр. Например, если
измерение отрезка на чертеже дало число 6,3 см, а измерение
длины поля дало число 254 м, надо признать, что второе при-
ближённое число точнее первого, так как в первом только две
значащие цифры, а во втором их три.
Если приближённое значение величины выражено целым чис-
лом, нули справа могут быть значащими цифрами, указывая на
отсутствие единиц соответствующих разрядов, но могут быть по-
ставлены взамен неизвестных или отброшенных цифр, и тогда в
счёт значащих цифр они не идут.
Если, например, приближённое значение веса 14,7 Г выразим
в миллиграммах, то получим число 14 700, в котором лишь три
значащие цифры. Если же вес в 14 700 мГ получен в результате
взвешивания на лабораторных весах, позволяющих находить мил-
лиграммы, то здесь приближённое число с пятью значащими циф-
рами. Переходя к граммам, его надо записать в виде 14,700 Г.
Чтобы устранить недоразумения, лучше избегать нулей, по-
ставленных взамен неизвестных или отброшенных цифр, перехо-
дя к более крупным единицам. Например, округляя число 83542
до сотен, не писать 83500, а писать 83,5 тысяч; вместо числа
3 569 000 кв. м, в котором три последних нуля поставлены вместо
неизвестных цифр, писать 3,569 кв. км и т. д.
В случаях, когда важно с полной ясностью указать, за какие
цифры данного приближённого числа мы не ручаемся, будем ста-
вить под этими цифрами чёрточку. Например, если х ~ 36 км, то
х~36 000 м; если £/ = 8,4 м, то у ~ 840 см, у ~ 8400 мм. Запись
36 км = 36000 м, применяемая, когда имеем дело с точными
числами, недопустима, если данные числа лишь приближённо
выражают значения величин.
Раздел 4. ЧЕТЫРЕ ДЕЙСТВИЯ НАД ПРИБЛИЖЁННЫМИ
ЧИСЛАМИ
§ 250. Сложение и вычитание. Имея два или более прибли-
жённых слагаемых, записанных по правилу академика Крылова и
данных с одним и тем же числом десятичных знаков, складывают
их по обычному правилу и получают в сумме приближённое
число, записанное согласно правилу академика Крылова.
Но если слагаемые даны с разным числом десятичных знаков,
полученная сумма содержит совершенно ненадёжные цифры и
нуждается в округлении.
Пусть, например, имеется прибор весом в 3,507 кГ (прибли-
жённое число с тремя десятичными знаками) и ящик с упако-
вочным материалом весом в 2,8 кГ (приближённое число с одним
220
десятичным знаком); сколько будет весить прибор вместе с упа-
ковкой?
, 3,507 , 3,507? , 3,507
2,8 2,8??? "* 2,8
6,307 6,3??? 6,307
6,3
Сделав сложение по обычному правилу, как показано слева,
мы получаем сумму, записанную с нарушением правила академи-
ка Крылова. Действительно, в первом слагаемом мы знаем целые,
десятые, сотые, тысячные, но не знаем десятитысячных, что отме-
чено (в средней записи) знаком вопроса; во втором слагаемом
знаем целые и десятые, но не знаем ни сотых, ни тысячных, ни
десятитысячных, что тоже отмечено знаками вопроса. Ясно, что
цифры сотых (0) и тысячных (7), полученные при сложении, ни-
какого доверия не заслуживают и должны быть отброшены. Сло-
жение надо выполнить так, как показано справа.
Для проверки проведём вычисления так:
, 3,5065 < а < 3,5075
+ 2,75 < Ь < 2,85
6,2565 < а + Ь < 6,3575
6,2 < а 4- Ь < 6,4
а + b ~ 6,3.
Точно так же обстоит дело и при вычитании. Приводим при-
мер, считая данные приближёнными числами, записанными со-
гласно правилу академика Крылова. Правильная запись только
в крайнем правом столбце.
42,7 42,7???
“ 14,2714 - 14,2714
28,4286 28,5???
42,7
“ 14,2714
28,4286
28,4
Для проверки проведём вычисления так:
Из меньшего, чем а,
вычитается
большее, чем Ь.
42,65 < а < 42,75
14,27145 > b > 14,27135
. 28,37855 < а — Ь < 28,47865
28,3 < а — Ь < 28,5
а — b ~ 28,4
Из большего, чем а,
вычитается
меньшее, чем Ь.
Сложение и вычитание цифр в каком-нибудь столбце, где
имеется хотя бы один знак вопроса, поставленный взамен неиз-
вестной цифры, делает цифру этого разряда в сумме и разности
вовсе не надёжной, а потому следует держаться такого правила.
При сложении и вычитании приближённых чисел в результате
следует сохранять столько десятичных знаков, сколько их в при-
ближённом данном с наименьшим числом десятичных знаков
(I правило округления суммы и разности приближённых чисел).
При применении этого правила следует избегать нулей, по-
ставленных взамен неизвестных или отброшенных цифр, выра-
жая приближённое число в более крупных единицах. Например,
221
если надо найти сумму трех слагаемых 54000, 29100, 1480, из
которых первое является результатом округления до разряда
тысяч, второе — до сотен, третье — до десятков, то лучше выра-
зить все три слагаемые в тысячах, а именно, в виде 54; 29,1;
1,48 (тысяч), и после получения суммы 84,58 (тысяч) округлить
её согласно правилу до целых (здесь приближённые слагаемые
имеют 0, 1, 2 десятичных знака), что даёт 85 (тысяч).
§ 251. Умножение и деление. Вернёмся к задаче, поставленной
в § 248: найти площадь прямоугольного поля, если его измерения
с точностью до метра равны 254 м и 194 м. Производя умножение,
получаем 49 276 кв. м, но ясно, что это число лишь приближённо
выражает искомую площадь и нуждается в округлении. Неизвест-
ные точные значения длины и ширины поля больше, чем 253,5 м
и 193,5 м, но меньше, чем 254,5 м и 194,5 м, а потому его
площадь больше, чем 49052,25 кв. м, и меньше, чем 49500,25 кв. м.
Имеем:
253,5 < а < 254,5
193,5 < b < 194,5
253,5 • 193,5 = 49052,25 < а • Ь < 254,5 • 194,5 = 49500,25
49000 < а • b < 49500
а • b ~ 49300
Таким образом, в найденном произведении 49 276, выражающем
приближённое значение площади, первые две цифры (4 и 9) без-
условно надёжны, третья же (2) не вполне надёжна. Согласно
правилу академика Крылова только эти три цифры и следует
сохранить, т. е. округлить найденное произведение до разряда
сотен, что даёт 49 300 кв. м, или 4,93 га.
Таким образом, перемножая два приближённых числа, имеющих
каждое по три значащие цифры, мы получили здесь приближён-
ное число, имеющее тоже три значащие цифры. К тому же резуль-
тату приводит и применение знаков вопроса взамен неизвестных
цифр:
254,?
194,?
??? ?
, 1016?
2286?
254?
493??,??
49300
Подобным же образом можно убедиться, что умножение двух
приближённых чисел, в одном из которых три, а в другом две
значащие цифры, даёт приближённое число с двумя значащими
цифрами; доказано, что умножение двух приближённых чисел
даёт всегда приближённое число, в котором столько заслуживаю-
щих доверия цифр, сколько их в том данном, в котором меньше
значащих цифр. Точно так же обстоит дело и с делением.
222
Отсюда правило: при умножении и делении приближённых
чисел в результате следует сохранять столько значащих цифр,
сколько их имеет приближённое данное с наименьшим числом
значащих цифр (II правило округления произведения и частного
приближённых чисел).
Рассмотрим две задачи на применение этого правила.
10 5
Задача I. Найти произведение 1 • 1 -g-, представляя дан-
ные в виде десятичных дробей и округляя множимое до четырёх,
а множитель до трёх значащих цифр.
Решение. 1 = 1,9090 ... = 1,909; 1 1.8333 ...= 1,83
11 о
1,909 • 1,83 = 3,49347 = 3,49.
Здесь сделано округление результата до трёх значащих цифр.
Для проверки сравниваем его с точным произведением, равным
10 5
1 уу • 1 -g = 3,5, и замечаем, что найденное приближённое произве-
дение 3,49347 отличается от этого точного меньше, чем на еди-
ницу разряда третьей значащей цифры, и что мы поступили
правильно, округлив его согласно правилу до трёх значащих
цифр.
Задача 2. Измерения показали, что кусок железа весит
491 Г и имеет объём 63 куб. см. Найти вес 1 куб. см этого куска.
Решение. 491 :63 = 7,79... = 7,8.
Здесь делимое и делитель — приближённые числа соответст-
венно с тремя и двумя значащими цифрами, поэтому округляем
частное до двух значащих цифр.
Для проверки предположим, что точное неизвестное нам зна-
чение веса больше, чем 490,5 Г, и меньше, чем 491,5 Г, а точное
неизвестное нам значение объёма больше, чем 62,5 куб. см, и
меньше, чем 63,5 куб. см.
Частное убывает при уменьшении делимого и увеличении
делителя, растёт при увеличении делимого и уменьшении дели-
теля (§ 81), а потому частное
490,5:63,5 = 7,724...
меньше искомого веса, частное же
491,5 : 62,5 = 7,864
больше его.
Имеем:
Меньшее ( ) Большее
делим < ; 490,5 < а < 491,51 делим
на большее I 63,5 > b > 62,5) на меньшее
490,5 : 63,5 = 7,724... < а : b < 7,864... = 491,5 : 62,5
7,7 < а : b < 7,9
а : b ~ 7,8
223
В найденном выше частном 491:63 = 7,79... первая цифра,
таким образом, безусловно надёжна, вторая не вполне надёжна,
третья и следующие — вовсе не надёжны, и мы поступили пра-
вильно, округлив его до двух значащих цифр. Теперь оно запи-
сано согласно правилу академика Крылова.
К тому же результату приводит и применение знаков вопроса
взамен неизвестных цифр:
491,? 1 63,?
441 ? I 7,8?
50??
— 504?
???
Отметим, что если одно из данных — число точное, то число
его цифр учитывать не надо. Так в произведении
6,789 • 53 = 359,817,
где множимое — приближённое число с четырьмя значащими
цифрами, а множитель 53 — число точное, сохранить надо четыре,
а не две значащие цифры, т. е. написать результат в виде 359,8.
§ 252. Совместные действия. Умея выполнять каждое из четы-
рёх действий над приближёнными числами, мы в состоянии ре-
шать и более сложные задачи, требующие выполнения двух и
более действий над такими числами.
Окончательный результат получается после выполнения по-
следнего действия, а предыдущие действия дают промежуточные
результаты.
Оказывается, что точность окончательного результата полу-
чается во многих случаях немного выше, если при вычислении
промежуточных результатов брать одной цифрой больше, чем
рекомендуют два предыдущих правила, т. е. брать их с одной
«запасной» цифрой (III правило округления промежуточных ре-
зультатов) .
В записи эту цифру можно как-нибудь выделять, например
подчёркивать. В окончательном результате она отбрасывается.
Проведём для примера вычисление значения
а Ь
х — ’
где
О 13 , 1 7 2
а~ 2 16 ’ — 18’ С~ 7 ’
взяв приближённые значения чисел а, Ь, с с точностью до сотых,
а именно:
а = 2,8125 ... ~ 2,81,6=1,3888 ... ~ 1,39, с = 0,2857 . . . ® 0,29.
224
Выполняем четыре указанных действия:
1) 2,81 • 1,39 2) 2,81 3) 1,42 • 0,29 4) 3,906 : 0,412 = 9,5
2529 I.39 , 1278 3906 : 412 — 9,48 ...
+ 843 1,42 + 284 3708
281 0,4118 1980
39059 0,412 1648
3,906 _ 3320
3296
Ответ. x=s9,5. 24
В первом действии мы перемножили два приближённых трёх-
значных числа и округлили произведение до четырёх значащих
цифр, отметив последнюю (6) как запасную.
Второе действие дало разность в виде приближённого числа
с двумя десятичными знаками (тремя значащими цифрами).
В третьем действии мы перемножили приближённые числа с
тремя и двумя значащими цифрами и округлили произведение
до трёх значащих цифр, отметив третью (2) как запасную.
Четвёртое действие состояло в делении приближённого числа
с тремя значащими цифрами на приближённое число с двумя
значащими цифрами (запасные цифры в счёт не идут); оно даёт
окончательный результат, а потому берём его без запасной цифры,
т. е. с двумя значащими цифрами.
Здесь мы имеем возможность для проверки найти точное зна-
чение х, проводя вычисление в обыкновенных дробях. Получаем
99
х = 9 164 = 9,603... и убеждаемся, что найденное приближённое
значение х, а именно 9,5, записано в соответствии с правилом
академика Крылова.
§ 253. Предварительное округление более точных данных.
Положим, требуется сложить три приближённых слагаемых, одно
из которых дано с одним десятичным знаком, а каждое из двух
других — с пятью.
Выполняя это сложение, округляем результат согласно пра-
вилу округления суммы (§ 250) и замечаем, что труд, потрачен-
ный на получение четырёх последних цифр, оказался напрасным.
Если округлять данные более точные слагаемые до выполне-
ния сложения, сохраняя в них только цифры тех разрядов, какие
имеются в наименее точном данном, результат получается не-
много менее точный.
Если же сохранить в более точных данных по одной лишней
(«запасной») цифре, то выигрыш в производстве вычисления полу-
чается без ущерба для точности. Приводим для сравнения все
три вычисления:
14,7 14,7 14,7
+ 2,04571 + 2,0 + 2,05
0,63059 0,6 0,63
17,37630 17,3 17,38
17.4 17,4
11 Арифметика
225
Подобное же положение встречается и при умножении. На-
пример, разыскивая произведение двух сомножителей, один из
которых является приближённым числом с двумя, а другой с
пятью значащими цифрами, мы должны округлить результат до
двух значащих цифр (§ 251).
Вычисление, произведённое ниже слева, показывает, что мы
напрасно затратили труд на получение многих цифр.
Если же округлить более точный сомножитель довыполнения
умножения, сохраняя в нём только две цифры, получаем резуль-
тат немного менее точный (вычисление ниже на середине).
Предварительное округление с сохранением одной лишней
(«запасной») значащей цифры, показанное ниже справа, обеспе-
чивает получение правильного результата при уменьшении
работы.
7,6483 • 4,8 , 611864 7,6 • 4,8 , 608 7,65 • 4,8 , 6120
+ 305932 + 304 + 3060
36,71184 36,48 36,720
37 36 37
Точно так же обстоит дело и с обратными действиями — вы-
читанием и делением. Предварительное округление более точных
данных полезно всегда, сохранение запасной цифры нередко
немного улучшает результат, а потому рекомендуется следующее
правило.
Если некоторые приближённые данные имеют больше деся-
тичных знаков (при сложении или вычитании) или больше знача-
щих цифр (при умножении и делении), чем другие, их следует
округлять раньше, чем производить действие, сохраняя лишь
одну запасную цифру по сравнению с менее точными данными
(IV правило предварительного округления более точных данных).
Пусть, например, требуется разделить приближённое значение
4
числа 4-д , взятое с двумя значащими цифрами, а именно 4,4 на
, •• 6
приближенное значение числа уу, взятое с шестью значащими
цифрами, а именно 0,545454.
Трудное деление 4,4 на 0,545454 даёт согласно правилу
округления частного, 8,1, но тот же результат получается гораздо
скорее после предварительного округления делителя до трёх
значащих цифр: 4,4 : 0,545 — 8,07... = 8,1. Предварительное округ-
ление без запасной цифры даёт несколько худший результат:
4,4 :0,55 = 8,0. Здесь можно найти и точное значение частного:
4У :п = 8й = 8>148148-
§ 254. Вычисление с наперёд назначенной точностью резуль-
тата. Употребление запасной цифры рекомендуется и в тех слу-
226
чаях, когда данные можно брать с произвольным числом цифр,
а результат надо получить с определённой наперёд указанной
точностью. Так, чтобы получить значение суммы
1 :1,1 + 1 :1,3 + 1 : 1,5 + 1 :1,7
с точностью до сотых, каждое слагаемое надо взять с точностью
до тысячных; это даст 2,933, или после округления 2,93 (вычи-
сление без запасной цифры даёт 2,94).
Чтобы найти произведение: 0,(5) = 0,5555... на 0,(6) = 0,6666...
с двумя значащими цифрами, достаточно взять сомножители с
тремя значащими цифрами:
0,556 - 0,667 = 0,370852 - 0,37.
Точное значение произведения
| = 0,370370...,
а вычисление без запасной цифры даёт:
0,56 • 0,67 = 0,3752 — 0,38.
Встречается немало случаев, когда вычисление с запасной
цифрой даёт то же самое, что и без неё, но брать её всё же
рекомендуется.
Раздел 5. НЕКОТОРЫЕ ЗАДАЧИ НА ИЗМЕРЕНИЕ ДЛИНЫ,
ПЛОЩАДИ И ОБЪЁМА
§ 255. Длина окружности. Решили устроить круговую дорож-
ку длиной 500 м, и требуется узнать, каков радиус такой окруж-
ности. Для этого надо предварительно выяснить, чему равно
отношение длины окружности к её диаметру. Сделать это можно
двумя способами — посредством измерений и по расчёту.
(=57tm
Рис. 80.
Возьмём какой-нибудь круглый предмет, например кастрюлю
(рис. 80), и измерим длину окружности её дна портновским санти-
метром или просто бумажной полоской, а затем длину диаметра
11
227
миллиметровой линейкой. Длина окружности кастрюли оказалась
равной (с точностью до миллиметра) 571 мм, а её диаметр 182 мм.
Теперь надо разделить первое из этих чисел на второе Замечая,
что оба данных — приближённые числа с тремя значащими циф-
рами каждое, применяем правило округления произведения и
частного (§ 251) и получаем 571 :182 — 3,14 (первые четыре цифры
частного 3,137..., округление до трёх значащих цифр даёт 3,14).
Измеряя другие круглые предметы, будем получать другие
значения длины окружности С и её диаметра d, но отношение
C:d оказывается каждый раз либо 3,14, либо немного меньше
или больше. Число 3,14 можно заменить числом Зу, так как
Зу = 3,142857... «3,14.
Объясняя расхождения неточностями измерения, приходим к
такому заключению: отношение длины С всякой окружности
к длине d её диаметра приближённо равно 3 у «3,14.
Число Зу называется «архимедовым числом» по имени грече-
ского учёного Архимеда, жившего больше 2000 лет назад и впер-
вые установившего, что это приближённое значение отношения
С к d заключено в таких границах:
31° <- -С <- 31
1371 < d 7 -
Архимед пользовался не тем способом измерений, о котором
сейчас шла речь, а другим способом точного расчёта. Этот вто-
рой способ позволяет установить, не прибегая ни к каким изме-
рениям, что отношение С: d в точности одинаково для всех
окружностей и что оно точно выражается десятичным непериоди-
ческим рядом, первые цифры которого приводим:
С :d — 3,1415926...
Округляя это число до трёх значащих цифр, получаем то са-
мое приближённое значение отношения С: d, какое легко найти
измерением (3,14). Чтобы понять этот второй способ получения
C:d, надо изучить такие разделы математики, какие входят в
программу IX и X классов.
Зная приближённое значение отношения С: d, легко решаем
задачу, приведённую в начале этого параграфа: чтобы получить
диаметр d такой окружности, длина С которой равна 500 м, надо
разделить 500 на 3,14, что даст 159,23...; здесь делимое (500) —
число точное, делитель (3,14) — приближённое с тремя значащи-
ми цифрами, а потому в частном берём три надёжные значащие
цифры и одну запасную (159,2); остаётся делением на 2 узнать
радиус: 159,2 : 2 = 79,6. Итак, чтобы круговая дорожка имела
длину в 500 м, её надо провести радиусом в 79,6 м.
Как выяснилось после Архимеда, это отношение длины окруж-
228
ности к диаметру точно выражается десятичным рядом, притом
непериодическим. Наш гениальный академик Леонард Эйлер
(1707—1783, Петербург) нашёл первых 153 десятичных знака
этого ряда. Он ввёл для обозначения отношения длины окруж-
ности к длине её диаметра греческую букву тс (читается «пи»).
Это обозначение в настоящее время принято во всех странах.
Приводим первые 32 десятичных знака числа тс:
тс = 3,14159265358979323846264338327950...
Итак, имеем:
длина окружности __ длина окружности
длина диаметра ’ удвоенная длина радиуса
Обозначая длину окружности буквой С, а длину её диаметра
буквой d, длину её радиуса буквой г (все в одних и тех же еди-
ницах), записываем эти соотношения формулами:
С с
—г = тс, или х- = тс.
d 2г
Основываясь на том, что делимое равно произведению дели-
теля на частное, получаем новые формулы:
С = тсс?,
(I)
откуда
d = C-.
7t
Формулу (I) можно записать иначе:
С = 2г.г,
(И)
откуда
2тс *
Если диаметр окружности равен 1, то С = тс, т. е. длина
окружности равна тс (тс — первая буква греческого слова «пере-
ферейя», что значит периферия, или граница, предполагается
круга, т. е. окружность, что и явилось поводом для обозначе-
ния отношения С к d через тс).
Полезно запомнить два следующих правила:
1) Чтобы найти длину окружности С, надо длину её диаметра
d умножить на тс:
С = тс-d; C^d 3 -J-; С ® d • 3,14; О d • 3,1416.
2) Чтобы найти диаметр окружности d, надо её длину С раз-
делить на тс:
й = С:тс; (1-С:3|; d~C:3,14; d'С: 3,1416.
Значение тс берут с большей или меньшей точностью в зави-
симости от точности данных или от желательной точности резуль-
тата (по правилам § 253 и 254). Например, зная d с двумя
22Э
значащими цифрами, достаточно для вычисления С взять п = 3,14,
или тс == 3 у, а если d найдено с четырьмя значащими цифрами,
надо взять 71 — 3,1416.
§ 256. Площадь многоугольника. Часть плоскости, ограни-
ченная со всех сторон отрезками, называется многоугольником.
Эти отрезки называются сторонами многоугольника, а те точки,
в которых отрезки попарно сходятся,— его вершинами.
Многоугольник может иметь сколько угодно сторон, начи-
ная с трёх. Треугольник, о площади которого мы уже говорили
(§ 149), есть не что иное, как многоугольник с тремя сторонами.
На рисунке 81 можно видеть многоугольник с шестью сторо-
нами и шестью вершинами, обозначенными буквами А, В, С,
D, Е, F. Его название — шестиугольник. Понятно, что такое
четырёхугольник, пятиугольник, семиугольник и т. д.
Умея находить площадь треугольника, мы можем найти пло-
щадь любого многоугольника, разрезая его (мысленно) на тре-
угольники. Покажем, как это сделать, находя площадь изобра-
жённого на рисунке 81 шестиугольника.
Разрезав шестиугольник, как показано на рисунке сплош-
ными тонкими линиями, на четыре треугольника, проведём в
каждом треугольнике высоту (прерывистые линии) и измерим
высоту и основание каждого треугольника. Работая остро отто-
ченным карандашом и пользуясь линейкой со скошенным краем,
можно добиться такой точности измерения, что найденные длины
будут отличаться от истинных их значений не больше, чем на
230
0,2 мм. Приведённая ниже примерная запись показывает весь
ход вычисления. (Рисунки 81 и 82 уменьшены в отношении 2 :3.)
Треугольник Основание (в мм) Высота (в мм) Площадь (в мм2)
АВН АН ~ 97,4 BG = 57,0 2776
CDH HD = 50,4 С1 » 45,2 1139
DEH DE ~ 53,0 НК ~ 16,2 429,3
AEF АЕх 114,2 FL = 38,6 2204
Площадь всего шестиугольника 6548,3 мм2;
после округления 6550 мм2; окончательно 65,5 см2.
Для проверки проведём вычисление вторично, разрезая дан-
ный многоугольник на треугольники по-другому, а именно, как
показано на рисунке 82. Теперь имеем следующее:
Треугольник Основание (в мм) Высота (в мм) Площадь (в льи2)
АВС АС 63,2 BP 32,4 1024
CDE СЕ 72,4 DQ - 34,6 1253
CEF FE ~ 101,2 CR -58,0 2935
ACF FC == 80,4 XS = 34,2 1375
Площадь всего шестиугольника 6587 Л.Ц2;
после округления 6590 мм2; окончательно 65,9 см2.
231
Расхождение между результатами, которые получились, объ-
ясняется неполной точностью чертежа н измерений по нему.
Оба результата заслуживают одинакового доверия, поэтому в
качестве окончательного ответа лучше всего взять их среднее:
(65,5 + 65,9): 2 = 65,7.
Итак, площадь данного шестиугольника составляет 65,7 см2,
причём цифра десятых не вполне надёжна.
Положим, что этот многоугольник изображён на плане с мас-
штабом в 1 :5000. Какова площадь соответствующего участка на
местности? Каждый отрезок, длиной 1 см на плане, изображает
отрезок, длиной 5000 см — 50 м на местности, а квадратный сан-
тиметр на плане изображает квадрат со стороной 50 м на мест-
ности. Но такой квадрат имеет площадь 50 - 50 = 2500 м2, или
0,25 га, а потому площадь участка равна 0,25 • 65,7 = 16,4 га,
причём цифра десятых долей гектара не вполне надёжна.
§ 257. Площадь круга. Если разрезать круг на большое
число равных частей, проводя в нём радиусы, как это показано
на рисунке 83, где получены 24 части (24 сектора1), то из этих
частей можно сложить фигуру, очень близкую к параллелограмму,
с основанием, равным длине полуокружности, и высотой, рав-
ной радиусу.
Рис. 83.
Этот приём был предложен гениальным итальянским худож-
ником, учёным и инженером Леонардо да Винчи (1452—1519).
Доказано, что площадь прямоугольника, у которого длина
равна полуокружности, а высота её радиусу, в точности равна
площади круга: площадь круга К равна площади прямоугольника
с измерениями, равными длине полуокружности и её радиусу.
Короче, К = • cj • г, где С — длина окружности; иначе
К = • 2 кг} • г = кг2.
Другими словами, чтобы получить площадь круга, достаточно
умножить г. на длину радиуса в квадрате.
1 Круговым сектором, или просто сектором, называется часть круга, огра-
ниченная двумя его радиусами и дугой.
232
Задача 1. Найти площадь круга, длина окружности кото-
рого равна 500 м.
Решение.
1) Диаметр окружности: 500 : 3,14 — 159,2 (м).
2) Радиус окружности: 159,2 : 2 = 79,60 (ли).
3) Площадь круга: 250 - 79,60=19900 (м2), или 1,99 га, или
почти 2 га.
Задача 2. Найти площадь круговой дорожки, если её
длина, измеренная по внешнему её краю, равна 500 м, а ши-
рина 6,0 м (рис. 84).
Решение.
1) Площадь круга, ограниченного
как установлено при решении за-
дачи 1, равна 1,99 га.
2) Диаметр окружности, ограни-
ченной внутренним краем дорожки:
159,2— 12,0= 147,2 (м).
3) Длина этой окружности:
147,2- 3,14 = 462,2 (м).
4) Площадь внутреннего круга:
231,1 - 73,6—17010 (jw2), или 1,70 га.
5) Площадь дорожки:
1,99—1,70 = 0,29 (га).
Как видим, найти площадь круга,
зная его радиус или диаметр, очень
легко. Значительно труднее обрат-
ная задача — нахождение радиуса
внешним краем дорожки,
круга, имеющего данную площадь: оно сводится к вычислению
стороны квадрата по данной его площади (§ 147) и решается
в нашем курсе арифметики только пробами или по таблицам.
Например: «На складе имеются трубы различных круговых
сечений. Как выбрать такую трубу, чтобы её сечение имело
300 см2?у>
Для этого достаточно найти диаметр сечения, что делается
так:
откуда
та-2 в зоо,
г2=-—=95,5.
7U
Подбором находим г:
9<г<10,
так как
92 = 81 < г2 = 95,5 < 100 = 102,
9,7 < г < 9,8, так как 9,72 = 94,09 < г2 = 95,5 < 96,04 = 9,82,
233
9,77 < г < 9,78, так как 9,772 = 95,45 < г2 = 95,5 < 95,65 == 9,782.
Итак, г «9,77 см\ 2г —d« 19,54 слг«19,5 см.
Это же можно скорее найти по таблице в книге В. М. Бра-
диса «Четырёхзначные математические таблицы».
§ 258. Площадь поверхности цилиндра. Выше уже упомина-
лось о цилиндрической поверхности (§ 131), какую представляют
собой, например, боковые стенки консервной банки, имеющей
обычно форму круглого цилиндра. Цилиндр имеет два одинако-
вых плоских основания, нижнее и верхнее, каждое из которых
имеет обычно форму круга. Расстояние между основаниями цилинд-
ра всюду одинаково и называется его высотой (обычное обозначе-
ние— /г, читается «аш»). Боковую поверхность прямого цилиндра
можно развернуть на плоскость: получается развёртка цилиндра
Рис. 85. Рис. 86.
цилиндра и его высоте
в виде прямоугольника со сторо-
нами, равными длине окружности
основания
(рис. 85).
Форму цилиндра имеют очень многие предметы: круглый ка-
рандаш, банка, железная труба, круглое полено и т. д. Не сле-
дует смешивать цилиндр с усечённым конусом, который отли-
чается от цилиндра тем, что верхнее его основание имеет другой
диаметр, чем нижнее. На рисунке 85 изображены два ведра, из
которых одно коническое, другое цилиндрическое.
Нередко возникает вопрос о площади поверхности цилиндра,
причём речь может идти о боковой поверхности цилиндра или о
полной его поверхности.
Как легко видеть по развёртке, площадь боковой поверх-
ности цилиндра равна произведению длины окружности основания
цилиндра С на высоту цилиндра h. Для получения площади полной
поверхности цилиндра надо к площади боковой поверхности доба-
вить удвоенную площадь основания.
Решим такую задачу. Сколько квадратных метров железных
листов потребуется на устройство цилиндрического бака для го-
рючего, если диаметр основания сделать равным 2,4 м, а вы-
соту 3,4 Л1?
Полагая данные числа точными и взяв л равным 3,14, за-
писываем всё решение в таком виде:
234
1. Длина окружности основания . . 2,4 3,14 = 7,536 ~ 7,54 (л)
2. Площадь боковой поверхности . . 7,54 • 3,4 = 25,62 (ж1 2)
3. Половина длины окружности ос-
нования ........................ 7,54 : 2 = 3,77 (л)
4. Радиус круга основания........2,4 : 2 = 1,2 (ле)
5. Площадь основания..............3,77 • 1,2 = 4,52 (ле2)
6. Площадь полной поверхности бака 25,6 + 4,52 + 4,52 ~ 34,6=35 (ле2)
§ 259. Объём цилиндра. Чтобы узнать объём цилиндра, на-
пример, чтобы узнать, сколько кубических единиц содержит
цилиндрическое ведро, мысленно разрежем этот цилиндр на оди-
наковые пластинки, имеющие одну и ту же толщину, равную
единице длины. Каждая такая пластинка представляет собой
тоже цилиндр; их выйдет столько, сколько
единиц длины содержит высота (рис. 87).
Каждую пластинку будем мысленно
разрезать на кубики с рёбрами, равными
единице длины (кубические единицы).
Каждый такой кубик займёт на основании
цилиндра квадрат со стороной, равной
единице длины (квадратную единицу), а
потому из каждой пластинки получим
столько кубических единиц, сколько квад-
ратных единиц содержит основание ци-
линдра.
Отсюда правило: чтобы найти объём
цилиндра в каких-нибудь кубических еди-
ницах, надо взять произведение числа,
выражающего площадь основания цилиндра
в соответствующих квадратных единицах, и числа, выражающего
высоту цилиндра в соответствующих линейных единицах. Короче:
объём цилиндра равен произведению площади его основания на
высоту х.
Если радиус основания цилиндра г, высота h, то площадь
основания равна лг2, объём цилиндра
V = ъгЧг.
Положим, надо найти вес круглого железного провода диа-
метром dг®4,50 мм и длиной А» 3,25 км, зная, что 1 куб. см.
железа весит 7,8 Г. Этот провод рассматриваем как цилиндр с
1 В приведённом рассуждении сделаны два допущения, упрощающие его,
но не вполне соответствующие действительности: предполагается, что высота
цилиндра содержит натуральное число единиц длины и что круг, являющийся
основанием цилиндра, содержит натуральное число единиц площади. Однако
в курсе математики IX класса доказывают, что приведённое здесь правило
даёт совершенно точное значение объёма цилиндра во всех случаях (т. е. при
любых числовых значениях высоты цилиндра и площади его основания).
235
диаметром основания d и высотой h. Приводим всё решение,
кроме некоторых выкладок, выполняемых на стороне.
1. Длина окружности основания . .4,50-3,14=14,13 (jhjk),
или = 1,413 (си)
2. Половина длины окружности ос-
нования .......................... 1,413 : 2 = 0,7065 (cjh)
3. Радиус круга (основания) .... 4,50 : 2 = 2,25 (льи),
или 0,225 (см)
4. Площадь основания............. 0,7065 - 0,225 = 0,1589625 =
= 0,1590 (см2)
5. Высота цилиндра в сантиметрах . 3,25 - 1000- 100 = 325 000,
или 325 тыс. (си)
6. Объём цилиндра................ 0,1590 • 325 000 ~ 51,675 тыс. см3 х
= 51,68 тыс. (cjh3)
7. Вес провода...................7,8 • 51,68 тыс. =403 000 Г,
или 403 кГ
Ответ. Провод весит около 400 кГ, или 0,40 Т.
Глава XIII. ПРЯМАЯ И ОБРАТНАЯ
ПРОПОРЦИОНАЛЬНОСТЬ
Раздел 1. ЗАВИСИМОСТЬ МЕЖДУ ВЕЛИЧИНАМИ
И ЕЁ НАГЛЯДНОЕ ИЗОБРАЖЕНИЕ
§ 260. Зависимые величины. Если при рассмотрении какого-
либо процесса приходится иметь дело с двумя и более величи-
нами, необходимо бывает выяснить, каковы зависимости между
ними. Пусть, например, строится прямоугольник, причём осно-
вание и высота берутся произвольно.
Эти две величины: длина основания и длина высоты — не за-
висят друг от друга.
Но площадь прямоугольника зависит от основания и высоты:
если основание равно, например, 6 см, а высота 5 см, то пло-
щадь получает при этом вполне определённое значение, а имен-
но, 6 • 5 - 30 кв. см.
Значение площади S при взятых значениях основания а и
высоты b уже нельзя взять по произволу, его надо вычислить
(формула: S = а Ь, § 144). Положение меняется, если надо по-
строить прямоугольник заданной площади, например в 50 кв. см.
Тогда по произволу можно брать лишь одну из сторон, напри-
мер основание, высоту же приходится вычислять: при основании
а = 5см высоту b надо взять равной 50 :5 = 10 (см), при основа-
нии 6 см b надо взять 50 : 6 = 8 (см) и т. д.; вообще
b = S : а.
Теперь высота является величиной, зависимой от основания.
Одной из важнейших задач математики является изучение тех
зависимостей, какие существуют между величинами. Настоящая
236
глава XIII рассматривает некоторые самые простые и в то же
время самые важные виды такой зависимости.
§ 261. Таблицы и графики. Рассмотрим следующую задачу
на движение. Из пункта А в 12 часов дня выходит пароход и
идёт по реке без остановок со скоростью 14 км/час1. Через два
часа из того же пункта в том же направлении выходит второй
пароход, стоявший до этого у пристани; он идёт тоже без оста-
новок, но со скоростью 18 км/час. Выяснить, какое расстояние
между пароходами будет в различные моменты времени до 12
часов ночи.
Здесь мы имеем всего четыре величины: 1) время, отсчиты-
ваемое от полудня; 2) расстояние, проходимое за это время пер-
вым пароходом; 3) расстояние, проходимое вторым пароходом;
4) расстояние между обоими пароходами. Три последние вели-
чины зависят от первой. Составляем следующую таблицу, содер-
жащую значения всех четырёх этих величин.
Время в часах Расстоя-х. НИЯ В КМ X. 12 1 2 3 4 5 6 7 8 9 10 11 12
Расстояния, проходимые первым па- роходом 0 14 28 42 56 70 84 98 112 126 140 154 168
Расстояния, проходимые вторым па- роходом 0 0 0 18 36 54 72 90 108 126 144 162 180
Расстояния между пер- вым и вторым пароходами 0 14 28 24 20 16 12 8 4 0 4 8 12
Таблица ясно показывает, как изменялось с течением времени
расстояние между пароходами: до 2 часов дня оно росло (I паро-
ход удалялся, а II стоял у пристани), а потом стало убывать
(II пароход догонял первый в каждый час на 18—14 = 4 км).
В 9 часов вечера расстояние обратилось в О (II пароход догнал I),
а после этого расстояние стало возрастать, но теперь впереди
был уже II пароход.
1 Запись 14 км/час означает скорость движения, в котором в каждый час
проходится 14 /си.
237
Составлять подобную таблицу полезно, когда рассматриваются
значения величин, изменяющихся при изменении других вели-
чин.
Ход изменения величин становится ещё более ясным, если
на основании таблицы построить график. На куске клетчатой
бумаги проведём две прямые под прямым углом друг к другу
(рис. 88).
На горизонтальной прямой, которую назовём первой осью, бу-
дем отмечать разные моменты времени, считая в одной клетке
Рис. 88.
по одному часу; на вертикаль-
ной прямой (на второй оси)
будем отмечать расстояния, счи-
тая в одной клетке 10 км. За
начало отсчёта берём точку
пересечения двух осей. Поло-
жение каждого парохода в 1 час
дня, в 2 часа дня и т. д. от-
мечаем точкой, которую ставим
над той точкой первой оси,
которая соответствует этому
моменту времени, и на такой
высоте над первой осью, какая
соответствует пройденному рас-
стоянию. Например, для 2 ча-
сов положение I парохода изо-
бражается точкой, находящейся
выше точки 2 первой оси на
2,8 клетки, так как к этому
времени будет пройдено 14-2=
= 28 км, а положение II паро-
хода точкой 2 первой оси, так
как в этот момент II пароход
только начинает движение. Все отмеченные на чертеже точки
соединяют сплошными линиями. Таким образом получаем график
движения I парохода в виде отрезка О А и график движения II
парохода в виде ломаной линии из двух отрезков ОВ и ВС.
Графики не только помогают наглядно представить измене-
ние рассматриваемых величин, но нередко дают и решение бо-
лее трудных вопросов. Рассмотрим, например, такую задачу.
Из пункта А в пункт Б и из пункта Б в пункт А ежедневно
в полдень отправляются поезда, прибывающие на место назна-
чения ровно через 7 суток. Сколько поездов противоположного
направления встречает каждый поезд, совершающий рейс от
А к Б?
График, показывающий движение этих поездов, изображён на
рисунке 89. Он ясно показывает, что каждый поезд, двигающийся
от А к Б, встретит один поезд противоположного направления
при своём отправлении из А, тринадцать таких же поездов в
238
пути, ещё один при прибытии в пункт Б, а всего 15 поездов
противоположного направления.
Рис. 89.
§ 262. Диаграммы. Кроме графиков, показывающих измене-
ние одной величины при изменении другой, часто употребляются
разного рода диаграммы. Диаграммой называется всякий чертёж
или рисунок, наглядно представляющий значения каких-либо ве-
личин.
На рисунках 90 и 91 даны две диаграммы, одна из прямо-
угольников, другая из секторов, наглядно показывающие, как
была написана одна и та же контрольная работа в двух классах
школы. В классе VI А эту работу писали 46 человек, причём
оценку «5» получили 5 учащихся, оценку «4» — 25, оценку «3» —
12, оценку «2» — 4 учащихся. В классе VI Б эту работу писал
239
41 человек, из которых 4 получили оценку «5», 28 — оценку «4»,
6—оценку «3», 3 — оценку «2». Считая число учащихся в каж-
дом классе за 100%, составляем следующую таблицу:
'х. Оценка Классы «5» «4» «3» «2» Всего
VI А П% 54% 26% 9% 100%
VI Б ю% 68% 15% 7% 100%
VIA vi-Б
Рис. 91.
Числа этой таблицы представлены наглядно на рисунке 90,
где каждый класс изображён столбиком
Расход воды
в мэ/сен
500“"
400- -
Г“1
(прямоугольником) высотой в 10 клеток,
так что каждая клетка по высоте изобра-
жает 10%.
На рисунке 91 эти же числа изобра-
жены секторами круга с различными
центральными углами. Весь круг имеет
при центре 360°, а потому каждый про-
цент изображается сектором с централь-
ным углом в 360° : 100 — 3°,6. Например,
число учащихся VI А
300- -
200--
класса, получивших
оценку «5», показано
в виде сектора, имею-
щего центральный угол
вЗ°,6. 11=39о,6~40°.
Расходом воды в
рис. 92. реке называется число,
показывающее сколь-
ко кубических метров воды протекает в каждую секунду через
поперечное сечение реки. Этот расход для данного места на реке
240
от месяца к месяцу меняется. На рисунке 92 наглядно пока-
зан расход воды в одной реке по месяцам до устройства плотины
и водохранилища (пунктирная линия) и после их устройства
(сплошная линия). Рассматривая эту диаграмму, легко видеть,
какие изменения произошли в течении реки в результате устрой-
ства плотины и водохранилища.
Раздел 2. ОТНОШЕНИЯ И ПРОПОРЦИИ
§ 263. Сравнение числовых значений величин. Сравнить два
значения одной и той же величины можно двумя способами.
Во-первых, узнать, на сколько одно из этих значений больше дру-
гого, а для этого из большего значения вычесть меньшее. Во-
вторых, узнать во сколько раз одно из этих значений больше дру-
гого или какую часть большего составляет меньшее, а для этого
одно значение делят на другое.
Таким образом, сравнение двух значений производится или
посредством вычитания, дающего разность этих значений, или
посредством деления, дающего их частное, или, что то же, от-
ношение одного из них к другому (§ 183).
Возьмём, например, рост числа учащихся за годы советской
власти. В царское время в России перед первой мировой войной
в начальных и средних школах было 8 млн. учащихся, а в СССР
к концу 1950 г. их было уже 37 млн. Второе из этих чисел
больше первого на 37 — 8 = 29 млн., в то же время его отноше-
ние к первому равно 37:8 = 4^-, или 4,625. Иногда говорят,
пользуясь не вполне точно словом «раз», что второе число (37 млн.)
больше первого (8 млн.) в 4-|- раза, или в 4,625 раза. Лучше
сказать, что отношение второго числа к первому равно 4,625.
Кроме двух указанных способов сравнения величин, часто
применяется следующий третий способ сравнения, представляю-
щий собой сочетание первого и второго способов: найдя деле-
нием отношение большего значения к меньшему, выражают это
отношение посредством умножения на 100 в процентах, а затем
из полученного числа вычитают 100. Полученная разность пока-
зывает, на сколько процентов большее число превосходит мень-
шее. В приведённом выше примере имеем отношение 4,625, а по-
тому второе число превосходит первое на 462,5— 100= 362,5%.
Итак, число учащихся в начальных и средних школах выросло
у нас с 1914 г. по 1950 г. на 362,5%.
Ещё пример. В высших учебных заведениях СССР в 1949 г.
было 1132 тыс. студентов, в 1950 г. их стало уже 1247 тыс.
Сравнивая эти числа тремя рассмотренными способами, имеем
по I способу число студентов за год выросло на 1247— 1132=
= 115 тыс.;
241
по II способу отношение числа студентов в 1950 г. к их чис-
лу в 1949 г. равно:
1247:1132— 1,1015...,
или, округляя до тысячных, равно 1,102;
по III способу число студентов за год выросло на 110,2 —
— 100 = Ю,2(%).
Результат, полученный по I способу, называют приростом, а
по III способу приростом в процентах.
Прирост в процентах можно получить немного скорее, если
выразить в процентах отношение прироста к меньшему числу.
В нашем примере имеем 115:1132 = 0,1015..., или 10,2%.
Этими же тремя способами сравнения двух значений одной
величины пользуются и тогда, когда речь идёт не о приросте,
а об убыли. Например, сравним лучшее время, показанное рус-
скими конькобежцами в 1914 г. на дистанцию в 500 м, а именно
49,5 секунды, и лучшее время, показанное на той же дистанции
советскими конькобежцами в 1946 г., а именно 45,1 секунды.
Как видим, второе значение меньше первого на 49,5—45,1=4,4 сек.
(I способ); отношение второго к первому равно 45,1:49,5 =
= 0,9111 ..., или после округления до тысячных 0,911 (II спо-
соб); второе меньше первого на 100 — 91,1=8,9% (III способ).
Здесь приходится брать отношение не большего к меньшему, а
меньшего к большему, и не вычитать 100%, а вычитать от 100%.
Правила применения трёх способов сравнения двух значений
одной величины можно записать коротко, применяя обозначение
чисел буквами, следующим образом: чтобы показать прирост Ь
по сравнению с а, берут
b — а (I способ),
или
(II способ),
или
100 • — 100(111 способ).
Последний результат можно получить также по формуле
Чтобы показать убыль Ь по сравнению с а, берут а — b (I спо-
соб), или (II способ), или 100 — — • 100 (III способ). Послед-
ний результат можно получить также по формуле а~Ь Ю0.
§ 264. Отношение. При делении натуральных чисел, когда
частное есть натуральное число, можно говорить, что частное
показывает, во сколько раз делимое больше делителя; например,
частное 45 :9 = 5 показывает, что 45 больше 9 в 5 раз.
242
При делении натуральных чисел, когда частное есть дробное
число, нельзя говорить, что частное показывает, во сколько раз
делимое больше делителя; например, о частном 9:45 = ^ = -i-
нельзя сказать, что показывает, что 9 больше 45 в у раза.
Отметим, что в нашем языке можно сочетать слово «раз» с
натуральными числами, т. е. можно говорить 1 раз, 2 раза,
1 2
3 раза, .... 1000 раз, ... , но нельзя говорить -% раза, у ра-
за, Зу раза и т. п., так же, как, например, нельзя побывать на
выставке у раза, в театре у раза и т. д.
А как же можно и должно говорить, что означает частное от
деления одного дробного числа на другое?
Для ответа на этот вопрос вводится понятие отношения
одного числа к другому; это понятие впервые было введено
в античном мире в IV и III вв. до и. э.
Отношением первого числа ко второму называется число, об-
ладающее тем свойством, что при умножении его на второе чис-
ло получится первое.
Например:
1) числа 150 и 5 имеют отношение 30, так как 5 • 30 = 150;
в этом случае вместо «отношение 150 к 5» можно говорить «150
больше 5 в 30 раз»;
2) числа 9 и 45 имеют отношение 4-, так как 45 • 4- = 9.
Итак, частное показывает отношение делимого к делителю.
TJ 3 5 3-11 33
Например, частное чисел у и уу , равное 4 . у— , пока-
3 5
зывает отношение числа у к числу уу.
В некоторых случаях отношение показывает, во сколько раз де-
лимое больше делителя; это будет тогда, когда частное полу-
о 15 3 15 4
чается в виде натурального числа. Например: у : у = у • - =
кс 15 з
= 5, где 5 показывает отношение у к у , но можно сказать,
С 15 ,
что 5 показывает, во сколько раз делимое у больше дели-
з
теля -г.
4
Зная определение отношения и зная взаимную связь делимого,
делителя и частного, выразим те же свойства, но в иных тер-
минах:
1) первый (предыдущий) член данного отношения равен произ-
ведению второго его члена на данное отношение;
2) второй (последующий) член данного отношения равен част-
ному от деления первого его члена на данное отношение;
243
3) отношение не изменяется, если о5а его члена умножить
или разделить на одно и то же число, отличное от нуля.
Применяя третье свойство, во многих случаях отношение
удаётся упростить, а именно: заменить первый и второй его члены
иными числами, меньшими или целыми вместо дробных, с со-
хранением того же отношения.
Например: 1) отношение 144:96 можно заменить отношением
3:2 (так как оба члена можно разделить на 48);
1 2
2) отношение 3= : 4-х- можно заменить (умножая оба члена
Л о
на 6) отношением 21 :28, а затем (разделив оба члена на 7) от-
ношением 3:4;
3) 6 см: 7 см заменить через 6:7;
4) латунь составляют так, чтобы в килограмм входило 650 Г
меди и 350 Г цинка. Найти отношение меди к цинку.
Ответ. 650 Г: 350 Г, короче 65 :35, ещё короче 13:7.
5) Если имеются два одинаковых сосуда, из которых один
наполнен керосином, а другой бензином, то отношение весов
этих жидкостей будет равно 8 :7 = 1-у .
Отношения широко применяются на практике. Например, по-
метка на карте «масштаб 1 : 20000», о которой была речь в § 130,
указывает, что отношение длины любого отрезка на карте к дли-
не того же отрезка на местности равно 1 : 20 000. Легко сообра-
зить, что значат такие выражения, как «увеличить в отношении
5; 3», «уменьшить в отношении 2:5» и т. д.
Переставляя члены данного отношения одно на место другого,
получаем новое отношение, которое называется обратным для
данного. Например, обратным для отношения 5 :4 является от-
ношение 4 :5, для отношения а : Ь отношение b : а.
§ 265. Определение пропорции. В жизни нередко приходится
сравнивать отношение двух значений одной величины с отноше-
нием двух значений другой величины. Например, в 1951 г. на
нужды просвещения в СССР было ассигновано 59 млрд. руб. из
общей суммы государственных расходов в 452 млрд. руб.; отноше-
ние расходов на просвещение к обшей сумме расходов состав-
ляло у нас в 1951 г., таким образом, 59 : 452 = 0,1305..., или с
точностью до тысячных 0,131, т. е. 13,1%. Совершенно иное на-
блюдается в капиталистических странах. Так, в США расходы
на просвещение составили в 1950—1951 гг. меньше 1% всех го-
сударственных расходов.
Сравнивая какие-нибудь два отношения, мы видим, что они
или равны, или неравны. Например, отношение чисел 15 :4 больше
отношения чисел 7 :2, а это последнее равно отношению 21 :6.
Записав эти два равных отношения рядом и поставив между
ними знак равенства, получаем пропорцию.
244
Итак, пропорцией называется равенство двух отношений, каж-
дое из которых задано своими двумя членами, как, например:
7 :2 = 21 : 6.
Как читать пропорции?
На примере: В общем виде:
10 : 2 = 30 : 6 а : b = с : d
читаем: 10 относится к 2 так же, как 30 читаем- а относится к Ь так же
относится к 6. как с относится к d.
Короче читаем: Отношение 10 к 2 равно отношению Отношение а к b равно отно
30 к 6. шению с к d.
В пропорции 15:5 = 6:2 числа 15 и 2 называются крайними
членами, числа 5 и 6 — средними членами этой пропорции В
пропорции a'.b — c.d крайними членами являются and, сред-
ними b и с.
Все члены пропорции могут быть отвлечёнными членами, как
во всех случаях, приведённых выше, но два члена одного отно-
шения могут быть и однородными именованными числами, т. е.
числами, выражающими значения одной и той же величины, как,
например:
12кГ:28 «Г = 3 : 7;
12 кГ: 28 кГ = 3 см : 7 см\
40 № : 400 № = 1 час. : 10 час. и т. д.
§ 266. Основное свойство пропорции. Как проверить правиль-
ность записи 4,8:0,02= 10,5:0,04375?
Это можно сделать двумя приёмами:
I. Путём нахождения I и II отношения:
4,8 :0,02 = 480 : 2 = 240
10,5 : 0,04375 = 240.
Следовательно, имеем пропорцию:
4,8 : 0,02 = 10,5 : 0,04375.
II. Путём нахождения произведений крайних и средних членов.
4,8-0,04375 = 0.21;
0,02- 10,5 = 0,21.
Как видим, здесь произведение крайних членов равно произ-
ведению средних членов. Этого достаточно, чтобы утверждать,
что имеет место пропорция:
4,8:0,02 = 10,5:0,04375.
Покажем, что в любой пропорции произведение крайних её
членов равно произведению средних членов (основное свойс гво
пропорции).
245
На примере:
Дана пропорция
12:3 = 20:5;
умножив оба её отношения на про-
изведение 3 • 5, получим равенство:
(12 :3) • (3 • 5) = (20 : 5) • (3 • 5),
которое можно записать в виде:
12 • 3 • 5_ 20 3 • 5
3 “ 5 ’
или, после сокращения, в виде;
12 • 5 = 20 • 3.
В общем виде:
Дана пропорция
а : b = с : d\
умножив оба её отношения на про-
изведение Ь • d, получим равенство:
(а : Ь) • Ь • d = (с : d) • b - d,
которое можно записать в виде:
а • b • d _ с b • d
b d '
или, после сокращения, в виде:
а • d = с • Ь.
Как видим, произведение крайних членов пропорции всегда
равно произведению средних её членов. Верно и обратное пред-
ложение: если произведение двух чисел равно произведению двух
других, то из них можно составить пропорцию.
На примере:
Дано равенство двух произве-
дений:
6 • 8 = 24 - 2;
разделив обе части этого равенства
на произведение 8 • 24, получаем:
6-8 _ 24 • 2
8 • 24 — 8 • 24 ’
а после сокращения:
6__^
24 ~ 8 ’
т. е. пропорцию
6 : 24 = 2 : 8.
В общем виде:
Дано равенство двух произве-
дений:
а • b = d • с;
разделив обе части этого равенства
на произведение b • d, получаем:
а • b_d с
b~-~d~ b^d'
а после сокращения:
а с
т. е. пропорцию
а : d = с : Ь.
Например, для проверки пропорции 0,1611 :0,4296 = 3:8 на-
ходим произведения 0,1611 8 = 1,2888 и 0,4296 • 3= 1,2888. Это
легче, чем находить оба отношения. Точно так же убеждаемся,
что пропорция 37 :14 = 8 :3 неверна (37 • 3 = 111, 14-8 = 112),
т. е. 37 : 14 =# 8 : 3.
§ 267. Нахождение неизвестного члена пропорции. Очень
часто, имея дело с четырьмя числами, составляющими пропор-
цию, приходится, зная три из них, находить четвёртое. Пусть,
например, имеется чертёж прибора с пометкой «масштаб 2 :5»,
и надо найти действительную длину х отрезка, равного на чер-
теже 35 мм. Пишем пропорцию
35 : х = 2 :5
и находим, что
откуда
х • 2 = 35 • 5 = 175,
х = 175 :2 — 87,5 (мм).
246
Как находить неизвестный крайний или неизвестный средний
член пропорции? Рассмотрим это.
На примере: 6 : х = 3 : 20. В общем виде: а : х = b : с.
По основному свойству пропорции имеем.
3 х = 6 • 20, Ъ • х = а • с.
откуда находим множитель х:
6-20 а • с
х~ з “ х- ь .
Как видим, чтобы найти неизвестный средний член пропор-
ции, достаточно разделить произведение крайних членов на дру-
гой средний.
х:9 = 50:6. | х:а = Ь:с.
По основному свойству пропорции имеем:
6 • х — 9 50, | с • х — а • Ь,
откуда находим множитель х:
9 • 50 __ I а Ь
х = —— =75. х =----.
6 | с
Как видим, чтобы найти неизвестный крайний член пропорции,
достаточно разделить произведение средних членов на другой
крайний.
Всякие четыре числа, из которых можно составить пропорцию,
называются пропорциональными числами. Разыскание неизвест-
ного члена пропорции по трём известным её членам называют по-
этому разысканием четвёртого пропорционального к трём данным
числам. Иначе это называют решением пропорции.
Каковы бы ни были три данных числа, всегда можно найти
к ним четвёртое пропорциональное. Надо только указать порядок,
в каком эти числа должны идти в пропорции, и помнить, что число
нуль вторым (последующим) членом отношения быть не может.
Обычно неизвестный член пропорции обозначают буквой х.
Приводим два примера разыскания четвёртого пропорциональ-
ного.
1. Найти х, если х : 36 = 5 :12.
Здесь х = = 3-5=15.
2. Найти х, если 14 : х = 35 :8.
Здесь х = = 3,2.
оо о
Разыскание четвёртого пропорционального выполняется, таким
образом, с помощью двух действий — одного умножения и одного
деления. Никогда не следует забывать, что здесь выгодно сперва
выполнить сокращение, если оно возможно, а потом уже умно-
247
жать и делить. Если то отношение, в котором оба члена известны,
не приведено к простейшему виду, надо начать с его упрощения
(§ 264). Приводим ещё примеры.
3. Найти х из пропорции 180 : 264 = х : 33.
Производя сокращение в первом отношении на 12, получаем
пропорцию 15 : 22 = х : 33, откуда х = 15^33 = 152' 3 = 22,5.
4. Найти х из пропорции 4^ :0,135= 1,25 :х.
Умножив оба члена первого отношения на 1000, а затем раз-
делив их на 5 и на 9, заменяем его равным ему отношением 100 ; 3.
Решая пропорцию 100 :3 = 1,25 :х, имеем:
3 - 1,25 3,75
X —------=------
100 — 100 — °’0375-
5. Вычислить с точностью до тысячных неизвестное х из
пропорции:
х: 59 = 13 : 37.
Здесь х = = 20.729.
§ 268. Перестановка членов пропорции. Если произведение
двух чисел равно произведению двух других чисел, то возникает
вопрос: сколько из этих четырёх чисел можно составить про-
порций?
Рассмотрим это на примере: даны
числа 8, 6, 20, 15, такие, что
8 • 15 = 6 20.
В общем виде; даны числа а, Ь,
с, d, такие, что
а • d = b • с.
a: b — c : d (I);
d : b = с : a (II).
Из предшествующего нам известно, что из таких чисел можно образовать
пропорцию. Действительно, имеем:
8 : 6 = 20 : 15 (I);
15 ; 6 = 20 : 8 (II);
Отметим, что (II) пропорция получена из (I) путём перестановки её край-
них членов.
8:20 = 6:15(111). | а : с = b : d (III).
Отметим, что (III) пропорция получена из (I) путём перестановки её сред-
них членов.
15:20 = 6:8 (IV). | d:c=6:a(IV).
Отметим, что (IV) пропорция получена из (I) путём переста-
новки и крайних и средних её членов,
Итак, имеем: из данных четырёх чисел, где произведение двух
чисел равно произведению двух других, можно составить 4 про-
порции, у котсрых различные отношения.
Меняя местами первые и вторые отношения в пропорциях I—IV,
получим ещё 4 пропорции:
20 : 15 = 8 : 6;
20 : 8=15: 6;
6 : 15 = 8 : 20;
6: 8=15:20.
c :d = a tb;
c :a = d'. b;
b :d = a :c;
b :a = d :c.
248
§ 269. Производные пропорции. Имея одну пропорцию, можно
получить из неё целый ряд новых, содержащих уже иные числа
и называемых производными пропорциями от данной пропорции.
Приводим три наиболее употребительные производные про-
порции.
Пусть дана пропорция:
15 : 6 = 20 : 8. |
Запишем её в виде равенства дробей:
15_20
6 - 8 ’
Прибавим по единице:
о о
иначе:
15 + 6 _ 20 + 8
6 ~ 8 '
Окончательный результат:
(15 + 6): 6 = (20 + 8) : 8. |
Видим, что сумма членов первого отношения так относится
к своему второму (последующему) члену, как сумма членов вто-
рого отношения относится к своему второму (последующему) члену
(I производная пропорция из данной).
Вычитая от тех же равных дробей по единице, имеем:
25-1 =20-1
6 8’
иначе:
15 — 6 20 — 8
6 “ 8 ’
Окончательный результат:
(15 —6) : 6 = (20 — 8): 8.
b 1 d 1
а— Ь с — d
~b~~~d~'
(а — Ь} -.b — (c — d) : d.
Видим, что разность членов первого отношения так относится
к своему второму (последующему) члену, как разность членов
второго отношения к своему второму (последующему) члену
(II производная пропорция из данной).
Разделив I производную пропорцию почленно на II, получим:
15 + 6. 15 —6 _ 20 + 8 . 20 —8
6 : 6 - 8 : 8
короче:
(15 + 6): (15 —6) =
= (20 + 8) : (20 — 8).
а + Ьа—b c+dc—d
~b~ : ~b~ d~ : ~d~f
(с + b): (a — b) = (c + d): (c — d).
Видим, что сумма членов первого отношения так относится
к их разности, как сумма членов второго отношения к их раз-
ности (III производная пропорция).
249
Как пример применения I производной пропорции решим за-
дачу: две семьи должны оплатить счёт за электроэнергию в сумме
60 руб.; сколько денег причитается с каждой семьи, если одна
пользуется семью лампочками, а другая — пятью такими же
лампочками?
Обозначая через х и у те суммы, какие должны внести
каждая семья, имеем пропорцию:
х : у = 7 :5,
откуда находим:
(* + У) : У = (7 + 5) : 5,
60:г/= 12:5; = 25; х = 60 —25 = 35.
Раздел 3. ВЕЛИЧИНА, ПРЯМО ПРОПОРЦИОНАЛЬНАЯ
ДРУГОЙ ВЕЛИЧИНЕ
§ 270. Определение и примеры прямой пропорциональности.
Хотя понятие пропорциональности в применении к частным
явлениям встречалось у нас и раньше, только теперь, после
необходимых обобщений, можно это понятие рассмотреть глубже
и основательнее.
Возьмём сначала пример. Рассмотрим равномерное движение
автомобиля.
Время движения (в часах) 2 1 4 2 2 1 2 3
Пройденный путь (в километрах) 30 60 90 120 150 180
Здесь имеются две величины: пройденный путь и время дви-
жения.
В первом ряду записано несколько значений первой величины,
во втором — соответствующие значения второй. Эти две величины
зависят одна от другой: взяв какое-нибудь произвольное число
километров пути, мы найдём время (делением на 60), а взяв
какое-нибудь произвольное число часов, найдём путь (умноже-
нием на 60). Взяв отношение каких-нибудь двух значений одной
величины, например 90 км : 150 км = 3 : 5 = 0,6, а также отно-
шение соответствующих значений другой, в данном случае
14-час.:2-^- час.= 3 :5 = 0,6, видим, что эти два отношения
2 2 II
равны, т. е. 90 км: 150 км = ly час.: 2у час., т. е. из четырёх
чисел можно составить пропорцию.
Величина прямо пропорциональна другой величине тогда и
только тогда, когда отношение двух произвольных значений одной
величины равно отношению двух соответствующих значений дру-
гой величины.
250
Другими словами: две величины называются прямо пропор-
циональными, если при изменении значений одной из них в ка-
ком-то произвольном отношении, в таком же отношении изме-
няется и другая величина.
Таким образом, путь при равномерном движении и время
этого движения — две прямо пропорциональные величины.
Можно указать сколько угодно других примеров прямо про-
порциональных величин: площадь поля и количество собранного
урожая (при условии, что с каждого квадратного метра поля со-
бирают поровну), объём и вес куска металла, взятого при одних
и тех же условиях, количество выполненной работы и её про-
должительность (при условии, что производительность работы
остаётся всё время одной и той же) и т. д.
Если имеются две величины, обладающие тем свойством, что
при увеличении любого значения одной из них соответствующее
значение другой тоже увеличивается, но не в том же отношении,
то такие две величины не будут прямо пропорциональными. Так,
например, по действующим у нас правилам за отправку теле-
граммы надо платить 1 руб. и по 30 коп. за каждое слово,
а потому за телеграмму из а слов платят b руб., причём значе-
ния а и Ь таковы:
а 5 6 7 8 9 10 11 12 13 14 15 16
ь 2,5 2,8 3,1 3,4 3,7 4,0 4,3 4,6 4,9 5,2 5,5 5,8
При увеличении числа слов вдвое, например с 5 до 10 слов,
плата растёт, но не вдвое, а только в отношении 4:2,5 = 8:5 =
= 1,6, т. е. медленнее, чем число слов. Плата за телеграмму
зависит от числа слов не по закону прямой пропорциональности.
Здесь другая зависимость, о которой речь будет дальше (§ 283).
Рассмотрим далее три такие величины: длину а стороны
квадрата, его периметр р, т. е. сумму всех его сторон, его пло-
щадь S. Легко проверить правильность следующей таблички,
содержащей соответствующие значения этих трёх величин.
а 1 2 3 4 5 6 7 8 9 10 11
р 4 8 12 16 20 24 28 32 36 40 44
S 1 4 9 16 25 36 49 64 81 100 121
Все три величины одновременно растут, но прямо пропор-
циональными являются только пара первых: сторона квадрата а
251
и его периметр р — 4а. При увеличении стороны в 2, 3, 4 и т. д.
раз площадь тоже растёт, но уже в 4, 9, 16 и т. д. раз; площадь
квадрата растёт быстрее, чем его сторона.
Чтобы узнать, являются ли две зависящие друг от друга
величины прямо пропорциональными, надо, таким образом, вы-
яснить два явления: во-первых, увеличиваются (уменьшаются) ли
значения одной величины при увеличении (уменьшении) значений
другой, и, во-вторых, равны ли отношения соответствующих зна-
чений.
Так, увеличивая в некотором отношении значение одного из
сомножителей, оставляя без изменения значение другого сомно-
жителя, известно, что произведение будет увеличиваться в том
же отношении (§ 80). Поэтому произведение прямо пропорци-
онально каждому из сомножителей (при условии, что другой со-
множитель не меняется).
Иначе обстоит дело с суммой: если увеличивать одно из
слагаемых, сохраняя другое без изменения, то сумма будет уве-
личиваться, но не в том же отношении, а меньшем, как это
легко видеть на любом примере. Так, если взять одно из сла-
гаемых равным 1, 2, 4, 8, 16, 32, а другое брать каждый раз
равным 10, то сумма получит значения 11, 12, 14, 18, 26, 42.
Сумма двух слагаемых растёт с увеличением одного из слагаемых,
но не прямо пропорциональна этому слагаемому.
§ 271. Свойства прямо пропорциональных величин. Рассматри-
вая табличку, приведённую в начале предыдущего параграфа,
легко заметить, что каждое значение первой величины (пройден-
ного пути) получается из соответствующего значения второй ве-
личины (времени движения) посредством умножения на одно
и то же число, а именно на 60:
60-1 = 30; 60-1 =60; 60 - 11 = 90 и т. д.
В этом заключается важное свойство любых двух величин,
связанных прямо пропорциональной зависимостью.
I. Все значения одной из двух прямо пропорциональных ве-
личин можно получить посредством умножения соответствующих
значений другой величины на одно и то же число, называемое
коэффициентом пропорциональности первой из взятых величин
относительно второй и обозначаемое обычно буквой k.
Так, в примере, рассмотренном в начале § 270, пройденный
путь получается посредством умножения 60 на время движения,
коэффициент пропорциональности здесь равен 60 км/час.
Обозначим буквами:
х — какое угодно значение первой величины,
у — соответствующее значение второй. Теперь, если положить
х=1, а у = k, то по определению пропорциональности имеем:
y:x — k:\, или y:x = k,
252
откуда
у — kx.
Таким образом, произвольное значение первой величины у равно
произведению соответствующего значения второй величины х на
один и тот же коэффициент пропорциональности k.
Коэффициентом пропорциональности двух величин, находя-
щихся в прямо пропорциональной зависимости, называется отно-
шение значения первой из них к соответствующему значению
второй,
Можно высказать обратное предложение к вышеустановлен-
ному 1 предложению.
II. Если все значения одной величины равны произведениям
соответствующих значений другой на одно и то же число, то эти
две величины прямо пропорциональны.
Действительно, возьмём две величины:
на примере:
I величина — время в часах;
II величина — путь в километрах
при равномерном движении, так что
путь равен постоянному числу 60
(скорости), умноженному на время.
в общем виде:
I величина — х\
II величина — у, причём
y=kx,
где k — постоянное число.
Дадим два значения первой из этих величин и найдём отношение второй
из них к первой:
время: -g- часа и 3 часа;
о 1
о часа : часа = 6.
х принимает значения:
*1 и х2;
Xt : xt.
Возьмём соответствующее значение второй из этих величин:
путь: 30 км и 180 км. | уг = kxj и (/2 = fex2-
Разделив полученное значение второй величины на первое её значение,
имеем:
180 км : 30 км — 6; [ Уг~У1 = kx2 : kxx = х2 : Хь
а потому имеем пропорцию:
180 км : 30 км = 3 часа : -^- часа. I Уг :yi = x2 : хъ
Итак, отношение у2: уг двух произвольных значений одной
величины у равно отношению х2 :хх двух соответствующих зна-
чений другой величины х, а потому эти две величины у и х на-
ходятся в прямой пропорциональной зависимости.
III. Свойства I и II позволяют дать другое определение пря-
мой пропорциональности: две величины называются прямо про-
порциональными, если любое значение у одной из них равно
произведению соответствующего значения другой х на одно и то же
число k, т. е. если у = kx, где k — постоянный коэффициент
пропорциональности.
253
Таким образом, для записи прямой пропорциональности двух
величин х и у удобно пользоваться формулой у = kx, где k —
постоянный коэффициент пропорциональности. Например, зави-
симость между временем х (в часах) и пройденным путём у
(в километрах) при постоянной скорости в 5 км[час можно вы-
разить формулой у = 5х. Зависимость между длиной стороны
квадрата х см и его периметром у см выражается формулой
у = 4х. Длина окружности С и её диаметр d связаны зависи-
мостью C~3,14d, или, точнее, С = та/, а потому эти две вели-
чины прямо пропорциональны.
IV. Если одна величина прямо пропорциональна другой с коэф-
фициентом пропорциональности k, то вторая прямо пропорци-
ональна первой с коэффициентом пропорциональности, равным
1 (т. е. обратным числом относительно k).
Действительно, если у есть величина, прямо пропорциональ-
ная х, a k — коэффициент пропорциональности, то имеем:
У — kx,
а потому
х = у : k,
или, что то же:
V. Если какая-то величина х принимает значения, например:
5; 7; 9; 11; 13; 15; 17; 19; 21; 23; . . ., то говорят, что она
растёт равномерно. Величина растёт равномерно, если она прини-
мает значения, из которых каждое последующее больше предыду-
щего на одно и то же число.
При равномерном росте одной из двух прямо пропорциональ-
ных величин другая величина растёт тоже равномерно.
В примере с пройденным путём и временем движения первая
из этих величин растёт равномерно, так как каждое её значение
на 0,5 часа больше предыдущего; равномерно же растёт и вторая:
каждое её значение на 30 км больше предыдущего.
На примере: у = 4х. | В общем виде: у = kx.
Будем равномерно изменять х на единицу в частном примере и на Л —
в общем виде:
х: х + 1; х 2; х + 3; ... | х; х + й; х 4- 2й; х 4- Зй; ...
Проверим соответствующие изменения у:
4х; 4(х + 1); 4 (х 4- 2); 4 (х +3); ... | kx; k(x + й); А (х 4- 2й): А (х 4- Зй); ...
у изменяется равномерно на 4 в частном примере и на АЛ в общем виде:
4 (х + 1) — 4х = 4
4 (х + 2) — 4 (х + 1) = 4
4 (х + 3) - 4 (х + 2) = 4
А (х -J- ft) — kx = Ай
А (х 4- 2й) — А (х 4- Л) = Ай
А (х 4- Зй) — А (х 4- 2h) = Ай
254
§ 272. Наглядное изображение прямой пропорциональности.
Применяя способ наглядного изображения изменяющихся вели-
чин посредством графиков (§ 261), покажем зависимость между
длиной куска ткани, изменяющейся от 0 до 10 м, и его стои-
мостью при цене 5 руб. за метр. На первой оси будем откла-
дывать число метров (в каждой
клетке 1 м), а по второй оси
число рублей (в каждой клетке
5 руб.).
Точки, выражающие стоимости
кусков от 1 до 10 м, заключены
в кружки (рис. 93). Как видим,
эти точки располагаются на одной
прямой линии, проходящей через
начальную точку отсчёта («на-
чало»).
Доказано, что во всех слу-
чаях прямой пропорциональности
точки графика располагаются на
одной прямой, проходящей через
начало.
Поэтому для вычерчивания гра-
фика любой прямо пропорциональной зависимости достаточно
найти какую-нибудь одну его точку и соединить её с началом.
Если зависимость отличается от
линию, не проходящую через начало, либо не прямую, а кри-
вую. На рисунке 94 изображён график зависимости между сла-
гаемым х и суммой у = 15 -|- х; на рисунке 95 — график зависи-
мости между стороной квадрата х и его площадью у — х2.
§ 273. Нахождение четвёртого пропорционального в случае
прямой пропорциональности. В жизни часто встречаются задачи,
в которых требуется найти значение некоторой величины, зная
соответствующее значение другой величины, прямо пропорцио-
нальной первой, и одну пару соответствующих значений обеих
этих величин.
255
Такова, например, задача: узнать, сколько придётся уплатить
за 8 кГ товара, если за 2,8 кГ этого товара уплатили 40 руб.
04 коп.
Здесь мы имеем две прямо пропорциональные величины —
количество товара и его стоимость, причём знаем одну пару
соответствующих значений этих величин (2,8 кГ и 40 руб.
0,4 коп.) и ещё одно значение первой величины (8 кГ), а найти
должны соответствующее значение другой — стоимость этих 8 кГ.
Всего, таким образом, даны три числа, и надо найти такое
четвёртое, которое вместе с первыми тремя составило бы про-
порцию. Задачи такого рода называются поэтому задачами на
нахождение четвёртого пропорционального (числа). Мы с ними
уже встречались (§ 267). Рассмотрим три способа решения по-
ставленной задачи.
I способ—решение отдельными действиями.
1) Сколько стоит 1 кГ товара, если за 2,8 кГ уплатили
40,04 руб.?
40,04 : 2,8 = 400,4 : 28 = 100,1 : 7 = 14,3 (руб.).
2) Сколько стоят 8 кг при цене 14,3 руб. за килограмм?
14,3 руб. • 8 = 114,4 руб.
Ответ. 114 руб. 40 коп.
II способ — решение приведением к единице.
Этот способ требует выполнения тех же двух действий, что
и первый, но без доведения первого действия до конца. Вот вся
запись решения задачи этим способом:
2,8 кГ — 40,04 руб.;
8 кГ — х руб.
Записав над чертой число 40,04, выражающее стоимость
2,8 кГ, пишем под чертой 2,8 и получаем, таким образом, стои-
, 40,04 и
мость 1 кГ в виде частного • Не производя деления, узнаем
стоимость 8 кГ, добавляя над чертой множитель 8. После этого
остаётся только освободиться от дробей и выполнить сокращения,
а затем получить искомое значение х.
40,04 • 8 4004 - 8 - 10 572 - 2 .... ... Л .п
Х=^йГ = 28 • 100 " = ~1б~ ~ 4,4 ИЛИ 114 РУ6' 40 К0П-
III способ — решение при помощи пропорций.
Замечая, что искомое значение х так относится к 40,04 руб.,
как 8 (кГ) относятся в 2,8 (кГ), пишем пропорцию
х : 40,04 = 8 : 2,8,
из которой находим:
40,04 • 8
Х ~ 2,8
и заканчиваем решение точно так, как во II способе. Чтобы не
ошибиться при записи пропорции, замечают, что в данном слу-
256
чае х больше, чем 40,04, а потому и во втором отношении пре-
дыдущий член должен быть больше последующего, т. е. х отно-
сится к 40,04 так же, как 8 относится к 2,8.
Способ приведения к единице и способ пропорций оказы-
ваются значительно более удобными, чем решение отдельными
действиями. Рекомендуется решать задачи на разыскание четвёр-
того пропорционального одним из этих двух способов, а решение
отдельными действиями использовать с целью проверки.
Вот ещё задача того же рода.
Автомобиль прошёл 39 км за 1 час. 12 мин. Сколько ему по-
надобится времени, чтобы при той же средней скорости пройти
94 кл<? Ответ дать с точностью до минуты.
Решение способом приведения к единице.
39 км—1 час 12 мин. =72 мин.;
94 км — х мин.
х = 72 ‘ 94 = = 173,5... = 174 мин., или 2 часа 54 мин.
оУ
Проверка. 1) Сколько времени в среднем нужно, чтобы
пройти 1 км?
72 : 39 = 1,8461... ~ 1,846 (мин.),
2) С колько времени надо, чтобы пройти при той же средней
скорости 94 км? 1,846 • 94 = 173,524... ~ 174 мин., или 2 часа
54 мин.
Раздел 4. ВЕЛИЧИНА, ОБРАТНО ПРОПОРЦИОНАЛЬНАЯ
ДРУГОЙ ВЕЛИЧИНЕ
§ 274. Определение и примеры обратной пропорциональности.
Рассмотрим два следующих ряда чисел, обладающих тем свой-
ством, что произведение каждых двух из них, подписанных одно
под другим, равно 24:
X 1 2 3 4 Б 6 7 8 9 10 11 12 13 14 15
У 24 12 8 6 4,8 4 со|г- СО 3 сч | со сч 2,4 сч 2 11* 13 4 1,6
Здесь мы имеем две величины: х и у, значения которых за-
писаны в этих двух рядах. Числа первого ряда можно считать,
например, значениями длины прямоугольника с площадью
24 кв. см, а числа второго ряда — значениями его высоты (то и
другое в сантиметрах).
Как видим, при увеличении значений одной величины значе-
ния другой уменьшаются, причём отношение любых двух значе-
ний х равно обратному отношению соответствующих значений у.
12 Арифметика
257
Например, взяв в верхнем ряду числа 4 и 12, отношение
которых
4:12 = 1
О
имеем в нижнем ряду соответствующие им числа 6 и 2 с отно-
шением
6:2 = 3.
Взяв эти же два числа 6 и 2 в обратном порядке, получаем
отношение 2:6, равное 1, т. е. равное отношению соответст-
вующих чисел верхнего ряда.
Величина обратно пропорциональна другой величине тогда и
только тогда, когда отношение двух произвольных значений одной
величины равно обратному отношению соответствующих значений
другой величины.
Другими словами: две величины называются обратно пропор-
циональными, если при изменении значения одной из них в каком-
нибудь отношении другая величина изменяется в обратном отно-
шении.
Выше мы имели пример такой зависимости: высота прямо-
угольника данной площади обратно пропорциональна его основа-
нию. Другой пример: количество товара, которое можно приоб-
рести, затратив какую-нибудь определённую сумму денег, напри-
мер 60 руб., обратно пропорционально цене этого товара. Дей-
ствительно, при цене в 5 руб. за килограмм на 60 руб. можно
купить 60:5= 12 кГ; при увеличении цены, например, в два
раза количество товара 60 : 10 = 6 кГ уменьшится во столько же
раз (§ 81).
Следует твёрдо помнить, что одна величина обратно пропор-
циональна другой лишь при выполнении условия: если в каком-
то отношении увеличить значение одной величины, то значение
другой уменьшится в том же отношении (и, наоборот, при умень-
шении значений одной в каком-то отношении значение другой
увеличится в том же отношении).
Можно привести ещё сколько угодно примеров величин, об-
ратно пропорциональных друг другу: количество метров ткани,
необходимое для пошивки платья, и ширина этой ткани; коли-
чество рабочих, нужных для выполнения некоторой определённой
работы, и время её выполнения; время, нужное для переезда из
одного пункта в другой, и скорость движения и т. д.
Какова зависимость между вычитаемым х и разностью у при
неизменном уменьшаемом, равном, например, 100?
X 1 2 4 8 16 32 64
у — 100 — х 99 98 96 92 84 68 36
258
При увеличении х разность 100 — х уменьшается, но обратной
пропорциональности здесь нет, так как при увеличении вычитае-
мого вдвое разность уменьшается не вдвое.
Например: х, = 4, х2 = 8, имеем: 8:4 = 2, а разность умень-
шается не вдвое (г/г = 96, у2 = 92, имеем: 96 : 92 = 1,0434... < 2).
§ 275. Свойства обратно пропорциональных величин. Возьмём
две величины, рассмотренные в § 274.
у — количество товара в килограммах 120 60 30 20 15 12 5
х — цена (в рублях на кило- грамм) товара, который можно в таком количестве купить иа 60 руб. 2 1 2 3 4 5 12
OU ии
Как видим, у = —, х = — .
1. Все значения величины, обратно пропорциональной другой
величине, можно получить посредством деления одного и того же
числа на соответствующие значения этой второй величины.
Так, в примере количество товара узнаём посредством деле-
ния 60 на его цену.
Если k есть то значение первой величины, которое соответ-
ствует значению 1 второй величины, у — какое угодно другое
значение первой величины, х — соответствующее значение вто-
рой, то
у : k = 1 : х,
а потому
У = k : х.
II. Если все значения одной величины (у) получены посред-
ством деления одного и того же числа k на соответствующие
значения второй величины (х), то эти две величины х и у обратно
пропорциональны.
Действительно, если
у = А :х,
то, обозначая буквами ух и уг два каких-нибудь значения первой
величины, а буквами хх и х2 соответствующие значения второй,
имеем:
откуда
У1 — k ' Xi", У2 — k : х2;
k k kx, x,
У1 У2 = — = — = x2: x>.
x, x2 kx, x, 2 1
Итак, отношение двух любых значений первой величины равно
обратному отношению соответствующих значений второй:
У1 Уъ — х2 : xlf
а потому эти две величины обратно пропорциональны.
12*
259
III. Если одна величина обратно пропорциональна другой с
коэффициентом обратной пропорциональности k, то и вторая
обратно пропорциональна первой, с тем же коэффициентом обрат-
ной пропорциональности.
Действительно, если у есть величина, обратно пропорциональ-
ная х, a k — коэффициент обратной пропорциональности, то имеем:
у = k : х,
откуда делитель х равен делимому k, разделённому на частное у,
т. е.
х = k : у.
IV. При равномерном росте величины х величина y = k’.x
убывает, но неравномерно.
В этом можно убедиться, рассматривая любой пример, хотя бы
взяв
60
у=~х
и полагая
х = 1, 2, 3, 4, 5 и т. д.,
т. е. х равномерно возрастает на единицу; тогда у получает зна-
чения:
у = 60, 30, 20, 15, 12 и т. д.,
т. е. у неравномерно убывает, а именно: на 30, 10, 5, 3 и т. д.
§ 276. Наглядное изображение обратной пропорциональности.
Применяя способ наглядного изображения зависимости двух вели-
чин, рассмотренный в § 261, покажем на графике зависимость
между основанием х и высотой у в прямоугольниках с площадью
в 6 кв. см.
Значения х будем брать от 1 до 6 см через каждые 0,5 см,
значения у вычислять с точностью до сотых долей сантиметра
(до десятых долей миллиметра). График будем строить на клет-
чатой бумаге, разграфлённой на квадраты со стороной в 5 мм.
Сначала составляем следующую табличку:
X 1 1,5 2 2,5 3 3,5 4 4,5 5 5,5 6
у = 6 :х 6,00 4,00 3,00 2,40 2,00 1,71 1,50 1,33 1,20 1,09 1,00
Точки, соответствующие этим значениям х и у, изображены
на рисунке 96. Как видим, они располагаются уже не на прямой
линии, как в случае прямой пропорциональности, а на некоторой
кривой, которую проводят от руки. Эту кривую называют ги-
перболой.
При уменьшении значений х точки этой кривой быстро под-
нимаются всё выше и выше; например, при х = 0,5 у = 12;
260
при х — 0,1 у — 60; при х = 0,01 у = 600 и т. д. На рисунке 96
эти точки не поместились. При увеличении значений х точки
кривой медленно опускаются, приближаясь всё ближе и ближе
к первой оси: при х = 10 у = 0,6;
при х = 60 у = 0,1; при х = 100
у = 0,06 и т. д. (на рисунке 96
эти точки не показаны).
§ 277. Нахождение четвёртого
пропорционального в случае обрат-
ной пропорциональности. Имея
пару обратно пропорциональных
величин, мы встречаемся с той же
задачей нахождения четвёртого
пропорционального числа, как и
в случае прямой пропорциональ-
ности: зная два соответствующих
значения этих величин и ещё ка-
кое-либо значение одной из них, Рис. 96.
найти новое значение второй ве-
личины, соответствующее данному значению первой.
Такова, например, задача: зная, что на устройство палатки
пошло 8 м полотна шириной 75 см, найти, сколько метров по-
лотна шириной 80 см пойдёт на устройство второй такой же
палатки.
Здесь мы имеем дело с длиной и шириной двух прямоугольни-
ков, имеющих одну и ту же площадь, т. е. с двумя обратно про-
порциональными величинами. Рассмотрим три способа решения
этой задачи.
I способ (отдельными действиями).
1) Какова площадь того полотна, которое пошло на устрой-
ство первой палатки?
75 см = 0,75 м\ 8 • 0,75 = 6 (кв. jw).
2) Какова длина прямоугольника, имеющего площадь 6 кв. м
при ширине 80 см?
80 см = 0,8 м; 6 :0,8 = 7,5 (jw).
Ответ. На устройство второй палатки надо 7,5 м полотна
шириной 80 см.
II способ (приведения к единице).
Длина того полотна, которое идёт на устройство палатки,
обратно пропорциональна его ширине. Если же при ширине
75 см нужно 8 м в длину, то при ширине 1 см материала пойдёт
в 75 раз больше, а при ширине 80 см — в 80 раз меньше. Обозна-
чая искомую длину буквой х, пишем:
8 • 75
Х~ 80 *
261
Дальше остаётся выполнить указанные действия, предварительно
производя сокращение, и мы получаем ответ: х = 7,5 м.
Разумеется, здесь мы выполняем те же два действия, что и в
первом способе, но не вычисляем до конца результат умножения,
а благодаря этому ответ получается несколько скорее.
III способ (способ пропорций).
Заметив, что длина полотна обратно пропорциональна его
ширине, сразу пишем пропорцию:
х : 8 = 75 :80
(отношение любых двух значений одной из двух обратно пропор-
циональных величин равно обратному отношению соответствую-
щих значений другой величины) и находим из этой пропорции:
8 • 75
Х ~ 80 ’
а дальше идёт то же, что и при способе приведения к единице.
Как показывает опыт, лучше всего применять способ приве-
дения к единице, а решением отдельными действиями пользо-
ваться при проверке.
Рассмотрим ещё такую задачу: колесо с поперечником в 86 см
сделало на некотором пути 4509 оборотов; сколько оборотов
сделает на том же пути колесо с поперечником в 72 см?
Число оборотов колеса на данном пути обратно пропорцио-
нально длине его окружности: в каком отношении увеличивается
длина окружности колеса, в том же отношении произойдёт умень-
шение числа оборотов на данном пути. Но длина окружности
колеса прямо пропорциональна его поперечнику (§ 255).
Итак, при увеличении поперечника окружности колеса в
каком-либо отношении длина его окружности увеличивается в
том же отношении, а число оборотов на данном пути умень-
шится в том же отношении. Таким образом поперечник колеса
обратно пропорционален числу оборотов, какое это колесо делает
на данном пути.
Способом приведения к единице поставленная задача решается
так: при поперечнике 86 см колесо делает 4509 оборотов; при
поперечнике в 1 см оно сделало бы оборотов в 86 раз больше;
при поперечнике в 72 см оно сделает оборотов в 72 раза меньше;
получаем запись:
4509 • 86
Х ~ 72
После сокращений (на 9 и на 2) имеем:
501 • 43 21500 сооп
х - —~ ~ 5380.
4 4 —
Округляя, получаем ответ: колесо с поперечником 72 см сделает
на том же пути 5380 оборотов.
262
Для проверки решим эту задачу ещё раз, выполняя отдель-
ные действия.
1. Какова длина окружности колеса при поперечнике 86 см?
86 см • 3,14 = 270,04 см~270,0 см.
2. Какой путь пройдёт это колесо, когда сделает 4509 обо-
ротов?
270 см 4509 = 1 217 430 см = 1 217 000 см.
3. Какова окружность колеса при поперечнике в 72 см?
72 см • 3,14 = 226,08 с>и~226 см.
4. Сколько оборотов сделает это колесо на пути в 1217 000 см?
1 217000 :226~ 5380 (оборотов).
В этом ответе надёжных цифр только три, так как число 3,14
выражает отношение окружности к диаметру только прибли-
жённо, а именно с тремя значащими цифрами.
Как видим, второе решение значительно сложнее первого.
На этой задаче хорошо видна выгода использования способа при-
ведения к единице при решении задач на пропорциональные
величины.
Раздел 5. ПРОПОРЦИОНАЛЬНОСТЬ ТРЁХ
И БОЛЕЕ ВЕЛИЧИН
§ 278. Примеры случаев, когда три и более величин связаны
попарно пропорциональной зависимостью. До сих пор мы рассмат-
ривали только такие задачи, в которых имели дело с двумя вели-
чинами, связанными прямой или обратной пропорциональностью.
Очень часто, однако, приходится рассматривать три и более
таких величины. Разберём несколько примеров.
I. Дан брус из какого-нибудь материала с площадью осно-
вания 5 кв. см, высотой h см, весом рГ. Если, сохраняя неиз-
менной площадь основания S, менять одну из двух остальных
величин h и р, то будет меняться и вторая из них; легко видеть,
что эти две величины h. и р прямо пропорциональны.
Если, сохраняя неизменной высоту h, менять одну из двух
остальных величин 5 и р, то будет меняться и вторая, причём
и здесь имеем прямую пропорциональность. Но если будем со-
хранять неизменным вес р, то при изменении одной из двух
остальных величин (площади основания или высоты) вторая будет
меняться уже не прямо, а обратно пропорционально первой.
Следующая табличка указывает зависимость между каждыми
двумя из трёх рассматриваемых величин.
263
Неизменная величина Площадь осно- вания S Высота h Вес Р
Изменяются вели- чины Высота и вес Площадь основа- ния и вес Площадь основа- ния и высота
Зависимость Прямая пропор- циональность Прямая пропор- циональность Обратная про- порциональность
Здесь могут возникнуть шесть задач: считая неизменной одну
из трёх величин: S, h, р, можно находить значение одной из
двух остальных.
Задачи 1 и 2. Если при неизменной площади основания
высота бруса равна 12,0 см и вес его равен 400 Г, то встаёт
два вопроса: 1) сколько будет весить брус из того же материала,
с той же площадью основания, при высоте 15,0 см и 2) какую
высоту должен иметь брус с той же площадью основания, чтобы
он весил 450 Г, если он изготовлен из того же материала?
Решение.
1) х Г: 400 Г = 15,0 см : 12,0 см — 5 : 4 (прямо пропорциональ-
ная зависимость);
х = = 500 (Г);
2) х см : 12,0 см = 450 Г : 400 Г = 9 :8;
12,0 -9 ,
X = —!g----= 13,5 (сщ.
Задачи 3 и 4. Если при данной высоте бруса площадь его
основания 25 см2. а вес 300 Г, то встаёт два вопроса: 1) сколько
будет весить брус с той же высотой при площади основания
36 см2 и 2) какова будет площадь при весе 480 Г, если они
изготовлены из одного и того же материала?
Решение.
1) х Г: 300 Г — 36 см2 : 25 см2 = 36 :25 (прямо пропорциональ-
ная зависимость);
х = = 432 (Г);
2) х см2 :25 см2 = 480 Г : 300 Г = 8 :5;
х = = 40 (см2).
Задачи 5 и 6. Если при данном весе бруса его высота
16,0 см и площадь основания 560 см2, то встаёт два вопроса:
264
I) какова будет высота, чтобы брус при том же весе имел пло-
щадь основания 420 сти2, и 2) какова площадь основания бруса
при том же весе при высоте 12,0 см, если они изготовлены из
одного и того же материала?
Решение.
1) х см: 16,0 см = 560 см2 :420 см2 = 4:3;
х= —з— = -J- = 21,3 (см) (обратно пропорциональная
зависимость);
2) х см2 : 560 см2 — 16,0 см : 12,0 см — 4:3 (то же)
560 • 4 2240
х = —=— = =« 747 (см2).
О о
II. Работают а землекопных машин (экскаваторов), каждая
вынимает за час Ь куб. м грунта; за с рабочих дней все они
вместе вынули V куб. м грунта.
Здесь всего четыре величины. Сохраняя неизменными значе-
ния каких-нибудь двух из них, например числа машин а и про-
изводительности каждой из них 6, будем менять значение одной
из двух остальных величин, например числа с рабочих дней;
тогда значение четвёртой величины, а именно объёма V всего
вынутого грунта, будет тоже меняться, притом прямо пропор-
ционально числу дней.
Подобным же образом найдём, что прямая пропорциональность
здесь имеется между b и V, между с и V, но между величинами
b и с, а и с, а и b зависимость оказывается уже иной, а именно,
обратно пропорциональной. Действительно, если мы будем сохра-
нять неизменными, например, число машин а и объём вынутого
грунта V, то при увеличении производительности каждой машины
во сколько-нибудь раз число дней работы во столько же раз
уменьшится, а потому эти две величины Ь и с обратно пропор-
циональны.
Следующая табличка указывает зависимость между каждыми
двумя из четырёх рассмотренных величин.
Неизменные величины а и b а и с а и V ft и с ft и и с и V
Меняются величины с и V Ъ и V Ь и с а и V а и с а и ft
Зависимость прямо пропори. прямо пропори. обратно пропори. прямо пропори. обратно пропори. обратно пропори.
265
Здесь могут возникнуть 12 задач, так как при каждой паре
неизменных величин, образуемых из четырёх данных, можно
находить одну из двух других.
III. Имеется брус с квадратным основанием; сторона этого
основания а см, высота бруса с см, объём бруса V куб. см.
Какова зависимость между каждыми двумя из этих трёх величин?
Неизменная величина а с V
Меняются величины с и V а и V а и с
Зависимость Прямая пропор- циональность Не прямая и не обратная про- порциональность Не прямая и не обратная про- порциональность
Здесь мы встречаемся с новыми, ещё не рассмотренными нами
зависимостями. Если сторону квадратного основания увеличить,
например, вдвое, то площадь основания увеличится вчетверо, во
столько же раз (при неизменной высоте) увеличится и объём; та-
ким образом, при увеличении стороны основания растёт и объём
бруса, но не в таком же отношении, а быстрее.
Если же сохранять неизменным объём, то при увеличении
стороны основания вдвое высоту бруса приходится уменьшать
во столько раз, во сколько раз увеличивается площадь основания,
т. е. вчетверо; при увеличении стороны квадратного основания
высота бруса неизменного объёма, таким образом, уменьшается,
но не в таком же отношении, а быстрее.
В обоих этих случаях мы встречаемся с зависимостью, отли-
чающейся от изученной нами прямой и обратной пропорциональ-
ности.
§ 279. Нахождение шестого пропорционального и другие более
сложные задачи на пропорциональную зависимость. Имея дело
с двумя величинами, из которых одна прямо или обратно пропор-
циональна другой, мы решали задачи на разыскание четвёртого
пропорционального числа.
Подобным же образом в случае трёх величин, связанных по-
парно прямой или обратной пропорциональностью, мы встречаемся
с задачей нахождения шестого пропорционального числа: даны по
одному значению каждой из трёх величин, а также по второму
значению двух из них (всего пять значений); найти соответст-
вующее значение третьей величины.
В случае четырёх попарно пропорциональных величин возни-
кает задача нахождения восьмого пропорционального числа, в слу-
чае пяти величин — десятого пропорционального числа и т. д.
266
Эти задачи можно решать любым из тех трёх способов, какими
мы решали задачи на разыскание четвёртого пропорционального
(§ 273 и 277).
Решим следующую задачу: железный брус с площадью осно-
вания в 54 кв. см и высотой 20 см весит 8,4 кГ; какую высоту
имеет брус из того же материала, если при основании в 64 кв. см
он весит 7,2 кГ?
I способ решения (отдельными действиями).
1. Каков объём первого бруса? 54 • 20 = 1080 (ел/3).
2. Сколько весит каждый кубический сантиметр железа?
8,4 кГ = 8400 Г; 8400 Г : 1080 = 7 Г.
3. Каков объём второго бруса?
7,2 кГ = 7200 Г;
7200 : 7-^ = 925 у (ел3).
4. Какова высота второго бруса?
925 у: 64= 14^14,4 (см).
Ответ. Второй брус имеет высоту 14,4 см.
II способ решения (приведением к единице).
Высота бруса прямо пропорциональна его весу (при неизмен-
ной площади основания) и обратно пропорциональна площади его
основания (при неизменном весе), как это мы видели в § 278.
При весе 8,4 кГ и площади основания 54 см2 высота бруса
ол / 20)
равна 20 см I пишем х = — 1.
При весе 1 кГ и той же площади основания 54 см2 высота
будет в 8,4 раза меньше (пишем 8,4 под чертой, имеем запись
20)
Х ~ 8,4/
При весе 7,2 кГ и той же площади основания высота будет
в 7,2 раза больше (пишем 7,2 над чертой, имеем запись: х ~
20 • 7,2 )
~ 8,4 /’
При весе 7,2 кГ и площади основания 1 см2 высота бу-
дет в 54 раза больше (пишем 54 над чертой, имеем запись:
20 • 7,2 • 54)
Х ~ 8,4 /‘
267
При весе 7,2 кГ и площади основания 64 см2 высота бу-
дет в 64 раза меньше ^пишем 64 внизу, получаем окончатель-
20 • 7,2.54\
ную запись: х———•
J 8,4 • 64 /
Если условие задачи записано в следующем виде:
54 см2 20 см 8,4 кГ;
64 см2 х см 7,2 кГ,
то оказывается, что по ходу только что выполненного рассужде-
ния мы постепенно «спускаемся вниз» (переходим от 8,4 через I к
7,2; от 54 через 1 к 64), а в результате получается переход от
данного значения высоты (20 см) к искомому её значению (х).
20 • 7 2 • 54
Придя к формуле х = 84’ —, производим упрощение и по-
лучаем окончательно:
v 5.9-9 405 .„13 к , .
X— 28 28 — ^28' (см)-
III способ (способ пропорций).
Находим сперва высоту у такого вспомогательного бруса, у
которого площадь основания, как у второго (64 кв. см), но вес, как
у первого (8,4кГ). Имеем такую запись условия:
54 см2 20 см 8,4 кГ-
64 см2 у см 8,4 кГ.
Не обращаем внимания на последний столбец и находим у,
как в § 273: составляем и решаем пропорцию:
ол гл сл 20-54 5 • 27 135
^:20 = 54:64; = =
Теперь переходим от вспомогательного бруса ко второму:
64 см2 у = см 8,4 кГ;
64 см2 хсм 7,2 кГ.
Не обращаем внимания на первый столбец и находим х, со-
ставляя и решая пропорцию
х;^ = 7,2:8,4;
135-7,2 _ 135-3_ 405 _ .13 И5, .
Х~ 8-8,4 ~ 4 - 7 28 14 2g _ 14,0 (СЛ!).
Способ приведения к единице имеет заметные преимущества
перед двумя другими. Им и рекомендуется постоянно пользовать-
ся, применяя наряду с ним первый способ (решение задачи от-
дельными действиями) для проверки.
268
Решим двумя способами (приведением к единице и отдель-
ными действиями) следующую задачу: 7 экскаваторов с ёмкостью
ковшей по 3,0 л<3 за 12 рабочих дней вынули 172 тыс. Т грунта;
сколько рабочих дней понадобится 6 новым мощным («шагающим»)
экскаваторам с ёмкостью ковшей по 14 м3, чтобы вынуть пол-
миллиона тонн грунта? Часовую производительность машины
можно считать прямо пропорциональной ёмкости её ковша.
Решение способом приведения к единице.
Как мы видели в § 278, число дней работы прямо пропорцио-
нально объёму вынутого грунта и обратно пропорционально как
числу машин, так и часовой их производительности.
Записав условие задачи в две строки:
7 экскаваторов 3,0 м3 12 рабочих дней 172 тыс. Т,
6 экскаваторов 14 м3 х рабочих дней 500 тыс. Т,
постепенно переходим сверху вниз, получая последовательно
записи:
12 12-7 12-7 12-7.3,0
X = —, X = ----, X = —с—, X = ----с--—,
О о
_ 12.7-3,0 12.7.3,0 12.7.3,0-500
Х~ 6-14 ’ Х ~ 6 • 14 • 172’ Х ~ 6- 14- 172 ’
и после сокращений имеем окончательно:
3,0-125 о 31 о „ . ,
х = —js— = 8 ти = 8,7 (рабочих дней).
Для проверки решим эту задачу ещё раз отдельными дейст-
виями.
1. Сколько грунта вынимают 7 экскаваторов с ёмкостью ковша
3,0 Л!3 за один рабочий день?
172:12 = 141 (ТЫС.
о
2. Сколько грунта вынимает за один рабочий день один такой
экскаватор?
141:7 = 21 (тыс. .и3).
О Z1
3. Сколько грунта вынимал бы за один рабочий день один
экскаватор с ёмкостью ковша 1 jw3?
2д :3 = §(ТЬ1С-л<3)-
4. Сколько грунта вынимает за один рабочий день один экска-
ватор с ёмкостью ковша 14 .и3?
|| • 14 = 9-1 (тыс. Л43).
269
5. Сколько грунта вынимают за один рабочий день 6 таких
экскаваторов?
94 • 6 = 574 (тыс. л3).
У о
6. Сколько рабочих дней надо этим 6 экскаваторам, чтобы вы-
нуть полмиллиона кубических метров грунта?
500 :57 -I- = 8 25 8,7 (рабочих дней).
Преимущества решения данной задачи способом приведения
к единице по сравнению с её решением отдельными действиями
бросаются в глаза. Однако, по крайней мере на первых порах,
рекомендуется каждую задачу решать обоими этими способами.
§ 280. Пропорциональное деление. Нередко приходится дан-
ное число делить на две и более неравных части, отношения
которых друг к другу заданы. Такое деление встречается, напри-
мер, в следующей задаче: четыре бригады школьников взялись
выполоть огород площадью в 21 а; какое задание следует дать
каждой бригаде, если в первой 5 человек, во второй 9, в третьей 17,
в четвёртой 25 и если считать, что все могут работать одинаково?
Здесь всего 5 4- 9 + 17 + 25 — 56 человек, на каждого при-
ходится 21 :56 = -g- = 0,375 а; задание первой бригаде составит
0,375 • 5 = 1,875 а, второй 0,375 • 9 = 3,375 а, третьей 0,375 • 17 =
= 6,375 а, четвёртой 0,375 • 25 = 9,375 а. Для проверки скла-
дываем все четыре полученных числа и находим сумму 21,000 а,
как и должно быть.
Здесь мы разделили число 21 пропорционально числам 5, 9,
17, 25. Задачи такого рода называют задачами на пропорцио-
нальное деление. Рассмотрим ещё несколько подобных задач.
Задача 1. Требуется изобразить круговой диаграммой (§ 262)
распределение посевных площадей в СССР в 1950 г. по культу-
рам, зная, что под зерновыми было занято 105,8 млн. га, под
техническими культурами 11,8 млн. га, под овоще-бахчевыми
12,5 млн. га, под кормовыми 28,4 млн. га. Найти с точностью
до десятых долей градуса центральные углы соответствующих
секторов.
Задача сводится к делению числа 360 пропорционально четырём
указанным числам. Не изменяя отношений между числами, умно-
жим их на 10, чтобы избежать дробей, и будем делить 360 про-
порционально числам 1058, 118, 125, 284, выражающим услов-
ное число паев, приходящихся на каждый из искомых углов. Всего,
таким образом, имеем 1585 паёв, на каждый пай приходится
360 :1585 = ~ градуса.
270
Сектор, изображающий площадь под зерновыми, должен иметь
угол:
72З,?0-8 = = 240,30... ~ 240°,3,
под техническими культурами: 723‘1718 = = 26,80... ~26°, 8,
ПОД овоще-бахчевыми: 72 • 125 9000 QQ qq qqo д 317 = 317 =28’39- 28 >4'
под кормовыми: 72 - 284 20448 „. сп 317 = 317 =64,50... ~64 ,5.
Для проверки подсчитываем сумму: 240°,3 + 26°,8+ 28°,4 + 64°,5
и убеждаемся, что она равна, как и должно бы быть, 36О°,О
(допустимо расхождение до 0,05 • 4 = 0°,2, обусловленное округ-
лением каждого слагаемого до десятых долей).
Здесь возможно другое решение, требующее меньшего числа
72
делений: найдя, что на один пай приходится градуса, выра-
жаем эту обыкновенную дробь в виде десятичной с точностью до
пяти значащих цифр = 0,227129... = 0,2271з), а затем умно-
жаем это приближённое её значение на числа 1058, 118, 125, 284.
После округления произведений до десятых получаем те же числа,
что и выше.
Задача 2. Расход по перевозке трёх грузов составил 1207 руб.,
причём первый груз весом в 14 Т был перевезён на 30 км, вто-
рой в 15 Т на 40 км, третий в 16 Т на 35 км. Распределить
этот расход между отправителями грузов пропорционально весу
и расстоянию с точностью до целых рублей.
Здесь надо исходить из расчёта стоимости каждого тонно-
километра, т. е. стоимости перевозки 1 Т на расстояние в 1 км:
подсчитав, сколько тонно-километров приходится на каждый груз,
а именно: 14-30 = 420 на первый, 15 - 40 = 600 на второй,
16 • 35 = 560 на третий, делим всю сумму 1207 руб. на три части
пропорционально числам 420, 600, 560 или 21, 30, 28, что даёт
при первом способе:
—79 21 = 320,8... ~321;
30 = 458,3... ^458;
120^-28.== 427,7... =^428.
Проверка. 321 + 458 + 428= 1207.
271
В итоге имеем:
Чтобы разделить число на части, пропорциональные данным
числам, достаточно разделить это число на сумму данных чисел
и полученное частное умножить на каждое из данных чисел.
Задача 3. Число 639 разделить на три такие части, чтобы
первая относилась ко второй, как 5 к 6, а вторая к третьей,
как 8 к 9.
Обозначая три искомых числа буквами х, у, г, имеем про-
порции:
ат : г/ = 5 : 6; г/: z = 8 :9.
Трудность здесь в том, что на второе число согласно первой
пропорции приходится шесть паёв, а согласно второй — восемь
паёв, так что здесь встречаются разные, а не одинаковые паи.
Чтобы сделать паи одинаковыми, заменим данные отношения
5:6 и 8:9 равными им такими, чтобы последующий член пер-
вого отношения стал равным предыдущему члену второго отно-
шения, а для этого берём
НОК (6; 8) = 24
и умножаем оба члена первого отношения на 24 : 6 = 4, оба члена
второго отношения на 24:8 = 3. Теперь имеем пропорции:
х : у — 5 : 6 = 20 : 24,
у ; z = 8 : 9 = 24 : 27,
из которых видно, что числа х, у, г имеют соответственно 20,
24, 27 одинаковых паёв, а всего 71 пай.
Остаётся разделить данное число 639 пропорционально чис-
лам 20, 24, 27, что мы уже умеем делать. Получив
х = 180, у = 216, z = 243,
производим проверку, находя сумму
180 4-216 + 243 = 639
и отношения
180:216 = 5 :6; 216 : 243 = 8 :9,
и убеждаемся, что все требования задачи выполнены.
Задача 4. Число 245 разделить обратно пропорционально
числам 5, 8, 12.
Здесь данное число 245 требуется разделить на такие три
части х, у, z, чтобы было
х:у = 8:5; у:г= 12:8 = 3:2.
272
Решая эту задачу тем же способом, что и предшествующую,
имеем:
НОК (5; 3) = 15;
х : у = 8 :5 = 24 :15;
t/: z = 3 : 2 = 15 :10;
24 4- 15 + 10 = 49; 245 :49 = 5;
х = 5 • 24 = 120; у = 5 • 15 = 75; z = 5 • 10 = 50.
Ответ. Искомые части числа 245 равны 120, 75 и 50.
Проверка. 120 4- 75 4- 50 = 245; х : у — 120: 75 — 8 :5 =
= ±:±; r/:z = 75:50 = 3:2= 12:8 = l:±.
В итоге имеем:
Чтобы разделить число на части, обратно пропорциональные
данным числам, достаточно разделить это число пропорционально
числам, обратным к данным числам.
Раздел 6. НЕКОТОРЫЕ ЗАВИСИМОСТИ, КОТОРЫЕ НАДО
ОТЛИЧАТЬ ОТ ПРЯМОЙ И ОБРАТНОЙ ПРОПОРЦИОНАЛЬНОСТИ
§ 281. Равномерное возрастание. При равномерном росте од-
ной из двух прямо пропорциональных величин другая растёт
тоже равномерно (§ 271). Однако таким равномерным ростом
обладают и некоторые величины, не связанные с другой вели-
чиной прямой пропорциональностью. Вот примеры.
1. Стоимость отправления телеграммы в другой город равно-
мерно растёт с увеличением числа слов: за каждое лишнее слово
приходится платить на 30 коп. больше. Но с каждой телеграммы
сверх пословной платы берётся ещё 1 руб.
Поэтому за телеграмму в 10 слов надо уплатить 30 • 10 4-
4- ЮО = 400 коп., или 4 руб., за телеграмму в 20 слов 30 • 20 -j-
4- 100 = 700 коп., или 7 руб.: при удвоении числа слов стои-
мость телеграммы возрастает несколько меньше, чем вдвое
(7:4 = 1|).
Итак, стоимость телеграммы и число слов в ней не прямо пропор-
циональны, хотя при равномерном росте числа слов стоимость
телеграммы растёт равномерно.
Действительно, при увеличении числа слов на одно стоимость
телеграммы возрастает на 30 коп., что хорошо видно из следую-
щей таблицы:
Число слов 1 2 3 4 5 6 7 8 9 10
Оплата в копейках 130 160 190 220 250 280 310 340 370 400
13 Арифметика
273
2. Если по плану надо изготовить за смену 200 деталей,
а рабочий перевыполнил план на а деталей, то план им выпол-
нен на р%, причём
при а — 10 20 30 40 50
имеем р = 105% 110% 115% 120% 125%,
так как каждая лишняя деталь прибавляет 0,5% к выполнению
плана, каждый лишний десяток деталей означает лишних 5%
выполнения плана.
Как видим, число деталей, изготовленных сверх плана (а2: аг=
— 20 :10 = 2), и процент выполнения плана (р2 : Pi = ПО : 105 —
= 1 не пропорциональны ^2 #= 1^j, но при равномерном росте
одной из этих двух величин другая растёт тоже равномерно.
3. Если одно из двух слагаемых остаётся без изменения, а
другое изменяется, то изменяется и их сумма, причём при рав-
номерном росте слагаемого сумма растёт тоже равномерно, но
пропорциональности между ними нет. В этом легко убедиться,
рассматривая таблицу, где взята сумма 25 а = Ь.
Первое слагаемое 25 25 25 25 25 25 25 25 25
Второе слагаемое (а) 4 8 12 16 20 24 28 32 36 растёт равномерно (по 4 единицы)
Сумма (t>) 29 33 37 41 45 49 53 57 61 растёт равномерно (по 4 единицы)
а пропорциональности нет, в самом деле:
а2: = 36 : 4 = 9,
Ь2 : Ь± = 61 : 29 = 2^ #= 9.
Итак, бывает такая зависимость между величинами, когда
при равномерном росте одной величины другая растёт тоже рав-
номерно, но прямой пропорциональности между ними нет.
§ 282. Равномерное убывание. Наряду с величинами, которые
равномерно возрастают при равномерном возрастании другой
величины, встречаются и величины, равномерно при этом убы-
вающие. Вот примеры.
1. Если надо пройти всего 32 км и каждый час проходить по
5 км, то с каждым часом остаток пути уменьшается равномерно.
Это показывает следующая табличка:
Продолжительность движения в часах 1 2 3 4 5 6
Остаток пути в километрах 27 22 17 12 7 2
274
При удвоении продолжительности движения, например с 2 до
4 часов, остаток пути уменьшается, но не вдвое, с 22 до 12,
22 5
т. е. J2 = 1-g-, а потому здесь зависимость, отличная от обратной
пропорциональности.
2. Некоторый товар продавался по 6 руб. за килограмм. Если
произошло снижение цен на несколько процентов, новая его цена
будет тем меньше, чем больше число процентов снижения; каж-
дый лишний процент уменьшает цену на 6 коп., так что здесь
мы имеем равномерное убывание цены при равномерном росте
числа процентов снижения.
Это хорошо показывает следующая табличка:
При снижении цен на: 5% ю% 15% 20%
Новая цена 5 р. 70 к. 5 р. 40 к. 5р. Юк. 4 р. 80 к.
Здесь тоже нет обратной пропорциональности.
Итак, бывают такие зависимости между величинами, когда
при равномерном росте одной величины другая равномерно же
убывает (уменьшается); такую зависимость не следует смеши-
вать с обратной пропорциональностью.
§ 283. Линейная зависимость. Если при равномерном росте
одной величины другая равномерно растёт или равномерно убы-
вает, то говорят, что эти две величины линейно зависят одна от
другой или что они связаны линейной зависимостью. В каждом
из пяти примеров, рассмотренных в двух предыдущих парагра
фах, мы имеем по паре величин,
связанных линейной зависи-
мостью.
Прямая пропорциональность
представляет собой особый слу-
чай линейной зависимости; об-
ратная же пропорциональность
не является линейной, так как
при равномерном росте одной
из двух обратно пропорциональ-
ных величин другая изменяется Рис. 97.
неравномерно (§ 275).
Изображая линейную зависимость графически, всегда получаем
ряд точек, расположенных на одной прямой линии, как на ри-
сунке 94 (стр. 255), где показана зависимость суммы у — 15 х от
слагаемого х. На рисунке 97 изображена зависимость между раз-
ностью у = 25 — х и её вычитаемым х. Этой прямолинейностью
графика объясняется и название зависимости — линейная.
Прямая пропорциональность — частный случай линейной за-
висимости. Её график имеет ту особенность, что проходит че-
13*
275
рез начало
ке 93 (стр.
Рис. 98.
отсчёта на обеих осях, как, например, на рисун-
255). Обратная пропорциональность не является ли-
нейной зависимостью; её график — не прямая, а
кривая (рис. 96 на стр. 261).
Приведём ещё пример линейной зависимости.
Для измерения температуры чаще всего употреб-
ляют термометр Цельзия (по имени шведского учё-
ного Цельзия, 1701 — 1744), но иногда и Фаренгейта
(по имени немецкого учёного, 1686—1736); на
рисунке 98 показано сходство и различие таких
термометров.
Зависимость между числами градусов по Цель-
зию и Фаренгейту, выражающими одну и ту же
температуру, является линейной, но не прямой про-
порциональностью, как это показывает, например,
следующая таблица:
Градусы Цельзия 0 20 40 60 80 100
Градусы Фаренгейта 32 68 104 140 176 212
Пропорциональности здесь нет, так как, напри-
мер, при увеличении числа градусов Цельзия с 20
до 40, т. е. вдвое, число градусов Фаренгейта растёт
в отношении 104 :68 = 1,529...
График зависимости между температурами поЦельзию и Фарен-
гейту дан на рисунке 99,
где F° = | С° + 32°.
§ 284. Примеры бо-
лее сложных зависимо-
стей. В школьном курсе
арифметики изучаются
рассмотренные нами са-
мые простые зависи-
мости между величи-
нами. Существует очень
много более сложных
зависимостей, которые
изучаются в других раз-
делах школьного курса
математики. Отметим
некоторые из таких
зависимостей, чтобы
устранить возможность
смешения их с тремя
рассмотренными.
276
1. Если сторона квадрата имеет а см, то его площадь S равна
а2. При увеличении стороны в 2, 3, 4 и т. д. раз его площадь
увеличивается в 4, 9, 16 и т. д. раз.
При равномерном росте стороны площадь квадрата растёт
не равномерно, а ускоренно: например, при стороне 1 см, 2 см,
3 см и т. д. площадь равна 1 см2, 4 см2, 9 см2 и т. д. Здесь нет
ни прямой пропорциональности, ни линейной зависимости. Это
новая, более сложная зависимость — пропорциональность квад-
рату (график на рис. 95, стр. 255).
2. Если ребро куба равно а см, то площадь S всех 6 его
граней выражается формулой S = 6а2. Зависимость между а
и S тоже является пропорциональностью квадрату, так как при
увеличении значения а в 2, 3, 4, 5, 6 и т. д. раз значение S
возрастает в 22 = 4, 32 = 9, 42 = 16, 52 = 25, 62 = 36 и т. д.
раз.
3. Если ребро куба равно а см, то его объём V см3 выра-
жается, как известно, формулой V = а3.
При а= 1 2 3 4 5 6 7 8 9 10
имеем V= 1 8 27 64 125 216 343 512 729 1000
Когда значение а увеличивается в 2; 3; 4 и т. д. раз, то
значение V — а3 увеличивается в отношении 23 —8; З3 = 27;
43 = 64 и т. д.
Такая зависимость носит название пропорциональности кубу.
4. Если к числителю и знаменателю какой-нибудь правиль-
2
ной дроби, например , прибавлять поровну, то получатся но-
вые дроби, возрастающие при увеличении прибавляемого числа,
но тоже меньшие единицы:
= 0,4000; = 1 = 0,5000; 0,5714. .. ;
О D + 1 Z О + Z /
Hi - 4=°’62б0; Ж=4=°'66136- • •
Щ = 7 = 0,7000; = п = °>7272- • •;
5 + 5 10 ’5 + 6 11
- 0,7500 и т. д.
5 + 7
Здесь новый вид зависимости, отличный от всех рассмотрен-
ных раньше — замедленный рост с неограниченным приближе-
нием к единице (прибавление 95 даёт = 0,97; прибавле-
\ О + Уо
(угуг- .. 2 + 995 n
ние 995 дает k ооё = 0,997 и т. д. I.
277
5. Положим, требуется огородить прямоугольный участок,
прилегающий одной стороной к зданию, так что ставить изго-
родь надо только по трём сторонам участка. Имеется материал
на устройство 20 м изгороди. Если стороны, идущие от здания,
сделать по 3 м, то на третью сторону останется 20—3-2 =
— 14 м, и площадь участка будет равна 3 - 14 = 42 кв. м.
При другой длине х каждой из сторон, идущих от здания,
получится другая длина у третьей стороны и другая площадь S
всего участка. Легко составить такую таблицу:
X (л) 1 2 3 4 5 6 7 8 9 10
у(м) 18 16 14 12 10 8 6 4 2 0
S (л«) 18 32 42 48 50 48 42 32 18 0
Рис. 100.
Значения у равномерно
убывают при равномерном
возрастании х — здесь встре-
чаемся с уже знакомой ли-
нейной зависимостью. Но за-
висимость S от х оказывается
более сложной: при равно-
мерном росте х площадь S
сперва растёт, притом замед-
ленно: при х = 5 получает
наибольшее (максимальное)
значение 50, затем начинает
убывать, причём чем даль-
ше, тем быстрее (ускоренно). Всё это хорошо видно по графику,
изображающему зависимость S от х (рис. 100).
Глава XIV. НЕКОТОРЫЕ ДОПОЛНИТЕЛЬНЫЕ
СВЕДЕНИЯ О ПРОЦЕНТАХ
Раздел!. ТРИ ОСНОВНЫЕ ЗАДАЧИ НА ПРОЦЕНТЫ
Понятие процент возникло в древней Греции и Риме в
связи с развитием торговли, особенно это понятие укрепилось
в городах средневековья. Слово «процент» образовано из двух
латинских слов про — на и центум — сто и в переводе значит:
на сто. Так, когда надо сказать, что на каждые 100 единиц
плана было перевыполнение на 5 единиц, говорят, что план пе-
ревыполнен на 5 процентов.
278
Процентом числа называется сотая доля этого числа. Из
итальянского слова cento получилось сокращение cto (с[о), а из
него знак %, который закрепился в печати в конце XVII века.
Вот почему ныне вместо записи 5 процентов применяется за-
пись 5%, где знак % означает множитель 0,01.
37
Например, дробь , т. е. тридцать семь сотых, можно про-
читать как «тридцать семь процентов» и записать без знамена-
теля в виде 37%. Запись 123% читается как «сто двадцать три про-
123
цента» и означает то же самое, что запись или 1,23. Если
сказано: «предприятие выполнило за неделю 27% месячного
плана», то это означает, что за неделю сделали 0,27 того, что
надо сделать за месяц.
Иногда употребляют понятие, близкое к проценту — промилль
(«на тысячу»).
Промиллем числа называется тысячная доля этого числа: так
0,005 есть пять промилле» и обозначается 5°/00, где знак °/00
означает множитель 0,001.
Можно различать три следующих типа задач на процентные
вычисления:
1. Нахождение процентного отношения первого данного числа
ко второму, т. е, выражение этого отношения в процентах.
2. Нахождение данного числа процентов от заданного числа.
3. Нахождение числа, если известно несколько процентов
этого числа.
Рассмотрим задачи каждого из этих трёх типов.
§ 285. Нахождение процентного отношения первого числа ко
второму.
На примере:
Куриное яйцо весит 60 Г, а его скор-
лупа 3 Г. Найти процентное отноше-
ние веса скорлупы к весу всего яйца.
1) Найдём отношение веса скор-
лупы к весу яйца:
3 Г : 60 Г = 1 : 20 = ^ = 0,05.
В общем виде:
Даны: I число а и II число Ь.
Найти процентное отношение I числа
ко II числу.
1) Найдём отношение 1 числа ко
II числу:
. а
а'ь~т'
2) Выразим найденное отношение в процентах:
0,05=5-0,01=5%. I а _ а • 100 а • 100
I У ~ ~Ь~ ' °’U1 “ —b /о'
Здесь знак % означает множитель 0,01.
Чтобы найти процентное отношение I числа ко II, достаточно:
1) разделить I число на II и 2) умножить полученное частное на
100 и на 0,01, передав последний множитель в виде знака %
(или выражая словом «процент»).
Например: 1) процентное отношение числа 34 к числу 40
выразится так: 34 • 0,01 =85 • 0,01 =85%;
279
2) процентное отношение числа 41 к 35 равно 41 • 0,01 =
= 117у • 0,01 = 117 у % ~ 117,14%.
Можно выразить правило нахождения процентного отношения
первого числа ко второму иначе:
Чтобы найти процентное отношение 1 числа ко II, достаточно:
1) разделить II число на 100 (узнается 1% II числа);
2) разделить I число на это частное (узнается, сколько
в I числе содержится процентов II числа);
3) поставить в найденном последнем частном множитель 0,01
в виде знака %.
Например, чтобы найти процентное отношение чисел 720
к 1800. нужно сделать следующее:
1) Найти 1% от 1800:
1800 : 100 = 18.
2) Найти отношение I числа к полученному частному:
720 :18 = 40.
3) Найти искомое процентное отношение: 40%.
Сравним вывод правила нахождения процентного отношения числа а
к числу b
в обыкновенных дробях:
а а • 100 а • 100 1
Т — b 100 — ~~Ь 100
_«• юо
/о'
в десятичных дробях:
. — 0,01 = —-— . 0 01 =
b b - 0,01 0,01 • b '
— а °/
0,01 • b /0‘
Во многих случаях легко установить устно, сколько процен-
тов второго данного числа составляет первое данное число. Вот
несколько примеров, в которых получение ответов не требует
никакой записи (расчёт делается в уме).
Выразить в % отношение 1 : 100 2 :100 9 : 100 10: 100 99 : 100
Ответ 1% 2% 9% ю% 99%
Выразить в % отношение 100 : 100 101 : 100 199 : 100 200 : 100 999 : 100
Ответ 100% 101% 199% 200% 999%
280
Выразить в % отношение 1000: 100 1,3: 100 0,4 :100 23,7 :100 2,43 :100
Ответ 1000% 1.3% 0,4% 23,7% 2,43%
Столь же просто выразить в процентах любую десятичную
дробь: для этого достаточно перенести знак дробности на два
места вправо. Например, 0,01 = 1%; 0,15=15%; 1,19=119%,
0,345 = 34,5%; 0,007 = 0,7%; 0,0002 = 0,02% и т. д.
Отметим некоторые обстоятельства, имеющие значение для
письменного решения задач на нахождение процентного отно-
шения.
Отношение двух чисел не изменяется, если оба числа уве-
личить или уменьшить в одно и то же число раз. Поэтому при
нахождении процентного отношения во многих случаях возможно
предварительное упрощение данных чисел.
Так, чтобы найти процентное отношение чисел 18000 и 16000,
делим сначала каждое из них на их НОД, равный 2000, а затем
находим отношение чисел 9 и 8, равное 1,125, или 112,5%.
Чтобы найти процентное отношение чисел 0,0014 и 0,0497,
умножаем каждое из них на 10000, а затем делим на 7; получив
таким путём числа 2 и 71, находим их отношение, равное
0,02816 ... , или, округляя до третьей значащей цифры, 0,0282,
т. е. 2,82%.
Если два данных числа мало отличаются одно от другого,
выгоднее сначала найти процентное отношение их разности
ко второму из них, а затем уже процентное отношение первого
из них ко второму (вычитанием из 100% или прибавлением
к 100%). Вот два примера.
1) Колхоз планировал улучшить 450 га лугов, а улучшил
473 га. На сколько процентов выполнен план улучшения лугов?
На этот вопрос можно ответить двумя способами:
во-первых, вычисляя (473 : 450) • 100% ~ 105,1%; во-вторых,
вычисляя [(473 — 450) : 450]% = [23 : 450] % ~ 5,1%, а затем взяв
100%+ 5,1%= 105,1%.
При втором способе можно вести расчёт иначе: надо
взять (23 : 450) - 100% = (46 : 900) • 100% = (46 :9)% = б! % =
= 5,111 ...% —5,1%.
2) Из 165 844 избирателей в выборах участвовали 165785 че-
ловек. Каков процент участия в голосовании?
Здесь лучше вычислять так: в голосовании не участвовало
165844—165785=59 человек, что составляет (59:165 844)-100% =
= 0,0355 ...%—0,04%, а участвовало 100% — 0,04% = 99,96%
всего числа избирателей.
281
Отметим ещё один часто встречающийся случай: дано не-
сколько чисел, и требуется установить, сколько процентов их
общей суммы составляет каждое из них. Это не что иное, как
задача на пропорциональное деление: число 100 надо разделить
пропорционально данным числам.
Приводим пример задачи такого рода. В помещенной ниже
табличке числа в столбце с заголовком «Сумма» являются дан-
ными, числа в столбце с заголовком «В % к итогу» появляются
в результате вычислений, проводимых с точностью до десятых
долей процента. Для проверки надо сложить числа этого столбца.
№ Виды хозяйства завода Сумма В % к итогу
1 Основные средства (здания и оборудо-
вание) 2 500000 56,4
2 Материалы и сырьё 245 000 5,7
3 Топливо 38 000 0,9
4 Касса 25 000 0,5
5 По счетам 435 000 9,8
6 Готовая продукция 580 000 13,0
7 Незавершённое производство 610 000 13,7
Итого 4 433 000 100,0%
В данной задаче получится итог ровно 100,0%, но возможно при
совершенно правильном решении небольшое отклонение от 100%
вследствие накопления ошибок округления. В таких случаях надо
провести вычисление немного точнее (скажем, до сотых процента),
а затем округлить результаты до требуемого десятичного знака,
допуская небольшое отступление от правил округления с тем,
чтобы получить в итоге ровно 100%.
§ 286. Как находить данное число процентов от заданного
числа? Научившись находить процентное отношение двух данных
чисел, перейдём к первой обратной задаче, а именно, к нахожде-
нию данного числа процентов от заданного числа.
В общем виде:
Чему равны р% от а? Иначе:
Р
наити от а.
На примере:
Чему равны 3% от 405? Иначе:
найти 0,03 от 405.
Известно, что эта задача решается умножением:
«5.0,03- 12J5. | =
Чтобы найти данное число процентов от заданного числа, до-
статочно умножить заданное число на сотую долю данного числа
процентов или, разделив заданное число на 100 (узнаётся 1% от
него), умножить полученное частное на данное число процентов
(узнаётся всё заданное число процентов от него).
282
Отметим, что задача нахождения дроби от числа и задача
нахождения данного числа процентов от заданного числа является
задачей одного типа, а потому и решается одним и тем же
приёмом.
Рассмотрим примеры письменного нахождения данного числа
процентов от заданного числа.
1) Найти 35% от 600,
Решение. 600 - 0,35 = 210,
или 6 • 35 = 210.
2) Найти 2,4% от 0,428.
Решение. 0,428 - 0,024 = 0,010272,
или 0,00428 • 2,4 = 0,010272.
3) Магнитный железняк (руда) содержит 65% железа. Сколько
будет железа в добытых 6 тыс. тонн руды?
6 тыс. Т • 0,65 = 3,9 тыс. Т ~ 4 тыс. Т.
Рассмотрим примеры устного нахождения данного числа про-
центов от заданного числа.
1) Легко находить устно 1% от любого натурального и дроб-
ного числа:
Найти Ответ
1% от 500 руб. 5 руб.
1% от 20 кГ 0,2 кГ
1% от 3 Т 0,03 Т
1% от 620 6,2
1% от 24 0,24
1% от 6 0,06
1% от 4,8 0,048
1% от 0,05 0,0005
1% от 5,06 0,0506
2) Нетрудно находить устно несколько процентов, когда число
их выражается однозначным или круглым числом:
Найти Ответ
6% от 500 руб. 5 руб. • 6 = 30 руб.
8% от 20 кГ 0,2 кГ 8=1,6кГ
4% от 3 Т 0,03 Т • 4 = 0,12 Т
6% от 6 0,06 - 6 = 0,36
5% от 1,4 0,014- 5 = 0,07
60% от 800 8 - 60 = 480
40% от 900 9 - 40 = 360
283
3) Надо научиться быстро выражать процентное отношение
в виде дроби и находить дробь от числа:
Найти Ответ
50% от 628 314, так как 50% есть 1
25% от 812 203, так как 25% есть -1
33-1% от 963 О 321, так как 33-1% есть 1. О о
12-1% от 1640 205, так как 12-1% есть _1 Z о
6-1% от 3216 201, так как 6-1% есть -1 4 1b
4) Полезно научиться находить заданное число процентов,
используя распределительное свойство:
9% от 650 руб.
11% от 850 кГ.
10% от 650 руб. равны 65 руб.
1% от 650 руб. равен 6 руб. 50 коп.
9% от 650 руб. равны 58 руб. 50 коп.
10% от 850 кГ равны 85 кГ
1% от 850 кГ равен 8,5 кГ
11% от 850 кГ равны 93,5 кГ
99% от 1500.
9-1% от 2400.
100% от 1500 1500 равны равен 1500 15
1% ОТ
99% от 1500 равны 1485.
ю% от 2400 равны 240
1°/ 4 /о от 2400 равна 6
9 3 о/ у4 /о от 2400 равны 234
§ 287. Как находить число, если известно несколько процентов
этого числа? Пусть а и b — два числа. Обозначим буквой р про-
центное отношение первого из них ко второму. Сначала мы рас-
смотрели (§ 285) задачу нахождения р по данным а и Ь, потом
первую обратную задачу (в § 286), а именно, задачу нахождения b
по данным аир. Остаётся рассмотреть вторую обратную задачу,
а именно, задачу разыскания а по данным b и р.
284
На примере: В общем виде:
Найти число, зная, что 15% от Найти число, зная, что р% от
него составляют 600. Иначе: найти число, зная, что 0,15 от него состав- ляют 600. Имеем: 0,15 х = 600, откуда х = 600 : 0,15 = 4000. него составляют а. Иначе: найти число, р зная, что от него составляют а. Имеем: 106 х = °” откуда р 100 х ~ а ’• 100 ~ а р ~ = (а : р) • 100.
Чтобы найти число, зная величину нескольких процентов этого
числа, достаточно разделить эту величину на сотую долю данного
числа процентов или, разделив эту величину на данное число
процентов (узнаётся 1% от известного числа), умножить получен-
ное частное на 100 (узнаётся всё число, или 100%).
Отметим, что задача нахождения числа, когда известно не-
сколько процентов этого числа, является задачей одного типа
с задачей нахождения числа, когда известна некоторая дробь от
этого числа, а потому и решается она одним и тем же приёмом.
Примеры письменного решения задач:
1) 35% от неизвестного числа равны 210; найти неизвестное
число.
(210 : 35) • 100 = 6 • 100 = 600,
иначе:
210 : 0,35 = 21 000 : 35 = 600.
2) 2,4% от х равны 0,010272; найти х.
х = (0,010272 :2,4) • 100 = 10,272 : 24 = 0,428,
иначе:
х = 0,010272 :0,024 = 10,272 :24 = 0,428.
3) Магнитный железняк (руда) содержит 65% железа. Сколько
надо добыть руды, чтобы иметь 4 тыс. Т железа?
(4 тыс. : 65) 100 = 0,06153 ... тыс. • 100 — 6,2 тыс. (Г).
Примеры устного решения задач:
1) Легко находить устно число, зная, чему равен 1% от него.
Найти х, зная, что Ответ
1% от х равен 40 х = 4000
1% от х равен 15 х = 1500
1% от х равен 6,3 х = 630
1% от х равен 0,7 х = 70
1% от х равен 0,11 х= 11
1% от х равен 0,054 х = 5,4
285
2) Нетрудно находить устно число, зная, чему равны несколько
процентов от него, когда данные выражены однозначными или
круглыми числами.
Найти х, зная, что Ответ
2% от х равны 40 х = (40 : 2) • 100 = 2000
15% от х равны 600 х = (600 : 15) • 100 = 4000
0,1% от х равна 35 х = 35 • 1000 = 35000
0,01% от х равна 8 х = 8 10 000 = 80 000
0,2% от х равны 4 х=2 1000 = 2000
3) Во многих случаях процентное отношение выражается
в виде некоторой доли, как, например, 50% — в виде 10% —
1 ~
в виде уд и т. д. 1огда надо выполнить такую замену и искать
число по данной его доле одним умножением.
Приводим примеры, когда решение легко выполняется устно.
Найти х, зная, что Иначе, Ответ
50% от х равны 16 j от л равна 16 х = 32
25% от х равны 250 от х равна 250 х = 1000
33-1-% от х равны 32 О 1- от х равна 32 О х = 96
12-i% от х равны 400 1 от х равна 400 О х = 3200
6-1-% от х равны 0,5 от х равна 0,5 х = 8
и т. д.
§ 288. Некоторые задачи на проценты, легко сводимые к трём
основным. Полезно сопоставить три рассмотренные основные задачи
на проценты. В каждой из них мы имеем дело с двумя числами
и с процентным отношением первого из них ко второму. Одно
из этих чисел (второе) является «стопроцентным»: оно прини-
мается за 100%.
В первой основной задаче мы знаем и первое и второе («сто-
процентное») число, а ищем процентное отношение первого числа
ко второму; задача решается делением первого числа на второе
и умножением частного на 100.
286
Во второй основной задаче дано второе («стопроцентное») число
и процентное отношение к нему первого (искомого) числа; задача
решается делением данного процентного отношения на 100 и умно-
жением данного «стопроцентного» числа на полученное частное.
В третьей основной задаче мы знаем первое число и процентное
его отношение ко второму (неизвестному «стопроцентному») числу
и ищем это последнее; задача решается делением данного про-
центного отношения на 100 и делением данного числа на полу-
ченное частное.
Рассмотрим некоторые задачи на проценты, встречающиеся
в жизненной практике, и покажем, как они сводятся к основным.
Задача 1. После снижения цены на 15% товар продаётся
по 4 руб. 25 коп. за 1 кГ. Какова была цена товара до сни-
жения?
Решение. Сниженная цена составляет 100% — 15% = 85%
старой. Следовательно, задача сводится к нахождению числа,
85% которого составляет 4 руб. 25 коп., или 425 коп. Это число
равно 425 :0,85 = 42 500 : 85 — 500.
Ответ. Прежняя цена была 5 руб. за 1 кГ.
Задача 2. За перевод денег по почте взимается 2% пере-
водимой суммы. Требуется перевести 500 руб. так, чтобы пере-
водимая сумма вместе с почтовыми расходами, включая стоимость
бланка (5 коп.) составила ровно 500 руб. На какую сумму надо
написать перевод?
Решение. Принимая неизвестную переводимую сумму за
100% и прибавляя 2% её, взимаемые почтой, получаем всего 102%.
Эти 102% равны 499 руб. 95 коп. (из 500 руб. вычитается стои-
мость бланка). Задача свелась к нахождению числа, 102% кото-
рого составляют 499 руб. 95 коп. Это число равно 499,95 : 102% —
= 490,147 ...
Ответ. Перевод надо написать па 490 руб. 15 коп.
Для проверки находим 2% этой суммы, что составляет
490,15 : 50 = 9,803 ___ или 9 руб. 80 коп. Всего имеем:
490 руб. 15 коп. -р 9 руб. 80 коп. -f- 5 коп. = 500 руб. 00 коп.
Задача 3. Свежие грибы содержат 90% влаги, сушёные —
12% влаги. Сколько сушёных грибов выйдет из 10 кГ свежих?
Сколько свежих грибов надо собрать, чтобы получить 10 кГ су-
шёных?
Решение. Сначала узнаем, сколько сухого вещества со-
держится в 10 кГ свежих грибов, т. е. сколько получилось бы
сухих грибов, если бы вся влага была удалена: (100% — 90%—
= 10%); 10% от 10 кГ составляют 1 кГ. Но в сушёных грибах
содержится 12% влаги, а сухое вещество составляет, следова-
тельно, 100% — 12% — 88%. Итак, первый вопрос задачи сво-
дится к тому, чтобы узнать число, 88% которого равны 1 кГ.
Находя его, получаем:
1 : 0,88 = 1,13636 ... — 1,136 (кГ).
287
Ответ. Из 10 кГ свежих грибов выйдет 1136 Г, или прибли-
жённо 1,1 кГ сушёных.
Для ответа на второй вопрос узнаем, сколько сухого веще-
ства содержится в 10 кГ сушёных грибов (88% от 10 кГ состав-
ляют 8,8 кГ). Но это сухое вещество составляет только 10% веса
свежих грибов, а потому для получения 10 кГ сушёных грибов
надо взять (8,8 : 10) • 100 = 8,8 • 10 = 88 кГ свежих.
Задача 4. Сберегательная касса начисляет 1 января каж-
дого года на каждый вклад процентные деньги из расчёта 2%
годовых для обыкновенного вклада и 3% для срочного вклада,
причем для упрощения расчётов год считается за 360 дней, каждый
месяц за 30 дней. Сколько процентных денег начислит сберкасса
на вклад в 1480 руб., внесённый 30 апреля предшествующего
года?
Замечая, что эти деньги были в сберкассе в течение 8 меся-
цев, находим, что если они были внесены как обыкновенный
2 - 1480 - 8 й -,о
вклад, на них надо начислить —ущ—j2~~ = 19 руб. 73коп., а если
и 3 • 1480 • 8
как срочный, то —— 29 руб. 60 коп.
Задача 5. Некоторое усовершенствование снизило себесто-
имость изделий (т. е. те расходы, какие песёт предприятие, чтобы
изготовить эти изделия) с 5000 руб. до 4000 руб. Какой процент
снижения себестоимости оно дало? На сколько процентов повы-
сится эта сниженная себестоимость, если отказаться от него,
т. е. вернуться к тому, что было до его введения?
При ответе на первый вопрос за 100% следует принять преж-
нюю себестоимость, т. е. 5000 руб.; снижение себестоимости со-
ставляет 5000 — 4000= 1000 руб., или 20% прежней себестои-
мости.
При ответе на второй вопрос за 100% принимается сни-
женная себестоимость (4000 руб.). Отказ от усовершенствования
повысит себестоимость на 1000 руб., или на 25%.
Отметим в заключение, что при решении всевозможных задач
на проценты делом первостепенной важности является выясне-
ние того, какое число, данное или искомое, принимается за 100%.
Раздел 2. НЕКОТОРЫЕ БОЛЕЕ СЛОЖНЫЕ ЗАДАЧИ
НА ПРОЦЕНТЫ
§ 289. Вычисление среднего процента. Чтобы найти среднее
из нескольких данных чисел, надо взять их сумму и разделить
её на число слагаемых. Но при вычислении среднего процента
во многих случаях приходится применять более сложный расчёт,
как это можно видеть на следующем примере.
Фабрика выпустила в I квартале 25 тыс. единиц продукции,
в том числе 40% первым сортом, а во II квартале уже 80 тыс.
единиц, причём первым сортом 90%. Каков в среднем за I и II
288
кварталы выпуск первосортной продукции в процентах от всего
количества выпущенной продукции?
Здесь надо узнать, сколько единиц первосортной продукции
было выпущено за каждый квартал в отдельности (40% от 25,
или 10 тыс. за I квартал, 90% от 80, или 72 тыс. за II квар-
тал) и сколько за I и II кварталы вместе (104-72=82 тыс.), а
затем найти процентное отношение выпущенной за оба квартала
первосортной продукции ко всему её количеству (25 4~ 80 = 105).
Получим (82:105)- 100 = 78,09 ...~78.1%.
Таков правильный ответ на поставленный вопрос. Взяв же
просто среднее из обоих указанных в условии процентных отно-
шений, мы получили бы неверный ответ, а именно (40% 4*
+ 90%): 2 = 65%. Его неправильность обусловлена тем, что 1%
продукции I квартала равен только 0,25 тыс. единиц, а 1 % про-
дукции II квартала гораздо больше 0,8 тыс. единиц; складывать
40% продукции I квартала и 90% продукции II квартала так же
бессмысленно, как при сложении 40 г и 90 кг получать сумму
404-90=130 (чего?).
При вычислении среднего процента по нескольким группам
простое среднее арифметическое из чисел, выражающих соответ-
ствующее процентное отношение по каждой группе в отдельности,
не даёт таким образом правильного результата. Здесь необхо-
димо вычисление взвешенного среднего: предварительно надо умно-
жить каждое процентное отношение на число, показывающее
численность соответствующей группы (её вес), а затем сумму всех
полученных произведений разделить на сумму численностей (сумму
весов) всех групп.
Если, например, имеются четыре группы численностью в 30,
75, 135, 160 предметов и требуется установить средний процент
по всем четырём группам, зная, что по отдельным группам он
равен 40%, 60%, 64%, 70%, то правильный результат даётся
формулой:
_ 40% - 30 + 60% • 75 + 64% 135 + 70% • 160 _ 25540% _ Ro/
Р 30 + 75 + 135 + 160 400 ~ ’ /о’
Обозначив процентное отношение по каждой группе буквами
Рх> Рз> • • »
а соответствующие веса (численности) групп буквами
аъ а2, а3, . , ak,
имеем следующую формулу взвешенного среднего р:
__Pi% • а1 4- Р2% • а2 4- Рз% • Дз 4~ • -4- Pk% ‘ ok
Р ~ Щ 4- а2 + а3 + . . . + ak
Если = а2 = а3 = ... = ak = а, то предшествующая формула
выразится так:
_ (pi% 4- Рг%4- • • • 4- Pfe%) • а_ Р1% 4- Pz% 4- • - - 4- Pk%
р____________________________a - k ~ k
289
§ 290. Понятие о сложных процентах. Рассмотрим такую за-
дачу: планом предусмотрено ежегодное увеличение суточного вы-
пуска продукции на 20%; какое увеличение суточной продукции
по сравнению с той, какая была к началу пятилетки, будет тем
самым обеспечено к её концу?
Казалось бы, ответить на этот вопрос очень просто: при 20%
увеличения продукции за год увеличение за 5 лет составит
20-5= 100%; к концу пятилетки продукция удвоится. Однако
этот ответ неверен, что показывает следующий подробный рас-
чёт.
Суточная продукция к началу I года принимается за 100%.
К концу I года будем иметь:
100% 4-20% от 100 равно 100% 4-20% = 120%;
к концу II года будем иметь:
120% 4- 20% от 120 равно 120% 4- 24% = 144%;
к концу III года будем иметь:
144% 4-20% от 144 равно 144% 4-28,8% = 172,8%;
к концу IV года будем иметь:
172,8% 4-20% от 172,8 равно 172,8% 4- 34,56% = 207,36%;
к концу V года будем иметь:
207,36% 4-20% от 207,36 равно 207,36% 4-41,472% = 248,832%
т. е. почти 249% того, что было в начале пятилетки. Итак, еже-
годный прирост в 20% означает, что за пятилетку произойдёт
увеличение не вдвое, как показывает простое умножение 20% на
5, а почти в 2~ раза.
Причина ошибочности первого расчёта в том, что прирост в
20% за каждый следующий год означает уже не такое прираще-
ние продукции, как в первый год, а большее. Как говорят, здесь
нужен расчёт не в простых, а в сложных процентах, или с учё-
том процентов на проценты.
Если 1 января положить в сберкассу некоторую сумму денег,
например 1000 руб., и 1 января каждого следующего года брать
те 30 руб., какие будут начислены за год на эту сумму (при
срочном вкладе), то за 10 лет мы возьмём всего 30 10 = 300 руб.,
так что вместе с той тысячей, какая была внесена, будем иметь
всего 1300 руб.
Получится более быстрый рост вклада, если начисленные
1 января деньги мы будем оставлять в сберкассе, так что в те-
чение следующего года процентные деньги будут начисляться
уже не только на ту сумму, какая была до 1 января, а и на
эти начисленные процентные деньги («проценты на проценты»),
290
Ведя расчёт для каждого года в отдельности, как это было
сделано выше при вычислении роста продукции, или применяя
более удобный способ вычисления сложных процентов, найдём,
что через 10 лет вклад составит уже не 1000 руб., а 1343 руб.
92 коп.
Рассмотрим ещё один вопрос, где опять придётся иметь дело
со сложными процентами. Положим, имеется зерноочистительная
машина, устроенная так, что каждый раз пропускаемое через
неё зерно теряет 90% примесей, т. е. того сора, который в ней
содержится. Что даст трёхкратное пропускание зерна через эту
машину? После первого пропускания в зерне останется только
100—90=10% примеси, какая была в нём первоначально. Второе
пропускание удалит 90% от этих 10% и оставит, следовательно,
только 1% примесей. После третьего пропускания получим зер-
но, содержащее лишь 0,1% тех примесей, какие оно содержало
до начала очистки.
С возрастанием и убыванием величин по закону сложных
процентов приходится встречаться при изучении многих явлений
природы и многих видов деятельности человека. Подробное изу-
чение этого закона относится к другой математической науке —
алгебре.
ПАМЯТКА
О ТОМ, СКОЛЬКО И КАКИХ НЕОБХОДИМО УСВОИТЬ «ЭЛЕМЕНТОВ
ЗНАНИЙ» И ПРИОБРЕСТИ УМЕНИЙ И НАВЫКОВ, СВЯЗАННЫХ
С ИЗУЧЕНИЕМ ОСНОВНОГО КУРСА АРИФМЕТИКИ
I. Умение подбирать примеры, поясняющие смысл тех понятий, которым
в этом пособии не дано определений, как-то: множество и элемент множества;
численность множества; натуральное число и натуральный ряд чисел; равное
и неравное, большее и меньшее множество элементов; общие элементы мно-
жеств; удаление части множества.
II. Знание определений понятий, рассмотренных в этом пособии, с уме-
нием пояснять их соответствующими примерами (напомним ещё раз, что до-
словного заучивания не требуется, определения можно излагать иначе, своими
словами, но непременно правильно);
1) Нуля; словесного исчисления; разряда и класса; письменной нумера-
ции; однозначного, двузначного и многозначного числа; круглого и разрядного
числа; количественных и порядковых чисел.
2) Суммы натуральных чисел; сложения; слагаемого; прибавление нуля;
разности; вычитания; уменьшаемого; вычитаемого; произведения; умножения;
множимого; множителя; сомножителей; умножения на единицу и нуль; част-
ного; деления без остатка; делимого; делителя; деления с остатком; простой
и составной задачи; числовой формулы.
3) Делителя и кратного; взаимно дополнительных делителей; признака
делимости; простого и составного числа; общего делителя и НОД; взаимно
простых чисел; общего кратного и НОК.
4) Отрезка; луча; метрических единиц длины; простого и составного име-
нованного числа; раздробления и превращения; окружности и круга; радиуса,
диаметра и хорды окружности; дуги и дугового градуса; угла, развёрнутого
и прямого угла, острого и тупого угла; угольника и эккера; транспортира;
прямоугольника и квадрата; вершин и сторон прямоугольника; квадратной
единицы и метрических квадратных единиц; площади фигуры; бруса и куба;
вершин, рёбер и граней бруса; кубических единиц; объёма тела; литра,
грамма и килограмма; суток; часа; минуты и секунды; недели, года и века;
месяца и квартала; старого и нового стиля; поясного времени.
5) Доли элемента; дроби; числителя и знаменателя; членов дроби; пра-
вильной и неправильной дробей; процента и промилля; отношения чисел;
сокращения дроби; суммы и разности дробей; умножения дроби на натураль-
ное число, большее единицы, на единицу и на нуль; деления дроби на нату-
ральное число; умножения на дробь; деления на дробь.
6) Десятичной дроби; периодического ряда; чистого и смешанного перио-
дического ряда; средне-арифметического; средне-взвешенного; приближённого
числа; десятичных знаков и значащих цифр.
7) Отношения величин; первого (предыдущего) и второго (последующего)
членов отношения; пропорции; средних и крайних членов пропорции; двух
пар пропорциональных чисел; прямой и обратной пропорциональности между
величинами; равномерного возрастания и убывания; линейной зависимости;
пропорциональности квадрату и кубу.
Ill. Знание предложений, в которых передаются связи одних понятий с
другими, вместе с умением (хотя бы на частных примерах) их выводить и
применять к упрощению вычислений:
292
I) Переместительного и сочетательного законов сложения и умножения;
распределительного закона умножения относительно суммы и разности; вычи-
тания суммы и из суммы, прибавления и вычитания разности; деления числа
на единицу и на само это число; деления нуля, невозможности деления на
нуль; деления суммы и разности; деления произведения и на произведение;
проверки сложения, вычитания, умножения и деления; числа цифр в произ-
ведении и частном; изменения суммы, разности, произведения и частного;
совместного изменения данных при сложении, вычитании, умножении и деле-
нии; чему равно слагаемое, уменьшаемое, вычитаемое; сомножитель; делимое
и делитель при делении без остатка и с остатком, если известны результат и
одно из двух данных.
2) Сравнительных свойств делителей и кратного; признаков делимости
суммы, разности и произведения; признаков делимости на 2, 5 и 10, на 4, 25
и 100, на 8, 125, 250, 500 и 1000, на 9 и 3, на 6, 12 и 15; бесконечности
множества всех составных и простых чисел; «Эратосфенова решета» при со-
ставлении таблицы простых чисел; взаимной связи составных и простых чисел;
общего признака делимости; четырёх свойств НОД; нахождения двумя приё-
мами НОД; трёх свойств НОК; нахождения двумя приёмами НОК.
3) Проверки линейки и угольника; свойств прямоугольника; нахождения
площади прямоугольника и квадрата; двух основных задач иа площади пря-
моугольника и квадрата; нахождения площади параллелограмма и треуголь-
ника; свойств бруса; нахождения объёма бруса и куба; трёх основных задач
на объём бруса и куба; трёх основных задач на нахождение временных про-
межутков, начала и конца события.
4) Деления множества на равные части; трёх возможных случаев нерав-
ных дробей; представления неправильной дроби в виде целого с дробью и
обратной задачи; деления натуральных чисел во множестве дробей; представ-
ления натуральных чисел в виде дробных; нахождения дроби от числа и на-
хождения числа, зная, чему равна указанная от него дробь; кратного изменения
числителя и знаменателя; совместного изменения членов дроби; основного
свойства дроби; сокращения дроби и условие несократимости дроби; приведе-
ния дробей к одному наименьшему знаменателю; как находить сумму и раз-
ность дробей; переместительного и сочетательного закона сложения и умно-
жения; распределительного закона относительно суммы и разности; пяти
свойств вычитания дробей; вывода площади прямоугольника и объёма бруса,
если стороны и рёбра их выражены дробными числами; шести свойств деления
дробных чисел.
5) Пяти свойств десятичных дробей; обоснования сложения и вычитания
десятичных дробей; умножения на разрядную единицу и умножения десятич-
ных дробей; деления иа разрядную единицу; деления в десятичных дробях —
три случая.
6) Возможности бесконечного деления; необходимых и достаточных усло-
вий возможности представления несократимых дробей в виде десятичных; не-
обходимых и достаточных условий получения чистого и смешанного периоди-
ческих рядов из данной дроби и обратные две задачи; округления по недо-
статку и избытку; сложения и вычитания, умножения и деления приближённых
чисел; длины окружности и диаметра её; площади многоугольника и круга;
площади поверхности цилиндра и объёма его.
7) Упрощения отношения; взаимной связи первого (предыдущего) и вто-
рого (последующего) членов отношения; основного свойства пропорции; не-
обходимых и достаточных условий возможности получения пропорции из
четырёх чисел; нахождения неизвестного члена пропорции; возможной пере-
становки членов пропорции; производных пропорций, получаемых из данной
пропорции; пяти свойств величин, находящихся в прямой пропорциональности;
четырёх свойств величин, находящихся в обратной пропорциональной зависи-
мости; сложных пропорциональных зависимостей.
IV. Устойчивые навыки культурных способов вычисления, рациональных
приёмов решения задач и сознательного пользования правилами, изложенными
в этом пособии, с умением их выводить хотя бы на частных примерах:
1) Чтение и запись натуральных чисел; сложение и вычитание: табличное.
293
круглых и многозначных чисел устно, письменно и инструментально; умно-
жение и деление: табличное, на разрядную единицу, круглых и многозначных
чисел (при делении — три случая) устно, письменно, инструментально и по
готовым таблицам.
2) Распознавание вида данного числа — простое оно или составное; тех-
ника разложения составного числа на произведение простых; техника нахож-
дения НОД и НОК-
3) Проведение прямых на бумаге и на земле; преобразование именован-
ных чисел; техника измерения отрезков и углов; построение развёртки бруса;
техника деления на равные части отрезка и прямоугольника, окружности и
круга.
4) Техника сокращения дробей и приведения их к одному наименьшему
знаменателю; техника сложения и вычитания дробей; правило умножения и
деления дробей на натуральные числа; правило умножения и деления дробей;
совместные действия.
5) Чтение и запись десятичных дробей; техника сложения, вычитания,
умножения и деления десятичных дробей устно, письменно и инструментально;
умножение и деление по готовым таблицам; совместные действия.
6) Четыре правила округления; вычисление с наперёд заданной точностью;
таблицы, графики и диаграммы при изучении зависимых величин; три вида
сравнений значений величин; техника нахождения четвёртого пропорциональ-
ного; техника наглядного изображения прямых и обратных пропорциональных
зависимостей, равномерного возрастания и убывания, линейной зависимости;
умение решать три основные задачи на проценты тремя способами и сводить
к ним другие встречающиеся задачи на проценты; умение решать три основ-
ные задачи на пропорциональное деление; умение иайти средний процент.
V. Знание общепринятых соглашений относительно введённых обозначений:
поместного значения цифр при записи натуральных чисел и десятичных дро-
бей; четырёх правил порядка действий в числовых формулах; соглашения
относительно горизонтальной черты как знака деления, когда это обозначение
входит в числовую формулу; запись приближённых чисел по правилу Кры-
лова, подчёркивание чёрточкой снизу тех разрядов, за которые не могут ру-
чаться; знаки % и °/00; знаки > и < ; римские числовые знаки.
СОДЕРЖАНИЕ
Предисловие...................................................... 2
К учащимся....................................................... 3
ЧАСТЬ 1. НАТУРАЛЬНЫЕ ЧИСЛА И НУЛЬ
Глава I. Нумерация
§ 1. Множество и его элементы.................................... 5
§ 2. Численность множества. Натуральные числа.................... —
§ 3. Порядок при подсчёте элементов множества.................... 6
§ 4. Натуральный ряд бесконечен.................................. —
§ 5. Число нуль.................................................. —
§ 6. Что такое словесная нумерация?.............................. —
§ 7. Разложение множества на десятки и образование разрядов в деся-
тичной нумерации. Счёт десятками................................. 7
§ 8. Составление множества из единиц, десятков и сотен. Образование
классов в десятичной нумерации................................... 8
§ 9. Что такое письменная нумерация?............................. 9
§ 10. Цифры и поместное значение цифр............................ —
§11. Виды чисел................................................. —
§12. Как прочитать число, записанное цифрами?.................. 10
§ 13. Как записать число цифрами?................................ —
§ 14. Количественные и порядковые натуральные числа............. 11
§ 15. Римская нумерация......................................... 12
Глава II. Сложение и вычитание
Раздел 7. Теория сложения
§16. Объединение множеств...................................... 13
§17. Сумма натуральных чисел................................... 14
§ 18. Обозначение суммы.................................... . —
§ 19. Переместительный закон сложения........................... 15
§ 20. Сочетательный закон сложения............................... —
§ 21. Сложение с числом нуль.................................... 16
Раздел 2. Техника устного и письменного сложения
§ 22. Сложение однозначных чисел, или табличное сложение........ 16
§ 23. Сложение круглых чисел.................................... 17
§ 24. Сложение многозначных чисел............................... 18
§ 25. Устное сложение........................................... 19
§ 26. Проверка сложения.......................................... —
Раздел 3. Теория вычитания
§ 27. Удаление части множества.................................. 19
§ 28. Разность натуральных чисел................................ 20
§ 29. Связь вычитания со сложением............................... —
295
§ 30. Вычитание суммы.......................................... 21
§ 31. Вычитание из суммы....................................... 22
§ 32. Прибавление разности...................................... —
§ 33. Вычитание разности....................................... 23
Раздел 4. Техника устного и письменного вычитания
§ 34. Табличное вычитание...................................... 23
§ 35. Вычитание многозначных чисел............................. 24
§ 36. Устное вычитание......................................... 25
§ 37. Вычитание по способу дополнения.......................... —
§ 38. Проверка вычитания и сложения ........................... 26
Раздел 5. Сложение и вычитание на приборах
§ 39. Русские счёты............................................ 26
§ 40. Арифмометр «Феликс»...................................... 28
Глава III. Умножение и деление
Раздел /.Теория умножения
§ 41. Объединение множеств одинаковой численности.............. 30
§ 42. Произведение натуральных чисел........................... 31
§ 43. Переместительный закон умножения.......................... —
§ 44. Сочетательный закон умножения............................ 33
§ 45. Распределительный закон умножения........................ 34
§ 46. Умножение на единицу..................................... 35
§ 47. Умножение нуля и умножение иа нуль....................... 36
Раздел 2. Техника устного и письменного умножения
§ 48. Табличное умножение...................................... 36
§ 49. Умножение круглых чисел.................................. 37
§ 50. Умножение многозначного числа на однозначное............. 38
§ 51. Умножение многозначных чисел.............................. —
§ 52. Число цифр в произведении................................ 39
§ 53. Устное умножение.......................................... —
§ 54. Проверка умножения....................................... 40
Раздел 3. Теория деления
§ 55. Разложение данного множества на новые множества одинаковой
численности ................................................... 41
§ 56. Частное натуральных чисел................................ 42
§ 57. Связь деления с умножением................................ —
§ 58. Особые случаи деления.................................... 43
§ 59. Деление суммы и разности ................................. —
§ 60. Деление произведения и деление на произведение........... 44
§ 61. Число цифр в частном..................................... 45
§ 62. Деление с остатком........................................ —
§ 63. Деление в широком смысле................................. 46
Раздел 4. Техника устного и письменного деления
§ 64. Табличное деление........................................ 46
§ 65. Деление на 10, 100, 1000 и т. д........................... —
§ 66. Деление круглых чисел...............................• . 47
§ 67. Деление на однозначное число.............................. —
§ 68. Деление многозначного числа в случае однозначного частного . . 48
296
§ 69. Деление произвольных многозначных чисел........ . . . 49
§ 70. Устное деление........................................... 50
§71. Проверка деления и умножения............................. 51
Раздел 5. Умножение и деление с помощью таблиц
и вычислительных приборов
§ 72. Таблицы произведений..................................... 51
§ 73. Русские счёты............................................ 52
§ 74. Арифмометр «Феликс».................................... 53
Глава IV. Совместные действия
Раздел 1. Взаимная связь данных и результатов
действий
§ 75. Сложение и вычитание..................................... 54
§ 76. Умножение и деление...................................... 55
§ 77. Деление с остатком....................................... 56
Раздел 2. Изменение результатов действий в зависи-
мости от изменения данных
§ 78. Изменение суммы.......................................... 57
§ 79. Изменение разности....................................... 58
§ 80. Изменение произведения.................................... —
§ 81. Изменение частного....................................... 59
Раздел 3. Задачи и запись их решений посредством
формул
§ 82. Задачи простые и составные.........................«... 60
§ 83. План решения составной задачи............................. —
§ 84. Вычисления согласно плану................................ 61
§ 85. Числовая формула.......................................... —
§ 86. Порядок действия в числовых формулах..................... 62
§ 87 Запись наименований...................................... 65
§ 88. Поиски плана решения задачи.............................. 66
Глава V. Делимость натуральных чисел
Раздел 1. Делители и кратные
§ 89. Делители данного натурального числа...................... 68
§ 90. Кратные данного натурального числа ....................... —
§ 91. Сравнительные свойства делителей и кратных данного натураль-
ного числа..................................................... 69
§ 92. Нахождение всех делителей данного натурального числа .... —
Раздел 2. Признаки делимости
§ 93. Что называется признаком делимости?...................... 70
§ 94. Признаки делимости суммы................................. 71
§ 95. Признак делимости разности............................... 72
§ 96. Признак делимости произведения........................... 73
§ 97. Признаки делимости на 2, 5, 10........................... 74
§ 98. Признаки делимости на 4, 25, 50, 100 .................... 75
§ 99. Признаки делимости на 8, 125, 250, 500, 1000 ............. —
§ 100. Признаки делимости на 3 и на 9.......................... 76
§ 101. Признаки делимости на 6, 12, 15......................... 77
297
Раздел 3. Числа простые и составные
§ 102. Три вида натуральных чисел.................................. 77
§ 103. Простые делители составного числа....................... 78
§ 104. Распознавание простых и составных чисел.................. —
§ 105. Бесконечность множества составных и множества простых чисел 80
§ 106. Составление таблицы простых чисел в промежутке от 1 до М . . —
§ 107. П. Л. Чебышев и И. М. Виноградов............................ 82
Раздел 4. Разложение чисел на простые множители
§ 108. Как выразить составное число в виде произведения простых
чисел?..................................................... 83
§ 109. Техника разложения составных чисел на простые множители . . 85
§ НО. Общий признак делимости...................................... 86
Глава VI. Наибольший общий делитель и наименьшее общее кратное
данных чисел
Раздел 1. Общи е делители и наибольший общий де-
литель
§111. Что называется общим делителем данных натуральных чисел?. . 86
§ 112. Что называется наибольшим общим делителем данных натураль-
ных чисел?................................................... 87
§ 113. Взаимно простые числа...................................... 88
§ 114. Некоторые свойства НОД...................................... 89
Раздел 2. Техника нахождения наибольшего общего
делителя
§ 115. Нахождение НОД посредством разложения на множители ... 90
§ 116. Нахождение всех общих делителей при помощи наибольшего
общего делителя............................................... —
§ 117. Способ нахождения наибольшего общего делителя, основанный на
последовательном делении..................................... 91
Раздел 3. Общие кратные и наименьшее общее крат-
ное данных чисел
§ 118. Что называется общим кратным данных натуральных чисел? . 93
§ 119. Что называется наименьшим общим кратным данных натураль-
ных чисел?................................................... 94
§ 120. Некоторые свойства НОК....................................... —
Раздел 4. Техника нахождения наименьшего общего
кратного
§ 121. Нахождение наименьшего общего кратного посредством разложе-
ния на простые множители..................................... 96
§ 122. Нахождение наименьшего общего кратного посредством наи-
большего общего делителя..................................... 97
ЧАСТЬ II. ДРОБНЫЕ ЧИСЛА
Глава VII. Величины и их значения
§ 123. Счёт и измерение........................................... 98
Раздел 1. Отрезок и его длина
§ 124. Прямая линия................................................ 98
§ 125. Отрезок и единицы длины.................................... 100
§ 126. Измерение длины.............................................. —
§ 127. Метрические меры длины..................................... 101
298
§ 128. Старые русские и некоторые зарубежные меры длины......... 101
§ 129. Простые и составные именованные числа. Раздробление и пре-
вращение ......................................................... —
§ 130. Измерения по плану и карте. Масштаб . . •................ 102
Раздел 2. Окружность
§ 131. Определение окружности................................... 102
§ 132. Циркуль.................................................. 103
§ 133. Дуга и дуговой градус.................................... 104
§ 134. Длина окружности и длина дуги окружности................. 105
§ 135. Происхождение метра....................................... —
Раздел 3. Угол и его измерение
§ 136. Луч...................................................... 106
§ 137. Угол....................................................... —
§ 138. Развёрнутый и прямой угол................................ 107
§ 139. Угольник................................................. 108
§ 140. Эккер.................................................... 109
§ 141. Измерение углов в градусах................................. —
Раздел 4. Площади
§ 142. Прямоугольник и квадрат................................... ПО
§ 143. Квадратные единицы......................................... —
§ 144. Площадь прямоугольника................................... 111
§ 145. Площадь квадрата......................................... 112
§ 146. Задачи на площадь прямоугольника......................... 113
§ 147. Задачи на площадь квадрата............................... 114
§ 148. Старые русские меры площади................................ —
§ 149. Площади параллелограмма и треугольника..................... —
Раздел 5. Брус и куб
§ 150 Брус............................................... 116
§ 151. Изготовление модели бруса........ —
§ 152. Куб............... 117
§ 153. Кубические единицы.............. —
§ 154. Объём бруса............... 118
§ 155. Объём куба............... 119
§ 156. Задачи на объём бруса................. —
§ 157. Задачи на объём бруса с квадратным основанием и на объём
куба............................................................ 120
Раздел 6. Объём жидких и сыпучих тел
§ 158. Литр..................................................... 121
§ 159. Старые русские меры ёмкости................................ —
Раздел 7. Вес
§ 160. Грамм, килограмм, тонна.................................. 121
§ 161. Другие метрические меры веса............................. 122
§ 162. Старые русские меры веса................................... —
Раздел 8. Время
§ 163. Сутки и части суток...................................... 123
§ 164. Неделя................................................... 124
§ 165. Год и век.................................................. —
§ 166. Месяц и квартал.......................................... 125
299
§ 167. Датирование................................................ 126
§ 168. Календарь. Старый и новый стиль............................ 127
§ 169. Поясное время.............................................. 128
§ 170. Задачи на время............................................ 129
Глава VIII. Множество долей и дроби
Раздел 1. Деление множества на равные части (доли)
§ 171. Доли элементов (предметов)............................. 130
§ 172. Деление отрезка и прямоугольника на равные части....... 131
§ 173. Деление окружности и круга на равные части............. 133
§ 174. Деление множества на равные части...................... 134
Раздел 2. Д р о б и, их равенство и неравенство
§ 175. Определение дроби...................................... 134
§ 176. Равенство и неравенство дробей......................... 135
§ 177. Дроби правильные и неправильные........................ 137
§ 178. Деление натуральных чисел.............................. 140
§ 179. Представление натурального числа в виде дроби.......... 141
§ 180. Проценты................................................. —
Раздел 5. Три основные задачи на дроби
§ 181. Нахождение дроби от числа ............................. 142
§ 182. Нахождение числа по его дроби............................ —
§ 183. Нахождение отношения двух чисел........................ 143
§ 184. Некоторые более сложные задачи на дроби, сводящиеся к ос-
новным .........................•............................. 144
Раздел 4. Свойства дробных чисел
§ 185. Кратное изменение числителя............................ 146
§ 186. Раздробление (размельчение) и укрупнение долей......... 147
§ 187. Кратное изменение знаменателя.......................... 149
§ 188. Основное свойство дроби.................................. —
§ 189. Сокращение дробей...................................... 150
§ 190. Приведение дробей к одному знаменателю................. 152
Глава IX. Сложение и вычитание дробей
Раздел 1. Сложение дробей
§ 191. Сумма дробей с равными знаменателями................... 154
§ 192. Сумма дробей с разными знаменателями................... 155
§ 193. Свойства сложения дробей............................... 156
§ 194. Техника сложения дробей................................ 157
§ 195. Проверка сложения дробей............................... 159
Раздел 2. Вычитание дробей
§ 19 G. Разность дробей....................................... 159
§ 197. Свойства вычитания дробей.............................. 160
§ 198. Техника вычитания дробей............................... 161
§ 199. Проверка вычитания дробей.............................. 162
§ 200. Совместное сложение и вычитание дробей................... —
300
Глава X. Умножение и деление дробей
Раздел 1. У м н о ж е н и е дроби на натуральное число
и на нуль и деление на натуральное число
§ 201. Определение умножения дроби иа натуральное число и на нуль 163
§ 202. Правило умножения дроби на натуральное число........... 164
§ 203. Деление дроби на натуральное число..................... 165
Раздел 2. Умножение на дробь
§ 204. Недостаточность прежнего определения умножения......... 167
§ 205. Новое определение действия умножения................... 168
§ 206. Правило умножения дробей............................... 169
§ 207. Свойства умножения дробей.............................. 171
§ 208. Техника умножения дробей............................... 173
§ 209. Вычисление площади прямоугольника и объёма бруса....... 174
Раздел 5. Деление на дробь
§210. Определение частного................................... 177
§ 211. Правило деления дробей................................... —
§ 212. Техника деления дробей................................. 178
§ 213. Что выражает частное?.................................. 179
§ 214. Свойства деления дробей.................................. —
§ 215. Задачи на площадь прямоугольника и объём бруса......... 182
§ 216. Совместные действия с дробями.......................... 183
Глава XI. Десятичные дроби
Раздел /.Определение и свойства десятичных дробей
§ 217. Почему действия с дробными числами проводятся значительно
сложнее, чем те же действия с натуральными числами?.......... 184
§218. Открытие десятичных дробей............................... —
§ 219. Определение десятичных дробей.......................... 186
§ 220. Чтение и запись десятичных дробей...................... 187
§ 221. Свойства десятичных дробей............................... —
§ 222. Проценты и промилли.................................... 190
Раздел 2. Сложение, вычитание, умножение и деление
десятичных дробей
§ 223. Сложение десятичных дробей............................. 190
§ 224. Вычитание десятичных дробей............................ 191
§ 225. Умножение и деление на 10, 100, 1000 и т. д............ 193
§ 226. Умножение десятичных дробей.............................. —
§ 227. Умножение десятичных дробей при помощи таблиц и вычисли-
тельных приборов. Проверка умножения......................... 194
§ 228. Деление натуральных чисел.............................. 195
§ 229. Деление десятичной дроби на натуральное число.......... 197
§ 230. Деление дроби на дробь................................... —
§ 231. Случай бесконечного деления............................ 198
Раздел 3. Представление обыкновенных дробей в
виде десятичных и обратная задача
§ 232. Представление обыкновенных дробей в виде десятичных спосо-
бом умножения................................................ 199
§ 233. Представление обыкновенных дробей в виде десятичных способом
деления ....................................................... —
301
§ 234. Обыкновенные дроби, не допускающие представления в виде де-
сятичных ................................................... 200
§ 235. Представление десятичной дроби в виде обыкновенной.. 201
Раздел 4. Периодические десятичные ряды
§ 236. Периодичность частного при бесконечном делении...... 202
§ 237. Получение чистого периодического десятичного ряда... 203
§ 238. Получение дроби, соответствующей данному чистому периодиче-
скому десятичному ряду...................................... 205
§ 239. Получение смешанного периодического десятичного ряда .... 206
§ 240. Получение дроби, соответствующей данному смешанному перио-
дическому десятичному ряду.................................. 207
Раздел 5. О совместных действиях с обыкновенными
и десятичными дробями
§ 241. Вычисления с обыкновенными дробями и целесообразность их
замены десятичными дробями.................................. 209
§ 242. Вычисления, когда в числовую формулу входят и обыкновенные
и десятичные дроби......................................... —
Глава XII. Приближённые значения величин н действия над ними
Раздел 1. Приближённые результаты счёта и
измерения
§ 243. Счёт элементов множества большой численности........ 211
§ 244. Точность измерения длины и других величин........... 213
§ 245. Запись результатов счёта и измерения. Повторные измерения . . 215
Раздел 2. Округление
§ 246. Округление по недостатку и по избытку............... 217
§ 247. Основное правило округления ........................ 218
Раздел 3. Приближённые числа и их точность
§ 248. Четыре источника получения приближённых чисел....... 219
§ 249. Десятичные знаки и значащие цифры..................... —
Раздел 4. Четыре действия над приближёнными
числами
§ 250. Сложение и вычитание................................ 220
§ 251. Умножение и деление................................. 222
§ 252. Совместные действия................................. 224
§ 253. Предварительное округление более точных данных...... 225
§ 254. Вычисление с наперёд назначенной точностью результата . . . 226
Раздел 5. Некоторые задачи на измерение длины,
площади и объёма
§ 255. Длина окружности.................................... 227
§ 256. Площадь многоугольника.............................. 230
§ 257. Площадь круга....................................... 232
§ 258. Площадь поверхности цилиндра ....................... 234
§ 259. Объём цилиндра...................................... 235
Глава XIII. Прямая и обратная пропорциональность
Раздел /.Зависимость между величинами и её
наглядное изображение
§ 260. Зависимые величины.................................. 236
§ 261. Таблицы и графики .................................. 237
§ 262. Диаграммы........................................... 239
202
Раздел 2. Отношения и пропорции
§ 263. Сравнение числовых значений величии................... 241
§ 264. Отношение............................................. 242
§ 265. Определение пропорции ................................ 244
§ 266. Основное свойство пропорции........................... 245
§ 267. Нахождение неизвестного члена пропорции............... 246
§ 268. Перестановка членов пропорции......................... 248
§ 269. Производные пропорции................................. 249
Раздел 3. Величина, прямо пропорциональная
другой величине
§ 270. Определение и примеры прямой пропорциональности....... 250
§ 271. Свойства прямо пропорциональных величин.............. 252
§ 272. Наглядное изображение прямой пропорциональности...... 255
§ 273. Нахождение четвёртого пропорционального в случае прямой
пропорциональности ......................................... —
Раздел 4. В е л и ч и н а, обратно пропорциональная
другой величине
§ 274. Определение и примеры обратной пропорциональности..... 257
§ 275. Свойства обратно пропорциональных величин............. 259
§ 276. Наглядное изображение обратной пропорциональности.... 260
§ 277. Нахождение четвёртого пропорционального в случае обратной
пропорциональности .......................................... 261
Раздел 5. П р о п о р ц и о н а л ь н о с ть трёх и более величин
§ 278. Примеры случаев, когда три и более величин связаны попарно
пропорциональной зависимостью............................... 263
§ 279. Нахождение шестого пропорционального и другие более сложные
задачи на пропорциональную зависимость....................... 266
§ 280. Пропорциональное деление.............................. 270
Раздел 6. Н е к ото р ы е зависимости, которые надо
отличать от прямой и обратной
пропорциональности
§ 281. Равномерное возрастание............................... 273
§ 282. Равномерное убывание.................................. 274
§ 283. Линейная зависимость.................................. 275
§ 284. Примеры более сложных зависимостей.................... 276
Глава XIV. Некоторые дополнительные сведения о процентах
Раздел /.Три основные задачи на проценты
§ 285. Нахождение процентного отношения первого числа ко второму . 279
§ 286. Как находить данное число процентов от заданного числа? . . . 282
§ 287. Как находить число, если известно несколько процентов этого
числа?....................................................... 284
§ 288. Некоторые задачи на проценты, легко сводимые к трём основным 286
Раздел 2. Некоторые более сложные задачи на
проценты
§ 289. Вычисление среднего процента.......................... 288
§ 290. Понятие о сложных процентах........................... 290
Памятка...................................................... 292
Иван Козьмич Андронов
и Владимир Модестович Брадис
Арифметика
(Пособие для средней школы)
Редактор В. С. Капустина
Художественный редактор Б. Л. Николаев
Технический редактор Г. И. Смирнов
Корректоры А. П. Тарасова и Л. Е. Плесская
*
Сдано в набор 17/1 1957 г. Подписано
к печати 8/VI11 1957 г. 60x92l/ie- Печ. л. 19.
Уч.-изд. л. 18,41. Тираж 30 000. А 07605.
*
Учпедгиз. Москва, Чистые пруды, 6.
Книжная фабрика им. Фрунзе Главиздата
Министерства культуры УССР, Харьков,
Донец-Захаржевская, 6/8. Зак. 167.
Цена без переплёта 4 р. 95 к.
Переплёт 80 к.