Текст
Б. И. АЛЕКСАНДРОВ и П. €. МОДЕНОВ
ПОСОБИЕ
по
МАТЕМАТИКЕ
ДЛЯ ПОДГОТОВИТЕЛЬНЫХ КУРаЧВ МГУ
ИЗДАТЕЛЬСТВО МОСКОВСКОГОХУНИВЕРСИТЕТА
1967
I
Б. И. АЛЕКСАНДРОВ и П. С. МОДЕНОВ
ПОСОБИЕ
ПО МАТЕМАТИКЕ
ДЛЯ ПОДГОТОВИТЕЛЬНЫХ КУРСОВ
МГУ
ИЗДАТЕЛЬСТВО
МОСКОВСКОГО УНИВЕРСИТЕТА
1967
Настоящая книга ставит своей целью помочь подготовиться
к конкурсным экзаменам на различные факультеты учащимся
подготовительных Курсов при Московском университете.
В книге приведены варианты письменных приемных экза-
менов по математике в МГУ в 1965 г., а по физическому
факультету, кроме того,— вопросы, предлагавшиеся на устном
экзамене.
Для самостоятельных упражнений имеется много приме-
ров и задач, взятых из различных руководств (§ 9). Часть
примеров разобрана. Для ряда примеров ответы даны непо-
средственно в тексте.
Для учащихся подготовительных курсов при МГУ поме-
щены темы контрольных работ. *
По просьбе дирекции курсов § 5, 6, 8 написаны М. К. По-
таповым и Г. В. Дорофеевым,
2-2-2
§ 1. ГЕОГРАФИЧЕСКИЙ ФАКУЛЬТЕТ
ВАРИАНТЫ ПИСЬМЕННЫХ ЭКЗАМЕНОВ
(дневное отделение)
Вариант 1
1. Если пароход и катер плывут по течению, то расстояние от
пункта А до пункта В пароход покрывает в полтора раза быстрее,
чем катер, при этом катер каждый час отстает от парохода на
8 км. Если же они плывут против течения, то пароход проходит
путь от В до Л в два раза быстрее катера. Найти скорости паро-
хода и катера в стоячей воде.
2. В окружность радиуса 1 вписан равнобедренный треугольник,
боковая сторона которого в два раза больше основания. В этот
треугольник вписана окружность. Найти ее радиус.
3. Найти все решения уравнения
5 4
1 — sin4 х--cos4 х = 0.
3
4. Решить неравенство
log^ (2х + 3)>0/
2
Вариант 2
5. Два тела движутся по окружности равномерно и в одну сто-
рону. Первое тело проходит окружность на 2 сек быстрее второго
и. догоняет второе тело каждые 12 сек. За какое время каждое те-
ло проходит окружность?
6. В четырехугольник, три последовательные стороны которого
равны соответственно 2, 3 и 4, вписана окружность радиуса 1,2.
Найти площадь этого четырехугольника.
3
7. Найти все решения уравнения
8 cos4 х — cos 4х = 1.
8. Решить неравенство
х4 — 5х2 + 4<0.
Вариант 3
9. Две суммы денег — всего 5000 руб. — положены на некото-
рые сроки в сберкассу из расчета 3% годовых (проценты начисля-
ются от первоначальной суммы в момент выдачи вклада пропор-
ционально времени пребывания вклада в сберкассе). Каждая из
этих сумм дала 60 руб. дохода. Первая сумма находилась в сбер-
кассе на четыре месяца меньше, чем вторая. Как велика каждая
сумма и на какой срок она была положена в сберкассу?
10. В ромб площадью 1 вписан круг площадью —. Определить
длину стороны ромба.
11. Найти все решения уравнения
cos х — У 2 sin — = 1.
2
12. Решить неравенство
log , (х2 —5х + 4)<0.
_з~
Вариант 4
13. Переднее колесо повозки на некотором пути сделало на
1000 оборотов больше заднего. Если бы длина окружности перед-
него колеса'была в полтора раза больше, то на том же пути оно
сделало бы на 200 оборотов больше заднего колеса. Чему равны
длины окружностей колес, если известно, что длина окружности
заднего колеса на 1,5 м больше длины окружности переднего ко-
леса?
14. В равнобочную трапецию, верхнее основание которой равно
единице, вписана окружность радиуса 1. Найти площадь тра-
пеции.
15. Найти все решения уравнения
cos2 (—---х\ —cos2 (— + лЛ =
\ 8 J \ 8 / 2
16. Решить неравенство
4^<2х+1 + 3.
4
Вариант 5
17. С двух участков земли собрано соответственно 140 т и 550 т
свеклы, причем с 1 м2 второго участка собрано на 2 кг меньше, чем
с 1 jk2 первого участка. После применения удобрений урожай на
первом участке удвоился, а на втором — утроился и с 1 м2 второго
участка собрали на 1 кг больше, чем с 1 м2 первого участка. Опре-
делить размеры участков
18. Радиус окружности, описанной около прямоугольного тре-
угольника, равен 5 см, а радиус окружности, вписанной в этот
треугольник, равен 2 см. Найти периметр этого треугольника.
19. Найти все решения уравнения
2 cos 2х = V6 (cos х — sin х).
20. Решить неравенство
2х + 1 х + 4
х —2 2х — 5
Решение варианта 1
1. Обозначим расстояние от Л до В через s км, скорость тече-
ния— через 01 км[час, скорость парохода в стоячей воде через
о2 км/час.
По условию задачи катер каждый час отстает от парохода на
8 км, следовательно, его скорость и2—8. Когда пароход и катер
плывут по течению реки, то скорость парохода равна vi + v2, а
скорость катера и2—8+»i.
Расстояние от пункта А до пункта В пароход покрывает в пол-
тора раза быстрее, чем катер, следовательно,
1,5s s ц)
^2 + ^1 Vz + vl — 8
Если же пароход и катер плывут против течения, то скорость
парохода v2—vlt а скорость катера v2—8—
По условию задачи пароход проходит путь от В до Л в два ра-
за быстрее катера, т. е.
v2— u2 —t»j—8 ’ '
Решая систему уравнений (1), (2), найдем
vr = 4 км/час, v2 = 20 км/час,
значит, скорость катера в стоячей воде равна 12 км/час.
2. Так как радиус окружности В, описанной вокруг треугольни-
ка ЛВС, равен 1, а основание Л В в два раза меньше боковой сто-
5
роны (ДС=СВ), то расстояние ОМ от центра окружности S до
стороны АС равно ~ (в силу подобия треугольников CAD и
СОМ), а значит СМ = (рис. 1).
4
Пусть 01 — центр окружности, вписанной в треугольник АВС.
Обозначая через г радиус этой окружности, имеем
АС = 4 = ^01 = С01
AD ~ . OtD г
Значит, С0|=4г, а. потому 0D=
= 5г—1 и, далее,
0Л=1.
8
Из прямоугольного треугольни-
ка AOD находим
(5г —1)2 = I2 — — = —,
' 64 64
3. Заменяя sin2* на 1—cos2*, получим
1 — (1 — cos2 х)2-cos4 * = О,
или
2 cos2 * —— cos4 х = 0.
3
3
Таким образом, либо cos * = 0, либо cos2 х == —, а потому * =
— -^-(26 + 1) и * = kit ± где k принимает все целые значения.
4. Областью определения функции log , (2* + 3) является интер-
2^
з
вал -------—. На основании свойств логарифмической функции, с ос-
нованием, меньшим единицы, данное неравенство равносильно системе
следующих неравенств:
х>—5-, 2* + 3< 1.
2
Отсюда
6
§ 2. ГЕОЛОГИЧЕСКИЙ ФАКУЛЬТЕТ
ВАРИАНТЫ ПИСЬМЕННЫХ ЭКЗАМЕНОВ
(дневное отделение)
• Вариант 1
. 1. Два туриста вышли из А в В одновременно, причем первый
турист каждый километр пути проходит на 5 мин быстрее второ-
го. Первый, пройдя пятую часть пути, вернулся в Л и, пробыв там
10 мин, снова пошел в В. При этом в В оба туриста пришли одно-
временно. Каково расстояние от А до В, если второй турист про-
шел его за 2,5 час?
2. На каждой медиане треугольника взята точка, делящая ме-
диану в отношении 1 :3, считая от вершины. Во сколько раз пло-
щадь треугольника с вершинами в этих трех точках меньше пло-
щади исходного треугольника?
3. Найти все решения уравнения
ctg2 х — tg2 х — 16 cos 2х.
4. Решить неравенство
Вариант 2
5. Пассажир, едущий из города А в город В, половину затра-
ченного на путь времени ехал на автобусе, а половину на автома-
шине. Если бы он весь путь от А до В проехал на автобусе, то это
заняло бы у него в полтора раза больше времени. Во сколько раз
быстрее проходит путь от А до В автомашина, чем автобус (пред-
полагается, что скорости автобуса и автомашины постоянны)?
6. В равнобедренный треугольник вписан квадрат единичной
площади, сторона которого лежит на основании треугольника.
Найти площадь треугольника, если известно, что центры тяжести
треугольника и квадрата совпадают (центр тяжести треугольника
лежит на пересечении его медиан).
7. Найти все решения уравнения
81П X + sin Зх — 4 cos’ X.
8. Решить неравенство
----5----<1.
3—2х —х2
7
Вариант 3
9. Из пункта А в пункт В против течения выехала моторная
лодка. В пути сломался мотор, и пока его 20 мин чинили, лодку
снесло вниз по реке. Определить, насколько позднее прибыла лод-
ка в пункт В, если известно, что обычно путь из Л в В лодка про-
ходит в полтора раза дольше, чем путь из В в Л.
10. В равнобедренном треугольнике высота, . опущенная на
основание, в полтора раза меньше радиуса описанной окружности.
Найти отношение основания к боковой стороне.
Ц. Найти все решения уравнения
&1п х + sin 2х = cos х 4- 2 с os2 х.
12. Решить неравенство
'2 — log2(x2 + Зх) >• 0.
Вариант 4
13. Из пунктов Л и В навстречу друг другу выехали одновре-
менно два автобуса, причем первый, имея вдвое большую ско-
рость, проехал весь путь на 1 час быстрее второго. На сколько
минут раньше произошла бы встреча этих автобусов, если бы ско-
рость второго автобуса увеличилась и стала бы равной скорости
первого автобуса?
v 14. Около окружности единичного радиуса описана равнобоч-
ная трапеция, у которой одно основание вдвое больше другого.
Определить среднюю линию трапеции.
15. Найти все решения уравнения
у cos Зх— 2 cos 2х 4- cos х — 0.
16. Решить неравенство
9х < 3х + 2.
Вариант 5
17. Двое рабочих, работая одновременно, выполнили всю рабо-
ту за 5 дней. Если бы первый рабочий работал в два раза быст-
рее, а второй в два раза медленнее, то всю работу они выполнили
бы за 4 дня. За сколько дней выполнил бы всю работу первый
рабочий?
18. В окружность радиуса 1 вписана трапеция, у которой ниж-
нее основание вдвое больше каждой из остальных сторон. Найти
площадь трапеции.
19. Найти все решения уравнения
1 + sin 2х = sin х + cos х.
20. Решить неравенство
r У* + 2>х.
8
Решение варианта 1
1. Положим АВ—х. Пусть t — время, за которое первый турист
проходит 1 км; тогда второй турист проходит
t 4- — час.
12
По условию задачи первый''турист, пройдя
АВ, вернулся в Л и, пробыв там — час, снова
6
один километр за .
пятую часть пути
пошел в В, следо-
7
вательно, первый турист прошел расстояние, равное —х.
5
Общее время нахождения первого туриста в пути (вместе с
о Л \ । 1
остановкой в пункте А) равно-------Ь —.
5 6
Таким образом, по условию задачи
5
2 ‘
7tx . 1
5 + 6
время
Второе уравнение, определяющее
туриста в пути, имеет вид
х(12^ + 1) _ 5
12 ~ 2 '
После упрощения получим систему
уравнений
нахождения второго
Рис. 2
. 5
XI = --,
3
х(12/+ 1) = 30.
Решая эту систему, найдем х=10 км.
2. Пусть АВС — произвольный треугольник, К, N, М — соот-
ветственно середины сторон ВС, С А и АВ, а О — точка пересечения
медиан АК, BN и СМ. Возьмем на медианах АК, ВК и СМ соот-
ветственно точки Ль Bi и Сь такие, что (рис. 2)
ЛЛ, = ВВ, _ СС, _ 1
. AtK B,N ~ (^М ~ 3 ‘ ..
Так как по свойству медиан треугольника
_ЛО_ =_ ВО = СО = 2
OK ON ОМ ~ ’
то из соотношений
ЛЛх _ 1
Л1К “ 3 ’
= 2, следовательно, ОК = —(^~
ОК 2
9
находим
откуда
ОА _5_
ОА 8 *
Аналогично доказывается, что <
OBi = 5 0С1 = 5
ОВ ~ 8 ’ ОС ~~ 8 ’
Таким образом, треугольник А1В1С1 получается из треугольни-
ка АВС подобным преобразованием с центром О и коэффициентом
подобия, равным 5/8. Поэтому отношение площади треугольника
AiBiCi к площади треугольника АВС равно квадрату коэффициен-
та подобия, т. е. 25/б4-
Отношение сходственных сторон треугольников AiBiCl и АВС
равно коэффициенту подобия, т. е. —.
3. Произведем над данным уравнением следующие эквивалент-
ные преобразования:
cos4 х — sin4 х , rj о
--------------— 16 cos 2х,
sin2 х cos2 jt
cos2 x — sin2 x , n n
------------= 16 cos 2x,
sin2 x cos2 x
cos 2x л o
-------= 4 cos 2x,
sin2 2jt
cos 2x (----------4 ) = 0,
\ sin2 2x J
' cos 2x f sin2 2x — —
------'---------£2 = o.
sin2 2x
Так как при sin 2x = 0 имеем cos 2x=±l и sin22x--------^-==-----p
то при sin2x = 0 числитель дроби, входящей в левую часть уравне-
ния, не равен нулю. Отсюда последнее уравнение, а следовательно
и данное, эквивалентно уравнению
cos 2х ^sin2 2х---= 0.
Отсюда либо cos 2х—0, следовательно,
2х = -у- + ka,
я , кя
х =-----------,
4 2
(1)
10
либо
sin8 2х — —,
4
откуда
2х = kn + —,
“ 6
. л
х = ---Ч------.
2 ~ 12
В формулах (1) и (2) k принимает все целые значения.
4. Так как основанием логарифма является число, большее 1,
то неравенство
г
(2)
1*2 ^-< 0
будет выполнено тогда и только тогда, когда
0 < -х-=-— < 1.
х + 2
х__3
Дробь—-j-y положительна, если или х<—2, или х>3.
Неравенство
А^-<1
преобразуем так:
х— 3 л 5
----->0, или -----
х, + 2 х +
<1
откуда
х>- — 2.
Таким образом, все решения данного неравенства
х> 3.
§ 3. БИОЛОГО-ПОЧВЕННЫЙ ФАКУЛЬТЕТ
?
ВАРИАНТЫ ПИСЬМЕННЫХ ЭКЗАМЕНОВ
(дневное отделение)
К
Вариант 1
1. Поле площадью 980 га обработано тремя бригадами, рабо-
тавшими последовательно одна за другой, причем каждая из них
затратила на работу свое число дней. Первая бригада обработала
70 га, вторая 280 га, а третья — остальную часть поля.
11
Если бы первая бригада работала столько дней, сколько затра-
тила на работу вторая, а вторая — сколько затратила первая, то
они обработали бы одинаковую площадь. Если бы вторая бригада
работала столько дней, сколько затратила третья, а третья —
сколько затратила вторая, то они также обработали бы одинако-
вую площадь. Сколько дней затратила на работу каждая бригада,
если известно, что три бригады, работая одновременно, могут об-
работать все поле за 14 дней.
} 2. Вокруг круга радиуса 1 описаны квадрат и равносторонний
треугольник, причем одна из сторон квадрата лежит на стороне
треугольника. Вычислить площадь общей части треугольника и
квадрата.
3. Найти все решения уравнения
cos2 х + cos2 + cos2 — + cos2 2.
4 2 4
4. Найти все решения уравнения
/1 + log2 х + /4 log4x —2 = 4.
Вариант 2
5. Два туриста вышли одновременно из пунктов А и В навстре-
чу друг другу. Они шли каждый со своей постоянной скоростью и
встретились в 4 км от пункта В. Достигнув соответственно пунк-
тов А и В, туристы немедленно повернули обратно и встретились
в 2 км от пункта А. Вторая встреча произошла через 2 час после
первой. Найти скорости движения туристов и расстояние между
пунктами А и В.
6. Заданы два равносторонних треугольника, каждый площа-
дью 1; второй получается из первого поворотом на угол 30° около
его центра. Вычислить площадь общей части этих треугольников.
7. Найти все решения уравнения
2 (sin х + cosx)2 = tg (45° + х). *
I 8. Найти все решения уравнения
Vnog9(9x3)] log3(9x) = log3 х2.,
Вариант 3
9. Из пункта А в направлении к пункту С выезжает автомаши-
на. Одновременно с ней Из пункта В, лежащего между А и С, так-
же в направлении к пункту С выезжает автобус. Автомашина че-
рез 12 мин достигает пункта В, и, продолжая движение, догоняет
автобус на расстоянии 50 км от пункта А. Если бы скорость авто-
буса была увеличена на 20 км/час, то автомашина догнала бы его
12
на расстоянии 100 км от пункта А. Определить скорость автома-
шины.
10. В круг радиуса 1 вписаны равносторонний треугольник и
квадрат, имеющие* общую вершину. Вычислить площадь общей
части треугольника и квадрата.
11. Найти все решения уравнения
sin2 х — sin2 2х + sin2 Зх = -* .
V 12. Найти все решения уравнения
2 log2 log2 х + log^ log2 (2/2x) = 1.
V
Вариант 4
13. Три насоса, которые выкачивают из реки воду для поливки,
начали работать одновременно. Первый и третий насосы закончи-
ли работу одновременно, а второй — через 2 час после начала ра-
боты. В результате первый насос выкачал 9 м3 воды, а второй и
третий — в сумме 28 л/3. Какое количество воды выкачивает за час
каждый насос, если известно, что третий насос за час выкачивает
на 3 м3 больше, чем первый, и что три насоса, работая вместе, вы-
качивают за час 14 ж3?
14. Вычислить площадь общей части двух ромбов, из которых
у первого диагонали равны 2 и 3, а второй получается поворотом
первого на 90° около его центра.
15. Найти все решения уравнения
cos Зх cos 4х 4- sin 2х sin 5х = (cos 2х + cos 4х).
16. Найти все решения уравнения
V 2 [10g2 (~бг) ~ 1 ] 12 + 10gl = 10g2 (2х)-
Вариант 5
17. Из пункта А в пункт В против течения реки на лодке отпра-
вилась группа туристов, которая проплыла это расстояние за
6 час. Обратно часть группы возвращалась на лодке, а часть на
плоту. Лодка прибыла в пункт А на 4 час раньше, чем плот. Сколь-
ко часов плыла лодка из пункта В в пункт А?
Примечание. Скорость плота относительно берега счи-
тается равной скорости течения.
18. Три окружности расположены на плоскости так, что каждая
из них касается двух других внешним образом. Две из них имеют
•радиус 3, а третья — радиус 1. Найти площадь треугольника АВС,
13
где А В и С — соответствующие точки касания трех окружностей.
19* Найти все решения уравнения
, 2 sinxcos2x 4- sin2x cosx = sin 4xcqs x.
20. Найти все решения уравнения
log, (х— l) + log, (х4-1) —log , (7—х) = 1.
V 2 • V2
Решение варианта 1
1. Пусть в первый раз первая бригада затратила на работу
х дней, вторая бригада у дней, третья бригада z дней. Тогда
70 280
га обработала первая бригада в 1 день, га обработала
х--------------------------------------------у
630
вторая бригада в 1 день,---- га обработала третья бригада в
1 день.
Если бы первая бригада работала столько дней, сколько затра-
70
тила на работу вторая, т. е. у дней, то она обработала бы-у га.
Если бы вторая бригада работала столько дней, сколько первая,
т. е. х дней, то она обработал^ бы--х га.
У
По условию задачи
70 280
----у =-------X.
X У
(1)
Если же вторая бригада работала бы столько дней, сколько
затратила третья, т. е. z дней, а третья — сколько затратила вто-
рая, т. е. у дней, то они также обработали бы одинаковую пло-
щадь. Таким образом, получаем второе уравнение
Если бы все три бригады работали вместе, то за один день они
обработали бы
70 . , 280 . 630
----Н---------1-------га,
х у г
а за 14 дней они обработали все поле.
Имеем третье уравнение:
l4f-™ +Ж+ ««.\_980.
\ X у г )
(3)
4
14
После упрощения система уравнений (1), (2), (3) имеет вид
у® = 4х2,
4z2 = 9у®,
— + — + — =1.
X у Z
Так как х, у и z положительны, то эта система уравнений экви-
валентна следующей:
' у = 2х,
. 2z = Зу,
— + — .+ — = 1.
X у г
Решая систему, получим х=6, у =12, z=18.
2. Пусть S-—окружность радиуса 1; АВС и EDD[K— соответ-
ственно равносторонний треугольник и квадрат, описанные вокруг
окружности S, причем сторона ЕК квадрата лежит на стороне АС
треугольника (рис. 3).
По условию задачи необходимо вычислить площадь общей час-
ти треугольника АВС и квадрата EDDiK, т. е. площадь шести-
угольника EMFFiMiK (М и — точ-
ки пересечения прямых АВ и ВС со
сторонами DE и DiK, a F и Fi — точки
пересечения прямой DDi с прямыми
АВ и ВС). Эту площадь можно опре-
делить как разность площади квадра-
та и площадей треугольников MDF и
MiDiFi.
Так как треугольник АВС правиль-
ный, то его высота BN есть ось симмет-
рии, проходящая через центр О кру-
га S.
Так как сторона ЕК квадрата
EDDiK, описанного вокруг окружно-
сти S, лежит на стороне АС треугольника и касается этой окружно-
сти в точке N, то прямая BN является осью симметрии и квадрата
EDDiK.
Из доказанного следует, что треугольники MDF и MiDiFi так-
же симметричны относительно прямой BN и потому равны.
Для определения площади треугольника MFD вычислим его
катеты DF и DM. Предварительно заметим, что BNi=ONt = l."} С
Из треугольника FBNi находим v ’
Рис. 3
FNt = BN j'Ctg 60° =
3
.15
и, следовательно, .
DF = DN. — FN. = 1 — .
11 3 .3
Из треугольника MDF находим
DM = DF-tg 602 э 4= -3 ~з’ - J/3.
Таким образом, площадь прямоугольного треугольника MDF
равна
— DF-DM = -~^3- 1/3 = -2у 3-3 -
2 6 3 3
Но так как площадь квадрата EDDiK равна 4, то площадь об-
щей части треугольника АВС и квадрата EDDJt равна
\-2 2/3-6
3 /з
Заметим еще, что площадь общей части правильного треуголь-
ника АВС и квадрата EDDXK можно определить как сумму пло-
щадей прямоугольника ЕММХК и трапеции MFFXMX.
3. Преобразуем данное уравнение следующим образом:
1 + cos 2х 2 . 1 4- cos х .
---------------------------------------|_ -------
2 2 2 2
или
cos 2х + cos-^- + cos х 4- cos — = 0.
2 2
Группируя первый член со вторым, а третий с четвертым, по-
лучим
2 cos 7х- 1?os — + 2 cos cos — = 0,
4 4 4 4
или
COS — ( cos + cos = 0,
4 \ 4 4 J
или
coscoscos = 0.
4 4 2
16
Решениями уравнений cos -у- = 0, cos-£- = 0, cos -^— = 0, а сле-
довательно и всеми решениями данного уравнения, будут
х = 2л (2А + 1), х = — (2& + 1), х = л (26+ 1),
5
где k принимает все целые значения.
4. .Так как Iog4x = log2x-log42 = “~log2x, то данное уравнение
можно переписать в виде
/1 + log2x + /21ogax —2 = 4.
Возводя в квадрат обе части этого уравнения, получим
3 log2 X - 1 + 2/21ogfx —2 = 16,
или f
2/2 log2x —2 = 17 — 3 log2 x.
Возводя в квадрат обе части этого уравнения, имеем
. 4 (2 log2x — 2)= 289 — 102 log2 х + 9 log2 х,
или
log2 х — 102 loga х + 297 = 0.
Корни этого уравнения:
log2 х = 3 и log2 х = 99,
откуда
х = 8, х = 2".
Среди этих значений х находятся все корни данного уравнения
(так как если какое-то число х=х0 является корнем уравнения
Л = то оно является и корнем уравнения Л2 = В2, но не наобо-
рот!). Поэтому числа х = 8 и х=2"(одно или даже оба!) могут и
не быть корнями данного уравнения. Подставляя в левую часть
данного уравнения 8 вместо х, получим
/1+ log28 + /2 log, 8-2 = /4 + /4 = 4,
так что х=8— корень данного уравнения. Подставляя х=2"г по-
лучим
У Л + log, 2" + /Hoga 289 —2 = V100 + /196 = 10 + 14 = 24,
т. е. х = 2" — не корень данного уравнения. Таким образом, дан-
ное уравнение имеет только один корень х=&
17
Замечание. Легко проверить, что х=2"— корень урав:
нения
— /1 + log2 х + /21og2x —2 = 4, (1)
однако х=8 — не корень уравнения (1).
При возведении в квадрат обеих, частей уравнения (1), получим
3 log2 х — 1 — 2 /flog**—2 = 16,
ИЛИ
2 /21ogfx- 2 = 3 logjX — 17. (2)
Число х=2" остается корнем уравнения (2), но х=8 — не ко-
рень. А при возведении обеих частей уравнения (2) в квадрат, по-
лучим уравнение, корни которого х=2" и х = 8. Как объяснить то
обстоятельство, что и в данном уравнении и в уравнении
— V1 + log2 х + /21og2x —2 = 4
при первом возведении в квадрат полученное уравнение оказы-
вается эквивалентным данному, а при вторичном возведении в
квадрат эквивалентность нарушается? § *
§ 4. ХИМИЧЕСКИЙ ФАКУЛЬТЕТ
ВАРИАНТЫ ПИСЬМЕННЫХ ЭКЗАМЕНОВ
(дневное отделение)
~ ? Вариант 1
1. Два одинаковых сосуда наполнены спиртом. Из первого со-
суда отлили а литров спирта и налили в него столько же литров
воды. Затем из полученной смеси водь! со спиртом отлили а лит-
ров и налили столько же литров воды. Из второго сосуда отлили
2а литров спирта и налили в него столько же литров воды. Затем
из полученной смеси воды со спиртом отлили 2а литров и налили
столько же литров воды. Определить, какую часть объема сосуда
составляют а литров, если крепость окончательной смеси в первом
сосуде в 25/ю раза больше крепости окончательной смеси во втором
сосуде.
2. Сторона основания правильной треугольной пирамиды рав-
на а, а высота, опущенная из какой-нибудь вершины основания
на противоположную ей боковую грань, равна Ь. Определить объем
пирамиды. *
18
3. Решить уравнение
sin I 2х—
— A + cos<2x — — A =/2cos<3x+— Y
12 ) \ 12 J \ 6/
4. Решить неравенство
2 log2 (x — 1) — log2 (2x — 4) > 1
Вариант 2
5. Три бригады, работая одновременно, обычно выполняют нор-
му по изготовлению деталей за несколько часов. Если бы первые
две бригады работали в два раза медленнее обычного, а третья
бригада — в 4 раза быстрее, то норма была бы выполнена за то
же время. Известно, что первая и вторая бригады при совместной
работе выполняют эту же норму в два раза быстрее, чем вторая
бригада совместно с третьей. Во сколько раз первая бригада за
один час делает деталей больше, чем третья?
6. Высота
плоские углы
7. Решить
правильной четырехугольной пирамиды
правильной четырехугольной пирамиды равна Л, а
при вершйне равны <р. Определить объем пирамиды,
уравнение
£
— X
— X
неравенство
1
1
8. Решить
2х + 3 2^+2 — 1 * °
Вариант 3
9. Из двух жидкостей, удельные веса которых 2 г/см3 и 3 г/см3,
составлена смесь. Сколько граммов взято каждой жидкости и ка-
ков удельный вес смеси, если 4 см3 смеси весят в 10 раз меньше,
чем вся первая жидкость, а 50 см3 смеси весят столько же, сколь-
ко вся вторая жидкость, входящая в ту же смесь? Предполагает-
ся, что объем смеси равен сумме объемов ее составных частей.
10. Дана прямая призма, у которой основанием служит пра-
вильный треугольник. Через одну из сторон нижнего основания и
противоположную вершину верхнего основания проведена плос-.
кость. Угол между этой плоскостью и основанием призмы равен а,
а площадь сечения призмы равна S. Определить объем призмы.
11. Решить уравнение
staf 2х+ — — 3cosf— — х^ = 1 +2 sinx.
\ 2 / \ 2 J
12. Решить неравенство
toga U2 — 3*) < 2.
19
Вариант 4
13. Даны три вещества с различными удельными весами. Из
них составлены три смеси: первая — из равных объемов второго и
третьего веществ, вторая — из равных объемов первого и третьего
веществ и третья — из равных объемов первого и второго веществ.
Удельные веса этих смесей находятся в отношении 7:6:3. Опре-
делить, во сколько раз удельный вес третьего вещества больше
удельного веса второго.
Объем смеси предполагается равным сумме объемов ее состав-
ных чабтей.
14. Определить объем параллелепипеда, у которого все ребра
равны 1, а все плоские углы при одной из вершин равны ср <90°.
15. Решить уравнение
tg Зя ~4Х--cos 2х = 21^3 cos2 (х + ~
16. Решить неравенство
logs х log2 х + 2 ’
Вариант 5
17. Два брата ходят вместе в школу из дома с'постоянной и
одинаковой для обоих скоростью. Однажды через 15 мин после
того,, как они вышли из дома, первый побежал домой, и» добежав
до дома, немедленно бросился догонять второго. Пока первый
брат отсутствовал, второй, уменьшив скорость ходьбы в два раза,
продолжал идти в школу. После того как первый брат догнал
второго, они пошли с первоначальной скоростью и пришли в шко-
лу на 6 мин позже, чем обычно. Определить, во сколько раз ско-
рость бега первого брата, которая считается постоянной, превосхо-
дит первоначальную скорость ходьбы братьев.
18. Определить синус угла между двумя высотами, опущенны-
ми из двух вершин правильного тетраэдра на противоположные
грани.
19. Решить уравнение
tgf = 3cfg-^.
20. Решить неравенство
V1 —уг5^х.
Решение варианта 1
1. Обозначим через х первоначальное количество спирта как
в первом, так и во втором сосудах (по условию задачи количество
спирта в обоих сосудах было одно и то же).
20
После первого отливания в первом сосуде осталось х—а лит-
ров спирта. После того как в сосуд добавили а литров воды, кре-
пость спирта, т. е. отношение объема спирта в первом сосуде к
объему смеси спирта с водой, стала равной ——— .Во второй раз
из первого сосуда отлили а литров, в. которых содержалось
х — а
-------а литров спирта и, значит, в первом сосуде осталось
X
х —а (х — а)2
х — а---------а = ~
X X
литров спирта. Крепость смеси з первом сосуде стала равной
(х — а)2
х2
После того как из второго сосуда отлили 2а литров спирта, в
нем осталось х—2а литров спирта, и когда второй сосуд дополни-
ли 2а литрами воды, то крепость смеси оказалась равной - ~~ — -.
X
Во второй раз из второго сосуда отлили 2а литров смеси, содер-
v х — 2а с, п (х — 2а) 2а
жащеи --------2а литров спирта, и в нем осталось х — 2а —------—. =
X X
(х__*2а)2
= -------литров спирта. Крепость смеси во втором сосуде оказалась
равной / -х .
По условию задачи
(х — а)2 . (х — 2а)2 __ 25 .
х2 х2 16
После упрощения получим уравнение
9х2 — 68ах + 84а2 = О,
откуда
х. = 6а, х9 = —а.
1 2 9
Так как х2 — 2а = а — 2а < 0, то х = -у- а не является ре-
шением данной задачи.
Таким образом, х = 6а и, значит,
а:х = 1 :6,
т. е. а литров составляет !/6 объема сосуда.
2. Пусть SABC — правильная треугольная пирамида, S — ее
вершина; АВС — равносторонний треугольник, лежащий в основа-
21
нии. Проекция О вершины S пирамиды SABC на плоскость ее
основания совпадает с точкой пересечения высот треугольника
АВС (так как проекции ОА, ОВ, ОС равных наклонных 5Л, SB, SC
равны между собой: ОА = ОВ = ОС). Прямая АО пересекает сто-
рону ВС в точке Е, являющейся серединой стороны ВС. Значит,
' SE — высота равнобедренного треуголь-
ника BSC (SEE ВС).
Пусть К — проекция точки А на пря-
мую SE. Так как SEA.ВС и АЕЕВС, то
прямая ВС перпендикулярна плоскости
треугольника AES. Но прямая АК ле-
жит в плоскости треугольника AES, сле-
довательно, скрещивающиеся прямые
АК и ВС взаимно перпендикулярны.
Итак, AKESE и АКЕВС, следователь-
но, прямая Л/С перпендикулярна плоско-
сти BSC (рис. 4).
Объем одной и той же пирамиды мож-
но определить при помощи формулы
У = — пл. Д ABC-h, (1)
3 \
где h — длина высоты SO, или при помощи формулы
V = у пл. Д CBS-b, (2)
где b — расстояние от вершины А до плоскости SBC, т. е. длина
отрезка Л/С Так как ДЛВС равносторонний, то его площадь рав-
на
£2/3
Далее, из прямоугольного треугольника OSE находим SE
л2 i
Ч-----' и, следовательно,
пл. /\SBC = — a-SE = — al/ ft2 +—•
2 2 У 12
Подставляя значения площадей треугольников АВС и CBS в
выражения объемов (1) и (2) и приравнивая результаты, получим
/3 _ ab >
12 6 V + 12 ’
откуда находим
у 3 • /За2 — 462
22
Подставляя значение h в формулу V = h объема пирамиды
SABC, получим
у _ а2/3
12
cflb
у^З"- |<3а2 — 4ft2 12 VЗа2 — 462
3. Преобразуем последовательно данное уравнение:
sin(2x-ir) . cos(2*~“ir) ,
' -7=-----— = COS ( Зх 4-
ab
/2
cos (2х---— | cos — 4- sin (2x —
I .12 I 4 \
= COS
(л Л* я
2х-------------
12 4
/ Л Л/ f О t
cos( 2х------) = cos ( Зх Ч---).
\ з J \ 6 /
Все решения этого уравнения находятся из соотношений
Зх + — + 2х— — = 2kn,
6 3
Зх + — 2х + — = 2ka,
6 3
откуда
л . 2&л
x = —— + 2ЙЛ,
2
где k принимает все целые значения.
4. Решениями данного неравенства могут быть только значе-
ния х, удовлетворяющие неравенствам
х—— 1>0, 2х — 4>0,
т. е. только х>2. Таким образом, данное неравенство эквивалент-
но смешанной системе
log> 0,
2 4(x—2)
x> 2,
или
(х-1)»
4(х-2)
1, x>2
23
или
х2 — 2х+ 1 >4х —8,
х> 2,
или
(х — 3)2>0,
х>2.
Отсюда следует, что решения последней системы, а значит и
все решения данного неравенства, таковы:
2<х<3, х>3.
§ 5. ФИЛОЛОГИЧЕСКИЙ ФАКУЛЬТЕТ
ВАРИАНТЫ ПИСЬМЕННЫХ ЭКЗАМЕНОВ
(дневное отделение)
Вариант 1
1. Две машинистки должны перепечатать, рукопись, состоящую
из трех глав, первая из которых вдвое короче второй и втрое длин-
нее трётьей. Работая вместе, машинистки перепечатали первую
главу за 3 нас 36 мин. Вторая глава была перепечатана за 8 час,
из которых 2 час работала только первая машинистка, а осталь-
ное время они работали вместе. Какое время потребуется второй
машинистке, чтобы перепечатать третью главу?
2. Решить уравнение
3 (log2 sin х)2 + log2 (1 — cos 2х) = 2.
3. Найти площадь треугольника АВС, если ZACB = 30°, АС=
= ВС и периметр треугольника равен 5.
4. При каких значениях у верно следующее утверждение: «су-
ществует хотя бы одно значение х, при котором неравенство
2 logo,5 У2 — 3 + 2х logo,5 У2 — х2 > О
выполняется»?
Вариант 2
5. Поступающие сдавали четыре экзамена. 20% из общего чис-
ла подавших заявления получили «неудовлетворительно» на пер-
вом экзамене. 90% выдержавших первый экзамен сдали также и
второй. На третьем экзамене отсеялась 718 часть оставшихся по-
24
еле второго экзамена, да еще 5 человек. Наконец, 8/9 от числа вы-
державших третий экзамен получили положительные оценки и на
четвертом. В результате оказалось, что число сдавших все экзаме-
ны вдвое больше числа мест, а число мест в полтора раза больше,
чем число получивших «неудовлетворительно» на первом экзамене.
Сколько заявлений было подано?
6. * Решить уравнение
sin (т-*)
1 2^ Л = 3 ♦ 4 cos х
7. Точка М лежит внутри равностороннего треугольника АВС.
Вычислить площадь этого треугольника, если известно, что
АМ = ВМ = 2, СМ= 1.
8. При каких значениях у верно следующее утверждение: «при
лйобом х неравенство
х2(2 — log2—£— 'j + 2х(1 + loga—J—) —2 (1 4- loga—
\ 0+1 J \ / \ i/4-i /
выполняется»?
Вариант 3 *
9. Для того чтобы из пункта А попасть в пункт В, нужно часть
пути от пункта А до пункта С проехать на поезде, а остальные
15 км от С до В — на автобусе. Вся поездка от А до В занимает
1 час 15 мин, причем автобус отправляется сразу после прихода
поезда, а временем, которое поезд и автобус тратят на остановки,
можно пренебречь. По ошибке пассажир сошел с поезда на оста-
новку раньше, прошел оставшийся путь до С длиной 5 км пешком
со скоростью 4 км) час, а затем еще 2Q мин ждал автобуса и в ре-
зультате попал в пункт В на 1 час 30 мин позже намеченного
срока. Найти расстояние от А до С, если известно, что скорость
поезда вдвое больше скорости автобуса.
10. Решить уравнение
(0,5)cos2x---.
\ ' ^Sin2X 2
11. Определить длину перпендикуляра ЕН, восставленного из
точки Е к стороне АВ треугольника АВС, гцеН — точка пересече-
ния данного перпендикуляра с одним из отрезков АС или СВ, зная
длины сторон АВ=4, АС=5, ВС = ]/~17 и зная, что данный пер-
пендикуляр делит треугольник на две фигуры равной площади.
12. Решить неравенство
25
. ' Вариант 4 *
13. Расстояние между пунктами Л и С равно 30 км. Из пунк-
та Л по направлению к С вышел лыжник, двигающийся со ско-
ростью 10 км/час. Через 15 мин навстречу ему из пункта С должен
был выйти другой лыжник с тем, чтобы, двигаясь с-постоянной
скоростью, встретиться с первым на середине пути. Однако второй
лыжник вышел с опозданием на 55 мин, вследствие чего встреча
произошла в другом пункте В. Чему равно расстояние от Л до В?.
14. Решить уравнение
— _|_ =------6—,
15. В треугольник АВС вписан квадрат таким образом, что
одна из его сторон лежит на стороне АВ треугольника АВС. Найти
сторону этого квадрата, если Л5=ЛС=8, а ВС = 81/ — •
г 5
16. Решить неравенство
log2 (х — 1) — Iog2 (х 4-1) 4- logx+i 2 > 0.
х— I
Решение варианта 1
Г. Пусть третья глава рукописи содержит х страниц, тогда пер-
вая содержит 3 х, а вторая 6 х страниц. Пусть первая машинистка
печатает за 1 час у страниц, а вторая z страниц. Работая вместе
3 час 36 мин, машинистки перепечатали первую главу, следова-
тельно, ,
-(z4-y) = Зх. ‘ (1)
О
Вторая глава была перепечатана за 8 час, из которых 2 час
работала только первая машинистка, а 6 час они работали вме-
сте, т. е. s
2у 4-6 (у 4~ z) = 6х. . (2)
Пусть одна вторая машинистка перепечатывает третью главу
за t час, тогда
tz — x. -
Подставляя tz вместо х в уравнения (1) и (2), получйм
6z 4- бу — 5tzt
+ = 3tz.
26
Умножая первое из этих уравнений на 2, а второе на—3 и скла-
дывая полученные при этом уравнения, будем иметь 3z=te, отку-
да /=3.
Итак, вторая машинистка перепечатает третью главу за 3 час,
2. Корнями данного уравнения могут быть только такие чис-
ла х, для которых sinx>0. Поэтому данное уравнение
3 (log2 sin х)2 + log2 (1 — cos 2х) = 2,
или
3 (log2 sin х)2 + log? (2siti2 x) — 2 = 0,
или
3 (log2 sin x)2 + 1 + 2 log21 sin x | — 2 = 0,
равносильно следующему:
3 (Iog2 sin x)2 + 2 log2 sin x — 1 = 0.
Рис. 5
Обозначай log2sinx через у и замечая, что в силу условия
sinx>0 величина у может принимать все значения, меньшие или
равные нулю, заключаем, что данное уравнение перепишется так:
3^ + 2у-1 = 0. ' (2)
Уравнение 3z/2 + 2у— 1 =0 имеет действительные корни разных
знаков — и — 1. Но так как у <С 0, то log2 sin х = — 1, sin х = —
3 2
и х = £л + (—1)А—, где k принимает все целые значения.
6
3. Так как угол АСВ равен 30°, то расстояние АР от верши-
ны Л треугольника АВС до стороны ВС в два раза меньше боко-
вой стороны АС треугольника АВС. Поэтому площадь S треуголь-
ника АВС равнаЛР-ВС =-^-ЛС2 (рис. 5). Для нахождения
АС воспользуемся тем, что периметр треугольника равен 5:
5 = АС + ВС + АВ = 2ЛС + 2ЛВ = 2ЛС (1 + sin 15°).
5
Отсюда АС —---------------- и так как
2(1+sin 15°)
ЯШ 15° - 1 / ^“s300 _ I/" 2-/3 ,
у 2 У 4
> СЖ '
г+'/г—/з 4(2+Тг2—/з )2 ’
* Можно иначе: sin 15°=sin(45°—30fO) ------*—и т. д. Ответ при этом не
4
упрощается, но и не содержит двойных радикамТов.
27
4. Перепишем данное неравенство так:
f (х) = х2 — 2х logo,51/2 + 3 — 2log0,5 у2 <0. (1)
Заметим, что функция y=x2+px+q, где р и q — действитель-
ные числа, отрицательна хотя бы при одном значении х; тогда и
только тогда, когда корни уравнения у=0 действительны и различ-
ны, т. е. тогда и только тогда, когда р2—4</>0.
Применяя это соображение, заключаем, что функция /(х), за-
данная соотношением (1), будет отрицательна хотя бы при одном
значении х тогда и только тогда, когда выполняется неравенство
(logo,5 У2)2 — 3 + 2 logo,5 f/2 > 0.
Перепишем это неравенство так:
(logo,5 У2 — 1) (logo,5 У2 + 3) > 0,
откуда либо logo,5 У2> 1, либо logo,5 у2<—3.
Неравенство
log0,5«/2> 1
выполняется тогда и только тогда, когда y=£Q и у2<0,5, т. е.
или —]/0,5 <{/< 0, или O<t/<Vo,5.
Неравенство logo,s*/2<—3 будет выполнено тогда и только
тогда, когда г/2>8, т. е. если или у<—2И2, или y>2\f2.
Итак, неравенство (1) выполняется хотя бы при одном значе-
нии х тогда и только тогда, когда у принадлежит одному из сле-
дующих интервалов:
у<-2/2’;--------+ <У<0~, 0<у< y>2V2.
у 2 у 2
§ 6. ЭКОНОМИЧЕСКИЙ ФАКУЛЬТЕТ
ВАРИАНТЫ ПИСЬМЕННЫХ ЭКЗАМЕНОВ
(дневное отделение) j
Вариант 1
1. Плоты шли из пункта А до устья реки вниз по течению. 1
В. устье реки их взял на буксир пароход и через 11 ~ суток после 1
выхода плотов из пункта А доставил по озеру в пункт В. Сколько
®Ремени пароход вел плоты от устья реки по озеру до В, если из-
40 ча°’ ЧТ° паР°ход тратит на рейс (без буксировки) от А до В
шается вдв ^8 ЧаС’ а СКОРОСТЬ во вРемя буксировки умень-
28
V2. Решить неравенство
log„ I —х~-— I <0.
ёо| 2х+1
\/3. Решить уравнение
/ л л- \ х о । sin5x — sinx n
(cos2x — cos4x)ctg3x -1--—— = 0.
8sin3x
'z4. Многочлен
2x3 + ax2 + bx -\-c
имеет два корня, равных — 3, и один корень, равный 2. Найти а\
Ь, с. * !
5. В точке М, находящейся на расстоянии 2 А от плоскости ос-
нования куба с ребром h и на расстоянии R>3h от центра куба,
помещен источник света. Доказать, что тень, отбрасываемая ку-
бом на плоскость основания, будет иметь наибольшую площадь,
когда плоскость, проходящая через центр куба, точку М и одну
из вершин, перпендикулярна плоскости основания.
Вариант 2
V&. От двух однородных кусков сплава с различным процентным
содержанием меди, весящих соответственно т и п кг, отрезано по
куску равного веса. Каждый из отрезанных кусков сплавили с
остатком другого куска, после чего процентное содержание меди
в получившихся сплавах стало одинаковым. Сколько весил каж-
дый из отрезанных кусков?
V 7. Решить неравенство
V 8. Решить уравнение
cos2 Зх — tg2 Зх — sin2 Зх + 1 = 0.
/9. Найти все действительные значения р и q, при которых х4+1
делится на x2 + px+q.
10. Дана правильная треугольная пирамида с центром основа-
ния О и плоскостью основания Р. В точке А, находящейся на рас-
стоянии h от плоскости Р и на расстоянии / от точки О, помещен
источник света. Доказать, что тень, отбрасываемая пирамидой на
плоскость Р, будет иметь наименьшую площадь, когда точка А
лежит в плоскости одной из боковых граней пирамиды.
Вариант 3
11. Из полного бака, содержащего 729 л кислоты, отлили
а литров и долили бак водой. После4 тщательного перемешивания
отлили а литров раствора и снова долили бак водой. После того
как такая процедура была повторена шесть раз, раствор в баке
содержал 64 л кислоты. Определить величину а.
29
\ 12. Найти положительные решения неравенства
' ' 2х—1
X 3~х > 1.
/
13. Решить уравнение
(1 -|-cosec2 х) sin 2х cos 2xtg3x = 0.
- 14. Многочлен х4+х3—х2+ах+Ь имеет два одинаковых корня,
равных 1. Найти а и Ь.
15. Ребра треугольной пирамиды, выходящие из вершины О,
попарно перпендикулярны, и их длины равны а, b и с. Найти объем
куба, вписанного в эту пирамиду так, что одна из его вершин
совпадает с вершиной О.
Вариант 4
16. Один сплав содержит медь и олово в отношении 2: 1, а дру-
гой — в отношении 3 :2. По скольку частей нужно взять каждого
из этих сплавов, чтобы получить третий сплав, в котором медь и
олово содержатся в отношении 27: 17?
17. Решить неравенство 1
log* к — 2 logl х — 3 < 0.
- 18. Решить уравнение
(1 + sec2x)sin 2xcos2xctg3x = 0.
19. Найти целые решения уравнения
(1— i)x = 2х
(комплексное число в нулевой степени считается равным 1).
** 20. В конус вписаны 4 шара радиуса г так, что каждый из них
касается конуса и трех других. Найти радиус основания конуса.
Решение варианта 1
1. Пусть скорость буксира v км/час, а скорость реки и км/час.
Пусть расстояние от пункта А до устья реки равно st км, а рас-
стояние от устья реки до пункта В по озеру равно s2 км. От пунк-
та А до устья реки плоты шли-^1- час, а от устья реки до пункта В
и
пароход доставил их за час. Всего же путь из А в В продол-
1 '
жался 11 —суток, т. е. 276 час, поэтому
= 276. (1)
и V
30
На путь от пункта А до устья реки пароход тратит
п So
от устья реки пункта В до—— час, поэтому
S1
u~\~v
час, а
*—Ь------1__^_ = 40. (2)
« + » V
Аналогично составляется уравнение
_£s_ _|_ _Л_ = 48. (3)
V V — U
Из системы уравнений (1), (2), (3) надо найти отношение
Из уравнений (2) и (3) находим
V
-1------------------------------!_\ = 8,
v — u V-\-U J
откуда
Складывая почленно уравнения (2) и (3), получим
2s2 ।2uS] ____gg
V V2 — и2
или в силу соотношения (4)
= 88-----= 88 — —. (5)
V D2 — и2 и
Подставляя в уравнение (1) вместо s1 и их выражения из
v
формул (4) и (5), получим
4 .<* 4- 88 — = 276,
и2 и
или
—-----2 —— 48 = 0.
и2 и
Положительный корень этого уравнения
— = 8,
V
следовательно,
-^- = 88 — 8-8 = 24.
v
31
2. Функция
1 х — 1 I
'"«• 2,-Г
определена при всех действительных значениях а и х, таких, что
а>0, а=#1, х#=1, х#=------
I. Случай а>1. В этом случае неравенство
log I Л-.1 |<о
°| 2x4-1 I
эквивалентно такому:
-——' < 1
2х-Н р
ИЛИ
\х- 1 |< |2х + 11. (1)
Корни функций 2х+1 и х—1 соответственно равны -—и 1,
поэтому естественно рассмотреть случаи
Г.'х< — —; 2°.-----3°. х>1.
2 2
1°. В случае х<--~ неравенство (1) эквивалентно неравенству
— х + 1 < — 2х— 1,
или
хК^ —2.
2°. В случае-----— <х<1 неравенство (1) эквивалентно нера-
венству
— х + 1 <С 2х -|” 1,
или
0<х.
Учитывая условия случая, получаем, что исходное неравенство
справедливо для х из промежутка 0<х<1.
32
3е. В случае х>1 неравенство (1) эквивалентно неравенству
х — 1<2х + 1,
или
х>— 2.
Решение же исходного неравенства х>1.
Итак, в случае а>1 все решения данного неравенства х<—2,
0<х<1 и х>1.
II. Случай 0<а<1. В этом случае неравенство
эквивалентно неравенству
лг~1 |>1,
2x4-1 К
или
|х—11 >|2х4-11. (2)
1°. Если х<—то неравенство (2) эквивалентно неравенству
— х4- 1 >— 2х— Г,
или
— 2<х.
Решением исходного неравенства будут все х из промежутка
— 2<х< — —.
2
2°. Если----— <х<1, то неравенство (2) эквивалентно нера-
венству
—— х 4~ I 2х 4~ 1 >
или
х<0.
В этом
случае решение исходного неравенства------
<х<0.
2 Зак. 351
33
3°. Если, наконец, х>1, то неравенство (2) эквивалентно не-
равенству
х — 1>2х+1,
откуда х < — 2. В случае 3° исходное неравенство не имеет реше-
ний, так как эта система неравенств х> 1 и х< — 2 несовместна.
Итак, в случае 0<а<>1 все решения данного неравенства
— 2<х<-------—,--
2 2
или все значения х из интервала (—2, 0), кроме л =----
Замечание. Неравенства
|х—1|<|2х+1| и |х — 1|>|2х+1|
хорошо интерпретируются геометри-
чески (рис. 6), если, конечно, счи-
тать, что х — действительное число
(это и предполагается в данной за-
даче) . Из рис. 6 видно, что если
х<—2, то 12х + 1|>|х—1 , если
—2<х<0, то ]2x4-1 |<|х—11, а ес-
ли х>0, то 12x4-1 |>|х—11.
3. Произведем над данным урав-
нением следующие эквивалентные
преобразования:
(О
г1 л • 9 /1 1 2 \2i cos3x . 2 sin 2дг cos Зх А
[1 — 2sin2x—(1 — sin2 xr}----------------------= 0,
v ' sin 3,r 8 sin 3x
sin4 x cos 3x j 4 sin x cos x cos 3x __ q
sin3x 8sin3x
sin x cos 3x (cos x — 2 sin3 x) _ q
8 sin 3x
Корни уравнения sinx = 0 не являются корнями данного урав-
нения, так как если sinx = 0, то и sin3x = 0.
Корни уравнения cos3x = 0, т. е.
л . fat
х =----------,
6 3 ’
где k принимает все целые значения, являются корнями данного
уравнения, так как если cos3x=0, то sin3x=±l, и знаменатель
уравнения (1) в нуль не обращается.
Пусть, наконец,
cosx —2sin3x = 0.
34
Имеем
' cosx — sinx 4-sinx — 2sin8x = 0,
cosx —sinx + sinx(l — 2sin2x) = 0,
cosx — sin x + sinx-cos 2x — 0,
cosx —sinx 4- sinx(cos2x— sin2x) = 0,
(cosx —sinx) (1 + sinxcosx + sin2x) = 0.
Отсюда
cosx — sinx = 0,
t. e.
tg*x = 1, x=ka +
где k принимает все целые значения. Все эти значения х — корни
данного уравнения, так как
sin Зх = sin (зйл + ¥= 0-
Остается решить уравнение
1 + sin xcosx + sin2x = 0.
Переписывая его в виде ’
fsinxq--^Y + l—^- = 0,
\ • 2 ) 4
заключаем, что оно не имеет решений.
Итак, все решения данного уравнения:
л । . Ал t л
х =-----------------------, х = kn 4-,
6 3 4
где k принимает все целые значения.
4. Пусть Xi =—3, х2 =— 3 и х3=2 — корни данного много-
члена. Тогда
2Х3 4- ах2 + Ьх + с = 2 (х + 3) (х 4- 3) (х — 2),
или
2Х3 4- ах2 4- Ьх 4- с = 2Х8 4- 8х2 — 6х—36.
Так как это тождество относительно х, то
а = 8, Ь = — 6, с——36.
Эту задачу можно решить иначе: так как xi = 2—корень данного
многочлена, то 164-4 а+2 Ь + с=О. Так как х2=—3 — корень дан-
2*
35
ного многочлена, то —54+9 а—Зб4-с=0. Затем перепишем дан-*
ный многочлен так:
2*34- ах2 + Ьх + с = (х 4- 3) [2х2 4-(а — 6) х 4- 6 — За 4- 18] 4-
4- —54 4-9а —36 4-с.
Так как —544-9 а—Зб4-с=0, то 2х3+а'х2+Ьх+с =
= (х4-3) [2х24- (а—6)х4-6—За4-18].
Поскольку данный многочлен имеет два корня, равных —3, то
Хз——3 есть корень многочлена 2х2+(а—6)х+Ь—За 4-18, т. е.
справедливо равенство
18—3 (а—6) 4-6—3 а 4-18=0.
Из системы трех уравнений
16 4- 4а 4- 26 4- с = 0,
54 4* 9а — 36 4- с — О,
18 —3(а —6)4-6 —За 4-18 = О
находим а=8, 6=—6, с=—36.
5. Пусть ABCDA\B\C\D\ — куб (рис. 7), ребра AAi, ВВ1г ССЬ •
DDi перпендикулярны плоскости л основания АВ CD.
Пусть точка О — центр куба. Тогда все точки М, удовлетво-
ряющие условию задачи, находятся на окружности S, лежащей в
плоскости Ль параллельной плоскости л и отстоящей от плоско-
сти л на расстоянии 2h. Центр О\ этой окружности является про-
екцией на плоскость ni центра О куба, а радиус г окружности S
определяется соотношением
г — R2 — ’ и так как Я > ЗА, то
г>1/' 962 — (— V
Г \ 2 ) 2
36
Ясно, что если мы из точки М проведем прямые, соединяющие
ее со всеми точками куба, то все точки пересечения этих прямых
с плоскостью я и дадут тень, отбрасываемую кубом. При этом
включим в тень и квадрат ABCD, лежащий в основании.
Для построения тени достаточно провести лишь прямые, сое-
диняющие точку М с вершинами куба, и найти точки их пересече-
ния с плоскостью л; соединив эти точки прямыми, получим контур
тени. .
Спроектируем окружность S на плоскость я; получим (рис. 8)
окружности радиуса г, внутри которой находится квадрат ABCD
со стороной h. Центром О2 окружности Si является проекция цент-
ра О куба на плоскость л.
Пусть Ki — произвольная точка пространства, отстоящая от
плоскости л на расстоянии, равном h. Обозначим через К ее пря-
моугольную проекцию на плоскость л.
Обозначим через К2 проекцию точки Ki из точки М на пло-
скость л. Тогда М[К2=2-М1К, где Mi—прямоугольная проекция
точки М на плоскость л (рис. 9).
37
Пусть А2, В2, С2, D2 — проекции точек Ait Blf Clf Di из точки М
на плоскость л; на основании сделанного замечания имеем
А2МХ = 2/Ш*, В2МХ = 2ВМ1г С2М± = 2СМ„ D2MX = 2DMV
Обозначим через N точку пересечения
окружности S с прямой, проходящей че-
рез точку О2 параллельно прямой DA, а
через L — точку пересечения окружности
S с прямой О2А (рис. 10).
Достаточно рассмотреть тень лишь
тогда, когда точка находится на дуге NL
окружности S.
Обозначим через Р точку пересечения
окружности S с прямой DA. Рассмотрим
два случая: Г точка Mi находится на ду-
ге PN-, 2° точка Mi находится на дуге PL.
1°. Пусть точка находится на дуге PN. Выясним, при ка-
ком положении точки Mi тень будет наибольшей. Если точка Mi
не совпадает с точкой Р, то тенью является шестиугольник
A2D2IIAD, В2С2]]ВС, D2C2\\DC\ соединив точки Л2 и В2, получим,
что тень состоит из квадрата ЛгВгСгДг со стороной 2ft и трапе-
ции АА2В2В с основаниями h и 2 Л и высотой, равной расстоянию
от точки Mi д.о прямой АВ.
38
Наибольшей эта высота будет тогда, когда точка Mi, переме-
щаясь по дуге PN, совпадает е точкой N, т. е. когда прямая М1О2
будет перпендикулярна ребру АВ (рис. 11). Значит, когда точ-
ка Mi движется по дуге NP от N к Р, площадь тени уменьшается,
и принимает наименьшее значение, когда точка Мг совпадает с точ-
кой Р. В этом случае тенью будет пятиугольник AD2C2B2B
(рис. 12), но его площадь также может быть найдена как площадь
квадрата A2B2C2D2 со стороной 2 h и трапеции АА2В2В с основа-
ниями h и 2h и высотой, равной расстоянию от точки Р до пря-
мой АВ.
2°. Посмотрим, как .будет изменяться площадь тени, если точ-
ка Mi движется по дуге PL. В этом случае тень ABB2C2D2D
(рис. 13) состоит из двух прямоугольных треугольников (ABD со
стороной h и B2C2D2 со стороной 2 Л) и трапеции BB2D2D, основа-
ния которой hY2 и 2/г]/2, а высота равна расстоянию от точ-
ки Mi до прямой BD.
Из точек дуги PL- наиболее удаленной от прямой DB является
точка L (рис. 14).
Для того чтобы найти наибольшую тень, остается сравнить
площади двух теней, отбрасываемых точкой М на плоскость л
в тех случаях, когда точка Mi совпадает либо с точкой N, либо с
точкой L. Пусть точка Mi совпадает с точкой N (см. рис. 11).
В этом случае тень состоит из квадрата A2B2C2D2 с площадью 4 №
39
Рис. 13
и трапеции АВВ2А2 с площадью й-NE (£ —проекция точки N
на прямую АВ).
Так как NE=NO2—ОгЕ=г—то площадь тени равна ,
2
4ft8 + —й /г——) = -Ц- й2 + —hr.
2 \ 2 / 4] 2 |
Пусть теперь точка Л41 совпадает с точкой L (см. рис. 14).
В этом случае тень состоит из треугольника ABD с площадью .
-1-й2, треугольника B2C2D2 с площадью 2й2 и трапеции BB2D2D
RD BnDa Т л
с площадью --~2 2 LO2.
Так как LO2=г, BD=hY2, BzD2=2h 1^2, то площадь тени
равна
— + 2й2 + -^-V2 hr = -5- h2 + —/2"hr.
2 2 2 2
Теперь сравним две эти площади. Составим разность площадей
и преобразуем ее последовательно:
-Lhi + —V'2hr—(—h2+ — hr'\ =
2 2 4 2 )
41
- - fh'+ДД w - 4- -1 > (r -h
' тг £ £• \ £• J
3t/~3
Выше было доказано, что r>——h. Но так как
ТО
/2+1 /,< 3/3 >,
2 2 П
r — h
значит,
J_ft2 + _L/2 hr— (—h*+ —hr\>0.
2 2 <4 2 • )
Таким образом, наибольшая площадь тени будет тогда, когда
точка ЛЬ совпадает с точкой L.
Остается заметить, что точка L, центр О куба и его вершина А
лежат в плоскости, перпендикулярной плоскости л основания.
Решение варианта 2
6. Обозначим через х вес одного из отрезанных кусков, через
и и о — количество меди в 1 кг соответственно первого и второго
кусков. Тогда в остатке первого куска содержится (т—х)и кг
меди; в остатке второго куска (п—x)v кг меди; в первом отрезан-
ном куске хи кг меди и, наконец,., во втором отрезанном куске
xv кг меди.
После того как куски снова сплавили, в первом куске оказа-
лось (т—x)u+xv кг меди, а во втором (и—x)v+xu кг меди. Со-
держание меди в первом куске (в процентах)
1ОО.±^^±^о/о,
т
а во втором 100 • .(п~х^~^хи По условию имеем уравнение
ЮО • (m~x)u + xv _ юс . (n — x)v + xu
т п '
ИЛИ
тли— хп(и— о.) = tniw + хт(и — о),
или
х(т + п)(и — v) = тп(и—v).
42
По условию процентное содержание меди в данных кусках
различно, т. е. u^=v. Поэтому из предыдущего уравнения находим
Л=_ тп.
m-j-n
7. Данное неравенство выполнено тогда и только тогда, когда
°<1°8а-75г<1« (О
Рассмотрим два случая.
I. 0<п<1.
Соотношения (1) равносильны следующим:
Л . 2х-3
а <-----г- < 1 •
х — 1
Поскольку. 3- = 2----—, то а < 2-----— < Г,
х—1 х—1 х—1
или
К—1-<2-а. (2)
X— 1
Из неравенства 1 < * —имеем 1<х^2 и обратно; поэтому
соотношения (2) эквивалентны таким:
0<х —1<1<(2 — а) (х—1).
Но 2—а>0 (так как а<1) и неравенство 1< (2—а) (х—1)
можно переписать так:
х—1>——,
2—a
3___а
откуда х > ———. Таким образом, имеем систему неравенств
1<х<2,
__________________ з—«
'________2 —a
Для решения этой системы нужно знать, как расположено чис-
ло ———относительно 1 и 2. Неравенство
3—а ।
2 —а
равносильно (поскольку 2—а>0) следующему: 3—а>2—а, т. е.
верно при любом а. Неравенство------>2 равносильно такому:
43
3—а^4—2а, или а>-1, что противоречит предположению 0<а<1.
Следовательно, для любого а, такого, что 0<а<1, справедливо
неравенство
1< 3—<2,
2 — а
и решением системы являются числа х из полуинтервала
3 —а
2 —а
х<2.
II. а>1.
В этом случае данное неравенство выполнено тогда и только
тогда, когда
(3)
или
или
(4)
Здесь рассмотрим три случая.
Пь 1<а<2.
В этом случае 2—а>0, и так как 1—(2—а)—а—il>0, то нера-
венствам (3) удовлетворяют только такие значения х, для которых
х—1>0. Поэтому
тогда, когда
соотношения (3) выполняются тогда и только
1
2 — а
или
3 — а
2 — а
П2. а>2.
Найдем сначала решения в области х>1 (см. соотношения (4)).
Так как 2—а<0<—-—, то неравенство
для всех рассматриваемых х, а-неравенство
следующему (х>1!):
2—а<—-— выполнено
х — 1
-----'С 1 равносильно
откуда х^2. Все х, удовлетворяющие этому неравенству, лежат
в рассматриваемой области х>1 и поэтому являются решениями
исходного неравенства.
44
Теперь, считая, конечно, по-прежнему а>2, найдем решение в
области х<1. Из соотношений (4) находим
1— (2 — а) = а— 1 >2,
поэтому существуют числа, большие 2—а и ^1. Так как х<1, то
неравенство —— выполняется. Решая же неравенство
х — 1
L_>2-a (х<1),
получим
Но
поэтому
X
3—а
2 —а
3~а- _ 1 =*—!— < О,
2—& 2 —а
%
3—а
2 — а
а так как мы ищем решения х<1 (и для случая л>2), то все они
будут
X
3 — а
2—а
Из. а=2.
В этом случае неравенства (4) принимают вид
0<—Ц-<1
х — 1
и решениями их являются все значения х, такие, что ,
х > 2.
Итак, если 0<а<1, то <х<2; если 1<а<2, то 2<
<х< 3~а ; если а = 2, то х>2; если а>2, то х< 3~~а ,
2—а 2—а
х>2.
8. Преобразуем левую часть данного уравнения следующим
образом:
cos2 Зх — tg2 Зх — sin2 Зх + 1 = cos2 Зх (1 — tg2 Зх) + 1 — tg2 Зх =
= (1— tg2 Зх) (1 +cos23x).
45
Имеем уравнение
(1 —tg23x)(l 4-cos23x) = 0.
Поскольку ни при каких значениях х 14-cos23x=/=0, то полу-
чаем уравнение
1— tg23x = 0,
эквивалентное данному, откуда tg23x=d, и следовательно, Зх=
= (2&4- 1)-^-,так что х = (2^4- где принимает все целые
значения.
9. Первое решение: разделив х44-1 на x2+px+q, полу-
чим в остатке
(<7 —р2)рх+ 1— p*q+q*.
Следовательно, х44-1 делится на x2+px+q в том и только в
том случае, когда
р(2<7 —р2) = 0,
.1 — Р2<7 4-<72 = 0;
р5^0,.так как в противном случае из второго уравнения получаем
1 + ^2_q( что не выполняется при действительных значениях q
(см. условие задачи). Значит, из первого уравнения p2=2q и под-
ставляя 2 q вместо р2 во второе уравнение, получим <?2=1. Но
q= >0, так что q= \ и р2=2. Таким образом, система (.1) имеет
два решения:
pt = V2, ^ = 1; р2 = — /2, <?2 = 1.
Итак, х4+1 делится на х24-х]/24-1 и на х2—х 1^24-1.
Второе решение. Многочлен х4 4-1 делится на x2+px+q
в том и только в том случае, когда существуют такие числа а и Ь,
что выполняется равенство многочленов
х4 + 1 = (х2 + рх -J- q) (х2 4- ах +Ь).
Раскрывая скобки в правой части, получим многочлен
х* + (Р + а) х3 4- (q +ар 4- Ь)х2 4- (aq 4- bp) х 4- bq.
Два многочлена равны тогда и только тогда, когда равны
коэффициенты при соответствующих степенях х. Таким образом,
р + а = 0,
q 4- ар 4- b = 0,
46
aq + bp = О,
bq = 1.
Из первого уравнения р = — а. Тогда
q — а2 + b = О,
a(q—b) = О,
bq = 1.
(1)
Если а=О, то из первого уравнения этой системы имеем
b + q=O, т. е. 6 =—q, а тогда третье принимает вид q2=—1, что
противоречит условию задачи. Значит, а=/=0. Тогда из второго
уравнения системы (1) находим q=b, а из третьего 62=1, значит,
а2=2&, так что 6>0. Следовательно, b=l, q=l, а2=2. Отсюда
01 = 1^2, а2=—1^2, Тт е. р\ =—1^2, р2=]/2. •
Таким образом, рассматриваемая система имеет два решения:
a1 = V2’. ^=1, Pi = —УХ <71 = 1;
a2 = — V~2, b2=l, р2--=У~2, <72=1.
Следовательно, при р=—]/2, q=l и при p=V2, q=l, и
толькр при таких значениях р и q существуют числа а и Ь, обла-
дающие требуемым свойством.
Третье решение. Многочлен х4 4-1 делится на x2+px+q
в том и только в том случае, когда оба корня этого трехчлена яв-
ляются его корнями. Решая биквадратное уравнение *
х4 + 1 = О,
получаем корни
Но коэффициенты трехчлена x2+px+q действительные, так
что его корни должны быть сопряженными. Следовательно, его
корни либо Xi и х2, либо х3 и х4. В первом случае р=—(xi+x2) =
= — ]/2, q=l, во втором р=—>(х34-х4) =У2, д=х3х4=1.
10. Пусть SK.LM. — правильная пирамида; S — ее вершина,
KLM — правильный треугольник, лежащий в основании. Пусть
О — прямоугольная проекция вершины S на плоскость Р.
Так как точка А отстоит от плоскости Р на расстоянии h, а от
точки О на расстоянии /, то точка А лежит на окружности л, кото-
рая расположена в плоскости Р', параллельной Р и отстоящей от
• = 0, Х*+ 2х2 + 1—2х2 = 0, (х2 + 1)2 — (х/2)2 = 0, х24-х/2 4- 1 = 0,
х2 — х /"2 4-1=0; отсюда получаются значения хх, х2, х;), х4, указанные в
тексте.
47
нее на расстоянии h (рис. 15). Центром С окружности я является
проекция точки О на плоскость Р'.
Рассмотрим только тот случай, когда h>SO и когда точки А
и S расположены по одну сторону от плоскости Р.
Если точка А перемещается по окружности л, то точка А' —
тень вершины S на плоскость Р перемещается по некоторой окруж-
ности я' (эта окружность я' является центральной проекцией из
точки S окружности л на плоскость Р').
На рис. 16 изображен вид рис. 15 по направлению прямой СО.
Пусть N — точка пересечения с окружностью л прямой, прохо-
Рис. 15
Рис. 16
дящей через точку О перпендикулярно ML, а В — точка пересече-
ния с окружностью л‘прямой, проходящей через точку О перпен-
дикулярно КМ.
Для решения задачи достаточно рассмотреть перемещение точ-
ки А лишь по дуге NB.
Из точки N не видна только сторона основания LM и поэтому
тенью от пирамиды является h.LN'M, где N' — тень вершины S.
Сам ZxKLM мы не будем относить к тени.
Пусть теперь точка А движется по окружности от N к В. Тень
А' вершины S при этом перемещается по окружности л' от N' к В'.
Пусть R' — точка окружности л', лежащая на прямой KL и R —
соответствующее положение точки А. Точка R лежит на прямой
SR' и точки S и R' лежат в плоскости грани KLS; следовательно,
и точка А лежит в плоскости грани KLS. Поэтому если точка А
занимает некоторое положение Q между N и R (включая самое
точку R), то из нее не видно только одной стороны основания LM,
и тенью пирамиды является A.LQ'M, площадь которого меньше
площади ALN'M, так как эти треугольники имеют общее основа-
ние, а высота треугольника LQ'M меньше высоты треугольника
48
Если же точка А занимает некоторое положение Т между R
и В, то из нее не видны стороны основания KL и LM. Поэтому теныр
пирамиды будет четырехугольник T'KLM; ARLM дополняет этот
четырехугольник до АКТ'М, и этот же треугольник дополняет
/\LR'M до Но, как и выше, площадь ЛКТ'М, очевидно/
больше, чем площадь /\KR'M, и поэтому площадь T'KLM больше
площади ALR'M. Л
Итак, когда точка А движется от N к R, площадь тени умень-..
шается, а когда она движется далее от R к В, площадь тени воз-
растает. Следовательно, площадь тени будет наименьшей, если
источник света находится в точке R, т. е. в плоскости грани RLS.
§ 7. ФИЗИЧЕСКИЙ ФАКУЛЬТЕТ
ВАРИАНТЫ ПИСЬМЕННЫХ ЭКЗАМЕНОВ
(дневное отделение)
s Вариант 1
1. Для каждого действительного числа а решить неравенство
. 1
ах>> —.
X
2. Найти все значения х и у (в том числе комплексные), такие,
что числа х, х+2у, 2х+у образуют арифметическую прогрессию,
а числа (z/+l)2, ху+5, (х+1)2 образуют геометрическую про-
грессию.
3. Решить уравнение
cos*х + sin* л = 2cos Г2x + — cosf2х-—.
\ 6 Л \ . 6 ;
4. В равнобедренном треугольнике дана боковая сторона Ъ
и угол при основании а. Вычислить расстояние от центра вписан-
ной окружности до центра описанной окружности.
5. Правильная пирамида, в основании которой лежит квадрат
со стороной а, вращается вокруг прямой, проходящей через ее
вершину. Эта прямая параллельна одной из сторон квадрата, ле-
жащего в основании пирамиды. Вычислить объем тела вращения,
если плоский угол при вершине пирамиды равен а.
Вариант 2
6. Для каждого действительного числа а решить уравнение
х | х + 11 + а = 0.
7. Решить неравенство
—-— < +2х — 1.
/27+9
49
8. Решить систему уравнений
sin(x— у) = 3 sinxcos у— 1,
sin (х + у) = — 2cosxsin у.
• 9. Из точки А, лежащей вне окружности радиуса г, проведена
секущая, не проходящая через центр О окружности. Пусть В и С—
точки, в которых секущая пересекает окружность. Найти
. ^АОВ . ^АОС
te—Y—-tg —J—.
если ОА=а.
10. Три шара касаются плоскости треугольника АВС в его вер-
шинах и попарно между собой. Найти радиусы .шаров, если из-
вестны длина с стороны АВ и прилежащие к ней углы А и В.
Вариант 3
11. Для каждого действительного а решить уравнение
V И + 1 — КМ -а.
(найти только действительные корни).
12. Решить систему уравненйй
cosx + cos у = 1,
cos — -р cos— = ----1.
2 2 2
13. Решить неравенство
' 3sin 2x>'stax + cosx + 1.
44. AOB — сектор круга радиуса г. Угол ХАОВ==а(а<я).
Найти радиус окружности, лежащей внутри этого сектора и ка-
сающейся хорды АВ, дуги АВ и биссектрисы угла АОВ.
15. Две равные сферы радиуса г касаются друг друга и граней
двугранного угла, величина которого равна а. Найти радиус сфе-
ры, которая касается граней двугранного угла и обеих данных
сфер.
Вариант 4
16. Для каждого действительного числа а решить уравнение
|cos2x| = | sin2 х — а| (0<х<2л).
17. Найти все действительные значения k, при которых, реше-
ние системы
х — 2у = k,
Зх + у = 8
50
удовлетворяет условию
у>а-
18. Решить уравнение
4slnx + 2cosx = 2 + 3 tgx.
19. Даны две концентрические окружности радиусов г и R,
r<R. Через некоторую точку Р меньшей окружности проведена
прямая, не проходящая через центр окружностей и пересекающая
большую окружность в точках В и С. Пусть перпендикуляр к ВС
в точке Р пересекает меньшую окружность в точке А. Найти сумму
РА2 + РВ2 + PC2.
Л
20. Дан угол а (а< —) осевого сечения прямого кругового ко-
2
нуса с вершиной S и образующей длины /. Через точку А, взятую
на основании конуса, проведена плоскость Р, которая перпендику-
лярна к образующей ВЛ. Через вершину конуса проведена пло-
скость Q. Эта плоскость перпендикулярна плоскости осевого сече-
ния конуса, проходящего через ВЛ, и составляет с образующей ВЛ
конуса угол 0 >(£<—). Плоскость Q рассекает конус по двум об-
разующим. Пусть продолжение этих образующих пересекает пло-
скость Р в точках Ci и С2. Найти длину отрезка CiC2.
Вариант 5
21. Для каждого положительного числа а (а =И= 1) решить урав-
нение
(loga sin х)2 + loge sin х — а = 0.
22. Решить неравенство
।cos д- 1'
4 cos2 х — 3 3 — 4 cos2 х ’
0<х <^л.
23. Найти коэффициент при хп в разложении
(1 + х + 2х2 + ... 4- пхп)2.
24. АВ и CD — два взаимно перпендикулярных диаметра ок-
ружности Sj. Окружность В2 имеет центр D и радиус DA. Из точ-
ки D проведены два луча, пересекающие окружность St в точках
Р и Q, а дугу АВ окружности S2, лежащую внутри окружности
Si, — в точках М и N. Пусть Р' и Q' — проекции точек Р и Q на
диаметр АВ. Доказать, что фигура, ограниченная дугами PQ, MN
и отрезками MP, NQ, равновелика треугольнику DP'Q'.
25. Три сферы радиусов г, г и R внешним образом касаются
друг друга и все касаются некоторой плоскости. Найти радиус
сферы, касающейся данных сфер и этой плоскости.
51
Вариант 6
26. Найти все действительные значения а, при которых корни
уравнения
х8 + х 4- а = О
действительные и оба корня больше а.
27. Решить неравенство
sin л* — 2 > g
4 sin2 х — 1
28. Решить уравнение
9-1*1 = (—Yx+11 +1 Х~х 1
к 2 ) ‘
29. Даны углы В и С треугольника ABC . Найти
котангенс острого угла, который образует медиана, выходящая из
вершины А, со стороной ВС.
30. Две равные сферы касаются друг друга и граней двугран-
ного угла. Третья сфера меньшего радиуса также касается граней
этого двугранного угла и обеих данных сфер. Дано отношение т
радиуса меньшей сферы к радиусу одной из равных сфер. Найти
величину а двугранного угла. В каких границах может изменять-
ся /п?
Вариант 7
31. Для каждого действительного числа а решить уравнение
(У + 2а -Ц^- + 1 = 0.
\ yf X ) у/~ X ‘
32. Решить неравенство
tg2* —2 1
t^x —1 2 ‘
33. Доказать, что число
111 ... 11 —222... 22
2л единиц л двоек
есть квадрат целого числа.
34. Из точки А, лежащей на окружности радиуса г, проведены
две хорды АС и АВ. Эти хорды лежат по одну сторону от диаметра
окружности, проходящего через точку А. Дана длина b большей
хорды и угол ХВАС=а. Найти радиус окружности, которая ка-
сается хорд АВ и АС и дуги ВС.
35; Два равных конуса имеют общую, вершину и касаются по
общей образующей. Угол осевого сечения конуса равен 2а. Найти
52
двугранный угол между двумя плоскостями, каждая из которых
касается обоих конусов, но не проходит через их общую обра-
зующую.
Вариант 8
36. Для каждого действительного числа а решить уравнение
х2 +1 х | + а = О
(найти только действительные корни).
37. Решить неравенство , '
tg* о
1-Hg*
38. Сколькими способами можно выбрать из ста первых нату-
ральных чисел три таких, сумма которых делилась бы на три? (по-
рядок слагаемых не учитывается).
39. На одной из сторон угла, равного а, даны две точки, рас-
стояния которых до другой стороны равны b и с. Найти радиус-
окружности, проходящей через эти две точки и касающейся дру-
гой стороны.
40. Угол между образующей прямого кругового конуса и его»
высотой равен а. Найти угол между двумя образующими этого»
конуса, если известно, что плоскости, касающиеся конуса по этим
образующим, взаимно перпендикулярны.
ВАРИАНТЫ ПИСЬМЕННЫХ ЭКЗАМЕНОВ
(вечернее отделение)
Вариант 1
41. Решить неравенство
logj, (х + 1) > log2 (2 — х).
2
42. Решить систему уравнений
sin х = sin 2w
(0<х<л, 0<у<л),
cos х = sin у.
43. Для каждого отрицательного числа т решить уравнение
4* — 4т • 2х + 2т + 2 = 0.
44. В треугольнике АВС даны углы А, В, С п радиус R описан-
ной вокруг него окружности. Внутри этого треугольника взяты две
55
точки Р и Q, такие, что ZPCA = ZQCB- —, Z.PAC=-^-,
3 3
ZQBC=—. Найти площадь треугольника PQC.
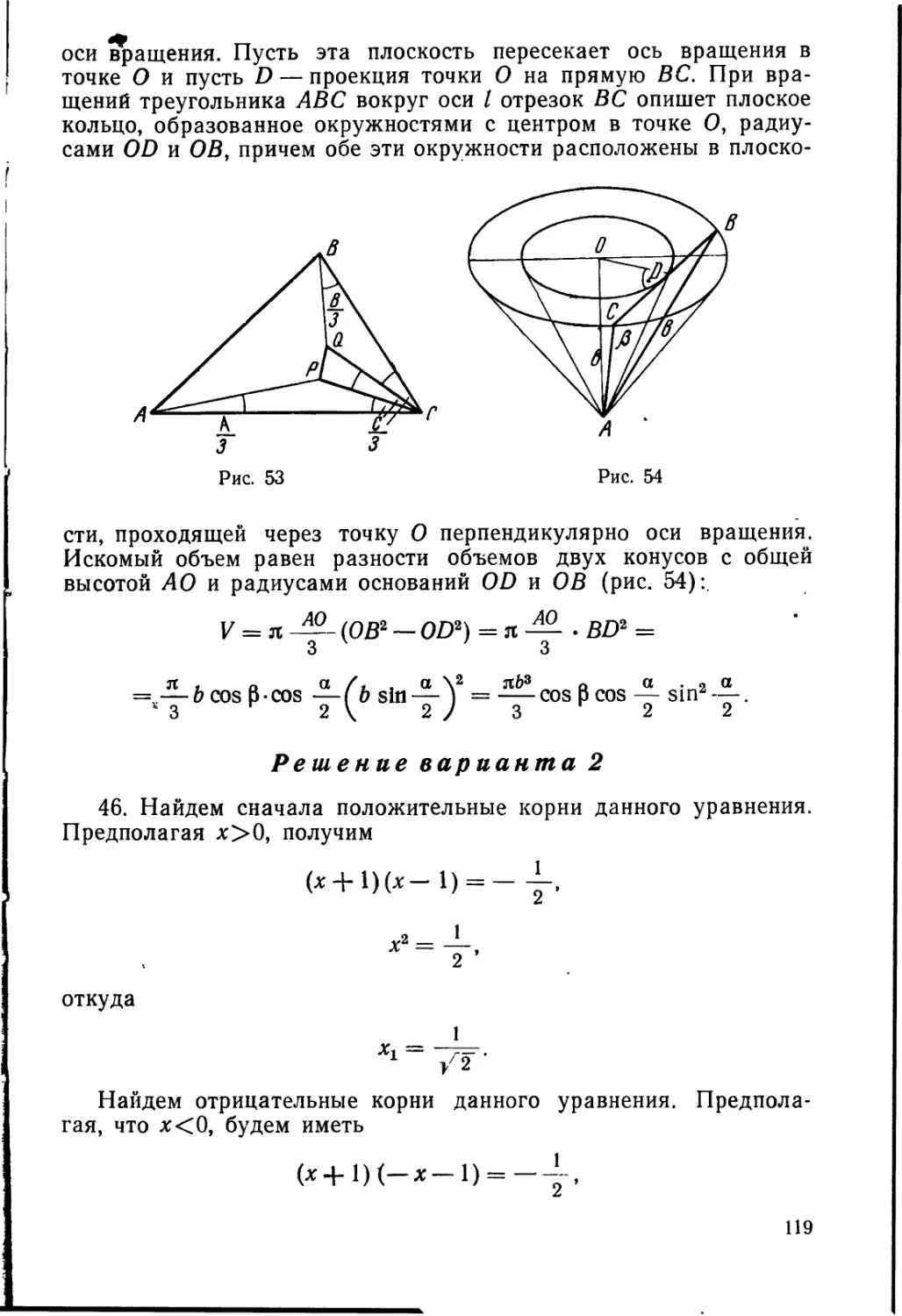
45. Дан равнобедренный треугольник АВС, АВ = АС=Ь, а угол
ВАС=а. Этот треугольник вращается вокруг оси, проходящей че-
рез вершину А так, что угол между этой осью и плоскостью тре-
угольника равен р, а основание треугольника перпендикулярно
оси. Вычислить объем тела, полученного при вращении треуголь-
ника АВС.
Вариант 2
46. Решить уравнение
(х+1)(|х|-1)=-4-.
47. Зная, что tga и tgp — корни квадратного уравнения ’
х2 + рх + q = О,
вычислить '
sin2 (a 4- Р) 4- р sin (a -|- P)cos (a 4- Р) 4- <?cos2 (a 4- P).
48. Решить неравенство
49. В круговой сектор, ограниченный радиусами ОА и ОВ
С. л \
a <-£-1, вписан квадрат так, что две его
соседние вершины лежат на радиусе ОА, третья вершина — на ра-
диусе OB, а четвертая вершина — на дуге АВ. Найти отношение
площадей квадрата и сектора.
50. Угол в осевом .сечении прямого кругового конуса равен а.
Через его вершину под углом р к оси конуса ( Р < —-) проведена
плоскость. Найти угол между двумя образующими конуса, по ко-
торым проведенная плоскость пересекает его поверхность
Вариант 3
51. Решить неравенство
— >*4-1.
X
52. Решить уравнение
Vsin х 4- cos х = 0.
54
53. Найти все действительные решения системы
2х2 = 2у2 = х
14-х» у’ 1 + j?
54. Внутри равнобедренного прямоугольного треугольника
АВС, катеты которого равны а (СА — СВ=а), взята точка Р, та-
кая, что Z.PAC=-^, ZPBC=-^. Найти расстояние от точки Р до
центра вписанной окружности.
55. В основании правильной четырехугольной пирамиды лежит
квадрат со стороной а. Высота пирамиды равна диагонали этого
квадрата. Пирамида рассечена плоскостью, параллельной ее вы-
соте и двум противоположным сторонам основания. Найти пери-
метр сечения, если известно, что в него можно вписать окружность.
Вариант 4
56. Решить неравенство
1
х U* • lgx< 1.
57. Решить уравнение
(sin х +’cos х)2 = tg х cos 2х.
58. Для каждого действительного числа а решить уравнение
1 [а~х _т*Л 9
V l-j-x |/ а — х
59. Три окружности расположены на плоскости так, что каж-
дая из них внешним образом касается двух других. Радиусы
окружностей относятся как 1 : 2 :3. Вычислить углы треугольника,
вершины которого расположены в точках касания.
60. Через середину диагонали куба перпендикулярно к ней
проведена плоскость. Определить площадь фигуры, получившейся
в сечении куба этой плоскостью, если ребро куба равно а.
Решение варианта I
(дневное отделение) 1
1. Перепишем данное неравенство в виде
1 . Л а№— 1 . п
ах---->0, или -------~>0.
х х
Если а^О, то все решения этого неравенства х<0. Если а>0,
то данное неравенство эквивалентно следующему:
55
Все решения данного неравенства (в случае а>0) образуют два
интервала’ (----(Ли/ -5-^, 4-оо\, или-------------
\ Vо, / \ /а / /а,
<х<Ч-оо. Результаты приведены на рис. 17.
[ 2. В соответствии с условием задачи имеем систему уравнений
х + 2х + у = 2(х + 2у),
(х+1)2(1/+1)8 = (х!/ + 5А
или
х = Зу,
(Зу+1)2(«/4-1)2 = (3«/2 + 5)2,
или
х = 3у,
I (3«/ + 1) (У + 1) + 3/ + 5] [ (Зу + 1) (у + 1) - 3/ - 5] = О,
или
X = Зу,
(6/ + 4у + 6) (4у— 4) = 0.
Эта система распадается на две:
х = Зу, ] х = 3у,\
3z/2 + 2i/+3 = 0 ) (1) И у=1. ) (2)
Отсюда находим три решения: хг = 3, «/1=1;
х2 = —1 + 2«/2, у2 = ~ 1 уИ-; х3 = - 1 -21 /2,
* о
_ -1-21/2 _
% .
3. Преобразуем данное уравнение следующим образом:
S6
(sin2 x + cos® x)2— 2sin2xcos2x = cos 4x4- cos ~
1----— sin2 2x = cos4x 4- -l-
2 2
1—^-(1 —cos4x) = cos 4x4-
_ л 1
Отсюда cos 4x = — и, следовательно,
3
fat , 1 1
x =------± — arc cos —
2 4 3
где k — любое целое число.
4. Пусть CD — высота равнобедренного треугольника АВС
{АС—ВС). Так как центры I и О вписанной и описанной окруж-
ностей лежат на луче CD, то расстояние d между ними всегда
равно | СО—CI |, независимо от того, лежит ли точка / между точ-
ками С и О, или точка О между точками Си/, или если точки F
и О совпадают (рис. 18). По теореме синусов
СО = /? = -?-,
2 sin а
CI = CD — ID = fcsina— ADtg— = fcsina — ftcosatg — „
2 < 2
так что
IO = d =
b'
2 sin a
b sin a 4- b cos a tg
— b
a a
„ sina cos — — cos a sin —
1 2 2
2 sin a a
cos —
2
57
= b
2 sin a a
cos —
2
b
2 sin a
1—4sin2 —
2
_A_|4COs2 — —3
2 sin a I 2
Ь I A О d О 01
4 cos3 3 cos —
a---------------------------2----2
2 sin a cos —
2
I 3a I
fr|C0S~T I
2 sin a cos —
2
Замечание. Из проведенных выкладок следует, что СО—
—С1>§ тогда и только тогда, когда cos-|-->0, а так как а —
острый угол, то это неравенство имеет место тогда и только тогда,
когда -у- < •—, т. е. а<С~-’ Таким образом, центр описанной
окружности равнобедренного треугольника лежит «ниже» центра
вписанной окружности тогда и только тогда, когда угол при осно-
вании равнобедренного треугольника меньше —, иначе угол при
3
вершине больше-^-. Если а= то треугольник равносторонний
и точки I и О совпадают.
Все это можно установить и геометрически. Прежде всего от-
метим, что условие
C> — эквивалентно (для равнобедренного
3
треугольника с вершиной С) следу-
ющему: с>Ь (где с и b — длины
сторон АВ и АС). Заметим, что
центр О окружности, описанной во-
круг равнобедренного треугольника
АВС (АС=ВС), является точкой
пересечения медиатрисы * стороны
АС с высотой, опущенной из верши-
ны С на сторону АВ. Если с>Ь, то
отношение
АВ' p — b
В'С р — с ’
в котором точка В' прикосновения к
стороне АС вписанной окружности
* Медиатрисой отрезка АВ называется
прямая, проходящая через середину этого
отрезка перпендикулярно к нему.
58
делит сторону АС, больше 1, а потому точка В' лежит между точ-
кой С и серединой В" отрезка Л С. Но так как В"0||В7, то точка /
лежит «выше» точки О. Аналогично доказывается, что в случае с<&
точка / лежит «ниже» точки О (в случае с=Ь точки О и / совпада-
ют) (см. рис. 18).
5. Пусть SABCD — данная пирамида (ЛBCD — квадрат со сто-
роной а), а /—ось вращения (рис. 19), параллельная АВ. При
вращении вокруг оси I отрезки AD и ВС опишут одинаковые плос-
кие кольца; радиус внутренней окружности кольца равен МР =
=NT=SP, где SP — высота пирамиды, а радиус внешней окруж-
ности кольца равен MA=NB=SQ, где SQ— апофема пирамиды.
Апофемы S/? и ST опишут равные конусы, высота каждого из
которых равна —, а радиус основания равен высоте SP пирами-
ды. Наконец, квадрат ABCD опишет полый цилиндр с внутрен^
ним радиусом SP и внешним SQ. Искомый объем V равен разно-
сти Vi—2У2, где Vi — объем цилиндра с радиусом SQ и высотой а,
а Уг — объем одного из указанных выше конусов. Итак,
V = л • SQ2a — 2 • — л • SP2 • ~;
3 2 ’
но
SQ = у ctg-p SP = У SQ2 — PQ2 = -у
следовательно,
т7 а2 , 2 « 2 _ a2 f . « а а
V = л---ctg2 — - а----л — ( ctg2-----1 )-----
4 6 2 3 4 \ 6 2 /2
Решение варианта 2
6. При решении этой и многих других задач, предлагавшихся
на физическом факультете, хорошо применять следующую теоре-
му: если корни квадратного уравнения x2+px+q — Q с действитель-
ными коэффициентами действительны и различны, то число X
меньше обоих корней тогда и только тогда, когда выполнены не-
равенства
А2 рА q 0, 2А-|-р<^0.
Число X больше одного из корней и меньше другого тогда и только^
тогда, когда выполнено неравенство
%2 -р рА q О»
59>
Число К больше обоих корней, если выполнены неравенства
Х® + рХ + ^>0, 2Х + р>0.
Доказательство этой теоремы таково: число X меньше обоих кор-
ней Xi и х2 (напомним читателю, что мы предполагаем, что эти
корни действительны и различны) тогда и только тогда, когда раз-
ности X—Xi и Л—х2— числа отрицательные, а это будет тогда и
Только тогда, когда их произведение положительно, а сумма отри-
цательна:
(K — xJlK — х2)>0, X — хг + X — х2<0,
«ли
№ — (xi + х2) X 4- х2х2 >0, 2Х — (хх + х2) < 0,
« так как xi+x2 = —Р, xxx2=q, то
Х® + рХ + ?>0, 2Х4-р<0.
Далее, число X больше одного корня и меньше другого тогда и
только тогда, когда разности X—Xi и X—х2 — числа разных знаков,
т. е. (X—Xi) (X—х2)<0, или Х2+рХ+^<0. Наконец, число X боль-
ше обоих корней Xi и х2 тогда и только тогда, когда числа X—xt и
X—х2 положительные, а это имеет место тогда и только тогда,
когда произведение и сумма этих чисел положительны:
(X — хх)(Х —х2)>0, X —Xj-4-Х—х2>0,
«ли
X® 4-рХ+ ^>0, 2Х + р>0.
Перейдем теперь к решению данной задачи. Заметим прежде
всего, что так как а действительное число, то данное уравнение не
может иметь мнимых корней. Далее, х=—1 является корнем дан-
ного уравнения тогда и только тогда, когда а=0; при этом уравне-
ние имеет еще корень х=0. Будем в дальнейшем считать, что а=#0.
Тогда х——1 не корень данного уравнения и, значит, если х.— ко-
рень данного уравнения, то х+1=#0. Итак, считая, что а=#0, най-
дем сначала те корни данного уравнения, для которых х>—1*т. е.
х-Ы>0. При этом условии |х+1| =х+1, и данное уравнение при-
нимает вид
х® + х + а = 0.
Мы должны исследовать, при каком условии это уравнение
имеет действительные корни, большие —1. Прежде всего должно
быть 1—4a^s0 (условие действительности корней), или а<—.
4
Если а= то-корни уравнения х2+х+а=0 будут Xi=x2=---------
60
это корни и данного уравнения, так как —— >—1. Будем считать,
что а<—. Тогда корни Х[ и х2 уравнения х2+х+а=0 действи-
4
тельны и различны. Они больше —1, если (см. теорему, сформули-
рованную в начале решения этого примера) выполняются нера-
венства
(х2 + х + а)ж=-1 > 0, (2х + 1 )хт_1 < О,
или (второе неравенство выполняется —1<0), а>0. Итак, если
0<а<—> то уравнение х2+х+а=0 имеет два действительных
4
корня:
х1>2 =--------------
и оба они больше —.1, а потому являются и корнями данного
уравнения.
Далее, число —1 будет заключено между корнями xt и х2 урав-
нения х2+х+а=0, если
(х2 4- х 4- a)x=-i < 0, или а < 0.
Рис. 20
Итак, если а<0,
тельных корня Xi и
то уравнение х24-х4-а=0 имеет два действи-
х2, но только больший из них
-1 4-/-1 -4д
больше —1, а потому только он будет корнем данного уравнения
(большим —1). На риС. 20 изображены результаты исследования
корней данного уравнения, больших —1 (а также для случая"
а=0).
61
Теперь исследуем корни уравнения, меньшие —.1. Для таких
корней х+1 <0, и данное уравнение принимает вид
— хъ—х4-а = 0, или х24-х— а = 0.
Теперь надо исследовать, когда это уравнение имеет действи-
тельные корни, меньшие —1. Прежде всего должно выполняться
условие
1 + 4а > 0, или а > —.
При а—----— уравнение принимает вид х2+х+ — =0 и имеет
4 4
корни Xi=x2=—— „ большие —1. Будем считать, что а>-----—.
2 4
Тогда корни уравнения х2+х—а=0 действительны и различны.
Оба корня будут меньше —>1, если выполняются условия
(х2 4- х — а)х—1 >0, (2х 4-1 )х=-1 > 0,
что не имеет места. Далее, число —1 заключено между корнями
уравнения х24-х—а=0 тогда и только тогда, когда (х2+х—
—а)ж=-1<0, или а>0.
Итак, в случае а>0 корни уравнения х24-х—а=0 действитель-
ны, различны и число —1 заключено между ними. Корнем данно-
го уравнения будет меньший корень, т. е.
— 1— /14-4а
/V - - - . . . - -L--- ф
2
На рис. 21 изображены результаты исследования наличия koi>-
ней данного уравнения, меньших —1.
Итог: если а<0, то данное уравнение имеет один корень
1+/Г^
Если а=0, то данное уравнение имеет два корня: 1
I
хх = 0, х2 = — 1. "1
62
Если 0<а<—, то данное уравнение имеет три корня:
4
Если
то
*
данное уравнение имеет два корня:
Если а>—, то данное уравнение имеет один корень
— 1 —-|Л1 4- 4а
2
Итог всех исследований дан на рис. 22.
Замечание. Изложенное решение показывает применение
общей теоремы, сформулированной перед изложением решения.
Эта теорема позволяет решить много подобных задач, где прихо-
Рис. 22-
дится исследовать расположение действительного числа относи-
тельно действительных корней квадратного уравнения. Если не
ставить цели показать применение общего метода, то эту задачу
можно решить и короче, например так: полагая x+l=z, приведем
данное уравнение к виду
(z—l)|z|+а = О,
и вопрос сведется к отысканию положительных корней уравнения
г2—z+a = 0 и отрицательных корней уравнения z2—z—а = 0 (ко-
нечно, надо еще рассмотреть случай а=0). Это исследование так-
же достаточно объемно, однако не придется применять указанную
выше общую теорему. Исследование предлагается провести чита-
телю самостоятельно.
63
Можно произвести и такую замену переменного:
• х -------— + г;
2
тогда данное уравнение примет вид
2+4~1+а=о’
а это уравнение эквивалентно следующим двум смешанным систе-
мам:
Таким образом, надо решить вопросы: при каком условии урав-
нение г2 = — — а имеет действительные корни, не меньшие-----—
4 2 ,
и при каком условии уравнение z2 = + а имеет действительные
1
корни, меньшие---
определяются затем из
Необходимо найти эти корни. Значения х
равенствах ------— -f-z. Это исследование
также предоставляется читателю.
В тех случаях, когда требуется найти только действительные
корни уравнения (или тогда, когда оно ймеет только действитель-
ные корни), интересно дать геометрическую интерпретацию реше-
нию. Остановимся на этом подробно (в применении к данному
примеру). Для этого построим график функции
i/ = x|x + 1 |.
Если х^—1, то уравнение принимает вид
у = —х2 —х.
Графиком является дуга АВ параболы с вершиной в точке
(---—, пересекающая ось Ох в двух точках В(—1, 0) и
О (0, 0). Повторяем, в силу условия х^—1 берется только ду-
64
га АВ параболы, соответствующая всем ее точкам с абсциссами
х^1—1.
Если х>—1, то уравнение z/=x|x+l | принимает вид
у = х2 + х.
Графиком является дуга BCOD параболы с вершиной в точке
с{----—,---—\ Таким образом, графиком функции у=х 1х+1|
\ 2 4 /
является линия ABCOD, состоящая из двух дуг АВ и BCOD двух.,
парабол, уравнения которых соответственно таковы:
у = — х2 — х и у = х2 4- х.
Данное уравнение
х\х + 1|4-а = 0
теперь можно переписать так:
у 4- а = 0, или у = —а;
таким образом, вопрос сводится к отысканию абсцисс точек пере-
сечения построенного графика ABCOD функции £/=х|х4-1 | с пря-
мой у — —а, параллельной оси Ох (и совпадающей с осью Ох в
случае а = 0). Теперь ясно, что следует рассмотреть пять случаев
положения прямой у=—а (рис. 23).
1) Если —а<-----— ,т. е. а>-^-,то прямая у=*—а пересекает
только дугу АВ параболы у——х2—х, и данное уравнение имеет
3 Зак. 351 , 65
один корень: это меньший корень уравнения —х2—х=—а, или
х24-х—а=0, т. е.
— 1 — т1 -г 4а
-«= -------------
1 ' 1
2) Если —а ------, т. е.а— “—, то прямая у=—а (т. е. у =
' 4 4
=----—пересекает дугу АВ и касается в точке С дуги BCOD.
4 /
Уравнение имеет два корня: меньший корень уравнения —х2—х=
= ——, или х24-х------— = 0, т. е.
4 4
— 1 — /2 1
х2 =----— и еще х3 ------
3) Если ——<—а<0, т. е. 0<а< —, то прямая «/ = —а пере-
4 4
секает дугу АВ в одной точке, а дугу BCOD в двух точках. Дан-
ное уравнение имеет три корня: меньший корень уравнения
— х2 — х = — а, т. е. х,='---—!— и еще
4 2
г____ г_____________ к
1—/)—4а 14-/1—4а
хч------о ’ Х6 ~ о
где xs и х6 — корни уравнения х2+х = —а.
4) Если а=0, то прямая у=—а, т. е. ось Ох пересекает график
функции в двух точках В и С; данное уравнение имеет два корня:
х7 = — 1, х8‘= 0.
5) Если, наконец, —а>0, т. е. а<0, то прямая у=—а пересе-
кает график ABCOD только в одной точке; данное уравнение име-
ет только один корень х9 — это больший корень уравнения х24-х=
= — а, т. е.
*9 —
— 1 + /1 —4а
2
Замечание. В приведенном геометрическом решении дан-
ной задачи пересечение прямой у = —а с построенным графиком
устанавливалось наглядными соображениями. Однако это должно
быть доказано аналитически. Отметим прежде всего следующее:
если а, Ь, с — любые действительные числа, причем а>0, то любая
прямая i/=l пересекает график функции
у = ах2 4- Ьх 4- с
06
в двух точках тогда и только тогда, когда
> 4ас — />2
4а
Эти две точки различны, если % > 4ас~б2 , и совпадают, если X =
4а
_ 4ac — fr^^B этом cjjyqae прямая у = X касается параболы у = ах2-г
4а
+ Ьх + с в ее вершине).
В самом деле, решая уравнение
ах2 4- Ьх + с = X,
получим
— b ± / ft2 — 4а(с- 1)
*' = " £ '
Корни и х2 будут действительны и различны, если Ь2— 4ас-)-
+ 4ак > 0, т. е. (а > 0) если X > 4ас~68 ]£ОрНИ Х1 и х* будут рав-
4а
ны между собой тогда и только тогда, когда Ь2— 4ас + 4аХ = 0, т. е.
. 4ас — Ь2
Л = -------•
4а
Аналогично доказывается, что в случае а<0 прямая пере-
секает график функции у=ах2+Ьх + с в двух различных точках
тогда и только тогда, когда Х<---------»и касается этого графика
4а
в одной точке (в вершине параболы) в случае
_ 4ас — Ь2
4а
В более сложных случаях (если, например, строятся графики
функций вида y=ax3 + bx2+cx+d, или y=ax4+bx3+cx2+dx+e
и т. д.) геометрические рассуждения, подобные проведенным вы-
ше, будут лишь интерпретацией, так как даже если проведено
исследование функции на возрастание и убывание, останется не
доказанным, проходит ли эта функция через все промежуточные
значения на сегменте, на котором она монотонна. Без такого дока-
зательства пересечение прямой у = к с построенным графиком
останется недоказанным. Наиболее естественно здесь было бы
обратиться к известному свойству непрерывной функции (прохо-
дить через все промежуточные значения); однако даже само поня-
тие непрерывности функции выходит за рамки средней школы. Для
целой рациональной функции у=ах2+Ьх + с второй степени, как
мы видим, указанное свойство удается доказать, притом эффектив-
но, т. е. указать те значения х, при которых функция у = ах2 + Ьх + с
принимает заданное значение из данного полуинтервала
Г 4ас — Ьа . \ . п\ / 4ас — b2 T z
-------, +°о ) (в случае а> 0), или ( —оо, ---------- (в случае
L 4а J \ 4а I
а < 0).
3*
67
7. Перепишем данное неравенство в виде
2х <2х
-/ 2х + 9 /1 + 2х + 1
ИЛИ
х(]/ 1 4-2х - V 2x4-9 + 1)<0.
Отметим, что радикалы будут действительными числами тогда
и только тогда, когда х >-. Рассмотрим два случая: 1) — у <С
Сх<0, тогда V 1 + 2х —]/ 2x4-9 4- 1 > 0; 2) х>0, тогда
/ 1 4-2х —V 2x4-9 4-1<0. _______
I) Решим неравенство V 1 4-2х — ]/ 2x4-9 4- 1>0, или
/ 1 + 2х 4-1 > V 2x4-9 .
Оно эквивалентно следующему:
1 4-2x4-2]/ 1 4-2х + 1 >2x4-9,
или
2]/ 14-2х>7;
отсюда *
45
,
8
а это противоречит условию
-у<х<о.
2) Решая неравенство -*
/ 1 4-2х — /2x4-9 4- 1 < 0,
45
получим х<—, но так как во втором случае мы считаем, что
8
х>0, то все решения данного неравенства
45
8
8. Перепишем данную систему так:
sin(x — у) =-|-sin(х 4-#) 4-sin(х — у) — 1,
sin (х 4- у) = sin (х — у) — sin (х 4- у).
68
Отсюда находим
sin(x+ у) = sin(x —у) =-^~,
5 о
следовательно,
2
х4- y = kx + (—1)4 arc sin—,
О
4
х — у = пл + (—1)" arc sin ,
5
значит,
х = k + nn + — (— 1)* arc sin— + — (— 1)" arc sin
2 2 ' 5 2 ' 5
у = — п-л 4- — (— 1)4arc sin—---— (— 1)" arc sin
a 2 2 5 2 5
где k и n — любые целые числа.
Замечание. Пользуясь формулами
si (х 4- у) = sin xcos у 4- sin у cos х,
si" (х — у) — sinx cos у — sin у cos х,
можно найти (решая данную систему) сначала sinxcosy и sint/cosx,
а затем sin(x+z/) и sin(x—у).
9. Первый способ решения. Проведем через точку Л
диаметр APOQ данной окружности (рис. 24). Полагая ЛАОВ — а,
Z А ОС=р, находим Z.BQP= -у, Z.CQP= так что искомое
произведение равно
, а . В РВ • PC пл. а ВРС
tg — tg — =---------------------------------,
s 2 s 2 QB QC пл. a BQC
так как ZBPC=ZBQC. Но треугольники ВРС и BQC имеют об-
щее основание ВС, значит, их площади относятся как расстояния
от точек Р и Q до прямой АВС; но отношение этих расстояний
равно отношению АР=а—г к AQ = a+r. Итак,
i ЛОВ 1. АОС а — г
tg------tg-------=----.
6 2 & 2 а+г
Второй способ решения. Пусть D — проекция точки О
на прямую АВС.
Применяя те же обозначения, будем иметь
^BOD = £=\ ^ОЛ£> = -я~Р~а
2 2
и, значит,
Р —а OD OD n . n а + Р '
cos -= , — = sin О AD = СО' . .
2га 2
69
Отсюда (почленно делим два последних равенства)
а
г
Р~а
COS------
2
р + а ’
COS------
2
значит (производная пропорция!)»
Третий способ решения. Так как^ЛОВ = а, ^ОАВ =
= —— а + Р и значит, АВО = — + ^~~а, то из Л АВО по тео-
2 2 2 2
реме синусов имеем
г
а
а-РР Р — а
cos------- cos----------
2 2
и далее, как во втором способе решения.
10. Сначала заметим, что если две сферы внешне касаются друг
друга и некоторой плоскости, то расстояние между точками каса-
ния равно 2 Vгхг2, где ц и г2 — радиусы сфер (рис. 25).
70
Обозначая через а, Ь и с длины сторон ВС, СА и АВ данного
треугольника, а через и, г2, г3 радиусы сфер, касающихся плоско-
сти треугольника АВС соответственно в точках А, В и С (причем
каждая сфера касается еще внешним образом двух других), на
основании сделанного замечания будем иметь
а = 2//у7, b = 2/zy7, с = 2]/"г^.
Перемножая почленно эти уравнения, получим
abc = в/уу,;
отсюда abc W3= 8 ,
а так как r2ra = = — “ 4
то г1 = 6с _ са _ 2а ’ 2 26 ’ 8 аЬ ~2с‘
Из треугольника АВС. по теореме синусов имеем
а __ Ь_________________________________с_____
sin Л sin В sin (Л + В) *
откуда
с sin Л 1 с sin В
а ------------, о *=----------,
sin (Л + 5) sin (Л + В)
значит, окончательно
Г — cs*n г _ с sin Л г _ с sin Л sin В
1 ~ 2зшЛ ’ 2 ~ 2sinB’ 3 “ 2sin2(Л + В)
Решение варианта 3
И. Так как У|х| + 1 — V\x\ > 0 при всех значёниях х, то дан-
ное уравнение не имеет решений, если а^О. Будем считать, что
а>0.
Перепишем данное уравнение в виде
УИ+1 = -ИТ|+а.
Так как при любом значении х (и а>0) левая и правая части —
положительные числа, то это уравнение эквивалентно тому, кето-
рое мы получим, возводя обе части последнего уравнения в квад-
рат:
|х| + 1 = |х| + 2аУ[х[ + а2,
71
или
2а/|х| = 1—а2.
Так как при любом значении х (и а>0) левая часть неотрица-
тельна, то уравнение не имеет решений, если я>1. Будем считать,
что 0<а^1. Тогда последнее уравнение эквивалентно уравне-
нию
4а21 х| = (1—а2)2,
откуда
и, следовательно,
х=±(1^_ (1)
Итак, если 0<а<1, то данное уравнение имеет два корня (фор-
мула (1)). Если а=1, то данное уравнение имеет один корень х = 0.
12. Перепишем данную систему в виде
2 cos2 —-Л + 2 cos2 —-----1 = 1,
2 2
1
s
x . у К 2 < cos F cos — = - — 1, 2 2 2 s
ИЛИ
2 x . л у 3 COS2 F cos2 — = , 2 2 2 ’1
X f У V 2 « cos F cos — = — 1, j 1
или !
/"cos — 4- cos— ¥ — 2 cos— cos— = —, < + 1
\ 2 2 J 2.22
r । у i/”2 < \
COS---kCOS— — —------1. 4
2 2 2 ;
Эта система уравнений эквивалентна следующей: 1
f /2 !\2 п х у 3 • :
k 2 J 2 2 2 1
x । у i' 2 <
cos---Feos- == ------1,
2 2 2
72
или после упрощений
х у 1^2
cos — cos — = —-—,
2 2 2
х . у -1Л2 <
COS-----L COS = JL---1.
2 2 2
Таким образом, cos и cos я шляются корнями квадратного
уравнения
_ iH— У— = о
\ 2 J 2
(если, конечно, оба корня этого уравнения по модулю не превос-
ходят 1). Решая уравнение, получим
х12 = А± _L(J—1/2 + А + =
2 \ 2 / Г 4 \ 2 ) 2
_2_f/1_1') + ±('/1 + 1\
2 \ 2 J ~ 2 \ 2 )
Ч = -~, ха = -1.
2
Итак,
х 1^2 ’ у , х , У ^2
COS - = —--, COS — = — 1, ИЛИ COS — = — 1, cos — = ——.
2 2 2 2 2 2
Следовательно,
х = 4kn±-^-, у = 2(2п4-1)л
и
х = 2 (2m + 1) л, у = 4зл + -у,
где k, п, т, s — произвольные целые числа.
13. При решении уравнений и неравенств, содержащих одновре-
менно sin2x и sinx+cosx, или sin2x и sinx—cosx, полезно ввести
новое неизвестное
и соответственно
sinx — cosx . / л \
у =-------—-----= sm х---------)
V 2 к 4 )
73
В первом случае
sin 2х = (sin х + cosx)2 — 1 = 2у2 — 1;
в* втором
sin2x = 1 —(sinx— cosx)a = 1 — 2у2.
Применяя это соображение к решению данного неравенства, т. е.
полагая
sin х 4- cos х . f , л \
У = ----т=----= sin ( х Н--,
/2 к 4 J
получим
sin 2х = 2у2 — 1,
3(2у2-1)>у/2+1,
или бу2 — yV2 — 4 >• О, причем — 1 < у < 1.
Решая уравнение
6«/2 —у/2 —4 = 0,
получим
Неравенства бу2—у V2—4>0, —1*0 <1 выполняются одновре-
менно в случае
или
- 1 <sin(xи Л!р_<81п(х+_5.)<1.
Для нахождения всех значений х, удовлетворяющих этим усло-
виям, полезно сначала найти на единичной окружности (тригоно-
метрический круг) точки, соответствующие углам, величины кото-
рых удовлетворяют этим соотношениям. Пусть (О) — единичная
окружность (рис. 26), радиус которой равен 1, PPi и MMi—два
ее взаимно перпендикулярных диаметра. На продолжении отрезка
РМ за точку М откладываем отрезок MS = PM. Тогда PS = 2 ]/2.
Делим отрезок PS на три равные части: PQ = QR—RS; тогда
21^7
PQ — —. Откладываем на радиусе ОР от точки О отрезок
ON=PQ и через точку N проводим прямую, перпендикулярную
74
прямой PPi. Пусть А и В — точки пересечения построенной прямой
2,Ло
с единичной окружностью. Тогда Z.MOB = arc sin ——, ХМОА =
3
= л—arcsin^^H все решения неравенства sin ^х +
соответствующие всем точкам открытой дуги АВ (т. е. точки А и
В исключаются), таковы:
2kit + arc sin ~2^— < (2k + 1) л — arc sin -2^
т. е.
2&л----— + arc sin 2 < х < 2/гл -I- — arc sin-2y 2 . (1)
4 3 4 3
Аналогично находим все решения неравенства
— 1< sin (х +
\ 4 7 2
п Зл . л п л
2ил------< х Ч----<Г 2пл------,
4 4 4
откуда
2шг —- 2/гл---(2)
Все решения данного неравенства даются неравенствами (1) и
(2), где k и п принимают все целые значения.
75
14. Обозначим расстояние от центра окружности до хорды АВ
через %:
к = ОС = г cos-у- (рис. 27).
Проведем прямую через точку
О и через центр искомой окруж-
ности. Пусть эта прямая пересе-
чет искомую окружность в точках
Р и Q.
Тогда
0P-6Q = OD2,
или
(г — 2х) г = (к + х)2,
или
х2 + 2 (г + Л).Х 4- к2 — г2 = 0.
Так как к<г (ОС<ОВ), то корни этого уравнения действитель-
ные и разных знаков. В качестве х следует взять положительный
корень
х = — (г + к) + /r2 + 2V + V —Х24-г2,
ИЛИ
х= /2г(г+Х)-(г + Х). (1)
Подставляя сюда К = rcos-~, получим
х =
2r-2r cos2 —---2г cos2 — =
4 4
= 2r cos — (1 —cos —= 4rcos — sin2—.
4 \ 4 J 4 8
Замечание. Формула (1) имеет следующую геометриче-
скую интерпретацию, позволяющую построить искомую окруж-
ность с помощью циркуля и линейки: пусть R — точка данной
окружности, лежащая на продолжении отрезка СО за точку О.
Тогда
RB2 = RC2 + СВ2 = (г + X)2 + ОВ2 — ОС2 =
= (г + М2 + г2 — X2 = 2г (г + X),
откуда
RB = У2г(г + к).
76
Так как
— г -}- X,
то радиус х искомой окружности равен разности RB—RC, иначе
говоря
RB = RD.
Таким образом, для построения центра по искомой окружности
строим окружность с центром в точке R и радиусом RB. Пусть D—
внутренняя точка данной окружности, в которой построенная
окружность пересекает диаметр данной окружности, проходящей
через точку R. Центр ® искомой окружности есть точка пересече-
ния прямой, проходящей через точку D перпендикулярно прямой
DR с биссектрисой угла DCB.
Читателю рекомендуется доказать правильность этого построе-
ния геометрически (это очень трудный вопрос).
15. Первый способ решения. Если сфера радиуса г
касается граней двугранного угла, величина которого равна а, то
расстояние от центра сферы до ребра двугранного угла равно
(рис. 28)
* . «
sm —
2
Далее, существуют две сферы, каждая из которых касается
двух данных сфер и граней двугранного угла. Проведем плоскость
через ребро данного двугранного угла, центры двух данных сфер
(радиуса г) и центры искомых сфер (рис. 29). Обозначим через х
77
радиус любой из искомых сфер. Так как расстояние от центра
сферы радиуса х, касающейся граней двугранного угла величи-
ны а, до ребра этого двугранного угла равно
х
sin —
2
то расстояние от центра С меньшей из искомых сфер до точки Р
касания данных сфер равно
г —х
»
а
sin —
а расстояние от центра D большей из искомых сфер до точки Р
равно
х — г
а
sin —-
2
Из прямоугольных треугольников СРВ и BPD получаем одно
и то же соотношение:
+ г2 = (г + х)2,
. « а
sm2 —
2
или
x2cos2 ----2r fl + sin2 — V + г2 = О,
2 \ 2 J
откуда
а а
1 4-sin2— ± sin -
2 2
*1,2 = Г------------------
а
sin2 —
2
« а
cos2 —
2
или
x1.2 = rfl+2tg2-^±tg-J-l/ 3 + 4tg2^-\
Второй способ решения. Если сферы радиуса г каса-
ются друг друга в точке Р, а сфера радиуса х с центром С касает-
ся их обоих, то (рис. 30)
СР = У СМ • CN = Ух (х + 2г) — Ух2 + 2гх.
78
Спроектируем две данные сферы, двугранный угол и две иско-
мые сферы в плоскость, проходящую через прямую CPD перпенди-
кулярно ребру данного двугранного угла (рис. 31). Так как дан-
ные сферы с искомыми имеют общие точки (точки касания), то при
указанном проектировании искомые сферы спроектируются в
окружности, пересекающие окружность, в которую спроектируют-
ся данные сферы. Теперь из рис. 31 находим
| х — г) = У 2гх + х2 sin у,
или
(х — Г)2 = (л2 + 2rx) sin2 -у,
а это уравнение, которое было получено выше.
Замечание. Если а стремится к л (развернутый двугран-
ный угол), то радиус
х± = г
а а / а
1 + sin2 — + sin — 1/ 3 -р sin2 —
2 2 V 1 2
а
cos2 —
2
неограниченно возрастает. Что касается Х2:
х2-=~г
а а
1 + sin2 — — sin —
2 2
3+sin»y-
а
cos2 —
2
79
го преобразуя его
х2 = г
а
cos2
2
а а
1 + sin^ — -J-sin —
j/^ 3 + sinS-y-
cl а
l+sm« — + sin —
т
заключаем, что х2 убывает и стремится к — . Случай а=л соот-
ветствует следующей задаче: найти радиус окружности, касаю-
щейся двух равных касающихся между собой окружностей и их
общей внешней касательной. Из рис. 32 находим
АВ = 2 Vхг = г, откуда х = —.
4
Таким образом, в данной нам задаче радиусы обеих сфер боль-
ше —. Установив это, можно еще раз доказать, что окружности,
являющиеся проекциями
искомых сфер в плоскость, перпендику-
лярную ребру данного двугранного уг-
ла, пересекают окружность, являющу-
юся проекцией в ту же плоскость дан-
ных сфер (см. рис. 31). Для этого надо
доказать, что .
| г — XI < ]/2гх + х2 < г -|- х,
или
(г — х)2 < 2гх + х2 < (г -}- х)2.
Неравенство 2rx-t-x2< (r+х)2, очевидно, выполняется. Что касает-
ся неравенства
(г — х)2 < 2гх + х2,
то оно приводится к виду х> а это по доказанному выше име-
ет место.
Решение варианта 4
16. Перепишем данное уравнение следующим образом:
| 2sin2x— 11 = | sln2x — а |.
80
1) Предположим, что sin2x>-^-, sin2x>a; тогда данное урав-
нение эквивалентно смешанной * системе
sin2x> —, sln2x>a, 2sin2x—1 = sin2x— a,
2
ИЛИ
sin2x>-^ , sin2x>tz, sln2x=l—a. (A)
Таким образом, должны выполняться неравенства
1 — а > 1 — а > а, откуда а <
Кроме того,
О < 1 —а < 1,
откуда
<Ка<у.
Итак, все соотношения (А) будут выполнены, если
2
При этом условии данное уравнение имеет четыре корня**:
х, = arc sin]/1 —а, х, = л — arc sin 1/1 —а,
1 ______________ _____________________ (1)
х3 = л -f- arcsin]/l —а, х4 = 2л — arc sin]/1 — а,
если 0<а< -у-, и два корня:
эт Ззт
Х1 = » Х2 = (2)
если а = 0.
1 '
2) Предположим, что sin2x< —, sin2x<a; то^да данное урав-
нение эквивалентно следующей смешанной системе:
sln2x<-~, sin2x<a, sin2x=l—а.
Из неравенств 1—1—а<а находим а из соотно-
шений 0 < 1 — а < 1 находим 0 < а < 1. Итак,
£
2
а< 1.
* Смешанной называется система, состоящая из .уравнений и неравенств.
** Речь все время идет о корнях, лежащих на сегменте [0,2л].
81
При этих условиях данное уравнение имеет четыре корня:
хх = arcsin]/ l—а, х4 = л— arcsinV4!—а,
х3 = л 4- arc sin У1 —а, х4 = 2л — arc sin У1 — а,
если < а < 1, и три корня:
хх = 0, х2 = л, х3 = 2л, (4)
если а= 1.
3) Предположим, что sin2x> a sin2x<a; тогда данное урав-
нение эквивалентно следующей смешанной системе:
sin2x> —, sln2x<a, 2sin2x—l=a — sin2x.
2
или
sin2x>—, sin2x<a, sin2x = 1 +a .
2 3
Из неравенств
находим a >-i-, а из неравенств
О
находим —1^а<2. Итак, если
тс данное уравнение имеет четыре корня:
хх = arc sin
х3 = л + arc sin
х2 = л — arc sin
а
—, х4 = 2л — arc sin
(5)
это в случае •< а < 2. Если же а = 2, то уравнение имеет
корня:
л Зл
1 2 2 2
два
(6)
82
4) Предположим, что sin2*<-|-, a sin2*>o; тогда данное урав-
нение эквивалентно следующей системе:
sin2*< —, sin2*>a, sin2* — -1
2 3
Из неравенств
14-а 1 14-а .
3 2 3
из неравенств 0 < --Th.?- 1 ( как и выше, на-
1
находим а < —, а
ходим — 1 <а<2.
Итак, если —то данное уравнение имеет четыре
корня:
это в случае — 1 < а < —; если же а = — 1, то три корня:
*х = 0, х2 = л, х3 = 2л. (8)
5) Заметим, что если sin2* = —, то а = —, а если sin2* = а, то
' 2 2
а = Поэтому остается рассмотреть случай а = В этом случае
данное уравнение принимает вид
откуда
значит,
|2sin2*—1| = sin2*—,
> 2 1
sln2* = —,
2
я Зя 5л 7л
*х — —, *2 _ 4 , *3 — 4 , *4 —.
Эти значения корней получаются из предыдущих (любой из
первых четырех случаев), если в окончательных формулах поло-
жить а= Отметим, что соотношения (2), (4), (6) и (8) сле-
дуют соответственно из соотношений (1), (3), (5) и (7), если поло-
жить в них а=0, а=1, а=2, а=—1 (окончательный итог дан в
таблице).
83
Таблица
Значения а Корни уравнения
1 1 V Н о « корней нет *1 = 0, х2 = Я, Хз — 2л
— 1 <а<0 • 1/ *+а . 1/ 1 + ® Xi = arc sin У " 3 » х2—л — arc sin у , Хз — л + arc sin , х4 — 2л —- arc sin ]/ ——
а = 0 л Зл .1 *1-"р *2 = -2 . ДГз-arcsin- yg- , • 1 । • 1 х4— л аге sin х5 — л + arc sin г— , уз у 3
°<“<т 1 х6 — 2л — arc sin У 3 xt = arc sin У 1 — a, x2 = л —arc sin}/ 1 — a , x3 = л + arc sin У 1—а , х4=2л— arc sin У 1—a , • 1/ 1+a • 1/ 1+a x5 — arc sin у 3 , x6 — л — arc sin у 3 ’ , , . 1/ 1+a „ . ]/ 1+a x7 — л 4- arc sin у g , x8 — 2л — arc sm у 3
1 Я~ 2 л Зл 5л 7л 1 4 4 4 4 '
т<а<1 Xj=arcsiny 1—a , x2 = л— arc sin У 1—a , x3 = л 4- arc sin 1 — a , x4 = 2л — arc sin У 1 — a , . 1/ 1+a . 1/ 1+a x5 — arc sin у £ , хб — л — arc sin у 3 ’ , . 1/ 1+a „ . 1/ l+a x7 — л 4- arc sin у £ , x8 — 2л — arc sin у
а~ 1 xx = 0, x2 = л, x3 = 2л, • 1/T • 1/"^ x4 = arc sin у -у, x5 — л — arc sin у -у, . 1/^2* . 1/"з” хб = л4-агс51п у -у, х7 = 2л —агезш у у
1 <а<2 хх — arc sin , х2 — л — arc sin ‘ , . 1/ 1+а „ . 1/' 1+а хз — л 4- arc sm у з » ~ 2л — arc sin у
а= 2 л *3л Х^Т’Х2 = Ч~
а>2 корней нет
84
17. Так как коэффициенты при х и у не пропорциональны, то
данная система имеет и притом только одно решение:
A-J-16 8 —ЗА
X =----!----, У — ------.
7 7
Остается решить систему неравенств
А + 16 1 8 —ЗА . 0
7 > А ’ 7
Из второго неравенства находим £< — 3 Первое неравенство пере-
пишем в виде
&+16 1_ 7 А 0, (1)
ИЛИ
А^+ 16А — 7 ► 0
k
или
... [А-(- 8-/71)][А-(- 8+ /71)1
А
Располагая корни числителя и знаменателя в порядке возрас-
тания
— 8—[/71, 0, —8 +/71,
заключаем, что все решения неравенства (1):
— 8- /71<А<0 и k> — 8 + /7Т.
g
Но кроме этого должно быть выполнено неравенство k<—.
Так как
— 8 +/71 </81 — 8= 1 < —,
3
то все значения k, удовлетворяющие условию задачи, таковы:
— 8 — /71 <Аг<0, /Л—8<Л<—.
3
18. Преобразуем данное уравнение следующим образом:
2cosx — 3 tg х + 4 sinx— 2 = 0,
85
2 cos2 x — 3 sin x
+ 2(2sinx— l)-0,
cos X
2 — 2 sin2 x — 3 sin x
cosx
+ 2(2sinx— l) = 0,
(Zsin^-DCsinx+Z) + 2(2stax-1) = 0,
COST
(2sinx— 1) (2— -in*+-2 > =0.
\ cos X J
Отсюда либо
2 sinx— 1 = 0,
t. e.
X = fel + (-l)‘-J-,
D
где k — любое целое число, либо
2_ sinxH-2 _ 0
COS X
Умножая левую часть на cosx, получим
2cosx — stax — 2 = 0.
Это уравнение эквивалентно предыдущему, так как, во-первых, оно
следует* из предыдущего, а во-вторых, уравнению 2cosx—sinx—
—2=0 не удовлетворяют те значения х, для которых cosx=0, а по-
тому из этого уравнения 2cosx—sinx—2=0 следует уравнение
2---?1П< + 2 = о Уравнение
COSX
2 cosx— stax — 2 = 0
решается так:
stax+ 2—2cosx =0,
2 sin —cos — + 4 sin2 — = 0,
2 2 2
sin — f cos — + 2 sin —= 0.
2 \ 2 2 J
* Будем говорить, что уравнение В=0 следует из уравнения Л=0 или урав-
нение В=0 является следствием уравнения Л=0, если все корни уравнения
являются корнями уравнения В=0.
86
Отеюда
sin — = О, х — 2fert;
2
cos — + 2 sin — = 0, tg — =---—, x = 2kn— 2arc tg —.
2 2- 6 2 2 s 2
Итак, все решения данного уравнения:
х = kn + (— 1)* -у-, х = 2kл, х — 2кл — arc tg
Замечание. Так как 0 < arc tgто 0< 2агс tg
л
—, а так как
2
1 4
4
1
то
1 4
2 arc tg — = arc tg —,
b 2 3
и последнюю формулу можно переписать так:
х — 2kn — arc tg —.
6 3
19. Обозначим через Q вторую точку пересечения прямой ВС
с меньшей окружностью. Тогда имеем
PQ = \BP — СР\
(знак модуля необходим, так как возможно, что ВР<СР). Возво-
дя в квадрат обе части этого равенства, получим
PQ2 = РВ2 + PC2 — 2РВ PC,
PQ2 = 4r2 - PA2.
Ho
PBPC = PM-PN = (R — r)(R + r)=R2 — r2
(рис. 33, M и N — концы диаметра большей окружности, проходя-
щего через точку Р). Таким образом,
4г2 — РА2 = РВ2 + PC2 — 2 (Я2 — г2),
откуда *
РА2 + РВ2 + PC2 = 2 (Я2 4- г2).
* Утверждение задачи верно и в том случае, когда прямая ВС касается мень-
шей окружности (доказать!).
87
20. На рис. 34 изображены сечения данной фигуры плоско-
стью, проходящей через образующую ВЛ и высоту конуса (при
этом плоскости Р и Q пересекутся по прямым AP1.SA и по прямой
SQ, такой, что ZXS7W=p), а также плоскостью основания конуса
(нижняя часть рис. 34). Имеем
ОМ = OStg (^-р) =
1 а
= I cos-----
2
Отсюда
ВгВг = 2МВг = 21/ /2 sin2— Z2cos2-^-ig2
=------------V sin (а —Р) sin р.
/а \
При проектировании из точки S на плоскость Р точка М спроек-
тируется в точку Л4', а точки Bi и В2 — в точки Ci и С2, о которых
говорится в условии задачи. При этом
СА _ SM' откула с С — В В
BLBa - sm ’ откуда SM •.
Далее находим
. а
, ~ *cos
SM' = —1—, SM --------—----- =-------------,
cos₽ ( а а о\
C0S\2~^J
88
так что
СхС2 — В± В2
а
cos — cos
2
Р
и окончательно
СХС2 = 2Z
/sin(а — Р) sin Р
а _
cos -^-C0S Р
Решение варианта 5
21. Так как а служит основанием системы логарифмов, то
должно быть а>0, Рассмотрим два случая: 0<а<1 и а>\.
рели 0<а<1 (и sinx>0), то' logasinx^0, значит, для данного
уравнения следует взять только неотрицательные корни уравнения
z2+z—а=0, где z=logasinx. Но при 0<а<1 корни данного урав-
нения разных знаков, значит, надо взять положительный корень
1 3 /Г+4^—1
loga sinx = ----•
Если а>1 (и sinx>0), то logasinx^0 и, значит, для данного
уравнения следует взять отрицательный корень
Итак, если 0<а< 1, то
V l+4a - 1
х = kn + (— l)*arcsina 2 ,
а если а>1, то
_ V l+4a+t
х = £л + (—1)* arc sin а 2 ;
в обоих случаях k принимает все целые значения.
22. Перепишем данное неравенство так:
1------+-----------------1----< о,
4 cos2 х — 3 4 cos2 х — 3
ИЛИ
4 cos2 х — cos х — 2 Q
4 cos2 х — 3
89
или
/ 1 — /33 \ f 1 + /33
( cosx---------cosx—-----------
\ 8 / \ 8
f/ =-------------—------------------
( /3 W _i_ У3 \
I cosx ——-—И COSX+—-— I
Отсюда
/3 . . 1 —/33 1 +1/33 _ /3
*-----— <2 cos x <”-----—, —— --------< cos x < ——
2 8 8 2
и, следовательно,
arc cos
1 — /33 , 5л
8 6 ’
— </ x < arc cos 1 (рис. 35).
6 8
23. Перепишем данное выражение в виде
. (1 +х + 2х*+ ... + лхп)(1 /х/2х2 + ... +пхп).
Отсюда сразу находим коэффициент при хп:
an=n-l +(п-1)-1+(п-2)-2 + (п-3)-3+ ... +
4-* [п — (п — 1)] (м — 1) -|-1 • п = 2м 4- п (1 4-2 4“?3 4~ - • • 4~ — 1) —
— 112 + 22 + 32 + .../(л— 1)г] = 2га+п—(1)
(л — 1) (2n — l)n n(n2/ll)
6 ~ 6
90
Замечание. Изложенный метод потребовал применения
формулы
s = I2 + 22 4- З2 + ... + п2 = + (2)
6
для суммы 12+22+32+... + (п—I)2. Формула (2) выводится так:
положим в тождестве
(k + I)3-+ 3k + 1
последовательно &=!, k=2,k = n; получим
23 — I3 = 3-12 4-3-1 + 1,
З3 — 23 = 3-22 + 3-2+ 1,
(n + I)3 — n3 = 3-n2 + 3-мЦ- 1.
Сложив полученные равенства, имеем
(п 4- I)3 — 1 = З-s + 3 w(-n2t~1) 4- п,
где $ — искомая сумма. Отсюда находим
Зв = (л 4-1)3 — А п (п 4-1) — (п 4- 1) =
= (л 4-1)(ла4-2л 4-1 —-у-— =
= (л 4-1)(«2 4- y) = -уп(п + 1)(2" +
и, значит,
s =-^-л(л 4-1)(2л 4-1).
О
Можно обойтись и без этой формулы.
Из формулы (1) имеем
Ол4-1 = 2 (п 4" 1) 4- (п 4-1) (1 4-2 4-3 4- ••• 4- п — 1 4- л) —
— (124- 22 + 324-•• • 4-(п—1)24-и2]. (3)
Из формул (1) и (3) находим
ая+1-а„=2 4-«24- 1 4-24-34-- + n-1 + л-л2 = 24- п(я+1).
91
Из этой формулы имеем
п . Ь2
а2 — ^ = 2+ —,
а3 —а2 = 2 4~,
п , 3-4
а4— а3 = 2 + —,
Л _ о । (« — !)«
ап ~ ап-1 — Т----2----•
Складывая эти равенства, получим
ал-а1 = 2(га-1)+-^-[1.2 + 2-3 + 3-4+... +(п-1)п]. (4)
Для вычисления суммы, стоящей в квадратных скобках, рассмот-
рим тождество
(k — l)k(k + 1) — (k — 2)\k — l)k = 3(k — 1)A.
Полагая в этом тождестве k=2, k = 3,k=n, получим
1-2-3 — 0-1-2 = 3-1-2,
2-3-4—1-2-3 = 3-2-3,
3-4-5 —2-3-4 = 3-3-4,
(n — l)n(n + 1) — (n —2)(n — l)n = 3(n— l)n.
Складывая почленно эти равенства, найдем
(п— 1)п(«+ 1) = 3[1-2 + 2-34-3-44- ... 4-(«—1)пГ,
отсюда
1-2 4-2-3 4-3-4 4- ... 4-(«— l)n= + .
3
Теперь заметим, что tii — это коэффициент при х в выражении
(14-х)2, т. е. «1=2. Таким образом, из формулы (4) находим
= 2 + 2(Л~ 1) + +
я v ' ' 6 6
24. Рассмотрим два случая: лучи DP и DQ находятся по одну
сторону от диаметра DC (рис. 36) и по разные стороны от него
(рис. 37). Так как площадь кругового сектора равна половине
квадрата радиуса, умноженной на угол сектора, то площади кру-
92
говых секторов MDN к OPQ равны между собой (Z POQ =
=2ZDPQ, но DM=0PV2J.
Далее, площадь, ojcoTopofl говорится в условии задачи, равна
разности площадей DPQ и DMN, или разности площадей DPQ. я
OPQ, или разности площадей треугольников DPQ и OPQ,
так как фигуры DPQ й OPQ имеют в качестве общей части сегмент
с хордой PQ. В случае, изображенном на рис. 36, разность площа-
дей треугольников DPQ и OPQ равна разности площадей тре-
угольников DPK и QKO (К — точка пересечения ОР и DQ),
Рис. 36 Рис. 37
или разности площадей треугольников DPO uDQO. Но пл. ADPO =
= пл. ADP'O, пл. Д£><20 = пл. ADQ'O, а разность площадей тре-
угольников DP'O и DQ'O равна площади треугольника DP'Q'.
В случае, изображенном на рис. 37, дело обстоит проще: раз-
ность площадей треугольников DPQ и OPQ равна сумме площа-
дей треугольников DPO и DQO, которые соответственно равно-
велики треугольникам DP'O и DQ'O. Сумма же Площадей по-
следних треугольников равна площади треугольника DP'Q'.
Замечание. Утверждение задачи верно и в том случае,
если одна из точек Р или Q совпадает с точкой С.
25. Если две сферы касаются одной и той же плоскости и друг
друга, то расстояние между точками касания равно 2 V Rr, где г
и R — радиусы сфер (см. последнюю задачу варианта 2 — зада-
чу № 10).
Пусть х — искомый радиус сферы р, которая касается трех
данных сфер а, 0 и у^(радиусы сфер а и у равны г, а радиус сфе-
ры 0 равен R) и данной плоскости. Обозначим точки прикоснове-
ния сфер а, ₽, у и р к данной плоскости соответственно через Л, В,
С&М. Тогда на основании замечания, сделанного в начале реше-
ния, будем иметь
АВ = 2У?Р, ВС = 2УгР, АС = 2г,
МА = 2Vxrt МС = 2Ухг, МВ = 2VxR.
93
Отсюда следует, что треугольник АВС равнобедренный (ВА =
= ВС) и что точка М лежит на медиатрисе его основания АС,
иначе на высоте, проходящей через вершину В. Для уточнения
положения точки М рассмотрим три случая:
Г АВ>АС, или R>r;
2° АВ<АС, или R<r,
3° АВ=АС, или R — r.
Заметим, что в случаях 1°, 2°
СА = МА V7 J
СВ ~ МВ ~ /я ’
значит, точки М и С лежат на окружности, являющейся геометри-
ческим
ний до
местом
точек А
точек, для каждой из которых отношение расстоя-
СА
равно —
н св
(это так называемая одна из трех
и В
окружностей Апполония для треуголь-
ника АВС). Эту окружность можно
построить так: пусть Р и Q — точки, в
которых биссектрисы внутреннего и
внешнего угла С треугольника АВС пе-
ресекают сторону АВ (рис. 38). Точки
Р и Q принадлежат окружности Аппо-
лония, проходящей через вершину С,
так как
РЛ (?Л _ СА
РВ QB СВ '
Окружность Апполония — это
окружность, построенная на отрезке
PQ как на диаметре.
Таким образом, с помощью цирку-
ля и линейки можно построить точки
прикосновения искомых сфер к данной
плоскости, если известны точки при-
косновения данных сфер к данной
плоскости.
Замечание. Конечно, приведенного только что рассужде-
ния от поступающих на физический факультет не требовалось.
Геометрически очевидно, что точки прикосновения искомых сфер
к данным и к данной плоскости лежат на медиатрисе отрезка АС.
1°. В случае АВ>АС, т. е. R>r (см. рис. 38), одна из точек М
прикосновения искомой сферы к данной плоскости лежит внутри
треугольника АВС, а другая М' — на продолжении луча BD за
точку D.
2°. В случае АВ<АС точки М и М' лежат по разные стороны
от точки В на медиатрисе отрезка АС. Если т-0 точка М
94
лежит на прямой АС, в случае <R<r точка М лежит внутри
О
треугольника АВС (рис. 39), а в случае точка М лежит
вне треугольника АВС (рис. 40).
Наконец, в случае АВ=АС (R=r) треугольник АВС — равно-
сторонний: точка М находится на равных расстояниях от его вер-
шины, т. е. является центром окружности, описанной вокруг тре-
Рис. 39 Рис. 40
угольника. В этом случае существует только одна сфера, удовлет-
воряющая условию задачи. Так кай расстояние от точки М до точ-
ки А равно 2 Vxr, а, с другой стороны, радиус окружности, опи-
гк 2г
санной вокруг треугольника со стороной 2г, равен то из ра-
венства
находим х= . Вернемся к общим случаям 1° и 2°. Предполо-
жим, что АВ>ВС (см. рис. 38). Находим
. BD = V АВ2 —AD2 - /4/?г —г4,
MD = BD — BM = V4Rr — r2 — 2VRx,
MD2 + DA2 = MA2, (1)
(\/ 4/?r —г4 - 2 VRx)2 + г4 = 4xr,
4Rr — r2 — 4 ]/4Rr — r2 + 4Rx + r2 = 4rx,
(R — r)x — VRr V4R — r ]Sx + Rr = 0.
95
Если повторить те же рассуждения для точки М', то получим
то же самое квадратное уравнение относительно Ух (так как
M'D—2VRx—У4Rr—г2). Отсюда следует, что корни послед-
него уравнения дают значения квадратных корней из радиусов х
искомых сфер, причем больший корень соответствует сфере с точ-
кой касания М' (так как она более удалена от точки А, а ее рас-
стояние до точки А равно 2 У#х). Решая последнее уравнение,
получим
2(R —г)
откуда
у _ pr (/4R— г + УЗг? .
Х1 2 W ,
4(7?.-г)2
знак минус соответствует сфере с точкой касания М, а знак
плюс — сфере с точкой касания М'.
Перейдем теперь к случаю АВ<АС, или /?<г; заметим, что в
этом случае точка М (см. рис. 39, 40) может лежать и на отрез-
ке BD, и на продолжении его за точку D, и даже совпадать с точ-
кой D. Вторая же точка касания сферы с тремя данными лежит на
продолжении отрезка DB за точку В. Точка М совпадает с точ-
кой D, если MC=DC, т. е. 2рЛхг=г, т. е. х=~. В этом случае
AD=AM=2 УхЯ= У&, и из прямоугольного треугольника
ADB находим
AD2 + DB2 = АВ2, г2 + rR = 4Rr,
откуда R = —. При таком значении R точка касания искомой сфе-
ры с данной плоскостью совпадает с тонкой D.
Считая R<r, заметим, что должно быть R так как —
4 4
есть радиус минимальной сферы, касающейся данной плоскости
и двух данных сфер радиуса г, касающихся между собой и этой
плоскости. Теперь, повторяя для точки М те же рассуждения, что
и выше в случае Г независимо от положения точки М на луче BD,
получим то же самое уравнение (1), которое лучше переписать в
виде
(г — R) х + УRr У 4R — г Ух — Rr = 0.
Это уравнение имеет действительные корни разных знаков; бе-
рем, естественно, только положительный корень:
х =
2 (г - Я)
96
откуда
x = Rr >4Я —г)3
4 (г — Я)*
Для точки М' получим уравнение
(г — /?) х—VRr VlR—г /х—Rr = О,
откуда
х = Rr
(/3r 4-/4R—г)*
4(г — Я)3
Остановимся еще на случае R ——
4
Тогда точки Л, В и С ле-
жат на
х—
одной прямой. В этом случае имеются две сферы радиусов
касающиеся трех данных; центры их симметричны относи-
тельно
прямой АС и отстоят от этой прямой на расстоянии ~7Z.
у 3
Отметим, что в конце концов задача во всех случаях имеет два
решения:
*1,2 = Rr
(/4R-r ±/Зг)3
4 (Я — г)3
конечно, в предположении, что R=^r, R>—.
4
Читателю рекомендуется произвести вычисления исходя из гео-
метрического построения точек М и М'. Знакомым с понятием сте-
пени точки относительно окружности можно рекомендовать такой
путь решения (что избавит от рассмотрения всевозможных част-
ных случаев); из соотношений
АР Уг AQ _ Уг
РВ ~ /Я ’ QB /Я
находим (положительное направление выберем от Л к В)
Далее,
Далее,
РВ = -2-f , QB =
УР + Уг х УР-У7
ВМ • ВМ’ = BP-BQ — -^~г :
где S — проекция центра О окружности Апполония на ось BD (по-
ложительное направление берем от В к D).
3
4 Зак. 351
97
Имеем
BP + BQ
BS BO BS 2 R
= -=- или - _l =------t=- =-----—;
BD BA }4rR —r2 —2/rR R — r
отсюда
as =
R — r
и, значит,
BM + BM' = 2?<4rj?-r2.
R-r
Таким образом, BM и BM' — корни уравнения
_ 2R V 4rR — r* 4R2r
R-r + R-r
ИЛИ
(/? - г) V — 2R /4/7? —r2l + 4/?2r = 0;
отсюда
R/r(/4R-r±/3r)
Корни Xi и 12 действительны (/? > — j. Если R>r, то они поло-
жительны, т. e. точки M и М' (ведь 1] = ЯА4, К2=ВМ') лежат на
луче BD. Если R<r, то корни разных знаков: одна из точек М
лежит на луче BD, другая — на его продолжении за точку В.
Найти значения радиусов сфер можно так: так как | XJ =ВМ =
^2VRxi, 1121 =BM'=*2VRx^ то радиусы сфер находятся из
соотношения
2VRx
RVr\y 4R — r±V3r\
откуда
_Rr(v 4R — r ±^3г)г
Xl-2~ 4(R —г)2
(все это в предположении R=£r и R^
98
Решение вар пакта 6
26. Корни данного уравнения
—1±/1 —4а
Л 1,2-----9
будут действительны тогда и только тогда, когда 1—4а:>0, т. е.
а<—. Оба корня больше а, если больше а меньший корень:
4
—1-/1 — 4а
2
а,
или
]/1 —4а< — 1—2а.
Если — 1 —2а < О, т. е. а> —и а < то это неравенст-
во не имеет места. Будем считать, что а<—— . Тогда —1—2а > О
и неравенство У1 — 4а < — 1 — 2а эквивалентно такому:
1 4а < 1 + 4а + 4а2,
или
а(а + 2)>0,
1
или, так как а <----:
2
[а + 2 < О,
т. е. а<—2. Таким образом, все значения а, при которых оба кор-
ня уравнения х2+х+а=0 будут больше а, таковы: а<—2.
Замечание. Эту задачу можно решить и так: 1—4а:>0—
условие действительности корней данного уравнения;
а2 4- 2а > 01 — условие того, что оба^корня данного уравнения
2а + 1 < 0 J (если они действительны) будут больше а (см. стр. 59).
27. Перепишем данное неравенство в виде
4 sin2 х — 1
или
sin х — 8 sin2*
4 sin2* — 1
ИЛИ
sin
* sin * —
1 \/ 1 \
sm * 4- — ( sin * — — I
2 2 /
4*
99
Отсюда— — <sinx<0n — <slnx<' —
2 8 2 •
Все решения:
2Z»t + arc sin— <x< — 4-26л,
8 6
2Лл 4- <x< (2k 4- 1) л— arcsin -i-,
(2A4- 1)я<x< (2k4- 1) л 4- —
6 *
2/гл—— <х<2£л,
6
где k принимает все целые значения
(рис. 41).
28. Перепишем данное уравнение
в виде
9W = 21*+’1+1*- Ч.
Корни выражений х, х4-1, х—1
таковы: 0,—1,1. Естественно поэто-
му рассмотреть следующие случаи:
1) х^—1; уравнение принимает
вид
9-*=
или
9х = 4Х‘,
отсюда х=0. Это противоречит условию х^.—1 таким образом,
уравнение не имеет корней, меньших или равных —1.
2) —1г£Гх<0. В этом случае уравнение принимает вид
9~* _ 2»+i-*+i,
или
3-2» = 22,
или
3* = 2-‘,
откуда
х = — log32.
Так как число—log32<0 и так как —log32—(—1) = 1—log32=
= log2 то —log32>—1. Таким образом, на сегменте [—1, 0]
данное уравнение имеет корень х=— log32.
100
3) 0^х<1. В этом случае данное уравнение примет вид
9* = 2Х+1~Х+1,
или
3* = 2,
откуда
х = log32,
и так как 0<loga2< 1, то x=log32— корень данного уравнения.
4) х^1. В этом случае данное уравнение примет вид
9* = 2х+'+х~1,
или
3* = 2х,
откуда х=0. Таким образом, данное уравнение не имеет корней в
полуинтервале (1, +оо).
Итак, данное уравнение имеет два корня:
хх----log32, xa = log32;
первый лежит в интервале (—1, 0), второй — в интервале (0, 1).
29. Предположим, что ZB> ZC nZB<-y- (рис. 42). Пусть
D—проекция вершины А на сторону ВС. Имеем
2 (BD + DM) = ВС = BD + DC,
откуда
DM = —(DC — DB).
Но DM—hc\.gx, DC=hctgC, DB — hcigB (h=AD). Поэтому
ctg x = _L (ctg C — ctg B).
Если ZB>-^~, то (рис. 43)
2(DM —DB) = BC = DC — DB,
101
откуда
DM = -у (DC + DB).
Но
DM = ftctgx, DC = ftctg C, DB = ftctg(n — B) = — ActgB,
значит,
ctg'x = у (ctg C — ctg B).
Читателю предлагается убедиться в том, что эта формула вер-
на и в случае ZB=—.
Аналогично в случае ZC>ZB получим формулу
ctgx = у (ctg В — ctg С);
наконец, она верна и в случае ZB = ZC. Итак, во всех случаях
ctgx = у
ctg В —ctg С
30. Эта задача решается аналогично последней задаче вариан-
та 3 (задача 15, рис. 31). Если сферы радиуса г касаются граней
данного двугранного угла и друг друга в точке Р, а сфера радиуса
х<г касается их обоих и граней того же двугранного угла, то, обо-
значая через С центр сферы радиуса х, как и в задаче 15 вариан-
та 3, находим PC— ]/гх2+2гх и теперь из рис. 31 находим
г — х = Vx2 + 2rxsin —
' 2 '
А так как — = т, то
Г
1 — tn = V т2 + 2т sin —,
2
откуда
(О
и так как 0<а<л (исключаем нулевой и развернутый двугран-
ные углы), то 0< — —, значит,
2 2
о<, 1~от <!.
Ут2 + 2т
102
Отсюда т<1 и, далее,
1 —/п< Ут2-[-2т,
1 — 2/и + /п2 < m2 + 2т,
1
.
4
Итак,
При выполнении этих неравенств из соотношения (1) находим
а = 2arcsin—..
/ т2-[2т
Решение варианта 7
31. Так как
= yU + J/V =(yF— 4^У + 2>2, .
V* ух \ y-xJ
то, полагая
получим квадратное уравнение
Х2 + 2аХ + 1 = 0; (1)
исследуем, при каком условии оно имеет действительные корни,
не меньшие двух. Прежде всего должно быть выполнено условие
а2 — 1 > О,
откуда или а^'—1, или а> 1. Если а> 1, то корни уравнения (1)
действительны, но отрицательны (х(х2=1, xi+x2=—2а<0), зна-
чит, должно быть а^1—1. При а =—1 корни уравнения (1) равны
между собой и равны 1 (а Должно быть Х^2).
Итак,
а< — 1.
Уравнение (1) имеет корень Х=2, если
5
4 + 4а + 1 =0, откуда а ---------.
4
Уравнение (1) принимает при этом следующий вид:
2
103
и имеет корни
X, = 2, Х„ = —
1 ’ « 2 ’
5
Итак, если а=------,
4
то данное уравнение приводится к виду
— =2,
V '
или
(/х — I)2 = О,
откуда .
х = 1.
к
Итак, если а =-------, то данное уравнение имеет только один
4
5
корень х=1. Будем считать, что а<—1 и а=Н=-------Тогда корни
Xi и Хг уравнения (1) действительны, различны, положительны и
ни один из них не равен 2. Данное уравнение имеет решения, если
или Хх < 2 < Х2, или 2 < Хх < Х2.
В первом случае только уравнение^!— = Х2, илих—X2j/x4-l = 0,
имеет различные действительные и положительные решения (относитель-
но /х).
Во втором случае этим свойством обладают оба уравнения:
Соотношения Х1<2<Хг будут выполнены тогда - и только тогда,
когда *
5
4 + 4а + 1 < 0, откуда а <-----
Итак, если а<?------, то
4
Х2 = /а2—1 - а,
(2)
* См. предварительное замечание к решению задачи 6 варианта 2, стр. 59.
104
и из уравнения (2), которое принимает вид
х — (]/а2 — 1 — а) Ух +1=0,
находим
Ух =
/а2 — 1 — а+Уэа* — 5 — 2а У'а2 — 1
2
значит,
х1>2 = +(/^Т-а±/2а2-5-2аК55^=Т )\ (3)
Неравенства 2<Xi<A.2 будут выполнены тогда и только тогда,
когда
4 + 4а + 1>0,
4 + 2а<0,
откуда
а>----J-, а<—2;
эта система неравенств несовместна.
Итак, если а<-----, то данное уравнение имеет два корня, за-
4
5
данные соотношением (3). Если а —--, то данное уравнение име-
4
5
ет один корень х= 1. Если а^>--то уравнение не имеет кор*
ней.
32. Перепишем данное неравенство так:
tg2x —2____L<o
tg2 х — 1 2
или
tg2 х — 3 Q
tg2X~ 1 ’
или *
(tgx + /3)'(tgx-/3~) <n
(tgx+l)(tgx — 1)
Отсюда
-/3<tgx<-l,
KtgxCVT,
105
следовательно (рис. 44):
kn---^<x<kn--^-,
3 4
/гл 4—у- < х < kn 4—
где k принимает все целые значения.
33. Будем обозначать через ап число
ааа . . .аа
п цифр; а—цифра
Имеем
12я - 2Я = -L • 92я---2-9Я = -1-(10*" - 1)--L (Ю« - 1) =
_ 10^” —2 • 10”4-1 _ / 10"—1 \2 _ / 9Я V _ 32
— 9 \ 3 7\37~'1'
Рис. 44 Рис. 45
34. Из рис. 45 находим (х — искомый радиус):
Ош = г — х, со/? = coQ 4- QR = г2-----------,
OR = PQ = AQ - АР = xctg-?--------Ьг.
Теперь из прямоугольного треугольника соО/? находим
(х ctg ------^-)2+(х + /г2-------у-/ = (г - X)2,
или
а а Ь2 л 1 ь2 о b2
x2ctg2-g---&xctg-^- + — + х2 + 2х]/ г2--------4- + Г2----
= г2 — 2гх + х2,
106
или
а а г hz
x2ctg2 - --&xctg-^“ + 2x у г2------= — 2rx,
или
x ctg2-j- = b ctg ---}Л4г2 — b2 — 2r,
значит,
x _ tg2 -^-(b ctg-^--У^г2 — b2 — 2rj.
Замечание. Для тех, кто знаком с преобразованием инвер-
сии и некоторыми ее свойствами, покажем, как с помощью цирку-
ля и линейки построить окружность, касающуюся хорд АС и АВ и
дуги ВС, а затем на этом пути вычислить радиус этой окружности.
Произведем инверсию с центром в точке А и степенью инвер-
сии, равной Л=4г2. При этой инверсии данная окружность перей-
дет в касательную t к ней, проведенной в точке D. Точки В и С
перейдут в точки В' и С' пересечения прямых АВ и АС с этой ка-
сательной и искомая окружность S перейдет в окружность S'
вневписанную в угол Л треугольника АВ'С'. Окружность S' легко
построить. Пусть окружность S' касается прямой / в точке /?'; пря-
мая R'A пересекает данную окружность в точке R, являющейся
точкой прикосновения искомой окружности с дугой ВС. Центр <о
искомой окружности лежит в точке пересечения прямой RO (О —
центр данной окружности) с биссектрисой угла ВАС (рис. 46).
107
Для вычисления радиуса окружности S заметим, что окруж-
ность S' из окружности S может быть получена гомотетией с цен-
тром А и коэффициентом гомотетии, равным —, где k — степень
инверсии, а о—степень точки А относительно окружности S. Зна-
чит, радиус х окружности S равен радиусу х' окружности S', умно-
О
женному на — :
k
t о
х = х----;
k
но
а = /1Q2 = x2ctg2 -—k = 4r2,
значит,
. а
х2 ctg2 -n
X = х' ------,
4f2
и потому
x = 4r2 tg2 -у- • —.
Остается вычислить x'. Радиус окружности, вневписанной в
угол А треугольника АВ'С', вычисляется по формуле
s'= (р'— а')х',
где s'—площадь треугольника АВ'С', р' — полупериметр, а' —
длина стороны В'С'. Имеем
s' = rDB’ —гDC' = r • 2rtg(a + (J) —г • 2rtg0 (0 = ^CAD),
или
s' = 2r2 ----.
cos (a 4- 0) cos 0
Далее, p'—a'= + AC' — B'C') =
2 L cos (« + 0) cos 0 cos 0 cos (a P) J
__cos 0 + cos (a 4~ 0) — sin a
cos 0 cos (a + P)
Итак,
, _ s'________________ 2r sin a ___
p'~a' cos P -J- cos (a 4" 0) ~ sin a-
a a a
4r sin— cos — zr sin —
2 2 2
/ a \ a Л . « a / a \ .a
2cos —4-0 cos——2sin — - cos— cos — 4“P —sin —
\ 2 1 / 2 2 2 \2irJ 2
108
значит,
f а . ft\ .а
cos —+ р —sin —
Л2+2а
х = 4r2 tg2--------------------
ь 2 а
2 2r sin —
2
= 2^Т
а а а
cos — cos В — sin — sin Р —• sin —
2 2 2
а
sin —
2
= 2г tg2 — ( ctg—cos P — sin p — A =
2 \ 2 J
л a I a b y<4r2 __ A2 * \
= 2rtg2T( ctg--.=
= tg2y (b ctg-| — /4г2 - b\— 2r у
35. Предположим, что 2 а< -у. Ha рис. 47 изображено сечение
конусов плоскостью, проходящей через их общую образующую ОА
и высоты ОС и ОС'. Это сечение дополнено прямой OD, лежащей
Рис. 47
в плоскости сечения и перпендикулярной их общей образую-
щей ОА. На рис. 48 изображено сечение одного из конусов пло-
скостью его основания. Считая высоты конусов равными 1, находим
АС = tga, О А = —-—, AD =----------, CD=ctga,
cos a sin a cos a
а из рис. 48
DK = VDC2 — CK* = Vctg2a — tg2a = A”82” .
r T 6 b sm a cos a
Теперь из пропорции
СК _ АР
DK AD
находим
АР — AD - =-----5-----Аа— sin a cos a = -t=S=t.
DK sin a cos a у cos 2a у cos 2a
109
Одна из плоскостей, касающаяся обоих конусов, — это пло-
скость, проходящая через прямые DO и DP. Угол этой плоскости
с плоскостью сечения, изображенного на рис. 47, и есть половина
одного из двугранных углов, которые образуют плоскости, касаю-
щиеся обоих конусов, но не проходящие через их общую образую-
щую АО. Обозначая этот угол через ф, имеем
. АР
АО
или
. sin а
tgq> = -v=r^-
У cos 2а
Замечание. Если 2а>-у-, то конусы не имеют общих ка-
сательных плоскостей (кроме одной, проходящей через их общую
образующую).
Решение варианта 8
36. Данное уравнение эквивалентно двум смешанным систе-
мам:
х>0, х2 + х 4- а — 0; (1)
х<0, х2—х+а=0. (2)
Решим смешанную систему (1). Из условия действительности кор-
ней
1— 4а >0
находим
4
Если 0<а^?—, то оба корня уравнения х2+х+а=0 отрицательны.
4
Если а —0, то х2+х=0, откуда надо взять только х=0. Если а<0,
то корни уравнения (1) разных знаков, но корнем данного уравне-
ния является только положительный корень
х— 2
Перейдем к системе (2). Условие действительности корней то же
самое: а^?—. Если 0<а<—, то корни уравнения х2—х+а=0
4 4
положительны и не являются корнями данного уравнения. Если
ПО
а<0, то корни уравнения х2—х+а = 0 разных знаков; корнем дан-
ного уравнения является отрицательный корень
1— /I— 4а
2
Итак, если а^О, то данное уравнение имеет два корня:
, VI—4а —1
*1,2 = ± —---------
2
а если а>0, то данное уравнение корней не имеет (если а=0, то
х=0).
Другой способ решения. Перепишем данное уравнение
в виде
Iх I2 + Iх I + а = °-
Если а>0, то |х|2+|х|+а>0 при всех значениях х. Если а<0,
го корни этого уравнения разных знаков, а так как |х| 3^0, то
откуда
. /Е=4а — 4
х = ± ----2----
Наконец, если а=0, то х=0.
37. Перепишем данное неравенство
в виде
или
или
tgx
14-tgx
2>0,
— 2 —tgjr
1 + tg X
tg-^ + 2
tgx+1^
Это неравенство выполнено тогда и только тогда, когда
— 2<tgx< —1,
значит, все решения данного неравенства
kn — arc tg 2 < х < kn —
4
где k принимает все целые значения (рис. 49).
111
38. Среди первых ста натуральных чисел имеется группа в
33 числа, делящихся на 3; группа в 33 числа, дающих при делении
на 3 в остатке 2, и группа в 34 числа, дающих при делении на 3
в остатке 1.
Для того чтобы сумма трех чисел из первых ста натуральных
разделилась на 3, необходимо и достаточно, чтобы они . были
выбраны все из одной группы или все из разных. Таким образом,
число всех возможных выборов равно
2 • С|з +С|4 + 33 • 33 • 34 = 53 922.
39. Прежде всего отметим, что искомая окружность может
быть построена с помощью циркуля и линейки исходя из следую-
щих соображений: пусть В и С — данные точки на одной из сто-
Рнс. 50
рон данного угла (на рис. 50 данный угол острый, на рис. 51 —
тупой). Тогда отрезок ДЗ касательной (S — точка касания), про-
веденной из точки А к любой окружности, проходящей через точ-
ки В и С, имеет постоянную величину АВ-АС). Построив
любую такую окружность и проведя к ней касательную из точки А,
строим окружность с центром А и радиусом ДЗ. Пусть Т — точка,
в которой эта окружность пересекает вторую сторону угла. Центр О
искомой окружности является точкой пересечения прямой, про-
ходящей через точку Т перпендикулярно АТ с медиатрисой отрез-
ка ВС. Для вычисления радиуса искомой окружности спроекти-
руем АТОМ (М — середина ВС) на прямую АВС. Считая сначала,
что данный угол острый (рис. 50), получим
ДТ-cosa + ОТ sin a = AM =
и так как
ДВ = -Л-, ДС = -Д-, ДТ = 4^,
sin a’ sm а ’ sin а
112
то
cos а + ОТ • sin а =
sin а 1
откуда
6 Н~с
2 sin а ’
пт* _ & 4" с — 2 be cos а
Ш “ 2 sin2 а
(1)
В случае, если а тупой угол (рис. 51), будем иметь
MR - Л/? = AM = - АВ^А—;
ИЛИ
ОТ • cos (а-----cos (л — а) = -4-t—,
\ 2 У sin а ' ' 2 sin а ’
откуда получаем для ОТ то же. самое выражение.
Полученная формула (1) верна и при а=—; ПРИ этом она
принимает вид
ОТ = -А±£_ ;
2
читателю рекомендуется сделать соответствующий чертеж.
40. Отложим на оси данного конуса от вершины в сторону осно-
вания отрезок ОЛ = 1. Опустим из точки А перпендикуляры на все
образующие данного конуса; получим конус,
образующая которого равна sin а, в то время
как проекция ОА на образующую данного ко-
нуса равна cos а. Таким образом, получаем
два конуса, имеющих общее основание, кото-
рые образуются вращением вокруг гипотенузы,
равной 1, прямоугольного треугольника с ка-
тетами cos а и sin а (рис. 52).
Плоскости, касающиеся данного конуса по
его образующим ОВ и ОС, будут перпендику-
лярны тогда и только тогда, когда перпенди-
кулярны образующие АВ и АС конуса с вер-
шиной Л, т. е. тогда и только тогда, когда
ВС =У~2 sin а. Теперь из равнобедренного тре-
угольника ОВС находим синус половины
угла <p=ZBOC:
, <р ВС tea
sin — = —: cos a =
2 2 <2
Заметим, что задача имеет решение тогда и только тогда, когда
на указанном выше конусе с вершиной А имеются две взаимно
перпендикулярные образующие, т. е. только тогда, когда угол в
из
осевом сечении этого конуса или тупой, или прямой. Это значит,
что угол в осевом сечении данного конуса должен быть острым
Л у- л Л / . ф 1 \
или прямым, т. е. а=С—. Если а=—, то <р= — ( sin — =------)
к ^4 4 ’ т 2 < 2 /2/
значит, взаимно перпендикулярные плоскости касаются данного
конуса по двум его образующим, полученным в осевом сечении.
Итак,
slflSL = !^,
2 /2
причем задача имеет решение только в случае 0<а^—.
4
Вечернее отделение
Решение варианта 1
41. Прежде всего отметим, что должны быть выполнены нера-
венства
х-|-1>0 и 2 — х>0,
откуда
— 1<х<2.
Теперь перепишем данное неравенство в виде
log2(x + 1 )logj_ 2 > log2 (2 — х),
2
или, так как log 12 = — 1, то
~2
log2—!—>10g2(2 —х);
х-Н
отсюда
и так как х+1 >0, то это неравенство эквивалентно следующему
(2-х)(х+1)<1,
или
х2 — х — 1 > 0.
Так как корни трехчлена х2—х—1 таковы: 1 , то неравен-
ство х2—х—1>0 будет выполнено тогда и только тогда, когда
1—/5 1+Z5
или х< £—, или х>— .
114
u , 1 “/5 1 + /5
Но так как — 1 < ——, 2 > —Ly—» 70 все решения данно-
го неравенства
— 1<х< -1+А<х<2
2 2
42. Перепишем уравнение sinx = sin2y, или sinx—sin2y=0,
в виде
2 sin cos = 0.
2 2
Отсюда либо х—2y=2kn, либо х+2у= (2п+ 1)л, где k и п прини-
мают все целые значения.
Аналогично переписывая уравнение cosx = sinz/, или
sin у — sin ( —-х ) = О,
\ 2 J
в виде
Iя Iя
х+у-~ у-*-\-~
2 sin----g--cos-----g-----= 0’
получаем
либо х + у —= 2т л, либо у — х + = (2s 4-1) л,
где т и s принимают все целые значения. Таким образом, все ре-
шения данной системы — это все решения следующих четырех
систем:
х — 2y = 2kn, х—2y = 2kn.,
х-\-у—у = 2/пл; (1) у — х 4-= (2s + 1) л;
х4- 2у = (2п 4-1) л, х 4-2# = (2п 4-1) я,
х + у—у = 2тл; у — х4- -^- = (2s4-l)n.
где k, т, п, s принимают все целые значения. По условию задачи
надо найти только те решения, которые удовлетворяют неравен-
ствам
0<х<л, 0 <у < л.
Решая систему (1), получим
х =Т 4-^(2/п4-*),
у = v + —
О о
115
теперь из неравенств
0<^- + ^(2/п + £)<л,
О о
о о
находим
—^-<2т4-Л<1, *
— -±-</п — /г<4~,
4 4 ’
а так как т и k целые числа, то
2m-}-k=0, или 2/и4-А=1,
и
т—k=Q, или т—k=1.
Система 2т+Л=0, т—k—Q имеет решение m=fe = 0. Система
2/п+А=0, т—k=\ не имеет решений в целых числах, как и си-
стемы 2/п 4'^=1, т—k=Q и 2tn+k=\, tn—k=l. Итак, система (1)
имеет в квадрате С<х<л, 0<#<лтолько одно решение:
х = — У= —
з ’ а 6 •
Решая систему (2), получим
х = л — 2kn — 2 (2s 4-1) л,
У~~----2&л — (2s 4- 1) л.
Неравенства 0<у<л принимают вид
0-С-^--2Ал — (2s 4- 1)л<л,
или
0<-^- —2fc —2s —1 <1,
0<1 — 4k — 4s — 2<2,
1< — 4k — 4s<3,
-4<* + s<—Г-
4 4
116
Нет ни одной совокупности целых чисел k и $, удовлетворяющих
этим условиям. Значит, система (2) в квадрате 0 <х<я, 0<«/<я
не имеет решений.
Решая систему (3), получим
х = я 4- 4/ил — (2п+ 1)л,
У = — (2п + О « — 2/пя.
Условия 0<х<л, 0<£/<ядают /п=п=0, так что система (3)
в квадрате 0<Сх<Сл, 0<у<я имеет только одно решение:
л я
Наконец, все решения системы (4):
л 2п4-1 2(2s+1)
Л — —t— ---- Jt '
3 3 3
я , 2п + 1 , 2s + 1
У 6 3 3
Решая систему неравенств 0<х<л, 0 <#< л, получим л=0, s = 0,
так что
я,
я.
л Л
х = 0, у = —,
. » 2
то же, что уже было получено при решении системы (3).
Итак, на квадрате 0 <Сх < л, 0 < у < л данная система имеет
только два решения:
= У1 = -Г И *2 = 0» & = V
О О Z
43. Полагая 2х—%, получим квадратное уравнение
%2 — 4/пХ + 2т + 2 = 0.
(1)
Дискриминант этого уравнения должен быть неотрицателен:
А = 4/п2 —2/и —2 = 4(/n — l)f/n + >0,
значит, или т<---или/п>1.Так как по условию задачи /п<0,
то остается/п<---Если/п =-----то уравнение (1) принимает
вид
А2 + 2Х + 1 = 0.
•417
Оба его корня отрицательны, но так как %=2Х>0, то при m *=-—
данное уравнение не имеет решений.Если— 1 ----то корни
уравнения (1) действительны и различны, и так как
“ 2/п -4" 2 О,
4~ ^*2 == 4/п
1 1 & 7
то Xi и Хг отрицательны. Данное уравнение опять не имеет корней.
При т =— 1 уравнение (1) принимает вид
X2 + 4Х = 0;
его корни Xi = 0, Ха =—4, исходное уравнение не имеет корней.
Если т<—1, то 2т+2<0, значит, корни уравнения (1) разных
знаков. Беря только положительный корень
X = 2х = 2т + V 4m2 — 2/П — 2,
находим
х = log2 (2m + УЧт2 — 2т — 2). (2)
Итак, только при т<—1 исходное уравнение имеет один корень
(2).
44. Из треугольников BQC и АРС по теореме синусов находим
(рис. 53)
CQ _ ВС PC _ АС
.В . / В С \' . 4 ~ f А С V
sin— sin ( — + — ) sin— sm —+ —-
3 4 3 3/ 3 3 3 /
Отсюда находим CQ и PC, а затем и площадь треугольника CPQ
по формуле: пл. ACPQ = — CQ-CPsin—. Итак,
2 3
пл. Л CPQ =
ВС AC-sin — sin — sin —
3 3 3
и так как BC = 2/?sin.4, ЛС=2/?з1пВ, то окончательно
пл. &CPQ — 2R2
45. Так как прямая ВС перпендикулярна оси вращения I, то
через прямую ВС можно провести плоскость, перпендикулярную
118*
оси вращения. Пусть эта плоскость пересекает ось вращения в
точке О и пусть D — проекция точки О на прямую ВС. При вра-
щений треугольника АВС вокруг оси / отрезок ВС опишет плоское
кольцо, образованное окружностями с центром в точке О, радиу-
сами OD и ОВ, причем обе эти окружности расположены в плоско-
сти, проходящей через точку О перпендикулярно оси вращения.
Искомый объем равен разности объемов двух конусов с общей
высотой АО и радиусами оснований OD и ОВ (рис. 54):.
V = л —- (ОВ2 — OD2) = л — • BD2 =
3 3
л , о а /, , а \2 л&3 о а . о а
==—& COS В-COS —(О sin— ) =----COS р COS — Sin2 —.
1 3 2 \ 2 J 3 2 2
Решение варианта 2
46. Найдем сначала положительные корни данного уравнения.
Предполагая х>0, получим
(х + 1)(х-1) = -±
откуда
Найдем отрицательные корни данного уравнения. Предпола-
гая, что х<0, будем иметь
(Х+1)(_Х_1) = _±>
119
(x+l)2 = J-,
x+1 = ± —4^,
/2
откуда
i , 1 t 1
X» = — 1 H--7^, X3 = — 1--
2 /2 3 /2
Заметим, что x=0— не корень данного уравнения, а также то,
что данное уравнение не имеет мнимых корней (докажите!).
47. Так как
р = — (tg а + tgp) =
sin (а + Р)
cos а cos р
Я = fg a tg 0,
то данное выражение можно переписать в виде
8|п= (а + ₽) - « + ?>«»(+ И> + tg а tg ₽ cos’ (а + Р) -
cos а cos Р
= sin’(U + в + + tg аtgP cos’ (а + Р) _
cos а cos р
= sin2 (а + 0) tg а tg 0 + cos2(a + 0) tg a tg 0 = tg a tg 0 = q.
48. Отметим прежде всего, что данные радикалы — действи-
тельные числа тогда и только тогда, когда
— 1<х<3.
При выполнении этих соотношений данное неравенство эквива-
лентно следующему:
/з^>^- + /7+7, (1)
ИЛИ
3 — х / % -J-1 -f- + 1 >
4
так как и левая, и правая части неравенства (1) состоят из неот-
рицательных чисел. Переписывая последнее неравенство в виде,
7 — 8х> 4/7+7, (2)
заключаем, что это неравенство не имеет решений среди всех зна-
7
чений х, для которых 7—8x^0, т. е.х> —. Итак, должно быть
8
— 1 <х<7-.
о
120
При выполнении этих условий неравенство (2) эквивалентно еле
дующему:
49 - 112х + 64х2 > 16х + 16,
или
64х2—128x4-33 >0. (3)
Корни уравнения
64х2 — 128х + 33 = 0
таковы:
Неравенство (3) выполнено тогда и только тогда, когда
или х< 1------------------или 1
8 8
тт 1 । 31^7 1 / 31 1
Но так как 1 + —— > —, то остается х < 1-; так как 1 —
_ 8^8 8
-/31 7
------<—, то окончательно все решения данного неравенства:
8 8
_1<x<1_X2L.
49. Покажем, как можно построить искомый квадрат (с по-
мощью циркуля и линейки): опустим из точки В перпендикуляр ВС
на прямую ОА. Отложим на продолжении отрезка ОС за точку С
отрезок CD—ВС. Проведем через точки В и D прямые, соответ-
ственно перпендикулярные прямым ВС и CD; пусть Е— точка пе-
ресечения построенных прямых. Произведем гомотетию с цен-
тром О, при которой точка Е квадрата BCDE перейдет в точку Е',
лежащую на дуге АВ; тогда квадрат BCDE перейдет в искомый
квадрат B'C'D'E' (точка Е' — точка пересечения прямой ОЕ и
дуги АВ; точка В'—-точка пересечения прямой О В с прямой, про-
ходящей через точку Е’ параллельно прямой О А; точки С' и D' —
проекции точек В' и Е' на прямую ОА). Не нарушая общности,
121
можно считать ОА = ОВ=\, Тогда BC=ED = CD = sin а, ОС=cos а,
значит, коэффициент гомотетии, при которой квадрат BCDE пере-
ходит в квадрат B'C'D'E', равен (рис. 55)
ь- 0£' - 1
ОЕ у (cos a -f- sin а)2 + sin2 а
Значит, сторона х квадрата B'C'D'E' равна
х== sing
Y1 + sin 2а + sin2 а
площади этого квадрата к площади сектора
а искомое отношение
ОАВ равно
2№ ______ 2 sin2 а
а а (1 + sin 2а + sin2 а)
X2
а
~2
(а — мера угла ZAOB в радианах).
50. Не нарушая общности, можно считать высоту конуса рав-
ной 1. Тогда радиус окружности, лежащей в основании конуса,
равен CM = tg-^-, а расстояние от центра О окружности, лежащей
в основании конуса до прямой, по которой указанная в условии
секущая плоскость пересекает основание конуса, равно OB =tgp.
Так как ZOB/1=—, то
2
sin
V 2 а
cos — cos р
Пусть S — вершина конуса, а х—искомый угол. Тогда Z.ASB =
__ _х_
“ 2 ’
и так как SB = —то (рис. 56)
& 2 BS
а
COS —
2
51.
Решение варианта 3
Перепишем данное неравенство так:
х + 1 — — <0,
X
или
х2 + х-2
122
или
(•у + 2)(х — 1) < о
X
Отсюда находим все решения данного неравенства: —оо<х<—2
и 0<х<1.
52. Данное уравнение эквивалентно следующей смешанной
системе:
cos х < О,
sin х > О,
(Vsin х)2 = (—cosx)2,
или
sin х > 0, cos х < 0, sin2 х + sin х — 1 =0.
Отсюда
. -^5 — 1
sinx = —------
2
и в силу условия'Чгоэх^О вге решения:
х = (2k + 1) л — arc sin
где k принимает все целые значения.
53. Систему рациональных уравнений естественно решать над
полем комплексных чисел. Поэтому найдем не только действитель-
ные, но и мнимые решения данной системы. Прежде всего заме-
тим, что данная система эквивалентна следующей:
2х2 = у(1 +х2), (1)
2у2 = х(1 + у2),
так как x=i не удовлетворяет первому из этих уравнений, a y=i—
второму (отсюда следует, что если х, у — решение системы (1),
то х, у является решением и данной системы). Система (1) экви-
валентна следующей:
2х2 - 2у2 = у (1 + х2) -х(1 + у2),
2у2 = х(1 + у2),
или
(х — у) (2х + 2у + 1 — ху) = 0,
2у2 = х(1 + у2).
123
Эта система распадается на две:
х — у = О,
2«/а = х(1 + i/2);
2х + 2у+1— ху = О,
2у2 = х(1 + у2).
Система (2) эквивалентна такой:
У = х,
2у* = У (Д + у*У,
отсюда
х^ = О, У1 = 0, х^ ~ 1, у% — 1 •
Система (3) эквивалентна следующей (докажите!):
2- -у2 - + 2# + 1 —у-^— =0,
1 + № 1+у2
2х+2у+1— ху = 0,
или
5//2 + 2у+ 1=0,
2х + 2у + 1 — ху = 0.
(2)
(3)
(4)
(5)
Из первого уравнения находим
Уз =
— 1+2/ —1—24
—Г-’ —
теперь из уравнения (5)
находим
2у+'
У-2
(6)
следовательно,
2/ —1
2 —
2/— 1
5
х3
__ _ 4/ + 3
2 2*‘“П
(4t+3) (2/ + Н) _ — 1 — 2/
—125 ~ 5
— 1 + 2/
5
124
Итак, данная система имеет четыре решения:
= 0, x2 = 1, — 1—2» X3 , 3 5 Fi = 0; Уг= 1; u -->+а. 5 ’
_ -1+2» □ — 1—2» 5 •
54. Из треугольника АРВ находим (рис. 57)
ВР а/2
sin 30° sin 67°30' ’
откуда
ВР = г-—--------------.
/2 cos22®30'
Далее,
BD = ВО cos 22°30',
и так как BD — то
/2
ВО = а-------------.
/2 cos 22°30'
Таким образом, АРВО равнобедренный, значит,
— = г- а-----sin 7°30';
2 /2 cos 22°30'
отсюда
’ ( л л
pQ____ а У2 sin 7°30' _,<2 \ 8 12
~ cos 22°30' “ У л
cos —
8
= aV 2 ftg — cos—-----sin =
<8 12 12 J
1 — cos----
4
я
sill-----
4
125
55. Пусть ABCD — квадрат, лежащий в основании пирамиды
SABCD (рис. 58). Проведем сечение, параллельное высоте и двум
сторонам квадрата АВ и CD. Пусть секущая плоскость пересечет
стороны SD и SC в точках Р и Q, а стороны основания ВС и DA
в точках R и S' (рис. 58). Сечение представляет собой трапецию:
PQ и RS'— основания, RQ и PS' — боковые стороны. Полагая
Рис. 58
PQ=x и замечая, что RS'=a, из условия, что в эту трапецию мож-
но вписать окружность, находим
PS’ = QR
Пусть Е — проекция точки S на' сторону'AD (SE — апофема
грани ASD). Так как высота пирамиды равна а ]^2, то
®=/т+2“1 = т“'Телерь прждем ,ери тачку Q п₽яму,°
QT\\PD (Т — точка, лежащая на стороне основания CD).
Из подобия треугольников находим
SE _ SD SD DC
PS ~ PD ~ QT ~~ ТС '
т. е.
3
— а
2 а
а + дг а —х ’
2^
откуда х = значит, периметр трапеции PQRS равен
2(х + а) = За.
126
Решение варианта 4
56. Так как при х>0 и х=£Л
1 . 1
:-------------------- lg X--.-
x,gx=10 iex= 10,
то данное неравенство эквивалентно следующей смешанной си-
стеме:
10 lg х< 1, х#=1.
Отсюда
0<х<1, 1<х<*^10.
57. Перепишем данное уравнение в виде
(cos х + siti х)2 - tg х (cos2 х — sin2 x);
отсюда
cos x-j-sinx = 0,
tgx= — 1,
X — kn— —.
4
Остается решить уравнение
cosx + sinx = tgx(cosx —slnx),
или
. . . sin2x
COS X + Sin X = sin X--,
COS X
или X
cosx
или
—?----= 0.
cosx
Это уравнение решений не имеет. Итак, все решения данного урав-
нения:
х = />*-^,
4
где k принимает все целые значения.
127
58. Прежде всего заметим, что данное уравнение может иметь
корни, заключенные между а и —1 (при а=—1 уравнение корней
не имеет). Пусть а<—1. Тогда корни данного уравнения должны
удовлетворять условию а<х<—1, так как при этих и только при
этих значениях х функция
принимает
положительные зна-
чения.
Полагая
а — х
ТТ7
и замечая, что Х>0, получим
X-----— = 2,
X
V —2Х —1 =0,
X = 1 + /2.
Таким образом, ,
1/^ = 1 +V2,
V Ч-х
значит,
^. = (1 + /2Г,
1 + х
а — х = (1 + /2)4 + х (1 +/2)4,
у__ Д-(1 + /2)\
1 + (1 +/2)<’
неравенства
а_(1+/2)4
а <---------< — 1
1 +(1 + /2)«
выполняются, так как неравенство
д-(/2+1)«
<1<' 1 + (/2+1)«
эквивалентно неравенству
(а+1)(1+/2)4<0,
которое в силу условия а<—1 выполняется. Неравенство
g-(l+/2)« t
128
или
а4~1
1 + (/2+1)<
О,
также выполняется.
Если а>—1, то корни данного уравнения должны удовлетво-
рять условию —1<х<а. Полагая, как и выше,
находим
Теперь находим
х+ 1
д —(1+/2)*
1 + (1 + /2)« ’
(1)
= —а+1 - >0,
1 + (1 + /2)4
А_ г = л - Д-О+/2)* _ (а+1)(1+/2)« . п
1+(1 + /2)4 1 + (1+/2)4
так что в случае а>—1 соотношением (1) определяется корень
данного уравнения.
Итак, если —1, то данное уравнение имеет один корень
г_ а-(1+/2)4
1 + (1 + /2)4 ’
Если а=—1, то данное уравнение не имеет корней.
59. Пусть (01), (О2), (О3) —окружности с центрами Оь О2, О3,
каждая из которых внешним образом касается двух других, при-
чем радиусы этих окружностей соответственно равны 1, 2 и 3
(рис. 59). Пусть А — точка касания окружностей (О2) и (О3),
В — точка касания окружностей (О3) и (Oi), а С — точка касания
окружностей (Oi) и (02). Положим О2О3=а, 030i = &, OiO2=c;
тогда OiC=OiB=p—а, О2А = О2С=р—Ь, ОъВ = О3А=р—с, где
р — полупериметр треугольника OiO2O3. Отсюда следует, что ок-
ружность (АВС), проходящая через точки А, В и С, является
окружностью, вписанной в треугольник OiO2O3. Последний тре-
угольник прямоугольный ^ZO2OiO3=-j-)c катетами OiO2=3,
OiO3=4 и гипотенузой О2О3=5. Пусть О — центр окружности
(АВС). Тогда
ВАС = — ВОС = —, АС В = —^АОВ = —(n-.-0j0302) =
2 4 2 2 4 13 2/
3 \ л lj3 л .1
л - arctg — = —-- arctg — = — - arctg — =
Т / £ ТЕ <3
5 Зак. 351
129
= arcctg —, СВ А = — СОА = — (л — О&Ог) =
3 2 2
=4- —4-=-т -arclg 4~=arcctg 4"=arctg 2-
Л А О £• Л i
Итак, углы треугольника АВС:
—, arctg 2 и arctg 3.
4
Рис. 60
60. Пусть О—середина диагонали MN куба (рис. 60). Пло-
скость Л1Л2Л3, проходящая через концы Ль А2, А3 ребер Л4ЛЬ МА2,
МА3 куба, отсекает от его диагонали MN отрезок ML =—MN (это
верно и для произвольного параллелепипеда!), а кроме того, пло-
скость AiA2A3 перпендикулярна диагонали куба (Л4/?±Л1Лз, следо-
вательно, и наклонная MN перпендикулярна Л]Л3 и т. д.). Отсюда
следует, что если продолжить отрезки МА\, МА2 и МА3 за точки
AltA2,A3 на расстояния МВ^ -^-MAt, МВ2=-~-МА2, МВ3==-^-МА3,
то плоскость В\В2В3 перпендикулярна диагонали MN и де-
лить ее пополам. Прямая В\В3 делит ребра RA{ и RA3 куба
пополам. Прямая В3В2 делит пополам ребра куба РА3 и РЛ2; нако-
нец, прямая В2ВГ делит пополам ребра QA2 и фЛь
Таким образом, в сечении получается шестиугольник, стороны
которого равны Этот шестиугольник правильный, так как
его противоположные стороны параллельны между собой и каж-
130
дая из них параллельна одной из сторон равностороннего тре-
угольника Лр42Лз. Площадь правильного шестиугольника со сто-
роной равна jjL3. е
ВОПРОСЫ, ПРЕДЛАГАВШИЕСЯ НА УСТНОМ ЭКЗАМЕНЕ
ПО МАТЕМАТИКЕ НА ФИЗИЧЕСКОМ ФАКУЛЬТЕТЕ
На устном экзамене по математике прежде всего предлагались
теоретические вопросы по программе для поступающих в высшие
учебные заведения. Помимо этих вопросов давались дополнитель-
ные вопросы. Некоторые из них мы и приводим ниже. К части этих
вопросов даны решения, к части — указания, а к части — ответы.
1. Найти на плоскости множество всех точек А4, координаты х
и у которых удовлетворяют следующему условию: число z2+z+l—
действительное и положительное (z=x+iy, где х и у — координаты
точки М).
Решение.
z2 + z+ 1 = (х4- 0i)2 + * + yi + 1 == № —/ + х+ 1 +(2*4- 1)0»-
Отсюда
(2x4-1)0 = О, (1)
х2 —1/2 + х4-1>0. (2)
Из соотношения (1) следует, что либо 0=0, либо 2х+1=0, т. е.
х ---—. Если 0=0, то неравенство (2) принимает вид х2+х+1 >0
и выполняется при всех действительных значениях х. Если
х =---—,то неравенство (2) принимает вид
А-.х,
откуда:
Таким образом, неравенство z24-z4-'l>0 выполняется тогда и
только тогда, когда точка М с координатами х и 0 или любая точ-
ка оси Ох (у=в), или любая точка отрезка АВ с концами
(1 тЛз* \ / 1 \
, -—к В(-, ——) (сами точки А и В исклю-
2------------------2 J \ 2-2/'
чаются). Читателю рекомендуется сделать чертеж.
2. Дано:—>—; что больше х или у?
X у
5*
131
Ответ. Если х и у одного знака, то х<у, а если х и у разных
знаков (т. е. х>0, a #<0), то'х>у.
3. Может ли простое число быть четным?
Ответ. ТоЯько число 2.
4. Рассмотрим два уравнения над полем действительных чисел:
А • В = 0 (1)
и
В = 0. (2)
Можно ли утверждать, что любой корень уравнения (1) яв-
ляется также корнем уравнения (2)?
Можно ли утверждать, что любой корень уравнения (2) яв-
ляется также корнем уравнения (1)?
Ответ. Неверно ни то, ни другое; примеры:
1) х(х— 1) = 0 (1). х—1 =0; (2)
2) (х — 2) arc sinx = 0 (1), х — 2 = 0. (2)
5. Рёшить неравенство sin х^ >а, (О
где а—действительный параметр.
Ответ. Если а<—1, то неравенство выполняется при всех
действительных значениях х. Если а=—1, то неравенство (1) вы-
полняется при всех действительных значениях х, кроме х—
=2ka—где k принимает все целые значения. Если —1 <а< 1,
то все решения данного неравенства:
2fert 4* arc sin а<^х < л — arc sin а + 2kn,
где k принимает все целые значения. Если а^1, то неравенство
(1) решений не имеет.
6. Найти на плоскости множество всех точек М, координаты х
и у которых удовлетворяют неравенству tgx>tgy.
Указание. Если — — , ——<«<' —, то из нера-
2 2 2 У2 г
венства tgx>tgy следует, что х>у, и обратно. Множество всех
точек, координаты х и у которых удовлетворяют неравенствам
состоит из всех точек, лежащих внутри квадрата с вершинами
132
(читателю рекомендуется сделать чертеж). Множество всех точек,
лежащих внутри этого квадрата, координаты которых удовлетво-
ряют условию х>у,— это множество всех точек, лежащих вну-
три треугольника CDA.
Разделим теперь всю плоскость на квадраты прямыми
х = -^- + Ал, у = + Где кип принимают все целые значе-
ния. Пусть /TB'C'D' — любой из этих квадратов (он получается из
квадрата ABCD переносом). Множество всех точек плоскости,
координаты которых удовлетворяют неравенству tgx>tgy, состоит
из всех точек, лежащих внутри всех треугольников C'D'A' (соответ-
ствующих всевозможным указанным выше переносам треугольника
CD А). Читателю рекомендуется сделать чертеж.
7. Решить уравнения:
1) tg (sinx) = 0;
2) sin (tg x) = 0.
Ответ: 1) x==fert, где k принимает все целые значения;
2) х = пл+arctg (for), где k и п принимают все целые значения.
8. Найти наименьшее значение функции у=х2+х+1, считая,
что х изменяется на сегменте а<х<6.
Ответ: Если ----------^-<6, то Данная Функция принимает
1
наименьшее значение при х =-----и это наименьшее значение
ж '1 1 I 1 з
функции равно —-----— + 1 = —-
Если а >----то наименьшее значение данной функции равно
'/min = a2 + a+1.
Если b <----то наименьшее значение данной функции равно
Ут1п = & + b + 1.
Читателю рекомендуется сделать соответствующие чертежи.
9. Найти наибольшее значение функции
у = х2 + х 4-1,
считая, что х изменяется на отрезке а i
Ответ: Если д + =-------—, или а + Ь=—1, то данная функция
принимает наибольшее значение при х=а и при х=Ь:
Упмх = а + 1 ~b* + b + l.
133
Если -a^b >-----или а + b> — 1, то ymax = &2 + b 4- 1. Ес-
ли а 4- b •< — 1, То утах = а2 4- а 4-1 • Читателю рекомендуется сде-
лать соответствующие чертежи.
10. Найти наименьшее значение функции
у = ах2 4- х 4- 1,
считая, что х изменяется на сегменте 2^х<;3.
_ Если а=0, то у=х+1, значит, t/min=24-l=3.
Если а
вале
• 2 < х < 3 таково: ymln = а • 22 4" 2 -f-1 == 4а 4* 3.
п 34-2 1 1
Если а < 0 и —1— =-------, т. е. а —-----,
2 2а 5
то наименьшее значение на сегменте [2, 3] данная функция
0, то функция у = ах2 4- х 4- 1 возрастает в полуинтер-
—5—, 4-©о\ значит, ее наименьшее значение на сегменте
2а /
У =----i-x24-*4~ 1
принимает при х=2 и при х=3:
ymIn=-4 + 2 + I = -T- + 3 + I =-?-•
О о о
с 3 + 2 Если —1—> 2 1 1 4 Л , т. е. <а<0, то данная функция 2а 5
у = ах2 4- х 4\1
принимает наименьшее значение при х=3:
l/min = 9a+4,
34-2 1
а если —— <-----------, т.
2 2а
. 1 ж
е. --------, то данная функция прини-
5
при х = 2;
мает наименьшее значение
Ут1п — 4а 4? 3.
11. Найти наибольшее значение функции
у = ах2 4- х 4- 1,
считая, что х изменяется на сегменте 2^x<i3.
Ответ: Если а=0, то у=х4-1, значит, г/тах=34-1=4. Если
а>0, то функция у=ах2+х+\ возрастаёт на полуинтервале
[---—Г 4-°°) и, значит, наибольшее значение данная функция при-
2а z
нимает при х=3:
Утах 4.
134
Если а <2 0 и если 2<С----— <3, т. е.
2а
то наибольшее значение данная функция принимает прих =---------:
2а
' __ 4а— 1
Утах •
4а
Если 2>------—, т. е. а <2—*-i-, то наибольшее значение дан-
20 4
ная функция принимает при х == 2, так как на полуинтервале
£---, 4- оо эта функция убывающая:
Утах = 4“ 3.
Наконец, если 3<2----т. е. а>--------то данная функция при-
нимает наибольшее значение при х = 3, так как на полуинтервале
—оо, —она возрастающая:
Утах ~ 4“
Читателю рекомендуется сделать соответствующие чертежи.
12. Решить неравенство
logsinx<l.
cos*
Ответ.-2-+ <х<-у 4-2&Л, где k принимает все целые
значения.
13. Решить неравенство
Ь = loga cos х > О,
где
a = logy^ tg x.
з
Решение. Если взять 0<х<2л, то из этих значений х толь-
ко при 0<х<-у существуют функции b и а. Итак, пусть 0<х<2
<2—. Тогда при 0<х<— будем иметь а>1, при х = — а = 1,
2 6 6
а при— < х <— будем иметь 0<а<1 и, наконец, при — <х<
6 4 4
<2-у будем иметь а <0. Надо оставить только а>1 и 0<2а<1,
135
т. е. 0<х< — и — <х<—. Но если а>1, то 1о&,со8х-<0
6 6 4
(считаем cosх>0), а если 0<а< 1, Tologecosx>0 (0<cosx< 1).
Итак, решениями исходного неравенства будут все значения х из ин-
тервала -^-<х<-^-, а все решения неравенства:
2Ал+ — <х<2£л-}-—,
6 4
где k принимает все целые значения.
14. Дано z =cos <р + i sin ф, где ф#=&л (Л — целое число). Най-
ти модуль и аргумент комплексного числа
Решение.
и =
ф ф ф
....................... 2 cos2 — 4- 2 sin — cos — i
cos ф + f sm qp -|- 1 _____2 2 2
cos ф-)-/sin ф — 1 л n ф , Л . ф ф .
Y Y — 2 sm2----f- 2 sin — cos - t
2 2 2
и так как sln^-^0 (ф^&л), то
ф ф
cos — 4- i sin —
. ф 2 2 ,
и = ctg ----------------------------- ctg
2 . ф . . Ф 2
-sm —+ «cos —
(Ф ф
— sin — 4-1 cos —
2 1 2
ф ф
— sin — 4- * cos --
2 1 2
= — ictg-y-
Отсюда следует, что
l“l = ctg-5-
и, далее, если ctg-5-О, т. е. если
2#л<ф<(2&+ 1)л,
где k — любое целое число, то
и = ctg — [cos (——4 i sin f — — 'j
6 2 L \ 2/ \ 2/
значит, аргумент и равен:
arg и = —+ 2&л,
где k принимает все целые значения.
136
Если же ctg-^-<0, т. е. если
(2k — 1)л<ср< 2kn,
где k— любое целое число, то
х ф ( Л ... Л
и = — ctg— cos---h i sin —
s 2 \ 2 2
значит,
arg и = 2ka -j- ,
где k принимает все целые значения.
15. Доказать, что если п— натуральное число, большее 5, то
2я • п! < пп.
Решение. Надо доказать, что если п>5, то
2я • п! .
пя
Рассмотрим последовательность
2я • п\
Имеем
/ 1 у
хп 2я-п!(п + 1)я+1 _1 + Г+...^
хя+1 па -2я+1(п+1)! 2 2
значит, xn>xn+i, т. е. хп — убывающая последовательность.
Далее находим
Х1 — 2 - 1 _ 1 — 2,
х2 4- 2 _ 4 2,
Х3 = 8 > 6 = 27 16 9 ’
= 16 • 24 44 _ _3_ 2 ’
хй = 32 • 120 55 __ 768 625
2е • 720 66 = — 81 <
1;
137
но х7<х6, значит, *7<1; x&<x-j, значит, х8<1 и т. д.; вообще хп<1
при л>5, а это и надо было доказать.
16. Найти знаменатель геометрической прогрессии, зная, что
сумма пяти ее членов, идущих подряд, равна 0.
Решение.
а 4- aq 4- аф + аф 4- aq* = 0.
Отсюда либо а = 0; тогда q — любое число. Либо, если а=/=0, то
^ + ^ + <72 + <7+1 =0,
(т’ + 1)! + ?(«2+1)-?, = 0,
(«*+1+4)‘—
(?s+l+4 + -^)(9!+l + 4--!yL) = 0.
Решая уравнения
+ о,
92+-^=^-<7+1 = О,
найдем четыре значения для q:
~ glt2 = -L (— 1 _ У5 ± i /10 — 2/5),
<73,4 = J-(_ 1 4- /5 ± i /104-2/5).
4
17. Сколько всего различных разбиений на пары можно сде-
лать из 10 человек?
Решение. Рассмотрим какую-нибудь одну (из 10!) переста-
новку из 10 лиц:
Поставим этой перестановке в соответствие следующее разбие-
ние на пары:
(av а2), (а3, аД (а6, аД (а7,а8), (а9, а10). (1)
Подсчитаем число всех перестановок, которым соответствует одно
и то же разбиение на пары. Эти перестановки мы получим, пере-
ставляя всеми способами пары (1); число всех таких перестановок
пар равно 5! —120.
Кроме того, внутри каждой пары можно менять местами поря-
док лиц; таким путем из одного и того же разбиения (1) можно
138
получить 25 перестановок, каждой из которых ставится в соответ-
ствие одно и то же разбиение (1) в пары. Итак, число различных
разбиений в пары будет
10! плк Л
------= 945 способов.
5! 25
18. Сколько существует на плоскости различных комбинаций
из пяти точек:
(+•+)> Л42(а8, а4), Л43(а5,ав), Л44(а7, аа), М6(а9, а10),
где все числа at, а2, а3, ait а5, ав, а2, а3, а9, аю отличны друг от друга
и каждое из них равно одному из чисел:
1,2, 3,4, 5, 6, 7,8,9, 10.
Ответ. -^1 = 30240 комбинаций (см. предыдущий вопрос).
5!
19. Вычислить следующую сумму:
s = 7-|-77 + 777+ ... 4-7„
(7 =777 ... 77).
п цифр
Решение.
s =-1 (9 + 99 + 999 + • • • +9п) =
= _1(Ю—1 + 100 —1 + 1000—1 +... + 10“—1)= .
=-1(1 + 10 + 102 + ... + 10" —п—1) =-^-(1„+1 —п — 1) =
У У
7 / 1 о „Л 7 /10л+1 —1 п
= — |----9П+, —п— 1 = —(-------------п— 11.
9 \ 9 / 9 \ 9 /
20. Доказать, что если последовательность ап — арифметичес-
кая прогрессия, то
Сл#2 Ц- Спи3 — ( 1 )л гап = 0.
Решение.
а3 — «2 =
а2 — ах = d.
Вычитая почленно, получим
ах — 2а24-а3 = 0.
139
Далее,
а2— 2а3 + ал = 0.
Вычитая почленно, получим
Oj “ 3^2 ~ЗП3 Л4 0 •
Далее,
а2 — За3 + За4 — а5 = 0.
Вычитая почленно, получим
ах — 4аа + 6а3 — 4а4 + а5 = 0.
Остается применить метод полной индукции.
21. Найти все рациональные значения х, при которых ]/х2 -|- х + 1
есть рациональное число. __________
Решение. Пусть х и Vх2 4- х 4- 1 — рациональные числа.
Тогда
Ух2 4- х + 1 — х = г (1)
число рациональное. Следствием соотношения (1) являются сле-
дующие:
Ух2 + х+1—x-j-r,
х2 + х 4-1 = х2 4- 2гх 4- г2,
х(1—2r) = r2—1.
г» 1
Равенство г = — невозможно, так как тогда
/х24-х4- 1 + у.
х2 4- х 4-1 ==х24**4- —,
4
1=±,
4
, 1
значит, ГФ— и потому
х =
г2 —1
1 —2г *
Обратно (это обязательно!—так как пока доказано, что если х и * 1
г2 — 1
----------------------------------------, где г — некоторое рацио-
г2 —1
нальное число, а нужно еще доказать, что если х =-----------, где
1 — 2г
+ х + 1 рациональны, то х
140
1
г — любое рациональное число, не равное —,
ло рациональное): пусть
ТО /х2 + X -V 1—чис-
г2 — !
х =-----------,
1 — 2г
. 1
где г — любое рациональное число, не равное —; тогда
1Z-y-----ГТ —12 । г2 — 1 I 1
у х2 4- х 4-1 = 1/ 3---— Ч---------h 1 —
г у (1—2г)2 1—2г
у74 — 2г3 4-Зг2—2г+Т _ | г2 _г-Н 1 I _ г2 —г+1
|1—2г| ”” |1—2г| ~ |1—2г| ’
так как г2—г+ 1>0 при любом рациональном числе г.
22. Вычислить
‘^0,9999999873.
с недостатком с семью верными знаками.
Ответ. 0,9999999, так как
0,9999999873 < ‘^0,9999999873 < 1.
23. Доказать, что при всех х выполняется неравенство
cos (sin х) > sin (cos х).
Решение.
cos (sin х) — sin (cos x) = sin -sin x) — sin (cos x) =
_ 2 sin (Д__sin*4-cos x\/Д_ I cosx—sin x\
\ 4 2 / \ 4 "* 2 /’
Далее,
то
и так как
141
Так как
2L_ > All >0,78 — 0,71 =0,07, 4 2 4 2 ^ л /’2 3,15 1,42 - “Т“ ' "Г" ‘ 4 2 4 2 ^
то Q Q7 Я cos X -|~ sin X <^15 ’ 4 2 ’
Оба угла 0,07 и 1,5 радиан находятся в интервале f0, значй¥,
Sjjj I п cos х -f- sin х \ q S\ 4 2 Л *
Аналогично доказывается, что в тех же пределах находится и
число л I cos х — sin х 4 * 2
значит, и /л . cos х — sin х \ . n cos I > 0. \ 4 2 /
Поэтому cos (sin x) — sin (cos x) > 0,
т. е. cos (sin x) > sin (cos x).
24. Выразить sin -у через sinx.
Решение, sin2 — 4- cos2 — = 1,
2 2
Отсюда 2 sin—cos— = sin x. 2 2 fsin— +cos— Y = 1 + sin x, \ 2 2 / ^Sin COS Y = 1 — Sin X.
142
Отсюда
sin — + COS — I = yi + sinx,
2 2 I
sin——cos — I = Vi — sinx.
2 2 |
. Л , Л A
b cos — и sin ——cos — естественно рассмотреть
Функция sill —+ cos— меняет знак при переходе — через зна-
2 2 2
чения---^-Ц-Ал, а функция sin —cos -у- меняет знак при пере-
ходе через значения + йл. Поэтому при исследовании знака
функций sin-j-H zzz * " — *
следующие сегменты изменения х:
Г——+ 2Ал,—+ 2£л],
L 2 2 J
+ 2£я,—+2£л1,
L 2 2 ~ J
— 4-2£л, — + 2fcn],
2 2 J
— 4-2£л, — + 2£л1.
2 2 I
1) Пусть —— + 26л < х < — + 26л; тогда
2 2
Sin — + cos — > О,
2 2
sin —-----COS — < О,
2 2
значит,
sin -|- + cos = У1 -f- sinx,
— sin -у- + cos -у- = ]/1 — sin х,
поэтому
sin — = — (V 1 + Sin X — J/ 1 — sinx).
2 2
2) Пусть — + 2£л < x < + 2&л; тогда
Sin — +.COS > 0,
2 2
sin ——cos-^- >0
2 2
143
следовательно,
sta-^- +cos-^- = /l 4-sinx,
sin—--COS— = УI —sinx,
2 2
и потому
sin 1 + sinx 4- У1 — sinx).
3) Пусть + 2kn < x < — 4- 2fat; тогда
sin — 4~ cos — < 0,
2 2
sin——cos— > 0,
2 2
и потому
sta-^- 4-cos-|- = —У1 4-stax,
sin——cos— = V1 — sinx,
2 2
значит,
sta-^- = (— У1 + sinx -) У1 —sinx).
4) Пусть,, наконец,
— + 2ka <x < — 4- 2£л;
2 2
тогда
sin — 4- cos — < 0,
2 2
sin—----cos— < 0,
2 2
поэтому
sin — 4- cos — = — УI 4- sinx,
2 2
sin —----cos — = —У1 — sinx,
2 2
значит,
sin — =-----— (У 1 4- sinx 4-/1 —sinx).
2 2
144
25. Вычислить без таблиц:
1) tg 20° tg40° tg 80°;
2) tg 10° tg 50° tg 70°;
3) tg 5° tg65° tg75°.
Решение. Каждый пример можно решить, опираясь на формулы:
sinacosP = -i- [siti(a + P) + sin(a — P)],
sinasinp = [cos (a — P) — cos(a + p)],
cos acos p = -y [cos (a — P) + cos (a + P)].
Мы дадим другое решёние, предварительно выведя одно тождество:
. о sin Зх 3 sin х — 4 sin3 х
tg Зх =--------------------------------------------
cos Зх 4 cos3 х — 3 cos х
3
— — sin2 x
4
— — sin2 x
4
, 3 — 4 sin2 x , 3 — 4 sin2 x .
= tg X--------------- = tgX----------------- = tgx
4 cos2 x — 3 1 — 4 sin2 x
. Л л . л . f л , \ . / л \
г sin2 ——sin2x sin — 4-x sm( — — x )
, 3 , к 3 1 J \ 3 J
= tg X -------------- = tg X--i
. . Я . / я , \ . f я X
sin2------sin2x sin ——f—x I sin (— — X ]
6 \ 6 J \ 6 /
(известно, что sin2 a — sin2 0 = sin (a + 0) sin (a— 0), этот вопрос за-
давался самостоятельно).
Итак,
tg Зх = tg х sin ^--^.sin ^^. = tg х tg (х + 60°) tg (60° - x).
cos (60° -f- x) cos (60 — x)
Полагая в этом тождестве х=20°, докажем, что первое из дан-
ных выражений равно 1^3. Полагая х=10°, докажем, что второе
из данных выражений равно Полагая, что х=5°, получим,
что третье из данных выражений равно,
tg 15° ^озЗО» = 2 _
sin 30°
26. Вычислить без таблиц
л . Зл . 5л . 7л , 9л .
х = cos----h cos----h cos-----h cos----h cos-----h
19 1 19 19 19 19
, 11л . 13л . 15л . 17л
+ COS------h COS----b COS-------h cos--.
19 19 19 19
145
Указание. Умножить обе части на и применить форму-
лу sin acos р = -у [sta (a + Р) + sin (a — Р)] (9 раз к правой части).
Ответ: х = —. Другой способ: просуммировать геометрическую
прогрессию:
л л Зл Зл 17л1 17л
СО8.-1д-+4 81П-|д-+СО8 -Н Slfl+ . . . Ц” COS —|д~ + I Sill ~jg~»
в результате получится комплексное число; х — действительная
часть этого числа.
27. Как должны быть расположены стороны прямого угла
относительно плоскости для того, чтобы в проекции угла на пло-
скость получились бы углы 1) острый, 2) тупой, 3) прямой.
Вершина данного прямого угла не лежит на данной плоскости.
Решение. 2) Докажем, что если стороны данного прямого
угла (или их продолжения) пересекают плоскость, то в проекции
получится тупой угол. Предположим, например, что данную пло-
скость пересекают стороны угла. Обозначим через А и В точки
пересечения. Тогда сфера с диаметром АВ пройдет через верши-
ну О данного прямого угла, и, значит, точка О на данную пло-
скость будет проектироваться в точку О', лежащую внутри боль-
шого круга сферы, по которому ее пересекает данная плоскость.
Отсюда следует, что ЛАО'В тупой. Аналогично доказывается, что
Х.АО'В тупой в случае, если данную плоскость пересекают про-
должения сторон данного прямого угла.
Теперь сразу легко установить, что если данную плоскость пе-
ресекает одна из сторон данного прямого угла и продолжение
другой, то в проекции получится острый угол (так как угол, смеж-
ный с данным, спроектируется в тупой).
Затем надо доказать, что если по крайней мере одна из сторон
данного прямого угла параллельна данной плоскости, а другая к
ней не перпендикулярна, то в проекции получится прямой угол.
Необходимость всех этих признаков доказывается сразу методом
от противного. 5
28. На плоскости найти геометрическое место точек, равноуда-
ленных от двух пересекающихся прямых.
Решение. Г. Пусть М — точка заданного геометрического
места точек, не совпадающая с точкой О пересечения данных пря-
мых I и tn. Обозначим через Р и Q проекции этой точки М соответ-
ственно на прямые / и tn. Тогда длины отрезков МР и MQ равны
между собой и, значит, прямоугольные треугольники ОМР и OMQ
равны между собой, так как у них равны катеты (МР и MQ) и они
имеют общую гипотенузу.
Отсюда следует, что ZMOP= ZMOQ и точка М лежит на од-
ной из биссектрис углов, образованных данными прямыми I и tn.
146
Замечание. Часто поступающие ограничивались только
что приведенным рассуждением. Однако из доказанного' не сле-
дует даже и то, что заданное геометрическое место имеет хотя бы
одну точку! В самом деле, ведь доказано только то, что если точ-
ка М принадлежит заданному геометрическому месту, то она ле-
жит на одной из биссектрис углов, образованных данными пря-
мыми.
2°. Докажем, что и обратно: если М — любая точка любой из
биссектрис углов, образованных прямыми I и т, то она принадле-
жит заданному геометрическому месту точек, т. е. ее расстояния
до данных прямых I и т равны между собой.
Сначала предположим, что точка М не совпадает с точкой О
(и лежит, конечно, на одной из биссектрис углов, образованных
данными прямыми). Пусть Р и Q — проекции точки М соответ-
ственно на прямые I и т. Тогда прямоугольные треугольники
ОМР и OMQ равны между собой, так как они имеют общую гипо-
тенузу ОМ и ZMOP= Z.MOQ.
Отсюда следует, что MP=MQ, т. е. точка М принадлежит за-
данному геометрическому месту точек.
Если точка М совпадает с точкой О, то ее расстояния до дан-
ных прямых также равны между собой.
Вот теперь можно утверждать, что заданное геометрическое
место точек состоит из всех точек обеих биссектрис углов между
двумя данными прямыми.
Аналогичные вопросы задавались для геометрического места
точек, равноудаленных от двух точек, и т. д.
29. На плоскости фиксированы две различные точки А и В.
Фиксирована прямая I. Найти на прямой I точку Af, для которой
сумма АМ2+ВМ2 имеет наименьшую величину.
Решение. Пусть М — произвольная точка. Обозначим се-
редину отрезка АВ через О, а через С — точку, симметричную
точке М относительно точки О. Имеем
2-AM2 + 2-ВМ2 = 4-ОМ2 + АВ2,
откуда
AM2 + BM2 = 2-ОМ2 + —.
2
Отсюда следует, что сумма АМ2+ВМ2 имеет наименьшее зна-
чение, если наименьшее значение имеет ОМ2 или ОМ. Значит, М—
это проекция точки О (середины отрезка АВ) на данную пря-
мую I.
30. В пространстве фиксированы две различные точки Л и В.
Фиксировано число k (положительное, отрицательное или нуль).
Найти геометрическое место точек М, для каждой из которых
AM2—BM2 = k.
147
Решение. Пусть М точка заданного геометрического места
точек, т. е.
AM2 — BM2 = k.
Проведем через точку М плоскость П, перпендикулярную прямой
АВ. Точку пересечения плоскости П с прямой АВ обозначим че-
рез Р. Тогда очевидно, что
AP2 — BP2 = AM2 — BM2 = k,
значит, точка Р так же, как и точка М, принадлежит заданному
геометрическому месту точек.
Заданному геометрическому месту точек принадлежит вся пло-
скость П, так как если W— любая точка этой плоскости, то
AN2 — BN2 — АР2 — BP2 = k.
Докажем теперь, что на прямой АВ существует и притом толь-
ко одна точка Р, такая, что
AP2 — BP2 = k. (1)
Пусть k>Q (случаи k=0 и &<0 предлагается исследовать чита-
телю самостоятельно). Тогда АР должно быть больше ВР и, зна-
чит, точка Р (если она существует) должна лежать на луче ОВ,
где О — середина отрезка АВ. Для того чтобы для точки, лежащей
на луче ОВ, было выполнено соотношение (1), необходимо и до-
статочно, чтобы было выполнено соотношение
(АР — BP) (AP + BP) = k,
или
АВ • 20Р = k,
или
Таким образом, имеется и притом только одна точка Р, лежа-
щая на луче ОВ, для которой выполняется равенство (1): эта
точка Р отстоит от точки О на расстоянии ——. Из доказанного
следует, что заданное геометрическое место точек есть пло-
скость П, перпендикулярная прямой АВ и проходящая через точ-
ку Р, так как проекция любой точки М, лежащей на плоскости П,
на прямую АВ совпадает с точкой Р и
МА2 — МВ2 = РА2 — РВ2 = k.
31. В пространстве заданы четыре точки А, В, С, D. Найти гео-
метрическое место точек М, для каждой из которых
AM2 + ВМ2 = СМ2 + DM2.
148
Решение.
AM2 + BM2 = 2 • 0±М2 4-
CM2 + DM2 = 2 • 02M2 +
где Oi — середина отрезка AB, a 02 — середина отрезка CD. Ра-
венство (1) будет выполнено тогда и только тогда, когда
2 • ОгМ2 + — = 2 • О2М2 + —,
т 2 а 2
или
п Л 42 Л Л 42 CD2 ~АВЗ
О.М2 — 09М2 ------------.
1 2 4
Отсюда следует, что заданное геометрическое место точек —
это плоскость, перпендикулярная к прямой OiO2, проходящей че-
рез середины отрезков АВ и CD (см. вопрос № 30) и проходящая:
через точку Р прямой О\О2, положение которой относительно то-
чек О] и О2 определено так, как указано в предыдущем вопросе.
32. Доказать, что для того чтобы треугольник был тупоуголь-
ный, необходимо и достаточно, чтобы его ортоцентр (точка пере-
сечения высот) лежал вне описанной окружности.
33. Стороны треугольника связаны соотношением
а2 + Ь2 + с2 = 97?2.
Доказать, что он равносторонний.
34. Доказать, что если А, В, С — углы треугольника, то
1) 8 sin — sin — sin — <1;
2 2 2
_ А В С 3/3
• 2) cos — cos — cos— < —-—;
’ 2 2 2 8
3) sin2 — + sin2 — -|- sin2 — > —.
’ 2 2 2 4
При каком условии имеет место знак равенства?
35. Две равные прямые круговые конические поверхности
имеют общую вершину, но не совпадают. Сколько общих образую-
щих могут иметь эти поверхности?
Ответ. От одной до четырех.
36. Где находится центр тяжести треугольника, сделанного из
однородной провол'оки?
Ответ. В центре окружности, вписанной в треугольник, вер-
шины которого — середины сторон данного.
149>
37. Постройте треугольник по двум сторонам а и b (а>0,
&>0) и углу А (0<Л<л), противолежащему стороне а.
Решение. Строим угол А. На одной из его сторон отклады-
ваем отрезок АС=Ь. Строим окружность с центром С и радиу-
сом а.
Случай I. А — острый угол. Тогда расстояние от точки С до
второй стороны угла А равно b sin А. Поэтому:
Г если а<Ь$\пА, то решений нет;
2° если a=b sin А, то решение одно; соответствующий тре-
угольник АВС прямоугольный, причем ZABC=-^-;
3° если b sin A<a<.b, то решений два: ACBt и ЛСВ2; один из
этих треугольников тупоугольный, другой — остроугольный (по-
чему?) ;
4°, 5° если а^Ь,то решение одно.
Случай II. Пусть Д = -^-.Повторяя предыдущее построение,
заключаем, что:
Г если то решений нет;
2° если а>Ь, то решение одно.
Случай III. -^-<Д<л — угол А тупой.
Повторяя предыдущие рассуждения, заключаем, что:
1° если а-^b, то решений нет;
2° если а>&, то всегда имеется одно решение.
Замечание. Если а>0, 6>0, 0<Д<л и а>Ь, то задача
всегда имеет и притом только одно решение.
38. Доказать, что окружность, проходящая через середины сто-
рон треугольника, касается окружности, вписанной в этот, тре-
угольник.
39. В треугольнике из трех проекций вершин на противолежа-
щие им стороны хотя бы одна лежит на соответствующей стороне
(а не на ее продолжении). Обладает ли аналогичным свойством
любой тетраэдр?
Ответ. Нет. Построить пример такого тетраэдра, для которого
проекции всех его вершин в плоскости противолежащих им граней
все лежат вне этих граней.
40. Доказать, что если высоты тетраэдра ABCD пересекаются
в одной точке, то AB1.CD, AC±BD и ADA.BC.
Обратно, если ABA.CD, AC1.BD и AD1.BC, то высоты тетра-
эдра ABCD пересекаются в одной точке; доказать, что при этом
вместо трех условий АВ ± CD, AC ± BD и AD ± ВС достаточно
потребовать выполнения только двух (любых).
41. Внутри треугольника АВС взяты три окружности, каждая
из которых касается двух сторон треугольника и окружности,
вписанной в этот треугольник. Зная радиусы г2 и г3 этих окруж-
150
ностей, вычислить радиус г окружности, вписанной в треугольник
АВС.
Ответ, г = Vr^ + Vv^+Vr^.
42. Даны два равных отрезка АВ и А'В'. Доказать, что поворо-
том плоскости вокруг некоторой точки можно совместить один
отрезок с другим. Сколько существует таких поворотов? Найти их
центры и углы поворота.
Решение. Существуют, вообще говоря, два поворота, каждый
из которых отрезок АВ переводит в отрезок А'В'. Центр Oi одно-
го из них есть точка пересечения медиатрис отрезков АА’ и ВВ'
(точки А и А' предполагаются различными, точки В и В' также
предполагаются различными. Кроме того, предполагается, что
медиатрисы отрезков АА' и ВВ' пересекаются). При повороте на
угол AOiA' точка А перейдет в точку А', а точка В — в точку В'.
Центр О2 другого поворота находится в точке пересечения ме-
диатрис отрезков ВА' и В'А (точки В и А' предполагаются различ-
ными, точки В' и А предполагаются также различными. Кроме
того, предполагается, что медиатрисы отрезков ВА' и В'А пересе-
каются). При повороте вокруг точки О2 на угол Z.AO2B' точка А
перейдет в точку В', а точка В в точку А'. Рассмотрение частных
случаев предоставляется читателю.
43. Доказать, что если вокруг сферы описан пространственный
четырехугольник ABCD (стороны АВ, ВС, CD, DA четырехуголь-
ника касаются сферы), то точки касания лежат в одной пло-
скости.
44. В треугольнике АВС длины сторон а, Ь, с и площадь S свя-
заны соотношением
S = a2 — (b — с)2.
Найти угол А.
Решение.
be sin А — Ь2 4- с2 — 2bc cos Л — Ь2 + 2Ьс — с2,
1 —cos Л = — sin Л,
4
1 — cos А 1
sin Л 4
А = 2 arc tg —.
45. В треугольнике АВС обозначим через т длину медианы,
выходящей из вершины А, а через а — длину стороны ВС. При
151
каком соотношении между т и а угол А будет острый? Прямой?
Тупой?
Ответ. т>-а-, А — острый угол, т = —, А — прямой, /п<
2 2
а А
< —, Я —тупой.
§ 8. МЕХАНИКО-МАТЕМАТИЧЕСКИЙ ФАКУЛЬТЕТ
ВАРИАНТЫ ПИСЬМЕННЫХ ЭКЗАМЕНОВ
(дневное отделение)
Вариант 1
1. Расстояние между двумя городами А и В пассажирский
поезд проходит на 4 час быстрее товарного. Если бы каждый
поезд шел то время, которое тратит другой поезд на путь от А
до В, то пассажирский поезд прошел бы на 280 км больше, чем
товарный. Если бы скорость каждого поезда была увеличена на
10 км/час, то пассажирский поезд прошел расстояние АВ на
2 час 24 мин быстрее товарного. Найти расстояние между города-
ми А и В.
2. Дана правильная четырехугольная пирамида SABCD с вер-
шиной S. Через точки А, В и середину ребра SC проведена пло-
скость. В каком отношении эта плоскость делит объем пирамиды?
3. Решить неравенство
logjlog2(4* — 6)] < 1.
4. Найти все пары чисел х, у, которые удовлетворяют урав-
нению
з
cos х +cos у—COS (х+ у) = —.
Вариант 2
5. Из города А в город В через равные промежутки времени и
с равной скоростью выезжает 21 автобус, каждый из которых про-
ходит путь АВ за 2 час 40 мин. При этом первый автобус прибы-
вает в город В в тот момент, когда из города А выезжает 21-й авто-
бус. Прибыв в город В, каждый автобус мгновенно поворачивается
и двигается к городу А.
Из города А одновременно с 21-м автобусом выезжает в го-
род В легковая машина, которая через t минут обгоняет 20-й авто-
бус. Найти t и время, за которое легковая машина преодолевает
152
расстояние АВ, если, встретив 1-й автобус, она встречает 2-й авто-
бус через t — 9 мин.
Примечание. Автобусы занумерованы в том порядке, в ка-
ком они выезжают из города А.
6. Дана правильная треугольная призма АВСА'В'С' с боковы-
ми ребрами АА', ВВ' и СС'. На продолжении ребра ВА взята точ-
ка М так, что AL4=AB (МВ=2 АВ). Через точки М, В' и середину
ребра АС проведена плоскость. В каком отношении эта плоскость
делит объем призмы?
7. Решить неравенство
log2 (]/х 4-3 — х — 1) < 0.
8. Найти все пары чисел х, у, которые удовлетворяют урав-
нению
sin2 х -1-J—Y -|- /cos2 х -|-J—У = 12 + — sin у.
sin2 х J \ cos2 х / 2
'Вариант 3
9. Города А и В расположены на берегу реки, причем город В
расположен ниже по течению. В 9 час утра из Л в В отправляется
плот, плывущий относительно берегов со скоростью течения реки.
В этот же момент из В в Л отправляется лодка, которая встре-
чается с плотом через 5 час. Доплыв до города А, лодка мгновенно
повернула обратно и приплыла в город В одновременно с плотом.
Успели ли лодка и плот прибыть в город В к 9 час вечера того же
дня?
10. Дана правильная четырехугольная пирамида SABCD с вер-
шиной S. На продолжении ребра СВ взята точка М так, что
1 3
МВ=— ВС (А1С= — ВС). Через точку Ми середины ребер АВ
и SC проведена плоскость. В каком отношении эта плоскость де-
лит объем пирамиды?
11. Решить неравенство
’ 12. Найти все решения уравнения
sin2x 4- — sin2 Зх = sinx • sin2 Зх.
4
Вариант 4
13. Два автобуса выезжают одновременно навстречу друг дру-
гу из пунктов Л и В и встречаются в 12 час дня. Если скорость
первого автобуса увеличить в два раза, а скорость второго оста-
153
вить прежней, то встреча произойдет на 56 мин раньше. Если же
увеличить в два раза скорость второго автобуса, оставив прежней
скорость первого, то встреча произойдет на 65 мин раньше. Опре-
делить время встречи, если увеличены вдвое скорости обоих авто-
бусов.
1 14. Дана правильная четырехугольная пирамида SABCD
с вершиной S. На продолжении ребра CD взята точка М так, что
DM=2 CD (CM=3CD). Через точки М, В и середину ребра SC
проведена плоскость. В каком отношении эта плоскость делит
Объем пирамиды?
15. Решить неравенство
4«<3-2/;+' + 4,+/‘.
16. Найти все пары чисел а, Ь, для которых всякая пара чисел
х, у (х^^-4-пл, +
где
п = 0, ±1, ± 2,...; т = 0, ±1, ± 2,...),
удовлетворяющая уравнению х+у=а, удовлетворяет также урав-
нению
tgx + tgi/4-tgxtgi/ = d. .
Вариант 5
затратил некоторую сумму денег на покупку
17. Школьник
Портфеля, авторучки и книги. Если бы портфель стоил в 5 раз де-
шевле, авторучка — в 2 раза дешевле, а книга — в 2,5 раза де-
шевле, то та же покупка стоила бы 8 руб. Если бы по сравнению
с первоначальной стоимостью портфель стоил в 2 раза дешевле,
авторучка — в 4 раза дешевле, а книга — в 3 раза дешевле, то за
ту же покупку школьник уплатил бы 12 руб. Сколько стоит покуп-
ка и что дороже: портфель или авторучка?
' 18. Дана правильная треугольная призма АВС А'В'С' с боко-
выми ребрами АА', ВВ' и СС'. На продолжении ребра А'В' взята
точка М так, что В'М=-±-А'В' (А'М=-^-А'В'). Через точку М и
середины ребер А'С' и В'В проведена плоскость. В каком отноше-
нии эта плоскость делит объем призмы?
19. Решить неравенство
log. + ? >0.
х2 4~ 1* — 5 |
20. Сколько решений на отрезке О^х^л имеет уравнение ,
sin х 4- 2 sin 2х = 3 + sin Зх.
154
Вариант 6
21. Города А и В расположены на берегу реки, причем го-
род А расположен ниже по течению. Из этих городов одновре-
менно выходят навстречу друг другу две лодки, которые встре-
чаются посредине между городами А и В. Продолжив свой путь
после встречи в прежних направлениях и достигнув соответственно
городов В и А, лодки мгновенно поворачивают обратно и встре-
чаются вновь на расстоянии 20 км от места первой встречи. Если
бы те же лодки, выйдя одновременно из городов А и В, поплыли
обе против течения, то лодка, вышедшая из А, догнала бы лодку,
вышедшую из В, в 150 км от В. Найти расстояние между города-
ми Л и В.
22. Дан куб ABCDA'B'C'D' с боковыми ребрами АА', ВВ', С С
и DD'. На продолжении ребер АВ, АА', AD отложены соответствен-
но отрезки BP, A'Q, DR длиной 1,5 АВ (AP=AQ=AR = 2,5 АВ).
Через точки Р, Q и R проведена плоскость. В каком отношении
эта плоскость делит объем куба?,
23. Решить неравенство
log* (2х) < ]/Tog*(2x3).
24. Найти все пары чисел х, у, которые удовлетворяют урав-
нению
tg4 х 4- tg4 у+ 2 ctg2x ctg2 у = 3 + sin2 (х 4- у).
Вариант 7
25. У школьника была некоторая сумма денег монетами до-
стоинством в 15 коп. и 20 коп., причем 20-копеечных монет было
больше, чем 15-копеечных. Пятую часть всех денег школьник
истратил, отдав 2 монеты за билет в кино. Половину оставшихся
у него денег он отдал за обед, оплатив его тремя монетами.
Сколько монет каждого достоинства было у школьника вначале?
' 26. В треугольной пирамиде все плоские углы при вершине
прямые. Доказать, что вершина пирамиды, точка пересечения
медиан основания и це’нтр описанного вокруг пирамиды шара ле-
жат на одной прямой.
27. Решить уравнение
— 2-
28. Найти все такие числа р, при которых уравнение
1 4- р sin х = р2 — sin2 х
имеет решение.
3Jc|J°g4U+2)—*°егх _ ।
155
ВАРИАНТЫ ПИСЬМЕННЫХ ЭКЗАМЕНОВ
(вечернее и заочное отделения)
Вариант 1
1. Велосипедист проехал из пункта А в пункт В по пути, состоя-
щему из подъема и спуска, общей длиной 60 км и потратил на
подъем и спуск одинаковое время. Дальше он проехал за 4 час
от пункта В до пункта С по ровной дороге, длина которой на 19 км
больше, чем длина подъема по пути из А в В. С какой скоростью
он ехал на подъеме, если известно, что скорость на спуске больше
скорости на подъеме на 6 км)час, а скорость по ровной дороге
равна среднему арифметическому из скоростей на подъеме и
«пуске.
2. Решить уравнение
sin у + cos Зу = 1 — 2 sin2 у + sin 2у.
3. Основанием четырехугольной пирамиды ОАВСЕ является
прямоугольник АВСЕ, а высота, опущенная из вершины О на осно-
вание, проходит через точку пересечения диагоналей основания.
Плоские углы АОВ и ВОС равны соответственно <р и ф, а высота
пирамиды равна Н. Найти объем пирамиды.
4. Решить неравенство
I 2лг — 11 <J_
№ — х — 2 2
Вариант 2
5. Имеются два куска ткани разных сортов. Первый кусок
стоит 90 руб., а второй— 105 руб. Если бы каждый из кусков был
меньше на 10 м, то первый кусок стоил бы на 10 руб. дороже вто-
рого. Если бы во втором куске ткани было на 5 м меньше, чем в
обоих кусках вместе, то он стоил бы 210 руб. Сколько метров ткани
в каждом куске?
6. Решить уравнение
sin2f— y^cosfe/---— \ = 1.
\ 4 /
7. Основанием четырехугольной пирамиды ОАВСЕ является
ромб, а высота, опущенная из вершины на основание, проходит
через точку пересечения диагоналей основания. Двугранные углы,
прилегающие к ребрам ОА и ОС, равны а, двугранные углы, при-
легающие к ребрам О В и ОЕ, равны р, а высота равна /. Опреде-
лить объем пирамиды.
8. Решить неравенство
(1о&х+б| 2) loga(x2 —х —2) > 1.
156
Вариант 3
9. Машинистка перепечатывала рукопись в течение 4 час,
после чего к ней присоединилась вторая машинистка, и, прорабо-
тав вместе 13~ час, они закончили перепечатку рукописи. Опре-
делить, сколько времени нужно каждой машинистке в отдельности
на перепечатку рукописи, если известно, что первой на перепечатку
половины рукописи надо на 2 час больше, чем второй на перепе-
чатку трети рукописи.
10. Решить уравнение
— 2 + 4 cos2 г = cos г + "/3 sinz.
11. У трехгранного угла О АВС угол между гранями О АВ и
ОВС прямой, а величина каждого из остальных двугранных углов
равна у. Найти величину плоского угла АОС.
12. Решить неравенство
(1 + х)(2 + х) > _ Зд.
х2 — |х| — 2
Вариант 4
13. Два поезда отправляются одновременно из пунктов А и В
навстречу друг другу. Скорость первого поезда на 40 км!час боль-
ше скорости второго. Они встречаются в пункте С, отстоящем на
60 км от середины пути АВ. Если бы первый поезд вышел на
1 час 15 мин позже второго, то они встретились бы в середине
пути АВ. Определить скорости поездов.
14. Решить уравнение
sin3/ • cos/ = ~ tg t. .
15. Высота трехгранной пирамиды О АВС, опущенная на осно-
вание АВС, падает в точку Р, лежащую внутри треугольника АВС.
Найти объем этой пирамиды, если известно, что пирамиды ОАВР,
ОВСР и ОСАР равновелики и что величины отрезков АР, ВР, СР
и ОР равны соответственно a, b, с, d.
16. Решить неравенство
х2 —1
/13—х2
>х—1.
Вариант 5
17. Одна чугунная болванка весит 40 кг, вторая — 50 кг. Погон-
ный метр первой болванки на 1,5 кг тяжелее погонного метра вто-
рой. Если бы вторая болванка была на 6 м длиннее первой, то ее
вес равнялся тем же 40 кг. Какова длина каждой болванки?
157
18. Решить уравнение
1 4- sin 2ф .
——-----— = COS® + sin®.
1 —Sin2<p
19. Основанием четырехугольной пирамиды является ромб, а
высота, опущенная из ее вершины на основание, проходитч через
точку пересечения диагоналей ромба. Боковая поверхность данной
пирамиды равна с. Через одну из сторон основания пирамиды про-
ведена плоскость, отсекающая от противоположной 'боковой грани
треугольник, площадь которого равна а. Найти боковую поверх-
ность пирамиды, которая отсечена от данной пирамиды проведен-
ной плоскостью.
20. Решить неравенство
(х2 —х—I)*-1 < 1.
ЗАДАЧИ НА СОСТАВЛЕНИЕ И РЕШЕНИЕ УРАВНЕНИЙ
Среди задач на составление и решение уравнений, предложен-
ных в этом году на механико-математическом факультете, было
немало таких, где неизвестных больше, чем уравнений. Однако из
полученных систем уравнений можно было определить то, что
требовалось в задаче.
Задачи, предлагавшиеся на дневном отделении, разобраны
ниже; задачи вечернего отделения предлагаются для самостоя-
тельного решения. В конце книги к ним даны ответы. Приступим
к решению задач.
Вариант 1. Пусть Vi км/час — скорость пассажирского поез-
да, о2 км/час — скорость товарного поезда, s км — расстояние-
между городами А и В.
Тогда расстояние АВ пассажирский поезд проходит за-^- час,
а товарный — за-^— час; из условия, что пассажирский поезд про-
о2
ходит это расстояние на 4 час быстрее товарного, получаем
«1 о2
Если бы каждый из поездов шел то время, которое тратит дру-
гой поезд на путь из А в В, то пассажирский поезд прошел бы
км, а товарный —— о2 км. Из условия, что пассажирский
V2 Vl
поезд прошел бы при этом на 280 км больше, чем товарный, имеем
— »! = —-f2 + 280.
О2 1>!
158
Если бы скорость каждого поезда увеличить на 10 км/час, то
пассажирский поезд проходил бы расстояние АВ за
товарный — за •— ------ час. Из условия задачи
о8 +10
а
----7~Г- 400 >
и1 + ю
следует, что
s________s_________2 24
• fli+io “ t»g+10 60 '
Перепишем теперь полученную систему уравнений следующим
образом:
— ol) = 280, Ult>2 s , ч 12 (Vi — IM = (O1+I0)(v2 + I0) V 1 27 5 • (1) (2) (3)
Из этой системы уравнений нам надо найти $. Предварительно
найдем и
Разделив почленно второе уравнение на первое, получим
= 70.
Разделив почленно третье уравнение на первое, получим
_______t/g____________ 3
(«1+10) («2+10) ” Т’
Отсюда
= 70,
о1о2= 1200.
Решив эту систему уравнений, найдем, что th=40, t»2=30.
Теперь, например, из уравнения (1) находим s=480.
(Вариант 2. Пусть скорость автобуса щ км/мин, легковой
машины — и2 км/мин. Из условия задачи следует, что расстоя-
ние АВ равно 160 Vi км и что автобусы выезжают через 8 мин один
за другим. Легковая машина за t мин проходит расстояние t>2 t км>
такое же, какое 20-й автобус преодолевает за Z+8 мин:
tV = M/ + 8). (1)
В момент встречи легковой машины с 1-м автобусом расстоя-
ние между легковой машиной и 2-м автобусом равно 8^ км. Че-
рез t — 9 мин после этого 2-й автобус пройдет (t — 9) о2 км, а.лег-
ковая машина (t — 9) Pi и встретит его, следовательно,
(/-9) ^ + (/-9)^ = 8^. (2)
159
Перепишем систему (1) и (2) так:
tV = M/ + 8), (Г)
v2(/-9) = O1(17-0. (2')
Разделив почленно уравнение (Г) на уравнение (2'), получим
t <+8
t — 9 “ 17—t '
решая которое, найдем ^ = 12 и t%=—3. Итак, /=12 мин.
Выясним теперь, за какое время легковая машина проезжает
расстояние АВ. Так как расстояние АВ равно 160 vlt а скорость i
легковой машины о2, то расстояние АВ легковая машина проез-
жает за «=160 — мин. Зная, что /=12, из уравнения (1) находим
«2 -1
=_t_ _ 12
V2 <4-8 60
12
Поэтому и = 160 • = 96, т. е. легковая машина проезжает рас-
стояние АВ за 1 час 36 мин.
* Вариант 3. Пусть скорость лодки в стоячей воде о км/час,
а скорость реки и км/час, и пусть расстояние АВ равно s км.
За 5 час лодка проплыла расстояние 5 (о—и) км, а плот 5 и км, ,
и так как через 5 час они встретились, то сумма этих двух расстоя-
ний есть расстояние АВ-.
s = 5u-f- 5 (о — и).
На путь из В в А лодка затратила —— час, а на путь из Л в В
v— и J
—-— час; на путь из А в В плот затратил — час. Так как по уело-
v~\-u и j
вию плот и лодка прибыли в В одновременно, то j
5 — s j s
и v — и vи ’
В задаче требуется узнать, успели ли лодка и плот прибыть в го- j
род В к 9 час вечера (того же дня). Другими словами, требуется ;
выяснить, будет ли время, затраченное плотом на путь из Л в В, j
т. е. —, не больше, чем 12 час (так как плот отправился в путь
в 9 час утра).
Итак, из системы уравнений }
5 = бы 4-5 (о — и), (1) |
и V — и v-\-u
160
требуется выяснить, будет ли отношение — меньше или равно 12,
или нет.
Найдем v из уравнения (1), v = и подставим"^- вместо v
в уравнение (2); получим
S s | s
и s s
или ’б'-" — -4-w 5
t ==- 4- t
. s
где t = —.
«
Это уравнение после упрощений приводится к виду
/2 —10/—25 = 0.
Корни этого уравнения действительны и разных знаков. Поло-
жительный корень t—5+1^50. Таким образом, время, затрачен-
ное плотом на путь из А в В, равно 5+]/50 час.
Так как 5+]/50=5+5/2>5+5-1,41 = 12,05, то время, за-
траченное плотом на путь из Л в В, больше 12 час. Значит, при-
быть в город В к 9 час вечера (того же дня) лодка и плот не
успеют.
-’Вариант 4. Пусть скорость первого автобуса t>i км)мин,
а второго »2 км/мин, и пусть расстояние от пункта А до пункта В
равно s км.
Пусть t мин есть время, затраченное автобусами в первый раз
на путь до встречи. В первый раз до встречи первый автобус
проехал Vi t-км, второй v2Ikm, а в сумме они проехали s км-.
s = t»1/+t>2/.. (1)
Во второй раз скорость первого автобуса была 2t»i км/мин,
а второго прежняя, на путь до встречи они затратили / — 56 мин-.
s = 2o1(/ —56) + »а(/ —56). (2)
Наконец, если бы скорость первого автобуса была прежней, а
второго 2 v2 км/минг то время, затраченное ими на путь до встречи,
равно /—.65 мин:
з = о1(/ —65) + 2о8(/-65). (3)
6 Зак. 351 161
Пусть время до встречи в случае, если увеличены вдвое скоро-
сти обоих автобусов, равно х мин-, тогда
s = 2хиг + 2хо2. (4)
Итак, мы получили систему четырех уравнений с пятью неиз-
вестными. Из этой системы нужно найти лишь неизвестные t и х.
Из уравнений (1) и (4) имеем
, s s
t = -------, X т= ----------,
01 + »2 +
следовательно,
t = 2x.
Перепишем уравнения (1) — (3) следующим образом:
s = (i>i + »2)7, (Г)
s = (2px + v2)(/—56), (2')
s = (vx + 2v2) (/—65). (3')
Исключая отсюда I, получим систему двух уравнений:
2oi + ti2 ох + о2
»l + 2O2 01+«2
>
Перепишем эту систему так:
--------------= 56, (4')
(2oi + o2)(t»! + o2)
--------------= 65. (5)
(»1 + 2u2)(0i + v2)
Разделив почленно первое из этих уравнений на второе, получим
(vlJr2v2) _ 56
^2(^1-\-у2) 65
ИЛИ
56f--Y—18~—65 = °-
\ 01 J ог
Это уравнение имеет действительные корни разных знаков. Его
положительный корень
02 _ _5_
0t 4
162
5
Подставляя значение v2 =—vL, например, в уравнение (4), по-
4
лучим
Теперь находим
X = —S = 819и1 - Q1
2(Px-bva) / 5 \
2-2 ( О1 + — t»i I
\ 4 /
Итак, х— 1 час 31 мин, значит, t=3 час 2 мин.
В задаче требуется узнать, когда встретились бы автобусы, если
их скорость увеличить вдвое? Для этого надо от 12 час отнять
(t—х) час. Таким образом, автобусы встретились бы в 10 час
29 мин.
Вариант 5. Пусть портфель стоит х руб., авторучка у руб.,
а книга z руб.
Первое уравнение составляется из условия, что покупка стоит
8 руб.:
2L + _L + _£_ = 8.
5 2 2,5
(1)
Аналогично составляется второе уравнение:
— + — + —=12. (2)
Упрощая уравнения (1) и (2), будем иметь
2х + by + 4z = 80,
6х + 3z/ +4z = 144.
Складывая почленно, получим
х + у + z = 28.
Таким образом, вся покупка стоила 28 рублей. Вычитая по-
членно из второго уравнения системы (3) первое, получим
2х — у = ^2. (4)
Предположим, что х^.у\ тогда уравнение (4) можно перепи-
сать так: х=32-Ь«/—х.
6*
163
В этом случае х^32 (так как, по предположению, у—х>0).
Но если х^32, то такое х не может удовлетворять уравнению (2)
(так как -^-^16, а числа у и г положительны), значит, этот слу-
чай невозможен.
Таким образом, остается лишь случай х>у, т. е. портфель до-
роже авторучки.
Выяснить, что дороже, портфель или авторучка, можно и так: из
2 1
системы (3) находим, что г/= 8-----z, а х = 20-----г; так как
3 3
2 1 1
х = 8-------Z-J-12 4--г — у 12-4-----2 и z> 0, то ясно, чтох>у.
3 3 3
Вариант 6. Пусть скорость реки v км1час, скорость первой
лодки в стоячей воде км/час, скорость второй лодки в стоячей
воде »2 км/час, и пусть расстояние между городами А и В равно
s км. На путь до первой встречи первая лодка затрачивает
----- час, а вторая ---час, откуда получаем первое
2(ох—о)----------------------------н 2(о24-о)-’ } н
уравнение
----?----.= ------. (1)
2(v24-o)--2(0! — v)
На путь до второй встречи первая лодка затрачивает ---------+
1^1 — V
т+20
-|-------час, считая от момента ее выезда из А, а вторая
014-0
4“ “20
s , 2
---------1----------час; отсюда получаем второе уравнение:
О24~О »2—»
Ох — О Oi4~O u2 4“U vS—°
Если бы обе лодки поплыли одновременно из пунктов А и В про-
тив течения, то на путь до встречи первая' лодка затратила бы
—-------час, а вторая-------час; таким образом, получаем третье
Ot — о о2 — о
уравнение:
s-|-150 150
01 — о о2 — о
Перепишем систему уравнений (1), (2) и (3) так:
V. = о. — 2и,
(3)
(Г)
164
s+40 = s —40
«14-0 f2 —° ’
8 = 150-. (3')
v2 — v
Отсюда
s+40 s —40
---!--—---------1 (4)
Ui+ v vY — 3u
s = 150 (5)
Из уравнения (4) находим
s = 20-^=^-. (6)
v
Из уравнений (5) и (6) имеем
20(ot —1>) = 150 2о
v Vi — Зи
ИЛИ
4_Е1--12 = 0.
\ о / о
Это уравнение имеет действительные корни разных знаков;
положительный корень
= 6.
V
Но тогда
s = 20 (ох — о) = 20-5о = 100
О V
Итак, расстояние между городами А и В равно 100 км.
Замечание. В предыдущих задачах число уравнений было
меньше, чем число неизвестных, до нам удавалось найти нужные
неизвестные из этих систем.
Большие трудности у поступающих вызывают задачи, которые
очень похожи на задачи на составление и решение уравнений, но
которые надо решать простым рассуждением, не составляя урав-
нений. Такова, например, следующая задача.
Вариант 7. Пусть у школьника было п монет достоинством
в 15 коп. и k монет достоинством в 20 коп., причем из условия за-
дачи n<k, За билет в кино школьник заплатив не менее 30 коп.
165
(15+15). За обед школьник заплатил в два раза дороже, чем за
билет в кино, т. е. не менее 60 коп., но известно, что за обед школь-
ник отдал 3 монеты, т. е. заплатил не более 60 коп. Отсюда ясно,
что за обед школьник заплатил 60 коп. (20+20 + 20), а за билет
в кино 30 коп. (15+15).
После того как школьник оплатил билет в кино и обед, у него
осталось 60 коп. Эти 60 коп. могут составить 4 монеты достоинст-
вом в 15 коп., или 3 монеты достоинством в 20 коп.
Если бы у него осталось 4 монеты достоинством в 15 коп. каж-
дая, то вначале у него было бы 6 монет достоинством в 15 коп. и
3 монеты достоинством в 20 коп., т. е. что противоречит усло-
вию задачи. Значит, у школьника осталось 3 монеты достоинством
в 20 коп.
Таким образом, у школьника вначале было 2 монеты достоинст-
вом в 15 коп. и 6 монет достоинством в 20 коп.
ГЕОМЕТРИЧЕСКИЕ ЗАДАЧИ
Почти во всех геометрических задачах, предлагавшихся на
дневном отделении механико-математического факультета, прово-
дилась некоторая плоскость сечения данного многогранника (куба,
пирамиды, призмы) и требовалось выяснить, в каком отношении
эта плоскость делит объем многогранника.
При решении подобных задач обычно возникает две трудности:
1. Как достаточно просто построить сечение.
2. Как вычислить объемы частей, на которые делит многогран-
ник плоскость сечения.
Однако в предлагаемых задачах трудности эти существенно
уменьшаются, если при решении задач делать дополнительные по-
строения вне рассматриваемого многогранника.
Как будет ясно из дальнейшего, эти дополнительные построе-
ния позволяют сравнительно просто построить сечение, т. е. найти
все точки пересечения с ребрами многогранника, и они же позво-
ляют вычислить объем одной из частей, на которые плоскость сече-
ния делит многогранник.
Ниже мы приведем решения всех таких задач и (для сравне-
ния) для некоторых из них дадим решения, не связанные с выхо-
дом за пределы рассматриваемого многогранника.
Заметим еще, что решения всех этих задач существенно не
меняются, а ответы остаются теми же, если предположить, что
рассматриваемые многогранники произвольные, а не правильные.
Однако мы приведем решения лишь для правильных много-
гранников, как и требуется в условиях задач.
И последнее, выход за пределы рассматриваемого тела оказы-
вается также полезным и при решении задач на доказательство,
как например, в одной из задач, предлагавшейся на дневном отде-
лении и разобранной ниже. Задачи, предлагавшиеся на вечернем
отделении, оставлены для самостоятельного разбора.
166
Вариант 1
Прежде всего отметим, что так как прямая АВ (рис. 61) парал-
лельна прямой DC, то она параллельна и плоскости боковой гра-
ни DSC. Тогда любая плоскость, проходящая через прямую АВ,
пересекает плоскость боковой грани DSC по прямой, параллель-
ной прямой АВ.
Следовательно, плоскость, проходящая через точки А, В и се-
редину (точку F) ребра SC, пересекает боковую грань DSC по
прямой EF, являющейся средней линией треугольника DSC.
Теперь найдем объем многогранника ABCDEF. Сделаем допол-
нительное построение: продолжим прямую
отрезок FK=EF, затем точку К соединим
прямыми с точками В и С.
Рассмотрим четырехугольник DCKE.
Это параллелограмм, так как в нем про-
тивоположные стороны DC и КЕ равны
и параллельны. А раз четырехугольник
DCKE есть параллелограмм, то в нем
противоположные стороны DE и СК рав-
ны и параллельны.
Аналогично показывается, что четы-
рехугольник АВКЕ есть параллелограмм
и в нем противоположные стороны АЕ и
ВК равны и параллельны.
Так как в основании нашей пирамиды
лежит квадрат, то DA и СВ также равны
EF и отложим на ней
и параллельны.
Итак, мы получили, что в треугольниках ADE и ВС К соответ-
ствующие стороны равны и параллельны, а это означает, что эти
треугольники равны, а их плоскости параллельны. Так как, кроме
того, DC=EK=AB и прямые DC, ЕК и АВ параллельны, то много-
гранник BCKADE есть треугольная призма с основаниями ADE
и ВСК.
Эту призму можно также рассматривать как половину парал-
лелепипеда, у которого в основании лежит квадрат ABCD, а одной
из боковых граней является параллелограмм DCKE. Поэтому
объем призмы CBKDAE равен половине объема этого параллеле-
пипеда, т. е. половине произведения площади квадрата ABCD на
высоту параллелепипеда, например, на высоту FM, опущенную из
точки F. на плоскость ABCD.
Из подобия треугольников OSC и MFC вытекает, что высота
нашего параллелепипеда равна половине высоты пирамиды.
Пусть V — объем пирамиды, Vi — объем призмы CBKDAE,
S — площадь квадрата ABCD, Н — высота пирамиды, тогда
s. А
17— SH iz 2 SH ,, 3 и _
v = - з , v х =------— = —— .откуда получаем, что V1 = — V, т.е.
167
объем призмы CBK.DAE составляет % объема пирамиды SABCD.
Теперь вспомним, что нам надо найти объем не призмы
CBKDAE, а многогранника ABCDEF, который есть разность приз-
мы CBKDAE и пирамиды BCKF. Поэтому для нахождения объе-
ма V3 многогранника ABCDEF надо из объема Vi призмы
CBKDAE вычесть объем V2 пирамиды BCKF.
Найдем объем V2 пирамиды BCKF. Пусть Si—площадь тре-
угольника CKF, ah — длина высоты, опущенной из вершины В
на плоскость треугольника CKF. Тогда
Syh z*\
’'= з
Но легко видеть, что призма CK.BDEA есть половина и такого
параллелепипеда: основание — параллелограмм DCKE, а квадрат
ABCD есть одна из боковых граней. Тогда в этом параллелепипеде
высота есть h, а площадь основания DCKJE — четыре площади
треугольника FK.C, поэтому объем призмы CK.BDEA можно запи-
сать и так:
V 4Sl-h
1 2 '
Отсюда, учитывая равенство (*), получаем
V = —
2 6
Теперь объем V3 многогранника ABCDEF найти легко:
о
3
Но так как Vx = —V, то окончательно получаем, что
4
т. е. объем многогранника ABCDEF составляет s/e объема пирами-
ды SABCD; но тогда объем многогранника SABFE составляет
3/3 объема пирамиды SABCD.
Следовательно, плоскость, проходящая через точки Л, В и се-
редину F ребра SC правильной четырехугольной пирамиды
SABCD, делит объем пирамиды в отношении 3: 5.
Эту задачу можно решить и без выхода за пределы рассматри-
ваемой пирамиды. Как уже показано выше, наша плоскость пере-
сечет плоскость боковой грани DSC по средней линии треуголь-
ника DSC. Для нахождения объема многогранника ABCDEF
проведем плоскость ADF. Тогда многогранник ABCDEF разобьет-
ся на две пирамиды FABCD и ADEF. Найдем теперь объемы этих
двух пирамид.
Так как у пирамиды FABCD высота равна половине высоты,
пирамиды SABCD, а основание то же самое, то объем Vi пирами-
168
ды FABCD равен половине объема V пирамиды SABCD, т. е.
Ki=v2v.
Для нахождения объема пирамиды ADEF проведем плоскость
ЗЛС. Тогда объем У2 пирамиды ADCS равен половине объема V
пирамиды SABCD, т. е. V2=1/2V.
В пирамиде ADCS точку А можно принять за вершину пира-
миды, а треугольник DCS — за основание. В пирамиде ADEF точ-
ка А также может быть принята за вершину, а треугольник DEF—
за основание. Тогда у пирамид ADEF и ADCS равные высоты.
Кроме того, очевидно, что площадь треугольника DEF равна
площади треугольника EFS, а последняя равна 'А площади тре-
угольника DCS. Значит, объем V3 пирамиды ADEF равен
*/4 объема Уг пирамиды ADCS, т. е. Уз= —V2=—V. Теперь объем
4 8
многогранника ABCDEF легко найти:.
К = |/+|/-1|/ + 1у = 1у.
4 13 2 8 8
Итак, объем многогранника ABCDEF равен 5/в объема данной
пирамиды SABCD, поэтому секущая плоскость делит объем дан-
ной пирамиды в отношении 3 : 5.
Ответ: 3:5.
Вариант 2
Пусть длина бокового ребра призмы АВСА\В\СХ (рис. 62) рав-
на Н, длина ребра основания равна а, а площадь основания
Зьавс, тогда объем V призмы ра-
вен: V=H-SbABC.
Пусть точка Е — середина ребра
АС. Точки Е и М лежат в плоскости
грани АВС, поэтому, соединив точ-
ки Е и М прямой, получим, что она
пересекает ребро ВС в точке D.
В треугольнике АВС проведем
среднюю линию ЕМ Получим подоб-
ные треугольники BMD и NED. Из
подобия этих треугольников полу-
чаем, что
BD _ ВМ
ND ~ NE ‘
Так как NE=BN=—, ВМ=2а, ND=BD—BN=BD—— ,то из
2 2
о
этого соотношения находим BD = — а, т. е. точка D делит реб-
ро ВС в отношении 2:1. Соединив точки Вх и М прямой, получим,
169
что она пересекает ребро AAt в точке К, причем ясно, что точка К
будет серединой ребра АА{.
Итак, наша плоскость разбила призму на 2 многогранника, от-
ношение объемов которых надо найти. Найдем сначала объем Vi
многогранника ABDEB\K, ограниченного треугольниками B\BD
и АКЕ, четырехугольниками ABDE, АВВ^К и BiKED. Объем этого
многогранника равен разности объемов двух треугольных пирамид
BtBDM и КАМЕ.
Найдем объем V2 пирамиды BiBDM:
= 4 BBL • 5д в dm •
О j
Площадь треугольника BDM равна половине произведения
основания ВМ на высоту, опущенную из точки D на основание.
Так как точка D делит ребро ВС в отношении 2 : 1, то высота,
опущенная из точки D на основание, равна 2/3 высоты h треуголь-
ника АВС. Поэтому
с 1 о,» 2 л 4 uh 4 q
BDM = — -2а- — Л = — • — == — дд АВС ,
z о о Z о
но тогда
^=4//-4s^bc=4v-
о о У
Так как Аем = 4 ‘ 4 ~ Авс и 4 то
объем Va пирамиды КАЕМ равен
v3=4‘4//-4s^bc=^v-
о Л Л
13
Тогда Vj,=V2— V3=-------V, т. е. плоскость делит объем призмы
36
в отношении 13: 23.
Найти объем 1Л многогранника ABDEBiK без выхода за пре-
делы призмы ЛВСД1В1С] можно, но это вычисление не будет ко-
роче. Убедимся в этом. *
* Проведя плоскость через точки A, Bt и Е, получим, что наш
многогранник разбился на 2 пирамиды: четырехугольную пирами-
ду ByABDE (Bi — вершина, четырехугольник ABDE — основание)
и треугольную пирамиду ЕАКВ\ (Е — вершина, треугольник
AKBi — основание).
Найдем объемы этих пирамид. У четырехугольной пирамиды
BXABDE высота есть ребро ВуВ, значит, высота равна Н.
Теперь найдем площадь четырехугольника ABDE. Она равна
площади треугольника АВС без площади треугольника EDC. Най-
дем площадь треугольника EDC. Так как точка D делит отре-
170
зок ВС в отношении 2:1, то высота, проведенная из точки D на
основание ЕС, равна */з высоты треугольника АВС.
Так как основание ЕС = 1/2АС, то площадь треугольника EDC
равна */б площади треугольника АВС. Значит, площадь четырех-
угольника ABDE равна 5/б площади треугольника АВС. Поэтому
объем V2 четырехугольной пирамиды BiABDE равен
у2=4-я.4$длвс=^-к,
оо 18
где V=H-S^abc есть объем призмы ABCA\BiCi. Нашу призму
ABCAiBiC\ можно рассматривать как половину параллелепипеда,
у которого основание — грань АВВ1А1, а боковая грань — четы-
рехугольник ACCtAi. Но тогда объем V призмы ABCAtB^i мож-
но посчитать и так: V=4zh-S abb,a,, где h — высота, опущенная
из точки С на грань АВВ1А\, причем ясно, что h — высота тре-
угольника АС В.
Теперь легко найти объем У3 треугольной пирамиды EAKBt.
Для этого надо найти площадь треугольника Л КВ] и высоту, опу-
щенйую из точки Е на грань ABBtAi. Очевидно, что так как точ-
ка В — середина ребра АС, то и высота, опущенная из точки Е на
грань ЛВВ1Л], равна половине высоты, опущенной из точки С на
грань ABBiAit т. е. равна h!2.
Так как К есть середина отрезка AAi (рис. 62), то площадь
треугольника AKBt равна половине площади треугольника АА1В1,
т. е. равна 1/4SxbbMi-
Значит,
Теперь объем У] многогранника ABDEBtK равен
у =у + УЭ = — V +—У = —У.
1 213 18 12 36
Следовательно, объем многогранника AiBtCiDCEK равен
— У, и плоскость делит объем призмы ЛВСЛ1В1С1 в отношении
36
13:23.
Ответ: 13:23.
Вариант 3
Пусть точка К есть середина ребра АВ (рис. 63). Плоскость
сечения пересекает плоскость ABCD по прямой КМ, которая пере-
секает ребро AD в точке F и продолжение реб))а CD в точке Е.
Легко показать, что точка F есть середина ребра AD и точка Е от-
стоит от точки D на '/2 DC, т. е.
ED = — DC (ЕС = — DC\
2 \ 2 J
171
Пусть точка W — середина ребра CS. Точки N и М лежат в пло-
скости грани SBC, поэтому прямая ММ пересекает ребро BS в не-
которой точке L.
Выясним теперь, в каком отношении точка L делит ребро BS.
Для этого проведем в треугольнике CSB среднюю линию NQ.
Тогда получим, что треугольники NQL и LBM равны, так как у них
BAf=ATQ = </2 СВ, ZLBM= ZNQL и Z.BML = Z.QNL, как накрест
лежащие углы при параллельных прямых WQ и СМ. Но из равен-
ства этих треугольников вытекает, что
BL = QL, откуда получаем: точка L делит
ребро SB в отношении 3:1.
Так как точки Е и N лежат в плоско-
сти грани SDC, то соединив эти точки,
получим, что прямая ЕМ пересечет ребро
SD в некоторой точке Р. Как легко пока-
зать, точка Р делит ребро SD также в от-
ношении 3:1.
Итак, мы построили сечение. Оказа-
лось, что плоскость сечения пересекает
пирамиду по пятиугольнику LK.FPN. Эта
плоскость делит пирамиду SABCD на два
многогранника, причем таких, что вычи-
слить их объемы сразу не представляется
возможным. Для того чтобы вычислить
объем хотя бы одного из этих многогран-
ников, нужно сделать дополнительные по-
строения и рассмотреть несколько пирамид.
Однако если внимательно посмотреть на чертеж (см. рис. 63),
то можно убедиться, что объем многогранника CDFKBLNP, огра-
ниченного треугольниками DFP и K.LB, четырехугольниками CNLB
и CNPD, пятиугольниками PFK.LM и DFKBC, равен объему тре-
угольной пирамиды NECM без объема двух треугольных пирамид
LKBM и PEDF. Вычислим теперь объемы этих пирамид.
Пусть высота нашей пирамиды SABCD равна Н, а ребро осно-
с^Н
вания равно а, тогда объем пирамиды SABCD равен: V=----. Так
о
как точка М есть середина ребра CS, то легко показать, что пер-
пендикуляр, опущенный из этой точки на плоскость ABCD, равен
половине перпендикуляра, опущенного из точки S на плоскость
ABCD, т. е. этот перпендикуляр равен Н/2. Столь же легко пока-
зать, что перпендикуляры, опущенные из точек L и Р на плоскость
ABCD, равны ~t
g
Площадь треугольника ЕСМ равна —а2. Площадь каждого из
8
треугольников DEF и ВМК равна . Теперь объем пирамиды NECM
8
172
1 ti 9 9
равен — - . — a2 = a объем каждой из пирамид PEFD и
LK.BM равен — . — . Поэтому объем V, нашего много-
3 4 8 32 J 1
гранника равен
Значит, наша плоскость делит объем пирамиды в отношении 1:1.
В этой задаче вычисление объема многогранника CDFK.BLNP
без выхода за пределы пирамиды и длиннее и, главное, менее гео-
метрически нагляднее, чем разобранное выше решение. Однако
приведем его.
Проведя плоскости через точки N, К, В и N, D, F, получим, что
многогранник CDFK.BLNP разбился на три пирамиды: пятиуголь-
ную пирамиду ND F КВ С (N — вершина, пятиугольник KBCDF—
основание), треугольную пирамиду NKBL (N — вершина, тре-
угольник KBL — основание) и треугольную пирамиду NPDF
(N — вершина, треугольник PDF — основание). Вычислим объемы
этих пирамид.
Так как точка N делит ребро CS пополам, то длина высоты,
опущенной из точки N на плоскость ABCD, равна половине высо-
ты, опущенной из точки S на ту же плоскость, т. е. равна Я/2.
Площадь пятиугольника KBCDF равна площади квадрата
ABCD без площади треугольника AKF:
Skbcdf -------а2.
Л Q О
Поэтому объем Vi пирамиды NKBCDF равен
• — а-
у,--'-.”..7-*- 7 v,
1 3 2 8 16
где V — объем пирамиды SABCD.
Заметим, что объем V пирамиды SABCD равен двум объемам
пирамиды SABC. Будем считать, что у пирамиды SABC точка С—
вершина, а треугольник ABS — основание. Пусть высота, опущен-
ная из точки С на грань ABS, равна Hi, а площадь треугольника
ЛВЗ равна S^ABs, тогда
L = ±Hi.S^abs, т. е. У =
Z о о
Так как точка N — середина ребра CS, то перпендикуляр, опу-
щенный из этой точки на плоскость ЛВЗ, равен -у- Hi.
173
Так как КВ' — — АВ, a BL = — BS, то
2 4
Зд KBL = у КВ-BL-sin KBL =
= -L.-L АВ-±В8-sin ^KBL = -±SaABS.
2 2 4 о
Поэтому объем У2 пирамиды NRBL равен
= Т V • Т5д4BS -‘IT • (тя‘5дЛВ5; - у-
Совершенно аналогичные рассуждения позволяют найти объем
Уз треугольной пирамиды NPDF:
Теперь объем У4 многогранника KBCDFPNL уже легко счи-
тается:
v. =v, + К +к = —У + —V + —V = —и,
4 1-Г 2 Г Л 16 32 32 2
т. е. плоскость сечения делит объем пирамиды пополам.
Ответ: 1:1.
Вариант 4
Точки М и В лежат в плоскости грани ABCD (рис. 64). Соеди-
нив их прямой, получим, что она пересекает ребро AD в точке К.
Рассматривая подобные треугольники МВС и MKD, получаем, что
/СР Л4Р ь'гч D/-* iz Л Pi
= уу откуда KD=—BC, т. е. точка К делит отрезок Аи
в отношении 1 :2. Пусть точка Е — середина ребра SC. Точки М
и Е лежат в плоскости грани SDC, поэтому, соединив эти точки
прямой, получим, что она пересечет ребро SD в точке Р. Пусть
точка О — середина ребра DC; соединив точки £ и О прямой, по-
лучим, что ОЕ есть средняя линия треугольника SDC, т. е. ОЕ=
= '/2DS.
Рассматривая подобные треугольники MPD и МЕО, получаем, что
"os' = ~мо ’ отКУда — уО£ = у DS, значит, точка Р делит
ребро SD в отношении 3:2.
Итак, плоскость сечения разделила пирамиду SABCD на два
многогранника. Один из них — многогранник BECKPD — ограни-
чен треугольниками ВЕС и KPD и четырехугольниками KDCB,
КВЕР и PDCE. Найдем его объем.
174
Этот многогранник равен разности двух треугольных пирамид
ЕМСВ и PMDK.. Поэтому найдем их объемы.
Для нахождения объема V] пирамиды ЕМСВ надо найти пло-
щадь основания — треугольника МВС и длину высоты, опущенной
из точки Е на основание, -г- на плоскость ABCD. Так как Е — сере-
дина ребра SC, то перпендикуляр, опущенный из этой точки, ра-
вен половине перпендикуляра Н, опущенного из точки 5 на плос-
кость ABCD, т, е. равен ///2.
Если ребро основания призмы равно а, то площадь прямо-
угольного треугольника МВС равна
5лМВс = -±-ВС-МС = -^а\
Поэтому
V1== -L.JL . А а2 = —V,
1 3 2 2 4
где V «*= есть объем пирамиды SABCD.
3
Теперь найдем объем пирамиды PMDK. Так как точка Р делит
ребро SD в отношении 3:2, то перпендикуляр, опущенный из этой
точки на основание — на плоскость ABCD,—равен 2Д перпендику-
ляра, опущенного из точки S на плоскость ABCD, т. е. равен 2/s Н.
Найдем площадь треугольника MDK
S^MDK = ^DKMD = -^a\
2 <3
Теперь объем V2 пирамиды PMKD легко находится:
V2 = — . Ан- — a2 = —V.
2 3 5 3 15
175
Итак, объем У3 многогранника BECKPD найден:
Va = = — V— -V V = — V.
8 1 2 4 15 60
31
Но тогда объем второго многогранника равен —V. Поэтому
г 60
плоскость сечения делит объем пирамиды в отношении 29:31.
Объем многогранника BECKPD может быть найден и без вы-
хода за пределы пирамиды SABCD. Для этого проведем плоскость
EKD. Тогда многогранник разобьется на две пирамиды: четырех-
угольную EDCBK и треугольную KDPE. Найдем их объемы.
Площадь четырехугольника—трапеции DKBC— равна:
Z о
Высота, опущенная из точки Е на плоскость ABCD, уже найдена
н *
и равна —. Поэтому объем Vi пирамиды EDCBK равен
V\ = —. — • — а2 = — V.
1 3 2 6 12
Пусть в пирамиде KDPE точка К — вершина, а треугольник
DPE — основание. Пусть в треугольнике DSC длина стороны DS
равна Ь, а длина высоты, опущенной из точки С на сторону DS,
равна h, тогда 5Д dsc ~ -у hb.
Так как точка Е — середина ребра SC, то перпендикуляр, опу-
щенный из точки Е на ребро DS равен половине перпендикуляра,
опущенного из точки С на ребро DS, т. е. равен h/2.
2 2
Так как, кроме того, DP = — DS = — Ь, то
5 5
5д DPE = "у DP’ ~~ = SaDSC-
Z Z О Z О
Точка К делит ребро AD в отношении 1 :2, поэтому перпен-
дикуляр, опущенный из точки К на плоскость SDC, равен 2/3 пер-
пендикуляра Hi, опущенного из точки А на плоскость SDC, т. е.
равен 2/3 Hi.
Поэтому объем V2 пирамиды KPDE равен
= Т • Ts^sc ='4 (тя1-5^с).
О О О 10 \ О /
Заметим, что объем V пирамиды SABCD равен двум объемам
пирамиды SACD. Кроме того, пирамиду 5ЛС£> можно рассматри-
176
вать и так: точка А — вершина, а треугольник SDC — основание,
тогда объем этой пирамиды равен:
-L^-Lh.-S^sdc, т. е. V-^-H^sdc.
2 «5 о
Поэтому V2=,/i5 V- Теперь объем Уз многогранника BCEKDP лег-
ко подсчитывается
V3 = V, + V = — V 4- -1-F = — V.
3 2 12 15 60
Значит, наша плоскость сечения делит объем пирамиды в отно-
шении 29: 31.
Ответ: 29:31.
Вариант 5
пересекает ребро
Пусть точка Е — середина ребра A{Ci (рис. 65). Так как точ-
ки Е и М лежат в плоскости грани AJitCi, то соединив эти точки
прямой, получим, что она пересечет ребро CiBi в точке К- Проведя
среднюю линию EQ треугольника AtBiCt, получим равные тре-
угольники EQK и КВ\М.
Из равенства этих треугольников вытекает, что KBi = QK, т. е.
что BiK=4i CtBi. Значит, плоскость сечения
CiB] в точке К, делящей это ребро в от-
ношении 3:1.
Пусть далее точка D есть середина
ребра ВВЬ Так как точки М и D лежат в
плоскости грани ABB^Ai, то, проведя
прямую MD, получим, что она пересечет
ребро АВ в точке N и продолжение ребра
AiA в точке L. Причем легко показать,
что точка ДО есть середина ребра АВ, а
точка L отстоит от точки А на половину
ребра ЛДь т. е. AL = ll2AAi и LA} =
Так как точки L и Е лежат в плоско-
сти грани ACCiAt, то соединив точки L
и Е прямой, получим, что она пересекает
ребро АС в точке F. Из подобия тре-
угольников LAF и LA[E вытекает, что
AF = — A,E= —(—AjCA = — АС..
з 1 з V 2 1 1 6 1
Значит, точка F делит ребро АС в отношении 1 :5. Итак, мы
нашли все точки пересечения плоскости сечения с ребрами призмы.
Сечение построено; оно разбило призму на два многогранника,
отношение объемов которых нам надо найти. Найдем объем
177
многогранника, ограниченного треугольниками AFN и KB\D, четы-
рехугольниками AAiEF и А\ЕКВ\, пятиугольниками AA\B\DN и
NFEKD.
Заметим, что объем этого многогранника можно получить так:
из объема треугольной пирамиды LA\EM отнять объем двух тре-
угольных пирамид LAFN и DKB\M.
Найдем теперь объемы всех этих трех пирамид. Пусть боковые
ребра призмы AAl=BBi — CCl = H, а площадь основания — тре-
угольника АВС—равна S; тогда объем призмы равен V—H'S.
Найдем объем Va пирамиды LAiEM. Так как прямая LAt пер-
пендикулярна по условию задачи плоскости AiEM, то LAt есть вы-
сота пирамиды LAiEM и М1 = 3/г Я.
Как следует из рис. 65, площадь треугольника Л^М равна
площади трапеции AiBiQE, т. е. равна 3/4 Здл^с, = 3А $•
Поэтому
о о
Далее, так как AF=4e АС, то высота треугольника AFN равна
1/в высоты треугольника АСВ, откуда, учитывая, что AN=l/3 АВ,
получаем:
S&AFN ~ S& АВС — -TT-S.
Так. как AL перпендикулярно плоскости AFN и так как AL =
= --ЛЛ4 = — Н,
2 1 2
то получаем, что объем У3 пирамиды LAFN
равен
1 я
3 2
V3 = ЛЛ-Зд AFN
О
—s = — V.
12 72
Наконец, так как точка D есть середина ребра ВВ} и прямая
ByD перпендикулярна плоскости KBiM, то высота пирамиды
DBiKM равна B\D = lla Н. Площадь треугольника В\МК равна
’/в 5дл1в1с1> т. е. S дв,мк =1/в S. Поэтому объем У4 пирамиды
DB\KM равен
V4 = ^-B,D. Зд BlUK = A-V.
о о z о До
Теперь найдем объем Vi нашего многогранника:
о / Z
— у = . -49 .. у
48 144
Значит, наша плоскость делит объем призмы ABCAiBtCi в отно-
шении 49 :95.
178
• Для нахождения объема многогранника AAiEKBiDNF без вы-
хода за пределы призмы ABCAiB^i проведем две плоскости: пер-
вую через точки D, Л1 и Е, вторую через точки D, А и F. Тогда наш
многогранник разобьется на три пирамиды: четырехугольную пи-
рамиду DAiEKBi (D — вершина, четырехугольник A^EKBi — осно-
вание), четырехугольную пирамиду DAA\EF (£> —вершина, четы-
рехугольник AA\EF — основание) и треугольную пирамиду DAFN
(D — вершина, треугольник AFN— основание). Найдем объемы
этих пирамид.
Так как точка D есть середина ребра BBi и ребро призмы пер-
пендикулярно плоскостям основания, то высоты пирамид DAFN и
DAxEKJBx равны Я/2.
Так как S/A л/w = S, то объем пирамиды DAFN:
1 3 2 12 72
Площадь четырехугольника AiEKBt равна площади треуголь-
ника без площади треугольника ЕС\К. Так как ECt = l/2
и Ci/<=3/4 CiBlt то площадь треугольника ЕС^Кг.
Sa EctK ;= 4- Е(\К, = SA л.ва-
2 о
Теперь
5
= Sд AiBtCt — 5д ECtK = ,
о
поэтому объем пирамиды DAiEKBi:
У2 = — . — . — S = — V.
2 3 2 8 48
Заметим теперь, что объем призмы ABCAiBiCt равен половине
объема параллелепипеда, у которого основание — грань АСС1А1, а
боковая грань — четырехугольник АВВ^, поэтому
У = 4--Л-5лсс.Лх»
где h — высота, опущенная из точки В на плоскость ACCiAi. Вы-
сота пирамиды DAAjEF, опущенная из точки D на плоскость
ACCxAi, равна h. Теперь найдем площадь четырехугольника
AAiEF. Четырехугольник AAtEF есть трапеция, поэтому
S^-^^.ЛЛ,.
179
И так как АгЕ =т^-.А1С1, a AF = ~ Afi^ то
А1С} 4~ -у- А&
SaaiEf. =---------------ААг = — 5лсс,л1 •
Л о
Теперь объем пирамиды DAA\EF равен
v3 = ±ab-sAAiEP = ^v,
о 9
и наконец, объем многогранника AAxEK.BiDNF
v. = v x + v 2 + vs = — v + — v +—v = —v.
4 1 2 72 48 9 144
Значит, наша плоскость делит объем призмы ABCA&Ct в от-
ношении 49:95.
Ответ: 49 :95.
Вариант 6
Прежде всего найдем точки пересечения плоскости сечения с
ребрами куба (рис. 66).
В плоскости грани AAiDtD лежат точки Q и Р. Соединив их
прямой, получим, что она пересечет продолжение ребра Л17)1 в
точке Е. Сравнивая подобные
треугольники EQAi и
получаем, что длина отрезка
AiE равна 3/2 AD. В плоскости
грани AA\BiB лежат точки Q и
Р. Соединив их прямой, полу-
чим, что она пересечет продол-
жение ребра в точке F.
Причем аналогично предыду-
щему Л1/?=3/2 АВ. Точки Р и R
лежат в плоскости грани
ABCD. Соединив их прямой, по-
лучим, что она пересечет про-
должение ребра DC в точке L.
Причем аналогично предыду-
щему DL—z/2 DC.
Точки Е и F лежат в плос-
кости грани AiBiCiDi. Соеди-
нив их прямой, получим, что
она пересечет ребра CiDj и
B{Ci в точках М и М Рассмат-
ривая треугольники MD^E,
180
FBtN1 и CiMN, приходим к выводу, что точки М и N есть середины
ребер CiD1 и BiCi.
Точки М и L лежат в плоскости грани CDD\Ci. Соединив их
прямой, получим, что она пересечет ребро CCi в точке К. Сравни-
вая треугольники С^МК и KCL, убеждаемся в том, что точка К
есть середина ребра CCi.
Итак, мы нашли сечение — это треугольник KMN, где точки
К, М и N1 есть середины ребер ССЬ CiDi и BiCb
Наша плоскость сечения отсекла от куба треугольную пирами-
ду C\KMN. Так как у этой пирамиды все плоские углы при верши-
не Ci прямые, то объем этой пирамиды равен
V, = —C,M-C1KC1N= — V,
1 6 1 1 48
где V — объем куба. Значит, наша плоскость делит объем куба в
отношении 1 :47.
Ответ: 1:47.
Вариант 7
Пусть у пирамиды ABCD (рис. 67) все плоские углы при вер-
шине А прямые Z ВАС = Z BAD = ZCAD=90°.
Пусть точка О есть центр описанного около пирамиды шара.
Тогда она является точкой пересечения всех плоскостей, проведен-
ных через середины ребер пирамиды
перпендикулярно этим ребрам. В
частности, отсюда следует, что пря-
мые, соединяющие точку О с середи-
нами ребер АВ, АС и AD, перпенди-
кулярны соответствующим ребрам
АВ, АС и AD.
Соединим точку О с вершиной А.
Нам надо доказать, что эта прямая
пересекает плоскость треугольника
BCD в точке пересечения медиан
этого треугольника. Для доказатель-
ства этого факта надо сделать до-
.полнительные построения. Как было
уже показано выше, очень часто ре-
шение той или иной задачи упрощается, если дополнительные по-
строения проводить вне тела, рассматриваемого в задаче. Поступим
так же и в этой задаче.
На диагонали АО отложим отрезок 0М=А0(АМ=2А0). Через
точку М проведем плоскость, перпендикулярную ребру АВ. Эта
плоскость пересечет ребро АВ в точке К., причем прямая МК будет
перпендикулярна ребру АВ. Пусть точка Е — середина отрезка
АВ, тогда, как уже было отмечено выше, прямая ОЕ также пер-
пендикулярна ребру АВ. Мы получили, что треугольники АОЕ и
181
АМК прямоугольные и имеют один общий угол, поэтому они по-
добны. Но из подобия следует, что А/(=2АЕ, т. е. АК=АВ. А это
означает, что точки К и В совпали.
Итак, плоскость, проходящая через точку М перпендикулярно
ребру АВ, пересекает ребро АВ в точке В. Аналогично показывает-
ся, что плоскости, проходящие через точку М перпендикулярно
ребрам АС и АО, пересекают эти ребра в точках С и О.
Но тогда при пересечении этих трех плоскостей с плоскостями
ABC, ABD и ACD боковых граней нашей пирамиды образуется
прямоугольный параллелепипед ABA\CDBXMCX с диагональю AM.
ч Теперь надо выяснить: в какой точке диагональ AM паралле-
лепипеда пересекает плоскость треугольника BCD?
Диагональ AM лежит в плоскости ADMAi. Эта плоскость пере-
секает отрезок ВС в его середине (диагонали параллелограмма
ACAiB, пересекаясь, делятся пополам). Поэтому плоскость ADMAi
пересекает плоскость BCD по прямой, соединяющей точку D с се-
рединой отрезка ВС, т. е. по медиане треугольника BCD. Значит,
точка пересечения диагонали AM с плоскостью треугольника BCD
лежит на одной медиане этого треугольника.
Аналогично доказывается, что точка пересечения диагонали AM
с плоскостью треугольника BCD лежит и на другой медиане этого
треугольника. Таким образом, доказано, что точка пересечения
диагонали AM с плоскостью треугольника BCD лежит на пересе-
чении медиан этого треугольника.
Значит, доказано, что в нашей пирамиде — вершина, точка пе-
ресечения медиан треугольника и центр описанного вокруг пира-
миды шара лежат на одной прямой. А это и требовалось доказать
в условии задачи.
Решение неравенств
Почти во всех вариантах письменных работ как на дневном,
так и на вечернем отделениях механико-математического факуль-
тета предлагалось решить неравенства.
Для решения этих неравенств надо хорошо знать свойства
логарифмической и показательной функции, отчетливо понимать
определение абсолютной величины действительного числа и пр.
Ниже мы разберем решение всех неравенств, предлагавшихся
на дневном отделении, оставив читателю неравенства, предлагав-
шиеся на вечернем отделении, для самостоятельного решения.
Напомним читателю, что областью определения функции у —
~f(x) называется множество всех тех значений х, каждому из
которых поставлено в соответствие число у.
1. Решить неравенство
logjlog2(4*-6)]<l.
182
Областью определения функции
у= log^logj^ — 6)]
являются все значения х, являющиеся решением системы нера-
венств:.
х>0, х=£1, log2(4* —6) > О, 4х — 6>0,
или
х>0, х=#1, 4х — 6>1.
Но система неравенств
0<х<1, 4*>7
несовместна. Значит, областью определения функции у является
множество всех чисел х, таких, что
x>log47.
Считая x>log47 и замечая, что log47>l, заключаем: данное
неравенство эквивалентно следующему неравенству:
log2(4* — 6)<х,
или
4х — 6 <2*,
Решая же неравенство
4х — 6 < 2х,
или
22* — 2х — 6<0,
ИЛИ , '
(2*4-2) (2х — 3)<0,
получим
x<log23,
и так как log47 = log2 ]/7 < log2.3, то решениями данного неравен-
ства будут все х из промежутка
log47<x<log23.
183
2. Решить неравенство
log2(]/x4-3 —х—1)<0.
Данное неравенство будет справедливо тогда и только тогда,
когда будут выполнены неравенства
х + 3>0, (1)
Ух 4-3 — х— 1>0, (2)
Ух4-3 — х— 1 < 1., (3)
Неравенство
']/' х 4- 3 х -J-1
выполняется, если —3^х<—1, так как при этих значениях х ле-
вая часть — неотрицательна, а правая — отрицательна. Если же
считать Х2>—1, то неравенство
/x-f- 3>х+ 1
эквивалентно неравенству
х + 3>х2 + 2х+ 1,
или
х2 + х — 2<0,
откуда
— 2<х<1,
т. е. в рассматриваемом случае решения неравенства (2)
— 1 <х< 1.
Итак, все решения неравенства (2):
— 3<х< 1.
Решим неравенство (3):
]/7+3<х + 2. (3')
Среди значений х, таких, что х^'—2, оно решений не имеет.
Считая х>—2 (и учитывая, что тогда х+3>0), заключаем, что
неравенство (3') эквивалентно неравенству
х Ц- 3 < х2 + 4х +4,
184
или
хг + Зх 4-1 > О,
откуда
х>
/5 —3
2
Все решения исходного неравенства — это все решения систе-
мы (1), (2), (3), т. е.
<х< 1.
3. Решить неравенство
logx,^z5_>_L
ё |х —2| 2
Областью определения функции
у = log*»
4х — 5
|х-2|
является множество всех решений системы неравенств:
х25^0, х2 #: 1, 4х — 5>0, х=#2,
т. е.
х>—, х^2.
4
5
Ноеслих>—и х =Ь 2, то во всяком случае х2 >• 1, и данное
4
неравенство эквивалентно неравенству
|х-2|
или
4х — 5>х|х — 2|.
Рассмотрим два случая:
(1)
х<2 и х>2.
185
5
Г. — <х<2. Тогда неравенство (1) эквивалентно следую-
4
тему:
4х — 5 > — х2 4- 2х,
или
х2 4- 2х — 5 > О,
или
[х_(_1_/б)] [х-(/б — 1)] > О,
или (так как х — (— 1 — p/6) = x-|-14“V/6 >0)
1.
Поскольку УТГ— 1>-^-,то решение исходного неравенства
/(Г—1<х<2.
2°. х>2. Тогда неравенство (1) эквивалентно следующему:
4х — 5 > х2— 2х»
или
х2 — 6х 4- 5 < О,
или
Значит, решение исходного неравенства
2<х< 5.
Итак, все решения исходного неравенства:
/б’-1<х<2, 2<х<5.
186
4; Решить неравенство
4'<3-2/г-2х + 4-4гг.
Ясно, что решениями этого неравенства могут быть только не-
отрицательные числа. Разделив обе части неравенства на 4^*,
получим неравенство
4-1’Л*’+*<3-2* ~ ^х +4,
равносильное данному, поскольку 4“>0 для всех х.
Полагая у — 2х ~ уГх , получаем неравенство
z/2-3r/-4<0.
Всеми решениями этого неравенства относительно у будут все у
из сегмента
-!<//< 4.
Значит, всеми решениями исходного неравенства будут все х,
удовлетворяющие неравенствам
— 1<2х-/7<4.
Но неравенство —^х выполняется для всех х^О, по-
этому решением исходного неравенства будут все х^О, удовле-
творяющие неравенству
2х -^<4.
Последнее неравенство равносильно следующему:
х — ’|/х‘-С2,
или
(/х + 1)(/Г-2)<0.
Так как х^О, то 1/х+1 >0, и значит, ]/х<2, т. е. х^4.
Итак, всеми решениями данного неравенства будут все х из сег-
мента 0^х<4.
5. Решить неравенство
I*2 —4х|-рЗ > 0
Х* + \Х — 5|
Совершенно очевидно, что для любого действительного х под
знаком логарифма стоит положительное число. На основании
свойств логарифмов с основанием, большим единицы, это нера-
венство равносильно следующему:
|^ — 4а-| + 3 > j
х2 | х — 5 |
187
Так как х24-|х—5| >0 для всех действительных значений х, то
это неравенство эквивалентно такому:
Гх||х~4| + 3>х2 + |х — 5|. (1)
Так как выражения х, х—4 и х—5, находящиеся под знаком
модуля, обращаются в нуль соответственно при х=0, х=4 и х=5,
то естественно исследовать неравенство (1) на промежутках
х<0, 0,<х<4 4<<х<5, х>5.
1°. х^О. Тогда неравенство (1) можно переписать так:
— х(4 — х) Ц- 3 > х2 — (х — 5).
Упростив это неравенство, получим х<-----—.
Так как все эти х удовлетворяют условию х^О, то все они яв-
ляются решениями данного неравенства.
2°. 0<х^4. Неравенство (1) в этом случае эквивалентно та-
кому:
х(4 — х) + 3 >х2 — (х — 5),
или
2х2 —5х + 2<0.
Всеми решениями этого неравенства будут все значения х из
сегмента —-Сх-С2. Так как все эти х удовлетворяют условию
0<х^4, то все они будут решениями исходного неравенства.
3°. 4<х^б. Неравенство (1) перепишется так:
х(х—4) +3<?х2—(х—5), или х<— —.
3
Так как все эти х не удовлетворяют условию 4<х^5, то в полу-
интервале 4<х^?5 нет решений исходного неравенства.
4°. х>5. Неравенство (1) примет вид х(х—4)+3^х2+х—5,
. 8
или х<-----.
5
Так как все эти х не удовлетворяют условию х>5, то в про-
межутке х>5 исходное неравенство не имеет решений.
Итак, все решения данного неравенства будут все х^?---и
3
все х из сегмента — <х<2.
2
6. Решить неравенство
log, (2х)< V \ogJ2^j~.
188
Область Di определения функции logx(2x) такова:
х^>0, х#=1.
Область £>2 определения функции ]/logz(2x3) находится из систе-
мы неравенств
х>0, х =# 1,1
logx(2x3) > 0. J
(1)
Если 0<х<1, то неравенство logx(2x3) ^0 эквивалентно 0<
<2х3^'1, т. е. в итоге 0<х<—^.Если же х>1, то неравенство
logx(2x3) ^0 эквивалентно 2х3^>1, т. е. х > —, что выполняется,
|/2
если х> 1.
Итак, множество всех решений системы (1), т. е. область Dz
определения функции yrlogz(2x3) , состоит из двух промежутков:
0 < х < —J—, х> 1.
у*
Множество всех значений из области D2 определения функции
V logx(2x3j входит в область D\ (х>0, х#=1) определения функ-
ции Togx(2x). Таким образом, все решения данного неравенства
входят в область £>2- Ясно, что все х из £>2, для которых
logx(2x)^0, являются решениями исходного неравенства.
Неравенство logx(2x)^0 выполняется для всех х из проме-
жутка ~ <х<1 и только для этих х. Следовательно, данное не-
равенство выполняется для всех х из этого промежутка, входя-
щих в £>2, т. е. для всех х из промежутка
Теперь предположим, что или 0<х<
1
2 ’
или х > 1
области £)2 после удаления из них промежутка
это часть
неравенства
Если или 0 < х < —, или х > 1, то обе части данного
положительны, поэтому после возведения неравенства в квадрат по-
лучим неравенство
(1+ logx2)*<3 + logx2,
1
эквивалентное данному (для значений х, таких, что или 0<х<^~»
илих>1).
J89
Перепишем это неравенство так:
(log, 2+ 2) (log, 2 — 1)<0. (1)
1°. Пусть х>1. Тогда logx2>0, значит, неравенство (1) равно-
сильно logx2—1гС0 или logx2<l. Отсюда получаем, что решением
данного неравенства будут все х^2.
2°. Пусть 0<х<-£-. Тогда logx2<0 и неравенство (1) эквива-
лентно logx2+2>0 или 2-Сх-2, но это неравенство выполняется
при всех х из интервала 0<х<-^-.
Объединяя все полученные результаты, заключаем, что все ре-
шения данного неравенства — это все значения х из промежутков
0<х< —и х> 2.
Решение нестандартных задач
Четвертые задачи в вариантах, предложенных на механико-
математическом факультете, были «нестандартными» в том смыс-
ле, что требовали для решения более искусственных методов и
более тонких рассуждений, чем обычно. В частности, в решениях
очень существенно использовались неравенства, и в особенности
два легко доказываемых, но очень важных неравенства
а2 + Ь2 > 21 а 11 b |, при любых а и Ь;
а + —>2, при а>0.
а
Кроме того, в решениях постоянно приходилось уделять особое
внимание тем случаям, когда имеют место знаки равенства: в пер-
вом неравенстве только при |а| = |^|, во втором — только при
й=1.
Мы подробно разбираем решения всех этих задач и в большин-
стве случаев приводим несколько решений. Заметим сразу же, что
решения этих задач сами по себе несложны. Поэтому мы рекомен-
дуем решить все эти задачи еще до того, как вы прочтете пх ре-
шения.
1. Сколько решений на отрезке 0^х<л имеет уравнение
sinx + 2 sin 2х‘= 3 + sin Зх.
Перепишем данное уравнение в виде
sin Зх — sinx — 2 sin 2х + 3 = О
190
и преобразуем левую часть:
2 sin х cos 2х — 4’sin х cosx 4- 3 = sin х (2 cos 2х — 4 cosx) + 3 ==
= sinх(4cos2х — 4cosx — 2) + 3 = sinx [(2cosx— I)2 —3] 4- 3.
Тогда будем иметь уравнение
sinx (2 cosx — I)2 + 3(1 — sinx) — 0.
По условию надо найти решения только на сегменте 0^х<л,
а на этом сегменте справедливо неравенство sinx:>0. Поэтому
оба слагаемых в получившемся у нас уравнении неотрицательны,
и оно удовлетворяется, таким образом, в том и только в том слу-
чае, когда эти слагаемые одновременно равны нулю. Таким обра-
зом, данное уравнение эквивалентно системе двух уравнений с
одним неизвестным
sinx(2cosx— I)2 = 0,
3(1 — sinx) = 0.
Из второго уравнения системы имеем sinx—1. Но тогда cosx = 0
и (2cosx—l)2=il#=0. Поэтому ни одно решение второго уравнения
не является решением первого, и, следовательно, система, а вме-
сте с ней и исходное уравнение, решений не имеет.
Замечание. В приведенном выше решении чрезвычайно
существенно то, что корни разыскивались только на отрезке
0<х<л, где sinx^O. Однако это условие дано лишь для облег-
чения задачи; в действительности и без этого ограничения можно
доказать, что и при sinx<0 уравнение не имеет решений.
В самом деле, если sinx<0, то
sin х 4- 2 sin 2х < 0 4- 2 = 2,
а
3 4-sin Зх > 3 4-(—1) = 2.
Можно рассуждать и так: преобразуем данное уравнение к
виду
sin х = 2(1 — sin 2х) 4- 1 4~ sin Зх;
отсюда следует, что sinx^O — противоречие с предположением
sinx<0.
Таким образом, данное уравнение не имеет корней не только
на отрезке 0^'х<л, но и вообще не имеет ни одного корня.
Отметим одну особенность этой задачи. В условии требуется
найти, сколько решений имеет это уравнение на отрезке 0^'х< я,
а оказывается, что оно вообще не имеет решений. Можно, конеч-
но, сказать, что уравнение имеет на указанном отрезке 0 корнай.
Это кажущееся противоречие между условием и ответом ставило
некоторых поступающих в тупик.
191
И в следующем уравнении, внешне совершенно обычном, ниче-
го не удается добиться стандартными приемами.
2. Решить уравнение
sin2 х + — sin2 Зх = sinx sin2 Зх.
4
Первое решение. Запишем уравнение в виде
sin2x— sinxsin23x4- ^-sin23x = О
и, рассматривая его левую часть как квадратный трехчлен относи-
тельно sinx, преобразуем уравнение следующим образом:
sin2x — slnxsln23x 4- —sin43x------- sin4 Зх 4-— sin2 Зх =
4 4 2
=^sln x---sin2 3xj2 4- sin2 3x (1 — sin2 3x) = 0.
В результате будем иметь уравнение
(sinx--— sin2 3xY 4—— sin2 6x = 0.
V 2 /16
Ясно, что это уравнение удовлетворяется в том и только в том
случае, когда оба слагаемых в левой части равны нулю, т. е. вы-
полняется система двух уравнений с одним неизвестным:
sinx = — sin23x,
2 (1)
sin6x = 0.
Решением второго уравнения является множество значений
йя' ,
х = где k принимает все целые значения.
Из этого множества надо выделить те числа, которые удовлет-
воряют и первому уравнению. Для нахождения соответствующих
значений k подставим вместо х в первое уравнение системы;
.6
получим
. kn 1 Зйя
sin — = — sin2----------
6 2 6
Заметим, что
— sin2 — = — sin2 — =
2 6 2 2
0, если k четно,
—, если k нечетно.
2
192
Если k четное, то sin = 0, что выполняется при = /л,
6 6
где I — любое целое число. Таким образом, среди четных значе-
ний k первому уравнению системы (1) удовлетворяют только чис-
ла # = 6/, где I — любое целое число. Если k — нечетное, то
sin2 = 1, и первое уравнение системы (1) принимает вид
. йл 1
sin----= —,
6 2
откуда —— = (—l)z — 4-/л, где I — любое целое число. Таким
6 6
образом, среди нечетных значений k первому уравнению системы
(1) удовлетворяют только числа & = 6/+(—l)z, где I — любое це-
лое число.
Итак, решениями данного уравнения являются следующие зна-
чения к
х — 1л, х — (—l)z—— 4-/л,
6
где I принимает все целые значения.
Второе решение. Заметим прежде всего, что левая часть
данного уравнения неотрицательна, поэтому мы должны иметь
sinxT^O. Легко проверить, что все корни уравнения sinx=0, т. е.
x=kn, где k — любое целое число, удовлетворяют уравнению. Най-
дем все остальные корни (для любого из них sinx=/=0).
Перенесем теперь в нашем уравнении все в левую часть и сум-
му квадратов дополним до полного квадрата, причем двумя спосо-
бами: до квадрата суммы и до квадрата разности; получим
1 \2
sinx+ — sln3xj 4-sinxsin3x(—1—sin3x) = 0 (2)
и
1 \2
sinx---— sin3xj 4-sinxsta3x(l—sin3x) = 0. (3)
Рассмотрим отдельно три случая.
Г. sin3x>0. Тогда оба слагаемых в левой части уравнения (3)
неотрицательны, т. е. данное уравнение эквивалентно в случае
sin3x>0 системе
sinx---i-sin3x = 0, (4)
sin х sin Зх (1 — sin Зх) = 0; (5)
7 Зак. 351
193
так как sinxy=O, sin3x>0, то из уравнения (5) имеем sin3x=l, а
тогда из уравнения (4) sinx~-^~.
Итак, надо решить систему
, 1
sinx = —,
2
sin Зх = 1.
Но если sinx=—, то sin3x=3sinx—4sin3x=l, т. е. всякое ре-
2
шение первого уравнения является решением второго уравнения и
система сводится к первому уравнению. Таким образом, ее реше-
ниями будут углы х из серии (—1)*—+&л, где k принимает все
6
целые значения.
2°. sin3x<0. В этом случае воспользуемся уравнением (2).
Поскольку —1—sin 3x^0, оба слагаемых в левой части уравне-
ния (2) неотрицательны, значит, данное уравнение при условии
sin3x<0 эквивалентно системе
sinx -j- sin3x = 0, (6)
sinx sin Зх(—1 — sin3x) = 0. (7)
Эта система эквивалентна такой:
. 1
sinx = —,
2
sin Зх — — 1,
которая не имеет решений, так как при sinx=-^- имеем sin3x=l.
3°. sin3x=0. В этом случае из данного уравнения следует, что
sinx=0, а мы сейчас находим корни, для которых sinx#=0.
Таким образом, все решения данного уравнения можно запи-
сать в видех «= kn, х = (— 1)* — kn, где k принимает все целые
значения.
Заметим, что это же самое решение можно несколько сокра-
тить. Именно, данное уравнение можно представить в виде
f sinx —~ | sin Зх |Y + sinx(| sinЗх| — sin2Зх) = 0.
Ho sin23x^ sin3x |, поэтому оба слагаемых неотрицательны, так
что данное уравнение эквивалентно системе
sinx----— sin3x = 0,
2
sinх (| sin Зх | — sin2 Зх) = 0.
194
Остается рассмотреть (как и выше) случаи sin3x>0, sin3x<0 и
bin3x=0.
Третье решение. Предположим, что данное уравнение
удовлетворяется некоторым числом х. Перепишем его в виде
sin2x = sin23x^sinx-----------------------
Отсюда ясно, что sinx--------- >0 fесли sinx----— = 0, то и
4 \ 4
sin х = — и sinx = o). Умножая неравенство sin23x<l на поло-
жительное выражение sinx----получим неравенство
sin23xf sinx---—^<slnx-------,
X. 4 J 4-
причем равенство достигается лишь при sin23x=l.
Следовательно, должно выполняться и неравенство
sin2x< sinx-------------------------—,
4
(1 \2
sinx----— j <0, которое справедливо >лишь при
sinx = —.
2
Итак, если некоторое число х удовлетворяет нашему уравне-
нию, то оно удовлетворяет системе
sin2 Зх = 1,
sinx = 1.
Обратное очевидно: если х удовлетворяет этой системе, то, под-
ставляя sinx=l и sin23x=l в исходное уравнение, убеждаемся, что
оно также удовлетворяется.
Таким образом, данное уравнение равносильно полученной си-
стеме, а эта система уже решена выше.
Этот же способ решения уравнения можно было бы несколько
видоизменить. Отнимем от обеих частей данного уравнения
sinx----получим
^sinx— = (sin23x— l)^sinx----------i-j.
Так как sinx----— *>0 (это было доказано выше), то правая
4
часть этого уравнения неположительна, а левая неотрицательна, поэ-
7* 195
тому уравнение удовлетворяется в том и только в том случае, когда
sinx = — и или sin2’3x = 1, или sinx-----— = 0.
2 k 4
Четвертое решение. Найдем корни данного уравнения,
отличные от корней x=kn, где k принимает все целые значения.
В этом случае (x=£kn,) имеем sinx=#0, sin3x=£0 и, поделив обе
части данного уравнения на произведение sinxsin3x, получим
sinx । 1 _।
sin2 Зх 4 sin х
Оба слагаемых в левой части положительны, поэтому можно
применить неравенство между средним арифметическим и средним
геометрическим двух положительных чисел:
_____ [ >21/ — 1 1
sin23x 4 sinx Y 4sin23x |sin3x|
В первом из написанных неравенств равенство достигается только
sinx 1 . , п I 1
при -------=--------, во втором —при I sin Зх I = 1.
sin23x 4 sinx
Поэтому левая часть равна 1 в том и только в том случае,
когда
4sin2x = sin2 Зх, ,Q4
(о)
| sin3x | = 1.
Подставляя из второго уравнения |sin3x| = l в первое, получим
4sin2x=l, откуда в силу sinx>0 будем иметь sinx=-~.
Таким образом, система (8) равносильна системе
, 1
sinx = —,
2
| sin Зх | = 1,
которую мы фактически выше уже исследовали.
Пятое решение. Как было доказано, корни данного урав-
нения удовлетворяют неравенству sinx^O. Пользуясь формулой
sin3x — 3sinx—4sin3x и обозначая sinx через t, после упрощений
получим уравнение седьмой степени относительно t: .
64Г — 16/6 — 96/5 + 24/4 + 36/3 — 13/2 = 0.
Очевидно, /=0 является корнем (притом двукратным) этого
уравнения и оно сводится к уравнению пятой степени:
64/5 — 16/4 — 96/3 + 24/2 + 36/ — 13 = 0.
196
Будем подбирать корни этого уравнения. Целыми его корнями
могут быть только ±1 и ±13; легко проверить, что ни одно из
этих чисел не является корнем. Будем подбирать рациональные
. » Р
корни, пользуясь следующей теоремой: «если число -— является
корнем многочлена с целыми коэффициентами, то р является дели-
телем свободного числа, a q — делителем старшего коэффициен-
та». Доказательство этой теоремы проводится аналогично доказа-
тельству теоремы о целых корнях целой рациональной функции с
целыми коэффициентами.
В данном случае р может принимать значения ±1, ±13; q —
значения ±2, ±4, ±8, ±16, ±32, ±64. Всего, таким образом, по-
надобится проверить не больше 48 чисел. Однако первое же испы-
тываемое число / = у является корнем, и левую часть уравнения
можно разложить на множители:
(/ — у)(64/4 + 16/3 — 88/2 — 20/ + 26) = 0.
Итак, t = Остается решить уравнение
32/4 4- 8 /3 — 44/2 -10/4- 13 = 0.
Оказывается, что /=у- является корнем и для этого уравнения, и
оно затем сведется к кубичному уравнению
16/з 4- 12/2—16/—13 = 0.
Представив левую часть в виде •>
16/(/2— 1)4- 12(/2 — 1)— 1 = — 16sinxcos2x— 12cos2x— 1 <0
(в силу условия sinx^O), заключаем, что уравнение 16/3+12/2—
—.16/—13 = 0 не имеет действительных корней на сегменте 0^/< 1
(/=sinx, sinx^O).
Окончательно имеем два корня: / = 0, / = —,
откуда и получаем
ответ: x — kn, х = (— 1)'— + 1л, где k и I принимают любые целые
6
значения.
При решении предыдущих задач мы сталкивались с системами
нескольких уравнений с одним неизвестным. В то же время пред-
лагались задачи, в которых требуется решить одно уравнение с
несколькими неизвестными.
3. Найти все пары чисел х, у, которые удовлетворяют урав-
нению
tg4 х 4- tg4 у 4- 2 ctg2 х ctg2 у = 3 4- sin2 (х 4- у).
197
Рассмотрим левую часть этого уравнения. Воспользовавшись
неравенством а4+64^2а262, справедливым, как легко видеть, для
любых а и Ь, будем иметь неравенство
tg4 х 4- tg4 г/ > 2 tg2 х tg2 у,
причем равенство достигается только при tg2x=tg2z/. Далее,
tg2 х tg2 у 4- ctg2 х ctg2 у > 2
как сумма взаимно обратных положительных величин, причем ра-
венство достигается лишь при tg2xtg2z/=l. Таким образом, левая
часть нашего уравнения больше или равна 4 и равна 4 только при
выполнении равенств
tg2x = tg2z/,
tg2xtg2z/=l.
С другой стороны, sin2(x+y) и, следовательно, правая
часть меньше или равна 4.
Таким образом, исходное уравнение удовлетворяется в том и
только в том случае, когда обе его части равны 4, так что оно
эквивалентно системе
(А) ‘ tg2x = tg2^,
(В) tg2xtg2f/=*l, (1)
(С) sin2 (х + у) = 1.
Из первых двух уравнений имеем tg2x=tg2z/ = 1, т. е.
tgx= ± 1, tgy = ± 1,
откуда х=— (2&+1), у= — (2п + 1), где k и п принимают все
4 4
целые значения. Из всех полученных таким образом пар значений
для х и у решение данного уравнения образуют только те, при
которых выполнено и третье уравнение системы (1). Заметим, что
>2/ , ч , 2 Г л /I. 1 1 1 \1 (1» если k + n+l нечетное,
sin2 (х + у) = sin2 — (k 4- п 4-1) = I '
L 2 J I 0, если &4-п 4-1 четное.
Отсюда следует, что из решений системы, состоящей из двух
уравнений (А) и (В), надо взять такие пары кип, для которых
сумма k+n=2m четная, т. е. п=2т—k, где т—любое целое число.
Итак, всеми решениями данного уравнения будут пары х, у
вида
х = 4(2*4- 1), t/ = 4(4/n-2*+1K
4 ,4
где т и k — любые целые числа.
198
Второе решение.
tg4 х + tg4 у + ctg2xctg2 у = (tg2 х — tg2 z/)2 +
+ 2(tg2xtg2z/ + ctg2xctg2i/) =
= (tg2 x — tg2z/)2 4- 2 (tg x tg у — ctgxctg y)2 + 4.
Данное уравнение принимает вид
(tg2x —tg2z/)2 + 2(tgxtgz/^ctgxctgz/)2 + 1 =sin2(x+^).
Левая часть этого уравнения больше или равна 1, а правая
меньше или равна 1. Поэтому уравнение удовлетворяется в том и
только в том случае, когда обе части равны 1, т. е. когда выпол-
няется система ,
tg2* — tg2z/ = O,
tg*tgz/ — ctgxctgz/ = O,
sin2(x + у) = 1.
Эта система решается так же, как и выше.
4. Найти все пары чисел х, у, которые удовлетворяют уравне-
нию
з
COS X + cos у — cos (х + у) = —.
Первое решение. Идея, которая может возникнуть при
решении одного уравнения с двумя неизвестными, такова: выра-
зить одно неизвестное через другое, и тогда, придавая всевозмож-
ные значения этому неизвестному, получать соответствующие зна-
чения другого. В данной задаче этот метод приводит к цели. Вы-
разим у через х. Перепишем данное уравнение так:
cos х + 2 sin (— + у\ sin — = —.
<2 / 2 2
л* / 3
Ясно, что sin— иначе cosx = —
и поэтому
з
T-cosx
2 sin —
2
(О
Отсюда можно найти у, если, конечно, правая часть по модулю
меньше или равна 1.
Решим неравенство
3
— — cos X
2 - 2sinT <1
199
Перепишем его в виде
—-----cos х | < 2 sin — ,
2 2
2
f з п\
или ( поскольку —-cos х>0 ]
-----cosx-<2|sin— .
2 | 2
i2-|-и, обозначая |sin-^-j через t, будем иметь
Но cosx = 1 —2sitr
неравенство
-i- 4- 2/2 < 2/,
или, что то же,
4/2 —4/4-1 <0, или (2/—1)2<0.
Отсюда
cos х = i, а тогда из уравнения (1) находим sin
2
Итак, правая часть уравнения (1) не превосходит по модулю 1
только при sin-|- =
чениях sin уравнение не имеет решений.
При sin-^- = —, — = (— 1)*-~ + или х = (— 1)*-у-.+ 2&л,
X 1
где k принимает все целые значения. Но если sin — = — , то
2 2
3 1
2 " 2 = j
*4 = '
1 X 1
—, т. е. при sin—=± —. При остальных зна-
у = 2пл4--у---гДе п — Л1°бое число.
При sin— =----—, т. е.—= (—1)*+*4"kn, или]
л - 1
х = (— 1)*+’--1- 2kn, где k — любое целое число, имеем cosx = — ,
а тогда
sin
3 1
2 2
2 •
200
и
и - 2пя — -------------— = 2пл------— (—1 )*+* —— kn,
а 2 2 2 6
где п — любое целое число.
Ответ:
х==(_1)йЛ + 2Лл, у = -J- + (- + (2п —k) л;
х = (- 1)*+14 + 2кл, у = -^ + + (2л - k) л,
о 2 о
где k, п принимают все целые значения.
Второе решение. Переносим все в левую часть и, поль-
зуясь тригонометрическими формулами, перепишем уравнение в
виде
п 9^+у 1 п х + у ^х—у 1 3 Л
2 cos2 —Г-?- — 1 — 2 cos - у cos-- Ч--= 0,
2 2 2 2
или
оХ-И х—у х + у . 1 Л
cos2 —— — cos---- cos - - Ч--=0.
2 2 2 4
Получившееся уравнение преобразуем следующим образом:
/ х + у 1 х — у . 1 9Х — у\ Л
( cos ——------cos---- Ч-----(I —cos2----- ) = 0.
v 2 2 2 J 4 \ 2 >
Поскольку оба слагаемых в левой части уравнения неотрица-
тельны, то данное уравнение эквивалентно системе уравнений
х + у 1 х — у
cos —— = — cos--------,
2 2 2
9 X — У <
cos2----- = 1.
2
Второе уравнение системы, очевидно, равносильно уравнению
sin у =0 и, решая его, получаем х—у=2пп. п — любое це-
лое число. Следовательно,
cos -~У- = cos ил = (— 1)п.
Рассмотрим отдельно четные и нечетные значения п. Если п — чет-
ное, n = 2k(k — любое целое число), то из первого уравнения имеем
201
х + у 1 , , 2л . л f . *
cos —, т. е. х + у = ± -у + 4л/, где / — любое целое чис-
ло, и таким образом, имеем систему
, 2л . . ,
х + У = ± — + 4л/,
О
х — у = 4лА.
*
Отсюда х = 2(k + /) л ± —, у = 2(1 — k) л ± —, где k и I — лю-
3 3
бые целые числа, причем перед -у в этих формулах берутся одно-
временно либо знак плюс, либо одновременно знак минус.
При п нечетном, п = 2k + 1, совершенно аналогично получаем
cos Х^У =------у т. е. х-f-у = ± у-4- 4л/, где / — любое целое
число, и, таким образом, имеем систему
х + у = ± -у- + 4л/,
х — у = 2(2k + 1) л.
Отсюда
х?= (2/ + 2& + 1)л ±-у,
у = (2l — 2k — 1)л ± -у,
где k и I принимают все целые значения, причем в этих формулах
2л ,
перед -у берется одновременно знак плюс или одновременно
знак минус.
Следующая задача такого типа сводится к тригонометрическо-
му неравенству, для доказательства которого требуется проявить
известную изобретательность.
5. Найти все пары чисел х, у, удовлетворяющие уравнению
1 \2 / 1 \2 1
sin2x4--------1 + |cos2x4----------) =12 + —-sinw.
sin2 x I I cos2 x / 2
Первое решение. Преобразуем левую часть данного урав-
нения следующим образом:
sin4 х 4--J--1- cos4 х 4-J------1- 4 =
sin4x cos4 х
= (sin4 х + cos4 х) (14------------!------+ 4 =
\ sin4 х cos4 х J
202
= (1 — 2 sin2x cos2x) f 1 +-----5-----+ 4 =
\ sinlr cos4x J
= (1-----— sin22x^ (1 -1---+ 4;
\ 2 ‘ / \ sin42x J
данное уравнение примет вид
(2 — sin22x) (1 Ч---Ц—= 16 + sin у.
\ sin42xy
Но 2 — sin22x> 1, 1 + . ’> 17, причем знаки равенства имеют
место тогда и только тогда, когда sin22x = 1. Поэтому левая часть
данного уравнения больше или равна 17, а правая часть меньше или
равна 17. Отсюда следует, что данное уравнение равносильно системе
sin22x = 1,
sin у = 1,
решение которой состоит из пар х, у вида х = -^-(2£ + 1), у = -j- +
+ 2пл, где k, п принимают все целые значения.
Второе решение. Преобразуем уравнение так же, как и
раньше. Обозначив для краткости sin22x через z, будем иметь
’ sin у = (2 — г) р + “М —! 16.
Это соотношение возможно тогда и только тогда, когда удов-
летворяется условие
-1<(2-г)(1 + -^-)-16<1,
\ г2 /
или после ряда преобразований
15г2 < — z3 + 2г2 — 16г + 32 < 17г2.
Перепишем эту систему двух неравенств так:
z3 + 15z24-16z — 32 > О, (1)
z3+ 13г2 + 16z — 32 <0. (2)
Так как z=l — корень функции z3+15z2+I6z—32, то неравен-
ство (1) можно переписать в виде
(z-l)(z2+ 16z-i-32)>0,
или
(z-l)[z-(8-4/2)][z-(8 + 4/2)].
203
Решая это неравенство, получаем
1 < z < 8 — 4 у 2, z > 8> 4У 2. (2')
Однако z=sin2 2x^1, так что из неравенства (2') следует, что
z=l. Таким образом, первое неравенство системы имеет единст-
венное решение z=<l. Непосредственной подстановкой проверяется,
что это решение z=l удовлетворяет и второму неравенству, т. е.
является решением системы (1), (2).
Итак, данное уравнение имеет решение только при sin22x=l.
Но тогда из него получаем, что sinz/= 1. В результате приходим к
прежней системе ,
sin2 2х = 1,
sin у = 1.
Заметим, что первое решение короче, но второе естественнее,
так как в нем более ясна цель того или иного рассуждения.
Очень серьезные трудности, причем самого главного, логиче-
ского, характера вызывают обычно уравнения и системы уравне-
ний с параметрами, в которых требуется найти такие значения этих
параметров, при которых выполняются указанные требования:
например, уравнение имеет единственное решение, или, наоборот,
удовлетворяется всеми допустимыми значениями, или всякое реше-
ние одной системы уравнений является решением другой системы
и т. п.
Эти задачи являются, пожалуй, наиболее трудными из всех,
которые мы здесь рассматриваем, именно потому, что они тре-
буют высокой логической культуры — того, чего не хватает многим
из поступающих. Чтобы решить такую задачу, необходимо в каж-
дый момент представлять себе, что уже сделано, что еще надо
сделать, что означают полученные результаты.
6. Найти все пары чисел а и Ь, для которых всякая пара чисел
х и у (х^=пл+~, У^=тл+^-; п, m = Q, ±1, ±2, ...), удовле-
творяющая уравнению
х + ^ = а, (1)
удовлетворяет также уравнению
tgx + tgy + lgxtgy = b. (2)
Решение*. Так как х#=пл+-у и у=^ тп + -у при всех це-
лых значениях п и т, то cosx#=0, cosy#;0, значит, умножая обе
части соотношения (2) на cosxcosz/, получаем соотношение, эквива-
лентное соотношению (2):
sin xcos z/+ sin у cos х + sinx sin у = & cosx cos у,
sin(x-f- у) — (cosx cost/ — sinx sin y) = (b — 1) cosx cos y,
* Решение принадлежит П. С. Моденову.
204
sin (x 4- у) — COS (x + y) = ~ (b — 1) [cos(x — y) + cos(x 4- y)],
2 sin (x + y) — (b + l)cos(x+t/) = (b — l)cos(x — y). (3)
Предположим, что существуют такие значения а и &, что из со-
отношения х+у = а, где х и у подчинены неравенствам, заданным
в условии задачи, следует соотношение (2), или, что то же самое,
соотношение (3). Но соотношение (3) при условии х+у=а прини-
мает вид
2 sin а — (b + l)cosa — (&— l)cos(x— у). (4)
Докажем, что если 6=#1, то существуют пары значений х, у,
удовлетворяющих условию х+у = а и неравенствам, данным в ус-
ловии задачи, при которых, однако, правая часть равенства (4)
принимает различные значения. В самом деле, каково бы ни бы-
ло число а, всегда можно найти таких два различных значения р
и q из интервалами, —J, что, полагая
а . а
Х! = — + Р, У^^-Р,
*2 = -f + <7. У2 = -^~Ч,
можно утверждать, что хь ylt х2, у2 удовлетворяют неравенствам,
данным в условии задачи.
Так как при этом
Х1 + У! = а,
х2 + у2 = а,
х1 — у1 = 2р,
x2~y2 = 2q
и оба числа 2р и 2q различны и лежат в интервале (0, л), то при
правая часть равенства (4), т. е. (Ь—l)cos(x—у), для х=Х|,
У —Ух принимает значение (Ь—4)cos2p, а при х=х2, у—у2— зна-
чение (6—1)cos2<7. Значит, Ь = 1. Но тогда из того же соотношения
(4) следует, что tga—1=0, откуда tga=l, т. е.
а = зл + —, *
4
где s — целое число.
Обратно, если s— любое целое число и 6=1, то из соотношения
х+у=а следует равенство
tg* 4- tg t/ -4- tgxtg г/ = 6,
205
так как оно эквивалентно соотношению (3), которое при 6 = 1,
а = ел 4- — обращается в тождество.
7. Найти, при каких значениях р уравнение
1 4- Р sin х — р2 = — sin2 х
имеет решение.
Запишем это уравнение в виде
sin2 х 4- р sinx 4-1 —р2 = 0.
Это уравнение квадратное относительно sinx, и для того чтобы
ответить на вопрос задачи, нужно найти значения, при которых
корни уравнения
t2 + pt 4- 1 — р2 = 0
действительны, и хотя бы один корень не превосходит по моду-
лю 1.
Проведем некоторые предварительные рассуждения. Рассмот-
рим квадратный трехчлен /2+р£+1—р2. Найдем все значения t,
при которых этот трехчлен имеет хотя бы один корень на сегменте
Для удобства дальнейших рассуждений сначала ограничимся
случаем, когда корни трехчлена отличны от —1 и 1. Тогда требуе-
мое условие выполняется в следующих трех случаях.
1°. Больший корень лежит в интервале —1</<1, а меньший —
меньше —1.
2°. Меньший корень лежит в интервале —1</<1, а больший —
больше 1.
3°. Оба корня лежат в интервале —1<7<1.
Случай Г выполняется тогда и только тогда, когда рассматри-
ваемый трехчлен отрицателен при t= — 1 и положителен при /=1,
т. е.
1—р4- 1—р2<0,
1 4-Р4- 1—р2>0,
ИЛИ
р2 4-р —2>0,
р2 — р — 2<0.
Решение этой системы: 1<р<2. Случай 2° выполняется тогда
и только тогда, когда рассматриваемый трехчлен положителен
при t = — 1 и отрицателен при f=l:
1 —р4-1 — р2>0,
1 4-Р4-1—Р2<0,
206
или
р2 + р—2<0,
р2— р — 2>0.
Решение этой системы: —2<р<—1.
В случае 3° трехчлен положителен и при7= — 1 и при t=\.
Однако это условие недостаточно для случая 3°; во-первых, надо
потребовать, чтобы корни были действительны (почему это не на-
до специально оговаривать в предыдущих случаях?), во-вторых,
это условие не исключает случаев, когда оба корня больше 1 и ког-
да они меньше 1. Ясно, что исключить последние два случая мож-
но, наложив условие, чтобы абсцисса вершины параболы, т. е.
число t——лежало в интервале —1</<1. Для действитель-
ности корней нужно потребовать, чтобы был неотрицателен дис-
криминант 5р2—4 данного трехчлена. Таким образом, имеем
систему неравенств
- 5р2 —4>0,
1—р+ 1—р2>0,
1 +р—1_р2>0,
или
\р\>-у=,
/ 5
|Р|>2,
р2 + р —2<0,
р2 —р —2<0.
Решение этой системы состоит из двух интервалов:
-1<Р<-------Д=-<р<1.
/5 V 5
Остается еще рассмотреть случай, когда трехчлен имеет корня-
ми числа —1 и 1. Очевидно, 1 является корнем при р=—1 и р=2,
а —1 является корнем при р=1 и р=—2. Эти четыре значения р
также удовлетворяют требуемым условиям.
207
Итак, все значения р, при которых данное уравнение имеет ре-
шение
— 2<р< ——^7-, -L-<P<2,
/5 /5
ИЛИ
-^<|р| <2.
у 5
§ 9. ДОПОЛНИТЕЛЬНЫЕ ПРИМЕРЫ И ЗАДАЧИ
АРИФМЕТИКА И АЛГЕБРА
I. Задачи по арифметике (с решениями)
1. а) Доказать, что если две правильные дроби в сумме равны
единице, то их знаменатели равны.
б) Пусть — и —---две положительные несократимые дроби,
с d
такие, что
р.у+р_у=1,
\ с / \ d J
Доказать, что одно из чисел а или b делится на 4 и что одно
из них делится на 3.
Решение: а) —4- —=1, — = Числам — Ь и d взаим-
с d с а
но простые, так как в противном случае числа d и b были бы не
взаимно простые. Следовательно, дробь
d — b
d
несократима, и потому c=d.
a b f а \ 2
б) Так как — и---правильные несократимые дроби, то ( —)
cd \ с J
f b \2 .
и ( — ) — также правильные несократимые дроби; но
\ d J
значит, на основании а) их знаменатели равны, т. е. c2=d2. Та-
ким образом,
а2 + Ь2 = с2; (2)
208
а и с — взаимно простые по условию; Ьис (d—c) также взаимно
простые. Значит, а и b — взаимно простые, так как если бы а и &
имели общий множитель k=/=\, то в силу равенства (2) с также
делилось бы на k. Но тогда а и с не были бы взаимно простыми.
Заметим теперь, что квадрат любого четного числа делится
на 4, а квадрат любого нечетного числа при делении на 4 в остат-
ке дает 1. Поэтому одно из чисел а или b должно быть четным, так
как в противном случае число с2, равное а24-62, при делении на 4
дало бы в остатке 2, что невозможно.
Предположим, что четным является число а, т. е. а=2а'; тогда
b и с — обязательно нечетные: 6 = 26'4-1 и с = 2с'+1. Тогда равен-
ство (2) примет вид
4а'2+(26'4-О2 = (2с'4-I)2,
или
4а'2 = (2с'+ I)2 — (26'+ I)2,
или
4а'я = (2с' + 2Ь’ 4- 2) (2с' — 26'),
а'2 = (с'+ 6'+ 1)(с'— 6').
Разность чисел с'+6'+1 и с'—Ь' равна 2 6'4-1, т. е. число не-
четное; значит, c'+b'+l и с'—Ь' имеют разную четность и одно из
них делится на 2.
Поэтому из равенства
а'2 = (с'4-6' + 1)(с'—&')
следует, что а' делится на 2.
Но а=2а', значит, а делится на 4. Теперь докажем, что одно
из чисел а или b делится на 3.
Докажем сначала, что если квадрат всякого натурального
числа не делится на 3, то при делении на 3 получается в остатке 1.
Действительно, все натуральные числа, не делящиеся на 3,
можно записать либо в виде 36 4-1, либо в виде ЗЛ + 2, где k — лю-
бое натуральное число.
Тогда
(ЗА+1)2 = 9А2 + б& + 1,
(3k + 2)2 = 9k2 4- 12&4-34-1.
Предположим, что ни а, ни b не делятся на 3. Пусть а = 3&+1,
6 = 3/4-1, тогда с2=а24-62=9А24-66+9/24-6/+2, значит, квадрат
нечетного числа при делении на 3 дает в остатке 2, что невозможно.
Пусть а=3&4-1, 6 = 3/4-2, тогда c2=a2+b2=9k2 + 6k+9l2+.
4-12/4-34-2, и мы приходим к тому же противоречию.
209
Аналогично выводится то же самое, если предположить, что
а=3&+2, 6=3/+1, или а=3&+2, 6=3/+2.
2. Есть ли 401 простое число? Решить уравнение
х* - у2 = 401
в целых положительных числах.
Решение. Число 401 не делится на числа 2, 3, 5, 7, 11, 13, 17
и 19, меньшие числа 20, которое является значением "И 401 с недо-
статком с точностью до 1. Значит, 401—число простое. Поэтому
из уравнения
(х — у)(х + у) = 401
следует, что
х — у= 1,
х+ у — 401
и, значит,
х = 201, у = 200.
3. 1°. Определить натуральное число п, такое, чтобы дробь
» + 4
п—3
была натуральным числом.
2°. Определить натуральное число п>3 так, чтобы дробь
» + 4
п — 3
была равна 1,24 с избытком с точностью до —.
100
Решение. 1°.
п — 3 п — 3
Отсюда или п—3=1, или п—3 = 7. Соответствующие значения
л=4 и п= 10.
2°. Из неравенств
1,23 <1+ —^—<1,25,
п —3
ИЛИ
0,23 <—— <0,25,
п — 3
210
находим
7
7
31<я<—4-3,
0,23
31<и<33,4.
Значит, существуют два значения п, удовлетворяющие условию
задачи: п=32, при котором
1,24
п — 3
с точностью до 0,01 с недостатком, и я=33, при котором
•^±1-1,24
п — 3
с избытком.
4. Найти все натуральные числа п, для которых натуральное
число /п=я2+я+1 делится на 13.
Решение. Число п2 + п+1 делится на 13 тогда и только тогда,
когда делится на 13 число
я24-я-|- 1— 13 = (я— 3)(« + 4),
г. е. когда
(я —3)(я4-4)= 13А.
Так как 13 простое число, то на 13 должно делиться либо я—3,
либо я+4, т. е.
или я—3= 13 р, или я+4=13р, откуда
я = 3 4- 1 Зр,
или
я = 13р— 4,
где р принимает все целые положительные значения (в соотноше-
нии же и=3+13р можно еще взять р=0; тогда я=3 и, действи-
тельно, при и=3 имеем п2+и+1 = 13).
5. Рассмотрим натуральное число яг=я4+п2+1, где я также
натуральное число.
1°. Разложить т в произведение двух множителей второй сте-
пени относительно я с целыми коэффициентами.
2°. Может ли число т быть простым?
Решение. Г, Разложение т на множители
m = я4 4- 2я2 4-1 — я2 = (я2 4- я 4-1) (я2 — я 4-1).
211
Введем обозначения
р = п? + n + 1, q = п2 — «4-1.
Общий делитель р и q должен быть делителем и чисел .
р + ? = 2(п2 + 1),
р — q = 2n.
Далее, каково бы ни было п, четное или нечетное, числа р и q
всегда нечетные; в самом деле,
р = n2 + n + 1 = п(п + 1) + 1,
7 = п2 — п + 1 = п(п — 1) + 1,
значит, общий делитель р и q не может быть равен 2, а значит,
общий делитель чисел p+q и р—q есть общий делитель чисел
п2+1 и п. Но если % этот общий делитель, т. е. п делится на Л, то
на Л делится и п2, значит, делится и п2+1, что возможно только
в случае Л=1. Итак, р и q — взаимно простые.
2°. Случай, когда т— простое число. Число т простое тогда
и только тогда, когда q=l, т. е. п2—п = 0; отсюда п=1 и, значит,
/п=3.
6. Шестизначное число N имеет вид
N = abcabc;
с — число единиц и число тысяч; b — число сотен и число десятков
тысяч, а — число сотен и число сотен тысяч (а+=0).
1°. Доказать, что Л/1 есть произведение числа abc на некоторое
натуральное число.
Доказать, что:
a) N делится на 7, 11 и 13;
Р) М не является квадратом натурального числа.
2°. Определить число N' указанного вида, обладающее одновре-
менно двумя свойствами:
a) N делится на 5;
Р) Ьс=2а.
Разложить полученное таким образом число на простые мно-
жители.
Решение. 1°. Вычисление N. abcabc=abc-1000+abc =
=о&с(1000 +1) =abc-1001.
a) N делится на 7, 11 и 13. Это следует из того, что 1001 =
=7-11-13.
Р) N не есть точный квадрат. Необходимое условие того, что
N есть точный квадрат, состоит в том, что в разложении N на про-
стые множители числа 7, 11 и 13 должны входить в четной степени.
Но N=abc-1001, значит, abc должно делиться на 7, 11, 13, т. е.
на 1001, что невозможно, так как abc трехзначное число.
212
2?. Вычисление 2V, удовлетворяющее соответствующим усло-
виям. N1 делится на 5 тогда и только тогда, _когда с=0 или с=5.
Но число с = 5 исключается в силу условия Ьс=2а, т. е. число Ьс
должно быть четным. Значит, с=0. С другой стороны, 2а —ЬО—
меньше 20, поэтому надо взять Ь=1, следовательно, а=5. Искомое
число
N = 510510.
Разложение N на простые множители. W=510 510= 1001-510=
= 51 • 10-1001, и так как 51 =3-17, то
510510=2-3-5-7-Ц.13-17
(произведение семи первых простых чисел!).
7. Доказать, что два последовательных целых положительных
числа — взаимно простые. Доказать, что если а и Ь — два нату-
ральных взаимно простых числа, то а и а + Ь— взаимно простые,
Ь и а+Ь — взаимно простые, ab и а+Ь— взаимно простые.
Может ли быть сократимой дробь
2п-)-5
(п + 2) (п + 3)
где п — натуральное число?
Решение. Свойство двух последовательных натуральных
чисел. Пусть £>(«, п+1)— наибольший общий делитель натураль-
ных чисел п и п+1. Тогда разность п+1—п=1 должна делиться
на D, т. е. £>=1, а значит, и и п+1—взаимно простые.
Изучение пар (а, а + Ь) и (Ь, а + Ь), если а и Ь — взаимно
простые натуральные числа. Пусть D(a, а+Ь)—наибольший об-
щий делитель чисел а и а+Ь. Тогда на D должны делиться чис-
ла а и а + Ь—а = Ь. Но так как а и Ь — взаимно простые, то £>=1.
Аналогично доказывается, что Ь и а+Ь — взаимно простые.
Замечание. Если D(a, Ь)—наибольший общий делитель
натуральных чисел а и Ь, то следующие положения эквивалентны:
D(a, b) = 1 ^.D(a, а + Ь) = D(b, а + Ь) = 1.
Изучение пары (ab, а + Ь). Заметим сначала, что наибольший
общий делитель двух натуральных чисел не изменится, если одно
из них разделить или умножить на число, взаимно простое с дру-
гим. Если а и Ь — взаимно простые натуральные числа, то а и
а + Ь — взаимно простые, значит, ab и а + Ь — взаимно простые.
Другое доказательство. На натуральное число D(ab, а+Ь) де-
лятся числа ab и а + Ь, следовательно, на число D разделятся чис-
ла а(а+Ь)—ab-а2 и Ь(а + Ь)—ab = b2, и так как а2 и Ь2 — взаимно
простые (в силу D (а, Ь) — 1), то D = 1.
Изучение дроби ——2” 5,—. Числа п+2 и п + 3 взаимно
(л + 2) (п + 3)
простые и, значит, взаимно простые пара чисел п + 2+и+3=2п+5
213
« (n+2) (n+3); таким образом, рассматриваемая дробь несокра-
тима.
8. Доказать, что если п — любое натуральное число, то п и п5
оканчиваются на одну и ту же цифру.
Доказательство; достаточно показать, что п5—п —
=п(п*—1) делится на 10. Сначала докажем, что если п не делится
на 5, то п4—1 делится на 5. В самом-деле, всякое натуральное чис-
ло п, не делящееся на 5, можно представить в одном из следующих
видов:
56+1, 56+ 2, 5^4-3, 56 + 4,
где k — любое натуральное число.
Теперь находим:
п4 — 1 =(14- 56)4 — 1 делится на 5,
п4 — 1 =(2 4- 56)4 — 1 делится на 5,
п4 — 1 =(3 4- 56)4 — 1 делится на 5,
п4 — 1 — (4 4- 56)4 — 1 делится на 5.
Далее, число п(п4—1) = (п—1)п(п+1) (п2+1) — четное, так
как из двух множителей п и n +1 один четный.
Итак, если п не делится на 5, то п5—п=п(п4—1) делится на 5
и на 2, следовательно, на 10. Но если п делится на 5, то п5—п=
= (п—1) п(п+1) (п4 + 1)—число четное, а значит, по-прежнему
«5—п делится на 10.
9. Доказать, что пр и пр+4, где пир — любые натуральные
числа, оканчиваются на одну и ту же цифру.
Доказательство: достаточно показать, что п₽+4—п? де-
лится на 10. Имеем
пр+4— пр = пр~1 • п(п^ — 1).
Но число и (и4—1) делится на 10 (см. предыдущую задачу).
10. Пусть п — произвольное натуральное число. Какие остатки
могут получиться при делении п4 на 5?
Решение. Если п делится на 5, то остаток равен 0. Если п
имеет вид 1+56, где 6 — любое натуральное число, то и4=1+4Х
Х56+... и, значит, п4 при делении на 5 дает в остатке 1.
Если п=2+56, то
п4 = 24 + 4 • 2® • 56 + ... = 1 + 15 +4 • 23 • 56 + ...
Отсюда видно, что остаток от деления п4 на 5 равен 1. Если
«=3+56, то
п4 = З4 + 4 • З3 • 56 + ... = 1 + 80 + 4 • З8 • 56 + ... ,
остаток от деления п на 5 равен 1.
214
Наконец, если п=4+5&, то
= 44 + 4 • 43 • 5&+ ... = 1 +255+ 4 • 43 • 5k+ ...
дает 1 в остатке от деления на 5.
Итак, остаток от деления п4 на 5, где п — произвольное нату-
ральное число, всегда равен или 0, или 1.
11. а) Определить возможно более'простым способом остатки
от деления на число 7 следующих чисел:
5 , 52, 53, 54, 5®, 5е и 57.
б) Найти все натуральные числа и, такие, что 19” при делении
на 7 дает в остатке 2.
в) Вычислить остаток от деления 1964 на 7.
Решение, а) Остаток от деления 5 на 7 равен 5. Остаток от
деления 52=25 на 7 равен 4. Теперь заметим, что если натураль-
ные числа тип при делении на натуральное число k дают остат-
ки, соответственно равные р и q, то остаток от деления тп на k ра-
вен остатку от деления pq на k. В самом деле,
тп = (тй + р) ink + q) = mnk? + (m+n)k + pq.
Значит, остаток от деления на 7 числа 53 равен остатку от деле-
ния числа 5-4=20 на 7, т. е. 6. Остаток от деления 54 на 7 равен
остатку от деления 5-6=30 на 7, т. е. 2. Остаток от деления 55
на 7 равен остатку от деления 5-2=40 на 7, т. е. 3. Остаток от
деления 56 на 7 равен остатку от деления на 7 числа 3-5=15,
т. е. 1, и, наконец, остаток от деления на 7 числа 57 равен снова 5.
Вообще, если п=6А+и', где k — любое натуральное число, а
п' равно одному из чисел 0, 1, 2, 3, 4, 5, 6, то остатки от деления
на 7 чисел 5П и 5я' равны между собой.
б) Отыскание натуральных чисел п, таких, что 19 при деле-
нии на 7 дает в остатке 2. Так как 19 при делении на 7 дает в.
остатке 5, то 19П и 5П при делении на 7 дают одни и те же остатки,
значит, 19п и 5”', где n=6k+n' (см. предыдущий параграф), при
делении на 7 дают один и тот же остаток. Но так как п'<7, то на
основании предыдущего параграфа остаток от деления 5я' на 7
будет равен 2 только при п'=4. Итак,
п = 6k + 4,
где k — любое натуральное число или нуль.
в) Остаток от деления 1964 на 7. Так как 64=6-10+4, то этот
остаток равен 2.
12. 1°. Найти общий наибольший делитель чисел 24 101 и 18 780.
2°. Найти все решения в целых числах уравнения
18 780х —24 101у = 313,
зная одно из решений
х = 9, у = 7.
215
Решение. 1°. D (24101, 18780) =313.
2°.’Данное уравнение принимает вид
60х — 77у = 1,
и так как
60-9 —77-7= 1,
то, вычитая почленно, будем иметь
60(х —9) —77(у —7) = 0. (1)
Но так как числа 60 и 77 взаимно простые, то х—9 должно де-
литься на 77, а у—7 — на 60, и эти частные в силу соотношения
(1) должны быть равны между собой:
= =п>
77 60
откуда
х = 9 + 77п,
у = 7 -|- 60п,
где п принимает все целые значения.
Замечание. Уравнение
60х — 77у — 1
в целых числах можно решать и так:
-77»+1-=i,+ l7|l+L
60 60
17у+1
60
9z—1 = t
17
г_ 171 + 1 =а+ -‘-+1
9 9 .
— t -|- 1
------- = И,
9
t = 1 — 9и,
значит,
z = 2 — 18п + п = 2 — 17п,
216
у = 6 — 51n -|-1 — 9n = 7 — 60га,
x = 2— 17ra 4-7 — 60ra = 9 — 77ra,
где n — любое целое число.
13. Даны четыре натуральных числа a, b, с, d, таких, что а>Ь>
>c>d.
1°. Доказать, что наибольший общий делитель D(a, b, с, d)
чисел a, b, с, d равен наибольшему общему делителю чисел а', Ь',
с', d, где а', Ь', с' — соответственно остатки от деления чисел а, Ь,
с на d.
2°. Приложить эту теорему для отыскания наибольшего общего
делителя чисел
58 212, 24 948, 21924 и 13608.
Решение. 1°. Отыскание D (a, b, с, d). Из соотношений
а = da 4- а', а' = а — da, b = dfi-\-b', или b'= b — dp, c = dy4~c'» с'=с— dy
следует, что общий делитель чисел a, b, с, d является общим дели-
телем чисел a', b', с', d и обратно.
Значит, D(a, b, с, d) = D(a', b', с', d).
2°. Имеем 58212= 13608-44-3780, 24948 = 13608- 1 4- 11340, 21924= 13608- 14-8316.
Итак, В (58 212, 24948, 21924, 13608) = = £>( 3 780, 11340, 8316, 13608).
Применяя доказанное в пункте 1°, еще раз получим
13608 = 3780-3 4-2268, 11340 = 3780-3, 8316 = 3780 - 2 4-756.
Значит, 0(3780, 11340, 8316, 13608) = = D (3780, 0,756, 2268) = =0(3780, 756, 2268). 217
Наконец,-
3780 = 756 • 5,
2268 = 756-3
я, значит,
£>(3780, 756, 2268)'= 756.
Окончательно: наибольший общий делитель данных чисел ра-
вен 756.
II. Задачи по арифметике (для самостоятельного решения)
I. Доказать, что если а и b — произвольные натуральные числа
(а>6) и а5 и Ь5 оканчиваются на одну и ту же цифру, то а—b де-
лится на 10, а2—Ь2 делится на 20.
2. Найти два целых положительных числа, зная, что их сумма
делится на 3 и что разность их квадратов равна 48.
Ответ. а = 8, 6=4 или а=13, 6=11.
3. Дано целое положительное число а. Существует ли целое
положительное число х, такое, что а+х2 является квадратом цело-
го положительного числа?
Решить задачу в трех случаях:
Га = 37; 2°а = 65; 3°а = 130.
Ответ. Г x=d8;,2° х=32, или х=4; 3° Нет решений.
4. Найти дробь~» равную дроби такую, что наибольший
г п 455
общий делитель D чисел тип равен 5. Найти наименьшее общее
кратное М чисел тип.
Ответ. D(60, 175) = 5, Л4(60, 175) = 2100.
5. Найти дробь, равную дроби
143
220 ’
такую, что наибольший общий делитель числителя и знаменателя
равен 25. Чему в таком случае равно наименьшее общее кратное
числителя и знаменателя?
Ответ. 6500.
500
6. Найти правильную дробь — (/п и п — натуральные числа и
п
т<п), зная, что наибольший общий делитель тип равен 12 и что
/им=5040.
218
7. Найти два натуральных числа, зная, что их наибольший об-
щий делитель равен 17, а разность квадратов равна 1445.
Ответ. 51 и 34. •
8. Г. Найти все общие делители чисел 4512 и 4128.
2°. Найти натуральное число п, такое, что если на него разде-
лить числа 4525 и 4147, то в остатке получатся 13 и 19.
Ответ. 1°. 1, 2, 3, 4, 6, 8, 12, 16, 24, 32, 48, 96.
2°. п = 24, п = 32, п = 48 и п = 96.
9. Дана дробь
п*+1
п (п2 — 1) ’
где п — натуральное число, большее 1. Доказать, что общий дели-
тель числителя и знаменателя является общим делителем чисел
п2—1 и 2 и обратно. Вывести отсюда, что если п — четное, то дробь,
несократима, если п — нечетное, то наибольший общий делитель
числителя и знаменателя равен 2.
10. Обозначим через аир два натуральных числа, а через.
d— общий делитель чисел а+р и ар.
Г. Доказать, что d является также общим делителем чисел
а2 и р2.
2°. Вывести из пункта 1°, что если, а и р взаимно простые, то>
а+р и ар также взаимно простые.
3°. Пусть а и Ь — два натуральных числа, Д — их наибольший
общий делитель, т — их наименьшее общее кратное.
тт а + b т ir »
Доказать, что два числа-- и — взаимно простые. Какой вы-
д д
вод отсюда можно сделать относительно наибольшего общего де-
лителя чисел а+b и т>
4°. Найти два натуральных числа а и Ь, зная их сумму 2704 в
наименьшее общее кратное 106 848.
Ответ. 3°. Наибольший общий делитель чисел а+Ь и т равен
наибольшему общему делителю чисел а и Ь:
D(a + b, m) = D(a, b).
4°. а =1008, 6=1696.
11. Доказать
V20 + 14/2 4- V20—14/2 =4.
12. У 38~+ 17/К = V 9 + 4/К.
13. ;+____________2-Гз _=Т/2.
/2 + /2 + /3 /2—/2 —/3
219
Указание. Решение упрощается, если учесть, что
4±2/3’ = (/'3± I)2.
Уничтожить иррациональность в знаменателе:
1 ж. , > •
14-/2 — /3 1+/24-/4 1—/24-/2
15. 4——.
y'a4-/ft + /f
16. Как геометрически интерпретируются сумма zi+z2 и раз*
тность Z\—z2 двух комплексных чисел Z\ и z2? Какой геометрический
смысл имеет |zi—z2|?
17. Привести к тригонометрической форме число
z = —cos 9 — isin0.
Ответ: cos(0+n) +i sin(0+jt).
18. Привести к тригонометрической форме число
z = 24-/3-Н.
Ответ. 2]/ 24- /3 (cos-^- 4- isin-^0.
19. Комплексные числа г удовлетворяют условию |z|=l. Где
расположены точки, изображающие эти числа z?
Л
20. Комплексные числа z удовлетворяют условию argz = —.
Где расположены точки, изображающие эти числа z?
21. Комплексные числа z удовлетворяют условию argz =—•
Где расположены точки, изображающие эти числа z?
22^ Комплексные числа z удовлетворяют условию |z+ 1 —I =
= ]/2. Где расположены точки, изображающие эти числа z?
23. Комплексные числа z удовлетворяют условию arg z=—
Где расположены точки, изображающие эти числа z?
24. Комплексные числа z удовлетворяют условию |z — i| =
= |z + 2|. Где расположены точки, изображающие эти числа z?
25. Комплексные числа z удовлетворяют условию | z + i |<| z — 2|.
Где расположены точки, изображающие эти числа z?
26. Комплексные числа z удовлетворяют условию|з+ 1 +i |<3.
Где расположены точки, изображающие эти числа z?
27. Найти тригонометрическую форму следующих комплексных
чисел: а) 1 + cos40°+Z sin40°; б) 1—cos40°+z sin40°.
28. Как расположены точки, изображающие корни четвертой
степени из единицы?
220
29. Начертить точки, соответствующие числам 2—i, 3(cos<p+
Ч-i sin <p).
30. Найти геометрические места точек на комплексной плоско-
сти, соответствующих комплексным числам, которые удовлетво-
ряют равенствам: a) |z| =/?, где R— данное вещественное чис-
ло, б) argz=<p, где ф — данный угол, в) arg (z—£1)=ф, где ф —
данный угол и Zi — данное комплексное число.
Указание к задаче «в». Обозначив z—Zi=z', найти гео-
метрическое место точек z', а затем найти z=z'+zi, складывая
z' и Zi, как векторы.
31. Записать число —1—i в тригонометрической форме. Вычис-
лить все три значения V —1 —i.
Ответ. 1/2 (cos—— -|-isin-^-1. Значения 1/"—1—i‘-
\ 4 4 / '
*/~л — 3/7
11[/3-1+Ц/3 + 1)], -L±-[_/3-l-H(l-/3)],
4 4
-^<1-0.
2 V '
32. Среди комплексных чисел г, удовлетворяющих условию
I 2 + 3t | ’С 1,
найти число, имеющее наименьший аргумент <р; 0^лр<2л.
III. Модуль, или абсолютная величина. Графики функций,
связанных с понятием модуля (задачи для самостоятельного
решения)
Построить графики следующих функций.
1. у = |2х —3| + |х + 4|, 9. У = logjjxl,
2. 3. у = |х — 11 — |х + 2|, z/ = x + |x— 11, 10. У = |log_i_|x||, 2
4. */ = |3—х2|, 11. У = |log8*|.
5. у = |х2+ 2х + 3 [ — 1, 12. У = |bg8|x||.
6. у — | х2 — 2х — 31 + х2 -|- 2х, 13. У = 1И-11-
7. i/ = 2|x|, 14. У = I sin X 1,
8. у = |10gj|_X|, 2 15. У = |cosx|.
221
IV. Квадратные уравнения и уравнения, приводящиеся
к квадратным (задачи с решениями)
1. Найти все значения т, при которых уравнение
х2 — 2f/"2x + m+ 1 = 0 (1)
имеет действительные и различные корни.
Определить, сколько корней этого уравнения находится в ин-
тервале (О,/2) в зависимости от т.
Решение.
А = (]/'2’)а —(m+ 1)= 1— т.
Корни Xi и х2 будут действительные и различные (xi<x2) тогда
и только тогда, когда
т<1.
Пусть это условие, выполнено, тогда один из корней данного
уравнения больше, а другой меньше У2, так как сумма их рав-
на 2)^2.
Итак,
хх У2 х%*
Значит, в интервал (0, )/2) может попасть только один мень-
ший корень. Ясно, что Xi находится в интервале (0; У 2), если
он положителен, т. е. одного знака с х2.
Но так как
хх+х2 = 2/‘2>0,
ххх2 = т 4- 1,
то оба корня X] и х2 положительны тогда и только тогда, когда
т+1>0, т. е. т>—1. _
Таким образом, в интервале (0; У2) может находиться толь-
ко один корень Xi уравнения (1); все значения т, при которых это
будет иметь место, образуют интервал
— 1 1.
Корень Xi, попадающий в интервал (0,У2), является мень-
шим корнем уравнения (1):
= У 2 — V 1—т.
2. Найти все значения а из сегмента (0, 2л], при которых корни
уравнения х2—2У2х+ l+2sina=0 действительны и различны.
Определить, сколько корней этого'уравнения находится в ин-
тервале (0, ]/2) в зависимости от значений а, лежащих на сег-
менте (0, 2л].
222
Решение. На оснований предыдущей задачи в интервале
(О, ]^2) будет находиться не более одного корня данного урав-
нения. Все значения а, при которых в этот интервал попадает один
корень, удовлетворяют неравенствам
— 1 <2sina< 1.
л > л 5л 7л 11л о
Отсюда 0 < а < —, -----< а <-----, ---< а < 2л.
6 6 6 6
Этот корень х± = У 2 — У1 — 2 siq а.
3. 1°. Решить и исследовать уравнение
2ы2(1 — cost) — 2usint + 1 = 0.
Вычислить в зависимости от значения sin-^-модуль и аргумент
каждого из корней.
2°. Во всем последующем предполагается, что t принадлежит
интервалу 0<t<2n. Обозначим через и' тот из корней данного
уравнения, который имеет аргумент—. Вычислить z = u —квад-
рат этого корня и придать этому выражению вид x+iiy (х и у дей-
ствительны) . Пусть г — модуль г, а 6 — аргумент z. Доказать, что
г=х+4-.
2
3°. Будем рассматривать t как время. Рассмотрим движущую-
ся точку /и(х, у), являющуюся изображением комплексного чис-
ла z. Какова будет траектория (Т) движущейся точки /и? В какой
момент времени точка т(х, у) будет занимать положение, для
которого X=~Y? Составить уравнение траектории (Г).
Решение. Г. Вычисляем дискриминант данного уравнения:
d = sin2t— 2(1 —cost) = —4sin4 -у.
Если cost=l, т. е. t=2kn, где k принимает все целые значения,
то в данном уравнении коэффициенты при и2 и и обращаются в
нуль, но свободный член 1=#0 — уравнение не имеет корней. Если
же costal, то sin — =#0; решая данное уравнение, будем иметь
t t t t . t t
sint±2tsin2— 2 sin —cos— + 2» sin2— cos— ±tsin—
u _ 2 _ 2 2 2 _ 2 2
2(1 —cost) . * t
4 sin2 2 sin —
2
223
Модуль и аргумент каждого решения. Рассмотрим два случая:
a) sin-^->0. Тогда оба корня имеют модуль
1
р = —г-
2sinT
Один из корней:
и' = ------( cos — + i sin — )
t \ 2 2 J
2sin —
2
имеет аргумент
— + 2ka,
2
где k принимает все целые значения.
Другой корень и", который мы перепишем в виде
= —Ч- [“’(—?)+ isin (“ т) ]'
2 sin —
2
имеет аргумент
---— + 2Ал,
2
где k принимает все целые значения.
б) sin-^-<0. В этом случае оба корня имеют модуль, равный
1
р=-—
2sinT
Переписывая первый корень в виде
и' -------!--Г cosf— + лЛ + i sin f — + л
2 sin —
2
заключаем, что аргумент и':
— + л + 2&л,
2
где k принимает все целые значения.
224
Второй корень
// 1 Г f
--------------- cos ( л —
2 sin —
2
л —
имеет аргумент
л----у + 2£л,
где k принимает все целые значения.
2°. Случай 0 < t < 2л. В этом случае 0 < — < л, значит, sin-y>0.
Корень данного уравнения, имеющий аргумент таков:
, 1 f t ... t \
и = --------- COS------hl Sin--- ).
t \ 2 2 /
2 sin —
Отсюда
/2
z = и
—у (cos t + i sin /),
4 sin2 —
2
следовательно,
-----!-y, argz = /.
4sin2 —
2
Перепишем выражение для z в следующем виде:
sin?
4 sin2y
cos t
z =-------------
t
4 sin2 —
2
Действительная часть числа z\
1 — 2 sin2 —
2
cos t
X = -------------
4 sin2 —
2
4 sin2 —
2
1
t
4sin2 —
2
1
---- = г
2
1
2 *
Отсюда
r = x + —.
2
3°. Траектория (T) точки m. Так как г = ]/ x2 + у2 и г = х +
1
2 ‘
2
8 Зак. 351
225
Возводя в квадрат обе части этого уравнения, получим
X2 + у2 =s X2+ х
4
или
это уравнение параболы (рис. 68). Важно
отметить, что, производя выкладки в обрат-
ном порядке, получим
Но так как
1
2
то знак модуля можно опустить и получим
2
С другой стороны, ясно, что при изменении t от 0 до 2л точка
т(х, у) опишет всю параболу у2 = * + ~ («против часовой стрел-
ки»). Таким образом, траектория (Т) точки т(х, у) —вся парабо-
ла у2 = .
V. Квадратные уравнения и уравнения, приводящиеся
к квадратным (задачи для самостоятельного решения)
1. Дано квадратное уравнение
(т— 1)х2— (2m— 1)х + т + 5 = 0.
1°. Найти все значения т, при которых это уравнение имеет
действительные корни Xi и х2.
2°. Предполагая, что т — любое действительное число, не рав-
ное единице, найти такое число а, чтобы произведение
(xi—a) (хз—а) не зависело от т.
Ответ. 1°. т<-^-.
20
2°. Указание. Дробно-линейная функция у — ах-~ — не за-
ух + д
висит от х
226
тогда и только тогда, когда аб—₽у=0.
Ответ, а = 6.
2. Не решая уравнение
/(х) = (х—1)(х —2) + (х —2)(х+1)+ (х+1)(х—1),
определить расположение корней этого уравнения относительно
— 1, 1 и 2.
Указание. f(—1)=6, f(l) =—2, f(2)=3, следовательно,
— 1<х1<1<х2<2.
3. Решить уравнение
У2* — 4m • 7* + 2m + 2 = 0.
Ответ. 1) Если т<—1, то уравнение имеет один корень:
х = log, (2т + У 4т2 — 2т — 2).
2) Если —1^т<1, то уравнение корней не имеет.
3) Если т>1, то уравнение имеет два корня:
*1,2 = log, (2т + У 4т2— 2т — 2).
При т=1 уравнение имеет один корень:
х = log, 2.
4. Найти все значения т, при которых корни Xi й х2 уравнения
тх2 — (т — 1) х -j- 2m — 1 = 0, где т + 0,
действительны и различны; предполагая, что т принимает только
такие значения, наити /и, при котором Xi +х2=4.
1— 2/2^ 1+2/2 2,2 л
Ответ. -----— <т<—!—-—, Xi + х2 = 4 только при т =
7 7
— —-— (Xi и х2 предполагаются действительными).
/7
5. Найти все значения /и, при которых уравнение
3mx2 — (7т + 1)х + 2т + 1 = 0 (1)
имеет действительные корни. Исследовать знаки корней.
Ответ. Если т<------Уравнение имеет два положительных
действительных корня х{ и х2 (которые мы получим, решив квад-
1 5
ратное уравнение (1)). При т—-----корни таковы: Х] = 0, х2= —.
2 3
Если — — <т<0, уравнение имеет два действительных корня раз-
ных знаков. Если т = 0, уравнение имеет один корень х=1. Если
^>0, то уравнение имеет два положительных корня.
8*
227
6. Решить уравнение
(1 — tn) sln2x — 2 (т 4-1 )cosx + Зт 4 4 = О,
где т—действительный параметр.
Ответ. 1°. Если т<_*— 3, уравнение не имеет решений.
2°. Если т = — 3, то х = 2£л + —.
3
3°. Если — 3 < /и < — 2, то
X = 2kn ± arc cos Д»+1 ± /.
tn — 1
4°. Еслит = — 2, то х = 2kn ± arc cos —.
з
5°. Если — 2</п<-----—, то
5
X = 2Ы ± arccos
т *«• 1
6°. Если т>----—, то уравнение не имеет решений.
5
7. 1°. Дано квадратное уравнение
/их2 4- 2х — 2т = 0, (1)
в котором т — действительный параметр, причем /п=#0. Найти
все значения т, при которых уравнение (1) имеет и притом толь-
ко один корень, заключенный между —1 и 1.
2°. Дано уравнение
mcos2x-4 4cosx — Зт — 0, (2)
в котором т — действительный параметр, а х — неизвестное.
Найти все значения т, при которых уравнение (2) имеет и при-
том только один корень, заключенный в интервале (0, л)?
2зт
3°. При каком значении т уравнение (2) имеет корень—?
О
Ответ. 1°. — 2<т<2. 2°. — 2<т<2. 3°. /и = —у. ,
8. Дано квадратное уравнение
(tn — 1) х2 — 2tnx + 2/п + 3 = 0, tn #= 1.
Найти все значения tn, при которых один из корней этого урав- ,
нения будет меньше 1, а другой больше 1, но меньше 2.
Ответ —2<т<—.
2
228
9. Решить уравнение
25х — (т+ 1)5* + 2(/п — 1) = О,
где т — действительный параметр, а х— неизвестное. Рассмот-
реть случай т=0.
Ответ. Если т>\, то уравнение имеет два корня:
x1 = log5(/n—1) и x2=logo2 (при т = 3 эти корни равны между со-
бой). Если /п^1, то уравнение имеет один корень x=logs2.
10. 1°. Составить квадратное уравнение, корни которого
х'=т + 3, х"=х'2—б-^+Ю, где т — действительный параметр.
2°. При каком условии полученное уравнение
а) имеет равные корни;
б) имеет корни х' и х", такие, что х"——х';
3°. имеет корень, равный нулю.
Ограничиться действительными корнями.
Ответ. 1°. х2 — (т2 + т -|- 4) х + (т 3) (т2 + 1) = 0.
2°. а) т = — 1, х' = х" = 2; т = 2, х’ = х" — 5; б)х' х"#:0.
3°. m = — 3, х' = 0, х" = 10.
11. Найти все значения а, при которых корни уравнения
(а — 2) х2 — 2ах + 2а — 3 = 0
действительны. Определить знаки корней.
12. Доказать, что корни уравнения
—+ -~ = 1,
X X — 1
где а и b — вещественные числа и а2+&2=/=0, действительны и раз-
личны.
13. Пусть Xi и х2— корни уравнения х2—ах+а—1=0, где а—
вещественное число. Найти значение а, при котором величина
х?+х2 будет наименьшей.
Указание. Выразить х?+х2 через коэффициенты трехчлена,
пользуясь теоремой Виета, и найти минимум квадратного трехчле-
на относительно а:
х21 + х2 = (хх + х2)2 — 2ххх2.
14. Доказать, что если хх и х2— корни уравнения х2 — сх— с =
= 0, где с — действительное число, не равное нулю, то х^-(-х|—
— х^х|> 0.
15. Пусть хх и х2 — корни уравнения х2 + рх + <? = 0. Выразить
через р и q следующие выражения:
х24-х2; х’4-хЗ; xf + x|; х^ + х^ —L- + —L-.
*1 4
229
Указание. Каждое из этих выражении нужно выразить че-
рез Х1+Х2 И Х1*2-
16. Найти все решения уравнений x6+5x®—24=0 и х6+
+ (с—Ь) х3—Ьс=О, где b и с — действительные числа.
17. Числа аир (а=#Р) являются корнями уравнения
х3 + рх + q = О
и удовлетворяют равенству аР + а+р=0. Найти соотношение меж
ду р и q и выразить третий корень через аир.
18. Решить уравнение
173x4-1 _ 2 К 174х+2 + 17Х+* = 0.
Ответ. х=0.
19. Решить уравнение
(х + а)4 + (х — а)4 = Ь,
где а и b — действительные параметры.
VI. Системы рациональных уравнений
(задачи для самостоятельного решения)
1. Исследовать систему уравне-
ний
ах — by = 0,
а2х— by = ab.
2. Исследовать систему уравне-
ний
ах— у = Ь,
х—ау = Ь.
Решить систему уравнений
3. х + у — а, х4 + ^ = а4.
4. ху + xz = а2, yz + ух = Ь2,
гх + zy = с2.
5. х2 + ху -|- 4xz — 4z2 = 0,
У2 + ху + 4уг — 8z2 = О,
xyz = 8.
6. (х + у)2 —z2 = 4,
(y + z)2 —х2 = 2,
(z + x)2-y2 = 3. .
7. xsy + tfx = (x + y)2,
x*y + yix = — (x + y)3.
□
8. xy + 24= —,
У
а У3
x
9. 2x2 + y2 + z2 = 9 + yz,
x2 + 2y2 + z2 = 6 + zx,
x2 + y2 + 2z2 = 3 + xy.
10. x + z/+2= 1,
xy + yz + zx = — 4,
x8 + y3 + z3 = 1.
11. xyz + xz2 = 2,
xy + 2xz = —-z,
х2уг — — 15.
230
12. -^— + ^±^=2,
х + 2у ху
ху _|_ х—2у _ 4
х — 2у ху
13. X2 + 2z/Z=l,
у2— 2zx = 2,
z2 + 2xy = 1.
14. (x + y)(x-\-z) = x,
(у + г)(у + х) = у,
(z + x) (z + У) = z.
15. (л8 + l)(jf + 1) = 18,
xy + x + у = 5.
16. x + y = Z,
y2 -|-Z2 = 13x2,
2(x34-z3) - 7г/3.
17. x — 2z/ + 3z = 9,
x2 + 4y2 + 9z2 = 189,
3xz = 4z/2.
18. x-\-y=\,
xz + yt = 2,
xz2 + yt2 = 5,
xz3 + yf3 = 14.
19. х* + у* = 17(x + y)2,
xy = 2(x + y).
20. x2 + if = x + y,
х* + У = -^(х + у)2.
21.
x2 + by2 4- 4z2 + 4xy-j-4yz=125,
x2 + 3y2 — 4za 4- 4xy — 4yz = 75,
x + y + z = 8.
22. 1°. -Найти действительные решения системы
х® — 15x4z/2 4- ISx2!/4 — уе = 0, (1)
6х®1/ — 20x?if 4- бхг/8 = 0. (2)
Доказать, что решение системы (1), (2) равносильно решению
уравнения
Ze= 1,
где z=x+yi.
Указан и’е. 2xy (Зх4 — 10x2y2 4- Зг/4) = 2ху (х2 — 3z/2) (Зх2 — у2) =
= 2ху(х 4- У/3)(х- у/3)(хУЗ 4- У) (х УЗ-у).
Ответ. Шесть решений: (1, 0), (— 1,0),
(___L (_______________L У3 \
\ 2 ’ 2 /’ \ 2 ’ 2 )'
23. Найти значения а, при которых система
х2 4- У* 4- 2х < 1,
х— г/4- а = О
имеет единственное действительное решение. -
Ответ. 1) а=3, при этом х=—2, «/=1; 2) а=—1, при этом
х=о, у=—1.
231
VII. Иррациональные уравнения и системы
(задачи для самостоятельного решения)
1. Решить уравнение
/x-2+]/2x-5+Kx +2 +3/27^5 = 7/2.
Ответ. х=15.
2. Решить уравнение
/х — а + х = О,
где а — действительный параметр.
Л г- 1 —/1—4а
Ответ. Если а<0, то х =----—------.
Если а=0, то х=0. Если а>0, то уравнение не имеет корней.
3. Решить уравнение
/х|х—1 \ = т,
где т — действительный параметр.
Ответ. Если/п<0, то уравнение не имеет корней. Если
то уравнение имеет три корня: два из них — это корни
уравнения
х2 — х + тг = О,
третий — это положительный корень уравнения
х2 — х — /п2 = 0.
„ . 1
Если т^>~, то уравнение имеет только один корень — это
положительный корень уравнения
х2 — х — /п2 = 0.
4. Решить уравнение
/х2 — 2ах — b —х,
где а и b — действительные параметры.
Ответ. 1) Если 6>0,или &<0, а не входит в полу-
Л Ь 1
интервал ^b, —j, то решении нет.
2) Если а = Ь = 0, то решением является любое неположитель-
ное число х.
232
3) Если а=И=6 = 0 или &>0, а не входит в полуинтервал^—, &j
или, наконец, если 6<0,&<а < —, то уравнение имеет единствен-
ный корень
62
х =--------.
2(Ь —а)
5. Решить систему уравнений
Vx2 + y2 + V^y = 2 /2,
6. Решить систему уравнений
/х + у | / х — у = 5
х—у V х + у 2 ’
х2 + у2 = 34.
VIII. Неравенства (задачи с решениями)
1. Доказать, что
1° Если х + у — а, то х2 + У2 >-у-«
2° Если х + у + z = а, то х2 4- у2 4- г2 —.
3
3°. Обобщить.
Решение. Г. (х + у)2 + (х — у)2 = 2(х2 4- у2).
Отсюда
2 1 2 (X 4“ У)2 Ч2
Х2 + У2< ,
причем знак равенства имеет место тогда и только тогда, когда
м а
х — у = 0, т. е. при х = у = —.
2°. х2 4- + г2 = 4- 1(х 4- у 4- z)2 4- (у - z)2 + (г - х)2 + (х - у)2].
О
Отсюда
Х2+ 2 + г2> (х + у + г?
3 3
причем знак равенства имеет место тогда и только тогда, когда
а
у 3
3°. Первое обобщение. Пусть
Х1 + Х2 + • • • + Хп ~ а'
233
Из тождества х^ + х| + ... + х2 = -i- К-Ч + *,+ ...+ х„)2 +
+ (хх — х2)2 + (хх — х3)2 + • • • + (*1 — хп)2 + (ха — х3)2 +
+ (х2 — х4)а + ... + (х2 —х„)2 + ... + (x„_i — х„)2]
находим
х*+х|+ ... +ха>-^-,
причем знак равенства имеет место тогда и только тогда, когда
а
Х1 — х2 — • • • — хп ~ •
п
Второе обобщение (из тождеств Лагранжа).
(а2 + &2) (х2 + у2) = (ах + by)2 + (ay — bx)2,
(а2 4- b2 + с2) (х2 + у2 + z2) = (ax-\-by + сг)2 +
+ (Ьх — ау)2 (су—bz)2 + (az — сх)2
(а2+а2+ ... 4-а2)(х2 + х24-... +х2) = (а1х14-а2х2+ ...о„х„)2 +
+ (а^ — ахх2)2 + (а3хг — ахх3)2 + • • • + (а„хх — а^)2 +
+...............................................+
+ • • ..........................+(anxn-i — an-1xn)2
следует, что если
ах + by «= с, то х2 + t/2 > —-—;
если
ах + by -|- сг = d,
то
и вообще, если
+ а2х2 + ... + апхп = d,
го
Х1 + Х2 + ’ ’ * +Хя “ _2 Т fl2 1 I 2 ’
+ Я2 + • • • "Г ап
причем знак равенства имеет место тогда и только тогда, когда
: х2 : • • • ’ хп ~ ai ’ ’• • • • ’ ап'
Замечание. Полагая а\=а2—... =ап = \, получим то, что
указано в первом обобщении.
2. Решить неравенство
у 1 — х2 < а — х,
где а — действительный параметр.____
Решение. Уравнение у—У 1 —х2 является уравнением полу-
окружности радиуса 1 с центром в начале координат, граничными
точками которой являются точки Л(—1, 0), В(0, 1), и которая про-
ходит через точку С(0, 1) (рис. 69).
Уравнение у=а—х есть уравнение прямой, проходящей через
точки (а, 0) и (0, а).
1°. Если а<—1, то неравенство решений не имеет.
2е. Если а=—1, то неравенство также решений не имеет.
3°. Если —1<а<1, то, решая совместно систему
у = |Л — х2, у = а — х,
или
+ У* = 1, х + у = а, у>0,
235
получим
(л + z/)2 — 2ху = 1,
х + у = а,
У>0;
Х +у = а,
У>0',
V —аХ+ а2-1 =0;
2
пусть X — отрицательный корень этого уравнения, т. е.
а —/2=^
Все решения неравенства в этом случае (3°):
а—/2—
2
4°. Если а=1, то все решения неравенства
— 1 <х< 1.
5°. Если 1 <а< J/2, то прямая у = а — х пересекает полуокруж-
-I /-т-------л а + У 2 — cP
ность у = У 1—х2 в двух точках, абсциссы которых -------.
Все решения данного неравенства в этом случае:
— 1<х< а +
6°. Если то решением является любое число, кроме
1
X = --т=-.
7°. Если а^>У2, то решением является любое число.
Замечание. Задача может быть решена и чисто аналити-
чески.
IX. Неравенства (задачи для самостоятельного решения)
1. Решить неравенство
]/х —2>х —4.
Ответ.
2 <х<6.
236
2. Найти наименьшее значение функции
у — \х— а | + | х— Ь| + |х— с| + |х — d|,
где a<.b<c<d. При каких значениях х эта функция принимает
наименьшее значение?
Ответ. z/min=d+c—b—а при всех х, таких, что &^х<с.
3. Доказать, что если п — натуральное число, большее 1, то
( "+1 у <п! < ( ” + 1 у
4. Решить неравенство
__________________________-> —
а х а
где а — действительный параметр, не равный нулю.
5. Найти области определения функций:
5°. У = \/ 1
J X2
6°. у= lglg2lgx,
7°. Уcos (sin х) —sin (cos х).
Ответ: —оо <х4" А.
2°. у = Ух + У— х,
3°. у — ]/ 1gsin г
4°. у = Vlogj sinx,
"2
6. Решить неравенство
____________________[
2х2 — 11 х-J- 12 2а-2-9x4-7 ’
7. Решить неравенство
/а2 — х2 4-2х > О,
где а — действительный параметр.
X. Графики функций (задачи с решениями)
1. Исследовать функцию
у = 8х* — 8х2 4- 1
на сегменте [—1, 1] и построить ее график.
1 °. _Доказать, что эта функция возрастающая на сегментах
Г /2 П1 г /2 ,1 х г , /2 1
I----—, 0 и -х-—, 1 и убывающая на сегментах —1,---------—
[1/^2 1
О, —— , Найти ее наибольшее и наименьшее значения на этом
2 J
сегменте. Построить ее график.
237
Решение. Полагая х — cos г, получим
8cos*z — 8 cos2 г 4- 1 = cos4z.
Считая, что 0<г<л, заключаем: 0<4г<4л.
Функция у = cos 4г при изменении г на сегменте 0<’г-<л обла-
дает следующими свойствами: на сегменте
она убывает от
1 до — 1, иначе (х=созг)на сегменте^-^—
— 1 до 1 и т. д.
1 она возрастает от
Из выражения z/=cos4z ясно также, что наименьшее значение
этой функции равно—1 (и оно достигается на сегменте 0 <г-<л
два раза) а наибольшее ее значение равно 1 (рис. 70).
Сегменты, на которых возрастает и убывает данная функция,
можно найти и иначе: полагая х2=н, получим
у = 8м2 — 8и 4-1,
причем в силу того, что —1^х-С1, имеем
Функция у—8и2—8и +1 убывает в полуинтервале —оо, и
возрастает в полуинтервале Ч-оо). Но так как значения и
ограничены 0^и<1, то ограничимся следующими выводами:
функция
у = 8и2 — 8и + 1
убывает на сегменте |о, и возрастает на сегменте lj.
Так как и=х2 и на сегменте [—1, 0] функция и=х2— убывающая,
238
а на сегменте [О, 1] — возрастающая, то мы приходим к тем же
выводам.
2. Исследовать функцию
z/=_2£±₽__
* *+р+1
(р — параметр) на возрастание и убывание.
Решение. Поделив числитель на' знаменатель, преобразуем
У к виду
Эта функция определена при всех значениях х#=—р—I.
В каждом из интервалов (—оо, —р—1) и (—р—1, 4-оо) функция
х+р + 1 возрастающая, а , *,— убывающая. Значит, если р>—2,
х + рф 1
то данная функция возрастающая в каждом из интервалов
(—оо, —р—1), (—р—1, +оо), а если р<—2, то убывающая. При
р=—2 у = 2 при всех х^= 1.
3. Рассмотрим следующий многочлен относительно х, коэффи-
циенты которого являются функциями параметра т:
у = (т— 1)х2Ч- (2/п— 3)х — 3m 4* 2.
Для каждого значения т#=1 это уравнение является уравне-
нием параболы, которую мы обозначим через П,п.
Г. Найти т, если известно, что вершины всех парабол Пт ле-
жат на прямой x=h, параллельной оси Оу (h — данное число, не
равное —1).
2°. Доказать, что все параболы Пт проходят через две фикси-
рованные точки.
3°. Доказать, исходя'из результата 2°, что все параболы Пт пе-
ресекают ось Ох в действительных точках. Доказать то же поло-
жение аналитически. Определить положение числа Х=—1 относи-
тельно корней уравнения у=0 (у — данная функция).
Ответы иуказания.
г./га = а±1.
2ft 4-2
2°. Перепишем данное уравнение тагб:
У + х2 + Зх — 2 = т (х2 4- 2х — 3).
Для того чтобы это уравнение выполнялось при всех значениях
т, необходимо и достаточно, чтобы х и у удовлетворяли уравне-
ниям
х2Ч- 2х — 3 = 0.
у4-х24-3х — 2 = 0
239
Решая эту систему, найдем две точки Р(—3, 2) и Q(l, —2).
Заметим, что при m—i данное уравнение принимает вид у — —х—1,
это уравнение прямой PQ.
3°. Так как ординаты точек Р и Q имеют разные знаки, то все
параболы Пт (и прямая П1) пересекают ось Ох в действительных
точках.
Аналитическое решение:
А = (2/п — З)2 —4(/и—1)(—Зт +2) = 16/и2 —32/и + 17>0
при всех действительных значениях т.
Переписывая уравнение у = 0 в виде
, . 2т— 3 . —3m+ 2 л
X2 Н-----— X + ----= О
т — 1 т — 1
и подставляя в левую часть х=%=—1, получим число —4<0. Зна-
чит, число %=—1 лежит между корнями любого из уравнений у = 0
(независимо от т).
4. Дано уравнение у=ах2 параболы (Р) (а>0). Проведем про-
извольную прямую (£>), Перпендикулярную оси параболы и пере-
секающую ось Оу в точке В (О, Ь). Пусть М — переменная точка
параболы, а (ЛГ) — окружность с центром М, касающаяся пря-
мой (D).
Г. Доказать, что на оси параболы, т. е. в данном случае на
оси Оу, существует точка К, обладающая следующим свойством:
длина KS отрезка касательной, проведенной из точки К, к окруж-
ности (Л4) (S — точка прикосновения), постоянна для всех окруж-
ностей (М).
2°. Как надо выбрать прямую (£>) для того, чтобы все окруж-
ности (Л4) проходили через одну и ту же точку?
Решение. 1°. Возьмем на оси Оу пока произвольную точ-
ку К с координатами х=0, y=k. Тогда, обозначая координаты
точки М через х и у, будем иметь (рис. 71).
KS2 - КМ2 — MS2 = КМ2 - МТ2 = x2 + (y — k)2 — (b — y)2 =
= x2 + 2(b—k)y + k2—b2,
и так как у=ах2, то
KS2 = -У- + 2(6 - k) у + k2 - b2 = (— + 26 — 2k)y + k2-b2.
а \ а /
Это выражение не зависит от положения точки М на параболе
тогда и только тогда, когда коэффициент при у равен нулю:
— + 26 - 2k = О,
а
откуда
240
При этом
KS2 = b2 4- — + —--Ь2 - 1+4а6
а 4а* 4а2
Отсюда следует, что задача возможна в случае
1 + 4а6>0,
г. е. в случае
6>-4-
4а
2°. Для каждой окружности (Л1), обладающей тем свойством,
1 -4-4аЬ
что KS2=——-----, существует ей симметричная относительно оси
4а2
параболы, обладающая, конечно, тем же свойством. Поэтому если
все окружности (Л!) проходят через одну и ту же точку, то она
должна лежать на оси параболы. Пусть С (0, с) —та фиксирован-
ная точка оси параболы, через которую проходят все окружности
(Л4). Тогда.
МС = МТ, или МС2 = МТ2,
241
или
х2 + (у — с)г = (у — Ь)2,
или, так как у = ах2:
х2 (1 — 2ас 4- 2аЬ) + с2 — Ь2 = 0.
соотношение должно выполняться
Это
что возможно только в случае
при всех значениях х,
1 - 2ас +{2аЬ = 0, с2- Ь2 = 0,
,или
2а (с — b) = 1, (с + 6)(с — &) = 0.
Из первого соотношения следует,
что с—Ь=£0, значит, с+Ь = О, и мы
находим
— 4ab = 1, b =----—, с = —.
4а 4а
Таким образом, если прямая (D) перпендикулярна оси парабо-
лы у —ах2 и пересекает ее в точке ^0,--—то все окружности
(7И) проходят через точку К ^0, В этом случае прямая (О)
называется директрисой параболы, а точка К — фокусом пара-
болы (рис. 72).
5. Доказать, что функция
х
1 + X2
в полуинтервалах (—оо, —1] и [1, +об) убывающая, а на сегмен-
те [—1, 1] возрастающая. __
Доказать, что в интервале (—оо, — р^З] эта функция обладает
следующим свойством: пусть Х\ и х2 — любые числа из этого ин-
тервала (xi=#x2); тогда
*1 , Х2 X! + х2
_х1 + 1 4 + 1 2 ,!.
2 Ц. (^+^‘ * 7
Доказать, что тем же свойством эта функция обладает на сег-
менте [O,/3J. На сегменте же [—р^З, 0] и на полусегменте
242
[]f 3, +oo) неравенство (1) заменяется на противоположное.
Дать всем этим фактам геометрическое истолкование и по-
строить график функции
у 14- *2 ’
6. Рассмотрим уравнение
2хи2— 2(х Ц- у — 3)и + у-\- 1 = 0, (1)
в котором и — неизвестное, а х и у — координаты переменной
точки М плоскости.
1°. Для каких положений точки М(х, у) уравнение (1) имеет
только один простой (не кратный) корень?
2°. Построить линию, для всех точек которой и только для та-
ких точек уравнение (1) имеет двойной корень.
Найти множество всех точек М(х, у), для координат которых
уравнение (1) имеет действительные и различные корни.
3°. Найти геометрическое место точек М(х, у), для каждой из
которых уравнение (1) имеет корень, равный нулю.
4°. Найти геометрическое место точек М(х, у), для каждой из
которых уравнение (1) имеет действительные корни противопо-
ложных знаков.
5°. Найти геометрическое место точек М (х, у), лежащих в пер-
вой четверти (х>0, у>0), для каждой из которых уравнение (1)
имеет действительные корни и исследовать знак этих корней в за-
висимости от положения точки М.
Решение. 1°. Уравнение (1) имеет только один простой ко-
рень, если коэффициент при и2 равен нулю, но коэффициент при и
не равен нулю, т. е.
х — 0,
значит, геометрическое место таких точек М состоит из всех точек
оси Оу, кроме точки (0, 3).
2°. Приравнивая нулю дискриминант, получим
(х + у-3)2-2х(у + 1) = О,
или
(д _ 4)2+ (0-3)2 = 42.
Это уравнение окружности (7) с центром в точке 7 (4,3) и ра-
диусом г=4. Эта окружность касается оси Оу в точке Л (0, 3), ко-
торая должна быть исключена из множества всех точек М окруж-
ности (7), так как при х=0, у=3 уравнение (1) не имеет корней.
Для того чтобы уравнение (1) имело действительные и различ-
ные корни, необходимо и достаточно, чтобы дискриминант данно-
243
го уравнения был положителен (и было выполнено неравенство
*¥=0):
(x-f-i/ —З)2 —2х(у4-1)>0,
или
(х-4)2 + («/-3)2>42.
Геометрическим местом точек М являются все точки плоскости,
лежащие вне окружности (/), за исключением всех точек оси Оу
(х¥=0) (рис. 73).
3°. Геометрическое место точек Л4(х, у), для которых данное
уравнение имеет корень, равный нулю, определяется из условия
«/+1=0. Это прямая, параллельная оси Ох
и пересекающая ось Оу в точке В (0, —1)
(точка В не исключается!).
4°. Сумма корней уравнения (1) равна
нулю, если
х + 0, х + у — 3 = 0.
Уравнение х+«/—3=0 есть уравнение
прямой А Т, проходящей через точки
Д(0, —3) и Т (3,0). Но так как по уело-
вию корни должны быть действительны, то
следует взять только часть этой прямой,
лежащую вне окружности (/) (если точка
Рис. 73 М совпадает с точкой Т (3,0), то уравнение
имеет двойной корень, равный нулю).
5°. Геометрическим местом точки М являются все точки, лежа-
щие в первой четверти и вне окружности (/). Произведение и сум-
ма корней в этом случае таковы:
p = -E±L, s== Л+у~3
2х х
Так как по условию х>0, «/>0, то р>0, значит, корни одинако-
вых знаков.
Выражениеs = ——отрицательно или положительно, если
соответственно «/<3—х или «/>3—х. Но в случае «/<3—х точка
М(х, у) лежит ниже прямой АТ, а в случае у>3—х — выше ее.
Значит, окончательно, геометрическое место точек М(х, у), лежа-
щих в первой четверти, для каждой из которых уравнение (1)
имеет отрицательные корни, является областью, ограниченной от-
резками ОН, О А и дугой АН окружности (/). Для всех остальных
положений точки М (х, у), лежащей в первой четверти и вне окруж-
ности (/), данное уравнение имеет положительные корни.
244
7. Дана функция
(1)
х2 4- Зх 4~ 4m
У х24-(5m4* 1)х4*3 ’
где т — действительный параметр. Доказать, что при любом т
график этой функции проходит через 3 фиксированные точки.
Решение. Возьмем произвольную точку М (хо, уо) и найдем
ту из кривых (1), которая проходит через точку Л4(хо, уо). Иначе
говоря, найдем то значение параметра т, при котором график
функции (1) проходит через точку ЛГ(х0, у0). Для этого, считая х0
и уо известными, надо решить уравнение (1) относительно т.
Имеем
Уо 1Ло + (5/п + 0*0 + 3] = хо + Зхо + 4т>
или
tn (5х0у0 — 4) 4- у0 (х2 4- х0 4- 3) — (х2 4- Зх0) = 0. (2)
Если 5хоу0—4=/=0, т. е. точка М (х.о, у0) не лежит на гиперболе
4
ху = то уравнение (2) является уравнением первой степени
5
относительно т и потому имеет только одно решение.
4
Значит, если точка М (х0, уо) не лежит на гиперболе ху = —,
5
то через нее проходит только одна кривая (1), соответствующая
единственному значению т, найденному из уравнения (2).
Поэтому найдем точки пересечения гиперболы ху = ~ с ли-
ниями (1), иначе говоря, решим систему
х2 4~ Зх 4~ 4m
x24-(5m4~ 1)х4-3 ’
4
ху = -.
У =
Имеем
4
5х
х2 4~ Зх 4~ 4т
х24-(5т4- 1)х4-3 ’
или
4х2 4- 4(5m 4-1)х4-12 = 5х3+ 15х2 4- 20/пх,
бх3 4- 11х2 — 4х — 12 = 0;
одним
Далее,
„ , 4
из корней этого уравнения является Xi = l, тогда уг — —
. 5
5х34- Их2 — 4х— 12 = (х— 1) (5х2 -|- 16x4- 12).
245
Решая уравнение
5Х2+ 16х+ 12 = 0,
получим
у __ __________9 и________— • х —___— и —_____—
•*2 - 2- Уг - 5 ’ *з - 5 ’ У» “ з •
Итак, графики всех данных функций проходят через три точки:
-и/!, f). м,(-2; - y} *»•(—Ь —
Все они расположены на гиперболе ху = —, причем точка All
5
лежит на одной ветви, проходящей в первой четверти, а точки Мг
и М3 — на другой ветви, проходящей в третьей четверти.
XI. Графики функций (задачи для самостоятельного решения)
1. Построить график функции
2. Построить график функции
X— 1
У =-------
|х+П
3. Обозначим через (Нт) график функции
(2т — 1)х + т
х — т
где т—действительный параметр. Доказать, что все линии (Нт) —
гиперболы и все проходят через одну и ту же фиксированную
точку.
Ответ. Все линии проходят через точку Д(0, 1).
4. Доказать, что функция
у = х3 — Зх + 2
возрастает на полуинтервалах (—оо, —1] и [1, +оо) и убывает на
сегменте [—1, 1].
Доказать, что для двух любых различных значений Xi и Хз из
полуинтервала (—оо, 0] имеем
х, — Зхд -|- 2 + х| — Зх2 4- 2 . / xt4~x2 \з_g xt-\-x2 . g
а для двух любых различных значений Х\ и х2 из полуинтервала
[0, 4-оо) имеет место противоположное неравенство.
Построить график этой функции.
246
5. Найти на плоскости множество всех точек М (х, у), коорди-
наты которых удовлетворяют уравнению
Указание. Преобразуем данное уравнение последовательно:
УЧу2—1) —х2(х2—1) = 0,
у4 —х4 —(t/2 —х2) = О,
(у2 - х2)(х2 + у2 - 1) = О,
(У — *) (У + *) (х2 + У2 — О = °-
Отсюда следует, что множество всех точек М, координаты х и у
которых удовлетворяют данному уравнению, состоит из всех точек
биссектрис
у = х и у=— х,
координаты углов и из всех точек окружности радиуса 1 с центром
в начале координат (х24-у2=1).
6. Парабола (С’ф) задана уравнением
у = 4х2 — 12х sinqi — 5 cos 2<р,
где ф—параметр. Будем считать, что 0^ф<2л.
1°. Доказать, что при любом значении ф парабола (Сф) пере-
секает ось Ох в двух различных точках А и В. Составить уравне-
ние, не зависящее от ф, которому удовлетворяют абсциссы точек
А и В.
2°. Вычислить в функции ф длину отрезка АВ. Для каких зна-
чений ф эта длина наименьшая? Построить графики соответст-
вующих парабол.
3°. Для каких значений ф парабола (Сф) проходит через нача-
ло координат? Построить соответствующие графики.
4°. Составить уравнение геометрического места вершины пара-
болы (Сф) при условии, что ф изменяется на сегменте [0, 2л].
Ответ. 1°. Д=4(5—э!п2ф)>0. Если х' и х" — корни функ-
ции у, то искомое соотношение
36х'х" - 10 (х' + х")2 4- 45 = 0.
2°. ЛВ- ]/5 — sinV, АВ минимально, если Ф = у- или Ф =
При ф — имеем у = 4х2 — 12х 4- 5, или у = (2х— З)2 — 4. Это
(3 \
—, —4k которая пересекает ось Оу
в точке (0, — 4). При ф = получаем у = 4х2 4- 12х 4- 5, это пара-
бола, симметричная параболе (Ся) относительно оси Оу.
247
3°. у = 4х2 — 6х У 2 (ср, = —, <р[ = — парабола с вершиной
_ \ 4 4 J
/3-^2 9\_ 5л , 7л л a t т/ п
(—-—,-----— 1. При <р2 = — и <р2 = — получаем у = 4х2 4 6х у 2 —
параболу, симметричную параболе (Сф1) относительно оси Оу.
4°. х2 — 5,----------(дУга параболы).
7. Г. Построить график (Я) функции
1+х
1 — X
2°. Обозначим через (D) биссектрису у=х координатных углов
I и III .четвертей. Пусть Р — какая-нибудь точка плоскости, не ле-
жащая на прямой (D). Проведем через точку Р прямую, парал-
лельную оси Ох, и пусть она пересекает прямую (D) в точке Р'.
Доказать, что абсцисса точки Р' равна ординате точки Р.
3°. Пусть теперь Р\—точка гиперболы (Н) с абсциссой ai—2.
Проведем через точку Рг прямую, параллельную оси Ох, и пусть
она пересечет прямую (D) в точке Pi'. Через точку Р/ проведем
прямую, параллельную оси Оу, и пусть она пересечет гиперболу
(Н) в точке Р2. Вычислить абсциссу а2 точки Р2. Теперь для точ-
ки Р2 повторим те же построения, т. е. проведем через точку Р2
прямую, параллельную оси Ох, которая пересечет прямую (D) в
точке Р2, а затем через точку Р2 проведем прямую, параллель-
ную оси Оу, которая пересечет гиперболу (Я) в точке Р3. Вычис-
лить абсциссу точки Р3. Подобным образом исходя из точки Р3
строится точка Рь, а затем исходя из точки Р4 — точка Р3. Вычис-
лить абсциссы а4 и а5 точек Р4 и Р3. Доказать, что точка Р5 совпа-
дает с точкой Рь
4°. Пусть теперь Я] — какое-нибудь число, отличное от —1, О
и 1. Рассмотрим на гиперболе (Н) точку с абсциссой а\. Повторим
построения предыдущего пункта; вычислить в функции at абсцис-
сы а2, аз, а4 и я5 точек Р2, Р3, Р4, Р5 и установить, что точка Р5 со-
впадает с точкой Рь
5°. Пусть 01 — произвольное число, не равное —1, О, 1. Сущест-
вует угол а, такой, что 02=tg(a-|- —). Дать аналогичные выраже-
\ 4 /
ния для о3, а4, а$ и установить снова, что Точки Р5 и Р] совпадают.
Обозначим через Ль Л2, Л3, Л4 ортогональные проекции на ось Ох
точек Рь Р2, Р3, Р4. Пусть 1 — точка оси Оу с ординатой, равной 1.
Используя выражение для й\, а2, аз, а^, через а (и тригонометриче-
ский круг с центром /,. касающийся оси Ох в точке О) установить,
как расположены друг относительно друга прямые /Ль /Л2, /Л3
и М4.
Ответ. 5°. Прямые /Л2 и /Л4 — биссектрисы углов, образо-
ванных прямыми lAi и IA3.
248
8. Построить графики следующих функций (1°—6°):
1°. у = 2~х — 1,
2°. у = 2х-\-2~х,
3°. у = 8 • 2х — 1 (указание: 8 • 2х = 2*+3),
___
4°. у = 22*-1 (указание: 22*-1 — 4* 2),
5°. у = 2^,
6°. Функция y=f(x) задана графически (рис. 74).
Рис. 74
Начертить на том же чертеже графики функций:
y = f(x) + a, y=f(ax + b),
y = f(x + a), . y = af(x) + b,
y = af(x), ^ = |/(x)|,
y — f(ax),
где а и b — данные вещественные числа.
- 7°. Построить график функции
# = cos(2x4--y).
Построить графики следующих функций:
8°. t/ = 3siti( 2х + — ) + 3,
9°. у = Ч — х2,
10°. у = 3-2*+ 1,
12°. у = lg(— х),
13°. у = log2(2x + 1)
указание: у = 1 + log2 6е + у
14°. у = sin х + cosх ( указание:
sin х 4- cos х = }^2cos (х j j,
15°. z/ = sin2x (указание:
. о 1 — cos 2х \
sin2 х =------------ ,
2 /
16°. y = cos2x,
17°. у = /ГП,
249
18°. у = V1—х2 (указание: рас-
стояние между точками графика
и началом координат равно 1,
так как х2 + у2 = 1),
19°. у= /1— 4х2,
20°. у= у]/1 —4х2,
21°. у = 1 +2х (указание:
х— 1 \
сравнить график этой функции
с графиком функции
1 + 2(х + 1) _
23°. у = х\
24°. у = frx,
25°. у = х4,
26°'. у = 1 V’
27°. у 1
28°. у 1
1—Х2 ’
29°. у 1
i-4-х2 ’
30°. у = 1 —C0S4X,
31°. у . 1
sin х *
32°. у 1
COS2X
33°. у =. 1 + tg X 1 —tgx ’
34°. у = log2X2,
35°. х = 21ogax,
36°. у = log2 (2x+ 1),
37°. у = 1 X^x.
XII. Прогрессии (задачи с решениями)
1. Пусть abed — четырехзначное число (d — число единиц, с —
число десятков, b — число сотен, а — число тысяч). Пусть Mi—
множество всех четырехзначных чисел, делящихся на 13.
Рассмотрим множество М2 всех таких четырехзначных чисел
abed, для которых
cd = 3 (ab 4- 2).
Требуется 1°. Расположить в порядке возрастания все числа
множества Мь
Что представляет собой полученная последовательность?
Сколько она содержит членов? Найти сумму всех чисел, входящих
в множество Mi.
2°. Решить все эти вопросы для чисел множества М2.
3°. Найти числа, входящие одновременно в множества Afi и М2.
Решение. 1°. Наименьшее четырехзначное число, делящееся
на 13, есть 1001:
1001 = 13-77.
250
Наибольшее четырехзначное число, делящееся на 13, есть 9997:
9997= 13-769.
Таким образом, все четырехзначные числа, делящиеся на 13 и
расположенные в порядке возрастания, образуют арифметическую
прогрессию, первый член которой равен 1001, последний 9997, а
разность равна 13. Число членов прогрессии равно
769 — 77+ 1 =693.
Сумма
1001+9997— 693 = 38 Ю 807.
2
2°. abed = 100а/? + cd = ЮОаб + 3 (ab + 2) = lOQab + Sab + 6 =
= 103a6 + 6.
Отсюда следует, что числа множества ЛГ2, расположенные в по-
рядке возрастания, также образуют арифметическую прогрессию
с разностью 103. _
Число 103 ab + 6 должно быть четырехзначное, a ab — двузнач-
ное. Наименьшее двузначное число 10. Значит, первый член про-
грессии 1036. Но так как cd<:99, то 3(а&+2)<99, или а& + 2<33,
или а&^31. ____
Итак, 10^а6< 31.
Отсюда следует, что последний член рассматриваемой прогрес-
сии 103-31+6=3199.
В этой прогрессии 22 члена (31 —10+1). Ее сумма
,='03в+3|99
2
3°. Числа, входящие в множества и М2, должны делиться на
13 и иметь вид 103 ab + 6.
Имеем
103ad + 6 = 104аЬ — а& + 6 = 13-8-а6 + 6 —об,
и, значит, 6—ab должно делиться на 13, т. е. иметь вид 13&, где
k — целое:
6 — ab = 13/г; ab = 6— 13£,
с другой стороны,
10<а6<31, или 10 <6—136 <31.
Решая эти неравенства, получим k = — \.
251
Таким образом,
ab = b — 13£= 19,
ё?=3(а6 + 2) = 3-21 =63,
значит, множества М\ и Л12 имеют только одно общее число 1963.
2. Найти геометрическую прогрессию из пяти членов, если из-
вестно, что
^1^5 = 25, Ц- и3 -|- . *
Решение. Пусть
их = a, и2 — aq, и3 = aq2, и4 = aq3, = aq*.
Тогда
aV = 25,
aq + си? + ас? = -у.
Эта система распадается на две
ао2 = 5.
35 (1)
aq + aq2 + aq3 = —
и
aq2 = — 5,
(2)
t 2 । з 35
aq + aq2 + acf =
Решая систему (1), находим
aq + aq2 ~\~aq3 _ 7
aq2 2 ’
2q2 — 5q + 2 = 0.
q' = 2, q" = —,
2
a' = —, a" = 20.
4
Соответствующие прогрессии:
—, —, 5, 10, 20;
.42
20, 10, 5, —, —.
2 4
252
* Решая систему (2), получим
2<72 + 9(? + 2 = 0, или q* + -|- q + 1 = 0.
Отсюда
а"' — — 9 —IV _ 1
4 4 ’ 4 q'" '
Отсюда находим еще две прогрессии.
3. Рассмотрим три числа а, &, с, заданные соотношениями
а = х— 3m, 6 —2х —4m, с = 4х—12.
1°. Определить х в функции т при условии, что числа а, 6, с.
взятые в этом порядке, образуют геометрическую прогрессию.
2°. Найти все целые значения т, при котором числа а, Ь, с бу-
дут также целыми и, взятые в указанном порядке, образуют гео-
метрическую прогрессию.
3°. При каких целых значениях т числа а, с, взятые в этом
порядке, образуют геометрическую прогрессию с целым знамена-
телем.
4°. При каких целых значениях т числа а, 6, с, взятые в этом
порядке, положительны и образуют геометрическую прогрессию с
целым знаменателем.
Решение. 1°. Три числа а, 6, с, взятые в этом порядке, обра-
зуют геометрическую прогрессию тогда и только тогда, когда
Ь2=ас, т. е. в данном случае
(2х — 4m)2 - (х — 3m) (4х — 12) = 0,
или
(т — 3) х = т (4т — 9).
Если т = 3, то это уравнение не имеет решений. Если т=/=3, то
% __ т (4/п — 9)
т — 3
для этого значения х:
/и2 _ 2т (2т — 3) _ 4 (2т — З)2
т — 3 т — 3 т — 3
Если исключить тривиальный случай т = 0 (тогда х = 0 и
я = 6 = с = 0), то знаменатель этой прогрессии равен
2(2m-3) .
т
2°. Пусть т — целое число. Тогда числа а, 6, с будут целые тог-
да и только тогда, когда х — целое.
253
Но так как
4ma-9m- = 4m + 3+—g—,
tn — 3 т—3
то х будет целым числом тогда и только тогда, когда 9 делится на
т—3. Это возможно только при следующих значениях т:
— 6, 0, 2, 4, 6, 12. (1)
3°. Пусть т — число целое. Тогда знаменатель
g 2(2т-3) =4__6_
т т
будет целым только для следующих значений т:
— 6, —3, —2, — 1, 1, 2, 6 (2)
(значение т=3 исключается!).
Все целые значения т, при которых и числа а, Ь, с, и знамена-
тель q будут целыми — это числа, которые входят и в множество
чисел (1), и в множество чисел (2), т. е. это такие значения т:
— 6, 2, 6.
4°. Однако из них только при /п=6 числа а, Ь, с будут положи-
тельными:
а — 12,6 = 36, с = 108.
Знаменатель q при этом равен 3.
XIII. Прогрессии (задачи для самостоятельного решения)
1. Найти корни уравнения
х3 — 14xai+ 56х — 64 = 0,
зная, что они образуют геометрическую прогрессию.
Указание. Обозначить корни так: a, aq, aq2.
Ответ. Х] = 2, х2=4, Хз=8.
2. Определить стороны треугольника, если они выражаются це-
лыми числами, образующими арифметическую прогрессию, при-
чем периметр треугольника равен 15.
Указание. Составить систему двух уравнений с тремя неиз-
вестными и выделить целые положительные решения.
3. Доказать, что если а>0, Ь>0, ОО соответственно /n-й, п-й,
р-й члены одновременно как арифметической, так и геометриче-
ской прогрессий, то
254
Указание. Представить а, Ь, с как члены геометрической
прогрессии и как члены арифметической прогрессии.
4. Числа ai, 02, аз, а4 образуют геометрическую прогрессию, а
числа fli—2, а2—1, аз—7, а4—27 образуют арифметическую про-
грессию. Найти числа ai, а2, а3, а4.
5. Доказать, что если члены ар, aq, ат и ап арифметической
прогрессии составляют геометрическую прогрессию, то р—q, q—tn,
т—п будут последовательными членами некоторой геометрической
прогрессии.
6. В арифметической прогрессии дан второй член — 5 и разность
d=5. Вычислить сумму п членов этой прогрессии.
5
Ответ. — п(п— 5).
7. Найти первый член и разность арифметической прогрессии,
зная, что сумма и ее первых членов равна 4п* 2 * + 5п.
Ответ. 9, 17, 25,..., (8n+1),...
8. Найти значение параметра р, при котором корни уравнения
х4 —(Зр4-4)х2 + р2 = 0
образуют арифметическую прогрессию.
Ответ. 1) р= 12; —6, —2, 2, 6; 2) р =-------------,
' н 19 /19
2 2 6
/19 ’ /19 ’ /19 '
9. 1°. Найти два положительных числа а и Ь, таких, что а,
а+2Ь, 2а + Ь образуют арифметическую прогрессию, а числа
(&+1)2, ab+5, (а+1)2 образуют геометрическую прогрессию.
2°, Сколько членов содержит указанные в пункте 1° прогрессии,
наибольший член каждой из которых не превосходит 10 000.
Ответ. Арифметическая прогрессия 3, 5, 7, 9, ... (1)
Геометрическая прогрессия 4, 8, 16, 32, ... (2)
Число членов арифметической прогрессии (1), меньших 10 000,
равно 4999.
Число членов геометрической прогрессии (2), меньших 10 000,
равно 11:
4, 8, 16, 32, 64, 128, 512, 1024, 2048, 4096, 8192.
10. Последовательность
«1, м2. и3,... ,ип,...
задана соотношением
4ип = «п-1 + 12, — 3.
1°. Вычислить и2, из, и4.
255
2°. Положим vn — tin—4. Доказать, что vn — геометрическая
прогрессия, и найти эту прогрессию.
~ 1О 15 63 255
Ответ: 1. и2 =------, и* =---, и. =----.
2 4 3 16 4 64
2°. vn = —Рл-ь причем и± = — 1.
4
XIV. Логарифмическая и показательная функции
(задачи с решениями)
1°. Разложить в произведение выражение
Ц = (х + У + z) (ху 4- yz + zx) — xyz.
2°. Даны три числа а, Ь, с, такие, что
О < а #= 1, 0<b =/= 1, 0 < с #= 1, 0 <abc-ф 1.
При каком соотношении между этими числами будет выпол-
няться равенство
log, х + log* х + logf х = loga6cx
при всех х>0.
Ответ. Г. и — (1/+ z) (z 4 х) (х 4- у).
2° 1g * । 1g х j Igx igx = 0
lg a 1g b 1g c lg a 4- 1g b + 1g c
Это верно при всех х>0 тогда и только тогда, когда
—-----1----!-1---5-----------!--------О,
Iga lg& Igc lga-|-lg6 + lgc
или
(Iga4 lg& + lgc)(lg&Igc4-Igclga4- Igalgf>) — Igalgft lgc = O,
ИЛИ
(Ig&4- lgc>) (lg c -J- lg a) (lg a -4- lgf>) = 0,
ИЛИ
IgbcAgca-lgab = 0,
т. e. одно из чисел be, ca или ab должно быть равно 1:
(be — 1)(ш— l)(a6— 1) = 0.
256
XV. Логарифмическая и показательная функции
(задачи для самостоятельного решения)
1. Доказать, что
loga* Nk = logaAT.
2. Доказать, что
loga/V* = -у- logaA\
3. Вычислить
, „.-₽log NV
(a“) as .
Ответ.
N s .
4. Всегда ли
\ogba2 = 2logba?
5. Вычислить
IglgW
a , 0<a^= 1.
Ответ. IgV.
6. Вычислить 4'°&5.
Ответ, 25.
7. Вычислить 2los»7.'
Находим, что
_L _L _L з _
21og,7 _ (g 3 )log,7 _ (81og„7) з = 7 з = j/ 7.
8. Вычислить 3 10g^6 .
Находим, что
3-log,/3-6 1 = 1 = 1 = 1 = 1
31Og/36 (/3)2l0g,/36 (/31Ogl<36 )2 & 36 *
9. Найти log54168, если log712=a и logi224 = Z>.
10. Доказать, что-если a2+b2=7 ab{ab^=Q), то
log J.ejH!.. = -L (Jog | a | + Jog | b I).
О Л
9 Зак. 351
257
Указание. Преобразовать и прологарифмировать данное
равенство.
11. Найти log3o8, если log3o3=a, log3o5 = &.
w о f 30 \8
Указание, о =. ( —— ) .
\ 3-5 /
12. Решить следующие уравнения:
1°. V logA. У Зх log3 х = — 1.
_ 1
Ответ, х = —.
9
2°. log, (5 /5) + logj/g (5 V5) log^x = — /б.
3°. 20logaxVx + 7loga^x3 = 3log_^x2, где 0 < аФ 1
Va
4°. logx21og2x2 = log4x2.
5°. 21g2 + lg(x2— l) = lg(4x—1).
3
Ответ. x = —.
2
13. Решить следующие уравнения:
1°. 5х + 5x+14- 5х '2 = 3х + 3x+14- Зх+2.
2°. 52*-i + 5Х+1 = 250.
3°. 3х 4-4х = 5х.
14. Решить следующие системы уравнений:
1°. %'gy = 4, ху = 40.
2°. у « = х, у3 - х2.
3°. log^x — log, у = ху = 16.
О
15. Решить следующие неравенства:
2°. 1-ogfl-(35~3:3)_^>3>
loga (5 — х)
3° 21og2(3x 4- 1) — 1 < д
‘ Iog2(3x4-1)-1
258
4°. Iogi_(2x+1)>-1.
3
5°. log2(2x Ц-1) < 1.
6°. log5 x > log125 (3x — 2).
Ответ. 0<x< —
2
2
Ответ. x>—,
3
ГЕОМЕТРИЯ, ПЛАНИМЕТРИЯ
XVI. Задачи по планиметрии с решениями
(без применения тригонометрии)
1. Даны две окружности (С) и (С') одного и того же радиу-
са R, касающиеся друг друга в точке А. Построить окружность ра-
диуса 2R, пересекающую под прямым углом окружность (С) и
пересекающую окружность (С') в двух диаметрально противопо-
ложных точках.
Решение. Пусть (у) — искомая окружность, ® — ее центр.
Обозначим через О и О' центры окружностей (С) и (О'). Так как
окружность (у) пересекает окружность (С) под прямым углом, то
<о02= (2R)2+R2, откуда 0ю=/?У5. Так как окружность (у) пере-
секает окружность (О') в двух диаметрально противоположных
точках, то
соО'2 = 4/?2 — R2 = 3R2,
откуда
(оО' = /?/3 .
Проведем теперь к окружностям (С) и (С') касательную^ точ-
ке А и отложим отрезок ЛВ = 2/? (рис. 75). Тогда За-
метим, что окружность с центром А и радиусом АВ пересекает
перпендикуляр, проведенный в точке О' к прямой 00' в точке В',
такой, что O'B' — RVz. Центр со искомой окружности есть точка
пересечения окружностей (S) и (S') с центрами О и О' и радиуса-
ми, соответственно равными ОВ и О'В'. Эти окружности пересека-
ются, притом в двух точках, так как расстояние 00'== 2/? между
их центрами заключено между разностью R (V Ъ—1/*3) и суммой
+1^3) радиусов окружностей (S) и (S').
2. Две точки М и АГ движутся соответственно по двум равным
окружностям С и С' в одном направлении и с одной и той же ско-
ростью. Доказать, что перпендикуляр к отрезку ММ' в его сере-
дине проходит через фиксированную точку /.
Решение. Угол а от ОМ до 0М\ взятый со знаком, сохра-
няет постоянную величину (так как точки М и М' движутся по
равным окружностям с одной и той же скоростью и в одном и том
9*
259
же направлении). Отметим на перпендикуляре I к отрезку ОО'
в его середине (О и О' — соответственно центры окружностей С
и С') точку 7, такую, что угол от 10 до 10' равен а. Произведем
поворот вокруг точки 7 на угол а.
Тогда окружность С совместит-
ся с окружностью С', точка О
совместится с точкой О', а точ-
ка М — с точкой М', так как угол
от ОМ до ОМ' равен а и
ОМ = ОМ'. Таким образом,ЫМО
совместится с треугольником
IM'O’, а потому 1М=1М'.
Итак, перпендикуляр к пере-
менному отрезку ММ' в его се-
редине проходит через фиксиро-
ванную точку 7, лежащую на
прямой I и определяемую тем
условием, что угол от отрезка
10 до отрезка 10' равен а
(рис. 76).
3. Даны две окружности (Ct)
и (С2), центры которых соответ-
ственно Oi и Ог, а радиусы Ri
и /?2, причем Эти две ок-
ружности пересекаются в точках
А и В.
Переменная точка Afi описывает окружность (Ci), а перемен-
ная точка М2 описывает окружность (С2), причем угол от направ-
ленного отрезка OiMt до направленного отрезка -О2М2 сохраняет
постоянную величину 0 (0=#О и 0#=л).
При каком преобразовании плоскости точка М} переходит в
точку М2? Имеет ли это преобразование двойную точку О (т. е. та-
260
кую, которая сама себе соответствует при этом преобразовании).
Каково геометрическое место точек О, если 0 изменяется от О
д° л? ;
Решение. Из равенств О2М2=О1М1 -£ и (ОрИь O2Af2)=0
следует, что точка Л41 переходит в точку М2 при преобразовании
подобия, причем коэффициент подобия k = а угол, на который
поворачивается плоскость, равен 0. Двойная точка этого подобия
определяется из условия
ОО. = ОО^,
т. е. точка О, если она существует, лежит на окружности Апполо-
ния (А), для которой k 1, а 01 и 02— предельные точки.
Обратно, пусть О — любая точка окружности (А). Если произ-
вести поворот на угол 0=(ООЬ 002), при котором точка 0\ перей-
дет в точку О* , лежащую на луче 002, а затем гомотетию с цент-
ром О и коэффициентом
ю точка 01 перейдет в 02. В результате этих двух преобразова-
ний окружность (Ci) перейдет в окружность (С2), а всякая точка
Мх окружности (Ci) перейдет в такую точку М2 окружности (С2),
что (01М1, О2М2)=0. Значит, геометрическое место двойных то-
чек О есть вся окружность (Д), за исключением точек ее пересе-
чения с прямой OiO2.
4. На оси Ох задана точка Н, та^ая, что 0Н=х. Через точку Н
проведена вторая ось Ни, такая, что угол от оси Ох до оси Ни ра-
вен 0. На этой оси берется точка М, определяемая соотношением
НМ = и.
"Г. Найти ориентированное расстояние у от точки О до прямой,
проходящей через точку М перпендикулярно оси НМ (указать, на
какой оси берется это расстояние у).
Рассмотрим окружность (О) радиуса R, пересекающую пря-
мую НМ в точках Д' и Д". Вычислить сумму и произведение вели-
чин НА' и НА"; составить уравнение второй степени, из которого
определяются НА' и НА". Исследовать, при каких случаях суще-
ствуют НА' и НА", считая, что R фиксировано, ахи 0 — перемен-
ные; интерпретировать результат исследования геометрически.
Составить квадратное уравнение, из которого находятся ориен-
тированные расстояния и' и и" от точки О до медиатрис отрезков
НА' и НА"; сравнить полученное уравнение с предыдущим; уста-
новить тождественность результатов.
261
2°. Существуют ли треугольники, вписанные в окружность ра-
диуса R с центром О, для которых Н — ортоцентр? Предполагая,
что точка А выбрана на описанной окружности, построить В и С.
Как связано с этим треугольником свойство, указанное в конце
пункта 1°?
Исследовать возможность построения одного или нескольких
треугольников АВС в зависимости от положения точки А на опи-
санной окружности и от относительного положения точки Н и
этой окружности.
Может ли треугольник АВС быть остроугольным?
Решение. Г. Вычисление у. Проектируя ломаную ОНМ и ее
замыкающую ОМ на ось ОК (К — проекция точки О на прямую,
проходящую через точку М перпендикулярно прямой НМ), полу-
чим (рис. 77)
ОЯ-cosO + НМ = ОК,
или
у —’XCOS0 + M.
Уравнение, корни которого НА' и НА". Положим к'=НА', )."=
*=НА" (рис. 78). Имеем
Л' к" = ОН2 — R2 = х2 — R2,
к' + к" = НА' + НА" = 2HL = — 2LH = — 2xcos9.
Таким образом, к' и к" — корни квадратного уравнения
V4-2Ucos0 4-x2 —/?2 = 0. (1)
Исследование. Вычисляем дискриминант этого уравнения:
А = х2 cos2 0 — (х2 — R2) - R2 — х2 sin2 0;
262
отрез-
значит, уравнение (1) имеет действительные корни тогда и только
тогда, когда
Д = #2 — x2sln29 >0. (2)
Замечая, что
OL2 = ОН2 — LH2 = х2 — х2 cos2 0 = х2 sin2 9,
заключаем, что соотношение Д^О означает: точка L должна ле-
жать внутри окружности (у) или на самой окружности. Это усло-
вие, очевидно, выполняется, если точка И лежит внутри окружно-
сти (у). Если же точка Н лежит вне окружности (у), то оно будет
выполняться тогда и только тогда, когда прямая Ни проходит
внутри того угла между касательными, проведенными из Н к (у),
в котором лежит точка О.
Уравнение, определяющее и' и и". Обозначим середины
ков НА' и НА" соответственно через /' и
Тогда
и' = П7 = LH~+ НГ = xcos0 + -у- ,
и" = LI" = LH + НТ = xcos 0 + -у-.
Отсюда находим
и' + и" = 2xcos0 + (А,' + X") = xcos0,
и' и" = x2cos20 -|- х -А-+2_ COS0 4- =
2 4
= X2COS20 — X2COS20 + -2TR2 = -x2~R-
4 4
и уравнение, из которого определяются и' и и", имеет вид
и2 — u xcos 0 4- x2~~R2 = о.
4
Мы получим корни этого уравнения, умножая на-
уравнения (1). В самом деле,
>>" — п и> I jjf! _
и и —----- и и -г- и =----------.
4^2
Геометрическая интерпретация. Произведем сначала симмет-
рию относительно точки L, а затем гомотетию с центром Н и коэф-
фициентом гомотетии, равным-}-—Произведение этих преобра-
(3)
корни
263
зований в указанном порядке есть гомотетия с коэффициентом
---Точки Я, А' и А" преобразуются соответственно в точки L,
Z" и значит,
а" =Ы" =------НА' =
2
и' = LF = ——НА”
2 2
2°. Изучение треугольников, вписанных в окружность (у), для
которых Н—ортоцентр. Пусть А — точка, лежащая на окружно-
сти (у), й At—точка (вообще говоря, единственная), в которой
прямая НА вторично пересекает окружность.
Если существует треугольник, удовлетворяющий условию за-
дачи, то точка, симметричная точке Н относительно стороны ВС,
есть точка 4ь Построим медиатрису отрезка HAi. Если она пере-
секает окружность (у) в двух точках В и С, то треугольник АВС
удовлетворяет условию задачи. Обозначим через К середину от-
резка ВС, иначе говоря, проекцию
Тогда ОХ= —-1-ЯЛ.
Исследование. Треугольник АВС
тогда, когда точка К лежит внутри
но, если НА<2R. Построим окружность
(Г) с центром Н и радиусом 2R (рис. 79).
Если OH<R, то любая точка А ок-
ружности (у) лежит внутри окружности
(Г); прямая АН однозначно определена,
и для выбранной точки А имеется толь-
ко один треугольник АВС.
Если OH=R, то надо рассмотреть
два случая.
1) Точка А совпадает с точкой Н.
В этом случае ей соответствует бесконеч-
ное множество треугольников АВС, по-
определена и решением является любой
А, две другие вершины которого В и С —
Рис. 79
прямая АН не
2 ’
X"
точки О на
существует
окружности
медиатрису НА\.
тогда и только
(у), следователь-
скольку
треугольник с вершиной
концы диаметра окружности (у).
2) Если же точка А совпадает с точкой, симметричной точке Н
относительно О, то ей соответствует вырожденный треугольник
АВС.
Если R<OH<3R, то окружность (Г) пересекает окружность
(у) в двух различных точках а и а'. Каждой точке А дуги аа'
окружности (у), лежащей внутри окружности (Г), соответствует
только один треугольник АВС (вырожденный в случае, если точ-
ка А совпадает с точкой а или с точкой а').
Если OH>3R, все точки (у) лежат вне окружности (Г); реше-
ний нет.
264
Если, наконец, OH—3R (предельный случай), то А есть точка
прикосновения окружностей (у) и (Г) (касающихся внешним об-
разом), получается вырожденный треугольник АВС.
Случай, когда все углы треугольника АВС острые. Пусть А —
наибольший угол треугольника АВС. Тогда углы В и С оба острые
и высота, опущенная из вершины А на сторону ВС, пересекает
отрезок ВС в некоторой точке /, расположенной между точками В
и С, причем точка I расположена между точками А и At, где Ai —
точка, в которой AI вторично пересекает окружность (у).
Если А — острый угол, то направленный отрезок ОК, следова-
тельно, и АН имеет то же направление, что и А/, и точка Н распо-
ложена между Ли/, следовательно, внутри (у).
Если А — тупой угол, то направленные отрезки ОК, следова-
тельно, и АН, направлены одинаково с IA, значит, точка Н лежит
вне окружности (у).
Наконец, если Л=
то Н совпадает с А.
Окончательно, все углы треугольника АВС будут острыми тог-
да и только тогда, когда точка Н лежит внутри окружности (у),
иначе говоря, если x<R.
5. На плоскости заданы два отрезка AtBi и Л2В2 разной длины:
А&
Построить на плоскости точку О, обладающую следующим
свойством: при повороте вокруг точки О на угол а (равный углу
между направленными отрезками Л1В1 и Л2В2) и при последую-
щей гомотетии с центром О и коэффициентом k отрезок AtBj пе-
рейдет в отрезок А2В2.
Решение. Предварительно решим следующую задачу: на
плоскости заданы две точки Ль Л2; кроме того, задан ориентиро-
ванный угол а и число 0<Л^1. Построить ^очку О, такую, что при
повороте вокруг нее на угол а и при последующей гомотетии с
центром О точка Л1 перешла бы в точку Л2.
Для решения этой задачи построим геометрическое место то-
чек М, для каждой из которых
MAt
1
ма2 k '
Это геометрическое место точек является окружностью (Л)
Апполония, для которой Л1 и Л2— предельные точки. Построим
дугу_AzC окружности, такую, что угол от направленного отрез-
ка СЛ, до направленного отрезка СЛ2 равен а. Эта дуга пересекает
окружность (Л) в некоторой точке О, так как один из ее концов Л]
лежит внутри окружности (Л), а другой Л2— вне ее.
265
При повороте вокруг точки на угол а, равный углу от направ-
ленного отрезка OAt до направленного отрезка ОА2, точка At
перейдет в точку До, лежащую на луче ОА2, причем, так как
ОА,, _ _1_
ОА2 k
то и
ОА0 ; 1
ОА2 k
Теперь при гомотетии (О, k) точка До перейдет в точку А2.
Данная задача решается так же, только надо выбрать
& __ А2В2
лд
и за угол а принять угол от направленного отрезка AiД до направ-
ленного отрезка А2В2. Тогда после проведения указанного пово-
рота и гомотетии не только точка At перейдет в точку А2, но точ-
ка Bi — в точку В2.
6. В точках А, В, С сосредоточены массы, соответственно рав-
ные а, р и у. Пусть й — центр тяжести системы этих материальных
точек, а М — любая точка (может и не лежащая в плоскости тре-
угольника АВС). Доказать, что
Л1Й« = «AM* + P-.MB* + y-.MC» _ ар А№ + Ру ВС2 + уаСА* (..
а + Р + у (а + Р + у)2 ’ (
Доказательство. Пусть О — точка, лежащая на прямой
АВ и делящая отрезок АВ в отношении —:
лб р
Тогда
Д0‘=—£—АВ, ОВ =
а
—-—АВ,
и применяя к треугольнику МАВ теорему Стюарта, получим
МО2-АВ = —— АВ-МА2 Н------АВ-МВ2---------— АВ3,
а+р а + р (а + р)2
откуда
МО2 = «УИЛ2 + РМВ2 ар .Ав2
а + р (аД-Р)2
(2)
266
Точка Q делит отрезок ОС в отношении —-—:
а + р
OQ __ у
ОС а + Р ’
значит,
ОС = ——ОС, OQ =-----------------ОС
a+P+Y а+Р+у
и, применяя теорему Стюарта для треугольника МОС, получим
Л4О1 2 ОС =--*-----МС2 ОС + —^iP—МО2-ОС —
« + Р + у • а + Р + у
У(« + Р) дез
(а + Р + у)2
или
MQ2 = —----------1---— МО2----------Y(a + P) ОС2. (3)
« + Р + У а + Р + у (a + P + Y)2
Наконец, из треугольника АВС по теореме Стюарта находим
СО2-АВ = СВ2 —АВ + СА2 —— АВ-------------АВ3,
а + Р a + Р (а 4- р)2
ИЛИ
СО2 = СВ2 —2— + С А2 — ---------АВ2. (4)
а + р а + р (а + Р)2
Подставляя в формулу (3) вместо МО2 и ОС2 их выражения
из формул (2) и (4), после упрощений получим формулу (1) (фор-
мула Лейбница).
Замечание. Среди масс a, р, у могут быть и отрицательные,
однако должно быть а+р+у=/=0. Центр тяжести О тогда опреде-
ляется формально (в случае, например, а<0 точка О берется на
продолжении отрезка АВ и т. д.). Проведенный выше вывод при
этом полностью сохраняется.
XVII. Задачи по планиметрии для самостоятельного решения
(без применения тригонометрии)
1. Дана прямоугольная трапеция ABCD (углы А и В прямые).
Пусть О — середина отрезка АВ. Дано
АВ = 2а, AD = Ь, ВС = с.
При каком необходимом и достаточном условии угол DOC
острый?
Ответ. Ьс>а2.
267
2. Построить окружность, касающуюся данной окружности и
данной прямой в данной на ней точке.
3. Построить окружность, касающуюся данной прямой и дан-
ной окружности в данной на ней точке.
4. Назовем расстоянием от точки до окружности длину наи-
меньшего отрезка, один конец которого является данной точкой, а
другой лежит на данной окружности. Построить окружность, рав-
ноудаленную от четырех данных точек плоскости.
5. На одной из сторон данного угла дан отрезок АВ. Построить
на второй стороне угла точку С, из которой отрезок АВ виден под
наибольшим углом.
6. Точка М лежит внутри треугольника АВС. Расстояния от
точки М до сторон ВС, СА и АВ треугольника АВС равны соответ-
ственно da, db,. dc. Обозначим через ha, hb, hc высоты треугольника
АВС. Доказать, что
Лд hb ha
7. По одну сторону от данной прямой ху расположены две точ-
ки Л и В. Построить на прямой ху отрезок MN данной длины I
так, чтобы ломаная AMNB имела наименьшую длину.
8. Центральный угол сектора равен 90°; радиус дуги сектора
равен 5. В сектор вписан прямоугольник, у которого одна сторона
в 6 раз больше другой. Найти стороны.
Ответ: 6 и 1.
9. В правильном треугольнике АВС' со стороной а проведена
средняя линия MN параллельно АС. Через точку А и середину MN
проведена прямая до пересечения с ВС в точке D. Найти длину
отрезка AD.
Ответ. • а^7—
О
10. В равнобедренном треугольнике АВС параллельно основа-
нию АС проведена средняя линия MN. Радиус окружности, описан-
ной около трапеции ACMN, в раз больше радиуса окружно-
сти, описанной около треугольника АВС. Найти углы треугольника
АВС.
О л л эт
твет. —, —, —,
2 4 4
11. Доказать, что если S(, S2, S3— площади, отсекаемые от
треугольника АВС касательными к вписанной окружности и соот-
ветственно параллельным сторонам а, Ь, с треугольника, то
268
Si : S2: S3 : S = (p—a)2: (p—ft)2: (p—с)2 : p2, где S — площадь тре-
угольника ABC.
12. В параллелограмме отношение сторон и отношение диаго-
налей одинаковы и равны —. Из вершины тупого угла А опущена
высота АЕ на большую сторону CD. Найти отношение длины от-
резка DE к длине СЕ.
13. На сторонах прямоугольного треугольника с катетами а и b
построены квадраты, лежащие вне треугольника. Найти площадь
треугольника с вершинами в центрах квадратов.
14. Найти площадь параллелограмма, если его большая диаго-
наль 5 см, а высоты 2 и 3 см.
Ответ. -^-(3V2T — 8).
15. В равнобедренном треугольнике с углом 120° радиус впи-
санной окружности равен /?. Внутри треугольника лежат два рав-
ных касающихся круга, каждый из которых касается одной боко-
вой стороны треугольника и вписанной в треугольник окружности.
Найти радиусы этих кругов. (Найти все решения.)
~ Я 3-2/Г п
Ответ, = =-----------R.
16. Около окружности описана равнобочная трапеция. Пло-
щадь четырехугольника с вершинами в точках касания составляет
— площади трапеции. Найти отношение оснований трапеции.
8
Ответ. 3.
17. В трапеции основания равны 84 и 42 см, а боковые стороны
39 и 45 см. Через точку пересечения диагоналей параллельно осно-
ваниям проведена прямая. Определить площади получившихся
трапеций.
Ответ. Si = 588, S2=1680.
18. В ДАВС ВС=а, АВ = с, АС=Ь. На ВС выбрана точка D
таким образом, что окружности, вписанные в AABD и AADC, ка-
саются. Найти BD.
19. В окружности радиуса R проведена хорда. Сумма ее длины
и расстояния от центра круга до хорды равна а. Найти длину
хорды.
20. Отрезки, образуемые на одной из сторон треугольника точ-
кой касания вписанной окружности, равны т и п, а противолежа-
щий этой стороне угол равен 60°. Найти площадь треугольника.
21. Вершины равностороннего треугольника расположены на
трех параллельных прямых. Расстояния от средней прямой до двух
крайних равны а и Ь. Найти сторону треугольника.
22. В полукруг вписан четырехугольник, три последовательные
стороны которого равны 2 1^5, 2}/~5, 6, а четвертая сторона яв-
ляется диаметром полукруга. Найти радиус полукруга.
269
23. Две окружности радиусов и и г2 касаются окружности ра-
диуса 7? внешним образом в точках, расстояние между которыми
равно а. Найти длину общей внешней касательной к первым двум
окружностям.
24. Определить стороны прямоугольного треугольника, если
его периметр равен 12 см, а площадь 6 см2.
Указание. Составить систему трех уравнений.
25. Определить вид треугольника, если длины а, Ь, с его сторон
связаны соотношением ai+bi + ci=a2b2+b2c2+c2a2.
Указание. Преобразовать данное равенство к виду
(а2 — 62)2 + (62 — с2)2 + (с2 — а2)2 = 0.
26. Внутри угла 60° расположена точка на расстоянии а и b от
его сторон. Найти расстояние от этой точки до вершины данного
угла.
Указание. Воспользоваться соотношением сторон прямо-
угольного треугольника с острым углом 30°.
27. Выразить через стороны треугольника:
а) высоты ha, h-ъ, hc;
б) радиус г вписанной окружности;
в) радиус R описанной окружности.
Примечание. Эти задачи следует решать без применения
тригонометрии.
28. На сторонах ВС, С А и АВ треугольника АВС взяты соответ-
ственно точки Р, Q и R, такие, что
м. = р, _d*_ = v.
PC QA r RB
Найти отношение площади треугольника PQR к площади тре-
угольника АВС.
Указание. Выразить через площадь ДЛВС площади тре-
угольников PCQ, QAR и RBP. Для вычисления площади APCQ,
например, рассмотреть ДЛРС.
29. Окружность касается двух смежных сторон квадрата и де-
лит третью на два отрезка а и Ь. Найти радиус этой окружности.
Указание. Центр окружности лежит на диагонали квадрата.
30. Круга радиуса г касаются внешним образом три равные
окружности, касающиеся, кроме того, попарно между собой. Найти
площади трех криволинейных треугольников, образованных ука-
занными окружностями.
Указание. Рассмотреть треугольник с вершинами в центрах
равных окружностей.
31. К двум внешне касающимся окружностям радиусов R и г
проведена общая касательная. Определить радиус окружности,
касающейся двух данных и их общей касательной. Вычислить при
270
32. Найти геометрическое место вершин В и С прямоугольного
треугольника ABC (Z.BAC=90P), если точка А фиксирована, ги-
потенуза ВС параллельна фиксированной прямой, а середина О
гипотенузы ВС описывает окружность с центром А.
Ответ. Две окружности, проходящие через точку А.
33. Дан равносторонний треугольник АВС. Окружность (р) ка-
сается стороны АВ в точке В; окружность (у) касается стороны АС
в точке С. Дано, что окружности (р) и (у) пересекаются. •
Г. а) Доказать, что точки их пересечения М и N и точка А при-
надлежат одной прямой.
2°. Дано, что окружности (р) и (у) касаются в некоторой точ-
ке Р; где находится их точка касания?
34. Пусть АВС — какой-нибудь треугольник. Обозначим через
At, Bi, Ct соответственно середины его сторон ВС, СА и АВ. Пусть
М — произвольная точка плоскости. Обозначим через А', В', С'
точки, симметричные точке М соответственно относительно точек
Ai, Bi, Ci. Доказать, что прямые АА', ВВ', СС' проходят через одну
и ту же точку М'. Доказать, что точки М, М' и центр тяжести G
треугольника АВС принадлежат одной прямой, причем точка М'
получается из точки М при гомотетии с центром в точке G и коэф-
фициентом гомотетии, равным —
35. Дан треугольник ABC, G — его центр тяжести. 1°. Выра-
зить
f (М) = МВ • МС cos ВМС + МС • МА cos СМА + МА • MB cos АМВ
только через длины отрезков MG, ВС, СА и АВ.
2°. Найти геометрическое место точек М, для каждой из кото-
рых f(Af)=O. Какая из точек этого геометрического места принад-
лежит окружности с диаметром ВС?
Ответ. 1°. /(Л4) = ЗЛ4С2 —— (ВС2СЛ2 + ЛВ2).
6
2°. Геометрическое место точек М, таких, что f(M)=0, являет-
ся окружностью (Г) с. центром Си радиусом
— ]/2(а2 + 624-с2) ;
6
где а = ВС, Ь = СА, с —АВ.
Точки окружности (Г), лежащие на окружности с диаметром
ВС, — это то же, что точки пересечения окружностей с диаметра-
ми ВС и АА' (А'—середина ВС). Если А — тупой угол, то точ-
ка Л лежит внутри окружности с диаметром ВС; решений нет.
Если Л — прямой угол, то условию задачи удовлетворяет только
она сама.
271
Если А — острый угол, то — два решения.
36. Решить треугольник по следующим данным:
1) а, А, 2р; 2) a, A, hb + hc — k\ 3) а, В, b 4- с = k.
СТЕРЕОМЕТРИЯ
XVIII. Задачи по стереометрии с решениями
(без применения тригонометрии)
1. В. пространстве даны два луча Ах и By, не лежащие в одной
плоскости; прямая АВ — их общий перпендикуляр. На лучах Ах
и By выбираются соответственно переменные точки М и Р таким
образом, что
АМ-ВР = — АВ2.
2
Доказать, что прямая МР касается фиксированной сферы.
Доказательство. Пусть М' — ортогональная проекция
точки М на плоскость, перпендикулярную к прямой АВ в точке В
(рис. 80). Точка М' лежит на луче
Вх', параллельном и одинаково на-
правленном с лучом Ах. Из прямо-
угольного треугольника МРМ' име-
ем
МР2 = ММ’2 + М’Р2 = АВ2 + М'Р2,
и так как треугольник РВМ' также
прямоугольный, то
[МР2 = АВ2 + ВМ’2 + ВР2,
или
МР2 = АВ2 + AM2 + ВР2,
или (в силу того, что АВ2=2АМ-ВР)
МР2 = (АМВР)2,
т. е. MP = AM 4- ВР.
Отложим теперь на отрезке МР от точки М к точке Р отрезок
МН=АМ (следовательно, РН=ВР), и пусть О — середина отрез-
ка АВ, а / — середина отрезка МР. Тогда
ОМ2 = О А2 + AM2 = О А2 + МН2,
OP2 = OB2 + ВР2 = ОВ2 4- PH2.
Отсюда
ОМ2 — ОР2 = НМ2 — HP2 = (НМ +~НР) (НМ — HP),
или
ОМ2 — ОР2 = 2МРЙН,
272
АМВР =
Значит, ОН _]_МР'. С другой стороны,
ОН2 = ОМ2 — МН2 = О А2 + AM2 — МН2,
и поскольку AM — МН, имеем ОН2 - - ОА2, то ОН = ОА.
Таким образом, ОНLMP и ОН=ОА, следовательно, пря-
мая МР касается в точке Н сферы с диаметром АВ.
Дополнительный вопрос. Решить задачу, считая, что
угол между осями Ах и By равен а и что
АВ?
а
4 cos2 —
2
2. АВ и ВС — две стороны квадрата ABCD. Этот квадрат яв-
ляется одной из граней куба ABCDEFGH, в котором ребра АЕ,
BF, CG и DH параллельны, О — центр куба; / — середина ребра
EF; J — середина ребра ЕН.
1°. Доказать, что IA = IG и JA=JG.
2°. Найти геометрическое место точек т, лежащих внутри квад-
рата EFGH, для каждой из которых tnA = mG.
3°. Найти геометрическое (е) точек М, лежащих внутри квад-
рата EFGH, для каждой из которых
MA<MG.
4°. Найти геометрическое место (е.') точек Р, лежащих внутри
квадрата EFGH, для каждой из которых выполнены четыре соот-
ношения:
PG<PA, РН^РВ, РЕ<РС, PF<PD.
Решение. 1°. Треугольники IEA, IFG, JEA, JHG прямоуголь-
ные, причем у каждого из них один катет равен ребру данного
куба, а другой — половине этого ребра. Значит, эти треугольники
равны (рис. 81) и потому
IA = IG = JA = JG.
2°. Геометрическое место точек, равноудаленных от точек А и G,
есть плоскость л, проходящая через середину О отрезка AG пер-
пендикулярно к этому отрезку. На основании доказанного выше
точки / и J лежат на плоскости л. Плоскость л пересекает грань
EFGH по отрезку П. Геометрическое место точек т состоит, та-
ким образом, из всех внутренних точек отрезка IJ.
3°. Геометрическое место точек М пространства, для каждой
из которых выполняется соотношение MA^.MG, состоит из всех
точек, лежащих на плоскости л, и всех точек М, лежащих по ту
сторону от плоскости л, где лежит точка А.
Отсюда следует, что геометрическое место точек М, лежащих
внутри квадрата EFGH, для каждой из которых MA^MG состоит
273
из всех точек, лежащих внутри треугольника EIJ, за исключением
точек / и J.
4°. Пусть /. — середина отрезка HG, а К—середина отрез-
ка GF. На основании предыдущего геометрическое место точек Р,
лежащих внутри квадрата EFGH. для каждой из которых выпол-
няются соотношения
PG<PA, РН^РВ9 РЕ<РС> PF^PD,
состоит из всех точек, лежащих внутри квадрата IJLK и на его
границе, за исключением вершин /, /, L, К (рис. 82).
Рис. 81 Рис. 82
3. ABCD — правильный тетраэдр, каждое ребро которого рав-
но а. Фиксировано число k. Найти геометрическое место точек М,
для каждой из которых
МА2 + МВ2 + МС2 + MD2 = k. (1)
Решение. Построим куб, такой, что стороны данного тетра-
эдра будут диагоналями его граней. Пусть М пока произвольная
точка пространства. Тогда, дополняя ДДВЛ4 до параллелограмма
(со сторонами МА и AfB), будем иметь (рис. 83): 4МО^ +АВ2=
= 2МА2 + 2МВ2, где Oi — середина отрезка АВ.
274
Аналогично 4AfO| +CD2=2AfC2+27WD2, где O2 — середина
отрезка CD.
Складывая полученные равенства и учитывая, что AB = CD = a,
получим
МА2 + MB2 + МС2 + ЛЮ2 = а2 + 2М0г{ + 2М(%.
Пусть О — середина отрезка OiO2. Дополняя ДЛЮ102 до па-
раллелограмма, получим
2ЛЮ? + 2MOl = 4МО2 + t>i С>2 = 4 ЛЮ2 + ,
и потому
МА2 + МВ2 + МС2 + MD2 = -|- а2 + 4М02.
Данное равенство (1) будет выполнено тогда и только тогда,
когда
k = — а2 + 4МО2,
2
или
МО2 =
т0-
заданное геометрическое место точек М пусто.
МО2 = О, МО = 0, значит, заданное геометриче-
Если k<Z — а2, то
2
з
Если k = —а2, то
2
ское место точек состоит из одной точки О (середины бимедианы
Ofiv т. е. отрезка, концами которого являются середины ребер АВ и
CD).
Если а2, то заданное геометрическое место точек есть сфе-
ра S радиуса
Р==
3 2
— а2
2
с центром в точке О.
Заметим, что диагональ d построенного куба равна
. , / а2 . а2 . а2 _ / 3
а = 1/---------------=1/ — а,
У 2 2 2 У 2
а значит, радиус R сферы S, описанной вокруг этого куба, равен
А а.
2
275
Сфера S совпадает со сферой S, если
1 п , 3 2
— 1/ k--------а2
2 V 2
а,
от худа
k = aV3 .
4. В плоскости (Р) задан прямоугольный треугольник АВС
с катетами ЛВ=За, АС=4а. На прямой (D), перпендикулярной в
точке-Л к плоскости (В), берется точка М, такая, что АМ=х.
1°. Построить центр сферы, описанной вокруг тетраэдра АВСМ
и вычислить ее радиус.
2°. Считая, что х изменяется, найти геометрическое место про-
екции В' точки В на прямую СМ.
Решение. 1°. Центр и радиус сферы, описанной вокруг тетра-
эдра МАВС. Множество
в
О
(Л)
(D)
Рис. 84
точек пространства, каждая из которых
равноотстоит от точек А, В, С, является
осью окружности (ЛВС)*. Так как центр
окружности (ЛВС) есть середина О отрез-
ка ВС, то ось (А) окружности (АВС) —
прямая-(А), проходящая через точку О
перпендикулярно плоскости (Р) (рис. 84).
Центр й сферы (МАВС)** лежит на
прямой (А). С другой стороны, множе-
ство точек, равноудаленных от точек Л
и М, есть плоскость-медиатриса отрез-
ка AM, т. е. плоскость, проходящая че-
рез середину I отрезка AM перпендику-
лярно отрезку AM. Эта плоскость пере-
секает плоскость, проходящую через па-
раллельные прямые (D) и (А) по пря-
мой I, проходящей через точку I параллельно АО; прямая I пере-
секает (А) в искомой точке й.
Радиус сферы (МАВС) равен ЙЛ:
ЙЛ2 = ОЛ2 4- ОЙ2.
Но ОА — медиана прямоугольного треугольника ЛВС и она
равна половине гипотенузы ВС, значит,
О А2 = = 9а2 + 16я2 = 25а2
4 4 4 4
* Символом (АВС) мы будем иногда обозначать окружность, проходящую
через точки Л, В и С. Осью окружности называется прямая, проходящая через
центр окружности перпендикулярно плоскости, в которой расположена эта ок-
ружность.
** (2ИДВС) — сфера, проходящая через точки М, А, В, С.
276
а так как
0Q = = —,
2
то окончательно
Я2 = ЙЛ2 =
4 4
откуда
Р = —/25а2 +х2 .
2
2°. Геометрическое место проекций точки В на прямую СМ
при условии, что х изменяется. Пусть В'—проекция точки В на
прямую СМ. Так как ВВ'±СМ и ABLCM, то прямая СМ перпен-
дикулярна плоскости АВВ', значит, СМ1.АВ' (рис. 85).
Таким образом, В' есть проекция точки А на переменную пря-
мую СМ\ /.САВ=Ч№, а точка В' лежит на окружности, лежащей
в плоскости САМ и построенной на АС, как на диаметре. Точка В'
Рис. 85
описывает эту окружность целиком при условии, что точка М опи-
сывает целиком прямую (D); в самом деле, любая прямая AM
имеет с окружностью S общую точку В'.
5. Дана плоскость (Р) и две точки Л и В. Точка А лежит на
плоскости (Р)-, точка В не лежит на этой плоскости. Дан угол а
прямой АВ с плоскостью (Р).
Найти на плоскости (Р) точки М, такие, что ЛАВМ равнобед-
ренный и прямоугольный (ZАВАЛ=90°).
Исследовать число решений в зависимости от значений а.
Решение. Угол В треугольника АВМ прямой тогда и только
тогда, когда точка М лежит в плоскости (П) на прямой, проходя-
щей через точку В перпендикулярно прямой АВ (рис. 86). С дру-
гой стороны, точка М должна лежать на плоскости (Р), значит,
277
она должна лежать на прямой (Д), по которой пересекаются пло-
скости (П) и (Р) (о<а< ~В плоскости (П) лежит перпен-
дикуляр ВН к прямой АВ, проведенный в плоскости, определяе-
мой прямой АВ и ее проекцией АВ' на плоскость (Р). Прямая (Д)
перпендикулярна АВ (так как она лежит в плоскости (П), перпен-
дикулярной АВ) и ортогональна ВВ' (так как (Д) лежит в пло-
скости (Р)). Значит, прямая (Д)перпендикулярна плоскости АВВ'
и (Д) .LAB'. Значит, (Д) есть прямая, лежащая в плоскости (Р)
и перпендикулярная АН. _
Треугольник АВМ будет равнобедренным, если АМ=АВ V2.
т. е. если точка М лежит на окружности (С) плоскости (Р) с цен-
тром А и радиусом
R = ABV2.
Так как
АН = -^-,
cos а
то приходим к следующим заключениям.
Если Р<Л/7, т. е. J/2 <—?—, или cosa< или, наконец,
cos а у 2
a~> —, то окружность (С) не имеет общих точек с прямой (Д); за-
4 . ,
дача не имеет ни одного решения.
Если R=AH, т. е. а=^-, то окружность (С) касается прямой
(Д) в точке Н\ существует только одна точка М (совпадающая !
с ТУ), удовлетворяющая условию задачи.
Если R>AH, т. е. а<—, то окружность (С) пересекает пря-
4 I
мую (Д) в двух точках; задача имеет два решения. |
XIX. Задачи по стереометрии для самостоятельного решения i
* (без применения тригонометрии) |
1. В плоскости л расположен равносторонний треугольник АВС у
со стороной а. На перпендикуляре и плоскости л в точке А отложен
отрезок AD = 2a. Определить положение центра Q и радиус./? сфе- j
ры, описанной вокруг пирамиды ABCD. d
Ответ. Точка £2 находится на луче Oz, выходящем из цен- f
тра О треугольника АВС в направлении луча AD; R =
у 3
2. Дан шар радиуса /?. Вычислить объем сферического слоя,
заключенного между двумя параллельными плоскостями, одна из .
278
которых проходит через центр шара, а другая делит пополам ра-
диус сферы, перпендикулярный к первой плоскости.
Ответ.
24
3. Рассмотрим тетраэдр ABCD. Пусть I — середина ребра AD,
J — середина ребра ВС, К — середина ребра АВ и L — середина
ребра CD. Доказать, что AC=BD тогда и только тогда, когда
KLVI1.
4. (Р) и (Q) — две взаимно перпендикулярные плоскости.
Пусть А и В — две произвольные точки, лежащие на линии их пе-
ресечения. Возьмем на плоскости Р точку, такую, что ХАВС=
В плоскости (Q) на отрезке АВ, как на диаметре, построим окруж-
ность. Пусть D — произвольная точка этой окружности, отличная
от точек А и В. Доказать, что треугольники CBD, ADB и ADC
прямоугольные.
5. Ребро правильного тетраэдра ABCD равно Ь. Найти радиус
шара, вписанного в трехгранный угол, образованный гранями
’тетраэдра с вершиной в точке А, и касающегося плоскости, прове-
денной через середины ребер АВ, AD и ВС.
6. В основании прямоугольного параллелепипеда лежит квад-
5
рат со стороной Ь, а высота параллелепипеда равна — Ь. Найти
4
радиус сферы, проходящей через концы стороны АВ основания и
касающейся граней параллелепипеда, параллельных АВ.
7. В треугольной пирамиде три грани взаимно перпендикуляр-
ны и их площади равны Si, S2, S3. Найти площадь четвертой грани.
8. В прямой круговой конус с высотой h и радиусом основания
2/г вписан шар. Найти площадь сечения этого шара плоскостью,
о ' Л/
проходящей через вершину конуса под углом — к его оси.
~ 3^2
Ответ. ---------
2(9 + 4/5)
9. Ребро куба ABCDA'B'C'D' равно а. Найти радиус сферы,
проходящей через середины ребер АА', ВВ' и через вершины
А и С'.
10. В правильную треугольную усеченную пирамиду с боковым
ребром I можно поместить шар, касающийся- всех граней, и шар,
касающийся всех ребер пирамиды. Найти длины сторон оснований
пирамиды.
И. В треугольной призме АВСА'В'С' боковое ребро равно Z.
В основании призмы лежит правильный треугольник со сторо-
ной 6, а прямая, проходящая через вершину В' и центр основания
АВС, перпендикулярна основаниям. Найти площадь сечения, про-
ходящего через ребро ВС и середину ребра АА'.
Ответ. -Ь- У15&2 4- 4Z2 .
8
279
12. В основании прямой треугольной призмы лежит равнобед-
ренный прямоугольный треугольник, гипотенуза которого равна с.
Через гипотенезу нижнего основания проведена плоскость так, что
в сечении призмы получился равносторонний треугольник. Извест-
но, что можно вписать шар, касающийся боковых граней призмы,
верхнего основания и сечения. Найти объем призмы.
Ответ. — (1+/6- —/3—/2).
8
13. В тетраэдре ABCD АВ = 8, CD=8, остальные ребра равны
V74. Найти радиус описанного шара.
14. Два шара радиуса г и два одинаковых шара неизвестного
радиуса расположены так, что каждый шар касается трех других
и данной плоскости. Найти радиусы двух последних шаров.
15. Ребро куба равно а. Найти радиус сферы, проходящей че-
рез вершины нижнего основания куба и касающейся ребер верх-
него его основания.
16. Диаметр шара является высотой правильного тетраэдра с
ребром а. Найти площадь поверхности тетраэдра, лежащей внутри
шара.
17. Около конуса с высотой 2 описана правильная треугольная
пирамида, сторона основания которой равна 3]^3. Найти радиус
шара, вписанного в трехгранный угол при основании пирамиды и
касающегося боковой поверхности конуса.
18. Ребро куба равно &. Найти объем конуса, у которого вер-
шина совпадает с вершиной А куба, а окружность основания про-
ходит через центры граней куба, не проходящих через вершину А.
XX. Задачи по тригонометрии с решениями
1. 1°. Найти три натуральных числа a, Ь, с при условии, что
число а не является точным квадратом и что существует острый
угол а, такой, что
о г-1Ла — 6
cos а = —--!—, cos 2а = —-------
с ’ с
Вычислить величину этого острого угла а.
2°. Доказать, что для острого угла а, определенного в 1°, вы-
полняются соотношения (для любого натурального п):
cos (22,г а) ~-, cos (22л+1 а) = JEJLzlL.
Вывести отсюда соотношения
cos2 acos4аcos 6аcos8а = —
16
280
и
cos 2а + cos 4а + cos 6а + cos 8а = — 1.
1°. Определение а, Ь, с. Имеем
а о 2 1 2 (а 4- b2 + 2b Va) л
cos 2а = 2cos2 а — 1 = ——Е—!=--— -----1 =
с2
_ 2(а + &2) —^ + 46/а
С2 9
и мы должны иметь
2 (а + b2) — c2-j-4byra _ yfa — b
с2 с
или
(с — 46) Уа = 2(а + &2)— с2 + 6с.
Так как У а.— число иррациональное, а числа а, Ь, с нату-
ральные, то последнее равенство возможно тогда и только тогда,
когда
с — 4Ь = О,
2(а + Ь2) — с2 + &с= 0;
отсюда
с = 4Ь, а = ЪЬ2
и, следовательно,
coSa - ЬУЬ+Ь _ /5+1
4b 4
о ь-Уб—ь Уб — 1
cos 2 a = —Цгт--= -— -----
4b 4
Вычисление а. Находим
COS4C - 2^2,,-| ---1 --++1.
16 4
Таким образом,
cos 4a = —cos a = cos (л— a).
Отсюда либо 4a = л — a + 26 л, т. е, a = — + ,
5 5
либо
4a = — (л — а) + 2&'л,
281
T. e. j
jt , 2 k'л л . 2k" л I
Так как, с другой стороны, а острый угол, то или а - — = 36°, ]
5 1
или а = -у- — 60°. Но это последнее значение а должно быть отбро- 1
шено, так как |
2°. Доказательство соотношений cos (а-22л) = — cos а и 1
cos (а • 22n+1) = cos 2а. Надо доказать, что для любого натурального п |
справедливы равенства |
cos(4 . 22л) = -У1±к и cos (4 • 22л+1) = i
\ 5 / 4 \ О 4
Равенства легко проверить: они верны, если п=1 и п=2, а за-
тем провести метод полной индукции. Но можно доказать эти
соотношения и непосредственно. >
Заметим сначала, что 22л — (— 1)ли 22л+1 — 2(— 1)л при любом на-
туральном п делятся на 5. В самом деле, это верно, если п = 1.
Далее,
22«+2 —(— l)«+i = 2-22л+1 —4(— 1)л + 4(— 1)л + (— 1)л = •
= 2 [22л+1 — 2(— 1И + 5 (— 1)л
делится на 5;
22л+3 — 2(— 1)л+1 = 8-22л — 8(— 1)л + 8(— 1)" + 2(— 1)" =
= 8[22л — (— 1)л] + 10 (— 1)л :
делится на 5. ;
Но так как числа 22л и 22л+1 четные, то i
22л = (— 1)л + 5(2^+ 1), ;
22л+1 = (—1)л.2 + 5-2£'. 1
Из последних равенств следует, что , «
22л- 21 = (_ 1 )«_££-_[_(2^ + 1)л, . j
5 5
22«+1 21 = (_ 1)" 4- 26'л,
5 ' ' 5
282
откуда
cos (4г • 22n) = — cos [(— 1)" 4г] = — cos + 1
\ 5 / L 5 J 5 4
COS • 22rt+1') = cos (— 1)" -4“] = COS-T~ = 1"
\ 5 / L '5 J 5 4
Примечание. Для a =имеем
2я /5—1
cos 2a = cos —=- = ——.
5 4
cos 4a = cos 22 — =-~ЬЛ,
5 4
(6я Юл \ , л Кб -4-1
-=—h -==— = cos 24 -=- = —y
5 5/ .5 4
8л „я т/б____________1
cos 8a = cos -=- = cos 2s — = 1—.-
5 5 4
Следовательно,
cos 2a cos 4a cos 6a cos 8a =
/5 — 1 /5+1 /5+1 /5—1 _ 1
4 4 4 4 16
и, далее,
cos 2a + cos 4a + cos 6a + cos 8a =
- "I /5+1 /5 +1 , /5 -1 ,
4 4 4 4
XXI. Задачи по тригонометрии для самостоятельного решения
1. Доказать, что sin(a+2p) =sin а, если ctg(a+P)=0.
Указание. Представить a+2p=2(al+p)—a.
2. Доказать, что
cos—-cos—= —
5 5 2
3. Доказать тождество
sina + slnfe + sine — sln(a + b + c) =
, . & + c , c + a , a-j-b
= 4sltl —-2- Sin —-I-------Sin —-t- .
2 2 2
283
Указание. Сгруппировать левую часть попарно.
4. Доказать, что если а+р+у = л, то имеет место тождество
sin2raa+sin2np+sin2ny= (—Ip+Msinnasinnpsinny, где п — це-
лое число.
Указание. Заменив у=л—(а4-р) и преобразовав левую
часть в произведение, заменить снова а+р=л—у и применить
формулы приведения.
5. Пусть x+y+z= Для каких целых значений k сумма
tgxtgy+tgz/tgz+tgztgx не будет зависеть от х, у, z>
Указание. Рассмотреть отдельно k=2k' и k=2k'+l. В пер-
вом случае легко убедиться, что при x=y=0, z=k'n и при х—у= —,
, 2л
г=кл------выражение принимает различные значения.
6. Доказать формулы;
а) sinarccosx — У1 —х2
b) cos arc sin х — У1 — х2
с) arc sin х 4- arc cos х = —
2
— 1<х<1-
7. Доказать, что если 0<х< 1 и а = 2arctg -~Ьх
Р = arc sin -—
1 + Х«
то а + Р = л.
8. Упростить выражения:
у — COS X ~|” cos Г X —-j cos ( X ----j,
\ 3 J \ 3 у
г = sinx 4- sinfx sin (х-f-
\ J \ 3 }
Ответ, у = 0, z = 0.
9. Решить уравнение
sin3 (х + = У 2 sinх.
10. Решить уравнение
4 sin xcos2 х = cosec х — sin х — cos х.
И. Решить уравнение
sin4хГ2-j-ctgх + ctgГ-j-— хМ = 2У2 (1 4- sln2x4-cos2x).
284
12. Решить уравнение
2 4- cos 4х = 5 cos 2х 4- 8 sin* х.
Ответ.-------1---,-----Ькл.
4 2 2
13. Решить уравнение
1 + 2cosx(l + sin2x) = (sin2x— cos2x).
14. Решить уравнение
35 4- 3 cos 4х — 12 sin2 2х — 32cos2 х «= 32 sin*х.
15. Решить уравнение
2 4- 4 cos 4х = tg х 4- ctgx.
О л । мл
твет.--------------.
12 3
16. Решить уравнение
sin3 х 4- cos8 х 4—7^ sin 2х sin f х 4~ — 1 = cos x 4- sin 3x. •
' /2 . \ 4 /
' Ответ. — 4- —kn.
4 2
17. Решить уравнение
* sin2 x 4- cos2 2x = sin2 3x 4- cos2 4x.
y-k kjt Л kft,
Ответ. ------1---------.
- 2 10 5
18. Решить уравнение
ctg x + ctg 3x = tg 2x.
Ответ. 4-kn, kn + kn ± arctg]/2 .
19. Решить уравнение
4cosx — 2cos 2x — cos4x = 1.
20. Решить уравнение
tg x = tg2 f x-—tg2 (x 4- —A 4- ctg x — 2 tg 2x.
\ 4 / \ 4 /
21. Решить уравнение
1 4- sin Зх = cos2x 4- sinx.
285
22. Решить уравнение
sin Зх 4- sin3x + sin 2х = 0.
23. Решить уравнение
2 sin Зх 4- 2 sin 2х 4- sin х = 0.
24. Решить уравнение
ctg2x = l±2!H£.
1 — sin х
Указание. Ограничив множество допустимых значений не-
равенством sinx=#0, перейти к уравнению относительно sinx и
cosx. Заметить, что
2 sinx cosx = (sinx + cosx)2 — 1.
25. Решить уравнение
sin8 х 4* cos3 x = 1--------------— sin 2x.
2
Указание. Разложить на множители левую часть.
26. Решить уравнение
sin2x— 12(sinx — cosx) 4- 12 = 0.
Указание. Заметить, что sin2x=l — (sinx—cosx)2.
27. Решить уравнение
cos 7х — sin 5х = Уз (cos 5х — sin 7х).
Указание. Сгруппировать cos7х и sin7х; cos5х и sin5х;
ввести вспомогательные углы.
28. Решить уравнение
. л X , Л х 5
sin4---h cos4-=-----.
3 3 8
Указание. Заметить, что
sin4 а + cos4 а = (sin2 а + cos2 а)2 — 2 sin2 а cos2 а =
= 1 — 2 sin2 а cos2 а = 1-- sin2 2а.
2
29. Решить уравнение
sinx t cosx о
sm a cos а
sina#:0, cosa^feO.
Ответ. x=a+2kn, x=2kn+a—За, где k принимает все целые
числовые значения.
286
30. Решить уравнение
x4cos2a— 2х2(1 + sill a cos b) -|- sin2 b - 0,
где а и b — параметры, a x — неизвестное.
Ответ. 1) Уравнение обращается в тождество, если а =— 4- 2&л,
b = л + 2sn, где k п s — любые целые числа.
2) Уравнение обращается в тождество, если а =------— + 2£л,
b = 2sn, где k и s — любые целые числа.
3) Если а = -у 4- 2&л, где k — любое целое число, но Ь=£ л -|~2зл
при всех целых числах s, то уравнение имеет два корня: Xi,2 =
= + sin —.
2
4) Если а =—4-2&л, где k — любое целое число, но &=# 2sn
, ь
при целых числах s, то уравнение имеет два корня: Xi,2 = ±cos—.
5) Если a=£2kit ± где k — любое целое число, то уравнение
имеет четыре корня:
-- ь
Y 2 cos —
, 2
*1,2 = ± --------------------
а а
cos — — sin —
2 2
Г- . Ь
K2sin —
*3,4 = ± ----------------
а а
cos — 4- sin —
2 2
31. Дано уравнение
2х2 — 2(2cosa— 1)х + 2 cos2 a — 5 cos a + 2 = 0,
причем a изменяется на сегменте [0, л]. Для каких значений а из
этого сегмента данное уравнение имеет два различных и действи-
тельных корня. Исследовать их знаки.
Ответ. 0<а<-^-; корни разных знаков.
32. Решить неравенство
sin х — Уз cos х ]/2, 0 < х < 2л.
Ответ. —<х<----------.
12 12
33. Решить неравенство
cos3 х cos Зх — sin3 х sin Зх > --
8
287
Указани.е. Представив cos3x=cosx(l—sin2x) и sin3x=
= sinx(l—cos2*), выразить левую часть через cos4x и решить не-
равенство относительно cos4x.
34. Решить неравенство
tg—*> te*-2
2 tgx + 2 ’
Указание. Решить неравенство относительно y=tg-~-.
35. Решить систему уравнений
tg* + tg!/= 1,
1
cosx cos у =
* /2
Указание. Разложив на множители tgx + tgz/, найти sin(x + z/)
и выразить у через х.
36. Решить систему уравнений
х + у = Р,
. ' cosxcost/ = a.
Указание. Разложить cosxcosу в сумму и найти cos(х—у).
37. Решить систему уравнений
sin х 4- sin у = sin (х + у),
И + |1/|=1-
Указание. Перенести sin(x4-z/) в левую часть, разложить
выражение на множители и подставить найденные решения во вто-
рое уравнение. Исключить посторонние решения первого урав-
нения.
38. Решить систему уравнений
cos2 у 4- 3 sin х sin у — 0,.
21 cos 2х — cos2 2# = 10.
39. Решить систему уравнений
х sin2 х — -1 = у cos2 у 4-,
\ 6 / \ 6 /
xcos2(x—= у sin2 (у 4- 4-).
40. Решить систему уравнений
sin х4- stay = —,
। /з
cos х 4- cos у = —
288
к I
41. Решить систему
2Sln*+cosj _ 2
42. Найти наибольшее и .наименьшее значения функции
<р (х) = sin6 х + cos6 х.
Ответ. <pmax = 1, <рт1п = ^-.
4
43. Найти все значения р, при которых уравнение
sec х + cosecx = р
имеет корень х, удовлетворяющий неравенству 0<х<-^-.
Ответ, р >21^2.
44. Найти соотношения между а=arc sin cos arc sinx и
Р = arc cos sin arc cos x.
Ответ, a 4- p = -y-.
45. Доказать, что cos x непериодическая функция.
XXII. Задачи по планиметрии с применением тригонометрии
(с решениями)
1. Доказать, что если а, Ь, с соответственно длины сторон ВС,
С А и АВ треугольника АВС, углы которого А, В, С, то
(— + — ^созЛ+ (— + —^cosB +(— + — ') cos С = 3.
\ с b J \ а с J \ b a J
Решение. Первый способ.
(— + — A cos Л + f — + — 'j cos В 4- (— + —^cosC =
\ с b J \ a c ) \ b a /
= — (Z>cosC4- ccosB) + — (ccosX+ acosC) 4-
a b
4- — (a cos В 4-6 cos 4). (1)
c
Ho
b cos C 4- c cos В = a,
c cos A 4- a cos C = b,
a cos В 4- b cos A ~= c,
поэтому сумма (1) равна 3.
Ю Зак. 351 ' 289
Второй способ. Так как стороны треугольника пропорцио-
нальны синусам противолежащих углов, то
cos С =
Г sin С sin Л
sin Л sin С
cos С =
>inC sin В J
1 / sin Л
V sin В
= —-— (sin В cos С + sin Ceos В) +
sin Л
+ —г— (sin С cos Л 4- sin Л cos С) 4-
sin В
4-------— (sin Л cos В 4-sin В cos Л) =
sin С
_ sin (В 4- С) । sin (С 4-^4) । sinQ44~B)
sin A sin В sin С
(2)
В силу соотношения Л + В,+С=л каждая из дробей, стоящих
в правой части равенства (2), равна 1, а потому их сумма равна 3.
2. ЛВС — произвольный треугольник, О — центр описанной
окружности, Я — его ортоцентр (точка пересечения высот),
1°, Доказать, что
ОЯ2 = 9£2 —(а24-д24-с2),
где R — радиус описанной окружности, а а, Ь, с — длины сторон
треугольника ЛВС:
ВС = а, СА = Ь, АВ = с.
2°. Доказать, что
ОН2 = /?2(1 —8 cos Л cos В cos С).
3°, Доказать, что треугольник ЛВС прямоугольный тогда и
только тогда, когда OH=R.
4°. Доказать, что
АН = 2R|"cosЛВЯ = 2tf|cosB|, CH = 2/?|cosC|.
5°. Вычислить угол О АН через углы Л, В, С треугольника ЛВС.
6°, Вычислить углы треугольника, если OH=2R и ЛО±ЛЯ,
Построить такой треугольник.
Решение. 1°. Применяя соотношение
МА2 4- МВ2 4- МС2 = 3MG2 4- .
290
где М — произвольная точка’ плоскости, а <3 — точка пересечения
медиан треугольника АВС, и считая, что точка М совпадает с цен-
тром О описанной окружности, находим
37?2 = 30G2 +
Но точки О, G, Н всегда принадлежат одной прямой, причем
ОН = 30G.
Значит, из последнего соотношения находим
3„а= О№ . а2 + &*+с*
3 "Г 3
поэтому
ОЯ2 = 9/?2 —(а24-624-с2).
2°. Замечая, что a=2₽siib4, 6 = 27?sinB, c=2/?sinC, из предыду-
щего пункта находим
ОЯ2 = 9/?2 — 4/?2 (sin2 Л’+ sin2 В]+ sin2 С).
Это выражение для ОН2 можно преобразовать к виду
ОН2 — ₽2(1 — 8 cos ЛсоэВсоэС)
(следует учесть, что Л+В,+ С=л).
3°. Если OH=R, то cos AcosBcos С=0, и обратно.
4°. Пусть М — середина ВС. Тогда АН=2 ОМ, значит,
АН = 2/ОВ2 —ВЛ42 = 2 1/R2 — — =
г 4
= 2 VR2 — 7?2sinM = 2R | cos А | и т. д.
5°. Из треугольника ОАН имеем
ОН2 = О А2 + АН2 — 20 А • АН • cos ОАН,
или
/?2(1 —8 cos Л cos В cos С) = R2 + 4/?2сов2Л — 2R-2R | cos Л| cos 0,
где 0 = •< ОАН.
Упрощая, получим
| cos Л |cos0 = cos2 Л + 2 cos Л cos В cos С.
Но
2 cos В cos С = cos (В + С) -|-cos (В — С) == —cos Л -|- cos (В — С),
10*
291
поэтому
| cos Л |cos6 — cos.4cos(B — C).
Если 0 < A < —, to
2
cos 9 = cos (B — C),
и считая, что B^C, находим 9 = В—С.
Если — <Л<я, то
2
cos 9 = —cos (В —С) = cos [я — (В — С)],
значит,
0 = я —(В —С)
(опять считаем, что В^С).
Замечание. Если А = -у, то АН=0, и угол О АН не опре-
делен.
6°, Если 0H=2R и АО1.АН, то Л =/= так как в противном
случае точка Н совпадала бы с точкой А, точка О совпадала бы с
серединой отрезка ВС, и мы имели бы OH—R.
Так как Z(MB=90o, то на основании пункта 5° cos(B—С) =0,
откуда (В^С)
В —С ==—.
2
(треугольники, обладающие этим свойством, называют тогда
квазмпрямоугольными).
С другой стороны, если OH=2R, то
1 — 8cos 4cosBcosC = 4,
8cos 4cos В cos С = — 3,
4 cos 4 [cos (В + С) + cos (В — С)] = —3,
и так как cos (В—С) =0, a cos 4 = —cos (В 4-С), то
cos2 (В + С) = у, cos (В + С) = ±
Но
В + С>В —С = —,
1 ' 2
292
значит,
. cos(B+ <?) = —
и потому
в + с = —
6
Окончательно находим
В =—, А = С = —
з 6
Построение треугольника не представляет затруднений.
3. На плоскости даны две оси Ох и Оу, такие, что угол от оси
Ох до оси Оу, отсчитываемый в положительном направлении (про-
тив часовой стрелки), равен '+—. Через точку А, лежащую на
оси Ох и имеющую положительную абсциссу а, проводится прямая,
параллельная оси Оу. Переменная окружность (С), касающаяся
в точке А оси Ох, пересекает вторично эту прямую в точке М.
Обозначим через <р угол от направленного отрезка ОА до направ-
ленного отрезка ОМ и будем брать для <р только значения из ин-
тервала —у <<р<-у. Прямая ОМ вторично пересекает окруж-
ность (С) в точке Р.
1°. Вычислить углы треугольника АРМ в функции <р (рассмот-
реть два случая: <р>0, <р<0). Вычислить ОМ, OP, AM, АР и ра-
диус Р окружности (С) в функции а и <р.
Определить ср, если ОР=ОМ.
Выразить через а и Р тангенс угла ОАР.
2°. Изучить функцию от <р:
У =.ОР 4- АР
при условии, что <р изменяется в интервале
2я л
“з
3°. Решить аналитически и исследовать уравнение
op + ap = -^L,
/3
где k — параметр.
Подтвердить правильность результатов при помощи графика
функции у=ОР+АР (см. 2°).
Г. Вычисление углов треугольника АРМ. Рассмотрим различ-
ные случаи для значений q>.
293
Если 0<q><-^- (рис. 87), то
-**'**• **7*'' rt
АРМ = хАМ = —.
О
—-—- rt
АМР = хАМ — <р = —— ф
О
rt
РАМ = — +ф.
О
Рис. 89
Если — — <ф<0 (рис. 88), то
3
АРМ = ОАМ =
О
-*-****. л
АМР = —— ф
и
294
и
*- РАМ = — + го. 3
Если —<ф<------------------— (рис. 89), то
3 3
АРМ = —. 3 2л АМР = ——|- ф
и Р4М = -(-^-+ф\
Окончательно, если оэ|а Л -е Л оэ | й
ТО л ЛРЛ1 = —, 3 АМР = — — <р, 3 л РАМ = h ф; 3 т
если _*L <ф<_ 3 3
то 7^- 2л АРМ 3 - 2л АМР = 4-Ф, и Л4М = +:ф).
Замечание. Если <р=0, то точки Р и М совпадают в точ-
кой А, а если <р=—у, то точки Р и М совпадают; прямая ОМ
в этом случае касается окружности (С) и треугольник ОАМ — раз-
носторонний. __
295
Вычисление ОМ, ОР, ДМ, АР и R. Во всех случаях (рис. 87—
89) из треугольника ОАМ находим
ОМ AM ОА
2л sm ф /л '
sin —- sin — — ф
3 \ 3 \
откуда
ауЗ
ф — sin ф
ДМ = fl|sin(p 1 = 2g Isin Ф ।
sin <p) cos Ф — sin <P
Далее, так как OM-OP = a2, то
ОР = sin f--------------<p\
3 \ з J
а так как (из треугольника ОАР)
АР = ОА
| sin ф_| . л
sin 3
то
ЛР=-^-|81Пф|.
О
Наконец, из треугольника АМР во всех случаях имеем
2Р = --М-
. Л
Sin —
3
откуда
АМ^З _ а^з1 |^пф| = 2а/3 Ыпф |
3 ” 3 /л \ ” 3 /Зсозф-^зШф
sinkT—фу
Вычисление ф в случае ОР = ОМ. Имеем
JL/Lsinfi _<Л _ Ш 1 .
3 ' 2 ,,п(т_ф)
296
откуда
sin2 Л ——q>A = —.
\ з ) 4
я
~3
л, поэтому sin
и из последнего
уравнения находим
. / л \ Уз «
sin (--ср ) = -— = sin—.
\ з / 2 з
следовательно, или ф=0 (результат, не представляющий интере-
са), или ф=—Таким образом, в этом случае ('ф=—пря-
мая ОМ касается окружности (С) (результат, который легко мож-
но было предвидеть).
Вычисление tg ОАР. В случае рис. 87 имеем
tg ОАР = tg (— — ф^ = 1/3-189 ,
<3 i + /3tg<₽
и так как
*
= 2а/3 sing) _ 2а/3 *£ Ф
’ 3 yr3cos ф — sin <р 3 3 — tg ф
ТО
3R + 2aV3
а значит,
tg ОЛР = УЗ(ЗН + 2аУЗ)-ЗЯУз = За
3R -I- 2а УЗ + 9R 6R4-a/3‘
В случае ——-<ф<0 (рис. 88) имеем
3
tg ОЛР =tg(^-ф
У з — tg ф
l+/3tgq>’
но теперь
= _ 2а/3 sin(P 2а/3 tg Ф
3 У3 cos <р—sin q> 3 —tg ф
откуда
. 3R/3
tg ф =------У—~,
3R — 2а УЗ
297
и, значит,
За
tg ОДР =----=..
ь 6R—а/3
Наконец, в случае —-^-<ф< — -2- (рис. 89) имеем
3 3
tgMP_ tgfа.+- ~^+'^ .
х 3 / i4-/3tg<p
откуда
3R — 2а /3
и, следовательно,
tg'OAP =-----
1 6R — аУЗ
Замечание. В двух последних случаях предполагалось, что
а Из =/= 6/?. Если а Из = 67?, то ОДР = —, и tg <р = —откуда
2 3
л
Ф =-----•
Y 6
2®. Изучение функции у = ОР + АР. Если-------— <<р < 0, то
о
з L \ 3
[и , то.
3
(а)
— Ф
2а
у = —
— Ф
2а У3 ( я \ zft\
Q--CO8(V~<P Г
Для построения графика функции </ = //(ф) следует воспользо-
2л
ваться формулой (а) для полуинтервала (——, 0] и формулой
О
(Р) для полуинтервала £о, -у-). График построен на рис. 90. Точка
(0, а) является угловой точкой графика.
3°. Решение уравнения ОР + АР = —7=-. Это уравнение распа-
дается на две системы:
. / Л X k
2л
— <Ф<0
□
COS Г —--ф
(I) и
0<Ф<-^-.
О
(И)
298
Предположим, что 0 <k <УЗ. Тогда из системы (I) находим
п , k Л . k
-----Ф = arc sin -7=-, откуда ф =------arc sin —~
6 у 3 6 у 3
Итак, система (I) имеет два решения* (различные или совпа-
дающие) при условии, что
-1^<Й<УЗ.
Теперь перейдем к исследованию системы (II). Предположим,
что 1. Тогда
----Ф = arc cos k, откуда ф = arc cos k,
6----6
либо
л я
——ф = —arccosA, откуда ф = — + arc cos й.
Найденные значения ф, притом оба, дают решение уравнения
у=ОР+АР тогда и только тогда, когда
-----7-< arc cos/г <
6 3
2
т. е.
299
и потому
OG< — <ОЛ'< —
з з
Отсюда следует, что точка А' не совпадает с точкой О, следова-
тельно, перпендикуляр к ОА' в точке А' вполне определен.
С другой стороны, из треугольника
OA'G имеем
ол;<оо+ол'</?.
Значит, точка А' лежит внутри ок-
ружности (Г), а потому прямая, прохо-
дящая через точку А' перпендикулярно
ОА', пересекает окружность (Г) в двух
'различных точках В и С.
Итак, с каждой точкой Л, лежащей
на окружности (Г), всегда ассоциирован
Рис. 91
и притом только один треугольник Т.
в) Геометрическое место точек А'. Точка А’ есть образ точки Л
при гомотетии ^G, —Если точка Л описывает целиком
окружность (Г), то точка А' описывает целиком окружность (у),
являющуюся образом окружности (Г) при гомотетии ^G, —
Центр <в окружности (у) есть образ точки О при гомотетии
Gca = —— GO;
2
отсюда, между прочим, следует, что радиус окружности (у) ра-
ил„ #
вен — •
2
р р
Поскольку GO<Z—, то 0<в<—, значит,
3 2
окружность (у) цели-
ком лежит внутри окружности (Г). Окружность (у) является окруж-
ностью Эйлера для всех треугольников Т.
с) Ортоцентр треугольника Т. Все треугольники Т имеют один
и тот же ортоцентр Н, поскольку
ОН = 3OG.
Отсюда также следует, что точка Н лежит внутри окружности,
описанной вокруг треугольника АВС, а потому все углы любого
из треугольников Т острые.
302
2°. а) Соотношение, относящееся к треугольникам t. Так как
точка g есть точка пересечения медиан треугольника АВС, то, за-
меняя в соотношении *..
МА2 + МВ* + МС2 — 3Mg2 = gA2 + gB2 + gC2
(M — любая точка, лежащая в плоскости треугольника АВС) точ-
ку М на точку О, получим
3Og2 + gA2 + gB2 + gC2 = 3R2. (1)
Равенство
BC2 + CA2 + AB2 = 9(R2 — Og2) (2)
по существу доказано в подстрочном примечании.
в) Условие того, что треугольник t равен треугольнику Т. Так
как BC=2RsinA, CA=2Rs'mB, AB — 2Rs\nC, то из соотношения (2)
следует -
Og2 = R2 [ 1 — у (sin2 А + sin2 В + sin2 С)]. (3)
Значит, треугольник t будет равен треугольнику Т тогда и только
D2
тогда, когда Og2 <-^-3
Отсюда и из соотношения (3) получаем необходимое и доста-
точное условие того, что треугольник t равен одному из треуголь-
ников Г:
1 — — (sin2 Л 4-sin2 В 4-sin2 С) <—,
9 9
или
sin2 Л + sin2 В 4-sin2 С > 2.
3°. а) Интервал I изменения В. Пусть заданы углы Л и В. Тогда
С=л—(Л-ьВ). Так как мы предположили, что В^С, то В<л—
— (Л4-В), откуда
* Соотношение
MH2 + MB2 + AiCa = 3AfG24-----TQ (1)
«5
верно для четырех любых точек плоскости; здесь G — центр тяжести системы из
трех точек, а а, b и с — соответственно длины отрезков ВС, С А и АВ. Соотноше-
ние (1) выводится легко, например, при помощи теоремы Стюарта. Далее, 4А'А2=
=2&2+2с2—а2, 4В'В2=2с2+2а2—&2, 4С'С2==2а2+262—с2, где Л', В', С' —соответ-
ственно середины отрезков ВС, СА и АВ. Складывая эти соотношения, получим
4ЛЛ'2 4- 4ВВ'2 + 4СС'2 = 3 (а2 4- &2 + с8)
или 3 (^Л2+^В2+^С2)==а2+62+с2.
303
Итак, угол В может изменятья в полуинтервале /:
Условие, при котором треугольник t равен одному из треуголь-
ников Т. Так как число k задано, то соотношение (3) можно пере-
писать в виде
А2 = 1 — у (sin2 Л 4-sin2 В 4-sin2 С). (3')
Но
sin2 В 4- sin2 С = у (2 — cos 2В — Cos 2С) = 1 — cos (В + С) cos (В—С),
и так как
В + С = л — А
и
В — С = В — (л — А — В) = 2В + Л — л,
то
sin2 В 4- sin2 С = 1—cos Лсов(2В + Л).
Соотношение (3') принимает теперь вид
k2 = 1 — у [sin2 Л 4- 1— cos Лсоэ(2В + Л)],
ИЛИ
1sin2 Л — совЛсоз(2В +Л)=—(1 — й2), где 0<В<^Д (4)
4 2
Итак, треугольник t в предположении В^С будет равен треуголь-
нику Т, если угол В принадлежит интервалу / и если выполнено
соотношение (4).
б) Изменение функции у. Если х изменяется от 0 до я , то
угол 2х+А изменяется от Л до л. Значит, соз(2х+Л) убывает от
созЛ до —1 и, значит, функция у возрастает от 14-э!п2Л—cosM до
l + sinM + cosA
Условие существования треугольников Т. Так как функция у
возрастает в полуинтервале /, уравнение (4) будет иметь реше-
ние и притом единственное тогда и только тогда, когда
1 + sin2 Л —cos2 Л < —(1 —k2) < 1 4-sln2 Л 4- cos Л.
304
Неравенство
1 Ц- sin2 Л — cos2 А < (1 — Л2)
можно переписать в виде
, л . 9А» — 1
cos2 А >----------
8
и оно выполняется, так как 0<^А<-^-.
Неравенство же
— (1 — А2) < 1 4- sin2 Л + cosH
приводится к виду
cos2 А —cos А + 1 ~9fe <С 0>
4
или
/ . 14-3k \/ л 1 —3k \ п
(cos Л---—— )(cos Л----------) < О
\ 2 Л 2 J
и, значит,
1 — 3k . . 14-ЗЛ
—-----<созл<—.
Заметим, что в силу условия 0<А< -у,
О1—3ft <* 1-*~ЗЛ <Г 1
2 2 ’
поэтому из последних неравенств следует, что
14-36 - . 1 — 36
arc cos —— < Л < аге cos —-—.
1 I 1__3k
Если Л = arccos —---, или Л = arc cos —--, функция у при-
нимает наибольшее значение, т. е.
В = х== и С = л —(Л + В) = В,
следовательно, треугольник ЛВС равнобедренный.
Окончательно: угол Л является углом треугольника Т тогда и
только тогда, когда он принадлежит сегменту.
Г 14-3* 1— 3k 1
arccos—4-—, arccos------- .
L 2 2 • J
Если величина угла Л совпадает с любой из границ этого сег-
мента, то соответствующий треугольник Т равнобедренный.
305
5. Рассмотрим треугольник ABC^ вписанный в окружность (О)
радиуса /?.
1°. Доказать, что точка О является центром тяжести масс, рав-
ных sin24, sin2B и sin2C и сосредоточенных соответственно в вер-
шинах А, В и С.
2°. Доказать, что если М — любая точка окружности (О), то
f(M) = МА2- sin24 + МВ2 • sin 2В + МС2 • sin 2С = 43,
где S — площадь треугольника АВС.
ю гт д. а-МЛЧ-рмВЧуМС2
Решение. 1 . Применим формулу Ми2=----------------——------------
а*т"Р + Y
__а (задача 6, стр. 266), полагая a=sin24, p = sin2B,
y=sin2C и считая, что точка Л! совпадает с точкой О; получим
QQ2 _ R2 sin 2Л sin 2В - с2 4~ sin 2В sin 2Cafi-f- sin 2С sin 2Л > 62 __
(sin 2Л + sin 2В + sin 2С)а
e R2 Л 4 sin 2Л sin 2В sina С 4 4 sin 2В sin 2 С sin2 Л 4 4 sin 2С sin 2Л sinaB) \
\ 16 sin2 Л sin2 В sin2 С )
__R2 Л cos Л cos В.sin С -р cos В cos С sin Л cos С cos Л sin В \
\ sin Л sin В sin С )
_ ^2 /1__ cos В sin (Л С) 4~ cos С cos Л sin В \ _
\ sin Л sin В sin С /
_ R2 Л cos В sin В 4~ cos С cos Л sin В \ __
\ sin Л sin В sin С /
__2^2 /1_ * 1 cos (Л Q 4 cos С cos Л _D2/1__i\___л
sin Л sin С /
т. е. точка G совпадает с точкой О.
2°, Соотношение f(M)=4S. Выберем теперь точку М. на окруж-
ности (О). Тогда
/(АО
R2 I ууц c2 sin 2Л sin 2В 4~а2 sin 2B sin 2C + 62sin2Csin24
sin 2A+sin 2B-|-sin 2C (sin 2A + sin 2B + sin 2C)a
R2 _f (M)R2 cos A cos В sin C 4- c°s В cosCsin Л -|-cos Cco s Л sinB
4 sin A sin В sin C sin A sin В sin C
= zw _ cos В sin (Л 4~ C) 4~ cos C cos A sin В
4 sin A sin В sin C sin A sin В sin C ’
R2 =
8 sin A sin В sin С
Таким образом,
f (M) = 8 sin A sin В sinC-7?2 = 8—-L . = 45.
' ' 2R 2R 2R R
306
XXIII. Задачи по планиметрии с применением тригонометрии
(для самостоятельного решения)
1. Возьмем внутри окружности (О) произвольную точку М.
Пусть АВ — диаметр этой окружности, проходящей через точку М,
a CD — хорда, перпендикулярная к АВ в точке М (С и D — концы
хорды). Дано отношение т площади треугольника ADC к площади
треугольника ODC.
Определить угол а= ZBAC Провести исследо-
вание, при каких значениях т задача имеет решения и найти эти
решения. Рассмотреть случай /п=3.
Указание. Вопрос сводится к решению уравнения
14- cos 2а л л
——---------= пг, 0 < а < —.
| cos 2а | 2
Ответ. Если 0</п^2, задача имеет одно решение:
а = — arc cos (------—\
2 \ m-f-1 J
Отметим, что если /и=1, то
1 / 1 \ я
а = — arc cos (---) = —,
2 \ 2 / з
т. е. точка М является серединой радиуса ОА.
Если т>2, задача имеет два решения:
1 / 1 \ 1 1
а. = — arc cos (-------) и а, = — arc cos-----.
1 2 \ «4-1 J 2 2 т — 1
В случае /п = 3 имеем два решения:
1 / 1 \ 1 1 я
а. = —arccost-----), а„ = —arc cos — =—.
1 2 \ 4 / 2 2 2 6
3R
В случае а = ах имеем AM = ——.
В случае а=аг течка М — середина радиуса ОВ.
2. Г. В треугольнике АВС высота АА' равна радиусу К описан-
ной окружности. Доказать, что произведение sinBsinC постоянно.
2°. Предполагая, что в таком треугольнике Л = 60°, вычислить
углы В и С.
3°. Предполагая, кроме того, что известна длина с стороны АВ,
вычислить длины а и b сторон ВС и СА.
Ответ. I9. sinBsinC = —. 29. В = —, С =—. 3°. а=с/3‘,
2 2 6
Ь = 2с.
307
3. В плоскости строится полуокружность с диаметром AB=2R.
На этой полуокружности берется переменная точка М. Положим
ЛВАМ=В. На перпендикуляре к плоскости (Р) в точке А берется
точка D, такая, что AD=BM.
1°. Выразить в функции R и 0 полную поверхность а тетраэдра
ABMD.
2°. При каком значении 0 имеем a=6/?2sin0?
Ответ. Г. <r=4/?2sin0(l 4-cos0). 2° 0 = -у.
4. Доказать, что в прямоугольном треугольнике (С — прямой
угол) имеет место соотношение
sin8 В cos8 В _ (62 — а8) с8
sin8 Л cos8 Л а8 Ь2
5. Доказать, что во всяком треугольнике имеет место соотно-
шение
6с cos2— -|- са cos2 — 4- об cos2 — = р2,
2 2 2
где р — полупериметр.
Указание. Перейти в этом выражении к соэЛ, cosB и cosC
и воспользоваться теоремой косинусов.
6. Острый угол прямоугольного треугольника равен а, а радиус
окружности, касающейся гипотенузы и продолжений двух катетов,
равен R. Найти длину гипотенузы этого треугольника.
7. Стороны параллелограмма равны а и Ь, а острый угол меж-
ду диагоналями равен а. Найти площадь параллелограмма.
XXIV. Задачи по стереометрии с применением тригонометрии
(для самостоятельного решения)
1. Радиус шара, описанного около правильной треугольной пи-
рамиды, равен R, а двугранный угол между двумя смежными бо-
ковыми гранями равен а. Найти сторону основания пирамиды.
2. В правильной четырехугольной пирамиде SABCD сторона
основания равна Ь, а угол между боковым ребром и плоскостью
2
основания равен arc cos —. Плоскость, параллельная диагонали
основания АС и боковому ребру BS, пересекает пирамиду так, что
в сечение можно вписать окружность. Определить радиус этой
окружности (найти все решения).
3. В треугольной пирамиде периметр основания равен 2р, ра-
диус вписанного шара равен R, а боковые грани образуют с осно-
ванием равные углы а. Найти объем пирамиды.
Ответ: p₽2tgactg2
4. Ребро куба равно а. Через диагональ АС грани ABCD прове-
дена плоскость так, что в сечении получилась трапеция, острый
308
угол которой равен arc cos Найти расстояние от вершины В
до секущей плоскости.
_ 2а
Ответ.—
з
5. В двугранный угол а вписаны два шара радиуса г, касающие-
ся друг друга. Найти радиус шара, касающегося граней угла и
данных шаров.
6. Объем правильной треугольной призмы равен v, угол между
диагоналями двух граней, проведенными из одной и той же вер-
шины, равен а. Найти сторону основания призмы.
Указание. Рассмотреть боковую грань и сечение, проходя-
щее через диагонали.
7. Вычислить объем правильной треугольной пирамиды, зная,
что плоский угол при вершине равен а, а радиус окружности, опи-
санной около боковой грани, равен г.
8. Конус и цилиндр имеют общее основание, а вершина конуса
находится в центре другого основания цилиндра. Чему равен угол
между осью конуса и его образующей, если известно, что полная
поверхность цилиндра относится к полной поверхности конуса
как 7:4.
Указание. Выразить обе поверхности через радиус основа-
ния и искомый угол.
9. В шар вписан правильный тетраэдр, затем в тетраэдр снова
вписан шар. Найти отношение поверхностей двух шаров.
Указание. Выразить радиусы шаров через ребро тетраэдра.
10. На плоскости лежат три равных шара радиуса R, попарно
касающиеся друг друга. Четвертый шар касается плоскости и каж-
дого из первых трех шаров. Найти радиус четвертого шара.
Указание. Рассмотреть проекцию на плоскость, перпенди-
кулярную данной плоскости и проходящую через центры одного
из данных шаров и четвертого шара.
11. Основанием пирамиды служит квадрат. Две боковые грани
перпендикулярны к плоскости основания, а две другие составляют
с ней углы, равные а. Чему равен двугранный угол между этими
последними гранями? Указание. Провести через диагональ
основания плоскость, перпендикулярную двум наклонным граням.
12. Дан прямоугольный треугольник ASB (Z.ASB=90°). На
перпендикуляре в точке S к плоскости этого треугольника откла-
дывается отрезок SC — a. Даны углы: 5СЛ = а и SCB = p.
1°. Выразить стороны треугольников SC4 и SCB через а, а и р.
Выразить через а, а и р длину отрезка АВ.
2°. Найти cosacosp, если дано, что Z.ACB=QQP.
Ответ. 1°. = atga, SB = atgp, SC = atgp, AC = ,
cos a
CB = ao , AB = a Vtg2a + tg2p. 2°. cosacosp = —.
cos p 2
309
§ 10. ТЕМЫ КОНТРОЛЬНЫХ РАБОТ
Контрольная работа № 1 (вариант 1)
1. Упростить выражение
-L^/1+Е, где х =-2-1/^?. •
1+ах У 1 — Ьх а у b
2. Найти все действительные числа т, для которых уравнение
х2 — (4/п + 6) х + 12 /п — 16 = 0
имеет положительные корни.
3. При каких действительных т один из корней уравнения
(/и2 — 5т + 3) x’i+ (Зт — 1) х + 2 = О
вдвое больше второго?
4. Решить уравнение
|3х— 3| — |2х4-6|= 1.
5. Решить систему уравнений
ху = 15.
6. Решить неравенство
|2л-1| <_1_
Xs — х — 2 Х 2
7. Найти все корни уравнения
logj(x— l)10^*-1)’] = 2.
8. Решить систему уравнений
log3(l-f- у) = 34-logax,
х2 + у2 = 629х2у2.
9. Решить уравнения
а) 3-16*+ 36* = 2-81*;
10. Решить неравенства
а) /7х— 13 —/Зх—19>/5х —27;
б) logix+ei2 • log, (х2 — х — 2) > 1.
310
11. Найти общий член последовательности х2, х3, ...» хп, ...»
если даны два первых члена Xi = a, Х2—Ь и известно, что каждый
член последовательности, начиная с третьего, равен полусумме
двух предыдущих:
д,_-й±й-,ж. = ^±5.Ят. д.
12. Найти все пары различных двузначных чисел, относительно
которых известно следующее: цифры единиц этих чисел равны.
Если первое число разделить на 9, то частное от деления равно
остатку, который получится от деления второго числа на 9, и, на-
оборот, частное от деления второго числа на 9 равно остатку от
деления первого числа на 9.
13. Река течет из Л в В, расстояние между которыми равно
12 км. Первая лодка выходит, против течения из В в Л в 12 час дня.
Через пять минут вслед за ней отправляется из В в Л вторая лод-
ка, которая догоняет первую в 1 км от В. Приплыв в Л, вторая
лодка мгновенно поворачивает обратно и встречает первую лодку
в 2 км от Л. Через 35 мин после того, как первая лодка придет
в Л, вторая лодка вернется в В. Найти время встреч обеих лодок
и скорость течения реки.
14. Построить графики:
а) 0 = |2х+4|-|Зх+1|4-|х|;
б) у = | ха — 6х + 81 — 2;
в) у= log_£|*+ 1|.
3
Контрольная работа № 1 (вариант 2)
1. Упростить выражение
______________________ 1 1
y = (x + 2Vx—\) 2+(Х_2/х_1) 2,
где х>1 и х=/=2.
2. При каких т уравнения
2ха — (Зт 4-2) х+ 12 = 0,
4№ — (9/п —2)х + 36 = 0
имеют общий корень?
3. Решить уравнение
Z2-|-|Z|2 = 0,
где z — комплексное число.
311
4. Решить неравенство
|3х —3| — |2х + 6 [<|х|.
5. Решить систему уравнений
х*+у = у12.
£*+* = х®.
6. Решить неравенство
х _|_х 35
+ /х2 —1 12 ‘
7. Найти все решений неравенства
(1+х)(2 + х) >_3х
х2 —|х|—2
8. Найти все корни уравнения
10gJ(x— 1)H<U-1)»| —2.
9. Решить систему уравнений
log4x+21og4z/ = 0,
z/2 + 36х = 13.
10. Решить уравнения:
а) //х+1-K/x-l = 3 _ ;
2И+/х
б) log2 (4* + 4) = х + log2 (2*+1 - 3);
в) 21g(x — 1) + lg(x-30)2 = 4.
11. Решить неравенства:
a) log/2 (5*— l)-log/2 -^9г> 2;
log 1 (Х’-Зх+I)
/IX
б)Ш <*•
12. Даны два положительных и неравных друг другу числа а
и Ь. Между ними вставлено п чисел (п — данное фиксированное
число) так, что числа a, Xi, Хг, ..., х„, Ъ образуют геометрическую
прогрессию. Найти произведение этих чисел
аххх2 ... хпЬ.
13. Некто купил 30 птиц за 30 монет. Из числа этих птиц за
каждых 3 воробьев заплачена 1 монета, за каждые 2 горлицы —
312
также 1 монета, за каждого голубя — 2 монеты. Сколько было
птиц каждой породы?
14. Построить графики:
а) у = \х—11 + Iх — 21 + |х — 3|;
б) у = 21 х | — х2;
в)
I X— 1 I , х-}"3
Hvrr I + — •
Контрольная работа № 2 (вариант 1)
1. Решить уравнение
sinx4-cos3x = 1—2sin2x + sin2x.
2. Решить уравнение
cos2 х 4-cosxcos у + cos2# = 0.
3. Решить неравенство
, X X
tgx>tg-^-
4. Хорда, стягивающая дугу окружности с центральным углом а,
равна Ь. Найти хорду, стягивающую дугу этой же окружности с
центральным углом 4а.
5. В параллелограмме дан острый угол а и расстояния а и b от
точки пересечения диагоналей до параллельных сторон. Вычис-
лить диагонали и площадь параллелограмма.
6. Боковое ребро правильной треугольной пирамиды равно а и
оно наклонено к плоскости основания под углом 0. Найти сторону
квадратного сечения, проведенного параллельно двум непересе-
кающимся ребрам пирамиды.
7. Дан конус, в осевом сечении которого при вершине угол а.
Через вершину проведена плоскость под углом р к высоте. Найти
угол между двумя образующими, по которым эта плоскость пере-
секает поверхность.
Контрольная работа № 2 (вариант 2)
1. Решить уравнение
siti3xcosx = — tg х.
2. Решить систему уравнений
cosx + cos у = а,
1 Я
х + у = —’
313
3. Решить неравенство
sin 1^64 — х2 >0.
4. Дана окружность радиуса /?. Из ее центра проведены два
радиуса О А и ОВ, образующие угол а. В. меньший сегмент круга,
отсекаемого хордой АВ, вписан равносторонний треугольник, одна
из сторон которого перпендикулярна хорде АВ. Найти сторону
этого треугольника.
5. Основанием прямой призмы служит ромб ABCD со сторо-
ной а и острым углом а (ЛАВС=а). Найти площадь сечения,
проходящего через диагональ АА' параллелепипеда параллельно
диагонали BD ромба. Высота параллелепипеда равна h.
6. Ребра ОА, ОВ, ОС прямоугольного параллелепипеда равны
соответственно 2, 4, 6. Найти косинус острого угла, образованного
плоскостью АВС с плоскостью О АВ.
7. Выразить объем сферического слоя через его высоту и ра-
диус г среднего сечения.
Контрольная работа № 3 (вариант /)
1. Из пункта А в пункт В выходит пешеход и одновременно на-
встречу ему из пункта В выезжает велосипедист. Пройдя 3 км,
пешеход сел в попутную машину и встретил велосипедиста посре-
дине между А и В. Если бы пешеход не воспользовался машиной,
то для того чтобы встретиться с велосипедистом в том же месте,
он должен был выйти на 2 час 40 мин раньше. Если бы машина
выехала из Л на 1 час 04 мин позднее велосипедиста из В, то их
встреча произошла бы на расстоянии 15 км от А. Найти скорость
пешехода, велосипедиста и машины, если расстояние АВ равно
40 км.
2. Найти все действительные значения р, при которых сумма
корней уравнения
рх2 + х — 8р + 4 = 0
меньше 1, а их произведение больше р.
3. Решить неравенство
log» С*2 — 4х + 3) < 1.
4. Решить уравнение
sin 2х sin 4х sin 6х = s*n4--» '
4
5. Найти все решения неравенства
^g|cosx+/3sinx] 2 0
из промежутка 0^х<2л.
314
6. В треугольнике АВС из вершины С проведены высота CD=h
и медиана CF. Найти радиус окружности, вписанной в треуголь-
ник CFD, если углы при вершинах А и В соответственно равны
а и р.
7. Из основания высоты правильной треугольной пирамиды на
ее боковую грань опущен перпендикуляр, равный а. Найти объем
пирамиды, если плоский угол при вершине этой пирамиды ра-
вен а.
Контрольная работа № 3 (вариант 2)
1. Если пассажир в городе А сядет в поезд, то он доберется
до В через 20 час. Если же он полетит самолетом, то он попадет
в В через 10 час после ухода поезда, причем ждать самолет ему
придется более 2 час. Во сколько раз скорость самолета превы-
шает скорость поезда, если известно, что самолет догоняет поезд
через 8/9 час после вылета?
2. Решить уравнение
6 — 3 + т/х — 2==5у/Г(х — 2)(х— 3).
3. Решить неравенство
2x4- /а2
— х2>0.
4. Решить неравенство
2sin2х 4- 2cos2x— (2 4- V%)cosx 4-V2>0.
5. Решить систему уравнений
sinx 4----— = 2,
cosy
sin x 1
cos у 2
6. В равнобедренный треугольник с основанием а вписана
окружность. Найти радиус этой окружности, если расстояние меж-
ду точками касания ее с боковыми сторонами треугольника рав-
но Ь.
7. -Из основания высоты правильной треугольной пирамиды
опущен перпендикуляр на боковое ребро, равный р. Найти объем
пирамиды, если двугранный угол между боковой гранью и основа-
нием пирамиды равен а.
ОТВЕТЫ К § 1 —6, 8
Л
§1 Вариант 2. 5. 6 сек, 4 сек. 6. 7,2 кв. ед. 7. х = л& ± —, где£—
любое целое число. 8. — 2 < х < — 1 и 1 < х < 2.
Вариант 3. 9. 3000 руб. 8 месяцев и 2000
11. x = 2nk, x = 2nk— (— 1)*““» где k — любое
руб. 1 ГОД. 10. Х= _ .
целое число. 12. x<*L~
2
Вариант 4. 13. 2 м 10 см и 3 м 60 см.
14. 5 кв. ед# 15. х == — -j-
где k — любое целое число. 16. x<log23.
л
Вариант 5. 17. 2 га и 11 га. 18. 24 см. 19. х = лЛ+ —;
4
л t л 1 5
± — + —, где k—любое целое число. 20. х<—; 2<х<—
6 4 3 2
х~ 2л& +
и х>3.
9
4
8. x<Z —3 и
§ 2Л Вариант 2. 5. В 2 раза. 6. — кв. ед.
+ где k — любое целое число.
7. х = л&4“
X = л£ +
+(-0*f
Вариант 3. 9. На 25 мин.
10. 11. Х1 = яЛ+-^-, х2 = 2яй±
F О 4
2л
± где я—любое целое число. 12. —4<х< — 3 и 0<х<1.
О
Вариант 4. 13. На 10 мин. 14. AlpL. 15. х = , х = 2л&,
где k — любое целое число. 16. x<Jog32.
3/3 л
Вариант 5« 17. За 10 дней. 18. —— кв. ед. 19. x = nk — -j-, х =
, я л
= 2nk ± — — —, где k — любое целое число. 20. — 2< х< 2.
4 4
< §3. Вариант 2. 5. 6 км/час, 4 км/час\ 10 км. 6. (/3—1) кв. ед.
л л
7. х = л£ — —; х = л£ ± , где k — любое целое число. 8. х — 9.
4 6
___________________________ 9 \ л лк
2/3 — — J кв. ед. 11. х=—
л
х = ± —— где А —любое целое число. 12. х = 8.
6
316
Вариант
2лк
х= где
5
12 л
4. 13. 3 м^нас, 5 м?!час и 6 мР/час. 14. —. 15. х = лк-}- —,
О Л
k — любое целое число. 16. 32.
9/7
Вариант 5. 17. 2 час. 18. —jg—. 19. х = —у-, где & — любое целое чис-
ло. 20. х — 3.
2 ф лк
§ 4. В а р и а н т. 2. 5. В 4 раза. 6. V = — /13 tg ф-tg —. 7. х =-------; х=
3 2 2
л 4
’.к ± —, где k — любое целое число. З^х < — 2,) х > log2 —.
о - О
Вариант 3.
9.
1080 1350 27 , t ,/ Seos а
— тг "’'-’К-ТГ'-
л - <•
11. х = л&; х = лк (— 1)* ~, где k — любое целое число. 12. — 1 < х < 0
о
и 3<х < 4. <
Вариант 4. 13. В 2,5 раза. 14. V = 2 sjn3 ,sjn3 JL . 15. х =
2 2
Л Лк л
= л^+—; х=——4- — , где —любое целое число. 16. 0< x<Z 1 и х > 2.
4 2 12
2/2
Вариант 5. 17. В 3 раза. 18. sin<р = ——. 19. х — 4л&; х = Ьлк ±
2л
± ——, где k — любое целое число. 20. — 1 < х < 1.
«5
§ 5. В ар иа н т 2. 5. 1000 заявлений. 6. х = — -|-&л, к = 0, ± 1, ± 2,...
7. ^-(9 + 3/5), 8. 0< у<1.
Вариант 3. 9. АС = 45 км. 10. х = — -|-, k = Q, +1, + 2, ...
4 2
11. 4 /2 . 12. -у <х< 1.
Вариант 4. 13. АВ = 20 км. 14. х = kn, х = (— l)ft 4* + 1) л,
fe = 0, ± 1, ±2, ... 15.3. 16. х>3.
§ 6. Вариант 3. 11. а = 243 л. 12. 0<х< 1<х<3. 14. а=—5.
6 = 4. 15. (-----------Y.
\ ab -j- Ьс + ас J
317
Вариант 4. 16. Первого сплава 9 частей, второго 35. 17. Если а > 1, то
а~ Уз ; если 0<а< 1, то а^3 < х<а~ . 18. х = “ + Т*»
4 %
х = —х — л-|-£ л, fe = 0, ±1, ±2,... 19. х = 0.
6 6
20. — • (3 /б + 3/24-4/3).
6
§ 8. (вечернее и заочное отделения).
* пл л л
Вариант 1. 1.о = 7 км/час* 2. y = 2nk, у=-т~ — —,у = 2тя——,
2 о 2
. ф . Ф
sin — sin —
4 2 2
где k. п, т принимают все целые числа. 3. V = — Н3-;— --—.
3 ф4-ф Ф—Ф
cos-----• cos----
2 2
4. х < «—4, — 1<х<2 и х>5.
Вариант 2. 5. 20 м и 15 м. 6. i = л^ + агс tg(l ± т^З), где fe —любое
а + Р а — р
cos-------------------------------»cos----------
I 2/3 2 2
целое число* 7. V= — 2pq — —-•------------------. 8. х< —7;
3 3 ар
cos — cos—
2 2
-5<х< ^-2 и х>4.
Вариант 3. 9. 26 час к 33 час.
k и п принимают все целые значения,
цательных решений нет*
2 л л
10. z = — Jtk + —; z = 2лп — —, где
3 9 3
АОС г______________
1g-----п---= v — cos2y- 12. Отри-
Вариант 4. 13. 80 км/час и 120 км/час. 14. х = £л ± —, где лю-
О
бое целое число. 15. V « d Р{р — ЬУ ip — с), где р = (а + Ь + с).
16. —Уг13<х< 1 я 2 < х</13.
л л
В а р и а н т 5* 17. фг = nk — —, <р2 = 2л^ — и <р3 = 2л£, где k — любое
4 2 _
целое число. 18. Лл —kn — + (— 1)* -j-. 19. s
20.
2
co
§ 1. Географический факультет ......................
§ 2. Геологический факультет........................
§ 3. Биолого-почвенный факультет ...................
§ 4. Химический факультет...........................
§ 5. Филологический факультет ......................
§ 6. Экономический факультет........................
§ 7. Физический факультет...........................
Вопросы, предлагавшиеся на устном экзамене по мате
матике на физическом факультете ....
§ 8. Механико-математический факультет..............
Задачи на составление и решение уравнений
Геометрические задачи..........................
Решение неравенств.............................
Решение нестандартных задач....................
§ 9. Дополнительные примеры и задачи................
Арифметика и алгебра...........................
Геометрия. Планиметрия ........................
Стереометрия ..................................
§ 10. Темы контрольных работ..................
Ответы ... .........................................
3
7
11
18
24
28
49
131
152
158
166
182
190
208
208
259
272
310
316
Борис Иванович Александров,
Петр Сергеевич Моденов
ПОСОБИЕ ПО МАТЕМАТИКЕ
ДЛЯ ПОДГОТОВИТЕЛЬНЫХ КУРСОВ
МГУ
4 заказное
Редактор Т. Г. Батенина Технический редактор Г. И. Георгиева
Корректоры С. С. Мазурская, М. И. Эльмус, Е. П. Утанина, И. С. Хлыстова
Сдано в набор 28/ХП * Подписано к печати 24/VII 1967 г.
Л-95651 Формат бОХЭО1/^ Бумага типогр. № 3 Физ. печ. л. 20,0
Уч.-изд. л. 15,86 Изд. № 37/зак.
Заказ 351 Тираж 40.000 Цена 70 коп.
Издательство Московского университета
Москва, Ленинские горы, Административный корпус.
Типография Изд-ва МГУ. Москва, Ленинские горы
Цена 7(дкоп