$
'	4
Решение
алгебраических
уравнений
Б БК 22.193
Б43
519.61
= ^=
х*! Беланов А, А. Решение алгебраических уравнений мето-
дом Лобачевского.— М.: Наука. Гл. ред. физ.-мат. лит., 1989,—
96 с. — ISBN 54)2-013961-0.
Изложен модернизированный метод Лобачевского отыскания
корней много членов. Модернизация позволила сделать метод эф-
фективным для решения задач на малых вычислительных устрой-
ствах и более простым в реализаций.
Имеются программы для микрокалькуляторов типа «Электро-
ника БЗ-34».
Приводится много примеров, поясняющих те или иные особен-
ности метода.
Для специалистов, выполняющих расчеты на малых вычисли-
те явных у стро йс тв а х.
Табл. 32, Ил. 10. Бибаиогр. 24 назв.
Рецензент
член-корреспондент АН СССР В. В, Воеводин
И ауянее и зда нив
&ЕЛАУЮВ Александр Андреевич
РЕШЕНИИ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЯ
МЕТОДОМ ЛОБАЧЕВСКОГО
Заведующий редакцией Е. Ю, Уойол
Редактор И. Е. Тьфтылиников
Художественный редактор Г. ..И. Коровина
Технический редактор в. и. Кондакова
Корректоры: Е. 10. Рычагова, ,1. С. Сомова
ИБ № 32687
Сдано и набор	Подписано н печати 22 1Н.8Н.
Формат 84x108/32. Бумаги кц .-журнальная
Гарнитура -обыкновеннаи ночам Печачч» ni.i<mc;i;i.
УСЛ. печ. Л. 5,04. Кр.-отг. =>JI;k Уч. н:ЧД .=|.
Тираде 17500 энз. Заказ М 1К«?. Ценз :;о ко;>.
Ордена Трудового Красного 3нами як |Г.1Д<т'яьст&о <<Наука»
Гл ав н ая ред а кция ф и з и ко - м ч г е м а т и ч < г ко i I л и тс ра т у ш .т
Ji 17071 Москва В-71, Ленинский irpuaiscKr, Г»
Вторая типография издательства «Лаука=.-
121099 Москва Г-99, Шуби некий нсу.т 6
„ 1602120000-605 t _
Б - iWHT" U9
ISBN 5-02-0139614)
2
Иа; V1 т ель етв о оИа у к а*>.
Главная редакция
из и i > о-ма тематнчес к ой
литературы, 1Н89
ОГЛАВЛЕНИЕ
Предисловие ..............<.............................. 4
§ 1.	Краткий обзор литературы но теории и применению
метода Лобачевского...................................... 7
§ 2.	Сущность и точность метода Лобачевского............ 9
§ 3.	Алгоритм квадрирования уравнения и его реализа-
ция па микрокалькуляторах типа «Электроника Б3-34» 1В
5 4. Алгоритмы разложения уравнения по степеням /Дву-
члена и определения знаков корней, Применение их
совместно с методом Лобачевского................... 23
§ 5я	Анализ некоторых способов вычисления комплексных
корней с различными модулями...................♦	. . .	32
§ 6.	Вычисление комплексных корней способом деквадри-
рования уравнений................<...................... 40
§ 7.	Теоремы о коэффициентах алгебраических уравнений,
имеющих корни с равными модулями. Способ расши-
рения области применения формул Энке , . . i. . ,	45
§ 8.	Уравнения, сопряженные с заданными уравнениями 51
§ 9.	Решение алгебраических уравнений различных типов
обобщенным (с двукратным кв адресованием) методом
Лобачевского...........................................  61
§ 10.	Сопоставление различных вариантов метода Лобачев-
ского с другими методами решения уравнений . . .	71
И р и л о ж ение. Программы для микрокалькулятора
«Электроника Б 3-34».............................   87
Список литературы	................... 96
ПРЕДИСЛОВИЕ	• л
Задачи, требующие решения нелинейных алгебраиче-
ских уравнений, встречаются во многих областях науки
и техники. Поэтому разработано большое число способов :
решения таких уравнений» ..
В связи с повсеместным распространением програм-
мируемых микрокалькуляторов и персональных микро*
ЭВМ возрос интерес к простым высокоточным способам
решения уравнений, реализуемым на этих вычислитель^ :
ных устройствах:, если уравнение с высокой точностью
можно решить на микрокалькуляторе в течение 15—30 мин, •
то обращение к более мощной ЭВМ становится нецело- •
сообразным — общие затраты времени на.решение урай- •
Нения с помощью этой техники коллективного польао- j
вания (подготовка программы, оформление заявки, ожи-
дание утвержденного исполнителю времени использования . 
ЭВМ и т, п»)л как правило, больше.
До середины 50-х годов метод Лобачевского считался .?
одним из самых совершенных способов решения ноли- 
нейных алгебраических уравнений [2, 3, 7, 17, 24]. Од-
нако попытки реализации его па ЭВМ не удались из-за .
недостаточной универсальности и громоздкости алгоритм
ма и низкой точности определения корней с близкими :
и равными модулями. Поэтому в настоящее время при :
решении уравнений как на ЭВМ, так и на микрокальку-
ляторах метод Лобачевского не используется [4, 14, 15, 
16, 22].
Для устранения недостатков метода Лобачевского раз-
работано несколько его вариантов [6,10]. Однако эти
варианты также не нашли широкого распространения
из-за наличия у них не только дополнительных достоинств
по сравнению с классическим методом, но и дополните ль- 
пых недостатков.
В настоящей работе проведен анализ погрешностей
метода, изучена зависимость между коэффициентами урав-
4
нений* имеющих корни о: равными щщудявд^'^
базе этих исследований предложены новые способы
шения метода Лобачевского: •
. 1) использование весьма простого признака наличия
в уравнении действительных и комплексных корней с раз* ; <
ными модулями; ..	...Л-.’	..
2)	вычисление действительных и комплексных корней
с равными модулями с помощью сопряженных уравнений,
корнями которых являются действительные части комп-
лексных корней или действительные корни, заданного •.
уравнения; •
3)	усовершенствование метода Энке и решение с по-
мощью этого метода уравнений с комплексными корнями,.  .
имеющими как различные, так и одинаковые модули;....
4)	решение уравнений с действительными и комплекс-
ными корнями, с различными и одинаковыми модулями
с помощью универсального обобщенного метода Лобачев-
ского — метода двукратного квадрирования (преимуще- .:
ства метода возрастают с увеличением степени уравнения); .
5)	определение комндекеных корней с различными
модулями весьма простым способом деквадрирования урав-
нений;
6)	определение наличия и места комплексных корней :.
в квадрированном уравнении способом* не требующим :-
информации о знаках коэффициентов уравнения в раз-: л.
личных циклах квадрирования;
7)	определение знаков действительных и комплексных:,
корней упрощенным способом*
Для повышения точности определения корней с близ-
кими модулями, в соответствий с рекомендациями работы:
1,24], детально рассмотрено применение разложения за^ . ‘
данного уравнения по -степеням: двучлена* !-
Целесообразность использования и высокая эффект у :
тивность перечисленных способов продемонстрирована на
конкретных примерах. Даны рекомендации по выбору
способов в различных условиях.
Кроме того, в работе проведен сравнительный анализ
модернизированного метода Лобачевского и широко ис-
пользуемых в настоящее время других методов решения
уравнений. Показано, что в одних случаях он не уступает*
а во многих других случаях — существенно превосходит: .:
применяемые методы. Анализ подтвердил5 также цела-. \
сообразность реализации метода Лобачевского на программ.
мируемых микрокалькуляторах типа «Электроника Б3-34й:: *.
при решении уравнений степени п 7* а если модули
5 
действительных и комплексных корней равны, — при
п 14.
Настоящая работа может служить пособием по изу-
чению метода Лобачевского, а также руководством по
решению нелинейных алгебраических уравнений па прог-
раммируемых микрокалькуляторах типа «Электроника
БЗ-34». В связи с этим прилагаются программы реализа-
ции как самого метода, так и перечисленных выше спосо-
бов повышения его эффективности. Программы решения
уравнений различных степеней однотипны: единообразно
вводятся исходные данные, используется одна инструк-
ция, по единой методике анализируются результаты вы-
числений. Кроме того, обеспечивается решение уравнений,
имеющих меньшую степень по орав нению со степенью,
указанной в названии программы.
Для облегчения составления программ решения алгеб-
раических уравнений высоких степеней на микро-ЭВМ
или на быстродействующих ЭВМ в работе содержится
подробное описание соответствующих алгоритмов.
Предложенный в работе способ решения алгебраиче-
ских уравнений с действительными и комплексными кор-
нями, имеющими равные модули, путем их надлежащего
распознавания, составления и решения сопряженных
уравнений может быть полезен также при использовании
других известных способов решения алгебраических уран
нений.
Автор считает приятной обязанностью выразить глу-
бо кую б л агод арность ч л. - кор р. ЛII СССР В, В .Воеводин у
за весьма ценные замечания и указания, реализация ко-
торых существенно улучшила содержание книги, а также
профессору МГУ д-ру физ. мат, паук Л. Г. Сухареву
и редактору книги канд. физ. мат. наук Е. Е. Ты рты ш-
НИКОВУ.
Л. А. Беланов
§	1, Краткий обзор литературы по теории
и применению метода Лобачевского
Одном из первых работ, в которой изложен рассмат-
риваемый метод, является «Алгебра» Н> И. Лобачевского
(опубликованная Казанским университетом в 1834 г.
II |). где была разъяснена сущность метода, приведены
формулы для преобразования {квадрировапия) урав-
нений, дан пример решения уравнения. Через три года
метод был вновь предложен швейцарским математиком
Греффе, а еще раньше, в 1826 г.,— французским матема-
тиком Дапделеном. Поэтому рассматриваемый метод иног-
да называется методом Лобачевского—Гроффе — Дандо-
лепа [11]. Существенный вклад в разработку метода внес
в 1841 г. немецкий астроном Энке.
Применительно к решению уравнений разных типов
метод подробно изложен академиком Л. II. Крыловым
в лекциях о приближенных вычислениях, впервые опуб-
ликовав них в 1911 г. [2].
В курсе высшей алгебры А. Г. Куроша отмечается,
что среди методов приближенного в ычисмепия корней
наиболее совершенным является метод Лобачевского [3|.
Аналогичная оценка этого метода содержится в работах
Л. К. Сушкевича. В. II. Демидовича и И. А. Марона,
В. Л. Загускина и др. [13, 7, 10|. При этом отмечаются
с ле ' (ующи в достоинст в а метода:
()	решение уравнений производится без выполнения
громоздких операций предварительного отделения корней;
2)	все корни уравнения определяются практически
одновременно;
3)	определяются различные типы корней — действи-
тельные, комплексные, с близкими и равными модулями;
4)	корни вычисляются, как правило, с весьма высокой
точностью;
5)	процесс вычислений всегда сходится.
7
. Однако во многих современных .руководствах по вы-
числительной математике метод Лобачевского излагается
весьма кратко или вообще не упоминается [4, 14, 15, 16, |
17]/Так, в широко распространенных справочниках по 1
высшей математике [8, 9] изложена лишь сущность ме- I
то да. Более подробно метод описан в справочнике ио ре- |
тению, алгебраических уравнений (10] и в руководстве J
по высшей математике [11]. Попытка использования ме-J
тода Лобачевского при решении уравнений с помощью
микрокалькуляторов предпринята в работе [23]. Эта
попытка, по-видимому, признана авторами работы не- j
удачной и в следующем издании книги [22] метод Лоба-
чевского отсутствует.
Наиболее часто отмечаются недостатки, сформулиро-
ванные в работе [6] следующим образом: «Метод пе явля-
ется универсальным, так как имеются уравнения, для/
отыскания корней которых он неприменим. Но и в слу- 
чаях его применимости, при наличии комплексных корней, j
его реализация на современных машинах сильно затруд- ;
йена. Из-за сложной логики практически невозможно j
составить достаточно универсальную программу решения :j
широкого класса уравнений по методу Лобачевского, j
Метод можно рекомендовать в основном для ручного счета <
при отыскании корней с невысокой точностью»..
Представляет определенный интерес анализ способов
преодоления трудностей, встречающихся при использо- }
вании метода Лобачевского,“которые^ екомендованы в ра- =
боте [2], и способов, предложенных в настоящей работе. .1
Чтобы убедиться в том, что уравнение имеет корни
с равными модулями, А. Н. Крылов [2] рекомендует •=
«поступать по известным приемам разыскания равных :
корней, отыскивая наибольший делитель между функцией 
f (<г) и ее производной». Вместо этой громоздкой операции,
как ' показано ниже, достаточно сопоставить отношения :..
определенных коэффициентов заданного уравнения.  ;
При решении уравнений с комплексными корнями \
в работе [2] рекомендуется использовать формулы Виета/
или Энке. В настоящей работе показано, что испольао- I
ванне формул Виета нецелесообразно, а методика Эпке /
может быть модернизирована с целью определения комп-
лексных корнем как с разными, так и с одинаковыми мо-j
дулями?Кроме того, для решения уравнений с разными^
типами корней -предложен весьма простой универсальный ?
метоп двукратного квадрировапия, достоинства которого,
проявляются тем больше, чем выше степень уравнения.
8
Большое внимание в лёкциях А. Н. Крылова уделено
обоснованию поправок вычисления комплексных корней
г близкими модулями. Ниже показано, что даже при
использовании современных микрокалькуляторов с весь -
ма ограниченной разрядностью чисел эти поправки не
нужны — в обоих вариантах погрешности вычисления
корней практически одинаковы............ ............
§ 2. Сущность и точность метода Лобачевского
Пусть задано алгебраическое уравнение
с^ха +	4* »• • 4"	4* ао 0 '	(2*1)
с действительными коэффициентами. Для определения
корней методом Лобачевского уравнение преобразовывают
так, чтобы каждый корень нового (квадрированного) "
уравнения был равен квадрату соответствующего корня
исходного уравнения. Затем полученное уравнение вновь
квадрируется, и через т циклов преобразования полу-
чается уравнение .
апт^П	+ • * ♦ + (—1)П<г0т =0-	(2-2)
Индекс п — i в уравнениях (2.1) и (2.2) означает
также номер ячейки ЭВМ (микрокалькулятора), в которую
записывается данный коэффициент, а индекс т коли-
чество циклов квадрирования, после которых получено
данное уравнение.
Корни нового уравнения (2.2) связаны с соответствую-
щими корнями уравнения (2.1):
1 « • ♦ j Zn — &п(2*3)
где N ~ т. — количество циклов квадрирования.
Из соотношений (2.3) видно, что в результате кв а др и-
ровапия корни уравнения (2.1) изменяются по-разному,
в зависимости от величины модулей. Рассмотрим способы
использования подобного изменения корней при решении
алгебраических уравнений.
Для уравнения (2.1) формулы Виета, выражающие
зависимость коэффициентов уравнения от его корней,
имеют следующий вид:	'
ап-а	।	t <
---= + + ..................................
п
йп~?	।	t	I
—~ ^=^2 4- жгг3 4- ... 4- Хг^Гп,
ап
9
— = a:xa;3j:s + si:r2r4 +	x„.-2xn^Tn,
71
(2-4)
(-l)"--^-V8...xn.
an
Формулы Виета для уравнения (2,2):
ап-1; т
а
nm
— zi d- Zz H”
"t ^n»
’	*1	F	1	t
-	---ZtZ2 -Г- z±z3 -r . . . 4- 2rt-iZn,
ПП1
™	~Z1Z2Z3 -4- 21Z2Z4 -j- - . . + Zn_.2Z-t^1Zn)
nm
(2-5)
— 7 7 7 7
nm
С учетом выражений (2,3) формулы (2.5) можно пре-
образовать к виду
ап-1; т
 д
w
хпх^1 J
^п-2; «I
а
пт
JV„N
(Г-л Л-п—1
а
пт.
ап-Э; т
хпхп- 2 У
%т
апт
N .\Т
= Т7Г .
.V .V
У'2	.
Рассмотрим наиболее характерные случаи.
1, В с о модули кор н е й р а з л и ч н ы, причем
I I I ^rt-l I	* Zz> 1	|-
При достаточно большом показателе степени
N r^-2Vv
’Un J
*n-i
. хп.......... .	,
бречь и уравнения (2.6) преобразовываются к
шениями
*1
можно
N отно-
прене-
виду
a-n~i; m
—-	^zn = xn>
<4*
nm
10
an-2; m
.V
^n-1»
а
пт
ап-?.\ m „ _	„	____
—-----=2= 2п4г(-*|2п^2	*^n '^n-l^-n-2*
апт
(2.7)
.52L~, , zz-A!' .т„К
37^77	-- *t’7L ^П-1 ’ • - Kl ♦
anm
Разделив 2-е уравнение (2«7) на 1-e, 3~e — на 2-е и т. д.
получим следующие соотношения:
an-l;m _	_ V
“Г----- — Zn---п ,
апт
ап~2; т
Лтг.-1; tn
an-3; m
~	___ .V
'= Z\i-2-----^n-2’
а-л-2; m
(2.8)
%г.
а1т
'^Z^Xy .
Следовательно, модули корней уравнения (2.1) таковы:
1 J	1/Лт		 1 InH п — |	/ йп \VxV ( Qm \ *
|^|== z1^'	|	Г а \ 1/1N f im , 1 1 as>m J
|.r3|=KK;(	' %п \i/N	(2.9) а	/	' < 3m /
I Д.'Л
V/N
апт J
Из формулы (2.6) следует, что в главном члене погреш-
ности определения f-ro корня имеют вид

(2.10)
У
При достаточно большом различии между корнями
или большом показателе N формула (2.10) упрощается:
/ X- \
; |^1К|.П|- (2ЛОа>
\ I /
11
Таблица 1
Относительные погрешности метода Лобачевского
Число ЦИКЛОй кзадряро- в ИН ИЯ ГИ	ОТПОШСПИР Л 1					
	0,9	0,8	5 0,1	0,6	0,5	1 од | i
!	4	0,1853	0,0281.	0,0033	0,0033	1,5 «10'"*	ЦЬ-И
1 i	0,0011	6,3«10“7	1,2'10“ ™ ,»ЛЛ»Л VAA«AV4»A4V*A....>.^—	8,3-10“^	5 «10^ !	Ю--’5
Погрешности Д$, рассчитанные по формуле (2.10а).
для уравнений 6-й степени при различных отношениях
и числе циклов кваэрирования	— 4, т2 6
приведены в табл. 1.
2. М о д у л и всех деист в и т е л ь и ы х к о р-
в е й о ди и а к о в ы:
I I I ♦ == \ *п !•
В этом случае при апт (2.6) имеют следующий вид: «П-1Г1К “ fl "Г (~~~ I + f • ж	X *♦ X п	„-Л.'Г* ’<j ( ~н.-2 \ «п-2; т - ••"?>. -л-i i |- I  J \ хп-1 / N Лг X; Г 4 . ( А m *“-?	1 1 Ч" 1 ’7" L	\ f п	4й .с"	 «0ГП	** 1 U !! "	। Здесь Ся =	, н щ	п\ Выр ажен и я (2,3} j ii м н и! м ? ‘“'д	 •Л?>1 и Н - Г: /П ^,.. ... ?.} » ...« -— 		 г л>'....2. Ц!г	1 коэффи)р4еиты уравнения \N	1	N 				J J_ w хп i	J ..]... f —LL?.l I ц.. v t ' k ' ’ J \,	f	•	\Д!	1 .......	|	W> .	J	|	«mJ ..	I	-, * 1	!	1	T	J	1 •2 /	X	’,zn-2	/	J  С», наг нпи .V ::	: ?/Г,- , _. (<) -г ’ t>] I  ' ’ ^.. 1 IL'] ;t;f, \ ^?7 '
1.2
_ Л’
Согласно (2.9) паходим (с точностью до знака) корни
щдаппого алгебраического уравнения:
(2.11)
Анализ выражении (2.11) позволяет сделать следую-
щие выводы.
1. При большом числе циклов квадрирования т,
г. е. при весьма большом показателе степени N = 2т,
пычислеппые значения корней будут отличаться от не-
ги иных. значений на сколь угодно малые величины, так
__	.,v	. / V/1V . / 1 X1/N .
как если/Уоо, то я?'- —> 1. (-----)	—) —>1,
' \ п /	\ п )
2. Наибольшие погрешности имеют корни с индек-
сами I = 1 и i — п. причем хп больше истинного значе-
нии. а т, меньше приблизительно на такую же величину.
Корень, имеющий индекс I ~ Л~ -|- 1? вычисляется е шь
шючьвюй точностью. Относительная погрешность вычис-
•ичппх корня хп равна
_ dT
<2Л2)
Я
IJ табл. 2 приведены относительные погрешности он-
ррд^.:1шшя хп для уравнений 4-й, 5-й и С й степеней, рас-
= читанные по формуле (2.12) при различных циклах квад-
рн ров а и и я. т.
В общем случае относительная плгрепптость вычисле-
ния модуля корня с индексом i равна
/ /и-1 x V/V
д„ I 'ti•	\	1	/О
13
Таблица 2
s
Наибольшие относительные погрешности метода
Лобачевского при определении корней с равными модулями
Степень уравнения п	Количеств* циклов квадрирования т 		 	 ....... 1			
	4	5	8	в. 1
4	0,0908	0,0443	0,0219	0,0054
5	0,1058	0.0516	0,0255	0,0063
6	0,1185	0,0576	0,0284	0,0070
Ж 
\Л:-
Ж
«
Относительная погрешность определения модулей, вы-
численная по формуле (2.13), приведена в табл. 3.
При использовании микрокалькулятора «Электрони-
ка БЗ-34» погрешности метода Лобачевского в случае
решения уравнения 6-й степени с действительными кор-
ними -г- з:0 -- 2 приведены в табл. 4.
Из сопоставления данных, приведенных в табл. 3, 4,
видно, что «теоретические» и «экспериментальные» зна-
чения совпадают с высокой точностью.
Из приведенных в табл. 2, 3 данных, кроме того,
следует, что при равных модулях корней погрешности
метода Лобачевского существенно больше, чем в случае
различных модулей. В связи с этим существует мнение,
что метод Лобачевского в некоторых случаях численно
расходится [12]. Ниже на конкретных примерах показано,
что даже при использовании микрокалькуляторов, имею-
щих небольшую разрядность чисел, численного расхож-
дения метода не наблюдается.
3- Уравнение 4-й степени имеет два действительных
корня {х} я х4) и пару комплексно-сопряженных корней
(.г2 — г соя ф -Ь ]r ein <р и — г cos ф — yr sin ф? где г —
модуль, ф — аргумент).
Положим, что хл У> г > а — 1. После т циклов
квадрирования получим
/	V	ЛУ	\
„ _,Л ,< г о со* м ,	]
аз?п — А 1 Т ——v------"1 ~7Г I ’
\	X*	X? <
/	jV	^N. V
= 2^V cos 2V<pi 1 + ттН-'ХГ +	..+ Чг Ь
\	2г4* соя дг<р совАф х^ /
(2.14)
с
о
S
«а
ф
©
«
Ф
Е
К •
с-
к
а,
к
©
S
ф
3
я
л
ф
В
о
к
i*
Q
к
в
я
ф
5Я
&
«
д
е
ф
и
ф
©
е -
н
ф
S
Я
S *
& *
5 «
а р?
Ъ
п
о
В
%
3
5В
и
05
Си
		
	•и и	СЛ SO О £3 о о 1 1
		
1 i 1	ос и	-0,0557 —0,0142
Модули х.	>?	сс IQ «с5 О о м* г- о о 5 i
	и 1 1	0,0181 0,0045
	 Л у.	0,0589 0,0144
		i I >Л' •<< оо оо ’г—1 03 г* О г г- О О 
	w вишшобиДКеая ffOHMMii он-коЯ	st О
st Р г; 'С' 03	* с^1 • fa 5 В X й 3 ” щ си « t « ** ф ф  а о н К № : - S s И я иС ж й. к В § * S к * © Е О Ф М S ф ф JT © ч « « ж ей £ и v И Ф /М J! А ^<4 54 ё »з “ 3 н ф т Ck S| Ф * Ф '1< х С эд ? ж я S “ ф >. Ж г4 © О К	Модули корней х. 						—			-г-			Т—		И	П г* hS 0 04 е-1 оо i i
			<t X ХС" Ю <&> LO '-r-i. о о ОС? 1 1
		«	о Л O-J тс CC QO t-- i.O 58 О о i 1
			0,01814375 0,00573905
		И	Ю QO О {"- ос oo 02 Оэ ос оэ i/J -*f”< oo oo
		к	0,118496 0,0284236
		Кол-во циклов квадрирования tn	Nt <o
15
л?
.. cos ZVrp
“рг~

r4>sW Г1-1 
«от —
• . ..
Из анализа выражений (2.14) Mdxpo сделать следую-
щие выводы.
Г. ;К^	уравнения из-за
присутствия сомножителя cos N^> могут принимать отри-;
дательные значения. Это свойство является одним :.’.йз-.
важнейших признаков наличия и места в квадрированном
у^адйевии комплексных корней. Остальные коэффициен-
ты при пь 1 положительны.
: ; 2. Отношения между некоторыми соседними коэф-
фициентами квадрированного уравнения
f“ •	..  .2^ cosjVq?	...	ri....,
+'л' '  ..
•1
a
2m .
Л'
i •	i	г
_ 2 C0S /V<₽ V + 2Л COS + zTfcosЛф T
*т г
441.:
(2-15)
Л \ >
Х1 I
4 / ’
rN
+ 2a?4 cos Лф “b
а
ап — r
П| - - —* —*** I
” й8ш •
I 4V
2 cos /Vcp I 1 -/ —]y 1	-
\ Sr-^cos/Vtp
л _l ? r* eos 2Vcp \ xi
1 4“z‘	Л
*4	-?*.
после извлечения корня TV-й степени с достаточно высокой
точностью равны г, независимо от соотношения между
действительными и мнимыми частями комплексных кор-^
ней. Это свойство обусловлено тем, что выражения (2,15) >
заключенные в квадратные скобки, будучи больше или
меньше 1, после извлечения корня N-й степени с высокой
точностью равны 1.
.. Поскольку в алгебраическом уравнении комплексные
корни являются попарно сопряженными с равными моду-
лями, в квадрированном уравнении два соседних отн<>
шения коэффициентов (2.15) имеют весьма близкие, зна-
чения, приближенно равные г. Следовательно, в том слу-
чае, если отношения коэффициентов (2.15) после извле-
чения корней У-й степени существенно различны, можно
полагать* что заданное уравнение не имеет комплексных
корней. ’.	. :
Как показано выше, модули всех корней кв а др про-
ванного уравнений, в том числе действительных и комп-
16
  .   
располагаются один за другим в строгом соот-
йх величиной,, причем если модули "корней
®||Л:йчнь^ то в соответствии, с формулой (2.10) погреш-
Ш^стй йх ’вычисления практически не «зависят от наличия
уравнении других корней. Благодаря этому свой-
можно полагать, что квадрированное уравнение
задается ца несколько практически независимых уран-.,
й 1-й/.2-й, s-й степеней, причем сумма степеней .
распавшихся уравнений равна степени и заданного
^Мнения. Действительно, ври разделении всех корней
^В^ношеиия (2.8) можно записать как совокупность
§Й0дапощйх уравнений. 1-й степени:
Ч" аот ~	•+ aim — 0, . . a.nmZ + ап-1; m ~ 0*
gg/Поскольку модули . комплексно-сопряженных корней
^Дньт; то при различии в модулях соседних пар комплекс
корней квадрированное уравнение (2.2) распада-
®ся па квадратные (практически независимые) уравнения:
а2т%2 4“	4~ дохн = 0
+ <W +	= 0
ж
• (2Л6)


ar.in^ Н“ «л-1;mz 4“ «n-а; т— 0.
1^/—Если заданное уравнение имеет одну или несколько
Вар действительных корней с близкими или равными
одулими. то квадрированное уравнение также распада*
,.^тся на квадратные уравнения типа (2.16). Для опредёле-
..яия корней в этом: случае необходимо, очевидно, найти
корни квадратных уравнений типа (2.16), а затем с по-
:||гощью формул (2.8) модули корней заданного урав-
нения.
ж- Необходимо отметить, что если в формуле
\ : .
-
	
gbn— ? “im	т (2 17)
дискриминант отрицателен, то это указывает на то, что
ц|аданпое уравнение содержит комплексно-сопряженную
гМару корней. Использование дискриминанта для расдо-
^Йрдиия комплексно-сопряженных корней весьма часто
^ЙЙтруднитеявно, из-за больших значений коэффициентов,
^следствие этого - квадраты и произведения коэффициен-
тов могут превышать допустимый для данной ЭВМ
^Япазоп чисел. Поэтому вместо определения «знака
...	:	. : . • • •	17
дискриминанта целесообразно рассмотреть условие
2 V^i-1; т *ги*	(?‘18)
Данное неравенство справедливо для всех комплексных
корней, а также может быть справедливо для действитель-
ных корней с равными или очень близкими модулями.
Поэтому применительно к микрокалькулятору «Электро-
ника БЗ-34» его необходимо дополнить условием
д	"К *4-1; t» * j/ гп
> 1СГ3.
(2.19)
Значение предложенного признака определения нали-
чия в заданном уравнении комплексных корней и их
места в квадрированном уравнении состоит в том, что
он позволяет полностью автоматизировать процесс квад-
рирования, отказавшись от запоминания знаков коэф-
фициентов в каждом цикле квадрирования. Последняя
информация полезна только в особо сложных случаях,
при наличии корней, с близкими и равными модулями.
. Количество циклов квадрирования целесообразно огра-
ничивать только возможностями ЭВМ, так как с увели-
чением т точность вычисления корней, как правило,
возрастает.
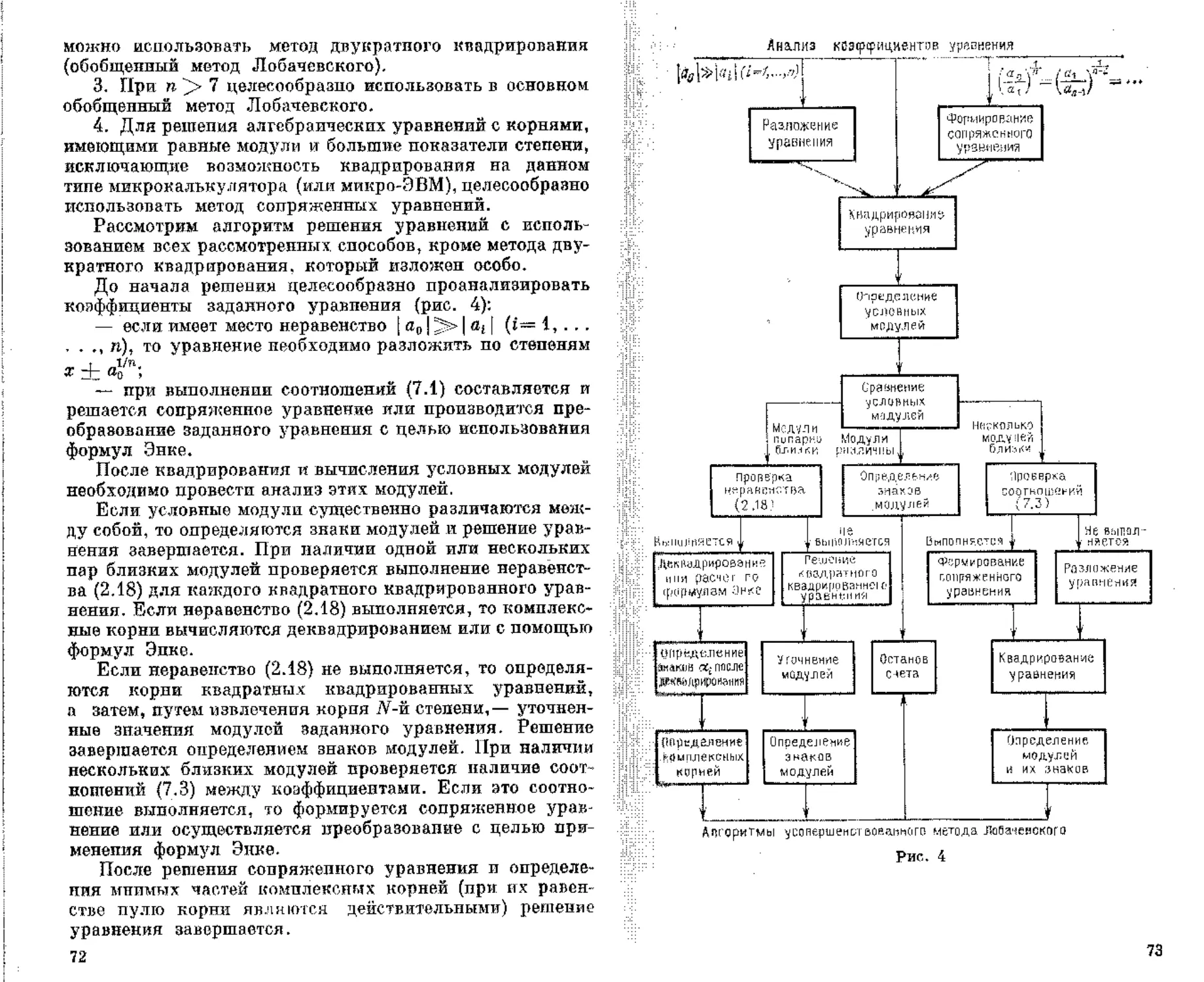
.. § 3. Алгоритм квадрирования уравнений и его
реализация на микрокалькуляторах типа
«Электроника БЗ-34»	. .
Коэффициенты квадрированного уравнения можно вы-
числить, представив заданное уравнение (2.1) в виде
ап (х + ху)(х + я2) . . . (я + хп) = 0. : (ЗЛ)
Умножим уравнение (3.1) на аналогичное уравнение
ап (^ — х)(.г2 — я)... (хп — х) = 0.	(3.2)
Произведение уравнений (ЗЛ) и (3.2) имеет вид
я* (х, — х-2)(х| — х?). . . (Хп — х2)	0.
Обозначим у — х\ — — х^ у2 = —	* < -? Уп ==
•— Хп и, повторив произведенные выше преобразования
т раз, получим уравнение
й/im .(^ "I” zl)(z ""Ь ^2) • • ♦ (2 “Г 2П)	0,
которое является аналогом уравнения (2.2). .
3 Выполним указанные выяге операции для уравнения
44 степени:
4-	а^х2 -г ахх 4- а0)*(а^4	й3^3 +	—
№"/<=•.	— Яд# + «Л) =* а£г8 — (4 — 2a2a4)j?e +
g||- . + («о — За-^з + 2а0й4)я4 — (4 — 2а0а2)х2 + 4 == 0.
Следовательно, после 1-го цикла преобразования по-
/ дучим уравнение, имеющее корни, равные квадратам
^корней заданного уравнения (со знаками «•—»):
<W4 +	-г «пу 4’ а01 = О,
У =* “	«41 = «4> ^31 = 4 — 2й2<74,	(3.3)
^21 ™ й2	4г 2й0й4, йц =	” 2й0Й2» &01 =* йд. .
Ж: Отсюда следует, что алгоритм определения коэффици-
;«адтов квадрированного уравнения весьма прост: каждый.
™ коэффициент преобразованного уравнения равен квад-
РатХ прежнего коэффициента минус удвоенное произ-
ведение соседних с ним коэффициентов, плюс удвоенное
Произведение следующих в порядке близости коэффициен-
тов и т. д. Этот алгоритм одинаков для всех циклов и для
'^уравнений любой степени.
При болыпих показателях степени п определение
Коэффициентов квадрированного уравнения целесообразно
4 производив без формул, с помощью двух полосок бумаги,
использование которых продемонстрируем на элемеятар-
. ном примере вычисления коэффициентов а1Х и я21 урав-
Нения 4-й степени (рис. 1).
4	3	2	1	0		
		0	1	2	3	4
life-- 	-2<го
......
4	л	2	1	0
0	1	2.	3	4
а21 “ «2-2а1а}+ 2«0а.
^еллл.’. У ’
^L...	• .	Рис. 1
IS?Предположим, что в ячейках ЭВМ 0~ 4 хранятся
рхфОтветствующие коэффициенты, а номера ячеек записаны
двух полосках бумаги в обычном и в обратном порядке.
2»
19
На рис. 1 показаны положения полосок бумаги при
определении коэффициентов аи и п.,} уравнения 4-й сте-
пени. В общем случае для определения z-ro коэффициента
уравнения (2.2) необходимо разместить полоски так,
чтобы клетки с номером i находились одна над другой.
Коэффициенты уравнения, записанные в ячейки ЭВМ.
номера которых находятся один пад другим, перемножа-
ются. Причем если I — четное число, то произведения
коэффициентов, записанные в четные номера ячеек, сумми-
руются, а я нечетные номера —вычитаются. При нечетном
i указанные действия производятся в обратном порядке.
Полученные в процессе квадрирования новые значе-
ния соответствующих коэффициентов записываются в дру-
гие ячейки памяти ЭВМ, а после определения всех коэф-
фициентов, кроме крайних (а01 и г/п1), записываются вместо
их предшествующих значений. Коэффициенты aQl и ап1
вычисляются последними и сразу записываются в ячейки
О и п.
Изложенный выше алгоритм реализован в прилагае-
мых программах квадрирования и определения модулей
корней уравнений 3~н7-й степеней, предназначенных для
микрокалькуляторов типа «Электропика БЗ-34», Про-
граммы для уравнений степеней от 3 -й до 6-й имеют иден-
тичные инструкции.
Коэффициенты уравнения при показателях степени
1 ч- п записываются в ячейки с такими же обозначениями.
Коэффициент при нулевой степени (свободный член) вместо
ячейки О необходимо затгисать в ячейку С. Ячейка О
используется для записи числа циклов т. которое можно
определить по соответствующей формуле или путем по-
следовательного возведения в квадрат коэффициента урав-
нения, имеющего наибольшую величину,— до тех пор,
пока порядок возводимого числа не превысит 50. Коли-
чество возведений в квадрат приблизительно равно числу
циклов квадрироваяия.
После прекращения квадрирования необходимо про-
верить порядок наибольшего коэффшщоита. Если этот
порядок меньше 50, то квадрировапие целесообразно
продолжить. Разделив все коэффициенты уравнения на
число порядка 1049 (если в уравнении нет коэффициента
п-от существенно меньше 1), можно провести еще один
цикл квадрированпя, которое, как правило, увеличивает
точность определения модулой корпел.
Если уравнение содержи!1 коэффициент а<у меньше 1
(при ап = 1), то необходимо также несколько раз возвести
20
в квадрат наименьший коэффициент. Процесс возведения
заканчивается, если наименьший коэффициент имеет по-
рядок меньше —49. Для дополнительного квадрирования
и атом случае необходимо все коэффициенты умножить
иа число 1019.
В общем случае при наличии в уравнении коэффициента
< 1 необходимо все коэффициенты уравнения разде-
лить па число (при ап = 1)
А		(3»4)
где агпах~ наибольший коэффициент заданного уравнения.
Из-за недостаточного количества ячеек памяти микро-
и°2^^7,1!_ИТОРОВ «Электроника БЗ-34»^программа решения
у равнений 7-й степени имеет следующие особенности.
Пуск программы производится после каждого цикла квад-
рировапия нажатием иа клавиши В/О, С/П. В ячейку 96
программной памяти записывается команда ИШ, где z—
ячейка памяти, в которой содержится наибольший (или
наименьший) коэффициент уравнения. Квадрировапие пре-
кращается, если порядок наибольшего коэффициента пре-
вышает 50, или в случае, если порядок наименьшего ко-
эффициента находится в интервале от —50 до —99. Ко-
личество циклов квадрирования запоминается. Затем вво-
дится программа автоматического определения модулей
корней (вместо части программы квадрирования), и даль-
нейшие действия оператора идентичны действиям при
решении уравнений 3-4-6-й степеней.
Для определения знаков корней можно использовать
следуиш^ую теорему Декарта: число положительных кор-
Ний многочлена f (х), засчитываемых каждый столько раз,
квковп его кратность, равно числу перемен знаков в сис-
чемо шюффгщиеятов этого многочлена (причем равные
яулн* коэффициенты не учитываются) или меньше этого
ЧИСлв на четное число.
Дополнительные рекомендации по использованию при-
айгешмых программ изложены в следующем примере.
П р и м е р 3.1. Решить уравнение
+ 175^ — 735,9? + 1624z2 -- 1764я + 720 = 0.
1. Запишем в памяти калькулятора программу № 4
(ги. н(miлг>лишне), а в ячейках 1™6 — коэффициенты при
« г шжапателями степени от 1-й до 6-й соответственно.
член записывается в ячейку С.
2 М:ян приближенного определения числа циклов
1ич?нцм1[мяшиия т раз возводим в квадрат коэффициент
21
Эту РйеЖцню	послё превши* ни я
порядка^^	способом определяем,;
$О: т	в ячейку 0.
•:;5 Мк: Наж атием W к л авййй В/О Г;СЙ1 - ’ производим « иго- :•
ШтачвсОе^квадр^^	w 4 время
СЯета:-дог:Ш^й	миШ ••
: ЙрйЖ-Ъ^	порядок нвиболь- .
шегокоэффициента?(нажатйем на клавиши ИЙ, 6). По- ;
рядок коэффициента оказалс я меньше 50.
: . 5;-< Для проведения ещё одного цикла квадрмрования
йажййаем клавиши B/O,/G/II.: .
7; :1х^	Д. записывается 
Показатель”:	/
I. ;-“Г‘ . Г :	.
\32..-
?:;:: 7« Для :определения модуля корня х1 необходимо::
няжатьяа клавиши ИПС, ИШ, С/П, После останова счета;
на индикаторе высвечивается значение этого модуля, /:
/•Д 8,: Дл>й: определения любого другого модуля, например ;;
необходимо нажать на . клавиши ИПЗ, ИП4, С/П.
.л: Отметим,.. что точность вычислений модулей повьппа-?
ется,.. если знаменаwtb показателя степени 1/Л' определи-
ется не с. помощью калькулятора (но формуле N 2™),/
д  по табл,’5. :
	Таблица 5
: . . Определение показателя а¥ по числу т	!
т.	.3..	. 4	5	6	7	8	9	. 10-:j
:W/:=	8	: 16	32	Й4	128	256	512	1024
Вычисленные значения модулей ч- хв при различных J
циклах квадрирования приведены в тдбл< 6; КДля осу-^Я
ществления 6-го цикла квадрирования все Коэффициенты-/1
после 5-го цикла были разделены нД число 1010.
Поскольку модули корней значительно отличаютсяй/1
один от другого, корни уравнения являются дойствитель- Ц
ными. Используя теорему Декарта, определяем, что урав^/i
нение имеет 6 перемен знаков коэффициентов, т. е. оно’
может иметь 6 положительных корней. Сопоставив сумму
корней с коэффициентом аъ = —21, убеждаемся в tom^-:i|
что. знаки , и модула определены правильна,
Сопоставив истинные значения модулей г вычислен- .|
ными, убеждаемся также в том, ЧТО фактические погрет-Ц-У
22

АЭ’Э'-йЬЖ? Ад? Г? д’ д б л-ад а 8
Йс^яй»«й1« те^вел^йя модуязК «грвей уравнения
(у-й степеви . 1 >--а.
Вели’Юа .	*: .* *•	.	(in	’					 	 	 -	 г::’’:’;' КОЛИЧССТВй ЦИИДОВ		
		:7т ^4 :>•	’ :Л»Ьй5-’ "Л j	* 	'
 ....: .	У.?	: :0,9Ш)99О	1,6000000	0,9999994
		1,9988698	1,9999998	2,0000103
y	1-.;			2,9999968	2,9999543
	4	3,9ЖЙ1^	3,9999132	
	Л,.••	4,9923168	4,9996675	4,9989175
	: : б : ..Г	6,0203344	::6,0(Ш78 .:	6,0000283
ности вычислений с высокой точностью совпадают с их
оценками по формулам: (2.10) и (2.10а). ;
А на л из погрешностей показыв аот, что в полном соот-
;'вететвнп с теорией погрешности опредегйний наибольших
модулей заметно больше других погрепшостей из-за того,
что относительные величины отличий этих ^(^улёй РйТ::
соседних наименьшие. Следовательно, для повышения
точности определения корней заданное уравнение целе-
•   сообразно преобразовать,(см. ниже) таким образом, чтобы
относительное различие в величине модулей, значения
которых наиболее близки, было как можно больше.
Точность вычисления модулей корней и xz можно
повысить, определив корни следующего квадратного урав-
: нений::••;/•••	А"	А 		::•'/'	А'.:' .<-
 	. a6mz? + a5niz 4- aim .*/ О.
- Для решения «того уравнения, имеющего весьма боль-
4 гаие значен и я корней, целее ообр а.зно предварительно р аз-
АА делить все коэффициенты на величину а9т. .Ay .у A; -АА,
Если решение квадратного уравнения (3.5) произвести
после 5-го цикла квадрирования, то будут получены
уточненные значения модулей- х&5,0001257;
= 6,0000016.4. (	\ .../ ^A-AAjAzAAW- /А^ААААА
:&
:й;

§4. Алгоритмы разложения уравнения по степеням
двучлена : и : определения, знаков корней J4;:	j ;4'<
Применение их совместно е методом Лобачевского
Разложение многочлена по степеням суммы или раз-
кости равнозначно смещению нуля по оси х, на которой
нанесены значения действительных корней или действи-
тельных частей комплексных корнн». ни .циннию пгли*
чину -Ьб. Вследствие зтон» <н :нп н и- । ил.-п lo uriniui раз-
л ичи я м оду.! i.e м с оседая х корпий м । > л j • । •-t j = >, . v нь г гисшю
увеличена, что позволяет увелячт г шчнт Hz («ирг.чочелия
модулей корней методом лЬыиниы.шп 1;'Н.
Для разложения много ч«нны ==<• « ыцИшм .?• 1 Ь, де-
ления многочлена на днучлен .=• \ Ь, >л •i.-in.-M- :пм кыню-
Ленин значения многочлен Л нрн м-ппчг.но =. ptnnui ;ЬЬ?
целесообразно непользояать «мыи п мы .м« «пгирмтм—
схему Горнера, которая сиг пни- н । :и-;н luhnui
Коэффициенты многочлена . iHPHtlhMi заннгьнииот-
СЯ В Строку. Слева- ЛИЖгзтнп ct porui ;НН(шыщипы1 Ч иг,ЛОЙ
С обратным знаком, Т- и;лп Ь :ын корень ПОДЛО-
жащий исключепшо из сразивши. п» л к гапмр Гор-
пера должен еовиздать г.о знлым корим Затем под
коэффициентом бь, запиг-ынаипм они- p,i = а т<ч же коэффи-
циент, ПОД коэфф 3 ЦНСНТОМ (f;< , и роилПОДеН Ur <An*b,
сложенное с коэффвэнюмтом- а„ н т. <». чигло nf -- anb -г
+ an-v Под коэффицисичом •_. .кипи-LHNIHK п число с2 —
— cLb ~г ^п-2 й т* Д‘ Значение миогоч.п нд при т- Ь рав-
но числу cn-i, а коэффициенты делимого знамен и нм ап
и q -7- сп. ^
b I an <1 ----- Ьап	bd ?	-г.-.. га...26-Ьй1
II р и м е р 4.1. Разделить многочлен
па двучлен х — 4 и определить его значение при х — 4.
Р е ш е в и с. Составляем схему Горнера:
Таким образом.
/ (х) = (2^2 + 8z -i- 29) (х.4) -Р 1.21;
/ (4) - 12U
Дл я вычисл ения коэффициентов разложения много-
члена / (х) по степеням двучлена х J- b пеобходи*мо после-
довательно разделить на этот двучлен:
а)	заданный многочлен;
б)	полученное частное (без последнего члена);
в)	вновь полученное частное (также без последнего
члена) и т. д.
24
Последние члены являются коэффициентами и сво-
бодным членом разложения заданного уравнения.
Пример 4.2. Разложить многочлен
/ (z)	2#3..3z + 5
по степеням двучлена х — 4.
Р е ш е н и е. Составляем полную схему Горнера,
в которой в первой строке записываются коэффициенты
уравнения, во второй строке — коэффициенты частного
н остаток и т. д.:
	^-4	0 — 3	5
4	2	8 29 121
	7	16 93
	2	24
	с	
Следовательно, / (z) ~ 2 (z — 4)3 + 24 (z — 4)2 +
+ 93 (z~~ 4) + 12L
Полная схема Горнера реализована в программе № 8
(см. приложение). При использовании этой программы без
изменений осуществляется разложение заданного уравне-
ния но степеням суммы или разности. Если необходимо
разделить заданное уравнение на двучлен, то в ячейку
21 следует записать новую команду: C/IL При вычисле-
нии значения многочлена / (Z>) в ячейки 15~~22 необхо-
димо, кроме того» записать ряд команд. В этом случае зна-
чения коэффициентов уравнения не меняются, а резуль-
тат / (6) записывается в ячейку С.
Во всех вариантах использования схемы Горнера
коэффициент а(, заданного уравнения должен^ быть запи-
сан в ячейку О.		1
Выбор оптимальной величины п знака параметра раз-
ложения h можно осуществить лишь в том случае, если
известны хотя бы приблизительно корни уравнения, т. е.
после приближенного решения заданного уравнения. За-
тем необходимо решить преобразованное уравнение.
Чтобы избежать увеличения объема вычислений в
2 раза, иногда целесообразно провести разложение уравне-
ния перед использованием метода Лобачевского. При этом
за ориентировочное значение параметра разложения Ъ
можно принять приближенное значение а знак Ъ
в схеме Горнера выбирается н ретиво пол оясным знаку коэф-
фициента Пн j решаемою уравнения.
Е<ли в результате разложения уравнения но степеням
z Ч- ;,i свободный член уравнения уменьшается пеапа-
25
чнтельио или даже возрастает, то методом Лобачевского
цел ес о обр а а л о р ешя ть нс пр е обра зова иное у । »а в 11 ение,
а исходное.
Продемонстрируем применение наложен пых выше ре-
комендаций на конкретных примерах.
П р и м е р 4.3. Решить уравнение
а? - 3221.г2 - I 3 454 21(k - 1,23321-1 (Р •• 0.
Р о щ е н и е. После 3-х циклон квадрирования поря-
док наибольшего коэффициента уравнения больше 50.
Поэтому разделим все коэффициенты уравнения на чис-
ло 10w и произведем еще один цикл квадрирования. За-
тем определяем модули корней:	980,34227;
1078,6986; х:х 1166,1624. Корпи вычислены с весь-
ма большими погрешностями, так как их истинные зна-
чения таковы: = 1000; х2 1110; ж3 1111.
При использовании разложения, уравнения параметр
b должен быть равен j/^-o	1072,37. Округляем, его
значение до величины Ъ -- 1100. В результате разложе-
ния заданного уравнения но степеням х у f 1100 по-
лучается уравнение
у3 -г 79г/'2 -•••- 1990// Ь 11000 - 0.
После 5-ти циклов квадрирования находим корни это-
го уравнения: z/x = 9,9855489; у2 -- 11,015918; у3
— —99,99998. Корпи заданного уравнения: -•••• ух 4-
+ Ъ - 1109,9855489; х. 1111,015918; х3 = 1000,00002.
Погрешности вычисления корней но превышают 1,5* 10~3.
Если из заданного уравнения исключит], корень хА
(поскольку модуль существенно отличается от других
модулей, и поэтому можно полагать, что оп вычислен
с большой точностью), а затем решить полученное квад-
ратное уравнение, то корни .г2 и .гл определяются безоши -
бочно.
11 р и м е р 4.4. Решить уравнение
— 65z2 Ч- Ю87.Г -- 1023 - 0.	(4.1)
Реше п и е. В согласии с изложенным выше поло-
жим Ъ 10. В результате разложения заданного урав-
нения по степеням х  у | 10 находим новое уравне-
ние
у3 ’"l- 85ул -р 1287.7 р 8347 - 0,	(4.2)
в котором свободный член значительно больше свободно-
го члена заданного уравнения. Поэтому квадрируем за-
26
данное уравнение. Отметим, что величину свободного чле-
на уравнения (4-2) можно определить проще; для ото го
достаточно вычислить значение / (/>) из уравнения (4.1).
После (5-ти циклов квадрирования уравнения (4.1)
пол учим
х, = 1; х2 - 30,991214; х3 - 33,009342.
Если исключить корень х1 из уравнения (4.1), вычис-
ленный с наибольшей точностью, так как его модуль су-
щественно отличается ст модулей других корней, то пос-
ле решения полученного квадратного уравнения находим,
что уточненные значения корней :с2 и х3 соответственно
равны 31 и 33, что совпадает’ с истинными значениями,
И.ч анализа корней уравнения (4.1) видно, что опти-
мальное значение параметра Ъ 34. При этом получает-
ся уравнение
у* + 37^ + 135?/ ф 99 -= 0.
После 5-ти циклов квадрирования находим
у. 1; ih г.= —2,9999996; у3 - -32,999995.
Следовательно, после обратной замены переменных по
формуле х - у г b корни уравнения (4.1) определяются
почти безошибочно.
Во многих случаях способ предварительного разложе-
ния заданного уравнения по стеиепям х + Ъ является
единственным, способом повышения точности метода Ло-
бачевского.
II р и м е р 4.5. Решить уравнение
,тз _ t5;t9z2 _|_ ум 118х - 1,2980924-10* - 0.
Р о th е и и е. Определяем значение параметра разло-
жения:
b у'а^ = f 1. ,2980924 • 10* = 506,33178.
Округлив полученную величину до b = 500. произве-
дем разложение заданного уравнения по степеням х =
-= у 4- 590; новое уравнение таково:
_ 19уз р 118? ... 240 = 0.
После 6-ти циклов квадрирования находим
уг - 4,9999992; у2 - (5,0000002; у3 - 7,9999993.
Истинные значения корней: 505, 506, 508. Следователь-
по, погрешности вычисления этих корней не превышают
1,6-104
27
: Если же заданное уравнение решать обычным способе^
без разложения уравнения ио степеням у Ь* то коей’
максимально возможного числа циклов квадрирован^
w ===== 4 определяем следующие значения модулей корней:
хх 472,70861; х2 = 506,33262; х3 = 542,34534. Мод^Й
и отличаются от истинных значений на такую болЖ
шую величину, что полагать заданное уравнение решёЖ
пым нет оснований,
Перейдем к определению знака корня. Известный спо-
соб — подстановка модуля в заданное уропепо ммЙЙ
следующие недостатки:	:|г’
.1) необходимо повторно записывать в ячейки С, 1 -НЙ
все коэффициенты заданного уравнения, так как посЙЙ
квадрирования в них содержатся другие значения коэф-
фициентов;
2) способ подстановки комплексного корпя в задан-
ное уравнение сложен в реализации на микрокалькуля-
торе; - •	......
3) вычисление значения / (^) на микрокалькуляторе
типа «Электроника БЗ-34» требует значительного вро*
мени.
Проанализируем абсолютные значения коэффициент##
частных, полученных от деления заданного уравнения на
.двучлены х •_.+ и х — где — наибольший модуль
корня решаемого уравнения.
Можно доказать, что при несовпадении знака xt дву4’
члена х + xt со знаком соответствующего корня абсрг
лютные значения коэффициентов частного Ап_2 -Ь А%-
меньше абсолютных значения соответствующих коэффй^
циентов при обратном знаке xt.
.. Действительно,	в первом варианте	?:
/(*<) = 0,	(4.3)
во втором варианте
/(-^) - \М |,-	(4,4)
где М — остаток, не равный нулю.
Поскольку М 0, коэффициенты частного (4.4) боль-
ще коэффициентов частного (4.3) — при условии, что мо-
дуль корней уравнения выбран наибольший.
Следовательно, сопоставляя значения (4,3) и (4.4), мож-
но определить знак, соответствующий знаку корня за-
данного уравнения.
•• После определения знака корня этот корень исклю-
чается из состава коэффициентов ап^ и (для опрей*
ления знаков другие корней). С помощью схемы Горне-
ра определяем повое значение коэффициента A^i
Ап-2 = (лп-1 ± xi)*(i xi) "г ^п-2-	(4-5)
При определении знаков действительных частей комп-
лексных корней изложенный алгоритм не меняется. Не-
обходимо лишь.вместо коэффициента ап^2 использовать
коэффициент	*
. ’ . • • . '   *  . .
&п-2 = ^п-2 “ 3 ri> '	(4.6)
i—1	’ •
где г I — кваДрат модуля комплексно-сопряженных кор-
ней г-й поры; к — количество пар комплексных корней.
.Предложенный алгоритм реализуется в прилагаемой
программе № 10, применение . которой продемонстри-
руем на следующих примерах.
Пример 4.6. . Решить уравнение
- 14,451*4 + 50,915376** - 76Д60098*2 +
+ 52,338867* - 13,640154 = 0.
Решение/ После округления получаем Ь == 1,7.
С помощью программы № 8 находим, что после разложе-
ния уравнение, имеет вид
г. / —	— 18,451424?э - 17,942021/ ~	
; ;	7,399709? - 1,117148 - 0. (4.7)
После 7-ми циклов квадрировапия определяем модули
корней уравнения (4.7):
= ?х = 0,47795757; у2 - 0,5800171; у3 = 0,59002974;
• ?4 = 0,81200553; ?5 - 8,409989.
При определении модуля уъ обычным способом на ин-
дикаторе высвечивается ERROR из-за превышения част-
ным диапазона чисел микрокалькулятора. В этом случае
• необходимо нажать на клавиши ИП4, 1, С/П и занести
полученное число в ячейку 7. Затем нажатием на клави-
щи 1, ИП5, СУП вычисляем .второе число - Перемножив
: полученные числа, определяем значение модуля ?б/
Для определения знаков модулей используем програм-
му №11, которая базируется только на двух коэффициентах
заданного, уравнения, засылаемых:	— в /ячейку 8,
^2 — в ячейку 9: . Модуль записывается  в ячейку А*
После нажатая на клавиши В/О, С/П и счета на индикато-
ре доявится модуль с соответствующим, злаком.
.29
Т а б л и ц а .7%:
Результаты решения уравнения пример» 4.6
Модули	Истинные значения корней	Без разложения уравнения		При разложении урдшиший: до степеням диучленоя ;х:--Ь7	
		Вычисленные модули:	Относитель- ные погреш- пости	Вычисленные модули	Относитель-”: НЫС ногреш-; : ногти
*1.	0,888	0,8870727.3	3,074 >10'5	0,8879945	п,2-1о-‘1 :
а;3	1,11	1,1087431	1/13-10 3	1,1099703	2Ji7J0’S
	1,1.2	1,1211676	1,04-1О-3	1,1199829	1,53. К)’8.
	1.222	1,2221484	1,2Ы(Н	1,2220427	3 49-10""® •
*5	10,111	10,110999	К)-’	W,110999	10-’
Данную программу целесообразно вводить с начала
программной памяти калькулятора, поело осуществления
квадрирования. В конце этой программы записывается
команда безусловного перехода на начало программы оп-
ределения модуля.
Изложенным выше способом определяем знаки всех
корней уравнения (4.7), а затем с помощью обратной под-
становки — корни заданного уравнения. Вычисленные
значения корней без разложения заданного уравнения
и с его разложением по степеням х — 1,7 приведены в
табл. 7.
При определении наиболее близких корней х2 и х3
обычным способом, т. е. путем исключения из заданного
уравнения корней х± и х$ с доследующим решени-
ем квадратного уравнения, получены значения
.т2 = 1,1097545;	- 1,1202092;
т. е. эти корни определены с большими погрешностями
(2,2-10 4 и 1,9* 10"4).
Еще один способ определения близких по модулю дей-
ствительных корней изложен в § 5.
Проведенный анализ точности определения близких
по модулю корней справедлив при условии, что использу-
ется микрокалькулятор «Электроника БЗ-34», имеющий
всего 8 разрядов мантиссы. С увеличением разрядности
чисел точность вычислений существенно возрастет.
При разложении заданного уравнения по степеням
двучлена необходимо обращать внимание на то, чтобы мо
дули корней преобразованного уравнения не были близ-
ки, так как это снизит точность вычислений. 
30
Пример 4.7. Решить уравнение
Х4 +	_ 1085л:2 - 711х + 289 800 - 0.
Решение. Параметр разложения b а^4 —
= 23,201955. Если выбрать значение параметра Ъ —
= +23,2 и произвести разложение заданного уравнения,
то получим повое уравнение
у* + 93,8/ + 2214,04/ + 502,392.? - 8635,33 = 0.
После 5-ти циклов квадрирования определяем корни
этого уравнения:
уг = 1,799908;	- —2,200111, у3 = 45,6145;
у4 = -47,805802.
Следовательно,
хг = У1 + ъ 1,799908 + 23,2 = 24,999908;
*2 -= У* + Ь = —2,200111 + 23,2 - 20,999889.
Истинные значения корней х± — 21, х2 = 25, т. е. по-
грешности вычислений составляют (3,7 4-5,3)* 10~в. Если
же исключить эти корни и определить два оставшихся
корня из полученного квадратного уравнения, то погреш-
ности вычисления корней х3 и гг4 возрастут до 4-10"4.
Различие между корнями уг и у3 преобразованного
уравнения возрастет, если выбрать параметр разложения
Ъ = 22. При этом получается уравнение
у4 + 89/ + 1885/ - 4413? - 6210 = 0.
После 5-ти циклов квадрирования определяем модули
корней преобразованного уравнения:
у1 - -I;1 у2 2,9999996.
С учетом округления чисел в микрокалькуляторе полу-
чим следующие значения модулей:
xY = yY + b — —1 + 22 — 21;
х2	У2 + Ь - 2,9999996 + 22 ^ 25.
Исключив эти корни из заданного уравнения, после
решения квадратного уравнения находим х3 — —23,
, %* = —24, что совпадает с истинными значениями.
31
§ 5.	Анализ некоторых способов вычисления
комплексных корней с различными модулями
Наличие и место квадратных квадрированных УраШ
нений с комплексными корнями определяете;! способам^
^ изложенными в § 2,
Если уравнение (2.1) имеет одну пару (но) комплект
но-сопряженных корней, то квадрат их модулой вычяД
ляется по формуле .
•	(5>|”
\ “г+1; т J
а действительные и мнимые частя этих корней опредёЖ-:
ютея с помощью формулы Виета [7|:
____п	м О
PjssWi— a*,	j:.:.;"
При наличии в уравнении (2.1) двух пар (Z-й и ;-й) К(Ш-
плексио-сопряженных корней их действительные чаей
вычисляются с помощью следующей системы линеййЙК
уравнений, получаемых также с помощью формул Виёйа.
U, 7]: '	./В'
Из формул (5.2) и (5.3) видно, что погрешности опреде-
ления действительных корней влияют па -погрешности вы-
числения комплексных корней, что является серьезным
недостатком этого метода.
В настоящее время весьма широко используются раз-
личные варианты определения трехчленов
х2 + ix + г2 0,	^5.4)
содержащих комплексно-сопряженные корпи.
Модули г этих трехчленов вычисляются по формуле
(5.1)т а коэффициент различными способами деления
нацело уравнения (24) на трехчлен (5.4) или с помощью
методов Бернулли; итераций, Лина, Налувера й др. ИЙ].
: 32-	'	 	• /Ж
Весьма эффективный, ио явно недооцениваемый метод
(изложен только в работе [2]) предложил немецкий мате?
матик и астроном Энке для уравнений (2.1) любой четной
степени.	...
Формулы Энке имеют следующий вид:
а)	для уравнений 4-й степени: .
₽х* + (Р2 - 2₽г2) - 0,	(5.5)
где р == 1 + аог"4, р! = а3 + ахг~2, р2 = 2а3;
yt — ?1 == 0,	(5.6)
где у 1 — ъ = а3 — ахг“2;
б)	для уравнений 6-й степени:
. Р/3 - р# + (Р2 - Зрг2) t - (р3 - 2рхг2) = 0,. (5.7)
:где . р = 1 4- рх =	р2 = а4 + ааг“2,
Р з 2(7'3 г
у*2 — у/ + (у2 — yr2) = Of	(5.8)
где у = 1 — yx ~ a5 — y2 .== a4 — a2r"2;
в)	для уравнения 8-й степени
р г4 ~ Р1*8 + (р2 - 4рг2) ? - (Р з - ЗРгГ2) t +
...	• + (Р4-2р2га +2рг4) = 0, (5.9)
где р = 1 + а0Г8> Pi = «7 + axr~e, ра =	+ а2г”4, р3 =
“=	~2? р4 2^^
.. ?^3 _ v^2 +	_ 2yr2) t — (Узу/2) = 0, (5.10)
где у = 1 — ц()г"8, yj -= а7 — а^, у2 — а2г^, уэ
:	аь — а3г 2;
Искомая величина t трехчлена (5.4) является общим
корнем обоих уравнений Энке для заданного уравнения
соответствующей степени, и для ее определения в работе
12] рекомендуется использовать деление одного уравнения
• на другое...
Ия анализа уравнений Энке для заданного уравнения
4-й степени можно сделать следующие выводы.
1. Неизвестный коэффициент t трехчлена (5.4) целе-
сообразно определять с помощью уравнения (5.6), которое
можно представить в следующем удобном для вычислений
виде, учитываяf что а — — -^г.
2 А. А. Беланов	33
Уравнение (5.5) пе содержит никакой дополнительной
информации.
•,,2.С помощью формулы (5.6а) можно решать также
уравнения 3-й степени (после умножения всех членов на¥;
учитывая, кроме того, что а0 — 0) и уравнения 5-й степе-
ни (после исключения действительного корня).
3.	Уравнения Энке можно использовать и в том слу-
чае, когда заданное уравнение имеет как комплексные
корни, так и действительные.	: хя
; 4. Уравнение Энке (5.6) целесообразно ис пользой®»:
и при наличии в заданном уравнении двух пар действи-
тельных корней, для которых известны величины и зра-
ки произведений пар корней.
5> Зйак при величине t, вычисляемый с помощью
вопий Эпке, однозначно определяет знаки соответствую-
щих корней заданного уравнения и дополнительных про-
верок не требуется.
6. Погрешности определения корней по формулам Энке
зависят только от погрешностей определения соответ-;
с.твующих модулей. Погрешности определения других:
корней влияния не оказывают.	Ж
7. Все коэффициенты уравнений Энке весьма просты
по структуре, что существенно облегчает их решение с йр-
мощью: ЭВМ.
При решении уравнений 5ч-7-й степеней также реле-
сообразно использовать только квадратное уравнение
(5.8) — его решение и исключение ненужного корня йе;
вызывает затруднений.
Уравнения (2.1) с показателями степени п > 8 целесо-
образно решать методом двукратного квадрирования
(см. § 9).
Если уравнение (2.1) имеет корни с равными модуля-
ми, то формулы Энке использовать нельзя. Однако ниже
будет показано, что после несложных преобразований
уравнения (2.1), с помощью формул Энке, имеющих коэф-
фициент у, можно одновременно определить все корни
кого уравнения.
Пример 5.1. Решить уравнение
.гл+ ж3 - Юж2 - 34т. - 26 = 0.
Решение, В результате квадрирования получена
информация о знаках коэффициентов заданного уравне-
ния (см. таблицу на с. 35).
Анализ информации о знаках коэффициентов показы-
вает. что квадрированное уравнение распадается на два
34:  :  -
I уравнения 1-й степени и одно уравнение 2-й степени,
р имеющее комплексные корни:
f: : а4а2 4” <^зв ~ 0, flge Z2 4~ а 26" ”1”	“0» aia2 4~ Одд =0.
| Из уравнений 1-й степени определяем xt — 1,142163;
[ х4 = 4,0104695.
f Квадрат модулей комплексных корней
[ i ,	г2 = (-515-У"'М = 5,6760998.
SX	.	•
|	. По формуле (5<6а) определяем величину и знак дейст-...
 вительной части сопряженных комплексных, корней:- . 
F г/« -	~~ Д’хГ	__ 4 (УМ 4 ЧЧЧ*
“	2 (1 - 4ог-<) ““ 2 (1 + 26.5,6760998-») “•	1,у341оЗЗ,
I	Р == /г2 - а2 = 1,6248105.
I : Следовательно, ж2,3 =—1,9341533 +/-1,6248105.
I Отметим, что	+ ж4 4- 2а = —1,0000001, т. е. поч-
I ти точно совпадает со значением коэффициента — а3.	Л
| Пример 5.2. Решить уравнение
|:	ж4 4- 2х9 4- Зх2 — 2х 4- 1 — 0.
!| Решение. После 7-ми циклов квадрирования оп-
Й ределяем предварительные значения модулей, т. е. зна-
: чения модулей при условии, что корни являются дейст-
вительными:
\ хг = 0,4962907; х2 = 0,46526936; хэ = 2,1492926;
х4 — 2,0149141.
Таким образом, квадрированное уравнение состоит из
двух уравнений 2-й степени с различными модулями:
•	“472й + aS7z 4- a27 = О,
L	.	Л472-4~. О»
!< \	2* ... 35 •
4=
= 0,3002425 ±/-0,37518945;
= -1,3002425 ± /-1,6248105.
/ В связи с близостью модулей каждого уравнения про^
; веряем с помощью неравенства (2.18) наличие в уравйен
ниях комплексных корней. Неравенство (2.18) выиовдф--
ется для обоих/ квадратных уравнений. Сяедовательщ^/
заданное уравнение имеет две пары комплексных корней!
модули которых равны
'^tjV12S =0,23091276;	.J/
, »27 /	’	’
'^Уй28 = 4,3306398.	:
V	1
,С< помощью формузш (5.6а) определяем ах = 0,3002428;
— “1 >300242^ . Мнимые части корней соответственна.
равны р х -У- г*— at 0,37518945; ра У	•;
— 1,6248105, Таким образом,
Отметки, что величина —2 (ах + сс2) равна коэффициенту;
.й3:—2л что свидетельствует о высокой точности метбдй?!
Лобачевского,. Если модули корней, в том числе койп^-
лёкснызц близки, : то ошибки их определения возрастаний..
В этом случае можно использовать поправки к вычислёцт:
ным значениям модулей гь. Для уравнений 4-й степени:-
с комплексными корнями исправленные значения мбду|::
лей вычисляются по: формулам
'	’	2; • : 2
rf—rlb 1 — 5
2iV-i
(5.11)
IilVaT
Г2Ь ) J
rib
Г2Ь
; П p п м e p 5.3. Решить уравнение
~ 4,04x3 + 8,1608s2 - 8?2416x + 4,1616 - O.|: </
Реше н и e. После 8-мициклов квадрирования одре-
деляем предварительные (при условии, что все корни яв7
•ляютсядействительными) значения модулей: :	.
х:! == 1,410452;	= 1,4177267; х3 = 1,4389353;
/=:„ '-•	- 1,4463327.	’’
: ; Модули корней ж, и х3 и х4 весьма близки. : • ;
С помощью. соотношения (2.18) убеждаемся, что урав-
нение содержит две п&ры комплексно ”сопряжённых кор-/
ней. Находим модули этих пар:
А ==У''25" == 1,9996355;
\ *ЗЬ /
А ~=/Л^у/а“ = 2,0811793.
. • .	.	\ <Чв. /
:• Согласно (5,6а) получаем:
.	 cq. ^ 6,99991049; а2 -1,020091 <
; |х - 0,99990724; ₽а = 1,0200949,
: Погрешности вычисления корней примерно равны 1O74;
истинные значения таковы:
.’•/ zit2 , == 1 4г 7-1;	= 1,02 4- / >1,02.
:. Исправленные значения модулей, вычисленные . пр
формулам (5,10). и- (5.11), соответственно равны т?- — /
±= 1,9999954; г| =• 2,0808049. Этим:. значениям соответ-
ствуют действительные части корней <хх — 1; а2 —
= 1,0200008, те. корни определяются с ошибками, нё.
превышающими А — 1(Г*. Следовательно, точность оп/
ределения корней вследствие использования .поправок
возросла на два порядка,'-
..Пример 5.4, Решить уравнение
....:	1,91^ ~~ 24,691s2 4- 51,356* - 25,755 - 0. • -
’ Решение. После 7-ми циклов квадрирования вьь
числяем предварительные модули:
xi = 0,99807511;. *а = <9970212;
^ = 1,0119479; *4 = 5/1030395.
С помощью соотношения (2.18) определяем, что, хотй-
модули корней и *2, .т3 и близки, все корни являются
действительными. Модули корней и *я можно ойрёдё- .
лить с погрешностями Дх = 2* 10"8, а модули корней
и *4-г с погрешностями Аа 610’4. .• •
: Продемонстрируем возможность уточнения модулей:
действительных корней с помощью формулы Энке (5.6а).
Сопоставляя моду ли. с коэффициентом а3 заданного .ур&и2
нения, определяем, что произведение модулей ^**
знак «+», а произведение модулей *3*4 —-зиак-«^^/•Ис-
пользуя эти произведения с соответствующйми^знаками
вместо значения:г2 в формуле (5.6а), находим, что коэф-
37
циенты I в трехчленах (5.4) равны tr = —2,01
ЖШйойШл.....
Решим квадратные уравнения
г
ж2 + 0,099999923s - 25,5 = 0.	. >
< Находим — 1; яа = 1,01; я3 = 5; х4 = 5,1, Эти знЙ^
зния модулей совпадают с истинными значениями. ":S
( П ри м е р 5-5. Решить одно из уравнений. Леверье,(
помощью которого была открыта планета Нептун;
’ + 4,224т56,5O71s* 4- 7,5013s3 + 8,4691s3 i • f f
+ 3,3641s 4- 1,6252 = Ш
Решение. После 7-ми, циклов квадрирования опре-
зляем предварительные модули корней, которые образу-
ттри близкихповеличине пары:
;J _«27^ + «172 4- в()7 = 0,
 ««Z2 4- «372 + д2,
•i
1=

— 0,

С помощью соотношения (2.18) определяем, что эти
п; нения имек^ комплексные корни. Находим квадра-
:.^бйуйй <
2 i «07 \ЪЧ2Я
'и
1,2965098; '
_ .	0,3053145;
r|8 ^.tey?23 == 4,1056652.
.	'		\ #67 / 	’  	 ' У
Этим значениям модулей соответствуют следующие
шнения (5.8) Энке:
а) 56,103734^ - 31,86493П 4- 4,102555 = 0;
б) : :0,2542738^ + 2,2226463г - 3,5479827 = 0
:::0;9765169«3 — 4,024427г 4- 0,4350647 = ®
:: 7 б) = 4,449043;), ' «м = 0,078406622; f.
... Я в).  «;б = ^2,0050522;:.0^ — 0,055550545." •- ?
Последовательно подставляя в заданное уравнение зна-
v I*  ' i	О О-/ • з •	•..
чения х-> ~ ri cos• фг = arccos'-—; к — показатель с»е~
пени данного члена уравнения), определяем истинные зна-.
чения а. Отметим, что ам>гЭ4, и можно поэтому пола-
гать, что а34 — ссм. Имеем 2 (а2 ~-аг — а8) = 4,2239998,
что с высокой точностью соответствует коэффициенту—a5.
Я прим ер 5.6. Решить уравнение (заимствованное из
лекций А. И. Крылова [2]), корни которого имеют близ-
кие модули: (	-АЯ
ЯЯ	. х1:.ЗЯ 4-	» 5х Ж-6'- = 0-: 	 •
. Р стен и е. Квадрируем уравнение с записью зна-
ков коэффициентов и реле; каждого цикла:
					rw : .						
т	atm-		•	.			aii]i	
i	’ Ч-/	• и^в		eB2‘	 .“₽ 			 4-:-” :
:-2-:		 ф-:<.	 4-- 	  : 		4“	•Ч-"-	 ¥'	
3	+	Jw •	 4*	’w'^e	  ’4^'	.. -4“ 		"P
4	ЛА.4	.	-zr		Ч’	 4*		’4”'.
5	• л.	 Л: ...	JL. .  J			. -К.		4”..
. fi.	:. .-Чг’ • 	.  :	4			4“	: 4* :	"" 4“;’:”
Л.	.=		 J. * : . <e"			4-		:.. -b .
Условные значения модулей корней:
1,0328279;Я	= t;2928559; X— 1,9624903,
'	.1,042455^'	1(2$9947&-: '  .
ж3 = 1,1080199; ze = 1,5378905; . •>,
Анализ значений модулей и знаков коэффициентов по-
казывает, что уравнение имеет три действительных корня
[ x-g, xs и ж?, а также две пары комплексно-сопряженных
; корней ;Tj и .г.,, и ,Т(;.
I Подстановкой действиталь1Пх1х: корней В ааданкиура®-
; некие убеждаемся в том, что наиболее точно определен
Г Я. •	.	: 39
<орець Исключив его, получим следующее уравнение?
Л+ 1,5878905^ + 0,365107b4 + 0,5614947а? - Э
	2,1364826^ + 0,7143238а; - 3,9014482 - Щ
Изложенным выше способом определяем уравнения-:
>5.8) Энке:
: .4,1258635г2 - 0,9216864/ - 2,0927827
?/..	1,843081^	1,280659/ ™ 1,4241711
 Корни уравнений:
//для (5Л2) 1Л 0,6092137; г2 0,83260605;
для (5.13) гх = 0,59778295; t2 —1,2926297.
Сопоставляя значения этих корней с величиной \ав
(^з 4? х« + определяем действительные части ком
Хпексных корпей xL1 х2 и х4, х5:
^1.0,60916737,
1 -1,2926389.
о,
о.
, Сумма значений и х, отличается от коэффициент^:.
Ze заданного уравнений, равного нулю, на относительней
1олйчину	.что почти совпадает с точность^/
вычислений этих величин, равной А2—3-10~6, выполнен?
аых в [2] с прмощью специальных поправок и семианач^
вдх таблиц логарифмов.
Отметим, что если исключить из заданного уравнения
действительные корни х* и jry, а затем решить полу?
ченное уравнение 4-й степени с помощью формулы (5.6а).
То точность определения корней уменьшится до А3=^
МСН,
Необходимо отметить также, что при использований
изложенного ниже обобщенного метода Лобачевского
объем вычислений уменьшается, а точность определения:
корней существенно увеличивается.
§ 6. Вычисление комплексных корней способом
деквадрнрования уравнений
• Сущность предлагаемого способа вычисления комп-
лексных корней состоит в следующем. После пъ Цййлш
вдадрйрованпя определяют квадратные уравнения, ‘ са-
держащие комплексные корни;
.	+ aM;mz:+ а^2;?п —0. ..'•	•	(6Л)
Затем с помощью формул Лобачевского преобразовы-
вают одно из квадратных квадрированных уравненийиг-го
цикла в уравнение, соответствующее, предыдущему
т— 1-му циклу квадрирования, т. е. в уравнение
.	•+ Лг-i; m-lz +	т-1	.	(6 <2}
w \	  
л.,• , —	1 л.	_ i У'**-*: ** •
’ :?im ;	’ г • im
• • ; г- " im
При деквадрировании крайние коэффициенты уравне-
ния (6.2) имеют знаки «+», а средний коэффициент дол-
жен иметь знак, совпадающий со знаком этого коэффи-
циента в соответствующем цикле квадрирования.
Пример 6.1. Способом деквадрироваиия решить
уравнение Леверье (см. пример 5.5)
4 4,224г6 + 6.507W + 7,5013г5 ! 8,4691а;2 +
>’+ 3,3641а; 4- 1,6252 =; 0.
Р е ш е н и в. Воспользуемся программой К* 9 (см?
приложение)»/...Квадрируем	уравнение С остановом
/после.: каждого Цикла для записи знаков коэффициентов
(для этого необходимо в ячейку 0 записать цифру .1,
а после каждого цикла квадрирования нажать на кла-
виши В/О; С/11):
т	а1т							
	а*т			азт	°2т		nom	
. 1	4‘.	4"			4*	«  »	4‘	
2 3	+	4		’4- 	4-		4	
		t	 • -h-		4-	. —	. 4	
4	4?:	Т“* .		’ .+“ -	4	4 ••	«J- 	
5	4- ’.		. • +. •	—-	4 •		н.	
6?	..4*	» »	:	*	-г—.	4	*	 4. ..	
7		4-	: 4-	—	'  “	4 .	4 ••	. в ✓
41
: Анализ изменений знаков коэффициентов показывай^...
его Уравнение распадается па три квадратных кнадрирЙ’:^
данных уравнения, содержащие комплексно -совряженйЫЙ :
горни; ••
.^27^^ "Г ^17* "I” ^07	0,
e47Z2 + «37Z -Г «27 == °,	(&.#.
. • ; ••••
flfl7z2 + ablz + ai7 = 0.	(6.6£
Для деквадрирования в ячейки 00 -4- 22 программной" .-
Щмяти калькулятора записывается программа № 9<_:
i также исходные данные. Если решается уравнение (6.3),
о в ячейку А записывается, отношение а17/аа7, в ячейку-
3— отношение .а07/а27, а в ячейку 0 — число циклов
п — 7.Деквадрировапие начинается нажатием на клави-
ни В/О, С/П.
Ио окончании. счета на индикаторе появится цифра
J — номер цикла квадрирования. Из информации о зна- •
sax коэффициентов уравнения видно, что в 6-м цикле
коэффициент aim имел знак «—». Поэтому при переходе
к следующему циклу необходимо нажать на клавиши 
—/;С/П (в 1-м цикле деквадрирования всегда нажи-
мается только клавиша С/П).
Если знак коэффициента ахга положительный (7-й,; .
1-й. 2-й циклы), то переход к следующему циклу деквад^:
шровайия производится нажатием на клавишу С/П.
... После появления на индикаторе цифры 0 процесс ' .
щквадрирования прекращается. При этом в ячейке А
)уДет число; равное 2aL (где ах — действительная’.
гаСть первой пары комплексных чисел), а в ячейке В —
шадрат модуля этой пары г?.
. Для деквадрирования уравнения (6.4) в яйчейку А.
1аййсывается отношение Оз?/а47, в ячейку В —• отношение.
а в ячейку 0 — тп — 7,
В результате деквадрирования уравнений (6.3)—(6.5)
Юлучий  соответственно
0,18535438; г? - 0,3053145; р£ - 0,5205365;
а2^ 0,07840679;	- 1,2965098; р2 = 1,1359411;
а^В'2,0050523;	=- 4,1056652; р3 = 0,29228496^
. . . .-	’ ’	— f’-
Сопоставление суммы аг + а2 + <х3 с величиной —
чтЦг^. и а3 имеют знаки а а2 — знак
«+»- Имеем —2 (ах + а2 ' ая) ~TW что свидетель-
ствует о высокой точности данного метода (если модули
корней существенно различны).
.. При мер 6.2. Решить уравнение примера 5.3 спо-
собом деквадрирования
_ 4,04г8 + 8,4608г2 - 8,2416г + 4,1616 - 0.
Решение. Результаты квадрирования этого урав-
нения с. остановом счета после каждого цикла следую-
щие:
По характеру флуктуаций знаков коэффициентов оп-
ределяем независимые квадратные квадрированные урав-
нения:
^28^	®08	0,	.
a48z2 + a9Sz + а28 ± 0;
Вот результаты деквадрирования этих уравнений:
ах = 1,00093; г?	1,9996354;	₽х = 1,0009299;
а2 = 1,0211669; г} = 2,0811793;	1,0211668,
Сопоставление вычисленных составляющих комплекс-
ных корней с истинными значениями и значениями,
вычисленными по формуле Энке (см. пример 5.3), пока-
зывает, *£то при малых различиях модулей Корпей способ
деквадрирования . заметно уступает, в точности . методу
Энке, причём могут быть получены и ошибочные значения.
Таким образом, вычисление комплексных корней спо-
собом деквадрирования целесообразно производить прг
большом различии между модулями корней.
Если модули комплексных корней уравнения блпакк
или равны, то, как показано в {21, эффективным спофбол
обеспечения большого различия между. модулями явля-
ется способ разложения уравнения по степеням двучлена
(см. § 4). Величина параметра разложения, как и ранее,
должна быть приблизительно равна а знак в схеме.
Горнера — соответствовать знаку при коэффициенте а^.
заданного уравнения.
К изложенному в работе [2] необходимо сделать одно
существенноев дополнение. Если модули комплексных:
корней равны, то, как показано ниже, производить раз-
ложение уравнения нецелесообразно. Без разложения
такие уравнения решаются быстрее и точнее.
Пример 6.3. Решить уравнение
+	+	+ i — 0.
Решение. После разложения заданного уравнения
по степеням х — у — 1 получим уравнение / — 5/ +
+ W - 13/ + 9/ - Зу + 1 - 0.
В результате квадрирования будет получена следую-
щая информация о знаках коэффициентов этого уравнения:
Анализ изменения знаков коэффициентов показывает,
что данное уравнение распадается на три квадратных
уравнения с комплексными корнями с квадратами моду-
лей, равными г{ = 0,19806226;	= 1,5549581; г* —
3,2469795. Поскольку модули существенно отличаются
друг от друга, применим способ деквадрироваиия урав-
нений
027z2 +	+ а07 ~ 0,	(6.6)
а47?2 +	— 0,	(6.7)
+ ®47 О-
(6.8)
В результате деквадрировапия этих уравнений на-
ходим
— для	(6.6)	<%1У = 0,09903113;	рг = 0,43388374;
. — для	(6.7)	а2у - 0,77747905;	р, = 0,97492789;
-для	(6.8)	a3:V - 1,6234898;	р3 -0,78183163.
Следовательно, действительные части комплексных кор-
ней заданного уравнения таковы:
ai “	— 1 = —0,9009689;
а2 — а2у — 1 — —0,222521;
аа — азу — 1 — — 0,6234898.
О высокой точности вычислений свидетельствуют ре-
зультаты ’ проверочных расчетов 2 (ссг + а2 + а3) =
= 1,0000002;	+ Pi = 1,0000001;	=
— 0,99999994; V + р3 — 1,0000001. Истинные значе-
ния вычисляемых величин равны 1.
Серьезным недостатком метода деквадрирования явля-
ется ограниченность области его применения. Как уже
отмечалось, различие между модулями пар комплексных
корней должно быть велико. Кроме того, при использо-
вании метода деквадрирования необходима информация
о знаках коэффициентов уравнения в.каждом цикле квад-
рирования*
§ 7. Теоремы о коэффициентах алгебраических
уравнений, имеющих корни с равными модулями.
Способ расширения области применения формул Энке
7.1. Теоремы о коэффициентах алгебраических урав-
нений, имеющих действительные и комплексные корни с
равными модулями. А. II. Крылов [2] отмечает, что при
использовании метода Лобачевского «самый невыгодный
случай тот, когда имеется несколько пар мнимых кор-
ней, имеющих равные модули». Суждения по этому воп-
росу других авторов аналогичны. В частности, в [6] отме-
чается: «Метод Лобачевского хорошо работает, если урав-
нение имеет только действительные корпи и не имеет
корней равных или близких но абсолютной величине»,
Способы решения уравнений, имеющих близкие корпи,
изложены выше. Исследуем уравнения, имеющие дейст-
вительные и комплексные корни с равными модулями.
м "4 -=:	ал^ращче-
"g::<^^'. уравнений* реющих	: или' комплек-
:=;=;;: .Й^ЙкОрНИ: с^раяШя^'-м^улями г;,и^	соорцно-
’: •• ' ' '   ? ‘ ''^
4^Ar : / :«v \1Дп-2) • • /	ДЗ/(п-4) . • --^. ..
SK.SW. =fcJ 'ГВД. ~"‘!^
.. ..^omppiie: в наглядной форме для уравнений и 7+й сте-
у 'пеней можно представить следующим образом-: .
: - а4х% a^xs +
«И	*—
агх*+' at х •+ ац
—Г 2----f
-г ----------
О
а7х7+ «ел:бч- а5х54- а4х4 + аях* 4 агхг^ а^х 4 а^-О
В соотношении (7.1) соответствующие пары коэффи-
циентов должны иметь одинаковые знаки.
Д о к а з а т е л ь с т в о. Заданное уравнение четной
степени представим как произведение трехчленов, кор-
нями которых являются комплексно-сопряженные или
действительные корни с модулями rn г2, . .	гп/2*
г2 +	>1 = О,
х2 + Цх {г* — О,
•	............. (7.2)
*г ~Н «и/2^ ~Ь гп/2 ~
Выразим коэффициенты заданного уравнения / (х) с
anw= 1 через коэффициенты трехчленов (7.2):
:: ^(*) ===. (*’ + 4х + ri)-(*2 +. «2^ 4 Л) • • - (*2 4 ««/г* 4 r2n/i) ==
. == жп 44«1 4 «г 4 • •  4 «п/г)-^1"1 4 •  • 4 («1гагз • • • ?"у/2 4
44ГМ   • г«/2 4 • • • 4 «n/a^i*г|... г2/2_1)ж 4.
4 /l-f2- • •Гп/2*-*®-
По условию rt = г2 — ... — Гп/2 = г. Поэтому
. / {«) — *п 4 («1 4 h 4 ..... 4 tn-i) 4............
; . 4 г«-2 («1 4 «а 4 ... 4 «п/г) # 4 г” = 0.
46
. Жмтывая принятые выше обозначения коэффядиМтоЬ..
уравнений:» получим ' \	.. :.С->:
% :5^:;. •	•••	... .,///.<
что равнозначно-соотношениям (7.1).
. Совершенно аналогично можно показать, что соот-
ношения (7.1) справедливы и при нечетной степени урав-
нения. .
Из теоремы 1 можно сделать следующие выводы.
Следствие 1. Корнями трехчленов (7.2) могут
бить также корни z^ квадрированных уравнений. Вслед-
ствие этого после квадрирования соотношения (7.1) между
коэффициентами уравнения, с учетом возведения корней
в степень N ~ 2т, сохраняются:
/ а„ \]/(^)	/ a, xi/(N(n-2))	, а \1/(ЖН)
р -	( ииг у	_ 1ГП I	___ /	, 2m _ \
\ апт )	\ en-i;7« J	х -:ап-ъ ™ )
(7-3)
Следствие 2. Если алгебраическое уравнение со-
держит несколько корней с одинаковыми модулями^ рав-
ными тх» и несколько корней, также действительных или
комплексных, с модулями, равными г2, то после квадриро-
вания это уравнение распадается на два независимых
уравнения, коэффициенты которых удовлетворяют соот-
ношениям (7.3).
Предположим^ что уравнение имеет три корня с рав-
ными модулями rt и четыре корня с равными модулями
г2. После квадрирования соотношения между коэффиг
циентдми этого уравнения будут следующими:
а) мри f\ >
A-WZ’+	«^Z + ^и//:1+Я,„?/;*+Й'4я^?+«1яУ+««Л*0
	-—.	 Jk	*	_ГЛ.	J 1 .  X • • 	- -,				r 1*   —f •'Я . б) при. /; < 1\ ! ,„//+	*f лм2 + a0^ 0
I	. <	11 f t 		L. 	J L__	„ZV............ J	;
47
Весьма важно, что приведенные соотношения ; (7Л)
между коэффициентами квадрированного уравнения вы-
полняются с высокой точностью. Сигналом для проверки
соотношений (7,1), (7.3) является наличие приближенного
равенства между условными (вычисленными при условии,
что все корни являются действительными) значениями '
модулей.
Теорема 2. Коэффициенты алгебраического урав-
нения степени с комплексными корнями, имеющими
разные модули, но одинаковые действительные и мнимые
части, удовлетворяют соотношениям (7.1).
Коэффициенты уравнений 6-й и более высоких степеней
С аналогичными корнями этим соотношениям не удов-
летворяют.
Доказательство. Уравнение 4-й степени с ком-
плексными корнями имеет два трехчлена. Если ах ~ |3lt
сс2 р2, то Г1 = 2<*j, г2 ~ 2«2‘ Следовательно,
(.г) — (х2 +	4- 2а?)(я2 + 2а2х + 2а|) =
-	+ 2	4* 2 (cti + а2)2лг2 4~
4-4а1а2(ах +	+ 4а^а2 == 0.
Таким образом,
-g-=4afa| ' Л,	== 2а1а,2 = ftr2.
Следовательно,
соответствует (7.1). Аналогичным образом можно
иться в том, что уравнение 6-й и более высоких сте-
й с комплексными корнями, имеющими равные деист-
льные и мнимые части, соотношениям (7.1) не удов-
• Теорема 3. Если алгебраические уравнения четной
степени п, имеющие корни с равными модулями г, содержат
пакже действительные корни, равные +г, то ап^ = 0.
Докажем теорему для простейшего случая — уравне-
1ия 4-й степени. Коэффициент а2 такого уравнения выра-
жается так
\	4- хгх3 4“ ЭД +	+ ЭД* .+• ^4*
Если х3 = — а знаки корней х3 и ^ одинаковы,
го выражение для а2 целесообразно записать в виде
48
(7.4)
Поскольку модули всёх корней одинаковы, то | хкх2 |=*
— ]: х3,т4 ), а знаки этих произведений противоположны
ио; условию. Равна нулю и сумма средних слагаемых.
Следовательно, а2 ~ 0.
. Теорема 1 и следствия 1,2 позволяют объяснить и
. .устранить причину, вследствие которой некоторые фор-
мулы Виета и уравнения Энке при наличии в уравнении
комплексных корней с равными модулями непригодны.
В известных работах |2, 5, 7] для решения уравнений
рекомендуется использовать следующие формулы Виета:
-XX	^=41(^0»
п	и
441(4),
"п; 1	{ п; 1
поскольку при их использовании получаются более прос-
тые аналитические зависимости, чем при использовании
других формул Виета. Однако при наличии в уравнении
корней с равными модулями коэффициенты . On-i и
и агд; ап_.2 и a.2f а также ряд других пар, согласно
теореме 1, отличаются друг от друга на постоянную ве-
личину. В связи с этим системы уравнений Виета (7.4)
содержат равносильные уравнения и решить заданное
уравнение с их помощью нельзя. Это замечание в равной
мере касается и уравнений Энке.
Таким образом, для решения алгебраических урав-
нений, имеющих корни не только с разными, но и с оди-
наковыми модулями, необходимо использовать формулы
Виета, связывающие корпи с независимыми во всех слу-
чаях коэффициентами аЛ-ь ап-2, * - • > а™/2-
Теорема 1, как показано ниже, позволяет также обо-
сновать алгоритм преобразования заданного уравнения
с корнями, имеющими равные модули, в такое уравнение,
которое можно решить с помощью формул Энке, причем
одновременно определить все комплексные корпи.
'7.2. Способ расширения области применения формул
Эмке. Выще изложены различные способы анализа и оп-
ределения корней алгебраического уравнения, которые
целесообразно использовать совместно с методом Лоба-
чевского для расширения диапазона его применения,
повышения точности и упрощения алгоритма. Выбор
тех или иных способов зависит от степени решаемого
уравнения истина его корней" (см. § 10).
49
Если модули комплексных корней равны (например,
в уравнении 4-й степени), то формулы типа. (5,6а) после
подстановки значений коэффициентов дают неопределен-
ность :вида 0/0..
• Для решения таких уравнений способом Энке эти
уравнения необходимо преобразовать путем умножения
на двучлен х1 — 1 или х2, + 1* Алгоритм такого преоб-
разования предельно прост: коэффициенты уравнения
записываются в строку, а затем со сдвигом на две пози-
ции записываются эти же коэффициенты со своими зна-
ками или с противоположными (для уравнений с равными
коэффициентами). После этого соответствующие слагае-
мые'суммируются, образуя ряд коэффициентов преобра-
зованного уравнения:
«л	йг1-2	♦.. &2	^0
1 Лть—2 * - • * «	#2	. Лф ••
ап &П“1 (fin Ч" &п-г) ....... Ч" ао) &Q ’
Преобразованное; уравнение решается так же, как
и . заданное.
Пример 7.1. Решить уравнение
х* + х3 + х2 + х Ц- 1 = 0.
Р е ш е н и е. Коэффициенты уравнения удовлетворяют
Соотношениям (7,1) и равны. Следовательно, умножаем
заданное уравнение на двучлен х2 — 1:
11.111
— 1 -^1	—.1 —1
11.0 О О -1	-1 • •  
Преобразованное уравнение имеет вид
+ хъ — х — 1 - 0.
Коэффициенты уравнения (5.8) для преобразованного
уравнения таковы: у — 2; ух = 2; уг = О.СледШа;тедаВо,-
/уравнение Энке (5.8) имеет вид — 2г — 2 А-О^’т, е,
г — i 1 — 0. Корни этого уравнения:
 f	’ r( _ < 1 1/3-.’
*1|S~--- 2	’ аК2--1- zfc & .!
’? Поскольку модуль определен безошибочно^ погреш-
ности определения корней равны нулю.
'SO."
• :Пр и м е р 7.2. Решить уравнение
~ 5,828427s* + 19,48528s4 - 40,627416s3 +
+ 58,455843s2 - 52,455843s + 27 ~ 0.
у/. Решение. Коэффициенты уравнения удовлетвори-
: ют соотношениям (7.1); Преобразуем заданное уравнение
•путем умножения его на двучлен х* + 1:
хВ 9 - 5,828427s7 + 20,485281s6 - 46,455843г6 +
+ 77,941124г4 — 93,083259г6 + 85,455843г2 —
— 52,455843г + 27 - 0.
. Коэффициенты уравнения Энке: у — 0,6666667;	==
- —3,885618;	10,990187; ь - -15,42809. Следо-
вательно,* уравнение Энке (38). имеет вид
0,6666667** + 3,885618*2 + 6,990187* + 3,771236 =Д
Методом Лобачевского определяем корни этого урав-
нения: *3 == 2,8284271; *2 — 2; tL = 1,0000002. Следова-
тельно, а3 = 1,4142135; а2 = 1; ах — 0,5000001. Невязка
коэффициента а5 составляет менее 10-7.
§ 8. Уравнения, сопряженные с заданными
уравнениями
В настоящей книге для заданных уравнений сопря-
женными называются такие уравнения, корнями которых
являются действительные части комплексных корней или
действительные корни с равными модулями,
Для уравнений (2.1) 4-й степени с комплексными кор-
нями имеют место следующие формулы Виета:
I •	«3
«1Пга2— ГХ’
r2i 4. Л -г-
(8-1)
Исходя из них, можно получить сопряженное уравнение
(справедливое, пр и условии а4 — 1):
~^-ааа + '4~(аг	~ г1) = ^"	(8.2)
Из структуры уравнения (8.2) видно, что его можно
использовать как при одинаковых, так и при разных зна-
чениях модулей корней.
61
С помощью сопряженного уравнения (8.2) можно
вычислять также действительные корпи, если определены
знаки и величины произведений пар модулей этих корней.
Действительно, при указанных условиях заданное
уравнение 4-й степени можно разложить на два квадрат-
ных уравнения (5.4), коэффициенты t которых определя-
ются (при а* = 1) с помощью уравнения
Z2 + a%t + (а2 — г*. — 4) — 0.	(8.2а)
где г, = г2 ==
Комплексные корни (2.1) уравнения 6-й степени свя-
заны с его независимыми коэффициентами формулами
Виета (ае = 1):
Ъ + а2 + а3 — — -g-a*,
4а}а2 + -г 4а2а3 4~ г2 4* г? -г т’з —	(8.3)
2а, (г! + гз) + 2а2 (г? + г3) + 2а, (tj 4- г*) 4-
+ 8а£ага^ = —а3.
Если Tj = г2 = гч = г, то уравнения (8.3) преобра-
зуются в сопряженное уравнение:
“3 -I 4 а5а> + ~Т ~	*• 4 ~ 2r2%)=0’ (8’4)
Сопряженное уравнение (8.4) можно решить методом
Лобачевского или любым другим известным методом,
так как с помощью соотношений (7.1) заданное уравнение
с корнями, имеющими равные модули, опознается, а мо-
дули вычисляются.
Сопряженное уравнение (8.4) и уравнения более вы-
соких степеней, полученные ниже, можно использовать
и для решения уравнений четной степени с действитель-
ными корпями, имеющими одинаковые модули и знаки.
Если же часть действительных корней имеет разные зна-
ки, то сопряженные уравнения использовать нельзя.
Опознавательным признаком наличия в заданном урав-
нении w пар корней с равными модулями, но разными
злаками является равенство нулю w коэффициентов ап 4-
4- ап/2 или ап;2 Использование этого признака
позволяет, совместно с соотношением (7.1), определить
корпи уравнения.
При решении уравнений с нечетными степенями,
имеющими корни с равными модулями, необходимо учи-
тывать* что по крайней мере один корень является дейСР
вительным. Его величина вычисляется также с помощью
соотношения (7.1). Определив знак и исключив этот
корень из заданного уравнения, можно, таким образом,
привести любое уравнение нечетной степени к четной,
для которых возможно получение сопряженных урав-
нений.
Если уравнение имеет три нары комплексных корней,
из которых две пары имеют модули, равные гъ а третья
пара — модули, равные г.2, то в этом случае сопряженное
уравнение имеет вид
гг + ~ аъа* -; -+- (а:1	2г; — г22) а +
+ .................<8-5>
Для заданных уравнений (2.1) степени п 8 сопря-
женные уравнения получены при условии, что модули
всех корней одинаковы. При п = 8 и аъ — 1 имеют место
следующие формулы Виета:
1	1
GC j (Хо “']	 Cf ji	““2"
1
ata2 -i схда3 4 сега4 --••• а2а3 4-	4 г* ~ ~г а,ы
(8.6)
(>г2 (а, 4 а2 4 а3 4 сс4) 4 8 (а^ад 4- <*1«2а4 4 сс3а5а4 4
+ а2а3а4) = — а5,
бг* -I 8г2 (а7а2 4	4 «1«4 4 а2а3 4 а2а4 + азаг) 4
4' 16а1а2а3а4 =
После соответствующих преобразований уравнений
(8.6) получается сопряженное уравнение
а’ -|  а7а3 (ай -..........4 г2)а3  | ~ (а5 — Згаа7)а • j
4	(а1 2г2а0 -!- 2г4) — 0.	(8.7)
Сопоставление структуры соответствующих коэффи-
циентов полученных сопряженных уравнений (8.2), (8.4),
(8.7) позволяет, не проводя весьма громоздких преобра-
зований формул Виета, для уравнений с п 10 получить
сопряженные уравнения 5-=-7-й и более высоких степеней.
Продемонстрируем этот способ на примере определе-
ния коэффициентов сопряженного уравнения 5-й степени.
Исходя из структуры ужо полученных сопряженных
уравнений, МОЖНО предположить, что сопряженное уран-
с: 9
UiJ
нешю 5'й степени для заданною уравнения (2.1) 10-й
степени будет следующим:
1	1	1
а5 -1 “у» а0а4 4-	(а8 — 5г2) а2 4	(а7 — 4г2л9) а2 4-
+ 4г " Зг2а« 1 Wr^ а ~$2~	""" 2г3й? ’’‘ zr4a^ ~ °’
(8.8)
где w и z — неизвестные коэффициенты.
Уравнение (8.8) представим в форме
а6 4- Ь4а4 + ^за3 + ^2а2 +	~ 0’ (8.8а)
Коэффициенты tv и z можно определить в том случае,
если окажется возможным для какого-либо уравнения
10-й степени найти коэффициенты Ьг и Ъь сопряженного
ему уравнения (8.8а).
Выберем в качестве заданного уравнение 10-й степени
с корнями лц — х2 = . . . = я1й — г = 1, так как такие
действительные корни являются частным случаем комп-
лексных корней, у которых мнимые части равны пулю:
*10 _	4"	— 120л:7 + 210^ - 252*® 4- 210г? —
- 120л? 4- 45л;2 — 10* 4п 1 - 0. (8.9)
Корни сопряженного уравнения известны: аг — а2 — ...
, # — сс5 = 1. Следовательно, само уравнение имеет
вид
а® - 5а4 + Юа3 — 10а2 + 5а — 1-0.	(8.10)
Приравняв коэффициенты при а и свободные члены
уравнений (8.8) и (8.10), получим уравнения
Ц* "	3(Zg “j- W’) ~— О,
1 . (8Л1)
(^5	^^7 "'Г	"—	Ь
из которых находим
w За8 - а0 4- 5И6 - 3-45 — 210 4- 80 - 5,
2а-..^-32 __ 2(..120) :«252--.32 _9
. аГ
Сопряженные уравнения имеют вид;
54
а)	для уравнений (2/1) 10-й степ э ни
/’ -|	«9а* 	(«„ 5/-) а:| -{•	{а- -- 4г2а#) и2 4
-I" + <««...3rS«» •" 5г’)“ + 4Нйь “	+ 2г*'Ы “ °’
(8.12)
б)	для уравнений (2.1) 12-й степени
сС
4" йИа3 +	(а^0 ~	•/ 4“ ^9 ” 5г3аи)а3 /
+ 4"(йв — 4г3 ®»т М*2/ ..1-(а7 —Зг2а04-5г‘ап) а
+ 4г (а* ~ 2ri(l» + 2г',а1» “ 2г^ “0; (813)
в)	для уравнений (2.1) 14-й степени
г'-"‘  । 4‘ •+• 4~ 7г^а& + 4" —а'1 1 
+ 4г ("«• — ')г*ап + 14Н) «“+ (as — 4r2ttn-! f,'"l«i3)aa-i-
+ -^-(as — ^-aio + 5r4«l3 — 7r«) а -H
-I-	-4г («т - 2r4 •)  2r^.lt - 2г«ам) = 0. (8.14)
Как уже отмечалось, сопряженные уравнения могут
быть решены не тол ько методом Лобачевского, по и лю-
бым другим способом.
Пример 8.1. Решить уравнение
- 4,828427а;3 + 9,656854г2 — 9,656854г + 4 = 0.
Р е ш е п и е. В результате квадрирования заданного
уравнения вычислены следующие предварительные (ус-
ловные) значения модулей (при пь 7):
- 1,3989878; г2 -= 1,409721; г3 - 1,4187094;
г4 = 1,429608.
Поскольку модули корней близки, проверяем выпол-
нение соотношений (7.1):
( 4 \74	[ 9/’56854 \^2	г-.
\ I / ™ \ 4,828427 )
(Соотношение (7.1) выполняется. Следовательно, мо-
дули корней равны ]/2. Сопряженное уравнение (8,2)
в данном случае имеет вид а2 — 2,4142135а + 1,4142135 =
0. Нго корни: ах — I; а2 = 1,4142135, Следовательно,
Корйи аадаййого уравнения определены практически без-
ошибочно
^1,2 = 1 zb 7 1;	— 1,4142135
(так как мнимая часть корней .г3 и равна нулю).
Если проверку соотношения (7.1) произвести до на-
чала квадрирования, то при решении данного уравнения
оно не требуется; "
П р и и е р 8.2. Решить уравнение
+ 2я8 — 2х - 1 - 0.
Решение. Коэффициенты уравнения удовлетворяют
соотношениям (7.1), а коэффициент а2, кроме того, равен
нулю. Следовательно, в соответствии с теоремой 3, урав-
нение имеет два действительных корня хг .= 1, х2 ==* — 1.
Разделив заданное уравнение на двучлен х2 — 1 и решив
полученное квадратное уравнение, определим два других
корня: х3 =*	“ —-1.
Необходимо отметить, что вопреки общепринятому
мнению заданное уравнение можно решить и непосред-
ственно методом Лобачевского. Действительно, после 1-го
цикла квадрирования получается уравнение
х* + 4х3 + баг2 + 4х + 1 = О,
которое в последующих циклах не меняется.
Предположим, что, несмотря на это, квадрирование бы-
ло продолжено до т == 50. При этом N = 2&0 = 1,125 ЛО15.
Следовательно, модули корней заданного уравнения та-
ковы:
/ 1 V/N —4 <_____I 4 V/1Y —4	— / 6 W‘Y— 4
» Х2 г“““ I £ )	- * ’	-\ 4 /	-- ’
Пример 8.3. Решить. уравнение
х1 4*- %* +	+ & + х3 + х1 + х + 1 === 0.
Решение. Корни уравнения удовлетворяют соот-
ношениям. (7.1).
Поскольку степень. уравнения нечетная, оно имеет
по крайней мере один действительный корень,., модуль
которого равен 1, а знак — отрицательный. Исключив
йот корень, получим новое уравнение
х* +	+ 1 — 0.
56
.Подставив коэффициенты этого уравнения в сопря-
женное уравнение (8.4). получим уравнение а3 4- 0,5 а — 0,
/Имеющее корни ах = 0, а2	У 0,5, а3 — —-]Ло,5.
л^аким образом, корни заданного уравнения будут вы-
н-^цслены безошибочно:
1* ^2	7>	~ ~~~]*> б 4х 1^0*6 + 7* ) 0>5;
. ^G,7 fi=.-’0,5 ± 7 V 0,5.
П р и м е р 8.4, Решить уравнение
. х* - 5,828427а* + 19,48528а;4 - 40,627416л* +
: • • + 58,455843л2 - 52,455843л + 27-0.
Решение. После 6-ти циклов квадрирования об-
наружим, что условные значения модулей корней близки.
. Поэтому проверим выполнение соотношения (7.1):
/^^^1,7320508; МЦ7‘== 1,7320508; ;
\	?	\ аь /	.
/^yZ1= 1,7320508.
Соотношения (7.1) выполняются. Если бы эта проверка
была произведена до решения уравнения, то квадрирова-
ГШе оказалось бы ненужным.
Составляем сопряженное уравнение
а3 - 2,9142135а2 + 2,6213202а - 0,70710675 = 0.
После 6-ти циклов квадрирования сопряженного урав-
нения определим модули его корней: ах= 1,4142136; а3 —
*** 0,9999998; а3 = 0,5000005. Для проверки точности рас-
четов вычислим 2(а/ + а2 + а3) = —5,8284266, что с вы-
. сокой точностью совпадает со значением коэффициента аб
Веданного уравнения. Вот вычисленные корни исходного
уравнения:
=* 1,4142136 + / 1;	- 0,9999998 ± / 1,4142137;
^Б,в -= 0,5000005 ± ] 1,6583122. •
. Истинные значения корней:
1^2 +; /; аг3,4 — 1	7 V2; хм ===0,5	7 V2Л75-
П р и м е р 8.5. Решить уравнение
«Н - 4,5144232а** + 14,760009а;12 - 38,836491а*1 +
...• + 93,2654а*0 - 198,58125х9 + 388,2677а;8 -
- 692,61131.x7 + 1164,8032а:6 — 1787,2307а* +
+ 2518,16б5а:4 — 3145,7547а;3 + 3583,6828а:2 —
3291л0144^ + 2187 = 0.
57
Р е ш е н и е. Коэффициенты заданного уравнения
удовлетворяют соотношениям
г-	/ 2137 у/к ( 3291,0144 ММ	/ 3586,«828 у/«
I	5 )	~ 1'4,5144232 / ~ V 14,760009 )
Следовательно, уравнение имеет корни с одним и тем
же модулем г J 3. Подставим численные значения ко-
эффициентов и модулей в сопряженное уравнение (8.14):
а? ~ 2,2572116а*	1,5599977а5	5,3028907а4 -
- 0,13312062а3 - 3,0691131 а" 0,37624218а +
+ 0,34061109 - 0,
Решим это уравнение методом Лобачевского. После
7-ми циклов квадрирования определим модули корней
сопряженного уравнения:
а7 - 1,6583167; ав - 1,4142006; а5 = 1,2247585;
а4 - 0,9999993: а3 0,79057076; а2 0,5000007;
сех - 0,30000034.
Истинные значения модулей:
а- - 1,6583123; ав - 1,4142135; а5 - 1,2247448;
а4 =- 1,0000000; а3 = 0,7905694; а2 - 0,5000000;
а, - 0,3000000.
Модули корней заданного уравнения определены без-
ошибочно. Поэтому оно решено с высокой точностью, при-
чем корни сопряженного уравнения являются действи-
тельными частями комплексных корней заданного урав-
нения.
II р и м е р 8.6. Решить уравнение
х* + 5^ + з/. __ 17Х4 _ 16жз 24х2 - 16х - 16 - 0.
Реше н ие. В результате квадрирования уравнения
определим, что коэффициенты во всех циклах положи-
тельны. Это означает, что корни уравнения являются дей-
ствительными.
Условные модули корней:
ъ - 0,98298076; х. - 0,9999998; х3 - 1,0173141;
= 1,9571455;	- 1,9873655; xQ - 2,012715;
х7 =: 2,0437937.
Первые три модуля и четыре последующих близки
между собой. Поэтому проверяет соотношения (7.3) меж-
ду коэффициентами квадрированного уравнения, индексы
58
которых указаны ниже:
7 б 5	4	3	2	10
'•	. I Н I	л
[урч,ооооооз J	[ о?то'Н)б
Z? -10,0 о О О О 5	/;4- 1,00 0 0000
Действия оператора при этом ничем не отличаются
от его действий при вычислении условных модулей. Так,
для определения отношения коэффициентов	не-
обходимо нажать на клавиши ИП, 4, ИП, 6, C/IL
Из приведенных выше отношений коэффициентов сле-
дует, что корни л\ х$ и л4 и- х7 имеют модули, равные
соответственно 1 и 2. Определив знаки модулей, нахо-
дим — л2 = л3 — 1; х4 — х5 — х6 х7 = —2.
Решим уравнения, имеющие корни различных типов —
действительные, комплексные, с одинаковыми и разными
модулями.
П р и мер 8.7. Решить уравнение
/' - 4,51лс - 14,995л6 + 74,67s4 + 16}935л3 —
- 265,43л2 + 408,93л - 144,36 = 0.
Р о пг е н и е. В результате квадрирования получим
следующие данные о знаках коэффициентов:
	4llm							
	а*	a«m		|T» •im		(l2m	%)1	
1	4	4		"I..	4’	f •VM	►	Л4*'
	4	>	-i-	....^	4	—		..
3	।		-J-	4			-L	
4	4	9	-j-	4		_L		1 "Г
•г>	<	1		-H		►	4	’1’
\ г> i	“Г"	4	4	4	4	1 "i”	4	4
Условные модули корней: хг = 0,<5; л2 — 1,3989796;
=: 1,4296134; л4 - 2,96767799; л5 - 3,0326727; л6 -
- 3,9616479; л? - 4,0488187.
Модуль л3 существенно отличается от остальных мо-
дулей. Поэтому полагаем, что он вычислен с высокой
игиннтыи и является действительным. Для уточнения
аюон*пий других модулей необходимо решать квадратные
59
квадрированные уравнения
#76^	*4“	“О,
#5<^2 ~Ь 4* #эе О,
имеющие действительные корни, а также квадратное квад-
рированное уравнение с комплексными корнями:
азв22 + a^z + «16 = 0.
Решая первые два квадратных уравнения обычным
способом, определим их корни z7, z6, «5, z4T а затем извле-
чем корни «ЛГ-й степени из полученных значений z$. Таким
образом, более, точно, х4 — 2,9993491; хъ — .3,0006515;
хе - 3,999885; х, -4,0101131. . ..	...
Уравнение с комплексными корнями решаем способом
деквадрирования, поскольку условные модули х2 и х3
существенно отличаются от соседних условных модулей.
В результате деквадрирования находим — 1,0000012;
р — 0,99999878. Определив знаки модулей, получим сле-
дующие значения корней:
xt 0,5; ^,3 - 1,0000012 ± /0,99999878; хл -
= -2,9993491; х$ - -3,0006515; х« - 3,9998851;
х7 - 4,0101131.	
Истинные значения корней заданного уравнения; .
хх = 0,5; а:2,з = 1± J-1; х4 = х& == ~3;	= 4,0;
х7 = 4,01. •
Пример 8.8. Решить уравнение [11]
х* _ 15^ + 56л;4 — 56л;3 - 56л:2 + 172л: - 120 - 0.
Решение. В результате квадрирования получена
следующая информация о знаках коэффициентов;
т	° i ni.						
	aem	®&пг	a4m	(}'3т'	а2т	fl. l?7l	айпг
1	Ч-	“Г	+	+  *	+	4-	
2		. +•.		—	—•	..4й	
3		+ ’		4-	4-	. -4*	
4	:Н" •		ч-		’Г ’	4-	• Ч- •
5					^|w.	’ • 4г	Ч'
60 .
th?- J Условные модули корней: хх ~ 1,3542558; . х* =*
1,3964068; х3 == 1,432247; х4 -= 1г4768261; х6 =
9999996;	- 10.
|Ир-Поскольку модули и существенно отличаются
ИЙан от другого п от других модулей, полагаем, что они
- вычислены с высокой точностью и являются действитель-
ними. Определив знаки и исключив корни хб и хъ из
заданного уравнения, получим новое уравнение
z4 — 2х8 + 0-х2 + 4х — 4 = 0.	(8.15)
р?:: Коэффициенты этого уравнения удовлетворяют соот-
У Ношениям (7.1), а средний коэффициент равен нулю. Сле-
| довательно, действительные корни таковы: х4 — — z3 “•
/2. Действительные части сопряженных
2
н комплексных корней: а — j" ~~	— 1, где b3 —
соответствующий коэффициент уравнения (8.15).
Таким образом, заданное уравнение имеет следующие
корни, вычисленные практически точно:
#Ь2 = 1 ± Д — — 1^2;	= У2; х6 == 2,9999996;
х& = 10.
§ 9. Решение алгебраических уравнений различных
типов обобщенным (с двукратным квадрировавшем)
методом Лобачевского
Рассмотренные выше новые и известные способы реше-
Имя алгебраических уравнений позволяют повысить точ-
ность определения корней определенного вида или упрос-
тить алгоритм расчетов. Однако эти способы имеют су-
^ЙЩетаенный недостаток — ограниченность применения.
^Вследствие этого возникает необходимость тщательного
РЭДМиза целесообразности применения того или иного
ОДлособа и особенностей программирования соответствую-
щих алгоритмов.
Выше было показано, что для повышения точности
Шйяислекия действительных корней с небольшим относи-
|«ЫШм различием модулей целесообразно использовать
ЙЙрйцию разложения уравнения по степеням двучлена,
& аатом — квадрироваиие и определение модулей.
Особенно эффективно применение операции разложе-
уравнения по степеням двучлена в том случае, если
.61
параметр разложения выбран оптимальным. Однако для
этого необходимо знание приближенных значений корней
или их модулей. Таким образом, для высокоточного опре-
деления действительных корней уравнения необходимо
квадрировать и определять модули корней дважды — до
и после разложения уравнения по степеням суммы или
разности.
Покажем, что подобное сочетание методов квадриро-
вания и разложения заданного уравнения позволяет так-
же с высокой точностью вычислить все комплексные кор-
ни алгебраического уравнения любой степени.
Разложение уравнения по степеням двучлена с пара-
метром Ъ означает смещение пуля отсчета действительных
корней и действительных частей комплексных корней ио
оси а на указанную величину влево или вправо, в зависи-
мости от знака параметра Ь, т. е. в точку О± или О2
(рис. 2).
Вычислим действительную часть а* комплексного кор-
ня Хг по информации о величине и знаке параметра Ъ,
а также по информации о значениях модуля комплексного
числа до разложения уравнения — п и после разложе-
ния — г\ или г2.
Из рис. 2 следует, что при Ъ > а
Р? = г? — а? = r“t2 — (b ± а)2,
т. е.
Аналогичное выражение имеет место и при b < а.
Весьма важно, что по формуле (9.1) определяется не
только величина, но и знак действительной части
62 •	•
комплексного корня. Точность вычисления величины аь
как следует из формулы (9.1), зависит от ошибок вычис-
ления модулой, определяемых дважды. Поскольку квад-
раты модулей вычитаются, ошибки вычисления модулей
частично компенсируются, что обусловливает сравнитель-
но высокую точность определения а даже при весьма
малых значениях параметра b (см. пример 9.3).
За счет смещения нуля отсчета модулей действитель-
ных корней последние после разложения уравнения умень-
шаются на величину Ъ, если знак b совпадает со знаком
корней, и увеличиваются при несовпадении знаков. Та-
ким образом, одновременно с вычислением комплексных
корней предложенный метод двукратного квадрирования
позволяет определить модули и знаки действительных
Корнеи, отличать их от комплексных корней.
Модуль каждого корня определяется дважды, За осно-
ву целесообразно. выбрать то значение, которое отяичан
ется от ближайших модулей на относительно большую
величину.
При реализации метода двукратного квадрирования
возникает проблема отождествления значений каждого
модуля действительных и комплексных корней, вычислен-
ных до и после разложения уравнения.
Отождествление значений модуля каждого действи-
тельного корня не представляет затруднений из-за раз-
личия между ними на заданную величину &.
Сравнительно просто решается и задача отождествле-
ния модулей комплексных корней, если п -<Г- 7. При этом
ft затруднительных случаях целесообразно использовать
метод проб с проверкой соотношения
’	.7
Ягг-i——	(9-2)
В сложных случаях, при больших п, отождествление
модулей целесообразно проводить по близости их значе-
ний, которая имеет место при разложении заданного урав-
нения по степеням двучлена с весьма малым значением
параметра 6. Однако при этом действительные части комп-
лексных корней щ вычисляются с ограниченной точно-
стью» Поэтому после повторного разложения заданного
.равнения с оптимальной величиной Ь. вычисляются
ЙЛЯениые значения комплексных корней (см. при-
мер’ 9.3),
В том случае, если относительное различие модулей
комплексных корней невелико (см. рис, 3, корни хг и х2),
63
за решаемое уравнение целесообразно выбрать не задан-
ное уравнение, а уравнение полученное после разложения
по степеням двучлена.. При смещении нуля отсчета из
точки О в точку О{ отношение модулей комплексных кор-
ней существенно возрастает, с r10/r20 ~ 1 до г1г/г21	1.
Ввиду малого относительного различия модулей кор-
ней исходного уравнения (г10 иг20). последние вычисля-
ются с заметными ошибками. После разложения уравне-
ния с параметром Ъ1 = О± —О модули корней ги и г21
отличаются существенно и вычисляются с высокой точ-
ностью. Если провести новое разложение исходного урав-
нения с параметром. Ъ2 = <92 — 0, то модули г12 и г22
также вычисляются с небольшими погрешностями. Поэто-
му использование двух разложений заданного уравнения
вместо одного существенно уменьшает ошибки определе-
ния комплексных корней xt и z2.
Для рассматриваемого варианта формула (9.1) транс-
формируется в формулы (9.3):
•	4+^2
1Х“	2.6.	’	(93)
— Г2 -5-7,2
__Г21	22 ’
- 2-Ьи .....— ’
где
ОСц — СД —* C/j, <Х21 — <Х2 — €/]_,	— С/2 —•
Комплексные корни заданного уравнения в рассмат-
риваемом варианте вычисляются по формулам (см. при-
мер 9.3)
•Л1 — ai ± 7₽1?	^2 “ а2 + /Рз’
+	«2—«si + ^i,	(9.4)
— Р» = ^4 — «п-
64
Если с помощью соотношения (7.1) может быть опре-
р: делено, что уравнение имеет корни с равными модулями,
. то предложенным методом все корни вычисляются после
Одного разложения и одного квадрирования (см. при-
ШР 9.1), причем проблема отождествления модулей в этом
случае отсутствует.
Несколько корней уравнения (действительных и
комплексных) могут иметь равные модули, а остальные
:р:^орни — различные модули. В этом случае после квад-
рирования уравнения с помощью соотношения (7.3) рас-
| Познаются корни с равными модулями и определяется их
;; значение. Затем производится разложение уравнения по
степеням двучлена, квадрирование и повторное определе-
|у ние модулей (см. примеры 9.2 и 9.4).
Продемонстрируем применение предложенного' обоб-
щенного метода Лобачевского на примерах решения
уравнений с различными типами корней.
Пример 9.1. Решить уравнение
+	+	+	+ + +	0.
Решение. Коэффициенты уравнения удовлетворя-
| Ют соотношению (7.1). Следовательно, модули всех корней
Йавны между’собой, причем их численное значение г — 1.
осле разложения уравнения по степеням разности с па-
раметром b = — 1 получим уравнение
_ 5уб + iiy4 _ 13у8 + д^2 _ Зу + 1 = 0
£•:' Квадрирование этого уравнения позволяет получить
1Лйдующую информацию о знаках коэффициентов:
ХХХХ .
' л ' ' ' .
 ' '
 > ' ' .
ХХХХХ.
«Г:
*ххх. .
еххх.
'/ '' 
•л>.лж.
йехх.
йехх.
’.ЖЖЖ.
ехххх
' УЛЛ л л л.
:хххх::.:. .
;хххх.
хЛхххх,
ххуххх:
: xzAxxx.
&W6SS:
.:хххх.:.:.
.:ххх::.:.:.
.:ххх.
fit	а1т						
		й5щ	aim	а3т	asm		a0m
** CQ X? СС •,		III II		Illi II		1 1 1 1 1 1	
И римечание. Знаки остальных коэффициентов
УроИшшя положительные.
| 4. А Велаяов
85
Квадраты модулей комплексных корней: rJk
= 0,19806228; 4 = 1,5549581;	= 3,2469793. По фор-
муле (9.1) вычисляем действительные части комплексных
корней:
а. = T-j2'1- Ь* -E_2^g^8+1 - 0.90096885:

2.(...... J.)
0.22252095;
2-(- 1)
Повязка коэффициента аъ равна 3-10~7, а модули комп-
лексных корней определены безошибочно. Следовательно,
уравнение решено с высокой точностью.
П р имр р 9.2. Решить уравнение
х1 _	_ 0?23^ + 0,188г4 — 0,23г3 + 0,188г2 —
-1,23х + 1,188 - 0.
Р е ш е и и е. После 9-ти циклов квадрирования полу-
чены следующие значения условных модулей:
хг 0,9; г, = 0,99864693; г3 = 0,99920822;
г4 = 1,0007923; г5 - 1,0013548; г6 = 1,1;
х7 = 1,2.
В связи с близостью условных модулей г2 -н г5 про-
веряем выполнение соотношения (7.3) для коэффициентов
квадрированного уравнения:
z4+ «4Sz’+ а„гг+ «,9z -t- «13 =0
1,0000001
Соотношения (7.3) выполняются, причем г, — 1; г? —
= 1.
В результате разложения заданного уравнения по сте-
пеням двучлепа с параметром Ъ = 1 получим новое урав-
нение:
у- -J- 6ys -I- И,77Г Т 19,038»/ 4- 13,222//» +
•t- 4,32б/г - 0,942// - 0,126	0.
60
После 6-ти циклив квадрирования определяем условные
модули корней:
у{ = 0,10000001; у2 0,2;	у3 == 1,0000001;
у* - 0,9999999;	уъ - 1,732051;	у« - 1,7320508;
У1 = 2,0999998,
Условные модули ?/3 и у4, уй и ?/6 близки, С помощью
неравенства (2.18) убеждаемся в том, что квадратные
квадрированные уравнения a4flz2 + a3fiz + а2С — 0, aQbz2 +
И	0 содержат комплексно-соиря/кснныо кор-
ни, Квадраты модулей этих корней: г|4 = 1;	=
* 3,0000001,
По формуле (9,1) определяем действительные части
комплексных корней:
г? -121 +
---
1 — 1 -Ь 1
= — 0,5.
После смещения пуля отсчета модулей на величину
b 1 модули Xj и х7 уменьшились, а модуль х6 увели*
пился. Следовательно, корни х3 и х7 имеют знаки «+».
а корень х$ — знак «—».
Вычисленные значения корней совпадают с истинными
величинами,
П р и м е р 9.3, Решить уравнение
г 0,6л6 + 0,18л6 - 0,72л* - 1,1251л3 +
+ 0,64566л2 — 0,786528л + 1,21176 - 0.
Р е тени е. После 9-ти циклов квадрирования вы-
числяем условные модули:
г, - 0,9;	х2 - 1,0028189; х3 - 0,9971926;
х4 - 1,0098586; хъ - 1,0100393; хв = 1,0999991;
х, 1,2000004,
В связи с близостью модулей х2 -н х5 проверяем вы-
ло л псине соотношения (7,3) между коэффициентами
3*
67
квадрированного уравнения:
-i	а.-^7Г-\- z •< О
Z’t = 1,0039507
Ц00703У)
Соотношение (7.3) не выполняется, по модуля корней
очень близки, причем г2<> — 0,99190063;	— 1,0419.
После разложения уравнения с параметром bt 0,5
вычисляем следующие значения модулей действительных
корней и действительных частей комплексных корней:
П21?> - 1,1; Щ- 1,62; а, - 0,1500036; а2 - 0,3500031.
Для повышения точности вычисления комплексны х
корней целесообразно егце раз разложить уравнение по
степеням двучлена с параметром Ь2 = 0,8. Аналогично
предыдущему определяем квадраты модулей комплексных,
корней: R\ — 1,4000001: Яп 2,2199998. Следовательно,
+	_м....1/Н. (()л8.0,5)* _
“х =":	2 (Й2 -	—	2 (0,8-0,5)	°’3а’
/;ж -	• i' W 1,62-2,2 (0.8-0,5)2	nQr.
а” 2(&а—&,)   	2(0,8- О,Г)'	~~иА '
pj = |/== |/1, 1 - (- 0,35)5 =;,. 0,9539392;
P1I — / Лз5 — 4i = /ШГ—Т^О^бр^ 0,72801098.
Действительные части и модули корней заданного
уравнения:
«I + br — —0,35 Ч- 0,5 = 0,15;
а2 = ап •+ Ь1 — —0,85 + 0,5 --- —0,35;
г] at + И °Л52 + 0,9539392* - 1;
г2 - а22 + рн = (-0,35)* + 0,72801098* - 1,02.
Истинные значения корней:
0,9; 1,2; -1,1; г? - 1; rl - 1,02;
0,15 ± /0,9539392; -0,35 -с /0,72801098-
Отметим, что если b = 0,01, то cq — —0,35032; а2 =
= 0,150355; если Ъ = 0,03, то - -0,35005166; а2 -
— 0,15005.
68
П ример 9.4. Решить уравнение Ц11
— 15.z5 -|- 56л:1 — 56х9 — 56а;2 + 172а? — 120 — 0.
Р еш ей и е. Условные модули корней, вычисленные
после 6-ти циклов квадрирования:
х. - 1,3839117; хг - 1,405278;	х3 - 1,4232045;
х4 = 1,4451802; хъ - 2,9999996;	- 9,9999999.
В связи с близостью условных модулей х± ~ х4 про-
веряем выполнение соотношения (7.3) для коэффициентов
квадрированного уравнения:
rz46zV	a^z + О
..	. f
Г"- 1,Н9Э39#2 :
л4— 4
Соотношение (7.3) выполняется. Следовательно., все
модули х± н- х4 равны )Л2. Модули корней х5 и х$ сущест-
венно различаются между собой и отличаются от других
условных модулей, т. е. соответствующие корни являются
действительными.
В результате разложения уравнения с параметром Ъ
2 получим уравнение
— Зг/6 — 34у4 — 48у3 — 8 г/2 4- 60у 4- 32 — 0.
После квадрирования определим значения условных
Модулей:
lh = 0,58578643; у2 - 1; у, = 1,3989797;
/д - 1,4296133; уб =- 3/142136; уб = 7,9999993.
Модули у3 и у4 близки, С помощью неравенства (2.18)
убеждаемся в том, что квадратное квадрированное урав-
нение a46z2 + a3ez 4~ а2в = 0 имеет комплексные корни.
Квадрат модулой этих корней равен — 2.
Учитывая сдвиг нуля отсчета на величину Ъ — 2Л оп-
ределяем, что действительные корни л:Б, х$ положительны.
Модули и у6 существенно различаются между собой
Л отличаются от других модулей. Поэтому они также
НПаяются действительными,; причем
Tl - yt b = 0,58578643 - 2 = -1,4142136;
уь ~ ь 3,4142136 - 2 — 1/1142136.
69
Действительные части комплексных корней, вьтч не леп-
ные по формуле (9.1), равны
’л~гм + />в	2—2 + 4	,
“ =------S------
Следовательно,
£ У г2 — а2 == У 2 — 1 = 1, т. е. х3>4 « 1 + pi.
Таким образом, несмотря на сочетание в данном урав-
нении действительных и комплексных корней с равными
и различными модулями, уравнение решено с весьма
высокой точностью.
Пример 9.5. Решить уравнение 121
х7 — 2х^ — Зя8 + 4я3 — 5я + 6 = 0.
Это уравнение рассмотрено в примере 5.6, где вычис-
лены следующие значения квадратов модулей комплекс-
ных корней: Г02 = 1,0766766;	== 1,666424,
Решение. После разложения уравнения с пара-
метром Ъ = 1,3 и определения модулей методом квадриро-
вания получим значения квадратов модулей комплексных
корней: Ни — 1,9747045; г4в = 5,0368429. По формуле
(9.1) вычисляем
г02	1,0766766 - 1,9747025 4- М2
2Л "	2-1,3
— 0,30460542;
а ~	5,0368429 +	_ 64631496.
—	2’6	2.1,3
. Действительные корни:
xt - 1,1080163; х2 = 1,5378905;	= —1,9624899»
Невязка коэффициента а6 равна 2,2’10"*, а невязка
свободного члена а0 равна 3,4 Л0“6.
Пример 9.6. Решить уравнение Леверье
х* + 4,224яБ + 6,5071я4 + 7,5013^ + 8,4691г2 +
+ 3,3641л + 1,6252 = 0,
которое в примерах 5.5, 6.1, 8.8 решено иными способами,
причем были вычислены следующие значения квадратов
модулей комплексных корней:
г? = 0,3053145; г| = 1,2965098;	= 4,1056652.
70
g; Решение. После разложения заданного уравнения
Д-;параметром 6 — —1,3 получим уравнение
2,424г5 + 1,5211^ + 2,95438.x3 + 4,212784г2 -
- 0,2382838^ + 1,2188261 -= 0.
II В результате квадрирования этого уравнения вычнс-
0|жйм значения квадратов модулей корней:
Ц	4 = 0,28410191; & = 1,4335538;
II	4 - 2,9926335.
н;_. По формуле (9.1) находим
а02 = -0,18535431; а24 = 0,07840666;
' а46 = -2,0050528.
Невязка коэффициента а-о равна 2-10-7.
Таким образом, несмотря на большое разнообразие
уравнений, решенных в примерах 9.1—9.6 методом дву-
йтного квадрирования, алгоритм вычислений остается
оьма простым изменяется незначительно.
Как показано ниже, недостатком метода двукратного
||Нвадрирования при п < 6 является большее время счета
|fci сравнению с аналогичным показателем остальных ва-
Л»антов метода Лобачевского, рассмотренных в данной
ж||^боте. При решении уравнений высоких степеней метод
Ц^укратного квадрировалия требует существенно мень-
Ijjifero времени по сравнению с любыми другими способами
>Шгределения комплексных корней.
10. Сопоставление различных вариантов
Щ- метода Лобачевского е другими методами
решения уравнений
|||/~ ЮЛ. Рекомендации ио использованию различных ва-
М|тптов метода Лобачевского, Выше были . рассмотрены
Кичине способы усовершенствования метода Лобачев-
о. Рекомендуется следующий порядок их использо-
я*
мр.-т. При .решении уравнений степени п 5 целесооб-
1|Йни применять квадрирование, формулы Энке, схему
Ленера, упрощенный алгоритм определения знаков кор-
2, Если значения показателя степени уравнения нахо-
ЖйШЙр в диапазоне 5 п 7, то дополнительно можно
{детендовать методы деквадрирования и сопряженных
||Йнений. Кроме того, вместо перечисленных способов
71
можно использовать метод двукратного квадрирования
(обобщенный метод Лобачевского),
3. При г?- > 7 целесообразно использовать в основном
обобщенный метод Лобачевского,
4. Для решения алгебраических уравнений с корнями,
имеющими равные модули и большие показатели степени,
исключающие возможность квадрирования на данном
типе микрокалькулятора (или микро-ЭВМ), целесообразно
использовать метод сопряженных уравнений.
Рассмотрим алгоритм решения уравнений с исполь-
зованием всех рассмотренных, способов, кроме метода дву-
кратного квадрирования, который изложен особо.
До начала решения целесообразно проанализировать
коэффициенты заданного уравнения (рис. 4):
—	если имеет место неравенство | а01	| а* | (i— 1,...
. .	п), то уравнение необходимо разложить по степеням
% iL «О >
—	при выполнении соотношений (7.1) составляется и
решается сопряженное уравнение или производится пре-
образование заданного уравнения с целью использования
формул Энке.
После квадрирования и вычисления условных модулей
необходимо провести анализ этих модулей.
Если условные модули существенно различаются меж-
ду собой, то определяются знаки модулей и решение урав-
нения завершается. При наличии одной или нескольких
пар близких модулей проверяется выполнение неравенст-
ва (2.18) для каждого квадратного квадрированного урав-
нения. Если неравенство (2.18) выполняется, то комплекс*
ные корни вычисляются деквадрированием или с помощью
формул Энке.
Если неравенство (2.18) не выполняется, то определя-
ются корни квадратных квадрированных уравнений,
а затем, путем извлечения корпя ТУ-й степени,— уточнен-
ные значения модулей заданного уравнения. Решение
завершается определением знаков модулей. При наличии
нескольких близких модулей проверяется наличие соот-
ношений (7.3) между коэффициентами. Если это соотно-
шение выполняется, то формируется сопряженное урав-
нение или осуществляется преобразование с целью при-
менения формул Энке.
После решения сопряженного уравнения и определе-
ния мнимых частей комплексных корней (при их равен-
стве пулю корни являются действительными) решение
уравнения завершается.
72
Диализ коэффициентов уравнения
(inp сделен не
.комплексных
корней
Определение
знаков
модулей
Определение
модулей
и их знаков

А ПРО ритм ь1 усопершенотвоааиногс метода -Лобачевского
Рис. 4
73
При певыполнепвм соотнотпений (7.1) заданное урав-
нение разлагается по степеням двучлена, квадрируется,
а затем вычисляются модули норией и их знаки.
В случае уравнений высокой степени могут встретить-
ся все рассмотренные варианты. Например, может быть
часть модулей, хорошо отделенных один от другого, дру-
гая часть модулей (условных) — попарно близких, а ос-
тавшиеся несколько модулей - с близкими значениями.
В этом случае останов счета по окончании вычислений
по данному варианту не производится: вычисления осу-
ществляются по другим вариантам - до завершения опре-
деления всех корней.
Изложенный алгоритм обеспечивает высокоточное оп-
ределение корней уравнения. Если высокая точность не
нужна, то алгоритм вычислений можно существенно упрос
титъ. Но и при реализации алгоритма в полном объеме,
как показано ниже, время счета по методу Лобачевского
меньше, а точность определения корней выше по сравне-
нию с соответствующими показателями применяемых в
настоящее время методов решения алгебраических урав-
нений.
Алгоритм решения алгебраических уравнения обобщенным ме-
тодом Лобачевского приводен на рис. 4. Решение уравнений целе-
сообразно начинать с проверки наличия в уравнения корней (дехг-
сгвительцых и комплексных) с равными модулями, т. е, с проверки
выполнения соотношений (7.1) между коэффициентами заддппогс
уравнения. При выпоипении соотношений (7.1) вычисляется точное
значение модулей корлей, Если соотношения (7/1) по выполняются,
проводится квадрирован не и определение ус ловных модулей.
В блоке сравнения условных модулей проводится разложение
уравнения по степеням двучлена, причем параметр ра ело же ни я Ь
можно принять равным а знак Ъ в схеме Горнера — еовпэ
дающим со знаком коэффициента an_L. Количество вычисленных
корней к сравнивается со степенью уравнения н, При к <; п про-
водится анализ относитедьшш: величины условного модуля и сосед-
них модулей. При г^/г-_х > 1.05 (для ILMK тина «Электроника
БЗ-34») можно полагать, что данный модуль соответствует действи-
тельному корню. Вычисление последнего завершается определении
знака (путем сопоставления с условным модулем, вычисленным
до разложения уравнения). Если rf./riz..J < 1,05, а модуль г- 2
отличается на 5% и более, то с помощью пера не яства (2.18) опре-
деляется тип корней. При небольшом различии нескольких услов-
ных модулей проверяется соотношение (7.3) между коэффициентами
квадрированного уравнения. При невыполнении соотношения (7.3)
проводится разложение заданного уравнения яс степеням двучлена,
а если это соотношение выполняется —- определяются модули кор
ней и вычисляются комплексные и действительные корни. Счет
прекращается, если количество вычисленных корней равно степени
п решаемого уравнения.
74
10,2. Сравнение метода 'Лобачевского с методами Нью-
тона и Липа. Сравним изложенные выше варианты метода
Лобачевского с наиболее распространенными в настоящее
время методами:
—	вычисления /действительных корней — методом
Ньютона;
—	вычисления комплексных корней — методом Лина;
-	- решения уравнении степени п 5 — специальным
методом выделения квадратичного множителя [22];
—	решения уравнений с показателем степени п 5 —
методом нелинейного программирования.
Для методов сопоставим следующие показатели:
—	точность вычисления модулей корней;
—	количество арифметических операций:
—	универсальность алгоритмов.
Количество арифметических действий в каждом цикле
квадрирования можно определить по формулам:
а)	количество умножений (делений):
7x42(1+(10.1)
з
б)	количество сложений (вычитаний):
(Л-Н)/2
S.^2 Jj 1-М\	(10.2)
л
[(п 1)/2 при п четном,
i 0 при п нечетном.
При использовании метода Ньютона значения функции
и сю производной целесообразно вычислять по схеме Гор-
нера. В этом случае в" каждом шаге (цикле) вычислений
модуля выполняется == 2п — 2 сложений (вычитаний)
и — 2п умножений (целений).
Рассчитанные по этим формулам количества арифме-
тических действий для вычисления всех корней алгебраи-
ческого уравнения приведены в табл. 8. Кроме того,
н табл. 9 представлены результаты вычисления модулей
шфпсй. уравнения 6-й степени, которое в примере 3.1
решено методом Лобачевского на микрокалькуляторе
« < t л о к трон ик а Б 3-34 ».
Из приведенных в табл. 9 данных следует: ирактичес-
тфн‘сдельная точность вычисл ения модулей корней имеет
моего после выполнения 5—6 шагов (циклов) расчета,
75
Таблица 8
м
Количество арифметических действий, необходимое для решения алгебраического уравнения
n-й степени методами Лобачевского и Ньютона
Степень уравнения	п = 3		п ™ 4		п “ э		71—6		п — 10	
Методы решения	Лоба- чев- ского	Ньютона	Лоба- чев- ского	Ньютона	Лоба- чев- ского	Ньютона	Лоба- чев- ского	- Ньютона	Лоба- чев- ского	Ньютона
Количество арифмети- че с к их деист вин: а) за один шаг (цикл) вычислений:										
— умножений	6	4	9	6	12	8	16	10	36	18
— сложений б) за 5—6 шагов (цик- лов) вычислений:	4	6	7	8	10	10	14	12	34	20
— умножений	30-36	20—24	45—54	30-36	60—72	40-48	80—96	50—60	180—216	90-108
— сложений в) для определения всех корней уравне- ния :	20-24	30—36	35-42	40—48	50-60	50—60	70-84	60-72	170—204	100—120
— умножений	33—39	60—72	49—58	120—144	65-77	200—288	86-92	300-360	190—226	900—1080
— сложений	20—24	90—108	35-42	160—192	50-60	250—300	70-84	360—432	170-204	1000—1200
— извлечения корня п-й степени:	3	—	4		5	—	6	——	10	—-
— всего арифмети- ческих действий	56—66	150—180	88-104	280-336	120—142	450—588	162—182	660—792	370—440	1900—2280


wewra wpaei ^агебравгческаго уравнения 6-й степени (пример 3.1) методом Ньютона
	—	Истинные значения корней						
тага (UFKJFil) расчета корней	1	1	2 5	3	.	4	5	6	7
	Принятые начальные значения						
	0,5	1,5	3,3	4,4	5,5	’ 7	10
1	0,76621082	2,1350761	2,8349067	3,7878025	4,8649298	6,5918367	8,995616
2	0.92564851	1,9679713	3,0029617	4,0506347	5,0321264	6,2958652	8,175322.1
3	0,98962695	1,9990018	3,0000273	4,0005825	5,0010101	6,1076175	7,5124809
4	0,99976203	2,0000017	3,0000315	3,9999186	4,9999948	6,0200848	6,9862875
<5	1,0000003	1,9999938	3,0000273	3,9999636	5,0000886	6,00086	6,581535
6	0,9999996	2,0000005		3,999817	5,0001199	6,000023	счет прекращен (см. столбец рядом) |
7	0,9999996	1,9999909			4,9999841	6,0000309	
8	0,99999965	2,0000042				6,0000267	
9	1,0000001	2,0000088				5,9999884	
						6,0000467	
Та б ?Ги ц а 10
если начальные значения корней выбраны достаточно
близкими к их истинным величинам* В противном случае
количество циклов расчета может существенно возрасти
(см* табл. 9 — вычисление корня. 6 при начальных значе-
ниях 7 и 10).
Из сопоставления результатов расчетов, приведенных
в табл. 6 и 9, видно также, что наибольшая точность
метода Ньютона не превосходит наибольшей точности
метода Лобачевского, если в обоих случаях используется
микрокалькулятор типа «Электроника БЗ-34»,
Анализ приведенных выше и других аналогичных дан-
ных показывает, что количество арифметических действий
по определению всех корней уравнения методом Ньютона
больше, чем при использовании метода Лобачевского, от
1,5—2 раз при стопени уравнения п ~ 3 до 4—5 раз при
п — 10.
Выше не учитывались арифметические действия , не-
обходимые;
—	для определения знаков модулей корней в методе
Лобачевского;
—	для определения начальных значений корней (от-
деления корней) в методе Ньютона*
При учете всего объема вычислений преимущество. ме-
тода Лобачевского в случае вычисления действительных
корней уравнений по сравнению с методом Ньютона воз-
растает еще больше.
Сопоставим метод Лобачевского с методом Лина, ко-
торый широко применяется для решения уравнений
с комплексными корнями.
Заимствованное из работы [10] уравнение Леверье
6-й степени в § 6 было решено методом Лобачевского
с использованием деквадрироваяия. Из формул (10.1)
и (10.2) видно, что при 7-ми циклах квадрирования не-
обходимо произвести 140 умножений и 126 сложений.
Вследствие этого на одну пару комплексно-сопряженных
корней приходится 47 умножений и 42 сложения. Кроме
того, в каждом цикле деквадрирования необходимо вы-
полнить 2 операции сложения, 1 операцию умножения
и 1 операцию извлечения корпя. Общее количество опе-
раций — 118.
Решим уравнение Леверье методом Лика.
Начальные значения коэффициентов трехчлена, вы-
деляемого из заданного уравнения, выбраны в соответст-
вии с рекомендациями работы [101, равными 2а0 = 4;
г© = 6. Вычисленные значения коэффициентов трехчле-
78

0
Г/ 2
И: 3
*  4
i. 5
: 6
’ 7
' 8
: 9
L ю
Значения коэффициентов 2а и г2 трехчлена, выделенного
. из уравнения Леверье методов! Лина
Коэффициент 2а	1 Коэффициент | rz	; Яв тага '	।	Коэффициент 2а	Коэффициент
4	б	1	11	0,37084656	0,30535815
2,1404102	0,81060995	12	0,3707371	0,30534076
1,8308649	0,82274822	13	0,37070707	0,30534076
0,47382056	0,99375138	14	0,37070544	0,30532307
0,36056875	0,42696489	15	0,37070666	0,30531419
0,34952847	0,32718088	16	0,37070815	0,30531418
0,34326751	0,30263147	•17	0,37070867	0,30531538
О; 362:14699.	0,30113645	18	0,37070877	0,30531449
0,36965148	0,30343437	19	0,37070875	0,30531452
О', 37116422	0,30483131	20	0,37070873	0,30531452
0,37107527	0,30528697	21	0,37070873	0,30531452
в различных циклах расчета приведены
Ш табл. 10.
Из табл. 10 видно, что для достижения почти предель-
ШШй точности вычислений достаточно выполнить 15—
1Ц шагов расчета. При* этом потребуется выполнить: умно-
, жепий — 120—152; сло'жоний —120—152. Таким образом,
для решения уравнений 6-й степени методом Лобачевско-
го требуется, при той же точности, в 2 раза мепыпе ариф-
метических действий ио сравнению с методом Лина.
Определить другие корни уравнения Леверье методом
Лина не представляется возможным, так как условия
Сходимости метода для этих корней ие выполняются даже
при весьма близких к истинным начальных значениях
' коэффициентов трехчленов.
В настоящей работе показано, что при решении урав-
1 й&йий с комплексными корнями, имеющими равные моду-
ЙВ» целесообразно применять сопряженные уравнения,
рмвющие действительные корни. Поэтому решение таких
уравнений сводится к рассмотренному выше случаю реше-
| ннн уравнений с действительными корнями.
На изложенного выше можно сделать следующие вы-
1,	При использовании микрокалькуляторов типа
ЛМтропика БЗ-34» точность методов Лобачевского, Нью-
гниц и Лина приблизительно одинакова.
79
2.	Метод Лобачевского требует от 1 л5 до 5 раз меньшего
объема вычисления всех корней уравнений степени 3
п 10.
3.	Существенным преимуществом метода Лобачевско-
го по сравнению с методами Ньютона, Лина и другими
является отсутствие необходимости:
а)	отделения корней;
б)	проверки сходимости метода;
в)	использования других методов, если данный метод
не сходится.
10 Л Сравнение метода Лобачевского с другими мето-
дами решения алгебраических уравнений. При решении
алгебраических уравнений на ЭВМ широко используются
методы парабол (Мюллера) и скорейшего спуска [18,19, 20].
Соответствующие программы характеризуются следую-
щими показателями:
— программа размещается на 250—300 ячейках памя-
ти 3-адресной ЭВМ; при использовании одноадресной ЭВМ
потребное количество ячеек памяти возрастает до 600—800;
— для определения корней многочлена 20-й степени
с действительными коэффициентами требуется 33—37 с,
если быстродействие ЭВМ составляет в среднем 20 000 опе-
раций в секунду. При этом относительная погрешность
равна 10~9;
— двукратные корни вычисляются с меньшей точ-
ностью: программы обеспечивают 5—6 верных знаков,
а яри счете трехкратных корней — 3—4 верных знака.
Из этих данных следует, что использование методов
Мюллера и скорейшего спуска в программах, предназна-
ченных для современных микрокалькуляторов, нецелесооб-
разно как вследствие весьма большого объема программ-
ной памяти, так и вследствие низкой точности вычисления
кратных корней.
В работах [21, 22] описаны предназначенные для мик-
рокалькуляторов типа «Электроника Б3-34э программы ре-
шения алгебраических уравнений 3—5-й степеней, в кото-
рых при п нечетном определяется и исключается действи-
тельный корень, а при п четном уравнение разлагается на
трехчлены типа (5.4). В работе [22] отмечается, что пред-
ложенный авторами новый алгоритм гарантирует сходи-
мость вычисления корней.
Проведем: сравнительный анализ метода Лобачевского
и упомянутого метода но следующим показателям:
— точность вычисления корней;
— время счета;
80
Т а б л и ца 11
Время счета по прилагаемым программам ва микро
калькуляторе «Электроника Г>3-34>>
xppjx:.:.:. i.xx:k:: ’.			Время счета, секунды				
XixXX.f..’.	Паммспованне и номер п р or раммы н ын iu лев и й	Количество циклов (шагов) счета	Степень уразко- пий п				
i;::xx:K:?‘ ’ zHHxH::?:  Xtxxx:. ’ I.xxx.:?’:			3	Г 1	а	В	7
: hxxh:.:.:  HxxXp:. “xxxiKH:: . ...:xxx.:.... Hxxx:;?:::	Кадрирование уравнении; программы № 1—5	1 5	12 60	18 90	24 120	34 170	43 215
i.HHxxxiH:.. xx::xxx?I ’ ?’:x:K:x! I ...:::::xx.. : Ихх:?:?:’: .•.::sx::.’. ...:::x.:.:. 'XxXXXX.. ’ Глх:?:??:.	Деквадрирование уравно- ним; программа №9	1 (для пары комн л. к орлей) п/2 шагов	W 10	10 20	10 20	10 30	10 30
хххп: .•.:::x.:.%. . .%:xx.:.... .;.:x.s...s.% ..	Извлечение корня Л-й сте- пени; программа №7	1 корень п корней	10 30	10 40	10 50	10 60	10 70
X:xZJ :s:sx:|:j:s:  . HxxH:.::: . ПННхл::?:. : ПхххШ.:.: .:x::x.:.:....	Определение знака корня автоматически; програм- ма № 10	1 п — 1	22 44	22 66	22 88	22 110	22 132
.:.:xx.:.:.. .:.:x::x...% . ,:::xxx.:.. xxxxx’:!:! I. .%:xx....... . ^лххлл’Л:: xx::.::::K:‘ xxx.:::?:*: ’ '..X.ixxX.:'"4'. * . .:xxx.:.... : xxxxxhl	Определение знака корня п оду автоматически; про- грамма №10	1 корень и корней	50 100	50 150	50 200	50 250	50 300
^Hixx:?:?:.’ * i.xxxxh: : .;.sx::x.:.. . .:.:xxx.:... .•xxxxx.. Hxxx::IK I. ::::xxx.:... xxxxx... . xxxxx..	Деления уравнения на двучлен; программа №8	1	30	37	43	50	60
xxxx::.:.:.. xxxxxx... xxxxxx.. xxxxx... xxxxxx.. xxxx::.... xxxxxx.. xxxxx... xxxx...... xxxxx... xxxxxx... XXxXXX... 'XXxxXX. xxxxx.:.. xxxxxx. xxxxxx. xxxx.:. 7//.XXX. .	Разложение уравнения «о степеням двучлена; программа №8	1	63	100	145	195	255
xxxxx... xxxxxx.. XXXXXXX.. xxixxx. xxxxx.... xxxxx.:.:.:.. . xxxxxxx... /xxxxx:	Рмешш квадратного урошшия «вручную»	1	40	40	40	40	40
xxxxxxx,: . XXtxXXXX. ’.. xxxxxxx’::.: . xxxxx.... : xxxixxx.:.. . xxxxxx.... . xxxxxxx. . . xxxxxx.. . XX.txXXX. ’. ’ . xxxxx.... I XXtxXX.: . ..xxxxx..	: Деление коэффициентов уравнения на заданное Число «вручную»	л-И коэффи- циентов	24	30	36	42	48
.•xxxxxx.. ijHxxx::::.	Деление коэффициентов уравнения на заданное 11 о программе № 6	П -1-1 коэфф и- ЦПонтов	12	15	18	21	24
81
Окончание табл. 11
• ] Ыи пешчяллис « iii'Mup л рея рам.мм Еьрн-кяенин	Кёаячг./гио iJMwroH (шагов) счета	Щн-МН i:4i:lo. < скулды				
		Щч-ILCHh урзвш.1- ллй и				
		3	4	V	6	7
Д в у к рат л о а к в а ।1 р i i,p < ы а  ние, раз ложен ле у рал пе- ни я нос г е«1 е ая м j 1 в у '[.ле и а, извлечен не корней	в	267	396	533	723	997
—	универсальность алгоритма; сходимость вы числ е-
ний;
—	степень автоматизации счета.
При сравнении методов целесообразно решать не толь-
ко сравнительно простые для метода Лобачевского урав-
нения, но и сложные — с корнями, имеющими равные
и близкие модули, с большими значениями модулей и т. и.
Время счета но прилагаемым программам па микро-
калькуляторе типа «Электроника БЗ-34» приведено в
табл. 11, причем эти данные получены с помощью одного
и того же микрокалькулятора, так как время счета на
разных экземплярах может существенно разд и чаться.
В табл. 11 приведено только время счета калькулятора,
потому что оно может быть объективно оценено. При оп-
ределении общего времени, необходимого для решения
у ра в пел и й, должно быть учтем о:
—	время ввода программы, которое составляет 4—
4,5 мип (при использовании всех ячеек программной па-
мяти калькулятора);
—	время ввода исходных данных, которое колеблется
в значительных пределах, его ос родненное значение мож-
по принять равным 1 мин;
—	время л орех ода от одном программы счета к дру-
гой — составляет 10-.20 с.
11 ри с р а в 1t еп и и методов 11 еоб х оу (нмо у чест ь, что я а
‘ )<8 я че й к а х 11 а м f i т и м и к р о к a j i ь i с у л я то р а, зам и м < i о м i .т х п р о -
граммов решения уравнении 5-й степени 1.221, .можно за-
к не ат ь с.: i ед у кн.ц и е п ри л а га ем ы е программ ы :
—	квадрирования уравнений 5-й степени и извлечения
корня Л'-й степени:;
—	р а зло- к e i i и я у р а в не и и я по сто п еня м дв у ч л е и а,
82
а также деления уравнения на дну член (исключения
нория).
Таким образом, для определения общего времени реше-
ния уравнения необходимо к времени счета» указанному
и табл. 11, прибавить 5—5,5 мин при использовании ме-
тода [22] и 6—6,5 мин при использования модернизиро-
ванного метода Лобачевского.
Точностные и временные показатели сравниваемых ме-
тодов приведены в табл. 12. Из анализа этих данных мож-
но сделать следующие выводы.
1.	Точность определения корней модернизпрованным
методом Лобачевского в ряде случаев существенно превы-
шает точность метода [22k а в: остальных случаях — не
шоке точности этого метода,
2.	Метод Лобачевского сходится при решении уравне-
ний с любыми типами корней» Метод [22], как следует из
представленных в табл. 12 данных, сходится не во всех
случаях. Причем информация оператору о выдаче ложных
значений корней не выдается. Это обусловливает необхо
димость проверки правильности решений даже в том слу-
чаем когда уравнение решено безошибочно.
3.	Бесспорным достоинством метода [22] является нрак-
тически'полная автоматизация процесса решения корней.
При использовании модернизированного метода Лобачев-
ского применяются различные программы, выбор которых
производится оператором. Несмотря на использование не-
скольких программ, общее время решения уравнения 3—
Гьй степеней методом Лобачевского в 1,5 раза меньше.
При решении уравнений 6-й и более высоких степеней
весьма часто используется, метод последовательного опре-
деления и исключения корней. В этом случае точность
вычисления корней уменьшается вследствие накопления
ошибок вычислений. Так, согласно данным работы" [22],
н уравнении 8-й степени последний из вычисленных кор-
мой может не содержать ни одной верной цифры. Для по-
еминшия точности вычислений рекомендуется повторять
щн четы, меняя каждый раз порядок определения корней,
hr чщ|гпше этого время решения уравнения существенно
рп ф;н = NHV|\
При решении уравнений степени 6 в работе [22]
рштмн иду стоя использовать метод нелинейного ирограм-
мнршшпия/ с помощью которого можно с высокой точ-
шитью определять коэффициенты трехчлена (32). После
иючемия его корней полученное уравнение 4.4-5-й
* НЧМЧ1ГЙ (при п — 6	7) решается с помощью упомяну-
83
Таблица 12
Точностные ц временные показатели методов решения алгебраических уравнений при использовании
микрокалькулятора «Электроника БЗ-34»
Номер примера) заданное уравнение	Истинные значе- ния модулей ;корней	Применяемые методы решения			Метод Лобачевского			
		Вычисленные значения модулей	Относит, погрешности	время счета ыин с)	Вычисленные : значения мо- дулей	Относит, погреш- ности	№ прог- раммы	Время счета С— мин
Пример 4.4 г3 _ 65г2+1087г — —1023 == 0	1 31 33	0,999999 31 33	10“7 0 0	5'30"	1 31 33	0 0 0	1,10,12	3'
Пример 4.5 г3 — 1519г2+769Н8г — —1,2980924*10^ — 0	505 506 508	504,83435 506,3082 507,8574	Ч< чЦ хЛ i । Г о о о «О СО СО	ТУУ	504,9999992 506,0000002 507,9999993	1,6Л0-й 4 Л 0-1о 1,4Л0^	8,1 10	4'
Пример 4,6 х3 — 3221г*+3453210г — —1,2332ЫО* = 0	1000 1110 1111	999,99545 1110,5022+ ±/0,70710678	4-10-° Неверно	5'	1000,00002 1110 1111	2Л0-и 0 0	8,1,10	4'
Пример 4.7 ж< + ^ —1085г2 —717г+ +289800 = 0	21 25 -23 • —24	21,00001 24.99999 —22,99995 —24,00005	5-Ю'7 4Л0“7 2Л(ГЙ 2Л0"е	12'30'	21 25 -23 —24	0 0 0 0	8,2 10,8	8'
г4 — 19,998^+ + 146,8842г2—. — 468,99507г+ + 548,47739 = 0 .: * ::::::: i:::: н*:+Г:*::	,‘’‘,’,’Г!’:*к:’:’:нн:ккск»** • ••*	3,333 4,444 5,555 6,666	3,333069 4,443967 5,5550455 6,6659804 £	X X	) 0,8880592 ’’ 1,096064 1,1204138 1,2219736	2Л0-*6 7Л0~* 8Л0~* ЗЛО"6 7Л0"* 1,3 ЛО"2 4ЛСН 2-10-Б •	12'30' ; О 9'	3,3329993 4,443996 5,5550102 6,6659934 ? - х	«Н| 0,88799978 1,1100553 1,1199374 1,2220076	2Л0-7 9Л0-7 2Л0“*6 ю-6 jxxxxxxxxxxx::xx::i8cxxs .xx;.x::::xx:n:::xxxxxxxS х:.:.хх:.:.::хххх::хххххх| 5.10-5 6 Л О-6 6Л0-6	2,10 1хЯК:.:.**Кхххххх9 X х X	. х . . ? 4 | sxxxxx:.xxxx::x:. х х х х \ X X ; 2/10	3'30" Illi 4 хх ' X
~	: а» I	1Д1 ЛЖМ'=Л	I 1J2 I i;222								
г*+г3+га — х — 1 ~ 0	—0,66099253 0,84873489 —0,59369115+ ±/1,1961583	6,66099252 0,84837486 -0,59369115+ ±/1,1961583	IO'7 IO”7	9'	0,66099253 0,84837487 0,59369115± ±/1,1961583	0 10-7	2,9,10	6'
г6+8г4+31г3 + 80г2+ +94г+20=0; см. [21]	-1±/3 —3,7320507 -2 -0,26794921	-1 ±/3,0000178 —3,7320507 —2,000032 —0,2679458	о+ю-« 10~« 1,5Л0“5 1,2Л0“®	17'	—1±/3 —3,7320502 —2,000000 -0,26794921	0+0 1.«Н 0 0	3,9,10	7'
г4—14,451^+ + 50,915376г3 — —76,160098г2 + +52,338867г — — 13,640154 ==0	.0,888 1,11 1,12 1,222 10,111	0,8612452 1,0985651 + {±/0,12176124 1,2816256 10,110999	ЗЛО"2 Неверно 5Л0~* 10-7	17'	0,8879945 1,1099703 1,1199829 1,2220424 10,110999	ь*- >-х СЛ	5° 5 О’  L—. |_Х ASS^<? 1 СЯ Й О» о»	8,3,10	8Г
Пример 6.3 гв+г5 + г4+г3+г2 + г + + 1 = 0			IO”* — для 1-го модуля [22]	19 + +11'	—0,9009689+ ±0,43388374 —0,222521 + ±0,97492789 0,6234898+ ±0,78183163	КГ7 для всех мо- дулей	8,4,9	9'
той ранее программы* Как показано в работе [22], для оп-
ределения этим методом трехчлена типа (5.4) уравнения
6-й степени (см. табл. 12) потребовалось 19 мин счета на
микрокалькуляторе. Невязка модуля равна 10"8, Еще
11 мин счета необходимо для исключения из заданного
уравнения вычисленного трехчлена и решения подучен-
ного уравнения 4-й степени. При решении заданного урав-
нения 6-й степени методом Лобачевского с деквадрирова-
нием требуется 9 мин счета (на разложение уравнения по
степеням двучлена, квадрирование и деквадрирование),
а невязка модулей равна 10‘7< С помощью сопряженного
уравнения корни этого уравнения можно определить за
4 мин при невязке модулей 1СГ7.
Из приведенных выше данных следует также, что метод
двукратного квадрирования при п < 6 требует заметно
большего времени счета по сравнению с другими вариан-
тами реализации метода Лобачевского. Но время счета по
этому метод у меньше, чем у широко используемых мето-
дов. Как уже отмечалось, алгоритм решения уравнений
с помощью метода двукратного квадрирования существен-
но проще алгоритма других вариантов метода Лобачев-
CzKoro, что имеет весьма важное значение. Высока и точ-
ность решения. Поэтому обобщенный метод Лобачевского
рекомендуется в качестве основного способа решения
уравнений с любыми типами корней.
ПРИЛОЖЕНИЕ
ПРОГРАММЫ ДЛЯ МИКРОКАЛЬКУЛЯТОРА
«ЭЛЕКТРОНИКА БЗ-34»
Программа 1. Вычисление модулей корней уравнений
3-й степени * *
азх3 4~ а^2 -|- а±х +	“ О
xj .:.:. .. Н:.: :. 1 я... . я.. ... . л::. * * * * ж::	а ф Е £		01	02	03	04	05	06	07	08	09
	00	ИП1	Fx2	И ПС	ИП2	X	2	X	’—	ПА	ИП2
	10 20	Ех2	ИП1	ипз	X	2	х	—	пв	И ПС	Fx2
		ПС	И113	Fx2	пз	НПА	П1	ипв	П2	FLO	ОО
	да	С/П	•	Fx<0	35	/-/	ИПД	ХУ	Fx*	С/П	Б11
	40	31									
Ввод исходных данных: а5 -г- ах — > Зч-i; а0 —> С.
Инструкция:
й) определение т: возведением т раз в квадрат ] атах | до тех
ti&fh Ж>ка порядок возводимого числа не превысит 50;
б) пасылка: т —> 0;
а) нуск: В/О; С/П;
г) йасылка: 1/2W—>Д;
Д) вычисление модуля нажать клавиши i — 1; С С/П.
86
87
Программа 2. Вычисление модулей корней уравнений
4-й степени
а&4 + а3х4 -|-	-|~ atx -|- а(1 — О
.Ns ячеек	00	01.	02	03	04	05	06	07	08	09
00	ИП1	Fx*	ИПС	ИП2	х	х.)	X	—..	ПА	ИП2
10	Fx2	ИПС	ИП4	х	И ГН	ипз	х	—'	2	X
20	4-	пв	И113	Ех*	ИП2	ИП4	X	2	X	—
30	П9	ИПС	Fx*	ПС	ИП4	Fx2	114	ИПА	П1	ипв
40	П2	ИП9	ИЗ	FLO	ОС)	С/П	• 1	Ех<0	50 1	^7„/
50	ипд	ХУ	Fx*	С/П	Г,П	46				
Ввод исходных данных: а4 4; а3 --* 3; а2 2; ах -*•* 1; «0 С.
Инструкция:
а)	определение т: возведением т раз в квадрат ! аПК1Х | до тех
нор, пока порядок числа не превысит 50;
б)	засылка: т -* 0;
в)	пуск: В/О; С/П;
г)	засылка: 1/2™ —> Д;
д)	вычисление модули хг: нажать клавиши i — 1; i\ С/П.
88’
Программа 3- Вычисление модулей корней уравнений
>•’ 5-й степени
£•	+ V8 + <М2 Н' rtir + йо ™ °
№ ячеек	00	01	02	03	04	05	06	07	08	09
00	ИПС	ИП2	X	2	X	1-1	П7	ИПС	ИШ	X
10	ИП1	И ИЗ	X		2		П8	ИП1	ИП5	X
20	И112	ИП4	\/ г %	-—	2	х	ПО	ипз	ИП5	х
30	2 4	X	/-/	ПА	6	П6	Сх	Л13	ИП6	5
40	* »*» **	ид	ктшд	Fx3	кипе		кпд	5	ИПД	
50	1’х-О	38	ИПС	Fx2	ПС	FL0	(К)	С/П	-4-	Fx<(
60 7» • % z V •	62	/-/	ипд	ХУ	Fxy	С/П	БИ 		58		
дай»* Ki
Ввод исходных данных: а5 —> 5; а< -- 4; д3 —> 3; й2 -+ 2;
'* 1; л0 > С*
И п с т р у к ц и я:
а)	определение т: возведением т раз в квадрат | атах | до тех
пока порядок числа по превысит 50;
6)	засылка: тп —* 0;
я) пуск: В/О; С/П;
г) засылка: 112т —> Д;
д) вычис ление модуля х,-: нажать клавиши i — 1; С С/П.
Программа 4. Вычисление модулей корней уравнений
6-й степени
ae.te + а5х5 + сцх4	+ «2.т2 +	+ л0 = 0
1 № ячеек	00	01	02	03	. 04	05	06	07	08	09
00	ИП1	Fx2	ИПС	ИП2	X	2	X	1 » •»	ПА	ЙП2
10	Fx2	И ПС	ИП4	X	ИП1	ИПЗ	X	.—	2	X
20	4-	ПВ	ИПЗ	Fx2	ИП1	И По	X	ИПС	ИП6	X
30	•—-	ИП2	ИП4	X	—	2	X	+	П9	ИП4
40	Fx?	ИП2	ИП6	X	ИПЗ	ИП5	X	 	•% 2	X
50	4-	П8	ИП5	Fx2	ИП4	ИП6	X	2	X	—
60	117	НПО	Fx2	Пб	ипе	Fx2	ПС	'И ПА	Ш	ИПВ
70	П2	ИП9	ПЗ	ИП8	П4	ИП7	П5	FLO	00	С/П
80	——	Fx<0	84		ипд	ХУ	Fxy	С/П	БП |	80
Виод исходных данных: аб 6;	—* 5;	—> 4; л3 3; а2 —*
—> 2; tij -** 1; Й0 ’“•'> С -
Инструкции:
а)	определение т: возведением т раз в квадрат | amax [ до
тех пор, пока нори док числа не превысит 50;
б)	засылка: w 0;
в)	пуск: В/О; СП;
г)	засылка: 1/2™ Д;
д)	вычисление модуля х-: нажать клавиши i -- 1; С С/П.
00
ii: 
i xbt • • •	•
///. .
I .. Программам» Квадрирование уравнений 7-й степени
а?х7 +	+ а^А 4- Л4Ж4 + а8лэ + д2я2 + агх -(- «0 = О
X.	№ ячеек	00	01	02	03	04 •	05	06	07	08	09
"s ;• • ’*. * f .	00	ИП1	Fx2	ИПС	ИП2	X	2	X	1	ПА	ИП2
	10	Fx2	ИПС	ИП4 к	X	ИП1	ИПЗ	X	—	2	X
	20		ПВ	ипз	Fx2	ИП1	ИП5	X	ИП2	ИП4	X
	80	ЖМкв	ИПС	ИП6	X		2	X	4"	ПО	ИП4
	<0	Fx2	ИП2	ИП6	X	ИП1	ИП7	X	-»—-	ИПЗ	ИП5
	•S0	X		2 	X	+	пд	ИП5	Fx2	ИПЗ	ИП7
	00	X	ИП4	ИП6	X	——	2	X	4-	П9	’НПО
:::х.:.:..... ;xxx::Z:Xi	W	Гх«	ЙП5	ИП7	X	2	X		П8	ИПС	Fx2
	•.:х:""’х «О	ПС	ИП7	Fx2	П7	ИПА	П1	ипв	П2	ипо	ИЗ
		И«Д	П4	ИП9	П5	ИП8	Ш6 •*—	uriz	С/П		1
ЙЙД исходных данных: а? —* 7; л9 — 6; аб —* 5, ал 4; а3
^2; at 1; а0 С; z — ячейка с | атах |.
^ИйУй Ш р У к ци я:
|И|ИИЗД' В/О; С/П;
ЙМСь знаков коэффициентов в данном цикле квадрирева-
шиьлиить и. а),
Д^1Е;;ШйДрйрование прекращается при атах > 106\
П р о г р а и м а (к Деление (умножение) коэффициентов урав-
нения на заданное число
№ ячеек	00	0:1	02	03	04	05	06	07	08	09
00	ипо	119	КИПУ	ИПА	“V	КП0	HLO	оо	.И ПС	И ПЛ
10		ПС	с/п							
Примечания: 1. При умножении коэффициентов в ячей-
ки 04 и 10 записывается команда «X». 2. При записи программы
с z-й: ячейки в (z + 08) записывается число г.
Ввод исходных данных: ап а} — в ячейки п 1} д0 С;
делитель — в ячейку А; п —* 0.
Инструкция: нуск: БП; z; С/П.
Программа 7. Извлечение корня TV-й степени
№ ячейки	00	01	02	03	04	05	06	07	08	09
00		Гх>0	04	/_ / )	ипд	ХУ	Fxy	с/п	БП	ОО
Примечания: 1, При записи программы с z-й ячейки:
в (z -И 03) записывается число (z 05); в (z + 10) записывается
число z. 2. Заслать 1/2™ в Д.
Инструкция при вычислении t-го модуля х^. нажать
на клавиши i — Г, С С/П.
92
Программа Разложение уравнения по степеням суммы
(разности); деление уравнения на двучлен; вычисление значения
многочлена
Ле	00	01	02	03	04	05	Об	07	08	09
00	Сх	ПС	ипд	IL9	ИПА	кипе	X	ПВ	ИПО	/
10		П9	киш	ипв	-1-	КП9	ИП9	ипс	—	Fx — 0
	04	МПС	!	+	ПС	ипд		Fx=0	02	С/П
	ПВ	C/1I								
Примечания: 1. Записанная программа осуществляв-
разложение уравнении но степеням двучлена. 2. При делении урав
Й<’нми на двучлен необходимо в ячейку 21 записать команду С/П.
И: При вычисления многочлена необходимо в ячейки 15 - 22 запи-
йпь команды: ПС; НПА; х; ПВ; И ПО; Fx~-0; 08; С/П. 4. При
Шш<ш программы с ячейки z записать: а) в ячейку (z +• 21) —
(> 4 4); б) в ячейку (z + 28) — число (г 4-002).
Пиод исходных данных: ап ч- а0 — в ячейки п ч- 0; параметр
jiOWWHUin Ъ (или кореш.; см. стр. 24) — в ячейку А; п > Д.
Инет р у к д и я: нажать на клавиши БП; z; С/П; значение
ffHHfuMitoiui / (6) *- а ячейке В.
XXX.-Х^
XXX
:хххх.-_
:ххххх
xxxxxxx
:.:хххххххххх.
:.:хххххххххх.
:ххххххххх
хххххххх
:.:.:ххххххх::хх.:.
.,хххххххх
:.:.:ххххххх::.:.:..
:.:::ххххххх.
:.:ххххххх::.
•.:.:ххххх::::.
.:.:хххх::::хх.
.:.:ххххххх::хх.:.
.гххххххххххх.:.
гххххххххххх.
..:ххххухх*ххххх.
.:ххух<ух4<хххх
:.:.:хххуу4<х>о«х .
. :ххх»ЛооЛх .
-.:ххххх>й<йЛ«х* :
-.:.:хххх4Лххх .
.:.:ххххЛххххх.
..r.rxxxjootxxxx .
. . хххф^ххххх.
. хххх>&«схххх .
.'ХХХХХ1ЙСХХХХ4.
. *ХХХ»УХХХХХ .
ixxxxxxx:
Програ м м а 9» Деквадрмроватше у рянмони п
'ЧпХ- I- »>_1; ,п.г +•	•••• о
\р	1 JN2 ячеек! *	00	01	02	03	04	05	(б	07	08	09
00	ипв	V’ V'	ПВ	2	х	И ПА	г.	!' Г	ПА	НПО
10	1	—.	по	С/П	1«х<0	00	ИПА	/—/	ПА	Г»П
20	00									
Примечания. 1. При записи программы с з-й ячейки
записать: а) я ячейку z -|- 16.- число z; б) в ячейку z + 21 —
число z.
Ввод исходных, данных:
• л.Л А	. ' ’ ♦ *>*/ "~~Г
И н с т р у К Ц и я:
а)	нажать па клавиши БII; з; С/П;
б)	затем — на С/П (в каждом цикле) или на / С/П -- до
появления О па индикаторе.
Результаты счета: в ячейке Л значение — 2cz; в ячейке В — г2.
94
Л р о г р а и м a IO. Онредолшпп- .шзкнк модулей автомати-
чески
И X а> Г е®‘	00	01	02	03	04	or,	06	07	08	09
00	Сх	ПС	ИИ А		ПА	ИП8		ИП/\	X	ИП9
ю	+	и в	ИПС	Fx—0	J9	1Ш.В	ПС	13П	02	
20	Fx2	F V	1		Fx >0	36	ИПС	П9	ИПА	/~/
30	ПЛ	ИП8	г •г	 118	ИПА	С/П 1	ИПВ	119	ИПЛ	БП
40	31									
Ввод исходных данных: а7гЛ8; («Ti...,2 •— £rf) •-* 9; | %i | или
| ?,а; 1 -* А.
И «стр у к ц и я: нажать на клавиши В/О; С/П.
После останова счета ла индикаторе высвечивается модуль
г соответствующим знаком.
Повторить для следующего корпя, написав его значение в А.
Содержимое ячеек 8 и 9 не менять! Счет начинать с модуля или
2а > имеющих наибольшие значения.
Н р о г р а м м a 1L Вычисление действительной части комп*
лнчочм* сопряженных корней по формуле (9.1)
I- к пй <Н •:51	02	03	04	05	06	07	08	09
НОННА	ППВ	Lx2			ПП 9			ИН9	..f.z*
!(> ШИ!] : <	С/П										
Нно.ч 1ь-ч’>Д11ык данных: b '- 9; г; •* .4; гь?.* В-
Ни- t р у i> п, и я: нажать на клавиши ВЛ>; С'[L
Но» 9И иг г;нн»нп В ячейке X (НИ	д.11 катере) будет хншеано
СПИСОК ЛИТЕРАТУРЫ
1.	Лобаче в с к и й Н, И, Полное собрашш сочи ионий. IV.—
М,— Л.: Гостехиздат, 1948.
2.	Крылов А. Н. Лекции о приближенных вычислениях,—
. М.-Ли ГИТТЛ, 1950,
3.	К у р о ш А. Г. Курс высшей алгебры..Ми Наука, 1975.
4.	Бахвалов Н. С. Численные методы. М.: Паука, 1975.
5,	Скарборо Дж. Численные методы .математического анали-
за,— М-— Л.: ГТТИ, 1934.
6.	Березин И. С., Жидков Н. II. Методы вычислений,-
Ми Наука, I960.
7,	Демидович Б. П., Марон И. А. Основы вычисли-
тельной математики.— М.: Наука, 1970.
8.	Бронштейн И. Н„ Семендяев К. А. Справочник
по математике для инженеров и учащихся втузов.— М.: Нау-
ка, 1986,
9.	К о р н Г., Корн Т. Справ оч ни к но математике для науч-
ных работников и инженеров.— Ми Наука, 1984.
10.	3 а г у с к ин В. Л. Справочник по численным методам реше-
ния алгебраических и трансцендентных уравнений,— Ми Физ-
матгиз, 1960.
11.	Андре А нго. Математика для электро- и радиоинжене-
ров,— Ми Наука, 1964.
12.	Энциклопедия математики. Т. 3.— Ми Сов. энциклопедия, 1980.
13.	С у ш к е в и ч А. К. Основы высшей алгебры. — Ми Гостех-
издат, 1932.
14.	Бут Э, Д. Численные методы.—М.: Фиаматгиз, 1959.
15.	Численные методы.-- М,: Высшая школа, 1976.
16.	Фильчаков П. Ф. Численные и графические методы при-
кладной математики.— Киев: Нау нова думка, 1970.
17.	Мишина А. П., Проскуряков И. В. Высшая ал-
гебра. Линейная алгебра, многочлены, общая алгебра,— Ми
Наука, 1965.
18.	Воеводин В, В. Численные методы алгебры. Теория и
алгорифмы.—М»: Наука, 1967.
19.	В о е в о д и и В. В., Б отацева Л. П. Стандартная под-
программа определения всех корней алгебраического много-
члена методом парабол.— Ми Изд-во МГУ, I960.
20.	Воеводин В. В. Стандартная подпрограмма определения
всех корней алгебраического многочлена.— Ми Изд-во МГУ,
1960.
21.	Дьяконов В. П. Справочник по расчетам "ла микрокаль-
куляторах. — Ми Наука, 1986.
22.	Т р о х и м е н к о Я. К„ Л ю б и ч Ф. Д. Инженерные рас-
четы на программируемых микрокалькуляторах,— Киев: Тех-
ника, 1985«
23.	Т рох яменк о Я. К,, Л ю б и ч Ф. Д. Инженерные рас-
четы на микрокалькуляторах,— Киев: Техника, 1980.
24,	Беэикович Я. С. Приближенные вычисления. — М.—
Ли Гостехиэдат, 1941.