СВОЙСТВА ФУНКЦИИ,
ЗАДАННОЙ ГРАФИКОМ
1.	Область определения: D = [-2; 4].
2.	Множество значений: Е = [-2,5; 3,5].
3.	Наибольшее значение у = 3,5 функция принима¬
ет в точке х = 3,5; наименьшее значение у = -2,5
функция принимает в точке х = -2.
4.	График функции пересекает ось Ох в точках
(-1,5; 0), (1; 0), (2,5; 0), а ось Оу — в точке (0; 0,5).
5.	Значения аргумента х = -1,5; х = 1; х = 2,5
являются нулями функции.
6.	Функция принимает отрицательные значения
на промежутках [-2; -1,5) и (1; 2,5)
и положительные значения на промежутках
(-1,5; 1) и (2,5; 4].
7.	Функция не является ни четной, ни нечетной.
8.	Функция является возрастающей на каждом из
промежутков [-2; -0,5], [2; 3,5] и убывающей на
каждом из промежутков [-0,5; 2], [3,5; 4].

СИСТЕМА ЛИНЕЙНЫХ УРАВНЕНИИ
С ДВУМЯ НЕИЗВЕСТНЫМИ (ПЕРЕМЕННЫМИ)
ахх + b1y = cv
а2х + Ь2у = с2
Пусть в системе ар Ьр ср а2, Ъ2, с2 отличны
от нуля, тогда верны утверждения:
б) если —1
а2
а) если —1
а2
то система имеет единственное решение;
С1
\ то система не имеет решении;
С2
а1
в) если —
«2
решений.
то система имеет бесконечно много
Решение систем линейных уравнений
Способ сложения
Способ подстановки
Зх + 2у = 5
5х + 7у = 1
•7,
•(-2);
Зх + 2у = 5,
5х + Чу = 1;
21х + 14у = 35,
-10х - 14у = -2;
Зх + 2у = 5,
Их =33;
3-3 + 2у = 5,
х =3;
х = 3,
у = -2.
5 - 2 (- 2)
5

УДК 51(075.3=161.1)
ББК 22.1я721
А34
Авторы:
Е. П. Кузнецова, Г. Л. Муравьева, Л. В. Шнеперман, Б. Ю. Япгин
Рецензенты:
кафедра алгебры и методики преподавания математики
Витебского государственного университета
им. П. М. Машерова (доктор пед. наук, профессор К. О. Ананченко);
учитель математики СШ № 153 г. Минска А. И. Абрамович
6'v
Навукова-педагагн;
Навукова-метадл;
«Национальны исты
Алгебра : учеб, пособие для 9-го кл. учрежде-
А34 ний, обеспечивающих получение общ. сред, об¬
разования, с рус. яз. обучения с 12-летним сро¬
ком обучения (базовый и повышенный уровни) /
Е. П. Кузнецова [и др.]; под ред. Л. Б. Шнепер-
I. асвета, 2006. —
; «Нацыяндг.ьны 1ь.стьттут укацьн»
j ф|л;ял N22
УДК 51(075.3=161.1)
ББК 22.1я721
ISBN 985-12-1461-2
© Оформление. УГ1 «Народная асве-
та», 2006

ОТ АВТОРОВ
В 9-м классе мы продолжим изучение алгебры. Здесь мы
познакомимся с понятием функции, научимся решать системы
уравнений с двумя неизвестными, подробно рассмотрим свой¬
ства квадратичной функции и особенности ее графика — па¬
раболы, разберемся с решением некоторых комбинаторных
задач.
Упражнения в этом учебном пособии нумеруются по гла¬
вам. Число перед точкой обозначает номер главы, число после
точки — номер упражнения в этой главе. Например, 3.14 —
это 14-е упражнение из 3-й главы. Аналогично нумеруются и
пункты теории. Пункт 2.4 обозначает 4-й пункт 2-й главы.
Как и в учебных пособиях «Математика, 7» и «Алгебра, 8»,
упражнения разделены натри группы. Задания, обозначенные
номерами с кружочками, например 1.12°, должен уметь ре¬
шать каждый, кто стремится знать алгебру хотя бы на 5—б
баллов. Все остальные задания предназначены для тех, кто же¬
лает углубить свои знания. Наиболее трудные задания отмече¬
ны номерами со звездочками, например 1.44*. Большинство
таких заданий помещено в сборнике задач, там же содержатся
и задания на повторение.
Теоретический материал, который выделен треугольника¬
ми ▲, предназначен тем, кто интересуется математикой и со¬
бирается изучать ее дальше.
Некоторые важные моменты в изложении теории отмечены
на полях восклицательным знаком
Весы
нарисованы там, где есть возможность сравни¬
вать варианты решения или доказательства.
Исторические сведения, которые встречаются в книге, от¬
мечены знаком
Квадрат с диагоналями И обозначает конец доказательства
теоремы.

От авторов
4
Пояснения к преобразованиям размещаются между двумя
вертикальными стрелками f ... f или I ... 1; направление
стрелок показывает, какое именно преобразование поясняется.
Материал на повторение отмечен специальным симво-
После каждого пункта теории помещены вопросы
под знаком

лава
Функции
О]
1.1.	Прямоугольная система координат
на плоскости
Положение точки на координатной прямой определяется ее
координатой. А как определить положение точки на плос¬
кости?
Для этого проведем две взаимно перпендикулярные прямые
(рис. 1). Точку пересечения этих прямых обозначим буквой О
и назовем началом координат. <hy точку возьмем за начало
отсчета на каждой из двух прямых и на каждой из них выберем
единицу длины и положительное направление.
Одну из прямых обозначим Ох и назовем осью абсцисс, дру¬
гую обозначим Оу и назовем осью ординат. Как правило, ось
абсцисс будем изображать горизонтальной прямой и направле¬
ние на ней выбирать слева направо, а ось ординат — верти¬
кальной прямой и направление на ней выбирать снизу вверх.
Итак, на каждой из осей Ох и Оу выбрано начало отсчета
(общая точка О), единица длины и положи¬
тельное направление, т. е. эти оси являются У 1
координатными прямыми. Их называют ося¬
ми координат. Говорят, что оси координат 1--
Ох и Оу образуют прямоугольную, или де¬
картову, систему координат на плоское- q *
ти, ее обозначают Оху. Плоскость, на кото¬
рой выбрана система координат, называется
координатной плоскостью.	рис. |

Функции
6
Система координат названа декартовой в честь вели¬
кого французского ученого Рене Декарта (1596—
1650). Метод координат был основным достижением
Декарта в математике. Он первым открыл, что «гео¬
метрические» кривые выражаются в прямоугольной
системе координат алгебраическими уравнениями.
Несмотря на то что система координат у Декарта была
несовершенной — в ней не рассматривались отрица¬
тельные числа,— труды Декарта оказывали огромное
влияние на развитие математики в течение почти
150 лет.
У
ъ
мг
м
1-
1
о
а	X
Рис. 2
Рассмотрим на координатной плоскости
некоторую точку М и опустим из нее перпен¬
дикуляры	и ММг на оси Ох и Оу
(рис. 2). Точки Мт и М2 — основания этих
перпендикуляров —■ называются проекция¬
ми точки М на оси координат.
Если точка М лежит на координатной
оси, то ее проекцией на эту ось является сама
точка М.
Точка Мг лежит на координатной прямой Ох, поэтому ей
соответствует определенное число а — ее координата на этой
прямой. Аналогично точке М2 соответствует определенное
число Ъ — ее координата на прямой Оу.
Рис. 3
Числа а и Ъ называются ко¬
ординатами точки М: число
а — абсциссой, а число b —
ординатой точки М.
То, что М — точка с коор¬
динатами а и Ъ, записывает¬
ся так: М(а; Ь). На первом
месте в скобках записывают
абсциссу, на втором — орди¬
нату. Например, на рисунке 3
изображены точки А(2; 3),
В(-2; 3), С(3; -2), Г>(-3; -2)
и Р(0; -2).

7 Прямоугольная система координат на плоскости
Заметим, что В(-2; 3) и С(3; —2) — различные точки.
В скобках стоят одни и те же числа -2 и 3, но в разном по¬
рядке; значит, в записи М(а; Ъ) имеют значение не только
числа а и Ь, но и порядок, в котором они записаны. Поэтому
пару (а; Ъ) называют упорядоченной.
Таким образом, каждой, точке М на координатной
плоскости соответствует упорядоченная пара чи¬
сел (а; Ь) — координаты этой точки.
Наоборот, каждой упорядоченной паре чисел (а; Ь)
соответствует определенная точка М на ко¬
ординатной плоскости — точка с координатами
(а-, Ь).
1.	Что такое координатная плоскость?
2.	На координатной плоскости отмечена точка М(а; Ь). Что назы¬
вается:
а) абсциссой точки М; б) ординатой точки М?
3.	Сравните с нулем координаты точки М(а; t>), лежащей:
а) на оси абсцисс; б) на оси ординат; в) на оси абсцисс и на оси
ординат; г) на оси абсцисс или на оси ординат.
Упражнения
1.1°. Найдите координаты отмеченных точек (рис. 4).
1)
.х
Рис. 4
1.2°. 1) Изобразите прямую, проходящую через точки АГ(О; 8)
и Р(~6; 8). Назовите ординату точки А(5; у), принадле¬
жащей прямой КР.
2)	Изобразите прямую, проходящую через точки
Л1(-3; 6) и Т(—3; 0). Назовите абсциссу точки В(х; -2),
принадлежащей прямой МТ.

8
1.3°. Начертите отрезок по координатам его концов:
2) С(0; -3) и .0(4; 2);
1) А(2; 7) и В(-6; 2);
3)	К(-6; 0) и Р(0; -2);	4) М(~2; -4) и Т(4; -3);
5) В(2; -1) и Х(-2; -4);	6) F(5; -3) и В(-5; 3).
1.4°. Начертите четырехугольник по координатам его вершин:
1)	А(-3; 0), В(—3; 6), С(0; 6), £>(0; 0);
2)	М(-1; -1), К(-1; 3); Р(5; 3), Т(5; -4).
1.5°. Начертите треугольник по координатам его вершин:
1)	А(3; 6), В(-5; -2), С(-1; 3);
2)	М(5; 4), Р(-6; 2), К(-3; -4).
1.6°. Отметьте на координатной плоскости точку, симметрич¬
ную данной точке относительно: а) оси Ох, б) оси Оу,
в) начала координат — и запишите ее координаты:
1) А(-5; -6);
3)	С(1; 7);
5)	Р(-4; 0);
2) В(-1; 6);
4)	В(3; -2);
6) Г(0; 5).
1.7.	На координатной плоскости расположены точки: А(2; 5),
В(-2; -5), Е(-2; 5), Р(3; -6), С(~3; 6), £>(2; -5), М(3; 6),
К(-3; -6). Не выполняя рисунка, найдите среди них
пары точек, симметричных относительно:
1) оси абсцисс; 2) оси ординат; 3) начала координат.
1.8.	Даны точки А(3; 2), В(4; -1), С(—1; -1), В(-2; 5).
1)	Найдите координаты проекций этих точек на оси Ох
и Оу, а также длины отрезков ОА, ОВ, ОС и OD.
2)	Начертите четырехугольник ABCD и симметричный
ему относительно оси Ох четырехугольник АДСрОр
3)	Начертите четырехугольник АзВзСгТ^, симметричный
четырехугольнику ABCD относительно оси Оу.
4)	Начертите четырехугольник А3В3С3В3, симметричный
четырехугольнику ABCD относительно начала коор¬
динат.
1.9.	Известны координаты трех вершин квадрата: А, В, С.
Найдите координаты четвертой вершины D, если:
1)	А(2; 0), В(0; -2), С(~2; 0);
2)	А(-1; 1), В(2; 1), С(-1; -2).

9	Координатные углы
1.2.	Координатные углы
Точка А (рис. 5) лежит на оси абсцисс. Ее координаты (3; 0).
Точка В(—4; 0) тоже лежит на оси абсцисс.
г Г’ ~
i	'	1
. -- -!	- ; ; 1- ! - 1
—
В
_ . i
д :	:
-6 _б	_з
' 1
I W 1 1	1	1 и
! 3 j 4 5	6 ,Х
.....	.	• -r -f
-	-	 L	'
... :
—
■ ■:

Рис
. 5
Мы видим, что если точка лежит на оси абсцисс, то
ее ордината равна нулю. И наоборот, если ордината
точки равна нулю, то точка лежит на оси абсцисс.
Точка С (рис. 6) лежит на оси ординат. Ее координаты (0; 3).
Точка D(Q; - 2) также лежит на оси ординат.
Мы видим, что если точка лежит на оси ординат,
то ее абсцисса равна нулю. И наоборот, если абсцисса
точки равна нулю, то точка лежит на оси ординат.
Начало координат — точка О имеет обе координаты, равные
нулю.
Оси координат образуют четыре прямых угла. Их называют
координатными углами.
Координатные углы нумеруют римскими цифрами I, II, III,
IV, как показано на рисунке 7, и называют первым, вторым,
третьим и четвертым координатными углами.

	!_°
Рассмотрим точки, не лежащие на осях координат.
Мы видим, что если точка М(а; Ъ) принадлежит I коорди¬
натному углу, то а > О, Ъ > 0 (рис. 8). И наоборот, если а О,
Ъ > 0, то точка М(а; Ъ) принадлежит I координатному углу.
: ,	У>.
ь
-h 11. ■
. а 1 о	х
Рис. 9
Если точка М(а; Ъ) принадлежит II координатному углу, то
а < О, Ь > О (рис. 9). И наоборот, если а < О, b > 0, то точка
М(а; Ъ) принадлежит II координатному углу.
Если точка М(а; Ъ) принадлежит III координатному углу,
то а < О, Ъ < 0. И наоборот, если а < 0, b < 0, то точка М(а; Ь)
принадлежит III координатному углу (рис. 10).
у.
■а \	.
-
- •; ж	°
I |	!^	!
U ■ 1.
ъ!
	Рис. ю
Если точка М(а; Ь) принадлежит IV координатному углу,
то а > 0, Ъ < 0. И наоборот, если а >0, Ъ < 0, то точка М(а; Ь)
принадлежит IV координатному углу (рис. 11).
Пример 1. Точка М(а; Ъ) не лежит на осях координат и
принадлежит III координатному углу. Какому координатному
углу принадлежат точки Мг(—а; Ъ), М2(а; —Ъ), М3(-а; ~Ь)?
Решение. Так как М(а; Ъ) принадлежит III координат¬
ному углу, то а < 0 и Ъ < 0, и, значит, Мх принадлежит IV ко¬
11
Координатные углы
ординатному углу, поскольку —а >0 и Ь i 0; М2 принадлежит
II координатному углу, поскольку а < 0 и > 0; М3 принадле¬
жит I координатному углу, поскольку ~а > 0 и —fe > 0.
Заметим, что точки М(а; Ь) и Му(~а; Ь) симметричны
относительно оси Оу; точки М(а; Ь) и М2(а; -Ь) сим¬
метричны относительно оси Ох; точки М(а; Ь) и
М3(—а; —Ь) симметричны относительно начала коор¬
динат — точки О.
▲ В самом деле, точки М
и Му лежат на прямой ММ у,
перпендикулярной оси Оу (по¬
чему?), причем расстояния от
М и Му до оси Оу равны
(рис. 12):
МК = МуК=\а\ = -а.
Аналогично доказывается,
что М и М2 симметричны от¬
носительно оси Ох (сделайте
это самостоятельно).
Для доказательства симметричности точек М и М3 относи¬
тельно начала координат надо доказать, что точки М, О и М3
лежат на одной прямой (т. е. АМОМ3 = 180°) и МО = ОМ3. Сде¬
лайте это, рассмотрев треугольники МОК и М3ОР (см.
рис. 12). ▲
Пример 2. Какую фигуру образуют на координатной
плоскости точки, абсциссы
которых удовлетворяют усло¬
вию:
а)	х < 3 или х > 6;
б)	1<х<2,5?
Решение, а) Условию
х < 3 или х > 6 соответству¬
ют точки двух полуплоско¬
стей, выделенных на рисун¬
ке 13 голубым цветом.

Функции	12
б) Условию 1 < х < 2,5 соответствует полоса между двумя
параллельными прямыми, выделенная голубым цветом на ри¬
сунке 14.
образуют точки, ординаты которых удовлетворяют условию:
а)	у>-3;	б)-4<1/-<1?
Решение, а) Условию у>~3 соответствует полуплос¬
кость, выделенная на рисунке 15 голубым цветом.
б)	Условию — 4 < у < 1 соответствует полоса между двумя
параллельными прямыми, выделенная на рисунке 16 голубым
цветом.
; у
L 1 L i i ;	1 I
uxu
' H , i
i i 'г
! jo
J 111
*
i !
!	i	;	i	!	!
I i
! i ; ' i ; .
'	' i-З'
1
-... .... .
- - - - -* - -r -- ■
	i _
L..	-
i
Рис. 15
i
	i у
_ i _	, t	■ i
i 1.
I I	:	;
■ i
1 ! 1 1 ! 1
1 Io
’l
'”i1 |11?
■
i
!
. 1 ■
■+-H
--Ь
:-4
■ '
— —
• - - •	-t • - •	•;
Рис. 16
1.	Где расположены точки:
а)	ординаты которых равны нулю;
б)	абсциссы которых равны нулю?
2.	Что можно сказать о координатах точки, если известно, что она
лежит:
а) на оси Оу,
б) на оси Ох?

13
Координатные углы Ц
3.	Что можно сказать о координатах точки, если известно, что она
принадлежит:
а) I координатному углу;	б) II координатному углу;
в)	Ш координатному углу;	г) IV координатному углу?
4.	Укажите координаты точки, симметричной точке М(а; Ь) отно¬
сительно:
а) оси Ох;	б) оси Оу;	в) начала координат.
Упражнения
1.10°. Какому координатному углу принадлежит точка:
1)	А(0; -1);	2) С(4; 0);
3)	В(0; 6);	4) К(-5; 0);
5) £(0; 0);	6) М(-2; 2);
7)	Р(2; 2);	8) Т(-3; -5);
9) В(-4; -4);	10) Е(4; -2)?
1.1Г. Начертите ломануюABCDE, если А(0; 0), В(1; 2), С(2; 0),
D(3; 2), Е(4; 0).
Какому координатному углу принадлежит эта ло¬
маная?
Как следует изменить знаки координат точек, чтобы ло¬
маная ABCDE разместилась:
1)	во II координатном угле;
2)	в III координатном угле;
3)	в IV координатном угле?
1.12°. Какому координатному углу принадлежит точка, если:
1)	абсцисса ее положительна, а ордината — отрица¬
тельна;
2)	и абсцисса, и ордината — отрицательны;
3)	ее абсцисса и ордината — противоположные числа;
4)	абсцисса равна 0, а ордината — отрицательна;
5)	абсцисса отрицательна, а ордината равна 0;
6)	и абсцисса, и ордината равны 0?
1.13°. Где на координатной плоскости лежат точки:
1)	абсциссы которых равны 4;
2)	ординаты которых равны -6?

Функции
14
1.14°. Сравните с нулем координаты точки М(х; у), если она
расположена:
1)	на оси Ох;
2)	на оси Оу;
3)	в I или II координатном угле;
4)	во II или III координатном угле;
5)	в III или IV координатном угле;
6)	в I или IV координатном угле.
115 Дана точка К(п; т). Сравните числа типе нулем и меж¬
ду собой, если точка К расположена на биссектрисе:
1)	I координатного угла;
2)	II координатного угла;
3)	III координатного угла,
4)	IV координатного утла.
1.16.	В каких координатных углах мемет находиться точка
Т(а; Ь), если:
1) а > 0;	2) а < 0;	3) b > 0;	4) b < 0?
1.17.	Какую фигуру образуют на координатной плоскости точ¬
ки, абсциссы которых удовлетворяют условию:
1)2<х<3;	2)~3<х<0;
3)х>- 4;	4)х<1;
5)	х < -1 или х > 5;	6) х < -2 или х > 4?
1.18.	Какую фигуру образуют на координатной плоскости точ¬
ки, ординаты которых удовлетворяют условию:
1)-6<г/^-3;	2)3^ у < 5;
3) у >2;	4)г/<-2;
5) у < -1 или у > 3;	6) у < -3 или у > 2?
1.19.	Какому условию удовлетворяют координаты точек ча¬
стей плоскости, выделенных на рисунке 17 голубым
цветом?
1.20.	Отметьте на координатной плоскости множество точек,
абсциссы которых удовлетворяют неравенству:
1)|х|<1;	2)|х|>3.
1.21.	Отметьте на координатной плоскости множество точек,
ординаты которых удовлетворяют неравенству:
1) \у\>2;	2)|у|<4.

15
Функция К
1) -
3d
2)
’1
yi
■З)
У1
.... .. ... -,
■ ’	I	i
1-
-1-
—
- 1-
J J
!
О
1
■ X'
'о
I I
1
х;
i 1 i — i
’ 1 'о
Il	’ X.
. J	„ -.
4)	/ У
l .	-5)i :	,y:
6)	. У.
4-i- •- -i - f
1
—i—1-
- 1	x - . i i
—
1 1 !o
—f	1

.. 1 .. x.’
- -I
Q
—
1
—
		„„ !
t -
l	p ■
i
■ i • • •	4
Рис. 17
1.3.	Функция
Рассмотрим сначала три примера.
Пример 1. Решим простую задачу.
Автомобиль едет из города А в город В, расстояние между
которыми 400 км, с постоянной скоростью 80 км/ч. На каком
расстоянии s км от города В будет автомобиль через t ч?
Решение. 3at4 автомобиль пройдет 80t км. Поэтому
s = 400 — 80t,
где множество значений, которые может принимать перемен¬
ная t,— это все числа от 0 до 5, т. е. промежуток [0; 5].
В этой формуле выражена зависимость между переменны¬
ми s и f. В ней указан закон, по которому каждому значению
t из промежутка [0; 5] ставится в соответствие одно определен¬
ное значение s.
Например, если t = 2, то s = 400 - 80 • 2 = 240.
Если t = 3,5, то s — 400 - 80 • 3,5 = 120.
Пр и м е р 2. Напомним теперь известную геометрическую
формулу. Пусть а — длина ребра куба, V— объем этого куба.
Тогда	у=
где множество значений, которые может принимать перемен¬
ная а,— это все положительные числа, т. е- промежуток
(0;+оо).
В этой формуле выражена зависимость между переменны¬
ми а и V. В ней указан закон, по которому каждому значению
а из промежутка (0; + °°) ставится в соответствие одно опреде¬
ленное значение V.
Пример 3. Известно, что число у на 5,7 больше утроен¬
ного числа х. Как найти число у, зная х?
Понятно, что число у находится по формуле
У = Зх + 5,7,
где множество значений, которые может принимать перемен¬
ная х,— это все действительные числа.
В этой формуле указан закон, по которому каждому дей¬
ствительному значению х ставится в соответствие одно опре¬
деленное значение у.
Таким образом, в каждом из рассмотренных примеров ука¬
зан закон, по которому каждому числу из некоторого множе¬
ства ставится в соответствие одно определенное число.
Определение. Закон (правило), по которому каждо¬
му значению х из множества чисел D ставится в соответ¬
ствие одно определенное значение у, называется функци¬
ей, заданной на множестве D.
При этом х называют независимой переменной или аргу¬
ментом, у — зависимой переменной или функцией от х, а
множество D — областью определения функции.
Разумеется, вместо букв х, у, D можно было употребить и
другие буквы.
Слово «функция» происходит от латинского functio,
что означает «совершение», «выполнение».
В математике термин «функция от х» первыми стали
употреблять ученые Готфрид Лейбниц (1646—1716) и
Иоганн Бернулли (1667—1748).
3 х
Пример 4. Дана функция у - с областью опре¬
деления D = (-оо; 0). Найти значения этой функции при х, рав¬
ном -5; -4; -3; —2; —1.

17
Функция
Решение. Пусть х1 = ~5; х2 — — 4, х3 — — 3, х4 — — 2;
r5 = —1. Соответствующие значения функций у обозначим yv
у2, Уз> У^ Уз- Тогда
■ ■ _3 -(■ 5)_ 8	3 .	_3 + 4 _ 7 _	, 3 .
5/1	5	_5 х 5 ’	&2	_4	_4 х 4 ’
г/з=1_3 = _2; у4 = 3_2 = _ 25; у5 = Ц1=-4.
Ответ:	~1у; ~2; -2,5; -4.
Пример 5. Дана функция у = —g— с областью опре¬
деления D = [1; 3]. Сравнить значения функции при х4 = 2 и
х2 — 3.
Решение. Соответствующие х4 и х2 значения функции у
обозначим уг и у2.
При хг = 2 соответствующее значение функции у равно
_-7 • 2 + 3 _ -14 + 3 _-11
2 2 2
При х2 = 3
_-7 • 3 + 3 _3(- 7 + 1) _3(-6) _
»2 г	2	2
Так как -5,5 > -9, то ух > у2.
Ответ: yY > у2.
л
Заметим, что в этой главе хх и yY(x2 и у2, х3иу3и т. д.)
будем обычно обозначать соответствующие значе¬
ния аргумента х и функции у. Аналогичные записи
употребляются и тогда, когда аргумент и функция вы¬
ражены другими-буквами.	;

f Нчукова-псдагапчная б1бл1ятэка
3.
1.	Сформулируйте	Установь1
2.	Назовите незави	i аждой из
мерах 1—3.
4. Назовите какие-нибудь пары соответствующих значений аргу¬
мента и функции в каждом,.из примеров 1—3.

18
Функции
У пражнения
1.22°. Дана функция у = с областью определения D =
= (—оо; 4), Найдите значения функции у при х, равном:
1)	-3; -f; 0;	; 1; 3; 4;
2)	—4; -1; f; 2; 3,9; 5.
1.23°. Найдите значение функции у — (х - 2)х с областью опре¬
деления В = N при:
1)х = 4;	2)х = 3.
1.24. Найдите значение функции у = х(5~х) с областью
определения В = Z при:
1)х = -5;	2)х = -1.
1.25°. Дана функция у = — 2х + 3 с областью определения D-R.
Сравните значения функции при:
1)х = 5их = 4;	2)х = -3их = 1;
3)	х = -|их = |;	4)х = —-|-их=-|-.
1.26.	Дана функция у = 4х — 1 с областью определения
В = [“10; 10]. Сравните значения этой функции при:
1)х = ~4их-—7;	2)х = 5их = 6;
3)х = -6их = 9;	4)х = -6их = —5.
1.27.	Дана функция у = хг с областью определения В = [—5; 5].
Найдите значения функции при х, равном:
1) -3;	2) 4;	3) 2;	4) -6;	5) 7;	6) 5.
1.28.	Дана функция	с областью определения В =
= (—1; +°о). Сравните значения функции при х, равных:
“Y и Т;	2)“уи-д-;
3) у и 3;	4) { и 4.

19	Функция
1.29.	Дана функция у = 6 + -i х с областью определения D- R.
Известно, что у принимает значения: 0; 3; —6; —9. Най¬
дите соответствующие значения аргумента х.
1.30.	Дана функция у с областью определения D-R. При
каком значении х значение функции у равно р, если:
1)	у = 2х — 4, р = 6;
2)	г/ = ~Зх + 4, р = 4;
3)	у = (2х-5)-|, р = 12;
4)	у = |(7-6х), р = -4?
1.31°. Сумма двух чисел равна 82. Одно из них равно х. Как
зависит значение второго числа у от первого? Является
ли эта зависимость функцией? Если да, то укажите об¬
ласть определения функции.
1.32°. Разность двух чисел равна 20. Вычитаемое равно х. Как
зависит уменьшаемое у от вычитаемого? Является ли эта
зависимость функцией? Если да, то укажите область оп¬
ределения функции.
1.33°. Забором длиной 80 м нужно огородить прямоугольную
площадку. Ширина площадки равна х. Как зависит дли¬
на площадки у от ширины? Является ли эта зависимость
функцией? Если да, то укажите область определения
этой функции, зная, что х — натуральное число.
1.34.	Одна сторона прямоугольника равна х см, а другая — на
2 см меньше.
1)	Найдите периметр у прямоугольника.
2)	Является ли у функцией от х?
3)	Укажите область определения D функции у.
4)	Найдите значения у, соответствующие значению х,
равному 5 см, 10 см, 14 см, 16 см.
1.35.	Сторона квадрата равна х см.
1)	Найдите площадь у этого квадрата.
2)	Является ли у функцией от х?
3)	Укажите область определения D функции у.
4)	Найдите значения у, соответствующие значению х,
равному 11 см, 15 см, 17 см, 21 см.

Функции
20
Укажите множество значений переменной х, при ко¬
торых выражение имеет смысл (т. е. естественную об¬
ласть определения выражения) (1.36—1.37).
1.36. 1) 2х+ 1;
оч	? •
Зх-6 ’
51	4	•
’ х(х-2) ’
7'1	■
' (2х-1)(х 8) ’
2) Зх - 2;
4)
5х- 1 .
4х + 16 ’
6) (х-З)х’
о\ 	Зх • 7

' (5х-6)(2х 10) ’
1.37. 1) л/Зх7^;
3) >/4-0,5х;
5)	7(х-б)2;
7) д/х2+7;
9)
2)	\/2х + 5;
4)	\/0,1 —8х;
6)	v(9 + хТ2;
8) д/(х - 112 + 12;
10) V2 ~ I х |.
1.4.	Задание функции формулой
Задать функцию — это значит указать ее область
определения D и закон (правило), по которому для
каждого значения аргумента х из множества D оп¬
ределяется одно значение функции у.
В алгебре основным способом задания функции явля¬
ется формула, левая часть которой — зависимая пе¬
ременная, а правая — выражение с независимой пере¬
менной. Во всех примерах предыдущего пункта функ¬
ция задавалась формулой.
Рассмотрим пример. Пусть функция задана на множестве
всех неотрицательных чисел, т. е. на промежутке [0; + оо),
формулой у — \х. Здесь область определения функции совпа¬
дает с естественной областью определения выражения у[х.
Когда функция задана формулой, то правая часть этой
формулы есть выражение с независимой переменной.
Если область определения функции совпадает с ес¬
тественной областью определения этого выражения,
то ее обычно не указывают.

21
Задание функции формулой
Например, когда мы говорим «функция у-\[х», это озна¬
чает, что указанной формулой задается функция на промежут¬
ке [0; +оо).
К
Еще один пример. Когда мы говорим «функция у = —— »,
х 4
это означает, что функция рассматривается на естественной об¬
ласти определения выражения , т. е. на множестве всех
х 4
чисел, кроме х = — 2 и х = 2 (эту область определения можно
записать так:	— 2) и (—2; 2) и (2; +°°)).
Выражать зависимость между переменными посред¬
ством формулы впервые стали Пьер Ферма и Рене Де¬
карт около 1637 г. А термин «функция» появился
только через 55 лет в 1692 г. в публикациях Готфрида
Лейбница.
1.	Что значит задать функцию?
2.	Почему в примере 2 из п. 1.3 областью определения функции
является промежуток (0; +°°), а в примере 3 — все дей¬
ствительные числа?
Упражнения
1.38°. Функция задана формулой у = х2 — 4. Укажите ее область
определения. Верно ли, что:
1)	у = 0 при х = —2;	2) у = 21 при х = -5;
3)	у = 30 при х = 6;	4) у - 4 при х = 0?
х3 3
1.39°. Функция задана формулой у = —g— . Укажите ее область
определения. Верно ли, что:
з
1) если х = 0, то у = - у ;	2) если х = —1, то у = ~2;
3) если х = 3, то у = 12;	4) если х = 2, то у = 2,5?
2х 3
1.40. Функция задана формулой у =	• Укажите ее область
определения. Найдите ее значение при:
1) х = — 1;	2)х = 2;	3)х = 3;	4)х = 0;
5)	х = а;	6) x = 3k;	7) х = — р;	8) х = ~2Ь.

^М^ФуНК^И	;	2
1.41°. Найдите значение х, при котором равны значения
функций:
1)	у = - Зх + 4 и у - 5х - 12;
2)	у = 4х — 7 и у = — 2х + 5;
3)	у — Зх2 — 5х + 6 и у = —4х + 5 + Зх2;
4)	у = 2 - 4х - Зх2 и у = 2х - Зх2 - 5.
1.42.	Функция задана формулой у = gx;g. Укажите ее область
определения. При каком значении аргумента значение
функции равно:
1)	-1;	2) 2;	3) 3;	4) 0;
5)	а;	6) 3k;	7) -р;	8) ~2Ь?
1.43.	При каком значении аргумента значение функции
У = Равно: 1) 2; 2) 0; 3) 0,5; 4) | ?
Укажите область определения этой функции.
1.44*. Функция задана формулой у = х2 на множестве D -
— [2; 10]. Сравните сумму значений функции при х = а
и х = Ьсо значением этой функции при х = а + b (аиЬ —
числа из D).
1.45.	Функция задана формулой у = -Зх + 5. Найдите все
значения х, при которых: 1) у < 0; 2) у > 0.
1.46.	Функция задана формулой у = (3 - \'Ю) (2х - 7). Найдите
все значения х, при которых значение функции неотри¬
цательно.
1.47.	Функция задана формулой у = (1~ у2) (4 - 5х). Найдите
все значения х, при которых значение функции отри¬
цательно.
Функция задана формулой. Укажите ее область определения.
(1.48—1.50).
1.48.
1)
ух + 6
(Х-1/-4
2)
<х-3
25- (х -3)'
3)1/ =
у2х-1
36 18х + 9х2 ’
х 4х - 39
49 - 28х + 4х2 ’
У =
9
У =

Задание функции таблицей Ц
23
1.49. 1)
2)
3)
4)
5)
4
г/ = ^т;
Vх
6)
_	2х-1
у	—тт
\(Х- 5)
1.50. 1)
3)
4)у=	/О-»'
8х214х-15
1.5.	Задание функции таблицей
Формула — это не единственный способ задания функции.
В этом пункте и в п. 1.7 мы познакомимся с двумя другими
способами.
Во многих случаях функция задается таблицей. Например,
в справочной литературе по закаливанию приводятся в виде
таблиц рекомендации по дозированию длительности первого
купания при разной температуре воды.
Обозначим температуру воды в водоеме, выраженную в
градусах по Цельсию, буквой t, а рекомендуемую врачами
длительность первого купания, выраженную в минутах,—
буквой q.
В таблице показана зависимость длительности купания q
от температуры воды t.
t.’C
12
13
14
15
16
17
18
19
20
21
22
23
24
Q, МИН
0,3
0,3
0,4
0,4
0,4
0,5
0,5
0,5
0,5
1
1
1
1,5
В этой таблице каждому значению t поставлено в соответ¬
ствие определенное значение q. Таким образом, таблицей зада¬
ется функция q от t.
Область определения этой функции образуют числа, стоя¬
щие в первой строке таблицы. А числа, стоящие во второй стро¬
ке,— те значения, которые может принимать функция

фу™ции
Определение. Множество всех значений, которые
может принимать функция, называется множеством, зна¬
чений функции.
В рассмотренном примере множество значений функции со¬
стоит из пяти чисел: 0,3; 0,4; 0,5; 1; 1,5.
Определение. Наименьшее число из множества зна¬
чений функции называется наименьшим значением фун¬
кции, а наибольшее число из этого множества — наиболь¬
шим значением функции.
В рассмотренном примере наименьшее значение функции
равно 0,3, функция принимает его в точках 12 и 13; наиболь¬
шее значение функции равно 1,5, функция принимает его в
точке 24.
Рассмотрим теперь таблицу из книги по географии.
Обозначим географическую широту точки земного шара,
выраженную в градусах, буквой Л, а длину дуги параллели на
этой широте, соответствующую одному градусу и выраженную
в километрах,— буквой I.
В таблице показана зависимость длины дуги параллели от
географической широты.
h,°
0
экватор
10
20
30
40
50
60
70
1, км
111,3
109,6
104,7
96,5
85,4
71,7
55,8
38,2
В этой таблице каждому значению h поставлено в соответ¬
ствие определенное значение I. Поэтому этой таблицей задана
функция I от h.
Область определения этой функции образуют числа, стоя¬
щие в первой строке таблицы. А во второй строке стоят все те
значения, которые может принимать функция. Они образуют
множество значений функции.
Наименьшее значение функции равно 38,2, она принимает
его в точке 70; наибольшее значение функции равно 111,3, она
принимает его в точке 0.

25
Задание функции таблицей
Покажем, как найти множество значений функции, задан
ной формулой.
Рассмотрим функцию
s = 400 - 801
из примера 1 п. 1.3. Область определения функции в этом
примере — промежуток [0; 5]. Заметим, что когда значение
аргумента t увеличивается от 0 до 5, то значения функции s
уменьшаются от 400 до 0. Таким образом, функция s может
принимать любое значение из промежутка [О; 400], т. е. этот
промежуток является множеством ее значений.
Ясно, что наименьшее значение s = 0 функция принимает
в точке t = 5, а наибольшее значение s = 400 функция прини¬
мает в точке t = 0.
1.	Приведите пример функции, заданной таблицей.
Назовите для нее:
а) область определения; б) множество значений; в) наимень¬
шее значение; г) наибольшее значение.
2.	Что называется множеством значений функции?
3.	Что называется наименьшим значением функции?
4.	Что называется наибольшим значением функции?
Упражнения
1.51°. Песок, нагретый до температуры 150 °C, остывал на воз¬
духе. Каждые 10 мин производился замер температуры
и данные заносились в таблицу.
t, мин
0
10
20
30
40
50
60
70
Т, °C
150
111
84
66
52
42
35
20
По таблице найдите:
1)	какую температуру имел песок через 10 мин, 30 мин,
40 мин, 60 мин после начала опыта;
2)	через сколько минут после начала опыта песок имел
температуру 111 °C, 66 °C, 52 °C, 35 °C;
3)	область определения и множество значений функции
от t, заданной этой таблицей;
4)	наибольшее и наименьшее значения функции от t, за¬
данной этой таблицей.

26
ЕМВУфункци|
1.52°. Таблица выражает зависимость силы давления F чело¬
века на пол кабины лифта, движущегося вверх с уско¬
рением 1,0 м/с2, от массы человека т.
т, кг
70
60
50
40
F, Н
756
648
540
432
По таблице найдите:
1)	силу давления на пол движущейся вверх кабины лиф¬
та человека, масса которого 60 кг, 50 кг;
2)	массу человека, поднимающегося в лифте, если его
давление на пол равно 756 Н, 432 Н, 540 Н;
3)	область определения и множество значений функции,
заданной этой таблицей;
4)	наибольшее и наименьшее значения функции, задан¬
ной этой таблицей.
1.53.	Уровень воды в реке с 1 по 12 мая изменялся по сравне¬
нию с ординаром1 следующим образом:
Дата
1
2
3
4
5
6
7
8
9
10
11
12
Уровень
воды, см
20
23
27
31
36
42
40
37
34
30
25
19
По таблице найдите:
1)	какой уровень воды относительно ординара был 2 мая,
9 мая, 12 мая;
2)	какого числа уровень воды относительно ординара со¬
ставлял 27 см, 42 см, 37 см, 19 см;
3)	область определения и множество значений функции,
заданной этой таблицей;
4)	наибольшее и наименьшее значения функции, задан¬
ной этой таблицей.
1 Ординар (от лат. ordinarus — обычный) — средний многолетний уровень
воды в реках, заливах и т. п.

Г рафик функции
1.54.	Масса ребенка от рождения до 8 лет изменяется в зави¬
симости от возраста в среднем следующим образом:
Возраст, годы
0
1
2
3
4
5
6
7
8
Масса, кг
3,3
9,2
11,9
12,9
14,3
15,4
16,8
18,4
20,5
По таблице найдите:
1)	среднюю массу ребенка в возрасте: 3 лет, 5 лет, 7 лет;
2)	в каком возрасте масса ребенка равна примерно
11,9 кг, 16,8 кг, 20,5 кг;
3)	на сколько килограммов увеличилась масса ребенка:
а)	за первые три года;
б)	с трех до шести лет;
в)	с четырех до восьми лет;
г)	с шести до восьми лет;
4)	на сколько килограммов увеличилась масса ребенка
за первый, третий, пятый, седьмой, восьмой год;
5)	область определения и множество значений функции,
заданной этой таблицей;
6)	наибольшее и наименьшее значения функции, задан¬
ной этой таблицей.
1.6.	График функции
Пусть функция задана на промежутке [2; 6] формулой
Найдем ее значения при значениях аргумента 2, 3, 4, 5, 6
и результаты поместим в таблицу:
X
2
3
4
5
6
У
ц
3 —
3 3
4
4
4
Для каждой упорядоченной пары (г; у) из полученной
таблицы отметим точку (х; у) на координатной плоскости

	!»■
Oxy (рис. 18). Рисунок дает некоторое наглядное представ¬
ление о множестве точек плоскости, координатами которых
являются соответствующие значения аргумента и функции:
первая координата — значение аргумента, а вторая — соответ-,
ствующее ему значение функции.
Наше представление будет тем точнее, чем «гуще» мы будем
выбирать значения аргумента, а следовательно, и значения
функции (рис. 19). На этом рисунке значения аргумента вы¬
браны через каждые 0,25 единицы длины.
х ' 7
Итак, мы видим, что функции у — —— с областью
определения [2; 6] на координатной плоскости соответствует
некоторое множество точек. Это множество точек называется
графиком данной функции.
Определение. Графиком функции называется мно¬
жество точек М(х; у) на координатной плоскости, где х при¬
нимает значения из области определения, ay — соответ¬
ствующие им значения функции.
х + 7
Чтобы изобразить график функции у = —, заданной на
промежутке [2; 6], мы должны вычислить для каждого дей¬
ствительного числа х из этого промежутка соответствующее
значение у и полученные точки (х; у) отметить на координат¬
29	Г рафик функции
ной плоскости. Множество всех этих точек и есть график на
шей функции.
Поскольку это множество бесконечное, то осущест¬
вить все указанные вычисления невозможно. Поэтому
график функции у = можно изобразить только
приближенно, соединяя отмеченные на плоскости
точки непрерывной плавной кривой (рис. 20).
Но даже это приближенное изображение дает хорошее пред¬
ставление о функции. Глядя на него, сразу можно сказать, что
наименьшее значение функции равно 2	, она принимает его
в точке 6, т. е. при х = 6.
Наибольшее значение функции равно 4	, она принимает
его в точке 2, т. е. при х = 2.
Множеством значений функции является промежуток
j 2	; 4	|. Кроме этого, видно, что график функции лежит в
I координатном угле, он не пересекается с осями коор¬
динат.
О точке М(а; Ъ), принадлежащей графику функции
у =	, говорят еще, что ее координаты удовлетво-
_хИ
ряют уравнению у =	.

Например, этому уравнению удовлетворяют координаты то'
чек (2; 4|), (з; 3А), (4; 2	), (5; 2| ), (б; 2-1).
В рассмотренном примере показано, как на координатной
плоскости изображается график функции, заданной форму¬
лой. Из этого же примера понятно, как изобразить график фун¬
кции, заданной таблицей. Надо для каждой упорядоченной
пары (х; у) из этой таблицы отметить на координатной плос¬
кости точку (х; у).
Например, на рисунке 21 изображен график функции, за¬
данной таблицей:
Пример 1. Функция задана формулой р = х2 - 3 на про¬
межутке [-2; 1]. Изобразить ее график.
Решение. Придадим переменной х несколько значений
и найдем соответствующие значения переменной у (см. таб¬
лицу).
X
-2
-1,5
-1
-0,5
0
0,5
1
У
1
3
4
-2
-4
-3
_2 —
Z 4
-2

31
График функции
Отметим точки (х; у), заданные
таблицей, на координатной плос¬
кости и соединим их непрерывной
плавной линией. Полученная кри¬
вая дает представление о графике
функции, заданной формулой
у-х2 — 3 на промежутке [—2; 1]
(рис. 22). Говорят также, что гра¬
фик построен по точкам.
График этой функции содержит
бесконечно много точек. Отметить
их все на координатной плоско¬
сти невозможно; приходится огра¬
ничиться лишь несколькими из них.
Пример 2. Функция задана формулой у — на проме¬
жутке [2; + оо). Изобразить ее график.
Решение. Придадим переменной х несколько значений
и найдем соответствующие значения переменной у (см. таб¬
лицу).
X
2
3
4
5
6
7
8
9
10
У
4
3 —
3 3
2 —
3 4
24
О
2 —
3 6
2
Отметим точки (х; у), заданные таблицей, на координатной
плоскости и соединим их плавной непрерывной кривой
(рис. 23).
Рис. 23

Функции
32
Так как областью определения функции является луч,
а его нельзя уместить на листе бумаги, то и изображе¬
ние графика функции нельзя уместить на листе бума¬
ги. Поэтому изобразить можно только часть гра¬
фика.
Пример 3. Изобразить график функции у = х3 — 4.
Решение. Поскольку область определения функции не
указана, то по договоренности это естественная область опре¬
деления выражения х3 — 4, т. е. в данном случае вся число¬
вая прямая R.
Придадим переменной х несколько значений и найдем со¬
ответствующие значения у (см. таблицу).
X
-3
-2
-1
0
1
2
3
4
У
00
1
_5±
& 3
"4
-4
-4
_2JL
3
1
2
ft 2
6Т
У


С
—
-5-
■■
Г
1
—
—
--


/ •
“Т"
-
> _
ю
L
! У
3 4*
-2
-
-
1
!
i
Чз
!
!
Рис. 24
По этим точкам построим график
функции у = -^-х3- 4 (рис, 24).
Пример 4. Функция задана фор¬
мулой у = д/9 — х3 на множестве чисел
{—3; —2; —1; 0; 1}. Изобразить ее
график.
Решение. Поскольку область опре¬
деления функции состоит из пяти зна¬
чений переменной х, то график функ¬
ции состоит всего из пяти точек
(см. таблицу, где квадратные корни
вычислены с точностью до 10"1, и
рис. 25).
X
-з
-2
-1
0
1
У
6
4,1
3,2
3
2,8

33	Г рафик
Пример 5. Функция задана фор¬
мулой у = 2х на множестве Z. Изобра¬
зить график этой функции.
Решение. Придадим переменной
х несколько значений из области опре¬
деления и найдем соответствующие зна¬
чения переменной у (см. таблицу).
X
-2
-1
0
1
2
3
У
1
4
1
2
1
2
4
8
Отметим эти точки на координатной
плоскости (рис. 26).
Построенные точки есть часть гра¬
фика функции у = 2х, заданной на об¬
ласти определения Z.
Пример 6. Функция задана фор¬
мулой у - Зх(х + 2). Принадлежит ли
графику этой функции точка:	рис. 26
а)	А(0; 2);	В(-4; 24)?
Решение, а) Подставим х = 0 и у = 2 — координаты точ¬
ки А в формулу, которой задана функция:
2 = 3-0(0+ 2),
откуда получим 2 = 0 — неверное числовое равенство.
Следовательно, точка А не принадлежит графику данной
функции.
Ответ: точка А(0; 2) не принадлежит графику функции
у - Зх(х + 2).
Покажем, как можно записать решение в тетради на
примере б).
б)	При х = -4 и у = 24 получим 24 = 3(-4)(-4 + 2), т. е.
24 = -12(-2) — верное числовое равенство.

Ответ: точка В(-4; 24) принадлежит графику функции
у ~ Зх(х + 2).
1.	Что называется графиком функции?
2.	Что означает выражение: «Координаты точки Л1(а; Ь) удовлетворя¬
ют уравнению у = Зхг — 5»?
Упражнения
1.55°. Функция задана формулой у = 2х(х - 4). Принадлежит
ли графику функции точка:
1)	А(-6; 2);	2) В(0; 0);	3) С(2,5; 3);
4) П(4; 3,6);	5) М(4; 0);	6) К(6; 9)?
1.56°. Функция задана формулой у = \ х2 — 1 + 3. Принадлежит
ли графику функции точка:
1)	А«10; 6);	2) В(-<5; 1);	3) С(0; 2);
4) D(-l; 1);	5) М(1; 3);	6) tf(ll; 13)?
1.57°. Функция задана формулой у ~ на промежутке
[1; Ю].
1)	Заполните таблицу:
X
1
2
3
4
5
6
7
8
9
10
У
2)	Для каждой пары (х; у) из таблицы изобразите на ко¬
ординатной плоскости точку.
3)	Соедините отмеченные точки непрерывной кривой.
4)	Назовите множество значений функции по изображе¬
нию графика.
5)	Назовите наименьшее и наибольшее значения функ¬
ции.
х2 I 9
1.58°. Функция задана формулой у = —2~ на промежутке [2; 5].
1)	Заполните таблицу:
X
2
2,5
3
3,5
4
4,5
5
У

35
Г рафик функции
2)	Изобразите график функции, используя данные таб¬
лицы.
3)	Назовите множество значений функции; наимень¬
шее значение функции, наибольшее значение функ¬
ции.
4)	В каких координатных углах расположен график
функции?
X2 ' 6
1.59°. Функция задана формулой у =
на множестве N.
Изобразите ее график.
1.60.	Функция задана формулой на множестве D.
а)	Изобразите график функции.
б)	Назовите область определения и множество значений
функции.
в)	Назовите наименьшее и наибольшее значения функ¬
ции.
г)	В каких координатных углах расположен график
функции?
д)	Пересекает ли график функции оси координат? Если
да, то в каких точках?
Выполните задания а) — д), если:
1)	у = х2 — 2х, D = [2; 4];
2)	у = |х3-4, П = [-2; 2].
1.61.	Функция задана формулой у = на промежутке
[-1; 4].
1)	Изобразите график функции.
2)	Назовите множество значений функции.
3)	Назовите наименьшее и наибольшее значения функ¬
ции.
4)	В каких координатных углах расположен график
функции?
5)	Пересекает ли график функции оси координат? Если
да, то в каких точках?

1.62.	Функция задана формулой на множестве {4; 4,25; 5; 5,21;
8; 8,41}. Изобразите график функции, если:
1)	у = 2\х — 4 + 1;	2) у = 2х — 3;
3)	у = (2 \ х - 4)2;	4) у = 1 - хх~4.
1.63.	Функция задана формулой на множестве [—2; +°°). Изоб¬
разите график функции, если:
1) у = 2х2~3;	2)у = 2х~3;
3) i/ = vr2T7;	=
1.64.	На множестве Z задана функция формулой:
1) у = х3+ 1;	2) у = 3х + 1;
3) </ = у + 1;	4)у = Зх + 1.
Изобразите график функции.
1.65*. Изобразите график функции, заданной на множестве
[1; 5] формулой:
_2х-1
!) У х ’
2)У=2-^-,
04	-Х2-1
3> у-—’
1.66. Функция задана формулой у = 7 \5~х + а.
Определите значение а, если ее график проходит через
точку:
1) (1; 16);	2) (-4; -12);	3) (-4; 7);_
4)	(-20; 3);	5) (0; 3 v 5);	6) (2; -4 х 3).
1.7.	Задание функции графиком
Выясним, может ли линия L
на рисунке 27 быть изображени¬
ем графика некоторой функ¬
ции?
Мы видим, что есть такое
значение х, например х = 3, ко¬
торому на линии L соответству¬
ют две различные точки, а зна¬
чит, два различных значения у.

Задание функции графиком
Но по определению функции каждому значению аргумента
ставится в соответствие только одно значение функции. Зна¬
чит, линия L не является изображением графика функции.
Сформулируем основное свойство графика функции:
на графике функции нет двух различных точек с од¬
ной и той же абсциссой.
А Действительно, если точка Т(а; Ь) принадлежит графику
функции, то это значит, что значению аргумента а соответ¬
ствует значение функции Ь. Но значению аргумента а может
соответствовать только одно значение функции, поэтому
Т(а; Ь) — единственная точка с абсциссой а. к.
Основное свойство графика функции можно сформу¬
лировать так: прямая, параллельная оси ординат, пе¬
ресекает график функции не более чем в одной
точке.
Таким образом, различные
точки графика функции имеют
различные абсциссы. Когда
множество М точек на коорди¬
натной плоскости обладает
этим свойством, то его можно
рассматривать как график не¬
которой функции. Областью
определения этой функции яв¬
ляется множество абсцисс всех
точек из множества М, и каж¬
дой абсциссе х точки из множества М ставится в соответствие
ее ордината у, эта ордината единственная благодаря свойству,
которым обладает множество М (рис. 28).
На практике изучение зависимостей между различными ве¬
личинами часто приводит к рассмотрению таких функций, ко¬
торые заданы графиками. Обычно график изображается с
помощью самописца, установленного на соответствующем
приборе.
Пример 1. На рисунке 29 изображен график изменения
толщины слоя I выпавших дождевых осадков в зависимости

Функции
3J
Плювиограф
от времени t. Этот график вычерчен самописцем специального
прибора — плювиографа* (см. рис.) в Белорусском гидромет¬
центре.
По графику (см. рис. 29) видно, что дождь начался в 5 ч
20 мин и прекратился в 7 ч
10 мин. Чтобы определить по
графику, сколько миллимет¬
ров осадков выпало к 6 ч, надо
из точки с координатой 6 на
оси абсцисс (здесь это ось Ot)
провести перпендикуляр к оси
Ot до пересечения с графиком
в точке Р. Получили, что зна¬
чению времени t = 6 ч соответ¬
ствует слой осадков I = 1,6 мм.
Итак, каждому значению
переменной t, взятому на оси
Ot из некоторого промежутка,
можно с помощью этого гра¬
фика найти соответствующее
определенное значение пере¬
менной I на оси 01. Поэтому этот график задает функцию I от t.
При задании функции графиком ее значения вычисляются,
как правило, приближенно. Эти значения зависят от точности
приборов и инструментов, которые используются для изобра¬
жения графика и последующих измерений при его чтении. За¬
дание функции графиком дает наглядное представление о
свойствах функции.
* Название прибора «плювиограф» происходит от латинского слова
pluvia — дождь.

39
Задание функции графиком К
По графику (см. рис. 29) можно увидеть, что его область
определения — это промежуток [б ; 7 Другими словами,
область определения функции, заданной графически,— это
проекция графика на ось абсцисс Ot (в нашем примере — это
тот промежуток времени, когда шел дождь).
Множество значений функции I на этом графике образуют
числа из промежутка [0; 2,6]. Этот промежуток является про¬
екцией графика на ось ор¬
динат О1.
Пример 2. С помощью
самописца, установленного на
приборе для регистрации ко¬
лебаний атмосферного давле¬
ния — барографе* (см. рис.),
при исследованиях с исполь¬
зованием воздушного зонда
получен график (рис. 30) из¬
менения атмосферного давле¬
ния р (в атмосферах) в зависи¬
мости от высоты h (в километ¬
рах) над уровнем моря.
Барограф
* Название прибора «барограф» происходит от латинского слова bans —
тяжесть, давление.

Чтобы определить по этому графику, каково атмосферное
давление на высоте 14 км над уровнем моря, надо из точки с
координатой 14 на оси абсцисс (здесь это ось Oh) провести пер¬
пендикуляр к оси Oh до пересечения с графиком в точке К.
Затем из точки К провести прямую, параллельную оси Oh, до
пересечения с осью ординат, т. е. найти ординату точки К. По¬
лучили, что значению высоты Л = 14 км соответствует дав¬
ление р = 0,2 атм. Итак, каждому значению переменной Л, взя¬
тому на оси Oh, можно с помощью графика найти соответст¬
вующее определенное значение переменной р на оси Ор, т. е.
этот график задает функцию р от Л.
По этому графику видно, что наименьшее значение, которое
может принимать аргумент h,— это 0, а наибольшее значе¬
ние — 20. Таким образом, все значения, которые может при¬
нимать аргумент Л,— это промежуток [0; 20], т. е. проекция
графика на ось абсцисс. Множество значений функции р на
этом графике образуют числа из промежутка [0,1; 1], т. е. про¬
екцию графика на ось ординат Ор.
1.	Сформулируйте основное свойство графика функции.
2.	Где на практике приходится рассматривать функции, заданные
графиком? Приведите примеры.
3.	Приведите пример линии, которая не может быть графиком
функции.
У пражнения
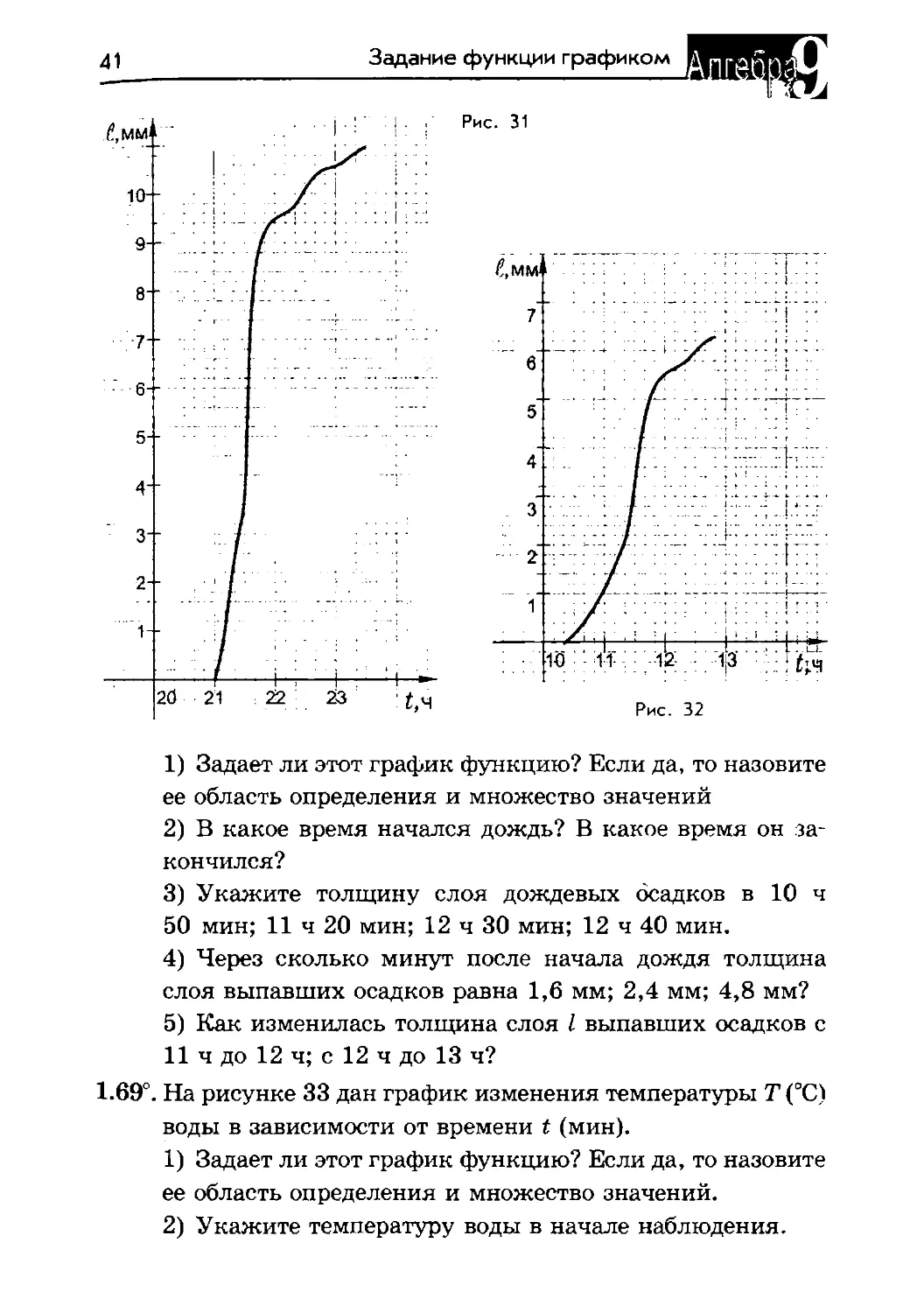
1.67°. На рисунке 31 дан график изменения толщины слоя
I (мм) выпавших дождевых осадков в зависимости от
времени t (ч).
1)	Задает ли этот график функцию? Если да, то назовите
ее область определения и множество значений.
2)	В какое время начался дождь? Когда он закончился?
3)	Укажите толщину слоя дождевых осадков в 21 ч
30 мин; 22 ч 10 мин; 22 ч 50 мин; 23 ч 30 мин.
4)	Через сколько минут после начала дождя толщина
слоя выпавших осадков равна 2 мм; 3 мм; 4,5 мм; 8 мм?
5)	Как изменилась толщина слоя I выпавших осадков за
первый час; за второй час?
1.68°. На рисунке 32 приведен график изменения слоя I (мм)
выпавших дождевых осадков в зависимости от времени
t (ч).

41
Задание функции графиком
1)	Задает ли этот график функцию? Если да, то назовите
ее область определения и множество значений
2)	В какое время начался дождь? В какое время он за¬
кончился?
3)	Укажите толщину слоя дождевых осадков в 10 ч
50 мин; 11 ч 20 мин; 12 ч 30 мин; 12 ч 40 мин.
4)	Через сколько минут после начала дождя толщина
слоя выпавших осадков равна 1,6 мм; 2,4 мм; 4,8 мм?
5)	Как изменилась толщина слоя I выпавших осадков с
11 ч до 12 ч; с 12 ч до 13 ч?
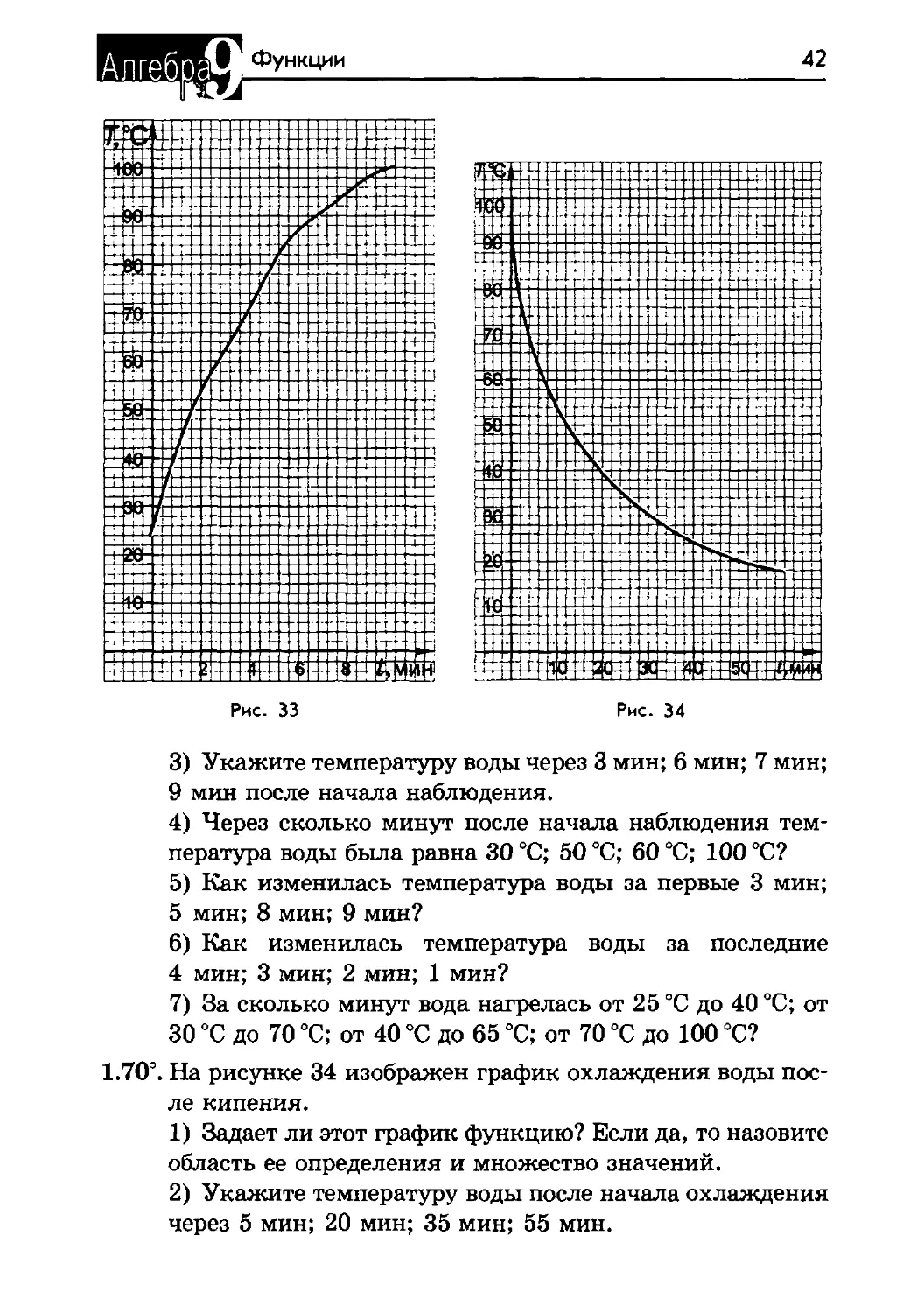
1.69°. На рисунке 33 дан график изменения температуры Т (°C)
воды в зависимости от времени t (мин).
1)	Задает ли этот график функцию? Если да, то назовите
ее область определения и множество значений.
2)	Укажите температуру воды в начале наблюдения.

Функции
42
Рис. 33
Рис. 34
3)	Укажите температуру воды через 3 мин; 6 мин; 7 мин;
9 мин после начала наблюдения.
4)	Через сколько минут после начала наблюдения тем¬
пература воды была равна 30 °C; 50 °C; 60 °C; 100 °C?
5)	Как изменилась температура воды за первые 3 мин;
5 мин; 8 мин; 9 мин?
6)	Как изменилась температура воды за последние
4 мин; 3 мин; 2 мин; 1 мин?
7)	За сколько минут вода нагрелась от 25 °C до 40 °C; от
30 °C до 70 °C; от 40 °C до 65 °C; от 70 °C до 100 °C?
1.70°. На рисунке 34 изображен график охлаждения воды пос¬
ле кипения.
1)	Задает ли этот график функцию? Если да, то назовите
область ее определения и множество значений.
2)	Укажите температуру воды после начала охлаждения
через 5 мин; 20 мин; 35 мин; 55 мин.

43
Задание функции графиком
3)	Через сколько минут после начала охлаждения тем¬
пература воды была равна 70 °C; 40 °C; 35 °C; 20 °C?
4)	На сколько градусов остыла вода за первые 10 мин;
20 мин; 30 мин; 45 мин?
5)	За сколько минут вода охладилась от 100 °C до 40 °C;
от 90 °C до 45 °C; от 80 °C до 35 °C; от 50 °C до 20 °C?
1.71.	Используя изображение графика функции (рис. 35), за¬
полните таблицу, перечертив ее в тетрадь:
X
- 2,5
-0,5
0
2
3
5
8
9,5
У
1)	Назовите область определения и множество значений
функции.
2)	Назовите наименьшее и наибольшее значения функ¬
ции.
1.72.	Используя изображение графика функции (рис. 36), за¬
полните таблицу, перечертив ее в тетрадь:
X
-з
-2
3,5
4
5
6,5
8
9
У
-2
1

44
1)	Назовите область определения и множество значений
функции.
2)	Назовите наименьшее и наибольшее значения
функции.
1.8.	Нули функции и промежутки
знакопостоянства
На рисунке 37 изображен график функции у = х2 — 4 с
областью определения — промежутком [—3; 1]. Этот гра¬
фик пересекается с осью абсцисс в точке с координатами
(-2; 0), т. е. при х = ~2 функция принимает значение
У = 0.
Определение. Значения аргумен¬
та, при которых функция принимает
значение, равное 0, называются нулями
функции.
Так, функция у = х2 - 4 с областью
определения D = [-3; 1] имеет единственный
нуль — число —2 (см. рис. 37).
А функция у = х2 - 4 с областью опре¬
деления D = [-3; 4] имеет два нуля — числа
—2 и 2 (поясните почему).

45
Нули функции и промежутки знакопостоянства
Пример 1. Найти нули функции, заданной формулой
у = х3 — 9х на множестве D, если:
а)	= (-оо; 1]; б) D = [-2; + оо); в) D = R- г) D = (-4; 0);
д) П = (3; 20].
Решение, а) Подставим у = 0 в формулу и найдем корни
полученного уравнения:
х3 - 9х = 0;
х(х2 - 9) = 0;
х(х - 3)(х + 3) = 0;
х = 0 или х — 3 = 0 или х + 3 = 0;
х = 0 или х = 3 или х — -3.
Из этих трех чисел промежутку (—1] принадлежат
только х = —3 и х = 0,— они и будут нулями функции
у = х3 — 9х, заданной на этом промежутке.
б)	Поскольку из трех найденных чисел промежутку
[-2; + оо) принадлежат только х = 0 и х = 3, то они и бу¬
дут нулями функции у = х3 — 9х, заданной на промежутке
D = [~2; + °о).
в)	Нулями рассматриваемой функции являются числа -3;
0; 3 (поясните почему).
г)	Рассматриваемая функция имеет единственный нуль —
это число -3 (поясните почему).
д)	Рассматриваемая функция нулей не имеет (поясните
почему).
Пример 2. Функция задана графиком на промежутке
D - [-7; 2] (рис. 38). Указать нули этой функции.
Рис. 38

46
Решение. Данная функция принимает значения, равные
нулю, в тех точках, где ее график пересекается с осью Ох.
Поскольку у = 0 при х, равном —6; —4,5; -3; —1 и 1,5, то числа
-6; -4,5; —3; —1 и 1,5 являются нулями данной функции.
Пример 3. Найти нули функции, заданной таблицей:
X
-9
-8
-7
-6
-5
—4
-3
-2
-1
0
1
2
3
4
5
У
2
0
0
1,3
1,7
3
5
2
1
-3
-2
0
1
3
2
Решение. Поскольку у - 0 при значениях х, равных —8;
-7 и 2, то числа -8; -7; 2 — нули данной функции.
Рассмотрим функцию, график которой изображен на рисун¬
ке 38. Мы видим, что на промежутке [-7; —6) значения этой
функции — только положительные числа; то же самое и на
промежутках (-4,5; -3) и (-1; 1,5). А на промежутках
(-6; -4,5), (-3; -1) и (1,5; 2] значения функции — только
отрицательные числа.
Такие промежутки значений аргумента, на которых значе¬
ния функции либо только положительные, либо только отри¬
цательные, называются промежутками знакопостоянства
функции.
1.	Что называется нулем функции?
2.	Какие промежутки называются промежутками знакопостоян¬
ства функции?
Упражнения
1.73°. Найдите нули функции, заданной формулой:
1)	у = Зх - 4;
2)	у = 5 - 2х;
3)	у = 9 — 4х на множестве D = N;
4)	у = 7 + Зх на множестве D — Z;
5)	у = —g на множестве D = [3; +°°);
6)	У = ~| на множестве D = (3; + °°);
х1 2 + 7х
7)	у = х+2 на множестве D = (-°°; -2);

Al
Нули функции и промежутки знакопостоянства
х* — 8х
8)	у = х 5 на множестве D = (5; +°°);
9) у =
хг-х~12
х-4
1.74°. На рисунке 39 функция задана графиком на промежут¬
ке D = [~4; 6], а на рисунке 40 — на промежутке
Л = [-6; 4,5]. Укажите для них:
1)	нули функции; 2) промежутки знакопостоянства.
1.75. Найдите нули функции, заданной таблицей:
X
-5
-4
-3
-2
-1
0
У
9
0
4
0
1,2
0
X
—2
-1
0
1
2
3
У
-3
-1.5
0
2
1
0
2)

1.76. Функция задана графиком, изображенным на’
1) рис. 22;	2) рис. 24;	3) рис 35;
4) рис. 36;	5) рис. 43, 1); 6) рис. 43, 2),
Назовите для этой функции:
а)	область определения;
б)	наименьшее и наибольшее значения;
в)	нули функции;
г)	промежутки знакопостоянства;
д)	множество значений.
1.9.	Возрастание и убывание функции
на промежутке
На рисунке 41 изображен график
функции, заданной формулой
у = ^^2 на промежутке [-1; 3].
Представим себе, что некоторая
точка М движется по графику так,
что ее абсцисса увеличивается, т. е.
движется слева направо. По рисунку
видно, что ординаты при таком дви¬
жении точки М будут увеличиваться,
т. е. точка М будет как бы «взбирать¬
ся» вверх по графику. Другими сло¬
вами, при увеличении значения аргу¬
мента х значение функции у увеличи¬
вается. Такую функцию называют
возрастающей,
Определение. Функция называется.возрастающей
на некотором промежутке, если большему значению
аргумента из этого промежутка соответствует большее
значение функции, т. е. для любых х, и х2, принадлежащих
промежутку, из того, что х2 > xv следует у2 > yv
На рисунке 42 изображен график функции, заданной фор¬
мулой у = у (х - З)2 на промежутке [0; 3].

49 Возрастание и убывание функции на промежутке
Представим теперь, что некоторая
точка М движется по данному гра¬
фику так, что ее абсцисса уве¬
личивается, т. е. движется слева на¬
право. По рисунку легко увидеть, что
ординаты при таком движении точки
будут уменьшаться; точка М будет
как бы «скатываться» по графику
вниз. Другими словами, при увеличе¬
нии значения аргумента х значе¬
ние функции у уменьшается. Такую
функцию называют убывающей.
Определение. Функция называется убывающей на
некотором промежутке, если большему значению аргу¬
мента из этого промежутка соответствует меньшее значе¬
ние функции, т. е. для любых и xv принадлежащих
промежутку, из того, что х2 > следует у2 < yv
▲ Когда функция задана формулой, то, чтобы выяснить,
является она возрастающей или убывающей на области опре¬
деления, не обязательно изображать ее график. Как это можно
сделать иначе, покажем на следующих примерах.
Пр и мер 1. Пусть функция задана на промежутке [—1; 3]
4х 1
формулой у = х 2 • Является ли эта функция возрастающей
(убывающей) на этом промежутке?
Решение. Пусть хг и х2 принадлежат промежутку [-1; 3]
и = t*1 2 *'- 2* ’ У2 =	• ЕСЛИ То ПОЛУ4™
Уг У1
4х2~1
х2 + 2
4х,-1
х, н 2
4х,х2
х, 8х2 - 2 ■ 4х^2 + х2 - 8xj + 2
(х1 + 2)(хг + 2)
9(х2- х,)
(X! + 2)(хг + 2)
Действительно, так как х2 > хр то х2 — хг > 0. Для любого
значения х из промежутка [—1; 3] сумма х + 2 > 0, значит,
2 >0 и г2 + 2 >0. Поэтому разность
_	_	9(х2 xt)
У2 У' (хг. 2)(х2-. 2)
положительное число. Следовательно, у2 > уг.

50
Функции
Таким образом, мы доказали, что если х2 > хр то у2 > Уц а
это значит, что функция у = х + 2 на промежутке [-1; 3] возра¬
стающая.
Пример 2. Пусть функция задана на промежутке [0; 3]
формулой у = у (х — З)2. Является ли функция возрастающей
(убывающей) на этом промежутке?
Решение. Пусть xt и х2 принадлежат промежутку [0; 3]
и yY - у (хг — З)2, у2 = у (х2 — З)2. Пусть х2 > хР Рассмотрим
разность у2 - у1 и определим ее знак:
У2 ~ У1 = у (х2 ~ З)2 - у (Xj - З)2 =
= ± ((х2 - 3) - (X! - 3))((х2 - 3) + (хх - 3)) =
= у (х2 - xL)(x2 + Xj - 6) < 0.
Действительно, так как х2 > хр то х2 — xt > 0. Для любого
значения х из промежутка [0; 3] разность х — 3 < 0. Значит,
х2 - 3 < 0, х1 - 3 < 0 (почему здесь строгое неравенство?) и
х2 + X; — 6 < 0. Поэтому разность у2 — уг — отрицательное чис¬
ло, следовательно, у2< у Р
Таким образом, мы доказали, что если х2 > хр то у2 < уг. Это
значит, что функция у — у (х - З)2 на промежутке [0; 3]
убывающая. ▲
1.	Какая функция называется возрастающей на промежутке?
2.	Какая функция называется убывающей на промежутке?
3*. Как доказывают, что функция является возрастающей (убы¬
вающей) на некотором промежутке?

51 Возрастание и убывание функции на промежутке р
У пражнения
1.77°. Функция задана графиком на рисунке 43. Назовите для
этой функции:
а)	промежутки возрастания;
б)	промежутки убывания.
1.78°. Функция задана формулой у = (х - 2)3. Сравните значе¬
ния функции У} и у2, если:
1)	хт = 0, х2 — 1;
3) хт = -4, х2 = 2;
2)	Х! = -3, х2 = -1;
4) Xj — —1, х2 = 6.
1.79.	Функция задана формулой у = 2 - \ х + 7. Сравните зна¬
чения функции и у2, если:
1) хт = 2, х2 = 9;	2) Xj = —3, х2 = —6;
3)	х, =-6, х2 = 2;	4) х1 = -7, х2= 18.
X + 1
1.80.	Функция задана формулой у = на промежутке
(—оо; 1). Сравните значения функции уг и у2, если:
1) Xj = -6, х2 = -4;	2) х^-3, х2 = -1;
3) Xj --1, х2 - 0,5;	4) хт = —4, х2 = 0.

52
Функции
1.81°. По изображению графика функции (рис. 44):
а)	укажите область определения и множество значений
функции;
б)	укажите нули функции:
в)	установите, является ли функция возрастающей (убы¬
вающей) на области определения.
1.82*. Докажите, что функция у = — у (х + I)2 на промежутке
[—10; —3] возрастающая. Найдите ее нули и наибольшее
значение.
1.83*. Докажите, что функция у = 4,5(4 - Зх)2 на промежутке
[—4; 1] убывающая. Найдите ее нули и наименьшее
значение.
1.84*. Докажите, что функция у = 4х2 — 1 на промежутке
[0; +°о) возрастающая; найдите ее нули.
1.85*. Докажите, что функция у = —Зх2 + 2 на промежутке
[0; +оо) убывающая; найдите ее нули.

Прямая пропорциональность р
53
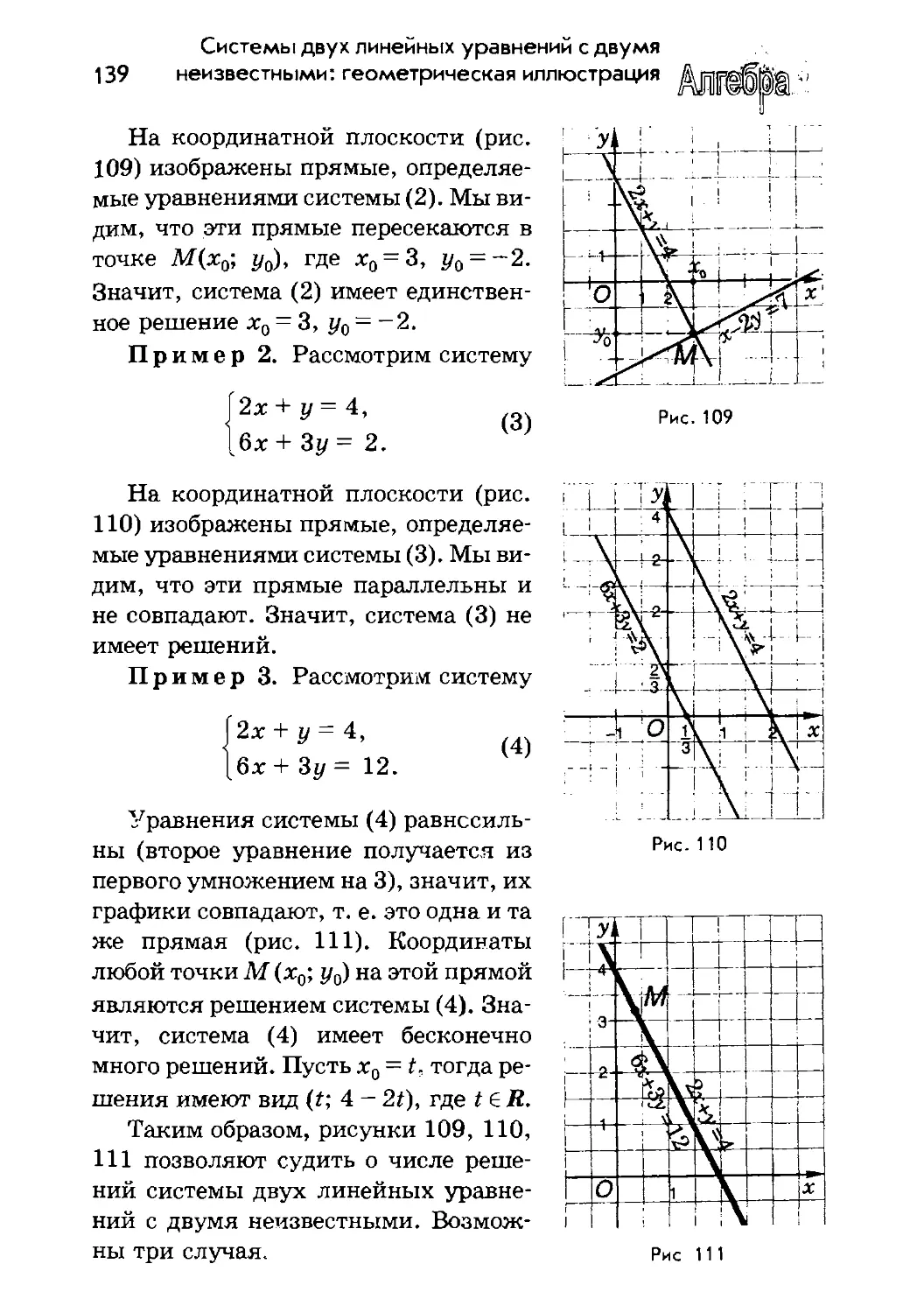
1.10.	Прямая пропорциональность
Определение. Прямой пропорциональностью на¬
зывается функция вида
y = kx,
где k * 0 — число.
Так как область определения функции не указана, то по до¬
говоренности (см. п. 1.4) — это естественная область определе¬
ния выражения kx, т. е. вся числовая прямая.
Очевидно, что прямая пропорциональность имеет единст¬
венный нуль — это точка х = 0.
Переменная у называется прямо пропорциональной пере¬
менной х (слово «прямо» часто опускается), а число k —
коэффициентом прямой пропорциональности.
Теорема. Если переменная у пропорциональна пере¬
менной х с коэффициентом k, то переменная х пропорци¬
ональна переменной у с коэффициентом -|-.
Доказательство. Переменная у пропорциональна пере¬
менной х с коэффициентом k, т. е. у - kx, /г * 0. Тогда
а это означает, что переменная х пропорциональна переменной
у с коэффициентом у .
Замечание. Доказанная теорема позволяет говорить, что пере¬
менные х и у (или у и х) пропорциональны.
в Прямая пропорциональность переменных х и у озна-
J чает, что их отношение постоянно, т. е. зависи
мость между ними при х * 0 выражена формулой
= k, k*0.
Напомним, что мы условились для значений аргумента
хх, х2 обозначать соответствующие значения функции уг, у2,
т. е. у, = kx}, у2 = kx2.

MiyjJ функции

Теорема. Пусть переменные х и у прямо пропорци¬
ональны. Тогда при х 0 для их соответствующих значений
верно равенство
У± _Xi
У1 *2 ‘
Доказательство. По условию у = kx — прямая пропор¬
циональность; значит, k * 0. А так как и х2 * 0, то у2 = kx2 * 0.
Следовательно, можно делить z/t на у2:
Pi _fe^i _х, га
Уг kx2 х2 ‘
Пример 1. Переменные а и b пропорциональны. Зная, что
= 37, а2 - 111, Ъ2 ~ 17, найти Ъх.
Решение. Поскольку а и b прямо пропорциональны, то
, а,д2 37 ■ 17	17 г 2
и, значит, ^1=^7=Л1Г = '3 = 5Т•
Ответ: = 5 у.
Пример 2. В таблице даны соответствующие значения
переменной р, которая зависит от переменной q.
У
3,2
4,1
р
12,8
16,4
5,0
7,6
8,4
20,0
26,6
33,6
Являются ли переменные р и q пропорциональными?
Решение. Переменные будут пропорциональны, если от¬
ношение -^- постоянно. Вычислим отношения соответствую¬
щих значений переменных р и q-.
Pi' 9i	12,8 • 3,2 — 4;	р$ • q% 20,0 • 5,0 — 4;
р2 :	~ 16,4 ■ 4,1 =4;	рА: q4 = 26,6 ■ 7,6 - 3,5.
Ответ: переменные р и q не пропорциональны, поскольку
не все отношения их соответствующих значений равны между
собой.

И
Прямая пропорциональность Д
55
Пример 3. В треугольнике АВС найти углы, если
известно, что их величины относятся как 2:3:4.
Решение. Величины углов треугольника пропорциональ¬
ны указанным числам 2, 3 и 4 с некоторым коэффициентом k,
т. е. АА = (/г-2)°; А В = (/? • 3)°; AC = (k- 4)°. Так как сумма
углов в треугольнике равна 180°, то получим:
2k + 3k + 4k — 180, откуда k = 20.
Таким образом, А А = (20 • 2)° = 40°; А В = (20 • 3)° = 60°:
А С = (20 • 4)° = 80°.
Ответ: 40°, 60°, 80°.
1.	Что называется прямой пропорциональностью?
2.	В каком случае переменная у называется прямо пропорциональ¬
ной переменной х?
3.	Как называется число k в формуле у = kx, если k * 0?
4.	Пропорциональны ли переменные х и у, если пропорциональны
переменные у и х?
5.	Что означает пропорциональность переменных х ку!
6.	Докажите свойство соответствующих значений прямо про¬
порциональных переменных.
Упражнения
1.86.	Верно ли, что прямо пропорциональны:
1)	периметр квадрата и его сторона;
2)	площадь квадрата и его сторона;
3)	длина окружности и ее радиус;
4)	сумма чисел и одно из слагаемых;
5)	делимое и частное, если делитель постоянный;
6)	возраст человека и его масса;
7)	высота и объем прямоугольного параллелепипеда,
если площадь основания постоянна;
8)	пройденный путь и время при постоянной скорости;
9)	число и 30 % этого числа;
10)	длина отрезка, измеренная в сантиметрах, и длина
этого отрезка, измеренная в метрах?
1.87.	Зависимость между переменными s и t выражается фор¬
мулой s = 75? — 126. Являются ли переменные t и s прямо
пропорциональными?

Функции
56
1.88.	Известно, что переменная а прямо пропорциональна пе¬
ременной Ъ. Что нужно знать, чтобы по заданному зна¬
чению b найти соответствующее значение а?
1.89°. Известно, что две переменные d и с прямо пропор¬
циональны и при d, равном 96, значение с равно 3-2.
Определите коэффициент пропорциональности. Вырази¬
те формулой зависимость с от d.
1.90°. Вместимость одной банки 3 л. Сколько потребуется
банок, чтобы разлить 6 л фруктового сока, 9 л, 12 л,
15 л? Составьте формулу, выражающую зависимость
между числом банок (п) и объемом сока (V)-
1.91°. Из 24 кг молока получается 3 кг сливок. Сколько
килограммов молока нужно для приготовления 6 кг
сливок, 12 кг, 15 кг, 24 кг?
Составьте формулу, выражающую зависимость между
массой молока (т) и массой сливок (Z).
1.92. Площадь треугольника выражается формулой S — ah,
где а — основание треугольника, h — зъкота. Верно ли,
что:
1)	при фиксированной высоте h площадь S и основа¬
ние а прямо пропорциональны;
2)	при фиксированном основании а площадь S и высота
h прямо пропорциональны;
3)	при фиксированной площади S основание а и высота
h прямо пропорциональны?
1.93°. Функция задана таблицей. Верно ли, что переменные х
и у прямо пропорциональны?
2)

Прямая пропорциональность Ц
57
X
1
2
3
4
5
6
У
1
4
9
16
П X
56
X
4
8
12
16
20
24
У
2
4
6
8
10
12
1.94°. Задает ли прямую пропорциональность формула:
X
У = ~~6’
7
1) у = ~6х;
2)
3)
4) у = 2х-1;
5)
6)
7) у = \ 2х;
10) р = 8,3х;
8)
И)
У = - \ Зх;
у = -5х + 3;
9)
12)
</ = 2х2;
X
У=~9’
-5
у = 4х3?
1.95. Начертите в тетради и заполните таблицу, если перемен¬
ные х и у прямо пропорциональны. Задайте функцию
формулой.
1)
X
0
1
9
2
9
1
3
1
2
4
4
У
0,5
2)
X
-3
-2,5
-2
-1,5
-1
1
1—,
1
8
0
У


0,8
1.96°. Функция задана формулой у = - у х.
1)	Найдите значение функции, если соответствующее
1	5
значение аргумента равно: —5; —1; —— ; 0;	; 4; 5; 10.
О	Z
2)	По значению функции —6; -4; 0; 1; 1,5; 2; 2,5; 8
найдите соответствующее значение аргумента.
1.97.	Число 60 представьте в виде двух слагаемых, отношение
которых равно: 1)1:2; 2) 2 '■ 3; 3)3:1; 4) 9 :11.

Д!И!^ функ^и

1.98.	Отрезок длиной 90 см разделили на две части. Найдите
длины полученных отрезков, если их отношение равно:
1)3:2; 2)1:4; 3)5:4; 4)7:3.
1.99.	Пятна от молока и супа на белых тканях можно вывести
протиранием их смесью, состоящей из 6 частей мыла,
1 части нашатырного спирта и 2 частей скипидара.
Сколько надо взять каждого из этих веществ, чтобы
приготовить 252 г смеси?
1.100.	Пятна на цветных шерстяных и шелковых тканях мож¬
но вывести протиранием пятен смесью, состоящей из
15 частей глицерина, 2 частей нашатырного спирта и
20 частей воды. Сколько надо взять каждого из этих ве¬
ществ, чтобы приготовить 296 г смеси?
1.101.	Для варки вишневого варенья было куплено 9 кг саха¬
ра. Сколько нужно взять вишни и сколько воды, чтобы
сварить варенье, если вишни, сахар и вода берутся в от¬
ношении 1 •' 1,5 : 0,15 соответственно?
1.102.	При варке варенья чернику, сахар и воду берут в отно¬
шении 2 : 2 : 0,1 соответственно. Сколько нужно сахара
и воды, чтобы сварить варенье из 8 кг черники?
1.11.	График и свойства функции у = kx (k^O)
Рассмотрим функцию
у = 2х.
Ее область определения — R, так как при любом значении
независимой переменной х существует, и притом единствен¬
ное, значение выражения 2х.
Чтобы получить представление о ее графике, поступим, как
в п. 1.6: придадим несколько значений аргументу х и вычис¬
лим соответствующие значения функции (результаты даны в
таблице).
X
-2
-1
0
1
2
3
У
-4
—2
0
2
4
6
Изобразим точки (х; у) с указанными координатами на
плоскости (рис. 45). Легко увидеть, что все они лежат на одной
прямой, проходящей через начало координат. Для этого доста¬
точно приложить к ним линейку.

Так как прямая определяется двумя точками, лежащими
на ней, то мы можем сказать, что графиком функции у = 2х
является прямая, проходящая через начало координат и точку
(1; 2) (рис. 46). Конечно, вместо точки (1; 2) можно указать
любую другую точку на этой прямой.
Если тем же способом изобразить графики функций у — kx
при значениях k, равных	; 3; 4, и при значениях k,
равных - 4; -3; -2; -	; - у, то легко убедиться, что каждый
из этих графиков является прямой, проходящей через начало
координат (рис. 47, 48).
Рис. 47
Рис. 48

Д!И!^ функ^и

1.98.	Отрезок длиной 90 см разделили на две части. Найдите
длины полученных отрезков, если их отношение равно:
1)3:2; 2)1:4; 3)5:4; 4)7:3.
1.99.	Пятна от молока и супа на белых тканях можно вывести
протиранием их смесью, состоящей из 6 частей мыла,
1 части нашатырного спирта и 2 частей скипидара.
Сколько надо взять каждого из этих веществ, чтобы
приготовить 252 г смеси?
1.100.	Пятна на цветных шерстяных и шелковых тканях мож¬
но вывести протиранием пятен смесью, состоящей из
15 частей глицерина, 2 частей нашатырного спирта и
20 частей воды. Сколько надо взять каждого из этих ве¬
ществ, чтобы приготовить 296 г смеси?
1.101.	Для варки вишневого варенья было куплено 9 кг саха¬
ра. Сколько нужно взять вишни и сколько воды, чтобы
сварить варенье, если вишни, сахар и вода берутся в от¬
ношении 1 •' 1,5 : 0,15 соответственно?
1.102.	При варке варенья чернику, сахар и воду берут в отно¬
шении 2 : 2 : 0,1 соответственно. Сколько нужно сахара
и воды, чтобы сварить варенье из 8 кг черники?
1.11.	График и свойства функции у = kx (k^O)
Рассмотрим функцию
у = 2х.
Ее область определения — R, так как при любом значении
независимой переменной х существует, и притом единствен¬
ное, значение выражения 2х.
Чтобы получить представление о ее графике, поступим, как
в п. 1.6: придадим несколько значений аргументу х и вычис¬
лим соответствующие значения функции (результаты даны в
таблице).
X
-2
-1
0
1
2
3
У
-4
—2
0
2
4
6
Изобразим точки (х; у) с указанными координатами на
плоскости (рис. 45). Легко увидеть, что все они лежат на одной
прямой, проходящей через начало координат. Для этого доста¬
точно приложить к ним линейку.

Так как прямая определяется двумя точками, лежащими
на ней, то мы можем сказать, что графиком функции у — 2х
является прямая, проходящая через начало координат и точку
(1; 2) (рис. 46). Конечно, вместо точки (1; 2) можно указать
любую другую точку на этой прямой.
Если тем же способом изобразить графики функций у — kx
при значениях k, равных	; 3; 4, и при значениях k,
равных -4;-3;-2;--|-;-у,то легко убедиться, что каждый
из этих графиков является прямой, проходящей через начало
координат (рис. 47, 48).
Рис. 47
Рис. 48

Функции
60
Итак, графиком прямой пропорциональности яв¬
ляется прямая, проходящая через начало коор¬
динат.
Заметим, что графиком прямой пропорциональности
у = kx (k * 0) может быть любая прямая, проходя¬
щая через начало координат, кроме осей коор¬
динат.
При k = 0 функция у — kx имеет вид у— 0. Но нам известно,
что все точки плоскости, ординаты которых равны нулю,
лежат на оси Ох, т. е. при k — 0 графиком функции у = kx
является ось Ох.
Мы уже говорили, что график функции дает нагляд¬
ное представление о ее свойствах. На рисунке 46 изобра¬
жен график функции у = 2х. На нем видно, что точка х = 0
является единственным нулем этой функции и что большим
значениям аргумента соответствуют большие значения функ¬
ции, т. е. что функция у = 2х возрастающая на области
определения.
И вообще, функция y — kx при /г > 0 является возраста¬
ющей на области определения (рис. 49).
Точно так же график функции у = ~2х (рис. 50)
сразу позволяет сказать, что у нее единственный нуль
(х = 0) и что эта функция убывающая на области опреде¬
ления.
Рис. 49
Рис. 50

61
Г рафик и свойства функции у = кх (к 0)
И вообще, функция y = kx
при k<0 является убываю¬
щей на области определения
(рис. 51).
Множество значений функ¬
ции у = kx при k * 0 — все дей¬
ствительные числа. Это свой¬
ство означает, что для любой
точки уг на оси Оу найдется
у- kx, k<0
У
такая точка х1 на оси Ох, что	Рис 51
</1 = kxY (см. рис. 49, 51).
Легко заметить по изображению графика (см. рис. 49 —
точки N и Т; рис. 51 —точки Р и L), что если значения аргу¬
мента функции у = kx (k * 0) отличаются только знаком, то и
значения функции отличаются только знаком, т. е. график
прямой пропорциональности симметричен относительно на¬
чала координат.
Это свойство функции у = kx (k 0) называется нечет¬
ностью.
Определение. Если значения функции, соответ¬
ствующие любым двум противоположным значениям аргу¬
мента (т. е. значениям а и —а), противоположны друг другу,
то такая функция называется нечетной.
g 1 Здесь, конечно, предполагается, что если число а при-
J < надлежит области определения функции, то и число
> ■ -а принадлежит этой области определения, т. е.
область определения нечетной функции должна
быть симметричной относительно нуля.
График любой нечетной функции симметричен
относительно начала координат.
Заметим также, что для прямой пропорциональности легко
указать и промежутки знакопостоянства. Например, функция
у = —17х принимает отрицательные значения (у < 0) на про¬
межутке (0; + оо), а положительные значения (у > 0) — на
промежутке (~°°; 0).
Сформулируем теперь свойства функции у = kx (k * 0) и
обоснуем их без помощи рисунков.

функ^и
Теорема (о свойствах функции у = kx, k * 0).
1.	Областью определения функции у = kx (k^O) явля¬
ется множество R всех действительных чисел.
2.	Множеством значений функции у = kx (/г	0) явля¬
ется множество R всех действительных чисел.
3.	Функция у = kx (k * 0) не имеет ни наименьшего, ни
наибольшего значений.
4.	График функции у = kx (k ^0) имеет единственную
точку пересечения с осями координат (0; 0) — начало
координат.
5.	Значение аргумента х = 0 является нулем функции
у - kx (k 0).
6.	Функция у — kx (k^ 0) является нечетной.
7.	Функция у = kx является возрастающей на области
определения, если k > 0, и убывающей, если k < 0.
8.	Функция у = kx (k > 0) принимает отрицательные
значения (у < 0) на промежутке (— 00; 0) и положительные
значения (у > 0) на промежутке (0; + °°), т. е. ее график
расположен в I и III координатных углах.
Функция у = kx (k < 0) принимает отрицательные
значения (у < 0) при х € (0; + о°) и положительные значения
(у > 0) при (-°о; 0), т. е. ее график расположен во II и
IV координатных углах.
▲ Доказательство свойства 2. Покажем, что функ¬
ция у = kx (fe * 0) может принять любое значение р при со¬
ответствующем значении аргумента. Чтобы найти это значение
аргумента, решим уравнение р = kx. Корнем этого уравнения
является число . При этом значении аргумента значение
функции равно р. И
Свойство 3 следует из свойства 2.
Свойства 4 и 5 докажите самостоятельно.
Доказательство свойства 6. Значениям аргумента а
и —а соответствуют значения функции ka и k (-а); но
k(-a) = — ka. Таким образом, значения функции, соответ¬
ствующие любым двум противоположным значениям аргу¬
мента (а и ~а), противоположны (ka n ~ka), т. е. функция
у = kx (k * 0) — нечетная. S

63
Г рафик и свойства функции у = кх (к 0)
Доказат ельство свойства 7. Напомним, что функция
называется возрастающей на области определения, если для
любых хр х2, принадлежащих области определения, из
неравенства х2 > хх следует неравенство у2 > у у, и убывающей,
если из неравенства х2 > хх следует неравенство у2 < уг. Итак,
пусть х2 > хР Рассмотрим разность у2 — уги определим ее знак:
У2 ~ Ух = kx2 ~kxt = k (х2 - xj.
Так как х2>хр то х2 — Xj > 0. Если k > 0, то разность
у2~ Уу = k (х2 - хх) — положительное число. Следовательно,
у2> Ух и функция у = kx — возрастающая на области опре¬
деления. Если же k < 0, то разность у2- уг — отрицательное
число. Значит, у2 < yY и функция у = kx — убывающая. К]
Свойство 8 докажите самостоятельно. ▲
1.	Что является графиком прямой пропорциональности9
2.	Перечислите свойства функции у = kx при:
а) k > 0; б) k < 0.
3.	Какая функция называется нечетной?
4.	Сформулируйте свойство графика нечетной функции.
5.	Сформулируйте теорему о свойствах функции у = kx (k * 0).
в*. Докажите свойства функции:
a) y = kx (k> 0); б) y = kx (k < 0).
Упражнения
1.103°. Принадлежит ли графику функции у = —3,5х точка:
1)	А(—1; 0);	2) В(2; -1);
3) 0(1; -3,5);	4) О(-2; 7);
5) М(0; 8);	6) К(~ 10; -35)?
1.104°. Прямая пропорциональность задана формулой:
1)	у = —|-х;	2)у=10х.
Какие из точек А (1; —5), В^2; у), С (10; -2), 0(0; 0),
Е(-1; —10), Р(5; -1) принадлежат графику данной
функции?

МИ^функции

1.105°. Изобразите график функции у = 4х. Определите:
1)	абсциссу точки графика, ордината которой равна 2;
4; -8; -4; 0; 1;
2)	проходит ли график функции через точки А(1; 4),
В(-1; 4), с(—2; -|), D(-3; -12), в(|; 1);
3)	есть ли на графике точка, абсцисса которой равна
100; 2000; ~300; -1200; если да, то какая у нее
ордината.
§
1.106. Изобразите график функции у = —-^х. Назовите не¬
сколько точек этого графика, координаты которых
являются целыми числами.
1.107°. Изобразите в одной системе координат графики
функций:
1)	у = -|-х; у = -2х; у = 5х;
2)	у = -^х; у = 2х; у = -5х;
3)	у = Зх; у = - х; у = бх;
4)	</ = |х; у = -3х; у = ~6х.
1.108. Существует ли такое значение аргумента, при котором
значение функции у =1,5х равно -600; -1200? Если да,
то найдите его.
2
1.109°. Изобразите график функции у = - —х. По графику
С
найдите:
1)	приближенное значение функции для значений ар-
к	о 1	2
гумента: -5; -2; у! у?
2)	приближенное значение аргумента для значений
функции: -3; 0,5; 2,5; 6.
1.110.	На рисунке 52 изображен график зависимости скорости
движения поезда от времени.
1)	Найдите промежуток времени, на котором зависи¬
мость была прямо пропорциональной.
2)	Какой была скорость поезда с 1 ч до 4 ч?

65
1.111.	На рисунке 53 изображены графики движения Маши и
Даши.
1)	Найдите по графику скорость движения каждой де¬
вочки.
2)	Напишите формулу пройденного каждой девочкой
пути в зависимости от времени.
1.112.	1) Прямая y — kx проходит через точку М(-4; 6). Про¬
ходит ли эта прямая через точку Р(6; -9)?
2)	Прямая y-kx проходит через точку ЛГ(—8; -5). Про¬
ходит ли эта прямая через точку А^ -|-; -|-)?
1.113.	График прямой пропорциональности проходит через
точку:
1)	М(2; -6);	2) К(~2; -8).
Изобразите график функции. Задайте ее формулой.
1.114.	График функции у = kx проходит через точку
1)	М(-24; -12);	2) Р(60; -12).
Найдите k.
1.115.	Изобразите график функции у = kx, если известно, что
ему принадлежит точка:
1) А(-6; 2);	2) В(5; -1);
3)	С(4; 8);	4) П(-3; -9).
1.116.	Стороны прямоугольника х см и 9 см. Площадь
прямоугольника S см2.

	61
1)	Запишите формулу, выражающую зависимость пло¬
щади прямоугольника от длины стороны.
2)	* Изобразите график этой зависимости при условии,
что 0 < х < 6.
1.117.	Масса одного карандаша 1,4 г. Масса п карандашей рав¬
на у г.
1)	Запишите формулу, выражающую зависимость мас¬
сы п карандашей от массы одного карандаша.
2)	Изобразите график этой зависимости при условии,
что п С 10.
1.118.	Изобразите график функции, заданной формулой
у = 0,6х на области определения:
1) R,	2) (0; +°°);	3) [-3; 5];
4)	{2; 3; 4; 5; 6; 7};	5) (-оо; 0];	6) Z.
1.119.	Изобразите график функции у = ах, если:
1)	а>0;
3)	0<а< 1;
5)	а < -1;
2)	а < 0;
4)	а>1;
6)	-1 < а '0
1.120.	На рисунке 54 изображе¬
ны графики прямых про¬
порциональностей. Для
каждой из функций напи¬
шите формулу, которой
можно ее задать.
1.121.	Изобразите график функ¬
ции:
1)	у = Зх;
2)	z/ = 3(-x);
3)	у = —Зх;
4)	г/ = — 3(—х).
1.122.	Изобразите в одной системе координат график функции
у = ах при:
1) а = -5;
3)	а = 4;
2)	а = -2;
4)	а = 10.

(>7	Г рафик и свойства функции у = кх (к 0)
1.123.	Укажите, при каких значениях а формулой задана воз¬
растающая функция:
1) у = а*х;	2) у = (5а + 4)х;
3)у = (9 — 3а)х;	4)у = а7х.
1.124.	Укажите, при каких значениях b формулой задана убы¬
вающая функция:
1) у = (4Ь~1)х;	2) у = (6~24Ь)х;
3)	У = ^х;	4) у = у)-Ь + 1х.
1.125.	Задайте формулой прямую пропорциональность, если
известно, что ее график проходит через точку:
1) М(2; -7);	2) N(-4; -2,5);
3)	Р(-8,5; 9);	4) 7(3,6; 1,8).
1.126.	На рисунке 55 изображены графики функций с обла¬
стью определения R. Какая из функций является не¬
четной?
1.127.	При каких значениях а функция является возрастаю¬
щей на области определения:
1) у = (а + 6)х;	2) у = (-3 + а)х;
3)	у = (а2 + 1)х;	4) у = (| а | - 1)х?

Функции
68
1.128.	При каких значениях а функция является убывающей
на области определения:
У~а^~2х’’
3) У~2\а\ 9Х;
1.129.	Изобразите схематично в одной системе координат гра¬
фики функций у = ах и у = Ьх, если:
1) а > О, b >	0, а > Ь;	2)	а	<	О,	b <	0, а < Ь;
3)	а > О, b <	0;	4)	а	<	О,	b >	0;
5)	а < О, b >	0, | а | = | b
6)	а > О, Ь <	0, | а | < 1, | Ы > 1.
1.12.	Линейная функция
Определение. Линейной функцией называется
функция вида
y = fex + b,
где k и Ь — числа.
Область определения линейной функции — это естествен¬
ная область определения выражения kx + b, т. е. множество R
всех действительных чисел, поскольку при любом значении
независимой переменной х существует, и притом единствен¬
ное, значение выражения kx + b.
Приведем примеры.
Пример 1. Линейными функциями являются функции
г/ = 2х + 3; у = —2х + 3; у = 2х~ 3;	У~~ 2х~ 3.
Пример 2. Функция г/ = йх(/г#О)— прямая пропорцио¬
нальность — это частный случай линейной функции y — kx + b
при k # О, Ь-0.
Пример 3. Еще один частный случай: когда k = О,
линейная функция принимает вид у = О • х + Ь, т. е. у — Ь.
Такая функция называется постоянной. При любом зна¬
чении аргумента х эта функция принимает одно и то же
значение Ь.

69	Линейная функция
Рассмотрим функцию
у - 2х — 3.
Составим таблицу значений этой функции и сравним ее с
таблицей значений функции у = 2х.
X
-2
-1
0
1
2
У = 2х
—4
-2
0
2
4
У = 2х - 3
-7
-5
-3
-1
1
Изобразим точки (х; у) с указанными координатами на
координатной плоскости (рис. 56, а).
Очевидно, что при каждом значении х значение функции
у = 2х - 3 меньше значения функции у = 2х на 3 единицы.
Поскольку графиком функции у = 2х является прямая, то и
график функции у = 2х — 3 — прямая (рис. 56, б).
Так как прямая определяется двумя точками, лежащими
на ней, то мы можем сказать, что графиком функции у = 2х — 3
является прямая, проходящая через точки (0; —3) и (1; —1)
(рис. 57). Конечно, вместо этих точек можно указать две любые
другие точки на этой прямой.
Рис. 56
Рис. 57

70
Легко убедиться,
что каждый из графиков
г/ = 2х + 3; у = —2х + 3; у = -2х~3
является прямой (рис. 58—60).
Прямая у — 2х + 3 параллельна прямой у = 2х
через точку (0; 3) (см. рис. 58).
Прямая у — — 2х + 3 параллельна прямой
проходит через точку (0; 3) (см. рис. 59).
Прямая у = - 2х - 3 параллельна прямой
проходит через точку (0; -3) (см. рис. 6^0).
▲
и проходит
у = ~2х и
у--2х и
Вообще, графиком линейной функции y = kx + b
является прямая, проходящая через точку (0; Ь) и
параллельная прямой у = kx.
Заметим, что если k = 0, то у — Ь, т. е.
постоянную (см. пример 3).
мы получаем
Графиком ее является прямая,
а)
У
б)
у=Ъ, Ъ>0
У .
с
О
С
X
ь
у=Ь, Ь<0
ь
Рис. 61
о
X

71
Линейная функция R
проходящая через точку С(0; Ь) и параллельная оси Ох
(рис. 61, а, б). При Ъ — 0 график совпадает с осью Ох. ▲
Как и график прямой пропорциональности, график линей¬
ной функции дает наглядное представление о ее свойствах. На
рисунке 57 изображен график функции у — 2х — 3. На нем
видно, что большему значению аргумента соответствует
большее значение функции, т. е. что функция у = 2х - 3
возрастающая на области определения, а число х=1,5
является ее единственным нулем.
И вообще, функция y — kx + b при k > 0 — возрастающая на
области определения (рис. 62).
Точно так же график функции у = -2х-3 (см. рис. 60)
сразу позволяет сказать, что эта функция — убывающая на
области определения и ее единственным нулем является число
х = —1,5.
И вообще, функция у — kx + Ь при k < 0 — убывающая на
области определения (рис. 63).
Нули линейной функции y — kx + b — это те значения х, при
которых она принимает значение 0, т. е. корни уравнения
kx + b - 0. При k * 0 получаем единственный нуль —
х=-у (см. рис. 62, 63).
Множество значений функций у = kx + b (k 0) — все
действительные числа. На графике функции это свойство
означает, что для любой точки ух на оси Оу найдется такая
точка хх на оси Ох, что ух = kx± + b.
Рис. 62
Рис. 63

Рис. 64
М8^|^функции

Заметим, что функция
у — kx + b (k 0) не принимает
ни наименьшего, ни наиболь¬
шего значения.
П р и м е р 4. Изобразить гра¬
фик функции У=— у х + 3 и
назвать ее свойства.
Решение. Графиком ли¬
нейной функции у — - у х + 3
является прямая, которая проходит через точки (0; 3) и (2; 2)
(рис. 64).
Свойства функции у = - у х + 3 следующие: область
определения — R; множество значений — R; ни наибольшего,
ни наименьшего значений функция не имеет; график функции
пересекает ось Ох в точке (6; 0) и ось Оу — в точке (0; 3);
значение аргумента х = 6 является нулем функции; функция
принимает положительные значения (у > 0) на промежутке
(- оо; 6) и отрицательные значения (у < 0) — на промежутке
(6; + оо); функция не является нечетной; функция убывающая
на области определения.
А Пример 5. Изобразить график функции у = -7 и
назвать ее свойства.
Решение. Графиком линейной функции у - -7 (по¬
стоянной) является прямая, которая проходит через точку
(0; —7) параллельно оси Ох (рис. 65). Функция у = -7 имеет
следующие свойства: область определения —
R; множество значений — множество, состоя¬
щее из одного числа —7; график функции
не пересекает ось Ох, а ось Оу пересекает
в точке (0; —7); функция не является не¬
четной (график не симметричен относительно
начала координат; график симметричен
относительно оси Оу); функция на области
определения не изменяет значений, поэтому
она не является ни возрастающей, ни убы¬
вающей. ▲
Рис. 65

73
Линейная функция
А Сформулируем теперь свойства линейной функции
у = kx + b при ft / 0 и Ь#0 (если Ъ = 0, то получается функция
у = kx, которая уже была рассмотрена в п. 1.11) и обоснуем их
без помощи рисунков.
Теорема 1 (о свойствах функции у = kx + b при k + О и
b * 0).
1.	Область определения функции у = kx + b — множе¬
ство R всех действительных чисел.
2.	Множеством значений функции у = kx + b (k +О) явля¬
ется множество R всех действительных чисел.
3.	Функция у = kx + b (k # 0) не принимает ни наиболь¬
шего, ни наименьшего значений.
4.	График функции у — kx + b (k^O) пересекает ось Ох в
точке 5 о), а ось Оу — в точке (0; &).
5.	Значение аргумента х — — является нулем функции
у = kx + b (k + 0).
6.	Функция y = kx + b(k+:O, b + 0) не является нечетной.
7.	Функция у - kx + Ъ является возрастающей на области
определения при k > 0 и убывающей при k < 0.
8.	Функция y — kx + b (k> 0) принимает отрицательные
значения (у<0) на промежутке	“у) и поло¬
жительные значения (у > 0) на промежутке (“у 5 + °°).
Функция y — kx + b (k < 0) принимает отрицательные
значения (у<0) при	+ °°^ и положительные
значения (у > 0) при х 6	00; - -у ).
Рассмотрим доказательства этих свойств.
Доказательство свойства 2. Покажем, что функция
у = kx + b (k + 0) может принять любое значение р при
соответствующем значении аргумента. Чтобы найти это
значение аргумента, решим уравнение
p = kx + b.

ВМЖГфункции	™
Корнем этого уравнения является число . При этом зна¬
чении аргумента значение функции равно р. И
Свойство 3 следует из свойства 2.
Доказательство свойств 4, 5. При у = 0 из формулы
у = kx + b (k * 0) получаем х — — у , а при х = 0 получаем у~Ь,
т. е. свойства 4 и 5 верны. И
Доказательство свойства 6. Пусть а и -а — значения
аргумента. Им соответствуют значения функции ka + b и
k(~a) + b, которые не являются противоположными числами,
поэтому функция у = kx + b не является нечетной. KI
Доказательство свойства 7. Пустьх2 > хг и у2 = kx2 + b,
Уг = kxv + Ъ.
Рассмотрим разность у2 - уг и определим ее знак:
у2—уг=kx2+b—(kxr + b) = kx2+b~kxr—b— kx2 ~kxY—k{x2~x^.
Так как x2>xp то х2~х\ > 0. Если k > 0, то разность
у2 - i/i=/?(x2-Xi) — положительное число, и поэтому у2> уг,
т. е. функция y = kx + b — возрастающая на области
определения. Если же k < 0, то разность у2 — у{ —
отрицательное число. Значит, у2 < уг и функция у = kx + b при
k < 0 — убывающая. И
Свойство 8 докажите самостоятельно.
Теорему 2 (о свойствах линейной функции у — kx + b (k — 0),
т. е. о свойствах функции у — Ъ, сформулируйте самостоя¬
тельно (см. пример 3). ▲
1.	Какая функция называется линейной?
2.	Покажите, что прямая пропорциональность — это частный слу¬
чай линейной функции.
3.	Покажите, что постоянная функция — это частный случай ли¬
нейной функции.
4.	Как расположены относительно друг друга графики функций:
линейной y — kx-УЬи прямой пропорциональности у = kxl
5.	Как изобразить график функции y = kx + b, если прямая у = kx
уже изображена?
6.	В каком случае график линейной функции совпадает с осью 0x1
7*. Сформулируйте теорему о свойствах линейной функции.

75
Линейная функция И
8'. Докажите свойства линейной функции:
а)	y = kx + b (k > О, Ь 0);
б)	у = kx + b (к < О, b * 0);
в)	у = kx + Ь (k = О, Ь * 0);
г)	у = kx + Ь (k = b = 0).
У пражнения
1.130°. Какой из формул задана линейная функция:
1)	у = х2 - 3 - (х + 2)2;
2)	у - 5 - х2 + (х - I)2;
3)	у = (2х - 5) - (Зх + 6);
4)	у = (-7х + 8) - (2х + 15);
5)	у = х(2 —х) + х2;
6)	у = х2 —х(8 + х);
7)	у = (х + 3) (3 - х) + 1;
8)	у = 5 — (х - 2) (х + 2);
9)	у = (х + 4)2 - (х + 4);
10)	у = (х — 7)2 — (х — 7)?
1.131. Существует ли такая линейная функция, что точки
(х; у) с координатами, указанными в таблице, принад¬
лежат ее графику?
X
-2
-1
0
1
2
3
4
У
2
0
—2
-4
-6
-8
-10
X
-2
-1
0
1
2
3
4 .
У
-3
0
3
6
9
12
18
1.132°. Верно ли, что графику линейной функции у = —Зх + 5
принадлежит точка:
1) А(0; 5);
4) D( -10; 0);
7) £(10; -25);
2) В(2; -1);
5) М(1; 2);
8) 7’(—10; 35);
3) С(2; -5);
6) £(-1; 11);
9) Р(3; -14)?

Функции
76
1.133°. Функция задана формулой у = 6х - 2.
1)	Найдите значение функции, если значение аргумен¬
та равно: -3; -2; -1; 0; 1; 2.
2)	При каком значении аргумента значение функции
равно: —4; -2; 0; 1; 3; 6?
3)	При каких значениях аргумента значения функции
положительны?
4)	При каких значениях аргумента значения функции
неположительны?
5)	Существует ли такое значение х, при котором зна¬
чение функции равно значению аргумента?
6)	Существует ли такое значение х, при котором зна¬
чение функции противоположно значению аргу¬
мента?
1.134°. В одной системе координат изобразите графики функ¬
ций, заданных формулами у — Зх и у — Зх — 2.
1.135. В одной системе координат изобразите графики функ¬
ций, заданных формулами:
1)	г/ = ух-2, у = {х + 2, у - -у х + 2, у = - |х - 2;
2)	у = 4х -1, у = 4х + 1, у = -4х + 1, у = -4х -1.
Назовите координаты точек пересечения каждого
графика с осями Ох и Оу.
1.136°. Изобразите в одной системе координат графики функ¬
ций:
1)	у= 5; г/ = — 5; у = 0;
2)	у = ~4; у = 4; у = -0.
1.137°. Верно ли, что функция, заданная следующей фор¬
мулой, является возрастающей на области опреде¬
ления:
1)	у = 4х - 10;
3)	у = -Зх-7;
5) I/ —15х;
7)	(/ = -11 + 4х;
_13х 4
9) у =	■
2)	у - -2х + 10;
4)	у - 5х - 6;
6) у = 18х;
8)	у = 8 - 7х;
10) 1/ = ^?
5

77	Линейная функция
1.138°. Верно ли, что функция, заданная следующей форму¬
лой, является убывающей на области определения:
1)	у = 0,2х —3;
2)	у = ~7,1х + 5;
5) у = 2,5х;
7) у = —4,9 - 5,2х;
9) у = 6-х;
2)	у = 0,Зх + 8;
4)	у = -3,9х + 25;
6) у = -4,7х;
8) у — -1,3 + 9,5х;
10) у = 5х —(10х— 1)?
1.139°. При каких значениях а функция, заданная формулой
у = ах + 3, будет:
1)	возрастающей на области определения;
2)	убывающей на области определения?
1.140°. При каком значении х равны значения функций, задан¬
ных формулами:
1)	у = 0,7х+ 14 и у = 0,2х- 1;
2)	у — -0,5х + 2,5 и у = —4,2х — 0,7;
3)	у = 1,6 - 0,8х и у = 2,4х + 1,2;
4)	у = 5,5 + 1,3х и у = 3,6 — 1,7х?
1.141°. При каких значениях х значения данной функции
а) положительны; б)	отрицательны:
1)	у - —1,5х + 3;	2)	у = 3,5х - 7;
3)	у = -6 + у х;	4)	у = -2х + 9,6;
5)	у = - у х - 4;	6)	у = |х + 2?
1.142.	Определите нули и
функции:
промежутки знакопостоянства
1)	у — -Зх + 15;
3)	у - 9 + 6х;
5)	у - 4х + 16;
7)	у = 25 - 50х;
2)	у = у х + 6;
4)	у = 4- 1,5х;
6)	у = 1,2х-3;
8)	у = ~18 + ух.
1.143.	Найдите координаты точек пересечения с осями Ох и
Оу графика функции, заданной формулой:
1)у = 0,6х—18;	2) у = 25 + 0,5х;
3)	у - 1,7х + 6,8;	4) у = -1,21х - 1,1.

Алгеб
1 Функции
1.144.	На рисунке 66 изображены прямые — графики линей¬
ных функций с областью определения й. Для каждой
78
Рис. 66
прямой напишите фор¬
мулу, задающую соот¬
ветствующую функцию.
1.145.	Найдите k и Ь, если
известно, что прямая
y = kx + b параллельна
прямой у = 2х и прохо¬
дит через точку:
1)	А(3; 10);
2)	С(-8; 4);
3)	; б);
4)	Р(1|;|).
1.146°. Верно ли, что график функции, заданной формулой
у = 2,7х - 8, параллелен графику функции:
1)	у = —2,7х + 3;	2) у = (-1)6 • 2,7х +	9;
3)	у = (—I)7 • 2,7х -	5;	4)i/ = 2,7x;
5)У = 1бх_2;	6)г/ = |^х + 1?
1.147.	Задайте формулой какую-нибудь линейную функцию,
график которой параллелен графику функции:
1)	у = 3,6х - 5;	2) у = —7,3х + 8;
3)	у - —4,4х - 2;	4) у = 6,2х + 3.
1.148.	Из функций у = 4х + 3, у — -4х + 3, у = -4x	3,
у^4х-3, у- -4х, у = -3, у = Зх - 4, у = Зх + 4, у = 4х,
у = Зх, у — — Зх — 4, у = — Зх + 4 выберите те, графики ко¬
торых:
1)	параллельные прямые;
2)	пересекающиеся прямые.
1.149.	Задайте формулой линейную функцию, график кото¬
рой пересекает ось Оу в той же точке, что и график
функции:

79
Линейная функция
1) у = -х — 3;	2) у = х + 5;
3)	у = 6х - 7;	4) у = -7х + 8.
1.150°. Найдите значение коэффициента а, если график функ¬
ции у = ах + 6 параллелен графику функции:
1) У = 2,8х;	2) у = -13,4х + 8;
3) у =-7,8х — 13;	4) у = 14,5.
1.151.	Графиком линейной функции является прямая, парал¬
лельная оси Ох и проходящая через точку:
1)	А(2; 7);	2) В(-15; -4);
3) С(6; -3,5);	4) £>(—100; 2).
Задайте формулой эту функцию и изобразите ее график.
1.152.	1) Функция задана формулой у = kx + 6,2. Найдите
значение k, если у = —3,2 при х = 10.
2)	Функция задана формулой у = 4,8х + Ь. Найдите
значение Ь, если у = 6,1 при х = -0,25.
1.153.	Функция задана формулой у = 4х + Ъ. Найдите значе¬
ние Ъ, если известно, что;
1)	при	значении	аргумента,	равном	2,	значение
функции равно 22;
2)	при	значении	аргумента,	равном	4,	значение
функции равно 3.
1.154.	Функция задана формулой y = kx + b. Известно, что ее
график проходит через точку В(-4; 2) и параллелен
графику функции у = 5х + 2. Изобразите график
заданной функции и укажите ее свойства.
1.155.	Функция задана формулой у = kx + b. Известно, что ее
график проходит через точку С( -4; -1) и параллелен
графику функции у = — Зх. Изобразите график заданной
функции и укажите ее свойства.
1.156*. При каких значениях а точка 1И(а; -2а) принадлежит
графику функции:
1) У = х;
ох   2	8
3)	y-ух-у;
_ 3	7
5)	у-ух-у;
2) у = -х;
4) у = -3,5х- 1;
6) у = 8х + 6?

Функции
80
1.157*. При каких значениях а точка #(а2; —2а) принадлежит
графику функции:
1)	2)у = -|-х;
3)у = -ух + 4;	4) г/ = -|-х-Ь 1у;
5)у-|х + 3;	6) у = - 1 у х -у ?
1.158*. При каких значениях а точка N(a~l; (а + 2)2) при¬
надлежит графику функции:
1)	у = -0,4х-0,6;	2) у = у х + 2~ ;
3)г/ = 6х + 13;	4) г/= —3,5х — 12?
1.159.	Изобразите график функции, заданной формулой на
множестве D; укажите ее нули, наибольшее и наимень¬
шее значения:
1)	у = | (8-х), D=[-5; 6];
2)	у = у (6-х), В=[-2; 8];
3)	у = —(—3 + х), D=[-4; 9];
4)	г/= —(—х — 5), Z) =[—6; 4].
1.13.	Функция у — | X I
Рассмотрим функцию у = | х
Областью определения этой функции является естественная
область определения выражения ] х |, т. е. множество R всех
действительных чисел, поскольку при любом значении
независимой переменной х существует, и притом единствен¬
ное, значение выражения | х |.
А как изобразить график функции у = | х |? Заметим, что
при неотрицательных значениях переменной х по определе¬
нию модуля | х | = х. Значит, при х > 0 этот график совпадает с
графиком функции у = х. Таким образом, при х > 0 графиком
функции у = | х | является биссектриса I координатного угла
(рис. 67).
При отрицательных значениях х по определению модуля
| х | = — х. Значит, при х < 0 график функции у — | х | совпадает

с графиком функции у = ~х. Таким образом, при х < 0 гра¬
фиком функции у = | х | является биссектриса II координатного
угла (рис. 68).
Итак, на множестве R всех действительных чисел для функ¬
ции у = | х | получается график, изображенный на рисунке 69.
Легко заметить по изображению графика, что если значе¬
ния аргумента отличаются только знаком, то соответству¬
ющие значения функции у = | х | равны, т. е. график функции
у = | х | симметричен относительно оси ординат. Это
свойство функции называется четностью.
Определение. Если значения функции, соответству¬
ющие любым двум противоположным значениям аргумен¬
та (т. е. значениям а и —а), равны между собой, то такая
функция называется четной.
Здесь, конечно, предполагается, что если число а при¬
надлежит области определения функции, то и число
-а принадлежит этой области определения, т. е. об¬
ласть определения четной функции должна быть
симметричной относительно нуля.
График любой четной функции симметричен относи¬
тельно оси ординат.
Например, на рисунках 55, 3) и 55, 4) изображены графики
четных функций. Четной является функция у = Ь (рис. 61).
Свойства функции у = kx нами изучены, а функция у = | х |
на промежутке (— ОО; 0] совпадает с функцией у = -х, а на
промежутке [0; + °°) совпадает с функцией у = х. Это дает
возможность установить свойства функции у = | х |.

WKg функции

Теорема (о свойствах функции у = | х |).
1.	Областью определения функции у = | х | является
множество R всех действительных чисел.
2.	Множеством значений функции у = \х\ является
промежуток [0; + 0°).
3.	Значение функции у = 0 является наименьшим,
наибольшего значения функция у = | х | не имеет.
4.	График функции у = | х | имеет с осями координат
единственную общую точку (0; 0) — начало координат.
5.	Значение аргумента х — 0 является нулем функции
У = I х
6.	Функция у = | х | принимает положительные значения
(у > 0) на множестве (- о°; 0) U (0; + о°), т. е. при х * 0 все
точки графика размещены в I и II координатных углах
(лежат над осью Ох).
7.	Функция у = | х | является четной.
8.	Функция у = | х | убывает от +“ до 0 на промежутке
(— оо; 0] и возрастает от 0 до + 00 на промежутке [0; + оо).
▲ Доказательство свойств 2—6 и 8 следует из свойств
прямой пропорциональности (см. п. 1.11).
Доказательство свойства 7. Пусть взяты противопо¬
ложные значения аргумента а и — а, тогда им соответствуют
значения функции | а | и | - а |. Но | а | — | -а |, и, таким образом,
значения функции, соответствующие любым двум противопо¬
ложным значениям аргумента, равны между собой, т. е.
функция четная. И ▲
Пр и м е р 1. На рисунке 70 изображены графики функций.
Какая из функций является: а) четной; б) нечетной; в) четной
и нечетной; г) ни четной, ни нечетной?
Решение, а) Четными являются функции, графики кото¬
рых изображены на рисунках 1), 2), 5), так как эти графики
симметричны относительно оси Оу.
б)	Нечетными являются функции, графики которых изоб¬
ражены на рисунках 2), 3), 6) (поясните почему).
в)	И четной, и нечетной является функция, график которой
изображен на рисунке 2) (поясните почему и задайте эту функ¬
цию формулой; какая у нее область определения?).

Функция у = | х | |!
83
Г
г)	Функция, график которой изображен на рисунке 4), не
является ни четной, ни нечетной (поясните почему).
1.	Как получить изображение графика функции у — | х | ?
2.	Изобразите график функции у = | х | и продемонстрируйте на нем
ее свойства.
3.	Какая функция называется четной?
4.	Сформулируйте свойство графика четной функции.
5.	Сформулируйте теорему о свойствах функции у = | х|.
6*. Докажите теорему о свойствах функции у = I х |.
Упражнения
1.160.	Можно ли функцию у — |х| задать формулой:
4) z/ = д/р;
1.161°. Принадлежит ли графику функции у — \х\ точка:
1)	А(-4; 4);	2) В(3; -3);	3) С(-12; 12);
4)	_D(2°; 1);	5) £((-2)5; 32);	6) К(43; (_2)6)?

84
Функции
1.162. Функция задана формулой у = |х - 1
1)	Найдите значение функции для каждого из значений
аргумента: -3; -2; -1; 0; 1; 2; 3.
2)	При каком значении аргумента функция принимает
значение: 0; 1; 2; 3; 12; 24; 49?
3)	При каких значениях аргумента функция принимает
положительные значения?
4)	При каких значениях аргумента функция принимает
неотрицательные значения?
5)	При каких значениях аргумента функция принимает
отрицательные значения?
1.163°. Изобразите график функции, заданной формулой на об¬
ласти определения D, и укажите свойства этой функ¬
ции, если:
1) у = |х|, £> = [-1; 4];	2) у = D = [-5; 2];
3) i/ = |x| + l,B = [-4; 4];	4) у = |х| - 2, D = [-3; 6].
1.164.	Найдите координаты точек пересечения графика функ¬
ции у = | х | с графиком функции, заданной формулой:
1) У = 6;
3) у = (-4)1 2;
5)	у = (-385,7)°;
7)	у = \/(-15)2;
2)	у = 1,2;
4)	z/ = (-3)3;
6)	у = (-0,734)°;
8)	У = \'(-3)2.
1.165.	При каких значениях а координаты точки удовлетво¬
ряют уравнению у -1 х | — 0:
1) Р(а2; -4а + 3);	2) М(а2; 7а - 12);
3)	К{2а2-, 6а + 8);	4) Т(3а2; -6а + 30)?
1.166*. Изобразите график функции и укажите ее свой¬
ства:
1) i/ = |x|;
4)	у = -\~х\;
2)	у = | -х|;
5)	I/ = 21 х |;
3)	I/ = — |х|;
6)	у = 0,51 х |;

Функция у = X2
7) у = -0,5| х|;
10) у = \ х~ 2 |;
8) у = -2|х|;	9) у = I х + 21;
11)	у = \х\~2;	12) у = |х| + 2.
1.167*. При каком значении а указанной формулой будет за¬
дана функция у = | х |:
1)	у = (а2 - 5а + 7) • | х |;
3)	у = (10 — а2) • | х |;
5)	У
7)	у ,|х|;
2)	р = (7а-а2-7)-|х|;
4)	у = (а4- 80)• |х|;
6) Р = (—д)_(а1~2)‘|х|;
8)р = ^-|х|?
1.14.	Функция у = х2
Рассмотрим функцию у — х2.
Ее область определения — это естественная область опре¬
деления выражения х2, т. е. множество R всех действитель¬
ных чисел, поскольку для любого значения независимой
переменной х существует, и притом единственное, значе¬
ние х2.
Чтобы изобразить график функции у = х2, придадим не¬
сколько значений аргументу и вычислим соответствующие
значения функции (см. таблицу):
X
0
±0,5
±1
±1,5
+2
±2,5
±3
У
0
0,25
1
2,25
4
6,25
9
Изобразим точки (х; у) с указанными координатами на
плоскости (рис. 71). Соединим эти точки плавной непрерывной
кривой. Эту кривую можно рассматривать как изображение
графика функции у = х2 (рис. 72).
График функции у = х2 называется параболой.

Функции
86
Теорема (о свойствах функции у - х2).
1.	Областью определения функции у-х2 является
множество R всех действительных чисел.
2.	Множеством значений функции г/ = х2 является про¬
межуток [0; +оо).
3.	Значение функции у = 0 является наименьшим, а наи¬
большего значения функция у = х2 не имеет.
4.	Парабола у — х2 имеет с осями координат единствен¬
ную общую точку (0; 0) — начало координат.
5.	Значение аргумента х = 0 является нулем функции.
6.	Функция у = х2 принимает положительные значения
на множестве (~°°; 0) U (0; +°°), т. е. все точки этой пара¬
болы, кроме начала координат, лежат выше оси Ох в I и II
координатных углах.
7.	Функция у = х2 — четная.

87
Функция у — х2 И
Изображение параболы позволяет наглядно представить
свойства, указанные в теореме. Разумеется, даже самый луч¬
ший рисунок не может служить доказательством.
На рисунке 72 видно, что парабола у — х2 имеет единствен¬
ную общую точку с осями координат — начало координат, а
остальные точки параболы лежат над осью абсцисс (свойства
4, 5, 6).
Множество значений функции
у — х2 — это проекция параболы на
ось Оу, а на рисунке 73 видно, что эта
проекция есть промежуток [0; +оо)
на оси Оу (свойства 2, 3). Это значит,
что для любой точки уА на оси Оу,
расположенной в верхней полуплос¬
кости, найдется такая точка хх на оси
Ох, что у у — Xi.
На рисунке 73 хорошо видно, что
найдутся даже две такие точки на
оси Ох: хх и х2.
Нетрудно заметить, что парабола симметрична относитель¬
но оси ординат (свойство 7).
Точка, в которой парабола пересекается со своей осью сим¬
метрии Оу, называется вершиной параболы, это начало коор¬
динат (0; 0).
Парабола у = х2 делится осью симметрии на две части; они
называются ветвями параболы. Принято говорить: «ветви па¬
раболы у = х2 направлены вверх».
▲ Приведем теперь доказательство теоремы о свойствах
функции у = х2, которое не опирается на изображение графика
функции.
Доказательство свойства 2. Функция у = х2 может
принимать только неотрицательные значения, т. е. только зна¬
чения из промежутка [0; +оо). Покажем, что она может при¬
нять любое значение b из этого промежутка при соответству¬
ющем значении аргумента.
Чтобы найти это значение аргумента, надо решить урав¬
нение	„
b — х .

Функции
88
Так как b > 0, то уравнение имеет два корня: - b и \Ь. При
каждом из этих значений аргумента значение функции рав¬
но Ь. И
Доказательство свойств 3 и 6. Так как у — х1 2 3 >0 при
любом значении х, то 0 — наименьшее значение функции. Кро¬
ме того, если мы возьмем любое положительное число а, то
всегда найдем такое число х, что будет верным числовое нера¬
венство х2 > а. Например, если а = 5, то значение х можно
взять 6 или еще большее. Ю
Свойства 4 и 5 легко проверить. Для этого надо в уравнение
у = х2 подставить соответствующие значения переменной х
(сделайте это самостоятельно).
Доказат е л ь с т в о свойства 7. Пусть значения аргумента
а и —а, тогда им соответствуют значения функции а2 и (—а)2.
Но а2 = (~а)2, и, таким образом, в точках а и -а функция у = х2
принимает одно и то же значение, т. е. она четная. Для гра¬
фика это означает, что парабола
симметрична относительно оси
ординат.
Действительно, если точка (а; Ь)
принадлежит параболе у = х2, т. е.
Ъ = а2, то и точка (~а; Ь) принадлежит
этой параболе, так как Ъ = (-а)2
(рис. 74).
Точки (а; Ь) и (-а; Ь) симметричны
относительно оси Оу. Значит, каждая
точка параболы у — х2 имеет на ней симметричную относитель¬
но оси Оу точку. Другими словами, парабола симметрична от¬
носительно оси Оу. И ▲
1.	Как называется график функции у = х2? Изобразите его.
2.	Продемонстрируйте свойства функции у-х2 на изображении
параболы.
3.	Сформулируйте теорему о свойствах функции у = хг.
4*. Докажите свойства функции у = х2.

89
Функция у = X1 2
1.168. Составьте формулу, выражающую зависимость значе¬
ния площади S закрашенной части фигуры от значения
радиуса круга R (рис. 75).
1.169. Составьте формулу, выражающую зависимость значе¬
ния площади S закрашенной части фигуры от значе¬
ния х (рис. 76).
Рис. 76
1.170°. Функция задана формулой у = х2. Сравните значения
функции при значениях аргумента, равных:
1)	-3 и -2;
4)	6 и -6;
7) -37,4 и 0;
10) -1 и 5;
2)	-4 и -5;
5)	2-| и2|;
8) 0 и -49,7;
11)	-3 и 7;
3)	-2 и 2;
6)	3| иЗу;
9)	28,7 и 0;
12)	12 и -8.

1.171“. При каком значении аргумента значение функции, за¬
данной формулой у = х2, равно:
1) 4;	2) 4 ;
3) 0,16;
4) 25;	5) 100;
6) 1,69?
!°. Какие из указанны
ции у = х2:
:х точек принадлежат графику функ-
1) А(-3; -9);
3) С(-1; 1);
5) F(12; 144);
7) Т(-6; -36);
9) N(9; 3);
11) F(-y6; -36);
2) В(3; 6);
4) ЛГ(—1,2; 1,44);
6) D(-13; 169);
8) Е(у/3; 3);
10) Р(~ 100; 10);
12) Q(yf7; у'49)?
>°. Укажите координаты точки, симметричной относитель¬
но оси Оу точке:
1) А(5; 25);
4) В(у'Б; 5);
7) Х(-4; -2);
10) В(2; -4);
2) В(-6; 36);
5) М(у6; 6);
8) Т(-7; -1);
11) F(3; -9);
3) С(13; 169);
6) Р(-1; 1);
9) 0(-1,5; 4,5);
12) N(20; 0).
1.174. Какие из указанных пар точек принадлежат графику
функции у = х2:
1)	А(-10; 100) и В(10; 100);
2)	М(-4; 32) и N(4; 32);
3)	С(—16; 4) и В (16; 4);
4)	-3) и Р(у'3; 3);
5)	Е(у[2 - 1; 3 -J<2) и Г(1 - у 2; 3 - 2у 2);
6)	+ yf2; 2у‘6 + 51 и Т(- <2 - <3; 2у 6 + 5)?
1.175°. Укажите абсциссы точек пересечения параболы, задан¬
ной формулой у = х2, с прямой:
1)	У =16;	2) у = 289;	3)у=196;
4)у = 100;	5)у = 5;	6) у = 7;
7)	у = 20;	8) у = 63.

91
1.176°. Пересекается ли график функции, заданной формулой
у — х2, с прямой:
1)	У = 63,7;	2) у = 29,1;	3) у = -5,2;
5) у = 0;
4) у = -8;
6) у = -0,0001?
1.177.	Изобразите график функции, заданной следующей фор¬
мулой, и укажите:
а)	область определения функции;
б)	множество значений функции;
в)	нули функции;
г)	промежутки знакопостоянства;
д)	координаты точек пересечения графика с осями Ох
и Оу.
1)	у - х(х + 4) - 4х;
2)	у = 5х - х(5 — х);
3)	у = (х - 9) (х + 9) + 81;
4)	у = 49 - (7 — х) (7 + х);
5)	у = (х - 2)2 - 4 + 4х;
6)	у — (х + З)2 - 6х - 9;
7)	у = (х + I)2 - 2(х + 2) + 3;
8)	у = (х - 2)2 + (х - 1) • 4.
1.178.	Изобразите график функции, заданной формулой у = х2
на множестве:
1) N-,	2) Z;
3)	всех четных чисел;
4)	всех нечетных чисел;
5)	[-1; 2];
7)	{-2; -1} U [0; 1];
9)	[-3; -1] U [1; + о°);
6)	[-3; 1];
8)	[-2; -1] U {0; 1};
10)	(-оо; -1] и [1; 2].
1.179*. Для функции у~х2 определите, при каких значениях
х значения функции: 1) меньше 9; 2) больше 4; 3) боль¬
ше 0; 4) меньше 16. Проиллюстрируйте результаты на
графике.

1.180.	На рисунке 77 изображены графики функций с симмет¬
ричной относительно нуля областью определения. Ка¬
кие из функций являются четными?
1.181.	Изобразите график функции и укажите ее свойства:
1)	у - (\'х2 - 2)2 + 2, если х € [2; 3];
2)	у = (д/х2 + 2)2 - 2, если х € [-2; 3];
3)	у - \Гх\ если х € [-3; 0];
4)	у = \1 х4, если х € [0; 3];
5)	у = рп + х2 + 1, если х € [-4; -1];
6)	у -	- 3 + х2, если х € [1; 3];
7)	у - х\! х2, если х > 0;
8)	у — х х2, если х < 0.
1.182*. Составив таблицу соответствующих значений х и у,
изобразите график функции и укажите ее свойства:
1) у = х2 + 2;	2) у - х2 + 3;	3) у = х2 - 3;
4) у = х2 - 2;	5) у = 3 - х2;	6) у = 2 - х2.

93
Функция у — х2: возрастание и убывание
¥
1.15.	Функция у = х2:
возрастание и убывание
Рассмотрим параболу у - х2 на про¬
межутке [0; +оо) (рис. 78). Представим
себе, что точка М(х; у) движется по ней
так, что ее абсцисса х увеличивается,
т. е. точка движется в направлении, вы¬
бранном на оси Ох,— слева направо.
Очевидно, что при таком движении ор¬
дината у точки М также будет увеличи¬
ваться, точка будет как бы «взбирать¬
ся» по параболе вверх.
Таким образом, при значениях х из промежутка
[0; + оо) большему значению х соответствует боль¬
шее значение у. Другими словами, функция у = х2 воз¬
растает на промежутке [0; +°о). Этот промежуток
называют промежутком возрастания функции
Рассмотрим теперь параболу у = х2
на промежутке (-°°; 0] (рис. 79). Пред¬
ставим себе, что точка Л1(х; у) движет¬
ся по ней так, что абсцисса х увеличи¬
вается, т. е. опять-таки слева направо.
Очевидно, что при таком движении
ордината у будет уменьшаться, точ¬
ка М будет как бы «скатываться» по па¬
раболе вниз.
Таким образом, при значениях х из промежутка
(-о®; 0] большему значению х соответствует мень¬
шее значение у. Другими словами, функция у = х2
убывает на промежутке (~°°; 0]. Этот промежу¬
ток называют промежутком убывания функции
Итак, теорему о свойствах функций у = х2 (см. п. 1.14) мож¬
но дополнить:

Функции
94
8. На промежутке	0] функция у = х2 убывает от
+оо до 0, а на промежутке [0; +°°) — возрастает от 0 до
+оо.
▲ Доказательство свойства 8 для промежутка
(-ОО; 0].
Пусть х2 > х1 — числа из промежутка (—°°; 0], т. е. неполо¬
жительные числа Им соответствуют значения функции
у2 = Хг, ух = х\. Надо доказать, что у2 < ух.
Рассмотрим разность у2~ у-,и определим ее знак:
у2 - ух = Хг - х? = (х2 - xj (х2 + хД
Так как х2> хр то х2 —Xj>0. По условию числа х2, хг
принадлежат промежутку (-°°; 0]. Значит, Xj < 0 и х2 < 0 (по¬
чему второе неравенство нестрогое?). Складывая эти неравен¬
ства, получаем х2 + х1 < 0.
Произведение положительного числа х2 — хг и отрица¬
тельного х2 + Xj есть число отрицательное, поэтому у2~у1-
= (х2 — xj (х2 + xj — отрицательное число. Следовательно,
у г < у р Значит, функция у ~ х2 убывает на промежутке
(-°°; 0].
Для промежутка [0; +°°) доказательство аналогичное —
проведите его самостоятельно. И ▲
Изучая в дальнейшем функции, мы будем указывать для
каждой из них:
1)	область определения;
2)	множество значений;
3)	наибольшее и наименьшее значения;
4)	точки пересечения графика с координатными осями;
5)	нули функции;
6)	промежутки знакопостоянства;
7)	наличие (либо отсутствие) четности, нечетности;
8)	промежутки возрастания, убывания.
Заметим, что когда предлагают найти промежутки
возрастания (убывания) функции, то принято указы¬
вать промежутки наибольшей длины.

95
Функция у = х2: возрастание и убывание И
Ж!
1.	Укажите для функции у — х2 промежуток:
а) возрастания;	б) убывания.
2.	На изображении параболы у = х2 поясните, почему промежуток
(-оо; 0] является промежутком убывания функции.
3.	На изображении параболы у = х2 поясните, почему промежуток
[0; +°°) является промежутком возрастания данной функции.
4*. Докажите, что функция у = хг:
а)	на промежутке (-<»; 0] убывает;
б)	на промежутке [0; +°°) возрастает.
Упражнения
1.183°. Функция задана графиком на рисунке 80. Укажите:
а) промежутки возрастания и б) промежутки убывания.
1.184°. Верно ли, что функция у — х2:
1)	возрастающая в области определения;
2)	убывающая в области определения;

Функции
96
3)	не является возрастающей в области определения;
4)	не является убывающей в области определения;
5)	возрастает на промежутке [5; 13];
6)	убывает на промежутке [-17; 1];
7)	возрастает на промежутке [-3; 10];
8)	убывает на промежутке [-29; -4]?
1.185°. Известно, что функция у = х2 задана на промежутке:
1) [2; 8];
2) [3; 7];
3) [-4;
0];
4) [-6; -1];
5) [-2; 5];
6) [-4;
3];
7) [-145; -21];
8) [69; 549];
9) [0; 49].
На каких из этих промежутков функция у =
х2:
а) возрастает;
б) убывает?
1.186.	Изобразите график функции, заданной формулой на
множестве D:
1)	у = (х - 5) (х + 2) + Зх + 10; D = [-1; 2];
2)	у = 7 + (х + 7) (х - 1) - 6х; D = [-3; 1];
3)	</ = ^; Р = [1; 2];
4)	1/ = ^^;7> = [-2; -1];
5)	у = V(x2 + 3)2-3; D = [0; 2];
6)	у = V(10 + x2)2- 10; D = [-3; 0];
7)	у = 7^7 + 4;2) = [“2: °];
8)	у = -+^5 + }Ох2 - 5; D = [-3; 0].
1.187.	По изображению графика функции из 1.186 укажите:
а)	множество значений функции;
б)	нули функции;
в)	промежутки знакопостоянства функции;
г)	промежутки возрастания;
д)	промежутки убывания.

Функция у — у/х
97
1.16.	Функция У =^Х
Рассмотрим формулу у - \х.
Выражение \/х имеет смысл только при неотрицательных,
значениях переменной х, его естественной областью определе¬
ния является промежуток [0; + °°). Для любого х из этого про¬
межутка существует, и притом единственное, значение ариф¬
метического квадратного корня — это число \Гх.
Таким образом, формула у = у'х задает функцию на проме¬
жутке [0; +оо).
Чтобы изобразить график функции у = у[х, придадим не¬
сколько значений аргументу х и вычислим (приближенно) со¬
ответствующие значения функции с помощью микрокальку¬
лятора или таблицы квадратных корней (см. таблицу):
X
0
0,5
1
1,5
2
2,5
3
3,5
4
4,5
5
5,5
6
У
0
0,7
1
1,2
1,4
1,6
1,7
1,9
2
2,1
2,2
2,3
2,4
Изобразим точки (х; у) с указанными координатами на
плоскости (рис. 81), соединим эти точки плавной непрерывной
кривой (рис. 82). Эту кривую можно рассматривать как изоб¬
ражение графика функции у = ух.
Теорема (о свойствах функции у = ух).
1.	Областью определения функции г/ = ух является мно¬
жество [0; +оо).
2.	Множеством значений функции у = yjx является мно¬
жество [0; +°°).

МИ^фУнк^и			п
3.	Значение функции у = 0 является наименьшим, а наи¬
большего значения функция у = у'х не имеет.
4.	График функции у = \Х имеет с осями координат
единственную общую точку (0; 0) — начало координат.
5.	Значение аргумента х = 0 является нулем функции
у = у'х.
6.	Функция у - ух принимает положительные значения
(у > 0) на промежутке (0; +°°), т. е. ее график расположен
в I координатном угле.
7.	Функция у = ух не является ни четной, ни нечетной.
8- Функция у = у[х возрастающая на области опреде¬
ления.
Изображение графика функции у = у х позволяет наглядно
представить свойства, указанные в теореме.
Множество значений функции у = \х — это проекция ее
графика на ось Оу. На рисунке 82 видно, что эта проекция есть
промежуток [0; +°о) на оси Оу (свойство 2). Таким образом,
для любой точки у1 на оси Оу, расположенной в верхней полу¬
плоскости, найдется такая точка xt на оси Ох, что у.. = у/х1
(рис. 83).
На этом рисунке видно, что график имеет единственную об¬
щую точку с осями координат — начало координат, а осталь¬
ные его точки лежат над осью абсцисс (свойства 3—6).
Таким образом, точка х = 0 является единственным нулем
функции, а на промежутке (0; + °°) функция у = \ Х принимает
только положительные значения.
Представим себе, что точка М(х; у) (рис. 84) движется по
графику функции у = у х так, что ее абсцисса х увеличивается,

Функция у = -Jx R
т. е. движется точка в направлении, выбранном на оси аб¬
сцисс,— слева направо. Очевидно, что ордината у при таком
движении точки также будет увеличиваться, значит, функция
у = у!х возрастающая (свойство 8).
▲ Приведем доказательства свойств, которые не опирают¬
ся на изображение графика функции.
Доказательство свойств 2 и 3. По определению значе¬
ния арифметического квадратного корня являются неотрица¬
тельными числами. Поэтому функция у = у’х может принимать
только неотрицательные значения, т. е. только значения из
промежутка [0; + °°); значит, число 0 — наименьшее значение.
Покажем, что у может принять любое значение Ъ из этого
промежутка при соответствующем значении аргумента.
Чтобы найти это значение аргумента, надо решить урав¬
нение	—
Ь = уХ.
Корнем данного уравнения является число Ь2. При этом зна¬
чении аргумента значение функции равно Ъ. И
Доказательство свойств 4, 5. Подставив в формулу
у = ух соответствующие значения переменной х, получим нуж¬
ные утверждения (убедитесь в этом).
Свойство 6 следует из свойств 4 и 5.
Доказательство свойства 7. Функция у = у'х не явля¬
ется четной и не является нечетной, поскольку ее область опре¬
деления несимметрична относительно нуля. И
Доказательство свойства 8. Когда увеличиваются зна¬
чения переменной х, то увеличиваются и значения у'х. В самом
деле, пусть числа хр х2 принадлежат промежутку [0; +°°), при¬
чем х2 > хг и у1 = \х1, у2 = \х2. Рассмотрим разность у2 — уг и
определим ее знак.
\Х2 \Хд)(<Хд+ \Х,)

улу + \Х,
- (уХг?-(\Х1)г - хг-х,
\Х2 + ух^	\.£ + уХ^
В этой дроби числитель х2 - хг — положительное число, так
как х2 > хР Знаменатель дроби у х2 + у хг — положительное чис-

функции	122
ло, поскольку \ix1 > 0, \ х2 > 0 (почему первое неравенство
нестрогое, а второе — строгое?). Следовательно, дробь
— — положительное число, т. е. разность у2~ У1 — поло-
д/х2 + ух,
жительное число. Значит, у2 > уг, т. е. функция у — \х возра¬
стает на промежутке [0; +<»). И ▲
1.	Изобразите график функции у = \ х.
2.	Сформулируйте теорему о свойствах функции у = \х.
3.	Продемонстрируйте на изображении графика функции у = \ix
ее свойства.
4 Докажите свойства функции у = \х.
Упражнения
1.188°. Составьте формулу зависимости площади поверхности
куба S от длины его ребра а. Найдите длину ребра куба,
зная, что площадь его поверхности равна: 36 см2; 96 см2;
150 см2; 30 м2.
1.189°. Площадь круга с радиусом г вычисляется по формуле
S = лг2. Составьте формулу зависимости радиуса г от
площади S. Найдите радиус круга, если площадь круга
равна: 25л см2; 64л см2; 0,01л см2; 90л м2.
1.190°. Используя график функции у - ^х (см. рис. 82), найди¬
те приближенное значение функции, если значение ар¬
гумента равно: 1,2; 3,6; 4,9; 6,7; 0,1; 1,8; 2,5; 3,9.
1.191°. Используя график функции у = ух (см. рис. 82), найди¬
те приближенное значение аргумента, если значение
функции равно: 0,6; 1,5; 1,8; 0,7; 2,2; 2,4.
1.192°. Функция задана формулой у = \х. При каком значении
функции значение аргумента равно: 4; 25; 49; 100; 625;
1000; 0,64; 0,81; f; 2,25; 2,89;
1.193°. Функция задана формулой у = \х. При каком значении
аргумента значение функции равно: 9; 14; 19; 0,1; 1,5;
4 7. 9Q. J_ . о А. . А . А 9

Функция у = -/х g
101
1.194°. Принадлежит ли графику функции у = ух точка:
1)	А(25; 5);	2) В(49; -7);
3)	С(0,25; 0,5);	4) .0(100; 10);
5)	М(-16; —4);	6) T(10 000; 100);
7) Е(-9; 3);	8) tf(-4; 4);
9) 0(0; 0);	10) Р(1; 1);
И) F(-l; -1);	12) Q(12; 144)?
1.195°. Пересекает ли график функции у = \[х график функции:
1)	У ~3,4;	2) у = 0,2;	3) у = -2,9;
4)г/ = 2,5;	5) у = 0;	6)y = S?
1.196°. Функция задана формулой у = \х. Сравните значения
функции, соответствующие значениям аргумента:
1)	5 и 6;
3)	0,2 и 0,1;
5)	6,2 и 6,3;
7) 91,2 и 90,2;
2)	8 и 10;
4)	0,3 и 0,4;
6)	9,5 и 10;
8) 145,7 и 142,9
1.197°. Изобразите график функции, заданной формулой у = ^х
на множестве:
1)	N; 2) {0; 2; 4; 6; 8}; 3) (1; 3; 5; 7; 9}; 4) Z;
5)	[0; 1]; 6) [1; 4]; 7) [0; 1) U (1; 4]; 8) [1; 4) U (4; 9].
1.198°. Укажите свойства функции и изобразите ее график,
если она задана следующей формулой на множестве D:
1)	z/ = (yx + l)2-(x + l)-yx, D = [1; 9];
2)	у = 5ух + (у'х - 2)2 - (х + 4), D = [0; 16];
3)	^ = 6^’D = [4; 16 *Ь
16]-
1.199. Может ли функция, заданная формулой у = ух, прини¬
мать значение, равное:
1) 344;
3)	т3, если т < 0;
5)	~р15, если р = -(136,7)°;
6)	р18, если р = (-263,4)°?
2) 127;
4) 4т4, если т 0;

М
Функции
102
1.200*. Найдите значение а, при котором графику функции
у = \ х принадлежит точка:
1)	М(а - 3; 4);
3) М(аг + 3а; 2);
5) М(2а2 + а + 3; а + 5);
7)	М(4 + 2а - а2; 2 - а);
2)	М(а + 6; 5);
4)	М(а2 + 6а; 4);
6)	М(2а2 - 7а + 5; а -1);
8)	М(6-4а-а2; -а-4).
1.201*. Составив таблицу соответствующих значений хну,
изобразите график функции и укажите ее свойства:
1)	У = \‘X + 3;
3)	у = у'х -2;
5)	у = 2 - у х;
7)	у = \~х;

9)	г/ = 3 - у-х;
2)	у = ух + 2;
4)	у = \х-3;
6)	у = 3 ~ ух;
8)	у = - \-х£
10)	у = 2 + у -х.
1.17.	Функция у — х3
Рассмотрим функцию у = х3.
Областью определения этой функции является естественная
область определения выражения х3, т. е. множество R всех
действительных чисел, поскольку для любого значения неза¬
висимой переменной х существует, и притом единственное,
значение выражения х3.
Чтобы изобразить график функции у = х3, придадим не¬
сколько значений аргументу и вычислим (приближенно) соот¬
ветствующие значения функции (см. таблицу).
X
-2
-1,5
-1
-0,5
0
0,5
1
1,5
2
У
-8
-3,38
-1
-0,13
0
0,13
1
3,38
8
Изобразим точки (х; у) с указанными координатами на
плоскости (рис. 85, а), соединим эти точки плавной непрерыв¬
ной кривой (рис. 85, б). Эту кривую можно рассматривать как
изображение графика функции у = х3.
График функции у - х3 называется кубической параболой.

103
Функция у = х3 И
--6-
• —8-
Рис. 85
Теорема (о свойствах функции у = х3).
1.	Областью определения функции у = х3 является мно¬
жество R всех действительных чисел.
2.	Множеством значений функции у = х3 является мно¬
жество R всех действительных чисел.
3.	Функция у = х3 наименьшего и наибольшего значений
не имеет.
4.	Кубическая парабола пересекает оси координат в
единственной точке (0; 0) — начале координат.
5.	Значение аргумента х — 0 является нулем функции
у = х3.
6.	Функция у = х3 принимает отрицательные значения
(у < 0) на промежутке (-°°; 0) и положительные значения
(у > 0) — на промежутке (0 +°°), т. е. кубическая парабола
расположена в I и III координатных углах.
7.	Функция у = х3 нечетная.
8.	Функция у = х3 возрастающая на области опреде¬
ления.

Функции	104
Все эти свойства функции у — х3 легко рассмотреть на изоб¬
ражении ее графика аналогично тому, как это сделано для
функций у = х2 и у = \ х.
В частности, график функции у = х3 симметричен отно¬
сительно начала координат.
Докажем это. Действительно, если
точка (а; Ь) принадлежит кубической
параболе у = х3, т. е. Ь = а3, то и точка
(-а; —Ь) принадлежит этой кубичес¬
кой параболе, так как -Ь = (-а)3
(рис. 86).
Точки (а; &) и (-а; -6) симметрич¬
ны относительно начала координат.
Значит, каждая точка кубической па¬
раболы у = х3 имеет на ней симмет¬
ричную относительно начала коорди¬
нат точку. Другими словами, куби¬
ческая парабола симметрична относи¬
тельно начала координат. И
Не опираясь на изображение графика, так же, как в пре¬
дыдущих пунктах, можно доказать свойства 4, 5, 6, 7, 8. Но
для доказательства свойства 2 необходимо понятие куби¬
ческого корня, с которым мы познакомимся в старших
классах.
▲ Самостоятельно выполните следующие задания.
а)	Рассмотрите свойства 4—8 функции у = х3 на изоб¬
ражении ее графика. Проведите рассуждения подобно
тому, как это сделано для других функций в пунктах
1.11—1.16.
б)	Укажите нули и промежутки знакопостоянства функции
у = х3.
в)	Докажите свойства 5 и 6 для функции у = х3
г)	Докажите свойство 7 подобно тому, как это сделано
в 1.11.
д)	Докажите, что функция у = х3 возрастающая (свой¬
ство 8).

Докажем свойство 3. Так как функция у = х3 возрастающая,
то при любом а имеем: а3 < (а + I)3. Следовательно, а3 не явля¬
ется наибольшим значением функции. И ▲
1.	Как называется график функции у = х3? Изобразите его.
2.	Сформулируйте теорему о свойствах функции у = х3.
3.	Продемонстрируйте на изображении кубической параболы ее
свойства.
4*. Докажите свойства функции у = х3.
Упражнения
1.202°. Используя изображение графика функции у = х3 (см.
рис. 85, б), найдите:
1)	приближенное значение у, если х равно: -1,7; -1,6;
-1,2; 0; 1,4; 1,8;
2)	приближенное значение х, если у равно: —6; —3,5;
-1,4; 0; 1,6; 2,8; 3,6.
1.203°. Используя изображение графика функции у = х3 (см.
рис. 85, б), сравните:
1) 0,83 и 1;
3' HPHf
5) (—2)3 и (~1,5)3;
1.204. Используя свойства функции у = х3, расположите в по¬
рядке возрастания числа: (-1,3)3; 0,43; (—1,6)3; 0,523;
(—1,5)3; 0,33; 1,23.
1.205°. Принадлежит ли графику функции у — х3 точка:
1) А(1; 1);	2) В(-2; 8);	3) С(-3; -27);
4)	D(5; 125);	5) М(-4; 64);	6) ЛД6; 216)?
1.206.	Укажите какое-нибудь значение аргумента, при кото¬
ром значение функции у — х3 больше: —2; —1; 0; 1; 2; 3.
1.207.	Укажите какое-нибудь значение аргумента, при кото¬
ром значение функции у = х3 меньше: 4; 3; 1; 0; —3; —4.
1.208.	Оцените значение выражения х3, если:
1)1<х<2,5;	2)~1<х<2;
3)	-2<х<0;	4) 0 < х < 3.

1.209.	Точка Q(m; ri) принадлежит графику функции у = х3.
Принадлежит ли графику этой функции точка:
1)	А(~т; -п);
3)	С(т; —п);
5)	Р(3т; 27п);
7)	#(0,1т; 0,001п);
2)	В(~т; п);
4)	D(n; т);
б>мНт;-<И
8)	т(-1у7п; -3-|п)?
1.210.	Укажите свойсть-а функции и изобразите ее график,
если функция задана формулой на множестве D:
1)	у = (х - 1) (х2 + х + 1) + (-14)°, D = [-2; 2];
2)	у = (х + 3) (х2 - Зх + 9) - З3, D - [0: 2];
3)	г/= (х — I)3 + 3(х + 1) (х - 2) + 7, Р = [-1; 2];
4)	у = (х + 2)3 - 6(х + 3) (х + 1) + 2(6х + 5), D = [-3; 1].
1.211.	При каком значении а графику функции у = х3 при¬
надлежит точка:
1)	К(2а+ 1; 8а3 + 18а + 1);
2)	К(а - 2; а3 + За2 + 11а + 5);
3)	#(а-1; а3-4а2 + За);
4)	К(3~2а; 11 - 6а - 8а3)?
1.18.	Обратная пропорциональность
Определение. Обратной пропорциональностью
называется функция вида
_ k
У--,
где k & 0 — число.
Переменная у называется обратно пропорциональной пере¬
менной х, а число k — коэффициентом обратной пропорцио¬
нальности.
Так как область определения функции не указана, то по до¬
говоренности (см. п. 1.4) — это естественная область определе-
k
ния выражения — , т. е. вся числовая прямая, кроме точки

107
Обратная пропорциональность И
Ж
х = 0. Для любого значения независимой переменной х 0 су-
k
ществует, и притом единственное, значение выражения —.
Теорема 1. Если переменная у обратно пропорцио¬
нальна переменной х с коэффициентом k, то переменная х
обратно пропорциональна переменной у с тем же коэффи¬
циентом k.
▲ Доказательство. Переменная у обратно пропор¬
циональна переменной х с коэффициентом k, т. е. у —	, k 0.
Тогда
ху = k, k * 0.
Значит, у*0 и, следовательно,
х — —, k 0.
у
А это означает, что переменная х обратно пропорциональна
переменной у с коэффициентом k. S ▲
Замечание. Доказанная теорема позволяет говорить, что пере¬
менные х и у (или у и х) обратно пропорциональны.
Обратная пропорциональность переменных х и у означает,
что их произведение постоянно и не равно нулю, т. е. зависи¬
мость между ними выражена формулой ху — k(k 0).
Теорема 2. Если переменные х и у обратно пропорци¬
ональны, то для их соответствующих значений верны ра¬
венства:
У± =х2.
У> х1 ’
1
б)
У'2	1
х2
т. е.
У1 ' У 2 х ■
*1
Х2
k
Доказательство, а) Пусть у = — , где /г^О. Если хр
м	k	k
х2 — два значения переменной х и уг ——, у2 -—, то
X]	х2
k
Pl - X, _ X,
Уг k_ ", '
Х2

IM^E^ Функции	108
б)	Пусть у = у, где к # 0. Если х2 — два значения пере¬
менной
и У1=~’ У2=~г> то
Х1 Х2
k 1
- =-т-=-т--
Уг А ±
Хг Х2
Таким образом, если переменные х и у обратно про
порционалъны, то значения ух и у2 прямо пропорцио¬
нальны числам — и — , т. е. у, : у2 = — : — .
X] Х-2	X, Х2
Пример 1. Переменныер и q обратно пропорциональны.
Найти р4, зная, что qY = 84, q2 = 42, р2 — 73.
Решение. Поскольку pviq обратно пропорциональны, то
<71 —Рг	ЧгРг 42 • 73	73 ос с
- = - и, значит, р,	=—^— =тг = 36,5.
7г Pi	7!	84	2
Ответ: 36,5.
Пример 2. Функция задана таблицей:
а
0,25
4
12
50
70
75
ь
20
1,25
5
12
0,1
1
14
1
15
Являются ли переменные Ъ и а обратно пропорциональ¬
ными?
Решение. Переменные будут обратно пропорциональны,
если Ьа = к, где к^О — постоянная. Вычислим произведение
соответствующих значений переменных b и а:
Ьгаг = 20 • 0,25 = 5;	= 1,25 • 4 — 5; Ь3а3 = • 12 = 5;
64а4 = 0,1 • 50 = 5; Ь5а5 = -^ • 70 = 5;	Ь6а6■ 75 = 5.
Ответ: переменные а и b обратно пропорциональны, так
как значения произведения ab — постоянны.

Обратная пропорциональность fi
109
Пример 3. Известно, что среди 26 кг конфет количество
мармелада, зефира и ириса обратно пропорционально числам
2, 3 и 4 соответственно. Сколько конфет каждого сорта?
Решение. Способ 1. Пусть мармелада было тп кг, зе¬
фира — р кг, ириса — t кг. Так как их массы обратно пропор¬
циональны числам 2, 3 и 4, то получим:
2т = 3р = 4t.
2 1
Отсюда легко найти, что р = -& т, t--^m. Так как всего
было 26 кг конфет, то т + р + t - 26, т. е.
т + -£-т + -^т = 26,
М1+1+4 )=26’
т = 26-™, т = 12.
Следовательно, р = 8 кг, t = 6 кг.
Ответ: 12 кг мармелада, 8 кг зефира, 6 кг ириса.
Способ 2. Согласно равенству б) из теоремы 2 для реше¬
ния задачи можно разделить 26 кг конфет прямо про-
порционально числам	.
Пусть мармелада т кг, зефира р кг, ириса t кг. Поскольку
их массы обратно пропорциональны числам 2, 3 и 4, то эти
массы прямо пропорциональны числам	. Таким об¬
разом, получим:
пг-р '■ t =
1_ . 1 . 1 _ 12 . 12 .12
2	3	4	2	3	4
= 6 : 4 ■ 3.
(Частное чисел не изменится, если каждое число умножить
на 12.) Итак, имеем: = -£• = -j- = k, где k — коэффициент про¬
порциональности. Тогда мармелада 6k кг, зефира 4k кг, ириса
3k кг. Так как всего 26 кг конфет, то получим уравнение
6k + 4k + 3k = 26; откуда k - 2.

222
Значит, т = 6k - 6 ■ 2 = 12 (кг), р = 4/г = 4- 2 = 8 (кг),
t = 3k = 3- 2 = 6 (кг).
Ответ: 12 кг мармелада, 8 кг зефира, 6 кг ириса.
1.	Какая зависимость называется обратной пропорциональностью?
2.	В каком случае переменная у называется обратно пропорцио¬
нальной переменной х?
3.	Как называется число k в формуле у =	, если k -л О?
4.	Будут ли обратно пропорциональными переменные х и у, если
обратно пропорциональны у и х?
5.	Что означает обратная пропорциональность переменных х и у?
6.	Сформулируйте свойство соответствующих значений обратно
пропорциональных переменных х и у.
Упражнения
1.212°. Найдите значения функции, заданной формулой у = — ,
если х принимает значения: -25; -10; -5; -1; 1; 5;
10; 25.
1.213°. Функция задана формулой у = -	. Найдите значения
у, если х принимает значения: -12; —6; -4; -3; -1; 1;
3; 4; 6; 12; 24.
1.214.	Найдите время t, которое необходимо для преодоления
расстояния в 900 км, если скорость поезда v равна:
30 км/ч; 40 км/ч; 45 км/ч; 60 км/ч.
1.215.	Маятник стенных часов делает 198 качаний за 3,3 мин.
Составьте формулу зависимости числа качаний маятни¬
ка Р от времени t. Определите количество качаний,
которое совершит маятник за: 3 мин 12 с; 5 мин 20 с;
6 мин 40 с; 10 мин 25 с.
1.216°. Обратная пропорциональность задана формулой у =	.
1)	Найдите значение функции, если значение аргумен¬
та равно: —100; —50; —30; —10; 5; 10; 60; 90; 120; 180.
2)	Найдите значение аргумента, если значение
функции равно: —240; —120; -90; -60; -30; -1; 1; 10;
60; 180.

111
Обратная пропорциональность П
1.217. Функция задана таблицей. Являются ли переменные х
и у обратно пропорциональными?
X
1
2
4
10
40
У
20
10
5
2
0,5
X
2
3
6
8
12
У
12
8
4
3
1
X
1
3
4
6
8
У
-1
-5
—7
-11
-15
X
-4
-з
—2
6
12
У
3
4
6
— 2
-1
1.218°. Принадлежит ли графику функции У~^ точка:
1)А(-5;-4);	2)в(-1;-±);
3)	С(40; 2);	4) Z>(25; f );
5)	-40);	6)m(|;7o)?
1.219°. Точка М(а; Ь) принадлежит графику функции
1)	Укажите значения а, если соответствующие значе¬
ния b равны: —6; —3; -2,4; 8; 12; 48.
2)	Укажите значения Ь, если соответствующие значе¬
ния а равны: -24; —8; —4; —0,5; 3; 6; 36.
1.220.	Точка Р(т; и) принадлежит графику функции У = ^ •
Принадлежит ли графику этой же функции точка:
1) А(~т; -п);
3) С(тп; -п);
5) тфт; |п);
2) В(~т; п);
4)	В(п; т);
6) м(-|т; -Зп)?
1.221.	Задайте функцию формулой, если известно, что она яв¬
ляется обратной пропорциональностью и значению ар¬
гумента, равному а, соответствует значение функции,
равное Ь:
2) а=|, Ь=12;
4) а — 15, Ь = 90.
1) а = 6, Ь = 3;
3) а = 0,1, Ь = 50;

функци-и	и?
1.222.	1) Переменные pwq обратно пропорциональны. Найди¬
те значение если р2 = 5, q^ = 3, q2 = 6.
2) Переменные тип обратно пропорциональны.
Найдите значение mv если т2 = 10, пг — 8, п2 = —4.
1.223.	1) Команды трех разных школ, участвуя в городских
спортивных соревнованиях, заняли 2, 3 и 5-е места и
набрали вместе 868 очков. Сколько очков набрала каж¬
дая команда, если известно, что число набранных очков
обратно пропорционально местам, занятым этими ко¬
мандами?
2) 286 калькуляторов разделили между тремя школа¬
ми, занявшими 1, 2 и 3-е места в районной математи¬
ческой олимпиаде. Сколько калькуляторов получила
каждая школа, если их число обратно пропорционально
месту, занятому командой?
1.224.	1) Число 680 разделите на три части обратно пропорци¬
онально числам 4-, ~	.
2	4	6
2) Число 1325 разделите на три части обратно
Q R 19
пропорционально числам — , — ,	.
1.225.	1) В четырехдневном походе турист был в движении
45 ч, проезжая ежедневно одно и то же расстояние, при
этом скорости его движения относились как 8 ■ 4 ■ 12 :6
(по дням движения). Сколько времени он был в
движении в каждый из четырех дней?
2) Три трактора одной мощности, находясь на поле одно
и то же время, вспахали 39 га. Сколько вспахал каждый
трактор, если время, затраченное на устранение не¬
исправностей во время работы каждого трактора, прямо
пропорционально числам 3; 4; 2?
1.226.	1) Для оклеивания стен помещения могут быть полно¬
стью использованы обои любого из трех узоров. Один
рулон обоев каждого из узоров покрывает соответствен¬
но площади: 4 м2, 6 м2 и 8 м2. Всего имеется 611 рулонов.
Сколько рулонов каждого узора?

113
Г рафик и свойства функции у =— (к 0)
2) В автобусном парке 60 автобусов трех типов: вме¬
стимостью 10, 50 и 75 человек. Вместе все 10-местные
автобусы парка за один рейс могут перевезти столько
же пассажиров, сколько все 50-местные или все 75-ме¬
стные. Сколько автобусов каждого типа в автобусном
парке?
1.19.	График и свойства функции у =— (k * 0)
Рассмотрим функцию у = — с областью определения
(-оо; 0) и (0; 4-ОО).
Чтобы получить представление о ее графике, поступим как
обычно: придадим несколько значений аргументу и вычислим
соответствующие значения функции. Сделаем это сначала для
положительных значений х и запишем результаты в таблицу.
X
0,5
1
1,5
2
2,5
3
3,5
4
4,5
5
5,5
6
У
6
3
2
3-
2
5
6
1
6
7
3
4
2
3
3
5
6
11
1
2
Изобразим точки (х; у) с указанными координатами на
плоскости (рис. 87). Соединим эти точки плавной непрерывной
кривой. Эту кривую можно рассматривать как изображение
графика функции У~~ при положительных значениях х
(рис. 88).
Рис. 87
Рис. 88

фун^ии:
Придадим аргументу несколько отрицательных значений и
составим таблицу соответствующих значений х и у:
X
-6
-5,5
-5
-4,5
—4
-3,5
-3
-2,5
—2
-1,5
-1
-0,5
У
1
2
6
11
3
5
2
3
3
4
6
7
-1
6
5
3
2
— 2
-3
-6
з
Изобразим график функции у-— при отрицательных
значениях х (рис. 89).
Объединяя на одном рисунке изображения графиков функ-
3
ции у — — при положительных и отрицательных значениях
аргумента, получаем изображение графика этой функции
(рис. 90).
Рис. 89
а
Таким образом, график функции у = — представляет собой
кривую, состоящую из двух ветвей, расположенных в I и
III координатных углах.
Если тем же способом изобразить графики функций
k	1
= — при k = ~2 , fe=l, А = 6, то легко убедиться, что каж¬
дый раз будет получаться похожая кривая, состоящая из
двух ветвей, расположенных в I и III координатных углах
(рис. 91).

Изображения графиков функций у - — при k = - -у ;
k = — 1, k~~6 будут расположены во II и IV координатных
углах (рис. 92).
Кривая, являющаяся графиком функции у = —, k О,
называется гиперболой.
k
Теорема (о свойствах функции У = ~ , А 0).
k
1.	Областью определения функции У = ~ (А 0) явля¬
ется множество всех действительных чисел, кроме х = 0
(т. е. х 0).
k
2.	Множеством значений функции у = — (А 0) явля¬
ется множество всех действительных чисел, кроме у = 0
(т. е. у^О).
3.	Наименьшего и наибольшего значений функция
k
У~~ (А т5 0) не имеет.
4.	Гипербола У~~ (А ^0) не пересекает координатных
осей.

	!1£
k
5.	Функция у = — (ft 5й 0) не имеет нулей.
6.	Функция у — — (ft > 0) принимает отрицательные зна¬
чения (у <0) на промежутке (—°°; 0) и принимает
положительные значения (с/>0) на промежутке (0; +°°),
т. е. ветви гиперболы располагаются в I и III координатных
углах.
Функция У~~ (ft < 0) принимает отрицательные значе¬
ния (у <0) при х € (0; +оо) и принимает положительные
значения (г/> 0) при х€(—оо; 0), т. е. ветви гиперболы
размещаются во II и IV координатных углах.
7.	Функция у - (ft 0) — нечетная.
8.	Функция у — — (ft > 0) на каждом из промежутков
(—оо; 0) и (0; +оо) является убывающей.
k
Функция у = — (ft < 0) на каждом из промежутков
(-оо; 0) и (0; +оо) является возрастающей.
Изображение гиперболы позволяет наглядно представить
£
эти свойства. На рисунке 93, где изображена гипербола у = —
(k > 0), видно, что она не пересекает осей координат, одна ветвь
гиперболы лежит в I координатном угле, а другая — в III
(свойства 4, 5, 6).
k
Множество значений функции у — — (ft > 0) (см. рис. 93) —
это проекция гиперболы на ось Оу. На рисунке видно, что эта
проекция есть вся ось без начала координат (свойство 2), т. е.
для любой точки j/j 0 на оси Оу найдется такая точка на
k
оси Ох, что уг = — (см. рис. 93).
*1
Нетрудно также заметить, что гипербола симметрична от¬
носительно начала координат (свойство 7).
Рассмотрим гиперболу у = (ft > 0) на промежутке (-оо; 0)
(рис. 94). Представим себе, что точка М(х‘, у) движется по
ней так, что асбцисса х увеличивается, т. е. точка М дви-

117
___	к
Г рафик и свойства функции у =— (к 5* 0)
Рис. 94
жется в направлении, выбранном на оси Ох,— слева направо.
Очевидно, что при таком движении ордината у будет умень¬
шаться, точка М будет как бы «скатываться» по гиперболе
вниз.
Таким образом, при значениях х из промежутка (-оо; 0)
большему значению х соответствует меньшее значение у.
k
Другими словами, функция у = — (к > 0) убывает на проме¬
жутке	0), что и отмечено в свойстве 8; на этом
промежутке она убывает от 0 до -оо.
Рассмотрим теперь гиперболу у = (k > 0) на промежутке
(0; +оо) (рис. 95). Представим себе, что точка М(х; у) движется
по ней так, что абсцисса х увеличивается, т. е. движется точка
М опять-таки слева направо. Очевидно, что при таком
движении ордината у будет уменьшаться, точка и здесь будет
как бы «скатываться» по гиперболе вниз.
Таким образом, при значениях х из промежутка (0; +оо)
большему значению х соответствует меньшее значение у.
k
Другими словами, функция у = — (к > 0) убывает на проме¬
жутке (0; +оо),— это также отмечено в свойстве 8; на этом
промежутке она убывает от +оо до 0.
▲ Приведем доказательства этих свойств, которые не опи¬
раются на изображение графика функции.
k
Доказательство свойства 2. Функция У = ~ (к ^0)
может принимать только значения, не равные нулю. Покажем,
Функции	118
что она может принять любое значение р 0 при соответ¬
ствующем значении аргумента. Чтобы найти это значение
аргумента, надо решить уравнение Р = ~ ■ Корнем этого урав¬
нения является число у. При этом значении аргумента
значение функции равно р. И
Свойство 3 непосредственно следует из свойства 2.
Свойства 4, 5 являются непосредственными следствиями из
свойств 1 и 2.
Доказательство свойства 6. Так как для точки (х; у)
k
на гиперболе у = — (k > 0) имеем ху — k > 0, то значения х и
у — это числа одного знака, т. е. точка (х; у) лежит в I или
III координатном угле. Ю
Доказательство свойства 7. Пусть значения аргумента
а и —а. Тогда им соответствуют значения функции и
k k
— =~~^ , они отличаются только знаком, т. е. являются про¬
тивоположными числами, следовательно, функция
(k 0) — нечетная. Ю
Для графика это означает, что гипер¬
бола симметрична относительно начала
координат (рис. 96). Докажите это само¬
стоятельно аналогично тому, как это сде¬
лано в п. 1.17.
Доказательство свойства 8. Дока-
k
жем, что функция у = — (k > 0) убывает на
промежутке( о°; 0). Пустьхр х2С(-°о; 0),
т. е. Xj и х2 — отрицательные числа, и
пусть х2 > хР
Рассмотрим разность у2 — ух и определим ее знак:
_	_ k_ _ k_ _ kXj kx2 _ A(x, -x?)
У2 Vt X2 Xi хгх2	XiX2
Так как x2 > xv то xx < x2 и, значит, хг — x2 < 0. Кроме того,
Xj и х2 — отрицательные числа, значит, их произведение
у х’ h
k>0 b
\(a;b)
/ \
-a j
’ 1
Оа X
-Ь
Рис
96

119
Г рафик и свойства функции у =— (к * 0)
положительно. По условию k >0, значит, разность у2 — уу =
к(хг -х2)
Х1*2
— отрицательное число. Следовательно, у2 < у у
Итак, для любых хг и х2 из промежутка (-оо; 0), если
х2 > Ху то у 2 < у у А это как раз и означает, что функция У ~~
(k >0) убывает на промежутке (-оо; 0). KI
Убывание этой функции на промежутке (0; +оо) дока¬
зывается аналогично. (Сделайте это самостоятельно.)
£
Заметим, что функция у = — (k > 0) — убывающая на
промежутке (—°°; 0) и убывающая на промежутке
(0; +оо). Но о ней нельзя сказать, что она убыва¬
ющая на всей области определения. На рисунке 97
х2 > хг и в то же время у2 > Уу
Аналогично свойства 1—8 можно обосновать для функции
у-4 ^<0)‘
£
По рисунку 98 поясните, почему функцию У = ~ (А < 0)
нельзя назвать возрастающей на всей области опреде¬
ления.
Поясните, как на рисунках 99, 100 проиллюстрированы
£
свойства 2 и 7 функции у = — (k < 0).

120
1.	Как называется график функции у = — (Л 0)?
2.	Сформулируйте и докажите свойства функции:
а) У = у (Л > 0);	б) у = ~ (Л <0).
k
3.	Используя изображение гиперболы у = — , продемонстрируйте
свойства соответствующей функции при: a) k > 0; б) h < 0.
Упражнения
15
1.227°. Принадлежит ли графику функции у = - — точка:
1)	А(-1; 15);	2) В(3; 5);
3) С(10; -1,5);	4) £>(—0,5; 30);
5)	; 45);	6) м(-|;-2б)?.
1.228°. 1) Функция задана формулой	Изобразите
график функции, предварительно заполнив в тетради
таблицу:
X
-8
-4
-2
-1
1
2
4
8
У
5
2) Функция задана формулой у = - — . Изобразите
график функции, предварительно заполнив в тетради
таблицу:
X
-10
-5
— 2
-1
1
2
5
10
У

121
Г рафик и свойства функции у —— (к 0)
О
1.229°. Используя изображение графика функции У=~ (см.
рис. 90), найдите:
1)	приближенное значение функции, если значение
аргумента равно: -6; —3; -1; 3; 6;
2)	приближенное значение аргумента, которое соответ¬
ствует значению функции: 6; 3; 1; -1; —3; -6.
1.230°. Для функции у = - найдите:
1)	значение функции, которое соответствует значению
аргумента: -8; -6; -3; 2; 4; 9;
2)	значение аргумента, которое соответствует значению
функции, равному: -10; —4; -2; -1; 2; 4; 6; 8.
1.231°. Задайте формулой обратную пропорциональность, если
известно, что ее график про¬
ходит через точку:
1)	4(12; 24); 2) В(-26; -13;);
3)	С(-30; 15); 4) Л(25; -5).
Изобразите график этой функ¬
ции и укажите ее свойства.
1.232°. На рисунке 101 изображен
график зависимости длины Ъ
прямоугольника с постоянной
площадью S от ширины а.
1) Какова ширина прямоуголь¬
ника, если длина равна: 2 см,
1,5 см, 4 см, 8 см?
2)	Какова длина прямоугольника, если ширина его рав¬
на: 1,5 см, 2,5 см, 4,5 см, 6,5 см?
3)	Каково значение площади прямоугольника 8?
1.233. Изобразите график функции, заданной формулой У ~~
на множестве:
1) N;
3)	{-5; -2; 2; 5; 6};
2) Z, х^0;
4) [-5; -1];

122
Функции
5) [|; 5);	6) {-4;-2;-1};
7) (-10; -5) U [1; 2);	8) [-5; 0) U (0; 10].
1.234*. Изобразите график функции, заданной формулой, и
укажите ее свойства:
1)
У =
	48	.
(2х - З)1 2 - (2х + З)2 ’
80 .
(5х-2)2-(2 + 5х)2’
_ х2 + 1 + 2х 12
У 6х+6	' х2+х’
2)
(х 5)2
25х 5х2 ‘
1.235. Известно, что графики функций
у--|- и у = kx + b
проходят через точку:
1)А(-1;-1);	2) _В(—1; 1);
3) С(-3; 1);	4) Z>(1;-5).
Найдите k и b.
1.236. При каких значениях а график обратной пропорцио¬
нальности, заданной формулой у =	, расположен в I и
III координатных углах, если:
1) k = 2а~ 12;
3) k = 5 - 10а;
5) k = | а | — 1;
2) k = 4а + 1;
4) k - 1,2 — 3,6а;
6) k = | а + 21 - 3?
1.237. При каких значениях а график обратной пропорцио-
k
нальности, заданной формулой у - — , расположен во II
и IV координатных углах, если:
1)	/? -= 12а- 1;
3) k = 1,4 -4,2а;
5)	k -1 а | - 4;
2)	k — 6 + За;
4)	/? = 3,9а-7,8;
6) k = | а - 11 - 5?
1.238. Найдите а, если графику функции У = ^г принадлежит
точка:
1)	К(а - 2; а - 1);	2) К(а + 2; а - 2,6);
3)	#(а-0,5; а + 3);	4) к(а - 4; а - 6-|-).

Системы уравнений
с двумя переменными
2.1.	Уравнения с двумя переменными
Определение. Равенство, содержащее две перемен¬
ные, называется уравнением с двумя переменными.
Переменные в уравнении называются также неизвест¬
ными.
Вот примеры уравнений с двумя неизвестными:
3х-р = 13;	(1)
3х-у*=13.	(2)
Формулы, которые задают различные функции |у = ух;
Р = х3; у ; у-Тх-3 и т. д.^, также являются примерами
уравнений с двумя переменными.
Отметим, что уравнение с двумя переменными описывает
определенную зависимость между этими переменными.
Определение. Упорядоченная пара значений неиз¬
вестных, при которых уравнение превращается в верное
числовое равенство, называется решением уравнения с
двумя неизвестными.
Например, упорядоченная пара (1; -10) является решением
уравнения (1). (Будем также писать х = 1, у — ~ 10.) Упоря-

J Системы уравнений с двумя переменными 124
доченная пара (у; 0^ тоже является решением этого урав¬
нения.
Упорядоченная пара (5; д/2) является решением уравнения
(2). Упорядоченная пара (7; —2 у[2) также является решением
уравнения (2).
Заметим, что термин корень уравнения применяется
только к уравнениям с одним неизвестным. Термин
решение уравнения применяется к уравнениям как с
одним неизвестным, так и с несколькими неизвест¬
ными.
Определение. Два уравнения с двумя неизвестными
называются равносильны ми, если каждое решение первого
уравнения является решением второго, и наоборот —
каждое решение второго уравнения является решением
первого, т. е. они имеют одни и те же решения.
Равносильными считаются и уравнения, которые не
имеют решений.
Например, уравнения
Зх — у = 13 и у = Зх — 13
равносильны (они имеют одни и те же решения), а уравнения
(1) и (2) такими не являются.
Уравнения
х2 + у2 = -1 и х2 + Зу2 = -1
тоже равносильны (они не имеют решений).
При решении уравнений с двумя неизвестными использу¬
ются те же свойства, что и при решении уравнений с одним
неизвестным.
1.	Если к обеим частям уравнения прибавить или из обеих
частей уравнения вычесть одно и то же число, то получим
уравнение, равносильное данному.
2.	Если обе части уравнения умножить или разделить на
одно и то же число, отличное от нуля, то получится уравне¬
ние, равносильное данному.

125	Уравнение с двумя переменными
Из первого свойства следует:
если в уравнении перенести слагаемое из одной части в дру¬
гую с противоположным знаком, то получится уравнение,
равносильное данному.
Пример 1. Решить уравнение с двумя переменными:
а)	2х2 + у2 = 0;
б)	4(х - 8)4 + (5 + у)2 = 0;
в)	х6 + 7у2 = -5.
Решение, а) Поскольку при любых значениях пере¬
менной х имеем 2х2 > 0 и при любых значениях переменной у
имеем у2 > 0, то уравнение а) обращается в верное числовое
равенство только тогда, когда х = 0 и у — 0.
Ответ: (0; 0).
б) Равенство 4(х - 8)4 + (5 + у)2 = 0 обращается в верное
числовое равенство только при х — 8 = 0 и 5 + у — 0.
Откуда имеем х = 8 и г/ = — 5.
Ответ: (8; -5).
в)	Поскольку левая часть равенства х6 + 7у2 принимает
неотрицательные значения при любых значениях пере¬
менных х и у, то принять значение —5 она не может.
Ответ: нет решений.
П р и м е р 2. Решить уравнение с двумя переменными:
а) 2х + у = 3;
б) Зх — 2у = 6.
Решение, а) Левая часть данного равенства может
принимать значение 3 в бесконечном количестве случаев,
например, когда х = 1 и у = 1, или х — 0 и у - 3, или х = 3 и
у = -3 и т. д.
Пусть t — некоторое действительное число (t ё Я). Подста¬
вив вместо переменной х в данное уравнение число t, получим
уравнение с одной переменной (с одним неизвестным) у:
2t + y = 3.
Откуда найдем значение у:
у = 3 — 2t.
Говорим, что мы выразили у через t из уравнения 2t + у = 3.

Системы уравнений с двумя переменными 126
Решением уравнения а) будут все упорядоченные числовые
пары вида (t; 3 - 2t).
Ответ: (?; 3 — 2t), где t € R.
б)	Способ 1. Пусть t&R. Подставив в уравнение б) вместо
х число t, получим уравнение 3t - 2у - 6, откуда вырасим у че-
.	6 -3t
рез t: у = —у .
Ответ:	уу^,где?€/?.
Способ 2. Пусть t QR. Подставив в уравнение б) вместо
у число t, получим уравнение Зх- 2t — 6, откуда
6 ' 2t
У = ~з~-
Ответ: ( 6	, где teR,
1.	Сформулируйте определение уравнения с двумя переменными.
2.	Что называется решением уравнения с двумя неизвестными?
3.	Можно ли решения уравнения с двумя неизвестными назвать
корнями уравнения?
4.	Какие два уравнения с двумя неизвестными называются равно¬
сильными?
5.	Могут ли равносильные уравнения не иметь решений?
6.	Перечислите преобразования уравнений, которые позволяют из
данного уравнения получать равносильное ему уравнение.
У пражнения
2.1°. Верно ли, что упорядоченная пара:
1)	(1; 3) — решение уравнения х + 2у = 7;
2)	(3; -1) — решение уравнения Зх~у = 10;
3)	(0; 15) — решение уравнения 7х + х = 15;
4)	(5; 3) — решение уравнения Зх - 5у = 0;
5)	(0; 0) — решение уравнения 5х + 8у = 0;
6)	^4; — у ) — решение уравнения 5у~7х = 21?
2.2°. Является ли решением уравнения 4х + Зу = 14 пара
чисел:
1)	х = 2, у = 3;
2)	х = 5, у = 0;

127
Уравнение с двумя переменными
3) х = 5, у = —2;
х 14 4t
5) x = t, у = —^—;
4)	х = 2,5, у = 1у ;
6) х = х0, у = 14 - 4х0?
2.3°. Укажите по три упорядоченных пары (х; у), удовлетво¬
ряющих уравнению:
1)	х-у = 0;	2)	х + у= 1;
3)	2х~7у — 3;	4)	5х — Зу = 4;
5)	0 • х + Зу = 6;	6)	4х + 0 • у = 0;
7)	у+-з=1;	8)	= 1;
9)f+|- = l;	10)f+f = -l.
2.4.	Равносильны ли уравнения:
1)	2х +Зу = 7 к у = ~ (7-2х);
2)	Зх + 2у = 9 и у = -|- - -|- х;
3)	5х - 8у = 6 и у =	(5х - 6);
4)	7х — 5у = 12 и у =	(7х — 12);
5)	7х - 4у = 3 и х = 3+74^;
6)	5х + Зг/ = 6 и х = 6 /У ;
7)	х2 + у2 + 25 = 0 и т/х + \1у +	= 0;
8)	I х + у | +1 х -у\ = -10 и д/(2х + У)2 + 36 = О?
2.5°. Выразите у через х из уравнения:
1) 2х + бу = 25;	2)	7х - 14у = 10;
3) 6х + 11у = -48;	4)-5х —14у = 8;
5)	8х + 7у = 3;	6)	9х + 5у = 2;
7)	9х — бу = 17;	8)	12х~ 9у = 8;
9)	10x4- 13у = 16;	10) 8х + 9у = 15.
2.6.	Запишите в общем виде решения уравнения упражнения
2,5.	Укажите решение этого уравнения, если:
1)х = 2;	2)х = -5;	3) х=р.

Системы уравнений с двумя переменными 128
2.7.	Решите уравнение:
1)	(2х - 7)2 + (Зг/ + 2)2 = 0;
2)	(4х + 5)2 + Q/-6)2 = 0;
3)	18х + 161 + I у + 41 = 0;
4)	|Зх-9| + |5г/- 151 = 0;
5)	у'х + 5 + | у - 1 | = 0;
6)	yjx~ 2 +1у +- 5 | = 0;
7)	х2 + г/2 + 10 = 2х + 6i/;
8)	х2 + г/2 + 34 = 10х - 6г/;
9)	л/2х - 7 + (у + 4)2 = -5;
10)	| 29х + 471 + (5г/ - 29)2 = -1.
2.8.	Является ли упорядоченная пара чисел (1; 0) решением
уравнения:
1)	I X — 1 | + 2 | у | = —1;
3) х2 + у2 - 1 = 0;
2)1^1 + 11^1 = 1;
4)	ху + х = 3?
2.2.	График уравнения с двумя переменными
Определение. Графиком уравнения с двумя пере¬
менными называется множество всех точек на координат¬
ной плоскости, координаты которых являются решениями
этого уравнения.
Очевидно, что графики равносильных уравнений сов¬
падают
Пример 1. Рассмотрим уравнение
Зх — 2у = 6.
Выразим из него у через х:
_ 3 о
У~~2 х_3-
(1)
(2)
Уравнения (1) и (2) равносильны, поэтому их графики сов¬
падают.
Теперь заметим, что формула (2) задает линейную фун¬
кцию, а график этой функции и график уравнения (1) — это

Г рафик уравнения с двумя переменными $
129
одно и то же множество точек на координатной
плоскости. Графиком линейной функции (2)
является прямая, изображенная на рисунке
102. Значит, эта прямая является графиком
уравнения (2), а следовательно, уравнения (1).
Поэтому уравнение (1) есть уравнение
прямой.
Пример 2. Рассмотрим уравнение
Ох - 2у = 6.	(3)
Оно равносильно уравнению у = ~3; по¬
этому графиком уравнения (3) является пря¬
мая, параллельная оси Ох (она изображена на
рисунке 103).
Пример 3. Рассмотрим уравнение
Зх - Оу = 6.	(4)
Оно равносильно уравнению х — 2; поэтому
графиком уравнения (4) является прямая,
параллельная оси Оу (она изображена на
рисунке 104). Заметим, что график уравнения
х + Оу = 2 с двумя переменными не является
графиком какой-либо функции (поясните
почему).
Определение. Линейным уравнени¬
ем с двумя неизвестными называется
уравнение вида
ах + by = с,
где а, Ь, с — числа, х ту — неизвестные.
Рис. 104
Примерами линейных уравнений с двумя неизвестными
являются уравнения (1), (2), (3), (4). Мы уже отмечали, что
уравнениями с двумя неизвестными (с двумя переменными)
являются и формулы изученных нами функций: у — х2; у = х3;
у=л]х; y = —(k^O) и т. д. Соответственно графики этих
функций являются и графиками, например, таких уравнений
с двумя переменными, как у - х2 - 0; Зу — Зх3 = 0;
2 (у - vx + 0,5) = 1; xy = k(k* 0).

Системы уравнений с двумя переменными
130
Пример 4. Изобразить график уравнения:
а)	Зх - 2у = Эх - 5у + 12;
б)	Зу - Зх3 = 0;
в)	2[у~\[х + 0,5J = 1;
г)	1 - ху = 0.
Решение, а) Перенесем (изменив соответственно знаки)
все слагаемые с переменной у в левую часть, а все остальные —
в правую:
~2у + 5у = 9х - Зх + 12;
| после приведения подобных членов, получим у
Зу — 6х + 12;
разделив обе части уравнения на 3, получим |
у = 2х + 4.
/Т"
т '
; -

- -4-
_ _ j

— L
.	—,
J_
. 1 . ...
	! -
Г 1'
L.
-1х
I '
/. ' 1
I -
Рис. 105
Теперь можно изобразить график данной
линейной функции — это прямая, которая
проходит через точки (—1; 2) и (0; 4)
(рис. 105).
б)	Выразим из данного уравнения перемен¬
ную у:
Зу — Зх3;
У = Xя.
Графиком этого уравнения является куби¬
ческая парабола (см. п. 1.17, рис. 85, б).
в) Выразим из данного уравнения переменную у.
г/- Vx + 0,5 = у ;
у = д/х-0,5 +-|-;
Изображение графика арифметического квадратного корня
нам известно (см. п. 1.16, рис. 82).
г) Выразим переменную у из данного уравнения, получим
Графиком этого
(см. п. 1.19, рис. 91).
уравнения является
гипербола

131
Г рафик уравнения с
▲ Пример 5. Изобразить график уравнения:
а)	(х + З)2 + (у - 8)4 = 0;
б)	х2 - у2 - 0.
Решение, а) Данному уравнению удовлетворяет только
одна упорядоченная пара чисел: х = — 3 и у = 8 (поясните
почему), значит, графиком этого уравнения является един¬
ственная точка (—3; 8) (рис. 106).
Рис. 106
б) Представив данное уравнение в виде
(х + у)(х — у) = 0,
можно увидеть, что его левая часть принимает значение 0, если
либо х + у — 0, либо х - у = 0.
Таким образом, график этого уравнения состоит сразу из
двух прямых у = — х и у = х (рис. 107). Обратите внимание:
уравнение не задает функцию (объясните почему). ▲
1.	Что называется графиком уравнения с двумя переменными?
2.	Приведите пример уравнения с двумя переменными, графиком
которого являются:
а) парабола; б) прямая; в) гипербола.
3*. Верно ли, что график уравнения с двумя переменными всегда
совпадает с графиком некоторой функции?
У пражнения
Изобразите график
(2.9—2.13).
2.9°. 1) Зх - 2у = 4;
3) f +f = 2;
уравнения с двумя переменными
2) 5х- г/= 4;
4) A +JL = !•
7 3	4	’

Системы уравнений с двумя переменными
132
5)	Зх + 2у = 5;	6) 4х + Зу = 2;
7)	0,5х - 0,Зу = 0,7;	8) 0,2х + 0,1 у = 0,6.
2.10°. 1) 6х + Зу = Зх - 12у + 5;
2)	7х - 2у - 6 = 4х - 2у - 1;
3)	2(х + у) - 10 = 8(х ~у) + 15х — у;
4)	5 - 6х = 3 (х — у) + 4(у — х) — 8;
3	5	15 ’
пч х-У-1 _ о = х + у + 5 +2L-JL
4	2	8	16 •
2.11.	1) 5(х - у) - 4(2х — Зу) = 3(2у — х);
2)	6(2х - Зу) - 3(3х - 2у) = 2 (х - бу),
3)	з(4 X-1|v)+2(y х+{?) =
= 4(у х-2у у);
4> f	+ 1 (тх+^) =
= у (у - 6х).
2.12.	1) 0-х + 5у = 10;
3)	4х + 0 • у = —8;
5)	у = ~5;
7)	х = 3;
2.13.	1) ху = 5;
3)	х2-у = 0;
5) у -|х| = 0;
7) у - х3 = 0;
9) ху 3 = 0;
2)	0 • х - Зу = 9;
4)	6х — 0 • у = 12;
6)	у = 5;
8)	х = -7.
2)	ху = -2-,
4)	vx -У = О;
6)	У - \Гх2 = 0;
8)	х-у = 0;
10)	4 —ху = 0.
В одной системе координат изобразите графики уравнений и
укажите координаты их точки пересечения (если она есть)
(2.14—2.15).
2.14.	1) 5х + Зу = 1 и 10х + бу = 2;
2)	2х + Зу = 2 и 6х + 9у = 4;
3)	2х — Зу — 1 и —4х — 2у = 3;

Системы двух линейных уравнений
с двумя неизвестными
133
4)	4х — 7у = 3 и —12х + 21i/ = 9;
5)	Зх — 4у = 3 и —6х + 8у = 5;
6)	5х + 2у = 2 и -Зх - 4i/ = 1.
2.15. 1) у — I х I = 0 и у - у'х - О;
2)	у - х3 = О и у - \/х2 = О;
3)	у - х2 = О и 4у - 2х = О;
4)	х3-у = 0иу = ~2;
5)	4i/ - д/16х2 = О и О • у + 4х = 8;
6)	\l25x2 - 5у = О и О • х - бу — 12.
2.3.	Системы двух линейных уравнений
с двумя неизвестными
В задачах, которые рассматривались в этой и предыдущей
главах, зависимость между переменными описывалась одним
уравнением. Но очень часто зависимость между двумя пере¬
менными описывается при помощи нескольких уравнений.
В таких случаях говорят о системе уравнений с двумя пере¬
менными. Переменные в уравнениях называют также неиз¬
вестными.
Обычно уравнения системы записывают в столбик одно под
другим и объединяют фигурной скобкой.
Примеры систем уравнений с двумя неизвестными х и у:
а) !2* + У = 4-
[х - Зу = -5;
[2х+у = 4,
\2х + у = 4;
|3x-2i/=3,
lx2 + ху = 4.
в)
2x + i/ = 4,
2х + у = 5;
Определение. Упорядоченная пара значений неиз¬
вестных, которые одновременно обращают каждое уравне¬
ние системы в верное числовое равенство, называется ре¬
шением системы.
Например, пара чисел (—1; —3), т. е. х = —1, у = -3, являет¬
ся решением системы г) (убедитесь в этом), но не является ре¬
шением ни одной из систем а) — в).

Системы уравнений с двумя переменными 134
Определение. Решить систему уравнений — это
значит найти все ее решения или доказать, что их нет.
Проще всего решить систему двух линейных уравнений с
двумя переменными, которую записывают в общем виде так:
fa,x+ Ь,у = с:,
\а2х + Ь2у = с2,
где ар Ьр ср а2, Ь2, с2 — числа.
Примерами систем линейных уравнений с двумя неизвест¬
ными х и у являются системы а) — в), а система г) к ним не
относится (поясните почему).
Определение. Две системы уравнений называются
равносильными, если каждое решение первой системы яв¬
ляется решением второй, и наоборот — каждое решение
второй системы является решением первой, т. е. они имеют
одни и те же решения.
Равносильными считаются и системы, которые не
имеют решений.
Теорема. Если одно из уравнений системы заменить
равносильным ему, то полученная система будет равносиль¬
на исходной.
Доказательство этой теоремы приводить не будем, но отме¬
тим, что она, вместе со свойствами 1 и 2 из п. 2.1, даст нам
возможность решать системы уравнений.
Система — слово греческого происхождения и в пе¬
реводе означает «составленное из частей», «соеди¬
нение».
Пример 1. Равносильны ли системы уравнений:
I 4х - бу = 10,
[Зх + Чу = 13
2х - Зу = 5,
Зх + Чу — 13;
[2х-Зг/=5,
[Зх+ Чу = 13
5,
?
7

Системы двух линейных уравнений
с двумя неизвестными
135
Решение, а) Уравнение 4х — бу = 10 получено из урав¬
нения 2х - Зу - 5 умножением его обеих частей на число 2,
значит, по свойству 2 из п. 2.1, эти уравнения равносильны.
Таким образом, по теореме предложенные системы равно¬
сильны.
13 Зх
б) Уравнение у — —?— получилось из уравнения
3x + 7i/ = 13 в результате следующих действий: сначала из
левой части в правую перенесли слагаемое Зх, изменив знак
на противоположный, а потом разделили обе части на число 7.
На основании следствия из свойства 1 и свойства 2 получи¬
ли равносильное исходному уравнение (см. п. 2.1). Следова¬
тельно, по теореме, данные системы равносильны.
Пример 2. Обосновать, что не являются равносильными
системы
2х + у = 3,	\у = 3 — 2х,
хг-уг = 4(х + у) И [х-у = 4.
Решение. Пара чисел (3; —3), т. е. х = 3, у = -3, является
решением первой системы, но не является решением второй
системы, значит, эти системы не равносильные.
1.	Что описывается системой уравнений с двумя переменными?
2.	Как записывают систему двух линейных уравнений с двумя пе¬
ременными?
3.	Что называется решением системы уравнений с двумя неизвест¬
ными?
4.	Что значит решить систему уравнений с двумя неизвестными?
5.	Какие две системы уравнений называются равносильными?
6.	Могут ли равносильные системы не иметь решений?
У пражнения
2.16°. Верно ли, что упорядоченная пара чисел (х0, i/0) является
решением системы:
[х + 2у = 5,	d „
1)	если х0=1, i/0 = 2;
(2х + у = 4,
[Зх - у = 6,	,	.
2)	„	„ если х0 = -1, у0 = 4;
|4х + 2у — 7,

3)
Системы уравнений с двумя переменными
136
4)
х + у = 12,
х - у = 2,
если х0 =11, уй = 1;
(2у - Зх = 1,
[Зх + 5у = 34,
если х0= 5, t/0 = 8;
j7x-3i/ = 4,
[2х + у = ~2,
(бх~5у=3,
[х + 2у = 8,
если х0 = 3, у0 = —2;
если х0 = 2, у0 — 3?
2.17°. Подберите какие-либо два решения системы уравнений:
[х + у = 3,	(х~ 2у= 1,
[,2х + 2у = 6;	[Зх - бу - 3;
fх = у,	\и = - 2х,
3)	4) Р 2
[у = х ;	[у = х .
2.18°. Дана система уравнений:
а)Р = 3 + 2!'-	5)Р = 8+2!/’
18у-4х = -12;	(2у- 4х = 5.
Верно ли, что ее решением является упорядоченная пара
чисел:
1)	(1;-1);	2) (-2; -2,5);
3) (5; 1);	4) (1; 5);
5)	(-1; -2);	6) (1; -3)?
2.19. Обоснуйте (устно), что система
4х - у = 5,
Зх + 8у = 11
равносиль¬
на каждой из следующих систем уравнений:
(4х = 5 + у,
[Зх = 11 - 8у;
3)	fy=4x-5,
[ 81/ = 11 - Зх;

Системы двух линейных уравнений
с двумя неизвестными
137
5)
12х — Зу — 15,
—12х — 32у = —44;
[ 32х ~8у = 40,
[Зх + 8у= 11.
2.20. Равносильны ли системы уравнений:
х + 5у = 7,	[х = 7 - 5у,
х - Зу = -1	[х - Зу = -1;
Зх + 2у = 10,	J 9х + бу = 30,
5х + Зу = 12	[10х + бу = 24;
3)
3(х - 1) = 4у + 1,
5(у - 1) = х + 1
и
Зх - 4у - 4 = О,
х = 5у - 6;
ГЗх + 2у = 10,
[5х + Зу = 12
_ 10-Зх
у

5х + Зу = 12;
“^3	, j[x = 3y + 6,
*+214У = 4 5 И [х = 9 - 14у;
6)
3	4	1
и
х + 5у = 48,
7х + у = 11?
2.21°. Выразите у через х и х через у в уравнении:
1) х + 2у = 8;
3) 5х — у = 3;
5)	2х — Зу — 7;
2)	х + у = 4;
4)	х + 2у = 4;
6)	5у + Зх = 2
2.22. Найдите значения тип, если известно, что решением
х — 2у = т,
системы <	являются:
[2х — у = п
1) х = 4, у = — 1;
3)	х = 0, у = 3;
5)	х = 9, у = 0;
2) х = -3, у = 1;
4)	х = -2, у = — 4;
6)	х = 8, у = -у.

Системы уравнений с двумя переменными
138
2.4.	Системы двух линейных уравнений
с двумя неизвестными:
геометрическая иллюстрация
Рассмотрим систему двух линейных уравнений с двумя не¬
известными
aix + biy = ci,
а2х + Ь2у = с2.
Будем считать, что хотя бы один из коэффициен¬
тов bY не равен нулю и что хотя бы один из коэффициен¬
тов а2, Ъ2 не равен нулю. Тогда каждое уравнение систе¬
мы (1) является уравнением прямой.
V
L:. Zjfc'
/ 1
/ 1
L	Ю
I 1lT"‘
j '
*4/ i
i +rf	-
i.. ■


Рис. 108
Если координаты точки М(х0; у0)
удовлетворяют первому уравнению
системы (1), то точка М лежит на
прямой, которая определяется пер¬
вым уравнением. Если координаты
точки М(х0; у о) удовлетворяют вто¬
рому уравнению системы (1), то точ¬
ка М лежит на прямой, которая
определяется вторым уравнением.
Значит, если координаты точки М
удовлетворяют обоим уравнениям
системы (1), т. е. (х0; у0) — решение этой системы, то точка М
лежит на обеих прямых (рис. 108).
Наоборот, если точка М(х0; г/0) лежит на обеих прямых, оп¬
ределяемых уравнениями системы (1), то ее координаты
(х0; у0) удовлетворяют каждому уравнению системы, т. е.
являются решением системы.
Приведем три примера — они соответствуют трем возмож¬
ным случаям взаимного расположения прямых, определяемых
уравнениями системы.
Пример 1. Рассмотрим систему
2х + у = 4,
x-2i/= 7.
(2)

Системы двух линейных уравнений с двумя
неизвестными: геометрическая иллюстрация
139
На координатной плоскости (рис.
109) изображены прямые, определяе¬
мые уравнениями системы (2). Мы ви¬
дим, что эти прямые пересекаются в
точке М(х0; у0), где х0 = 3, у0 = ~2.
Значит, система (2) имеет единствен¬
ное решение х0 = 3, у0 = -2.
Пр и м е р 2. Рассмотрим систему
2*+!/=4,	(3)
6х + Зу = 2.
На координатной плоскости (рис.
110) изображены прямые, определяе¬
мые уравнениями системы (3). Мы ви¬
дим, что эти прямые параллельны и
не совпадают. Значит, система (3) не
имеет решений.
Пример 3. Рассмотрим систему
f2x + i/=4,
[бх+ Зу = 12.
Уравнения системы (4) равносиль¬
ны (второе уравнение получается из
первого умножением на 3), значит, их
графики совпадают, т. е. это одна и та
же прямая (рис. 111). Координаты
любой точки М (х0; у0) на этой прямой
являются решением системы (4). Зна¬
чит, система (4) имеет бесконечно
много решений. Пусть х0 = t, тогда ре¬
шения имеют вид (t; 4 - 2t), где teR.
Таким образом, рисунки 109, 110,
111 позволяют судить о числе реше¬
ний системы двух линейных уравне¬
ний с двумя неизвестными. Возмож¬
ны три случая.
Рис 111

Системы уравнений с двумя переменными 140
1.	Система имеет единственное решение, когда прямые,
определяемые уравнениями системы, пересекаются.
2.	Система не имеет решений, когда прямые, определяе¬
мые уравнениями системы, параллельны и не совпадают.
3.	Система имеет бесконечно много решений, когда пря¬
мые, определяемые уравнениями системы, совпадают.
Судить о числе решений системы двух линейных
уравнений с двумя неизвестными можно и не прибе¬
гая к геометрической иллюстрации. Из разобранных
примеров видно, что случаи 2 и 3 имеют место, когда
коэффициенты при неизвестных в уравнениях систе¬
мы пропорциональны. Если при этом свободные чле¬
ны и коэффициенты при неизвестных не пропорцио¬
нальны, то система не имеет решений. А если свобод¬
ные члены и коэффициенты при неизвестных пропор¬
циональны, то система имеет бесконечно много реше¬
ний. В случае 1 коэффициенты при неизвестных не
пропорциональны.
Когда в системе (1) все коэффициенты при неизвестных и
свободные члены отличны от нуля, это можно записать так:
1.	Система (1) имеет единственное решение, когда
(2 2
(Это условие можно записать в виде
агЬ2 - а2Ьх О,
не накладывая при этом на коэффициенты никаких ограни¬
чений.)
2.	Система (1) не имеет решений, когда
ai _ b_i с,
^2 ^2 ^2
3.	Система (1) имеет бесконечно много решений, когда
Д1 	bi 	Ci
а2 Ь2 сг ’
Замечание. Графики уравнений можно использовать и для ре¬
шения систем. Однако следует помнить, что решение при этом, как
правило, получается приближенным, поскольку решения зависят от
точности приборов и инструментов, которые используются для изоб¬
ражения графика и последующих измерений при его чтении.

Системы двух линейных уравнений с двумя
неизвестными: геометрическая иллюстрация
141
1.	В каком случае система линейных уравнений с двумя неизвест¬
ными:
а)	имеет единственное решение;
б)	не имеет решений;
в)	имеет бесконечно много решений?
2.	В каком случае линейными уравнениями системы
|а;х + Ь]У= с,,
[а2х+ Ь2у = с2
определяются две прямые, которые;
а) пересекаются;	б) параллельны;	в) совпадают?
Упражнения
2.23°. Изобразите прямые, уравнения которых записаны в си¬
стеме, и укажите число решений системы:
у = Зх,
2)
1 у = 8х,
у = ~2+ х;
[у + х = 2:
у = 5 - 2х,
4)
\у = 6-х,
х- у= 1;
[х + у = 2
х - 2у = 4,
6)
\х + 2у =
,2х - у = 3;
(Зх + у =
2.24°. Изобразите в одной системе координат прямые у — 4х и
у - х — 3. Имеют ли они точки пересечения? Укажите
координаты точки, которая обращает каждое из урав¬
нений в верное равенство.
2.25°. Изобразите прямые, уравнения которых записаны в сис¬
теме, и укажите число решений системы:
(2х + у = 6,
[2х - у = 4;
2)
Зх + у = 4,
х + 2у= -4;
[2х + у = 2,
(Зг/ + 6х = 6;
4)
4х - у + 5 = О,
х + 2у - 4 = 0;
5)
х + у = 6,
2х + 2у = 4;
6)
х + Зу - 6 = 0,
Зх + 9у - 4 = 0.

Системы уравнений с двумя переменными
142
2.26°. Покажите, используя
что система уравнений
геометрическую иллюстрацию,
не имеет решений:
3)
4х
(4х - у = 5;
х + у = 6,
2х = 1 - 2у;
у - х = О,
2) 1
|4х- 4г/ = -у,
4) Н'
[2х = 1 + 2у.
2.27°. Покажите, используя геометрическую иллюстрацию,
что система уравнений имеет бесконечно много решений:
1)
X + у = О,
5х + 5у = 0;
2)
X- у = з,
6х - бу = 18;
(2х~ у= 3,
[4х - 2у - 6;
4) |7х + у = 14,
[14х + 2у = 28.
2.28°. Запишите решение каждой системы уравнений из 2.27
(см. пример 3 в п. 2.4).
2.29°. Покажите, используя геометрическую иллюстрацию,
что система уравнений имеет единственное решение:
1)
5х + 2у — 13,
2х - у = 3;
2)
4х + Зу - 6,
2х + у = 4;
3)
7х - 4у = 5,
х + 2у - 3;
4) f’3x-4i/= 2,
[x-3j/= 1.
2.30. Не прибегая к геометрической иллюстрации, укажите,
какие из систем уравнений: а) не имеют решений;
б)	имеют единственное решение; в) имеют бесконечно
много решений.
1)	1х + У=4’	2) |х + У=3’
[х- у = 12;	[х + у= 5;
3) 1Х~У=^	4) /* + ^8’
[х - у = 4;	[2х -I- 2у = 16;

Системы двух линейных уравнений с двумя
неизвестными: геометрическая иллюстрация
143
х + у = 3,
6)
J х + 2у = 1,
х-у= 8;
(х- у= 4;
2х-у= 2,
8)
\х~у= 5,
2х + у = 14;
[4х - 4у = 20;
х-у = 4,
Ю)
(х = 4~ у,
2х-2у= 5;
Ь = 4- х;
2х + у = 15,
12)
[2х = 1 - у,
У = Зх;
[i/ = x- 5.
2.31*. Какой из рисунков (рис
уравнений:
1)
2х + 5у = т2,
4х + Юг/ = 2т2;
112) иллюстрирует систему
\2х+5у= т2,
Их + Юг/ -т2 + 2;
2х — 5у = т2,
х+7у= т2 + 2?
3)
2.32*. Известно, что система двух линейных уравнений с двумя
неизвестными хну
тх + пу = k,
рх + ly= q
(т, п, k,p, I, q — отличны от нуля) имеет бесконечно мно¬
го решений. Верно ли, что:
1) любая упорядоченная пара чисел является решением
этой системы;

Системы уравнений с двумя переменными
144
2)	решения системы можно записать в виде
гДе t € Я;
3)	решения системы можно записать в виде
(*;	), где teR;
4)	решения системы можно записать в виде (х0; у0), где
Xq € R, у0 £ R,
5)
имеет
место
п _ k
равенство 	— ;
6)	имеет место равенство pk = mq;
7)	имеет место равенство тп =pl;
О\	q-px0_k-mxa , 00
8)	имеет место равенство	-—-— , х0€л?
2.33*. При каких значениях k система уравнений
(2х - 2у ~ 7 k,
[х - у = О
имеет решения?
2.34*. При каких значениях k система уравнений
|4х + 4у = 5k,
[у = - х + 1
не имеет решений?
2.5.	Решение систем линейных уравнений
способом сложения
Для решения систем линейных уравнений мы будем поль¬
зоваться двумя способами. Каждый из них опирается на свой¬
ства 1 и 2 из п. 2.1 и теорему из п. 2.3. Рассмотрим решение
систем линейных уравнений с двумя неизвестными способом
сложения.

Решение систем линейных уравнений
способом сложения
145
Пример 1. Решить систему уравнений
Г4х - 5у = 3,
[2х + Зу = 7.
Решение. Преобразуем уравнения данной системы так,
чтобы коэффициенты при у стали противоположными. Для
этого обе части первого уравнения умножим на 3, а обе части
второго уравнения — на 5; это удобно при решении обозначать
так, как показано ниже:
[4х - 5у = 3, -3,
[2х + Зу = 7	-5.
После умножения уравнений системы на указанные
числа получим систему, равносильную данной (см. тео¬
рему из п. 2.3)
12х — 15у = 9,
10х + 15у= 35.
(1)
Первое уравнение следующей системы перепишем
из данной системы. Сложив почленно уравнения сис¬
темы (1), запишем результат во второй строке,—
получили систему, равносильную данной:
4х - 5у = 3,
22х = 44;
разделив обе части второго уравнения на 22, получим
4х - 5у = 3,
х = 2;
| подставим 2 вместо х в первое уравнение |
[8- 5у = 3,
[х — 2.
Откуда имеем
\у= 1.
[х= 2.
Ответ: (2; 1).

Системы уравнений с двумя переменными
146
▲ Докажем, что при замене одного из уравнений систе¬
мы (1) уравнением, полученным от сложения левых и сложе¬
ния правых частей уравнений этой системы, получится равно¬
сильная ей система уравнений
12х - 15у = 9,
(12х - 15(/) +(10х + 15(/) =9 + 35.
(3)
(4)
Допустим, что система (1) имеет решение — пару чисел
(х0; (/0). Это значит, что
12х0—15(/0 = 9 и 1Охо + 15z/0 = 35 •—
верные числовые равенства. Тогда
12х0- 15(/0 = 9,
(12х0 - 15г/0) + (1Охо + 15г/0) = 9 + 35 -
тоже верные числовые равенства. Таким образом, каждое ре¬
шение системы (1) является решением системы (2).
Наоборот, пусть система (2) имеет решение и этим решени¬
ем является пара чисел (х0; у0). Значит, равенства (4) — вер¬
ные числовые равенства. Тогда равенства (3) — тоже верные
числовые равенства (равенства (4) получаются из равенств (3)
посредством сложения, а равенства (3) получаются из равенст¬
ва (4) посредством вычитания). Таким образом, каждое реше¬
ние системы (2) является решением системы (1).
Итак, мы доказали, что системы (1) и (2) равносильны. И
Заметим, что уравнения системы из примера 1 можно
было бы преобразовать так, чтобы коэффициенты
при х стали противоположными числами. Рассуждения были
бы совершенно аналогичными, и мы получили бы то же самое
решение — (2; 1). ▲
На примере 2 покажем, как можно оформить запись реше¬
ния системы линейных уравнений в тетради
Пример 2. Решить систему уравнений
Зх + у — 4,
12х+ 7у= 10.

Решение систем линейных уравнений
147	способом сложения
Решение.
ГЗх + р-4,	|-(-4)
[12х + 7у = 10;
[-12х - 4у = -16,
[12х + 7у = 10;
I Зх + у = 4,
[Зу = -6;
|3х + у= 4,
Ь = -2;
|3х- 2= 4,
[У = “2;
fx= 2,
[У = -2.
Ответ: (2; —2).
Пример 3. Составить уравнение прямой, проходящей че¬
рез точки (1; 3) и (~2; 7).
Решение. Уравнение прямой имеет вид у = ах + Ъ.
Поскольку эта прямая проходит через точку (1; 3), то будет
верным числовое равенство
3 = а • 1 + Ь.
Поскольку прямой принадлежит и точка (—2; 7), то верным
является числовое равенство
7 = а(—2) + 6.
Имеем систему уравнений с двумя неизвестными а и Ь:
13 = а + Ь,
[7 = ~2а + Ь.
Решив ее, находим:
а=-1|;&=4|.

Системы уравнений с двумя переменными 148
Таким образом, уравнение искомой прямой имеет вид
1 1	. л 1
=	х + 4-g .
Ответ: у = - 1-|- х + 4у .
1.	В чем заключается способ сложения при решении систем ли¬
нейных уравнений?
2.	Обязательно ли, используя способ сложения при решении сис¬
тем линейных уравнений, преобразовывать уравнения так, что¬
бы противоположными стали коэффициенты именно при у?
3*. На чем основан способ сложения при решении систем линей¬
ных уравнений?
У пражнения
Решите систему линейных уравнений способом сложения
(2.35—2.36).
2.35°. 1)
х + у = 30,
х - у = 20;
2)
х + у = 40,
у - х = 16;
3)
5у + х = 44,
х + у = 16;
4)
х — 3i/ — 4,
х - у = 14;
5)
Зх + 8г/ — 19,
6х - у = 4;
J3x + 4у = 85,
]_5х - Зу = 105;
7)
х + 5у = 25,
Зх + 2у = — 3;
8)
5х + 7у = 141,
7х - у = 3;
|3х + 8у = -7,
|бх + 5у = -58;
Ю)
12х — 7у = 88,
13х + 14г/ = 9.
2.36.	цИх-Зу + ^О,
|4х - 5г/ + 17 = 0;
25х - 4у + 1 = 0,
31х - 5г/ + 16 =0;

Решение систем линейных уравнений
149	способом сложения
5(3х + у) — 8 (х - бу) = 46,
4(2х - Зу) - 13(х - у) = 6;
4 |10(х - у) -4(1-х) = ±у,
[7(х + 2у) + 4(3х - у) = у - х.
2.37.	Укажите номера тех систем уравнений, которые:
а) имеют бесконечно много решений; б) не имеют реше¬
ний; в) имеют единственное решение.
|2х + 4у = 6,
[у + 0,5х = 0;
Г l,5i/ + X = 0,5,
[2х + Зу = - 1;
\бу - 15х = 0,
[9у - Зх - 18;
|8г/ — 2х = 24,
1 Зг/ + х = -3;
9) Н-!' = 5^
[6 = х + у;
И [8х + 20г/ = 3,
[2х+ бу = 16;
2)	[8 + Х = 2У’
[х + 4г/ = 10;
4) [3У = П-2х,
[8х = 44 - 12 у,
f 12х - Зу = 5,
[бу + 10 = 24х;
8) J3x = 2’
[— Зх + 2у = - 2;
10) !5х + 2у = _18’
|15х + бу = -54;
12)	Ь+1=в»>
[2х = 3 + Юг/.
2.38.	Запишите решения тех систем из упражнения 2.37, ко¬
торые имеют бесконечно много решений.
2.39.	Решите систему уравнений:
рЗг/ - 4х = 17,
!) 1 8х - Зу _ у - 4х - 7 _ -1.
5	10
_ 2х 6 _ х - 2
“У о	9	’
2)
У = г _ Зх 6
2Х 2 ‘

Системы уравнений с двумя переменными 150
2.40*. При каких значениях а система уравнений имеет един¬
ственное решение:
ах + 2у = 3,	2 f ах + 2у = 3,
Зх - ар = 7;	[Зх + ау — 7;
[7х + 2р = 1,	|7х —Зу = а,
[2х + 7р = а;	[21х - 9у = 9?
2.41*. При каких значениях т система уравнений имеет бес¬
конечно много решений:
х + 2у = Зт,
Зх + 2 ту ~ 9;
2)
х + ту = 3,
2х + 2ту = 4zn;
3)
тх - 2ту = 6,
5х — бту = 15;
4х - у ту = 8,
тх - 27у = 2т?
2.42*. Составьте уравнение прямой, проходящей через точки:
1)	(1; 2)и(-1; 8);	2) (4; 6) и (2; 12);
3)	(-6; 1) и (-5; -8);	4) (3; -1) и (-6; 1).
2.43*. Существуют ли такие значения т, при которых прямая
(т + 3)х + ту = т + 1:
1)	параллельна прямой Зх - 2у = 7;
2)	пересекает прямую 5х + 4у = 1;
3)	совпадает с прямой 9х — бу = 7;
4)	параллельна прямой 4х — Зу = 5;
5)	пересекает прямую 2х + 5р = 2;
6)	совпадает с прямой 5х — 2у = 3?
2.6.	Решение систем линейных уравнений
способом подстановки
Разберем на примерах еще один способ решения систем ли¬
нейных уравнений — способ подстановки.
При мер 1. Решим систему уравнений
(Зх - у = 7,
[2х + Зу = —10.
(1)

Решение систем линейных уравнений
151	способом подстановки
Преобразуем первое уравнение системы, выразив у через х:
у = 3х~ 7.
Так как это уравнение равносильно первому уравнению сис¬
темы (1), то согласно теореме из п 2.3 система
fу = Зх - 7,
[2х + Зу = -10
равносильна системе (1).
Подставим во второе уравнение системы (2) вместо у выра¬
жение Зх — 7. Получим систему
у = Зх-7,
2х + 3(3х - 7) = -10.
Система (3) равносильна системе (2).
Преобразуя второе уравнение системы (3), получаем равно¬
сильную ей систему
|!/-Зх-7,	(4)
[х = 1.
Подставим значение х = 1 в первое уравнение системы (4)
и решим полученное уравнение с неизвестным у:
У = 3-1-7,
у--4.
Пара чисел х = 1, у = — 4 является единственным решением
системы (4), а следовательно, и равносильной ей системы (1).
Ответ: (1; -4).
Решение системы уравнений способом подстановки можно
оформить, например, так.
Пример 2. Решить систему уравнений
2х — 5у = 6,
4х + 2у = 9.

Системы уравнений с двумя переменными
152
Решение. Данная система уравнений равносильна сле¬
дующей:
X = 3 + у у,
4(3 +-|-г/) + 2г/=9.
Решим второе уравнение этой системы:
4(6 + 5у) + 2 • 2у = 9 • 2,
24 + 201/ + 4у = 18,
24г/ = -6,
1
Итак, получили:
х = 3 + -|г/,
1
[У =
г^. —2—
X z 8 ,
1
Ответ: (г-|;
Современные записи решений уравнений восходят к
XVIII в. При решении систем уравнений первым по¬
явился способ сложения, а затем способ подстановки.
Во «Всеобщей арифметике» Ньютона (XVII в.) встре¬
чаются уже все способы решения систем уравнений,
применяемые ныне в школе.
ПримерЗ. Решить систему уравнений:
а) |2л + !/ = 7’	б)[21 + !/ = 7’	в)>Рх + » = 7’
[2х + у = 5;	[2х + у = 7;	[ 2х + у = а.
Решение, а) Коэффициенты уравнений системы удовлет¬
воряют условию
2 _ J_ 7_
2	1	5 •

Решение систем линейных уравнений
способом подстановки
153
Поэтому согласно результатам п. 2.4 система не имеет ре¬
шений.
Ответ: нет решений.
К этому же выводу можно прийти, решая систему спо¬
собом сложения или способом подстановки.
Решим ее, например, способом сложения:
2х + у = 7, | • (-1)
2х + у — 5;
Ох + Ог/=~2,
2х + у = 5.
-J
Уравнение 0 - х + 0" у = - 2 этой системы не имеет решений,
поскольку при любых значениях х и у оно обращается в
неверное числовое равенство 0 = — 2.
Значит, не имеет решений и сама система, а следовательно,
и равносильная ей система а).
Ответ: нет решений.
б) Решения каждого из уравнений этой системы, которые
можно записать в виде (t; 7 - 2t), t<=R (см. п. 2.1, пример 2),
и являются решениями системы.
Ответ: (t; 7 — 2t), ttR.
Эти же решения получаются, когда систему решают
способом сложения или способом подстановки. Решим
ее, например, способом подстановки:
\у = 7 - 2х,
[2х + (7 - 2х) = 7;
у = 7 - 2х,
О х = 0.
Второе уравнение этой системы обращается в верное число¬
вое равенство при любых значениях х и у, а решениями пер¬
вого уравнения являются пары (f, 7 - 2t), где t€R.
Ответ: (t; 7 ~2t), t eR.

Системы уравнений с двумя переменными 154
▲ в) Решим систему способом подстановки:
\у = 7 - 2х,
] 2х + 7 - 2х = а;
\у = 7~2х,	(5)
[0х = а-7.	(6)
Если а - 7 = 0, т. е. а - 7, то решением уравнения (6)
является любое значение х = t и тогда из уравнения (5)
находим у = 7 - 2t, где t € R.
Если а — 7 * 0, т. е. а * 7, то уравнение (6) не имеет решений
и, значит, не имеет решения и система в).
Ответ: если а — 7, то (t; 7 — 2t), где t & R; если а 7, то нет
решений.
Учитывая, что коэффициенты при х и у в уравнениях
системы в) равны, можно (используя результаты
у
п. 2.4) утверждать, что система не имеет решений при —	1
и имеет бесконечно много решений при = 1. ▲
1. В чем заключается способ подстановки при решении системы
линейных уравнений с двумя переменными?
2*. На чем основано решение системы уравнений способом подста¬
новки?
3. Обязательно ли, решая систему линейных уравнений способом
подстановки, выражать из уравнения именно у через х?
Упражнения
Решите систему линейных уравнений способом подстановки
(2.44—2.45).
2 44° 1) > У 15,
]7х-3£/=10;
13х - 5у = 31,
J [2х + 7у = -31;
ГЗг/ — 4х= 1,
13х + 4t/ = 28;
2 |5t/ + 4x = 18,
[Зу + х = 8;
|2х - 7у = -25,
[4t/— 9х = 30;
J 6х - 4у = 15,
J [8х - Зу = 9.

Решение систем линейных уравнений
способом подстановки
155
2.45°. 1)
3)
5)
- + ^ = 8
2	3	°’
2х _ JL = о.
3	4
+ х = 14,
У ~Чг = 12;
2)
4)
+ ^ = 17
+ f = 6
Л. _ JL = I
2	3	±’
2х- 1 _ Зу- 1	_5_
2	3	6 ’
= Ю
6 2
2.46.	Какие из систем уравнений: а) имеют бесконечно много
решений; б) имеют единственное решение; в) не имеют
решений:
1)
7х - Зу = 3,
4х + 5у = —24;
2)
7х - Зу = 3,
21х — 9у — 9;
3)
7х — Зу = 3,
14х — бу = 9;
4)
8х + 2у = 3,
4х + у = -3;
|2х - Зу = 5,
[—4х + бу = - 10;
6)
2х + Зу = 0,
7х - 2у = 0;
7)
X + у + 1 = 1,
2х + 2у + 2 = 2;
8;
13х - 2у — 3,
1,3х - 0,2у = -16?
2.47.	1) Решите систему уравнений (а — число)
5у - 4х = 7,
2х + ау = - 5,
зная, что прямая ах + 5у = 9 проходит через точку
К(2; 3).

Системы уравнений с двумя переменными 156
2) Решите систему уравнений (Ь — число)
Зх — 4у = 5,
Зу + Ьх = - 9,
зная, что прямая 2х + by = 6 проходит через точку
А7(-3; 4).
2.48.	1) Прямая у = kx проходит через точку пересечения
прямых Зх — у = 20 и 5у + 7х = —12. Найдите к.
2) Прямая у = kx проходит через точку пересечения
прямых у — 5х — 3 и 2у - Зх = 15. Найдите k.
2.49*. Решите систему уравнений (а и b — числа):
х - у ~ 5а — 36,	[4х - Зу - 5а + 36,
2х + у = 4а — 66;	{зх - 4у = 5а —36;
х + у = За - 56,	[6(х + у) = 4а + 96,
у - х = а + 76;	[4х + 9у = 6а + 66.
2.50.	Решите систему уравнений (тп — число)
2х + ту — 11,
4х + бу = 6,
если известно, что пара (2; 1) является решением первого
уравнения системы.
2.51.	Решите систему уравнений (а — число)
5х + 2у = 12,
ах + Зу = 11,
если известно, что пара (5; -3) является решением вто¬
рого уравнения системы.
2.52*. Укажите значения а, 6 и с, при которых система урав¬
нений: а) имеет единственное решение; б) не имеет ре¬
шений:
4х + ау - 6,
6х + 8у = с.
ах + Зу = с,
2х + by = 2;

Расстояние между двумя точками.
Уравнение окружности
157
2.53.	При каких значениях а решением системы уравнений яв¬
ляется упорядоченная пара положительных чисел:
1)
X + у = а,
Зх - 2у = 10;
2 |7х - ау = 1,
’ [5х —9у = 9?
2.54.	При каких значениях а решением системы уравнений яв¬
ляется упорядоченная пара отрицательных чисел:
р |4х + 5у = 15,	|4х-3у = 6,
[Зх + 2у = а;	5х — ау = 8?
2.55.	При каких значениях а система уравнений не имеет ре¬
шений:
1)
Зх - 7у = 15,
6х + ау = 60;
2)
2х + 5у = 7,
7х — ау = 9?
2.56.	При каких значениях а и & система уравнений имеет бес¬
конечно много решений:
ах - бу = 15,	Г ах - у = Ъ,
4х + by = 2;	[4х + Зу = 10?
2.7.	Расстояние между двумя точками.
Уравнение окружности
Выведем формулы для вычисления расстояния между дву¬
мя точками на координатной прямой и на координатной
плоскости.
Теорема1. ПустьA(xJ и В(х2) — точки на координат¬
ной прямой. Тогда расстояние между этими точками нахо¬
дится по формуле
АВ = | х2 - Xj |.

Системы уравнений с двумя переменными
156
2) Решите систему уравнений (Ь — число)
Зх — 4у = 5,
Зу + Ьх = - 9,
зная, что прямая 2х + by = 6 проходит через точку
4).
2.48.	1) Прямая у = kx проходит через точку пересечения
прямых Зх — у = 20 и 5у + 7х — —12. Найдите k.
2) Прямая у = kx проходит через точку пересечения
прямых у = 5х — 3 и 2у - Зх - 15. Найдите k.
2.49*. Решите систему уравнений (а и Ь — числа):
х - у = 5а — ЗЬ,	(4х - Зу = 5а + ЗЬ,
2х + у = 4а — 65;	{зх - 4у = 5а —ЗЬ;
х + у = За - 5Ь,	[6(х + у) = 4а + 95,
у - х = а + 75;	[4х + 9у = 6а + 65.
2.50.	Решите систему уравнений (иг — число)
2х + ту — 11,
4х + бу = 6,
если известно, что пара (2; 1) является решением первого
уравнения системы.
2.51.	Решите систему уравнений (а — число)
5х + 2у = 12,
ах + Зу = 11,
если известно, что пара (5; —3) является решением вто¬
рого уравнения системы.
2.52*. Укажите значения а, 5 и с, при которых система урав¬
нений: а) имеет единственное решение; б) не имеет ре¬
шений:
4х + ау - 6,
Ьх + Зу = с.
ах + Зу = с,
2х + by = 2;

Расстояние между двумя точками.
Уравнение окружности
157
2.53.	При каких значениях а решением системы уравнений яв¬
ляется упорядоченная пара положительных чисел:
1)
X + у = а,
Зх - 2у = 10;
2 |7х - ау = 1,
’ [5х —9у = 9?
2.54.	При каких значениях а решением системы уравнений яв¬
ляется упорядоченная пара отрицательных чисел:
р |4х + 5у = 15,	|4х-3у = 6,
[Зх + 2у = а;	5х — ау = 8?
2.55.	При каких значениях а система уравнений не имеет ре¬
шений:
1)
Зх - 7у = 15,
6х + ау = 60;
2)
2х + 5у = 7,
7х — ау = 9?
2.56.	При каких значениях а и & система уравнений имеет бес¬
конечно много решений:
ах - бу = 15,	Г ах - у = Ъ,
4х + by = 2;	[4х + Зу = 10?
2.7.	Расстояние между двумя точками.
Уравнение окружности
Выведем формулы для вычисления расстояния между дву¬
мя точками на координатной прямой и на координатной
плоскости.
Теорема1. ПустьA(xJ и В(х2) — точки на координат¬
ной прямой. Тогда расстояние между этими точками нахо¬
дится по формуле
АВ = | х2 - Xj |.

Системы уравнений с двумя переменными
158
Доказательство. На рисунке 113 (а — е) изображе¬
ны все возможные случаи взаимного расположения точек А, В
и О (начало координат). Напомним, что АО = ОА = | хх | и
ВО — OB = I х21.
а<4
В
О
6)А
О
В

в) О
А
В t
X,
*2
о
Хх
0
X?
0
X,
х?
г)
д)
е)
В
О
{
А ,
В
А
О
О
В
А ,
*2
0
X,
*2
X,
0 *
0
х?
X,
Рис. 113
Рассмотрим случай а): Поскольку хг < 0, х2 < 0 и хг < х2 , то
имеем АВ=ОА-ОВ= | хх ]— | х21 =-х1-(-х2)=х2-х1=| х2-хг |.
Убедитесь, что в каждом из случаев б) — е) расстояние АВ
также равно значению выражения | х2—хт |. й
Теорема 2. Пусть А(хт; i/J и В(х2; у2)— точки на ко¬
ординатной плоскости. Тогда расстояние между этими точ¬
ками находится по формуле
АВ = V(x2 - хх)2 + (у2 - yj2.
^Доказательство. Пусть А и В расположены на ко¬
ординатной плоскости так, как это изображено на рисунке 114.
Обозначим буквами Д и А
натные оси Ох и Оу, буквами
Рис. 1U
.2 проекции точки А на коорди-
В1 и В2 — проекции точки В на
оси Ох и Оу, а буквой С — точ¬
ку пересечения прямых АА1
и ВВ2.
Длины отрезков АС и А^
равны, а согласно теореме 1
длина отрезка А^В2 равна
I у2~ Уг !•
Таким образом,
АС = А^В2 = | у2-уг I.
Аналогично
ВС=А1В1 = |х2-х1|.

Расстояние между двумя точками.
Уравнение окружности g
159
Из прямоугольного треугольника АВС по теореме Пифагора
имеем
АВ2 =АС2 + ВС2 = (у2 - у,)2 + (х2 - х,)2.
Откуда находим
АВ = \/(х2 ~ *i)2 + (У2 “ У1)2- И
Заметим, что все наши рассуждения остаются в силе и для
любого другого расположения точек на координатной плоскос¬
ти, когда отрезок АВ не параллелен ни одной из координатных
осей.
Докажите самостоятельно, что по формуле
АВ = \(х2 - xt)2 + (z/2 - у J2
можно находить расстояние между двумя точками и тогда,
когда отрезок АВ параллелен одной из координатных осей. ▲
Напомним теперь определение окружности.
Окружность — это множест¬
во всех точек плоскости, рас¬
стояние которых до некоторой
точки К (центра окружности)
равно числу R (радиусу окруж¬
ности). Значит, если точка
М(х; у) лежит на окружности с
центром в точке К(а; Ь) и ради¬
усом R, то МК = R (рис. 115).
Наоборот, если МК = R, то
точка М(х; у) лежит на окруж¬
ности с центром в точке К (а; Ъ)
и радиусом R.
Расстояние между точками М и К определяется по формуле
МК = х (х - а)2 + (у - Ь)2.
Значит, условие того, что точка М(х; у) лежит на окруж¬
ности с центром в точке К (а; Ь) и радиусом R, выражается ра¬
венством

\'(х - а)2 + (у~ b)2 = R,
которое обычно записывают в виде
(х - а)2 + (у- b)2 = R2.

160
Системы уравнений с двумя переменными
Эго равенство называется уравнением окружности с цент¬
ром в точке К (а; Ь) и радиусом R.
Пример 1. Записать уравнение окружности с центром в
точке К и радиусом R, если:
а)	К(~5; -3), 7? = 4;	б) К(0-, 0), R = 7;
в) К(~2; 4), В=1;	г) К(1', 1), = 0,5.
Решение, а) Подставив в уравнение окружности с цент¬
ром в точке К(а; Ь) и радиусом R значения а = — 5, Ъ — — 3 и
R = 4, получим уравнение данной окружности
(х + 5)2 + (у + З)2 = 16.
Аналогично запишем:
б)	х2 + у2 = 49;
в)	(х2 + 2)2 + (у — 4)2 = 1;
г)	(х — I)2 + (у — I)2 = 0,25.
Заметим также, что равенство x2 + y2 = R? является
уравнением окружности с центром в начале коор¬
динат и радиусом R (см. б)).
^Пример 2. Указать координаты точек пересечения
окружности
(х - 2)2 + {у + I)2 = 5
с осями координат и найти расстояние между каждыми двумя
из этих точек.
Решение. Поскольку все точки на оси Ох имеют ордина¬
ту, равную нулю, и у = 0 — уравнение оси Ох, то координаты
точек пересечения данной окружности с осью Ох находим из
системы уравнений
|(х — 2)2 + (у + 1)2 = 5,
Ь = 0.
Откуда получим и решим уравнение:
(х - 2)2 + 1 = 5;
(х-2)2 = 4;
|х-2| = 2;
х — 2 = —2 или х — 2 = 2;
х = 0 или х = 4.

Расстояние между двумя точками.
Таким образом, имеем две точки пересечения окружности
с осью Ох: Р(4; 0) и 0(0; 0).
Аналогично координаты точек пересечения окружности с
осью Оу находим из системы (объясните почему)
f(x - 2)2 + (у + 1)2 = Е,
]х = 0.
Получили (~2)2 + (у + I)2 = 5, откуда находим
(г/ + 1)2=1;
li/+ 11 = 1;
у + 1 = -1 или у + 1 = 1;
у = ~2 или у — 0.
Таким образом, с осью Оу окружность также пересекается
в двух точках М(0; —2) и 0(0; 0).
Затем вычисляем все расстояния между точками.
МО = д/(0 - О)2 + (0 + 2)2 = 2;
MP = V(4-0)2 + (0 + 2)2 = л/16 + 4 = \Г20 = 2^5;
РО = Т(0-4)2 + (0~0)2 = 4.
Ответ: Р(4; 0); 0(0; 0); М(0; -2);
МО = 2; МР = 2 Тб; РО = 4.
АПримерЗ. Доказать, что уравнение
у2 - 4у + 10х + х2 + 13 = 0
является уравнением окружности.
Доказательство. Преобразуем левую часть данного
уравнения, выделяя в ней полные квадраты двучленов:
у2 - 4у + 10х + х2 + 13 =
= у2 - 2 ’ 2у + 22 - 22 + х2 + 2 • 5 • х + 52 - 52 + 13 =
= (у - 2)2 - 4 + (х + 5)2 -25 + 13-
= (у - 2)2 + (х + 5)2 - 16.
Таким образом, исходное уравнение можно записать в виде
(х + 5)2 + (у- 2)2 = 16.
Это уравнение окружности с центром в точке К(— 5; 2) и
радиусом R = 4. И ▲

Системы уравнений с двумя переменными
162
1.	Запишите формулу расстояния между точками: a) A(x^ и В(х2);
б)А(х1; у}) и В(х2; уг).
2.	Запишите уравнение окружности: а) с центром в точке Р(т; t)
и радиусом R; б) с центром в точке 0(0; 0) и радиусом R.
3*. Докажите теорему 1 для каждого из возможных шести случаев
размещения точек А и В на координатной прямой относительно
точки О.
4*. Докажите теорему о расстоянии между точками A(xt; у,) и
•В(х2; у2).
5*. Докажите, что если точка М(х0; у0) принадлежит окружности
с центром в точке P(t; k) и радиусом R, то ее координаты удов¬
летворяют уравнению (х — t)2 + (у - А)2 = R2.
6*. Докажите, что если координаты точки У(х,; yj удовлетворяют
уравнению (х — t)2 + (у ~ А)2 = Я2, то точка N принадлежит
окружности с центром в точке P(t; k) и радиусом R.
Упражнения
2.57°. Найдите расстояние между точками А и В на координат
ной прямой, если:
1)	А(—6) и В(12);
3)	А(-18) и В(—35);
5)Л(1|)ИВ(8^):
7)л(94)ив(-4^);
2)	А(14) и В(~9);
4)	А(8) и В(-17);
6)	л(-14-|)яВ(-з£);
8М(-49£)ИВ(171|).
2.58 . Найдите расстояние между точками А и В на координат
ной плоскости, если:
1)	А(-4; 2)иВ(-3; 9);
3)	А(12; 4) и В(-1; 5);
5)	А(2; -5) и В(0; 3);
7) А(5; -3) и В(0; 0);
2) А(1; 8) и В(9; -3);
4) А(-3; 12) и В(7; 8);
6) А(1; 2) и В(-6; 0);
8) А(-2|; |)иВ(-1; 1).
2.59. Запишите уравнение окружности с центром в точке В и
радиусом R, если:
1)	Р(—2;	10), Я = 6;	2)	Р(0; 6), Я = 5;
3) Р(3; 0), R = 1;	4)	Р(-1; -1), R = 3;
5) Р(—4;	-8), R = V3;	6)	Р(8; -9), R = ^5;
7)	Р(—3;	1), Я = Т7 + 1;	8)	Р(3; 3), R = j2. - 1.

Расстояние между двумя точками.
2.60*. Укажите координаты точек пересечения окружности с
осями Ох и Оу:
1)	(х — З)1 2 + (у + 5)2 = 36;
2)	(х + 6)2 + (у - I)2 = 49;
3)	(х - I)2 + (у + I)2 = 9;
4)	(х~2)2 + (у —2)2 = 25;
5)	(х + З)2 + (у — 4)2 = 100;
6)	(х - 6)2 + (у + 5)2 = 81.
2.61*. Докажите, что указанное уравнение является уравнени¬
ем окружности:
1)	х2 - 2х + у2 + бу = -9;
2)	х2 + 6х + у2 - 2у + 1 = 0;
3)	х2 + у2 - 10х + 2у + 10 = 0;
4)	х2 + у2 - 2х - 20г/ + 97 = 0;
5)	х2 + у2 + 12х + 10у = -60;
6)	х2 + у2 —8х + 8у = —23.
2.62. Имеет ли общие точки график уравнения х2 + у2 — 9
с графиком функции:
1)	У = 4;
3) у = х2 + 2;
5) у = —х2-3;
2)	1/ = -3;
4)	у = х2 + 4;
6)	у=—х2 —4?
Если да, то укажите число общих точек.
2.63*. Запишите уравнение окружности с диаметром АВ, если:
1) А(1; 3), В(—7; -3);	2) А(3; -2), В(-5; -8);
3)	А(-2; 7), В(6; 1);	4) А(-4; -5), В(-2; 3).
2.64. Запишите уравнение окружности с центром в начале
координат и проходящей через точку:
1) М(-3; 4);	2) Р(2; -7);
3) К(-5; -3);	4) Т(-1; -9).

164
2.8.	Системы, состоящие из уравнения первой
и уравнения второй степени с двумя неизвестными
Определение. Уравнением первой степени с двумя
неизвестными хи у называется уравнение вида
ах + by = с,
где хотя бы один из коэффициентов а, Ь не равен нулю.
Таким образом, линейное уравнение с двумя неизвестными,
у которого хотя бы один из коэффициентов при неизвестных
не равен нулю, является уравнением первой степени с двумя
неизвестными.
Определение. Уравнением второй степени с двумя
неизвестными хи у называется уравнение вида
ох2 + Ъху + су1 + dx + ey + f = 0,
где хотя бы один из коэффициентов а, Ь, с не равен нулю.
Рассмотрим системы, состоящие из уравнения первой сте¬
пени и уравнения второй степени. Такие системы всегда можно
решить способом подстановки.
При мер 1. Решить систему уравнений
12х2 + 8ху — 2у2 + Зх — у - 2 = О,
\2x-y = 1.
Решение. Преобразуем второе уравнение данной систе¬
мы, выразив у через х:
у = 2х-1.
Подставим это выражение вместо у в первое уравнение дан¬
ной системы:
2х2 + 8х(2х - 1) - 2(2х - I)2 + Зх - (2х - 1) - 2 = 0.
После преобразований получим
10х2 + х - 3 = 0.
Корни этого квадратного уравнения:
Xj = -0,6; х2 = 0,5.

Системы, состоящие из уравнения первой и
165 уравнения второй степени с двумя неизвестными
Вычислим соответствующие значения у:
у^-2,2; у2 = 0.
Ответ: (-0,6; —2,2), (0,5; 0).
Пример 2. Решить систему уравнений
Решение.
Зх - 2у = 1,
5х2 + 4xi/+ 13 = 0.
Зх - 2у = 1,
5х2 + 4xi/ + 13 = 0;
У =
Зх-1
2 ’
5х2 + 4x(^^j + 13 =0.
(1)
(2)
Решим уравнение (2):
5х2 + 6х2 - 2х + 13 = 0,
Их2 —2х + 13 = 0,
Л = 4 — 4-11,13<0, значит, корней нет и система не имеет
решений.
Ответ: решений нет.
Пример 3. Сумма двух целых чисел равна 79, а их про¬
изведение равно 1254. Найти эти числа.
Решение. Пусть х — одно из чисел, а у — второе. Тогда
по условию задачи составим систему уравнений
|х + у = 79,
[ху = 1254.
Решим эту систему:
х = 79 - у,
(79 - г/)г/ = 1254.
(3)
(4)

Системы уравнений с двумя переменными
166
Решим уравнение (4):
79z/ - у2 = 1254,
у2 - 79у + 1254 = О,
D = 792 - 4 • 1254 = 6241 - 5016 = 1225,
JD = 35,
.. _79-35 _оо	79 + 35 _ 114 _
2 2 2
Из уравнения (3) получим соответственно:
хг = 57, х2 = 22.
Ответ: 22 и 57.
▲
В некоторых случаях можно решить систему урав¬
нений и более рациональным способом, чем способ
подстановки.
Пример 4. Решить систему уравнений
{ЗХг+2’ = \	(5)
[9х2 - 35 - 4/ = 0.
Решение. Система уравнений (5) равносильна системе
|3х + 2у = 7,
((Зх + 2у) (Зх - 2у) = 35.
Подставив во второе уравнение вместо Зх + 2у число 7 и раз¬
делив обе части этого уравнения на 7, получим систему, рав¬
носильную заданной:
ГЗх + 2у - 7,
(Зх - 2у = 5.
Применив способ сложения, переходим к системе
6х = 12,
4г/ = 2,
откуда находим х = 2 и у = 0,5.
Ответ: (2; 0,5). ▲

Системы, состоящие из уравнения первой и
167 уравнения второй степени с двумя неизвестными
1.	Что называется уравнением первой степени с двумя неизвест¬
ными?
2.	Что называется уравнением второй степени с двумя неизвест¬
ными?
3.	Что значит решить систему уравнений с двумя неизвестными?
4.	Что называется решением системы уравнений с двумя неизвест¬
ными?
5*. Обоснуйте, почему способом подстановки всегда можно решить
систему уравнений с двумя неизвестными, состоящую из урав¬
нений второй и первой степени.
Упражнения
2.65°. Установите, какую степень (первую или вторую) имеет
уравнение с двумя неизвестными хну:
1)	а2х - ЗЬу = 5;
2)	4х — 5ху = 7;
3)	(х - у)2 + 5х — 7у = (у ~ х)2;
4)	4х + у2 - Зху = 2у~у(3х~ у);
5)	5х — 7у2 — Зху = 2у + у (Зх — 1);
6)	(х + у)2 —(х-у)2 = 3х + 4у-1;
7)	(х - 1) (у + 2) = ху - 5х2;
8)	(х + 4) (у - 1) = 7у + ху.
2.66. Найдите координаты точек пересечения:
1)	окружности (х + 5)2 + (у - 4)2 = 25 и прямой у = х + 2;
2)	окружности (х — 8)2 + (у + 4)2 = 13 и прямой у = х — 7;
3)	окружности (х — З)2 + (у — 8)2 = 36 и прямой
Зх — 4у = 7;
4)	прямой 5х + 12у = 14 и окружности
(х - I)2 + (у - З)2 = 4.
Решите систему уравнений (2.67—2.70).
2.67°. 1)
х + у = 6,
2	2 __ ч л
X - У - 12;
2х - у = 3,
4х2 - уг - 15 = 0;
Зх + у — 7,
9х2 — у2 + 7 = 0.

Системы уравнений с двумя переменными
168
2.68. 1)
Зх - 4у = 5,
Зх2 - 4ху + 4у2 - 5х — 1;
2)
2х + Зу = 5,
4х2 + 12xi/ + 8у2 — 5у = 10;
3)
4х2 - 9у2 + 4х — 8у = 5,
2х - Зу = 1;
4)
9х2 + 16z/2 - 24xi/ + 7у = 9,
Зх - 4у = 10.
2.69. 1)
2х2 — Зу2 + 4х- 8у = 5,
2х — Зу = 1;
2)
Зх2 + 2у2 - ху + 7у = 9,
Зх - 4у = 10;
3)
Зх + 4/ _ 2х2-4г/ _ __2
6	5	15’
Зх — 2у = 4;
4)
Ту2-Ту - 4х^+2х£ = 0 4
7	5	’’
2х + 5у = — 1;
5)
х2 + 9х + Qy = 12,
х + Зу , х- 7у _ к_5_,
2	3	6 ’
2уг- 5у+ 17х = 100,
8х + 9у _ х- 7у _ 1 о.
6	4	1О’
х2 - ху -2х - у _ 4у2- 2хг + 9х + 4,у _ 1
6	3	2 ’
2х + 4 у _ Зх+ 7у _ _4_.
3	5	15’
6)

169
Использоваййетзчсге»»гтк=»^___
при решении текстовых задач
8)
х2 + у2 + 2х - Зу - 4 , llx-y + xy _ 9Q
3	6
2х - 4у _ 5х - 11у _ 5
3
12’
8
2.70.
х + 2у = 3,
2х + 5| у\ = 7;
2)
2х + Чу = 5,
3]х| + у = 4;
3)
Зх + 4у = 10,
4x+3|i/| =11;
Гбх + бг/ = 28,
’ [|х| + 9г/ = 29.
2.71. 1) Сумма двух целых чисел равна—15, а их произведение
равно —184. Найдите эти числа.
2) Разность двух целых неотрицательных чисел рав¬
на 29, а их произведение равно 210. Найдите эти числа.
2.9.	Использование систем уравнений
при решении текстовых задач
Покажем на конкретных примерах, как можно использо¬
вать системы уравнений при решении текстовых задач.
Пример 1. Степа и Настя, готовясь к олимпиаде по ма¬
тематике, обменивались еженедельно информацией о числе ре¬
шенных задач из сборника. В первую неделю выяснилось, что
Настя решила на 24 задачи больше, чем Степа. В следующую
неделю, после того как каждый решил еще по 19 задач, ока¬
залось, что Степа решил в два раза меньше задач, чем Настя.
Сколько задач решил каждый?
Решение. Пусть Степа решил в первую неделю х задач,
а Настя — у задач. Согласно условию у - х = 24. За две не¬
дели Степа решил х + 19, а Настя у + 19 задач. По условию
2(х + 19) = у + 19. Таким образом,
у — х = 24,
2(х+ 19) = у+ 19.

Решим эту систему способом подстановки:
у = 24 + х,
2(х + 19) = 24 + х + 19;
\у = 24-!-х,
[х = 5;
(у = 29,
[х = 5.
Степа решил всего х + 19 задач, т. е. 5 + 19 = 24, а Настя
решила всего у + 19 задач, т. е. 29 + 19 = 48.
Ответ: 24; 48.
Пример 2. Конфеты «Белорусские» и «Ласунак» расфа¬
сованы в коробки разной вместимости. Известно, что 4 коробки
«Белорусских» и 5 коробок «Ласунка» имеют массу 55 кг, а
если в этом наборе три коробки «Ласунка» заменить на три
коробки «Белорусских», то масса всех конфет будет 49 кг. Най¬
ти массу одной коробки с конфетами «Белорусские» и коробки
с конфетами «Ласунак».
Решение. Пусть х кг — масса коробки с конфетами «Бе¬
лорусские», а у кг — с конфетами «Ласунак». По условию за¬
дачи запишем уравнение 4х + 5у = 55, а после обмена коробок
получим уравнение вида 7х + 2у = 49.
Таким образом, имеем
4х + 5у = 55,
7х + 2 у = 49.
Решим эту систему методом сложения:

■	i vddia	IKHHHBK'WF
Из второго уравнения системы находим х = 5.
Подставив х = 5 в уравнение (1), получим:
y = ll-f •5 = 7.
Ответ: 5 кг — масса коробки с конфетами «Белорусские»,
7 кг — масса коробки с конфетами «Ласунак».
Задачи, решение которых можно свести к решению
систем уравнений с несколькими неизвестными,
встречаются уже в произведениях древних авторов.
Задача Бхаскары (XII в.). Некто сказал другу: «Дай
мне 100 рупий, и я буду вдвое богаче тебя». Друг от¬
ветил: «Дай мне только 10 рупий, и я стану в 6 раз
богаче тебя». Сколько было рупий у каждого?
Решим эту задачу. Пусть некто имеет х рупий, а у его
друга — у рупий. По условию задачи запишем систе¬
му уравнений:
[х + 100 = 2(у- 100),
U + 10 = 6(х- 10).
Решим эту систему методом подстановки:
у = 6х - 70,
х + 100 = 2(6х - 70 - 100).
Из второго уравнения имеем х = 40, а из первого по¬
лучаем у —170.
Ответ: 40 рупий; 170 рупий.
1.	Составьте три различные задачи, каждая из которых решается
„ |х + Зу = 17,
при помощи системы уравнении (
17х + 2у = 24.
2.	С чего начинается решение задачи при помощи системы урав¬
нений?

172
АИГ®0|р8 Системы уравнений с двумя переменными
Упражнения
2.72°. 1) Сколько писем написала Лена Юре и сколько раз Юра
ответил Лене, если известно, что сумма числа ее писем
и его ответов равна 152, а их разность равна 68?
2) Найдите возраст собаки Найды и кота Пушка, если
Найда старше Пушка, причем произведение их возрастов
равно 72, а сумма равна 18.
2.73°. 1) По скольку окуней поймали Володя и Андрей, если
известно, что разность между количеством Володиных и
Андрюшиных окуней равна 3, а произведение этих чисел
равно 54?
2) Сколько записок написал Ярослав Даше и сколько раз
Даша написала ответы, если известно, что разность этих
чисел равна 64, а их частное равно 17?
2.74°. 1) В двузначном числе десятков на 5 больше, чем содер¬
жится единиц в разряде единиц. Произведение цифр чис¬
ла на 58 меньше самого числа. Найдите это число.
2) В двузначном числе десятков на 3 меньше, чем содер¬
жится единиц в разряде единиц. Найдите число, если
произведение его цифр меньше самого числа на 15.
2.75°. 1) Нам вдвоем 63 года. Сейчас я на 3 года старше, чем
был тогда, когда мне было столько, сколько тебе теперь.
Сколько лет нам сейчас?
2) Мне сейчас на 6 лет больше, чем тебе было тогда, когда
мне было столько, сколько тебе сейчас. Когда тебе будет
столько, сколько мне сейчас, то нам вместе будет 60 лет.
Сколько лет нам сейчас?
2.76°. 1) Произведение возрастов Нины и Веры равно 420. Из¬
вестно, что Вера на год старше Нины. Найдите сумму их
возрастов.
2) Среднее арифметическое числа примеров, которые
Тима решил сам, и числа примеров, решенных с по¬
мощью бабушки Тамары Петровны, равно 23, а произве¬
дение этих чисел равно 480. Сколько примеров Тима ре¬
шил самостоятельно, а сколько вместе с бабушкой, если
Тима самостоятельно решил большую часть примеров?
2.77.	1) Сумма двух чисел равна 2,53. Если в большем из них
перенести запятую на один знак влево, то получится
меньшее число. Найдите эти. числа.

Использование систем уравнений
2) Разность двух чисел равна 103,95. Если в вычитаемом
перенести запятую на два знака вправо, то получится
уменьшаемое. Найдите эти числа.
2.78.	1) Лодка с постоянной собственной скоростью плывет по
течению от деревни Бахтино до деревни Караневичи 3 ч,
а обратное возвращение в Бахтино занимает 4 ч. Сколько
времени понадобится, чтобы проплыть этот же путь до
деревни Караневичи по течению на плоту?
2) Лодка с постоянной собственной скоростью плывет от
деревни Гагики до деревни Машки по течению реки Оль
2 ч, а возвращается за 3 ч. Сколько времени плыла
бы лодка от Гагиков до Машков, если бы не было те¬
чения?
2.79.	1) В карьере работают самосвалы двух грузоподъемно¬
стей; Три самосвала одной грузоподъемности и два —
другой за один раз перевозят 55 т груза, а пять самосва¬
лов первого типа и семь — другого за один раз перевозят
110 т груза. Найдите грузоподъемности самосвалов.
2) Маршрут обслуживается двумя автобусами с различ¬
ным числом посадочных мест. За 5 рейсов они могут пе¬
ревезти, будучи заполненными, 535 человек. Если один
автобус выполнит 12 рейсов, а другой — 8 рейсов, то они
перевезут, будучи заполненными, 1104 человека. Найди¬
те, сколько мест в каждом автобусе.
2.80.	1) Одна автомашина перевезла 672 т груза, а вторая —
700 т. Первая автомашина перевозила ежедневно на 3 т
груза меньше, чем вторая. По скольку тонн груза пере¬
возила ежедневно каждая автомашина, если первая ра¬
ботала на 1 день больше, чем вторая?
2) Для наполнения водоема поставлено 2 насоса. После
двух часов совместной работы первый насос был отклю¬
чен и второй закончил наполнение оставшейся части
водоема. За сколько часов каждый из насосов, работая
отдельно, может наполнить водоем, если первому насосу
на выполнение этой работы требуется на 8 ч меньше, чем
второму?
2.81.	1) Два поезда, выехав одновременно навстречу друг дру¬
гу из пунктов Толино и Зылево, расстояние между кото-

Системы уравнений с двумя переменными
174
рыми 900 км, встретятся через 5 ч. Если один из них
увеличит скорость на 10 км/ч, а другой уменьшит ско¬
рость на 40 км/ч, то к моменту встречи один из них про¬
едет на 180 км больше, чем другой. Найдите скорости
поездов.
2) Катер, двигаясь по течению, преодолевает расстояние
между пунктами Артемьево и Коптево за 3 ч. На обрат¬
ный путь при движении против течения, двигаясь с той
же собственной скоростью, катер затрачивает на 2 ч боль¬
ше. За какое время вернулся бы катер при отсутствии
течения?
2.82.	1) Степиной бабушке Лидии Васильевне больше 40 лет,
причем сумма цифр ее возраста равна 10, а разность цифр
равна 4. Сколько лет Степиной бабушке?
2) Степиной маме Ирине Станиславовне меньше 40 лет,
причем сумма цифр в записи ее возраста равна 10, а раз¬
ность цифр равна 6. Сколько лет Степиной маме?
2.83.	1) Имеются 15- и 25-процентные растворы кислоты.
Сколько граммов каждого раствора надо взять, чтобы по¬
лучить 400 г 20-процентного раствора?
2) В одном сплаве содержится 40 % меди, а в другом —
60 %. Сколько килограммов каждого сплава надо взять,
чтобы получить 70 кг нового сплава, в котором медь со¬
ставляет 45 % ?
▲ 2.10. Некоторые приемы решения
систем уравнений
Рассмотрим несколько более сложных примеров решения
систем уравнений.
При мер 1. Решить систему уравнений
(х2 + у2 + 2ху - X- у = 6,
l7r-3z/ = 26.
Решение. Обозначим х + у = и, тогда первое уравнение
системы примет вид
и2 — и — 6 = 0.

175 Некоторые приемы решения систем уравнений
Решив это квадратное уравнение, получим = —2, и2 = 3.
Таким образом, решение данной системы сводится к реше¬
нию двух систем уравнений
\х + у = -2, [х + г/ = 3,
(7х —Зг/ = 26	[7х- Зу = 26.
Решите их самостоятельно.
Ответ: (2;—4), (3,5;—0,5).
Пример 2. Решить систему уравнений
Решение. Обозначим —= и,
х + у
система уравнений примет вид
а х - у = v, тогда данная
8и + -%■ = 2,
24и--^- = 1.
Решением этой системы линейных уравнений является
пара чисел и=^ и v = 4 (убедитесь в этом).
Учитывая введенные обозначения, получим систему урав¬
нений
1 = 1
х + у 8 ’
х-у = 4,
х + у = 8,
откуда имеем <
[х~у = 4,
(х = 6,
\у = 2.
Ответ: (6; 2).
Пример 3*. Решить систему уравнений
х2 - ху + у2 = 19,
х3 + у3 = -19.

Системы уравнений с двумя переменными
176
Решение. Применив в левой части второго уравнения
системы формулу суммы кубов, получим
х2 - ху + у2 = 19,
(х + у) (х2 - ху + у2) = -19.
Используя первое уравнение системы, заменим во втором
уравнении множитель х2 — ху + у2 числом 19; тогда получим
(х + у)- 19 = -19,
откуда у = —х - 1.
Итак, получили систему уравнений, равносильную данной:
х2 - ху + у2 = 19,
у = -х - 1.
Решим эту систему способом подстановки:
у = -х - 1,
х2 - х(-х — 1) + (-х — I)2 = 19.
Из второго уравнения имеем хг = — 3, х2 — 2.
Таким образом, решение данной системы сводится к реше¬
нию двух систем:
Ответ: (—3; 2), (2; -3).
Пример 4*. Решить систему уравнений
х3 + у3 + х2 у + ху2 = 5,
х2 + 8ху + у2— —11.
Решение. В левых частях первого и второго уравнений
системы
(х + у)2:
выделим соответственно выражения (х + у)3 и

177 Некоторые приемы решения систем уравнений И
f(x3 + у3 + Зх2у + Зху2) — 2х2у — 2ху2 = 5,
Цх2 + 2ху + у2) + бху = -11;
((х + у)3 - 2ху (х + у) = 5,
](х + у)2 + бху = -11.
Пусть х + у = и, a. xy = v, тогда система примет вид
(и3 — 2uv = 5,	(1)
lu2 + 6u = -ll.	(2)
Из уравнения (1) следует, что переменная и не может при¬
нимать значение, равное нулю.
Умножив обе части уравнения (1) на 3, а обе части уравне¬
ния (2) на переменную и (и 0), получим систему, равносиль¬
ную системе уравнений (1) и (2):
Зи3 — 6uv = 15,	(3)
и3 + 6uv = - Пи.	(4)
Сложив левые и сложив правые части уравнений (3) и (4),
придем к уравнению
4u3 = 15-llu.
Решим его:
4и3 — 4 + llu — 11 = 0,
4(и3 — 1) + ll(u — 1) = 0,
4(u - 1) (u2 + u + 1) + 11(и - 1) = 0,
(и - 1) (4и2 + 4и + 15) = 0.
Отсюда и = 1 (квадратный трехчлен 4и2 + 4и + 15 не имеет
корней).
Подставив u = 1 в уравнение (1), получим
1 - 2и = 5,
т.е. v = -2.
Учитывая обозначения, получим систему уравнений
(х + у = 1,
\ху = -2.

Системы уравнений с двумя переменными
178
Решением этой системы являются пары чисел
Х! = -1, уY = 2 и х2 = 2, г/2 = -1.
Ответ: (-1; 2), (2; -1).
Пример 5*. Решить систему уравнений
\/5x-4i/ + a/2x+8i/ = 8,
7х + 4у = 32.
Решение. Заметим, что сумма подкоренных выражений
(5х - 4у) + (2х + Sy) равна 7х + 4у, а это левая часть второго
уравнения системы. Введем новые переменные. Пусть
\/5х — 4у = и, а \/2х + Sy = v, тогда имеем
и2 + v2 = (-у/бх - 4г/)2 + (V2x + Sy )2 = 7х + 4у.
Таким образом, данная система примет вид
и + v = 8,
, , Т- е-
и + v = 32,
и + v = 8,
(u + v)2 — 2uv = 32.
(и + v = 8,	fu + v = 8,
Тогда имеем	т. е. {
I.82 - 2ui? = 32,	|zw = 16,
откуда получим и = 4, v = 4.
С учетом обозначений переменных имеем систему урав¬
нений
7бх - 4у =4,
\/2х + Sy = 4.
Из этой системы получим
5х - 4у = 16,
2х + Sy = 16,
откуда находим х = 4, у = 1 (убедитесь в этом).
Ответ: (4; 1).

179 Некоторые приемы решения систем уравнений
Пример 6*. Решить систему уравнений
2\х — у\ + 3| 2х - 3//| = 51,
3| х — у\ + 6| Зу — 2х| = 96.
Решение. Пусть lx~yl = u, a i 2х — Зг/1 = V. Тогда, по¬
скольку | 2х - Зу | = | Зу — 2х | = v, получим
f2u + 3v = 51,
| Зи + 6v = 96.
Решив эту систему, получим и — 6, v = 13.
Учитывая введенные обозначения, получим систему урав¬
нений
|х - j/| =6,
12х — Зг/ ] = 13,
решение которой сводится к решению совокупности четырех
систем уравнений (поясните почему):
х - у = -6,	[ х - у = 6,	Гх - у = -6,
2х — Зу -13;	[2х - Зу = —13;	[2х — Зу - 13;
х - у = 6,
2х — Зу = 13.
Из этих систем уравнений получим соответственно:
X - -5,	[х = 31,	[х = -31,	[х = 5,
t/ = l;	[у = 25;	[// = -25;	= —1.
Ответ: (-5; 1), (31; 25), (-31; -25), (5; -1).
1.	Сколько решений может иметь система из двух уравнений с
двумя неизвестными?
2.	Может ли система из двух уравнений с двумя неизвестными
иметь ровно три решения?

’ Системы уравнений с двумя переменными 180
i
Упражнения
Решите систему уравнений (2.84—2.85).
2.84.
1)
3)
2.85.
1)
2)
2.86.
Найдите все пары чисел (х; у), которые удовлетворяют
уравнению:
1)	(10 - 2х - Зу)1 2 3 4 + (—х + 5у- 8)2 = 0;
2)	(-Зх + 4у - 15)2 + (2х - у + 5)2 = 0;
3)	+ У +	+
4)	(^±^)2 + (2^5)2 = 0.
Решите систему уравнений (2.87—2.93).

181
Некоторые приемы решения систем уравнений
5)
f х2 + 2 у + 1 — 0,
1у2 + 2х + 1=0;
х2 + 2у = 6,
у2 + Зх2 = 9;
х2 + у2 + 2ху
X - у = 1;
9,
6)
Х2 + у2 - 2ху
X + у = 3.
1,
х2 - у2 = 3,
2)
(х2 -у2 = 5,
X - у = 3;
[х + у = -1,
х + у =1,
4)
ху = -2;
[ху = 6;
X - у =2,
6)
[х + у =3,
х3~у3 = 26;
V + У3 = 9;
х + у = 5,
8)
(х ~ у =3,
х3 + у3 = 35;
V - у3 = 63.

sjlfc Системы уравнений с двумя переменными 182
2.91.
2)
4)
2.92.
+ ху =
5,
7;
-	х - у
-	ху =
= 18,
13;
2.93.
-2.x =
О,
2.94*. Решите систему уравнений относительно х и у:
х Гх+г/ = (а + Ь)3,	2) fax + by = а3 + b3,
1х — у = (а - Ъ]3',	li/ - х = 3 (а2 - &2).
▲ 2.11. Уравнения, содержащие переменную
в знаменателе и под знаком радикала
Рассмотрим несколько примеров уравнений с перемен¬
ной (неизвестным) в знаменателе и (или) под знаком ради¬
кала.
Пример 1. Решить уравнение
(2х-3) 7x^=0.
(1)

Уравнения, содержащие переменную
183	в знаменателе и под знаком радикала
Решение. Способ 1. Если при некотором значении х про¬
изведение равно нулю, то один из множителей равен нулю, т. е.
2х — 3 = 0 или д/х — 5 = 0.
Таким образом, корни уравнения (1) находятся среди корней
этих уравнений. Решив их, получим хг = 1,5, х2 = 5.
Но проверка показывает, что хг — 1,5 не является корнем
уравнения (1), так как при этом значении х левая часть урав¬
нения (1) не имеет смысла (объясните почему).
Ответ: 5.
Итак, при таком методе решения уравнения проверка най¬
денных значений переменной по условию является необходи¬
мой частью решения уравнения (1).
Заметим, что при решении уравнения (1) способом 1 мы
пользовались следующим утверждением.
Если значение произведения выражений равно нулю,
то хотя бы один из множителей равен нулю.
Способ 2. Исходное уравнение
(2х-3)7^5 = 0
равносильно тому, что
или -\Jx — 5 = 0
х~ 5 > 0
(объясните почему).
Система не имеет решений, поскольку корень уравнения
2х — 3 — 0 не удовлетворяет неравенству х > 5. А уравнение
л/х - 5 = 0 имеет корень х = 5.
Ответ: 5.
В тетради это решение можно записать так:
(2х - 3) 7х - 5 = 0;
Г 2 х — 3 = 0,	I	_
или Ух - 5 = 0;
х-5>0
х = 1,5,
х > 5
или х = 5;
нет решений или х = 5.
Ответ: 5.

Системы уравнений с двумя переменными 184
В этой записи каждые два последовательных утверждения
равносильны. Поэтому в проверке найденных значений пере¬
менной по условию нет необходимости.
Заметим, что при решении уравнения (1) способом 2 мы
пользовались следующим утверждением:
Значение произведения равно нулю тогда и только
тогда, когда хотя бы один из множителей равен ну¬
лю, а остальные при этом имеют смысл.
П р и м е р 2. Решить уравнение
хг-Зх-18 = Q	^2)
ух - 5
Решение. Способ 1. Умножив обе части уравнения (2) на
знаменатель -.jx — 5, получим квадратное уравнение
х2 - Зх - 18 = О,
корнями которого являются
хг = -3; х2 = 6.
Проверим эти значения переменной х по исходному урав¬
нению (2): при х — — 3 левая часть уравнения -== не имеет
смысла, значит, число -3 не является корнем уравнения (2);
при х — 6 получим -2= = 0 — верное числовое равенство, зна-
v 1
чит, число 6 — корень уравнения (2).
Ответ: 6.
Заметим, что проверку можно не записывать так подробно,
но обязательно надо отметить, что она была выполнена (иначе
решение не будет обоснованным). Например, можно было бы
написать «Проверка показывает, что только значение 6 удов¬
летворяет уравнению (2)».
Можно решить уравнение (2), пользуясь и следующим
утверждением:
Значение дроби равно нулю тогда и только тогда,
когда числитель равен нулю, а знаменатель имеет
смысл и не равен нулю.

Уравнения, содержащие переменную
в знаменателе и под знаком радикала
185
Способ 2. Согласно условию равенства дроби нулю
уравнение (2) равносильно тому, что: х2 - Зх — 18 = О,
х - 5 > О, д/х — 5^0.
Таким образом, уравнение (2) равносильно тому, что:
(х = - 3 или х = 6),
х > 5.
Откуда х = 6.
Ответ: 6.
В тетради это решение можно записать так:
х2- Зх - 18 _ q.
Vx — 5
х2 - Зх - 18 = 0,
х - 5 > 0;
(х = - 3 или х = 6),
х > 5;
х = 6.
Ответ: 6.
Пример 3. Решить уравнение
(х2 - 4х- 12) д/х - 5 _ q
\'2 - х
(3)
Решение. Способ 1. Из уравнения (3) следует:
х2 - 4х - 12 - 0 или д/х — 5 = 0;
х = - 2 или х = 6 или х = 5.
Проверка показывает, что все эти значения не удовлетво¬
ряют уравнению (3), значит, оно не имеет решений.
Ответ: нет решений.
Способ 2.
(х2-4х- 12) у'х-5 _ q.
\'2 - х
(х2 - 4х - 12) д/х - 5= 0,
2 - х > 0;

Системы уравнений
с двумя переменными
186
х2 - 4х - 12 =0,
' х - 5 > 0,
2 — х > О
или
ух — 5 = О,
2 - х > 0;
/х = 5,
ИЛИ 5
|х<2;
(х — —2 или х = 6),
- х > 5,
х < 2
обе системы не имеют решений.
Ответ: нет решений.
Способ 3. Корни уравнения (3) находятся в области оп¬
ределения выражения, стоящего в его левой части,
т. е. удовлетворяют системе неравенств
х - 5 > 0,
2 - х > 0.
Но эта система равносильна системе
[х < 2,
которая не имеет решений, значит, не имеет решений и урав¬
нение (3).
Ответ: нет решений.
Пример 4. Решить уравнение
х +	- 12 | ^х 2	 х

2х-12	13-	7 и-	w
Решение. Внимательно посмотрев на левую часть урав¬
нения (4), можно заметить, что его корни должны удовле¬
творять системе неравенств
[х - 2 > 0,
[2 - х > 0,
т. е. х = 2. Другие значения переменной х корнями быть не
могут.

Уравнения, содержащие переменную
187	в знаменателе и под знаком радикала
Проверим, является ли значение х = 2 корнем уравнения
(4), подставив это значение в уравнение (4):
2г + 4-2-12
2-2-12
13
Получили	= 0 — верное равенство, значит,
число 2 — корень уравнения (4).
Ответ: 2.
1.	При каких условиях может быть равным нулю значение произ¬
ведения выражений с переменной?
2.	Сформулируйте условие равенства дроби нулю.
3.	Когда при решении уравнения можно обойтись без проверки?
4.	В каких случаях проверка является необходимой частью реше¬
ния уравнения?
Упражнения
Решите уравнение (2.95—2.103).
2.95. 1) (7х + 12)^'х774 = 0;
2)	(3x-4)Vxzrl = 0;
3)	(3x-2)V2x = 0;
4)	(6х + 5)= 0;
5)	(х2- 7x + l)VxTT=0;
6)	(- Зх2 - 6х + 3) Jx=2 = 0;
7)	[х2 - хV2 + у )V2x3 + 4х = 0;
8)	(х2 — хV2”- 4) у/бх2 + 10х = 0.
(х-2)2 + 5_а.
5)

Системы уравнений с двумя переменными
188
2.97. 1)
(6х2 + х- 1)У2х — 1 л.
х2 + Зх
2)
7х2 + Зх-4
(8х2 + 14х- 15)\/х - 0,5
3)
	х(х+2)-3	_Q.
(4х2 - 4х + 1)-\/2 -1x1	’
4)
(х2- 10х+ 25)-\/б - 31x1
х(х + 3) - 4
5)
(х(х - 5) + 4)^1 х 1 — 3
9х2- 6х+ 1
6)
(2х2 + 7x)V51 х| - 10
х(х-4) + 3
2.98. 1) (^^-а)7з^=0;
2)	4-8±х-2)л/5х-30 = 0.
2.99. 1)
(х2 - 4х - 12)у х2 — 36 _ n
2х-12	U
(х2 + Их + 28)\/х2 — 49 _ п
)	21 + Зх
2.100. 1) г = 0;
VI — х
2.101. 1) уТтт5 = /Ггх;
3)	V4 + 2х = v’-З - х;
91 (%5 - х )У4 х __ л
vx^s	и-
2)	V16-X = Vx-36;
4)	V-6-12x = V3x^ 9
2.102.
2\ (х2 + 11х+ 18)УЗ-х _ q
J	ух-8
2.103. 1)
х2-16х + 60 , уХ^То уПЙ^х^л
5х-30	12	5 U
х2 + 9х + 20
8х + 32
ух + 5 у -25 - 5х _ п
9	7 U
2)

Уравнения, неравенства, функции,
189 содержащие выражения со знаком модуля
▲ 2.12. Уравнения, неравенства, функции,
содержащие выражения со знаком модуля
Вы уже умеете изображать график функции у = | х |, а также
решать простые уравнения и неравенства, содержащие выра¬
жения под знаком модуля. Например,
|х| = 7; |х —2| = 4;	| х2 + 5х + 71 = 1;
|х|>3; lx|<4; I х + 51 > 6; |х-2|<4.
(Вспомните, как решаются такие уравнения и неравенства.)
Рассмотрим несколько более сложных примеров.
Пример 1. Решить уравнение
Зх + |х| = 4.	(1)
Решение. Использовав определение модуля, заменим
уравнение (1) равносильной ему совокупностью двух систем:
х > 0,	[х<0,
или <
Зх + х = 4	[Зх —х = 4.
Решив обе системы, получим х = 1 (поясните почему).
Ответ: 1.
П р и м е р 2. Решить уравнение
Зх +1 х —21 = 4.	(2)
Решение. Использовав определение модуля, заменим
уравнение (2) равносильной ему совокупностью двух систем:
jx-2 >0,
(Зх + х — 2 = 4
или
1х-2 < 0,
[Зх - (х - 2) = 4
Решим эти системы:
fx>2,
[х < 2,
или
L1;
[х = 1,5
нет решений
или
х = 1.
Ответ: 1.

ft- Системы уравнений с двумя переменными 190
ПримерЗ. Решить неравенство
Зх +1 х - 21 > 4.
(3)
Решение. Использовав определение модуля, заменим не¬
равенство (3) равносильной ему совокупностью двух систем:
или
Решим эти системы:
или
или
х\
х—2: -
Рис. 116
О
2
+
+
+
х - 21 + 8.	(4)
Решение. В этом нера¬
венстве уже два выражения с
переменной стоят под знаком
модуля. На координатной пря¬
мой (рис. 116) отметим точки
0 и 2, в которых соответст¬
венно равны нулю значения
выражений х и х — 2.
На рисунке указаны знаки значений каждого из этих вы¬
ражений на каждом из трех образовавшихся числовых про¬
межутков: (—оо; 0), (0; 2), (2; +<»). Используя эту информацию
и определение модуля, заменяем уравнение (4) равносильной
ему совокупностью трех систем:
[х > 2,
ИЛИ (
[х + 4х > х - 2 + 8.

Уравнения, неравенства, функции,
содержащие выражения со знаком модуля
191
Решим эти системы:
fx < О,
[х > 2,5
или
Jx > 2,
или <!
[х > 1,5;
нет решений или
или хе(2;+оо).
Ответ:
Пример 5*. Изобразить график функции
г/ = |х| —[х —2| —1.	(5)
Решение. Используя ри¬
сунок 116 и определение моду¬
ля, рассмотрим функцию (5) на
промежутках (—°°; 0], (0; 2] и
(2; +оо).
Если х е (—°°; 0], то у =
= -х + х - 2 - 1, т. е. у = -3.
Если х€(0; 2], то у =
= х + х - 2 - 1, т. е. у = 2х -3.
Если х е (2; +оо), то у ~ х — (х — 2) — 1, т. е. у — 1.
Изобразив на каждом из трех промежутков координат¬
ной плоскости Оху часть соответствующей прямой, получим
изображение графика функции (5) (см. рис. 117).
1.	Приведите пример уравнения (неравенства), содержащего:
а)	два выражения с переменной, одно из которых под знаком
модуля;
б)	три выражения с переменной, два из которых под знаком мо¬
дуля.
2.	Сколько решений может иметь уравнение | х — 21 = а?
Упражнения
Решите уравнение (2.104—2.112).
2.104.	1) 14х ~ 51 = 8;	2) 12х + 31 = 4;
3)	| х + 11 = 0;	4) ] х — 21 = 0;
5)	I Зх + 71 = -7;	6) I 5х + 21 = -2;
7) 12х - 11 + 1 = 0;	8) I 7х - 41 + 4 = 0;
9)	4-Ц-Зх| = 5.

9 Системы уравнений с двумя переменными 192
2.105.	1) (| х — 71 — 4)(3х - 2) = 0;
2)	(4х + 3)( | х + 51 — 2) = 0;
3)	(6 -1 2х + 11 )(6х + 3) = 0;
4)	(9-12х)(8-|4-2х|) = 0.
2.106. 1) ||х| + 4| = 4;
3)||х|-7|=7;	4)||
2) |5 + |х|| = 5;
4) ||х|-2| = 2;
5)|2-|х||-4 = 0;	6)|3-|х||-5 = 0.
2.107.	1) | х + 21 = 6 - 2х;	2) 41 х - 31 = 7х - 11;
3)	16х - 11 - Зх = 4;	4) 12х - 51 - 1 = Зх.
2.108.	1) V(2x + З)2 - Зх + 2 = 0;
2)	V(3x - 2)2 + 2х - 3 = 0;
3)	V*2 - 4х + 4 = Зх - 4;
4)	д/х2 + 6х + 9 = 4х + 3.
2.109.	1) 2(х+ I)2 + 1 х + 11- 1 = 0;
2)	(х —З)2 — 21 х - 31 - 3 = 0;
3)	(х-4)2- 51 х- 41 = 6;
4)	(х + 5)2 + 31 х + 51 = 4.
2.110.	1) х2-31х| + 4= 0;
2)	х2-5|х|-6 = 0;
3)	х2 - 41 х + 11 + 2х + 4 = 0;
4)	х2 - 31 х - 11 - 2х + 3 = 0.
2.111.	1) |х-21 = | 1 -4х|;	2)	12 + Зх| = |2 + х|;
3) |х + 41 —1x1 = 2;	4)	12х — 61 — |х + 11 = 5;
5)	| х - 5 | +14х + 11 = 6;	6)	| х + 71 +1 Зх - 4 | = 9;
7) |х-2| = |х|-2;	8)	|х| + 3 = |х + 3|.
2.112*. 1) [ Зх — 21 — 313 - 2х| + х = 4;
2)	|Зх + 21 + х = 5 — 12х— 11;
3)	д/9х2 — 6х + 1 - у) х2 + 2х + 1 = 2х + 3;
4)	д/4Х2 + 4х + 1 + \/х2 - 6х + 9 = 5х - 4.

Уравнения, неравенства, функции,
193 содержащие выражения со знаком модуля
Решите неравенство (2.113—2.114).
2.113.	1) | Зх + 41 < 5;	2)	| 2х - 51 > 2;
3) 16х - 2 | < 0;	4)	| 5х - 31 > 0;
5)	| 2 - 8х| >-2;	6)	| 7х + 2 | < -3;
7) V (х - З)2 < 3;	8)	V (2-х)2 >2;
9) \/ 9х2 - 6х + 1 < 1.
2.114.	1) | 2х — 71 < х;	2) | Зх + 41 > 2х;
3) | 5 - 2х| > х + 6;	4) | 3 - 2х| < 4х - 1;
5)|3х+1|<у;	6) |4x-l|>f;
7) д/(х — I)2 > х — 1;	8) ^х2 +2х+1 < х-2;
9) д/ х2 - 4х + 4 < х - 4.
Решите уравнение (2.115—2.117).
2.115.	1) | Зх + 81 = -8 - Зх;	2) | 5 — 7х [ = 7х — 5;
3) 14х — 3 | = 4х — 3;	4) | 5х + 41 = 4 + 5х.
2.116.	1) \Мх2 - 4х + 1 = 2х — 1;
1	=	I	.
\'х2 + Юх + 25 1х + 5|’
2) 7 9х2 _ 6х + 1 = 1 - Зх;
4) .	1	-	1
\!х2- 14х + 49 Iх 7|
2.117*. 1) | 2 (\/х )2 - 321 = 32 - 2х;
2)	| 3 (\/х")2 — 12 | = Зх — 12;
3)	| 3 x/х2 - 6 | = 3 | х | - 6;
4)	| 2 ^х2 — 81 = 8 — 21 х |;
5)	13 x/х2 - 61 = Зх + 6;
6)	| 2 ух2 + 81 = 8 - 2х.
2.118. Решите неравенство:
1)	|х+1|- 3|х- 2|>х + 4;
2)	31х- 3| -14 + Зх| < х + 3;
3)	] х | — 21 х — 41 > 5х;
4)	41 х - 31 +1 х | Зх - 1;

Системы уравнений с двумя переменными
194
5)	| х | — 21 х — 21 + 31 х + 51 < 2х;
6)	2 | х | - 31 х - 11 + 4 | х - 31 > 6х.
Изобразите график функции (2.119—2.121).
2.119.
1)
У =
1 х + 11;
2) У =
1 х -г 3 |;
3)
У = \
|х-4|;
4) У =
| 7 - х|.
2.120.
1)
У =
|х + 2|_
6 + 2х;
2) у = \х~ 11 + 3 — 2х;
3)
У = \
6х — 11 ■
- Зх + 4;
4) г/ = 2х — 51 — 1 — Зх-
2.121.
1)
У =
|х + 4|-
1 х ] — 2;
2) у = | х +' 3 | -1 х'| + 2-
а 2.13. Уравнения с параметром
Пример 1. Решить уравнение с неизвестным х:
(а-3)х + 4 = а+1.	(1)
Решение. В данном уравнении буквой а обозначено
некоторое число. Уравнение (1) равносильно линейному урав¬
нению вида
(а ~3)х-а~ 3.	(2)
Если а 3, то уравнение (2), а значит и уравнение (1), имеет
-	а - 3	ч
единственный корень х = —z , т. е. х = 1.
CL — О
Если а = 3, то уравнение (2), а значит и уравнение (1),
равносильно уравнению 0 • х = 0, корнем которого является
любое число.
Ответ: х = 1 при а^З;
х — любое число при а = 3.
Пример 2. Решить уравнение с неизвестным х:
т2х - т = 4х + 2.	(3)
Решение. В данном уравнении буквой т обозначено
некоторое число. Таким образом, решаем линейное уравнение
с неизвестным х:
т2х — тп = 4х + 2;
т2х - 4х = тп + 2;
(тп2 - 4) х = т + 2.
(4)

195	Уравнения с параметром
Когда /п2-4^0, т. е. тп^-2 и т*2, то уравнение (4), а
значит и уравнение (3), имеет единственный корень
Если т2 —4 = 0, то т — — 2 или т = 2.
Когда т = — 2, то уравнение (4), а значит и уравнение (3),
равносильно уравнению 0 • х = О, корнем которого является
любое действительное число.
Когда т = 2, то уравнение (4), а значит и уравнение (3),
равносильно уравнению 0 • х = 4, которое не имеет корней.
Ответ: х —при т — 2 и т 2;
х — любое число при т = — 2;
нет корней при т = 2.
Уравнения, в записи которых, кроме неизвестного, есть
буква, обозначающая число (а, т — в примерах 1 и 2), назы¬
вают уравнениями с параметром*.
Уравнения с параметром встречались нам и раньше. Напри¬
мер, в линейном уравнении ах = Ь с неизвестным х, решение
которого в общем виде рассматривалось в 7-м классе, даже два
параметра — а и Ь.
Рассмотрим еще несколько примеров.
ПримерЗ. При каких значениях параметра а квадратное
уравнение
х2 + 4(а — 1)х + а2 — О
имеет единственное решение?
Решение. Найдем дискриминант данного квадратного
уравнения:
D = 4(а2 - 2а + 1) - 4а2 = -8а + 4.
Поскольку квадратное уравнение имеет два равных корня
(т. е. единственное решение) при D = 0, то найдем нужное
значение параметра, решив уравнение -8а-1-4 = 0. Таким об¬
разом, а = 0,5.
Ответ: при а = 0,5.
* Слово «параметр» происходит от греческого слова parametron —отме¬
ривающий.

Системы уравнений с двумя переменными
196
Пример 4*. Решить уравнение с параметром а:
ах2 + (4а - 1)х + 4а = 0.
(5)
Решение. Если значение старшего коэффициента а равно
нулю, то уравнение (5) имеет вид
0 • х2 - х = 0,
откуда х = 0.
Если значение старшего коэффициента а отлично от нуля,
то уравнение (5) — квадратное, и его решение зависит от зна¬
чений дискриминанта D. Найдем этот дискриминант:
D = 16а2 - 8а + 1 — 4а • 4а = -8а + 1.
Когда D > 0, т. е. а < (напомним, что а 0), то
- 4a + 1 ± \ 1 - 8а
Х1-2	2а
Когда D = 0, т. е. а =	, то х1 л = ~ 4 °д+ 1 .
Когда D < 0, т. е. а > -g-, то уравнение (5) корней не имеет.
Ответ: xl 2 = ~ 4a+ 12±^-1~g~ при а G (-оо; 0) U (о?	);
х = 0 при а — 0;
нет корней при а€ ; + оо^;
- 4а + 1	1
х1.2 = ~2^ при а .
Решить уравнение с параметром — это значит ука¬
зать значения параметра, при которых уравнение
имеет корни, и для этих значений параметра найти
корни уравнения, а также указать, при каких значе¬
ниях параметра решений нет.
Другими словами, решить уравнение с параметром —
это значит решить данное уравнение при каждом зна¬
чении параметра.
При мер 5*. Решить уравнение с параметром k:
9х+ 2 _
kx+ 2

197
Уравнения с параметром
Решение.
9х+ 2
kx + 2
9х+ 2 - k2x - 2k _ р.
kx+2 —U
(9- fe2)x+ 2(1- /г) _ п
kx + 2	U
По условию равенства дроби нулю запишем систему, рав¬
носильную этому уравнению:
[(9 - k2)x + 2(1 - к) = 0,	(6)
1 kx + 2 * 0.
Решим первое уравнение этой системы.
При k — 3 оно имеет вид 0 • х — 4 — 0 и корней не имеет.
При k = — 3 оно имеет вид 0 • х + 8 = 0 и корней не имеет.
Значит, при к — ± 3 система (6) решений не имеет, а при
к * ± 3 она равносильна системе
х=2(^1>
9 -/г2 ’
2(fe- 1)
9-Л2
+ 2*0.
(7)
Из второго условия системы (7) после преобразований по¬
лучаем
2(9^0,
9 - k2
откуда находим k * 9.
Ответ: х = 2	~ при /г*±ЗиА1*9;
9 — k
нет корней при k Е {—3; 3; 9}.
Пример 6*. При каких значениях параметра а один из
корней уравнения
х2 + (2а - 1)х + а2 = 0	(8)
равен утроенному другому?
Решение. Квадратное уравнение (8) имеет корни, если
D = (2а - I)2- 4а2 = 1 - 4а > 0, т. е. а<-|-.

Системы уравнений с двумя переменными
198
Пусть хг и х2 — корни уравнении (8), По условию х2 = 3х1
и, согласно теореме Виета, имеем:
|Xj + 3Xi = 1 - 2а,
txi • 3xj = а2;
|4xi = 1 - 2а,
[Зх2! = а2;
Г 1 2а
*1 =
(9)
Из второго уравнения системы (9) находим значения пара¬
метра а:
аг = ~^ -^3; a2 = --|-+V3
(убедитесь в правильности вычислений).
Понятно, что ах < -j-. Покажем, что а2 , т. е. 1 - 4а2	0:
1 - 4а2 = 1 - 4(- у + уЗ) = 7 — 4уЗ = 7 — \13 • 16 =
= Л'49 -V48>0.
Ответ: аг = --|- -уЗ; a2-~-^- + \j3.
9
1.	Приведите пример уравнения с параметром.
2.	Что значит решить уравнение с параметром?
Упражнения
2.122°. 1) При каких значениях параметра а уравнение
х2 = а — 6:
а) имеет два различных корня; б) имеет два равных
корня; в) не имеет корней?
2) При каких значениях параметра а уравнение
4х2 = а + 5:
а) имеет два различных корня; б) имеет два равных
корня; в) не имеет корней?

199
а)	имеет два различных корня; б) имеет два равных кор¬
ня; в) не имеет корней?
2) При каких значениях параметра а уравнение
х2 — 10а — 25 — а2:
а)	имеет два различных корня; б) имеет два равных
корня; в) не имеет корней?
Решите уравнение с неизвестным х (2.124—2.131).
2.124.
2.125.
2.126.
2.127.
2) ах = -3;
4) (5 —а)х = 1.
2) (а2 - 16)х = а-4;
4) (а + 2)х = а2 —4.
- 1;	2) (а2 - 8а + 12)х = а - 6.
2) т2х ~т = 16х + 4;
1т;	4) 9х - 4т2х - 2т = 3.
2.128.
2.129.
х-а
2)
4)
4x-5_fc.
kx-5 R’
Fnr_2fe = 0-
4-kx
2-131*-1)	=
2.132*. 1) При каких значениях параметра а один из корней
уравнения ах2 + (За - 1)х + 50а = 0 равен удвоенному
другому?
2)
4)

Системы уравнений с двумя переменными
200
2) При каких значениях параметра а один из корней
уравнения ах4 — (2а + 3)х + 48а = 0 равен утроенному
другому?
Решите уравнение с параметром т (2.133—2.134).
2.133. 1) т\х = 0;
3) (т + 2) \'х = 0;
5) (х - 2) у/т + х = 0;
2) т v'-x = 0;
4) (т - 5) \1х = 0;
6) (х + 3) \1т - х = 0;
9)
х+3
10) ~=L = 0.
ух + т
2.134.	1) |x| = zn + 5;
3) | х - 11 + т61 х | = 0;
2) | х | = т - 7;
4) | х - 2 | + т41 х | = 0-
а 2.14. Системы уравнений с параметром
Пример 1. Найти все значения а, при которых система
уравнений
2х - у = 3,
ах + 4 z/ = 1
имеет единственное решение.
Решение. Система имеет единственное решение, когда
-у *	(п. 2.4), т. е. а* -8.
Ответ: при а-8.
Пример 2. Решить систему уравнений с неизвестными
х и у.
\рх + у = 3,
\2х + (2р - 3)у = 1.
(1)

201
Системы уравнений с параметром
Решение.
Будем решать систему (1) методом подста¬
новки:
\рх + у = 3,
\2х + (2р - 3)у = 1;
1у = 3-рх,
[2х + (2р ~ 3)у= 1;
у = 3~рх,
2х + (2р —3)(3—рх) = 1
Преобразуем второе уравнение системы (2):
2х + 6р — 9 - 2р2х + Зрх - 1:
(—2р2 + Зр + 2)х + 6р - 10 = 0.	(3)
Получили линейное уравнение с неизвестным х и парамет¬
ром р. Решим его.
Пусть ~2р2 + Зр + 2 = 0, тогда р = - 0,5 или р = 2.
Когда р = -0,5, то линейное уравнение (3) имеет вид
0'Х —13 = 0,— у этого уравнения нет корней, значит, нет
решений и у системы (1).
Когда р = 2, то линейное уравнение (3) имеет вид
0 • х + 2 = 0,— у этого уравнения также нет корней, значит, нет
решений и у системы (1).
Когдар -0,5 ир * 2, то линейное уравнение (3) имеет один
корень
х- ю-бр
- 2р2 +■ Зр + 2
Из первого уравнения системы (2) находим:
10р-6р2	.
-2р2 + Зр + 2’
У =
Р-6

2р’ - Зр - 2
Ответ: х =
10-6Р	■ ц
- 2р2 + 3р+ 2 ’ У
	£_6

2р2-Зр-2
при р * -0,5 и р * 2;
система не имеет решений при р = -0,5 или р — 2.

Системы уравнений с двумя переменными
202
Системы уравнений, в записи которых, кроме неизвестных,
есть буквы, обозначающие числа (как а и р в примерах 1 и 2),
называют системами уравнений с параметром.
Решить систему уравнений с параметром — это
значит указать значения параметра, при которых сис¬
тема уравнений имеет решения, и для этих значений
параметра найти решения системы, а также указать,
при каких значениях параметра система уравнений
решений не имеет.
Другими словами, решить систему уравнений с
параметром — это значит решить данную систему
уравнений при каждом значении параметра.
При мер 3*. Решить систему уравнений с параметром k:
(2k - 1) х + у = k,
2k2x + (1 + k)y = 2.
(4)
Решение,
новки:
Будем решать систему (4) методом подста-
f(2k - 1) х + у = k,
\2k2x + (1 + k) у = 2;
у — k — (2k — 1) x,
2k2x + (l +k)(k~(2k~ l)x) = 2.
Преобразовав второе уравнение системы (5), получим:
(l-k)x=2-k-k2.	(6)
Получили линейное уравнение с неизвестным х и парамет¬
ром k. Решим его.
Если коэффициент при х равен нулю, т. е. k = 1, то урав¬
нение (6) имеет вид
0-х = 0.
Любое действительное число является корнем этого уравне¬
ния. И тогда при k - 1 значение неизвестного у мы выразим
через значение х из первого уравнения системы (4): у = 1 — х.

203
Системы уравнений с параметром
Если коэффициент при х в уравнении (6) отличен от нуля,
т. е. k * 1, то это уравнение имеет единственное решение
2-А-А2.
Л 1-А	’
х = k + 2.
Из первого уравнения системы (5) находим значение неиз¬
вестного у‘.	ni.2ni.tn
v	y = ~2kz~2k + 2.
Ответ: если k = 1, то х — любое число; у = 1 — х;
если k * 1, то х — k + 2; у = -2kz — 2k + 2.
Этот ответ можно записать и так: если k = 1, то (х; 1 — х),
x€R; если k * 1, то (k + 2; ~2kz — 2k + 2).
Пример 4*. При каких значениях параметра а система
уравнений
(а + 1)х + ау = 4а + 1,
(а - 3)х + (За - 4)г/ = а - 6
а)	имеет единственное решение;
б)	имеет бесконечно много решений;
в)	не имеет решений?
Решение, а) Система (7) имеет единственное решение,
когда
(а + 1)(За-4)-а(а-3)^0.	(8)
После преобразований получим:
а2 + а- 2^0, а^—2 и а^1.
б), в) Итак, когда а *~2 и 1, система (7) имеет един¬
ственное решение. А при а — —2 она имеет вид
[—х —2z/ = —7,
[-5х- 10 г/ = —8
и, как легко убедиться (сделайте это), не имеет решений.
При а = 1 система (7) имеет вид
I 2х + у = 5,
[-2х- z/ = -5
и, как можно убедиться (сделайте это), имеет бесконечно много
решений.

Системы уравнений с двумя переменными 204
Ответ: а) единственное решение при а^—2 и а^1;
б)	бесконечно много решений при а = 1;
в)	нет решений при а = — 2.
1.	Приведите пример системы уравнений с параметром.
2.	Что значит решить систему уравнений с параметром?
У пражнения
2.135.	Найдите все значения параметра а, при каждом из ко¬
торых система уравнений имеет единственное решение:
1)
2х + бу = 15,
ах + 12у = 5;
2)
Зх + 4ау = 7,
9х - 2у = 14;
3)
Зах - у = а + 2,
х - 4ау = а + 3;
4)
12х + 2ау = а - 1,
ах + бу = ~а - 5.
2.136. Найдите все значения параметра а, при каждом из ко¬
торых система уравнений не имеет решений:
1)
х - а2у = -16,
ах - 4ау = 8;
2)
а2х + 12у = -7,
— Зах - 4ау = 8;
3)
4х + (а + 1)у = 8 + а,
9х + Зу = 2а - 4;
I (а — 3)х + 14у = 5 - а,
[2х - 7у = ба + 11.
2.137. Найдите все значения параметра а, при каждом из ко¬
торых система уравнений имеет бесконечно много ре¬
шений:
Зх + ау = 7,
15х + 10у = 35;
|7х + у = 15,
[ах + 5у = 75;
(а - 2)х + Зу = 7,
(а - 2)3х + ау = 7;
ах + (а + 1)3у = 13,
4х + 25(а + 1)у = 13.
1)
3)
4)

205
Системы уравнений с параметром
Решите систему уравнений с неизвестными х и у
(2.138—2.139).
2.138. 1)
тх + у = 2,
х~у = 3;
2)
х - ту = 4,
2х + у = 3;
\рх + 4у = 4,
[Зх = 1-у,
4)
5х + 3 = - 2ру,
— 10х + у = 6.
2.139*. 1)
Зх + (i — l)z/ = t + 1,
(t + 1)х = 3 - у;
[(2 + t)x + 5у = 6t + 7,
1(2 - t)y = x~5;
3)	|2x - (2 — 9k2)y = 3k,
[x + y = 1;
4)	P“9 = -3’
1(254" - 4)4- 5i/= 54 - 12.
2.140.	1) Брат старше сестры на 4 года. Вместе им п лет.
Сколько лет каждому? При каком значении п брат будет
старше сестры в 2 раза?
2) Один арбуз на 3 кг тяжелее другого, масса двух ар¬
бузов равна а кг. Какова масса каждого арбуза? При ка¬
ком значении а масса одного арбуза будет в 4 раза пре¬
восходить массу другого арбуза?
2.141.	1) Периметр прямоугольника равен 300 м, длина на I м
больше его ширины. Какова площадь прямоугольника?
При каком значении I площадь прямоугольника будет
наибольшей?
2) Сумма высоты и основания треугольника равна
24 см, основание больше высоты на т см. Какова пло¬
щадь треугольника? При каком значении т площадь
треугольника будет наибольшей?
2.142.	1) Общая длина двух веревок равна 70 м. После того
как от одной веревки отрезали а м, она стала короче дру¬
гой в 3 раза. Каковы были первоначальные длины ве¬
А[п1[г©[^иа Системы уравнений с двумя переменными 206
ревок? При каком значении а обе веревки имели равные
длины?
2) Строители вымостили плиткой два тротуара общей
длиной 800 м. После реконструкции длину одного из
тротуаров увеличили на а м, и тротуар стал вдвое длин¬
нее другого. Каковы были длины двух тротуаров до
реконструкции? При каком значении а обе длины были
равными перед реконструкцией?
2.143.	1) Один кран наполняет бассейн за 5 ч, другому крану
для этого надо на t ч больше. За какое время два крана
наполнят бассейн? При каком значении t задача не име¬
ет решения?
2) Один рабочий выполняет работу за 7 ч, а вместе с дру¬
гим рабочим он выполняет работу за п ч. За какое время
второй рабочий выполнит эту работу? При каких зна¬
чениях п задача не имеет решения?

Квадратичная функция
3.1.	Функция у-ах2
Определение. Квадратичной функцией называется
функция вида
у = ах2 + Ьх + с (а, Ь, с — числа, а * 0).
Область определения этой функции — множество R всех
действительных чисел, поскольку при любом значении неза¬
висимой переменной х существует, и притом единственное,
значение выражения ах2 + Ьх + с.
Функция у = х2 является частным случаем квадра¬
тичной функции у — ах2 + Ьх + с при а —1, 6 = 0,
с = 0.
График квадратичной функции (как и график функции
у = х2) называют параболой, а уравнение у = ах2 + Ьх + с
(а * 0) — уравнением этой параболы.
График квадратичной функции и ее свойства мы будем из¬
учать, используя график и свойства функции у = х2.
Рассмотрим еще один частный случай квадратичной функ¬
ции у = ах2 + Ьх + с при 6 = 0, с = 0, т. е. функцию у — ах2
(а * 0). Сначала рассмотрим эту функцию при а > 0. Приведем
два примера такой функции — при а > 1 и при 0 < а < 1.
Пр и мер 1. Рассмотрим функцию у = 2х2. Составим таб¬
лицу значений этой функции и сравним ее с таблицей значений
функции у = х2.

Квадратичная функция	208
X
0
+0,5
+ 1
±1,5
±2
у = хг
0
0,25
1
2,25
4
у — 2х2
0
0,5
2
4,5
8
Воспользовавшись таблицей, изобразим на одном рисунке
параболы у = х2 и у = 2х2 (рис. 118).
Очевидно, что при каждом значении х значение функции
у — 2х2 в 2 раза больше значения функции у - х2. Значит, при
одной и той же абсциссе х0 ордината точки М на параболе
у = 2х2 в 2 раза больше ординаты точки N на параболе у — х2
(рис. 119). Поэтому любую точку М на параболе у = 2х2 можно
получить из соответствующей точки N на параболе у = х2,
увеличив ординату точки N в 2 раза.
Говорят, что парабола у = 2х2 получается из параболы у = х2
растяжением в 2 раза вдоль оси Оу. Заметим, что при
растяжении параболы у = х2 вц,олъ оси Оу ее вершина является
неподвижной точкой (поясните почему).
Пример 2. Рассмотрим функцию у =	х2.
Составим таблицу значений этой функции и сравним ее с
таблицей значений функции у = х2.
X
0
±0,5
±1
±1,5
±2
У = х?
0
0,25
1
2,25
4
1 2
0
0,125
0,5
1,125
2

209
Функция у = ах2
Воспользовавшись таблицей, изобразим на одном рисунке
параболы у — х2 и у = х2 (рис. 120).
Очевидно, что при каждом значении х значение функции
у = х2 в 2 раза меньше значения функции у = х2. Значит, при
одной и той же абсциссе х0 ордината точки М на параболе
у = х2 в 2 раза меньше ординаты точки N на параболе у = х2
(рис. 121). Поэтому любую точку М на параболе у = ~х2
можно получить из соответствующей точки N на параболе
у = х2, уменьшив ординату точки N в 2 раза.
Говорят, что парабола ц = у х2 получается из параболы
у = х2 сжатием в 2 раза вдоль оси Оу. Заметим, что при сжатии
параболы у = х2 вдоль оси Оу ее вершина является
неподвижной точкой (поясните почему).
Соображения, которые были приведены при рассмотрении
примеров 1 и 2, показывают, что:
если а>1, то парабола у = ах2 получается из
параболы у = х2 растяжением в а раз вдоль оси Оу;
если 0<а<1, то парабола у = ах2 получается из
параболы у — х2 сжатием в раз вдоль оси Оу.
Функция у = ах2 (а > 0) обладает теми же свойствами, что
и функция у — х2 (см. п. 1.14), и доказываются они так же, как
для функции у = х2.

Квадратичная функция	210
Рассмотрим функцию
у — ах2 {а < 0).
В качестве примера приведем функцию у = -2х2. Сравним
ее с функцией у = 2х2, которую мы уже изучили.
Заметим, что I - 2х21 — I 2х21 при любом значении х. Поэтому
у точек М(х0; — 2х2) и 2V(x0; 2х2) с равными абсциссами
ординаты — противоположные числа. Значит, эти точки сим¬
метричны относительно оси Ох (рис. 122). Таким образом,
графики функции у = —2х2 и у = 2х2 симметричны относитель¬
но оси Ох.
Приведенные в этом примере соображения показывают, что
парабола у = ах2 (а < 0) симметрична параболе у = I а I х2 от¬
носительно оси Ох (рис. 123). Из этой симметрии следуют
свойства функции у = ах2 (а < 0).
Приведем без доказательства теорему о свойствах функции
у = ах2 (а < 0).
Теорема.
1.	Областью определения функции у = ах2 (а < 0) явля¬
ется множество R всех действительных чисел.
2.	Множеством значений функции у = ах2 (а < 0) являет¬
ся промежуток (- оо; 0].

211
Функция у = ах2 ИИУ
3.	Значение у = 0 является наибольшим значением
функции у — ах2 (а < 0), а наименьшего значения функция
не имеет.
4.	График функции у = ах2 (а < 0) пересекается с осями
координат в единственной точке (0; 0) — начале координат.
5.	Значение аргумента х = 0 является нулем функции
у = ах2 (а < 0).
6.	Функции у = ах2(а<0) принимает отрицательные
значения (у < 0) на множестве (—	0) U (0; + °°), т. е. па¬
рабола расположена в III и IV координатных углах.
7.	Функции у = ах2 (а < 0) четная.
8.	Функции у = ах2 (а < 0) возрастает от — °о до 0 на про¬
межутке (— 00; 0] и убывает от 0 до - 00 на промежутке
[0; +оо).
Мы видели, что при а > 0 и а < 0 парабола у = ах2
симметрична относительно оси Оу (см. рис. 122, 123). Таким
образом, ось Оу является осью симметрии параболы
у — ах2 (а 0).
Точка, в которой парабола пересекается со своей осью сим¬
метрии, называется вершиной параболы.
Вершиной параболы у = ах2 является начало координат.
Ветви параболы у = ах2 (а > 0) направлены вверх (рис. 124), а
ветви параболы у = ах2 (а < 0) направлены вниз (рис. 125).
Пример 3. Найти координаты точек пересечения парабо¬
лы у — 5х2 и прямой у = 2х + 3.

функция
212
Решение. Координаты точек пересечения графиков фун¬
кций являются решениями системы уравнений
У = 5х1 2 3 4,
у = 2х + 3.
(1)
Из этой системы следует уравнение
5х2 - 2х — 3 = 0, его корни хх = —	,
х2 = 1.
Из системы (1) получим:
^ = 5 6(~т)2 = т; ^ = 5-
Ответ:	(1; 5).
Замечание. Если графики функций у = 5х2 и у = 2х + 3
изображены в одной системе координат (рис. 126), то по
рисунку можно найти координаты точек пересечения этих
графиков; обычно это удается сделать только приближенно.
1.	Какая функция называется квадратичной?
2.	Как называется график квадратичной функции?
3.	Почему функция у = ах2 (а * 0) является квадратичной?
4.	Сформулируйте свойства функции у -ах2 при:
а) а > 0; б) а < 0.
5.	Как получается парабола у = ах2 из параболы у = х2, если:
а)а>1;	б)0<а<1?
6.	Проиллюстрируйте на рисунке свойства функции у =ах2 при:
а) а > 0;	б) а < 0.
7*. Докажите, свойства функции у = ах2 при:
а) а > 0; б) а < 0.
Упражнения
3.1°. Даны функции: у —	х2; у = х2; у = 4х2. Изобразите на
одном чертеже графики зтих функций и укажите для
каждой из функций ее свойства.

213
Функция у = ах1
3.2°. Верно ли, что графику функции у = 4х2 принадлежит
точка:
1)А(-1;-4);	2) В(0,5; 2);
3)	С(0,1; 0,4);	4) Г»(-2; 16)?
3.3. Функция задана формулой у =-|- х2 на множестве:
1)[0;+со);	2)(-оо;0];	3) ЛГ;
4)	Z;	5) [-4; 3];	6) [-2; 4].
Укажите наибольшее и наименьшее значения заданной
функции, изобразив предварительно ее график.
3.4°. Найдите координаты общих точек (если они есть) пара¬
болы у = 2х2 и прямой:
1)	£/ = 25;	2) £/= 1020;	3) £/ = -16;
4)	у = -2870;	5) у = 0;	6) у = 2460.
3.5.	Укажите свойства функции и изобразите ее график:
=	2) £/= 6х2;
3)£/ = 3х2;	4) £/ = ух2.
3.6.	Функция задана формулой у = х2 на множестве
{-4; -3; -2; —1; 0; 1; 2; 3; 4}. Укажите множество, на
котором функция:
а)	возрастает; б) убывает.
3.7.	Найдите значение а, если известно, что парабола у = ах2
проходит через точку:
1)	(1; 5);	2) (2; 16);
3) (0; 0);	4) (3; 1);
5)	(-2; 1);	6) (-5; 125).
3.8.	Запишите уравнение параболы, полученной из параболы
у = 2х2:
1)	растяжением в 2 раза вдоль оси Оу;
2)	растяжением в 4 раза вдоль оси Оу;
3)	сжатием в 4 раза вдоль оси Оу;
4)	сжатием в 2 раза вдоль оси Оу.

Квадратичная функция
214
3.9.	Задайте формулой с соответствующей областью опреде¬
ления функцию, график которой — часть параболы —
изображен на рисунке 127.
Рис 127
3.10.	Изобразите в одной системе координат графики функций
у = у х2 и у =- у х2. Укажите для обеих функций:
а)	область определения;
б)	множество значений;
в)	ось симметрии графика;
г)	наибольшее значение;
д)	наименьшее значение;
е)	промежуток убывания;
ж)	промежуток возрастания.
3.11°. Принадлежит ли параболе у = -250х2 точка:
1) Х(-1;	-250);	2)	Л7(-3;	-2250);
з)	Т(\/2;	-500);	4)	Р(0,2; -10);
5)	£(0,1;	-2,5);	6)	В(-3; 750)?
3.12.	При каких значениях параметра а функция у = (а + 3)х2
имеет:
1)	наибольшее значение;
2)	наименьшее значение;

Функция у — ах2
215
3)	графиком параболу;
4)	графиком прямую?
3.13.	На рисунке 128 изображен график функции у — ах2. Ука¬
жите значение а.
3.14.	Укажите значения параметра k, при которых функция
у = (/г-4)х2:
1)	является квадратичной и имеет наибольшее значение;
2)	является квадратичной и не имеет наибольшего зна¬
чения;
3)	не является квадратичной;
4)	имеет график, симметричный относительно оси Оу,
5)	имеет график, симметричный относительно начала
координат;
6)	является четной.
3.15.	Верно ли, что ось Оу является осью симметрии графика
функции, заданной формулой на множестве D, если:
1)	у = Зх2, 7) = [—5; 2];
2)	у = ~2х2, D = [-7; 7];
3)	у = -0,8х2, D = [3; 15];

216
Квадратичная функция
y=±x2,D = [-5-, 0];
у = 5х2, £> = [-4,7; 4,7];
1/=-7х2, £) = [—11; —2];
г/= —112х2, £> = [-6; 6);
у = 4,39х2, £> = (-4; 4);
z/ = f х2, £> = (-v5; у 5);
у = ~8х2, £> = (-9; 9]?
1)
3)
1)
2)
3)
4)
4)
5)
6)
7)
8)
9)
Ю)
3.16*. Изобразите график функции:
у = 2x1 xl, х > 0;
2)	у — у xlxl, х€ {0; 1; 2; 3};
у = -2x1 х I, х < 0;
4)	i/ = -y xlxl, х€{—4; -3; -2; -1}.
3.17*. При каких значениях параметра р не является квадра¬
тичной функция:
у = (Зр2 - 5р + 8)х2 + 4х - 1;
у = (~2р2 + Зр -1)х2 - 6х + 5;
у = (~5р2 - 4р -1)х2 + 7х + 3;
у = (4р2 -7р + 3)х2 - 5х - 2?
3.2.	Функция у = ах2 + с
Рассмотрим частный случай квадратичной функции
у = ах2 + Ьх + с при b = 0, т. е. функцию
у = ах2 + с,
где а 0, с 0.
Приведем
знаков чисел
четыре примера с различными комбинациями
а и с.
1. Рассмотрим функцию у - у хг + 3 (здесь
Пример
а = у > 0, с = 3 > 0). Сравним ее с функцией у = у х2. При каж¬
дом значении х значение функции у = х2 + 3 больше значе-

217
Функция у =	+ с
ния функции у = х2 на 3 еди¬
ницы. Следовательно, каждая
точка М параболы у = -^-х2 + 3
получается из соответствую¬
щей точки N параболы у = -|- х2
сдвигом на 3 единицы вверх
(рис. 129). Это значит, что па¬
рабола у =-^- х2 + 3 получается
из параболы у = х2 сдвигом
на 3 единицы вверх вдоль
оси Оу.
Поэтому осью симметрии
параболы у = -^- х2 + 3 так же, к
и осью симметрии параболы
у =	х2, является ось Оу, т. е. данная функция четная.
Вершина рассматриваемой параболы — точка (0; 3); она по¬
лучается из точки (0; 0) — вершины параболы у = х2 — сдви¬
гом на 3 единицы вверх. Ветви параболы у = -^- х2 + 3 направ¬
лены вверх.
Используя свойства функции у = хг, получаем и другие
свойства функции у = ± х2 + 3.
Функция г/ =-|- х2 + 3 не имеет нулей. Наименьшее значе¬
ние этой функции равно 3, наибольшего значения функция не
имеет.
Множеством значений функции у = -^-хг + 3 является про¬
межуток [3; + ©о).
При любых значениях х значения функции — положитель¬
ные числа.
На промежутке (—0°; 0] функция у = -^- х2 + 3 убывает от
+ со до 3, а на промежутке [0; + °°) возрастает от 3 до + °°.

Квадратичная функция
218
Пример 2. Рассмотрим
функцию у = у х2 - 3 (здесь
а = у > 0, с = -3 < 0). Сравним
ее с функцией у - хг. При
каждом значении х значение
функции у-~х2~3 меньше
1 2
значения функции у - х на
3 единицы. Следовательно,
каждая точка М параболы
у = у х2 - 3 получается из со¬
ответствующей точки N параболы у = -~х2 сдвигом на 3 еди¬
ницы вниз (рис. 130). Это значит, что парабола у х2 — 3 по¬
лучается из параболы у =-^ х 2 сдвигом на 3 единицы вниз
вдоль оси Оу. Поэтому осью симметрии параболы у = у х2 - 3
так же, как и осью симметрии параболы у =	х2, является ось
Оу, т. е. данная функция четная.
Вершина рассматриваемой параболы — точка (0; -3); она
получается из точки (0; 0) — вершины параболы г/=ух2—
сдвигом на 3 единицы вниз. Ветви параболы у = -- х2 - 3 на¬
правлены вверх.
Нули функции у = у х2 — 3 — это корни уравнения
у х2 - 3 = 0, т. е. числа хт = - \ 6 , х2 = у 6 .
На промежутках	— \ 6 ) и (у6; +°°) значения функции
положительны, а на промежутке (- \ 6 ; \ 6 ) значения функции
отрицательны.
Наименьшее значение этой функции равно -3, а наиболь¬
шего значения функция не имеет.

219
Функция у = ах2 + с
Множеством значений функции у = х2 - 3 является про¬
межуток [-3; +оо).
На промежутке (- °°; 0] функция у = ± х2 - 3 убывает от
+ оо до — 3, а на промежутке [0; + оо) возрастает от — 3 до + оо.
Пример 3. Рассмотрим функцию у-~-~х2 + 3 (здесь
а = ~ у < 0, с = 3 > 0). Сравним
эту функцию с функцией
у = — -^х2 по аналогии с при¬
мером 1. Мы видим, что пара¬
бола I/ = — у х2 + 3 получается
сдвигом параболы у = - у х2
на 3 единицы вверх вдоль оси
Оу (рис. 131).
Пример 4. Рассмотрим
функцию у = — у х2 - 3 (здесь
a — — у<0, с=-3<0). Срав¬
ним эту функцию с функцией
у = - у х2 по аналогии с при¬
мером 1. Мы видим, что пара¬
бола I/ = - у х2 - 3 получается
сдвигом параболы у = - у х2
на 3 единицы вниз вдоль оси
Оу (рис. 132).
Для каждой из функций в
примерах 3 и 4 назовите:
а)	координаты вершины па¬
раболы;
б)	уравнение оси симмет¬
рии параболы;

220
в)	направление ветвей параболы;
г)	нули функции;
д)	промежутки знакопостоянства функции;
е)	наименьшее значение функции;
ж)	наибольшее значение функции;
з)	множество значений функции;
и)	промежуток возрастания;
к)	промежуток убывания.
Соображения, которые были приведены при рассмотрении
примеров 1—4, показывают, что
парабола у = ах2 + с получается сдвигом параболы
у = ах2 вдоль оси Оу.
при с> 0 на с единиц вверх;
при с < 0 на I с I единиц вниз.
1.	Каким преобразованием можно получить параболу у = ах2 + с
из параболы у = ах2"!
2,	Назовите для параболы у = ах2 + с свойства а) — к) (см. с. 219—
220) в случае, когда: а > 0, а < 0.
Упражнения
3.18°. Изобразите график функции, заданной формулой, и ука¬
жите ее свойства:
1)	у = у х2 - 4;	2)	у = -j- х2 + 4;
3) г/= Зх2 + 1;	4)	г/ = 3х2 —1;
5)	у = - у х2 + 3;	6)	у = - у х2 - 3;
7)у = — 4х2-2;	8)у	=	~4х2 + 2.
3.19. Как из графика функции у — 2х2 можно получить график
функции:
1)у = 2х2 + 1;	2) у = 2х2 — 1;
3) у = - 6 + 2х2;	4) у = 2х2 + 9?
3.20°. Запишите уравнение параболы, полученной из параболы
у = 7х2 сдвигом вдоль оси Оу на:

221
Функция у = ах2 + с
1) 3 единицы вверх;
3) 7 единиц вниз;
5) 2,1 единицы вниз;
7) 0,9 единицы вверх;
2)	5 единиц вниз;
4)	4 единицы вверх;
6)	8,4 единицы вниз;
8)	0,3 единицы вверх.
3.21°. Запишите уравнение параболы, полученной из параболы
у = - 3,2х2 сдвигом вдоль оси Оу на:
1) 6 единиц вверх;	2) 4,6 единицы вниз;
3)	2,4 единицы вниз; 6) 7 единиц вверх.
3.22.	Как надо преобразовать параболу у = -0,73х2, чтобы
уравнение полученной параболы имело вид:
1) у = -0,73х2 + 6^_	2) г/= — 0,73х2 - 27;
3) у = -0,73хг-\3;	4) у = ~0,73х2 + х/5 ?
3.23.	Как надо преобразовать параболу у = х2, чтобы уравнение
полученной параболы имело вид:
1) у = -7х2 + 3;	2)у = 5х2-6;
3)	y=|x2-(v5)2;	4) у = -±х2 + (у7)4?
3.24.	Используя изображение параболы на рисунке 133, задай¬
те формулой ее уравнение.
4) У.
3.25.	Для каждой функции из упражнения 3.24 укажите:
а)	множество значений;
б)	наибольшее (наименьшее) значение;
в)	промежуток убывания;
г)	промежуток возрастания;
д)	координаты вершины параболы;

Квадратичная функция
222
е)	ось симметрии параболы;
ж)	координаты точек пересечения с осями Ох и Оу,
з)	промежутки знакопостоянства.
3.26.	Найдите точки пересечения параболы и прямой:
1)
= 1-х2
и
у = -8;
2)
у~-
-х2 - 4
и
У = 5;
3)
У =
= х2 + 2
и
у = 4х - 3;
4)
У =
= 6х2 - 1
и
у = 5х;
5)
У =
= 5х2 + 1
и
у = 6х;
6)
У =
- 2х2 - 4
и
У = х-4;
7)
У =
= 8х2 -1
и
у = - 3 - 8х:
8)
У =
: | х2 + i
и
2
у = -тх.
3.27.	Имеет ли парабола у = 6х2 — 1 общие точки с прямой-
1)у = 8;	2) у = 0;	3)^=1;
4)у = -1;	5) £/ = -10;	6) у = ~3?
Если да, то найдите их координаты.
3.28.	Имеет ли парабола у — - Зх2 + 2 общие точки с прямой:
1) у = 0;	2) у = 2;	3) у = 9;
4) у = —1;	5) у = -10;	6) у = 1,025?
Если да, то найдите их координаты.
3.29.	При каких значениях р парабола у = х2 + р проходит' че¬
рез точку:
1)А(0;-3);	2) В(-4; 17);
3) х(|; |);	4) М(-0,5;-6,45)?
3.30.	При каких значениях аир парабола у = ах2 + р проходит
через точки:
1)	А(0; ~1)иВ(1; 2);
2)	М(1; 0) и N(-3; 24);
3)	Т(-2; 3)иХ(-1; 4);
4)	Е(-3; 2) иР(3; -1)?

223
Функция у = а (х — s)2
3.3.	Функция у = а (х — s)2
Рассмотрим функцию у = а(х~ s)2, где а 0 и s 0.
Приведем четыре примера с различными комбинациями
знаков чисел а и s.
Пример 1. Рассмотрим функцию у--^-(х-З)2 (здесь
а = у >0; s = 3 >о).
Воспользовавшись таблицей, изобразим на одном рисунке
график этой функции и график функции у = у х2 (рис. 134).
X
- 1
1
2
0
1
2
1
4
2
4
3
4
4
1 2
1
1
0
1
1
, 1
ч 1
4 1
4
8
У 2 х
2
8
8
2
1 8
3 8
4 2
у=у(х-3)2
8
4
4
3 —
3 8
2
4
1
2
1
8
0
1
8
1
2
Если внимательно посмотреть на рисунок, то связь между
графиками функций становится очевидной: парабола
у = у (х - З)2 сдвинута относительно параболы у = у х2 на
3 единицы вправо вдоль оси
Ох.
Поэтому ось симметрии па¬
раболы у = у (х — З)2 получит¬
ся, если сдвинуть ось симмет¬
рии параболы у = у х2 на 3
единицы вправо вдоль оси Ох.
Значит, ось симметрии параболы у — у (х - З)2 — это прямая
х — 3, она параллельна оси Оу и проходит через точку (3; 0).
По изображению параболы можно увидеть, что:
а)	точка (3; 0) — вершина параболы;
б)	х = 3 — уравнение оси симметрии параболы;

Квадратичная функция	224
в)	ветви параболы направлены вверх;
г)	значение абсциссы х = 3 — нуль функции;
д)	значения функции положительны (у > 0) на множестве
(-оо; 3) и (3; +оо);
е)	у — 0 — наименьшее значение функции;
ж)	наибольшего значения функция не имеет;
з)	множеством значений функции у - (х - З)2 является
промежуток [0; +°°);
и)	на промежутке (—°°; 3] функция убывает от +°° до 0;
к)	на промежутке [3; +оо) функция возрастает от 0
ДО + оо.
▲ Чтобы исследовать функцию у = у (х - З)2, сравним ее
с функцией У = у х2. Значе-
_ 1 2
ние функции у - ~2 хz в точке
х0 обозначим у0, т. е. Уо~
=	х2. Значит, точка А(х0; z/0)
лежит на. параболе У = у х2
(рис. 135).
Значение функции у = у (х - З)2 в точке х0 + 3 равно
у ((*0 + 3) - З)2 = у х2 = Уо. Значит, точка B(xQ + 3; Уо) лежит
на параболе у = у (х - З)2 (см. рис. 135).
Теперь заметим, что точка В получилась из точки А сдви¬
гом на 3 единицы вправо вдоль оси Ох, т. е. каждая точка па¬
раболы г/ = у (х — З)2 получается из соответствующей точки
параболы г/ = у х2 сдвигом на 3 единицы вправо вдоль оси
Ох. Поэтому и вся парабола у = у (х - З)2 получится, если
сдвинуть параболу У = у х2 на 3 единицы вправо вдоль
оси Ох. ▲

225
Функция у = а (х — $)2
Пример 2. Рассмотрим функцию у=-|-(х + 2)2 (здесь
а= у >0; s = —2 <о).
Используя таблицу, изобразим на одном рисунке графики
указанных в ней функций (рис. 136).
X
-З.т
-3
-21
-2
-1!
-1
1
2
0
1
2
1
„ 1
, 1
91
, 1
3
1
1
0
1
1
I/	3 X2
412
2 12
1 3
4
3
12
12
3
р=у(х+2)2
3
4
1
3
1
12
0
1
12
1
3
3
4
2J_
Z12
3
По рисунку легко заметить, что парабола у = (х + 2)2
сдвинута относительно параболы у = х2 на 2 единицы влево
вдоль оси Ох.
По изображению параболы у = (х + 2)2 на рисунке 136
можно указать свойства а) — и) (см. ц. 3.2), а также уравнение
ее оси симметрии:
а)	(—2; 0) — координаты вершины параболы и х = -2 —
уравнение ее оси симметрии;
б)	ветви параболы направлены вверх;

91 Квадратичная функция
226
в)	нуль функции у = (х + 2)2 — это число х0 = — 2;
г)	при х € (—оо; —2) U (—2; +оо) значения функции положи¬
тельны, т. е. у > 0;
д)	наименьшее значение функции равно нулю;
е)	наибольшего значения функция не имеет;
ж)	промежуток [0; +оо) — множество значений функции;
з)	на промежутке [—2;+°о) функция у= (х + 2)2 возрас¬
тает от 0 до +оо.
и)	на промежутке (— оо; —2] функция убывает от +оо до 0.
Пример 3. Рассмотрим функцию г/ = - (х — -|- ) (здесь
а = —< 0; s = -| > о).
Изобразив на одном рисунке графики функций у = - х2
и у = ~	можно увидеть, что парабола
у = — -у (х —|-) сдвинута относительно параболы у = — х2 на
у единицы вправо вдоль оси Ох (рис. 137).
а = -у <0; s = --|- <о).

227
Изобразим на одном рисунке графики функций у = — у х2
иу = _-|-(х + -|-)2 (рис. 138). По рисунку видно, что парабола
у = - у (х + -у) сдвинута относительно параболы у = — -у х2
на у единицы влево вдоль оси Ох.
По изображениям на рисунках 137 и 138 парабол
1 / з \2	1 / , з V
у = -у lx-~2 I и у = -у (х+ ~2 I можно указать свойства
а) — к) (см. п. 3.2).
Например, для функции у = ~ у ^х—|- ) по рисунку 137
укажем:
а)	(-у; о) — координаты вершины параболы;
б)	уравнение оси симметрии параболы х = у;
в)	ветви параболы у = — у I х —% \ направлены ьниз:
г)	нуль функции — это число х0 — -у ;
д)	при хе(-°°; у)	+°°) значения функции отри¬
цательны, т. е. у < 0;

Квадратичная функция
228
е)	наименьшего значения функция у = -
не
имеет;
ж)	наибольшее значение функции равно нулю;
з)	промежуток (—°°; 0] — множество значений функции;
и)	на промежутке	-|-1 функция у = — -|-
воз-
растает от - оо до 0;
к)	на промежутке ; +оо) функция убывает от 0 до - оо.
Для функции из примера 4 аналогичные свойства а) — к)
сформулируйте самостоятельно.
Соображения, приведенные при рассмотрении приме¬
ров 1—4, показывают, что парабола у = а(х — s)1 2 по¬
лучается сдвигом параболы у = ах2 вдоль оси Ох на
s единиц вправо, когда s > 0, и на Is I единиц влево,
когда s < 0.
1. Каким преобразованием можно получить параболу у = а(х - s)2
из параболы у = ах?Ч
2*. Назовите для параболы у = а(х — s)2 свойства а) — к)
(см. с. 227—228) в случае, когда а > 0, а < 0.
Упражнения
3.31.	Как из графика функции у = 5х2 можно получить график
функции:
1)	у = 5(х- З)2;
3) z/ — 5х2 + 10х + 5;
5) у = 5х2 - 50х + 125;
7)	у = 5х2 + Юу'Тх + 35;
2)	z/ = 5(x + 7)2;
4)	у = 5х2 - 40х + 80;
6)	у = 5х2 - 20х + 20;
8)	у = 5х2 + 10<Зх + 15?
3.32.	Запишите уравнение параболы, полученной из параболы
у = 2,3x2 сдвигом вдоль оси Ох на:
1)	4 единицы влево;
3)	3 единицы вправо;
5)	1,5 единицы влево;
7)	0,7 единицы вправо;
2)	5 единиц вправо;
4)	7 единиц влево;
6)	0,4 единицы вправо;
8)	2,3 единицы влево.

229
Функция у = а(х — $)2 й
3.33.	Как надо преобразовать параболу у = — 0,4х2, чтобы полу¬
чилась парабола:
1)	У = ~0,4(х - 2)2;	2) у = -0,4(х + 6,8)2;
3)	у - —0,4(х + 7,3)2;	4) у = -0,4(х - 9)2?
3.34.	Как надо преобразовать параболу у = 27х2, чтобы полу¬
чилась парабола:
1)	у = 27(х + 92)2;	2) у = 27(х - 670)2;
3) у = 27(х - 530)2;	4) у = 27(х + З1)2?
3.35°. Изобразите график функции, заданной формулой, и ука¬
жите ее свойства:
1) у=±(х + 2)2-,
3) у = 3(х —1,5)2;
5)	у = - у (4 - х)2;
7)	у = -5(х+ I)2;
2)	У=у (х —2)2;
4)	у = 3(х + 1,5)2;
6)	у=- у (х+4)2;
8)	у = -5(1- х)2.
3.36°. Найдите координаты точек пересечения графиков функ¬
ций:
1)	у = (2 + х)2 и у = 4;
2)	у = (х - 4)2 и у = 9;
3)	у = (3 —2х)2 и у = 1;
4)	у = (6х — 4)2 и у = 16;
5)	у = (4х — 5)2 и у = 8х + 25;
6)	у = (3 — 8х)2 и у = 9 + 16х.
3.37°. Укажите вершину параболы:
1) y = 4(x+f )2;	2)	у = 2,4(х — 2,5)2;
3)	у = -9(х-|)2;	4)	у = -0,1(0,75-х)2;
5)	У=у(4 + х)2;	6)	у = ^-(х + 0,8)2;
7)	у = х2 - 4х + 4;	8)	у = х2 + 25 - 10х.

3.38.	Задайте формулой квадратичную функцию, график ко¬
торой изображен на рисунке 139.
3.39.	Для каждой функции из упражнения 3.37 укажите ее
свойства.
3.40.	Укажите свойства функции, заданной формулой, и изоб¬
разите ее график:
1)у = (х-5)2;	2) у = ~(х + 4)2;
3) у =-3(х + 2)2;	4) i/= 2(х — З)2.
3.41°. Дана функция у=(х —) . Принадлежит ’ли графику
функции точка:
3) 0(3,5; 9);	4) К(-7,5; -49)?
3.42°. Запишите уравнение оси симметрии параболы:
1) у=р(х + 5)2;	2)z/=px2 —4;

231	Функция у = а(х — s)2
3)	у = рх2 + -|-;	4) у=р(х + 1,8)2;
5)	у = (х-р)2;	6) у = (х +р)2;
7)	у = ~х2 —р;	8) у = —(х — р)2;
9)	у = ~(х + р)2;	10)у=-х2+р.
3.43.	Верно ли, что при любом значении параметра р график
функции (см. упражнение 3.42) не имеет общих точек с
прямой:
а) у =-374; б) у=0; в) у =128?
3.44.	При каком значении к графику функции у = 5 (х + к)2
принадлежит точка:
1) (0; 5);	2) (-7; 5);	3) (7; -5);
4)	(7; 5);	5)(|;б);	6) (0,5;-5)?
3.45.	На рисунке 140 изображена парабола р = Ь(х + с)2. Опре¬
делите знаки чисел Ь и с
Рис. 140

Квадратичная функция
232
3.4.	Функция у — а(х — s)2 +1
Рассмотрим функцию у = а(х — s)2 + t, где а 0, s 0, t О.
Приведем четыре примера такой функции.
Пример 1. Рассмотрим функцию у = (х - I)2 + 3 (здесь
a = -j>0;s = l>0;t=3>0).
Ее график можно получить из параболы у = у х2
следующим образом. Сдвинем параболу у = х2 вдоль оси Ох
на 1 единицу вправо. В
Рис. 141
у = у (х — I)2 + 3 легко
функции (см. рис. 141).
Назовите:
увидеть
результате получим параболу
у = -у (х - I)2. Теперь сдвинем
эту параболу вдоль оси Оу на
3 единицы вверх. Соображе¬
ния, которые были приведены
при рассмотрении примера 1 из
п. 3.2, показывают, что в ре¬
зультате получится парабола
у = у (х -.I)2 + 3. Каждая точ¬
ка этой параболы получается
из соответствующей точки па¬
раболы у — у (х - I)2 сдвигом
на 3 единицы вверх вдоль
оси Оу (рис. 141).
По изображению параболы
свойства соответствующей
а)	координаты вершины параболы;
б)	уравнение оси симметрии параболы;
в)	направление ветвей параболы;
г)	нули функции;
д)	промежутки знакопостоянства функции;

233	Функция у = а(х — л)2 + t
е)	наименьшее значение функции;
ж)	наибольшее значение функции;
з)	множество значений функции;
и)	промежуток возрастания функции;
к)	промежуток убывания функции.
П р и м е р 2. Рассмотрим функцию у = у (х + I)2 - 3 (здесь
а = у >0; s = -l<0; f = -3<0).
Ее график можно получить из параболы у — х2
следующим образом. Сдвинем параболу у =~х2 вдоль оси Ох
на 1 единицу влево. В
результате получим параболу
у = у (х + I)2. Теперь сдвинем
эту параболу вдоль оси Оу на
3 единицы вниз. Те же сообра¬
жения, что и в примере 2 из
п. 3.2, показывают, что в ре¬
зультате получится парабола
у = у (х + I)2 — 3. Каждая точ¬
ка этой параболы получается
из соответствующей точки па¬
раболы у — у (х + I)2 сдвигом
на 3 единицы вниз вдоль оси Оу
(рис. 142).
Используя изображение параболы у=у(х + 1)2 — 3, назо¬
вите для соответствующей функции свойства а) — к), пере¬
численные в примере 1.
Пример 3. Рассмотрим функцию у = - у (х - I)2 + 3
(здесь а = - у < 0; $ = 1 > 0; t - 3 > 0).
Соображения, которые были приведены при рассмотрении
примера 1, показывают, что график этой функции получается

из параболы у = — х2 сдвигом на 1 единицу вправо вдоль оси
Ох и на 3 единицы вверх вдоль оси Оу (рис. 143).
Пример 4. Рассмотрим функцию у = — -у (х + I)2 - 3
(здесь а =	< 0; а = -1 < 0; f = -3 < 0).
Соображения, которые были приведены при рассмотрении
примера 2, показывают, что ее график получается из параболы
у = — х2 сдвигом на 1 единицу влево вдоль оси Ох и на 3
единицы вниз вдоль оси Оу (рис. 144).
Используя изображения парабол из примеров 3 и 4 на ри¬
сунках 143 и 144, назовите для каждой из соответствующих
функций свойства, перечисленные в примере 1.
Соображения, которые были приведены при рассмотрении
примеров 1—4, показывают, что
т
парабола y~a{x~s)2 + t получается сдвигом пара¬
болы у = ах2: вдоль оси Ох на | s | единиц (вправо, когда
s > 0, и влево, когда s < 0J; вдоль оси Оу na\t \ единиц
(вверх, когда t> 0, и вниз, когда t < О/
Осью симметрии параболы у = а(х~s)2 + t является
прямая х = s (эта прямая параллельна оси Оу).

235	Функция у = а(х - s)2 + t
Ось симмещрии пересекает параболу у = а(х - s)2 + t
в точке P(s; t), и эта точка является вершиной
параболы.
Ветви, параболы у = а(х — s)2 + t направлены вверх,
когда а > 0, и направлены вниз, когда а < О.
П р и м е р 5. Какими преобразованиями (сдвигами) можно
из параболы у = х2 получить параболу:
а)	г/=(х + 6)2 — 8; б) у =(х - 4)2 - 13?
Решение, а) Приведем формулу у —(х + 6)2 — 8 к виду
у = а(х - s)2 + t:
г/= 1(х —(—6))2+(—8).
Таким образом, имеем: а = 1 > 0; s = -6 <0; t = -8 < 0.
Так как парабола у = а(х — s)2 + t получается из параболы
у = ах2 сдвигом вдоль оси Ох влево на | s I единиц при s < 0 и
сдвигом вдоль оси Оу вниз на 111 единиц при t < 0, то парабола
у = 1(х -(—6))2 +(—8) получается из параболы у = 1 • х2 сдвигом
вдоль оси Ох на 6 единиц влево и вниз вдоль оси Оу на 8
единиц.
б)	Приведем формулу у =(х — 4)2 — 13 к виду у=а(х — s)2 + t:
у=(х-4)г+(~13),
здесь а = 1 > 0; s = 4 > 0; t = -13 < 0.
Таким образом, парабола г/=(х-4)2+(~13) получена из
параболы у = х2 сдвигом вдоль оси Ох вправо на 4 единицы и
вниз вдоль оси Оу на 13 единиц.
Пример 6. Пересекает ли парабола у = — 0,38(х + 4)2 + 7
прямую:
а) г/= —10,3; б) у = 17,3; в)у = 0>
Р’в ш е н и е. Поскольку а = —0,38 <0, то ветви параболы
направлены вниз; вершина параболы — точка (—4; 7); ось
симметрии параболы — прямая х = —4.
Изобразив параболу (сделайте это), можно увидеть, что
она пересекается с прямыми у = -10,3 и у = 0 и не может
иметь общих точек с прямой у — 17,3. Так как множеством
Квадратичная функция
236
значений функции у = -0,38(х + 4)2 + 7 является промежуток
(—00; 7], то, следовательно, 7 — это наибольшее значение
функции.
1.	Каким преобразованием из параболы у = ах2 можно получить
параболу у = а(х — sf + t из параболы у = ах2?
2.	Назовите для параболы у = а(х — s)2 +1 свойства а) — к) (см.
с. 232—233) в случае, когда а > 0, а < 0.
У пражнения
3.46.	Какими преобразованиями (сдвигами) из параболы у = х2
можно получить параболу:
1)	у=(х-5)2 +1;	2)	у =(х + З)2 - 4;
3)	у =(х + 2)2 — 7;	4)	у =(х — I)2 + 5;
5) у = 8 + (х - 9)2;	6)	у =-6 + (х + 8)2?
3.47.	Какими преобразованиями (сдвигами) из параболы
у = — х2 можно получить параболу:
1)	у = -(х + 3)2-1;	2) у = 5-(х-2)2;
3)	у = 6-(х-4)2;	4) у = —(х + 9)2 — 7?
3.48.	Запишите уравнение параболы, полученной из параболы
у = 7х2 сдвигом вдоль оси Ох и вдоль оси Оу
соответственно на:
1)	3 единицы влево и 2 единицы вниз;
2)	5 единиц вправо и 6 единиц вниз;
3)	0,5 единицы вправо и 5 единиц вверх;
4)	3,5 единицы влево и 2 единицы вверх.
3.49°. Определите по изображению графика функции
у = у (х — I)2 + 3 (см. рис. 141), при каких значениях х
функция принимает:
1)	положительные значения;
2)	отрицательные значения;
3)	значения, равные нулю;
4)	значения, не большие нуля.

237
Функция у = а(х — s)2 + t
3.50.	Определите по изображению графика функции
(см. рис. 144) свойства функции, заданной формулой
у = - | (х + I)1 2 - 3.
3.51.	Какими преобразованиями (сдвигами) из параболы
у = 6х2 можно получить параболу:
1)у = 6х2 —3;	2)у = 6(х —I)2;
3)	у = 6(х - I)2 - 3?
3.52.	Какими преобразованиями (сдвигами) из параболы
у = ~ (х + 6)2 можно получить параболу:
1)	у = у(х + 6)2-5;	2) у = у (х + 6)2 + 7;
3) у =-у (х + 6)2 + 10;	4) у = -|(х + 6)2~12?
3.53.	Какими преобразованиями (сдвигами) из параболы
у = -3(х - 4)2 можно получить параболу:
1)	у = -3(х-4)2 + 8;	2)	у = —3(х — 4)2 — 9;
3) у = 3(х-4)2-24;	4)	у = 3(х - 4)2 + 16?
3.54.	Укажите уравнение оси симметрии параболы:
1)	у = 3(х —4)2-2;	2)	у = -6(х + 2)2 + 6;
3) у = —2(х + 7)2 + 1;	4)	у = 4(х - З)2 + 5.
3.55.	Найдите координаты вершины параболы:
1)	у = 5(х —8)2 + 2;
3) у = -у (х + 2)2 + 6;
5)	у = -4(х + у j2-y;
7)	у =(х + а)2 - Ъ;
9) у = k(x-p)2 + t;
2)	у =-2(х + З)2 —5;
4)	у = у (х - 6)2 - 3;
6)	у = 8(х--|)2 + -|-;
8)	у=(х-с)2-р;
10)	у = т(х + п)2 + р.
3.56 . Изобразите схематично параболу:
1)	у=(х-4)2 + 3;
3)	у =(3 — х)2 — 3,5;
5)	у = -(х + 0,75)2 + -|;
7)	у =-(х + 2)2-1;
2)	у =(х + 2,5)2 ~ 1;
4)	у=(5-х)2 + 2;
6)	у = -(х-0,25)2-у;
8)	у = —(х —З)2 —4.

Квадратичная функция
238
3.57.	Для каждой функции (см. упражнение 3.56) укажите:
а)	множество значений;
б)	промежуток убывания;
в)	промежуток возрастания;
г)	уравнение оси симметрии;
д)	наибольшее (наименьшее) значение;
е)	значения х, при которых у > 0;
ж)	значения х, при которых у < 0;
з)	координаты точек пересечения с осями Ох и Оу.
3.58.	Задайте формулой квадратичную функцию, график ко¬
торой изображен на рисунке 145, и укажите ее свойства.
3.59°. Принадлежит ли графику функции у = (х — I)1 2 + 4 точка:
1)	А(-3; 20);	2) В(0; 3);
3) С(1; 16);	4) D(2; 5)?
3.60.	Имеет ли график функции у = 0,8(х — 6)2 + 5 общие
точки с прямой:
1) У = -Ю;
3) у = 0;
5)	у = 5;
2)	у = 100;
4)	у = 4;
6)	у = б?
3.61.	Имеет ли график функции у = — 6,2(х + 8)2 — 3 общие
точки с прямой:
1)у = 200;	2) у = -300;
3)у = 0;	4)у = —2;
5)у = -3;	6)у = 8?

239
Функция у = а(х — s)2 + t
3.62.	При каких значениях параметра р указанная точка при¬
надлежит графику функции у = 3(х + р)2 - 2:
1) (1; 10); 2) (-2; -2);
3) (-3; 5);	4) (2; 10)?
3.63. При каких значениях параметра р данная функция при¬
нимает только отрицательные значения:
1) г/=р(х - 7)2 — 3;
2) г/=р(х — 4)2 + 5;
3) у = 2(х+р)2 — 1;
4) у = -7(х + р)2~3;
5) у = -5(х + 1)2-р;
6) у = 6(х + 2)2 — р;
7) у = -0,3(х + 8)2 + р;
8) у =	(х-9)2+р?
3.64. Верно ли, что при
любом значении р парабола
(см. упражнение 3.63) имеет общие точки с прямой:
а) у = -10; б) у = 0;	в) у = 27?
3.65. Назовите, при каких условиях вершина параболы
у = а(х - s)2 + t будет расположена:
1)	в I координатном угле;
2)	во II координатном угле;
3)	в III или IV координатном угле;
4)	не в I координатном угле;
5)	не в IV координатном угле;
6)	во II или III координатном угле.
3.5.	Квадратичная функция
Рассмотрим функцию
у — ах2 + Ьх + с,
где а, Ъ, с — числа (а 0). Напомним, что она называется
квадратичной.
Приведем два примера квадратичной функции.
Пример 1. Рассмотрим функцию
г/= х2 — 4х + 3.	(1)
Преобразуем формулу (1) к виду, изученному в п. 3.4. Для
этого из квадратного трехчлена х2 — 4х + 3 выделим полный
квадрат
х2 — 4х + 3 = х2 - 4х + 4 - 4 + 3 = (х - 2)2 - 1.

Квадратичная функция
238
3.57. Для каждой функции (см. упражнение 3.56) укажите:
а)	множество значений;
б)	промежуток убывания;
в)	промежуток возрастания;
г)	уравнение оси симметрии;
д)	наибольшее (наименьшее) значение;
е)	значения х, при которых у > 0;
ж)	значения х, при которых у < 0;
з)	координаты точек пересечения с осями Ох и Оу.
3.58.	Задайте формулой квадратичную функцию, график ко¬
торой изображен на рисунке 145, и укажите ее свойства.
3.59°. Принадлежит ли графику функции у = (х - I)1 2 + 4 точка:
1)	А(-3; 20);	2) В(0; 3);
3) 0(1; 16);	4) 0(2; 5)?
3.60.	Имеет ли график
точки с прямой:
функции у = 0,8(х - 6)2 + 5 общие
1) У = -Ю;
3) у = 0;
5)	у = 5;
2)	у =100;
4)	у = 4;
6)	у = 6?
3.61.	Имеет ли график функции у = — 6,2(х + 8)2 — 3 общие
точки с прямой:
1) г/= 200;	2) у = -300;
3)	у = 0;	4) у = ~2;
5)у = -3;	6)г/ = 8?

239
Функция у = а(х — s)2 + t И
И®
3.62.	При каких значениях параметра р указанная точка при¬
надлежит графику функции у - 3(х + р)2 - 2:
1) (1; Ю);
3) (-3; 5);
2)	(-2; -2);
4)	(2; 10)?
3.63.	При каких значениях параметра р данная функция при¬
нимает только отрицательные значения:
1) г/=р(х - 7)2 — 3;
3)	г/= 2(х+р)2 — 1;
5)	г/ = —5(х + 1)2-р;
7)	г/ = -0,3(х + 8)2+р;
2)	z/=p(x-4)2 + 5;
4)	г/ = ~7(х + р)2-3;
6)	г/= 6(х + 2)2 — р;
8)	У = --^ (х-9)2+р?
3.64.	Верно ли, что при любом значении р парабола
(см. упражнение 3.63) имеет общие точки с прямой:
а)	г/ = —10;	б) у = 0;	в) у = 27?
3.65.	Назовите, при каких условиях вершина параболы
у = а(х — s)2 + t будет расположена:
1)	в I координатном угле;
2)	во II координатном угле;
3)	в III или IV координатном угле;
4)	не в I координатном угле;
5)	не в IV координатном угле;
б)	во II или III координатном угле.
3.5.	Квадратичная функция
Рассмотрим функцию
у - ах2 + Ьх + с.
где а, Ъ, с — числа (а^О). Напомним, что она называется
квадратичной.
Приведем два примера квадратичной функции.
Пример 1. Рассмотрим функцию
у = х2 - 4х + 3.
(1)
Преобразуем формулу (1) к виду, изученному в п. 3.4. Для
этого из квадратного трехчлена х2 — 4х + 3 выделим полный
квадрат
х2 - 4х + 3 = х2 ~ 4х + 4 - 4 + 3 = (х - 2)2 ~ 1.

Квадратичная функция
240
Я
■ . ■ 1 ! !
1 : 1 1
-
-
3
f-
—
■■
ixxxf
1 I/' I 1
—
t
О.
л
1	! 4..
X


г
4X1J XI
Рис. 146
Таким образом, формулу (1) мож¬
но записать в виде
у = (х — 2)2 — 1.
Следовательно, графиком квадра¬
тичной функции (1) является пара¬
бола с вершиной в точке (2; -1);
ее ось симметрии — прямая х = 2 —
проходит через эту точку парал¬
лельно оси Оу, а ветви направлены
вверх (рис. 146).
Так как вершина параболы лежит ниже оси Ох, а ветви ее
направлены вверх, то рисунок дает наглядное представление
о том, что парабола пересекает ось Ох в двух точках.
Конечно, это можно установить и не прибегая к рисунку.
Достаточно заметить, что точки пересечения параболы с осью
Ох — это те точки параболы, ординаты которых равны нулю.
Тогда, полагая у = 0 в формуле (1), получаем, что абсциссы
точек пересечения удовлетворяют уравнению
О = х2 - 4х + 3.
Решая это уравнение, получаем хг = 1, х2 = 3.
Полагая х = 0в формуле (1), получаем точку пересечения
параболы с осью Оу: (0; 3).
На параболе есть еще одна точка с ординатой 3, симметрич¬
ная точке (0; 3). Абсциссу ее можно найти, полагая у = 3 в фор¬
муле (1). Из уравнения 3 = х2 — 4х + 3 находим х = 4.
Итак:
1)	отмечаем на координатной плоскости вершину
параболы — точку (2; - 1);
2)	проводим через эту точку ось параболы — прямую х = 2;
3)	отмечаем точки пересечения параболы с осью Ох — это
точки (1; 0) и (3; 0);
4)	отмечаем точку пересечения параболы с осью Оу — это
точка (0; 3);
5)	отмечаем симметричную ей точку параболы — это
точка (4; 3).
Изображаем параболу, проходящую через отмеченные точ¬
ки. Такое изображение будем называть схематичным.

241	Квадратичная функция
Пример 2. Изобразить схематично график функции
у = -2х2 + 10х - 13.	(2)
Решение. Преобразуем формулу (2) к виду, изученному
в предыдущем пункте. Для этого вынесем за скобки старший
коэффициент —2:
у = -2 (х2 — 5х + у ).
Теперь из квадратного трехчлена, стоящего в скобках, вы¬
делим полный квадрат:
х2 - 5х + у
Итак, получаем
Следовательно, графиком квадратичной функции (2) явля¬
ется парабола с вершиной в точке
ее ось симмет-
5
рии — прямая х = -g	проходит через вершину параллельно
оси Оу, а ветви направлены вниз.
Так как вершина параболы лежит ниже оси Ох и ветви ее
направлены вниз, то легко представить, что парабола не пере¬
секает ось Ох. Это можно установить, не прибегая к рисунку.
Мы уже знаем, что точки пересечения параболы с осью Ох —
это те точки параболы, ордината которых равна 0. Но если в
формуле (2) положить у — 0, то получим квадратное уравнение
0 =-2х2 + 10х — 13.
Его дискриминант D = 102 — 4 • 2 • 13 — —4. Следовательно,
это уравнение не имеет корней, а, значит, парабола не имеет
точек пересечения с осью Ох.
Чтобы найти точку пересечения параболы (2) с осью Оу, за¬
мечаем, что абсцисса этой точки равна 0. Полагая х = 0 в
формуле (2), получаем у = —13, значит, точка пересечения
параболы с осью Оу — это точка (0; -13). Точка, симмет-

Квадратичная функция
242
Рис. 147
ричная ей относительно оси симметрии
параболы, имеет ординату -13. Поэтому,
полагая у = —13 в формуле (2), получаем,
что ее абсцисса удовлетворяет уравнению
—13 = —2х2 + 10х - 13.
Решая это уравнение, получим хт = О,
х2 = 5. Значит, на параболе лежит и
точка (5; -13).
Схематическое изображение парабо¬
лы (2) показано на рисунке 147.
ПримерЗ. Изобразить график функ¬
ции
у = Зх2 + Зх - 6.
Решение. 1) Зх2+Зх-6 = 3(х2+х-2)=з(х2+2-у х+ у -
-Г-2)=з(х + |)2-2г’ = з(х + |)2-б|.
/	1 \2	з
Таким образом, у — 31 х + у I - бу .
Вершина параболы—-точка	у; ~6у ].
2)	Ось симметрии параболы — прямая х = — у .
3)	Найдем точки пересечения параболы с осью Ох. Абсцис¬
сы этих точек — корни уравнения Зх2 + Зх — 6 = 0. Откуда для
равносильного ему уравнения х2 + х —2 = 0 имеем хх = —2,
х2= 1.
Получили точки (-2; 0) и (1; 0).
4)	Найдем точку пересечения с осью Оу. При х = 0 получим
у = -6, т. е. точку (0; -6).
5)	Найдем точку, симметричную точке (0; —6) относительно
оси параболы, решив уравнение — 6 = Зх2 + Зх — 6, т. е.
Зх2 + Зх = 0. Откуда находим хг = 0, х2 = -1.
Таким образом, искомая точка — точка (—1; —6).
Изобразим схематично параболу у — Зх2 + Зх - 6 (рис. 148).

243
Квадратичная функция ш
и
[и
Заметим, что х0 — абсциссу вер¬
шины параболы у — ах2 + Ъх + с
можно найти по формуле
х° = 2а (пРовеРьте эту формулу
по примерам 1—3).
1.	Какая функция называется квадра¬
тичной?
2.	Как для параболы у = ах2 + Ьх + с
найти:
а) координаты вершины; б) коорди¬
наты точки пересечения с осью Оу;
в) координаты точек пересечения с
осью Ох; г) координаты точек пере¬
сечения с прямой у = <Я
3.	Какие из точек, перечисленных в
вопросе 2, имеются у любой пара¬
болы у = ах2 + bx + сг!
4.	Как изобразить график функции у = ах2 + Ьх + сЧ
Упражнения
Используя метод выделения полного квадрата, приведите фор¬
мулу к виду у — а(х - s)2 + t (3.66—3.67).
3.66°. 1) у = х2 + 20х + 6;
3)	у = —х2 — 8х + 3;
5)	у = х2~ 13х + 1;
7)	у = -Зх2 + 12х - 9;
9)	г/= 4х2 - 12х + 8;
3.67. 1) у--^-х2 + 2х;
3) у = (~2х - 7)х;
5)	у = х(7 - О,3х)-2;
2) у = х2 - 6х + 10;
4) у = х2 - 12х - 7;
6) у = -х2 - Их - 20;
8) у = 5х2 + 15х + 2;
10) у = -6х2 - 18х + 5.
2) у — х2 + Зх;
4) у = (-3х + 2)х;
6) I/= —х(5 + 0,2х)—5
3.68. Укажите координаты вершины данной параболы и коор¬
динаты точек ее пересечения с осями Ох и Оу, приведя
ее уравнение к виду у = а(х — s)2 + t:
1) у = х2 - 10х + 27;	2)	у = х2 + 6х + 5;
3) у - 8х - 15 - х2;	4)	у = 14х - х2 - 45;
5) у - 9х2 + 6х - 3;	6)	у - 4х2 + 12х - 7;
7)	у = х2 + 2 - х;	8)	у = -у х2 + х - 8.

Квадратичная функция
244
3.69°. Найдите координаты вершины параболы:
1) у = х1 2 - 24х + 108;	2)	у = х2 + 26х - 120;
3) у = х2 + 34х + 280;	4)	у = х2 - 16х - 132;
5) у = 42 + х - х2;	6) у = 6 - х - х2;
7) у — 18 — х2 - 7х;	8)	у = 13х — 30 — х2;
9) у = х2 + 20 - 9х;	10)	у = х2 - 24 + 5х.
3.70°. Найдите координаты точек пересечения с осями Ох и Оу
графика функции:
1) у = у х2 + 2х-2у;
3) у = —2х2 — Зх + 14;
5) у = х2 + 2,5х — 9;
7) у = 15х2 + 34х + 15;
9) у = -х2 — 15х - 44;
3.71. Изобразите схематично
свойства:
2)	у = —2х2 + 4х + 16;
4)	у = х2 + 2х - 8;
6)	у = у х2 - Зх + 4-|-;
8)	у = ЗОх2 + 37х + 10;
10)	у = х2 - 13х + 22.
график функции и укажите ее
1) у = —Зх2 — 6х — 5;
3)	у = х2 — 2х - 2;
5)	у = —2х2 + Зх + 2;
7)	у = 4х2 + 4х - 3;
9)	у = 5х2 — 8х + 3;
2) у = 2х2 - 4х + 5;
4)	у — Зх2 + 2х — 1;
6)	у = —Зх2 + 8х — 4;
8)	у = -4х2 + 4х- 1;
10)	у = 3х2- 2х- 7.
▲ 3.6. Исследование квадратичной функции
Формулу, задающую квадратичную функцию
у — ах2 + Ъх + с,
преобразуем таким же образом, как в примерах п. 3.5.
Вынесем за скобки старший коэффициент а:
y = n(x2 + |x + f ).

245
а
Далее из квадратного трехчлена, стоящего в скобках, выделим
полный квадрат:
D
4.аг ’
где D = b2 — 4ас — дискриминант квадратного трехчлена
ах2 + Ьх + с.
Отсюда получаем
Таким образом, вершиной параболы у = ах2 + Ьх + с
lb D \
является точка I —	ее ось симметрии — пря-
Ь
мая х = -	— проходит через вершину и параллельна
оси Оу.
Ветви параболы направлены вверх, когда а > 0, и вниз,
когда а < 0.
Корни Xj и х2 квадратного уравнения ах2 + Ьх + с = 0 (если
они существуют, т. е. если D > 0) являются абсциссами точек
пересечения параболы с осью Ох.
Легко найти точки пересечения параболы с прямой у = с.
Абсциссы этих точек находят из уравнения
ах2 + Ьх + с = с,
решая которое получают: х = 0 или х = -	. Значит, искомые
точки — (0; с) и -у ; с). Заметим, что точка (0; с) лежит на
оси Оу.
Все это позволяет дать схематичное изображение параболы
у - ах2 + Ьх + с, не выделяя предварительно из квадратного
трехчлена полный квадрат.

Квадратичная функция
246
Пример 1. Изобразить схематично
параболу
у = 5х2 + 10х + 8.	(1)
Решение. D = 102 — 4• 5 • 8 = 100 —
— 160 = — 60 < 0, значит, точек пересече¬
ния параболы с осью Ох нет; а = 5 > О,
значит, ветви параболы направлены
вверх.
Найдем координаты вершины пара¬
болы. По формуле х0 = имеем
х0 = g-g = -1; подставив х = -1 в уравне¬
ние (1), находим г/0=5(-1)2+1О(~1)+8=3
(или по формуле у0 = получим
Рис. 149	= Таким образом, вершина
параболы — точка (-1; 3). Ось симметрии параболы — прямая
х = —1.
Найдем координаты точек пересечения параболы с прямой
у = с, т. е. с прямой у = 8. Решив уравнение 5х2 + 10х + 8 = 8,
получим х = 0 или х = — 2. Таким образом, имеем точку (0; 8)
(эта точка лежит на оси Оу) и точку ( — 2; 8).
Изобразим график функции у = 5х2 + 10х + 8 схематично
(рис. 149).
Пример 2. Изобразить схематично график функции
у = ~3х2 + 3х + 6.
Решение. D = З2 - 4(-3)6 = 9(1 + 8) = 81 > 0; а = -3<0,
значит, ветви параболы направлены вниз. Найдем координаты
вершины параболы по формулам х0 =	, у0 =	:
3 _ 1	_ -81 _ 27	3
Х° 2(3)	2 ’	4(-3)	4	0 4 ’
Вершина параболы — точка (; 6	.
g I | Заметим, что ординату вершины уа можно найти ина-
ф I че: подставив х = х0 в трехчлен -3х2 + 3х + 6,
получим
+ 3--5- +6 = б4.
2	4
Уо = _3(т)2

247
Исследование квадратичной функции
Прямая х — у —ось симметрии па¬
раболы.
Найдем координаты точек пересече¬
ния параболы с осью Ох. Решив уравне¬
ние —Зх2 + Зх + 6 = О, получим х^-1,
х2 = 2. Таким образом, имеем точки
(-1; 0) и (2; 0).
Найдем координаты точек пере¬
сечения параболы с прямой у = 6. Решив
уравнение — Зх2 + Зх + 6 = 6, получим
х = 0 или х = 1. Таким образом, имеем
точки (0; 6) и (1; 6).
Изобразим схематично параболу
у = -Зх2 + Зх + 6 (рис. 150).
I Можно получить схематичное изображение параболы
00) у = ах2 + Ьх + с и несколько иначе. Например, можно,
найдя координаты вершины параболы, просто вычислить
дополнительно координаты еще нескольких произвольных
На рисунках 151, 152, 153 показаны схематичные изобра¬
жения парабол:
а) у = у х2 + 4х + 8; б) у = - у х2 + Зх - 5;
в) у — — х2 + 4х — 8.

Квадратичная функция
248
Определите, на каком именно из ри¬
сунков изображена каждая из этих пара¬
бол. Как это легче всего установить?
По изображению параболы, используя
координаты трех ее точек, можно восста¬
новить и уравнение параболы.
Пример 3*. Определить, каким
уравнением задана парабола, изображен¬
ная на рисунке 154.
Решение. Подставив в уравнение
параболы у — ах2 + Ъх + с координаты
трех ее точек (—2; 0), (1; -3), (0; —6),
получим систему уравнений с тремя
неизвестными а, b и с:
4а — 2Ь + с - 0,
' а +Ь + с = — 3,
с — — 6.
Решим ее:
4а — 2Ь = 6,
а + b — 3,
с = —6;
4а — 2(3 - а) = 6,
- Ъ - 3 - а,
с = -6;
6а = 12,
а = 2,
Ь = 1,
с - —6;
с — -6.
< b = 3 — а,
Таким образом, парабола, изображенная на рисунке 154,
задана уравнением у - 2х2 + х — 6.
Рассмотрим теперь все возможные случаи изображения па¬
раболы у = ах2 + Ьх + с. Они сведены в таблицу (рис. 155).
Дадим к этой таблице некоторые пояснения.
Когда а > 0, ветви параболы направлены вверх. При этом
для дискриминанта D возможны три случая:
1)0 0;	2) £) = 0;	3) D < 0.
Рассмотрим особенности этих случаев.
Случай 1). Если а > 0 и D > 0, то у0 — ордината вершины
D
- отрицательна, и, следовательно, вершина расположена

ниже оси абсцисс. Поэтому парабола пересекает ось Ох в двух
точках, абсциссы которых хр х2 являются корнями квадрат¬
ного трехчлена ах2 + Ъх + с (х0 = Xi%X2 — абсцисса вершины).
Случай 2). Если а >0 и .0 = 0, то у0— ордината вершины
D
-	равна нулю, и, следовательно, вершина лежит на оси
абсцисс. Поэтому парабола имеет с осью Ох только одну общую
точку, абсцисса которой Xj является единственным корнем
квадратного трехчлена ах2 + Ъх + с (х0 = хг — абсцисса вер¬
шины).
Случай 3). Если а > 0 и О < 0, то у0 — ордината вершины
D
-	положительна, и, значит, вершина расположена выше
оси абсцисс. Поэтому парабола не пересекается с осью Ох, а
квадратный трехчлен ах2 + Ъх + с не имеет корней (х0 =	).

250
V Квадратичная функция
Когда а < 0, ветви параболы направлены вниз. При этом для
дискриминанта D возможны три случая:
4) D > 0;	5) D = 0;	6) D < 0.
Рассмотрим особенности этих случаев.
Случай 4). Если а < 0 и D > 0, то у0 — ордината вершины
—	положительна, и, следовательно, вершина расположена
выше оси абсцисс. Поэтому парабола пересекает ось Ох в двух
точках, абсциссы которых хг, х2 являются корнями
квадратного трехчлена ах2 + Ъх + с (х0 = Xl-^X2 ).
Случай 5). Если а < 0 и D = 0, то у0 — ордината вершины
D
—	равна нулю, и, следовательно, вершина лежит на оси
абсцисс. Поэтому парабола имеет с осью Ох только одну общую
точку, абсцисса которой хг является единственным корнем
квадратного трехчлена ах2 + Ьх + с (х0 = xj.
Случай 6). Если а < 0 и D < 0, то у0 — ордината вершины
D
—	отрицательна, и, следовательно, вершина расположена ни¬
же оси абсцисс. Поэтому парабола не пересекается с осью Ох, а
квадратный трехчлен ах2 + Ъх + с не имеет корней (х0 = ).
1.	Изобразите график функции у = ах2 + Ьх + с, если:
а)	а > 0, D = 0;	б) а < 0, D = 0;	в) а > 0, D < 0;
г) а > 0, D > 0;	д) а < 0, D > 0;	е) а < 0, D < 0.
2.	Дана парабола y=px2 + kx + m. Укажите возможные значения
дискриминанта D, если вершина параболы размещена:
а)	в I координатном угле, причем р > 0, т > 0;
б)	во II координатном угле, причем р < 0, т < 0;
в)	в III координатном угле, причем т. < 0;
г)	в IV координатном угле, причем т > 0,
Упражнения
3.72°. Изобразите схематично график заданной функции и,
используя полученный рисунок, укажите, при каких
значениях х значения функции а) отрицательны; б) рав¬
ны нулю; в) положительны, если:

251
Исследование квадратичной функции
1)	у = х2 + 6х - 4;	2) у = х2 - 4х + 3;
3) у = Зх2 — 6х + 7;	4) у = — 2х2 — 4х + 5;
5) у =-4х2 + 5;	6)у = —Зх2 —6.
Докажите, что указанная парабола не пересекается с осью Ох
(3.73—3.74).
3.73.	1) у = 2х2 - Зх + 6;	2) у = -7х2 + 5х - 2;
3) у = -9х2 - 8х - 3;	4) у = 4х2 + 9х + 6.
3.74.	1) у - -4х2 - 2х - 7;	2) у - 7х2 + 15х + 14;
3) у = 7х2 - 9х + 12;	4) у - -6х2 - 4х - 9.
3.75.	При каких значениях р указанная парабола пересекается
с осью Ох: а) в одной точке; б) в двух точках:
1)	У — (Р — 2)х2 +(р + 1)х - 0,2;
2)	у = (р + 2)х2 +(р + 7)х + 9;
3)	у = х2 + 2(р - 3)х + Зр + 1;
4)	у = х2 + 2(р + 2)х + Зр + 4?
3.76.	При каких значениях параметра р вершина данной па¬
раболы расположена а) ниже оси Ох; б) выше оси Ох;
в) на оси Ох:
1)	у - —Зрх2 — 2х — 5;
2)	у = -|- х2 - 4рх + 3;
3)	у =-0,9х2 - 2х - 5р;
4)	у = —1,5рх2 + х — 2?
3.77.	На рисунке 156 изображен график функции
у - х2 +рх + q. Определите значения р и q.
Рис. 156

Квадратичная функция
252
3.78.	Какому координатному углу принадлежит вершина па¬
раболы у = тх2 +рх + k, если:
1) т> 0, р> 0, k> 0;
3) т > 0, р > 0, k < 0;
5)	т < 0, р < 0, k < 0;
7) т < 0, р < 0, k > 0;
2)	т> 0, р < 0, k> 0;
4) т > 0, р < 0, k < 0;
6)	т < 0, р > 0, k > 0;
8) т < 0, р> 0, k < О?
3.79.	Укажите знаки чисел а, Ь,
с, если ветви параболы
у = ах2 + Ьх + с направлены
параболы принадлежит:
1)	II координатному углу;
2)	I координатному углу;
3)	IV координатному углу;
4)	III координатному углу.
вверх, а вершина этой
3.80.	Укажите знаки чисел тп, п и k, если ветви параболы
у = тх2 + пх + k направлены вниз, а вершина этой
параболы принадлежит:
1)	I координатному углу;
2)	II координатному углу;
3)	III координатному углу;
4)	IV координатному углу.
3.81.	На рисунке 157 изображена парабола у = ах2 + Ъх +с.
Укажите знаки чисел а, Ь, с.
Рис. 157

Преобразования графиков функций Ц
253
▲ 3.7. Преобразования графиков функций
1. Некоторые обозначения
Будем обозначать функцию какой-нибудь буквой, скажем
f, а ее значение в точке х будем обозначать f(x) (читается «эф
от икс»).
При таких обозначениях аргумента и функции тот факт,
что у является функцией от х, записывается в виде равенства
y = f(x), а функцию f называют еще «функция f(x)» или
«функция y = f(x)». Пишут также у(х).
Заметим, что для обозначения функции можно употреблять
и другие буквы, например g, h, и и т. п.
Рассмотрим примеры конкретных функций.
Пример 1. Для функции f, заданной формулой у = х2,
символ f означает возведение аргумента в квадрат, a f(x) = х2.
Пример 2. Для функции f, заданной формулой у =	,
символ f означает отыскание числа, обратного аргументу, а
Лх)=|.
Пример 3. Для функции f, заданной формулой у — \1х,
символ f означает извлечение арифметического квадратного
корня из аргумента, a f (х) = \гх.
Если с — некоторое число, то запись f(c) означает числен¬
ное значение функции f(x), соответствующее значению х,
равному с.
Так, в примере 1:
Д3) = 32 = 9;	/(—3) = (—З)2 = 9;	Д0) = 02 = 0.
В примере 2:
/(3) = -|-;	/(-3)=rg = --|-;	f(O)=-y—не имеет смысла.
В примере 3:
f (3) = у' 3; f (- 3) = у - 3 — не имеет смысла; f (0) =	= 0.
Область определения функции f обозначается D(f).
Если функция f задана формулой у — f(x), а ее область
определения не указана, то считается, что она
состоит из тех значений х, при которых выражение
f(x) имеет смысл.

Квадратичная функция
254
Таким образом, в этом случае D(f) совпадает с естественной
областью определения выражения f(x). Когда в задании тре¬
буется найти область определения функции у = /(х), то име¬
ется в виду указание в виде числового множества (про¬
межутка) именно естественной области определения выраже¬
ния /(х).
Так, в примере 1 область определения D(f) = R.
В примере 2 область определения D(f) = (-°°; 0) U (0; +<»).
В примере 3 область определения D(f) = [0; +оо).
Множество значений функции f обозначается E(f).
Так, в примере 1 множество значений E(f)- [0; +о°).
В примере 2 множество значений E(f) = (-°°; 0) U (0; +оо).
В примере 3 множество значений E(f) = [0; +°°).
2. График функции у - ~f(x)
В предыдущих пунктах мы научились из графика функции
у = х2 различными преобразованиями получать графики дру¬
гих квадратичных функций.
Покажем теперь, как из графика произвольной функции
у = /(х) с помощью различных преобразований получать гра¬
фики некоторых других функций.
На рисунке 158 синей линией изображен график некоторой
функции у = /(х). Координаты точки М графика этой функции
имеют вид (a; f(a)), где a
Точка Мг(а; ~f(a)) принадлежит графику функции
y — -f(x), и координаты каждой точки этого графика имеют
такой же вид. Точка Мг симметрична точке М относительно
оси Ох. Значит, каждую точку Мг
графика функции y = -f(x) можно
получить из некоторой точки М
графика функции у = /(х), отобра¬
зив точку М симметрично отно¬
сительно оси Ох (см. рис. 158).
Таким образом, график
функции у — —f(х) может
быть получен из графика
функции у = f(x) симмет¬
ричным отображением
относительно оси Ох.

255
Преобразования графиков функций
Пример 4. Изобразить график
функции у — — \1Х.
Решение. Изобразим синей
линией график функции у = \!~х
(рис. 159). Отобразим эту линию
симметрично относительно оси Ох.
Полученная кривая и будет изобра¬
жением графика функции у = —ух
(на рисунке она красного цвета).
3. График функции У = f(~x)	Рис. 159
На рисунке 160 синей линией изображен график некоторой
функции y = f(x). Координаты точки М графика этой функ¬
ции имеют вид (а; /(а)), где a &D(f). Точка ~а принадлежит
области определения функции у = f(~x), и точка Мг(~а; f(a))
принадлежит графику функции у — f(—x). Заметим, что ко¬
ординаты каждой точки этого графика имеют такой же вид.
Точка Мг симметрична точке М относительно оси Оу. Значит,
каждую точку Мг графика функции у = f(~x) можно получить
из некоторой точки М графика функции у = f(x), отобразив
точку М симметрично относительно оси Оу (см. рис. 160).
I Таким образом, график функции y = f(~x) может
быть получен из графика функции у = f(x) симмет-
I ричным отображением относительно оси Оу.
Пример 5. Изобразить график функции у = у]-х.
Решение. Изобразим синей линией график функции
у = у[х (рис. 161). Отобразим эту линию симметрично отно¬
сительно оси Оу. Полученная кривая и будет изображением
графика функции у = \]—х (на рисунке она красного цвета).
Рис. 161
Рис. 160

Квадратичная функция	256
4.	График функции у = f(x) + t
На рисунке 162 синей линией изображен график некоторой
функции у = f(x). Координаты точки М графика этой функции
имеют вид (а; /(а)), где а е D(f).
у
f(a)+t
S.’	*
L	y=if(x)+t, t>Q
-Да)
S	I
. «.• r' '	J
■: о
y=f\x)
a \ ' x
Рис. 162
Рис. 163
Точка М-.(а; f(a) + t) получается из точки М сдвигом едоль
оси Оу на расстояние t вверх при t > 0 (см. рис. 162) или на 111
вниз при t < 0 (рис. 163). Точка MY(a; f(a) +1) принадлежит
графику функции у = f(x) + t, и координаты каждой точки
этого графика имеют такой же вид.
Таким образом, график функции у = f(x) +1 получа¬
ется сдвигом графика функции у = f(x) вдоль оси Оу
на расстояние 111 (вверх при t > 0; вниз при t < 0).
Пример 6. Изобразить график функции:
а) у = у[х + 2; б) у = Jx - 2.
Решение, а) Изобразим синей линией график функции
у = (рис. 164). Сдвинув его на 2 единицы вверх, получим
график функции у — Jx~ + 2 (красная линия на рис. 164).
О
х
+-
1
Рис. 165

257
б)
Преобразования графиков функций
График функции у=\х~2 изображен на рисунке 165
красной линией.
5.	График функции у = f(x — s)
На рисунке 166 синей линией изображен график некоторой
функции у = f(x). Координаты точки М графика этой функции
имеют вид (a;	где а € D(f). Так как
f((a + s) - s) = f(a),
то точка а + s принадлежит области определения функции
у = f(x - s) и точка Mr(a + s; /(а)) принадлежит графику
функции y = f(x~s). Точка M^a + s; /(а)) получается из
точки М(а; f(a)) сдвигом вдоль оси Ох на s единиц впра¬
во при s > 0 (см. рис. 166) или на | s | единиц влево при
s < 0 (рис. 167).
Заметим, что каждую точку (а + s, f(a)) графика функции
у = f(x — s) можно получить из некоторой точки М графика
функции у = f(x), сдвинув точку М вдоль оси Ох на | s | единиц
(вправо при s > 0 и влево при s < 0).
и
Таким образом, график функции y = f(x~s) получа¬
ется сдвигом графика функции у = f(x) вдоль оси Ох
на | s | единиц (вправо при s > 0, влево при s < 0).
Пример 7. Изобразить график функции:
а)	у = \ х + 2; б) у = у'х ~ 2.

Квадратичная функция	258
Решение, а) Изобразим синей линией график функции
у = у[х (рис. 168). Поскольку уравнение у = ^х + 2 можно
представить в виде у = 'Jx — (—2), то график этой функции
получаем сдвигом графика функции у = \Гх на 2 единицы влево
вдоль оси Ох (красная линия на рис. 168).
б) График функции у = \х~2 изображен на рисунке 169
красной линией.
6.	График функции у = kf(x) (k > 0)
На рисунке 170 синей линией изображен график некоторой
функции у = f(x). Координаты точки М графика этой функции
имеют вид (a; f(a)), где а € D(f). Точка М,(а; kf (а)) принад¬
лежит графику функции у — kf(x), и координаты каждой точки
этого графика имеют такой же вид.
Таким образом, если умножить ординату каждой
точки графика функции y=f(x) на число k (это значит
выполнить растяжение (или сжатие) вдоль оси Оу), то
получим точки графика y = kf{x),— он изображен
красной линией. Если k > 1, то говорят о растяжении
вдоль оси Оу в k раз (см. рис. 170). Если же 0 < k < 1,
то говорят о сжатии вдоль оси Оу в у- раз (рис. 171).

259
Преобразования графиков функций
Пример 8. Изобразить график функции:
а)у = 2<х; б) у = ± v'x.
Решение, а) Изобразим синей линией график функции
у = \х (рис. 172). Проделаем с каждой точкой на этом графике
следующие преобразования: оставим ее абсциссу без измене¬
ния, а ординату увеличим в
растянется вдвое вдоль оси Оу
у = 2 \Х (красная линия на рис
2 раза. В результате график
и получится график функции
172).
Рис. 172
б) График функции У = у
Рис. 173
х изображен на рисунке 173
красной линией.
7.	График функции у = f (-^0, где т > О
На рисунке 174 синей линией изображен график некоторой
функции у = f(x). Координаты точки М графика этой функции
имеют вид (а; /(а)), где а 6 D(f). Так как f = f(a), то число
та принадлежит области определения функции y = f\~)и
точка Мг(та; f (а)) принадлежит графику функции у = ц —
и координаты каждой точки этого графика имеют такой
же вид.
Таким образом, если умножить абсциссы каждой
точки графика функции у = /(х) на число т (это
значит выполнить растяжение (или сжатие) вдоль оси
Ох), то получим точки графика y=f[^-~^, он
изображен красной линией. Если т > 1, то говорят о

В Квадратичная функция
260
Рис. 175
растяжении вдоль оси Ох в траз (см. рис. 174). Если
же 0 < т < 1, то говорят о сжатии вдоль оси Ох в
раз (рис. 175).
Пример 9. Изобразить график функции:
а) у = VЗх + 2; б) у = д/ у х + 2.
Решение, а) Изобразим синей линией график функции
у = \/ х + 2 (см. пример 7). Проделаем с каждой точкой на этом
графике следующее преобразование: уменьшим ее абсциссу в
3 раза, а ординату оставим без изменения. В результате график
как бы «сожмется», втрое вдоль оси Ох и получится график
функции у = \ Зх + 2 (красная линия на рис. 176). Итак, если
f (х) = yx+T, то V&ET2 =^/| + 2 = f^ = f (3х)-
б)	График функции у = х + 2 изображен на рисунке
177 красной линией.
Рис. 176
Рис. 177

261	Преобразования графиков функций
8.	График функции у = | f(x) |
На рисунке 178 синей линией изображен график некоторой
функции у — f(x).
Рассмотрим функцию у = I f(x) |.
На тех промежутках, где точки графика функции у — f(x)
лежат выше оси абсцисс или на ней, значения функции
неотрицательные, т. е. /(х) > 0. Но тогда | /(х) | = /(х) и график
функции у = | /(х) | совпадает на этих промежутках с графиком
функции у = /(х).
На тех промежутках, где точки графика функции у = /(х)
лежат ниже оси абсцисс, значения функции отрицательные,
т. е. f(x) < 0. Но тогда \f(x)\~—f(x) и график функции
у — I /(х) | совпадает на этих промежутках с графиком функции
у = — /(х). Таким образом, на этих промежутках график функ¬
ции у = | /(х) | симметричен графику функции у = f(x) относи¬
тельно оси абсцисс.
Таким образом, чтобы изобразить график функции
у = | f(x) |, можно части графика функции у = /(х), ле¬
жащие выше оси абсцисс или на ней, оставить без
изменения, а части, лежащие ниже оси абсцисс,
отобразить симметрично относительно этой оси.
Пример 10. Изобразить график функции:
а) у = | Зх - 2 |;	б) у = 11 Зх — 21 — 11.
Решение, а) Изобразим синей линией график функции
у — Зх — 2 (рис. 179, а). Часть этого графика, лежащую ниже
оси Ох, отобразим симметрично относительно оси Ох. Полу-

ченная красная линия и будет изображением графика функ¬
ции у = | Зх - 2 | (рис. 179, б).
б)	Изобразим красной линией график функции у -
= I Зх — 21 — 1 (рис. 180, а). Часть этого графика, лежащую
ниже оси Ох, отобразим симметрично относительно оси Ох.
Полученная линия (рис. 180, б) и будет изображением графика
функции у = 11 Зх - 2 I - 11.
9. График функции у — f(\x\)
На рисунке 181 синей линией изображен график функции
у - f(x). При значениях аргумента х > 0 имеем f( | х |) = f(x).
Значит, при неотрицательных
значениях аргумента график
функции y—f(\x\) совпадает с
графиком функции у = f(x).
Заметим, что f( | х |) =
= f( I ~х |), значит, функция
y=f(\x\) четная и ее график
симметричен относительно оси
Оу (красная линия на рисун¬
ке 181)
Таким образом, чтобы изобразить график функции
y~f(\x\), можно часть графика функции y = f(x) с
неотрицательными абсциссами оставить без изме¬
нения, часть графика функции у = f( | х |) с отрица¬
тельными абсциссами получить из первой части
симметричным отображением относительно оси Оу.

Преобразования графиков функций
263
Заметим, что часть графика функции у = f(x) с отри¬
цательными абсциссами при изображении графика
у — /“(| х |) не используется.
Пример 11. Изобразить график функции:
а) у = 31 х| - 2;
б) у = \ I х |;
Решение, а) Изобразим синей
линией график функции у — Зх — 2
(см. рис. 179, а). Часть этого графика,
лежащую правее оси Оу, выделим
красной линией как первую часть
графика функции у = 3|х| — 2. Дру¬
гая часть искомого графика получа¬
ется из первой части симметричным
отображением относительно оси Оу.
Полученная красная линия (рис.
182), симметричная относительно
оси Оу, и будет изображением гра¬
фика функции у = 3|х|-2. (Часть
графика, расположенную левее оси
в) у = | VTxT-1
Оу, не используем,— ее можно вообще не изображать.)
б) Изобразим синей линией график функции у = \[х (рис.
183, а). Весь этот график лежит правее оси Оу — выделим его
красной линией как первую часть графика функции у — \ I х |
(рис. 183, б). А вторую часть получим симметричным отобра¬
жением первой части относительно оси Оу. Полученная
красная линия, симметричная относительно оси Оу, является
изображением графика функции у = д/|х| (см. рис. 183, б).
Рис. 183

Квадратичная функция
264
в)	Изобразим синей линией график функции у = ух - 1
(рис. 184, а). Весь этот график лежит правее оси Оу — выделим
его зеленой линией как первую часть графика функции
у = 1 х | — 1. А вторую часть получим из первой симметричным
отображением относительно оси Оу. Полученная зеленая
линия, симметричная относительно оси Оу, является изоб¬
ражением графика функции у = у/1 х I - 1 (рис. 184, б).
В)
17
-1 о
1 х
Затем часть графика у = у/ТхТ~ 1, лежащую ниже оси Ох,
отобразим симметрично относительно оси Ох. Полученная
кривая и будет изображением графика функции у = | у/| х | — 11
(рис. 184, в).
1.	Каким преобразованием из графика'функции y = f(x) можно
получить график функции:
a) y = ~f(x);	6)y=f(-x);	в) y = -f(-x)?
2.	Каким преобразованием из графика функции y = f(x) можно
получить график функции:
a) y = f(x)~3;	б) y = f(x + 4);	в) y = f(x-2) + 57
3.	Каким преобразованием из графика функции у = f (х) можно
получить график функции:
a)f/ = 3/(x);	=	в) у=± f (5х)?
4.	Каким преобразованием из графика функции у = f (х) можно по¬
лучить график функции:
а) {/ = |/(х)|;	б) i/ = 7(|x|);	в) =

265
Преобразования графиков функций
Упражнения
Укажите, используя числовые промежутки, область определе¬
ния функции, заданной формулой у = f(x) (3.82—3.83).
3.82°. 1) f(x) = х2 + 6;
4) /(Х) = ?Т1;
7) ftx) = VT+2;
3.83. 1) /(х) = I х + 41;
3) /(X) = v'l-|х|;
2)/(х) = х2 —7;	3)/(x) = ^;
5)	f(x) =	;	6) /(х) =	2;
X - 1О	0-Х
8) ftx) = V3=x + l.
2)	/(х) = |х-2| + 2;
4)	ftx) = V|x|-l;
6)	=
3.84. Найдите множество значений функции /(х), если:
1)	/(х) = х2-2;
3)	/(х) = ух + 4;
5)	/(х) = -1 х — 5
7)	f(x) = ^;
2)	=
4)	ftx) = -<T=T;
6)	/(х) = |х-7|;
8)	Лх) = |^.
Изобразите график функции у = f(x) (3.85—3.93).
3.85. 1) Лх) = ^;
3)	/(х) = ^ + 3;
5)	f(x) = ^ + l;
7)	Лх) = -^3;
2) Лх)=^;
4)	Лх)=-7-4;
6) Лх) = -|;
5)	f(x) = -£_3~2.
3.86. 1) /(х) = |х + 11;
3)	/(х) = | х | + 3;
5) ftx) = |x + 3|-2;
7)	/(х) = -||х-б|:
2) /(х) = | х - 41;
4)	/(х) = | х | — 3;
6)	f(x) = -1| х |;
8)	/(х) = - ||х-5 | + 1.

И® Квадра1и_чна1функция
266
3.87.
1) f(x) = \lx~l;
3) f(x) = Vx + 3;
5) fix) = Vx + 2 — 2;
7) /(x) = -v 3x + 3;
2) fix) = yix+l;
4) ftx) = Vx-4;
6) f(x) = -V3x;
8) fix) = - V 3x + 3 J. 4.
3.88.
1) /(x) = V'2-x;
2) /(x) = V-x-l;
3) /(x) = V-x + 3;
4) f(x) = yj-x- 1;
5) fix) = V —x + 2 - 2;
6) /(x) = -V~2x;
7) /(x) = -V -2x + 3;
8) ftx) = -V~2x + 3 + 4.
3.89.
1) fix) = (x + 2)3;
2) ftx) = (x~4)3;
3) /(x) = x3+l;
4) fix) = x3 -4;
5) /(x) = (x+l)3 r2;
6) /(x) = -yx3;
7) /(x) = -|(x + 2)3;
8) /(x) = -f (x + 2)3-l.
3.90.
1) f(x) = ']\x\ + 2;
2) /(x) = V|x|-4;
3) f(x)=VM + i;
4) fix) = V|x| - 2;
5) /(x) = V+ 2-2;
6) f(x) = —2 Vl x |;
7) f(x) = —2 Vl x| + 3;
8) /(x) = -2V|x| + 3-l.
3.91.
!)
2) f(x)=	;
3) МАЧ
4)/W = |7i7-2|;
5) Ж> = |т74 -3;
6)/W ||x|\4	3|.
3,92.
1) fix) = | x31;
2) fix) = | x31 + 1;
3) fix) = | (x + l)31;
4) fix) = | x3 + 21;
5) fix) = | x31 - 2;
6) ftx) = |lx3| - 2 |;
7) f(x) = | (x + l)31 + 2;
8) /(x) = -|x3|.
3.93.
1) fix) = I VIX | - 4 |;
2) /(x) = |V|x|-2|;
3) f(x) = | VW-- 2 | + 1;
4) fix) = \ V|x| + l|;
5) fix) = | VI x - 411;
6) /(x) = |Vlx+3||.

Комбинаторика
и теория вероятностей
4.1. Правило умножения
В 8-м классе мы решали комбинаторные задачи, используя
правило умножения. Сформулируем это правило.
Пусть последовательно осуществляется к выборов. Если
первый из них можно осуществить пу способами, второй — пг
способами и т. д., кй выбор — способами, то все к выборов
можно осуществить
способами.	.	2 '
Пример 1. Сколько существует пятизначных чисел:
а) кратных 3; б) кратных 7?
Решение. Составляя из цифр пятизначное число, в каче¬
стве первой цифры записи этого числа можно выбрать любую
из девяти отличных от нуля цифр. К каждой из них на второе,
третье, четвертое и пятое места можно приписать любую из 10
цифр. Поэтому количество различных пятизначных чисел рав¬
но 9 • 10 • 10 • 10 • 10, т. е. 90 000.
а)	Из любых трех чисел, идущих подряд, одно и только одно
делится на три. Так как различных пятизначных чисел 90 000,
то среди них будет 90 000:3 = 30 000 чисел, кратных трем.
б)	Чтобы найти количество пятизначных чисел, кратных се¬
ми, надо разделить 90 000 на 7 (поясните почему). Здесь воз¬
можно лишь деление с остатком: 90 000 = 7-12 857 + 1.
Значит, количество пятизначных чисел, кратных 7, равно
12 857.

Комбинаторика и теория вероятностей	268
Пример 2. Какое из чисел 4840 или 1944 имеет больше
натуральных делителей?
Решение. Разложим эти числа на простые множи¬
тели:
4840 = 23 • 5 • II1 2; 1944 = 23-35.
Число 23 имеет четыре натуральных делителя (а именно:
1, 2, 22, 23), число 5 — два натуральных делителя, число
II2 — три натуральных делителя (назовите их). Каждый
натуральный делитель числа 4840 можно получить, взяв
по одному натуральному делителю каждого из чисел 23, 5,
II2 и перемножив их. А согласно правилу умножения вы¬
брать по одному натуральному делителю каждого из этих
чисел можно 4 • 2 • 3 способами, т. е. всего 24 способами.
Таким образом, число 4840 имеет 24 натуральных дели¬
теля.
Аналогично подсчитываем (сделайте это самостоятельно),
что число 1944 также имеет 24 натуральных делителя.
Значит, числа 4840 и 1944 имеют равное число дели¬
телей.
Пример 3. Из пункта А в пункт В ведет на 5 дорог боль¬
ше, чем из пункта В в пункт С. Известно, что можно составить
36 маршрутов, ведущих из А в С через В. Сколько дорог ведет
из А в В?
Решение. Пусть из пункта А в пункт В ведет п дорог. Тог¬
да из В в С ведет п — 5 дорог. Согласно правилу умножения
можно составить п (п — 5) маршрутов из А в С. По условию
п (п — 5) = 36.
Корни этого уравнения: nY = — 4, п2 = 9.
Поскольку значение п должно быть натуральным числом,
то получаем п = 9.
Ответ: 9 дорог.
1.	Сформулируйте правило умножения для последовательного вы¬
бора:
а) двух объектов; б) трех объектов.
2.	Приведите свой пример задачи на применение правила умноже¬
ния.

269
Правило умножения
У пражнения
4.1.	Сколько существует четырехзначных чисел:
1) кратных 2;	2) кратных 5;
3) кратных 2 и 3;	4) кратных 5 и 7?
4.2.	Сколько натуральных делителей имеет число:
1) 25-36;	2) 36-47;	3) 36-47-610;	4) 47-25-64?
4.3.	Номерной знак машины содержит серию из трех, букв ла¬
тинского алфавита. Для нумерации машин используются
20 букв латинского алфавита. Сколько различных серий
можно составить, если каждая буква содержится в записи
серии не более одного раза?
4.4.	В киоске продаются тюльпаны пяти цветов: желтые, бе¬
лые, розовые, бордовые и красные. Какое наибольшее чис¬
ло букетов из трех тюльпанов разного цвета можно соста¬
вить, чтобы любые два букета отличались цветом хотя бы
одного тюльпана?
4.5.	Продавец ларька решил сделать наборы из двух ручек со
стержнями разных цветов так, чтобы два набора различа¬
лись цветом хотя бы одного стержня. Продавец составил
наибольшее число возможных наборов, это число 21.
Стержни скольких различных цветов были в ларьке (кор¬
пуса всех ручек одинаковые)?
4.6.	На конференции 16 ее участников обменялись визитными
карточками. Сколько визитных карточек для этого пона¬
добилось?
4.7.	В турнире приняли участие 16 шахматистов, и каждый с
каждым сыграл по одной партии. Сколько всего партий
было сыграно?
4.8.	В футбольном турнире сыграно всего 210 матчей, причем
каждые две команды встречались дважды. Сколько всего
команд участвовало в турнире?
4.9.	В меню столовой первых блюд на 3 меньше, чем вторых.
Оказалось возможным составить 28 различных обедов из
двух блюд (первого и второго). Сколько в меню первых
блюд и сколько вторых?

Комбинаторика и теория вероятностей
270
а 4.2. Перестановки
На уроке физкультуры учащихся можно построить по
росту, по алфавиту или в каком-нибудь другом порядке. Дру¬
гими словами, учеников можно упорядочить различными
способами. Каждое такое упорядочение учащихся (располо¬
жение в определенном порядке) называется их переста¬
новкой.
Пример 1. Множество, состоящее из одного элемента, на¬
пример из буквы А, можно, очевидно, упорядочить единствен¬
ным образом.
Пример 2. Множество, состоящее из двух элементов, на¬
пример из букв А и В, можно упорядочить двумя способами;
из элементов этого множества можно составить ровно две пе¬
рестановки:
АВиВА.
Пример 3. Множество, состоящее из трех элементов, на¬
пример из букв А, В, С, можно упорядочить шестью различ¬
ными способами; из элементов этого множества можно соста¬
вить ровно шесть перестановок:
АВС; А С В; В С А; ВАС; С А В; С В А.
Множество, состоящее из п элементов, будем называть
п-элементным множеством.
В примерах 1, 2, 3 мы рассматривали соответственно
одноэлементное, двухэлементное и трехэлементное множе¬
ства.
В комбинаторике упорядочение п-элементного множества
(т. е. расположение элементов п-элементного множества в
определенном порядке) называется перестановкой его эле¬
ментов (перестановкой из п элементов).
Число перестановок из п элементов обозначается Рп.
. Термин «перестановка» впервые употребил в одном
! из своих популярных учебников по арифметике пре¬
подаватель математики из Антверпена Андре Таке
(1612—1660, Голландия).
Обозначение числа перестановок именно буквой Р
объясняется тем, что в переводе с французского слово
permutation означает перемещение, перестановка.

271	Перестановки
Пример 4. Сколько перестановок можно составить из пя¬
тиэлементного множества?
Решение. Как можно составить перестановку из пяти эле¬
ментов? На первое место можно поставить любой из этих эле¬
ментов; значит, элемент, стоящий на первом месте, можно вы¬
брать пятью способами. После того как выбран элемент, стоя¬
щий на первом месте, на второе место можно поставить любой
из оставшихся четырех элементов; значит, элемент, стоящий
на втором месте, можно выбрать четырьмя способами. Соответ¬
ственно элемент на третье место можно выбрать тремя спосо¬
бами, на четвертое место — двумя способами и на последнее,
пятое, место остается единственный элемент.
Согласно правилу умножения, 5 элементов можно упорядо¬
чить 5 • 4 • 3 • 2 • 1 способами, т. е. Р5 = 5 • 4 • 3 • 2 • 1 = 120.
Теорема. Число перестановок из п элементов находит¬
ся пс формуле
Рл= 1 • 2 • 3 •... • и.	(1)
Доказательство. Как можно составить перестановку из
элементов «-элементного множества? На первое место можно
поставить любой из п элементов этого множества; значит,
элемент, стоящий на первом месте, можно выбрать п спо¬
собами. После того как выбран элемент, стоящий на первом
месте, на второе место можно поставить любой из оставшихся
п~ 1 элементов; значит, элемент, стоящий на втором месте,
можно выбрать п — 1 способами и т. д.
Согласно правилу умножения, п элементов можно упоря¬
дочить
п • (п — 1) • (ге - 2) •... • 3 • 2 • 1
способами, т. е.
Рп = п • (п - 1) • (п - 2) •... • 3 • 2 • 1. И
Произведение всех натуральных чисел от 1 до п
обозначается ге! (читается «эн-факториал» ). т. е.
n! = 1 • 2 • 3 •... • (п — 1) • п.
Пользуясь этим обозначением, формулу (1) можно записать
в виде

Комбинаторика и теория вероятностей
272
Слово «факториал» (factorial) — английское слово, в
переводе означает «множитель».
П ример 5. Сколькими способами можно раздать четыре
разные кружки четверым гостям?
Решение. Число способов раздачи кружек гостям равно
числу перестановок из четырех элементов, т. е.
Р4 = 1 • 2 • 3 • 4 = 24.
Ответ: 24.
Пример 6. Сколькими способами можно составить распи¬
сание из семи разных уроков, чтобы алгебра и геометрия сто¬
яли рядом?
Решение. Способ 1. Допустим, что в расписании алгебра
и геометрия стоят рядом и алгебра стоит перед геометрией.
При этом алгебра может стоять на первом уроке, на втором,
на третьем, ..., на шестом уроке (на седьмом уроке алгебра
стоять не может, почему?). Значит, упорядоченная пара (ал¬
гебра, геометрия) может разместиться в расписании шестью
способами. При каждом из этих способов оставшиеся пять
предметов могут образовывать 5! перестановок. Таким обра¬
зом, число перестановок, в которых алгебра и геометрия стоят
рядом и алгебра стоит перед геометрией, равно 6 • 5!, т. е. 6!.
Такое же число перестановок, в которых алгебра и геометрия
стоят рядом и геометрия стоит перед алгеброй. Следовательно,
число перестановок, в которых алгебра и геометрия стоят ря¬
дом, равно
2 • 6! = 1440.
Ответ: 1440.
Способ 2. Будем считать алгебру и геометрию, стоящие
в расписании рядом, одним длинным уроком матема¬
тики. Тогда расписание возможно составить 6! различными
способами. При каждом таком способе из алгебры и геометрии
можно составить 2 перестановки. Значит, расписание, в кото¬
ром алгебра и геометрия стоят рядом, можно составить 2 • 6!
способами.
А составить расписание из семи разных уроков так, чтобы
алгебра и геометрия не стояли рядом, можно (7! — 2 • 6!) спо¬
собами (объясните почему).

273
Перестановки JI
Пример 7*. Сколько существует перестановок из п
элементов, в которых данные два элемента стоят рядом?
Решение. Способ 1. Пусть данные два элемента — это р
и q. Допустим, что в перестановке они стоят рядом и р стоит
перед q. При этом р может стоять на первом месте, на втором
месте, на третьем месте, ..., на (и — 1) месте (на п местер стоять
не может, почему?). Значит, упорядоченная пара (р, q) может
разместиться в перестановке (п - 1) способом.
При каждом из этих способов оставшиеся п — 2 элемента
могут образовывать (и - 2)! перестановок. Таким образом,
число перестановок, в которых р и q стоят рядом и р стоит
перед q, равно
(и- 1)(п-2)!, т. е. (п-1)!.
Такое же число перестановок, в которых р и q стоят рядом
и q стоит перед р. Следовательно, число перестановок, в кото¬
рых р и q стоят рядом, равно
2(п- 1)1.
Ответ: 2(п-1)!.
Способ 2. Будем считать элементы р и q, стоящие в пе¬
рестановке рядом, одним «склеенным» элементом. То¬
гда элементов будет п — 1, и из них можно составить (и - 1)!
перестановок. В каждой такой перестановке элементы р и q
можно расположить рядом двумя способами: (р, q) и (q, р).
Поэтому число перестановок, в которых р и q стоят рядом,
равно 2(п — 1)!.
1.	Сформулируйте определение n-элементного множества.
2.	Что называется перестановкой из п элементов?
3.	Как обозначается и чему равно число перестановок из п эле¬
ментов?
4*. Докажите формулу для числа перестановок Рп.
5. Как читается и что обозначает символ п!?

Комбинаторика и теория вероятностей
274
Упражнения
4.10. Найдите значение выражения:
14! .
12! ’
19!
17!
4.11. Упростите выражение:
п (р 2)!.
' ~ р! ’
о\ (Р 7 3)!	,
J (р 1)! (р2 -4) ’
4.12. Сравните числа:
1) 2! • 5! и 2 • 5!;
3) 2-5! и (2-5)!;
5) 2! ■ 5! и (2 • 5)!;
ол (р + 1)! .
J (Р-2)! ’
.. (р + 2)!(р2-9)
' (р + 4)!
2) 3! - 2! и 3! - 2;
4) (3 • 4)! и 3 • 4!;
6) 3! • 4! и (3 • 4)!.
4) A2L.
7 614!
4.13. Сравните числа при р, равном 1; 2; 3:
1)	Зр! и (Зр)!;	2) 3!р! и (Зр)!;
3) 4!р! и (4р)!;	4) 4р! и (4р)!.
4.14.
Выполните действия:
4.15.
1) —-— +—-—■
> (t + З)! (t : 3)! ’
1 ~ 1	.
’ (t + 1)!	(t -1)! ’
Решите уравнение:
1) (Ц2)! = 72;
2)
2)
4)
1
(<-2)!
4.16.
Сколькими способами
1) 7 разных книг;
можно разместить на полке:
2)	9 разных книг?
4.17.	Во вторник в 9 А классе все уроки разные. Завуч сказал,
что из этих уроков расписание можно составить 120 спо¬
собами. Сколько уроков в 9 А во вторник?
4.18.	Сколькими способами могут разместиться:
1)	4 пассажира в четырехместном купе;
2)	6 пассажиров в шестиместной каюте;
3)	10 пассажиров в десятиместном мини-автобусе?

275
1)	п = 7;
4.19. Сколькими способами можно рассадить на скамейке п че¬
ловек, если:
2)	и = 5?
4.20. Сколькими способами можно рассадить за круглым сто¬
лом п гостей, если два способа, при которых у каждого
гостя слева и справа одни и те же соседи, считаются оди¬
наковыми. Решите задачу при:
1)	п = 7;	2) и = 5;	3) и = 17;	4) и = 9.
4.21 На полке стоят 15 различных книг: 7 в синих переплетах
и 8 в красных. Сколькими способами можно разместить
эти книги, чтобы:
1)	первые 8 мест занимали книги в красных переплетах;
2)	книги в синих и красных переплетах чередовались?
4.22.	Сколько существует перестановок букв а, Ъ, с, d, е, f, k, I,
tn, n, таких, что:
1)	буква k занимает второе место, а буква b — седьмое;
2)	буква k занимает одно из первых трех мест, а буква
Ъ — одно из последних двух мест;
3)	буква b следует непосредственно за буквой k;
4)	буквы b и k стоят рядом?
▲ 4.3. Событие, вероятность события
Напомним некоторые сведения о случайных событиях и ве¬
роятностях событий, с которыми мы познакомились в восьмом
классе. Начнем с примера.
П р и м е р 1, Двенадцать не различимых на ощупь карточек
занумерованы числами от 1 до 12 и помещены в ящик.
Проделаем следующий опыт: вынем наугад одну карточку
из ящика. При этом возможны 12 исходов, каждый из которых
характеризуется номером вынутой карточки. Все эти исходы
равновозможны. К тому же все они несовместны (никакие два
не могут произойти вместе, поскольку вынутая карточка имеет
только один номер).

Комбинаторика и теория вероятностей	276
Каждый из рассмотренных 12 равновозможных несовмест¬
ных исходов называется элементарным событием (элемен¬
тарным исходом).
Рассмотрим событие (обозначим его буквой А): «номер
вынутой карточки делится на 3». Оно произойдет, если
номером вынутой карточки будет одно из чисел: 3, 6, 9, 12.
Говорят, что каждое из этих четырех элементарных событий
благоприятствует событию А. Эти четыре события называют
благоприятствующими событию А.
Событием, противоположным событию А (обозначается
А, читается «А с чертой»), называется событие, которому
благоприятствуют все те элементарные исходы, которые не
благоприятствуют событию А
В нашем опыте А означает: «номер вынутой карточки не
делится на 3». Оно произойдет, если номером вынутой
карточки будет одно из чисел: 1, 2, 4, 5, 7, 8, 10, 11. Каждое
из этих восьми элементарных событий не благоприятствует
событию А (и благоприятствует событию А).
Вероятностью события А (обозначается Р(А)) называ¬
ется отношение числа элементарных исходов, благоприят¬
ствующих событию А, к общему числу элементарных исходов.
Это определение вероятности называется классическим.
В нашем опыте вероятность события А равна = у, т. е.
Р(А) - ^2 ~ у •
Вероятность события А равна , поскольку Р(А) =	= -|-.
Вообще, для любого события А верно равенство
Р(А) = 1- Р(А).
Пусть в нашем опыте событие В означает: «номер вынутой
карточки делится на 1». Это событие произойдет при любом
исходе. Такое событие называется достоверным.
А событие С — «номер вынутой карточки делится на 13» —
не может произойти ни при каком исходе. Такое событие на¬
зывается невозможным.

277
Событие, вероятность события
Событие называется достоверным (будем обозначать его
буквой U), если в результате опыта оно обязательно произой¬
дет. Таким образом, все элементарные исходы являются бла¬
гоприятствующими событию U, и поэтому P(U) = 1.
Событие называется невозможным (будем обозначать его
буквой О), если в результате опыта оно не может произойти.
Таким образом, ни один элементарный исход не будет благо¬
приятствовать событию О, и поэтому Р(О) = 0.
1.	Дайте определение случайного события.
2.	Какое событие называется противоположным событию А?
3.	Что называется вероятностью события А?
4.	Чему равна вероятность:
а)	невозможного события;
б)	достоверного события?
5.	Какое событие называется:
а)	невозможным;
б)	достоверным?
6.	Запишите формулу для вычисления вероятности события, про¬
тивоположного событию А.
Упражнения
4.23.	В ящике находятся карточки, занумерованные двузнач¬
ными числами, причем использованы все двузначные
числа и разные карточки имеют разные номера. Опыт за¬
ключается в том, что вынимают наугад одну карточку.
Какова вероятность того, что номер вынутой карточки:
1) делится на 9;
3)	делится на 17;
5)	не делится на 24;
2) делится на 7;
4) делится на 19;
6)	не делится на 36?
4.24.	Если расписание из пяти уроков: алгебра, геометрия,
физкультура, литература и химия — составляется на¬
угад, то какова вероятность, что:
1)	алгебра будет на первом уроке;
2)	математика будет на первом уроке;
3)	алгебры не будет на первом уроке;
4)	математики не будет на первом уроке?
4.25.	Из букв разрезной азбуки сложили слово «мама». Затем
четыре карточки, на которых написаны эти буквы, по-

Комбинаторика и теория вероятностей
278
дожили в ящик и тщательно перемешали. Если эти кар¬
точки вынуть наугад и расположить в порядке появле¬
ния, то какова вероятность, что опять получится слово
«мама»?
4.26.	Из букв разрезной азбуки сложили слово «карта». Затем
пять карточек, на которых написаны эти буквы, поло¬
жили в ящик и тщательно перемешали. Если эти кар¬
точки вынуть наугад и расположить в порядке появле¬
ния, то какова вероятность, что опять получится слово
«карта»?
4.27.	Бросаются одновременно три игральные кости*. Какова
вероятность, что сумма выпавших очков равна: 1) 9;
2) 10; 3) 11; 4) 12?
4.28.	В каждом из трех ящиков находятся по три шарика —
два белых и один красный. Какова вероятность того, что
если из каждого ящика вынуть наугад по одному шари¬
ку, то хотя бы один из трех вынутых шариков будет:
1) красным; 2) белым?
4.29.	На книжную полку поставили произвольно п книг, среди
которых трехтомник А. П. Чехова. Какова вероятность
того, что три томика А. П. Чехова будут стоять рядом,
если: 1) п - 10; 2) п = 11; 3) п = 13; 4) п = 12?
Рис. 18S
* Игральная кость — это кубик, на гранях которого отмечены точки:
одна, две, три, четыре, пять, шесть (рис. 185).

279
Справочные материалы
Справочные материалы
Основные свойства сложения и умножения
1.	Переместительный закон
а + Ь = Ь + а; аЪ-Ъа
2.	Сочетательный закон
(а + Ь) + с - а + (Ь + с); (ab)c = a(bc).
3.	Распределительный закон
(а + b)c = ас + Ъс.
4—5. Существуют числа 0 (нуль) и 1 (единица), такие, что
для любого числа а верны равенства
а + 0 = о, о-1-а.
6.	Для любого числа а существует противоположное число
-а, такое, что
а + (-а) = 0.
7.	Для любого числа а 0 существует обратное число
а-1 =— , такое, что
а • а'1 = 1.
Свойства степеней с целыми показателями
При а * 0, п натуральном:
1.	а1 = а.
2.	ап= а а-а-...а (п > 1).
п раз
3.	а°=1.
4.	ап = -„ (п>1).
а
При а * О, Ь 0 и I, ;п целых:
5.	aLam~ а1+т.
6.	а1 ■ ат = а‘~т.

Справочные материалы
280
7.	(al)m = alm.
8.	(ab)'n = ambm.
Q (	= —
■ \ b J bm'
Формулы сокращенного умножения
1.	Квадрат суммы: (а + b)2 = a2 + b2 + 2аЬ.
2.	Квадрат разности: (а - Ь)2 — а2 + Ъ2 — 2аЪ.
3.	Разность квадратов: а2 - Ь2 = (а - Ъ)(а + Ъ).
4.	Куб суммы: (а + Ь)3 = а3 + За2Ь + ЗаЬ2 + Ь3 =
= a3 + b3 + ЗаЬ(а + Ь).
5.	Куб разности: (а — Ь)3 — а3 — За2Ь + ЗаЬ2 — Ъ3-
— а3 — Ъ3 — ЗаЬ(а — Ь).
6.	Сумма кубов: а3 + Ь3 = (а + b) (а2 — ab + Ь2).
7.	Разность кубов: a3 — b3 = (a — b) (а2 + ab + Ь2).
Свойства алгебраических дробей
1 ~А = — = —-4
В -В В‘
О А .С _АР + ВС
В Р В Р
5 А.С -А'С
в' Р В Р’
9 АК-А
1 ВК В'
л А _С _ АР-ВС
В D В Р
й А ■ С — А Р
B D ВС'
Квадраты и кубы натуральных чисел
от 1 до 10
п
1
2
3
4
5
6
7
8
9
10
п2
1
4
9
16
25
36
49
64
81
100
п3
1
8
27
64
125
216
343
512
729
1000

281
Справочные материалы
Степени чисел 2, 3, 5
п
1
2
3
4
5
6
7
8
9
10
2"
2
4
8
16
32
64
128
256
512
1024
3"
3
9
27
81
243
729
2187
6561
19 683
59 049
5"
5
25
125
625
3125
15 625
Таблица квадратов натуральных чисел от 10 до 99
Десятки
Единицы
0
1
2
3
4
5
6
7
8
9
1
100
121
144
169
196
225
256
289
324
361
2
400
441
484
529
576
625
676
729
784
841
3
900
961
1024
1089
1156
1225
1296
1369
1444
1521
4
1600
1681
1764
1849
1936
2025
2116
2209
2304
2401
5
2500
2601
2704
2809
2916
3025
3136
3249
3364
3481
6
3600
3721
3844
3969
4096
4225
4356
4489
4624
4761
7
4900
5041
5184
5329
5476
5625
5776
5929
6084
6241
8
6400
6561
6724
6889
7056
7225
7396
7569
7744
7921
9
8100
8281
8464
8649
8836
9025
9216
9409
9604
9801
Квадратные уравнения
ах2 + Ьх + с = 0 (а * 0) — квадратное уравнение относительно х,
D — b2- 4ас — дискриминант.
Если Z) > 0, то х12 — ~b2aD'	корни квадратного уравнения.

Справочные материалы
282
Если D < 0, то уравнение не имеет корней.
Если b = 2k, k^.Z, то удобно вычислять корни по формуле
Разложение квадратного трехчлена на множители
Если хр х2 — корни квадратного трехчлена, то
ах2 + Ьх + с = а(х - х:)(х - х2).
Выделение полного квадрата
ах2 + bx + с-а(х +	+ с .
\	2а)	4а
Приведенное квадратное уравнение
х2 +рх + q = 0;
D = p2~4q.
Если D > 0, то Xj 2 = Р±2^ — корни приведенного квадрат¬
ного уравнения.
Если D < 0, то уравнение не имеет корней.
Теорема Виета
Если xL х2 — корни квадратного уравнения х2 +рх + q = 0,
то
X] + х2 = ~ р; Xj • х2 = q.
Если Xj, х2 — корни квадратного уравнения ах2 + Ьх + с = 0,
то

283
Справочные материалы
Основные свойства числовых неравенств
1.	Если а> Ь, то b < а.
2.	Если а > b и b > с, то а > с.
3.	Если а > Ь, то а + с > b + с.
4.	Если а > b и с > 0, то ас > Ьс.
5.	Если а > b и с < 0, то ас < Ьс.
6.	Если а> Ь и ab > 0, то — < — .
а ь
7.	Если а > Ь и Ь > 0, то ап > b", ntN.
8.	Если а> Ь и с > d, то а + с> b + d.
9.	Если a>b, с > d и a, b, с, d — положительные числа, то
ас > bd.
10.	I а + b I < I а\ +1 b I, I а I -1 b I < I а + b I.
Модуль числа
а
а, если а > 0,
-а, если а < 0.
Решение неравенств с модулем
I xl < 4,
- 4<х^4
1x1 < 3,
-3<х<3
-3	3
Ответ: (-3; 3).
1x1 > 3,
х < -3 или х > 3
////////,	{///////£.
-3	3
J///Z//////,	.
-4	4
Ответ: [-4; 4],
I xl > 4,
х < —4 или х > 4
-4	4
Ответ:	—3] U [3;+°°). Ответ: (—оо; — 4) и (4;+°°).

Справочные материалы
284
Свойства арифметических квадратных корней
1.
2.
3.
4.
5.
6.
(Та )2~а(а> 0).
То2 = I а I.
Если -\[а > \lb, то а> Ь; если а > Ь, то у[а > \fb (а > 0, Ь > 0).
Таблица квадратных корней
72*1,414
73* 1,732
75* 2,236
76*2,449
77*2,646
710* 3,162
711 *3,317
713*3,606
714* 3,742
715* 3,873
717*4,123
719*4,359
720 * 4,472
Комбинаторика и теория вероятностей
Число перестановок из п элементов
Р,= 1-2-3-... -n = nl.
Вероятность события А
где п — общее число элементарных исходов, k — число эле¬
ментарных исходов, способствующих событию А.

285	Справочные материалы
Вероятность события А, противоположного событию А,
равна
Р(А) = 1 - Р(А).
Факториалы натуральных чисел от 1 до 10
п
1
2
3
4
5
5
7
8
9
10
п!
1
2
6
24
120
720
5040
40 320
362 880
3 628 800

Справочные материалы
286
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Абсцисса 6
Аргумент 16
Вероятность события 276
Вершина параболы 87
Ветви параболы 87
График функции 28
Гипербола 115
Значение функции
	наибольшее 24
	наименьшее 24
Исход элементарный 276
Координаты точки 6
Коэффициент обратной пропорцио¬
нальности 106
—	прямой пропорционально¬
сти 53
Множество значений функции 24
—	п-элементное 270
Начало координат 5
Нуль функции 44
Область определения функции 16
Обратная пропорциональность 106
Ордината 6
Парабола 86, 207
—	кубическая 102
Параметр 197
Переменная зависимая 16
—	независимая 16
Переменные обратно пропорцио¬
нальные 106
—прямо пропорциональные 53
Перестановка 270
Плоскость координатная 5
Правило умножения 267
Промежутки знакопостоянства
функции 46
Промежуток возрастания функ¬
ции 93
—	убывания функции 93
Прямая пропорциональность 53
Расстояние между двумя точка¬
ми 157
Решение системы уравнений с дву¬
мя переменными 133
—	уравнения с двумя неизвест¬
ными 123
Система двух линейных уравнений
с двумя неизвестными (перемен¬
ными) 133
—	координат на плоскости 5
	 	 (декартова) 5
—		(прямоугольная) 5
Системы уравнений равносиль¬
ные 134
Событие благоприятствующее со¬
бытию А 276
—	достоверное 276, 277
—	невозможное 276, 277
—	противоположное 276
—	элементарное 276
Углы координатные 9
Уравнение окружности 157
Уравнение с двумя неизвестны¬
ми 123
	второй степени 164
	 линейное 129
	первой степени 164
Уравнения равносильные 124
Функция 16
—	возрастающая 48
	на промежутке 48
—	линейная 68
—	квадратичная 207, 239
—	нечетная 61
—	постоянная 68
—	четная 81
—	убывающая 49
	на промежутке 49

2&7
Ответы к упражнениям
ОТВЕТЫ
Глава I
1.2. 1) 8; 2) -3.
1.6.	1) а) А,(-5; 6), б) Д„(5; -6), в) Д,(5; 6); 3) а) С,(1; -7), б) С/-1; 7),
в)	Со(-1; -7); 6) а) Г,(0; -5), б) Г„(0; 5), в) Г0(О; -5).
1.7.	1) А и D; В и £; Р и М; С и К; 2) В и D; Р и К', С и М; 3) Е п D-, Р и
С; М и К.
1.8.	1) АДЗ^ Д,(2), ОА = уТЗ; ВД4), ВД-1), 0В= х17; СД-1), С„( 1),
ОС = у 2; D/-2), Dy(5), 0D = х 29.
1.9.	1) (0; 2); 2) (2; -2).
1.10.	1) III и IV; 3) I и II; 5) I, II, III, IV; 7) I; 9) III.
1.12.	2) III; 4) III и IV; 6) I, II, III, IV.
1.13.	1) На прямой х = 4; 2) на прямой у - -6.
1.14.	2) х = 0, у — любое; 4) х < 0, у — любое; 6) х > 0, у — любое.
1.15.	1) п = т > 0; 3) п = т < 0.
1.16.	2) 2 или 3; 4) 3 или 4.
1.17.	1) Полоса; 3) полуплоскость; 5) две полуплоскости.
1.18.	2) Полоса; 4) полуплоскость; 6) две полуплоскости.
1.19.	1) х < 0 или х > 2; 3) -2 < у < -1 или 3 < у < 4; 5) х < 0 или 2 < х < 3.
7	19
1.22.	2) 0; -0,6; —д-; - уд ; -3; -79; не определено.
1.23.	1) 8.
1.24.	2) -6.
1.25.	1) Меньше; 3) больше.
1.26.	2) Меньше; 4) меньше.
1.27.	1) 9; 3) 4; 5) не существует.
1.28.	2) Больше; 4) больше.
1.29.	-18; -9; -36; -45.
1.30.	1) 5; 3) 20,5.
1.31.	у = 82 - х; да; все числа.
1.32.	у = х + 20; да; все числа.
1.33.	у = 40 - х; да; 0 < х < 40.
1.34.	1) у = 4х-4; 2) да; 3) х>2; 4) 16; 36; 52; 60.
1.35.	1) х2; 2) да; 3) х > 0; 4) 121 см2, 225 см2, 289 см2, 441 см’.
1.36.	1) Л; 3) (—°°; 2) U (2; +°°);	5) (—°°; —2) U (—2; 0) U (0;+°°);
7) (-оо; 0,5) U (0,5; 8) U (8; +оо).
1.37.	2) [-2,5; +°°); 4) (-оо; 0,0125]; 6) R; 8) Л; 10) [- 2; 2].
1.38.	2) Верно; 4) неверно.
1.39.	1) Верно; 3) верно.

Ответы к упражнениям
288
1.40.2) 0,25:4) 1,5;6)	; 8)	.
1.41.	1) 2; 3) 1у.
40 ол ". « 4 .	18*+ 4 . Оч 4 -125
1.42.	2) -16, 4) у , 6) y-g* ; 8) -jy^- .
1.43.	1) -у; 3) у.
1.44.	Больше.
1.45.	1) х > у ; 2) х • у .
1.46.	3,5.
1.47.	х < 0,8.
1.48.	2) [3; 8) U (8; +°°); 4) [9,75; +оо).
1.49.	1) R; 3) (-оо; 0) U (0; +°о); 5) (-оо; 0) U (0; +оо).
1.50.	2) (-оо;-у) и (-у; l)U(l;+oo); 4) (-оо;-0,75) U (-0,75; 2,5) и
U (2,5; +ОО).
1.52. 1) 648; 540; 2) 70; 40; 50; 3) область определения {40; 50; 60; 70}; мно¬
жество значений {432; 540; 648; 756}; 4) 756; 432.
1.55.	2) Да; 4) нет; 6) нет.
1.56.	1) Да; 3) нет; 5) да.
1.57.	4) Область определения [1; 10], множество значений [1,6; 7]; 5) 1,6; 7.
1.58.	3) [3; 3,4], наименьшее значение равно 3, наибольшее равно 3,4;
4) график расположен в I координатном угле.
1.60.	2) б) Р = [-2; 2], Е = [-8; 0]; в) -8; 0; г) 1; 3; 4; д) (0; -4), (2; 0).
1.61.	2) [-6; -1]; 3) -6; -1; 4) 3 и 4; 5) (0; 3).
1.66. 1) 2; 3) -14; 5) -4<5?
1.69. 1) Да, D = [0; 10], Е = [24; 100]; 2) 24°; 3) через 7 мин температура будет
приближенно равна 92°; 4) температура 60° будет достигнута прибли¬
женно через 3,4 мин; 5) за первые 8 мин температура увеличится при¬
ближенно на 70°; 6) за последние 2 мин температура увеличится
приближенно на 6°; 7) с 40° до 65’ вода нагрелась приближенно за
2,4 мин.
1.71.	1) [-2,5; 10], [-1,5; 2,5]; 2) -1,5; 2,5.
1.72.	1) [-3; 9], [-2; 3]; 2) -2; 3.
1.73.	2) 2,5; 4) нет; 6) нет; 8) 8.
1.74.	Рис. 39: 1) -4; -2; 3; 5,5; 2) (-4; -2), (-2; 0), (0; 3), (3; 5,5), (5,5; 6].
1.75.	2) 0; 3.
1.76.	3) Рис. 35: а) [-2,5; 9,5]; б) -1,5; 2,5; в) 3; 8; г) [-2,5; 3), (3; 8), (8; 9,5];
' д) [-1,5; 2,5]; 5) рис. 39: а) [-4; 6]; б) -2; 2; в) -4; -2; 0; 3; 5,5;
г)	( -4; -2), ( -2; 0), (0; 3), (3; 5,5), (5,5; 6]; д) [-2; 2].
1.77.	1) а) [-5; -3], [0; 3]; б) [-6; -5], [-3; 0], [3; 5].
1.78.	1) у1 < у2; 3) у, < уг.

289
Ответы к упражнениям
1.79.	2) у, < у2; 4) у, > уг.
1.80.	1) у, > у2; 3) у, > у2.
1.81.	2) а) [0,5; 2], [-1; 1,5]; б) ~0,7; в) возрастающая;
4) а) [-1,5; 1,5], [-0,5; 2]; б) 1; в) убывающая.
1.86.	2) Нет; 4) нет; 6) нет; 8) да; 10) да.
1.87.	Нет.
1.88.	Коэффициент пропорциональности.
1.89.	c = f ;* = |.
р
1.90.	И -д- .
1.91.	48 кг; 96 кг; 120 кг; 192 кг; т — 81.
1.92.	1) Да; 3) нет.
1.93.	2) Да; 4) да.
1.94.	1) Да; 3) нет; 5) нет; 7) да; 9) нет; 11) нет.
1.95.	2) у = -3,2х.
1.96.	2) 15; 10; 0; -2,5; -3,75; 5; 6,25; 20.
1.97.	2) 24 + 36; 4) 27 + 33.
1.98.	1) 54 см; 36 см; 3) 50 см; 40 см.
1.99.	168 г, 28 г, 56 г.
1.100.	120 г, 16 г, 160 г.
1.101.	6 кг вишни, 0,9 кг воды.
1.102.	8 кг сахара, 0,4 кг воды.
1.103.	2) Нет; 4) да; 6) нет.
1.104.	2) D, Е.
1.108. -400; -800.
1.110.	1) [0; 1]; 2) 60 км/ч.
1.111.	1) Скорость Даши 8 км/ч, скорость Маши 3 км/ч; 2) s = 8x, s = 3x.
1.112.	1) Да; 2) да.
1.113.	2) у = 4х.
1.114.	1) 0,5.
1.116.	1) S = 9x.
1.117.	1) у = 1,4п.
1.120. а) у = 2х; в) у = у х; д) у = -х.
1.123.	2) а >-0,8; 4) а > 0.
1.124.	1) Ь < 0,25; 3) Ь < 0.
1.125.	2) у = 0,625х; 4) у = 0,5х.
1.126.	1), 4).
1.127.	2) а > 3; 4) а < -1 или a > 1.
1.128.	1) а < -2; 3) а 0, а < -4,5 или а > 4,5.
1.130.	1), 2), 3), 4), 5), 6).
1.131.	2) Нет.
1.132.	1) Да; 3) нет; 5) да; 7) да; 9) нет.

Ответы к упражнениям
290
1.133.	1) -20; -14; -8; -2; 4; 10; 2) -у; 0; у ; у ; у ; у ; 3) х>у ;
4) х < у ; 5) у ; 6) у •
1.135. 2) (0; -1), (0,25; 0); (0; 1), ( 0,25; 0); (0; 1), (0,25; 0); (0; -1), (-0,25; 0).
1.137.	2) Нет; 4) да; 6) да; 8) нет; 10) да.
1.138.	1) Нет; 3) да; 5) нет; 7) да; 9) да.
1.139.	2) а < 0.
1.140.	1) -30; 3) 0,125.
1.141.	2) а) х > 2; б) х < 2; 4) а) х < 4,8; б) х > 4,8; 6) а) х > - 8; б) х < - 8.
1.142.	1) 5; (-оо; 5), (5; 4-оо); 3) -1,5; (-оо; -1,5), (-1,5; +оо); 5) -4;
(- ОО; -4), (- 4; -ТОО); 7) 0,5; (-оо; 0,5), (0,5; +оо).
1.143.	2) (0; 25), (-50; 0); 4) (0; -1,1), ( у ; о).
2
1.144.	а) у = 2х + 2; б) у = у х — 2; в) у = -0,5х + 1; г) у = -х - 3.
1.145.	1) у = 2х + 4; 3) у = 2х + 7.
1.146.	2) Да; 4) да; 6) нет.
1.150.	2) -13,4; 4) 0.
1.151.	1) у = 7; 3) у =---3,5.
1.152.	2) 7,3.
1.153.	1) 14.
1.154.	у = Их+ 22. Функция возрастающая; область определения R; множе¬
ство значений R; - 4,4 — нуль функции; (-оо; -4,4), (-4,4; +°о) —
интервалы знакопостоянства.
1.155.	у = -3х- 13.
1.156.	2) 0; 4) - у ; 6) -0,6.
1.157.	1) - у ; 0; 3) -1; 4; 5) -3; -1.
1.158.	2) - 2; -1,25; 4) -5; - 2,5.
1.159.	1) Нулей нет; 3,25 — наибольшее значение; 0,5 — наименьшее значе¬
ние; 3) 3 — нуль функции; 7 — наибольшее значение; —6—наимень¬
шее значение.
1.160.	1) Нет; 3) да; 5) нет.
1.161.	2) Нет; 4) да; 6) да.
1.162.	1) 4, 3, 2, 1, 0, 1, 2; 2) 1; 0 или 2;
—1 или 3; -2 или 4; -11 или 13;
—23 или 25; - 48 или 50; 3) х * 1;
4) при любых; 5) ни при каких.
1.164.	1) (-6; 6), (6; 6); 3) (-16; 16), (16; 16); 5) ( 1; 1), (1; 1); 7) (-15; 15),
(15; 15).
1.165.	2) 3; 4; 4) -5; 3.
1.167. 1) 2; 3; 3) -3; 3; 5) 0; 7) а — любое, кроме -7.

291
Ответы к упражнениям
1.168.	2) S = (4-7t)/?.
1.169.	2) S=108-4x2.
1.170.	2) Меньше; 4) равны; 6) больше; 8) меньше; 10) меньше; 12) больше.
1.171.	1) ±2; 3) ±0,4; 5) ±10.
1.172.	С, М, К, D, Е, Q.
1.173.	2) (6; 36); 4) (-/5; 5); 6) (1; 1); 8) (7; -1); 10) (-2; -4); 12) (-20; 0).
1.174.	1), 5), 6).
1.175.	1) ±4; 3) ±14; 5) ±^5; 7) г 2/5.
1.176.	2) Да; 4) нет; 6) нет.
1.177.	2) у = х2; a) R-, б) [0; ± оо); в) 0; г) (-оо; 0), (0; +°о); д) (0; 0);
4), 6), 8) см. ответы к заданию 2).
1.179.	1) -3 < х < 3; 2) х < -2 или х > 2; 3) х * 0; 4) -4 < х < 4.
1.180.	3), 6).
1.181.	1) у = х2 для х € [2; 3]; 3) у = х2 для х С [-3; 0].
6)	у = х2 для х ё [1; 3]; 8) у = -х2 для х € (-оо; 0).
1.183.	1) а) [0; 5]; б) [-4; 0]; 3) а) [-5; -3], [-2; 0], [2; 3]; б) [-3; -2],
[0; 2], [3; 6].
1.184.	2) Нет; 4) да; 6) нет; 8) да.
1.185.	а) 1), 2), 8), 9); б) 3), 4), 7).
1.186.	1) у = х‘, хе[—1; 2]; 3) j/ = x2, хе[1; 2]; 5) г/ = х2, хё[0; 2];
7)	у = х2, х€[—2; 0].
1.187.	2) у = х2 для х€[-3; 1]; а) [0; 9]; б) 0; в) [-3; 0), (0; 1]; г) [0; 1];
д)	[-3; 0].
1.188.	S = 6а2; -/б см; 4 см; 5 см; /5 м.
1.189.	r = yj ; 5 см; 8 см; 0,1 см; Зл/10 м.
1 192. 2: 5; 7, 10; 25; 10<10; 0,8; 0,9;	; 1,5; 1,7;	.
1.193.81; 196; 361; 0,01; 2,25; 22,09; 529; 0,25; 5-|- ;	~ .
1.194.	2) Нет; 4) да; 6) да; 8) нет; 10) да; 12) нет.
1.195.	1) Да; 3) нет; 5) да.
1.196.	2) Меньше; 4) меньше; 6) меньше; 8) больше.
1.198.	1) у = \Гх, хё[1; 9]; 3) у = у[х, х<=[4; 16].
1.199.	2) Да; 4) да; в) да.
1.200.	1) 19; 3) -4 или 1; 6) 1 или 4; 8) -5.
1.204.	(-1,6)3; (-1.5)3; (~1,3)3; 0,33; 0,43; 0,523; 1,23.
1.205.	1) Да; 3) да; 5) нет.
1.208.	2) -1 < х3 < 8; 4) 0 < х3 < 27.
1.209.	1) Да; 3) нет (кроме т = п = 0); 5) да; 7) да.
1.210.	2) у = х3; 4) у = х3.
1.211.	1) 0 или 1; 3) ± 1.
1.212.	-0,2; -0,5; -1; -5; 5; 1: 0,5; 0,2.

Ответы к упражнениям
292
1.214.	30 ч; 22,5 ч; 20 ч; 15 ч.
1.215.	P = 60t; 192; 320; 400; 625.
1.217.	2) Нет; 4) да.
1.218.	1) Да; 3) нет; 5) да.
1.220. 1) Да; 3) нет; 5) да.
1.221.
2) у-
1.222.	1) 10.
1.223.	1) 420; 280; 168; 2) 156; 78; 52.
1.224.	1) 300; 200; 180; 2) 500; 550; 275.
1.225.	1) 9 ч; 18 ч; 6 ч; 12 ч; 2) 12 га; 8 га; 16 га.
1.226.	1) 282; 188; 141; 2) 45; 9; 6.
1.227.	2) Нет; 4) да; 6) да.
1.231.
_338 ..	_ 125
2) у = —; 4) У = ~~
1.232. 1) 4 см; ~ 5,3 см; 2 см; 1 см; 3) 8 см2.
1.234.	2) у-~ ; 4) у = --^ .
1.235.	1) k = 1, b = 0; 3) k = -3, Ъ = -8.
1.236.	2) а > -0,25; 4) а '	; 6) а ■. • 5 или а > 1.
1.238. 2) -2,4; 3; 4) 3-|-; 7.
Глава 2
2.1.	2) Да; 4) да; 6) да.
2.2.	1) Нет; 3) да; 5) да.
2.4. 2) Да; 4) да; 6) да; 8) да.
2.5.
1)
25-2х
3)
- 6х - 48
11
5) У
3-8х
7
Ч)У =
9х- 17
6
9) У-
16- 10х
13
2-6. 2) (х0;
7х0- 10
14
ШЭД
4) (х0;
^),(2;-4),(-5;ЙНп-^-8);
У =
6)	(х0;	), (2; -3,2), (-5; 9,4), (t;	);

293
Ответы к упражнениям
8) (х0;
12t-8)
9 Г
Ю) (х0;
15-8М
9	)■
2,7.	1)	3) (-2; -4); 5) (-5; 1); 7) (1; 3); 9) нет решений.
2.8.	2) Да; 4) нет.
2.10.	1) Зх + 20t/ = 5; 3) 21х - lit/ + 10 = 0; 5) 2х + бу + 1 = 0.
2.11.	2) х = 0; 4) х = 0.
2.14.	1) Графики совпадают; 3)	; - уj; 5) графики параллельны.
2.15.	2) (0; 0), (1; 1); 4) (~\12; -2); 6) нет точек пересечения.
2.16.	1) Да; 3) нет; 5) нет.
2.17.	2) (1; 0), (3; 1); 4) (0; 0), (-2; 4).
2.18.	а) 1) Да; 3) нет; 5) нет; б) 1) нет; 3) нет; 5) нет.
2.20.	2) Да; 4) да; 6) нет.
2.21.	1) у =	, х = 8 - 2у; 3) у = 5х - 3, х =	; 5) у = 2*3 7 ,
2.22.	2) т = -5, п = -7; 4) т = 6, п = 0; 6) т = 9, п = 16,5.
2.23.	2) 1; 4) 0; 6) 1.
2.24.	(1; 4).
2.25.	1) 1; 3) бесконечно много; 5) 0.
2.28. 2) (t + 3; i), tR; 4) (t; 14 - 7t), t e R.
2.30.	a) 2), 3), 9); 6) 1), 5), 6), 7), 11), 12); в) 4), 8), 10).	_
2.31.	1) если m - 0, то б), если т * 0, то д); 2) а) при т* + \/2; б) при
т = ± v 2; 3) г).
2.32.	1) Нет; 2) да; 3) да; 4) нет; 5) да; 6) да; 7) нет; 8) да.
2.33.	k = 0.
2.34.	k *0,8.
2.35.1) (25; 5); 3) (9; 7); 5) (1; 2); 7) ( 5; 6); 9) (-13; 4).
2.36.	2) (5; 6); 4)(^;-^).
2.37.	а)	4), 6), 10); б) 1), 3), 11); в) 2), 5), 7),	8), 9), 12).
2.38.	4)	(t;	); /ей; 6) (t; ^у-^ ); t	-.R ; 10)	(t;	-	5<	);
2.39.	1) (4; 11); 2) (6; 0).	_
2.40.	1)	а — любое; 2) а * ± \/ 6; 3) а — любое; 4) нет	таких.
2.41.	1)	Нет таких; 2) 1,5; 3) 2; 4) ±9.
2.42.	2) Зх + у - 18 = 0; 4) 2х + 9у + 3 = 0.
2.43.	1) т = ~ 1,2; 3) нет; 5) тп*-5.
2.44.	2) (2; 2); 4) (-2; 3); 6)	; ~4у ).

Ответы к упражнениям
294
2.45.	1) (8,64; 11,04); 3) (7,2; 13,2); 5) (18; 6).
2.46.	а) 2), 5), 7); б) 1), 6); в) 3), 4), 8).
2.47.	2) (-1; -2).
2.48.	1) -2.
2.49.	1) (За-36; -2а); 2) (5а + 21д; -$а+21Ь g)	2а + Ь);
2.50.	(-1,5; 2).
2.51.	(2; 1).
2.52.	2) а) Например, а = 1; 5 = 2; с = 3; б) например, а - 2; Ь = 16; с = 5.
2.53.	1)а>3у;2) а >12,6.
2.54.	1) Ни при каких; 2) -4 < а < 3,75.
2.55.	1) -14; 2) -17,5.
4	10
2.56.	1) а = 30; 6 = -0,8; 2) а = -у ; 6 = -у .
2.57.	1) 18; 3) 17; 5) 7~^ ; 7) 131|.
2.58.	2) /185; 4) 2^29; 6)	8) Л'2^5.
2.59.	1) (х + 2)2 + (у - 10)2 = 36; 3) (х - З)2 + у2 = 1; 5) (х + 4)2 +
+ (у + 8)2 = 3; 7) (х + З)2 + (у - I)2 = 8 + 2/7.
2.60.	2) (0; 1 ± >/13), (—6 ±4/7; 0); 4) (0; 2 ±/21), (2 ±/21; 0);
6)	(0; -5 ± з/б), (6 ± 2/14; 0).
2.62.	1) Нет; 3) да; 2; 5) да; 2.
2.63.	1) (х + З)2 + у2 = 25; 3) (х - 2)2 + (у - 4)2 = 25.
2.64.	2)х2 + г/2 = 53; 4) х2+у2 = &2.
2.65.	2) 2; 4) 1; 6) 2; 8) 1.
2.66.	1) (—2; 0), (-1; 1); 2) (5; -2), (6; -1); 3) (6,6; 3,2); 4) нет.
2.67.	1) (4; 2); 3) (2; 1).
2.68.	1) (1; —|-), (у; у); 2) (-2; 3), (14,5; -8); 3) (у; у);
4) (-14; -13).
2.69.	1) (-2; -у ), (2; 1); 3) (1; -у ), (	); 5) (-18; -25), (3; -4);
7)	(4,75; 0,75), (5; 1).
2.70.	1) (1; 1), (у ; - у ); 2) (-1; 1), ( g ; ^ ); 3) (2; 1); 4) (2; 3).
2.71.	1) -23 и 8; 2) 35 и 6.
2.72.	1) 42 и 110; 2) 6 и 12.
2.73.	1) 6 и 9; 2) 4 и 68.
2.74.	1) 72 или 94; 2) 25 или 69.
2.75.	1) 30 и 33; 2) 27 и 21.

295
Ответы к упражнениям
2.76.	1) 41; 2) 16 и 30.
2.77.	1) 0,23 и 2,3; 2) 105 и 1,05.
2.78.	1) 24 ч; 2) 12 ч.
2.79.	1) 15 т, 5 т; 2) 62 и 45.
2.80.	1) 32 и 35; 2) 4 и 12.
2.81.	1) 80 км/ч, 100 км/ч; 2) 3 ч 45 мин.
2.82.	1) 73; 2) 28.
2.83.	1) 200 г; 200 г; 2) 52,5 кг; 17,5 кг.
2.84.	1) (1; -1); (1; 1); 3) (-2; -3), (2; 3).
2.85.	1) (Щ ; ||), (7; 5); 2) (-2; 3).
2.86.	1) (2; 2); 2) (-1; 3); 3) (1,3; -0,1); 4) (2,2; -0,6).
2.87.	1) (0,5; 5,5), (1,5; 5,5); 2) (-0,5; 1,5), (- 0,5; 2,5).
2.89.	1) (2; -1); 2) (-3; 2); 3) (-1; 2), (2; -1); 4) (-2; -3), (3; 2); 5) (-1; -3);
(3; 1), 6) (2; 1), (1; 2); 7) (2; 3), (3; 2); 8) (-1; -4), (4; 1).
2.90.	1) (-3; 1), (1; -3); 2) (-1; -2), (2; 1); 3) (2; 1); 4) (2; -0,5); 5) (2; 3), (3;
2)	; 6) (-2; -1), (1; 2); 7) (1; 2), (3; 4); 8) (-5; -1), (3; 7).
2.91.	1) (-1; -2), (-1; 2), (1; -2), (1; 2); 2) (-2; 1), (-1; 2), (1; -2), (2; -1);
3)	(-1; —2), (-1; 2), (1; -2), (1; 2); 4) (-2; 5), (2; 1).	_	_
2.92.	1) (1; 2)^(2; 1); 2) (1; 3), (3; 1); 3) Ф4),_(4; 3), (-2 - \ 3^_-2 + \_3),
(-2 + V 3; —2 - /3) ; 4) (-5; 3), (- V17; х/17), (3; -5), (у 17; - у17).
2.93.	1) (1; 1); 2) (-4; -2), (-2; -4), (2; 4), (4; 2); 3) (-3; -1), (3; 1), (-12;
3,5), (12; -3,5); 4) (-2; -1), (-2; 0), (1; - 1), (1; 0).
2.94.	1) (а3 + Зад2; За2Ь + Ь3); 2) если а — Ь = 0 или а = - д, то (t; t), t С R, иначе
((а - 2ЬУ; (2а - Ь)г).
2.95.	1) 4; 3) 0; у ; 5)	; -1; 7) -2; 0;	.
2.96.	2) ± у^7; 4) -2; 1,75; 6) нет решений.
2.97.	1) 0,5; 3) 1; 5) -3; 3; 4.
2.98.	2) 6.
2.99.	1) -6.
2.100.	2) 4.
2.101.	1) 6; 3) нет решений
2.102.	2) нет решений.
2.103.	1) 10.
2.104.	1) -0,75; 3,25; 2) - 3,5; 0,5; 3) -1; 4) 2; 5) 0; 6) 0; 7) 0; 8) 0; 9) 0.
2.105.	1) у; 3; 11; 2) -7; -3; -0,75; 3) -3,5; -0,5; 2,5; 4) -2; 0,75; 6.
2.106.	1) 0; 2) 0; 3) -14; 0; 14; 4) • 4; 0; 4; 5) -6; 6; 6) - 8; 8.
2.107.	1)	у ; 2)	; 3)	-у ; у ; 4) 0,8.
2.108.	1)	5; 2) -1; 1; 3)	1,5; 4) 0.
2.109.	1)	-1,5; -0,5; 2)	0; 6; 3) -2; 10; 4) -6;	-4.
2.110.	1)	0; 2) -6; 6; 3)	-2; 0; 2; 4; 4) -1;	0;	2;	3.

Ответы к упражнениям
296
2.111.	1) -у ; у ; 2) -1; 0; 3) -1; 4) 0; 10; 5) -0,4; 0; 6) 1; 1,5; 7) [2; +°°);
8)	[0; +оо).
2.112.	1) 1,5; 2) - у ; у ; 3) -0,5; 4) 2.
2.113.	1) (—3; у); 2) (-оо; 1,5) U (3,5; + оо); 3) у ; 4) х*0,6; 5) Я; 6) 0;
7)	[0; 6]; 8) (-оо; 0] U [4; +°°); 9) (в; у ).
2.114.	1)[у; 7^; 2) Я; 3) ( — ОО;	] О [11; +°°); 4) [у; + оо^; 5) 0;
б)	(-°°;	) и (и : +оо): 7) (_00; 1); 8) 0; 9) 0-
2.115.	1) (-ОО; -у j; 2) [у ; +оо); 3) [0,75; +оо); 4) [-0,8; +оо).
2.116.	1) [0,5; +оо); 2) (-оо; - у]; 3)х*-5; 4)х*7.
2.117.	1) [0; 16]; 2) [4; +оо); 3) (-оо; -2) U [2; +оо); 4) [-4; 4].
2.118.	1)0; 2)(у;+оо^;3) (-оо;-2); 4) [у! у]; 5)0; 6) (-оо;
2.122.	1) а) а > 6; б) а = 6; в) а < 6; 2) а) а > -5; б) а = -5; в) а < -5.
2.123.	1) а) а * у ; б) а = у ; в) ни при каких; 2) а) ни при каких; б) а = 5;
в)	а * 5.
2	3
2.124.	1) — , если а * 0; 0, если а = 0; 2) - — , если а * 0; 0, если а = 0;
3) — . , если а * -4; 0, если а = -4; 4) -	, если а * 5; 0, если а = 5.
2.125.	1) —, если а * ± 3; 0, если а = 3; х —любое, если а = -3; 2)	. ,
а - 3	а + 4
если а * ± 4; 0, если а = —4; х — любое, если а = 4; 3) а + 5, если а * 5;
х — любое, если а = 5; 4) а - 2, если а * -2; х — любое, если а = -2.
2.126.	1) —, если а * 1, а * 5; 0, если а = 5; х — любое, если а = 1; 2) —,
d - и	d — л
если а * 2, а 6; 0, если а = 2; х — любое, если а = 6.
2.127.	1) ——-л , если т & ± 3; 0, если т = — 3; х — любое, если т. = 3; 2) ——;,
тп + З	’ ' т-1
если т * ± 4; 0, если т = 4; х — любое, если т = -4; 3) 2т\ 7 ’ е*2-™
297
Ответы к упражнениям
т * ± 3,5; 0, если т = -3,5; х — любое, если т = 3,5; 4) х—Д—, если
о — Л тп
т * ±1,5; 0, если т = 1,5; х — любое, если т = -1,5.
1 - За + \/ ба2 — ба + 1	,	1 Г 3 +-\/3	\
1)	 2^	> еслиа е(-°°; 0)Ul 0; —j?- lul—g*-; + ool.
( 3 - \1з 3 + \/3	_ 2а + 3 + \1-12аг + 12а + 9
0, если a e I —g~ ; —g— I; 0, если а = 0; 2)	—	•
если а = 0.
2.130.	1) x = a, если а * -3, а * -1; 0, если а = -3, а = -1; 2) х = -а, если
а * 3, а * 4; 0, если а = 3, а = 4; 3) х = 1 и х = 3, если а * -1, а * -3;
х = 1, если а = —3; х = 3, если а = -1; 4) х = — 3 и х = 6, если а * —24,
а * 12; х = -3, если а - —24; х = 6, если а = 12.
2.131.	1) х = Д;, если k * 9, k * ± 3; 0, если k = ± 3, k = 9; 2)	> если
2k - 4	г-
k^ + 2, k^4; 0, если k = ± 2, k = 4; 3) —	, если k^± \[7, k # 3,5;
k - 7
2.133.	1) х = 0, если т — любое; х > 0, если т = 0; 2) если т * 0, то х = 0; если
т = 0, то х С 0; 3) если т # -2, то х = 0; если т = -2, то х > 0; 4) если
т * 5, то х = 0; если т = 5, то х > 0; 5) если т < -2, то х = — т; если
т = -2, то х = 2; если т > -2, то х = 2 и х = ~т; 6) если т < -3, то
х — т; если т = -3, то х = —3; если т > —3, то х = —3 и х = т; 7) если
т * -2, то х = 0; если т = -2, то решений нет; 8) если т # 1, то х = 0;
если т = 1, то решений нет; 9) если т # —3, то х = т; если т = — 3, то
решений нет; 10) если т > -4, то х = 4; если т < -4, то решений нет.
2.134.	1) ± (т + 5), если т> -5; 0, если т< -5; 2) ± (тп - 7), если т > 7; 0,
если т < 7; 3) х = 1, если т = 0; 0, если т * 0; 4) х = 2, если т = 0; 0,
если т * 0.
2.135. 1) а * 4; 2) а * - у ; 3)
2.136.	1) -2; 0; 2; 2) -3; 0; 3; 3) у; 4) -1.
2.137.	1) 2; 2) 35; 3) 3; 4) 4.

Ответы к упражнениям
298
2.138.
2.139.
( 5	2-Зт\	.	. (Зт + 4	-5	\
)’ е™ т * -1’’ 0> если т =	2)	)>
если т * -0,5; 0, если т = -0,5; 3) (0; 1), если р * 12; (t; 1 - 3t \ t е Я),
если р=12; 4) (-0,6; 0), если р^-0,25; (t; 10t + 611 е Я), если
р = - 0,25.
1) Если t ± 2, то ( ^2 ; уТ~2 )> №ля t = -2, то нет решений; если
t = 2, то (к; 3 - k | к € Я); 2) если t * ± 3, то (	; - ^g j; если
2
t = -3, то нет решений; если t = 3, то (/г; 5 - k | к Ч R); 3) если к * ± "д' ,
/З/г+1	1	\	2	2
то \ 3fe+ 2’ 3fe + 2/; если k = ~~3 ’ то нет Ре™615™; ес-™ fe = lf > то
,	.	_	3	(	1	15*-.8\	3
(я; 1 - п I п е Я); 4) если k * ± "д", то I д^ _ д; д^_ д I; если к=~§ ,
то
2.140.
1)
2.141
2.142.
2.143.
3
нет решений; если k = — ~^ , то (р; р + 31р е Я).
^•5
2
- см2; 0.
п±4;п^4.12; 2)о + 3.
- м2; 0; 2) 576 ~
22500 - е'
4
За + 70
4
каких.
5(t + 5)
> f + 10
1)
1)
8
210-За „„ 1 „ч 1600 +а 800-а
м, 		 м, 23 -д- м; 2) 	д  м, —д— м, ни при
7 - п
ч, ни при каких; 2)	, а 7.
Глава 3
3.2.	2) Нет; 4) да.
3.3.	1) Наименьшее 0, наибольшего нет; 3) наименьшее , наибольшего
нет; 5) наибольшее 5-|-, наименьшее 0.
3.4.	2) (± \/510; 1020); 4) нет; 6) (± v1230; 2460).
3.6.	а) {0; 1; 2; 3; 4}; б) {-4; -3; -2; -1; 0}.
3.7.	2) 4; 4)	; 6) 5.
3.8.	1) р = 4х2; 3) р = 0,5.x2.
3.9.	2)у = ±х2, [-3; 3]; 4) у = 2х2, [-1; 1]; 6)р = 0,5х2, {-2; -1; 0; 1; 2; 3}.
3.11.	1) Да; 3) да; 5) да.
3.12.	1) а < 3; 2) а > -3; 4) а = -3; 3) а * -3.
3.13.	1) -4; 3)--1-.
3.14.	1) /г >4; 3) /г = 4; 5) /г = 4.

299
Ответы к упражнениям
3.15.	2) Да; 4) нет; 6) нет; 8) да; 10) нет.
3.17. 1) Ни при каких; 3) ни при каких.
3.19.	2) Сдвиг на 1 вниз; 4) сдвиг на 9 вверх.
3.20.	1)	у = 7х2 + 3; 3) у = 7х: - 7; 5) у = 7х2	- 2,1;	7)	у =	7х2 + 0,9.
3.21.	2)	у = -3,2х2 - 4,6; 4) у = -3,2х2 + 7.
3.22.	1)	На 6 вверх; 3) на ■ \ 3 вниз.
3.23.	2)	Растяжение вдоль оси Оу в 5 раз,	сдвиг	вдоль	оси	Оу	на 6 единиц
вниз; 4) сжатие вдоль оси Оу в 9 раз, симметричное отображение отно¬
сительно оси Ох, сдвиг вдоль оси Оу на 49 единиц вверх.
3.24.	1) у = х2 + 3; 3) у =-х2 + 4.
3.25.	2) а) [—4; +°°); б) -4 — наименьшее значение, наибольшего значения
нет; в) (-оо; 0]; г) [0; + оо); д) (0; -4); е) х = 0; ж) (0; -4), (-2; 0), (2; 0);
з) (—оо; -2), (-2; 72), (2; +°°); 4) а) (—°°; —1]; б) -1 — наибольшее зна¬
чение, наименьшего значения нет; в) [0; +°°); г) (-оо; 0]; д) (0; -1);
е) х = 0; ж) (0; -1); з) (~°о; +оо).
3.26.	1) (±3; -8); 3) нет; 5) (0,2; 1,2), (1; 6); 7) (-0,5; 1).
3.27.	2) Да;	4) да; (0; -1); 6) нет.
3.28.	1) Да;	joj; 3) нет; 5) да; (+2; —10).
3.29.	1) -3; 2) 1; 3)	! 4) ~6,7.
3.30.	1) а = 3, р = -1; 2) а = 3, р = -3; 3) а = -у, р = 4 у ; 4) ни при каких.
3.31.	1) Сдвиг на 3 вправо; 3) сдвиг на 1 влево; 5) сдвиг на 5 вправо; 7) сдвиг
на \ 7 влево.
3.32.	2) р = 2,3(х - 5)2; 4) р = 2,3(х+7)2; 6) у = 2,3(х - 0,4)2; 8) р = 2,3(х +
+ 2,3)2.
3.33.	1) Сдвиг на 2 вправо; 3) сдвиг на 7,3 влево.
3.34.	2) Сдвиг на 1 вправо; 4) сдвиг на 81 влево.
3.36.	1) (-4; 4); (0; 4); 3) (1; 1), (2; 1); 5) (0; 25), (3; 49).
3.37.	1)(-у ;о); 3) (0,75; 0); 5) (-4; 0); 7) (2; 0).
3.38.	2) у = —0,25(х - 2)2; 4) у = 1,25(х + 2)2.
3.41.	2) Нет; 4) нет.
3.42.	2) х = 0; 4) х = -1,8; 6) х = -р; 8) х =р; 10) х = 0.
3.43.	1)	а) Нет; б) нет;	в) нет; 3) а) нет; б) нет; в)	нет;	5)	а) да;	б)	нет;	в) нет;
7)	а) нет; б) нет;	8) нет; 9) а) нет; б) нет; в)	да.
3.44.	2) 6 и 8; 4) -8 и -6; 6) ни при каком.
3.45.	1)	b < 0; с > 0; 3)	b < 0; с = 0; 5) b > 0; с > 0.
3.46.	2)	Сдвиг на 3 влево и на 4 вниз; 4) сдвиг	на	1	вправо	и	на	5	вверх;
6) сдвиг на 8 влево и на 6 вниз.
3.47.	1) Сдвиг на 3 влево и на 1 вниз; 3) сдвиг на 4 вправо и на 6 вверх.

Ответы к упражнениям
300
3.48.
3.51.
3.52.
3.53.
3.54.
3.55.
3.58.
3.59.
3.60.
3.61.
3.62.
3.63.
3.64.
3.65.
3.66.
3.67.
3.68.
3.69.
3.70.
3.75.
3.76.
3.77.
3.78.
3.79.
3.80.
3.81.
3.82.
2)	у = (х - 5)2 * * * * 7 - 6; 4) у 7(х	3,5)2 ? 2.
1)	Сдвиг на 3 вниз; 3) сдвиг на 1 вправо и на 3 вниз.
2)	Сдвиг на 7 вверх; 4) сдвиг на 12 вверх и симметрия относительно
оси Ох.
1) Сдвиг на 8 вверх; 2) сдвиг на 24 вверх и симметрия относительно
оси Ох.
2) х = -2; 4) х = 3.
1)	(8; 2); 3) (- 2; 6); 5) ( -0,25; -0,5); 7) (-а; ~Ь); 9) (р; i).
2)	у = - х2 - 2х; 4) у = -х? + 6х — 8.
1)	Да; 3) нет.
2)	Да; 4) нет; 6) да.
1)	Нет; 3) нет; 5) да.
2)	2; 4) -4 или 0.
1)	р < 0; 3) ни при каких; 5) р > 0; 7) р ■ 0.
2)	а) Нет; б) нет; в) нет; 4) а) да; б) нет; в) нет; 6) а) нет; б) нет; в) нет;
8)	а) нет; б) нет; в) нет.
1) s > 0, t > 0; 3) s — любое, КО; 5) з > 0, t ' 0.
1) у = (х + 10)2- 94; 3) р = —(х + 4)2 + 19; 5) у - (х-6,5)2- 41,25; 7) у =
= —3(х - 2)2 ■< 3; 9) у = 4(х - 1,5)2 - 1.
2)р = 0,5(х
З)2 - 4,5; 4) у -- -3 (х - у ) " у ; 6) у = -0,2(х - 12,5)2 +
+ 26,25.
1) У = (х - 5)? 2 2; (5; 2), (О; 27); 3) у - -(х - 4)2 + 1; (4; 1), (3; 0), (5; 0),
(0; -15); 5) р-Э^х + у -4; (-1; -4), (-1; 0), (у; о), (0; -3);
7) у =у (х -4,5)2- 0,25; (4,5; -0,25), (3; 0), (6; 0), (0; 2).
2) (-13; -289); 4) (8; -196); 6) (-0,5; 6,25); 8) (6,5; 12,25); 10) (-2,5;
-30,25).
1)	(-5; 0), (1; 0), (0; -2,5); 3) (-3,5; 0), (2; 0), (0; 14); 5) (-4,5; 0), (2; 0),
(0; -9); 7) ( у ; о), (-0,6; 0), (0; 15); 9) (-11; 0), (-4; 0), (0; -44).
2)	а) -1; 23; б) р < -1, р > 23; 4) а) -1; 0; б) р < -1, р > 0.
1) а) р < 0, р? А; б) 0 <р<Д; в) р = Д; 3) а) р>-|; б) р<-|;
2) р = -8, q = 16; 4) р - - 4, q = -1.
1)	2 или 3; 3) 3; 5) 2 или 3; 7) 2.
2)	а > 0, Ь < 0, с > 0; 4) а > 0, b < 0, с — любое.
1)	лг < 0, п > 0, k — любое; 3) т < 0, п< 0, k 0.
2)	а > 0, Ь < 0, с > 0; 4) а > 0, b < 0, с < 0; 6) а > 0, b > 0, с < 0; 8) а > 0,
b < 0, е>0.
1) (-ОО; +0О); 3) (-ОО; 3) U (3; +оо); 5) (-оо; —4) U (—4; 4) U (4; +оо);
7) [-2; +о°).

301
Ответы к упражнениям
3.83.
3.84.
4.1.
4.2.
4.3.
4.4.
4.5.
4.6.
4.7.
4.8.
4.9.
4.10.
4.11.
4.12.
4.13.
4.14.
4.15.
4.16.
4.17.
4.18.
4.19.
4.20.
4.21.
4.22.
4.23.
4.24.
4.25.
4.26.
4.27.
4.28.
4.29.
2) (-оо; +°°); 4) (-оо; -1] U [1; +оо); 6) (-0О; -5) U (-5; -1) и (-1; +оо).
1) (-оо; 1]; 2) [-2; +°°); 3) (-оо; 0) и (0; +°°); 4) [0; +оо); 5) (-оо; 0);
6) (-оо; 0]; 7) [0; +оо); 8) (0; +оо); 9) (0; +оо).
Глава 4
1) 4500; 2) 1800; 3) 1500; 4) 257.
1) 42; 2) 56; 3) 425; 4) 120.
6840.
10.
7.
240.
120.
15.
7 и 4.
1) 182; 2) 342; 3) 126; 4) 210.
1) Равны; 2) равны; 3) меньше; 4) больше: 5) меньше; 6) меньше.
1) Меньше; 2) при р = 1 равны; при р - 2 и при р = 3 меньше; 3) при
р ~ 1 равны; при р = 2 и при р = 3 меньше; 4) меньше.
t2+ 1 .	t2+ 1 . ..	-2t
(1+1)! ’ (t + 1)!’ ’ (t+ 1)1 ’
1) 7; 2) 5.
1) 5040; 2) 362 880.
5.
1) 24; 2) 720; 3) 3 628 800.
1) 5040; 2) 120.
1) 720; 2) 24; 3) 161; 4) 40 320.
1) 71-81; 2) 2-7! 81.
1) 81; 2) 6-81; 3) 91; 4) 2-91.
1) 0,2; 2) 0,4; 3) 0,8; 4) 0,6.
6 ‘
_1
60'
25	1	1 л \ 25
1}Лб;2) 8-;3) 8-;4)216
1) 19 . 2) 26
'27’ ’ 27'
15 1 2) 55'' 3) 26 ’ 4) 22 ’

Содержание
302
СОДЕРЖАНИЕ
От авторов	3
Глава 1. ФУНКЦИИ
1.1.	Прямоугольная система координат	на	плоскости	 5
1.2.	Координатные углы	 9
1.3.	Функция	 15
1.4.	Задание	функции	формулой	 20
1.5.	Задание	функции	таблицей	 23
1.6.	График	функции	 27
1.7.	Задание	функции	графиком	 36
1.8.	Нули функции и промежутки знакопостоянства	 44
1.9.	Возрастание и убывание функции на промежутке	 48
1.10.	Прямая пропорциональность	 53
1.11.	График и свойства функции у = kx (k * 0)	 58
1.12.	Линейная функция	 68
1.13.	Функция у = | х I	 80
1.14.	Функция у — хг	 85
1.15.	Функция у = х2: возрастание и убывание	 93
1.16.	Функция у = \ix	 97
1.17.	Функция у = х3............................... 102
1.18.	Обратная пропорциональность 	106
k
1.19.	График и свойства функции у = — (k * 0)	 113
Глава 2. СИСТЕМЫ УРАВНЕНИЙ С ДВУМЯ ПЕРЕМЕННЫМИ
2.1.	Уравнения с двумя переменными	123
2.2.	График уравнения с двумя переменными	128
2.3.	Системы двух линейных уравнений с двумя неизвестными .... 133
2.4.	Системы двух линейных уравнений с двумя неизвестными:
геометрическая иллюстрация	138
2.5.	Решение систем линейных уравнений способом сложения	144
2.6.	Решение систем линейных уравнений способом подстановки . . . 150
2.7.	Расстояние между двумя точками. Уравнение окружности	157
2.8.	Системы, состоящие из уравнения первой и уравнения второй
степени с двумя неизвестными	164
2.9.	Использование систем уравнений при решении текстовых задач 169
А 2.10. Некоторые приемы решения систем уравнений	174
А 2.11. Уравнения, содержащие переменную в знаменателе и под зна¬
ком радикала	182
А 2.12. Уравнения, неравенства, функции, содержащие выражения со
знаком модуля	189
А 2.13. Уравнения с параметром 	194
А 2.14. Системы уравнений с параметром	200

303	Содержание
Глава 3. КВАДРАТИЧНАЯ ФУНКЦИЯ
3.1.	Функция у = ах1 2 3	207
3.2.	Функция у = ах2 + с	216
3.3.	Функция у = a(x-s)2	223
Функция у = а(х - s)2 + t	232
Квадратичная функция	239
6.	Исследование квадратичной	функции	244
7.	Преобразования графиков функций	25^
Глава 4. КОМБИНАТОРИКА
И ТЕОРИЯ ВЕРОЯТНОСТЕЙ	]
1.	Правило умножения	267
2.	Перестановки	270
3.	Событие, вероятность события	275
Справочные материалы	279
Предметный указатель	286
Ответы	287
► ► ►	► ► со со
rfx	СО СО СЛ

ФУНКЦИИ И ИХ ГРАФИКИ

УРАВНЕНИЕ ОКРУЖНОСТИ
С РАДИУСОМ R
КВАДРАТИЧНАЯ ФУНКЦИЯ
у = ах2+ Ьх + с (а 0)
Х1-2_ 2а ’
х _ _Ь_
Х°~ 2а’
i/0 = ах2+ Ьх0+ с.
2/j
У
\
; L !
Уо
/*Т\
/ 2 а \	г
с’
\	2а J
о
С1
хо	X
О
хХ х° /х2
X
Уо
а > 0, D > 0
а < 0, D > 0

ISBN 985 12-1461-2
I 11 Л fJL 1