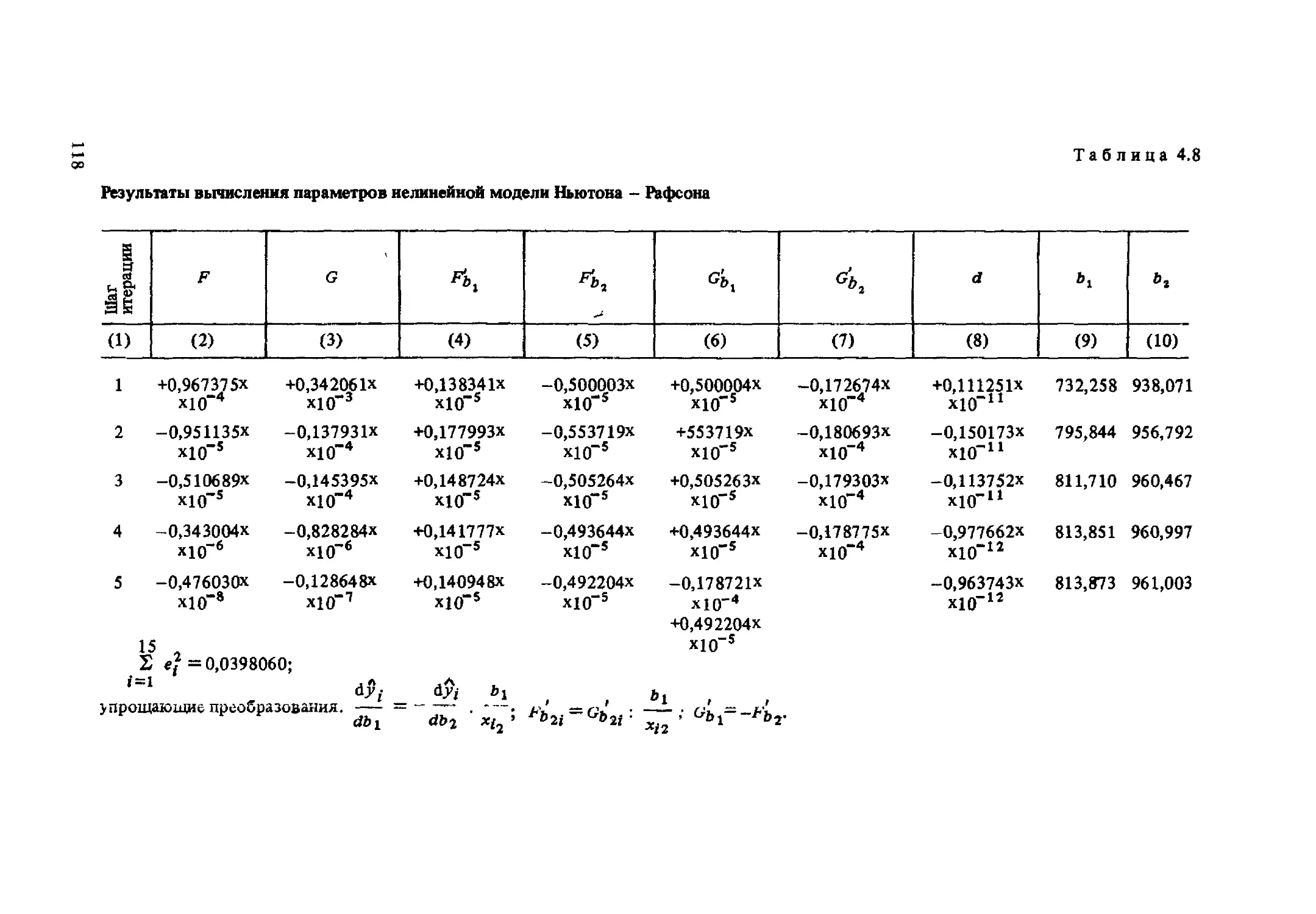
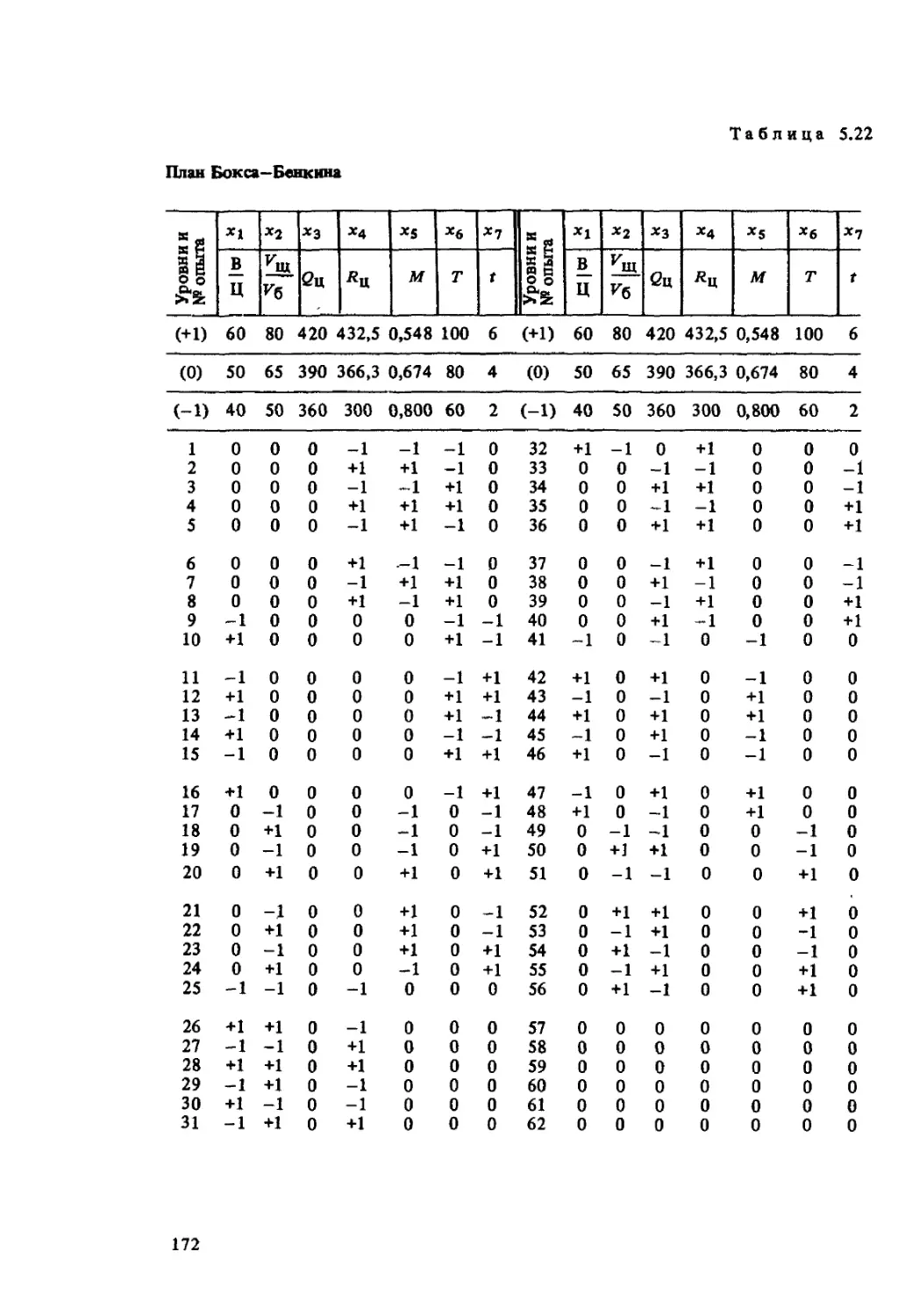
Текст
Е. Н. Львовский
СТАТИСТИЧЕСКИЕ МЕТОДЫ
ПОСТРОЕНИЯ
ЭМПИРИЧЕСКИХ ФОРМУЛ
Издание второе, переработанное и дополненное
Допущено Министерством высшего и среднего
специального образования СССР
в качестве учебного пособия
для студентов
высших технических учебных заведений
ББК22.1
Л89
УДК 51(075)
Рецензенты: кафедра прикладной математики Московского инженерно-
строительного института (зав. кафедрой - д-р физ.-мат. наук, проф. В.В. Куче-
ренко) и д-р техн, наук, проф. Ю.В. Зайцев (Всесоюзный заочный политехни-
ческий институт)
Львовский Е.Н.
Л89 Статистические методы построения эмпирических формул: Учеб,
пособие для втузов. — 2-е изд., перераб. и доп. - М.: Высш, шк., 1988,—
239 с.: ил.
ISBN 5-06-001264-6
Во 2-м издании пособия (1-е - 1982 г.) изложены основные методы обра-
ботки опйтных данных. Подробно описаны способы предварительной обработ-
ки результатов наблюдений. Рассмотрены статистические методы построения
эмпирических формул, метод максимума правдоподобия, метод средних и
конфлюэнтный анализ. Освещена методика планирования и обработки актив-
ных экспериментов. Даны основы дисперсионного анализа.
1502000000(4509000000) - 430
001 (01) - 88
35-88
ББК 22.1
51
ISBN 5—06—001264—6 _ ©Издательство ’’Высшая школа”, 1982
<© Издательство ’’Высшая школа”, 1988 с изменениями
ОГЛАВЛЕНИЕ
Предисловие........................................................... 5
Введение. Краткие сведения из теории вероятностей и математической стати-
стики.......................................f..........1 . ........... 7
§ В.1. Случайные события (7) § В.2. Относительная частота и вероятность слу-
чайных событий (8). § В.З. Сложение и умножение вероятностей (10).
§ В.4. Дискретно распределенные случайные величины (13). § В.5. Непрерывно
распределенные случайные величины (14). § В.6. Система обозначений (16).
Глава I. Предварительная обработка экспериментальных данных.......... 17
§ 1.1. Цели предварительной обработки опытных данных (17). § 1.2. Генераль-
ная совокупность и выборка (17). § 1.3. Вычисление характеристик эмпири-
ческих распределений (выборочных характеристик). Моменты (18). § 1.4. От-
сев грубых погрешностей (23). § 1.5. Полигон и гистограмма частот распреде-
ления (25). § 1.6. Проверка гипотезы нормального распределения (28).
§ 1.7. Преобразование распределений к нормальному (32). § 1.8. Алгоритм и
блок-схема алгоритма предварительной обработки экспериментальных дан-
ных (37).
Глава И. Статистические методы построения преобразования и оценки пар-
ных зависимостей по экспериментальным данным......................... 41
§ 2.1. Метод наименьших квадратов в простейшем случае двумерного простран-
ства (на плоскости). Уравнение регрессии (41). § 2.2. Геометрическая интер-
претация коэффициентов регрессии. Дополнительные разъяснения (44).
§ 2.3. Парная корреляция. Статистическое оценивание парной корреляции и
регрессии (46). § 2.4. Числовой пример выполнения парного линейного регрес-
сионного и корреляционного анализов. Статистическое оценивание результатов
расчетов (49). § 2.5. Оценка линейности регрессии (53). § 2.6. Нелинейная пар-
ная регрессия (55). § 2.7. Другие формы нелинейной парной регрессии. Выбор
оптимальной формы (59). § 2.8. Алгоритм и укрупненная блок-схема алгорит-
ма расчета на ЭВМ оптимальной формы связи между двумя переменными фи-
зическими величинами (60). § 2.9. Методика предсказания предельных значе-
ний величин, изменяющихся по экспоненте (61).
Глава III. Множественный регрессионный и корреляционный анализ. Много-
факторные эмпирические зависимости................................ 64
§ 3.1. Линейный множественный регрессионный анализ (64). § 3.2. Проверка
значимости уравнения регрессии и коэффициентов уравнения регрессии (67).
§ 3.3. Множественный корреляционный анализ (68). § 3.4. Множественный
нелинейный регрессионный анализ (73). § 3.5. Выбор оптимальной формы урав-
нения регрессии в множественной ситуации. Различные методы решения задачи
(74). § 3.6, Примеры множественного регрессионного анализа (78). § 3.7. Ме-
тодика отыскания комбинаций значений факторов, максимизирующих и мини-
мизирующих функцию отклика (80). § 3.8. Алгоритмы и укрупненные блок-
схемы алгоритмов множественного корреляционного и множественных рег-
рессионных анализов, выполняемых методом исключения и методом включе-
ния переменных (85).
Глава IV. Дополнительные сведения о построении эмпирических зависимос-
тей по опытным данным............................................... 87
§ 4.1. Предварительные соображения (87). § 4.2. Построение нелинейных эмпи-
рических зависимостей с использованием ортогональных полиномов Чебышева
(параболическое интерполирование) (87). § 4.3. Значение остатков при изуче-
нии результатов регрессионного анализа [43] (93). § 4.4. Интерпретация урав-
нения регрессии (95). § 4.5. Метод средних (101). § 4.6. Метод максимума
правдоподобия. Регрессионный и конфлюэнтный анализы как частные случаи
метода максимума правдоподобия (104). § 4.7. Модели, нелинейные по пара-
метрам (112). § 4.8. Сравнение данных (130).
Глава V. Построение эмпирических формул по результатам активных
(специальным образом спланированных) экспериментов......................137
§ 5.1. Активные эксперименты - эффективный исследовательский метод
естествоиспытателей (137). § 5.2. Отсеивающие эксперименты (145).
§ 5.3. Экстремальные эксперименты (152). § 5.4, Дисперсионный анализ (175).
§ 5.5. Некоторое понятие об оптимальном планировании экспериментов (184).
§ 5.6. Планирование экспериментов на симплексе для оптимизации составов
смесей (192).
Послесловие...........................................................196
Приложения ......................................................... 197
Литература.......................................................... 234
ПРЕДИСЛОВИЕ
... знание людей заслуживает имени
Науки в зависимости от того, какую
роль играет в нем число.
Э. Борель
Технический прогресс немыслим без развития науки, а развитие науки
невозможно без грамотно спланированных и поставленных эксперимен-
тов, без обработки их результатов для получения максимально возможного
количества информации.
В свете реформы высшей школы в вузах нашей страны все большее
внимание уделяется научной работе студентов. Широкое распространение
получает сравнительно новая форма этой работы — УИРС (учебно-иссле-
довательская работа студентов). В учебных планах некоторых специаль-
ностей уже уделено время для УИРС. УИРС - это занятия студентов под
руководством опытных педагогов, ставящие своей целью привить навыки
научного творчества. Однако научное творчество невозможно без умело
поставленных экспериментов и грамотной обработки их результатов, кото-
рая позволяет извлечь из проделанной работы максимум формализован-
ной, численно выраженной информации.
В нашей стране и за рубежом издано большое количество литературы
по методике экспериментирования и обработке экспериментальных данных
для построения эмпирических зависимостей (см. список литературы, при-
веденный в конце пособия), однако студентам будет полезна книга неболь-
шого объема, в которой освещены основные вопросы статистической обра-
ботки экспериментальных данных для построения эмпирических зависи-
мостей. Этим и руководствовался автор при написании данного учебного
пособия.
Материал пособия излагается в рецептурном плане, т.е. непосредственно
для практического применения методом индукции (от простого к слож-
ному). В литературе [4, 8, 37, 43, 52, 60, 66, 69, 76, 102] можно найти
математически строгое изложение некоторых вопросов, затронутых в на-
стоящем пособии.
Автор ставил перед собой цель изложить материал в максимально
доступной и понятной форме. Каждый новый термин выделен и подробно
пояснен либо во введении, либо в основном тексте. Следует помнить, что
самый лучший способ освоить трудный раздел — самостоятельно решить
числовые примеры.
При описании статистических методов построения эмпирических зави-
симостей материал изложен так, что для его понимания достаточно тех
разделов математики, которые изучаются в старших классах средней
школы.
В настоящее время научная работа невозможна без применения ЭВМ.
Поэтому там, где в этом есть необходимость, приведены алгоритмы и
укрупненные блок-схемы. Если же не требуется применения больших
5
ЭВМ, то рекомендуется использовать настольную вычислительную тех-
нику.
Материал пособия изложен в том порядке, в котором его обычно при-
меняют при обработке экспериментальных данных. Рассмотрено много
числовых примеров, взятых из практики обработки экспериментов и ис-
кусственно синтезированных. В связи с тем что у не имеющих математи-
ческого образования экспериментаторов могут возникнуть трудности,
связанные с терминологией, перед основным материалом помещено вве-
дение, в котором содержатся основные сведения из теории вероятностей.
В гл. I изложена методика предварительной обработки эксперимен-
тальных данных. В гл. II описаны наиболее простые, а в гл. III - более
сложные случаи применения метода наименьших квадратов для построе-
ния эмпирических зависимостей. В гл. IV рассмотрены специальные во-
просы теории обработки экспериментов. Гл. V посвящена перспективным
методам построения эмпирических зависимостей по результатам активных,
спланированных экспериментов. В приложениях содержатся таблицы, не-
обходимые для построения и статистической оценки эмпирических зави-
симостей.
В настоящее время ставят эксперименты и по их результатам строят
модели почти во всех областях науки. Медики и биологи, агрономы и пси-
хологи, физики и инженеры не могут обойтись без статистической обра-
ботки результатов наблюдений и измерений. Данное пособие и предназна-
чено для студентов самых различных специальностей. Оно будет также
полезно преподавателям, читающим курсы УИРС, ’’Введение в научные ис-
следования”, ’’Основы научных исследований”, и начинающим эксперимен-
таторам.
Время, затраченное на изучение статистических методов обработки
наблюдений, окупится за счет экономии средств и времени при постановке
экспериментов и обработке их результатов. Стоимость обработки экспе-
риментов составляет незначительную часть стоимости эксперимента в це-
лом, но может значительно повысить ценность полученных результатов.
Этому вопросу часто не уделяют должного внимания, и нередки случаи,
когда результаты дорогостоящих экспериментов не подвергают даже прос-
тейшей обработке; при этом, как следствие, теряется огромное количест-
во полезной информации. Культуру экспериментирования и умение обра-
батывать результаты опытов для получения максимально возможной ин-
формации надо прививать еще в вузе.
Главная задача настоящего пособия — популяризация методов построе-
ния эмпирических зависимостей по результатам экспериментов. Пособие
содержит большой список литературы (164 наименования). Начиная с
1961 г. в журнале ’’Заводская лаборатория” публикуются статьи методо-
логического характера по обработке результатов эксперимента. Перечень
этих работ дан в П 14.
Во втором издании книги исправлены замеченные опечатки, расширен
наиболее сложный раздел о нелинейном оценивании данных экспериментов
Приведен новый параграф, посвященный методике сравнения опытных и
теоретических данных. А
ВВЕДЕНИЕ
КРАТКИЕ СВЕДЕНИЯ ИЗ ТЕОРИИ ВЕРОЯТНОСТЕЙ
И МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ
Методы обработки данных наблюдений базируются на положениях теории
вероятностей и математической статистики. Студенты большинства спе-
циальностей либо не изучают теорию вероятностей вообще, Либо знакомят-
ся с этой дисциплиной при изучении курса высшей математики в очень
небольшом объеме.
Необходимость предварительно перед чтением литературы по ме-
тодам обработки данных наблюдений ознакомиться с основными поло-
жениями теории вероятностей, как правило, отпугивает эксперимента-
торов от специальной литературы по этому вопросу. Настоящее учеб-
ное пособие предназначено для преодоления этого своеобразного линг-
вистического и психологического барьера. Читателям на выбор предла-
гается один из двух возможных методов изучения материала книги.
Первый метод (традициойный). Материал изучают по порядку.
Сначала знакомятся с введением, а затем изучают основной материал
книги.
Второй метод. Изучение материала начинают сразу с гл. I, а к
введению возвращаются по мере необходимости только тогда, когда в
тексте встречаются понятия,- требующие дополнительного разъяснения.
Для облегчения и организации этого процесса материал введения
разделен на части, на которые в необходимых местах даются ссылки с по-
мощью скобок О в отличие от ссылок на литературу [ ] и ссылок на фор-
мулы ( ).
Все положения введения приведены без доказательств.
§ В.1. Случайные события
1.1. Испытания. Для изучения тех или иных явлений природы и об-
щества производят опыты или наблюдения.
С семантической точки зрения слова «опыт» и «наблюдение» неравно-
значны. По-видимому, при проведении опыта естествоиспытатель играет
более активную роль, чем при наблюдении того или иного явления. Можно
также отметить, что в понятие «опыт» как составная часть входит понятие
«наблюдение» и еще нечто, относящееся к искусственному воспроизве-
дению условий для наблюдения.
7
Испытанием в теории вероятностей называется осуществление ка-
кого-нибудь комплекса условий, который может быть воспроизведен
сколь угодно большое число раз. О всяком новом испытании говорится как
о повторении прежнего, чтобы лишний раз подчеркнуть, что испытания
происходят в одних и тех же условиях. При этом не следует забывать, что
о воспроизведении условий испытания можно говорить только в прибли-
женном смысле. При повторном бросании игральных костей, успеет (хотя
и крайне незначительно) измениться температура воздуха, направление
его движения; изменится (на доли миллиграмма) и вес самих костей в
результате налипания пылевых частиц.
Испытание в отличие от опыта не обязательно предполагает наличие
наблюдателя. Как испытания квалифицируются самые разнообразные
явления, в которых одни и те же условия реализуются многократно.
1.2. События. Результатом испытаний являются события. Некоторые
события происходят неизбежно в результате каждого испытания, и поэ-
тому они называются достоверными. Другие события вовсе не могут про-
изойти, и поэтому их называют невозможными.
В результате испытания в связи с изменением случайных обстоятельств
может произойти то или иное событие из множества событий возможных
при данном испытании [138]. Это множество событий называется полем
событий, связанных с испытанием, а события'этого поля — случайными.
События называют несовместимыми, если появление одного из них
исключает появление других событий в одном и том же испытании. На-
пример, появление «герба» при бросании монеты исключает появление
надписи, определяющей достоинство монеты.
События называют равновозможными, если есть основания считать,
что одао из них не более возможно, чем другое. Например, если в урне
находится одинаковое количество тщательно перемешанных шаров раз-
ного цвета, то возможность вынуть шар любого цвета одинакова. Равно-
возможны выпадения «герба» и «надписи» при бросании монеты или появ-
ление того или иного числа очков при бросании игральных костей.
§ В.2. Относительная частота и вероятность случайных событий
2.1, Относительная частота. Относительной частотой Wn(AJ (или час-
тостью) случайного события А называется отношение числа пА появлений
этого события к общему числу произведенных испытаний:
(B.i)
Важно отметить, что частость в весьма обширном и важном классе
случаев, - в длинных повторных сериях испытаний, обладает статистиче-
ской устойчивостью. Например, при многократном бросании правильной
игральной кости относительная частота выпадения каждого числа очков от
1 до 6 колеблется около одного и того же числа 1/6.
Нетрудно заметить, что
(В.2)
8
Если событие А невозможно, то в любой серии выполненных испыта-
ний пА = 0 и Wn(A) — 0. Если событие А достоверно, то всегда пА — п и
Устойчивость относительной частоты отражает некоторое объективное
свойство случайного события, заключающееся в определенной степени
его возможности [134] . Например, приблизительное равенство относитель-
ных частот выпадения очков от 1 до 6 при бросании правильной игральной
кости отражает то обстоятельство, что центр тяжести совпадает с геомет-
рическим центром костяного кубика, что делает одинаково возможным
выпадение каждого числа очков.
2.2. Вероятность. Мера объективной возможности появления случайного
события А называется его вероятностью и обозначается символом Р(А).
Около числа Р(А ) группируются относительные частоты события А.
Благодаря устойчивости и близости относительной частоты WnfAJ,
полученной из достаточно длинной серии испытаний, к вероятности Р(А)
относительная частота может служить приближенной оценкой вероятности,
тем бодее точной, чем больше число испытаний в серии. В свою очередь,
знание вероятности наступления события А позволяет предсказывать с
той или иной надежностью его относительную частоту в предстоящих испы-
таниях, по крайней мере при больших п [138] .
2.3. Основные аксиомы теории вероятностей. Эти аксиомы представ-
ляют интерес прежде всего потому, что позволяют по-другому и более
строго сформулировать понятие вероятности.
Аксиома 1. С каждым событием А данного поля испытаний связы-
вается число Р(А), называемое вероятностью и удовлетворяющее условию
0<Р(А)<1. (В.З)
Для относительной частоты такое же условие выполняется естествен-
ным образом [см. формулу (В.2) ] .
Аксиома 2. Вероятность достоверного события Uполя равна единице
и, следовательно,
P(U)=1. (В.4)
Это требование также соответствует очевидному свойству относительной
частоты достоверного события.
Аксиома 3. (Правило сложения вероятностей несовместимых собы-
тий). Если событие S поля подразделяется на несовместимые события
Ai, А2, Ат того же поля, т.е. представляет собой сумму этих событий,
так что 5’ = Л1 + Л2+... + Ат и А^- = И при любых i и j ft, j = 1,2,...,
т), то
P(S=Ai + А2 + ...+Am) =P(Ai) +Р(Л2) + ... + Р(Лш), (В.5)
т.е. вероятность суммы несовместимых [138] событий равна сумме их
вероятностей.
Если поле содержит бесконечное множество событий, то событие 5
может быть представлено как сумма бесконечной последовательности
Е1г Е2, ..., Еп, ... несовместимых событий данного поля. Предполагается,
9
что и в этом случае выполняется правил^ сложения:
P(S> = Р(ЕГ +Е2 +...Еп + ...) = Р(Ег) + Р(Е2) + ... +/>(£„)+ ...,(В.6)
где бесконечный ряд в правой части сходится.
В формулах (В.4) и (В.5) через U и V обозначены соответственно до-
стоверные и невозможные события.
Аксиоматическое построение теории вероятностей разработано из-
вестным советским математиком академиком А.Н. Колмогоровым. Опре-
делить понятие «вероятность», являющееся неотъемлемым свойством слу-
чайного события, не просто.
Как отмечалось выше, повторение опытов при неизмененных усло-
виях представляет собой основной инструмент познания природы.
С другой стороны, как бы ни стараться сохранить неизменными усло-
вия опыта, его результаты всегда имеют некоторый разброс: таким обра-
зом, никогда невозможно заранее предсказать точное числовое значение
результата предстоящего наблюдения. Однако из сказанного вовсе не
следует, что результаты наблюдений не подчиняются никакому закону.
Наоборот, при их анализе явственно выявляются две основные тенденции:
1) большинство результатов наблюдений тесно группируется около
среднего значения всей серии наблюдений;
2) чем больше отклонение результата от среднего значения, тем мень-
ше частость (вероятность) его появления.
§ В.З. Сложение и умножение вероятностей
3.1. Вероятности в полной группе событий. Случайные события обра-
зуют полную группу, если при каждом повторении испытания должно
произойти хотя бы одно из них. Например, если X — число очков, выпадаю-
щее на верхней грани игральной кости, то события X = 1, X = 2, X - 3,
Х=4, Х=5,Х=6 образуют полную группу. Однако полную группу обра-
зуют и следующие события: Xчетно, Xнечетно, а также X = 1; 1 < Х< 6;
Х=6.
Таким образом, из системы событий, связанных с данным испытанием,
можно различным образом конструировать полные группы событий.
Сумма вероятностей несовместимых событий, образующих полную
группу, равна единице:
P(Ai) + Р(Л2) + ...+P(AS)= 1. (В.7)
Особый интерес представляет случай, когда полная группа событий
состоит из двух несовместимых событий (X четно, X нечетно), так что
появление одного из них означает непоявление другого. Такие события
называют взаимно противоположными.
Если одно из пары таких событий обозначить через Л, то другое можно
обозначить через А (следует читать: «не Л»). Сумма вероятностей двух
взаимно противоположных событий равна единице:
Р(А}+Р(А) = 1. (В.7а)
10
Формула (В.7а) позволяет вычислить вероятность одного из двух
противоположных событий, если известна вероятность другого [134].
3.2. Условные вероятности. Если при вычислении вероятности события
кроме условий S никаких других ограничений не накладывается, то такая
вероятность называется безусловной. Однако иногда возникает необходи-
мость вычислить вероятность некоторого события Я*, при дополнительном
условии, что другое событие А уже произошло.
Условной вероятностью РА(В) называют вероятность события В, вычис-
ленную в предположении, что событие А уже наступило.
Если, например, в урне находилось первоначально 6 шаров (3 белых и
3 черных) и известно, что первый вынутый шар - черный (событие Л), то
можно определить вероятность появления белого шара при втором испытании
(событие В), если установить, что шары вынимают без возвращения. После
первого испытания в урне осталось 5 шаров и три из них — белые. Услов-
ная вероятность РА(В) — 3/5. Такой же результат можно получить и по
формуле
РЛ (В) = №А) > 0) • (В-8)
Вероятность появления белого шара при первом испытании Р(А) =
= 3/6= 1/2.
Вероятность Р(АВ), того, что в первом испытании появится черный
шар, а во втором — белый, можно определить следующим образом: общее
число исходов совместного появления двух шаров любого цвета равно
числу размещений: А% = 6-5 = 30. Из этого числа исходов событию АВ
благоприятствуют 3-3 = 9 исходов; следовательно,
Р(АВ) = 9/30 = 3/10.
Искомая условная вероятность
р /Д) _ р(АВ> з/ю _ 2
А ' Р(А) 1/2 5 ’
т.е. полученд-от же результат.
В этом примере затронут очень важный вопрос о характере выборки,
которая может быть с возвращением и без возвращения вынутых эле-
ментов.
3.3. Свойства условных вероятностей. Правило умножения и общее
правило сложения вероятностей. Запишем формулу (В.8) в виде
Р(АВ) =P(A)Pa(B). (В.9)
Это равенство представляет собой так называемое правило умножения
вероятностей: вероятность совместного появления двух событий равна
произведению вероятности одного из них на условную вероятность другого,
вычисленную в предположении, что первое событие уже произошло.
Это правило можно распространить и на большее число событий: веро-
ятность совместного появления нескольких событий равна произведению
вероятности одного из них на условные вероятности всех остальных, при-
чем вероятность каждого последующего события вычисляется в предпо-
11
ложении, что все предыдущие события уже появились:
^641^2^3 = P(Ax)Pa t (Дг^АхАг (A*)— ^AiA2...An_i (Дп)>
(В.1ф
где РА i а2 .... л ~i (А») ~ вероятность события Ап, вычисленная в пред-
положении, что события Л J, А2,.... Лл _ t наступили. Для трех событий фор-
мула (В. 10) принимает вид
Р(АВС) = Р(А)Ра(В)Рав(С). (В. 10а)
Общее правило сложения вероятностей можно сформулировать так:
вероятность суммы двух событий (совместимых или несовместимых)
равна сумме вероятностей этих событий без вероятности их совместного
наступления:
Р(А+В) =Р(А)+Р(В) ~ Р(АВ). (ВЛ)
Если события несовместимы и, следовательно, Р(АВ) = 0, то формула
(В.11) приводится к (В.5) (третья аксиома) при пт = 2.
3.4. Независимые события. Умножение вероятностей независимых
событий. Событие В называют независимым от события А, если появление
события А не изменяет вероятность события В. Другими словами, услов-
ная вероятность события В равна его безусловной вероятности:
РА(В)=Р(В). (В. 12)
Вероятность совместного появления нескольких событий, независи-
мых в совокупности, равна произведению вероятностей этих событий:
Р{АхА2 ...Ап} = P(Ai)P(A2) ...Р(Ап). (В.13)
Это так называемое правило умножения вероятностей независимых со-
бытий.
3.5. Формула полной вероятности. Вероятность события А, которое
может наступить лишь при условии появления одного из несовместимых
событий Bi, В2...Вт, образующих полную группу (п. 3.1),равна сумме
произведений вероятностей каждого из этих событий на соответствующую
условную вероятность события А:
Р(А) =P(Bi) РВ1(А)+ Р(В2)РВ2(А) + ... +Р(Вп)РВп(А). (В.14)
3.6. Вероятность гипотез. Формулы Байеса. Предположим, что собы-
тие А может наступить при условии появления одного из несовместимых
событий Bit В2...Вт, образующих полную группу. Так как заранее не
известно, какое из этих событий наступит в действительности, эти события
называют гипотезами. Вероятность появления события А определяется по
формуле полной вероятности (В.14):
Р(А) = Р(В1)Рв> (А) *Р(Вг)РВ1 (А) + ... ^Р(Вп)РВп(А).
Если теперь предположить, что событие А уже произошло, то можно
поставить задачу выяснить, как изменились (в связи с тем, что событие
А уже наступило) вероятности гипотез. Другими словами, следует найти
12
условные вероятно РА (Вх), РА (В2),РА (Вп). По формуле умножения
вероятностей,
Р/АВг) = Р(А )РА(В,) = Р(В, )РВ1 (А),
рткуда
Р(В,)РВ1(А)
Р(А)
Подставляя вместо Р(А) значение из формулы полной вероятности
(В. 14), имеем
р(Вх)РВх(А^Р(В2)РВ2(А)+..ЛР(Вп)РВп(А) ’
Точно так же можно вывести формулы, определяющие условные вероят-
ности остальных гипотез Bt (i ~ 1, п):
P(Bj)PBi(A)
Г{В1)РВ1<А)
(В.15)
Ра Р(В2)РВх(А) + Р(В2)РВ2(А) + ...+ Р(Вп)РВп(А) ’
Это и есть формулы Байеса, позволяющие переоценить вероятности гипо-
тез после того, как становится известным результат испытания, в итоге
которого появилось событие А [28].
§ В.4. Дискретно распределенные случайные величины
Случайная величина — это переменная, принимающая в результате
испытания то или иное числовое значение в зависимости от случайного
исхода испытания [138]. Другими словами, случайная величина рассмат-
ривается как функция, аргументом которой служит элементарное случай-
ное событие поля испытания.
Случайные величины могут быть: 1) дискретными; 2) непрерывны-
ми (непрерывно распределенными).
Случайная величина, которая может принимать конечное или бесконеч-
ное счетное множество значений, элементы которого могут быть зануме-
рованы и выписаны в последовательность *1, х2,хп, называется дискрет-
ной (дискретно распределенной). На практике часто встречаются дискрет-
ные случайные величины, принимающие лишь целочисленные значения.
Если известны все возможные значения хь х2, ...» хп, принимаемые
дискретной случайной величиной, и вероятности p(Xj) для каждого собы-
тия X = Xi поля испытания, то распределение этой величины считают теоре-
тически заданным. Так как эти события составляют полную группу, то в
соответствии с формулой (В.7)
2^=1. (В.16)
।
Общая масса вероятности, равная единице при дискретном распределении,
сосредоточена в счетной или конечной системе точек х/, т.е. имеет место
точечное распределение массы вероятности.
Так как предмет настоящего учебного пособия — изучение методов
статистической обработки результатов экспериментов (погрешностей
13
измерения), которые по своей природе являются непрерывно распреде-
ленными величинами, то основное внимание следует уделить именно этому
типу случайных величин.
В противоположность дискретно распределенным случайным вели-
чинам масса вероятности непрерывно распределенных случайных величии
распределена сплошной полосой по всей оси Ох или по некоторым участ-
кам этой оси с определенной плотностью [138].
§ В.5. Непрерывно распределенные случайные величины
5.1. Эмпирическое и теоретическое распределение. Распределение от-
носительных частот (частостей) называется эмпирическим. Распределе-
ние вероятностей называется теоретическим распределением.
5.2. Теоретические характеристики непрерывно распределенной случай-
ной величины. Функция распределения вероятности и плотность распреде-
ления. Квантили. Медиана. Непрерывная случайная величина — это такая
величина, которая может принимать любые значения в одном или несколь-
ких заданных интервалах или областях плоскости или пространства. Су-
щественным здесь является то обстоятельство, что эти значения образуют
несчетное бесконечное множество, которое называют континуумом [138].
Выше отмечалось, что дискретная случайная величина может быть
задана перечислением всех ее возможных значений. Из определения непре-
рывной случайной величины ясно, что для нее подобная операция неосу-
ществима. Если рассмотреть непрерывную случайную величину X, возмож-
ные значения которой сплошь заполняют интервал (а, Ь), то возникает
вопрос: можно ли перечислить все возможные значения X? Ответ, безуслов-
но, отрицателен, так как этот перечень составляет несчетное бесконечное
множество. Необходимо ввести более общий метод задания случайных
величин, пригодный для любых типов таких величин.
Пусть х — действительное число. Вероятность события, состоящего в
том, что X примет значение, меньшее х, т.е. вероятность события X < х,
обозначают через F(x). С изменением х изменяется и F(x}, т.е. F(x) — функ-
ция от х.
Функцией распределения называют вероятность того, что случайная
величина Xв результате испытания примет значение, меньшее х:
F(x) = P(X<x). (В. 17)
Функцию F(x) иногда называют интегральной функцией.
Функция распределения имеет следующие свойства.
1°. Значения функции распределения принадлежат отрезку [0, 1] :
о<ад<1.
2°. Функция F(x} - неубывающая функция, т.е. F(х2) > Ffxy) ', если
х2 >хх.
Эти же свойства можно сформулировать и по-другому [ 138] :
1°. Имеет место соотношение
lim F(x) = 0, lim F(x) = 1.
Х~*—оо оо
14
2°. Функция F(x) - непрерывная и возрастающая; ее приращение в
промежутке (xi, х2) равно вероятности для величины X попасть в этот
промежуток.
Плотностью распределения вероятностей непрерывной случайной ве-
личины называют функцию f(x) - первую производную функции распреде-
ления F(x):
f(x) = F'(x); (В-17а)
ffx) иногда называют дифференциальной функцией распределения.
При описании непрерывного распределения часто используют так
называемые квантили. Квантилем, отвечающим заданному уровню вероят-
ности р, называют такое значение .х = хр, при котором функция распределе-
ния принимает значение, равное р, т.е. F(xp) = р. Некоторые квантили име-
ют особое название. Так, например, медианой распределения МеХ называет-
ся квантиль, отвечающий значению р = 1/2. Квантили, соответствующие
значениям р — 1/4 и р = 3/4, называют соответственно нижним и верхним
квантилями. Если, например, р = 90, р = 95, то получаем соответственно
90%-ные и 95%-ные квантили. Указанные квантили называют еще соот-
ветственно 10%-ными, 5%-ными верхними точками распределения, а кван-
тили, отвечающие, например, значениям р — 0,10, р — 0,05, — 10%-ными,
5%-ными нижними точками распределения [138].
53. Моменты непрерывного распределения. Математическое ожидание
и дисперсия. Если обозначить через f(x) Дх элементарную вероятность, то
математическое ожидание MX непрерывно распределенной величины X
можно определить по формуле
MX = xf(x) dx, (В.18)
предполагая, что этот интеграл сходится абсолютно.
Математическое ожидание функции Y — Ф(А) величины X
МУ = М[ФХ] =7ад/Гх/(к. (В.19)
—о»
В частности, если Ф (Л) = Хк, то получаем выражение для fc-ro началь-
ного момента:
vk = lxktfx)Ax. (В.20)
—со
Центральный момент &-го порядка
Д* = 7 (х - vf fix) dx. (В.21)
Дисперсию (второй центральный момент) находят по формуле
DX = р2 =а2 = °$(х - v}2flxj dx. (В.22)
—со
Модой непрерывного распределения называют значение аргумента,
при котором плотность распределения fix) достигает максимума.
15
§ В.6. Система обозначений
В заключение введения обратим особое внимание на наиболее употре-
бительную систему обозначений, принятую в математической статистике
[П.14.2] *
Теоретические характеристики обозначают буквами греческого алфа-
вита, выборочные оценки (характеристики эмпирического распределен
ния) — соответствующими буквами латинского алфавита. Примеры га-
ких обозначений даны в табл. ВЛ, при составлении которой использован^
работа [П.14.2] .
Обозначения, принятые в математической статистике
Таблица В.1
Наименование величины Теоретические характеристики Выборочные оценки
Средние значения случайной величины У, MX, Ml, М<х> х
Дисперсия 02,DX,Dl, о2 <х> S2
Квадратичная ошибка (среднеквадрати-
ческое отклонение) а S
Коэффициент вариации У V
Коэффициенты корреляции Р г
Коэффициенты регрессии а, Mo, Pj а, Ь, с, bo, Ь]
Зависимая переменная П У
Независимая переменная £ X
Часто в литературе для обозначения теоретических характеристик рас-
пределений (параметров) используют греческие буквы (например, ??, £),
а символы т?, ? — для обозначения выборочных значений или оценок. Иногда
обозначения оценок даются с указанием объема выборки % (п)),
а иногда — без него (т?, £). Эта система обозначений может показаться раз-
норечивой, однако специфика изложения вопросов математической статис-
тики такова, что в одной работе, как правило, приходится использовать
все указанные виды обозначений.
В этом разделе приведены лишь некоторые сведения из теории вероят-
ностей и математической статистики. При желании можно легко пополнить
знания по этим вопросам. Рекомендуем, например, следующие работы:
[12, 17, 19, 22, 27, 28, 36-38, 41, 47, 52, 54, 55, 58, 67, 72, 74, 92, 100,
109, 113,128-130, 134,138,139,147] .
* Ссылка на приложение 14.
Глава I
ПРЕДВАРИТЕЛЬНАЯ ОБРАБОТКА ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ
§ 1.1. Цели предварительной обработки опытных данных
Предварительная обработка результатов измерений или наблюдений необ-
ходима для того, чтобы в дальнейшем с наибольшей эффективностью,
а главное — корректно, использовать для построения эмпирических зави-
симостей статистические методы.
Содержание предварительной обработки в основном состоит в от-
сеивании грубых погрешностей измерения или погрешностей, неизбеж-
но имеющих место при переписывании цифрового материала или при
вводе информации в считывающее устройство ЭВМ.
Грубые погрешности измерения (аномальные, йли сильно выделяю-
щиеся, значения) очень плохо поддаются определению, хотя интуитивно
каждому экспериментатору ясно, что это такое.
Можно встретить указание [П.14.24], что аномальные значения из-
меряемой величины получаются в результате изменения условий экспери-
мента, однако это определение неполное.
Пожалуй, лучше поясняет сущность грубых погрешностей следую-
щий [П.14.23] пример: если допустить, что 10 % измерений, представляю-
щих собой аномальные значения, отстоят от среднего более чем на 31 (I —
отрезок на оси Ох), а остальные наблюдения располагаются в пределах I,
то при оценке дисперсии <5.3> через S2 (см. § 1.3) эти 10 % наблюдений
по меньшей мере удваивают оценку.
Другим важным моментом предварительной обработки данных яв-
ляется проверка соответствия распределения результатов измерения зако-
ну нормального распределения. Если эта гипотеза неприемлема, то следует
определить, какому закону распределения подчиняются опытные данные,
и, если это возможно, преобразовать данное распределение к нормальному.
Только после выполнения перечисленных выше операций можно перейти
к построению эмпирических формул, применяя, например, метод наимень-
ших квадратов.
§ 1.2. Генеральная совокупность и выборка
Генеральной называют совокупность всех мыслимых значений наблю-
дений, которые мргли бы быть сделаны при данном комплексе условий
ГП 14.53]. О комплексе условий сказано выше <1.1>.
17
Генеральная совокупность может быть конечной и бесконечной. Дан-,
ное выше определение генеральной совокупности можно считать строго
обоснованным только для случаев конечных генеральных совокупностей
Понятие бесконечной генеральной совокупности — математическая
абстракция, как и представление о том, что измерить случайную величину
<1.2> можно бесконечное число раз. Приближенно бесконечную генераль-
ную совокупность можно истолковать как предельный случай конечной
генеральной совокупности [П.14.53]. Результаты ограниченного ряда
наблюдений х2, хп случайной величины можно рассматривать как
выборку из данной генеральной совокупности.
Во введении дано понятие относительной частоты и вероятности слу-
чайных событий <2>. Относительные частоты можно истолковать как
выборочные значения вероятностей случайных событий.
Если говорить о характеристиках распределений вероятностей, то
характеристики теоретических распределений <5.1> можно рассматривать
как характеристики, существующие в генеральной совокупности, а харак-
теристики эмпирических распределений — как выборочные характеристики.
Можно встретить [52] и другую терминологию. Характеристики
распределения вероятностей в генеральной совокупности называют пара-
метрами, а выборочные (эмпирические) значения характеристик — оцен-
ками или статистиками.
Параметры <5.4> обозначаются буквами греческого алфавита, а оцен-
ки — соответствующими буквами латинского алфавита.
§ 1.3. Вычисление характеристик эмпирических распределений
(выборочных характеристик). Моменты
Необходимо прежде всего отметить, что здесь и в дальнейшем речь
идет только о непрерывно распределенных случайных величинах <5>.
Пусть имеется ограниченный ряд наблюдений х2, .... хп случай-
ной величины £. Среднее значение наблюдаемого признака можно опре-
делить по формуле
дГ= — S xit i — 1, н. (1.1)
Л /=1
Таким образом, х представляет собой эмпирическое, или выборочное,
среднее. Если вычислено среднее, то легко найти отклонение каждого
наблюдения dj от среднего:
dj = Xj-x. (1.2)
Величину
s2= п А ал
18
называют дисперсией или вторым центральным моментом эмпирического
распределения <5.3>: S2 = т2.
В случае одномерного эмпирического распределения произвольным
моментом порядка к [46] называется сумма к-х степеней отклонений
результатов наблюдений от произвольного числа с, деленная на объем
выборки п:
(1.4)
п 1=1
где к может принимать любые значения натурального ряда чисел. Если
с = 0, то момент называют начальным. Начальным моментом первого
порядка является выборочное среднее х. Действительно, х можно опреде-
лить и по формуле
х= - S (х, —О)1, (1.5)
п ,- = t
которая равносильна формуле (1.1).
При с = х, как уже отмечалось при рассмотрении формулы (1.3),
момент называется центральным. Первый центральный момент
mv = - S (х^-х)1 =0. (1.6)
” i=l
Второй центральный момент [см. формулу (1.3)]
т2 = — S (xz- - х)2
представляет собой дисперсию S2 эмпирического распределения.
Несмещенную оценку для о2 (а2 — дисперсия теоретического рас-
пределения) , определение которой дано ниже, можно найти по формуле
7= 2(х/-5)2. (1.7)
Выборочные среднеквадратические отклонения соответственно могут
быть найдены по формулам
5 = ^2, (1.8) S^^S2. (1.9)
Из других моментов чаще всего используют моменты третьего и чет-
вертого порядка:
/из = “ S (xz -x)3, (1.10)
” <=1
/и4 = 7 2 (1.11)
п 1=1
Выборочное значение коэффициента вариации v, являющееся мерой
относительной изменчивости наблюдаемой случайной величины, вычисляют
по формуле
v=S/x. (1.12)
Коэффициент вариации может быть вычислен и в процентах:
и=|100. (1.13)
19
Выборочные значения характеристик распределения имеет смысл
вычислять только в том случае, если выборка является случайной. Обыч-
но на практике наблюдаемые значения xJt х2, хп — величины случайные
<4> и отклонения их от среднего значения обусловлены погрешностями
измерения, «ошибками природы» и т.д. В свою очередь, погрешности - ре-
зультат действия многих факторов.
Если имеет место такой редкий случай, когда в распоряжении иссле-
дователя имеется вся генеральная совокупность и необходимо сделать из
нее выборку, то используют один из методов рандомизации (случайного
выбора). Удобнее всего при этом пользоваться таблицей случайных чисел
(см. табл. П.1).
Следует отметить, что к оценкам предъявляются требования состоя-
тельности, несмещенности и эффективности. Оценка параметра называется
состоятельной [4] , если по мере роста числа наблюдений п (т.е. при п -*
-> N в случае конечной генеральной совокупности объема N и при п -* °° в
случае бесконечной генеральной совокупности) она (оценка) стремится
к оцениваемому теоретическому значению параметра. Например, для
дисперсии lim S2 (и) = а2. Оценка параметра называется несмещенной,
если при любом числе наблюдений п ее математическое ожидание точно
равно значению оцениваемого параметра [4]. Удовлетворение требова-
нию несмещенности устраняет систематическую погрешность, которая
зависит от объема выборки ни в случае состоятельности стремится к нулю
при п -* 00.
Следует четко разделять понятия состоятельности и несмещенности.
Выше [см. формулы (1.3) и (1.7)] были определены две оценки для
дисперсии: S2 и S2. Обе эти оценки состоятельны, но только вторая являет-
ся несмещенной, так как первая содержит систематическую отрицатель-
ную погрешность — о2/п (поскольку математическое ожидание MSjn, =
= а2 — о2 /п), которая с ростом п монотонно убывает. Из этого следует,
что требование несмещенности особенно важно при малом количестве
наблюдений.
Оценка параметра называется эффективной, если среди прочих оценок
того же параметра она обладает наименьшей дисперсией [4].
Если имеется выборка Xi, х2....хп из нормальной генеральной сово-
купности, то среднее можно оценить двумя способами: по формуле (1.1)
и с помощью выражения [xmnfw/ + *тахМ] /2- Обе эти оценки обладают
свойствами состоятельности и несмещенности, однако можно показать,
что дисперсия при первом способе оцейки равна а2/и, а при втором равна
it2 а2 / (24 In п), т.е. существенно больше, так как первая оценка подвержена
меньшим случайным колебаниям вокруг неизвестного истинного значения
оцениваемого параметра.
Таким образом, первый способ оценки теоретического среднего являет-
ся состоятельным, несмещенным и эффективным, а второй способ — толь-
ко состоятельным и несмещенным.
Классическим примером, на основе которого были впервые получены
многие положения математической статистики, является вычисление выбо-
20
рочных значений характеристик распределения признаков случайно состав-
ленной группы сверстников (например, группы новобранцев).
Наглядный пример вычисления х, 5, S моментов и v можно получить,
если использовать данные наблюдения роста группы двадцатилетних юно-
шей — студентов-третьекурсников. Вычисления удобно производить в
табличной форме (см. табл. 1.1). Обычно все вычисления в математической
статистике проводят в табличной форме, которая наиболее удобна, так как
обладает наглядностью, обозримостью и позволяет проверять вычисления
Таблица 1.1
Данные для вычисления х? S, S, mv и и
№п/п Рост, м-102 di, м-102 "4 №п/п Рост, м-102 di м-102 di *2
(1) (2) (3) (4) (5) (6) (7) (8)
1 183 +7,34 53,88 31 172 -3,66 13,40
2 170 -5,66 32,04 32 176 +0,34 0,12
3 176 +0,34 0,12 33 167 -8,66 74,99
4 178 +2,34 5,48 34 166 -9f66 93,32
5 176 +0,34 0,12 35 180 +4,34 18,84
6 180 +4,34 18,84 36 183 +7,34 53,88
7 176 +0,34 0,12 37 176 +0,34 0,12
8 185 +9,34 87,23 38 182 +6,34 40,19
9 184 +8,34 69,56 39 178 +2,34 5,48
10 174 -1,66 2,75 40 172 -3,66 13,40
11 168 -7,66 58,68 41 185 +9,34 87,23
12 174 -1,66 2,75 42 183 +7,34 53,88
13 189 +13,34 177,95 43 175 -0,66 0,43
14 172 -3,66 13,39 44 174 -1,66 2,75
15 175 -0,66 0,43 45 180 +4,34 18,84
16 167 -8,66 74,99 46 166 -9,66 93,32
17 179 +3,34 11,16 47 169 -6,66 44,36
18 176 +0,34 0,12 48 171 -4,66 21,71
19 169 -6,66 44,35 49 178 +2,34 5,48
20 178 +2,34 5,48 50 169 -6,66 44,36
21 169 -6,66 44,35 51 170 -5,66 32,04
22 171 -4,66 21,72 52 179 +3,34 11,16
23 170 -5,66 32,04 53 171 -4,66 21,72
24 - 177 +1,34 1,79 54 178 +2,34 5,48
25 176 +0,34 0,12 55 173 -2,66 7,07
26 179 +3,34 11,16 56 177 +1,34 1,79
27 174 -1,66 2,75
28 176 +0 34 0 12
29 188 +12,34 152,27
30 178 +2,34 5,48 Г 9837 +0,04 1695,90
* Множитель 102 введен для сближения порядка величин массы (кг) и роста (м).
21
на каждом этапе. Некоторые таблицы довольно громоздкие, но такова
специфика статистических вычислений. В настоящее время при наличии
большого количества настольных и карманных компьютеров заполнение
таких таблиц не встречает принципиальных, трудностей. Особенно удобно
использовать компьютеры, специально предназначенные для статистических
вычислений.
В табл. 1.1 приведены цифры, обозначающие рост двадцатилетних сту-
дентов [столбцы (2) и (6) J. При комплектовании лекционных потоков
меньше всего учитывается рост студентов, поэтому выборку можно счи-
тать случайной. Примером грубой ошибки в подобной ситуации было бы.
вычисление выборочных характеристик с использованием наблюдений
роста солдат Преображенского полка царской гвардии. Сумма столбцов
(3) и (7) должна теоретически быть равна нулю (центральный момент
первого порядка), и это может служить промежуточной проверкой пра-
вильности вычислений. Однако при вычислении с точностью до четырех
знаков всегда имеет место небольшая невязка, несмотря на соблюдение
известного правила вычислений (чередование округлений с избытком и с
недостатком). Средний рост группы, состоящей из 56 студентов, оказался
равным 1,7566 м.
Специалисты по демографии утверждают, что если бы подобное наблю-
дение было произведено 100 лет назад, то, вероятно, эта величина не до-
стигла бы и 1,7 м. Тенденция увеличения среднего роста людей в европейс-
ких странах общеизвестна. Вспомним хотя бы о; рыцарских доспехах,, ко-
торые пришлись бы впору в настоящее время только детям. Это типичный
пример временного «дрейфа средней». Далее будет показано, что если
хотя бы умозрительно построить закон «дрейфа» и провести измерения
через определенные промежутки времени, то можно сделать попытку
прогноза. На практике чаще всего «дрейф средней»'имеет случайный, не-
упорядоченный характер.
Результаты вычисления выборочных характеристик, упомянутых выше,
по данным табл. 1.1 приведены в табл. 1.2.
Выборочные характеристики распределения
Таблица 1.2
X S 5 т2 тз т4 и %
175,66 5,50 5,55 +0,04 ~ 0 30,28 45,14 2356,27 3,00
В этой таблвде имеются значения средней х, среднеквадратических
отклонений 5 и 5, четырех моментов и коэффициента вариации и. Для
теоретического нормального распределения значения нечетных моментов
равны нулю.
Как видно из табл. 1.2, относительный показатель изменчивости наблю-
даемого признака v не так уж велик. Увеличения значения и можно ожи-
дать при увеличении объема выборки. На практике можно встретить и
22
большие значения v, в том числе и более 33 %. Этот показатель, как будет
показано ниже, имеет важное значение, так как позволяет судить о харак-
тере распределения случайной величины.
Все сказанное выше относится к равноточным измерениям и наблюде-
ниям, т.е. к измерениям, которые содержат только случайную погрешность,
подчиняющуюся закону нормального распределения, о котором подробно
сказано ниже.
В практической работе бывают случаи [160], когда для наиболее на-
дежного определения некоторой величины собирают измерений различ-
ного происхождения, выполненные разными инструментами и методами.
Результаты таких измерений называют неравнотЬчными.
Если результаты неравноточных измерений xif х2,хп [133] можно
рассматривать как средние для серий равноточных измерений и точность
измерений в каждой серии одинакова, а количество измерений в каж-
дой серии известно (ту), то основные выборочные характеристики можно
определить по формулам
| (1J>)
S = S тД/ хД (1.4а)
И - 1 / = 1
п
где7У= S т?
1 1
Используя понятия весов измерений wb запишем эти формулы в виде
- W1X1+W2X2 + •• +™пхп 1 ”
Х = --------:-------------=--- S W/X/,
И’1 + w2 + - + wn W /=1
n
где w = S wb
i=l
(1.16)
w(n - 1)
(1-46)
mi 2 i mi 0 --- -------
где w, = — ; Sf. = ------- S (xtj-Xi)\ i = 1, n, j = 1, mb т.е.xn, xi2,.... x«,
Si mi-\j=i >
xtmi — результаты измерений в Лй серии со средним значением хь
§ 1.4. Отсев грубых погрешностей
Можно встретить большое количество различных рекомендаций для
проведения отсева грубых погрешностей наблюдения (аномальных значе-
ний) [П. 14.24]. Предложим для практического использования наиболее
простые методы отсева грубых погрешностей. Если в распоряжении экс-
периментатора имеется выборка небольшого объема п < 25, то можно
воспользоваться методом вычисления максимального относительного
отклонения [127]:
(1.14)
23
где Xj — крайний (наибольший или наименьший) элемент выборки, по
которой подсчитывались х и S [см. формулы (1.1) и (1.9)] ; т^_р ~
табличное значение статистики т, вычисленной при доверительной вероят-
ности q = 1 - р.
Таким образом, для выделения аномального значения вычисляют
т = lxt- - х|/5, (1.15)
которое затем сравнивают с табличным значением ?! _р:
rCTj.p. (1.16)
Если это неравенство соблюдается, то наблюдение не отсеивают, если не
соблюдается, то наблюдение исключают. После исключения того или иного
наблюдения или нескольких наблюдений характеристики эмпирического
распределения должны быть перечитаны по данным сокращенной выборки.
Квантили распределения статистики т при уровнях значимости р — 0,10,
р = 0,05, р = 0,025, р = 0,01 или доверительной вероятности 1 р = q —
= 0,90, 0,95, 0,975, 0,99 <5.2> даны в П.2. На практике обычно исполь-
зуют уровень значимости р = 0,05 (результат получается с 95%-й дове-
рительной вероятностью).
Процедуру отсева можно повторить и для следующего по абсолютной
величине максимального относительного отклонения, но предварительно
необходимо пересчитать хи S для выборки нового объема п — 1.
Рассмотрим другой метод отсева грубых погрешностей для малой
выборки [60]. В этом случае вычисляют
1-ху - х|
х/(п -1) /н 5
(1.17)
и полученный результат сравнивают с критическим значением, взятым из
П.З при соответствующих п и 1 — р. В формулу (1.17) по сравнению с
формулой (1.15) введен уточняющий коэффициент 1/V(л — 1)/н7
Отсев грубых погрешностей можно провести и для больших выборок.
Для практических целей лучше всего использовать таблицы распределения
Стьюдента. Этот метод исключения аномальных значений для выборок
большого объема отличается простотой, а таблицы распределения Стьюден-
та имеются практически в любой книге по математической статистике.
Распределение Стьюдента относится к категории распределений, связан-
ных с нормальным распределением. Подробно эти распределения рассмот-
рены в учебниках по математической статистике.
Известно, что критическое значение тр (р — процентная точка норми-
рованного выборочного отклонения) выражается через критическое значе-
ние распределения Стьюдента tp п_2 [17]:
_ Чр. п-2)^п~ 1
т(р, п)
(1.18)
Учитывая это, можно предложить следующую процедуру отсева грубых
погрешностей измерения для больших выборок:
24
1) из табл. 1.1 выбирают наблюдение, имеющее наибольшее отклоне-
ние: 1,89- 1,7566 = 0,1334;
2) по формуле (1.15) вычисляют
т = |х/ - xl/S = 0,1334/0,0555 = 2,40;
3) по табл. П.4 находят процентные точки ^-распределения Стьюдента
t(p, п-2): ^(5%, 54) = 1*6735, /(од %,54) = 3,2574;
4) по формуле (1.18) вычисляют соответствующие точки ^(5%f 56) =
— 1,647, т(01 %, 56) = 3,005.
Значение т = 2,40 находится между двумя табличными критическими
зна гениями: 1,647 < 2,40 < 3,005. В этом случае от отсева выделяющегося
наблюдения лучше всего воздержаться.
Предположим, что при переписывании табл. 1.1 действительно вкра-
лась грубая ошибка; например, в строке 13 вместо 1,89 м записано 2,89 м
(людей такого роста практически нет). Тогда т = (2,89 — 1,7566)/0,0555 =
- 20,42. Полученное значение относительного отклонения безусловно
больше критического табличного значения при любом значении р\
следовательно, такое наблюдение должно быть отсеяно как грубая погреш-
ность. Как видно из приведенного выше примера, рекомендуемый метод
отсева грубых погрешностей удобен еще тем, что максимальные относи-
тельные отклонения в процессе вычисления могут быть разделены на три
группы: 1) и). 2) Т(5%>и) <т <7(0}1%> „); 3) 7>Т(0>1%и).
Наблюдения, попавшие в первую* группу, нельзя отсеивать ни в коем
случае. Наблюдения второй группы можно отсеять, если в пользу этой
процедуры имеются еще и другие соображения экспериментатора (напри-
мер, заключения, сделанные на основе изучения физических, химических и
других свойств изучаемого явления). Наблюдения третьей группы, по-
видимому, отсеивают всегда.
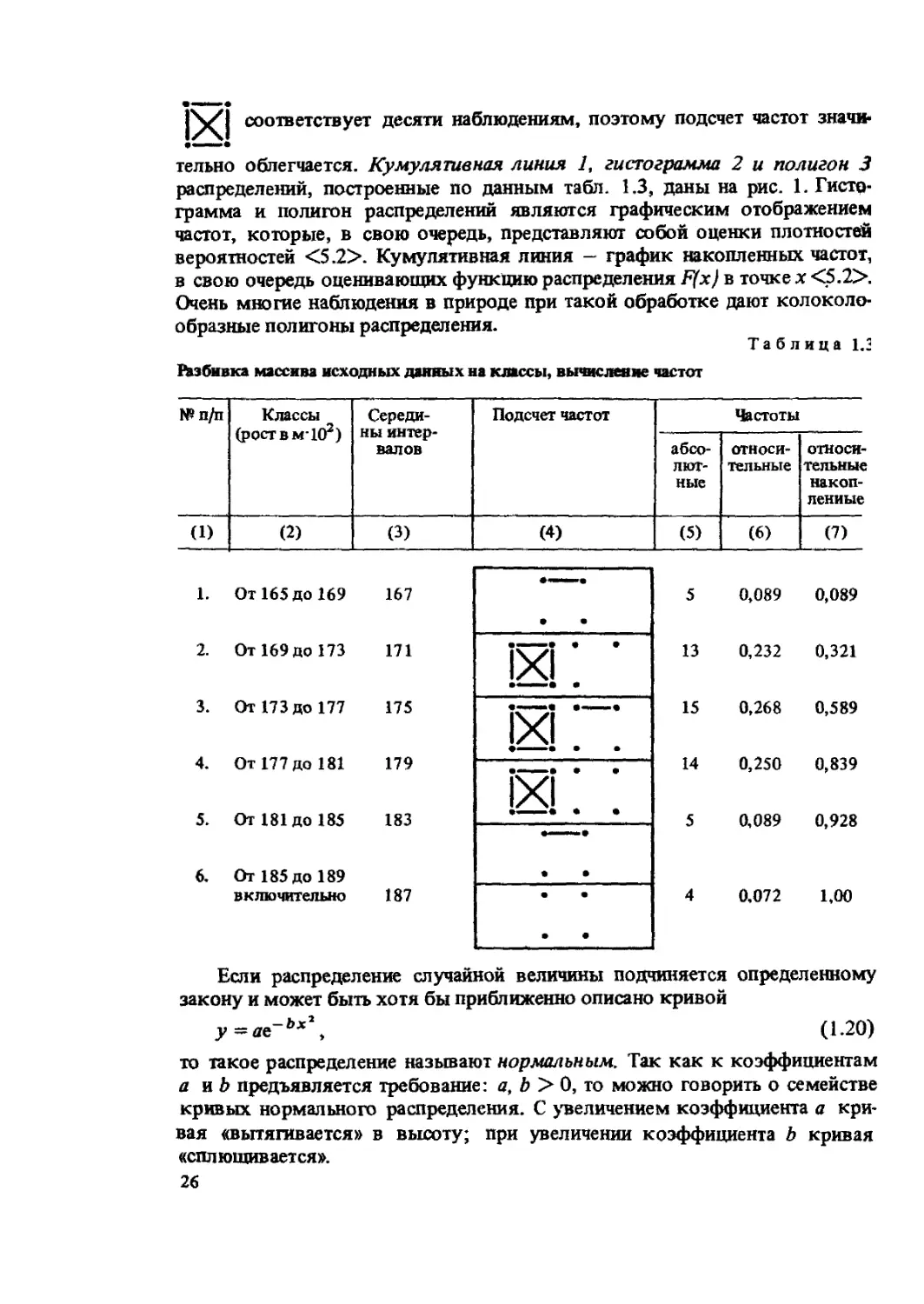
§ 1.5. Полигон и гистограмма частот распределения
Если данные табл. 1.1 (наблюдения роста студентов-ровесников в
лекционном потоке) разделить на классы, то можно построить полигон
и гистограмму частот.
Разбиение на классы можно выполнить по правилу Штюргеса [52].
Число классов
к * 1 + 3,32 1g л. (1.19)
В данном случае к = 1 + 3,32-1,75 = 6,81.
С другой стороны, разница между хтах и xmjn (размах варьирования)
составляет 189 — 166 = 23 см. Исходя из этого, примем число классов
равным 6 со ступенями, равными 4 см: 4*6 = 24 ~ 23 см. Разбиение на
классы приведено в табл. 1.3. Здесь же дана методика подчета частот [163].
Поясним эту методику. Табл. 1.1 просматривают по порядку от первой
До последней строчки и при чтении каждого результата соответствующую
метку (точку или черточку) заносят в тот класс, к которому относится
Данное наблюдение (эту работу удобно выполнять вдвоем). Каждый знак
25
соответствует десяти наблюдениям, поэтому подсчет частот значи*
«III
тельно облегчается. Кумулятивная линия 1, гистограмма 2 и полигон 3
распределений, построенные по данным табл. 1.3, даны на рис. 1. Гисто-
грамма и полигон распределений являются графическим отображением
частот, которые, в свою очередь, представляют собой оценки плотностей
вероятностей <5.2>. Кумулятивная линия — график накопленных частот,
в свою очередь оценивающих функцию распределения F(x) в точке х <5.2>.
Очень многие наблюдения в природе при такой обработке дают колоколо-
образные полигоны распределения.
Таблица 1.3
взбивка массива исходных данных на классы, вычисление частот
№п/п Классы (роствмЮ2) Середи- ны интер- валов Подсчет частот Частоты
абсо- лют- ные относи- тельные относи- тельные накоп- ленные
(1) (2) (3) (4) (5) (6) (7)
•««а
1. От 165 до 169 167 • • 5 0,089 0,089
2. От 169 до 173 171 • • 13 0,232 0,321
•
3. От 173 до 177 175 ivi 15 0,268 0,589
4. От 177 до 181 |/\| • • 0,250
179 — * * * 14 0,839
1X1
5. От 181 до 185 183 • • 5 0,089 0 928
6. От 185 до 189 • •
включительно 187 • • 4 0,072 1,00
• •
Если распределение случайной величины подчиняется определенному
закону и может быть хотя бы приближенно описано кривой
у~ ае~Ьх\ (1-20)
то такое распределение называют нормальным. Так как к коэффициентам
а и b предъявляется требование: а, b > 0, то можно говорить о семействе
кривых нормального распределения. С увеличением коэффициента а кри-
вая «вытягивается» в высоту; при увеличении коэффициента b кривая
«сплющивается».
26
165167169111115 115111119181183185181189
Рис. 1
Нормальное распределение обладает и другими важными свойствами,
которые позволяют считать это распределение основой математической
статистики. Рассмотрим эти свойства.
1 °. Ордината у, которая определяет высоту кривой для каждой точки
оси Ох (абсциссы), представляет собой плотность вероятности <5.2>
некоторого значения переменной х и определяется [52] следующей фор-
мулой:
У —f(x) = е 2 ° (—00 <х< + °°, а> 0). (1.21)
где о — среднеквадратическое отклонение теоретического распределения;
д - среднее значение (математическое ожидание) теоретического распре-
деления.
Из формулы (1.21) следует, что нормальное распределение полностью
определяется величинами д и ст (я = 3,141593... и е = 2,718282... — матема-
тические постоянные). Математическое ожидание р. определяет положение
кривой распределения относительно оси Ох. Среднеквадратическое откло-
нение ст определяет форму кривой. Чем больше ст (разброс данных), тем
кривая становится более пологой (ее основание более широкое).
2°. Кривая нормального распределения симметрична относительно
среднего значения.
3°. Максимум ординаты кривой
утах=—1=, (1.22)
а у/2-п
что при о — 1 составляет примерно 0,4. Если х + ± «>, то у + 0. Другими
словами, очень большие и очень малые значения переменной х маловеро-
ятны.
4°. Примерно 2/3 всех наблюдений лежит в площади, отсекаемой пер-
пендикулярами к оси Ox (р ± ст). При большом объеме выборки примерно
90 % всех наблюдений лежит между — 1,64ст и + 1,64ст. Границы - О,675ст и
+ 0,675ст называют вероятными отклонениями; в этом интервале находится
около 50 % всех наблюдений.
Для нормального распределения среднее, мода и медиана совпадают
<5.3>.
27
Для статистических методов построения эмпирических зависимостей
очень важно, чтобы результаты наблюдений подчинялись нормальному
закону распределения, поэтому проверка нормальности распределения -
основное содержание предварительной обработки результатов наблюде-
ний.
§ 1.6. Проверка гипотезы нормальности распределения
Для не очень больших выборок (и < 120) можно найти [52] простые
рекомендации по проверке нормальности распределения. Для этого необ-
ходимо вычислить среднее абсолютное отклонение (САО) по формуле
САО= S|xz-x|/n. (1.23)
Для выборки, имеющей приближенно нормальный закон распределе-
ния, должно быть справедливо выражение
ICAO/S - 0,79791 < 0,4 Д/лГ. (1.24)
По данным табл. 1.1, CAO = S [х/ - х\/п = 247/56 = 4,41. Подставим это
значение в формулу (1.24):
14,41/5,55 - 0,7979| < 0,4/>/56; 0,0032 < 0,0535.
Следовательно, гипотеза нормальности распределения выборки данных
приведенных в табл. 1.1, принимается.
Быструю проверку гипотезы нормальности распределения для срав-
нительно широкого класса выборок 3 < п < 1000 можно выполнить с
помощью метода, изложенного _в [52], используя размах варьирования
R. Подсчитывают отношение R/S и сопоставляют с критическими верхни-
ми и нижними границами этого отношения, приведенными в табл. П.6.
Если R/S меньше нижней или больше верхней границы, то нормального
распределения нет. Особенно важно, чтобы это условие соблюдалось при
р — 0,10 (10%-ный уровень значимости). В рассмотренном примере R/S =
= 23/5,55 = 4,144. При п = 56 и р = 0,10 нижняя и верхняя границы по
указанной таблице соответственно равны 4,03 и 5,23, т.е. 4,03 < 4,144 <
< 5,23. Следовательно, гипотеза нормальности распределения подтверж-
дается и по этому критерию.
Некоторое представление о близости эмпирического распределения
к нормальному может дать анализ показателей асимметрии и эксцесса.
Показатель асимметрии можно определить, используя данные табл. 1.2,
по формуле
gi=m3/mli2. (1-25)
Для симметричных распределений т3 = 0 и gx = 0. Для нормального рас-
пределения т^/т^ =3.
Для удобства сравнения эмпирического распределения и нормального
в качестве показателя эксцесса принимают величину
g2=m^lm2-3. (1.26)
28
в рассматриваемом примере
gl = т3/т32'2 = 45,14/166,62 = 0,27 ¥= 0.
Следовательно, некоторая асимметрия имеет место
g2 = m^ml - 3 = 2356,27/916,88 - 3 = 2,57 - 3 = - 0,43 < 0. Имеется
также и небольшой эксцесс.
Несмещенные оценки для показателей асимметрии и эксцесса опреде-
ляют по формулам
Gi =
х/п(п-1)
п— 2
gl-
(1-27)
(1-28)
В данном случае = 0,28, G2 - — 0,35.
Для проверки гипотезы нормальности, распределения следует также
вычислить среднеквадратические отклонения для показателей асимметрии
и эксцесса:
с - / 6и(”~ D__Г
G» v (п- 2) (п+1) (п+3) ’
с = / 24п(п-1)2
V (и-3)(п-2)(п+3)(п+5) ’
(1-29)
(1.30)
Имеем Sgt = 0,32, SG # = 0,63.
Бели выполняются условия
KAIC3SG,, (1.31) |G2|<55Gj, (1.32)
то гипотеза нормальности исследуемого распределения может быть при-
нята. В данном примере 0,28 <0,96 и 0,35 <3,15; следовательно, выполне-
ние указанных условий свидетельствует, что гипотеза нормальности распре-
деления может быть принята.
Рассмотрим методику проверки гипотезы нормальности распределения
по х2'Критерию. Применение критерия х2 предполагает также использова-
ние свойств так называемого стандартного нормального распределения
[52]. Уравнение кривой стандартного нормального распределения имеет
вид 2 ,
2 ~0,4е 2. (1.33)
гдег =(х- д)/а.
Значения ординат кривой стандартного нормального распределения
протабулированы и приведены в табл. П.7.
Расчеты выполняют в табличной форме, используя данные табл. 1.3.
Методика и результаты расчетов даны в табл. 1.4. В этой таблице значе-
ния х2 вычислены по формуле
Х2 = S (В—Е)2/Е,
(всех классов)
(1.34)
29
где В — наблюдаемая абсолютная частота (табл. 1.3); Е - ожидаемая по
стандартному нормально мураспределению частота.
В табл. 1.4 критерий х2 = 0,651. Число степеней свободы и = —
— 1 — 2, так как оцениваются два параметра: х и & [якл — число классов
(интервалов)]. По табл. П.8 находим табличное значение:
Х(2; Ю) =4.605 »о,651 =5?.
Таким образом, гипотеза о том, что наблюдаемые частоты распреде-
лены нормально, принимается на 10 %-ном уровне [52].
Данные табл. 1.4 можно использовать и для проверки гипотезы нор-
мальности распределения с помощью критерия согласия Колмогорова-
Смирнова (К-С-критерия); для этого вычисляют [52]
л= (1.35)
где FB — накопленная наблюдаемая частота; F& — накопленная ожидаемая
частота.
Вычисления приведены в табл. 1.5. Данные для В и £ в табл. 1.5 взяты
из табл. 1.4; FB и FE получены накоплением частот В и Е. Затем выбирают
максимальное значение F^ — FE и по нему определяют критерий согласия
Колмогорова—Смирнова D. Полученное значение сравнивают с критичес-
ким, взятым из табл. П.9 (Ь <Z?T). Имеем £>(56; 0,ю) “ 0,167> 0,05 =
= D, т.е. можно сделать тот же вывод, что и выше: гипотеза нормального
распределения на достаточно «жестком» 10 %-ном уровне принимается.
Таковы наиболее часто используемые методы проверки гипотезы
нормальности распределения. Важность обязательного проведения этой
процедуры при предварительной обработке опытных данных можно про-
иллюстрировать следующей цитатой [76] : «Как оказывается в весьма
широком классе несмещенных оценок, оценки, найденные по методу
наименьших квадратов могут быть совместно эффективными, лишь если
вектор погрешностей Д нормален. Таким образом, наличие оптималь-
ных свойств у метода наименьших квадратов тесно связано с нормаль-
ностью вектора погрешностей».
Выше изложены пять методик проверки гипотезы нормальности рас-
пределения: по среднему абсолютному отклонению (САО), по размаху
варьирования R, по показателям асимметрии и эксцесса, по х2 -критерию
и по критерию Колмогорова-Смирнова (К-С-критерию). Возникает
вопрос: как использовать эти методики и какие из них предпочтительны
в тех или иных случаях?
Методика проверки нормальности распределения по показателям
асимметрии и эксцесса очень хорошо иллюстрирует использование мо-
ментов, а также очень удобна при проведении расчетов на ЭВМ [46] . Про-
верку по К-С-критерию проводят только в редких случаях. Для практи-
ческого применения (особенно при расчетах с использованием настольных
ЭВМ) рекомендуются в основном две методики: по размаху варьирования
и по х2 -критерию, причем первая служит для быстрой «прикидочной» про-
верки, а вторая — для основательной проверки нормальности распреде-
ления.
30
2
Процедура вычисления критерия х
№ клас- са Середины интерва- лов X Частоты В х2 Вх Вх2 - X - X
(1) (2) (3) (4) (5) (6) (7)
1 167 5 27 889 *835 139 445 -8,93
2 171 13 29 241 2223 380 133 -4,93
3 175 15 30 625 2625 459 375 -0,93
. 4 179 14 32041 2506 448 574 3,07
5 183 5 33 489 915 167 445 7,07
6 187 4 34 969 748 139 876 11,07
S 56 9852 1 743 848
х = Е Вх/п = 9852/56 = 175,93; k'^nb/S = 56*4/5,39 = 41,6; S = \
Таблица 1.4
1 _ 1 1* ' м 1 -Ь LJL_ Ординаты f(z) из табл. П.7 Е В—Е (В-Е)г (В-Е)г Е
(8) (9) (Ю) (11) (12) (13) (14)
1,66 0,1006 4,18 4,18 0,82 0,67 0,16
0,91 0,2637 10,97 10,97 2,03 4,12 0,38
0,17 0,3932 16,37 16,37 -1,37 1,88 0,11
0,57 0,3391 14,11 14,11 -0,11 0,01 0,0007
1,31 0,1691 7,03 9,06 -0,06 0,004 0,0004
2,05 0,0488 2,0Г
0,651
/ Д Вх1 - Д(Дх)2/и
п - 1
= -^1600/55 =5,39; Ъ - размер класса.
Таблица 1.5
Результаты вычисления К — С-критерня
В 5 13 15 14 5 4
Е 4,18 , 10,97 16,37 14,11 7,03 2,03
FB 5 18 33 47 52 56
^Е 4,18 15,15 31,52 45,63 52,66 54,69
\Fb~Fe\ 0,82 2,85 1,48 1,37 0,66 1,31
£>=2,85/56 =0,05
§ 1.7. Преобразование распределений к нормальному
Если исследователь, использовав методы, изложенные в предыдущем
параграфе, убедился, что гипотеза нормальности распределения не может
быть принята, то может быть, что с помощью существующих методов
удастся так преобразовать исходные данные, что их распределение будет
подчиняться нормальному закону. Напомним, что после получения окон-
чательного результата надо не забыть выполнить обратное преобразование.
В самом начале операции преобразования данных большую помощь
могут оказать гистограмма и полигон распределения, приведенные на
рис. 1. При обработке результатов наблюдений в медицине, биологии,
материаловедении, экономике и других отраслях знаний встречаются
логарифмические нормальные распределения, особенностью которых
является крутая левая ветвь полигона и пологая правая (полигон явно
асимметричен). Логарифмические нормальные распределения играют
большую роль в математической статистике, так как встречаются очень
часто в практике обработки наблюдений и легко преобразуются к нормаль-
ному распределению. Для экспериментатора было бы непростительно
провести, например, регрессионный анализ (см. гл. II) по результатам
наблюдений, распределенных логарифмически нормально, без их предва-
рительного преобразования.
При логарифмировании исходных данных левая ветвь кривой распре-
деления сильно растягивается и распределение принимает приближенно
нормальный характер. Если при преобразовании х' = 1g х получаются значе-
ния, расположенные между 0 и 1, то все вновь полученные значения ддя
удобства расчетов и во избежание получения отрицательных параметров
необходимо умножить на 10 в соответствующей степени, чтобы все цифры
были больше единицы, т.е. выполнить преобразование х" = Igx • 10я.
Асимметричное распределение с одной вершиной часто приводится к
нормальному преобразованием х' = 1g (х ± а). В отдельных случаях можно
применять и другие преобразования:
а) обратная величина
х'=11х; (1.36^
б) обратное значение квадратных корней
х'=1/у/х. (1.37)
Преобразование «обратная величина» является наиболее «сильным». Сред-
нее положение между логарифмическим преобразованием и «обратной
32
величиной» занимает преобразование «обратное значение квадратных
корней» [52] .
Для нормализации смещенного вправо распределения служат триго-
нометрические преобразования, а также степенные преобразования х —
= При этом для а принимают значения: а =1,5 при умеренном и а =
= 2 при сильно выраженном правом смещении. Рекомендуем самостоятель-
но придумать такие преобразования, которые удовлетворяли бы иссле-
дователя в том или ином случае.
Проследим на числовом примере, как асимметричное распределение
можно преобразовать В нормальное. Пример^ приведенный ниже, искусст-
венно синтезирован с помощью обычной миллиметровки.
Кривая распределения, приведенная на рис. 2, имеет очень крутую
левую и пологую правую ветвь. Можно ожидать, что такое распределение
будет отличаться от нормального. Это предположение можно проверить,
сравнивая ординаты кривой, данной на рис. 2, с ординатами кривой стан-
дартного нормального распределения с помощью х2 -критерия. В третьем
столбце табл. 1.6 приведены частоты распределения, точно соответствующие
кривея!, изображенной на рис. 2.
Полученная по результатам расчетов величина х2 = 20,86 > х2 (ю; одо) =
= 15,987; следовательно, исследуемое распределение не является нормаль-
ным. Число степеней свободы v = 13 — 3 = 10, так как три последних клас-
са объединены (Ь < 4); кроме того, по данным табл. 1.6 вычисляют коэф-
фициент вариации и = 38 % > 33 %, что является признаком логарифмичес-
ки нормального распределения [52].
Для выполнения операции преобразования коллектив данных распи-
сывают до Полного состава и каждое наблюдение трансформируют с по-
мощью логарифмического преобразования х' = Igx. Для удобства расчетов
полученные результаты умножают на 100. Эти операции приведены в
табл.1.7.
33
Таблица 1.6
Проверка гипотезы нормальности для непреобразованных данных
№ класса Классы Середины классов х хг Вх Вх2 х-х х-х Ордината fW Е В—Е (В-Ер Е
(1) (2) (3) (4) (5) (6) (7) (8) (9) (Ю) (И) (12) (13) (14) (15)
1 40-50 14 45 2 025 630 28 350 -47,17 1,35 0,1604 6,32 6,32 7,68 58,98 9,33
2 50-60 15 55 3 025 825 45 375 -37,17 1,06 0,2275 8,96 8,96 6,04 36,48 4,06
3 60-70 16 65 4 225 1040 67 600 -27,17 0,78 0,2943 11,59 11,59 4?41 19,45 1,68
4 70-80 15 75 5 625 1125 84 375 -17,17 0,49 0,3538 13,93 13,93 1,07 1,14 0,08
5 80-90 14 85 7 225 1190 101 150 -7,17 0,20 0,3910 15,40 15,40 -1,40 1,96 0,13
6 90-100 12 95 9025 1140 108 300 2,83 0,08 0,3977 15,66 15,66 -3,66 13,40 0,86
7 100-110 11 105 11025 1155 121 275 12,83 0,37 0,3725 14,67 14,67 -3,67 13,47 0,92
8 110-120 10 115 13 225 1150 132 250 22,83 0,65 0,3230 12,72 12,72 -2,72 7,40 0,58
9 120-130 8 125 15 625 1000 125 000 32,83 0,94 0,2565 10,10 10,10 -2,10 4,41 0,44
10 130-140 7 135 18 225 945 127 575 42,83 1,22 0,1895 7,46 7,46 -0,46 0,21 0,03
11 140-150 6 145 21 025 870 126 150 52,83 1,51 0,1276 5,02 5,02 +0,98 0,96 0,19
12 150-160 4 155 24 025 620 96 100 62,83 1,79 0,0804 3,17 3,17 +0,83 0,69 0,22
13 160-170 3 165 27 225 495 81 675 72,83 2,08 0,0459 1,81 3,25 +2,75 7,56 2,34
14 170-180 2 175 30 625 350 61 250 82,83 2,36 0,0246 0,97
15 180-190 1 185 34 225 185 34 225 92,83 2,65 0,0119 0,47
Б 138 12720 1 340 650 ? =20,86
и =s/x = 35,04/92,17 * 100 =
х- 12 720/138 =92,17; S = V(1340650 - 161798400/138)/137 =35,04; к = 138*10/35,04 = 39,38;
= 38 % > 33 %; x2J2. од) = 15,987; 20,86 > 15,987.
Преобразование данных
Таблица 1.7
1 № п/п 1 X x'=lg X ff X = =х'-10С -Н. и % X x'=lgX tf X = =х'-100 № п/п | X xf = lgx ff X ~ =x'-100 п/u aN X x =lgx x = =x'-100 № n/n X x = Igx x” = = x'-100
(1) (2) (3) (4) (5) (6) (7) (8) (9) (10) (11) (12) (13) (14) (15) (16) (17) (18) (19) (20)
UJ
и»
1 40 1,60206 160,21 29 59 1,77085 177,09 57 78 1,89209 189,21 85 98 1,99123 199,12 113 127 2,10380 210,38
2 41 1,61278 161,28 30 60 1,77815 177,82 58 78 1,89209 189,21 86 99 1,99564 199,56 114 128 2,10721 210,72
3 41 1,61278 161,28 31 60 1,77815 177,82 59 79 1,89763 189,76 87 100 2,00000 200,00 115 129 2,11059 211,06
4 42 1,62325 162,33 32 61 1,78533 178,53 60 79 1,89763 189,76 88 101 2,00432 200,43 116 130 2,11394 211,39
5 43 1,63347 163,35 33 62 1,79239 179,24 61 80 1,90309 190,31 89 102 2,00860 200,86 117 131 2,11727 211,73
6 44 1,64345 164,35 34 62 1,79239 179,24 62 81 1,90849 190,85 90 103 2,01284 201,28 118 133 2,12385 212,39
7 44 1,64345 164,35 35 63 1,79934 179,93 63 81 1,90849 190,85 91 104 2,01703 201,70 119 134 2,12711 212,71
8 45 1,65321 165,32 36 63 1,79934 179,93 64 82 1,91381 191,38 92 105 2,02119 202,12 120 136 2,13354 213,35
9 46 1,66276 166,28 37 64 1,80618 180,62 65 83 1,91908 191,91 93 106 2,02531 202,53 121 137 2,13672 213,67
10 47 1,67210 167,21 38 65 1,81291 181,29 66 83 1,91908 191,91 94 106 2,02531 202,53 122 139 2,14302 214,30
11 48 1,68124 168,12 39 66 1,81954 181,95 67 84 1,92428 192,43 95 107 2Д32938 292,94 123 140 ,2,14613 214,61
12 48 1,68124 168,12 40 66 1,81954 181,95 68 85 1,92942 192,94 96 108 2,03342, 203,34 124 143 2,15534 215,53
13 49 1,69020 169,02 41 67 1,82607 182,61 • 69 85 1,92942 192,94 97 109 2,03743 203,74 125 144 2,15836 215,84
14 49 1,69020 169,02 42 68 1,83251 183,25 70 86 1,93450 193,45 98 110 2,04139 204,14 126 146 2,16435 216,44
15 50 1,69897 169,90 43 68 1,83251 183,25 71 86 1,93450 193,45 99 111 2,04532 204,53 127 147 2,16732 216,73
16 51 1,70757 170,76 44 69 1,83885 183,89 72 87 1,93952 193,95 100 112 2,04922 204,92 128 149 2,17319 217,32
17 51 1,70757 170,76 45 69 1,83885 183,89 73 88 1,94448 194,45 101 113 2,05308 205,31 129 151 2,17898 217,90
18 52 1,71600 171,60 46 70 1,84510 184,51 74 89 1,94939 194,94 102 114 2,05691 205,69 130 155 2,19033 219.03
19 52 1,71600 171,60 47 71 1,85126 185,13 75 90 1,95424 195,42 103 115 2,06070 206,07 131 157 2,19590 219,59
20 53 1,72428 172,43 48 71 1,85126 185,13 76 91 1,95904 195,90 104 116 2,06446 206,45 132 158 2,19866 219,87
21 54 1,73239 173,24 49 72 1,85733 185,73 77 92 1,96379 196,38 105 117 2,06819 206,82 133 162 2,20952 220,95
22 54 1,73239 173,24 50 73 1,86332 186,33 78 93 1,96848 196,85 106 118 2,07188 207,19 134 166 2,22011 222,01
23 55 1,74 046 174,04 51 73 1,86332 186,33 79 93 1,96848 196,85 107 119 2,07555 207,56 135 168 2,22531 222,53
24 56 1,74819 174,82 52 74 1,86923 186,92 80 94 1,97313 197,31 108 120 2,07918 207,92 136 174 2,24055 224,06
25 57 1,75587 175,59 53 75 1,87506 187,51 81 95 1,97772 197,77 109 121 2,08279 208,28 137 177 2,24797 224,80
26 57 1,75587 175,59 .54 76 1,88081 188,08 82 96 1,98227 198,23 110 123 2,08991 208,99 138 186 2,26951 226.95
27 58 1,76343 176,34 55 76 1,88081 188,08 83 97 1,98677 198,68 111 124 2,09342 209,34
28 59 Г,77 085 177,09 56 77 1,88649 188,65 84 97 1,98677 198,68 112 125 2,09691 209,69
w
Таблица 1.8
Проверка гипотезы нормальности для данных, преобразованных по формуле х" = In х • 100
№ класса Классы Частоты В Середины классов х х2 Вх Вх2 X — X х-х s Ордина- ты f(z) Е В-Е (В-Е)2 (В-Е)2 Е
(1) (2) (3) (4) (5) (6) (7) (8) (9) (10) (И) (12) (13) (14) (15)
1 160-164,4 7 162,2 26308,84 1135,4 184 161,88 -30,83 1,83 0,0748 2,70 2,70 4,30 18,49 6,85
2 164,4-168,8 5 166,6 27755,56 833,0 138777,80 -26,43 1,57 0,1163 4,20 4,20 0,80 0,64 0,15
3 168,8-173,2 8 171,0 29241,00 1368,0 233928,00 -22,03 1,31 0,1691 6,10 6,10 1,90 3,61 0,59
4 173,2-177,6 9 175,4 30765,16 1578,6 276886,44 -17,63 1,05 0,2299 8,29 8,29 0,71 0,50 0,06
5 177,6-182,0 11 179,8 32328,04 1977,8 355608,44 -13,23 0,79 0,2920 10,54 10,54 0,46 0,21 0,02
6 182,0-186,4 И 184,2 33929,64 2026,2 373226,04 -8,83 0,52 0,3485 12,57 12,57 -1,57 2,46 0,20
7 186,4-190,8 10 188,6 35569,96 1886,0 355696,60 -4,43 0,26 0,3857 13,92 13,92 -3,92 15,37 1,10
8 190,8-195,2 13 193,0 37249,00 2509,0 484237,00 -0,03 0,002 0,3989 14,39 14,39 -1,39 1,93 0,13
9 195,2-199,6 12 197,4 38966,76 2368,8 467601,12 4,37 0,26 0,3857 13,92 13,92 -1,92 3,69 0,27
10 199,6-204,0 И 201,8 40723,24 2219,8 447955,64 8,77 0,52 0,3485 12,57 12,57 -1,57 2,46 0,20
11 204,0-208,4 12 206,2 42518,44 2474,4 510221,28 13,17 0,78 0,2943 10,62 10,62 1,38 1,90 0,18
12 208,4-212,8 10 210,6 44352,36 2106,0 443523,60 17,57 1,04 0,2323 8,38 8,38 1,62 2,62 0,31
13 212,8-217,2 8 215,0 46225,00 1720,0 369800,00 21,97 1,31 0,1691 6,10 6,10 1,90 3,61 0,59
14 217,2-221,6 6 219,4 48136,36 1316,4 288818,16 26,37 1,57 0,1163 4,20 4,20 1,80 3,24 0,77
15 221,6-226 5 223,8 50086,44 1119,0 250432,20 30,77 1,83 0,0748 2,70 2,70 2,30 5,29 1,96
X 138 26638,4 5180874,2 13,38
х= S Вх/п = 193,03; к =nb/S = 36,08; Ь—4,4; п = 138; и = 16,83/193,03 = 8,7 %; 5 =х/(5180874,2 - 5142060,55)/137 = 16,83.
Новые данные изменяются от 160 до 226. Разделим этот диапазон на
15 новых класов и проверим гипотезу нормальности распределения для
вновь полученных частот. Уже одного взгляда на распределение частот
(табл. 1.8) достаточно, чтобы определить, что распределение стало почти
симметричным. Левая ветвь значительно «растянулась^ и центр распределе-
ния сместился вправо. Процедура проверки гипотезы нормальности рас-
пределения преобразованных данных дана в табл. 1.8. Полученная в этой
таблице величинах1 2 = 13,38 < X(i2; ою) = 18>549 (см. П.8); следователь-
но, для преобразованных данных гипотеза нормальности подтверждается.
Коэффициент вариации после преобразования данных снизился с 38 до
8,7 %.
Таким образом, наглядно показано, как можно преобразовать данные,
не подчиняющиеся закону нормального распределения, чтобы распределе-
ние новых, преобразованных данных стало нормальным.
§ 1.8. Алгоритм и блок-схема алгоритма
предварительной обработки экспериментальных
данных
При объеме выборки, превышающем 100—150 наблюдений, как будет
показано ниже, оптимальные эмпирические зависимости, отвечающие
современному уровню знаний, можно построить только с помощью ЭВМ.
Поэтому целесообразно включить в программу машинной обработки
наблюдений также и предварительную обработку экспериментальных
данных. Ниже даны алгоритм и блок-схема алгоритма предварительной
обработки наблюдений.
1. Вычисление выборочных характеристик х, №, S, S, mlt т2, т3, т4
и и соответственно по следующим формулам:
п
i ft
* = ; S2 = m2 = ~ 2 (Xj - x)2;
5=V- S (х/-х)2, 5=>/-Ь- S^-x)2,
" i=i л- 1 i=i
1 n _ in _
= — S (x, -x); m3 — — S (x, -x)3;
ni=i n I=i
1 n F
= 7 S (xz-x)4; и =4.
n f=i x
2. Отсев грубых погрешностей: а) вычисляют наибольшее отклонение;
^max ~ lxmax(min) *~х|;
б) вычисляют т = ^тад/Х'
в) по табл. П.4 находят процентные точки f-распределения Стьюдента
г(р;п-2)’ а именно: „_2) и г^0>1 „_2);
г) вычисляют соответствующие точки :
37
’ ” '/t" 2> + l,(S%; »-2) I2
_ f(<M %; и-2)У”~~1 .
7(0,1 * " 7("-2)i-u(0,i%; „_2)f ’
д) сравнивают результаты вычислений по п. 26) и 2г); принимают
окончательное решение об отсеве первой грубой погрешности, если резуль-
тат по п. 26) значительно больше результатов по п. 2г); _
е) пересчитывают выборочные характеристики хи 5 для нового масси-
ва данных (без отсеянного значения Xj) при объеме массива п — 1;
ж) повторяют процедуру от п. 2а) до п. 2д) для следующего по абсо-
лютной величине наибольшего отклонения dmax.
3. Проверка нормальности распределения (проводят только при v <
<33 %): а) вычисляют wg2 по формулам
gi = т3/т2/2; g2 =т4/т% - 3;
б) находят несмещенные оценки для показателей асимметрии и экс-
цесса:
<?• = g2 = "-1 [(„+ I)g, + 6];
Л— 2 (И— Z)(n—3)
в) определяют среднеквадратические отклонения:
6л(и-1)______
(и-2)(л+1)(л+3) ’
5 — У 24л(и-1)2
V (л-3) (п-2) (и+3) (л+5) ’
г) проверяют условия |G\ | < 3<Sg\ , и |(72| < 5Sq2 (соблюдение этих
условий говорит о возможности принятия гипотезы нормального распре-
деления) ;
д) разбивают массив исходных данных на классы:
к = 1 + 3,321g п;
е) определяют середины классов х;
ж) подсчитывают частоты для всех классов В;
з) вычисляют для всех классов Вх и Вх2;
и) находят хи 5?
ЯВх ~ / ЕВх2-(ЕБх)2/п
и л-1
к) вычисляют к' — nb/S; _
л) определяют z ~ (х - x)/S,
м) формируют с помощью табл. П.7 вектор-столбец/fz);
н) вычисляют для всех классов Е —f(z)k, В - Е, (В ~ Е)2;
о) вычисляют х2 по формуле
X2 = S (В - Е) 2/Е;
38
п) проверяют, используя табл. П.8, условие х2 < ’ v ~ Лкл — “
— 2; р = 0, 10 (если это условие соблюдается, то гипотеза нормальности
распределения может быть принята на 10 %-ном уровне);
р) вычисляют накопленные частоты FbkFe, используя частоты В и Е;
с) находят
£ maxlF^-F^I
*** а
л л
т) проверяют с помощью табл. П.9 условие D < ^(^o,io) (если это
условие соблюдается, то гипотеза нормальности распределения может быть
принята на 10 %-ном уровне).
4. Преобразование распределений к нормальному. Для распределений,
имеющих крутую левую ветвь гистограммы и пологую правую, выпол-
СНачало
I
да
У Ввод исходных
/(Г) данных Xi
вычисление выборочных характеристик
(Т) распределения (п.1 !с Выдачей их но печать * 1
Подготовка к отсеву грубой ошибки
(3) наблюдения (п.2а~2г)
^Лроберкб^
условии .
&Т(5Ъ,п)
ммлЬ
да.
ПроВерка
условия
v7. *35
^^ровер^.
условий
п. 3 2),(n.3pLs?
(?) ЛГ нет
[Конец J t.
/Формирование нового
нет / вектор-столбца
исходных данных
\ (Вез отсеянного
\ элемента)
да
вычисление крите-
риев G4,Gltsc,SF.
(п 32^ (п.Зр)1,
~ в (п.зу)
(7)
Т
&
Рис. 3
39
няют преобразования матрицы и сходных данных по формулам: х =
= 1g (х ± а) • 10й, х = 1/х, х' = 1/х/х; посте каждого преобразования
реализуют процедуру вычисления х2 (от п. З.д) до п. З.н)) и окончательно
принимают то преобразование, которое дает минимальное х2 • Для распре-
делений, смещенных вправо, матрицу исходных данных преобразуют по
формуле х' = ха (при в = 1,5; 2) и после каждого преобразования повто-
ряют процедуру вычисления х2 • Для принятия гипотезы нормальности
преобразованного распределения должно соблюдаться условие х2 <
<Х(».Р) [п.Зн)].
Укрупненная блок-схема алгоритма предварительной обработки опыт-
ных данных приведена на рис. 3.
Глава II
СТАТИСТИЧЕСКИЕ МЕТОДЫ ПОСТРОЕНИЯ
ПРЕОБРАЗОВАНИЯ И ОЦЕНКИ ПАРНЫХ ЗАВИСИМОСТЕЙ
ПО ЭКСПЕРИМЕНТАЛЬНЫМ ДАННЫМ
§ 2.1. Метод наименьших квадратов в простейшем случае
двумерного пространства (на плоскости).
Уравнение регрессии
К так называемым парным зависимостям типа .у =f(x) относится подавляю-
щее большинство всех формул, используемых в естественно-научных и
технических дисциплинах. По результатам экспериментов такие формулы
обычно строили, применяя метод наименьших квадратов, однако только
в последнее время с появлением новейших ЭВМ, пригодных для выполне-
ния расчетов очень большого объема, удается построить парные зависи-
мости оптимальной формы. Поэтому рекомендации, данные в настоящей
главе, можно использовать не только для построения новых парных зави-
симостей, но и для пересмотра старых, в том числе и тех, которые приве-
дены в учебниках.
Сама по себе процедура линейного парного регрессионного анализа
(метода наименьших квадратов на плоскости) очень проста, и для ее вы-
полнения достаточно настольной ЭВМ. (Эту процедуру можно выполнять
и вручную). Большие ЭВМ требуются только для поиска оптимальной
формы парной зависимости.
Пусть имеется п пар наблюде-
ний значений функции отклика yz-,
полученных при фиксированных (в
смысле записанных) значениях не-
зависимой переменной фактора Xj.
Для графического изображения этих
пар наблюдений в виде эксперимен-
тальных точек с координатами х;
у на плоскости применяется систе-
ма декартовых координат (рис. 4).
Координаты точек 1 -8, изобра-
женных на рис. 4, приведены в
табл. 2.1. Такие результаты наблю-
дений могут быть получены в
любой экспериментальной ра-
боте.
Рис. 4
41
Таблица 2.1
Координаты точек
1 2 3 4 5 6 7 8
X 1,5 4,0 5,0 7,0 8,5 10,0 11,0 12,5
У 5,0 4,5 7,0 6,5 9,5 9,0 11,0 9,0
Собственно говоря, естествоиспытатели на протяжении столетий наблю-
дают, что произойдет с интересующим их явлением (функцией отклика
, если изменить независимую переменную (фактор х).
Задача линейного регрессионного анализа (метода наименьших квад-
ратов) состоит в том, чтобы, зная положение точек 1-8 на плоскости, так
провести линию регрессии, чтобы сумма квадратов отклонений Д? вдоль
оси Оу (ординаты) этих точек U от проведенной прямой была минималь-
ной.
Для проведения вычислений по классическому методу наименьших
квадратов (для проведения регрессионного анализа) к выдвигаемой гипо-
тезе (к форме уравнения регрессии) предъявляется такое требование:
это уравнение должно быть линейным по параметрам или допускать воз-
можность линеаризации. Так, например, процедура проведения регрессион-
ного анализа одинакова для уравнений у = Ьо + Ьх и у — b0 + bz2, так как
подстановка х = z2 приводит второе уравнение к первому. Этот вопрос
подробнее рассмотрен ниже. Здесь же для простоты и более легкого освое-
ния методики регрессионного анализа предположим (на первых порах),
что при проведении парного линейного регрессионного анализа имеем дело
только с уравнением прямой линии (следует помнить, что это допущение
делается только для упрощения усвоения начальных элементарных сведе-
ний по методике построения формул по опытным данным).
Уравнение прямой на плоскости в декартовых координатах
у = Ь0 + Ьгх, (2.1)
где bo, bi — постоянные числа, геометрическая интерпретация которых
дана ниже. Учитывая это, задачу метода наименьших квадратов аналити-
чески можно выразить следующим образом:
й
U= S [yz-(i0 (2.2)
1 = 1
гдеyj - (Ьо + biXj) = Д,-, или
п „ ___
U— S Д? . , 1 = 1, л. (2.3)
;=1 ‘mm ’ v '
Формулы (2.2) и (2.3) словами кратко можно выразить так: сумма
квадратов отклонений вдоль оси Оу должна быть минимальной (принцип
Лежандра).
Построенная таким образом линия регрессии позволяет в данном слу-
чае с некоторой вероятностью предсказать в интервале от х — 1,5 до х =
42
= 12,5 любые значения функции у при отсутствующих в табл. 2.1 значениях
фактора х.
Для решения задачи, поставленной в формуле (2.2), необходимо в
каждом конкретном случае вычислить значения коэффициентов Ьо и д15
минимизирующие сумму отклонений U. Для этого, как известно из мате-
матического анализа, необходимо вычислить частные производные функции
U по коэффициентам Ьо и bi и приравнять их нулю:
(2.4)
^-=0.
I 6Ь0
) =0.
I дЬ 1
Решая эту систему уравнений, находим искомые значения Ьо и Ьг. Систему
(2.4) называют системой нормальных уравнений. В формулу (2.4) под-
ставляют значение U из формулы (2.2) и одновременно выполняют опе-
рацию дифференцирования:
I = 2 l>z ~ (*о + brxi) ] = 0,
I 000 1=1
1 4г = [П'-(Ьо+ *.*>) 1^=0.
1=1
Преобразуем полученную систему нормальных уравнений:
bon + bi Sx/ = Sy/,
b0 Sx/ + bt ^xi = S (y^i) •
(2.5)
(2.6)
В формуле (2.6) и далее для краткости у знака суммы S опущены индек-
сы. Систему (2.6) решаем с помощью определителей
Z>o = ©i/0, bi = ©2/©, (2.7)
где 0 — главный определитель. Имеем:
0 = п Sx Sx Sx2 = nSx2 —(Sx)2, (2.8)
©1 = Sy Sx Sxy Sx2 = SySx2 — Sxy Sx, (2.9)
©2 = n Sy Sx Sxy =«Sxy - SxSy, (2.Ю)
откуда Ьо = Sj»Sx2 - SxjSx (2.11)
nSx2 -(2x)2
bi = n£xy — SxSy (2.12)
nEx2 — (Sx)2
Как и другие статистические расчеты, вычисление коэффициентов рег-
рессии удобно проводить в табличной форме. На примере построения линии
регрессии по данным табл. 2.1 можно рассмотреть практическую методику
вычисления коэффициентов,регрессии, которая приведена в табл. 2.2.
43
Таблица 2.2
Методика вычисления коэффициентов регрессии
№п/п X У х2 У2 ХУ х + у /X + у)2
(1) (2) (3) (4) (5) (6) (7) (8)
1 1,5 5,0 2,25 25,0 7,50 6,50 42,25
2 4,0 4,5 16,00 20,25 18,00 8,50 72,25
3 5,0 7,0 25,00 49,00 35,00 12,00 144,00
4 7,0 6,5 49,00 42,25 45,50 13,50 182,25
5 8,5 9,5 72,25 90,25 80,75 18,00 324,00
6 10,0 9,0 100,00 81,00 90,00 19,00 361,00
7 11,0 11,0 121,00 121,00 121,00 22,00 484,00
8 12,5 9,0 156,25 81,00 112,50 21,5 462,25
S 59,5 61,5 541,75 509,25 510,25 121,00 2072,00
х = 7,4375, 7 = 7,6875
Для проверки правильности вычислений в табл. 2.2 можно использо-
вать выражение
S (х/ + у i) 2 = Sx 2 + 2 Sxip i + Zyf. (2.13)
Значения сумм подставляем в формулу (2.13). Получаем 2072,00 = 541,75+
+ 2-510,25 + 509,75; 2072,00 = 2072,00. Следовательно, вычисления выпол-
нены правильно. В формулу (2.11) и формулу (2.12) подставляем найден-
ные значения для сумм из табл. 2.2, в результате получаем
Ьо = (61,50 • 541,75 - 510,25 • 59,50)/(8-541,75 - 3540,25) = 3,73,
Ьг =(8 -510,25 - 59,50 • 61,50)/(8 541,75 - 3540,25) = 0,53.
Уравнение регрессии или формула, которая отображает с некоторой
вероятностью зависимость у от х, построенная по экспериментальным
точкам, изображенным на рис. 4, имеет вид
у = 3,73 + 0,53х. (2.14)
Это пример парной линейной зависимости.
§ 2.2. Геометрическая интерпретация коэффициентов
регрессии. Дополнительные разъяснения
Коэффициент Ьо (свободный член уравнения регрессии) геометричес-
ки представляет собой расстояние от начала координат до точки пересече-
ния линии регрессии с ординатой или, другими словами, это отрезок, отсе-
каемый на ординате линией регрессии.
Коэффициент Z>i представляет собой тангенс угла наклона линии рег-
рессии к оси абсцисс: tga = 0,53; а = 27°55' (рис. 5). На этом рисунке
изображено «облако» точек с явно выраженной тенденцией (чем больше х,
тем больше у), хотя и имеются некоторые отклонения от этого закона.
Линия регрессии проведена через «облако» точек, при этом соблюден прин-
44
цип Лежандра. Положение линии в системе координат на плоскости пол-
ностью определяется коэффициентами bG и Ьх.
Различают два вида связи: функциональную и стохастическую. Линей-
ная функциональная связь в данном случае имела бы место, если бы все эти
точки (рис. 5) располагались на прямой регрессии. При наличие погрешнос-
тей измерения связь между у и х является стохастической (вероятностной).
Для функциональной связи понятие корреляции практически не имеет
смысла (коэффициент парной корреляции всегда равен 1). Для стохасти-
ческой связи вычисление коэффициента парной корреляции г между у и
х и его статистическая оценка — важная процедура, результаты проведения
которой позволяют судить о тесноте связи. Коэффициент г может изме-
няться от -1 до 1. Чем ближе г к единице, тем ближе изучаемая зависи-
мость к функциональной. Целесообразно рассмотреть терминологию, свя-
занную с регрессионным и корреляционным анализом.
Рис. 5
Для у в литературе можно встретить следующие наименования: функ-
ция отклика, зависимая переменная, предикатор; х называют входной пе-
ременной, независимой переменной, фактором, регрессором. Если перемен-
ные у и х представляют двумерную нормально распределенную случайную
величину, то существует две регрессии [52]. Одна определяет зависимость
v_ot х, а другая — хот у. Прямые регрессии пересекаются в центре тяжести
(х; у) и образуют «ножницы». Чем уже «ножницы», тем ближе стохастичес-
кая связь с функциональной. При функциональной связи обе прямые сли-
ваются.
На рис. 6, а-г даны некоторые характерные положения прямой ли-
нейной регрессии в зависимости от значений коэффициентов регрессии. То
обстоятельство, что прямые пересекаются в точке с координатами (х; j?),
45
можно использовать для быстрого построения линий регрессии. Достаточно
по формулам (2.11) и (2.15) вычислить Ь0(у; х) и b0(x, j), нанести в сис-
теме координат точку О (х; у), как обе линии регрессии оказываются по-
строенными; bt(y; х) и bifx; у) определяют графическим методом, изме-
ряя углы между линиями регрессии и осью абсцисс.
§ 2.3. Парная корреляция. Статистическое оценивание
парной корреляции и регрессии
Существует две модели регрессии. Условно можно модель 2 = (ух) +
+ bi (уХ)Х назвать прямой регрессией, а модель х = Ьо (Ху), + Ьг (ху) у -
обратной. Это означает, что уравнение у — b0 + bix не является алгебраичес-
ким, из которого непосредственно можно найти х, так как эта модель полу-
чена минимизацией суммы квадратов отклонений вдоль оси Оу.
Чтобы вычислить х и у (обратная регрессия), следует минимизировать
сумму квадратов отклонений вдоль оси Ох. Выбор того или иного уравне-
ния регрессии произволен [95] и зависит от того, какую из случайных
величин, х или у, считают заданной (независимой переменной). Такая си-
туация вызывает возражения экспериментаторов [4].
В принципе можно записать выражение для ортогональной регрессии
(к этому вопросу вернемся после рассмотрения коэффициента корреля-
ции) , однако ортогональная регрессия, где расстояния от эксперименталь-
ных точек до прямой регрессии измеряют по перпендикуляру к этой пря-
мой, находит ограниченное применение, так как положение линии регрес-
сии в системе координат зависит от выбранного по осям масштаба. Так,
например, если исследуется зависимость сопротивления проводника от
температуры, то получают разные модели ортогональной регрессии при
использовании шкал Цельсия или Фаренгейта, что недопустимо.
Однако если, например, исследуется влияние температуры внешней
среды на температуру тела земноводных и используется одна и та же шкала,
то ортогональная регрессия может быть использована на практике.
Формулы для вычисления коэффициентов Ьо и bi в случае прямой
регрессии даны выше [формулы (2.11) и (2.12)]. При обратной регрес-
сии коэффициенты вычисляют по формулам
^O(xy) “ 2 ExSy —ЕхуЕу (215)
лЕу2—(Еу)2
(ху) = лЕху-ЕхЕу nSy2—(Еу)2 ’ (2.16)
Таким образом, в дополнение к определителям 0, 0Г, 02 получают
второй главный определитель
©' = п Ъу Sj 1 Ej2l (2.17)
и определи гель Ех Sj |
©1 = Еху Ej2 1 • (2.18)
46
Учитывая это, формулы (2.15) и (2.16) запишем в виде
*о(х,) (219) " »1<хЯ=в2/в'-
Коэффициент парной корреляции
___________nZxy - SXEy
/ее' v/[n sx2-<sx)2 ][л sy 2-(Еу)2 ]
(2.20)
(2.21)
Если в формуле (2.21) числитель и знаменатель разделить на п, то
получим
а в _ ъху - (1/*)(£х)(Ду)
(l/n)(sx)a J[sy2- (1/л)<Ёу)’ 1
(2.22)
В литературе можно встретить следующую формулу для вычисления
г (с использованием средних):
А S(X-X)(y-y)
(2.23)
Зная формулы для нахождения коэффициента парной корреляции, можно
вернуться к вопросу об ортогональной регрессии, модель которой строится
по формуле Л
Y— у +---у: ~НХ-х), (2.24)
5о+ч/5о + 4г2
где S<t = Sx/Sy-Sy=y/S^, -(I/в) £ /i-хД S’ =
= (1/л) £ (у-уР [см. формулу (1.3)1.
/ = 1
С понятиями ортогональной, прямой и обратной регрессии тесно связано
понятие эллипса рассеяния.
Линия ортогональной регрессии, задаваемая соотношением (2.24),
является одной из главных осей эллипса рассеяния, а две другие линии
регрессии — диаметры этого эллипса [4].
Уравнение эллипса рассеяния имеет вид
1(^1 = 4 2) (2.и)
(индексы суммирования опущены). Здесь х<р — процентная точка
X2-распределения с двумя степенями свободы, которая берется по табл. П.8.
Процедуры вычисления коэффициентов регрессии, корреляции и не-
которых других величин, необходимых для их статистического оценива-
ния с использованием данных табл. 2.2, можно упростить, если вычислить
следующие промежуточные величины:
Qx -4/п = Sx2 - (1 /и) (Бх) 2, (2.26)
Qy = е’/л _(1/л) (ад2, (2.27)
Qxy = е2/и = Бху - (1/и) (Бх) (Бу). (2.28)
47
Проверка вычислений:
S(х + у)1 -(1/и) [S(x+rt] 2 =Q, + Qy + 2Qxy. (2.29)
Далее вычисления проводят в следующем порядке [52] : а) находят
средние значения:
(2.30) у=2у/и; (2.31)
б) вычисляют коэффициенты регрессии Ьй^уХу, bx (ху)Л^о (ху)д^1 (ху) >
коэффициент корреляции г, Qyx, стандартные ошибки SXf Sy, Sxy, Syx,
$Ь0(ух) ** (ух) •
(ух) Qxy/Qx’ (2.32)
60(ух) =У~Ь1(уХ)Х, (2.34)
r = Qxy/x/Q^Qr; (2.36)
«х =>/&/(>>-О, (2.38)
^ = С^/£«-1), (2-40)
Sm(,x)=W^ (2'42'
Проверка вычислений:
Г~ ~ Qxy^QxQy = $ху/8Х8у ~
Sbnf г \ = fa-
°0 (ух) (ух) v '
(ху) -QxylQy'^ (2.33)
^о(ху) — х ~ (xy)F (2-^5)
Qyx ~ Qy ~ (ух) Оху ’ (2.37)
Sy=VQ~/(n-i), (2.39)
S_yx =y/Qyx/(n-2), (2.41)
Sb0(yx) ^Syxy/lln + ^/Qx. (2.43)
(yx)^i (xy) ’ (2.44)
(2.45)
Для статистического оценивания коэффициентов регрессии проверяют
нуль-гипотезу Яо: Р ~ 0> т-е- проверяют, отличается ли статистически значи-
мо оценка коэффициента регрессии от нуля [52] . Границу значимости уста-
навливают на основании распределения Стьюдента:
(2.46)
где Р — значение коэффициента регрессии в генеральной совокупности;
Ъ — выборочная оценка коэффициента регрессии; р находят по
табл. П.4. Если условие (2.46) соблюдается, то можно сделать вывод, что
(3 значимо отличается от нуля. Оценку значимости коэффициента парной
корреляции (проверку наличия корреляции) выполняют по формуле
А г>/ п - 2
г---у 2; р) • (2.47)
\jl-r
Если это условие выполняется, то гипотезу Но' г =0 отклоняют. Для этой
же цели можно использовать табл. П.10. По этой таблице значение коэффи-
циента корреляции сравнивают с его критическим значением (г > г крит) •
Для проверки значимости уравнения регрессии в целом с использова-
нием F-критерия Фишера общую дисперсию 5^ сравнивают с остаточной
дисперсией 5^ Ост?которую можно вычислить в табличной форме (табл. 2.3).
Вычисление ^ост, или сокращенно 5^.т, имеет большое значение в тео-
рии статистических методов построения эмпирических зависимостей. В
литературе можно встретить различные наименования для (остаточная
48
Таблица 2.3
Вычисление остаточной дисперсии с использованием данных табл. 2.2 и формулы
у = 3,73 + 0,53л:
№ п/п у X у =3,73 + 0,53х .У - У (у -у)2
(1) (2) (3) (4) (5) (6)
1 5,0 1,5 3,73 + 0,53- 1,5 =4,53 +0,47 0,2209
2 4,5 4,0 3,73 + 0,53-4,0=5,85 -1,35 1,8225
3 7,0 5,0 3,73 + 0,53-5,0=6,38 +0,62 0,3844
4 6,5 7,0 3,73 + 0,53-7,0=7,44 -0,94 0,8836
5 9,5 8,5 3,73 + 0,53- 8,5 =8,24 + 1,26 1,5876
6 9,0 10,0 3,73 + 0,53- 10,0 = 9,03 -0,03 0,0009
7 11,0 11,0 3,73 + 0,53- 11,0 = 9,56 +1,44 2,0736
8 9,0 12,5 3,73 + 0,53 - 12,5 = 10,35 -1,35 1,8225
S 61,5 59,5 0,12 8,8
дисперсия, сумма квадратов остатков, остаточная сумма квадратов);
5?ст представляет собой показатель ошибки предсказания уравнением
регрессии результатов опытов. Качество предсказания определяют, срав-
нивая 52ст с Sy, другими словами F-критерий Фишера показывает, во сколь-
ко раз уравнение регрессии предсказывает результаты опытов лучше, чем
среднее у:
= 5,28,
у J п— 1 п ~ 1
й _ W-УУ _ 8,8 _
Sy™~ п 2 ~ 6 -1’46’
Р = = 3,62 CAJ. 6. 5%) = 4,06.
(2.48)
(2.49)
Для того чтобы уравнение (2.14) адекватно описывало результаты экс-
периментов, необходимо, чтобы это уравнение при 5%-ном уровне значи-
мости описывало результаты опытов в 4,06 раза лучше среднего
У в- 5%) = 4,06). Фактическое же значение F = 3,62 меньше таблично-
го. При 10 %-ном уровне значимости F - 3,62 >FJ7, 6.= 2,93; уравне-
ние (2.14) статистически значимо описывает результаты экспериментов;
^табп берутиз табл. П.11.
§ 2.4. Числовой пример выполнения парного линейного
регрессионного и корреляционного анализов.
Статистическое оценивание результатов расчетов
Для решения примеров можно использовать данные, которые рассмат-
ривались в гл. I (рост двадцатилетних студентов в м-102 в лекционном по-
токе — вектор-столбец у, их масса в кг — вектор-столбец х).
Нормальность распределения данных вектор-столбца у проверена в
гл. I. Для проверки нормальности распределения данных вектор-столбца
х воспользуемся наиболее простым методом, т.е. проверим, находится ли
49
отношение R/S в допустимых пределах
(в 10 %-ных границах). Имеем R/S=
= 25/5^86 = 4,27. Критические значения
(10 %-ные границы) по табл. П.9 равны
4,022 и 5,220, т.е. 4,022 < 4,27 < 5,220;
следовательно, гипотезу нормальности рас-
пределения можно принять. Таким образом,
наблюдения роста и массы двадцатилетних
мужчин являются двумерной нормально рас-
пределенной величиной и имеет место вто-
рой тип регрессии, при котором могут быть
исследованы прямая у = f(x) и обратная
х — fly) регрессии и выполнен корреля-
ционный анализ.
Расчет коэффициентов уравнений рег-
рессии и коэффициента корреляции с
применением настольных калькуляторов
лучше всего выполнять в табличной фор-
ме. Результаты таких расчетов приведены
в табл. 2.4. В этой таблице 14 столбцов, и на первый взгляд она может
показаться очень громоздкой. Однако при этом необходимо учитывать,
что столбцы (1)-(6) нужны непосредственно для построения уравнений
регрессии и вычисления коэффициента парной корреляции. Столбцы (7)
и (8) используют для проверки правильности вычислений, а столбцы
(9) - (14) — для проверки адекватности уравнений регрессии.
По данным табл. 2.4 найдем следующие суммы: Sx = 4069, Sy =
= 9837, Sx2 = 297545, Sy2 - 1 729 671, Sxy = 7J5 587, S(x + y)2 =
= 3 458 390, S(y - y)2 = 1281,35, S(x -2)2 = 1503,54, средние значе-
ния x — 72,66,у = 175,66; промежуточные величины:
Qx = Sx2 —(Sx)2/w = 297545 - 16556761/56 = 1889,
Qy = Sy2 - (Sy)2/n = 1729671 - 96766569/56 = 1697,
Qxy = Sxy- (Sx) (Sy)/«= 715587 - 40026753;
коэффициенты уравнений регрессии:
bI (>X) = Qxy/Qx = 824/1889 = 0,436,
bi (Xy) = Qxy!Qy ~ 824/1697 - 0,486,
bo(yx) =y - bl (yx)* = 175,660- 0,436 • 72,660 = 143,980,
b0(xy) =* - bt (х>)У = 72,660 - 0,486 • 175,660 = -12,711.
Таким образом, в рассматриваемом примере уравнения прямой и обрат-
ной регрессии имеют соответственно вид
у = 143,980 + 0,436х; (2.50) х = -12,711 + 0,486у. (2.51)
Проверим правильность вычислений: 297 545 + 2 715 587 + 1 729 671 =
= 3 458 390, 3 458 390 = 3 458 390; следовательно, вычисления выпол-
нены правильно.
50
Таблица 2.4
Расчет данных для парного линейного регрессионного и корреляционного анализа
№ п/п х, кг у, м-102 хг У2 ху х + у /х + у/ Ж У У~У (У~У? X х-х (х-х)2
(1) (2) (3) (4) (5) (6) (7) (8) (9) (Ю) (11) (12) (13) (14)
1 72 183 5184 33 489 13 176 255 65 025 175,372 7,628 58,22 76,227 -4,227 17,87
2 70 170 4900 28 900 11 900 240 57 600 174,500 -4,500 20,25 73,909 -3,909 15,28
3 83 176 6889 30 976 14 608 259 67 081 180,168 -4,168 17,39 72,825 10,175 103,43
4 68 178 4624 31684 12 104 246 65 016 173,628 4,372 19,09 73,797 -5,797 33,61
5 69 176 4761 30 976 12 144 245 60 025 174,064 1,936 3,75 72,825 -3,825 14,63
6 83 180 6889 32 400 14 940 263 69 169 180,168 -0,168 0,03 74,769 8,231 67,75
7 74 176 5476 30 976 13 024 250 62 500 176,244 -0,244 0,06 72,825 1,175 1,38
8 79 185 6241 34 225 14 615 264 69 696 178,424 174,936 6,576 43,24 77,199 1,801 3,24
9 71 184 5041 33 856 13 064 255 65 025 9,064 82.16 76,713 -5,713 32,63
10 68 174 4624 30 276 11 832 242 58 564 173,628 0,372 0,14 71,853 -3,853 14,85
11 70 168 4900 28 224 11 760 238 56 644 174,500 -6,500 42,25 68,937 1,063 1,13
12 70 174 4900 30 276 12 180 244 59 536 174,500 -0,500 0,25 71,853 -1,853 3,43
13 85 189 7225 35 721 16 065 274 75 076 181,040 7,960 63,36 79,143 5,857 34,30
14 83 172 6889 29 548 14 276 255 65 025 180,168 -8,168 74,88 70,881 12,119 146.87
15 85 175 7225 30 625 14 875 260 67 600 181,040 -6,040 36,48 72,339 12,661 160,30
16 60 167 3600 27 889 10 020 227 51 529 170,140 -3,140 9,86 68,451 -8,451 71,42
17 74 179 5476 32 041 13 246 253 64 009 176,244 2,756 7,59 74,283 -0,283 0,08
18 69 176 4761 30 976 12 144 245 60 025 174,064 1,936 3,75 72,825 -3.825 14,63
19 68 169 4624 28 561 11492 237 56 169 173,628 -4,628 21,42 69,423 -1,423 2,02
20 74 178 5476 31 684 13 172 252 63 504 176,244 1,756 3,08 73,797 ‘ 0,203 0,04
21 65 169 4225 28 561 10 985 234 54 756 172,320 -3,320 11,02 69,423 -4,423 19,56
22 69 171 4761 29 241 11 799 240 57 600 174,064 -3,064 9,39 70,395 -1,395 1,95
23 65 170 4225 28 900 11 050 235 55 225 172,320 -2,320 5,38 69,909 -4,909 24,10
24 79 177 6241 31 329 13 983 256 65 536 178,424 -1,424 2,03 73,311 5,689 32,36
25 84 176 7056 30 976 14 784 260 67 600 180,604 -4,604 21,19 72,825 11,175 124.88
Продолжение табл. 2.4
(1) (2) (3) (4) (5) (6) (7) (8) (9) (10) (И) (12) (13) (14)
26 80 179 6400 32 041 14 320 259 67 081 178,860 0,140 0,02 74,283 5,717 32,68
27 71 174 5041 30 276 12 354 245 60 025 174,936 -0,936 0,88 71,583 -0,583 0,34
28 76 176 5776 30 976 13 376 252 63 504 177,116 -1,116 1,25 72,825 3,175 10,08
29 73 188 5329 35 344 13 724 261 68 121 178,808 9,192 84,49 78,657 -5,657 32,00
30 72 178 5184 31684 12 816 250 62 500 175,372 2,628 6,91 73,797 -1,797 3,23
31 68 172 4624 29 584 11 696 240 57 600 173,628 -1,628 2,65 70,881 -2,881 8.30
32 67 176 4489 30 976 11 792 243 59 049 173,192 2,808 7,88 72,825 -5,825 33,93
33 65 167 4225 27 889 10 855 232 53 824 172,320 -5,320 28,30 68,451 -3.451 11,91
34 74 166 5476 27 556 12 284 240 57 600 176,244 -10,244 104,86 67,965 6,035 36,42
35 70 180 4900 32 400 12 600 250 62 500 174,500 5,500 30,25 74,769 -4,769 22,74
36 82 183 6724 33 489 15 006 265 70 225 179,732 3.268 10,68 76,227 5,773 33,33
37 71 176 5041 30 976 12 496 247 61 009 174,936 1,064 1,13 72,825 -1,825 3,33
38 72 182 5184 33 124 13 104 254 64 516 175,372 6,628 43,93 75,741 -3.741 14,00
39 68 178 4624 31 684 12 104 246 60 516 173,628 4,372 19,11 73,797 -5,797 33.61
40 78 172 6084 29 584 13 416 250 62 500 177,988 -5,988 35,86 79,881 7,119 50,68
41 74 185 5476 34 225 13 690 259 67 081 176,244 8,756 76,67 77,199 3,199 10,23
42 72 183 5184 33 489 13 176 255 65 025 175,372 7,628 58,19 76,227 4,227 17,87
43 72 175 5184 30 625 12 600 247 61 009 175,372 -0,372 0,14 72,339 -0.339 0,11
44 71 174 5041 30 276 12 354 245 60 025 174,936 -0,936 0,88 71,853 -0,853 0,73
45 75 180 5625 32 400 13 500 255 65 025 176,680 3,320 11,02 74,769 0.231 0.05
46 62 166 3844 27 556 10 292 228 51 984 171,012 -5,012 25,12 67,965 -5,965 35,58
47 67 169 4489 28 561 11 323 236 55 696 173,192 -4,192 17,57 69,423 -2,423 5,87
48 82 171 6724 29 241 14 022 253 64 009 179,732 -8,732 76,24 70,395 11,605 134,68
49 76 178 5776 31 684 13 528 254 64 516 177,116 0,884 0,78 73,797 2,203 4,85
50 69 169 4761 28 561 И 661 238 56 644 174,064 -5,064 25,64 69,423 -0,423 0,18
51 68 170 4624 28 900 11 560 238 56 644 173,628 -3,628 13,16 69,909 -1,909 3,64
52 72 179 5184 32 041 12 888 251 63 001 175,372 3,628 13,16 74,283 -2,283 5,21
53 69 171 4761 29 241 11 799 240 57 600 174,064 -3,064 9,39 70,395 -1,395 1,95
54 73 178 5329 31684 12 994 251 63 001 175,808 2,192 4,80 73,797 -0,797 0,64
55 73 173 5329 29 929 12 629 246 60 516 175,808 -2,808 7,88 71,367 1,633 2,67
56 70 177 4900 31 329 12 390 247 61009 174,500 2,500 6,25 73,311 -3,311 10.96
Для иллюстрации можно изобразить две линии регрессии (рис. 7);
угол (3 между ними дает представление о коэффициенте парной корреля-
ции. При /3 = 90° у и х независимы. При /3=0° между у и х существует
функциональная связь (у полностью зависит от х).
Для оценки статистической значимости уравнений регрессии и коэф-
фициентов уравнений вычислим следующие показатели:-
<2ух = бу -Д1(у«> Qxy = 1697 - 0,436 824= 1337,74;
£« = V6J(»-0 = 5,86; Sy = Vg,/(»-l) =5,55;
Sxy = бху/(»-1) = 14,98; Syx -x/Qyxl(n-2) = 4,98^
SiiO-x) =WV&=4,98/43,46 = 0,1146; = 8ухх/Цп + х*/вх=
= 8,35; £*=34,35; £j = 30,85; ^ = S (y-y)*/(n - 2) = 23,73;
5*^.= S(x - x)*/(n- 2) = 27,84.
Адекватность уравнений проверим по критерию Фишера:
Fy = 5J/^OCT = 30,85/23,73 = 1,34, Fx = S2X/^XOCT = 34,35/27,84 = 1,23.
Табличное значение FT находим по табл. П.11, из которой видно, что полу-
ченные нами уравнения регрессии значимы только при 10%-м уровне
значимости (90 %-й доверительной вероятности).
Значимость коэффициентов регрессии проверим по r-критерию Стью-
дента:
^ьо(ух) ~ (ух)/$ь 1 (ух) —0,436/0,1146 — 3,80,
~ Ьо (ух) /$bQ (ух) = 143,980/8,35 = 17,24.
Табличное значение Ат находим по табл. П.4. При 5 %-ном уровне значимос-
ти и п — 56 табличное значение f(S6j5%) = 1»67; следовательно, найденные
значения коэффициентов регрессии статистически значимы.
Окончательную проверку правильности вычислений выполняем по
формулам
г ~ S ~ О'*) (*•»*) ’
х у
14,98/32,52 = х/0,436-0,486; 0,46 = 0,46;
sb0(yx)/Sbl (ух) =VSx2/n; 8,3552456/0,1146 = 72,89241; 72,88356 =
= 72,89241;
следовательно, все вычисления выполнены правильно.
В рассмотренном примере выполнен парный линейный корреляцион-
ный и регрессионный анализ зависимости между ростом и массой двадца-
тилетних студентов.
§2.5 . Оценка линейности регрессии
Оценка линейности регрессии может быть выполнена в том случае,
если общее число значений у больше, чем число к значений х. Каждому
значению х( соответствует и/ значений у [52]. На практике при проведе-
нии измерений или наблюдений так чаще всего и бывает.
53
Таблица 2.5
Расчет данных для проверки линейности регрессии
"в Z Хг Л/ я/ Уг Я 1 <?s 1 1 Г (Уц-У)2 1 ч> м
(1) (2) (3) (4) (5) (6) (7) (8) (9) (10) (И) (12)
1 60 167 I 167,00 170,14 3,14 9,86 9,86 0 0 0
2 62 166 1 166,00 171,01 5,01 25,10 25,10 0 0 0
3 65 169, 170, 167 3 168,67 172,32 3,65 13,32 39,96 0,33; 1,33; 1,67 0,109; 1,769; 2,789 12,250; 12,250 4,449
4 67 176, 169 2 172,50 173,19 0,69 0,48 0,96 3,50; 3,50 24,500
5 68 178, 174, 169, 172, 178, 170 6 173,50 173,63 0,13 0,02 0,12 4,50; 0,50; 4,50; 1,50; 4,50; 3,50 20,250; 0,250; 20,250; 2,250; 20,250; 12,250 75,500
6 69 176, 176, 171, 169, 171 5 172,60 174,06 1,46 2,13 10,65 3,40; 3,40; 1,60; 3,60; 1,60 11,560; 11,560; 2,500; 12,96; 2,56 41,200
7 70 170, 168, 174, 180, 177 5 173,80 174,50 0,70 0,49 2,45 3,80; 5,80; 0,20; 6,20; 3,20 14,440; 33,640; 0,040; 38,440; 10,240 96,800
8 71 184, 174, 176, 174 4 177,00 174,94 2,06 4,24 16,96 7,00;'3,00; 1,00; 3,00 49,000; 9,000; 1,000; 9,000 68,000
9 72 183, 178, 182, 183, 175,179 6 180,00 175,37 4,63 21,44 128,64 3,00; 2,00; 2,00; 3,00; 5,00; 1,00 9,000; 4,000; 4,000; 9,000; 25,000; 1,000 52.000
10 73 188, 178, 173 3 179,67 175,81 3,86 14,90 44,70 8,33; 1,67; 6,67 69,389; 2,789; 44,489 116,667
11 74 176, 179, 178, 166, 185 5 176,80 176,24 0,56 0,31 1,55 0,80; 2,20; 1,20; 10,80; 8,2 0,640; 4,840; 1,440; 116,640; 67,24 190,800
12 75 180 1 180,00 176,68 3,32 11,02 11,02 0 0 0
13 76 176, 178 2 177,00 177,12 0,12 0,01 0,02 1,00; 1,00 1,000; 1.000 2,000
14 78 172 1 172,00 177,99 5,99 35,88 35,88 0 0 0
15 79 185, 177 2 181,00 178,42 2,58 6,66 13,32 4,00; 4,00 16,000; 16,000 32,000
16 80 179 1 179,00 178,86 0,14 0,02 0,02 0 0 0
17 82 183, 171 2 177,00 179,73 2,73 7,45 14,90 6,00; 6,00 36,000; 36,000 72,000
18 83 176, 180, 172 3 176,00 180,17 4,17 17,39 52,17 0; 4,00; 4,00 0; 16,000; 16,000 32,000
19 84 176 1 176,00 180,60 4,60 21,16 21,16 0 0 0
20 85 189, 175 2 182,00 181,04 0,96 0,92 1,84 7,00; 7,00 49,000; 49,000 98,000
431,25
905,916
S
Данные табл. 2.4 (масса х и рост у двадцатилетних студентов) с учетом
сказанного выше представлены в табл. 2.5. В столбце (4) этой таблицы
даны количества значений соответствующие каждому значению х/.
В столбце (8) подсчитываются отклонения групповых средних значений
У1 от прямой регрессии, в столбце (11) - отклонения значений у от группо-
вых средних.
Если статистика [52]
(2.52)
т.е. сумма отклонений групповых средних от прямой регрессии, делен-
ная на сумму отклонений значений у от групповых средних со степенями
свободы в числителе = к — 2 и в знаменателе v2 ~ п - к, достигает или
превосходит границу значимости, то гипотезу о линейности нужно отбро-
сить. л
В данном случае F =[1/(20 - 2)-431,259]/[ 1/(56-20)-905,916)] =
= 0,952 не достигает границы значимости, так как F^v v ;S96j >1; сле-
довательно, гипотеза линейности связи у =f(x) не может (эыть отброшена.
§ 2.6. Нелинейная парная регрессия
В том случае, когда по правилам, изложенным в предыдущем парагра-
фе, гипотеза линейности может быть отброшена или когда при графическом
изображении точек нелинейность явно просматривается «на глаз», есть
смысл получить по экспериментальным данным нелинейную (квадратич-
ную или высших порядков) формулу парной зависимости. При этом можно
рассчитывать, что нелинейная формула даст меньшую остаточную диспер-
сию 5^, т.е. лучше предскажет результаты опытов. Следует только очень
хорошо помнить, что речь идет о зависимости, Нелинейной по фактору
х. По параметрам зависимость останется линейной.
Для того чтобы отличить квадратичную парную регрессию от мно-
жественной, которая будет рассмотрена ниже, целесообразно изменить
принятую в первых параграфах гл. II систему обозначений коэффициентов
регрессии. С учетом этой оговорки формулу парной квадратичной регрес-
сии можно представить в виде
у =д+ Ьх+ сх2. (2.53)
Аналогично запишем формулу кубичной регрессии:
у =a + bx+ сх2 + dx3. (2.54)
Однако надо иметь в виду, что уже парный регрессионный анализ
третьего порядка (кубичная регрессия) трудно выполнить вручную.
При наличии в распоряжении исследователя большой ЭВМ теоретичес-
ки можно получить формулу парной зависимости любого порядка, однако
с некоторого момента при повышении порядка уравнения регрессии оста-
55
точная дисперсия вместо того, чтобы уменьшаться, может увеличиваться.
Это, как правило, и является условием прекращения счета.
Коэффициенты квадратичного уравнения а, Ь-, с можно найти, решая
следующую систему трех нормальных уравнений с тремя неизвестными:
ап + bSx + cSx2 = Sy,
aSx + bSx2 + cSx3 == Sxy, (2.55)
aSx2 + bS^ + cSx4 = Sx2y.
Нетрудно заметить, что можно написать аналогичную систему уравне-
ний для получения уравнения парной зависимости любого порядка. На-
пример, для определения коэффициентов кубичной парной регрессии
можно методом экстраполяции получить систему нормальных уравнений
вида
ап + bSx + cSx2 + dSx3 = Sy,
aSx + bSx2 + cSx3 + dSx4 = Sxy,
aSx2 + bS^ + cSx4 + dSxs = Sx2y, (2.56)
aSx3 + bSx4 + cSx5 + dSx* = Sx3y
и тд. для уравнения регрессии любого порядка.
Для иллюстрации решим простой пример, исходные данные для реше-
ния которого (результаты наблюдений) приведены в табл. 2.6.
Таблица 2.6
Исходные данные для решения примера по парной квадратичной регрессии
X 1,7 - 3,4 4 4,1 5,3
У 25 34 57 82 98
Восстановить квадратичную парную зависимость — это значит найти
коэффициенты а, b и с уравнения (2.53). Предварительно вычисляют сум-
мы в табличной форме (табл. 2.7).
Затем следует довольно сложная процедура решения системы алгеб-
раических уравнений, которую нужно выполнять очень внимательно, так
как можно допустить ошибку, обнаружить которую можно только полным
повторением расчета (в этом и состоит недостаток метода построения
квадратичных полиномов).
С ростом степени полинома всю процедуру приходится повторять за-
ново и снова вычислять все коэффициенты. Используя ортогональные поли-
номы Чебышева, перечисленные недостатки можно устранить (методика
изложена в гл. IV). '
Взятые из табл. 2.7 значения сумм подставляем в нормальные уравне-
ния (2.55):
5,00а + 18,50* + 75,35с = 296,00, (1)
18,50я + 75,35* + 326,01с = 1241,70, (2)
75,35а + 326,01* + 1469,60с = 5508,53. (3)
56
Таблица 2.7
Суммы, необходимые для вычисления коэффициентов а, b и с
№ п/п X У ху х2 х2у х3 х4
(1) (2) (3) (4) (5) (6) ч (7) (8)
1 1,7 25 42,5 2,89 72,25 4,91 8,35
2 3,4 34 115,6 11,56 393,04 39,30 133,62
3 4 57 * 228,0 16,00 912,00 64,00 256,00
4 4,1 82 336,2 16,81 1378,42 68,92 282,57
5 5,3 98 519,4 28,09 2752,12 148,88 789,06
S 18,5 296 1241,7 75,35 5508,53 326,01 1469,60
Систему решаем методом исключения переменных. Все члены первого
уравнения умножаем на 3,7:
18,50а + 68,456 + 278,80с = 1095,20,
18,5 07 + 75,356 + 326,01с = 1241,70, ,..
__________________’_________(4)
6,906 +47,21с = 146,5.
Далее исключаем а из уравнений (2) и (3). Для этого умножим все
члены уравнения (4) на 2,073;
18,5 07 + 75,356 + 326,01с = 1241,70,
75,35а + 326,016 + 1469,60с =5508,53,
75,35а + 306,906 + 1327,84с = 5057,44, (5)
75,35а + 326,016 + 1469,60с = 5508,33,
19,116+ 141,76с = 451,09.
Из уравнений (4) и (5) исключаем 6 и определяем с:
6,906 + 47,21с = 146,5, | * 2,77,
19,116 + 141,76с = 451,09,
19,116+ 130,77с = 405,81,
19,116+ 141,76с = 451,09,
10,99с = 45,28,
с = 4,1200;
19,116 + 141,76 - 4,12 = 451,09, 19,116 =-132,96,
6 = -6,9576;
5,00а - 18,50 • 6,9576 + 75,35 • 4,1200= 296,
5,00а + 181,72 = 296, а = 22,856.
57
Для проверки найденные значения коэффициентов подставляются в
одно из исходных уравнений:
18,50 • 22,8560 - 75,35 • 6,9576 + 326,01 • 4,1200 = 1241,70;
1241,70= 1241,70.
Таблица 2.8
Вычисление остаточной дисперсии и дисперсии у
№ n/n У У |у-у| i Л,2 (У-УГ У-У (у -у)2
(1) (2) (3) (4) (5) (6) (7)
1 25 22,935 2,065 4,264 34,2 1169,64
2 34 46,827 12,827 164,532 25,2 635,04
3 57 60,946 3,946 15,571 2,2 4,84
4 82 63,587 18,413 339,039 22,8 519,84
5 98 101,712 3,712 13,779 45,421 22063,067
S 296 537,185 4392,427
у =59,2
Таблица 2.9
Функции и нормальные уравнения
№п/п Функции Нормальные уравнения
1 у = в + bx ел + bSx — Sy a Ex + bSx2 = S(xy)
2 Igy =a+ bx an + bSx = S Igy aSx + ftSx* = S (xIgy)
3 у —а + b \%х
(tn + 6 s lg x = Sy
aS lgx + 6S(lgx)a = S(ylgx)
4 Igy -а + b Igx
у —abx или
Igy — Iga + x lgZ>
6
у — a + bx + cxa
an + £»S Igx = S Igy
aSlgxdS (tgx)’ = S (Igx Igy)
5
n Igfl + lg6Sx = S Igy
IgaEx + 1g 6sxa - S (lgxIgy)
an + bSx + cSx* = Sy
aSx + ftsx* + cSx3 = Sxy
a Ex’ + dSx* + cSx4 = S (x*y)
an + ftsx + cs y/x — Sy
aSx + bSx1 + cS = Sxy
aS y/x + bs \/x* + cSx => S x/xy
8 у = ai¥’ или
lgy=lge+xlgx+x*lgc
n lg a + lg bSx + IgcSx1 = S Igy
IgaSx + IgftSx* + IgcSx3 = S (x Igy)
IgaSx* + IgbSx’ + IgcSx* = S(x* Igy)
58
Окончательно получаем квадратичное уравнение
у = 22,8560 - 6,9576х + 4,1200х2. (2.57)
Вычисляем предсказанные значения у:
pi = 22,8560 - 6,9576 1,7 + 4,1200 • 2,89 = 22,935,
у 2 = 22,8560 - 6,9576 • 3,4 + 4,1200 • 11,56 = 46,827, ‘
р3 = 22,8560 - 6,9576 • 4 + 4,1200 • 16 = 60,946, (2.58)
у4 = 22,8560 - 6,9576 4,1 + 4,1200 • 16,81 = 63,587,
у5 = 22,8560 - 6,9576 • 5,3 +4,1200 • 28,09 = 101,712.
Процедура вычисления остаточной дисперсии дана в табл. 2.8:
= 537, 185/3 = 179,062, 3J =* 4392,427/4 = 1098,107,
F = 1098,107/179,062 = 6,133.
Таким образом, полученное уравнение предсказывает результаты опы-
тов в шесть раз лучше среднего у.
§ 2.7. Другие формы нелинейной парной регрессии.
Выбор оптимальной формы
Используя метод наименьших квадратов, можно построить практи-
чески любые формы нелинейной парной связи. Для этого используют ли-
неаризующие преобразс ания, так как только линейные по параметрам
функции восстанавливаются методом наименьших квадратов.
В табл. 2.10 приведены часто встречающиеся парные зависимости и
линеаризующие преобразования переменных^ Качество предсказания ре-
зультатов проверяют с помощью уравнения у' = Ь'о + Ъ\х . После вычисле-
ния коэффициентов б'о и Ь\ по методу наименьших квадратов (как для
парной линейной зависимости) выполняют обратные преобразования, т.е.
по б'о и Ь\ определяют Ьо и Ъх в соответствии с указаниями табл. 2.10. Таким
образом, парная зависимость может иметь разнообразную форму.
До тех пор пока не проверены все известные формы связи, исследова-
тель не может быть уверен, что выбрана лучшая форма (с точки зрения точ-
ности предсказания результатов опытов). Исключение — случай, когда
облако точек имеет определенную и интерпретируемую форму.
Выполнение расчетов по отысканию оптимальной формы связи при
большом числе исходных данных вручную и с применением малых ЭВМ,
как указывалось выше, теоретически возможно, но практически требует
такого количества времени, что задача становится нереальной.
В работе [78] предложен метод обработки на больших ЭВМ опытных
данных для получения оптимальной формы парной зависимости. С по-
мощью этого метода была, например, уточнена известная в строительстве
парная связь между модулем деформаций бетона и его прочностью. При
числе пар наблюдений п = 48 линейная форма зависимости имела вид
£'б = 86,74 + 0,95/?пр; остаточная дисперсия = 1918,34. Полученная
расчетом оптимальная форма связи Еъ = 8,716Л^55; остаточная диспер-
сия^ = 1826, 30.
Разработана [ЮЗ] программа для ЭВМ ЕС 1020, проверяющая 19
59
Таблица 2.10
Функции и линеаризующие преобразования
№ п/п Функция Линеаризующие преобразования
преобразование пере- менных выражения для величин Ьо и bi
У' 1 X b<f b\
(1) (2) (3) (4) (5) (6)
1 у = Ь„ + /X У 1/х ь0 bt
2 у= l/(b0 + blx'j 1/У X ь0
3 У = x/(b0 + ^х)’ х/у X Ьд ьх
4 у = ь<Ах igy X Ig^o Igb,
5 у = Ьое^х 1пу X 1пдс bi
6 У = 1/(&0 + &ie"X). i/y е-х Ьд bi
7 igy lgb0 bi
8 У = Ьд + ftJgX У Igx *0 bi
9 y = b0/(bt + х) i/y X 1/bo
10 у = Ьох/(6х + х) 1/У 1/х bjbo 1/&O
11 у - 1пу 1/х 1п60 bi
12 У = ь0 + У Xй ъ. bi
различных форм связи, включая линейную и квадратичную формы. В том
случае, когда при увеличении показателя степени остаточная дисперсия
уменьшается, число проверяемых функций увеличивается за счет нелиней-
ных функций высших порядков. По этой программе были проверены зави-
симости и полученные выше вручную у (рост), х (масса) двадцатилетних
студентов в лекционном потоке. Получены следующие оптимальные формы
связи:
у = 209,811 - 2464,690/х, (2.59)
х = 159,466 - 15235,200/у, (2.60)
где у — в м-101 2, х — в кг. Однако остаточные дисперсии для этих формул не-
значительно отличаются от соответствующих остаточных дисперсий линей-
ных форм, что лишний раз подтверждает доказанную выше гипотезу о ли-
нейности связи между ростом и весом мужчин.
§ 2.8. Алгоритм и укрупненная блок-схема алгоритма
расчета на ЭВМ оптимальной формы связи
между двумя переменными физическими величинами
1. Вычисление сумм Sx, Sy, Sx2, Sy2 и Sxy и средних значений у и
х; проверка вычислений.
2. Вычисление промежуточных величин:
60
Qx = ^x2 - (l/n)(Sx)2,
ey = S/-(l/«)(2>*2),
Qxy = %ХУ “ Ufa) (s*) (2^)-
3. Вычисление коэффициентов
линейной регрессии:
bx = Qxy/Qx, bo^y-bxx.
4. Вычисление остаточной дис-
персии для линейной формы:
^ = Ъ(у-уУ/(п-2).
5, Вычисление промежуточной
величины:
QyX ~ Qy ~ bi Qxy •
6. Вычисление коэффициента
корреляции:
г = Qxy/\/QxQy
7. Сравнение г с гт. Если г > гт,
то имеется статистически значимая
линейная связь между величинами
у и х. Не выполняться это условие
может по двум причинам: 1) ме-
жду изучаемыми переменными нет
связи; 2) связь есть, но нелинейная.
8. Проверка гипотезы линейно-
сти связи (выполнение всех ране-
тов по табл. 2.5 и сравнение F с
F1).
С начало
♦
/С В бод исходных
/& донных (Xj,yt)
|0 вычисление, сумм (п. 1) ]
|Вычисление промежуточных величинХ
|Ф Qx,9u,Qtu(n.2) I
- ..............Г . ,......- , .
Вычисление коэффициентов линейной
модели bt ubB, промежуточной величины
©и остаточной дисперсии t
линейной формы tn. 5,4.5)
оберко
Конец
Расчет коэффициентов
Ф нелинейных моделей
(п. 9, 10)
выбор оптимальной связи по
^наименьшей остаточной
© дисперсии (п.ц)
родерк.
(тХ гипотезы линей"-
Юности связи
п 8}
нет
нет
у
„ У Выдача но печати,
коэффициента аыд
/Чу) нои модели и Sett
{ Конец )
Рис. 8
9. Расчет по уравнениям (2.56), (2.57) и т.д. коэффициентов квадра-
тичной, кубичной и тщ. форм связи до тех пор, пока не начнет увели-
чиваться.
10. Проверка функций по табл. 2.9 и 2.10 (вычисление коэффициентов
и остаточных дисперсий).
11. Выбор оптимальной формы связи по минимальной остаточной дис-
персии.
Блок-схема алгоритма приведена на рис. 8.
§ 2.9. Методика предсказания предельных значений величин,
изменяющихся по экспоненте
Часто при изучении явлений природы и развития цивилизации можно
встретить величины, изменяющиеся с течением времени по экспоненте.
Используя изложенную в настоящей главе методику парного регрессион-
ного анализа, можно попытаться предсказать предельные значения изучае-
мых переменных.
61
Чтобы лучше понять свойства величины, изменяющейся по экспоненте,
рассмотрим рис. 9. Такая величина имеет начальное значение у0 и предел,
к которому стремится в бесконечности упред; с течением времени она
может увеличиваться (рис. 9) или уменьшаться. К подобным величинам
относятся уже упомянутый выше средний рост мужчин в европейских
странах, большинство спортивных рекордов (прыжки в высоту, штанга,
бег и тд.), средняя урожайность сельскохозяйственных культур и т.д.
Эти величины имеют тенденцию роста с течением времени, однако ясно, что
этот рост имеет затухающий характер. Кривая, приведенная на рис. 9, мо-
жет, например, быть аналитически выражена уравнением, если ввести обо-
значение упред = b 0:
у =Уо + Ьо(1 - e“ft»f). (2.60)
Можно привести еще много аналитических выражений для величин, изме-
няющихся по экспоненте. Как будет доказано, финишные участки такой
кривой хорошо аппроксимируются [78] гиперболической зависимостью
У = t/(b0+bit) (2.61)
(строка 3 табл. 2.10). Разделив числитель и знаменатель правой части вы-
ражения (2.61) на t, получим
у = !/(*„/»+»,). (2.62)
При t -» » кривая (рис. 9) стремится к асимптоте и у "*УшВДД.
у = 1/(&оА + Й1)^Упред = (2.63)
Формулу (2.61) преобразуем следующим образом: t = -jЬ0/Ьг +(\!bi)(t/y).
Введем линеаризующую замену переменных в соответствии с табл. 2.10:
х' = t; у — t/y; -Ь^/Ъ t = Z>'0; 1 /Z>i ^Упред- ® результате получаем выражение
х = Ьо + Упр^у'. (2.64)
По наблюдениям х и у' можно по формуле (2.53) определить Упрел:
Упрел ~ Qx*y' ’iQy1'
Рассмотрим эту методику подробнее на примере вычисления предель-
ных деформаций ползучести бетона (способности деформироваться при
Рис. 9
Рис. 10
62
неизменной нагрузке). Эти деформации имеют затухающий характер при
нагрузках, не превышающих половины предела прочности, и развиваются
по экспоненте. Расчеты приведены в табл. 2.11.
Таблица 2.11
Расчеты по предсказанию предельного значения величины, изменяющейся по
экспоненте (предельные деформации ползучести бетона)
№ п/п х' У' ,3 X ,2 У х’у‘ х' + у' (х‘ + у'Г
(1) (2) (3) (4) (5) (6) (7) (8)
1 50 51,546 2 500 2656,99 2577,30 101,546 10311,59
2 70 61,838 4 900 3823,94 4328,66 131,838 17381,26
3 90 73,230 8 100 5362,63 6590,70 163,230 26644,03
4 100 77,339 10 000 5981,32 7733,90 177,339 31449,12
5 200 115,607 40 000 13364,98 23121,40 315,607 99607,78
S 510 379,56 65500 31189,86 44351,96 185393,78
Р = 102,7 = 75,91
Так как зависимость трансформирована в линейную, то расчеты, дан*
ные в табл. 2.11, представляют собой подготовительные операции для
проведения обычной процедуры вычисления коэффициентов линейного
уравнения регрессии. Таким образом, сложный вопрос предсказания пре-
дельных значений физических величин при известной тенденции их изме-
нения во времени сводится к простой процедуре линейного регрессионного
анализа.
Проверим правильность вычислений:
Sx2 + 2Sxy' + Sy'2 « S(x +у')2;
65 500 + 2*44351,96 + 31189,86 = 185^93,78; 185393,78 = 185393,78;
Qx'y' = Zx'y' - (1/л) (Sx') (Sy'); Qxy = 5636,84;
Qy = Sy2 - (l/п) (Sy2) = 2376,70; yw = 2,37.
Таким образом, предельные относительные деформации ползучести
бетона выбранного состава должны составить У^д — - 2,37 * 1<Г5.
Доказательством того, что финишные участки экспоненты хорошо аппро-
ксимируются гиперболой, является то обстоятельство, что если в декар-
товой системе координат нанести точки с координатами х' и у', то они рас-
положатся Приблизительно на прямой линии (рис. 10).
Аналогично можно предсказывать предельные значения для любых
других величин, изменяющихся по экспоненте.
Глава Ш
МНОЖЕСТВЕННЫЙ РЕГРЕССИОННЫЙ И КОРРЕЛЯЦИОННЫЙ АНАЛИЗЫ.
МНОГОФАКТОРНЫЕ ЭМПИРИЧЕСКИЕ ЗАВИСИМОСТИ
§ 3.1. Линейный множественный регрессионный анализ
В гл. II рассмотрение парного регрессионного анализа было начато с графи-
ческой интерпретации (что удобнее всего для понимания сущности метода
наименьших квадратов). При изучении множественного регрессионного
анализа такой возможности нет, так как не существует графической интер-
претации многомерного пространства. Ясно, что р-мерное пространство —
это только математический прием, экстраполяция свойств двумерного
пространства на р-мерное. Если при этом не стараться наглядно представить
себе р-мерное пространство, то никаких затруднений для понимания мно-
жественного регрессионного анализа не возникает.
На практике при анализе результатов научных исследований часто
имеет место ситуация, когда количественное изменение изучаемого явле-
ния {функции откликц} зависит не от одной, а от нескольких причин
(факторов). При проведении экспериментов в такой множественной
ситуации исследователь записывает показания приборов о состоянии функ-
ции отклика (у) и всех факторов, от которых она зависит (ху). Результата-
ми наблюдений являются уже не два вектор-столбца (у и х), как при про-
ведении парного регрессионного анализа, а матрица результатов наблю-
дений
У1 Хц *12 Х13 .. ... xlp
У2 Х21 *2 2 Х23 • .. X2j ... Х2р
Уз Хз1 х32 *33 . .. X3j ... хзр
Уг Хп хц xie . Xif ... xip
Уп Xni ХП2 *из • Xnj ... хпр
(3.1)
где п — количество опытов; р — число факторов; хц — значение /-го фак-
тора для f-го опыта; у^ — значение функции отклика для /-го опыта.
Задача множественного регрессионного анализа состоит, вностроении
такого уравнения плоскости в (р + 1)-мерном пространстве, отклонения
результатов наблюдений у,- от коброй были бы минимальными. Или,
64
другими словами, следует вычислить значения коэффициентов b0, bj в ли-
нейном полиноме
у = fro+ 2 Ъ.х., (3.2)
i=i 1 '
что равносильно минимизации выражения*
п А п
2 = 2 — (Ьо + + b2xi2 + b3xi3 + ... +
i-1 i = l
+ bjXij + ... + bpXjp) ] 2, (3'3)
A
где yj — вычисляемые, предсказываемые, выравненные значения иссле-
дуемой характеристики.
Для отыскания минимума выражения (3.3) необходимо найти част-
ные производные по всем неизвестным Ьо, Ь±, Ь2, Ь.3,bj, Ьр и при-
равнять их нулю. Полученные уравнения образуют систему нормальных
уравнений:
nb0 + bi Sxn + b2l,xi2 + ... + bjl,Xij + ... + bp'ZXfp = Sy,-;
fr0Sxfl + bi Sx2i + b2 ^ХцХ(2 + ... + bjZXiiXjj + ... + bpZxjiXjp = SyiX/i,
fro ^xij+ fri £хцХц + b2Zxi2Xij + ... + bj’Zxy + ... + bp ZxjpXij = Sy,- x,j,
Ьо^Х[р + bi ^ХцХ(р + £>2 ^xj2Xjp + ... + bj^tXijXip + ... + bp^>Xjp = 2У|Хф,
(3.4)
или в матричной форме
(X * Х)В = X * Y, (3.5)
где В — вектор-столбец искомых коэффициентов аппроксимирующего
полинома (3.2):
В =
b2
(3.6)
ьр
X — матрица всех значений всех рассматриваемых факторов, полученных
при проведении измерений или наблюдений:
*В дальнейшем индексы при знаке S опущены.
65
*10 *20 *11 *21 *12 *22 ... *1/ - ... Х2/ . -- х1р *2р
х = XiO ХЦ */2 ... X// .. *1р >
хпо хп 1 *«2 — *п/ - •• *пр
(3.7)
Х{ о - вектор-столбец, определяющий свободный чДен уравнения регрессии.
В матрице исходных данных этот столбец состоит из единиц; Y - вектор-
столбец опытных значений изучаемой характеристики
У1
У?
У1
(3.8)
Уп
X* - матрица, транспонированная к матрице X:
Х*Х-
п S*ii S*/2 2»Х/1 ^Xj2 ••• 2*A 2xflxf2... Sx/2xnSxf22 ... 2*f/ ... Sx/ix/y — 2xi2x/y ... Sx^p 2*/2*ip
2*// SXf/Xfi SXijXi2 ... 2*J ... l*XijXip
2*/р Sx/pXnSXfpX^ ... ZXipXij ... 24
Sy,
%У1Хц
^ixi2
ZyiXij
ZyiXip
(3.9)
X*Y =
(3.10)
Для решения системы нормальных уравнений в матричной форме
(3.5) следует умножить ее слева на матрицу, обратную матрице системы
нормальных уравнений, если таковая существует:
(Х*Х)-1 (Х*Х)В = (Х»Х)-> (X*Y), (3,1 J)
(X*X)"1(X*X) =Е, (3.12)
где Е — единичная матрица.
Таким образом, решение системы нормальных уравнений в матричной
форме запишется следующим образом:
В =(Х*Х)"1 (X*Y). (3.13)
66
Каждый коэффициент уравнения регрессии можно найти по формуле
Ь, = _ £ y,xl7> (3.14)
где ctj — элементы обратной матрицы (X * X)”1.
В результате проведения всех этих операций получаем полином первой
степени (3.2) с известными коэффициентами b0, bj. Этот полином является
аппроксимацией функции у = f(xlf х2, х3, хр хр), вид которой не-
известен. Уже при п > 20 ир> 3 расчеты коэффициентов уравнения регрес-
сии вручную и с применением настольных ЭВМ весьма затруднительны.
При п > 500 и р > 10 расчеты вручную для одной только задачи можно
проводить в течение многих лет, поэтому процедура множественного рег-
рессионного анализа ориентирована главным образом на применение боль-
ших ЭВМ.
Теоретически точность аппроксимации можно повысить, повышая
степень полинома, однако практически для полиномов высоких степеней
при проведении матричных операций на ЭВМ накапливаются столь значи-
тельные погрешности округления, что решение становится невозможным.
Этот вопрос будет подробно рассмотрен в гл. IV. На практике обычно
ограничиваются построением полинома второго порядка и проведением
шагового регрессионного анализа с включением или исключением пере-
менных. Строят также множественные нелинейные модели, поддающиеся
линеаризации.
Целесообразно напомнить еще раз, что обычным методом наименьших
квадратов можно построить только линейные по параметрам модели (пар-
ные и множественные).
§ 3.2. Проверка значимости уравнения регрессии
и коэффициентов уравнения регрессии
Проверка значимости (качества предсказания) множественного урав-
нения регрессии в принципе мало отличается от соответствующей провер-
ки парной зависимости (см. § 2.3). Вычисляют остаточную дисперсию по
формуле
(3.15)
мост
П А -
п - р - 1
которую затем сравнивают с дисперсией среднего с помощью F-крите-
рия Фишера
£ = (3.16)
с числом степеней свободы в числителе v t = п — 1 и в знаменателе v2 -
- п - р - 1. Считают, что уравнение (3.2) предсказывает результаты опы-
тов лучше среднего, если F достигает или превышает границу значимости
при выбранном уровне значимости (обычно принимаютр — 1 q = 5 %).
Далее будет показано, что существуют и другие методы оценки ка-
67
чества предсказания уравнением регрессии результатов опыта (например,
оценка коэффициента множественной корреляции и т.д.).
Значимость коэффициентов регрессии b0, bj проверяют по критерию
Стьюдента:
(3.17)
погрешность коэффициента регрессии
где Cjj — диагональный элемент матрицы, обратной матрице нормальных
уравнений. Вычисленное значение t сравнивают с tT при числе степеней
свободыv-n -р - 1.
Доверительный интервал для коэффициентов регрессии
Ь, - eSb^i <b,+ t'Sb., (3.19)
где j3/ — значение для коэффициентов регрессии в генеральной совокуп-
ности.
§ 3.3. Множественный корреляционный анализ
Расчеты обычно начинают с вычисления парных коэффициентов кор-
реляции, характеризующих тесноту связи между двумя величинами. В
множественной ситуации вычисляют два типа парных коэффициентов
корреляции:
1) fyxj ~ коэффициенты, определяющие тесноту связи между функ-
цией отклика у и одним из факторов х7-;
2) rxjxm — коэффициенты, показывающие тесноту связи между одним
из факторов Xj и фактором хт (j, т = 1,р).
Формула для вычисления гух. отличается от формулы (2.36), предназ-
наченной для вычисления коэффициента парной корреляции, только индек-
сом при х:
ryXj = Qxjy/'^QxjQy t (3.20)
где QXjy = Sx,y -(1/к) (2xf) (Sy), (3.21)
eJt. = Sx;-(l/n)(j:x/)2, (3.22) Й^ = Е^2-(1/п)(£^)2. (3.23)
Следует напомнить, что суммы записаны в сокращенном виде, например
hxjy = S хцУ1. Коэффициент парной корреляции
^хгхт~ (l/n)(Zxj)(Zxm)
гх.х = - - - - •л-, —-у (3 24)
lm J[£xj- (lM)(Sxz)aH2^- (W(^xmy]
Если ввести обозначения
Qxmxj ~ ^xmxj ~ (11п) (Sx^j) (Sxz), (3.25)
Qxm = Ъх2т -(1/м) (Sxm)2, (3.26)
то формулу (3.24) можно привести к принятому в данном пособии стан-
дартному виду:
Гх)хт = Qxmxj/y/Q^Q^> (3.27)
68
Значение парного коэффициента корреляции, как указывалось выше,
изменяется от — 1 до +1. Если, например, коэффициент гух. - величина
отрицательная, то это значит, что х}- уменьшается с увеличением у. Если
гух. положителен, то Xj увеличивается с увеличением у.
1 Значимость парных коэффициентов корреляции можно проверить дву-
мя способами:
1) сравнением с табличными значениями гт:
Р >гт, ' (3.28)
2) по Г-критерию Стьюдента:
? = r/Sr>fT, (3.29)
где Sr — среднеквадратическая погрешность выборочного парного коэф-
фициента корреляции:
= (1 - 1- (З.ЗО)
Здесь fT определяют по таблице с числом степеней свободы v = п — 2.
Доверительный интервал для парных коэффициентов корреляции
Гуху — tTSr ^Ipyxj ^Fyxj + (3.31)
где рух. — парный коэффициент корреляции в генеральной совокупности.
Если один из коэффициентов rXjxm окажется равным 1, то это означает,
что факторы Xj и хт функционально (не вероятностно) связаны между
собой и тогда целесообразно один из них исключить из рассмотрения, при-
чем оставляют тот фактор, у которого коэффициент гух. больше.
После вычисления всех парных коэффициентов корреляции и исключе-
ния из рассмотрения того или иного фактора можно построить матрицу
коэффициентов корреляции вида
1 ^ух2 ••• ryXj — гухр
гхху 1 ГХ\Х2 — ГХ\Х] — гхгхр
ГХ2У ГХ2Х1 1 -• rX2Xj — ГХ2Хр
(3.32)
rXjy rXfXi rXjX2 ... 1 ... rx.Xp
rxpy rXpX1 rXpX2 ... rXpX. ... 1
Используя матрицу (332), можно вычислить частные коэффициенты
корреляции, которые показывают степень влияния одного из факторов
Xj на функцию отклика у при условии, что остальные факторы закреплены
на постоянном уровне. Формула для вычисления частных коэффициентов
корреляции такова:
ГУ'Х 1, х2, х3, .... Xj, хр
(3.33)
гдеЛ^ - определитель матрицы, образованной из матрицы (3.32) вычер-
киванием 1-й строки /-го столбца. Определители DY х и Djj вычисляют ана-
69
логично. Как и парные коэффициенты, частные коэффициенты корреляции
изменяются от -1 до +1.
Значимость и доверительный Интервал для коэффициентов частной кор-
реляции определяются так же, кай для коэффициентов парной корреляции,
только число степеней свободы вычисляют по формуле
у = и-к-2, (3.34)
где к = р — 1 — порядок частного коэффициента парной корреляции.
Для изучения тесноты связи между функцией отклика у и несколь-
кими факторами х2, х3,..., хр.... хр используют коэффициент множест-
венной корреляции R. Коэффициент множественной корреляции служит,
как указывалось выше, и для оценки качества предсказания; R всегда по-
ложителен и изменяется от 0 до 1. Чем больше R, тем лучше качество пред-
сказаний данной моделью опытных данных.
Для вычисления коэффициента множественной корреляции исполь-
зуют матрицу (3.32):
Ryxi, Х2> Х3, Xj, ..., Хр = — 1 j (3.35)
R можно также найти [46] по формуле
R (3.36)
или вычислить величину
/ Д (?г-й)а
«'“Vl-Jj2---------. (3.37)
S О,—у)2
св язанную с R соотношением
R = У1-^Ц(1-(Я’)2] • (3-38)
п—р — 1
Значимость коэффициента множественной корреляции проверяют
по r-критерию Стьюдента:
?R=«/SR>rI(„_p_1), (3.39)
где SR — среднеквадратическая погрешность коэффициента множественной
корреляции,
Sr = (1 - Л2)/\/«“Р- 1; (3.40)
значимость R можно проверить также и по F-критерию Фишера:
Аг = Г • (3-41)
Полученное значение FR сравнивают с табличным FT при выбранном уров-
не значимости и теслах степеней свободы Pj = и- р-1ир2 =р. Если рас-
четное значение rR превышает табличное, то гипотезу g равенстве коэф-
фициента множественной корреляции нулю отвергают и связь считают
статистически значимой.
70
Величину R2 называют множественным коэффициентом детермина-
ции; она показывает, какая часть дисперсии функции отклика объясняется
вариацией линейной комбинации выбранных факторов хь х2, х3, ...
...ХР-
В [78] приведены результаты множественного корреляционного
анализа влияния 10 факторов на удельные относительные деформации
ползучести бетона
В матрицу исходных данных, вводимых в ЭВМ, включены результаты
367 опытов над бетонными образцами (и = 367 - в матрице 367 строк),
в которых фиксировались значения у « C(tr Т), и следующих 10 факторов:
— отношение массы цемента к массе заполнителя в 1 м3 бетона (Ц/3), %;
х2 - расход цемента на 1 м3 бетона (Ц), кг; х3 - влажность среды (ИО, %;
х4 — масштабный фактор (М),м-102;х5—водоцементноеотношение (В/Ц),
%; х6 — возраст бетона в момент загружения (г), сут; х7 ~ время дейст-
вия нагрузки (t — т), сут; х8 — нормальная густота цементного теста
(НГ), %; х9 — значение напряжений (о), мПа-10; х10 - модуль упругости
заполнителя (Е3), МПа-1(Г2.
В табл. 3.1 приведена треугольная мат-
рица парных коэффициентов корреляции.
Матрица коэффициентов корреляции (3.32)
симметрична, поэтому ее нижнюю поло-
вину можно не приводить, так как гХ1Х2 =
= тХ2Х1 и т.д. Коэффициент корреляции
гХ1х2 близок к единице, поэтому фактор
х2 исключен из рассмотрения; статистически
значимые коэффициенты парною корреляции
в табл. 3.1 подчеркнуты. *
Значимые, связи для наглядности удобно
изображать в виде графа (рис. И). Исполь-
зуя методы теории графов, можно построить
таблицу, наглядно показывающую количест-
во статистически значимых связей меж-
*9
Рис. 11
Таблица 3.1
Матрица коэффициентов парной корреляции
X. У *1 Х3 х4 XS х6 х8 х» Хю
у 1 -0,199 -0,263 -0,065 +0,520 -0,209 +0.292 -0,184 -0,219 +0,170
X! 1 +0,253 -0,056 -0,539 -0,039 -0,440 +0,046 +0,076 -0,054
Х3 1
х4 -0,146 -0,030 -0,005 -0,358 -0,133 -0,00 +0,116
1 -0,051 +0,051 -Q0065 -0,015 -0,080 +0,150
Х5 1 -0,033 +0,252 -0,344 -0,345 +0,283
Хб 1 +0,033 +0,035 +0,149 +0,003
X? 1 -0,046 -0,074 -0,045
х8 1 +0,297 -0,149
х9 1 -0,108
Хю , 1
71
ду функцией отклика и факторами (табл. 3.2). Такую таблицу называют
еще матрицей смежности вершин.
Там, где есть статистически значимая связь, в табл. 3.2 стоит 1, где та-
кой связи нет — 0. По этой таблице легко подсчитать число связей (локаль-
ных степеней) и проранжировать факторы по числу таких степеней. Факто-
ры, имеющие большое число локальных степеней, можно в других задачах
рассматривать как функции отклика.
Таблица 3.2
Матрица смежности вершин
У *1 (Ц/З) х3 (Ю *4 (АО *5 (В/Ц) х6 (т) *7 (f-r) *8 (НГ) х9 (») *10 (Е3) локаль- 1 ные сте- '
У c(t,r) X 1 1 0 1 1 1 1 1 1 8
*1 ц/з 1 X 1 0 1 0 1 0 0 0 4
Хз W 1 1 X 1 0 0 1 1 0 1 6
х4 М 0 0 1 X 0 0 0 0 0 1 2
Х5 в/ц 1 1 0 0 X 0 1 1 1 1 6
Хб т 1 0 0 0 0 X 0 0 1 0 2
Х7 t ~т 1 1 1 0 1 0 X 0 0 0 4
Х& НГ 1 0 1 0 1 0 0 X 1 1 5
х9 а 1 0 0 0 1 1 0 1 X 1 5
*10 Е3 1 0 1 1 1 0 0 1 1 X 6
Локальные степени 8 . 4 6 2 6 2 4 5 5 6
пени
В табл. 3.3 проведено ранжирование факторов по числу локальных
степеней. Полученная таким образом исходная информация дает возмож-
ность использовать для изучения результатов корреляционного анализа
методы теории графов и множеств. Особенно это полезно при сравнении
данных решения нескольких похожих задач [78].
Таблица 3.3
Ранжирование по числу локальных степеней
1 2 3 4 5 6 7 8 9 10
Факторы или функ- ция С(Лт) В/Ц W Е3 НГ а Ц/з t — 7 г м
Число локальных степеней 8 6 6 6 5 5 4 4 2 2
72
В этой работе исследовано влияние 10 факторов X/ на три разные функ-
ции отклика у! - С(Ь т), у2 - Еъ (модуль деформации бетона), у3 - R
(прочность бетона), другими словами, изучалось влияние 10 факторов на
прочностные и деформативные характеристики бетона.
Методами теории множеств и графов было математически доказано,
что факторы по-разному влияют на прочностные и деформативные харак-
теристики бетона. 4
§ 3.4. Множественный нелинейный регрессионный анализ
Первый этап нелинейного множественного регрессионного анализа —
это получение так называемой квадратичной формы. Для этого определяют
коэффициенты регрессии b0, bj, bjm и Ьц в полиноме:
у = b0 + biXi + b2x2 + ... + bj-Xf + ... + ЬрХр + bi + Ь22х2 + ... +
+ bjjxf + ... + ЬррХр + bi 2Х1Х2 + bi 3XiX3 + ... . (3.42)
Степень уравнения можно повышать до тех пор, пока уменьшается
остаточная дисперсия Начиная со второго шага каждому повышению
степени полинома предшествует замена переменных, линеаризующая функ-
ции хр+1 = Xi, Хр+2 = х2, Хр+з =х| и т.д., после чего коэффициенты но-
вого «расширенного» линейного полинома определяют по формулам (3.3) —
(3.14).
Для практических целей, как правило, ограничиваются квадратичной
формой. Как указывалось выше, при достаточно большом числе обраба-
тываемых опытных данных (и > 500) и числе факторов р> 10 повышение
степени полинома становится невозможным, так как эта задача находится
за пределами возможностей современных больших ЭВМ, если не исполь-
зовать процедуру, предложенную академиком Чебышевым, о которой бу-
дет сказано в гл. iy.
Другой формой проведения нелинейного регрессионного анализа
является использование так называемых «внутренне линейных» форм
уравнений, т.е. форм, которые легко линеаризуются логарифмированием
или другим преобразованием. К таким моделям относится прежде всего
[43] мультипликативная модель:
у = Z>ox?1 х22 ... хД. хьрр; (3.43)
логарифмируя это уравнение по основанию е, переводят его в линейную
форму:
In у = 1пй0 + bi Inxi + b2 lnx2 + ... + (3 44)
+ bj 1 nxj + ... + bp In xp .
Далее производят замену переменных: у’ — In у, bo =1п Ло, х[ =ln xIf х2 =
= in х2 и т.д. Затем выполняют все операции множественного линейного
регрессионного анализа. В конце расчетов производят только одно обрат-
ное преобразование для получения величины Ьо.
Другим примером внутреннелинейных форм уравнений являются
следующие экспоненциальные модели:
73
1) у = exp (&0 + ^1*1 + + - + bjXj + ... + bpXp),
In у =b0 + btXi + b2x2 + ...+ b/Xj + ... + bpxp;
2) у = b0 exp bi exp b2 ... exp bj ... exp bpy
Iny =ln bo + biXi + b2x2 + — + bjXj + ... + bpXp',
3) у = ------------------------------------—
1 + ехр(&0+Л1%1+й2х2+...+bjXj+,..+bpXp)
ln(x- — 1)= bQ + biXi + b2x2 + ... + b/Xj + ... + bpXp .
Наконец, можно упомянуть об обратной модели:
_____________________1________________
? b0 ♦ biXi + b2x2+...+bjXj + ... + ЬрХр ’
i = b0 + biXi + b2x2 + ... + bjXj + ... + bpXp .
(3.45)
(3.46)
(3.47)
(3.48)
(3.49)
(3.50)
(3.51)
(3.52)
Таким образом, ясно, как вычислить коэффициенты регрессии в при-
веденных выше моделях. Например, для уравнения (3.46) достаточно вы-
числить вектор-столбец In у, затем решить систему нормальных уравнений;
аналогично, для модели (3.52) следует перед решением системы нормаль-
ных уравнении вычислить вектор-столбец значений 1 (у.
Мерой тесноты связи в Нелинейной зависимости служит множествен-
ное корреляционное отношение, которое вычисляют по формуле (3.37),
но используя, для вычисления у нелинейную форму уравнения. Сравнение
множественного корреляционного отношения с коэффициентом множест-
венной корреляции, вычисленным по линейной форме, дает некоторое
представление о «кривизне» изучаемой зависимости.
Следует отметить одно важно обстоятельство. В гл. I было дано поня-
тие о результатах неравноточных наблюдений, т.е. результатах, полученных
на разных приборах, разных испытательных машинах и т.д. Оказывается,
что такие наблюдения можно объединить в одну матрицу исходных данных,
если ввести фиктивную переменную. Фиктивная переменная имеет два зна-
чения: 0 или 1. Число фиктивных переменных на единицу меньше числа
использованных приборов, литературных источников и тд. Значимость
фиктивного фактора (проверяемая по r-критерию) говорит о значимости
различий между наблюдениями, выполненными разными способами. Если
фиктивный фактор окажется незначимым, то все наблюдения можно счи-
тать равноточными, что позволяет использовать эти наблюдения совместно
при проведении множественного регрессивного анализа.
§ 3.5. Выбор оптимальной формы уравнения регрессии
в множественной ситуации. Различные методы
решения задачи
Для выбора оптимальной формы регрессии было бы лучше всего
просто вычислить на ЭВМ коэффициенты всех возможных уравнений
регрессии, как это делалось при парном анализе, а затем выбрать «луч-
74
шее» уравнение по минимальной остаточной дисперсии или значению коэф-
фициента множественной корреляции, однако такая постановка решения
задачи не всегда реальна.
Рассмотрим простой пример. Имеется вектор-столбец наблюдений
функции отклика у, которая зависит от четырех факторов: х2, х3 и
х4. Запишем все возможные формы только линейных*уравнений регрессии
для этого случая:
1) У + bxxi;
3)у = й0 + Ь3х3 ;
5) У = Ьо + b^xi + Ь2х2
7) у = Ьо + biXi + Z>4x4;
9) у - b0 + Ь2х2 + Ь4х4;
11) у=Ь0+ biX! + Ь2х2 + Ь3х3;
13) у = Ьо + Ь\ХХ + Ь3х3 + Ь4х4;
15) у - Ьо + £>1*1 + Ь2х2 + Ь3х3 + Ь4х4-}
2) у = Ьо + Ъ2х2;
4) у = Ьо + Ь4х4;
6) у = Ьо + biXi + b3x3',
8) у=Ь0 + Ь2х2 +Ь3х3-,
10) у =Ь0 + Ь3х3 + Ь4х4\
12) у -Ьо + biXi + Ь2х2 + Ь4х4
14) у = Ьо + Ь2х2 + Ь3х3 + Ь4х4
16) у = Ь0 или у =у.
Общее число уравнений в этом случае равно 16 (р = 4; 2₽ = 16).
Простой подсчет показывает [43], что уже при р = 10 число возмож-
ных линейных вариантов уравнений составит 210 = 1024. Если вспомнить
еще о нелинейных формах уравнений, то чисто техническая трудность ре-
шения такой задачи понятна, однако имеется еще одна трудность. Может
оказаться, что для нескольких уравнений показатели S^, R2 одинаковы,
тогда возникает вопрос, какое из уравнений выбрать. Аналогично, показа-
тели статистической оценки значимости двух факторов также могут быть
одинаковы.
Для решения вопроса о том, какой фактор следует Предпочесть, ис-
пользуют прежде всего формальные методы. Вычисляются парные коэф-
фициенты корреляции гуХ}., частные коэффициенты корреляции, /-критерии
Стьюдента для каждого фактора. Можно еще построить два’ частных урав-
нения регрессии, в которые входили бы только сравниваемые факторы:
У = bo + bjXh у = Ьо + Ьтхт, (3.53)
- и затем вычислить остаточные дисперсии S^. и частные /^-критерии Фи-
шера для каждого из уравнений.
Таким образом, для сравнения важности факторов имеются пять пока-
зателей: 1) коэффициенты парной корреляции между функцией отклика
и изучаемым фактором; 2) частные коэффициенты корреляции; 3) /-кри-
терии Стьюдента; 4) остаточные дисперсии 3^', 5) частные F-критерии
Фишера.
Вероятность того, что все эти критерии для двух сравниваемых факто-
ров одинаковы практически, равна нулю. Однако ситуация, когда по неко-
торым критериям кажется более предпочтительным первый фактор, а по
другим, наоборот, второй, встречается довольно часто. В этом случае можно
предложить суммирование результатов. Пусть, например, при решении
задачи было получено, что:
75
xj xm
ryxj = 0,3 5; гУхт ~ 0’^8;
rчасти ~ 0,44^ f части “ 0,41,
^bj = 2,56; *ът = 2,70;
&т = 184; gCT = 190;
A-4,65; Я =4,73.
Перед сложением оба значения S^. целесообразно вычесть из какого-
либо постоянного числа, например из 300, и результат разделить на 100.
Имеем: 300 - 184 = 116: 100 = 1,16; 300 - 190= 110 : 100 = 1,10. Скла-
дывая результаты, получаем: Sy = 9,16, Sm = 9,45. Следовательно, второй
фактор предпочтительнее, однако эта процедура малоэффективна.
Решающее значение при выборе того или иного фактора (в том случае,
когда при введении их в уравнение регрессии получают одинаковые оста-
точную дисперсию и коэффициент множественной корреляции) имеют
физико-химические или даже интуитивные представления о важности этих
факторов.
В литературе [43, 46] рассмотрены различные методики проведения
множественного регрессионного анализа. Однако все они, по-видимому,
могут быть сведены к трем разновидностям: 1) методу всех регрессий;
2) методу исключения переменных; 3) методу включения переменных.
Метод всех регрессий достаточно подробно описан выше. Кроме того,
как уже указывалось, технически он может быть использован при неболь-
ших значениях п (числе опытов) и р (числе факторов).
Целесообразно более подробно остановиться на двух последних мето-
дах. При использовании метода исключения переменных уравнение регрес-
сии расширяют сразу до полной квадратичной или, если возможно, до
полной кубической формы. Однако необходимо помнить, что расширению
модели должны предшествовать предварительная обработка результатов
наблюдений (см- гл. I), построение линейной модели, вычисление парных
и частных коэффициентов корреляции, предварительное исключение одного
из сильно коррелированных факторов, вычисление остаточной дисперсии
5^ст, коэффициента множественной корреляции R и F-критерия Фишера
по линейной модели.
Исключение начинают с фактора, имеющего наименьший критерий
Стьюдента. На каждом этапе после исключения каждого фактора для но-
вого уравнения регрессии вычисляют множественный коэффициент корре-
ляции, остаточную дисперсию и F-критерий Фишера. Наибольшую трудность
представляет решение вопроса, на каком этапе прекратить исключение
факторов. Здесь возможны следующие подходы:
1) прекратить исключение факторов, когда остаточная дисперсия
начнет увеличиваться;
2) назначить уровень значимости р % при вычислении /-критерия Стью-
дента для последнего оставляемого фактора.
Во втором случае целесообразно перед началом отсева факторов по-
строить диаграмму ранжирования /-критериев Стьюдента для всех факто-
76
ров и эффектов (совместных факторов)
расширенной модели. Практика показывает,
что при этом могут встретиться диаграм-
мы трех типов (рис. 12). Если имеет
место диаграмма первого типа, то момент
прекращения отсева факторов определить
легко. Он соответствует скачку в диаграм-
ме (рис. 12, а, б, в).
Диаграмма второго типа характеризует-
ся тем, что если соединить середины верх-
них концов столбиков, то получается экспо-
нента. По этой диаграмме (с меньшей уве-
ренностью) также можно определить, где
следует закончить отсев факторов.
Диаграмма третьего типа, у которой в
результате соединения середин верхних
концов столбиков получается прямая, не
дает информации о моменте окончания от-
сева факторов. В этом случае для прекра-
щения отсева назначают предельный уро-
вень значимости при вычислении Г-крите-
рия Стьюдента для факторов, остающихся
в модели р — 5 %. Рис-12
Если теперь рассмотреть метод включения факторов, то можно от-
метить, что его основные принципы уже изложены выше. Действительно,
при использовании процедуры включения факторов, важнее всего знать,
какой из них является наиболее предпочтительным, т.е/ ’какой фактор
включить в модель в первую очередь. Подробно процедура метода вклю-
чения изложена в [43] : на первом этапе выбирают фактор, у которого
гух^ наибольший (предположим, что это Лл), и строят линейное уравнение
= / (xj). Затем вычисляют частный коэффициент корреляции. В матема-
тическом отношении это эквивалентно вычислению корреляции между ос-
татками е( от регрессии у = / (хг) и регрессии х;- = (xi), которая факти-
чески не определяется. Затем выбирают величину Ху (предположим, что это
х2), которая отличается наибольшим частным коэффициентом корреляции
с функцией отклика .у, и находят второе уравнение регрессии у =/(XjX2)
ИТ. д.
При использовании метода включения переменных также проводят
все перечисленные выше предварительные вычисления для метода исключе-
ния переменных, кроме расширения модели. Основным критерием для
определения порядка включения факторов является, как отмечалось выше,
значение частного коэффициента корреляции, поэтому метод включения
используют в основном при построении линейных или внутреннелинейных
моделей (мультипликативных, обратных, экспоненциальных).
Для квадратичных форм и форм высших порядков частные коэффи-
циенты корреляции вычислить невозможно, для этих моделей применяют
метод исключения факторов.
77
При проведении множественного регрессионного диализа методом
включения факторов операции на ЭВМ целесообразно выполнять в следую-
щем порядке:
1) построить линейную модель;
2) построить матрицу коэффициентов парной корреляции;
3) вычислить частные коэффициенты корреляции;
4) вычислить критерии для оценки качества предсказания результатов
опыта полной линейной моделью (Л, R2, S2,^);
5) построить линейную модель с одним фактором, у которого част-
ный коэффициент корреляции наибольший;
6) вычислить R, R2 и 5^. для полученной в п. 5 модели.
Если для двух или нескольких факторов получены одинаковые част-
ные коэффициенты корреляции, то для определения порядка включения
факторов вводят в действие описанную выше процедуру сравнения факто-
ров по пяти критериям. Включение факторов продолжают до тех пор,
пока R, R2 и S2^ полученных моделей улучшаются, и может быть закон-
чено, когда включение нового фактора приводит к незначительному увели-
чению R, R2 и уменьшению S2^ или даже к ухудшению этих показателей.
§ 3.6. Примеры множественного регрессионного анализа
Метод исключения эффектов (факторов и парных взаимодействий)
можно рассмотреть на примере построения модели для вычисления пол-
зучести бетона [78], исходные данные которой приведены в § 3.2. В этой
задаче строилась зависимость удельных относительных деформаций ползу-
чести бетона С(;г Г) от девяти факторов: хь х3, х4, х5, х6, х7, х8, х9, xi0.
Расшифровка факторов дана в § 3.3. На первом этапе на ЭВМ была построе-
на полная квадратичная модель с 54 эффектами вида
y=bQ + &iXi + b2x2 + ... +ЬрХр + bx lx] + Ь22х2 + ... + ЬррХр +
+ Z>i2xix2 + bi3xxx3 + ....
j =-3518,754 +7,798Xi + 10,888x3 + 179,306x4 + 10,434x5-
—l,229x6 + 0,268x7 + 287,590x8 + 5,442x9 - 12,OO3xio - 0,562x? -
—0,125xiX3 — 0,309xiX4 — 0,013x3 — 0,017x3x4 + 0,071x4 - 0,036xiX5 -
— 0,0007xi x6 — 0,003xi x7 — 0,062x3xs + 0,004x3x6 + 0,0002x3x7 —
— 0,438x4xs — 0,016r4x6 + 0,0003x4x7 — 0,010xtx8 — 0,051xiX9 + (3.54)
+ 0,087xiXi о — 0,177x3x8 + 0,004x3x9 - 0,001x3Xi 0 — 4,377x4x8 —
— 0,057x4x9 — 0,102r4Xi 0 — 0,017x| - 0,010x5x6 — 0,003x5x7 +
+ 0,0009xi - 0,00005x6x7 — 0,00003x7 + 0,115xsx8 — 0,024x5x9 +
+ 0,010x5Xi о + 0,063x6x8 + 0,001x6x9 — 0,001x6Xi 0 + 0,004x7x8 +
+ 0,0002x7x9 — 0,0005х7хю — 0,083х| — 0,145x8x9 + 0,503х8Хю +
+ 0,002x9 + 0,0004x9Xi o + 0,0002xiO;
критерий Фишера для этой модели
F = 4506,774/1489,286 = 3,026 > FT = 1,02.
78
Затем был произведен 11-ступенчатый отсев незначимых эффектов, в про-
цессе которого было исключено 28 статистически незначимых по г-крите-
рию Стьюдента эффектов, в результате была получена модель с 26 эффек-
тами:
f у =-6411,454+З.9б8х3 + 137,328*4 + 9,223xs + 0,371х7 + 473,002х8 -
-5,915х1О — 0,460*1 —0,107*1*3 +0,074*3 — 0,002*i*7' —
- 0,065*3*5 + 0,004*з*6 ~ 0,334*4*5 + 0,001*6 — 0,070*7*ю - (3.55)
- 3,007*4*8 ~ 1,122*4*1 о - 0,018*5*6 - 0,00002*7 + O,OO7xsxlo +
+ 0,0003х7*9 - 0,0006*7*ю - 10,653*1 - 0,039х8*9 + 0,285*8*, 0 + 0,003*|;
F =4506,774/1483,727 = 3,038 >FT = 1,02.
После дешифровки уравнение (3.55) приняло вид
С(ЛТ) = [-64! 1,454 + 3,968^ + 137,328М + 9,223 (В/Ц) + 0,371 (1т) +
+ 473,002 НГ - 5,915£з - 0,460(Ц/3)2 - 0,107(Ц/3) W + 0,074(Л/)2 -
- 0,002(Ц/3)(Г-т)—0,065И/(В/Ц)+0,004И/г 0,334Л/- (В/Ц) + 0,070(Ц/З)^ -
- 3,007 ЛЦНГ) - 1,122AFЕ3 - 0,018 (В/Ц)т + 0,001 (т)2 - 0,00002 (г-т)2 +
+ 0,007 (В/Ц)£3 + 0,0003(т - т) а - 0,0006(г - т)Е3 - 10,653 (НГ)2 -
- 0,039 (НГ) а + 0,285 (НГ)Е3 + 0,003 (а) 2 ] • 1 (Г 7; (3.56)
F-критерий Фишера уравнения (3.50) увеличился незначительно (F =
= 3,038), другие показатели оказались хорошими (R = 0,840, R2 - 0,706).
Уравнение (3.56) имеет явно нелинейный характер. Из 26 оставшихся
в уравнении эффектов линейные только 6.
В табл. 3.4 приведены пределы вариации у, *;- в матрице исходной ин-
формации, а также пределы, в которых рекомендуется использовать фор-
мулу (3.55).
Лучше всего любое уравнение регрессии предсказывает в центре фак-
торного пространства с координатами Yf. По мере удаления от этого центра
Таблица 3.4
Пределы вариации у, Xj
С (t, т) ц/з W М В/Ц т t-r НГ а Ез
Единица величины (МПах х Ю)4 % % М’101 % сут сут % МПах х 10 МПах х Ю"2
Пределы измене- 7,5 5,5 35 27 1 6 3800 24 16,6 300
ния факторов в исход- ном материале 480 34,5 105 80 105 365 28 250 900
Пределы, в кото- min 14 50 10 40 14 14 24 24 320
рых рекомендуется max 25 90 20 70 115 1700 27,5 110 570
иедользовать форму-
лу (3 155)
* Числа первого столбца таблицы следует умножить на 10 7.
79
качество предсказания ухудшается. При очень большом Удалении с помо-
щью уравнения регрессии можно получить нелепые результаты. Как видно
из табл. 3.4, пределы, в которых рекомендуется использовать формулу
(3.55), определены с большой осторожностью, и они значительно меньше
пределов изменчивости факторов в исходном экспериментальном материа-
ле. Однако и указанная величина интервала достаточна для практического
применения формулы (3.55),
Метод включения факторов использован в работе [158], в которой
исследовано влияние 22 факторов на усадку (уменьшение объема с тече-
нием времени) цементно-песчаных растворов. Окончательно сохранено
8 факторов, и линейное уравнение регрессии имеет вид
у= — 234,7 + 144х2 - 486х7 - 1465xi 0 + 218%! 2 + 5,68а1] 3 +
+ 5,46a'iS - 13,3х18 + 164х22, (3-57)
где у — относительные деформации усадки цементно-песчаного раствора
(Еу 10е); х2 — суммарное содержание щелочей, приведенное к экви-
валентному содержанию Na2O(R2O), %; х7 — структурный коэффициент
Шейнина (Л),
к = (0,5С35 + 0,2C25)/(0,75C3S + C2S);
X] 0 — максимальная крупность песка, соответствующая полному остат-
ку на сите < 5 % (атах), м-103, х12 — модуль крупности песка (Мкр);
X] 3 — коэффициент поверхности песка (A:1I(jB); X] s — расход воды в смеси
(В), л/м3;х18 — влажность воздуха в лаборатории (0), %; х22 — разница
между фактическим и оптимальным содержанием серного ангидрида
(ASO3 = |SO3 - SO2nTl), %.
Уравнение (3.57) приведено для иллюстрации возможностей регрес-
сионного анализа, а также для иллюстрации того обстоятельства, что в ка-
честве факторов иногда можно использовать достаточно сложные функции.
Вычисленное для уравнения (3.57) F-отношение равно 3.71 и значительно
превышает границу значимости.
Множественный корреляционный и регрессионный анализы при их
умелом использовании являются мощным аппаратом познания явлений
природы и общества.
§ 3.7. Методика отыскания комбинаций значений факторов,
максимизирующих и минимизирующих функцию отклика
Нелинейное уравнение регрессии можно использовать для решения
очень важной задачи, часто встречающейся в естественно-научных иссле-
дованиях. Задача состоит в отыскании максимума и минимума той или
иной функции отклика.
Для определения типа многомерной поверхности следует квадратичное
уравнение регрессии привести к канонической форме.
Встречаются следующие многомерные поверхности [102] ;
1) поверхности, имеющие один экстремум — максимум или мини-
мум; в этом случае все коэффициенты канонической формы имеют оди-
наковый знак, центр фигуры находится вблизи центра эксперимента;
80
2) поверхности типа минимакса — коэффициенты канонической формы
имеют разные знаки, центр фигуры расположен вблизи центра экспери-
мента;
3) поверхности типа возрастающего возвышения («гребня») — центр
фигуры удален от центра эксперимента, часть коэффициентов каноничес-
кой формы близка к нулю.
После определения формы многомерной поверхности, если окажется,
что исследуемая поверхность относится ко второму или третьему классу,
можно попытаться отыскать условный максимум и минимум. Если для
проведения этих операций воспользоваться, например, уравнением регрес-
сии (3.58), то целесообразно условный экстремум искать в пределах ги-
перпространственной сферы с радиусом, равным y/S2., и центром в точке
с координатами xj. Для нахождения условного экстремума в заданной
области факторного многомерного пространства можно воспользоваться
методом перебора всех комбинаций независимых переменных, при этом
переменные на интервале варьирования квантуют произвольно.
Полином второго порядка при р переменных вида
у =Ъ0 + + Ь2х2 + ... + ЬрХр + bi ixj + b22x2 + ... + ЬррХ2 +
+ b12XiX2 + Wi*3 + -
можно представить в канонической форме:
Y-YS = B21X2, + B22Xl + ... + Bl>pXj. (3.58)
Если обозначить а0 = Ьо - у, За? = bj,3ajm = bjm, ajj = bjj, то уравнение
(3.42) принимает вид
До + £ ЗарС} + £ 2ajmXjXm + £ UjjxJ = 0. (3.59)
/ = 1 /, «i=i i = i
Чтобы преобразовать это уравнение к канонической форме, составляют
характеристические уравнения вида
2 Хр~г /г = 0, г = СКр, (3.60)
где 1Г — инварианты поверхности (некоторые функции коэффициентов
aj, ajmt Иц, не меняющие значения при переносе начала координат и повороте
осей). Отметим, что 1р равен взятой с множителем (— I)2 сумме всех
(Р) главных миноров определителя, составлено из коэффициентов д/;- и
а^т. Корни характеристического уравнения 1, Х21, ..., Хр являются коэф-
фициентами при новых переменных Л) в канонической форме.
Координаты центра
YS =f(Xls,X2s,..., xps) (3.61)
определяют из системы уравнений
£-=(),/=Ё£, (3.62)
дх1
81
или, что то же самое,
ZaijXj+ 01 =0,
/
2 a2fXf + а2 = О,
i
2 OpjXj + Op = 0. (3.63)
/
Каноническая форма имеет вид
У-У5 = 2Х.Л?. (3.64)
/
Новые переменные Xj связаны со старыми Xj следующими соотноше-
ниями:
Xj=T,CjmXj. (3.65)
Коэффициенты Cjm определяют из системы нормированных уравнений,
включающих значения корней X/ характеристического уравнения. Эти
операции обычно выполняют на ЭВМ.
Таблица 3.5
Матрица коэффициентов при парных взаимодействиях уравнения (3.55)
Код Х1 *3 *4 Xs *6 *7 *8 *9 *10
*1 -0,460 -0,214 0 0 0 -0,004 0 0 +0,140
*3 0 0 -0,130 +0,008 0 0 0 0
*4 +0,074 -0,668 0 0 -6,014 0 -0,244
0 -0,036 0 0 0 +0,014
+0,001 0 0 0 0
Хд -0,00002 0 +0.0006 -0,0012
*8 -10,653 -0,078 0,570
*9 +0,003 0
*10 0
Порядок выполнения операций покажем на примере приведения к ка-
ноническому виду уже знакомого уравнения (3.55). На первом этапе сос-
тавляем матрицу коэффициентов при парных взаимодействиях факторов
уравнения (3.55) (см. табл. 3.5). Все элементы матрицы, кроме диагональ-
ных, удваиваем.
Нулевые значения в ячейках табл. 3.5 поставлены там, где коэффициен-
ты при парных взаимодействиях статистически незначимы. Опыт пока-
82
зал, что можно было бы учесть и незначимые по Меритерию коэффициенты
и это мало изменило бы результат вычислений. Расчеты можно провести,
учитывая и не учитывая незначимые коэффициенты, а затем полученные
результаты проанализировать и выбрать лучший (с точки зрения иссле-
дователя) .
Далее составляем систему уравнений в частных пройзводных:
—0,92Qxi — 0,107х3 — 0,002х7 + 0,07Qxi о = О,
3,968 - 0,107X1 - 0,065xs + 0,004х6 =0,
137,328 + 0,148X4 - 0,334х5 - 3,007х8 - 0,122X10 =0,
9,223 — 0,065х3 — 0,334xs — 0,018х6 — 0,007xi 0 =0,
0,004 - 0,01 8х5 + 0,002х6 =0,
0,371 - 0,002xj - 0,00002х7 + 0,0003х9 - 0,0006xi 0 =0,
483,002 - 3,007x4 - 21,306х8 - 0,039х9 + 0,285хХ0 =0,
0,0003х7 - 0,039х8 + 0,006х9 =0,
-5,915 + 0,07Qxi - 0,122X4 + 0,007xs - 0,0006х7 + 0,285х8 =0.
Решая систему, находим координаты центра: хх = 26,10; х3 = 13,09; х4 =
= 17,43; х5 = 36,91; х6 = 306,00; х7 = 2083,02; х8 = 25,28; х9 =60,19;
х10 =422,56. По формуле (3.51) вычисляем Y$ = 11,285.
Уравнение регрессии в канонической форме имеет вид
У - 11,285 = - 0,59 АГ? + 0,18 + 2,96 Х24 - 0,20 Xj + 0,002 Xj -
- 0,0002 Х$ - 13,37 Xl + 0,004 Xl - 0,034 Xj 0, (3-66)
где новые переменные Xопределяются следующими уравнениями:
Xi =0,88xi + 0,35х3 — 0,06х4 + 0,15xs + 0,0045х6 +
+ 0,0Q55x7 + 0,02xs + 0,0028х9 — 0,26xi о,
Х3 = —0,32X1 + 0,70х3 + 0,023х4 — 0,46х5 + 0,12х6 +
+ 0,0097х7 — 0,04х8 + 0,01 5х9 — 0,42хх 0,
Х4 = -0,006xi - 0,008х3 + 0,88х4 + 0,20xs - 0,002х6 +
+ 0,0001х7 — 0,40х8 + 0,104х9 — 0,15xi 0,
Х5 =—0,33X1 + 0,18х3 — 0,20х4 + 0,82xs + 0,14х6 —
—0,0087х7 + 0,096х8 + 0,04х9 — 0,34хю,
Х6 = 0,066xi - 0,124х3 + 0,020х4 - 0,05 5х5 + 0,83х6 -
—0,26х7 - 0,0068хв - 0,47х9 + 0,021X10, • (3-67)
Хг = -0,0099х! - 0,049х3 + 0,0008х4 - 0,005xs + 0,19х6 +
+0,96х7 + 0,Q0007x8 — 0,18х9 — 0,015xi 0,
Хя = 0,00034хг - 0,00019х3 + 0,41х4 - 0,0204х5 - 0,00006х6 -
— 0,00005 Зх7 + 0,91х8 + 0,005х9 — 0,031хх о,
Х9 = 0,054xi — 0,088х3 + 0_,0077х4 — 0,057xs + 0,48х6 +
+ 0,064х7 — 0,008х8 + 0,86х9 + 0,047X10,
Хю = —0,029X1 + 0,57х3 — 0,09х4 + 0,20xs + 0,08х6 — 0,024х7 —
- 0,008х8 — 0,016х9 + 0,78xi 0.
83
Каноническое уравнение (3.66) имеет члены, близкие к нулю; сле-
довательно, оно описывает в многомерном пространстве фигуру третьего
типа (типа «гребня»). Характер полученного канонического уравнения
дает возможность перейти к анализу уравнения регрессии (3.55) методом
квантования переменных.
Квантование переменных выполняем следующим образом (см. табл.
3.4):
X! (Ц/З) - 14; 16,2; 18,4; 20,6; 22,8; 25;
х3 (ИО - 50; 58; 66; 74; 82; 90;
х4(Л1) - 10; 12; 14; 16; 18; 20;
х5 (В/Ц) -40; 46; 52; 58; 64; 70;
х6 (т) -14,0; 34,2; 54,4; 74,6; 94,8; 115,0;
х7 (Г - т) - 14,0; 351,2; 688,4; 1025,6; 1362,8; 1700,0;
х8(НГ) -24; 24,7; 25,4; 26,1; 26,8; 27,5;
х9 (о) -24; 41,2; 58,4; 75,6; 92,8; ПО;
хю (£3) -32°; 37°; 42°; 47°; 52°; 57°-
Исходя из физических представлений о сущности явления, можно сле-
дующим образом характеризовать влияние факторов на удельные относи-
тельные деформации ползучести бетона:
1) с уменьшением влажности среды W увеличивается C(t гу,
2) с уменьшением размеров образца (масштабного фактора М) Т)
увеличивается;
3) с увеличением В/Ц увеличивается ту,
4) $ течением времени (г - г) увеличивается C(f> ту}
5) с уменьшением НГ увеличивается C^t Tyt
6) с увеличением Е3 уменьшается C(t,rY>
7) с увеличением Ц/З увеличивается C(f> ту,
8) с увеличением напряжений и увеличивается C(f> гу
9) с увеличением возраста бетона т уменьшается
При расчете на ЭВМ перебирают все возможные комбинации кванто-
ванных значений факторов. Число комбинаций определяется формулой
m — г/, где п — число квантов в интервалах варьирования факторов,/ -
число факторов. На печать выводят максимальные и минимальные значе-
ния функции отклика и максимизирующие и минимизирующие значения
факторов. Приведем результаты решения: 1) максимизирующие значения
факторов: W = 50 %, М = 10 мЮ2, В/Ц = 70 %, (t - г) = 1700 сут, НГ =
= 24 %, Е3 = 570 МПа-1(Г 2, Ц/З = 25 %, а = 110 МПа-10, т = 14 сут, макси-
мальное значение функции отклика т) = 182,68-10’ 7 (МПа-10)’1;
2) минимизирующие значения факторов: W = 90 %, М = 20 М-102,
В/Ц = 40 %, (г - т) = 14 сут, НГ = 27,5 %, Е3 = 570 МПа-10’2, Ц/З = 14 %,
а = 24 МПа-10, т = 115 сут, минимальное значение функции отклика
C(fjT) = 33,10-Ю’7 (МПа-10)’1.
84
Таким образом, полученное математическое направление действия
факторов точно соответствует изложенным выше физическим представ-
лениям.
§ 3.8. Алгоритмы и укрупненные блок-схемы алгоритмов
множественного корреляционного и множественных
регрессионных анализов, выполняемых методом
исключения и методом включения переменных
Анализ методом исключения переменных включает следующие опе-
рации:
1) предварительную обработку исходных данных (см. формулы гл. I) ;
2) построение линейной многофакторной модели [формулы (3.3) —
(3.14)];
3) проверку статистической значимости факторов и, модели в целом
[формулы (3.15)-(3.19)] ;
4) вычисление коэффициентов парной корреляции [формулы (3.20)-
(3.27)] и проверку их значимости [формулы (3.28) —(3.31)] ;
Рис. 13
Рис. 14
85
5) вычисление частных коэффициентов корреляции и проверку их
значимости (формулы (3.33) и (3.34) ] ;
6) вычисление множественных коэффициентов корреляции и детерми-
нации и проверку их значимости [формулы (3.35) — (3.41) ] ;
7) построение квадратичной формы [формула (3.42) ];
8) ступенчатый отсев незначимых факторов с вычислением на каждой
ступени характеристик 5^, ft, R, R2 нового уравнения;
9) выбор момента прекращения отсева;
10) исследование окончательного уравнения регрессии (см. п. 3).
При анализе методом включения факторов пункты с 1-го по 6-й вклю-
чительно предыдущей методики можно сохранить. Отличия начинаются с
7-го пункта:
7а) выбор первого фактора для включения в модель (3.21);
8а) включение факторов в разных комбинациях с вычислением на каж-
дой ступени характеристик F, R, R2 нового уравнения;
9а) исследование окончательного уравнения регрессии (п.З).
Укрупненные блок-схемы алгоритмов приведены на рис. 13 и 14.
Глава IV
ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ О ПОСТРОЕНИИ
ЭМПИРИЧЕСКИХ ЗАВИСИМОСТЕЙ ПО ОПЫТНЫМ ДАННЫМ
§ 4.1. Предварительные соображения
На первом этапе ознакомления с методикой обработки экспериментальных
данных и построения эмпирических формул по результатам традиционных
«пассивных» экспериментов достаточно изучить материал первых трех
глав настоящего пособия.
Желающим глубже изучить этот вопрос необходимо ознакомиться и с
материалами данной главы, в которой изложены некоторые специальные
аспекты и методы построения эмпирических зависимостей по эксперимен-
тальным данным.
§ 4.2. Построение нелинейных эмпирических зависимостей
с использованием ортогональных полиномов Чебышева
(параболическое интерполирование)
Выше указывалось, что аппроксимирующий нелинейный полином вида
у = До + aix + а2х2 + ... + д3х3 + ... + (4.1)
может быть любой степени, но при построении полинома высоких степе-
ней ошибки округления начинают играть заметную роль.
Более существенно то, что при каждом повышении степени полинома
приходится не только вычислять новый коэффициент, но и пересчитывать
все остальные коэффициенты. Пусть, например, по экспериментальным
данным построен полиному = а0 + агх + а2х2. Для того чтобы построить
полином вида у = а0 + aix + а2х2 + а3х3, необходимо не только вычис-
лить коэффициент а3, но и пересчитать а0, at и а2.
Способ Чебышева позволяет значительно упростить этот процесс [37] .
Аппроксимирующий многочлен строится в виде суммы повышающих сте-
пеней, причем добавление новых слагаемых не изменяет вычисленных ранее
коэффициентов. Прибавляя таким образом член за членом к многочлену,
можно наблюдать, как убывает остаточная дисперсия; таким образом, об-
легчается и процесс выбора степени многочлена.
Рассмотрим построение парной нелинейной зависимости. Исходными
данными являются два вектор-столбца п наблюдений х и у. Требуется по-
строить нелинейный параболический полином степени т с числом неиз-
87
вестных коэффициентов т + 1. При этом, как правило, т < п. Сущность
способа Чебышева состоит в том, что аппроксимирующий многочлен отыст
кивают не непосредственно в виде суммы степеней х, а в виде комбинации
многочленов, которые выбирают специальным образом.
Можно записать [37] искомый многочлен в виде
У =аоФо (х) + <?i0i (х) + ... + атфт(х), (4.2)
где 0о(х) = 1, (х) — х + аг ... и вообще 0/ (х) - многочлен степени / вида
0/(х) =xl + afl) х1 1 + ... (4.3)
со старшим коэффициентом, равным единице. Способ построения этих
многочленов рассмотрен ниже.
Если предположить, что многочлены уже построены, то можно отыски-
вать значения коэффициентов а0, ах, а2, а3.ат. Для этого, как и в гл. II,
по принципу Лежандра необходимо найти минимум функции:
U= J2 - [аофо (ху) + (цфг (ху) + ... + атфт (ху) ]j 2. (4.4)
Вычисление частных производных функции U по всем коэффициентам
а0, ai, а2, ..., ат дает возможность построить систему нормальных уравне-
ний метода наименьших квадратов [37] :
аоЪ [0О (ху) ] 2 + ai 20о (ху) 01 (ху) + а2 20о (х,)02 (ху) + ... +
+ От 20о (х/)Фт (Ху) = ЪУ1ф0 (Ху) ,
<7OS0O (х,)01 (Ху) + 01 2 [01 (Ху) ] 2 + а2 ЪФ1 (х/)0з (Ху) + ... +
+ ага20! (ху)фш (ху) = Syy0i (ху),
aoS0o (ху)0/ (ху) + 01 201 (Ху)0у (Ху) + ... + ау2 [0/(ху) ]2 +
+ ... + От £ф1 (Х()фт (Ху) = (Ху) ,
й0 S0o (Ху)0га (Ху) + 01 201 (ху)0т (ху) + ... + От 2 [Фт (Ху) ] 2 —
= 2j'y0w (Ху).
Решая эту систему, можно получить значения коэффициентов полинома
(4.2). Многочлены 0о(х), 0i(x), ..., фт (х) следует выбирать так, чтобы
можно было упростить систему (4.4а). Для этого необходимо подобрать
многочлены, удовлетворяющие условиям
20/ (ху)0л(ху) = 0, I Фк,
2 [0z (ху) ] 2 * 0, I = 0, т. (4-5)
Последнее означает, что хотя бы в одной из точек ху, i = 1, п, многочлен
0/(х) =#= 0. Такие многочлены называют ортогональными многочленами
Чебышева.
Понятие ортогональности — это экстраполяция понятия перпендикуляр-
ности векторов на плоскости в многомерное пространство. При выполне-
нии условий (4.5) в левой части каждого из уравнений системы (4.4)
88
остается только один член, так что сразу можно написать выражение для
искомых коэффициентов
1 ^1Ф1(х()]г
где I = 0, т.
Теперь следует убедиться, что условия (4.5) выполнимы, и найти
соответствующее им выражение для ортогональных многочленов Чебы-
шева при заданных точках хг-.
Ранее было принято Фо(х) = 1. Из условия (4.5), полагая I = 0, к = 1
для многочлена ф\ (х), получаем
S0i(x/)=O. (4.7)
Так как ф\(х) = х + «1 (см. формулу (4.2)), то условие (4.7) переписы-
ваем в виде
S (х/ + СЦ ) =0.
Откуда
Sx, + =0, или = — (1/«)2хг-. (4.8)
Нетрудно заметить, что это среднее значение х с противоположным знаком:
«1 = -х. Окончательно получаем
Ф1(х) =х —(1/я) Sx,. (4.9)
Для построения многочлена ф2(х) необходимо положить в условиях
(4.5) последовательно I = 0, к — 2 и затем I = 1 ,к = 2. В результате полу-
чаем два уравнения:
1Еф2(Х{) = 0,
\Ui(.Xi^2(xi) =0, (4.10)
где ф2(х) — многочлен второй степени со старшим коэффициентом, рав-
ным единице. Этот многочлен можно записать в виде
ф2(х) = (х+02)0х(х) + у2Фо(х), (4.11)
где фо (х) = 1.
Подставим выражение (4.11) в систему (4.10):
ГSx,-0i (xj) + 02 Еф1 (х^ + пу2 =0.
ISx, [фх(х0] 2 + 02S[0i(xI)]2 + 72S0i(x/) =0. (4‘12'
Учитывая выражение (4.7), запишем формулы (4.12) в виде
fSxf0 i (xf) + пу2 =0,
|SXf [Фг (Xi) ] 2 + 02 S [фХ (Xi) ] 2 = 0. (41
Решая систему (4.13), получаем
— (х/)12 1
02 = ---------”, 7г =-------SXj^^Xf), (4.14)
22[Ф1(^г)12 п
89
где Sxf0i (х,-) = Sx,- (х,- + аг) = Sx? + ai Sx,-,
S [0i07)]2 = 2(x,- + «i)0i(x/) = Sx,-0i(x,-),
Sx,- [0i (x,-) ]2 = 2 (x?+ aiXj) Ф1 (x,) =
= Sx? + ai Sx? + «i Sx,- 0i (x,-). ( • )
Таким образом построены многочлены ф0(х), Ф1 (х) и ф2 (х).
Приведем без доказательства рекуррентную формулу, с помощью
которой можно построить любой последующий многочлен, если известны
два предыдущих:
фг +1 (х) = (х+ Зг +1 )Фг (х) + 1г + 1 Фг -I (х) , (4.15)
Е^ЯФгСч)]2 Ех,фг_1 (х,)фг(х,)
0г +1 =---------------, 1г +1 =-------------------• (4‘16)
Е[ФгСч)Г Е{фг_1(х,)]
Формулы (4.14) являются частным случаем формул (4.16) при г = 1.
Вычисление по формулам (4.16) сводится к нахождению сумм степеней
х,-:
2 [Фг Ы]2 = S^0r(xf).= Sx?r + ar(1) Sx?'”1 + - +<г?2х£,
Sx,-0r_i (X, )фг (X,) — SXf фг(х),
2x,[0r(x,)]2 =S(x71 + a<1)x^0r(x,-) =
= Sx?r+1 + aj1) Sx2r + ... + «^Sx;+1 + aru)Sx^(xf). (4.17)
Формулы (4.14a) получаются из формул (4.17) при г = 1.
Используя изложенную методику, по данным табл. 2.6 (см. гл. П,
§ 2.6) можно построить нелинейный полином вида у = а + Ьх + сх2 + ...,
или, что то же самое, у = а0 + агх + а2х2 + ... + атхт. (При использовании
ортогональных ^многочленов Чебышева удобнее принять второй тип обо-
значений.) На первом этапе можно построить многочлен первой степени
(л = 5); суммы степеней х вычислены в табл. 2.7, По формуле (4.9) имеем
0i(x) = х -(l/«)Sx,- = х — 18,5/5 =х- 3,70;
следовательно, = - 3,70; фх (х) = х + .
Вычислим свободный член полинома: п0 = Ъу^п = 296/5 = 59,20. Для
определения ах по формуле (4.14а) найдем
2 [01 to)]2 = 2х? + «1 Sx,- = 75,35 + (-3,70) -18,50 = 6,90.
Далее определяем
2у,-0 1 (х,-)= Sj,-x,- + «1 S^ = 1241,701 (-3,70) -296 = 146,50;
=146,50/6,90 = 21,23.
Таким образом, аппроксимирующий многочлен первой степени имеет вид
у = 59,20+ 21,2301 (х), (4.18)
или
у = 59,20 + 21,23 (х- 3,70) = 59,20+ 21,23х - 78,55;
у = -19,35 +21,23х. (4.19)
90
Остаточная дисперсия этого уравнения = S(yz -y)2/(jt — 2) = 241,94.
Дисперсия среднего Sy = S(yz- -у)2/(п - 1) = 1098,11.
На втором этапе можно построить многочлен второй степени. При этом
необходимо вычислить только многочлен ф2(х) и коэффициент а2. Опреде-
ляем коэффициенты /32 и у2, используя ранее вычисленное выражение
2х,ф i(X|) = S [Ф1 (х/) ] 2 ~ 6,90, и находим
Sx(- [01 (xt) ]2 = 'Zxf + »i Sx2 + ai 2*/0i (*i) = 326,01 +
+ (-3,70) 75,35 +(-3,70)-6,90 = 326,01 - 278,80 - 25,53 = 21,68.
По формулам (4.14) имеем /32 = — 21,68/6,90 — —3,14, у2 =— 6,90/5 =
= —1,38. Многочлен ф2(х) имеет вид
ф2(х) = (x-02)0i(x) -72 = (х - 3,14) (х-3,70) -1,38 =
= х2 — 3,14х— 3,70г + 11,62- 1,38= х2 - 6,84х + 10,24. ( J
Далее находим
S^fo) «2у,х?+ 4° Ху/х/ +а<2) = 5508,53 +(-6,84)-1241,70 +
+ 10,24 • 296 = 46,34;
ар) = —6,84; ар) = 10,24 [см. формулу (4.20)] .
По формуле (4.17) имеем
S [ф2(х<) ]2 = Sx2 ф2(х/) = Sx* + ар) Sxf + ар) Sx? =
= 1469,60+ (-6,84)-326,01 + 10,24 • 75,35 = 11,27;
а2 = 46,34/11,27 = 4,11.
Таким образом, аппроксимирующий многочлен второго порядка
у = 59,2+ 21,23 ф1(х)+4,11 ф2(х). (4.21)
Если сравнить уравнения (4.18) и (4.21), то нетрудно заметить, что два
первых члена в правых частях одинаковы. Подставляя в уравнение (4.21)
найденные ранее значения ортогональных полиномов Чебышева Ф1(х) и
ф2(х), получаем
у = 59,20 + 21,23(х — 3,70) +4,11 (х2 -6,84х+ 10,24).
В результате алгебраических преобразований окончательно имеем
у = 22,74-6,88х +4,1 lx2. (4.22)
Сравнивая полином [см. формулу (2.58)] у = 22,8560 — 6,9576х +
+ 4,1200х2 с полиномом (4.22), полученным обычным способом, заме-
чаем, что они почти идентичны. Различия в десятичных знаках, по-види-
мому, можно объяснить ошибками округления.
Для полинома (4.22) 52ст = 179,069; для полинома (2.58) S2CT =
= 179,062; следовательно, качество предсказания обоих уравнений прак-
тически одинаково. При этом надо помнить, что при вычислении полинома
(2.58) были удержаны четыре знака после запятой, а при вьтчислении поли-
нома (4.22) — только два знака. Это сделано умышленно, чтобы проил-
люстрировать значение точности вычислений в статистических расчетах.
91
Следует также отметить, что поли-
ном второго порядка значительно лучше
предсказывает результаты опытов, чем по-
лином первого порядка, и тем более луч-
ше чем среднее значение у : 179,069 <
<241,940 <1098,110.
Нет никакого сомнения, что полином
(4.22) получен с меньшими трудовыми за-
тратами на расчетные операции- Ясно так-
же, что этот выигрыш резко возрастает с
увеличением степени полинома. Для того
чтобы построить полином третьей степени
обычным способом, необходимо решить
четыре уравнения с четырьмя неизвестны-
ми. Для построения такого же полинома
с помощью ортогональных многочленов
Чебышева нужно вычислить только Фз(х)
и а3 по готовым формулам.
Для полного освоения методики по-
строения нелинейных полиномов с помощью
ортогональных многочленов Чебышева
целесообразно построить полином третьей
степени. Это необходимо также для того,
чтобы определить, насколько возрастает
качество предсказания с повышением сте-
пени полинома еще на одну степень.
Вычисления начнем с определения J33 и у3, используя при этом ранее
полученное выражение Sxz-02(xf) = S [02(*i)l 2 = 11,27. Далее находим
[ф2 (х,)] 2 = Sx? + а2(1> Sx*+a}2) Sx3 +
+ a2(1) Ъх&2(Х1) = 6833,06 +(-6,84)-1469,60 + 10,24 326,01 +
+ (-6,84)-11,27 = 42,19,
Рз =-42,19/11,27 = -3,74, ?3 =-11,27/6,90 = -1,63.
Многочлен Фз(х), вычисленный с помощью рекуррентной формулы
(4.15), имеет вид
ф3(х) = (х+03)ф2(х) +7зФ1(х) =
= (х - 3,74) (х - 6,84х + 10,24)+ (-1,63) (х - 3,70) =
= х3 - 6,84х2+ 10,24х— 3,74х2 + 25,58х- 38,30 - 1,63х +
+ 6,03 =х3 - 10,58х2 + 34,19х-32,27;
a3(1 )=-Ю,58, а<2) =+34,19, а3(3) =-32,27.
Далее определяем:
£>703(л) = S^x? + а3(1) S^x2 + а| SytXf + «з(3) tyt = 2548,63 +
+ (-10,58) -5508,53 + 34,19-1241,70 + (-32,27) -296,00 = -29,814.
1098,110
Среднее
значение у
2Ы.940
Полином
первой
степени
179,069
Лолином
Второй
степени
Рис. 15
132,212
Полином
третьей
степени
92
По формуле (4.17) находим
2 [03(xf) ]2 = Sx?03(xf) = Exf + а3(1> Exf + а3(2) Ex? + а3(3) Ex? =
= 32579,48 +(-10,58)-6833,06 + 34,19-1469,60 4 (-32,27)-326,01 =
= 10,988;
а3 =—29,814/10,988 =—2,713 =*-2,71.
Полином третьей степени имеет вид
у =59,20+ 21,230!(х)+4,11ф2(х)~ 2,710э(х).
Подставим вместо 01 (х), ф2 (х), 03(х) их значения:
у = 59,20+21,23 (х —3,70)+4,11 (х2 -6,84х+ 10,24)-2,71 (х3 -
- 10.58Х2 + 34,19х — 32,27) = 59,200 + 21,230х-78,551 + 4,1 IQx2 -
- 28,112х+42,086-2,71QX3 + 28,672х2 - 92,655х + 87,452 =
= 110,187 - 99,537х + 32,782х* - 2.71Х3;
у = 110,187 - 99,537х + 32,782х2 - 2J1X3. (4.23)
Остаточная дисперсия для этого полинома 5^ст = 132,212; 132,212 <
< 179,069 <241,940 <1098,110 (рис. 15).
§ 4.3. Значение остатков при изучении результатов
регрессионного анализа [43]
Остатки представляют собой разницу между наблюдаемым значением
функции отклика у, в точках, в которых измеряется значение функции,
и предсказываемыми уравнением регрессии значениями функции отклика
у( в этих же точках:
ее=У<-Уь (4.24)
где г = 1,п.
Как указывалось выше, эти остатки используют в первую очередь
для вычисления остаточной дисперсии, но в них содержится и другая ин-
формация. Остатки — это то, что нельзя объяснить уравнением регрессии,
их можно квалифицировать как «шум», помехи или погрешности, если
само уравнение получено правильно.
При проведении регрессионного анализа считают, что погрешности
независимы, имеют нулевые средние, одинаковую (постоянную) диспер-
сию и подчиняются закону нормального распределения. Подтверждение
перечисленных свойств остатков служит доказательством того, что модель
построена правильно. Следовательно, прежде всего проверяют условие
е - 'Lejn — 0.
Затем по правилам, изложенные в гл. I, проверяют нормальность распре-
деления остатков. Кроме того [43], можно построить графики остатков
следующих типов:
1) в зависимости от времени, если известна последовательность наблю-
дений;
93
2) в зависимости от предсказываемых значений у;
3) в зависимости от факторов xj(j = 17р);
4) отдельно для каждого прибора или исследователя;
5) общий график остатков.
При построении графика остатков в зависимости от времени, если
все остатки расположены в пределах равномерной полосы (двух параллель-
ных линий), то это означает, что временной дрейф не оказывает влияния
на результат наблюдений. Если остатки на временной последовательности
располагаются на поверхности, напоминающей прямолинейный или криво-
линейный треугольник, то это означает, что в модель следует включить фак-
тор времени.
При построении общего графика остатков сразу видно, какие наблю-
дения резко выделяются (выпадают из общей картины). Следует проанали-
зировать причины такого явления и при необходимости построить модель,
исключая подобные наблюдения.
*Ю-
*4-
О -
•2~-
-4 -
6-
-»F
-----*-
у или Xj
а)
б)
Рис. 16
Выше уже говорилось о процедуре введения фиктивных факторов при
проведении множественного регрессионного анализа. О необходимости
использования этой процедуры можно судить, анализируя график остат-
ков четвертого типа (график, составленный с выделением опытов каждого
исследователя). Если окажется (рис. 16, б), что остатки опытных значений
параметров у какого-либо исследователя резко выделяются (отклоняются
влево или вправо), то зто говорит о необходимости введения фиктивных
факторов.
На трафиках типа, изображенного на рис. 16,а, остатки должны распо-
лагаться в пределах горизонтальной полосы. Нарушение этого закона может
означать следующее:
1) дисперсия не постоянна, как постулировалось; необходимо учесть
неоднородность наблюдений или преобразовать исходные данные до начала
обработки;
94
2) анализ ошибочен; отклонения от уравнения регрессии носят систе-
матический характер; большим значениям у, соответствуют большие откло-
нения ej, и наоборот;
3) модель неадекватна; необходимо внести дополнительные члены или
преобразовать исходные данные до начала анализа.
Если на графиках типа, изображенных на рис. 16, исследуются зависи-
мости остатков от х/, то выход остатков за пределы горизонтальной полосы
может еще означать, что допущена погрешность в вычислениях, линейный
эффект исключен неверно.
При проведении расчетов на ЭВМ обычно программируют выдачу гра-
фиков остатков на печать.
§ 4.4. Интерпретация уравнения регрессии
Проще всего было бы никак не интерпретировать коэффициенты
аппроксимирующих полиномов (уравнений регрессии), а рассматривать
их как некоторые числа, позволяющие вычислить значения функции откли-
ка у,- в точках, в которых эксперимент не ставился.
При выполнении регрессионного анализа, как правило, имеет место
ситуация, когда истинная форма функции отклика неизвестна и аппрокси-
мирующий полином является как бы разложением в ряд неизвестной функ-
ции для приближенного вычисления ее значений на участке определения
функции. Однако такой чисто формальный подход к трактовке коэффи-
циентов регрессии зачастую не удовлетворяет экспериментаторов.
Для «повышения доверия» к изложенным выше статистическим мето-
дам построения эмпирических зависимостей выполним небольшой матема-
тический эксперимент, из анализа результатов которого станет ясно, что
коэффициенты регрессии, полученные по результатам регрессионного ана-
лиза, соответствуют числам, которые отражают истинную форму функции
отклика, являются вполне однозначными и состоятельными оценками
коэффициентов регрессии в генеральной совокупности. Попутно рассмот-
рим примеры искусственного синтезирования задач в математической ста-
тистике. Если предположить, что функция отклика, отображающая какой-
либо процесс, имеет вид
у = 10 + 10х, (4.25)
то, имея такое уравнение, легко, задаваясь значениями х, найти соответ-
ствующие значения у. Полученные таким образом вектор-столбцы х и у
приведены в табл. 4.1.
Искусственно синтезированные для анализа данные
Таблица 4.1
№ 1 2 3 4 5 б 7 8
X 2 3 4 5 6 7 8 9
У 30 40 50 60 70 80 90 100
95
Так как зависимость (4.25) имеет детерминированный характер, то,
используя данные табл. 4.2 и формулы парного линейного регрессионного
анализа, можно получить выражение, идентичное формуле (4.25).
Таблица 4.2
Вычисление сумм степеней х и у
№п/п X У ХУ х2 у2 х+у (х+у}2 № X У ху х2 у2 х+у (х+У)2
(1) (2) (3) (4) (5) (6) (7) (8) (1) (2) (3) (4) (5) (6) (7) (8)
1 2 30 60 4 900 32 1024 2 3 40 120 9 1600 43 1849 3 4 50 200 16 2500 54 2916 4 5 60 300 25 3600 65 4225 5 6 70 420 36 4900 76 5776 6 7 80 560 49 6400 87 7569 7 8 90 720 64 8100 98 9604 8 9 100 900 81 10000 109 11881 Е 44 520 3280 284 38000 44844
х = 5,5;у=65; Ех3 + 2Еху + Еу2 = Е(х + у)2; 284 + 6560 + 38000 = 44844;
44844 = 44844.
Вычисление сумм степеней хи .у и проверку правильности этих вычис-
лений, как указывалось выше, удобно проводить в табличной форме (см,
табл. 4.2). Коэффициенты регрессии
, = £ху-(1/и)(Ех)(Еу) = 3280-(1/8) (44-520) _ 420 _
1 Ех3-(1/л)(Ех)3 284- (1/8)-1936 42 ’
/?о ~У - ЬхХ = 65 — 10 • 5,5 = 10.
Таким образом, получено уравнение (4.25): у = 10 + 10х. Коэффициент
парной корреляции равен единице, что является признаком функциональ-
ной детерминированной зависимости:
г = QxyhJQx- Qy ='420/V42 • 4200 = 420/420 = 1.
Искусственно синтезированной задаче, можно придать и вероятност-
ный характер, если к числам вектор-столбца х прибавлять или вычитать
искусственную «погрешность» Д, = 0,04 по таблице случайных чисел ПД.
(Если случайное число оканчивается на четную цифру или нуль, то прибав-
ляют 0,04; если на нечетную цифру — вычитают 0,04.) Такую я® операцию
проводят с вектор-столбцом у, только здесь искусственная «погрешность»
Д,- = у/0,04. Преобразованные таким образом данные табл. 4.1 приведены
в табл. 4.3.
Данные с искусственными погрешностями
Таблица 4.3
1 2 3 4 5 6 7 8
X 1,96 3,04 3,96 4,96 6,04 7,04 7,96 9,04
У 29,8 40,2 50,2 59,8 69,8 80,2 90,2 100,2
96
Расчеты по новым данным приведены в табл. 4.4. Коэффициенты рег-
рессии
_ Zxy-l/n(Zx)(Zy) _ 3286,016- (1/8) (44 520,4) _ 423,816 =
Ь1~ Ex2-l/n(Sjc)a ” 284,4928-(1/8) 1936 “ 42,4928 “
= 9,9738;
bo =У~ bix = 65,05 - 9,9738 - 5,5 = 10,1939.
Уравнение регрессии имеет вид
у = 10,1939 + 9,9738х (4.26)
и достаточно близко к исходному уравнению (4.25).
Таблица 4.4
Нахождение суммы степеней х и у с искусственными погрешностями
№п/п X У ху х2 уг х + у (х + у)2
1 2 3 4 5 6 7 8
1 1,96 29,8 58,408 3,8416 888,04 31.76 1008,6976
2 3,04 40,2 122,208 9,2416 1616,04 43.24 1869.6976
3 3,96 50,2 198,792 15,6816 2520,04 54,16 2933,3056
4 4,96 59,8 296,608 24,6016 3576,04 64,76 4193.8576
5 6,04 69,8 421.592 36,4816 4872,04 75,84 5751,7056
6 7,04 80,2 564,608 49,5616 6432,04 87.24 7610,8176
7 7,96 90,2 717,992 63,3616 8136.04 98,16 9635,3856
8 9,04 100,2 905,808 81,7216 10040.04 109,24 11933,3776
Z 44 520,4 3286,016 284,4928 38080.32 44 936.84 4 8
х = 5,5; у =65,05; Zx2 + 2Zxy + Zy1 = Z(x + у)2;
284,4928 + 6572,032+ 38080,32 =44936,8448; 44936,8448 = 44936,8448.
Рассмотрим, как повлияли искусственно введенные ошибки на зна-
чения коэффициента корреляции:
г = ~ХУ- = ; 423-81,60........... = 0,9997697.
x/QxQy 7424928-4228,3000
Коэффициент корреляции не намного отличается от единицы. Для большей
убедительности изложенный выше прием можно повторить и для нелиней-
ного парного регрессионного анализа. В качестве исходной формулы можно
взять зависимость
у = 1 +х + х2. (4.27)
Данные, полученные по этой формуле, приведены в табл. 4.5.
Суммы степеней для х и у даны в табл. 4.6. Для построения квадратич-
ного полинома по данным тагбл. 4.6 целесообразно воспользоваться мето-
дом ортогональных полиномов Чебышева. Расчеты приведены ниже; число
«опытов»/? = 6: 97
4-579
Таблица 4.5
Данные, полученные по формуле (4.27)
1 2 3 4 5 6
X 2 3 4 5 6 7
У 7 13 21 31 43 57
Таблица 4.6
Суммы степеней для квадратичной зависимости
№пД! X У xy x 2 у2 x2y x3 J3 x4 xy2 x+y (x+y/ /х+у/
(1) (2) (3) (4) (5) (6) (7) (8) (9) (10) (11) (12) (13) (14)
1 2 7 14 4 49 28 8 343 16 98 9 81 729
2 3 13 39 ' 9 169 117 27 2 197 81 507 16 256 4096
3 4 21 84 16 441 336 64 9 261 256 1764 25 625 15625
4 5 31 155 25 961 775 125 29 791 625 4805 36 1296 46656
5 6 43 258 36 1849 1548 216 79 507 1296 11094 49 2401 117649
6 7 57 399 49 3249 2793 343 185 193 2401 22743 64 4096 262144
E 27 172 949 139 6718 5597 783 306 292 4675 41011 8755 446899
<t>i(x) ~х-х~х -45; 01 =-4,5; а0 =у = 28,6666;
Sx? + £4 Sx,- = 139 + (-4,5) ♦ 27 = 17,5;
SW = «1 Sji = 949 +(-4,5) • 172 = 175; a2 = 175/17,5 = 10.
Полином первой степени
У = 28,6666 + 1O0i(x), или у = 286666 + 10(х- 4,5) = -16,3334+ 10х.
Далее,
£[Ф1(х/)]2=17,5;
Sx/ + Oj £х/ + at Sx,-0i(x/) = 783 + (-4,5)439 +(-4,5)-17,5 = 78,75;
02 =-78,75/17,5 « —4,5; y2 =-17,5/6 = -2,9167;
<h(*) - (x - 02)0i(x)- 72 =(x - 4,5) (x - 4,5) - 2,9167 =
= x2 ~9x+ 17,3333;
Sj/x? + Oj1) Sy,-x, + a<2> Syt = 5597 + (-9) -949 +
+ 17,3333 • 172 = 37,3276;
0,(0 =-9; a(2) =+173333;
Sx* + apy Ixf + Sx? = 4675 + (-9) -783 + 17,3333439 = 37,3287;
a2 = 37,3276/37,3276 = 1.
7-4,5; 7=28,6666; Sx2 + 2Sxy+ Sy2 = (x + y)2;
139+1898 + 6718 = 8755; 8755 = 8755;
Sx2 + SSx2^ + 3Sxy2 + Sy3 = S(x + y)3; 783 + 16791 + 123033 +
+ 306292 = 446899; 446899 = 446899.
98
Полином второго порядка имеет вид
у = 28,6666+ 10ф1(х) + ф2(х) =28,6666+ 10(х —4,5) +х2 -
— 9х + 17,3333 = 0,9999+х + х2 ~ 1 + х + х2.
По данным табл. 4.1 легко восстановить детерминированную зависи-
мость (4.27) с помощью методики, которая изложена в курсе алгебры
средней школы, однако важно, что и сравнительно сложные статистические
методы приводят к тем же результатам в граничном случае, когда рассмат-
ривается функциональная связь.
На практике имеют дело с наблюдениями, имеющими случайный харак-
тер. Погрешности этих наблюдений зависят от многих факторов, и иссле-
дователю необходимо знать, может ли восстановленная им эмпирическая
зависимость быть использована для аппроксимации функции отклика,
Продолжая рассматривать вопрос об интерпретации коэффициентов
регрессии, можно отметить, что если факторы в уравнении множественной
регрессии не коррелированы, уравнение линейно и в него включены все
основные определяющие процесс факторы, а коэффициент множественной
детерминации R2 близок к единице, то можно решить следующие вопросы
интерпретации коэффициентов регрессии:
1) интерпретацию знаков; знак минус при коэффициенте bj означает,
что при уменьшении Xj функция отклика у увеличивается; знак плюс
означает, что у увеличивается с увеличением ху;
2) интерпретацию значения коэффициентов регрессии [46]; если урав-
нение регрессии имеет вид
у = b0 + biXt + b2x2 + — + bjXj + ... + hpXp, (4.28)
то чистая регрессия у на Xj получается, если в уравнение (4.28) цодставить
средние значения всех факторов, кроме Xj:
9(i) = (b0 + ^bjXj)+ b^i. (4.29)
Аналогично можно получить уравнение чистой регрессии для всех дру-
гих р — 1 факторов. С помощью таких уравнений каждый из коэффициен-
тов регрессии blt b2.bj,..., bp интерпретируют как величину, показываю-
щую, на сколько в среднем изменяется зависимая переменная у (функция
отклика) при изменении данного фактора х; на единицу измерения при
фиксированных значениях других р - 1 факторов.
Если факторы сильно коррелированы между собой, то интерпрета-
ция может оказаться несостоятельной. Рассмотрена [46] методика, позво-
ляющая получить некоррелированные оценки коэффициентов регрессии,
которые затем можно интерпретировать. Эту процедуру называют каскад-
ным регрессионным анализом, который состоит в следующем. Предполо-
жим, что результаты наблюдений описываются уравнением
У = Ь0 + biXi + b2x2. (4.30)
Предположим также, что факторы Xi и х2 коррелированы между собой
(коэффициент корреляции ri 2 статистически значим) и это не противоре-
99
чит физическому смыслу изучаемого явления. Если есть основания пола-
гать, что вариация xt приводит не только к изменению .у, но и к изменению
х2, то кроме уравнения регрессии (4.30) можно записать уравнение
х2 =Ь'0+ д'ххх . (4.31)
При Г! 2, близком к единице, уравнение (4.31) становится функциональным
и вместо уравнения (4.30) достаточно рассмотреть уравнение у = Ьо +
+ bjXi или у = Ьо + Ь2х2, т.е. один из факторов хх или х2 исключить из
рассмотрения. При гх 2 > т.е. когда гх 2 статистически незначим, факторы
хх и х2 можно считать некоррелированными и уравнение (4.30) поддается
четкой интерпретации. Каждый из коэффициентов регрессии £>х и Ь2 в этом
случае показывает, на сколько в среднем изменяется функция отклика
у при изменении соответствующих факторов хх их2 на единицу измерения.
Если же гт < г 12 < 1, то, как указывалось выше, интерпретация по методу
чистых регрессий неправомерна. В этом случае, для того чтобы узнать, как
сказывается влияние вариации хх и у, можно выполнить следующие опе-
рации: задавшись каким-либо значением хгх, следует подставить его в урав-
нение (4.31) и найти среднее значение х2. Затем, подставляя значения
х'х и х2 в уравнение (4.30), можно найти среднее значение у х, соответствую-
щее значению х'х. Повторяя эту операцию для другого значения хх, можно
определить значение у2. Разность^2 - yi и является средним эффектом
изменения хх на величину х'х' - хх. Можно также интерпретировать видо-
измененное уравнение двух факторов:
У=Ь0 + biXi + £>2Дх2, (4.32)
где Дх2 — остаток, представляющий собой отклонения фактических наблю-
дений значений х2 от соответствующих расчетных значений х2 по уравне-
нию (4.31):
Дх2 =х2 —(£>о + £’1ХХ). (4.33)
Это еще один пример использования остатков (см. § 4.3). Переменные
хх и Дх2 в уравнении (4.32) уже не коррелированы между собой, и коэф-
фициенты bt и Ь2 в уравнении (4.32) определяют независимо друг от дру-
га. Интерпретация коэффициента £>х в этом случае такая же, как для урав-
нения с некоррелированными факторами, а коэффициент Ь2 определяет
действие вариации х2 на у при отклонении от среднего уровня, определяе-
мого уравнением (4.31), т.е. при |Дх2| > 0. Эти рассуждения можно рас-
пространить на любое число факторов и на нелинейную зависимость.
Факторы, влияющие на функцию отклика у, могут быть четырех типов:
1) управляемые факторы, которые можно изменять в широких пре-
делах;
2) ограниченно управляемые факторы, значения которых коррели-
рованы с другими факторами и которые можно варьировать лишь в опре-
деленных пределах;
3) неуправляемые факторы, значения которых не коррелированы с
другими факторами и изменяются независимо от воли экспериментатора;
100
4) неуправляемые факторы, значения которых коррелированы с дру-
гими факторами и изменяются независимо от воли экспериментатора.
При интерпретации факторы первого и третьего видов включают в
управнение в натуральном виде, а второго и четвертого — в виде величин
Дху. Графическая интерпретация коэффициентов линейных парных уравне-
ний регрессии дана в гл. II. Некоторое отношение к вопросу интерпретации
имеет также процедура приведения уравнений к каноническому виду,
изложения в гл. III.
§ 4.5. Метод средних
Для построения эмпирических зависимостей кроме подробно рассмот-
ренного метода наименьших квадратов существует еще один более простой,
но менее строгий метод — так называемый метод средних. Этот метод
имеет, кроме того, и более ограниченное применение. По-видимому, его
можно эффективно использовать только в парной ситуации: у = f(x). Одна-
ко для ориентации в специальной литературе полезно ознакомиться с ос-
новными принципами этого метода.
Метод средних состоит в том, что параметры эмпирической формулы
определяются, по существу, только из одного условия, а именно условия
равенства нулю суммы всех отклонений наблюдаемой величины от средне-
го значения [ 164] :
S = 0, (4.34)
1 = 1
где dj — yi - у. Определенные приемы позволяют вычислять до трех пара-
метров с помощью только одной зависимости (4.32). Наиболее эффекти-
вен этот метод в простейшей ситуации, когда нужно построить зависимость
вида
У=Ьхх. (4.35)
Вычислим коэффициент Ьх; учитывая, что сумма отклонений наблю-
дений от среднего равна нулю, запишем
2 (Ь1Х, -Л) =0, (4.36)
i=i
откуда
bx = S yt / S Xi; (4.37)
i=l i=l
если числитель и знаменатель этой дроби разделить на п, то получим
*1 =у/*> (4.38)
гдех=(1/и) S xit у = (1/и) Z уi.
l=i i=i
Преимущество метода средних в данном случае заключается в его
простоте ив том, что он не накладывает ограничений на исходные опыт-
101
ные данные (например, не требует, чтобы эти данные имели нормальное
распределение).
Если требуется построить линейную парную зависимость у = Ьо + bix,
то вычисления по методу средних не намного сложнее. Здесь требуется
вычислить коэффициенты 0 и .
Для получения нужного количества уравнений выбирают из общего
количества пар наблюдений примерно половину и сумму их отклонений
приравнивают нулю. Затем приравнивают нулю сумму прочих отклонений:
S (Z>0 + Ьгх{ - j) =0; S (60 + бхХ/- j) = 0. (4.39)
1=1 f=m+l
Таким образом, получаем систему двух уравнений:
bi X Xi + mb$ - S yit
i=i i-i
n n
Ьг S +(« - = E Л,
i=m +1 i—m +1
(4.39a)
где m = и/2 при четном пи т = (и + 1)/2 при п нечетном. Сложим оба урав-
нения (4.39а) почленно:
л л
bi S Xi + nb0 = S yi.
<=i i=i
Разделив все члены этого уравнения на п, окончательно имеем
b0 =у - biX,
т.е. получена формула (2.34), выведенная методом наименьших квадра-
тов.
Если представить линейную зависимость в виде у-у -bi(x — х), то
bi можно вычислить по одной из следующих формул:
(4.40)
(4.40а)
На практике при нечетном т обычно второе из уравнений (4.39а) сос-
тавляют в виде
bi S Xi+(n-m +1) bo= S yh (4.41)
i —m i—m
т.е. одно из отклонений учитывают в обоих уравнениях системы.
102
Этот прием ликвидирует возможность произвольного деления выбор-
ки на части и делает метод средних однозначным.
Для получения нужного количества уравнений при построении зависи-
мости у = а + Ьх + сх2 множество всех отклонений разбивают на три при-
мерно равных массива и в каждом из них приравнивают нулю сумму от-
клонений. В результате для вычисления параметров а, Ь, с получают сле-
дующую систему:
т т т 1
с S х? + b S xt + тха = S у,,
1=1 1=1 i=l
m2 тя тг
с S х} + b S x/ + (m2 + m1)a= S yf-, (4.42)
i=mt +1 f=m,+l /=mx +1
n n n
c S X{ + b S Xi + (л — тг) a = S Л7 •
i—m2 + l f=ma + l f=m2+l
При использовании этого метода вычисления менее трудоемки, но,
как указывалось выше, он обладает меньшей строгостью и универсаль-
ностью, чем метод наименьших квадратов. Решая пример, рассмотренный
ранее (исходные данные приведены в табл. 4.4), методом средних, мож-
но сравнить результаты решений, полученных с помощью метода наимень-
ших квадратов и метода средних.
Опыт показывает, что при использовании метода средних для построе-
ния полинома у = b0 + btx нужно иметь в виду три ограничения:
1) метод можно использовать, если имеет место только регрессия
первого типа (х(- — фиксированные значения фактора; у/ — наблюдаемые
случайные значения функции отклика у);
2) исходные данные перед обработкой должны быть расположены по
увеличивающимся значениям х;
3) дисперсия у должна быть постоянна и не очень велика (при построе-
нии уравнения типа у = Ь^х таких ограничений не было).
Указанным требованиям соответствуют данные рассмотренной выше
искусственно синтезированной задачи (см. табл. 4.4). Все операции прово-
дят в табличной форме (табл. 4.7).
Из табл. 4.7 следует, что как по формуле (4.40), так и по формуле
(4.40а) получено одной то же уравнение:
у = 10,4586 + 9,9257х (4.43)
Формула (4.26), полученная с помощью метода наименьших квадра-
тов, имеет виду = 10,1939 + 9,9738хи несколько ближе к исходной фор-
муле у = 10+ 10х.
Использовать метод средних для построения линейного уравнения
типа у = Ьо + Ьх по данным табл. 2.4 нельзя. Более того, с увеличением
п числитель и знаменатель формулы (4.406) в этом случае стремились бы
к нулю. Отсюда следует упомянутая выше неуниверсальность метода сред-
них по сравнению с методом наименьших квадратов, и применять его мож-
но рекомендовать только при построении формул вида у = Z>iX
103
Таблица 4.7
Вычисления по методу средних
№ п/п х у х^ — х yi - У Вычисления
(1) (2) (3) (4) (5) Формула (4.40)
1 1,96 29,8 -3,54 -35,25 2 3,04 40,2 -2,46 -24,85 3 3,96 50,2 -1,54 -14,85 4 4,96 59,8 -0,54 -5,25 -80,2 41 - -8,08 -9'9257- bQ =65,05 - 9,9257*5,5 = 10,4586; Формула (4.40а) 13,93 - 30,08 =-16,16; 180,0- 340,4 =-160,4; bt = 9,9257; b0 = 65,05 - 9,9257'5,5 = = 10,4586.
т X 13,92 180,0 -8,08 -80,2 /=1
5 6,04 69,8 6 7,04 80,2 7 7,96 90,2 8 9,04 100,2 п S 30,08 340,4 i—m+1 X 44 ' 520,4 х =5,5; у = 65,05
§ 4.6. Метод максимума правдоподобия. Регрессионный
и конфлюэнтный анализы как частные случаи
метода максимума правдоподобия
Если бы материал в настоящем пособии излагался методом дедукции
(от сложного к простому), то этот параграф следовало бы поместить в
начале гл. II, а затем изложить методику построения эмпирических зависи-
мостей по результатам пассивных экспериментов. Однако поскольку ма-
териал излагается методом индукции и в рецептурном плане, то этот срав-
нительно сложный материал рассматривается именно здесь, когда основ-
ные вопросы, связанные с построением эмпирических зависимостей по
результатам пассивных экспериментов, уже изучены.
Принцип максимума правдоподобия может рассматриваться [66]
как основная идея всех методов и приемов, положенных в основу стати-
стической обработки экспериментальных данных для построения эмпи-
рических зависимостей. В общем виде принцип максимума правдоподо-
бия можно сформулировать так [66]: наилучшее описание явления то,
которое дает наибольшую вероятность получить в результате измерений
именно те значения, которые и были фактически получены.
Если рассматривать полный эксперимент (число независимых наблю-
дений больше числа определяемых величин: п > р, т.е. нет алгебраической
104
неоднозначности), то проведение измерений с абсолютной точностью озна-
чало бы, что из всех возможных гипотез относительно исследуемого явле-
ния можно было бы выбрать только одну гипотезу, которая соответствова-
ла бы экспериментальным данным. Однако в действительности, как ука-
зывалось в предыдущих главах, наблюдения и измерения всегда содержат
погрешности. В связи с этим имеет место множество‘гипотез, не противо-
речащих опытным данным. Принцип максимума правдоподобия состоит
в выборе такой гипотезы, при которой вероятность получить в процессе
измерения фактически наблюдаемые величины была бы максимальной.
Предположим, что функция отклика у (исследуемое явление) — вели-
чина непрерывная. Вероятность того, что в генеральной совокупности эта
функция примет определенное значение, равна Р(у, 0) dy <5.2>, где Р —
неизвестный параметр, подлежащий определению. Предположим, что при
случайном выборе объема п из этой генеральной совокупности найдены
значения ylt у2, уп- При этом процесс извлечения членов выборки дол-
жен быть таким, чтобы вероятность получить новое значение у не зависела
от полученных ранее величин. Вероятность получить значения yit у2, Уп
равна
dP = £djidy2 ... dy„,
где
L (У1, Уг, Уп; » = ^{у 1. Р{ У г 0 } ... Р {у„, 0} (4.44)
Функция L называется функцией правдоподобия. Выборочной оцен-
кой параметра Р является параметр Ъ. На практике удобнее иметь дело не
с самой функцией, а с ее логарифмом, поэтому оценку параметра р можно
получить, решая уравнение
=0 (4.45)
дЬ
Если распределение величины у в генеральной совокупности является
нормальным, то вероятность найти у между у и у + dy равна
р{у. ч; 4 dy = dy.
Для случайной выборки объема п запишем равенство
L (у;ч; о2) = * пП exp I- 7“ S (У/ - я)2
(2№)"'2 I 2<г’ /=1
Функция правдоподобия L достигает максимума, если стоящая в по-
казателе формулы (4.46) сумма квадратов отклонений минимальна:
(4.46)
U= S - чЙ*)]2, (4.47)
1=1
где т] (Р, х) — функция от независимой переменной х любого вида с систе-
мой коэффициентов р, постоянных для каждого вида функции и подлежа-
щих определению.
105
При линейной параметризации
s 4-[yf-(Po+
/=1 a2yt /=1' '
(4-48)
где W{ = — вектор-столбец весов, о котором сказано ниже;
i = Т, п — общее число опытов; j — 1,р — число факторов в множественной
ситуации.
Выражение (4.47) и есть основная зависимость метода наименьших
квадратов. Таким образом, метод наименьших квадратов — это частный
случай метода максимума правдоподобия при нормальном распределении.
Для того чтобы вычислить минимум выражения (4.48), следует, как уже
указывалось выше, взять частные производные Этого выражения по всем
параметрам (коэффициентам) и приравнять их нулю, одновременно
заменяя значения параметров их выборочными оценками. Полученная
система называется системой нормальных уравнений; в матричной форме
она имеет вид
( X*WX)B = X*WY. (4.49)
Формула (4.49) отличается от формулы (3.5) только диагональной
матрицей весов:
Wj О
W =
W/
wn
(4.50)
Расшифровка остальных обозначений формулы (4.49) дана в гл. III.
Для простейшего случая, когда имеют место парная зависимость вида
У —ffx) и линейная параметризация, формула (4.47) принимает вид
U~ SWffo- (Ро+Мг)]2, (4.51)
/=1
Соответственно система нормальных уравнений имеет более простой вид:
S [у, -(д0 + М/) Is 0,
< /=; (4.52)
S wt [у, -(д0 + ] xt = 0.
j=i
Если каждому фиксированному значению фактора х соответствует
только одно наблюдение зависимой переменной у, то дисперсия у отсут-
ствует и необходимость во взвешивании отпадает, а формула (4.52) при-
водится к формуле (2.5):
106
In
s !>«—(^o +
i — 1
S 0i-(^0 + M/)]** =0.
1=1
Рассмотрим теперь для простейшего случая парной линейной связи
классификацию ситуаций, которые могут иметь место при проведений
экспериментов.
Классификацию способов наблюдений, которые не обязательно зави-
сят от воли экспериментатора, а часто обусловленьгособенностями объек-
та наблюдения, для наглядности представим в виде графических схем.
На рис. 17 изображена экспериментальная ситуация первого типа. Здесь
каждому фиксированному значению фактора х соответствует только одно
наблюдение (измерение) зависимой переменной у. Система нормальных
/равнений метода наименьших квадратов имеет самый простой вид (2.5).
Рис. 18
На рис. 18 изображена экспериментальная ситуация второго типа, когда
каждому фиксированному значению фактора х соответствуют к значений
зависимой переменной у, имеющих нормальное распределение, матема-
тическое ожидание и дисперсию Оу.. Здесь i = 1, п — общее число опытов;
/ = 1, к — число наблюдений в каждом опыте (не путать с / = 1, р — чис-
лом факторов).
Для оценки параметров служит система нормальных уравнений (4.52)
со взвешиванием. На рис. 19 изображена экспериментальная ситуация треть-
107
его типа. Здесь фактор х, так же как и
независимая переменная у, измеряется с
погрешностями. Вместо одного фикси-
рованного значения фактора х в каждом
опыте имеется к значений фактора х,
имеющих нормальное распределение, ма-
тематическое ожидание и дисперсию
6*.. Здесь i — 1, п — общее число опытов:
/ = 1, к у — число наблюдений в каждом
опыте дня зависимой переменной у,
j — 1, kx — число наблюдений в каждом
опыте для фактора х. Распределение
х не коррелировало с распределением у.
Для оценки коэффициентов 0о> 01 в
этой ситуации метод наименьших квад-
ратов мало эффективен, поэтому исполь-
зуют другой частный случай метода мак-
симума правдоподобия.
Эти рассуждения можно распростра-
нить на любой вид зависимости у от
х и на р-мерное факторное простран-
ство. Изложим основные принципы
Рис. 19
этого частного случая. Как уже указывалось, вместо одного элементарного
измерения фактора х имеется совокупность элементарных измерений, для
которой, если считать распределение нормальным, известны генеральное
среднее и генеральная дисперсия так, что можно найти зависящие от
статистики уровни для выборочного среднего х,- и выборочной дисперсии
SXf, либо эти величины оценивают на основании достаточно большой неза-
висимой выборки [66].
Каждому взвешенному экспериментальному измерению величины у
приписываются определенное значение фактора х, являющегося оценкой
среднего для всех элементарных наблюдений, и дисперсия этого сред-
него.
Этот случай анализа наблюдений называется конфлюэнтным (от франц,
confluer — сливаться), так как если бы совокупность наблюдений фактора
х с известной оценкой среднего и дисперсии слились в одну точку, то имел
бы место обычный регрессионный анализ (вторая экспериментальная
ситуация; см. рис. 18).
Метод максимума правдоподобия при определенных условиях может
привести задачу конфлюэнтного анализа к методу наименьших квадратов
с использованием последовательных приближений [66]. Напомним, что
рассматривается простейшая парная ситуация у — f(x). Разделение этих
двух переменных на зависимую и независимую теряет смысл при случай-
ных колебаниях обеих величин.
Здесь рассматривается также такой чаще всего встречающийся случай,
когда распределения х и у не коррелированы.
Плотность вероятности найти измеряемую точку (центр выборки)
108
в генеральной совокупности около х, и уг- при двумерном нормальном рас-
пределении равна <5.2>, <3.4>
Р(хьуг, Ьп} = Р{ур =
(4.53)
1 2 сгх^ 2 ау1
если центром распределения в генеральной совокупности являются точки
tn- „
Интенсивность источника плотности вероятности наити событие в точке
х$>1 пропорциональна длине элемента теоретической кривой и некоторой
функции 0(0-
Полная плотность вероятности найти событие в точке определяет-
ся интегрированием по дуге кривой:
=J <№{*<,л; S ’!®} Ф«). (4.54)
где элемент дуги кривой
о2
dS2 = d$2 + dr?2 (4.55)
°yi
имеет ту же размерность, что и d£.
Функция 0(0 представляет собой плотность источников точек, полу-
чающихся при измерении, и может быть определена после детального ана-
лиза физического смысла плотности вероятности:
0п(0) • (4.56)
Функция правдоподобия равна плотности вероятности найти одновре-
менно все точки в тех местах, где они обнаружены, и, следовательно (так
как измерения независимы), при разных х/ имеет вид произведения инте-
гралов (4.54), взятого по всем наблюдаемым событиям.
При некоторых условиях, которые обычно выполняются в экспери-
ментах, конфлюэнтную задачу можно свести к последовательности регрес-
сионных задач. Если на участке кривой, находящейся в интервале от — оХ{
до +oXi и от —oyi до +а^, наклон и кривизна изменяются мало (кривая
достаточно гладкая), то при вычислении интеграла (4.54) в случае нор-
мального распределения можно ограничиться участком кривой около точ-
ки xfyf.
Другим условием, позволяющим свести конфлюэнтную задачу к по-
следовательности регрессионных задач, является требование, чтобы точка
xtyt не находилась ближе от конца теоретической кривой, чем на ох.. При
этих условиях можно представить плотность распределения в виде плот-
ности частного распределения наблюдений У/ при фиксированных xf, имею-
щего вид, близкий к плотности нормального распределения.
На небольшом участке кривой в окрестностях точки х^ теоретическую
кривую можно приближенно представить первыми тремя членами ряда
Тейлора:
П (О = ?(*/) + (5 - r{ (xt) + - (Я), (4.57)
109
где характеристики кривой т?(£) заменяются характеристиками ее оценки
%(х). Если подставить (4.57) в (4.53), а (4.53) в (4.56), разлагая (4.53)
по степеням 1? в предположении, что "* т? < 1, и интегрируя практичес-
аУ1
ки в бесконечных пределах до величины порядка ц", то получим
* f" rAr, •. . 1 Ан 2,2 /»1Аг2 -21
1 1 [л (*/)-У/+-j-Л oxi(°yi~^axf1i ) ai ]
-----— exp ------------------------г--------------------
<7 у V 2ff Z Oj
4 2 1
x [1+^"(й(х|)-л) й; .
°i ,
где а] = Uyf + ty2 Qxp a Vi и ty* - значения первой и второй производной
оценки кривой регрессии при х ~ х,.
В формулу (4.58) в качестве ненормированных весов входят
1+п" (л/ ~Ji^)
wt = -------------------%— . (4.59)
Кроме того, центром распределения для у/ является сдвинутая оценка кри-
вой регрессии г] (*/) + о,, где
gf = /2^ (4.60)
Так как производные т?'- и т)/ и отклонения Ду, = т?(ху) -у,- до проведения
анализа неизвестны, то на первый взгляд может показаться, что возникает
ситуация, которая носит название «заколдованный круг». Из этого «кругах
можно выйти с помощью последовательных приближений, используя тот
факт, что функция правдоподобия слабее зависит от изменения весов при
подборе кривой регрессии, чем от разностей у, — т? (xf).
Нулевое приближение можно получить, проведя «на глаз» кривую через
экспериментальные точки. Первую производную, получаемую дифференци-
рованием кривой нулевого приближения, подставляют в знаменатель вы-
ражения (4.59), вторую производную заменяют нулем и анализируют вновь
полученные веса.
Дифференцирование кривой регрессии первого приближения позво-
ляет найти величины , 17/ и Ду/, с помощью которых вновь пересчитывают
веса и оценивают сдвиги (4.60).
Эту процедуру уточнения кривой и весов продолжают до тех пор,
пока изменения весов не станут меньше заранее назначенной величины,
отражающей точность проводимых расчетов. При достаточно малых
ZT „2
°Х t °Х и
— и —- г} сходимость процесса итерации должна быть достаточно
°У Оу
быстрой.
Как указывалось выше, в расчетном отношении конфлюэнтная задача
110
эквивалентна последовательности регрессионных задач. При ох 0, т.е.
если наблюдения х, являются фиксированными адсламм, все формулы
конфлюэнтного анализа автоматически переходят в формулы регрессион-
ного анализа (вторая экспериментальная ситуация).
Конфлюэнтный анализ подробно описан в [66, 106, 144, 145, П.14.64,
П. 14.69, П.14.77]. В литературе приводятся также примеры решения искус-
ственно синтезированных задач методом регрессионного и конфлюэнтного
анализов с сопоставлением результатов [144].
Разработана программа для ЭВМ по множественному регрессионному
и конфлюэнтному анализу [106]. Здесь же изложен порядок решения за-
дачи конфлюэнтного анализа методом последовательных приближений
(итерации) в многофакторной ситуации:
1) отыскивают значения /F — нулевая оценка вектор-столбца коэф-
фициентов регрессии fy, при которых достигается минимум функционала
(4.48) при постоянных весах wt = l/Oy{);
2) в каждой экспериментальной точке х, подсчитывают величины ве-
сов и смещений:
yi jt=i дхк
2 -I
. = £ f
1 *=1 ^kdxk tk
(4.61)
(4.62)
где aX{k — дисперсия определения Ar-й координаты z-й точки xz. Частные
производные находят методом численного дифференцирования по фор-
мулам
* А>-
£ x~Xi я
—4(0,’ Ху, xik - Л) ] — (?,’ Ху, ;
А О О
Д I [4(1; xif;xtk - Л)+ 2tj(0;Ху, х{к) +
* / 2 Я
+ чЙ xif,xik + Л)]— ^t?IV(0;xz/; $/fc).
(4.63)
(4.64)
Шаг дифференцирования h выбирают, учитывая погрешности расчета
производных. Влияние шага на точность проверяют повторным обраще-
нием к программе с уменьшением шага h;
1
3) отыскивают значения при которых достигается минимум функ-
ционала Ui при постоянных весах :
ui = S wf \yt - i?(0; xjj - a‘] 2.
i— 1 , *•
(4.65)
111
л Я
Операции 2) и 3) повторяют соответственно при р и (3 и т.д. до тех пор,
пока Процесс не сойдется:
JP 1
ft. - Pi
max 7J- — <£, (4.66)
7 ft
где / = 1, p - количество неизвестных параметров: € — наперед заданное
положительное число, величина которого сравнима с возможной погреш-
' 53
ностью вычислений. Значение р, для которого выполняется условие (4.66),
принимают за оценку искомых коэффициентов р полинома при конфэлю-
энтном анализе [106] .
§ 4.7. Модели, нелинейные по параметрам
Ранее рассматривались только линейные по параметрам модели, кото-
рые строились путем анализа экспериментальных данных. Отмечалось,
что модели вида
у = Ьо + Ъх,
у =bo+ biXj. + b2x2 + ... + ЬрХр,
у = а+ Ьх+ сх2 + dx3 + ..., (4.63а)
У = b0 + biXi + b2x2 + ... + ЬрХр + ... + Ьцх2 + Ь22х2 + ... + ЬррХ2 +
+ + Ь13ХгХ3 + ...,
•... -xbpp>
у = exp (ро + ftjXi + Ь2хг + ... + ЬрХр)
являются линейными по параметрам Ьо, (У = 1, р).
В последние годы появились публикации [И, П.14.18, П.14.80,
П.14.99], в которых даны рекомендации по построению эмпирических фор-
мул, нелинейных по параметрам.
При линейной параметризации без взвешивания (погрешности х пре-
небрежимо малы, а погрешности у независимы и имеют одинаковые стан-
дартные отклонения) формула (4.48) принимает вид
[У,--Wo +‘£ 0/,/)] 2. (4.64а)
Как указывалось, для вычисления оценок коэффициентов j30, fy в пред-
положении минимума выражения в квадратных скобках формулы (4.64а)
составляют систему нормальных уравнений метода наименьших квадра-
тов, вычисляя частые производные по всем параметрам Ь, Ьр и прирав-
нивают полученные выражения нулю. Вычисление значений коэффициентов
bo, bj (решение системы нормальных уравнении) сводится к использова-
нию методов линейной алгебры, в частости к проведению операций транс-
понирования и обращения матриц [формулы (3.4) —(3.14)].
112
При нелинейной параметризации дело обстоит сложнее. Приходится
решать систему нелинейных уравнений. Для этого можно использовать
методы последовательного приближения. Исходные данные примера по-
строения нелинейной по параметрам модели, который рассмотрен ниже
исключительно для сравнения окончательных результатов, взяты из книги
[11]. В этой работе пример решен на ЭВМ IBM/360 с использованием мат-
ричных операций. Приведены только конечные результаты. Поэтому этот
пример нельзя использовать для обучения начинающих экспериментаторов.
В настоящей работе нелинейные уравнения решались методом Ньюто-
на—Рафсона, все этапы решения сохранены. Вычисления проводились в
системе FORTRAN ЕС 1022, использовался также настольный компьютер
«Texas Instruments SR-50-А», позволяющий легко выполнять операции с
экспонентами.
Предположим, что у (функция отклика) — доля химического вещества
А, оставшаяся к моменту времени xt в результате реакции типа А -> В.
Зависимая переменная у удовлетворяет дифференциальному уравнению
[11]
где К — константа скорости.
Решение этого уравнения при следующих начальных условиях: у = 1,
если Xj - 0, — имеет вид
у = exp (- Kxi).
Константа скорости К зависит от абсолютной температуры х2 следующим
образом:
К = b 1 ехр (~Ь 2/х2 ), (4.66)
где Ьг — предэкспоненциальный множитель; Ъ2 — энергия активации. Мо-
дель процесса принимает вид
х2, blf Z>2) = exp ехр (-Ь2/х2)]. (4.67)
Формула (4.67) является нелинейной по параметрам bt и Ь2 моделью
изучаемого процесса.
Для того чтобы хорошо предсказать результаты опытов у/, модель
(4.67) должна давать значения у,, имеющие минимально возможные рас-
хождения с результатами опытов yit т.е. сумма квадратов отклонений
U{b)= S е] (6) = S fo-Jrf»/)2. (4.68)
1=1 i=l
yt(b) = ехр [-biXji exp (~b2/xi2)] (4.69)
должна был» минимальной. Другими словами, параметры bt и Ь2 должны
быть вычислены так, чтобы сумма квадратов отклонений (4.68) была ми-
нимальной.
Для отыскания минимума функции U(b) по параметрам bi и Ь2 следу-
ет взять ее частные производные по этим параметрам и приравнять их нулю:
113
ди л
5гг°-
^ = 0. ’
У
Далее, учитывая (4.68), можно записать:
п де/
S 2е, —1 -О,
/=1 дг>1 I
п де/
S 2е{ — =0,
/=1 дЬ2
те^у^-у^
def дг л \ ^У1
< J»i dbt дь1
д , л dyt
- ТГ- = -тг (У1-У1) =- — ,
ОО 2 О&2 ^2
(4.70)
(4.71)
(4.72)
(4.73)
так как у у (вектор наблюдений) не зависит от bt и Z>2- Уравнения (4.71)
записаны в общем виде. А
Если учесть конкретную форму нелинейной модели у/ [формула
(4.69)] и подставить ее в систему (4.71), принимая во внимание (4.72),
то полечим
ду{ Ь2 Ь 2
~1 =ехр[-Ь1х11 ехр(- —)] [-хп ехр(- — )] =
dbi xi2 xi2
= ~xit ехрНчхд ехр(— ^-)] ехр(- ^-),
хп хт
- ~^expH>ixn ехр(-—)] [-Ь1Хц ехр(- ~-)(- -Ц] =
db2 Xf2 Х/2 х12
*2 *2 ч
--------exp [-biXu ехр(~—)]ехр(- —)
Х/2-----*/2 х12
ИЛИ а
дУ{ А . ь3 *
— =-Х/1У/ехр(- “—),
obi Х{2
&У1 z *2Ч|
дЬг ж/i Xf2 J .
Систему (4.71), учитывая формулу (4.75), запишем в виде
(4.74)
(4.75)
” л &2
+2 L et yt ехр(- = О,
i=l fi2
и а *2
—2 Е е((^-4 у, ехр(— ) =0.
/ = 1 х12 xi2
(4.76)
114
Система (4.76) является системой двух нелинейных уравнений с двумя
неизвестными (bi и b2); ее можно решить методом Ньютона—Рафсона.
Для того чтобы рассмотреть процедуру метода Ньютона—Рафсона, вве-
дем следующие обозначения:
ПА
F(bi, b2) = S ехр(-------) Хц =0,
i = 1 xi2
п Ь1ХЦ А *2
G(bi, b2) = Sef(----)у;ехр(-----)=0. (4.77)
1 = 1 x12 xi2
Таким образом, чтобы определить неизвестные параметры bi и Ь2,
следует решить систему нелинейных уравнений:
F(h,62) = 0, <7(61,62)=0. (4.78)
Эти уравнения можно переписать в другом виде, выделяя параметры
bi, b2'
bl =Ф1(*., ь2). Ь2=Ф2 (bl, *,). (4.79)
Обычная итерационная схема имеет вид
^+1)=Ф1 ,*<*>), Ь<*+1)=Ф2 (t,(k\b^)2 (4.80)
[вычисление (Л: + 1)-го приближения по Аг-му]. Пусть известны некото-
рые приближенные значения Ь^ и Ь^, в частности некоторые начальные
приближения bi и Ь2. Обозначим разность между точными значениями кор-
ней bi и Ь2 и их приближенными значениями и Ь^ через Д&1 и Д62,
т.е. полагаем
bi =b{k> + &bi,b2=b<2k> + Ab2. (4.81)
Подставляя значения корней Ьъ Ь2 в формулу (4.78), получаем
F(Ъ<к> + Ддь- Ъ<к> + Д62) = 0,
G (Ь<к> + ДЛЬ- Ъ<к> + Дд2) = 0. <4-82)
Используем разложение Тейлора для функции двух переменных в
окрестности точки с координатами (Ь°; д2):
Ь —ь
f(bi, b2)=f(bt, Ы) + -—-)?»,)(»?.6?) +~7—2/('„,)(«’!. ь°2)+ ....
(4.83)
где . Положим bi = b2 = b^; bi - b2=bi ~ b^ ~ Abt;
Ь2 - Ь2 = Ъ2 - Ь^ = ДЬ2. Тогда разложение (4.83) для функций (4.82)
принимает вид
F(b(V + Д6Ь b™ + Ab2) = F(b^, b^ + Д^ (/>(*< b^) +
+ дд2кь;(д(*<&^) + ...=о,
G (Ь^ + ЛЬ1, Ь^^ + Д62) = G (Ь(к>, Ъ<к>) + Ддх Gb’fb(k>, b<k>) +
+ Д62 &ьз(Ь<к>, Ь<к>) + ... =0. * (4.84)
115
Сохраняя в этом разложении только первый член, приближенно полу-
чаем
ДЬ^ч-Ab2F£>a ® -F^iG^+^G'b^-G. (4.85)
Здесь функции F и G и их производные подсчитывают в точках Ь^,
Решая (4.85), найдем
ЛК (GF^-FG/,,) {FG’b-GF'b)
Д/>, ss ---Я-----, Д62 as -------*----
d d
r^fid-F>bi G'b2- GbtFb2.
Подставляя эти приближенные значения в формулу (4.81) и обозна-
чая полученные значения корней (параметров) через Ьр+1> и
окончательно получаем рекуррентную формулу
(4.86)
4(*+i)=4(*;+ о^ъ-fgi,, (4.87)
11 d ’ 2 2 d ’
где F, Fb', Fb'2, G, Gb'lt Gb2 вычисляют в точке b^k\ т.е. при значениях
bt и Ъ2 на предыдущем шаге.
Используя формулы (4.69), (4.75) и (4.76), запишем выражения для
производныхFbFb2, Gb\ И Gb'2‘
S. b2 де. Гл ду, 1
Fftl=-Sx/iexp(-—) ~ =
i = l xi2 dftxV dbi)
n dy{ f A |
=+ S xn e*p(-b2/xi2) — < -у,- + e/ ;
i=i dbi [ J
def д% Л
учитывая, что —— — — —— и в/ = еу{ - yh получаем
ub} дЪI
^Ь1 JeXP (“*«/•*«) ] 2yi (ei ~ yi) ;
= S хп < ~у/ exp (-д2/х/2)+
1=1 |O&2
+ ТГ exp (-Ь2/хц) + ем exp (-b2/xi2) (-----) -
O»2 X/2
v / л dft dyt Ail
= S S -У/ — + et — - e^i — > exp (~b2/xi2);
i=l । OO2 Od2 X/2 I
G»! = s <
f=l
(4.88)
(4.89)
(4.90)
де{
db i x/2
* exp (-d2Ал) = S <
&1Х/1 Л ХЦ Ь1Х/1 ду.
Xj2 Х/2 до 1
*1^/1 л Л Х/1
-------Т- (е/ - У/) + в/ У/ —
х/2 дЬ 1 Х/2
exp (-62 A/2);
(4-91)
116
Gt>2
+
n bixn дел л
= 2 (------—1у1ехр(-й2/х,-2) +
i = l xi2 db2
ду- а 1
—1~ exp (- b2/xi2) + e,yf exp (~b2/xi2) (- —)
db2 *l2
f -Л A ‘ 1
и biXii dyt л et yt I
= S (--------) exp (-b2/xi2) < —L fa - y,) ~ —------ к
f = l xi2 db2 X{2 I-
(4.92)
dei
где — -
db i
db i
л det dy{
+ хцу1 exp (~b2/xi2); = - —-
do 2 do 2
*1*11 A z , / X
=--------yt exp (-b2/xi2);
*12
на каждом шаге итерации вычисляют значения F, G, Fb'v Fb'2, Gb ,
Gb’2, которые подставляют в формулу (4.87), учитывая формулу (4.85),
и вычисляют новые значения параметров Ъ2 и 62. Процесс продолжают до
тех пор, пока |6*+1 - bk\ не будет меньше заранее заданной величины,
назначаемой сообразно точности проводимых расчетов.
Начальные (нулевые) значения параметров Ь\ и Ь2 могут быть полу-
чены методом линеаризации функции (4.67) [И] :
In (—In у) = In b2 - b2jx2 + In x! (4.93)
или
fr=b\+b2x\ (4.94)
где
y+ ~ In (—Iny), x+ = l/x2, bi = In bit b2 = b2. (4.95)
Модель (4.94) линейна по параметрам, и коэффициенты b\ и Ь2 мож-
но вычислить по обычной методике линейного парного регрессионного ана-
лиза (см. гл П): Ь\ = 6,643963; Ь2 = 928,6492. Возвращаясь к прежним
параметрам, получаем b° = exp Ь2 = 768,1331; Ь2 ~ Ь2 = 928,6492.
Вычисления по формулам (4.89) —(4.92) на первый взгляд могут пока-
заться очень сложными. Однако их анализ и внимательное сравнение дают
возможность вычислять значения F, G, Fb'v Fb', Gb'v Gb2 с помощью
сравнительно простой расчетной процедуры. На каждом шаге итерации
достаточно вычислить промежуточные величины у/, е,-, е?, у/в/, - у^,
dy,
—г и затем подставить их в формулы (4.68), (4.88), (4.89), (4.90),
do2
(4.91), (4.92) и (4.87), чтобы получить величины суммы квадратов остат-
ков и параметров Ьх и Ъ2 на данном шаге.
При начальных значениях параметров = 768,1331, b2 = 928,6492,
принимая |Z>i+1 - < 0,2, \Ьк2 2 - Ь^\ < 0,2, можно получить значения
параметров на каждом из пяти шагов итерации, приведенные в табл. 4.8.
Значения промежуточных величин даны для тех, кто захочет самостоятель-
но повторить решения примера с применением настольной ЭВМ. Нетрудно
117
Таблица 4.8
QO
Результаты вычисления параметров нелинейной модели Ньютона - Рафсона
Шаг итерации L F G G'bx d *2
(1) (2) (3) (4) (5) (6) (7) (8) (9) (Ю)
1 +0,96737 5х XI 0“4 +0,342061х хЮ"3 +0Д38341Х хЮ"5 -0,500003х хЮ"5 +0,500004х хю"5 -0Д72674Х ХЮ"4 +0Д11251Х хЮ"11 732,258 938,071
2 -0.951135Х ХЮ"5 -0,137931х XI О"4 +0Д77993Х хЮ"5 -0,553719х хЮ"5 +553719Х ХЮ"5 -0Д80693Х х10"4 - 0Д50173Х хЮ"11 795,844 956,792
3 —0,510689х xl О"5 -0,145395х ХЮ"4 +0Д48724Х хЮ"5 —0,505264х хю"5 +0,50526 Зх ХЮ"5 -0Д79303Х ХЮ"4 -ОД13752Х хЮ"11 811,710 960,467
4 0,34 3004х ХЮ"6 -0,828284х хЮ"6 +0,141777х хЮ"5 -0,493644х х10"5 +0.493644Х Х10"5 -0Д78775Х XI О"4 -0,977662х ХЮ"12 813,851 960,997
5 -0,476030х ХЮ"8 -0,12864 8х хЮ"1 +0,14094 8х ХЮ"5 -0,492204х ХЮ"5 -0Д78721Х xl О-4 -0,963743х хЮ"12 813,873 961,003
+0.492204Х
15 „ Х10-5
2 - 0,0398060;
*=1 Р , bl ,
упрощающие преобразования. ~ ~ ~ F&2/ -G^.: — ; Gb=-F'br
заметить, что |813,873 - 813,8511 = 0,022 < 0,2, |961,003 - 960,997| =
= 0,0006 < 0,2. Для сравнения значения bi на первой итерации можно
вычислить на малой ЭВМ
b'l =b°i +(GF&'2 - FG^JId = 768,1331 +
+ 34,2061 1 (Г s(-0,500003 10~5)-9,67375-10"5 •(—1,726741(Г5) _
0,11125110г11
= 768,1331 ♦ -17^153Хя4^511(Г10 =768’1331 -
-35,8740 = 732,2591.
Числа, полученные на 5-й итерации (табл. 4.8), почти точно совпадают
с аналогичными числами, полученными Й. Бардом [11] на 6-й итерации
(вычисления проводились другим методом на другой ЭВМ и начаты с
другого начального приближения: й? = 750; Ъ% = 1200; Ъ\ = 813,4583;
Z>2 = 960,9063; S ej ~ 0,03980599). Такие благоприятные результаты
/=1
получаются не всегда [П.14.18].
Поверхность отклика кроме глобального может иметь и локальные
экстремумы, поэтому нет никакой уверенности, что получен именно тот
результат, к которому стремился исследователь. При этом следует пом-
нить, что выбор числа параметров зависит от интуитивных представлений и
является процедурой произвольной.
С технической точки зрения при выполнении операций с экспонентами
встречается еще одна трудность. Промежуточные результаты часто имеют
очень малые значения (например, 0,1 • 1(Г200), т.е. возникает ситуация,
именуемая «машинный нуль».
Поэтому задачу построения модели, нелинейной по параметрам, как
правило, решают на ЭВМ многократно, варьируя число параметров раз-
ными способами и с различными начальными приближениями. Укрупнен-
ная блок-схема программы построения на ЭВМ ЕС 1022 нелинейной по па-
раметрам модели методом Ньютона—Рафсона приведена на рис. 20.
Выше рассмотрена методика построения нелинейной по параметрам
модели при числе параметров р = 2. Метод решения нелинейных уравнений
Ньютона—Рафсона может быть использован также для любого числа пара-
метров.
Частное дифференцирование выражения (4.47) при нелинейной пара-
метризации по всем параметрам и приравнивание каждого полученного
выражения нулю позволяют записать систему нелинейных алгебраических
уравнений:
M>i. Ь2,...,Ьр) = 0,
* ^2, —, Ьр) = 0» (4.96)
fp(bi, ,dpj = O.’
119
Ясно, что кроме параметров bj в уравнениях (4.96) присутствуют также
независимые переменные Ху и зависимые переменные yi, которые для
краткости опущены, поскольку дифференцирование проводилось по пара-
метрам bj.
Требуется найти значение В, удовлетворяющее системе (4.96), где В
представляет собой р-мерный вектор неизвестных параметров:
bi
Ьг
(4.97)
bp
Систему (4.96) можно переписать в виде р-мерного векторного уравнения
F(B) = 0. (4.98)
Предположим, что разность между начальным приближением В0 и
решением системы нелинейных уравнений является малым вектором ДВ.
Если функция F(B) достаточное число раз дифференцируема в В0, то можно
воспользоваться разложением Тейлора:
Рис. 20
F(B) = F(B° + ДВ) =
= F(B°) +J0(B-B°) + ... = 0,
где Jo — матрица Якоби в точке В0;
dfi
д/2
О
Ob 1
dfi dfj,
db2 db°
df2 df2
(4.99)
(4.100)
dfp dfp dfp
db? d&i d bp
Если в разложении (4.99) ограничиться
только линейными членами, то получим
O^F(B°) + Jo (В-В°), (4.101
откуда В = В0 — J©1 F(B°). Это значение В
приближенное, но его можно использо-
вать в качестве начального на следующем
шаге итерации. В общем случае получаем
рекуррентную формулу
Bfc+l=Bfc-Jfc1F(Bfc). (4.102)
Процесс повторяют до тех пор, пока не получают | ДВ| <£ для некото-
рого заранее заданного £, выбранного в соответствии с точностью вычисле-
ний.
120
Материал, изложенный в данном параграфе, наряду с конфлюэнтным
анализом, по-видимому, отличается наибольшей сложностью. Для облегче-
ния усвоения этого материала целесообразно привести конкретный пример
построения нелинейной по параметрам модели для вычисления деформаций
ползучести бетонов. В качестве независимых переменных xj в модели
фигурируют факторы: т — возраст бетона к моменту ,загружения и (Z - т) —
время наблюдения в сутках. Данный пример тем более интересен, что для
получения результатов при решении системы нелинейных алгебраических
уравнений пришлось кроме метода Ньютона—Рафсона использовать еще и
метод наискорейшего спуска.
При выборе формы модели был использован кусочный метод описания
кривых ползучести бетонов- И.Е. Прокоповича. Сущность этого метода в
том, что бетоны с точки зрения их возраста при загружении подразделяют-
ся на три категории:
1) старые бетоны — тх > 360 сут;
2) стареющие бетоны — 28 < тх < 360 сут;
3) интенсивно стареющие бетоны — rt < 28 сут.
Поэтому для аппроксимации кривых ползучести первых двух катего-
рий бетонов при наличии в модели не более трех параметров можно исполь-
зовать следующие формулы:
1)т, >360сут; С(,= (4.103)
2) 28 < Ti < 360 сут;
С«,г)=0(г/(<-г)=<С» + Ле'”)[1-Де-1'1(’" °1- (4104)
Выражения (4.103) и (4.104) охватывают бетоны, загруженные в воз-
расте более 28 сут, т.е. подавляющее большинство встречающихся на прак-
тике случаев.
Для Ti < 28 сут (случай, редко встречающийся на практике) в настоя-
щее время используют более сложные формулы с большим числом коэф-
фициентов. Методику вычисления такого количества коэффициентов с
помощью нелинейного оценивания еще предстоит разработать.
Если ввести обозначения, обычно используемые при построении эмпи-
рических формул статистическими методами, а именно: у = C(tj т), х =
= (t - т),Ьо=В,Ъ1 = , то формула (4.103) принимает вид
У =со (1 -Ьое-*У * * * 1Х). (4.103а)
Для формулы (4.104) также можно ввести следующие обозначения:
У = C(t) т)/ Xi = т; х2 = (Г - т); Ьо = В; Ьг - у; b2 - ; в этом случае она
принимает, вид
У =(С0 + Ле-*»*1 ) (1 -г>ое-Ьг*г)- (4.104а)
Выражения (4.103а) и (4.104а) нелинейны по параметрам b0, bif b2.
Если имеются вектор-столбцы наблюдений у, Со, х для формулы (4.103а),
можно методами нелинейного оценивания вычислить значения параметров
Ьо и Ь2.
Если имеются вектор-столбцы наблюдений у, Со, х1г х2, А для форму-
121
лы (4.104а), можно методами нелинейного оценивания вычислить пара-
метры Ьо, Ъ2 иЬ2.
В экспериментальных работах по исследованию ползучести бетона уда-
лось обнаружить пока всего несколько опытов с возрастом бетона rt >
> 360 сут.
Для надежного оценивания значений параметров Ьо и bi необходимо
провести хотя бы несколько десятков опытов. Если удастся в дальней-
шем собрать необходимую информацию, то решение задачи нелинейного
оценивания параметров Ьо и bt для модели ползучести старого бетона
будет легко разрешимо. Одновременно можно будет проверить гипотезу
Ьо=О.
Стареющий бетон (28 < Ti < 360 сут) исследован достаточно, и поэ-
тому задачу нелинейного оценивания коэффициентов b0, bi, Ь2 в формуле
(4.104а) удалось решить.
Значения Со, А в формуле (4.104а) получены следующим образом:
Со=0,50Ск,28); Л = 0,70С(в$ 28), (4.105)
где 28) — предельнее значения удельных относительных деформа-
ций ползучести бетона, определенные по методике И.Е. Прокоповича:
с(«, 28) =63’6 ’10"7 'Д kf, (4.106)
где kf — независимые коэффициенты, определяющие влияние факторов.
Для вычислений использованы результаты опытов С.В. Александровс-
кого и Э.Я. Багрия, Глэнвиля, Дэвиса, Дютрона, К.С. Карапетяна, Мамийа-
на, И.И. Улицкого, П.Я. Панарина. И.Е. Прокоповича, Росса, автора книги
(всего 141 опыт). __
Исходные данные (значения^, х2(, 28), Соь Ai, i = 1,и, п = 141)
приведены в табл. 4.9.
Используя принцип Лежандра, можно записать, что сумма квадратов
отклонений значений, вычисленных по формуле (4.104а) от эксперимен-
тальных значений у / должна быть минимальной:
(4.107)
где
У/ =(С0/ + (1 - Ьое"д2*29- (4.108)
Другими словами, нужно подобрать такие значения параметров b0, b2, b2,
которые минимизировали бы сумму квадратов отклонений U. Таким обра-
зом, задача сводится к отысканию минимума функций U(b). Найдем част-
ные производные и приравняем их нулю:
^=0; «='0; ^1=0. (4.109)
ODq ot>i ob2
Если ввести обозначения
et(b^yi-%(bk (4.110)
122
Таблица 4.9
Но- мер опыта С(С т) t °-5С(«.г) Значение по формуле (4.104а) Отклонение
У1 *21 Со А Л ei =У1~У1
1 2 3 4 5 6 7 8
1 20 28 12 28,2 39,6 11,81 8,19
2 23 28 32 28,2 39,6 16,86 6,14
3 26 28 52 28,2 39,6 21,35 4,65
4 28 28 82 28,2 39,6 27,14 0,86
5 18 40 10 24,0 33,6 8,93 9,07
6 21 40 20 24,0 33,6 11,12 9,98
7 24 40 40 24,0 33,6 14,84 9,16
8 26 40 70 24,0 33,6 19,77 6,23
9 20 77 33 20,9 29,3 9,85 10,15
10 50 90 710 25,1 35,1 36,57 13,43
И 50 90 710 25,1 35,1 36,57 13,43
12 25 90 710 15,95 22,3 23,24 1,76
13 30 90 710 15,95 22,3 23,24 6,76
14 74,5 98 700 37,6 52,6 74,23 0,27
15 69 28 700 37,6 52,6 74,23 -5,23
16 185 28 2700 93,0 130,2 186,24 -1,04
17 71 28 1800 56,6 79,2 113,19 -42,19
18 51 90 90 39,6 55,4 29,48 21,52
19 114 28 27 57,5 80,5 115,03 -1,03
20 124 28 33 76,2 106,7 134,56 -1,56
21 107 28 330 76,2 106,7 134,56 -27,56
22 95 28 330 76,2 106,7 134,56 -39,56
23 98 28 330 76,2 106,7 134,56 -36,56
24 104,0 28 330 76,2 106,7 134,56 -30,56
25 76 28 730 55,4 77,6 109,67 -33,67
26 186 28 27 93,0 130,2 186,04 -1,04
27 140 28 150 110,1 154,7 144,40 -4,4
28 185 28 2700 93,0 130,2 186,04 -1,04
29 76 28 2400 38,5 53,9 77,02 -1,02
30 95 28 1300 48,0 67,2 95,99 -0,99
31 115 28 2400 58,0 81,2 116,03 -1,03
32 66 90 1300 33,5 46,9 49,41 16,59
33 73 90 1300 37,0 51,8 54,57 18,43
34 75 90 2400 38,0 53,2 56,07 18,93
35 49 98 1000 25,0 35,0 49,91 -0,92
36 104,0 29 340 58,6 82,2 104,31 -0,31
37 31,2 28 340 24,0 33,6 42,70 -11,5
38 112 28 340 62,2 87,1 11,69 0,31
39 34 28 340 25,4 35,6 45,22 -11,22
40 176 28 2700 88,5 123,9 177,04 -1,04
123
Продолжение табл. 4.9
1 2 3 4 5 6 7 8
41 18 28 1400 90,5 126,7 181,01 — 1,01
42 179 28 2700 90,0 426,0 180,04 -1,04
43 162,0 28 1300 81,5 114,1 162,97 -0,97
44 122 28 1000 61,5 86,1 122,76 -0,76
45 247,0 28 1900 142,6 199,6 285,24 -38,24
46 198,0 28 1900 74,5 104,3 149,03 -1,03
47 105,0 28 1900 65,6 91,8 131,20 -26,20
48 60 60 900 30,5 42,7 51,09 8,91
49 29 60 900 15,0 21,0 25,12 3,88
50 25 60 900 14,0 19,6 23,45 1,55
51 28 60 900 15,0 21,0 25,12 2,88
52 186 29 600 98,8 138,3 191,89 -5,89
53 104 95 500 69,2 96,8 95,92 8,08
54 52 185 300 60,3 84,4 59,71 -7,71
55 59 28 570 37,0 51,8 71,96 -12,96
56 54,5 28 570 27,9 39,1 54,29 0,21
57 23 28 570 19,1 21,1 29,34 -6,34
58 20 28 570 13,1 18,4 25,52 -5,52
59 18 365 307 16,1 22,5 14,17 3,83
60 24 365 307 16,1 22,5 14,17 9,83
61 26 365 307 16,1 22,5 14,17 11,83
62 25 28 571 15,1 21,2 29,41 -4,41
63 15 365 307 7,5 10,6 6,60 8,40
64 25 28 571 15,1 21,2 29,41 -4,41
65 10 365 307 7,5 10,6 6,60 3,40
66 24 28 571 15,1 24,2 29,41 -5,41
67 12 365 307 7,9 10,6 6,6 5,40
68 36,4 28 230 29,4 41,2 46,26 -9,86
69 26,6 60 198 22,7 31,8 28,28 -1,68
70 26,2 90 168 20,6 28,8 20,95 5,25
71 13,4 181 77,0 18,0 25,1 9,69 3,71
72 37,3 33 284 22,4 31,4 36,80 0,50
73 16,4 60 267 17,2 24,2 24,02 -7,62
74 6,4 196 126 13,4 18,8 9,13 -2,73
75 13,8 60 213 15,4 21,5 19,73 -5,93
76 8,2 181 94 12,2 17,0 7,3 0,90
77 22,7 182 348 14,1 19,7 14,6 8,1
78 38,2 90 440 14,1 19,7 19,53 18,67
79 25,7 182 348 15,3 21,4 15,84 9,86
80 38,0 60 471 21,0 29,4 33,53 4,47
81 23,5 28 100 14,7 20,6 19,24 4,25
82 23,1 28 150 17,5 24,5 22,91 0,19
83 14,7 90 113 12,2 17,1 10,24 4,46
84 17,4 28 150 44,4 66,3 62,02 -44,62
85 10,8 90 113 47,4 66,3 33,74 -28,94
124
Продолжение табл. 4.9
1 2 3 4 5 6 7 8
86 12,0 28 30 47,4 66,3 27,49 -15,49
87 25,0 28 40 47,4 66,3 >1,41 -6,41
88 40,0 28 50 47,4 66,3 35,09 4,91
89 50,0 28 60 47,4 66,3 38,57 11,43
90 57,0 28 70 47,4 66,3 41,81 15,16
91 68,0 28 80 47,4 66.3 44,93 23,07
92 77,0 28 90 47,4 66,3 44,83 29,17
93 80,0 28 10 47,4 66,3 50,56 29,44
94 25,0 9 10 33,2 46,4 26,12 -1,12
95 32,0 90 110 33,2 46,4 27,45 4,55
96 41,0 90 120 33,2 46,4 28,70 12,30
97 55,0 90 140 33,2 46,4 30,99 24,01
98 66,7 28 135 35,4 49,5 44,01 22,69
99 24,8 28 235 37,0 51,9 58,71 -33,91
100 17,7 50 235 29,6 41,5 41,50 -23,80
101 16,7 90 235 26,0 36,3 30,37 -13,67
102 10,0 28 12 30,5 42,8 12,77 -2,77
103 13,2 28 22 30,5 42,8 15,58 -2,38
104 16,0 28 92 30,5 42,8 31,19 -15,19
105 16,5 28 132 30,5 42,8 37,57 -21,07
106 17,0 28 172 30,5 42,8 42,58 -25,58
107 10,0 60 20 23,5 32,9 9,72 0,28
108 12,0 60 60 23,5 32,9 16,08 -4,08
109 13,1 60 100 23,5 32,9 21,08 -7,98
ПО 13,7 60 140 23,5 32,9 25,01 -11,31
111 7,5 91 29 21,4 30,0 8,99 -1,49
112 8,5 91 69 21,4 30,0 13,79 -5,29
ИЗ 10,0 91 109 21 >4 30,0 17,56 -7,56
114 81,0 28 2000 41,0 57,4 82,02 -1,02
115 60,0 28 2000 30,5 42,7 61,01 -1,01
116 50,0 90 2000 25,5 35,7 37,62 12,38
117 36,0 90 2000 18,7 26,3 27,63 8,37
118 34,0 365 2000 17,5 24,5 17,81 16,19
119 28,0 365 2000 14,5 20,3 14,75 13,25
120 40,0 90 2000 28,4 39,7 41,88 -1,88
121 70,5 28 2000 36,5 49,7 72,02 -1,52
122 40,0 90 2000 23,5 32,8 34,64 5,36
123 34,0 365 2000 17,5 24,5 17,81 16,19
124 28,0 365 2000 14,5 20,3 14,75 13,15
125 47,0 28 3800 24,3 34,0 48,60 1,6
126 51,0 28 3800 26,2 36,8 52,50 -1,5
127 75,5 28 3800 38,0 53,2 76,02 -0,52
128 77,0 28 3800 41,4 58,0 82,85 -5,85
129 81,0 28 3800 41,4 58,0 82,85 -1,85
130 15,4 34 67 48,0 67,1 39,95 -24,55
125
Продолжение табл. 4.9
1 2 3 4 5 6 7 8
131 11,5 70 62 37,0 51,7 24,56 -13,06
132 4,9 51 31 20,6 28,8 10,66 -5,76
133 10,5 29 44 25,3 35,4 17,46 -6,96
134 36,8 28 100 21,4 29,96 22,84 13,96
135 45,9 28 200 23,5 32,9 34,97 10,93
136 9,9 28 100 10,0 14,0 10,67 -0,77
137 46,4 28 200 29,5 41,3 43,90 2,5
138 52,4 28 100 31,0 43,3 33,04 19,36
139 29,8 28 200 24,5 34,3 36,46 -6,66
140 38,4 28 200 39,6 55,4 58,92 -2,52
141 1,4 28 100 ИД 15,5 11,83 -10,43
то формулу (4.107) можно переписать в виде
И А
U(b)= S ё}(Ь).
f=i
(4.111)
Далее вычислим:
дЩЬ) дь^ n deifb J f=l dbo
< dU(b) дьг ди(Ь) db% _ V /hi dei<b) i=l o*l - v a) де*(Ъ} — S 2e^(b) 1=1 0*2 (4.112)
Учитывая (4.110), можно получить
det(b) dbg tetfb) <>*1 dyj(b) db0 ’ dpjfb) dbi * (4.ПЗ)
det(b) db2 dyj(b) db 2
Подставляя вместо у^Ь) его значение из выражения (4.108), получим
де^Ь)
dbQ
ЩЪ)
дЬ 1
ЩЬ)
дЬ%
=e-ft2*2(C0< + Ле“ь»х”);
= хи Afe-6ixi*(l-boe~b^i);
= ьо e~b^i(Coi + Ai e~b i*»).
(4.114)
Подставляя (4.112) в (4.109) и учитывая (4.114), получаем систем)
уравнений:
126
S e;(bj e~b2X2i(Coi + Ле-ь»хИ) =0;
i=l
J Se/Z>Mif^e~bl*u(l-^oe"b2X29=0; (4.115)
f=i
-S e^b) x2iboe~b2X2i (Coi + Л/е-*!*!') =0.
i=i
Это система алгебраических уравнений, нелинейных по параметрам bQ, bi,
b2 Однако ее решение не просто, поскольку здесь сходимость зависит от
выбранного метода решения и взятых начальных приближений коэффи-
циентов 50, di, д2.
При первой попытке решения задачи за первичные (начальные) при-
ближения взяты те значения параметров, которые обычно встречаются в
работах по исследованию ползучести бетона: Ьо =В = 0,25; 5? = 7 = 0,012;
b2 - 71 = 0,006. На основе начальных приближений вычислены значения
yj(b) и е^Ь) (табл. 4.9). При этом S [е? fbj] 0 - 23067,64.
i=i
Попытка решить систему (4.115) методом Ньютона—Рафсона с ука-
занными начальными приближениями успеха не имела, так как решение
расходилось.
Далее была сделана вторая попытка решить систему методом скорей-
шего спуска; при этом получено стабильное решение. Вновь найденные
значения параметров были взяты за начальное приближение при повтор-
ном использовании метода Ньютона—Рафсона и получено быстросходя-
щееся решение, признанное окончательным.
Рассмотрим методику применения метода скорейшего спуска в данной
задаче. Чтобы упростить изложение алгоритма решения, введем обозна-
чения
М>о, *1. Ь2)= £ e,We-‘2X2'(C0/ + Л(е-‘2Д;‘>);
Л(*о, bl, М= 2 -6„е-‘2*2'); (4.116)
i = l
f2(b0, blf b2)=-^ei(b)x2ibo e~b^i(CQi +
и перепишем систему (4.115) в виде
M>o,blfb2^0-, fi(b0,bl,b2) = Q; Л(Ь0, d„ Ь2) = 0. (4.117)
Введем также новую функцию
Ф(Ьо, blt Ь2)=/о (50, bu b2) + /К*о, d2) + f2(b0, blt d2). (4.118)
Формула (4.118) принимает минимальное значение при тех и только тех
значениях параметров b0, bi и Ь2, которые удовлетворяют уравнениям сис-
темы (4.115). Вычисления производятся по следующим формулам:
^oi Дг+1 -Ьо, к ~ ;
127
bi, fc+i - bi, fc - Xjt
i>it k> b2, jt)
dbi
(4.119)
, . дф(Ьо, k> bi, k>' *2, fc)
° 2, fc+1 к “ Afc ---------------
Obz
Здесь
0(6 0, fc> bi, fc> 6 2, Jlc)
Ль- _ -----------------------—
A + B + C
где
Л = [
дф(.ьо, к> ь 1, V ь2, *) , о
--------------------------1 ;
дф(.ьо, k:bi, к' ь2, к), 2
1 dbi 1 1
дф(Ь0, к; bit к; Ь2, Jt) 2
С 1 лх. J ’
(4.120)
(4.121)
db2
Из формулы (4.118) видно, что
дф(Ь0, ь 1»ь2) д * *
----п-------= 7^- [Со (Ьо,Ь1,Ьг)+Яфо,Ь1,Ь1) +
Ob0 Obo
+ /? Фо, *2) ] = 2 [/-„(й», Ь2, bt) + (4.122)
Obo
dfl(bQ., bl> bl) д/2(Ь0, Ь\, bi)
+ Л Фо, bi, bi) +fi(bQ, bi, b2) °- ];
ODq ODq
дф(Ьл, b 1 , bl) A
----ТГ------— = —- L/o Фо, bi, bi) + /12 фо, bi, bi) +
ODj---------Q&j
_Л д/л(Ьл, Ь», bi)
+ /?<bo,bi,l>2)] = 2|/o(io,b1,i2)------------- + (4.123)
UO x
U A A d/1(b°’bl’b2)x/-/K A К df2(b0,bi,bi)
+/1Фо, bi, b2) — +АФо, bi, b2) ],
ob1 obi
дф(Ьп, bl, b2) A - -
US (bo. bi, b2) + fl фо, bl, bi)+
o&2 O&2
<УЬ(Ьо» bj, bo)
+ /? Фо,»!.»,)]-2 --------- + (4.124)
OD 2
, dfi (bo, b 1, b 2) ^/2(^01^1,62)
+/1Ф0, bl, bi) ° + fifbo, bl, bi) - ---------- .
dbi Obi
В формулах (4.122) — (4.124)
ЬМЪо,Ь1, t,j)_ £e-2b2x2,(C(). + 4.e-»i*H)J; (4.125)
db0 f=i
d/o(bo,bb ь2) _ £ Х1/Л.е-(Ь1*11+ b2*2f) X
dbi 1=1
x [(i -b0e-b2x*i)(C0i+ Л/е”6^1')- e{fb)]; (4.126)
128
db2 i=l
х [ejfb) + Z>0 е"62*2i(COl- + А, е~ь 1 х»«); (4.127)
<Vi(bo> ь2) __ _£/о(^о>_*1д£22_. (4 128)
дЬо
ОЛ<»..»».Ъ> _ g х1/4 e-»>xii(i -й.е-»^») х
<Э»1 (=1 '
х H,e->1X1'(l-M_#’X2')-e/Wl; (4129>
»^.ъ.,ъг) = » „
X [(Со/+A-e-b»xH)(i_boe-b2*29-efW]; (4-130)
дЛ(Ьр, & ь bi) __ <?Л(&о. ь1>ь2) (4 131)
dbo дЬ2
дЛ(&о, bi> ь2) _ <У1(Ьо» Ьь ь2) (4 132)
дЪ1 дь2
Д/2(Ьо.ь,1:.^= £ x22i6oe-^^-(Co + А''-’’'*'1) х
дь2 i=i
X [й<,е-'’«’[’<(Со( + Л/е-»>х>9 + е/ГЬЛ]. (4-133)
Алгоритм решения системы нелинейных уравнений методом Ньюто-
на—Рафсона приведен выше. Как уже отмечалось, попытка использовать
метод Ньютона-Рафсона сразу для решения системы (4.115) при началь-
ных приближениях & § = 0,85; й? = 0,012; Ь2 = 0,006 оказалась безуспеш-
ной. Возможно, эти приближения были слишком далеки от истинных значе-
ний параметров и вектор ДВ не был слишком малой величиной.
На втором этапе была предпринята попытка решить систему (4.115)
методом скорейшего спуска при тех же начальных приближениях. Вычис-
ления производились в системе FORTRAN ЕС 1022 при числе наблюдений
«=141.
Результаты вычислений, оказавшиеся весьма обнадеживающими, пока-
зывают хорошую сходимость метода скорейшего спуска при решении
подобных задач.
Уже на 8-й итерации абсолютная погрешность к+1 - к соста-
вила: для Ьо - 4,21-1СГ5%; для bt — 0,0493 %; для Ь2 - 0,905 %; полу-
чены следующие значения.параметров: bl = 0,85; bl =0,0143; b2 =0,0047.
Эти значения параметров взяты за начальные при повторном использовании
метода Ньютона-Рафсона. На 7-й итерации абсолютная погрешность £,
составила: для Ьо — 8,76-10-6%; для Ьг — 0 %; для b2 — 1,35-1СГ5%; по-
лучены следующие значения параметров: Ьо = 0,683; Z>i = 0,0134; b2 =
= 0,00344. Эти значения можно рассматривать как окончательные для взя-
того массива экспериментальных данных. Таким образом, формула (4.104)
принимает вид С(t, т) =(С0 + Ле-0’0134т) [1 - 0,683е“°’°0344 .
5 - 579 129
Как уже указывалось, при начальных приближениях сумма квадратов
отклонений составила 28067,64.
Расчет по методу скорейшего спуска дал возможность снизить сумму
квадратов до 25391,6 L
После уточнения величин параметров по методу Ньютона—Рафсона
окончательно получено Sc; = 23887,52.
Автор надеется, что изучение материала данного параграфа даст воз-
можность читателям самостоятельно решать задачи построения нелиней-
ных по параметрам моделей.
§ 4.8. Сравнение данных
Задача статистического сравнения данных очень часто возникает при
обработке результатов экспериментов. Ситуация, когда необходимо срав-
нить между собой теоретические и экспериментальные данные, встречается
практически в каждой научной работе. Как же решается эта задача в настоя-
щее время большинством исследователей? Например, по результатам опы-
та критическая сила при сжатии стержня составила 12 560 Н. Теория при
этом дает другой результат — 11 500 Н.
Являются ди эти результаты достаточно близкими между собой? И,
вообще, можно ли считать результат эксперимента удовлетворительным?
Абсолютная разница составляет 1 060 Н; относительная разница — 8,4 %.
Нельзя сказать, много это или мало; существенна разница между экспери-
ментальным и теоретическим результатом или нет? Однако в подавляющем
большинстве научных работ на этом и заканчивается сравнение теоретичес-
ких и экспериментальных данных.
В некоторых работах делается грубейшая методологическая ошибка:
сравнение теоретических и экспериментальных данных производят графи-
чески. На графике одним цветом изображают теоретическую кривую, а
другим цветом - ломаную линию, полученную по результатам эксперимен-
тов. Такое сравнение не только ни о чем не говорит, ио и вообще может
ввести в заблуждение, так как показатели такого сравнения зависят от
масштаба чертежа.
Еще более сложная задача возникает, когда необходимо сравнить меж-
ду собой два массива экспериментальных данных, полученных в разных
условиях, и требуется при этом определить, существенно ли влияет изме-
нение условий на полученные результаты. Например, известно, что проч-
ность бетона с течением времени увеличивается. Некоторые исследователи
заметили, что прочность нагруженного бетона увеличивается значительнее,
чем прочность ненагруженного бетона. Однако результаты неоднозначны и
зачастую противоречивы. В одних работах четко проявляется эффект
ускоренного увеличения прочности пригруженных бетонных образцов с
течением времени, в других такой эффект не наблюдается. Ниже будет
сделана попытка дать практические рекомендации для решения подобных
задач.
Прежде чем приступить к любому сравнению результатов, следует
определить погрешность эксперимента. Именно с погрешностью экспери-
130
мента следует сравнивать разницу между полученными результатами.
Наиболее простой и часто встречающийся случай состоит в том, что погреш-
ность эксперимента вычисляют по результатам экспериментов, выполнен-
ных в одной ’’точке”, например испытываются образцы из одного замеса
бетона, древесина из одинаковых слоев дерева и т.д. Пусть из одного заме-
са бетона были изготовлены восемь образцов в виде призм. Испытание этих
образцов на сжатие позволило определить призменную прочность бетона
Апр. Полученные результаты и вычисление по ним погрешности экспери-
мента приведены в табл. 4.10.
Из табл. 4.10 видно, что квадратическая погрешность эксперимента
представляет собой сумму квадратов разностей между i-й и средним ре-
зультатом наблюдений, деленную на число измерений в данной точке и
уменьшенную на единицу.
Таблица 4.10
Вычисление погрешности эксперимента по результатам
опытов, поставленных в одной "точке”
№ п/п Результаты экспериментов по определению 7?пр, МПа* 10 А^пр ~^npi ~ ^пр (ДАпр)2
1 -Л 3 4
1 221,4 0,1 0,01
2 230,4 9,1 82,81
3 210,8 -10,5 110,25
4 217,9 -3,4 11,56
5 227,3 6,0 36,00
6 230,3 9,0 81,00
7 213,6 -7,7 59,29
8 218,7 -2,6 6,76
1770,4 0,0 387,68
- 1770,4 .
^пр ~ g —221,3 ,
S/?np=%^38 = 7,44;
Результаты вычислений:
387,68
S2 =-------L2-S5538.
«пр 7
=0,034; v% = 3,4.
221,3
Понятие «погрешность эксперимента» является очень важным для
всех экспериментаторов. При постановке любых опытов всегда необходи-
мо поставить некоторое количество опытов в одной точке (не меньше
шести) для вычисления погрешности эксперимента. При этом такие опыты
желательно поставить по возможности ближе к центру эксперимента.
131
Так, если при проведении экспериментов по определению прочност-
ных характеристик бетона призменная прочность бетона изменяется в пре-
делах от 10 до 30 МПа, то погрешность эксперимента целесообразно вычис-
лять по результатам испытания образцов, имеющих призменную прочность
около 20 МПа.
Значение коэффициента вариации v зависит от тщательности проведе-
ния экспериментов. Так, например, общепринято, что v % для бетона состав-
ляет 7-9 %. В нашем случае (см. табл. 4.10) получилось v % — 3,4 только
потому, что эксперимент проводился с особой тщательностью в лаборатор-
ных условиях и были приняты специальные меры для уменьшения разбро-
са результатов. Погрешность эксперимента можно вычислить и по «неравно-
точным» измерениям, но объем вычислений при этом увеличивается [127].
Рассмотрим пример вычисления погрешности эксперимента по резуль-
татам неравноточных измерений, при этом процедуре вычисления ошибки
эксперимента предшествует проверка однородности результатов. Данные
для вычислений даны в табл. 4.11.
Погрешность эксперимента с использованием этих данных находится
по следующей методике:
а) вычисляется G-критерий Кохрена для проверки однородности ряда
дисперсий:
G = = ,3.65>77 = 0,207;
N 2 1762,2 ’
б) сравнивается G и G^n — 0,3915 (число степеней свободы v = 48,
16,32):
G = 0,207 <GTaftl =0,3915;
(0,01; 2)
следовательно, ряд дисперсий однороден;
в) вычисляется квадратичная погрешность эксперимента;
S2
2 _ W 1762,2 _ПП17.
SM~ N " 16 “110’17>
г) вычисляется погрешность эксперимента:
Sy = 10,50.
Как видно из табл. 4.11, общее число образцов п = 48, число точек
измерений N = 16. Квадратичная погрешность здесь вдвое больше, чем та,
которая вычислялась по результатам равноточных измерений.
Как отмечалось выше, прочность бетона, хранимого в соответствую-
щих условиях, с течением времени увеличивается. При этом некоторыми
специалистами выдвигается гипотеза, что прочностные и деформативные
характеристики загруженных бетонных образцов изменяются с течением
времени существеннее, чем у незагруженных образцов. Следует прове-
рить эту гипотезу, сравнивая результаты испытаний незагруженных и
132
Таблица 4.11
Данные для вычисление погрешности эксперимента по результатам
неравноточных измерений
№ опы- та Марка образца и суммы м*г& 1Д7?пр1 |ДЯцр|3 &(у{) Ti гтабл Марка отбро- шенно- го об- разца Окон- чатель- ный ре- зультат
1 2 3 4 5 6 7 8 9 10 11
1 П-1-1 П-1-2 П-1-3 155,4 162,2 138,2 3,5 10,3 13,7 12,25 106,09 187,69 153,02 12,40 1,11 1,41 - 151,9
455,8 151,9 306,03
2 П-2-1 П-2-2 П-2-3 239,7 247,0 259,7 8,1 0,8 8,9 65,61 0,64 79,27 72,73 8,53 1,04 1,41 - 247,8
743,4 247,8 145,46
3 П-3-1 П-3-2 П-3-3 95,0 86,4 89,9 4,6 4,0 0,5 217,6 16,0 0,25 18,71 4,33 1,06 1,41 - 90,4
271,3 90,4 37,41
4 П-4-1 П-4-2 П-4-3 161,8 164,9 164,3 1,9 1,2 0,6 3,61 1,44 0,36 2,71 1,65 1,15 1,41 - 163,7
491,0 163,7 5,41
5 П-5-1 П-5-2 П-5-3 234,4 250,5 269,8 17,2 1,1 18,2 295,84 1,21 336,24 314,14 17,7 1,03 1,41 - 251,6
754,7 251,6 628,29
6 П-6-1 П-6-2 П-6-3 169,8 161,8 177,9 0 , 8,0 8,1 0,00 64,00 65,61 64,81 8,04 1,01 1,41 - 169,8
509,5 169,8 129,61
7 П-7-1 П-7-2 П-7-3 217,3 205,9 235,5 2,3 13,7 15,9 5,29 187,69 252,81 222,89 14,88 1,07 1,41 - 219,6
658,7 219,6 445,79
8 П-8-1 П-8-2 П-8-3 412,3 112,7 109,3 0,9 1,3 2,1 0,81 1,69 4,41 3,46 1,86 1,13 1,41 — 11,4
133
Продолжение табл. 11.4
1 2 3 4 5 6 7 8 9 10 11
334,3 111,4 6,91
9 П-9-1 П-9-2 П-9-3 83,3 77,3 88,7 0,2 5,8 5,6 0,04 33,64 31,36 32,52 5,71 1,02 1,41 - 83,1
249,3 . 83,1 65,04
10 П-10-1 П-10-2 П-10-3 173,6 155,0 168,6 7,8 10,8 2,8 60,84 116,64 7,84 92,66 9,65 1,13 1,41 165,8
497,2 165,8 185,32
11 П-11-1 П-11-2 П-11-3 173,0 186,4 181,8 7,4 6,0 1,4 54,76 36,00 1,96 46,36 6,81 1,08 1,41 - 180,4
541,2 180,2 92,72
12 П-12-1 П-12-2 П-12-3 258,8 265,9 294,9 14,4 7,3 21,7 207,36 53,29 470,89 365,77 19,1 •1,14 1,41 - 273
819,6 273,2 731,54
13 П-13-1 П-13-2 П-13-3 203,0 202,6 227,2 7,9 8,3 16,3 62,41 68,89 265,69 19&50 14,10 1,16 1,41 - 210,9
632,8 210,9
14 П-14-1 П-14-2 П-14-3 150,8 150,8 134,1 5,6 5,6 11,1 31,36 31,36 123,21 92,97 9,66 1,15 1,41 - 145,2
435,7 145,2 185,93
15 П-15-1 П-15-2 П-15-3 268,5 281,5 271,4 5,3 7,7 2,4 28,09 59,29 5,76 46,57 6,82 1,13 1,41 - 273,8
821,4 273,8 93,14
16 П-16-1 П-16-2 П-16-3 137,8 144,2 149,6 6,1 0,3 5,7 37,21 0,09 32,49 34,90 5,8 1,05 1,41 — 143,9
431,6 143,9 69,79 1762,72
134
Таблица 4.12
Исходные данные для сравнения результатов испытаний загруженных
и незагруженных образцов
№ п/п Уровень затру- жения а//?Пр ЛПр, МПа-10 Еъ, МПа-10"2
не загру- жен загру- жен не загру- жен загру- жен не загру- жен загру- жен
1 2 3 4 5 6 7 8
1 од 168,6 168,1 174,0 187,5 0,203 0,217
2 0,3 165,5 179,9 170,0 185,0 0,198 0,203
3 0,5 164,6 186,3 170,0 172,0 0,193 0,216
Таблица 4.13
Сравнение результатов испытаний
Наимено- вание ха- ракте- ристики Незагру- женные образцы Загру- женные образцы Разность 1Д1 |Д|2 Диспер- сия Квадра- тичная ошибка экспери- мента Расчет- ное зна- чение F- крите- рия Таблич- ные зна- чения F- критерия при р=5%
1 2 3 4 5 6 7 8 9
л {4 _ 168,6 168,1 0,5 0,25
Ж Q —J S 165,5 179,9 14,4 207,36 339,25 55,38 6,13 4,74
с е 164,6 186,3 21,7 470,89
174,0 187,5 13,5 209,25
Модуль формац МПа-10 170,0 185,0 15,0 225,00 219,13 87,34 2,51 5,79
170,0 172,0 2,0 4,00
0,203 0,217 0,014 0,000196
Л К о * *5 0,198 0,203 0,005 0,000025 0,000375. 0,000055 6,82 5,79
0,193 0,213 0,023 0.00052S
загруженных образцов. Исходные данные для сравнения приведены в
табл. 4.12.
Операции сравнения с использованием F-критерия в табличной фор-
ме приведены в табл. 4.13. В этой таблице для призменной прочности бе-
тона в столбце 7 приведена квадратичная погрешность эксперимента,
вычисленная в табл. 4.10. В этом же столбце даны квадратичные погреш-
135
ности для модуля деформаций и коэффициента Пуассона, вычисленные по
этой же методике.
Из табл. 4.13 видно, что для призменной прочности расчетное значе-
ние F-критерия больше табличного:
F = 6 13 >FT =474
Г -^г(2; 7; 0,05)
Для модуля деформаций, наоборот, расчетное значение F-критерия
меньше табличного:
5.w5)=5,79.
Для коэффициента Пуассона расчетное значение F-критерия больше
табличного:
F = 6,82>F’.5;o,O5)=5,79.
Таким образом можно сделать вывод, что нагрузка существенно влия-
ет на изменение прочности и коэффициента Пуассона бетона, но несущест-
венно влияет на изменение модуля деформаций.
Так следует проводить сравнение результатов и ни в коем случае не
ограничиваться вычислением процента различия или тем более графичес-
ким сравнением результатов.
Глава V
ПОСТРОЕНИЕ ЭМПИРИЧЕСКИХ ФОРМУЛ ПО РЕЗУЛЬТАТАМ
АКТИВНЫХ (СПЕЦИАЛЬНЫМ ОБРАЗОМ СПЛАНИРОВАННЫХ) ЭКСПЕРИМЕНТОВ
§ 5.1. Активные эксперименты — эффективный
исследовательский метод естествоиспытателей
В первых четырех главах рассматривались статистические методы обработ-
ки экспериментальных данных, предназначенные для построения эмпири-
ческих зависимостей. Это дает возможность перейти к рассмотрению прин-
ципиально нового подхода к экспериментированию, который состоит в
том, что в каждом опыте варьируют одновременно все независимые пере-
менные (факторы) по специальному плану.
Эксперименты, поставленные таким образом, называют активными
в отличие от обычных, традиционных, пассивных экспериментов, при поста-
новке которых в каждом отдельном опыте варьирует только один фактор.
Активные эксперименты обладают следующими преимуществами:
1) многомерный регрессионный анализ чувствителен к соблюдению
исходных предпосылок, четко сформулированных в книге [102] ;
а) результаты наблюдений у у2,уп представляют собой независи-
мые, нормально распределенные случайные величины;
б) дисперсии равны друг другу (выборочные оценки Sy. однородны),
или, другими словами, если производить многократные повторные наблю-
дения над величиной у,- при некотором определенном наборе значений
ха, хп> ...» xtp, то дисперсия о у. не будет отличаться от дисперсии о^,
полученной при повторных наблюдениях для любого другого набора зна-
чений независимых переменных, х^,xJp;
в) независимые переменные х2,..., хр измеряются с пренебрежимо
малой погрешностью по сравнению с погрешностью в определении у.
Ясно, что эти требования могут быть выполнены только при актив-
ном эксперименте, кроме того, активный эксперимент просто лучше орга-
низован [97] ;
2) поскольку план экспериментов составляет заранее, перед началом
опытов, то ничто не мешает так составить этот план, чтобы максимально
упростить последующую обработку экспериментов для построения регрес-
сионных моделей;
3) оптимальное использование факторного пространства при активном
экспериментировании позволяет при минимальных затратах (минималь-
ном количестве экспериментов) получить максимум информации об изу-
137
чаемых явлениях, однако следует отметить, что вопрос использования
факторного пространства — один из самых сложных в планировании экспе-
риментов. Планы строят на р-мерных кубах, сферах, симплексах и других
фигурах. При планировании, например, на сфере, вписанной в куб, не ис-
пользуются угловые участки факторного пространства;
4) при планировании экстремальных экспериментов кроме аппрокси-
мации функции отклика (построения эмпирической зависимости) попутно
можно решить порой более важные для исследователя задачи — поиск
экстремума (максимума или минимума) в р-мерном факторном простран-
стве и задачу оптимального управления процессами;
5) методы планирования экспериментов позволяют опытным путем
проранжировать факторы по степени их влияния на функцию отклика;
6) планируемые эксперименты позволяют получить математическое
описание таких процессов, которое ранее было затруднительным (напри-
мер, при изучении диаграмм состав—свойство), и формализовать мето-
дами дисперсионного анализа изучение явлений, зависящих от качествен-
ных факторов;
7) планирование эксперимента позволяет изучать и математически
описывать процессы и явления при неполном знании их механизма.
Эти и некоторые другие особенности активных экспериментов под-
робно изучены ниже. Отметим, что активные эксперименты — мощное
средство познания природы, и нет сомнений, что этому способу эксперимен-
тирования принадлежит большое будущее.
В 30-х годах методы планирования экспериментов использовал Р. Фи-
шер применительно к решению агробиологических задач. Он же разработал
основные вопросы дисперсионного анализа [102].
Термин «дисперсионный анализ» в литературе применяется в смысле
сопоставления дисперсий и в смысле специального планирования и обра-
ботки экспериментов, позволяющих учесть влияние на функцию отклика
количественных и качественных факторов [149]. В настоящей работе тер-
мин употребляется во втором смысле.
Большая заслуга в дальнейшем развитии идей и методов планирования
экспериментов принадлежит Боксу, его сотрудникам, ученикам и последо-
вателям (Уилсону, Хантеру, Бенкину и др.). В нашей стране большой
вклад в популяризацию и дальнейшее развитие новых методов постановки
и обработки экспериментов принадлежит ВБ. Налимову [95, 96,97,102].
Ему же принадлежит первая в нашей стране статья по этому вопросу.
Область применения планируемых экспериментов распространяется на все
явления, которые зависят от управляемых факторов, т.е. таких факторов,
которые можно изменять и поддерживать на определенных уровнях. Экс-
перименты такого рода проводят при изучении физических, химических,
медико-биологических явлений. Такие ситуации встречаются во всех тех-
нических и инженерных дисциплинах. Планируемые эксперименты можно
подразделить на:
1) отсеивающие эксперименты, предназначенные для ранжирования
факторов;
2) экстремальные эксперименты;
138
3) ме^рды планирования экспериментов для дисперсионного анализа;
4) методы планирования экспериментов для специальных случаев
(изучение диаграмм состав—свойство и др.).
Для того чтобы нагляднее представить себе отличительные особенности
и преимущества новых методов экспериментирования, рассмотрим сущ-
ность метода Бокса—Уилсона, относящегося к области экстремальных
экспериментов.
Пусть, например, требуется построить математическую модель проч-
ности бетона или металлического сплава или любого другого материала в
зависимости от факторов, определяющих это очень важное свойство кон-
струкционных материалов, и затем использовать полученную модель для
оптимизации свойств интересующего исследователя материала. Задачу
можно решать двумя способами. Первый из них — традиционный — пред-
полагает постановку обычных пассивных экспериментов. Ставят некото-
рое количество опытов, в которых изучают, например, влияние водоцемент-
ного отношения (В/Ц) на прочность бетона. При постановке опытов варьи-
руют только В/Ц, остальные факторы поддерживают на постоянном уровне.
Затем ставят вторую группу экспериментов, в которой изучают влия-
ние возраста бетона т на прочность. В третьей группе опытов изучают влия-
ние активности цемента Лц на прочность и т.д.
Полученные результаты составляют матрицу результатов измерений X
и вектор-столбец Y. Результаты обрабатывают на ЭВМ по программе, опи-
санной в гл. III, в результате получают вектор-столбец параметров (коэф-
фициентов) bj
В = (Х*Х)”1 (X*Y),
т.е. строят множественное уравнение регрессии, например уравнение (3.55).
Используя это уравнение, можно реализовать процедуру поиска экстрему-
ма по результатам пассивных экспериментов, изложенную в гл. III, но уве-
ренности, что это и есть истинный экстремум, не будет.
При использовании второго способа (активные эксперименты) все
факторы, от которых зависит, например, прочность бетона: 1) В/Ц — водо-
цементное отношение, %; 2) г — возраст бетона к моменту испытания;
3) 7?ц — активность цемента; 4) Ц/З — отношение по весу цемента
к крупному заполнителю; 5) R3 — прочность крупного заполнителя;
6) <^тах — максимальная крупность заполнителя; 7) JVC —
влажность среды, в которой хранятся образцы; 8) tc — температура
среды, °C; 9) v — скорость загружения образца во время испытаний
варьируют одновременно в каждом опыте по специальному плану.
По полученным результатам экспериментов вручную в течение нес-
кольких минут можно вычислить вектор-столбец коэффициентов регрес-
сионной модели bj, но это не главное преимущество второго способа. Глав-
ное преимущество состоит в том, что, используя вторую регрессионную
модель, можно реализовать эффективный алгоритм поиска экстремума,
так называемый метод крутого восхождения, сущность которого рассмот-
рена ниже. Здесь же отметим, что при использовании этого способа поиска
экстремума реализуется идея «черного ящика» (исследование явления при
139
неполном знании его механизма), схема которого приведена на рис. 21.
В этом случае задачу решают поэтапно:
1) варьируют входы (в каждом опыте все одновременно) и наблю-
дают за изменением выхода (первая серия экспериментов);
2) строят первую математическую модель (уравнение регрессии);
3) корректируют входы, проводят другую серию экспериментов, и
так до достижения оптимума (экстремума).
Ниже наглядно показано, что этот способ поиска оптимума намного
эффективнее первого.
В ситуации, когда прочность металлического сплава зависит, напри-
мер, от факторов %i и х2, содержания железа (%), содержания хрома (%),
изложенные выше подходы к проведению экспериментов и поиску опти-
мума можно изобразить графически. На рис. 22 с помощью горизонталей
изображена поверхность отклика в двухфакторном пространстве. Точке
Опт соответствует максимальная прочность сплава.
Начиная эксперименты традиционным способом, берут исходный сплав
(точка А), содержание хрома сохраняют на постоянном уровне, а содержа-
ние железа варьируют. Двигаясь вправо вдоль линии абсцисс, довольно
быстро устанавливают бесперспективность этого направления движения.
При движении влево прочность сплава сначала увеличивается, а затем
уменьшается. Там, где прочность сплава на этой линии максимальна, нахо-
дится точка В — сплав, являющийся отправной точкой для новых поисков.
Из точки В проверяют два направления движения (вниз и вверх вдоль оси
ординат), при этом закрепляют на постоянном уровне содержание железа,
а изменяют содержание хрома.
При движении вверх находят новую перспективную точку С, от кото-
рой снова, переходя к варьированию содержания железа, приходят в опти-
мум — точку Опт.
Рис. 22 дает представление о следующих особенностях пассивных
экспериментов;
1) линии, изображенные пунктиром, отображают эксперимент, про-
веденный впустую (ошибочные направления движения к оптимуму);
140
2) поиск оптимума ведется фактически вслепую, методом попыток;
3) сплошная линия, представляющая собой правильное направление
движения к оптимуму, не является кратчайшим расстоянием от точки
А до точки Ощ.;
4) при увеличении числа факторов ху процедура поиска оптимума
резко усложнится и тут мало поможет даже сама по себе очень сложная
методика поиска оптимума, изложенная в гл. III.
При постановке активных экспериментов на небольшом участке в
окрестностях точки (рис. 23) поверхность отклика аппроксимируют
плоскостью, для чего ставят четыре опыта по плану, приведенному в
табл. 5.1. Знак плюс означает, что фактор ху поддерживается на верхнем
Таблица 5.1
План активных экспериментов
- *1 Х1 У
1 — + У1
2 + + Уз
3 + — Уз
4 — — —
уровне, знак минус указывает на нижний уровень фактора. По результатам
экспериментов строят линейный полином вида
у =bQ + + b2x2. (5.1)
Затем отыскивают градиент уравнения (5.1) или то направление даль-
нейшего движения по поверхности отклика, которое приводит к увеличе-
нию (самый «крутой склон»). Движение по «крутому склону» продолжают
до точки В, в окрестностях которой снова ставят четыре опыта и строят
полином
У = &о + b’lXi + Ь2х2. (5.2)
141
Далее движение продолжают по градиенту по точки О^, в окрестнос-
тях которой ставят большее количество опытов для нелинейного описа-
ния «почти стационарной области»—части поверхности отклика, близкой к
экстремуму и имеющей явно нелинейный характер. Схема движения по
градиенту и описание «почти стационарной области» приведены на рис. 24.
Особенности такого способа экспериментирования состоят в следующем:
1) ставят минимальное количество опытов;
2) движение от точки А до точки От осуществляют по кратчайшему
пути;
3) попутно получают нелинейное уравнение, описывающее функцию
отклика в «почти стационарной области», которое в случае необходимости
можно использовать для управления процессом.
Для иллюстрации этих основных особенностей активного эксперимен-
тирования рассмотрим числовой пример*.
Решается задача об оптимизации качества шва при сварке никеля.
Требуется найти состав и условия приготовления покрытия электродов для
сварки никеля с целью получения возможно меньшего числа пор в свар-
ном шве. Исследуется зависимость функции отклика у (число пор в участ-
ке сварного шва) от шести факторов, из которых один качественный.
Порядок решения задачи:
1) выбор исходной точки (нулевого уровня);
2) выбор интервалов варьирования факторов;
3) постановка первой небольшой серии опытов (8 опытов);
4) определение коэффициентов регрессии и запись линейного уравне-
ния регрессии в виде
У ~ bo + biXi + b2x2 + b3x3 + b4x4 + bsx5 + b6x6;
5) определение направления, дающего наименьшее значение у и начало
движения по градиенту (выполнение мысленных опытов);
6) повторение п. 3), 4) и 5) до достижения области минимума пор в
сварном стыке.
Методика и результаты решения задачи приведены в табл. 5.2. В этой
таблице показана реализация схемы экспериментирования, приведенной
на рис. 23. В таблице 9 столбцов и 50 строк.
В 1-й строке содержится основной уровень — исходный состав обмаз-
ки электродов, который давал большое количество пор. Задача опытов
состояла в том, чтобы свести это количество до минимума, а лучше всего
до нуля.
Во 2-й строке приведен интервал варьирования (7). В 3-й и 4-й строках
даны соответственно верхний (+1) и нижний (—1) уровни варьирования
факторов при планировании экспериментов. Далее в матрице планирования
эти уровни показаны в сокращенном виде. Вместо +1 написано а
вместо —1 написано
В строках 5—12 дана» ортогональная матрица планирования экспери-
*Пример заимствован из публичной лекции Ф.С. Новика.
142
Таблица 5.2
Методика и результаты проведения активных экспериментов
U/Ц оЫ Факторы и функция отклика Криолит, % Титан, % Алюминий, % Фтористый Натрий, % Длина дуги Время про- калки, мин Число пор (рентгено- скопия)
Код *1 *2 *3 х4 *5 х6 У
(1) (2) (3) (4) (5) (6) (7) (8) (9)
1 Основной уровень (о) 14 5 6 6 120 2 Интервал варьирова- ния (1) 2 1 1,5 2 15 3 Верхний уровень (+1) 16 6 7,5 8 Длинная 135г дуга 4 Нижний уровень (-1) 12 4 4,5 4 Короткая 105 дуга 5 1 ------ 275 6 Первая серия из 2+ - + - + - 181 7 восьми опытов поЗ- + -+ + - 185 8 плану 4+ + + + - -65 9 5+--+- + 142 10 6 --++ + + 301 11 7 + + + +304 12 8 - + +--+ 223 13 Коэффициенты моде- ли -36,5 -15,2 -17,0 -36,2 +33,2 +24,0 14 bjXI -73 -15,2 -25,5 -72,4 - +360 15 шаг движения по гра- диенту +0,63 +0,13 +0,2 +0,62 - -3 16 Вычисление шага -73 •(—1)=+73 1 14,63 5,13 6,2 6,62 Короткая 117 17 +73:100 = 0,7 3 2 15,26 5,26 6,4 7,24 ” 114 18 0,73-0,1 =0,63 3 15,89 . 5,39 6,6 7,86 ” 111 19 Десять мысленных опытов ' I 4 16,52 5,52 6,8 8,48 ” 108 58 20 (движение по град иен-5 17,15 5,65 7,0 9,10 ” 105 21 ту) II 6 17,78 5,78 7,2 9,72 и 102 35(min) 22 Опыты4, би 8 7 18,41 5,91 7,4 10,34 ” 99 23 выполняют на III 8 19,04 6,04 7,5 10,96 ” 96 64 24 самом деле 9 19,67 6,17 7,8 11,58 ” 93 25 10 20,3 6,3 8,0 12,20 ” 90 26 Новый (О) 18 6 7,5 10 ” 100 27 Интервал варьирова- ния (2) 0,5 Потолок, 0,5 0,5 - 5 больше нельзя 28 Верхний уровень (+1) 18,5 6 8 10,5 - 105 29 Нижний уровень (-1) 17,5 6 7,0 9,5 Короткая 95
143
Продолжение табл. 5 2
(1) (2) (3) (4) (5) (6) (7) (8) (9)
30 1 — Не варь- — Не варь- — 66
31 Вторая серия из 2 + ируется + — ируется — 40
32 восьыи опытов по 3 + — + (-1) — 44
33 плану 4 — + + — 52
34 5 + — + 39
35 6 + — + 69
36 7 — — + 72
37 8 + + + + 41
38 Коэффициенты мо- -11,9 -2,4 -0,6 +2,4
цепи bf
39 bf*I -5,95 -1,2 -0,3 +12
40 Шаг движения по гра-
диенту +1,0 +0,2 +0,05 -2
41 1 19 6 7,7 10 Короткая 98
42 Мысленные опыты I 2
(движение по гради- 20 6 7,9 10 99 96 12
43 енту) II 3 21 6 8,1 10 99 94 4
44 4 22 6 8,3 10 99 92
45 IV 5 23 6 8,5 10 95 90 0
46 Опыты 2, 3, 5 и 6 24 6 8,7 10 99 88
47 7 выполнены III 7 25 6 8,9 10 9» 86 0
48 8 26 6 9,1 10 99 84
49 9 27 6 9,3 10 99 82
50 10 28 6 9,5 10 80
Всего выполнено 23 опыта
ментов и результаты опытов [столбец (9) ], полученные при уровнях варь-
ирования, указанных в матрице.
В 13-й строке приведены значения коэффициентов линейной регрес-
сионной модели, полученной при обработке результатов восьми опытов:
у = 60-36,5*! - 15,2х2 — 17,0*3 — 36,2*4 — 33,2х5 + 24,0х6. (5.3)
В 14-й и 15-й строках определены направление и шаг движения по гра-
диенту («крутому склону»). Направление соответствует обратному знаку
коэффициентов регрессии: если имеется знак минус, как, например, при
bi, то при движении по градиенту надо прибавить шаг к основному уровню.
Сложнее обстоит дело при определении шага. Здесь за основу берут проце-
дуру перемножения значения коэффициента регрессии бу на интервал варь-
ирования (J), но затем производят округление, для которого требуются
интуитивные представления о существе изучаемого процесса, т.е. эта опера-
ция доступна только специалисту.
В таблице подробно описано получение шага движения по градиенту
для фактора *i. Качественный фактор *5 в дальнейшем не варьируется,
так как лучшие результаты получаются при короткой дуге.
144
В строках 16—25 расписаны уровни факторов Xj для десяти мысленных
опытов.
Три мысленных опыта (4, 6 и 8) выполнены в действительности в по-
рядке, показанном римскими цифрами. Опыт 6 (строка 21) дал минималь-
ное число пор. Этот опыт и принимают за основу при установлении нового
исходного основного уровня (строка 26) для постановки новой серии из
8 опытов по плану.
Числа строки 26 являются округленными числами строки 21 — шесто-
го мысленного опыта, после осуществления которого получено минималь-
ное количество пор.
В строках 30—37 даются матрица планирования и результаты второй
серии из восьми опытов.
Коэффициенты bj новой модели даны в строке 38. Строки 39 и 40
дают направление и шаг последнего движения по градиенту.
В строках 41—50 записаны мысленные опыты (движение по градиенту).
Опыты 2, 3, 5 и 7 выполнены в действительности в порядке, указанном
римскими цифрами. Опыты 5 и 7 дали сварной шов без пор, т.е. достигну-
та область оптимума.
Фактор х2 не варьируют после строки 29, так как при большем содер-
жании этого компонента процесс не может быть осуществлен. Окончатель-
но уравнение регрессии имеет вид
y=b0 — 1 l,9Xi — 2,4х3 — 0,6х4 + 2,4хб. (5.4)
Специфика этой задачи такова, что не требуется описание почти стацио-
нарной области полиномом второго порядка.
Таким образом, всего за 23 опыта получен высококачественный свар-
ной шов без пор.
Этот пример дает некоторое представление о возможностях актив-
ных экспериментов. Следует отметить, что процедура такого эксперимен-
тирования не носит формальный характер. Опыты могут быть поставле-
ны только хорошим специалистом. Строки 2, 15 , 26, 27 и 40 табл. 5.2 мо-
гут быть получены только при наличии хороших интуитивных представ-
лений о механизме изучаемого явления.
Однако процедура активного экспериментирования позволяет наи-
лучшим образом использовать знания, имеющиеся a priori об изучаемом
явлении. Это еще одна важная особенность планируемых экспериментов.
Ознакомившись с отличительными чертами планируемых активных экс-
периментов, подробно опишем методику их проведения и получения по
результатам их эмпирических зависимостей.
§ 5.2. Отсеивающие эксперименты
Матрица отсеивающих экспериментов состоит из двух блоков. Пер-
вый блок получают методом рандомизации — методом случайного выбора,
например путем бросания монеты или с помощью таблицы случайных
чисел. «Орел» соответствует знаку плюс в матрице планирования, «реш-
ка» — знаку минус.
145
Четная цифра в таблице случайных чисел — знак плюс, нечетная -
знак минус. Первый блок матрицы может быть также сформирован при
менительно к свойствам планов с минимальной неортогональностью [102]
Первый блок матрицы планирования служит для выделения линейных
эффектов.
Второй блок матрицы получают попеременным перемножением вектор^
столбцов первого блока и служит для выделения парных эффектов ("пар-
ных взаимодействий факторов). Матрица X = (хд) имеет размеры: i= 1,п-
число опытов, / = 1, к — число эффектов (факторов и их парных вза-
имодействий). Если р — число факторов, то к > р. Число вектор-столбцов
второго блока матрицыX:г =к- р — CJ.
Реализуя серию отсеивающих экспериментов в соответствии с первым
блоком матрицы X, который является матрицей планирования, получают
дектор-столбец результатов опытов у0, который используют для перво-
начального выделения факторов и парных взаимодействий.
Процедуру первоначального выделения факторов и парных взаимо-
действий в терминах факторного анализа можно выразить следующим
образом:
она станет понятной только при изучении числового примера. В формуле
(5.5) ху — +1 и Ху = — 1 — элементы матрицы; у° — элементы вектор-
столбца результатов экспериментов.
Группу наибольших по абсолютной величине линейных эффектов и
парных взаимодействий выделяют; и на втором этапе решения уточняют с
помощью множественного регрессионного анализа [78].
Наибольшую трудность представляет определение числа эффектов
т, которые нужно взять для регрессионного анализа. Как показал опыт,
не при всяком т задача решается (при некоторых т матрица нормаль-
ных уравнений не обращается).
В каждой конкретной задаче оптимальное т может быть определено
следующим образом: назначают т - 2, 3, 4, ..., к и применяют шаговый
метод поиска оптимального т, который продолжают до получения доста-
точно малой остаточной дисперсии 5^. или до переполнения машины.
Регрессионный анализ выполняют в обычном порядке по формулам
(3.5)—(3.14). Значимые эффекты выделяют по Г-критерию Стьюдента при
п-т—1 степенях свободы и 5%-ном уровне значимости:
^крит ~ Sbft » (5.6)
где
(5.7)
Все эффекты Zy > £>крит признают статистически значимыми и выде-
ляют.
146
Далее корректируют вектор-столбец результатов экспериментов jv0,
ликвидируя влияние выделенных эффектов, по формуле
т, х.. + 1 т j
у] - S L, -S-----------=уЧ - S bj^, + 1). (5.8)
1=1 1 /—1
Процесс [формулы (5.5)-(5.8)] повторяют др выделения всех зна-
чимых эффектов. Для проверки изложенного метода была решена искус-
ственно синтезированная задача с 36 эффектами (8 линейных эффектов
и 28 парных взаимодействий [78] ). Эффекты вводились методом решения
неполной квадратичной полиномиальной модели с заданными коэффици-
ентами bj. В табл. 5.3 сравнены введенные эффекты и полученные по про-
цедуре, изложенной выше. Эффекты в табл. 5.3 даны в терминах регрес-
сионного анализа в порядке их выделения.
Изложенный метод обработки результатов отсеивающих эксперимен-
тов не включает, подобно другим методам, трудно машинизируемую опе-
рацию «распознавания зрительного образа» и предназначен для реализации
на ЭВМ.
К сожалению, процедура обработки отсеивающих экспериментов очень
плохо воспринимается при простом чтении ее описания. Для того чтобы
было можно в практических целях воспользоваться изложенной методи-
кой, решим небольшой искусственно синтезированный пример.
Таблица 5.3
Сравнение искусственно введенных и выделенных эффектов
Обозначение эффектов *56 *4 *6 ьз *5 *35 *34 *45 *14 *57
Введенные bj —7 18 -5 -15 20 -9 -8 3 1 2
Выделенные bj -7,596 20,750- -5,827 -1Z911 20,922 -9,734 -7,663 2,203 1,411 2,754
Эффекты и их парные взаимодействия введем с помощью полинома
у =— 5,0xi + 15,0х2 + 3,0*з + 6,0*1*2 + 0,5x^3 + 2,0*2*з- (5.9)
В табл. 5.4 приведены блоки матрицы X. Исключительно для упроще-
ния расчетов [чтобы избежать выполнения вручную процедуры множест-
венного регрессионного анализа по формулам (3.5)—(3.15)], так как здесь
не стоит вопрос об экономии количества экспериментов (пример искус-
ственно синтезирован), можно взять в качестве матрицы планирования
план полного факторного эксперимента с числом строк п>к.
Обычно на практике для уменьшения числа опытов используют не-
насыщенное планирование п < к, но в этом случае план не обладает свойст-
вами, позволяющими упростить процедуру регрессионного анализа. При
обработке результатов отсеивающих экспериментов на ЭВМ такое упроще-
ние не актуально. Методика построения планов подробно рассмотрена в
следующих параграфах настоящей главы.
147
Таблица 5.4
Исходные данные для обработки отсеивающих экспериментов
№п/п Первый блок Второй блок У°
*1 *2 *3 *1*2 *1*3 *2*3
(1) (2) (3) (4) (5) (6) (7) (8)
1 — — — + + + 35,8
2 + — — — + 3,8
3 — + — + — 40,2
4 + — + — — 42,2
5 — + — — 27,8
6 — + — + — 4,8
7 — + + — -*• + 49,8
8 + + + + + 51,2
-6,45 +13,5 +1,45 +7,3 +1,05 +3,2 Выделенные эффекты
-5,0 +15,0 +3,0 +6,0 -0,5 +2,0 Введенные эффекты
Таблица 5.5
Вычисление у° введением эффектов с помощью уравнения (5.9)
№п/п *1*1 *2*2 *з*з
(1) (2) (3) (4)
1 -5,0 (-1) =+5,0 15,0 (-1) =-15,0 3,0 (-1) =-3,0
2 -5,0 (+1) =-5,0 15,0(-1) =-15,0 3,0 (-1) =-3,0
3 -5,0 (-1) =+5,0 15,0 (+1) =+15,0 3,0 (-1) =-3,0
4 -5,0 (+1) =-5,0 15,0 (+1) =+15,0 3,0 (-1) =-з,о_^
5 -5,0 (-1) =+5,0 15,0 (-1) =-15,0 3,0 (+1) =+3,0
6 -5,0 (+1) =-5,0 15,0(-1) =-15,0 3,0 (+1) =+3,0
7 -5,0 (-1) =+5,0 15,0 (+1) =+15,0 3,0(+1) =+3,0
8 -5,0 (+1) =-5,0 15,0 (+1) =+15,0 3,0 (+1) =+3,0
Продолжение табл. 5.5
*12 *1*2 *13 *1*3 *23 *2*3 У / У У°
(5) (6) (7) (8) (9) (Ю)
6,0 (+1) =+6,0 -0,5 (+1) = -0,5 2,0 (+1) =+2,0 -5,5 36,0 35,8
6,0 (-1) =-6,0 -0,5 (-1) =+0,5 2,0 (+1) =+2,0 -26,5 4,0 3,8
6,0 (-1) =-6,0 -0,5 (+1) =-0,5 2,0 (-1) =-2,0 +9,5 40,0 40,2
6,0 (+1) =+6,0 -0,5 (-1) =+0,5 2,0 (-1) =-2,0 +11,5 42,0 42,2
6,0 (+1) =+6,0 -0,5 (-1) =+0,5 2,0 (-1) =-2,0 -2,5 28,0 27,8
6,0 (-1) =-6,0 -0,5 (+1) =-0,5 2,0 (-1) =-2,0 -25,5 5,0 4,8
6,0 (-1) =-6,0 -0,5 (-1) =+0,5 2,0 (+1) =+2,0 +19,5 50,0 49,8
6,0 (+1) =+6,0 -0,5 (+1) = -0,5 2,0 (+1) =+2,0 +20,5 51,0 51,2
148
Процедура вычисления элементов вектор-столбца j’0 с введением эф-
фектов с помощью уравнения (5.6) и использованием матрицы X из табл. 5.4
приведена в табл. 5.5. В полученный вектор-столбец результатов вводят
погрешности (± 0,2) по изложенной в гл. IV методике, применяя табли-
цу случайных чисел П.1, в результате получают вектор-столбец данных
у°. В последних двух строках табл. 5.4 сравнены выделенные и введен-
ные эффекты. Данный пример рассмотрен в основном для того, чтобы
привести табл. 5.6, которая является реализацией процедуры предваритель-
ного выделения эффектов по формуле (5.2). Формула (5.2) малопонятна,
а табл. 5.6 читается легко.
Группу наибольших по абсолютной величине эффектов выделяют и
уточняют с помощью регрессионного анализа. Специальный план, взятый
в данном примере, позволяет вычислить эффекты по формуле
(5.9а)
я
Ь/=(2*//Л)/л-
Вопрос о том, почему коэффициенты йу в данном случае вычисляются
так просто, рассмотрен в следующем параграфе. Таблица 56
Процедура предварительного выделения эффектов
№ п/п *1 х2 хз Х1Х2 *1*3 *1*3 У°
+ — + — + — + — + — + — (1) (2) (3) (4) (5) (6) (7) (8) (9) (10) (11) (12) (13) (14) 1 35,8 35,8 35,8 35,8 35,8 35,8 35,8 2 3,8 3,8 3,8 3,8 3,8 3,8 3,8 3 40,2 40,2 40,2 40,2 40,2 40,2 40,2 4 42,2 42,2 42,2 42,2 42,2 42,2 42,2 5 27,8 27,8 27,8 27,8 27,8 27,8 27,8 6 4,8 4,8 4,8 4,8 4,8 4,8 4,8 7 49,8 49,8 49,8 49,8 49,8 49,8 49,8 8 51,2 51,2 51,2 51,2 51,2 51,2 51,2 9 102 153,6 183,4 72,2 133,6 122,0 157 98,6 132 123,6 140,6 115,0 255,6 Ю 25,5 38,4 45,85 18,05 33,4 30,5 39,25 24,65 33,0 30,9 35,15 28,75 11 -12,9 +27,8 +2,9 +14,6 +2,1 +6,4 12 -6,45 +13,9 +1,45 +7,3 +1,05 +3,2
В строке 10 табл. 5.6 приведены результаты строки 9, деленные на
и/2 = 4. В строке 11 даны выделенные эффекты Lj в терминах факторного
анализа.
149
Из изложенного выше ясно, что отношение между эффектами в терми-
нах регрессионного и факторного анализов следующее: bj = Ljl'2.^ — причем
при неортогональном плане это равенство является приближенным.
В строке 12 табл. 5.6 приведены выделенные эффекты в терминах
регрессионного анализа. С табл. 5.6 начинается собственно методика обра-
ботки отсеивающих экспериментов. Предшествующие действия служили
только для синтезирования примера.
В реальных задачах после «выравнивания» вектор-столбца по формуле
(5.5)' процедуру повторяют до выделения всех значимых эффектов. В
рассматриваемом искусственно синтезированном примере это делать нет
смысла.
В работе [78] даны результаты отсеивающих экспериментов, постав?
ленных для выявления важнейших факторов, влияющих на модуль дефор-
маций и прочность бетона, и произведена обработка результатов на ЭВМ.
Рандомизированная матрица планирования для девяти факторов, из кото-
рых три качественных, и результаты экспериментов приведены в табл. 5.7;
В эксперименте, как видно из этой таблицы, варьировались по матрице
планирования следующие факторы:
Таблица 5.7
Матрица планирования и результаты отсеивающих экспериментов
в/ц Яц 6ц Вид це- мента т Порода за- полнителя й? йГ W Способ ускорения твердения *6
Я пр
+1 0,6 400 440 Портланд- 50 Гранит 0,8 70 % Естествен-
цемент ный
-1 0,4 300 350 Шлако- 7 Извест- 0,5 Вода Пропарен- портланд- няк ный цемент
Код № п/п *1 х2 ^3 *4 *5 *6 *7 *8 х9 У1 У2
(1) (2) (3) (4) (5) (6) (7) (8) (9) (10) (11) (12)
1+ + + - - - - + + 134,3 101,8 2 — + + + + + + - + 264,1 256,1. 3+ + - - + + + + + 305,3 214,9 4 + + — - + - + - 211,0 162,3 5 — + + - - + + + + 274,6 198,7 6 + - + + - -- + - - 105,3 47,5 7 - - - + + + + + + 317,5 246,4 8 - + - + - + + - - 254,9 126,7 9 + - + _ - - + + + 113,3 73,1 10+- - + + - + - - 169,7 119,9 11+- - + + + - - 162,7 101,1 12 + + + + - + - - - 181,5 94,1 13 -- + + + - + + + 263,8 305,2 14 - + - + + - - + + 168,7 126,0 15+- - - - - - - 86,1 31,9 16 - + - + - + + - + 272,9 165,1
150
1) В/Ц — водоцементное отношение, %;
2) Ац — активность цемента, МПа* 10;
3) — количество цемента на 1 м3 бетона, кг;
4) вид цемента (качественный фактор);
5) г — возраст бетона к моменту испытания, сут;
6) порода крупного заполнителя бетона (качественный фактор);
7) Кщ/Кб - отношение объема крупного заполнителя к объему бетона;
8) W — влажность среды, в которой сохранялись образцы, %;
9) способ ускорения твердения бетона (качественный фактор).
Модуль деформаций Eq (МПа-10-2) и прочность бетона R8 (МПа-10)
найдены по результатам испытания трех бетонных призм размером 10x1 Ох
х40 см в каждом опыте.
Следует обратить особое внимание на тот факт, что, поскольку фак-
торы рассматривают в кодированном обозначении (+1 — верхний уровень
—1 — нижний уровень), при постановке отсеивающих экспериментов может
быть изучена степень влияния на исследуемое явление не только количест-
венных, но и качественных факторов.
Если бы и в описываемом реальном примере использовался полный
ортогональный план, то число опытов было бы равно 29 =512. Ясно, что
здесь целесообразно использовать ненасыщенное и неортогональное плани-
рование с сокращением числа опытов до 16 и проведением множественного
регрессионного анализа на ЭВМ. Этого небольшого количества опытов
оказалось достаточно для получения нужной информации.
При обработке результатов отсеивающих экспериментов (табл. 5.7)
на ЭВМ для изучения степени влияния факторов на модуль деформации
бетона на первом этапе эффекты начали выделяться при числе эффектов
т = 8, а при т = 16 матрица нормальных уравнений не обращалась.
Анализ показал, что оптимальным можно считать т = 12. При этом
эффекты выделились в следующем порядке:
первый цикл: 1) х6, 2) хп 3) х7, 4) х9, 5) х2х8,6) х7х9, 7) х2,8) xs,
9) XiXs, 10) х3х7,11) xvx2,12) х2х3;
второй цикл: 13) х2х3,14) х2х9 и 15) х3х8.
Всего за два цикла выделилось 15 эффектов из 45 возможных. Из 9
линейных эффектов статистически незначимыми оказались только эффек-
ты х3 их8.
При обработке результатов экспериментов на ЭВМ в задаче, предназ-
наченной для изучения степени влияния 9 факторов на прочность бетона,
эффекты начали выделяться уже при т = 5, а при т = 14 матрица нормаль-
ных уравнений не обращалась; оптимальным являлось ли = 10.
Эффекты выделялись в следующем порядке:
первый цикл: 1) х15 2) xs, 3) х7,4) х7х9, 5) Xjx2;
второй цикл: 6) х4х8,7) х4х9,8) х2х9, 9) х6;
третий цикл: 10) х3х9.
Всего за 3 цикла выделилось 10 эффектов из 45 возможных. Стати-
стически незначимыми для этого случая оказались 5 линейных эффектов из 9.
Алгоритмы машинной обработки отсеивающих экспериментов:
1)п ервоначальное выделение эффектов по формуле (5.2) (см. табл. 5.6);
151
©
X
С Начало )
4 I---------------
/ Ввод исходных данных
г© (х, Y, размер задачи)
Предварительная обработка
исходных данных (n.t)
Рие. 25
2) выбор оптимального числа
выделившихся эффектов для провес
дения регрессионного анализа.
3) регрессионный анализ [фор»
мулы (3.5)-(3.14)] ;
4) оценка значимости эффек-
тов с помощью /-критерия Стью-
дента по формулам (5.3) и
(5.4);
5) корректировка [выравни-
вание вектор-столбца у0 по фор-
муле (5.5)] ;
6) повторение п. 1)—5) дд
выделения всех статистически зна-
чимых эффектов.
Если есть возможным подсчи-
тать величину /-критерия Стьюдента
для каждого выделившегося эф-
фекта, то эти данные также можно
выдать на печать для построения
гистограммы ранжирования эффек-
тов.
Укрупненная блок-схема алго-
ритма обработки на ЭВМ резуль-
татов отсеивающих экспериментов
приведена на рис. 25.
§ 5.3. Экстремальные эксперименты
Рассмотрение экстремальных экспериментов, некоторое представле-
ние о которых было получено при изучении § 5.1, м'ожно начать с мето-
дики составления планов полного факторного эксперимента (ПФЭ) и
дробных реплик от него.
Перед началом работы с планом экспериментатор должен знать, сколь-
ко и какие именно факторы он собирается варьировать. Для решения этой
задачи нужно иметь опыт специалиста, а также знать и уметь использовать
материал предыдущего параграфа. Факторы должны быть количественными
и контролируемыми (изменяться и поддерживаться на постоянном уровне
по воле экспериментатора), а результаты опытов — воспроизводимыми.
Погрешности экспериментов предполагают небольшими, подчиняющимися
закону нормального распределения.
Устанавливают основной уровень факторов (0) — центр эксперимента
(исходная точка, начало движения по поверхности отклика) и интервалы
варьирования факторов (7), которые должны быть достаточно большими,
но не максимальными. Выбор максимальных интервалов варьирования
при составлении линейных планов не позволит перейти затем к планам
152
второго порядка. Вычисляют верхний (+1) и нижний (—1) уровни варьи-
рования факторов.
Для построения регрессионного уравнения с двумя факторами
и %2 вида
у = bo + z>i*i + ъ2х2 + £12*1*2 (5.9б)
можно предложить план ПФЭ, приведенный в табл. 5.8. Предположим, что
варьируются два фактора: фактор - водоцементное отношение (В/Ц)
и фактор х2 — возраст бетона (т), функция отклика у — прочность бето-
на (^пр ) •
В табл. 5.8 ПФЭ приведен в форме, удобной непосредственно для поста-
новки экспериментов; х0 — это фиктивный фактор, который необходим
для вычисления свободного члена полинома £0; + 1 и —1 — кодированные
обозначения уровней факторов. Столбец (6) матрицы X получается пере-
множением столбца (4) на столбец (5).
План полного факторного эксперимента (ПФЭ) 22
Таблица 5.8
Факторы и функция отклика В/Ц г (В/Ц)'Т Обозначения строк мат- рицы X *пр
Код *0 *1 *2 *1*2 У
Единицы величины % Сутки
Основной уровень (0) 50 28
Интервал варьирова-
ния (/) 20 14 мПа-10
Верхний уровень (+1) 70 42
Нижний уровень (-1) 30 14
(1) (2) (3) (4) (5) , (6) (7) (8)
№ опыта 1 +1 -1 -1 +1 (1) У1
2 +1 • +1 -1 -1 а У2
3 +1 -1 +1 -1 Ъ Уз
4 +1 +1 +1 +1 аЪ У4
План 22 Планирование Матрица X Вектор выхода Y
Как видно из табл. 5.8, собственно для планирования служат только
столбцы (4) и (5). В табл. 5.9 эти столбцы воспроизведены отдельно, при
этом вместо +1 написано а вместо —1 написано
Чтобы получить планирование (23) для трех факторов: х1г х2 и х3, —
следует табл. 5.9 переписать еще раз и к ней справа добавить еще один
столбец с четырьмя знаками минус и четырьмя знаками плюс. Такое пла-
нирование (23) показано в табл. 5.10, где двойной линией очерчены повто-
ряемые матрицы.
153
Таблица 5.9
Таблица 5.1$
Планирование 22 Планирование 23
Точно так же поступают, если нужно получить планирование для четы-
рех факторов 24 (2 — число уровней варьирования, 4 — число факторов;
24 = 16 - число опытов); матрицу из табл. 5.10 повторяют два раза и
справа приписывают столбец с восемью минусами и восемью плюсами.
В табл. 5.11 двойной линией очерчены повторяющиеся матрицы.
Правило составления планирования можно сформулировать и по-дру-
гому: в столбце Xj знаки минус и плюс чередуются; в столбце х3 чере-
дуются два минуса и два плюса; в столбце х3 чередуются четыре минуса и
четыре плюса; в столбце х4 чередуются восемь минусов и восемь плюсов
и т д. с удвоением количества чередующихся знаков.
Отметим, что при планировании с любым количеством факторов в
плане ПФЭ в первой строке всегда будут только минусы, а в последней —
только плюсы.
Нет сомнения, что теперь можно составить планирование для любого
количества факторов 2Р. Если обозначить, как в табл. 5.11, факторы ма-
лыми буквами латинского алфавита, то можно записать планирование в
буквенном обозначении. Если строка обозначена буквой а, то это значит,
что только фактор х} взят на верхнем уровне +1, а остальные факторы
взяты на нижнем уровне —1. Если строка обозначена буквой Ъ, то только
фактор х2 взят на верхнем уровне, а остальные — на нижнем. Обозначение
ab означает, что только факторы хг и х2 взяты на верхнем уровне. Если
все факторы взяты на нижнем уровне, как в первой строке, то эту строку
обозначают знаком (1).
, Например, планирование для двух факторов 22 (табл. 5.9) можно
обозначить так: (1), a, b, ab; для трех факторов 23: (1), а, Ъ, ab, с, ас,
be, abc; для четырех факторов: (1), a, b, ab, с, ас, be, abc, d, ad, bd, abd,
cd, acd, bed, abed и тд. Отметим, что принята такая система обозначений,
что обозначение начальных строк всех планов повторяется.
Для рассмотрения вопроса о степенях свободы [102] в табл. 5.12
приведен в упрощенном (по сравнению с табл. 5.8) виде план ПФЭ для
трех факторов 23. Используя этот план, можно независимо оценить коэф-
фициенты регрессии b0, bif b2, Ь3, bi2, bi3, b23 иЬ123. Если ограничиться
линейным приближением (оценивать только линейные эффекты bo, bit
154
Таблица 5.11
Планирование 24
а ь с d \ Буквенные обо-
№ п/п
*2 Хз Х4
1 — - — — (1)
2 + — — — а
3 — 4- — — b
4 + 4- — — ab
5 — — + — с
6 4- — 4- — ас
7 — 4- 4- — Ьа
8 + + + abc
9 — — — + d
10 4- — — + ad
11 — + — + bd
12 + + — + abd
13 — — + + cd
14 + — + 4- acd
15 — + + + bed
16 4- 4- + 4- abed
Таблица 5.12
План ПФЭ 23
№ n/n Матрица X Планирование Буквен- ные обо- значения строк Вектор выхода Y
xq *1 X2 Хз *1*2 *1X3 *2*3 *1*2*3
(1) (2) (3) (4) (S) (6) (7) (8) (9) (10) (ID
1 + — — — + + + (1) У1
2 4- + — — — — + + a У2
3 4- — + — + — 4- b Уз
4 + 4- + — 4- —— — ab У4
5 + — + 4- — — + c У5
6 4- 4- — + — 4- — ac Уб
7 + — 4- + — — + — be У?
8 + + 4- + + 4- 4* 4- abc Уъ
Ь2 и Z>3), то четыре степени свободы останутся для проверки адекватности
(статистической оценки) уравнения регрессии. Можно оценивать только
линейные эффекты и парные взаимодействия, тогда только одна степень
свободы останется для проверки адекватности.
Нетрудно заметить, что с увеличением числа факторов р количество
экспериментов резко возрастает: п = 2Р. Уже для пяти факторов при реали-
155
зации ПФЭ надо поставить 32 эксперимента. Если учесть, что еще хотя
бы 6 опытов нужно поставить в центре эксперимента [основной уро-
вень (0)] для вычисления погрешности эксперимента (этот вопрос под-
робно рассмотрен ниже), то ясно, что количество экспериментов при
осуществлении ПФЭ достаточно велико.
Для уменьшения числа опытов вместо полного факторного экспери-
мента используют дробные реплики от него, которые позволяют знаодтель-
но экономить количество опытов при небольшой потере информации, если
при решении той или иной задачи можно ограничиться построением линей-
ной формы уравнения регрессии или оценивать независимо не все эффекты
(бывают ситуации, когда оценивать те или иные взаимодействия не имеет
смысла).
Для полуреплики от ПФЭ с тремя факторами количество эксперимен-
тов п — 23-1 = 4; для ситуации, в которой оцениваются шесть факторов,
1/2 ПФЭ 2б“1 =32; */4 ПФЭ+26"2 = 16; 1/8 ПФЭ26~2 = 8.
Полуреплику, например, от ПФЭ 23 получают делением матрицы на две
части. Если ПФЭ 23 в буквенном обозначении записан (табл. 5.12) в виде
(1), b, b, ab, с, ас, be, abc, то полуреплики таковы:
1) первая полуреплика с, a, b, abc;
2) вторая полуреплика (1), ас, be, ab.
Эти полуреплики в развернутом виде приведены в табл .5.13.
Таблица 5.13
Определяющий контраст Определяющий контраст
J=X!X2X3 / = -х1х2х3
Правила составления полуреплик можно сформулировать так.
1. Вновь полученные дробные реплики должны обладать всеми мате-
матическими свойствами ПФЭ, о которых подробно сказано ниже.
2. Каждое парное взаимодействие может оцениваться совместно с од-
ним из линейных эффектов, т.е. если, например, в первой полуреплике
перемножить вектор-столбцы на х2, то получится вектор-столбец х3,
и т.д.
156
Если коэффициенты при парных взаимодействиях не строго равны ну-
лю, то коэффициенты регрессии являются оценками совместных эффек-
тов [83] для первой полуреплики:
+ 023f t>2 02 +01Э> + Pi 2; (5.9в)
для второй полу реплики
Ь" ~*Р1 ~023г &2->02“013> ^3"*’Рз—Р12- (5.10)
Если после постановки первой полуреплики у экспериментатора воз-
никает сомнение в том, что коэффициенты при парных взаимодействиях
равны нулю, то можно поставить еще четыре опыта (вторую полуреплику).
Среднее из суммы и разности для первой и второй систем совместных
оценок дает независимую оценку всех эффектов (и линейных и парных
взаимодействий):
= (Я + Ъг = (Ь'2 + ь;'У2, Ъ, = (Ъ'3 + 6з)/2; ,, . п
^23 ~ (b2 ~~ ^i)/2, Ь1з =(^2 “ ^2)/2, Ьц = (Ь3 — Ьз)/2.
Проводя расчеты по формулам (5.11), можно окончательно убедиться,
равны ли коэффициенты bi 2, Ь\ з, Ъ23 нулю.
Отметим важную особенность активных экспериментов: при обса^--
ке последующей серии экспериментов полностью используется информа-
ция, полученная при обработке предыдущей серии. Планы экспериментов
именно так и составлены, чтобы эксперименты, которые проводят во вто-
рую очередь, дополняли эксперименты, сделанные в начале исследования.
Объединение двух полуреплик, приведенных в табл. 5.13, дает план
ПФЭ (табл. 5.12), поэтому понятно, что при реализации экспериментов по
первой и второй полурепликам получаются независимые оценки эффектов.
Сформулируем третье правило формирования полуреплик, которое
фактически является следствием двух первых:
3. В первую полуреплику берут строки с нечетным числом латинских
букв, что соответствует требованию х3 =х1х2, а во вторую полуреплику —
строки с четным числом латинских букв и строку (1), что соответствует
требованию х3=-х1х2 .
В задаче с четырьмя независимыми факторами ПФЭ также может быть
разбит на две полуреплики: 1 (1), ad, bd, ab, cd, ас, be, abed; 2) d, a, b,
abd, c, acd, bed, abc, Первая полуреплика получается умножением на d не-
четного сочетания букв в записи ПФЭ 2Э (1) a, b, ab, с, ас, be, abc, а вто-
рая — умножением на d четного сочетания букв и (1) в этом же плане [83].
Можно привести еще пример 1/«-реплики от ПФЭ 2s (табл. 5.14).
Какие эффекты смешаны в плане, приведенном в табл. 5.14, можно узнать
из определяющего контраста
I = xix2x4 =x2x2x3xs =x3x4xs. (5.12)
Для того чтобы рассмотреть сущность определяющего контраста,
введем понятие так называемых генерирующих соотношений, которыми
задаются полуреплики. Например, две полуреплики 23"1, приведенные в
табл. 5.13, заданы следующими генерирующими соотношениями:
*з =ххх2; х3 = -ххх^ (5,13)
157
Таблица 5.14
S""2
Дробная реплика 2
Словами эти формулы можно выразить так: в первой полуреплике век-
тор-столбец х3 получается умножением вектор-столбца xt на вектор-стол-
бец х2; во второй полуреплике вектор-столбец х3 получается умножением
элементов столбца хх на соответствующие элементы столбца х2; знак каж-
дого элемента вновь полученного столбца меняется на обратный.
Если обозначить элементы первого столбца матрицы х0 знаком I (все
они всегда равны +1), то, чтобы получить соотношения, определяющие эле-
менты первого столбца для каждой из полуреплик (т.е. соотношения, даю-
щие при перемножении +1), нужно умножить на х3 левые и правые части
записанных выше генерирующих соотношений (5.13):
х3 = xlx2x3; xl ~ -Х1Х2Х3. (5.14)
Любой элемент матрицы X, возведенный в квадрат, дает +1; следовательно,
х3 = Z=x1x2x3; х3 =Z=-XiX2x3. (5.15)
В формуле (5.15) получены определяющие контрасты двух полуреп-
лик от ПЭФ 23, записанные ранее в табл. 5.13 без объяснения.
Для того чтобы узнать, какие эффекты определяются совместно (сме-
шаны), нужно последовательно умножить все факторы на определяющий
контраст. Проделаем эту операцию для формулы (5.15):
первая полуреплика
Zxi =х?х2х3, тл. b'i ->0i + 023,
Zx2 =х2х2х3, т.е. b2 ->02 + 013,
Zx3 =ххх2х1, т.е. Ь3 ->03 + 012;
вторая полуреплика
Zxt =-xlx2x3, т.е. bi ->0i -023,
Zx2 =-х2х1х3, т.е. b2 ~>02_01з,
1х3=~х2х2х1, т.е. Z>3^J33-012.
Таким образом, из определяющих контрастов (5.15) вновь получены соот-
ношения (5.9в) и (5.10),показывающие, какие эффекты смешаны.
Теперь рассмотрим обобщенный определяющий контраст (5.12) для
*/4-реплики 25-2, планирование которой дано в табл. 5.14. Здесь два
158
(5.16)
последних эффекта оценивают совместно с взаимодействиями. Несущест-
венным предполагают прежде всего тройное взаимодействие, также пре-
небрегают одним из парных взаимодействий. Это взаимодействие можно
выбрать на основании физического смысла изучаемого явления, а если
такой информации нет, то методом рандомизации (случайного выбора).
Если, например, решено пренебречь взаимодействуем xtx2, то можно
построить четыре 1/4-реплики со следующими генерирующими соотно-
шениями:
х4 =XiX2t xs =XiX2x3;
Х4 =XiX2, Х5 = —Х1Х2Х3
Х4 =-Х1Х2, Х5 =Х1Х2Х3
Х4~-Х1Х2, Х5 =-ХуХ2Х3.
Определяющие контрасты для этих реплик таковы:
/=х1х2х4, / = Х1Х2ХзХ5;
Z = x1x2x4, /=-XiX2X3X5; (5 17)
1= -XiX2x4, Z=x1x2x3xs;
Z=-XiX2X4, / = ~Х1Х2ХзХ5.
Если перемножить попарно эти определяющие контрасты, то для каж-
дой реплики получится третье соотношение, также задающее элементы
столбца xQ =1. Поэтому, чтобы полностью охарактеризовать разрешающую
способность реплик, вводят обобщающие определяющие контрасты:
/ = Х1Х2Х4 =Х1Х2Х3Х5 -х3х4х5,
Z = XiX2x4 == -Х!Х2ХзХ5 = -х3х4х5, (5.18)
Z=-XiX2X4 =Х!Х2ХзХ5 =~ХзХ4Х5,
Z=-X1X2X4 =XtX2X3Xs =X3X4X5.
Первый из этих определяющих контрастов был приведен выше [см.
формулу (5.12)]. Перемножая этот обобщающий определяющий контраст
на каждый из факторов ху, получаем совместные оценки для эффектов при
планировании по дробной реплике, приведенной в табл. 5.14. Для повы-
шения разрешающей способности опытов можно поставить еще одну чет-
вертьреплику 2s-2, чтобы оценить независимо все линейные эффекты по
методике, изложенной выше. Готовые планы дробных реплик приведены
в табл. П.12.
Выше отмечалось, что планы ПФЭ и дробных реплик составлены таким
образом, чтобы максимально упростить вычисление коэффициентов регрес-
сии bj и проверку адекватности уравнений. С математической точки зрения
планы можно рассматривать как линейные, поскольку произведения факто-
ров всегда можно заменить новым линейным эффектом. Такая процедура
применялась в § 3.3 при рассмотрении множественного нелинейного рег-
рессионного анализа. В этом случае число линейных эффектов р увеличи-
вается до к линейных эффектов, где к>р. Если учесть это обстоятельство,
159
то можно сформулировать следующие свойства планов ПФЭ и дробных реп-
лик:
1°. Скалярное произведение всех вектор-столбцов равно нулю (свой-
ство ортогональности).
2°. Значения факторов симметрично располагаются вокруг центра экс-
перимента.
3°. Сумма квадратов элементов всех столбцов матрицы X одинакова.
Из свойства 1° следует, что матрица коэффициентов нормальных урав-
нений Х*Х диагональна. Из свойства 3° следует, что все диагональные эле-
менты этой матрицы равны числу опытов п, а диагональные элементы об-
ратной матрицы (Х*Х)-1 - Cjj ~ Ijn, поэтому для проведения регрессион-
ного анализа по результатам активных экспериментов имеют место очень
простые упомянутые выше формулы [см. формулу (5.7) ].
Коэффициенты регрессии
п - —
bj = < !П> 7 = °’ к-
Погрешности коэффициентов регрессии
/=6Т (5.19)
Остаточная дисперсия
— л л _
b*)((n-k- 1). (5.20)
i = l 7=0 ’
F-отношение Фишера
= ' (5-21)
Обратим внимание на то, что если ранее рассматоивалось «верхнее»
F-отношение, когда для отбрасывания нуль-гипотезы F > F9, то формула
(5.21) представляет собой нижнее F-отношение, когда для отбрасывания
нуль-гипотезы F < FT при принятом уровне значимости и степенях сво-
боды в числителе п - к - 1 и в знаменателе «(0) — 1. Здесь под пони-
мают не дисперсию вектор-столбца у, а погрешность эксперимента; кото-
рая найдена по некоторому числу опытов и (о), поставленному в центре
эксперимента [все факторы поддерживаются на основном уровне (0) ].
Значимость коэффициентов регрессии bj оценивают по формуле
tj = b/y/n/S^. (5.22)
Найденное «значение f-критерия Стьюдента сравнивают с табличным; tj >
> tт при принятом уровне значимости и числе степеней свободы, при кото-
ром была определена ошибка эксперимента, т.е. v = П(0) — 1»
Пример вычисления погрешности эксперимента Sryjno данным опытов,
поставленных в центре эксперимента [основной уровень (0) ], приведен
в табл. 4.10. Если погрешность экспериментов вычислена, то по формулам
(5.21) и (5.22) можно проверить адекватность уравнения регрессии и Зна-
чимость коэффициентов уравнения bj.
160 у
Если требуется поставить большое количество длительных опытов,
то возникает опасность временного дрейфа функции отклика за счет изме-
нения условий изготовления опытных образцов, влияния изменившихся
погодных условий, износа или разладки оборудования, изменения свойств
материалов, например реактивизации цемента, хранящегося на открытом
воздухе, и тщ.
Для исключения влияния временного дрейфа полный факторный
эксперимент и дробные реплики разбивают на блоки. Так, например, план
ПФЭ 2Э, приведенный в табл. 5.12, целесообразно разбить на два блока.
Для оценки межблокового эффекта вводят фиктивный фактор xg, кото-
рый считают смешанным с тем взаимодействием, которым можно пре-
небречь (для рассматриваемого случая это тройное взаимодействие
Х1Х2Х3).
План разбивают на два блока таким образом, чтобы в верхнем блоке
взаимодействие xjx2x3 поддерживалось только в верхнем уровне (+1),
а в нижнем блоке — только на нижнем уровне.
Таким образом, в верхний блок попадают строки 2, 3, 5 и 8 из
табл. 5.12, остальные строки попадают в нижний блок (табл. 5.15).
В табл. 5.15 те же номера опытов, что в табл. 5.12. Нетрудно заметить,
что разбиение в табл. 5.16 на два блока совпадает с разбиением на две полу-
реплики: а, Ъ, с, abc и (1), ab, ас, Ъс. Коэффициенты регрессии, полученные
по табл. 5.16, являются оценками для следующих эффектов:
bo ~*0о, bi ~*0i, Ь2 ~>02, Ь3 ~>03;
Ь12 Ра, Ь13Р13, Ь23->р23, Ъх23 -> 0123 + 0б«
Если предположить, что Pi23 близок к нулю, то значимость й123 го-
ворит о значимости межблокового эффекта 0q, отображающего временной
дрейф. Все остальные коэффициенты регрессии определяются независимо,
поэтому при таком планировании влияние временного дрейфа исключается.
Избиение плана ПФЭ на два блока
Таблица 5.15
№ опы- та Матрица X Планирование Буквенные обозначе- ния строк | Вектор Y |
*0 *1 *2 *3 *1*2 *1*3 *2*3 *1*2*3
(1) (2) (3) (4) (5) (б) (7) (8) (9) (10) (И) (12)
2 + + — — — — + + а У2
1 3 + — + — — + — + b УЗ
I блок 5 + — — + + — — + с У5
8 + + + + + + + + abc У8
1 + — — л* + + + л* (1) У1
4 ч* + + — + — — — ab У4
'П блок 6 + + — + — + — — ас Уб
7 + — + + — — + — be У?
6-579
161
Таблица 5.16
Планирование опытов по исследованию влияния факторов
на удельные относительные деформации ползучести бетона
Факторы *1 % 70 10 80 60 W в/ц Г-т 7Ц т *1*5 *2*6 *3*7 *1*6 *2*5 *4*7 *1*7 *3*5 *4*6 *2*7 *4*6 *3*6
Код Единица величины (0) (/) (+1) (1) *0 *2 % 97,5 7,5 105 90 *3 % 50 10 60 40 *4 сут 150 50 200 100 *5 % 6,36 0,44 5,92 6,80 *6 л МПа-10”2 425 25 450 400 *7 сут 17,5 10,5 28 7
(1) (2) (3) (4) (5) (6) (7) (8) (9) (Ю) (И) (12) (13)
1 + — — — — — + + + +
2 + — — — — + + + — — — —
3 + + + + + — — — — — — —
4 + + + + ч* + + + + + + +
5 + + + — — — — + — -м. + +
6 + — — ч* + — + + + — —
7 + + + — + + — + + — —
8 + — + + + + — — —- + +
9 + + — + — — + — — + — +
10 + — + — + — + — Ч" — + —
11 + + — + — Ч" + + + —
12 + — + — + + — + — + — +
13 + ч* — — + ч* — — + —. — +
14 + — + + — ч* — — — + + —
15 + ч* — — + — + + — + + —
16 + — + + — — + + + - — +
— j
Планирование
Матрица X
По результатам активных экспериментов была построена [78] модель
относительных деформаций ползучести бетона Т) в зависимости от семи
факторов, выбранных по результатам предварительной оценки важности
факторов, в том числе с помощью приведенных в гл. И! моделей, которые
были получены по результатам пассивных экспериментов, и с помощью
отсеивающих экспериментов: 1) jcj — отношение объема крупного запол-
нителя к объему бетона Иш/Кб, %; 2) х2 — влажность среды W, %; 3) х3 —
водоцементное отношение В/Ц, %; 4) х4 — время действия нагрузки, t - т,
сут; 5) х5 — количественный показатель вида цемента /ц, вычисленный
с учетом активности цемента и нормальной густоты цементного теста:
/ц = НГ ' ^И3г/^СЖ>
где НГ — нормальная густота цементного теста, %; ЛиЭГ — прочность образ-
цов при изгибе, МПа-10; R^ — прочность образцов при сжатии, МПа-10;
162
6) %б — модуль упругости заполнителя Еэ, МПа-10"2; 7) х7 — возраст бе-
тона в момент загружения т, сут.
Для планирования выбрана1 /8-реплика от ПФЭ типа 27"3 с определяю-
щим контрастом (см. табл. П.12):
J = XtX2X3X4 = XiX2X5X6 =XiX3X5X7 = х1х4х6х7 = х2х3хбх7 =
= х2х4х5х7 = х3х4х5хб.
Если положить, что все взаимодействия выше второго порядка незначимы,
то можно определить (перемножая определяющий контраст на каждый
фактор), что в этой дробной реплике смешаны следующие эффекты парных
взаимодействий:
~Х2Х6 =Х3Х7, XiX6 =х2х5 =х4х7, х,х7 -x3xs =х4х6, , .
(3 *24J
Х2Х7=Х4Х5 = Х3Х6*
На основании физических представлений о сущности явления, а также
методом попыток из этих взаимодействий выбирались значимые (одно
из трех): в готовое уравнение подставляли все взаимодействия поочередно
до получения правильного направления действия факторов в окончатель-
ном уравнении. Планирование экспериментов, факторы, единицы вели-
чин, основной уровень, интервалы варьирования, верхний и нижний уровни
факторов приведены в табл. 5.17. Кроме основных результатов опытов
получены еще девять векторов выхода.
Часть результатов, которые получены при реализации плана, приведен-
ного табл. 5.17, дана в табл. 5.18. Здесь приведены векторы выхода Су, т) -
относительные удельные деформации ползучести бетона (у3), Еб — модуль
деформаций бетона (ух), Rb — призменная прочность бетона (у2) и уь —
плотность бетона (у4). Обработка данных табл. 5.17 и 5.18 по формулам
(5.17)—(5.22) дает возможность построить полиномиальные модели для
описания изучаемых функций отклика. Например, для удельных относи-
тельных деформаций ползучести бетона Cyt ту получена модель со значи-
мыми Йу
т) = (+2,255 - 0,679х2 + 0,430х3 + 0,522к4 + 0,686х5 +
+ 1,006х7 +0,472XiX7 — 0,409х3х6)-1(Гб,
которая дана в кодированных обозначениях факторов ху — +1. Для пере-
хода к натуральным обозначениям служат следующие формулы:
х\ —70 х^ —97,5 хз — 50 —150
Xi = •----, Х2 = --------, Х3 = ------, Х4 = -------,
10 2 7,5 3 10 4 100
6,36-х5 ?б-425 х^—17,5 (5.26)
Xs = Хб = : *’= •
Здесь в числителе основной уровень (0), а в знаменателе — интервал варьи-
рования (У).
Подставляя в формулу (5.25) значения хиз (5.26), получаем модель
в натуральных обозначениях факторов:
Таблица 5.17
Результаты активных экспериментов
Исследуемые параметры Еь С (t, т)' 19 7б
Единица величины МПа-10"2 МПа-10 (МПа-10)"1 кг/м3 • 10"3
Код У1 Уз У4
(1) (2) (3) (4) (5)
1 228,7 151,9 0,634 2,198
2 313,7 247,8 3,680 2,320
3 206,0 90,4 0,535 2,260
4 253,9 163,7 4,590 2,355
5 293,3 251,6 0,985 2,308
я 6 218,0 1 169,8 4,636 2,138
2 7 299,1 219,6 1Д76 2,394
§ 8 221,7 111,4 4,327 2,268
з 9 200,1 83,1 0,799 2,310
S 10 310,9 165,8 0,987 2,324
S 11 223,4 180,4 5,236 2,200
12 288,0 273,0 2,932 2,248
3 13 262,9 210,9 0,316 2,265
й 14 209,8 145,2 1,217 2,254
15 326,6 273,8 3,841 2,390
16 262,2 143,9 0,139 2,354
Ошибка эксперимента
9,57 11,20 0,501 0,0412
Число степеней свободы
при определении 32 32 5 5
— —
C(f т) = (-13,7470 - 0,0786x1 - 0,0905 х2 + 0,7400 х3 +
+ 0,0104 х4 - 1,5590 х5 - 0,0820хб - 0,2180х7 + 0,0045 xlx7 - (5.27)
- 0,00164х3х6)10Гб.
Характеристика модели и сводка результатов даны в табл. 5.18.
Деформацию ползучести бетона измеряли в течение 200 сут. За этот
срок было выполнено несколько наблюдений.
Используя процедуру, изложенную в § 2.8, предсказали предельные
значения удельных относительных деформаций ползучести бетона т).
По этим данным была получена модель ту [91,68] :
С(оо, г) = (+35,7314- 1,0045 Гщ/Кб - 0.1269W + 1,0743 • £ -
- 0,9931Ju - 0,0270Е3 - 0,1474т - 0,0031 • • т +
Ц
+ 0,0021 (Кщ/Кб) Е3 + 0,0064(Кщ/Fg)т — 0,0024 • А- - /Г3) -1 (Г6.
Н.Х. Арутюняном для определения удельных относительных деформа-
ций ползучести бетона предложена следующая зависимость:
164
Таблица 5.18
Модели, построенные по результатам активного эксперимента
Иссле- Факторы и пар- дуе- ные взаимо- мый действия Гщ/Уб W в/ц Т—т 7Ц Е3 т В/ЦХт Уб Х£з ГЩ х т V5 ЦХ£»
пара- " метр единицы вели- чины % % % сутки —• МПа-10-2 сутки
(0) 70 97,5 50 150 63,6 425 17,5
<Z> 10 7,5 10 50 0,44 25 10,5
+1 80 105 60 200 5,92 450 28
-1 60 90 40 100 6,80 400 7
Переменные в кодированном обозначении хо XI х2 х3 х4 xs Хб х7 х3х7 Х1Х6 XjX7 X3X5
Значимые bj +2,255х - -0.679Х +0,430х +0,522х +0,68бх - +1,00бх - +0,472х -0,409х ХЮ-6 хю“6 ХЮ”6 ХЮ”6 хЮ-6 ХЮ-6 ХЮ’6 хЮ-6
Статистичес- кие оценки мо- дели »1=8; р2=5; =О,5ОЗХ1О-6; S2 =0,251х10-12; sJCT = 0,769xl0-12 £=3,062; =10,29; 3,062<10,29
Переход к абсолютным пе- ременным %-70 *2-97,5 хэ-50 xq—150 6,36-% %-17,5 10,5
10 7,5 10 150 0,44
Вид форму- лы в абсолют- ных значениях С(Г> г) =(-13,7470 - 0,0786x1 - 0,0905х2 + 0,7400х3 + 0,0104х4 - l,5590xs + + 0,0820х6 - 0,21805(7 + 0,0045xix7 - 0,0016хэхб)- 10-6
CU. Г) = с(~. г)(1 -е-”''-7’). (5.29)
По результатам активных экспериментов построена многофакторная мо-
дель и для вычисления коэффициентов 7 в формуле (5.29):
7 = (15,880 + 2,368 + 6,943 х5 + 2,032 — 5,540 х7 +
+ 2,725 — 2,475x^7 — 5,721х3хб) 10"3.
В формуле (5.30) факторы даны в кодированных обозначениях. Переход
к натуральным обозначениям факторов осуществляют по формуле (5.26).
Здесь показана новая возможность вычисления коэффициентов полу-
эмпирических зависимостей типа (5.29) по многофакторным моделям.
Действительно, в формуле (5.29) величину ту можно вычислить с по-
мощью модели (5.28), а коэффициент 7 — по модели (5.30). Эти величины
зависят от многих факторов, и для них нельзя назначать постоянные значе-
ния, поэтому предложено каждый раз при использовании этой формулы
определять т) и 7 из опыта. Модели (5.28) и (5.30) позволяют обой-
тись без этой трудоемкой процедуры.
Таким образом, подробно рассмотрена методика использования линей-
ных планов при постановке экспериментов. После получения линейной моде-
ли (а иногда и модели, содержащей парные эффекты) можно перейти, если
есть необходимость, к движению по градиенту (крутому склону) поверх-
ности отклика по методике, изложенной в § 5.1.
Для более полного описания почти стационарной области поверхности
отклика и области экстремума целесообразно поставить эксперименты по
планам второго порядка.
Из рис. 24 следует, что область экстремума трудно аппроксимировать
с помощью линейных планов с варьированием факторов на двух уровнях.
Эту область функции отклика следует аппроксимировать нелинейными
планами с варьированием факторов хотя бы на трех уровнях. Действитель-
но, через три точки на небольшом участке кривую можно провести почти
с такой же уверенностью, как прямую через две точки. Однако если для
этой цели использовать планы ПФЭ с варьированием факторов на трех уров-
нях типа Зр, то количество опытов будет очень велико. Уже при р = 5
п — 243. Поэтому разработаны различные приемы, позволяющие сократить
число опытов в нелинейных планах. К таким планам относится, например,
центральное композиционное планирование, разработанное Боксом и
Уилсоном [102, 16]. Если рассматривать трехфакторную ситуацию (коли-
чество факторов, для которого план еще можно изобразить графически
в трехмерном пространстве), то идея центрального композиционного пла-
нирования состоит в том, что ставят серию из 8 опытов, располагая каждый
опыт в вершине куба, т.е. реализуется линейный план ПФЭ 23 = 8. Затем к
этим точкам добавляют еще шесть звездных точек, находящихся на ли-
ниях, которые выходят из центра куба. В центре ставят еще одну точку.
Количество точек равно 8 + 6+1 = 15. Для ПФЭ З3 это количество равно
27. Таким образом, удается сэкономить почти половину опытов. Звезд-
ные точки образуют октаэдр и располагаются на расстоянии а от центра
166
куба. Число нулевых точек в центре экс-
перимента может быть и больше единицы.
План, изображенный на рис. 26,
позволяет оценить коэффициенты мо-
дели:
y=tfo + di*! + b2x2 + b3x3 +
+ bi2xix2 + bi3xix3 + 623*2*3 +
+ 6цХ? + 622*2 + 633х|. (5.31)
В этой модели нужно оценить 10 коэф-
фициентов; три степени свободы оста-
нутся для проверки адекватности мо-
дели.
В общем случае центральный ком-
позиционный план неортогонален.
Ортогональность достигается специальным образом выбранным звездным
плечом си преобразованием квадратичных значений факторов. В табл. 5.19,
заимствованной из [102], даны величины а для некоторых значений р.
Выше отмечалось, что для ортогональных планов все коэффициенты опре-
деляют независимо по формуле
и и
(5.32)
Таблица 5.19
Значения а при р = 2, 3, 4, 5
Число факторов
2 3 4 5
Ядро планирования 22 23 24 2s"1 (Z=xix2x3x4x5)
Величина а 1,000 1,215 1,414 1,547
Погрешности коэффициентов регрессии вычисляют по формуле
(5.33)
Остаточная дисперсия определяется формулой (5.20).
Для приведения плана к ортогональному виду квадратичные значения
факторов преобразуют. Поэтому по формуле (5.32) получается уравнение
регрессии в трансформированном виде:
У =6о + 61X1 + ... + Ьр Хр + ... + 612*12 + ... + 6(р_!)р Хр_1 Хр + ... +
+ 6n(xJ -Х12)+ ... +bpptf> -Хр2). (5.34)
Для перехода к обычной форме уравнения регрессии нужно опреде-
лить новое значение свободного члена:
b0=b'0 - Ьцх? - ... - bppx*-, (5.35)
оно оценивается с погрешностью
+•••+<x₽)2SU <5 * * В-эд
Пример ортогонального центрального композиционного плана для
четырех факторов приведен в табл. 5.20 [102]. Для реализаАщи этого
плана нужно выполнить 25 опытов вместо Зр — 81 опыта по ПФЭ Зр. Эко-
номия составляет 56 опытов.
Практика показала, что ортогональность плана не является достаточ-
ным критерием оптимальности. Потребовалось ввести еще понятие рота-
табелъности [102, 15] . Ротатабельным называют планирование, для
которого дисперсия выходного параметра у, предсказанного уравнением
регрессии, постоянна для всех точек, находящихся на равном расстоянии
от центра эксперимента.
Экспериментатору заранее не известно, где находится та часть поверх-
ности отклика, которая представляет для него особый интерес, поэтому
следует стремиться к тому, чтобы количество информации, содержащееся
в уравнении регрессии, было одинаковым для всех равноотстоящих от
центра экспериментальных точек.
Ротатабельным является планирование, обратная матрица которого
(Х*Х)~1 инварианта к ортогональному вращению координат. Для планов
второго порядка это условие удовлетворяется, если все нечетные моменты
(формулы для вычисления моментов приведены в гл. 1) вплоть до мо-
ментов 4-го порядка равны 0, а для четных моментов имеют место соот-
ношения
л ---
Я xfr = п\2, j = 1,р;
S хЛ = 3 S xft х^ - ЗиХ4, /, г = 1, р, / Ф г „ (5.37)
/=1 1 i=l ’
где Х2 и Х4 — произвольные постоянные, удовлетворяющие неравенству
Х4Х2 >р/(р+2). (5.38)
Увеличивая количество точек, поставленных в центре эксперимента,
можно усилить неравенство (5.38), так как его левая часть — величина пер-
вого порядка относительно п.
Для случая р = 3 было показано, что центральный композиционный
план есть комбинация куба, октаэдра и центральной точки. В общем случае
при р > 3 центральный композиционный план строится на гиперкубе и
р-мерном аналоге октаэдра, при этом величина звездного плеча определяет-
ся из условия ротатабельности
а = 2₽/4. (5.39)
При р = 5 вместо ПФЭ 2s можно использовать полуреплику типа 25”1 с
определяющим контрастом I = х ix2x3x4x5, тогда а = 2 (р~1 '4.
В табл. 5.21 дан образец центрального композиционного ротатабель-
ного униформ-планирования второго порядка при р = 3 [102]. Коэф-
168
Таблица 5.20
Ортогональный центральный композиционный план при р =4
№ опыта *0 *1 х2 *3 «4 ж?— -0,8 х2— -0,8 4— -0,8 4” -0,8 ххх2 Х1Х3 XjX4 *2*3 х2х4 х3х4 Вектор Y
(1) (2) (3) (4) (5) (6) (7) (8) (9) (10) (И) (12) (13) (14) (15) (16) (17) (18)
Централь- ная точка 0 +1 0 0 0 0 -0,8 -0,8 -0,8 -0,8 0 0 0 0 0 0 У0
1 +1 -1 -1 -1 -1 0,2 0,2 0,2 0,2 +1 +1 +1 +1 +1 +1 У1
2 +1 +1 -1 -1 -1 0,2 0,2 0,2 0,2 -1 -1 -1 +1 +1 +1 У2
3 +1 -1 +1 -1 -1 0,2 0,2 0,2 0,2 -1 +1 + 1 -1 -1 +1 УЗ
4 +1 +1 +1 -1 -1 0,2 0,2 0,2 0,2 +1 -1 -1 -1 -1 + 1 У4
5 +1 -1 -1 +1 -1 0,2 0,2 0,2 0,2 +1 -1 +1 -1 +1 -1 У$
6 +1 +1 -1 +1 -1 0,2 0,2 0,2 0,2 -1 +1 -1 -1 +1 -1 Уб
7 +1 -1 +1 +1 -1 0,2 0,2 0,2 0,2 -1 -1 +1 +1 -1 -1 Уп
План 8 +1 +1 +1 +1 -1 0,2 0,2 0,2 0,2 +1 +1 -1 +1 -1 -1 У»
ПФЭ 24 9 +1 -1 -1 -1 +1 0,2 0,2 0,2 0,2 + 1 +1 -1 +1 -1 -1 У9
10 +1 +1 -1 -1 +1 0,2 0,2 0,2 0,2 -1 -1 +1 +1 -1 -1 У10
11 +1 -1 +1 -1 +1 0,2 0,2 0,2 0,2 -1 + 1 -1 -1 +1 -1 У11
12 +1 +1 +1 -1 +1 0,2 0,2 0,2 0,2 +1 -1 +1 -1 +1 -1 У12
13 +1 -1 -1 +1 +1 0,2 0,2 0,2 0,2 +1 -1 -1 -1 -1 +1 У13
14 +1 +1 -1 +1 +1 0,2 0,2 0,2 0,2 -1 +1 +1 -1 -1 +1 У14
15 +1 -1 +1 +1 +1 0,2 0,2 0,2 0,2 -1 -1 -1 +1 +1 +1 У15
16 +1 +1 +1 +1 +1 0,2 0,2 0,2 0,2 +1 +1 +1 +1 +1 ,+1 У16
17 +1 -1,4142 0 0 0 1,2 -0,8 -0,8 -0,8 0 0 0 0 0 0 У17
18 +1 +1,4142 0 0 0 1,2 -0,8 -0,8 -0,8 0 0 0 0 0 0 У18
19 +1 0 -1,4142 0 0 -0,8 1,2 -0,8 -0,8 0 0 0 0 0 0 У19
Звездные 20 +1 0 +1,4142 0 0 -0,8 1,2 -0,8 -0,8 0 0 0 0 0 0 Уто
точки 21 +1 0 0 -1,4142 0 -0,8 -0,8 1,2 -0,8 0 0 0 0 0 0 У21
22 +1 0 0 +1,4142 0 -0,8 -0,8 1,2 -0,8 0 0 0 0 0 0 У22
23 +1 0 0 0 -1,4142 -0,8 -0,8 -0,8 1,2 0 0 0 0 0 0 У23
04 чО 24 +1 0 0 0 +1,4142 -0,8 -0,8 -0,8 1,2 0 0 0 0 0 0 У24
Таблица 5.21
Центральное композиционное униформ-планирование второго порядка при р = 1
Матрицах Планирование Вектор ¥
№ опыта «0 *1 *2 «3 2 2 *2 4 *1*2 *1*3 «2*3
(1) (2) (3) (4) (5) (6) (7) (8) (9) (10) (11) (12) (13)
Опыты в центре экспе- римен- та 110 0 0 0 00000 У1 210 0 0 0 0 0 0 0 0 у2 310 0 0 0 00000 Уз 410 0 0 0 0 0 0 0 0 у4 510 0 0 0 0 0 0 0 0 ys 610 0 0 0 00000 Уб
План типа 23 7 1-1-1-1 1 1 1 1 1 1 У7 8 11-1-1 1 1 1 -1 -1 1 у8 9 1-11 -1 1 1 1 -1 1 -1 у9 10 1 1 1 -1 1 1 1 1 -1 -1 ую И 1 -1 -1 1 1 111-1-1 уп 12 1 1 -1 1 1 1 1 -1 1 -1 уп 13 1 -1 1 1 1 1 1 -1 -1 1 уп 14 1 1 1 1 1 1 1 1 1 1 У14
Звезд- ные точки й — 15 1 —1,682 0 0 2,828 0 0 0 0 0 у15 16 1 1,682 0 0 2,828 0 0 0 0 0 у16 17 1 0 -1,682 0 0 2,828 0 0 0 0 уп 18 1 0 1,682 0 0 2,828 0 0 0 0 yt8 19 1 0 0 -1,682 0 0 2,828 0 0 0 yi9 20 1 0 0 1,682 0 0 2,828 0 0 0 у20
фициенты уравнения регрессии для этого плана могут быть найдены по
следующим формулам:
б0 = 0,166338(6»- 0,056791 S (fly),
7-1
67-= 0,073224(7»,
р
bff = 0,062500 (ду) + 0,006889 S (jjy) - 0,056791 (Оу),
7=1
bjr = 0,125000(71», (5.40)
п п п . п
где (Оу) = S уь (/» = S xfi yh <jjy) = S xly,, (jry) = S xfi xri yb j * r,i =
i-1 7=1 7 = 1 * 7 = 1
= iTnf i=Vp.
Коэффициенты в формулах (5.40) подсчитаны с помощью ЭВМ [102].
Из этих формул видно, что коэффициенты бу и bjr вычисляются независимо,
а коэффициенты Ьц коррелированы между собой и корреляционно связаны
170
со свободным членом b0. Формулы (5.40) можно представить и в общем
виде для любого р [83] :
60 = - (2XJ (р + 2) (ОД - 2Л4 С £ (йу) ]; (5.41)
Л 1 = 1
bj^-Цу)-, (5.42)
•f п
b« = - (с2 [(р+ 2) К, -р] (ОД+С* (1 — Х4) S й»-2Х4С(од) ;
” 1 7 = 1 Х5.43)
сг
(5.44)
21^41. (5.45) Slr^; (5.46)
= (5 д7) = ; (5 48)
С=——; (5.49) А = -~— -----------. (5.50)
"2 2Х4[(р+2П4-р] 1 }
т х •-
fit 71
В работе [14] приведены почти ортогональные ротатабельные планы
второго порядка, рассчитанные на ЭВМ без звездных точек. Планы такого
типа только и могут быть использованы при построении моделей прочност-
ных и деформативных характеристик бетона в зависимости от определяю-
щих их факторов, так как варьирование факторов в пределах | ±3| = 6(7),
как это требуется, например, в плане, приведенном в табл. 5.21, невозмож-
но, когда речь идет о задачах, связанных с составом бетона.
Такие планы были использованы в работах [82—85], цель которых —
построение моделей второго порядка для вычисления и прогнозирования
прочностных и деформативных характеристик бетона в зависимости от
семи факторов. Набор факторов менялся для различных характеристик.
В моделях для вычисления и прогнозирования предельных удельных
относительных деформаций ползучести, пропаренного бетона варьирова-
лись следующие семь факторов: 1) Xi — водоцементное отношение (В/Ц),
%; 2) х2 - отношение объема шебня без пустот к объему бетона (Ищ/Кб),
%; 3) х3 — количество цемента в одном кубометре бетона (2ц), кг; 4)х4 —
активность цемента (Яц),МПа • 10; 5) х5 — масштабный фактор образцов
(М), М = fyF/V, где F — площадь поверхности образца, V — объем образца;
6) — температура изотермического процесса (Г), °C; 7) х7 — длитель-
ность изотермического процесса (Т), ч.
Планы Бокса—Бенкина представляют собой выборку строк из плана
ПФЭ ЗР. Принцип построения такого плана — комбинирование матриц типа
25 на ЭВМ по сбалансированной схеме неполных блоков. Во всех строках
полученной при этом матрицы отличны от нуля только по три элемента.
В этом плане число строк (число опытов) и = 62 по сравнению с и = 92
Для центрального композиционного ротатабельного плана при числе фак-
торов р = 7. План приведен в табл. 5.22 в сокращенном виде.
171
Таблица 5.22
План Бокса—Бенкина
Уровни и : № опыта i - xi *2 *3 х4 xs *6 *7 Уровни и № опыта *1 Х2 ^3 х4 *5 Хб хп
_В Ц F6 бц Яц м т Г Ц *Щ F6 бц Яц м Т t
(+1) 60 80 420 432,5 0,548 100 6 (+1) 60 80 420 432,5 0,548 100 6 (0) 50 65 390 366,3 0,674 80 4 (0) 50 65 390 366,3 0,674 80 4 (-1) 40 50 360 300 0,800 60 2 (-1) 40 50 360 300 0,800 60 2 1 0 0 0 -1 -1 -1 0 32 +1 -1 0 +1 0 0 0 2 0 0 0 +1 +1 -1 0 33 0 0 -1 -1 0 0 -1 3 0 0 0 -1 1 +1 0 34 0 0 +1 +1 0 0 -1 4 0 0 0 +1 +1 +1 0 35 0 0 1 -1 0 0 +1 5 0 0 0 -1 +1 -1 0 36 0 0 +1 +1 0 0 +1 6 0 0 0 +1 -1 -1 0 37 0 0 -1 +1 0 0 -1 7 0 0 0 -1 +1 +1 0 38 0 0 +1 -1 0 0 -1 8 0 0 0 +1 -1 +1 0 39 0 0 -1 +1 0 0 +1 9 -1 0 0 0 0 -1 -1 40 0 0 +1 -1 0 0 +1 10 +1 0 0 0 0 +1 -1 41 -1 0 -1 0 -1 0 0 11 -1 0 0 0 0 -1 +1 42 +1 0 +1 0 -1 0 0 12 +1 0 0 0 0 +1 +1 43 -1 0 -1 0 +1 0 0 13 -1 0 0 0 0 +1 -1 44 +1 0 +1 0 +1 0 0 14 +1 0 0 0 0 -1 -1 45 -1 0 +1 0 -1 0 0 15 -1 0 0 0 0 +1 +1 46 +1 0 -1 0 -1 0 0 16 +1 0 0 0 0 -1 +1 47 -1 0 +1 0 +1 0 0 17 0 -1 0 0 -1 0 -1 48 +1 0 -1 0 +1 0 0 18 0 +1 0 0 -1 0 -1 49 0 -1 -1 0 0 -1 0 19 0 -1 0 0 -1 0 +1 50 0 +1 +1 0 0 -1 0 20 0 +1 0 0 +1 0 +1 51 0 -1 -1 0 0 +1 0 21 0 -1 0 0 +1 0 -1 52 0 +1 +1 0 0 +1 0 22 0 +1 0 0 +1 0 -1 53 0 -1 +1 0 0 -1 0 23 0 -1 0 0 +1 0 +1 54 0 +1 -1 0 0 -1 0 24 0 +1 0 0 -1 0 +1 55 0 -1 +1 0 0 +1 0 25 -1 -1 0 -1 0 0 0 56 0 +1 -1 0 0 +1 0 26 +1 +1 0 -1 0 0 0 57 0 0 0 0 0 0 0 27 -1 -1 0 +1 0 0 0 58 0 0 0 0 0 0 0 28 +1 +1 0 +1 0 0 0 59 0 0 0 0 0 0 0 29 -1 +1 0 -1 0 0 0 60 0 0 0 0 0 0 0 30 +1 -1 0 -1 0 0 0 61 0 0 0 0 0 0 0 31 -1 +1 о +1 0 0 0 62 0 0 0 0 0 0 0
172
Для вычисления коэффициентов регрессии, проверки их значимости
и проверки адекватности уравнения при использовании плана, приведен-
но го в табл. 5.22, используют следующие формулы: Ьо=Уо, (5.51)
где у о — среднее значение наблюдений, сделанных в центре эксперимента;
Л bj = A S п „ Р п уо Ъп = Billxnyi + С1Д “ “Т ’ (5.52) (5.53)
fyr =Di^^XjiXriyi’t (5.54) = где п0 — число опытов в центре эксперимента; (5'56) ’^1= л — 2 S (У01-У0) (5-58) 4)• (5-55) (5.57) (5.59)
После вычисления коэффициентов регрессии можно вычислить свя-
занную с ними сумму квадратов
— Р п р 1 л л 5012=Л s (S х„у^2+П1 S S (XjiXrtyi)2+d0 S J/+ /=1 / = 1 7 / = 1 /=1 1—1 + Д,,.5//<л » с числом степеней свободы (5.60)
Л12=(р + 2)(р+1)/2-1, (5.61)
где Pi — число парных взаимодействий. Остаточная сумма квадратов
Г Л 2 .Л . J, [.=/?№>/) 1 г2 _ *=1 * = 1 с ° ОСТ “ п ^012 с числом степеней свободы (5*62)
Дет =л-(р+ 2) (р+1)/2. (5.63)
Значимость коэффициентов регрессии проверяют по формуле ?>ГТ, где (5.64) (5.65) 173
Выше указывалось, что [см. формулу (5.59)] ошибка эксперимента
-2 _ ^(°) (уо/-уо)2
1=1 «(о) ~ 1
Разность между остаточной дисперсией и ошибкой эксперимента
S2 =S2 (5.66)
разн ‘-’ост (У) 4
со степенями свободы
/разн = л- (р+ 1) (р+ 2)/2. (5.67)
Отношение Фишера
F = <5-68)
СО степенями свободы Vi -/разн’ V1 = п (0) — а
Адекватность уравнения проверяют с помощью формулы F < FT.
Если это условие соблюдается при принятом уровне значимости, то счи-
тается, что уравнение адекватно представляет результаты экспериментов.
В формулах (5.52) —(5.60) буквенные обозначения для рассматриваемого
плана (р = 7) таковы: А — 1/24; В = 1/16; С\ = 1/144; Z>i = 1/8; 5—3;
i = 1, п, j, г = 1, р, j ¥= г, где п — число опытов, р — число факторов.
Таблица 5.23
Модели, полученные по плану Бокса - Бенкина
-5. к & Коэффи- циенты регрессии £<~’т)х Ml X Ю5 х Ю6 'с' Коэффи- циенты регрессии X Ю5 г) х х Ю6 Фео* Ю
(1) (2) (3) (4) (5) (1) (2) (3) (4) (5)
1 *0 +34,2161 -10,520 +19,121 19 *15 +0,8491 0,9196 +0,8620
2 Ь1 +2,7183 +4,7634 +3,9668 20 *16- +2,1667 -0,6305 -0,4783
3 *2 -0,9991 +0,5351 -1,1262 21 *17 -1,0737 -1,4045 -3,3871
4 ь3 + 1,3833 +0,7157 +1,2032 22 *23 -0,8855 +0,9685 -1,5020
5 *4 -2,2657 -2,4090 -4,3274 23 *24 +1,1737 +1,1835 +2,8981
6 *5 -1,5808 -1,3093 +1,8042 24 *25 -0,1052 -0,6391 -0,5855
7 Ь6 -0,8356 -0,5595 -2,8047 25 *26 +1,2515 -0,0340 +0,9792
8 *7 -1,6338 -1,4877 -2,2347 26 *27 -0,3935 -0,4130 +0,4130
9 *11 -0,2172 +1,4493 +2,5043 27 *34 +2,4006 +0,2135 +0,1382
10 *22 +1,0958 +0,7901 -0,5079 28 *35 -3,6241 -1,3547 -0,3335
11 Ь33 -1,4144 -0,3665 -0,2346 29 *36 -1,7317 -0,2815 -0,5225
12 *44 +1,9635 +1,2278 +3,5311 30 *37 -3,2171 -1,1071 -1,4295
13 *55 -2,9882 -2,3007 -1,6349 31 *45 -0,3082 +0,2520 +0,7463
14 b66 -1,4320 +0,7567 +2,1356 32 *46 -1,3502 -0,1882 +0,0756
15 ЬТ1 +0,0760 -0,4847 +0,9199 33 *47 -0,0591 +0,3760 +0,5875
16 *12 —0,0647 +1,7080 +1,0033 34 *56 -0,6332 +0,0047 -1,2715
17 *13 +1,1851 +1,4777 +0,4127 35 *57 +0,6682 +0,3501 -0,0107.
18 174 *14 +5,8260 +0,9423 +3,9643 36 *67 +1,3977 +2,2255 -0,6041
По этому плану с помощью методики предсказания предельных значе-
ний величин, изменяющихся по экспоненте, рассмотренной в гл. II, были
получены модели следующих предельных характеристик ползучести про-
паренных бетонов: — относительных деформаций ползучести; —
удельных относительных деформаций (меры) ползучести; 0^-характерис-
тики ползучести.
Модели приведены в табл. 5.23. В этой таблице коэффициенты регрес-
сии, незначимые по Лкритерию, подчеркнуты. К этим моделям легко
применить процедуру приведения к канонической форме, рассмотренную
в гл. Ш, при нахождении области экстремума.
Планы экстремальных экспериментов, разработанные в основном
школой Бокса и описанные в данном параграфе, имеют одну особенность:
оптимальность планов достигается на интуитивном уровне исходя из опыта
экспериментатора. Сначала оптимальными планами считали ортогональные
планы, позже — ротатабельные.
Одновременно с развитием идей Бокса [108] развивалось и направ-
ление, возглавляемое американским математиком Кифером, в котором
использовались новейшие разделы математики (теория множеств, теория
меры и т.д.), получившее название концепции D-оптимальности. Подробнее
вопрос об оптимальном планировании рассмотрен в § 5.5. Большой вклад
в развитие этой теории внесли советские ученые [108,145].
§ 5.4. Дисперсионный анализ
В § 5.1 рассмотрена методика отбора важнейших факторов и их вза-
имодействия в многофакторной ситуации (путем постановки отсеивающих
экспериментов). Эта методика допускает рассмотрение качественных фак-
торов. С помощью дисперсионного анализа можно решать как эти задачи,
так и некоторые другие. Теория дисперсионного анализа — один из самых
подробно разработанных разделов прикладной математической статистики
[149, 156]. Здесь приводятся только основные положения дисперсионного
анализа и на числовом примере рассматривается методика его проведения.
При проведении дисперсионного анализа можно получить математическую
модель, но это не является главной целью, так как при наличии качествен-
ных факторов эту модель нельзя использовать для прогнозирования значе-
ний функции отклика, не найденных из эксперимента.
Дисперсионный анализ как уже сказано, позволяет выделить главные
факторы их взаимодействия, дает возможность с помощью рандомизации
исключить влияние временного дрейфа неконтролируемых факторов и
оценить ошибки эксперимента.
Схема проведения эксперимента для дисперсионного анализа по пла-
ну ПФЭ 24 изображена на рис. 27. На этом рисунке показано 16 различных
сочетаний уровней четырех факторов А, В, С, D, что соответствует плану
ПФЭ 24; — верхний уровень для фактора А; Аг - нижний уровень,
и т.д.
Если рассматривать конкретный опыт, например опыт 6, то нетрудно,
используя схему, приведенную на рис. 27, расписать уровни варьирования
175
I Эксперимент 1
Рис. 27
факторов по знакомой методике:
*1 х2 х3 х4
А1 В С1 £)2
+ 1 -1 +1 -1
Аналогично можно расписать и остальные опыты и тем самым прийти
к планированию типа ПФЭ 24.
Главное в дисперсионном анализе — рандомизация (случайный выбор
сочетаний уровней факторов для их реализации). Если для рандомизации
16 опытов, изображенных на рис. 27, воспользоваться таблицей случайных
чисел, то получим следующий порядок их проведения по времени: 1) 3,
2) 2, 3) 7, 4) 10, 5) 4, 6) 12, 7) 9, 8) 6, 9) 8, 10) 1, 11) 13,12) 16,13) 5,
14) 11,15) 14,16) 15.
Порядок проведения дисперсионного анализа легче всего пояснить на
конкретном примере. Пусть, например, требуется исследовать влияние
факторов и их взаимодействий на очень важное в строительстве явление —
сцепление нового (уложенного позже) бетона со старым [84].
Предварительные исследования позволили выбрать из всего много-
образия факторов, влияющих на это явление, четыре основных. Перечень
факторов, их шифровка в терминах дисперсионного и регрессионного ана-
лизов, уровни варьирования факторов приведены в табл. 5.24. Как видно'
из этой таблицы, фактор А — качественный, остальные — количественные.
В соответствий со схемой, изображенной на рис. 27, было поставлено
16 опытов. В каждой точке (ячейке) испытывалось по 3 образца. Общее
количество образцов составило 48.
Результаты экспериментов, расположенные по схеме дисперсионного
анализа приведены в табл. 5.25. Для сокращения трудоемкости расчетов,
эти результаты можно закодировать, что не повлияет на результаты рас-
четов. В табл. 5.25 кодирование выполнено по схеме у} — 15. В этой ж&-
176
таблице даны суммы кодированных данных в каждой ячейке. В прямо-
угольничках даны суммы квадратов этих данных. Таким образом, в
табл. 5.25 имеются все данные, необходимые для дисперсионного анализа.
Таблица 5.24
Факторы и уровни варьирования
№п/п Факторы Код Уровни варьирования
регрес- сион- ный диспер- сион- ный верхний +1 нижний 1
(1) (2) (3) (4) (5) (О
1 Тип поверхности старого (легкого) *1 А Шерохо- Гладкая
бетона ватая (Дх) (а2)
2 Консистенция старого бетона (осад- ка конуса), м-102 *2 В 10-11 (51) 3-4 (В2)
3 Консистенция нового (тяжелого) бе- тона (осадка конуса), м-102 «3 С 14-16 (С1) 4-6 (С2)
4 Водоцементное отношение нового бетона (В/Ц) *4 D 0,55 (51) 0,85 (52)
Дисперсионный анализ плана 24 проводят по модели
Х=ц + А + В + С+ D + АВ+ АС+ AD+ ВС+ BD +
+ CD+ АВС + ABD + ACD+ BCD + ABCD + €, <5 69)
f V- J
т.е. оценивают независимо среднее д, четыре основных эффекта (А, В,
С, D), шесть парных и четыре тройных взаимодействия. Так как число воз-
можных статистических испытаний для оценки эффектов и погрешности
е, возникающей за счет влияния неучтенных факторов, составляет 24 — 1 =
= 15, то при таком планировании эффект взаимодействия ABCD и погреш-
ности £ смешаны и оцениваются совместно.
Эффекты оценивают, вычисляя соответствующие суммы квадратов.
Общая сумма квадратов
£5общ = 1668,62 - 292/48 = 1668,62 - 17,52083 = 1651,0992.
Число 1668,62 получается в результате сложения всех чисел, помещенных
в прямоугольничках табл. 5.26, число 29 — сумма сумм закодированных
наблюдений во всех ячейках той же таблицы, 48 — общее количество наблю-
дений.
Сумма квадратов типа поверхности (Д)
5-5 = -10-7)2£ -~-7)2-----~ = 680,57416 - 17,52083 = 663,05333.
А 24 48 ’
Сумма квадрата консистенции старого бетона (5)
„ _ (11,7)2+(17,3)2 292
SSB---------М-------------°’65334-
7- 579
177
Таблица 5.25
Исходные данные для дисперсионного анализа
Л1
*1 В2
С1 с2 С1 02
01 02 01 02 01 02 01 02
16,7 16,3 18,3 18,5 23,6 12,7 13,9 32,2
16,5 17,5 19,2 19,5 22,6 13,9 15,1 31,6
15,7 18,5 18,9 20,2 23,1 14,2 13,0 32,0
Преобразованные данные (из каждого наблюдения вычтено 15)
1,7 1,3 3,3 3,5 8,6 -2,3 -1,1 17,2
1,5 2,5 4,2 4,5 7,6 -1,1 0,1 16,6
(5,63| (20,19 1 |43,74 | |59,54| 1197,33 [7,14| |5,22 1 i860,4 j
0,7 3,5 3,9 5,2 8,1 -0,8 -2,0 17,0
——— ____ в——
3,9 7,3 11,4 13,2 24,3 -4,2 -3,0 50,8
Bi Н2
Cl С2 Ci С2
D1 02 01 02 01 02 01 Z>3
11,9 17,1 11,3 10,3 7,9 7,1 15,9 12,2
13,9 18,3 11,9 9,3 8,2 6,4 14,3 12,7
12,7 16,4 11,6 11,2 9,4 7,8 13,3 14,2
Преобразованные данные (из каждого наблюдения вычтено-15)
-3,1 2,1 -3,7 -4,7 -7,1 -7,9 0,9 -2,8
-1,1 3,3 -3,1 -5,7 -6,8 -8,6 -0,7 -2,3
|16,11| 1 1 34,861 | (69,02) 1128,01| |186,21| (4,19| 1 |13,7?|
-2.3 1,4 -3,4 -3.8 -5.6 -7.2 -1,7 -0.8
-6,5 5Л -10,2 -14,2 -19,5 -23,7 -1,5 —5,9
Сумма квадратов консистенции нового бетона (С)
се - (4,6)2 + (40,6)2 292 _
~ й--------------48“ 52’04250-
Сумма квадратов В/Ц нового бетона (D)
-4=20^8000.
178
Суммы квадратов парных взаимодействий
(SXtBi)’ + (EHiB2)3 + (S^2Bi)a + (ЕЛ2В2)3
SSAB = 12
292 сс сс _ (35,8)2 +(67,9)2 + (-24,1) 2 +(50,6) 2
48 55 А ^В 12 .
од2
-663,05333 - 0,65334 = 71,54081;
48
UiCir+UiC^+^Cir+^hCb)1 292
“ 12 48
сс с-с- - <31»3)2 *(72,4)2 +(-42,9)2 +(-31,8)2 _
12
- 292/48 - 663,05333 - 52,04250 = 23,47500;
(ЕА^О3 + (ЕА i£>2)3 + (EA2Di)3 + (SA2D2)3
SSAD ~ 12
_ _ SSD = (36,6)2 +(67,1)2i+(-37,7)2 +(-37)2 __
- 663,05333 - 20,28000 = 18,50084;
(SB1C1)3 + (SB1C2)2 + (SB2Ci)3 + (SB2C2)3 292 „„
^ВС 12 48 ** ~ SSC ~
- (11,5)2 +(0,2)2 +(—23,1)2 +(40,4)2 _ _
-52,04250= 138,80916;
(Е В1D О3 + (EBiD2)3 + (EB2Dx)3 + (EB2D2)3
55^ _ _ _
_ 292 co cc _ (-1,4)2+(13,1)2 +(0,3)2+(17)2
48 п
- 292/48 - 0,65334 - 20,28000 = 0,10083;
ГП _ + (SC1D2)3 + (EC2D1)3 + (EC2D2)3
SSCD "12
- _ SSC - SSD = _ 29,/48 _
- 52,04250 - 20,28000 = 87,93833.
Суммы квадратов тройных взаимодействий
_ (E^iBjCx)3 + (ЕЛ1В3С1)а + (EXiB2C2)3 + (SXjBjCj)’
Ъ^АВС “ 6 +
(E^BtCj)3 + (£Л2Д2С1)3 + (£Л2В2С2)3 + (ЕЛ1ВгГ2)3
- ~
- 292/48 —iSS. - SSn - SSr ~SS.B- SS .r - SSne =
A D C AD AC DL
179
(11,2) 2 + (20,1) 2 + (47,8) 2 + (24,6) 2 + (0,3) 2
=------------------------------------- +
+ 03,2)2 4^7,1)14-24,4)1 _ 292/48 _ 663 05333 _
- 0,65334 - 52,04250 - 71,54081 - 23,475 - 138,80916 = 22,22169;
(ZAiBiDi)* + (ЕЛ1В2^1)1 + (£Л1В2О2)3 + (lAiBiZM3
SSABD 6 +
(2Л2В1Р1)а + (£Л2В2^1)’ + (EA2B2D2)a + (ЕЛ2В1Р2)2
+ 6
-29V4S~SSa-SSb~SSd~SSab-SSad-SSbd =
__ (15,З)2 + (21,3)2 + (46,6)2 + (20,5)2 +(-16,7)2 +(-21)2 +(-29,6)2 -(-7,4)2 _
6
- 292/48 - 663,05333 - 0,65334 - 20,28000 - 71,54081 + 18,50084 -
- 0,10083 = 30,08335;
- <s^icipi)a * (s^CaDi)3 + (SyltCaDa)2 + (^tCiP2)2
^ACD ~ 6 +
(SXaCiPi)3 + (2Л2С2Р1)а + (ЕЛ2СаР2)а + (£Л2С|Ра)2
+ _
- 292/48 - - SSC - SSD - SSAC - SSAD - SSCD fe
- (28,2) 2 +(8,4) 2 +(64,0)2 +(3,1)2 +(-26,0)2 +(-11,7)2 +(-20,1)2 +(-16,9)2
“ 6
- 292/48 - 663,05333 - 52,04250 - 20,28000 - 23,47500 - 18,50084 -
- 87,93833 = 196,17577;
_ (SBiQPi)2 + (EBxCaPi)1 + (SBiCaPn2 + (SBiCiP2)a
ddBCP---------------------------ё----------------------- +
(SBa^iPi)3 + &B2C2Dif + &B2c2Ptf + (SBaCt^a)2
- 292/48 - SSa - SS„ - 55^ - SSD„ -SSnr- SS„n =
i vw c D BC BD CD
_ (-2,6)2 +(1,2)2 +(-l)2 +(14,1)2 + (4,8)2 + (—4,5)2 +(44,9)2 +(-27,9)2 _
6
- 292/48 - 0,65334 - 52,04250 - 20,28000 - 138,80916 - 0,10083 -
- 87,93833 = 190,27501.
Буквенные обозначения в предыдущих вычислениях не очень коррект-
ны с математической точки зрения, но без них впервые занимающемуся
дисперсионным анализом практически невозможно разобраться в приве-
денном примере.
180
Как уже отмечалось, 55ОШИб смешано с SSABCD и может быть вычис-
лено вычитанием из ЗЗобщ всех вычисленных выше сумм квадратов:
55ошиб = 55общ - 1515,1499 = 1651,0992 - 1515,1499 = 135,94930.
Если принять весьма вероятную гипотезу о незначимости суммы квад-
ратов взаимодействия SSABCD, то полученное значение &>Ошиб можно ис-
пользовать для проверки статистических гипотез о влиянии факторов и
их взаимодействии на сцепление нового бетона со старым по F-критерию
Фишера.
Результаты дисперсионного анализа и проверка гипотез даны в
табл. 5.26. При значении Fjf. 33. = 4,1451 можно принять нуль-гипо-
тезы о том, что на сцепление нового бетона со старым не влияют эффекты
В и BD. При более «жестком» 1%-ном уровне значимости Г1 = 7,4881
можно исключить еще как незначимые эффекты D, AC, AD, ABC, ABD.
Оставшиеся 7 эффектов вполне согласуются с физическими представле-
ниями о сущности изучаемого явления. Гипотеза о незначимости эффекта
ABCD принята априори.
На рис. 28 дано ранжирование эффектов по F-критерию. Легко заме-
тить, что эффект А (тип поверхности старого бетона) резко выделяется
среди других. Это естественно, так как заранее можно было бы предполо-
жить, что тип поверхности окажет решающее влияние на прочность сцепле-
ния нового бетона со старым.
Сводка результатов дисперсионного анализа
Таблица 5.26
№п/п Источник изменчивости Степень свободы Сумма квадратов Средний квадрат F (верхнее)
(1) (2) (3) (4) (5) (6)
1 Тип поверхности старого бетона (Л) 1 663,05333 663,05 160,93
2 Консистенция старого бетона (В) 1 0,65334 0,65 0,16
3 Консистенция нового бетона (С) 1 52,04250 52,04 12,63
4 Водоцементное отношение нового
бетона (D) 1 20,28000 20,28 4,92
5 Взаимодействие (ЛВ) 1 71,54081 71,54 17,36
6 Взаимодействие (ЛС) 1 23,47500 23,48 5,79
7 Взаимодействие (Л£>) 1 18,50084 18,50 4,49
8 Взаимодействие (ВС) 1 138,80916 138,81 33,54
9 Взаимодействие (BD) 1 0,10083 0,10 0,02
10 Взаимодействие (CD) 1 87,93833 87,94 21,34
11 Взаимодействие (ЛВС) 1 22,22169 22,22 5,39
12 Взаимодействие (ABD) 1 30,08335 30,08 7,30
13 Взаимодействие (ЛСО) 1 196,17577 196,18 47.62
14 Взаимодействие (BCD) 1 190,27501 190.28 46.32
15 Ошибка Се) 33 135,94930 4,12
Сумма 5Вобщ 47 1651,09920
181
Таблица 5.27
Матрица X и результаты наблюдший прочности стыка на сдвиг
№ опыта Планирование Матрица X Y (7?сдв)
*0 *1 *2 *3 *4 *1*2 *1*3 *1*4 *2*3 Х2Х4 *3*1 Л Я К К frx^xlx х Л X >•4 К X Л X и X
(1) (2) (3) (4) (5) (6) (7) (8) (9) (Ю) (11) (12) (13) (14) (15) (16) (17)
1 + — — — — + -к + + + + __ — 13,03
2 + + — — —• + + + + + + — 31,93
3 + «г, — — — + + — — + + + — + 10,27
4 + + + — — + — — — — + — — 4* + 19,40
5 + — — + — + — + — + — + — + + 7,10
6 + + — + — — + — — + — — + — + 13,60
7 + — + + •— — + + — — + + — 17,27
8 + + + — + + * — + — — + — — — 17,50
9 + — — — + + + — + — — — + + + 14,50
10 + + — + — + + — — + — — + 14,00
11 + — + -Г + — — — + — + — + — 11,60
12 + + + — 4* + — + — + — — + — — 18,80
13 + — —f + + — — — + + + __ 8,50
14 + + — + + —• + + — — + — + 23,10
15 + — + + + — — — + + + — — + 12,83
16 + + + + + + + + + + + + + + 16,30
ЮО
50
1 2 3+567891011 12
Рис. 28
Фактор А — качественный, и для
построения математической модели
процесса и поиска области оптимума
его следовало бы исключить. Выпол-
ненный дисперсионный анализ показы-
вает, что это невозможно.
Дисперсионный анализ выполнял-
ся по плану ПФЭ 24, поэтому его
результаты можно обработать мето-
дами регрессионного анализа. Резуль-
таты наблюдений и матрица планиро-
вания приведены в табл. 5.27.
Коэффициенты регрессионной мо-
дели, найденные по формуле (5.28) по
данным табл. 5.27, приведены в табл.
5.28 [столбец (5)]. Здесь же даны
подсчитанные для каждого коэффици-
ента величины /-критериев Стьюдента.
В табл. 5.28 выполнено сравнение ран-
жирования эффектов по F-критерию
182
Таблица 5.28
Сравнение результатов дисперсионного (ДА) и регрессионного (РА) анализов
№п/п Дисперсионный анализ Регрессионный анализ Ранжирование “по ДА Ранжирова- вание по РА
эффект F эффект 6/ */
(1) (2) (3) (4) (5) (6) 47) (8)
1 А 160,93 +3,721 +20,558 1 1
2 В 0,16 *2 -0,112 -0,619 13 13
3 С 12,63 *3 -1,083 -5,983 7 7
4 D 4,92 *4 -0,654 -3,613 11 10
5 АВ 17,36 *1*2 -1,217 -6,724 6 6
6 АС 5,79 *1*3 -0,621 -3,431 9 12
7 AD 4,49 *1*4 +0,624 -3,448 12 И
8 ВС 33,54 *2*3 +1,562 +8,630 4 4
9 BD 0,02 *2*4 +0,041 +0,227 14 14
10 CD 21,34 *3*4 +1,312 +7,249 ' 5 5
11 АВС 5,39 *1*2*3 +0,958 +5,293 10 8
12 ABD 7,30 *1*2*4 +0,788 +4,354 8 9
13 ACD 47,62 *1*3*4 +2,042 +11,282 2 3
14 BCD 46,32 *2*3*4 -2,108 -11,646 3 2
Фишера (дисперсионный анализ) и по (-критерию Стьюдента (регрессион-
ный анализ) [см. столбцы (7) и (8) табл. 5.28]. Результаты ранжирования,
выполненного двумя различными методами, почти совпадают. Чтобы оце-
нить слово «почти», вычислим коэффициент парной ранговой корреляции
по Спирмену: \
л (1/6)(п3-п) - S(d2)
р = --------------------
(1/6) (л3 - л)
(5.70)
или р = 1 —
6S(da)
л (л ~ 1)
[40], что то ж₽ самое. Здесь л— число сопоставляе-
мых результатов; 5(J2) — сумма квадратов отклонений. Величина Sid2)
подсчитана в табл. 5.29;
Р = «/б) (М3 = 45Щ8 =
(1/6) (143 - 14) 457.333
При полном совпадении рангов р = 1: следовательно, слово «почти»
оценивается в 0,0396, или около 4 %.
Насколько можно судить по данным табл. 5.27 при оценке вклада
эффектов, дисперсионный анализ обладает большей чувствительностью,
чем регрессионный анализ.
Дисперсионный анализ опытов, выполненных по ортогональному пла-
ну, более трудоемок, чем регрессионный, однако есть планы [149], кото-
рые предназначены специально только для дисперсионного анализа. При
183
Таблица 5.29
Данные для расчета коэффициента ранговой корреляции
*1*3
*1*4
*2*3
*2*4
*3*4
2
Эффек-
ты
Ранги
по ДА Ранги 1 13 7 11 6 9 12 4 14 5 10 8 2 3
по РА 1 13 7 10 6 12 11 4 14 5 8 9 3 2
d 0 0 0 1 0 -3 1 0 0 0 2 1 -1 1
d2 0 0 0 1 0 9 1 0 0 0 4 1 1 1 18
проведении дисперсионного анализа большое значение имеет рандоми-
зация и учитывается количество наблюдений, выполненных в каждой экспе-
риментальной точке.
§ 5.5. Некоторое понятие об оптимальном
планировании экспериментов
Как указывается в работах [97, 108, П.14.16], взгляды на вопрос
оптимальности планов менялись с течением времени. Вначале оптимальны-
ми считали ортогональные планы, позднее — ротатабельные. Линейные пла-
ны, построенные на основе матриц Адамара, обладают рядом оптимальных
свойств: ортогональностью, ротатабельностью и минимальной дисперсией
оценок коэффициентов регрессии [108]. Центральные композиционные
ротатабельные планы [15] не ортогональны и не минимизировали диспер-
сию оценок коэффициентов регрессии. Все эти критерии оптимальности
интуитивные и не являются логическим продолжением основных идей
математической статистики.
Теория оптимального эксперимента Кифера—Федорова, включающая
принцип D-оптимальности, восполняет этот пробел. Концепция D-оптималь-
ности может рассматриваться как концепция совместных эффективных
оценок. Можно считать, что она является естественным продолжением одно-
го из основных направлений современной математической статистики —
теории эффективных дценок Фишера. В этой теории эффективность оценок
задается только оптимальным способом обработки результатов наблюде-
ний. В концепции Кифера эффективность обусловлена еще и оптимальным
расположением точек в пространстве факторов (независимых переменных)
[108].
В более поздней работе [П.14.16] говорится об эквивалентности D-
и G-оптимальных планов Кифера и Вольфковица.
В.В. Федоров [145] обобщил зту теорему на случай линейных функ-
ционалов ковариационных матриц (/.-оптимальность) и на случай выпук-
лых функционалов (Ф-оптимапьность). Благодаря наличию большого оде-
ла разновидностей планов в настоящее время появилась возможность выбо-
184
ра компромиссных планов, достаточно хороших с позиции разных крите-
риев. В настоящем пособии нет возможности подробно рассмотреть все
эти вопросы. Вкратце коснемся некоторых из них. Одной из первых работ
на русском языке по данной проблеме является работа [108].
Планирование экспериментов, при котором объем эллипсоида рас-
сеяния оценок параметров минимизируется на множестве планов в задан-
ной области, называется D-оптимальным.
Для отдельных частных видов регрессии одни и те же планы могут
отвечать одновременно нескольким критериям оптимальности. Для случая
полиномиальной регрессии на шаре ротатабельность плана — необходимое
условие D-оптимальности.
Понятие эллипсоида рассеяния — экстраполяция приведенного в гл. II
понятия эллипса рассеяния на плоскости в р-мерное факторное простран-
ство.
Для того чтобы рассмотреть вопрос о критериях оптимальности, необ-
ходимо ввести новые понятия и прежде всего понятия информационной
матрицы системы нормальных уравнений и понятие ковариационной мат-
рицы (матрицы ошибок; дисперсионной матрицы) лучших линейных оце-
нок параметров Зу-
Ковариацией называется второй смешанный центральный момент
<5.3> — корреляционный момент случайных величин х и у:
cov (ху) = • (5.71)
Корреляционный момент можно записать и для двух оценок коэффици-
ентов регрессии: cov (3;3i) •
Лучшими оценками параметров модели являются несмещенные, сос-
тоятельные и эффективные оценки. О несмещенных, состоятельных и эф-
фективных оценках параметров распределений говорилось в гл. I. Для
параметров модели понятия несмещенности, состоятельности и эффектив-
ности изложены в работе [145] .
Оценки р являются несмещенными, если их математические ожидания
равны истинным значениям параметров:
М [3] =3ист- (5.72)
Оценки 3„ состоятельные, если они сходятся по вероятности к истин-
ным значениям параметров:
lim Р [Зи ~ Зист] *(3и Зист) ] = (5.73)
П~* ж
где € — любое наперед заданное положительное число. Индекс п означает,
что оценка получена после измерений. Величина Р [А >£] есть вероят-
ность того, что А > £. Л
Несмещенные оценки 3 являются эффективными, если имеет место
неравенство
D(3)<D(3), (5.74)
185
где Z>(0) — дисперсионная матрица оценок р, Р (3) — дисперсионная мат-
рица любых других несмещенных оценок; D(fl) называют еще [102, 108]
ковариационной матрицей и матрицей ошибок.
Если модель линейна по параметрам, то, используя результаты, полу-
ченные в гл. III, можно сделать следующий вывод: лучшими линейными
оценками для неизвестных параметров 3 являются оценки
3 = M-1(X*WY), (5.75)
ще M=(X*WX). (5.76)
Здесь Х*Х — матрица системы нормальных уравнений, которая распи-
сана в гл. Ill; W — вектор весов w; (ю/ = а~Y — вектор наблюденийур
Матрица (X*WY) рассмотрена в § 4.6; 3 - вектор оценок неизвестных
параметров.
В формулах (5.75) и (5.76), как и во всей книге, постулируется нор-
мальное распределение. В работе [145] рассмотрен более общий случай.
Условимся в дальнейшем называть матрицу М информационной, а об-
ратную ей матрицу
D(3)=M"1 (5-77)
- ковариационной
Теперь дадим определение некоторых принципов оптимальности. План
называется D-оптимальным, если ему соответствует ковариационная мат-
рица с наименьшим значением определителя (или, что то же, информацион-
ная матрица с наибольшим значением определителя). D-оптимальный план
минимизирует обобщенную дисперсию, или, как указывалось выше, эллип-
соид рассеяния оценок параметров. ,
План называется Л-оптимальным, если его ковариационная матрица
имеет наименьший след — сумму диагональных элементов. Л-оптималь-
ный план минимизирует среднюю дисперсию лучших линейных оценок па-
раметров. План называется G-оптимальным, если обеспечивает наименьшую
по всем планам максимальную величину дисперсии предсказанных значений
в заданной области планирования. План называется D-оптимальным, если
максимальное характеристическое значение соответствующей ему кова-
риационной матрицы оценок параметров минимально. D-оптимальный план
минимизирует максимальную ось эллипсоида рассеяния параметров.
Критерии D-, А- и D-оптимальности эквивалентны, если ковариацион-
ная матрица оценок коэффициентов имеет наиболее простой'вид, а именно
когда М“1 = Z Е, где Z - константа, Е - единичная матрица. Такой план
одновременно является и ортогональным и ротатабельным [ 108].
Еще в 1967 г. [П. 14.124] была сделана попытка построить на пяти-
мерном кубе план второго порядка, близкий к D-оптимальному, и срав-
нить этот план с другими планами, в том числе с D-оптимальным планом
Кифера.
В табл. 5.30, заимствованной из [П. 14.124], приведены результаты
этого сравнения. Из таблицы видно, что определитель информационной мат-
рицы у почти D-оптимального плана (VI) не намного меньше, чем соответ-
186
Таблица 5.30
Сравнение планов
Обозначения пла- на, принятые в П. 14.124 Тип плана Число на- блю- дений Величина опреде- лителя инфор- мационной матрицы м Средняя диспер- сия
I Ротатабельный план Бокса 52 0,596-10" 2 89,30
II План Дрейпера-Лоуренса при Р=5,а =2,3780 с = 1,2572 52 0,194-Ю1 52,76
III План с точками, случайно раз- бросанными на кубе, с равномер- ным законом распределения 52 0,152-108 35,46
IV То же 32 0,160-105 75,87
V План с точками в вершинах пя- тимерного куба и в серединах гра- ней 42 0,148-Ю20 14,09
VI План, близкий к D-оптималь- нэму 52 0,474-Ю20 18,133
VII D-оптимальный план Кифера 3000 0,136-Ю21 15,51
Таблица 5.31
№ п/п *1 *2 хз х4 № п/п *1 *2 *3 x4 xs
1 а а а а а 18 —а а fl a -a
2 а а а а -а 19 ~а а a -a a
3 а а а -а а 20 -а а a -a
4 а а а -а -а 21 -а а a a
5 а а -а а а 22 -а а a -a
6 а а -а а -а 23 -в а -a -a a
7 а а -а -а а 24 -а а s -a —a
8 а а -а -а -а 25 -а a a a
9 а -а а а а 26 -а —fl a a —d
10 а -а а а —а 27 -а -fl a -a a
11 а -а а —О а 28 —а -fl fl ’ -a -a
12 а -а а -~й -а 29 ЛД -fl -fl a a
13 а -а а а 30 -а -fl -fl a -a
14 а -а -а а -а 31 -а -fl -a ~a a
15 а -а ~а -а а 32 -а -a -fl -a -a
16 а -а -а -а -а 33 0 0 fl a a
17 -а а а а а 34 в 0 0 a a
187
Продолжение табп. 5.31
№ п/п • *2 хз х4 х$ №п/п Ч Х2 *3 х4 *5
35 0 0 -а а 44 0 а 0 -а а
36 —а —а а 0 0 45 а 0 0 -а а
37 0 -а 0 а а 46 -а 0 а 0 -а
38 -а 0 0 а а 47 0 а и -а 0
39 -а 0 а а 0 48 а а ~а 0 0
40 —а а 0 а 0 49 а а 0 -а 0
41 а 0 0 —d -а 50 0 -а а 0 -а
42 а 0 -а 0 -а 51 -а 0 —d 0 -а
43 Л_ 0 а -а а 0 52 -а 0 -а -а 0
Таблица 5.32
р = 4
Название плана п |М(О1 ^ср ^шах ^min
D-оптимальный - 0.22-10"4 11,1 15 7,7
План на кубе, близкий к D-оптималъному 24 0,80-10”5 8,5 18,5 4,8
План Коно 21 0,23* 10"6 21,4 89,0* 8,4*
План Кифера 27 0,77'Ю"5 13,0 - -
План Кифера 27 0,81-10"s 13,1 24,0* 7,0*
План Хартли-Коно 18 0,10-10~6 20,8 138,0* 6,5*
План Хартли 17 0,10’Ю"7 17,1 118,6* 3,2*
План Дрейпера-Л буренса 31 0,38-Ю”13 18,79 112,0 3,8
Ротатабелы/ый Бокса 31 0,18-Ю"16 36,5 267,2 4,2
Ортогональный 25 0,18-Ю”10 13,2 66,5 6,4
р = 5
D-оптимальный 0,63-Ю"6 15,5 21 10,7
План на кубе, близкий к D-оптимальному 42 0,68-10"7 14,1 34,2 6,0
План Кифера 26 0,44-10~7 21,9 58,0* 10,0*
188
Продолжение табл. 5.32
Название плана п \М (01 ^ср ^тах ^min
План Кифера 26 0,53-10"7 23,2 58,0* 8,0*
План Кифера 26 0,59*10”7 23,0-. - -
План Кифера 52 0,22-10“6 18,1 34,5* 11,0*
План Хартли 27 0,17-Ю"7 11,0 27,4 2,7
План Вестлейка 23 0,61-10"8 37,0 195,5* 4,5*
План со случайным выбо- ром точек на кубе 52 0,70-Ю"19 35,5 290,0* 7,5*
То же 32 0.74-10’22 75,9 - -
План Дрейпера-Лоуренса 52 0,90-10“26 52,8 286,8 4,7
Ротатабельный Бокса 52 0,28-10"28 89,3 692,4 5,0
Ротатабельный Бокса (с полурепликой) 32 0,55-10“28 85,9 665,7 4,9
Ортогональный 43 0,40-10"18 25,1 149,2 9,0
Ортогональный (с полу- репликой) 27 0,10-10"17 23,0 144,8 6,8
р = 6 D-оптимальный 0,15ь10”7 20,6 28 14,2
План на кубе, близкий к D-оптимальному 76 0,23-10"9 27,5 66,5 7,9
План Хартли-Коно 44 0,37-10“10 29,3 77,0* 16,7*
План Хартли- Коно 44 0,20-10“10 31,1 55,6* 11,4*
План Коно 88 0,21-10“8 25,7 42,6* 14,5*
План Хартли 29 0,59-10“17 52,0 152,0* 3,3*
План Дрейпера-Лоуренса 91 0,11-10“37 56,2 719,2 5,8
Ротатабельный Бокса 91 0,59-10"45 261,1 1726,4 5,5
Ротатабельный Бокса (с полурепликой) 53 0,25-10“39 126,7 1007,5 5,7
Ортогональный 77 0,22-Ю-28 48,0 312,1 12,8
Ортогональный (с полу- репликой) 45 0,15-Ю"27 31,4 277,6 9.5
189
Таблица 5.33
План на кубе, близкий к D-оптимальному с варьированием четырех факторов
и *1 х2 хз х4 J п *1 Х2 ХЗ Х4 и *1 Х2 Хз х4
111 1 19-11 1 1 17 1 0 00 2 11 1 -1 10 -1 1 1 -1 18 -1 0 0 0 3 1 1 -1 1 И -1 1 -1 1 19 0 1 0 0 4 1 1 -1 -1 12 -1 1 -1 -1 20 0 -1 0 0 5 1-11 1 13 -1 -1 1 1 21 0 0 10 6 1 -1 1 -1 14 -1 -1 1 -1 22 0 0 -1 0 7 1 -1 -1 1 15 -1 -1 -1 1 23 0 0 0 1 8 1 -1 -1 -1 16 -1 -1 -1 -1 24 0 0 0 -1 План Хартли-Коно 11-1-1-17-1-11 1 13 -11-10 2-11-1-181 1 1 1 14 -1 0 11 3 -1 -1 1 -1 9 0 0 0 0 15 0 1 1 -1 4 11 1 -1 10 0 1 -1 1 16 1 -1 1 0 5 1-1-1 1 11 -1 0 -1 -1 17 1 -1 0 1 6 -1 1 -1 1 12 1 0 1 1 18 0 -1 1 -1 План на кубе, близкий к D-оптимальному с варьированием пяти факторов
п *1 х2 *3 *5 п Xl Х2 Хз Х4 Х5 п Xl Х2 Хз х4 Xs
1 1 1 1 1 1 15 1 -1 -1 -1 1 29 -1 -1 -1 1 1 2 1 1 1 1 -1 16 1 -1 -1 -1 -1 30 -1 -1 -1 1 -1 3 1 1 1 -1 1 17 -1 1 1 1 1 31 -1 -1 -1 -1 1 4 1 1 1 -1 -1 18 -1 1 1 1 -1 32 -1 -1 -1 -1 -1 5 1 1 -1 1 1 19 -1 1 1 -1 1 33 1 0 0 0 0 6 1 1 -1 1 -1 20 -1 1 1 -1 -1 34 -1 0 0 0 0 7 1 1 -1 -1 1 21 -1 1 -1 1 1 35 0 1 0 0 0 8 1 1 -1 -1 -1 22 -1 1 -1 1 -1 36 0 -1 0 0 0 9 1-11 1 1 23 -1 1 -1 -1 1 37 0 0 1 0 0 10 1 -1 1 1 -1 24 -1 1 -1 -1 -1 38 0 0 -1 0 0 11 1 -1 1 -1 1 25 -1 -1 1 1 1 39 0 0 0 1 0 12 1—1 1 -1 -1 26 -1 -1 1 1 -1 40 0 0 0 -1 0 13 1 -1 -1 1 1 27 -1 -1 1 -1 1 41 0 0 0 0 1 14 1 -1 -1 1 -1 28 -1 -1 1 -1 -1 42 0 0 0 0 -1 План Хартли 1 1 1 1 1 1 10 1 -1 1 1 -1 19 -1 0 0 0 0 2 -1 -1 1 1 1 11 1 1 -1 -1 1 20 0 1 0 0 0 3-11-1 -1 -1 12 -1 -1 -1 -1 1 21 0 -1 0 0 0 4 1 -1 -1 -1 -1 13 -1 1 1 -1 1 22 0 0 1 1 0 5 -1 1 -1 1 1 14 1 -1 1 -1 1 23 0 0 -1 0 0 6 1 -1 -1 1 1 15 1 1 -1 1 -1 24 0 0 0 1 0 7 1 1 1 -1 -1 16 -1 -1 -1 1 -1 25 0 0 0 -1 0 8 -1 -1 1 -1 -1 17 0 0 0 0 0 26 0 0 0 0 1 9-11'1 1 -1 18 1 0 0 0 0 27 0 0 0 0 -1 План Кифера 1 1 1 1 1 1 19 -1 1 1 -1 1 36 -1 -1 1 0 0 2 1 1 1 1 -1 20 -1 1 1 -1 -1 37 0 -1 0 1 1 3 1 1 1 -1 1 21 -1 1 -1 1 1 38 -1 0 0 1 1 4 1 1 1 -1 -1 22 -1 1 -1 1 -1 39 -1 0 1 1 0 5 1 1 -1 1 1 23 -1 1 -1 -1 1 40 -1 1 0 1 0 190
Продолжение табл. 5.33
п *1 *2 *3 х4 Xs п х2 хз *4 *5 л Х2 *3 х4 Х$
6 1 1 -1 1 -1 24 -1 1 -1 -1 -1 41 1 0 0 -1 -1
7 1 1 -1 -1 1 25 1 -1 1 1 1 42 1 0 -1 0 -1
8 1 1 -1 -1 -1 26 -1 -1 1 1 -1 4i 0 1 -1 1 0
9 1 -1 1 1 1 27 -1 -1 1 -1 1 44‘ 0 1 0 -1 1
10 1 -1 1 1 „1 28 -1 -1 1 1 -1 45 1 0 0 -1 1
И 1 -1 1 -1 1 29 -1 -1 -1 1 1 46 -1 0 1 0 -1
12 1 1 1 -1 -1 30 -1 „1 -1 1 -1 47 0 1 1 -1 0
13 1 -1 1 1 1 31 -1 -1 -1 -1 1 48 1 1 -1 0 0
14 1 -1 -1 1 -1 32 -1 -1 -1 -1 -1 49 1 1 0 -1 0
15 1 -1 -1 1 1 33 0 0 1 1 1 50 0 -1 -1 0 -1
16 1 -1 -1 -1 -1 34 1 0 0 1 1 51 -1 0 -1 0 -1
17 -1 1 1 1 1 35 0 0 -1 -1 1 52 -1 0 -1 -1 0
18 -1 1 1 1 -1
План Вестлейка
1 1 1 1 1 -1 9 -1 1 -1 -1 1 17 0 0 1 0 0
2 1 1 -1 -1 -1 10 -1 1 1 1 1 18 0 0 -1 0 0
3 -1 1 1 1 -1 11 1 1 -1 1 1 19 0 0 0 1 0
4 -1 1 -1 1 -1 12 1 1 -1 -1 1 20 0 0 0 -1 0
5 1 1 1 1 1 13 1 0 0 0 0 21 0 0 0 0 1
6 1 -1 -1 -1 1 14 -1 0 0 0 0 22 0 0 0 0 -1
7 -1 -1 1 -1 1 15 0 1 0 0 0 23 0 0 0 0 0
8 -1 -1 -1 1 1 16 0 -1 0 0 0
План Коно
п *1 х2 хз х4 XS *6 п *1 х2 *3 х4 xs Хб
1 -1 1 -1 -1 -1 -1 23 1 1 1 1 -1 -1
2 1 1 -1 -1 1 1 24 -1 -1 1 1 1 1
3 1 -1 1 1 1 -1 25 1 -1 -1 1 -1 -1
4 -1 1 1 1 -1 1 26 -1 -1 1 -1 1 -1
5 1 1 -1 -1 -1 -1 27 1 1 1 -1 -1 1
6 -1 -1 -1 -1 1 1 28 -1 1 -1 1 1 1
7 1 -1 1 1 -1 1 29 -1 1 -1 1 -1 -1
8 -1 1 1 1 1 -1 30 -1 -1 1 -1 -1 1
9 1 -1 1 -1 -1 -1 31 1 1 1 -1 1 -1
10 -1 -1 -1 1 1 -1 32 1 -1 -1 1 1 1
И 1 1 -1 1 -1 1 33 0 0 0 0 0 0
12 -1 1 1 -1 1 1 34 0 0 0 0 0 0
13 -1 1 1 -1 -1 -1 35 -1 -1 0 1 1 -1
14 -1 -1 -1 1 -1 1 36 1 1 0 1 1 1
15 1 -1 1 -1 1 1 37 1 -1 0 -1 -1 -1
16 1 1 -1 1 1 -1 38 -1 -1 -1 -1 -1 0
17 1 -1 -1 -1 1 -1 39 0 1 -1 1 1 1
18 -1 1 -1 -1 -1 1 40 1 -1 1 1 1 0
19 -1 -1 1 1 -1 -1 41 0 1 -1 -1 1 -1
20 1 1 1 1 1 1 42 0 1 1 -1 1 1
21 1 -1 -1 -1 -1 1 43 1 0 -1 1 -1 -1
22 -1 1 -1 -1 1 -1 44 -1 -1 1 1 1 0
191
Продолжение табл. 5.33
План Хартли
п *2 *3 *5 *6 П *1 Х2 *3 *5 *6
1 -1 -1 -1 -1 1 1 16 1 1 1 1 1 1
2 -1 -1 -1 1 -1 1 17 0 0 0 0 0 0
3 -1 -1 1 -1 -1 1 18 1 0 0 0 0 0
4 -1 -1 1 1 1 1 19 -1 0 0 0 0 0
5 -1 1 -1 -1 1 -1 20 0 1 0 0 0 0
6 -1 1 -1 1 -1 -1 21 0 -1 0 0 0 0
7 -1 1 1 -1 -1 -1 22 0 0 1 0 0 0
8 -1 1 1 1 1 -1 23 0 0 -1 0 0 0
9 1 -1 -1 -1 1 -1 24 0 0 0 0 0 0
10 1 -1 -1 1 -1 -1 25 0 0 0 1 0 0
11 1 -1 1 „1 -1 -1 26 0 0 0 „1 0 0
12 1 -1 1 1' 1 -1 27 0 0 0 0 1 0
13 1 1 -1 -1 1 1 28 0 0 0 0 -1 0
14 1 1 -1 1 -1 1 29 0 0 0 0 0 1
15 1 1 1 -1 -1 1 0 0 0 0 -1
ствующий показатель плана Кифера, а средняя дисперсия соответственно
немногим больше, зато число наблюдений этого плана намного меньше
(52 -< 3000). Близкий к /^оптимальному план на пятимерном кубе пре-
восходит по своим показателям остальные планы. Этот план приведен в
табл. 5.31. Для удобства сравнения с планом Бокса а принято равным
2,378.
В работе [108] приведена более подробная таблица сравнения пла-
нов. Здесь сравниваются 36 планов с числом варьируемых факторов р =
= 4, р = 5ир=6. Эту таблицу, которая воспроизведена в табл. 5.32, можно
рекомендовать экспериментаторам для изучения в процессе выбора стра-
тегии планирования экспериментов.
В табл. 5.33 даны координаты планов, лучших с точки зрения их срав-
нения с ^оптимальными планами.
§ 5.6. Планирование экспериментов на симплексе
для оптимизации составов смесей
Симплексный метод применяют для описания поверхности отклика в
задачах оптимизации составов смесей (сплавы, полимеры, бетоны и др.),
а также для любых других задач, в которых
р
Sxz=l. (5.78)
Содержание всех компонентов в любой смеси составляет 100 % [Ю2] .
Из ограничения (5.78) следует, что ковариационная матрица оказывает-
ся вырожденной, если в матрицу независимых переменных включить стол-
бец, состоящий из единиц (свободный член модели). Эта же матрица яв-
ляется вырожденной, если в матрицу факторов включить квадраты и пар-
192
ные произведения факторов (ху х/, х?). С другой стороны, поверхность от-
клика в подобных задачах имеет сложную конфигурацию, поэтому для ее
описания целесообразно использовать модели высоких порядков.
Если прибегнуть к преобразованию независимых переменных, то
ограничение (5.78), которое на первый взгляд кажется недостатком,
можно превратить в преимущество [П.14.174]. Рассмотрим этот вопрос на
примере квадратичной формы. Для трех компонентов полная квадратичная
форма имеет вид
у-b0 + Z>iXi + b2x2 + b3x3 + bi2XiX2 + 3*1X3 + Ь23х2х3 +
+ Ьцх21 + Ь22х% + Ь33х3. (5-79)
Из формулы (5.78) следует, что
*1 + х2 + х3 = 1, (5.80)
поэтому можно записать
Z»o*i + Ъох2 + ЬоХз -Ъо. (5.81)
Используя формулу (5.81), уравнение (5.79) запишем в виде
р = (Ьо + bi)Xi +(Ь0 + Ь2)х2 +(Ь0 + &3)*з + ^12*1*2 +
+ 2>1зХ1Хз + Ь23х2х3 + Ьцх1 + b22x% + Ь33х3. (5.82)
Умножая обе части выражения (5.80) последовательно на х2, х2 и х3, по-
лучаем:
Xi =Xi - XiX2 - XiX3,
х2 =х2 - XiX2 - х2х3,
х3 = х3 -хгх3 -Х2Х3.
Подставляя эти выражения в уравнение (5.82), имеем
у = (b0 + bi + bi i)Xi +(й0 + b2 + b22)x2 +(Z»0 + b3 + b33)x3 +
+ (fc12 - Ьц - Ь22)Х1Х2 +(Ь13-Ьц -Ь33)Х1Х3 +(b23 +
(5.o3J
+ b22 +b33)x2x3.
Если произвести замену в (5.83):
b'i = Ьц + bi + bi 1, b2 = bo + b2 + b22,
b3-bo+b3+b33, bi2 — bi2 — Ьц — b22,
bi3=bi3—Ьц—b33, b23=b23 — b22—b33,
то модель (5.83) принимает вид
y=b'i Xi + b2x2 + b3x3 +b'i2XiX2 +b'i3xix3 +b23x2x3. (5.84)
Для этой модели ковариационная матрица не является вырожденной. Глав-
ное преимущество модели (5.84) в том, что по сравнению с уравнением
(5.79) по экспериментальным данным в этой модели оценивают на четыре
параметра меньше.
193
В общем случае для ^компонентов модели выглядят следующим обра-
зом [П. 14.74]: 1) квадратичная модель
У- S fyxf+ S fyiXjXr, (5.85)
1</<р 1 1 ' 1
2) неполная кубическая модель
7 = S &xz+ S 0//х/х,+ S fytkxixk. (5.86)
1</<р !</</<₽ l</<Z<Jt<p
Метод планирования называется симплексным, так как эксперимен-
тальные точки располагаются на симплексах или симплексных решетках.
Варианты симплексных решеток показаны на рис. 29, а-е.
а) 5) в) г) д)'"* е)
Рис. 29
В табл. 5.34 дано число опытов в зависимости от числа компонентов
смеси и степени полинома, описывающего поверхность отклика. Коэффи-
циенты уравнений регрессии вычисляют по результатам экспериментов из
простых соотношений.
При*! = 1,х2 -0, х3 = 0 формула (5.84) принимает вид
b’i =Уъ Ь'2 =У2 и Ь3 =у3;
при Xi =/1/2, х2 =1/2 и х3 =0
Z>i2 -4^12 —271 —272, b'i3 = 4у13 —271 — 2у3,
Ьгз ~4у23 — 2у2 — 2у3.
Для р-компонентной системы коэффициенты квадратичной формулы
ь/ =Уу bjl = 4У/1 ~ 2>7 - 2?1-
Таблица 5.34
Число опытов для построения моделей разных степеней для описания
поверхностей отклика многокомпонентных систем
Число компонентов Степень полинома
вторая третья неполная третья четвертая
1 2 3 4 5
3 б 7 10 15
4 10 14 20 35
5 15 25 35 70
6 21 41 56 126
8 36 92 120 330
10 55 175 220 715
194
Планы на симплексе являются насыщенными, поэтому для проверки
адекватности ставят дополнительные опыты (проверочные точки).
Порядок расчетов рассмотрим на примере квадратичной модели. Как
указывается в работе [108], коэффициенты bj и bji являются линейными
комбинациями значений yj и yjl-, наблюдаемых в точках симплексной ре-
шетки [формула (5.84)], поэтому уравнение (5.84) мйжно записать в виде
у= S ДуУу + S Ojiyji. (5.87)
1</<р 1 ' 1<}<1<р 1 7
Если предположить, что уу и уу/ — усредненные результаты гу и гу/ наблю-
дений в каждой точке решетки, то
°уГ °у!1 = (5-88)
дисперсия предсказанного значения
оЯ = п2[ S S (5.89)
Л 1</<р rj l<j<Kp rjl
где
aj = Xj (2xy - 1), aji = 4xj xi; (5.90)
здесь a2 — ошибка эксперимента.
Если число опытов в каждой точке одинаково, то выражение (5.89)
принимает вид
^-(а2/г)(Ха? + Say2). (5.91)
Более подробно симплексный метод и практические примеры даны в
[102,108, П.14.174] .
ПОСЛЕСЛОВИЕ
Рйс. 30
Внимательно прочитавшие эту
книгу должны овладеть наибо-
лее употребительными метода-
ми обработки эксперименталь-
ных данных, используемыми
для построения эмпирических
зависимостей.
Чтобы не нарушать строй-
ность изложения, автор недоста-
точное внимание уделил двум
важным для экспериментатора
разделам прикладной матема-
тической статистики, а именно:
статистическому оцениванию и
статистическому сопоставлению
результатов наблюдений. Под-
робные сведения по этим вопро-
сам можно найти в [52]. Не-
достаточно подробно изложен и
дисперсионный анализ, который
хорошо описан в [149, 156].
Материал книги позволяет
составить генеральную схему
методики обработки экспери-
ментальных данных для по-
строения эмпирических зависимостей. Такая схема изображена на рис. 30.
Однако эта схема вовсе не обязывает экспериментатора пройти весь наме-
ченный путь. Каждый выбирает стратегию экспериментирования в зависи-
мости от задач, которые нужно решить в каждом конкретном исследо-
вании.
Генеральная схема отображает оптимальную, по мнению автора, ме-
тодику поведения исследователя в ситуации, когда имеется масса экспери-
ментального материала, полученного другими исследователями, когда
изучается достаточно сложное явление, которое зависит от многих факто-
ров. Такие типы задач очень часто встречаются в науке.
Автор заранее благодарен за все замечания и предложения по данной
работе, которые просит высылать в адрес редакции.
Автор
196
Приложения
ILL Случайные числа*
44 983 33 834 54 280 67 850 96 025 96 117 00 768 14 821 69 029 25 453 48 798 15 486
89 494 34 431 44 890 59 890 79 682 20 308 82 510 53 609 13 258 89 631 80 497 49 167
54 430 52632 94 126 95 597 48 338 67 645 44 676 14 730 22 642 21 919 21 050 87 791
96 999 42 104 34 377 63 309 82 181 00 278 28 209 95 629 75 818 09 043 48 564 8 / 355
87 947 09 427 32 380 43 636 58-578 07 761 28 456 46 570 11 623 50 417 37 763 30 136
30 238 46 126 85 306 37 114 22 718 50 584 92 291 56 575 24 075 43 889 40 909 18 741
22 938 13 073 32 066 43 098 75 738 94 910 15 403 89 151 73 322 18 370 90 586 46 115
89 182 27 750 63 314 87 302 49 472 24 885 79 506 60 638 07 132 00 908 92 035 75 518
16 187 03 303 40 287 52 435 23 926 92 544 54 099 31497 06 863 22 864 72 620 74 169
21 526 07 401 30 925 46 148 20 138 33 874 56 715 38 424 38 273 11 361 15 203 64 912
42 907 95 158 27 146 37 012 43 361 03 173 97 911 71 313 44 256 66 609 42 504 76 799
21 479 48 265 01 674 47 274 56 350 37 512 14 883 99 673 62 298 33 948 32 456 28 675
90 076 70 233 76 730 25 043 16 686 54 737 57 341 01 786 20 803 69 465 37 970 05 673
93 202 25 355 94 941 84 434 22 384 13 240 93 617 51 549 28 532 57 150 77 261 62 643
46 059 72 208 90 475 10 341 39 703 83 224 37 858 61 657 04 184 15 597 29 448 01 922
38 220 13 972 86 115 17 196 24 568 26 820 66 299 39 960 02 489 53 079 72 789 22 562
82 618 85 756 51 156 74 037 12 501 94 162 42 006 16 135 82 797 31 296 93 268 10 104
07 896 74 085 59 886 03 051 78 702 13 402 74 318 10 870 72 107 11 550 61 175 33 345
95 241 84 360 13 960 95 736 43 637 60 399 19 080 60 261 11 207 73 065 48 286 57 057
53 849 26 578 39 954 86 726 91 039 13 884 25 376 36 880 02 564 96 978 62 332 77 321
72 967 53 031 47 906 99 501 27 7 53 69 946 66 875 25 601 30 038 78 786 65 194' 65 283
87 910 89 260 66 444 15 979 83 469 96 952 50 065 72 802 70 630 87 336 16 385 32 784
10482 34 277 40 177 01 081 57 788 08 612 39 886 42 234 04 905 83 274 22 459 75 032
68 034 98 561 46 747 30 655 41 878 93 610 51 745 41 771 61 398 98 154 61 644 12 405
80 277 92 450 60 888 18 689 45 966 25 837 70 906 60 733 11 765 09 293 70 076 40 751
59 896 78 185 60 268 03 650 36 814 88 460 34 049 09 111 64 205 77 930 32 391 69 076
78 369 04 163 77 673 73 342 78 915 _ - - 20 537 06 126 27 222 17 378 59 359 00 055 66 780
23 015 54 261 95 020 77 705 81 682 96 907 37 411 93 548 87 546 07 687 47 338 12 240
55 171 85 448 12 545 75 992 08 790 88 992 69 756 18 960 85 182 02 245 11 566 52 527
58 095 62 204 69 319 00 672 96 037 78 680 98 744 83 719 40 702 79 038 68 639 63 329
19 700 98 193 37 600 70 617 58 959 45 486 58 338 84 563 62 071 17 799 96 994 41635
12 666 87 597 23 190 26 243 36 690 75 829 71 060 32 257 15 699 02 654 83 110 44 278
66 685 05 344 71 633 68 536 18786 28 575 08 455 79 261 49 705 31491 25 318 52 586
72 590 47 283 45 445 35 611 98 354 53 680 45 747 60 026 13 032 14 048 16 304 11 959
30 286 06 434 50 229 09 070 44 848 09 996 77 753 05 018 92 605 10 316 07 351 78 020
87 494 95 585 25 547 53 500 45 047 08 406 66 984 63 390 48 093 02 366 05 407 08 325
32 301 25 923 76 556 13 274 39 776 97 027 56 919 17 792 09 214 53 781 90 102 25 774
70711 37 921 54 289 17 828 60 976 57 662 61 757 93 272 09 887 04 196 98 251 52 453
36 086 05 468 41 631 95 632 78154 38 634 47 463 37 514 24 437 01 316 04 777 06 534
37 403 42 231 17 073 49 097 54 147 03 656 14 735 06 370 81 703 90 858 55 130 40 869
41 022 76 893 29 200 82 747 97 297 74 420 18 783 93 571 89 055 56 413 77 817 10 655
70 978 57 385 70532 46 978 87 390 53 319 90 155 03 154 20 301 47 831 86 786 И 284
19 207 41 684 20 288 19 783 83 215 35 810 39 852 43 795 21 530 96 315 55 657 76 473
50172 23 114 28 745 12 249 35 844 63 255 26 451 06 896 06 707 99 251 06 260 74 779
43 112 94 833 72 864 58 785 53 473 06 308 56 788 30 474 57 277 23 425 27 092 47 759
64 031 41 740 69 680 69373 73 674 97 914 77 989 47 280 71 804 74 587 70 563 77 813
92 357 38 870 73 884 95 662 83 923 90 790 49474 11 901 30 322 80 254 99 608 17 019
79 945 42 580 86 605 97 758 08 206 54 199 41 327 01 170 21 745 71 318 07 978 35 440
48 030 05 125 70 866 72 154 86 385 39 490 57 482 32 921 33 795 43 155 30 432 48 384
80 016 81 500 48 061 25 583 74 101 87 573 01 556 89 184 64 830 16 779 35 724 ( 82 103
32 265 65 728 89 776 04 006 06 089 84 076 12 445 47 416 83 620 49151 97 420 23 689
82 534 76 335 21 108 42 302 79 496 21 054 80 132 67 719 72 662 58 360 57 384 65 406
72 055 61 146 82 780 89 411 53 131 57 879 39 099 42 715 24 830 60 045 23 250 39 847
26 999 96 294 20 431 30 114 23 035 30 380 76 272 60 343 57 572 42 492 47 962 21 439
01 628 47 335 17 893 53 176 07 436 14 799 78 197 48 601 97 557 89 917 20 530 61 565
66 322 27 390 37 834 73 494 21 527 93 579 20 949 85 666 25 102 64 733 93 872 72 693
96 239 18 521 67 354 41 883 58 939 36 222 43 935 36 272 47 817 90 287 91 434 86 453
10 497 83 617 39 176 45 062 63 903 33 862 14 903 38 996 60 027 41 702 78 189 28 598
69 712 33 438 85 908 58 620 50 646 47 857 96 024 58 568 67 614 44 370 40 276 85 964
51 375 42 451 76 889 68 096 80 657 91 046 95 340 70 209 23 825 46 031 45 306 64 476
Таблица заимствована из [52], с. 58,
П.2. Квантили распределения максимального относительного отклонения _р
п Уровни значимости Р п Уровни значимости Р
0,10 0,05 0,025 0,01 0,10 0,05 0,025 0,01
3 1,41 1,41 1,41 1,41 15 2,33 2,49 2,64 2,80
4 1,65 1,69 1,71 1,72 16 2,35 2,52 2,67 2,84
5 1,79 1,87 1,92 1,96 17 2,38 2,55 2,70 2,87
6 1,89 2,00 2,07 2,13 18 2,40 2,58 2,73 2,90
7 1,97 2,09 2,18 2,27 19 2,43 2,60 2,75 2,93
8 2,04 2,17 2,27 2,37 20 2,45 2,62 2,78 2,96
9 2,10 2,24 2,35 2,46 21 2,47 2,64 2,80 2,98
10 2,15 2,29 2,41 2,54 22 2,49 2,66 2,82 3,01
11 2,19 2,34 2,47 2,61 23 2,50 2,68 2,84 3,03
12 2,23 2,39 2,52 2,66 24 2,52 2,70 2,86 3,05
13 2,26 2,43 2,56 2,71 25 2.54 2,72 2,88 3,07
14 2,30 2,46 2,60 2,76
41 * Таблица заимствована из [127], с. 283.
П.З. Квантили распределения величины Tj _р
п 1 -Р=0,90, Р=0,10 1 — Р—0,95, Р=0,05 1-Р =0,99, Р=0,01
3 1,41 1,41 1,41
4 1,64 1,69 1,72
5 1,79 1,87 1,96
6 1,89 2,00 2,13
7 1,97 2,09 2,26
8 2,04 2,17 2,37
9 2,10 2,24 2,46
10 2,15 2,29 2,54
Таблица заимствована из [60], с. 50.
П.4. Процентные точки распределения Стьюдента’
V 40% 25% 10% 5 % 2,5% 1 % 0,5% 0,25% 0,1% 0,05 %
1 0,3249 1,0000 3,0777 6,3138 12,7062 31,8205 63,6567 127,3213 318,3088 636,6192
2 2887 0,8165 1,8856 2,9200 4,3027 6,9646 9,9248 14,0890 22,3271 31,5991
3 2767 7649 6377 3534 3,1824 4,5407 5,8409 7,4533 10,2145 12,9240
4 2707 7407 5332 1318 2,7764 3,7469 4,6041 5,5976 7,1732 8,6103
5 2672 7267 4759 2,0150 5706 3649 4,0321 4,7733 5,8934 6,8688
6 0,2648 0,7176 1,4398 1,9432 2,4469 3,1427 2,7074 4,3168 5,2076 5,9588
7 2632 7111 4149 • 8946 3646 2,9980 4995 4,0293 4,7853 4079
8 2619 7064 3968 8595 3060 8965 3554 3,8325 5008 5,0413
9 2610 7027 3830 8331 2622 8214 2498 6897 2968 4,7809
10 2602 6998 3722 8125 2281 7638 1693 5814 1437 5869
11 0,2596 0,6974 1,3634 1,7959 2,2010 2,7181 3,1058 3,4966 4,0247 4,4370
12 2590 6955 3562 7823 1788 6810 0545 4284 3,9296 3178
13 2586 6938 3502 7709 1604 6503 3,0123 3725 8520 2208
14 2582 6924 3450 7613 1448 6245 2,9768 3257 7874 1405
15 2679 6912 3406 7530 1314 6025 9467 2860 7328 0728
16 0,2576 0,6901 1,3368 1,7459 2,1199 2,5835 2,9208 3,2520 3,6862 4,0150
17 2573 6892 3334 7396 1098 5669 8982 2224 6458 3,9651
18 2571 6884 3304 7341 1009 5524 8784 1966 6105 9216
19 2569 6876 3277 7291 0930 5395 8609 1-737 5794 8834
20 2567 6870 3253 7247 0860 5280 8453 1534 5518 8495
21 0,2566 0,6864 1,3232 1,7207 2,0796 2,5176 2,8314 3,1352 3,5272 3,8193
22 2564 6858 3212 7171 0739 5083 8188 1188 5050 7921
23 2563 6853 3195 7139 0687 4999 8703 1040 4850 7676
24 2562 6848 3178 7109 0639 4922 7969 0905 4668 7454
25 2561 6844 3163 7081 0595 4851 7874 0782 4502 7251
Продолжение табл. П. 4
>х 40 1_- 10 91 5 7с 2,5 % 1 1 7с 0,5 % 0,25 % 0.1 % 0.05 %
26 0.2 560 0.6840 1.3150 1,7056 2.0555 2,4786 2,7787 3,0669 3,4350 3.7066
2559 6837 3137 7033 0518 4727 7707 0565 4210 6896
28 2558 6 834 3125 7011 0484 4671 7633 0469 4082 6739
29 2557 6830 3114 6991 0452 4620 7564 0380 3962 6594
30 2556 6828 3104 6973 0423 4573 7500 0298 3852 6460
3 э 0.2555 0.6822 1,3086 1.6939 2.0369 2.4487 2,7385 3.0149 3,3653 3.6218
34 7 S 3 6818 3070 6909 0322 4411 7284 3.0020 3479 6007
36 255 2 6 814 3055 6883 0281 4345 7195 2.9905 3326 5821
3 8 2551 6810 3042 6860 0244 4286 7116 9803 3190 5657
40 25 5< । 6807 3031 6839 0211 4233 7045 9712 3069 5510
42 0.2559 0.6 804 1.3020 1.6820 2.0181 2.4185 2,6981 2,9630 3.2960 3,5377
44 254 9 ^«01 30 1 1 6802 0154 4141 6923 9555 2861 5258
46 2 .'44 6 7 99 3002 6787 0129 4102 6870 9488 2771 5150
48 254 v 67 96 2994 67 72 0106 4066 6822 9426 2689 5051
50 25-4' 67 94 2987 67 59 0086 4033 6778 9370 2614 4960
s S 0.2546 0.6 790 1.297 1 1.6730 2.0040 2.3961 2.6682 2.9247 3,2561 3.4764
60 254 < 67 86 2958 6706 2.0003 3901 6603 9146 2317 4602
65 2544 67 83 2947 66 86 1.9971 3851 65 36 9060 2204 4466
70 254 3. 67 80 2938 6669 9944 3808 6479 8987 2108 4350
80 0.254 2 0.6776 1.2922 1.6641 1.9901 2.3739 2,6387 2.8870 3.1953 3,4163
90 254 1 6 7 72 29 10 66 20 9867 3685 6316 8779 1833 4019
100 2540 67 70 2901 6602 9840 364 2 6259 8707 1737 3905
1 20 25 39 6 765 2886 65 77 9799 3578 6174 8599 1595 3735
;0 25 38 676! 2872 6551 9759 35 15 6090 8492 1455 3566
Зои 253 7 675 1 28^8 65 2^ 9719 3451 6006 8385 1315 3398
2 50 25 Зб 6755 2849 65 О' 9695 34 14 5956 8322 1232 3299
он) 2' ’6 67 53 2844 6499 96 79 3388 5923 8279 1176 32.33
411'1 2 67 S] 2837 64 87 9659 33 57 5882 8227 1107 3150
'60 0 ?' 0.6750 1 2832 1.647 9 1.9647 2.3338 2.5857 2.8195 3.1066 3.3101
6. и 11 .тми в мм1!и [ 1 7 | . с. 240.
202
П.5. Коэффициенты для определения 95 %-ных доверительных границ
для среднего значения по САО*
п Коэффициент й Коэффициент п Коэффициент
2 12,71 9 1,00 20 0,60
3 3,45 10 0,93 25 0,53
4 2,16 11 0,87 30 0,48
5 1,66 12 0,82 40 0,41
6 1,40 13 0,78 60 0,33
7 1,21 14 0,75 120 0,23
8 1,09 15 0,71
* Таблица заимствована из [52], с. 235.
П.6. Критические границы отношения R/S*
Объем выбор- ки п Нижние границы Верхние границы
Вероятность эшибки
0,000 0,005 0,01 0.025 0,05 0,10 0,10 0,05 0,025 0,01 0,005 0,000
3 1,732 1,735 1,737 1,745 1.758 1,782 1,997 1,999 2,000 2,000 2,000 2,000
4 1,732 1,83 1,87 1,93 1,98 2,04 2,409 2,429 2,439 2,445 2,447 2,449
5 1,826 1,98 2.02 2,09 2,15 2,22 2.712 2.753 2,782 2,803 2,813 2,828
6 1.826 2,11 2,15 2,22 2,28 2,37 2,949 3,012 3,056 3,095 3,115 3,162
7 1.871 2,22 2,26 2.33 2,40 2,49 3,143 3,222 3,282 ~ 3,338 3,369 3,465
8 1,871 2,31 2.35 2.43 2,50 2,59 3,308 3,399 3.471 3,543 3,585 3,742
9 1.897 2,39 2,44 2,51 2,59 2,68 3.449 3,552 3,634 3,720 3,772 4,000
10 1,897 2.46 2,51 2,59 2,67 2,76 3,57 3,685 3.777 3,875 3,935 4,243
11 1,915 2,53 2,58 2,66 2,74 2,84 3,68 3,80 3,903 4,012 4.079 4.472
12 1,915 2,59 2,64 2,72 2,80 2,90 3.78 3,91 4,02 4,134 4,208 4,690
13 1,927 2,64 2,70 2,78 2,86 2,96 3,87 4,00 4,12 4,244 4,325 4.899
14 1,927 2,70 2,75 2,83 2,92 3,02 3.95 4.09 4,21 4.34 4.431 5.099
15 1,936 2,74 2,80 2,88 2,97 3.07 4,02 4,17 4,29 4,44 4,53 5.292
16 1,936 2,79 2,84 2,93 3,01 3,12 4,09 4,24 4.37 4,52 4.62 5.477
17 1,944 2,83 2,88 2,97 3,06 3,17 4.15 4,31 4,44 4.60 4,70 5.657
18 1,944 2,87 2,92 3,01 3,10 3.21 4,21 4,37 4.51 4,67 4.78 5,831
19 1,949 2,90 2,96 3,05 3,14 3,25 4,27 4,43 4.57 4,74 4,85 6.000
20 1,949 2,94 2,99 3,09 3,18 3,29 4,32 4,49 4,63 4,80 4,91 6,164
25 1,961 3,09 3,15 3,24 3,34 3,45 4,53 4,71 4.87 5.06 5.19 6.93
30 1,966 3,21 3,27 3,37 3,47 3,59 4,70 4,89 - 5.06 5.26 5,40 7.62
35 1,972 3,32 3,38 3,48 3,58 3,70 4.84 5,04 5,21 5,42 5,57 8.25
40 1,975 3,41 3,47 3,57 3,67 3,79 4.96 5,16 5.34 5,56 5,71 8.83
45 1,978 3,49 3,55 3,66 3,75 3,88 5.06 5,26 5.45 5,67 5.83 9,38
50 1,980 3,56 3,62 3,73 3,83 3,95 5.14 5.35 5.54 5,77 5.93 9,90
55 1,982 3,62 3,69 3,80 3,90 4,02 5.22 5,43 5,63 5,86 6.02 10.39
'60 1,983 3,68 3,75 3,86 3,96 4,08 5.29 5,51 5.70 5,94 6,10 10.86
65 1,985 3,74 3,80 3,91 4,01 4,14 5,35 5,57 5,77 6,01 6,17 11.31
70 1,986 3,79 3,85 3,96 4,06 4,19 5.41 5,63 5,83 6,07 6.24 11.75
75 1,987 3,83 3,90 4,01 4,11 4,24 5,46 5,68 5,88 6,13 6.30 12.17
80 1,987 3,88 3,94 4,05 4,16 4,28 5,51 5,73 5,93 6,18 6.35 12.57
85 1,988 3,92 3,99 4,09 4,20 4,33 5.56 5,78 5.98 6.23 6,40 12,96
90 1,989 3,96 4,02 4,13 4,24 4,36 5.60 5,82 6,03 6,27 6,45 13.34
95 1,990 3,99 4,06 4,17 4,27 4,40 5,64 5,86 6.07 6,32 6.49 13.71
100 1,990 4,03 4,10 4,21 4,31 . 4,44 5,68 5,90 6.11 6,36 6.53 14.07
150 1,993 4,32 4,38 4,48 4,59 4,72 5,96 6,18 6,39 6,64 6,82 17.26
200 1,995 4,53 4,59 4,68 4,78 4,90 6,15 6,39 6.60 6.84 7.01 19.95
500 1,998 5,06 5,13 5,25 5,37 5,49 6,7 2 6,94 7.15 7.42 7.60 31.59
1000 1,999 5,50 5,57 5.68 5,79 5.92 7.11 7.33 7.54 7,80 7.99 44.70
* Таблица заимствована из [52], с, 299.
203
204
П.7. Ординаты стандартной нормальной кривой*
Z 0.00 0.01 0.02 0.03 0,04 0.05 0.06 0,07 0.08 0.09
0.0 0,3989 0.3989 0.3989 0,3988 0,3986 0,3984 0,3982 0,3080 0,3977 0.3973
0.1 0.3970 0,3965 0.3961 0,3956 0.3951 0.3945 0,3939 ' 0,3932 0.3925 0,3918
0,2 0,3910 0.3902 0,3894 0.3885 0.3876 0,3867 0.3857 0.3847 0.3836 0.3825
0.3 0.3814 0,3802 0,3790 0.3778 0.3765 0,3752 0.3739 0.3725 0.37 1 2 0.3697
0.4 0,3683 0.3668 0.3653 0,3637 0,3621 0.3605 0,3589 0.357 2 0.3555 0.35 3 8
0,5 0,3521 0.3503 0,3485 0.3467 0,3448 0,3429 0.3410 0.3391 0.3372 0.3352
0,6 0.3332 0,3312 0,3292 0,3271 0.3251 0.3230 0.3209 0.3187 0.3166 0.3144
0.7 0.3123 0,3101 0,3079 0.3056 0.3034 0.3011 0.2989 0.2966 0,2943 0.2920
0.8 0.2897 0,2874 0,2850 0.2827 0,2803 0.2780 0,2756 0.2732 0.2709 0.2685
0,9 0.2661 0,2637 0,2613 0.2589 0.2565 0,2541 0,2516 0,2492 0.2468 0.2444
1,0 0,2420 0,2396 0.2371 0,2347 0.2323 0.2299 0.2275 0,2251 0.2227 0,22г?
1,1 0,2179 0.2155 0.2131 0.2107 0.2083 0,2059 0.2036 0.2012 0.1989 0,1965
1.2 0.1942 0.1919 0.1895 0.1872 0.1849 0,1826 0.1 804 0.1781 0 1758 0.1736
1,3 0,1714 0,1691 0,1669 0.1647 0,1626 0.1604 0,1582 0,1561 0.1539 0.15 1 8
1.4 0,1497 0.1476 0.1456 0.1435 0.1415 0.1 394 0.1374 0.1 354 0.1334 0 1315
1.5 0,1295 0.1276 0.1257 0.1238 0.1219 0.1 200 0,1182 0.1 163 0.1145 O.IJ27
1,6 0,1 109 0,1092 0,1074 0.1057 0 1 040 0,1023 0.1006 0.0989 0.0973 0.0957
1,7 0,0940 0.0925 0,0909 0.0893 0.0878 0.0863 0.0848 0.0833 0.0818 О.0804
1,8 0,0790 0,0775 0.0761 0,0748 0.0734 0.0721 0,0707 0.0694 0.0681 0.0669
1.9 0,0656 0.0644 0.0632 0.0620 0,0608 0.0596 0.0584 0.0573 0.0562 0,0551
2.0 0.0540 0,0529 0,0519 0.0508 0.0498 0.0488 0,0478 1 0.0468 0.0459 0.044 9
2.1 0.0440 0,0431 0,0422 0.0413 0.0404 0,0396 0.0387 (1,0379 0.0371 0.036
2.2 0,0355 0,0347 0.0339 0.0332 0,0325 0.0317 0.0310 О.ОЗОЗ 0.0297 0.029.
2.3 0.0283 0.0277 0,0270 0,0264 0.0258 0.0252 0.0246 0.0241 0,0235 0.0229
2,4 0.0224 0,0219 0,0213 0.0208 0.0203 0.0198 0.0194 0.0189 0.0184 0.0180
2,5 0,0175 0,0171 0,0167 0,0163 0.0158 0.0154 0.0151 0.0147 0.0143 0.0139
2.6 0.0136 0,0132 0,0129 0.0126 0.0122 0.0119 0.01 16 0.0113 0.01 10 0.0107
2.7 0,0104 0,0101 0.0099 0,0096 0.0093 0.0091 0.0088 0.0086 0.0084 00081
2,8 0,0079 0,0077 0,0075 0,0073 0,0071 0,0069 0,0067 0,0065 0,0063 0,0061
2,9 0,0060 0,0058 0,0056 0,0055 0,0053 0,0051 0,0050 0,0048 0,0047 0,0046
3,0 0,0044 0,0043 0,0042 0,0040 0,0039 0,0038 0,0037 0,0036 0,0035 0,0034
зд 0,0033 0,0032 0,0031 0,0030 0,0029 0,0028 0,0027 0,0026 0,0025 0,0025
3,2 0,0024 0,0023 0,0022 0,0022 0,0021 0,0020 0,0020 0,0019 0,0018 0,0018
3,3 0,0017 0,0017 0,0016 0,0016 0,0015 0,0015 0,0014 0,0014 0,0013 0,0013
3,4 0,0012 0,0012 0,0012 0,0011 0,0011 0,0010 0,0010 0,0010 0,0009 0,0009
3,5 0,0009 0,0008 0,0008 0,0008 0,0008 0,0007 0,0007 0,0007 0,0007 0,0006
3,6 0,0006 0,0006 0,0006 0,0005 0,0005 0,0005 0,0005 0,0005 0,0005 0,0004
3,7 0,0004 0,0004 0,0004 0,0004 0,0004 0,0004 0,0003 0,0003 0,0003 0,0003
3,8 0,0001 0,0003 0,0003 0,0003 0,0003 0,0002 0,0002 0,0002 0,0002 0,0002
3,9 0,0002 0,0002 0,0002 0,0002 0,0002 0,0002 0,0002 0,0002 0,0001 0,0001
4,0 0,0001 0,0001 0,0001 0,0001 0,0001 0,0001 0,0001 0,0001 0,0001 0,0001
Z 0,00 0,01 0,02 0,03 0,04 0,05 0,06 0,07 0,08 0,09
* Таблица заимствована из [52], с. 82.
А
П.8. Процентные точки распределения х *
\Р-1 Л ^>4^ 99,95 % 99,9% 99,5% 99% 97,5% 95 % 90% 80% 70% 60% 50%
1 0,0393 0,0157 0,0393 0,0157 0,0982 0,0393 0,0158 0,0642 0,148 0,275 0,455
2 0,0100 0,0200 0,0100 0,0201 0,0506 0,103 0,211 0,446 0,713 Г,'022 1,386
3 0,0153 0,0243 0,0717 0,115 0,216 0,352 0,584 1,005 1,424 1,869 2,366
4 0,0639 0,0908 0,207 0,297 0,484 0,711 1,064 1,649 2,195 2,753 3,357
5 0,158 0,210 0,412 0,554 0,831 1,145 1,610 2,343 3,000 3,655 4,351
6 0,299 0,381 0,676 0,872 1,237 1,635 2,204 3,070 3,828 4,570 5,348
7 0,485 0,598 0,989 1,239 1,690 2,167 2,833 3,822 4,671 5,493 6,346
8 0,710 0,857 1,344 1,646 2,180 2,733 3,490 4,594 5,527 6,423 7,344
9 0,972 1,153 1,735 2,088 2,700 3,325 4,168 5,380 6,393 7,357 8,343
10 1,265 1,479 2,156 2,558 3,247 3,940 4,865 6,179 7,267 8,295 9,342
205
Продолжение табл. П.8
206
\р-1 99,95 % 99,9% 99,5% 99% 97,5% 95% 90% 80% 70% 60% 50%
н 1,587 1,834 2,603 3,053 3,816 4,575 5,578 6,989 8,148 9,237 10,341
12 1,934 2,214 3,074 3,571 4,404 5,226 6,304 7,807 9,034 10,182 11,340
13 2,305 2,617 3,565 4,107 5,009 5,892 7,042 8,634 9,926 11,129 12,340
14 2,697 3,041 4,075 4,660 5,629 6,571 7,790 9,467 10,821 12,079 13,339
15 3,108 3,483 4,601 5,229 6,262 7,261 8,547 10,307 11,721 13,030 14,339
16 3,536 3,942 5,142 5,812 6,908 7,962 9,312 11,152 12,624 13,983 15,338
17 3,980 4,416 5,697 6,408 7,564 8,672 10,085 12,002 13,531 14,937 16,338
18 4,439 4,905 6,265 7,015 8,231 9,390 10,865 12,857 14,440 15,893 17,338
19 4,912 5,407 6,844 7,633 8,907 10,117 11,651 13,716 15,352 16,850 18,338
20 5,398 5,921 7,434 8,260 9,591 10,851 12,443 14,578 16,266 17,809 19,337
21 5,896 6,447 8,034 8,897 10,283 11,591 13,240 15,445 17,182 18,768 20,337
22 6,404 6,983 8,643 9,542 10,982 12,338 14,041 16,314 18,101 19,729 21,337
23 6,924 7,529 9,260 10,196 11,688 13,091 14,848 17,187 19,021 20,690 22,337
24 7,453 8,085 9,886 10,856 12,401 13,848 15,659 18,062 19,943 21,652 23,337
25 7,991 8,649 10,520 11,524 13,120 14,611 16,473 18,940 20,867 22,616 24,337
26 8,538 9,222 11,160 12,198 13,844 15,379 17,292 19,820 21,792 23,579 25,336
27 9,093 9,803 11,808 12,879 14,573 16,151 18,114 20,703 22,719 24,544 26,336
28 9,656 10,391 12,461 13,565 15,308 16,928 18,939 21,588 23,647 25,509 27,336
29 10,227 10,986 13,121 14,256 16,047 17,708 19,768 22,475 24,577 26,475 28,336
30 10,804 11,588 13,787 14,953 16,791 18,493 20,599 23,364 25,508 27,442 29,336
31 11,389 12,196 14,458 15,655 17,539 19,281 21,434 24,255 26,440 28,409 30,336
32 11,979 12,811 15,134 16,362 18,291 20,072 22,271 25,148 27,373 29,376 31,336
33 12,576 13,431 15,815 17,073 19,047 20,867 23,110 26,042 28,307 30,344 32,336
34 13,179 14,057 16,501 17,789 19,806 21,664 23,952 26,938 29,242 31,313 33,336
35 13,788 14,688 17,192 18,509 20,569 22,465 24,797 27,836 30,178 32,282 34,336
36 14,401 15,324 17,887 19,233 21,336 23,269 25,643 28,735 31,115 33,252 35,336
37 15,020 15,965 18,586 19,960 22,106 24,075 26,492 29,635 32,053 34,222 36,336
38 15,644 16,611 19,289 20,691 22,878 24,884 27,343 30,537 32,992 35,192 37,335
39 16,273 17,262 19,996 21,426 23,654 25,695 28,196 31,441 33,932 36,163 38,335
40 16,906 17,916 20,707 22,164 24,453 26,509 29.051 32,345 34,872 37,134 35,335
Продолжение табл. П.8
40% 30% 20% 10% 5 % 2,5% 1% 0,5% 0,1 % 0,05%
0,708 1,074 1,642 2,706 3,841 5,024 6,635 7,879 10,828 12,116 1
1,833 2,408 3,219 4,605 5,991 7,378 9,210 10,597 13,816 15,202 2
2,946 3,665 4,642 6,251 7,815 9,348 11,345 12,838 16,266 17,730 3
4,045 4,878 5,989 7,779 9,488 11,143 13,277 14,860 18,467 19,997 4
5,132 6,064 7,289 9,236 11,070 12,832 15,086 16,750 20,515 22,105 5
6,211 7,231 8,558 10,645 12,592 14,449 16,812 18,548 22,458 24,103 6
7,283 8,383 9,803 12,017 14,067 16,013 18,475 20,278 24,322 26,018 7
8,351 9,524 11,030 13,362 15,507 17,535 20,090 21,955 26,125 27,868 8
9,414 10,656 12,242 14,684 16,919 19,023 21,666 23,589 27,877 29,666 9
10,473 11,781 13,442 15,987 18,307 20,483 23,209 25,188 29,588 31,420 10
11,530 12,899 14,631 17,275 19,675 21,920 24,725 26,757 31,264 33,136 11
12,584 14,011 15,812 18,549 21,026 23,336 26,217 28,300 32,909 34,821 12
13,636 15,119 16,985 19,812 22,362 24,736 27,688 29,819 34,528 36,478 13
14,685 16,222 18,151 21,064 23,685 26,119 29,141 31,319 36,123 38,109 14
15,733 17,322 19,311 22,307 24,996 27,488 30,578 32,801 37,697 39,719 15
16,780 18,418 20,465 23,542 26,296 28,845 32.000 34,267 39,252 41,308 16
17,824 19,511 21,615 24,769 27,587 30,191 33,409 35,718 40,790 42,879 17
18,868 20,601 22,760 25,989 28,869 31,526 34,805 37,156 42,312 44,434 18
19,910 21,689 23,900 27,204 30,144 32,852 36,191 38,582 43,820 45,973 19
20,951 22,775 25,038 28,412 31,410 34,170 37,566 39,997 45,315 47,498 20
21,991 23,858 26,171 29,615 32,671 35,479 38;932 41,401 46,797 49,610 21
23,031 24,939 27,301 30,813 33,924 36,781 40,289 42,796 48,268 50,511 22
24,069 26,018 28,429 32,007 35,172 38,076 41,638 44,181 49,728 52,000 23
26,106 27,096 29,553 33,196 36,415 39,364 42,980 45,558 51,179 53,479 24
26,143 28,172 30,675 34,382 37,652 40,646 44,314 46,928 52,620 54,947 25
о Продолжение табл. П.8
00 40% 30% 20% 10% 5 % 2,5% 1% 0,5% 0,1 % 0,05 %
27,179 29,246 31,795 35,563 38,885 41,923 45,642 48,290 54,052 56,407 26
28,214 30,319 32,912 36,741 40,113 43,194 46,963 49,645 55,476 57,858 27
29,249 31,391 34,027 37,916 41,337 44,461 48,278 50,993 56,892 59,300 28
30,283 32,461 35,139 39,087 42,557 45,722 49,588 52,336 58,301 60,735 29
31,316 33,530 36,250 40,256 43,773 46,979 50,892 53,672 59,703 62,162 30
32,349 34,598 37,359 41,422 44,985 48,232 52,191 55,003 61,098 63,582 31
33,381 35,665 38,466 42,585 46,194 49,480 53,486 56,328 62,487 64,995 32
34,413 36,731 39,572 43,745 47,400 50,725 54,776 57,648 63,870 66,402 33
35,444 37,795 40,676 44,903 48,602 51,966 56,061 58,964 65,247 67,803 34
36,475 38,859 41,778 46,059 49,802 53,203 57,342 60,275 66,619 69,199 35
37,505 39,922 42,879 47,212 50,998 54,437 58,619 61,581 67,985 70,588 36
38,535 40,984 43,978 48,363 52,192 55,668 59,892 62,882 69,346 71,972 37
39,564 42,045 45,076 49,513 53,384 56,895 61,162 64,181 70,703 73,351 38
40,593 43,105 46,173 50,660 54,572 58,120 62,428 65,476 72,055 74,725 39
41,622 44,165 47,269 51,805 55,758 59,342 62,691 66,766 73,402 76,095 40
* Таблица заимств овака из [17], с. 228.
П.9. Критические значения ЛГ-С-критерия
п D0,10 £*0,05 п £*0,10 £*0,05 п D0,10 £*0,05 п £*о,ю Do, 05 п Do, ю £*0,05 п £*о,ю Z>0,05
3 0,636 0,708 10 0,369 0,409 17 0,286 0,318 24 0,242 0,269 31 0,214 0,238 38 0,194 0,215
4 0,565 0,624 11 0,352 0,391 18 0,278 0,309 25 0,238 0.264 32 0,211 0,234 39 0,191 0,213
5 0,509 0,563 12 0,338 0,375 19 0,271 0,301 26 0,233 0,259 33 0,208 0,231 40 0,189 0,210
6 0,468 0,519 13 0,325 0,361 20 0,265 0,294 27 0,229 0,254 34 0,205 0,227 50 0,170 0,177
7 0,436 0,483 14 0,314 0,349 21 0,259 0,287 28 0,225 0,250 35 0,202 0,224 100 0,121 0,134
8 0,410 0,454 15 0,304 0,338 22 0,253 0,281 29 0,221 0,246 36 0,199 0,221
9 0,387 0,430 16 0,295 0,327 23 0,247 0,275 30 0,218 0,242 37- 0,196 0,218
* Таблица заимствована из [52], с. 302.
П.10. Проверка коэффициента корреляции на значимость относительно нуля*
Число степеней свободы (1) Двусторонний критерий Односторонний критерий
5% 1 % 0,1 % 5% 1 % 0,1 %
(2) (3) (4) (5) ‘ (6) (7)
1 0,9969 А* В* 0,9877 0,9995 С*
2 0,9500 0,9900 0,9990 0,9000 0,9800 0,9980
3 0,8783 0,9587 0,9911 0,805 0,934 0,986
4 0,811 0,917 0,974 0,729 0,882 0,963
5 0,754 0,875 0,951 0,669 0,833 0,935
6 0,707 0,834 0,925 0,621 0,789 0,905
7 0,666 0,798 0,898 0,582 0,750 0,875 .
8 0,632 0,765 0,872 0,549 0,715 0,847
9 0,602 0,735 0,847 0,521 0,685 0,820
10 0,576 0,708 0,823 0,497 0,658 0,795
11 0,553 0,684 0,801 0,476 0,634 0,772
12 0,532 0,661 0,780 0,457 0,612 0,750
13 0,514 0,641 0,760 0,441 0,592 0,730
14 0,497 0,623 0,742 0,426 0,574 0,711
15 0,482 0,606 0,725 0,412 0,558 0,694
16 0,468 0,590 0,708 0,400 0,543 0,678
17 0,456 0,575 0,693 0,389 0,529 0,662
18 0,444 0,561 0,679 0,378 0,516 0,648
19 0,433 0,549 0,665 0,369 0,503 0,635
20 0,423 0,537 0,652 0,360 0,492 0,622
21 0,413 0,526 0,640 0,352 0,482 0,610
22 0,404 0,515 0,629 0,344 0,472 0,599
23 0,396 0,505 0,618 0,337 0,462 0,588
24 0,388 0,496 0,607 0,330 0,453 0,578
25 0,381 0,487 0,597 0,323 0,445 0,568
26 0,374 0,478 0,588 0,317 0,437 0,559
27 0,367 0,470 0,579 0,311 0,430 0,550
28 0,361 0,463 0,570 0,306 0,423 0,541
29 0,355 0,456 0,562 0,301 0,416 0,533
30 0,349 0,449 0,554 0,296 0,409 0,526
35 0,325 9,418 0,519 0,275 0,381 0,492
40 0,304 0,393 0,490 0,257 0,358 0,463
50 0,273 0,354 0,443 ’ 0,231 0,322 0,419
60 0,250 0,325 0,408 0,211 0,295 0,385
70 0,232 0,302 0,380 0,195 0,274 0,358
80 0,217 0,283 0,357 0,183 0,257 0,336
90 0,205 0,267 0,338 0,173 0,242 0,318
100 0,195 0,254 0,321 0,164 0,230 0,302
120 0,178 0,232 0,294 0,150 0,210 0,277
150 0,159 0,208 0,263 0,134 0,189 0,249
200 0,138 0,181 0,230 0,116 0,164 0,216
250 0,124 0,162 0,206 0,104 0,146 0,194
300 0,113 0,148 0,188 0,095 0,134 0,177
350 0,105 0,137 0,175 0,0878 0,124 0,164
400 0,0978 0,128 0,164 * Таблица заимствована из [52] , с. 392. 8-579 0,0822 0,116 0,154 209
Продолжение табл. П.10.
(1) (2) (3) (4) (5) (6) (7)
500 0,0875 0,115 0,146 0,0735 0,104 0,138
700 0,0740 0,0972 0,124 0,0621 0,0878 0,216
1000 0,0619 0,0813 0,104 0,0520 0,0735 0,0975
1500 0,0505 0,0664 0,0847 0,0424 0,0600 0,0795
2000 0,0438 0,0575 0,0734 0,0368 0,0519 0,0689
А* = 0,999877, В* = 0,99999877, С* = 0,9999951.
ПЛ 1. Процентные точки F-распределения Фишер», р = 10 %*
v2 \ 1 2 3 4 5 6 7 8 9
1 39,846 49,500 53,593 55,833 57,241 58,204 58,906 59,439 59,858
2 8,5263 9,0000 9,1618 9,2434 9,2926 9,3255 9,3491 9,3668 9,3805
3 5,5383 5,4624 5,3908 5,3427 5,3092 5,2847 5,2662 5,2517 5,2400
4 4,5448 4,3246 4,1908 4,1073 4,0506 4,0098 3,9790 3,9549 3,9357
5 4,0604 3,7797 3,6195 3,5202 3,4530 3,4045 3,3679 3,3393 3,3163
6 3,7760 3,4633 3,2888 3,1808 3,1075 3,0546 2,0145 3,9830 2,9577
7 3,5894 3,2574 3,0741 2,9605 2,8833 2,8274 2,7849 2,7516 2,7247
8 3,4579 3,1131 2,9238 2,8064 2,7265 2,6683 2,6241 2,5893 2,5612
9 3,3603 3,0065 2,8129 2,6927 2,6106 2,5509 2,5053 2,4694 2,4403
10 3,2850 2,9345 2,7277 2,6053 2,5216 2,4606 2,4140 2,3772 2,3473
11 3,2252 2,8595 2,6602 2,5362 2,4512 2,3891 2,3416 2,3040 2,2735
12 2,1765 2,8068 2,6055 2,4801 2,3940 2,3310 2,2828 2,2446 2,2135
13 3,1362 2,7632 2,5603 2,4337 2,3467 2,3830 2,2341 2,1953 2,1638
14 3,1022 2,7275 2,5222 2,3947 2,3069 2,2426 2,1931 2,1539 2,1220
15 3,0732 2,6952 2,4898 2,3614 2,2730 2,2081 2,1582 2,1185 2,0862
16 3,0481 2,6682 2,4618 2,3327 2,2438 2,7849 2,1280 2,0880 2,0553
17 3,0262 2,6446 2,4374 2,3077 2,2183 2,1524 2,1017 2,0613 2,0284
18 3,0070 2,6239 2,4160 2,2858 2,1958 2,1296 2,0785 2,0379 2,0047
19 2,9899 2,6055 8,3970 2,2663 2,1760 2,1094 2,0580 2,0171 1,9836
20 2,9747 2,5893 2,3801 2,2489 2,1582 2,0913 2,0397 1,9985 1,9649
21 2,9609 2,5746 2,3649 2,2333 2,1423 2,0751 2,0232 1,9819 1,9480
22 2,9486 2,5613 2,3512 2,2193 2,1279 2,0605 2,0084 1,9668 1,9327
23 2,9374 2,5493 2,3387 2,2065 2,1149 2,0472 1,9949 1,9531 1,9189
24 2,9271 2,5383 2,3274 2,1949 2,1030 2,0351 1,9826 1,9407 1,9063
25 2,9177 2,5283 2,3170 2,1843 2,0922 2,0241 1,9714 1,9292 1,8947
26 2,9091 2,5191 2,3075 2,1745 2,0822 2,0139 1,9640 1,9188 1,8841
27 2,9012 2,5106 2,2987 2,1655 2,0730 2,0045 1,9515 1,9091 1,8743
28 2,8939 2,5028 2,2906 2,1571 2,0645 1,9959 1,9427 1,9001 1,8652
29 2,8871 2,4950 2,2831 2,1494 2,0566 1,9878 1,9345 1,8918 1,8568
30 2,8807 2,4887 2,2761 2,1422 2,0492 1,9803 1,9269 1,8841 1,8490
40 2,8354 2,4404 2,2261 2,0909 1,9968 1,9269 1,8725 1,8289 1,7929
60 2,7914 2,3933 2,1774 2,0410 1,9457 1,8747 1,8194 1,7748 1,7380
120 2,7478 2,3473 2,1300 1,9923 1,8959 1,8238 1,7675 1,7220 1,6843
оо 2,7055 2,3026 2,0838 1,9449 1,8473 1,7741 1,7167 1,6702 1,6315
♦Таблица заимствована из (17], с. 272.
210
10 12 15 20 24 30 40 60 120 оо
60,195 60,705 61,220 61,740 62,002 62,265 62,529 62,794 63,061 63,328
9,3916 9,4081 9,4247 9,4413 9,4496 9,4579 9,4663 9,4746 9,4829 9,4913
5,2304 5,2156 5,2003 5,1845 5,1764 5,1681 5,1597 5,1512 5,1425 5,1337
3,9199 3,8955 3,8703 3,8443 3,8310 3,8174 3,8036 3,7896 3,7753 3,7607
3,2974 3,2682 3,2380 3,2067 3,1905 3,1741 2,1573 3,1402 3,1228 3,1050
2,93б9 2,9047 2,8712 2,8363 2,8183 2,8000 2,7812 2,7620 2,7423 2,7222
2,7025 2,6681 2,6322 2,2547 2,5753 2,5555 2,5351 2,5142 2,4928 2,4708
2,5380 2,5020 2,4642 2,4246 2,4041 2,3830 2,3614 2,3391 2,3162 2,2926
2,4163 2,3789 2,3396 2,2983 2,2768 1,2547 2,2320 2,2085 2,1843 2,1592
2,3226 2,2841 2,2435 2,2007 2,1784 2,1554 2,1317 2,1072 2,0818 2,0554
2,24 82 2,2087 2,1671 2,1230 2,1000 2,0762 2,0516 2,0261 1,9997 1,9721
2,1878 2,1474 2,1049 2,0597 2,0360 2,0115 1,9861 1,9597 1,9323 1,9036
2,1376 2,0966 2,0532 2,0070 1,9827 1,9576 1,9315 1,9043 1,8759 1,8462
2,0954 2,0537 2,0095 1,9625 1,9377 1,9119 1,8852 1,8572 1,8230 1,7973
2,0593 2,0171 1,9722 1,9243 1,8990 1,8728 1,8454 1,8168 1,7867 1,7551
2,0281 1,9854 1,9399 1,8913 1,8656 1,8388 1,8108 1,7816 1,7507 1,7182
2,0009 1,9577 1,9117 1,8624 1,8362 1,8090 1,7805 1,7506 1,7191 1,6856
1,9770 1,9333 1,8868 1,8368 1,8103 1,7827 1,7537 1,7232 1,6910 1,6567
1,9557 1,9117 1,8647 1,8142 1,7873 1,7592 1,7298 1,6988 1,6659 1,6308
1,9367 1,8924 1,8449 1,7938 1,7667 1,7382 1,7083 1,6768 1,6433 1,6074
1,9197 1,8750 1,8272 1,7756 1,7481 1,7193 1,6890 1,6569 1,6228 1,5862
1,9043 1,8593 1,8111 1,7590 1,7312 1,7021 1,6714 1,6389 1,6042 1,5668
1,8903 1,8450 1,7964 1,7439 1,7159 1,6964 1,6554 1,6224 1,5871 1,5490
1,8775 1,8319 1,7831 1,7302 1,7019 1,6701 1,6407 1,6073 1,5715 1,5327
1,8658 1,8200 1,7708 1,7175 1,6890 1,6589 1,6272 1,5934 1,5570 1,5176
1,8550 1,8090 1,7596 1,7059 1,6771 1,6468 1,6147 1,5805 1,5437 1,5036
1,8451 1,7989 1,7492 1,6951 1,6662 1,6356 1,6032 1,5686 1,5313 1,4906
1,8359 1,7895 1,7395 1,6852 1,6560 1,6252 1,5925 1,5575 1,5198 1,4784
1,8274 1,7808 1,7306 1,6759 1,6465 1,6155 1,5855 1,5472 1,5090 1,4670
1,8195 1,7727 1,7223 1,6673 1,6377 1,6065 1,5732 1,5376 1,4989 1,4564
1,7627 1,7146 1,6624 1,6052 1,5741 1,5411 1,5056 1,4672 1,4248 1,3769
1,7070 1,6574 1,6034 1,5435 1,5107 1,4755 1,4373 1,3952 1,3476 1,2915
1,6524 1,6012 1,5450 1,4821 1,4472 1,4094 1,3676 1,3203 1,2646 1,1926
1,5987 1,5458 1,4871 1,4206 1,3832 1,3419 1,2951 1,2400 1,1686 1,1000
211
Процентные точки ^’-распределения Фишера, р =5 %
v2 \ 1 2 3 4 5 6 7 8 9
1 161,45 199,50 215,71 224,58 230,16 233,99 236,77 238,88 140,54
2 18,513 19,000 19,164 19,247 19,296 19,330 19,353 19,371 19,385
3 10,128 9,5521 9,2766 9,1172 9,0135 8,9406 8,8868 8,8452 8,8123
4 7,7086 6,9443 6,5914 6,3883 6,2560 6,1631 6,0942 6,0410 5,9988
5 6,6079 5,7861 5,4095 5,1922 5,0503 4,9503 4,8759 4,8183 4,7725
6 5,9874 5,1433 4,7571 4,5337 4,3874 4,2839 4,2066 4,1468 4,0990
7 5,5914 4,7374 4,3468 4,1203 3,9715 3,8660 3,7870 3,7257 3,6767
8 5,3177 4,4590 4,0662 3,8378 3,6875 3,5806 3,5005 3,4381 3,3881
9 5,1174 4,2565 3,8626 3,6331 3,4817 3,3738 3,2927 3,2296 3,1789
10 4,9646 4,1028 3,7083 3,4780 3,3258 3,2172 3,1355 3,0717 3,0204
11 4,8443 3,9823 3,5874 3,3567 3,2039 2,0946 3,0123 2,9480 2,8962
12 4,7472 3,8853 3,4903 3,2592 3,1059 2,9961 2,9134 2,8486 2,7964
13 4,6672 3,8056 3,4105 3,1791 3,0254 2,9153 2,8321 2,7669 2,7144
14 4,6001 3,7389 3,3439 3,1122 2,9582 2,8477 2,7642 2,6987 2,6458
15 4,5431 3,6823 3,2974 3,0556 2,9013 2,7905 2,7066 2,6408 2,5876
16 4,4940 3,6337 3,2389 3,0069 2,8524 2,7413 2,6572 2,5911 2,5377
17 4,4513 3,5915 3,1968 2,9647 2,8100 2,6987 2,6143 2,5480 2,4943
18 4,4139 3,5546 3,1599 2,9277 2,7729 2,6613 2,5767 2,5102 2,4563
19 4,3808 3,5219 3,1274 2,8951 2,7401 2,6283 2,5435 2,4768 2,4227
20 4,3513 3,4928 3,0984 2,8661 2,7109 2,5990 2,5140 2,4471 2,3928
21 4,3248 3,4668 3,0725 2,8401 2,6848 2,5727 2,4876 2,4205 2,3661
22 4,3009 3,4434 3,0491 2,8167 2,6613 2,5491 2,4638 2,3965 2,3419
23 4,2793 3,4221 3,0280 2,7955 2,6400 2,5277 2,4422 2,3748 2,3201
24 4,2597 3,4028 3,0088 2,7763 2,6207 2,5082 2,4226 2,3551 2,3002
25 4,2417 3,3852 2,9912 2,7587 2,6030 2,4904 2,4047 2,3371 2,2821
26 4,2252 3,3690 3,9751 2,7426 2,5868 2,4741 2,3883 2,3205 2,2655
27 4,2100 3,3541 2,9604 2,7278 2,5719 2,4591 2,3732 2,3053 2,2501
28 4,1960 3,3404 2,9467 2,7141 2,5581 2,4453 2,3593 2,2913 2,2360
29 4,1830 3,3277 2,9340 2,7014 2,5454 2,4324 2,3463 2,2782 2,2229
30 4,1709 3,3158 2,9223 2,6896 2,5336 2,4205 2,3343 2,2662 2,2107
40 4,0848 3,2317 2,8387 2,6060 2,4495 2,3359 2,2490 2,1802 2,1240
60 4,0012 3,1504 2,7581 2,5252 2,3683 2,2540 2,1665 2,0970 2,0401
120 3,9201 3,0718 2,6802 2,4472 2,2900 2,1750 2,0867 2,0164 1,9588
©О 3,8415 2,9957 2,6049 2,3719 2,2141 2,0986 2,0096 1,9384 1,8799
212
10 12 15 20 24 30 40 60 120 оо
241,88 243,91 245,95 248,01 249,05 250,09 251,14 252,20 253,25 254,32
19,396 19,413 19,429 19,446 19,454 19,462 19,471 19,479 19,487 19,496
8,7855 8,7446 8,7029 8,6602 8,6385 8,6166 8,5944 8,5720 8,5494 8,5265
5,9644 5,9117 5,8578 5,8025 5,7744 5,7459 5,71.70 5,6870 5,6581 5,6281
4,7351 4,6777 4,6188 4,5581 4,5272 4,4957 4,4638 4,4314 4,3984 4,3650
4,0600 3,9999 3,9381 3,8742 3,8415 3,8082 3,7743 3,7398 3,7047 3,6688
3,6365 3,5747 3,5108 3,4445 3,4105 3,3758 3,3404 3,3043 3,2674 3,2298
3,3472 3,2840 3,2184 3,1503 3,1152 3,0794 3,0428 3,0053 2,9669 2,9276
3,1373 3,0729 3,0061 2,9365 2,9005 2,8637 2,8259 2,7872 2,7475 2,7067
2,9782 2,9130 2,8450 2,7740 2,7372 2,6996 2,6609 2,6211 2,5801 2,5379
2,8536 2,7876 2,7186 2,6464 2,6090 2,5705 2,5309 2,4901 2,4480 2,4045
2,7534 2,6866 2,6169 2,5436 2,5055 2,4663 2,4259 2,3842 2,3410 2,2962
2,6710 2,6037 2,5331 2,4589 2,4202 2,3803 2,3392 2,2966 2,2524 2,2064
2,6021 2,5342 2,4630 2,3879 2,3487 2,3082 2,2664 2,2230 2,1778 2,1307
2,5437 2,4753 2,4035 2,3275 2,2878 2,246 8 2,2043 2,1601 2,1141 2,0658
2,4935 2,4247 2,3522 2,2756 2,2354 2,1938 2,1507 2,1058 2,0589 2,0096
2,4499 2,3807 2,3977 2,2304 2,1898 2,1477 2,1040 2,0584 2,0107 1,9604
2,4117 2,3421 2,2686 2,1906 2,1497 2,1071 2,0629 2,0166 1,9681 1,9168
2,3779 2,3080 2,2341 2,1555 2,1141 2,0712 2,0264 1,9796 1,9302 1,8780
2,3479 2,2776 2,2033 2,1242 2,0825 2,0391 1,9938 1,9464 1,8961 1,8432
2,3210 2,2504 2,1757 2,0960 2,0540 2,0102 1,9645 1,9165 1,8657 1,8117
2,2967 2,2258 2,1508 2,0707 2,0283 1,9842 1,9380 1,8895 1,8380 1,7831
2,2747 2,2036 2,1282 2,0476 2,0050 1,9605 1,9139 1,8649 1,8128 1,7570
2,2547 2,1834 2,1077 2,0267 1,9838 1,9390 1,8920 1,8424 1,7897 1,7331
2,2365 2,1649 2,0889 2,0075 1,9643 1,9192 1,8778 1,8217 1,7684 1,7110
2,2197 2,1479 2,0716 1,9898 1,9464 1,9010 1,8533 1,8027 1.7488 1,6906
2,2043 2,1323 2,0558 1,9736 1,9299 1,8842 1,8361 1,7851 1,7307 1,6717
2,1900 2,1179 2,0411 1,9586 1,9147 1,8687 1,8203 1,7689 1,7138 1,6541
2,1768 2,1045 2,0275 1,9446 1,9005 1,8543 1,8055 1,7537 1,6981 1,6377
2,1646 2,0921 2,0148 1,9317 1,8874 1,8409 1,7918 1,7396 1,6835 1,6223
2,0772 2,0035 1,9245 1,8389 1,7929 1,7444 1,6928 1,6373 1,5766 1,5089
1,9926 1,9174 1,8364 1,7480 1,7001 1,6491 1,5943 1,5343 1,4673 1,3893
1,9105 1,8337 1,7505 1,6587 1,6084 1,5543 1,4952 1,4290 1,3519 1,2539
1,8307 1,7522 1,6664 1,5705 1,5173 1,4591 1,3940 1,3180 1,2214 1,0000
213
Процентные точки F-распределения Фишера, р — 2,5 %
1 2 3 4 5 6 7 8 9
1 647,79 799,50 864,16 899,58 921,85 937,11 948,22 956,66 963,28
2 38,506 39,000 39,165 39,248 39,298 39,331 39,355 39,373 39,387
3 17,443 16,044 15,439 15,101 14,885 14,735 14,624 14,540 14,473
4 12,218 10,649 9,9792 9,6045 9,3645 9,1973 9,0741 8,9796 8,9047
5 10,007 8,4336 7,7636 7,3879 7,1464 6,9777 6,8531 6,7572 6,6810
6 8,8131 7,2598 6,5988 6,2272 5,9876 5,8197 5,6955 5,5996 5,5234
7 8,0727 6,5415 5,8898 5,5226 5,2852 5,1186 4,9949 4,8994 4,8232
8 7,5709 6,0595 5,4160 5,0526 4,8173 4,6517 4,5286 4,4332 4,3572
9 7,2093 5,7147 5,0781 4,7181 4,4844 4,3197 4,1971 4,1020 4,0260
10 6,9367 5,4564 4,8256 4,4683 4,2361 4,0721 3,9498 3,8549 3,7790
11 6,7241 5,2559 4,6300 4,2751 4,0440 3,8807 3,7586 3,6638 3,5879
12 6,5538 5,0959 4,4742 4,1212 3,8911 3,7283 3,6065 3,5118 3,4358
13 6,4143 4,9653 4,3472 3,9959 3,7667 3,6043 3,4827 3,3880 3,3120
14 6,2979 4,8567 4,2417 3,8919 3,6634 3,5014 3,3799 3,2853 3,2093
15 6,1995 4,7650 4,1528 3,8043 3,5764 3,4147 3,2934 3,1987 3,1227
16 6,1151 4,6867 4,0768 3,7294 3,5021 3,3406 3,2194 3,1248 3,0488
17 6,0420 4,6189 4,0112 3,6648 3,4379 3,2767 3,1556 3,0610 2,9849
18 5,9781 4,5597 3,9593 3,6083 3,3820 3,2209 3,0999 3,0053 2,9291
19 5,9216 4,5075 3,9034 3,5587 3,3327 3,1718 3,0509 2,9563 2,8800
20 5,8715 4,4613 3,8587 3,5147 3,2891 3,1283 3,0074 2,9128 2,8365
21 5,8266 4,4199 3,8188 3,4754 3,2501 3,0895 2,9686 2,8740 2,7977
22 5,7863 4,3828 3,7829 3,4401 3,2151 3,0546 2,9338 2,8392 2,7628
23 5,7498 4,3492 3,7505 3,4083 3,1835 3,0232 2,9024 2,8077 2,7313
24 5,7167 4,3187 3,7211 3,3794 3,1548 2,9946 2,8738 2,7791 2,7027
25 5,6864 4,2909 3,6943 3,3530 3,1287 2,9685 2,8478 2,7531 2,6766
26 5,6586 4,2655 3,6697 3,3289 3,1048 2,9447 2,8240 2,7293 2,6528
27 5,6331 4,2421 3,6472 3,3067 3,0828 2,9228 2,8021 2,7074 2,6309
28 5,6096 4,2205 3,6264 3,2863 3,0625 2,9027 2,7820 2,6872 2,6106
29 5,5878 4,2006 3,6072 3,2674 3,0438 2,8840 2,7633 2,6686 2,5919
30 5,5675 4,1821 3,5894 3,2499 3,0265 2,8667 2,7460 2,6513 2,5746
40 5,4239 4,0510 3,4633 3,1261 2,9037 2,7444 2,6238 2,5289 2,4519
60 5,2857 3,9253 3,3425 3,0077 2,7853 2,6274 2,5068 2,4117 2,3344
120 5,1525 3,8046 3,2270 2,8943 2,6740 2,5154 2,3948 2,2994 2,2217
оо 5,0239 3,6869 3,1161 2,7858 2,5665 2,4082 2,2875 2,1918 2,1136
214
10 12 15 20 24 30 40 60 120 oo
968,63 976,71 984,87 993,10 997,25 1001,4 1005,6 1009,8 1014,0 1018,3
39,398 39,415 39,431 39,448 39,456 39,465 39Д73 39,481 39,490 39,498
14,419 14,337 14,253 14,167 14,124 14,081 14,037 13,992 13,947 13,902
8,8439 8,7512 8,6565 8,5599 8,5109 8,4613 8,4111 8,3604 8,3092 8,2573
6,6192 6,5246 6,4227 6,3285 6,2780 6,2269 6,1751 6,1225 6,0693 6,0153
5,4613 5,3662 5,2687 5,1684 5,1172 5,0652 5,0125 4,9589 4,9045 4,8491
4,7611 4,6658 4,5678 4,4667 4,4150 4,3624 4,3089 4,2544 4,1989 4,1423
4,2951 4,1997 4,1012 3,9995 3,9472 3,8940 3,8398 3,7844 3,7279 3,6702
3,9639 3,8682 3,7694 3,6669 3,6142 3,5604 3,5055 3,4493 3,3918 3,3329
3,7168 3,6209 3,5217 3,4186 3,3654 3,3110 3,2554 3,1984 3,1399 3,0798
3,5257 3,4296 3,3299 3,2261 3,1725 3,1176 3,0613 3,0035 2,9441 2,8828
3,3736 3,2773 3,1772 3,0728 3,0187 2,9633 2,9063 2,8478 2,7874 2,7249
3,2497 3,1532 3,0527 2,9477 2,8932 2,8373 2,7797 2,7204 2,6590 2,^955
3,1469 3,0501 2,9493 2,8437 2,7888 2,7324 2,6742 2,6142 2,5519 2,4872
3,0602 2,9633 2,8621 2,7559 2,7006 2,6437 2,5850 2,5242 2,4611 2,3953
2,9862 2,8890 2,7875 2,6808 2,6252 2,5678 2,5085 2,4471 2,3831 2,3163
2,9222 2,8249 2,7230 2,6158 2,5598 2,5021 2,4422 2,3801 2,3153 2,2474
2,8664 2,7689 2,6667 2,5590 2,5027 2,4445 2,3842 2,3214 2,2558 2,1869
2,8173 2,7196 2,6171 2,5089 2,4523 2,3937 2,3329 2,1695 2,2032 2,1333
2,7737 2,6758 2,5731 2,4645 2,4076 2,3486 2,2873 2,2234 2,1562 2,0853
2,7348 2,6368 2,5338 2,4247 2,3675 2,3082 2,2465 2,1819 2,1141 2,0422
2,6998 2,6017 2,4984 2,3890 2,3315 2,2718 2,2097 2,1446 2,0760 2,0032
2,6682 2,5699 2,4665 2,3567 2,2989 2,2389 2,1763 2,1107 2,0415 1,9677
2,6396 2,5412 2,4374 2,3273 2,2693 2,2090 2,1460 2,0799 2,0099 1,9353
2,6135 2,5149 2,4110 2,3005 2,2422 2,1816 2,1183 2,0517 1,9811 1,9055
2,5895 2,4909 2,3867 2,2759 2,2174 2,1565 2,0928 2r0257 1,9545 1,8781
2,5676 2,4688 2,3644 2,2533 2,1946 2,1334 2,0693 2,0018 1,9299 1,8527
2,5473 2,4484 2,3438 2,2324 2,1735 2,1121 2,0477 1,9^96 1,9072 1,8291
2,5286 2,4295 2,3248 2,2131 2,1540 2,0923 2,0276 1,9591 1,8861 1,8072
2,5112 2,4120 2,3072 2,1952 2,1359 2,0739 2,0089 1,9400 1,8664 1,7867
2,3882 2,2882 2,1819 2,0677 2,0069 1,9429 1,8752 1,8028 1,7242 1,6371
2,2702 2,1692 2,0613 1,9445 1,8817 1,8152 1,7440 1,6668 1,5810 1,4822
2,1570 2,0548 1,9450 1,8249 1,7597 1,6899 1,6141 1,5299 1,4327 1,3104
2,0843 1,9447 1,8326 1,7085 1,6402 1,5660 1,4835 1,3883 1,2684 1,0000
215
Процентные точки F-распределения Фишера, р = 1 %
Е2_ 1 2 3 4 5 6 7 8 9
1 4052,2 4999,5 5403,3 5624,6 5763,7 5859,0 5928,3 5981,1 6022,5
2 98,503 99,000 99,166 99,249 99,299 99,332 99,356 99,374 99,388
3 34,116 30,817 29,457 28,457 28,237 27,911 27,672 27,489 27,345
4 21,198 18,000 16,694 15,977 15,522 15,207 14,976 14,799 14,659
5 16,258 13,274 12,060 11,392 10,967 10,672 10,456 10,289 10,158
6 13,745 10,925 9,7795 9,1483 8,7459 8,4661 8,2600 8,1016 7,9761
7 12,246 9,5466 8,4513 7,8467 7,4604 7,1914 6,9928 6,8401 6,7188
8 11,259 8,6491 7,5910 7,0060 6,6318 6,3707 6,1776 6,0289 5,9106
9 10,561 8,0215 6,9919 6,4221 6,0569 5,8018 5,6129 5,4671 5,3511
10 10,044 7,5594 6,5523 5,9943 5,6363 5,3858 5,2001 5,0567 4,9424
11 9,6460 7,2057 6,2167 5,6683 5,3160 5,0692 4,8861 4,7445 4,6315
12 9,3302 6,9266 5,9526 5,4119 5,0643 4,8206 4,6395 4,4994 4,3875
13 9,0738 6,7010 5,7394 5,2053 4,8616 4,6204 4,4410 4,3021 4,1911
14 8,8616 6,5149 5,5639 5,0354 4,6950 4,4558 4,2779 4,1399 4,0297
15 8,6831 6,3589 5,4170 4,8932 4,5556 4,3183 4,1415 4,0045 3,8948
16 8,5310 6,2262 5,2922 4,7726 4,4374 4,2016 4,0259 3,8896 3,7804
17 8,3997 6,1121 5,1850 4,6690 4,3359 4,1015 3,9267 3,7910 3,6822
18 8,2854 6,0129 5,0919 4,5790 4,2479 4,0146 3,8406 3,7054 3,5971
19 8,1850 5,9259 5,0103 4,5003 4,1708 3,9386 3,7653 3,6305 3,5225
20 8,0960 5,8489 4,9382 4,4307 4,1027 3,8714 3,6987 3,5644 3,4567
21 8,0166 5,7804 4,8740 4,3688 4,0421 3,8117 3,6396 3,5056 3,3981
22 7,9454 5,7190 4,8166 4,3134 3,9880 3,7583 3,5867 3,4530 3,3458
23 7,8811 5,6637 4,7649 4,2635 3,9392 3,7102 3,5390 3,4057 3,2986
24 7,8229 5,6136 4,7181 4,2184 3,8951 3,6667 3,4959 3,3629 3,2560
25 7,7698 5,5680 4,6755 4,1774 3,8550 3,6272 3,4568 3,3239 3,2172
26 7,7213 5,5263 4,6366 4,1400 3,8183 3,5911 3,4210 3,2884 3,1818
27 7,6767 5,4881 4,6009 4,1056 3,7848 3,5580 3,3882 3,2558 3,1494
28 7,6356 5,4529 4,5681 4,0740 3,7539 3,5276 3,3581 3,2259 3,1195
29 7,5976 5,4205 4,5378 4,0449 3,7254 3,4995 3,3302 3,1982 3,0920
30 7,5625 5,3903 4,5097 4,0179 3,6990 3,4735 3,3045 3,1726 3,0665
40 7,3141 5,1785 4,3126 3,8283 3,5138 3,2910 3,1238 2,9930 2,8876
60 7,0771 4,9774 4,1259 3,6491 3,3389 3,1187 2,9530 2,8233 2,7185
120 6,8510 4,7865 3,9491 3,4796 3,1735 2,9559 2,7918 2,6629 2,5586
оо 6,6349 4,6052 3,7816 3,3192 3,0173 2,8020 2,6393 2,5113 2,4073
216
10 12 15 20 24 30 40 60 120 оо
6055,8 6106,3 6157,3 6208,7 6234,6 6260,7 6286,8 6313,0 6339,4 6366,0
99,399 99,416 99,432 99,449 99,458 99,466 99,474. 99,483 99,491 99,499
27,229 27,052 26,872 26,690 26,598 26,505 26,411 26,316 26,221 26,125
14,546 14,374 14,198 14,020 13,929 13,838 13,746 13,652 13,558 13,463
10,051 9,8883 9,7222 9,5527 9,4665 9,3793 9,2912 9,2020 9,1118 9,0204
7,8741 7,7183 7,5590 7,3958 7,3127 7,2285 7,1432 7,0568 6,9690 6,8801
6,6201 6,4691 6,3143 6,1554 6,0743 5,9921 5,9084 5,8236 5,7372 5,6495
5,8143 5,6668 5,5151 5,3591 5,2793 5,1981 5,1156 5,0316 4,9460 4,8588
5,2565 5,1114 4,9621 4,8080 4,7290 4,6486 4,5667 4,4831 4,3978 4,3105
4,8492 4,7059 4,5582 4,4054 4,3269 4,2469 4,1653 4,0819 3,9965 3,9090
4,5393 4,3974 4,2509 4,0990 4,0209 3,9411 3,8596 3,7761 3,6904 3,6025
4,2961 4,1553 4,0096 3,8584 3,7805 3,7008 3,6192 3,5355 3,4494 3,3608
4,1003 3,9603 3,8154 3,6646 3,5868 3,5070 3,4253 3,3413 3,2548 3,1654
3,9394 3,8001 3,6557 3,5052 3,4274 3,3476 3,2656 3,1813 3,0942 3,0040
3,8049 3,6662 3,5222 3,3719 3,2940 3,2141 3,1319 3,0471 2,9595 2,8684
3,6909 3,5527 3,4089 3,2588 3,1808 3,1007 3,0182 2,9330 2,8447 2,7528
3,5931 3,4552 3,3117 3,1615 3,0835 3,0032 2,9205 2,8348 2,7459 2,6530
3,5082 3,3706 3,3373 3,0771 2,9990 2,9185 2,8354 2,7493 2,6597 2,5660
3,4338 3,2965 3,1533 3,0031 2,9249 2,8442 2,7608 2,6742 2,5839 2,4893
3,3682 3,2311 3,0880 2,9377 2,8594 2,7785 2,6947 2,6077 2,5168 2,4212
3,3098 3,1729 3,0299 2,8796 2,8011 2,7200 2,6359 2,5484 2,4568 2,3603
3,2576 3,1209 2,9780 2,8444 2,7488 2,6675 2,5831 2,4951 2,4029 2,3055
3,2106 3,0740 2,9311 2,7805 2,7017 2,6206 2,5355 2,4471 2,3542 2,2559
3,1681 3,0316 2,8887 2,7380 2,6591 2,5773 2,4923 2,4035 2,3099 2,2107
3,1294 2,9931 2,8502 2,6993 2,6203 2,5383 2,4530 2,3637 2,2695 2,1694
3,0941 2,9579 2,8150 2,6640 ‘ 2,5848 2,5026 2,4170 2,3273 2,2325 2,1315
3,0618 2,9256 2,7827 2,6316 2,5522 2,4699 2,3840 2,2938 2,1984 2,0965
3,0320 2,8959 2,7530 2,6017 2,5223 2,4397 2,3535 2,2629 2,1670 2,0642
3,0045 2,8685 2,7256 2,5742 2,4946 2,4118 2,3253 2,2344 2,1378 2,0342
2,9791 2,8431 2,7002 2,5487 2,4689 2,3860 2,2992 2,2079 2,1107 2,0062
2,8005 2,6648 2,5216 2,3689 2,2880 2,2034 2,1142 2,0194 1,9172 1,8047
2,6318 2,4961 2,3523 2,1978 2,1150 2,0285 1,9360 1,8363 1,7263 1,6006
2,4721 2,3363 2,1915 2,0346 1,9500 1,8600 1,7628 1,6557 1,5330 1,3805
2,3209 2,1848 2,0385 1,8783 1,7908 1,6964 1,5923 1,4730 1,3246 1,0000
217
ПЛ2. Планы дробных решнж*
1. Полуреплика типа 24-1 с определяющим контрастом I =xjx2x3X4. Оценивают-
ся линейные эффекты н смешанные парные взаимодействия Х4Х2 =х3Х4, Х]Х3 =х2хз,
*1*4 =х2х3.
(1) Эффекты Степени свободы
Линейные 4
ас Парные взаимодействия 3
ad __________________
Всего 7
Ьс
bd
cd
abed
2. Четвертьреплика типа 2s’2 с определяющим контрастом/==х2х2Х5 —х3X4X5 ~
— Х1Х2Х3Х4. Линейные эффекты оцениваются совместно с парными взаимодействия-
ми. Из парных взаимодействий оцениваются только х2х3 —х^х^ х}х4 =х2х3.
(D
аЪ Эффекты Степени свободы
Линейные 5
же Парные взаимодействия 2
bee __________________
Всего 7
ade
bde
abed
3. Полуреплика типа 2s**1 с определяющим контрастом 1 — х3х2х 5X4X5.1) Опы-
ты разбиты на четыре блока. Определяются линейные эффекты и парные взаимодейст-
вия, кроме Х3Х4, Х3Х5 и Х4Х5, которые смешаны с межблоковым эффектом.
Блоки
1 2 3 4
(1) ас ae ad
ab Ьс be bd
acde de cd ce
bede abde abed abce
Эффекты Степени свободы
Межблоковый дрейф 3
Линейные 5
Парные взаимодействия 7
Всего 15
♦ПЛ 2. заимствовано из [102], с. 317.
218
2) Опыты разбиты на два блока. Оцениваются линейные эффекты и все парные
взаимодействия, кроме х4х5. Первый блок объединяется со вторым, третий - с чет-
вертым.
Эффекты Степени свободы
Межблоковый дрейф Линейные Парные взаимодействия 1 5 9
Всего 15
3) Опыты не разбиваются на блоки. Оцениваются все линейные эффекты и все
парные взаимодействия. Все четыре блока объединяются вместе.
Эффекты Степени свободы
Линейные 5
Парные взаимодействия 10
Всего 15
4. Ув-реплика типа 26’3 с определяющим контрастом I ~ XiX3Xj = *1*4*6 =
= х2х3хб = х2х4х5 = х2х2х3х4 = XiX2x5x6 = х3х4х$хб. Оцениваются линейные эф-
фекты совместно с парными взаимодействиями и три смешанных парных взаимо-
действия.
(1)
acf
ade Эффекты Степени свободы
^се Линейные 6
bdf
abed Парные взаимодействия 1
а&е/ ------------------
cdef Всего 7
5. У4фепликатипа 26 2 с определяющим контрастом I = xix2x3x5 =xjx2x4x6 =
= x3x4x5xe. 1) Опыты разбиваются на четыре блока. Оцениваются все линейные эф-
фекты и смешанные парные взаимодействия х2х3 = х2х5, х2х4 = x2xe, xjx^ =х2х3,
*1*6 = *2*4, *3*4 =*5*6. *3*6 =*4*5-
Блоки
1 2 3 4 Эффекты Степени свободы
— Межблоковый дрейф 3
(1) acd ab acf Линейные 6
abce aef ce ade Парные взаимодействия 6
abdf bef df bed —
cdef bde abedef bef Всего 15
219
С межблоковым эффектом смешаны х>х2, Х1*эхб> х2хз*б-
2) Опыты разбиваются на два блока. Оцениваются те же эффекты, что и в пре-
дыдущем планировании, и еще три смешанных парных взаимодействия xjx2 =х3х5 =
=х4х6. Первый блок объединен со вторым, третий - с четвертым.
Эффекты Межблоковый дрейф Линейные Парные взаимодействия Тройные взаимодействия Степени свободы 1 б 7 1 Всего 15
Тройное взаимодействие *1X3X6 смешано с межблоковым эффектом.
3) Опыты не разбиваются на блоки. Оцениваются те же эффекты, что при раз-
биении на два блока. Все четыре блока объединяются вместе.
Эффекты Линейные Парные взаимодействия Тройные взаимодействия Степени свободы 6 7 2 Всего 15
6. %-реплика типа 26""1, определяющий контраст I = xlX2X3x4xsx6. 1) Опыты
разбиваются на восемь блоков. Оцениваются все линейные эффекты и парные взаимо-
действия, кроме Х1Х5, х2х$ и Х3Х4, которые смешиваются с межблоковым эффектом.
Блоки
1 2 3 4 5 6 7 8
(Г) ab ac be ae af ad bd
abef ef de df bf be ce cf
acde acdf abdf acef cd abed abef abce
bedf bcde beef abde abedef cdef bdef abef
С межблоковым эффектом смешаны xix$, х2хб, х3, х4, xix2x3, xix2x4, xix3x6,
XiX4X6.
Эффекты Степени свободы
Межблоковый дрейф 7
Линейные 6
Парные взаимодействия 12
Взаимодействия высшего
порядка 6
Всего 31
2) Опыты разбиваются на четыре блока. Оцениваются: линейные эффекты и вое
парные взаимодействия, кроме х3х4. Первый блок объединяется со вторым, третий —
с четвертым, пятый — с шестым, седьмой - с восьмым.
С межблоковым эффектом смешаны х3х4, xjx2x3, xix2x4.
220
Эффекты
Степени свободы
Межблоковый Дрейф 3
Линейные б
Парные взаимодействия 14
Взаимодействия высшего
порядка 8
Всего 31
3) Опыты разбиваются на два блока. Оцениваются все линейные эффекты и все
парные взаимодействия. С межблоковым эффектом связаны два тройных взаимо-
действия: х3х2хз = *4*5*6» остальные тройные взаимодействия смешаны попарно.
Объединяются блоки 1-4 и блоки 5-8.
Эффекты Степени свободы
Межблоковый дрейф 1
Линейные б
Парные взаимодействия 15
Тройны взаимодействия 9
Всего 31
4) Опыты не разбиваются на блоки. Оцениваются все линейные эффекты, все
парные взаимодействия и 10 пар тройных взаимодействий. Все восемь блоков объе-
диняются вместе.
Эффекты Степени свободы
Линейные б
Парные взаимодействия 15
Тройные взаимодействия 10
II II
Всего 31
7- Vi $-реплика типа 2 7-4 с определяющим контрастом I = XjX2x7 =х1хз*5 ~
*1*4*6 =*2*3*6 =*2*4*5 = *3*4*7 = *5*6*7 = *1*2*3*4 = *1*2*6*7 = *1*3*6*7 =
*1*4*5*7 = *2*3*5*7 = *2*4*6*7 =*3*4*5*6 = *1*2*з*4*5Хб*7- Оцениваются ЛН-
нейные эффекты, смешанные с парными взаимодействиями.
(Z)
abed
abef
acfg Эффекты Степени свободы
abeg Линейные 7
aceg -------------------
abfg Всего 7
cdef
8. 7g-реплика типа 27-3 с определяющим контрастом I = *i*2*3*4 =xjx2xsxe =
= *1*3*5*7 = *1*4*6*7 " *2*3*6*7 = *2*4*5*7 =*3*4*5*б- U ОПЫТЫ разбиваются На
четыре блока. Оцениваются все линейные эффекты и смешанные парные взаимо-
действия Х}Х3 “X2Xg Х3Х7, XjXg *2*5 *4*7' *1*5 *3*5 ~ *4*6’ *2*7 *4*5
=*3*6-
221
Блоки
1 2 3 4
(I) abg acf ef edg bdf abed abef aceg abedefg adef bdeg ade bee adfg befg
Смешаны с межблоковым эффектом х^х2 = х3х4 = xsx6; xxx3 = х2х4 = х5х7;
Х1Х4 =х2х3 =хбх7.
Эффекты Межблоковый дрейф Линейные Парные взаимодействия Взаимодействия высшего порядка Степени свободы 3 7 4 1
Всего 15
2) Опыты разбиваются на два блока. Оцениваются те же эффекты, что и раньше,
и еще совместные парные взаимодействия XjX2 = х3х4 = xgx6; XjX3 = х2х4 =х5х7;
Х1Х4 =х2х3 =х6х7.
Блоки
1 2
(I) abg
abed acf
abef ade
aceg bee
abfg bdf
befg edg
bdeg efg
cdef abedefg
С межблоковым эффектом смешано тройное взаимодействие xjx2x7.
Эффекты Межблоковый дрейф Линейные Парные взаимодействия Степени свободы 1 7 7 Всего 15
3) Опыты не разбиваются на блоки. Оцениваются те же эффекты, что и при раз- -
биении на два блока. Оба блока по восемь наблюдений объединяются вместе.
Эффекты Степени свободы
Линейные Парные взаимодействия Взаимодействия высшего порядка 7 7 1
Всего 15
222
9. 1Д-реплика типа 27-2 с определяющим контрастом I = xjx2x3x4X5 =
-x^x^x^x^Xf =X4X3XfiXf. 1) СМ1ьггы разбиваются на восемь блоков. Оцениваются все ли-
нейные эффекты и все парные взаимодействия, кроме xlxit *1*3» х2х3 и х^х6 =х5х7,
которые оказываются смешанными с межблоковыми эффектами. Из оцениваемых
парных взаимодействий только две пары задаются совместными оценками х^х$ —
И *4X7 =Х5Х6.
Блоки
1 2 3 4 5 6 7 8
(J) de аЬ cdg ас bdg be abg
defg fg cdf cef bdf bef adf aef
abcdf abcdg ceg abde beg acde aeg befg
abceg abcef abdefg abfg acdefg acfg bedefg bcde
С межблоковым дрейфом X2X4X7, x3x4x7. Эффекты Межблоковый дрейф Линейные Парные взаимодействия Взаимодействия высшего порядка смешаны Xjx2, Степени свободы 7 7 14 3 XJX3, x2x3 1, *4*6 = X$X7, XjX4X7,
Всего 31
2) Опыты разбиваются на четыре блока. Оцениваются все линейные эффекты и
парные взаимодействия, кроме х4х6 = х5х7, смешанных с межблоковым дрейфом.
Две пары парных взаимодействий задаются совместными оценками х4х3 = х^х7,
*4* 7 =*5*6-
Блоки
1 2 3 4
W ab de
be bef ac fg
adf cef bdf adg
aeg abfg beg aef
defg acfg cdf bcde
abcdf abde ceg bsfg
abceg acde acdefg abcdg
bedefg cdg abdefg abcef
С межблоковым эффектом смешаны х4х6 =х5х7, xix4x5, xix5x$,
Эффекты Степени свободы
Межблоковый дрейф 3
Линейные 7
Парные взаимодействия 17
Взаимодействия высшего
порядка 4
Всего 31
223
3) Опыты разбиваются на два блока. Оцениваются все линейные эффекты и все
парные взаимодействия. Часть парных взаимодействий задается совместными оцен-
ками х4х5 =*6*7. х4*7 =х5х6, х4х6 = х5х7. Первый блок объединяется со вторым,
третий — с четвертым.
Эффекты Степени свободы
Межблоковый дрейф 1
Линейные 7
Парные взаимодействия 18
Взаимодействия высшего
порядка 5
Всего 31
4) Опыты не разбиваются на блоки. Оцениваются те же эффекты, что и при раз-
биении на два блока.
Эффекты Степени свободы
Линейные 7
Парные взаимодействия 18
Взаимодействия высшего
порядка 6
Всего 31
10. */1-реплика 27"1 с определяющим контрастом 1=Х1Х2Х$х4х5х6х7.1) Опыты
разбиваются на 16 блоков. Определяются все линейные эффекты и все парные взаимо-
действия, кроме Х}Х2, *1*3, х2хз, х5хб» xsx7 и хбх7> которые оказываются смешан-
ными с межблоковым эффектом.
1 Блоки 8
2 3 4 5 6 7
ab ac be ae be ce abce
abed cd bd ad bede acde abde de
defg abdefg acdefg bedefg adfg bdfg edfg abedfg
abcefg cefg befg aefg befg aefg abfg fg
9 10 11 12 13 14 15 16
af bf cf abef ef abef acef beef
bedf aedf abdf df abedef cdef bdef adef
adeg bdeg cdeg abedeg dg abdg aedg bedg
bceg aceg abeg eg abeg eg bg ag
С межблоковым эффектом здесь смешаны xjx2, Х1Х3, х2хз, xjXg, х5х7,
ХбХ7, Х1Х4Х5, Х1Х4Х6, XjX4X7, Х2Х4Х5, Х2Х4Х6, Х2Х4Х7, Х3Х4Х5, Х3Х4Х6, X3X4X7.
Эффекты
Степени свободы
Межблоковый дрейф
Линейные
Парные взаимодействия
Взаимодействия высшего
порядка
15
7
15
26
Всего 63
224
2) Опыты разбиваются на восемь блоков. Оцениваются все линейные эффекты,
«се парные взаимодействия и все тройные взаимодействия, кроме Х1Х2Х3,
XiX^x7, х2х4х6, x2xsx7, х3х4х7 и х3х5хб, которые оказываются смешанными с
межблоковыми дрейфом.
Блоки
1 2 3 4 5 6 7 8
(I) be ac ab ag af ae ad
abdg de de dg bg be bf bg
abef eg eg ef ce cd eg cf
acdf abdf abde acde abef abeg abeg abce
aceg abeg abfg acfg adef abeg adfg aefg
bcde aedg bedg bedf befg bdfg bdeg bdef
befg acef beef bceg cdfg cefg cdef cdeg
befg bedefg acdefg abdefg abedeg abedef abcefg abedfg
Эффекты Степени свободы
Межблоковый дрейф 7
Линейные 7
Парные взаимодействия 21
Тройные взаимодействия 28
Всего 63
3) Опыты разбиваются на четыре блока. Оцениваются все линейные эффекты, все
парные взаимодействия, все тройные взаимодействия, кроме Х|Х2Хз, х1х4х5 и х1л6л7,
которые оказываются смешанными с межблоковым дрейфом. Объединяются: первый
блок — со вторым, третий - с четвертым, пятый - с шестым, седьмой — с восьмым.
Эффекты Степени свободы
Межблоковый дрейф 3
Линейные 7
Парные взаимодействия 21
Взаимодействия высшего
порядка 32
Всего 63
4) Опыты разбиваются на два блока. Оцениваются: все линейные эффекты, все
парные взаимодействия и все тройные взаимодействия, кроме XjX2x3, которые ока-
зываются смешанными с межблоковым эффектом. Объединяются: первый блок -
с четвертым и пятый блок - с восьмым.
Эффекты
Степени свободы
Межблоковый дрейф 3
Линейные 7
Парные взаимодействия 21
Тройные взаимодействия 34
Всего 63
225
5) Опыты не разбиваются на блоки. Оцениваются все линейные эффекты, все
парные взаимодействия и все тройные взаимодействия. Объединяются все блоки
вместе.
Эффекты Линейные Парные взаимодействия Тройные взаимодействия Степени свободы 7 21 35 Всего 63
ПЛЗ. Центральное композиционное ротатабельное планирование второго порядка и планирование с разбиением на ортогональные блоки (лс - число точек гиперкуба; ла - число звездных точек; н (0) - число точек в центре эксперимента; а - величина звездного плеча)*
Ротатабельное планирование Разбиение на блоки (все дробные реплики от р пспа л (о) Na 2р-факторного эксперимента должны оставлять все основные эффекты взаимнонесмешанными)
24 4 5 13 1,414 1. Четыре точки квадрата плюс две центральные точки. II. Четыре звездные точки плюс две централь- ные точки. Блоки ортогональны при а = 1,414. Общее число точек в блоках 12.
3 8 6 6 20 1,682 I, II. Полуреплики от факторного эксперимен- та типа 23, каждая с двумя точками в центре. III. Шесть звездных точек плюс две централь- ные точки. Для разбиения на ортогональные блоки а = = 1,633. Общее число точек в блоках 20.
4 16 8 7 31 2,000 1, П. Полуреплики от факторного эксперимен- та типа 24, каждая с двумя центральными точками. Ш. Восемь звездных точек плюс две централь- ные точки. Блоки ортогональны при а = 2,000. Общее число точек в блоках 30.
5 321010 52 2,378 I, П, III, IV. % -реплики от факторного экспе- римента типа 2 , каждая с двумя центральными точками. V. 10 звездйых точек плюс четыре центральные точки. Для разбиения на ортогональные блоки а — = 2,366. Общее число точек в блоках 54.
5 16 106 32 2,000 (полу реплика) I. 16 точек полуреплики от факторного экспе- римента типа 2s плюс шесть центральных точек. II. 10 звездных точек плюс одна центральная точка. Для разбиения на ортогональные блоки а = ~ 2,000. Общее число точек в блоках 33.
226
6 64 12 15 91 2,828 I, II, III, IV, V, VI, VII, VIII. 1/8-реплики от факторного эксперимента типа 2б, каждая с од- ной центральной точкой, всего по девять точек в каждом блоке. IX. 12 звездных точек плюс шесть нулевых точек. Для разбиения на ортогональные блоки а = = 2,828. Общее число точек в блоках 90.
6 32 12 9 53 2,378 (полу реплика) I, II. 1/2 от полуреплики факторного экспери- мента типа 26, каждый такой блок содержит 16 точек плюс дополнительно четыре центральные точки. III. 12 звездных точек плюс две центральные точки. Для разбиения на ортогональные блоки а = = 2,366. Общее число в блоках 54.
7 128 14 21 163 3,333 Блоки с I по XVI. 1/6-реплики от факторного эксперимента типа 27, каждый блок содержит по восемь точек плюс одну центральную точку. XVII. 14 звездных точек плюс 11 центральных точек. Для разбиения на ортогональные блоки а = = 3,33^3. Общее число точек в блоках 54.
7 64 14 14 92 2,828 Блоки с I по Vin. 1/8 от 1/2-реплики от фак- торного эксперимента типа 2 . В каждом таком блоке по восемь точек плюс одна дополнительная точка в центре. IX. 14 звездных точек плюс четыре централь- ные точки. Для разбиения на ортогональные блоки а = = 2,828. Общее число точек в блоках 90.
* Таблица заимствована из [102] , с. 92.
1114. Указатель 200 работ методологического характера по обработке
результатов и планированию экспериментов, опубликованных в журнале
"Заводская лаборатория”
А. Основополагающие и обобщающие статьи
1. Гнеденко Б.В. Математическая статистика - мощное орудие в работе заводс-
кой лаборатории. 1961, № 10, с. 1251. 2. Налимов В.В. О стандартизации способов
Представления экспериментального материала. 1961, № 10, с. 1268. 3. Мешалкин Л.Д
Обсуждение книг по математической статистике. 1961, № 10, с. 1279. 4. Передовая.
Методы кибернетики - в практику лабораторий. 1962, № 7, с. 771. 5. Налимов В.В.
Статистические методы планирования экспериметов при математическом описании
Процессов. 1962, № 1, с. 5. 6. Слободчикова Р.И. Применение различных методов к
исследованию поверхности отклика. 1966, № 10, с. 1234. 7. Айвазян С.А. Математико-
статистические методы в лабораторной практике. 1967, № 10, с. 1293. 8. Маркова Е.В.,
Адлер Ю.П., Преображенская Г.Б. Развитие методов планирования экспериментов в
СССР. 1967, № 10, с. 1300. 9. Федоров В.В. Планирование экспериментов при изучении
227
механизма явлений. 1968, № 3, с. 314.10. Веселая Г.Н. Лапина З.С., Слободчикова Р.Н.
О программах по математической статистике на ЭВМ ”Минск-22”. 1970, № 1, с. 74.
11. Налимов В.В. Влияние математической статистики и кибернетики на методологию
научных исследований. 1970, № 10, С. 1218. 12. Федоров В.В. Планирование экспери-
ментов по различению гипотез кривых при помощи метода отношения вероятностей.
1968, № 3, с. 320. 13. Новик Ф.С. К вопросу о возможности использования метода
симплексных решеток для изучения диаграммы состояний. 1968, № 10, с. 1223. 14. Се-
дунов Е.В. Обобщение задачи Бокса-Драйпера в планировании регрессионных экс-
периментов. 1973, № 3, с. 308. 15. Горский В.Г., Грановский Ю.В., Журавлева Т.Г.
О работе школы-семинара ’’Планирование экспериментов при изучении механизма
явлений”, 1974, № 3, с. 345. 16. Налимов В.В., Голикова Т.Н. Теория планирования
экспериментов: достигнутое и ожидаемое. 1977, № 10, с. 1247. 17. Адлер Ю.П., Гра-
новский Ю.В. Методология и практика планирования экспериментов за десять лет.
1977, № 10, с. 1253. 18. Налимов В.В. Анализ трудностей, связанных с построением
нелинейных по параметрам моделей в задачах химической кинетики. 1978, № 3, с. 325.
Б. Предварительная обработка результатов наблюдений
19. Воробьев Г.Г. Применение перфорированных карт в промышленных и иссле-
довательских лабораториях (обзор). 1962, 3, с. 316. 20. Гринзайд Е.Л. Оценка вос-
производимости результатов анализа по расхождению параллельных определений.
1962, № 7, с. 840. 21. Айвазян С.А., Кацев П.Г. Метод определения существенных
различий между двумя средними показателями (реферат). 1962, № 7, с. 843. 22. Рос-
товцев А.М. Быстрый метод расчета числовых характеристик рядов распределения
экспериментальных данных. 1963, № 7, с. 853. 23. Бровмак М.Я., РИмек В.Х. Об оцен-
ке резко выделяющихся опытных данных при механических испытаниях. 1964, № 7,
с. 861. 24. Микешина Н.Г. Выявление и исключение аномальных значений (обзор).
1966, № 3, с. 310. 25. Шенявский Л.А. Метод приближенного расчета площадей двух
перекрывающихся гауссовых пиков. 1966, № 7, с. 851. 26. Кретов В.И., Дыхович-
ный А.А., Бевз А.А. Применение распределейия Вейбулла к анализу прочности бетона.
1967, № 5, с. 604. 27. Бродский В.П. О расчете показателя однородности. 1967, № 7,
с. 851. 28. Шейнина Г.А., Шейнин А. Б. Некоторые приемы статистической обработки
архивного материала лабораторного контроля. 1969, № 1, с. 80. 29. Гольдберг Ю.И.
Графический метод выявления и учета систематических погрешностей результатов
количественных определений. 1969, № 3, с. 330. 30. Благовещенский Ю.Н. О прогнозе
числа экспериментов для достижения заданной относительной погрешности при опре-
делении среднего. 1969, № 5, с. 587. 31. Мешалкин Л.Д., Смирнов Н.П., Сосновс-
кий М.Н. Об устойчивости оценок центра распределения (обзор). 1969, № 5, с. 594.
32. Славный В.А. Количественные критерии точности и чувствительности и возмож-
ность учета априорной информации при анализе вещества. 1969, № 7, с. 818. 33. Благо-
вещенский Ю.Н. Эффективность среднего как оценка для математического ожидания
логарифмически нормального распределения. 1970, № 5, с. 568. 34. Розанов Г.В.,
Френкель А. А. Об одной многоэтапной процедуре формализации априорной информа-
ции. 1970, № 3, с. 319. 35. Архаров Л.В. О некотором критерии для проверки гипотезы
о независимости наблюдений. 1971, № 3, с. 332. 36. Парамонов Ю.М. Об оценке кван-
тиля, не смещенной по вероятности. 1971, № 3, с. 336. 37. Гутер Р.С., Муратова Т.А.,
Полунов Ю.Л. О подборе параметров для кривых распределения Пирсона. 1971, № 5,
с. 582. 38. Гутер Р.С. Об одном тесте для проверки программы псевдослучайных
чисел. 1973, N® 3, с. 326. 39. Логинова Г.Л., Логинов Э.А. Интервальная оценка сред-
него случайной переменной при неслучайном аргументе. 1973, № 10, с. 1237.40. Бенья-
минов Б.Б. Применение последовательного анализа для проверки гипотезы о нераз-
личимости измерений. 1975, № 7, с. 841. 41. Киселев И.И. Построение доверительных
областей для параметров асимптотических распределений экстремальных значений.
1975, № 10, с. 1230. 42. Мельников Н.Н., Мироненко Л.Н. Некоторые задачи нахожде-
ния параметров распределения. 1976, № 10, с. 1229. 43. Закгейм А.Ю. Интервальные
оценки для средних при внутренней неоднородности образцов, 1977, № 1, с. 77.
44. Ращ Д Нецентральные распределения (обзор). 1977, № 3, с. 317. 45. Бостанд-
228
жиян В.А. Математическое ожидание и дисперсия выборочных характеристик из лога-
рифмической совокупности. 1977, № 7, с. 878. 46. Назик А.Е., Приходько Ю.Г., Зай-
чик В.С и др. Оценка параметров распределения Вейбулла по цензурированным вы-
боркам. 1978, № 1, с. 66. 47. Володин И.Н. К оценке среднего значения нормального
распределения с гарантированными ограничениями на относительную ошибку оцени-
вания. 1978, № 1, с. 69. 48. Свалов С.Н. Уточнение метода линеаризации для оценки
моментов. 1978, № 5, с. 593. 49. Орлов А.Г. О сравнении экспериментальных данных
двух литературных источников статистическими методами. 1978, № 7, с. 852. 50. Шак-
леин С.В. Выявление систематических ошибок в многократных неравноточных рядах
измерений. 1978, № 5, с. 422. 51. Кутенков П.Р. Анализ устойчивости размера и мощ-
ности ряда статистических критериев сравнения дисперсий к нарушению нормальности
распределения. 1979, № 10, с. 930.
В. Статистические методы построения и оценивания эмпирических зависимостей
по экспериментальным данным
52. Хлопотов О.Д. Построение эмпирических зависимостей методом осреднения.
1963, № 10, с. 1215. 53. Айвазян С.А. Применение методов корреляционного и регрес-
сионного анализов к обработке результатов экспериментов (обзор) Ч. I. 1964, № 7,
с. 832. 54. Айвазян С.А. Применение методов корреляционного и регрессионного ана-
лизов к обработке результатов экспериментов (обзор). Ч. II. 1964, № 8, с. 973. 55.
Самойленко А.И. Учет погрешности измерения в уравнениях регрессии при линейном
характере связи. 1965, № 10, с. 1226. 56. Веселая Г.Н. О применении многомерного
регрессионного анализа при исследовании технологических процессов. 1966, № 3,
с. 327. 57. Петерсен И.Ф. К применению регрессионного анализа в проблемах оптими-
зации. 1967, № 5, с. 594. 58. Лелянов СП. Определение параметров нелинейной регрес-
сии методом наименьших квадратов. 1967, № И, с. 1417. 59. Олевская И.В. Об одном
частом случае применения линейной регрессии при обработке экспериментальных дан-
ных. 1967, № 11, с. 1420. 60. Кац Л.А. Фокальный метод в корреляционном анализе.
1968, № 1, с. 75. 61. Масленников И.М., Галицкий А.Я., Полянский В.П. Об одном
методе представления искомой функции в регрессионном анализе и его применении.
1968, № 7, с. 845. 62. Олевская И.В. Определение линии регрессии по методу танген-
сов. 1968, № 10, с. 1217. 63. Липкин М.И., Шилова Г.С., Острейко И.А. и др. Разработка
и применение универсальной программы множественного регрессионного анализа.
1968, № 10, с. 1233. 64. Андрукович П.Ф., Николаева Л.С., Федоров В.В. Программы по
регрессионному и конфлюэнтному анализу. 1969, № 1, с. 84. 65. Гурин Л.С. Соло-
дун Л.А. Об аппроксимации некоторого класса функций методом наименьших квад-
> ратов. 1969, № 5, с. 597. 66. Андрукович П.Ф, Один алгоритм поиска наибольших и
наименьших значений функции. 1970, № 1, с. 60. 67. Бородюк В.П. Влияние ошибок
регистрации переменных на точность регрессионного уравнения. 1970, № 1, с. 62.
68. Андрукович П.Ф. Применение метода главных компонентов в регрессионном ана-
лизе. 1970, № 3, с. 312. 69. Николаева Л.С, Федоров В.В. Использование методов кон-
флюэнтного анализа при линейной параметризации поверхности отклика. 1970, № 1,
с. 68. 70. Андельсон-Вельский Г.М., Бекетов Н.В., Чернышева.И.Б. О вычислении об-
ратной матрицы к матрице частных вторых производных. 1971, № 1, с. 68. 71. Райс-
кая Н.Н., Терехин А.Т., Френкель А.А. Кластерный анализ и его применения (обзор).
1972, № 10, с. 1222. 72. Маньковский В. А., Михай лид иВ. А. Об одном способе обработ-
ки экспериментальных данных. 1972, № 10, с. 1232. 73. Апраушева Н.Н., Конаков В.Д
Использование непараметрических оценок в регрессионном анализе. 1973, № 5, с. 566.
74. Бородюк В.П., Вощинин А.П. Ошибки регистрации независимых переменных в
задачах множественной регрессии. 1973, № 7, с. 831. 75. Дубов Э.Л. Регрессионный
анализ при погрешностях в фиксации части аргументов поверхности отклика. 1974,
№ 1, с. 67. 76. Веселая Г.Н. Реализация метода наименьших квадратов на ЭВМ. 1974,
№ 1, с. 79. 77. Айвазян С А., Бограновский И.М. Методы статистического исследова-
ния конфлюэнтного анализа и их применение. 1974, № 3, с. 285. 78. Щербакова Э.С.,
Музиченко Л.А. Об одном алгоритме поиска локального экстремума функции мно-
гих переменных. 1974, № 3, с. 295. 79. Райская Н.Н., Терехин А.Т., Френкель А.А.
Об использовании кластерного анализа при построении регрессионных моделей,
229
1974, № 5, с. 573. 80. Израилевич М.Я., Волков В.А., Полисар Л.М. Статистический
анализ эмпирических зависимостей, нелинейных относительно искомых параметров.
1974, № 5, с. 583. 81. Епишин Ю.Г. Регрессионный метод наименьших абсолютных
отклонений. 1974, № 10, с. 1227. 82. Маневич В.А, Аппроксимация точек на плоскости
выпуклым полиномом. 1974, № 10, с. 1232. 83. Шумский В.М., Грановский Ю.В.,
Сгерликова И.В. Анализ одного способа оценивания координат экстремума по экспе-
риментальным данным. 1974, № 1, с. 84. 84. Липовецкий С.С. Метод многофакторной
квазиортогональной регрессии. 1975, № 5, с. 577. 85. Комяков А.А., Маньковский В.А.
Единый метод определения параметров эмпирических формул с помощью номограмм.
1975, № 5, с. 589. 86. Дронов В.С., Целищев Ю.В. О сглаживании экспериментальных
зависимостей методом однозначной аппроксимации. 1975, № 7, с. 844. 87. Кабанова
О.В., Слободчикова Р.И. Построение нелинейных моделей с помощью алгоритмов пре-
образования переменных. 1975, № 10, с. 1242. 88. Поздняков В.В., Лученко В.И. О схо-
димости метода последовательного построения регрессионных зависимостей. 1976,
№ 1, с. 65. 89^Мухина Л.Г., Самарин Ю.П. О непараметрическом выравнивании экспе-
риментальных зависимостей. 1976, № 3, с. 325. 90. Липовецкий С.С. К статистическому
оцениванию единого уравнения взаимосвязи произвольного числа факторов, подвер-
женных влиянию ошибок измерения. 1976, № 5, с. 576. 91. Тулунчук Ю.М. Анализ
надежности принятия решения о типе уравнения регрессии с использованием прове-
рочных выборок при нормальной аддитивной помехе. 1976, № 10, с. 1233. 92. Лисен-
ков А.Н., Кодкинд Г.Х., Басиева Т.Х и др. Об алгоритмическом обеспечении для за-
дач статистического анализа многофакторных экспериментов. 1976, № 7, с. 859. 93.
Фуксман Я.Л. Точечно-несмещенное описание поверхности отклика, 1977, № 1, с. 61.
94. Целищев В.Д, Дронов В.С. К вопросу об определении области применения и ин-
формативности метода однозначной аппроксимации. 1977, № 5, с. 584. 95. Сысоев В.В.,
Самойлов В.М., Величко ДА. О целесообразности исследования математических мо-
делей по остаткам. 1977, № 5, с. 600. 96. Липовецкий С.С. Построение главных компо-
нент на основе качественного анализа корреляционных матриц. 1977, № 7, с. 865.
97. Липовецкий С.С. Некоторые вопросы построения корреляционных моделей. 1978,
№ 1, с. 62. 98. Писаренко В.Н., Мержанова Р.Ф., Жукова Т.Б. и др. Об эффективности
статистических дискриминирующих методов проверки гипотез. 1978, № 3, с. 331.
99. Кабанова О.В., Слободчикова Р.И. Нетрадиционный метод поиска параметров не-
линейных моделей. 1978, № 3, с. 334. 100. Балк П.И., Балк Т.В. О восстановлении
экспериментальных зависимостей при неизвестном законе распределения ошибок из-
мерений. 1978, № 3, с. 339. 101. Майданчик Б.И., Раев А.Г., Строганов Ю.А, О восста-
новлении функции по ограниченной выборке. 1978, № 5, с. 589. 102. Бреев И.М. Метод
усредненных сглаживающих Полиномов. 1978, № 7, с. 850. 103. Сурков А.В., Ново-
жилов Н.М., Аносов Н.П. и др. О точности определения эмпирических зависимостей,
полученных ускоренными способами исследований. 1978, № 10, с. 1247. 104. Дубо-
ва И.С., Федорова Г.С., Федоров В.В. Системы оптимальных опорных траекторий в
регрессионных задачах с временной зависимостью. 1978, № 1, с. 71. 105. Кабанова О.В.
Критерии и методы преобразования переменных при построении статистических мо-
делей. 1979, № 3, с. 245. 106. Пасутман Б.В. О применении критерия знаков и после-
довательного анализа Вальда. 1979, № 3, с. 257. 107. Перельман И.И. Адаптивный экс-
потенциально взвешенный метод наименьших квадратов для оценки дрейфующих
параметров. 1979, № 7, с. 633. 108. Липовецкий С.С. Регрессионные модели неявных
функций. 1979, № 10, с. 925. 109. Слотин Ю.С. Преобразование полиномиальных мо-
делей. 1980, № 1, с. 57. НО. Закгейм А.Ю., Быстров Л.В. Интервальные оценки для
абсцисс регрессионных зависимостей. 1980, № 1, с. 65.
Г. Планирование и обработка отсеивающих экспериментов
111. Слободчикова Р.И., Фрейдлина В.Л., Лапина Э.С. и др. Отсеивающие экспе-
рименты. Повышение эффективности метода случайного баланса путем применения
ветвящейся стратегии if использования вычислительных машин. 1966, № 1, с. 53.
112. Мешалкин Л.Д. К обоснованию метода случайного баланса. 1970, № 3, с. 316.
113. Максимов В.И. Приспособление для визуального отбора значимых эффектов
230
при обработке результатов эксперимента методом случайного баланса. 1971, № 5,
с. 573. 114. Лапина З.С, Слободчикова Р.И. Исследование границ применимости
алгоритма случайного баланса. 1971, № 7, с. 818. 115. Барский В.Д., Забелло Л.А.,
Аксенина А.А. и др. К вопросу о построении матрицы планирования отсеивающего
эксперимента. 1971, № 7, с. 821. 116. Слободчикова Р.И. Выделение значимых факто-
ров методом случайного баланса с помощью многоуровневых планов. 1973, № 1,
с. 53. 117. Козырев В.П., Герасимова М.Ф., Автономова А.Ф. О выделении существен-
ных факторов. 1974, № 3, с. 305. 118. Кац М.Д. Выделение значимых факторов мето-
дом обучения распознаванию образов. 1975, № 1, с. 85. 119. Седунов Е.В. Оценка
метода воспроизводящих ядер в сверхнасыщенном планировании регрессионных
экспериментов. 1976, N* 7, с. 584. 12а Розендорн Н.Н., Розендорн Э.Р. Алгебраическое
обоснование применимости сверхнасыщенных планов в условиях шума. 1976, № 10,
с. 1219. 121. Малолеткин Г.Н., Мельников Н.Н. Математическое обеспечение ЕС ЭВМ
для выделения существенных факторов. 1979, № 7, с. 648. 122. Еханин М.В.,
чикова Р.И. Разработка многоуровневых сверхнасыщенных планов для технологичес
ких процессов. 198а N* 1, с. 50.
Д. Планирование экспериментов с количественными уровнями варьирования
123. Голикова Т.И., Микешина Н.Г. Сравнение D-оптимальных планов второго
порядка на Л’-мерном шаре с ротатабельными планами Бокса- 1967, № 5, с. 591. 124.
Голикова Т.И., Микешина Н.Г., Налимов В.В. и др. Построение на кубе планов второ-
го порядка, близких к D-оптимальным. 1967, № 7, с. 847.125. Лисенков А.Н. К вопро-
су об использовании некоторых планов второго порядка. 1969, № 1, с. 67. 126. Весе-
лая Г.Н, Лапина З.С. Вычисление коэффициентов регрессии при ротатабелъном пла-
нировании. 1961, № 1, с. 87. 127. Федорова Г.С., Игошина И.В. Информационный под-
ход к планированию регрессионных экспериментов. 1970, № 5, с. 571.128. Тийтс Т.В.,
Петерсен И.Ф. Регрессионные планы третьего порядка для круга с малым количест-
вом экспериментов. 1971, № 1, с. 55. 129. Петерсен И.Ф., Кукс Я.П. Метод прямых про-
изведений для построения планов регрессионных экспериментов. 1971, № 1, с. 157.
130. Кириченко Г.С., Макалец Б. И., Немцева Л.М. Принятие решений при изменении
пределов варьирования независимых переменных в планируемом эксперименте. 1971,
№ 5, с. 573. 131. Вучков И.Н„ Круг Г.К., Лецкий Э.К. и др. D-оптимальные планы для
кубической регрессии. 1971, № 7, с. 815.132. Кудрявцева Б.М., Плотицина Л.Б. Иссле-
дование влияния добавления ортогонализирующих экспериментов на качество исход-
ного статистического материала. 1971, № 10, с. 1233.133. Горский В.Г., Бродский В.З.
О регрессионном анализе при планировании второго порядка. 1972, № 1, с. 61.134. Со-
лянки Б.Л. Оптимальное планирование по отношению к производной от полинома.
1972, № 5, с. 577. 135. Рейзлин А.С. Об ортогональных ротатабельных планах второго
порядка. 1972, № 5, с. 588. 136. Ротко Ю.М., Котляр Л.И., Вайнберг А.А. Применение
квази-D-оптимального плана В при исследовании питающих устройств для сыпучих
материалов. 1972, № 7, с. 839. 137. Бенцианов Ю.В., Кафаров В.В., Свердлов В.П.
Сравнение некоторых невыраженных планов второго порядка на трехмерном кубе.
1973, № 5, с. 575. 138. Совельянов В.П. Об одном полезном следствии симметрии пол-
ного факторного эксперимента типа 2 . 1973, № 5, с. 584. 139. Рогинский Л.В., Стрель-
цов А.А. Метод анализа уравнения регрессии, заданного на гиперкубе. 1973, № 7, с. 841.
14а Тийтс Т.В., Петерсен И.Ф. Минимаксные регрессионные планы для квадрата с ма-
лым количеством экспериментов. 1973, № 10, с. 1219. 141. Ермаков С.М., МеласВ.Б.
Об одном подходе к планированию экспериментов при нелинейной параметризации.
1973, № 10, с. 1222. 142. Лецкий Э.К., Никифорова ЕС Об использовании спектров
непрерывных D-оптимальных планов при построении точных планов. 1974, № 5, с. 562.
143. Седунов ЕВ. Сравнение характеристик несмещенных планов регрессионных
экспериментов и планов в классической постановке. 1975, № 1, с. 76. 144. Береж-
ной Ю.И., Деревянко Л.И. D-оптимальные планы для полиномиальной регрессии.
1975, № 3, с. 326. 145. Берсенев СМ., Саблин Н.И. Планирование помехоустойчивых
регрессионных экспериментов. 1976, № 3, с. 314. 146. Слотин Ю.С. Построение ком-
позиционных локально-ортогональных планов третьего порядка. 1977, № 5, с. 592.
231
147. Ермаков СМ., Махмудов А.А. О планах регрессионных экспериментов, мини-
мизирующих систематическую ошибку. 1977, № 7, с. 854. 148. Круг Г.К., Кайшев В.К.
D-оптимальные планы для одного класса регрессионных функций. 1977, № 7, с. 858.
149. Седунов Е.В. О практическом применении несмещенных планов регрессионных
экспериментов. 1978, № 7, с. 829. 150. Фомин Г.А., Фомина Е.С. Построение оптималь-
ных планов для моделей, нелинейных по параметрам. 1978, № 7, с. 848. 151. Седу-
нов Е.В. Планирование и анализ регрессионных экспериментов с учетом систематичес-
кой ошибки. 1979, № 1, с. 65. 152. Жиглявский А.А. Об итерационном методе нахож-
дения оптимальных планов регрессионных экспериментов. 1979, № 1, с. 63. 153. Дани-
ленко Е.Л., Ляшенко Т.В. Расчет точных оптимальных планов на выпуклых много-
гранниках. 1979, № 3, с. 249. 154. Грановский Ю.В. О принятии решений при исполь-
зовании методов Б окса-Уилсона. 1979, № 5, с. 419. 155. Николаева Л.С., Федоров В.В.,
Евсеев А.М. и др. Построение оптимальных планов при усложнении структуры мо-
дели физико-химической равновесной системы. 1979, № 10, с. 940.
Е. Планирование факторных экспериментов с качественными
и комбинированными уровнями варьирования.
f
156. Маркова Е.В. Латинские квадраты в планировании эксперимента. 1968,
№ 1, с. 60. 157. Маркова Е.В. Латинские прямоугольники и кубы в планировании
эксперимента. 1968, № 6, с. 832. 158. Солодун Л.А. Об определении взаимодействия
между двумя факторами при наличии в таблице дисперсионного анализа пустых кле-
ток. 1968, № 10, с. 1220. 159. Маркова Е.В. BIB-схемы в планируемых экспериментах
(обзор). 1970, № 7, с. 834. 160. Маркова Е-В. О структурной связи между факторными
экспериментами и латинскими квадратами. 1971, № 1, с. 60. 161. Маркова Е.В. Стати-
стический анализ сбалансированных неполноблочных планов (обзор). 1971, № 7, с. 807.
162. Пен Р.З. Факторный анализ результатов активного эксперимента. 1972, № 1, с. 70.
163. Маркова Е.В. О выдвижении дополнительных гипотез при применении латинских
квадратов, кубов и параллелепипедов. 1972, № 3, с. 318. 164. Маркова Е.В. РВ1В-схе-
мы в планировании экспериментов (обзор). 172, № 5, с. 584. 165. Рузинов Л.П. К во-
просу о тройных и четверных эффектах взаимодействия факторов. 1972, № 7, с. 840.
166. Горский В.Г., Адлер Ю.П., Бродский В.З. и др. Линейные планы с целочислен-
ными уровнями. 1973, № 5, с. 579. 167. Маневич М.С. Опыт применения квазирандо-
мизационного метода планирования экспериментов. 1977, № 1, с. 66. 168. Марко-
ва Е.В., Прис Д.А. Латинские кубы и связанные с ними планы. 1978, № 10, с. 1231.
169. Консон Е.Д. Устойчивое оценивание на блоках факторного эксперимента. 1978,
№ 10, с. 1243. 170. Носов В.В. Применение теории кодирования при построении не-
которых геометрических факторных планов. 1979, № 7, с. 642.
Ж. Симплексный метод планирования экспериментов.
171. Горский В.Г., Бродский В.З. Симплексный метод планирования экстремаль-
ных экспериментов. 1965, № 7, с. 831. 172. Маркова Е.В. Сравнение симплексного ме-
тода с методом Бокса-Уилсона, на примере химической реакции. 1965, № 7, с. 835.
173. Налимов В.В. Еще раз’о сравнении случайного поиска с методом градиента в сим-
плексном планировании. 1966, № 7, с. 854. 174. Новик Ф.С., Минц Р.С., Малков Ю.С.
Применение метода симплексных решеток для построения диаграмм состав - свойст-
во. 1967, № 7, с. 840. 175. Горский В.Г., Бродский В.З. Некоторые вопросы примене-
ния симплекс-планов. 1968, № 7, с. 838. 176. Чугунков В.И., Бродский В.З., Горс-
кий В.Г. Об одном методе композиционного построения ротатабельного симплекс-
суммируемого плана второго порядка. 1969, № 3, с. 323. 177. Орехов А.А., Корни-
лова С.И. Оптимизация процесса с помощью случайного симплекса с учетом веса
функции отклика в его вершинах. 1969, № 3, с. 326. 178. Векслер М.А., Горский В.Г.,
Бродский В.З. Экспериментальная проверка ортогонального плана первого порядка
и несимметричного симплекс-суммированного плана. 1970, № 5, с. 578. 180. Иза-
ков Ф.Я. Об одном практическом приеме симплекс-планирования при поиске опти-
мальных режимов технологических процессов. 1971, № 3, с. 330. 181. Рогинский Л.В.,
232
Стрельцов А.А. Оптимизация многофакторных процессов со многими выходными
параметрами методом симплекс-планирования. 1972, № 1, с. 66. 182. Должанский Ю,М.,
Никитина Е.П., Мержанова Р.Ф. и др. Симплекс-пропорциональные планы на плос-
кости. 1978, № 10, с. 1240. 183. Ильенко А.В., Кацев П.Г. Модификация симплексного
метода в задачах оптимизации. 1980, № 1, с. 54.
3. Работы по другим вопросам, связанным с планированием и
обработкой экспериментов
184. Петлюк Ф.Б., Платонов В.М. Решение общей задачи аппроксимации методом
быстрейшего спуска. 1963, № 10, с. 1221. 185. Мешалкин Л.Д., Нгуен Динь Хьен. Срав-
нение двух методов оптимизации. 1966, № 1, с. 64. 186. Растригин Л.А. О критериях
Сопоставления методов поиска экстремума. 1966, № 10, с. 1248. 187. Лисенков А.Н.,
Круг Г.К., Коршунов М.А. и др. О применении планируемых экспериментов в усло-
виях временного дрейфа. 1967, № 5, с. 598. 188. Иващенко А.И., Новик Ф.С., Чуй-
ко Г.П. К вопросу математического планирования экспериментов при исследовании
многокомпонентных систем. 1970, № 7, с. 834. 189. Горский В.Г., Адлер Ю.П. О мето-
дологии регрессионного и дисперсионного анализа при планировании экспериментов
с неравномерным дублированием опытов. 1971, № 3, с. 319. 190. Кудрявцев Б.М.
К вопросу о оптимизации производственных процессов статистическими методами.
1971, № 10, с. 1226. 191. Веников В.А., Кулиев А.М. О применении теории подобия
При экспериментально-статистических методах анализа. 1972, № 7, с. 842. 192. Кац
М.Д., Щеглов В.Н. Применение булевой алгебры для анализа многокомпонентных
смесей по спектрам поглощения. 1973, № 3, с. 317. 193. Колосов В.В., Растригин Л.А.
Применение методов случайного поиска при последовательном планировании опти-
мальных экспериментов. 1974, № 3, с. 302. 194. Воронков О.Г. Об одном алгоритме
матриц Адамара. 1974, № 10, с. 1244. 195. Ясаков А.И. Применение методов квази-
крутого восхождения для оптимизации процессов с двумя параметрами выхода.
1?76, № 1, с. 78. 196. Цэранка Б. Некоторые свойства блочных планов. 1976, № 10,
С. 1216. 197. Бродский В.З., Кузнецов В.С Об оптимальном преобразовании регуляр-
ных планов главных эффектов. 1976, № 3, с. 317. 198. Даниленко Е.Л. Критерии
охвата области действия модели областью планирования (S'-критерии), 1977, № 7,
с. 860. 199. Дворкин Л.И., Файнер М.Ш., Мироненко А.В. Опыт применения методов
математической теории эксперимента при планировании и оптимизации инженерных
расчетов. 1978, № 5, с. 586. 200. Вощинин А.П. Планирование экспериментов при
айализе знаков регрессионных коэффициентов. 1979, № 7, с. 638.
Литература
1. Адлер ЮЛ. Введение в планирование эксперимента. - М.: Металлургия, 1969.
2. Адлер ЮЛ., Грановский Ю.В. Обзор прикладных работ по планированию
эксперимента. Препринт. - М.: Изд-во МГУ, 1967.
3. Адлер ЮЛ, Маркова Е.В., Грановский Ю.В. Планирование эксперимента при
поиске оптимальных условий. 2-е изд. - М.: Наука, 1976.
4. Айвазян С.А. Статистические исследования зависимостей. Применение методов
корреляционного и регрессионного анализа при обработке результатов эксперимен-
тов. - М.: Металлургия, 1968.
5. Айвазян С. А., Бежаева З.И., Староверов О-В. Классификация многомерных
наблюдений. - М.: Статистика, 1974.
6. Алберт А. Регрессия, псевдоинверсия и рекуррентное оценивание. - М.: Наука,
1977.
7. Алексеев ГЛ. Объективные методы выравнивания и оптимизации корреля-
ционных связей. - JL: Гидрометеоиздат, 1971.
8. Лндероон Т. Введение в многомерный статистический анализ. - М.: Физмат-
гнз, 1963.
9. Андрукович П. Применение метода главных компонент в практических иссле-
дованиях. - М.: Изд-во МГУ, 1973.
10. Ашмарин ИЛ. и рр. Быстрые методы статистической обработки и планирова-
ния экспериментов. - Л.: Изд-во ЛГУ, 1975.
11. Бард Й. Нелинейное оценивание параметров. - М.: Статистика, 1979.
12. Бернстейн А. Справочник статистических решений. - М.: Статистика, 1968.
13. Бирюков В.В. Практическое руководство по применению математических
методов планирования эксперимента для поиска оптимальных условий в многофак-
торных процессах. - Рига: Зинатне, 1969.
14. Box G. Е.Р., Behnken D.W. Some New Three Level Desing for Study of Quantitive
Variables. Technometries, vol. 2, 1960, № 4.
15. Box G.E.P., Hanter J.S. Multifactor Experimental Desings for Exploring Response
Surface?. Annals of Mathematical Statistics, 1957, 28, № 1,195.
16. Box G.E J*., Wilson K.B. On the Experimental Attainement, of Optimum Conditions.
Journal of the Royal Statistical society, series B, 13, № 1,1.
17. Большее Л.Н., Смирнов H.B. Таблицы математической статистики. - М.:
Вычислительный центр АН СССР, 1968.
18. Брандт 3. Статистические методы анализа наблюдений. - М.: Мир, 1975.
19. Браунли К.А. Статистическая теория и методология в науке и технике. - М.:
Наука, 1977.
20. Бродский В.З. Введение в факторное планирование эксперимента. - М.: Нау-
ка, 1976.
21. Бродский В.З. Многофакторные регулярные планы. - М.: Изд-во МГУ, 1972.
22. Бродский А.Д., Кан В.Л. Краткий справочник по математической обработке
результатов измерений. - М.: Стандартно, 1960.
23. Бурмистров ГЛ. Основы метода наименьших квадратов. - М.: Госгеолтех-
издат, 1963.
24. Вапник ВЛ. Восстановление зависимостей по эмпирическим данным. — М.:
Наука, 1979.
25. Великанов М.Л.;Ошибки измерения и эмпирические зависимости. — Л.: Гидро-
метеоиздат, 1962.
26. Винарский М.С., Лурье М.В. Планирование экспериментов в технологических
исследованиях. - Киев: Техника, 1975.
234
27. Гнеденко Б.В. Беседы о математической статистике. - М.. Знание, 1968.
28. Гмурман В.Е. Теория вероятностей и математическая статистика. - М.: Выс-
шая школа, 1977.
29. Голикова Т.И., Панченко Л.А., Фридман М.З. Каталог планов второго порядка
Ч. I и II. - М.: Изд-во МГУ, 1975.
30. Головенко А.Г Математическая обработка опытных данных. - Минск: Изд-во
БПИ, 1960.
31. Гольцман Ф.М. Статистические модели интерпретации. - М.: Наука, 1971.
32. Горя В.С. Алгоритмы математической обработки результатов исследований. -
Кишинев: Штиинца, 1978.
33. Грановский Ю.Ф., Любимова Т.Н., Мурашова Т.И., Стахов А.Б. Планирование
эксперимента. - Библиография прикладных работ за 1969-1970 гг. - М.: Изд-во
МГУ, 1974.
34. Грановский Ю.Ф., Мурашова Т.И., Стахов А.Б., Адлер Ю.П. Планирование
эксперимента. - Библиография прикладных работ за 1966-1968 гг. - М.: Изд-во
МГУ, 1971.
' 35. Гришин В.К. Статистические методы анализа и планирования экспериментов.
- М.: Изд-во МГУ, 1975.
36. Гроот Моррис. Оптимальные статистические решения. — М.: Мир, 1974.
37. Гутер Р.С., Овчинский Б.В. Элементы численного анализа и математической
обработки результатов опыта. - М.: Наука, 1970.
38. Даименд С. Мир вероятности и статистики в йауке. - М.: Статистика, 1970.
39. Денисов В.И. Математическое обеспечение системы ЭВМ - эксперимента-
тор. - М.: Наука, 1977.
40. Денисов В.И., Попов А.А. А-, Е- оптимальные и ортогональные планы регрес-
сионных экспериментов для полиномиальных моделей. Препринт. - М.: Изд-во Науч-
ного Совета по кибернетике, 1976.
41. Длин А.М. Математическая статистика в технике. - М.: Советская наука,
1958.
42. Долинский Е.Ф. Обработка результатов измерений. - М.: Изд-во стандартов.
1973.
43. Дрейпер Н. и Смит Г Прикладной регрессионный анализ. - М.: Статистика,
1973.
44. Дроздов Н.Д. Линейная алгебра в теории уравнивания измерений. - М.:
Недра, 1972.
45. Дружинин Н.К Выборочное наблюдение и эксперимент. - М.: Статистика,
1977.
46. Дукарский О.М., Закурдаев А.Г. Статистический анализ и обработка наблю-
дений на ЭВМ ”Минск-22”— М.: Статистика, 1971.
47. ДюгеД. Теоретическая и прикладная статистика. - М.: Наука, 1972.
48. Ермаков С.М. Метод Монте-Карло и смежные вопросы. - М.: Наука, 1971.
49. Ермольев Ю.М., Ляшко И.И., Михалевич В.С. и др. Математические методы
исследования операций. - Киев: Вища школа, 1979.
50. Ефимова М.Р. Множественная корреляция. - М.: Изд-во МИУ, 1977.
51. Ефимова М.Р. Теория корреляции (Парная зависимость). - М.: Изд-во МИУ,
1976.
52. Закс Лотар. Статистическое оценивание. - М.: Статистика, 1976.
53. Зедгинидзе И.Г Математическое планирование эксперимента для исследова-
ния и оптимизации свойств смесей. - Тбилиси: Мецниереба, 1971.
54. Зингер А.А. Элементы теории статистических решений. - Л.: Изд-во ЛЭТИ,
1977.
55. Иванов А. Статистические методы в инженерных исследованиях. - М.: Изд-во
МЭИ, 1976.
56. Ильин И.Р. Таблицы для статистической обработки экспериментальных дан-
ных. - Кишинев: Штиинца, 1976.
57. Инструкция и описание программ для статистической обработки малой вы-
борки. - Л.: Судостроение, 1977.
235
58. Исмаилов Ш.Ю. Математическая статистика и обработка результатов измере-
ний. - Л.: Изд-во ЛЭТИ, 1977.
59. Карлин С., Стадден В. Чебышевские системы и их применение в анализе и
статистике. - М.: Наука, 1976.
60. Кассандрова О.Н., Лебедев В.В. Обработка результатов наблюдений. - М.:
Наука, 1970.
61. Кемниц Ю.В. Определение параметров эмпирических формул методом наи-
меньших квадратов. - М,: Недра, 1964.
62. Кендэл М. Дж. Ранговая корреляция. - М.: Статистика, 1975.
63. Кендэл М. Дж. Многомерный статистический анализ и временные ряды. -
М.: Наука, 1976.
64. Кендэл М. Дж., Стюарт А. Статистические выводы и связи. - М.: Наука, 1973.
65. Клейнен Дж. Статистические методы в имитационном моделировании. - М.:
Статистика, 1978.
66. Клепиков Н.П., Соколов С.Н. Анализ и планирование экспериментов методом
максимума правдоподобия. - М.: Наука, 1964.
67. КоксД.В., Хинкли Д. Теоретическая статистика. - М.: Мир. 1978.
68. Колесников А.Ф. Основы математической обработки результатов измерений.
Томск: Изд-во ТГУ, 1963.
69. Кол кот Э. Проверка значимости. - М.: Статистика, 1978.
70. Конюховский В.В. Критерии согласия однородности и независимости. - М.:
Изд-во МГУ, 1970.
71. Коуден Д Статистические методы контроля качества. - М.: Физматгиз, 1961.
72. Крамер Г. Математические методы статистики. - М.: Мир, 1975.
73. Круг Г.К., Сосулин Ю.А., Фатуев В.А. Планирование эксперимента в задачах
идентификации и экстраполяции. - М.: Наука, 1977.
74. Леонтьев Н.Л. Техника статистических вычислений. - М.: Лесная промыш-
ленность, 1966.
75. Леман Э.Л. Проверка статистических гипотез. - М.: Наука, 1964.
76. Линник Ю.В. Метод наименьших квадратов и основы теории обработки наблю-
дений. - М.: Физматгиз, 1962.
77. Лаули Д.И. и Максвелл А.Э. Факторный анализ. Статистический метод. - М.:
Мир, 1967.
78. Львовский Е.Н. Пассивный и активный эксперимент при изучении механи-
ческих характеристик бетона. — Кишинев: Картя Молдовеняска, 1970.
79. Львовский Е.Н. Исследование механических характеристик бетона с приме-
нением ЭВМ статистических методов и активных экспериментов. - Кишинев: Изд-во
КПИ, 1970.
80. ЛитЛгр E.N. Research of Mechanical Characteristics of concrete using Computer,
Statistical Methods and . Active Experiments Summaries Rilem Symposium. - Copenhagen,
1971. - •
81. Lvovskiy E.N. Calculation of Prestressing Lossesin Fitting caused by Greep of
Concrete using Multifactor Models, VIII International Congress of the Federation Inter-
national de la Precontrainte. - London, 1978.
82. Львовский E.H., Бордеяну Г.В. Экспериментально-статистические исследова-
ния деформаций ползучести бетона с построением математических моделей второго
порядка для их вычисления и прогнозирования. - В сб.: Прочность, деформативность
и устойчивость строительных конструкций. - Кишинев: Штиинца, 1977.
83. Lvovskiy E.N., Bordeyanou G. V. Une methode statistique nouvelle pour le calcul
des caracteristiques de fluage des betons. Bulletin de liaison de laboratoires des pouts et
chaussees, N 91, 1977.
34. Львовский Ё.Н., Бордеяну Г.В., Которобай B.M. и др. Планирование экспери-
ментов и статистическая обработка их результатов при исследовании механических
характеристик бетона и* железобетонных конструкций, — Известия вузов. Строитель-
ство и архитектура, 1976, № 6.
85. Львовский Е.Н., Которобай В.М. Экспериментально-статистические иссле-
дования начального модуля упругости пропаренных заводских бетонов с построением
236
многофакторных математических моделей для его вычисления. - В об.: Прочность,
деформативн*сть и устойчивость строительных конструкций. - Кишинев: Штиинца,
1977.
86. Мазмишвили А.И., Беляев Б.И. Сборник задач по теории ошибок и способу
наименьших квадратов. - М.: Изд-во Московского горного института, 1960.
37. Маркова Е.В. Руководство по применению латинских квадратов при пла-
нировании эксперимента с качественными факторами. — Челябинск: Изд-во УралНИИ-
стройпроекта, 1971.
88. Маркова Е.В., Лисенков А.Н. Планирование эксперимента в условиях неодно-
родностей. -- М.: Наука, 1973.
89. Математическая статистика и планирование эксперимента. Библиографичес-
кий указатель отечественной и иностранной литературы. 1960-1969 гг. - М.: Изд-во
МЭИ, 1970.
90. Материалы второй всесоюзной конференции по планированию эксперимента.
- М.: Изд-во МЭИ, 1968.
91. Методика статистической обработки эмпирических данных. - М.: Стандарт-
гиз, 1963.
92. Митропольский А.К. Введение в статистическое исчисление. - Л.: Изд-во
ВЗЛТИ, 1955.
93. Митропольский А.К. Техника статистических вычислений. - М.: Наука, 1971.
94. Мудрое В.И. Методы обработки наблюдений (квазиправдоподобные оценки).
- М.: Советское радио, 1976.
95. Налимов В.В. Применение математической статистики при анализе вещества.
- М.: Физматгиз, 1960.
96. Налимов В.В. Статистические методы описания химических и металлургичес-
ких процессов. - М.: Металлу ргиз дат, 1963.
97. Налимов В.В. Теория эксперимента. - М.: Наука, 1971.
98. Налимов В.В. Логические основания прикладной математики. Препринт. -
М.: Изд-во МГУ, 1971, № 24.
99. Налимов В.В. Вероятностная модель языка. - М.: Наука, 1975.
100. Налимов В. В. Язык вероятностных представлений. - Препринт. - М.: Изд-во
научного совета по кибернетике, 1976.
101. Налимов В.В., Голикова Т.Н Логические основания планирования экспери-
мента. - М.: Металлургия, 1976.
102. Налимов В.В., Чернова НА. Статистические методы планирования экстре-
мальных экспериментов. - М.: Наука, 1965.
103. Негура НГ. Разработка алгоритма и программы анализа и выбора опти-
мальных парных зависимостей в теории бетона и железобетона. — Доклады республи-
канской конференции ’’Повышение качества и эффективности бетонных конструкций
и изделий на базе применения передовой технологии”. Кишинев, 1978.
104. Немчинов В.С. Полиномы Чебышева и математическая статистика. - М.:
Тип. ”Красное знамя”, 1946.
105. Никитина ЕЛ Планирование и анализ эксперимента (модели третьего по-
рядка). - М.: Изд-во МГУ, 1976.
106. Николаева Л.С. Программы по регрессионному и конфлюэнтному анализу.
Препринт. - М.: Изд-во МГУ, 1969, № 9.
107. Новик Ф.С. Планирование эксперимента в металловедении. - М.: Машино-
строение, 1974.
108. Новые идеи в планировании эксперимента / Под ред. В.В. Налимова. - М.:
Наука, 1969.
109.0 преподавании математической статистики экспериментаторам. — М.:
Изд-во МГУ, 1971.
110. Орлова Л. Линейный регрессионный анализ. - М.: Изд-во МГУ, 1971.
111. Пазман А., Федоров В.В. Планирование физических экспериментов. Обзор.
- Дубна: Объединенный институт ядерных исследований, 1967.
112. Ратшпп NJ., Lvovskiy E.N. Mehrfaktorenmodelle Zur Bestimmung der Kriech-
kennwerte von Beton. Bauplanung Bautechnik, N 7,1972.
237
113. Пасхавер И. С. Закон больших чисел и статистические закономерности. -
М.: Статистика, 1974.
114. Пирятин В.Д. Обработка результатов экспериментальных исследований, -
Харьков: Изд-во ХГУ, 1967.
115. Планирование оптимальных экспериментов / Под ред. М.Б. Малютова. - М.;
Изд-во МГУ, 1975, № 48.
116. Планирование эксперимента. Литература на русском и украинском языках
за 1965-1969 гг. - М.: Гос. публ. науч.-техн. б-ка СССР, 1969.
117. Планирование эксперимента. Список литературы на иностранных языках
за 1965-1970 гг. - М.: Гос. публ. науч.-техн. б-ка СССР, 1973.
118. Планирование эксперимента. Указатель литературы на русском и украинс-
ком языках за 1970-1971 гг. - М.: Гос. публ. науч.-техн. б-ка СССР, 1972.
119. Плескунин В.И., Воронина Е.Д. Теоретические основы организации и анализа
выборочных данных в эксперименте. - Л.: Изд-во ЛГУ, 1979.
120. Померанцев В.В. Практическая методика корреляционного анализа. - М.:
Экономиздат, 1963.
121. Прикладная статистика. Анализ и оценка на ЭЦВМ регрессионных зависи-
мостей. - М.: Изд-во стандаров, 1975.
- 122. Прикладные программы по математической статистике для ЭВМ ”Минск-32”.
- Таллин: Изд-во АН ЭССР, 1977.
123. Прикладной многомерный статистический анализ. - Сб. тр. - М.: Наука,
1978.
124. Проблемы планирования эксперимента / Под ред. Г.К. Круга. - М.: Наука,
1969.
125. Программы по математической статистике для ЭВМ ”Минск-22”. - М.:
ОНТИ, 1969.
126. Протодьяконов М.М., Тядер Р.П. Методика рационального планирования
экспериментов. - М.: Наука, 1970.
127. Пустыльник Е.И. Статистические методы анализа и обработки наблюдений.
- М-: Наука, 1968.
128. Рао С.Р. Линейные статистические методы и их применения. - М.: Наука, 1968.
129. Романовскиц В.И. Математическая статистика. Т. I. - Ташкент: Изд-во АН
Уз. ССР, 1961.
130. Романовский В.И. Математическая статистика. Т. II. - Ташкент: Изд-во
АН Уз. ССР, 1963.
131. Романовский В.И. Применение математической статистики в опытом деле. -
М. - Л.: Гостехиздат, 1947.
132. Рохвангер А.Е., Шевяков А.Ю. Математическое планирование научно-техни-
ческих исследований (статистический подход). - М.: Наука, 1975.
133. Румшиский ЛЗ. Математическая обработка результатов эксперимента. -
М.: Наука, 1971.
134. Румшиский ЛЗ. Элементы теории вероятностей. - М.: Наука, 1970.
135. Румшиский Л.З., Смирнов С.Н. Методы обработки результатов экспери-
ментов. - М.: Изд-во МИСиС., 1973.
136. Саульев В.К. Математическая обработка результатов наблюдений. - М.:
Изд-во МАИ, 1974.
137. Синдлер Ю.Б. Метод двуступенчатого статистического анализа и его прило-
жение в технике. - М.: Наука, 1973.
138. Смирнов Н.В., Дунин-Барковский И.В. Курс теории вероятности и мате-
матической статистики для технических приложений. - М.: Наука, 1969.
139. Справочник по теории вероятности и математической статистике. - Киев:
Наукова Думка, 1978.
140. Стойкова Л.С. Экстраполяция по методу наименьших квадратов с приме-
нением симметричных полиномов Чебышева - Лежандра. Препринт. - Киев: Изд-во
АН УССР, 1972, №72-7$.
141. Теория и практика измерения статистических характеристик. - Труды I
Всесоюзной конференции. Л., 1972.
238
142. Уорсинг А., Геффнер Дж. Методы обработки экспериментальных данных. -
М.: ИЛ, 1953.
143. Успенский А.Б., Федоров В.В Вычислительные аспекты метода наименьших
квадратов при анализе и планировании регрессионных экспериментов. - М.: Изд-во
МГУ, 1976.
144. Федоров В.В. Анализ экспериментов при наличии ошибок в контролируемых
переменных. Препринт. - М.: Изд-во МГУ, 1968, № 2.
145. Федоров В-В. Теория оптимального эксперимента. — М.: Наука, 1971.
146. (Й/ш Д Введение в теорию планирования эксперимента. - М.: Наука, 1970.
147. Хальд А. Математическая статистика с техническими приложениями. - М.:
ИЛ, 1956.
148. Хан Г., Шапиро С. Статистические модели в инженерных задачах. - М.: Мир,
1969.
149. Хикс Ч. Основные принципы планирования эксперимента. - М.: Мир, 1967.
150. Химмелъблау Д Актив процессов статистическими методами. — М.: Мир,
1973.
151. Хо томский В.И. Выравнивание статистических рядов по методу наимень-
ших квадратов (способ Чебышева) и таблицы для нахождения уравнений параболичес-
ких кривых. - М.: Госстацдартиздат, 1959.
152. Хьюстон А. Дисперсионный анализ. - М.: Статистика, 1971.
153. Численные методы математической статистики. Алгоритмы и программы. -
М-: Изд-во МГУ, 1976.
154. Чупров А. Л. Основные проблемы теоршт корреляции. - М.: Госстатиздат,
1960.
155. Шенк X. Теория инженерного эксперимента. — М.: Мир, 1972.
156. ШеффеД. Дисперсионный анализ. - М.: Физматгиз, 1963.
157. Ширяев А.Н. Статистический последовательный анализ. Оптимальные пра-
вила остановки. - М.: Наука, 1976.
158. Щербаков Е.Н., Сырбу Ф.П. Многофакторный статистический анализ влия-
ния качества цемента на величину усадки цементно-песчанных растворов. Труды
ЦНИИС Минтрасстроя. - М., 1974, выл. 77.
159. Щербаков Е.Н., Сырбу Ф.П. Эффективная методика многофакторного стати-
стического анализа физико-механических свойств бетона с помощью ЭВМ - В сб.г
Исследование надежности и качества железобетонных конструкций. - Куйбышев:
Изд-во Куйбышевского университета, 1978.
160. Щиголев Б.М. Математическая обработка наблюдений. - М.: Наука, 1969.
, 161. Яковлев КП. Математическая обработка результатов измерений. — М.:
Гостехиздат, 1953.
162. Яноши Л. Теория и практика обработки результатов измерений. - М.: Мир,
1968.
163. Яснопольский С,Л. Первичная обработка статистических данных. — М.*.
ЙВД-во МИСнС, 1971.
164. Яснопольский С. Л. Построение эмпирических формул и подбор их пара-
метров методом наименьших квадратов и методом средних. - М.: Изд-во МИСиС,
1972.
Учебное издание
Евгений Николаевич Львовский
Статистические методы построения
эмпирических формул
Зав. редакцией Е.С. Гридасова
Редактор Ж.И. Яковлева
Мл. редакторы Н.П. Майкова, Г.В. Вятоха
Художник В.И. Казакова
Художественный редактор В.И. Пономаренко
Технические редакторы Л.А. Муравьева, Л.М. Матюшина
Корректор Г.И. Кострикова
Оператор О.М. Есипова
ИБ№6160
Изд. № ФМ-863. Сдано в набор 26.11.87. Подл, в печать 14.07.88.
Формат 60x88/16. Бум. офсетная № 2. Гарнитура Пресс-Роман, Печать офсетная,
объем 14,70 усл. печ. л. 14,70 усл. кр.-отт. 15,06 уч. изд. л.
Тираж 20 000 экз. Зак. № 579. Цена 80 коп.
Издательство ’’Высшая школа”, 101430, Москва, ГСП-4, Неглинная ул., д. 29/14.
Набрано на набдрно-пишущих машинах издательства.
Отпечатано в Московской типографии № 8 Союзполиграфпрома при Государственном
комитете СССР по делам издательств , полиграфии и книжной торговли. 101898,
Москва, Хохловский пер., 7.