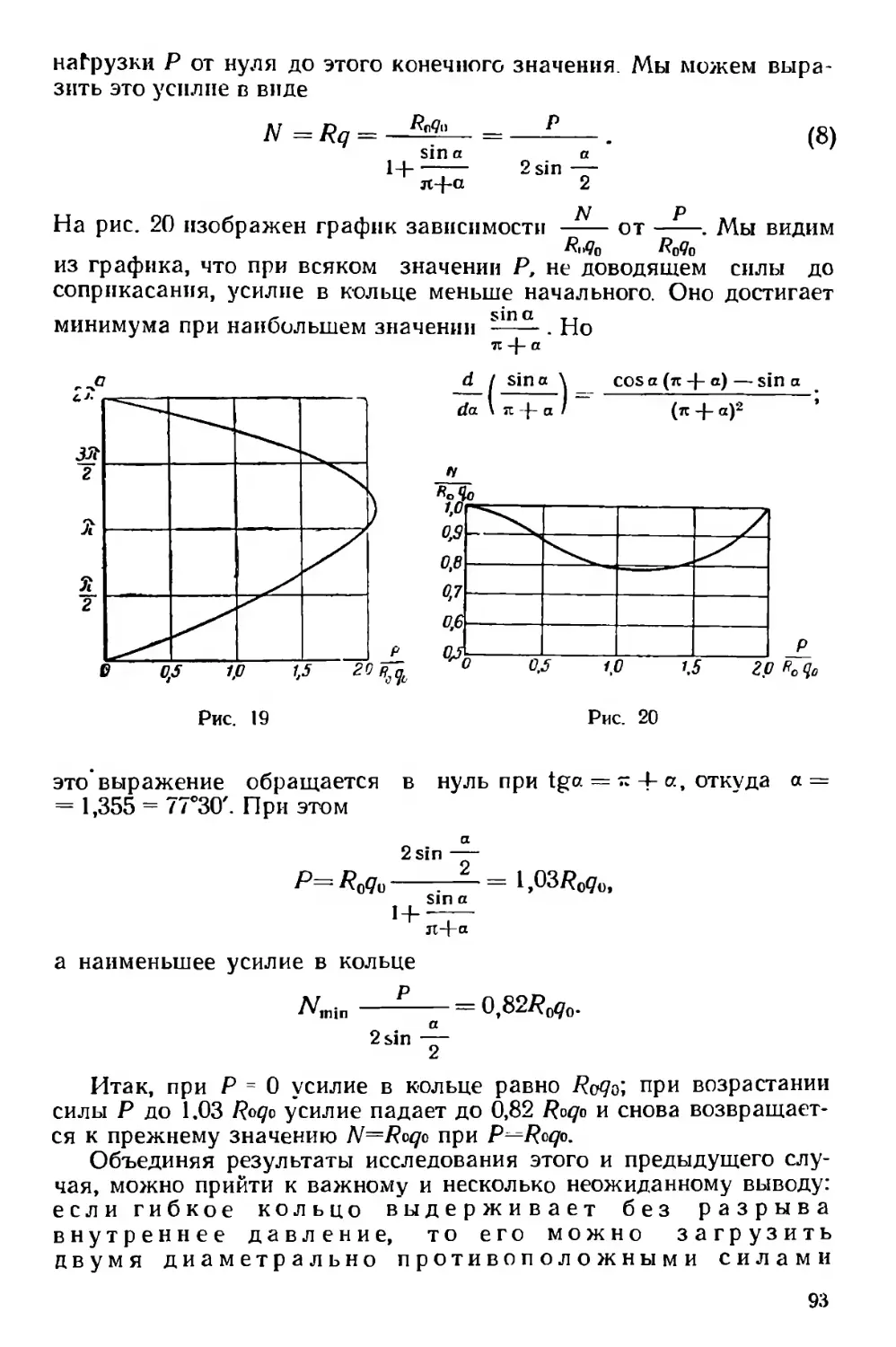
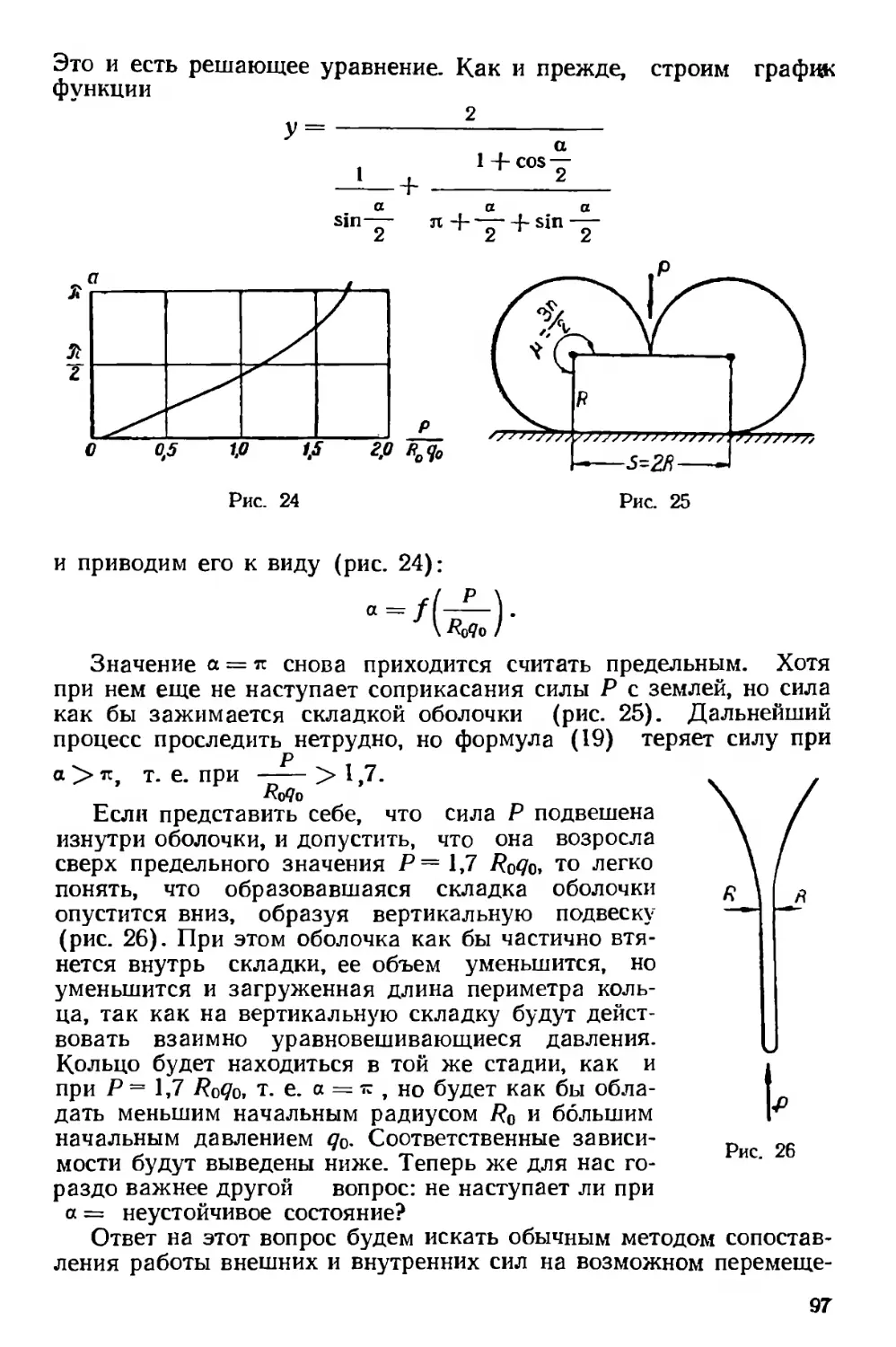
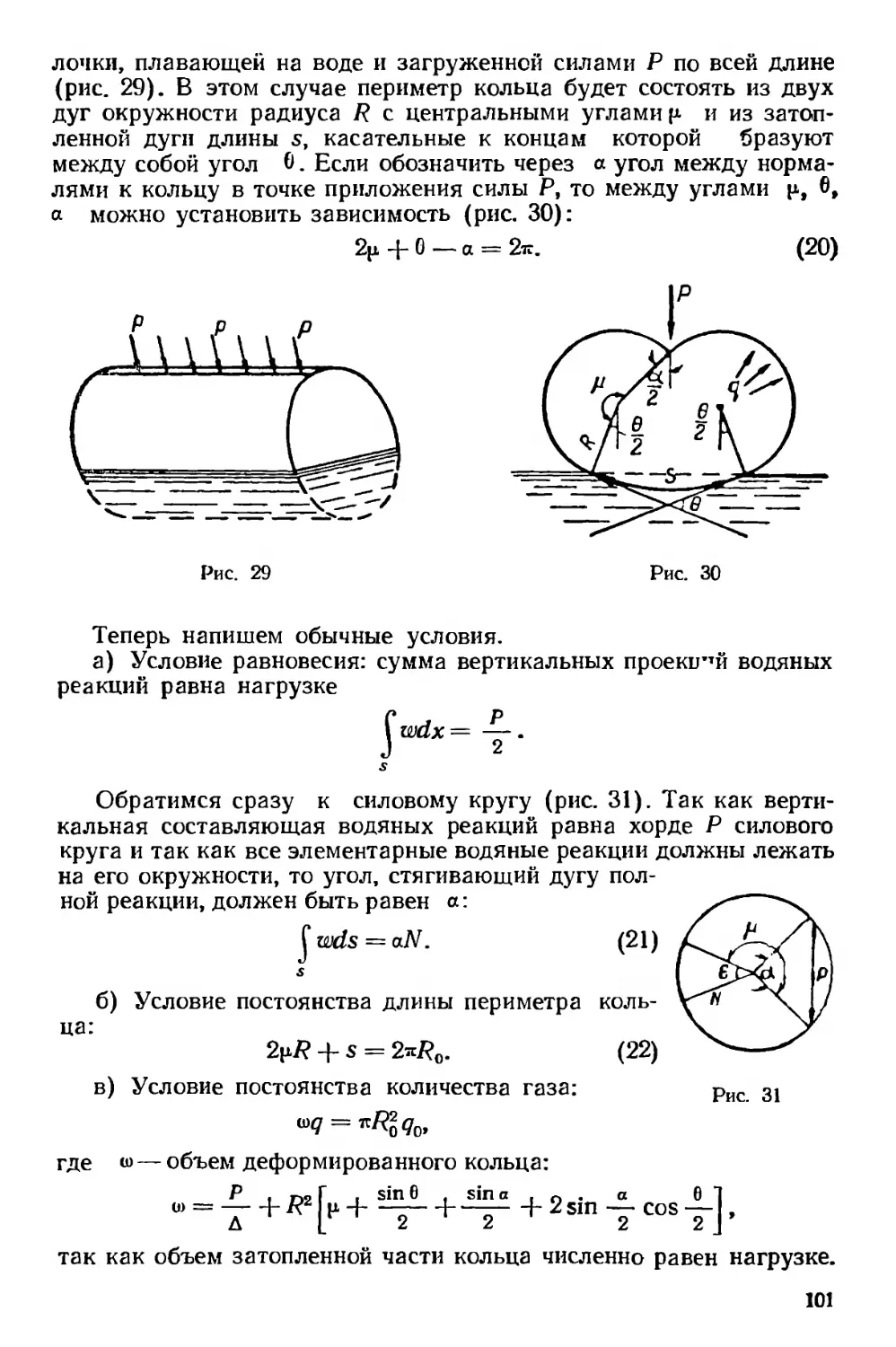
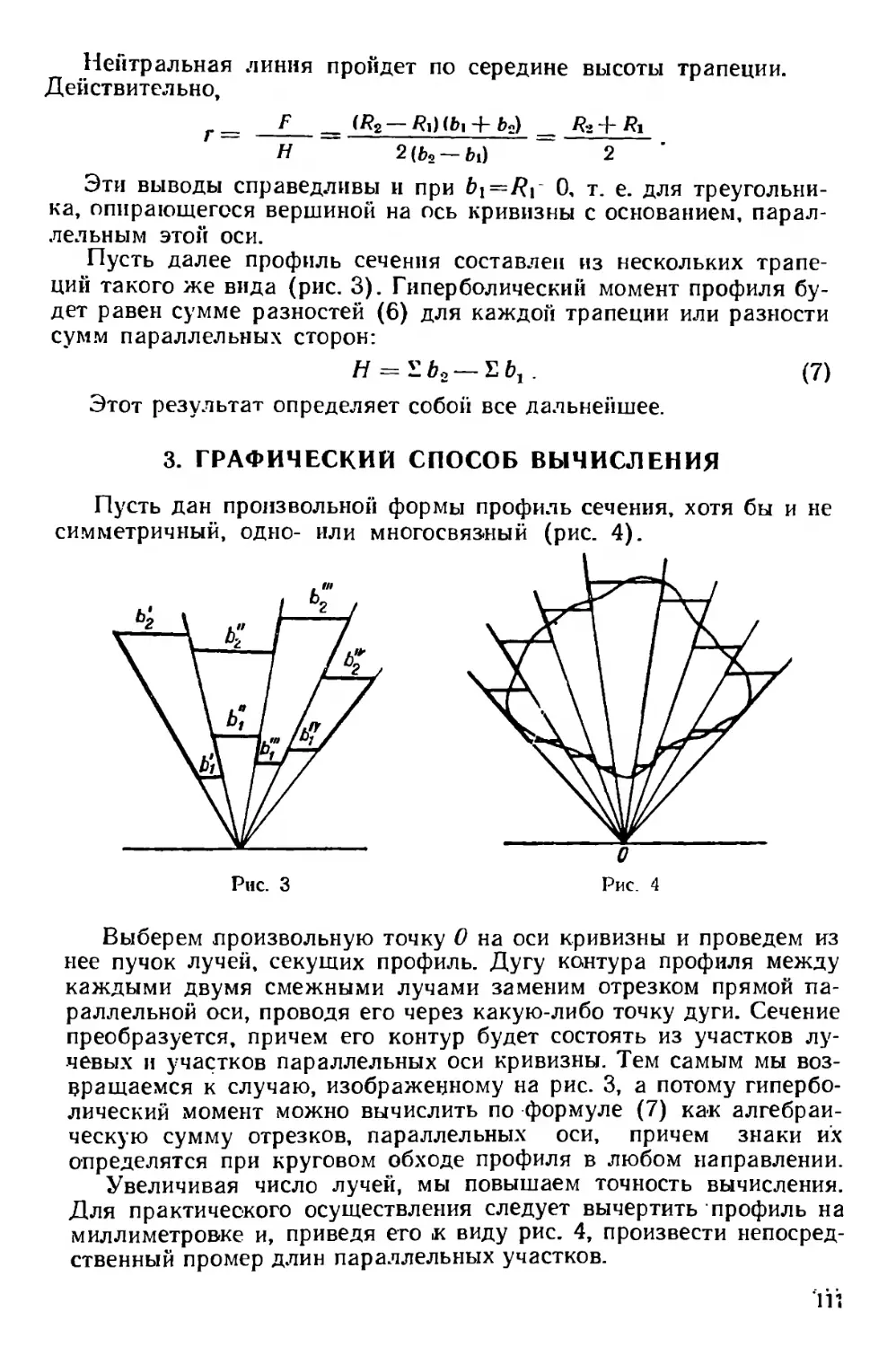
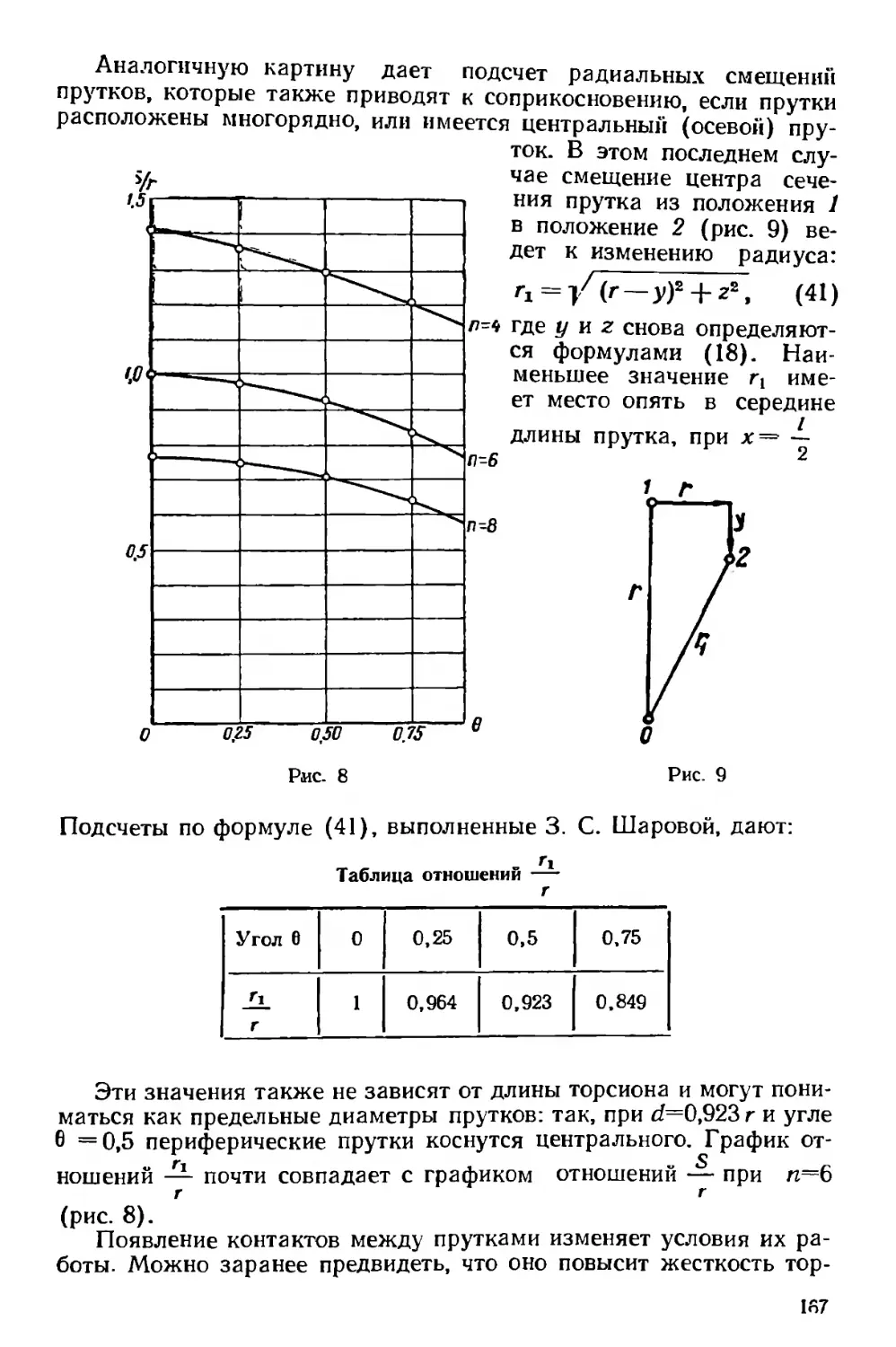
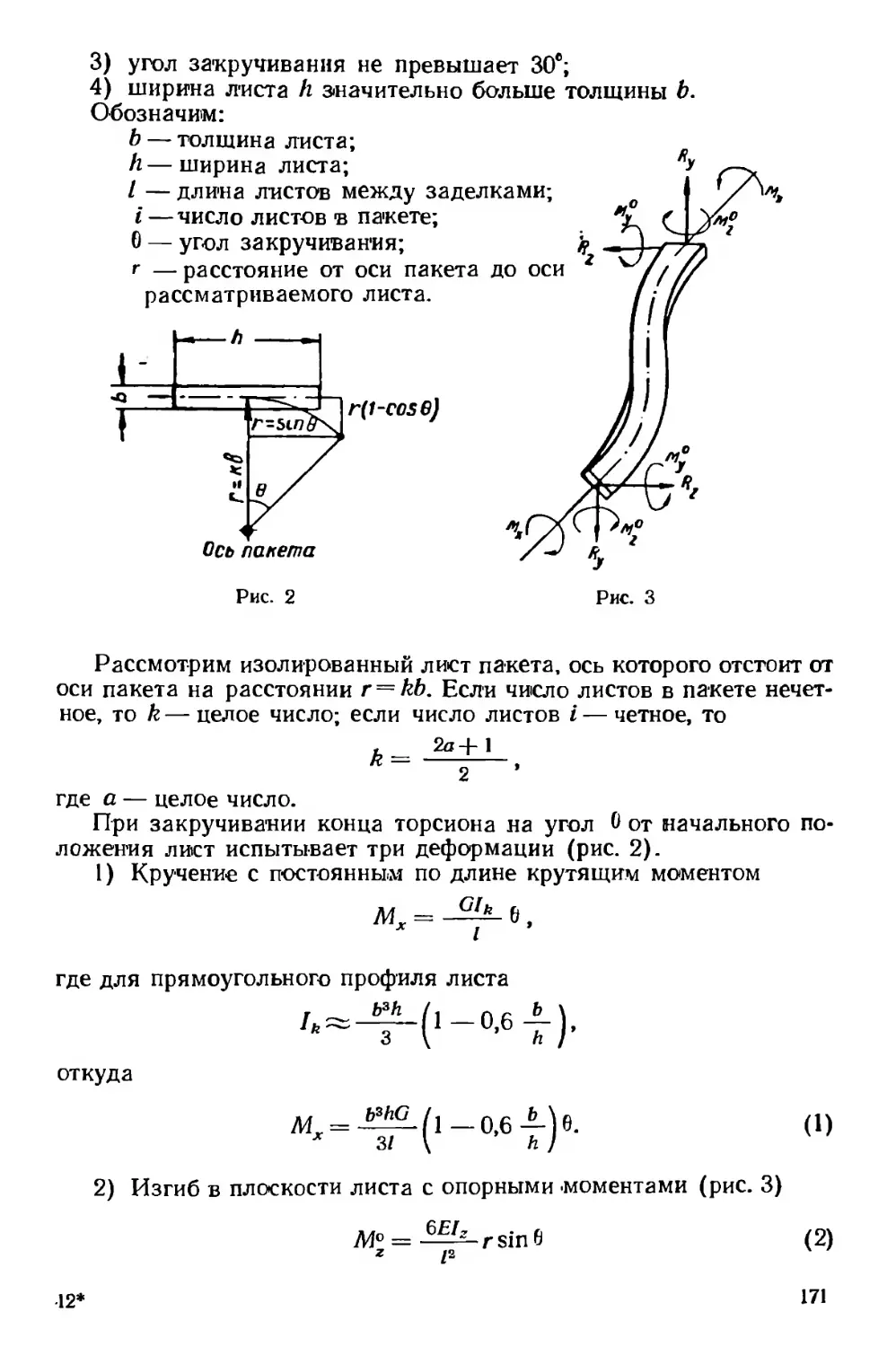
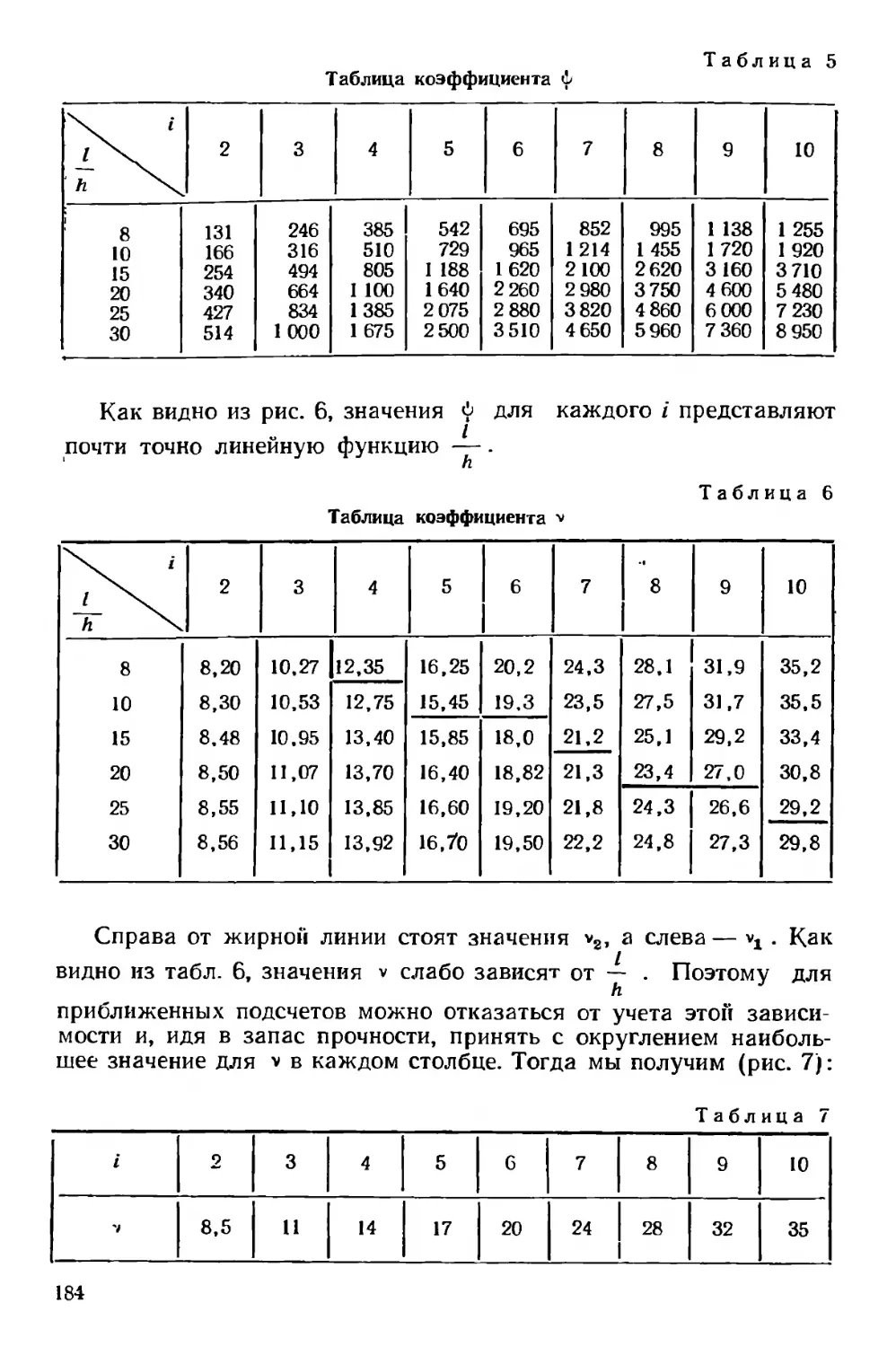
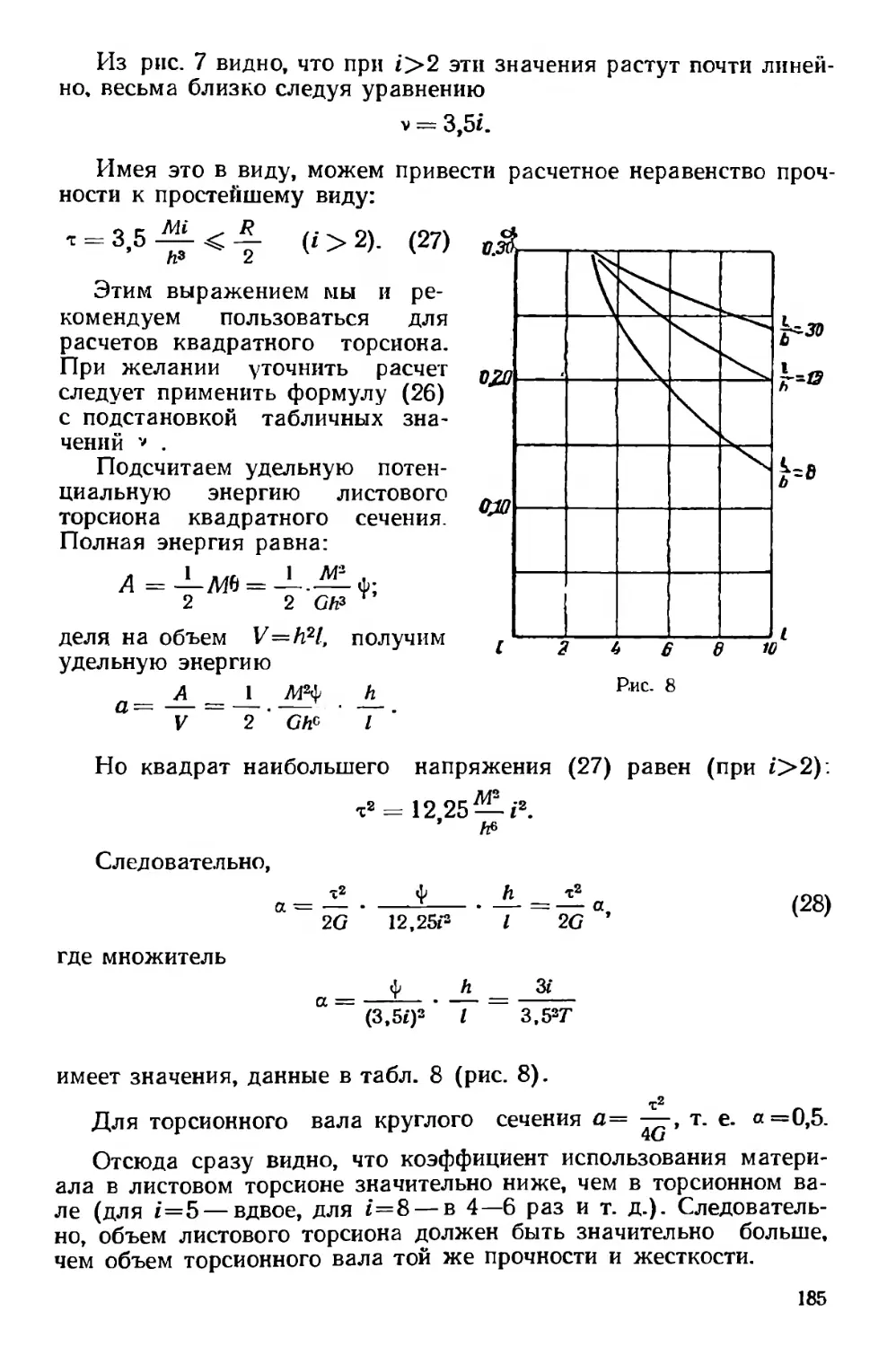
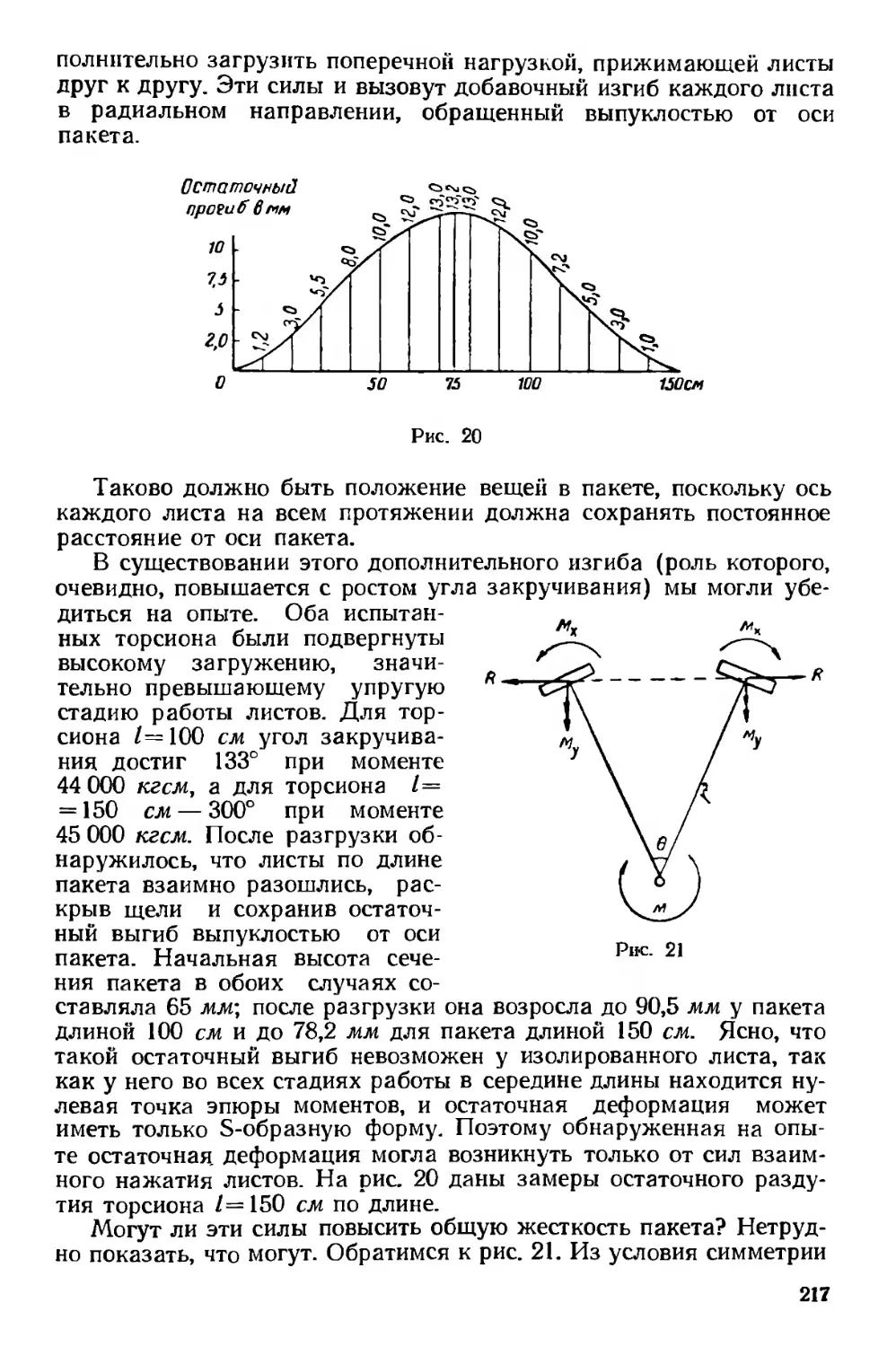
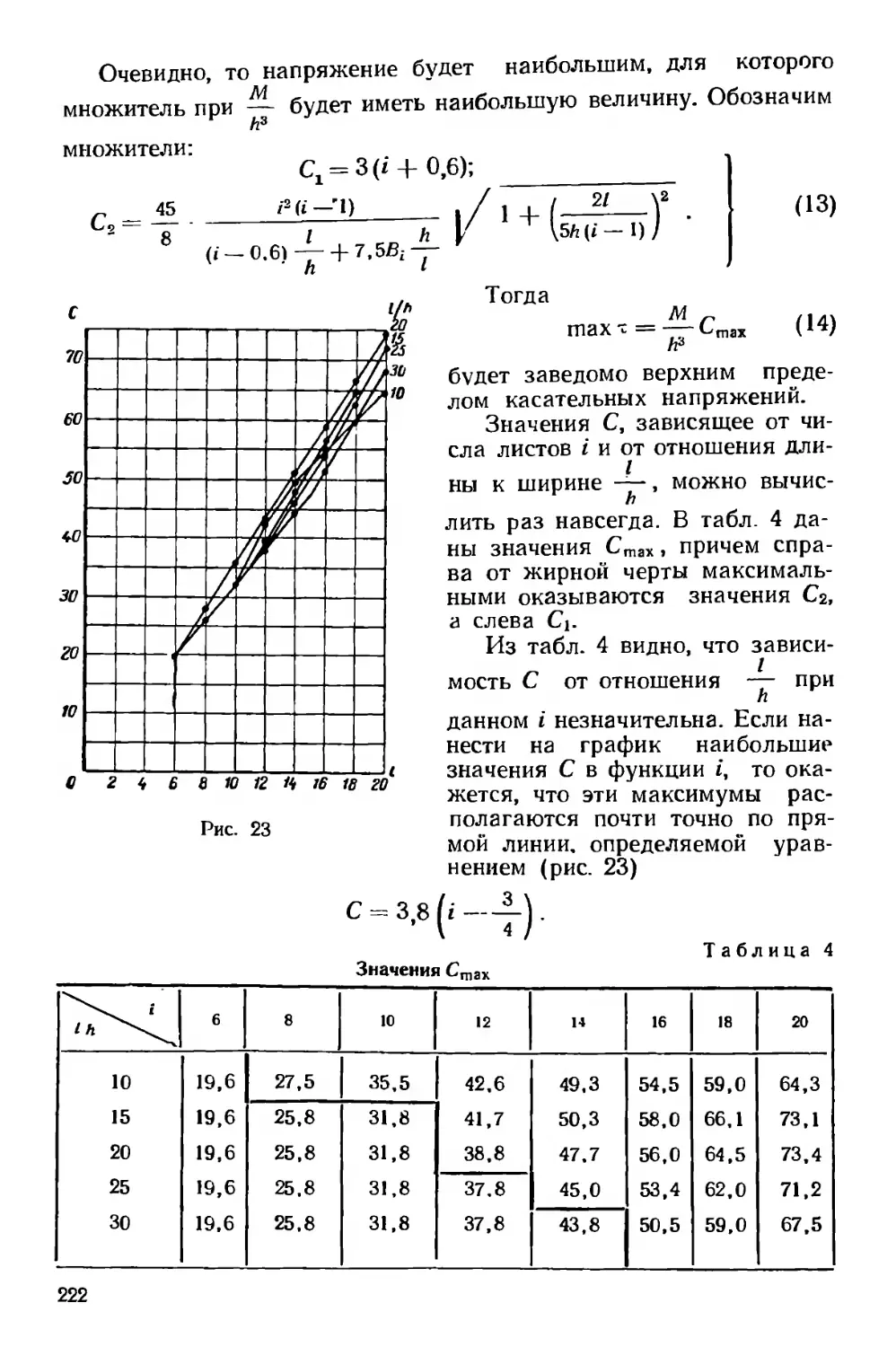
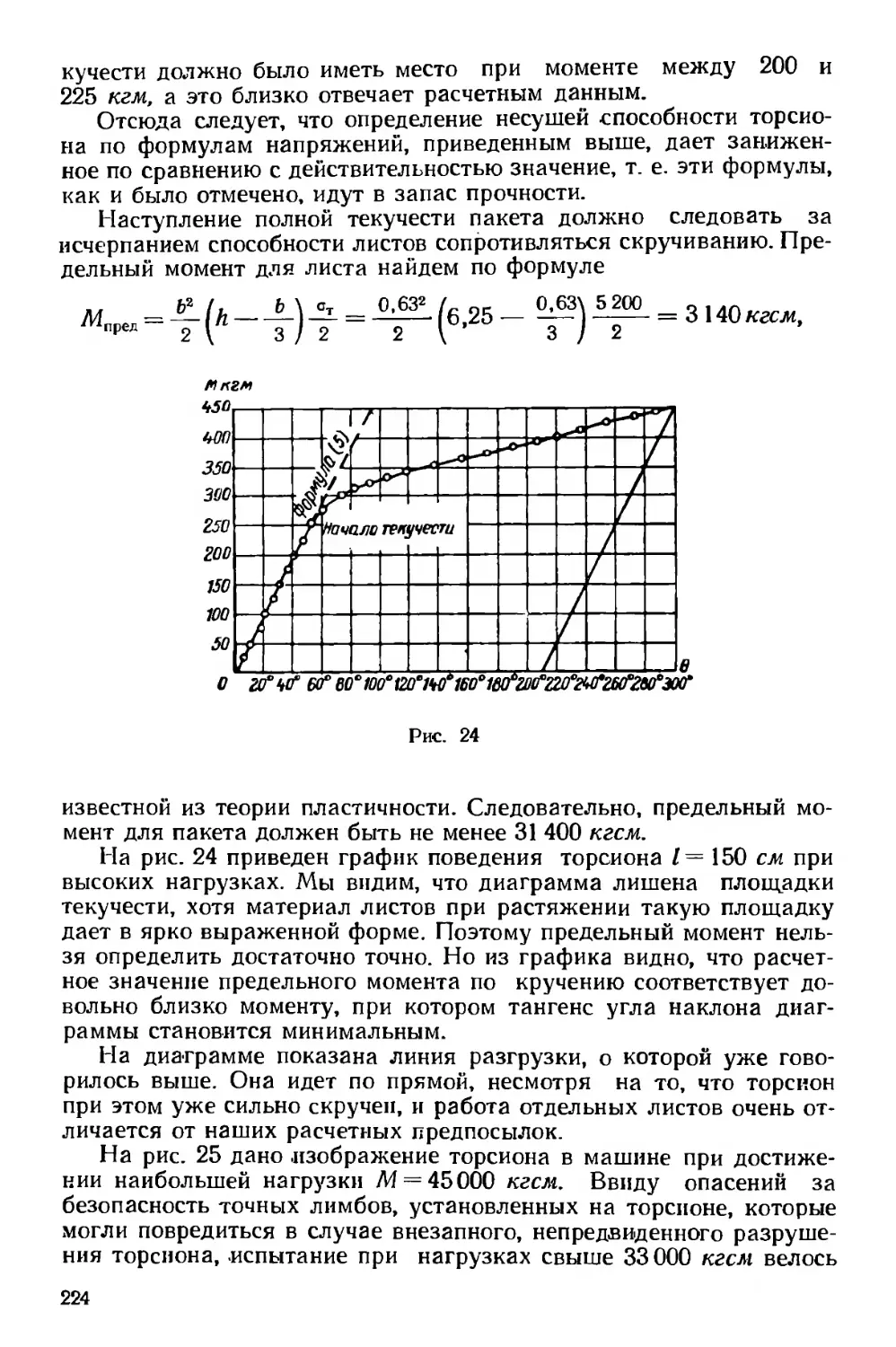
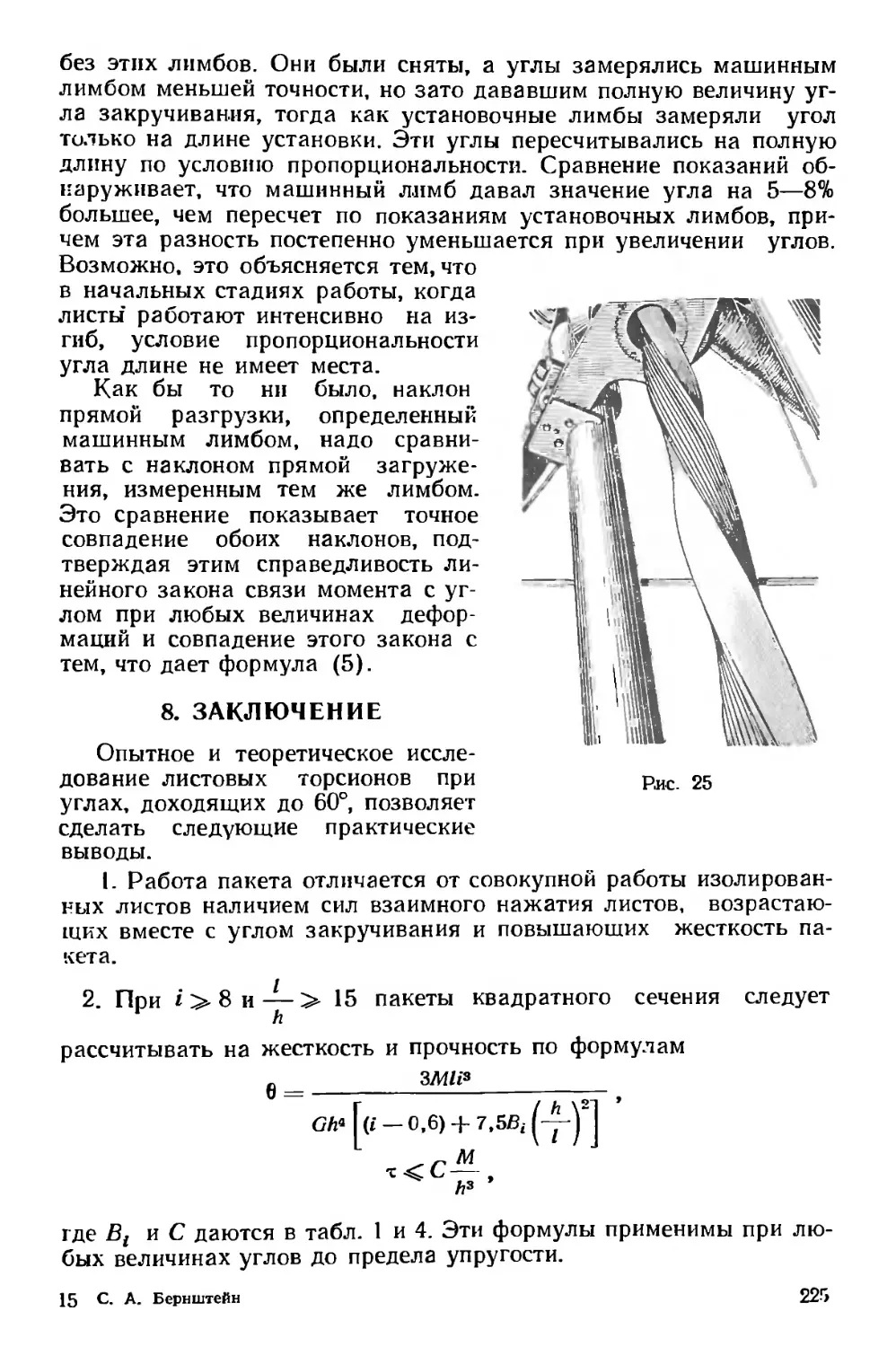
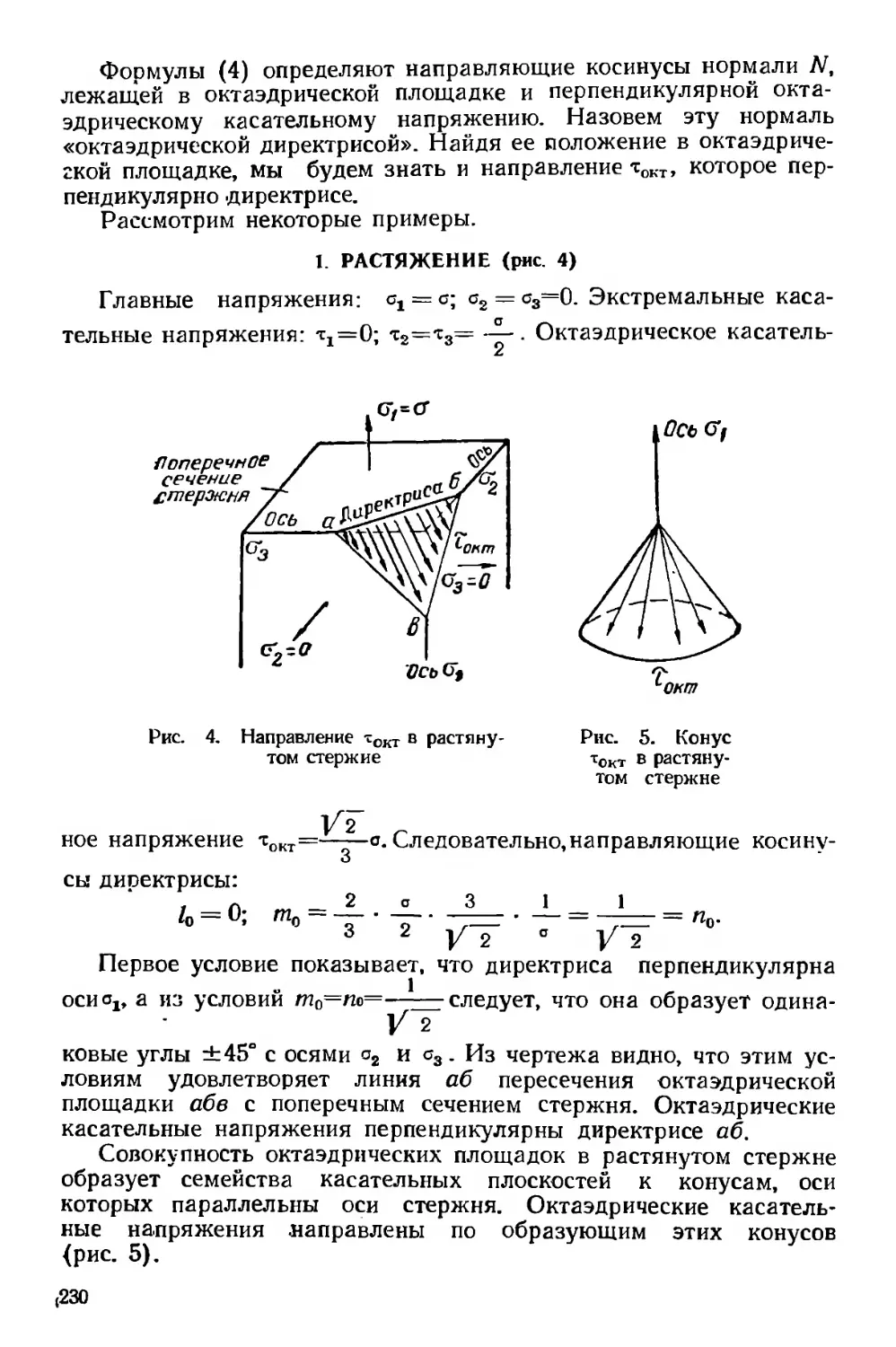
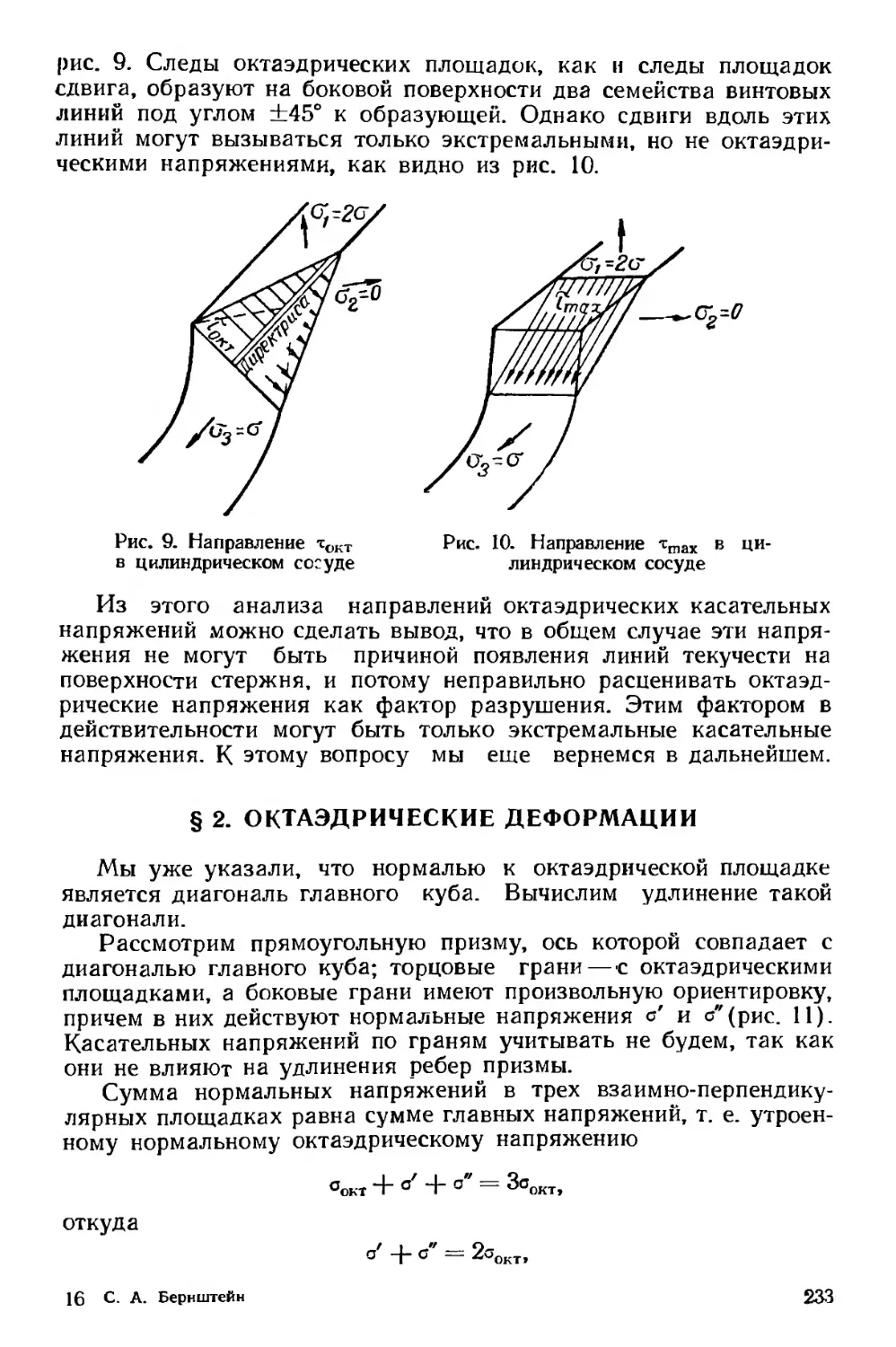
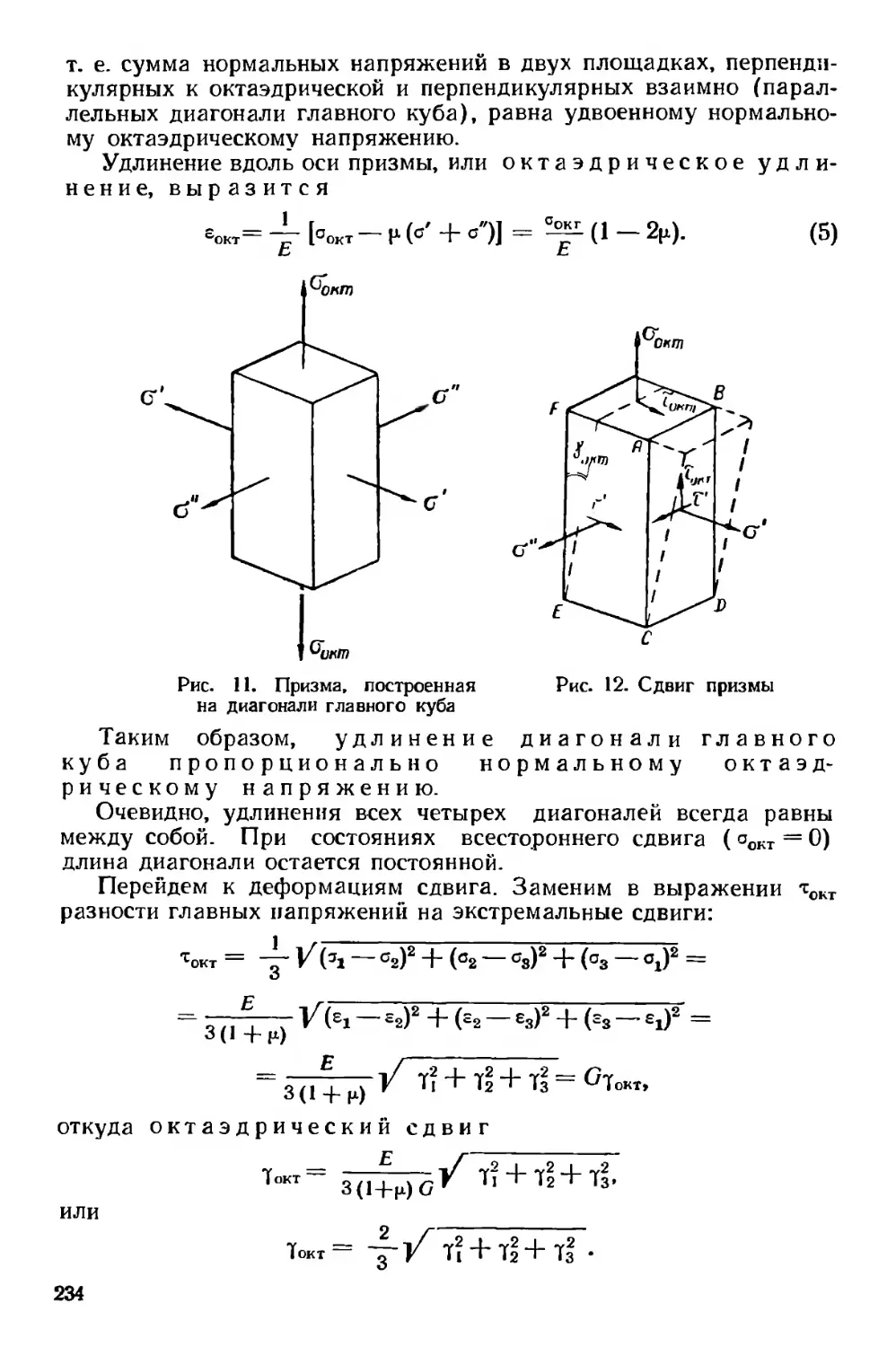
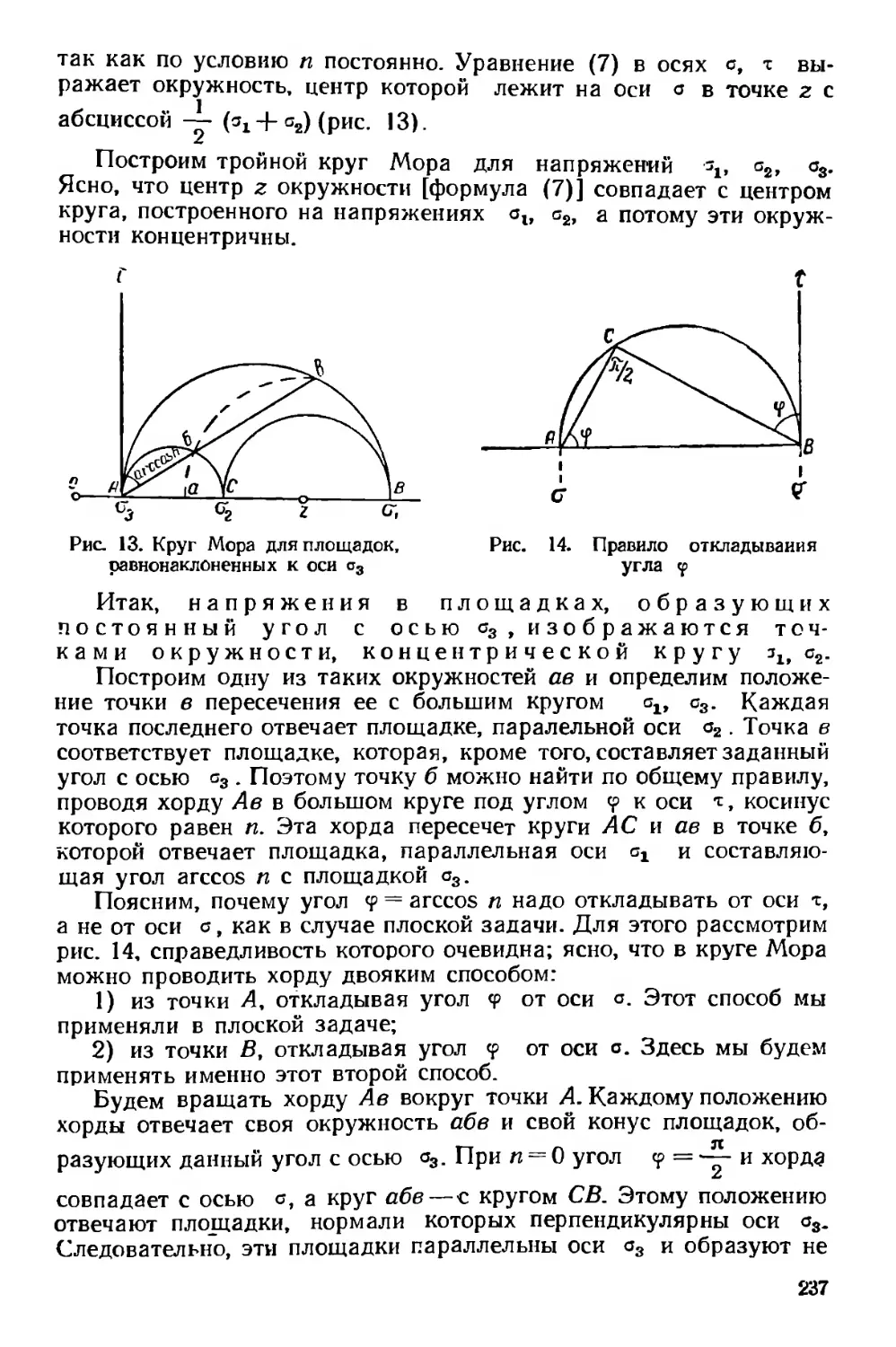
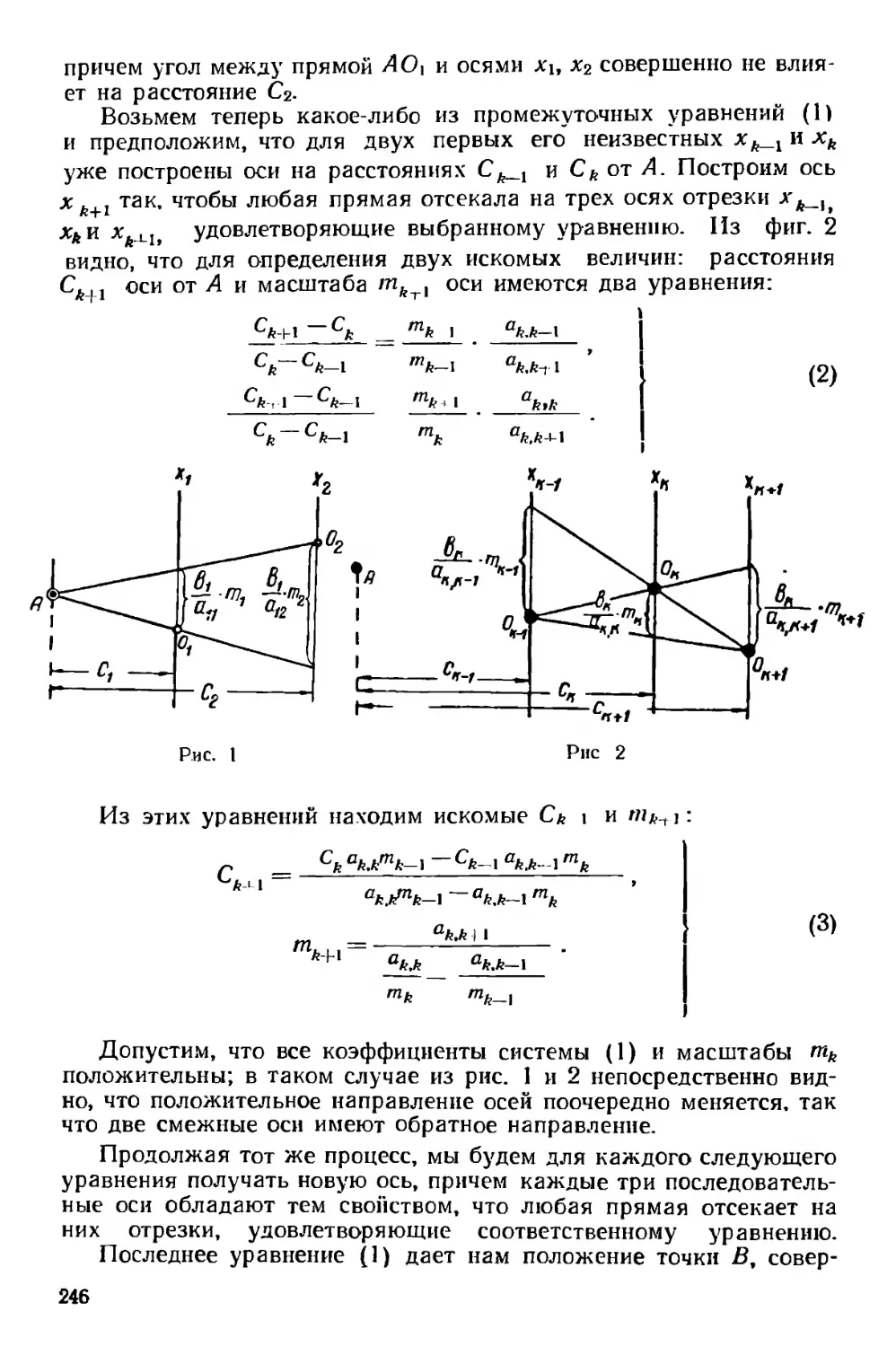
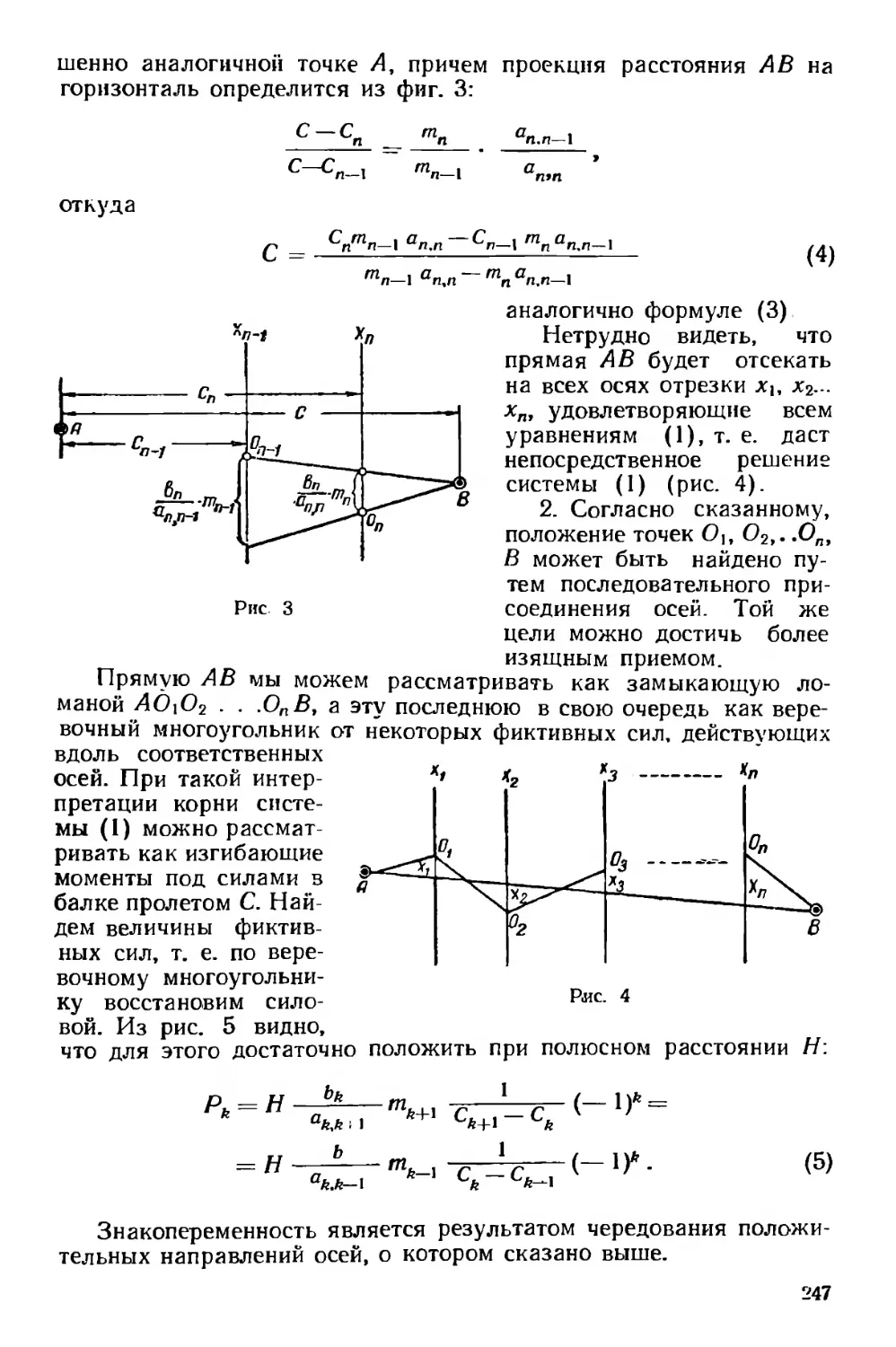
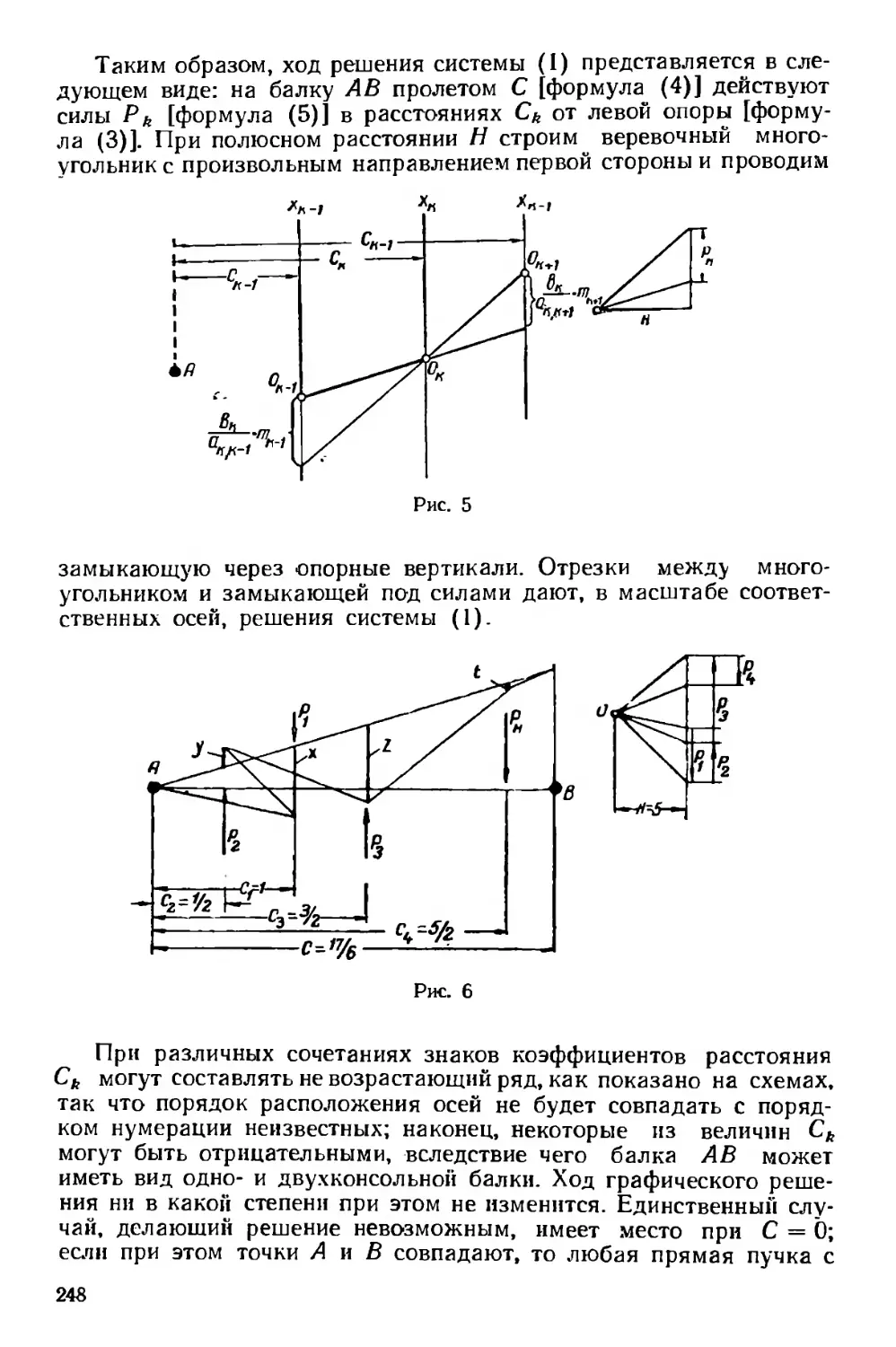
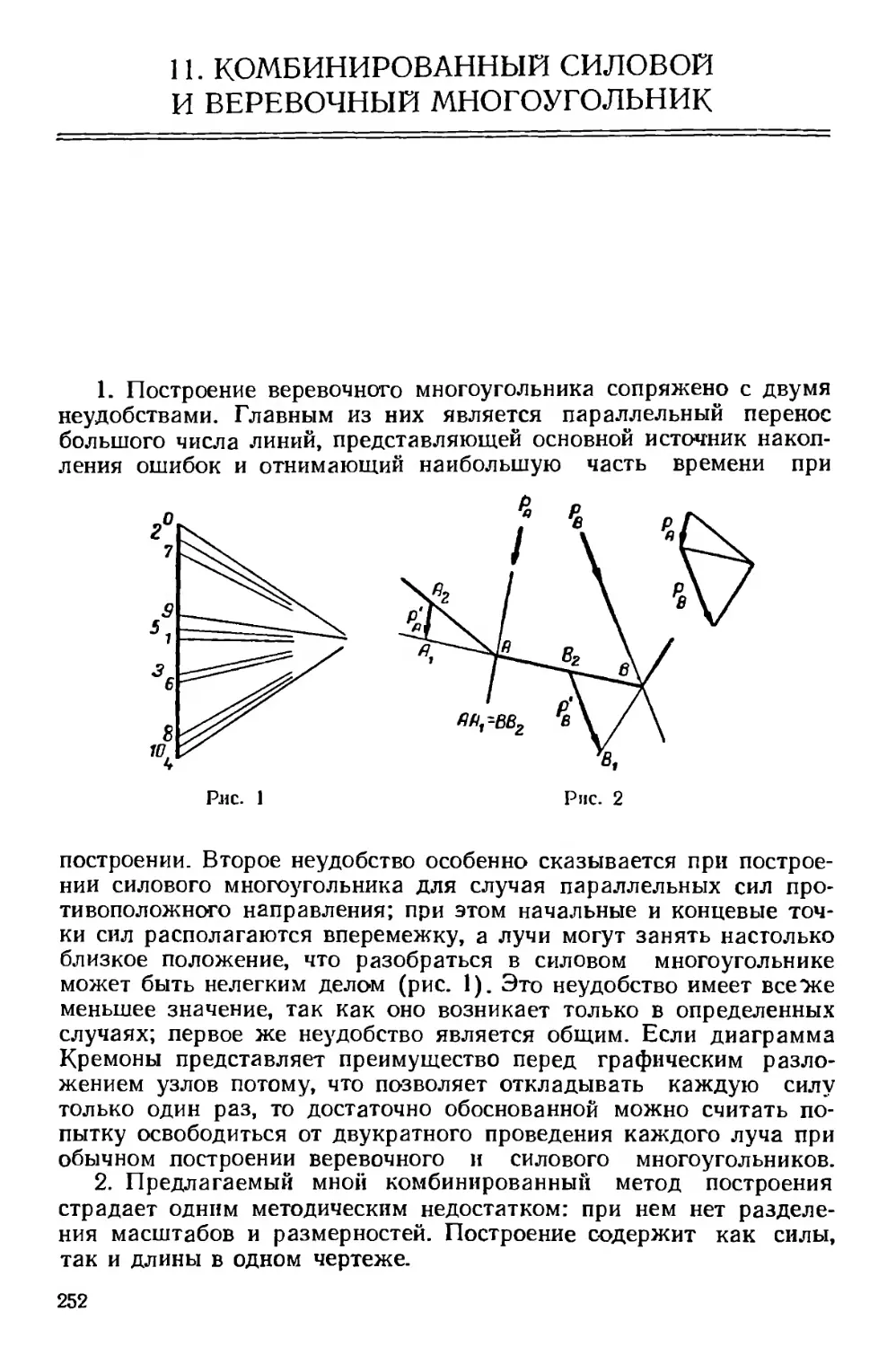
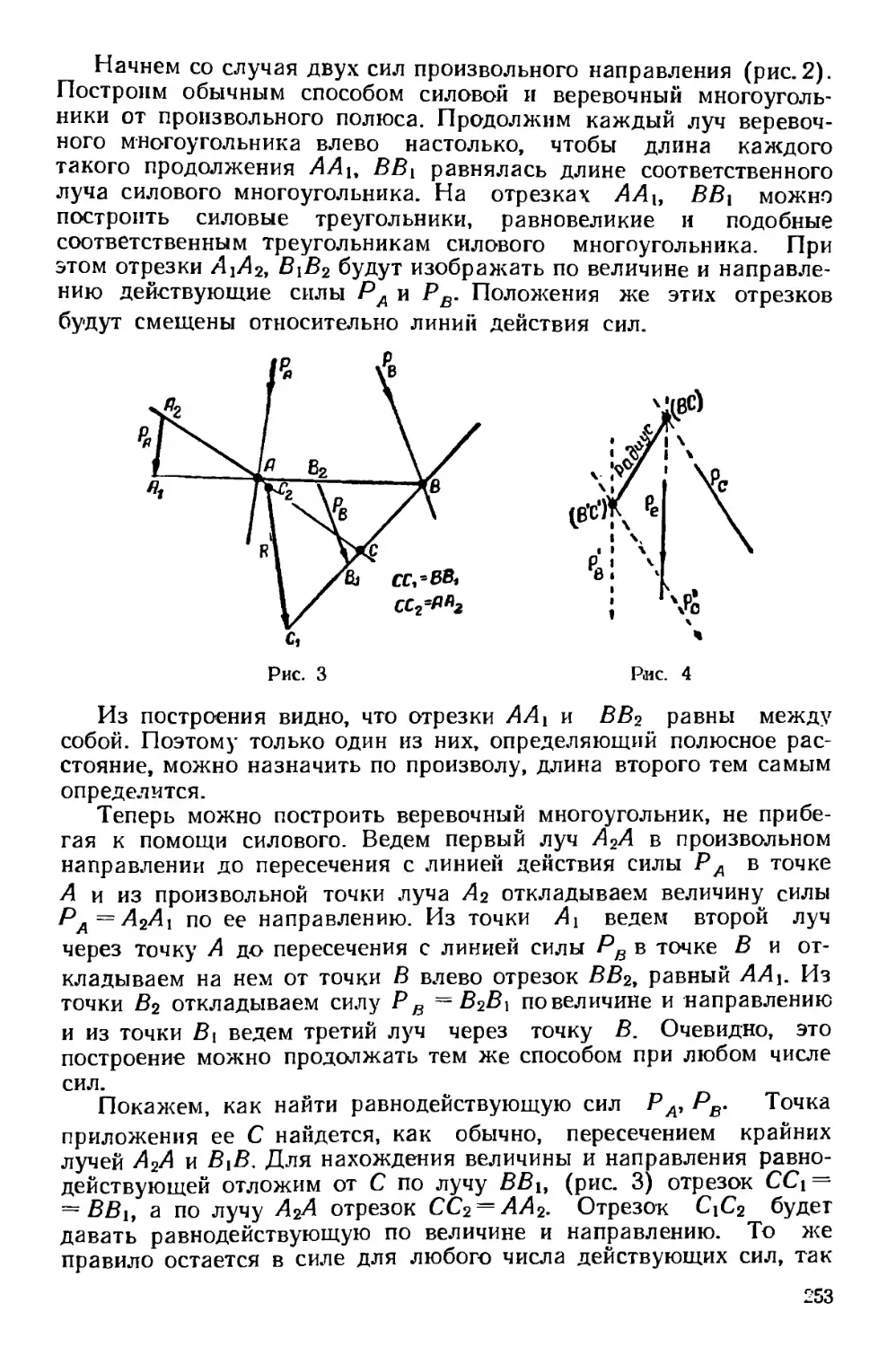
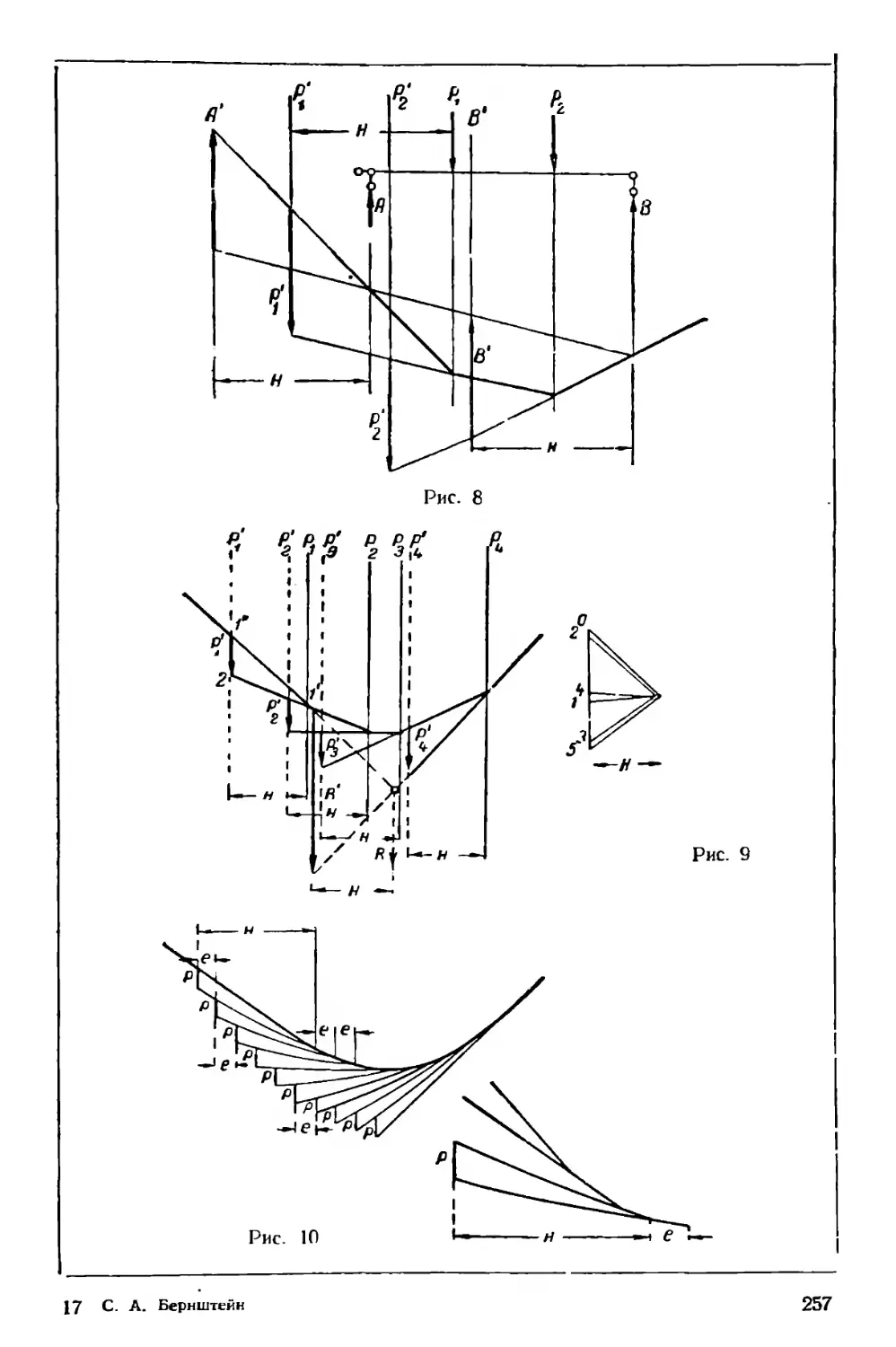
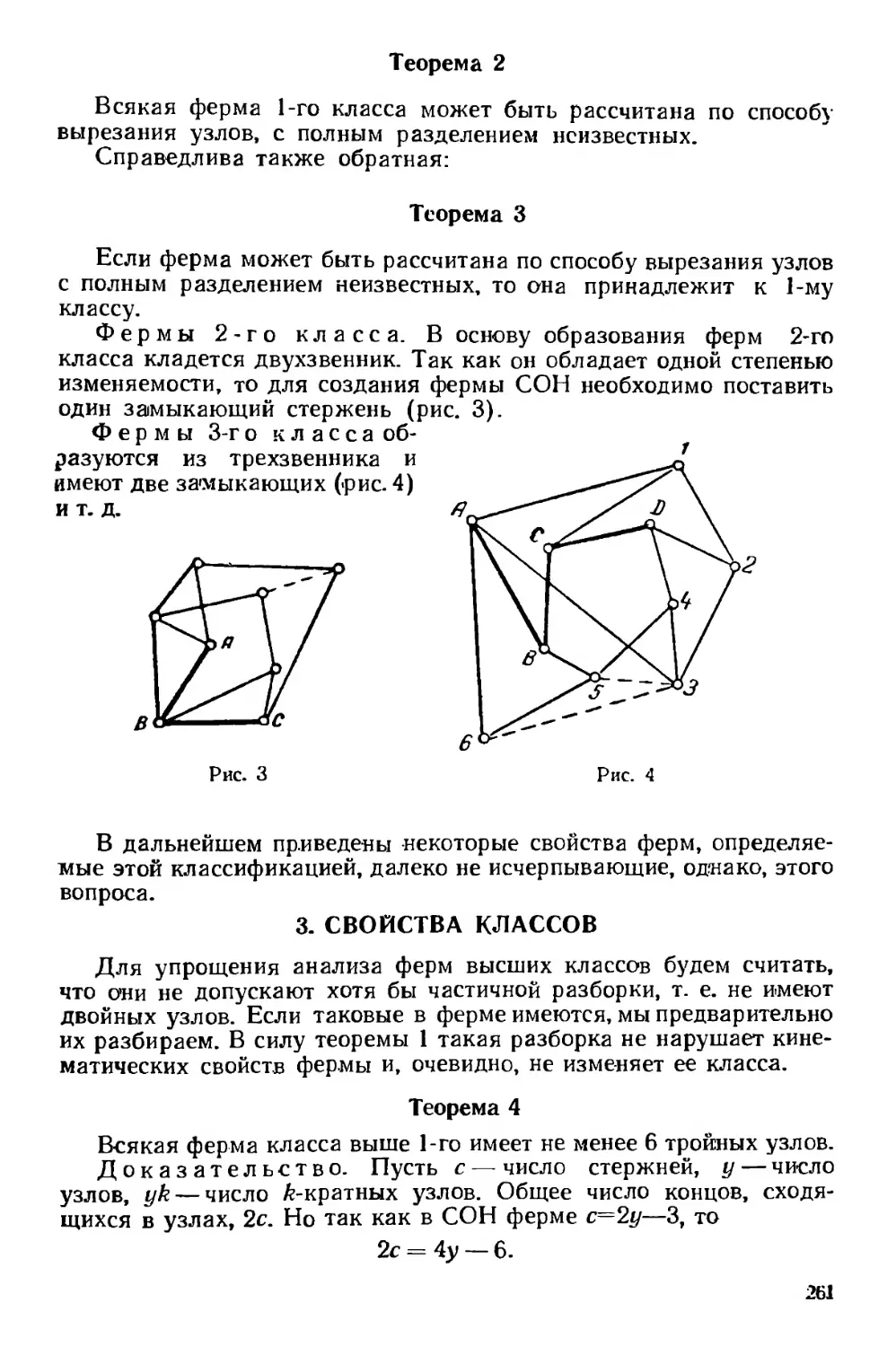
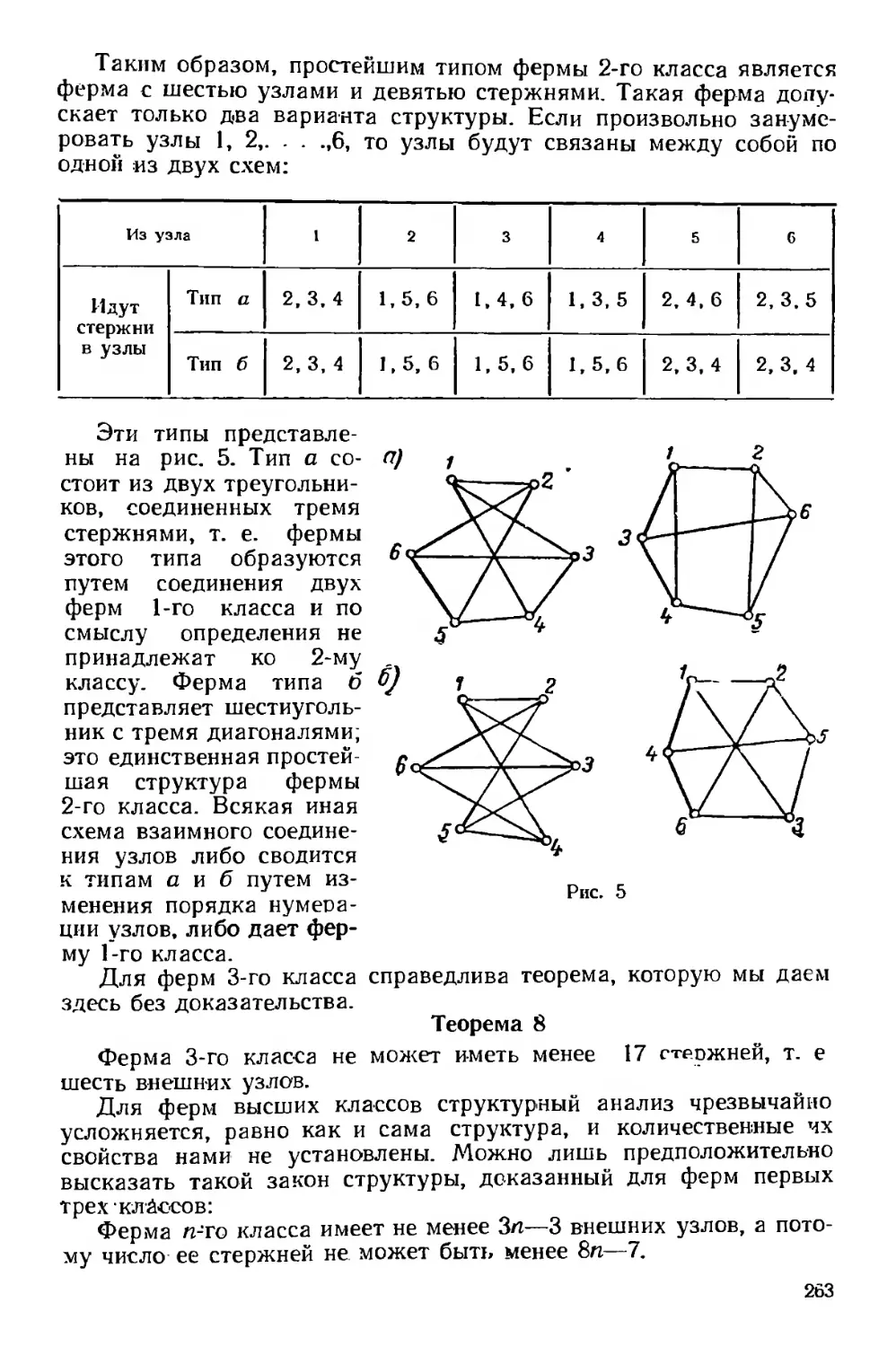
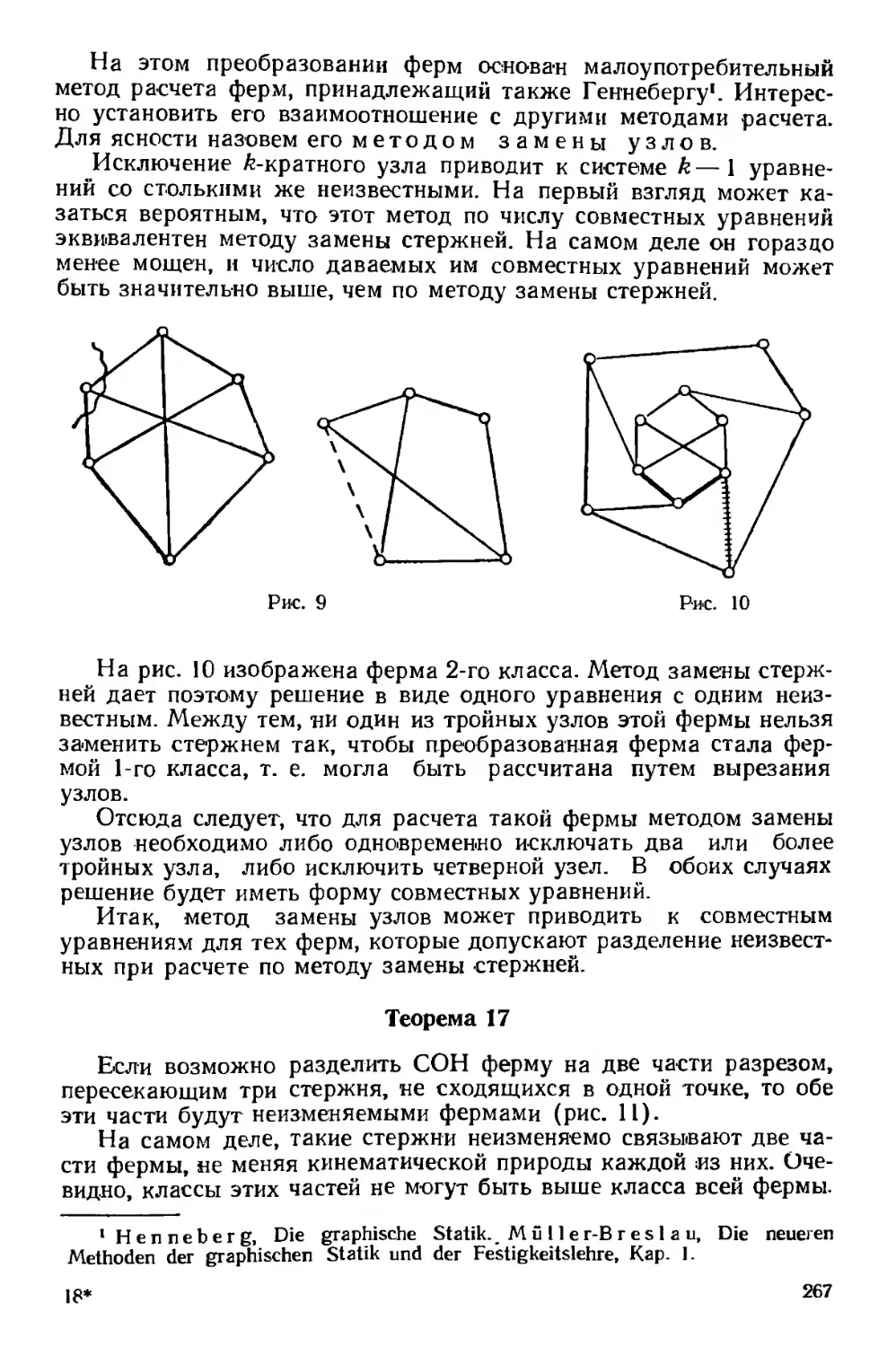
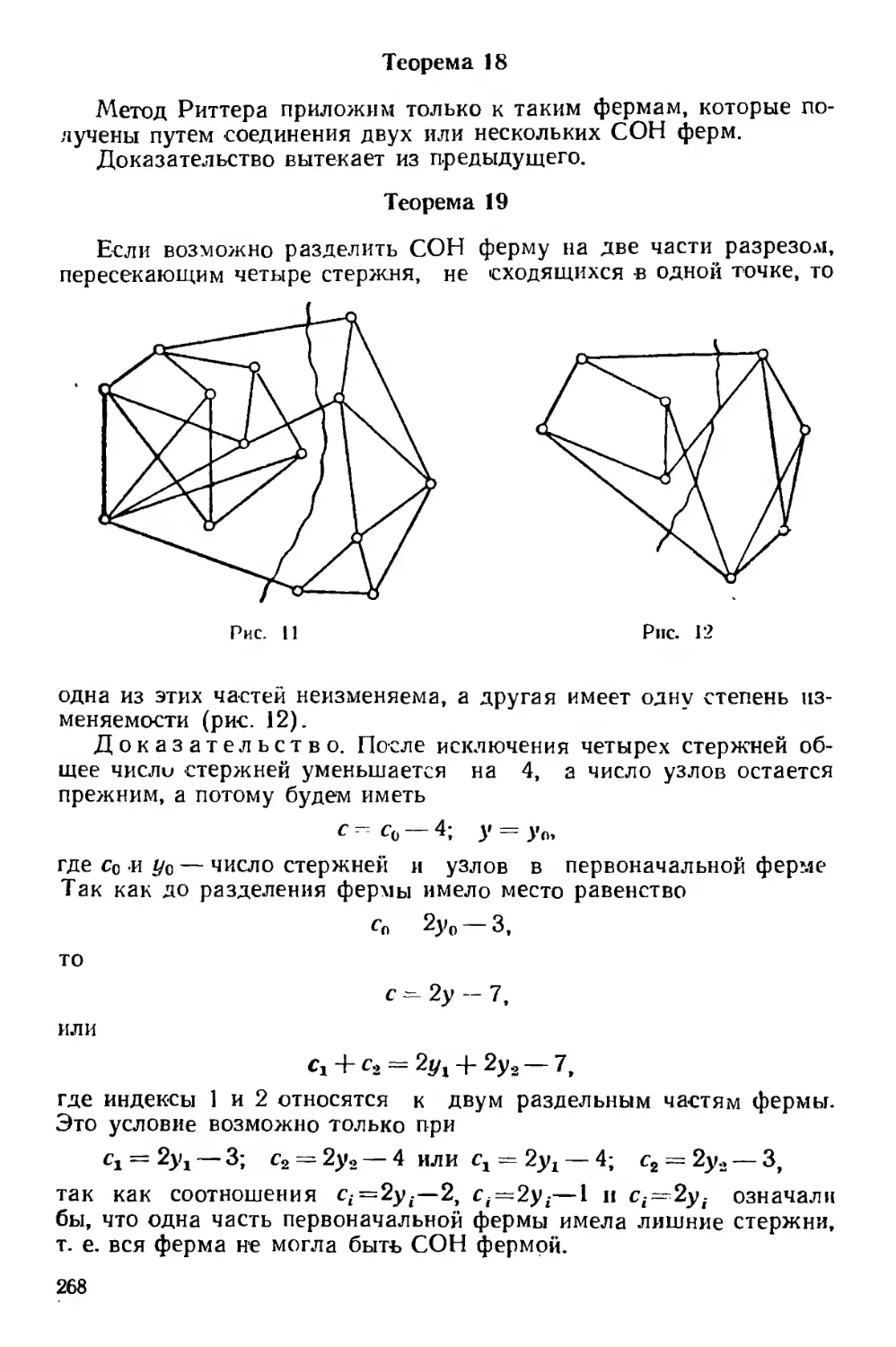
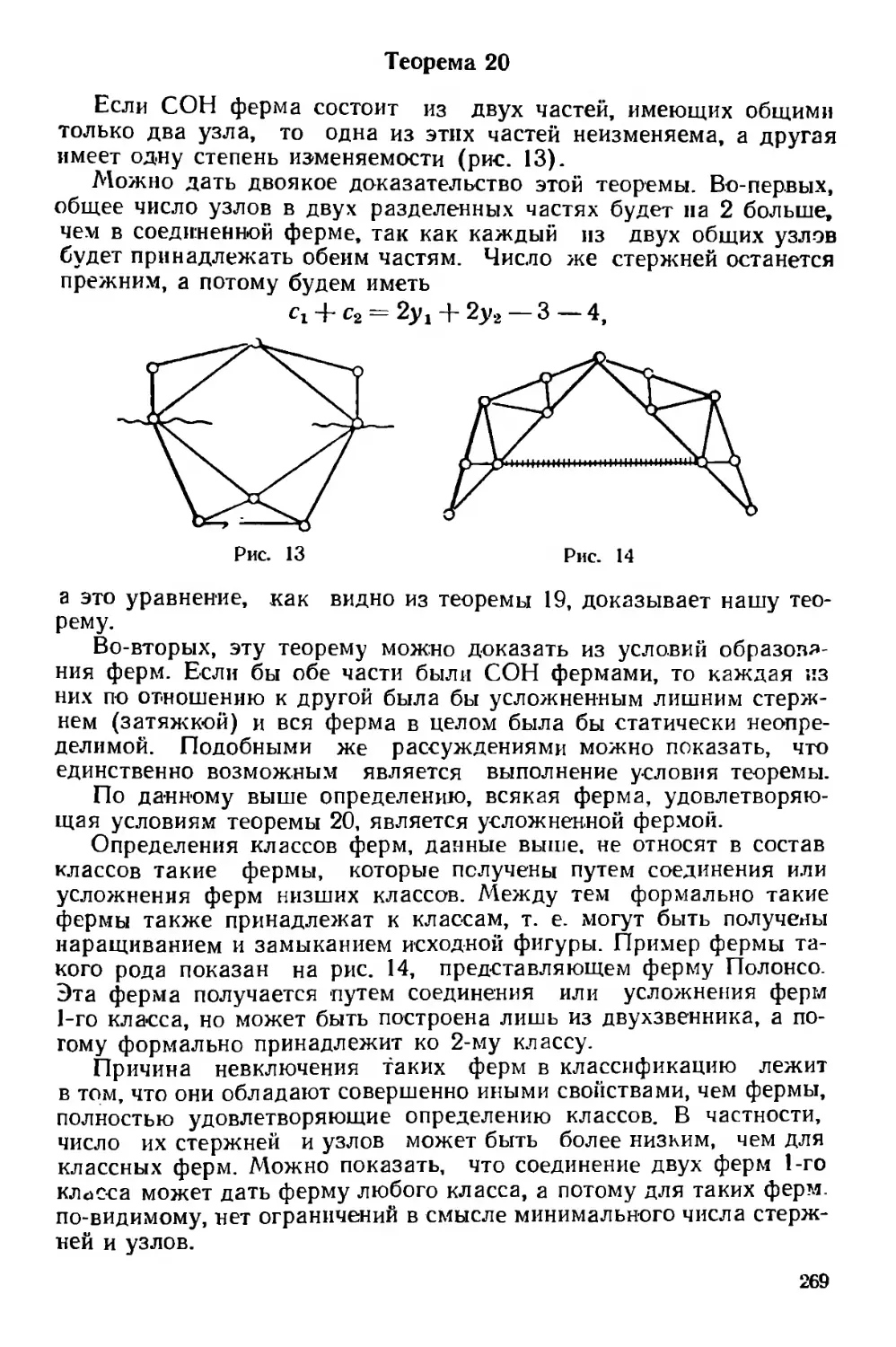
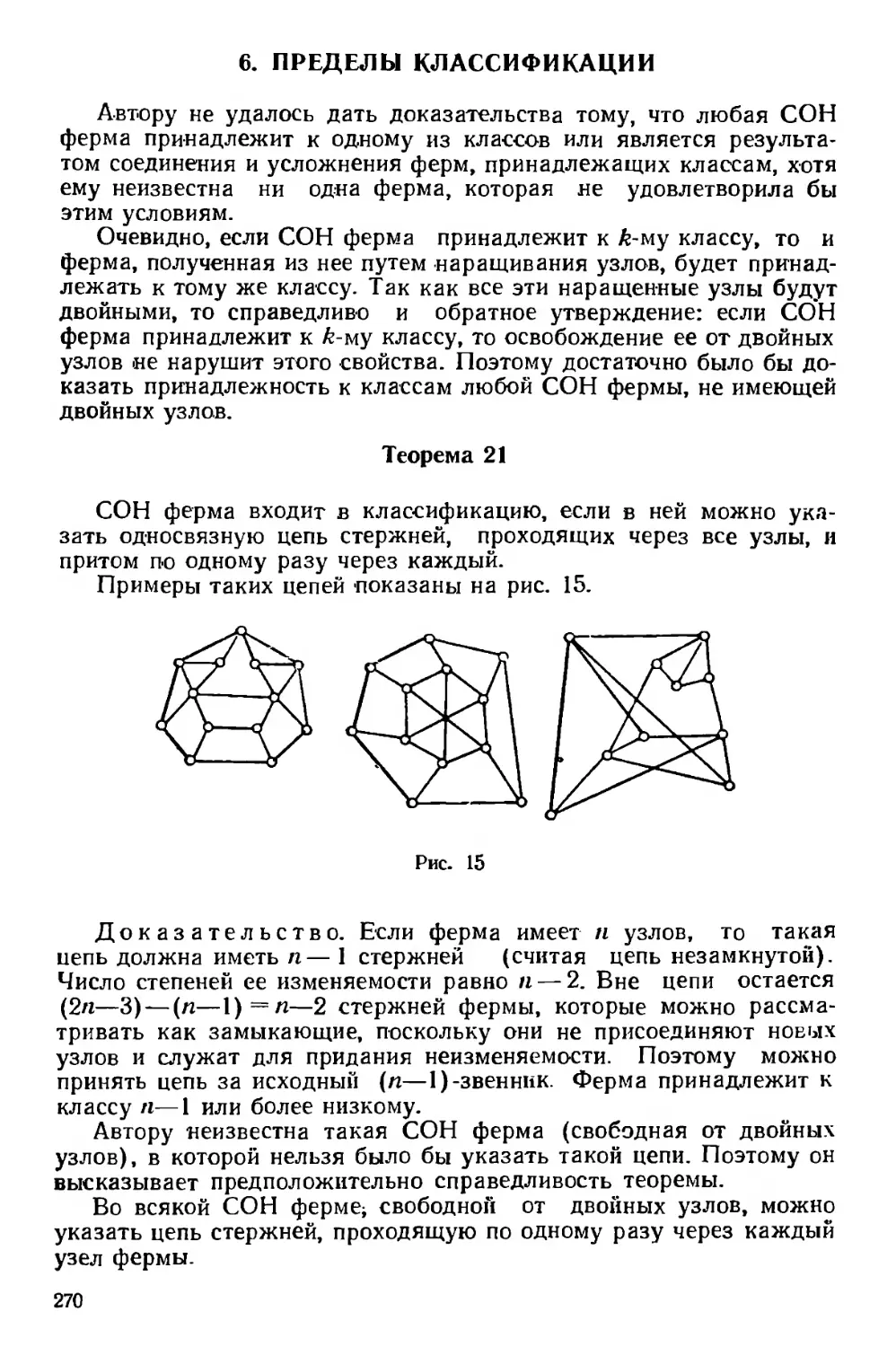
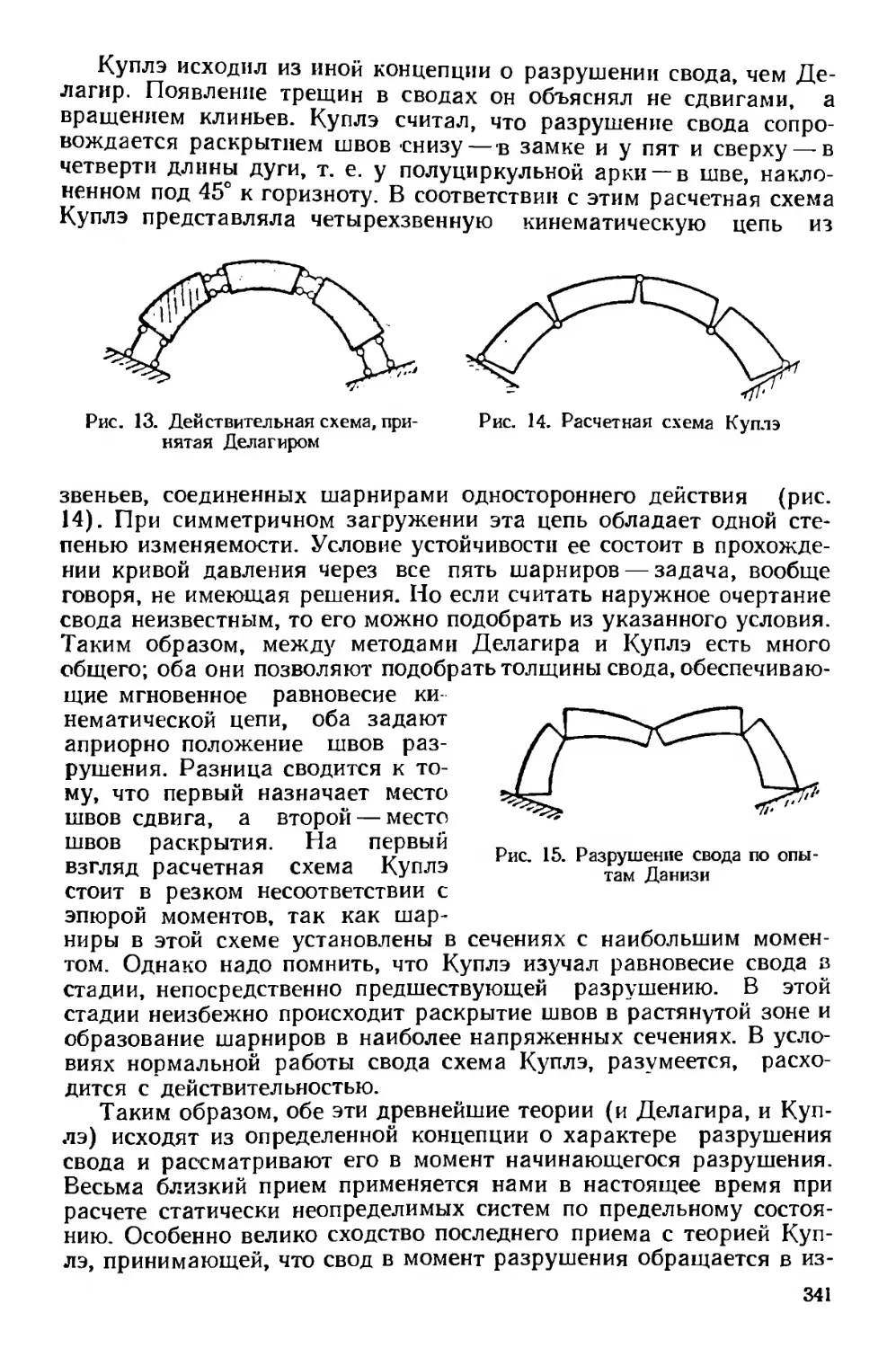
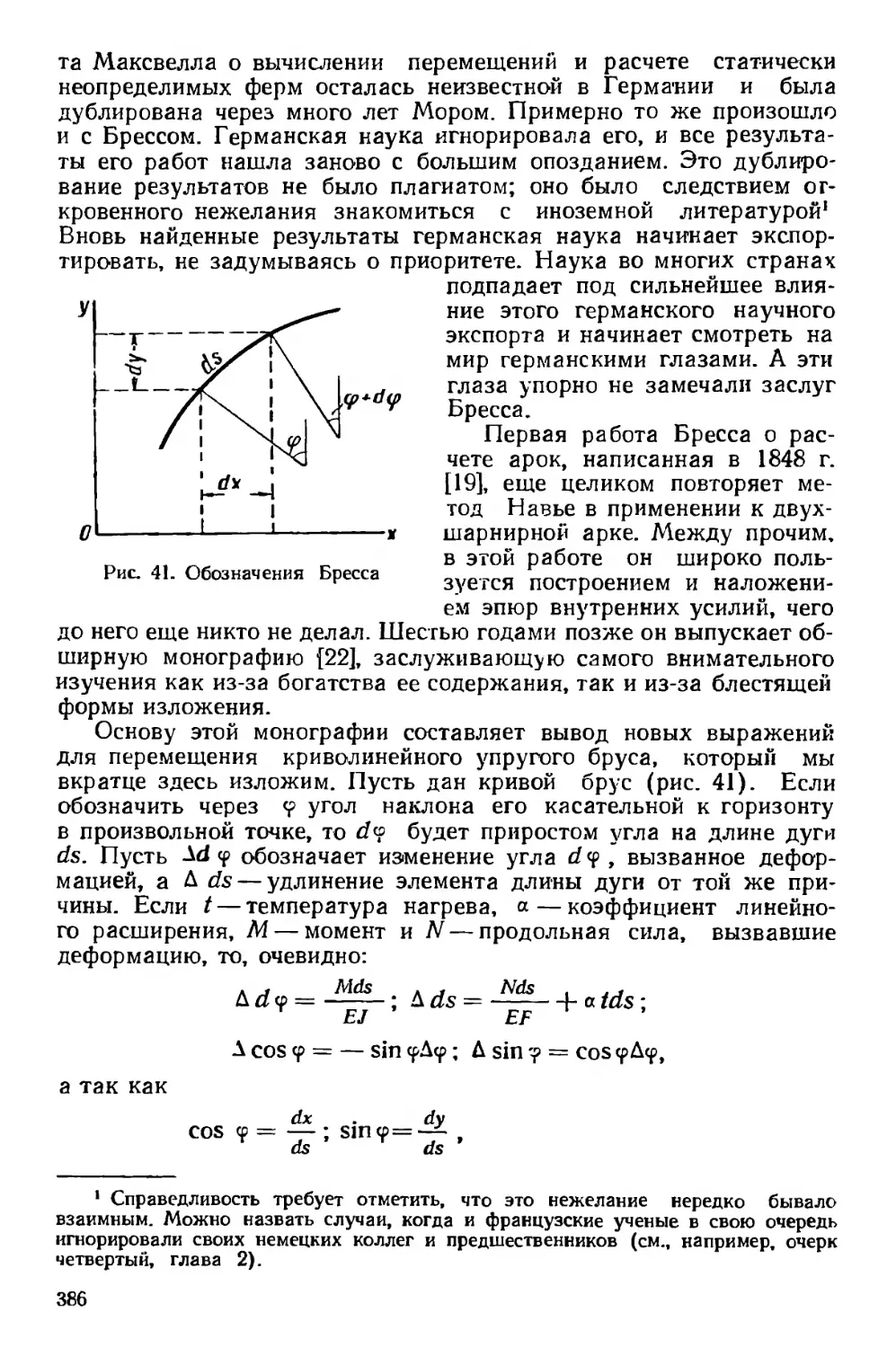
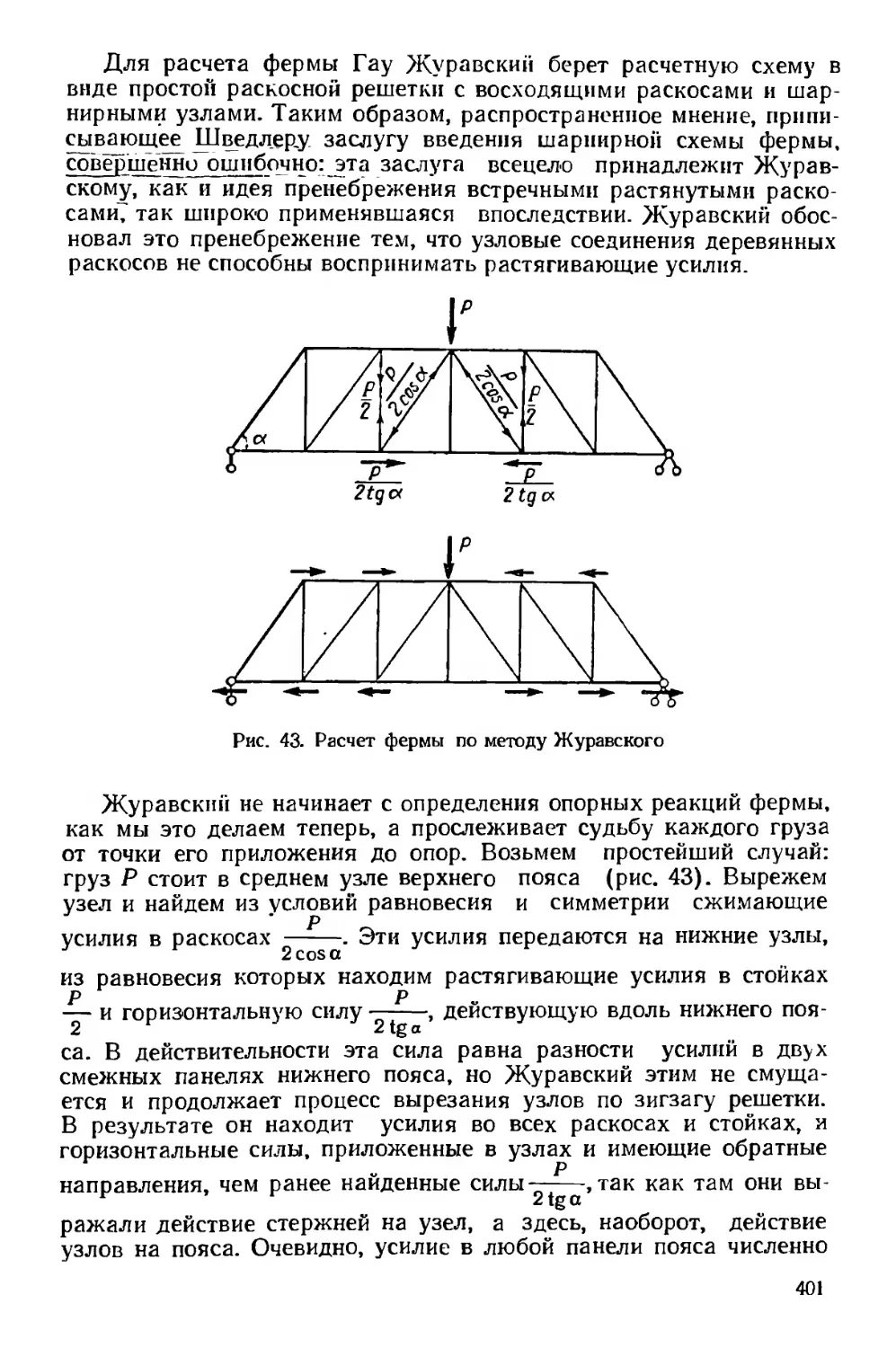
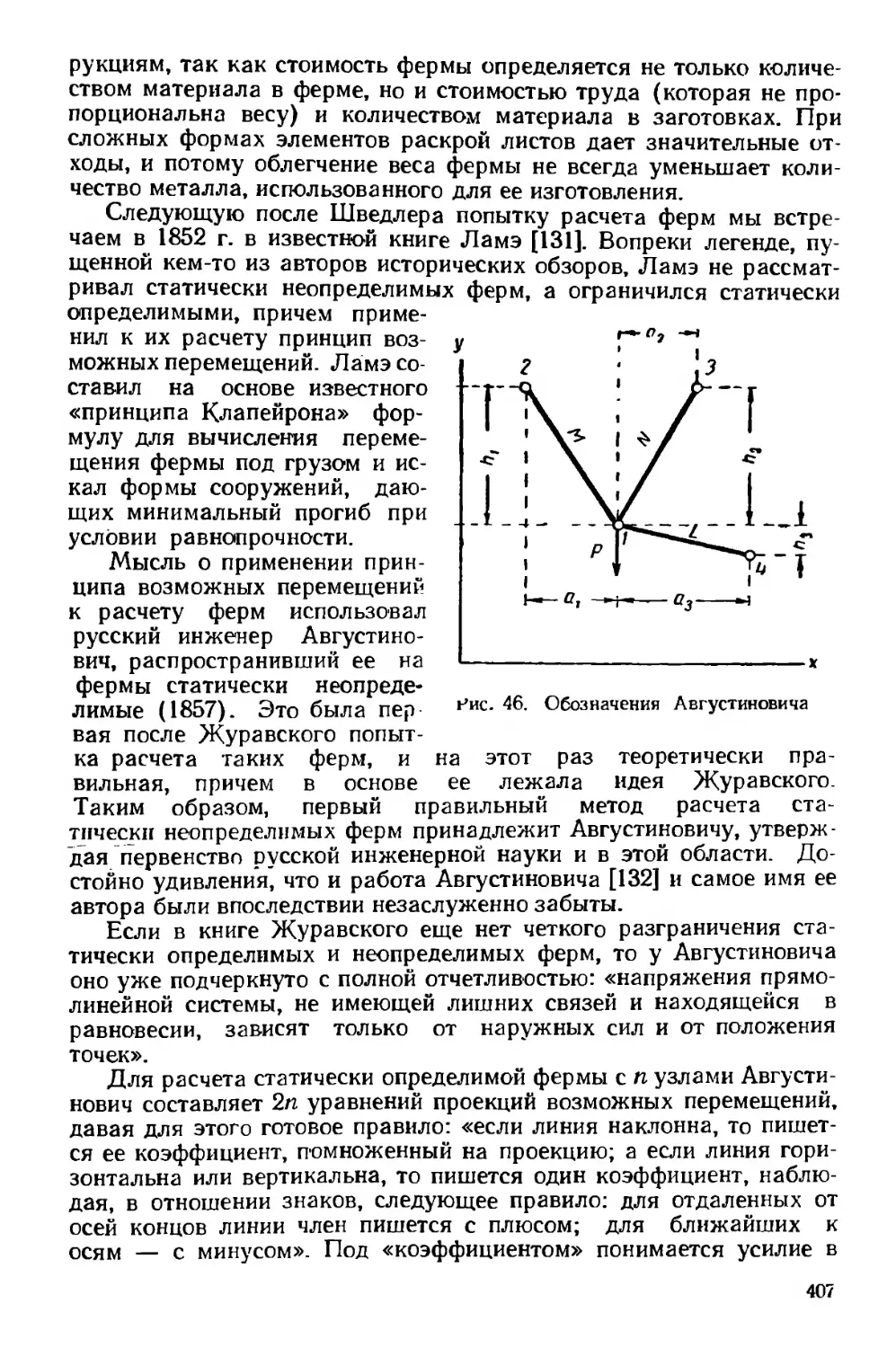
Текст
Проф. С. А. БЕРНШТЕЙН
ИЗБРАННЫЕ
ТРУДЫ
по
СТРОИТЕЛЬНОЙ
МЕХАНИКЕ
(Подбор статей произведен
проф. И. М. РАБИНОВИЧЕМ)
ГОСУДАРСТВЕННОЕ ИЗДАТЕЛЬСТВО
ЛИТЕРАТУРЫ ПО СТРОИТЕЛЬСТВУ, АРХИТЕКТУРЕ
И СТРОИТЕЛЬНЫМ МАТЕРИАЛАМ
Москва — 1961
РЕЦЕНЗЕНТЫ
КАФЕДРА СТРОИТЕЛЬНОЙ МЕХАНИКИ
ВОЕННО-ИНЖЕНЕРНОЙ АКАДЕМИИ
ИМЕНИ В. В. КУЙБЫШЕВА
СЕКЦИЯ ТЕОРИИ СООРУЖЕНИЙ
Ученого Совета
ЦЕНТРАЛЬНОГО НАУЧНО-ИССЛЕДОВАТЕЛЬСКОГО
ИНСТИТУТА СТРОИТЕЛЬНЫХ КОНСТРУКЦИЙ
АСиА СССР
Статьи проф С. А. Бернштейна, включенные в дан-
ный сборник, выбраны из числа работ, опубликованных
им в период 1931—1958 гг., и содержат материалы, по-
священные вопросам расчета сооружений на устойчи-
вость, на динамическое действце нагрузки, на работу
их за пределом упругости, а также вопросам теории
прочности, теории ферм, кривых стержней и др. Поме-
щена также его известная монография по истории строи-
тельной механики.
Книга рассчитана на инженеров-проектировщиков,
строителей, научных работников и учащихся строитель-
ных вузов.
ОПЕЧАТКИ
Стршнца Строка Напечатано 1 | Должно быть
97 3 снизу е= а=л
102 14 сверху на угол на угоч fl
107 8 снизу трехфазных трехзначных
114 2 сверху (пот Приняв для Приняв яля G
тсбчицей) выражение выражение
153 15 сверху Лг=0
d-h d-u
310 8 снизу dydz dydz
44G 8 снизу 1967 1867
БИОГРАФИЧЕСКИЙ ОЧЕРК
(26/1V-1901—21/IV-1958)
Сергей Александрович
БЕРНШТЕЙН родился в Моск-
ве. Среднее образование полу-
чил в Московской 9-й гимназии
в 1918 г.; высшее — на физи-
ко-математическом факультете
Московского Государственного
университета, курс которого
окончил по специальности чис-
той математики в 1921 г., и на
строительном отделении Мо-
сковского института путей со-
общения, курс которого закон-
чил в 1926 г.
С весны 1926 г., еще сту
дентом, начал работать в Мо-
стоиспытательном бюро науч-
но-технического комитета На-
родного Комиссариата путей
сообщения, где проработал до
конца 1932 г., занимая после-
довательно должности от тех-
ника до заведующего бюро.
С 1929 г. начал препода-
вать строительную механику в
московских высших учебных
заведениях, с 1932 г. — в Во-
енно-инженерной академии
имени Куйбышева; с 1938 г. перешел на должность начальника кафедры «Сопро-
тивления материалов» в Военную академию бронетанковых и моторизованных
войск Советской Армии, где проработал до лета 1957 г., когда тяжелая болезнь
вынудила его выйти в отставку.
Научно-исследовательская работа С. А. Бернштейна протекала по двум лини-
ям: экспериментальной и теоретической. В дореволюционной России эксперимен-
тальное исследование и испытание сооружений, можно сказать, отсутствовало.
3
В первые же годы Советской власти начало создаваться это дело, причем пио-
нером в этой области был созданный в 1918 г. Институт инженерных исследо-
ваний HKJ1C, в состав которого входили три мостоиспытательные станции.
Здесь впервые были заложены основы методологии испытаний, проектиро-
валась и изготовлялась измерительная аппаратура, производилось массовое
обследование и испытание железнодорожных мостов на всей территории СССР.
В этой научно-экспериментальной работе С. А. Бернштейн принимал деятель-
ное и всестороннее участие.
Накопленный им большой опыт экспериментального исследования крупных
сооружений в натурных условиях был эффективно использован им впоследст-
вии в 1935—1937 гг. в другой области — в исследовании стальных конструкций
тяжелых цехов; в эти годы он руководил лабораторией стальных конструкций
Центрального научно-исследовательского института промышленных сооружений
(ЦНИПС).
Многие теоретические работы С. А. Бернштейна были связаны с его экспе-
риментальными исследованиями. В период 1927—1932 гг. он опубликовал боль-
шую серию статей, в которых освещались различные вопросы статики и дина-
мики пролетных строений мостов как пространственных конструкций.
Дальнейшие работы С. А. Бернштейна, охватывающие примерно двадцати-
пятилетний период, посвящены различным вопросам расчета сооружений и их
элементов: расчету прочности и устойчивости сложных ферм, теории ледяных
переправ как пластинок на упругом основании, охватывающей вопросы расчета,
конструирования и эксплуатации переправ; расчету ферм за пределом упругости;
теории пластичности; расчету гибких упругих стержней переменного сечения
и др. Примером оригинальности его трактовки проблем могут служить публикуе-
мая в данном сборнике статья «О расчете гибкого кольца» и его главный науч-
ный труд «Новый метод определения частот колебаний упругих систем», защи-
щенный им в 1938 г. в качестве докторской диссертации.
С. А. Бернштейн был блестящим лектором, а также автором интересных
учебных руководств («Основы расчета статически неопределимых систем», «Ос-
новы динамики сооружений», «Сопротивление материалов»).
Он обладал в высокой степени талантом литературного изложения. Образ
цом такого изложения является его переизданная в данном сборнике книга:
^Очерки по истории строительной механики», которая заслуживает занять по-
четное место в научно-исторической литературе.
Сергей Александрович Бернштейн был верным сыном нашей Родины, отдавав-
шим свои силы советской науке и воспитанию инженерных кадров, достойных
страны социализма.
И. М. РАБИНОВИЧ
1. НОВЫЙ МЕТОД ВЫЧИСЛЕНИЯ ЧАСТОТ
КОЛЕБАНИЙ УПРУГИХ СИСТЕМ
И ЕГО ПРИЛОЖЕНИЕ К ЗАДАЧАМ УСТОЙЧИВОСТИ
Расчет конструкций, выполняемый по способам строительной
механики и сопротивления материалов, до последнего времени
ограничивается статическими приемами и лишь в особых слу-
чаях учитывает динамичность нагрузок, притом обычно несовер-
шенными способами. Между тем рост скоростей механизмов и дей-
ствующих на них нагрузок делает все более насущной потребно-
стью для расчетчика использование методов динамики сооружений.
Известно, что всякая задача динамики упругой системы, будь
то задача об ударе снаряда в сооружение или задача о движении
машины по неровной поверхности, требует в первую очередь раз-
решения вопроса о частоте свободных колебаний системы. Поэтому
выработка удобного, точного и надежного метода вычисления
частот колебаний может считаться предпосылкой для возможности
практического расчета конструкций на динамическую нагрузку.
Современные методы вычисления частот свободных колебаний
упругих систем можно разбить на две группы. В одну из них вой-
дут точные методы, основанные на решении дифференциальных
уравнений свободных колебаний, в другую — приближенные мето-
ды, характеризующиеся априорным назначением ожидаемой фор-
мы стоячей волны. Общим для всех этих методов является то, что
.они позволяют вычислить частоту лишь после установления формы
стоячей волны, и в этом смысле все они могут быть названы кос-
венными методами.
Между тем очевидно, что частоты свободных колебаний пред-
ставляют собой величины, полностью определяемые массами си-
стемы и ее упругими характеристиками (статическими жесткостя-
ми или перемещениями); равным образом и форма стоячей волны
зависит только от этих факторов. Поэтому естественно стремиться
к нахождению прямого метода вычисления частот, .позволяю-
щего определить частоты непосредственно через массы и переме-
щения.
Автор поставил перед собой задачу нахождения такого метода,
который бы:
1) был прямым, т. е. допускал -непосредственное вычисление
частот через выражения масс и статических перемещений;
2) был универсальным, т. е. давал единую форму решения
для любой стержневой системы, каково бы ни было число ее сте-
пеней свободы;
3) в случае невозможности получения точных значений частот
в виде замкнутых конечных формул допускал приближенное вы-
числение частот с любой степенью точности, давая на каждой сту-
пени приближения возможность оценки степени допущенной по-
грешности.
Задача нахождения такого метода оказалась разрешимой.
1. СПЕКТРАЛЬНАЯ ФУНКЦИЯ
Пусть стержневая система имеет п степеней свободы, причем
направления характеризующих ее независимых смещений обозна-
чены /, 2.. .,п, а массы, совершающие работу на этих смещениях,
названы ти т2,..., тп. Система дифференциальных уравнений
свободных незатухающих колебаний может быть записана в виде:
У = т1 6Л1 + т2 --------Ь d йлл
1 dt2, 1 2 dt1 пл in др пп
(1)
где уъ...,уп — величины смещений по соответственным направлени-
ям, a —перемещение по f-му направлению от единичной силы,
приложенной по £-му направлению.
Уравнения (1) допускают решения вида
y* = Cftsin(<ft+ >),
если частота удовлетворяет так называемому вековому уравне-
нию, которое мы запишем в виде детерминанта, обозначая z=cp2,
S(z) = тА1г — 1 т2Ь12г m<A22z—1 -0 (2)
mnt>nnz—\.
Как известно, уравнение (2) дает для z п действительных поло-
жительных корней 2Ь z2i..., 2„, равных квадратам частот колеба-
ний системы, причем коэффициентами уравнения являются выра-
жения, зависящие только от масс и статических перемещений
системы. Таким образом, этот классический метод вычисления ча-
стот является, по нашему определению, прямым методом, но, к
сожалению, практически непригодным при п>2, так как и вычис-
6
ление коэффициентов и тем более решение уравнения (2) пред-
ставляют задачу чрезвычайной сложности. Автору удалось дока-
зать, однако, что для определения низших, наиболее важных в
практике частот нет необходимости ни в вычислении всех коэффи-
циентов уравнения (2), ни в его полном решении, благодаря чему
метод векового уравнения впервые становится практически прием-
лемым и притом удобным методом.
Развертывая детерминант (2) по степеням z=<p2, получаем зна-
копеременный полином п-й степени:
S(z) = 1 — Агг 4- A2z2---+ (— l)"A„z" = 0, (3)
где любой член уравнения Ak определяется формулами
Аг = S mfiii
п i—I
i=l Л=1
^kAkk
Легко видеть, что все Ak положительны. Установим зависи-
мость между их величинами. Рассмотрим для этого детерминант
перемещений
^11^12............^1п
^21^22 • • • - 62rt
и будем считать, что он отвечает канонической системе уравнений
метода сил для некоторой стержневой n-кратно статически неоп-
ределимой системы. Применяя алгоритм Гаусса для решения этих
уравнений, можно привести детерминант (5) к виду
^11^12.........\п
.........«
О О............{(1.2. -П-1)
= в„«2’--Л;2-"-”. (6)
где верхние индексы указывают закрепленные направления. Тач,
йз 2) выражает перемещение 3-й точки от единичной силы в той же
точке для системы с закрепленными точками l-й, 2-й и т. д. Заме-
тим, что выражение (6) инвариантно относительно порядка нуме-
рации точек и что всегда
7
Рассмотрим выражение коэффициента Лг и преобразуем его,
используя формулы (6) и (7):
1=21>А!а=
2=1 /?=1 £=! Л=1
= — V V т.т. б.. бР> < — У т. б.. У т. Ъ =
2 XU 1 к и kk 2 1 11 & №
2=1 А=1 2=1 Л=1
=4-(SmA^ = ТЛ?' (8)
С помощью аналогичных преобразований можно доказать, что
вообще
Ak
А*<1Г’ <9>
откуда следует, что коэффициенты Ak для любой стержневой си-
стемы образуют быстро убывающую последовательность.
Разложение (3) и формулы (4) можно немедленно распростра-
нить вместе с неравенством (9) на системы с бесконечным числом
степеней свободы.
В этом случае система дифференциальных уравнений (1) пре-
вратится в одно интегральное уравнение Фредгольма второго рода:
y(s) = zJy(/)6s,m(f)dZ, (1')
где m(t) —погонная масса в точке t, а б5/—функция влияния пе-
ремещения, т. е. перемещение точки s от единичной силы в точке t.
Полином (3) при этом обратится в бесконечный ряд:
5(2) = 1 - ЛХ2 4- Л222-ч- (-1)^4- • • •, (10)
носящий в теории интегральных уравнений название ряда Фред-
гольма. В дальнейшем он будет попрежнему называться спект-
ральной функцией; по определению, корни уравнения (10)
равны квадратам частот колебаний системы. Они все будут дейст-
вительными положительными числами.
Коэффициенты ряда (10) выразятся формулами:
Аг = J т (х) 6VJzZx f
А>= J | J W>dxdy dz,
(11)
8
из которых непосредственно вытекает справедливость неравенств
(9). В выражениях (И) интеграция распространяется на длину
всех стержней системы.
Неравенства (9) показывают, что ряд (10) сходится равномер-
но и абсолютно в любой точке z, а потому спектральная функция
представляет собой целую аналитическую функцию1.
Обозначим корни спектральной функции (10) zb z2...; в таком
случае можно доказать справедливость равенства
Л.= У—, (12)
zk
правая часть которого представляет сходящийся ряд. Этот резуль-
тат можно сформулировать иначе: сумма квадратов перио-
дов колебаний любой стержневой системы есть
сходящийся ряд.
Из сходимости ряда (12) можно вывести еще одно важное не-
равенство, связывающее величины коэффициентов Ak:
a, A i<—~А1, (13)
и показывающее, что коэффициенты спектральной функции (10)
убывают ускоренно.
2. ЗАКОНЫ СХОДИМОСТИ КОРНЕЙ
Из сходимости ряда (10) следует, что головные полиномы
S„(z) = 1 - A1Z + Aza + (—1)"Anz", (14)
получаемые из спектральной функции после отбрасывания оста-
точного члена, будут тем менее отклоняться от самой функции
S(z), чем выше п. Следовательно, и корни полинома Sn (г) будут
тем менее отклоняться от первых п корней спектральной функции,
чем выше п. Это свойство позволяет аппроксимировать корни zk
спектральной функции посредством последовательности корней
Zkn полиномов Sn(z). При этом обнаруживается весьма важный
закон приближения корней.
Установим пределы, между которыми заключены корни z по-
линома Sn (z)., предполагая сперва, что все они действительны. Из
условия
1 Строгие математические доказательства приводимых здесь утверждений
даны в работе автора «Новый метод определения частот колебаний упругих си-
стем», изд. ВИА РККА, 1939.
9
находим
С другой стороны, приводя полином (14) к виду
5„(2)=(-1рЛ„2» (i- .A+^=L._L -+(-1^.^) , (15)
найдем, что старший корень полинома (14) znn будет равен обрат-
ной величине младшего корня многочлена, заключенного r скобки
в формуле (15), и, следовательно,
Отсюда заключаем, что вне пределов интервала
полином (14) заведомо не имеет действительных корней, причем
это рассуждение сохранится в силе и в том случае, когда среди
корней z„ есть мнимые числа.
Рассмотрим теперь разность двух полиномов, преобразуя ее:
Sn+k (Z) - S„-l (2) = AnZ" ( 1 - 2 4- z‘--------+
+ (— 1)*A+»- 2*1
4л /
Согласно сказанному, младший корень разности будет удовлет-
ворять неравенству
(16)
Ai-h
если он действителен, если же он окажется мнимым числом, то
можно утверждать, что все действительные корни разности удов-
летворяют неравенству (16).
С другой стороны, все действительные корни полинома Sn-i (г),
согласно доказанному выше, удовлетворяют неравенству
Но в силу неравенств (13)
4П_| > /х-|_ д -4л__2 > 4п_2
л л л п—1 ’ л л ’
Лл+> Лн Лл—1 Лл— 1
откуда
10
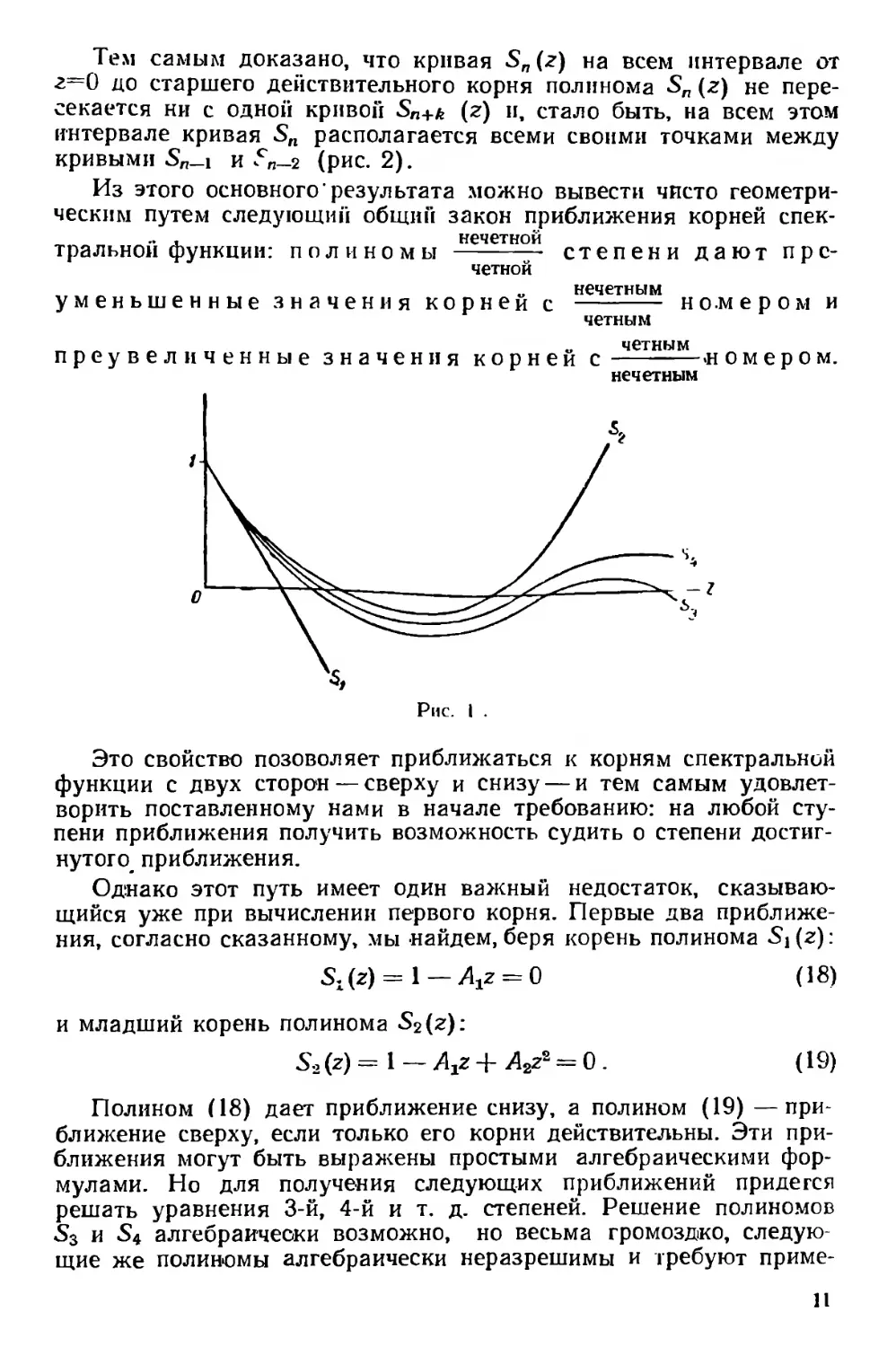
Тем самым доказано, что кривая S„ (z) на всем интервале от
2=0 до старшего действительного корня полинома S„ (z) не пере-
секается ни с одной кривой Sn+k (2) и, стало быть, на всем этом
интервале кривая Sn располагается всеми своими точками между
кривыми 5Л_1 и 5п-2 (рис. 2).
Из этого основного’результата можно вывести чисто геометри-
ческим путем следующий общин закон приближения корней спек-
.. , нечетной
тральной функции: полиномы -------- степени дают пре-
четной
„ нечетным
уменьшенные значения корней с -------------- номером и
четным
____ „ „ четным
преувеличенные значения корней с---------------и омером.
нечетным
Это свойство позоволяет приближаться к корням спектральной
функции с двух сторон — сверху и снизу — и тем самым удовлет-
ворить поставленному нами в начале требованию: на любой сту-
пени приближения получить возможность судить о степени достиг-
нутого приближения.
Однако этот путь имеет один важный недостаток, сказываю-
щийся уже при вычислении первого корня. Первые два приближе-
ния, согласно сказанному, мы найдем, беря корень полинома Si(z):
Sl(z) = \ — A1z = Q (18)
и младший корень полинома S2(z):
S2(z) =1 — A1z+ A2z2 = 0 . (19)
Полином (18) дает приближение снизу, а полином (19) —при-
ближение сверху, если только его корни действительны. Эти при-
ближения могут быть выражены простыми алгебраическими фор-
мулами. Но для получения следующих приближений придется
решать уравнения 3-й, 4-й и т. д. степеней. Решение полиномов
S3 и S4 алгебраически возможно, но весьма громоздко, следую-
щие же полиномы алгебраически неразрешимы и требуют приме-
11
нения приближенных приемов для нахождения корней. Тем самым
на одно приближение (вычисление корней спектральной функции)
накладывается другое приближение (вычисление корней прибли-
жающих полиномов), вследствие чего мы теряем право утверждать
о найденных приближениях корней, являются ли они приближени-
ями снизу или сверху. К этому недостатку присоединяется еще
один. Коэффициенты Ak представляют интегралы (или суммы) из
детерминантов, так что подинтегральное выражение представляет
собой разность двух чисел, причем эти числа велики, а разность их
мала. Вследствие этого для сколько-нибудь надежного определе-
ния коэффициентов Ak требуется производить вычисления с тем
большим числом знаков, чем выше номер коэффициента, а это
значительно осложняет работу.
3. ТРАНСФОРМИРОВАННАЯ СПЕКТРАЛЬНАЯ ФУНКЦИЯ
Для устранения первого недостатка автором предложен -метод
трансформации спектральной функции, основанный на преобразо-
вании независимого переменного. Второй недостаток устраняется
переходом от коэффициентов A k к новым коэффициентам Вк.
Мы начнем с этого последнего преобразования.
Если представить спектральную функцию в виде бесконечного
произведения
S(z) - П (1 — —
(20)
сходимость которого вытекает из сходимости ряда (12), и прирав-
нять коэффициенты при одинаковых степенях z в разложении (10)
и в (произведении (20), то мы найдем формулы, связывающие ко-
эффициенты Ak и корни zk, причем они будут вполне подобны ана-
логичным формулам для многочленов:
Введем обозначение
(21)
15
В таком случае, обобщая формулы Ньютона для многочленов
на случай целой функции, найдем:
4 = 4,
В2 = Д2 —2Д,,
в3 = дз - ЗД,Л2+ЗА,,
откуда обратно:
-4. = Вг,
Л3=4-(В?-В2).
4 = ± (ВЗ-ЗВД+2В,) ,
О!
(22)
Вернемся теперь к выражениям (11), связывающим коэффи-
циенты л4Л с массами и перемещениями, и преобразуем их, заме-
няя произведения перемещений на детерминанты перемещений,
согласно общей формуле (6). Выражение Aj при этом не изменит-
ся, а коэффициент Л2 приведется *к виду
4= ~ JJ т (х)т (у) [ 6хх - «у dxdy =
= -у [J т W 6„ dx]----у JJ m (*)«(У) ^dxdy = -j- (4~С,),
где через С2 обозначен интеграл вычитаемого:
с2 = J J т (х) т (у) &ydxdy .
Обозначим аналогично:
(23)
Ся = jJ J т (х)т (у) т (z) ^xy^y^xdxdydz ,
и преобразуем выражение А3;
л=4г ПН(х) т (у) т (z) f < S“8w _ +
+ % 8ух 8« - 8УУ - 8zx 8yz ]dxdydz .
Разлагая интеграл на сумму интегралов, найдем, что
ш
m (х) т (у) т (г)
[^(^\y-^)ldxdydz = 2A,A2,
J f f т (х) т (у) т (г) Ъуу Vjlxdydz =
6« Zyzdxdydz = А1С2
а поэтому
а3 = 4- (44 - 4Q + Q= V (4 ~ 3^.с2 + 2Сз) •
О О!
(24)
13
Сопоставляя выражения (23) и (24) с (22), устанавливаем
немедленно тождественность коэффициентов Bk и Ск, откуда вы-
текают замечательные соотношения между корнями, массами и
перемещения ми:
m(x)bXJIdx,
m(x)m(y)t>xyZyxdxdy,
(25)
в3=
т (х) т (у) т (z) bvftyjs,jlxdydz,
Заметим при этом, что числа Bk в отличие от Ак представля-
ют собой интегралы произведений, а не разности, а потому могут
быть вычислены со значительно большей достоверностью при той
же затрате труда. Если мы сумеем определять корни непосредст-
венно через числа Bk, минуя вычисление коэффициентов Ак9 то
второй из упомянутых ранее недостатков будет устранен.
В теории интегральных уравнений числа Вк называются «сле-
дами» ядра.
Перейдем от спектральной функции, выраженной бесконечным
произведением (20), к «трансформированной спектральной функ-
ции с показателем л»:
7’<")(z)= п(1— — V (26)
*-'1
Легко понять, что этот переход сводится к преобразованию не-
га /
зависимого переменного: вместо оси z мы берем ось V z, понимая
под этим радикалом только его действительное значение. Выраже-
ние (26) показывает, что корни функции 7(n)(z) соответственно
равны и-м степеням корней функции S(z). Если разложить функ-
цию (26) в ряд
TW (z) = 1 — A^z + A™z2 • • - ,
то, как нетрудно убедиться, между коэффициентами разложения
и корнями будут существовать зависимости, вполне аналогич-
ные (22):
д<1”) = в„,
Л<">= 1 (27)
Л<”)= <5 — (В^ — ЗВ В -|-2В ) , \ П П 2п • ЗП/ ’
но отличающиеся тем, что индексы чисел Вк в правых частях ра-
венств (22) придется умножить на п.
14
Таким образом,
Т<~> (Z) = 1 - В„2 4- -2- (BJ — ) Z2 —
-^-(B3n-3fi„B2n + 2B3„)23+---,
(28)
причем, полагая п— 1, мы возвращаемся к спектральной функции
Легко показать, что быстрота сходимости ряда (28) увеличи-
вается вместе с л, а отсюда следует, что в области своих корней
головной полином T^n,(z) будет тем меньше отклоняться от суммы
всего ряда (28), чем выше п, каково бы ни было k. Иными слова-
ми, корни полиномов (z) при данном k будут тем менее откло-
няться от первых k корней функции T(n)(z), чем выше л, причем
эта сходимость будет монотонной.
Тем самым мы получаем возможность приближения корня zk
спектральной функции через полиномы степени не выше £+!;
именно — старшие корни полиномов
ухо, т™. • -
дадут приближение корня zk снизу, а вторые по старшинству кор-
ни полиномов
т<1)
л+1»
Т(2) т(3) . .
1 4+1» 1 /г+1
дадут приближение корня zk сверху.
4. ПРАКТИЧЕСКИЕ ПРИЕМЫ ВЫЧИСЛЕНИЯ КОРНЕЙ
Применим эти результаты к вычислению первого корня z.
спектральной функции, равного квадрату частоты основного тона
колебаний. Для приближения его снизу берем последовательность
полиномов T<n>(z):
7'[1) = 1 _ , 7р=1—B2z- - ,
откуда находим последовательные приближения корня, извлекая
радикалы п-й степени:
— -2— —!——1— ... (29)
’ V ~в, ’ ’ "г—
v '• V в3 Ув„
Приближение сверху найдем из последовательности полиномов
7<">(z):
7Х*)= 1 - В,2+ -2-(В?-В2) г2,
7f» = 1— В2г + -2-(В| — , (30)
15
младшие корни которых по извлечении радикала м-й степени дают:
Объединяя последовательности (29) и (31), найдем основное
двустороннее неравенство для определения первого корня z^.
Пределы этого неравенства монотонно сближаются с ростом и.
Практически вполне удовлетворительную степень приближения
первого корня дает уже простейшее неравенство, которое полу-
чается из неравенства (32) при я= 1:
(33)
для получения которого достаточно вычислить только два числа
В, и В2. Переход к более высоким значениям п в неравенстве (32)
становится необходимым, только если радикал в знаменателе пра-
вой части (33) будет мнимым. Как нам удалось показать, появле-
ние мнимости связано с уменьшением быстроты возрастания кор-
ней zk в функции их номера; в частности, взаимная близость двух
первых корней zx и z2 неизбежно дает мнимное выражение в правой
части (33), заставляющее переходить к значению п=2 или выше.
Интересно отметить, что первое, самое грубое приближение
первого корня снизу в последовательности (29)
1 1
> — =------------
J ™ ИЪХЛdx
представляет собой известную приближенную формулу Донкерли
(Dunkerley).
Для приближения второго корня снизу достаточно снова вер-
нуться к полиномам (30) и взять их старшие корни, извлекая из
них опять радикал п-и степени:
16
2
Приближение второго корня сверху требует решения уравне-
ний третьей степени, т. е. применения формулы Кардана. Но так
как использование ее достаточно громоздко и так как в огромном
большинстве задач из инженерной практики основное значение
имеет первая частота, тогда ка»к вторую обычно достаточно оце-
нить ориентировочно, то мы не приводим развернутого выражения
двустороннего неравенства для второго корня.
Заметим еще, что двустороннее неравенство вида (32) можно
построить для определения любого старшего корня, если считать
младшие корн-и определенными предварительно.
Этот метод позволяет с большой простотой и высокой степенью
точности вычислять частоты колебаний даже таких систем, для
которых точное решение либо невыполнимо, либо весьма сложно.
Примеры вычисления частот этим методом приведены в книге
автора1.
5. СЛУЧАЙ СОВМЕСТНЫХ ИНТЕГРАЛЬНЫХ УРАВНЕНИЙ
Удобство вычисления, высокая точность и универсальность
нового метода заставляют поднять вопрос о распространении это-
го метода на ряд других задач, относящихся к динамике и устой-
чивости конструкций и сводящихся к проблеме собственных зна-
чений. Такое распространение и составляет задачу настоящей
работы.
Мы начнем со случая совместных интегральных уравнений,
который не получил разрешения в предыдущих работах автора.
Пусть каждая точка системы обладает двумя степенями свобо-
ды, причем действующие на нее силы инерции вызывают одновре-
1 С. А. Бернштейн. Новый метод -определения частот колебаний упругих
систем, изд. ВИА РККА. 1939.
17
менные .перемещения по двум «взаимно-перпендикулярным направ-
лениям. Такой случай встречается, например, в задаче о колебани-
ях кривого бруса.
Введем обозначения;
y(s) —вертикальное смещение точки s;
x(s) —горизонтальное смещение точки $;
о (sy, ty) — вертикальное перемещение точки s от единичной вер-
тикальной силы в точке /;
о (sx> М — горизонтальное перемещение той же точки от той же
силы;
& (sy, tx)—вертикальное перемещение точки s от единичной гори-
зонтальной силы в точке t\
6 (sx, tx) —горизонтальное перемещение той же точки от той же
силы.
Между этими четырьмя функциями влияния существуют сле-
дующие свойства взаимности:
8 (sy, 9 = 8 (G,s,);8 («жА)=8 (бАг);
8 (sj, О = 8 A, s,); 8 (sA, ty) = 8 (ty,sx).
Обозначая т (s) погонную массу в точке s, напишем два урав-
нения перемещений от инерционных сил:
У (s) = z J т (I) |у (<) 8 (sy,ty) + X (/) 8 dt,
О
I
x(s)= z f -8(sv,9 + x(t)-8(s^)|dt.
(36)
Пределы интеграции здесь выставлены условно. Интеграция
должна производиться по всей длине стержней системы, если она
имеет стержневую структуру. Для системы поверхностного или
объемного строения интеграция распространяется на всю поверх-
ность или весь объем.
Мы получили два совместных однородных интегральных урав-
нения, из которых требуется найти собственные значения z=zft,
равные квадратам частот колебаний системы.
Так как с механической точки зрения задача не имеет прин-
ципиального отличия от обычной задачи, то можно ожидать, что
метод спектральной функции окажется и здесь применимым для
нахождения собственных значений. Так оно в действительности
и есть.
Для доказательства данную упругую систему с дважды беско-
нечным числом степеней свободы заменим системой с конечным
их числом, сосредоточивая массу в п отдельных точках. Такая из-
мененная система будет иметь не менее 2/г степеней свободы, так
как каждая точка имеет две степени свободы по условию. Для
простоты записи предположим, что система -имеет в точности 2п
степеней свободы. Вековое yjpa-внение для этой системы примет
вид
18
II
19
Развертывая этот детерминант по степеням z, получим спект-
ральную функцию обычного вида:
Sn(z) = I - ----+ AS„.^", (37)
коэффициенты которой выразятся суммами:
А1П^ f т (k) [6 (Лу Д) + 8 (МЛ .
4-1
Лг«=vid ij га(*и(«) Iе (kyM [ (s,9+
+ 8<*y’(wJj+8(fc,A> ,
(38)
где верхние индексы (&у), (kx) означают, что перемещение вычис-
ляется для системы, у которой точка k дополнительно закреплена
против вертикальных или соответственно горизонтальных сме-
щений.
Следы Bkn для такой системы получат выражения:
в1п= А„= Е m(k> R(*,A) + SAA)J.
k=\
- 2д2„ = v £ т(k} т(i, (г. (1уЛ) +
Л=1 1=1
+ 82 (*Л) 4- *2 (^у) + г2 (S А)1 ,
(39)
Формулы (38) превращаются в обычные формулы (И), если
перенумеровать подряд все 2 п степеней свободы, не делая разли-
чия между вертикальными и горизонтальными направлениями.
Будем теперь увеличивать п и перейдем к пределу. В пределе
получим исходную систему, спектральная функция для которой
будет пределом спектральных функций Sn:
S (z) = hm Sn (z)= 1 — ATz -f- Z2z2-, (40)
причем коэффициенты также будут равны пределам последова-
тельностей соответствующих коэффициентов:
Ak = Игл АЛп .
п- '
Мы не даем строгого доказательства существования всех упо-
мянутых пределов, так как оно совершенно тождественно с дока-
зательством, приведенным для простого случая в цитированной
работе автора.
20
При переходе к пределу получим такие выражения для коэф-
фициентов:
А= j m(s) |g(sy,sv) + S(sr,sJJ ds,
0
I I
Лз= 2!" J J m(s)m(t) (8(sy>sy) |Л>«уЛ) +
0 0
+8<M (1Л,1 v)] +S >(/,,9+8<4Wll<fcA,
и для следов:
В1= ] m(s) |8 (sy>sy) + 8(sy,sJ]</s,
О
Вг= J’ f '"(s)'n(O [S2(Vy)+82(Mx) +
(41)
(42)
+ 82(sx,/y) + 8*(Sy,/v)lrfs<&,
Нетрудно убедиться, что неравенства
остаются в силе, так как они основаны на очевидных неравенствах
вида
Отсюда следует, что спектральная функция (40) обладает со-
вершенно такими же свойствами, как и функция (10), и, стало
быть, метод нахождения частот через последовательности корней
спектральных полиномов остается применимым и к задаче о сов-
местных интегральных уравнениях. В частности, низшая частота
будет определяться неравенством (32) или (33) с подстановкой
в них выражений (42) для следов Bk.
Нетрудно видеть, что мы пришли бы к такому же выводу, если
бы предположили, что каждая точ-ка (вернее, каждое сечение) уп-
ругой системы обладает не двумя, а произвольным числом N сте-
пеней свободы. В этом случае задача свелась бы к системе N
совместных однородных интегральных уравнений, но решение ее
по методу спектральной функции имело бы ту же форму. Разу-
меется, выражения Ак и Bk усложнились бы, но закон их построе-
ния настолько очевиден, что мы не будем приводить развернутых
форму I для них в самом общем виде.
21
6. ПРОСТЕЙШАЯ ЗАДАЧА УСТОЙЧИВОСТИ
Задача определения частот свободных колебаний упругой си-
стемы представляет частный случай общей проблемы математиче-
ской физики о собственных значениях. Ввиду этого естественно
пытаться перенести метод спектральной функции на другие задачи
о собственных значениях и в .первую очередь на задачи устойчи-
вости упругих систем.
Критерием применимости нашего метода является возможность
приведения задачи к однородному интегральному уравнению ти-
па (Г), ядром которого является функция влияния какого-либо
перемещения или ее произведение на призвольную положительную
и ограниченную функцию одного переменного. Если задача может
быть сведена к такому уравнению, то метод спектральной функции
полностью приложим к нахождению собственных значений, какова
бы ни была физическая природа задачи.
Простейшим примером задачи устойчивости, приводимой к
уравнению (1), является задача о продольном изгибе центрально
загруженного стержня с шарнирными концами. Эта задача до-
пускает двоякий способ построения уравнения (1').
Дифференциальное уравнение изогнутой оси принимает для
такого стержня известную форму
EJ-^ + Py = O. (43)
Обозначим через q(x) фиктивную поперечную нагрузку, спо-
собную изогнуть стержень по такой же кривой при отсутствии
продольной силы. Из условия М = Ру найдем
q (х)= Р =------— у . (44)
4 dx2 Е J у к ’
С другой стороны, прогиб у(х) стержня можно выразить ин-
тегральным уравнением, как принято говорить в математической
физике, истокообразно:
i
у (х) — j* q (s) & (xts) ds ,
d
или, подставляя выражение (44) для q (s),
у (x) = — P2 f у (s) О (x,s) ds , (45)
J EJ (s)
причем J(s) можно рассматривать как переменную величину.
Уравнение (45) имеет ту же структуру, что и (1'). Сходство
обратится в тождество, если положить т (s) = —-— . Тогда мы
EJ(s)
получим такой результат: критическая сила центрально-сжатого
шарнирно-опертого стержня равна частоте поперечных колеба-
ний такого же стержня, загруженного массами /n(s) = —?— .
22
В частности, п,ри J = const мы получаем формулу Эйлера
п __ л3 , f EJ _ л-EJ
кр~ i* V т ~~-
Очевидно, что подобие уравнений (Г) и (45) ведет за собой
полную применимость метода спектральной функции. Более того,
при этом остаются в силе все формулы, приведенные выше, с за-
меной в них лишь m(s) на —?— .
7 EJ(s)
Так как задача о шарнирно-опертом стержне имеет особо важное
практическое значение, то этот вывод существенен, так как он
позволяет находить надежные двусторонние приближения крити-
ческой силы для стержней переменного сечения.
Та же задача может быть приведена к другому интегральномv
уравнению того же типа. Этот путь указал Трефц1. Его особен-
ность состоит в том, что истокообразному определению подвергает-
ся не прогиб оси стержня, а угол поворота касательной к оси.
Пусть ? — угол поворота оси в точке х. Проектируем продоль-
ную силу Р на нормаль к оси, заменяя благодаря незначительно-
сти угла синус тангенсом:
Psin<f = P<e = P-^- =Q.
dx
Это выражение дает величину поперечной силы в сечении.
Умножая ее на длину элемента dx, «получим элементарную пару
P-^-dx = Ру' (х) dx.
dx
Обозначим через 0 (s, t) угол поворота касательной в точке s
от действия единичной пары в точке t. Тогда угол поворота от про-
дольной силы выразится:
yz (s) = Р Jy'(O^ (s,t)dt. (46)
Это уравнение снова имеет форму (Г), а потому вычисление
критической силы может быть выполнено по методу спектральной
функции. Очевидно, уравнению (46) будет отвечать иная спек-
тральная функция, чем уравнению (45). Интересно выяснить их
взаимное соотношение.
Спектральная функция для уравнения (45) имеет вид
S(P) = \ —А1Р2 + А2Р4------,
где
С f (47)
1 J EJ (s) 2! J J EJ (s) EJ (t)
1 Treff tz. Zeitschrift fur angewandteMathematik und Mechanik, t. 3, стр. 272,
1923; см. также Я. Л. Нудельман, Интегральные уравнения в теории про-
дольного изгиба, «Прикладная математика и механика», т. III вып. 1, 1936.
23
Спектральную функцию уравнения (46) запишем в виде
О(Р)= 1-а1Р + а2Р2-----------------------,
где
«Xi = JН(s,s)ds; а2 = j J 0(s,s)(ttt)dsdt- • (48)
Обозначим, кроме того, следы уравнения (45), как обычно,
через Bk , а следы уравнения (46)—через ₽*. Так как спектр
системы, т. е. совокупность собственных значений P = Pk, в обоих
случаях одинаков, то между корнями Pk и следами существует
зависимость
£ *k ‘k
и, с другой стороны,
1 1 рГ 2j Pl 1
Отсюда следует, что
fl„ = ₽2„, (49)
и, следовательно,
A = ₽3; (50)
Из сопоставления равенств (49) и (50) с (27) видно, что функ-
ция S(P) является по отношению к с(Р) трансформированной
функцией с показателем 2. По доказанному автором свойству та-
ких функций, их сходимость ускоряется с ростом показателя
трансформации. Таким образом, вычисление критической силы
через корни функции °(Р), отвечающей уравнению Трефца, дает
менее быструю сходимость, чем использование для той же цели
функции S(P), отвечающей уравнению (45).
Напишем развернутые выражения следов
Pi = j 0(s,s)ds ; ₽2 = J J ®2(s,f)dsdt; - - • (51)
Соотношение (49) приводит к интересным интегральным тож-
дествам:
f8(s-s)^4Je2(s’0<Zsd<’
dsdl =
J J EJ(s)EJtt)
= J J | |0(s,/)H (t,u)ty(utv)ti(v,s)dsdtdudv,
(52)
24
Было бы интересно получить эти тождества прямым путем»
вскрывая их физической смысл.
Покажем на примере .вычисление критической силы для шар-
нирно-опертого центрально-сжатого стержня, исходя из обычной
спектральной функции (47) и из функции (48), отвечающей
интегральному уравнению Трефца.
1-й способ. Заимствуем значения Bit В2 из упомянутой ра-
боты автора:
J £7 90 (£7)2 *
J J (£7)з 9 450 £7/
Отсюда
или, переходя от z к PkP = ]/z и подставляя Bit В2,
9,862 — < Ркв < 9,88 — ;
> J2 RP /2
при точном значении множителя
я2 = 9,8696-
2-й способ (через уравнение Трефца). Находим значения
0(s, s) 0(s, Z), пользуясь формулой Мора:
0 (5>0= 3/4? Is3+(z -s)3 —г <z - s> i(z -s) <2s - z>+
+ (Z — Z) (2Z — s)) I при s < t.
Определяем Pi, P2:
0
0 0
откуда
25
или
Рлр>9,49^.
Верхний предел в этом приближении вычислить нельзя, так
как он получает мнимое выражение.
Сопоставляя оба способа, мы обнаруживаем подтверждение
наших теоретических выводов:
1) числа Bi и ₽2 равны между собой [равенство (49)];
2) первый способ дает более быструю сходимость прибли-
жений.
Автор показал в своей предшествующей работе, что появление
мнимых корней у полинома второй степени свидетельствует о том
что корни спектральной функции возрастают медленнее членов
геометрической прогрессии с знаменателем 3. При оперировании
со спектральной функцией, отвечающей уравнению Трефца, этот
знаменатель повышается до 32 = 9, так что вероятность встретить
мнимное выражение в правой части неравенства (33) резко возра-
стает. Яркий пример этого мы видели в только что разрешенной
обоими способами задаче.
7. УСТОЙЧИВОСТЬ консольного СТЕРЖНЯ
Рис. 2
Установленное нами преимущество первого способа становится
спорным или даже исчезает, как только мы переходим от шарнир-
но-опертого стержня к стержню с
другими краевыми условиями.
Пусть стержень имеет один ко-
нец свободный, а другой защемлен-
ный (рис. 2). Изгибающий момент
при продольном изгибе выразится:
M = P(f—y),
а потому фиктивная поперечная нагрузка определится из
Выражая прогиб истокообразно через нагрузку q (х), получим
неоднородное интегральное уравнение
y(x) = J<7(s)8(x>s)ds = -P» J I/-y(s)l • (53)
отличное по структуре от уравнения (!'). Уравнение (53) можно
привести к однородной форме, но ценой отказа от симметрии ядра
и основных его свойств. На самом деле, положим в уравнении (53)
Х=/, I/ (') =/-•
/= -Р2 f If-У(«)] -^7^ , (54)
J EJ (S)
26
и вычтем почленно уравнение (53) из (54):
f-У (х) = - Р2 J [f-y (s)l —ds,
или, обозначая f — у (х) = ц(х):
1 (х) = - Р8 С ч (s) [8 (!,s) - В (X.S)] . (55)
J EJ (s)
Это уравнение однородно и формально сходно с (Г), но его
ядро обладает существенно иными свойствами.
Обозначая б (l,s) —&(x,s) = К (x,s), перечислим эти отличия:
1) К (х,$) #=К($,х);
2) условие К (х, х) > 0 может не соблюдаться;
3) детерминант, составленный из ядер, может не быть положи-
тельным, т. е. возможно соотношение
К(х1,х1) K(xltx2)-- К(х2,хх) К(х2,х2)-- K(xi.x„) К (x,,xn)
К(х„,х^ К(х„,х2)-- • К (хпгхр)
4) нельзя утверждать справедливости неравенства
Dn К (Х2,Х2) • • • /С (хп,хп).
Эти изменения в свойствах ядра приводят к тому, что формаль-
но построенная спектральная функция может оказаться расходя-
щейся и, во всяком случае, не будет удовлетворять тем законам
сходимости, которые делают возможным двустороннее приближе-
ние корней. Короче говоря, к уравнению (55), так же как и к (53),
неприменим метод спектральной функции.
Это затруднение можно обойти, применяя условный прием пе-
рехода к измененной фиктивной схеме стержня. Подобный прием,
как известно, успешно применяется в графоаналитическом методе
определения деформаций балок и служит для выравнивания крае-
вых условий двух различных дифференциальных уравнений. Здесь
этот прием послужит для придания однородности интегральному
уравнению изгиба.
Для осуществления этой задачи достаточно создать такие
условия, при которых прогиб будет пропорционален моменту
а для этого нужно, чтобы прогиб отсчитывался от оси, совпадаю-
щей с направлением действия силы. Если это направление не
смещается при потере устойчивости (случай шарнирно-опертого
стержня), условие (56) само собой выполняется; в консольном
27
стержне, однако, направление силы смещается, и интегральное
уравнение получается неоднородным.
Пусть же точка приложения продольной силы к стержню будет
закреплена от поперечных смещений, а место заделки, напротив,
освобождено от такого закрепления (рис. 3). Нетрудно видеть, что
для такой фиктивной схемы соблюдается условие (56), а потому
интегральное уравнение продольного изгиба примет форму урав-
нения (Г) или (45).
Две схемы рис. 2 и 3 облада-
ют следующими интересными
свойствами:
1) форма продольного изгиба
и величины критической силы у
обеих схем одинаковы;
Рис- 3 2) форма поперечного изгиба
от одинаковой поперечной на-
грузки у обеих схем различна;
3) как следствие, частоты поперечных колебаний у двух схем
различны;
4) критическая сила для схемы рис. 2 равна частоте попереч-
ных колебаний схемы рис. 3 при загружении ее массой
/ Ч 1
т (X) = —-— и обратно.
£ J (х)
Эти свойства вытекают из того, что краевые условия обеих
схем одинаковы относительно продольной нагрузки, но различны
относительно поперечной нагрузки.
Таким образом, для вычисления критической силы по методу
спектральной функции приходится переходить к фиктивной схеме,,
если исходить из интегрального уравнения прогиба.
Теперь обратимся к интегральному уравнению Трефца, выра-
жающему истокообразно угол поворота. Нетрудно убедиться, что
это уравнение будет однородным, так как угол поворота не меня-
ется при параллельном смещении осей координат. Действительно,
условие
Q.
р
/ =
(57)
получающееся из равенства (56) в силу теоремы Швеллера —Жу-
равского, останется справедливым при любом параллельном пере-
носе силы Р. Следовательно, уравнение Трефца и для стержня
по рис. 2 получит форму уравнения (46). Хотя спектральная
функция, построенная для уравнения (46), как всегда, обладает
более медленной сходимостью, чем для уравнения (45), но зато
применение уравнения (46) не требует перехода к фиктивной схе-
ме, а это является, конечно, важным практическим и принципиаль-
ным преимуществом.
Определим критическую силу для стержня по рис. 2 обоими
способами.
28
1-й способ. Переходим к фиктивной схеме по рис. 3 и вы-
числяем для нее перемещения 6(s, s), 0, полагая начало
координат на правой опоре:
8(M = ^-(3/-2s);
«М = ^7 + -77- [«(/-s) + 4<s2~’
Вычисляем Bi, В2:
i
о о
Отсюда
при точном значении коэффициента -=2,4673---
2-й способ. Вычисляем значения 6 (s,s), 6(s, t) для схемы
рис. 2, принимая начало координат в заделке:
0(s,z)==ir (s<°-
Отсюда
p,=^(S,S)ds^^.-,
О о
Следовательно:
29
Сопоставляя оба способа, мы убеждаемся, что в этом случае
вычисления по второму способу значительно проще, чем по перво-
му, хотя, как всегда, дают меньшую точность.
8. ЗАКЛЮЧЕНИЕ
Предложенный метод, помимо своего удобства и универсаль
ности, обладает еще одним существенным достоинством. Позволяя
выразить значение частоты или критической силы в явной форме
через числа Вп, этот метод в сильной степени облегчает анализ
свойств частот и дает возможность исследовать в общем виде их
зависимость от различных факторов. Удачные примеры таких ис-
следований дают диссертации аспирантов Грузинского индустри-
ального института, выполненные под руководством автора1.
Несомненно, что этот метод может найти себе применение не
только в инженерных задачах, но и в ряде проблем математиче-
ской физики и астрономии, сводящихся к определению собствен-
ных значений ограниченного ядра. Но, разумеется, основным
полем его применения будут динамические расчеты в инженерных
задачах.
1 А. Н. Размадзе, Динамическая работа висячих металлических мостов
(кандидатская диссертация), 1939.
В. И. Бацикадзе, Колебания статически определимых ферм (кандидат-
ская диссертация), 1939.
Р. С. Лордкипанидзе, Вычисление частот колебаний стержней пере-
менного сечения (кандидатская диссертация), 1940.
2. РАБОТА СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫХ ФЕРМ
В УПРУГО-ПЛАСТИЧЕСКОЙ СТАДИИ
А. ПОВЕДЕНИЕ СЖАТОГО СТЕРЖНЯ ПОСЛЕ ПОТЕРИ
УСТОЙЧИВОСТИ
§ 1. ПОСТАНОВКА ЗАДАЧИ
Расчет статически неопределимых ферм по методу упругой де-
формации обладает тем же недостатком, что и расчет всякой стати-
чески неопределимой системы: юн позволяет проследить поведение
системы только до первого нарушения
упругости. Если даже принять для
упрощения график удлинений Пранд-
тля, поднимающий предел упругости
до предела текучести, то все же даль-
нейшее поведение системы не может
быть установлено упругим методом
расчета. Между тем реальная величи-
на коэффициента запаса требует для
своего установления знания предель-
ной нагрузки, т. е. верхнего предела
нагрузки, которую может выдержи-
вать сооружение. Эта предельная на-
грузка всегда выше той, при которой появляется первая текучесть,
но раздвиг между обеими нагрузками может иметь самую различ-
ную величину. Другими словами, упругая стадия работы может
составлять большую или меньшую долю от полной работоспособ-
ности сооружения.
Соображения о необходимости расчета сооружений по предель-
ному состоянию возникли уже давно. Как известно, Грюнинг1 ука-
зал новый путь такого расчета, перейдя к рассмотрению пластиче-
ских деформаций.
Классическая теория пластических деформаций основана на
графике удлинений Прандтля (рис. 1). Так как этот график уста-
навливает независимость величины удлинения от напряжения, коль
1 М. G г й n i n g, Die Tragfahigkeit statisch unbestimmter Tragwerke aus Stahl
bei beliebig haufig wiederholter Belastung, Berlin, 1926.
31.
скоро последнее достигло предела текучести, то при расчете стати-
чески неопределимых систем на послеупругую нагрузку исчезает
необходимость в удовлетворении условиям деформации по мере
перехода в пластическое состояние статически избыточных эле-
ментов. Когда все такие элементы перейдут в пластическое состоя-
ние, то отпадут все условия, связывающие деформативность систе-
мы, и она сможет быть рассчитана с помощью только одних условий
равновесия.
Этот метод расчета с успехом применен к неразрезным бал-
кам1 и отчасти к рамам2. Достоинства его общеизвестны. Примене-
ние же этого метода к фермам сталкивается с серьезными принци-
пиальными трудностями, которых недооценил Грюнинг, несмотря
на то, что свои рассуждения он вел применительно именно к стати-
чески неопределимым фермам.
Основная трудность заключается в том, что стержни фермы вы-
ходят из упругой стадии работы не только путем перехода в пласти-
ческое состояние, но и путем потери устойчивости, причем, как будет
показано ниже, зависимость между нагрузкой и укорочением сжа-
того стержня, потерявшего устойчивость, не отвечает диаграмме
Прандтля. Следовательно, мы должны будем оперировать с графи-
ками удлинений двух различных типов.
Это осложнение, заставляющее учитывать знаки усилий в стерж-
нях ферм, ведет за собой вторую расчетную трудность.
Известно, что статически неопределимую систему любого типа
нельзя в общем случае запроектировать как систему равного сопро-
тивления. Для ферм это обстоятельство доказывается теоремой
Мориса Леви3.
При расчете неразрезной балки по методу пластических дефор-
маций отсутствие равнопрочности в упругой стадии нас мало сму-
щает. Мы можем задаться уравновешенной эпюрой моментов для
нагрузки предельного состояния и подобрать сечения по максималь-
ным ординатам этой эпюры. В предельном состоянии конструктив-
ная балка приобретает ту самую эпюру, которой мы задались, хотя
для ряда сечений (включая нулевые точки эпюры) это состояние
и не исчерпывает несущей способности. Иными словами, наличие
местных конструктивных запасов в неразрезной балке не
снижает и не повышает предельной нагрузки, детерминированной
мощностью сечений в точках с максимальными моментами.
Если мы попробуем применить такой прием расчета к ферм^
т. е. зададимся уравновешенным распределением усилий в стерж-
нях и подберем их сечения по предельной нагрузке, предположи-
тельно устанавливая знаки усилий, то мы встретимся с затрудне-
1 Работы Maier—Leibnitz, Fritsche, Абрикосова, ^Кудина, Туркина и др.
2 К- Girkmann, Bemessung von Rahmentragwerken unter Zugrundelegung
eines ideal plastischen Stahles. Akad. d. Wiss. in Wien, «Math.-nat. Klasse», Bd.
9 10, 140, 1931. См. также статью Л. И. Маламента в сборнике «Расчет метал-
лических конструкций с учетом пластических деформаций» под ред. С Берн-
штейна, Госстройиздат, 1938.
3 М. Levy, La statigue graphique. См. также сноску следующей страницы.
32
нпем: эти знаки в предельном состоянии могут измениться против
предположенных1. А это будет означать, что действительное пре-
дельное состояние не совпадает с ожидаемым, ибо. как уже было
сказано, поведение и предельная нагрузка не одинаковы для рас-
тянутого стержня, перешедшего в пластическое состояние, и для
сжатого стержня, потерявшего устойчивость. Равным образом уве-
личение местных конструктивных запасов может привести к такому
же результату, изменив предельную нагрузку.
Наконец, .последнее затруднение, вытекающее снова из различия
в поведении сжатых и растянутых стержней, таково. Если мы под-
нимем нагрузку на ферму выше упругой стадии ее работы и если
даже при этом ни один сжатый стержень не потеряет устойчивости,
но какой-либо растянутый стержень потечет, то после разгрузки
этот стержень получит остаточное сжимающее усилие, которое мо-
жет лишить его устойчивости. С подобным явлением мы также не
встречаемся при расчете балок и рам. Даже если в ферме (напри-
мер, вантовой) все стержни в упругой стадии работы растянуты и
сконструированы так, что они не способны работать на сжатие, то
появление текучести в отдельных стержнях может привести при
разгрузке к появлению сжимающих усилий в других стержнях, т. е.
к выключению их из работы. Таким -образом, и в этих фермах имеет
место двоякая природа работы стержней в неупругой стадии.
Приведенные соображения показывают, что задача расчета
ферм по предельному состоянию несравненно сложнее аналогичной
задачи для неразрезных балок и раь|. Для ее разрешения необхо-
димо в первую очередь установить зависимость между нагрузкой и
укорочением сжатого стержня до и после потери устойчивости. Эта
зависимость должна дополнить диаграмму Прандтля, которую мы
будем считать справедливой только для растянутых стержней.
§ 2. ПРЕДЕЛЬНОЕ СОСТОЯНИЕ СЖАТО-ИЗОГНУТОГО СТЕРЖНЯ
При обычном методе расчета продольный изгиб стержня
означает прекращение его существования, и потому вопрос
о поведении стержня после потери устойчивости лишен смысла.
Действительно, вообразим себе свободно стоящий центрально
сжатый стержень с шарнирными концами. Чем точнее центри-
ровка и чем совершеннее форма и структура стержня, тем
ближе к критической силе может быть подведена нагрузка.
При подходе к критической силе начинается быстрый реет
выгиба, а стало быть, и момента, неизбежно дсхводящий стержень
до катастрофы, так как нагрузка на свободно стоящий стержень
не уменьшится в результате его выгиба.
Иначе обстоит дело, если концы сжатого стержня взаимно
соединены добавочными связями, ограничивающими свободу
сближения этих концов. Такой случай мы имеем в испытатель-
ных машинах. Известно, что появление продольного изгиба
1 И. М. Рабинович,К теории статически неопределимых ферм, М.» 1933.
3J
сигнализируется в этих машинах падением нагрузки, так что
равновесие стержня после потерн устойчивости, вообще говоря,
возможно, но лишь при снижении нагрузки ниже критической.
Уменьшение продольной силы позволяет опасному сечению
выдержать момент при большей стреле выгиба, нежели в слу-
чае постоянной нагрузки, а потому в машине излом стержня
(или переход в пластическое состояние) произойдет при боль-
шей стреле выгиба, чем в случае свободного стержня. Те же
соображения относятся и к .сжатому стержню в статически
неопределимой ферме.
Проф. И. М. Рабинович1 доказал, что наличие дополнитель-
ных связей не изменяет величины критической силы для сжа-
того стержня. Он установил далее, что нагрузка, воспринимае-
мая сжатым стержнем статически неопределимой фермы,
и после потери устойчивости остается равной критической
силе до появления в опасном сечении напряжений текучести,
после чего нагрузка начинает убывать. Падение несущей спо-
собности сжатого стержня после потери устойчивости еще
раньше обнаружил Кацинчи2. Сходный результат получил и Хвал-
ла3, проверявший результаты Кацинчи на простейшем эксперименте.
Мы выведем этот результат независимым путем, придав ему об-
щую расчетную форму, отсутствующую у упомянутых выше ав-
торов.
В поведении гибкого сжатого стержня можно установить следу-
ющие этапы:
1) упругое центральное сжатие вплоть до критической силы;
2) упругий выгиб, заканчивающийся появлением напряжений,
равных пределу текучести в крайних фибрах опасного сечения;
3) распространение пластичности по опасному сечению, завер-
шающееся полной пропиткой сечения пластичностью, т. е. образо-
ванием шарнира текучести;
4) распространение зоны текучести по длине стержня при сох-
ранении шарнира текучести в опасном сечении.
В стержнях малой гибкости второй этап будет отсутствовать.
Наиболее характерными моментами являются конечные ста-
дии первых трех этапов: достижение критической силы, появление
фибровой пластичности и образование шарнира текучести. Иссле-
дуем эти три стадии.
Если придерживаться концепции идеального упруго-пластич-
ного материала, для которого справедлива диаграмма Прандтля.
1 II. М Рабинович, Об устойчивости стержней в статически неопредели-
мых системах, AL, 1932.
2 G. К a z i п с z у, Bemessung von statisch unbestimmten Konstruktionen unter
Berucksichtigung der bleibenden Defomiationen, Liege, 1930.
о cIVv?,,a’ Theorie des aussermittig gedruckten Stabes aus Baustahl,
«Stahlbau» № 21—23, 1934.
E; C11У a]1 a- Drei Beitrage zur Frage des Tragvermogens statisch unbe-
stimmter Stahltragwerke, «Abhandl. d. Intern. Ver. f. BrGckenbau u. Hochbau»
34
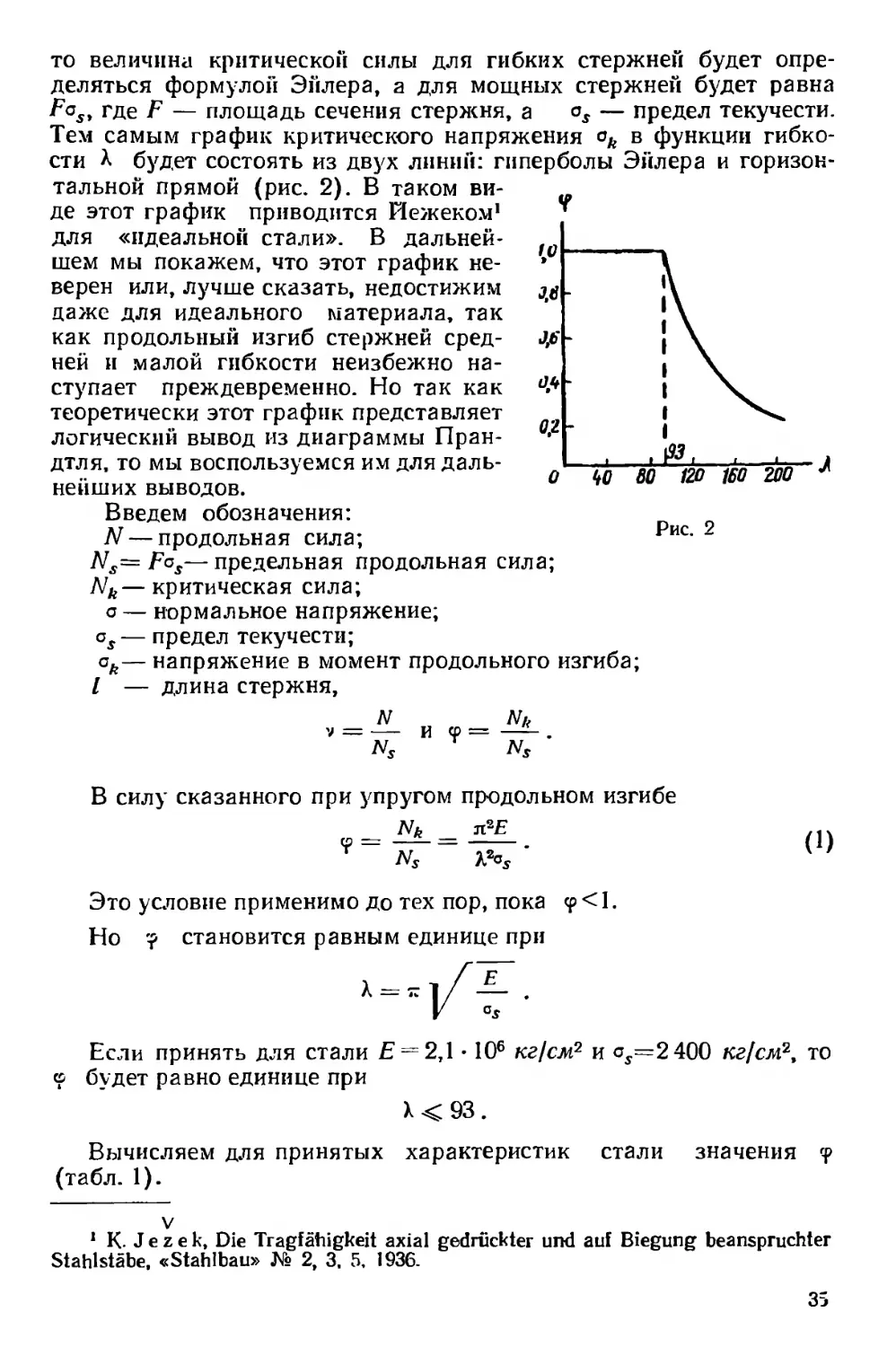
то величина критической силы для гибких стержней будет опре-
деляться формулой Эйлера, а для мощных стержней будет равна
Fas, где F — площадь сечения стержня, a os — предел текучести.
Тем самым график критического напряжения ok в функции гибко-
сти А будет состоять из двух линий: гиперболы Эйлера и горизон-
тальной прямой (рис. 2). В таком ви-
де этот график приводится Иежеком* 1
для «идеальной стали». В дальней-
шем мы покажем, что этот график не-
верен или, лучше сказать, недостижим
даже для идеального материала, так
как продольный изгиб стержней сред-
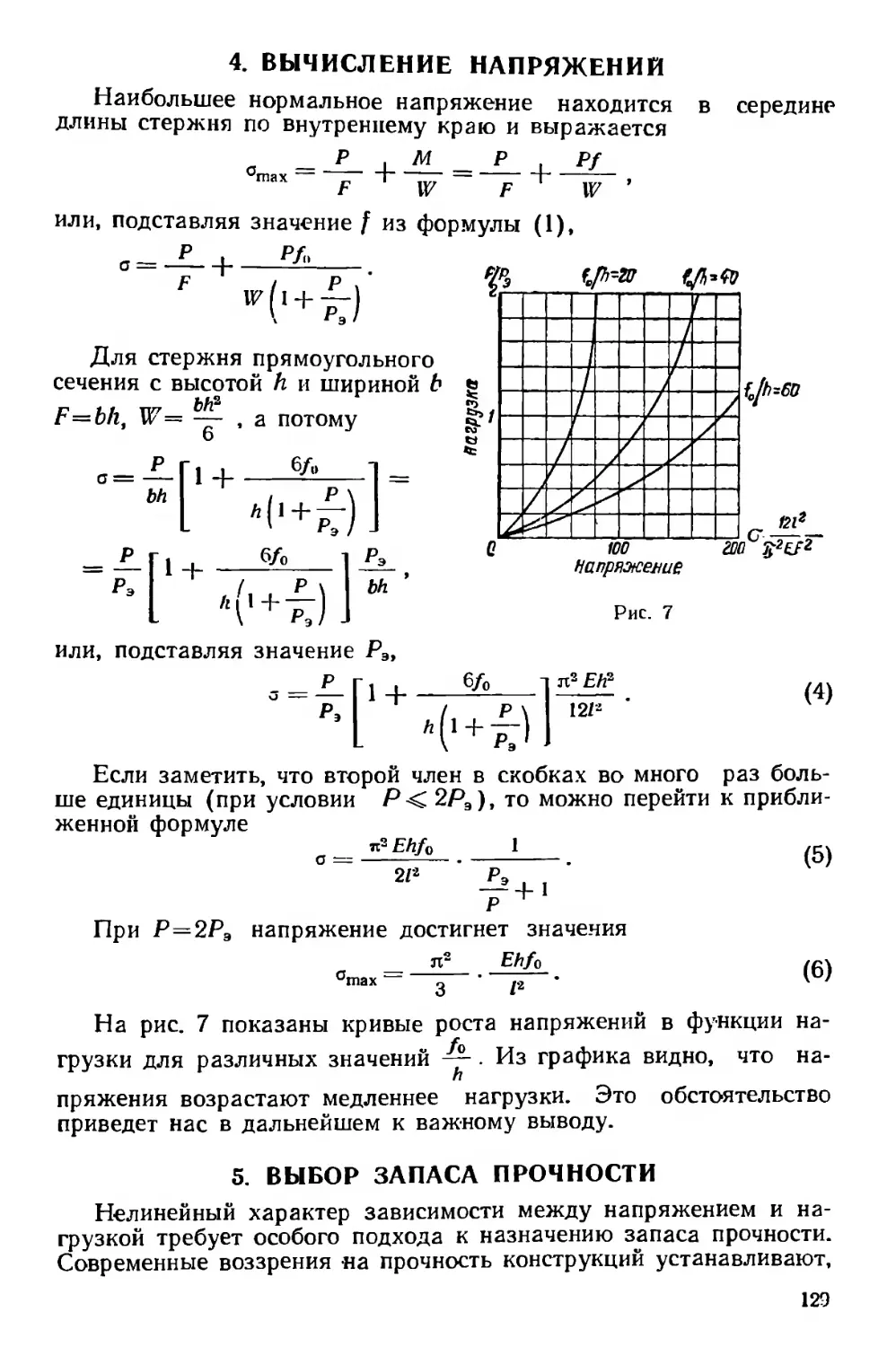
ней и малой гибкости неизбежно на-
ступает преждевременно. Но так как
теоретически этот график представляет
логический вывод из диаграммы Пран-
дтля, то мы воспользуемся им для даль-
нейших выводов.
Введем обозначения:
N — продольная сила;
Ns= Fcs— предельная продольная сила;
Nk—критическая сила;
о — нормальное напряжение;
cs— предел текучести;
ak— напряжение в момент продольного изгиба;
I — длина стержня,
W Nk
v =--- И Ф = —— .
Ns т Ns
В силу сказанного при упругом продольном изгибе
_ Nk _ п2Е
? “ Ns ~ 14 ’
(О
Это условие применимо до тех пор, пока <р <1.
Но ? становится равным единице при
Если принять для стали Е = 2,1 • 106 кг/см2 и as=2400 кг/см2, то
ф будет равно единице при
X < 93.
Вычисляем для принятых характеристик стали значения
(табл. 1).
v
1 К. J е z е k, Die Tragfahigkeit axial gedriickter und auf Biegung beanspruchter
Stahlstabe, «Stahlbau» № 2, 3, 5, 1936.
35
Таблица 1
X 93 100 120 140 160 180 200
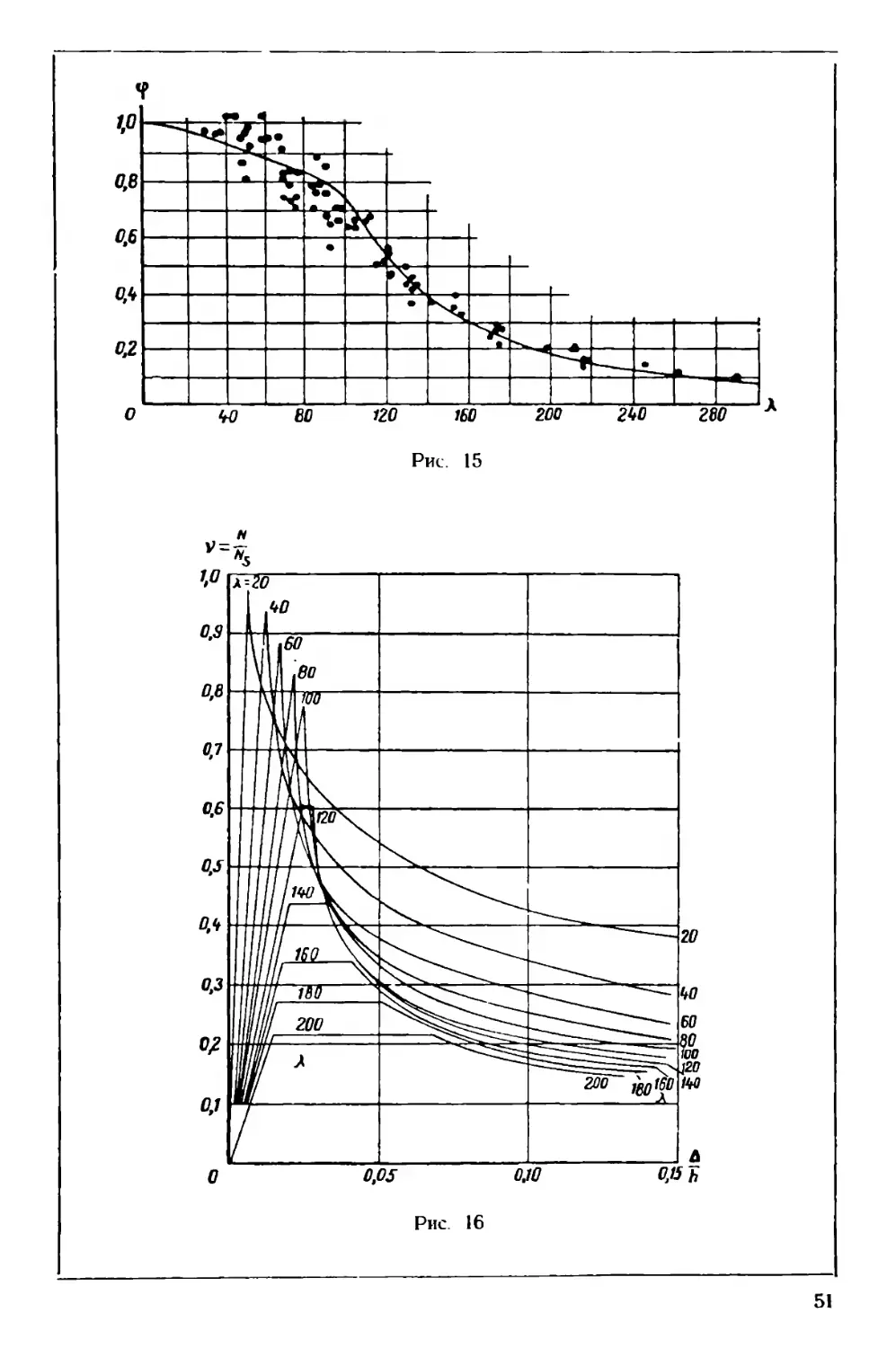
¥ 1,0 0,863 0,600 0,440 0,337 0,226 0,216
Итак, первый этап характеризуется условием
N<Nk
ИЛИ
(2)
Перейдем ко второму этапу. Петерявший устойчивость стер-
жень начинает изгибаться, приобретая стрелу выгиба /, а следова-
тельно, работает на сложное сопротивление с моментом M = Nf.
Конец этапа найдем из условия
N . М
о =--------
F W
(3)
где W — момент сопротивления, или
где с — расстояние от нейтральной оси до обращенной к центру
кривизны крайней фибры сечения, аг — радиус инерции сечения.
Введя обозначения
— = о и— = v
F oj
получим
или
(4)
Такова величина стрелы в конце второго этапа. Соответствую-
щую ей нагрузку мы найдем позже.
Третий этап характеризуется дальнейшим ростом момента, в
связи с чем пластичность распространяется в глубь сечения, и эпю-
ра напряжений становится ломаной. Этот этап заканчивается
образованием пластического шарнира, т. е. переходом наиболее
напряженного сечения в такое состояние, при котором все волокна
испытывают предельное напряжение, равное положительному или
отрицательному пределу текучести. Для начала будем считать оба
предела равными между собой. Нашей задачей является установ-
36
ление зависимости между продольной силой и моментом в предель-
ном состоянии. Задача эта была решена Гиркманном1 * * для некото-
рых форм сечения. Скромной заслугой автора является применение
более удобных обозначений.
Однако это упрощение формы
позволило значительно дальше
углубиться в анализ явления.
Пусть hi и h2 — расстояния
от центра тяжести сечения до
крайних фибр, а и—расстояние
от того же центра до нейтраль-
ной оси сечения (рис. 3). Усло-
вия равновесия позволяют напи-
сать два уравнения, связывающие
продольную силу К, момент М и
расстояние и:
N = о,
(pf —р/7) = Ф1(и),
—hi и
7И — оД j ydF + J ydF} = Ф2 (и).
—hl и
(5)
Исключая из этих двух уравнений и, мы получим зависимость
вида
Ф = (NfM) = 0 ,
связывающую значения N и М в предельном состоянии, т. е. при
наличии пластического шарнира в сечении.
Особенно просто эта операция выполняется для прямоугольного
сечения. Если h — высота прямоугольника, а b — его ширина, то
уравнения (5) примут вид:
N = cs.2bu,
M=C'b(— — u
Исключая и, получим уравнение Гиркманна
м = —"Ц.
(6)
Заметим теперь, что
а = М и bho = N
О «3 о о
будут равны предельным значениям момента и продольной силы,
вызывающим порознь предельное состояние сечения.
1 К. G i г k m a n n, Bemessung von Rahmentragwerken unter Zugrundelegung
eines ideal plastischen Stahles. Akad. d. Wiss. in Wien «Math.-nat. Klasse»,
Bd. 9—10, 140, 4931.
37
Обозначая р = — и подставляя в выражение (6), полечим
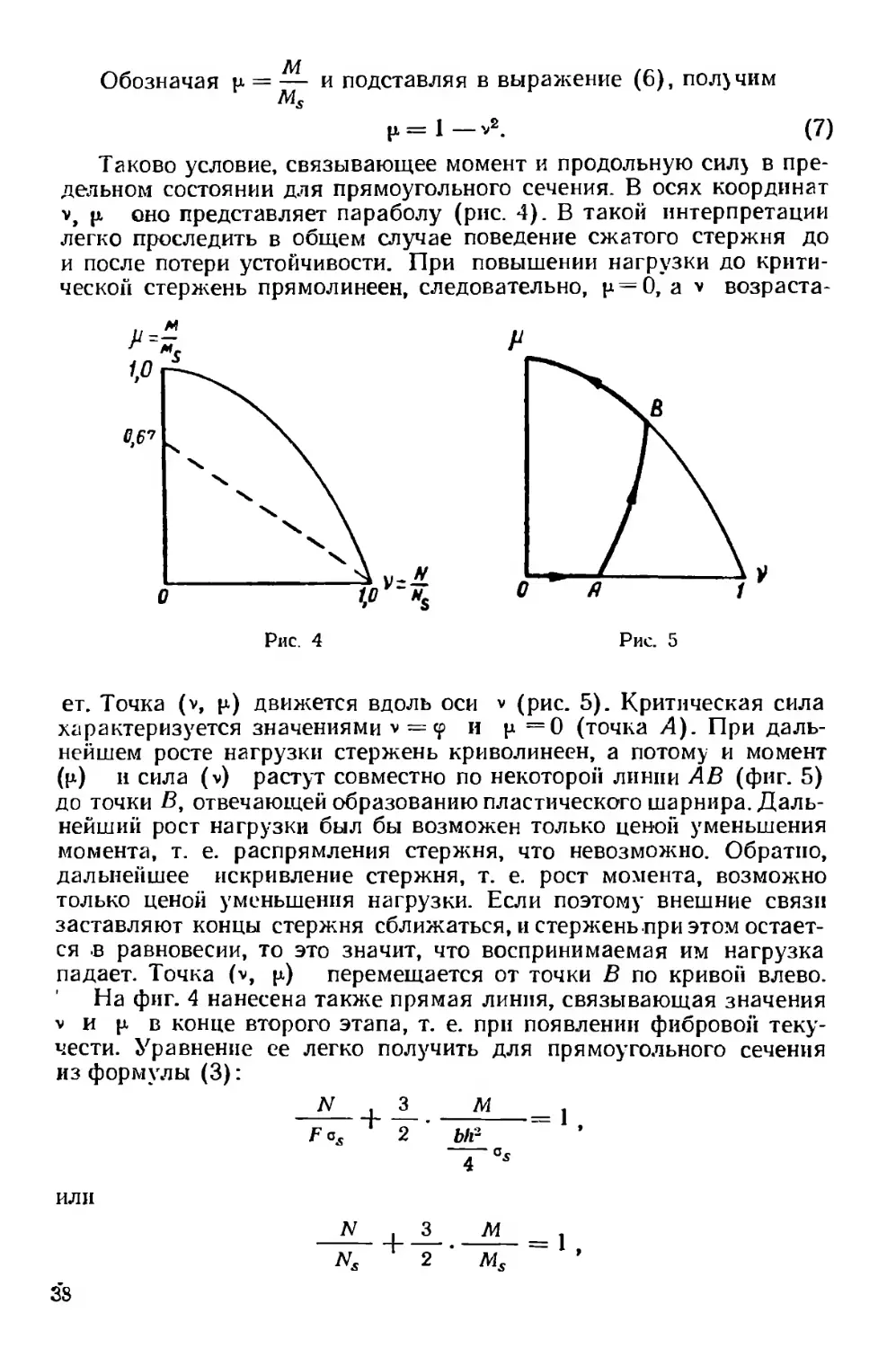
P=l-v2. (7)
Таково условие, связывающее момент и продольную сил} в пре-
дельном состоянии для прямоугольного сечения. В осях координат
v, р оно представляет параболу (рис. 4). В такой интерпретации
легко проследить в общем случае поведение сжатого стержня до
и после потери устойчивости. При повышении нагрузки до крити-
ческой стержень прямолинеен, следовательно, р = 0, a v возраста-
ет. Точка (v, р) движется вдоль оси v (рис. 5). Критическая сила
характеризуется значениями * = и р = 0 (точка Д). При даль-
нейшем росте нагрузки стержень криволинеен, а потому и момент
(р) и сила (v) растут совместно по некоторой линии АВ (фиг. 5)
до точки В, отвечающей образованию пластического шарнира. Даль-
нейший рост нагрузки был бы возможен только ценой уменьшения
момента, т. е. распрямления стержня, что невозможно. Обратно,
дальнейшее искривление стержня, т. е. рост момента, возможно
только ценой уменьшения нагрузки. Если поэтому внешние связи
заставляют концы стержня сближаться, и стержень при этом остает-
ся .в равновесии, то это значит, что воспринимаемая им нагрузка
падает. Точка (v, р) перемещается от точки В по кривой влево.
На фиг. 4 нанесена также прямая линия, связывающая значения
v и р в конце второго этапа, т. е. при появлении фибровой теку-
чести. Уравнение ее легко получить для прямоугольного сечения
из формулы (3):
JV_ 3 м
Fcs + 2 ЬК-
4 °s
или
N 3 М
N* 2 ' Ms
38
или, наконец,
. 3 i
> + -!л=1
(8)
Эта прямая ограничивает расчетное состояние опасного сечения,
тогда как парабола изображает геометрическое место предельных
состояний.
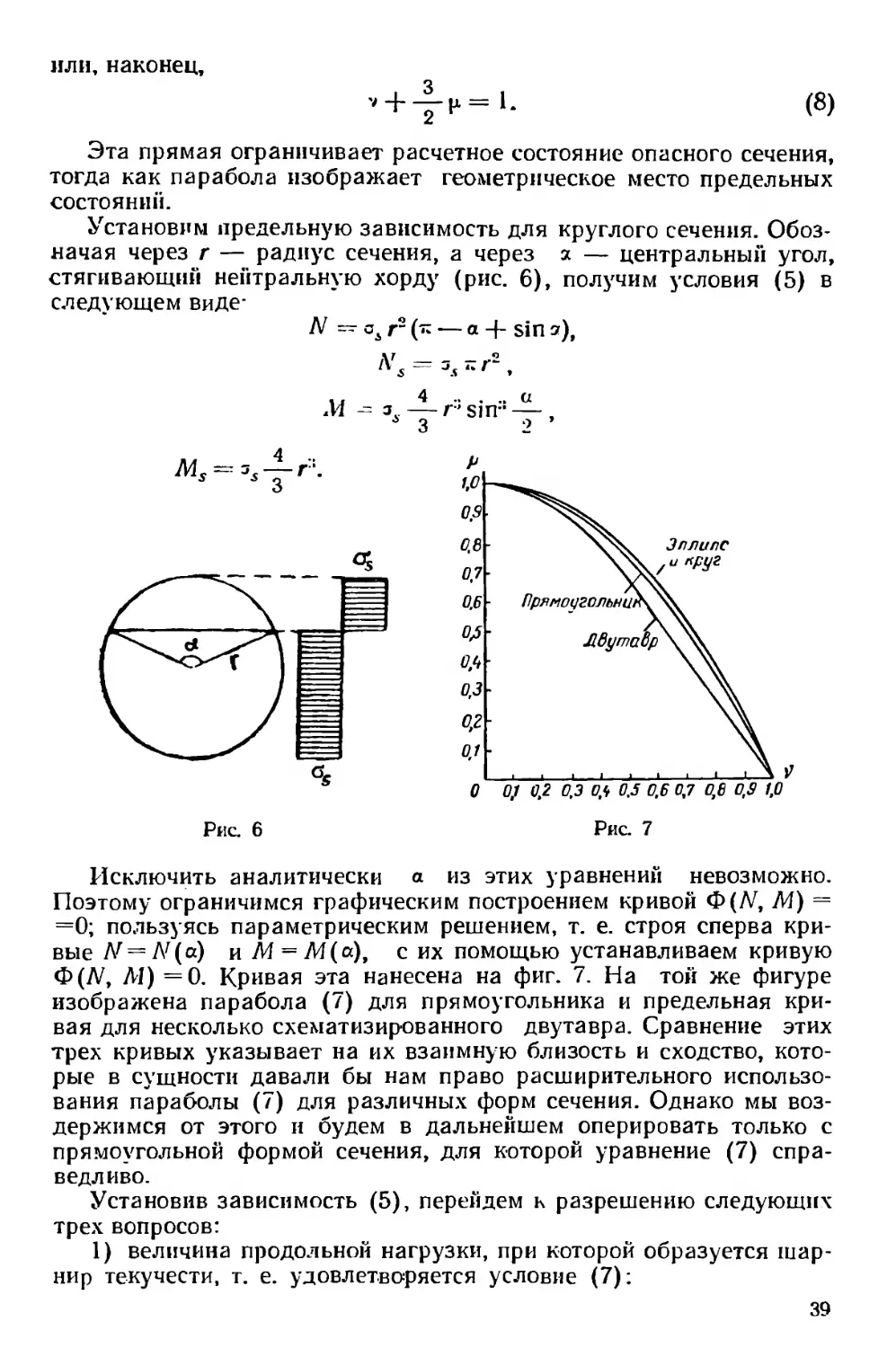
Установим предельную зависимость для круглого сечения. Обоз-
начая через г — радиус сечения, а через а — центральный угол,
стягивающий нейтральную хорду (рис. 6), получим условия (5) в
следующем виде-
ла (к — а + sin з),
г*,
•, 4 и
М - — г- sin- — ,
Л 3 2
Рис. 7
Рис. 6
Исключить аналитически а из этих уравнений невозможно.
Поэтому ограничимся графическим построением кривой Ф(М, 7И) =
=0; пользуясь параметрическим решением, т. е. строя сперва кри-
вые № = N(a) и М = М(а), с их помощью устанавливаем кривую
Ф(Л\ М) =0. Кривая эта нанесена на фиг. 7. На той же фигуре
изображена парабола (7) для прямоугольника и предельная кри-
вая для несколько схематизированного двутавра. Сравнение этих
трех кривых указывает на их взаимную близость и сходство, кото-
рые в сущности давали бы нам право расширительного использо-
вания параболы (7) для различных форм сечения. Однако мы воз-
держимся от этого и будем в дальнейшем оперировать только с
прямоугольной формой сечения, для которой уравнение (7) спра-
ведливо.
Установив зависимость (5), перейдем к разрешению следующих
трех вопросов:
1) величина продольной нагрузки, при которой образуется шар-
нир текучести, т. е. удовлетворяется условие (7):
39
2) величина стрелы изгиба при образовании шарнира текучести:
3) величина укорочения хорды стержня в той же стадии.
§ 3. ПРЕДЕЛЬНАЯ ПРОДОЛЬНАЯ СИЛА
Пусть продольный изгиб наступил, и стержень изогнулся под
силой 7V, дав стрелу прогиба /. Момент в опасном сечении будет
М = Nf. Если гибкость стержня X > тг 1 / — > так что Ь т0 в
1/ os
момент продольного изгиба все сечения стержня уже находятся в
предельном состоянии, а потому в этом случае предельная нагрузка
совпадает с критической:
vnpen 1
ИЛИ
^пред = Nь Ns .
Поэтому достаточно ограничиться исследованием продольного
изгиба, возникающего при упругой работе стержня. До тех пор пока
в опасном сечении выпучившегося стержня нет пластических дефор-
маций, мы можем выразить стрелу прогиба приближенной форму-
лой Мизеса1
-£--1 =—Ч,/2—1 •
31 [ Nk л f
Появление пластических деформаций в опасном сечении уве-
личит деформативность стержня, а потому в третьей стадии стрела
выгиба выразится
/W=/,«+/,«.
где/1 (>) определяется формулой Мизеса, а /г (v) есть некоторая
возрастающая функция нагрузки v. Отсюда следует, что приня-
тие формулы Мизеса в третьей стадии дает преуменьшенную вели-
чину стрелы при данной нагрузке и, обратно, преувеличенную
величину нагрузки при данной стреле. С другой стороны, нагрузка
в третьем этапе не может быть меньше критической силы » = <р,
так как до образования пластического шарнира несущая способ-
ность стержня не исчерпана. Таким образом, истинная величина
усилия v в момент образования пластического шарнира, т. е. в
конце третьей стадии, лежит между двумя пределами, причем ниж-
ним пределом является * = а верхним — то значение *, кото-
рое дается формулой Мизеса при предельной величине стрелы.
Из формулы Мизеса
м=лу -LLW‘VZ|/---i= —
________ п N/г V rf Я |/ ?
1 R. von Mises, Ausbiegung eincs auf Knickung beanspruchten Stabes.
«Zeitschr. f. angew. Math. u. Meeh.», Bd 4, 435, 1924.
40
Разделим момент М на предельный момент Л^ = —
|л = - = J-2L. 4W*. — 1/г__1.
к ъНг as <р у <р
Но А?Л = <fbh 3S и 7- = — . — = —, а потому:
Л г h (-12
и .1. ,/ZZT= А./Zxv 1/ZT7=
л h ybh as | <p n 3 }f tf>
= l,04Xv 2----1 . (9)
В предельном состоянии * и р связаны, кроме того, еще усло-
вием (7). Решая оба уравнения совместно, получим
(1 — V2)s= l,08XVp--1)
или
и— 1ДЭ8 —к3(i,08X2 — 2)v2+ 1 =0.
При <р=1, т. е. X < 93, уравнение (10) удовлетворится значе-
нием v =<р=1, или Л/Г11рсд= = Ns, как и следовало ожидать. Для
общего решения уравнения НО) преобразуем его, полагая g=—
v
и обозначая левую его часть через у:
у = __ 1,08о2ХТ + <Р2 (1,08Х2 — 2)2 + 1 = 0 .
Применим для решения способ Ньютона, ограничиваясь вторым
приближением для корня и принимая за первое приближение
значение £ = 1. Тогда второе приближение даст
5=1—рД2_1
(10)
но
5,(1) = т4„2?2 4- 1 = (1 — <Р2)2,
у '(g) = 4'Л3 — 3,24?2X2g2 + 2?s (1,08Х2 — 2) g,
у'(1) = т2 (4<р2 — 1,08Х2— 4) — 1,08 X V.
Последнее допущение основано на том, что 4(1—<р2) заведомо
меньше 4, тогда как 1,08 X2 заведомо больше 1,08-932=9 300.
Отсюда
5 =
1.08XV
или
v = = Т +
П - У2)2
1,08Х2<р
41
Нетрудно видеть, что второй член правой части ничтожно
мал сравнительно с первым. Ниже даны значения £, подсчитан-
ные по первой из этих формул для разных гибкостей (табл. 2).
Та блица 2
X <93 100 120 140 160 180 200
е 1.0 1+0,84-Ю-5 И 7.3-Ю-5 HI5.8-10-5 1+24,3-10“5 1+34.10“5 1+46-10“5
Это значит, что верхний предел нагрузки превосходит нижний
предел (критическую силу) в практических случаях на сотые
доли процента, и, следовательно, мы можем смело считать, что
истинная нагрузка совпадает с нижним пределом, т. е. что кри-
тическая сила есть наивысшая сила, воспринимаемая стержнем
до или после потери устойчивости.
Иными словами, второй и третий этапы характеризуются
постоянством усилия v = ф, а соответствующий им участок графи-
ка укорочений должен изображаться горизонтальной прямой, ко-
торую можно уподобить площадке текучести растянутого стержня.
На фиг. 5 этим этапам будет отвечать вертикальная прямая.
§ 4. СТРЕЛА ВЫГИБА В ПРЕДЕЛЬНОМ СОСТОЯНИИ
Теперь мы можем найти стрелу прогиба f при достижении
предельного состояния. Отметим, что никаких гипотез о форме
линии изгиба для этого не требуется.
Стрела f определяется из выражения
г М М Ns Ms |i Мх
N ~ Ms ' N ' Ns ~ “7' Ws ’
HO
Mx = M2
Ns 4bhas 4 ’
а из формулы (7)
p = I — v2.
Поэтому
или
так как в предельном состоянии Ниже даны значения
для разных гибкостей (табл. 3).
42
Таблица 3
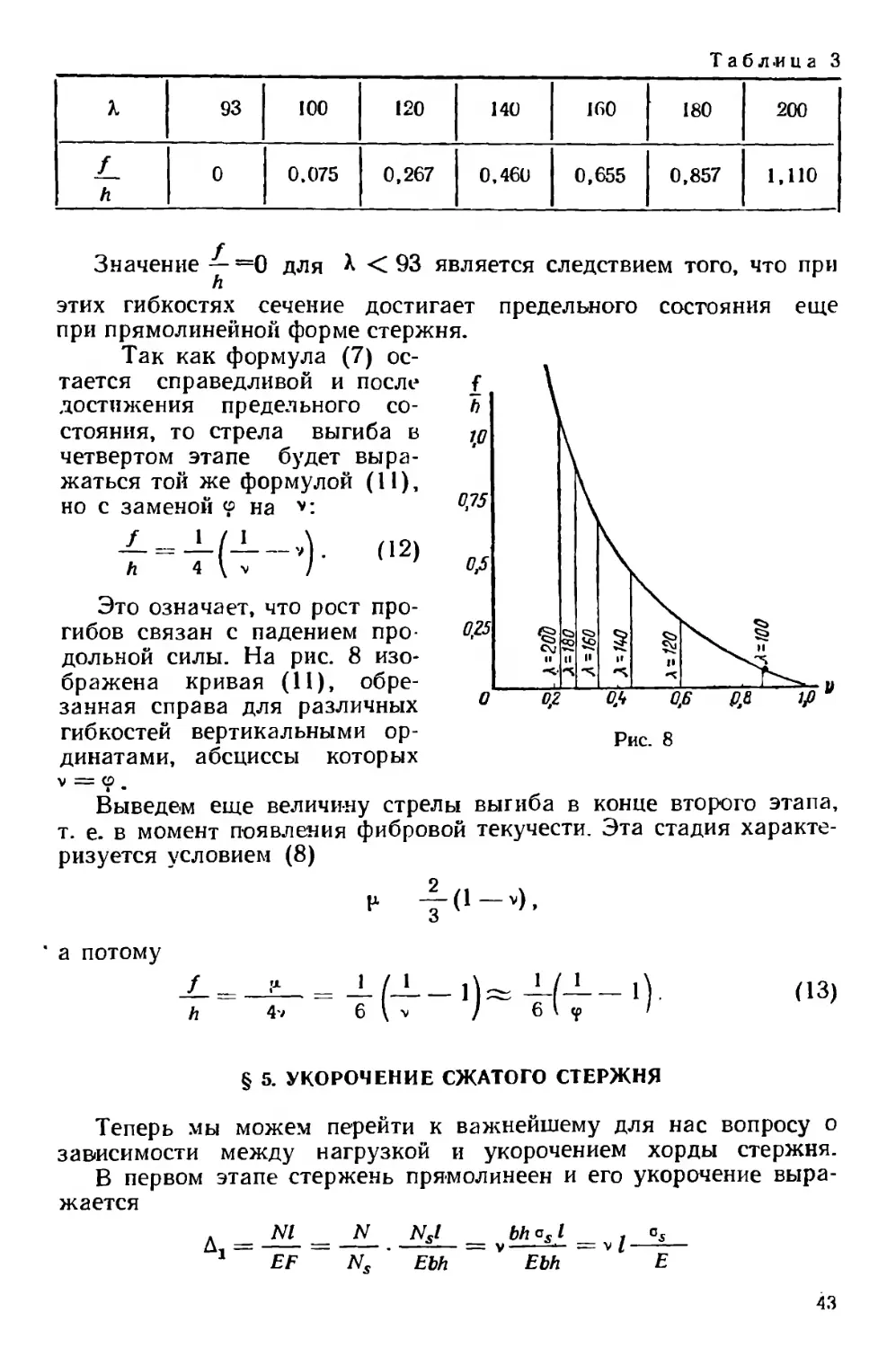
1 93 100 120 140 160 180 200
f h 0 0.075 0,267 0,460 0,655 0,857 1,110
Значение — =0 для X < 93 является следствием того, что при
h
этих гибкостях сечение достигает предельного состояния еще
при прямолинейной форме стержня.
Так как формула (7) ос-
тается справедливой и после
достижения предельного со-
стояния, то стрела выгиба в
четвертом этапе будет выра-
жаться той же формулой (11),
но с заменой на
Это означает, что рост про-
гибов связан с падением про-
дольной силы. На рис. 8 изо-
бражена кривая (11), обре-
занная справа для различных
гибкостей вертикальными ор-
динатами, абсциссы которых
v — и .
Выведем еще величину стрелы выгиба в конце второго этапа,
т. е. в момент появления фибровой текучести. Эта стадия характе-
ризуется условием (8)
’ а потому
§ 5. УКОРОЧЕНИЕ СЖАТОГО СТЕРЖНЯ
(13)
Теперь мы можем перейти к важнейшему для нас вопросу о
зависимости между нагрузкой и укорочением хорды стержня.
В первом этапе стержень прямолинеен и его укорочение выра-
жается
Nl_ _ JV_ Nsl _ ybh as l =
EF ~~ Ns Ebh ~ V Ebh E
43
или
Al
~~h
а в конце первого
= V— .-^- = vX-----= 3,3-10“4 vX,
h Е eV 12
этапа
= 3,3- 1(Г4 Х<р.
Л
этапах укорочение слагается из укорочения оси,
(14)
(15)
В дальнейших
определяемого по-прежнему формулой (14), и из отрезка, выра-
жающего разность между длиной искривленной оси и длиной хор-
ды. На первый взгляд применение формулы( 14), т. е. закона Гука,
к неупрупим этапам кажется незаконным. Однако можно доказать
справедливость формулы (14) и в этих этапах. В предельном со-
стоя-нии в наиболее напряженном среднем сечении включается
пластический шарнир, благодаря чему в сечении устраняется одна
связь, препятствующая свободе вращения смежных сечений. Про-
дольная связь шарниром не нарушается, так как протяженность
шарнира по длине стержня бесконечно мала. Поэтому продольные
пластические укорочения оси невозможны; они остаются упругими
для всех точек параболы уравнения (7), кроме точки >=1,р=0.
Применимость формулы (14) для третьего и четвертого этапов
может быть доказана также и тем, что третий этап протекает при
практически постоянной величине продольной силы, а стало быть,
и укорочения оси стержня; четвертый же этап сопровождается раз-
грузкой и удлинением оси стержня, происходящим, разумеется, по
упругому закону.
Для определения укорочения в следующих этапах воспользуем-
ся формулой разности длин дуги и хорды:
Тр'2<гх.
о
где у(х) — уравнение линии изгиба.
Законность применения этой приближенной формулы может
возбудить сомнения, которые, однако, легко рассеять. Приближен-
ность формулы состоит в замене синуса на тангенс. Тем самым
формула применима при достаточно малых углах поворота сечений.
Зададимся допустимой мерой ошибки в 3%. При а =15°, sina =0,259,
tga =0,268. Таким образом, можно принять угол 15° за предел при-
менимости формулы.
Но при изгибе по синусоиде (невыгоднейшее предположение)
наибольший тангенс угла наклона (на конце стержня) выразится
tea- _*_=_52
Б I h I h
Приравняем его предельному допустимому значению tg 15°:
12
- —— = 0,268
h X
44
или
= 0,0246 х ,
Л
откуда видим, что формула укорочения при изгибе верна до дости-
жения следующих величин стрел выгиба:
при л = 20 60 100 140 200
-^- = 0,49 1,47 2,46 3,44 4,92
h
Из сопоставления этих данных с графиком рис. 8 мы видим, что
область законности взятой под сомнение формулы простирается
значительно дальше практической необходимости.
Выполнение интеграции требует знания уравнения у (х). Во
втором этапе, пока изгиб упруг, можно принять линию «изгиба за
синусоиду
а это дает
y=/sin-y- ,
4Z ’
и поэтому укорочение в конце второго этапа, взятое по
формуле (13), будет
= з.з -1 ст4 х<р + (-L — 1V — =
Л т 144 \ т ) I
= 3,310“4 + (16)
Рис. 9
Второй член выражает добавочное укорочение, полученное
хордой на протяжении второго этапа.
В третьем этапе, а тем более в четвертом, т. е. когда уже обра-
зовался шарнир текучести, синусоидальная форма изгиба перехо-
дит в некоторую другую, характеризующуюся увеличением
кривизны в окрестностях опасного сечения. Легко понять, что но-
вая линия изгиба будет менее выпуклой, чем синусоида, и более
выпуклой, чем треугольник. Иными словами, если принять одина-
ковую стрелу выгиба для синусоиды, истинной кривой и треуголь-
ника, то истинная кривая во всех остальных точках будет иметь
ординаты меньшие, чем синусоида, и большие, чем треугольник
(рис. 9). Поэтому закономерности, общие для синусоиды и тре-
угольника, тем самым будут справедливы и для истинной кривой,
а величины параметров будут иметь для нее некоторые средние
значения.
Принимая в третьем этапе синусоидальную форму, найдем
укорочение в конце этого этапа, т. е. в предельном состоянии
[по формуле (10)]:
- 3.3- + -£(4- ~,)-А_ 3.3. W-х, +
45
и в четвертом этапе
-^- = 3,3-io-4xv + -5i21^-L — vpnpn v (17)
Если же принять другой предельный случай — изгиб по тре-
2/2
6= —, и в конце третьего этапа получим
угольнику, то
а в четвертом этапе будет
А. = 3,3- 1СГ4 Xv + (18)
Расхождение во втором члене формул
(17) и (18) составляет около 20% для двух
крайних случаев. Так как истинная величи-
на укорочения должна лежать между зна-
чениями (17) и (18), то, принимая для ко-
эффициента второго члена среднюю вели-
чину 0,48, мы получим ошибку заведомо
меньшую 10% во втором члене, и, стало
быть, еще меньшую для полной величины
укорочения. Этот коэффициент мы обозна-
чим буквой k и назовем его «коэффициен-
том формы».
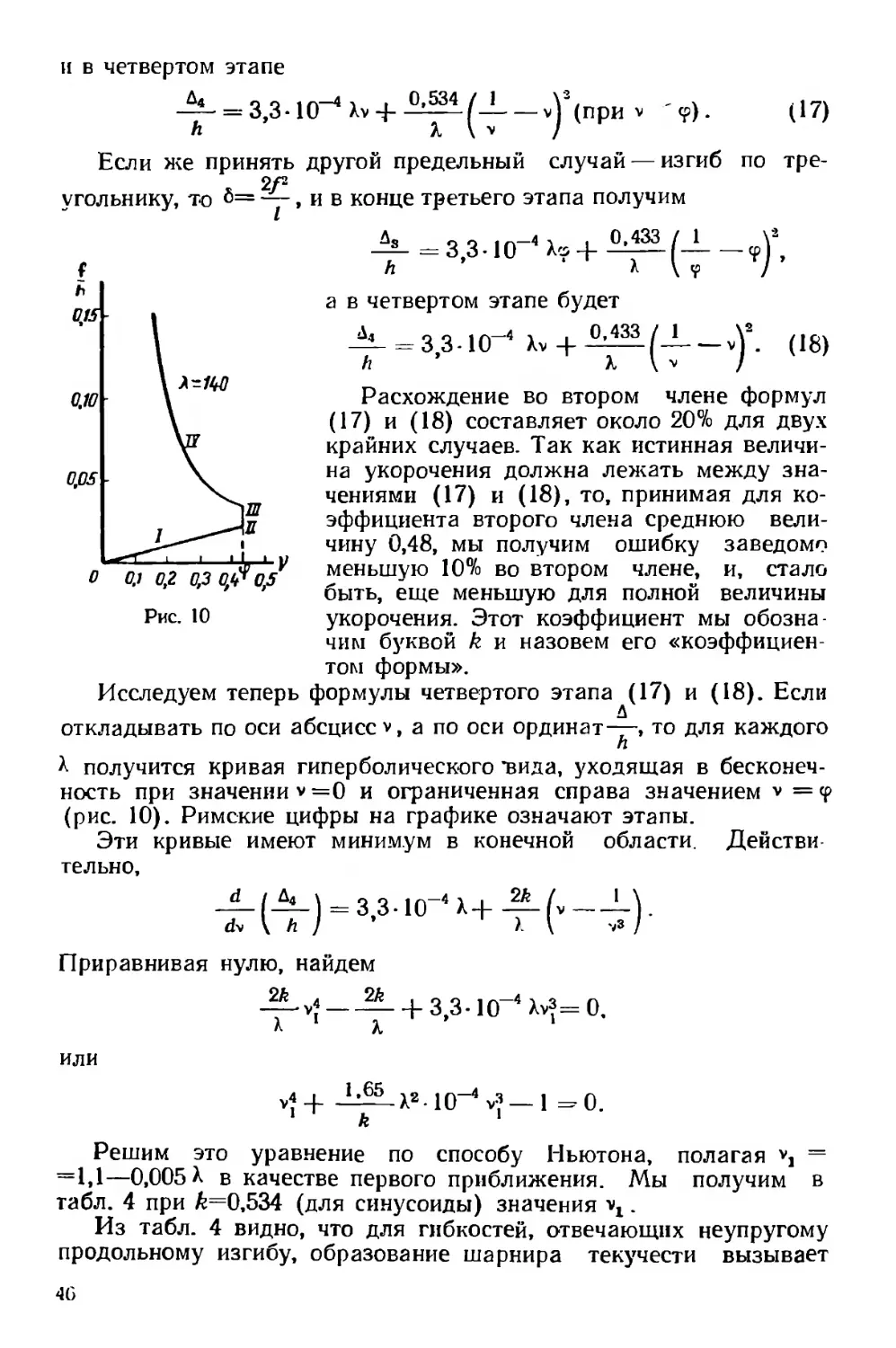
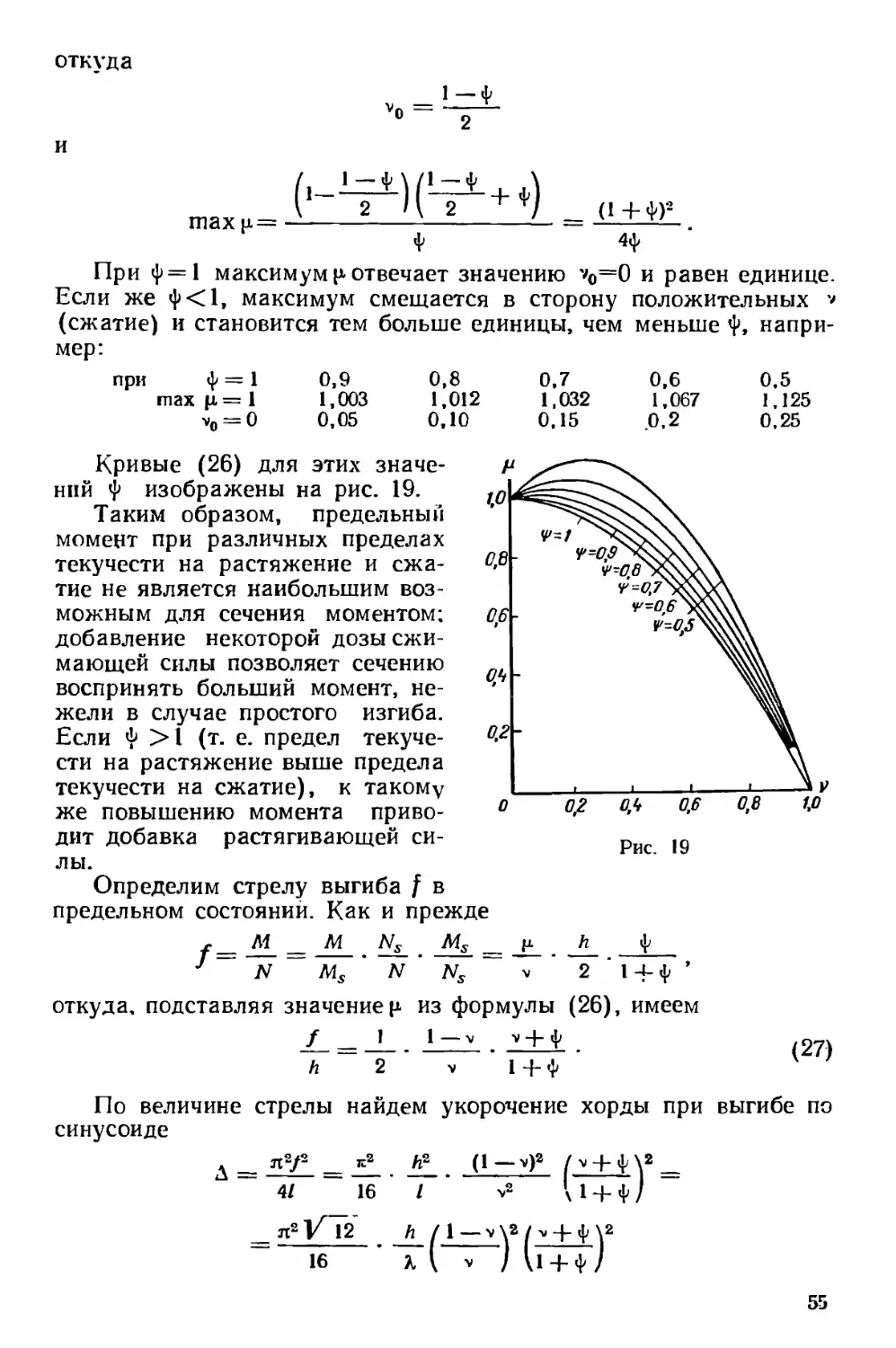
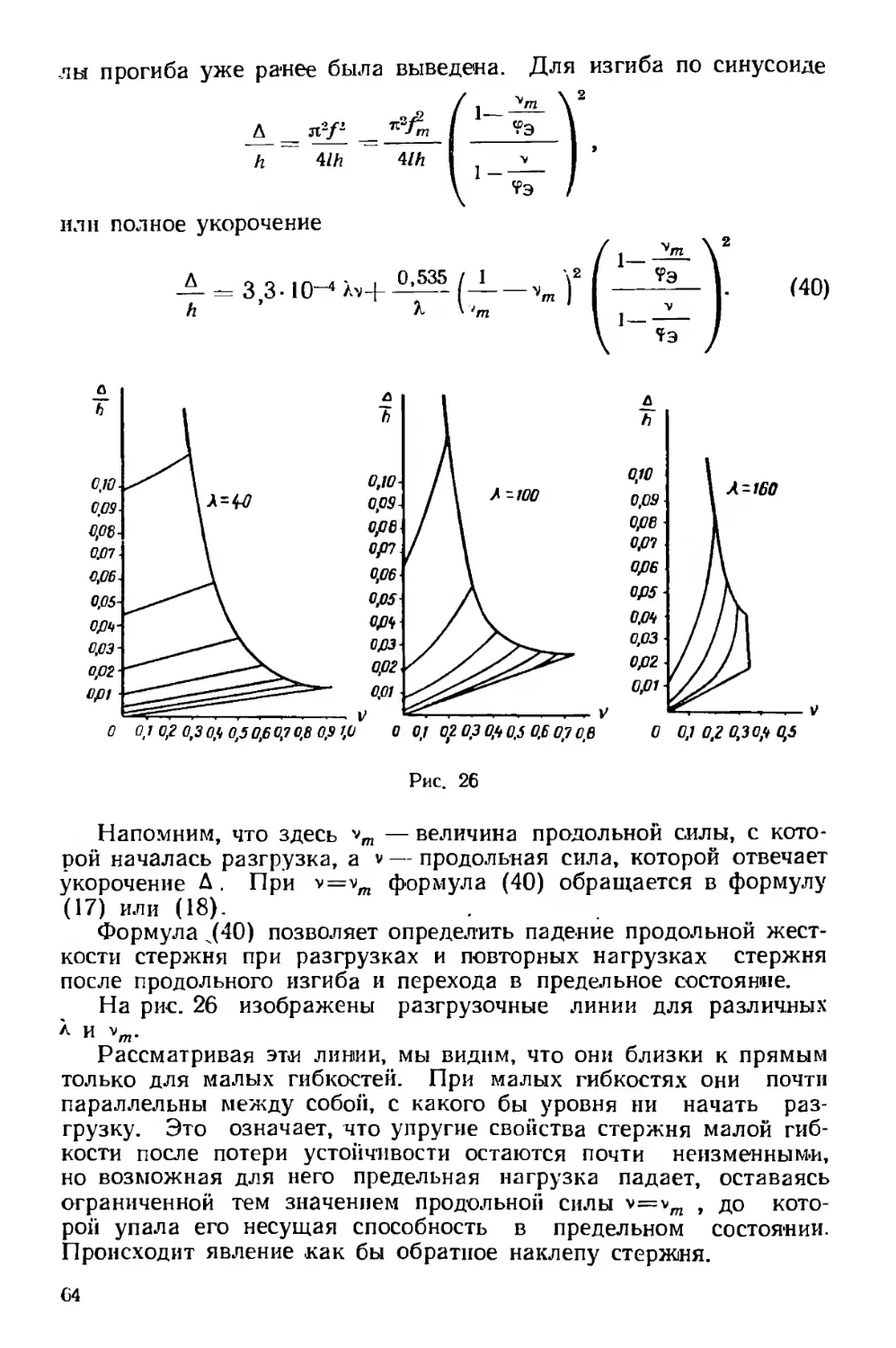
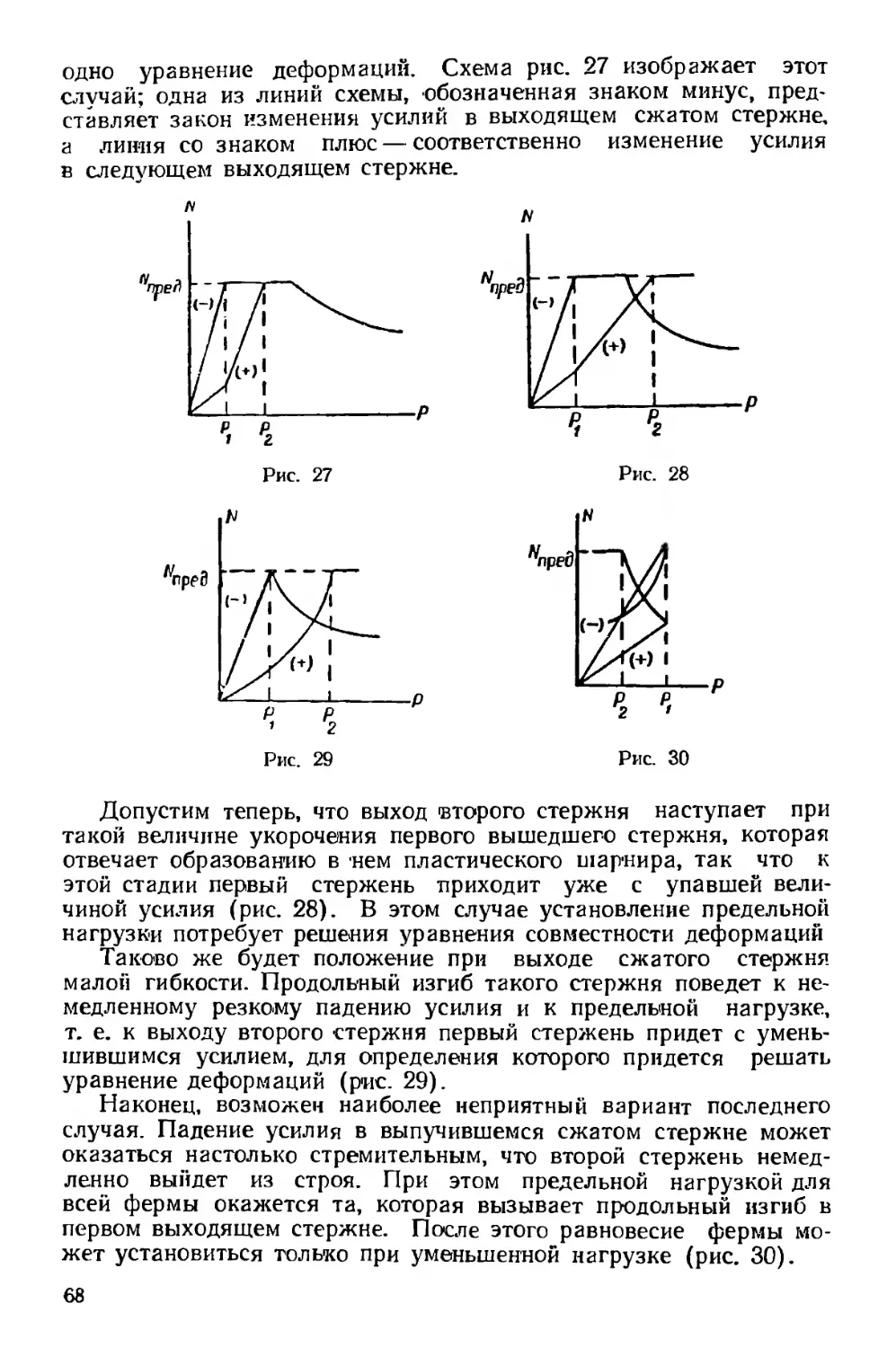
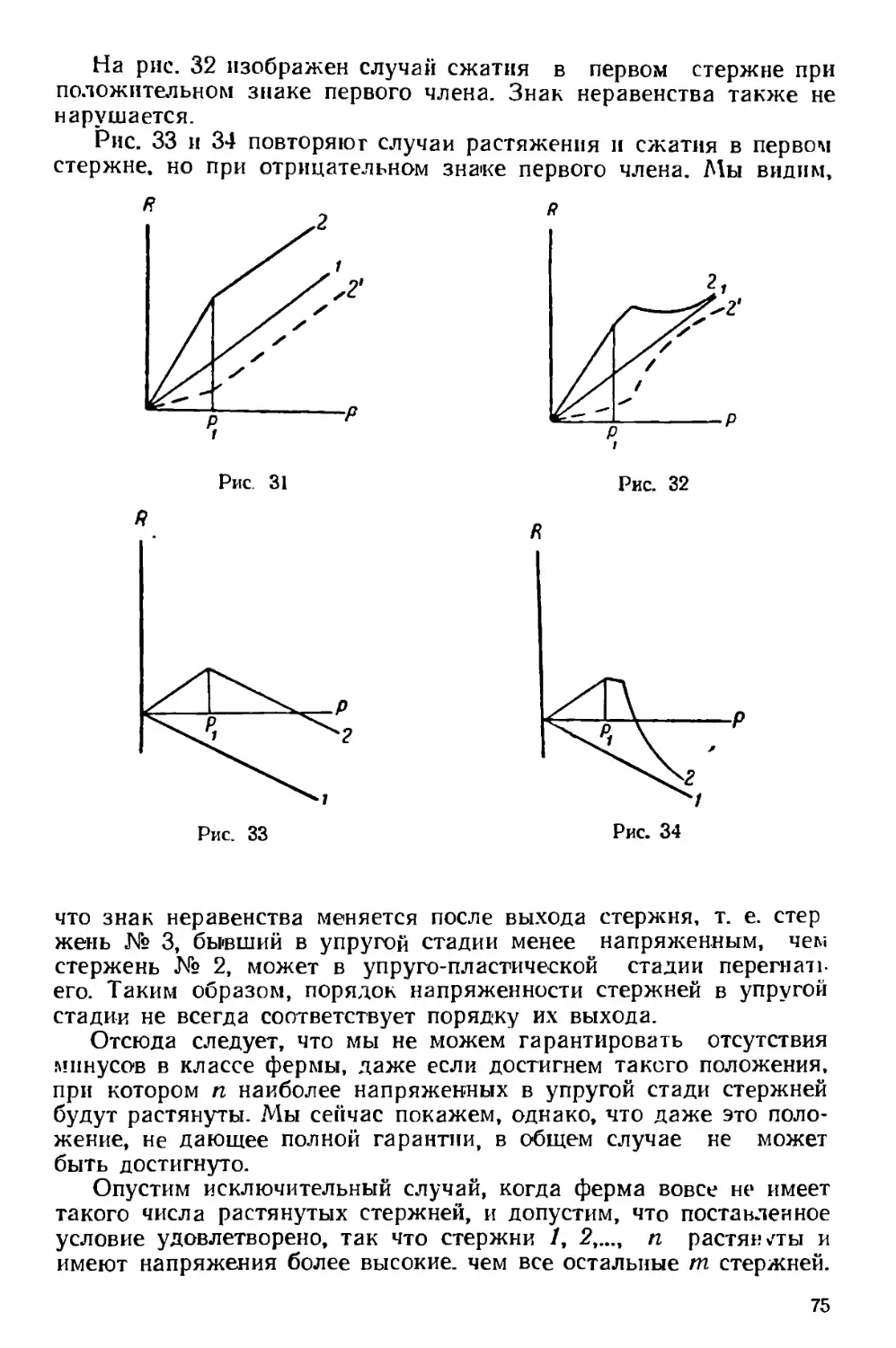
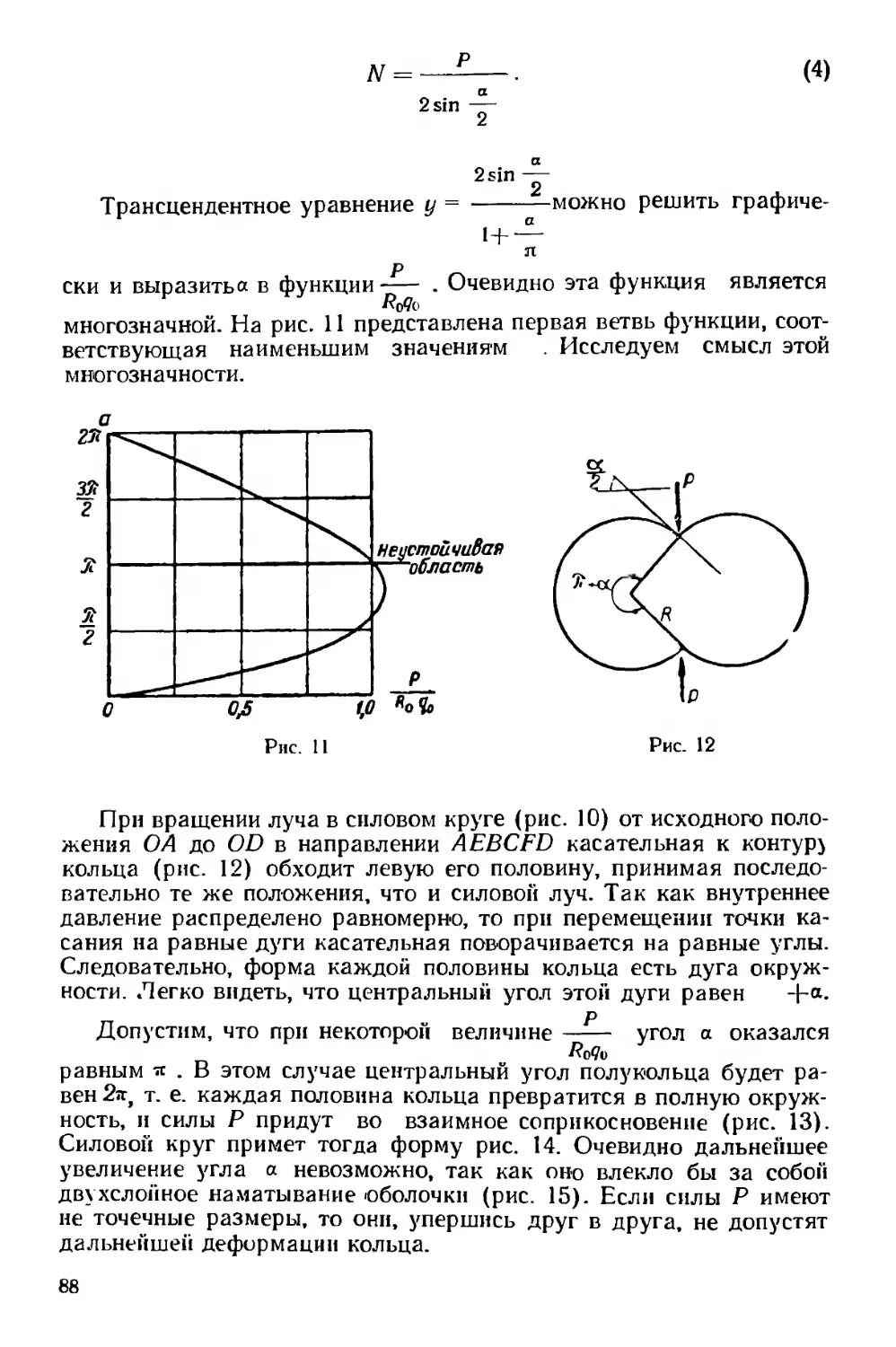
Исследуем теперь формулы четвертого этапа (17) и (18). Если
д
откладывать по оси абсцисс *, а по оси ординат—, то для каждого
h
Л получится кривая гиперболического *вида, уходящая в бесконеч-
ность при значении v=0 и ограниченная справа значением v =<р
(рис. 10). Римские цифры на графике означают этапы.
Эти кривые имеют минимум в конечной области. Действн
тельно,
Приравнивая нулю, найдем
— И-------— + 3,3- 10-4 М= 0.
X 1 X
или
. —1 =о.
1 к 1
Решим это уравнение по способу Ньютона, полагая =
=1,1—0,005 X в качестве первого приближения. Мы получим в
табл. 4 при £=0,534 (для синусоиды) значения .
Из табл. 4 видно, что для гибкостей, отвечающих неупругому
продольному изгибу, образование шарнира текучести вызывает
4G
настолько быстрое падение несущей способности, что хорда
стержня после потери устойчивости начинает удлиняться.
Действительно, приведенные в табл. 4 значения соответствую-
щие наибольшей длине хорды (наименьшему укорочению), ниже
значений <р, при которых происходит потеря устойчивости. (Для
А <93, ; :1; для А. = ЮО, <р =0,863). Следовательно, укорочение в
предельном состоянии после потери устойчивости (конец третьего
Таблица 4
X 0 20 40 60 80 100
1-е приближение 1,10 1.00 1.00 0,90 0,80 0,70 0,60
2-е 0,972 0,896 0,804 0,718 0,648
3-е 1,00 0,971 0,896 0,805 0,718 0,644
этапа) будет уменьшаться до достижения продольной силой
табличного значения vlt после чего начнет снова увеличиваться.
Математически это объясняется тем, что —, определяемое форму-
h
лой (17), есть сумма возрастающей прямой и убывающей кривой,
причем последняя обращена выпуклостью книзу.
Прежде чем давать объяснение по существу этому странному
явлению, заметим, что принятие другого коэффициента при вто-
ром члене формулы (17), т. е. другой формы изгиба, приводит к
такому же результату, причем значениям, отвечающие минималь-
ному укорочению, оказываются чрезвычайно близкими к ранее
вычисленным. Так, для изгиба по треугольнику при k “0,433 имеем
значения приведенные в табл. 5.
Таблица 5
0 20 40 60 80 100
1,00 0,966 0,881 0,777 0,691 0,637
Следовательно, для истинной формы изгиба минимум укороче-
ния также будет иметь место при нагрузке меньшей критической,
причем для этой истинной кривой, занимающей промежуточное
положение между синусоидой и треугольником, можно принять
округленно следующие средние значения (табл. 6, рис. 11).
Таблица 6
0 20 40 60 80 100 120
1,0 0,97 0,89 0,79 0,70 0,64 0,57
47
На рис. 11 нанесена также кривая <р. Из сопоставления обеих
кривых видно, что для гибкостей X > 120 минимум укорочения со-
ответствует значению т. е. является недостижимым.
Таким образом, зависимость укорочений от нагрузки в урав-
новешенных состояниях может иметь двоякую природу, изобра-
женную на рис. 12 и 13.
В случае упругого продольного изги-
ба (рис. 12) укорочения возрастают ли-
нейно до v = <р (состояние продольного
изгиба) (точка 7), после чего они растут
при постоянном значении силы v = <р до достижения предельного
состояния (точка 2). Дальнейший рост укорочений сопровождает-
ся падением нагрузки.
При неупругом продольном изгибе (рис. 13) укорочения также
растут линейно до значения v = <р (точка 7), но еще до дости-
жения этого значения, соответствующего предельному состоянию,
график укорочения достигает характерной точки (точка 2) при
?=/. При этом величина укорочения уравнивается с наименьшей
его величиной, достигаемой в послекритической стадии (точка <?).
Состояние v — / характеризуется тем, что одной и той же длине
хорды стержня соответствуют две формы равновесия: прямоли-
нейная с нагрузкой / и криволинейная с нагрузкой Vj < </.
Далее заметим, что при нагрузке * < / каждой величине уко-
рочения, т. е. каждой длине стержня, соответствует единственная
форма равновесия; при *><р' таких форм оказывается две.
Можно доказать, что это свидетельствует о неустойчивости
равновесия во всей области /О<<р, так что действительный про-
дольный изгиб становится возможным уже при v = ср'.
Это доказательство вытекает из соображения о необратимо-
сти процесса перехода из одного состояния равновесия в другое1.
Допустим, что сжатый стержень вставлен в пресс винтового дей-
ствия, так что величина укорочения стержня предопределена хо-
дом винта. Пусть стержень достиг состояния/, т. е. усилие в нем
1 Более строгое доказательство автором дано в статье «К расчету статически
неопределимых ферм по разрушающей нагрузке», «Проект и стандарт» № 7, 1937.
48
равно ?'Л^. Стержень прямолинеен и упруг. Дадим ему искривле-
ние. Так как длина стержня фиксирована прессом, то точка на
диаграмме, изображающая состояние стержня (рис. 13), будет пе-
ремещаться из точки 2 в точку 3. Если стрела изгиба достигнет
значения — = —-------vij, то стержень придет снова в состояние
равновесия (точка 5), -но это будет предельное состояние с образо-
ванием пластического шарнира в стержне. Обратный переход в точ-
ку 2 станет невозможным именно вследствие развития остаточных
деформаций. Строго говоря, процесс становится необратимым уже
с момента появления фибровой текучести, для образования кото-
f 1 / 1 - \
рои нужна еще меньшая стрела — = —[---------1 | , где v2 лежит
А 6 \ /
между и
Итак, случайное искривление стержня при нагрузке v>cp' мо-
жет привести стержень в криволинейную форму равновесия. Это
значит, что продольный изгиб наступит именно при v=?', т. е. ранее
предельного состояния v=<p = 1.
Дело не изменится существенным образом, если предположить,
что концы стержня соединены упругой связью, жесткость которой
значительно превосходит продольную жесткость стержня. С этим
случаем мы встречаемся в статически неопределимых фермах.
При этом переход из одной формы равновесия в другую будет со-
вершаться не по горизонтальной прямой 2—3, а по некоторой
кривой, касательные к которой образуют с осью * углы значитель-
но меньшие, чем прямая 0—1 (рис. 13).
Определим теперь значение?', т. е. реальный коэффициент
продольного изгиба. Для этого надо приравнять упругое укороче-
ние стержня при v=<pz минимальному укорочению хорды, получаю-
щемуся при v=Vi. Мы используем для этого формулы (14) и (17)
или (18), взяв средний коэффициент 0,48 для второго члена по-
следней формулы, как более отвечающий истинной средней кривой
изгиба. Приравнивая, получим
з,з- ю-4 <р'х = з,з- io-4 ^х + 2^?
откуда
Подставляя табличные значения vt, получим табл. 7.
Таблица 7
0 20 40 60 80 100
т' 1,00 0,98 0,94 0,88 0,83 0.77
49
Таковы реальные значения коэффициента продольного изгиба
Приводим для сравнения значения </, подсчитанные для двух
крайних случаев—синусоиды и треугольника. Это сравнение по-
казывает, что точная форма кривой выгиба слабо влияет на ве-
личины <р' (табл. 8).
Таблица 8
1 0 20 40 60 80 100
Синусоида Треугольник 1,0 1,0 0,986 0,981 0,945 0,924 0,891 0,871 0,834 0,808 0,778 0,751
Мы видим, что даже при л=Ч00, т. е. в случае упругого про-
дольного изгиба, значение <р' оказывается ниже эйлеровского.
Нанесем значения <? и <р на
график (рис. 14) и сопоставим
их с опытными данными1 (рис.
15). Мы немедленно убеждаемся
в близком соответствии нашего
графика с опытом и в сходстве
его с кривой Энгессера—Карма-
на. Это показывает, что даже
идеальная упруго-пластичная
сталь дает такую же форму гра-
фика, как действительная сталь,
в расхождение с мнением йеже-
ка, принявшего для идеальной
стали график по рис. 2. Этот ре-
зультат, насколько мне известно,
отсутствует в литературе.
Наш вывод позволяет, кроме
того, пояснить разбросанность
опытных точек в области неупругого продольного изгиба при
а <100. Мы видели, что этим гибкостям отвечает не одна опреде-
ленная величина критической силы, а целая область критических
значений, при которых продольный изгиб становится если не обя-
зательным, то возможным. Совпадение опытной критической силы
с одним из теоретических значений этой области определяется
рядом индивидуальных особенностей опытного образца и обстоя-
тельств эксперимента.
Вернемся к графику удлинений и внесем в него исправления,
срезая горизонтальными прямыми заостренные концы линий для
Х<120. Затем повернем график, меняя местами оси* и —(рис. 16).
h
В последней форме график является окончательным инструментом
для расчета статически неопределимых ферм, стержни которых
1 Заимствованы из работ Ясинского.
50
ч
Рис. 16
51
имеют прямоугольное сечение. Этот график служит дополнением к
графику Прандтля; последний относится к растянутым стержням,
а полученный — к сжатым.
Смысл графика рис. 16 таков. Если сжатый стержень полу-
л
чил укорочение, равное —, и если он находится в равновесии, то
продольная сила в нем равна где * — ордината точки кривой
с абсциссой —.
h
Все выводы этого параграфа относятся исключительно к пря-
моугольному сечению. Аналитическое решение для иных форм се-
чения, кроме круглого, очень осложняется. Для круглого сечения
решение сохранит ту же форму, если, основываясь на взаимной
близости кривых предельного состояния на фиг. 7, принять для
круглого сечения уравнение предельного состояния в виде
р. — 1 — V2.
При этом условии уравнения для круглого сечения будут отли-
чаться от вышеприведенных только численными значениями коэф-
фициентов. Так, формулы укорочений (17) — (18) примут вид
-у = 2,85-10-4vX4-A^2__vy> (20)
где d — диаметр сечения;
k=0,445 при выгибе по синусоиде;
k=0,361 при выгибе по треугольнику.
Если с помощью уравнения (20) подсчитать значения и
принимая среднюю величину коэффициента формы Л = 0,4, мы
получим весьма близкие цифры к тем, которые ранее были выве-
дены для прямоугольного сечения (табл. 9).
Таблица 9
Л 20 40 60 80 100
0,968 0,980 0,886 0,936 0,787 0,880 0,700 0,820 0,625 0,758
Таким образом, кривые истинных значений для идеальной
упруго-пластичной стали для прямоугольного и круглого сечений
практически совпадают, хотя, строго говоря, они несколько раз-
личны в области неупругого продольного изгиба. Этот результат
показывает, что гибкость не является единственным аргументом,
определяющим коэффициент продольного изгиба; последний за-
висит также от формы сечения.
График укорочений для стержней круглого сечения будет,
разумеется, несколько отличаться от рис. 16, хотя общий его ха-
рактер будет таков же.
52
§ 6. РАЗЛИЧИЕ ПРЕДЕЛОВ ТЕКУЧЕСТИ ПРИ СЖАТИИ И РАСТЯЖЕНИИ
ВЛИЯНИЕ ВЕЛИЧИНЫ ПРЕДЕЛА ТЕКУЧЕСТИ
Истинные значения пределов текучести при сжатии и растя
жении у мягких сталей несколько расходятся между собой. Иссле-
дуем, какие -изменения вносит в предыдущие выводы это расхож-
дение.
Допустим, что пределы текучести материала при растяжении
и сжатии различны и равны соответственно о, и
Рис 18
Отношение пределов текучести обозначим
Для стали ф< 1.
Если прямоугольное сечение работает в предельном состоянии
только на момент, то нейтральная ось пройдет не через центр
тяжести сечения, а сместится в сторону сжатых волокон (рис. 17),
так как > о2. Положение оси найдем из условия равенства пло-
щадей эпюры
oda = o2(h— а),
откуда
, cz а
ф = — =--------
h — a
И
а = (21)
1 4-ф
Предельный момент найдем из формулы
(22)
При равенстве пределов текучести, т. е. ф=1, получим обычное вы-
ражение Мs = •
Предельная продольная сжимающая сила будет равна:
Ns = bhvd. (23)
53
Возьмем теперь произвольное предельное состояние при сов-
местном действии изгиба и сжатия (рис. 18). Найдем напряжение
о от осевой силы исходя из условия равенства площадей:
(с, + — u)b = (ad — о) ub,
откуда
и
W = = ♦(•-“)]• (24)
Момент определим из формулы
Введем прежние обозначения:
N М
V = -- U = ----- .
Тогда из выражения (24) имеем
у=т(1 + <1')~'?-
или
и _ * + ф
h 1 + ф ’
Подставим это выражение в формулу (25):
(l = l±i(i_v)2±±
ф '1 + ф
или
рассматриваемого
(l-4fr-M)
Ф
Таково уравнение предельных состояний для
случая. При ф = 1 оно принимает прежний вид:
|Х= 1 — А
Уравнение (26) опять выражает параболу,
относительно нормального положения. Анализ полученного урав-
нения (26) приводит к неожиданному на первый взгляд резуль-
тату. Найдем максимум приравнивая нулю производную —:
d't
(26)
но повернутую
_ — Пп+ Ф)+ (1 — >о) _ , 1 । J__2j0 _
dv ф ф ф ’
54
откуда
v _1-Ф
°““Г”
(1 + ф)2
4ф
При ф=1 максимум р отвечает значению vo=0 и равен единице.
Если же ф<1, максимум смещается в сторону положительных *
(сжатие) и становится тем больше единицы, чем меньше ф, напри-
мер:
при ф = 1
max р, = 1
vo = O
0,9 0,8 0,7 0,6 0,5
1,003 1,012 1,032 1,067 1,125
0,05 0,10 0,15 0.2 0.25
этих значе-
Кривые (26) для
ннй ф изображены на рис. 19.
Таким образом, предельный
момент при различных пределах
текучести на растяжение и сжа-
тие не является наибольшим воз-
можным для сечения моментом;
добавление некоторой дозы сжи-
мающей силы позволяет сечению
воспринять больший момент, не-
жели в случае простого изгиба.
Если ф >1 (т. е. предел текуче-
сти на растяжение выше предела
текучести на сжатие), к такому
же повышению момента приво-
дит добавка растягивающей си-
лы.
Определим стрелу выгиба f в
предельном состояний. Как и прежде
. =
из формулы
f_M__ М Ns
N ~ Ms ' N
откуда, подставляя значениер
Р>
h
2
(26), имеем
A = _L. . 2±±
h 2 v 14-ф
(27)
Ф
По величине стрелы найдем укорочение хорды при выгибе по
синусоиде
Л = = *2 . . О-*)2 р + Ф\2 =
4/ 16 / \ 14- ф)
= л2У 12 h / 1 — у \ а р + ф \2
16 X ( у Ц1 + Ф/
55
или
A = 2,138 /1-у\2р + ф\2 =
h к \ » ] Ч + Ф/
(тН1
Первый множитель правой части равен укорочению хорды для
прежнего случая приф=1; второй множитель дает поправку за
счет неравенства пределов текучести. Очевидно, выражение этого
второго множителя не зависит от формы изгиба. Обозначая его
через В(ф), запишем выражение укорочения хорды при изгибе
по кривой любой формы в виде
А(|) = А (1)В(ф). (28)
Функция В (ф) = (-А-)2 у
для всякого ф<1 представ-
ляет возрастающую функцию от v. На рис. 20 изображены эти
функции для различных ф.
Полное укорочение в предельном состоянии выразится
— = —-----vX + ^111В (ф).
h £|/TF h
(29)
Сравнение полученной формулы с выражением укорочения
при ф = 1, т. е. az~cd~aSj приводит к следующим выводам. Будем
считать т. е. имеющим одинаковую величину в обоих слу-
чаях, a oz < cd. В этом предположении мы найдем, что первый
член формулы (29), выражающий укорочение оси, одинаков в
обоих случаях, так что укорочения в первом этапе совпадают.
Укорочение же хорды в следующих этапах будет происходить тем
менее интенсивно, чем меньше ф, т. е. чем больше разница между
пределами текучести. Уменьшение укорочений скажется особенно
сильно при больших гибкостях, т. е. малых v, так как В(Ф) для
малых v уменьшается. Это означает, что протяженность второго л
третьего этапов, или площадки «текучести» на графике укороче-
ний, уменьшается вместе с Ф, а дальнейший спад нагрузки проис-
ходит более интенсивно. Очевидно, предположение ф>1 при
прежнем значении приведет нас к обратным выводам.
Здесь уместно осветить также -роль абсолютной величины пре-
дела текучести для случая ф=1, которую в предыдущих выводах
мы принимали равной 2 400 кг}см2. Как видно из формулы (17)
или (18),
А = vX + A(_L (30)
h Е V 12 V v /
которую мы здесь приводим для наглядности в более общем виде,
величина предела текучести явно входит только в первый член,
выражающий укорочение оси. Поэтому наклон первой прямоли-
56
нсйной ветви графика укорочении, отвечающий первому этапу,
будет уменьшаться с ростом (если говорить о наклоне между
этой прямой и осью деформаций на графике). По так как
равно напряжению при сжатии, то увеличение приведет к про-
порциональному уменьшению коэффициента продольного изгиба
а потому укорочение при достижении критической силы не зави-
сит от величины Это обстоятельство наглядно изображено нз
Второй же член формулы (30), выражающий укорочение хор
ды, не зависит явным образом от о, хотя
, _ _о_
Ns CS
является функцией as. Поэтому в осях координат гипербола,
изображающая сумму обоих членов, будет смещаться вправо г
увеличением при заданной гибкости. Отсюда следует, что длина
горизонтальной площадки «текучести» для данной гибкости воз-
растает с повышением предела текучести материала, т. е. между
наступлением продольного изгиба и образованием пластического
шарнира происходит тем большее накопление деформаций, чеч:
выше предел текучести.
§ 7. РАЗГРУЗКА СТЕРЖНЯ ПОСЛЕ ПЕРЕХОДА ЕГО В ПРЕДЕЛЬНОЕ
СОСТОЯНИЕ
Исследуем теперь деформации сжатого стержня, подвергаемо-
го разгрузке после потери устойчивости и перехода в предельное
состояние.
Пусть стержень находится в предельном состоянии, т. е. имеет
пластический шарнир в среднем сечении. Воспринимаемая им про-
57
дольная сила упала с наибольшего значения Д/=Д/Л до некоторого
значения N=Nm<Nb а стрела выгиба приняла величину h=fm-
Произведем постепенную разгрузку стержня и будем искать из-
менение стрелы.
Поставленную задачу нельзя решать обычными приемами,
так как она не удовлетворяет закону независимости действия сил.
Но при бесконечно малых изменениях сил этот закон может быть
признан справедливым, а потому любой из способов вычисления
перемещений может быть применен, если придать ему дифферен-
циальную форму. с
Приложим по концам искривленного
и сжатого силами 7V стержня растягива- / [
ющие силы dN (рис. 22), которые частич- —/у г*
но распрямят стержень, уменьшив его o-i I i
A ! I
с<л/ * I \!
» I . —*• I gfr-A—r~
л du
Рис. 22
Рис. 23
прогиб у в любой точке на dy, а стрелу f на df. Будем считать это
изменение формы за возможное перемещение искривленного стер-
жня. При этом перемещении в стержне появятся добавочные внут-
ренние усилия
dMr = ydN + Ndy
и
dNj = —dN cos a.
Будем считать моменты положительными, если они отвечают
распрямлению стержня, продольные силы положительными при
сжатии и приращения стрел выгиба положительными при рас-
прямлении стержня.
В качестве другого состояния возьмем ненапряженный стер-
жень с той же формой искривления (приведя его к этой форме,
например, путем соответственного нагрева) и приложим в его
средней точке поперечную нагрузку Р=1 (рис. 23), вызывающую
внутренние усилия
М, - —
2 ’
/
где — и
2
/V» = sin a.
58
Приравняем работу внешних и внутренних сил этого состояния
на перемещениях первого состояния, отбрасывая интеграл попереч-
ных сил:
i
\df=2 ам^2 ~
о
2
+ 2 С dNtN, —
J 1 “ EF
о
или, подставляя выражения усилий,
i i
2 2
df — С x(Ndy + ydN) —-----2f d/Vsin a cos a . (31)
J EJ J EF
0 0
В этом уравнении следовало бы вести интеграцию по длине
дуги ds. Переходя к дифференциалу dx, мы пренебрегаем величи-
ной ~^У'2- Если даже принять максимальное значение я=15°, т. е.
у= tga--0,268, то 0,036, и ошибка будет заведомо меньше
3,6%. В § 5 было показано, что такая величина угла я относится к
случаям искривления, не имеющим практического значения. По-
этому замена ds на dx представляется нам приемлемой, равно как
и принятие верхнего предела интегралов равным половине началь-
ной длины.
Разделив все члены уравнения (31) на df, получим
i _L L
2 2 2
1 лт С dy dx , dN С dx о dN С . dx /ооч
1=W х-£-—+— ху—-2— sinacosa —. (32)
J df EJ df J EJ df J EF
0 0 0
Если считать, что при малых деформациях форма изгиба
остается неизменной, то при любой форме изгиба уравнение изог-
нутой оси может быть представлено в виде
y(x) = fy1(x).
где </1 (х) не зависит от стрелы прогиба /, а потому
^ = у,-
df /
Заменим далее sin я cos я заведомо преувеличенным выраже-
нием tg я = у' и приведем выражение (32) к виду
i i
Д = fxv^-^ f2v'— =
\ f df1 } ' EJ df J ' EF
f df)J df1
59
где fa и fb — числовые значения интегралов, зависящие только
от формы искривления.
Отсюда
*HLtfa-fb) + Na-l = 0, (33)
df
или
Обращая члены, получим
df _ dN
(a—b)f ~ 1-aN ’
откуда
1п/= — k [In (1 — aN) + In С],
где k- 1 — — и С— произвольная постоянная, или, освобождаясь
ь
от знака логарифма,
' = (34)
Постоянную С* найдем из начальных условий.
При N=Nm, f=fm
откуда
Теперь окончательно получим
м-О- (35>
Найдем пределы значений а и Ь, считая за возможные предель-
ные формы искривления синусоиду -и треугольник.
При
г . ЯЛ
y=/sin —
f . six dx
а = I х sin — - —
’ l EJ
о
x?EJ ~
где N3 —эйлеровская критическая сила.
60
b =
2
P nx dx 2
COS---•----=------
) I EF EF
о
k= 1---= 1
Ь
2 л" J j 2jv
PF ~ X*
Второй член для реальных гибкостей весьма мал по сравнении)
о единицей. При =20 он равен 0,049, а для ^=100 он составит
всего 0,002. Поэтому этот член, выражающий работу продольны.х
сил, можно отбросить и дать окончательное выражение стрелы
прогиба в виде
(36)
*-мг
Заметим, что здесь Мэ= есть величина, численно равная
энлеровской критической силе только для упругого продольного
изгиба; при неупругом продольном изгибе выражение Nэ не имеет
физического истолкования и должно рассматриваться как некото
рый числовой коэффициент.
Для треугольника, т. е. при y=f — I*
i
2
’ _ С 2х* dx — f~ — 0,82
° J I ' EJ ~ 12EJ ~ ’
0
I
b= f A.
J l EF EF
0
, , 2-12EJ , 24
PEF X2
•Отбрасывая снова второй член, получим для треугольника
1-0,82-^
'-о-82 £
(37)
В действительности форма изгиба, оставаясь заключенно:»
между синусоидой и треугольником, не является постоянной, а по-
тому коэффициент -при втором члене числителя и знаменателя
61
должен рассматриваться как переменная величина, зависящая от
Nm и N заключенная между 1 и 0,82. Пренебрегая для ориенти-
ровочного расчета этой зависимостью, мы должны были бы при-
нять некоторое среднее значение коэффициента порядка 0,9. Для
упрощения мы возьмем значение коэффициента, отвечающее выги-
бу по синусоиде, и будем в дальнейшем оперировать с выражением
(36). Совершаемая при этом ошибка будет всего сильнее сказы-
ваться при Nm , близких к Лэ , т. е. если при больших гибкостях
разгрузка начата вскоре после перехода в предельное состояние,
и при N, близких к Nm , что соответствует началу разгрузки.
Дальнейшие и более поздние стадии разгрузки будут давать прак-
тически совпадающие результаты по формулам (36) и (37). Обе
формулы дадут также хорошее совпадение для стержней малой
гибкости (л <100), где Nm всегда значительно ниже Л/э .
Из формулы (36) можно найти зависимость между продольной
силой и моментом при разгрузке:
M = Nft
или для прямоугольника
Ж _ _ N Ns * J f
Ms ~ Ns ' MJ ~ Ns ’ /2
откуда
1——
!x=vJL/=4^v
Л л 1--^-
¥э
где
Но в начальный момент
м — д/™. v 1 ______________________у2
И™ — * л — 1 —
Поэтому
На рис. 24, изображающем предельную зависимость »х=1—
нанесены разгрузочные кривые по формуле (38) для X =100, т. е?
?э =0,863. Стрелки на кривых означают возможное направление
процесса. Отметим еще раз, что <?э не совпадает с действительным
коэффициентом продольного изгиба » при А 100.
Процесс разгрузки теоретически является вполне обратимым.
Поэтому повторное загружение до v<vm должно пойти по той
62
же кривой. Попытка увеличить нагрузку выше '<'=vrj приведет к
включению пластического шарнира, падению несущей способности»
увеличению стрелы прогиба и перемещению точки (*,•*) влево по
предельной кривой. Последний процесс, разумеется, необратим.
Мы видим, что значение является критическим для стерж-
ня, ранее достигшего этого значения. Состояние можнг
вполне уподобить продольному изгибу, хотя оно характеризуется
Из формулы (36) можно найти также величину остаточного
прогиба, полагая * =0:
Остаточный прогиб будет тем больше, чем дальше успела пе-
реместиться изображающая точка по предельной кривой —>2,
т. е. чем больше fm и, следовательно, чем меньше . На рис. 25
представлена зависимость остаточного прогиба от *да для ?э =
=0,863 (Л = ЮО).
Теперь перейдем к определению укорочений стержня при раз
грузке. Величина укорочения стержня, как и при нагрузке, сла-
гается из двух частей: укорочения оси, выражаемого -прежней
формулой
А = з 3-10--1
h
и сокращения хорды при изгибе по кривой у = у(х) со стрелой про
гиба f. Зависимость между сокращением хорды и величиной стре
63
Рис. 26
Напомним, что здесь ''т — величина продольной силы, с кото-
рой началась разгрузка, а * — продольная сила, которой отвечает
укорочение Д . При формула (40) обращается в формулу
(17) или (18).
Формула J40) позволяет определить падение продольной жест-
кости стержня при разгрузках и повторных нагрузках стержня
после продольного изгиба и перехода в предельное состояние.
На рис. 26 изображены разгрузочные линии для различных
Л и ут.
Рассматривая эта линии, мы видим, что они близки к прямым
только для малых гибкостей. При малых гибкостях они почти
параллельны между собой, с какого бы уровня ни начать раз-
грузку. Это означает, что упругие свойства стержня малой гиб-
кости после потери устойчивости остаются почти неизменными,
но возможная для него предельная нагрузка падает, оставаясь
ограниченной тем значением продольной силы , до кото-
рой упала его несущая способность в предельном состоянии.
Происходит явление как бы обратное наклепу стержня.
64
Чем больше гибкость стержня, тем заметнее снижается его
продольная жесткость по мере продвижения по предельной кри-
вой. Иными словами, чем сильнее развились деформации изгиба
после потери устойчивости, тем меньше становится «модуль упру-
гости» стержня. Явление «обратного наклепа», разумеется, имеет
место и здесь.
Все эти свойства достаточно очевидны, и большинство из них
могло бы быть предсказано интуитивно. Автор видит свою заслугу
лишь в том, что ему удалось впервые подвергнуть эти явления
анализу и придать нм форму простых математических закономер-
ностей, хотя бы и приближенных.
Выведенные законы поведения сжатого стержня после потери
устойчивости позволяют дать исчерпывающее теоретическое ре-
шение задачи о действительной предельной нагрузке для стати-
чески неопределимой фермы.
Б. РАБОТА СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫХ ФЕРМ
§ 8. КЛАССИФИКАЦИЯ СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫХ ФЕРМ
Если бы диаграмма укорочений сжатого стержня обладала
неограниченной площадкой текучести, подобно тому, как мы
принимаем для растянутого стержня, то расчет статически неопре-
делимой фермы по предельному состоянию можно было бы вести
тем же путем, как и расчет балочно-рамных систем. Достаточно
было бы задаться уравновешенным распределением усилий при
предельной нагрузке и подобрать сечения стержней, пользуясь
одними только уравнениями равновесия. Именно так предлагал в
свое время рассчитывать статически неопределимые фермы проф.
Завриев1. Действительная работа фермы в этом случае состояла
бы в постепенном переходе лишних стержней в пластическое со-
стояние с сохранением в них постоянного предельного усилия.
Уже ряд ранее опубликованных работ установил ошибочность
такого подхода. Из работ проф. И. М. Рабиновича2, А. А. Гвозде-
ва3, Хвалла4 и др. бесспорно выяснилось, что для сжатых стерж-
ней нагрузка раньше -или позже становится убывающей функцией
укорочения, а потому потерявший устойчивость сжатый стержень
при дальнейшем росте нагрузки на ферму будет принимать все
меньшее участие в работе фермы и к предельному для фермы со-
стоянию придет с усилием, меньшим, чем его собственная макси-
мальная несущая способность.
1 К- С. Завриев, Новый прием расчета статически неопределимых ферм
«Проект и стандарт» № 8, 1934.
2 И. М. Рабинович, Устойчивость стержней в статически неопределимых
системах, М.., 1932.
3 А. А. Гвоздев, Определение величины разрушающей нагрузки, «Проект
и стандарт» № 8, 1934.
4 См. Е. С h w а 11 а, цит. соч.
65
Однако перечисленные авторы не дали аналитических выра-
жений для закона падения нагрузки в сжатом стержне, так как
не оперировали с диаграммой Прандтля. Хвалла построил графики
укорочений, аналогичные нашим, но основанные на истинных
диаграммах удлинений. Вопрос о том, какие трафики «вернее»,
совершенно неправомочен, так как, разумеется, графики Хвалла
для той именно партии стали, которой он пользовался, должны
дать лучшее совпадение с действительностью. Степень же их при-
годности для какой-либо другой партии или марки стали не более
очевидна, чем пригодность наших отвлеченных графиков. Здесь
важно лишь то, что наш метод, как уже было указано выше, дает
аналитические выражения для графиков укорочений, не встречаю-
щиеся у Хвалла и позволяющие построить общую теорию расчета
статически неопределимых ферм.
Пусть дана произвольная статически- неопределимая ферма с
п лишними стержнями, несущая постоянную нагрузку Р посте-
пенно возрастающей интенсивности. По мере роста нагрузки
один стержень за другим будет выходить из упругой стадии
работы; растянутые стержни будут достигать пластического со-
стояния, а сжатые будут терять устойчивость и переходить в
предельное состояние. Стержни обоих типов назовем для крат-
кости «выходящими».
Предельной для фермы нагрузкой Рпред будет та, при которой
выйдет (п+1)-й стержень.
Мы будем классифицировать фермы с точки зрения порядка
чередования растянутых и сжатых стержней в числе выходящих
и символически обозначать класс фермы последовательностью
из п знаков плюс и минус, указывающих на порядок знаков вы-
ходящих -стержней вплоть до превращения фермы в статически
определимую.
Так, ферма с одним лишним стержнем может принадлежать к
классу ( + ) или (—); фермы с двумя лишними стержнями обра-
зуют четыре класса: (++), (Ч—), (—+) и (——). В общем
случае ферма с п лишними стержнями может принадлежать к
одному из 2П различных классов.
Фермы разных классов различны с точки зрения своей работы
и расчета. Если класс фермы обозначен серией одних только плю-
сов, т. е. все выходящие стержни растянуты, то ферма может
быть рассчитана классическим способом предельных нагрузок с
использованием только одних уравнений равновесия. Если же
обозначение класса содержит хотя бы один знак минус, т. е. среди
выходящих стержней есть хотя бы один сжатый стержень, то урав-
нения равновесия становятся недостаточными для расчета и дол-
жны быть дополнены условиями совместности деформаций, число
которых равно числу минусов в классе фермы. Иными словами,
статически неопределимая ферма, обозначенная серией плюсов,
является статически определимой при расчете по предельной ста-
дии; наличие т минусов в классе фермы придает ей /п-кратную
статическую неопределимость при предельном расчете. Очевидно,
66
т < /г, где п — степень статической неопределимости при упругом
расчете. Знак равенства имеет место для ферм, класс которых со-
держит только минусы.
Ясно, что класс характеризуется не одной только геометри-
ческой схемой фермы, но и нагрузкой. При разных видах загру-
жения одна и та же ферма будет принадлежать к разным классам.
Эти предварительные соображения показывают, что с точки
зрения трудоемкости расчета выгодно стремиться к уменьшению
числа минусов в классе фермы. Поэтому в дальнейшем изложении
будет особо разобран вопрос о возможности уничтожения минусов.
Попытаемся разрешить в этой главе следующие задачи:
1) анализ поведения ферм различных классов при увеличении
нагрузки;
2) выработку метода расчета ферм различных классов по
предельной нагрузке;
3) исследование возможности уничтожения минусов в классе
фермы;
4) поведение фермы при разгрузке.
§ 9. РАБОТА ОДНОКРАТНО СТАТИЧЕСКИ НЕОПРЕДЕЛИМОЙ ФЕРМЫ
При п=\ число классов равно 2Л=2. Один из классов обозна-
чается знаком плюс, другой—знаком минус.
1. Ферма класса плюс. При повышении нагрузки упругий
этап работы заканчивается появлением текучести в растянутом
стержне. Начиная с этой стадии, усилие в нем фискируется вели-
чиной N=F?S, и при дальнейшем росте нагрузки ферма работает
уже как статически определимая с добавочной узловой нагрузкой
Fcs. Выход еще одного стержня (безразлично — растянутого или
сжатого) будет означать достижение предельного для фермы со-
стояния. Так как число минусов в классе фермы /и=-0, то в пре-
дельном состоянии она может быть рассчитана с помощью только
одних уравнений равновесия.
2. Ферма класса минус. Концом упругого этапа работы
является продольный изгиб сжатого стержня. Дальнейшая работа
фермы может протекать по нескольким вариантам. Если гибкость
выпучившегося стержня велика, так что площадка «текучести»
в его графике достаточно протяженна, то при дальнейшем росте
нагрузки усилие в этом стержне будет оставаться постоянным
до достижения определенной величины укорочения, соответствую-
щего образованию в стержне пластического шарнира. При этом
может случиться, что какой-либо из остальных стержней фермы
выйдет из работы при меньшей величине укорочения рассматри-
ваемого стержня, т. е. еще до полной проработки его площадки
«текучести». В таком случае ферма по своей работе не будет
отличаться от класса плюс и может быть рассчитана в предель-
ном состоянии как статически определимая, хотя для установле
ния того обстоятельства, что площадка «текучести» не исчерпы-
вается до перехода к предельной нагрузке, придется составить
67
одно уравнение деформаций. Схема рис. 27 изображает этот
случай; одна из линий схемы, обозначенная знаком минус, пред-
ставляет закон изменения усилий в выходящем сжатом стержне,
а линия со знаком плюс — соответственно изменение усилия
в следующем выходящем стержне.
Рис. 30
Допустим теперь, что выход второго стержня наступает при
такой величине укорочения первого вышедшего стержня, которая
отвечает образованию в нем пластического шарнира, так что к
этой стадии первый стержень приходит уже с упавшей вели-
чиной усилия (рис. 28). В этом случае установление предельной
нагрузки потребует решения уравнения совместности деформаций
Таково же будет положение при выходе сжатого стержня
малой гибкости. Продольный изгиб такого стержня поведет к не-
медленному резкому падению усилия и к предельной нагрузке,
т. е. к выходу второго стержня первый стержень придет с умень-
шившимся усилием, для определения которого придется решать
уравнение деформаций (рис. 29).
Наконец, возможен наиболее неприятный вариант последнего
случая. Падение усилия в выпучившемся сжатом стержне может
оказаться настолько стремительным, что второй стержень немед-
ленно выйдет из строя. При этом предельной нагрузкой для
всей фермы окажется та, которая вызывает продольный изгиб в
первом выходящем стержне. После этого равновесие фермы мо-
жет установиться только при уменьшенной нагрузке (рис. 30).
68
§ W. РАСЧЕТ ОДНОКРАТНО СТАТИЧЕСКИ НЕОПРЕДЕЛИМОЙ ФЕРМЫ
Будем решать задачу поверочного расчета фермы, т. е. будем
предполагать сечения всех стержней и тип нагрузки заданными.
Требуется установить предельную величину нагрузки.
Обозначим: Р] — нагрузку, вызывающую выход первого
стержня; Р2=Рщеа — нагрузку, вызывающую выход второго
стержня и являющуюся предельной 1нагрузкой для фермы.
Первым этапом расчета является обычный расчет по упругой
теории, позволяющий установить принадлежность фермы к классу
плюс или минус, т. е. определить, какой стержень будет первым
выходящим, каков его знак и какова нагрузка, вызывающая его
выход.
Приемы решения этой задачи не требуют пояснений.
Если первый выходящий стержень окажется растянутым,
т. е. ферма принадлежит к классу плюс, то для определения на-
грузки Ръ следует фиксировать усилие в этом стержне значени-
ем и произвести вторичный расчет фермы уже как стати-
чески определимой. Наименьшая нагрузка, вызывающая выход
второго стержня, и будет предельной нагрузкой.
Если же первый выходящий стержень сжат, так что ферма
принадлежит к классу минус, задача значительно усложняется.
Усилие в вышедшем стержне, уже не остается постоянным
а падает (сразу или после проработки площадки «текучести»).
Назовем это усилие X. Тем самым в дальнейшей стадии расчета
мы снова имеем дело со статически неопределимой задачей,
путь решения которой таков.
Отбросим из фермы выпучившийся сжатый стержень и заме-
ним его силами X, приложенными в узлах по концам стержня.
Причисляя X к внешней нагрузке,, найдем сближение узлов от
совместного действия внешних сил:
6.v₽=X^/=A(P>X)- (4>)
Здесь Np—усилия в стержнях основной системы от нагрузки Р
и сил X; —то же, от сил X=l; I — длины стержней. Укороче-
ние (41) является линейной функцией двух неизвестных Р и X.
Очевидно, каждому Р отвечает единственное значение X. По-
этому между Р и X должно существовать еще одно уравнение.
Этим уравнением будет условие равновесия.
Произведем подсчет нагрузки Р2, вызывающей выход какого-
нибудь второго стержня S&. Предельное усилие для этого стержня
известно и равно Fkos , если он растянут, и ^F^s, если он сжат.
С другой стороны, это же усилие может быть выражено линейно
через Р и X:
или
(42)
69
Это >и есть искомое условие равновесия. Из двух уравнений
{41) и (42) исключаем Р и получаем линейное уравнение отно-
сительно X, ахр с известными числовыми коэффициентами:
Ъхр = аХ + Ь. (43)
Усилие X в выпучившемся стержне можно представить в виде
X = vFxis.
Этому усилию отвечает укорочение самого стержня
-*)2]=/з(Х). (44)
Следовательно, условие совместности деформаций
д = \р (45)
представится как уравнение 3-й степени относительно X. Решая
его, найдем величину сжимающего усилия в выпучившемся
стержне в момент появления предельного усилия (42) в стержне
Sk при условии, что все прочие стержни работают вплоть до
этого момента упруго «и устойчиво. После этого из формулы (42)
найдем соответствующую предельную нагрузку по стержню Sk.
Этот расчет, начиная с уравнений (42), следует повторить
для каждого стержня основной системы и из полученных пре-
дельных нагрузок выбрать наименьшую. Она и будет предельной’
нагрузкой Рпред для фермы.
При этом может оказаться, что РПред <Рь Это будет озна-
чать, что уже выход первого стержня представляет предельное
состояние для фермы, так как следующее за этим выходом стре-
мительное падение несущей способности стержня немедленно
доводит какой-либо другой стержень до предельного состояния.
Решение уравнения (45), т. е. совместное решение уравнений
(43) и (44), удобнее произвести графическим путем, используя
график укорочений рис. 16, на котором л-инии (44) построены.
Достаточно провести прямую (43) и -найти абсциссу v точки ее
пересечения с кривой графика для соответственого X, чтобы оп-
ределить X=»Fxas . Разумеется, для этого уравнение (43) следует
привести к виду
= а,у+ blf (46)
п
где аг = ~Fxas, h— наименьшая высота прямоугольного
сечения стержня X. Таким графическим приемом пользовался
Хвалла, не имевший в своем распоряжении аналитического вы-
ражения (44).
70
Таким образом, мы видим, что расчет фермы с одним лишним
стержнем по предельной нагрузке значительно сложнее обычною
упругого расчета, особенно для фермы класса минус.
§ 11. РАСЧЕТ МНОГОКРАТНО СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫХ ФЕРМ
Мы ограничимся случаем фермы с двумя лишними стержнями.
Расчет такой фермы будет состоять из нескольких этапов, зави-
сящих от класса фермы. Первый этап расчета — обычный упру-
гий расчет, позволяющий определить первый выходящий стержень,
его знак и соответствующую моменту его выхода нагрузку Pi.
Если этот стержень растянут, т. е. ферма имеет класс (+ + ) или
(-!—), мы можем его отбросить, заменив постоянным усилием
Fas . Остальные -стержни образуют уже однократно статически
неопределимую ферму, а потому дальнейший расчет будет вес-
тись по способам § 10.
Если же первый выходящий стержень сжат, т. е. ферма при-
надлежит к классу (—Ь) или (------), задача неимоверно ослож-
няется. Отбросим снова этот стержень и заменим неизвестной
силой Xi. Рассчитаем основную однократно неопределимую си-
стему на совместное действие сил Р и и определим усилия
Np, вызванные этой нагрузкой в стержнях фермы, а также уси-
лия М, вызванные силой Х]=1.
Затем найдем сближение узлов в виде линейной функции Р
и Xi:
= (47>
Заметим, что составление этого уравнения потребует дву-
кратного расчета фермы с одним лишним стержнем, помимо ранее
произведенного расчета фермы .с двумя лишними стержнями.
Теперь необходимо произвести поверку по предельному
усилию для каждою стержня фермы. Эта поверка совершается
по способу § 10 и дает величину нагрузки Р2» вызывающей выход
второго стержня.
Если этот второй стержень растянут [класс фермы (—F)], то
следует его снова отбросить, заменив силами Fcs t и произвести
новую поверку по всем прочим стержням по способу § 10 для
установления предельной для фермы нагрузки Р$.
Если же этот второй стержень сжат [класс (-----)], то мы
вынуждены, отбрасывая его, ввести новые неизвестные силы Х2
и произвести поверку по всем стержням оставшейся статически
определимой фермы несколько иным путем. Рассчитаем эту
ферму трижды:
1) на совместное действие сил Х2, Р (обозначим усилия в
стержнях Np);
2) на действие силы Xi=l (усилия 2Vj);
3) на действие силы Х2 = 1 (усилия N2).
Неоудобство всех этих расчетов состоит в том, что они должны
вестись в алгебраическом, а не численном виде.
71
Теперь определим сближения узлов по концам
по концам стержня Х2:
б2₽=Х^/=/2(^Л1.^)-
г С.Г
стержня Xt и
(48)
Далее приравниваем расчетное усилие от нагрузки Р, Х2 в
каком-либо стержне, подвергаемом проверке, его по предельному
усилию
(49)
л;=/з(Л^Л2)=^
или для сжатого стержня
Np=f3(P,X1,X2) = ^s.
Из этих уравнений (48) и (49) исключим Р и получим для
62Р два линейных выражения с числовыми коэффициентами:
(50)
\р — аП^1 4" fl12^ 2 + fl13i |
b.>p = flojXj -|- fl22-^2 + ^23- I
„ „ Xi
Дополним их двумя нелинейными относительно -у^-
X
= —— уравнениями укорочений вышедших стержней:
P2°S
Д1 = й1[з,з.1о-’Л1Ч+ A/J—,\21
Д2 — А2
'2
(51)
и составим уравнения совместности деформаций:
^2р — I
Из этих совместных уравнений 3-й степени относительно Хь
Х2 найдем Xit Х2, а стало-быть, и нагрузку Р. Этот расчет, начи-
ная с уравнения (49), следует повторить для каждого стержня
основной системы и из полученных нагрузок выбрать наимень-
шую. Она и будет предельной нагрузкой для фермы.
Мы видим, как велики расчетные трудности даже для фермы
с двумя лишними стержнями. Эти трудности еще усугубляются
невозможностью графического решения уравнений (52)*. Правда,
в результате такого расчета полностью выясняется весь процесс
перехода фермы от упругой стадии к предельному состоянию.
* Благодаря этому Хвалла, имевший в своем распоряжении только графики
укорочений, но не их аналитические выражения, не мог дать способа расчета
фермы с несколькими лишними стержнями.
(52)
72
Очевидно, с увеличением числа лишних стержней в ферме та-
кой ход расчета становится совершенно неосуществимым на
практике, особенно если в обозначении класса фермы много мину-
сов и, главное, если эти минусы занимают не последние -по поряд-
ку места. Чем меньше минусов и чем позже они встречаются в
классе, тем расчет проще; чем больше минусов и чем раньше они
появляются, тем расчет сложнее.
В общем случае, если класс содержит т минусов, расчет будег
содержать, помимо прочих этапов, решение ряда систем из т сов-
местных уравнений 3-й степен-и, причем число этих систем урав-
нений равно числу стержней в основной статически определимой
системе.
Мы рассмотрели здесь только задачу поверочного расчета
фермы, сечения которой заданы, так как задача подбора сечений
этим методом не может быть решена.
§ 12. НЕКОТОРЫЕ СТРУКТУРНЫЕ СВОЙСТВА СТАТИЧЕСКИ
НЕОПРЕДЕЛИМЫХ ФЕРМ
Приведенный выше метод поверочного расчета ферм по пре-
дельной стадии обладет только одним недостатком, хотя и весьма
серьезным: он крайне сложен. Эта сложность присуща самой
ферме, если в числе выходящих стержней имеются сжатые. По-
этому весьма соблазнительной представляется задача такого
подбора сечений, при котором ферма достигла бы предельного
состояния, не имея выходящих сжатых стержней. Попытаемся
выяснить, разрешима ли такая задача в общем случае.
Мы могли бы помириться со следующими вариантами работы
фермы:
1) все выходящие стержни растянуты, кроме последнего, при
надлежащего уже к основной системе, который м-ожет быть сжат;
2) все выходящие стержни, включая последний, достигают
одновременно критического состояния. В этом случае знаки уси-
лий в выходящих стержнях безразличны.
Действительно, при удовлетворении первого условия класс
фермы состоял бы из одних плюсов, и последняя основная систе-
ма рассчитывалась бы на предельную нагрузку с помощью одних
только уравнений равновесия
Во втором случае предельное состояние фермы совпадало бы
с предельным состоянием каждого выходящего стержня, а пото-
му обычный упругий расчет позволил бы найти предельную на-
грузку. Ферма была бы равнопрочной относительно лишних стер-
жней, и теория пластических деформаций оказалась бы излишней.
Разберем первый вариант. Для проверки знака выходящих
стержней в n-кратно статически неопределимой ферме нам
пришлось бы рассчитать ее п раз, постепенно выключая выходя-
щие стержни. Этот путь весьма сложен, так как обнаружение
сжатия в каком-нибудь &-м выходящем стержне заставит заме-
нять сечения стержней и начинать всю работу сначала.
73
Крайне заманчивым было бы принять, что порядок выхода
стержней соответствует порядку их напряженности в упругой
стадии. Иными словами, если в упругой стадии мы выпишем но-
мера стержней в порядке убывающей напряженности, то соблаз-
нительно было бы считать, что они будут выходить из работы в
этом именно порядке. К сожалению, это не всегда верно.
Возьмем ферму с одним лишним стержнем и положим, что в
упругой стадии самым напряженным является стержень № 1, а
вторым по величине напряжения — стержень № 2. Пусть стержень
№ 1 вышел из работы и при некоторой нагрузке Р имеет усилие
Если он растянут, то 5i= а если же он сжат, то Si=—
где v — коэффициент падения усилия. Напишем выражения усилий
при этой нагрузке для стержня № 2 и для произвольного стерж-
ня № 3:
= S2p + «SiSai, $з=$зр + ЗДа-
Здесь S2p, S3p —усилия от нагрузки, a S2i, S3i — от единич-
ной силы Si 1 в основной системе. Перейдем к напряжениям:
°2 — —— (S-2P + ^Ai); °з= ($зр +
Л#2 р f3v3
Здесь коэффициенты rf2> ?з вставлены для общности. Для случая
растяжения будем считать <?2=Тз
По условию в упругой стадии о2>а3 . Сохранится ли это не-
равенство и после выхода первого стержня?
Напишем это неравенство в виде
Я = (S2p - CS3p) 4- (S2J - CS3l) > 0, (53)
где C= .
F 3*3
Первый член левой части есть линейная возрастающая функ-
ция нагрузки:
S2p-CS3p = kP.
Второй член также есть линейная возрастающая функция от
нагрузки в упругой стадии. После выхода первого стержня этот
член .останется величиной постоянной, если вышедший стержень
был растянут, и станет убывающей функцией нагрузки, если он
был сжат.
Изобразим процесс графически, откладывая по оси абсцисс
нагрузку Р, а по оси ординат величину R, равную левой части не
равенства (53). На рис. 31—34 изображены четыре возможных
случая.
Рис. 31 относится к случаю, когда первый стержень растянут и
первый член неравенства (53) положителен. Прямая линия 1 изо-
бражает этот первый член, а ломаная линия 2 выражает сумму
обоих членов. При отрицательном знаке второго члена линия 2
пойдет ниже прямой 1 (линия 2'). Знак неравенства не нарушает-
ся после выхода первого стержня.
74
На рис. 32 изображен случай сжатия в первом стержне при
положительном знаке первого члена. Знак неравенства также не
нарушается.
Рис. 33 и 34 повторяют случаи растяжения и сжатия в первом
стержне, но при отрицательном знаке первого члена. Мы видим.
Рис. 32
что знак неравенства меняется после выхода стержня, т. е. стер
жень № 3, бывший в упругой стадии менее напряженным, чем
стержень № 2, может в упруго-пластической стадии перегнан-
его. Таким образом, порядок напряженности стержней в упругой
стадии не всегда соответствует порядку их выхода.
Отсюда следует, что мы не можем гарантировать отсутствия
минусов в классе фермы, даже если достигнем такого положения,
при котором п наиболее напряженных в упругой стади стержней
будут растянуты. Мы сейчас покажем, однако, что даже это поло-
жение, не дающее полной гарантии, в общем случае не может
быть достигнуто.
Опустим исключительный случай, когда ферма вовсе не имеет
такого числа растянутых стержней, и допустим, что поставленное
условие удовлетворено, так что стержни /, 2,..., п растянуты и
имеют напряжения более высокие, чем все остальные т стержней.
75
Назовем выбранные стержни «лишними» и обозначим их удлине-
ния через
*1» *2> • • • > 1п‘
Напишем канонические уравнения в той форме, которую дает
им метод заданных напряжений:
yi NjpNji [ I Ы _ Q
EFj 7 EFt
(54)
NjpNjn » I Xnln _ Q
EFj EFn
Здесь j—номер основного стержня;
Njp — полное усилие в этом стержне от нагрузки и всех лиш-
них неизвестных;
Nn—усилия в нем от единичных значений неизвестных
Хл = 1;
— длины стержней;
Fj—их площади.
Суммирование распространяется на все основные стержни.
Заменим отношения через удлинения Q., разделим каждое
EFk
уравнение соответственно на /ь /2, и обозначим
Njp „
efJ ~ €j' ik lk ~~ Qjk'
Тогда уравнения примут вид:
m
S °/ie/+ h = °>
/=i
(55)
S ‘„=o.
Значения ik (удлинения лишних стержней) еще не вполне оп-
ределяют величины Cj (удлинения основных стержней), так как
последние зависят от усилий Xk , а не от удлинений /Л. Поэтому
каждому подбору сечений Fk лишних стержней будут отвечать
76
свои значения еу. Коэффициенты же aik от сечений Fk не зависят;
они зависят только от геометрической формы и от того, какие
стержни приняты за лишние.
Посмотрим, можно ли удовлетворить уравнениям (55), если
наложить на значения ej дополнительные требования:
(56)
при любых значениях / и k. Неравенства (56) выражают условие
недонапряженности основных стержней по
ными лишними стержнями в упругой стадии.
Пусть fmjn есть наименьшее из чисел гь
/г, • • in. Тогда совместное решение усло-
вий (55) и (56) можно трактовать геометри-
чески следующим образом. Каждое уравне-
ние (55) в m-мерном пространстве выража-
ет (т—1)-мерную «плоскость». Совокуп-
ность их определяет (т—п)-мерную «ли-
нию», координаты которой е2,..., ет удов-
летворяют уравнениям (55). В том же про-
странстве неравенства (56) выражают т-
мерный «куб» с центром в начале коорди-
нат и со стороной, равной 2imiri. Условия
сравнению с выбран-
(55) и (56), взятые вместе, требуют «пересечения «линии» (55) с
«кубом». Легко видеть, что это, вообще говоря, неосуществимо.
Пусть ферма имеет один лишний стержень (?г=1) и два основ-
ных (т = 2). Тогда единственное уравнение (55) выразит прямую
линию на плоскости еь е2, которая должна пересекаться с квадра-
том (56), имеющим сторону 2Ц (рис. 35). Пусть при некотором
подборе сечений это пересечение не осуществилось. Возможно ли
его достигнуть измененным подбором сечений? Легко видеть, что
это невозможно. Если при новом подборе сечения F лишнего
стержня мы -потребуем сохранения его напряженности, т. е. удли-
нения i*i, то ни размер квадрата, ни положение прямой, определяе-
мое коэффициентами ап, а2ь не зависящими от площадей, не изме-
няется. Попробуем изменить сечение Fi так, чтобы его напряжен-
ность, т. е. удлинение А, возросла или уменьшилась в k раз. Напи-
шем единственное уравнение (55) в виде
— е1+-^е2=1.
Это есть уравнение прямой в отрезках, причем отсекаемые ею
й й
на осях отрезки равны-----и------.
ан ад
Изменим в k раз удлинение лишнего стержня й:
-^-ех+ -^1—е2=1.
-ki! 1 ~kh 2
Отрезки на осях возросли (или уменьшились) в k раз, но во
столько же раз возросла (или уменьшилась) сторона квадрата
77
f56). Поэтому если пересечения прямой с квадратом не было, то
его не будет и при изменении ii-
Мы вели несколько упрощенно наше рассуждение. На самом
деле условия (55) и (56) должны быть дополнены еще добавоч-
ными неравенствами, фиксирующими обязательные знаки усилий
Njp , т. е. удлинений основных стержней ej , поскольку они вполне
определены подбором сечений лишних стержней. Геометрически
это значит, что «линия» (55) должна да ер ес екать «куб» (56) не где
угодно, а в совершенно определенном «квадранте». Это условие
еще более стесняет возможность совместного удовлетворения урав-
нений (55) и неравенств (56).
Это рассуждение показывает, что мы не в силах
заставить произвольно выбранную группу лишних
стержней иметь напряжения более высокие, чем у
всех основных стержней, варьируя только площади
сечений. Этого результата можно достигнуть толь-
ко для некоторых основных систем. Интересной за-
дачей было бы изыскание регулярного процесса на-
хождения таких недонапряженных основных си-
стем. Задачи этой мы здесь касаться не будем. Но
так как эта основная система должна быть не толь-
Рис. 36 ко недонапряженной по сравнению с лишними
стержнями, но мы еще требуем растягивающих
усилий от этих лишних стержней, то, вообще
говоря, эта задача явится неразрешимой для произвольной
фермы.
Вот простой пример. Ферма имеет один лишний стержень и два
основных (рис. 36). Один стержень растянут и два — сжаты. Мож-
но ли заставить единственный растянутый стержень иметь более
высокое напряжение, чем оба сжатых стержня?
Уравнение (55) для этого случая примет вид
2 sin2 ае2 — е3= —
Удовлетворить этому уравнению значениями
1«1|<4, |е3|<«1
возможно только, если 2 sin2a>l, т. е. а >45°. При а <45° ни-
каким подбором сечений нельзя избежать того, что продольный
изгиб в одном из сжатых стержней наступит ранее перехода рас-
тянутого стержня в пластическое состояние. Ферма имеет класс
минус.
Наш геометрический путь доказательства позволяет очень легко
доказать обратную теорему, выведенную Морисом Леви и утверж-
дающую возможность недонапряженности лишних стержней по
сравнению с основной системой. Для доказательства этой теоремы
изменим знак неравенств (56) на обратный. Тогда эти неравенства
будут выражать уже не внутреннюю полость «куба», а внешнюю
часть пространства, через которую, разумеется, пройдет любая
«линия» (55), что и доказывает теорему Леви.
78
Таким образом, первый из намеченных нами улучшенных вари-
антов работы фермы в общем случае не может быть реализован.
Легко видеть, что также обстоит дело и со вторым. В этом вариан-
те мы отказываемся от фиксации знака усилия в выходящих
стержнях, но зато требуем одновременности их выхода, т. е. равйо-
напряженности в упругом состоянии. При этом уравнения (55)
принимают еще более простой вид:
Еал5/=±1,
............................. (57)
+ 1,
где 67 = -р-, a i0 — удлинение (укорочение) лишних стержней.
ио|
Неравенства (56) также упростятся:
16/10- (58)
Смысл условий (57) и (58) остается прежним: они требуют пе-
ресечения «линии» (57) с определенным «квадрантом» «куба» (58),
имеющего стороны, равные двум. Эти требования в общем случае
также неосуществимы, как условия (55) и (56) для первого вари-
анта.
Резюмируя все вышесказанное, приходится признать, что осво-
бодиться от сложностей, вносимых поведением сжатых стержней,
при расчете фермы по предельной стадии в общем случае невоз-
можно. Указанный нами в § 11 способ расчета является поэтому
единственным правильным способом.
Жертвуя точностью определения истинных запасов, можно было
бы попытаться пойти по упрощенному пути, предложенному проф.
Стрелецким. Он высказал мысль о сходстве поведения пластичного
сжатого стержня после потери устойчивости с поведением стержня
из хрупкого материала и предложил вовсе исключать их из рас-
смотрения после потери устойчивости, считая их перерезанными.
Вряд ли, однако, этот путь может привести к удовлетворительным
результатам, так как, во-первых, полное исключение сжатых стер-
жней будет настолько перегружать последующие системы, что мы
не получим ощутимого повышения запаса, а во-вторых, порядок вы-
хода стержней все же нельзя будет установить из упругого расчета,
так как полное исключение сжатых стержней в еще большей степе-
ни сможет перепутать этот порядок, чем в действительном случае,
рассмотренном выше.
§ 13. РАЗГРУЗКА ФЕРМЫ
Как было уже указано в начале этой работы, разгрузка фермы
после выхода каких-либо стержней не всегда явится безобидным
процессом.
Рассмотрим ферму с любым числом лишних стержней и допу-
стим, что первым выходящим стержнем будет растянутый. Мы мо-
79
жем принять его за единственный лишний стержень и написать
уравнение деформаций в таком виде:
Ал ~ ^Ф>
где —удлинение лишнего стержня, а —расхождение его
концевых узлов в основной системе, полученной после удаления
этого стержня.
До тех пор пока не вышел еще один стержень, основная система
работает упруго, а потому любая ее деформация будет линейной
функцией усилий в лишнем стержне N и нагрузки Р:
4- k2P.
Пусть первый стержень перешел в пластическое состояние и по-
лучил остаточное удлинение Длп , сверх полного упругого удлине-
ния Длу (рис. 37). Это произошло при некоторой нагрузке Рь ве-
личину которой найдем из
Алп + Длу = +^2^1,
здесь Ns — предельное усилие в лишнем стержне.
Если бы этот стержень был беспредельно упругим, то той же
нагрузке Pi отвечало бы большее усилие в стержне Ni>Ns и
меньшее полное удлинение Длу4-Дпу, которое было бы зато впол-
не упругим:
Напишем такое же выражение для нагрузки Ps, означающей
конеи упругой работы лишнего стержня:
Из рис. 37 видно, что
A.jy 4~ Длу _yVj
Д./у
80
или
откуда следует, что
М = frM + Л2Р1
Ns kiNs + k.Ps ’
1 5 Ps
Если теперь произвести разгрузку фермы, то в лишнем стержне
появится усилие обратного знака, равное
A^-jVx=-(V, (59)
и тем большее, чем выше была нагруз-
ка Р\ против нагрузки Ps, обращаю-
щей лишний стержень в пластическое
состояние.
Если воздействие такого сжимаю-
щего усилия пройдет для стержня без-
болезненно, то в дальнейшем он будет
работать вполне упруго до нагрузки
Pi. Всякое новое превышение этой на-
грузки будет вызывать добавочное ос-
таточное удлинение, а разгрузка —
добавочное сжатие.
Может случиться, что остаточное
сжатие — (М—Ns) превзойдет критическую силу для стержня, и
он выпучится. Так как для критического усилия мы можем напи-
сать выражение
то из сопоставления этого выражения с равенством (59) найдем,
что продольный изгиб при разгрузке наступит, если
откуда
Рг> РД1 +<?)•
(60)
Итак, если лишний стержень начнет течь при нагрузке Ps на
ферму, и мы поднимем эту нагрузку более чем в 1 + раз, где —
коэффициент продольного изгиба для этого стержня, то при раз-
грузке он неизбежно выпучится. Ферма будет хорошо вести себя
при высокой нагрузке, но ее нельзя будет разгрузить без выпучи-
вания стержня. Как видно из рис. 38, остаточное удлинение стер-
жня почти исчезнет за счет его искривления, а остаточное сжатие
81
сильно уменьшится за счет изгиба. Попытка вторичного загруже-
ния фермы покажет, что искривившийся стержень участвует в ра-
боте фермы много слабее, чем раньше, за счет падения его про-
дольной жесткости, так что вторичное загружение прилагается уже
в ферме иной схемы, чем прежняя ферма.
Такое же изменение схемы последует и в том случае, если пер-
вым выходящим стержнем был сжатый. На рис. 39 показана схема
работы стержня при последовательно возрастающих загружениях
и разгрузках.
§ 14. О ВОЗМОЖНОСТИ ЭКСПЛУАТАЦИИ ФЕРМЫ
В УПРУГО-ПЛАСТИЧЕСКОЙ СТАДИИ
Когда мы исследуем область упруго-пластической работы не-
разрезной балки с целью выяснения предельного состояния, то мы
имеем в виду установление истинного запаса прочности такой бал-
ки. Иными словами, мы при этом предполагаем, что именно пре-
дельное состояние, т. е. обращение балки в изменяемую систем}
за счет включения ряда пластических шарниров, есть то состояние,
которое можно уподобить достижению площадки текучести в растя-
гиваемом образце. Поэтому вполне обоснованным является отне-
сение коэффициента запаса к этому предельному состоянию.
Отдельные случаи эксплуатационного углубления в упруго-пласти-
ческую стадию не будут вызывать никаких осложнений, кроме не-
значительного прироста остаточных прогибов, не более вредных,
чем остаточные прогибы при раскружаливании. Опасность потери
устойчивости в балке является совершенно особой опасностью, и
проверка на устойчивость может быть вполне отделена от проверки
на прочность.
В ферме эти две проверки неразделимы, так как потеря устой-
чивости сжатого стержня есть в то же время его естественный
предел прочности. Поэтому для фермы случайное углубление в
упруго-пластическую стадию почти всегда неотрывно связано с
появлением продольного изгиба в сжатых стержнях либо при заг-
ружении выше упругого предела, либо при разгрузке из этого сос-
тояния. Но продольный изгиб, как мы видели, приводит к сущест-
венному изменению самой схемы фермы, искривляя стержни,
которые по роду своей работы обязаны быть прямыми, а потому
уменьшая их продольную жесткость и долю участия в работе
фермы.
Разумеется, возможны различные взгляды на допустимость
таких изменений. Нормы расчета в отличие от методов расчета
всегда содержат субъективные моменты. Автор полагает со своей
стороны, что установленные им законы поведения сжатых стержней
с достаточной определенностью свидетельствуют о невозможности
использования упруго-пластической работы ферм в случае потери
устойчивости. Единственный случай, когда такое углубление в
упруго-пластическую стадию не влечет за собой потери устойчиво-
82
сги, — это случай фермы, все выходящие стержни которой растя-
нуты, т. е. класс которой состоит из одних плюсов. Но как мы
только что видели, и в этом случае нас подстерегает враг — про-
дольный изгиб, если не на фронте загружения, то в тылу разгрузки.
В силу сказанного приходим к заключению, что исчисление
коэффициента запаса по отношению к предельному состоянию для
статически неопределимой фермы должно производиться гораздо
осторожнее, чем для балочно-рамных систем, работающих на изгиб.
3. О РАСЧЕТЕ ГИБКОГО КОЛЬЦА
Рис. I
L Под гибким кольцом мы понимаем замкнутую нить, способ-
ную работать только на растяжение. Примером такого кольца может
служить элемент гибкой цилиндрической оболочки, выделенный
двумя параллельными плоскостями, нормальными к оси цилиндра
(рис. 1). Такие оболочки применяются в воздухоплавании и в пере-
правочном деле (лодка А-3) и находятся под действием внешних сил
и внутреннего давления воздуха или
иного газа.
Задача расчета такого гибкого
кольца осложняется тем, что деформа-
ции его велики, и потому положение и
даже направление действующих на
кольцо сил зависит от его окончатель-
ной формы равновесия, а эта послед-
няя определяется силами. Таким обра-
зом закон независимости действия сил
здесь неприложим.
Задачу расчета можно решить на основе теории веревочного
многоугольника. Действительно, так как кольцо способно воспри-
нимать лишь растягивающие напряжения, то его форму равнове-
сия можно уподобить некоторому веревочному многоугольнику, по-
строенному для данных нагрузок. Лучи соответственного силового
многоугольника выразят в силовом масштабе усилия в контуре
кольца. Таким образом, по форме равновесия можно найти усилия,
возникающие в кольце, а по силовому многоугольнику, наоборот,
можно найти форму равновесия.
Если бы направление внешних сил не зависело от формы равно-
весия, то силовой многоугольник можно было бы построить непос-
редственно, не зная формы равновесия. После этого достаточно бы-
ло бы подобрать положение полюса, при котором контур веревочно-
го многоугольника имел бы заданную длину—длину контура кольца,
и задача была бы решена вполне точно. Так именно ее можно решить
для случая жесткого кольца. Задача такого построения много ус-
ложняется для гибкого кольца, так как силового многоугольника
нельзя построить, не зная предварительно формы равновесия. Это
затруднение снова вытекает из неприменимости закона независи-
мости действия сил. Однако задача и в этом случае разрешима
вполне точно.
84
2. Как сказано, задача распадается на две части: построение
силового многоугольника и отыскание его полюса. Начнем с общих
соображений относительно положения полюса.
Рис. 2 Рис- 3
Пусть на кольцо действуют произвольные взаимно урав-
новешенные силы. Какова бы ни была форма равновесия коль-
ца, соответствующий ей силовой многоугольник будет замкнутой
односвязной или многосвязной фигурой. Контур ее будет составлен
из действующих на кольцо сил, а лучи будут выражать усилия в
соответственных элементах кольца. Покажем, что положение полю-
са должно удовлетворять тому условию, чтобы направление обхода
всех силовых треугольников, состоящих из двух лучей и внешней
силы, было одинаковым.
Рис. 4 Рис. 3 Рис. 6
На самом деле, пусть два силовых треугольника ОАВ и OCD
(рис. 2) имеют противоположные направления обхода. О — полюс,
АВ и CD — силы, ОА, ОВ, ОС, OD — лучи. На рис. 3 показаны
соответствующие силы в веревочном многоугольнике, откуда видно,
что если обход силового треугольника по часовой стрелке дает
растягивающие усилия в соответственном элементе веревочного
многоугольника, то обратное направление обхода дает усилия
сжимающие, и наоборот. Но так как в кольце могут иметь место
лишь растягивающие усилия, то предположение о наличии силовых
треугольников с различным направлением обхода отпадает.
Отсюда легко вывести два единственно возможных случая топо-
логического расположения полюса в силовом многоугольнике.
Случай I. Все части контура силового многоугольника имеют
относительно полюса кривизну одного знака, т. е. обращены к по-
люсу вогнутой стороной (рис. 4) или выпуклой (рис. 5).
Случай II. Если контур имеет точки перегиба, то положение
полюса определяется тем условием, что ни один луч не должен
пересекать контура (рис. 6).
85
Покажем, что этих указаний достаточно для ориентировочной
оценки верхнего предела величины усилия в кольце.
Пусть кольцо загружено по рис. 7 силой Р, внутренним давле-
нием q и водяной реактивной нагрузкой W. Для упрощения примера
допустим, что деформации кольца невелики, а потому силы после
деформации сохраняют свое направление. Это предположение будет
справедливо, если q велико, а Р и, стало быть, W— малы. Найдя ве-
личины водяных реакций из условий равновесия, мы можем пост-
роить силовой многоугольник (рис. 8). Помещая полюс внутри петли
А, мы удовлетворим требования случая I. Легко видеть, что полюс
не может занять никакого иного положения. Самым неблагопри-
ятным положением полюса будет точка О, а верхним пределом
усилий в кольце — длина луча ОМ.
3. От этого приближенного решения можно перейти к точному,
если дополнительно предположить, что внешние силы не могут
иметь составляющих вдоль контура кольца, т. е. всегда направлены
по нормали к нему. Это предположение справедливо для большин-
ства случаев и, в частности, для случая давления на кольцо жидко-
стей и газов. Допустим также, что продольными удлинениями обо-
лочки кольца можно пренебречь.
При первом предположении лучи силового многоугольника дол-
жны быть нормальны к его сторонам, так как лучи параллельны
касательным к контуру кольца, а стороны параллельны силам,
направленным по нормали к кольцу. С другой стороны, все лучи
пересекаются в одной точке — полюсе силового многогугольника.
Итак, силовой многоугольник есть фигура, все нормали которой
пересекаются в одной точке. Единственной такой фигурой является
окружность.
Мы получили первый важный вывод: Каковы бы ни бы-
ли силы, действующие на кольцо в направлении
нормалей, силовой многоугольник представляет
окружность (или часть окружности) с цент-
ром в полюсе.
Отсюда следует также, что при любой нагрузке такого типа
усилие во всех частях контура кольца имеет постоянную величину.
86
Рис. 9
не зависит от
внутренним
q0 и двумя
Эта теорема позволяет дать точное решение задачи для любого
случая загружения. Мы покажем ее применение на нескольких
простых примерах.
4. Пример 1. Кольцо находится под действием сплошной
равномерной нормальной нагрузки q0, направленной наружу (дав-
ление газа). Длину контура кольца обозначим 2^RG. Длина сило-
вой окружности равна сумме всех сил, т. е. 2^RoqOt откуда ее ради-
ус, равный усилию в коль-
це, выразится:
Форма равновесия
есть окружность радиуса
Яо.
Пример 2. Кольцо
нагружено
давлением
равными и противополож-
ными силами Р, действу-
ющими по диаметру коль-
ца (рис. 9). Предположим
сперва, что давление qG внутри кольца постоянно и
нагрузки. Такой случай имеет место, если цилиндрическая оболоч-
ка, загруженная по всей длине силами Р, соединена с обширным
резервуаром, объем которого значительно превосходит объем обо-
лочки, так что давление газа в этой системе можно считать постоян-
ным. Мы делаем это предположение для упрощения с тем, чтобы в
следующем примере от него отказаться.
Так как концы всех силовых векторов в силовом многоугольнике
должны лежать на одной окружности радиуса N, то силы Р пред-
ставят симметрично расположенные вертикальные хорды этого си-
лового круга (рис. 10). Порядок обхода силового круга таков:
AEBCFDCFDAEBA.
Обозначим через N радиус силового круга, а через а — цент-
ральный угол, стянутый хордой Р. Тогда
P=2Psin—,
2
а
(2я + 2а)М = 2^0, (2)
т. е. длина контура силового круга с учетом двукратного обхода
дуг, опирающихся на угол а, равна сумме внутренних давлений.
Исключим из формул (1) и (2) радиус Л':
а
2 sin —
— =--------— (3)
Prfo j.|. g
3t
87
(4)
2siny
Трансцендентное уравнение у = ------можно решить графиче-
1+ —
Л
ски и выразить а в функции^— . Очевидно эта функция является
многозначной. На рис. 11 представлена первая ветвь функции, соот-
ветствующая наименьшим значениям . Исследуем смысл этой
многозначности.
При вращении луча в силовом круге (рис. 10) от исходного поло-
жения ОА до OD в направлении AEBCFD касательная к контуру
кольца (рис. 12) обходит левую его половину, принимая последо-
вательно те же положения, что и силовой луч. Так как внутреннее
давление распределено равномерно, то при перемещении точки ка-
сания на равные дуги касательная поворачивается на равные углы.
Следовательно, форма каждой половины кольца есть дуга окруж-
ности. Легко видеть, что центральный угол этой дуги равен +а.
Допустим, что при некоторой величине —— угол а оказался
равным я . В этом случае центральный угол полукольца будет ра-
вен т. е. каждая половина кольца превратится в полную окруж-
ность, и силы Р придут во взаимное соприкосновение (рис. 13).
Силовой круг примет тогда форму рис. 14. Очевидно дальнейшее
увеличение угла а невозможно, так как оно влекло бы за собой
двухслойное наматывание оболочки (рис. 15). Если силы Р имеют
не точечные размеры, то они, упершись друг в друга, не допустят
дальнейшей деформации кольца.
88
Отсюда следует, что из всех ветвей функции а=/ I-------)реаль-
ный смысл имеют только те, для которых 0 < а < тс. Этот вывод,
однако, еще не устраняет полностью неопределенности решения.
Р
При значениях------ от 1 до 1,05 угол а может иметь два значения;
при больших величинах-------угол становится отрицательным. Отри-
цательное значение указывает на то, что центральный угол полу-
кольца меньше тс , т. е. силы Р как бы растягивают кольцо, что
о Р
лишено смысла. Значению-------= I соответствуют два значения а:
РоЧо
ах 0,6тс;
а2 = тс.
Таким образом, при P = Rogo возможны две различные формы
равновесия кольца, причем вторая из них соответствует рассмот-
ренному выше случаю смыкания двух половин кольца (фиг. 13).
Но возможность существования двух разных форм равновесия при
одной и той же нагрузке свидетельствует о неустойчивости равно-
весия: кольцо уже неспособно удержать на себе силы Р и допускает
Рис. 13 Рис. 14 Рис. 15
их взаимное соприкасание. Очевидно, при Р > Rcq0 тем более долж-
на наступить потеря устойчивости. Этот случай интересен тем,
что явление потери устойчивости происходит при наличии растяже-
ния во всех частях оболочки.
Итак, гибкое кольцо радиуса Ro, находящееся
под действием постоянного внутреннего давле-
ния q0 и двух диаметрально противоположных
сил Р, теряет устойчивость при Ркрит = Rogo-
Критической силе Ркрит соответствует радиус силового круга
дг _ Р _ РоУо
2 2
Таково будет растягивающее усилие во всех частях оболочки.
Смысл этой формулы ясен: она выражает усилие от внутреннего
давления в кольце половинного радиуса, так как оболочка как бы
распалась на два таких кольца.
Существование зоны неустойчивого равновесия при а от 0,6 тс
до тс означает следующее. Пусть на кольцо действуют определен-
89
ные силы Р и давление до, причем P<Rogn. Начнем уменьшать внут-
реннее давление. В тот момент, когда наступит равенство P~Rogo
кольцо потеряет устойчивость и силы Р придут в соприкосновение.
Если после этого снова начать повышать внутреннее давление, то
кольцо сразу расправится, и угол внедрения а вернется к критиче-
скому значению а =0,6 тс.
Найдем предельное расстояние d, на котором могут удерживать-
ся силы (рис. 16). Этот предельный раздвиг получается из условия
d = 2R sin = 2R sin я~2°’— =2Я sin -5-.
Радиус R деформированного полукольца определим из условия
постоянства длины периметра полукольца:
(тс 4- 0,6тс) = тс/?0,
откуда
Подставляя эти значения в выражение для d, найдем
й = —“sin — = 0,737?о.
1,6 5
Это и есть минимальное расстояние, на котором могут удержи-
ваться силы Р.
Итак, при постоянном внутреннем давлении картина работы
кольца представляется в следующем виде. Наибольшее усилие в
кольце имеет место при отсутствии внешней нагрузки. По мере
увеличения сил Р усилие в кольце падает, а точки приложения сил
сближаются. При P = Rogo сближение достигает критической вели-
чины d = G,73 Ro, после чего кольцо теряет устойчивость и силы
сближаются до соприкосновения. Усилие в кольце принимает наи-
меньшее значение, равное половине первоначального, и уже не
меняется при дальнейшем росте нагрузки.
5. Перейдем к рассмотрению другого случая, когда внутреннее
давление является функцией объема оболочки, т. е. количество
газа, наполняющего цилиндрическую оболочку, постоянно.
90
Сперва перечислим некоторые общие свойства замкнутого гиб-
кого кольца.
1. Если участок контура кольца загружен только равномерным
внутренним давлением, то формой равновесия этого участка яв-
ляется дуга окружности, и наоборот.
2. Касательная к кольцу испытывает скачки только в точках
приложения сосредоточенных сил.
3. Если формой равновесия участка контура кольца является
прямая линия, то на этот участок действуют с обеих сторон равные
и противоположные силы, и наоборот.
Эти свойства настолько очевидны, что можно не приводить.их
доказательств.
Итак, пусть кольцо с периметром 2к^0 находится под действием
внутреннего давления qo. К кольцу прикладываются две диамет-
рально противоположные силы Р. Как следует из предыдущего,
кольцо, деформируясь, принимает вид двух дуг с центральным
углом тг + а, описанных радиусом R, меньшим, чем 7?о, а внутрен-
нее давление повышается с qo до q (рис. 17). Мы можем составить
следующие уравнения:
а) условие постоянства длины контура полу-
кольца: v
/ \ ❖/ \
/?(* + а) = Я07г, L сффс р]
откуда \ / X. /
R = ——; (5) ----'
1+ — Рис 18
71
б) условие постоянства количества газа в оболочке:
<7® = q0^Rl,
где <о— площадь деформированного кольца:
со — R2 (к 4- а 4- sin а),
откуда
л *
или, подставляя из равенства (5)
— = 1 + —,
/? л
/ а \2 а
14-— 14- —
__ \ 71 / __ Л
а srna sin а
14- 4- 14- ,
71 71 л+а
в) из силового круга (рис. 18) имеем
Р = 2N sin —
2
(6)
91
и
откуда
а
2 sin ——
Р 2
1+JL
Л
или в силу равенства (6)
а
2 sin —
Р = ________2_
Яо<7о 1+s»na
(7)
Это уравнение решает задачу. Подобно тому, как это было
прежде, строим график функции:
2 sin —
________2_
и приводим его к виду a=sf(~—)(РИС- 19). Применяя к этому гра-
\ “о<7о /
фику прежние рассуждения, придем к следующим выводам.
Прежде всего явление неустойчивого равновесия здесь отсутст-
вует, так как функция а является однозначной при а О.
\ RoQo I
Оболочка оказывается устойчивой до самого момента соприкосно-
вения сил Р, наступающего при
Р ==
т. е. при двойней нагрузке сравнительно с прежним случаем.
Усилие в кольце при этом равно:
л тс Z
2sin —
2
т. е. равно начальному усилию. Таким образом, при выпускании
газа из надутой цилиндрической оболочки, загруженной силами Р,
оболочка упруго удерживает грузы, плавно допуская их до сопри-
касания. Если после наступившего соприкасания сил снова повы-
сить внутреннее давление, то оболочка расправится и разведет
грузы.
Мы видели, что усилие в кольце в момент соприкасания сил Р
равно начальному усилию от одного внутреннего давления. Отсюда
не следует, что усилие это остается постоянным при возрастании
92
наГрузки Р от нуля до этого конечного значения. Мы можем выра-
зить это усилие в виде
N = Rq = —
Sin а
л-f-a
Р
а
2 sin —
2
На рис. 20 изображен график зависимости --------от------. Мы видим
Riflo PqQo
из графика, что при всяком значении Р, не доводящем силы до
соприкасания, усилие в кольце меньше начального. Оно достигает
это’выражение обращается в нуль при tga = к 4- а, откуда а =
- 1,355 = 77°30'. При этом
a
2 sin —
PoQd-----;----= 1,03/?0go,
sin a
14-—
Jl-J-a
а наименьшее усилие в кольце
AU--------= 0.82^.
2 sin -у-
Итак, при Р = 0 усилие в кольце равно Roqo’, при возрастании
силы Р до 1.03 Roqo усилие падает до 0,82 Roqo и снова возвращает-
ся к прежнему значению N=Roqc при P Rcqo.
Объединяя результаты исследования этого и предыдущего слу-
чая, можно прийти к важному и несколько неожиданному выводу:
если гибкое кольцо выдерживает без разрыва
внутреннее давление, то его можно загрузить
двумя диаметрально противоположными силами
93
любой величины без всякой опасности для проч-
ности кольца.
6. Попробуем рассчитать надутую оболочку, лежащую на земле
и загруженную сверху силой Р (рис. 21). Часть кольца, соприкаса-
ющаяся с землей, должна иметь прямолинейную форму. На осно-
вании ска-занного в § 5 заключаем, что реактивное давление земли
должно быть равно внутреннему давлению q.
Но так как полная реакция земли должна уравновесить нагруз-
ку Р, то длина сплющенной части кольца s, лежащей на земле,
определится из условия равновесия
sq = P. (9)
Остальная часть кольца образует две дуги радиуса R с цент-
ральными углами (рис. 22). Эти дуги должны иметь согласно
сказанному в начале § 5 горизонтальную касательную в месте
примыкания их к сплющенной части кольца, а потому центры дуг
находятся на вертикалях, восставленных в местах примыкания.
s
т. е. на расстояниях — от оси симметрии.
Подобно прежнему обозначим через Ro, q0 начальный радиус
кольца и начальное внутреннее давление (в отсутствии нагрузки).
Как и в предыдущей задаче, мы можем составить условия:
а) постоянства длины периметра кольца
2р/? + 5 = 2кР0; (10)
б) постоянства количества газа в оболочке:
где <о — площадь деформированного кольца, равная:
.ш = ^2 + 3|(2 + со8-2-).
Но так как s = 2R sin — , то
2
со = R2 + 2 sin 4- -i- sin а
94
и условие постоянства количества газа дает
/ Р \2 _ go _______________________
\ Яо / q . о . <* . 1 .
р. 4- 2 sin — 4- — Sin a
(11)
Подставляя значение s, преобразуем (10):
2|x/? + 2/?siny=2rc/?0, (10)
откуда
R
Л)
(12)
F + sin
Теперь обращаемся к силовому кругу (рис. 23). Сила Р обра-
зует его вертикальную хорду. Так как нагрузка обладает только
одной осью симметрии — вертикальной, то силовой круг симметри-
чен только относительно горизонтальной оси.
Это — общее свойство: оси симметрии нагруз-
ки и силового круга взаимно-перпендикуляр-
ны. Сплющенной горизонтальной части кольца
будет соответствовать один единственный го-
ризонтальный луч в силовом круге; равные и
противоположные давления q, действующие с
обеих сторон на эту часть кольца, сливаются в
одну точку А.
Из силового круга берем соотношение
Рис. 23
(13)
Кроме того, длина силовой окружности с двукратным проходом ду-
ги а равна внутренним давлениям, действующим на криволинейные
части контура кольца:
(2z4-a)W = 2?,Rq. (14)
Но так как в силу симметрии силового круга
P = 2W sin — .
2
то условие (14) принимает вид
(15)
как и в предыдущих задачах. Подставим найденное значение в
формулу (12):
R =----------- (16)
а а
я+v+sinv
95
и (11);
___ Яо 9о _____________________
~ R2 ' а а 1
л-Ь —+2sin — + — sma
= q0
а а
"+T+sinT
л
2
Л
«+“-+2sin ~sina
(«+-|- + sin -у)‘
=чо -----------—------—---------• (п:
"[("+ V+sin v) +sin т (‘+ cos т)]
Перемножая равенства (16) и (17), получим выражение для N:
N = Rq---------- • — X
а ал
-+v+sinV
/ а а \2
______(”+Т+”пт)
Г/ а а \ а / a
lr + T + sinTrsinT(1 + cosT,
= ^0 ' - •
sin -f (,+cost)
’H-V+sinT
Подставим это значение в формулу (13):
а
sin --------------------------------
Р = 27?о<7о------------------
sin —(i+cos —
1+-----:-2------
а а
я + —+ sin —
или
л аГ а “ 1
Р 2sln-r[" + T + sin—]
n+'7 + sin^’+sin-7(I + c°sy-)
________________2_______
! l + cos-=-
ч----------------
. О. а а
s,nY "+-£- +sin-
US)
(19)
96
Это и есть решающее уравнение. Как и прежде, строим график
функции
1 4 l+cost
а а а
и приводим его к виду (рис. 24):
Значение а =« снова приходится считать предельным. Хотя
при нем еще не наступает соприкасания силы Р с землей, но сила
как бы зажимается складкой оболочки (рис. 25). Дальнейший
процесс проследить нетрудно, но формула (19) теряет силу при
Р
а > т. е. при ------>1,7. . ,
/?о7о \ /
Если представить себе, что сила Р подвешена \ /
изнутри оболочки, и допустить, что она возросла \ /
сверх предельного значения Р=1,7 Ро<7о. то легко \ /
понять, что образовавшаяся складка оболочки д \ Л
опустится вниз, образуя вертикальную подвеску "
(рис. 26). При этом оболочка как бы частично втя-
нется внутрь складки, ее объем уменьшится, но
уменьшится и загруженная длина периметра коль-
ца, так как на вертикальную складку будут дейст-
вовать взаимно уравновешивающиеся давления.
Кольцо будет находиться в той же стадии, как и i
при Р = 1,7 Ро<7о, т. е. а = т: , но будет как бы обла- |
дать меньшим начальным радиусом Ro и большим г
начальным давлением qD. Соответственные зависи- рис 26
мости будут выведены ниже. Теперь же для нас го- и *
раздо важнее другой вопрос: не наступает ли при
а — неустойчивое состояние?
Ответ на этот вопрос будем искать обычным методом сопостав-
ления работы внешних и внутренних сил на возможном перемеще-
97
нии. Если dAe — приращение работы внешних сил, a dAt — то
же, внутренних сил, то устойчивое равновесие характеризуется не-
равенством
dAt > dAe,
а неустойчивое — обратным неравенством.
Рассмотрим кольцо в состоянии а = к, Р = 1,7 RQqQ и дадим силе
Р малое перемещение вниз на длину 6.
Работа внешних сил (внутреннее давление относим к внутрен-
ним силам) выразится
dAe = P^
Перемещение 6 сократит рабочий периметр кольца на 26, а ра-
диус R — на dR. Давление q возрастает на dq. Формула (10х) для
длины кольца примет вид
2р. (R — dR) + 2(R — dR) sin = 2^0 — 28,
или, так как
2 ~ 2 ’
ТО
(R — dR) (Зя + 2) = 2к/?0 — 28.
Но так как до перемещения, т. е. при 6 = 0 и dR -^Q, было
/?(Зн+2) = 2н/?0,
то, вычитая почленно, получим
(te + 2)dR= 28,
или
dR = -^—ti.
Зл + 2
Новый объем станет равен:
о — d(o=(R — dR)2 4- 2 sin sin aj ,
откуда, отбрасывая вторые степени приращений,
~du> = —2RdR pi + 2 sin sin a| = — 2RdR py + 2
или
d0,=2'?dMv’' + 2) 2/?o = 2,352/?6.
Приращение внутреннего давления найдем из условия постоян-
ства количества газа:
(q 4- dq) (со — d<o) = qwt
откуда, снова пренебрегая высшими порядками малости,
qdw —
или
dq = ч— = Я. 2,352/?5 = _У?'352^ = о 35 .
ш to по / 3 , о \ ’ Я
Приращение работы внутренних давлений выразится:
dAl = (q + ^dv>^ad«> = 2,352Rqi.
Но
а потому
dA t = 2,352 — = 1,176РБ > РБ = dAe.
1 2 e
Таким образом, оболочка не теряет устойчивости при образо-
вании складки, когда a — tz.
Теперь вернемся к исследованию поведения кольца при нагруз-
ке 1,7 RoqG. Как было сказано, после того как угол внедрения а
примет значение тг, дальнейшее возрастание нагрузки вызовет об-
разование подвески (рис. 26). Часть кольца под грузом сложится
в виде складки, а угол внедрения будет оставаться постоянным
(а = к). Такое переходное состояние имеет пределом тот момент,
когда нижняя часть подвески опустится до земли и сила Р пол-
ностью уравновесится сосредоточенной реакцией земли. В мгнове-
ние, непосредственно предшествующее этому соприкасанию, длина
подвески становится равной радиусу R (рис. 27). Условие постоян-
ства длины периметра принимает вид:
2/? -|- s -|- 3tzR = 2тй/?0,
а так как при а = к
S--2/?,
R =
Ro
99
Объем кольца будет при этом равен:
w = 2/?2 + = *2 (2+ т)=
2 + п
Условие постоянства количества газа выразится:
з , 2
—(т+т)-
Усилие в кольце при этом будет:
* = Я<7 = Мт + 4) =
о Z \ Z Л /
Т + V
т. е. равно начальному усилию в отсутствии нагрузки, а нагрузка
P = 2/V sin=2Яо<7о.
«Легко показать, что при всякой другой нагрузке Р < 2/?одо уси-
лие в кольце будет меньше начального. Это непосредственно видно
из формулы (18), в которой знаменатель больше единицы для
всякого На рис. 28 приведен график —— в функции от
р
-—, изображающий характер изменений усилия в кольце. Мы снова
получаем тот же неожиданный результат, что и раньше: если ци-
линдрическая оболочка, лежащая на земле, вы-
держивает без разрыва внутреннее давление,
то она не лопнет и от загружения ее по длине
любыми силами Р.
7. В заключение рассмотрим наиболее сложный случай, имею-
щий особо важное значение, — случай надутой цилиндрической обо-
100
лочки, плавающей на воде и загруженной силами Р по всей длине
(рис. 29). В этом случае периметр кольца будет состоять из двух
дуг окружности радиуса R с центральными углами р и из затоп-
ленной дуги длины s, касательные к концам которой бразуют
между собой угол 0. Если обозначить через а угол между норма-
лями к кольцу в точке приложения силы Р, то между углами jx, 6,
а можно установить зависимость (рис. 30):
2И + G — а = 2тс. (20)
Теперь напишем обычные условия.
а) Условие равновесия: сумма вертикальных проекций водяных
реакций равна нагрузке
, Р
wdx= —.
2
л
Обратимся сразу к силовому кругу (рис. 31). Так как верти-
кальная составляющая водяных реакций равна хорде Р силового
круга и так как все элементарные водяные реакции должны лежать
на его окружности, то угол, стягивающий дугу пол-
ной реакции, должен быть равен а:
j* wds = aN.
б) Условие постоянства длины периметра
ца:
2?# 4- s = 2я/?0.
в) Условие постоянства количества газа:
=
где w — объем деформированного кольца:
Р f ТУ2 Г I Sin 6 I S*n а I П • « 6 1
w = _+^+— +_ -f-2sin — cos —j,
так как объем затопленной части кольца численно равен нагрузке.
101
Здесь Д=1—объемный вес воды. Выражая из равенства (20) р
через а и 6, найдем
Г , а — 6 , sin 0 . sin а о . а 0 1 , Р
<» = /?*[«+ — + — +— +2sln — c°S—] + —.
Искомое условие принимает вид:
^L + ^L + ^ + ^ + 2sin^-cos±]+^=^0
или
а = . (23)
Из силового круга находим
Р = 2N sin —
2
И
qs — J wds = ON.
s
Это последнее условие выражает, что совокупность внешних
сил, действующих на затопленную дугу s, вызывает на протяжении
этой дуги поворот нормали на угол . Используя (21), найдем
qs = (0 + a)N,
откуда
s== (6 + °)Ar
Q
N
Но, как всегда, N=Rq, а потому—=R. Находим окончательно
Q
длину дуги 5:
$-7?(б + а)
и подставляем ее в (22):
2и/? + Я(а4-б) = 2пЯ0
или
/?(2тс + а-6 + а + 6) = 2тг7?0,
откуда
(25
(26)
Если подставить это значение R в формулу (23) и перемножить
равенства (23) и (26), мы получим значение N=qR. Приравняв
его выражению N, взятому из формулы (24), мы выразим Р з
102
функции ROt q0, а и 6, как это делали и в предыдущих задачах.
Отличие от них заключается в лишнем аргументе б, который делае:
решение неопределенным. Для исключения угла 0 необходимо вы-
разить через а и б площадь затопленной части кольца, равную в
то же время —. Эта площадь может быть выражена эллиптиче-
ским интегралом следующим образом.
Отрежем от деформированно-
го кольца часть, показанную на
рис. 32. Новыми обозначениями
здесь являются: t — глубина за-
топления в произвольной точке,
— угол наклона касательной к
Рис. 33
Рис. 32
горизонту в той же точке. На отсеченную часть кольца действуют
силы AZ, А; по касательным к контуру в местах разреза, водяное
давление и внутреннее давление. Составим условие равновесия
всех сил относительно горизонтальной оси. Для этого заметим, что
горизонтальное водяное давление характеризуется треугольной
эпюрой с высотой и основанием, равными глубине /, а горизон-
тальная составляющая внутренних давлений равна произведению
интенсивности q на вертикальную проекцию длины отсеченной
части контура. Поэтому условие равновесия напишется так:
А/ coSy + N cos <? = g | A? (cos у + cos -y-j + /j —у,
откуда, заменяя А/ через Rqt
t2 — 2qt — 2qR (cos ---cos = 0,
или _______________________
t = q— g2+ 2qR (cos --------cos. (27)
Знак минус перед радикалом выбран потому, что q всегда боль-
ше, чем t, так как иначе затопленная часть оболочки оказалась
бы обращенной выпуклостью наверх, чего никогда не бывает.
103
Площадь затопленной части кольца выражается:
и* = J tdx.
Но
dx = ds cos — —— d ocos
я — t
так как между нагрузкой на затопленную дугу q—t и радиусом ее
кривизны р существует общая зависимость:
Таким образом площадь <о' выражается эллиптическим инте-
гралом: е
и* = — — — N С cos <р do + qN С ----- * со. у rfy-----. ^g)
Л I * I Г / 6 \
I ) 1/ q*+2qR (cos ~2 ~~ cos ?/
О V G Г
~~ 2 2
Этот интеграл и дает искомую дополнительную зависимость
между а и б, так как q, N и R выражены через а и 6. Вычисление
этого интеграла не представляет особых трудностей, но мы не бу-
дем приводить этого вычисления, ограничиваясь ориентировочным
сравнительным расчетом.
Отправными пунктами нашего сравнительного расчета будут
формулы (25) и (26). Вторая из них показывает, что между радиу-
сом деформированного кольца и углом внедрения нагрузки суще-
ствует точно такая же связь, как и в задаче о двух диаметрально
противоположных силах, рассмотренной в § 5. Из первой же фор-
мулы видно, что длина затопленной дуги как раз такова, как
если бы круглую часть деформированного полукольца продлить
тем же радиусом и на затопленную часть.
На рис. 33 изображены два состояния кольца. В первом состоя-
нии кольцо загружено по § 5 двумя равными диаметрально проти-
воположными силами Р и имеет деформированный радиус R и
угол внедрения нагрузки а Во втором состоянии кольцо плавает
и загружено сверху такой же силой Р. Его радиус и угол внедре-
ния таковы же, как в первом состоянии.
Возможны ли два таких состояния? Очевидно да, так как
длина периметра в обоих состояниях одинакова, а формы дефор-
мации соответствуют формам равновесия. Допустим теперь, что и
внутренние давления q после деформации одинаковы в обоих со-
стояниях. Тогда и усилия в контуре N=Rq будут одинаковы.
Теперь разгрузим кольцо от силы Р в том и другом случаях.
Находясь под действием одного лишь внутреннего давления, коль-
ца превратятся в окружности одинакового радиуса RQ, определяе-
104
мого через R и а по формуле (26), и, стало быть, одинаковой пло-
1цади. Но площадь плавающего кольца была больше, чем площадь
опертого кольца, как сразу видно из фиг. 33. Следовательно, при
раагружении площадь плавающего кольца увеличится в меньшей
мере, чем площадь опертого, а потому начальное давление в не-
загруженном плавающем кольце будет больше, чем в другом.
Итак, равные нагрузки Р вызовут в обоих кольцах равные уси-
лия N только в том случае, если начальное давление до в плаваю-
щем кольце выше начального давления
в опертом кольце. Следовательно, при
равных начальных давлениях д0 давление
д под нагрузкой в плавающем кольце
будет ниже, чем в опертом, а так как уси-
лия /V в контуре пропорциональны давле-
ниям, то усилие в плавающем кольце бу-
дет всегда меньше, чем в опертом кольце,
при равных Р, до и Ро.
Если же вспомнить, что усилие в за-
груженном опертом кольце не может пре-
восходить начального усилия в отсутствии
нагрузки, то можно сделать вывод, анало-
гичный установленному в § 5.
Если плавающее кольцо выдерживает без раз-
рыва внутреннее давление д0, то оно не лопнет ни
при какой нагрузке Р.
Возникает вопрос о пределе загружения. В задаче 5 пределом
являлась та нагрузка Р, при которой происходило соприкасание
сил Р. В плавающем кольце пределом является нагрузка, затоп-
ляющая кольцо. Найти эту нагрузку можно, если заметить, что при
ней б =2тс. Подставляя это значение, мы сможем выразить пре-
дельную нагрузку через Ро и д0.
8. Полученные выводы оправдывают принятую нами с самого
начала гипотезу о нерастяжимости оболочки кольца. Действитель-
но, усилие в кольце во всех рассмотренных случаях загружения
уменьшается от нагрузки. Следовательно, окончательная длина
оболочки заключена между ее теоретической длиной и длиной
в надутом, но незагруженном состоянии, причем она весьма близка
к этой последней. Но уменьшение усилия от нагрузки, вызывая
незначительное сокращение длины периметра, ведет к уменьшению
объема и увеличению внутреннего давления. Тем самым усилие
в кольце несколько повышается и снова удлиняет периметр обо-
лочки. Действительная длина периметра будет еще ближе к на-
чальной, чем это вытекает из наших расчетов.
Допущенная нами ошибка не превосходит 2—3%.
Во всех рассмотренных задачах мы игнорировали собственный
вес кольца. Силы веса не являются радиальными; их направление
постоянно и не зависит от формы равновесия. Вследствие этого
силовой многоугольник перестает быть кругом и превращается в
«яйцо» (рис. 34), узкий конец которого относится к верхней части
105
кольца, а широкий — к нижней. Усилия в кольце перестают быть
постоянной величиной, а меняются от максимума в точках верхней
части с горизонтальной касательной и до минимума в таких же
точках нижней части кольца. Наибольшее и наименьшее усилия
выражаются горизонтальными полуосями силового «яйца». Услож-
нение формы силового многоугольника сильно осложняет аналити-
ческое решение в этом случае. Но, руководствуясь изложенным
выше методом решения, приближенный расчет кольца с учетом
собственного веса произвести сравнительно просто.
Важно то, что и при учете собственного веса наш основной вы-
вод останется в силе: разрушающей нагрузкой для гибкого кольца,
а стало быть, и для гибкой цилиндрической оболочки являются не
внешние силы, а внутреннее давление.
Этот вывод распространяется на цилиндрическую оболочку
лишь в том случае, если действующие на нее внешние силы равно-
мерно распределены по ее длине и не вызывают изгиба этой
«колбасы» по длине. Сосредоточенное же давление, приложенное
в отдельных точках оболочки, резко ухудшает условия ее работы,
вызывая потерю устойчивости и образование складок. Целый ряд
известных случаев разрыва оболочек под нагрузкой объясняется
именно наличием таких нагрузок. Наш анализ показывает, что
случаи разрыва могут быть совершенно устранены из практики,
если, не меняя оболочки, удовлетворить одному требованию: рав-
номерно распределять по всей длине оболочки действующие на
нее силы.
4. ГРАФОАНАЛИТИЧЕСКИЙ РАСЧЕТ
КРИВОГО БРУСА НА ИЗГИБ
Аналитический метод расчета кривого бруса на изгиб, данный
Винклером, обладает серьезным практическим неудобством. Оты-
скание положения нейтральной линии в сечении требует вычи-
сления интеграла, который даже для простейшей формы про-
филя — прямоугольника — приводит к логарифмическим формулам,
а для сколько-нибудь сложных профилей вообще не поддается
вычислению в конечном виде. Как следствие этого, проектировщи-
ку приходится прибегать к помощи специальных таблиц, не обес-
печивающих достаточной точности. Не имея под рукой таких таб-
лиц в нужную минуту или не найдя в них значений для нужного
профиля, проектировщик часто вообще отказывается от учета
кривизны бруса и рассчитывает его по формулам обычного изгиба.
Как известно, это во всех случаях ведет к .недооценке .напряжений
и подчас очень значительной.
Добавим еще, что известные графические приемы для решения
этой задачи практически сложны и ведут к потере точности.
В настоящей работе автор предлагает несколько приемов рас-
чета, сочетающих практическую простоту с высокой точностью.
Исходя из аналитического решения для частного случая, автор
дает общий графический прием расчета, который в дальнейшем
облекает снова в аналитическую форму. Ввиду этого автор считает
оправданным применение термина «графоаналитический расчет».
Техника применения и точность вычисления показаны на ряде при-
меров. Из них видно, что предлагаемый метод, хотя и является при-
ближенным, но дает даже в простейших случаях точность более
высокую, чем вычисление обычным аналитическим методом с при-
менением трехфазных таблиц логарифмов.
1. ВЫВОД ОСНОВНЫХ ФОРМУЛ
Для лучшего понимания предлагаемого способа мы приведем
здесь известный вывод основных формул изгиба кривого бруса,
отличающийся от общепринятого только иным выбором начала
координат, позволяющим несколько упростить изложение.
Исходим из предпосылок:
1) ось бруса есть плоская кривая;
107
2) профиль бруса имеет ось симметрии в плоскости кривизны;
3) нагрузка расположена в той же плоскости.
Рассмотрим элемент бруса 1Г—22' (рис. 1) с центральным
углом db и радиусами кромок: внутренним Ri и наружным /?2-
Радиус произвольного волокна обозначим R, радиус нейтрального
слоя — г.
Принимая гипотезу Бернулли о сохранении плоскости сечений,
допустим, что сечение /—Г закреплено, а сечение 2—2' поверну-
лось вокруг точки нейтрального слоя и приняло положение 3—3'.
Отрезки волокон между линиями 2—2' и 3—3' выразят полные уд-
линения этих волокон:
Д^ = Л(Я-г),
где k — неизвестный постоян-
ный множитель. Делим удли-
нение волокна с радиусом R
на начальную его длину Rdb,
чтобы получить относительное
удлинение
= k R~r
"R dG ‘ 7?
На основании закона Гука получаем выражение напряжения
з=Ег = = С(1 — —(1)
R R dfi R 1 R J ’ V '
где C — новый постоянный множитель.
Выражение (1) содержит два неизвестных: радиус нейтрально-
го слоя г и множитель С. Для их вычисления составим два урав-
нения равновесия. Сумма проекций всех внутренних сил на каса-
тельную к оси бруса равна нулю, если брус испытывает только
изгиб:
F F
откуда
F F
ИЛИ
г = —— , (2)
где F—площадь поперечного сечения бруса и
.) R
’1П8
Сумма моментов внутренних сил (приводящихся к паре сил.
как следует из первого уравнения равновесия) относительно лю-
бой точки плоскости равна изгибающему моменту М в данном
сечении. Составляем эту сумму относительно центра кривизны:
М = [aKRdF = С (1 - —) RdF=C ^(R — r)dF = CS,
f F F
где —r)dF — статический момент площади сечения отно-
сительно нейтральной линии. Поэтому С — и из (1) оконча-
тельно
(3)
Основное затруднение при использовании этой известной фор-
мулы состоит в вычислении радиуса нейтрального слоя г по фор-
муле (2), а следовательно, в вычислении интеграла Н.
Предлагаемый нами графоаналитический прием служит имен-
но для решения этой задачи.
2. ГИПЕРБОЛИЧЕСКИЙ МОМЕНТ СЕЧЕНИЯ
Интеграл Н, стоящий в знаменателе формулы (2),
= С dF
J R
(4)
можно истолковать как момент минус первой степени от площа-
ди сечения, взятый относительно оси кривизны. Назовем его
поэтому гиперболическим моментом сечения*. Он имеет размер-
ность длины и может вычисляться для частей сечения в отдельно-
сти.
Отношение (2), определяющее радиус кривизны нейтрального
слоя
представляет некоторую аналогию с формулой, определяющей
расстояние до центра тяжести сечения,
Обе формулы совпадут при АН const, т. е. для профиля, вы-
1 Проф. Урбан называет этот интеграл «радиальной площадью».
См. И. В. Урбан, Расчет брусьев большой кривизны методом радиальных
характеристик. Труды Московского авиационного института, 1943.
109
тянутого параллельно оси, высота которого весьма мала по срав-
нению с радиусом кривизны. Этот вывод хорошо известен: при
неограниченном увеличении радиуса кривизны нейтральный слой
стремится к центру тяжести.
Это свойство указывает на невозможность расширенного тол-
кования аналогии уравнений (2) и (5): центр тяжести, определяе-
постоянная точка, положение которой не
зависит от выбора координатных осей;
напротив, уравнение (2) не определяет
никакой инвариантной точки, геометри-
чески присущей профилю сечения.
Ввиду этого невозможно выразить в
элементарном виде зависимость между
гиперболическими моментами для вза-
имно-параллельных осей подобную тем,
которые управляют величинами стати-
ческих моментов,
(теорема Штейнера) и вообще момен-
тов положительных порядков. Это обсто-
ятельство крайне невыгодно с практиче-
ски расчетной точки зрения.
Аналогию между уравнениями (2) и
(5) можно тем не менее использовать
мый формулой (5), есть
моментов инерции
для графического решения, преобразуя профиль сечения и опре-
деляя центр тяжести или площадь преобразованного сечения.
На этой идее основан ряд графических приемов1. При несомнен-
ном изяществе приемы эти, однако, практически неудобны пото-
му, что преобразуют прямолинейные участки контура сечения
в криволинейные, т. е. заменяют простое очертание сложным, вы-
числительная обработка которого по необходимости может быть
только приближенной. Тем самым эти приемы ведут к потере точ-
ности. Между тем вычисление нейтрального слоя требует большой
точности, трудно достижимой при таких графических операциях.
В основу предлагаемого нами метода положим результат вы-
числения гиперболического момента для трапеции с точкой схода
на оси кривизны и основаниями и параллельными этой оси
(рис. 2). В этом случае
а поэтому
dF -=bdR = ~—RdR,
Н=-^- f = ft
R2 .! R 2 ' ’
П1
(6)
e. гиперболический момент такой трапеции равен разности длин
оснований.
1 Н. Б е л я е в, Сопротивление материалов, Тех.-теоретизДат, М., 1939, стр. 475.
С. Тимошенко, Курс сопротивления материалов, § 134 ОГИЗ, Н. Т. 1931.
А. Попов, Расчет бруса и оболочки большой кривизны ДА., 1935, стр. 9.
ПО
Нейтральная линия пройдет по середине высоты трапеции.
Действительно,
r== F __ (fi> —+ M _ /?-> !-/?!
н 2(b.~ bi) 2
Эти выводы справедливы и при &i=/?r 0, т. е. для треугольни-
ка, опирающегося вершиной на ось кривизны с основанием, парал-
лельным этой оси.
Пусть далее профиль сечения составлен из нескольких трапе-
ций такого же вида (рис. 3). Гиперболический момент профиля бу-
дет равен сумме разностей (6) для каждой трапеции или разности
сумм параллельных сторон:
Н = £Ь2 — ^Ьг. (7)
Этот результат определяет собой все дальнейшее.
3. ГРАФИЧЕСКИЙ СПОСОБ ВЫЧИСЛЕНИЯ
Пусть дан произвольной формы профиль сечения, хотя бы и не
симметричный, одно- или многосвязный (рис. 4).
Выберем произвольную точку О на оси кривизны и проведем из
нее пучок лучей, секущих профиль. Дугу контура профиля между
каждыми двумя смежными лучами заменим отрезком прямой па-
раллельной оси, проводя его через какую-либо точку дуги. Сечение
преобразуется, причем его контур будет состоять из участков лу-
чевых и участков параллельных оси кривизны. Тем самым мы воз-
вращаемся к случаю, изображенному на рис. 3, а потому гипербо-
лический момент можно вычислить по формуле (7) как алгебраи-
ческую сумму отрезков, параллельных оси, причем знаки их
определятся при круговом обходе профиля в любом направлении.
Увеличивая число лучей, мы повышаем точность вычисления.
Для практического осуществления следует вычертить профиль на
миллиметров-ке и, приведя его .к виду рис. 4, произвести непосред-
ственный промер длин параллельных участков.
lii
Как видим, прием технически весьма прост и одинаково удобо-
лрименим для профиля любой формы.
4. ГРАФОАНАЛИТИЧЕСКИЙ СПОСОБ
Очевидно быстрота сходимости процесса приближения зависит
от удачного выбора той точки на дуге, через которую проводится
параллельный оси отрезок. Для вывода правила, обеспечивающе-
го удачный выбор, проведем ана-
литический расчет.
Будем считать лучи прове-
денными настолько часто, что
отрезки контура профиля между
смежными лучами можно при-
нять за прямолинейные. Разу-
меется, при наличии углов пере-
лома у контура лучи следует про-
вести через их вершины. Рас-
смотрим такой отрезок контура
АВ, ограниченный лучами ОА,
ОВ (рис. 5), и обозначим через
расстояние от оси до ближай-
шей к нему точки контура В, че-
рез b — длину основания треугольника АСВ и через h — его вы-
соту. Продолжим луч ОВ и проведем линию, параллельную оси.
через какую-либо точку отрезка АВ, на расстоянии у от оси. Дли-
ну отрезка этой линии DE между лучами обозначим через х.
Очевидно отрезок х будет равен гиперболическому моменту
треугольника ODE. Выясним, при каком значении у отрезок х бу-
дет равен гиперболическому моменту треугольника ОАВ. Легко
видеть, что при этом будет иметь место равенство гиперболических
моментов треугольника АСВ и трапеции DECB.
Длины х и у связаны очевидным соотношением
х = -^
Ri ’
и, следовательно, гиперболический момент трапеции DEC В, имею-
щий точку схода на оси, равен:
Н = х
У
Ri
С другой стороны, ширина треугольника АСВ на произвольном
расстоянии у от оси выразится: ~(Ri+h—у), а потому гиперболи-
h
ческий момент этого треугольника будет равен:
/?+ h
У
(8)
1п*±2!
Я1
(9)
Н =
112
Приравнивая значения Н из формул (8) и (9). получим
.У __ Ri~{- h
Ri h /?i ’
откуда
Итак, для того чтобы гиперболические моменты треугольников
О АВ и ODE были равны между собой, необходимо провести отре-
зок DE на расстоянии у от оси,определяемом формулой (10). Уста-
новим, в каком отношении делит этот отрезок высоту треугольника
АСВ. Для этого преобразуем выражение (10):
Геометрический смысл коэффициента у таков: он выражает
отношение расстояния отрезка DE от основания СВ к высоте
треугольника АСВ, Так, если бы получилось, например, у = ,
то это значило бы, что отрезок DE проходит через центр тяжести
треугольника.
Мы видим, что Tj есть функция отношения Для выражения ее
Ri
в конечном виде можно было бы разложить логарифм в ряд и
ограничиться несколькими первыми членами. Мы предлагаем дру-
гой путь, дающий лучшее приближение. Вычислим значения •»] для
h . Л
различных —, нанесем их на график и попробуем заменить полу-
Ал
ченную кривую прямой линией. Это оказывается вполне возмож-
ным и достаточно точным, если заранее ограничить пределы значе-
ний Хотя для точности построения высота зазубрин заменяю-
щего контура (рис. 4) должна быть достаточно малой, мы возь-
h
мем очень щедрый предел: —-
высоты зазубрин не превосходили расстояния от
h
края зазубрины. Нижний предел отношения —
Ri
исходя из практических условий построения.
При таких пределах оказывается возможным
жение (11) простой линейной формулой
1, т. е. будем требовать, чтобы
оси до нижнего
установим в Vio
тп= 0,49—0,1 —
Ri ’
заменить выра-
(12)
В приводимой ниже таблице дано сравнение точных значений
ij по формуле (11) и приближенных — по формуле (12) в указан-
ных выше пределах.
из
h Вл 0,10 0,20 0,30 0,40 0,50 0,60 0,70 0,80 0,90 1,00
tq точное 0,483 0,467 0,455 0,444 0,433 0,423 0.413 0,404 0,395 0,386
>] прибли- женное 0,480 0,470 0,460 0,450 0,440 0,430 0,420 0,410 0,400 0,390
Мы видим, что расхождения лежат в пределах 1,5%.
Приняв для выражение (12), выразим через него длины отрез-
ков у и х:
гл f by г bh
у R - - Ъ /7 X = ----— = Ь ---------т, ,
1 /?. Rx
Рис 6 Рис. 7
откуда гиперболический момент треугольника ДСВ с высотой
и основанием Ь, отстоящим на R\ от оси, равен
Я = (13)
Пусть теперь смежные лучи ОА, О В выделяют из контура две
дуги, которые мы заменяем хордами АВ и А'В' (рис. 6). Приме-
няя к треугольнику А'В'С' те же обозначения, что и для АВС, но
со штрихом, найдем, что
11 АВА'В’ ~ 1 откуда АВА'В' ~ или Н АВА'В’ = АВС * П СВС'В' ПА'В' С » R1 R,
1'14
Очевидно при многосвязных контурах, дающих более двух пе-
ресечений с лучами, в эту формулу войдут добавочные члены того
же вида.
Таким образом, пет необходимости в проведении отрезков х.
параллельных оси, и превращении контура в зазубренную фигурх
(рис. 4); достаточно заменить контур многоугольником, вершины
которого лежат на лучах и произвести обмер треугольников типа
АВС, заштрихованных на рис. 7: нужно знать их высоты h, основа-
ния b и расстояния последних от —
оси. После этого гиперболический мо- //
мент профиля выразится алгебраиче- —---------SL—
ской суммой Л V.
«-и(1 + 4г'Ь "4| / \
причем треугольники, входящие в со- (Г [Г
отав профиля, дают положительные у]______________1/
члены, а треугольники, расположен- Vs.
ные вне профиля,— отрицательные чле
ны. Коэффициент у для каждого тре- — -----
угольника вычисляется по формуле
(12) в функции от его размеров h и
Некоторым недостатком этого при- ---------—-------------
ома является то, что он выражает ги- рис §
перболический момент в виде разно-
сти. Как известно, точность таких вычислений всегда ниже, чем
точность вычисления сумм. От этого недостатка можно избавить-
ся следующим образом. Вместо проведения лучей рассечем про-
филь линиями, параллельными оси, и заменим отрезки контура
прямыми (рис. 8). Тогда профиль окажется составленным из ряда
трапеций с основаниями, параллельными оси, причем высоты, дли-
ны оснований и расстояния их от оси могут быть определены гра-
фически или аналитически. Если мы сумеем вычислить на основе
предыдущих рассуждений гиперболический момент для трапеции
такого вида, то момент любого профиля возможно будет опреде-
лить простым суммированием полученных выражений.
Оба эти приема — суммирование по треугольникам и по тра-
пециям — являются уже не графическими, а графоаналитиче-
скими.
5. РЕШЕНИЕ ДЛЯ ТРАПЕЦИИ
Возьмем трапецию, обращенную к оси кривизны широким ос-
нованием (рис. 9). Такой профиль обычно применяется для крю-
ков. Проведем из произвольной точки оси О лучи в вершины тра-
пеции, разделяющие ее на два треугольника, и трапецию с точкой
схода на оси. Лучи делят основание трапеции на отрезки KL, LM,
MN, причем, как видно из чертежа,
115
а отрезки KL, MN при соответственном выборе точки 0 можно счи-
тать одинаковыми и равными:
Гиперболический момент каждого треугольника будет равен
[формула (13)]:
R2—R1 \
------г
а для трапеции PQLM [формула (6)]
HpQLM = ^2 (1 ) •
Общий гиперболический момент всего профиля будет равен:
или, преобразуя и обозначая высоту трапеции h=R2—R\,
Я = лМ!_11 + -|Ч1 _,))]. (15)
L Ri Rs J
Эта формула справедлива и для трапеции, обращенной к оси
узким основанием (bi<b2).
Из общей формулы (15)
получаем решение для част-
ных случаев
1) Прямоугольник.
Полагаем в формуле (15)61=
= b2 = b:
<16>
откуда радиус нейтрального
слоя
г = —— = —lfe , (17)
2. Треугольник, обращенный к оси вершиной, с основанием
параллельным оси. Полагаем в формуле (15) 61 = 0, b2= 6:
Я=-^-(1-Ч), (18)
откуда
3- Треугольник, обращенный к оси основанием. Полагая в
формуле (15) 62 = 0, 61 = 6, получим формулу (13)
116
Н=^-Т), (20)
Al
откуда
Напомним, что при пользовании формулами (15) и (21) коэффи-
циент т] можно определять из уравнения (12) только при условии
1 h । g,
1 ’ ПРИ более высоких профилях нужно разбивать их
линиями, параллельными оси, на части, для каждой из которых это
неравенство удовлетворяется. Для улучшения точности выгодно,
если ближайшие к оси кривизны части имеют высоту меньшую,
чем удаленные части.
Обращаясь к рис. 9, мы видим, что гиперболический момент
произвольного профиля, разделенного параллелями к оси на тра-
пеции, может быть вычислен суммированием формулы (15)
W = n-r-£-7j + (22)
L Al A2 J
причем индексы 1 относятся к ближайшему к оси основанию тра-
пеции и ее радиусу, а индексы 2 — к удаленному. Коэффициент
тд вычисляется по формуле (12) для каждой трапеции отдельно.
Этот прием позволяет еще более повысить точность и дать дву-
стороннее приближение, если заменить дуги контура в одном слу-
чае хордами, а в другом — касательными, т. е. произвести вычис-
ление гиперболического момента по формуле (22) сначала для
вписанного многоугольника, а затем для описанного. Истинное
значение, очевидно, будет заключаться между обоими, так что
степень приближения будет известна.
Поясняем, что для вычисления гиперболического момента необ-
ходима высокая точность, так как в формулу напряжения (3) вхо-
дит выражение статического момента профиля относительно ней-
тральной линии, равного произведению площади профиля на раз-
ность радиусов нейтрального слоя г и оси бруса г0- Вычисление
разности взаимно близких чисел требует, как известно, большой
точности в определении каждого из них.
Степень точности, даваемой предлагаемым нами приемом, вид-
на из следующих примеров.
6. ПРИМЕРЫ ВЫЧИСЛЕНИЯ
1. Дан прямоугольный профиль с размерами: Л = 8 см, /?1 = 4см,
/?2И2 см, b = 3 см (пример, разобранный у проф. Беляева в
«Сопротивлении материалов», стр. 481—482).
Так как—= —>1, разобьем прямоугольник на два прямо-
Ri 4
угольника равной высоты Л = 4 см, проведя разделяющую парал-
лель через середину высоты.
117
Нижний прямоугольник:
-А_ = А= 1- ч = 049 —0,1-1 =0,39, /?1 = 4<-ж, R2=8cm.
ft 4
По фр муле (16)
//,=3-4
= 12-0,1737 см.
Верхний прямоугольник: — = ~^- = 0,5;ц 0,49—0,1-0,5 = 0,44;
/?1 = 8 см, R2 = 12 см.
И2 =
/72 = 3.4|А1£ +JL|!L| = 12-0,1017
Гиперболический момент всего прямоугольника
и =- Нг + Н2 = 12-0,2754 = 3,3072 см.
Радиус нейтрального слоя
CM.
—— = 7,2762 см.
И 3,3072
Точное решение (по четырехзначным таблицам натуральных
логарифмов)
Н = Яп—^- = 3-1 0986 = 3,2958 см,
Rx
94
г = —-— = 7,282 см.
3,2958
Расхождение 0,8%. Отмечаем, что Беляев, пользуясь трех-
значными логарифмами, получил значение г =7,29 см. Отсюда
видно, что точность нашего приближенного метода не меньше
точности практических вычислений по аналитическому методу.
2. Трапеция, обращенная к оси широким основанием, 61 = 8 см,
b2^?> см, h=\2 см, /?1=8 см, /?г = 20 см (Беляев, «Сопротив-
ление материалов», стр. 483).
-г h 12 .
Так как — = —>1, разбиваем трапецию на две части нерав-
Ri 8
ной высоты; для ближайшей к оси части примем h = 4 см, для
удаленной h = 8 см.
Нижняя трапеция: Ь\ = 8 см, Ь2 = 6,33 см, Ri = % см, 12 см,
h = 4 см, — = ~ = 0,5, т( = 0,49 — 0,1-0,5 = 0,44.
/?> 8
По формуле (15)
Я;
0,44 + 0,5б| =
2,9416 см.
Верхняя трапеция:
Ьг — 6,33см, Ь2 — 3см, Rr= 12см, /?2 = 20см,
h 8
h = &CM, — = —= 0,67, ^ = 0,49-0,1-0,67 = 0,42.
/?i 12
= 8 Г_М£ 0,42 + -^—0,581 =
[12 ’ 1 20 ’ ]
Н2
2,4G8Qcm.
118
Гиперболический момент всей трапеции
Н = Н1+ Н. = 5,4W6 см,
площадь трапеции
F= ^±^-12 = 66 см-,
2
радиус нейтрального слоя
г = —— = 12,2005 см.
н
Вычисление по точной логарифмической формуле с четырех-
значными логарифмами дает
Н — 5,3817 см;
г= 12 262 см.
Расхождение 0,5%. В курсе Беляева применены вспомогатель-
ные таблицы Иллинойского университета, которые дали г =
= 12,14 см с отклонением, в 2 раза превосходящим наше.
3. Двутавровый профиль № 10 по союзному ОСТ с радиусом
кривизны внутренней кромки /?i = 5 см и размерами: h = 10 см.
ширина полки 6,8 см, толщина полки 0,76 см, толщина стенки
0,45 см. Вычисление проводим по частям, разделяя стенку по вы-
h 8,48 .
соте на две равные части, так как для всей стенки — =------->1.
Ri 5,76
Верхняя полка:
6 = 6,8, Л = 0,76, ^=14,24, /?2=15,
ч = 0,49 — 0,1 = 0,485.
' ’ 14,24
Н,= 6,8-0,76[ + °|515- I = 0,353см.
1 ’ ’ [ 14,24 15 J ’
Нижняя полка:
b = 6,8, Л = 0,76, = 5, Я2 = 5,76,
71 = 0,49 — 0,1 = 0,475.
1 ’5
Н. = 6,8-0,76Г ?’4— + °'^-1 = 0,963 см.
[ 5 5,76 J
Верхняя часть стенки:
fc = 0,45, h = 4,24, К, = 10, Я2 =14,24,
Ч = 0,49 — 0 1 —— = 0,448.
Н3 = 0,45-4,24[-^- + 4g-] = 0,159™.
119
Нижняя часть стенки:
b = 0,45, h = 4,24, RT = 5,76, Я2 = 10,
1) = 0 49 — 0,1 -1^- = 0,417 .
4 ’ ’ 5,76
= 0,45-4,24 Г-0,417-+ 0-583 ] = 0,249ел.
4 ’ I 5,76 10 J
Для всего двутавра
Н = 0,353 4- 0,963 -j- 0,159 + 0,249 = 1,724 см.
Площадь двутавра
/л'F = 14,3 см2.
Д/ \\ Радиус нейтрального слоя
Т \К--га 4/ Г = —— = 8,295 см.
\\ /7 Н
-М Вычисление для трех прямо-
та____________________угольников по точной логарифми-
I ческой формуле дает /7=1,722 см,
G г 8,304 см.
1 Расхождение 0,1%.
J 4. Круг радиуса а, радиус кри-
рис 10 визны оси бруса 2а.
с‘ Применяем общий прием заме-
ны контура многоугольником, при-
чем ограничиваемся первым грубым приближением, но двусто-
ронним: заменяем круг вписанным и описанным правильными
шестиугольниками и разбиваем каждый из них на две трапеции
средней параллелью (рис. 10). Размеры определяем геометриче-
ски. Для простоты примем а=1.
Вписанный шестиугольник. Верхняя трапеция:
h = 0,866, b. = 2, b2 = 1, R.= 2, R,= 2 866 — = 0 433,
Ri
•>j = 0,49 — 0,1 -0,43 = 0,45.
= 0,866-0,6419.
Нг = 0,866 Г— 0,45 4- —— 0 551
[ 2 2.866 ’ J
Нижняя трапеция:
h = 0,866, 6j= 1, b.=2, Я.= 1,133 R.,= 2 А = о,76,
Rt
т) = 0,49—0,1-0,76 = 0,41.
0,866 0,9518.
0,41 + -|- 0,5э] =
Н» = 0,866 [—!—
[ 1,133
Для всего шестиугольника
Н = Я, + Н2 = 0,866-1,5937 = 1,3804,
120
площадь его
p^08 0,44 + JJ54 0,56| = 0 7212
F = 6 — 0,866 = 2,598,
радиус нейтрального слоя
г = —£_ = 1,882.
Н
Описанный шестиугольник. Верхняя трапеция:
й = 1, 6,= 2,308, 62= 1,154, /?! = 2, /?2=3, — =0,5,
Ri
т] = 0,49 — 0,1.0,5 = 0,44.
Нг = 1
Нижняя трапеция:
h= I, Ьг= 1,154, *2= 2,308, /?,= 1, /?2>2, -^-= 1,
, = 0,49 — 0,1-1 =0,39.
Н2 = 1 0,39+ -ур-0,61] = 1,1540.
Для всего шестиугольника
Н=Н1~^Н2= 1,8752,
площадь его
F = 6 — 1,154-1 =3,462,
радиус нейтрального слоя
г = —— = 1,846.
И
Таким образом, для радиуса нейтрального слоя круга уста-
навливаются пределы
1,846 <г< 1,882,
раздвиг между которыми составляет менее 2% от их величины.
Приняв среднее значение г =1,864, будем иметь погрешность, не
превышающую ±1%.
Подсчет по точной формуле дает (см. Беляев, «Сопротивление
материалов», стр. 474)
г =---------- — =-----!— - = 1,864,
4 [ta — Vi-4а2 — 4а2] 4-2^3
совпадая полностью с нашим средним значением.
Отмечаем, что столь высокая точность результата получена,
несмотря на то, что замена круга шестиугольником представ-
ляет весьма грубый прием. Тем не менее он оказывается со-
вершенно достаточным по точности при двусторонней оценке.
121
Разумеется, для круглого профиля, допускающего вычисление
радиуса нейтрального слоя по сравнительно простой формуле,
нет основания прибегать к графоаналитическому приему. Этот
пример приведен нами только для возможности сравнения ре-
зультатов вычисления с точным методом. Из него видно, что
применение графоаналитического метода к криволинейным про-
филям дает весьма высокую точность.
7. ВЫВОДЫ
Из предложенных выше расчетных приемов самым практич-
ным оказывается расчет по трапециям, выполняемый следую-
щим образом:
1. Профиль сечения разделяется на части параллелями к оси
кривизны, расстояния между которыми h могут быть различны,
но должны удовлетворять условию
где Ri — расстояния от оси до параллелей.
2. Контур сечения заменяется многоугольником с вершинами
на параллелях — вписанным или описанным (для лучшей точ-
ности вычисление проводится для обоих), и длины параллелей
между вершинами вычисляются или измеряются (рис. 8). Таким
образом, профиль распадается на ряд трапеций.
3. Для каждой трапеции с высотой h и расстоянием R\ от оси
кривизны до ближайшего основания вычисляется коэффициент :
71= 0,49 — 0,1 ——.
Rl
4. Обозначая для каждой трапеции через Ri длину бли-
жайшего к оси основания и расстояние до него, через 62, R2 —
то же для удаленного основания, вычисляем гиперболический
момент k-й трапеции (рис. 10):
Hk = h ,)1.
L № Кз J
5. Суммируем гиперболические моменты трапеций:
вычисляем площадь многоугольника F и определяем радиус ней-
трального слоя:
При вычислении по вписанному и описанному многоугольни-
кам истинный радиус лежит между значениями, полученными
для них по предыдущей формуле, и может быть принят равным
их полусумме.
5. ДУГОВАЯ РЕССОРА С НЕЛИНЕЙНОЙ
ХАРАКТЕРИСТИКОЙ
Подвеска с нелинейной характеристикой обладает несомнен-
ными преимуществами. Если ее жесткость возрастает с нагруз-
кой, она становится самотормозящей и не нуждается в упорных
устройствах. Ее колебания имеют псевдо-гармонический характер
и поэтому резонанса в обычном смысле не может возникнуть.
Возможны две принципиальные схемы нелинейной подвески. В
первой схеме нелинейность достигается последовательным вклю-
чением упругих элементов, вследствие чего характеристика
имеет вид ломаной линии. Такая схема обладает неизбежным не-
достатком: при включении добавочных элементов может возникать
удар. Другая схема приводит к конструкции, не следующей зако-
ну Гука и дающей непрерывный криволинейный график зависи-
мости между нагрузкой и деформацией. Эта схема несомненно
выгоднее первой, и в настоящее время известно несколько конст-
рукций, работающих по ней.
Целью настоящей статьи является разработка метода расчета
новой простой схемы нелинейной подвески возрастающей жест-
кости непрерывного действия, т. е. не требующей последователь-
ного включения дополнительных упругих элементов.
1. ДУГОВАЯ РЕССОРА
Представим себе ненапряженный тонкий стержень криволиней-
ного очертания, выгнутый по дуге синусоиды, к концам которого
приложены растягивающие силы, стремящиеся его распрямить
(рис. 1). Под действием сил стрела дуги будет уменьшаться, бла-
годаря чему изгибающие моменты будут возрастать не пропорци-
онально нагрузке, а замедленно. Поэтому и перемещения всех
точек стержня, в том числе и расхождение концов, будут не ли-
нейными, а замедленными функциями нагрузки. Эта схема и при-
водит нас к подвеске с нелинейной характеристикой, которую мы
назовем «дуговой рессорой».
Конструктивное применение дуговой рессоры может осущест-
вляться по одному из двух типов, показанных на рис. 2, т.е. при
вертикальном или горизонтальном ее расположении.
123
В разделах 2—6 проводится расчет дуговой рессоры постоян-
ного сечения, в разделе 7 совершается переход к листовой дуговой
рессоре равного сопротивления, в 8—10 даны
правила и примеры расчета, а в 11 приводятся
некоторые соображения о возможном конструк-
тивном и технологическом осуществлении таких
рессор.
Рис. 2
2. ВЫЧИСЛЕНИЕ СТРЕЛЫ
Обозначим:
I— длина хорды рессоры в ненагруженном состоянии;
/о — стрела выгиба „
f (Р) — то же, под нагрузкой;
Д —удлинение рессоры, т. е. расхождение ее концов;
Р — нагрузка;
Л, b — высота и ширина прямоугольного сечения.
Так как начальной формой дуги стержня является синусоида,
то, как известно, стержень будет сохранять синусоидальную фор-
му и при нагружении. Поэтому уравнение оси стержня под на-
грузкой будет
если направить оси координат согласно рис. 3.
При возрастании нагрузки стрела стержня будет уменьшаться
по нелинейному закону. Для ее вычисления используем прием,
предложенный автором в 1938 г. для аналогичной задачи1. Необ-
ходимость в особом приеме вытекает из нелинейности задачи,
из-за которой обычные методы вычисления перемещений, основан-
ные на применении принципа независимости действия сил, оказы-
ваются незаконными. Однако, как нами было показано, эти
методы сохраняют справедливость для бесконечно малых прира-
щений нагрузки.
1 Проф. С. А. Бернштейн, Работа статически-неопределимых ферм в
упруго-пластической стадии, § 7. Сборник «Расчет металлических конструкций
с учетом пластических деформаций», Госстройиздат, 1938.
121
Рассмотрим два состояния стержня. В первом состоянии стер-
жень, загруженный силами Р, получает дополнительную нагрузку
dP, которая вызывает возможное перемещение точек стержня,
изменяя его стрелу f(P) на df, а прогиб у в любой точке на dy
(рис. 4).
Во втором состоянии рассматри-
вается ненапряженный стержень с той
же стрелой f(P) (можно было бы при-
нять его даже прямолинейным, так
как в дальнейшем мы пренебрегаем
работой продольных сил), к которо-
му приложена в середине длины поперечно направленная единич-
ная сила.
Приравняем выражения работы внешних и внутренних сил вто-
рого состояния на возможном перемещении первого состояния,
отбрасывая члены, зависящие от продольных и поперечных сил, и
замечая, что стрела получает на рассматриваемом возможном пе-
ремещении отрицательное приращение
i
2
О
Здесь dMi — приращение момента первого состояния, а М2—
момент второго состояния.
Очевидно,
Mi = Ру,
dMr = d (Ру) = Pdy -pydP,
.. X , I
M2 = —у- , при х < —,
откуда
-d/=J x(Pdy + ydP),
О
125
или
С dy_ dx
J df ' El
О
2
[* dx
I ХУ — •
J
о
— 1
Строго говоря, интеграцию следует вести по длине дуги, но
ошибка, происходящая от замены ds на dx, мала и не имеет су-
щественного значения.
Заметим теперь, что
dy .их у
df If'
а потому
0
df ) л2El
Множитель при скобке равен обратной величине эйлеровской
критической силы:
л2 EI
I2
Поэтому
dP
df
= 0,
или
^- + -^- = 0,
-ЬРэ f
откуда
1п(Р + Рэ) +ln/= InC,
или
где С — произвольная постоянная, определяемая из начального
условия: при Р=0, f=foz
С
126
откуда
/=—V-
1+^г
Итак, стрела связана с нагрузкой гиперболическим законом
(рис. 5). в
3. ВЫЧИСЛЕНИЕ УДЛИНЕНИЯ
Возвратимся к первому состоянию рис. 4 и подсчитаем ра-
боту внешних и внутренних сил на перемещениях этого состоя-
ния. Работа внешних сил
dAe = (Р + dP) dL Pd Д ,
если отбросить малые второго порядка. Работа внутренних сил
i
dAt = j MdM ,
О
где по-прежнему
М = Ру, dM = Pdy 4- ydP.
Приравниваем оба выражения работы:
i
Pdb — ^Py (Pdy + ydP) ,
О
откуда
=Pfy ^1. Л£+ Су»-*-.
dP iy dP El J J El
о о
Ho
dy — =-^L У-
dP dP S I dP ' f ’
а потому
— =(— . + 1) C/2sin2 — =
dP \f dP )jJ I El
0
= Pd/+ fdP pl = fl d(Pf)
fdP ' 2EI 2EI ' dP
Подставляем выражение (1) для стрелы J:
127
Интегрируя, найдем удлинение Д:
р
или, подставляя значение Рв,
(2)
К этому выражению следовало бы добавить удлинение от рас-
тяжения стержня —, но оно ничтожно мало по сравнению с
EF
Формула (2) позволяет построить график характеристики ду-
говой рессоры (рис. 6), из которого видно, что жесткость рес-
соры непрерывно возрастает, и уже при — =2 становится пра-
* э
ктически бесконечно большой. Поэтому значение Р=2Р можно
принять за предельную расчетную величину нагрузки, при кото-
рой рост деформаций почти прекращается и рессора как бы дохо-
дит до упора. Соответственное предельное значение удлинения
равно:
Дщах = — = 2,19—^—.
тах 9 I I
(3)
Из этой формулы видно, что удлинение в основном зависит
от начальной стрелы стержня и явным образом не зависит от раз-
меров сечения.
Для каждого конкретного проектного задания можно выбрать
на графике (рис. 6) тот участок, в пределах которого должна
расположиться работа рессоры от постоянной нагрузки и от дина-
мической перегрузки.
128
4. ВЫЧИСЛЕНИЕ НАПРЯЖЕНИЙ
Наибольшее нормальное напряжение находится
длины стержня по внутреннему краю и выражается
М =_Р_ , Р/
W F ' W ’
середине
°max —
или, подставляя значение f из формулы (1),
или, подставляя значение Рэ,
Если заметить, что второй член в скобках во много раз боль-
ше единицы (при условии 2РЭ), то можно перейти к прибли-
женной формуле
„ = ----1-- (5)
2/2 2-’+1
р
При Р=2РЭ напряжение достигнет значения
На рис. 7 показаны кривые роста напряжений в функции на-
грузки для различных значений . Из графика видно, что на-
пряжения возрастают медленнее нагрузки. Это обстоятельство
приведет нас в дальнейшем к важному выводу.
5. ВЫБОР ЗАПАСА ПРОЧНОСТИ
Нелинейный характер зависимости между напряжением и на-
грузкой требует особого подхода к назначению запаса прочности.
Современные воззрения на прочность конструкций устанавливают,
129
что запас прочности должен исчисляться как отношение предель-
ной (разрушающей) нагрузки к рабочей (расчетной) нагрузке
п __ ЛфСД .
Рраб
При линейной зависимости между нагрузкой и напряжением,
сохраняющейся до разрушения (или до наступления текучести),
запас по напряжениям будет в точности таков же, как по на-
грузкам. На этом и основан обычный метод расчета конструкций
по допускаемым напряжениям. Однако, как известно, для стати-
чески неопределимых систем, изготовленных из пластичного мате-
риала, это совпадение не имеет места, и назначение запаса проч-
ности должно исходить из сравнения нагрузок, а не напряжений.
На этой точке зрения стоит современная теория расчета сооруже-
ний по предельным нагрузкам.
Для рассматриваемой дуговой рессоры с нелинейной характе-
ристикой запас по напряжениям также не равен запасу по нагруз-
кам, так как напряжения растут медленнее нагрузок.
Если принять ^-кратный запас по нагрузкам, т. е. положить
Р , = Р = 2пР
* раб э > 'прел ,
то напряжения будут соответственно равны:
. _ 0Г1 I 6А 1 «
°ра6-2[ 1 + —]——
^пред -р
6/0 I л2 ЕР
(14-2и)й ] 12/2 *
так что запас прочности по напряжениям будет выражаться
1 + —6А -
„ _ °пРеД _____(1 + 2П) h
° °Раб t 6Д
+ ЗЛ
причем его значение убывает с ростом —. Если принять наимень-
А
шее реальное значение -у1, при котором рессора еще обладает
h
достаточной эластичностью, равным 20, то
1+-™-
п<п______! + *-.
° 41
Подсчет по этой формуле дает
при п = 2, 3,
по=1,22, 1,33,
4, 5, ..., 10
1,40, 1,45,..., 1,64
Таким образом, даже 10-кратное увеличение нагруз-
ки против расчетной дает перенапряжение всего
130
н а 64%. При больших значениях — величина по становится еще
Л
меньше, быстро приближаясь к предельному значению
.. Зя
lim п =--------.
А °
Отсюда с неизбежностью следует вывод, что запас по на-
пряжениям для дуговой рессоры должен быть
взят значительно ниже, чем для любой подвески
с линейной характеристикой из того же матери-
ала, т. е. допускаемые напряжения могут и должны быть значи-
тельно повышены.
Примем за основу трехкратный запас по нагрузкам, т. е. при-
знаем возможной случайную трехкратную перегрузку опорного
катка против наибольшей расчетной (учитывающей динамику).
Соответственный запас по напряжениям будет равен или меньше
1,33, поэтому допускаемое напряжение можно смело взять рав-
ным 3/4 от предела выносливости при одностороннем цикле нагруз-
ки, или около половины временного сопротивления. Однако и та-
кое значение следует считать чрезмерно осторожным, так как в
высшей степени невероятно, чтобы трехкратная перегрузка против
расчетной происходила достаточно много раз (миллионы раз!)
для возможности развития усталостной трещины. Поэтому мы по-
лагаем возможным ограничиться еще меньшим запасом по напря-
жениям и принять допускаемое напряжение равным 0,7 от времен-
ного сопротивления.
Разумеется, это предложение должно быть проверено на опыте
эксплуатации, так как лабораторные эксперименты не могут
воспроизвести реальных условий работы подвески. Но во вяском
случае несомненно, что дуговая рессора является не только само-
тормозящей по деформациям, а и самоупрочняющейся и что поэ-
тому даже при более высоких допускаемых напряжениях возмож-
ность ее разрушения значительно менее вероятна, чем у подвески
с линейной характеристикой.
6. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ
Вследствие нелинейности задачи принцип Клапейрона оказы-
вается неприложпмым, и потенциальную энергию приходится под-
считывать по формуле
о о
отбрасывая по-прежнему деформацию чистого удлинения.
Из уравнения (2)
dA А) I
2£/(,+х)!
13!
Поэтому
Зависимость запаса потенциальной энергии от нагрузки пред
ставлена на графике (рис. 8).
Вычислим отношение потенциальной энергии к удлинению
представляя последнее в виде
Р.ис. 8
При этом
А __ 1г Р1
Д *?Е1 ’ Р Р1
2----+-----
Pl
Р
откуда
Таким образом, потенциальная энергия не может быть выра-
жена произведением силы на удлинение с постоянным коэффици-
ентом. Множитель при РА убывает с ростом нагрузки от началь-
ного значения 1/2 до нуля. При Р=2РЭ, т. е. при принятом нами
л
расчетном пределе нагружения, А = — , т. е. при равных значе-
ниях Р и Д она вдвое ниже, чем у линейных систем. При меньших
нагрузках запас энергии относительно выше.
Для подсчета удельной величины потенциальной энергии вы-
132
числим отношение энергии к квадрату напряжения, принимая
для последнего приближенное выражение (5). Это допустимо,
так как даже при наименьшем реальном значении — =20 вто-
рой член в формуле (4) превосходит первый в 120 раз в начале
загружения и в 40 раз при предельной нагрузке.
А = к4 Elfp 41* _ Il _ b№l _ bhl
°2 ~ 4/3 л4£2й2^ ~ ЕН2 ~ \2Ehz “ 12Е
Обозначая объем рессоры bhl=V, получаем
А =
12Е
откуда удельная потенциальная энергия
а—------
I2E
(9)
Сравним это значение с тем, которое имеет место в подвесках
с линейной характеристикой. Плоская рессора постоянного се-
чения при поперечном загружении дает
т. е. в 17г раза меньше. Но так как для нее энергия выражается
формулой Клапейрона А = РД, то объем ее будет превосходить
объем дуговой рессоры не в Р/2, а в 3 раза, если даже исходить из
одинаковых допускаемых напряжений, что конечно неверно: для
дуговой рессоры они могут быть взяты более высокими.
Цилиндрическая винтовая пружина и торсионный вал дают
или, подставляя
т = — и G = — Е.
2 8
т. е. в 2 раза больше, чем у дуговой рессоры. Это приводит к ра-
венству их объемов (при равных напряжениях).
Таким образом, по весовым показателям дуговая рессора экви-
валентна винтовой пружине и торсиону.
7. ДУГОВАЯ РЕССОРА РАВНОГО СОПРОТИВЛЕНИЯ
При расчете дуговых рессор постоянного сечения их ширина
обычно получается довольно значительной, что имеет несомнен-
ное неудобство. Поэтому целесообразно перейти к рессоре равного
сопротивления, конструируя ее как листовую рессору.
133
При постоянной высоте сечения h ширина дуговой рессоры
равного сопротивления должна меняться, как и изгибающий мо-
мент, по закону синуса
в « • 5Т х,
b = Ьо sm —-—.
Разумеется, на концах ширина не будет сходить к нулю, а оста-
нется на крайних участках постоянной. Мы можем не вводить эту
поправку в расчет, так как с самого начала отказались от учета
продольных сил и удлинений.
Итак, для рессоры равного сопротивления получим
г / \ г - л х f bf}
I(х) = /osm —у—, /е =
Расчетные формулы при этом несколько изменятся: в них
появятся новые значения числовых коэффициентов. Не повторяя
выводов, в которых следует лишь при интегрировании работы
внести вместо постоянного I переменное /(х), приведем оконча-
тельные расчетные формулы.
Введем вместо эйлеровской силы Рэ новое обозначение:
_ 8Е10
6 /2 ’
Тогда стрела дуги выразится прежней формулой (I)
в которой, как и в дальнейших, вместо Рэ введено Ре.
Удлинение рессоры выразится
л/
(2')
Здесь изменился также числовой коэффициент: вместо —=2,45
4
8 г-г-
стоит —=2,55.
л
Предельное удлинение при Р=2Ре »
64/2 А
Атах =-^=2,26-^. (3')
УЛ* *
Числовой множитель здесь несколько повысился.
Наибольшее напряжение
134
При предельной нагрузке Р=2РС
„ _ 8 Efoh
°max — у • — • (6 )
Значение запаса прочности в напряжениях остается прежним.
Потенциальная энергия
А = -^~
E‘ofl
(T)
P
Формула (8) остается в силе, если заменить Рв на Ре.
Удельная потенциальная энергия оказывается вдвое большей,
чем при постоянном сечении,
a = —^—a2
6E
(9')
3ZZE
Рис. 9
£
а потому дуговая рессора равно-
го сопротивления по объему
вдвое меньше торсиона или вин-
товой пружины, даже если не
учитывать возможность сниже-
ния запаса прочности для пер-
вой.
Возникает естественный вопрос: нельзя ли превратить дуговую
рессору равного сопротивления в листовую пакетную рессору, по-
добно поперечной рессоре. На первый взгляд кажется, что это не-
возможно, так как при этом на растяжение будет работать только
один коренной лист, все же прочие листы будут работать лишь на
изгиб. Это обстоятельство, однако, можно считать несуществен-
ным, так как из предыдущего видно, что напряжения от растяже-
ния составляют ничтожную долю от напряжений изгиба. Более
существенным является вопрос о том, в какой мере дополнитель-
ные листы будут разгружать коренной лист от напряжений изгиба.
Мы считаем возможным использовать для ответа на этот вопрос
ту гипотезу, которая кладется в основу расчета поперечных ли-
стовых рессор; контакт между всеми листами сохраняется по всей
длине на «всех стадиях загружения. Из этой гипотезы следует
тождественность форм упругих линий всех листов, а значит и сов-
падение кривизн всех листов в каждом сечении рессоры. Но в та-
ком случае и изгибающие моменты в каждом сечении поровну
распределятся между всеми листами, и листовая рессора будет
работать как рессора равного сопротивления, хотя, разумеется,
растяжение будет восприниматься только коренным листом.
Разница в очертании между дуговой и поперечной пакетной
рессорой будет заключаться лишь в том, что у дуговой рессоры
длины листов должны убывать неравномерно. Из рис. 9 видно,
что места обрыва листов определяются формулой
Ьо sin ——Bi > i = 1,2,3f...,n—1,
135
пользование которой при наличии таблиц синусов очень просто.
Здесь п — число листов в рессоре, В= —ширина каждого
листа.
За предельную расчетную нагрузку для листовой рессоры мы
принимаем Р=2Ре, из тех же соображений, что и для рессоры
постоянного сечения. Заметим, что при этой нагрузке стрела
рессоры уменьшится втрое против начальной величины. Распря-
мить рессору полностью возможно лишь после появления в ней
пластических деформаций.
Приводимая таблица позволяет непосредственно определить
длины листов, суммарную их длину и объем рессоры равного со-
противления при числе листов от 3 до 8.
Таблица длин листов и объемов дуговых рессор равного сопротивления
Число листов Длины листов 3 4 5 6 7 8 Множитель
1 z6 'я: 1 0,784 0,534 1 0,842 0,667 0,460 1 0,872 0,740 0,592 0,408 1 0,894 0,784 0,667 0,534 0,372 1 0,910 0,816 0,718 0,612 0,494 0,340 1 0,920 0,842 0,754 0,667 0,572 0,460 0,320 1 XI 1
Сумма длин . 2,318 2,969 3,612 4,251 4,890 5,535 XI
Объем 0,77 0,74 0,72 0,71 0,70 0,69 XIF
8. ПОРЯДОК РАСЧЕТА ПРИ ПРОСТОМ ЗАДАНИИ
Под расчетом при простом задании мы будем понимать назна-
чение размеров рессоры по одному заданному условию: при за-
данной нагрузке Р деформация рессоры должна получить задан-
ное значение , а напряжение должно быть равно допускаемому.
Заданное значение Р является предельным; поэтому оно не
должно превосходить 2Р , но может быть меньше. Именно, если
желательно, чтобы рессора при предельном загружении сохрани-
ла значительную эластичность, то надо снизить значение — -
Рэ
Зато при этом объем рессоры возрастет, предел прочности по
напряжениям придется повысить, а рессору снабдить ограничи-
телем хода.
136
Примем значение Р~2РЭ , при котором рессора будет самотор-
мозящей, т. е. положим
Р—о л°Е/ _ *?ЕЫ* _ n~EF / h \2
Z2 6Z7 8 * * ~ 6 ( / / "
Задавшись гибкостью —, определим потребную площадь
h
сечения F. Значение гибкости целесообразно принимать не менее
100—150. Тогда
Из условия прочности при предельной нагрузке и данном до-
пускаемом напряжении [о]
О - . . - Ы
3 Z2 11
найдем отношение стрелы к длине:
/о < 3 [а1 zg\
I к2£ ' h
По заданной деформации
Д = 2,19——
найдем стрелу
(В)
после чего вычислим
fo 1 h
Для рессоры равного сопротивления формулы (А), (Б), (В)
заменяются соответственно следующими:
/о < 3 М I
I 8Е h ’
(А')
(Б')
(В')
7 2,26 А
Объем рессоры не зависит от принятого значения гибкости
(он зависит от отношения -£-) и при Р=2РЭ имеет постоянное
значение:
_ ЗРА£
[»)’
137
Объем рессоры равного сопротивления теоретически в 2 раза
меньше, в действительности же, из-за необходимости сохранить
постоянную ширину листа, получается несколько больше полови-
ны объема рессоры постоянного сечения.
Из постоянства объема следует, что для сокращения длины
рессоры надо увеличить площадь ее сечения. Но увеличение пло-
щади требует увеличения гибкости. Поэтому уменьшение длины
приводит к уменьшению высоты и увеличению ширины сечения.
Чем рессора длиннее, тем ее сечение ближе к квадрату, а чем она
короче, тем сечение становится более плоским и широким.
Пример 1. Подобрать дуговую рессору постоянного сечения
при [о] =5 000 кг/см2, которая при Р=200 кг дает удлинение
Д =4 см.
Задаемся гибкостью —= 200. Тогда из формулы (А)
Л
„ 6-200 ОПП2 п л »
F =---------2002 — 2,4 см2.
л2-2-10«
Из формулы (Б)
fo 3-5 000 олл_________ 3
/ л2-2-106 ~ 20
Из формулы (В)
г 4 20 1 о о
Л ~ ТБГ “ - 12’2<7jm-
Отсюда
/=-у-12,2 = 81,5 см,
Ь = —2,4 = 6 см,
0,4
V = 6 0,4-81,5 = 196см3.
Пример 2. Подобрать дуговую рессору равного сопротивле-
ния при данных примера 1.
Задаемся той же гибкостью -^-=200 и находим из форму-
лы (А')
F =---3-200 2002 =
4-2-10е
Из формулы (Б')
/и < 3-5 000 200— 3
I 8-2-106 ~ 16
138
Из формулы (В')
4 16 Q _
„ „ ---------= 9,5 см.
2,26 3
Отсюда
1 = ~^~ 9,5 50 см,
h = -22- - 0,25 см,
200
6«=^г=12сл-
Составим рессору из четырех листов 0,25X3 см. Места обрыва
листов найдем из условий:
sin
= ——, £=1, 2 3.
4
При
£ = 1 f= 0,25, Х1 =
50-0,25 А
— ---------= 4 см\
£ = 2, = 0,52,
50-0,52 о „
Хо —--------= 8,3 см\
л
i = з, = 0,85, ха = 50'0-85 = 13,5 ГЛ.
I л
Длины листов соответственно равны: 50 см (50—2-4) =42 см.
(50 — 2• 8,3) =33,4 см и (50 — 2-13,5) =23 см.
Объем рессоры
V = — (50 + 42 + 33,4 + 27) = 111 сл3.
4
Теоретический объем равен:
V = —. Р—- = 96 он3.
2 [ор
Схема рессоры дана на рис. 10.
9. РАСЧЕТ ПРИ ДВОЙНОМ ЗАДАНИИ
В этом случае назначение размеров рессоры производится по
двум заданным условиям:
1) при Р=РЬ А —Ах;
2) при P=P2>Pi, А = А2 > Аъ ° = [°]
139
В подвесках с линейной характеристикой такие условия будут
совместными только при наличии пропорциональности
Рг __ Д2
Л “ Д1 ’
если полагать, что подвеска не имеет начального обжима.
Напротив, дуговая рессора может удовлетворить заданным
условиям при довольно широком диапазоне соотношений нагрузок
и деформаций. Однако при этом предельная нагрузка Р2, вообще
говоря, не будет иметь же-
лаемого значения 2РЭ, и
.г. .г. Р-2
потому коэффициент z= —
Рэ
является неизвестной вели-
чиной.
Обозначим отношение
нагрузок и деформаций:
-А_ = я> -^ = ?,
Pi А1
причем аир всегда боль-
ше 1. Построим график уд-
линений рессоры (рис. 11).
Разрешить поставлен-
двойную задачу — значит найти на кривой рис. 11 две точки 1
координаты которых удовлетворяют условиям
-*t- = a, -^-=р.
У1 Xi
Очевидно, задача разрешима не при всяких значениях аир.
Так, она не имеет решения при р>а. Но и в случае принципиаль-
ной разрешимости отыскание точек 1 и 2 на графике путем проб
было бы крайне неудобным делом. Нам удалось найти простой
метод решения задачи, позволяющий по данным аир сразу найти
положение точки 2, после чего точка 1 может быть определена без
труда.
Составим выражение :
Д1
ную
и 2,
pt :г
(1-HO2
(I + о2
где для сокращения обозначено t = — /или — —для рессоры
Рз ' Р с
равного сопротивления). Приведем к более простому виду
а(2 + а/)(1 + 02
d + «02(2 + 0
(10)
140
Мы получили уравнение 3-й степени относительно t. Отсюда
видно, что каждой паре значений а, Р отвечают три корня для /,
среди которых могут быть и мнимые и отрицательные. Решение
этого уравнения по формуле Кардана крайне неудобно. Поэтому
проще построить сетку кривых t = t(a, р), которая давала бы
графическое решение задачи. Однако выгоднее поступить иначе.
Фиксируем положение верхней точки 2 на графике (см. рис. 11),
отвечающей значениям Р2 = а Pi и Д2 =₽Д1,т. е. положим
Р-з Pi <
---~ = а----— = a t = Z.
Рэ Рэ
где z — постоянное число, и подставим z= at в уравнение (10):
/ 2 \2
a
Вычтем из этого выражения единицу и разделим на a —1, т. е.
С__ I
составим выражение --- . После упрощений найдем
/ \ р —1 1
т (z, a) - ----= ----------
‘ ' a —1 (14-z)2
2(а-1) + г
(И)
2(а-1)4-г
(г, a) «почти» не зависит от а ,
Можно показать, что функция у
т. е. при данном z имеет для любого а почти постоянное значение.
Действительно, рассмотрим производную — :
да
Ъ =
да
Производная представляет точный квадрат, а потому функция
(11) монотонно возрастает вместе с a . Дадим аргументу a
крайние значения a= 1 и а=со. В первом случае, раскрывая не-
определенность по Лопиталю, найдем
min т (z,1) =------------- .
(l+z)(2 + z)
Во втором случае, деля числитель и знаменатель выражения
(11) на а, получим
тахт<2’оо) = ^ГТ^-
Возьмем отношение обоих крайних значений:
7 (г, о°) _ (2 4-г)2
Т(г, 1) 4(1 + *)’
141
Это отношение равно:
при z = 0 1,0 2,0
Т|(г. °°) . д 0 । 12 133.
T(z. О
Это и показывает, что функция (11) практически зависит только
от z, но не от а. Даже при наибольшем значении з = 2 (которому
отвечает предельное условие Рг= 2РЭ) > эта функция возрастает
всего на 33% при изменении аргумента а от 1 до со . Если ограни-
читься наибольшим значением
т. е.
то при з = 2
функция ------ будет меняться в
а — 1
пределах от 0,17 до 0,20.
г. В— I
Ввиду этого можно принять для у = -— значения, отвечающие
а—1
полусумме значений при а = 1 и а= со , или, что проще и дает
вполне достаточное приближение, значения, отвечающие а = 2, т. е.
z ч ₽—I 1 2+ l,5z
а—1 (1 + Z)2 2+о.5г
Эти значения нанесены на графике (рис. 12), который и дает
искомое решение задачи.
•Действительно, достаточно по заданным а и В вычислить
В— 1
7 =------- и взять из графика соответствующее значение з. чтобы
а — I
найти положение точек 1 и 2, так как Р2 = %Р3 и Р\=— Р3-
а
Из графика видно, что задача имеет решение лишь при тех
значениях а и Р , которые удовлетворяют неравенству
0,185 1.
а— 1
Решение будет тем выгоднее, чем больше з, т. е. чем меньше
Р — 1
у, так как при этом объем рессоры получается меньшим, и
142
возможно будет принять меньший запас прочности в напряжениях,
как показано ниже.
Обнаруженное нами постоянство отношения ——- имеет инте-
а — 1
ресный геометрический смысл.
Фиксируем на характеристике рессоры (см. рис. 11) верхнюю
точку 2 и возьмем произвольную нижнюю точку 1. Проведем хорды
01 и 12 и вычислим их угловые коэффициенты.
Для хорды 01:
Для хорды 12:
X Р2 — Л
tg%=—р—
Д2 ' Рэ 4/Дх
— — I
Я2/о
41Д>
4/(Дг-Д1)
=0^
Фиксированной точке 2
Р2 а — 1
—, при котором -—
отвечает определенное значение z =
const. Следовательно, при фиксации
точки 2 отношение угловых коэффициентов хорд 01 и 12 не зависит
от положения точки 1 на кривой и остается «почти» постоянным
для любого ее положения.
При двойном задании мы уже не можем назначить по произ-
волу верхнюю точку (предельное загружение), как это мы делали
при простом задании. Ее положение единственным образом опреде-
ляется заданными значениями а, ₽ . Поэтому каждой паре этих
значений отвечает своя величина потребного запаса прочности в
напряжениях па .
Действительно,
обозначение z= —
Р э
напишем выражение этого запаса, сохраняя
п = п
6/о
(1 + zn) h
6/о ’
(14- г) h
или при min = 20, п = 3 (запас в нагрузках),
„ 121+Зг I 4- г _ о 1 + г
п = о .--------о-----------
° 121+г 1 + Зг 1 + 32
(12)
На рис. 13 построена зависимость пд от отношения —р (кото-
рое само есть функция г), из которой особенно отчетливо видно,
что рессора будет тем выгоднее, чем меньше —р .
143
Потенциальная энергия при предельной нагрузке Р2 выразится
Р Р-2
формулой (8), если подставить вместо — значение — — z:
Рэ *э
Но так как при всякой нагрузке А = ~ V,
то
1/ = |2Р—£.. (13)
(2 +г) с2
Таким образом, и объем рессоры уменьшается вместе с -Р~~ j
даже при условии равенства допускаемых напряжений.
10. ПОРЯДОК РАСЧЕТА ПРИ ДВОЙНОМ ЗАДАНИИ
Если требуется, чтобы дуговая рессора давала:
при Р = Рг деформацию Д = Aj,
„ P = Pz . А = Д2,
и имела при Р2 напряжение, равное допускаемому [ с ], то нужно
вычислить отношения больших значений нагрузки и деформации
к меньшим:
a=Aj₽=^ л=^1
1Д а —1
Очевидно, у есть отношение прироста деформации к приросту
нагрузки в процентах.
Далее, по графику (рис. 12) находим для данного у значение
р%
z=-p~3 •
После этого приступаем к подбору размеров. Задаемся гиб-
костью рессоры—> 100 и находим площадь сечения из условия
(Г)
F_ 12Р-2 7 I у
т&Ег \ h / ’
Затем из условия прочности определяем — :
/о
/ П2£ й
Наконец, по деформации Д2 ищем стрелу f0:
f __ 4Д« 1
(Е)
(1 + гГ
(Ж)
144
При подобранных по этим формулам размерах рессора удовлет-
ворит обоим расчетным заданиям.
Объем рессоры будет равен
V = -12Ргйг£ . (3)
(2 +г) (ср ’
Для дуговой рессоры равного сопротивления формулы (Д),
(Е), (Ж) принимают соответственно вид:
2Ez I h / ’
(Д')
I
I ' 4£
z- лДз 1
f°=—•— 1 -
(1-hz)*
Объем рессоры равного сопротивления будет несколько более
половины объема рессоры постоянного сечения.
Пример 3. Подо-брать размеры дуговой рессоры равного со-
противления по двойному заданию:
при Рг = 1 800 кг, Дг = 7,5 см,
„ Р2 = 3500 кг, Д2=10гл!,
если допускаемое напряжение [о ] = 8 000 кг/см2.
Вычисляем отношения:
а=_3500 = 1 94 P = J2_=133; 1=jhJ. = ^1=0,35.
1800 ’ 1 7,5 • ’ * a —1 094
По графику (см. рис. 12) находим z = 1, т. е. Р%^РЭ- Задаемся
гибкостью — -= ПО и находим площадь F из формулы (Д')
h
F = 3~3500 110s = 31,8 си2.
2-2-10М
Из формулы (Е')
Q + О^ПО^О 22.
I 4-2-Юе
Из формулы (Ж')
откуда
_и17_ = 108 A =
0,22 ПО
/о = -^«32с№.
145
Составляем рессору из четырех листов 1X8 см и находим их
длину из таблицы:
Zx = 108cjh, Z2 = 0,842-108= 91 см, 13 = 0,667-108 = 72см,
/4 = О,46О -108 = 50 см.
Объем рессоры равен:
V = 0,74 -108 • 32 = 2 560 см*.
Торсион, рассчитанный на ту же нагрузку Р2 = 3 500 кг и де-
формацию Дг= Ю см при [т] =-i-[a]=4 000 кг!см2 и радиусе
балансира г=25 см, будет иметь размеры: d = 4,8 см, Z=190 см
и объем 3 400 см3.
11. О КОНСТРУКЦИИ И ИЗГОТОВЛЕНИИ ДУГОВЫХ
РЕССОР
Листы дуговой рессоры следует выгибать в холодном состоя-
нии. Так как синусоидальная форма выгиба соответствует де-
формации продольного изгиба, то листы целесообразно выгибать
путем продольного сжатия, устраивая специальные рамки с вин-
товой передачей траверсы. После выгиба листы отжигают в изо-
гнутом состоянии для освобождения от напряжений и затем закали-
вают и шлифуют.
Для крепления концов рессоры край листа следует отогнуть
в горячем состоянии (до выгиба листа), с образованием крюка
(см. рис. 10). В загнутые концы закладывают болты, к которым
крепят серьги балансира.
При сборке рессоры равного сопротивления листы наклады-
вают на выпуклую сторону основного листа со смазкой и стяги-
вают по середине длины скобой (см. рис. 10).
Все эти технологические приемы и конструктивные формы
достаточно просто осуществить.
При выкройке листов рессор следует помнить, что расчетная
длина I — есть длина хорды листа. Действительная длина листа
выражается через эту длину и стрелу выгиба f0 формулой
По этой же формуле следует вычислять длины листов рессоры
равного сопротивления, подставляя вместо f0 начальную стрелу
каждого листа.
К определенным таким образом длинам следует добавить дли-
ну загибов по обоим концам основного листа.
Заметим, что формулы и подсчеты объемов рессор в этой
статье составлены по длинам хорд листов, а не по их действитель-
ным длинам, и потому носят теоретический характер. Для получе-
ния истинных объемов результаты этих подсчетов надо умножить
на 1 + №-1*.
6. к РАСЧЕТУ ПРУТКОВЫХ ТОРСИОНОВ
Поиски новых, улучшенных типов подвесок для гусеничных
машин привели конструкторскую мысль к ряду новых схем. Одной
из таких схем является прутковый торсион. Элементарный расчет
этой схемы был дан Доброгаевым, на работу которого мы будем
ссылаться в дальнейшем. Этот расчет основан на некоторых до-
пущениях, которые не являются вполне бесспорными. Цель настоя-
щей статьи заключается в выводе уточненного расчета и проверке
решения Доброгаева.
1. РАСЧЕТНАЯ СХЕМА
Прутковым торсионом называется система параллельных стерж-
ней (прутков), жестко заделанных в концевые диски (рис. 1).
Такая система является геометрически неиз-
меняемой (жесткой) и способна воспринимать
скручивающие моменты, приложенные к кон-
цевым дискам. Схема расположения прутков
и их число могут быть произвольными. Обыч-
но предполагается осевая симметрия, т. е- рас-
положение по окружности (одной или нес-
кольким концентрическим). Возможно нали-
чие осевого прутка. Конструкция торсиона
должна предусмотреть возможность замены
отдельных прутков в случае их повреждения.
Нетрудно понять, что при действии скру-
чивающих моментов прутки торсиона будут
работать на кручение и изгиб. Это показано
на рис. 2, изображающем пруток в плане и с
Ряс. I
торца до деформации (1) и после скручива-
ния торсиона на угол б (2). Очевидно, пруток скрутился на тот же
угол, вследствие чего в нем возник постоянный по длине крутящий
момент
(1)
где Iр— полярный момент инерции сечения прутка, которое пред-
полагается круглым, I — его длина и G — модуль сдвига.
14”
Кроме того, пруток изгибается от смещения его конца на 6 ;
вследствие этого в нем возникают изгибающие моменты, меняю-
щиеся по длине по линейному закону и достигающие максимума
по концам:
Рис. 2
где / — осевой момент инерции сечения прут-
ка, Я—линейное смещение прутка, равное
6 = 2rsin — , г—расстояние от центра прут-
ка до оси торсиона.
На концах прутка возникнут также опор-
ные реакции, направленные вдоль смещения
конца и равные:
R = 12 6 Е/ (3)
/з '
Поэтому для поворота концевого диска на
угол О требуется приложить скручивающий
момент
iz-zr sin —
.. .. । „ 6 Gir, ь . 2 е
М — Мх + rcos— = —6 ч---------------------------------г cos — =
х 2 I & 2
Gin ь I 12Е7 2 - ь
= ----2- 6 Ч----------г2 Sin б,
I Р
на каждый пруток, расположенный по окружности радиуса г. При
п прутках на окружности
м = + r*sin()j. (4)
Таким образом, торсион обладает нелинейной характеристикой
и жесткость его падает по мере роста деформации.
Расчет на прочность следует вести по 3-й теории прочности:
N ’
где Wр—полярный момент сопротивления прутка, а [т]— допускае-
мое напряжение на срез. Подставим выражения моментов (1—2)’
(?-r?2+(^>sin4 (5)
Приведенные здесь формулы составляют основу метода рас-
счета прутковых торсионов, данного Доброгаевым. Анализируя этот
148
метод, мы обнаружим наличие двух скрытых допущений, содержа-
щихся в нем.
1. Прутки торсиона предполагаются работающими изолиро-
ванно, т. е. не приходящими во взаимное соприкосновение.
2. Деформации торсиона предполагаются малыми (как обычно
в сопротивлении материалов), ввиду чего кручение и изгиб прутков
можно изучать независимо друг от друга.
Оба эти допущения законны при весьма малых углах закручи-
вания 0. При больших же углах (на практике могут встретиться
углы порядка 40—50°) они теряют справедливость, так как прутки
начинают нажимать друг на друга, а за счет их искривления кру-
чение частично преобразуется в изгиб и обратно.
Задача нашей работы:
1) вывести уравнения деформации прутка, справедливые при
любых углах, т. е. учитывающие преобразование деформаций;
2) изучить взаимное смещение осей прутков по окружному
и радиальному направлениям и тем самым установить пределы
допустимости рассмотрения прутков, как работающих изолиро-
ванно.
2. ВЫВОД УРАВНЕНИЙ ДЕФОРМАЦИИ
ИЗОЛИРОВАННОГО ПРУТКА
Пусть задний конец торсиона неподвижен, а к переднему при-
ложен скручивающий момент М (рис. 3). Рассмотрим отдельный
пруток, центр которого до деформации находился на верхнем
конце вертикального радиуса
г. Начало координат поместим
в центре заднего неподвижно-
го сечения прутка, а оси нап-
равим: х—по оси прутка впе-
ред, у — вдоль радиуса торси-
она вверх, z—перпендикуляр-
но радиусу вправо.
При повороте переднего
конца на угол 0 по часовой
стрелке на концах прутка воз-
никнут опорные реакции
R2 вдоль соответствующих
осей, опорные изгибающие мо-
менты в двух плоскостях Му ,
и крутящий момент Мх.
Очевидно, благодаря ис-
кривлению прутка концевые
крутящие моменты будут вы-
зывать не только кручение, но и
опорные моменты будут
чение.
изгиб, и обратно,— изгибающие
вызывать не только изгиб, но и кру-
!49
Если бы пруток оставался прямым, то опорный крутящий мо-
мент был бы равен Л/д. = [формула (1)] и таков же был бы
крутящий момент по всей длине прутка. Обозначим через <р угол
наклона плоскости поперечного сечения прутка к плоскости yz. В
таком сечении возникнут и крутящий и изгибающий моменты:
Л4„зг = Мх sin <р;
Л4кр = 7ИЛсо5<р.
Покажем, что несмотря на это, формула (1) остается доста-
точно точной. Для этого вычислим потенциальную энергию круче-
ния прутка, полагая
G/p =-i-Е/(так как /р= 2/; G =-|-Ej;
i i
Лкр= — Мх 6 = — f Ml sin2 <р + — (* М? cos2 =
р 2 х 2 J х Г Е1 2 J r Glp
о о
=f (sinS ’ + fcosS ’)dx=-£г (т1 - т/ sin“ ’ dx)
о о
Величина второго члена в скобках очень мала по сравнению
с величиной первого члена. Действительно, sin <tg<?, a tg<p
достигает максимума в среднем сечении, где он равен:
3 ь
maxtgcp = — . — ,
если б — взаимное смещение концов прутка. Поэтому
и, стало быть, для потенциальной энергии справедливо двусторон-
нее неравенство
5 Г.__________£/_з_ AVI л 5
8 El [ 5 U ' l Л 8 El '
Если даже принять сравнительно большое отношение —у — -~
(это будет, например, при 1=Е>г и 6 = тс), то вычитаемое в левой
части будет меьше 3% и может быть отброшено. Итак, энергия кру-
тящего момента определяется собственно кручением, и потому
150
формулу (1) можно считать справедливой, а крутящий момент
— постоянным по длине прутка. Напротив, изгибающие момен-
ты будут меняться от кручения.
Основные дифференциальные уравнения изгиба прутка в двух
плоскостях получим, составляя суммы моментов относительно
осей z и у:
= - & -%- = -Ч + Ryx + Мх^- ;
Му=~Е/-^- = -М’у + ^х~М^-
Здесь у и z — смещения оси прутка, а последние члены представ-
ляют изгибающие моменты в сечении, вызванные опорными крутя-
щими моментами вследствие деформации прутка.
Наличие этих членов отличает уравнения (6) от обычных урав-
нений изгиба, справедливых для малых деформаций.
Уравнения (6) — совместные. Чтобы сделать их независимыми,
интегрируем их один раз:
^-Mlx + R^+M^ + K.El-,
-EI-^- = -M;x + Rx £--Мху+КуЕ1,
где Kzt Ку— произвольные постоянные. Легко видеть, что они
равны нулю, так как при х = 0 мы должны иметь у = 0, z = О,
— = 0 и — = 0 (условия защемления).
dx dx
г-, dy dz
Подставим полученные значения —, — в первые части урав-
dx dx
нений (6):
— EI = —М + Ryx + х — ^^ ~ + ;
2 У * EI EI 2 * Е!
-ElS = ~My + ^x~Mx^Fx + Mxlf4 + MxW
или
*У I = fgy I V I **!& -*
dx* \Е1 ) У EI \Е1 (Ely ] (Е1У 2 ’
— = К —
d^+\EI) El \ EI (Ely ) (EI}2 2
151
Обозначим постоянные коэффициенты сокращенно:
Мг
—— = а.
EI
Л_=Ь
EI °’
-(А-+ ) = &1,
\ Е1 (£/)5 I
Л1^- = Ь2,
2 (Ely
М'у _с
~1Г е’
— (•&----) = <i,
\ EI (Е1У )
М.? Ну _
2 (Ely 2'
Тогда получим окончательные уравнения изгиба в виде
у" + а2у = b0 -f- brx + b2x2 ; |
z" + a2z = cQ + сгх + с2х2. J
(7)
(8)
Заметим, что между коэффициентами а, Ь, с существуют две за-
висимости:
2Ь3 <
аЬ$ — q ;
а
2с2 ,
-------ас0 = — bt.
а
(9)
3. ИНТЕГРИРОВАНИЕ ОСНОВНЫХ УРАВНЕНИЙ ИЗГИБА
Общие интегралы уравнений (8) имеют вид:
у = cos ах + Ву sin ах 4-
+ (1 — cos ах) + Ь± (х-— sin axj +
+ b2 р2— (1 —cosox)^j;
z = A, cos ах + В, sin ах +
4- "ArpoU — cosax) 4- ct^x---— sin ax) 4-
4- c2 p2--т (1 — cos ax)]j.
где Ay, Byt As, Bz— четыре произвольные постоянные.
152
Таким образом, в уравнения (10) входят десять неизвестных
величин: четыре произвольных постоянных и шесть коэффициентов
Ь, с (7). Учитывая зависимости (9), заключаем, что необходимо
составить еще восемь уравнении для нахождения всех неизвестных.
Эти уравнения получим из краевых условий. Напоминаем, что коэф-
фициент а имеет известную величину, так как мы доказали воз-
можность вычисления Мх по формуле (1).
Искомые краевые условия таковы:
при х = 0, у = 0, у' = 0;
z = 0, z' = 0.
При х = I, у = г (1 — cos 6); у* = 0;
Z = г sin 0; z' = 0.
Используем эти условия:
1) При х = 0, у ~ 0. Подстановка в уравнении (10) дает =0.
2) При х = 0, 2 = 0. Подстановка в уравнения (10) дает Л2= 0.
3) При х = 0, у' = 0. Составляем выражение прозводной, исполь-
зуя условие 1:
у’ = аВу cos ах + sin ах + Ьг — br cos ах + 262х— — sin ах\^
откуда Ву = 0.
4) При х = 0, z' 0 аналогично получаем В^ = 0.
5) При .г = l,y = /'(1—cos6) = :
р>0(1 — cosaZ) + Ь1 (/ — -у sin +
+ Z>2[z2--|-(l-cosaZ)]|. (11)
6) При х = /, у' = 0:
О = p60sina/ 4- 6Х(1 —cosa/) + 262 (l — • U2)
7) При х = I, z = г sin 6 = 6г:
*г= -2- |Со(1 - cosaZ) + Ci(z —-i-sin azj +
т^гр2 —-^-(1—coscZ)j|. (13)
8) При х = /, z,= 0:
О = -L-|ac0 sin al-\- cx(l —cosa/) -f-2c2^/ — si”j | • (14)
Пользуясь уравнениями (9), исключим из уравнений (11) — (14)
b\ и Ci. После преобразований получим:
153
b^\ — cosaZ)— coa^l----i-sinaZ^ +
4- b2 p2-у (1 — cos aZ)j 4- c2 — p-------— sin alj = a2 6y ;
boa sin al — coa (1 — cos al) + Z>22 p-sin azj 4-
4-c2— (1 —cosaZ) = 0;
a
(1 \ 2 / 1 \ (15)
Z------sin al\ 4- c0 (1 — cosaZ) — b2 — IZ — — sin alj 4-
4- cz p2--(1 — cos al)| = a2bz ;
2
Z>oa(l —cosaZ) 4- Cousin a/— b2 —(1 —cosaZ) 4-
a
+ c2-2p-----sin ozj = 0.
Решая совместно уравнения (15) относительно bOt b2, cOt c2 и
обозначая
£ = (16)
получим:
Подставим эти значения в уравнения (10):
у = ? ([т в‘-+ М(1 _ cos ах)+
+ [—r6v- + тМ (х- 4sincx) +
+£4*2_4(,-cosax)]l:
г=41 [~ir6- т М(1 ~cos “*)+
+[-т6^' T6--+4P#-Tsino*b
-£4x2_4(1-coscx)]|-
154
Преобразуя и вводя обозначения:
а
2L ~Р'
1
aL
(17)
qby —S&., = и;
q\ + sby = v,
получим окончательные уравнения изгиба:
У ~ Л *2+ и^х----sin ах} + cos ах 4- —;
г = —p6yx2-}- ----— rfiycosах---------—.
(18)
Нетрудно видеть, что отношение прогибов —---величина пере-
менная, зависящая от х. Отсюда следует, что линия прогиба прутка
не лежит в одной плоскости, являясь линией двоякой кривизны.
Таково первое отличие результатов нашего анализа от упрощенно-
го решения Доброгаева, согласно которому пруток изгибается по
плоской кривой.
4. ОПОРНЫЕ МОМЕНТЫ И РЕАКЦИИ
Значение опорных изгибающих моментов и реакций получим из
уравнений (7), подставляя в них значения коэффициентов Ь, с
(19)
где
а = =-|--у-(формула 1),
6у = г(1 — cos 6), d, = г sin 6.
155
Формулы (19) отличаются от формул (2) — (3), полученных по
Доброгаеву. Чтобы удобнее сопоставить те и другие, произведем
некоторые преобразования.
В формулы реакций (19) входит отношение — Используя вы-
ражение (16) для Л, представим его в виде
4пЧа_________1___________ 4
4/з ‘ al . al. ~ /з
1 — — ctg-----
2 S 2
al . al
TctgT
__4_ (0,4 6)2
“ /з ' 1 —O,40ctgO,4O *
так как
al = Ao
2 5
Поэтому
_ д2Е/ _ 12Е/ (0,4 6)2
L y~ P y 1—0,4 6 ctg 0,4 0
(20)
1
7
(21)
fi(0)
L - 13 1 v ’
где
Ш = ---------------------
3 I —0,40 ctg 0,40
Эта функция имеет значения (см. рис. 4):
при 6 = 0 0,25 0,5 0,75 1,0 1,25 1,5
Л(6) = 0 0,835 0,948 1,005 0,992 0,982 0,973
1,75
0,967
При расчете по Доброгаеву /?= -----6, а потому fi(0)=l.
/з
Таким образом, реакции при углах до 0,7 (-40°) в действитель-
ности меньше, чем по этому расчету, и связаны со смещением нели-
нейной зависимостью. В этом — второе отличие наших результатов.
Переходим к опорным моментам. Подставляя в их выражения
д 4
(19) значения — = — 6, — из (20), в, и бг, приведем их к виду:
* Р [ 5
Л10 = 4^гв
У 12
sin0 + A._P<'-«*°) 1 =
25 1— 0,4Octg0,40 J
= -^Л(в).
-cos6) + JL.
0 sin 0
0,4 0 ctg 0,4 0
(22)
156
157
где через /z(6), /у(6) обозначены произведения 6 на двучлены в
квадратных скобках.
При расчете по Доброгаеву [формула (2)]
Л1" = (1 — cos 6) = —1,5 (1 — cos 6),
ЛГ = ——sin 6 = 1,5 sin 6.
у /3 I2
Сравнение результатов подсчетов
6 0 0.1 0,2 0,3 0,4 0,5 0,6 0,7
Для А(б) 0 0,0111 0,0396 0,0854 0,1502 0,2319 0,3298 0,4440
м'г 1,5(1— cos6) 0 0,0074 0,0299 0,0670 0,1184 0,1837 0,2620 0,3528
Для 0 0,1816 0,3048 0,4461 0,5808 0,7080 0,8262 0,9331
Му 1,5 sin 6 0 0,1491 0,2974 0,4431 0,5841 0,7191 0,8470 0,9661
Графики функций, помещенных в этой таблице, даны на рис. 5.
Таким образом, опорный момент М * больше, чем при расчете
по Доброгаеву, а момент Л4у при малых углах больше и при боль-
ших — меньше, чем по этому расчету. Таково третье отличие.
5. РАСЧЕТ НА ПРОЧНОСТЬ И ЖЕСТКОСТЬ
Зависимость между внешним скручивающим моментом и углом
закручивания дается формулой (4), которая для одиночного прут-
ка примет вид
М = Мх + R,г = ~г2sin 6,
а2
или, подставляя значение — и преобразуя:
м [1 + ± /X f_______________1 =
5/ L 5 \ Z ) 1 — 0.4 6 cig0.4 О J
где
р . 4_______6 s*n е_
К 5 ‘ I — O,4ectgO,4 6
При расчете по Доброгаеву
M=±.^L+-^r2sine = ^[1+(i)=15^]. (24)
158
Сопоставление формул (23) и (24)
(рис. 6)
6 0.1 0.2 0,3 0,4 0.5 0.6 0.7
F(6) sin 0 ,5— 18,16 14,98 15,28 14,89 14,96 14,77 14,68 14,59 14,40 14,38 14,12 14,11 13,80 13,80
Таким образом, расхож-
дение в определении жест-
кости обоими способами не-
велико и имеет место толь-
ко при малых углах: дейст-
вительная жесткость при
таких углах несколько
больше, чем по Доброгае-
ву. Оба расчета практиче-
ски совпадают при 0 > 0,4.
Так как функция F( в )
имеет (кроме самых малых
углов) почти постоянное
значение, можно принять
приближенно
Е (6)^15,
откуда получим
и обратно
е = —
4EI
так что с достаточной точностью можно считать пруток следующим
линейной характеристике.
При п прутках, расположенных по окружности радиуса г,
51 1 — м.
2
(26)
1+15
Если, кроме того, имеется пруток по оси торсиона, то
е = -01—.------------------------------!---------м.
4Е1 . . Г. . г VI
(27)
Аналогичную более общую формулу для случая расположения
прутков по нескольким концентрическим окружностям получить
нетрудно.
159
Прочность прутка следует проверять по 3-й теории прочности,
т. е. по наибольшему касательному напряжению, пользуясь извест-
ной формулой
< Н•
wp wpr * у z
Нетрудно понять, что наибольшие изгибающие моменты имеют
место в опорных сечениях, т. е.
max Му = М°у и max Мг = М°г.
Подставляя их значения (22) в .неравенство, преобразуем подра-
дикальное выражение
Ml = Ml + + М? = +
16г»^(Е/у 1Г p 2 6(1—cost) 1°
25/4 |L 5 L 1—0.40ctg0,40 J
+ [- (1- cos6) + -|-.
0 sin 0
1 —0,4 OctgO,4 0
16(E/)2 02
25Z3
1 + -cos6)[l 4-
0,4 0 \al[
— 0,4 OctgO,4 0 ) ]|
16 (E/)2 03
25Z2
[' + (т)Ч(ч].
где
Поэтому
ф(6) = 2(1 — cosO) 1 +
0,40
— 0,40ctg0,40
1+1тН
(28)
(29)
Значения функции <Ь (0)
0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8
82 59 57,2 56,4 55,4 54,8 54,1 53,3
Приближенно полагая ф(6) —55 (это дает достаточную точ-
ность, кроме самых малых углов), получим
"• - /1+551т)‘
(30)
160
Но 6 можно выразить через внешний момент М из равенства
(25), а потому
Мо = -----
1+ 15
-1— м.
2
(31)
Множитель при М весьма 'мало отличается от единицы:
расчет прутка по внешнему моменту.
Ввиду этого окончательно получим: при п прутках по одной ок-
ружности неравенство прочности имеет вид (подставляя Wp=-^~
гдеd — диаметр прутка):
16М
(32)
а угол закручивания торсиона выражается
с 80 Ml
и = ----------------
+ 15 (-4)
(33)
Могут вызвать сомнение произведенные нами замены различных
функций от 6 постоянными значениями и в особенности двоякая
замена, примененная в формуле (31). В действительности следовало
бы написать
м0 =
Гф(6)
--------м,
2
где ф(6) и F (в) определяются формулами (23) и (28). Множи-
тель при М зависит, таким образом, не только от -у-, но и от угла 6.
Наибольшего отклонения от единицы он достигает при -у- — ~ и
самых малых углах ( 6 < 0,1, или около 6°). Это отклонение состав-
ляет 1,2. Уже при угле 0,2 оно падает до 1,14. Формула (31) дает
для этого случая 1,12.
П С. А. Бернштейн
161
Следует отметить, что все произведенные упрощения не даю’’
искажений закономерностей, а лишь заменяют слабо искривленные
линии прямыми.
6. ОБЪЕМ ТОРСИОНА И ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ
При п прутках диаметра d и длины I объем прутков торсиона
(без концевых дисков) выразится:
17 nd? .
V = п------I.
4
Выразим диаметр через момент и допускаемое напряжение, поль-
зуясь условием (32)
Г 16Л4 12/3
L J
Поэтому
* - Т (тТ' ™
где
kn= 2,525 п .
Объем равнопрочного сплошного торсиона той же длины
у _______________________ nd4 ,
с~ 4 ’
при
т. е. при п=},
Vf= 2,525
Подсчет дает:
п= 1 3 4 6 8 10
kn= 2,525 3,64 4,01 4,60 5,05 5,64
Vc~ 1 1,44 1,59 1,82 2 2,23
Таким образом, весовые показатели кажутся неблагоприятными:
при четырех прутках прутковый торсион на 59% превосходит по
весу равнопрочный сплошной торсион той же длины, а при вось-
ми прутках — вдвое. Но дело в том, что равнопрочный сплошной
162
торсион той же длины будет более жестким. Поэтому прутковый
торсион при топ же жесткости следует сделать короче сплошного.
Произведем сравнение торсионов равной прочности и равной
жесткости. Для этого представим формулу (33) в новом виде, ис-
пользуя выражение т (32):
с. 5Н i
Ed
1 + 15
I
I r
Аналогичная формула для сплошного торсиона длины 1е и диа-
метра de будет
6r = -^-4
r Edc c
откуда при равной жесткости и прочности
/г _ I
Но для равнопрочности между диаметрами должно быть соот-
ношение
з _
dc = d yf п
где п — число прутков.
Поэтому длина пруткового торсиона I связала с длиной /с рав-
нопрочного и равножесткого торсиона условием
1 =
(35)
Отношение объемов
зится:
__V =
У С
или при
г _ 1 1
I ~ 40 20
— = 1,01 1,04
сплошного торсиона и пруткового выра-
3
_EZ._L = 1 + 15(-02 (36)
1 1 1 1 1
10 5 4 3 2
1,15 1,60 2,07 2,67 4,75
Таким образом, мы приходим к следующим выводам:
1. Объем пруткового торсиона всегда больше, чем равнопроч-
ного и равножесткого сплошного торсиона.
2. Отношение объемов не зависит от числа прутков (при распо-
ложении по одной окружности), а только от отношения радиуса
пучка к длине.
П*
163
3. При-у-< оба типа торсионов имеют практически одинако-
вый объем; при увеличении— отношение объемов резко возрастает.
4. Длина пруткового торсиона меньше, чем сплошного той же
жесткости [формула (35)]. Так, при-у-= —, Z~0,5Zc при п=8,
и 1С при п=4.
Потенциальная энергия пруткового торсиона определяется из
А = — .
2 я &пЕ [1 + 15 (—П
Деля на объем, получим удельную энергию
_________160Л12__________________ 256 М2_________ _
я2<£Елф+__________________________________________1.6п*Ер + 15(y) j
=№ (37)
'6£[1 + 15(тЛ
Удельная энергия сплошного торсиона
а __ 256ЛГ [Ч2
GE ~ 1.6Е ‘
Поэтому удельная энергия пруткового торсиона всегда меньше,
чем у сплошного; их отношение обратно отношению объемов (36):
а.
и составляет
1+15(тГ
(38)
10
— =0,99 0,96 0 87
ас
Эти подсчеты также показывают,
1 1 1 1 1 1 1
5 4 3 2
0,62 0,51 0,38 0,21.
что прутковые торсионы вы-
годны только при малых ~ (до .
При таких значениях член 15 (-у-)2 может быть отброшен по
сравнению с единицей, и расчетные формулы еще упростятся.
Угол закручивания
164
Длина пруткового торсиона
4
(35')
7. ПРЕДЕЛЫ ПРИМЕНИМОСТИ РАСЧЕТНЫХ ФОРМУЛ
Выведенные выше формулы можно считать справедливыми при
выполнении трех условий:
1) прутки работают при напряжениях, не превосходящих пре-
дела пропорциональности;
2) концевые диски обеспечивают глухую
3) смежные прутки не приходят в
соприкосновение.
Первое условие проверяется расчет-
ным неравенством прочности; второе
обеспечивается конструктивными меро-
приятиями; третье требует специального
анализа.
Очевидно, смежные прутки могут
прийти в соприкосновение, если расстоя-
ния между центрами их сечений убыва-
ют с ростом угла закручивания. Это яв-
ление действительно имеет место. При
скручивании пруткового торсиона его
прутки взаимно сближаются как в направлении окружности, так и
в радиальном направлении.
Начнем с анализа сближения по окружному направлению.
Пусть прутки располагаются по одной окружности с централь-
ным углом Р между, радиусами-векторами их центров (рис. 7).
Очевидно, р = — , где п — число прутков. Начальное расстоя-
п
ние между центрами смежных прутков равно So=2r sin .
Для каждого прутка можно составить уравнения деформаций
(18) в своих собственных координатных осях, располагая их, как
показано на рис. 7.
Пользуясь уравнениями преобразования координат:
у2 = г(1 —cos р) + Vi cos р — ZjSinp,
z2 = — г sin р + z± cos P + У1 sin p ,
(39)
можно выразить перемещения второго прутка в координатных осях
первого прутка. Для этого надо лишь подставить в равенства (39)
вместо увыражения (18), и мы получим уравнения смещений
второго прутка z2,1/2-
165
После этого можно вычислить расстояние между центрами прут-
ков в любом сечении по их длине по формуле
S = ]/ (у2 — Ух)2 + (Z2 — 21 )2
Если S<S0, то прутки сближаются.
Подставляя в выражение для S разности смещений из равенств
(39) и опуская индексы при yi, получим •
5 = [(г—у)(1—cos₽)—zsin₽]24- [(г—y)sin₽4-г(1 — cosp)]2. (40)
Расстояние S является функцией трех аргументов: угла р , т. е.
числа прутков на окружности, угла закручивания в и положения
сечения по длине прутка, т. е. координаты х. Формула (40) позво-
ляет найти числовые значения S, пользуясь выражениями (18) для
у и z.
Нетрудно понять, что сближение прутков должно иметь макси-
мум в середине длины прутка. Это следует из того, что сближения
по концам равны нулю и распределяются по симметричному зако-
ну. Поэтому достаточно ограничиться подсчетами для среднего се-
чения, т. е. -Л Подсчеты расстояний для различных р и 6 , от-
личающиеся чрезвычайной трудоемкостью, произведены преподава-
телем кафедры 3. С. Шаровой и представлены в таблице и на рис. 8.
Таблица значений
Угол закру- чивания 6 3 0 0,25 0,50 0,75
п Т'" = 4 1,415 1,362 1,296 1,207
f.n = 6 1 0,960 0.924 0.840
f’"=8 0,766 0,747 0,710 0,647
Из приведенной таблицы видно, что расстояния между прутка-
ми убывают по мере роста угла закручивания при любом числе
прутков. Далее очевидно, что каждое число таблицы указывает
предельную величину диаметра прутка dt которая дает со-
прикосновение прутков при соответствующем угле 6 . Так, давая
прутку диаметр 2/=1,296г при /г=4 пруткам, мы получим соприкос-
новение прутков при угле в = 0,5, т. е. 28,5°. Этот угол и будет пре-
дельным, так как при больших углах наши расчетные формулы те-
ряют силу.
Важно отметить, что числа, приведенные в таблице, не зависят от
длины прутка; иными словами, длинные и короткие пучки при оди-
наковых углах дают одинаковое сближение.
166
Аналогичную картину дает подсчет радиальных смещений
прутков, которые также приводят к соприкосновению, если прутки
расположены многорядно, или имеется центральный (осевой) пру-
ток. В этом последнем слу-
Рис. 8
чае смещение центра сече-
ния прутка из положения 1
в положение 2 (рис. 9) ве-
дет к изменению радиуса:
Л = /(r — y)2 + z2, (41)
где у и z снова определяют-
ся формулами (18). Наи-
меньшее значение и име-
ет место опять в середине
длины прутка, при
Рис. 9
Подсчеты по формуле (41), выполненные 3. С. Шаровой, дают:
Таблица отношений —-
Угол 6 0 0,25 0,5 0,75
_П_ г 1 0,964 0,923 0,849
Эти значения также не зависят от длины торсиона и могут пони-
маться как предельные диаметры прутков: так, при с?=0,923г и угле
6 =0,5 периферические прутки коснутся центрального. График от-
ношений — почти совпадает с графиком отношений — при п=6
(рис. 8).
Появление контактов между прутками изменяет условия их ра-
боты. Можно заранее предвидеть, что оно повысит жесткость тор-
167
сиона при больших углах, и в этом смысле будет оценено конст-
рукторами положительным образом.
Однако не исключена возможность быстрого выхода торсиона из
строя после появления контактов вследствие потери устойчивости:
нажимающие друг на друга прутки будут выдавливаться с окруж-
ности. Возможность такого явления следует проверить экспери-
ментально, как и общий характер работы пучка после появления
контактов.
8. ПРИМЕР РАСЧЕТА ПРУТКОВОГО ТОРСИОНА
Имеется сплошной торсион длины 1С = 190 см, диаметра dc=
=4,8 см. Требуется подобрать размеры для эквивалентного прутко-
вого торсиона. Примем п=4 прутка.
Полярный момент сопротивления сплошного торсиона
Wp = ^- = ^ = 21,8слЛ
F 16 16
Допускаемый крутящий момент
Л1ДОП = 21,8т кгсм ,
где т — допускаемое напряжение в кг{см2.
Полярный момент инерции торсиона
t ndc 7t-4,84 .
I •-= ---= —~ ~ 52,4 см*.
р ' 32
Угол закручивания при допускаемом напряжении
е= М
32
GIp 8-10^-52,4
Объем сплошного торсиона
,г тт-4 82
Vc =---с- lc= 5-^1 190 = 3 430 см\
с 4 с 4
Рассчитываем эквивалентный прутковый торсион. Диаметр най-
дем из условия
, de 4,8 q
а — —с =--------= 3 см.
3 _ 3
1^4
Располагаем прутки по окружности радиуса г = 2,5 см на взаим-
ных расстояниях между центрами 5= 1,415г=3,54 см.
Определяем длину пруткового торсиона из условия равенства
жесткостей (35):
168
Объем пруткового торсиона
V = = 4 -^-121 = 3440сл::,
4 4
т. е. практически совпадает с объемом эквивалентного сплошного
торсиона. Фактически он будет больше за счет концевых дисков и
креплений.
Пусть допускаемое напряжение [т] -5000 кг/см2. Тогда пре-
дельный угол закручивания 105-0=9,9 [т]= 49 500, или 0 = 0,495.
Отношение диаметра прутка d к радиусу пучка г
— = —5— = 1,2
г 2,5
меньше предельного значения 1,296, которое находим в таблице
значений — для случая п =4, 0 = 0,5. Поэтому прутки будут рабо-
тать без контактов вплоть до предельного допускаемого скручива-
ющего момента.
7. РАСЧЕТ ЛИСТОВОГО ТОРСИОНА
Листовым торсионом будем называть пакет полос прямоуголь-
ного сечения, связанный по концам обоймами и работающий на
кручение (рис. 1). К этой форме торсиона обратилась конструктор-
ская мысль в поисках новых типов
подвесок, обладающих большей
деформативностыо, чем обычный
торсионный вал той же длины.
Ввиду этого мы сочли целесооб-
разным дать способ расчета та-
кого торсиона, не предрешая во-
проса о рациональности его при-
менения в отдельных случаях.
Произведенное нами иссле-
дование подтвердило предполо-
жение о высокой деформативно-
сти этой конструкции. Вместе с
тем расчеты показали, что по весовому признаку листовой торси-
он неизбежно будет менее рационален, чем торсионный вал рав-
ной прочности и равной жесткости, вследствие весьма низкой проч-
ности на кручение тонких листов прямоугольного сечения. Поэтому
единственным преимуществом листового торсиона перед валом яв-
ляется то, что он позволяет значительно увеличить деформацию
подвески при сохранении длины, обусловленной шириной корпуса
танка, хотя и ценой утяжеления. С точки зрения конструктивной
листовой торсион весьма удобен тем, что делает излишним устрой-
ство шлицев по концам, требующее горячей высадки.
Точный расчет листового торсиона весьма осложняется трением,
которое может возникать между листами, и зависит от состояния
поверхностей. Поэтому мы ограничились приближенным расчетом,
основанным на ряде допущений. Приемлемость этих допущений бы-
ла проверена и оправдана опытами, основные результаты кото-
рых приводятся ниже.
1. ВЫВОД ВЫРАЖЕНИЯ УГЛА ЗАКРУЧИВАНИЯ
В основу расчета кладем четыре допущения:
1) силы трения между листами отсутствуют;
2) деформации изгиба и кручения листов можно рассматри-
вать раздельно, применяя к ним принцип наложения;
170
3) угол закручивания не превышает 30е;
4) ширина листа h значительно больше толщины Ь.
Обозначим:
Рис. 2
Рис. з
Рассмотрим изолированный лист пакета, ось которого отстоит от
оси пакета на расстоянии r = kb. Если число листов в пакете нечет-
ное, то k — целое число; если число листов i — четное, то
л=^+2-,
2
где а — целое число.
При закручивании конца торсиона на угол 0 от начального по-
ложения лист испытывает три деформации (рис. 2).
1) Кручение с постоянным по длине крутящим моментом
Мх = 6 ,
х I
где для прямоугольного профиля листа
откуда
м oe-L }е. (1)
* 31 \ h )
2) Изгиб в плоскости листа с опорными -моментами (рис. 3)
Mo = ^_rsinf) (2)
Z /2
12*
171
и опорными реакциями
n 12EZ- .
7?, —------ г sin 6,
/з
где
г = bh3
г 12
Уравнение изгибающего момента по длине листа имеет вид
Mz — M°z — Rzx = - г sin 0 (1 — 2 -у j .
Здесь х—абсцисса сечения, отсчитываемая от одного из концов
пакета.
3) Изгиб в радиальном направлении с опорными моментами
М° — г(1—cos 6) (4)
и опорными реакциями
r(l—cos6), (5)
где
j _ b3h
12 ’
Уравнение изгибающего момента по длине листа
Му = Му — Ryx =
= -^r(l-cos6)(l-2-^).
Формулы (2) — (5) получены в предположении, что листы ра-
ботают на изгиб, как балки с заделанными концами, смещающими-
ся взаимно в направлении перпендикуляра к оси на расстояние
г sin6 и г(1 —cos6) соответственно.
Вычислим потенциальную энергию всех трех деформаций, рас-
сматривая их раздельно (второе допущение).
Энергия кручения
мс8= 1,3/1062 71 —0,6— .
2 6/ \ ’ h
Энергия изгиба в плоскости листа
(3)
172
Энергия радиального изгиба
]’Ч2тНЧ
-ЧЧт)’"
ИЛИ
Суммируем три выражения Ах, Ау, Az и приравниваем сумму
работе внешнего момента М на угле закручивания 6:
Ах + Ay + AZ = ~M4,
откуда
ЧЖ)!1
или, используя формулу (1),
М = мх
1 +
(6)
При 0, меняющемся в пределах от 0 до — (3-е допущение),
6
/I—cosC '2 _ /sin 6\2
(-------j меняется от 0 до 0,06, a 1 —— ) от 1,0 до 0,91. Если
I л V
учесть, кроме того, что 1 — 1 значительно больше единицы (4-е до-
пущение) „то можно приближенно положить
sin 6 __ 1 1 — cos 6 __ q
6 ~ ’ 6 ‘
Тогда получ-им из формулы (6):
М = МХ
(7)
а по подстановке выражений (1) и г —kb,
173
Нетрудно понять, что для целого пакета, состоящего из i листов,
Эта зависимость примет ©ид
где ££2 распространяется на все листы пакета. Обозначая для
краткости
Е k2 = В,
найдем значения В простым подсчетом. Так, например, для пяти
листов
В = 0 + 2(12 + 22) = 10;
для шести листов
Значения чисел В приведены в табл. 1.
Таблица 1
i 2 3 4 5 6 7 8 9 10
В 0.5 2 5 10 17,5 28 42 60 82,5
Окончательно получим
откуда находим искомое выражение угла закручивания пакета
Мы видим, что листовой торсион обладает линейной характери-
стикой. Но это явилось следствием допущенных нами приближений.
В действительности, при коэффициенте В в формулах (8) и (9)
имеется добавочный множитель, равный:
который мы приняли постоянным и равным единице. Для оценки
возможной погрешности возьмем случай квадратного пакета
(bi = h)t наибольший угол 6=-^- и наибольшее конструктивно-обо-
снованное значение -у-=0,1. Подсчет дает такие значения макси-
мальных ошибок в величине угла:
при i = 3 5 7 9
ошибка = 0,4% 1,2% 2,1% 3,2%,
174
причем для 0—0 ошибка обращается в 0. При реальных соотноше-
h 1 1
ниях порядка — = — или — ошибка будет значительно меньше.
Ввиду этого мы полагаем возможным сохранить сделанные прибли-
жения я использовать для целей расчета линейные зависимости
(8) и (9).
2. НАПРЯЖЕНИЯ
Опасным сечением для листового торсиона является сечение
в заделке, а наиболее напряженными листами — крайние. Внутрен-
ние усилия здесь будут:
Крутящий момент
Изгибающие моменты:
м» = -^-мх = ме '^6(1-со5.6> .,
т)
всь оаьетО.
Р<ис. 4
Л1О = 2k Mr = ^_15Ws.n6 _
4bZ 6^1 —0,6-^-j
причем k = ——, где i— число листов, а В берется из табл. 1.
_ sin О
Положим, как и раньше, -у- = 1 и, кроме того, примем
-—cosQ . Максимальная ошибка приб=— составит для пер-
0 2 6
вой замены 5%, а для второй 2%, в обоих случаях в сторону пре-
увеличения, т. е. в запас прочности.
Тогда запишем:
м° = мх
15fe& 6
М° = МХ
I5fefe-
4bl(l-0,б4)
В прямоугольном сечении листа имеются три точки, которые
следует подвергнуть поверке прочности, как опасные. Эти точки
отмечены на рис. 4 цифрами /, 2 и 3.
175
В точке 1 сочетаются: максимум касательного напряжения от
кручения:
Л4Г
где
b2h
з(1 + °.6^) ’
и максимум нормального напряжения от радиального изгиба:
М°
UZy ’
где
Применяя третью теорию прочности, получим расчетное нера-
венство для точки 1:
'. у г'
мг
2b2h
где R — основное допускаемое -напряжение на растяжение.
Преобразуем это выражение:
Т- <п)
В точке 2 сочетаются максимумы нормальных напряжений от
двух изгибов:
М° М°
'о =-----------;--
UZ, 1 wy
где
или
Mxk
b~hl
45
°2” 2
h + ~bb
1 — 0,6 —
h
или, переходя
преобразуя.
для единообразия к касательным напряжениям и
45 Мх k (2h +5 6)
8 0,6-^-j
(12)
176
Наконец, в точке 3 сочетаются максимум нормального напряже-
ния от изгиба в плоскости листа
0=2£
U7-
и местный максимум касательного напряжения от кручения, кого-
равным 0,75 от
рый можно принять ДЛЯ ТОНКИХ ЛИСТОВ -
а-бсолютлого максимума:
9Л1
ИЛИ
. R
•Т* (13)
Нам предстоит выяснить, какое из напряжений (11) — (13) яв-
ляется расчетным.
Обозначим для краткости
-------------= и, — = V, 1—0,36 — = W.
/ b \ / й2
v262 ч- 4V72;
(14)
Тогда:
^=4w(2+-t);
г, = ±и }/52V’- + U72.
Выражения эти допускают упрощение. Прежде всего заметим,
что W весьма близко к единице. Если принять— -С-т-» т0
п о
г, /
0,96<W< 1. Далее, если ограничиваться углами 0 , то — <
<— . --0,174 и, следовательно, мало по сравнению с двойкой
3 6
(формула т 2).
177
Наконец, в формуле первый член под радикалом будет при тех
h 1
же ограничениях и условии — меньшие величины:
f—/_LV(0,174)2 = 0.0043Л2
и даже при весьма большом числе листов (например, /=11, #=5)
составит ничтожную долю от второго члена, равного 4. Ввиду это-
го мы заменим выражения (13) приближенными упрощенными
формулами:
С77 ЗЛ1Г
4 = 0/ =--------;
45Mrk
(15)
:з —
9M
I Ь \ у Z2
4fc2hfl—0,6—j r
Теперь сразу видно, что напряжение т2 всегда
поэтому может быть исключено из дальнейшего
Далее, напряжение ^3 будет больше, чем *4, если
25l/2+ 1 >6,
т. e.
V > = 0,176.
15
Но V= ~у— ~ 2/>Й • Таким образом, при
чет следует вести по напряжениям т3 , а при
меньше т3, и
рассмотрения.
>0,35 рас-
<0,35 —по
напряжениям
Представим эти напряжения в окончательном виде, подстав-
ляя выражение (10) для Мх.
При (t'~l>ft<0,35
Здесь М — внешний скручивающий момент.
178
3. АНАЛИЗ ПОЛУЧЕННЫХ РЕЗУЛЬТАТОВ
В выведенных нами формулах угла закручивания (9) и напря-
жений (16) основную роль играет стоящее в знаменателе выраже-
ние
^ = (1-о,б4)г + 7,5(4-уВ,
(17)
зависящее от трех параметров: числа листов i и отношений — ,
h h
— . Исследуем это выражение.
1. При данных i и ~ Т есть убывающая линейная функция—
« h
2. При данных / и — Т есть возрастающая квадратичная
, h
функция —.
3. При данных -7- и —
h I
функция i.
Заметим, что зависимость
. Ь
обычных соотношениях — от
h
няться в пределах от 0,85 до
Т есть возрастающая нелинейная
Т от весьма слаба, так как при
h
*/4 до 71о член 1—0,6 — будет ме-
h
0,94. Пусть, например, -у- =7го (при
больших
значениях — влияние — , очевидно, еще меньше). Тог-
1 h
да найдем:
Таблица 2
ь h i = 4 6 8 10
V4 7 = 3,48 5,43 7,60 10,07
"/io 7 = 3,84 5,98 8,32 10,97
Расхождение не превышает 10%. Следовательно, если заменить
член 1—0,6— его средним значением 0,9, то ошибка не превысит
h
5%. Мы не имеем в виду рекомендовать такую замену в расчет-
ных целях, так как вычисление Т по формуле (17) очень неслож-
но. Но она уместна в целях анализа влияния различных факторов
на жесткость и прочность листового торсиона.
179
Итак, заменим выражение (17) упрощенным:
Т = 0,9( + 7,5(— f В,
(18)
h
содержащим лишь два аргумента: i и — о
Заметим далее, что Ы есть высота сечения пакета, и, стало
бьпь, отношение — = Ф есть коэффициент, характеризующий
h
форму сечения. Для квадрата Ф =1, для широкого пакета Ф<1,
для высокого Ф>1.
Теперь возьмем выражение угла закручивания (9) и преобра-
зуем:
0 = 2™.
ьзиат
ЗМР
>______
иют
= (19)
---TOP
фз
-у-, i и коэффициента формы. Будем считать /»
придем к следующим выводам:
где ф зависит от
постоянным. Тогда
1) Влияние формы пакета: торсион тем жестче, чем сечение его
выше и уже. Квадратный пакет имеет среднюю жесткость.
2) Влияние числа листов: так как и числитель и знаменатель
суть возрастающие функции /, то оценим влияние i непосредст-
венным подсчетом для разных t и для крайних значении — = ,/1о
и 7зо (табл. 3).
Табл иц а 3
i = 2 4 6 8 10
h _ —’/10 /3 = 4,36 T 16,1 32,2 51,2 65,8
h / ='/m I3 — = 4,45 T 16,5 39,0 68,3 103,2
Таким образом, угол резко возрастает с увеличением числа
листов, т. е. при нарезке пакета данной формы на большее число
листов.
3) Влияние -у- характеризуется произведением -у-Т, стоящим
в знаменателе. Это произведение есть возрастающая функция ;
следовательно, при данном h угол возрастает вместе с длиной, что,
впрочем, очевидно.
Итак, окончательно приходим к выводу: листовой торсион да-
ет тем большую деформацию, чем шире его форма, чем больше
число листов и чем больше длина (рис. 5).
180
Переходим к анализу прочности листового торсиона. Для этого
преобразуем формулы (16):
при (1—1)-^-<0,35
• = 3M _ м 3/3 .
b~hT ~ № ТФ- ’
при (t—1) — > 0,35
(20)
и исследуем их, полагая Л посто-
янным. Тогда приходим к следу-
ющим выводам:
1. Влияние формы пакета:
торсион тем прочнее, чем боль-
ше^ Ф, т. е. чем его сечение выше
и уже. Однако эта зависимость
сказывается слабее, чем для де-
формации, так как Ф входит в
формулы напряжений во второй
степени, а в формулу угла — в
Рис. 5
третьей степени.
2. Влияние числа листов характеризуем таблицей, в которой
даны значения т с точностью до постоянного множителя:
Таблица 4
i — 2 4 6 8 10
h = V10 2,18 4.08 8,58 12,86 16,21
h у- = 1/30 т = 2,22 4,40 6,51 8,54 10,32
При составлении таблицы учтены обе формулы (20). Значения,
стоящие слева от вертикальных черт, получены по первой форму-
ле, справа —по второй.
Мы видим, что напряжения возрастают с увеличением числа
листов, причем каждая из формул (20) дает скорость роста, близ-
кую к линейной, но вторая дает более быстрый рост, чем первая.
Отсюда заключаем, во-первых, что увеличение числа листов сни-
жает прочность, и, во-вторых, что применение торсионов, удовлет-
воряющих условию (I—1) у <0,35, целесообразно.
181
3. Влияние — оказывается различным при разном числе ли-
r h 0,35
стов, как видно из предыдущей таблицы. Если — < —р т0 на‘
пряжения слабо возрастают с уменьшением —, т. е. с ростом
h „ 0,35
длины. Если же —, возрастая, превзойдет величину т—р то вли-
яние длины становится обратным, и напряжения увеличиваются
с уменьшением длины.
4. СЛУЧАЙ КВАДРАТНОГО ТОРСИОНА
Листовой торсион квадратного сечения имеет несомненные
преимущества конструктивного характера. Поэтому полезно при-
менить к нему выведенные нами формулы, тем более, что им при
этом удается придать более простую форму.
Для квадратного торсиона коэффициент формы Ф =1, а — =
h
— —у . Поэтому
T = (i — 0,6)+ 7,5 (-у-)2 В,
6 = м 31-3 [
Gh? Т h ’
Ai it2
i = — —
h’ T
при (i— 1)у <0,35,
т=^.-^|/25[»-1)Ч2+1
Л» 4Т V I 2/ J
при (1—1)— > 0,35.
Обозначим:
(21)
(22)
(23)
Тогда получим простую форму записи:
(24)
fi М !
и =-------ф.
СЛз Т1
(25)
м
Л3
(26)
h Коэффициенты <р, и *2, зависящие от двух аргументов: i и
— , даем в форме табл. 5—6 и графиков (рис. 6—7).
182
Рис. 6
Таблица 5
Таблица коэффициента
X. i й ^Х 2 3 4 5 6 7 8 9 10
! 8 131 246 385 542 695 852 995 1 138 1 255
10 166 316 510 729 965 1214 1455 1720 1 920
15 254 494 805 I 188 1620 2100 2620 3 160 3 710
20 340 664 I 100 1640 2 260 2 980 3 750 4600 5 480
25 427 834 1385 2 075 2 880 3 820 4 860 6 000 7 230
30 514 1000 1 675 2 500 3510 4 650 5960 7 360 8 950
Как видно из рис. 6, значения б для каждого i представляют
почти точно линейную функцию —.
Таблица 6
Таблица коэффициента v
X. L 1 \ h X 2 3 4 5 6 7 8 9 10
8 8,20 10,27 12,35 16,25 20,2 24,3 28.1 31,9 35,2
10 8,30 10,53 12,75 15,45 19,3 23,5 27,5 31,7 35,5
15 8,48 10,95 13,40 15,85 18,0 21,2 25,1 29,2 33,4
20 8,50 11,07 13,70 16,40 18,82 21,3 23,4 27,0 30,8
25 8,55 11,10 13,85 16,60 19,20 21,8 24,3 26,6 29,2
30 8,56 11,15 13,92 16,70 19,50 22,2 24,8 27,3 29,8
Справа от жирной линии стоят значения *2, а слева — vx . Как
видно из табл. 6, значения v слабо зависят от — . Поэтому для
h
приближенных подсчетов можно отказаться от учета этой зависи-
мости и, идя в запас прочности, принять с округлением наиболь-
шее значение для v в каждом столбце. Тогда мы получим (рис. 7):
Т аблица 7
1 2 3 4 5 6 7 8 9 10
у 8,5 11 14 17 20 24 28 32 35
184
Из рис. 7 видно, что при i>2 эти значения растут почти линей-
но, весьма близко следуя уравнению
v — 3t5i.
Имея это в виду, можем
ности к простейшему виду:
т = 3,5 — < -5- (i > 2). (27)
Этим выражением мы и ре-
комендуем пользоваться для
расчетов квадратного торсиона.
При желании уточнить расчет
следует применить формулу (26)
с подстановкой табличных зна-
чений V .
Подсчитаем удельную потен-
циальную энергию листового
торсиона квадратного сечения.
Полная энергия равна:
А = _Lm6 = _L.^;
2 2 Gh* т
деля на объем V—h2l, получим
удельную энергию
_ Д = 1 At2ф
” V ~ 2 ' G№ I '
привести расчетное неравенство проч
Но квадрат наибольшего напряжения (27) равен (при г>2).
т2 = 12 25 —i2.
Следовательно,
. _1—. (28)
20 12,25i2 I 2G ’
где множитель
— Ф h — &
а ~ (3,5i)3 ' I 3,52Г
имеет значения, данные в табл. 8 (рис. 8).
Для торсионного вала круглого сечения а= —, т. е. а =0,5.
Отсюда сразу видно, что коэффициент использования матери-
ала в листовом торсионе значительно ниже, чем в торсионном ва-
ле (для /=5 — вдвое, для i=8— в 4—6 раз и т. д.). Следователь-
но, объем листового торсиона должен быть значительно больше,
чем объем торсионного вала той же прочности и жесткости.
185
Таблица 8
Таблица значения коэффициента а
h \ 3 4 5 6 7 8 9 10
8 0,29 0,24 0,22 0,19 0,18 0,16 0,14 0,13
10 0,29 0,26 0,24 0,22 0,20 0,19 0,17 0,16
15 0,30 0,27 0,26 0,25 0,23 0,22 0,21 0,20
20 0,30 0,28 0,27 0,25 0,25 0,24 0,23 0,22
25 0,30 0,28 0,27 0,26 0,26 0,25 0,24 0,23
30 0,30 0,28 0,27 0,27 0,26 0,25 0,25 0,24
5. ПРИМЕРЫ РАСЧЕТА
1) Подобрать размеры сечения листового торсиона квадратно-
го сечения из четырех листов при Я = 5 000 кг/сж2, дающего угол
закручивания 0,25° при моменте 500 кгсм и способного воспринять
момент Л1=20000 кгсм.
Определяем ширину сечения h по формуле (27)
3,5М < R
Л8 2 ’
откуда
. -3/ 3.5М-2 ?/”7-20000-4 . о
h> I/ —-------- = I/ ----------- = 4,8СМ,-
F R К 5 000
и толщина листов
a h 4.8 1 о
о = — = — = 1,2 fAt.
i 4
Потребную длину торсиона определим из формулы (25)
6 = — ф =------—— ф = —— = 0,0043,
Gh* 8-10^-4,83 Т 4-180
откуда
0,0043-8-1^.4,83 _
500
По графику ф при 4=4 находим -^- = 14,2, и, следова-
тельно,
Z= 14,2h = 14,2-4,8 = 68,2^.
Объем торсиона
V = th* = 68,2-4,82 = 1 570см*.
186
Эквивалентный по прочности и жесткости торсионный вал
круглого сечения будет иметь диаметр d=3,45 см, длину 1=95,5 см
и объем V= =890 см3, т. е. в 1,76 раза меньше.
2) Рассчитаем листовой торсион квадратного сечения, эквива-
лентный по прочности торсионному валу диаметром /2 = 4,8 см.
Приравнивая выражения наибольших напряжений в обоих слу-
чаях, получим условие равной прочности:
16Л1 _ 3,5М
ЯбР — Лз ’
или при rf=4,8 см,
~ = 4,2^Т
Поэтому при различном числе листов i получим такие разме-
ры листового торсиона (с округлением):
г=3 4 5 6 7 8 9 10
Л=6,05 6,70 7,20 7,60 8,0 8,40 8,75 9,0 см
b=2fi 1,70 1,45 1,30 1,10 1,05 0,95 0,90cjw
Пусть длина вала /в = 190 см. Определим эквивалентную по
жесткости длину /л листового торсиона из условия равенства
углов:
32ЛЯВ_ м
Gnd* ~ Gh*
откуда
з___
ф=/ . 3? = 190 . & = 270».
Y в cP я 4,8* я
Пользуясь графиком функции ф, находим соответствующие
значения отношений — , а, стало быть, и длины /л:
h
i = 3 4 5 6 7 8 9 10
А = 24 2 19.6 16,8 15,0 13,8 13,2 12,5 12,4
h
/л= 146,5 131,2 121,0 114,0 110,2 109 108 ПО см
Таким образом, длина листового торсиона значительно мень-
ше, чем длина эквивалентного вала; она падает с ростом числа
листов до некоторого минимума, на котором удерживается.
Объем вала равен
V, - ZB = 190 = 3 440 см3.
187
Объемы эквивалентных листовых торсионов вычислим по фор-
муле УЛ=Л2/Л:
/= 3 4 5 6 7 8 9 10
Ул= 5 350 5 850 6 260 6 590 7 050 7 700 8 300 8 900 см?
Таким образом, как мы и предвидели, объем листового торси-
она превосходит объем вала тем больше, чем больше число листов.
Основной выигрыш получается только в длине, благодаря чему
при данной ширине корпуса танка можно получить значительно
большую деформацию, чем при равнопрочном вале.
Так, придавая листовому торсиону длину /л=/в=190 см, полу-
чим углы закручивания, выраженные в долях угла закручивания
вала:
i= 3 5 7 9
— = 1,35 1,62 1,88 2,08.
6. ОПЫТНАЯ ПРОВЕРКА ТЕОРИИ
Для проверки изложенного выше метода расчета нами был
проведен ряд экспериментов. Задачей экспериментов было преж-
де всего, выяснение приемлемости двух основных допущений:
пренебрежения силами трения и раздельного учета изгиба и кру-
чения. Очевидно, влияние этих допущений должно прежде всего
сказаться на зависимости между моментом и углом, которая тео-
ретически выражается формулой (9), полученной ценой ряда до-
бавочных упрощений. Поэтому основным содержанием экспери-
мента была проверка этой формулы.
Модели торсионов собирались из стальных полос 0,6X3,0 см.
Механические свойства этой стали были определены испытанием
на прессе Гагарина пяти образцов, давшем результаты:
Таблица 9
№ образца 1 2 3 4 5 Среднее
Предел пропорциональности .... 2 480 2 550 2 445 — 2 695 2540
Предел текучести 2 780 3 050 2 770 2 770 2 875 2850
Временное сопротивление 4600 4830 4 460 4 570 4 680 4 630
Как видно из диаграммы испытания образца № 2 (рис. 9),
сталь обладает высокой степенью пластичности. Это обстоятель-
ство не дало возможности проверить расчетную формулу при
188
больших углах, так. как материал достигал состояния текучести
уже при сравнительно небольших углах закручивания.
наибольшей нагрузки Л1-25 кгм. Шкала машины позволяет от-
считывать 0,25 кгм (малое деление лимба), так что точность ре-
гистрации нагрузки более чем достаточна. Торсионы закладыва-
лись в рифленые губки, исклю-
чавшие возможность поворота
листов вокруг поперечной оси.
Это оказалось существенным:
при закладке в гладкие губки
контрольные тензометры с не-
сомненностью показали, что
листы имеют по концам упру-
гую, а не жесткую заделку.
Измерение угла закручива-
ния торсиона производилось р.ис щ
при помощи зеркального при
бора. По длине торсиона,
вблизи концов, устанавливались на струбцинах зеркальца, и на-
блюдение велось через зрительные трубы по миллиметровой шка-
ле с расстояния 1 м. Точность регистрации углов при этом состав-
ляет 0,5 • 10 4 радиана.
Кроме того, на крайнем листе у заделки устанавливался тензо-
метр Гугенбергера на базе 2 см на узкой грани. Этот тензометр
позволял проверить величину опорного изгибающего момента и
тем самым давал оценку работы листа на изгиб.
Контрольное наблюдение за углом закручивания образца в
целом велось по лимбу машины, дающему невысокую точность
(до 0,5°).
189
Схема модели торсиона с установленными приборами дана
на рис. 10.
Как следует из данного выше анализа, основными параметра-
ми, от которых зависит жесткость торсиона, являются число ли-
стов i и отношение —. Поэтому мы испытали модели торсионов с
h
различным числом листов — 4, 5 и 6 и двумя значениями —: 10
h
и 20.
Приводим результаты опытов и теоретического расчета моде-
лей.
1. Одиночная полоса 3,0X 0,6 см, длина между заделками
Z=30 см. Испытание преследовало двоякую цель: сравнение с из-
вестной для этого случая расчетной формулой давало дополни-
тельную калибровку материала и, с другой стороны, позволяло
изучить работу полосы за пределом текучести.
Угол закручивания определяется формулой
в -------55"------=------з/и-зо----= j ggg. 10_„ м
№6 (.-0.6^-)
а на длине 20 см, соответствующей расстоянию между зеркалами,
е = — 1 965- ю-* М = 1,31 10-4 м.
3 ’
Опытные значения углов даны в табл. 10.
Таблица 10
Опыт № 16/3
м в кгсм Измеренный угол 0о Теоретиче- ский угол Вт во вт Прирост угла опыт- ный ДВО Прирост угла теоре- тический Д0т
100 1,74-10“2 1,31-10“2 1,33 1,74-10“2
200 3,14-10“ 2 2,62-10“2 1,20 1,40-10“2
300 4,39-10“2 3 93-10“2 1,12 1,25-10“2 1,31-10“2
400 5,73-10“2 5,24-10“2 1,09 !,34-10“2
500 6,91-10“2 6,55-10“2 1,05 1.18-10-2
600 8.18-10-2 7,86-10^2 1,04 1,27-10“2
Среднее . . . 1,14 1,36-КГ"2 1,31-10“2
Отношение приростов угла — Д0: >- = 1^ = 1 038. г 1,31 *
190
Таким образом, среднее расхождение составляет 3,8%. Это по-
казывает, что принятое в расчете значение (7 = 8-105 кг/см2 доста-
точно близко к действительному и что работа одиночной полосы
вполне отвечает теории.
Определим крутящий момент Мт, соответствующий текучести
полосы. Как известно, для пластического материала этот момент
не обусловливается достижением текучести в наиболее напряжен-
ной точке сечения, так как после этой стадии начинается перерас-
пределение напряжений и их выравнивание. Предельный момент
определяется удвоенным объемом поверхности равного ската, по-
строенной на сечении. Для прямоугольного профиля этой поверх-
ностью будет четырехскатная крыша с наклоном граней 45°. Ее
удвоенный объем, умноженный на предел текучести тт = -у, даст
предельный момент
& /. 0.62 /Q 0,6X2 850
ЛЕ= —lh-------= —-— 3---------— ------- 7\7 кгсм
т 2 \ 3 / т 3 \ 3/2
Опыт № 16/3 дал значение /Ит^700 кгсм.
2. Модель № 10. Составлена из 6 листов 0,6X3,0 см, длина
между заделками 60 см. Зеркала измеряют угол на длине 50 см
(отступы по 5 см от концов), тензометр установлен на растянутой
кромке крайнего листа в расстоянии 2,5 см от заделки.
Производим расчет модели, принимая значение (7=8 • 105 кг{см2.
По формуле (9) определим угол закручивания на длине /=50 см
(при /=6, В=17,5):
37V1-5O
0.63-3-8-1О-
--------------------------=0,515- 10-4М.
/ 0,6 /3 \2
(1-0.6у 6 + 7.5(¥) 17.5
Для одной ступени загружения, т. е. при М = 500 кгсм, имеем
В = 0,515- 1О'"-500 = 2,57-10-2.
Нормальное напряжение в заделке крайнего листа от изгиба в
его плоскости определяется формулой (§ 3)
_ М®_____________45М(f—1)__________
4^[(1-о.бА),-+7,5(А)2в]
откуда
о = 0.465М,
а при М=500 кгсм и на расстоянии 2,5 см от заделки, т. е. 27,5 см
от середины торсиона (от нулевой точки эпюры моментов)
о = 2Л5 о 465.500 = 213 кг!см2.
30
Результаты испытания даны в табл. 11.
191
Т а блица 11
Опыт № 10/2
м в кгсм Измеренный угол ео Теоретиче- ский угол Вт 6Т Измерен- ное нап- ряжение °о Теорети- ческое напряже- ние от °о °т део Дсо
500 2,77-102 2,57-10“2 1,08 260 213 1,22 2,77-10“2 200
1 000 5,05-10“2 5,14-10“2 0,98 452 426 1,06 2,28-10“2 192
1500 7,52-1(Г2 7,71-10“2 0,97 653 639 1,02 2,47-10”2 201
2 000 9,87-10-2 10,28-10“2 0,96 855 852 1,00 2,35-10“2 202
2500 12,36-10-2 12,85-10“2 0,96 1050 1065 0,98 2,49-10“2 195
Среднее 0,99 1 Среднее 1,0б| 2,472-10“2 210
Как видно из табл. И, совпадение между опытом и теорией
почти полное. Некоторое отклонение получается только от перво-
го этапа загружения и может объясняться наличием мертвого хода
в машине. Для устранения этого влияния следует взять среднее
значение прироста угла и напряжения при изменении момента на
одну ступень, т. е. на 500 кгсм.
Средний прирост угла на 500 кгм
Д60 = 2,472- КГ2.
Отношение опытного прироста напряжения к теоретическому
——=0,961.
2,57
Средний прирост напряжения Л? =210 кг/см2.
Отношение опытного прироста напряжения к теоретическому
3. Модель № 9. Составлена из 5 листов 0,6X3,0 см (квадрат-
ное сечение), длиной 60 см. Установка приборов такая же, как в
10-й модели.
Расчетный угол на длине /=50 см (при i=5, В=10):
6=--------------------=°-630-1(^4 м-
0,88-54-7,5— 10
400
а при М=500 кгсм:
6 = 0,630-10“4-500 = 3,15-10~2.
Теоретическое напряжение в заделке
45Л4 (5—1)
О =---------------1----------------= 0,455Л4,
4-0,62-3-60 [о,88-54- 7,5 10 j
192
а при M — 500 кгсм и на расстоянии 2,5 см от заделки
с = — 0,455-500 =208 кг!см2.
30
Результаты испытания даны в табл. 12.
Таблица 12
Опыт № 9/3
М в кгсм Измерен- ный угол ео Теоретиче- ский угол 6Т ео ет Измерен- ное нап- ряжение °о Теорети- ческое напря- жение ат °о ат део д°о
500 3,61-10“2 3,15-10“2 1,14 225 208 1,08 3,61-Ю"2 225
1 000 6,83-10“2 6,30-10“2 1,08 429 416 1,03 3,22-10“2 204
1500 9.91-10~2 9,45-10“'2 1,05 631 624 1,01 3.08-10“2 202
2 000 13,01-10“2 12,60-10“2 1,03 835 832 1,0 3,10-10“2 204
2 500 16,01-10“2 15,75-10“2 1,02 1 040 1 040 1,0 3,00-10“2 205
Среднее 1,06 |1,024 3,20-10“2 208
Совпадение в величинах углов и здесь весьма близкое, кроме
крайних ступеней. Подсчитываем средние приросты.
Средний прирост угла Д6о=3,20-I0-2.
Отношение опытного прироста угла к теоретическому
1 015.
3.15
Средний прирост напряжения Дсо=208 кг!см2.
Отношение опытного прироста напряжения к теоретическому
™=10.
208
4. Модель № 11. Составлена из 4 листов 0,6X3,0 см, длиной
60 см. Зеркала установлены на базе 45 см, тензометр отстоит на
5 см от заделки.
Расчетный угол на длине I = 45 см (при i =-4, В~5)
6 = ЗЛ^----------------*---------= 0,724- io-4 м,
0.65-3-8-1№ 1 .
0.88-4+7.5 5
а при М =500* кгсм
6 = 0,724-10^-500 = 3,62-10-2.
Теоретическое напряжение в заделке
а __45М(4-1)---------------------= О43Ш>
4-0,62-3-60 Го,88-4+7,5 -i-5 ]
13 С. А. Бернштейн
193
а при M = 500 кгсм и на расстоянии 25 см от середины длины
о = — 0,434 • 500 = 181 кг 'см2.
30
Результаты опыта даны в табл. 13.
Таблица 13
Опыт № 11/2
М в кгсм Измеренный угол ео Теоретиче- ский угол 6О ет Измерен- ное нап- ряжение °о Теорети- ческое напряже- ние GT °о °т део Дсо
500 3,85-10“2 3,62-10“2 1,06 172 181 0,95 3.85-10“2 172
1 000 7,27-10~2 7,24-10“2 1,00 375 362 1,03 3,42-10“2 203
1 500 10,98-10“2 10.86-10“2 1,01 569 543 1,05 3,71-10“2 194
2 000 14,63-10“2 14,48-10“2 1,01 718 724 0,99 3,65-Ю“2 149
2 500 18,20-10“2 18,10-10-2 1,00 910 905 1,0 3,57-10“2 192
Среднее | 1,016 1 1,004 3,64-10“2 | 182
В этом случае совпадение по углам и напряжениям особенно
близкое.
Средний прирост угла
де0 = з,б4-ю~2.
Отношение опытного прироста угла к теоретическому
— = 1,003.
3,62
Средний прирост напряжения Аао = 182 кг]см2.
Отношение опытного прироста напряжения к теоретическому
— = 1,005.
181
5. Модель № 12. Составлена из 6 листов 0,6X3,0 см, длиной
30 см. Зеркала установлены на базе 20 см\ тензометры не стави-
лись.
Расчетный угол на длине 20 см
п ЗЛ1’20 1 1 -г щ Ч лл
и =-------------- ------------------= 1,75-10~5 М.
0.63-3-8- ](£ 1 ’
0,88-64-7,5—17,5
100
При Л1=500 кгсм
6 = 1,75-1 (Г5-500 = 0,875-1 (Г2.
194
Таблица 14
Опыт № 12/2
/Ив кгсм Измеренный угол ео Теоретиче- ский угол ет 6Т -“о
500 0,80-102 0,875-10“2 0,91 0,80-10“2
1 000 1,58-10~2 1,75 -10“2 0,90 0,78-10“2
1 500 2,41-К»-2 2,62 -10“2 0,92 0,83-КГ2
2 000 3,20-10“2 3,50 -10“2 0,91 0,79-10“2
2 500 4,27-10“2 4,37 -10“2 0,98 1,07-1 ОТ"2
Среднее 0,924 0,854-10“2
Отношение приростов углов
Дв^ = 054 =о>975
Дбт 0,875
6. Модель № 14. Составлена из 5 листов 0,6X3,0 см, длиной
30 см. Зеркала установлены на базе 20 см.
Расчетный угол на этой длине
6 = 3|М'20-------------!---------= 2,24-10-5 М.
0,88-5 + 7.54-10
100
При 7И=5ОО кгсм
6= 2,24-10 5-500 = 1,12-ЮЛ
Таблица 15
Опыт № 14/3
М в кгсм Измерен- ный угол «о Теорети- ческий угол 6Т 0о 6Т дво
500 1,30- Ю' 2 1,12-КГ"2 1,16 1,30-10~2
1 000 2,42-10“2 2,24-10“2 1,08 1,12-10—2
1 500 3,48-10“2 3,36-Ю“2 1,03 1,06-10“2
2000 4,54-102 4,48-КГ"2 1,01 1,06-КГ2
2 500 5,56-10' 2 5,60-Ю2 0.99 1.02-10-2
3 000 6,65-10 2 6,72-10“2 0,99 1,09-1(Г2
Среднее 1,04 1,11-10“2
I33
195
Отношение приростов углов
*1!°. = кН = 0 99.
дет 1.12
7. Модель № 13. Составлена из 4 листов 0,6X3,0, длина 30см.
Зеркала установлены на базе 15 см.
Расчетный угол на этой длине
с ЗМ-15 1
и ==---------• ---------------
= 2,22-IO”6 M.
При М = 500 кгсм
е =2.22-1(Г5-500=1,11 Ю-2.
Таблица 16
Опыт № 13/2
М в кгсм Измерен- ный угол ео Теоретиче- ский угол 6Т 6о ет А0о
500 1, io-io—2 1,1Ы0“2 0,99 1,10-Ю-2
1000 2,15. ИГ2 2,22-10~2 0,97 1,05-10“2
1 500 3,20-10“2 3,33-10“2 0,96 1.05-10-2
2 000 4,33-10“2 4,44-10“2 0,98 1,13-10“2
Среднее 0,975 1,08-10“2
Отношение приростов углов
= Ь08 =о 9у5
Двт 1,11
Результаты испытаний шести моделей сведены в табл. 17, в ко-
торой даны отношения средних приростов углов.
Таблица 17
Отношения --—
Д6Т
h 4 5 6
20 1,003 1,015 0,961
10 0,975 0,990 0,975
196
Из табл. 17 видно, что выведенная нами формула угла закручи-
вания листового торсиона весьма близко соответствует опыту. Тем
самым можно признать оправданными допущения, положенные в
основу ее вывода, и, в частности, гипотезу незначительности сил
трения между листами.
8. Исследование влияния трения между листами.
Для оценки влияния трения были специально испытаны две моде-
ли, составленные из одних и тех же пяти полос 0,6x3,0 см, дли-
ной 60 см. В модели № 9 листы были сложены, как обычно, вплот-
ную. В модели № 8 между листами в заделках были проложены
стальные прокладки толщиной 1,2 мм, так что листы на всем про-
тяжении свободной длины не соприкасались между собой. Зеркала
устанавливались на расстоянии 50 см.
Теоретический угол закручивания на длине 50 см для модели
№ 9 (без прокладок) был подсчитан выше:
6 = 0,630- ю-4 Л4,
и при М = 500 кгсм
6 = 0,630- Ю-4 • 500 = 3,15.10-2 .
Результаты испытания были приведены выше. Средний опытный
прирост угла по опыту № 9/3 оказался равным 3,20.10-2, так что
отношение приростов
=?д?9=1 015.
дбт 3,15
Модель № 8 (с прокладками) требует особого расчета, так как
наличие прокладок увеличило высоту сечения. Число В определится
из
В = ЕЛ2 = 0+2( °’6+^2-)2 + 2( lt20+6?’-M-)8 = 14,40,
а потому
6 = ЗЛ1-50-------------!------------ 0,617 • 10-« М
0,63.3-8-105 1
’ 0,88-5+7,5--14,40
400
и при М = 500 кгсм
е = 0,618- Ю^-БОО = 3,035- ю-2.
Результаты испытания модели № 8 даны в табл. 18.
Отношение приростов углов
= =0,954.
дет 3,085
Таким образом, опытные приросты углов при наличии прокла-
док, т. е. с исключенным трением, оказались меньшими, чем приро-
сты углов без прокладок, т. е. с-существующим трением:
без трения ^2 ==0,954,
Д6Т
с трением =1,015,
Д0Т
197
Таблица i8
Опыт № 8/2
М в кгсм Измерен- ный угол Во Теоретиче- ский угол 6т 6р ет Д«о
500 3,16-10“2 3,08-10“2 1,02 3,16-10“2
1000 5,99-10“2 6.17-10-2 0,97 2,83-10“2
1 500 8,92-10“2 9,25-10“2 0,96 2,93-10“2
2 000 11,84-10“2 12,34-10“2 0,96 2,92-10“2
2 500 14,71-10“2 15,42-10“2 0,95 2,87-10“2
Среднее 0,97 2,94-10—2
хотя обе модели состояли из тех же листов. Несомненно, наличие
сил трения должно было бы дать обратную картину, т. е. уменьшить
углы против расчета. Разумеется, из полученного результата нельзя
Рис. 11
сделать вывод, что трение умень-
шает жесткость пакета. Можно
лишь утверждать, что влияние
сил трения настолько мало, что
покрывается другими случайны-
ми влияниями.
Следует оговориться, что этот
вывод получен при малых углах
закручивания (порядка 10°),
влияние сил трения, безусловно,
будет сказываться при очень
больших углах, когда листы, за-
кручиваясь, будут взаимно обжиматься. Однако это может иметь
место лишь при углах, превосходящих 90°.
9. Испытание при высоких нагрузках. Для опыт-
ного изучения работы листовых торсионов при высоких нагрузках
были проведены испытания двух одинаковых моделей № 4 и № 15
из 5 листов 0,6x3,0 см, длиной 30 см. Первая испытывалась в глад-
ких губках, вторая — в рифленых. Задачей испытания было, во-пер-
вых, установление момента перехода пакета в пластическое со-
стояние и, во-вторых, выяснение характера разрушения.
Очевидно, предельный крутящий момент 7ИТ, отвечающий пере-
ходу пакета в состояние текучести, не может быть подсчитан по
формуле наибольшего напряжения по той же причине, как и для
одиночной полосы. Решение задачи о предельном состоянии стерж-
ня прямоугольного сечения, работающего на изгиб с кручением, нам
неизвестно. Поэтому мы ограничились ориентировочной теоретиче-
ской оценкой предельного момента исходя из следующих сообра-
жений.
198
Предельный крутящий момент для одиночной полосы, подсчи-
танный выше, равен 717 кгсм. Для пакета из 5 листов он будет
равен:
Л4«руч = 5717 = 3 ЬЪЪкгсм.
Однако достижение в каждой полосе состояния пластичности
за счет кручения, равносильное включению в каждом листе шарни-
ра текучести с осью, направленной вдоль листа, еще не дает свобо-
ды перемещения пакету в целом, если сопротивление листов изгибу
не исчерпано. Поэтому можно утверждать, что предельный момент
для пакета
Л4Т >3 585 кгсм.
Подсчитаем предельный момент по изгибу.
Если принять, что опорные сечения двух верхних и двух нижних
листов перешли полностью в пластическое состояние изгиба с
вертикальной нейтральной линией (средний лист на изгиб не рабо-
тает), то, как видно из рис. 11, опорный предельный изгибающий
момент каждой пары листов равен:
Л4"зг = а -26— • — = — ат.
1 т 2 2 2 1
Эти моменты создают опорные реакции
а реакции приводятся к крутящему моменту
докруч = Р ы = аг = 3'0--62'- 2 850 = 922 кгсм.
т т I т 30
Очевидно, предельный момент для пакета будет меньше суммы
обоих значений:
Л4Т < 3 585 -+- 922 = 4 507кгсм,
так как появление двух взаимно-перпендикулярных пластических
шарниров (продольного и поперечного) привело бы к появлению
в главных площадках напряжений выше предела текучести. Таким
образом, для предельного момента находим две границы:
3 585 < Мт < 4 507 кгсм.
Как уже сказано, предельный момент был получен эксперимен-
тально при испытании двух одинаковых моделей:
модель №4: Л4Т = 4 150кгсм\
модель № 15 : 7ИТ = 4 200 кгсм
в соответствии с установленными границами.
199
На рис. 12 дана диаграм-ма зависимости между углом и момен-
том для модели № 4.
После перехода в пластическое состояние пакеты оказываются
способными выдержать весьма высокую нагрузку. Модель № 4 раз-
рушилась при М = 20 000 кгсм, когда угол закручивания достиг
674°. Разрушение произошло от разрыва крайних листов у заделки
в растянутой зоне (рис. 13). Модель № 15 выдержала без разру-
шения предельную нагрузку, даваемую машиной — 30 000 кгсм,
закрутившись на угол 1080°. Различие в поведении обеих моделей
Рис. 13
объясняется тем, что первая была установлена в гладких губках,
а вторая —в рифленых, причем кромки листов во второй модели
срезались рифами, и концы листов значительно сдвинулись взаим-
но. По-видимому, появление этих сдвигов повело к уменьшению
изгибающих моментов в крайних листах и повысило разрушающую
нагрузку.
Таким образом, запас прочности, отнесенный к временному со-
противлению, оказывается очень высоким. Разумеется, при изго-
товлении листов из закаленной стали этого пластического резерва
прочности не будет, и предельная нагрузка для таких торсионов
будет исчисляться по данной в § 3 формуле наибольших напряже-
ний (16).
200
Подводя итоги результатам испытаний, мы считаем возможным
отметить, что соответствие между теорией и опытом оказалось
значительно более высоким, чем можно было ожидать от прибли-
женного расчета. Столь близкие к единице значения поправки
редко получаются при испытаниях даже тех конструкций, расчет
которых мы привыкли принимать за точный (например, изгиб ба-
лок круглого, а тем более двутаврового сечения). Ввиду этого мы
считаем принятые нами расчетные допущения вполне оправданны-
ми на опыте, а выведенные из них расчетные формулы полностью
подтвержденными экспериментально.
8. ИССЛЕДОВАНИЕ ЛИСТОВЫХ ТОРСИОНОВ
ПРИ БОЛЬШИХ ДЕФОРМАЦИЯХ
В № 6 «Трудов Академии» за 1948 г. в статье «Расчет листового
торсиона» был изложен общий метод расчета подвесок этого типа
на прочность и на жесткость. Статья эта вызвала ряд откликов,
свидетельствующих о проявленном конструкторами интересе к этой
системе подвески. Одновременно были высказаны пожелания о
проверке возможности применения выведенных автором расчетных
формул при больших деформациях. Учитывая это, автор провел
дополнительные теоретические и экспериментальные исследования
и изложил их в настоящей статье.
Необходимость в этих новых исследованиях вызвана тем, что
предложенный автором способ расчета листовых торсионов был
выведен ценой принятия ряда допущений, приемлемых лишь при
углах закручивания, не превышающих 30°. Опытную проверку
пришлось ограничить еще меньшими углами (порядка 10—12°), так
как при больших углах закручивания напряжения в образцах до-
стигали предела текучести.
Своей основной задачей автор считал проверку и уточнение за-
кона, связывающего момент и угол закручивания торсиона, так как
этим законом определяется по существу вся работа системы. Мы
начнем с исследования этого закона для изолированного листа
пакета.
1. РАСЧЕТ ИЗОЛИРОВАННОГО ЛИСТА. ПЕРВЫЙ СПОСОБ
Простейший способ расчета изолированного листа, входящего
в состав листового торсиона, основан на допущении о применимо-
сти к нему принципа раздельного рассмотрения деформаций изгиба
и кручения. Этот способ и был приведен в упомянутой статье. Здесь
мы дадим значительно более простой вывод уравнения деформации
листа.
Рассмотрим отдельный лист пакета толщины ft, ширины h и
длины /, ось которого отстоит от оси пакета на расстоянии г. Кон-
цы листа считаем защемленными. Пусть этот лист получил дефор-
мацию, связанную с взаимным закручиванием концов пакета на
угол В таком случае концевые сечения листа займут положения,
показанные на рис. 1.
202
Деформацию листа можно считать слагающейся:
а) из взаимного смещения опорных сечений на Л= 2r sin в
плоскости наибольшей жесткости листа;
б) взаимного поворота опорных сечений на угол 6 вокруг про-
дольной оси листа.
В пояснение такой трактовки предлагаем считать ось наиболь-
шей жесткости сечения листа совпадающей до деформации с на-
правлением смещения 8. Затем концы листа разводятся от началь-
о 6
ных положении на — каждый и поворачиваются в разные стороны
Ряс. 1 Рис. 2
Первая деформация вызывает плоский изгиб листа, причем
опорные моменты в плоскости наибольшей жесткости равны:
лл 6Е/« х
М, =------- д.
у Г2
Эти моменты показаны на рис. 2 векторами с двойным острием.
Опорные реакции в той же плоскости получают следующее выра-
жение:
л 12E/V А 24ЕД,г . 6
7? -- ----^6 =--------- sin----
/3 /3 2
Вторая деформация вызывает кручение листа, причем опорные
крутящие моменты будут равны:
м GM.
I ’
где /к—фактор крутильной жесткости прямоугольного профиля,
имеющий значение:
Поэтому
'-irt'-».'!)-
«,.«(1-0,6-Ц».
3/ \ h/
203
14*
Приближенность такого приема раздельного рассмотрения де-
формаций очевидна -из рис. 2, который показывает, что после де-
формации кручения опорные реакции R уже не будут лежать в
плоскости наибольшей жесткости листа.
Теперь составим уравнение равновесия, освобождая один конец
листа от закрепления и приравнивая момент приложенных к нему
реактивных усилий общему моменту М, вызвавшему деформацию:
М = М.. + Rr cos — =
Л 2
= -g^L/i_Q6 — )0 4--12£^<sin6,
3/ ’ й / Р
или, подставляя Л = ^-
у 12
Обозначим далее r = kb и учтем, что £^2,56:
М = — 0,6 -у) 6 + 7,5Л2 (-у)2 sin е1 (D
Наконец, учитывая взаимную близость sin 6 и 6, тем более что
второе слагаемое в скобках всегда в несколько раз меньше перво-
го, получим окончательно формулу:
Л1= -^-[(1-°.6-у) + 7’5лг('г)2]е’ (2)
дающую линейную зависимость М от б. Эта формула и была пред-
ложена автором в упомянутой статье.
2. РАСЧЕТ ИЗОЛИРОВАННОГО ЛИСТА. ВТОРОЙ СПОСОБ
Второй способ, более точный, хотя и приближенный, отличает-
ся от первого тем, что деформацию изгиба мы считаем приложен-
ной к первоначально закрученному листу, так что учитывается
меняющееся по длине листа положение главных осей сечения. При
этом деформации изгиба и кручения уже не рассматриваются раз-
дельно, но их взаимодействие все же учтено не полностью: мы учи-
тываем влияние кручения на изгиб, но оставляем без учета вторич-
ное воздействие изгиба на деформацию кручения. Иными словами,
эта последняя принимается независящей от изгиба листа.
Обращаемся снова к схеме (см. рис. 2). Из условия заделки
обоих концов и геометрической тождественности обеих половин
длины стержня следует, что эпюра изгибающих моментов кососим-
метрична, и в середине длины момент равен нулю. Разрезаем лист
в этой точке плоскостью, параллельной концевым заделкам. В этом
сечении будут действовать только поперечная сила Q = R и крутя-
щий момент причем сила Q направлена по глав-ной оси сече-
ния z.
204
Плоскость разреза не есть поперечное сечение листа, но прини-
мается нами за таковое ввиду малости угла наклона. Действитель-
но, наибольшее возможное смещение концов равно г |/ 2 при
О = — . При этом смещение среднего сечения относительно заделки
составит--—z, а тангенс угла поворота хорды листа будет равен
_ 2
- V2. . При рациональном конструировании, даже для крайнего
листа пакета, можно принять, что — < — < а потому г^-- <
I 21 30 ’ /
I т_г 1
< —. Но для угла, тангенс которого меньше —, можно смело
положить косинус равным 1, т. е. пренебречь тем, что проведенный
нами разрез не совпадает с попе-
речным сечением.
Теперь исследуем деформацию
изгиба закрученного листа,
относительную координату
У
7
вводя
х — I %,
повер-
нуты на угол относительно сред-
него сечения (рис. 3). Поэтому со-
ставляющие изгибающего момента
по главным осям будут равны:
МТ1 (£) = /?£ cos в£,
В сечении, отстоящем на
от середины, главные оси
Рис. з
Л4С (g) = Z?ZB sin 6^.
л
Эти моменты вызовут поворот сечения вокруг соответственных
осей на углы
М„ 1 „
Е/у
. _ 1 Л
и перемещения среднего сечения по направлениям осей
rf/c = /grf.pT,
df^ = -Rd4,
или
4Л= —l2cos6K
# =-^2sine5dg.
‘ tig
205
Полное перемещение среднего сечения в направлении силы /?,
т. е. оси z, будет равно:
V-z
Л= i(d/ccos6g-d/4sin6E)rfg,
б
или, подставляя выражения dfz, dfr и обозначая 7 = — ,
* ^z
’/з
f. = f g2(cos26g + T Sin2eg)d5.
' £/d
TT Г - О
Но смешение /,=rsin —, а потому получим после интегриро-
вания
W3 Гт-. 1
8Е7у [ 6
е
г sin —
2
откуда, обозначая
,,sin 0 cos в sine
6(6)- + ----V’
получим окончательно
/3
Отсюда легко найти зависимость между углом закручивания и
внешним моментом М для изолированного листа. Очевидно,
М = Мх + Rr cos ,
или, подставляя выражения Мх и R,
дд______________ ^Е1у)Г~ . _____sin 6_______
“ I /з у _|_ j
(т-още)
Подставим далее выражения
— ; Е = 2,50; r=kb;
12
G&h
М = р 1 — 0,6 0+2,5k2
sin О
-4—-(7-1)47(0)
О
Функция (7(0), входящая в это выражение, при 6=0 принимает
определенный вид, а потому точность ее вычисления при малых
.206
значениях 6 невелика. Ввиду этого разложим функцию в ряд
почленно и ограничимся членами 4-й степени:
Поэтому знаменатель второго члена в формуле момента примет
вид
или (с достаточной точностью для углов ДО б =
_1_[1 +О,15(Т- 1)6»].
Окончательно получаем уравнение деформации листа в виде
М = ГА _ 0 6 —16 + 7,5Л2 /—У--------------—---------1. (3)
з/ |Д h ) \ z ) 1 + о. 15 (Т - 1) е3 J
3. РАСЧЕТ ПАКЕТА
Мы получили три разные формы (1) — (3) уравнения, связыва-
ющего момент и угол закручивания изолированного листа. Эти три
формулы различаются только выражением второго слагаемого в
скобках и потому могут быть записаны в общем виде так:
м = -^- (!-°.6 y)® + 7’5^ (т)г/?(6)]’ (4)
где F(9) имеет три разных значения, занумерованных соответст-
венно трем уравнениям:
Г* (б) = sin в, F2 (б) = б,
F (6) =-------5*2®-----э
' l + 0,15(f — I) в2
причем у
Заметим сразу, что при малых углах все три выражения прак-
тически совпадают. Поэтому характеристика листа, построенная в
осях б, 7И, будет во всех трех случаях иметь общую касательную
в начале координат. Ясно, далее, что по уравнению (2) эта каса-
тельная совпадает с характеристикой на всем протяжении, так как
последняя — линейна; характеристики же по уравнениям (1) и (3)
будут постепенно отставать от касательной, проходя ниже ее,
207
причем характеристика 3 пройдет ниже характеристики /. Принци-
пиальная схема всех трех характеристик дана на рис. 4. На этом
рисунке показана еще одна прямая линия, отмеченная буквой k.
Она соответствует значению F = 0. Поясним ее смысл.
Нетрудно видеть, что первое слагаемое общей формулы (4)
выражает долю внешнего момента, идущую на скручивание листа,
а второе —долю, идущую на изгиб листа. Поэтому разница между
формулами (1), (2), (3) сводится к различной оценке роли изгиба.
Далее заметим, что формула (1), а тем более формула (2), дает
максимальную оценку возможной доли изгиба, так как при ее вы-
воде мы считали, что изгиб полностью совершается в плоскости
наибольшей жесткости листа. Полагая Г = 0, мы получим другую
предельную оценку, пренебрегающую изгибом и учитывающую
только работу листа на кручение. Этому предположению и отвечает
прямая k. Ясно, что истинная характеристика будет заключена в
вилке между прямыми 2 и k.
Однако при любой форме функции F/6) уравнение изолиро-
ванного листа позволяет перейти к уравнению пакета, состоящего
из i листов.
В этом случае момент, вызывающий закручивание пакета на
угол б, будет равен сумме моментов, необходимых для такой же
деформации отдельных листов, если только допустить что между
листами пакета нет сил взаимодействия.
Применяя для такого суммирования формулу (4), получим:
м = [(1 - °,6 -J-) /6 + 7,5 tfF (6) ].
Введем, как и в предыдущей работе автора, обозначение:
*. = !>= 2(т)2.
где В[ есть число, зависящее только от количества листов в паке-
те. Его можно легко найти непосредственным подсчетом или взять
из табл. 1.
208
Таблица I
i 4 5 6 7 8 9 10 12 14 16 18 20
Bi 5 10 17,5 28 42 60 82,5 143 227,5 340 484,5 645
После этого уравнение пакета представляется в общем виде:
М = ™ К1 -°>6 т)й + 7-5В- (тУг(6)] •
При подстановке соответственных значений F(6) получим
верхний предел момента
7И = -?-|(1-о'6т)/+7>5В-(тЛ0: <5>
нижний предел момента
M = _^L(l_0>6A)ie. (6>
Уточненное значение момента, отвечающее второму выводу,
гл = 171 _ 0,6 —) № + 7,5В,. I—V--—--------. (7>
31 L\ h) ‘\ I ) 1 + 0,15(7— 1)02
Выбор между формулами может быть сделан только на осно-
вании опыта. Характеристики пакета, построенные по этим форму-
лам, расположатся взаимно так же, как и характеристики отдель-
ного листа на рис. 4. Мы оставим без внимания характеристику па-
кета, получаемую из уравнения листа /, так как она практически
совпадает с характеристикой 5.
Необходимо отметить еще, что нижняя предельная прямая 6.
соответствующая чистому кручению, является асимптотой, к кото-
рой стремится при больших углах кривая 7. Это следует из того,
что при больших углах 6 второе слагаемое в формуле (7) стре-
мится к нулю. Таким образом, действительная схема характери-
стик пакета принимает вид, показанный на рис. 5. Мы видим, что
в начале координат кривая 7 касается верхней прямой, а с ростом
угла отстает от нее и приближается к нижней прямой асимптоти-
чески.
4. ОПЫТНОЕ ИССЛЕДОВАНИЕ ИЗОЛИРОВАННОГО ЛИСТА
Как уже было сказано, вопрос о выборе между формулами
(5) — (7) должен быть решен опытом. Однако и опытное решение
получить не так просто. Прежде всего все опытные результаты,
приведенные в первой статье автора, несмотря на многочислен-
ность их, не позволяют разрешить этот вопрос, так как при тех
величинах углов, которые были достигнуты в этих опытах, форму-
лы (5) и (7) дают практически совпадающие значения. Поэтому
пришлось ставить специальные опыты, стремясь к увеличению
209
углов закручивания. При этом нужно было подобрать параметры
пакета так, чтобы вторые слагаемые в формулах, выражающие
роль изгиба, получили возможно большую величину, потому что
только при этом условии можно было надеяться получить из опыта
указание, какая из формул ближе отвечает действительности. Но,
как видно из формул, для увеличения второго слагаемого следует:
а) увеличить число листов, так как множитель возрастает
в функции числа листов весьма быстро (эта возможность была ис-
пользована, и число листов было увеличено с шести при прежних
опытах до десяти);
б) увеличить отношение -у-, т. е. увеличить h или уменьшить I.
Однако оба эти пути повышают общую жесткость и напряжен-
ность пакета, т. е. препятствуют получению достаточно больших
деформаций в упругих пределах. Поэтому для достижения боль-
ших углов при заведомо упругой работе пакета пришлось пойти на
увеличение длины (с 60 до 100 и даже до 150 см), хотя этим по-
нижалась относительная величина спорного второго слагаемого в
формулах.
Это затруднение заставило нас произвести добавочную серию ис-
пытаний, а именно испытания изолированных листов.
Для этой цели был применен один из листов, приготовленных
для пакета, который при помощи концевых прокладок можно было
устанавливать в крутильную машину в различных положениях от-
носительно оси машины: по оси и со смещениями от оси, отвечаю-
щими положениям 1, 2, 3, 4 и 5 листов в пакете, считая от его оси.
Таким образом, значения k для разных позиций листа были та-
ковы:
№ позиции • - 0 1 2 3 4 5
k .........0 0,5 1,5 2,5 3,5 4,5
В нулевой позиции лист работал на простое кручение. С ростом
номера позиции возрастала и доля изгиба. Испытание листа в ну-
левой позиции позволило определить значение модуля сдвига. Он
оказался равным:
для листа / = 100см, G = 7,05-105кг см2;
„ „ I = 150 см, G = 7,38 -105 кг 'см2.
Оба значения, особенно первое, — меньше обычного для стали,
но так как они определены непосредственно из опыта, то и поло-
жены в основу дальнейших подсчетов.
На рис. 6—10 даны графики испытаний листа /=100 см в пози-
циях 1—5, а на рис. 11—15—то же, для листа /=150 см. Опытные
точки нанесены кружками, а сплошные линии соответствуют теоре-
тическому подсчету по уточненной формуле (3) с подстановкой
опытных значений модуля сдвига. Из графиков видно, что эта фор-
мула во всех случаях дает весьма удовлетворительное совпадение
с опытом. Следует заметить, впрочем, что различия между расчет-
210
1-я позиция
2li
212
ними значениями моментов, подсчитанных по формулам (2) и (3),
даже для наибольших углов, достигнутых при испытании, не пре-
восходят 2,5°/о, так что на основании этих опытов еще нельзя уста-
новить, которая из этих двух формул ближе к действительности.
5. ОПЫТНОЕ ИССЛЕДОВАНИЕ ПАКЕТА
Испытанию были подвергнуты два пакета из 10 листов каждый,
со следующими размерами:
длина в свету между захватами машины 1 = 100 см 150 см
ширина листов h= 6,3 см 6,25 см
толщина листов />=0,65 см 0,63 см
квадрат отношения ширины к толщине квадрат отношения длины к ширине 7= 94 (-К-251 98,5 576
модуль сдвига G = 7,05-105— 7,38-106 —
СМ2 см2
средний предел пропорциональности оп — 4 300 кг!см2
средний предел текучести от = 5 200 кг!см2
предел прочности ов = 9 100 кг! см2
Приведенные здесь средние механические характеристики полу-
чены из испытания пяти гагаринских образцов, вырезанных из ма-
териала листа. Сталь обладает значительной пластичностью и вы-
сокой прочностью, причем диаграммы показывают хорошо выра-
женную площадку текучести.
Концы листов, входящие в зажимы машины, были связаны
шпильками, обеспечивающими от взаимного сдвига листов в задел-
ках. Испытание производилось на крутильной машине мощностью
600 кгм. Углы измерялись при помощи двух лимбов, расположен-
ных вблизи заделок, так что замеренные по ним углы пересчитыва-
лись на полную длину пакета. Кроме того, отдельный лимб мень-
шей точности давал контрольную величину полного угла закручи-
вания.
Общий вид установки показан на рис. 16, а вид пакета в машине
до испытания — на рис. 17.
Графики испытания пакетов представлены на рис. 18 и 19. Опыт-
ные значения нанесены кружками, а теоретические, подсчитанные
по формулам (5) и (7), — сплошными линиями с теми же номерами.
Эти линии в пределах опытных углов выглядят обе прямолинейны-
ми, хотя только верхняя из них выражается уравнением первой сте-
пени. Пунктиром проведена прямая 6.
Из графиков сразу видно, что в обоих случаях опытные точки
располагаются между обеими теоретическими линиями, причем для
торсина /=150 см они лежат ближе к прямой 5, чем к уточненной
кривой 7. Таким образом, прямая 5, как мы и ожидали, переоцени-
вает изгибную жесткость пакета, но формула 7 ее недооценивает.
Это представляется несколько неожиданным.
Как же объяснить это несоответствие работы пакета с формулой
(7). если опыты с изолированными листами дали столь близкое сов-
213
падение с ней? Для объяснения приведем еще один характерный
подсчет.
Подсчитаем сумму опытных значений моментов при данном угле
6 для всех пяти позиций изолированного листа и удвоим ее. Полу-
Рис. -16
Рис. 17
ченные значения дадут опытные величины моментов для совокупно-
сти 10 листов, отличающейся от такого же пакета заведомым от-
сутствием сил взаимодействия между листами. Назовем эти значе-
ния Alio и сравним их с опытными значениями Mntполученными из
испытания целого пакета.
Эти данные приведены в табл. 2 и 3 вместе с теоретическими,
подсчитанными по формуле (5). Они обозначены М (5) и М (7).
214
Таблица 2
Моменты для торсиона I => 100 см
Угол б{ 12 18е 24 30°
М10 4 720 9 000 13 160 17 180
4 800 9 400 14 000 18 300 23 200
Л1(5) 5 040 10 080 15 120 20160 25 200
М(7) 4914 9 262 13 304 17 156 21 026
Таблица 3
Моменты для торсиона /=150 см
Угол 6° 12° 18е 24° зс 36° 42 48
2580 5 340 7 880 10460 12 960 15 400 18 140 20280
мп 2600 5 800 8 450 11 300 14000 16 600 19 400 21 900
М5) 2 800 5600 8 400 11 200 14 000 16 800 19 600 22 400
М(7) 2 780 5 400 7920 10 400 12 840 15 350 17 850 20300
Изучение этих таблиц приводит к следующим выводам:
1. Работа пакета из 10 листов отличается от работы совокупно-
сти 10 изолированных листов, причем пакет обладает на 6 8°/о бо-
лее высокой жесткостью.
215
2. Работа совокупности 10 изолированных листов весьма
близко отвечает теоретической картине, выраженной формулой (7),
но резко отличается от данных формулы (5).
3. Работа целого пакета соответствует в большей степени под-
счетам по формуле (5), чем по формуле (7).
Это означает, что при кручении листового торсиона между его
листами возникают силы взаимодействия, повышающие его общую
жесткость. По этой-то причине формула (7), выведенная для изо-
лированного листа, хорошо отвечает работе такого листа, но недо-
оценивает жесткость целого пакета.
Вопрос о вероятной природе этих сил взаимодействия рассмот-
рен ниже. Пока отметим только практически важный вывод: упро-
щенная формула (5), предложенная автором в 1948 г., дает не худ-
шее, а в некоторых случаях и лучшее соответствие с опытом, чем
более точная и сложная формула (7).
Существенным оказывается также факт сохранения линейной
зазисимости между моментом и углом закручивания для больших
деформаций. В описанных выше опытах, иллюстрированных рис.
18—-19, линейная зависимость прослежена до углов порядка 50°.
Дальнейший рост углов привел бы к текучести материала, как вид-
но из приведенного ниже описания опыта при высоких нагрузках.
Но, как известно, упругие деформации при разгрузке из любого
состояния следуют начальному закону Гука. Поэтому важным под-
тверждением справедливости (вернее, достаточной точности) ли-
нейной зависимости оказывается то, что при разгрузке из сильно
закрученного состояния (момент 450 кати, угол закручивания 300°)
пакет длиной 150 см показал остаточный угол 21 Г, или 89:450=
0,2° на 1 кгм, т. е. почти столько же, как и при начальном загруже-
нии: 0,218° на 1 кгм по опыту и 0,214° по формуле (5). Как будет
показано ниже, небольшое расхождение вполне покрывается неко-
торым различием в показании лимбов разного устройства, по ко-
торым брались отсчеты при нагружении и разгрузке.
6. О СИЛАХ ВЗАИМОДЕЙСТВИЯ МЕЖДУ ЛИСТАМИ
Опыт доказал с несомненностью, что между листами пакета при
его закручивании возникают силы взаимодействия. Что это за си-
лы? Силы трения, или силы взаимного нажатия листов? Не отрицая
наличия сил трения, мы считаем, что основную роль играют силы
взаимного нажатия.
Прежде всего можно показать, что при тех теоретических зна-
чениях реакций, изгибающих и крутящих моментов, которые были
найдены выше при выводе формулы (3), стрела радиального выги-
ба листа будет меньше, чем г(1 —cos-^-),t. е. изогнутую ось листа
нельзя наложить на поверхность цилиндра с радиусом г. Контакт
будет иметь место только в средней точке оси, а концы оси будут
отставать от поверхности цилиндра. Следовательно, для создания
контакта по всей длине деформированный лист пришлось бы до-
216
полнительно загрузить поперечной нагрузкой, прижимающей листы
друг к другу. Эти силы и вызовут добавочный изгиб каждого листа
в радиальном направлении, обращенный выпуклостью от оси
пакета.
Рис. 20
Таково должно быть положение вещей в пакете, поскольку ось
каждого листа на всем протяжении должна сохранять постоянное
расстояние от оси пакета.
В существовании этого дополнительного изгиба (роль которого,
очевидно, повышается с ростом угла закручивания) мы могли убе-
диться на опыте. Оба испытан-
ных торсиона были подвергнуты
высокому за гружению, значи-
тельно превышающему упругую
стадию работы листов. Для тор-
сиона /—100 см угол закручива-
ния достиг 133° при моменте
44 000 кгсм, а для торсиона /=
= 150 см — 300° при моменте
45 000 кгсм. После разгрузки об-
наружилось, что листы по длине
пакета взаимно разошлись, рас-
крыв щели и сохранив остаточ-
ный выгиб выпуклостью от оси
пакета. Начальная высота сече-
Рис. 21
ния пакета в обоих случаях со-
ставляла 65 мм\ после разгрузки она возросла до 90,5 мм у пакета
длиной 100 см и до 78,2 мм для пакета длиной 150 см. Ясно, что
такой остаточный выгиб невозможен у изолированного листа, так
как у него во всех стадиях работы в середине длины находится ну-
левая точка эпюры моментов, и остаточная деформация может
иметь только S-образную форму. Поэтому обнаруженная на опы-
те остаточная деформация могла возникнуть только от сил взаим-
ного нажатия листов. На рис. 20 даны замеры остаточного разду-
тия торсиона /=150 см по длине.
Могут ли эти силы повысить общую жесткость пакета? Нетруд-
но показать, что могут. Обратимся к рис. 21. Из условия симметрии
217
следует, что равнодействующая сил нажатия на лист направлена
по биссектрисе центрального угла; таково же будет направление
дополнительных реакций D (на схеме показан крайний лист пакета,
испытывающий одностороннее нажатие от нижележащего листа).
Условие равновесия даст
М = Мх + Rr cos + Dr sin ,
тогда как нами ранее были учтены только два первых члена правой
части. Отсюда видно, что при данном угле в общий момент будет
больше, чем следовало по нашим выводам, т. е. жесткость пакета
превышает жесткость совокупности изолированных листов. Ясно,
что наличие этой дополнительной деформации внесет изменения во
всю картину работы пакета, вызывая снижение крутящих моментов
и увеличение реакций, т. е. усиливая относительную долю изгиба в
общей деформации.
Этим и объясняется, что формула (5), заведомо переоцениваю-
щая роль изгиба в работе изолированного листа, даст столь близкое
соответствие с опытом для целого пакета, в то время как формула
(7), более точно оценивающая изгиб в изолированном листе, недо-
оценивает его в работе пакета.
Но это соответствие формулы (5) с опытом для пакета прихо-
дится теперь рассматривать, как соответствие до некоторой степени
случайное, являющееся следствием удачной взаимной компенсации
неточностей, допущенных при ее выводе. Тем самым формулу (5)
надо расценивать как формулу наполовину эмпирическую, оправ-
данную опытом, несмотря на ее нестрогость, в определенных гра-
ницах. Оценим эти границы.
Формула (5) имеет вид
М = ; (1 _ 0.6 JL.) i + 7,5В, (А-)8] 6. (5)
Во всех опытах эта формула дала точное соответствие при ма-
лых углах. Следовательно, множитель перед скобкой (общий для
формул (5) и (7) может не вызывать сомнений. Первый член в
скобках, выражающий скручивающий момент, в реальных условиях
(особенно для пакетов квадратного сечения) будет иметь достаточ-
но стабильную величину, близкую к той, которую имели испытан-
ные торсионы.
Второй член, оценивающий долю изгиба, в наших опытах имел
величину.
торсион I = 100 см.............7,5В, ~ 2>46
торсион /= 150 см......... . • 7,5В; =
при одинаковой величине первого члена (1—0,6 -у-р = 9,40.
Таким образом, формула (5) дает хорошее соответствие с опы-
том при достаточно широком диапазоне изменения второго члена.
218
Ее точность, очевидно, будет повышаться по мере убывания этого
члена. Но приведенное выше значение его 2,46 отвечает условиям:
i=10, ib = h, — =16.
h
Поэтому мы считаем себя вправе утверждать, что формула (5),
безусловно, даст высокое соответствие с опытом при следующих
условиях:
а) квадратное сечение пакета;
б) число листов не менее десяти;
в) длина пакета превышает ширину листа по крайней мере в
15 раз.
При этих условиях применимость формулы (5) не ограничена
величиной угла закручивания (разумеется, при упругих деформаци-
ях). Впрочем, автор убежден, что область ее применимости значи-
тельно шире тех пределов, в которых она проверена на опыте.
7. НАПРЯЖЕНИЯ И ПРОЧНОСТЬ
Поскольку опыт оправдал применимость формулы (5) при боль-
ших деформациях, встает естественный вопрос о применимости вы-
веденных на ее основе выражений расчетных напряжений. Вопрос
этот имеет значение только для больших углов закручивания.
Мы подойдем к этому вопросу исходя из очевидного теоретиче-
ски и подтвержденного опытом положения, что истинная характе-
ристика торсиона заключена между двумя прямыми с уравнениями
М2=^|1 — 0,6 —1«6, (6)
3/ ' h /
причем всегда
Как было указано, М2 отвечает работе листов только на круче-
ние, и потому соответственный крутящий момент будет верхним
пределом крутящего момента в листах. ЛЛ отвечает работе на кру-
чение с наиболее интенсивным изгибом, а потому соответственный
изгибающий момент будет наибольшим возможным, а крутящий—
наименьшим. Иными словами, истинная характеристика торсиона
взята нами в вилку.
На основании этого можно и для напряжений установить пре-
делы. При этом, однако, надо помнить, что расчет на прочность
требует установления верхнего предела напряжений, а поэтому за-
ключение напряжения в двусторонние пределы не обязательно.
Рассмотрим опасные точки сечения наиболее напряженного
крайнего листа (рис. 22).
В точке 1 возникнут касательные напряжения от кручения, кото-
рые будут наибольшими при расчете по формуле (6), так как кру-
219
тящий момент при этом состоянии наибольший. Нормальных напря-
жений в точке 1 не учитываем, так как вывод формулы (5) пред-
полагает изгиб листа в плоскости наибольшей жесткости.
В точке 2 возникнут нормальные напряжения от изгиба, которые
будут наибольшими при расчете по формуле (5), и касательные
напряжения от кручения, которые следует определять из той же
формулы.
У Наибольшее касательное напряже-
ние, отвечающее этой комбинации, надо
1 сопоставить с касательным напряжени-
р I 12 ем в точке 1. Наибольшее из двух напря-
I______ т 4 жений даст заведомый максимум и бу-
дет расчетным. Истинный максимум на-
р,ис- 22 пряжения будет ниже наибольшего из
этих напряжений и, по всей вероятности,
заключен в вилке между ними.
Расчет основываем на третьей теории прочности.
Если листы работают только на кручение, то крутящий момент
в одном листе определится из условия
i
а наибольшее касательное напряжение в точке 1 будет равно:
где
откуда
з(1 + 0,6^
37И (1 + 0,бу-
т
(8)
Если листы работают на изгиб с кручением по формуле (5), то
крутящий момент в листе равен:
л I
Л-0,6 —V
31 I h )
Подставляя из формулы (5) значение —получим
(9)
i+ 7,5В,
М =
220
Касательное напряжение в точке 2 можно определить из
2 4 U4 4 trh \ ' ft J
Изгибающий опорный момент найдем из условия
и, подставляя выражение для Мх, а также £=2,56, /у= —,r=kb
6 0, х 12
и sin —(в запас прочности), получим
м _ 15 . Мх
Нормальное напряжение в точке 2 будет равно:
г_____________ Mv __ 6Л/У _ 45 k Мх
~ ~ЬЧ ' 6_ь_ ’
’ h
Наибольшее касательное напряжение в точке 2 будет
ts= 4'1/Л(О2)2 + 4«)2 =
= А.---------------./ 25(^)! + (1-0,Зб4У ’
4 Ы У 1
или, заменяя в запас прочности второе слагаемое под радикалом
на единицу,
Наибольшее из напряжений т2, выражаемых формулами (8)
и (10), и будет расчетным. Значение Мх берется по формуле (9).
Дальнейшее исследование проведем для случая торсиона с
квадратным сечением, для которого ih^b, А>=-^—.Тогда формулы
(8) и (10) примут вид:
= -тг(' + °.6). (Н)
й3
* 8 (i_0,6)_L+7.5BiA V Umz-d/
h I
221
Очевидно, то напряжение будет наибольшим, для которого
множитель при — будет иметь наибольшую величину. Обозначим
множители:
С, = 3 (/ + 0,6); ______________
/2й-1)
(13)
45
8
(»-
0.6) —— + 7,5В/
' h I
Рис. 23
Тогда
max т =Стах (14)
№
будет заведомо верхним преде-
лом касательных напряжений.
Значения С, зависящее от чи-
сла листов i и от отношения дли-
I
ны к ширине —, можно вычис-
лить раз навсегда. В табл. 4 да-
ны значения Стах, причем спра-
ва от жирной черты максималь-
ными оказываются значения Сг,
а слева Ср
Из табл. 4 видно, что зависи-
мость С от отношения при
h
данном i незначительна. Если на-
нести на график наибольшие
значения С в функции i, то ока-
жется, что эти максимумы рас-
полагаются почти точно по пря-
мой линии, определяемой урав-
нением (рис. 23)
Таблица 4
Значения Стах
6 8 10 12 14 16 18 20
10 19,6 27,5 35,5 42,6 49,3 54,5 59,0 64,3
15 19,6 25,8 31,8 41,7 50,3 58,0 66,1 73,1
20 19,6 25,8 31,8 38,8 47.7 56,0 64,5 73,4
25 19,6 25.8 31,8 37.8 45,0 53,4 62,0 71,2
30 19,6 25.8 31,8 37,8 43,8 50,5 59,0 67,5
222
Поэтому, идя в запас прочности, можно пренебречь влиянием —
h
и вести расчет по формуле
т < 3,8 (/
3 \ Л/
4 / Л3
(15)
Автор рекомендует эту формулу для ориентировочных подсчетов.
Более точные результаты даст применение формулы (14) и таблич-
ных значений С. Формула (15) должна заменить собой данную ав-
тором в первой статье формулу1, в которой было принято С = 3.5/.
Расхождение между прежними и новыми выражениями невелико,
но при большом числе листов новая формула дает более надежный
максимум.
Проведенные нами испытания торсиона при высоких нагрузках
позволяют проверить общую прочность пакета и сравнить ее с тео-
ретической. Так как материал листов обладает значительной пла-
стичностью, то предельным состоянием будет не разрушение тор-
сиона, а переход в пластическое состояние.
Подсчитаем величину момента, при которой в крайних листах
появятся напряжения текучести. Для торсиона 1= 150 см имеем:
1 = 10, — =24, Й = 6,25С1И, а, = 5200 —.
’ h см2
Находим из табл. 4 значение С = 31,8 и подставляем в форму-
лу (14)
Л1Т > =---------— = 20 000 кгсм.
С 31,8
При испытании пакета были замерены следующие приросты
угла закручивания на ступень загружения:
Таблица 5
м == 25 50 75 100 125 150 175 200 225 250 кгм
Д6 = 5,4° 5,5° 5,5° 5,2° 5,6° 5,5° 5,4° 5.8° 6,2°
При следующей ступени нагружения М = 250 кгм прирост угла
составил 8,6°, а нагрузка начала сдавать — верный признак наступ-
ления текучести. Но из табл. 5 видно, что появление фибровой те-
1 См. формулу (-27) на стр. 58 «Труды Академии», сборник № 6 за 1948 г.
223
кучести должно было иметь место при моменте между 200 и
225 кгм, а это близко отвечает расчетным данным.
Отсюда следует, что определение несушей способности торсио-
на по формулам напряжений, приведенным выше, дает занижен-
ное по сравнению с действительностью значение, т. е. эти формулы,
как и было отмечено, идут в запас прочности.
Наступление полной текучести пакета должно следовать за
исчерпанием способности листов сопротивляться скручиванию. Пре-
дельный момент для листа найдем по формуле
м = lh —Ь-}± = (б ,25 - = 3 140 кгсм,
пред 2 \ 3/2 2 \ 3/2
известной из теории пластичности. Следовательно, предельный мо-
мент для пакета должен быть не менее 31 400 кгсм.
На рис. 24 приведен график поведения торсиона 1= 150 см при
высоких нагрузках. Мы видим, что диаграмма лишена площадки
текучести, хотя материал листов при растяжении такую площадку
дает в ярко выраженной форме. Поэтому предельный момент нель-
зя определить достаточно точно. Но из графика видно, что расчет-
ное значение предельного момента по кручению соответствует до-
вольно близко моменту, при котором тангенс угла наклона диаг-
раммы становится минимальным.
На диаграмме показана линия разгрузки, о которой уже гово-
рилось выше. Она идет по прямой, несмотря на то, что торснон
при этом уже сильно скручен, и работа отдельных листов очень от-
личается от наших расчетных предпосылок.
На рис. 25 дано .изображение торсиона в машине при достиже-
нии наибольшей нагрузки М = 45000 кгсм. Ввиду опасений за
безопасность точных лимбов, установленных на торсионе, которые
могли повредиться в случае внезапного, непредвиденного разруше-
ния торсиона, .испытание при нагрузках свыше 33000 кгсм велось
224
без этих лимбов. Они были сняты, а углы замерялись машинным
лимбом меньшей точности, но зато дававшим полную величину уг-
ла закручивания, тогда как установочные лимбы замеряли угол
только на длине установки. Эти углы пересчитывались на полную
длину по условию пропорциональности. Сравнение показаний об-
наруживает, что машинный лимб давал значение угла на 5—8%
большее, чем пересчет по показаниям установочных лимбов, при-
чем эта разность постепенно уменьшается при увеличении углов.
Возможно, это объясняется тем, что
в начальных стадиях работы, когда
листы работают интенсивно на из-
гиб, условие пропорциональности
угла длине не имеет места.
Как бы то ни было, наклон
прямой разгрузки, определенный
машинным лимбом, надо сравни-
вать с наклоном прямой загруже-
ния, измеренным тем же лимбом.
Это сравнение показывает точное
совпадение обоих наклонов, под-
тверждая этим справедливость ли-
нейного закона связи момента с уг-
лом при любых величинах дефор-
маций и совпадение этого закона с
тем, что дает формула (5).
8. ЗАКЛЮЧЕНИЕ
Опытное и теоретическое иссле-
Рис. 25
дование листовых торсионов при
углах, доходящих до 60°, позволяет
сделать следующие практические
ВЫВОДЫ.
1. Работа пакета отличается от совокупной работы изолирован-
ных листов наличием сил взаимного нажатия листов, возрастаю-
щих вместе с углом закручивания и повышающих жесткость па-
кета.
2. При / >8иу> 15 пакеты квадратного сечения следует
рассчитывать на жесткость и прочность по формулам
л ЗЛШ3
и =---------------------------f
Gh' Г(» - 0,6) + 7.5В(
„ М
х с -—,
й3
где В{ и С даются в табл. 1 и 4. Эти формулы применимы при лю-
бых величинах углов до предела упругости.
15 С. А. Бернштейн
225
Мы считаем, что дальнейшее уточнение теоретического расчета
листового торсиона было бы бесцельным ввиду невозможности
предусмотреть расчетом два обстоятельства:
а) опыт показал, что значения модуля сдвига для листово-
го материала гораздо менее стабильны, чем для обычных круглых
образцов, и потому без опытного определения этого модуля для
данной партии листового материала расчет не может обеспечить
высокой точности результатов;
б) и характеристика жесткости, и величины напряжений при
больших деформациях существенно зависят от степени начальной
правки листов, т. е. от плотности их взаимного прилегания, которую
невозможно учесть расчетом.
9. ОБОБЩЕНИЕ ОКТАЭДРИЧЕСКОЙ ТЕОРИИ
ПЛАСТИЧНОСТИ
В настоящее время наибольшим распространением среди тео-
рий пластичности (прочности) пользуется теория энергии формо-
изменения или, что то же, теория октаэдрических касательных на-
пряжений. Ее особенностью является, как известно, неучет нор-
мального октаэдрического напряжения. Кроме того, в основе этой
теории лежит общее для большинства теорий прочности условие
Сен-Венана о том, что предельное значение решающего напряже-
ния (в данном случае октаэдрического касательного) есть величи-
на постоянная для данного материала и не зависит от вида напря-
женного состояния.
Автор считает, что оба эти условия идут не на пользу данной
теории пластичности, и имеет в виду изложить свои соображения
о создании более общей октаэдрической теории прочности
(пластичности), свободной от обоих ограничений. Однако предва-
рительно считаем целесообразным несколько детальнее углубить-
ся в анализ геометрической и физической сущности октаэдрических
напряжений, чем это обычно делается, чтобы привыкнуть видеть
в них не только формальные образы тензорного исчисления.
§ 1. НАПРАВЛЕНИЕ ОКТАЭДРИЧЕСКОГО КАСАТЕЛЬНОГО
НАПРЯЖЕНИЯ
Начнем с уточнения вопросов, связанных с положением октаэд-
рических площадок. Как известно, октаэдрическими площадками
называются площадки, равнонаклоненные ко всем трем главным
площадкам. Если представить себе куб, ориентированный по глав-
ным площадкам (будем его называть «главный куб»), то четыре
октаэдрические площадки срежут четыре его верхних угла, остав-
ляя на гранях следы под углом 45° к ребрам (рис. 1), подобно ме-
таллическим оковкам на углах сундука. Четыре нижних угла бу-
дут срезаны такими же четырьмя площадками, попарно совпадаю-
щими с верхними, а потому действительно различных октаэдричес-
ких площадок будет только четыре.
Хотя такое представление октаэдрических площадок является
достаточно наглядным, но полезно усвоить и другое геометричес-
15* 227
кое представление о них: октаэдрические площадки нормальны к
диагоналям главного куба (рис. 2).
Теперь перейдем к вопросу о направлении октаэдрического ка-
сательного напряжения. Обозначим:
рокт —полное октаэдрическое напряжение;
сокт—нормальное октаэдрическое напряжение;
токт —касательное октаэдрическое напряжение;
сз—главные напряжения.
Рис. 3. Директриса октаэдрических
напряжений
Рис. I. Положение
октаэдрических
площадок
Рис. 2. Октаэдри-
ческая площадка
перпендикулярна
диагонали главного
куба
Октаэдрические напряжения определяются известными форму-
лами:
Рокт= -7=/ + + ;
V 3
°окт= + 32 + °з);
Токт = "у — Д2)2 + (С2 — *3)2 + (С3 — °1)2-
Направление сотк совпадает с нормалью к октаэдрической
площадке, направляющие косинусы которой равны между собой:
1=т=п= — р потому оно вполне определено. Но направле-
]/ 3
ния токт, и стало быть рокт, остаются неизвестными. Для их на-
хождения проведем нормаль N к плоскости октаэдрических напря-
жений оокт, токт, лежащую в октаэдрической площадке (рис. 3),
и обозначим направляющие косинусы этой нормали через /0, т°, п0.
Условие взаимной перпендикулярности двух плоскостей (октаэд-
рической площадки и плоскости напряжений) выразится формулой
О = //0 + -|- пя0 = —1—(Zn + /и0 4- n0),
откуда ]/ з (1)
Zo 4~ /ио + ло = 0.
Далее, проекция полного октаэдрического напряжения рокт на
нормаль N также равна нулю. Составим и приравняем нулю сум-
228
му проекций на N усилий в трех главных площадках тетраэдра:
О = (cxZ) /0 + (с2т) т0 + (osn) и0 = —(ог/0 + J- с3и0),
V 3
откуда
ci4 + С2^о + С3«0 = °- (2)
Уравнений (1) и (2) вместе с условием
Z + 'nl + n^l (3)
достаточно для определения /о, то, по.
Исключим из уравнения (1) величину п0:
п0 = — (10 + т0)
и подставим это значение в уравнение (2)
*14 + С2^0 — °3 (/о + ™о) = О
ИЛИ
4 (С1 — сз) — то (сз — *г) = О,
откуда
и, следовательно,
al „ X „ ™ °2-с3 °1-°2
о ‘ ^о) - ' ^0 ^0 — ^0 -
Подставим эти выражения в условие (3)
1
откуда найдем значение т0:
pg —
т0= _____________________
У (°1 — Ог)3 + (с2 — Рз)3 — (°з
где т2 — — (о3 —Oj). Обозначая аналогично
сокт
два остальных
2
3
экстремальных касательных напряжения:
и = у- (с2 — °з); Ч = -j- (°i — °г)
и применяя круговую перестановку индексов, получим оконча-
тельно
t 2 ?! 2 ?2
---Г ‘ ’ т°~~ 3 ’ ? ’
о токт о токт
Знаки экстремальных касательных
мулах мы будем определять исходя
нумеров главных напряжений 1, 2, 3.
"о=Т
•С2
токт
(4)
напряжений в этих фор-
из циклического порядка
229
Формулы (4) определяют направляющие косинусы нормали N,
лежащей в октаэдрической площадке и перпендикулярной окта-
эдрическому касательному напряжению. Назовем эту нормаль
«октаэдрической директрисой». Найдя ее положение в октаэдриче-
ской площадке, мы будем знать и направление токт, которое пер-
пендикулярно директрисе.
Рассмотрим некоторые примеры.
I. РАСТЯЖЕНИЕ (рис. 4)
Главные напряжения: 4 — 0; с2 = с3=0. Экстремальные каса-
тельные напряжения: '4=0; Т2=тз~ ~ Октаэдрическое касатель-
Рис. 4. Направление токт в растяну-
том стержне
! 0С6 (ff
Рис. 5. Конус
токт в растяну-
том стержне
/2 г
ное напряжение токт=—— а. Следовательно,направляющие косину-
сы директрисы:
Первое условие показывает, что директриса перпендикулярна
ochoj, а из условий то=по=—— следует, что она образует одина-
V 2
ковые углы ±45° с осями о2 и сз - Из чертежа видно, что этим ус-
ловиям удовлетворяет линия аб пересечения октаэдрической
площадки абв с поперечным сечением стержня. Октаэдрические
касательные напряжения перпендикулярны директрисе аб.
Совокупность октаэдрических площадок в растянутом стержне
образует семейства касательных плоскостей к конусам, оси
которых параллельны оси стержня. Октаэдрические касатель-
ные напряжения направлены по образующим этих конусов
(рис. 5).
<230
Хотя следы октаэдрических площадок на боковой поверхности
стержня совпадают со следами площадок наибольших сдвигов, но
ясно, что октаэдрические напряжения не вызывают сдвигов вдоль
этих следов; такие сдвиги могут быть вызваны только действием
экстремальных касательных напряжений.
2. СЛУЧАЙ РАВЕНСТВА ДВУХ ГЛАВНЫХ НАПРЯЖЕНИЙ
Рис. 6. Направление}
тОкт в сферической
оболочке
Если на заданное напряженное состояние наложить всесторон-
нее растяжение или сжатие, то направление токт не изменится.
Это следует из того, что при таком наложении меняется только
ооКт . Поэтому направление т0КТ, найденное
для случая одноосного растяжения, сохранит-
ся при наложении всестороннего растяжения.
При этом все три главных напряжения будут
в общем случае отличны от нуля, но два из
них будут иметь одинаковую величину:
N I
°1 = — “Г °о! С2 = С3 = С0-
г
- Л
Если, в частности, о0 =------, то = 0;
F
N
°2 =сз=-----> и мы получим случаи сжатого
F
сферического тонкостенного сосуда. С
точки зрения октаэдрических касательных напряжений эта задача
эквивалентна простому растяжению, а случай растянутого сфери-
ческого сосуда эквивалентен простому сжатию.
При любом' напряженном состоянии такого типа директриса
составляет углы +45° с направлениями обоих взаимно-равных
главных напряжений и нормальна к третьему главному напряже-
нию.
Случай сферического сосуда при растяжении изображен на рис. 6.
3. ЧИСТЫЙ СДВИГ
В этом случае == — с2 = + о, с8 = 0;
Поэтому направляющие косинусы директрисы равны:
Директриса образует одинаковые углы с осями и с . Можно
показать, что она является высотой аг октаэдрического треуголь-
ника обе, основание бв которого лежит в плоскости нулевого глав-
ного напряжения (рис. 7).
231
Действительно, если сторона куба рвна 1, то
ав = бв = аб = \г 2 ; вг = ’>
аг = V^(oe)2—(вг)2= j/^ 2 — -±- = -|- -
Рис. 7. Направление тОкт при
чистом сдвиге
Рис. 8. Направление ттах при
чистом сдвиге
Опустим из точки г нормаль
нить, что она пересечет ребро в
на ребро куба ад\ нетрудно по-
точке £, лежащей посередине вы-
1
2
соты, так что ае=
. Поэтому
cos (аг, ае) = ~
аг
-ч/-=^=.
2 2
Такова же величина косинуса угла между директрисой и го-
ризонтальным ребром куба аж. Поэтому третий косинус (угла
директрисы с ребром вд) равен:
и требовалось доказать.
2
- /г ’ что
Касательные октаэдрические напряжения перпендикулярны
директрисе, т. е. параллельны стороне бв, лежащей в незагружен-
ной главной площадке. Эта сторона в скрученном стержне совпада-
ет с поперечной или продольной риской на поверхности, и потому
сдвиги вдоль этих рисок могут вызываться как экстремальны-
ми, так и октаэдрическими напряжениями (рис. 8).
Наложим на чистый сдвиг всестороннее растяжение с напряже-
нием о. Тогда
ох = с -р о = 2о; с2 = — а + с = 0; с3 — 0 + о = с.
Это состояние отвечает тонкостенному растянутому цилиндри-
ческому резервуару, у которого ось о совпадает с продольной
осью, а ось о направлена по радиусу. Построение показано на
232
рис. 9. Следы октаэдрических площадок, как и следы площадок
сдвига, образуют на боковой поверхности два семейства винтовых
линий под углом ±45° к образующей. Однако сдвиги вдоль этих
линий могут вызываться только экстремальными, но не октаэдри-
ческими напряжениями, как видно из рис. 10.
Рис. 9. Направление токт
в цилиндрическом сосуде
Рис. 10. Направление ттах в ци-
линдрическом сосуде
Из этого анализа направлений октаэдрических касательных
напряжений можно сделать вывод, что в общем случае эти напря-
жения не могут быть причиной появления линий текучести на
поверхности стержня, и потому неправильно расценивать октаэд-
рические напряжения как фактор разрушения. Этим фактором в
действительности могут быть только экстремальные касательные
напряжения. К этому вопросу мы еще вернемся в дальнейшем.
§ 2. ОКТАЭДРИЧЕСКИЕ ДЕФОРМАЦИИ
Мы уже указали, что нормалью к октаэдрической площадке
является диагональ главного куба. Вычислим удлинение такой
диагонали.
Рассмотрим прямоугольную призму, ось которой совпадает с
диагональю главного куба; торцовые грани—-с октаэдрическими
площадками, а боковые грани имеют произвольную ориентировку,
причем в них действуют нормальные напряжения с' и с"(рис. 11).
Касательных напряжений по граням учитывать не будем, так как
они не влияют на удлинения ребер призмы.
Сумма нормальных напряжений в трех взаимно-перпендику-
лярных площадках равна сумме главных напряжений, т. е. утроен-
ному нормальному октаэдрическому напряжению
°окт + °' + Q" = 3°окт,
откуда
d + С" — 2^окт»
16 С. А. Бернштейн
233
т. е. сумма нормальных напряжении в двух площадках, перпенди-
кулярных к октаэдрической и перпендикулярных взаимно (парал-
лельных диагонали главного куба), равна удвоенному нормально-
му октаэдрическому напряжению.
Удлинение вдоль оси призмы, или октаэдрическое удли-
нение, выразится
£окт= [°ОКТ Р (с с )]
Рис. 11. Призма, построенная Рис. 12. Сдвиг призмы
на диагонали главного куба
Таким образом, удлинение диагонали главного
куба пропорционально нормальному октаэд-
рическому напряжению.
Очевидно, удлинения всех четырех диагоналей всегда равны
между собой. При состояниях всестороннего сдвига (оокт — 0)
длина диагонали остается постоянной.
Перейдем к деформациям сдвига. Заменим в выражении т0КТ
разности главных напряжений на экстремальные сдвиги:
%КТ= -у V(’l — °г)2 + (°2 — Сз)2 + (°3 — °1)2 =
= З--,* VOh - *з)2 + (з2 - е3)2 + (е, - Ч)2 =
= = оТоК1>
откуда октаэдрический сдвиг
-ri + ii+т!.
или
2 /-------------
Токт = -у у т? + т|+тг| •
234
Геометрический смысл октаэдрического сдвига можно понять,
исследуя деформации призмы, которую мы рассмотрели выше.
Повернем ее вокруг продольной оси так, чтобы октаэдрическое
касательное напряжение в торцовых гранях было перпендикулярно
одному из ребер, например АВ (рис. 12). Иными словами, пусть
ребро АВ есть директриса для т0к7. По закону взаимности каса-
тельное напряжение т' в грани ACEF может быть направлено
только параллельно напряжению токт. Этим определяется направ-
ление составляющих т'/соктв грани A BCD.
Призма испытывает двойной сдвиг от напряжений т' и токт. Но
первый сдвиг, вызывая искажение (перекос) сечения призмы, не
изменяет направления ее оси. Напротив, второй сдвиг искажает
боковую грань ACEF и вызывает поворот оси призмы на угол т0КТ,
Итак, октаэдрический сдвиг равен углу пово-
рота диагонали главного куба.
Отсюда следует, что угол поворота диагонали
главного куба пропорционален касательному
октаэдрическому напряжению.
При всестороннем растяжении или сжатии диагональ куба не
поворачивается, а только изменяет длину, и главный куб сохраняет
кубическую форму.
При всестороннем сдвиге диагональ главного куба не изменяет
длины, но поворачивается, *и куб деформируется в параллелепипед.
В общем случае напряженного состояния деформация всегда
может быть сведена к удлинению (укорочению) и повороту
диагоналей главного куба.
При таком чисто геометрическом подходе легко понять, к чему
сводится энергия деформации, выраженная через октаэдрические
напряжения. Энергия изменения длины диагонали куба
~ 2 Сокт~окт
есть энергия изменения объема. Энергия поворота диагонали
^ОКтТокт
есть энергия изменения формы. Полная энергия выразится их сум-
мой
э = э0 + Эф.
§ 3. ГРАФИЧЕСКОЕ ПОСТРОЕНИЕ ОКТАЭДРИЧЕСКИХ
НАПРЯЖЕНИЙ С ПОМОЩЬЮ КРУГА МОРА
Графический прием построения октаэдрических напряжений на
круге Мора очень прост; к сожалению, обоснование его довольно
сложно, так как требует знакомства с применением круга Мора
для более общей задачи — нахождения напряжений в площадке,
ориентированной .произвольным образом. Эта задача обычно не
16*
235
разбирается в учебниках по сопротивлению материалов, а ее обо-
снование, предложенное самим Мором, нам кажется излишне гро-
моздким. Поэтому мы сочли целесообразным привести здесь иное
обоснование.
Поясним, что обычное использование тройного круга Мора,
сводящееся к проведению в них хорд, параллельных той или иной
площадке, приемлемо только для серий площадок, перпендикуляр-
ных одной из главных. Можно вообразить себе книгу, поставлен-
ную на одну из главных площадок, крышки переплета которой
развернуты на прямой угол по двум остальным главным площад-
кам. Тогда раскинувшиеся веером листы книги изобразят те пло-
щадки, в которых можно найти напряжения обычным построением
круга Мора.
Рассмотрим теперь совокупность площадок, для которых один
из направляющих косинусов, например и, имеет постоянное зна-
чение. Все эти площадки образуют конус, ось которого совпадает
с направлением с3, т. е. с нормалью к главной площадке 3.
Составим выражение квадрата полного напряжения р в таких
площадках
р2 = о2 4- т2 - - о2/2 -|- с2т2 4- а2/?2.
Наложим на заданное напряженное состояние всестороннее
сжатие с напряжением . Тогда квадрат полного напряжения р{
выразится
Р? = (° — °о)2 + = ( °! — %)2 Р + ( °2 —°о)2 т2 +
+ (Зз— °о)~п2. (6)
Подберем значение с0 так, чтобы множители при Z2 и т2 были
равны между собой:
(31 — °о)2 = (°2 — «о)2-
Так как то —со — —(с2—°о)» откуда
___ °1 4~ °2
0 ~ 2 ’
Тогда
(ci — °о)2 = (°2 — со)2 = »
и, подставляя в выражение (6),
Но 12 + т2 = 1—и2, а потому
236
так как по условию п постоянно. Уравнение (7) в осях с, т вы-
ражает окружность, центр которой лежит на оси о в точке z с
абсциссой —• (31 + с2)(рис. 13).
Построим тройной круг Мора для напряжений о2, о3.
Ясно, что центр z окружности [формула (7)] совпадает с центром
круга, построенного на напряжениях <зъ о2, а потому эти окруж-
ности концентричны.
Рис. 13. Круг Мора для площадок. Рис. 14. Правило откладывания
равнонаклоненных к оси а3 угла у
Итак, напряжения в площадках, образующих
постоянный угол с осью с3 , изображаются точ-
ками окружности, концентрической кругу с2.
Построим одну из таких окружностей ав и определим положе-
ние точки в пересечения ее с большим кругом а1, с3. Каждая
точка последнего отвечает площадке, паралельной оси <з2 . Точка в
соответствует площадке, которая, кроме того, составляет заданный
угол с осью з3 . Поэтому точку б можно найти по общему правилу,
проводя хорду Ав в большом круге под углом к оси т, косинус
которого равен п. Эта хорда пересечет круги АС и ав в точке б,
которой отвечает площадка, параллельная оси и составляю-
щая угол arccos п с площадкой о3.
Поясним, почему угол <р = arccos п надо откладывать от оси т,
а не от оси о, как в случае плоской задачи. Для этого рассмотрим
рис. 14, справедливость которого очевидна; ясно, что в круге Мора
можно проводить хорду двояким способом:
1) из точки Л, откладывая угол <р от оси о. Этот способ мы
применяли в плоской задаче;
2) из точки В, откладывая угол от оси а. Здесь мы будем
применять именно этот второй способ.
Будем вращать хорду Ав вокруг точки А. Каждому положению
хорды отвечает своя окружность абв и свой конус площадок, об-
разующих данный угол с осью <з3. При п = 0 угол ~ и хордз
совпадает с осью о, а круг абв—с кругом СВ. Этому положению
отвечают площадки, нормали которых перпендикулярны оси <з3_
Следовательно, эти площадки параллельны оси о3 и образуют не
237
конус, а цилиндр с осью 03. При п=\ хорда совпадаете осью т, а
круг абв обратится в одну точки А. Этому случаю отвечает единст-
венная площадка, нормаль к которой параллельна оси <з3, т е.
главная площадка.
площадки
Положение произвольной площадки определяется значениями
двух направляющих косинусов, например п и т, так как третий
косинус связан с ними условием /2= 1 — (щ2+п2). Площадки с за-
Рис. 16. Упрощенное построение
данным п изобразятся
кругом ав, построенным
выше. Площадки с задан-
ным т изобразятся ок-
ружностью гд, концент-
ричной кругу з3. Точно
так же площадки с за-
данным / изобразятся
окружностью еж, концент-
ричной кругу с2 с3 . При
данных I, т, п, удовлет-
воряющих условию
/24-/п2+л2=1, все три ок-
ружности пересекут-
ся в одной точке Р, абсцисса и ордината которой равны о и соот-
ветственно т в данной площадке (рис. 15).
Как видно из чертежа, наибольшую точность построения точки
Р дают окружности, концентрические двум малым кругам, т. е.
определяемые косинусами I и п (рис. 16).
Применим эти рассуждения к построению октаэдрических на-
пряжений.Так как при этом 1 = т = п =—то точки е и в зави-
I 3
мают на большом круге симметричное постоянное положение. На-
хождение этих точек упрощается в силу следующего соображения.
Пусть Е и £> —точки на большом круге, определяемые углами
наклона хорд AD, BE, которые равны = arccos —-— (рис. 17).
Уз
238
Очевидно, точка Е представляет крайнее возможное положение
точки Р, изображающей октаэдрическую площадку, которое имеет
место, если левый малый круг обратится в точку Л, а правый круг
совпадает с большим кругом АВ. Но такой вид круга Мора отве-
чает случаю простого растяжения, при котором нормальное окта-
эдрическое напряжение °окт = “^“с. а полюс находится в точке А.
Таким образом, абсцисса AEt точки Е равна одной трети диа-
метра АВ. Точно так же абсцисса AD} точки D равна двум третям
d -
Рис. 17. Крайние положения октаэд-
рических напряжений в круге Мора
Рис. 18. Г рафическое построение ок-
таэдрических напряжений
диаметра. Поэтому построение октаэдрических напряжений полу-
чает следующий вид (рис. 18): делим диаметр АВ большого
круга на три равные части и из точек деления Еь восставляем
перпендикуляры к оси до пересечения с большим кругом в точках
Е, D. Из центра левого малого круга засекаем дугу через левую
точку Е, а из центра правого круга — через правую точку D.
Абсцисса и ордината точки Р пересечения этих дуг равны соот-
ветственно оокт и токт
Пусть при заданном диаметре большого круга АВ точка С
меняет положение, так что среднее главное напряжение о2 изме-
няется. Тогда точка Р будет перемещаться по некоторой кривой —
геометрическому месту точек, изображающих октаэдрические пло-
щадки при всевозможных видах напряженного состояния. Пока-
жем, что эта кривая есть гипербола.
Будем считать и с3 постоянными, а о2 — переменным и на-
пишем выражения октаэдрических напряжений в измененной
форме:
°окт = + 32 + = + °3^ + V 32 ’
о О О
= V «°1 - ==)2 + + (°® - °Х>21 =
= V[(°?+^-°3°l)+°2— МОз + 31)] '
239
Исключим из этих уравнений переменное о2 > подставляя его
значение из первого уравнения во второе:
32 = Ззокг — ( °3 + °1) : в2 = ^ОКТ — 6%кт ( °3 + °1) + ( 3з+°1)2 ;
= V [( 3?+3з-’з °.) + 9^ - 6%кт ( Э3+а,) +
+ (°3 + а1)2 — Ззокт (°3 4- °1) 4- Оз + °1)2| =
= -у ( °? + °1 + °3 °1) + 2 [ °окт - °окт ( »1 - ’з)] •
Мы получили уравнение гиперболы в осях оокт, токт:
Чкт - Токг - 2зокт ( °1 + °з) + -| ( 3Т+’1+°> °з) = 0
Преобразуем его, перенося начало координат в центр большого
круга:
°окт 2 (°1 4- Сз) Х t 'окт — V .
Тогда
°окт = Х + 4"( °1 + Зз) ; °Lr= х2 + 4"( °1 + ’з)2+ Х( 31 + °з)
и уравнение гиперболы примет вид
2х2 + (с14-®з)24-2л:(а14-аз) — у2 — 2х(а, + з3) —
9
- (’.+ Зз)2+ y(’i + ’i + 3, Зз) = о
или
о 1
2х= - У2 + т ( 3* + О* + ,, 33) - -L ( о, + оз)2 = о,
откуда
2х2-у2 + А.(31_Оз)2=0.
О
Обозначим
Тогда
радиус
большого круга
через = а3)-
2хг— у2+ -1/?2=0.
Ордината .вершины гиперболы дает значение тОКт при чистом
сдвиге:
при х = 0 у
240
Точки пересечения Е, D гиперболы с большим кругом отвечают
растяжению и сжатию:
при X = ± —
В этих точках касательные к гиперболе нормальны к хордам
АЕ и BD (рис. 19). Действительно, дифференцируем уравнение
гиперболы
4xdx — 2ydy — 0,
откуда
dy ___________ 2х
dx у
В точках Е, D при
отрезки
АЕ, = BD.= R = 2х.
1 3
Рис. 19 Геометрическое место точек,
изображающих октаэдрические на-
пряжения
Из рис. 19 видно, что тангенс угла а наклона хорды АЕ к оси
равени стало быть этот угол равен углу наклона касательной
к гиперболе в точке Е с осью у. Отсюда следует, что хорды АЕ* BD
являются нормалями к гиперболе, и, стало быть, хорды AD, BE —
касательными к ней в точках D, Е.
Таким образом, касательные октаэдрические напряжения (при
меняющемся среднем главном напряжении о2 ) выражаются ор-
динатами точек дуги гиперболы ED, а нормальные октаэдрические
напряжения — абсциссами этих точек. Поэтому при состояниях
всестороннего сдвига полюсы кругов Мора лежат в пределах сред-
ней трети диаметра большого круга.
Обратная теорема не верна, т. е. не всякое напряженное состоя-
ние, при котором полюс находится в средней трети, представляет
всесторонний сдвиг. Вот простейший пример. Пусть о2 = о3 = —о1.
Полюс находится в центре большого круга, но 4-о2+о3=о3=/=0.
§ 4. ОБОБЩЕНИЕ ОКТАЭДРИЧЕСКОЙ ТЕОРИИ
ПРОЧНОСТИ
Из рис. 19 отчетливо видна область расхождения двух теорий
пластичности: теории наибольших касательных напряжений и тео-
рии октаэдрических касательных напряжений. В точках Е и D ок-
241
таэдрическое касательное напряжение токт достигает наибольшей
возможной доли от экстремального ттах, равного радиусу большого
круга. Это отвечает случаям одноосного растяжения или сжатия.
Наименьшую долю от ттах октаэдрическое касательное напряже-
ние составляет в случае чистого сдвига (кручение).
По третьей теории прочности (пластичности) предельная вели-
чина ^гпах полагается неизменной и не зависящей от вида напряжен-
ного состояния. Но при этом предельное значение токт для разных
видов напряженного состояния будет различно. Поэтому третью
теорию можно трактовать как теорию октаэдрическую, но допол-
ненную учетом вида напряженного состояния.
Точно так же по октаэдрической теории предельная величина
Токт принимается постоянной и не зависящей от вида напряженного
состояния. Но при этом предельное ттах оказывается величиной
переменной, принимающей разные значения для различных видов
напряженного состояния. Поэтому октаэдрическую теорию можно
трактовать как теорию наибольших касательных напряжений, до-
полненную учетом вида напряженного состояния.
Именно под этим углом зрения и надо рассматривать октаэдри-
ческую теорию. Мы уже указывали, что истинной причиной на-
ступления текучести всегда будут экстремальные касательные на-
пряжения, но октаэдрическая теория позволяет давать их предель-
ным значениям не стабильную, а вариантную величину, учитыва-
ющую вид напряженного состояния. В этом смысле обе теории
пластичности оказываются принципиально эквивалентными между
собой. Однако и та и другая теории исходят из допущения о неиз-
менности предельного значения своего решающего напряжения, об
его независимости от вида напряженного состояния. Таким обра-
зом, обе теории цепко держатся за уже упоминавшийся нами прин-
цип Сен-Венана.
Единственная теория прочности, которая в свое время пыталась
освободиться от этого принципа, была теория прочности Мора.
Внешне связанная с графическим представлением кругов Мора и
их объемлющей, эта теория в действительности сочетала между
собой предельные значения нормального и касательного напряже-
ний некоторой аналитической зависимостью вида
°тах) = 0 ,
так что каждому роду напряженного состояния отвечала своя пара
значений этих предельных величин. Известно, что Мор считал воз-
можным представить эту зависимость, по крайней мере на некото-
ром участке, уравнением прямой линии.
Теория прочности Мора позволяла учесть возможное различие
прочности материала при растяжении и сжатии и исходила из
весьма правдоподобного предположения, что растягивающие на-
пряжения в площадках сдвига должны снижать сопротивление
сдвигу, а сжимающие, напротив, повышать его.
Нам представляется, что все эти положительные особенности
242
теории iMopa следует сохранить, применив их к октаэдрической
теории прочности. Заметим, что использование кругов Мора яв-
ляется совершенно необязательным и может быть заменено постро
ением простого графика напряженных состояний в осях оокт, тОК1
(рис. 20). При этом с особой наглядностью выступает удобство
применения октаэдрических напряжений как характеристик на-
пряженного состояния: они позволяют изобразить трехмерное мно-
гообразие напряженных состояний на плоском графике.
Очевидно, ось ординат на графике изобразит состояния всесто-
роннего сдвига, при которых оокт=0, а полуоси абсцисс — состоя-
ния всестороннего растяжения и соответственно сжатия, при ко-
f-CKfn
Рис. 20. Обобщенная октаэдрическая теория прочности
торых токт=0. Одноосному растяжению и сжатию будут отвечать
лучи ОР, ОС, наклон которых к оси абсцисс определяется тем, что
при этих состояниях 5ОКТ = 0.47 а и стало быть tga=
= 'WL =_£1£_з= 1 41 .
сокт I
Границу области безопасных состояний, впредь до опытного
уточнения, можно принять, как и в теории Мора, по прямой, прохо-
дящей через точки С и Р или точки полуосей, отвечающие допус-
каемым значениям [%кТ] и [Токт] при всестороннем растяжении и
всестороннем сдвиге:
~окт | °ПКТ __ |
[Токт1 [°окт]
Простые геометрические соображения показывают:
, , = 2 1°1р[°1с .
1 окт1 з Wc-Hp ’
f i _____ в Fclp[°]c
Гокт1 ~ з * Mc+Hp
При взаимном равенстве допускаемых напряжений на растя-
жение и на сжатие [о]р - [’]с . найдем для кручения
243
как в обычной октаэдрической теории.
Подставляя выражения [сокт], Ьокт] в уравнение граничной пря-
мой, после преобразований получим
('•“Tsfb-'+f1-'”
[°1с— Нр
°]с|°]р '
= 1 .
В этой формуле отчетливо выступает зависимость между каса-
тельным и нормальным октаэдрическими напряжениями, которую
автор рекомендует считать предельной. Приняв ее, мы тем самым
откажемся и от идеи независимости предельных напряжений от
вида напряженного состояния и от неучета растягивающего окта-
эдрического напряжения, которое, по нашему мнению, небезраз-
лично для прочности. Однако это последнее условие не является
постулатом, искусственно придаваемым к этой теории прочности.
Как видно из структуры второго члена последней формулы, учет
сокт становится необходимым, только если опыты устанавливают
для данного материала различие прочности при одноосном растя-
жении и сжатии. Если такого различия не обнаружено из опыта,
то и учет оокт отпадает.
Условность сохраняется лишь в одном — в форме граничной
линии области безопасных состояний. Если принятие прямолиней-
ной границы приемлемо для областей, смежных с осью ординат,
ю по мере удаления от нее прямолинейность границы становится
все менее вероятной. Разумеется, по графику (рис. 20) нельзя оп-
ределить значение [сокт] при всестороннем растяжении, так как это
значение слишком сильно зависит от формы границы. Нам пред-
ставляется, что целесообразно поставить систематические опыты
над материалами разного типа, чтобы установить не только форму
границы для каждого материала в отдельности, но и общие законы,
управляющие образованием этой формы.
10. ПРИМЕНЕНИЕ ГРАФОСТАТИКИ К РЕШЕНИЮ
СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ
1. Числовое решение системы линейных уравнений часто
осложняется тем, что неизбежное при решении накопление ошибок
приводит к результатам, не удовлетворяющим исходной системе
уравнений. Предлагаемый ниже способ, использующий методы но-
мографии и графостатики, дает в некоторых случаях возможность
более удобного и простого решения системы.
Пусть дана система п линейных уравнений с п неизвестными,
приведенная к виду:
а11Х1 + 6212*2 " ,
floj* 1 ~|~ 6^22*2 —I- 6Z23X3 —
(1)
62п—1,н—2Хп—2 62п—1,л—1 *п—1 —1,пХп&п—1,
62п,л—1*п—1 “F 62л,п Хп &л -
Известно, что всякую систему линейных уравнений возможно
привести к виду (1). Помимо того, ряд задач статики непосред-
ственно приводит к системе этого типа.
Возьмем точку А на плоскости и две параллельных оси Xiiix2
отстоящие от А на расстояния Cj и С2, с нанесенными на них чис-
ловыми шкалами в масштабах и т2 (рис. 1). Определим эти
4 величины так, чтобы любая прямая, проходящая через точку Л,
отсекала на осях отрезки xt и х2, удовлетворяющие первому урав-
нению (1). Из фиг. I видно, что для этого достаточно положить
С2 /Л-2
Ci mi
Qu
Я12
При выбранном положении начала любые три числа /П1,т2,
С] определяют число С2, удовлетворяющее поставленному требо-
ванию. Поэтому тремя величинами т2 и Ci мы можем задаться
по произволу. Положим, например, Ci = 1, mi=m2 = 1 = масшта-
бу расстояния Сь Тогда
245
причем угол между прямой А0х и осями Хь х2 совершенно не влия-
ет на расстояние С2.
Возьмем теперь какое-либо из промежуточных уравнений (1)
и предположим, что для двух первых его неизвестных хЛ1 и xk
уже построены оси на расстояниях и Ck от А. Построим ось
х k+1 так, чтобы любая прямая отсекала на трех осях отрезки х^,
хЛи xftLI> удовлетворяющие выбранному уравнению. Из фиг. 2
видно, что для определения двух искомых величин: расстояния
СЛ |1 оси от А и масштаба оси имеются два уравнения:
Из этих уравнений находим искомые С* i и
съ ak,kmk-\ ~ ck-i ak.k-\ mk
~ ak,k~\ mk
(3)
m k mk—\
Допустим, что все коэффициенты системы (1) и масштабы mk
положительны; в таком случае из рис. 1 и 2 непосредственно вид-
но, что положительное направление осей поочередно меняется, так
что две смежные оси имеют обратное направление.
Продолжая тот же процесс, мы будем для каждого следующего
уравнения получать новую ось, причем каждые три последователь-
ные оси обладают тем свойством, что любая прямая отсекает на
них отрезки, удовлетворяющие соответственному уравнению.
Последнее уравнение (1) дает нам положение точки В, совер-
246
шенно аналогичной точке Л, причем проекция расстояния АВ на
горизонталь определится из фиг. 3:
откуда
1 ап,п ^п—\ гппап,п—}
(4)
П,п п П,П—1
Рис 3
аналогично формуле (3)
Нетрудно видеть, что
прямая АВ будет отсекать
на всех осях отрезки хь х2...
хл, удовлетворяющие всем
уравнениям (1), т. е. даст
непосредственное решение
системы (1) (рис. 4).
2. Согласно сказанному,
положение точек Оь О2,. .Ол,
В может быть найдено пу-
тем последовательного при-
соединения осей. Той же
цели можно достичь более
изящным приемом.
Прямую АВ мы можем рассматривать как замыкающую ло-
маной АО]О2 . . .ОпВ, а эту последнюю в свою очередь как вере-
вочный многоугольник от некоторых фиктивных сил, действующих
вдоль соответственных
осей. При такой интер-
претации корни систе-
мы (1) можно рассмат-
ривать как изгибающие
моменты под силами в
балке пролетом С. Най-
дем величины фиктив-
ных сил, т. е. по вере-
вочному многоугольни-
ку восстановим сило-
вой. Из рис. 5 видно,
что для этого достаточно положить при полюсном расстоянии Н:
Рк = Н
bk
ak,k1
1
(-1)*=
ь
ak.k—\
mk-\
(—>)*-
(5)
^+1
= Н
Знакопеременность является результатом чередования положи-
тельных направлений осей, о котором сказано выше.
247
Таким образом, ход решения системы (1) представляется в сле-
дующем виде: на балку АВ пролетом С [формула (4)] действуют
силы [формула (5)] в расстояниях Ck от левой опоры [форму-
ла (3)]. При полюсном расстоянии Н строим веревочный много-
угольник с произвольным направлением первой стороны и проводим
замыкающую через опорные вертикали. Отрезки между много-
угольником и замыкающей под силами дают, в масштабе соответ-
ственных осей, решения системы (1).
При различных сочетаниях знаков коэффициентов расстояния
Ck могут составлять не возрастающий ряд, как показано на схемах,
так что порядок расположения осей не будет совпадать с поряд-
ком нумерации неизвестных; наконец, некоторые из величин Ck
могут быть отрицательными, вследствие чего балка АВ может
иметь вид одно- и двухконсольной балки. Ход графического реше-
ния ни в какой степени при этом не изменится. Единственный слу-
чай, делающий решение невозможным, имеет место при С = 0;
если при этом точки А и В совпадают, то любая прямая пучка с
248
центром А дает решение системы; при этом неизвестные оказыва-
ются определенными лишь с точностью до сомножителя К. Иными
словами, из системы возможно определить лишь отношение всех
неизвестных к какому-либо одному; если же при С = 0 имеет
место несовпадение точек А и В, то единственная прямая, прохо-
дящая через точки А и В, будет параллельна осям, и система будет
несовместна.
В процессе решения знаменатели отдельных значений mh и Ck
могут обратиться в нуль; в этом случае следует изменить одну из
произвольных начальных постоянных, например т2.
Рассмотрим пример решения системы с четырьмя неизвест-
ными:
х + 2у = 4,
2х + у —z = 3,
у 4~ 2z +1 = 6,
z -Ь 4/ = 2.
Положим mi = т2 = Cj = 1.
Тогда
тз = П-----Г = 1 ’ = ~2 ’
4-Ы — 1-2-1
1 1 2 3
4 2/1 —1/1 11-2-1 2
3 1 5 3
С = = 5 . с = ~2~41~~ 2 11 = 17 .
4~ 2-1 — 11 2 ’ 4-1 —Ы 6 ’
Рг = Н — - —j-J------ — 4/7; Р3 = Н -у-------!- = 6/7;
Р. = —Н Л . J- =з/7; Р4 = — В ------------- = —2Н.
—1 1 * 4 11
Построение дано на рис. 6.
Жирными линиями на осях отмечена система решений уравне-
ний (6). Так как полюсное расстояние для удобства чертежа
принято нами /7 = 5, то отрезки на осях, измеренные в масштабе
длин € k, должны быть умножены на Н и разделены на соответ-
ственные масштабы осей mk, в нашем частном случае равные 1.
Знаки решений определяются следующим образом:
1) отсчеты на всех осях ведутся от веревочного многоугольника
до замыкающей;
2) положительные направления осей определяются по форму-
ле (— так что при положительных масштабах mk направ-
ление меняется поочередно;
249
3) на первой оси положительное направление назначается по
произволу, в соответствии с чем берется и направление действия
сил Pk.
В нашем примере положительное направление на оси х приня-
то кверху, и таково же положительное направление действия сил.
Так как все масштабы tnk положительны (и равны 1), то направ-
ления осей чередуются: на 2-й (оси у) — книзу, на 3-й (г) — квер-
ху, на 4-й (0 — книзу. Окончательно находим величины неизве-
стных:
х = 0,49-5 = 2,45; z = 0,54-5 = 2,70;
у = 0,15-5 =0,76; t= -0,03-5 = —0,15.
Точные значения, полученные алгебраическим решением, та-
ковы:
х = 2,47; у = 0,76; z=— 2,71; * = —0,17,
так что даже построение в небольшом масштабе дает достаточно
точный результат.
3. Покажем применение изложенного способа к графиче-
скому расчету неразрезных балок. Нетрудно видеть,
что уравнения трех моментов для балки с п + 1 пролетом имеют
как раз вид системы (1), причем неизвестными являются опорные
моменты Mk. Обозначая пролеты через Z*, а условные опорные
реакции через Bk и A^+i для опоры, расположенной между &-ым
и (k + 1)-ым пролетами, имеем:
ЪМХ (/, + /2) + М21г = - 6 (В1 + Л2),
Мг12 + 2М2 (/2 + /3) 4- /И3/3 = - 6 (В2+Л3),
(7)
1п + 2Л1„ ( Z„ + Z„+I) = - 6 (В„ + Л„+1).
При этом величины Ck, tnk и Pk выразятся через коэффициенты:
ak,k ak.k^-\ Ч+и ak,k~\~
следующим образом:
250
CI = 1. сг=2(,>+^:
Q __ 2Ck ( lk^~ ^+1)^—1 ~Ck—l lkmk .
"" 2('(t + WOm*-i-ztm* ’
m = lk+\mk-lmk.
4+1 2('*+'*+1)т*-|-'л ’
P^i-iy'+'H- 6(В*+л^)т*-'т*_______!_
Сл+1-С„’
(8)
причем ход решения остается тем же, что и раньше: к балке про-
летом C = Cn+i прикладываем в расстояниях Ck от левой опоры
силы Pk’> строим веревочный многоугольник с полюсным расстоя-
нием Н и замыкаем его на опорных вертикалях. Отрезки между
многоугольником и замыкающей под силами, т. е. моменты под
силами, дают величины соответственных опорных моментов в мас-
zr (—mk ez
штабах —£—как изложено в разборе числового примера
п
в п. 2.
11. КОМБИНИРОВАННЫЙ СИЛОВОЙ
И ВЕРЕВОЧНЫЙ МНОГОУГОЛЬНИК
1. Построение веревочного многоугольника сопряжено с двумя
неудобствами. Главным из них является параллельный перенос
большого числа линий, представляющей основной источник накоп-
ления ошибок и отнимающий наибольшую часть времени при
построении. Второе неудобство особенно сказывается при построе-
нии силового многоугольника для случая параллельных сил про-
тивоположного направления; при этом начальные и концевые точ-
ки сил располагаются вперемежку, а лучи могут занять настолько
близкое положение, что разобраться в силовом многоугольнике
может быть нелегким делом (рис. 1). Это неудобство имеет все'Же
меньшее значение, так как оно возникает только в определенных
случаях; первое же неудобство является общим. Если диаграмма
Кремоны представляет преимущество перед графическим разло-
жением узлов потому, что позволяет откладывать каждую силу
только один раз, то достаточно обоснованной можно считать по-
пытку освободиться от двукратного проведения каждого луча при
обычном построении веревочного и силового многоугольников.
2. Предлагаемый мной комбинированный метод построения
страдает одним методическим недостатком: при нем нет разделе-
ния масштабов и размерностей. Построение содержит как силы,
так и длины в одном чертеже.
252
Начнем со случая двух сил произвольного направления (рис. 2).
Построим обычным способом силовой и веревочный многоуголь-
ники от произвольного полюса. Продолжим каждый луч веревоч-
ного многоугольника влево настолько, чтобы длина каждого
такого продолжения /4Л1, ВВ[ равнялась длине соответственного
луча силового многоугольника. На отрезках ЛЛЬ BBi можно
построить силовые треугольники, равновеликие и подобные
соответственным треугольникам силового многоугольника. При
этом отрезки Л]Л2, В\В2 будут изображать по величине и направле-
нию действующие силы РА и Р в. Положения же этих отрезков
будут смещены относительно линий действия сил.
Рис. 4
Из построения видно, что отрезки AAi и ВВ2 равны между
собой. Поэтому только один из них, определяющий полюсное рас-
стояние, можно назначить по произволу, длина второго тем самым
определится.
Теперь можно построить веревочный многоугольник, не прибе-
гая к помощи силового. Ведем первый луч Л2Л в произвольном
направлении до пересечения с линией действия силы РА в точке
Л и из произвольной точки луча Л2 откладываем величину силы
Pa=A2Ai по ее направлению. Из точки А[ ведем второй луч
через точку А до пересечения с линией силы Рв в точке В и от-
кладываем на нем от точки В влево отрезок ВВ2, равный AAj. Из
точки В2 откладываем силу Рв = В2В} повеличине и направлению
и из точки Bi ведем третий луч через точку В. Очевидно, это
построение можно продолжать тем же способом при любом числе
сил.
Покажем, как найти равнодействующую сил РА, Рв. Точка
приложения ее С найдется, как обычно, пересечением крайних
лучей А2А и В]В. Для нахождения величины и направления равно-
действующей отложим от С по лучу BBi, (рис. 3) отрезок СС\ =
= BBh а по лучу А2А отрезок СС2 = АА2. Отрезок С\С2 будет
давать равнодействующую по величине и направлению. То же
правило остается в силе для любого числа действующих сил, так-
253
B'C”
Рис. 5
как в построении равнодействующей участвуют только край-
ние лучи веревочного многоугольника.
3. В описанном построении все силы откладываются по своему
направлению, но .в смещенном положении. Установим зависимость
между величиной смещения различных сил. Для удобства форму-
лировок назовем смещен-
ную силу отображенной
силой.
Рассмотрим две любые
силы, например Рв и Рс,
и соответственные отобра-
женные силы Р 'в и Р'с
(рис. 4). Найдем точки
пересечения направлений
действительных сил (ВС)
и отображенных сил
(В'С'). Назовем линию,
соединяющую эти две
точки, радиусом сил Рв ,
Рс . Докажем теорему:
радиусы всех сил
пересекаютсяв од-
ной точке.
Пусть даны три силы
Рл, Рв, Рс , для которых
сделано построение ком-
бинированного много-
угольника (рис. 5). Най-
дем точки пересечения
каждой пары действитель-
ных сил (АВ), (ВС) и (С4) и отображенных сил (А'В'), (В'С'),
(С'А'). Эти тройки точек, вообще говоря, не сливаются в одну точку,
т. е. образуют два подобных и подобно расположенных треугольни-
ка, так как соответственные стороны их параллельны. Отсюда сле-
дует, что прямые, соединяющие соответственные вершины обоих тре-
угольников, пересекаются в одной точке. Но эти прямые и будут, по
нашему определению, радиусами сил РА, Рв), (Рв, Рс), (Рс, РА}.
Эти два треугольника обладают следующим свойством. Возь-
мем в них две соответственно расположенные точки а и а'. Если
точка а лежит на направлении действительной силы, то точка а'
лежит на направлении отображенной силы.
Докажем теперь такую теорему: радиус сил Распарал-
лелен лучу веревочного многоугольника, идуще-
му между силами Pz, Pk.
Рассмотрим радиус сил (Рв, Рс) (рис. 6) и два подобных тре-
угольника, стронами которых служат направления действительных
и отображенных сил Рв и Рс, Р'в и Р’с и луч веревочного много-
254
угольника, расположенный между силами Рв и Рс На чертеже эти
треугольники обозначены вершинами (ВС), В, С и (В'С'), ВЬС2.
Согласно правилу построения комбинированного многоугольника
отрезки В\В и С2С равны между собой. Прибавляя к обоим отрез-
кам общую часть С2В, найдем, что равны между собой и отрезки
В\С2 и ВС. Итак, у двух рассмотренных подобных треугольников
имеется одна сторона одинаковая. Следовательно, треугольники
равны, и линия, соединяющая их вершины (ВС), (В'С'), т. е. радиус
сил (Рв, Рс), параллельна основанию, т. е. лучу комбинированно-
го многоугольника.
Из доказанных двух теорем следует, что точка пересечения
радиусов есть полюс силового многоугольника, сами же радиусы
являются его лучами. Отсюда вытекает, между прочим, и то, что
взаимное расположение отображенных и действительных сил раз-
лично; они образуют проективную группу.
4. Подобие расположения действительных и отображенных сил
будет иметь место только в одном случае, имеющем, правда, особо
важное значение на практике, — в случае параллельных сил. При
этом взаимные расстояния отображенных и действительных сил
будут одинаковы; каждая отображенная сила сместится относи-
тельно одноименной действительной силы на одинаковую длину,
равную полюсному расстоянию. Благодаря этому построение зна-
чительно упростится и примет такой вид (рис. 7).
Дана система параллельных сил Рь Р2, Р$, Р4. Задаваясь по-
люсным расстоянием (здесь было бы уместнее употребить иной
термин, например расстояние смещения) Н, сдвигаем все силы по
перпендикуляру к их направлению вправо или влево на расстоя-
ние Н. Новые положения сил будут отображениями. Ведем в про-
извольном направлении первый луч /"—Г до пересечения с дей-
ствительной силой Pi. Следует лишь помнить, что, сдвигая силы
255
влево, рекомендуется давать первому лучу нисходящее вправо
направление, а сдвигая вправо, — восходящее направление, так
как иначе форма комбинированного многоугольника окажется
неудобной.
По направлению отображенной силы Р'у откладываем ее ве-
личину (/"—2) =Pj от первого луча и соединяем точки 2,Г пря-
мой, которая и будет вторым лучом. От второго луча откладываем
по направлению второй отображенной силы Рг ее величину и про-
должаем тот же процесс, ясный из чертежа.
Покажем, как определяются в этом случае равнодействующая
и реакции простой балки.
Для нахождения величины равнодействующей, приложенной,
как всегда, в точке пересечения крайних лучей, следует отложить
от этой точки влево или вправо (в зависимости от принятого на-
правления смещения) величину смещения Н (полюсного расстоя-
ния) (рис. 7). Отрезок, проходящий через найденную точку в на-
правлении сил и заключенный между крайними лучами, дает
величину равнодействующей.
Нахождение опорных реакций ведется сходным образом. Пусть
АВ — балка (рис. 8), нагруженная параллельными силами Pi, Рг,
для которых построен комбинированный многоугольник со смеще-
нием влево на расстояние Н. Проводим по обычному правилу
замыкающую А'В' и продолжаем ее влево до пересечения с отобра-
жением А' реакции А. Это отображение получается, как и отобра-
жения сил, смещением реакции влево (в нашем случае) на рас-
стояние Н. Отрезок направления отображенной реакции, заключен-
ный между замыкающей и первым лучом, дает величину левой
реакции. Правая реакция найдется на направлении правой отобра-
женной реакции и будет равна отрезку, заключенному между
замыкающей и последним лучом.
На рис. 9 дано построение комбинированного многоугольника
для параллельных сил разного направления. Для сравнения приве-
дено построение силового многоугольника. Нельзя не согласиться,
что построение обычного веревочного многоугольника в этом слу-
чае привело бы к значительным неудобствам из-за взаимной бли-
зости и перемешанное™ лучей; построение комбинированного
многоугольника свободно от этих неудобств.
5. Мы отметили ранее, что объединение в одном чертеже линий,
выражающих силы и длины, методически невыгодно. Но в этом
сочетании разных размерностей есть и удобство. Именно, вывод
формулы для момента М = уН может быть сделан из сопостав-
ления подобных треугольников, расположенных так, что углы при
одной из вершин являются вертикальными. Благодаря этому вывод
получает большую наглядность, чем тогда, когда два сравниваемых
треугольника заимствованы из различных чертежей.
Из построения комбинированного многоугольника вытекает
изящный графический прием построения параболы. Так как эпюра
моментов от сплошной равномерной нагрузки есть парабола, то
достаточно принять за нагрузку равные и равноотстоящие силы.
256
17 С. А. Бернштейн
257
чтобы комбинированный многоугольник дал семейство касательных
к параболе. Задаемся величиной погонной нагрузки р, единицей
длины, т. е. расстоянием между силами е, и расстоянием смещения
(полюсным расстоянием) И. Построение параболы приведено на
рис. 10 и ясно без комментариев.
6. Мы не видим необходимости в проведении интерпретации
общеизвестных свойств веревочного многоугольника на графиче-
ский язык комбинированного многоугольника. Читатель без труда
убедится, что все практические задачи, с которыми приходится
встречаться, легко осуществимы в оформлении комбинированного
многоугольника. К числу таких задач относится, например, построе-
ние кривой давления для трехшарнирной арки.
В нашу задачу входила лишь пропаганда комбинированного
многоугольника как удобного практического приема, который поз-
воляет ускорить и уточнить графическое построение.
Следует добавить, что комбинированный многоугольник позво-
ляет особенно просто решать обратную задачу — восстановление
действующих сил по заданному веревочному многоугольнику.
12. О КЛАССИФИКАЦИИ ПЛОСКИХ
СТАТИЧЕСКИ ОПРЕДЕЛИМЫХ ФЕРМ
Несмотря на огромное разнообразие структурных типов плос-
ких статически определимых ферм можно дать некоторый общий
закон их образования и на основе этого закона произвести клас-
сификацию таких ферм и их расчетных свойств.
В дальнейшем я рассматриваю исключительно фермы, обладаю-
щие внутренней неизменяемостью, т. е. представляющие собой
диск. Для опирания таких ферм нужны три опорных стержня, рас-
положение которых должно удовлетворять известным условиям.
Для простоты я исключаю в дальнейшем из рассмотрения опорные
стержни, и чертежи ферм не изображают точек опоры. Читатель
может мысленно считать их совпадающими с любыми узлами
фермы. Точно также внешняя нагрузка считается приложенной в
любых узлах.
Поскольку речь пойдет о дескриптивных структурных свойствах
ферм, постольку фермы неизменяемые и мгновенно изменяемые в
дальнейшем неразличимы. Известно, что любую мгновенно изменя-
емую ферму можно преобразовать в неизменяемую путем измене-
ния направлений стержней без изменения ее структуры. Я изучаю
только структуру, а не направления стержней.
Для краткости статически определимые неизменяемые (или
мгновенно изменяемые) фермы называются в дальнейшем
«фермы СОН».
1 ОПРЕДЕЛЕНИЯ
Назовем наращиванием фермы процесс последователь-
ного присоединения новых узлов с помощью двух стержней;
. разборкой фермы — процесс последовательного откидыва-
ния узлов, в которых сходятся два стержня;
замыканием фермы — постановку одного или нескольких
стержней между наращенными узлами, служащих для прида-
ния ферме неизменяемости; эти стержни назовем замыкаю-
щими;
размыканием фермы — удаление замыкающих;
соединением ферм — процесс соединения двух ферм с
помощью трех стержней или стержня и шарнира;
17*
259
усложнением ферм — замену одного или нескольких стерж-
ней фермочками.
Узел назовем двойным, тр о й н ы м... k-к р ат-н ы м, если
в нем сходятся два, три,..., k стержней.
Наконец, назовем многозвенником (двухзвенником, трех-,...,
й-звенником) односвязную разомкнутую кинематическую цепь
(рис. 1). л-звенник есть система, обладающая п—1 степенями из-
меняемости. Наращивая к n-звеннику новые
« ci узлы, будем получать системы также с п—1
j'4***^ степенями изменяемости в силу теоремы 1.
jL I Теорема 1
/ | Наращивание и разборка узлов не меня-
°------ ют кинематических свойств системы.
Многозвенник представляет ядро образо-
вания фермы. Из теоремы 1 следует, что
Рис. 1 процесс наращивания узлов к п-звеннику
не может дать неизменяемой фермы, если
л>1. Для придания системе неизменяемости необходимо ее замк-
нуть путем постановки п—1 замыкающих. Процесс образования
фермы принимает такой вид: к исходному n-звеннику на-
ращиваются узлы, после чего в систему включа-
ются п—1 замыкающих. После постановки замыкающих си-
стема обращается в ферму СОН и может быть снова наращена.
2 . КЛАССЫ ФЕРМ
Определение. Ферма принадлежит к n-му классу, если
она образована из n-звенника, но не может быть получена из
многозвенника с меньшим числом звеньев, а
ния или усложнения ферм низших классов.
Фермы 1-го класса. Исходной фи-
гурой для образования ферм 1-го класса яв-
ляется однозвенник, т. е. стержень. Так как
стержень есть диск, т. е. не имеет внутрен-
них степеней свободы, то процесс образова-
ния ферм 1-го класса ограничивается нара-
щением узлов и не нуждается в замыкании.
Легко видеть, что все фермы, составленные
из треугольников, принадлежат к 1-му клас-
равно и из соедине-
Рис. 2
су. Однако содержание класса не ограничивается такими фермами.
На рис. 2 представлена ферма, не состоящая из треугольников, но
принадлежащая к 1-му классу. Исходная фигура, как и на всех
последующих чертежах, показана жирными линиями.
Так как фермы 1-го класса не имеют замыкающих, то они мо-
гут быть разобраны в порядке, обратном наращиванию. Легко ви-
деть, что процесс разборки узла со статической точки зрения
равносилен расчету усилий в стержнях узла путем -его вырезания.
Отсюда вытекает:
260
Теорема 2
Всякая ферма 1-го класса может быть рассчитана по способу
вырезания узлов, с полным разделением неизвестных.
Справедлива также обратная:
Теорема 3
Если ферма может быть рассчитана по способу вырезания узлов
с полным разделением неизвестных, то она принадлежит к 1-му
классу.
Фермы 2-го класса. В основу образования ферм 2-го
класса кладется двухзвенник. Так как он обладает одной степенью
изменяемости, то для создания фермы СОН необходимо поставить
один замыкающий стержень (рис. 3).
Фермы 3-го класса об-
разуются из трехзвенника и
имеют две замыкающих (рис. 4)
и т. д.
В дальнейшем приведены некоторые свойства ферм, определяе-
мые этой классификацией, далеко не исчерпывающие, однако, этого
вопроса.
3. СВОЙСТВА КЛАССОВ
Для упрощения анализа ферм высших классов будем считать,
что они не допускают хотя бы частичной разборки, т. е. не имеют
двойных узлов. Если таковые в ферме имеются, мы предварительно
их разбираем. В силу теоремы 1 такая разборка не нарушает кине-
матических свойств фермы и, очевидно, не изменяет ее класса.
Теорема 4
Всякая ферма класса выше l-ro имеет не менее 6 тройных узлов.
Доказательство. Пусть с —число стержней, у — число
узлов, yk— число ^-кратных узлов. Общее число концов, сходя-
щихся в узлах, 2с. Но так как в СОН ферме с=2«/—3, то
2с = 4у — 6.
261
Но
У=Уз + У4 + У5 + ---, (>)
так как по условию двойных узлов в ферме нет и
2с = 4у — 6 = Зу3 + 4у4 4- 5ys + ... (2
Из (1) имеем
Уг = У~ (Ус +Уз+
Подставляем в равенство (2):
4у-6=Зу-3(у4 + у5 + ...) + 4у4 + 5у5+...,
или
У — 6 — у4 + 2у5 + Зус 4- — ,
откуда
У = 6 4~ у4 4- 2у5 4~ Зу6 + - • • (3)
Приравниваем правые части (1) и (3):
6 4~ 2у5 4~ Зу6 -— Уз 4- у5 4- ус...,
или
Уз —6 = у54-2у64-... (4)
Так как сумма в правой части (4) не может быть отрицатель-
ной, то что и требовалось доказать. Из (4) видно, кроме того,
что:
1) число тройных узло<в может быть больше шести только при
наличии пятерных, шестерных и т. д. узлов;
2) если в ферме нет узлов сложнее четверных, то число трой-
ных узлов всегда равно шести.
Теорема 5
Ферма класса выше 1-го не может иметь менее девяти стержней.
На самом деле, число тройных узлов в такой ферме не менее
шести, а потому число стержней не может быть менее 2-6—3^9.
Отсюда вытекает:
Теорема 6
Всякая ферма с числом стержней менее девяти решается выре-
занием узлов.
Назовем внешним узлом фермы узел, не принадлеж.ащнй
к исходному многозвеннику. Очевидно, многие узлы фермы могут
являться внешними и внутренними одновременно, так как в основу
образования фермы можно положить различные многозвенники.
Теорема 7
Ферма 2-го класса имеет не менее трех внешних узлов.
Доказательство вытекает из теоремы 5.
262
Таким образом, простейшим типом фермы 2-го класса является
ферма с шестью узлами и девятью стержнями. Такая ферма допу-
скает только два варианта структуры. Если произвольно зануме-
ровать узлы 1, 2,. . . .,6, то узлы будут связаны между собой по
одной из двух схем:
Из узла 1 2 3 4 5 6
Идут стержни в узлы Тип а 2, 3, 4 1,5, 6 1, 4, 6 1, з, 5 2, 4, 6 2,3.5
Тип б 2, 3, 4 1,5, 6 1, 5, 6 1, 5, 6 2,3,4 2,3,4
Эти типы представле-
ны на рис. 5. Тип а со-
стоит из двух треугольни-
ков, соединенных тремя
стержнями, т. е. фермы
этого типа образуются
путем соединения двух
ферм 1-го класса и по
смыслу определения не
принадлежат ко 2-му
классу. Ферма типа б
представляет шестиуголь-
ник с тремя диагоналями;
это единственная простей-
шая структура фермы
2-го класса. Всякая иная
схема взаимного соедине-
ния узлов либо сводится
к типам а и б путем из-
менения порядка нумера-
ции узлов, либо дает фер-
му l-ro класса.
Для ферм 3-го класса
здесь без доказательства.
Рис. 5
справедлива теорема, которую мы даем
Теорема 8
Ферма 3-го класса не может иметь менее 17 стержней, т. е
шесть внешних узлов.
Для ферм высших классов структурный анализ чрезвычайно
усложняется, равно как и сама структура, и количественные чх
свойства нами не установлены. Можно лишь предположительно
высказать такой закон структуры, доказанный для ферм первых
трех классов:
Ферма п-го класса имеет не менее 3/?—3 внешних узлов, а пото-
му число ее стержней не может быть менее 8п—7.
263
Из рис. 4 видно, насколько сложны очертания фермы 3-го клас-
са. Поэтому можно считать, что фермы высших классов не могут
иметь практического применения.
4. РАСЧЕТНЫЕ СВОЙСТВА КЛАССОВ
Теорема 9
Всякая ферма n-го класса может быть разобрана по снятии
п—1 замыкающих стержней.
Доказательство непосредственно вытекает из процесса образо-
вания ферм. Так как постановке замыкающих предшествует на-
ращивание исходной фигуры, т. е. последовательное присоединение
узлов двумя стержнями, то эта стадия образования фермы может
быть повторена в обратном порядке, если замыкающие будут сня-
ты. Отсюда вытекает:
Теорема 10
Если усилия во всех п—1 замыкающих известны, то ферма п-го
класса решается вырезанием узлов.
Из этой теоремы следует, что если принять усилия во всех за-
мыкающих за независимые переменные и последовательным выре-
занием узлов выразить усилия в остальных стержнях через эти не-
зависимые переменные, то получится система совместных уравне-
ний, число которых равно числу замыкающих, т. е. на единицу
меньше номера класса.
Этой теоремой устанавливается связь между классами ферм
и тем способом расчета ферм, который носит у различных авторов
название метода ложных положений, метода заданных усилий и
т. д. Принимая это последнее название, выразим полученный ре-
зультат в виде теоремы.
Теорема 11
Расчет фермы n-го класса по методу заданных усилий приводит
к системе п—1 совместных уравнений.
Теорема 12
Заменой одного стержня можно снизить класс фермы на еди-
ницу.
Доказательство. Снимем одну из замыкающих и заменим
ее стержнем, соединяющим два узла исходного многозвенника, рас-
положенные через один. Причисляя новый стержень к многозвен-
нику взамен двух стержней, первоначально связывавших эти два
узла, увидим, что число его звеньев от этого уменьшилось на еди-
ницу, а два звена, обойденных новым стержнем, превратились
в наращенный узел. Очевидно, исходя из этой фигуры можно в
прежнем порядке нарастить все узлы фермы. Для замыкания по-
264
требуется на единицу меньшее число стержней, чем ранее. Тем са-
мым класс фермы снизился на единицу.
На рис. 6 дан пример такой замены, обращающий ферму 2-го
класса в ферму 1-го класса. Исходная фигура показана жирно, за-
мыкающая заштрихована, а порядок наращивания узлов обозна-
чен номерами. Те же обозначения применены на дальнейших чер-
тежах.
Теорема 13
Заменой п—1 стержней можно превратить ферму «-го класса
в ферму 1-го класса.
Доказательство вытекает из предыдущего. Для такого преоб-
разования фермы следует п—1 ее за-
мыкающих заменить стержнями, свя-
зующими через один узлы исходно-
го многозвенника. Очевидно, таких
связующих стержней в и-звенникс
можно поставить как раз п— 1. После
этого многозвенный превратится в не-
изменяемую цепь треугольников, т. е.
в ферму 1-го класса.
Пример преобразования фермы
3-го класса в ферм) 1-го класса путем
замены двух стержней дан на рис. 7.
Но так как ферма 1-го класса ре-
шается путем непосредственного вы-
резания узлов, то следствием доказан-
ного является:
Рпс 7
Теорема 14
Расчет фермы /z-го класса по спо-
собу замены стержней (Геннеберга)
требует замены п—1 стержней, а пото-
му приводится к системе п—1 совместных уравнений.
18 С. А. Бернштейн
265
Сопоставляя эту теорему с теоремой 11, получаем:
Теорема 15
вых, а потому, они
Рас. 6
Способ Геннеберга и способ заданных усилий дают для каждой
фермы системы уравнений с одинаковым числом неизвест-
эквивалентны в расчетном смысле.
Наш подход к классификации ферм поз-
воляет значительно упростить процесс замены
стержней при использовании способа Генне-
берга, так как на место исследования кинема-
тических свойств фермы и отдельных стерж-
ней подставляет анализ образования фермы,
обладающий значительно большей простотой.
При некотором навыке исходный многозвен-
ник нащупывается без труда, тем более что
в одной и той же ферме целый ряд многозвен-
ников может быть взят за основу образова-
ния фермы. Проследив затем процесс наращи-
вания узлов, мы выделяем все стержни, ос-
тавшиеся неприсоединенными. Эти стержни и
являются замыкающими. Их следует устра-
нить из фермы, заменив их стержнями, соеди-
няющими через один узлы исходного много-
звенника. Преобразованная ферма решается
путем вырезания узлов.
Классификация ферм позволяет также избежать излишних за-
мен стержней, от которых нелегко уберечься при обычном подходе.
Так, например, в учебниках строительной механики нередко случай
двойной замены стержней при решении по способу Геннеберга ил-
люстрируется фермой рис. 8, которая принадлежит ко 2-му классу,
как видно хотя бы из числа ее стержней, а потому требует замены
лишь одного стержня.
5. ПРЕОБРАЗОВАНИЕ ФЕРМ
Теорема 16
Если исключить из СОН фермы ^-кратный узел, соединив
попарно узлы, к которым шли из него стержни, k — 2 новыми
стержнями, то получится снова ферма СОН (рис. 9).
Действительно, при этом этом число узлов снижается на 1, а
число стержней на 2, так что условие с = 2у—3 остается в силе.
Так, например, исключение двойного узла возможно без всякой ком-
пенсации; исключение тройного узла требует постановки одного
нового стержня между любой парой узлов, к которым шли стержни
от исключенного узла, и т. д.
266
На этом преобразовании ферм основан малоупотребительный
метод расчета ферм, принадлежащий также Геннебергу1. Интерес-
но установить его взаимоотношение с другими методами расчета.
Для ясности назовем его методом замены узлов.
Исключение Л-кратного узла приводит к системе k—1 уравне-
ний со столькими же неизвестными. На первый взгляд может ка-
заться вероятным, что этот метод по числу совместных уравнений
эквивалентен методу замены стержней. На самом деле он горазцо
менее мощен, и число даваемых им совместных уравнений может
быть значительно выше, чем по методу замены стержней.
На рис. 10 изображена ферма 2-го класса. Метод замены стерж-
ней дает поэтому решение в виде одного уравнения с одним неиз-
вестным. Между тем, ни один из тройных узлов этой фермы нельзя
заменить стержнем так, чтобы преобразованная ферма стала фер-
мой 1-го класса, т. е. могла быть рассчитана путем вырезания
узлов.
Отсюда следует, что для расчета такой фермы методом замены
узлов необходимо либо одновременно исключать два или более
тройных узла, либо исключить четверной узел. В обоих случаях
решение будет иметь форму совместных уравнений.
Итак, метод замены узлов может приводить к совместным
уравнениям для тех ферм, которые допускают разделение неизвест-
ных при расчете по методу замены стержней.
Теорема 17
Если возможно разделить СОН ферму на две части разрезом,
пересекающим три стержня, не сходящихся в одной точке, то обе
эти части будут неизменяемыми фермами (рис. 11).
На самом деле, такие стержни неизменяемо связывают две ча-
сти фермы, не меняя кинематической природы каждой из них. Оче-
видно, классы этих частей не могут быть выше класса всей фермы.
1 Henneberg, Die graphische Statik. . M u 11 e r-B r e s I a u, Die neueren
Methoden der graphischen Statik und der Festigkeitslehre, Кар. 1.
18*
267
Теорема 18
Метод Риттера приложим только к таким фермам, которые по-
лучены путем соединения двух или нескольких СОН ферм.
Доказательство вытекает из предыдущего.
Теорема 19
Если возможно разделить СОН
пересекающим четыре стержня, не
ферму на две части разрезол!,
сходящихся в одной точке, то
одна из этих частей неизменяема, а другая имеет одну степень из-
меняемости (рис. 12).
Доказательство. После исключения четырех стержней об-
щее числи стержней уменьшается на 4, а число узлов остается
прежним, а потому будем иметь
с - с0 — 4; у = у0,
где с0 и ус — число стержней и узлов в первоначальной ферме
Так как до разделения фермы имело место равенство
Сп 2у0 3,
то
с — 2у — 7,
или
G + = ^У\ + 2У-> — 7,
где индексы 1 и 2 относятся к двум раздельным частям фермы.
Это условие возможно только при
Q = 2У1 — 3; с2 = 2у2 — 4 или q = 2yL — 4; q = 2у2 — 3,
так как соотношения ci=2yi—2, ci~2yi—1 п ci—2yi означали
бы, что одна часть первоначальной фермы имела лишние стержни,
т. е. вся ферма не могла быть СОН фермой.
268
Теорема 20
Если СОН ферма состоит из двух частей, имеющих общими
только два узла, то одна из этих частей неизменяема, а другая
имеет одну степень изменяемости (рис. 13).
Можно дать двоякое доказательство этой теоремы. Во-первых,
общее число узлов в двух разделенных частях будет па 2 больше»
чем в соединенной ферме, так как каждый из двух общих узлов
будет принадлежать обеим частям. Число же стержней останется
прежним, а потому будем иметь
+ с2 = 2у1 4- 2у.» — 3 — 4,
Рис. 14
а это уравнение, как видно из теоремы 19, доказывает нашу тео-
рему.
Во-вторых, эту теорему можно доказать из условий образова-
ния ферм. Если бы обе части были СОН фермами, то каждая из
них по отношению к другой была бы усложненным лишним стерж-
нем (затяжкой) и вся ферма в целом была бы статически неопре-
делимой. Подобными же рассуждениями можно показать, что
единственно возможным является выполнение условия теоремы.
По данному выше определению, всякая ферма, удовлетворяю-
щая условиям теоремы 20, является усложненной фермой.
Определения классов ферм, данные выше, не относят в состав
классов такие фермы, которые получены путем соединения или
усложнения ферм низших классов. Между тем формально такие
фермы также принадлежат к классам, т. е. могут быть получены
наращиванием и замыканием исходной фигуры. Пример фермы та-
кого рода показан на рис. 14, представляющем ферму Полонсо.
Эта ферма получается путем соединения или усложнения ферм
1-го класса, но может быть построена лишь из двухзвенника, а по-
тому формально принадлежит ко 2-му классу.
Причина невключения таких ферм в классификацию лежит
в том, что они обладают совершенно иными свойствами, чем фермы,
полностью удовлетворяющие определению классов. В частности,
число их стержней и узлов может быть более низким, чем для
классных ферм. Можно показать, что соединение двух ферм 1-го
класса может дать ферму любого класса, а потому для таких ферм,
по-видимому, нет ограничений в смысле минимального числа стерж-
ней и узлов.
269
6. ПРЕДЕЛЫ КЛАССИФИКАЦИИ
Автору не удалось дать доказательства тому, что любая СОН
ферма принадлежит к одному из классов или является результа-
том соединения и усложнения ферм, принадлежащих классам, хотя
ему неизвестна ни одна ферма, которая не удовлетворила бы
этим условиям.
Очевидно, если СОН ферма принадлежит к Л-му классу, то и
ферма, полученная из нее путем наращивания узлов, будет принад-
лежать к тому же классу. Так как все эти наращенные узлы будут
двойными, то справедливо и обратное утверждение: если СОН
ферма принадлежит к Л-му классу, то освобождение ее от двойных
узлов не нарушит этого свойства. Поэтому достаточно было бы до-
казать принадлежность к классам любой СОН фермы, не имеющей
двойных узлов.
Теорема 21
СОН ферма входит в классификацию, если в ней можно ука-
зать односвязную цепь стержней, проходящих через все узлы, и
притом по одному разу через каждый.
Примеры таких цепей -показаны на рис. 15.
Рис. 15
Доказательство. Если ферма имеет п узлов, то такая
цепь должна иметь п— 1 стержней (считая цепь незамкнутой).
Число степеней ее изменяемости равно п — 2. Вне цепи остается
(2п—3) — (п—1)=п—2 стержней фермы, которые можно рассма-
тривать как замыкающие, поскольку они не присоединяют новых
узлов и служат для придания неизменяемости. Поэтому можно
принять цепь за исходный (п—1)-звенник. Ферма принадлежит к
классу п—1 или более низкому.
Автору неизвестна такая СОН ферма (свободная от двойных
узлов), в которой нельзя было бы указать такой цепи. Поэтому он
высказывает предположительно справедливость теоремы.
Во всякой СОН ферме; свободной от двойных узлов, можно
указать цепь стержней, проходящую по одному разу через каждый
узел фермы.
270
Дать доказательство этой теоремы автору .не удалось. Но если
она окажется справедливой, то тем самым в силу теоремы 21 бу-
дет доказана полнота данной классификации: вне классов не оста-
нется ни одной СОН фермы.
Изложенные здесь свойства классов и вытекающие из них рас-
четные свойства ферм далеко -не исчерпывают того обширного ма-
териала, который может быть выведен на основе данной нами
классификации.
13. ОЧЕРКИ ПО ИСТОРИИ
СТРОИТЕЛЬНОЙ МЕХАНИКИ
«Чтобы понять современное
состояние мысли, вернейший
путь — вспомнить, как челове-
чество дошло до него».
А. И. Герцен
ВВЕДЕНИЕ
Изложение строительной механики в современных учебниках,
методически продуманное и стройное, не всегда дает почувствовать
читателю, сколько труда было затрачено поколениями ученых, что-
бы дойти до современных удобных и надежных методов расчета
сооружений на прочность, сколько 'на этом пути пришлось преодо-
леть ошибок и заблуждений. Разумеется, нельзя требовать от инже-
нера, чтобы он при расчете каждой балки думал об истории
двухсотлетних исканий, плодом которых явилась знакомая ему
расчетная формула о = ^-. Но знать об этих исканиях полезно каж-
дому инженеру.
Для сознательного применения методов строительной механики
не только полезно, но и необходимо знакомство с историей разви-
тия этих методов. Без такого знакомства нельзя подойти с крити-
ческой оценкой и к современному состоянию науки. Более того, для
дальнейшего развития науки обязательно знакомство с ее историей,
если мы хотим избежать повторения старых ошибок, которые в
былое время тормозили научный прогресс. С другой стороны, изве-
стный интерес могут представлять даже те методы, которые в свое
время были отброшены, так как среди них подчас обнаруживаются
полезные способы, которые можно с успехом применить в наше
время, на изменившемся уровне развития науки.
Более 20 лет назад, приступив к изучению давно забытых ис-
следований по строительной механике давно забытых ученых
XVII—XVIII веков, автор с удивлением обнаружил, что их методы
расчета, забракованные в XIX веке, имеют неожиданное сходство
с некоторыми новейшими методами нашего времени — с методами,
основанными на учете пластических деформаций. Это было тем бо-
лее неожиданным, что в ту далекую эпоху ученые не только не име-
ли понятия о пластических деформациях, но и свойство упругости
еще не умели использовать при расчетах на прочность. И несмотря
на это, те методы, которые наука выдвинула за последние десятиле-
тия как принципиальное новшество, оказались в известном смысле
воскресшими давно забытыми методами XVIII века.
272
Дальнейшее изучение истории строительной механики показало,
что в 20—30-х годах XIX века произошла коренная ломка основного
подхода к проблеме прочности. В эту пору старинные методы
XVIII века быстро исчезли, «вымерли», уступив место новым мето-
дам, которые безраздельно господствовали в строительной механи-
ке в течение последующего столетия. Лишь в последнее время
они вновь подвергаются пересмотру, означающему начало нового
этапа в науке.
Таким образом, оказалось возможным разделить историю строи
тельной механики на три основных этапа1.
Первый этап начался с трудов Галилея, опубликованных
в 1638 г. В первом очерке мы подробно ознакомимся с этими тру-
дами, а здесь отметим только самое существенное: Галилей ставил
вопрос о прочности тел, рассматривая их в момент разрушения,
или, как мы говорим теперь, в предельном состоянии. Его
совершенно не интересовало, каким путем и через какие этапы
тело дошло до этого состояния. Подход Галилея был принят без
возражений всей последующей плеядой ученых XVII—XVIII веков,
занимавшихся вопросами прочности, во главе с Мариоттом, Яковом
и Даниилом Бернулли, Лейбницем, Эйлером и получил наиболее
законченную форму в работах Кулона. Все немногочисленные в ту
эпоху эксперименты ставились с единственной целью — найти вели-
чину разрушающего груза и форму разрушения; все многочислен-
ные теории пытались предсказать эту форму и найти по ней вели-
чину разрушающей нагрузки. С особой отчетливостью своеобразие
этого подхода видно из истории расчета арок. Во втором очерке
читатель увидит, что десятки исследований в XVIII и начале XIX
века основаны на умозрительных гипотезах о форме разрушения
арки.
Этот подход был обречен на бесплодность в силу ряда причин,
о которых мы подробнее расскажем в дальнейших очерках. Одной
из важнейших причин было то, что метод предельного состояния
по самой своей природе не мог дать никаких сведений о поведении
сооружения при той -нагрузке, для которой оно создавалось, о по-
ведении его в рабочем состоянии. Следствием этого явился резкий
отрыв строительной механики XVIII века от жизни, от практиче
ских задач техники. Такая наука могла существовать только до
тех пор, пока в ней не было настоящей практической потребности.
В дальнейшем мы постараемся показать, почему в XVIII веке
практика не ставила серьезных требований к строительной механи-
ке и почему эти требования возникли в начале XIX века. И то, и
другое объясняется историческими причинами социально-экономи-
ческого порядка: сменой господствующего класса и начинающимся
расцветом буржуазии. Как сказал Ф. Энгельс, «вместе с расцветом
буржуазии шаг за шагом шел гигантский рост науки. Возобнови-
лись занятия астрономией, механикой, физикой, анатомией, физио-
1 Проф. С. А. Бернштейн, Очерк истории расчета свода, сборник «Иссле-
дования по теории сооружений», ОНТИ. 1936, стр. 228.
273
логией. Буржуазии для развития ее промышленности нужна была
наука, которая исследовала бы свойства физических тел и формы
проявления сил природы» («Развитие социализма от утопии к нау-
ке», изд. 1940 г., стр. 22).
Эти слова Энгельса самым прямым образом применимы и к
строительной механике. Развитие промышленности приводит к по-
явлению новых строительных материалов — чугуна и сварочного
железа, приводит к развитию путей сообщения, к усиленному
строительству мостов: сперва для шоссейных дорог, а с 30-х годов
XIX века и для железных. И тогда оказывается, что строительная
механика XVIII века с ее умозрительными приемами поисков пре-
дельного состояния не способна решить простейшую задачу — рас-
считать простую балку на изгиб, и не способна именно потому, что
не может ответить на вопрос: как же работает балка под той на-
грузкой, для несения которой она создана?
Запросы практики растут быстрее, чем строительная механика
может их разрешить, и к 20-м годам XIX века ее задолженность пе-
ред практикой достигает нетерпимых размеров. В науке созревает
необходимость коренной ломки. Эту ломку начал Кулибин, а завер-
шил Навье, который решительно встал на путь изучения действи-
тельной работы сооружения под нагрузкой, на путь его расчета по
рабочему состоянию.
Так начался второй этап в истории строительной механи-
ки. Плодотворность нового подхода обеспечила быстрое развитие
науки, которая к 70-м годам XIX века .не только полностью ликви-
дировала свою задолженность перед строительной практикой, но
даже начала сама вести ее вперед. ’
Однако и расчет по рабочему состоянию (иначе называемый
расчетом по допускаемым напряжениям) имеет свои недостатки.
Он не позволяет достаточно точно установить величину действи-
тельного запаса прочности и -не позволяет именно потому, что в от-
личие от первого подхода недостаточно интересуется предельным
состоянием сооружения. Любопытно, что этот недостаток отчетливо
сознавал уже Кулибин, первым применивший новый подход при
расчете знаменитого моста через Неву. Только совместный учет
поведения сооружения и в рабочем и в предельном состоянии спо-
собен дать точный ответ о величине истинного запаса прочности,
обеспечив наивысшую экономичность сооружения без ущерба для
его прочности и долговечности.
Вопросы экономичности и рационализации имеют особую важ-
ность для нашей Родины, а потому естественно, что недостатки
расчета по рабочему состоянию, заставляющего мириться с избы-
точными запасами, вызывали особенно серьезную критику именно
в Советском Союзе, где и получили успешное развитие новая ветвь
науки — теория пластичности и новое направление в строительной
механике — расчет сооружений по предельному состоянию с уче-
том пластических деформаций. Но это не есть возврат к старым
приемам расчета по предельному состоянию, имевшим лишь умо-
зрительную основу. Теперь предельное состояние изучают во все-
274
оружии современных знаний о рабочем состоянии с использовани-
ем и теории пластичности, и теории упругости, изучают на новой
научно-технической основе. И хотя новый подход приводит иногда
к приемам, напоминающим забытые приемы инженеров XVIII века,
но это, конечно, не есть возврат к старому, а подъем науки на
следующую, более высокую ступень, подобный восхождению по
спирали. В этом подъеме науки одно из первых мест по праву зани-
мают советские ученые, начинающие третий этап в истории
строительной механики.
Этот третий этап было бы неправильно расценивать как отказ
от ра-счета по рабочему состоянию и полный переход к расчету по
предельному состоянию. Это не всегда возможно и не всегда целе-
сообразно. По нашему мнению, попытка подобной полной пере-
стройки (имеющая своих приверженцев) была бы ошибочной. Но-
вый этап должен, на наш взгляд, синтезировать оба метода расчета,
сочетать расчет по рабочему и по предельному состояниям, исполь-
зуя достоинства обоих подходов и освобождаясь от их недостатков.
Таковы основные этапы в истории строительной механики.
В дальнейших^ очерках^мы подробно остановимся на основных осо-
бенностях ..-
В настоят
эти три
костью, хо
ной нами
поправки.
иными. Только Леопардо-да-Винчи, этот универсаль-
который изучал все (и ни одного исследования не довел
занимался проблемой прочности и устойчивости ранее
его труд остался неопубликованным и потому не оказал
развитие науки о прочности.
юружений на прочность настолько внедрился в созна-
нного инженера, чго самая мысль о постройке ответ-
«оружения без такого расчета с трудом укладывается в
и. А ведь только 130 лет назад Навье писал в преди-
ому изданию своего курса (1826): «Большинство кон-
танавливают размеры частей машин и сооружений
уществленных конструкций. Они редко подвергают
дующие на эти детали силы или величину сопротивле-
ей».
;ать несомненным, что до начала XIX века и зодче-
троение руководствовались в основном только тради-
птами, накопленными в течение ряда столетий, и как
разнообразны архитектурные формы сооружений, они
„и точки зрения представляли обычно лишь под ража-
ним, зарекомендовавшим себя, образцам.
шется, возведение сооружений без знания строительной
I возможно (до некоторого предела). Но оно, во-первых,
тирует от аварий, во-вторых, до крайности ограничивает
размеры сооружений, и, в-третьих, оно чрезвычайно неэко-
Именно этот последний недостаток эмпирического строи-
послужил поводом и причиной развития науки о прочно-
ужений, и, конечно, не случайно время зарождения этой
.уки совпадает с эпохой распада феодально-крепостничес-
хества и появления капиталистической системы хозяйства.
277
ОЧЕРК ПЕРВЫЙ
ИЗ ИСТОРИИ СОПРОТИВЛЕНИЯ МАТЕРИАЛОВ
«Прочность подобных тел не
сохраняет того оке отношения,
которое существует меокду ве-
личиною тел»
• Галилей
«Во всяком деле надо знать
историю его развития».
Максим Горький
Глава 1
РОЖДЕНИЕ НАУКИ О ПРОЧНОСТИ
В 1638 г. на уединенную виллу Арчетри близ Флоренции, где до-
живал свои дни опальный Галилей, доставили из далекого голланд-
ского города Лейдена связку экземпляров книги, только что отпе-
чатанной на итальянском языке в типографии Эльзевиров: «Беседы
шил Навье, который решительно встал на путь изучен'
тельной работы сооружения под нагрузкой, на путь его,
рабочемусостоянию. *
Так начался второй этап в истории строитель!
ки. Плодотворность нового подхода обеспечила быстрс
науки, которая к 70-м годам XIX века не только полно<
дировала свою задолженность перед строительной пр<
даже начала сама вести ее вперед. '
Однако и расчет по рабочему состоянию (и'на
расчетом по допускаемым напряжениям) имеет св
Он не позволяет достаточно точно установить вел!
тельного запаса прочности и не позволяет именно по-
личие от первого подхода недостаточно интересуете
состоянием сооружения. Любопытно, что этот недостс
сознавал уже Кулибин, первым применивший новь
расчете знаменитого моста через Неву. Только сов
поведения сооружения и в рабочем и в предельном ci
собен дать точный ответ о величине истинного запас
обеспечив наивысшую экономичность сооружения без
его прочности и долговечности.
Вопросы экономичности и рационализации имеют <
ность для нашей Родины, а потому естественно, что
расчета по рабочему состоянию, заставляющего мирит
точными запасами, вызывали особенно серьезную Крит
в Советском Союзе, где и получили успешное развитие
науки — теория пластичности и новое направление в -ст
механике —расчет сооружений по предельному состоя
том пластических деформаций. Но это не есть возврат
приемам расчета по предельному состоянию, имевшим
зрительную основу. Теперь предельное состояние изуча
274
и математические доказательства, касающиеся двух новых отрас-
лей науки» [1]. По всей Европе пришлось искать издателя, который
согласился бы напечатать новый труд осужденного инквизицией
ученого. Семндесятичетырехлетний Галилей взял книгу, ощупал ее
руками, погладил пергамент переплета и отложил в сторону. Ему
не пришлось увидеть свою последнюю книгу: уже год, как он ослеп.
В этой книге Галилей заложил основы «двух новых отраслей
наук»: динамики и учения о прочности.
Далеко не для всякой науки можно прямо назвать имя ее осно-
воположника. В большинстве случаев новая ветвь науки лишь по-
степенно отходит ют старого ствола. И это неудивительно: для со-
здания новой науки нужно увидеть новые пути, нужно сказать прин
ципиально новое слово, а это под силу только великим ученым. Га-
лилей сказал такое новое слово: сн первый в истории человечества
поставил вопрос о прочности тел и первый попытался его разрешить.
Может показаться странным, чго этот вопрос не ставился до Га-
лилея на протяжении долгих столетий истории человеческой культу-
ры, хотя от античной древности и средневековья дошли, до наших
дней замечательные образцы зодчества и мостостроения. И тем не
менее попытки найти догалилеевские работы о прочности остались
безрезультатными. Только Леонардо-да Винчи, этот универсаль-
ный гений, который изучал все (и ни одного исследования не довел
до конца), занимался проблемой прочности и устойчивости ранее
Галилея, но его труд остался неопубликованным и потому не оказал
влияния на развитие науки о прочности.
Расчет сооружений на прочность настолько внедрился в созна-
ние современного инженера, что самая мысль о постройке ответ-
ственного сооружения без такого расчета с трудом укладывается в
представлении. А -ведь только 130 лет назад Навье писал в преди-
словии к первому изданию своего курса (1826): «Большинство кон-
структоров устанавливают размеры частей машин и сооружений
по образцу осуществленных конструкций. Они редко подвергают
расчету действующие на эти детали силы или величину сопротивле-
ния этих деталей».
Нужно считать несомненным, что до начала XIX века и зодче-
ство, и мостостроение руководствовались в основном только тради-
циями и рецептами, накопленными в течение ряда столетий, и как
бы ни были разнообразны архитектурные формы сооружений, они
с инженерной точки зрения представляли обычно лишь подража-
ние прежним, зарекомендовавшим себя, образцам.
Разумеется, возведение сооружений без знания строительной
механики возможно (до некоторого предела). Но оно, во-первых,
не гарантирует от аварий, во-вторых, до крайности ограничивает
формы и размеры сооружений, и, в-третьих, оно чрезвычайно неэко-
номично. Именно этот последний недостаток эмпирического строи-
тельства послужил поводом и причиной развития науки о прочно-
сти сооружений, и, конечно, не случайно время зарождения этой
новой науки совпадает с эпохой распада феодально-крепостничес-
кого общества и появления капиталистической системы хозяйства.
277
Что привело Галилея к постановке проблемы прочности? С име-
нем Галилея в нашем представлении связываются прежде всего
его знаменитая борьба за учение Коперника и те бессмертные
DX SCORS1
в
DIMOSTRAZIONI
М А Т Е М A Г I С Н Е,
interned due пиоке feitnze
Attenenti alia
М Ес AN I С А Ос 1 МОViMfc NT! L о 4 • р ц
'MSigtor
GALILEO GALILEI LIN СЕ О
Fdofofoc MitcrnA'UcoprimanoddScrcrLiHimo
Gtand Ducadi Tcfaunx
-v«4 typepdice&lrijmc d’attaa Sc&at
IN U. I D A,
ApprcHb gli Ellevtrii. м d c rxxvn
Заглавный лист книги Галилея
астрономические открытия, которые он сделал с помощью созданно-
го им же телескопа: лунные горы, фазы Венеры, спутники Юпитера,
пятна на солнце и его вращение вокруг собственной оси—откры-
тия, послужившие ему опытными доказательствами в борьбе против
геоцентрического миропонимания. Но при этом часто упускают из
виду, что Галилей был не только астрономом, но и выдающимся
инженером, изучавшим вопросы баллистики и гидравлики, форти-
278
фикации и судостроения. Именно практические запросы судострое-
ния и побудили Галилея заняться вопросами прочности. Это было
еще в первом десятилетии XVII века, задолго до столкновения с
инквизицией.
Каков же был подход Галилея к проблеме прочности? Выяснить
это особенно интересно именно потому, что то был первый шаг к
новой науке.
Галилей рассмотрел два вида деформации стержня: растяжение
и изгиб, и в обоих случаях искал величину разрушающей на-
грузки. Его совершенно не интересовали ни поведение стержня в
нормальных условиях, ни величина и распределение усилий при
обычной нагрузке, ни характер перехода от нормального прочного
состояния к разрушению. Это необходимо особо подчеркнуть: пер-
вое исследование прочности исходило из пре-
дельного состояния стержня.
Абсолютные характеристики
прочности, т. е. прочностные свой- I
ства материалов, Галилею не бы- I
ли известны, и он с большой на- <| т
учной проницательностью ограни-
чился изучением относительных,
сравнительных оценок прочности.
Для случая растяжения Галилей ------*7----------
принимал несущую способность $
пропорциональной площади сече- \
НИЯ стержня, и МОЖНО полагать, Рис. 1. Схема изгиба по Галилею
судя по тону изложения, что это
свойство растянутых стержней во времена Галилея было уже обще-
известным. Вероятно, сведения о нем переходили из поколения в
поколение, от учителя к ученику, с очень давней поры.
Новое слово было сказано Галилеем в задаче изгиба. Он теоре-
тически исследовал сравнительную прочность геометрически подоб-
ных стержней на изгиб, с учетом и без учета собственного веса. Для
такой оценки необходимо было задаться законом распределения
усилий в опасном сечении при изломе. Галилей принял эти усилия
равномерно распределенными по сечению и притом растягивающи-
ми (рис. 1), считая, что излом консоли происходит путем раскрытия
трещины сверху и вращения вокруг нижнего ребра сечения.
Составляя условие равенства моментов относительно этого реб-
ра, Галилей нашел, что прочность стержня прямоугольного сечения
пропорциональна ширине и квадрату высоты, а круглого сечения —
кубу диаметра. Оба вывода совершенно правильны, но ошибочная
предпосылка о распределении усилий привела Галилея к следую-
щим значениям момента сопротивления (по современной термино-
логии) :
для прямоугольника W = ;
iV7 nd3
для круга W = .
8
279
Это решение заслуживает внимательною анализа. На первый
взгляд оно кажется грубо ошибочным: в нем не удовлетворены ни
условия равновесия, ни условия деформации. Прочность балки пря-
моугольного профиля переоценена втрое, а балки круглого профи-
ля — вчетверо. И тем не менее это первое решение по-своему пра-
вильно, если только вспомнить постановку задачи.
Галилей ставил вопрос не об абсолютной, а о сравнительной
прочности геометрически подобных стержней. И эту задачу он пра-
вильно разрешил для каждого вида профиля в отдельности. Най-
денные им закономерности сравнительной оценки не зависят от ве-
личины числового коэффициента в выражении момента сопротивле-
ния, и потому произвольно принятый Галиднем закон распределе-
ния усилий по сечению не искажает условий подобия.
Здесь уместно отметить обстоятельство, не кажущееся с первого
взгляда очевидным: каков бы ни был закон распределения напря-
жений в сечении о f(y) и где бы ни проходила нейтральная линия,
, и- bh2
момент сопротивления прямоугольного профиля выразится U ”
/и ,
а круглого— W= причем числа т и п будут функционалами от
л
f (у), не зависящими от размеров сечения. Эту любопытную теоре-
му впервые доказал Паран для прямоугольного профиля в 1713 г.
В дальнейшем ходе развития науки о сопротивлении материалов
последовательно сменилось несколько законов распределения на-
пряжений. Галилей принял f(y) C, Марнотт и Лейбниц — закон
f(y)~ Су, полагая начало координат на краю сечения, Паран—тот
же закон, но с началом координат по середине высоты, и, наконец.
Навье перенес начало координат (нейтральную линию) в центр тя-
жести сечения. В соответствии с этим коэффициенты т и п для пря-
моугольного и круглого профилей принимали значения:
Галилей
т 2
п 8
Вопрос о правильности
нюдь не столь очевиден, как это кажется с первого взгляда, хотя
современный инженер из этих значений выберет последние. Но не
надо забывать, что эти последние значения можно считать правиль-
ными, только если балка находится в упругом состоянии. В этом
случае значения коэффициентов т и п можно проверить опытом,
измерив тензометрами удлинения крайних волокон. Однако за пре-
делами справедливости закона Гука функция f(y) начинает непре-
рывно изменять свой вид, а потому и числа т, п получают перемен-
ные значения. А ведь Галилея интересовало именно предельное со-
стояние балки, которое для большинства материалов наступает
далеко за пределами закона пропорциональности. Поэтому для за-
дачи, поставленной Галилеем, наши привычные значения ш^б и
п = 32 отнюдь не обладают большей достоверностью, чем получен-
ные им значения. Известно, что современная теория пластичности
(приближенная) дает в предельном состоянии значения и
Мариотт
3
12,8
того или иного варианта решения от-
Паран
6
32
280
/г=18,84. Каковы будут истинные значения этих коэффициентов в
предельном состоянии для конкретного вида материала с заданной
диаграммой растяжения, не обладающей площадкой текучести, нам
и до сих пор неизвестно. Эти значения можно найти только опыт-
ным путем.
Таким образом, своеобразие постановки задачи позволило Гали-
лею .избежать как определения прочностных свойств материалов,
так и изыскания истинного закона распределения напряжений. За-
дача о сравнительной прочности геометрически подобных тел не
требовала ни того, ни другого, а потому была решена Галилеем со-
вершенно правильно.
Ставил ли Галилей опыты со стержнями? Большинство авторов,
пишущих о Галилее, отвечает на этот вопрос утвердительно. Меж-
ду тем в «Беседах» нет почти ни одного указания на опыты, если не
считать двух числовых примеров, касающихся прочности мрамора
и меди. Но и эти примеры говорят скорее против предположения об
опытах Галилея. На самом деле, Галилей оценил прочность мра-
мора на разрыв в 5 кг/см2, т. е. примерно в 3—4 раза ниже истин-
ного значения. Прочность медной проволоки он определил через
предельную длину, при которой наступает разрыв от собственного
веса, оценив ее в 4 801 локоть. Но длина старинной итальянской
меры «локоть» (braccia) составляла около 119 см. Поэтому времен-
ное сопротивление меди получается равным 5 100 кг 1см2, или в
2—3 раза больше истинного. Трудно думать, что неточность в по-
становке экспериментов могла дать такие грубые ошибки в разные
стороны1.
С другой стороны, если бы Галилей провел сравнительные испы-
тания теоретически равных по прочности балок прямоугольного и
круглого профиля из любого материала, то он неизбежно обнару-
жил бы расхождение со своими расчетами. Он убедился бы в этом
также, если бы сопоставил опытные значения прочности стержня из
данного материала на изгиб и растяжение. Однако такое сопостав-
ление впервые сделал только Мариотт на полвека позже, обнару-
жив при этом ошибку Галилея. Отсутствие у Галилея сомнений в
правильности его расчетов, отчетливо видное из текста «Бесед»,
на наш взгляд, говорит о тем, что он не ставил таких опытов. Осно-
ву его исследования вероятно составляли не эксперименты, а наб-
людения.
Как бы то ни было, Галилей совершенно правильно оценил роль
ширины и высоты прямоугольного сечения в сопротивлении балки
излому. Судя по характеру диалога в «Беседах», можно заключить,
что Галилей действительно впервые установил эту зависимость,
ранее неизвестную и ощущавшуюся строителями лишь интуитивно.
Можно полагать даже, что именно это специфическое различие
участия ширины и высоты сечения в сопротивлении изгибу, обнару-
1 В примечаниях к русскому изданию книги Галилея А. Н. Долгов без под-
счета утверждает, что оценка Галилея близка к истине. Вероятно, А. Н. Долгов
исходил из старинного русского значения меры «локоть», составлявшего около
45 см. Такое же утверждение приводится в новой книге проф. Е. С. Аицелиновича,
Галилео Галилей, Учпедгиз, 1955, стр. 88—89.
281
женнсе Галилеем, послужило для него исходным толчком для поста-
новки проблемы прочности в целом. Интересно, что исходя из своей
теории Галилей дал правильное решение задачи о балке равного
сопротивления (для случая прямоугольного профиля постоянной
ширины).
Вернемся теперь к анализу основного допущения Галилея о
постоянстве растягивающих напряжений в сечении балки. Это до-
пущение было сделано им не случайно. Оно отражает воззрение
Галилея на природу прочности и разрушения, то воззрение, которое
в наше время называется «первой теорией прочности». По мнению
Галилея, всякое разрушение происходит путем отрыва и обуслов-
ливается действием растягивающих сил. Вот почему и разрушение
от изгиба было для Галилея результатом действия растягивающих
сил, превзошедших некоторый постоянный для данного материала
предел.
Как же объяснил Галилей причину прочности и разрушения?
В научной деятельности Галилея нас поражает смешение новых,
революционных для свего времени идей с обветшавшими схоласти-
ческими воззрениями, сохранившимися в изуродованном виде со
времен Аристотеля. Галилей развенчал нашу планету, сведя ее с
центра вселенной на роль скромного спутника, не побоялся дать
верное истолкование своим астрономическим открытиям (фазы
Венеры, спутники Юпитера и т. д.). Н-о наряду с этим он без крити-
ки повторял аристотелевскую басню о том, что кометы — это
освещенные солнцем вредные испарения Земли, не смущаясь тем,
что отсутствие параллакса заставляло отодвигать эти «вредные
испарения» на огромное расстояние от Земли. Подобно этому,
смело создавая новую науку о прочности, Галилей объяснил проч-
ность тел аристотелевской «боязнью пустоты», хотя и пытался хит-
роумными схоластическими аналогиями придать этой «боязни»
некое уточненное и расширенное толкование.
Классические примеры «боязни пустоты» относились обычно к
явлениям, вызываемым давлением воздуха, о котором во времена
Галилея еще не подозревали, хотя именно Галилей впервые дока-
зал, что воздух имеет вес. Галилей объяснил той же «боязнью
пусоты» и взаимное сцепление гладких притертых мраморных
пластинок, которое в действительности имеет совершенно иную
природу. Любопытно, что через 100 лет после смерти Галилея, когда
опыт Торичелли уже доказал существование давления воздуха и
прекратил толки о «боязни пустоты», новым объяснением заменили
прежнее во всех случаях, причем Христиан Вольф, учитель Ломо-
носова, в своем учебнике «Cosm-ologia Generalis» (1737), по кото-
рому, вероятно, учился и Ломоносов, объяснял сцепление мрамор-
ных пластинок именно давлением воздуха.
Галилей умер через 4 года после опубликования «Бесед». Две
новые отрасли наук, созданные им в этой бессмертной книге, неиз-
меримо разрослись за три века, прошедшие со дня его смерти. Раз-
витие динамики и науки о прочности привело к современным бле-
стящим успехам машиностроения, транспорта и- строительной тех-
282
ники. Однако по основному, коренному вопросу о природе прочности,
который уже Галилей пытался ставить, мы не имеем иного ответа,
кроме некоторых гипотез качественного характера, не допускающих
количественной оценки. Проблема прочности материала, впервые
поставленная Галилеем, будет разрешена только тогда, когда
ученые по известным физико-химическим и структурным свойствам
материала смогут предсказывать его прочностные свойства. Тогда
покажется наивным и несовершенным современный эмпирический
способ подбора состава прочных сплавов; он будет заменен точным
предварительным расчетом, основанным на законах молекулярной
и ядерной физики и способным создавать новые материалы еще не-
виданной прочности.
Важные исследования прочности монокристаллов, проведенные
за последние годы советскими учеными, представляют быть может
первые шаги к такому разрешению проблемы о прочности веще-
ства.
«От живого созерцания к
абстрактному мышлению и от
него к практике — таков диа-
лектический путь познания
истины, познания объективной
реальности».
В. И. Ленин
(Филос. тетр., 1947, стр.
146—147).
Глава 2
НАУКА, УТРАТИВШАЯ СВЯЗЬ С ПРАКТИКОЙ
В 1826 г. Навье издал первый систематический курс сопротивле-
ния материалов. К этому времени прошло почти 200 лет после опуб-
ликования «Бесед» Галилея, заложивших основу новой прикладной
науки. В ее дальнейшей разработке приняли участие крупнейшие
ученые Европы: Мариотт и Лейбниц, братья Бернулли и Эйлер,
Лагранж и Кулон. Казалось бы за это время скопился богатейший
запас знаний для применения к нуждам техники, и эмпирический
период строительства остался давно позади. А между тем Навье с
грустью признается в своем курсе, что конструкторы редко прибе-
гают к расчету и что до сих пор от трудов его предшественников
больше пользы получила математика, чем архитектура и техника.
Чем это объяснить?
Кто был виноват в том, что наука не дошла до строителя? Если
говорить о вине, то, несомненно, были виноваты обе стороны. Не
подлежит сомнению, что строители проявили значительную кос-
ность, недоверие к новым затеям и расчетным методам, придержи-
вались рутины и профессиональных традиций. Они еще не осознали,
283
чем может быть для них наука, и не научились предъявлять ей тре-
бования. В этом вина строителей, в оправдание которых нужно
вспомнить, что и социально-экономическая обстановка в Европе
XVII—XVIII веков не способствовала прогрессу техники.
А в чем же была вина науки?
Вина науки, или вернее вина ученых, изучавших законы сопро-
тивления твердых тел, состояла в глубоком отрыве от практики-
Этот отрыв, вообще характерный для западно-европейской культу-
ры XVIII века, нигде быть может не сказался так отчетливо, как
именно в области строительной механики. Нельзя дать правильный,
исторический обзор, не подчеркивая этого обстоятельства.
Галилея нельзя упрекнуть в таком отрыве. Его натолкнула на
проблему прочности практика, и свои выводы он дал в такой фор-
ме, что практика могла ими воспользоваться. Правильный путь-
научного развития его .идей требовал в первую очередь опытов,,
опытов и еще раз опытов для проверки допущений Галилея и оцен-
ки прочности различных материалов в различных условиях. Но ни-
кто из учеников Галилея на протяжении десятилетий не подумал,
об этом.
Отрыв строительной механики от жизни остро чувствовали сов-
ременники: и инженеры, и публицисты. Резкий выпад против такого
отрыва мы находим в одной из самых замечательных книг, вышед-
ших в XVIII веке, — в «Путешествиях Гулливера» Свифта. Эта
жестокая сатира беспощадно бичевала недостатки современного,
Свифту политического и общественного строя, и каждая насмешка
в ней представляла удар по реальным порокам общества. В треть-
ем путешествии Гулливер посетил Лапуту, жители которой были
так страстно увлечены математикой, что даже за обедом не могли
отказаться от созерцания геометрических образов. И вот что рас-
сказывает Гулливер о «строительной технике» лапутян: «Дома ла-
путян построены очень скверно; стены поставлены криво, во всем
здании нельзя найти ни одного прямого угла; эти недостатки объ-
ясняются презрительным их отношением к прикладной геометрии,
которую они считают наукой вульгарной и ремесленной; указания,
которые они делают, слишком утонченны и недоступны для рабо-
чих, что служит источником беспрестанных ошибок».
Для тех читателей, которые полагают, что нельзя основывать
серьезные научные утверждения на таком полемическом, «несерь-
езном» сочинении, как «Путешествия Гулливера», можно привести
еще одну цитату, на этот раз из вполне «серьезного источника»: из
«Диссертации о толщине мостовых сводов» Готье [2], опубликован-
ной в том же 1727 г., что и книга Свифта. Вот что пишет Готье о
работе своего предшественника Делагира по расчету сводов:
«Я честно сознаюсь, что я не достаточно учен, чтобы понять ее.
Я не смог даже проследить вывод автора, настолько он мне пока-
зался сложным; и я считаю все, что он написал, такой вещью, кото-
рой не смогут йонять ни полу-ученые, ни тем более рабочие. Ибо-
если для понимания его выводов надо обязательно* знать алгебру,,
которой он пользуется, то не думаю, чтобы каменщпюили-а_рхитек-
284
тор, для которых такого сорта работы должны были бы писаться,
могли когда нибудьих использовать»1.
Содержание этой жалобы инж. Готье поразительно близко под-
ходит к насмешке памфлетиста Свифта.
А вот выдержка из «Курса мостостроения» Э. Готэ [3], написан-
ного в конце XVIII века (но изданного только в 1809—1813 гг.):
«Всякий строитель оценивает, сколь важно для него знать в
точности меру прочности материалов, и потому та ветвь механики,
которая известна под названием сопротивления твердых тел, обе-
щает самые плодотворные приложения. Но хотя многие занимались
этой наукой, и хотя Эйлер и Лагранж не побрезговали (курсив мой
С. Б.) сделать из нее предмет своих исследований, полученные
результаты не дают почти никакой помощи строительству. Анали-
тические формулы бесполезны, пока не будут определены значения
постоянных, в них содержащихся; но до сих пор попытка их опре-
деления осталась почти бесплодной».
Эта жалоба была написана через 150 лет после того, как Гали-
лей основал науку о прочности. Неужели за этот долгий срок новая
наука действительно не развивалась? Такое заключение было бы
совершенно неверным. XVIII век был эпохой достаточно быстрого
роста науки о прочности, но в са-мой основе этой науки лежала
причина отрыва ее от практики. Причину эту мы постараемся
вскрыть из анализа развития науки.
Почти 40 лет отделяют книгу Галилея от следующего шага в
•строительной механике. В Западной Европе XVII века, разоренной
Тридцатилетней войной и отсталыми формами феодально-крепост-
нического хозяйства, новая наука не находит плодородной почвы
для развития.
Этим следующим шагом было установление закона пропорцио-
нальности между нагрузкой и деформацией. Роберт Гук открыл
•его еще в 1660 г., но опубликовал — и то в виде анаграммы2 —
лишь в 1676 г. Расшифровка этой анаграммы, данная Гуком в 1678 г.
J4], звучит неясно и сама кажется зашифрованной формулировкой
того ясного и простого положения, которое мы теперь называем
законом Гука: «Ut tensio, sic vis», т. e. «каково удлинение, такова
•сила». Этим законом были установлены два новых свойства тел:
.пропорциональность между нагрузкой и деформацией и упругость.
Нельзя не отметить, что статья Гука была написана на латинском
языке — языке ученой касты, тогда как «Беседы» Галилея — на
народном итальянском языке. Галилей хотел сделать свой труд
1 В наше время и нашему читателю странно слышать такие жалобы, так как
•со введением всеобщего семилетнего обучения алгебра стала достоянием каждого
•советского человека. Но не забудем, что для современных капиталистических
стран жалоба Готье не потеряла остроты и сегодня.
2 Для составления анаграммы все буквы, входящие в состав фразы, подби-
рались в алфавитном порядке, причем каждая повторялась столько же раз, как
•и в исходной фразе. Получившийся бессмысленный набор букв публиковался как
•предварительная заявка на еще не проверенное открытие. Такой способ публика-
ции был очень распространен в XVII веке.
285
достоянием широких кругов техников, а у Гука такого намерения
не было.
Надо мысленно перенестись в условия материальной культуры
XVII века, чтобы оценить заслугу Гука. В то время в быту почти
не было предметов, обнаруживающих заметное на глаз или на
ощупь свойство упругости. В наши дни слово «упругость» невольно
сочетается в представлении со свойствами резины. Даже школьное
название резинки для стирания карандаша «ластик» есть иска-
женное слово «эластик», т. е. упругий1. Но резина стала известна в
Европе только в 20-годах XIX века. Сбросим ее со счетов. Гибких
стальных изделий (кроме только рапиры или шпаги) в XVII веке
также еще не было. Какие же иные предметы обихода проявляют
заметное свойство упругости? Винтовая пружина, самое название
которой говорит об упругости, а применение в весах — о законе
пропорциональности. Но винтовая пружина по некоторым данным
была изобретена именно Гуком. Ему пришлось изобрести сильно
деформирующееся упругое тело, чтобы из наблюдения над ним
установить свой закон пропорциональности.
Понятие упругости быстро переносится после Гука на тонкие
металлические и деревянные стержни (по тогдашней терминологии
«пластины»), но долгое время представляется совершенно непри-
менимым к камню и чугуну — важнейшим строительным материа-
лам для ответственных сооружений на континенте и особенно в
Англии, где строевого леса уже тогда было мало. На протяжении
всего XVIII века камень принято считать абсолютно твердым телом,
хотя Иоганн Бернулли [5] уже в начале века утверждал и доказы-
вал теоретически, что таких тел быть не может. Упругость камня
была установлена опытным путем только в XIX веке.
Любопытно, что значительно ранее была обнаружена упругость
льда как строительного материала. Это открытие сделал в 1740 г.
петербургский академик Г. В. Крафт в связи с постройкой извест-
ного «Ледяного дома» на Неве [6]:
«В жестокую стужу и лед на подобие других твердых тел силь-
ное сопротивление показывает; и я сам неложными над ледяными
шарами учиненными опытами узнал, что лед нарочитую эластиче-
скую силу имеет, и оною несколько раздается, а потом опять преж-
нюю свою величину получает».
Обнаруженное новое свойство упругости естественно возбудило
интерес физиков и философов. На рубеже XVII и XVIII веков по-
является ряд попыток объяснить природу упругости. Объяснения
эти очень разнообразны. Среди них есть и ссылки на свойства
«симпатии и антипатии», якобы просущие твердым телам, и отве-
чающие духу времени теории «весьма тонкой упругой материи»,
проникающей все опоры вещества и движущейся сквозь них, вовле-
кая в круговое вращение «корпускулы» материи (И. Бернулли, 1726).
1 Известно, что в течение долгих лет после своего появления в Европе рези-
на не находила другого практического применения, кроме стирания карандаш-
ных записей.
286
Общим для всех этих теорий являются их умозрительность и глубо-
кая схоластичность, а потому они не заслуживают анализа.
Важно подчеркнуть другое. Свойство упругости и закон Гука,
теряющие справедливость задолго до разрушения материала, со-
вершенно не увязываются в эту эпоху с проблемой прочности,
поскольку последняя, развиваясь по пути, указанному Галилеем,
рассматривает лишь предельное состояние тела. Кроме того, как
уже было сказано, эти свойства не считаются приложимыми к
камню и чугуну. Поэтому вплоть до начала XIX века научные
изыскания, основанные на законе Гука, остаются вне поля зрения
инженеров-строителей и кажутся им надуманными, абстрактными,
оторванными от жизни и не применимыми на практике.
Современное учение о сопротивлении материалов представляет
стройное сочетание теории упругости с учением о прочности. В
XVII—XVIII веках эти два направления совершенно чужды одно
другому и развиваются самостоятельно. С «одной стороны, исследо-
ванию подвергаются упругие деформации стержней, с другой сто-
роны, затрачиваются усилия на отыскание предельных состояний
сооружений (излом балки, разрушение свода). Первые изыскания
не связываются с прочностью, а вторые остаются чуждыми поня-
тию упругости. Этот взаимный разрыв двух ветвей одной науки и
был одной из важных причин, -обесплодивших строительную меха-
нику XVIII века как прикладную науку.
Почти одновременно с Гуком закон пропорциональности обна-
ружил французский физик Мариотт [7] (1680), не знавший о рабо-
тах Гука. Надо помнить, что в те времена еще не существовало
научных журналов, и связь между учеными могла поддерживаться
только путем обмена письмами. Мариотт изучал деформации дере-
вянных, железных и стеклянных стержней и установил, что даже
«самые твердые тела» — стекло и железо — деформируются при-
мерно пропорционально нагрузке и восстанавливают первоначаль-
ную форму после устранения нагрузки. Таким образом, закон про-
порциональности в конце XVII века был установлен достаточно
твердо. Это не помешало Якову Бернулли в 1705 г. пытаться
опровергать этот закон умозрительными соображениями. Я- Бер-
нулли утверждал [8], что деформации должны расти медленнее на-
грузки, так как иначе при сжатии волокно должно будет укоротить-
ся более, чем на свою первоначальную длину. Любопытный пример
для коллекции научных заблуждений, хотя для случая сжатия при
больших деформациях закон Гука разумеется нарушается.
Мариотт высказал еще одно предположение, которому суждено
было в течение двух столетий владеть умами инженеров. Речь идет
о той гипотезе, которая ныне называется второй теорией прочности.
Мариотт утверждал, что растянутый стержень разорвется, когда
его удлинение превысит некоторый безопасный предел, и основывал
свое утверждение на рассуждениях о силах притяжения между
частицами тела, которые ослабевают при их взаимном удалении.
Таким образом, за первые 50 лет существования новой науки было
высказано уже две теории прочности: первая (Галилея) о разру-
2b7
шении от растягивающих усилий и вторая (Мариотта)—о разру-
шении от удлинений.
Важнейшим выводом из закона Гука — Мариотта было уста-
новление пропорциональности между изгибающим моментом и кри-
визной линии прогиба. Это положение было найдено Яковом Бер-
нулли, который опубликовал его сперва в виде анаграммы (1691),
а потом открыто (1694), и, наконец, дал доказательство (1695)
исходя из гипотезы плоских сеч ени й. Это было первым
правильным подходом к вопросу о перемещениях балки при изги-
бе (Галилей считал линию прогиба балки под грузом за квадрат-
ную параболу). Я- Бернулли получил тем самым дифференциальное
уравнение изгиба и интегрировал его в рядах с помощью линейных
подставок. При этом он брал точное выражение кривизны, не за-
меняя его на вторую производную прогиба, как это делаем мы в
большинстве задач со времен Навье.
Интересно, что и это решение, если не вводить гипотезы малых
перемещений, оказывается расчетом, балки по предельному, или,
точнее, по конечному состоянию. Смысл уравнения Бернулли таков:
ЕСЛИ балка под некоторой нагрузкой изогнулась, получив в сече-
ниях заданные кривизны, ТО изгибающие моменты будут им. про-
порциональны. Балка рассматривается в том конечном состоянии^
которое она приняла в результате изгиба. Таким образом, это ре-
шение по своему подходу вполне соответствует духу времени и пути,
указанному Галилеем.
Для современной науки задача о деформации изгиба имеет ог-
ромную важность, так как на ее решении в конечном счете основана
вся теория статически неопределимых балок и рам, т. е. почти все
современное строительство. Но в условиях XVII века эта задача
еще не могла найти себе применения. Она оказалась преждевре-
менной и надолго осталась по преимуществу предметом отвлечен-
ных упражнений математиков.
Нельзя разумеется, отрицать важность и пользу теоретических
научных исследований, если они опережают свое время и не могут
найти немедленного практического применения. Было бы очень
печально, если бы наука шла непрерывно на поводу у практики,
разрешая только задачи сегодняшнего дня и не создавая перспек-
тив. Но истинная наука не должна и не может существовать в
отрыве от жизни, и задачей каждого ученого должно быть всемер-
ное старание довести свои исследования до возможности их приме-
нения в жизни. Особо важным это становится для науки приклад-
ной по самому существу своему, какой является строительная меха-
ника. И этого именно стремления связаться с жизнью мы не видим
у ученых XVIII века.
Исследования упругих деформаций оставались в течение-XVIII
века чисто физической проблемой. Технической задачей были по-
пытки разрешить вопрос о прочности балки и свода. Длительная
история этих попыток рассмотрена ниже — рачет балки в отдельной
главе, а расчет свода — в отдельном очерке.
«Из наблюдений установлять
теорию, через теорию исправ-
лять наблюдения, — есть луч-
ший из всех способов изы-
скания правды».
М. В. Ломоносов
Глава 3
ЗАДАЧА О ПРОЧНОСТИ БАЛКИ
В главе I мы разобрали сделанную Галилеем первую попытку
рассчитать балку на прочность, отметили ее положительные и отри-
цательные стороны и указали, что достаточно было бы поставить
простой опыт, чтобы обна- - -= —-
ружить ошибочную установ- @ ©
ку Галилея — гипотезу о
равномерном распределении у
усилий в опасном сечении. < ?
Ошибку Галилея обна- ______
ружил на опыте Мариотт.
Он сравнил прочность Рис. 2. Схема изгиба по Мариотту
стержней на изгиб и растя-
жение и установил, что отно-
шение разрывающего груза к ломающему в действительности
больше, чем полагал Галилей, т. е., что Галилей переоценивал
прочность балки при изгибе. Этот опыт Мариотта подтверждает
не только ошибочность выводов Галилея, но и тот странный факт,
что ни Галилей, ни его ученики не проделали такой проверки.
Мариотт попробовал исправить теорию Галилея, приняв иной
закон распределения усилий в сечении изогнутого стержня. С его
попытки начинается длительная история задачи о прочности бал-
ки, полная чередования правильных передовых мыслей и странных
заблуждений.
Оставаясь на позициях Галилея о предельном состоянии стерж-
ня, Мариотт показал сперва, что если разрушение при изгибе про-
исходит путем вращения вокруг сжатого ребра (как полагал Га-
лилей), то усилия в опасном сечении должны меняться по линей-
ному закону (рис. 2,а), а не оставаться постоянными. Такую же
треугольную эпюру усилий после Мариотта принимали Лейбниц
(1684) и Вариньон (1702). Несколько позже Мариотт исправил эту
эпюру и поместил нулевую точку в середине высоты стержня
(рис. 2,6), признав тем самым наличие сжатия при изгибе, о ко-
тором ранее не думали, и подойдя вплотную к истине1.
Однако при этом произошел досадный случай. Вычисляя сопро-
тивление стержня прямоугольного профиля изгибу по двузначной
1 В современных учебниках открытие сжатия волокон при изгибе нередко
неправильно приписывают Дюгамелю (1767).
19 С. А. Бернштейн 289
эпюре напряжений из условия равенства моментов внешних и
внутренних сил, Мариотт допустил алгебраическую ошибку и ввел в
расчет лишнюю двойку. В результате этой ошибки Мариотт пришел
к выводу, что прочность стержня при изгибе будет одинакова в обо-
их предположениях: при принятии треугольной эпюры и двузначной
эпюры с нулем по середине высоты. В обоих предположениях он
получил значение момента сопротивления прямоугольного профиля
bh2 „
— , тогда как для двузначной эпюры должно было получиться
3 ~
bh~
значение —.
6
Но еще более удивительно, что этой ошибке суждено было еще
раз исказить расчет через 25 лет после Мариотта и оттянуть на це-
лое столетие правильное решение задачи. В 1705 г. Яков Бернуллц
вернулся к задаче изгиба (уже после того, как он установил важ-
ный закон о пропорциональности между изгибающим моментом и
кривизной стержня). Можно думать, что он не знал работ Мариот-
та, так как приписывал заслугу открытия сжатых волокон при изги-
бе исключительно себе. Как и Мариотт, Бернулли сопоставил треу-
гольную и двузначную эпюры напряжений, и тоже ошибся в 2 раза
в том же самом месте при оценке прочности по двузначной эпюре.
Была ли эта ошибка совершена им самостоятельно, или он списал
вывод Мариотта, не проверив его, — сказать трудно, да это и не
столь существенно. Важно для дальнейшего то, что на основе свое-
го ошибочного расчета он высказал удивительную теорему: по мне-
нию Бернулли, положение нулевой точки в линейной эпюре напря-
жений вообще не оказывает никакого влияния на сопротивление
изгибу, и потому нет надобности уточнять положение этой точки.
Вот эта неверная теорема, подкрепленная авторитетом имени Якова
Бернулли, и оказалась вредным тормозом, задержав на целое сто-
летие развитие учения об изгибе.
Прославленным корифеям европейской науки XVIII века под-
час случалось впадать в удивительные заблуждения!
Первое правильное решение задачи о прочности балки при из-
гибе дал французский военный инженер Паран [9] в 1713 г. Он
указал, что треугольная эпюра невозможна, так как, приняв ее,
приходится допустить, что сжимающая сила сосредоточена на
кромке сечения, которая при этом неизбежно будет разрушена, так
что в предельном состоянии эпюра уже не будет треугольной. Па-
ран впервые указал, что между растягивающими и сжимающими
усилиями при изгибе должно существовать равновесие, откуда
следует, что в симметричном профиле нулевая точка эпюры распо-
ложится по середине высоты. Таким образом, Паран получил пра-
вильную форму эпюры, и, что всего важнее, не ошибся при вычис-
лении в 2 раза, как Мариотт и Бернулли. Между прочим Парану
принадлежит первое решение известной задачи о том, как вырезать
из круглого бревна прямоугольный брус наибольшей прочности при
изгибе.
290
Правильное решение Парана, давшее для прямоугольного сече-
b№
ния выражение момента сопротивления — , повторил и подтвер-
дил в 1729 г. петербургский академик Бильфингер. Его работа [10].
опубликованная в Известиях Академии наук в 1735 г. (на латин-
ском языке), была первой работой по строительной механике, из-
данной в России.
Казалось бы, трудами Парана и Бильфингера задача прочности
балки решена полностью. На самом деле этой задаче предстояла
еще долгая и сложная судьба.
Через 60 лет после Парана его выводы повторил (не зная рабо-
ты Парана) Кулон [11], о котором мы еще будем говорить в даль-
нейшем. Он также воспользовался для вывода положения нулевой
точки эпюры условиями равновесия (в те времена они применялись
редко и не казались обязательными) и также отмечал невозмож-
ность сосредоточения сжимающего усилия на кромке без ее разру-
шения. Замечательно, что Кулон поставил положение нейтральной
линии в связь с законом Гука. Он указал, что если закон Гука пере-
станет действовать ранее разрушения, то нейтральная линия при
разрушении займет иное положение. Это замечание Кулона являет-
ся одним из первых по времени указаний на существенное различие
между рабочим и предельным состояниями.
Таким образом, Кулон в 1773 г. полностью подтвердил правиль-
ность забытой работы Парана 1713 г. Но, как говорил Сен-Венан,
работа Кулона содержала так много идей в малом объеме, что
внимание инженеров и ученых в течение следующего полустолетия
не могло остановиться ни на одной из них.
Через 25 лет после работы Кулона вышел курс сопротивления
материалов Жирара [12] (1798). Мы вернемся к нему в очерке IV,
так как этот курс содержит самую раннюю попытку расчета ста-
тически неопределимых балок. Жирар ссылается на Кулона при
решении задачи изгиба, но, несмотря на эту ссылку, помещает
нулевую точку эпюры на край сечения и повторяет ошибочное ут-
верждение Якова Бернулли о безразличности положения этой нуле-
вой точки. Странно, что к книге Жирара приложен протокол засе-
дания Национального института наук и искусств, из которого вид-
но, что эта книга получила одобрительный отзыв Кулона. Может
быть Кулон написал этот отзыв, недостаточно внимательно прочи-
тав книгу Жирара?
Как бы то ни было, Жирар своей книгой вернул задачу изгиба
к тому уровню, на каком она была до 1713 г. — регресс на 85 лет» и
к тому же санкционированный Кулоном. Кулон сам пожертвовал
своим научным достижением в пользу авторитета Бернулли.
Проходит еще 15 лет. Навье в одной из своих первых работ
(1813 г.) все еще придерживается теоремы Бернулли (ровно через
100 лет после того, как Паран доказал ее ошибочность). Такой
упорный застой в науке убедительно говорит об умозрительности
подхода к задаче изгиба: к ее решению не привлекается ни опыт,
ни обоснованная теория.
19:
291
В 1820 г. мы встречаем еще одно ошибочное решение задачи,
на этот раз уже для общего случая несимметричного профиля. Дю-
ло выступил с утверждением, что положение нулевой точки в эпю-
ре напряжений должно определяться из условия равенства момен-
тов растягивающих и сжимающих напряжений, а не равенства са-
мих усилий. Посмотрим, к чему приводит это допущение. Если
уравнение линейной эпюры напряжений написать в виде a~ky, то
условие Дюло выразится
f aydF = f oydF,
р с
где буквы «р» и «с» под интегралами указывают, что областями
интегрирования являются растянутая и соответственно сжатая зо-
ны сечения. Подставляя уравнение напряжения, получим
т. е. моменты инерции этих двух зон сечения равны между собой. Оче-
видно, это верно только для симметричного профиля. Этот же ре-
зультат почти в то же время высказал Тредгольд [13] (предложив-
ший термин «нейтральной линии»), придав ему несколько иную
трактовку: по его формулировке, «нейтральная линия делит сече-
ние на такие две части, что если каждую из них симметрично отра-
зить по другую сторону нейтральной линии, то оба симметричных
профиля будут иметь одинаковое сопротивление». Мы видим, что
это правило эквивалентно выводу Дюло, если уточнить неопреде-
ленный термин «сопротивление». Жесткости обоих профилей, пост-
роенных таким образом, будут одинаковы, но прочность их будет
различна. По-видимому, идея Дюло — Тредгольда была последним
заблуждением в истории расчета балки на прочность. В 1826 г.
Навье дал, наконец, правильное решение, хотя перед этим и он не
избежал кратковременного увлечения теорией Дюло.
Итак, для решения этой задачи потребовалось без малого два
столетия, 188 лет, если считать от даты опубликования «Бесед»
Галилея, где была сделана первая попытка расчета балки на
прочность. Характерный пример того тернистого пути, по которо-
му развивалась наука в XVIII столетии.
К этому обзору надо добавить еще одно замечание. На протяже-
нии всего XVIII столетия понятия момента инерции и момента соп-
ротивления сечения еще не разделены. Дело не в том, что этих тер-
минов тогда еще не было в употреблении, а в том, что характери-
стика прочности и характеристика жескости балки при изгибе не
считаются различными, несмотря на явное различие в размер-
ности. Из-за этого возникает теоретическая путаница, разобраться
в которой не под силу инженеру-практику. А ученые теоретики, как
мы увидим ниже, удовлетворялись тем, что вводили ту или иную
характеристику в уравнения в виде нерасшифрованной алгебраи-
ческой величины, отнюдь не интересуясь ее реальным содержанием.
В результате такого подхода даже совершенно конкретная практи-
ческая задача оказывалась неприменимой к строительной практике.
«Мы возьмем от прошлого
огонь, но не пепел».
Жан Жорес
Глава 4
ЗАДАЧА О ПРОДОЛЬНОМ ИЗГИБЕ, ИТОГИ XVIII ВЕКА
У нас нет сведений, чтобы кто-нибудь ставил систематические
опытные исследования прочности материалов ранее Питера Мушен-
брука [14] (1692—1761). Отдельные опыты ставили и Мариотт, и
Рис. 3. Испытательная машина Мушенбрука, 1729 г.
Гук, а может быть и Галилей. Но Мушенбрук был первым настоя-
щим врожденным экспериментатором. Он был профессором универ-
ситета в том самом городе Лейдене, где когда-то была напечатана
книга Галилея, и обессмертил этот город названием изобретенной
им лейденской банки.
Мушенбрук построил первую серьезную испытательную маши-
ну (рис. 3), на которой испытывал прочность всего, что ему попада-
лось под руку, — по-видимому, из чистой любознательности. Вряд
ли кому-нибудь после Мушенбрука приходила, например, фантазия
испытывать на разрыв коровьи рога. Этой любознательностью он
несколько похож на своего соотечественника и современника Ле-
венгука, открывшего мир бактерий, который также внимательно
разглядывал в свой удивительный микроскоп все, что ему попадало
под руку, наблюдал, записывал и не делал никаких выводов.
Но один вывод Мушенбрук все же сделал. Он испытывал на
сжатие длинные стержни, обнаружил при этом явление продоль-
ного изгиба и установил, что критическая сила обратно пропорцио-
нальна квадрату длины стержня. Труд Мушенбрука был издан в
1729 г.
293
Эйлер (1707—1783)
294
Впервые продольным изгибом заинтересовался еще Леонардо-да-
Винчи почти на столетие раньше Галилея, но его исследования ос-
тались в рукописи и стали известными только в XIX веке. Вот по-
чему надо считать, что именно Мушенбрук положил начало изуче-
нию этой важной задачи строительной механики, которая разви-
лась впоследствии в обширную проблему устойчивости сооруже-
ний. В эту главу науки русские ученые вписали немало славных
страниц. А первое решение задачи о продольном изгибе дал, как
известно, великий ученый Леонард Эйлер [15], на всю жизнь свя-
завший свою судьбу с Российской академией наук и сыгравший
важнейшую роль в деле развития нашей отечественной науки.
Леонард Эйлер родился в г. Базеле (Швейцария) в 1707 г. Он
очень рано пристрастился к математике, которой обучался у Ио-
ганна Бернулли в Базельском университете. Эйлер окончил уни-
верситет 18 лет и сразу по окончании получил приглашение во
вновь создаваемую Петербургскую академию наук. Его рекомен-
довал Бернулли.
Любопытно, что единственной вакантной должностью в акаде-
мии была кафедра физиологии. Бернулли советовал своему ученику
не смущаться этим, и Эйлер на несколько месяцев погрузился в
изучение анатомии и физиологии. Впрочем, когда Эйлер приехал
в Петербург в 1727 г., о физиологии уже не было разговора, и
Эйлер сразу стал работать в родной ему математической области.
По-видимому, его первые впечатления от России не были осо-
бенно благоприятными. Академик А. Н. Крылов пишет по этому
поводу1: «Попал он в эту страну из маленькой Швейцарии, где
культура восходила от Юлия Цезаря и древних римлян, построив-
ших в ней такие дороги и мосты, которые почти без ремонта стоят
и поныне...». В России же «не только не было науки, но даже само-
го этого слова не существовало в тогдашнем русском языке, и Ака-
демия наук именовалась «де сиякс академия», а ее ученики — «еле-
вами»... Дороги в стране были таковы, что для сколь-нибудь даль-
ней поездки выжидали зимнего пути...».
К этому надо добавить, что никакое ученое звание не гаранти-
ровало от телесных наказаний: при Бироне были биты батогами
академические переводчики Барков и Лебедев, а профессор
Тредьяковский избит лично кабинетминистром.
Несмотря на тяжелую обстановку и атмосферу бесправия, от
которого могли спасать только личные связи с влиятельными вре-
менщиками, Эйлер с большим рвением принялся за работу в акаде-
мии, еще не думая, что Россия станет ему второй родиной. Это рве-
ние послужило причиной серьезного несчастья. В 1736 г. Эйлер
взялся выполнить за три дня срочную вычислительную работу, на
которую другие математики запрашивали три месяца. Свое обеща-
ние он выполнил ценой потери правого глаза из-за переутомления.
В 1741 г., в смутные дни правления Анны Леопольдовны,
Эйлер уехал из России. По его переписке можно заключить, что он
1 Статья акад А. Н. Крылова об Эйлере в сборнике, изданном Институтом
истории науки и техники к 150-летию со дня смерти Эйлера в 193а г.
295
METHODUS
INEEXIENDJ
! \ E A S C U R V A S
Max M«'r'.r.' c.prcprietatc gaudoncs.
SIPE
S О L и T I О
xOBLEMATIS ISOPRRI&! ETRICI
L * s i « o s £ ь s и accfpte
ЛVCTOй£
N!! A RDO EU L E R Q
Satrma-
rum r^TROTOLTTAN^ Sitd®.
MDCCXLM;
Заглавный лист книги Эйлера
296
опасался и за судьбу академии, и за свою личную судьбу в связи
с начавшимися повальными арестами и ссылками. Эйлер перешел
работать в Берлинскую академию наук, сохранив в то же время
звание члена Петербургской академии, и ежегодно направлял в Пе-
тербург десятки научных работ в течение всех 25 лет, проведенных
им в Берлине.
Русское правительство неоднократно возобновляло переговоры
о возвращении Эйлера в Россию. В 1766 г., вскоре после смерти
Ломоносова, он вернулся в Петербург, и на этот раз навсегда. Но
в тот же год его постигло новое несчастье: Эйлер заболел и почти
ослеп на левый глаз. Всю остальную часть жизни— 17 лет (!) —он
работал слепым, диктуя свои труды родным. Он продиктовал не ме-
нее десяти томов отдельных сочинений и несколько сот статей. По-
разительный пример преданности науке и силы духа.
Эйлер умер в 1783 г., умер внезапно, за чайным столом. Как
сказал Кондорсе, «Эйлер прекратил вычислять и жить». Его похо-
ронили в Петербурге, на Смоленском кладбище, а дети и внуки
его навсегда остались в России. Один из отдаленных потомков ве-
ликого ученого, мичман Эйлер, служил в 1904 г. на героическом
крейсере «Варяг».
Эйлера можно по справедливости считать одним из основопо-
ложников русской науки, так как он никогда не принадлежал к
«немецкой партии» в Академии наук и оказывал всяческую под-
держку русским ученым. Известно, с каким огромным уважением
он относился к Ломоносову. Известно, что он, единственный из
всей академии, энергично помог Кулибину, стремясь добиться осу-
ществления его проекта моста через Неву (об этом мы расскажем
в очерке втором).
Имя Эйлера в строительной механике неразрывно связано с
задачей продольного изгиба, хотя Эйлер вовсе не искал решения
этой задачи и пришел к ней случайно. Он заинтересовался указа-
нием своего друга Даниила Бернулли (это уже третий ученый из
семьи Бернулли, которого нам приходится упоминать), что «по-
Г ds
тенциальная сила» изогнутой пластинки 1 ~ получает наимень-
шее значение для истинной линии прогиба (при постоянстве сече-
ния, длины и заданных краевых условиях). Нетрудно видеть, что
эта «потенциальная сила» отличается от потенциальной энергии
EJ
изогнутого стержня только множителем 2 •
Эйлер был создателем вариационного исчисления, и его живо
интересовали применения этого нового метода к естествознанию.
Поэтому он внимательно изучил формы упругих кривых, удовлет-
воряющих этому условию минимума, и по этим формам восстанав-
ливал уравновешивающую нагрузку. Одна из девяти изученных им
форм уравновешивалась двумя равными и противоположными
сжимающими силами, приложенными по концам дуги, и равными
—, где Ek2—по терминологии Эйлера «абсолютная упру-
20 С. А. Бернштейн
297
гость пластинки», а / — длина. С замечательной прозорливостью
Эйлер заметил, что этот случай отвечает задаче продольного изги-
ба или, по его выражению, «задаче о силе колонн». Приводим с
некоторыми сокращениями эти несколько строк из книги Эйлера
1744 г.:
«Пусть АВ — колонна, установленная вертикально на основа-
нии А и несущая груз Р. Если колонна установлена так, что она
упасть не может, то со стороны груза Р, если он будет
слишком велик, можно опасаться только изгиба ко-
Рис. 4. Схе-
ма ‘колонны
по Эйлеру
лонны; в этом случае, следовательно, можно будет
рассматривать колонну как обладающую упругостью...
Мы видели в § 25, что сила, требующаяся для самого
малого наклонения колонны, равна -р Ekz. Следова-
ла
тельно, если груз Р не будет превышать— Е£2, то
можно будет не опасаться никакого решительно изги-
ба; наоборот, если груз Р будет больше, то колонна
не может сопротивляться изгибу... Все это можно ис-
пользовать преимущественно в отношении деревянных
колонн, как подверженных изгибу».
В своих дальнейших работах по продольному из-
гибу Эйлер развил эту теорию и исправил некоторые
свои ошибки. Одной из таких ошибок, нам кажется,
является несоответствие решения Эйлера и рассмотренной им рас-
четной схемы. Для колонны по схеме, приведенной Эйлером
(рис. 4), критическая сила будет вчетверо меньше, чем указано
Эйлером- Выведенное им выражение справедливо для шарнирно-
опертой колонны, но не для стойки, закрепленной одним концом1.
Но здесь нас должно интересовать другое. Во-первых, указа-
ние Эйлера на применимость его решения к деревянным колоннам,
«как подверженным изгибу», говорит о том, что способность камен-
ных и чугунных колонн к упругой деформации во времена Эйлера
еще не была осознана. Во-вторых, интересно, как Эйлер трактовал
величину «абсолютной упругости» Ek2. Приводим подлинный текст:
«Эта абсолютная упругость Ek2 зависит, во-первых, от природы
вещества, из которого изготовлена пластинка; поэтому принято
говорить, что одно вещество в большей, а другое в меньшей степени
обладает возбудителем упругости. Во-вторых, она так зависит от
ширины пластинки, что выражение Ek2 везде должно быть пропор-
ционально ширине пластинки, если остальные условия равны. В-
третьих же, весьма большое значение для определения Ek2 имеет
толщина пластинки, которая, по-видимому, влияет таким образом,
что Ek2 пропорционально квадрату толщины... Отсюда можно бу-
дет посредством опытов, позволяющих измерить ширину и толщи-
ну, сравнивать между собой и определять упругости всех веществ».
1 Решение задачи продольного изгиба при различных краевых условиях дал
Лагранж в 1770 г.
298
Эта выписка подтверждает наше замечание о том, что в XVIII
веке существовало смешение понятий момента инерции и момента
сопротивления сечения. Размерность «абсолютной упругости», со-
общаемая Эйлером, отвечает моменту сопротивления, тогда как в
действительности в «формулу Эйлера» должен входить момент
инерции. Иными словами, «толщина пластинки» должна входить
в выражение «абсолютной упругости» не во второй, а в третьей
степени. Если бы кто-нибудь попробовал «определять упругости
веществ» посредством опытов, рекомендуемых Эйлером, то ре-
зультатом таких опытов была бы полная путаница.
Теперь попробуем встать на точку зрения строителя XVIII ве-
ка. Пусть это будет культурный, начитанный инженер, знающий
алгебру (вспомним цитату из книги Готэ на стр. 285), сознающий
опасность продольного изгиба и желающий ее избежать. Что он
может извлечь для своей практической задачи из труда Эйлера?
Вывод, что критическая сила обратно пропорциональна квадрату
длины? Но этот результат уже известен из экспериментальных
(и потому более убедительных) работ Мушенбрука. Зависимость
от ширины и толщины? Но всякий грамотный строитель придаст
деревянной колонне или круглое, или квадратное сечение. Какова
же для этих профилей зависимость критической силы от ширины
или диаметра? Это остается неизвестным. Если строитель, дове-
ряясь осторожному высказыванию Эйлера, примет, что эта зави-
симость выражается третьей степенью ширины или диаметра, то
он, как мы знаем, ошибется, так как эта зависимость для квадра-
та и круга выражается четвертой степенью.
Мы останавливаемся на этом, с тем чтобы еще раз показать на
примере продольного изгиба, как глубок был разрыв между нау-
кой и жизнью в XVIII веке. Верное по существу решение Эйлера
(и гениальное по своему методу) невозможно применить на прак-
тике, и ни Эйлера, ни его соратников не интересовала необходи-
мость довести это решение до возможности практического исполь-
зования.
Можно ли поэтому удивляться, что решение Эйлера долго не
находило применения? Даже такой крупный ученый, как Кулон,
сомневался в справедливости этого решения и, как это ни странно,
в существовании самого явления продольного изгиба. В своей ра-
боте 1776 г. он утверждал со ссылкой на собственные опыты, что
прочность сжатых стержней не зависит от их длины. Вероятно
Кулон испытывал только чугунные или каменные стержни малой
длины, для которых разрушение путем сдвига предшествует по-
тере устойчивости.
Эйлер дважды возвращался к задаче продольного изгиба —
в 1757 и 1778 гг. В последней работе [16] он исправил свои прежние
ошибки, указав, что для круглого профиля «упругость» пропор-
циональна 4-й степени диаметра (как известно, истинное выраже-
-nd? ч
ние будет )
64
Другая ошибка, исправленная Эйлером, особенно
удивительна. В 1744 г. Эйлер утверждал, что колонна якобы не
20*
299
может потерять устойчивости под действием собственного веса, но
если ее перерезать по середине длины, т. е. свободно поставить друг
на друга две полуколонны, то потеря устойчивости станет воз-
можной. Эйлер убедился в ошибочности этого суждения в работе
1778 г.
Но все эти критические замечания представляют лишь мелоч-
ные придирки по сравнению с гениальной смелостью решения за-
дачи о продольном изгибе. Необходимо подчеркнуть, что решение
Эйлера было расчетом по предельному состоянию, и таким остает-
ся до сих пор каждое решение всякой проблемы устойчивости. Кри-
тическая нагрузка может быть определена, только если известна
форма потери устойчивости, если эта потеря устойчивости уже
произошла или происходит. Таким образом, это замечательное
решение по самому своему подходу всецело отвечает идее расчета
по предельному состоянию, свойственному эпохе.
Работу Эйлера по продольному изгибу продолжил и развил
Лагранж [17] (1770). Он дал точный интеграл уравнения продоль-
ного изгиба и вывел связь между величинами нагрузки и стрелы
прогиба. При силе, меньшей критической, стрела получила мни-
мое выражение. Лагранж впервые обнаружил возможность про-
дольного изгиба по нескольким полуволнам и дал значение крити-
ческой силы при различных концевых закреплениях.
Однако и Лагранжа совершенно не интересовал вопрос о зна-
чении упругой константы, входящей в решение, и потому его ис-
следования не помогли приблизить решение к строительной прак-
тике.
Перенесемся еще на четверть века вперед, в 1798 г. В этом
году вышла уже упоминавшаяся нами книга Жирара [12], который
зачеркнул весь прогресс XVIII века в учении об изгибе и вернулся
к ошибочным мнениям Бернулли начала столетия. В такой же
мере регрессивным Жирар проявил себя и в задаче продольного
изгиба, которая трудами Эйлера и Лагранжа была к этому време-
ни разрешена полностью (для упругого случая), так как еще в
1778 году Эйлер указал, наконец, правильную размерность коэф-
фициента жесткости.
Но Жирар не согласен с новыми работами Эйлера. Он снисхо-
дительно упрекает Эйлера за измену своему прежнему ошибочно-
му мнению и утверждает, что критическая сила пропорциональна
третьей степени диаметра, ссылаясь при этом на авторитет Якова
Бернулли. Мало того, Жирар пытается «объяснить» явление про-
дольного изгиба уже известным в то время поперечным расшире-
нием сжатых стержней, которые при наличии торцового трения
принимают бочкообразную форму. Жирар полагал, что в резуль-
тате такого бочкования либо произойдет разрыв стержня вдоль
его оси, либо одни искривившиеся продольные волокна «перетянут»
другие в свою сторону и вызовут продольный изгиб. Таким обра-
зом, и решение задачи продольного изгиба к концу века старания-
ми Жирара было испорчено, хотя его книга, как уже было ска-
зано, заслужила одобрение Кулона.
300
Между тем Кулону в истории строительной механики принад-
лежит бесспорно прогрессивная роль. Во втором очерке мы бу-
дем говорить об его работах по расчету свода. Его замечательный
метод расчета подпорных стенок, применяемый по настоящее вре-
мя, остается вне рамок этой книги. Здесь уместно перечислить
достижения этого выдающегося физика и военного инженера в
области сопротивления материалов.
Мы уже отметили, что Кулон дал правильное решение задачи о
прочности балки. Кроме того, ему принадлежали еще три важных
открытия. Во-первых, он открыл существование касательных на-
пряжений. Вероятно это открытие стояло в связи с его известными
исследованиями в областии трения. Кулон показал, что раз-
рушение сжатых стержней очень часто происходит путем сдвига и
высказал предположение, что именно сдвиги являются причиной
всякого разрушения. Это предположение мы называем теперь
третьей теорией прочности и очень широко применяем в расчет-
ной практике.
Интересно, что Кулон придал задаче о касательных напряже-
ниях в сжатом стержне форму задачи на минимум, как и всем
другим проблемам строительной механики, рассмотренным в его
работе, имевшей характерное заглавие: «Применение правил на-
хождения максимумов и минимумов к некоторым задачам статики,
относящимся к архитектуре». Вот подлинный текст этой задачи:
«Чтобы определить наибольший вес, который может выдержать
устой, надо найти такое сечение, в котором силы сцепления спо-
собны уравновесить наименьший вес». Этот минимальный вес для
опасного сечения будет максимальным безопасным весом нагрузки
для устоя в целом. Тот же своеобразный подход — определение
максимальной (предельной) нагрузки как минимума некоторой
функции — Кулон применил и к расчету подпорных стенок и сво-
дов. Это был последовательно проведенный путь расчета по пре-
дельному состоянию.
Во-вторых, Кулон дал первое решние задачи о кручении (1784).
Он изучил кручение тонких проволок круглого сечения и вывел для
них правильные расчетные формулы, которыми мы постоянно поль-
зуемся, не думая об их авторе. Кулон установил, что крутящий мо-
мент пропорционален углу закручивания и четвертой степени диа-
метра. Мы сказали бы сейчас, что угол закручивания пропорциона-
лен крутящему моменту. Но для Кулона расчетным состоянием
было конечное состояние стержня, уже получившего деформацию.
По этой деформации Кулон определял вызвавший ее крутящий
момент. Совершенно так же подходили предшественники Кулона к
задаче о деформациях балки: по заданной деформации они опре-
деляли вызвавшую ее нагрузку. Подход, характерный для всего
XVIII века.
В-третьих, Кулон из опытов на изгиб и кручение вывел закон о
пропорциональности между нагрузкой и упругой частью деформа-
ции вплоть до разрушения — закон, неправильно называемый у
нас законом Герстнера.
•3Q1
Замечательные открытия Кулона были последними важными
исследованиями в области строительной механики в XVIII веке.
После них, как мы уже сказали, наступил регресс, отчетливо вид-
ный из книги Жирара.
Мы дошли до начала XIX века — преддверия работ Навье, с
имени которого мы начали обзор послегалилеевского периода ис-
тории науки. Подведем теперь некоторые итоги. Имел ли действи-
тельно право Навье жаловаться, что от трудов его предшественни-
ков инженеры получили мало пользы? Попробуем перечислить
окончательные плоды науки к этому времени.
По изгибу: разноречивые способы расчета на прочность балки,
дающие для балки прямоугольного профиля расхождение в 2 раза.
Задача изгиба решается только для балок прямоугольного и круг-
лого профиля и только при простейших случаях загружения: кон-
соль с грузом на конце, простая балка с грузом посередине. Вы-
числение перемещений осуществляется чрезвычайно сложно, путем
интегрирования в рядах точного уравнения кривизны, но не дает
количественного результата, так как значение коэффициента жест-
кости еще не известно. Самые понятия коэффициента жесткости
при изгибе (момент инерции сечения) и коэффициента прочности
(момент сопротивления) смешиваются, и даже их размерность оп-
ределяется ошибочно. Значения модуля упругости не известны еще
даже для самых распространенных материалов, да и само понятие
модуля упругости еще не установлено.
По продольному изгибу: правильное теоретическое решение
Эйлера — Лагранжа для упругого случая при невозможности ко-
личественной оценки по той же причине, что и для поперечного
изгиба.
По кручению: правильное решение Кулона для круглого про-
филя, но не дающее количественной оценки прочности и жестко-
сти, так как ни сопротивление материалов срезу, ни модуль сдвига
не известны.
Три разноречивые теории прочности.
Этот обзор доказывает правоту Навье: возможность практи-
ческого использования основных теоретических исследований
XVIII века в области сопротивления материалов действительно
крайне ограничена. Наука была оторвана от практики.
Решительный поворот науки к жизни начал осуществляться в
первой четверти XIX века и тесно связан с именем Навье. Для его
осуществления необходимо было отказаться от основного подхода
к проблеме прочности, указанного Галилеем,—от расчета по пре-
дельному состоянию, и заменить его новым, более прогрессивным
подходом.
Уместно поставить вопрос: почему же этот отрыв науки от жиз-
ни смог продержаться так долго? Мы не раз отмечали, что строи-
тельная механика — наука прикладная, тесно связанная с задача-
ми, выдвигаемыми жизнью. Два фактора двигают эту науку: по-
требность создания новых форм сооружений (или увеличение их
размеров) и экономика. Первый фактор начал действовать в сущ-
302
ности только с 20-х годов XIX века, когда появление железных
дорог и новых строительных материалов (чугуна, а потом свароч-
ного железа) потребовали создания новых необычных типов соору-
жении (в первую очередь мостов), способных выдерживать резко
увеличенные нагрузки. Этого стимула к развитию строительной
механики не было на протяжении всего XVIII века. Второй фак-
тор — экономический — постепенно начинал сказываться на строи-
тельстве в связи с развитием буржуазно-капиталистических произ-
водственных отношений. Однако в большинстве европейских стран
в XVIII веке феодальные формы хозяйства господствовали еще
почти неограниченно. И в России, и в Западной Европе того вре-
мени мосты, дворцы и заводы строились крепостными; на фабриках
и в копях трудились те же крепостные, приписанные к заводу или
составлявшие собственность заводовладельца. Неограниченная
эксплуатация рабочих давала хозяевам такие огромные прибыли,
что соображения экономии, рационализации строительства не
только не стояли в порядке дня, а встречали к себе враждебное
отношение. Крепостное право было тормозом для развития про-
мышленности, а стало быть и прикладной науки. Таким образом,
экономические условия XVIII века не стимулировали развития
строительной механики. Поэтому она и не искала сближения с
практикой.
«Французских математиков
всегда упрекают в том, что они
слишком отвлеченно рассматри-
вают свой предмет и что их тео-
рии мало приносят пользы, об-
ществу. Ныне... уже многие
ученые, увлекаемые общим на-
правлением народной потреб-
ности, решились сойти в мир
вещественный, ознакомиться с
ним и озарить его светильни-
ком своих умозрений».
Подполковник М. С. Вол-
ков (Журнал путей со-
общения, 1838, т. 2,
стр. 166).
Глава 5
РАБОТЫ НАВЬЕ И РЕФОРМА СТРОИТЕЛЬНОЙ МЕХАНИКИ
К началу XIX века состояние строительной механики приходит
в резкое несоответствие с требованиями техники и экономики и
требует решительной перестройки, решительного поворота к нуж-
дам практики. Такая перестройка строительной механики была
303
осуществлена в 20-х годах XIX века и связана с именем француз-
ского инженера путей сообщения Навье.
Историческая закономерность этой реформы несомненна и не
случайно, что она имела место именно во Франции. К этому вре-
Навье (1785—1836)
мепи во Франции назрел ряд важных социально-экономических и
технических причин, настоятельно требовавших разработки надеж-
ных методов расчета конструкций на прочность- Французская ре-
волюция, разгромившая феодализм, привела к власти буржуазию,
а последующие события в истории Франции — континентальная
блокада и ограбление завоеванных Наполеоном европейских
стран — способствовали небывалому обогащению буржуазии и
содействовали быстрому- росту промышленности. А рост промыш-
304
ленности потребовал, с одной стороны, скорейшего развития техни-
ческой мысли, а с другой — изыскания способов удешевления стро-
ительства ради повышения прибылей.
Непосредственной технической причиной, вызвавшей реформу
строительной механики, было появление и широкое применение в
технике новых материалов — сперва чугуна, а затем сварочного
железа. Дороговизна, тяжесть и хрупкость чугуна в особенности
настоятельно требовали значительно более внимательного отноше-
ния к расчету, чем это было принято для камня и дерева. Непра-
вильно ставить эту реформу в связь с появлением железных дорог,
как это иногда делается, так как она фактически предшествовала
открытию первых регулярных железных дорог. Железнодорожное
строительство оказало мощное влияние на развитие строительной
механики в последующий период, начиная с 30-х годов. Но основ-
ные работы Навье и его школы появились ранее, когда еще не-
возможно было предугадать тех огромных запросов и требований,
которые новый вид транспорта предъявит к науке. Первопричи-
ной же реформы были, как сказано, социально-экономические
сдвиги.
Не вполне ясно, почему эти сдвиги привели к реформе строи-
тельной науки во Франции, а не в Англии, где они наступили
раньше и позволили Англии занять первое по тому времени место
в мире в техническом и промышленном отношении. В силу каких-
то причин развитие строительной механики в Англии на всем про-
тяжении XIX века сильно отставало от уровня строительной тех-
ники в той же Англии и не может идти ни в какое сравнение с
успехами строительной механики во Франции. Можно высказать
лишь одну гипотезу: быть может на развитие строительной меха-
ники влияло не только состояние промышленности и техники
в каждую эпоху, но и скорость их развития. Скорость же эта
во Франции в начале прошлого века была значительно выше, чем
в Англии, по причинам, уже ранее названным. В результате пере-
чень имен ученых, вложивших свой труд в создание классического
курса сопротивления материалов, содержит много французов и
очень мало англичан. Можно утверждать даже, что английский
вклад в эту науку в XIX веке, в пору наибольшего расцвета анг-
лийской промышленности, уступает по важности русскому вкладу
в эту же эпоху, хотя в промышленном отношении Россия XIX ве-
ка сильно отставала от Западной Европы, особенно к концу царст-
вования Николая I, сознательно тормозившего развитие отечест-
венной промышленности из боязни революции.
Надо сказать, впрочем, что прославленное превосходство
строительной техники в Англии XIX века не оправдывается при
более внимательном изучении вопроса. Вот характерное высказы-
вание по этому поводу, которое мы находим в журнале Главного
управления путей сообщения и публичных зданий за 1853 г., стр. 3
(без подписи автора):
«Прямые чугунные балки различных сечений и форм уже при-
чинили в- Англии переломом своим разные несчастья. Несмотря на
305
это во Франции следовали и до сих пор следуют без всякого раз-
бора примеру англичан, употребляя при сооружении мостов эту
систему, исполненную недостатков. Там, где чугун обходится очень
дорого, употребление прямых балок в мостах обнаруживает мла-
денчество искусства. Введение подобных балок может быть припи-
сано заводчикам, имевшим при этом в виду увеличение сбыта
чугуна».
Эта последняя фраза, написанная неизвестным русским инже-
нером 100 лет назад, удивительным образом не утратила своей
социальной остроты и вполне применима к современной капита-
листической технике.
В чем же состояла реформа строительной механики, связанная
с именем Навье?
Сущность этой реформы, по настоящему понятая лишь много
позже, состояла, во-первых, в отказе от расчета по предельному
состоянию, господствовавшему в науке со времени Галилея, и в
переходе всей строительной механики на принцип расчета по рабо-
чему состоянию.
Сущность этой реформы состояла, во-вторых, в провозглашении
принципа малости перемещений, который позволил вести расчет не
по неизвестному конечному деформированному состоянию систе-
мы, а по заданному начальному состоянию.
Обе эти стороны реформы Навье тесно связаны между со-
бой. Это именно две стороны одной и той же идеи — перехода от
конечного состояния к начальному и в усилиях, и в переме-
щениях.
Различие между обоими принципами можно формулировать
следующим образом.
Принцип предельного или конечного состояния исходит из
схемы вероятного разрушения конструкции и определяет величи-
ну нагрузки, при которой такое разрушение может произойти.
Допускаемая нагрузка определяется делением предельной нагруз-
ки на запас прочности.
Принцип рабочего или начального состояния определяет на-
пряженное и деформативное состояние конструкции при рабочей,
действительной нагрузке, принимая, что предельное состояние
полностью подобно рабочему, так что отношение нагрузок, усилий,
напряжений и перемещений в обоих состояниях одинаково и равно
запасу прочности.
При этом подходе нет надобности задаваться видом предель-
ного состояния и изучать его; достаточно изучить рабочее состоя-
ние, т. е. напряжения и перемещения при расчетной нагрузке, и
найти их отношения к предельным. Так как при этом предпола-
гается известной из опыта предельная величина напряжения для
данного материала, которая при делении на запас прочности дает
так называемое допускаемое напряжение, то весь расчет сводится
к сравнению действительных рабочих напряжений с допускаемыми
напряжениями. По этой причине расчет по рабочему состоянию
часто называют расчетом по допускаемым напряжениям. Надо
306
подчеркнуть, что самое понятие напряжения впервые ввел сам
Навье.
Для рассматриваемой эпохи переход к новому принципу расче-
та по рабочему состоянию был безусловно глубоко прогрессивным.
Отсутствие экспериментальных данных о поведении конструкций
при высоких нагрузках вынуждало прибегать к более или менее
вероятным гипотезам о схеме разрушения, внося этим в расчет
элемент условности и произвола. С особой отчетливостью это вид-
но в истории расчета арок (очерк II). Напротив, изучение дейст-
вительного состояния конструкции позволяло обойтись без таких
произвольных гипотез, опираясь на несложный эксперимент и
применяя расчетный аппарат математической теории упругости, ос-
новоположником которой явился тот же Навье.
Введение понятия напряжения, возможность элементарного вы-
числения его для большинства практических задач и прямого
сопоставления с полученным из опытных данных допускаемым
напряжением внесли в строительную механику рациональный эле-
мент и дали инженерам ощущение небывалой до этого надежности
расчета, свободного от всякого произвола. Так именно была вос-
принята эта важнейшая реформа (разумеется, не сразу), опреде-
лившая пути развития строительной механики на целое столетие
вперед. С момента перехода на принцип рабочего состояния
строительная механика впервые стала, наконец, прикладной нау-
кой, способной удовлетворять практическим нуждам техники.
Если Галилей был основоположником науки о прочности, то Навье
впервые сумел связать ее с жизнью, а потому 1826 г. — дата вы-
хода в свет книги Навье — не менее важен в истории этой науки,
чем 1638 г. — дата ее рождения.
Сейчас мы уже можем более спокойно и критически отнестись
к реформе Навье, так как за последние годы строительная меха-
ника переживает новую важную реформу, поднимаясь на следую-
щую, более высокую ступень. Об этой реформе, заключающейся
кажущимся образом в возрождении принципа предельного состоя-
ния, подробно сказано в дальнейших главах. Пока отметим лишь,
что «объективность» нового принципа рабочего состояния и сво-
бода его от произвольных допущений на самом деле были фикци-
ей. В основе этого принципа лежит совершенно произ-
вольное допущение о полном подобии рабочего и предельного
состояний. В действительности о таком подобии, т. е. о пропорцио-
нальности между величинами нагрузки, с одной стороны, и вели-
чинами напряжений и перемещений, с другой, можно говорить (и
то с оговорками) лишь в пределах справедливости закона Гука1.
Но действие закона Гука у всех материалов прекращается ранее
разрушения, а потому предельное состояние любой конструкции
не будет подобно ее состоянию при расчетной нагрузке. Мы вида-
ли, что это обстоятельство отмечал еще Кулон в применении к про-
1 Для контактной задачи этой пропорциональности нет даже при соблюдении
закона Гука.
307
стейшей задаче изгиба. Однако в общем виде порочность идеи
подобия двух состояний начала сознаваться только через много
десятилетий после смерти Навье.
Но если в действительности переход к новому принципу и озна-
чал замену одной условности на другую, то между этими услов-
ностями была и существенная разница. Во-первых, поиски предель-
ных состояний требовали введения гипотез о форме разрушения,
зависевших от схемы самого сооружения, так что число этих ги-
потез было равно числу различных видов конструкций. Новый
принцип вводил только одну общую гипотезу — условие подобия
двух состояний, и стало быть элемент условности в новом принци-
пе был несравненно менее субъективным, чем в старом. А во-вто-
рых, фактическое нарушение условия подобия приводит (за ред-
чайшими исключениями) к тому, что новый принцип дает не-
сколько преувеличенный запас прочности, так что расчет по нему
дает безусловную гарантию безопасности. Вот этой гарантии ста-
рый расчет по предельному состоянию был неспособен дать, и
именно в этом различии между ними заключается основное преи-
мущество расчета по рабочему состоянию, обеспечившее превра-
щение строительной механики в важнейшую для практики при-
кладную науку.
=5: *
*
Луи Навье родился в 1785 г. в семье адвоката. Он рано лишил-
ся отца и был воспитан своим дядей, видным инженером мосто-
строителем Готэ. Это родство определило будущую специальность
Навье. Он обучался в парижской Школе мостов и дорог, соответст-
вовавшей по профилю нашему Институту инженеров путей сооб-
щения, и окончил ее в 1808 г. Сперва Навье занялся практической
строительной работой, специализировавшись на висячих мостах.
Но здесь его вскоре постигла неудача, в которой он не был пови-
нен. Он приступил к постройке большого висячего моста через Се-
ну в Париже, но когда работы уже близились к окончанию, обна-
ружилась осадка устоя, подмытого вследствие аварии водопровода.
Навье быстро составил проект усиления устоя, но правительствен-
ная комиссия отказалась отпустить добавочную сумму и распоря-
дилась разобрать почти готовый мост. Можно представить себе,
каким ударом это было для молодого талантливого инженера и
сколько незаслуженной клеветы свалилось на его голову. После
этой неудачи он отказался от практической работы и занялся ис-
ключительно научными исследованиями. Прежде всего, как дань
уважения к своему покойному воспитателю (Готэ умер в 1806 г.).
Навье издает на собственный счет двухтомный курс мостов Готэ
[3], снабдив его своими примечаниями (надо сказать, что издание
это резко выделяется из современных технических изданий своей
роскошью). Затем в журналах начинают появляться оригинальные
научные работы Навье, и он приобретает известность как ученый-
инженер. В 1819 г. он становится профессором Школы мостов п
308
дорог, а в 1824 г. — академиком. Навье умер неожиданно рано, в
1836 г. в возрасте 51 года. Его курс лекций по прикладной механи-
ке издавался трижды: в 1826, в 1833 и — посмертное издание — в
1864 г., под редакцией его ученика Сен-Вена на, снабдившего клас-
сический труд своего учителя примечаниями и комментариями, зна-
чительно превышавшими по объему текст Навье.
Такова биографическая канва жизни Навье.
Обзор его научной деятельности и изучение подлинных работ
производят несколько странное, двойственное впечатление. Наряду
с важнейшими открытиями, которые, как мы уже сказали, опре-
делили путь дальнейшего развития науки на целое столетие, в его
трудах встречаются странные ошибки, грубо неправильные ут-
верждения, ошибочность которых немедленно вскрывается эле-
ментарной проверкой расчетным или опытным путем. Были ли эти
ошибки результатом небрежности, невнимательности или Навье
чрезмерно доверялся своей интуиции — сказать трудно. Но вернее
предположить, что Навье был человеком способным страстно увле-
каться в научной деятельности и забывать при этом необходимую
для ученого осторожность и осмотрительность. Невольно вспоми-
нается, сколько ошибок сделал его великий соотечественник Па-
стер по этой же причине.
Первые работы Навье относятся к пресловутой задаче изгиба,
к которой он подходит еще со старых позиций предельного состоя-
ния. Повторяя мнения своего воспитателя Готэ, он в 1813 г. ут-
верждает, что нет смысла учитывать сжатие волокон при изгибе,
так как положение нейтральной линии не влияет на сопротивление
изгибу. Мы видели, что эту ошибочную мысль впервые высказал
ровно за 100 лет Яков Бернулли. Позже он развивает другую оши-
бочную идею Готэ о том, что при изгибе бруса каждое волокно
работает на растяжение и изгиб. В 1819 г. Навье получает, нако-
нец, правильное выражение момента сопротивления для симметрич-
ных профилей, но повторяет ошибку Дюло в отношении несим-
метричных профилей, определяя положение нейтральной линии из
условия равенства моментов растягивающих и сжимающих усилий
в сечении.
Правильное решение задачи изгиба Навье удалось дать только
в курсе лекций 1826 г. Он отверг разделявшееся большинством уче-
ных мнение Дюло и один среди всех определил положение нейт-
ральной линии из условия равенства усилий, а не их моментов в
сечении. Мы знаем, что так поступали задолго до Навье Паран и
Кулон, но только применительно к симметричным профилям. Реше-
ние Навье оказалось верным для профиля любой формы, причем
он первый нашел, что нейтральная линия проходит через центр
тяжести сечения, «если закон Гука верен». Эта оговорка принад-
лежит самому Навье, который ясно сознавал, что отныне он обре-
кает себя на рассмотрение только чисто упругой стадии работы
конструкции.
Интересно, что Навье не заметил, что фактор изгибной жест-
кости можно вычислять как момент инерции сечения и даже не
309
сумел дать для него удобный способ записи. Вместо привычной для
нас записи выражения момента инерции Jи = J* v2dF он писал так:
b ftu b fyi
$du J dvv2 + J du J dvv2,
где b = a fiU и f%u — ординаты, ограничивающие растянутую
и сжатую зоны сечения по оси v. Этим он даже усложнил запись,
встречающуюся в изданном им курсе мостов Готэ: jj duv2dv. Но
надо помнить, что в те времена понятия дифференциала площади
еще не существовало, и возможность представления интеграла по
площади в виде простого, не двойного интеграла не была известна.
Уподобление фактора жесткости моменту инерции сечения сделал
соратник Навье по Школе мостов и дорог Перси, и Коши уже при-
менил этот термин в своей работе по кручению 1829 г. Тем не ме-
нее во втором издании курса лекций 1833 г. Навье не употребляет
этого термина1.
Успешное разрешение задачи изгиба и применимость получен-
ного решения к профилям любого вида соблазнили Навье дать
общее решение и для задачи кручения. Но здесь он совершил гру-
бую ошибку, предложив распространить решение Кулона для
стержня круглого профиля на профиль любой формы. Известно,
в чем состоит разница между задачами изгиба и кручения: при
изгибе стержни любого профиля сохраняют в пределах малых де-
формаций плоские поперечные сечения, и потому формулы изгиба
применимы к любым профилям. При кручении же плоские сечения
сохраняются только у стержня круглого профиля, и потому осно-
ванная на гипотезе плоских сечений элементарная теория кручения
верна только для круглого профиля. Это обстоятельство в то вре-
мя еще не было известно, хотя уже упоминавшийся нами Дюло еще
в 1813 г. производил опыты на кручение стержней круглого, квад-
ратного и прямоугольного профиля, результаты которых, как го-
ворит Сен-Венан, «удивили Навье». Несмотря на это «удивление»,
он в первом издании курса не делает никаких оговорок по поводу
ограниченной применимости элементарной формулы кручения.
В 1829 г. Коши попробовал решить задачу о кручении стержня
прямоугольного профиля. Это решение оказалось неверным, и сам
Коши через четверть века (в 1854 г.) от него отрекся. Решение Ко-
ши исходило из уравнения
d"h Jj Jо q
dydz Л 4- Ji
где у, z — оси координат сечения;
и — смещение вдоль оси стержня;
1 Для характеристики заблуждений, с которыми приходилось бороться Навье,
укажем, что Тредгольд считал круглый профиль единственным, обладающим
одинаковой жесткостью на изгиб по всем направлениям. Навье опроверг это мне-
ние и указал целый ряд профилем, обладающих этим свойством (квадрат и всякие
симметричные комбинации круга н квадрата).
310
/i и /2 — главные моменты инерции сечения;
0 —угол закручивания.
Это уравнение показывает, что Коши обнаружил нарушение
закона плоскости сечений, но из него следует также, что по Коши
сечения, у которых главные моменты инерции равны между собой
(например, квадрат, симметричный крест и т. д.), остаются при
кручении плоскими, а это неверно. Для прямоугольника Коши
получил формулу
где b и с — стороны сечения. Эта -формула пригодна только для
очень узкого прямоугольника, когда с во много раз больше 6; она
дает для этого случая известное выражение
I 3
Во втором издании лекций Навье, признавая, что гипотеза
плоских сечений для кручения «не вполне точна», приводит для
прямоугольника вышенаписанную формулу Коши, но для квадрата
сохраняет свое прежнее решение по гипотезе плоских сечений
m = gq—
и 9
которое, впрочем, получается и из формулы Коши, так как по
решению последнего, как сказано, квадратные сечения остаются
плоскими. Как известно, правильное решение для квадрата содер-
жат в знаменателе последней формулы множитель 7,5 вместо 6,
так что Навье и Коши переоценили крутильную жесткость стержня
квадратного профиля на 25%.
Таким образом, Навье не удалось дать общего правильного
решения задачи о кручении; оно появилось только через 30 лет в
трудах Сен-Венана. Интересно, что порочность решения, по-види-
мому, мало беспокоила инженеров на протяжении этих десятиле-
тий; очевидно, это объясняется тем, что вопрос о кручении стерж-
ней некруглого сечения не имел в то время практической важ-
ности1.
Задача продольного изгиба также не получает у Навье оконча-
тельного решения. К тому времени многочисленные опыты Одри,
Жирара, Ламандэ, Ронделэ, Дюло и др. твердо установили, что
решение Эйлера по непонятной причине непригодно для стержней
средней длины. Навье приводит в своем курсе вывод формулы
Эйлера, а затем, не пытаясь вскрыть причину ее несоответствия с
опытами, дает следующие указания.
1 В качестве исторического курьеза упомянем о теории Тредгольда (1826),
который пробовал рассматривать кручение прямоугольного стержня как изгиб
относительно диагонали, соединяющей угловую точку одного концевого сечения
с противоположной точкой другого концевого сечения.
311
1. Формула Эйлера верна, если длина превосходит толщину в
20 раз и более.
2. Для коротких стержней расчет надо вести на раздавливание,
по допускаемому напряжению /?.
3. Для дерева при / = V2d надо брать а при /=24(7—Vs/?;
4. Для кованого железа при / = \2d надо брать Б/е/?, а при
/ = 24d——.
2
5. Для литого железа при l = 4d надо брать %/?, при /=&/—
при /=36(/---
Интересно признание, которым Навье сопровождает эти ука-
зания: «Опыты не дают возможности точно вычислить сопротив-
ление в промежуточных случаях». При этом он рекомендует вво-
дить запас прочности, равный 10 для дерева, 4 или 5 — для железа.
Сопоставляя эти рекомендации с современными нормами рас-
чета на устойчивость, можно заметить очень значительное расхож-
дение, причем для железа Навье переоценивает опасность потери
устойчивости, а для дерева—недооценивает ее. Приводим резуль-
таты сравнения в таблице:
Материал Гибкость Коэффициент ф снижения до- пускаемого напряжения
по Навье по нормам
Литое железо1 16 0,67 0,98
32 0,50 0,93
144 0,067 0,34
Кованое железо1 48 96 0,62 0,50 0,90 0,63
Дерево 48 96 0,83 0,50 0,82 0.33
* Сравниваем с нормами для стали марки Ст. 3.
С современной точки зрения приходится признать рекомендации
Навье весьма неудовлетворительными.
Навье принадлежит далее решение задачи о балке, загружен-
ной произвольным образом. По-видимому, это было первое по вре-
мени решение; до Навье ограничивались случаем сосредоточен-
ного груза в середине пролета (или на конце консоли). Но и здесь
Навье допустил странную ошибку: он утверждал, что опасное сече-
ние двухопорной балки (сечение с наибольшей кривизной) всегда
лежит на вертикали центра тяжести нагрузки (т. 1, стр. 234, изд.
1833 г.). Это, разумеется, совершенно неверно: вспомним, напри-
мер, Ч7о при действии на балку двух сосредоточенных грузов опас-
312
мое сечение находится под одним из них, а не под общим центром
тяжести. Достаточно было бы построить эпюру моментов или про-
делать несложные подсчеты, чтобы убедиться в ошибочности этого
утверждения. Но ни самому Навье, ни его последователям на про-
тяжении двух десятилетий не приходило в голову строить эпюры
моментов и вообще прибегать к помощи графиков для придания
наглядности аналитическим расчетам. Возможно, что в этом
сказалось влияние школы Лагранжа, который был убежденным
противником геометрических методов. От этого влияния было не-
легко освободиться: впервые эпюры моментов построил для арки
Бресс [19] только в 1848 г. Одно из самых ранних построений эпю-
ры моментов для балки мы находим в книге русского инж. Беспа-
лова [20], вышедшей в 1855 г.
К работам Навье мы еще вернемся в дальнейших очерках, где
расскажем о том, что он дал первый расчет двухшарнирной арки и
второй по времени (хотя и независимый от предшественника)
расчет неразрезной балки. В области сопротивления материалов
его достижения ограничиваются тем, что выше изложено.
Однако это изложение было бы односторонним, если бы мы не
подчеркнули главного: при решении всякой задачи (было ли оно
верным или ошибочным) Навье делал упор на определение дейст-
вительных напряжений, возникающих при действии рабочей на-
грузки. Он впервые ввел и самое понятие допускаемого напряже-
ния, легшее в основу нового принципа расчета, и даже обозначение
его буквой /?, которое до последнего времени применялось в на-
шей технической литературе.
Любопытно, что для железа с пределом прочности 4 000 кг! см2
Навье рекомендовал допускаемое напряжение на изгиб
1 300 кг(см2, что весьма близко к нашим современным нормам для
такой стали. Для растяжения он снижал эту величину до 1 000 и да-
же до 600 кг!см\
Навье совершенно четко формулировал смысл осуществляемой
им реформы: «Сопротивление разрушению недостаточно для про-
ектирования, так как надо знать не разрушающую силу, а ту, кото-
рою можно нагрузить элемент без того, чтобы возникающее в нем
изменение возрастало со временем».
Столь же последовательно Навье поставил вопрос о малых
перемещениях. Он показал, что все девять форм изгиба, изучав-
шихся Эйлером, интегрируются в этом случае в конечном виде
при любой нагрузке. Для этого достаточно заменить дифференци-
ал дуги на дифференциал ее проекции на ось абсцисс. В том же
предположении малости деформаций Навье свел к квадратурам
задачу изгиба криволинейного стержня (см. очерк II) и случай
продольного изгиба при весьма малом эксцентрицитете.
Надо заметить, впрочем, что мысль о применении малых пере-
мещений впервые была высказана еще Готэ, учителем Навье, но
первое последовательное приложение ее и полный отказ от рас-
смотрения больших перемещений составляет всецело заслугу
Навье. По тому времени это было большой заслугой, так как по-
313
зволило простым путем разрешить важные практические задачи
и тем самым приблизить науку к жизни. Сам Навье придавал вы-
числению деформаций едва ли не большее значение, чем вычисле-
нию напряжений. Это объясняется тем, что он был убежденным
сторонником второй теории прочности, высказанной Мариоттом.
Поэтому Навье настаивал на нормировании в первую очередь
именно относительных удлинений, и вся позднейшая французская
школа, включая Сен-Венана, так упорно придерживалась 2-й
теории прочности, иногда вопреки очевидности.
Новый подход к строительной механике ни в чем, быть может,
не отразился с такой отчетливостью, как в новой отрасли этой нау-
ки— теории упругости, основоположником которой явился тот же
Навье (1819), и которая в трудах Коши быстро встала на верный
путь. Для этой новой науки, основанной на неограниченной спра-
ведливости закона Гука и принципа малости перемещений, особо
характерен полный добровольный отказ от рассмотрения поведе-
ния конструкции вблизи ее предельного состояния или состояния
разрушения. Теория упругости с первых своих шагов стала на путь
изучения рабочего состояния конструкции, и в этом была ее сила,
но в этом же впоследствии оказалась и ее слабость, так как от-
каз от изучения условий разрушения неизбежно уводил ее от
жизни, от возможности приложения на практике. Замечательна
эта диалектическая двойственность: переход на принцип расчета
по рабочему состоянию в сопротивлении материалов сблизил эту
науку с практикой, но тот же принцип, примененный в неограничен-
ной форме к теории упругости, оказал обратное действие, отдалив
ее от практики.
«Европа в отношении к Рос-
сии всегда была столь же неве-
жественна, как и неблагодарна».
А. С. Пушкин
Глава 6
ЗАВЕРШЕНИЕ ТЕОРИИ ИЗГИБА
Навье умер в 1836 г., когда уже во всех странах Европы зады-
мили первые паровозы. Перед мостостроителями встала совершен-
но новая задача — обеспечить прочность мостов при действии пе-
ремещающейся нагрузки, вес которой велик по сравнению с весом
пролетного строения. К решению этой задачи наука оказалась не-
подготовленной. Все, чем она овладела к 30-м годам XIX века в об-
ласти теории изгиба, сводилось к уменью вычислить перемещения и
нормальные напряжения при простейших случаях загружения бал-
ки. Естественно, что именно задача поперечного изгиба потребова-
ла первоочередного развития.
Следующий шаг после Навье в этой области сделал Перси [21],
314
который ввел понятие момента ‘инерции сечения, разработал тео-
рию моментов инерции и указал на то, что теория изгиба Навье
верна лишь при совпадении нейтральной линии с главной осью
сечения (1834).
Еще через 9 лет Сен-Венан разрешил задачу косого изгиба
(1843), введя два уравнения моментов относительно обеих главных
осей. Он же дал решение для задачи об изгибе с растяжением, ис-
пользовав для этого впервые принцип наложения малых дефор-
маций.
Поразительно, что понадобилось 20 лет со времени появления
первых уравнений теории упругости, прежде чем их линейность
навела на мысль о возможности такого наложения. Еще порази-
тельнее то, что мысль о возможности наложения нагрузок возникла
еще позже, к концу 1840-х годов, когда ее одновременно использо-
вали Журавский и Бресс. Напомним, что линейность уравнений
теории упругости явилась следствием принятия условия малых де-
формаций и неограниченной справедливости закона Гука, т. е. тех
самых допущений, которые составили существо переворота в строи-
тельной механике,— перехода от принципа предельного состояния
к расчету по начальному рабочему состоянию. Добавочный выи-
грыш, полученный при этом переходе, состоял именно в линейности
всех уравнений, и это как раз не было понято и использовано в те-
чение двух деся гилей.
Задачу о внецентренном растяжении или сжатии решил в об-
щем виде Бресс [22], установивший понятие ядра сечения и изучив-
ший его свойства (1854).
Однако все эти труды французской школы относились только к
случаю чистого изгиба и не учитывали сдвигов. Первое решение
задачи о поперечном изгибе дал замечательный русский ученый
Дмитрий Иванович Журавский.
Наличие сдвигов при изгибе было подмечено задолго до рас-
сматриваемого периода. Первое указание дал, по-видимому, Дю-
гамель в 1767 г., заметив, что только сдвигами можно объяснить
различие прочности и жесткости у целой балки и у балки, распи-
ленной на продольные слои. Позже Кулон указал, что данный им
расчет на изгиб верен только в тех случаях, когда плечо силы мно-
го больше высоты сечения (или, по современной терминологии, если
влияние поперечной силы на прочность невелико). Понятие среза
при изгибе встречается затем у Юнга, сравнивавшего это явление
с действием ножниц. Термин поперечной силы при изгибе ввел Ви-
ка, изучавший опытным путем сдвиги при изгибе (1833). Таким
образом, явление сдвигов при поперечном изгибе было уже давно
известно, когда Журавский впервые попытался подойти к нему
расчетным путем и дал свое знаменитое решение [23].
Задача о касательных напряжениях при изгибе была для Журав-
ского побочной задачей, встретившейся ему при разрешении более
общего вопроса о расчете мостовых деревянных ферм. Поэтому
более подробный рассказ о деятельности этого выдающегося чело-
века мы дадим в очерке III. Но поскольку мы здесь впервые ветре-
315
чаемся с русским ученым в области строительной механики, умест-
но коснуться вопроса о развитии этой науки в России к рассматри-
ваемому периоду.
В 1810 г. в России открылось первое высшее техническое учебное
заведение — Институт инженеров путей сообщения в Петербурге,
явившееся колыбелью русской технической науки. Из-за отсутствия
отечественных кадров создание его было доверено представителям
самой передовой для того времени научной школы — французской.
Выбор был сделан правильно, так как ни немецкая, ни английская
школы в то время не могли состязаться с французской. В Россию
был приглашен ряд видных французских инженеров — Бетанкур,
Базен и др., среди которых мы встречаем в 20-х годах имена таких
первоклассных ученых, как Ламэ и Клапейрон.
Однако последующая правительственная политика превратила
разумное начинание во вредную бессмыслицу. Вместо того, чтобы
постепенно заменять иностранцев русскими инженерами, окончив-
шими институт, правительство Александра I и особенно Николая I
сознательно препятствовало этому процессу, всячески поддерживая
иноземцев и всемерно противодействуя русским. Преподавание в
институте велось исключительно на французском языке, и ученые
труды института печатались по-французски. От этого времени до
нас дошел целый ряд укоренившихся в русском языке французских
терминов, вроде слова «эпюра», означавшего по французски просто
«чертеж», но получившего „специфический смысл в начертательной
геометрии и сопротивлении материалов. Кстати, названия обеих
этих наук дословно переведены с французского. Нельзя не упомя-
нуть, что автору первого русского курса механики, замечательному
ученому Остроградскому, было предложено перевести на француз-
ский язык этот учебник, поскольку он предназначался для Путей-
ского института.
С начала 1830-х годов дело обернулось еще хуже. Николай I,
раздраженный французской июльской революцией 1830 г., изгнал
из института французских инженеров, в том числе Ламэ и Клапей-
рона, и заменил их немецкими инженерами. Они стояли несравнен
но ниже своих предшественников по научному уровню, но зато
были политически благонадежными. Институт был объявлен кра-
мольным учреждением; в нем завели казарменную муштру и даже
телесные наказания для студентов. Русских инженеров старались
не допускать к ответственным работам, ,и постройку первой желез-
ной дороги — Царскосельской — поручили чешскому инженеру
Франтишеку Антонину Герстнеру (младшему).
Однако политика зажима и репрессий не могла справиться с
мощным ростом технического уровня русских инженеров. С 1834 г.
правительству пришлось пойти на уступки. В институте был вве-
ден русский язык и появились первые русские профессора. Не-
смотря на сопротивление иностранной профессуры, вводятся кур-
сы передовой техники — изучение железных дорог и паровозов. К
этому периоду относится и появление первых русских учебных
пособий и научных трудов по строительной механике.
316
Современникам следует знать имена первою русского профессо-
ра строительной механики Матвея Степановича Волкова (1802—
1878), одного из основоположников железнодорожного дела в
России1, и Николая Феликсовича Ястржембского, автора первого
русского учебника сопротивления материалов [24], вышедшего в
свет в год смерти Пушкина. Мы не случайно упомянули здесь имя
ГЕ П. Мельников (1807—1880)
великого поэта: в последние годы жизни он принял участие в кам-
пании за строительство железных дорог в России-
В середине 1840-х годов, когда началась научная деятельность
Журавского, русская техническая школа, несмотря на постоянное
противодействие царского правительства, уже твердо стояла на
ногах и пользовалась широкой поддержкой и защитой со стороны
русской общественности (упомянем в этой связи имя Белинского,
живо интересовавшегося строительством Петербургско-московской
железной дороги) и молодой либеральной буржуазии, которой
была необходима отечественная техника. Именно эта поддержка
была причиной крупнейшей победы русских инженеров: несмотря
1 Некоторые данные об его деятельности см. в книге В .С. Виргинского,
Возникновение железных дорог в России, Гострансиздат, М., 1949, стр. 97—99.
317
на открытое предпочтение, оказываемое иностранцам, правитель-
ству пришлось отказаться от предложений Герстена и поручить
сооружение величайшей в мире по тому времени железной дороги
из Петербурга в Москву русским инженерам Павлу Петровичу
Н. О. Крафт (1798—1857)
Мельникову (1807—1880) и Николаю Осиповичу Крафту (1798—
1857), которые блестяще справились с этой грандиозной задачей
и создали магистраль, которая и сейчас по своим техническим ка-
чествам заслуженно считается лучшей железной дорогой Совет-
ского Союза.
В числе помощников Мельникова и Крафта был Дмитрий Ива-
нович Журавский (1821—1891), руководивший мостовым отделом
строительства.
Журавский был инженером-практиком, строителем мостов, и в
своей научной деятельности он оставался таким же убежденным
практиком. В его трудах не следует искать теоретических обоб-
щений, которые смогут пригодиться когда-нибудь впоследствии
Он исходил из потребностей строительства и старался удовлетво-
рить их с удивительной смелостью, не смущаясь никакими труд-
ностями. Его научная 'интуиция и находчивость были поразитель-
ны, и именно эти свойства позволили ему решить задачу о сдви-
318
гах при изгибе. Для оценки его заслуги в этой области надо
вспомнить, что более простая задача о нормальных напряжениях
при изгибе потребовала 200 лет
Галилея до Навье, прежде чем
удалось получить верное решение.
Журавский поставил и решил за-
дачу о сдвигах совершенно само-
стоятельно, не имея даже наме-
ка на метод решения в трудах
своих предшественников.
Журавский рассмотрел одну
частную задачу: консоль прямо-
угольного профиля с грузом на
конце (рис. 5). Если отделить
консоль от заделки и приложить
труда крупнейших ученых, от
Р
Рис. 5. Схема Журавского для вычис-
ления касательных напряжений при
изгибе
вместо опорного момента распре-
деленные по двузначной эпюре
нормальные усилия в опорном
сечении, то станет ясно, что эти
нормальные усилия, направлен-
ные в разные стороны, вызывают срез вдоль нейтрального слоя. Ве-
личина срезающего усилия Q определяется из уравнения равно-
весия
Л/2 Л 2
Q = J idF = -у- \ydF = yL.
О о
На первый взгляд это решение может показаться странным и
даже неверным, так как срезающая сила оказывается пропорцио-
нальной изгибающему моменту. Но это сомнение объясняется
просто; на свободном конце консоли момент равен нулю, а если
бы он был отличен от нуля, то по методу Журавского срезающая
сила получилась бы пропорциональной разности моментов, или,
точнее,— производной от момента. Как известно, этот последний
вывод часто называется теоремой Журавского, хотя прямого дока-
зательства ее он не дал.
Из формулы срезающего усилия можно получить и выражение
касательного напряжения в нейтральном слое, но для этого надо
положить, что напряжения равномерно распределены по ширине-
консоли b и ее длине I
Журавский дал и более общее решение для касательного на-
пряжения в произвольном слое, которое приводит после деления
на b и I к известной формуле
ЬЛз \ 4 У I Jb
3J9
Надо заметить, однако, что прием решения, основанный на до-
пущении о равномерном распределении касательных напряжений
по длине балки, справедлив только для участка балки, не несуще-
го местной нагрузки. Журавский рассмотрел именно этот случай,
но не оговорил этого условия.
В зарубежной литературе формула касательных напряжений,
выведенная Журавским, встречается впервые у Ренкина [25] в
1862 г. (решение Журавского было опубликовано в 1855 г.). Из-
вестно, что формула Журавского является приближенной, так как
требует принятия гипотезы о равномерном распределении каса-
тельных напряжений по ширине прямоугольного профиля. Точное
решение, полученное впоследствии Сен-Венаном методами теории
упругости, показало высокую степень приближения формулы Жу-
равского для прямоугольных профилей, у которых высота равна
или больше ширины, т. е. для всех практически важных случаев.
Теперь мы смело применяем формулу Журавского и для более
сложных форм профилей — двутавровых, швеллерных и т. п., так
что это решение оказалось значительно более общим, чем предпо-
лагал Журавский. И особенно важно подчеркнуть, что решение
Журавского осталось единственным практическим методом вычис-
ления касательных напряжений при изгибе.
В результате работы Журавского, разрешившего вопрос о ка-
сательных напряжениях при изгибе, и деятельности французской
школы, давшей решение для нормальных напряжений при любой
форме профиля, проблема изгиба прямолинейного стержня к се-
редине 1850-х годов оказалась разрешенной достаточно полно.
Теория изгиба криволинейных стержней была разработана не-
сколько позже1. Первое приближенное решение дал в 1868 г. Ип-
полит Антонович Евневич (1831—1903) [26]. Это решение в 1871 г.
упростил Иван Алексеевич Вышнеградский (1831—1895) [27], пред-
ложивший отбросить учет поперечной деформации стержня. Реше-
нием Вышнеградского (в несколько преобразованной форме) до
сих пор пользуются в курсах сопротивления материалов. Первое
точное решение методами теории упругости дал в 1880 г. Харлам-
пий Сергеевич Головин (1844—1904) [28].
Таким образом, из основных задач изгиба значительно запоз-
дала только проблема продольного изгиба. Мы видели, что Навье
пользовался формулой Эйлера для критической силы при боль-
ших гибкостях, дополняя ее числовыми данными для некоторых
конкретных значений средней и малой гибкости. Но к середине
XIX века, как это ни странно, формула Эйлера совершенно выхо-
дит из употребления. Явное несоответстствие ее с опытными данны-
ми при средних и малых гибкостях подрывает к ней доверие, так
как причина этого несоответствия ускользает от понимания инже-
неров. Нам сейчас нелегко понять, как могло случиться, что в те-
1 Исторический обзор решений этой задачи см. в статье Е. С. Янушевича
«О расчете бруса большой кривизны», в сборнике «Расчеты на прочность, жест-
кость, устойчивость и колебания», Машгиз, М., 1955.
320
чение десятилетий никому не пришло в голову, что наличие мно
жителя Е в формуле Эйлера обусловливает упругую работу стер-
жня и тем самым ограничивает значени'е гибкости, ниже которого
эта формула теряет смысл1- Однако именно это непонимание при-
роды формулы Эйлера привело к полному разочарованию в ней.
Вместо формулы Эйлера в середине XIX века появляются много-
численные полуэмпирическ1ие формулы, пытающиеся удовлетво-
рить опытным данным при всех значениях гибкости, т. е. и в не-
упругой, и в упругой области. Такова, например, формула Репки-
на для допускаемого напряжения на сжатие
(ас| = |Ор| ,
1 U 1+-JX2 ’
где — гибкость, а р —число, постоянное для данного материала.
Однако формула Ренкина не является чисто эмпирической.
Она исходит из совершенно произвольного допущения, что сила Р
имеет некоторый эксцентрицитет а, который связан с размерами
стержня уравнением
где ₽ — опытный коэффициент; I — длина; h — расстояние от цент-
ра тяжести сечения до крайнего волокна на вогнутой стороне. В
таком случае краевое напряженке выразится
а при подстановке выражения для а
0=^(1 +₽*2),
откуда критическое напряжение
_ Р _ о
°к— F ~ 1+рХ2
Эксперимент показывает, что эта формула не может отвечать
опыту ни при каком постоянном значении р, так что она принци-
пиально неправильна. В упругой области она дает слишком высо-
кие значения критического напряжения, а в неупругой области —
слишком низкие. Несмотря на это, формула Ренкина .до сих пор
находит приверженцев: ею пользуются в машиностроении. Она ши-
роко применяется также в США2.
Первую попытку получить теоретическое решение задачи о
1 По-видимому, впервые это понял и объяснил Ламарль [29] в 1846 г.
2 Американский институт стальных конструкций ввел в 1928 г. формулу
_ |о1=—L?*!— (при 1>бо).
Ренкина в виде L°cl yi
1 + 18 000
21 с. А. Бернштейн
321
продольном изгибе в неупругой области сделал Энгессер [30]
(1889). Он предложил заменить постоянный модуль упругости
Е переменной величиной Е-=~ , геометрически выражающей
de
тангенс угла наклона касательной в диаграмме растяжения (рис.
6). Энгессер считал, что при этом можно будет определять крити-
ческую нагрузку по формуле Эйлера, заменяя Е на Ес:
р ___ECJ
^кр — /3 •
Ошибочность этого мнения впервые была вскрыта выдающим-
ся русским ученым Феликсом Станиславовичем Ясинским (1856—
Рис. 6. Ошибочное опре-
деление „приведенного мо-
дуля" по Энгессеру
место занимает его
1899), внесшим ценный вклад в изучение
вопросов устойчивости. Можно без пре-
увеличения сказать, что Ясинский зало-
жил основу современных инженерных
методов расчета на устойчивость.
Ф. С. Ясинский получил образование
в Петербургском институте инженеров
путей сообщения, после чего более 10 лет
работал путевым инженером в провин-
ции. Его научная деятельность началась
с 1890 г., когда он был переведен в Пе-
тербург, и продолжалась менее 10 лет.
Она была оборвана в 1899 г. преждевре-
менной смертью1.
Среди трудов Ясинского, очень раз-
нообразных по тематике, центральное
диссертация «О сопротивлении продоль-
ному изгибу» 131], изданная в 1894 г. В этом труде Ясинский
поставил и разрешил целый ряд вопросов устойчивости..
Между ними было и исправление теории Энгессера. Ясинский
указал, что при выходе стержня из прямолинейного состояния его
слои на выпуклой стороне будут разгружаться, следуя закону
Гука, а на вогнутой стороне — загружаться, отходя от линейного
закона. Поэтому материал стержня имеет одновременно два раз-
личных модуля. В 1895—1898 гг. Ясинский дал теоретическое ре-
шение в этом предположении [32]. Значительно позже — в 1910 г. —
аналогичное решение выполнил Карман. В иностранной литерату-
ре такой путь решения задачи продольного изгиба называется
методом Энгессера — Кармана, несмотря на то, что работы Ясин-
ского конца 1890-х годов были напечатаны в распространенном
швейцарском журнале (Schweizerische Bauzeitung) — характерный
пример замалчивания достижений русских ученых.
Однако сам Ясинский понимал, что такой путь решения нель-
зя признать удачным и правильным. В основу его должна быть
1 Деятельность Ясинского подробно описана в биографическом очерке
А. Н. Митинского, приложенном к книге «Избранные работы по устойчивости
сжатых стержней» Ф. С. Ясинского, изданной в 1952 г.
322
взята опытная диаграмма растяжения, которая для каждого об-
разца обладает некоторыми индивидуальными особенностями, и
потому требует осреднения для нескольких образцов — прием
спорного свойства, поскольку эта осредненная диаграмма в даль-
Ф. С. Ясинский (1856—1899)
нейшем подвергается теоретической обработке. Полученные в ре-
зультате такой (весьма трудоемкой) обработки числовые значения
критической силы, разумеется, должны быть снова проверены
прямыми опытами на продольный изгиб.
Поэтому Ясинский встал на путь непосредственного опытного
определения критического напряжения для неупругой области.
Обработка результатов многочисленных опытов над сталью опре-
деленной марки привела его к построению линейной формулы вида
ок = а —
21*
323
Несколько ранее аналогичную формулу дал швейцарский про-
фессор Тетмайер для другой марки стали.
Ясинскому принадлежит также мысль о введении коэффици-
ента снижения допускаемого напряжения при продольном изгибе,
который лежит теперь в основе всякой проверки на устойчивость.
Интересно, что самое обозначение этого коэффициента буквой е,
укоренившееся в нашей практике расчета, бы-ло введено Ясинским.
Подсчитанные им значения коэффициента <р применялись у нас до
конца 1920-х годов, когда были пересчитаны в связи с изменением
свойств строительной стали.
Помимо этих основных результатов, мы обязаны Ясинскому
еще целым рядом важных достижений в области устойчивости
Так, он впервые решил задачу о продольном изгибе стержня с
промежуточными упругими опорами, применив ее к расчету сжа-
тых поясов открытых мостовых пролетных строений и сжатых
раскосов многорешетчатых и многораскосных ферм. Ясинский
ввел также известное понятие «приведенной длины» стержня, ко-
торое позволило представить единой формулой выражение крити-
ческой силы при любых концевых и промежуточных условиях за-
крепления стержня.
Работы Ясинского имели большое принципиальное значение.
Они установили этот метод решения задач устойчивости, которым
в настоящее время пользуются во всем мире. Основная особен-
ность этого метода заключается, однако, не в то-м, что для вычис-
ления критической силы используется та или иная формула, или
опытные данные. Существо метода заключается в приведении за-
дачи устойчивости к эквивалентной задаче прочности путем уста-
новления переменных допускаемых напряжений, зависящих от
гибкости.
В самом деле, когда мы ведем расчет сжатого стержня по
формуле Ясинского
У
то это означает именно установление эквивалентности между дей-
ствительным сжатым стержнем, теряющим устойчивость при кри-
тическом напряжении |ос] и, и условным растянутым стержнем из
условного материала, имеющего предельное напряжение, равное
fap]?7*- Здесь через п обозначен запас прочности.
Тем самым Ясинский дал решению задачи устойчивости форму
расчета по допускаемому напряжению и окончательно завершил
начатый Навье переход сопротивления материалов на принцип
расчета по рабочему состоянию. Этот процесс перехода рас-
тянулся, таким образом, на 70 лет.
Эта методическая завершенность науки о сопротивлении мате-
риалов привела к тому, что литература по этой науке приобрела
значительную стабильность содержания и формы. Сравнение кур-
сов сопротивления материалов 90-х годов прошлого века и 20-х
годов нынешнего века показывает, что между ними нет принци-
324
пиальных различий. Основные установки за этот период не измс-
няются и не подвергаются никаким сомнениям. Поэтому решение
всякой новой задачи о прочности, расчет всякой новой конструк-
тивной схемы без раздумий укладываются в привычную удобную
форму расчета по допускаемым напряжениям.
И подобно тому как это не раз случалось с другими отраслями
науки, эта мнимая завершенность привела к новому кризису, раз-
вивающемуся в наше время.
^Сколько бы ни было точно
математическое решение, оно
не может быть точнее тех приб-
лиженных предпосылок, на ко-
их оно основано».
Акад. А. Н. Крылов
Глава 7
НОВЫЕ ПУТИ
Конец XIX и начало XX века были периодом неограниченного и
полного господства принципа рабочего состояния во всех разделах
строительной механики. Это были года 'быстрого развития тео-
рии упругости, учения об устойчивости конструкций, накопления
громадного арсенала опытных данных об усталости, пластичности
и прочности материалов. Но этот период был в то же время пери-
одом постепенного обнаружения фактов, не укладывавшихся в
схему расчета по рабочему состоянию.
В основе принципа расчета по рабочему состоянию лежат три
скрытых допущения, и именно их условность привела к постепен-
ному накоплению противоречий между расчетом и опытом. Обна-
ружение этих противоречий, вскрытие условных допущений и, как
результат, переход строительной механики на новую, высшую
ступень развития составляют, на наш взгляд, наиболее существен-
ное достижение науки о прочности за последние десятилетия.
Теперь, когда эта перестройка науки уже частично заверши-
лась, нетрудно дать анализ этих допущений, лежащих в основе
расчета по рабочему состоянию, и это необходимо сделать, чтобы
понять смысл перехода науки на новые пути.
Расчет по рабочему состоянию заключается в том, что наиболь-
шие напряжения, возникающие при расчетной нагрузке, сравни-
ваются с допускаемыми напряжениями для данного материала.
Эта формулировка уже содержит два положения, требующих
уточнения.
1. Какие напряжения подлежат сравнению?
2. Как устанавливается величина допускаемого напряжения?
325
Ответ на первый вопрос требует принятия некоторой теории
прочности, и в этом заключается первое допущение. В предыду-
щих главах мы встретились с тремя старейшими «классическими»
теориями прочности. Для основных «галилеевских» задач сопро-
тивления материалов — растяжения и изгиба — выбор теории
прочности не имеет существенного значения, так как обе задачи
приводятся к линейному напряженному состоянию и эквивалентны
между собой. На протяжении двух первых столетий развития на-
уки о прочности только эти линейные задачи составляли предмет
изучения, и потому спор о преимуществах той или иной теории
прочности носил чисто академический характер. Собственно гово-
ря, особых споров и, не было.
Но в середине XIX века развитие техники заставляет науку о
прочности обратиться к изучению конструкций, испытывающих не
линейное, а плоское или объемное напряженное состояние. Сюда
относятся не только двухмерные и трехмерные тела (пластинки,
резервуары и т. п.), но и такая простая схема, как стержень, ра
ботающий на кручение. Расчет таких систем по принципу рабоче-
го состояния требует принятия определенной теории прочности,
устанавливающей переход к эквивалентному линейному состоя-
нию— простому растяжению или сжатию. По этой причине во
второй половине XIX века теории прочности начинают привлекать
пристальное внимание ученых, а в начале XX века появляются
новые теории прочности.
Всякая теория прочности принимает за причину разрушения
и критерий прочности некоторое напряжение, которое можно на-
звать «решающим». По первой теории решающим напряжением
будет наибольшее нормальное, по второй теории — «приведенное»
нормальное напряжение (равное наибольшему удлинению, умно-
женному на модуль упругости), по третьей теории—наибольшее
касательное напряжение и т. д. Если обозначить решающее на-
пряжение через /?, а его допускаемое значение при простом рас-
тяжении через [7?р], то расчет по рабочему состоянию для любой
теории прочности приводит к неравенству
max Я < [Яр]. (1)
Пусть первое допущение сделано, некоторая теория прочности
выбрана и тем самым левая часть неравенства (1) установлена.
Попробуем ответить теперь на второй вопрос: как же определяет-
ся допускаемое напряжение, т. е. правая часть неравенства (1)?
Допускаемым напряжением мы называем отношение предель-
ного (разрушающего) напряжения к запасу прочности. Величина
предельного напряжения устанавливается из эксперимента (ис-
пытание лабораторных образцов), а величина запаса прочности
из опыта эксплуатации. Казалось бы, все этапы расчета контро-
лируются опытом и не содержат никаких условных допущений.
Однако такое допущение содержится в правой части неравенства
(1): допущение о возможности ограничиться определением допу-
скаемого напряжения для простого растяжения (или сжатия).
326
Впервые это допущение высказал в явной форме Сен-Венан в
1870-х годах, дав этим окончательное идейное обоснование само-
го принципа рабочего состояния.
Условие Сен-Венана можно формулировать так: предель-
ное значение решающего напряжения не зависит
от в-и да напряженного состояния и является для дан-
ного материала постоянной величиной.
Иными словами, если из опыта с растянутым образцом уста-
новлена величина предельного решающего напряжения /?прсд, то
любая конструкция из данного материала при любом напряжен-
ном состоянии достигнет предельного состояния, как только наи-
большее решающее напряжение достигнет того же самого
значения /?пред.
Однако и условие Сен-Венана оказывается недостаточным дл*^
обоснования принципа рабочего состояния. Неравенство (1) по-
зволяет судить о прочности конструкции только в том случае, ес-
ли равенство наибольших решающих напряжений у растянутого
образца и у конструкции произвольного вида приводит к равенст-
ву их запасов прочности. Таким образом, одно допущение необ-
ходимо для обоснования левой части неравенства (теория прочно-
сти), другое — для обоснования его правой части (условие Сен-Ве-
нана) и третье допущение необходимо для оправдания самого не-
равенства (1). Это третье допущение формулируется так: дости-
жение решающим напряжением предельного
значения хотя бы в одной единственной точке
конструкции означает достижение предельного
состояния для всей конструкции.
Легко понять, что это условие выполняется только для совер-
шенно хрупкого материала, который следует закону Гука вплоть
до разрушения. Поэтому третье допущение мы будем называть
условием хрупкости.
Итак, в основе расчета по рабочему состоянию лежат три до-
пущения:
1) теория прочности;
2) условие Сен-Венана;
3) условие хрупкости.
Нетрудно сообразить, что мы действительно используем все
три допущения при каждом расчете на прочность конструкции,
испытывающей плоское -или объемное напряженное состояние, при
каждом расчете стержня на изгиб с кручением, при расчете резер-
вуара, толстостенного цилиндра, пластинки и т. п. А на каком
основании?
Прежде всею, откуда следует, что условие Сен-Венана спра-
ведливо? Почему величину предельного напряжения материала
следует считать за неизменное, внутренне присущее материалу
имманентное свойство? Не правильнее ли предположить, что оно
является изменчивой величиной, зависящей от вида напряженно-
го состояния?
327
Эти сомнения начали появляться еще с конца прошлого века и с
особой остротой подвергли критике наиболее распространенную
теорию прочности — третью, теорию наибольших касательных на-
пряжений. Действительно, опыт не подтверждал условия Сен-Ве-
нана для этой теории: предельное касательное напряжение при
кручении по опыту оказывалось выше, чем при растяжении.
Устранить это несоответствие можно было двумя путями: испра-
вить теорию прочности, чтобы сохранить в неприкосновенности
условие Сен-Венана, или, наоборот, сохранить третью теорию
прочности, но отказаться от условия Сен-Венана.
Первый путь привел к созданию новой теории прочности, ко-
торую разновременно и в разной форме предложили Губер, Мизес
и Генки. По этой теории решающим напряжением является каса-
тельное напряжение в октаэдрической площадке, т. е. в площад-
ке, равнонаклоненной к трем главным площадкам. Эта теория поз-
воляла объяснить, почему наибольшее касательное напряже-
ние в предельном состоянии различно для растяжения и кручения.
Но зато теперь октаэдрическое касательное напряжение
объявлялось постоянным и независящим от вида напряженного
состояния, без всякого обоснования этого привычного условия
Сен-Венана.
На другой путь встал Мор, который первым попытался освобо-
диться от условия Сен-Венана. Теория прочности Мора [33] оста-
вила за наибольшим касательным напряжением смысл решающего
напряжения, но ввела переменное допускаемое напряжение, зави-
сящее от вида напряженного состояния. В сущности теория Мора
есть третья теория прочности без условия Сен-Венана, и нам
представляется, что отказ от этого сомнительного условия дает
теории прочности Мора принципиальное преимущество перед тео-
рией октаэдрических напряжений. Преимуществом последней яв-
ляется только ее удобная аналитическая форма, из-за которой эта
теория и приобрела распространение.
Несомненно, что в дальнейшем от условия Сен-Венана придет-
ся отказаться, так как все большее число опытных фактов ему
противоречит1. Именно этим вызвано появление за последнее
время новых комбинированных теорий упругости Н. Н. Давиден-
кова, Я. Б. Фридмана [34] и др.
Условие хрупкости также пришло в противоречие с опытом еще
в конце прошлою века. Одним из первых сигналов его ошибочно-
сти был результат попытки уточнить расчет ферм путем учета
жесткости узлов. Первую такую попытку сделал Мандерла в
1880 г. Он установил, что влияние жесткости узлов приводит к зна-
чительному повышению напряжений в стержнях фермы вследст-
вие их изгиба по сравнению с расчетными величинами, получа
емыми обычным путем из гипотезы шарнирных узлов. Это озна-
чало, что последовательное применение расчета по рабочему со-
1 См. книгу С. И. Ратнер, Прочность и пластичность металлов. Гос. изд
обор, пром., 1949.
328
стоянию, основанного на условии хрупкости, требует значительно-
го увеличения запаса прочности по сравнению с установившейся
традицией. Вывод был настолько абсурден, что практика, к
счастью, ему не поверила и не приняла его1.
Вторым случаем, противоречившим условию хрупкости, оказа-
лась частная задача о расчете заклепок. Решение этой задачи
дал в 1840-х годах известный английский мостостроитель Роберт
Стефенсон (сын строителя паровозов). Основываясь на опытах,
поставленных им во время работ по сооружению трубчатых мо-
стов, и придерживаясь старого принципа предельного состояния.
Стефенсон установил, что прочность стержня заклепки на срез
составляет около трех четвертей от его прочности на разрыв. Это
означало, что стержень заклепки можно рассчитывать на срез
так же, как на растяжение, т. е. по среднему напряжению, но с
принятием допускаемого напряжения, равного 0,75 от допускаемо-
го напряжения на растяжение. Тем самым этому расчету придава-
лась видимость расчета по рабочему состоянию, но только види-
мость, так как величины и распределение действительных напря-
жений в рабочем состоянии оставались неизвестными. Стефенсона
не интересовало даже, какой природы будут эти напряжения—ка-
сательные или нормальные.
Выпадение этой задачи из общей схемы расчета по рабочему
состоянию авторы курсов сопротивления материалов на рубеже
XIX—XX веков конфузливо обходили, именуя расчет заклепок
«условным» или «грубо приближенным». Такая высокомерная
оценка была, разумеется, непрайильна. Стефенсоновский способ
расчета заклепок есть классический пример расчета по предель-
ному состоянию, характерного для предшествующего периода в
науке. Но к концу XIX века в результате успехов теории упруго-
сти самая идея такого расчета была забыта. Когда же заклепоч-
ное соединение попробовали рассчитать поточнее, с привлечением
математической теории упругости и усовершенствованных экспе-
риментальных методов, то обнаружилось странное обстоятельст-
во. Касательные напряжения в сечении заклепки оказались рас-
пределенными неравномерно, причем максимальное их значение
было намного выше среднего. Поэтому заклепочное соединение,
рассчитанное «условным» Стефенсоновским способом и десятки
лет благополучно работающее в любом стальном мосту, оказыва-
лось непрочным при проверке его «точными» методами теории
упругости. Повторилось то же недоразумение, что и при расчете
ферм с жесткими узлами: «условный» способ расчета оказывался
правильнее «точного». Разумеется, в этом противоречии была ви-
новата не теория упругости, а то третье допущение, которое мы
привели выше, — условие хрупкости. Из этого противоречия выте-
кало прямое опровержение этого условия, т. е. вывод о возможном
неравенстве запасов прочности при равенстве наибольших напря-
1 Если не считать глубоко ошибочных попыток сооружать фермы с болтовы-
ми шарнирными узлами, имевших место в США (см. очерк III).
22 С. А. Бернштейн
329
жений. Такой вывод, очевидно, подрывал принцип расчета по ра-
оочему состоянию.
В данном случае перед инженерами фактически встала любо-
пытная дилемма: либо сохранить «условный» Стефенсоновский
способ расчета заклепок по предельному состоянию и этой ценой
спасти принцип рабочего состояния со всеми его допущениями,
либо во имя единства ’методики перейти к точному способу расче-
та заклепок, но зато пожертвовать самим принципом рабочего
состояния. Разумеется, был выбран первый путь. Мы до сих пор
рассчитываем заклепки по предельному состоянию, делая вид, что
считаем их по рабочему состоянию.
Следующий удар по принципу рабочего состояния был нанесен
в результате опытного изучения поведения конструкций из пла-
стичных материалов при высоких нагрузках. При этом отчетливо
обнаружилось, что работа статически неопределимых конструк-
ций испытывает качественное изменение после выхода из чисто
упругой области. Так, в изогнутом стержне начальный линейный
закон распределения напряжения сменяется нелинейным после
появления текучести в крайних волокнах, и истинный момент со-
противления в предельном состоянии отличен от его начального
значения. В неразрезной балке или раме происходит перераспре-
деление изгибающих моментов, причем к предельному состоянию
она приходит со статически определимой схемой, имеющей в наи-
более напряженных сечениях пластические шарниры с выравнен-
ными значениями моментов.
Смысл всех этих явлений один и тот же: из равенства наиболь-
ших напряжений не вытекает равенство запасов прочности или.
иначе, подобие между рабочим и предельным состоянием возмож-
но лишь для идеально упругого вполне хрупкого материала. При
отклонении поведения материала от закона Гука это подобие ис-
чезает. Это означает, что расчетный запас прочности, определя-
емый расчетом по рабочему состоянию, не равен истинному запасу,
а, как правило, ниже последнего, так что расчет по рабочему со-
стоянию дает .избыточный запас и потому неэкономичен.
Именно этот последний вывод положил конец неограниченно-
му господству принципа рабочего состояния в строительной меха-
нике, так как он был сделан в ту эпоху, когда вопросы экономики
строительства получили первенствующее значение.
Формулируя назначение строительной механики, мы говорим,
что эта наука позволяет обеспечивать достаточную прочность кон-
струкций при наименьшем расходе материала, т. е. в нашем пред-
ставлении экономический эффект расчета неотделим от техниче-
ского. Однако этот подход в прошлом столетии еще не имел такой
четкой направленности. Реформа. Навье дала впервые возмож-
ность обеспечить заведомую прочность сооружения, и этот важ-
нейший ее результат на долгое время имел преобладающее зна-
чение в глазах инженеров. Обеспечить прочность любой ценой—
таков был общий лозунг, хотя бы эта цена была значительно выше
возможного минимума. Практически говоря, это означало приня-
330
тие излишне высоких запасов прочности, как заведомой гарантии
от разрушения. В известном смысле мы можем быть благодарны
строителям прошлого века за такую чрезмерную осторожность,
так как она позволила нам использовать железнодорожные мосты
восьмидесятилетие!о возраста, пропуская по ним нагрузку, в 2—
3 раза большую, чем та, для которой они по проекту предназна-
чались.
Однако к 20-м годам нашего столетия такая расточительность
стала немыслимой в силу причин и технического и социально-эко-
номического порядка. Технической причиной была необходимость
возведения сооружений резко возросшего масштаба и под резко
возросшую нагрузку, а экономической причиной было исчерпание
материальных ресурсов в европейских странах в результате пер-
вой мировой войны. Особую остроту экономическая сторона строи-
тельства получила в Советском Союзе, так как, во-первых, наша
Родина поставила перед собой высокую задачу скорейшего по-
строения социализма, а во-вторых, она пострадала от войны и им-
периалистической интервенции в несравненно большей степени,
чем другие страны Европы от войны, и не могла рассчитывать на
помощь извне. Тем самым в Советском Союзе сочетались гранди-
озный размах строительства и необходимость беречь каждую ко-
пейку и каждый килограмм строительного материала Ввиду этих
особых условий неудивительно, что попытки изменения основного
расчетного подхода, сулившие избавление от избыточного запаса
(а заодно и упрощение техники расчета), возникнув почти одно-
временно во всех странах Европы в конце 1920-х годов, получили
особое развитие и плодотворное применение именно в Советском
Союзе.
Но если признание необходимости пересмотра основных пози-
ций нашей науки были единодушным, то пути разрешения этой
проблемы раздвоились. Одно направление пошло по линии рас-
пространения теоретических решений теории упругости на пласти-
ческую область и привело к созданию теории пластичности. Осно-
вой этого направления были отказ от простой формы закона Гука
и замена его более сложной зависимостью между напряжением,
деформацией и их изменением во времени. Целью этого направле-
ния является создание возможности предсказать поведение кон-
струкции на всем этапе от начального до предельного состояния.
Разработка теории пластичности была результатом трудов мно-
гих ученых — Надаи [35], Прагера, Мизеса, Генки, Ильюшина [36],
Соколовского [37], Лейбензона [38], Михлина [39] и многих других.
Другое направление исходит из предельного состояния кон-
струкции и позволяет установить предельную нагрузку для той новой
схемы, которую приобрела конструкция в предельном состоянии.
По своему основному подходу этот путь бесспорно представляет
возрождение старого принципа расчета по предельному состоянию,
но на новой основе. Этим новым, существенно отличающим совре-
менный подход от приемов XVIII века, является то, что установ-
ление предельной схемы конструкции производится на основании
22*
331
точных сведений об ее поведении в начальной упругой стадии.
Так, для неразрезной балки предельной схемой будет балка с
шарнирами, размещение которых осуществляется не умозритель-
но, как поступали в XVIII веке при расчете арок (см. очерк II),
а в соответствии с положением сечений, имеющих наибольшие мо-
менты в начальной упругой стадии работы.
Это направление, известное под названием расчета сооружений
с учетом пластических деформаций и зародившееся в трудах Грю-
нинга [40], ЛАайера, Фриче, Канна и др., получило особо широкое
развитие и практическое применение в Советском Союзе в* трудах
Стрелецкого [41 и 41а], Горбунова [416], Назарова [41в], Жудина
[41г] и особенно Гвоздева [42], разработавшего общую стройную тео-
рию расчета по предельному состоянию. В результате этих работ Со-
ветский Союз стал первой в мире страной, включившей этот про-
грессивный метод расчета в нормы проектирования сооружений.
Увлечение новым принципом расчета привело некоторых его
горячих сторонников к представлению с своевременности и необ-
ходимости полного отказа от расчета по рабочему состоянию, о
необходимости исключения из технического обихода самого поня-
тия допускаемого напряжения. Нам представляется, что такое
мнение совершенно неправильно и необоснованно.
Прежде всего, надо учесть, что вся обширная область маши-
ностроения не может отказаться от расчета по рабочему состоя-
нию, потому что она имеет дело в основном с малопластичными
закаленными сталями и сплавами, для которых условие хрупкости
достаточно близко к действительности. Во-вторых, нельзя забы-
вать, что при действии переменных нагрузок даже самый пластич-
ный материал дает хрупкие формы разрушения. Если при стати-
ческом загружении пластичного 'материала происходит выравни-
вание местных напряжений, позволяющее не думать об их наличии
в начальной стадии, то при переменном и динамическом загруже-
нии даже пластичной стали (а тем более закаленной) наличие
концентрации напряжений представляет реальную опасность, при-
водящую при высоких нагрузках не к выравниванию их, а к преж-
девременному разрушению.
Поэтому мы считаем, что происходящую сейчас перестройку
строительной механики, в частности учения о сопротивлении ма-
териалов, не следует понимать, как отказ от принципа рабочего
состояния и полный переход к принципу предельного состояния.
Правильнее рассматривать наступающую новую — третью — эру
в этой науке, как эру синтеза обоих направлений, с отведением
каждому из них своего заслуженного места в расчетах на проч-
ность.
Нам кажется, что правильное понимание диалектической двой-
ственности новой эры в сопротивлении материалов может способст-
вовать его успешному развитию и удержать от скороспелых оши-
бочных суждений.
ОЧЕРК ВТОРОЙ
ИСТОРИЯ РАСЧЕТА АРОК
«Две слабости, опираясь друг
на друга, рождают крепость.
Так половина мира, опираясь на
другую, делается устойчивой».
Леонардо-да-Винчи
Глава 1
ВВЕДЕНИЕ
Задача о расчете арки занимает совершенно особое место в
истории строительной механики как по количеству посвященных
ей работ, так и по своеобразию предложенных методов. На протя-
жении всего XVIII века и первой половины XIX века бесшарнирная
арка — свод — оказывается почти единственным строительным
объектом, к которому устремлено внимание ученых — и инженеров,
и математиков, и физиков. Такое преимущественное внимание к
своду объясняется несколькими причинами. Во-первых, свод пред-
ставлял тогда наиболее ответственную строительную форму и
единственную, допускавшую перекрытие больших пролетов. Возве-
дение свода требовало особо высокого искусства строителя, и в
неумелых руках нередко оканчивалось обрушением. Во-вторых,
важные экономические причины побуждали искать новые, более
рациональные типы сводов, и это стояло в связи с появлением но-
вого заказчика.
Основными строительными сооружениями, требовавшими при-
менения свода, были до середины XVIII века церкви, дворцы и
мосты. Поэтому своды возводились в основном строителями с ху-
дожественным уклоном, охотно использовавшими в новых объектах
элементы готовых технических решений. Несомненно, что расту-
щие требования экономики в связи со вздорожанием материалов и
рабочей силы рано или поздно привели бы к необходимости расче-
та свода, даже как элемента дворцового и церковного строитель-
ства, а тем более мостового. Но эта необходимость возникла ско-
рее ввиду появления совершенно нового потребителя сводов.
Таким новым потребителем оказались военные инженеры. Это об-
стоятельство до сего времени не получило исторической оценки.
Историки архитектуры не упоминают о нем, так как военному
строительству уже тогда были чужды художественные задачи,
историки строительной механики интересуются преимущественно
методикой расчета и умалчивают о потребителе. Не исключена
возможность, что в этой книге впервые упоминается о важной роли,
которую сыграло военно-инженерное дело в развитии теории свода.
Новым объектом для применения свода явился пороховой по-
333
греб. При сооружении этого объекта строитель встретился с совер-
шенно новыми задачами. Во-первых, необходимо было обеспечить
прочность свода от артиллерийского обстрела. Во-вторых, необ-
ходимо было дать возможно более компактное решение, чтобы
уменьшить объем земляных работ и увеличить полезную кубатуру
погреба. В-третьих, надо было соблюдать экономию, так как пра-
вительства в XVIII веке скупее финансировали невзрачное военное
строительство, чем дворцы и соборы, которые своим величием
призваны были поддерживать падающий престиж монархического
абсолютизма и церкви. Совокупность этих трех требований — по-
вышенной прочности, компактности и экономии — послужила актив-
ным стимулом для развития теории свода. Среди имен ученых,
работавших над этой теорией с конца XVIII века до 40-х годов
XIX века, имена военных инженеров решительно преобладают.
В 30-х годах XIX века происходит новая смена преобладающего
потребителя, вызванная начавшимся повсеместно строительством
железных дорог, предъявившим резко повышенные требования к
прочности, размерам и экономике арочных мостов. Появляются и
применяются в строительстве сводов новые материалы — чугун и
сварочное железо. Возникает необходимость в строительстве поло-
гих сводов, и притом работающих на перемещающуюся временную
нагрузку. Военные инженеры, как ведущие деятели строительной
механики, сходят со сцены, уступая первое место путейцам, и уже
более не возвращаются к ведущей роли. Напротив, мостостроители
постепенно монополизируют применение свода, вытесняемого из
гражданской архитектуры плоскими перекрытиями.
Новые требования ставят новые расчетные задачи. Если до 30-х
годов XIX века своды рассчитываются только на симметричную
постоянную нагрузку, то с этого времени появляются приемы рас-
чета сводов на отдельную сосредоточенную силу, занимающую
произвольное положение на своде. Эти приемы приводят к изобре'
тению линий влияния; впервые понятие о линии влияния (точнее,
о числах влияния) появилось именно в расчете свода (1854).
Задача о расчете свода обладает коварным свойством — казать-
ся более простой, чем она есть на самом деле. Этим объясняется
то, что к ее решению неоднократно приступали с недостаточными
или просто негодными средствами, получая суррогаты решения,
которые часто не удовлетворяли никого, кроме их авторов. В связи
с этим количество предложенных методов очень велико, хотя это
изобилие часто только кажущееся. Если ограничиваться знакомст-
вом с предисловиями к подлинным работам, в которых авторы с
большей или меньшей степенью высокомерия отвергают методы
своих предшественников, обещая дать совершенно новый и вполне
точный метод решения задачи, то читателя может охватить трепет
перед разнообразием методов. Но в большинстве случаев ознаком-
ление с самой работой обнаруживает ближайшее ее родство с тру-
дами отвергнутых предшественников. Нередко отличие от них сво-
дится к простому преобразованию формул или даже изменению
обозначений. Любопытно, что чем широковещательнее предисловие
334
автора, чем больше его суровость к предшественникам, тем обычно
менее оригинальной оказывается сама работа. Действительно цен-
ные исследования по этой теме (да и по всякой другой) отлича-
ются скромностью и серьезностью изложения.
В действительности задача о своде принадлежит к числу труд
нейших задач строительной механики, и ее нельзя считать пол-
ностью разрешенной и до настоящего времени, даже если предпола-
гать материал свода совершенно упругим. В дальнейшем мы оста-
новимся подробнее на специфической трудности этой задачи. Но
трудности эти еще неизмеримо возрастают, если рассматривать
свод так, как это делали все исследователи до середины XIX века
Эта «классическая» концепция принимает свод за совокупность
абсолютно твердых клиньев, соединенных в швах весьма слабым
раствором, который способен работать только на сжатие и срез.
Неспособность раствора сопротивляться растяжению и весьма сла-
бое его сопротивление срезу делают швы связями одностороннего
действия, способными сдвигаться ш раскрываться при неблагопри-
ятном положении нагрузки, причем свод обращается в кинемати-
ческую цепь с несколькими степенями подвижности. Ввиду этого
расчет свода преследует единственную цель: обеспечить при данной
нагрузке статическую и кинематическую неподвижность, или, по
старинной терминолгии, «устойчивость» свода. Проблема прочности
при этом долгое время остается вне пределов изучения.
Концепцией абсолютно твердых клиньев предопределяется мате-
матический аппарат решения: уравнения равновесия или эквива-
лентные им уравнения возможных перемещений — вот единствен-
ные условия, которыми может воспользоваться теория. Но так как
свод трижды статически неопределим (при симметричной на-
грузке-— дважды), то этих условий явным образом недостаточно
для решения.
Исследователи XVIII и начала XIX века пытаются избежать
этого затруднения (не вполне ясного для них, так как понятие ста-
тической неопределимости в XVIII веке еще не усвоено) тем, что
рассматривают свод в состоянии предельного равновесия, на грани
раскрытия или сдвига швов. Если известны места этих швов (кото-
рым отвечают положения нулевых точек эпюр осевых или фибро-
вых1 моментов и поперечных сил в предельном состоянии), то за-
дача оказывается статически определимой. Мы знаем, что и упру-
гую арку можно рассчитать с помощью уравнений равновесия,
если известно положение нулевых точек эпюры моментов: для этого
достаточно включить в этих точках шарниры. Но статическая не-
определимость состоит именно в невозможности нахождения этих
точек из условий равновесия.
1 Фибровым моментом называют момент левых или правых внешних сил
относительно какой-либо нецентральной оси сечения, т. е. оси, не проходящей
через центр тяжести сечения. Фибровые моменты для разных осей различны и не
совпадают с осевым моментом (т. е. моментом относительно центральной оси),
так как сечение свода испытывает изгиб и сжатие. Очевидно, фибровые моменты
равны нулю во всех точках кривой давления.
335
Все старинные методы расчета арок и сводов, несмотря на ка-
жущееся их многообразие, могут быть сведены в две категории в
зависимости от решения задачи нахождения нулевых точек.
Методы первой категории назначают положение швов раскры-
тия или сдвига произвольно, исходя из умозрительных соображений.
/Методы второй категории пытаются устранить произвол, опре-
деляя положение или границы положения швов раскрытия и сдвига
из различных экстремальных условий. Эти методы ведут начало от
Кулона.
Но для обеих категорий общим остается то, что свод рассматри-
вается в состоянии предельного равновесия, в момент разрушения.
Ни один из исследователей свода на протяжении всего XVIII века
и первых десятилетий XIX века не ставит перед собой задачу изуче-
ния действительной работы свода под рабочей нагрузкой ни опыт-
ным, ни теоретическим путем. Все заинтересованы только одним
предельным состоянием и яростно спорят между собой, опровергая
чужие умозрительные соображения о виде разрушения и отстаивая
свои столь же умозрительные гипотезы.
Характерный для первого периода истории строительной меха-
ники принцип расчета по предельному состоянию с особой отчетли-
востью выступает именно в истории расчета арок.
Когда в 20-х годах XIX века происходит смена основного на-
правления и расчет по предельному состоянию начинает заменяться
расчетом по рабочему состоянию, свод остается единственной систе-
мой, для которой пытаются сохранить старый подход вопреки здра-
вому смыслу. Период с 20-х до 50-х годов XIX века особенно любо-
пытен, как отражение этой борьбы старого с новым. Сторонники
расчета по предельному состоянию делают отчаянные попытки най-
ти новые принципы, открыть новые законы статики, для того чтобы
дать расчет свода чисто статическим путем, не используя условий
деформации. Эта борьба заканчивается, конечно, победой нового
направления, после того как Бресс дает в 1854 г. расчет бесшар-
нирной арки как упругой статически неопределимой системы.
Мы сказали, что никто из исследователей арки в XVIII веке
не заинтересовался условиями действительной ее работы под на-
грузкой. Это верно в отношении западно-европейской науки. Но на-
шелся один человек, который смело свернул с пути, указанного
Галилеем, и на полвека раньше Навье встал на путь изучения
рабочего состояния арки. Это был замечательный русский механик
Иван Петрович Кулибин.
Глава 2
ПЕРИОД УМОЗРИТЕЛЬНЫХ КОНЦЕПЦИЙ
Первое по времени высказывание о характере работы арки при-
надлежит известному архитектору эпохи Возрождения Леону-Бат-
тисте Альберти. В его книге, написанной в 1452 г. [43], мы находим
следующие рассуждения.
336
Полуциркульная арка, по мнению Альберти, «самая крепкая
из всех, это само собою явствует, а также обнаруживается путем
рассуждения и доказательства. Ведь я не вижу, как она могла бы
сама распасться, разве только один клин вытолкнет другой, но от
этой беды они настолько далеки, что скорее наоборот — один укреп-
ляется поддержкой другого... Ибо каким образом верхний клин,
который в спине, может один оказаться настолько сильным, чтобы
вытолкнуть смежные клинья? Или как можно под их давлением
вытолкнуть его с занимаемого места?».
Проф. И. М . Рабинович1 дает яркую оценку этой характерной
для своей эпохи тирады: «Казалось бы, вместо того, чтобы расто-
чать в пространство свои патетические вопросы, в которых одно-
временно содержатся и совершенно превратные ответы, достаточ-
но было бы Альберти произвести несколько опытов разрушения
арок, и он мог бы воочию увидеть механизм разрушения таковых, —
однако такой метод решения был не в духе того времени».
Хотя труд Альберти на два столетия предшествует работам Га-
лилея, вполне основательно признавать последнего за зачинателя
строительной механики, так как восклицания Альберти стоят еще
вне науки. Нужно добавить, что эти восклицания принесли впослед-
ствии немалый вред: благодаря авторитету Альберти среди архи-
текторов, усердно копировавших орнаменты из его увража,
сомнение в существовании распора в полуциркульных арках
удержалось до конца XVIII века, затормозив этим развитие
науки.
Старейшей работой по расчету арок, о которой нам удалось
найти упоминание, была работа Деванна 1643 г. В ней предлага-
лись формулы для определения толщины пят свода, которые впо-
следствии были признаны неверными. Где эта работа опубликована
и как были обоснованы формулы Дева на, нам неизвестно. Она от-
носится, так сказать, к доисторическому периоду, сведения о ко-
тором чрезвычайно скудны.
Исторический период в области расчета сводов начинается в
J695 г. с первой теории французского инженера Филиппа Делагира
[441 (1640—1718). Делагир рассматривал свод как совокупность
идеально гладких клиньев, свободно соприкасающихся в швах без
трения и сцепления. Из этой предпосылки следует, что давление
между отдельными клиньями направлено нормально к поверхности
шва. Иными словами, расчетная схема свода в предельном состоя-
нии представляет кинематическую цепь, число звеньев которой рав-
но числу клиньев, причем звенья соединены между собой шарнир-
ными параллелограммами (рис. 7). Мы знаем, что такая цепь будет
находиться в мгновенном равновесии, если можно построить ве-
ревочный многоугольник, стороны которого будут нормальны к
соответствующим швам. Обратно, построив такой многоугольник,
легко вывести зависимость между углами наклона швов и весами
1 И М. Рабинович, Курс строительной механики стержневых систем,
ч. II, 1940, стр. 229.
337
клиньев и отсюда найти закон изменения толщины свода. Нетрудно
сообразить, что веса клиньев Рп должны выражаться
Рп = и (ctg <Р„+, — ctg?„), (1)
где оп, — углы наклона к горизонту двух швов, ограничи-
вающих данный клин, а Н — распор (рис. 8).
Основываясь на этой зависимости, Паран в 1704 г. дал способ
построения наружного очертания для свода с полуциркульным
внутренним очертанием.
Эта первая теория Делагира была
вытеснена через 17 лет второй теорией
того же автора и надолго, почти на
100 лет, погрузилась в забвение. Пра-
вильнее будет даже сказать, что она бы-
ла забыта навсегда, так как при вторич-
Рис. 7. Расчетная схема по первой
теории Делагира
Рис. 8. Определение
распора по первой
теории Делагира
ном своем появлении на свет в трудах Эйтельвейна (глава 5) она
была принята за новую теорию. В своем втором воплощении она
пользовалась широким признанием, а потому заслуживает анализа.
Мы видим, что Делагир не ограничился удалением двух лишних
связей и приведением свода к статически определимой схеме. Он
пошел далее и удалил так много связей, что превратил арку в
многократно-изменяемую кинематическую цепь. Легко понять, что
его теория подходит под первую категорию, упомянутую в главе 1,
так как места швов сдвига он назначил произвольно. При этом он
установил места нулевых точек эпюры поперечных сил, а не момен-
тов, так как исходил из теории сдвига клиньев. Очевидно, опреде-
лив по уравнению (1) закон изменения толщины свода, Делагир
мог отказаться от первоначального размещения швов, расставив
их произвольным образом и лишь сохранив их ортогональность к
внутреннему очертанию свода. При таком произвольном смещении
швов зависимость (1) почти не нарушится, и кинематическая цепь
останется в состоянии, весьма близком к мгновенному равновесию.
Первая теория Делагира должна быть признана крайне неудов-
летворительной.
На самом деле в основе ее лежит предположение о свободно со-
прикасающихся идеально гладких клиньях. Не говоря уже о том,
что клинья свода обладают грубошероховатой поверхностью,
338
полуциркульного свода и не за-
а)
Рис. 9. Схема образования трещин в
своде
нельзя забывать, что они соединяются раствором. Как бы ни был
слаб этот раствор, он все же оказывает весьма значительное сопро-
тивление сдвигу, и потому предпосылки Делагира чрезвычайно
далеки от действительности. Кроме того, расчет полуциркульного
свода по этой теории приводит к неожиданному затруднению: тол-
щина свода у опор обращается в бесконечность.
Каким образом при этих условиях упомянутый нами Паран дал
построение наружного очертания
метил несообразности результа-
та, нам неизвестно; работы Пара-
на мы не видели, а Боссю уже в
1774 г. сомневался, была ли она
вообще напечатана.
Необходимо оговориться, что
все теории расчета свода мы из-
лагаем здесь с нашей современ-
ной точки зрения, пользуясь сов-
ременными понятиями и терми-
нами. Не следует забывать, что
во времена Делагира веревочный
многоугольник еще не был изве-
стен. Вследствие этого теория
Делагира (по существу очень
простая и почти не требующая
формул) в подлинных работах
изложена сложно и запутанно.
Это замечание относится и ко
всем последующим методам.
В 1712 г. Делагир опублико-
вал свою вторую теорию [45]. Эта теория оказалась (по крайней
мере в XVIII веке) гораздо жизнеспособнее первой. Она произ-
вела на современников сильное впечатление и удержалась без
серьезных соперников до конца XVIII века. В большинстве истори-
ческих обзоров по теории свода под названием теории Делагира
упоминается только эта вторая теория.
Вторая теория Делагира значительно остроумнее первой, хотя
она основана на неверном умозаключении.
Эпюра моментов от сплошной равномерной нагрузки для свода
имеет очертание, изображенное на рис. 9, а. Такому загружению
соответствует деформация свода по рис. 9, б. Допустим, что свод
имеет каменную надстройку, обычную для XVIII века, и наметим
на нем возможные места появления трещин (рис. 9, в) исходя из
характера деформации. Мы видим, что свод имеет тенденцию рас-
крываться снизу—в замке и пятах и сверху— вблизи четвертей
пролета. Однако наличие каменной надстройки затрудняет образо-
вание трещин внизу, и, наоборот, ускоряет образование тре-
щин вверху свода и в самой надстройке. Таким образом,
весьма естественно ждать в таких сводах появления вблизи четвер-
тей пролета трещин, распространяющихся через всю надстройку.
339
Весьма вероятно, что именно наблюдение таких трещин навело
Делагира на мысль, что разрушение свода происходит всегда в
четвертях пролета. Но оставаясь верным приверженцем теории сдви-
гов, он приписал эти трещины действию сдвига.
Рис. 10. Сдвиг свода по Делагиру
Рис. 11. Расчетная схема по вто-
рой теории Делагира
В своей второй теории Делагир уже не расчленяет свод на от-
дельные клинья по числу камней. Он рассматривает свод в предель-
ном состоянии, как совокупность всего трех звеньев- среднего и двух
крайних, причем разделяющие их швы помещает в четвертях про-
лета (точнее — в четвертях длины дуги свода). Средняя часть сво-
Рия. 12. Определе-
ние распора по вто-
рой теории Делаги-
ра
да, действуя как клин, стремится опуститься,
раздвигая крайние части (рис. 10). Так как тре-
ние по-прежнему не учитывается, то в четвертях
пролета поперечная сила равна нулю, а потому
в этих сечениях снова можно вставить шарнир-
ные параллелограммы. Расчетная схема прини-
мает вид рис. 11.
Ясно, что лучи силового многоугольника, со-
ответствующие четвертям пролета, будут при
этом иметь заданные направления (рис. 12), и
точка их пересечения однозначно определит по-
ложение полюса О кривой давления, а стало
быть, и величину распора. Таким образом, рас-
четная схема рис. 11 позволяет найти распор
чисто статическим путем, хотя она и остается
один раз статически неопределимой. Однако, ес-
ли отвлечься от трения в опорах, т. е. привести
расчетную схему рис. 11 к виду рис. 13, то она
станет механизмом и будет обладать всеми недостатками первой
теории Делагира; в частности, толщина опор у полуциркульного
свода снова обратится в бесконечность.
Вторая теория Делагира дает яркий пример теории первой кате-
гории: положение швов разрушения назначается априорно.
Эта теория подверглась дальнейшей разработке со стороны ря-
да исследователей, из которых можно упомянуть Куплэ 1461, Бели-
дора [47], Хеттона [48], Боссю (49), Апфальтерна [50] и Маскерони
[51]. Наибольший интерес среди них представляет вторая работа
Куплэ [46], появившаяся в 1730 г.
340
Куплэ исходил из иной концепции о разрушении свода, чем Де-
лагнр. Появление трещин в сводах он объяснял не сдвигами, а
вращением клиньев. Куплэ считал, что разрушение свода сопро-
вождается раскрытием швов -снизу — в замке и у пят и сверху — в
четверти длины дуги, т. е. у полуциркульной арки —в шве, накло-
ненном под 45 к горизноту. В соответствии с этим расчетная схема
Куплэ представляла четырехзвенную кинематическую цепь из
Рис. 13. Действительная схема, при-
нятая Делагиром
Рис. 14. Расчетная схема Куплэ
звеньев, соединенных шарнирами одностороннего действия (рис.
14). При симметричном загружении эта цепь обладает одной сте-
пенью изменяемости. Условие устойчивости ее состоит в прохожде-
нии кривой давления через все пять шарниров — задача, вообще
говоря, не имеющая решения. Но если считать наружное очертание
свода неизвестным, то его можно подобрать из указанного условия.
Таким образом, между методами Делагира и Куплэ есть много
общего; оба они позволяют подобрать толщины свода, обеспечиваю-
щие мгновенное равновесие ки
нематической цепи, оба задают
априорно положение швов раз-
рушения. Разница сводится к то-
му, что первый назначает место
швов сдвига, а второй — место
швов раскрытия. На первый
взгляд расчетная схема Куплэ
стоит в резком несоответствии с
Рис. 15. Разрушение свода по опы-
там Данизи
эпюрой моментов, так как шар-
ниры в этой схеме установлены в сечениях с наибольшим момен-
том. Однако надо помнить, что Куплэ изучал равновесие свода в
стадии, непосредственно предшествующей разрушению. В этой
стадии неизбежно происходит раскрытие швов в растянутой зоне и
образование шарниров в наиболее напряженных сечениях. В усло-
виях нормальной работы свода схема Куплэ, разумеется, расхо-
дится с действительностью.
Таким образом, обе эти древнейшие теории (и Делагира, и Куп-
лэ) исходят из определенной концепции о характере разрушения
свода и рассматривают его в момент начинающегося разрушения.
Весьма близкий прием применяется нами в настоящее время при
расчете статически неопределимых систем по предельному состоя-
нию. Особенно велико сходство последнего приема с теорией Куп-
лэ, принимающей, что свод в момент разрушения обращается в из-
341
меняемую систему путем образования шарниров, как это требуется
по новейшей из современных теорий.
Теории Делагира и Куплэ представляют собой эмбрионы всех
позднейших методов расчета свода по предельному состоянию, как
читатель убедится из дальнейшего изложения.
В 1732 г. Данизи поставил при академии в Монпелье опыты над
разрушением небольших моделей арки (521. По-видимому, это была
первая экспериментальная работа, посвященная аркам. Эти опыты
показали, что гипотеза Делагира о разрушении арки путем разде-
ления ее на три части не соответствует действительности. Данизи
установил, что арка при разрушении разделяется на четыре куска,
причем в замке и пятах происходит раскрытие швов снизу, а вбли-
зи четвертей — сверху (рис. 15), т. е. так, как предположил Куплэ,
хотя истинное положение промежуточного шва не постоянно: она
зависит от размеров свода и обычно лежит ниже шва, наклонен-
ного под 45° к горизонту. Данизи не обнаружил никаких сдвигов
при разрушении арки в значительной мере вследствие малого мас-
штаба моделей, и потому он считал, что сдвигов нет вообще, а раз-
рушение происходит только путем вращения отдельных частей
свода.
Несмотря на такой результат эксперимента, популярность вто-
рой теории Делагира ничуть не поколебалась; более того (вопреки
очевидности), она совершенно вытеснила теорию Куплэ. До неко-
торой степени это может объясниться несколько большей просто-
той теории Делагира, а также тем, что ее сторонником был знаме-
нитый строитель арочных мостов Перронэ [53] (1708—1794), кото-
рый составил таблицы для расчета сводов именно на основе теории
Делагира1. Эти таблицы пользовались в конце XVIII века большой
известностью.
Вторая теория Делагира дожила до конца XVIII века и затем
была отвергнута навсегда, уступив свое преобладающее место
частью первой теории того же Делагира, частью многочисленным
методам, возникшим из круга идей Кулона. Любопытно отметить,
что одним из последних ее приверженцев был русский военный ин-
женер, преподаватель военных наук в Московском университет-
ском пансионе Гавриил Иванович Мягков Г541, работа которого,
опубликованная в 1825 г., является одной из первых по времени
русских исследований по строительной механике.
Прежде чем переходить к следующей главе истории — работе
Кулона, следует вкратце упомянуть о ранней попытке применения
к расчету сводов теории цепной линии. Цепная линия, т. е. форма
равновесия бесконечно тонкой весомой нити, была открыта Яковом
Бернулли и Лейбницем в конце XVII века. В 1707 г. Давид Грего-
ри 155] (1661 1710) предложил рассматривать свод как опрокину-
тую нить и указал, что свод, состоящий из бесконечно тонких
клиньев одинакового веса, будет находиться в равновесии, если
1 В Ленинграде сохранились до сих пор два арочных моста через Фонтанку,
построенных Перронэ: Чернышев и Калинкин, Прежде их было семь.
342
примет форму цепной линии. Насколько нам известно, идея эта не
получила дальнейшего распространения до работ Герстнера
(1831).
Глава 3
ТЕОРИЯ КУЛОНА
В 1773 г. военный инженер Шарль-Огюстен Кулон (1736—
1806) представил в Парижскую академию наук свою работу [11],
озаглавленную «Применение правил нахождения максимумов и
минимумов к некоторым
задачам статики, относя-
щимся к архитектуре».
Этой работе суждено бы-
ло впоследствии нало-
жить глубокий отпечаток
на развитие теории свода
и подпорных стенок. До
настоящего времени тео-
рия свода Кулона изла-
гается в некоторых учеб-
ных руководствах: в при-
менении же к расчету
подпорных стенок метод
Кулона и доныне господ-
ствует почти безраздель-
но. Такая живучесть ме-
тода Кулона неудивитель-
на; этому крупнейшему
физику, обессмертившему
себя исследованиями в
области трения и электри-
чества, удалось построить
весьма остроумную при-
ближенную теорию сво-
дов [56] и подпорных сте-
нок в предельном состоя-
нии. Кулон (1736—1806)
В соответствии с на-
шей установкой, мы изло-
жим метод Кулона с современной точки зрения.
Кулон объединил обе теории Делагира с теорией Куплэ и про-
изводил проверку арок как на сдвиги, так и на вращение. Начнем
со второй проверки. Допустим, что арка находится в состоянии
предельного равновесия, т. е. на грани разрушения, которое про-
343
изойдет так, как следует из опытов Данизи. При разрушении свод
раскроется снизу—в замке (это следует из условий симметрии) и
вблизи опор и сверху — в.близи четвертей пролета. Таким обра-
зом, в пяти швах раскрытия, положение одного из которых извест-
но, в момент разрушения включатся односторонние шарниры, при-
чем свод разделится на четыре звена. Два средних звена образуют
трехшарнирную арку, которую можно будет рассчитать статически,
если будет известно положение промежуточного шва разрушения
и положения шарниров в швах.
—Н
Рис. 16. Раскрытие шарнира по Кулону
Рис. 17. Схема Кулона
Если кривая давления пересечет шов разрушения в пределах
толщины свода, то шарнир останется запертым. Он станет шар-
ниром, если кривая давления выйдет из свода так, что шарнир ока-
жется между кривой давления и осью свода (рис. 16). При этом
шов раскроется и произойдет разрушение свода. Состояние пре-
дельного равновесия наступит в тот момент, когда кривая давле-
ния пройдет через шарнир.
Поскольку четвертной шов раскрывается сверху, постольку
можно считать, что шарнир в этом шве расположен на внутреннем
очертании свода. Если раскрытие замкового шва начнется одновре-
менно с раскрытием четвертного шва, то замковый шарнир следует
поместить на наружном очертании (рис. 14). Если же раскрытие
замкового шва запаздывает, то замковый шарнир может оказаться
помещенным в некоторой неизвестной точке замкового шва между
обоими очертаниями свода. Таким образом, задача является дваж-
ды статически неопределимой: неизвестными служат положение
четвертного шва и положение замкового шарнира. Следует отме-
тить, что Кулон первый правильно оценил порядок статической не-
определимости задачи.
С одним неизвестным — положением замкового шарнира — Ку-
лон справился просто: он заявил, что на практике можно считать
этот шарнир помещенным в верхней точке замкового шва. Для
отыскания второго неизвестного он применил метод максимумов и
минимумов.
Кулон разрезает арку в замке, отбрасывает одну ее половину
и заменяет одной горизонтальной силой Н — распором (рис. 17),
приложенным в верхней точке шва, т. е. в шарнире. Где бы ни на-
ходился промежуточный четвертной шов разрушения, т. е. шарнир,
344
два средних звена свода образуют трехшарнирную арку, для ко-
торой величина распора может быть найдена из уравнений стати-
ки. Следовательно, распор является статической функцией поло-
жения четвертного- шва разрушения. Кулон составляет выражение
этой функции и находит аналитическим путем значение аргумента,
т. е. положение шва разрушения, обращающее в максимум величи-
ну распора. Если считать, что образование промежуточного одно-
стороннего шарнира возможно в каждом шве, т. е. если считать
свод за многозвенную кинематическую цепь с односторонними
шарнирами, то очевидно, что при всяком меньшем значении распо-
ра свод будет раскрываться в одном из промежуточных швов. На-
Рис. 18. Разрушение свода от чрез-
мерной величины распора
Рис. 19. Вторая схема Кулона
против, при значении распора, большем, чем найденный максимум,
ни один шов не раскроется, и кривая давления на всем протяжении
пройдет внутри тела свода. Следовательно, найденное максималь-
ное значение распора является в действительности минимумом,
г. е. наименьшим возможным значением распора для свода, не по-
терявшего устойчивости.
Этот нижний предел можно найти, не прибегая к высшей ма-
тематике. Для этого достаточно последовательно определять зна-
чение распора, способного уравновесить от вращения вокруг ниж-
них ребер швов один клин, два первых клина и т. д., с учетом дей-
ствующей на них нагрузки, после чего из найденных значений
следует взять наибольшее.
Аналогичным образом Кулон определил верхний предел распо-
ра. Для этого он искал наименьшее значение распора, способного
опрокинуть полуарку наружу, т. е. раскрыть четвертной шов сни-
зу, а замковый —сверху (рис. 18). В соответствии с этой новой
концепцией о характере разрушения Кулон помещал четвертной
шарнир в верхнюю точку шва, замковый же шарнир переносил
на нижнее очертание свода (рис. 19).
Новая схема (рис. 19) опять позволила вычислять распор, как
статическую функцию положения четвертного шва; Кулон находил
минимальное значение этой функции. Очевидно, при всяком боль-
шем значении распора произойдет раскрытие снизу одного из про-
межуточных швов, тогда как при меньших значениях кривая дав-
ления пройдет внутри тела свода, и он останется в равновесии.
Следовательно, найденный минимум представляет в действитель-
ности максимум распора, возможного в устойчивом своде.
345
Рис. 20. Третья и четвертая
схемы Кулона
Таким образом, в отличие от теории Куплэ, априорно назначав-
шей положение шва разрушения, теория Кулона определяет поло-
жение таких швов из экстремальных условий и находит два преде-
ла, между которыми лежит действительное значение распора.
Теория Кулона по нашей классификации принадлежит ко второй
категории.
Таким же способом Кулон преобра-
зовал вторую теорию Делагира, отказав-
шись от априорного значения промежу-
точного шва сдвига и дополнив расчет
Делагира учетом трения между клинь-
ями1.
Совершенно так же, как и в провер-
ке на вращения, Кулон определил мак-
симальную величину распора, способно-
го удержать от сдвига полуарку с про-
извольно расположенным швом сдвига
(рис. 20), и минимальную величину рас-
пора, способного выдавить кверху сред-
нюю часть арки. Первое значение слу-
жит нижним пределом возможного рас-
пора, а второе — верхним.
четыре предельных значения для распора:
два предела Н™'т, — по вращениям и два предела
/7™ах — по сдвигам. Если оба нижних предела меньше обоих верх-
них, например, если
fjmin fjmin yymax jyrnax
Итого Кулон нашел
то равновесие свода возможно, причем истинный распор будет за-
ключаться между внутренними членами этой цепи неравенств; если
же один из нижних пределов больше одного из верхних, то равно-
весие невозможно.
Мы видим, что теория Кулона не давала однозначного опреде-
ленного решения задачи. Это было приближенное решение, осно-
ванное на неравенствах и устанавливающее пределы, между кото-
рыми должен заключаться распор. Преимущества теории Кулона
над предшествующими неоспоримы, и остроумие, с которым он по-
дошел к решению задачи, заслуживает высокой оценки.
Однако в теории Кулона есть слабое место, которое он сам со-
знавал. Кулону было ясно, что прохождение равнодействующей
через крайнюю точку шва, т. е. через ребро клина, неизбежно вы-
зовет раздавливание материала в этом ребре, а потому устойчивое
и прочное состояние свода требует, чтобы равнодействующая от-
ступила от ребра внутрь на некоторое расстояние, величина которо-
го остается совершенно неопределенной.
1 Напомним, что Кулон был автором первой и существующей до сих пор
теории трения. _
346
Эта неопределенность сильно повредила теории Кулона и задер-
жала ее распространение на долгие годы. Сам Кулон не очень за-
ботился о придании своему исследованию вполне конкретного
прикладного характера; его более всего интересовала принципи-
альная сторона задачи, как видно и из заглавия его работы. Мы
снова встречаемся здесь с примером того отрыва науки от жизни,
о котором уже говорили в очерке первом.
Отметим еще одну особенность теории Кулона. Определение
границ значения распора по Кулону производится из условий рав-
новесия средних частей арки, от промежуточных швов разрушения
до замка. Поведение и природа крайних частей свода, т. е. их на-
грузка, форма и т. п., в сущности не играют почти никакой роли.
Они являются лишь консольными опорами для той трехшарнирноч
арки, в которую превращается средняя часть свода в предельном
состоянии.
Последним спорным местом теории Кулона является вопрос о
том, заключен ли действительно истинный распор между экстрему-
мами, вычисленными по способу Кулона. В сущности это положе-
ние не было доказано Кулоном, хотя и кажется весьма правдопо-
добным. Между тем оно в общем случае неверно, и кулоновские
условия не являются ни необходимыми, ни достаточными. Впервые
это было доказано русским военным инженером Германом Егоро-
вичем Паукером (см. главу 7).
«Противу мнения и чаяния
многих, толь довольно предки
наши оставили на память, чти
применяясь к летописателям
других народов, на своих жало-
ваться не найдем причины. Не
мало имеем свидетельств, что в
России толь великой тьмы не-
вежества не было, какую пред-
ставляют многие внешние писа-
тели».
М. В. Ломоносов (Избр.
филос. сочин., стр 298)
Глава 4
ТРУДЫ ИВАНА ПЕТРОВИЧА КУЛИБИНА
В то время, когда Кулон писал в Париже свой труд, в далекой
северной столице, в тесной мастерской Академии наук на Василь-
евском острове, совершались удивительные дела. Дела эти настоль-
ко опережали свой век, что автор испытал большие затруднения,
347
стараясь найти подходящее место в очерке истории расчета арок
для этой главы —она решительно выпадала из общего плана изло-
жения. В конце концов автор решил поместить ее здесь исходя
только из хронологического признака. Но по своему содержанию
эта глава все же никак не может быть привязана к общей истории
расчета арок: настолько своеобразен был ум у Ивана Петровича
Иван Петрович Кулибин (1735—1818)
Кулибина. Вместе с тем именно такое хронологическое сопоставле-
ние дает особенно отчетливо почувствовать новаторство Кулибина.
История жизни Кулибина достаточно широко известна [57], и
мы ограничимся здесь краткими сведениями из его биографии.
И. П. Кулибин родился в 1735 г. в Нижнем-Новгороде в семье мел-
кого торговца-раскольника. Он нигде не учился и своим развитием
обязан был только себе — чтению книг и газет. Кулибин очень рано
высказал любовь к механике и необыкновенные способности к ней.
и когда в 1769 г. он получил должность механика при Академии
наук, о нем уже шла широкая молва по России, как о механике-
чудодее, строителе удивительных часов, оптических приборов и
автоматов. Под руководством Кулибина академические мастерские
достигли небывалого расцвета и стали выпускать для академии и
на продажу научные приборы, в том числе отличные телескопы и
микроскопы.
348
В Академии наук Кулибину пришлось испытать на себе наци-
ональное и классовое презрение иноземных академиков к «борода-
тому русскому мужику»1. Только один из этих иноземцев принял
в Кулибине участие и всячески его поддерживал. Но зато этот
«один» был величайшим математиком XVIII века, основоположни-
ком русской математической школы. Это был Леонард Эйлер.
После 3U лет работы в Академии наук Кулибина при неясных
обстоятельствах в 1801 г. выжили из академии. Он вернулся в род-
ной город, где работал над созданием «водоходного судна». В
1818 г. он умер в совершенной нищете. Чтобы достать денег на по-
хороны, вдове Кулибина пришлось продать стенные часы его
работы.
Когда Кулибин в 1769 г. приехал в Петербург, он сразу же ув-
лекся идеей сооружения постоянного моста через Неву. В Петер-
бурге через Неву существовал только наплавной мост, разводив-
шийся весной и осенью. В эти периоды переправа совершалась на
лодках и была нередко сопряжена с опасностью для жизни. Чита-
тели «Медного всадника» вспомнят, что положение не изменилось
и через 50 лет после Кулибина.
Кулибин считал сооружение промежуточных опор неосуществи-
мым из-за быстроты течения, большой глубины реки и ледоходов.
Поэтому он остановился на схеме однопролетного арочного моста
небывалого в те времена пролета — 300 м, выполненного из дерева.
Выбор материала понятен: сооружение каменного моста такого
пролета невозможно, а железо в те времена еще не пытались при-
менять для мостсв. Впрочем, мысль о железе как наиболее подхо-
дящем материале для мостов была впервые высказана тем же
Кулибиным на несколько десятилетий раньше появления первых
железных мостов в Западной Европе.
Кулибин последовательно разработал три варианта моста, и по
третьему варианту была построена знаменитая модель, о которой
речь ниже. Рисунок этого третьего варианта широко известен по
многочисленным воспроизведениям в популярных изданиях (рис.
21). Но в этих изданиях обычно ничего не говорится о расчете мос-
та, и потому труд Кулибина нередко воспринимается как полуфан-
тастическая идея прожектера-изобретателя. Между тем Кулибин
сумел рассчитать это гигантское сооружение и вложил в этот рас-
чет столько идей и новшеств, что правильно было бы считать его
работу одним из важнейших трудов по строительной механике в
XVIII веке, если бы только он своевременно стал всеобщим досто-
янием. К несчастью, Кулибин ограничился тем, что опубликовал
свою работу отдельной брошюрой, изданной только в 1799 г. [58]
и не обращавшей на себя внимания современников в течение деся-
тилетий. Первую справедливую оценку труда Кулибина дали в
50-х годах XIX столетия Журавский и Собко. В наше время пре-
красный анализ этой работы произвел Якубовский [59], к содержа-
тельной статье которого мы отсылаем интересующихся конструк-
* Правительство Екатерины II предложило Кулибину потомственное дворян-
ство при условии снятия бороды. Кулибин отказался.
349
тивной стороной кулибинских проектов. Однако только рассмотре-
ние работ Кулибина в историческом разрезе на фоне всей истории
строительной механики может полностью осветить научную роль
Кулибина.
По своей конструкции кулибинская арка во всех вариантах
представляла арочную ферму постоянной высоты с заделанными
пятами (неподвижные опоры по концам обоих поясов) и с много-
Рис. 21. Проект арочного моста Кулибина
решетчатым заполнением. Фермы такого типа стали применяться
в мостостроении только с 1820 г. под именем ферм Тауна; по спра-
ведливости их следует называть фермами Кулибина.
Кулибин не получил систематического научного образования
и не был знаком с теоретическими основами механики. Но это не
помешало ему разбираться в механических законах лучше и пра-
вильнее, чем это удавалось многим из тех, которые такое образова-
ние получили и глядели на Кулибина с презрительным высокоме-
рием, как на «самоучку». Кулибин решил сам дойти до познания
законов механики, и притом не умозрительным, а опытным путем.
Для этого ему пришлось исследовать, как работает арка под на-
грузкой. А этот путь был путем изучения рабочего состояния арки,
а не ее предельного состояния. Вот первая причина, по которой эта
глава истории так резко выпадает из общего плана. Если все уче-
ные, от Делагира до Кульмана, на протяжении почти двух столе-
тий упорно и тщетно пытались изучать арку с позиций предельного
состояния и так и не справились с этой задачей, то Кулибин, пред-
восхищая на полстолетия реформу Навье, сразу встал на правиль-
ный и плодотворный путь изучения рабочего состояния. В этом его
первая и важная заслуга, оставшаяся неоцененной и даже не отме-
ченной ни в одном из обзоров его деятельности вплоть до наших
дней.
350
Кулибин фактически принял схему своей арки за трехшарнир-
ную, хотя она была бесшарнирной. Разумеется, в те времена еще
не существовало ни термина, ни самой конструктивной схемы трех-
шарнирной арки. Такая замена не может, конечно, быть признана
точной. Однако, если очертание арки принято по кривой давления
от нагрузки, разница в величине распора у трехшарнпрной и бес-
шарнирной арки получится только за счет продольных деформаций
последней. Это обстоятельство было понято только через 100 лет
после Кулибина. Но Кулибин с помощью простого здравого смысла
увидел то, чего не видели его предшественники и современники:
сходство между аркой и парой стропильных ног, связанных в замке
и имеющих неподвижные опоры. Это сходство состояло в распор-
ности обеих систем. Поэтому первый опыт Кулибина имел целью
Рис. 22. Опытное определение
распора по Кулибину,
Рис. 23. Определение распора с помощью
веревочного многоугольника (осуществлено
Кулибиным)
измерение распора, даваемого весом наклонной стропильной ноги.
Схема опыта дана на рис. 22 и понятна без пояснений. Произведя
серию опытов при разном наклоне и разном весе ноги, Кулибин
установил следующие зависимости:
1) при данном угле наклона отношение распора к вертикаль-
ной реакции постоянно и не зависит от веса полуарки;
2) отношение распора к весу полуарки в 4 раза меньше отно-
шения пролета арки к стреле = —
3) величина распора зависит от положения груза в пролете.
Это последнее положение Кулибин вывел из опыта, поставлен-
ного по схеме рис. 23. Иными словами, он использовал для на-
хождения распора веревочный многоугольник. Но ту же идею Ку-
либин применил и для более сложной задачи: нахождения опти-
мального очертания арки, и притом при неравномерной ее нагруз-
ке. Стремясь уменьшить распор, Кулибин облегчил среднюю часть
арки, уменьшая сечения всех элементов от опор к замку, так что
площади сечений изменялись от трех единиц у опор до двух еди-
ниц у замка. Затем он подобрал серию гирек, вес которых менялся
по тому же закону, подвесил их к веревке, как показано на рис. 24,
добился натяжением .веревки нужного ему провеса и прочертил
контур получившегося веревочного многоугольника. Этот контур он
351
я принял за очертание оси арки, справедливо считая, что при этом
она будет работать только на осевое сжатие. Иными словами, очер-
тание оси он взял по кривой давления от нагрузки и применил для
нахождения кривой давления веревочный многоугольник. Это было
в 1772 г.
Для оценки этого достижения Кулибина надо учесть, что в то
время теория веревочного многоугольника еще не была известна.
Ее разработали впервые Ламэ и Клапейрон в 1823 г., а первое
приложение этой теории к расчету арок относится только к 30-м
годам XIX века.
Таким образом, идея при-
менения веревочного много-
угольника к расчету арок, без-
условно, представляет само-
стоятельное творчество Кули
бина и в этом его вторая важ-
ная заслуга.
Выбрав очертание оси ар-
ки по кривой давления1 2, Ку-
либин нашел с помощью ве-
Рис. 24. Веревочный многоугольник, при-
мененный Кулибиным для нахождения
оптимального очертания оси арки
ревочного многоугольника
распор при заданном законе
изменения собственного веса. Полученная им цифра — 385 ОСО пу-
дов— дает абсолютно точное значение распора для трехшарнирной
арки.
Если вспомнить, что в это время в западно-европейской науке
даже простую балку умели рассчитывать только на действие со-
средоточенного груза в середине пролета, что в курсе мостов Готье
1755 г. мы находим фантастическое утверждение о зависимости
вертикальной реакции наклонной балки при вертикальной нагруз-
ке от величины угла наклона, что через полвека после Кулибина
знаменитый Навье совершит грубую ошибку, пытаясь рассчитать
простую балку на действие произвольной нагрузки, — если вспом-
нить все это и сравнить с научным результатом Кулибина, само-
стоятельно решившего несравненно более сложную задачу и при-
том абсолютно точно, то историческая роль Кулибина получит
правильную оценку.
Но и это еще не все. Кулибина приходится считать основателем
научной теории моделирования.
Имея в виду проверить свои расчеты на модели, Кулибин учел,
что при изменении всех линейных размеров в п раз собственный
вес изменится в л3 раз, а площади сечений элементов — только в
л2 раз. Это значит, что и прочность элементов, работающих на
растяжение и сжатие, изменится в п2 раз2-
Следовательно, модель фермы в — натуральной величины
1 Первая попытка решения этой задачи (и притом неправильная) в западно-
европейской литературе была сделана Салимбени в 1787 г.
2 Это верно и в отношении устойчивости сжатых стержней, так как их гиб-
кость при пропорциональном изменении всех размеров остается постоянной.
352
имеет напряжения от собственного веса, в п раз меньше, чем
ферма в натуральную величину, и потом}' для уподобления усло-
вий работы фермы и модели необходимо загрузить последнюю до-
бавочной нагрузкой, превосходящей вес модели g в п раз. Если
мост несет, кроме собственного веса, полезный груз Р. то к модели
должна быть приложена полезная нагрузка —, а всего
/p=«g+-^-}
Таково рассуждение Кулибина, получившее полное одобрение со
стороны старика Эйлера. Сейчас мы похвалили бы инженера, ко-
торый так грамотно применяет в своей диссертации теорию мо-
делирования. Следует по достоинству оценить эту третью заслугу
Кулибина, который впервые в истории строительной механики
поставил и правильно разрешил задачу моделирования.
К этим трем заслугам надо, однако, прибавить еще четвертую.
Кулибин не был первым экспериментатором в строительной ме-
ханике. Мы уже упоминали об опытах над сводами, поставленных
в 1732 г. Данизи; известно, что еще Мариотт испытывал прочность
балок шарнирно-опертых и с двусторонней заделкой. Но все эти
опыты преследовали цель нахождения предельной, разрушающей
нагрузки и вида разрушения. Никому из предшественников Кули-
бина, изобретавших различные умозрительные теории свода, не
пришло в голову поставить опыт для измерения действительной
величины распора в своде в его рабочем состоянии. В этом и
состоит четвертая крупная заслуга Кулибина: он первый в истории
строительной механики встал на путь опытной проверки действи-
тельной работы сооружения, и потому его труды и достижения в
области расчета арок так же резко отличаются от работ большин-
ства его предшественников и современников, как химия от алхи-
мии или астрономия от астрологии. Если бы труды Кулибина не
остались без использования, а нашли продолжателей, то его смело
можно было бы назвать одним из основателей научной строитель-
ной механики. Но для этого он родился слишком рано...
Как известно, испытание модели увенчалось полным успехом
Кулибина. Модель была построена в 1775—1776 гг. в ’/ю натураль-
ной величины, так что она представляла сама по себе громадный
арочный мост пролетом в 30 м и весом в 330 пудов. Ассигнований
правительства на постройку модели оказалось недостаточно, и
есть данные полагать, что Кулибин вложил в нее значительные
личные средства, вследствие чего ему и пришлось так бедствовать
всю дальнейшую жизнь.
По условию подобия модель должна была выдержать десяти-
кратный собственный вес, т. е. 3 300 пудов, воспроизводивших ус-
ловия работы моста на постоянную нагрузку. Модель выдержала
без всяких признаков повреждений нагрузку в 3 870 пудов (больше
не оказалось под рукой балласта), и потому избыток в 570 пудов
для модели отвечал безопасной 100-кратной полезной нагрузке для
23 С. А, Бернштейн
353
моста, т. е. 57000 пудов (900 т, или 3 т на 1 пог. м), что значи-
тельно превосходило действительную потребность по тому време-
ни. Вся нагрузка была уложена невыгоднейшим образом — в зам-
ке арки, чем обеспечивался добавочный запас прочности для мо-
ста, и была выдержана на модели 28 дней без каких-либо призна-
ков повреждения.
Современники оставили нам краткие, но выразительные описа-
ния этого знаменательного испытания; отрывки из них уместно
привести здесь.
«День осмотра модели был назначен 27 декабря 1776 г. Испы-
тателями были назначены: академики Эйлер—отец, И. Л. Эй-
лер — сын его1, С. Котельников2, Ст. Разумовский, В. Л. Крафт,
А. И. Лексель; адъюнкты: Петр Иноходцев, Н. Фус и М. Головин.
Пробная тяжесть долженствовала быть 3 300 пудов. Сначала все
сомневались и подсмеивались над Кулибиным; он молчал. Но по-
том, когда вся установленная тяжесть была положена и модель
выдержала, он велел положить на нее все оставшиеся полосы
железа, потом кирпич, который по какому-то случаю был нало-
жен на дворе, и таким образом тяжесть дошла до 3 870 пудов, и
модель не трогалась. 28 дней стояла она под тяжестью и даже не
погнулась. Знаменитый проект Кулибина много шума наделал и
заграницей. Лондонская академия молчала»3 (П. И. Мельников,
Нижегородские ведомости, 1845).
«Старик Эйлер сам первый взобрался на модель^ когда кон-
чился весь балласт для нагрузки модели, и протянул оттуда руку
Кулибину, как победителю» (Павел Свиньин, Жизнь русского ме-
ханика Кулибина и его изобретения, Спб., 1819).
Интересно, что восторженная заметка об испытании, помещен-
ная в «Санкт-Петербургских ведомостях» за 1777 г., № 12, заканчи-
вается словами: «Впрочем нельзя было определить, какой тягостью
мост сей поколебаться может; следственно справедливое о сем
удивление еще бы могло умножиться, когда бы исследовано было
все пространство его силы».
Это замечание вполне справедливо. Действительно, опыт с
моделью не позволил установить ее истинного запаса прочности,
и в этом можно усмотреть неполноту опыта. Но, с другой стороны,
для всей концепции Кулибина очень характерно, что его интересо-
вало только рабочее, а не предельное состояние конструкции, как
мы уже не раз подчеркивали. Кроме того, ему, вероятно, было
1 Иван Леонардович Эйлер, профессор Академии наук по кафедре фи-
зики.
2 В 1774 г вышел курс механики С. Котельникова: «Книга, содержа-
щая в себе учение о равновесии и движении тел». В ней содержатся, между про-
чим, расчет висячего моста с помощью цепной линии и опытные данные о проч-
ности проволок, дерева и канатов. Котельников считал, что «всякое тело твердое
состоит из волокон, соединенных между собою по длине своей».
3 Упоминание о «молчании» Лондонской академии очень знаменательно. В
1772 г. Лондонская академия объявила конкурс на проект однопролетного ароч-
ного моста через Темзу. Кулибин знал об этом конкурсе, так как о нем печатали
в русских газетах, но не пожелал отдать свой проект заграницу.
354
жаль ломать модель. Заметим еще, что если модель при соответст-
венном подборе нагрузки воспроизводила условия работы моста
в рабочем состоянии, или, иными словами, в области преобла-
дания упругих деформаций, то для предельного состояния элемен-
тарные законы моделирования вряд ли применимы. Масштабный
фактор оказывает сильное и не поддающееся точному учету влия-
ние на прочность деревянных конструкций и особенно их соеди-
нений, и потому из установления опытной, предельной нагрузки
для модели еще нельзя было бы определить с точностью вели-
чину разрушающей нагрузки для моста в натуральную величину.
Кулибинская модель просуществовала не менее 30 лет. В 90-х
годах XVIII века она была перевезена под руководством Кулибина
в Таврический сад и установлена там на одном из каналов. Сколь-
ко лет она после этого простояла и каков был ее конец, — неизвесг-
но. А мост? Мост так и не был построен. Несмотря на блестящий
успех испытания модели, «наделавший шуму заграницей», прави-
тельство Екатерины II и не подумало даже поставить вопрос об
его постройке. Ассигнования были прекращены прежде, чем Кули-
бину удалось покрыть расходы на сооружение модели. Ему не
заплатили даже за работу по перевозке и установке модели в
Таврическом саду.
Первый постоянный мост через Неву (с чугунными арками)
был построен только в 1850 г. Станиславом Валерьяновичем Кер-
бедзом.
Чудесный талант Кулибина опередил свое время по крайней
мере на полстолетия и не нашел своевременной поддержки, разви-
тия и применения. Его судьба, как и судьба его выдающихся сов-
ременников — Ползунова, Фролова, Баженова, вечным укором
лежит на русском царизме1.
Глава 5
ПОСЛЕКУЛОНОВСКИЙ ПЕРИОД
Теперь мы вернемся к изложению дальнейшего развития науч-
ной мысли в Западной Европе. Надо сознаться, что после свежих
приемов Кулибина этот возврат несколько напоминает переход
из цветущего сада в душную комнату, и труды европейских уче-
ных конца XVIII и начала XIX века по расчету сводов кажутся
схоластическими, надуманными и ненаучными. Автор сознавал,
как невыгоден такой переход с точки зрения компоновки книги;
1 Существует мнение, будто кулибинский проект моста не был осуществлен
потому, что имел чрезмерно крутой подъем проезжей части. Это совершенно не-
верно. Проезжая часть располагалась не по верхнему очертанию арки, а между
поясами, и имела очень незначительный подъем.
23*
355
но труды Кулибина таковы, что нелегко подыскать для него до-
стойных соратников в строительной механике XVIII века.
Теория Кулона долгие годы оставалась без применения, не-
смотря на то, что она стояла несравненно выше теорий Делагира и
Куплэ. Нам кажется, что в этом идейном превосходстве и заклю-
чалась причина ее непопулярности. Теория Кулона оказалась слиш-
ком мудреной для его современников-строителей.
Нам трудно теперь составить себе представление о скромном
уровне теоретического развития инженеров-строителей XVIII века.
Они были в гораздо большей степени художниками, чем инженера-
ми, и в гораздо большей степени производителями работ, чем
математиками1. Строителю XVIII века нужна была формула, до-
пускающая подбор толщины свода. Эту формулу давали ему таб-
лицы Перронэ, осно-ванные на второй теории Делагира. Нужды
нет, что эта формула требовала излишнего расхода материала; в
условиях XVIII века это обстоятельство еще мало тревожило
строителей. Неопределенный метод Кулона, насыщенный матема-
тикой и не дающий готовых формул, не мог рассчитывать на быст-
рое признание и успех. Это признание пришло через 35—40 лет,
когда архитекторы-художники как основные строители сводов
уступили место военным инженерам и путейцам, обладавшим зна-
чительно более высокой степенью технической подготовки.
Для того чтобы не потерять ориентировки среди огромного ко-
личества методов расчета сводов, появившихся в Западной Евро-
пе в начале XIX века, необходимо выделить несколько основных
ведущих имен, которые могут служить опорными вехами в этом
изобилии методов. Мы уже миновали три таких вехи: Делагира,
Куплэ и Кулона.
После Кулона, который возвышается в этом лесу, как могучий
дуб, мы вступаем в полосу мелколесья, простирающуюся от Куло-
на до Навье. Как и в других разделах строительной механики, эта
пора оказывается периодом застоя и даже попятного движения.
По-видимому, итальянцем Салимбени [60] было впервые введено
понятие оси свода (1798). Это понятие для тех форм свода, какие
были в ходу в XVIII веке, является очень сложным и допускает
различные определения. Вот почему в XVIII веке под очертанием
свода понимали не очертание оси, как это мы делаем теперь, а
внутреннее очертание. Установление понятия оси свода было боль-
шим шагом вперед на пути выяснения расчетной схемы свода, п
после работ Салимбени им все чаще начинают пользоваться.
1 История сохранила нам рассказ о знаменитом архитекторе Матвее Федо-
ровиче Казакове (1738—1812), построившем московское здание Сената (ныне
здание Верховного Совета в Кремле), увенчанное чрезвычайно смелым по своему
времени куполом, который, разумеется, был спроектирован без расчета. При
раскружаливании купола опасения среди рабочих за целость купола едва не пре-
вратились в панику. Уверенный в себе Казаков сам взошел на верх купола и ос-
тавался на нем до полного освобождения кружал, чтобы мужественным примером
восстановить в строителях веру в прочность его создания. Он, вероятно, только
засмеялся бы, если бы кто-нибудь предложил ему заменить расчетом такой риско-
ванный способ проверки прочности.
356
Тот же Салимбени попытался решить задачу подбора очерта-
ния аркь, которую впервые разрешил задолго до него Кулибин.
Салимбени не учитывал трения и сцепления между клиньями арки
и считал, что каждый клин должен быть в равновесии под дейст-
вием собственного веса и давлений, производимых на него сосед-
ними клиньями. Давления эти в виду отсутствия трения направ-
лены по нормалям к швам. Салимбени предположил далее, что эти
давления пересекаются в центре тяжести клина, т. е. на оси свода.
Это означает, что кривая давления совпадает с осью свода На-
грузку же Салимбени направлял нормально к наружному очерта-
нию свода, приравнивая ее действие
к гидростатическому. Исходя из
этих предпосылок Салимбени со-
ставил дифференциальное уравне-
ние оси свода и проинтегрировал
его в неопределенном виде, без оп-
ределения постоянных интегрирова-
ния. Обширная (более 300 страниц)
и тяжеловесная по изложению ра-
бота Салимбени содержит ряд тео-
рем о равновесии сводов различной
зданной формы, для которых совпа-
дение кривой давления с осью не мо-
жет иметь
посылки и
повторены
лимбени.
Рис. 25. Схема Буатара
места. Любопытно, что через 60 лет расчетные пред-
ход рассуждений Салимбени были почти полностью
в работе Вилларсо 1846 г. без упоминания о Са-
Начало XIX века знаменуется постановкой обширных опытов
над разрушением больших моделей арок. Эту экспериментальную
работу выполнили в 1800 г. Буатар [61], Готэ [62] и Ронделэ [63].
Опыты подтвердили полностью факт разрушения арки путем раз-
деления ее на четыре части от вращения, и тем самым окончатель-
но забраковали вторую теорию Делагира, хотя они не обнаружили
сдвигов при разрушении, как и опыты Данизи. Но уже в следую-
щем году Атвуд [64] опубликовал результаты своих опытов, по-
ставленных со специальной целью обнаружения сдвигов. В своих
моделях Атвуд обивал швы полированной медью, чтобы умень-
шить силы трения, и получил бесспорное доказательство наличия
сдвигов.
На основе собственных опытов Буатар построил новую теорию,
о которой стоит вкратце упомянуть. Подобно Кулону, Буатар при-
нимает, что арка в момент разрушения обращается в четырехзвен-
ную кинематическую шарнирную цепь, причем он размещает зам-
ковый и пятовые шарниры на наружной поверхности свода, а про-
межуточный— на внутренней (рис. 25). Эту цепь Буатар рассмат-
ривает как систему рычагов и определяет усилия, действующие
на промежуточный шарнир: распор Н от вышележащей трехшар-
нирной арки и вертикальное давление V от весов Vj, Уг. двух
звеньев 0-1, 1-2, соединяющихся в этом шарнире. Затем Буатар
357
определяет коэффициент устойчивости на опрокидывание звена 0-1
вокруг пятового шарнира 0, т. е. отношение моментов
Это отношение яв-
ляется функцией поло-
жения промежуточно-
го шва разрушения.
Буатар принимает за
опасный шов тот, для
которого это отноше-
ние обращается в ми-
нимум. Найдя такой
шов, Буатар опреде-
ляет соответственный
распор, принимая его
за истинный распор
арки.
Мы видим, что сме-
лая мысль Кулона —
рассчитывать арку из
экстремальных усло-
вий - характеризует и
теорию Буатар а; ее
также следует отнести
ко второй категории
методов. Однако меж-
ду обеими теориями
есть ряд различий. Во-
первых, Буатар огра-
ничился нахождением
нижнего предела рас-
пора и принял этот
k== M0(V) > J
МЛН)
Ламэ (1795—1870)
предел за истинное зна-
чение распора. Бо-вторых, Буатар полностью отказался от учета
сдвигов, основываясь на результатах своих несовершенных опытов.
В-третьих, Буатар изучал устойчивость крайних частей арки, тогда
как Кулон рассматривал только ее средние части.
Поэтому значения распора, определяемые методами Кулона и
Буатара, вообще говоря, не совпадают, причем коэффициент k
преимущественно зависит от вида крайних частей арки. Следует
заметить, что Буатар не вводил термина «коэффициент устойчи-
вости», он употреблен нами для большей ясности.
Любопытно, что Буатар попробовал проверить по своему ме-
тоду устойчивость арок моста в Немуре и нашел, что они должны
были бы обрушиться, если бы не было сил сцепления между клинь-
ями. Это была первая в истории свода попытка учесть влияние
сил сцепления.
358
Теория Буатара не удовлетворила современников. Как и теория
Кулона, она не давала конкретных указаний о необходимых раз-
мерах утолщения сводов к пятам. Более того, из этой теории
вообще не вытекала необходимость такого утолщения, давно уста-
новленная на опыте. Готэ объяснил эту необходимость главным
образом недостатками грунта, т. е. возможностью смещения опор.
Мы видим, что теория Буатара, несмотря на более примитив-
ные, чем у Кулона, предпосылки и рассуждения, выдвинула два
новых обстоятельства: она указала на необходимость учета сил
сцепления, хотя и не дала для этого регулярного метода, и ввела в
рассмотрение поведение опорных частей арки, не учитывавшихся
Кулоном.
Теория Буатара получила известность только во Франции; его
непосредственными преемниками были Одуа, Ламэ и Клапейрон
(см. главу 6). Германская наука пошла по другой дороге.
Первый директор Берлинской строительной академии Эйтель-
вейн (1764—1848), которого история помнит как автора первого
метода расчета неразрезных балок, выступил в 1808 г. со своей
теорией расчета сводов [65]. Вернее сказать, он дал две теории.
Во-первых, он воскресил первую теорию Делагира, т. е. теорию
сдвига свободно соприкасающихся клиньев. Авторство Делагира к
этому времени было уже забыто, и современники приписали за-
слугу изобретения этого метода Эйтельвейну. В изложении Эйтель-
вейна (к слову сказать, в высшей степени неуклюжем и запутан-
ном) эта простая теория пришлась по вкусу современникам, и на
долгие годы заняла почетное место в немецких курсах строитель-
ной механики; последнее по времени изложение ее встречается в
50-х годах у Вейсбаха [66]. Из работ, претендовавших на ориги-
нальность, эта теория повторяется у Рэслинга [67], Кнохенгауэра
[68] и в скучнейшей и бездарной работе Камерлоэра [69], носящей
громкое название («Разоблаченные тайны, или новая теория все-
возможных сводов, выведенная из правильных принципов с уче-
том опыта»). Каждый из этих авторов выдает эту старую прими-
тивную теорию за свое изобретение.
Во втором своем методе. Эйтельвейн попытался дополнить тео-
рию свободных клиньев, введя в рассмотрение силы трения в швах.
При этом Эйтельвейн допустил ошибку, так как полагал давления
между клиньями нормальными к швам, несмотря на наличие тре-
ния. Кроме того, он нарушил закон равенства между действием и
противодействием, допустив, что давления, взаимно оказываемые
двумя смежными клиньями, не равны между собой, и определяя
сумму моментов избыточных неуравновешенных давлений относи-
тельно пяты свода. Ввиду явной незаконности обоих допущений
нет нужды подробнее останавливаться на этом методе.
Мы видим что Эйтельвейн всецело стоит на старых позициях;
его теория не пользуется экстремальным методом. По своему
научному уровню работа Эйтельвейна резко отстает от современ-
ных ей французских исследований (положение, характерное для
немецкой науки первой четверти XIX века).
359
Чтобы завершить обзор методов, не следующих по кулонов-
скому пути, надо рассмотреть еще одну теорию, появившуюся
вскоре после Эйтельвейна. Хотя она не получила распространения
и в настоящее время совершенно забыта, но заслуживает упоми-
нания из-за некоторых содержащихся в ней особенностей.
Автором этой теории был немецкий инженер Рейхенбах [70]
(1811). Он поставил себе задачу, отличную от обычных задач рас-
чета арки. Во-первых, объектом его расчета были, помимо камен-
ных сводов, чугунные трубчатые арки; во-вторых, он задался целью
рассчитать арку на действие произвольно расположенного сосре-
доточенного груза. Эта последняя задача ни разу не рассматрива-
лась до Рейхенбаха, поскольку временная нагрузка на каменные
арки составляла ничтожную часть собственного веса. Для чугун-
ной арки соотношение меняется, и временную сосредоточенную
нагрузку необходимо учитывать. Таким образом, появление нового
материала вызвало потребность в постановке новых расчетных
задач.
В соответствии с материалом Рейхенбах различал два рода
сводов: своды, свободно составленные из клиньев, и сплошные сво-
ды. При расчете первых он придерживается первой теории Делаги-
ра (Эйтельвейна) для подбора весов последовательных клиньев;
для поверки же свода на сосредоточенную силу он ограничивается
требованием о невыходе кривой давления из тела свода при любом
положении силы. Это первый известный нам случай применения
кривой давления к расчету арки (после Кулибина), хотя Рейхенбах
еще не употребляет этого термина1.
Для сплошного свода при действии сосредоточенной силы в
точке В (рис. 26) Рейхенбах рисует на глаз форму упругой линии
и намечает четыре опасных сечения: в пятах (А, 7)), под грузом
(В) и посередине между грузом и дальней опорой (С). Затем Рей-
хенбах полагает, что разрушающий груз Р можно считать состав-
ленным из четырех частей:
Р-РА + Рв + Рс + Р^
где РА, Рв, Рс, PD—грузы, способные порознь вызвать разруше-
ние в сечениях А, В, С, D. Для нахождения каждого из них он об-
ращает свод в трехшарнирную арку, размещая шарниры в трех
остальных сечениях. Так, для определения РА он принимает схему
рис. 27,с, считая, что в сечениях В, Ct D уже включились шарниры
вследствие раскрытия сечений, т. е. разрушения. Для определения
Рс, PD выбираются схемы рис. 27,6, 27,с, 27 Д
1 Кому в действительности принадлежит заслуга введения понятия о кривой
давления, сказать довольно трудно. Феппль указывает на Мозлея (1835), Пере-
дерий— на Мери (1827), Черепашинскпй— на Клапейрона (1823), а Понселе —
на Кулона (1773). Ссылка Передерия (Курс мостов больших пролетов, ч. II,
Каменные мосты, стр. 148, Л., 1925) вызывает серьезные сомнения, так как из-
вестная работа Мери вышла только в 1840 г., на работу же Мери 1827 г. мы не
нашли нигде никаких ссылок. Вдобавок в 1827 г. Мери был 22-летннм юношей, и
маловероятно, чтобы в этом возрасте он уже выступил с самостоятельным иссле-
дованием.
360
Разумеется, этот способ расчета неверен, так как в представле-
нии Рейхенбаха свод является системой с переменным числом свя-
зей, а для таких систем неприменим закон независимости действия
сил, а стало быть незаконно и разложение разрушающего груза
на четыре указанные составляющие. Однако в методе Рейхенбаха
заложены идеи, которые для своего
времени следует признать передо-
выми. К числу их, помимо уже
упомянутых новшеств — рассмот-
рения сплошного свода и попыт-
ки расчета его на произвольно
расположенную сосредоточенную
силу, надо отнести, во-первых,
Рис. 26. Схема деформации по Рейхенбаху
довольно чаткое представление о расчетной схеме и, во-вторых,
ту мысль, что разрушение свода произойдет лишь при появлении
четвертого шарнира, тогда как включение первых трех шарниров
для свода не опасно. В этой идее нетрудно усмотреть зародыш той
мысли, которая легла в основу современных методов расчета ста-
тически неопределимых систем по предельному состоянию. Эти-то
новые и оригинальные идеи и заставили автора несколько подроб-
нее остановиться на работе Рейхенбаха, несмотря на содержа-
щиеся в ней ошибки.
Все перечисленные нами методы не являются продолжением и
развитием идей Кулона, и, видимо, их авторы в большинстве вооб-
ще не были знакомы с работой Кулона. Следующий этап истории
характеризуется победным шествием метода Кулона, кладущего
сильный отпечаток на все последующие теории в течение десяти-
летий.
Глава 6
ВОЗРОЖДЕНИЕ И РАСЦВЕТ ИДЕЙ КУЛОНА
Кому первому принадлежит заслуга извлечения из-под спуда
забытой теории Кулона, сказать довольно -трудно. Французы при-
писывают эту заслугу Одуа [71] (1820); но в немецкой литературе
24 С. А. Бернштейн
361
имеются более ранние изложения этой теории у Шульца [72]
(1808), Майяра [73] (1817) и Лангсдорфа [74] (1817). Однако не-
мецкие авторы, излагая теорию Кулона, не упоминают его имени.
Возможно, что они не были знакомы с работами Кулона и разра-
ботали его теорию самостоятельно, но вернее, что мы имеем здесь
случай простой научной недобросовестности.
В этом смысле правы те, кто считает военного инженера Одуа
первым, обратившим общее внимание на теорию Кулона, так как
он не только отметил авторство Кулона, но и указал, что ряд пос-
ледующих теорий и прежде всего теория Буатара являются след-
ствием и частным случаем теории Кулона, а опыты Буатара и
Готэ ее вполне подтверждают.
Одуа не ограничился пересказом теории Кулона и пошел не-
сколько дальше. Он ввел понятие о коэффициенте устойчивости,
зародыш которого в неявной форме мы видели еще у. Буатара.
Установлением этого понятия Одуа рассчитывал устранить неопре-
деленность кулоновского решения, дающего лишь пределы воз-
можной величины распора. Из примеров осуществленных сводов
Одуа вывел путем довольно сомнительных умозаключений, что
истинный распор должен примерно вдвое превышать кулоновский
нижний предел. Этот множитель — 2 — Одуа и назвал коэффи-
циентом устойчивости и считал его достаточным во всех случаях.
Весьма близко к Одуа й по времени и по содержанию стоит
небольшая работа Ламэ и Клапейрона [75], опубликованная в
1823 г. Ламэ и Клапейрон работали в это время в Петербурге на
постройке Исаакиевского собора, и их исследование состоит в пря-
мой связи с этой деятельностью. Они рассматривали буатаровскую
четырехзвенную расчетную схему и искали положение промежу-
точных швов разрушения, обращая в минимум сумму моментов
сил, приложенных к промежуточному шарниру, относительно пято
вого шарнира.
min [Л10(У) — МС(Н)\ .
Таким образом, при обозначениях рис. 25 истинный распор по
теории Ламэ и Клапейрона обращает в минимум разность
К (ср) = V(<p) х(?) — Н(о) у(ф),
тогда как Буатар минимизирует отношение
Очевидно, что решения в общем случае будут различны, хотя
обе теории определяют степень устойчивости свода по избытку
удерживающего момента над опрокидывающим, как это мы дела-
ем и теперь при расчете подпорных стенок.
В работе Ламэ и Клапейрона есть несколько интересных момен-
тов. Во-первых, они отступили от традиционного деления свода
на клинья путем проведения швов, нормальных к внутреннему
очертанию, и приняли все швы вертикальными, надеясь таким nv-
362
тем упростить формулы. Хотя особого упрощения и не получилось,
так как в вопросах сдвигов и скольжения приходилось возвра-
щаться к нормальным швам, однако этот прием неоднократно по-
вторяется в работах позднейших исследователей (Карвалло,
Хаген, Феппль и др.). Во-вторых, они вывели для круговой арки
теорему, позволяющую найти положение шва разрушения графи-
ческим путем. Теорема эта такова (рис. 28):
«Касательная к внутреннему очертанию арки в промежуточном
шве разрушения пересекает горизонталь, проходящую через верх-
нюю точку замкового сечения, на вер-
тикали центра тяжести части свода, _____
расположенной между этим швом раз-
рушения и замком». /$/—
В-третьих, и это наиболее для нас
интересно, они указали на величайшую
важность установления закона распре-
деления напряжений в действительных
швах, хотя и не предложили для этого
никакой теории. Это была первая, еще *—1,
робкая попытка свернуть с пути, про-
ложенного Делагиром и Куплэ, и от Рис._28. Теорема Ламэ и Клапей-
расчета арки по предельному состоя- Р0113
нию перейти к расчету по рабочему со-
стоянию. По-настоящему эту задачу поставил Навье.
Однако прежде чем переходить к работам Навье, которые на-
чинают новую главу истории расчета арок, следует вкратце пере-
числить работы комментаторов Одуа, который в свою очередь был
лишь комментатором Кулона.
Дело в том, что простая с принципиальной точки зрения теория
Кулона очень тяжела для практического вычисления. Условие ми-
нимума даже для простейшего очертания — кругового — приводит
к сложному трансцендентному уравнению. Поэтому задачи прак-
тики требовали неотложного упрощения кулоновских формул и
составления вспомогательных таблиц для расчета свода. Начиная
с Одуа, ряд инженеров (по преимуществу военных) идет по этому
пути. Из них надо прежде всего назвать Гариделя [76], который
преобразовал формулы Одуа, воспользовавшись разложением в
ряд условия минимума, и свел расчет к определению некоторых
тригонометрических функций угла наклона шва разрушения, даз
таблицы для расчета. Для некоторых частных случаев он составил
приближенные формулы, позволяющие найти нижний предел рас-
пора и положение шва разрушения непосредственно или после не-
сложных подстановок. Кроме того, он дал решения по методу
Кулона для сводов с эллиптическим внутренним очертанием и
эллиптическим или треугольным внешним очертанием, чего не де-
лал Одуа. Однако для нас самое любопытное в работе Гариделя —
это его признание, что по-настоящему свод является упругим,
сжимаемым телом, так что соприкасание клиньев происходит фак-
тически по некоторой поверхности, причем плоскости швов пово-
363
рачиваются вокруг неизвестного центра. Где будет находиться
этот центр поворота? Гаридель расценивает эту задачу безнадеж-
но: «Этого мы не знаем, и не узнаем никогда». Такого рода песси-
мизм встречается и у позднейших авторов, как естественное след-
ствие бесплодности попыток -расчета арки по предельному состоя-
НИЮ.
Несколько ранее работ Гариделя вышел курс статики соору-
, .х j расчета сводов целиком опи-
рающийся на метод Куло-
на. Новой идеей у Перси
является попытка избавить-
ся от произвола, вносимо-
го в метод Кулона благода-
ря приложению распора в
верхней точке замкового
сечения. Перси попробовал
исключить этот произвол
путем вторичного миними-
зирования распора, т. е. оп-
ределял точку приложения
жений Перги [21] (1834), в области
Рис. 29. Схема Перси
распора и положение шва разрушения как аргументы, дающие ми-
нимум миниморум распора. Между прочим при расчете сводов с
каменной забуткой Перси, как и Кулон, помещал шарниры на очер-
таниях самого свода (рис. 29), не думая о сопротивлении, которое
будет оказывать забутка раскрыванию швов снизу свода.
Понселе [77] (1835) попробовал дать обобщение гипотез Одуа,
предположив, что крайние швы разрушения могут не совпадать с
пятами арки. Он же дал графическое построение для определения
максимального распора, шва разрушения и статических моментов
веса клиньев (не пользуясь веревочным многоугольником). Как
большинство построений Понселе, оно является геометрическим,
а не графостатическим, и потому не представляет для нас интере-
са. Вдобавок построение это чрезвычайно сложное и запутанное,
чем вероятно и объясняется то, что оно не вошло в употребление.
Веревочный многоугольник для определения статических мо-
ментов весов клиньев впервые применил Мишон [78], выпустивший
новые таблицы для расчета сводов в 1848 г.
Перечень имен последователей Кулона показывает явное пре-
обладание французских авторов. Это не является результатом слу-
чайного подбора имен. Действительно, в германских государствах
теория Кулона пользовалась слабым признанием; более популяр-
ной была теория Эйтельвейна. Кроме того, до середины 30-х годов
германская инженерная наука вообще отставала от французской
и в области расчета сводов в частности. С конца 30-х годов в ней
наступает оживление, но расчет сводов направляется по своеобраз-
ному пути, который будет рассмотрен в главах 8 и 9.
Глава 7
РАБОТЫ НАВЬЕ И ЕГО ПОСЛЕДОВАТЕЛЕЙ
В 1825 1826 гг. Навье читал лекции о расчете сводов в париж-
ской Школе мостов и дорог, вошедшие в его известный курс при-
кладной механики [18]. В большинстве обзоров истории расчета
свода идеям Навье уделяется немного места. Действительно, если
подходить формально, то можно расценить работы Навье как не-
которое развитие и уточнение теории Кулона. Но если подойти по
существу, то роль Навье предстанет совсем в ином свете.
Мы уже подробно освещали эту 'роль в очерке первом, под-
черкнув глубокий смысл коренной реформы, проведенной Навье
в сопротивлении материалов: эта реформа состояла в переходе от
расчета по предельному (разрушающему) состоянию к расчету по
действительному состоянию системы под расчетной нагрузкой.
Мы видели, что Навье упорно стремился перевести все основные
задачи сопротивления материалов на новый путь — путь вычисле-
ния напряжений в рабочем состоянии. Естественно ожидать по-
этому, что и задачу расчета свода он перевел на тот же путь.
Однако он не сумел этого сделать, и его работы по расчету свода
представляют странное смешение новых и старых идей.
Новой идеей был отказ от абсолютно жестких клиньев и учет
их упругой деформируемости. Новой идеей (высказанной еще
Кулоном) была мысль о неизбежности разрушения материала сво-
да в случае совпадения точек кривой давления с ребрами швов и
о необходимости расчета свода на прочность. Этот расчет в соот-
ветствии с общим смыслом реформы Навье должен был дать зна-
чения напряжений в действительном состоянии.
Но все эти новые мысли Навье втиснул в старую чужеродную
форму расчета по предельному состоянию. Вместо того чтобы най-
ти напряжения в рабочем состоянии, он искал напряжения в пре-
дельном состоянии.
Если до Навье предельное состояние свода понимается чисто
кинематически, как раскрытие швов и вращение звеньев вокруг
шарниров, то для Навье оно приобретает силовой смысл и насту-
пает тогда, когда краевые сжимающие напряжения в швах падают
до нуля, так как раствор по старой концепции не способен работать
на растяжение. Поэтому в состоянии предельного равновесия
эпюра напряжений в швах разрушения принимает треугольную
форму (рис. 30), и, следовательно, равнодействующая отходит от
ребра сечения внутрь на Уз толщины свода, т. е. по современной
терминологии совпадает с ядровой точкой1. Таким образом, Навье
впервые вводит в рассмотрение изгиб свода. С расчетной точки
зрения идея Навье приводит к сужению полосы, внутри которой
обязана лежать кривая давления. Если прежние теории требовали,
чтобы кривая давления не выходила из тела свода, то по теории
Навье она не должна выходить из пределов средней трети толщи-
1 Понятие ядра сечения введено Брессом в 1854 г.
365
ны свода. Выход ее из этих пределов означает для Навье разруше-
ние свода, но не от нарушения его геометрической неизменяемо-
сти, а от разрыва материала свода или раствора в швах.
Расчетной схемой Навье является такая же трехшарнирная
арка, как у Кулона, но с шарнирами, расположенными йена очер-
таниях свода, а на линиях, ограничивающих ядровую полосу
(рис. 31).
Теория Навье в сущности не дала расчета свода, хотя его вы-
вод о невыходе кривой давления из средней трети был совершенно
правилен (для материала, не способного работать на растяжение).
Сохранение старых идей о предельном состоянии не позволило
ему найти истинную величину распора, т. е. зависимость между
Рис. 30. Работа свода на
изгиб по Навье
Рпс. 31. Расчетная схема Навье
распором и нагрузкой1. Поэтому теория Навье носит половинча-
тый компромиссный характер.
С нашей современной точки зрения использование понятия
предельного состояния для расчета является правильным и про-
грессивным приемом. Но правильность его основана на ясном
представлении о характере работы сооружения в упругой ста-
дии и о поведении материала при высоких нагрузках. Во вре-
мена Навье ни то, ни другое еще не было изучено, и понятие пре-
дельного состояния оставалось совершенно умозрительным. По-
этому в ту эпоху прогрессивным был отказ от преждевременного
обращения к предельному состоянию, и правильным был путь изу-
чения напряжения и деформаций в рабочем состоянии. Навье не
сумел встать при расчете свода на этот путь, им же указанный, и
попытался влить новое вино в старые мехи. А ведь Навье был
очень близок от доведения до конца задачи расчета упругого сво-
да. В его распоряжении был созданный им самим метод вычисле-
ния упругих перемещений для криволинейного стержня, который
он и использовал, дав впервые точный метод расчета двухшарнир-
ной арки.
Мы не будем здесь подробно излагать этого метода. По су-
ществу это был старый аналитический способ интегрирования
дифференциального уравнения изогнутой оси бруса, который
1 Вспомним, что Кулибин сумел решить эту задачу для трехшарнирной арки
за 50 лет до Навье, так как его ум не был скован традициями расчета по пре-
дельному состоянию.
366
Навье обобщил для случая кривого бруса малой кривизны и для
сил, действующих по взаимно-перпендикулярным направлениям.
Вместо одного дифференциального уравнения прогиба Навье со-
ставил два уравнения: для вертикальной и горизонтальной состав-
ляющих перемещения, которые он интегрировал порознь. Прирав-
нивая затем нулю горизонтальное расхождение опор двухшарнир-
ной арки, он находил значение распора. Этим же методом Навье
(и раньше его Эйтельвейн) .рассчитывал неразрезные балки, при-
равнивая нулю прогиб на опорах и угол поворота в заделках.
Таким образом, в распоряжении Навье действительно имелся весь
арсенал расчетных приемов, необходимых для расчета бесшар-
нирной арки-свода, и, несмотря на это, ни он сам, ни его
последователи в течение целых 30 лет не замечали этой возмож-
ности.
После Навье его идеи получили дальнейшее развитие в ряде
работ, использовавших понятие кривой давления. В хронологиче-
ском порядке заслуживают упоминания Кайзер [79] (1836); Мери
[80] (1840), изучавший формы сводов, у которых кривые давления,
соответствующие нижнему и верхнему пределам распора, совпада-
ют между собой; Дежарден [81] (1845), рассматривавший круговой
свод в момент освобождения от кружал и давший формулу распо-
ра, который он называет «мертвым давлением» в отличие от «жи-
вогд давления», передающегося на кружала; Вилларсо [82] (1846).
который по существу повторил старинную работу Салимбени, опре-
деляя наивыгоднейшую форму свода из условия совпадения кривой
давления с осью и направляя внешнюю нагрузку по нормалям к
наружному очертанию свода; Сен-Гилем [83], несколько упростив-
ший решение Вилларсо; Беланже [84] (1847), обобщивший гипо-
тезу Навье о распределении напряжений и заменивший треуголь-
ную эпюру напряжений трапецеидальной; Карвалло [85] (1853),
установивший некоторые геометрические свойства швов разруше-
ния и давший таблицы для расчета и, наконец, американец Вуд-
бери [86] (1858), излагающий теорию Навье под видом собственно-
го изобретения, но с опозданием на 30 лет.
С 30-х годов прошлого столетия в связи с развитием железно-
дорожного строительства начинаются особенно усиленные поиски
метода расчета свода. Число работ, посвященных этой теме, резко
возрастает, хотя их авторы по преимуществу занимаются комбини-
рованием различных методов, принадлежащих их предшественни-
кам. Поэтому методическая систематизация работ последующего
периода очень затруднительна; методы наслаиваются и перепле-
таются между собой. Детальное изложение всех этих вариантов,
обычно представляющихся самим авторам последним словом науки,
помимо неизбежной скуки, создало бы у читателя крайне пеструю
и запутанную картину. Поэтому мы выберем несколько основных
методических направлений и выделим в них наиболее оригиналь-
ные с методической точки зрения работы, с тем чтобы рассмотреть
их подробнее; все же прочие работы упомянем мельком, давая им
лишь краткую характеристику.
367
Прежде всего, следует остановиться на своеобразном направ-
лении, которое, к сожалению, получило малое развитие в дальней-
шем. Речь идет о кинематическом методе расчета свода, основан-
ном на принципе возможных перемещений. История применения
этого принципа к расчету сооружений гораздо старше, чем приня-
то думать.
Родоначальником этого направления был французский воен^
ный инженер Ламбель [87], из скромности не выставивший своего
имени на титульном листе своей книги, вышедшей в 1822 г., и
лишь подписавшийся под предисловием. Работа эта, написанная
чрезвычайно серьезно, с обстоятельным пониманием аксиом ме-
ханики, в наше время, к сожалению, совершенно забыта. Она
имела целью усовершенствовать Вобанов-ский тип порохового
погреба.
Ламбель исходит из классической четырехзвенной предельной
схемы Кулона, рассчитывая ее на сдвиги и вращения, но самый
расчет проводит кинематически, определяя чисто геометрическим
путем перемещения шарниров при возможной форме смещения.
Таким образом, ему* принадлежит первый кинематический расчет
трехшарнирной арки', и, насколько нам известно, первый после ры-
чага (балки) кинематический расчет сооружения вообще. Заме-
тим, что искомыми величинами в расчете Ламбеля являются не
усилия, а размеры пят и опор, определяемые кулоновским прие-
мом из условия устойчивости на сдвиг и опрокидывание.
Нам известны еще только два автора, подхвативших идею
Ламбеля и приложивших кинематический метод к расчету свода.
Интересно, что оба эти автора были русские военные инженеры
Кербедз и Паукер.
О роли первого из них, строителе первого .в России металли-
ческого моста через Неву в Ленинграде, нам известно лишь то,
что в своих лекциях по механике, читанных в Николаевском инже-
нерном училище, он применял кинематический метод к расчету
свода по кулоновскому способу. Были ли эти лекции изданы, нам
не удалось выяснить. О работе Германа Егоровича Паукера
(1822—1889) следует рассказать подробнее. Г. Е. Паукер был од-
ним из наиболее выдающихся русских инженеров прошлого века
как по обширности и многосторонности знаний, так и по громад-
ному практическому опыту1. В 1849 г. он опубликовал работу «О
проверке устойчивости цилиндрических сводов» [88], которая, по-
мимо изложения его новой теории, содержала обширный и очень
ценный обзор истории расчета свода. Исследование Паукера пред-
ставляет значительный интерес из-за ряда своеобразных приемов,
им примененных.
Паукер поставил себе задачу проверить устойчивость свода при
раскружаливании, не вводя гипотез о форме излома, и пришел к
1 Жизнеописание и оценку деятельности Г. Е. Паукера см. проф. И. М. Р а-
б и н о в и ч , Деятели русской строительной механики XIX столетия. «Вестник
Военно-инженерной академии», вып. 43. изд. ВИА, 1945, стр. 7—13.
368
заключению, что концепция Куплэ — Кулона о характере разру-
шения свода не всегда справедлива, и в некоторых случаях свод
может разделиться на большее число звеньев частью путем вра-
щений, частью путем сдвигов. Так, на рис. 32 изображен случай
разрушения свода по шести швам, хотя при кулоновском расчете
по пяти швам он оказывается устойчивым. Таким образом, Паукер
впервые показал, что выполнение неравенства Кулона не является
еще ни необходимым, ни достаточным условием устойчивости.
Этот вывод получен Паукером двумя методами — статическим
и кинематическим. Мы изложим подробнее только первый из них,
так как они оба совершенно однородны. Метод этот отличается
Рис. 32. Пример, приведенный
Паукером в опровержение теории
Кулона
Рис. 33. Метод расчета Паукера
Симметричный свод дважды статически неопределим. Предше-
ственники Паукера (например, Перси) выбирали в качестве неиз-
вестных величин распор и точку его приложения в замке (Кулон
задавался этим последним неизвестным). Таким образом, эти
неизвестные, определявшиеся путем экстремирования, были раз-
нородными по природе и размерности: одно являлось силовым, а
другое — геометрическим фактором. Благодаря этому и неравенст-
ва равновесия получались неоднородными и даже нелинейными
относительно неизвестных. Паукеру пришла счастливая мысль
ввести два однородных неизвестных, и в качестве таковых он выб-
рал две параллельные составляющие распора и и у*, приложенные
в верхней и нижней точках замкового сечения (рис. 33). Наметим
произвольный шо*в разрушения, наклоненный под углом ? к вер-
тикали, и пусть Р — вес части свода, расположенной между этим
швом и замком, К — коэффициент трения в шве,
У и у — ординаты верхней и нижней точек шва, Уо и уо— то же,
для замка, X и х — плечи силы Р относительно верхней и нижней
точек шва. Для того чтобы шов не раскрылся сверху, должно быть
u(Y„ —y) + v(y<,~ у)>Рх; (1)
♦ Обозначения наши. Паукер называет их X и .
36Э
чтобы он не раскрылся снизу
u(YB-Y) + v(yv-Y)<PX;
чтобы верхняя часть свода не сползла вниз
(2)
(3)
sin + К cos « ’
Г. Е. Паукер (1822—1889)
чтобы она не сдвинулась
кверху
и -г и \ :-------г;------
sin ср — К COS<p
Условия (1)—(4)
представляют преобразо-
ванные кулоновские не-
равенства. Но Кулон
включал в них только
одно неизвестное (рас-
пор), которое определял
путем варьирования ар-
гумента (положения
шва); неравенства же
Паукера содержат два
неизвестных, от которых
не так просто отделаться.
Тогда Паукер применяет
своеобразный прием: он
принимает составляю-
щие распора w, v за ко-
ординаты точки на плос-
кости. При этом каждое
из неравенств (1)—(4)
обращается в уравнение
точек полуплоскости, ле-
жащих по одну сторону от прямых, определяемых равенствами:
u(YB — у)+ v(yQ —у) -=Рх,
/г(У0-У) + о(ус-У)=РХ,
v -- J
sin + К cos <р
. Р
и + V =----------------------.
sin у — /Ccos<p
(5)
Каждому положению шва разрушения соответствуют четыре
прямые (5), выделяющие из плоскости некоторую область (рис.
34); внутри этой области лежат точки, координаты и, v которых
удовлетворяют неравенствам (1) — (4). При изменении положения
шва эти прямые смещаются, и ограниченная ими область меняет
форму. Наложим друг на друга все такие области, соответствую-
370
щие всевозможным положениям шва разрушения. Если не найдет-
ся ни одной точки, общей всем этим областям, то свод не может
быть устойчив; если общей является только одна точка, то свод
находится в состоянии мгновенного равновесия; если же имеется
целая область ю, входящая в состав всех частных областей, то свод
будет устойчив, причем возможно бесчисленное множество реше-
ний н, и, удовлетворяющих неравенствам (1) —(4) для любого
шва разрушения. Из этих решений Паукер выбирает то, для кото-
у
Рис. 34. Графическое решение
Паукера
Рис. 35. Нахождение мини-
мального распора по Паукеру
рого сумма u+v имеет наименьшее значение; очевидно, ему соот-
ветствует та точка области <о, которая лежит на ближайшей к на-
чалу координат прямой, отсекающей на положительных направ-
лениях осей равные отрезки (рис. 35).
Совершенно тем же путем Паукер проводит и кинематический
расчет свода, но вместо неравенств равновесия составляет нера-
венства возможных перемещений клиньев. Между прочим он вво-
дит при этом в рассмотрение сцепление в швах, предполагая нали-
чие железных скреп между клиньями, а равно и силы трения в
швах; поэтому сдвиги и расхождения по оси являются для него
невозможными перемещениями, если соответственные усилия
меньше сил сцепления и трения.
. Глава 8
МЕТОДЫ, ОСНОВАННЫЕ НА ОТЫСКАНИИ ИСТИННОЙ
КРИВОЙ ДАВЛЕНИЯ
Мы уже упоминали, что представление о кривой давления в
своде появилось довольно рано. Однако лишь в 30-х годах XIX ве-
ка кривая давления становится в центре внимания, и прежние за-
24* 371
дачи — определение толщины пят и вычисление распора — за-
меняются более общей и глубокой задачей — нахождения действи-
тельной кривой давления.
К этому периоду различие между статически определимыми и
неопределимыми системами и их расчетные особенности являются
уже вполне установленными. Пуансо [89] еще в начале XIX века
указал, что решение статически неопределимых систем становится
возможным лишь при учете упругих деформаций. Расчет нераз-
резной балки, произведенный Эйтельвейном, и двухшарнирной ар-
ки. выполненный Навье, подтвердил справедливость указания
Пуансо. Казалось бы, остается распространить тот же метод рас^
чета на свод, и решение будет найдено. После работ Навье эта
возможность становится особенно близкой и легко достижимой.
Однако именно в это время теория свода делает крутой поворот в
сторону и пытается найти решение без рассмотрения упругих де-
формаций и без эксперимента, на основе чистой спекуляции.
С тех пор как было усвоено понятие кривой давления, стати-
ческая неопределимость свода стала пониматься как возможность
проведения в своде бесконечного множества кривых давления,
вполне равноправных с точки зрения статики. Среди этого множе-
ства кривых имеется одна истинная. К ее нахождению и применяют
разнообразные умозрительные приемы.
Эти приемы можно разделить на две категории. К первой от-
носятся те методы, которые, оставаясь на базе классической ста-
тики, пытаются уничтожить неопределенность введением различ-
ных допущений геометрического свойства о форме кривой давле-
ния и о характере работы свода. Под эту рубрику отчасти подходят
уже упоминавшиеся нами работы Мери, Вилларсо и других фран-
цузских инженеров. Другая категория методов, столь же по суще-
ству не обоснованных, значительно более любопытна с философской
точки зрения. Первым выразителем идей, характеризующих это
направление, можно считать Даламбера, который еще во второй
половине XVIII века высказывал ошибочную мысль, что статиче-
ская неразрешимость задачи о двухпролетной неразрезной балке
свидетельствует якобы о неполноте системы аксиом статики. Уси-
лия представителей второй категории методов направлены на
поиски тех недостающих аксиом, с помощью которых можно найти
истинную кривую давления.
Ввиду совершенной разнородности методов этих двух катего-
рий мы рассмотрим сперва методы первой категории, а затем —
методы второй категории, ввиду чего хронологическую -последова-
тельность придется нарушить.
Любопытно, что эта глава истории будет содержать почти ис-
ключительно имена немецких инженеров. Мы лишь упоминаем об
этом факте, воздерживаясь от соблазнительной мысли поставить
его в соответствие с идеалистическим умозрительным направлени-
ем германской философии рассматриваемого периода.
Современная теория свода понимает под кривой давления оги-
бающую равнодействующих усилий, проведенных во всевозмож-
372
ных сечениях свода. Сто лет назад теория свода рассматривала
две различные кривые, характеризующие -работу свода: одну на-
зывали «кривая давления», а другую — «кривая сопротивления».
Эта вторая линия, забытая в наше время, определялась как гео-
метрическое место точек пересечения равнодействующих со шва-
ми. Очевидно, кривая давления не зависит от направления швов
свода, а потому вполне определяется формой свода и нагрузкой.
Напротив, кривая сопротивления зависит от направления швов,
а потому таких кривых можно провести сколько угодно, сообразно
с выбранным направлением швов. Если принять швы вертикаль-
ными, то при действии вертикальной на-
грузки соответственная кривая сопротивле-
ния совпадает с кривой давления, т. е. с ве-
ревочным многоугольником от нагрузки.
При наклонных швах этого совпадения не
будет.
Это несовпадение обеих кривых принес-
ло авторам методов расчета свода немало
огорчений, так как кулоновская теория
приводила не к кривой давления, а именно
к кривой сопротивления. На почве этого
несовпадения появляются ошибки в рас-
суждениях, яростно разоблачаемые автора-
ми-соперниками; на той же почве возника-
ют различные ухищрения подчас сомни-
тельного свойства — вроде прямого отказа
от наклонных швов в пользу вертикальных, совершенно не вяжу-
щихся с концепцией свода, как совокупности свободных клиньев.
Нам нет необходимости разбираться подробно в этих разногла-
сиях. Добавим, что кривая сопротивления была применена раньше
кривой давления.
Первая из двух перечисленных нами категорий методов ведет
начало от известного чешского инженера Франтишка Йозефа Гер-
стнера старшего [90] (1756—1832). Он рассматривал своды без
учета трения в швах и принимал за работающую часть свода толь-
ко ту полосу, которая лежит между двумя кривыми сопротивле-
ния/соответствующими кулоновским пределам распора. Остальные
части свода он считал как бы подвешенными к работающей по-
лосе и загружающими ее, но не участвующими в работе свода.
Основная идея Герстнера сводилась к тому, что кривую сопро-
тивления можно принять за форму цепи, несущей заданные на-
грузки, и в этом предположении он вывел уравнение кривой
сопротивления, подхватив, таким образом, идеи Бернулли и Грего-
ри. Легко видеть, в чем ошибка этого предположения: в том, что в
действительности грузы от забутки смещены относительно соот-
ветствующих участков кривой сопротивления (рис. 36). Ту же
ошибку, от которой можно было бы освободиться, приняв верти-
кальные швы, повторили Кнохенгауер [91] и Барлоу [92]. Шуберт
[93] попробовал выйти из затруднения тем, что добавил неизвестно
373
Ф. И. Герстнер (17.гю—1Я32)
откуда взявшиеся боковые усилия, компенсировавшие смещение
направлений нагрузки. Хаген [94] принял швы вертикальными и
тем освободился от ошибки Герстнера, но зато предположил, что
кривая сопротивления совпадает с осью свода в замке и пятах.
Гипотезу вертикальных швов он считал безобидной, так как пола-
гал, что опасаться скольжения клиньев в швах не приходится.
Хаген пытался провести кривую сопротивления через центры всех
швов и предлагал выпра-
вить форму свода в тех
местах, где эта кривая
приближается к очерта-
нию свода. Подобную же
попытку сделали Бауэрн-
фейнд [95], который шел
обратным путем, и по за-
данной оси свода подби-
рал кривую нагрузки
т. е. необходимую высоту
забутки, из условий сов-
падения кривой сопро-
тивления с осью, и Гоф-
ман [96], который рассчи-
тывал свод как брус рав-
ного сопротивления,
предполагая такое же
совпадение обеих кри-
вых. Заметим, что все
перечисленные работы не
пользуются кулоновским
методом экстремирова-
ния и априорно задаются
положением некоторых
точек кривой сопротив-
ления. В этом смысле
они менее совершенны,
чем метод Кулона, не го-
воря уже о Навье, и восходят к Делагиру. Можно сказать, что все
эти методы даже менее надежны, чем метод Делагира, поскольку
последний исходил из приближенной оценки, а перечисленные ме-
тоды являются плодом чистой спекуляции.
Гораздо более совершенными являются позднейшие методы
той же категории, относящиеся к 60-м и к 70-м годам прошлого
века. Авторами этих методов являются Шведлер [97], Дюран-Клэ
[98], Кульман [99], Феппль [100] и др. При оценке этих работ сле-
дует иметь в виду, что они написаны уже после того, как появил-
ся точный расчет свода как упругого бруса, данный Брессом (1854)
и после него Ренкином (1862). По существу они являлись запозда-
лыми п потому ненужными приближенными методами и заслужи-
374
вают упоминания лишь из-за своеобразия примененных пх авто-
рами приемов.
Так, Дюран-Клэ [98] применяет для нахождения кривой давле-
ния следующее рассуждение. Выделим часть свода cdcadv (рис. 37),
ограниченную замком corfo и произвольным швом. В силу симмет-
рии свода и нагрузки кривая давления нормальна к шву ccdc, но
пересекает этот шов, равно как и шов cd, в неизвестных точках ао
и а. Таким образом, Дюран-Клэ, как и Паукер, выбирает две
однородные неизвестные
величины, но не силово-
го, а геометрического по-
рядка. Пусть Р — вес
звена cdcGdG, приложен-
ный в его центре тяже-
сти. Фиксируем положе-
ние точки а. Если кривая
давления пересекает
замковый шов Codo в точ-
ке do, то мы можем наме-
тить ее крайние лучи
dGe, еа и найти соответ-
ственный распор. ~
так же, если она прохо-
дит через точку
можем провести крайние лучи qa, £\а и снова определить р""—р
Отложим соответственные распоры duAo и соВо по перпендикулярам
к замковому шву от предположенных точек приложения. При из-
менении точки пересечения кривой давления с замковым швом рас-
пор будет меняться по некоторой кривой AqB0. Этим значениям рас-
пора соответствуют различные величины нормальных давлений на
шов cd
Точно
Со, МЫ
распор.
в точке а, которые мы откладываем на перпендикуляре в
этой точке. Концы соответственных ординат
укладываются в отрезке АВ. Таким обрззом,
каждой точке а шва cd соответствует своя
кривая А0В0 и свой отрезок АВ. Если варь-
ировать положение точки а, то кривые
AqBq будут меняться от а0₽ ДО 7обо, а отре-
зок АВ своими концами опишет кривые а?
и . Между этими двумя сериями кривы к
имеется следующая зависимость: каждой
кривой одной серии соответствует ордина-
та, заключенная между крайними кривыми
другой серии. Как бы ни проходила истин-
ная кривая давления, концы ординат, вы-
ражающих распор и нормальное давление в шве cd, окажутся
внутри соответственных площадей аоРо7<Д) и аР7^-
Далее Дюран-Клэ вводит ограничение величины наибольшего
напряжения, продолжая рассуждать геометрически. Пусть cd —
сечение свода (рис. 38). Если R — допускаемое давление на сече-
Рис. 38. График допу-
скаемых давлений на се-
чение
375
ние при центральном сжатии, то при действии силы в ядровой точ-
ке допускаемое давление будет —; вообще каждой точке сечения
соответствует допускаемая величина давления, приложенного в
этой точке. График этих предельных давлений, имеющий вид колпа-
ка, изображен на рис. 38. Теперь наложим этот колпак cdf на рис. 37
так, чтобы точки с и d совпали (рис. 39). Очевидно, этот колпак
вырежет из площади часть ротш, внутри которой обязаны ле-
жать концы ординат давления.
не превосходящего допускаемое;
наоборот, остальные части пло-
щади отвечают недопустимым
давлениям. Площадке Ротш будет
отвечать в замковой площади
ао₽оТ<Д) часть Ро°отЛ, из которой
колпак to^ofo, наложенный на
замковое сечение, выделит новую
часть Х<ЛоНо7о-
Теперь будем варьировать по-
ложение шва cd и следить за из-
менением площадки X</oHovo в
замке. Если эти площадки, пост-
роенные при всевозможных поло-
жениях шва cd, будут иметь об-
щие горизонтальные отрезки, то
свод устойчив и прочен, и из
этих общих отрезков можно выб-
рать минимум и максимум рас-
пора.
Нет спора, что этот метод
расчета чрезвычайно сложен для
практического применения, но
ему нельзя отказать в изяще-
4 4 Я ао 4
Рис. 39. Графическое решение
Дюран-Клэ
стве.
Август Феппль [100] (1881) применил для приближенного рас-
чета свода понятие «площади давления», т. е. области свода, про-
низанной возможными с точки зрения равновесия кривыми давле-
ния. Эта область ограничена частями дуг кривой давления и ча-
стями очертаний свода. Феппль утверждает, что наиболее эконом-
ным будет то очертание свода, при котором очертание площади
давления совпадет с контуром свода или ядровой полосы. По су-
ществу площадь давления Феппля вполне эквивалентна рабочей
части свода в представлении Герстнера.
Единственным действительно интересным результатом работ
Феппля является доказательство того, что при параллельном про-
ектировании овода кривая давления отображается снова в кривую
давления. Этот вывод позволил Фепплю изучать равновесие эл-
липтических сводов, преобразуя их путем параллельной проекции
в круговые. Ту же идею использует так называемое преобразова-
376
ние Фуллера [101], при котором кривые давления путем парал-
лельной проекции отображаются в прямые линии.
Методы Феппля и Фуллера переносят нас в область графиче-
ских приемов расчета свода; для полноты следует назвать еще
ряд подобных приемов, которые были в тот же период предложе-
ны Кульманом [99], Штейнером [102], Эдди [103] и сводились к пра-
вилам построения кривой давления, вписанной в ядровую полосу
и касающейся ее контура в трех точках.
Глава 9
поиски НЕДОСТАЮЩЕЙ аксиомы статики
Вторая категория методов, распространившихся в период с
30-х до 70-х годов, характеризуется, как мы говорили, представ-
лением о недостаточности системы аксиом статики твердого тела
и попытками изобрести тот недостающий принцип, с помощью ко-
торого расчет статически неопределимой абсолютно твердой си-
стемы удастся провести чисто статическим путем. Этот недостаю-
щий принцип, призванный устранить множественность и неопре-
деленность статического решения, очевидно, должен был устанав-
ливать правило выбора единственного истинного решения из мно-
жества возможных. Совершенно естественно, что такому правилу
выбора присваивался вариационный характер, так что единствен-
ное истинное решение рассматривалось как минимальное значе-
ние некоторой силовой функции. Такое воззрение хорошо увязы-
валось с философской концепцией о том, что природа стремится к
наименьшим затратам, получившей подтверждение в ряде задач
вариационного исчисления. В такой форме впервые высказывал
эти идеи Мопертюи [104] в 1764 г., предложивший «принцип наи-
меньшего действия».
Мы видели, что еще Кулон применил для расчета свода метод
экстремирования, т. е. отыскания наименьшего и наибольшего
значения распора. Однако метод Кулона совершенно чужд тем
идеям, о которых мы только что говорили. Кулон не искал истин-
ного решения; он ясно сознавал, что его метод направлен лишь на
отыскание возможных пределов, между которыми заключено не-
известное ему истинное решение. Точно так же он подходил и п
расчету подпорных стенок при определении активного и пассивно-
го давлений, которые он считал за пределы истинного давления.
Укоренившийся в наших учебниках способ изложения, трактую-
щий активное и пассивное давление как истинные значения, исхо-
дит не от Кулона, а от Ребхана [105] (1871), который в сущности
исказил идею Кулона.
377
Первая попытка применения к расчету свода принципа наи-
меньшего действия, насколько нам удалось установить, принадле-
жит Берару [106] и относится к 1810 г. Берар формулировал этот
принцип так: «Сила тяжести всегда стремится создать максимум
или минимум» и, основываясь на нем, требовал, чтобы боковое
давление клина в своде было наименьшим. Работа Бера-ра содер-
жит ряд весьма наивных рассуждений, приводящих к явно оши-
бочным следствиям, поэтому она заслуживает упоминания лишь
из-за ее приоритета в этой серии глубоко порочных по своей уста-
новке исследований.
Через 23 года после Берара, в 1833 г., профессор Оксфордско-
го университета Генри Мозлей (1802—1872) опубликовал изобре-
тенный им «принцип наименьшего сопротивления», а двумя года-
ми позже применил его к расчету свода [107]. Мозлей был неза-
урядным ученым с большой склонностью к абстрактным методам
рассуждения. Его метод расчета свода породил целую школу, хо-
тя и на иноземной почве; наибольшим признанием и популярно-
стью он пользовался в Германии, где проводником его идей был
мало талантливый Шеффлер, переведший на немецкий язык курс
строительной механики Мозлея и развивавший его идеи в своих
работах.
Забытый в наше время «принцип наименьшего сопротивления»
мы приводим здесь в дословной формулировке Мозлея:
«Если дана уравновешенная система давлений, в числе кото-
рых имеется некоторое количество сопротивлений, то каждое из
последних должно иметь минимальную величину, -при условии
соблюдения равновесия системы в целом».
В применении к своду этот принцип принимает такую форму:
Из всех значений распора, которые могут действовать на замко-
вое сечение полусвода и различаются между собой по величине
и точке приложения, но не нарушают равновесия полусвода, — тс
значение распора, которое действует на замок от второго такого
же полусвода, является наименьшим».
Таким образом, с точки зрения Мозлея, распор является тем
сопротивлением, которое должно быть минимальным. С нашей
точки зрения, это утверждение является более чем спорным, хотя
бы потому, что распор в своде не есть единственное «сопротивле-
ние»; с таким же правом Мозлей мог бы требовать минимальных
значений для опорных моментов свода и вообще для любого внут-
реннего усилия.
Посмотрим, однако, как Мозлей использовал свой принцип.
Возьмем полусвод и приложим распор в произвольной точке зам-
кового сечения. Если начать уменьшать распор, то кривая давле-
ния (которой Мозлей широко пользуется) будет становиться все
более подъемистой и, наконец, в некоторой точке коснется внут-
реннего очертания свода (рис. 40). Соответственное значение рас
пора является наименьшим возможным для данной точки прило-
жения распора. Каждой точке замкового сечения соответствует
таким образом свой минимум распора. Мозлей еще раз применяет
378
экстремирование и выбирает наименьший из этих минимумов, ко-
торый он и принимает за истинный распор, приложенный уже во
вполне определенной точке.
Таким образом, с расчетной точки зрения, метод Мозлея весь-
ма напоминает метод Кулона; кулоновская идея экстремирования
здесь лишь дублируется, повторяется дважды для исключения
двух неизвестных из неравенств равновесия, как это делал не-
сколько раньше Перси. Мы уже видели иные приемы для дости-
жения той же цели в работах Паукера и Дюран-Клэ, обладаю-
щие большей оригинальностью
метод Мозлея может пока-
заться простым использова-
нием и повторением способа
Кулона. На самом же деле
между ними имеется глубо-
чайшее принципиальное раз-
личие, о котором мы уже го-
ворили. Метод Кулона приво-
дил к нахождению нижнего и
верхнего пределов распора;
для Мозлея же найденный им
минимальный распор (даже
если он совпадает с кулонов-
ским нижним пределом) яв-
ляется истинным значением
и смелостью. На первый взгляд
Рис. 40. Кривая давления, отвечающая
наименьшему значению распора, касает-
ся внутреннего очертания свода (Мозлей)
распора. Мы видим, что Кулоновский метод строже метода Моз-
лея, так как не пользуется никакими добавочными аксиомами.
Но методу Мозлея присущ еще один порок. Мы уже указали,
что второй этап расчетов Мозлея состоит в отыскании той точки
замкового сечения, которой отвечает наименьший из минимумов
распора. Если эта точка выходила за пределы толщины свода в
замке (а выходить она могла, очевидно, только кверху), то Моз-
лей полагал распор приложенным в верхней точке замкового шва,
и соответственный минимальный распор принимал за истинный.
Между тем минимальный распор, как функция положения точки
приложения в замке, не имеет минимума в конечной области; эта
функция является монотонно убывающей. Поэтому точка сечения,
соответствующая абсолютному минимуму распора, всегда уходит
в бесконечность, причем распор обращается в нуль, так что
Мозлею во всех случаях приходится прилагать распор в верхней
точке замка, т. е. получать значение распора, в точности совпада-
ющее с нижним пределом Кулона. Таким образом, Мозлей в дей-
ствительности нисколько не сдвинулся вперед по сравнению с
Кулоном, и одним из двух неизвестных — положением кривой дав-
ления в замке — он по существу просто задается, как и Кулон,
хотя и маскирует эту условность видимостью вариационного рас-
чета.
Как же произошло, что Мозлей сам не заметил отсутствия ми-
нимума у наименьшего распора? После чтения подлинных работ
379
Мозлея этот промах становится отчасти понятным. Мозлей изла-
гал свои работы необычайно сухо и абстрактно, без всяких попы-
ток практического применения. Весь стиль изложения, включая
характер рисунков, изображающих необыкновенно корявые
«обобщенные» своды, свидетельствует об отвлеченности крута идей
Мозлея. Работы его исключительно трудны для понимания. Этой
отвлеченностью мы и объясняем то, что Мозлей не обратил вни-
мания на такую «мелочь», как отсутствие минимума у функции,
написанной им в развернутом виде. Он ограничился лаконической
df г\
записью — =U, долженствующей определить минимум, но не по-
интересовался решением этого уравнения.
Несомненно, что абстрактный и неопределенный метод Мозлея,
к тому же изложенный крайне тяжелым языком, оказался бы об-
реченным на забвение, если бы не пропаганда Шеффлера. В изло-
жении Шеффлера он нашел весьма благоприятную почву для рас-
пространения в Германии, заинтересовав германских ученых
именно своей сомнительной философской стороной. Это увлечение,
с нашей точки зрения, было чрезвычайно вредным. Во-первых,
оно исходило из ложной предпосылки о неполноте системы акси-
ом статики и о возможности строгого расчета абсолютно твердого
свода при условии добавления новой аксиомы. Во-вторых, оно да-
вало повод к возникновению метафизических идей о поведении
усилий в своде, принимавших подчас почти мистический характер.
К счастью, эта «болезнь» была строго локализована и за преде-
лами Германии не получила распространения.
Первой жертвой был, как уже сказано, Шеффлер [108]. Он
попытался усовершенствовать метод Мозлея учетом прочности
материала. Мозлей рассуждал так: представим себе свод, лежа-
щий на кружалах. Распор равен нулю. При раскружаливании
распор постепенно возрастает, пока не достигнет того наименьше-
го значения, при котором обеспечивается равновесие, и дальше
возрастать не будет. Шеффлер показал, что при этом наименьшем
значении распора кривая давления коснется верхнего очертанич
свода в замке, а это будет означать раздавливание материала по
ребру шва. Поэтому Шеффлер вынужден был предположить, что
распор не удержится на наименьшем значении, а еще несколько
возрастает, в связи с чем кривая давления в опасных сечениях от-
ступит в глубь тела свода. Это отступление кривой давления было
вместе с тем отступлением теории Мозлея от прежних позиций,
окончательно ее обесценившим.
Действительно, изобретенный Мозлеем «принцип наименьшего
сопротивления» был привлечен им к расчету свода именно в на-
дежде получения единственного, совершенно определенного реше-
ния. Поправка Шеффлера снова внесла неопределенность, лишив
найденное Мозлеем решение свойства единственности. Таким об-
разом, новая аксиома не принесла тех плодов, ради которых она
была создана. Следовательно, сама эта аксиома нуждалась в ис-
правлении. Шеффлеру не удалось исправить ее, быть может, пото-
380
му, что он не признавал теории Навье о плоском графике напря-
жений, и ограничился бездоказательным утверждением об от-
ступлении истинной кривой давления в опасных сечениях в глубь
свода на ’/< его толщины.
Исправить аксиому Мозлея попытался Хаген во втором изда-
нии своей книги [94], вышедшем в 1862 г. Он предложил «закон
наивыгоднейшего напряжения», сводившийся к утверждению,
будто бы истинная кривая давления будет отступать от ребер
швов в глубь свода до тех пор, пока краевые напряжения в опас-
ных сечениях не примут наименьших возможных величин. Из это-
го закона следовало, что наименьшие вертикальные расстояния ог
кривой давления до ближайшего очертания свода во всех трех
опасных сечениях — замке, пяте и промежуточном шве разруше-
ния— должны быть одинаковы.
Это рассуждение вызывает ряд недоуменных вопросов. Поче-
му отступление кривой давления остановится именно в этот мо-
мент? Почему она не уйдет еще глубже в тело свода, так что кра-
евые напряжения снова возрастут? Каков тот таинственный
механизм, который удержит ее в момент достижения наименьших
краевых напряжений? Все эти вопросы остаются без ответа.
Почти в той же форме эта полумистическая аксиома повто-
ряется в первом издании «Графической статики» Кульмана [99]
(1866). Кульман в отличие от Шеффлера был сторонником теории
Навье и попытался объединить две концепции свода: представле-
ние о своде, как об упругом теле, ^неспособном сопротивляться
растяжению, для которого поэтому выход кривой давления из яд-
ровой полосы означал разрушение, и представление об абсолютно
жестком своде, нуждающемся для статического расчета в созда-
нии специальной аксиомы. Из такого- смешения двух диаметраль-
но противоположных концепций не могло выйти ничего хорошего.
Ошибочный путь, принятый Кульманом, тем более заслуживает
порицания, что за 8 лет до него Менабреа [109] опубликовал прин-
цип наименьшей работы, подводивший научную базу под долго-
летние поиски экстремальных свойств внутренних усилий, а за
12 лет до Кульмана Брессом уже был дан точный и, как следует
быть, простой метод расчета упругого свода. Поэтому во времена
Кульмана заниматься изобретением новых метафизических акси-
ом для расчета свода было уже поздно.
Аксиома Кульмана в дословном переводе такова:
«Из всех кривых давления, которые могут быть вписаны в
свод, та является действительной кривой давления свода, которая
ближе всех прижимается к оси свода, в том смысле, что при ней
обращаются в минимум напряжения в наиболее напряженных
ребрах швов».
Эта аксиома почти совпадает с утверждением Хагена. Однако
сам Кульман не считает ее за аксиому и пытается дать доказа-
тельство. Доказательство это стоит привести как пример заблуж-
дения, в которое может впасть даже такой крупный ученый, как
Кульман.
381
Вообразим себе свод, говорит Кульман, изготовленный из ма-
териала настолько «мягкого» (weich), что в него можно вписать
только одну кривую давления, не вызывающую разрушения. За-
тем мысленно представим себе, что свод постепенно «отверде-
вает» (erhartet), но так, что при этом ни его вес, ни модуль упру-
гости (!) не изменяются. Процесс отвердевания не заставит кри-
вую давления сместиться, а потому и в самом твердом сво-
де она пройдет именно так, как этого требует высказанное утверж-
дение.
Это доказательство содержит целый ряд скрытых допущений.
Прежде всего, под «мягким» и «твердым» материалами Кульман,
очевидно, понимает материалы с низким и высоким временным
сопротивлением. Только при таком понимании приобретает смысл
предположение о существовании «мягкого» свода с единственной
возможной кривой давления; всякое иное положение ее вызовет
разрушение материала. Но основное допущение Кульмана состо-
ит именно в предположении, что эта кривая давления в «мягком»
своде и будет его истинной кривой давления. Очевидно, это скры-
тое допущение совершенно эквивалентно аксиоме, которую Куль-
ман пытается доказать. В сущности Кульман доказал лишь оче-
видный факт, что положение кривой давления при прочих равных
условиях не зависит от временного сопротивления материала.
Но, помимо ошибочности доказательства Кульмана, самое его
утверждение является неверным. Мы знаем, например, что кривая
давления в параболическом своде от сплошной равномерной на-
грузки, имеющая также параболическое очертание, не совпадает
с осью свода, так что краевые напряжения имеют величины боль-
шие, чем было бы в случае совпадения обеих линий. Следователь-
но, истинная кривая давления вовсе не заботится об обращении в
минимум краевых напряжений.
Надо сказать, что Кульман не дал никаких указаний на способ
отыскания такой кривой давления. Приводимое им графическое
построение «наивыгоднейшей кривой давления» очень изящно, но
дает не ту кривую давления, свойство которой постулирует Куль-
ман, а кривую давления, вписанную в ядровую полосу и касаю-
щуюся ее контура в замке и шве разрушения. Таким образом,
Кульман приходит к расчетной схеме Навье, а потому найденный
им распор не есть истинный распор, а лишь нижний предел распо-
ра в кулоновском смысле, для которого Кульман вводит двойной
коэффициент запаса, как это делал Одуа еще в 20-х годах.
Во втором издании своей «Графической статики» (1875) Куль-
ман сам отказался от гипотезы наименьших напряжений и заме-
нил ее более углубленным изучением работы свода. Он сделал по-
пытку учесть усадку свода за счет обжатия раствора в швах,
полагая клинья свода по-прежнему абсолютно твердыми. Отступ-
ление кривой давления в глубь тела свода он объяснил раздавли-
ванием раствора у краев швов и включением в работу следующих
слоев его, лежащих ближе к оси. Эта вторая теория Кульмана по
результатам приближается к точной и неплохо отвечает обычным
382
производственным условиям того времени, когда было принято
раскружаливать своды до полного затвердения раствора.
Интересно, что мысль Кульмана о наибольшем сближении
истинной кривой давления с осью свода возродилась через нес-
колько лет в иной форме. Винклер, рассчитавший еще в 1867 г.
свод как упругое тело и признаваемый некоторыми немецкими
учеными (например, Мертенсом) за автора первого точного рас-
чета свода (хотя Бресс дал такой расчет еще в 1854 г.), подошел
к определению истинного положения кривой давления более стро-
гим путем [110]. Он высказал теорему о том, что при постоянной
толщине свода истинной кривой давления будет та, для которой
среднее квадратичное отклонение от оси свода будет минималь-
ным. Эту теорему легко вывести из принципа наименьшей рабо-
ты, если пренебречь той частью потенциальной энергии, которая
вызвана продольными и поперечными деформациями. Действи-
тельно, потенциальная энергия свода при этом условии будет
равна:
где Н — распор;
I — постоянный момент инерции;
М
z=—-— вертикальное отклонение кривой давления от оси свода
п
Минимум сокращенного выражения потенциальной энергии
имеет место при наименьшем квадратичном отклонении обеих ли-
ний. Эта интересная теорема, забытая в наше время, дает хоро-
шее приближение к действительности для сводов с небольшим
отношением толщины в замке к стреле.
Разумеется, теорема Винклера не имеет никакого отношения к
поискам недостающей аксиомы статики; после Кульмана этот
ложный путь решения был оставлен навсегда.
Глава 10
РАСЧЕТ СВОДА КАК УПРУГОГО ТЕЛА
Мы бегло ознакомились с разнообразными попытками дать
расчет свода без учета упругих свойств материала. Эти попытки в
истории расчета свода играют такую же роль, как алхимия в
истории химии. Они характеризуются умозрительным направле-
нием, наличием предвзятых гипотез и пренебрежением к система-
тическому эксперименту. Действительно, достойно удивления, что
литература по расчету сводов не содержит ни одного упоминания
об опытном изучении их работы после опытов Буатара и др., от-
383
носящихся к 1800 г., вплоть до опыта Удри, изучавшего в 60-х го-
дах на модели в натуральную величину действие температуры на
свод, придавая ему деформации, аналогичные температурным, с
помощью парных клиньев в опорах. Никому из деятелей этого
«средневековья» не приходила в голову возможность непосредст-
венной поверки гипотез путем простого измерения распора в мо-
мент раскружаливания, как это сделал Кулибин в предыдущем
столетии для расчета своей арки.
Но так же, как точная химия пользуется результатами беспо-
рядочных работ искателей эликсира жизни, строительная механи-
ка не могла не применить тех результатов, к которым пришли
искатели истинной кривой давления.
Трудами этих искателей природа свода, роль его геометриче-
ских форм, характер и положение кривой давления были глубоко
проанализированы, и представление о характере работы свода до-
стигло высокой степени развития.
Однако эти побочные успехи были достигнуты дорогой ценой
бесплодных трудов многих ученых на протяжении нескольких
десятилетий. В чем причина этой бесплодности? Разумеется, в
том, что они не разглядели того передового направления, на кото-
рое встала строительная механика после Навье, и пытались во что
бы то ни стало удержаться на старых отживших позициях расчета
по предельному состоянию. Тем самым роль Мозлея, Шеффлера,
Хагена и всех их приверженцев следует оценить как реакцион-
ную: они тянули науку не вперед, а назад. Поэтому вполне закон-
ным финалом их реакционной деятельности было скатывание в
мистический идеализм. Мы хорошо знаем, что таков бесславный
и неизбежный конец всякого реакционного направления в науке.
Сознание неизбежности учета упругих свойств материала сво-
да в сочетании с преувеличенным представлением о трудности та-
кого учета появляется впервые у Ламэ и Клапейрона [75] (1823 г.)
и затем повторяется у Навье [18] (1826), Гариделя [76] (1835),
Вилларсо [82] (1853), Понселе [77] (1852), Коллиньона [111] (1889)
и др. Действительно, трудность задачи довольно велика благодаря
наличию швов, заполненных слабым раствором. Наука до поры
до времени уклоняется от решения этой задачи, пока появление
бетонных сплошных сводов и металлических арок с заделанными
пятами не делает дальнейшее уклонение невозможным. Первым
отважился подойти к решению упругой арки с заделанными пя-
тами французский ученый, инженер путей сообщения Шарль Бресс
(1822—1883). ученик Клапейрона.
Судьба работ Бресса почти загадочна. Его имени нет ни в од-
ном русском энциклопедическом словаре. Оно сохранилось толь-
ко в. курсах гидравлики. Редкому преподавателю строительной ме-
ханики, не говоря уже о строителях-практиках, известно это имя и
те выдающиеся заслуги, с которыми оно связано1. Вот краткий пе-
речень того, что сделано Брессом в 1848—1865 гг.
1 Несмотря на длительные поиски, не удалось найти даже портрета Бресса.
384
1) Бресс нашел моментные фокусы в неразрезной балке
(1865).
2) Бресс вдел понятие ядра речения (1854).
3) Бресс дал первое построение объемлющей эпюры для нераз-
резной балки (1859).
4)^ Бресс впервые стал учитывать влияние продольных дефор-
маций и температурных удлинений при вычислении упругих пере-
мещений (1854).
5) Бресс преобразовал дифференциальные уравнения изогну-
той оси бруса (прямого или кривого), приведя их к интегральной
форме, весьма близкой к формуле Мора и служащей переходным
звеном между этой последней и графоаналитическим методом,
открытым много позже (1854).
6) _Бресс_дал впервые общую постановку задачи расчета стати-
чески неопределимых систем методом сил, указав способы подсче-
та числа лишних неизвестных и введя понятие уравнений дефор-
маций, которыми до него никто не пользовался (1854).
7) Бресс предложил метод группирования нагрузки при расче-
те симметричных арок (1854). Немецкие авторы приписывают эту
заслугу Шведлеру [97] (1868) и иногда Толкмнтту [112] (1876), а
у нас этот прием почему-то называется методом Андре (1919).
8) Бресс предложил метод группировки неизвестных при рас-
чете симметричных арок (1854).
9) Бресс впервые рассчитал двухшарнирную арку с затяжкой
(1854).
10) Бресс впервые стал применять эпюры моментов и других
внутренних усилий (1848).
И) Бресс впервые употребил_«числа влияния», т. е. ординаты
линии влияния распора для двухшарнйрной арки, составив для
них таблицы (1854). Этот факт также искажается немецкими уче-
ными, считающими за изобретателей линий влияния Винклера и
Мора (1868). По-видимому, германской науке в этой области при-
надлежит первенство лишь терминологическое: название линий
влияния (Influenzlinien) исходит от Вейрауха [113] (1873).
12) Бресс, наконец, рассчитал впервые бесшарнирную арку
(1854).
Половины этого перечня было бы достаточно, чтобы обессмер-
тить имя Бресса и создать целую школу, разрабатывающую идеи,
которые Бресс с такой щедростью разбрасывал на страницах
своих книг. Вместо этого его ожидало почти полное забвение.
Объяснение этому странному факту можно усмотреть только в
том, что как раз в эту эпоху французская наука в ряде отраслей
стала уступать свое вековое первенство молодой германской на-
уке. Эта смена ролей, несомненно, стоит в связи с внешнеполити-
ческими событиями — начинающимся объединением Германии и
выходом ее в ряды мировых держав.
Шовинистическая гордость, охватывающая германских ученых,
в ряде случаев приводит к полному игнорированию ими иноземной
науки. Мы считаем не случайным тот факт, что знаменитая рабо-
25 С. А. Бернштейн
385
та Максвелла о вычислении перемещений и расчете статически
неопределимых ферм осталась неизвестной в Германии и была
дублирована через много лет Мором. Примерно то же произошло
и с Брессом. Германская наука игнорировала его, и все результа-
ты его работ нашла заново с большим опозданием. Это дублиро-
вание результатов не было плагиатом; оно было следствием от-
кровенного нежелания знакомиться с иноземной литературой1
Вновь найденные результаты германская наука начинает экспор-
тировать, не задумываясь о приоритете. Наука во многих странах
подпадает под сильнейшее влия-
ние этого германского научного
экспорта и начинает смотреть на
мир германскими глазами. А эти
глаза упорно не замечали заслуг
Бресса.
Первая работа Бресса о рас-
чете арок, написанная в 1848 г.
[19], еще целиком повторяет ме-
тод Навье в применении к двух-
шарнирной арке. Между прочим,
в этой работе он широко поль-
Рис. 41. Обозначения Бресса зуется построением и наложени-
ем эпюр внутренних усилий, чего
до него еще никто не делал. Шестью годами позже он выпускает об-
ширную монографию [22], заслуживающую самого внимательного
изучения как из-за богатства ее содержания, так и из-за блестящей
формы изложения.
Основу этой монографии составляет вывод новых выражений
для перемещения криволинейного упругого бруса, который мы
вкратце здесь изложим. Пусть дан кривой брус (рис. 41). Если
обозначить через у угол наклона его касательной к горизонту
в произвольной точке, то d® будет приростом угла на длине дуги
ds. Пусть Ad ср обозначает изменение угла dcp , вызванное дефор-
мацией, a A ds — удлинение элемента длины дуги от той же при-
чины. Если t — температура нагрева, а—коэффициент линейно-
го расширения, М — момент и N — продольная сила, вызвавшие
деформацию, то, очевидно:
A cos ср = — sin срДср; A sin ? = cos ср Аср,
а так как
их . иу
COS ср = -; sincp=-i ,
ds ds
1 Справедливость требует отметить, что это нежелание нередко бывало
взаимным. Можно назвать случаи, когда и французские ученые в свою очередь
игнорировали своих немецких коллег и предшественников (см., например, очерк
четвертый, глава 2).
386
ds ds ds ds T
Дифференцируем левые части этих равенств как дроби, считая
Д за символ дифференцирования:
ds Д dx — dx Д ds dv .
—s—=—±^’
ds &dy — dy b ds _ dx >
~ ~ds~
ds*
Подставим значение
* , Nds . ,,
^ds —-------- a Ids
EF
и сократим на ds:
Ldx~ — dy Дер Н—dx + a tdx;
&dy = dx Д<р --— dy 4- a tdy.
EF
Интегрируем по частям первые члены правых частей:
J dy by — у Д<р — J у A d ср = у Ьу — J у^- ds;
J dx Д<р = х Дер — JxAdcp = xA<p —J d s.
Поэтому интегралы выражений (а) примут вид:
Дх = — уД<р + £ ds + J —dx + a tx + С,;
Ду = хby — d& + ^dy + aty + C2 .
(а)
(6)
Пусть начальная точка so(xo, уо) в результате деформации
переместилась на Д хо, Д#о> & касательная к ней повернулась на
угол Дср0. Тогда линейные перемещения точки s (х, у) выразятся:
Дх = Дх0 —(у —у0) Д<р0+ J Mds +
+ С cos<p- Nds + a t (х — х0);
J EF
•So
Д у = Д Уо + (х — х0) Дср0 — JMds +
+ J -^~^ds+ at(y~yn),
So
25*
(в)
387
а если хо=уо=0 и Дх0 = Ду0 = О, т. е. начальная точка неподвиж-
на и совпадает с началом координат, то:
д*= — уДто+ ( Np°s<P & + а<х;
J hJ J Lt
°, °. (г)
Ду = хД%—+J-^^-ds + aZy.
о о
Таковы окончательные формулы перемещений, данные Брес-
сом. Они представляют огромный шаг вперед по сравнению с
обычным аналитическим методом, так как, во-первых, сводят дву-
кратную интеграцию к однократной и, во-вторых, учитывают про-
дольные деформации. Если ограничиться двумя первыми членами
формул (г), мы получим выражение графоаналитического метода;
для этого останется лишь дать интегралам графическое истолко-
вание.
Второй и третий члены этих формул вполне соответствуют
формуле Мора с откинутым интегралом поперечных сил, так как
сомножители у, х, cos ср и sin ср при усилиях под знаками интегра-
лов соответственно равны усилиям того же рода, вызванным еди-
ничной горизонтальной или вертикальной силой.
Бресс не сумел вывести из формул (г) ни графоаналитического
метода, ни формулы Мора, хотя и до одного, и до другой оставал-
ся буквально один шаг. Это есть пример своеобразной научной
близорукости, нередко встречающейся в истории науки. Несомнен-
но, что и мы теперь на каждом шагу проходим мимо замечатель-
ных открытий, от которых нас отделяет ничтожное расстояние, _и
не видим их. Наши потомки будут также удивляться нашей близо-
рукости, как мы удивляемся близорукости наших предков.
Сам Бресс не придавал большого принципиального значения
своему преобразованию и писал о нем так: «...это преобразование
не имеет теоретической важности, но приобретает ценность в при-
ложениях, допуская и облегчая аналитические вычисления, кото-
рые без него были бы почти невыполнимы по своей длительности».
Владея этими удобными формулами, Бресс без труда получает
решение для двухшарнирной арки, выбирая распор Н за лишнее
неизвестное и приравнивая нулю горизонтальное расхождение
опор [первая из формул (г)]:
М = Л40 — Ну,
N = — Н cos ср;
л С Мо —Ну , । f Aq — Н cos у j t
o = j ——-cos<fds + aW>
О о
388
откуда
s J
С уМ0 J , C N0cosv
|_ЁГЛ + ] —
0
t. e. известное решение без учета поперечных деформаций.
Среди прочих примеров Бресс решает (так сказать, мимоходом)
и бесшарнирную арку, т. е. сплошной свод, или, го его терминоло-
гии, арку с защемленными пятами, для случая симметричной н i-
грузки и накопит два уравнения для определения распора Н
опорного момента Л1:
Л1(—ds+Н [-^-ds~— [—ds-
J EJ J EJ J EJ
0 0 0
0 0 0
= a и _ f A ds + ds,
J EJ J EF
0 c
t. e. наши обычные канонические уравнения. Весь расчет, которо-
го искали со времен Делагира в продолжение 150 лет, занимает
Х-Бресса всего полторы сграницы.
Но самое замечательное и удивительное это то, что ни Бресс,
ни его последователи не поняли значения и смысла того, что он
сделал. Они не поняли, что Бресс нашел решение для свода. Вот
подлинные слова Бресса, с которых он начинает расчет бесшар-
нирной арки: «Так как этот случай имеет малое практическое
значение (1), то мы ограничим задачу, рассматривая симметрич-
ную арку под симметричной нагрузкой».
Надо быть справедливым. Свода Делагира — Кулона, свобод-
но составленного из абсолютно жестких клиньев, Бресс действи-
тельно не рассчитал, и вряд ли эту фиктивную схему кто-либо су-
меет точно рассчитать. Бресс не рассчитал и того свода из упру-
гих камней на слабом растворе, который было принято раскружа-
ливать пораньше, пока раствор еще не отвердел. Но Бресс рассчи-
тал тот свод, в котором возраст придал раствору прочность камня;
тот свод, который нельзя разобрать по кирпичику. Нет никакого
сомнения, что именно такой свод и следует рассчитывать. Расчет-
ная концепция Бресса, разумеется, ближе к истине, чем концеп-
ция Кулона, даже для свода, сложенного из отдельных камней,
не говоря уже о кирпичных и бетонных сводах.
389
Но Бресс не понял и этого. Он продолжал считать, что его
расчет годится лишь для деревянных и металлических арок. А так
как такие арки редко осуществляют бесшарнирными, то и весь
расчет имеет «малое практическое значение». Бресс настолько
мало придавал значения своему расчету бесшарнирной арки, что
даже не включил его в свой курс прикладной механики [114]. Не-
сомненно, это тоже способствовало тому, что расчет Бресса не
привлек к себе широкого внимания, так как его монография
пользовалась, конечно, гораздо меньшим распространением, чем
курс механики.
Метод Бресса осторожно развивал его ученик и последователь
Альбарэ [115] (1860), ограничившийся расчетом двухшарнирных
арок и использовавший линию влияния распора, данную Брессом,
для определения невыгоднейшего загружения. Альбарэ еще полон
пиетета к своему учителю и постоянно ссылается на него. Но уже
Фабрэ [116] (1859) и Беланже [117] (1862), приводя расчет бесшар-
нирных арок по Брессу, умалчивают об его авторе. Немудрено,
что вне пределов Франции авторство Бресса остается неизвестным,
если даже на родине по прошествии всего нескольких лет имя его
не связывают с результатами его работ. И во всей позднейшей
литературе по сводам (расчетной и исторической) имя Бресса бо-
лее не появляется. По-видимому, восстановление исторической
справедливости и приоритета Бресса впервые довелось выполнить
автору этой книги1.
Любопытно, что Мертенс [118], приписывая Винклеру заслугу
первого расчета бесшарнирной арки, упоминает Бресса как авто-
ра первого расчета двухшарнирной арки. Мы уже знаем, что ее
впервые рассчитал Навье. Этот пример показывает, с какой осто-
рожностью нужно подходить к сведениям, приводимым в истори-
ческих обзорах, составленных без изучения подлинных работ.
Следующим по времени методом расчета упругого свода был
метод известного английского ученого Ренкина [25]. По существу
он исходит из тех же предпосылок и приходит к тем же результа-
там, что и Бресс, но выбранный им путь несравненно менее изящен.
Ренкин разлагает вертикальную нагрузку р на две составляю-
щие: нагрузку pi, вызывающую только продольное сжатие арки и
потому равную:
где Н—распор и остальную часть нагрузки р—pit вызывающую
только изгиб:
Р-Р1=Р — Н-^-.
ах2
1 С. А. Бернштейн, Очерк истории расчета свода, сборник «Исследования
по теории сооружений» под ред. А. А. Гвоздева, И. М. Рабиновича и М. М Фи
лоненко-Бородича, ОНТИ, 1936, стр 241—244.
390
Для этой второй части Ренкин определяет путем последова-
тельного интегрирования:
1) вертикальную поперечную силу
0 0 0
+ Н&--------
\ dx dx0 )
здесь А — левая вертикальная реакция, а = tg <?о,
dx0
где ср0— угол наклона оси арки у опоры;
2) изгибающий момент
М = Мл + J Qvdx = МА + Ах — pdx* +
О 0 0
+ н(у-х-^-],
dx?.
где Л/д — опорный момент;
3) угол поворота
6 = 6 - f — ds,
А J EJ
о
где Од — угол поворота на опоре и, наконец,
4) прогиб
v = J 0 dx.
о
Эти четыре уравнения содержат четыре неизвестных: распор,
вертикальную реакцию, опорный момент и угол поворота на опо-
ре. Для двухшарнирной арки исчезает МА , а для бесшарнирной —
исчезает Од , так что во всех случаях Ренкин имеет дело с тремя
неизвестными. Принимая х = Z он получает еще три уравнения с
тремя неизвестными: В, Мв (или &в) и V в (вертикальное сме-
щение правой опоры). Полагая VB= О и 6В = О (или Мв =0),
будем иметь два числовых уравнения для определения трех
неизвестных: Н, А (или В), МА (или Л/в) — для бесшарнирной
арки или Я, А (или В),6д (или 6В)— для двухшарнирной. Для
составления третьего уравнения Ренкин рассматривает укороче-
ние dt элемента дуги ds за счет сжатия
di =Н
ds cos (f EF
39!
и горизонтальное смещение и произвольной точки арки. Из ра-
венств
ds2 — dx2 + dy2
и
(ds 4- dt)2 = (dx 4- du)2 + (dy 4- dv)2
X. С. Головин (1844—1904)
выводим, отбрасывая квадраты дифференциалов,
ds dt = dxdu 4 dydv ,
откуда
du = -^—dt----— dv,
dx dx
или
du —------ ——--------6 tg <p dx
EF cos3 <f>
392
и третье уравнение, выражающее неизменность длины пролета,
принимает вид
i
и = f [— - ——--------F 0 igср]dx = 0.
J [ EF cos3 у ь т I
о
Таким образом, Ренкин не дает развернутой формы уравнений
деформаций, как это сделал Бресс, а потому его метод несравнен-
но сложнее для расчетов. По своей природе он ближе к методу
Навье. Внимания в нем заслуживает лишь весьма раннее приме-
нение известного уравнения
d~M
dx-
Заблуждений может быть сколько угодно, но истина едина, а
потому все способы расчета упругого свода приводят к одинако-
вым результатам. После Ренкина расчет свода как упругого бру-
са повторили Винклер [119] (1867) и Мор [120] (1870).
Мы пользуемся в настоящее время классическим методом Мо-
ра, который предполагается известным читателю. Мору же при-
надлежит известный графический прием построения линий влияния
для бесшарнирного свода с помощью веревочного многоугольни-
ка. Головин [28] и Феппль [100] произвели в 1880—1881 гг. расчет
свода по точным методам теории упругости; но этот расчет не по-
лучил дальнейшего распространения. В общем можно сказать, что
к 1880 г. окончательно установился тот метод расчета свода, ко-
торым мы пользуемся теперь; даже способ выноса неизвестных
в упругий центр тяжести с помощью бесконечно жестких консо-
лей к этому времени уже стал известным (Крон [121], 1880).
Глава 11
ЗАКЛЮЧЕНИЕ
Расчет бесшарнирной арки, данный Брессом, Ренкином ч
Мором, появился в те десятилетия, когда интерес строителей
к этой системе значительно понизился вследствие общего увлече-
ния балочными фермами. Увлечение это временами доходило до
настоящего абсурда: случалось, что в горных ущельях строили
металлические балочные мосты, с великими трудностями достав-
ляя металл по горным дорогам, хотя камень был под рукой, а
26 С. А. Бернштейн
392
скала обеспечивала надежность опор для сооружения арки. Воз-
рождение интереса к арке связано с появлением нового строитель-
ного материала — железобетона. Любопытно, что успешное
применение железобетона в арочных мостах содействовало раз-
витию строительства арок и из старых материалов (камня и ме-
талла), достигшему в первые десятилетия нашего века больших
успехов.
Применение железобетона позволило сразу резко увеличить
пролеты арочных мостов и значительно уменьшить толщины сво-
дов, а это поставило перед строительной механикой новые задачи.
Положение кривой давления в тонком своде приобрело особую
важность, так как уже незначительное отклонение ее от оси вы-
зывало резкое увеличение фибровых напряжений. Поэтому тех-
ника ставит перед наукой вопрос о способе подбора очертания оси
арки, наименее отклоняющейся от кривой давления. Мы видели,
что задача эта имеет почтенный возраст, и, тем не менее, до сих
пор она получила только приближенное решение, хотя степень
приближения может считаться удовлетворительной. Как известно,
существует несколько таких приближенных приемов, различаю-
щихся математическим выражением кривой, принимаемой за ось
арки. За последние десятилетия появились новые работы Руднева
[122] и Киселева [123] на эту тему.
Однако задача расчета арки до сих пор не может считаться
разрешенной полностью, так как существующие методы расчета не
учитывают изменения формы оси арки под нагрузкой. Между тем
в пологих сводах даже незначительные упругие перемещения оси
создают заметное расхождение между осью и кривой давления,
вызывая появление дополнительных изгибающих моментов. Эта
задача еще ждет решения; трудности ее чрезвычайно велики, так
как она нелинейна и требует учета изменения самой расчетной
схемы под нагрузкой. До сего времени существуют только первые
попытки решения [124].
Второй новой задачей, возникшей в результате применения
пологих тонких сводов, была проблема устойчивости свода, вызвав-
шая целый ряд исследований. Впервые она была решена в частном
случае С. П. Тимошенко [125] (1910), но наиболее полное освеще-
ние получила в трудах А. Н. Динника [126], И. Я- Штаермана [127],
А. Г. Локшина [128] и др.
Очередную задачу составляет распространение на арку мето-
дов расчета по предельному равновесию, разработанных
А. А. Гвоздевым [42] и другими и знаменующих собой отказ от
расчета по рабочему состоянию.
ОЧЕРК ТРЕТИЙ
ИЗ ИСТОРИИ РАСЧЕТА ФЕРМ
«Нет такой системы, по кото-
рой могли бы строить мосты без
страха, чтобы они не провали-
лись, ежели не будут обращать
внимание на размеры, придава-
емые частям моста».
Д. И. Журавский (жур-
нал Главного управления
путей сообщения и пу-
бличных зданий, т. XVI,
1852, стр. 120).
Глава 1
ВВЕДЕНИЕ
Поиски метода расчета свода продолжались более 150 лет.
Поиски метода расчета ферм уложились в срок, вдесятеро меньший:
от первого метода, данного Журавским, до разработанных Макс-
веллом графического расчета статически определимых ферм и об-
щей теории расчета статически неопределимых ферм прошло толь-
ко 15 лет.
Такая необычайная в строительной механике стремительность
овладения новой областью объясняется .в первую очередь тем, что
разработка методов расчета ферм очень сильно запоздала по
сравнению с практической потребностью. Начавшееся в 30-х годах
XIX века сооружение железных дорог поставило перед мостострои-
телями совершенно новые задачи. Если в мостах под гужевые до-
роги вес временной нагрузки составлял малую долю собственного
веса пролетного строения (а в каменных арочных мостах — ничтож-
но малую), то в железнодорожных мостах соотношение изменилось
в обратную сторону. Вес поезда оказался величиной того же поряд-
ка, что и постоянная нагрузка, а в деревянных мостах он стал
превосходить последнюю. Но так как положение поезда на мосту
может меняться, то перед проектировщиками мостов встала задача
изыскания самого невыгодного положения поезда на мосту и рас-
чета пролетного строения при таком, вообще говоря, несимметрич-
ном положении нагрузки.
К решению этой задачи строительная механика оказалась совер-
шенно неподготовленной даже применительно к простейшей схеме
моста — балке на двух опорах. Достаточно напомнить, что даже во
2-м издании курса Навье, появившемся в 1833 г., когда в России
уже побежал по рельсам паровоз Черепанова, содержится совер-
шенно ложное утверждение о работе балки: Навье полагал, что
опасное сечение, т. е. сечение с наибольшим моментом, всегда на-
26*
395
ходится под центром тяжести внешней нагрузки (иными словами,
максимум в эпюре моментов якобы находится на вертикали, где
пересекаются крайние ее лучи).
Но если для балки расчетные возможности все же существова-
ли, то для фермы не было вообще никаких расчетных методов.
В том же курсе Навье [18] (1833), в курсе Перси [21] (1834) ив дру-
гих современных книгах рассмотрены только простейшие ри-
гельно-подкосные схемы, для которых дается грубо условный спо-
соб расчета, и простая треугольная стропильная ферма. Для балоч-
ных ферм до второй половины 40-х годов не существовало никако-
го способа расчета1. Между тем именно балочная ферма оказалась
особенно пригодной для мостов под железные дороги. Схема такой
фермы, состоящая из параллельных поясов, соединенных решет-
кой, впервые была предложена, по-видимому, Палладио в XVI
веке, но не нашла широкого применения до появления железных
дорог. В 1820 г. Таун дал конструкцию балочной фермы с многоре-
шетчатым заполнением, известную до сих пор под названием фер-
мы Тауна, хотя по справедливости ее надо называть фермой Кули-
бина, который применил эту же конструкцию в своем арочном
мосту еще в 1772 г. Затем появляются одна за другой схемы Лонга
и Гау, а Роберт Стефенсон строит известные трубчатые мосты
«Британия» и Конуэйский, заменив решетчатое заполнение сплош-
ной стенкой. Надо считать несомненным, что именно эти схемы
явились родоначальниками современных балочных ферм, хотя не-
редко высказывают мнение об отсутствии между ними родовой
преемственной связи. В действительности же первые балочные
фермы рассматривались современниками именно как балка со
сквозной стенкой, а не как новый самостоятельный тип сооруже-
ния. Характерной в этом смысле является интересная статья
М. С. Волкова, первого русского профессора строительной механи-
ки, опубликованная в 1838 г. [129]. Волков называет такие фермы
«связями» и считает их за балку с выброшенной стенкой. Взамен
стенки в «связи» поставлены стойки и раскосы, причем последние
служат для предотвращения «скользения». Волков указывает, что
если соединить между собой концы обоих поясов, то возможность
«скользения» устранится, и раскосы станут излишними. Он пред-
лагает ряд таких безраскосных схем (рис. 42) и рекомендует при-
менять две первые из них, как безраспорные, в мостостроении. Эта
1 Когда знаменитый зодчий К. И. Росси строил в 1830 г. в Петербурге здание
Александрийского театра (ныне театр имени А. С. Пушкина), то многие видные
инженеры во главе с известным Базеном усомнились в прочности громадных же-
лезных стропильных арочных ферм, запроектированных Росси, и добились при-
остановки строительства. Оскорбленный, но уверенный в своей интуиции Росси
написал министру двора письмо, в котором мы находим характерное заявление:
«... В случае, когда бы в упомянутом здании от устройства металлической крыши
произошло какое-либо несчастье, то в пример для других пусть тотчас же меня
повесят на одной из стропил». Этот аргумент, по-видимому, подействовал не
менее убедительно, чем расчетная проверка, которую нельзя было применить
для решения спора, так как метода расчета таких ферм ле существовало (см. Н.
Вейнерт, Росси, изд. «Искусство», 1939, стр. 108—111).
396
статья Волкова представляет, по-видимому, первую в строительной
механике попытку анализа работы ферм разной схемы, хотя мето-
да расчета их она еще не дает.
Расчет ферм запоздал, однако, не только потому, что практиче-
ская необходимость в нем возникла позже, чем, например, для
арок. К этой задаче наука не могла подступиться, оставаясь на
старых позициях предельного состояния. Для расчета свода ио
предельному состоянию можно было без особого труда выдумы-
вать более или менее правдоподобные формы разрушения, и рас-
считывать их статически в состоянии
предельного равновесия. Но задача о
предельном состоянии статически не-
определимой фермы (а именно тако-
вы были фермы Палладио и выросшие
из них фермы Кулибина—Тауна, Га>
и др.)» задача о виде ее разрушения
настолько сложна, что и сейчас она
представляет для нас почти непреодо-
лимые трудности, хотя мы подходим
к ней во всеоружии современных зна-
ний. Для умозрительной науки XVIII
века эти задачи были совершенно не-
приступны. Поэтому первые методы
расчета ферм могли появиться только
тогда, когда завершился переход нау-
ки на путь расчета по рабочему состоя-
нию, т. е. не ранее 30—40-х годов
XIX века. Интересно, что первые пра-
вильные методы расчета ферм, как ста-
Рис. 42. Схемы „связей"
(ферм) по Волкову
тически определимых, так и статически
неопределимых, были даны русскими инженерами.
Мы начали наш рассказ с параллели между историей расчета
ферм и историей расчета сводов. Закончим вводную главу другим
сопоставлением ферм и сводов. Схема арки или свода, появивша-
яся в далекой древности, не подверглась существенному измене-
нию до наших дней. Достижения строительной механики позволили
в высокой степени рационализировать ее конструкцию, уменьшить
сечения, резко увеличить пролет, но самая схема арки осталась
прежней. В этом смысле можно сказать, что задачей науки в об-
ласти арок была разработка метода расчета системы с заданной
схемой.
В противоположность этому схемы ферм непрерывно изменя-
лись параллельно с успехами их расчета. Развитие строительной
механики активно влияло на изменение самих схем ферм, а из-
менение этих схем в свою очередь побуждало к дальнейшему про-
грессу строительной механики. Это активное воздействие теории
на практику и привело к тому, что при взгляде на современные
легкие, стройные и рациональные мостовые фермы мы отказываем-
ся признавать их родство с неуклюжими предками.
Глава 2
РАБОТЫ Д. И. ЖУРАВСКОГО
Имя Дмитрия Ивановича Журавского достаточно широко из-
вестно из книг по истории русской техники. Краткая оценка-его
работ в области расчета ферм приведена в «Курсе строительной
Дмитрий Иванович Журавский (1821—1891)
механики стержневых
систем» проф. И. М.
Рабиновича (ч. 1,
1950, стр. 279—280).
Однако в широких
** кругах инженеров-
строителей с именем
Журавского обычно
связывают только «те^
орему „ Журавского»
(производна я от из ги
бающего момента рав-
на поперечной силе),
которой он не откры-
вал и никогда не при-
менял в своих иссле-
дованиях. Между тем
научные заслуги Жу-
равского настолько
велики, что о них дол-
жен знать каждый ин-
женер-строитель.
Дмитрий Иванович
Журавский родился в
1821 г. и обучался в
Петербургском инсти-
туте путей сообщения.
Немедленно по окон-
чании курса (1842 г.)
он был направлен на
изыскания Петербург-
ско - Московской же-
i лезной дороги, а за-
тем переведен в отдел
проектирования мостов
для этой линии. За
образец мостовой фер-
мы ему было предложено взять незадолго до этого появившуюся
систему Гау, состоявшую из параллельных поясов, деревянных пе-
рекрестных раскосов и железных болтовых стоек-стяжек. Метода
расчета этой системы не существовало, и представление об ее ра-
боте было весьма смутным. Молодой инженер не испугался теоре-
тической трудности и самостоятельно разработал метод расчета
398
фермы Гау на нагрузку, занимающую произвольное положение в
пролете, и даже попытался дать расчет многопролетной неразрез-
нои фермы такой схемы. Это был первый в истории науки метод
расчета фермы^ и мы подробнее скажем о нем дальше.
Проектная и строительная работа над мостами Петербургско-
Московской железной дороги1 послужила источником для всей на-
учной деятельности Журавского. Результаты ее были опубликова-
ны сперва в журнале Главного управления путей сообщения в виде
трех статей в 1850, 1852 и 1855 гг., а затем изданы отдельной книгой
в 1855 г. под названием «О мостах раскосной системы Гау» [23].
Этот труд был премирован Академией наук. После этого Журав-
ский напечатал выдержки из своего труда в известном французском
журнале «Annales des ponts et chaussees» (1856).
По-видимому, в дальнейшие годы жизни Журавский самостоя-
тельных научных исследований почти не вел. Он не был професси-
оналом-ученым и свою замечательную работу выполнил, когда по-
чувствовал в этом практическую необходимость. Впоследствии Жу-
равский, как признанный крупнейший авторитет, занимал руково-
дящие должности в Министерстве путей сообщения и был под
конец жизни директором Департамента железных дорог. Он умер
в 1891 г.
Перейдем к общему обзору его научной деятельности. На осно-
вании результатов расчета фермы Журавский впервые обнаружил
ряд особенностей в работе ферм до этого неизвестных, в частности
явление_убывания усилий в стойках раскосной фермы от опор к
середине пролета при сплошной нагрузке. Этот вывод Журавского
показался в ту пору до такой степени странным, что ему пришлось
поставить специальный публичный опыт для доказательства своей
правоты. Этот опыт был настолько остроумен и эффектен, что о нем
необходимо рассказать, тем более, что это было после Кулибина
едва ли не первое опытное изучение работы целого сооружения.
Журавский построил небольшую модель фермы Гау, заменив в
ней растянутые болтовые стойки проволоками одинакового сече-
ния. Эти проволоки он натянул так, что при отсутствии нагрузки
г на ферме они издавали звук одинаковой высоты. Затем Журавский
загрузил ферму и провел по проволочным стойкам смычком. При
этом проволоки запели на разные голоса: самый высокий тон изда-
вали стойки у опор, а чем ближе к середине пролета, тем тон стойки
оказался ниже2.
Книга Журавского содержит, помимо расчета ферм, также
теорию работы и способ расчета шпоночных соединений. В этой
области ему также удалось сказать первое слово. В одном из при-
ложений к книге Журавский дал то решение задачи о касательных
1 Под руководством Журавского производилась постройка моста через Ве-
ребьинской овраг близ станции Малая Вишера. Впоследствии трасса линии была
изменена и овраг перейден по громадной иасыпи.
2 Этот рассказ заимствован из книги Л. Ф. Николаи, Краткие исторические
данные о развитии мостового дела в России, Спб., 1898.
399
напряжениях при изгибе, о котором мы уже упоминали в очерке
первом. В связи с этим нужно сказать, что впоследствии Журавский
вернулся к этой задаче (1860) и изучал сдвиги в стенке двутавро-
вой балки. Так как наблюдение этих сдвигов в железной балке было
затруднительно, то Журавский изготовил и испытал двутавровую
балку из картона, справедливо полагая, что характер явления не
должен зависеть от рода материала. Это был первый в истории нау-
ки пример замены материала для изучения работы конструк-
ции, широко применявшийся впоследствии, в частности при иссле-
довании конструкций оптическим методом. Кроме того, Журавский
впервые поставил вопрос об электросварке рельсов, задолго до при-
менения этого процесса заграницей.
Теперь обратимся к анализу того первого в истории метода рас-
чета ферм, который был дан Журавским, и начнем с цитаты из
введения к его книге, подчеркивающей приоритет русской науки:
^Исследование балок, состоящих из брусьев раскошенных и свя-
занных между собой, было сделано в России прежде, чем о том
было напечатано на английском, французском или немецком язы-
ках; сочинения американского инженера Лонга и австрийского Гега
вовсе не давали понятия об распределении напряжений по всем
частям составной балки». Журавский отмечает далее, что его пер-
вые опыты и расчеты относятся к 1845 г., тогда как первая иност-
ранная статья Кульмана о расчете ферм появилась в 1851 г.
Журавский указывает, что владея расчетом, он доказал непра-
вильность конструкции стефенсоновских трубчатых мостов, оши-
бочность мнения Лонга о влиянии предварительного натяжения
болтов и ошибочность американских воззрений на сопротивление
поясов.
Указание на ошибку Лонга интересно, так как в этой задаче
Журовский сделал существенное открытие. Речь идет о работе бол-
товой стяжки, имеющей начальное натяжение. В то время было
принято считать, основываясь на мнении Лонга, что усилие в болте
от продольной растягивающей нагрузки складывается с усилием от
начального натяжения. Журавский доказал, наоборот, что «напря-
жение болтов при нагрузке не состоит из суммы предварительного
напряжения от завинчивания болтов и напряжения, производимого
собственно нагрузкой, как это могло бы показаться с первого
взгляда». Это высказывание Журавского и данный им расчетный
анализ совершенно правильны: если к головкам болта приложить
растягивающую силу, то условие в болте начнет возрастать лишь
после того, как стянутые начальным натяжением болта элементы
восстановят свои первоначальные размеры. Очевидно, это произой-
дет, когда внешняя сила станет равна начальному натяжению.
Этот важный вывод Журавского, очевидно, в такой же мере
относится к расчету заклепок на отрыв головок. Любопытно, что в
английской литературе по расчету заклепок он впервые появился
только в конце 20-х годов нашего столетия и возбудил за рубежом
целую дискуссию.
Переходим к изложению расчетного метода Журавского.
400
Для расчета фермы Гау Журавский берет расчетную схему в
виде простой раскосной решетки с восходящими раскосами и шар-
нирными узлами. Таким образом, распространенное мнение, припи-
сывающее Швеллеру заслугу введения шарнирной схемы фермы,
совершенно ошибочно: эта заслуга всецело принадлежит Журав-
скому, как и идея пренебрежения встречными растянутыми раско-
сами? так широко применявшаяся впоследствии. Журавский обос-
новал это пренебрежение тем, что узловые соединения деревянных
раскосов не способны воспринимать растягивающие усилия.
Рис. 43. Расчет фермы по методу Журавского
Журавский не начинает с определения опорных реакций фермы,
как мы это делаем теперь, а прослеживает судьбу каждого груза
от точки его приложения до опор. Возьмем простейший случай:
груз Р стоит в среднем узле верхнего пояса (рис. 43). Вырежем
узел и найдем из условий равновесия и симметрии сжимающие
Р
усилия в раскосах ----. Эти усилия передаются на нижние узлы,
из равновесия которых находим растягивающие усилия в стойках
у- и горизонтальную силу ? , действующую вдоль нижнего поя-
са. В действительности эта сила равна разности усилий в двух
смежных панелях нижнего пояса, но Журавский этим не смуща-
ется и продолжает процесс вырезания узлов по зигзагу решетки.
В результате он находит усилия во всех раскосах и стойках, и
горизонтальные силы, приложенные в узлах и имеющие обратные
направления, чем ранее найденные силы ~2't , так как там они вы-
ражали действие стержней на узел, а здесь, наоборот, действие
узлов на пояса. Очевидно, усилие в любой панели пояса численно
401
равно сумме горизонтальных сил, приложенных к узлам по одну
сторону от панели, и решение получается совершенно точным, не-
смотря на то, что реакции предварительно не были определены.
Этот метод расчета интересен с двух точек зрения. Во-первых, он
основан на идее вырезания узлов и составлении условий равно-
весия, и, таким образом, открытие и первое применение _ метода
вырезания узлов, безусловно, принадлежат Журавскому.
Во-вторых (и в этом он отличается от современной формы метода
вырезания узлов, идущей от Кульмана и Шведлера), Журавский не
ищет при вырезании узлов усилий в элементах пояса, а находит
разность (равнодействующую) усилий в двух смежных панелях,
и это его освобождает от необходимости решения совместных урав-
нений, хотя в каждом следующем узле встречаются три неизвест-
ных усилия. Нам кажется, что эта идея Журавского незаслуженно
подверглась впоследствии забвению и могла бы найти и теперь
удачное применение при расчете сложных ферм.
Но как же применить этот способ расчета, если сила Р стоит не
в среднем узле? В этом случае Журавский разбивает силу на две
части у Р и (1—у)Р, где у — неопределенный множитель, и ведет
разложение каждой составляющей по узлам в свою сторону. Затем
он составляет уравнение равновесия горизонтальных узловых сил и
находит из него значение у. Легко видеть, что у Р и (1—у)Р будут
равны опорным реакциям. По поводу этого результата Журавский
с некоторым удивлением замечает:
«Оказывается, что груз... производит на опоры давления, обратно
пропорциональные расстояниям точек опоры от точки приложения
груза, т. е. система передает давление на точки опоры точно
так, как цельный брус». Это несколько наивное замечание Журав-
ского очень характерно. Оно показывает, что 100 лет назад смысл
условий равновесий не был вполне ясен не только рядовому инже-
неру, но даже такому выдающемуся исследователю, как Журав-
ский. С другой стороны, оно объясняет, почему Журавский ведет
разложение сил от загруженного узла к опорам, а не обратно (что
было бы проще): самое определение реакций фермы в те времена
вызывало затруднения.
Мы не будем останавливаться на решении Журавского для слу-
чая произвольного расположения узловой нагрузки; здесь возника-
ет затруднение при выборе того узла, с которого следует начать раз-
ложение в -обе стороны. Это затруднение приходится решать путем
проб, причем контролем служат уравнения равновесия узловых по-
ясных сил. Характерно, что возможность расчленения нагрузки и
применения принципа наложения Журавским не использована;
впервые эта идея встречается у Августиновича, который продолжил
цело Журавского в области расчета ферм.
Расчет раскосной фермы, данный Журавским, вполне точен при
любом расположении нагрузки. В частности, при равномерном за-
гружении всех узлов наибольшее усилие в поясе оказывается рав-
Р1п п
НЫМ ~8h ’ ГДе г — узловая нагрузка, I — пролет, п — число узлов.
402
h — высота фермы (Журавский указывает, что это выражение впер-
вые вывел капитан Хржановский). Но, разумеется, этот расчет ока-
зывается условным для фермы с перекрестными раскосами, так как
выбор однораскосной схемы должен предшествовать расчету, а до
производства расчета нельзя установить, какой раскос в каждой
панели окажется сжатым. Правда, если в результате расчета ка-
кой-либо раскос окажется растянутым, то не представит труда ис-
править расчет, заменив в схеме этот раскос на встречный. При ус-
ловии такой поправки расчет фермы г перекрестными раскосами
также будет точным, поскольку раскосы не способны работать на
растяжение.
Журавский сделал далее попытку разрешить
гораздо более сложную задачу — рассчитать мно-
гопролетную неразрезную ферму. Если вспомнить,
что в то время существовало решение только двух
статически неопределимых задач — неразрезной
балки и двухшарнирной арки, то смелость, с кото-
рой молодой инженер взялся за столь сложную про-
блему, и совершенное своеобразие подхода до-
стойны быть отмеченными. Хотя Журавский нигде
не останавливается на различии между статически
определимой и неопределимой системой, но для не-
го это различие ясно, поскольку он прибегает для рас-
чета неразрезной фермы к условиям деформации.
Вспомним, что при расчете фермы по методу
Журавского усилия в раскосах и стойках опреде-
Р
Рис. 44. За-
дача Жу-
равского
ляются непосредственно из равновесия узлов, а
усилия в поясах вычисляются, как суммы левых
(или правых) горизонтальных узловых составляющих. Такой спо-
соб расчета поясов возможен, однако, только в однопролетной
ферме. Журавский указывает, что в многопролетной ферме в каж-
дом пролете существует по крайней мере одно сечение пояса, не
совершающее продольных перемещений под нагрузкой. Участок
пояса между двумя такими «сечениями раздела грузов» (по тер-
минологии Журавского) находится в таких же условиях, как
стержень с обоими неподвижными концами, по длине которого
приложены осевые силы (рис. 44). Эта последняя задача стати-
чески неопределима, и Журавский решает ее, применив впервые
в истории науки метод/дефолмаций.
Таким образом, неправильно мнение, приписывающее первое
применение метода деформаций Винклеру (1862) или Брессу (1865).
Журавский принимает за неизвестную величину перемещение X
точки приложения силы Р и находит его из условия равновесия
EFl , EFl
h
устанавливая отсюда, что сила Р распределяется между участками
стержня обратно пропорционально их длинам. Эта задача, обычно
рассматриваемая во всех учебниках сопротивления материалов, за-
403
служивает названия задачи Журавского, так как именно он впер-
вые дал ее решение.
Если положение «сечений раздела грузов» в пролетах известно,
то предыдущее решение позволяет распределить узловые горизон-
тальные составляющие между обоими такими сечениями и найти
отсюда усилия в поясах. Слабым местом в методе Журавского ока-
зывается именно порядок нахождения этих сечений, для которого
он предлагает способ проб, недостаточно обоснованный теоретиче-
ски1. Таким образом, надо признать, что Журавскому принадлежит
первая попытка расчета статически неопределимых ферм, но не
первое правильное решение этой задачи. В Западной Европе в это
время еще никто не умел рассчитывать даже статически опреде-
лимые фермы. Первый правильный расчет статически неопредели-
мой фермы дал РА сский инженер Августинович.
Из этого обзора деятельности Журавского видно, как велики и
разнообразны его научные заслуги в истории строительной механи-
ки. Журавский значительно опередил западноевропейскую науку,
и мы вправе гордиться им, как замечательным русским ученым.
Глава 3
РАБОТЫ ШВЕДЛЕРА И АВГУСТИНОВИЧА
Мы уже объяснили, почему 50-е годы прошлого столетия яв-
ляются периодом чрезвычайно интенсивных поисков метода расчета
ферм: быстрое развитие железнодорожной сети и успешное приме-
нение балочных ферм в мостостроении настоятельно требуют ско-
рейшего изыскания способа их расчета. В 1850 г. исполнилось 25 лет
со дня открытия первой железной дороги в Англии; во Франции,
Германии, Бельгии и США они насчитывают к этому времени поч-
ти 20 лет существования. Тем более любопытно, что первый метод
расчета ферм появился в России, где он предшествовал открытию
первой большой железной дороги (опыт постройки Царскосельской
1 Для неразрезной балочной схемы такими сечениями будут те, в которых
касательные к линии прогиба взаимно параллельны. Действительно, условие по-
стоянства длины продольного волокна, отстоящего на у от нейтральной линии,
на участке от Xj до х2 выразится
о = j zdx = j dx у Jjjdx = у [<р(х2) — ¥(%!)],
откуда углы наклона касательной в точках Xi и х2 равны между собой. Оче-
видно, таких пар сечений может быть бесконечное множество, и потому одним из
них в каждом пролете можно задаться.
404
ж. д., открытой в 1837 г., не идет в счет, так как на ней не было
ни одного большого моста).
В 1851 г. вышла статья Швеллера [130], содержавшая метод рас-
чета статически определимых ферм, известный теперь под именем
«метода вырезания узлов» и основанный на составлении уравнений
равновесия для усилий в каждом узле фермы, в предположении его
шарнирности. Это был именно тот метод, которым ранее пользовал-
ся Журавский. Экземпляр журнала со статьей Швеллера, достав-
ленный в библиотеку Московского университета из Петербурга, про-
путешествовал в почтовом вагоне, пересекая реки и овраги по мос-
там, рассчитанным Журавским тем самым способом, о котором го-
ворилось в этой статье
Швеллера.
Но между методами
Журавского и Швеллера
есть и различие. Метод
Швеллера позволяет
обойтись без совместных
уравнений лишь в том
случае, если возможен
такой порядок обхода уз-
лов фермы, при котором
в каждом следующем уз-
ле встречаются только
Рис. 45. Пример фермы, которую легче
рассчитать методом Журавского, чем но
способу вырезания узлов Шведлера
два неизвестных усилия
В противном случае он приводит к совместным уравне-
ниям, число которых равно числу стержней. Метод Жу-
равского для ферм с параллельными поясами позволяет обой-
тись без совместных уравнений и в более сложных случаях. Так,
для фермы по рис. 45 метод вырезания узлов Шведлера в про-
стой форме неприменим, так как он приводит к 15 совместным урав-
нениям с таким же числом неизвестных (при несимметричной на-
грузке). Метод вырезания узлов Журавского позволяет сразу вы-
числить усилия в раскосах и стойках и найти узловые горизонталь-
ные составляющие, суммирование которых дает усилия в поясах,
без всяких совместных уравнений. Таким образом, способ Журав-
ского дает более широкие возможности, и потому следует пожалеть,
что он забыт и не излагается в учебниках.
Но если предложенный Шведлером метод вырезания узлов яв-
ляется фактически лишь повторением способа, ранее найденного
Журавским, и притом в указанном смысле повторением менее
удобным, то бесспорная и важная заслуга Шведлера состояла в
том, что он впервые привлек общее внимание к статически опреде-
лимым схемам ферм и указал на их преимущества. Это был пер-
вый пример активного воздействия строительной механики на кон-
структивную форму сооружений в области расчета ферм. Если до
этого времени мостовые фермы сохраняли свою родовую связь с
балкой (таковы многорешетчатые фермы типа Гау и Кулибина—
Тауна), то предложенные Шведлером схемы ферм, образованных из
405
Шведлер (1823—1879)
плохо, так как
треугольников, внеся ясность в структуру и распределение усилии,
совершенно порвали эту родовую связь. Схемы, данные Шведлером,
далеко не сразу получили популярность среди инженеров. В Рос-
сии и Западной Европе многорешетчатые и многораскосные фермы
(усовершенствованные в России проф. Белелюбским, учеником Жу-
равского) продолжали
применяться до конца
XIX столетия наряду
с новыми статически
определимыми схема-
ми, постепенно вытес-
няясь последними. В
консервативной Англии
многораскосные фер-
мы строились до кон-
ца 20-х годов нашего
века, когда в России
они уже давно стали
анахронизмом.
Американская тех-
ника, заинтересовав-
шись преимуществами
статически определи-
мых ферм, встала во
второй половине XIX
века на своеобразный
и глубоко неверный
путь приближения кон-
струкции ферм к их
расчетной схеме и за-
менила жесткие узлы
болтовыми шарнира-
ми. Разумеется, такие
фермы обладали пони-
женной жесткостью и
постоянно расстраива-
лись и требовали непрерывного наблюдения и ухода, но тем не ме-
нее они применялись в США очень упорно. Это один из немногих
примеров в истории строительной механики неправильного понима-
ния взаимной связи между конструкцией и расчетной схемой.
Надо -отметить, что Шведлер, увлекаясь изобретенным им спосо-
бом образования новых схем ферм, попробовал искать оптималь-
ные схемы, удовлетворяющие наперед заданным условиям: условию
постоянства усилий в элементах пояса фермы с полигональным
очертанием (так называемая «ферма Шведлера»), условию мини-
мума веса и т. п. Однако эти поиски часто приводили к схемам, не-
удобным в конструктивном отношении, и потому почти не нашли
применения. Кроме того, идея создания фермы наименьшего теоре-
тического веса не всегда приводит к наиболее экономичным конст-
406
рукциям, так как стоимость фермы определяется не только количе-
ством материала в ферме, но и стоимостью труда (которая не про-
порциональна весу) и количеством материала в заготовках. При
сложных формах элементов раскрой листов дает значительные от-
ходы, и потому облегчение веса фермы не всегда уменьшает коли-
чество металла, использованного для ее изготовления.
Следующую после Шведлера попытку расчета ферм мы встре-
чаем в 1852 г. в известной книге Ламэ [131]. Вопреки легенде, пу-
щенной кем-то из авторов исторических обзоров, Ламэ не рассмат-
ривал статически неопределимых ферм, а ограничился статически
определимыми, причем приме-
нил к их расчету принцип воз-
можных перемещений. Ламэ со-
став-ил на основе известного
«принципа Клапейрона» фор-
мулу для вычисления переме-
щения фермы под грузом и ис-
кал формы сооружений, даю-
щих минимальный прогиб при
условии равнопрочности.
Мысль о применении прин-
ципа возможных перемещений
к расчету ферм использовал
русский инженер Августино-
вич, распространивший ее на
фермы статически неопреде-
лимые (1857). Это была пер
вая после Журавского попыт-
ка расчета таких ферм, и на этот раз теоретически пра-
вильная, причем в основе ее лежала идея Журавского.
Таким образом, первый правильный метод расчета ста-
тически неопределимых ферм принадлежит Августиновичу, утверж-
дая первенство русской инженерной науки и в этой области. До-
стойно удивления, что и работа Августиновича [132] и самое имя ее
автора были впоследствии незаслуженно забыты.
Если в книге Журавского еще нет четкого разграничения ста-
тически определимых и неопределимых ферм, то у Августиновича
оно уже подчеркнуто с полной отчетливостью: «напряжения прямо-
линейной системы, не имеющей лишних связей и находящейся в
равновесии, зависят только от наружных сил и от положения
точек».
Для расчета статически определимой фермы с п узлами Августи-
нович составляет 2п уравнений проекций возможных перемещений,
давая для этого готовое правило: «если линия наклонна, то пишет-
ся ее коэффициент, помноженный на проекцию; а если линия гори-
зонтальна или вертикальна, то пишется один коэффициент, наблю-
дая, в отношении знаков, следующее правило: для отдаленных от
осей концов линии член пишется с плюсом; для ближайших к
осям — с минусом». Под «коэффициентом» понимается усилие в
407
стержне или величина, ему пропорциональная; в приведенных Ав-
густиновичем примерах эти «коэффициенты» равны усилиям в
стержнях, деленным на их длины.
По этому правилу уравнения перемещений для узла 1 (рис. 46)
напишутся так:
4- ахМ — a2N — a3L — 0;
— Р — hxM — h2N + h^L = 0.
Если сюда подставить вместо Л4, A, L усилия в стержнях, делен-
ные на длины, то мы получим обычные уравнения равновесия.
Рис. 47. Первая статически неопределимая ферма, которую уда-
лось правильно рассчитать (Августинович)
Разумеется, составление и решение системы 2п уравнений для
фермы с п узлами очень трудоемко (как и метод вырезания узлов
в общем случае). Августинович сознает это неудобство и приводит
характерное соображение:
«Если бы существовал другой способ, более простой, тогда не-
зачем было бы прибегать к способу возможных перемещений; но
при составлении проектов часто, глядя только на чертеж, судят о
степени прочности системы, или стараются уподобить ее фигуре,
несколько похожей на проектированную, и таким образом делают
выводы, не всегда согласные с действительностью».
Это признание интересно не только потому, что оно подтверж-
дает распространенность в 50-х годах прошлого века способа про-
ектирования мостовых ферм без расчета; оно показывает также, что
методы расчета, предложенные Журавским и Шведлером, не дошли
еще в то время до рядового проектировщика и казались ему непо-
стижимо мудреными. Конечно, способ, рекомендованный Августи-
новичем, не облегчал внедрения расчета ферм в проектную практи-
ку; с точки зрения трудоемкости он даже представлял некоторый
шаг назад. Но зато чрезвычайно оригинален данный Августинови-
чем способ расчета статически неопределимых ферм, поясненный
им на примере фермы по рис. 47.
408
Эта распорная ферма имеет при симметричном загружении два
лишних неизвестных Q и Для их определения необходимо со-
ставить два условия деформации, выражающие постоянство длин
проекций на горизонтальную ось обоих поясов. Теперь мы решили
бы эту задачу очень просто. При постоянной длине панели и равен-
Рис. 48. Лемма Авгу-
стиновича
бы эту задачу очень просто. При постоянной
стве сечений элементов пояса (таковы
допущения Августиновича) мы состави-
ли бы условие равенства нулю суммы
проекций удлинений поясов в виде
у. Ns cos а _ут Nd ___ d у дг _ q
2j — — 7EF ~£F ~ ’
откуда S №=0, т. е. алгебраическая сум-
ма усилий в элементах каждого пояса
должна быть равна нулю.
Здесь $ — длина элемента пояса;
scos a=d— длина панели; N—усилие
в элементе пояса.
Вместо этого Августинович вспомина-
ет «задачу Журавского» о действии осе-
вых сил на стержень с заделанными
концами и обобщает ее, полагая, что к
стержню приложены на равных расстоя-
ниях продольные силы Рь Р2, ...» Р n-i •
Применяя закон наложения нагрузок (едва ли не первый в исто-
рии пример использования этого закона), Августинович вычисляет
реакции по концам стержня:
А = - Л + — Р2+- + — Р
п п п
в = ^11р1 + ^1р2-1-----h-Lp
п п п т
Затем он доказывает, что это решение останется справедливым,
если стержень имеет ломаную форму: проекции удлинения системы
abcde (рис. 48) таковы, как если бы прямой стержень af был на-
тянут силой Р. Отсюда он заключает, что вышенаписанные урав-
нения останутся справедливыми, если вместо сил Р подставить в
них горизонтальные составляющие узловых поясных сил, как это
делал и Журавский; при этом реакции, вычисленные по этим
уравнениям, будут равны искомым реакциям ферм Q и Qi в зави-
симости от того, для какого пояса взяты узлы.
Этому способу решения никак нельзя отказать в своеобразии, и
если он не нашел распространения, то только из-за общей трудо-
емкости расчета. Как бы то ни было, именно этот способ является
самым ранним правильным способом расчета статически неопре-
делимой фермы.
Глава 4
Ревкину
Рис. 49. Графический расчет фер-
мы по "
ПОЯВЛЕНИЕ КЛАССИЧЕСКИХ МЕТОДОВ РАСЧЕТА ФЕРМ
Одновременно с работой Августиновича, содержащей первый
правильный способ расчета статически неопределимой фермы, в
том же 1857 г. вышла книга Шеффлера [108], предлагавшая совер-
шенно неверный метод расчета многорешетчатых ферм, основан-
ный на учете изгиба всей фермы как балки. Шеффлер почему-то
решил, что при изгибе фермы с радиусом кривизны R каждый рас-
кос также изогнется с радиусом кривизны г= —, где а — угол
cos2 а
наклона раскоса к поясу. Исходя из этого предположения, он под-
считывал общий момент изгиба
всей фермы — поясов и раскосов
Насколько нам известно, к этому
странному способу расчета никто
впоследствии не возвращался, и
он был заслуженно забыт. Мы
вспоминаем его здесь, как исто-
рический курьез. Взамен этого
для расчета многорешетчатых
ферм в позднейших трудах (Гер-
бер [133], 1865, Лесль и Шюблер
[134], 1871) окончательно устано-
вился тот условный способ, кото-
рый с некоторыми поправками
дожил до наших дней: пояса рас-
считываются по изгибающим мо-
ментам, а раскосы — по попереч-
ной силе, деленной на число ре-
шеток.
В 1858 г^ появляется новая
, которая поз-
привела к открытию Максвеллом знамени-
расчета статически определимой фермы,
(1864)
графического приема, известного под именем диаграммы
идея
же
ТОГО . ж
Кремоны—Максвелла. Это новая идея принадлежала-Ренки ну [25]
и была позднее (1862) изложена им в его широко известном в свое
время «Руководстве для инженеров-строителей» (таково заглавие
этой книги в русском переводе инженера Андреева, изданном в
1870 г. в Петербурге).
Идея Ренкина состоит в том, что ферма рассматривается как ве-
ревочный многоугольник, по которому строится силовой многоуголь-
ник. Этот прием поясняется примером, приведенным в книге Рен-
кина (стр. 196—198 русского издания). Для стропильной фермы
(рис. 49) строим силовой многоугольник с полюсом О, проводя лу-
чи, параллельные элементам наружного обвода фермы. При этом
отрезки АВ и DE, очевидно, выразят реакции опор, а их сумма рав-
на грузу Р. Весь отрезок, по словам Ренкина, «...означает то, чем
должен быть груз в точке 1 для того, чтобы условия равновесия
410
брусьев А и Е были исполнены, и, следовательно, BD представляет
недостаток действительного груза в точке 1 или придаточную отвес-
ную силу, действующую вниз: она-то и должна быть заменена рас-
кашиванием. BD, противоположное и равное DB, представляет рав-
нодействующую недостатка поддерживающих усилий в точках 3 и
4, в которых нет действительных грузов». Проводя лучи DC и ВС, па-
раллельные раскосам, до пересечения в точке С, мы найдем усилия
во всех стержнях фермы.
Идея Ренкина ясна, несмотря на старомодный язык переводчика.
Она состоит в построении графика, в котором отрезки параллельны
соответственным стержням фермы и равны усилиям в них (при опре-
деленном силовом масштабе), причем график не содержит пи одной
лишней линии. В этом смысле график Ренкина является прямым
предтечей диаграммы Кремоны. Но если последняя представляет
многоугольник, взаимный с фермой, в том смысле, что каждому
узлу -одной фигуры отвечает замкнутый многоугольник другой, и
обратно, то диаграмма Ренкина этим свойством взаимности не об-
ладает, и потому ее нельзя построить путем последовательного об-
хода узлов фермы. По-видимому, она не получила распространения,
хотя несомненно, что Максвелл был знаком с методом Ренкина.
В 1862 г. вышла книга Августа Риттера [135], в которой был
впервые изложен метод сечений или моментных точек. Мы полага-
ем, что читатели с ним достаточно хорошо знакомы, и потому не
излагаем его содержания. В отличие от метода вырезания узлов
этот метод позволял (по крайней мере для ферм, образованных из
треугольников) непосредственно вычислить усилие в любом стерж-
не независимо от прочих и без решения совместных уравнений.
Этим резко снижалась трудоемкость расчета; по существу это был
первый действительно удобный и общедоступный способ расчета
ферм. Кроме того, его важным достоинством была возможность
представления усилия в любом стержне стандартным выражением
N =— где М — момент внешних сил относительно моментной точ-
г
ки, а г —плечо стержня относительно той же точки. Такое пред-
ставление способствовало уяснению характера работы каждого
стержня и его роли в работе всей фермы. Впоследствии оно сильно
упростило задачу построения линий влияния для стержней ферм.
Неудивительно, что метод сечений сразу приобрел очень широкую
популярность среди инженеров-проектировщиков.
Проходят еще 2 года, и классические методы расчета ферм по-
лучают завершение в знаменитой работе Максвелла 1864 г., всего
через 14 лет после опубликования первой статьи Журавского.
Работа Максвелла [136] испытала на себе странную судьбу, ко-
торая иногда обрекает на непонятное невнимание выдающиеся на-
учные открытия. Действительно, об этой работе вспомнили только
тогда, когда все основные результаты Максвелла были вновь от-
крыты другими учеными, не знавшими его работы, вследствие чего
эти результаты носят двойное наименование. Так, предложенный
Максвеллом способ графического расчета ферм был вновь открыт
411
через 8 лет итальянцем Кремоной [137] (1872) и называется диаг-
раммой Кремоны—Максвелла (сам Кремона охотно признал прио-
ритет Максвелла, хотя не был знаком с его работой, когда писал
Максвелл (1831—1879)
свою книгу «О взаимных фигурах в графической статике»). От-
крытый Максвеллом способ вычисления перемещений ферм был
заново открыт в более общем виде Мором [138] (1874) и известен
под названием формулы Мора—Максвелла или даже просто фор-
мулы Мора. Открытый Максвеллом закон взаимности перемещений
стал известен только после того, как Бетти доказал более общую
теорему о взаимности работ [139] (1872), причем ни Мор, ни Бетти
не были знакомы с работой Максвелла.
412
Очень трудно понять, почему труд Максвелла не был оценен и
даже замечен современниками. Вряд ли можно видеть причину в
малом знакомстве ученых Европы того времени с английским язы-
ком1. Ведь столь же м алоза меченной прошла и выдающаяся рабо-
та Бресса (1854), о которой рассказано в очерке втором, хотя фран-
цузский язык, на котором она написана, был достаточно известен
европейским ученым, а тем более, надо полагать, соотечественникам
Бресса, которые тоже не обратили на эту работу должного вни-
мания.
Вернее всего причиной, обусловившей малую известность рабо-
ты Максвелла, было то, что она слишком резко поднималась над
общим бесцветным уровнем английской литературы по строитель-
ной механике, и потому не была понята в Англии и не привлекла к
себе внимания на континенте, где от английской научной литера-
туры не привыкли ждать важных открытий. Как бы то ни было, о
работе Максвелла сами англичане вспомнили только тогда, когда
его открытия были заново открыты на континенте Европы. Общий
ход развития науки задержался вследствие этого на десяток лет и
на столько же опоздало внедрение методов Максвелла в расчетную
практику.
Мы не останавливаемся на открытом Максвеллом графическом
расчете ферм, так как он известен студентам втузов с первого кур-
са и так часто вызывает при первом знакомстве чувство изумлен-
ного восхищения своей стройностью. Скажем несколько подробнее
о методе расчета статически неопределимых ферм, данном Макс-
веллом. Его особенностями были представление уравнений дефор-
маций в канонической форме и указание общего метода вычисления
перемещений, которые являются коэффициентами в этих уравне-
ниях.
В настоящее время под каноническими уравнениями метода сил
мы понимаем систему уравнений вида
Xi бц + Х2 ^12 + • Ч- Хп Ь1п — о,
*Ат + Х26л2 + • - - + = о,
выражающих условия отсутствия перемещений по направлениям
лишних связей в n-кратно статически неопределимой системе. Здесь
Xi,..., Хп — неизвестные усилия в лишних связях; §ik — перемеще-
ние по направлению связи i от единичной силы в связи k\ &io —
перемещение от внешней нагрузки по направлению связи L Дове-
ряясь немецкой научной литературе, нередко называют автором ка-
нонических уравнений Мюллера-Бреслау2. В действительности,
первая идея придания уравнениям метода сил канонической формы
1 Проф. И. М. Рабинович отметил в своем курсе [140], что даже известней-
ший английский физик Рэлей не был знаком с работой Максвелла.
2 Сам Мюллер-Бреслау называл их «уравнениями Максвелла» («Графическая
статика сооружений», т. II, ч. 1, Спб., 1910, стр. 19).
413
принадлежит Брессу [22] (1854), применившему эти уравнения в
расчете бесшарнирной арки. Вторым по времени и более общим бы-
ло решение Максвелла (1864), составившего канонические уравне-
ния для статически неопределимых ферм в развернутом виде, т. е.
с готовыми выражениями коэффициентов. Вот запись уравнений
Максвелла в подлинных обозначениях:
R S ег2 4- S Ъ ers -|- Т S ert 4-4- Р S ерг — 0;
R S ers + S Ses2 4- Т L est 4- - • 4- рХeps = 0;
/?Sert + S Ses/+TSe/2+-------|-PSepZ = 0.
Здесь P — нагрузка; /?, S, T,... — усилия в лишних связях;
г, s, /,..., р — усилия в стержнях от единичных сил /?=1, $4, Т=1,...,
Р=1; е — удлинения стержней от единичного в них усилия.
В переводе на наши обычные обозначения получим
е= -1—: г = N ' S = N/ = р = N.,
EF г S' t, > Г р,
и, следовательно, коэффициенты уравнений Максвелла выразятся
V *> V 1 х V Vaw ж
Z^er- = ; Jjers = -j-jp = И т. д.
Таким образом, Максвелл сумел дать необыкновенно простой и
общий способ вычисления перемещений для ферм. Из этого способа
сразу вытекает теорема о взаимности перемещений. Действительно:
= S ers = — esr = dsr.
Работы Риттера, Максвелла и его «дублеров» — Кремоны и
Мора — завершили стремительные поиски удобных и надежных
методов расчета ферм как статически определимых, так и статиче-
ски неопределимых. В 70-х годах XIX века этот расчет уже не вы-
зывает у проектировщиков никаких затруднений.
Глава 5
НОВЫЕ МЕТОДЫ
Появление тех общеизвестных методов расчета ферм, которые
в предыдущей главе были названы «классическими», дало возмож-
ность инженерам рассчитывать фермы обоих классов — и статиче-
ски определимые, и статически неопределимые. Однако это расчет-
ное «равноправие» ферм двух классов было лишь кажущимся, так
как степень трудоемкости их расчета совершенно различна.
414
Начать с того, что у ферм, статически определимых, расчет пред-
шествует подбору сечений, так что конструктор подбирает эти се-
чения, точно зная величины усилий в каждом элементе. У ферм ста-
тически неопределимых подбор сечений должен предшествовать
расчету, т. е. этими сечениями необходимо задаться предварительно,
не имея еще представления о величинах усилий. Поэтому последую-
щий расчет обычно показывает несоответствие между усилиями и
сечениями стержней, и их приходится изменять, а затем снова про-
изводить расчет. Эту операцию иногда необходимо повторять не-
сколько раз, прежде чем будет достигнуто достаточное соответствие
между усилиями и сечениями.
Далее сам процесс расчета статически неопределимой фермы не-
сравненно сложнее, чем для статически определимой, особенно при
наличии нескольких лишних связей, приводящем к системе совмест-
ных уравнений.
Наконец, если речь идет о расчете на подвижную нагрузку (а
эта задача для мостов является основной), то добавочное осложне-
ние в статически неопределимых фермах вызывается криволинейно-
стью (точнее, мнюгоугольностыо) очертания линий влияния, которое
не дает возможности так просто находить невыгоднейшее положе-
ние нагрузки и производить подсчет усилий, как в статически опре-
делимых фермах, где линии влияния состоят из двух—трех прямо-
линейных отрезков.
Но строительная механика — это наука, предъявляющая особую
требовательность в отношении простоты расчетных методов. Ее ис-
тория показывает, что недостаточно найти «какой-нибудь» расчет-
ный метод; необходимо позаботиться, чтобы он был «удобным», т. е.
сводился к ряду возможно более простых операций минимальной
трудоемкости. Всю историю строительной механики можно было
бы условно трактовать, как историю поисков удобных расчетных
приемов, настолько важное место занимает в ней стремление к
сниже'нию трудоемкости расчетов. Разумеется, с общим ростом ма-
тематической культуры инженеров изменяется оценка «трудности»
расчетов; приемы, затруднявшие передовых инженеров 100 лет на-
зад, теперь не кажутся трудными рядовому технику. Но тенденция
к упрощению расчетных приемов продолжает существовать и веро-
ятно никогда не исчезнет. Если перед инженером имеются два ва-
рианта сооружения, более или менее равноценные по всем показа-
телям, но с резко различной степенью трудоемкости расчета, он
обычно предпочтет вариант, допускающий более простой расчет.
Именно этим приходится объяснять явное предпочтение строи-
тельству статически определимых ферм в последней четверти XIX
века и потерю вкуса к статически неопределимым фермам. Создает-
ся своеобразное положение, которое уже отмечалось в исторической
литературе: пока инженеры вообще не умели рассчитывать фермы,
они строили исключительно статически неопределимые фермы;
когда же им указали, как надо такие фермы рассчитывать, они пе-
рестали их применять. Этому несомненному факту не противоречит
продолжавшееся до конца века применение двухраскосных ферм,
415
хотя в быстро убывающем количестве; дело в том, что расчет та-
ких ферм осуществлялся путем разложения на простые решетки,
т. е. их рассчитывали как статически определимые. Зато совершен-
но исчезают неразрезные балочные фермы, а арки с затяжкой или
двухшарнирные возводятся единицами.
Ввиду такого различия в подходе мы рассмотрим дальнейшую
историю расчета ферм раздельно для обоих классов, начав со ста-
тически определимых.
Применение ферм в мостостроении поставило перед инженерной
наукой очередную задачу — расчет ферм на подвижную нагрузку.
Эту задачу пытался разрешить еще Журавский, , но это ему не
удалось, и решение затянулось на многие годы, пока не было най-
дено в методе линий влияния.
Важнейшая в строительной механике методика построения и
применения линий влияния зародилась значительно раньше, чем
обычно полагают. Еще в 1854 г. Бресс [22] составил таблицы «чисел
влияния» для распора и опорных моментов бесшарнирной арки,
вполне отчетливо высказывая идею их использования путем нало-
жения отдельных сил. Мы уже отмечали в очерке втором, что Бресс
вообще очень широко применял принцип независимости действия
сил, вытекающий из линейности основных уравнений строительной
механики. В этом направлении он значительно опередил свой век,
и потому его приоритет был забыт так же основательно, как и в
большинстве других задач, для которых он дал первое решение.
Правда, Бресс не построил графика чисел влияния, т. е. самой «ли-
нии влияния».
Через 13 лет после Бресса линии влияния для балки с заделан-
ными концами построил Винклер [119] (1867); в1868 г. он построил
их для арки, доведя до конца идею Бресса четырнадцатилетней дав-
ности и заслужив за это в немецкой литературе славу изобретателя
линий влияния.
Любопытно, что все эти первые попытки построения линий влия-
ния относились только к статически неопределимым системам, и
прошло еще много лет, прежде чем додумались до их применения
к статически определимой балке (Френкель [141], 1876). После этого
перейти к балочной ферме было уже нетрудно, так как метод мо-
ментных точек фактически сводил задачу расчета фермы к расчету
простой балки. К началу 80-х годов построение и применение линий
влияния для статически определимых ферм было уже достаточно
широко известно.
Совокупность всех этих расчетных приемов: диаграммы Макс-
велла—Кремоны, метода моментных точек и метода расчета по ли-
ниям влияния, давала настолько широкие возможности расчета ста-
тически определимых ферм любого типа и в любых условиях (и
притом ценой малой трудоемкости), что задачу такого расчета к
концу 80-х годов можно считать доведенной до конца. Неудивитель-
но, что последующие десятилетия добавили к этому вопросу мало
нового.
416
В сущности основные усилия в этот последующий период (при-
менительно к статически определимым фермам) были направлены
на расчет сложных ферм этого класса, структурные особенности ко-
торых заключаются в том, что они не образованы из треугольников.
Ввиду этого расчет их по способу вырезания узлов или по способу
моментных точек приводит к совместным уравнениям. Этот резуль-
тат настолько неприятен, что нередко высказывается суждение о
«^неприменимости» этих способов к расчету таких ферм, что конечно
неправильно, и только подтверждает нашу мысль о нетерпимом от-
ношении инженеров к расчетным осложнениям. Необходимо при-
знать, что такие сложные статически определимые фермы почти не
нашли применения в строительстве, так как не обладали никакими
преимуществами перед простыми фермами, образованными из тре-
угольников. Поэтому изыскание удобного метода их расчета состав-
ляло несколько отвлеченную, хотя и очень интересную задачу. Для
ее решения было предложено несколько приемов: одни сводились к
обобщению метода моментных точек (Мюллер-Бреслау [142], 1887;
Абрамов [143], 1935); другие применяли новую идею временного
изменения схемы фермы с последующим исправлением этой замены
(метод замены стержней Геннеберга [144], 1886, метод замены свя-
зей, 1901): третьи использовали в разных вариациях «метод лож-
ного положения». Мы не останавливаемся на этих методах именно
вследствие малой практической актуальности самой задачи.
В отличие от теории статически определимых ферм, доведенной
еще в конце прошлого века до совершенства, история расчета ста-
тически неопределимых ферм не остановилась на методе Максвел-
ла—Мора и далека от завершения и в наши дни. Причиной этого
была, как сказано, высокая трудоемкость расчета таких ферм, пре-
пятствовавшая практическому внедрению его в строительство в
течение долгих лет. Автор вспоминает, что всего лет 25 назад к не-
му обратились инженеры одной крупной строительной организации
с просьбой прочесть им несколько лекций о расчете статически не-
определимых ферм, настолько мало был еще тогда известен этот
расчет в среде инженеров-строителей.
Интересно, что расчет статически неопределимых ферм в ряде
случаев сопряжен со специфической трудностью. Если увеличить
площадь сечения одного лишнего стержня, оставив сечения всех
прочих стержней неизменными, то усилие в этом стержне возрастет;
если уменьшить его сечение, то уменьшится и усилие (наподобие
труб водопровода, по которым протекает тем больше воды, чем
больше их сечение). При малых размерах сечения изменение его
приводит к быстрому изменению усилия; но при достаточно боль-
ших размерах сечения достигается стабильность усилия, и на его
величину не влияет даже значительное изменение размеров сечения.
Напряжение в лишнем стержне также является функцией сечения,
асимптотически убывающей до нуля при росте сечения. Эти законо-
мерности для фермы с одним лишним стержнем (например, арки
с затяжкой) представлены на принципиальном графике рис. 50. Ес-
ли поэтому напряжение в лишнем стержне оказалось слишком вы-
27 С. А. Бернштейн
417
Рис. 50. Зависимость уси-
лия и напряжения в лиш-
нем стержне от площади
его сечения
соким, то в некоторых случаях снизить его до нужной величины воз-
можно только путем увеличения сечения в несколько раз, а это мо-
жет оказаться неосуществимым с конструктивной точки зрения.
В других случаях может оказаться недостижимым поднятие напря-
жения до допускаемой нормы, так как даже уменьшение площади
сечения до нуля, т. е. полное устранение стержня, не приводит к це-
ли. Незнакомство с этой особенностью статически неопределимых
ферм способно вызвать недоразумения. Так, в одной американской
книге по расчету арочных ферм, вышедшей в 20-х годах нашего
столетия, мы нашли недоуменные жало-
бы на трудность расчета арки с затяж-
кой: автор указывал с удивлением, что,
уменьшая избыточные размеры сечения
затяжки, можно дойти до полного ее
вырождения и обращения арки с затяж-
кой в простую балочную ферму. Причина
этого ясна из графика рис. 50; она выте-
кает как частный случай из известной
теоремы Мориса .Леви о невозможности
обеспечить для лишних стержней напря-
жения заданной величины.
Важнейшей попыткой устранить прак-
тические неудобства метода Максвелла—
Мора следует считать «метод заданных
напряжений». Он был впервые предло-
жен в 1928 г. немецким инженером Гей-
маном [145] и получил значительное раз-
витие в целом ряде работ отечествен
. Рабинович [146], К М. Хуберян [147],
Ю. А. Радциг [148] и др.). Метод этот состоит в том, что мы за-
даемся не размерами сечений,. а величинами напряжений во
всех основных стержнях, после чего усилия в лишних стержнях
определяются из разделенных уравнений без необходимости сов-
местного решения системы канонических уравнений. Крупным до-
стоинством этого метода является его однократность, так как юн пе
требует повторных пересчетов. Основной его недостаток в том, что
его затруднительно применить к важнейшей задаче расчета ферм
на подвижную нагрузку.
Появление новых расчетных идей, связанных с учетом пластич-
ности материала и переходом на принцип расчета по предельному
состоянию, пробудило естественные надежды, что этот путь позво-
лит дать более простой и удобный способ расчета статически неоп-
ределимых ферм. Для этого казалось достаточным найти предель-
ные усилия в лишних стержнях исходя из заданных для них раз-
меров сечений, а затем рассчитать совокупность основных стержней,
образующих статически определимую систему, на совместное дей-
ствие предельной нагрузки и предельных усилий в лишних стерж-
нях. Хотя этот путь можно было применить только к неподвижной
нагрузке, но он казался очень многообещающим. К сожалению, эти
ных ученых (nood). И. М
418
надежды потускнели, когда проф. И. М. Рабинович [149] обратил
внимание на падение несущей способности сжатых стержней после
потери устойчивости, а автор настоящей книги доказал эксперимен-
тально и теоретически [150], что это падение несущей способности
сжатых стержней эквивалентно их хрупкому излому, т. е. мгновен-
ному выходу из строя. Ввиду этого оказалось, что расчет ферм по
предельному состоянию возможен лишь в том случае, если в про-
цессе перехода фермы от рабочего к предельному состоянию ни
один сжатый стержень не потеряет устойчивости. Однако этот слу-
чай для ряда схем ферм вообще не может иметь места. За послед-
ние годы появилась интересная работа проф. Н. С. Стрелецкого
[151], пытающаяся обойти это принципиальное затруднение.
В результате приходится признать, что задача расчета статиче-
ски неопределимых ферм до сих пор не имеет еще достаточно удоб-
ного решения, в особенности для случая подвижной нагрузки, и
представляет интересное и благодарное поле для научной деятель-
ности.
9 Ч Е г Е ЧЕТВЕРТЬ! Г
ИСТОРИЯ РАСЧЕТА НЕРАЗРЕЗНОЙ БАЛКИ
«Почему дерево, чем оно
длиннее, тем слабее, и больше
прогибается при подъеме его?»
Аристотель. Проблемы
механики, гл. XVII
Глава 1
ПЕРВЫЕ ПОПЫТКИ РАСЧЕТ*
Неразрезная балка играла и до сих пор играет в строительной
механике своеобразную роль пробного камня: всякий новый метод
расчета статически неопределимых систем ичн вариант такого мето-
ла, или графическое построение в первую очередь и обязательно
проверялись на нерасоезной балке. Причина такого предпочтения
заключается, очевидно, в том, что из всех статически неопределимых
систем неразрезные пал.ат обладают наибольшей простотой и зако-
номерностью образования при любом числе лишних неизвестных.
Ввиду этого рассказать историю расчета неразрезных балок
значит в сущности рассказать историю расчета статически неопре-
делимых систем вообще А так как такой расчет обязательно связан
410
с вычислением перемещений, то нам придется говорить и об исто-
рии методов вычисления перемещений. Таким образом, в этом очер-
ке мы рассматриваем очень широкий круг вопросов, хотя по загла-
вию он может показаться узким и специальным.
Если не считать свода, за которым в течение полутора столетий
ученые не желали признавать специфики, свойственной статически
неопределимым системам и который упорно пытались рассчитывать
с помощью уравнений равновесия, сдобренных сомнительными ги-
потезами, то неразрезная балка является первой статически неопре-
делимой системой, за которой признали это свойство, первой такой
системой, которую попытались рассчитать, и первой системой, ко-
торую действительно сумели рассчитать правильно. А первым, кто
обратил внимание на неразрезную балку, был основоположник уче-
ния о прочности Галилей.
В «Беседах» Галилея приводится очень поучительный рассказ,
вызывающий недоумение собеседников: на некоем строительстве за-
готовленная впрок мраморная колонна была уложена на две де-
ревянные опоры, расположенные вблизи ее концов. По истечении
нескольких месяцев строитель, опасаясь за прочность колонны,
подвел под ее середину третью опору. После этого колонна немед-
ленно треснула над средней опорой. Галилей правильно объясняет
причину печального исхода такого «усиления»: старые опоры успе-
ли обмяться и осесть, а потому колонна легла не на три опоры, а
на две — среднюю и одну из крайних. Половина длины колонны об-
разовала консоль, которая и переломилась у средней опоры. Дейст-
. PZ2
вительно, изгибающии момент в этом сечении равен --- , если
/ — длина всей колонны; когда же колонна была оперта на две
опоры вблизи концов, то наибольший момент имел меньшую вели-
Р(1~ 2а)2
чину -------, где а — расстояние от края колонны до центра кон-
цевой опоры. Таких формул у Галилея, разумеется, нет, и он огра-
ничивается качественной оценкой.
Этот рассказ интересен в двух отношениях. Во-первых, он пока-
зывает, что Галилей чувствовал, какую опасность для неразрезной
балки таит возможность осадки опор. Во-вторых, он дает первый в
истории пример аварии, которая вызвана неудачным усилением.
Уместно подчеркнуть еще одну особенность рассказа Галилея.
Его интересует не то, как работала колонна в первом благополуч-
ном этапе, а только то, как она разрушилась. Во всех немногочис-
ленных рассмотренных задачах о прочности Галилей остается верен
себе и изучает всякое тело только в состоянии разрушения. Мы уже
неоднократно подчеркивали, что именно авторитету Галилея обяза-
на строительная механика своим неуклонным курсом предельного
состояния на протяжении почти двух последующих столетий.
Следующее по времени упоминание о статически неопределимой
балке мы находим у Мариотта [7], почти через полвека после смерти
Галилея. Мариотт исследовал экспериментальным путем балку с
двусторонней заделкой, загруженную в середине пролета, и нашел,
420
что ее прочность в 2 раза выше, чем у балки, опертой по концам.
Как известно, это соответствует теоретическому решению, так как
Р1
наибольший изгибающий момент в первом случае равен— , а во
8
Р1 тт
втором — . Надо отметить,
впрочем, что такого четкого соответ-
ствия не получилось бы, если бы Мариотт испытывал балки из вяз-
кого материала, например железа. К счастью для себя, он работал
только с хрупким материалом — стеклом, для которого закон Гука
можно считать справедливым вплоть до разрушения. Правда, через
несколько десятилетий Мушенбрук [14] подтвердил правильность
наблюдения Мариотта из опыта над деревянными стержнями. Ве-
роятно, он брал хорошо высушенный дуб или бук, потому что в XIX
веке Барлоу [152] также на основании опытов с деревянными стерж-
нями опровергал данные Мариотта и Мушенбрука и утверждал, что
соотношение прочностей составляет не 2, а только 1,5. Возможно,
что в опытах Барлоу не была достигнута полная заделка концов.
После Мушенбрука мы не встречаем больше ни одного рассуж-
дения о статически неопределимых балках на протяжении всего
XVIII века, вплоть до самого его конца. Но зато в конце века по-
является первая попытка расчета, о которой до сих пор не упомина-
лось в исторической литературе.
Эта попытка содержится в книге Жирара [12], вышедшей в
1798 г. Бури Французской революции к этому времени уже отгре-
мели, но от них еще уцелела своеобразная терминология. В прило-
женном книге протоколе заседания Национального института на-
ук и искусств от «11 вентоза 6-го года» изложено, как «гражданин
Прони» сообщил, что ему и «гражданину Кулону» было поручено
ознакомиться с этой книгой, которая им очень понравилась.
Жирар понимает, что статически неопределимую балку нельзя
рассчитать без учета ее деформации. Поэтому он применяет анали-
тический метод вычисления перемещений, основанный на прибли-
жу М
женном уравнении т. е- принимает гипотезу малых пере-
мещений, которая к концу XVIII века постепенно начинает нахо-
дить приверженцев.
Жирар рассматривает две задачи: балку с двусторонней задел-
кой и балку с заделкой на одном конце и шарнирной опорой на дру-
гом. В обоих случаях нагрузкой является сила в середине пролета,
и в обоих случаях он принимает, что загруженное сечение не может
поворачиваться, так что в нем касательная к линии прогиба гори-
зонтальна. Для первой задачи — балки с двусторонней заделкой —
это верно в силу симметрии схемы, и потому Жирар получает пра-
Р1
вильное выражение опорных моментов и момента под грузом: — .
8
Но для второго случая это, очевидно, неверно, так как схема несим-
метрична (рис. 51). Условие горизонтальности касательной под
грузом приводит Жирара к равенству моментов под грузом и в
28 С. А. Бернштейн
421
Pl
заделке, величина которых получается равной —. Как известно,
момент в заделке имеет в действительности величину-^-Р/, а момент
5
под грузом —
Р1.
Рис. 51. Расчет стати-
чески неопределимой бал-
ки по Жирару
Таким образом, первая попытка расчета привела лишь к частич-
ному успеху. Однако ошибочность решения второй задачи наводит
на любопытные соображения. С точки зрения современного расчета
по состоянию предельного равновесия
(с учетом пластических деформаций),
вторая задача решена Жираром совер-
шенно правильно, так как он рассмат-
ривает балку в состоянии, когда опорный
и пролетный моменты стали равными
между собой. В очерке втором мы уже
отмечали неожиданное сходство расчет-
ных методов XVIII века и наиболее пе-
редовых современных расчетных прие-
мов. Теперь мы встречаемся еще раз с таким совпадением. Разу-
меется, здесь это совпадение носит случайный характер, так ка*<
решение Жирара основано на совершенно произвольной и невер-
ной гипотезе. Поэтому мы останавливаемся на этом только для
того, чтобы отметить условный смысл понятия правильности ре-
шения, если оно основано на условных допущениях: решение Жи-
рара, которое в конце XIX века вызвало бы только презритель-
ную усмешку со стороны последователя Навье, может теперь
возбудить гораздо более внимательное отношение.
Глава 2
ПЕРВЫЙ РАСЧЕТ НЕРАЗРЕЗНОЙ БАЛКИ
Работой Жирара заканчивается «предистория» статически неоп-
ределимых балок. Его работа была напечатана, когда Наполеон
одерживал свои первые победы над австрийцами в Северной Ита-
лии. Следующая работа, с которой начинается собственно истори-
ческий период, появилась в 1808 г. в Берлине, в пору наивысшего
блеска Наполеоновской империи и полного разгрома Пруссии.
Это был 2-й том «Курса статики твердых тел» Эйтельвейна [65],
президента Берлинской строительной академии. Эйтельвейн решил
задачу о двухпролетной неразрезнон балке, загруженной собствен-
ным весом и одним сосредоточенным грузом в произвольной точке
каждого пролета. Длины пролетов и величины грузов он принимает
различными, так что схема несимметрична (рис. 52).
422
Для решения этой задачи (такой простой с современной точки
зрения) Эйтельвейн имеет в своем распоряжении только один ана-
литический метод вычисления перемещений, которым пользовался и
Жирар. Но Эйтельвейн не делает никаких гипотез. Он составляет
четыре уравнения изгибающих моментов по числу участков, дваж-
ды их интегрирует и получает
четыре уравнения линии прогиба
с восемью произвольными пос-
тоянными и тремя неизвестными
реакциями. Для определения
этих 11 величин он составляет
три опорных условия, шесть ус-
ловий сопряжения под грузами и
на средней опоре и два уравне-
ния равновесия и решает совмест-
но все 11 уравнений. В резуль-
тате он получает готовые выра-
жения опорных реакций, кото-
рые имеют, конечно, очень
сложный вид. Так, левая реакция
(в подлинных обозначениях)
Рис. 52. Неразрезная балка,
рассчитанная Эйтельвейном
балки по рис. 52 выражается
Q = [/(« — а) (2се — ас — а2)Р +
с(Ь — с) (е — b}(b + с — 2е) Р' +
-|- J- cef (с2 — Зсе — е2) G].
Здесь G — погонный вес. Характерно, что в этом решении еще
совершенно отсутствует понятие об основной системе; уравнения
равновесия и деформаций решаются совместно. Нетрудно предста-
вить себе, как велика трудоеглкость решения задачи пю способу Эй-
тельвейна. Очевидно, она4 будет быстро возрастать с увеличением
числа пролетов и числа грузов в каждом пролете. Так, для расчета
четырехпролетной балки с тремя грузами в каждом пролете придет-
ся решать совместно 37 уравнений со столькими же неизвестными.
Теперь эта задача требует совместного решения всего трех уравне-
ний с тремя неизвестными.
Математик считает задачу решенной, когда указан принципиаль-
ный путь решения. Эйтельвейн дал даже больше: он выполнил ре-
шение для определенной схемы и вывел готовые формулы реакций.
И тем не менее для инженера такое решение нельзя признать при-
годным, и не приходится удивляться, что правильное решение Эй-
тельвейна в течение десятилетий не находило применения. Оно
чересчур сложно, непомерно трудоемко. Разумеется, теперь инжене-
рам приходится рассчитывать системы, приводящие даже не к де-
сяткам, а к сотням совместных уравнений. Но не надо забывать,
что, во-первых, уровень математического развития современных ин-
женеров неизмеримо выше, чем у их предшественников начала про-
шлого века, а во-вторых, что должно существовать некоторое ра-
28*
423
зумное соответствие между степенью сложности рассчитываемой
системы и степенью сложности расчетного метода. Для расчета та-
кой сложной системы, как каркас 30-этажного здания, «не обидно»
решить систему из нескольких десятков уравнений, но применить
столь же громоздкий расчетный аппарат для четырехпролетной не-
разрезной балки показалось бы неоправданным даже современно-
му инженеру, не боящемуся сложных расчетов. Вот почему в такой
прикладной науке, как строительная механика, недостаточно ука-
зать правильный способ расчета; надо дать возможно более простой
и удобный метод расчета, и только после этого проблема может
считаться разрешенной. Эйтельвейн выполнил первое условие, но
не выполнил второго.
Необходимо подчеркнуть еще одну особенность расчета Энтель-
вейна: он полностью основан на рассмотрении действительного,
рабочего, состояния балки. Тем самым этот расчет представляет
одну из первых ласточек новой эры в строительной механике, одно-
го из предвестников реформы Навье. Мы показали в очерке втором,
что первым предвестником были труды Кулибина 1772—1775 гг.
Проходит еще 18 лет. Наполеон давно умер в изгнании, во Фран-
ции опять правят Бурбоны. В истории Европы произошли крупней-
шие события. Но расчет неразрезной балки за эти бурные 18 лет
не сдвинулся с места, к нему вообще никто не обращался. Эти 18
лет отделяют книгу Эйтельвейна от первого издания курса лекций
Навье [18] 1826 г. Навье рассчитывает неразрезную балку почти в
точности так же, как Эйтельвейн, но ни словом о нем не упоминает.
Есть все основания считать, что Навье вообще не был знаком с
работой прусского профессора и самостоятельно встал на тот же
путь, которым шел Эйтельвейн. Но любопытно, что и в позднейших
исторических обзорах честь первого расчета неразре^пой балки не-
изменно приписывается Навье. Приоритет Эйтельвейна был впервые
восстановлен проф. И. М. Рабиновичем1. На решении Навье следу-
ет остановиться несколько подробнее и начать с примененного им
способа нахождения линии прогиба простой балки.
Пусть простая балка несет сосредоточенный груз в произвольной
точке С. Навье полагает сечение С заделанным (как делал и Жи-
рар), ищет линию прогиба каждой ветви, как консоли, загружен-
ной реакцией на свободном конце, и затем выравнивает балку из
условий равенства прогибов и углов наклона. Очевидно, этот прием
не хуже всякого другого. В случае более сложной нагрузки (напри-
мер, сплошной равномерной на участке балки) Навье полагает за-
деланным сечение под центром тяжести нагрузки и применяет преж-
ний прием. По-видимому, этот путь и привел его к высказыванию
грубо ошибочного утверждения, о котором мы говорили в очерке
первом, якобы опасное сечение балки всегда находится под цент-
ром тяжести нагрузки. После этого Навье переходит к статически
неопределимым балкам. Балку с заделкой и шарнирной опорой он
рассчитывает правильно, отбрасывая шарнирную опору и находя
1 Проф. И. М. Рабинович, Основы новейших методов расчета рамных
систем, ч. 1, Госстройиздат, 1933, стр. 11.
424
величину реакции из условия отсутствия прогиба на конце консоли.
Таким образом, у Навье уже есть понимание необходимости разде-
ления условии равновесия и условий деформации, которого не было
у Эйтельвейна, т. е. зародыш идеи об основной системе.
Весьма своеобразен способ, каким Навье решал балку с двусто-
ронней заделкой. Он заменял одну из заделок на опору с консолью,
несущей на конце груз (рис. 53), величину которого он определял
из условия отсутствия угла поворота на опоре В. При этом он не
исключал из решения длину услов-
ной консоли я, так что и реак-
ция В, и условный груз X определя-
лись в функции а. Навье полагал,
что заделку вообще нельзя мыслить
сосредоточенной в одном сечении,
так как силы X и В обраща-
ются в бесконечность при я=0. По-
разительно, как Навье не • заметил
при этом, что произведение Ха
остается постоянным и выражает
Рис. 53. Расчет балки с дву-
сторонней заделкой по Навье
опорный момент в заделке.
При расчете неразрезной балки Навье ограничился значительно
более простой схемой, чем та, на которую в свое время отважился
Эйтельвейн: он взял двухпролетную балку с равными пролетами, с
грузами в серединах пролетов и без учета собственного веса. Для
расчета он полагал (по своему обыкновению) сечение над средней
опорой заделанным (хотя величины грузов неодинаковы) и прирав-
нивал нулю прогибы на крайних опорах. Это позволяло ему найти
и реакции, и угол наклона среднего сечения.
Мы уже знаем (очерк второй), что Навье дал первый расчет
двухшарнирной арки, где идея основной системы также чувствует-
ся достаточно ясно. Но очень важно отметить, что Навье впервые
отметил принципиальную разрешимость любой статически неопре-
делимой системы. Это высказано им в отношении именно неразрез-
рой балки: «Если жесткий нагруженный стержень оперт более чем
в двух точках, реакции опор неопределенны... Но если стержень
упруг, неопределенность полностью исчезнет».
Глава 3
УРАВНЕНИЕ ТРЕХ МОМЕНТОВ
Шли годы. Во всех странах Европы усиленно строились желез-
ные дороги; мостостроители особенно охотно применяли для желез-
нодорожных мостов неразрезные балки, но решением Эйтельвей-
на— Навье при этом не пользовались. Это точное решение было
совершенно не приемлемо по своей сложности, а ученые не утруж-
дали себя поисками более удобных способов в течение десятилетий,
несмотря на явную потребность в них. Чтобы выйти из положения,
425
строители-практики выработали упрощенный прием расчета нераз-
резных балок. Кем и когда этот прием предложен, установить не
удалось. Вероятно, он создавался постепенно, и имена его авторов
забыты. Но прием этот устойчиво держался до 60-х годов XIX века.
В основе его лежит допуще-
ние о горизонтальности касательной
к линии прогиба на промежуточ-
ных опорах. Если пролеты балки
равны между собой, нагрузка
Рис. 54. Приближенный рас-
чет неразрезной балки
распределена равномерно, и по кон-
цам балки имеются заделки, то это
допущение отвечает истине. В
этом случае, очевидно, каждый пролет можно рассматривать как
самостоятельную балку с двусторонней заделкой. Но этот прием
без смущения применялся и при неравных пролетах, и при наличии
шарнирных опор по концам, что, конечно, решительно неверно, но
зато подкупающе просто: реакции в крайних шарнирных опорах
принимаются равными % от нагрузки одного пролета. Так, для бал-
ки по схеме рис. 54 значения реакций слева направо можно напи-
сать сразу:
3 , / 5 । J
8 ql' ( 8 + 2
9 , ,9,3,
о о о
Это, конечно, чрезвычайно удобный способ, хотя весьма далекий
от точности — истинные значения реакций будут
31 , 52 , 58 , 52 , 31 ,
xql'^ql’liql'Mql’ttql
и соответственные отношения реакций, определенных приближен-
ным способом, к точным значениям равны
0,68; 1,21; 0,97; 1,21; 0,68.
Трудно признать такие расхождения терпимыми. Тем не менее
на протяжении десятилетий строители были вынуждены рассчиты-
вать неразрезную балку этим грубейшим способом. Несомненно,
в данном случае реальная потребность в точном и удобном способе
расчета существовала. Но, к сожалению, не всегда наука достаточно
охотно и торопливо отзывается на запросы жизни; неотзывчивость
строительной механики всегда приводит к излишнему расходу ма-
териала’.
1 В книге ГО. Вейсбаха [66] «Теоретическая и практическая механика», т. II,
1853 (русское издание Вольфа, 1861 г.) читаем по поводу этого приема расчета:
«Формулы, выведенные в предыдущих параграфах, основаны на предположениях,
не вполне точных для некоторых случаев; поэтому выводы оттуда получаемые
разнятся от действительных иногда на 10% и 20%. Но как при постройках раз-
меры, придаваемые частям, берутся всегда увеличенные против получаемых по
расчетам, то означенная выше неточность не может иметь влияния на прочность
постройки». Из приведенного выше примера видно, что ошибка может быть зна-
чительно более 20%.
426
Следующий этап в истории неразрезн-ой балки относится к па-
мятному 1848 г. и тесно связан с событиями, ознаменовавшими этот
год в истории человечества. Во время революционных боев восстав-
шего французского народа с правительственными войсками был
серьезно поврежден пятипролетный неразрезной мост через Сену
у Аньера. К восстановлению моста привлекли светило французской
науки — самого Клапейрона, который, по-видимому, впервые прак-
тически встретился при этом с неразрезной системой и заинтересо-
вался ее расчетом. Решать пятипролетную балку по способу Навье
было бы чрезвычайно сложно, и Клапейрон в поисках более удобного
пути набрел на счастливую мысль: принять за основную систему
разрезную схему, включив над промежуточными опорами шарниры.
Хорошо известно, в чем преимущества этой основной системы: она
взаимно изолирует пролеты, вследствие чего большое количество
побочных коэффициентов в канонических уравнениях обращается
в нуль. Клапейрон встал на тот путь, который впоследствии привел
к получению знаменитых уравнений трех моментов, но удивитель-
ным образом не сразу дошел до них. А произошло это потому, что
он принял двойную систему неизвестных: не только опорные момен-
ты подлежат определению в его первом методе, но и углы поворота
балки на опорах.
Уравнение трех моментов составляется для промежуточной опо-
ры балки и выражает четкое условие: взаимное равенство углов на-
клона касательной слева и справа от опоры. Первоначальные урав-
нения Клапейрона составлялись для каждого пролета (по два) и
выражали величину левого и соответственно правого опорного угла
поворота. Если обозначить эти углы через а и а', углы в основной
системе от нагрузки ар' и ар, левый и правый опорные моменты
М и то эти уравнения имели почти тривиальный вид:
Ml M'l , Ml , M'l
а = а---------------; а = а Ч-------------.
р 3EJ 6EJ р 6EJ 3EJ
Сейчас такие уравнения можно написать сразу, пользуясь графо-
аналитическим методом. Клапейрон выводил их аналитическим пу-
тем, и потому его вывод занимает почти две страницы формул и пре-
образований.
Непостижимо, как Клапейрон не заметил, что в этих уравнениях
углы исключаются, если рассмотреть пару смежных пролетов. Одна-
ко ему потребовалось 9 лет, прежде чем он усмотрел эту возмож-
ность. В таком виде число уравнений и неизвестных для расчета
неразрезной балки вдвое превышало число пролетов, но и это было
огромным успехом после метода Эйтельвейна — Навье.
Клапейрон не опубликовал этого первого своего решения, и мы
можем познакомиться с ним только в чужом изложении [153]. Уже
из этого можно заключить, что он не делал из него тайны и доста-
точно -охотно делился им со своими учениками и друзьями. Вообще
есть основания считать, что знакомое сочетание имен «Ламэ и Кла-
пейрон» не было случайностью. По-видимому, Клапейрон не очень
42"
любил публиковать свои работы, и нередко Ламэ побуждал его к это-
му и отчасти пропагандировал достижения своего друга. Поэтому
вполне вероятно, что Клапейрон дошел до идеи исключения углов
из своих уравнений, т. е. до настоящих уравнений трех моментов,
задолго до того, как его уговорили (с опозданием) опубликовать
этот окончательный и столь важный результат, и что он был изве-
стен в окружении Клапейрона значительно ранее. Вероятно, этим и
объясняется последовавшая далее загадочная история.
15 июня 1855 г. в Париже состоялось заседание Общества граж-
данских инженеров. Последним пунктом повестки стоял доклад ни-
кому неведомого инженера Берто. Повестка была перегружена, за-
седание затянулось, и доклад Берто хотели вообще снять с обсуж-
дения. Однако он очень настаивал, и ему дали самое минимальное
время, за которое он только успел сказать, что нашел новый способ
расчета неразрезных балок. Тогда его доклад решили перенести
на следующее заседание — 6 июля. Этот доклад был опубликован
[154]. Он содержит словесную формулировку уравнения трех
моментов для балки постоянного сечения под сплошной равномер-
ной нагрузкой ( без всякого вывода или обоснования) и напоминает
авторскую заявку. Создается впечатление, что Берто спешил закре-
пить за собой славу открытия этого уравнения.
Берто сам был мостостроитель, путейский инженер. По-видимо-
му, он был учеником Клапейрона или по крайней мере вращался
в непосредственном его окружении. И тут невольно возникают два
вопроса.
1. Почему Берто, будучи путейским инженером, так добивался
постановки своего доклада во второстепенном по значению Обще-
стве гражданских инженеров, а не в Школе дорог и мостов?
2. Почему Берто, сумев блестящим образом разрешить одну из
важнейших задач строительной механики, за всю дальнейшую
жизнь не написал больше ни одной работы, и его имя навсегда исче-
зает из летописей науки?
Пусть каждый читатель этой книги попробует сам ответить на
эти вопросы и оценить роль Берто в соответствии со своим ответом.
Прошло еще 2 года. На страницах самого авторитетного фран-
цузского журнала «Известия Академии наук» в 1857 г. появляется
небольшая статья Клапейрона [155], где он излагает способ расчета
неразрезных балок с помощью уравнений трех моментов. В этой
статье перечислены многие предшественники Клапейрона, изучав-
шие неразрезную балку, но Берто среди них не упомянут.
К числу выше поставленных вопросов можно добавить еще один:
почему Клапейрон не упомянул о приоритете Берто, и почему Бер-
то не выступил с протестом против этого? Как бы то ни было, в
1855—1857 гг. уравнение трех моментов стало общеизвестным и
немедленно вошло в расчетную практику, так как инженеры сразу .
оценили огромные преимущества этого замечательного по своему
остроумию приема, впервые сделавшего расчет неразрезной балки
428
общедоступным. В позднейшей литературе за уравнением трех мо-
ментов прочно установилось название «уравнения Клапейрона»1.
Была ли этим восстановлена, или, наоборот, нарушена истори-
ческая справедливость?
Клапейрон (1779—1864)
В том же 1857 г. Бресс самостоятельно получил то же уравнение
и излагал его в своих лекциях в Школе мостов и дорог. Он опубли-
ковал его [114] в 1859 г. со ссылкой на Клапейрона и без упомина-
ния о Берто. А в 1858 г. инженер Мадрасской железной дороги в
Индии Хеппель [156], не имея в своем распоряжении литературы,
самостоятельно вывел уравнение трех моментов для расчета пяти-
пролетного моста. Когда идея созрела и когда в ней есть практиче-
ская потребность, она может одновременно осенить несколько умов
в разных концах земного шара.
1 Это название привилось не сразу. Коллиньон, в своей книге, изданной в
Петербурге в 1860 г. (Collignon, Ports, metalliques a poutres droites continues),
считает Клапейрона автором первого метода (с неисключенными углами), а
уравнение трех моментов приписывает Брессу (не Берто’). В курсе сопротивле-
ния материалов Беланже 1862 г. утверждается, что это уравнение впервые дал
Клапейрон. В этой книге также нет упоминания о Берто.
Глава 4
ПОИСКИ УДОБНОГО МЕТОДА ВЫЧИСЛЕНИЯ ПЕРЕМЕЩЕНИЙ
И Берто, н Клапейрон дали выражение уравнения трех моментов
только для одного частного случая — сплошной равномерной -на-
грузки на балке. Для дальнейшего обобщения необходимо было
О. Мор (1835-1918)
научиться вычислять углы поворота на опорах простой балки от
произвольной нагрузки, так как именно эти углы входят в правые
части уравнений.
Классический аналитический метод был крайне неудобен для ре-
шения этой задачи. Действительно, он давал гораздо больше, чем
430
для нее было нужно, — уравнение всей линии прогиба, из которой
требуется определить только углы поворота по концам, — и за эту
избыточную полноту решения приходилось расплачиваться чрезмер-
ной трудоемкостью вычислений, от которой лишь частично избавлял
метод интегрирования Клебша. Необходимо было найти прямой
метод вычисления, позволяющий сразу получить нужные переме-
щения, — в данном случае углы поворота. От нахождения такого
прямого метода зависела возможность практического расчета лю-
бой статически неопределимой системы, работающей на изгиб.
В настоящее время мы применяем для этого формулу Мора —
Максвелла в аналитической или графоаналитической форме. Для
балок столь же простое решение дает графоаналитический метод
?4ора. Но было бы ошибкой думать, что оба эти приема родились
внезапно и не имели предшественинков.
В действительности, такие предшественники были, хотя они за-
быты и, если можно так выразиться, «забиты» формулой Мора. Мы
считаем уместным, хотя бы отчасти, воскресить забытую историю
поисков удобного метода вычисления перемещений, которые завер-
шились в работах Мора.
Первый шаг сделал в 1854 г. Бресс [22], и мы уже приводили
в очерке втором выведенные им формулы для вычисления переме-
щений криволинейного стержня. Применительно к прямому стерж-
ню (балке) эти формулы дают выражение прогиба и угла поворота
в виде
(* дТИ »
у = хч>(1 —I—— dx,
о
С Л4 и
О
где <р0— угол поворота на левой опоре, с которой совпадает начало
координат. Несомненно, эти формулы представляют очень значи-
тельный прогресс по сравнению с аналитическим методом двукрат-
ного интегрирования, так как они дают возможность прямого вы-
числения прогиба и угла поворота в любом сечении балки, не тре-
буют определения произвольных постоянных и заменяют двукрат-
ное интегрирование однократным. По существу в этих формулах
полностью заключен будущий графоаналитический способ Мора,
так как первая из них, очевидно, выражает момент от фиктивной
М
нагрузки —,
а вторая — поперечную силу от той же нагрузки. Но
хотя Бресс был первым ученым, которому пришла в голову счаст-
ливая мысль изображать закон изменения изгибающего момента в
виде графика (эпюры), но он не сумел дать графостатическое ис-
толкование своих формул. Сейчас нам даже странно представить
себе, что для этого потребовалось еще 14 лет: графоаналитический
метод Мора был опубликован в 1868 г.
29*
431
Идея использования эпюры моментов как инструмента для вычис-
ления прогиба, т. е. идея графоаналитического метода, возникла
однако за 13 лет до Мора: впервые ее применил русский инженер
Беспалов [20] в 1855 г. Это имя давно забыто и ни разу не встреча-
лось нам ни в одной книге по строительной механике. Маленькая
книжечка Беспалова, изданная в год Крымской войны, содержит
Рис. 55. Способ „перемноже-
ния эпюр" по Беспалову
(1855)
элементарное изложение основных
задач сопротивления материалов,
полностью стоящее на уровне
своего времени, но не представ-
ляющее ничего оригинального,
кроме нескольких страниц (стр. 26—
30), где изложен совершенно не-
обычный прием вычисления проги-
ба консоли, основанный на методе
приравнивания работы внешних
и внутренних сил (как известно,
этот метод был предложен Клапей-
роном). Для вычисления работы
внутренних сил Ess* Беспалов
строит две эпюры: эпюру напря-
жения о и эпюру удлинения для
произвольного волокна по длине
консоли (рис. 55), а затем соче-
тает их в одну эпюру, откладывая
по оси абсцисс удлинения, а по оси
ординат напряжения. Беспалов без труда доказывает, что контур
этого нового графика очерчен по дуге параболы, а потому его пло-
щадь, выражающая работу, равна 2/3 ^max Отсюда он получает
правильное выражение прогиба консоли.
В этом приеме можно, пожалуй, увидеть зародыш будущего ме-
тода «перемножения эпюр», данного впоследствии Мюллером-Брес-
лау на основе формулы Мора. Беспалов первым догадался исполь-
зовать эпюры, т. е. графики внутренних усилий, для графоаналити-
ческого вычисления прогиба. И хотя примененный нм для этого
прием может показаться сейчас несовершенным, не надо забы-
вать, что эта мысль никому не приходила в голову ранее Беспалова,
и что после него прошли три десятилетия, прежде чем она была
применена в общем виде Мюллером-Бреслау (1884).
Через 3 года после Беспалова (работа которого, по-видимому,
осталась незамеченной и в иностранной, и даже в русской науке)
мы встречаем в курсе прикладной механики Магистра [157] новую
идею. Для того же случая консоли с грузом на конце Магистр полу-
чает формулу прогиба в виде
i
Р С 9
У = ~EJ-J Х dX’
о
* Множитель 72 У Беспалова пропущен.
432
используя уравнение Бресса, и вычисляет этот интеграл, как стати-
ческий момент фиктивных сил xdx. Магистр ссылается при этом
на Понселе, но без указания на источник, которого нам разыскать
не удалось. Кому бы ни принадлежала эта идея — Магистру
или Понселе, — она очень интересна, так как представляет еще
один подход к графоаналитическому методу. Но в проти-
воположность Беспалову, который исходит из эпюры, Магистр не
замечает, что треугольный график фиктивной нагрузки х, от кото-
рой он берет статический момент, представляет собой эпюру момен-
тов. Таким образом, идеи Беспалова п Магистра (или Понселе) как
бы взаимно дополняют друг друга; казалось бы достаточно было
положить перед собой на стол эти две книжки, раскрыв первую на
странице 26, а вторую на странице 537, чтобы додуматься до
графоаналитического метода. Но Мор додумался до него только
через 10 лет.
В истории строительной механики мы уже не раз отмечали
случаи, когда тот или иной ученый стоит перед готовым созревшим
открытием и не видит его. История поисков метода вычисления пе-
ремещений особенно богата примерами такой близорукости. Бресс
дал готовые формулы графоаналитического метода; Магистр пока-
зал их графостатический смысл, а Беспалов дал пример использо-
вания эпюр для вычисления прогиба. Предложение Магистра сразу
переводило задачу вычисления прогиба в область графической ста-
тики, где применение веревочного многоугольника для вычисления
статических моментов уже было к этому времени известно. И тем
не менее, когда Кульман выпустил в 1866 г. свою известную книгу
по графической статике [99], в которой он придал графическим
методам небывалую до этого общность и стройность, он не только не
перевел приема Магистра на графический язык, но безапелляцион-
но заявил, что задача вычисления прогибов балки навсегда останет-
ся недоступной для применения графических методов, так как эти
прогибы ничтожно малы по сравнению с длиной балки. Открытый
Мором двумя годами позже графический метод построения линии
прогиба с помощью веревочного многоугольника дал хороший урок
Кульману. Но, помимо оплошного утверждения Кульмана, самая
его мотивировка вызывает крайнее удивление: неужели Кульман не
знал, что продольный профиль проектируемой железнодорожной
линии вычерчивается инженерами в разных масштабах по верти-
кальной и горизонтальной оси, и что их, таким образом, ничуть не
смущает ничтожная разница вертикальных отметок по сравнению
с длиной линии?
После появления работы Мора 1868 г. [158], содержащей графи-
ческий метод построения линии прогиба (который вскоре же был
превращен в графоаналитический), дальнейшие открытия следуют
одно за другим. В 1874 г. Мор дает обобщение формулы Максвелла,
известное под названием формулы Мора — Максвелла [138], а в
1875 г. Кастилиано [159] публикует свою теорему. Все эти методы
вычисления перемещений мы считаем достаточно известными чита-
телю, и потому на них не останавливаемся.
433
Рис. 55. Способ „пере-
множения эпюр“ по Мюл-
Таким образом, задача нахождения удобного -метода вычисле-
ния перемещений была решена к началу 70-х годов.
Надо подчеркнуть, что вычисление перемещений путем непосред-
ственного интегрирования формулы Мора, несмотря на математи-
ческую простоту, все же не удовлетворило инженеров и применя-
лось неохотно, пока не был найден способ освободиться от этого
интегрирования. Первый такой способ дал Мюллер-Бреслау; он ос-
нован на условии линейности уравнения
момента от единичной силы и использу-
ет графическое представление моментов
в виде эпюр. Если — эпюра моментов
от единичной силы, линейная на рас-
сматриваемом участке, а Мр — эпюра
моментов от нагрузки (рис. 56), то по
Мюллеру-Бреслау интеграл Мора
J М\М dx (жесткость EJ опускаем) ра-
вен сумме произведений фиктивных реак-
ций от эпюры Мр на крайние ординаты
эпюры М\.
леру-Бреслау j' dx = .
Но и этот, несомненно, простой способ не нашел широкого рас-
пространения, и формуле Мора в течение нескольких десятилетий
/пришлось выдерживать трудную борьбу с ее конкурентом — теоре-
мой Кастильяно. Окончательную победу формула Мора смогла
сдержать только с помощью способа вычисления, данного молодым
советским инженером Верещагиным [161]. Этот способ хорошо изве-
стен: он сводит вычисление интеграла Мора к умножению площади
эпюры Мр на ординату линейной эпюры М^ находящуюся против
центра тяжести этой площади. Нетрудно установить переход от
приема Мюллера-Бреслау к приему Верещагина; но интересно, что
только последний получил сразу широчайшую популярность и со-
действовал быстрому освоению метода Мора в кругах инженеров-
строителей1.
Для балок вычисление перемещений графоаналитическим спо-
собом Мора получило в России широкое распространение немед-
ленно после его опубликования, приняв несколько своеобразную
трактовку «шести строк» (нагрузка, поперечная сила, изгибающий
момент, кривизна, угол поворота и прогиб), которая способствовала
глубокому пониманию существа этого метода и достаточно хорошо
известна читателям. Именно это понимание существа было причи-
ной того недоумения, с которым было встречено в наших научных
кругах наивное «открытие» американской науки 1930-х годов [162],
предлагавшее принимать за фиктивную нагрузку не эпюру мо-
ментов, а эпюру поперечной силы, причем из восторженного тона
1 Возможно, что этому способствовала самая форма способа Верещагина,
напоминавшая хорошо знакомый прием загружения линий влияния.
434
американских журналов можно было заключить, что обычный
графоаналитический метод Мора за океаном к тому времени еще
не был известен.
Глава 5
ЗАВЕРШЕНИЕ ТЕОРИИ НЕРАЗРЕЗНЫХ БАЛОК И НОВЫЕ МЕТОДЫ
Нахождение удобного метода вычисления перемещении устрани-
ло одно из главных осложнений, стоявших на пути расчета нераз-
резной балки. Но осталось другое осложнение, не менее серьезное:
при большом числе пролетов задача сводилась к системе совмест-
ных уравнений с большим числом неизвестных. Хотя эти уравнения
были трехчленными, но процесс их разрушения представлял доста-
точно трудоемкую и ненадежную в смысле точности операцию.
Дело в том, что решение совместных линейных уравнений сопря-
жено всегда с вычислением разностей больших чисел, а эта опера
ция во многих случаях крайне неблагоприятно отражается на точ-
ности вычислений. Ввиду этого значения свободных членов и коэф-
фициентов при неизвестных приходится вычислять с большим
числом знаков, чем сильно осложняется процесс решения, и тем нс
менее точность результата может оказаться невысокой. Этот во-
прос в строительной механике является поистине больным вопро-
сом, и на протяжении многих десятилетий история этой науки изо-
билует попытками избавиться от совместных уравнений при расчете
статически неопределимых систем. В сущности именно этим стрем-
лением порождено изобилие методов в современной теории расчета
рам. Ввиду важности этого стимула в развитии нашей науки уме-
стно привести убедительный пример.
Дана система канонических уравнении:
5Хг + 7Х3 4- 6Х3 -г 5Х4 - 23 ;
7Х2 + 10Х2 4- 8Х3 + 7Х> = 32 ;
(«X! + 8Х2+10Х3 -|- 9Х4 - 33 ;
5Х, 4- 7Х2 9Х3 г10Х4 = 31 ,
точное решение которой таково: Л'1 = Х9= X3 = X4= 1. Однако, если
подставить в уравнения значения
14,6; Х2 = — 7,2; Х3=— 2,5; Х4 = 3,1,
то они будут удовлетворены с точностью до Уз %, так как правые
части получат значения соответственно: 23,1; 31,9; 32,9; 31,1. Если
повысить требование точности до */зо% (0,00031), то уравнения удов-
летворяются такими значениями неизвестных:
Х1 = 2,36; Х2 = 0,18; Х3 = О,65; Х4 = 1,21,
435
а правые части соответственно будут равны: 23,01; 31,99; 32,99,
31,01.
Повысим точность еще в 10 раз, до Vsoo»- Тогда значения не-
известных будут таковы:
Xj = 1,136; Х2 = 0,918; Х3 = 0,965; Х4 = 1,021 ,
т. е. ошибка в их величинах против точных значений составляет от
2 до 14%, хотя правые части ничтожно отклоняются от заданных
значений:’23,001; 31,999; 32,999; 31,001. Из этого примера ясно, как
ненадежен может быть в смысле точности результат решения сов-
местных линейных уравнений. Разумеется, этот пример подобран
искусственно (хотя уравнения по структуре являются канонически-
ми, удовлетворяя условию взаимности коэффициентов); но нет
никакой гарантии в том, что уравнения, составленные для задан-
ной статически неопределимой системы, не обладают подобной ко-
варной породой, хотя бы и не в столь сильной степени. Поэтому
стремление строительной механики освободиться от совместных
уравнений объясняется не только постоянной тягой этой науки к
снижению трудоемкости вычислений, но и беспокойством за досто-
верность числовых результатов этих вычислений. В истории расче-
та неразрезной балки это стремление имело ярко выраженный и
многосторонний характер.
Первую такую попытку сделал Бресс, и она привела его к важ-
нейшему открытию. Получив одновременно с Клапейроном уравне-
ния трех моментов, Бресс задался целью выяснить, нельзя ли
уменьшить число неизвестных в уравнениях, если пренебречь влия-
нием удаленных пролетов. На этот путь его натолкнуло постоянно
проявлявшееся им стремление принять принцип независимости дей-
ствия сил. В данном случае оно привело его к идее загружения од-
ного единственного пролета балки. Результаты этого анализа он
опубликовал в 1859 г. в I томе своего курса прикладной механики
[П4] (глава III).
Бресс принял все пролеты, кроме одного, свободными от нагруз-
ки и приравнял левые части уравнений трех моментов нулю. Этот
хорошо известный нам прием показал ему, что опорные моменты в
незагруженных пролетах находятся в постоянном соотношении, че-
редуются по знаку и быстро убывают по мере удаления от загру-
женного пролета. Бресс вывел рекуррентную формулу этих отно-
шений моментов, которые впоследствии получили название фокус-
ных отношений, но он не заметил, что из постоянства их величин
вытекает наличие постоянных нулевых точек эпюры моментов в не-
загруженных пролетах. В данном случае его интересовала только
количественная оценка возможности пренебрежения влиянием уда-
ленных пролетов, которую он и получил.
Продолжая в последующие годы работу в том же направлении,
Бресс довел задачу до конца, и в 1865 г. в III томе своего курса
указал на существование этих нулевых точек. Тем самым он стал
основоположником нового важного метода в строительной механи-
ке метода моментных фокусов. Метод этот получил свое полное
436
развитие в позднейших работах Винклера [163], Кульмана [99] и
Мориса Леви [164], но, безусловно, ошибочно распространенное в
немецкой литературе мнение, приписывающее заслугу открытия
метода фокусов Кульману; эта заслуга всецело принадлежит
Брессу.
Одним из важнейших достоинств метода моментных фокусов
является, как известно, то, что он позволяет свести задачу к реше-
нию всего двух уравнений с двумя неизвестными (для каждого
загруженного пролета), т. е. совершенно устраняет все неприятно-
сти, связанные с решением совместных уравнений. Кроме того, он,
естественно, подсказывает мысль о графическом построении эпюры
моментов с использованием положения фокусных точек. Эта мысль
получила в дальнейшем широкое развитие, причем весь расчет ие-
разрезной балки удалось перевести на графический пут >. Из раз-
личных вариантов такого графического расчета автор считает
наиболее удобным и совершенным способ проф. Б. Н. Жемочкина
[165].
Чтобы не возвращаться более к имени Бресса, отметим здесь,
что он дал в 1854 г. общую постановку задачи расчета статически
неопределимых систем любого вида. Он показал, что число урав-
нений метода сил всегда равно числу лишних неизвестных, и что эти
уравнения будут линейными. Бресс очень широко использовал воз-
можности, даваемые этой линейностью уравнений. Он выразил
внутренние усилия и перемещения в виде линейной функции внеш-
них сил. ввел понятие чисел влияния (т. е. ординат линий влияния),
применил закон независимости действия сил и предложил приемы
группирования неизвестных и разложения нагрузки на симметрич-
ную и обратно симметричную составляющие. Таким образом, Брес-
са следут считать основоположником общей теории расчета ста-
тически неопределимых систем.
Последним вкладом Бресса в расчет неразрезных балок было
применение теории конечных разностей к решению уравнений трех
моментов для балки с равными пролетами и указание способа
построения объемлющей эпюры. Второй случай применения конеч-
ных разностей к расчету неразрезной балки мы находим в курсе
проф. И. А. Евневича [26] 1868 г. Евневич между прочим представил
в новой своеобразной форме задачу интегрирования дифференци-
ального уравнения изгиба для балки, несущей любое число сосре-
доточенных сил Рк, приложенных в точках с абсциссами хк :
Ж = х);
-ш») = т)]+=
EJ(y— ---?)] + Т
437
Где а — угол наклона касательной в начале координат. Этим пу-
тем он избавился от необходимости вычисления произвольных пос-
тоянных при любом числе сил. Но наиболее интересным результа-
том Евневича было составление уравнения трех реакций,
справедливого для равнопролетной балки при сплошной равномер-
ной нагрузке1:
+ - -6Q-
И. А. Евневич (1831—1Г03)
Здесь Q — нагруз-
ка одного пролета.
Евневич решал его
как уравнение в конеч-
ных разностях 2-го
порядка. Это уравне-
ние незаслуженно за-
быто в наши дни, как
и имя его автора. Это
тем более обидно, что
в курсе механики Кол-
линьона [111] (3-е изда-
ние 1885 г.) уравнение
трех реакций приписы-
вается испанскому ин-
женеру дон Пабло де
Альзола, книга которо-
го о расчете балок [166]
вышла в 1869 г., т. е. на
год позже курса Евне-
вича.
Открытие метода
моментных фокусов
вместе с новыми удоб-
ными методами вычис-
ления перемещений
окончательно устрани-
ло все трудности в деле
расчета неразрезной
балки. И, несмотря на это, судьба неразрезной балки как
строительной формы напоминает судьбу статических неопре-
делимых ферм: открытие удобного метода расчета совпада-
ет по времени с упадком популярности неразрезнон балки среди
строителей. Вообще последние десятилетня прошлого века пред-
ставляют период временного разочарования в статиче-
ски неопределимых системах всякого рода и явного пред-
почтения, отдаваемого системам, статически определимым. В этот
период мостовые фермы окончательно отказываются от сложной
решетки н приобретают простейшие треугольные схемы; в этот
1 Это уравнение справедливо п для несколько более общего случая.
438
период в США появляются абсурдные фермы с болтовыми шарнир-
ными узлами; в этот период особенно охотно возводятся трехшар-
нирные арки, вытесняя собой беошарнирные. И в этот период
неразрезная балка почти сходит со сцены, вытесняясь неожидан-
ным соперником — шарнирно-консольной многопролетной балкой,
часто именуемой балкой Гербера, метод расчета которой впервые
дал русский инженер Семиколенов [167].
Причина этого всеобщего охлаждения к статически неопреде-
лимым системам, наступившего именно в ту пору, когда, наконец,
был найден способ их расчета, не вполне ясна. Легко понять, по-
чему в предшествующую эпоху они, напротив, столь широко при-
менялись: это объяснялось стремлением увеличить надежность
сооружений добавлением избыточных связей, поскольку действи-
тельный характер работы сооружений еще оставался неясным для
строителей. Можно полагать, что увлечение статически определи-
мыми системами, наступившее впоследствии, обусловлено именно
тем, что характер их работы стал абсолютно ясен для инженеров
(чего нельзя было сказать про статически неопределимые системы),
и потому применение их связывалось с чувством полной уверен-
ности в их надежности при всех обстоятельствах.
Трудно сказать, как долго продолжалась бы эта «статически
определимая полоса» в строительстве, если бы не появление нового
строительного материала — железобетона.
По самой своей природе железобетон подсказывает применение
монолитных форм сооружений и чужд идее шарнира. Поэтому
появление железобетона оказалось сильнейшим стимулом для при-
менения статически неопределимых систем, а стало быть п для
развитиямстодов их расчета. Так еще раз на судьбу строительной
"механики оказала влияние технология строительных материалов.
' Последовавшие за открытием железобетона десятилетия пред-
ставляют любопытную картину борьбы нового со старым в строи-
тельной технике. Новым являлось логическое применение статиче-
ски неопределимых схем железобетонных сооружений; старым —
пережитки «статически определимой полосы» в строительстве, при-
вившей инженерам вкус и исключительное пристрастие к статиче-
ской определимости. Как и всегда бывает в такой борьбе, новое,
прогрессивное направление победило, и памятником этой борьбы
остались только отдельные уродливые сооружения вроде железо-
бетонных ферм или трехшариирных железобетонных арок. Инте-
ресно, что возрождение статически неопределимого строительства,
вызванное спецификой железобетона, распространилось и на преж-
ние материалы (сталь и даже дерево), из которых в последнее
время охотно возводят статически неопределимые системы.
Для неразрезной балки новый материал дал неограниченные
возможности применения, легко оттеснив конкуренцию шарнирно-
консольных балок. В связи с этим интерес к задаче расчета нераз-
резной балки ничуть не ослабел, хотя эта задача уже к 70-м годам
прошлого века могла считаться успешно разрешенной. Действи-
тельно, количество работ, посвященных этой теме, остается исклю-
439
чительно большим до последнего времени, и разобраться в этом
изобилии нелегко. Одни работы давали существенное дополнение
к методу Клапейрона — это были труды, позволившие учитывать
осадку опор и влияние их упругости (уравнение пяти моментов);
другие предлагали новые варианты решения основной задачи о
неразрезной балке. Число этик последних попыток особенно вели-
ко, хотя почти ни одна из них не привилась на практике.
Из них нужно упомянуть «теорему о двух моментах», данную
Морисом Леви [164] (1886), и «уравнение трех перемещений», по-
лученное А. А. Поповым [168] (1933) путем применения к нераз-
резной балке метода деформаций. Весьма существенным вкладом
в общую теорию расчета статически неопределимых систем яви-
лась разработка метода угловых фокусов (Жемочкин [169], 1929).
приложимого и к неразрезной балке.
Мы уже отметили, что неразрезная балка служит своеобразным
пробным камнем для всякого нового метода расчета статически
неопределимых систем. Поэтому именно к ней в первую очередь
были применены новые идеи расчета, возникшие из рассмотрения
пластических деформаций материала. Теоретический анализ по-
казал, что при наличии площадки текучести у материала рост из-
гибающих моментов в наиболее напряженных сечениях при высо-
ких нагрузках сперва замедляется, а затем и вовсе останавливает-
ся, причем моменты в этих сечениях приобретают постоянную пре-
дельную величину, а сами сечения не участвуют в восприятии даль-
нейшего роста нагрузки и играют роль шарниров с постоянной
величиной момента. Если число таких упруго-пластических шарни-
ров станет равным степени статической неопределимости балки, то
в дальнейшей стадии работы ее можно рассчитывать как статиче-
ски определимую вплоть до предельного состояния, которое насту-
пит при включении еще одного шарнира, обращающего балку в
механизм, не способный сопротивляться действию нагрузки.
Из этой теоретической схемы следует, во-первых, что истинный
запас прочности в неразрезной балке значительно выше, чем выте-
кает из обычного «упругого» расчета, и, во-вторых, что переходом
к расчету по предельному состоянию можно вообще освободиться
от осложнений, связанных со статической неопределимостью балки,
и рассчитывать ее статически. Все эти обстоятельства достаточно
широко известны, и поэтому мы лишь вкратце излагаем эту
теорию.
Экспериментальная проверка, произведенная инж. В. С. Турки-
ным [170] (1936), показала, что действительное поведение неразрез-
ной балки несколько отличается от этой теоретической схехмы, так
как выравнивание моментов в наиболее напряженных сечениях
не происходит вследствие упрочнения материала, прошедшего пло-
щадку текучести. Благодаря этому истинный запас прочности еще
несколько выше, чем следует из теоретического расчета. Наиболее
существенным следствием этих опытов явилось, однако, установ-
ление того факта, что неразрезная балка, как правило, теряет
устойчивость ранее достижения предельного состояния по прочно-
440
сти. Тем самым оказалось (как и в случае статически неопредели-
мой фермы), что расчет по предельному состоянию с учетом плас-
тичности материала не отделим от поверки на устойчивость в упру-
го-пластическом состоянии.
Однако и поверка на устойчивость, как мы уже неоднократно
указывали, есть также расчет по предельному состоянию. Поэтому
сейчас нет спора относительно целесообразности применения рас-
чета по предельному состоянию к статически неопределимым си-
стемам из пластичного материала; есть лишь вопрос о том, каково
будет это состояние в каждом отдельном случае, т. е. обусловлено
ли его наступление исчерпанием прочности или потерей устойчиво-
сти. Бесспорно, однако, что необходимость учета опасности потери
устойчивости в ряде случаев исключает возможность ограничиться
статическим расчетом сооружения, как это казалось по началу.
В особенности это относится к стальным сооружениям, для кото-
рых в большинстве случаев решающим будет расчет на устойчи-
вость. Для железобетонных сооружений с их массивными форма-
ми, особенно для неразрезных балок, опасность потери устойчиво-
сти обычно отсутствует, и потому нет оснований отказываться от
их расчета по предельному состоянию, осуществляемого статиче-
ским путем.
Эти соображения четко диктуют направление дальнейших ис-
следований. Очередными проблемами являются, с одной стороны,
разрешение задач устойчивости в упруго-пластической стадии, и,
с~другойТ— завершение расчета по предельному состоянию на
случаи действия подвижной и переменной нагрузки. Естественно,
что именно в этих направлениях за последние годы проведено осо-
бенно много исследований и в Советском Союзе, и за рубежом.
БИБЛИОГРАФИЯ
А. РАБОТЫ ПО ИСТОРИИ СТРОИТЕЛЬНОЙ МЕХАНИКИ
-Литература по истории строительной механики довольно обширна, хотя в
большинстве имеет обзорный характер. Специальных сочинений по истории можно
\казать три:
Timoshenko, History of the strength of materials, New York, 1953.
Tod hunter and Pearson, A history of the theory of elasticity, 1886—1893.
R u h I m a n n, Vortrage uber die Geschichte der technischen Mechanik, Leipzig,
1885.
Кроме того, ряд ценных исторических обзоров имеется в следующих книгах.
Проф. И. М. Рабинович, Курс строительной механики стержневых систем
изд. 1, Госстройиздат, 1938 1940, и изд. 2, Госстройиздат—Гос. изд-во литера-
туры по строительству и архитектуре, 1950—1954.
А. Л я в. Математическая теория упругости (русский перевод), ОНТИ, 1935.
N a v i е г. Resume des lemons, donnees a 1’ecole des ponts et chaussees sur
Г application de la mecanique a I’etablissement des constructions et des machines,
Paris, 3-me edition, vol. 1. 1864. В этом издании книги Навье помещен обширный и
весьма интересный исторический обзор, написанный Сен-Венаном.
Специальные обзоры по истории расчета сводов приведены в трудах:
Г. Е. Паукер, О поверке устойчивости цилиндрических сводов, «Инженер-
ные записки Военно-Ученого комитета», часть XXXIII, кн. 1, стр. 1, Спб., 1849.
Р о п с е 1 е t, Examen critique et historique des principals theories ou solutions
л
concernant 1’equilibre des voutes. Compt. Rend, de I’Acad. d. Sciences de Paris.
T- XXXV, № 15—47, стр. 494, 531, 577. Имеется переработанный русский перевод
этой статьи без указания автора и переводчика, выполненный Домерщиковым:
«Краткий исторический и критический обзор главнейших теорий устойчивости
сводов», «Инженерные записки Военно-Ученого комитета», 1854, часть XLI.
кн. 2, стр. 179.
Lahmeyer, Geschichtliche Notizen uber die Theorie der Kreies gewolbe,
Journ. f. die Baukunst von Crelle, 1843, Bd. XVIII, стр. 207.
Б. ПОДЛИННЫЕ ТРУДЫ
1. Галилео Галилей, Беседы и математические доказательства, касаю-
щиеся двух новых отраслей науки, относящихся к механике и местному движе-
нию. Русское издание в переводе С. Н. Долгова, ГТТИ, 1934. Подлинник издан
в Лейдене в 1638 г.
2. Gautier, Dissertation sur 1’epaisseur des culees des ponts. Paris, 1727,
Присоединено к 3-му изданию его курса «Traite des Ponts». Paris, 1755.
3. E. Gau they, Traite de la construction des ponts. Publie par Navier, Paris,
1809—1813.
4. Robert Hooke, De potentia restitutiva or of springs, explaining the po-
wer of springing bodies. London, 1678.
5. Иоганн Бернулли, Избранные сочинения по механике. Перевод под
ред. В. П. Егоршина, ГТТИ, 1937, стр. 43—58.
442
6. Подлинное и обстоятельное описание построенного в Санкт-Петербурге в
январе месяце 1740 года Ледяного дома,... сочиненное для охотников до нату-
ральной науки через Георга Вольфганга Крафта, Санкт-Петербургские Академии
наук члена н физика профессора, Спб., 1741.
7. Е. Mariotte, Traite du mouvement des eaux. Paris, 1686.
8 J. Bernoulli, Veritable hypothese de la resistance des solides, avec la
demonstration de la courbure des corps, qui font ressort, 1705, Oeuvres compL,
t. 2, Geneve, 1744.
9. P are n t, De la veritable mecanique de resistance relative des soli'des, Essais
et reherches des mathematiques et des physiques. III-е vol., XVI-e memoire, Pa-
ris, 1713.
10. G. В. Bulffinger, De solidorum resistentia specimen. Comment, Acad.
Scient. Petropol ad annum 1729, т. IV, p. 164—181, Спб., 1735.
11. C. A. Coulomb. Application des regies de maximis et minimis a quelques
problemcs de statique, relatifs а Г architecture, Memoire des savants etrangers de
i’Acad. des Sciences de Paris, 1773.
12. P. S. Girard, Traite analytique de la resistance des solides et des solides
d'egale resistance, Paris, an VI (1798).
13. T. Tredgold, A practical essay on the strength of cast iron, 1821.
14. Piler van Musschenbroek. Introductio ad cohaerentiam conporum
firmorum, Leyden, 1729.
15. Леонард Эйлер, Метод нахождения кривых линий, обладающих
свойствами максимума либо минимума. Русское изд. ГТТИ, 1934. Подлинник из-
дан в Лозанне в 1744 г.
16. L. Е u 1 е г, Acta Acad. Petropol, 1778, Paris prior, p. 121—193.
17. Lagrange, Sur la figure des colonnes, Miscellanea Taurinensia, t. 5,
Paris, 1770—1773.
18. Navi er, Resume des lemons, donnees a 1’ecole des ponts et chaussees sur
1’application de la mecanique a I’etabl-issement des constructions et des machines,
Paris, 1-е изд. 1826, 2-е изд. 1833, 3-е изд. 1864.
19. Bresse, Etudes theoriques sur la resistance des arcs employes dans les
ponts en fonte ouen bois, Ann. des Ponts et chaussees, 2-e serie, 1848, I semestre.
N 191.
20. Инженер-подполковник Беспалов, Элементарный способ решения воп-
росов, относительно сопротивления материалов и устойчивости сооружений, Спб.,
1855.
21. N. Persy, Cours destabilite des constructions. Metz., 1834.
22. Bresse. Recherches analytiques sur la flexion et la resistance des pieces
courbes. Paris, 1854.
23. Д. И. Журавский, О мостах раскосной системы Гау, Спб., 1855
24. Н Ястржембский. Курс практической механики, ч. I—II, Спб.,
1837—1838.
25. W. Rankine, Manual of civil engineering, 1862. Вышло -русское издание
этой книги в переводе мнж. Андреева: У. Рен к ин. Руководство для инжене-
ров-строителей, Спб., 1870.
26. И. А. Евневич, Руководство к изучению законов сопротивлений строи-
тельных материалов с присоединением общих начал теории упругости, Спб., 1868.
27. И. А. Вышнеградский, Курс подъемных машин, ч. I, 1872.
28. X. С. Головин. Одна из задач статики упругого тела, «Известия Санкт-
Петербургского практического технологического института», т. 3, 1880—1881.
29. La marie, Annales des travaux publics de Belgique, t. 3, 1845, p. 1—64;
t. 4, 1846, p. 1—36.
30. F. Engesser, Ober bie Knickfestigkeit gerader Stabe, Zt. Arch. Ing.,
1889, S. 455.
31. Ф. С. Ясинский. О сопротивлении продольному изгибу, Спб., 1894.
32. Ф С. Я с и н с к и й, Избранные работы по устойчивости сжатых стержней,
ГТТИ, М —П., 1952.
33. О. Мор, Чем обусловлены предел упругости и временное сопротивление
материала? сборник «Новые идеи в технике», № 1, «Теории прочности», под ред.
проф. С. П. Тимошенко. Петроград, 1915. Подлинная статья помешена в журнале
Zeitschrift des Vereines deutscher Ingenieure, '1900.
443
34. Я. Б. Фридман, Механические свойства металлов, Оборонгиз, 1952.
35. А. Нада и, Пластичность (русский перевод), ОНТИ, 1936. Подлинник
вышел в 1931 г.
36. А. А. Ильюшин, Некоторые вопросы теории пластических деформаций,
«Прикладная механика», т. VII, вып. 4, 1943. Его же, К теории малых упруго-
пластических деформаций, там же, т. X, вып. 3, 1946.
37. В В. Соколовский, Теория пластичности, изд. АН СССР, 1946.
38. Л. С. Л ей бен зон. Элементы математической теории пластичности,
ГТТИ, 1943.
39. С. Г. Михлин, Основные уравнения математической теории пластич-
ности, изд. АН СССР, 1934.
40. М. Grunin g, Die Tragfahigkeit statisch unbestimmter Tragwerke aus
Stahl bei beliebig haufig wiederholter Belastung, Berlin, 1926.
41. H. С. Стрелецкий, Об исчислении запасов прочности сооружений,
сборник трудов Моск. инж.-стр. ин-та имени Куйбышева, № 1, М., 1938.
41а . Его же, К вопросу установления коэффициента запаса сооружений,
Известия АН СССР, Отд. техн, наук № 1, 1947.
416. Б. Н. Горбунов. К вопросу о коэффициенте запаса при расчете
по теории пластических деформаций, «Труды конференции по пластическим дефор-
мациям», изд. АН СССР. 1938.
41в. А. Г. Низа ров, О применении понятия идеального профиля к анали-
зу несущей способности статически неопределимых систем, «Труды конференции
по пластическим деформациям», 1938.
41г. Н. Д. Жудин, Расчет стальных конструкций с учетом пластических
деформаций, сборник трудов Киевского строительного ин-та, вып. 2, 1935.
42. А. А. Гвоздев, Расчет несущей способности конструкций по методу
предельного равновесия, Стройиздат, 1949.
43. Л. Б Альберти, Десять книг о зодчестве, М., 1935. стр. 96. Подлин-
ник издан в 1452 г.
44. Р. D е 1 а Нуге, Traite de Mecanique, Paris, 1695.
45. P. Del a H у re,Sur la construction des vofites dans les edifices, Memoi-
res de 1’Acad. des Sciences de Paris, 1712, p. 91.
46. Couplet, De la poussee des vofites, Mem. de 1’Acad. d. Sciences de Paris,
1729—1730.
47. Belidor, La science des ingenieurs dans la conduite des travaux de
fortification et d’architecture civile, Paris. 1729. Переиздано в 1830 г. под редак-
цией «и с .дополнениями Навье.
48. Hutton, The principles of bridges, London, '1772; 2-d ed. 1801.
49. Boss ut. Recherches sur 1’equilibre des vofites, Mem. de 1’Acad. des Scien-
ces de Paris, 1774.
50. A p f a 11 e r n, Abhandlung von dem Drucke der Gewolbe auf ihre Seiten-
mauern, Wien, 1782.
51. Mascheroni, Nuove richerche sull’equilibrio delle volte, Bergame, 1785.
52. Об опытах Данизи см. A. F. F г ё z i е г, La Theorie et la pratique de la
coupe des pierres et des bois, ou traite de stereotomie, Srassburg, 1738—1739, t. III.
53. Perronet, Description des projets et de la construction des ponts, Paris.
1738; Memoire sur le cintrement et decintrement des ponts, Paris, 1777.
54. Г. И. Мягков, Теория о механизме сводов, Москва, 1825.
55. D. Gregory, Philosoph, transactions, 1707.
56. С. A. Coulomb, La statique des vofites, Paris, 1776.
57. H. II. Коч ин, Кулибин, «Жизнь замечательных людей», серия биогра-
фии, вып. 7 (163), изд-во «Молодая гвардия», М., 1940.
58. Описание представленного на чертеже моста, простирающегося из одной
дуги на 140 сажен, изобретенного механиком Иваном Кулибиным, с разными
вычислениями состоящих в нем тяжестей. Спб., 1799. Рукописи Кулибина были
изданы только в наше время: «Рукописные материалы И. П. Кулибина», нзд.
АН СССР. 1953.
59. Б. В. Якубовски й. Проекты мостов Кулибина. Архив истории науки
и техники, внп. 8.'изд. АН СССР, 1936.
60. S а 1 i m b е n i. Degli archi e delle volte. Verona, 1787.
61. Boistard. Recueil d’experiences et observations. 1800, p. 95.
444
62. G a u t h е у, Dissertation sur les degradations du Pantheon Francais, Pa-
ris, 1800, p. 111.
63. R о n d e 1 e t, Art de batir, t. Ill, p. 236.
64. G. Atwood, A dissertation on the construction and properties of ar-
ches, >1801.
65. I. A. E у te I wei n. Handbuch der Statik fester Korper, Berlin, 1808, Bd. Il,
§ 374—399.
66. J. W e i s b a c h, Lehrbuch der Ingenieur-und Maschinen-Mechanik, Braun-
schweig, 1853. Эта книга была переведена на русский язык: Ю. Вейсбах, Теорети-
ческая и практическая механика, Изд. Вольфа, Слб., 1859—1861.
67. R б s 1 i n g, Unterricht im Gewolb-und Bogenbau, 1829.
68. К- W. Knochenhauer, Die Statik der Gewolbe mit Rucksicht auf ihre
Anwendung, Berlin, 1842.
69. A. Ritter von Camerloher, Enthullte Geheimnisse, oder neue, aus
richtigen Prinzipien mit Rucksicht auf Erfahrungen abgeleitete Theorie aller Gewol-
barten, Landshut, 1833.
70. Georg Reichenbach, Theorie der Briickenbogen und Vorschlage zu
eisernen Brucken in jeder beliebigen Grosse, Munchen, 1811.
71. Audoy, Memoires sur la poussee des vofites en berceau. Memorial de
1’Officier du Genie, Paris, 1820, № 4.
72. Schulz, Versuch einiger Beitrage zur hydraulischen Architektur, 1808.
73. S. Ma ill a rd, Die Mechanik der Gewolbe in ihrem ganzen Umfange
abgehandelt, Pesth, 1817. Русский перевод этой работы помещен в XXI части «Ин-
женерных записок Военно-ученого комитета», 1839. В XXIV части «Инженерных
записок», 1842, кн. 2, стр. 306, приведен подробный анализ работы Майяра.
74. La ngs dorf, Anleitung zum Strassen-und Bruckenbau, 1817.
75. Подполковники Ламе и Клапейрон, Об устойчивости сводов, Жур-
нал путей сообщения, 1826, кн. 2 и 3. Ранее опубликовано в «Annales des mines»
sai 1823 г.
76. G a r i d e 1, Memoire sur le calcul des vofites en berceau, Memorial de
I’Officier du Genie, 1835; № 12, p. 7; Tables les poussee des voutes en plein cintre,
Paris, 1837.
77. Poncelet, Solution graphique des principales questions sur la stabilite
des vofites, Mem. de I’Officier du Genie, 1835, № 12, p. 151.
78. M i c h о n, Tables et formules pratiques pour I’etablissement des vofites
cylindriques, Mem. de I’Officier du Genie, 1848, № 15, p. 7.
79. Kaiser, Handbuch der Statik, 1836.
80. Mery, Sur 1’equilibre des vofites en berceau, Ann. des Ponts et chaussfees,
1-e serie, >1840, 1-r semestre, p. 50.
81. Dej ardin, Routine de I’etablissement des vofites, Paris, 1845.
82. Villarceau, Sur I’etablissement des arches de pont, envisage de point
de vue de la plus grande stabilite. Compt. Rend, de 1’Acad. des Sciences de Paris,
t. XXIII, 1846, Nov., 9. Отдельное издание 1853.
83. P. Sain t-G u i 1 h e m, Memoire sur I’etablissement des arches de pont
assujetties aux conditions du maximum de stabilite, Ann. des ponts et chaussees,
t. XVII, № 227, p. 83.
84. Belanger, Cours de mecanique, Paris, 1847.
85. C ar v a Ho, Etude sur la stabilite. des voutes, Ann. des ponts et chaus-
sees, 1853.
86. D. P. Woodbury, Treatise on the various elements of stability in the
well-proportioned arch., New York, 1858.
87. L a m b e I, Applications du principe des vitesses virtuelies a la poussee des
terres et des vofites, Par un Directeur des fortifications, Metz, 1822.
88. Г. E. Паукер, О поверке устойчивости цилиндрических сводов, Инже-
нерные записки, т. XXXIII, кн. 1, Спб., 1849.
89. Р о i n s о t, Principes de statique, Paris, 1803. Эта книга неоднократно
издавалась в русском переводе под заглавием: «Пуансо, Основы статики». Пер-
вое русское издание вышло в 40-х годах XIX века, последнее—в 1922 г.
90. F. J. Ritter von Gerstner, Handbuch der Mechanik, Bd. I, p. 404,
Prag, 1831.
91. Knochenhauer, Statik der Gewolbe, Berlin, 1842.
445
92. Barlow, Mechanical principles, The Civil Eng. and Archit. Journal,
July, 1847.
93. Schubert, Theorie der Konstruktion steinerner Bogenbrucken,
Berlin, 1847.
' 94. Hagen, Ober Form und Starke gewolbter Bogen und Kuppeln,
Berlin, 1844. -
95. В a u e г n f e i n d, Stuttgart. Eisenbahnzeitung, 1846, № 34, S. 299.
96. Hoffmann, Ober Form und Starke gewolbter Bogen, Berlin, 4853.
97. S c h w e d 1 e r, Theorie der Stutzlinie, ein Beitrag zur Form und Starke
gewolbter Bogen, Zeitschr. f. Bauwesen, 1859, S. 109.
98. Duran d-C 1 a у e, Sur la verification de la stabilite des vofites en ma-
^onnerie et sur 1’emploi des courbes de pression. Ann. des Ponts et Chauss., 1867,
1-e partie, p. 63; 1868, 1-e partie, p. 109; 1880, '1-e partie, p. 416.
99. К. C u 1 m a n n, Die graphische Statik, Zurich, 1866 (2-te Ausg., 1875).
100. A. Fop pl, Theorie der Gewolbe, Leipzig, 1881.
101. См. В. Кирпичев, Основания графической статики, § 89. Гос. Тех.
Теор. Изд. 1933.
102. Steiner, Ober graphische Behandlung des Bogentragers von konstantem
Querschnitt ohne Gelenk, Allg. Bauzeitung, 1878, S. 21.
103. Eddy, Neue Constructionen aus der graphischen statik, Leipzig, 1880.
104. Maupertuis, Les loix du mouvement et du repos deduites d’un prin-
cipe metaphysique. Memoiren der Berliner Akademie, 1746, S. 265.
105. R e b h a n n, Theorie des Erddruckes und der Futtermauern, Wien, 1871.
106. J. B. Berard, Statique des vofites, contenant I’essai d’une nouvelle theo-
rie de la poussee, Paris, 1810.
107. Henry Moseley, On the equilibrium of the arch. Transact, of the Cam-
bridge Philosoph. Society, vol. V, part III, p. 293, Cambridge, 1835; On the equili-
brium of bodies in contact. Ibid., vol. VI, part III, p. 463, Cambridge, 1838; The
Mechanical principles of engineering and architecture, London, 1844.
108 H. Scheffler, Theorie der Gewolbe, Futtermauern und eisernen Brucken,
Braunschweig, 1857.
109. Menabrea, Nouveau principe sur la distribution des tensions dans les
systemes elastiques. Compt. Rend, de 1’Acad. des Sciences de Paris, vol. 46, 1858,
p. 1056.
110. Winkler, Lage der Stutzlinie im Gewolbe, Deutsche Bauzeitung, 1879,
S. 117, 127, 139; 1880, S. 58, 184, 210, 243.
111. E. Collignon, Cours de mecanique, appliquee aux constructions, Pa-
ris. 1869 (3-e ed., 1885).
112. Tolkmitt, Beitrag zur Theorie gewolbter Bogen, Zeitschr. f. Bauwesen,
1876, S. 402; Die Berechnung der Gewolbestarke und Bogenform massiver Brucken.
Zt. d. Arch. u. Ing. Ver. zu Hannover, 1878, S. 452.
H3. Weyrauch, Allgemeine Theorie und Berechnung der kontinuierlichen
und einfachen Trager, Leipzig, 1873.
114. Bresse, Cours de Mecanique appliquee, t. I—III, Paris, 1859—1865-
115. Al ba ret, Calculs des arcs metalliques a section constante et a section
variables, Memoires et documents des Ann. des Ponts et Chaussees, t. II, № 46,
p. 90—124, 1860.
.116 . Fabre, Theorie des vofites elastiques et dilatables d’une application spe-
ciale aux arcs metalliques, Paris, 1859.
117. Beran ger, Theorie de la resistance de la torsion et de la feexion plane
des solides, Paris, 1862.
418. M e h r t e n s, Vorlesungen uber Statik der Baukonstruktionen und Festig-
keitslehre, Leipzig, 1903.
119. Winkler, Die Lehre von der Elastizitat und Festigkeit, Prag, 1967.
120. Mohr, Beitrag zur Theorie elastischer Bogentrager. Zt. d. Arch. u.
Ing. Ver. zu Hannover, 1870, S. 239. Эта статья была издана на русском языке
в 1870 г. в Петербурге в переводе Недзялковского.
121. Krohn, Beitrag zur Theorie der elastischen Bogentrager. Zeitschr. f. Bau-
kunde, 4880, S. 219.
122. В. И. Руднев. О рациональной форме сплошной упругой арки в
связи с современными методами возведения, Труды МИИТ, вып. 15, 1930.
446
123. В. А. Киселев, О рациональной оси свода, там же.
124. Bernhard Fritz, Theorie und Berechnung vollwandiger Bogentrager
bei Berucksichtigung des Einflusses der Systemverformung, Berlin, 1934.
125. С. П. Тимошенко, Известия киевского политехнического ин-та, 1910
126. А. Н. Д и н н и к. Устойчивость арок, ГТТИ, 1946.
127. И. Я. Ш т а е р м а н и А. А. Пиковский, Основы теории устойчи-
вости строительных конструкций, Стройиздат, 1939.
128. А. Г. Л о к ш и н , Об устойчивости стержня с криволинейной осью. При-
кладная математика и механика, т. И, № 1, 1934.
129. Подполковник Волков, Записка о системах связей, не производящих
на упоры их горизонтального действия. Журнал путей сообщения, 1838.
130. Schwedler, Theorie der Briickenbalkensysteme, Zt. f. Bauwesen, 1851.
131. Lame, Lemons sur la theorie mathematique de I’elasticite des corps solides,
Paris. '1852.
132. Инженер-подполковник Августинович, Вычисления напряжений
раскосных мостов. Журнал Главного управления путей сообщения и публичных
зданий, 1857, кн IV.
133. Гербер, Расчет мостовых ферм. Перевод Недзялковского, Спб., 1870.
В подлиннике опубликовано в 1865 г.
134. L a i s s I е und S с h u b I е г, Der Bau der Bruckentrager, Stutgart, 1871.
135. A. Ritter, Elementare Theorie und Berechnung eiserner Dach-und Bru-
ckenkonstruktionen, Hannover, 1862.
Русское издание: Август Риттер, Элементарная теория и расчет железных
стропильных и мостовых ферм. Перевод инж. Л. Вурцеля, Спб., 1875.
136. W. Maxwell, On the calculation of the equilibrium and stiffness of
frames. The London Philosoph. Magazine, 1864, April, p. 294.
137. Кремона, Взаимные фигуры в графической статике, М., 1936. Под
линник издан в -Милане в 1872 г.
138. Mohr, Beitrag zur Theorie des Fachwerks, Zeitschrift d. Arch. u. Ing.—
Vereines zu Hannover, '1874—1875.
139. Betti, Teoria dell’elasticita, II nuovo cimento, 1872, t. VII—VIII.
140. И. M. Рабинович, Курс строительной механики стержневых систем,
Стройиздат. 1938—1940.
141. Frankel, Uber die Ungunstigste Einstellung eines Systems von Ein-
zellasten auf Fachwerktragern mit Hilfe von Influenzkurven, Ziviling, 1876, S. 441.
142. Muller-Breslau, Beitrag zur Theorie des ebenen Fachwerks, Schweiz.
Bauzeitung, 1887, № 9—40.
143. Г. Д. Абрамов, Исследование и расчет плоских ферм способом вы-
бранных сечений, Труды Московского авиационного института, № 1—3, 1935.
144. Henneberg, Statik der starren Systeme, Darmstadt, 1886, S. 229.
145. Heimann, Beitrag zur Berechnung statisch unbestimmter Fachwerke,
Berlin, 1928.
146. И. M. P а б и н о в и 4, К теории статически неопределимых ферм, Транс-
желдориздат, 1933.
147. К. М. X у б е р я н, К расчету статически неопределимых ферм, Тбилис-
ский научно-исследовательский институт сооружений, вып. 32, Тбилиси, 1938.
148. Ю. А. Радциг, Об определении наименьшего объема статически не
определимых ферм, Труды Казанского авиационного института, т. XVII, Казань,
1946.
149. И. М. Р а б и н о в и ч , Об устойчивости стержней в статически неопреде-
лимых системах, Стройиздат, 1932.
150. С. А. Бернштейн, Работа статически неопределимых ферм в упру-
го-пластической стадии, сборник «Расчет металлических конструкций с учетом
пластических деформаций», Стройиздат, 1938.
151. Н. С. Стрелецкий, К вопросу о разрушении ферм под циклической
нагрузкой. Известия АН СССР, Отд. техи. наук, № 12. 1946.
152. Barlow, Essay on the strength and stress of timber.
153. Molinos et Pronnier, Traite theorique et pratique de la construc-
tion des ponts metalliques, Paris, 1857, p. 34. См. также (134) т. .1, стр. 30.
154- Memories et comptes rendus des trsvsux de 1з societe des ingenietirs civils,
1855, p. 278—280. Протоколы заседаний от 15 июня и 6 июля 1855 года. В СССР
447
единственный экземпляр этого редкого журнала имеется в библиотеке Ленин-
градского института инженеров железнодорожного транспорта.
155. Clapeyron, Calcul d’une poutre elastique reposant librement sur des
appuis inegalement espaces, Comptes Rendus de I’Acad. des Sciences de Paris,
1857, p. 1076—1080.
156. Hep pel. On the theory of continuous beams, Proc, of the Royal Society,
vol. XIX. № 123. June, 1870.
157. M. Mahistre, Cours de Mecanique appliqu’ee Paris, 1858.
158. O. Mohr, Beitrag zur Theorie der Holz- und Eisenkonstruktionen. Zeitschr.
d. Arch. u. Ing. Ver. zu Hannover, 1868.
159. C a s t i g 1 i a n o, Nuova teoria interne dell’equilibrio dei sistemi elastic!,
Atti della Academia delle scienze. Torino, 1875.
160. M u 11 e г-В г e s 1 a u, Die neueren Methoden der Festigkeitslehre, 1886.
161. А. Верещагин, Новые методы расчета статически неопределимых
систем, «Строительная промышленность» № 9, 1925.
162. Н. В. Compton and С. О. Dohrenwend, The sheararea method.
Proc, of the Amer. Soc. of Civil Engineers May, 1935.
163. Winkler, Beitrage zur Theorie der continuierlichen Balkentrager. Der
Civiling., 1862, S. 135—182.
164. Maurice Levy, La sttique graphique, Paris, 1886.
165. Б. H. Же м очкин, Графические способы определения моментов и по-
перечных сил в неразрезных балках, Труды МНИТ, вып. X. 1929.
166. Don Pablo deAlzola, Teoria del calculo de las vigas rectas, Mad-
rid, 1869.
167. Гавриил Семиколено в. Теория уравновешенных балок, Журнал
Министерства путей сообщения, т. 19. Спб., 1871.
168. А. А. Попов, Метод трех перемещений, Труды Научно-исследователь
ского ин-та тяги НКПС, сборн. 14, 1933.
169. Б. Н. Ж е м о ч к и н , Расчет статически неопределимых рамных систем.
Метод угловых фокусов, Л!., 1929.
170. В. С. Ту рки н, Исследование упруго-пластической работы стальных не-
разрезных балок, сборник «Расчет металлических конструкций с учетом пласти
ческих деформаций» под ред. проф. С. А. Бернштейна, Стройиздат, 1938.
СЕРГЕИ АЛЕКСАНДРОВИЧ
БЕРНШТЕЙН
ИЗБРАННЫЕ ТРУДЫ
ПО СТРОИТЕЛЬНОЙ МЕХАНИКЕ
* * *
Госстройиздат
Москва, Третьяковский проезд, д. I
4с * #
Редактор издательства Т. В. Горячева
Переплет художника С. А. Киреева
Технический редактор Л. М. О с е н к о
Корректоры Г. А. Лебедева и М. А. Шифрина
Сдано в набор 7/IV— 1961 г. Подписано к печати 28/VII—1961 г.
Т 08291. Бумага 60х921',е=14.1“бум. л.—28.25 п. ч. (28,1 .уч.-изд. л.) .
Тираж ЗБООэкэ. Изд. № VII1-5452- Зак. № 957.
Цена 1 р. 41 к. 4- переплет № 5—10 коп.
Типография JMv 1 Государственного издательства литературы
по строительству, архитектуре и строительным материалам,
г. Владимир
СПИСОК НАУЧНЫХ ТРУДОВ
проф. С. А. БЕРНШТЕЙНА
1. Обработка результатов массовых психологических измерений.
Практикум по экспериментальной психологии, МГУ, 1927.
2. Опытное исследование работы верхнего пояса открытого мо-
ста. Труды Научно-технического комитета НКПС, вып. 60, 1927.
3. Uber frei Horizontalschwingungen eiserner Brucken, Труды
Научно-технического комитета НКПС, вып. 89, 1928.
4. Ледяная железнодорожная переправа (теория и расчет ледя-
ного слоя), Труды Научно-технического комитета НКПС. выл. 84,
1928.
5. Временные правила сооружения, содержания и эксплуатации
железнодорожных ледяных переправ. Труды Научно-технического
комитета НКПС, вып. 84, 1929.
6. Исследование свободных поперечных колебаний пролетных
строений, Труды Научно-технического комитета НКПС, вып. 88,1929.
7. Напряжения в мостах, Техническая энциклопедия, «Мосты»,
1930.
8. Теория боковой качкч железных мостов. Труды Центрального
научно-исследовательского управления НКПС, вып. ПО, 1930.
9. Применение графостатики к решению систем линейных урав-
нений, Труды МИИТ, вып. 18, 1931.
10. О работе .металлических мостов под динамической нагрузкой.
Труды Центрального планово-экономического управления НКПС,
вып. 143, 1931.
11. О мостах с последующим усилением, Приложение к «Строи-
тельному Бюллетеню» НКПС № 4, 1931.
12. Расчет ферм с крестовой решеткой, Труды Центрального
института железнодорожного строительства НКПС, 1932.
13. Авторизованный перевод книги Блейх «Теория и расчет же-
лезных мостов», Гострансиздат, 1931-
14. Приближенный способ расчета распора в балочных фермах
с подпружной аркой. Вестник Военно-инженерной академии № 3»
1934.
15. Комбинированный силовой и веревочный многоугольник,
Вестник Военно-инженерной академии № 3, 1934.
16. О классификации плоских статически-определимых ферм.
Вестник Военно-инженерной академии № 3, 1934.
17. Меп»ды расчета статически-определимых систем. Справочник
инженера ср- ‘чтчровщика промсооружений, Госстройиздат, 1934
18. Линии или,-»ия. Справочник инженера-проектировщика, Гос-
стройиздат, 1934.
19. О расчете гибк. кольца, сборник по теории сооружений,
Госстройиздат, 1935.
20. Очерк истории расчета свода, сборник по теории сооруже-
ний, Госстройиздат, 1935.
21. К расчету прочности ледяного слоя на переправе, Вестник
Военно-инженерной академии № 8, 1935.
22. Основы расчета статически неопределимых систем, ОНТИ,
1936.
23. Опытное исслед.^ание металлоконструкций промышленных
цехов, «Проект и стандарт» № 5, 1936.
24. Методы и задачи исследования действительной работы со-
оружений, сборник «Исследование действительной работы стальных
промышленных цехов» под ред. С. Бернштейна, Госстройиздат, 1938.
25. Расчет устойчивости раскосов в многорешетчатых фермах.
Издание Военно-инженерной академии, 1936.
26. К расчету статически-неопределимых ферм по разрушающей
нагрузке «Проект и стандарт», № 5, 1937.
449
27. О расчете статически-неопределимых ферм в пластической
стадии, Труды конференции по пластическим деформациям Академии
наук, 193Я
28. Экспериментально-теоретические исследования упруго-пла-
стической работы стальных балок. (Совместно .с инж. Туркиным),
Труды конференции по пластическим деформациям Академии наук,
1938.
29. Конференция по пластическим деформациям, «Проект и стан-
дарт» № 2, 1937.
30. Предпосылки к расчету сооружений по разрушающей на-
грузке, Сборник «Расчет металлических конструкций с учетом пла-
стических деформаций» под ред. С. Бернштейна, Госстройиздат,
1938.
31. Работа статически-неопределимых ферм в упруго-пластиче-
ской стадии, Сборник «Расчет металлических конструкций с учетом
пластических деформаций» под ред. С. Бернштейна, Госстройиздат,
1938.
32. Основы динамики сооружений, ОНТИ, 1938.
33. Новый метод определения частот колебаний упругих систем,
Издание Военно-инженерной академии, 1939.
34. Новый метод вычисления частот колебаний упругих систем и
его приложение к задачам устойчивости, Труды Военной академии
механизации и моторизации, юбилейный сборник, 1940.
35. Основы динамики сооружений, 2-ое издание, исправленное и
дополненное, ОНТИ, 1941.
36. Переправа танков по льду, сборник по эксплуатации танков,
изд. Управления эксплуатации танков, № 2—3, 1945.
37. Сопротивление материалов, учебник, Издание Военной ака-
демии бронетанковых и механизированных войск Советской Армии,
1946.
38. Сопротивление материалов, Дополнения к учебнику, Издание
Академии БТиМВ СА, 1949.
39. Сопротивление материалов, Конспект лекций, вып. 2, Изда-
ние Академии БТиМВ СА, 1953.
40. Расчет листового торсиона. Труды Академии БТиМВ СА,
сборник № 6 (57), 1948.
41. Сопротивление материалов, Конспект лекций, вып. 3, Изда-
ние Академии БТиМВ С А, 1954.
42. Сопротивление материалов. Учебник, изд. 2-е, Издание Ака-
демии БТиМВ СА, 1955.
43. Очерки по истории строительной механики, Стройиздат, 1957.
44. Обобщение октаэдрической теории пластичности, Известия
Артиллерийской инженерной академии, т. 109, 1958.
НЕОПУБЛИКОВАННЫЕ РАБОТЫ
1. К существованию тригонометрических рядов, не суммируемых
по Пуасону, 1921.
2. О тригонометрических рядах обладающих дифференциальны-
ми свойствами, 1923.
3. Инструкция по расчету ферм с крестовой решеткой, 1932.
4. История расчета сводов, 1937.
5. Достижения и задачи современной теории пластических де-
формаций, 1938.
6. О некоторых интегральных соотношениях в строительной
механике, 1938.
ОГЛАВЛЕНИЕ
Биографический очерк........................................... 3
1. Новый метод вычисления частот колебаний упругих систем и его
приложение к задачам устойчивости............................. 5
2. Работа статически неопределимых ферм в упруго-пластической
стадии...................................................... 31
А. Поведение сжатого стержня после потери устойчивости —
Б. Работа статически неопределимых ферм 65
3. О расчете гибкого кольца.................................... 84
4. Графоаналитический расчет кривого бруса на изгиб 107
5. Дуговая рессора с нелинейной характеристикой 123
6. К расчету прутковых торсионов............................... 147
7. Расчет листового торсиона................................... 170
8. Исследование листовых торсионов при больших деформациях 202
9. Обобщение октаэдрической теории пластичности ..... - 227
10. Применение графостатики к решению систем линейных уравнений 245
11. Комбинированный силовой и веревочный многоугольник 252
12. О классификации плоских статически определимых ферм 259
13. Очерки по истории строительной механики 272
Введение .......... —
ОЧЕРК ПЕРВЫЙ. Из истории сопротивления материалов
Глава I. Рождение науки о прочности .... 275
Глава 2. Наука, утратившая связь с практикой 283
Глава 3. Задача о прочности балки................ 289
Глава 4. Задача о продольном изгибе. Итоги XVIII века 293
Глава 5. Работы Навье и реформа строительной механики 303
Глава 6. Завершение теории изгиба.............. 314
Глава 7. Новые пути . ...................................325
ОЧЕРК ВТОРОЙ. История расчета арок
Глава L Введение....................................... 333
Глава 2. Период умозрительных концепций 336
Глава 3. Теория Кулона................................. 343
Глава 4. Труды Ивана Петровича Кулибина 347
Глава 5. Послекулоновский период................... . 355
Глава 6. Возрождение и расцвет идей Кулона . 361
Глава 7. Работы Навье и его последователей..............365
Глава 8. Методы, основанные на отыскании истинной кри-
вой давления......................................... 371
Глава 9. Поиски недостающей аксиомы статики . 377
Глава 10. Расчет свода как упругого тела ... 383
Глава 11. Заключение........................... 393
ОЧЕРК ТРЕТИЙ. Из истории расчета ферм
Глава 1. Введение..................................... 395
Глава 2. Работы Д. И. Журавского................ 398
Глава 3. Работы Шведлера и Августиновича .... 404
Глава 4. Появление классических методов расчета ферм 410
Глава 5. Новые методы........................... 414
ОЧЕРК ЧЕТВЕРТЫЙ. История расчета неразрезной балки
Глава 1. Первые попытки расчета .... 419
Глава 2. Первый расчет неразрезной балки 422
Глава 3. Уравнение трех моментов.................... 425
Глава 4. Поиски удобного метода вычисления перемещений 430
Глава 5. Завершение теории неразрезных балок и новые
методы ........ - - 435
Библиография
А. Работы по истории строительной механики , 442
Б. Подлинные труды......................
Список научных трудов С. А. Бернштейна . . 449