Автор: Данилина Н.И. Дубровская Н.С. Кваша О.П. Смирнов Г.Л. Феклисов Г.И.
Теги: математика вычислительная математика
Год: 1976
Текст
518
Ч—67
УДК 518 (075.8)
И. И. Данилина, Н. С. Дубровская, О. П. Кваша,
Г. Л. Смирнов, Г. И. Феклисов
Рецензенты; доц. Данелян Т. Я. и препод. Данилова А. Н.
Численные методы. Учебник для техникумов. М., «Высш.
' школа», 1976.
368 с. с ил.
На обороте тит. л. авт.: Н. И. Данилина, Н. С. Дубровская, О. П Ква-
ша [и др.]
В книге излагаются основы вычислительной математики и численные методы
математического анализа в объеме, необходимом технику-программисту для работы
на электронных вычислительных машинах.
Учебник написан в понятной и доступной для изучения форме. Теоретический
материал сопровождается многочисленными примерами, а также упражнениями для
самостоятельной работы.
Предназначается для учащихся средних специальных учебных заведений.
Ч _20203— 240 240_76 518
001(01)—76
© Издательство «Высшая школа», 1976 г.
ОГЛАВЛЕНИЕ
Стр.
Предисловие. .................................... 7
Раздел первый
ПРИБЛИЖЕННЫЕ ВЫЧИСЛЕНИЯ
Глава I
Элементарная теория погрешностей
§ 1.1. Точные и приближенные числа. Источники погрешностей. Клас-
сификация погрешностей............................................ 8
§ 1.2, Абсолютная и относительная погрешности................... 10
§ 1.3. Десятичная запись приближенных чисел. Значащая цифра числа.
Верная значащая цифра ............................................13
£ 1.4. Округление чисел......................................... 16
$ 1.5. Связь между числом верных знаков и погрешностью числа ... 18
§ 1.6. Погрешности суммы и разности...............................20
§ 1.7. Погрешность произведения. Число верных знаков произведения 24
§ 1.8. Погрешность частного. Число верных знаков частного.........29
§ 1.9. Погрешности степени и корня ...............................31
§ 1.10. Правила подсчета цифр.....................................32
Упражнения........................................................34
Глава II
Методы решения систем линейных уравнений
§ 2.1. Матрицы и векторы, Основные действия над матрицами и векто-
рами .............................................................35
§ 2.2. Определитель матрицы. Свойства определителя и методы его вы-
числения..........................................................41
§ 2.3. Ранг матрицы........................................... 48
§ 2.4. Обратная матрица......................................... 49
§ 2.5. Абсолютная величина и норма матрицы......................52
§ 2.6. Клеточные матрицы. Действия над клеточными матрицами ... 54
§ 2.7. Треугольные матрицы. Разложение матрицы на произведение
двух треугольных матриц...........................................64
§ 2.8. Понятие о системе линейных уравнений.......................68
§ 2.9. Матричная форма записи системы линейных уравнений. Решение
матричных уравнений............................................. 69
§ 2.10. Формулы Крамера для решения системы линейных уравнений 73
§ 2.11. Решение системы линейных уравнений методом последовательного
исключения неизвестных (методом Гаусса). .........................75
§ 2.12. Вычисление определителей с помощью схемы Гаусса...........85
§ 2.13. Обращение матрицы с помощью схемы Гаусса ................86
§ 2.14. Понятие предела для векторов и матриц................... 89
§ 2.15. Приближенные методы решения систем линейных уравнений . . 90
§ 2.16. Условия сходимости итерационного процесса.................94
§ 2.17. Оценка погрешности приближенного процесса метода итерации 95
§ 2.18. Метод Зейделя. Условия сходимости процесса Зейделя .... 96
3
Стр.
§ 2.19. Оценка погрешности процесса Зейделя......................99
§ 2.20. Приведение системы линейных уравнений к виду, удобному для
итераций........................................................100
§ 2.21. Исправление элементов приближенной обратной матрицы . . . 102
Упражнения.......................................................ЮЗ
Глава III
Методы решения нелинейных уравнений
§3.1. Алгебраические и трансцендентные уравнения...............108
§ 3.2. Графические методы решения уравнений и систем............112
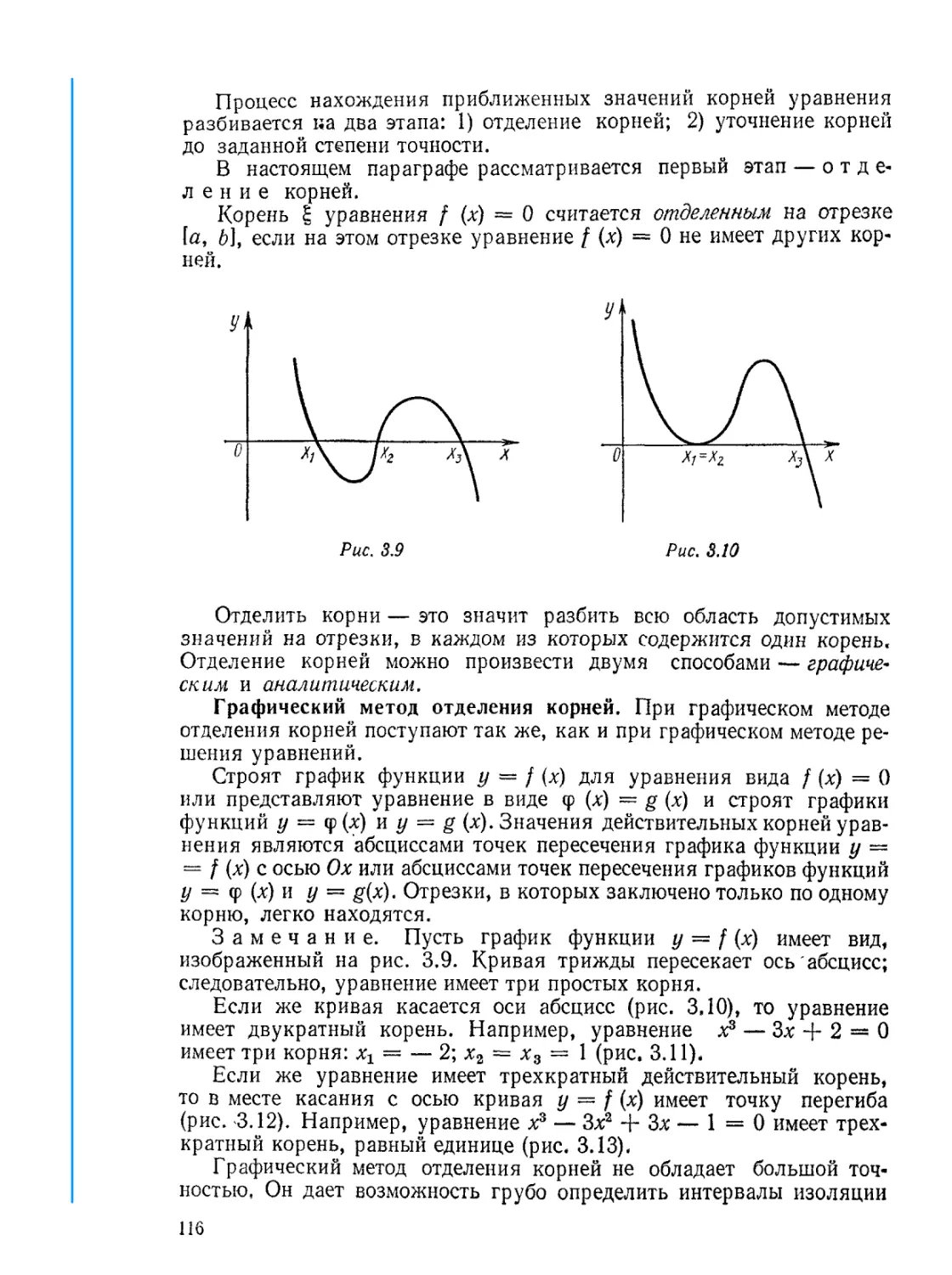
§ 3.3. Отделение корней.........................................115
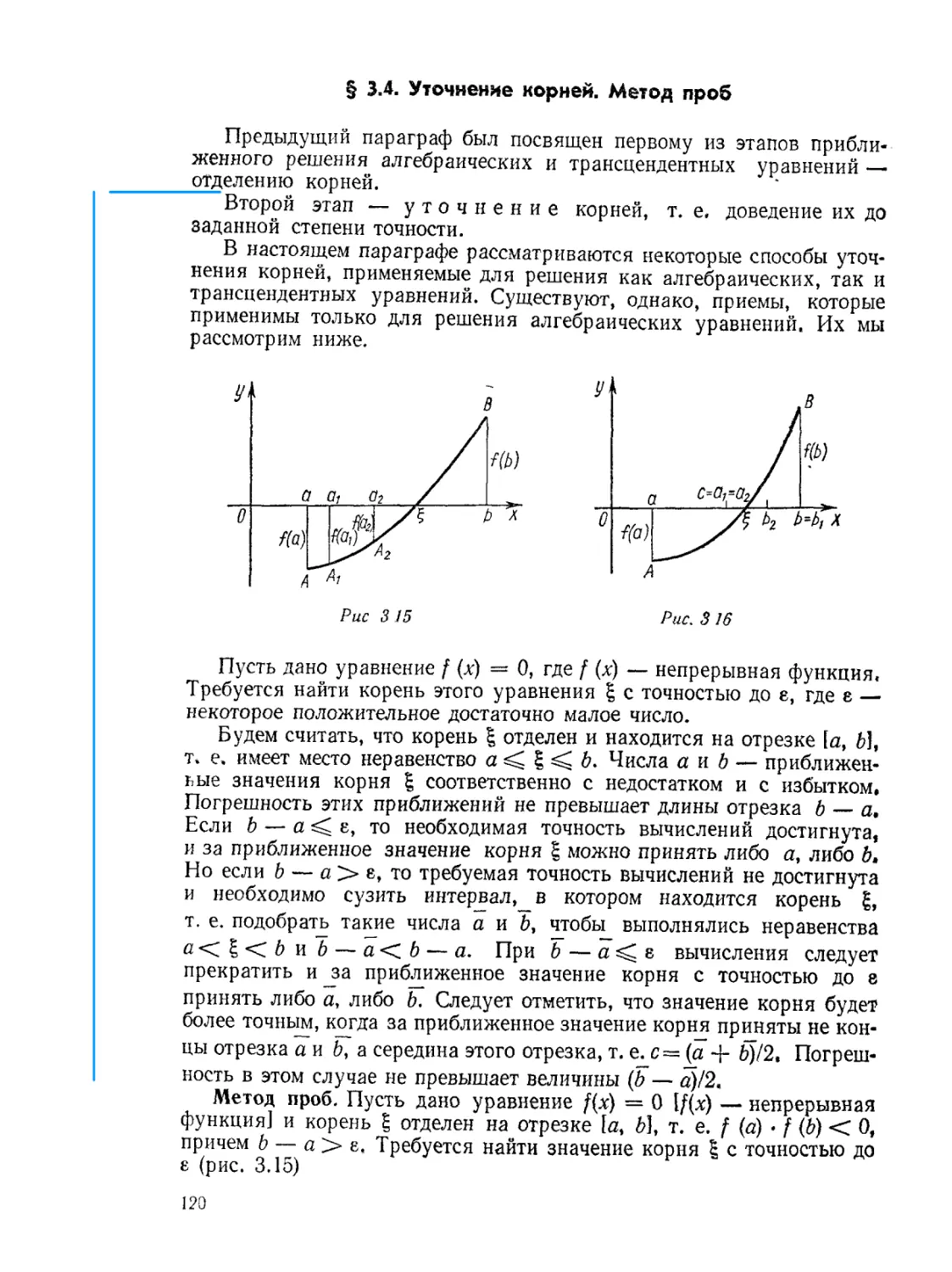
§ 3.4. Уточнение корней. Метод проб.............................120
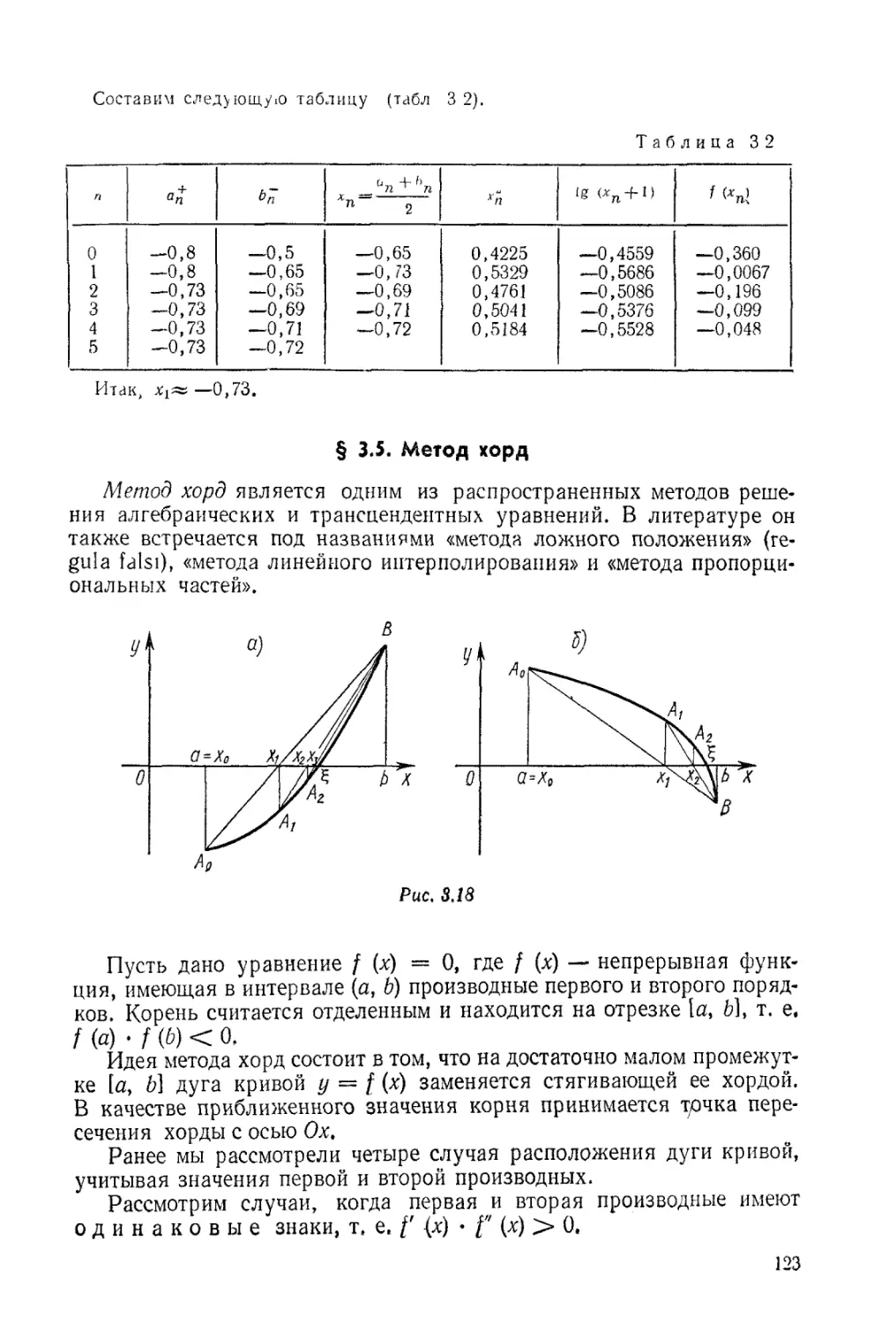
§ 3.5. Метод хорд...............................................123
§ 3.6. Метод Ньютона (метод касательных)........................127
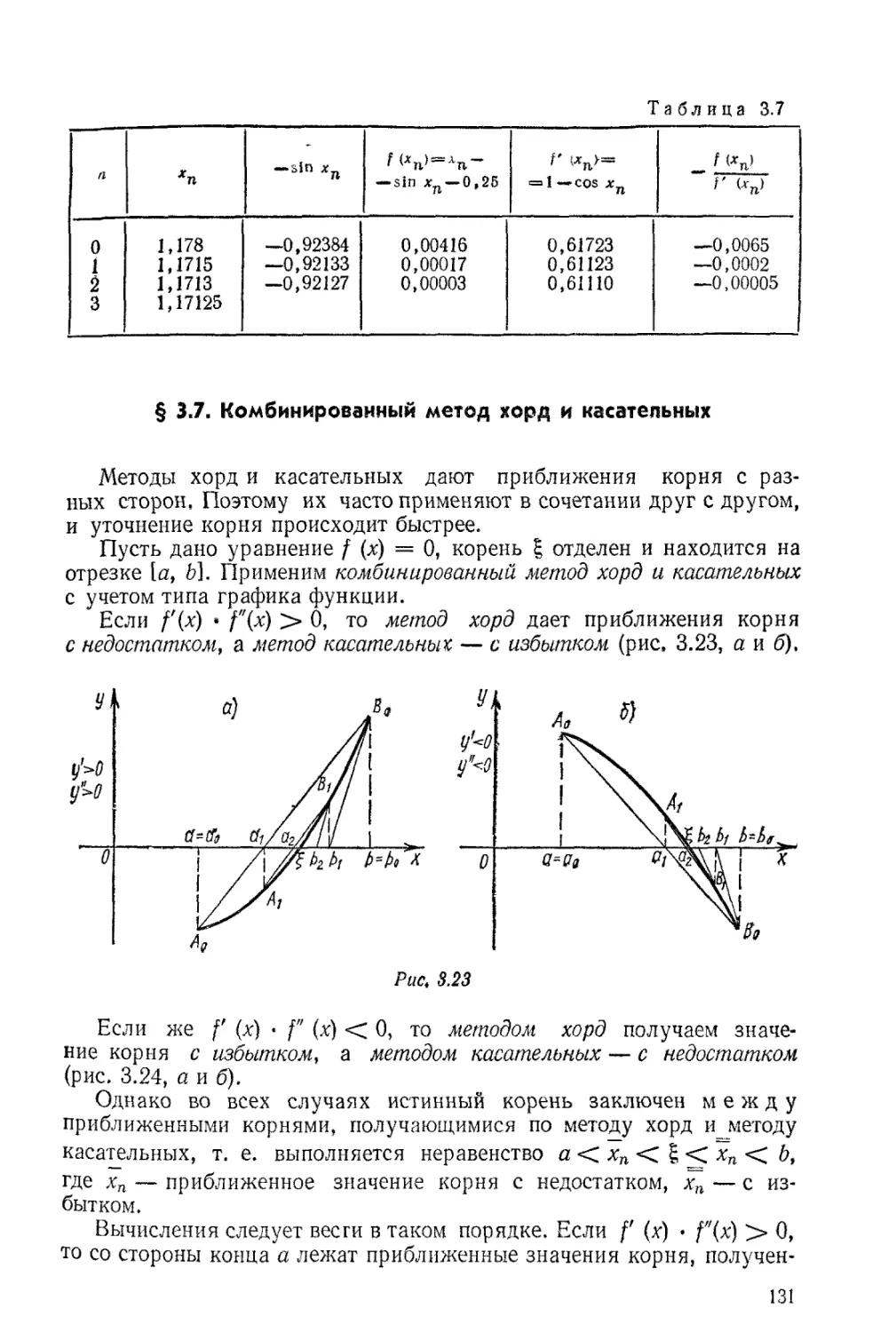
§ 3.7. Комбинированный метод хорд и касательных.................131
§ 3.8. Метод итерации (метод последовательных приближений) .... 135
§ 3.9. Приближенное решение систем уравнений. Метод Ньютона для
системы двух уравнений. ...................................... 139
§ 3.10. Метод итерации для нелинейной системы уравнений.........142
§ 3.11. Общие свойства алгебраических уравнений. Определение числа
действительных корней алгебраического уравнения.................144
§ 3.12. Нахождение области существования корней алгебраического
уравнения..................................................... 147
§ 3.13. Вычисление значений многочлена. Схема Горнера...........150
§ 3.14. Схема деления многочлена на квадратный трехчлен.........153
§ 3.15. Выделение квадратного трехчлена по методу Хичкока.......156
Упражнения. . . ................................................160
Глава IV
Интерполирование и экстраполирование
§ 4.1. Способы задания функций . ...............................161
§ 4.2. Математические таблицы................................. 163
§ 4.3. Математическая постановка задачи интерполирования . . . . 168
§ 4.4. Интерполяционный многочлен Лагранжа.................... 169
§ 4.5. Оценка погрешности интерполяционного многочлена Лагранжа 174
§ 4.6. Конечные разности........................................176
§ 4.7. Первая интерполяционная формула Ньютона для равноотстоящих
узлов интерполяции............................................ 182
§ 4.8. Вторая интерполяционная формула Ньютона ......... 185
§ 4.9. Оценки погрешностей интерполяционных формул Ньютона . . 187
§ 4.10. Единственность интерполяционного многочлена........... 189
§ 4.11. Интерполирование в таблицах.............................189
§ 4.12. Линейное интерполирование по Эйткину....................192
§ 4.13. Разделенные разности. . ................................194
§ 4.14. Первая интерполяционная формула Ньютона для неравноотстоя-
щих узлов интерполяции.........................................«196
§ 4.15. Интерполяционные формулы Гаусса........................«197
§ 4.16. Интерполирование с помощью многочленов Чебышева.........199
§ 4.17. Обратное интерполирование............................. 201
Упражнения....................................................... 204
Глава V
Определение собственных чисел и собственных векторов матрицы
§5.1. Характеристический многочлен и методы определения его коэф-
фициентов ......................................................208
§ 5.2. Метод непосредственного развертывания ............ 210
4
Стр.
§ 5.3. Метод Крылова для развертывания характеристического опреде-
лителя ................................................ ........ 212
§ 5.4. Вычисление собственных векторов по методу Крылова.219
§ 5.5. Метод Данилевского.................................... ..220
§ 5.6. Вычисление собственных векторов по методу Данилевского . . . 232
§ 5.7. Метод Леверрье — Фаддеева.................................234
§ 5.8. Метод интерполяции...................................... 236
§ 5.9. Определение первого собственного числа матрицы методом ите-
рации......................................................... 239
§ 5.10. Определение последующих собственных чисел и принадлежащих
им собственных векторов............................... 241
Упражнения......................................................... 243
Глава VI
Математическая обработка данных
§ 6.1. Постановка задачи........................................... 244
§ 6.2. Построение эмпирических линейных зависимостей. Методы уточ-
нения параметров этих зависимостей . . .........................246
§ 6.3. Выбор эмпирических формул для нелинейных зависимостей . . 253
§ 6.4. Преобразование координат......................................257
§ 6.5. Эмпирические формулы, содержащие три параметра.............259
Упражнения...........................................................261
Раздел второй
ЧИСЛЕННЫЕ МЕТОДЫ МАТЕМАТИЧЕСКОГО
АН АЛИЗА
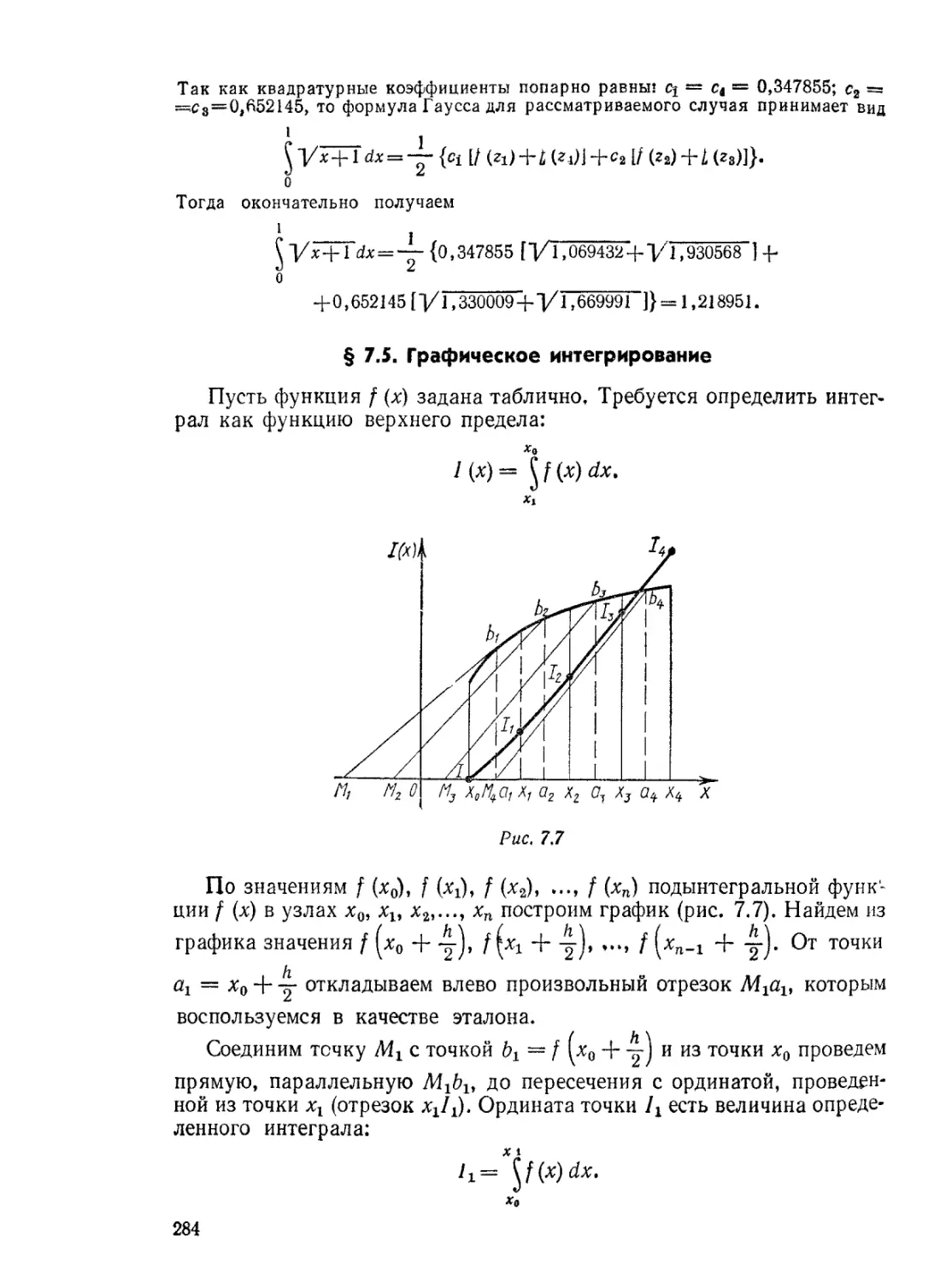
Т"Л’з-Впа Л7!!
Численное интегрирование и дифференцирование
§ 7.1. Численное интегрирование. Простейшие квадратурные формулы 265
*§ 7.2. Обобщенная формула численного интегрирования Ньютона—Котеса 271
§ 7.3. Квадратурная формула Чебышева..........................274
§ 7*4. Квадратурная формула Гаусса............................277
§ 7.5. Графическое интегрирование.............................284
§ 7.6. Численное дифференцирование. Формулы приближенного диф-
ференцирования, основанные на интерполяционных формулах
Ньютона........................................................285
§ 7.7. Формула приближенного дифференцирования, основанная на
интерполяционной формуле Лагранжа.......................287
§ 7.8. Графическое дифференцирование..........................289
Упражнения. ,............................................... 289
Глава VIII
Ряды Фурье
§ 8.1. Понятие последовательности и ряда......................290
§ 8.2. Разложение функций в ряд Фурье. Теорема Дирихле........294
§ 8.3. Интегрирование и дифференцирование рядов Фурье.........300
§ 8.4. Численный гармонический анализ. Тригонометрическое интер-
полирование ................................................. 302
§ 8.5. Численные методы определения коэффициентов Фурье .... 306
Упражнения.................................................. 310
5
Стр.
Глава IX
Приближенное решение обыкновенных дифференциальных уравнений
§ 9.1. Понятие о дифференциальном уравнении................. * 311
§ 9.2. Метод последовательных приближений (метод Пикара) .... 314
§ 9.3. Интегрирование дифференциальных уравнений с помощью степен-
ных рядов................................................. 317
§ 9.4. Численное интегрирование дифференциальных уравнений. Метод
Эйлера........................................................318
§ 9.5. Модификации метода Эйлера.............................322
§ 9.6. Метод Рунге — Кутта...................................326
§ 9.7. Экстраполяционный метод Адамса.........................332
Упражнения. ................................................ 337
Глава X
Приближенное решение дифференциальных уравнений в частных произ-
водных
§ 10.1 Классификация дифференциальных уравнений в частных произ-
водных................................................. ........ 338
§ 10.2. Конечно-разностные аппроксимации ......................341
§ 10.3. Аппроксимация эллиптических дифференциальных уравнений
в частных производных...........................................347
§ 10.4. Решение разностных уравнений для эллиптических дифферен-
циальных уравнений..............................................349
§ 10.5. Влияние криволинейных граничных условий................352
§ 10.6 Аппроксимация параболических и гиперболических дифферен-
циальных уравнений в частных производных...............356
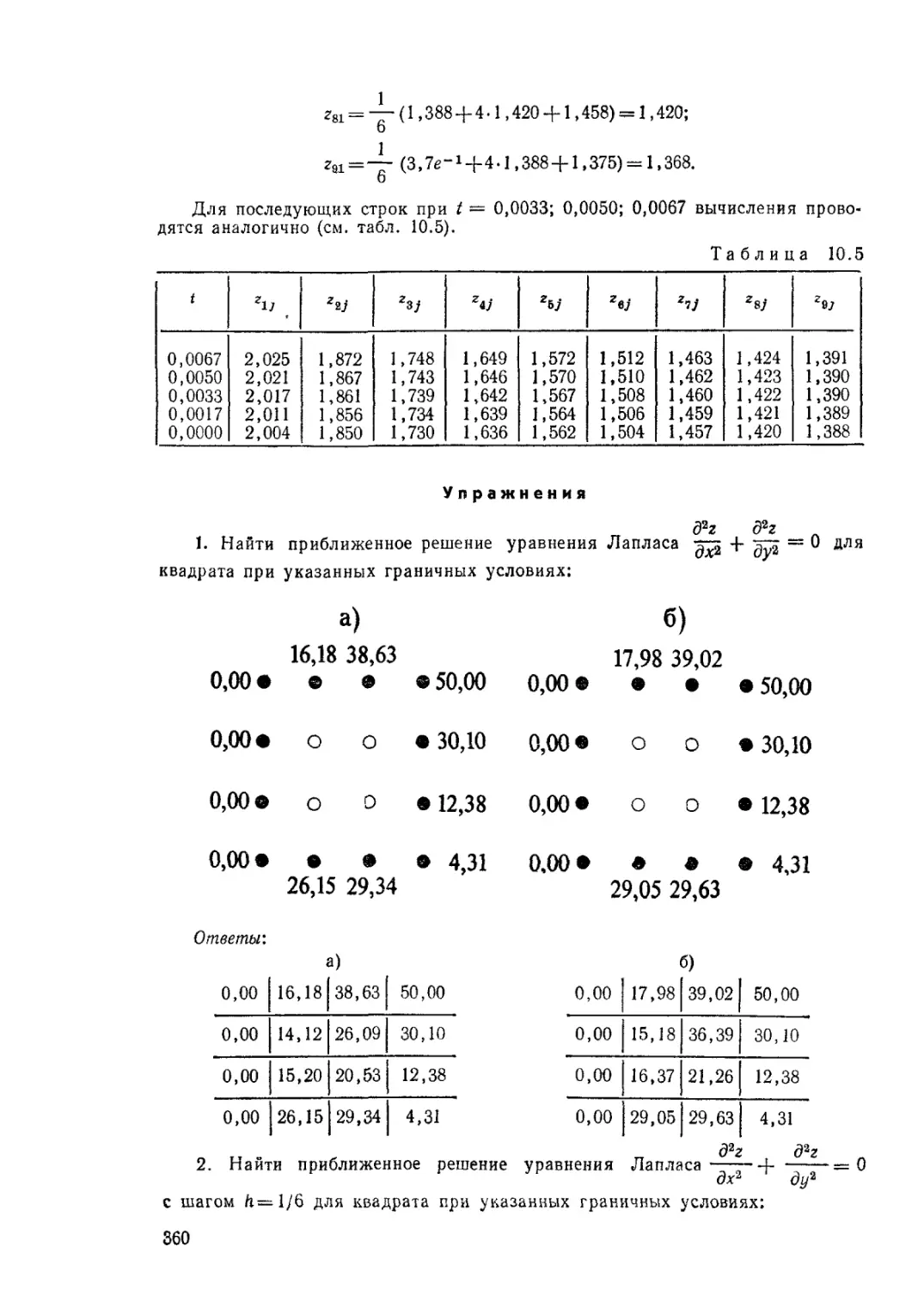
Упражнения.......................................................360
Литература......................................................363
Предметный указатель.......................................... 364
ПРЕДИСЛОВИЕ
Курс «Численные методы» является одной из основных дисцип-
лин, необходимых для подготовки программистов среднего звена.
Он имеет своей целью изучение учащимися основ и методики ре-
шения задач прикладной математики с приближенными вычис-
лениями и численными методами математического анализа в объ-
еме, необходимом технику-программисту для работы на электрон-
ных вычислительных машинах.
Настоящая книга — первая попытка создания учебника для изу-
чения вычислительной математики в средних специальных учебных
заведениях.
В результате изучения этого курса учащиеся должны знать чис-
ленные методы, уметь применять их при решении задач и приме-
ров, уметь составлять и применять вычислительные бланки и таб-
лицы для дальнейшего программирования на ЭВМ.
По своему содержанию учебник разбит на два больших разде-
ла: «Приближенные вычисления» и «Численные методы математи-
ческого анализа». Первый раздел включает шесть глав: «Элемен-
тарная теория погрешностей»; «Методы решения систем линейных
уравнений»; «Методы решения нелинейных уравнений»; «Интерпо-
лирование и экстраполирование»; «Определение собственных чисел
и собственных векторов матрицы»; «Математическая обработка
данных». Второй раздел содержит четыре главы: «Численное ин-
тегрирование и дифференцирование»; «Ряды Фурье»; «Приб-
лиженное решение обыкновенных дифференциальных урав-
нений»; «Приближенное решение дифференциальных уравнений в
частных производных».
Изучение численных методов немыслимо без решения значи-
тельного количества задач. Теоретический материал иллюстриру-
ется многочисленными примерами. В конце каждой главы приво-
дятся упражнения, решение которых должно способствовать луч-
шему усвоению излагаемого материала.
Работа над учебником проводилась в следующем порядке: гла-
вы I, III и IX написала О. П. Кваша, главы II и V — Н. С. Дубров-
ская, главы IV, VI и VII — Н. И. Данилина, главу VIII — Г. Л.
Смирнов, главу X — Г. И. Феклисов.
Авторы выражают свою признательность рецензентам Т. Да-
нелян и А. Д. Даниловой, внимательно прочитавшим рукопись и
сделавшим ряд ценных замечаний, а также редактору книги А. М.
Суходскому, чья работа во многом способствовала улучшению
книги.
Авторы
Раздел первый
ПРИБЛИЖЕННЫЕ ВЫЧИСЛЕНИЯ
Глава I
ЭЛЕМЕНТАРНАЯ ТЕОРИЯ ПОГРЕШНОСТЕЙ
§ 1.1. Точные и приближенные числа. Источники погрешностей.
Классификация погрешностей
В процессе решения задачи вычислитель сталкивается с различ-
ными числами, которые могут быть точными или приближенными. Точ-
ные числа дают истинное значение величины числа, приближенные —
близкое к истинному, причем степень близости определяется погреш-
ностью вычисления.
Например, в утверждениях: «куб имеет 6 граней»; «на руке 5 паль-
цев»; «в классе 32 ученика»; «в книге 582 страницы» числа 6, 5, 32,
582—точные. В утверждениях: «ширина дома 14,25 м»; «вес коробки
50 г»; «в лесу около 5000 деревьев» числа 14,25; 50; 5000—приближен-
ные. Измерение ширины дома производится измерительными средст-
вами, которые сами могут быть неточными; кроме того, измеритель при
измерении допускает ошибку (погрешность). При взвешивании коробки
также допускается ошибка, так как автоматические весы не чувстви-
тельны к увеличению или уменьшению веса на 0,5 г. Произвести точно
подсчет количества деревьев в лесу невозможно, так как некоторые
деревья могут быть подсчитаны дважды; другие совсем не включались
в счет; некоторые деревья были отнесены к кустарникам и исключены
из счета, и, наоборот, кустарники включены в счет количества
деревьев.
Во многих случаях жизни невозможно найти точное значение вели-
чины числа и вычислителю приходится довольствоваться его прибли-
женным значением. Кроме того, очень часто вычислитель сознатель-
но заменяет точное значение приближенным в целях упрощения вычис-
лений.
Таким образом, приближенным числом а называется число, незна-
чительно отличающееся от точного числа А и заменяющее последнее
в вычислениях.
При решении той или иной задачи вручную или на вычислительной
машине мы получаем числовой результат, который, как правило, не
является точным, так как при постановке задачи и в ходе вычислений
возникают погрешности. Поэтому любая задача, связанная с массовы-
ми действиями над числами, может быть решена стой или иной степенью
точности. В связи с этим при постановке задачи должна быть указана
точность ее решения, т, е. задана погрешность, максимально допусти-
мая в процессе всех вычислений.
8
Источниками погрешностей (ошибок) могут быть.
1) неточное отображение реальных процессов с помощью матема-
тики, в связи с чем рассматривается не сам процесс, а его идеализиро-
ванная математическая модель. Не всегда реальные явления природы
можно точно отобразить математически. Поэтому принимаются усло-
вия, упрощающие решение задачи, что вызывает появление погрешно-
стей. Некоторые задачи невозможно решить в точной постановке и они
могут заменяться другими задачами, близкими по результатам первым.
При этом также возникают погрешности;
2) приближенное выражение величин, входящих в условие за-
дачи, вследствие их неточного измерения. Это погрешности исходных
данных, физических констант, чисел л, е и др.;
3) замена бесконечных процессов, пределами которых являются
искомые величины, конечной последовательностью действий. Сюда
относятся погрешности, образующиеся в результате обрыва какого-то
бесконечного процесса на некотором этапе. Например, если в ряде
длЗ уЪ
sin х~х----------------1---------------Н
31 5! 71
взять определенное количество членов и принять их сумму за sin х»
то мы, естественно, допуск аем погрешность;
4) округление исходных данных, промежуточных или окончатель-
ных результатов, когда при вычислениях используется лишь конечное
число цифр числа.
При отбрасывании младших разрядов числа имеет место погреш-
ность. Пусть, например, число 0,7835478931 требуется записать в ячей-
ку электронной цифровой вычислительной машины «Минск 1». Раз-
рядная сетка машины допускает запись семизначного десятичного чис-
ла. Поэтому данное число нужно округлить так, чтобы в нем осталось
не более семи знаков после запятой. Тогда округленное число примет
следующий вид: 0,7835479;
5) кроме указанных выше случаев, погрешности могут появлять-
ся в результате действий над приближенными числами. В этом случае
погрешности исходных данных в какой-то мере переносятся на резуль-
тат вычислений.
Полная погрешность является результатом сложного взаимодей-
ствия всех видов погрешностей. При решении конкретных задач те
или иные погрешности могут отсутствовать или мало влиять на обра-
зование полной погрешности. Однако для полного анализа погрешно-
стей необходимо учитывать все их виды.
Во всех случаях полная погрешность не может превышать по своей
абсолютной величине суммы абсолютных величин всех видов погреш-
ностей, но обычно она редко достигает такой максимальной величины.
Таким образом, погрешности можно подразделить на три большие
группы:
1) исходные, или неустранимые, к которым относятся погрешности,
возникающие в результате приближенного описания реальных про-
цессов и неточного задания исходных данных, а также погрешности,
9
связанные с действиями над приближенными числами. Эти погрешно-
сти проходят через все вычисления и являются неустранимыми;
2) погрешности округления (зарождающиеся), которые появляются
в результате округления исходных данных, промежуточных и оконча-
тельных результатов;
3) остаточные, возникающие в результате замены бесконечных
процессов конечной последовательностью действий.
Оценка погрешности может быть произведена: с помощью абсолют-
ной погрешности; с помощью относительной погрешности; с помощью
остаточного члена; с помощью статистических оценок.
При работе с приближенными величинами вычислитель должен
уметь:
а) давать математические характеристики точности приближенных
величин;
б) зная степень точности исходных данных, оценить степень точ-
ности результатов;
в) брать исходные данные с такой степенью точности, чтобы обес-
печить заданную точность результата. В этом случае не следует слиш-
ком завышать точность исходных данных, чтобы избавить вычисли-
теля от бесполезных расчетов;
г) уметь правильно построить вычислительный процесс, чтобы
избавить его от тех выкладок, которые не окажут влияния на точные
цифры результата.
§ 1.2. Абсолютная и относительная погрешности
В § 1.1 было дано определение приближенного числа: приближен-
ным числом а называется число, незначительно отличающееся от точ-
ного числа А и заменяющее его в вычислениях.
Если А, то говорят, что число а является приближенным зна-
чением числа А по недостатку; если а > А — приближенным значением
по избытку.
Разность между точным числом А и его приближенным значением
а составляет ошибку, или погрешность. Если a<Z А, то А — а > 0;
если а> А, то А—п<0.
Как правило, знак ошибки вычислителя не интересует, поэтому
пользуются абсолютной ошибкой, или абсолютной погрешностью.
Абсолютная величина разности между точным числом А и его
приближенным значением а называется абсолютной погрешностью
приближенного числа а:
Аа = 1 Л —«(1)
Здесь возможны два случая.
1. Точное число А нам известно. Тогда абсолютная погрешность
приближенного числа легко находится по формуле (1).
Пример 1. Пусть А = 784,2737, а — 784,274; тогда абсолютная погрешность
= | А — а 1 = I 784,2737—784,274 | = 0,0003,
10
2, Точное число Л нам неизвестно, тогда вычислить абсолютную по-
грешность по формуле (1) нельзя. Поэтому пользуются понятием гра-
ницы абсолютной погрешности, удовлетворяющей неравенству
|Л-а|<Д;.
Граница абсолютной погрешности, т. е. число, заведомо превышаю-
щее абсолютную погрешность (или в крайнем случае равное ей), назы-
вается предельной абсолютной погрешностью.
Следовательно, если — предельная абсолютная погрешность, то
(2)
Значение точного числа А всегда заключено в следующих границах;
а —Д*^Л<а + Д*. (3)
Выражение а—есть приближение числа А по недостатку, а
а + Д£ — приближение числа А по избытку. Значение числа А за-
писывается так:
А “ а + Да. (3 )
Пример 2. Число 45,3 получено округлением. Точное значение числа неиз
вестно, однако, пользуясь правилами округления чисел, можно сказать, что аб-
солютная погрешность не превышает (меньше или равна) 0,05
Следовательно, границей абсолютной погрешности (предельной абсолютной
погрешностью) можно считать 0,05. Записывают это так: 45,3 ( ±0,05). Скобки
часто опускают, так что запись 45,3 ± 0,05 означает то же самое. Двойной знак
± означает, что отклонение приближенного значения числа от точного возмож-
но в обе стороны.,В качестве границы абсолютной погрешности берут по возмож-
ности наименьшее число.
Пример 3. При измерении длины отрезка оказалось, что ошибка, допущенная
нами, не превышает 0,5 см; тем более она не превышает 1, 2 или 3 см. Каждое
из этих чисел можно считать границей абсолютной погрешности. Однако нужно
указать наименьшую из них, так как чем меньше граница абсолютной погрешно-
сти, тем точнее выражается приближенное значение числа. В записи приближен-
ного числа, полученного в результате измерения, обычно отмечают ею предель-
ную абсолютную погрешность.
На практике часто применяют выражения типа: «с точностью до
0,01»; «с точностью до 1 см» и т. д. Это означает, что предельная абсо-
лютная погрешность соответственно равна 0,01; 1 см и т. д.
Пример 4. Если длина отрезка I = 184 см измерена с точностью до 0,05 см,
то* пишут I == 184 см ± 0,05 см. Здесь предельная абсолютная погрешность
= 0,05 см, а точная величина длины I отрезка заключена в следующих грани-
цах: 183,95 см < I < 184,05 см.
По абсолютной и предельной абсолютной погрешностям нельзя
судить о том, хорошо или плохо произведено измерение.
Пример 5. Пусть при измерении книги и длины стола были получены резуль-
таты: = 28,4 ± 0,1 (см) и /2 = 110,3 ± 0,1 (см). И в первом, и во втором слу-
чае предельная абсолютная погрешность составляет ОД см. Однако второе из-
мерение было произведено более точно, чем первое.
И
Для того чтобы определить качество произведенных измерений,
необходимо определить, какую долю составляет абсолютная или
предельная абсолютная погрешность от измеряемой величины.
В связи с этим вводится понятие относительной погрешности.
Относительной погрешностью 6а приближенного числа а называет-
ся отношение абсолютной погрешности Ла к модулю точного числа
А (Л 0), т. е.
б (4)
а М|
Отсюда
Аа = | А |ба. (4')
Число 6J, заведомо превышающее относительную погрешность
(или в крайнем случае равное ей), называется предельной относитель-
ной погрешностью: 1
аа < 8*. (5)
Из соотношений (4) и (5) вытекает, что
I А I
Из определения предельной абсолютной погрешности следует, что
Аа AJ. Тогда можно записать
= М iss (6)
и за предельную относительную погрешность приближенного числа
а можно принять
Л*
= ттг • С)
Ml
Учитывая, что А, как правило, неизвестно и что A tv а, равенства
(6) и (7) можно записать так:
Да = |а|6а. (6')
И
Возвращаясь к примеру 5, найдем предельные относительные погрешности
измерения книги и стола.
е* 0.1 (см)
% = ' ^0,0035, или 0,35%;
1 28,4 (см)
с 0,1 (см) п.
6* = 7 ^0,009, или 0,09%.
1‘ 110,3 (см)
Таким образом, измерение стола было произведено намного точнее.
Очевидно, что как относительная погрешность, так и предельная
относительная погрешность представляют собой отвлеченные числа,
не зависящие от единиц, в которых выражаются результаты измере-
ний,
12
Пример 6. Определить (в процентах) предельную относительную погрешность
приближенного числа а ~ 35,148 ± 0,00074
решение. Воспользуемся формулой (7). Тогда
_ д2 0,00074
б^ = —— = 4—— = 0,000021 ® 0,0021%.
а |а| 35,148
Пример 7. Определить предельную абсолютную погрешность приближенного
числа а = 4,123, если = 0,01%.
Решение. Запишем проценты в виде десятичной дроби и для определения
предельной абсолютной погрешности воспользуемся формулой (6'); тогда
Да = | а I 62 = 4,123 • 0,0001 = 0,00042.
Пример 8. Определить относительные погрешности чисел х и yt полученных
при измерении углов Какой из результатов более точный?
X У
50°30'10" 3" 45°15'36” 2"
Решение. Переведем заданные значения х и у в секунды и определим
относительные погрешности измерений. Более точным измерением будет то, где
относительная погрешность меньше. Имеем:
х= 181810" ± 3", = 3/181810 « 0,000017 = 0,0017%;
у =162936" ± 2\ = 2/162936 w 0,000013 = 0,0013%.
Измерение у произведено более точно.
Пример 9. Определить, какое равенство точнее: at = 13/19 ж 0,684 или
а2 = У52 ~ 7,21?
Решение. Для нахождения предельных абсолютных погрешностей берем
числа и а2 с большим числом десятичных знаков: 13/19 zz 0,68421; ~\/52 »
7,2111. Определяем предельные абсолютные погрешности, округляя их с из-
бытком:
А* = I 0,68421 —0,684 I < 0,00022; А* = ] 7,2111 —7,21 I < 0,0012.
Находим предельные относительные погрешности:
ба, = Да,/^=0,00022/0,684 ~ 0,00033 = 0,033%;
ба,= Да2/аг = 0,0012/7,21 X 0,00017 = 0,017%.
Второе равенство является более точным, поскольку 6as < 6av
§ 1.3. Десятичная запись приближенных чисел.
Значащая цифра числа. Верная значащая цифра
Системой счисления, или нумерацией, называется совокупность
правил, служащих для наименования и обозначения чисел. Цифра-
ми называются условные знаки, используемые при обозначении чисел.
При записи чисел в десятичной системе счисления пользуются десятью
13
цифрами: О, 1, 2, 3, 4, 5, 6, 7, 8, 9. Десятичная система является по-
зиционной: значение каждой цифры в числе зависит от ее положения
среди других цифр этого числа. Так, в числе 7777, 77 имеются шесть
цифр 7. Но все они имеют разные значения. Значение первой слева
цифры — 7000, второй — 700, третьей — 70, четвертой — 7, пятой —
0,7, шестой — 0,07, Число 1П1.П является сокращенной записью
следующей суммы:
7777,77 = 7 . 103 + 7 * 103 + 7 • 101 + 7 . 10° + 7 . 10’1 + 7 ЮЛ
В десятичном числе единица каждого разряда равна десяти едини-
цам предыдущего разряда. Вообще, всякое десятичное положительное
число а может быть представлено в виде конечной или бесконечной де-
сятичной дроби:
a = a1‘10w + <z2* 10'””1+сс3* 1О'П"2 + ... +aJ0^+’+ ..., (1)
где — цифры числа (I = 1, 2, осм и), причем =/= 0, а т — стар-
ший десятичный разряд числа а.
Значение единицы соответствующего разряда есть цена разряда.
Так, цена первого (слева) разряда приближенного числа а есть 10w,
второго Ю^-1, п-го 10'™+Ч
При решении задач очень часто ставится условие: вычислить резуль-
тат с точностью до одной десятой, одной сотой и т. д. Создается впечат-
ление, что точность вычислений определяется числом десятичных зна-
ков после запятой. Это неправильно, так как число десятичных знаков
зависит от единицы, выбранной для измерения.
Определяющим точность вычисления является не число десятичных
знаков, а число значащих цифр результата
Значащими цифрами приближенного числа а называются все циф-
ры в его десятичном изображении, отличные от нуля, и нули, если они
содержатся между значащими цифрами или расположены в конце
числа и указывают на сохранение разряда точности. Нули, стоящие
левее первой отличной от нуля цифры, не являются значащи-
ми цифрами,
Пример 1, Числа 0,001403 и 6,0300 имеют соответственно 4 и 5 значащих
цифр. Нуль, записанный в конце десятичной дроби, всегда значащая цифра (иначе
его просто бы не писали). В данном примере в числе 3,0300 последний нуль по-
казывает, что число задано с точностью до десятитысячных.
При написании целых чисел нули справа могут быть в одних слу-
чаях значащей цифрой, в других — незначащей. Если число 835 000
задано с точностью до единиц, то все три нуля справа—значащие цифры.
Если же это число задано с точностью до сотен, то последние два ну-
ля — незначащие цифры, а нуль в разряде сотен—значащая цифра.
Пример 2. Число 399 837 округлили до тысяч, получили 400 000. Нуль в раз-
ряде тысяч является значащей цифрой, так как стоит в разряде точности. Все
остальные цифры стоящие левее нуля, находящегося в разряде точности, являют-
ся также значащими. Последние три нуля — незначащие цифры.
14
Для того чтобы по записи числа можно было бы определить, явля-
ются ли крайние правые нули значащими или нет, рекомендуется числа
представлять в виде произведения двух сомножителей, например:
400 • Ю3, или 40,0 • 104, или 4,00 • 105. Последняя форма записи, ког-
да запятая поставлена после первой слева значащей цифры, называет-
ся нормальной и является предпочтительной. В таком представлении
количество значащих цифр числа равно количеству значащих цифр
первого сомножителя.
Однако точность приближенного числа зависит не от того, сколько
в этом числе значащих цифр, а от того, сколько значащих цифр заслу-
живают доверия, т. е. от количества верных значащих цифр.
Приближенное число а = • 10т + а2 • 10mel + ... + ccn X
X 10'л-л+1 + ... содержит п верных значащих цифр в узком смысле,
если абсолютная погрешность этого числа не превосходит половины
единицы десятичного разряда, выражаемого п-й значащей цифрой,
считая слева направо, т, е. если выполняется неравенство
Да< 0,5. (2)
Если это неравенство не выполняется, то цифру называют сомни-
тельной, Очевидно, что если цифра ап — верная, то и все предшествую
щие ей цифры тоже верные. Таким образом, среди верных цифр всегда
можно указать последнюю.
Пример 3 Для точного числа А = 17,976 число а = 17,98 является прибли-
жением с четырьмя верными знаками в узком смысле, так как Да = | А — а | =
= 0,004 < 0,5-0,01.
В математических таблицах все помещенные значащие цифры —
верные. Так, в известных таблицах В, М. Брадиса значения синуса даны
с абсолютной погрешностью, не превышающей 0,5 • 10“4, т. е. с че-
тырьмя верными значащими цифрами в узком смысле. В последнее
время стали использоваться таблицы (таблицы различных физических
величин, экспериментально составленные таблицы), в которых абсо-
лютные погрешности чисел не превосходят единицы последнего разряда.
Приближенное число
а = аг10ш + сс2*10т"’1+ ... + 10Z7I*n+I + ...
содержит п верных значащих цифр в широком смысле, если абсолютная
погрешность этого числа не превосходит единицы десятичного разряда,
выражаемого п-й значащей цифрой, считая слева направо, т. е. если
выполняется неравенство
Да<Ы0'”-"+1. (3)
Пример 4. Для точного числа А = 17,976 число а — 17,97 является прибли-
женным с четырьмя верными цифрами в широком смысле, так как Да —
I А — а | == 0,006 < 1 < 0,01.
Неравенства (2) и (3) можно записать в виде Да со * куп-n+i,
где параметр со, принимающий значения 0,5 со 1, указывает на
характер проводимых вычислений. Если приближенные числа появ-
15
ляюгся в результате вычислений по формулам с точными значениями
исходных данных (например, при составлении таблиц трансцендент-
ных функций), иными словами, когда можно практически достигнуть
любой заданной точности, то выгоднее брать меньшее значение пара-
метра to, т. е. со = 0,5.
Если же приближенные числа получаются в результате вычисле-
ний с недостаточно точными исходными данными, то параметр со при-
нимается равным единице. В этом случае малые значения параметра
со связаны с необходимостью производить округления, которые сни-
жают точность результатов и поэтому являются невыгодными. Если
указано, что цифры приближенного числа верные и со = 0,5, то это оз-
начает, что цифры числа верны в узком смысле; если же со = 1, то
в широком смысле.
Пример 5. Сколько верных значащих цифр содержит приближенное число
а = 85,267 i 0,0084: 1) в узком смысле; 2) в широком смысле?
Решение. 1) Из условия видно, что погрешность Аа — 0,0084 < 0,05.
Следовательно, верными в узком смысле будут цифры 8, 5, 2.
2) Поскольку Аа = 0,0084 < 0,01, верными в широком смысле будут цифры
8, 5, 2, 6
Пример 6. Определить предельные абсолютные погрешности приближенных
чисел а = 96,387 и b = 9,32, если они содержат только верные цифры в узком и
широком смысле соответственно.
Р е ш е н и е. 1) Так как для числа а — 96,387 последняя цифра 7, стоящая
в разряде тысячных долей, является верной значащей цифрой в узком смысле,
то Att < 0,5 • 0,001, т. е. Аа < 0,0005, или A J = 0,0005. Тогда число а можно
записать так: 96,387 ± 0,0005.
2) Последняя цифра приближенного числа b — 9,32 стоит в разряде сотых
долей. Так как это число содержит верные цифры в широком смысле, то, следова-
тельно, А& < 1 • 0,01, т. е. Аь < 0,01, или А* = 0,01. Числов можно записать
так: 9,32 ± 0,01.
§ 1.4. Округление чисел
В приближенных вычислениях часто приходится округлять числа
как приближенные, так и точные, т. е. отбрасывать одну или несколько
последних цифр и при необходимости заменять их нулями. При округ-
лении числа мы заменяем его приближенным числом с меньшим коли-
чеством значащих цифр, в результате чего возникает погрешность ок-
ругления. Чтобы эта погрешность была минимальной, нужно придер-
живаться некоторых правил округления (по дополнению).
Правило I. Если первая слева из отбрасываемых цифр больше
5, то последняя из сохраняемых цифр усиливается, т.е. увеличивается
на единицу. Усиление производится и тогда, когда первая слева из от-
брасываемых цифр равна 5, а за ней следуют отличные от нуля цифры.
Пример 1. Округляя до десятых долей число 73,473, получим 73,5. Послед-
няя из оставшихся цифр усилена, так как 7 > 5.
Правило II. Если первая из отброшенных цифр меньше 5, то
последняя из оставшихся цифр не усиливается, т, е< остается без
изменения.
Пример 2. Округляя до сотых долей число 73,473, получим 73,47,
16
Правило III. Если первая слева из отброшенных цифр равна
5 и за ней не следуют отличные от нуля цифры, то последняя остав-
шаяся цифра усиливается, если она нечетная, и остается без изменения,
если она четная (правило четной цифры).
Пример 3. Округляя число 5,785 до сотых долей, получаем 5,78. Усиления
не делаем, так как последняя сохраняемая цифра 8 — четная. Округляя число
5,775 до второго десятичного знака, имеем 5,78. Последняя сохраняемая цифра 7
увеличивается на единицу, поскольку она нечетная.
При применении правила III к округлению одного числа мы фак-
тически не увеличиваем точность вычислений, однако при многочис-
ленных округлениях избыточные числа встречаются примерно так же
часто, как и недостаточные. Происходит взаимная компенсация погреш-
ностей, результат оказывается более точным.
Таким образом, при применении выше рассмотренных правил ок-
ругления абсолютная погрешность округления не превосходит полови-
ны единицы разряда, определяемого последней оставленной значащей
цифрой.
Если точное число А округляется до п значащих цифр по правилу
дополнения, то получаемое приближенное число а имеет абсолютную
погрешность, равную погрешности округления. В этом случае прибли-
женное число а имеет п верных значащих цифр в узком смысле.
Пример 4. Округляя число А — 26,837 до трех значащих цифр, получим
а = 26,8, откуда
Ла = | Л—а | = | 26,837—26,81 = 0»037 <0,05,
т. е. число а имеет три верные значащие цифры в узком смысле.
При округлении приближенного числа аг получаем новое прибли-
женное число абсолютная погрешность которого складывается из
абсолютной погрешности первоначального числа ах и погрешности
округления, т, е.
“ Aqi 4" ^окр* (1)
Пример 5. Округлить сомнительные цифры числа сц = 34 124 ( ± 0,021).
Определить абсолютную погрешность результата.
Решение. Приближенное число щ имеет три верные цифры в узком смыс-
ле. 3, 4, 1, так как Да = 0,021 <0,05 Применяя правила округления, найдем
приближенное значение сохранив десятые доли: а2 == 34,1. Теперь получаем
Дай= Д^ 4- докр = 0,021 + 0,024 =» 0,045 < 0,05.
Таким образом, все значащие цифры числа а2 верные (в узком смысле), т. е.
= 34,1.
Однако при округлении приближенного числа аъ имеющего п вер-
ных значащих цифр (в узком смысле), до п значащих цифр может ока-
заться, что округленное число а% будет иметь п верных значащих цифр
в широком смысле.
Пример 6. Приближенное число щ ~ 15,3654 ± 0,0018 имеет четыре верные
значащие цифры в узком смысле (1, 5, 3, 6), так как Д — 0,0018 < 0,005. При
округлении до четырех значащих цифр получим а2 “ 15,37 и
Д^ = + Докр -0,0018+0,0046 0,0064.
17
Очевидно, что 0,005 < 0,0064 < 0,01. Следователь но, число 15,37 ± 0,0064
имеет четыре верные цифры в широком смысле.
Пример 7. Округлить сомнительные цифры числа а± = 26,7245 ± 0,0026*
оставив верные зизкп в узком смысле. Определить абсолютную погрешность ре-
зультата.
Решение. По условию Да = 0,0026 < 0,005, следовательно, в числе
26,7245 верными в узком смысле являются цифры 2, 6, 7, 2. Используя правила
округления, найдем приближенное значение а2, сохранив сотые доли: а2 ~ 26,72,
Далее, имеем
ДДг = Докр^О,0026+0,0045 = 0,0071.
Полученная погрешность больше 0,005 (0,005 < 0,0071), поэтому уменьшим чис-
ло цифр в приближенном числе до трех: а3 == 26.7. Находим
ЛДз= Да1 + ДОкр = 0,0026+0,0245 = 0,0271,
т. е. ДЦз < 0,05. Следовательно, оставшиеся три цифры верны в узком смысле.
Пример 8. Округлить сомнительные цифры числа ~ 22,7314, оставив
верные знаки в узком смысле. Определить абсолютную погрешность числа, если
Решение. Запишем & в виде десятичной дроби: — 0,002 и опреде-
лим Д по формуле (6') § 1.2:
Дд = । «I I = 22,7314 . 0,002 = 0,0455.
U| х I «1 7 7 7
Так как Дд = 0,0455 < 0,05, то верными в этом числе будут три цифры: 2, 2, 7.
Округлим число 22,7314, сохранив в нем десятые доли: а2 = 22,7. Тогда
ДДг=Дй1+Докр = 0,0455+0,0314 = 0,0769.
Поскольку полученная’погрешность больше 0,05, уменьшаем число цифр в приб-
лиженном числе до двух: а3 = 23; тогда
ДДз = ДД1+Докр = 0,0455+0,2686 = 0,3141,
т. е. ДДз < 0,5. Таким образом, в полученном округленном числе 23 обе цифры
являются верными в узком смысле.
Пример 9. Округлить сомнительные цифры числа а± = 5,273, оставив верные
знаки в ^широком смысле. Определить абсолютную погрешность числа, если
Решение. Находим
A*t = | «1 =5,273-0,001 =0,0053.
В числе аг верными в широком смысле являются три цифры (5, 2, 7), поэтому ок-
ругляем его до трех значащих цифр: а2 = 5,27; отсюда
ДДг= ДО1+Докр = 0,0053 + 0,003 = 0,0083 < 0,01.
Следовательно, округленное число 5,27 имеет три верные цифры в широком
смысле.
§ 1.5. Связь между числом верных знаков и погрешностью числа
Абсолютная погрешность приближенного числа связана с числом
верных знаков соотношением
Аа< и» Ю"2—"+1, (1)
что следует из определения верной значащей цифры,
18
В какой же зависимости от числа верных значащих цифр находится
относительная погрешность?
Запишем приближенное число
a = a1"10"’ + a2-10f’!—1 + ... + an-10m-n+1 + ... (2)
(cq ф 0), все цифры которого при данном выборе параметра со верные
(0,5 < со < 1).
Разделив обе части неравенства (1) на | а |, получим
Ад ___________________т-10т-'г+1________________< со- КУ”-м-1 =
|а| |a1.10'«4-a2.10"'-,+ ... +ап-10т-'г+1+ ... | cq-lO”
_ co-10m со
“а1-10"г-10'1~1 ~ aj. 10п~1 ’
т. е.
где а, — первая значащая цифра числа; п — количество верных
значащих цифр.
За предельную относительную погрешность можно принять
6£ = —-—.
aj.lO"-1
Пример 1. Какова предельная относительная погрешность приближенного
числа а ~ 4,176, если оно имеет только верные цифры в узком смысле?
Решение. Так как в числе 4,176 все четыре цифры верны в узком смысле,
то выбираем со = 0,5. По формуле (4) находим предельную относительную пог-
решность
в*а=---_ =----------+ = 0,000125 = 0,0125%,
ссг 10"“х 2*4* 103
Заметим, что предельную относительную погрешность числа а можно найти,
пользуясь формулой 6a— Д^/| а [. Так как в данном числе а все цифры верны
в узком смысле, то — 0,0005, Тогда
6a =0,0005/4,176 ~ 0,000120 =0,0120%.
Как видим, разница невелика, но применение формулы (4) несколько упро-
гцает вычисление 6д.
Пример 2. Какова предельная относительная погрешность числа а = 14,278,
если оно имеет только верные цифры в широком смысле?
Решение. Так как все пять цифр числа верны в широком смысле^ то
о) — 1, Тогда
со___________1__
aj. 104 = 1 • 104
= 0,0001 =0,01%,
Пример 3. Со сколькими верными десятичными знаками в узком смысле надо
взять Т/18, чтобы погрешность не превышала 0,1%?
Решение, Здесь а ~ ~[/18 ж 4, ...» 6a < 0,1%, т. е. 6S <0,001; со = 0,5,
имеем 6а == ""qh- 1 0,001, откуда
125 < Ю"’1; 1,25-102 < и—1; 1g 1,25 + 2 < п — 1; п>3 + 1g 1,25,
т. е. п > з> где п — наименьший целочисленный аргумент, Для большей точности
можно принять п = 4.
19
§ 1.6. Погрешности суммы и разности
Теорема. Абсолютная погрешность алгебраической суммы несколь-
ких приближенных чисел не превышает суммы абсолютных погрешно-
стей этих чисел.
Доказательство. Пусть А = Xt + Х2 + *»* + Хп
— сумма точных чисел, причем величины Хг-могут быть любого знака;
а = + х2 + + хп — сумма приближенных значений этих чисел.
Абсолютные погрешности их соответственно равны ДЖ1, ДЖ2, *.,,Дхп.
Вычитая из точного значения суммы приближенное ее значение,
имеем
А — а — (Хх—xj + (Х2—х2) 4~... + (Хп — хп).
Переходя к модулям, получим
|А — а | | Хг—Xj ] +1Х2—х2|4- +
Следовательно,
Aa^ А^4-Д*г4- ••• 4-АХп, 0)
что и требовалось доказать.
Следствие. Предельная абсолютная погрешность алгебраичес-
кой суммы равна сумме предельных абсолютных погрешностей сла-
гаемых.
Действительно, имеем ДЖ1 Д*р АЖ1 AJ3, ДАп Д1п.
Подставляя значения предельных абсолютных погрешностей в нера-
венство (1), мы еще более усилим его:
Аа А % 4-А^2 4- ••• + А^,
или
Дй-Д^4-А:24- ... 4-А:п. (2)
Из последней формулы следует, что предельная абсолютная по-
грешность алгебраической суммы не может быть меньше предельной
абсолютной погрешности наименее точного из слагаемых, так как уве-
личение точности за счет остальных слагаемых невозможно. Поэтому,
чтобы не производить лишних вычислений, не следует сохранять лиш-
ние знаки и в более точных слагаемых.
При сложении чисел различной абсолютной точности рекомендуется
поступать следующим образом:
1) выделить число (или числа) наименьшей абсолютной точности
(т. е. число, имеющее наибольшую абсолютную погрешность);
2) наиболее точные числа округлить таким образом, чтобы сохра-
нить в них на один знак больше, чем в выделенном числе (т. е. оставить
один запасной знак);
3) произвести сложение, учитывая все сохраненные знаки;
4) полученный результат округлить на один знак.
Пример 1. Сложить несколько приближенных чисел:
а = 0,1732 + 17,45 4~ 0,000333 4" 204,4 + 7,25 +
4- 144,2 4- 0,0112 4- 0,634 4- 0,0771.
В каждом из приведенных чисел верны все значащие цифры (в широком смысле).
20
Решение, Выделяем два числа наименьшей точности: 204,4 и 144,2. Оба
они верны с точностью до ОД. Следовательно, остальные числа следует округлить
с точностью до 0,01. Округлим и сложим эти числа:
ОД
17,4
0,0
204,4
7,2
144,2
0,0
0,6
0,0
374,1
7
5
0
5
1
3
9
Округляя полученное число до ОД, окончательно получим а = 374,2.
Оценим точность результата. Для этого найдем полную погрешность, которая
состоит из трех слагаемых;
1) суммы предельных погрешностей исходных данных
Ах = 0,0001 + 0,01 + 0,000001 + ОД + 0,01 + ОД + 0,0001 + 0,001 +
+ 0,0001 = 0,221301 < 0,222;
2) абсолютной величины суммы ошибок (с учетом их знаков) округления
слагаемых
Д2 = | 0,00324-0,000333+0,00124-0,004—0,0029 | =
= 0,005833 < 0,006;
3) заключительной погрешности округления результата А3 — 0,010.
Следовательно,
Да = Дх + д2 + 0,222 + 0,006 + 0,010 = 0,238 < 0,3.
Искомая сумма есть 374,2 ± 0,3.
Таким образом, убеждаемся, что окончательная погрешность не меньше
предельной абсолютной погрешности наименее точного из слагаемых (действи-
тельно, 0,3 > ОД).
Определим предельную относительную погрешность суммы несколь-
ких приближенных чисел.
Здесь следует различать два случая: 1) все слагаемые имеют одина-
ковые знаки; 2) слагаемые имеют разные знаки.
Рассмотрим первый случай, Пусть а — хг 4- х2 4- ... + хп,
где приближенные числа Xf 1, 2, *..,«) имеют соответственно
предельные абсолютные погрешности Д^, Д*2> Д£п, Положим
для простоты Xt > 0; тогда
л *
* _ Дд
>а~ ~-
(3)
Но, согласно формуле (2)
= Ajj + Д* 4- ••• + Д*.
п
Подставляя Да в формулу (3) и заменяя а суммой У xit получим
21
s
. (3')
n
i — 1
Так как Ах. = л;гб*., то
2 xi&*,
62 = —---------. (3я)
n
2 xi
1=1
«Обозначим через бтах и 6min наибольшее и наименьшее из чисел
б*г; тогда имеем
2 Xi 8* 6max Xi
с*___ г=1 -- £—1 ___£*
иа — << — итах»
п п
2 xi 2 Xi
i = 1 i = 1
Аналогично можно получить, что 6д > 6min. Таким образом,
Smin < $д <С бтах • И)
Следовательно, предельная относительная погрешность суммы
слагаемых одного знака заключена между наименьшей и наибольшей
предельными относительными погрешностями слагаемых.
Пример 2. Оценить относительную погрешность суммы чисел в примере 1 и
сравнить ее с относительными погрешностями слагаемых.
Решение. Относительная погрешность суммы а такова:
б* = 0,3/374,2 = 0,0008 = 0,08%.
Предельные относительные погрешности слагаемых составляют соответственно
1/1732 = 0,058%; 1/1745 = 0,057%; 1/333 = 0,3%;
1/2044 = 0,049%; 1/725 = 0,14%; 1/1442 = 0,069%;
1/112 = 0,89%; 1/634 = 0,16%; 1/771=0,13%;
бтах = 0,89%; бт in = 0,049%; ба = 0,08%.
Итак, 0,049 < 0,08 < 0,89, т. е. предельная относительная погрешность заклю-
чена между наименьшей и наибольшей предельными относительными погрешно-
стями слагаемых.
Рассмотрим второй случай (разность). Пусть х > 0,
у > 0 и а = х — у. Тогда, сохраняя прежние обозначения, получим
Ла Дх -р Ду
|а| |х—1/|
(5)
22
Таким образом, если числа х и у мало отличаются друг от друга, то даже
при малых погрешностях AJ и величина предельной относительной
погрешности разности может оказаться значительной.
Пример 3. Пусть х~ 5,125, у ~ 5,135; здесь A j = 0,0005, Aj = 0,0005,
62^6^0,01%. Предельная же относительная погрешность разности а =
= х — у равна
0,0005+0,0005
62 = ------—------- ♦ 100 = 10%.
0,01
Очевидно, что в результате вычитания двух близких чисел может
произойти большая потеря точности. Чтобы не допустить этого, следует
попытаться так преобразовать вычислительную схему, чтобы малые
разности величин вычислялись непосредственно.
Пример 4. Найти разность и = Уб,27 — Уб,26 с тремя верными знаками.
Решение. Возьмем Уб,27 и Уб,26 с достаточно большим количеством
верных значащих цифр, так как при вычитании близких друг другу чисел первые
несколько цифр могут пропасть:
"1/6/27 —2,503997...; 2,501999... .
Получим
н = У+27—/6,26 = 0,001998 ~ 0,00200 = 2,00. Ю“3.
Однако вычислительную схему можно изменить и взять квадратные корни только
стремя верными знаками:
C|/6^7-V6^6)(V6^7 + Z6j6)
и = у 6,27 — /6,26 =--------------------------=
V 6,27 + Уб,26
_ 6,27 — 6,26
Уб?27 + Уб/26
Это выражение, кроме разности данных чисел, никаких других разностей не со-
держит. В результате получаем
0,01
2,50 + 2,50
0,01
=0,00200 = 2,00-Ю-3,
5,00
как и прежде.
Пример 5. Вычислить значение функции у — 1 — cos х для следующих зна-
чений аргумента: 1) х — 80°; 2) х = 1°. Подсчитать предельные абсолютную и
относительную погрешности результата.
Решение. 1) По «Четырехзначным математическим таблицам» Брадиса
находим: cos 80° = 0,1736 и поскольку все цифры этого числа верны в узком смыс-
ле, то Acos 80° — 0,00005. Тогда ух = 1 — cos 80°= 1—0,1736 — 0,8264 и А^ —
= 0,00005 (из точного числа, равного единице, вычитается приближенное число
с абсолютной погрешностью, не превышающей 0,00005). Следовательно,
6^=0,00005/0,8264 = 0,00006 = 0,006%.
2) Имеем cos 1° — 0,9998; Acos 1° — 0,00005; у2 = 1 — cos 1° —
= 1—0,9998 = 0,0002; Л^2 — 0,00005; значит,
6^3 = 0,00005/0,0002 = 0,25 = 25%.
23
Из приведенных примеров видно, что для малых значений аргумента непо-
средственный расчет по формуле у = 1 — cos х дает относительную погрешность
порядка 25%. Для х~ 80° такая погрешность составляет всего лишь 0,006%.
Изменим вычислительную схему и для вычисления значений функции у =
= 1 — cos х при малых значениях аргумента воспользуемся формулой у — 1 —
—cos x=2sina~-. Обозначим я = sin 0°30' = 0,0087. Тогда Да = 0,00005; 6а —
= 0,5/87 = 0,58%. Но
у2 = 1 — cos X -= 1 — cos 1° 2 sin2 0°30' == 2 . 0,00872 = 0,000151;
6^8 — 6д2 =2бд =; 1,16%.
(см. ниже, § 1.7). В результате получаем
д*2 = ^26*2 0,000151 • 0,0116 == 0,0000018
(а ранее имели Да = 0,00005). Таким образом, простое преобразование расчет-
ной формулы позволило по тем же четырехзначным таблицам получить большую
точность.
Однако преобразовать вычислительную схему не всегда возможно.
Поэтому при вычитании близких друг другу чисел необходимо их брать
с достаточным числом запасных верных знаков (если это возможно).
Если известно, что первые tn значащих цифр могут пропасть, а резуль-
тат нужно получить с п верными значащими цифрами, то исходные дан-
ные необходимо брать с т + п верными значащими цифрами, как было
сделано’ в примере 4.
§ 1J. Погрешность произведения. Число верных знаков
произведения
Ранее были получены формулы для определения абсолютной по-
грешности алгебраической суммы нескольких приближенных чисел.
Для нахождения абсолютной погрешности произведения и =
х2...хп и частного и~х!у также можно получить соответствующие
формулы, однако они являются более сложными, и поэтому абсолют-
ную погрешность произведения и частного удобно находить через
относительную погрешность, используя формулу Ди = | и | би. В свя-
зи с этим выведем формулу для определения относительной погреш-
ности произведения.
Погрешность произведения. Теорема. Относительная погрешность
произведения нескольких приближенных чисел, отличных от нуля, не
превышает суммы относительных погрешностей этих чисел.
Доказательство. Пусть
U == Х]Х2 *$« Xji * (1)
Для определенности положим, что приближенные числа х19 х2, хп
положительны и имеют абсолютные погрешности ДЛ1, ДХ2, Д^п со-
ответственно.
Для оценки погрешности произведения прологарифмируем выраже-
ние (1):
In и = In Xi + In х2 + ... + In хп. (2)
24
Абсолютная погрешность алгебраической суммы нескольких прибли-
женных чисел (2) не превосходит суммы абсолютных погрешностей
слагаемых, т. е. (3)
А1п и Д In ЛГ1 + Ain х2 + ... +Д1пхп.
Используя приближенную формулу
Д1п*~ | d Inx | = И ’ (4)
получим и Xi х2 + —, (5)
откуда • < бХ14-6. ч- ... + 8V . 1 п (6)
Заметим, что знак модуля в выражении (5) опущен, так как было при-
нято, что > 0 (/ = 1, 2, ♦ п).
Формула (6), очевидно, остается верной и в том случае, если х£
имеют разные знаки.
Следствие. Предельная относительная погрешность произве-
дения равна сумме предельных относительных погрешностей сомно-
жителей.
Действительно,
61 >6., 61>6Х„ б* > 6Г • (7)
-М Л. г, л-2' ’ > Л'П, *"П '
Подставляя значения предельных относительных погрешностей в не-
равенство (6), мы еще более усилим его, т. е.
би б^ + б£2 + •••
или
б^б^+бХ + ... +6Jn. (8)
Если все сомножители, кроме одного, являются точными числами,
то из формулы (8) следует, что предельная относительная погрешность
произведения совпадает с предельной относительной погрешностью
приближенного сомножителя. Таким образом, если приближенным
числом является лишь значение множителя хг то
6^ = 6^. (9)
Замечание. При умножении приближенного числа х на точ-
ный сомножитель k предельная относительная погрешность произве-
дения равна предельной относительной погрешности приближенного
числа х, а предельная абсолютная погрешность в | k | раз больше пре-
дельной абсолютной погрешности приближенного сомножителя,
25
Действительно, пусть а ~ kx, где k— точный сомножитель, отлич-
ный от пуля, Тогда согласно формуле (9) имеем Sfi = 6*, или
AS = 1 = |6^ = | fexj -Ц- = |
|х| *
т. е.
Д£ = | &| А*- (Ю)
Зная предельную относительную погрешность 6*, произведения и,
можно определить его абсолютную погрешность по формуле Д« —
- ! и |
Из формулы (8) видно, что предельная относительная погрешность
произведения не может быть меньше, чем предельная относительная
погрешность наименее точного из сомножителей. Поэтому при перемно-
жении чисел разной относительной точности (т. е. имеющих разное
число верных значащих цифр) выполняют следующие действия по вы-
числению произведения:
1) выделяют число с наименьшим количеством верных значащих
цифр (наименее точное число);
2) округляют оставшиеся сомножители таким образом, чтобы они
содержали на одну значащую цифру больше, чем количество верных
значащих цифр в выделенном числе;
3) сохраняют в произведении столько значащих цифр, сколько вер-
ных значащих цифр имеет наименее точный из сомножителей (выделен-
ное число).
Пример 1. Найти произведение приближенных чисел Xj = 3,6 их2 - 84,489,
все цифры которых верны
Решение. В первом числе две верные значащие цифры, а во втором —
пять. Поэтому второе число округляем до трех значащих цифр. После округле-
ния имеем Xj = 3,6; х« — 84,5. Отсюда
хл = 3,6 . 84,5 = 294,20 2,9 ПО2.
В результате оставлены две значащие цифры, т. е. столько, сколько их имел
сомножитель с наименьшим количеством верных значащих цифр.
Пример 2. Определить произведение и приближенных чисел Xj “ 12,4 и
х2 = 65,54 и число верных знаков в нем, если все написанные цифры сомножи-
телей верны (в узком смысле).
Решение. В первом из чисел три верные значащие цифры, во втором —
четыре; можно перемножить числа без предварительного округления: Xj • х2 =
= 12,4 • 65,54 = 712,696. Следует оставить три значащие цифры, так как наи-
менее точный из сомножителей имеет столько же верных значащих цифр; таким
образом, и — 713. Подсчитаем погрешность:
0,05 0,005
6“ = 6* + S* = + 7^54 =0’0041,
Тогда Дм = 713 . 0,0041 3. Значит, произведение и имеет два верных знака и
его следует записать так, и = 713 ± 3.
26
Число верных знаков произведения. Пусть дано произведение
k сомножителей (й 10):
k
и = хех2... Хк = П X;.
1=1
где xt =И= 0. Каждый из сомножителей содержит не менее чем п верных
цифр (п > 1).
Пусть каждый из сомножителей имеет вид:
KK+pj-lO'*-1 +у1-Юг--2+ ....
• хг = а2-10^ + р2. КУ’-1 + у2-10^~2 + ....
х^ад.ЮЧ^-Ю'^'+^Ю'^Ч ....
т. е.
x! = «!.10^ + ₽i.10/~1 + Ys.10?-2 + ... (Z=l, 2, ..., k).
Здесь аь а2, ak — первые значащие цифры приближенных сом-
ножителей, записанных в десятичной системе счисления.
Для предельной относительной погрешности приближенного числа,
имеющего п верных знаков, используем формулу
6* =----2— (f-1, 2, k).
1 arlO"-1
Тогда предельная относительная погрешность произведения k при-
ближенных чисел, имеющих по п верных значащих цифр, равна
б* = у б:=у—= (П)
г jw ocr10rt“1 10n-1 ос.
1=1 1 t=\ 1
* 1
Учитывая, что сомножителей не более 10 (k 10), имеем V — ^10
z—1 Q'4
и, следовательно,
6*
(12)
Таким образом, если все сомножители имеют /г верных значащих
цифр и число сомножителей не более 10, то число верных знаков произ
ведения на одну или на две единицы меньше п. В том случае, если сом
ножители имеют различную точность, под п следует понимать чис-
ло верных знаков наименее точного из сомножителей.
Пример 3. Определить предельную относительную погрешность и количество
верных цифр произведения и = 84,76 • 8,436, где все цифры сомножителей вер-
ны в узком смысле.
Решение. Оба сомножителя имеют по четыре верные цифры в узком смыс-
ле, т, е, п = 4 и со = 0,5. Тогда по формуле (11) имеем
6и= 2-Ю3 (~8~) = ~ ' 10 3<:Т 10-3’
Следовательно, произведение имеет до меньшей мере гри верные цифры в узком
смысле.
27
Проверим, так ли это. Найдем произведение данных приближенных чисел;
оно равно и = 714,1. Определим предельную абсолютную погрешность по форму*
ле “ 1 и | 6»; получим А/Г = 714,1 • 0,125 • 10”3 0,09. Тогда и — 714,1 ±
± 0,09. Отсюда следует, что произведение имеет три верные цифры в узком
смысле.
Пример 4. Определить предельную относительную погрешность произведения
и — 145,35 • 1,24386 и число верных цифр в нем, если числа даны с верными
знаками в узком смысле.
Решение. Здесь Xj = 145,35; =5; х2 — 1,24386; п2 ” 6; со = 0,5.
Данные числа имеют различное количество верных значащих цифр, выбираем
п == 5. Находим
® / 1 . , 1 f J_ ,
и 10"-1 \ ai а-2 / 2*104 \ 1 * 1 /
= 1 • 10-4 < — -10-3.
2
Мы видим, что произведение имеет четыре верные значащие цифры в широком или
три в узком смысле.
Таким образом, в самом неблагоприятном случае, когда первые значащие
цифры сомножителей равны единице, произведение будет иметь по меньшей мере
п — 2 верные значащие цифры (где п — наименьшее число верных значащих
цифр данных сомножителей).
Пример 5. Определить предельную относительную погрешность произведе-
ния и = 4,387 • 593,6 и число верных знаков в нем, если числа содержат только
верные цифры в широком смысле
Решение. Имеем а3 = 4, пх = 4, а2 = 5, и2 = 4, со — 1. Тогда
б*=---— f— + —)= -A- f — 4- — ) = 10-3-0,45< 1-Ю-8.
“ 10""1 \ И1 а2 / 103 \ 4 5 /
Произведение содержит три верные значащие цифры в широком смысле, т. е. на
одну меньше, чем каждый из сомножителей.
Замечание. Рассмотрим случай, когда находится произведе-
ние большого числа приближенных чисел
U = Х1Х2 • •• хъ (k > 10).
Предельная относительная погрешность согласно формуле (8) равна
“ 6*, + + ... + бду
Однако при большом числе k удобнее пользоваться статистической
оценкой, учитывающей частичную компенсацию погрешностей разных
знаков. Если предельные относительные погрешности сомножителей
примерно одинаковы и равны б£\ то для определения предельной отно-
сительной погрешности произведения можно воспользоваться формулой
6* = /ЗЬ6г*. (13)
Если же предельная относительная погрешность одного из чисел
значительно превышает погрешности остальных сомножителей, то
предельная относительная погрешность произведения принимается
равной этой максимальной погрешности.
28
§ 1.8. Погрешность частного. Число верных знаков частного
Погрешность частного. Теорема. Относительная погрешность
частного не превышает суммы относительных погрешностей делимого
и делителя.
Доказательство. Пусть х и у — приближенные числа,
а Ах и — абсолютные погрешности. Для определенности положим
%Д> 0, £/> 0. Требуется найти погрешность частного
. (1)
У
Прологарифмировав*выражение (1), получим
In и = In х — In у. (2)
Абсолютная погрешность алгебраической суммы приближенных чи-
сел не превосходит суммы абсолютных погрешностей слагаемых, поэ-
тому
Ainu А1П х -J- A in у
(3)
Применяя приближенную формулу
Д1пИ « | d In и | =
получим
Ад Ау । Ау
и х у
(4)
или
Sg
(4')
Знак модуля в равенстве (4) опущен, так как мы положили х>0,
У>0.
Формула (4), очевидно, будет верной и тогда, когда делимое и дели-
тель имеют разные знаки.
Следствие. Предельная относительная погрешность частного
равна сумме предельных относительных погрешностей делимого и де-
лителя.
Действительно, 8У т. е. би + 6J,
«Я-
(5)
Замечание. Все правила приближенных вычислений, сфор-
мулированные для умножения, распространяются и на случай деления.
В частности, если одно из чисел (делимое или делитель) относительно
точнее другого, то более точное число округляется так, чтобы в нем
оказалось на одну значащую цифру больше, чем количество верных
значащих цифр наименее точного из чисел. Это же правило распрост-
раняется на случай, когда приходится перемножать или делить не-
сколько чисел. Окончательный результат, как правило, записывается
с абсолютной или предельной абсолютной погрешностью, Поэтому,
29
зная относительную или предельную относительную погрешность част-
ного, легко определить абсолютную или предельную абсолютную
погрешность результата по формуле
Пример 1, Вычислить частное и =* г/у приближенных чисел х = 5,735 и
у — 1,23, если все цифры делимого и делитепя верны в широком смысле. Опре-
делить предельные относительную и абсолютную погрешности.
Решение. Сначала вычислим частное. Делимое х = 5,735 содержит че-
тыре верные значащие цифры, делитель — три; поэтому можно проводить деление
без предварительного округления: и == 5,735 : 1,23 = 4,66. В результате остав-
лены три значащие цифры, так как наименее точное число (делитель) содержит
три верные значащие цифры.
2) Подсчитаем предельную относительную погрешность частного по фор-
муле (5), учитывая, что Ах — 0,001, А^ = 0,01:
6*= 6*4-6*-= —“—“ = 0,000184-0,00813 = 0,00831 =0,83 %,
о/Зэ 123
3) Определим предельную абсолютную погрешность
Aw =| и | 6* = 4,66’0,0083 = 0,04.
Окончательный результат следует записать так: и = 4,66 ± 0,04.
Заметим, что цифра сотых долей является сомнительной, поскольку 0,04 >
> 0,01. Если записать результат только с верными значащими цифрами, то не-
обходимо произвести округление и учесть погрешность округления, т. е. щ =
= 4,7; == 4- Аокр = 0,04 4- 0,04 = 0,08 « 0,1. Тогда и = 4,7 ± 0,1.
Однако на самом деле предельная абсолютная погрешность несколько ниже
Число верных знаков частного. Пусть приближенные числа х и у
имеют по п верных значащих цифр и пусть
х = ар КУ* 4-^2* ;
z/ = Рр 1О^4-₽2-.
Тогда, используя равенства
6;=——,6’
арЮ"-1
---------- (О,5<со< 1),
Pi-10'1-1
найдем предельную относительную погрешность частного
с. os СО СО (0 / 1 , I \
Оу — Ох 4“ Оу----------1- ... — |----------------1.
у cq 10”-1 PrlO"-1 Ю"-1 \ ₽i J
Следовательно, если 2 и 2, то частное имеет п — 1 вер-
ную значащую цифру. Если же 04 = 1 и = 1, то частное может иметь
п — 2 верные значащие цифры.
Пример 2. Вычислить частное и ~ 39,356 : 2,21 и определить, сколько в нем
содержится верных значащих цифр, если в делимом и делителе все цифры вер-
ные (в узком смысле).
Решение. 1) Поскольку в делителе три верные значащие цифры, а в де-
лимом — пять, делимое округляем до четырех значащих цифр и производим де-
ление: и = 39,36 : 2,21 = 17,81 ж 17,8 (в результате оставляем столько знача-
щих цифр, сколько их имеется в числе с меньшим количеством верных значащих
цифр).
30
2) Подсчет предельной относительной погрешности произведем по формуле
(6), где со = 0,5, поскольку делимое и делитель содержат верные цифры в узком
смысле; и == 3, так как менее точное число содержит три верные цифры; cq = 3;
= 2. Следовательно,
юп—1 \ ctj
1 /1 1 \ в
—Цг ( — + “ - —.Ю-2 = 0,42 %.
2-102 \ 3 2 ) 12
Таким образом, частное содержит две верные значащие цифры (в узком смыс-
ле), т. е. на одну значащую цифру меньше, чем у приближенного числа (делителя)
с меньшим количеством верных значащих цифр.
Пример 3. Определить предельную относительную погрешность частного
и = 15,834 : 1,72 и количество верных значащих цифр в нем, если делимое и де-
литель содержат верные значащие цифры в широком смысле.
Решение. Наименее точное число содержит три верные значащие цифры.
Определим предельную относительную погрешность по формуле (6), приняв
со = 1 (числа содержат верные цифры в широком смыле):
б“ 10n~l \ а, + ₽! J 10а ( 1 + 1 J Ю2 °’2’10
Мы видим, что частное содержит только одну верную значащую цифру, т. е-
на две верные значащие цифры меньше, чем у наименее точного числа.
§ 1.9. Погрешности степени и корня
Погрешность степени. Теорема. Предельная относительная по-
грешность т-й степени приближенного числа (т — натуральное)
в т раз больше предельной относительной погрешности самого числа.
Доказательство. Пусть и = Тогда
и = х • х... х.
f т сомножителей
Найдем предельную относительную погрешность произведения:
= б; + б* + ... + ^ =
т слагаемых
т. е.
= (1)
что и требовалось доказать. Из равенства (1) вытекает, что при возведе-
нии приближенного числа в степень в результате следует оставить
столько значащих цифр, сколько верных значащих цифр содержится
в основании степени.
Пример 1. Сторона квадрата а = 36,5 см (с точностью до 1 мм). Найти пло-
щадь квадрата, относительную и абсолютную погрешности и число верных зна-
ков результата.
Решение. 1) Вычислим площадь квадрата
S = 36,52 = 1332 = 1,33 . 103 (см2).
2) Определим предельную’-ютносительную погрешность площади
= 26; =2.2^7- -0,0054.
00. о
31
3) Определим предельную абсолютную погрешность площади
Д|= 1,33* 103*0,0054 = 0,72* 10 « 8 см3.
Окончательный ответ можно записать так:
S « (1,33 ± 0,008) . 103 (см2).
Таким образом, результат имеет три верные значащие цифры в широком
смысле.
Погрешность корня. Теорема. Предельная относительная погреш-
ность корня пг-й степени в т раз меньше предельной относительной
погрешности подкоренного числа.
Доказательство, Пусть и = j/x, тогда х == и”\ Отсюда
получаем 6J ~ тд^ Тс е*
(2)
tn
что и требовалось доказать^
Из равенства (2) вытекает, что при извлечении корня m-й степени
из приближенного числа в результате следует брать столько значащих
цифр, сколько верных значащих цифр имеет подкоренное число.
Пример 2. Определить, с какой относительной погрешностью и со сколькими
верными цифрами можно найти сторону квадрата, если его площадь S =
= 16,45 см2 (о точностью до 0,01).
Решение, Имеем а ~ = 4,056 (см)|
с 1 с 1 0,01
6« = v6s = V ДГ7Т=0’0003=0’03 /о!
Д2 = 4,056 0,0003 = 1,2 • 10-3 » 0,002.
Таким образом, а — 4,056 ± 0,002 (см), откуда п = 3.
§ 1.10. Правила подсчета цифр
При вычислениях, если не проводится строгий подсчет погрешно-
стей, рекомендуется пользоваться правилами подсчета цифр. Эти пра-
вила указывают, как следует проводить округление всех результатов,
чтобы, во-первых, обеспечить заданную точность окончательного ре-
зультата и, во-вторых, не производить вычислений с лишними знаками,
не оказывающими влияние на верные знаки результата,
Приведем правила подсчета цифр, данные В. М. Бра-
•дисом.
1. При сложении и вычитании приближенных чисел в результате
следует сохранить столько десятичных знаков, сколько их в прибли-
женном данном с наименьшим числом десятичных знаков.
2. При умножении и делении в результате следует сохранить столь-
ко значащих цифр, сколько их в приближенном данном с наименьшим
числом верных значащих цифр.
3. При возведении приближенного числа в квадрат или куб в ре-
зультате следует сохранить столько значащих цифр, сколько их в ос-
новании степени.
32
4. При извлечении квадратного и кубического корней из прибли-
женного числа в результате следует сохранить столько значащих цифр,
сколько их в подкоренном числе.
5. При вычислении промежуточных результатов следует сохранить
на одну цифру больше, чем рекомендуют правила 1—4. В окончатель-
ном результате эта «запасная цифра» отбрасывается*
6. Если некоторые данные имеют больше десятичных знаков (при
сложении и вычитании) или больше значащих цифр (при других дей-
ствиях), чем другие, то их предварительно следует округлить, сохраняя
лишь одну «запасную цифру»с
7. При вычислении с помощью логарифмов одночленного выраже-
ния рекомендуется подсчитать число значащих цифр в приближенном
данном, имеющем наименьшее число значащих цифр, и воспользовать-
ся таблицей логарифмов с числом десятичных знаков на единицу
большим. В окончательном результате последняя значащая цифра от-
брасывается.
8. Если данные можно брать с произвольной точностью, то для
получения результата с т верными цифрами исходные данные следует
брать с таким числом цифр, которые согласно предыдущим правилам
обеспечивают т + 1 цифру в результате.
Эти правила даются в предположении, что компоненты действий
содержат только верные цифры и число действий невелико.
Пример 1. Вычислить X = , где а =7,45 (±0,01), b — 50,46 ( ± 0,02),
с2
о — 15,4 ( ± 0,03). Определить погрешность результата.
Решение. При вычислении промежуточных результатов будем сохранять
одну «запасную цифру», т. е. если по общему правилу следует оставить п знача-
щих цифр, то в промежуточных результатах сохраним и + 1 цифру. Имеем
а3 = 413,5, 1/6=7,1035, c3 = 237,2i =12,4.
В результате оставлены три значащие цифры, так как наименьшее число зна-
чащих цифр в сомножителях равно трем
Подсчитаем погрешности результата:
6^ = 36* 4- -Ь 6*-|-2б^ =0,004054-0,0001954-0,0038 «0,0081!
Д^ = 12,4-0,0081 «0,11.
Итак, получаем ответ: X = 12,4 ± 0,11; бх — 0,81%.
Пример 2, Вычислить Х = где а = 2,754 ( ± 0,001), b = 11,7
(с — d)2
( ± 0,04), т = 0,56 ( ± 0,005), с = 10,536 ( ± 0,002), d = 6,32 ( ± 0,008).
Определить погрешность результата.
Решение. Находим
а + b = 2,75 + 11,7 = 14,45;
Ла ± ъ = Да + Ль + Локр = 0,001 + 0,04 + 0,004 = 0,045;
g — d = 10,536—6,32 = 4,216; Дс « d = 0,002 + 0,008 = 0,010.
Следовательно,
14,45*0,56
4,2162
14,45*0,56
17,75
= 0,456^ 0,46 = 4,6.10-1;
33
= 0,045 _0.005_ _0;ОА„ =о,ОО311 +0,00894+0,00474 = 0,01679»
х 14,45 0,56 4,216 ’ -г • 1
« 1,68%)
Дх = 0,46 • 0,0168 = 0,0077.
Итак, получаем ответ; X == 0,46 ( ± 0,0077); == 1,68%.
Пример 3. Пользуясь правилами подсчета цифр, вычислить
У = лЛ2 (fl—
\ ** 7
где h = 11,8, л -= 3,142, R = 23,67.
Решение. Находим
3,142 . 11,82 (23,67—3,933) = 3,142 . II,82 • 19,737 =
==3,142 . 139,2* 19,737 = 437,37 . 19,737 =* 8630 ^8,63 • 10\
Упражнения
1. Выполнить последовательные округления следующих чисел; а) 2,75464;
б) 3,14159; в) 0,56453; г) 4,1945; д) 0,60653.
Ответы: а) 2,7546; 2,755; 2,75; 2,8; 3; б) 3,1416; 3,142; 3,14; 3,1; 3; в) 0,5645;
0,565; 0,56; 0,6; 1; г) 4,194, 4,19; 4,2; 4; д) 0,6065; 0,607; 0,61; 0,6; L
2. Округляя следующие числа до трех значащих цифр, определить абсолют-
ную Да и относительную (в процентах) 6а погрешности полученных приближе-
ний: а) 1,1426; б) 0,01015; в) 0,1245; г) 921,55; д) 0,002462.
Ответы: а) 1,14; Да = 0,0026; 6а = 0,23%; б) 0,0102; Да = 0,00005; 6Й =
- 0,5%; в) 0,124; Да = 0,0005; 6а = 0,41%; г) 922; Да = 0,45; 6а = 0,049%;
д) 0,00246; Дя = 0,000002; 6f = 0,082%
3. Определить абсолютную погрешность Дх следующих приближенных чисел
по их относительной погрешности 6Х: а) х = 2,52; 6Х == 0.7%; б) х — 0,986;
6V = 10%; в) х = 46,72; 6Х = 1%; г) х = 199.1; 6Х = 0,01; д) х = 0,86341;
6Х - 0,0004.
Ответы: а) 0,018; б) 0,099; в) 0,047; г) 2,0; д) 0,00035.
4. Определить количество верных значащих цифр в узком и широком смысле
для следующих приближенных чисел; а) 39,285 ± 0,034; б) 1,2785 ± 0,0007;
в) 183,3 ± 0,1; г) 0,056 ± 0,0003; д) 84,17 ± 0,0073.
Ответы: а) 3 и 3; б) 4 и 4; в) 3 и 4; г) 2 и 2; д) 3 и 4.
5. Определить, какое из равенств точнее: а) 6/25 ~ или 1/3 ж 0,333;
б) 1/9 «0,1 или 1/3 0,33; в)_ 15/7 «2,14 или 1/9 «0,11; г) 6/7 « 0,86 или
л 22/7; д) л = 3,142 или /10 3,1623.
У Казани е. Предварительно найти предельные относительные погреш-
ности. Более точным является то равенство, предельная относительная погреш-
ность которого меньше.
Ответы: а) второе; б) второе; в) первое; г) второе; д) второе.
6. Округлить сомнительные цифры числа а == 47,453 ± 0,024, оставив в нем
верные знаки в узком смысле.
Ответ: а — 47,5.
7. Округлить сомнительные цифры числа а = 46,3852 ± 0,0031, оставив
в нем верные знаки в широком смысле.
Ответ: 46,39.
8. Округлить сомнительные цифры приближенного числа а = 3,2873, если
6а = СГ, 1%, оставив в нем верные знаки в широком смысле.
Ответ: 3,29.
9. Найти предельные абсолютные и относительные погрешности приближен-
ных чисел, если они имеют только верные цифры: а) а = 0,7538 (в узком смыс-
ле); б) а = 17,354 (в широком смысле).
У Казани е. Использовать формулу (4) § 1.5.
Ответы: а) Д^ = 0,00005; f= 0,0075%; б) Да = 0,001; 6а ===== 0,01%.
31
10. Со сколькими верными значащими цифрами надо взять результаты ука-
занных ниже операций, чтобы их предельные относительные погрешности не пре-
вышали &%?
а) а=1/3, 6S = O,1%3 б) а=-|/29; 62 = 0,1%;
в) а=5/27, 62 = 0,1%; Р) 0=^347, б’а=0,1%; д) а = ^33, ба =0,1%.
Указание. Воспользоваться формулой (4) § 1.5.
Ответы*, а) 4; б) 3; в) 4; г) 3; д) 4.
11. Вычислить следующие выражения с оценкой погрешностей. В ответе
сохранить все верные цифры и одну сомнительную. Все числа даны с верными
цифрами.
„ 3,07-326 36-245*85
а) у у .
36,4'323 ^75-642
37,24-458,67 96,891—4,25
в) Y —----------------; г) Y =---------------,
7 36,5.246 33,34-0,426
Ответы: а) У =0,085; Лу = 0,0012; бу = 1,4%; б) У = 1,20; Ду = 0,056;
бу =4,7%; в) У = 0,0552; Ду = 0,00043; бу =0,77%, г) У = 2,747; Ду=0,0090;
бу = 0,33.
12. Пользуясь правилами подсчета цифр, вычислить:
А2 а2 Ц-4аЬ Ц- Ь1
a) S —-------—“----—----, где А =2,73; а = 0,152; 6 = 0,328;
18 (а-^Ь)2
б) S = — л (D2 — d2), где 0 = 0,937; d = 0,0630.
4
Ответы: a) S ~ 0^594; б) 5 — 0,687.
Глава I!
МЕТОДЫ РЕШЕНИЯ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ
§ 2.1. Матрицы и векторы. Основные действия
над матрицами и векторами
Прямоугольная таблица, составленная из элементов (в частном
случае чисел) и имеющая т строк и п столбцов, называется матрицей
типа т X п. Элементы матрицы обозначаются через где I — номер
строки, а / — номер столбца, на пересечении которых находится этот
элемент»
Например,
#п я12 6z13 ... а1п
#21 #22 #23 ••• #2п
А —
#31 #32 #33 •••#3п
— #ml #тп2 #m3***#m7i —
матрица типа т X п, имеющая т строк и п столбцов.
Сокращенная запись матрицы имеет вид Л—[ао], где i==l,
/ 1, 2, гц
35
Если в матрице tn Ф п, т. е.число строк не равно числу столбцов,
то матрица называется прямоугольной.
Матрица, имеющая только одну строку, т. е. т = 1, называется
матрицей-строкой, или вектором-строкой; например,
А = [цп nmJ или А — [1 2 34]>
Матрица, имеющая только один столбец, т» е, п — 1, называется
матрицей-столбцом, или вектором-столбцом; например,
В дальнейшем матрицу-строку или матрицу-столбец будем называть
pi 1
; или X = х2
-хп J
называются элементами, или координатами, вектора X» Так как чис-
вектором и обозначать X —
xnL Числа xlfx2, *tt9xn
ло координат вектора есть, по определению, его размерность, то вектор
X является и-мерным*
Если в матрице
аи а12 п1п
#21 а2п
_ ^7П1 ^ТП2 ЩгПП —
типа т х п поменять местами строки и столбцы, то получится матрица
аи Й21 •••
Д' = а12 ^22 ••• ат2
« ♦ • • • • •
_ д1п а2п
типа т X и, которая называется транспонированной по
к А.
отношению
Пример 1. Для матрицы
' I
2
О
2
Л = 2
1
-3 5
4 2
3 4
типа 3x4 транспонированной является матрица
Г 12 1
л/ 2 0 2
А* =
.—343
5 2 4
типа 4x3.
36
Транспонирование матрицы-столбца дает матрицу-строку, и нао-
борот. Если в матрице число строк равно числу столбцов, т. е. т = п,
то матрица называется квадратной. Такую матрицу можно записать
в виде
а1п
^21 ^22 **• ^2л
_ ^nl ••• ®пп _
Для квадратной матрицы общее число строк или столбцов называется
порядком матрицы.
Главной диагональю квадратной матрицы называется диагональ,
проходящая через верхний левый и нижний правый угол, т. е. сово-
купность элементов вида ail} где I = 1, 2t ..., п.
Квадратная матрица, у которой все элементы, расположенные
вне главной диагонали, равны нулю, называется диагональной. Эта
матрица имеет следующий вид:
“аи 0 0 ...0
О, О ...О
О 0 а33... О
-О 0 0 ...апп_
Диагональная матрица, у которой все элементы, стоящие на глав-
ной диагонали, равны единице, называется единичной. Единичная
матрица обозначается символом Е и имеет вид
I 0 0...0-
О 1 0...0
О 0 1... о
О 0 0... 1
Индекс п указывает на порядок единичной матрицы. В матричном
исчислении единичная матрица играет роль единицы.
Матрица, все элементы которой равны нулю, называется нулевой
и обозначается через 0. Если нужно указать число строк и столбцов
то п»ишут OmXn!
О
тпХ п
ГО
о
0...0"
0...0
0...0
Квадратная матрица, в которой все элементы расположены сим-
метрично относительно главной диагонали, называется симметричной.
Для симметричной матрицы имеет место равенство = ац.
37
Например,
2 4"
3 5
5 6
есть симметричная матрица»
Две матрицы А — [а^] и В = называются равными, если:
1) они одного и того же типа, т. е. число строк матрицы А равно числу
строк матрицы В и число столбцов матрицы А равно числу столбцов
матрицы В; 2) соответствующие элементы этих матриц равны между
собой. Таким образом, если
типа, элементы которой равны суммам соответствующих элементов
аи и Ьц матриц А и В, т, е. Сц = аи + Ьц.
Разность матриц определяется аналогично сумме, только у элемен-
тов вычитаемой матрицы знак меняется на противоположный: D
= Л — В; du = atj — Ьц (I = 1, 2, ш; i = 1, 2, ri).
Пример 2» Пусть
1
—2
—7
1
А=
3
4
1
4
4
5
2
3
в=
Тогда
2
2
—6
3
1
3
о
2
5
2
1
8
—3
1
1
—2
— 1 2 —7 ~
3 —2 —4
—6 0 — 1
3 4—5
О 3 1 11
—6—369
—8 12 1 3
-1 —408
С=д+В=
2
О
6
4
2
О==Л—В =
Сложение матриц подчиняется следующим законам:
1) А + (В + С) - (Л + В) + С; 2) А + В - В + Л; 3) А +0 = Л.
Произведением матрицы А = [at J на число а называется матрица,
элементы которой получены умножением всех элементов матрицы А
на число а:
Аа —
ааи аа12 ... оео1п
СШ21 CttZ22 ^^2/1
L aami аат^аатп
38
Произведение Аа подчиняется следующим законам:
1) 1 • А = Л; 2) 0 • А = 0; 3) а (рЛ) = («₽) • Л.
'Матрица — Л = ( — 1) Л называется противоположной матрице А,
Пример 3. Произведение матрицы
на число 2 есть матрица
2 6
О 2
—6 2
— 8
~4
10
Произведением матрицы А = на матрицу В = 1Ьц]РХд
называется матрица С = 1сИ\тхг
Произведение АВ двух матриц в указанном порядке возможно
в том и только в том случае, когда число столбцов матрицы Л равно
числу строк матрицы В. Есльщтип матрицы Л равен т X п, а тип
матрицы В равен р X q, то матрица С = АВ имеет тип т X q, т. е.
в матрице-произведении число строк равно числу строк левого со-
множителя, а число столбцов — числу столбцов правого сомножителя:
це произведения АВ, нужно элементы i-й строки матрицы А умно-
жить на соответствующие элементы j-го столбца матрицы В и полу-
ченные произведения сложить'.
С~АВ =
4*^12^21 4" ••• + pl ^11^12 + ^12^22+ ••• A~ainb Р2
а2^п + й22^21 + ->‘ + а2пЬр1 a2lbl2-\-a22b22-[- ... -sra2nbP2...
*.*4“^mn^PI ^ml^l2~h^m2^22 Ч* ••• Ч* ^тп^Р2'**
••• an^iq + о1262(7 + ...+ alnbPq
... a21blq 4- a22b2g 4*...+ a2nbPq
Ч” ^тп2 &2q Ч* * • Ч~ ^mrfipq —
т. е. = anbXj 4- а^Ь^ 4- ... 4- ainbn}, где I = 1, 2, .... пц
/= 1, 2, .... q.
Например, с23 = а21Ь13 4- с22623 4- ... 4- a2nbnS.
39
Примеры.
4.
2
ГЗ 2 8 11 1—3
АВ «= * =»
[1 —4 0 3 J О 1
Ь 1 _
“3.2+2.1+8.04-ЬЗ 3( —1)4-2.(—3)4-8.1 + 14 1ГИ 0 '
Ь2+(—4).1+0.0 + 3.3 1 •( — !)+(— 4)-(—3)+0-1+3-1 J [ 7 14,
Здесь ДВ = [а^]2Х4 4^гЛ4х2=С —[С^]2Х2.
Г1 2 31
5. АВ = 4 5 6
7 8 9
’ 1 Я Г Ь1+2.2 + 3-3"
2 = 4.1+5.2+6-3
_3 J |_7-1+8.2+9.3-
" 14"
32
50
Здесь ЛВ=[а^]зхз- [Ьг^зх! — [cijJ3X 1.
6.
5 6"
7 8
2"
4
1
3
"5 6*
.7 8
2T
4J
__ Г1-5 + 2.7 1.6 + 2-8'
= [3-5 + 4-7 3-6 + 4-8_
'5-1 +6.3 5.2+6-4]
,7-1+8-3 7.2 + 8.4J =
Г19 22]
= [43 50] ’
Г 23 341
, т. е. АВ + ВЛ.
[31 46]
7. АВ =
Г1 2 3'
[4 5 6^
"3 2 4‘
2 1 3
4 3 0
'ЬЗ+2-2 + 3.4 1.2+2-1+3-3 1-4+2.3+3.0 3 Г 19 13 10 ‘
,4.3 + 5-2+6-4 4«2 + 5.1+6'3 4-4+5.3+6-0 J ~ [ 46 31 31 _
ГЗ 2 4"1
ВЛ = 2 1 3
4 3 0
1 2 31
не существует.
4 5 6J
Матричные произведения подчиняются следующим законам:
1) А(ВС) = (АВ)С\ 2) сс(АВ) = (аА)В; 3) (Л + В)С = АС + ВС\
4) С(А + В) = СА + СВ.
Отметим, что АВ =+ ВЛ, т. е. произведение двух матриц в общем
случае не обладает свойством переместительности. Значит, в общем
случае нельзя менять местами матрицы-сомножители, не изменив их
произведения.
Если изменить порядок сомножителей, то может оказаться, что
произвести умножение матриц вообще невозможно.
О произведении АВ двух матриц А и В будем говорить, что матрица
В умножается на матрицу А слева, или что матрица А умножается на
матрицу В справа.
Произведение нескольких матриц АВС следует понимать так:
матрица А умножается справа на матрицу В, а полученная матрица
умножается справа на матрицу С и т. д. Количество перемножаемых
матриц может быть любым, лишь бы можно было перемножать каж-
дые две рядом стоящие матрицы.
40
Матрица Ап называется п-й степенью матрицы А. Если Д —квад-
ратная матрица, а п — целое положительное число, то
Ап - А * А • А:..,А.
п множителей
Действия сложения и умножения на число над матрицами-столб-
цами и матрицами-строками (т. е. векторами) производятся аналогич-
но соответствующим действиям над квадратными матрицами. Так,
суммой двух векторов X и у% ••• Уп\ будет вектор
Z = [z1z2...znl с координатами = х.+Уъ z2 ~ х2 + у2, zn =
= хп 4- уп, произведением вектора X = 1хт х2хп1 на число а —
вектор Z = аХ = |аххах2... ахп].
Пример 8. Сумма векторов Л —[12 3]
Z~[~ 4 0 7]; произведением век юра Х =
и У = [ — 5—2 4] есть вектор
I П
2 на число а —2 является
вектор Z —
§ 2.2. Определитель матрицы. Свойства определителя
и методы его вычисления
С квадратной матрицей А ~ hfJ-] связан определитель (детерми-
нант), который обозначается det А или | А |:
det Л = М [ =
гг12 ... aln
^21 ^22 • * • й2П
&п1 &пп
Определитель матрицы есть число, вычисляемое по некоторым прави-
лам, которые мы рассмотрим ниже.
В определителе различают две диагонали: главную и побочную.
Главная диагональ, так же как и в квадратной матрице, состоит из эле-
ментов ati, где I = 1, 2, п. Побочная диагональ проходит перпенди-
кулярно главной, из верхнего правого угла определителя в нижний
левый.
Порядок определителя соответствует порядку матрицы, определи-
телем которой он является»
Определитель второго порядка равен произведению элементов глав-
ной диагонали минус произведение элементов побочной диагонали:
det 4 =
ап
а21
й12
^22
“ Й11 ^22 ~ ^21 Д12’
41
Пример 1.
<НЛ = Р 4 = 5—8=—3.
|4 5|
Определителем третьего порядка называется число
det Л-
#11 #12 #13
#21 #22 #23
#31 #32 #33
— #11 #33 4“ #13 #21 #32 4" #12 #23 #31
— #13 CZ22 a&i — #21 #12 #33 #32 #23 #11*
Таким образом, каждый член определителя третьего порядка пред-
ставляет собой произведение трех его элементов, взятых по одному
из каждой строки и каждого столбца, Эти произведения берутся с оп-
ределенными знаками: со знаком плюс — три члена, состоящие из эле-
ментов главной диагонали и из элементов, расположенных в вершинах
равнобедренных треугольников с основаниями, параллельными глав-
ной диагонали (рис. 2.1); со знаком минус — три члена, расположен-
ные аналогичным образом относительно побочной диагонали (рис. 2.2),
Указанное правило называется правилом треугольников.
Пример 2.
1 2
4еМ = —4 5
3
— 1 - Ь5.2 + З.Ь( —4)+2.( —1).2—2.5.3— Ь(— I)-1 —
2 1
2
—2<( — 4).2=—19.
Перечислим теперь свойства определителя.
1. Определитель не меняется при транспонировании:
det А =
#н ап ...#1П
#21 #22 ••• #2п
#П1 #П2 ••• #пп
#11 #21 — #nl
#12 #22 #П2
#1П #2п ••• #пп
42
Например,
2 3
5 —1
1 2
1
— 4
2
1 —4 2
det А =
2 5 1
3—12
= 1.5.2+3.{-4)-1+2.( —1).2—.
—3-5*2— Ь( — 1). 1—2. (—4)-2= —19.
2. Если одна из строк или один из столбцов определителя состоит
из нулей, то определитель равен нулю.
Например,
О 1 2
det 4= О 3 4
= 0-3-154-0-1-44-0.2.10—0-3-2—о. 1.15—0-4-10 = 0,
О 10 15
3. От перестановки двух строк или двух столбцов определитель
меняет только знак.
Например,
3
1 2
2 I
— 4 5
det Л =
2 =Ы.( —1)4-2-2-(—4) + 2.5*3—3*Ь( —4) —
— 1
— 5*2*1— 2.2. ( —1) = 19
(ср. с примером, иллюстрирующим свойство 1).
4. Определитель содержащий две одинаковые строки или два оди-
наковых столбца, равен нулю.
Например,
1
2 3
det Л = 1
2 3
1 2
= 1.2.2+2.3.2+ЬЬЗ—2.2.3—1*2.2 —1*ЬЗ = 0.
5. Если все элементы некоторой строки или столбца определителя
умножить на число k Ф 0, то сам определитель умножится на это
число.
Иначе это свойство можно сформулировать так: общий множитель
всех элементов некоторой строки или некоторого столбца можно вы-
нести за знак определителя.
Например,
3 6 9 1 2 3
det А — 2 1 2 = з. 2 1 2 = 3-19 = 57
—4 5 —1 — 4 5 —1
(ср. с примером, иллюстрирующим свойство 3).
6. Определитель, содержащий две пропорциональные строки, равен
нулю,
43
Например,
det Л==
12 3 =3»
2 1 2
= 3*0 = 0.
3 6 9
1 2 3
1 2 3
2 1 2
7. Если все элементы i-й строки определителя п-го порядка пред-
ставлены в виде суммы двух слагаемых: а^ = Ьц + «и (/ = 1, 2, п),
то данный определитель равен сумме двух определителей, у которых
все строки, кроме i-й. такие же. как и в заданном определителе, а 1-я
строка в одном из слагаемых состоит из элементов Ьц, а в другом —
из элементов ctj. т. е,
det 4 =
аА «12 а\3 • • ‘ а1п
«21 = ^21 4~ «21 «22 ~ ^22 4* «22 «23 “ ^23 4 «23 • • * «2п ~ ^2 Л 4* «2П
«эх <732 «зз ... а3п
^П2 &ПЗ ••• «пп
«11 «12 «13 * ••«tn «11 «12 «13 ... «1п
^21 ^22 ^23 • •• ^2П «21 «22 «гз ... «2п
31 «32 «зз . •* «Зп 4- «31 «32 «33 ••• «ЗП
«п! «п2 «пЗ • »• ^ПП «П2 «пЗ •• • «пп
2 7 9
1 3 4
1 0 2
Например,
det Л =
8. Если одна из строк определителя представляет сумму других
строк или сумму произведений других строк определителя на число
k. то определитель равен нулю, (Это следует из свойств 6 и 7 опреде-
лителя.)
Например^
1 2 3
det А = 3 2 7
1 0 2
1 2 3 1 2 3 + 2- 1 2 3 1 0 2 = 04-2.0 = 0
1 0 2 1 0 2
9. Определитель не изменится, если к элементам одной из его строк
(столбцов) прибавить соответственные элементы другой строки
(столбца), умноженные на одно и то же число.
Например;
2 7 9
det Л = 1 3 4 = —1
1 0 2
44
(см. пример, иллюстрирующий свойство 7). Умножим третью строку на 3 и при-
бавим ко второй строке; тогда
2 7 9
4 3 10
1 0 2
det 4 =
= 2.3-2 + 1.7.10+4.0.9 —Ь3*9—4-7*2—2.0-10= — I.
Применяя вышеуказанные свойства определителей, можно упро-
стить задачу вычисления определителей и-го порядка.
Определитель n-го порядка может быть выражен через определи-
тели более низких порядков.
Для этого необходимо ввести понятия минора и алгебраического
дополнения. Пусть дан некоторый определитель n-го порядка. Мино-
ром А-го порядка (1 <1 k п — 1) определителя d называется опреде-
литель, получающийся после вычеркивания в исходном определителе
некоторых п — k строк мп — k столбцов.
Так, например, минором й-го порядка определителя
^12 а1з «14
d = ^21 а23 С?24
^31 а32 ^33 П34
П41 п43 ^44
при k — 1 является определитель с вычеркнутыми тремя строками
и тремя столбцами, при k — 2 — определитель с вычеркнутыми двумя
строками и двумя столбцами и при k — 3 — определитель с вычерк-
нутой строкой и столбцом.
Максимальное число k для определителя и-го порядка может быть
равно п — 1. При k = п — 1 вычеркиваются только одна строка
и один столбец.
В частности, если в определителе n-го порядка вычеркивается толь-
ко одна строка (i-я) и один столбец (/-й), то на их пересечении ока-
жется единственный элемент и полученный минор (и — 1)-го по-
рядка называется соответствующим этому элементу и обозначается
через Mih
Например, элементу ап соответствует минор
Мц =
^22
^32
^42
#23
^33
а 43
#24
Й34
П44
так как элемент ап лежит на пересечении первой строки и первого
столбца.
Если присвоить минору знак « +» или « — », в зависимости от
суммы номеров строк и столбцов, на пересечении которых находится
соответствующий этому минору элемент, то данный минор называется
алгебраическим дополнением и обозначается Ац = (—l)z+' М^.
Очевидно, если сумма i + / четная, то алгебраическое дополнение
имеет тот же знак, что и минор; если же сумма i + j нечетная, то знак
изменится на противоположный,
45
Пример 3. Для определителя
2—15
d= 6 2 1
1 4 3
алгебраическое дополнение элемента вычисляется таким образом:
Л§1 = (-1/+?Мг.,-=(-1)8Л121 = (-1)8|~4 =( —1) (—3—20) = 23.
Вообще, определитель равен сумме всех произведений элементов
какой-либо строки или столбца на соответствующие им алгебраине*
ские дополнения, а именно:
d =
Яд ^12 ••• &\п
^21 ^22 ••• ^2П
= а11 Al + aiz •••
(1)
^n2 ••• &пп
ИЛИ
d ~ a1jA1j + a2jA2j + ,,, + unjAnj9 0^
где формула (1) дает разложение определителя d по элементам t-й
строки, а формула (Г) — по элементам /-го столбца.
Пример 4, Вычислить определитель
разложив его по элементам второй строки
Решение. Имеем d = a21A2i + а22Д22 + а2эА23} откуда
1__2 ___31 II ____31 1 ___*21
_ +5 +4 I = (—6)-235* 14-{-4* 17 ==
I и — / I | ( — / J t О |
= —138 + 70 + 68 = 0.
Применяя свойство 8 определителя, мы бы могли сразу сказать, что этот
определитель равен нулю, так как вторая строка его представляет собой сумму
третьей и первой строки, умноженной на — 1.
Пример 5, Вычислить определитель
1111
12 3 4
1 3 6 10
1 4 10 20
разложив его по элементам первого столбца,
Решен
2
Ац —
и е.
3
6
1) Имеем d — оцАц + 6z2iA2i + + лл A1]t Находим
4
10
20
=2»2*
10
3
4
2
3
3
6
2
5
= 4
2
5
5
= 4(2.5—3*5 + 2.3)^4.
46
Мы вынесли за знак определителя Ап общий множитель 2 из третьей строки и
общий множитель 2 из третьего столбца и разложили получившийся определи-
тель по элементам первой строки
2) Находим
1
А1~ 3
4
1
6
10
1 1 1
10 ^—2- 3 6
20 2 5
1
10
10
/16 101 13 101 13 6|\
ЮГ |2 ЮГ |2 5|J
- — 2(10—104-3)=-—6.
Мы вынесли общий множитель 2 из третьей строки и разложили определитель
по элементам первой строки.
3) Аналогично получаем
1
/31 = 2
4
1 1 3 4 10 20 = 2* 1 1 1 2 3 4 2 5 10 /13 4 12 41 12 3 = 2 — + \ 15 10 | |2 101 12 5
= 2 (10 - -124-4) = 4.
4) Наконец, нахо им
1 1 1
2 3 4
3 6 10
I3 4| I2 41
|б ю|+|з 10|
—
[2 31
= -6 + 8-3 = -1.
I О о I
5) Раскладывая определитель А по элементам первой строки, окончательно
получим
det Л — 1 • 4 4~ 1 • ( — 6) + 1 4 4- 1 • ( — 1) = 1.
Пример 6. Вычислить определитель, заданный в предыдущем примере, при-
меняя преобразования, основанные на свойствах определителя (так называемые
элементарны* преобразования)
Р е ш е н и е. 1) Если мы оставим первую строку определителя без изменения
и, умножив ее на — 1, прибавим сначала ко второй, а затем к третьей и четвер-
той строкам, то определитель не изменится (свойство 9):
1111 12 3 4 1 3 6 10 1 4 10 20 1111 0 12 3 0 2 5 9 0 3 9 19 •
2) Раскладываем полученный определитель по элементам первого столбца:
d ~ ДцАи Чг ^21^21 4“ #41А 11. Так как = 0, = 0, — 0,
то d = ац4п
3) Оставляем без изменения первую строку, затем, умножив ее на — 2, при-
бавим ко второй строке и, наконец, умножив на — 3, прибавим к третьей строке.
Согласно свойству 9, определитель от этих преобразований не изменится. Полу-
чаем
1 2 3
d= 0 1 3
0 3 10
4) Раскладывая последний определитель снова по элементам первого столб-
ца, имеем d = + ^21^21 + зъ но так как azi “ 0 и a3i = то
d = -'114i-
47
5) Вычисляем полученный в результате преобразований определитель вто-
рого порядка!
I 1
|з
3
10
Таким образом, мы рассмотрели два из существующих методов вычисления
определителей n-го порядка
§ 2.3. Ранг матрицы
Рангом матрицы называется наибольший порядок миноров данной
матрицы, отличных от нуля. Из определения следует, что если ранг
матрицы равен г, то в матрице можно найти хотя бы один минор г-го
порядка не равный нулю, а все миноры (г + 1)-го порядка равны
нулю. Отметим, что ранг нулевой матрицы равен нулю, а ранг матри-
цы-строки (или матрицы-столбца) равен единице.
При нахождении ранга переходят от миноров меньших порядков
к минорам больших порядков и придерживаются следующего правила:
пусть найден минор г-го порядка отличный от нуля, тогда нужно
вычислить лишь миноры (г + 1)-го порядка, окаймляющие данный
минор Ми. Если все эти миноры равны нулю, то ранг матрицы равен
г; если же хотя бы один из них отличен от нуля, то эту операцию сле-
дует применить к нему, причем в этом случае ранг матрицы заведомо
больше г.
Пример. Найти ранг матрицы
2 4 10
2 4 10
1—231
0 0 7 2
Решение. 1) Находим минор второго порядка, не равный нулю:
=/= 0.
Этот минор находится на пересечении второй и третьей строк и второго и третьего
столбцов.
2) Найдем миноры третьего порядка, окаймляющие данный, семи возмож-
ными способами. Составляем М2 и из-второй, третьей и четвертой строк;
2
-1
М2 =
о
4
—2
0
1
3 =0
7
(так как третья строка равна сумме первой и удвоенной второй);
4 1 0
М3= —2 3
0 7
1 =0
2
(по той же причине).
48
Окаймляющие миноры из первой, второй и третьей строк не составляем,
так как они равны нулю (первая и вторая строки равны). Таким образом, все ми*
норы третьего порядка равны нулю. Миноры четвертого порядка уже не вычис-
ляем, все они также равны нулю. Следовательно, г = 2.
§ 2.4. Обратная матрица
Матрица называется обратной по отношению к данной, если ее ум-
ножение как справа, так и слева на данную матрицу, дает единичную
матрицу.
Для матрицы А обратная матрица обозначается Л‘\ По опреде-
лению,
АА"1 = А~*А - Е.
Нахождение обратной матрицы называется обращением данной
матрицы.
Квадратная матрица называется неособенной, или невырожден-
ной, если ее определитель не равен нулю. Если же определитель мат-
рицы равен нулю, то матрица называется особенной, или вырожден-
ной. Всякая неособенная матрица имеет обратную.
Пусть дана матрица
ап а12
Д _ Й21 ^22 й23 а24
а31 @3'2 @33 @34
^41 ^42 ^43 @44 _
Обратную матрицу А~1 находят по следующей схеме:
1ш а г. Вычисляют определитель
Пц й12 аи
| ДI — ^21 ^22 ^23 0,24
^32 ^33 @34
^41 fl42 ^43 ^4->
II шаг. Вычисляют алгебраические дополнения к элементам
матрицы А и составляют матрицу, союзную по отношению к данной.
Если из алгебраических дополнений всех элементов матрицы А со-
ставить новую матрицу и транспонировать ее, то полученная матрица
называется союзной по отношению к данной и обозначается А:
Ли Л21
Л12 Л 22
^13 ^23
Л u Л 24
^31
^32
АзЗ
^34
А]
Л42
Аз
Л 44
49
Ill шаг. Находят обратную матрицу по формуле Л’1 = -j—p ♦ Л:
-ЛП/|Л| Л21/|Л| Л31/|Л| Л41/|Л|“1
Д-1 [ ^22/1 I ^32/i f ^42/1 I
Аз/I а । лаз/| л । л33/| л | л43/| л |
Л14/|Л| Л4/М1 Лт/М|
Если порядок матрицы А большой, то этот метод обращения матрицы
требует сложной вычислительной работы. Существуют другие способы
обращения матрицы, рассмотренные ниже.
Нахождение обратной матрицы Л"1 имеет исключительно важное
значение для решения систем линейных уравнений*
Пример. Обратить матрицу
1 2 4 2
3 1 1—3
= —2 3 — 1 1
— 12 0 1
Решение 1шаг. Вычисляем
12 4 2
< , 3 1 1—3
det А —
—2 3 — 1 1
— 12 0 1
для чего разложим определитель
по элементам первой строки. Имеем
Следовательно
det Л — Ь (—8)4-2- (—1)+4.7+2>(-6)=6.
50
II шаг.
матрицы Л:
Вычисляем остальные алгебраические дополнения
элементов
Л21 —
2
3
2
4
2
= - (-2 + 8 + 4-12)=2; Л22 =
О
1
Л2з= — -—2
-1
Л24 —
^31 —
^Зй== —
^зз =
= — 1—4—1;
2
3
2
2
1
1
1
—2
— 1
4
— 1
О
2
1
1
=~ —(3—2 — 84-6 + 4—2) = — U
I
—2
— 1
2
3
2
4
— 1
О
^2 — 164-124-2 = 0;
2
1
2
4
1
О
2
—3
1
= 2—24—4—4=—30;
1
3
-1
4
1
О
2
—3
1
= —(1 + 12+2—12) = —3;
3
—1
2
1
2
2
—3
1
= 1+6 + 12+2 + 6—6 = 21;
Лз4= —
1
3
— 1
2
1
2
4
1
О
= —(—2+24+4—2)= —24;
Ди= —
2
1
3
4
1
— 1
2
— 3
1
. ,„(2—36—2—6—6—4) = 52,
Л4§ =
43 —
1
3
-2
4
1
— 1
2
-3
1
= 1+24—6+4—12—3 = 8;
1
3
—2
2
1
3
2
—3
1
= —(1 + 12 + 18+4+9—6) = —38
Л44 =
1
3
—2
2
1
3
4
1
— 1
—4 + 36+8—3+6 = 42.
51
Ill шаг. Составляем союзную матрицу
Проверка:
1 2 4 2" ~ — 8/6 2/6 -30/6 52/6"
3 1 1 -3 -1/6 1/6 — 3/6 8/6
— 2 3 —1 1 7/6 -1/6 21/6 —38/6
_-1 2 0 _ — 6/6 0 -24/6 42/6
"—8—2+28 — 12 2 + 2 —4 + 0 —30 — 6 + 84 — 48 52+16 — 152+84"
6 6 6 6
-24—1+7+18 6+1 —1+0 —90 — 3 + 21+72 156 + 8—38—126
6 6 6 6
16 — 3 — 7—6 —4 + 3+1+0 60—9—21—24 —104 + 24+38+42
6 6 6 6
8 —2 + 0—6 —2 + 2 + 0 + 0 30 — 6+0 — 24 —52 + 16 +0 + 42
6 6 6 6
~1 0 0 0"
= 0 0 1 о ^Е'
0 0 0 1
§ 2.5. Абсолютная величина и норма матрицы
Под абсолютной величиной (модулем) матрицы А — [а^] пони-
мается матрица | А | — [ | ап [ ], где все элементы | аг> | есть модули эле-
ментов матрицы Д.
Под нормой матрицы А = понимается действительное число
|| Я ||, удовлетворяющее следующим условиям:
1) || А || 0 (причем || А || = 0 тогда и только тогда, когда А — 0);
2) || аА || — | а | • || А ||, где а — число (причем || — А || = || А Ц);
3) || А + В || ^|| А || + || В ||;
4) 11 л . В II < II д ц. II В II,
52
где Л и В — матрицы, для которых соответствующие операции имеют
смысл.
Матрица А — 1а^] определяется тремя нормами:
1) || Л ||1 —= max 2 I aij 1 — норма 1 — максимальная сумма моду-
i /
лей элементов матрицы по строкам',
2) || А || а = шах 2 I аи I — норма 2 — максимальная сумма моду-
1 i
лей элементов матрицы по столбцам.
3) || А ||3 — j/*2 ~ЙГГ2 — норма 3 — корень квадратный из сум-
мы квадратов модулей всех элементов матрицы.
Пример 1. Для матрицы
А =
2
5
6
вычислить II А II I, II А II2 и II А || 3.
Решение. Находим
— 1
3
— 7
4
2
3
|] Л || 1 -шах (2 + 1 + 4, 5 + 3 + 2,
6+7 + 3) — max (7, 10, 16) = 16,
4+2+3) -max (13, 11, 9) — 13,
I! А || з == V22+К+ 42 + 52 + З3+22 + 62 + 72 + З2 = V153 - 12,2.
*2
Для вектора X = ;
эти нормы вычисляются по следующим
формулам:
|| X Jj = max | Xi | — максимальная из координат век-
тора, взятая по модулю',
||X||2 = | | -f- | х2 | Ц- ... + | хп [ — сумма модулей координат вектора',
|| X Ц-з = ]/1 хх |2+1 х |2+... +1 хп 12 — корень квадратный из суммы квад-
ратов модулей координат вектора.
Норма ||Х||з называется абсолютной величиной вектора.
Пример 2. Для вектора
Х =
1
2
3
— 5
вычислить IIXlit, ||Х||2 и ||Х||з.
Решение. Имеем
||Х [|t = max (1, 2, 3, 5) = 5;
||Х||2= 1+2 + 3+5= 11;
|| X ||з = У12+22 + 32 + 53 = Д/ 39 = 6,2.
53
§ 2.6. Клеточные матрицы. Действия над клеточными матрицами
При выполнении вычислений над матрицами высоких порядков
целесообразно разбить их на клетки (блоки) с помощью горизонталь-
ных и вертикальных перегородок, идущих вдоль и поперек всей мат-
рицы. Таким образом, каждая матрица разбивается на подматрицы
меньших порядков, вычислительные действия над которыми произво-
дить значительно проще.
Разбиение квадратных матриц на клетки. Рассмотрим два метода
разбиения квадратных матриц на клетки.
Первый метод, Данную матрицу S четвертого порядка мож-
но разбить на четыре квадратные матрицы А, В, С, D второго порядка:
3 =
S11 S12 $33 $14
$21 $22 $23 $24
$31 $32 $33 $34
. $41 S42 $43 $44
В -
D
где
Над клеточными матрицами такого типа можно производить операции
сложения и умножения, оперируя с клетками матрицы, как с элемен-
тами обычной матрицы.
Пусть
— клеточные матрицы одного и того же типа и разбиения, тогда
S + P =
А+К B+L
S-P =
АК+ВМ AL + BN
СА-М
СКА-DM CLA-DN
Пример 1. Матрицы
5
7
6
8
7
6
4
5
—3
«4
- 3
—6
А =
разбить на квадратные клетки и вычислить А-]-В и АВ.
54
Решение. 1)
Разобьем матрицы Ли В на квадратные клетки следующим
образом:
Г 5 7—3
Г лп
Л = —
_ Л21
7 6
6 4
8 5
—4
— 3
— 6
Г Ви
; в= —
, ^21
“1 2
2 3
1 3
J 4
3 4~
4 5
5 7
6 8__
2) Находим
Л + В-
Ли + Вц
л21+ B2i
Л1з + В12
Л224-В22,
"6 9
9 9
7 7
10 9
0 0"
о о
2 5
О 7
3) Имеем
лв-
Лц Вц + Лх2 #21
Л27 Вц +Л22 B2J
Лц В12 + Л12 в22
Лз1 В12 + Л22 В22
Последовательно получаем
Л2/ Вц 4“ Л22 В21 —
Г8
Ь
61
0J
4ц ВГ2--
'5 7
7 6
Г 43 55'
[45 58~
Л12 В22"
Л11 В124~Л12 В22 =
— 39 —53 1
Л 21 Bia =
’6
8
Л21 В12+Л22В22 —
Таким образом,
34
44
Г5
7’
8
ЛВ-
'8 6 4 2
5 0 —5 -10
7 7 7 7
.10 9 8 7.
55
Второй метод, Можно разбить матрицу n-го порядка
на клетки так называемым окаймлением, т. е. на квадратную матрицу
(п — 1)-го порядка, окаймленную матрицей-строкой (п — 1)-го по-
рядка, матрицей-столбцом (п — 1)-го порядка и матрицей первого
порядка — числом:
где Лп_х — квадратная матрица (п — 1)-го порядка; Un-i — мат“
рица-столбец (п— 1)-го порядка; Vn_x—матрица-строка (п — 1)-го
порядка; апп—число.
Действия над окаймленными матрицами производятся так же, как
действия над клеточными матрицами.
Пусть
л ГМ£71 В=ГРУ1
V а X Ь
— две окаймленные матрицы n-го порядка, Тогда
М + Р t/4-У] AB[MP + UX MY + Ub
_ V-YX a-Yb _ ’ _ VP-^aX VY-Yab
где MP и UX — матрицы (п — 1)-го порядка; MY и Ub — матрицы-
столбцы (п — 1)-го порядка; VP и аХ — матрицы-строки (п — 1)-го
порядка; VY и ab — числа.
Пример 2. Матрицы
5
6
4
8
9
7
А =
— 4
—5
—3
2 5’
— 1 3
6 5
3
4
9
разбить на клетки окаймлением и вычислить А + В и АВ.
Решение. 1) Разбиваем матрицы А и В с помощью окаймления!
2) Находим
“ М + Р
V4-X
U+У ~
а+Ь
8 10 1 -
10 8 —2
13 13 2
56
3) Имеем
MP + UX MY + Ub
VP + aX VY + ab
Последовательно получаем
5 81 [*3
21
— 1]
'47 2 ‘
54 3
— 24 ’
— 30
MP + UX^
MF-
5 81
6 9]
49
57
7]‘
Г 29
L
= [4
= [40 1], aX = (-3M9
VP + aX = [13 —17];
6] = [—27 -18],
VF = [4 7] .
VF+a&=26.
Таким образом,
= 41,
ab — (~ 3)*5= —15,
~11 —22 29
АВ^ 9 —27 32
J3 -17 26
3
4
ГЛ I Bi
Обращение матриц разбиением на клетки. Пусть S == [g~hd —
клеточная матрица, в которой А и D — квадратные клетки порядков
р и q (где p-{-q = ri)b Нам нужно найти обратную матрицу З”1^
в которой К и N — квадратные матрицы также порядков р и q.
По определению обратной матрицы, S3”1 — Еп. Но единичная
матрица в данном случае тоже будет разбита на клетки аналогичным
Г£ 0 }
образом, т, е. Еп = |opeJ » где Ер и Ео — единичные матрицы, соот-
ветственно порядков р и q. Тогда
SS-! =
'АВ'
CD
'KL1]AK + BM ALA-BN ] _ ГЕР О’
/И AJ [СК + ОЛ1 CL + DN ] ” [0 Eq
Приравнивая элементы матрицы-произведения элементам единич-
ной матрицы, выводим следующие формулы для определения клеток
обратной матрицы.
Первая группа формул (обращение начинается с вычисления X-1):
N — (D—С А~1 В)"1,
M=-NCA~\
L^—A-'BN,
К^А-^-А-'ВМ.
(1)
57
Вторая группа формул (обращение начинается с вычисления О-1):
K = (A—BD-lC)-\
L=-KBD-\
N = D~1—D~1CB. ;
Эти формулы выведены в предположении, что все указанные обраще-
ния матриц выполнимы. Таким образом, обращение матрицы порядка
п сводится к обращению двух матриц порядков р и q и к нескольким
матричным умножениям.
Пример 3. Обратить матрицу
10 12
— 12 3 1
4 0—21
0 2 12
при помощи разбиения на клетки.
Решение. 1) Разбиваем данную матрицу S н<. клетки:
Для вычислений возьмем первую группу формул.
2) Вычисляем матрицу А~2:
^12! Г 10 1’
Л — 11 = 1 о ’ 1^ 1 = 2;
_«21 ^22.1 L — 1 2 J
Л it Л21
I Л | | Л | . Лп=а22г=2, Л21 “—й12~0,
Л] 2 Л22 Л12= Л22 = ^и = 1;
|л| |Л|
следовательно^
’ 2/2 0 I Г 1 0 1
1/2 1/2J= [l/2 V2 J
Образуем произведения
’ 1
.1/2
Г<
СЛ"1-:!
о
л-1в=
(СА“1)В =
0
1/2
0'
2
‘4
1
C(A-LB)=:
0“
1_
°]
2
Г1 :
[з
1
1/2
Г1
' [з
1
2
1 2
2 3/2
0’
1г
81
3J*
Г4 81
2]
1J
0
1/2
2“
. т
2 __
3/2J [4 3
"4
.1
'4
4
о
58
[для контроля вычисляем последнюю матрицу дважды — как (СЛ-1 )В и
как С(Л“Х В)].
3) Составим матрицу
и находим обратную ей матрицу /V = (D —
Имеем det (D — СА~1В) — 6—21 = — 15. Обозначим
—6 —71^ Грц р12
— 3 —1J [р21 Р22
тогда алгебраические дополнения Ptj — р22 “ — И P2j “ — р13 = 7, Р12
= — P2I “ 3; Р2з — Рп = — 6. Следовательно,
— СЛ"1 В)-1 =
1/15 —7/151 _ Г 1/15 — 7/151
—3/15 6/15] “ [ —1/5 2/5]’
4) Вычисляем матрицы
= — жл-1^ — Г
L —1/5
_ Г—3/15 —7/151 _
“ 2/5 2/5 ]“
1 Г1 2 1
L——Л"I л л .
[2 3/2
— 7/151 Г4 0]
2/5J ’ [1 1]
"1/5 7/15 ’]
.2/5 —2/5 ]’
' 1/15 —7/15'
. — 1/5 2/5 .
5/15" _
—5/15]
2 1
3/2] '
0 ’
V2 _
-5/15
—5/30
"1
2
1
U/2
А-'ВМ^
К^А-' — А-1 ВМ =
1/5
2/5
Г1
’ 11
1/3 — 1/3 1
1/6 i/з f
7/15 *] Г1 — 1/31
—2/5 [1 1/3 J’
—1/3 ] Г 0 1/3]
1/3 [ — 1/2 1/6J’
В
результате получаем
ГК L~
[ М N .
0 1/3 1/3 -1/3
-1/2 1/6 1/6 1/3
1/5 7/15 1/15 — 7/15
2/5 —2/5 —1/5* 2/5
Обращение клеточных окаймленных матриц, Пусть
" «11 п12 «1, п-1 ^1п
а 21 cz23 ••• а1, п-1 ^2п ^п-1
А = an-i, 1 ^п-1? 2*** ^n*lj п-1 ^n-lfn = Лп-1 ^пп _
(7п2 ••• ^п( п-1 ^пп _
Будем считать, что данная матрица А получена в результате окаймле-
ния матрицы порядка п— 1 матрицей-строкой Va-i =
59
= [ап1 апъ... дП| n_J, матрицей-столбцом
Un-l
-ащ
&2П
-&П-1, П“*
также
имеющими порядок п — 1, и числом апп.
Матрица обратная данной, тоже имеет вид окаймленной мат-
рицы
'Р П-4 ^П~1
Qn-i-----
ап
в которой искомые величины таковы: — матрица (п — 1)-го
порядка; 7?п-1 — матрица-столбец (п — 1)-го порядка; Qn_] — мат-
рица-строка (п — 1)-го порядка; ---число*
czn
Применяя правило умножения окаймленных матриц, имеем
A^P^ + U^Q^ A^R^ + ^L
ап
Vn-iPn-i + annQn^
an
= 0 ]
О 1
Приравнивая элементы матрицы-произведения соответствующим
элементам единичной матрицы, получаем следующие формулы для
вычисления элементов обратной матрицы Л"1:
^пп I п—! Дм — 1
Rn-1 — — I п — 1 ап
л __ Ап- 1
Ч'п-!”’-----------------»
атъ
( . ^n-1 Un-1 Vn-1 ДГ-Н
n-1 == 1 П----------------------
(3)
Таким образом, обращение окаймленной матрицы n-го порядка
сводится к обращению одной матрицы (п — 1)-го порядка и нескольким
матричным умножениям.
При этом для нахождения элементов обратной матрицы Л”1 при-
меняется следующая схема.
1. Пусть элементы матрицы Л"1 обозначены через (lt j — 1,
2,,*s, n), а элементы матрицы ДТ-i через d'^ (r, j = 1, 2, ttt, n — 1),
60
Тогда
d{\
^21
di2 ... d{ n—i
^22 ... d2i n-i
dn— I, i dn—J t 2 ««* dn^i^
2. Вычисляют элементы строки-произведения — и
столбца-произведения — AnhUn-i> обозначив их соответственно
^п-1 1 1Тп1Тп2*** Уп, Л—1]»
Pin
р2п
-Xn-21t/n.1 =
i n
3< Определяют число ant
n—1
П—1
Ctn «nn + 2 ^ni Pin ann+ 2 Уп1*
Двойное вычисление числа ап служит контролем предшествующих
вычислений.
4. Находят все элементы матрицы Д*1 по следующим формулам:
= + —n— (i, k^n—iy,
ап
rfio = —. dnh=^- (i, k^n-Di
<xn an
dnn = ~.
Пример. Методом окаймления обратить матрицу
(4)
тН со ю со сч со 1 5 1 — 1 0 ” 1 2 = ^п-1 -Кп-1 1 1 «
. 3—1 4 1 „
Решение, I эта п, Обращаем матрицу Лп_11
1) Находим матрицу Лд—2, Имеем
Лп-2 —
'3
2
det АПяя2= — 1; Лц = —3, Л21 = 4,
Л12 = —2, Л22 — 3;
61
следовательно^
^2 = [2
—4*1
—3j
2) Производя матричные умножения, получаем
дения и столбца-произведения:
элементы строки-произве-
[?3i Y32I — —^n-2 ~[3
Г 1______и___________Г3
1М П-2 П^2" [2
—41
J-U —3L
““О J
5Г”111
1 1“ 1—7 J
8) Находим число двумя способами!
«3=^33 + #31 йз+аз2 Р^з“ —1 +3»(—11)+(—5)*(—7) = 1;
аз “ #зз + #13 Ysi+#23 V32 = — 1 +^* 1 +1 •(—3) = 1.
4) По формулам (4) вычисляем элементы матрицы A”J.p
, ,, , P13T3I й
^11—+---------=3+-----;--=~8;
«3 1
+^._(+!=аии
«3 1
. ./ . РгзУз! п , ( —7).1
+------= 2 + ; = —5;
а3 1
. ' , &23V32 . , (—7).(—3)
^22 = ^2 2 +-= “ 3 + --- = 18;
<х3 1
Таким образом, получаем
29 —11
18 —7
—3 1
II э т а п. Обращаем матрицу Л:
—4 5 0 ~
— 3 11 г А я V =»
_ I un-i
~5 -1 2 “ L Vn-1 апп
3—1 4 1
1) Матрица была определена на I этапе.
2) Производим матричные умножения:
—8 29
— 11
[?41 ?42 ?431— ——[3 —1 4]* —5
= [15 —57 22)|
62
3) Вычисляем а4!
cQ==a44+ Рм+tys Рз&~1 +3«(—-7)(—1)*(—4) + 1 *4= —12;
а4 = а44 + а14 у«+«24 у42+а34 у43 = 1+0.15 + 1.(—57)+2-22= —12.
4) Обозначив
$11 $12 $13 $14
-1 — 5__ 521 $22 525 524
$31 $32 $33 S34
_$4Х s&2 $43 $Д4_
до формулам (4) определяем элементы матрицы Л-1:
Р14 Yu я , (-7)-15 9
$11 — “11 "Г — —8+ - - - - - = т
а4 — 12 12
с <Г I. Р14 ?42 gQ , , (—7)-(—57) 51
$12 — й12 ;
— 12 12 ’
Л-. , я т 314 ?43 (-7)-22 22
$13 — а13~г А
сс4 — 12 12
Р24У 41 . 5, (-4)-15 о-
$21 “ “21 “Г — — D+ —V,
^4 — 12
с А I Р24 У 42 (-4) (-57) 12
$22 — а22Г -18Н‘ -12 12 ;
£ - г! Л . Р24 У 43 , , (-4)-22 4
$23 “ а23 "Г «4 --14 -12 ~ ~12~ 5
г» -- /У 1 Р34 ?41 . . , ±11 . 3
$31 — “31 т «4 ~ ’ + -12 " 12 ’ Г
Рз4 Т42 21
$32 ~ “32 1 ‘ &4 12
Р34 ?43 Ь22 Ю I»
$зз ~^зз+ СС4 —12 12
Р14 7 ₽24 4 , _ Рз4 1
$14 — ос4 12 ' s-=—=лг! $34 = 12
Vri 15 Уи 57_ *
$41 — СС4 ~ 12 "• S42~ а4 12 ’
?43 22 1 1
$43 — сс4 = ~ 12 * а4 ” 12 *
Итак, окончательно находим
— 9—51 22 7'
A-^S: 0 —12 4 4
” 12 —3 21 —10 - -1
— 15 57 —22 -
63
Матрицы более высоких порядков обращаются аналогично, посте-
пенным увеличением порядка окаймленной матрицы, т, е, увеличением
числа матричных умножений,
§ 2.7, Треугольные матрицы. Разложение матрицы
на произведение двух треугольных матриц
Квадратная матрица называется треугольной, если элементы, стоя-
щие выше или ниже главной диагонали, равны нулю. Если равны нулю
элементы, стоящие выше главной диагонали, то матрица называется
нижней треугольной*, такова, например, матрица
0 .... О
^21 ^22 О
/п1 ^п2 ••• ^пп
Если же равны нулю элементы, стоящие ниже главной диагонали,
то матрица называется верхней треугольной; такова, например, матрица
'll Г12 ••• rm
О г22... г2п
Определитель треугольной матрицы равен произведению ее диаго-
нальных элементов. Если Т = [//J — треугольная матрица, то
Обратная матрица неособенной треугольной матрицы есть также
треугольная матрица того же типа и структуры,
Если квадратная матрица
А =
а11 Й12 ••• а1п
^21 ^22 •”
^п2 ••• ^пп
имеет отличные от нуля диагональные миноры (так называются миноры
определителя матрицы, у которых на главных диагоналях стоят диаго-
нальные элементы матрицы), т. е.
О,
.... det4=#O,
то ее можно разложить на произведение двух треугольных матриц
(верхней и нижней). Это разложение будет единственным, если диа-
гональным элементам одной из треугольных матриц заранее дать от-
личные от нуля значения (например, положить их равными единице).
64
Пусть А = ТХТ2, где
0 0 ... 0 “
1 Г12 Г13 ••• Г1п
Т, = ^21 ^22 0 ••• О
J 1
7\ = 0 1 ^*23 ••• Г2п
/п1 ^п2 ^пЗ ••• ^ПП —
Lo о о... 1 J
Искомые элементы треугольных матриц 7\ и 7\ находят следующим
образом:
1) Перемножают матрицы 7\ и Т2 (на примере матрицы четвертого
порядка).
“ Gi 0 0 0 " 1 Г12 Г13 Г14
л-л= ^21 ^22 0 0 0 1 r23 r24
hi hi hs 0 0 0 1 rS4
_ ^41 hi Ьз _ _ 0 0 0 1 _
^11^12 hiri3 hiru
4= ^21 ^21Г12 4~ ^22 ' hihs 4“ ^22^23 hirU 4“ ^22r24
hi hlT 12 4“ ^32 j h^r 13 4~ 23 4* hs hihi 4~ hi^24 4“ hzhz
_/41 ^41^12 + ^42 J h\r 13 4~ hiT 23 4“ h$ ^41H4 4442^24 4~ ^43r34 4" ^44
2) Приравнивают соответствующие
ния элементам матрицы
элементы матрицы-произведе-
ЙЦ Й12 6Zts
^21 ^22 ^23 ^24
а31 ^32 &33 ^84
^41 ^42 ^43 ^44.
а именно /ц — йц" /21 — ^21» Gi ®3i> ^41 “ ^41» ^11^12 — ^12» • После
этого решают сначала одночленные, затем двучленные и т, д. уравне-
ния.
Пример 1. Матрицу
1
2 —3~
2 —4
— 1 1
разложить на произведение двух треугольных матриц.
Решение. I) Введем обозначения
Произведем матричное умножение:
/11 0 0 1 Г12 Г13 /11 /11 /цг13
ЛТг= ^21 /22 0 0 1 Г23 /21 /21 Г12+ /22 /21г13 4" /22Г23
/з! /32 /зз 0 0 1 /зХ /31 /'12 4"/з2 /з1 г 13 + /з2г23 4" /зз
65
2) Составим уравнения
6.1 = 1; 2; 6iri3 =—3$
/21 = 3; 6i ^12 +/22=2; 61 63 + 6263 =—4:
Лп .^2; ?31 г12 + /32==—1; 6i 6.3 + 62 6з + бз = !•
3) Решаем эти уравнения:
2 л —3
61 — Ь 62 = =2; 6з — j =—3;
, -з- / -2-3.2_______4’ г -4~3-(-3) Л,
— 4 4
5*5
/31 —2; /32 — — 1 2*2 = 5; 6з = 1 —2-( —3) — = 4 •
Таким образом,
Пользуясь разложением квадратной матрицы А на произведение
двух треугольных, можно легко вычислять обратную матрицу А~\
а именно, если А = ТгТ2, то
Л“1-72” 7г1.
Обратные матрицы для треугольных находятся сравнительно просто.
Пример 2. Для матрицы
— 3 1
-5 2
— 7 3
найти обратную, разложив данную матрицу на произведение двух треугольных.
Решение. 1) Сначала вычисляем
det А —
2 —3 1
4—5 2
5—7 2
= _зо__зо—28+25 + 48+28= 13^=0.
2) Данную матрицу разбиваем на произведение двух треугольных:
1
о
о
71 =
61
61
61
61
/21
61
О О
62 б ;
62 6з
61 г 12
61 г1г + 6г
61 62+62
Г12
1
о
Г13
Г 23
1
61 г 13
61 63+62 6з
61 г1з + б2 бз + бз
Tj т2 =
Л =
66
доставляем уравнения;
/ц — 2; fa rig= — 3;
ta~4; £2f —5;
*31 = 5j /з! ГГз-р/зг—*“7j
fit из — h
*21 Из + *22 Пз=2|
*31 rld+*32 Г2з+*3§~ 3
Решая эти уравнения, находим
?22=-Нб=1; л23= 2-2 = 0;
== 3—5/2 = 1/2, Следовательно,
*11 ^21 Из =__
*31 — *32 —
— 3/2; ri3 = 1/2; /21 = 4;
— 7 + 15/2 = 1/2; /33 =
—3/2 1/2
1 О
О 1
3) Для нахождения обратной матрицы Д"1 = T^1Tf1 необходимо опре-
делить Т^1 и Tf1.
Обратим матрицу Т2', обратной для нее является верхняя треугольная мат-
рица, элементы главной диагонали которой равны 1. Положим
1
о
о
’Н§
I
о
г1§
Г23
1
Тогда Т2Т2Х =Е t или
1
О
о
Т2Т^ =
3
Г12~ 2
1
о
—3/2
1
О
Составляем уравнения
3
г 12— “0;
Отсюда находим г12 = 3/2;
г1з =
1
О
о
1/2
О
1 J
3
Г13 —~ г2з +
Г23
1
Г23 = 0.
3 1
Т'’2з+Т=0:
— 1/2. Следовательно)
3/2
1
0
— 1/2
О
1
1
о
о
7V =
Переходим к нахождению матрицы, обратной по отношению к 7\; Гр1 так-
же будет верхьей треугольной матрицей. Положим
Тогда
Л’1-
tn
*21
*31
0 0
*22 0
*32 *33
67
2/11
4/ц+ ?2i
е , 1 1
5/ц +~ *21 + *31
О
/22
1 1
/22 + 2 I32
О
О
1
у «33
1 О о
О 1 о
О О 1
Составляем уравнения:
2/п=1; 4/п +/21 = 0; /22= И
1 1 ~ 1 I Л I
5*11 + q *2i + Q *31 — 01 9 /22+ 0 /32—0» "7"/зз=1»
Отсюда находим
/и = 1/2; /21 = (-4).(1/2) = -2; /22=1;1
(-5).(1/2)-(1/2)-(-2) , . -1/2
' 172 “~3; '32~ 1/2
-1; /зз = -^-=2.
Следовательно,
О О
1 О
— 1 2
4) Теперь можно найти матрицу, обратную данной:
1 3/2 —1/2
О 1 О
О 0 1
— 1 2 — J
—2 10-
—3 —1 2
§ 2.8. Понятие о системе линейных уравнений
В общем виде система т линейных уравнений о п неизвестными
записывается так:
auxI + al2x2 + ... + аиХ] 4-... +а1пхп = Ьь
а21 Х1 + й22 4" ••+ + ••• + ^2П %П — ^2>
анх1 + а12ха+ ••• ••• ^ainxn~^ii
k &т] Х1 4“ ^тп2 ^2 4" ••• 4“ %j 4“ 4“ ^mn %n “ ^тп*
Уравнения системы считаются пронумерованными: первое, второе,
m-е. Числа х2, хп называются неизвестными системы;
Лц> #12, ^тп — коэффициентами при неизвестных системы.
Коэффициент при неизвестном хц в /-м уравнении обозначается
через ац, где первый индекс i указывает номер уравнения, в котором
находится данный коэффициент, а второй индекс / — номер неизвест-
ного, при котором находится данный коэффициент. Например, коэф-
фициент 023 находится во втором уравнении системы при неизвестном х3.
Числа &х, fe2, ,,м Ьт называются свободными членами системы.
68
Кратко система (1) может быть записана так:
2^^ = ^ (<=1,2.......... т). (Г)
;=|
Решением системы линейных уравнений (1) называется любая сово-
купность чисел аъ а2> .*., ап, которая будучи подставленной на место
неизвестных xlt х2, ..., хп в уравнения данной системы, обращает все
эти уравнения в тождества.
Система линейных уравнений (1) называется совместной, если она
имеет решение. Если система линейных уравнений не имеет решения,
то она называется несовместной, или противоречивой.
Совместная система линейных уравнений может иметь одно или не-
сколько решений и называется определенной, если ♦ имеет одно единст-
венное решение, и неопределенной, если имеет больше одного решения.
Две системы линейных уравнений с одним и тем же числом неиз-
вестных* называется эквивалентными, если они или обе несовместны,
или обе совместны и имеют одни и те же решения.
В этой главе мы будем рассматривать системы и линейных уравне-
ний с п неизвестными, т. е. системы вида
। а11х1 + а12ха+ .-+auX7 + ... + ainxn = ^,
021 Х1 + а22 Х2 + - + a2i Xj + — + а2п ХП = &2>
< ............................................... (2)
а11 *1 + 0/2 Х2 + ••• 4“ 0Ц */4~ ••• 4“ а1пХп~&1>
0д1 Х1 4“ 0/i2 Х2 4“ • ’• + anj Х] 4* •**А~&ппХп
§ 2.9. Матричная форма записи системы линейных уравнений.
Решение матричных уравнений
Пусть дана определенная система п линейных уравнений
0ц xi + 012 х2 + ••• + 0щ хп = blt
021 Х1 "4” 022 Х2 4* • 4“ 02л Хп = ^2»
0?ii xi 4* 0^.2Хп 4" • • • 4~ 0#п %п
Данную систему, пользуясь матричными обозначениями, можно за-
писать в следующем виде:
где
АХ = В,
69
Квадратная матрица А называется матрицей системы (1), а векторы
X и В — соответственно вектором-столбцом неизвестных системы
и вектором-столбцом ее свободных членов.
В матричном виде систему (1) можно записать и так:
ап ^22 1 с е • •*» см * « • 1 еч . Л . * 1 = гм (20
_^тг1 ^п2 1 ••• апп_ -Хп_
Рассмотрим три вида матричных уравнений и способы их решения,
I. Матричное уравнение вида АХ В, Для решения данного
уравнения умножим слева обе его части на Л-1:
д-MX = А-'В,
Но произведение А"1 А = Е, следовательно, EX = A~1Bt откуда
X - А^В. (3)
Пример 1. Используя матричную запись, решить систему линейных урав*
нений
Х1 +х2 4“2хз= — 1,
2xj — х2 -|-2хз =—4,
„ 4xi Ч- ^2 4хз — — 2.
Решение. Запишем систему в виде АХ ~ Eh
'1 1
2 —1
4 1
'хГ
х2
Лз_
Находим Д-1:
1 1 2
deM= 2—12 =6;
Ли — —6; Д 2f = —2; Дд^ = 4;
4 I 4
Л12 —0; —4; Дз2 = 2; Дтз —6; Д2д=3; Дзз =—3;
—1/3 2/3"
—2/3 1/3
1/2 —1/2_
Теперь, пользуясь формулой (3), получаем
1 —1/3
Х~А~1В = 0 —2/3
1 1/2
2/3"
1/3
-1/2
" Г
2
—2
Окончательный ответ: Xi — 1; х^ —2; х3 ——2.
Если имеется несколько систем линейных уравнений, имеющих
одинаковые матрицы системы, то их можно объединить в одно матрич-
ное уравнение и решать одновременно.
70
Пример 2. Даны три системы линейных уравнений:
Г Xi Зх2 ^Xg = 1, | х^• Зхб 2xg = 5, Г х?—3xg -р 2х9 = —~ 5,
/3X1—Ах% =2, < Зх4—4х5 =7, < Зх7—4х8 — — 2,
t 2xi—5х2 + — 2; [ 2х4—бх5-}-Зх6 = 9; 12х7—5х8 + Зх9 = — 7.
Найти их решения.
Решение. Составляем матричное уравнение АХ —
в, где
А = “1—3 2" 3—4 0 2—5 3 Х-^ х^ х^ Х2 Х5 Xg х3 х@ х9~ 1 1 Ю NO *- СО *4 СП 1 1 1 о КЗ ел ! 1
имеет вид X = А^В.
— соответственно матрица системы, матрица неизвестных и матрица свободных
членов. Матрица-решение имеет вид X — А^В.
Находим А-1:
det А —
Аха= — 9;
1
3
2
А<
—з
—4
—5
•22 “ “
2
О =1;
3,
1; Аз2 = 6; Au —
Г —12
—9
—7
Ац=—12; А21——1; А31 — 8;
А-1 =4 =
7; А2з==“1;
8’
6 .
5
А33 —
—1
—1
Таким образом,
—1
—1
—1
Л~ Л-1/? —
'—12
—9
—7
8"
6
5
—5"
—2
—7
“2
1
1
6"
5
2
Следовательно, решения данных
X] — 2, х2
II. Матричное уравнение вида ХА = В.
умножим справа обе его части на Л”1:
ХАЛ"1 = ВА~\
систем
гаковы:
— 1, х8 *—* 1, х$ ~~ 5, Х5 — 2, х$ 3; х? — 6, х8 — 5, Хд — 2.
Для решения уравнения
Значит, ХЕ = ВЛ"1, откуда
Х = ВА~1
(4)
Пример 3. Решить матричное
X-
уравнение
~6
6
.8
2
1
—1
Решен
1
2
1
det А =
и е. Находим
1
—1
О
А"1:
3; Ан — — 1; A2j — —1; Азх = 0; Ai2 —
1;
А22 — 2; А32 —
А~
1
-1
1
“3;
О’
—3
-3
Aj3— 1; А2з= 1;
’ 1/3
1/3
1/3
А"1-
A33— —3;
1/3 О'
—2/3 1 ♦
—1/3 1
—1
1
1
2
1
1
—1
О
— 1
2
1
1
1
1
2
2
5
7
9
5
2
3
4
71
По формуле (4) получаем
X = BA~^
2 —11 Г 1/3
1 1 • 1/3
—1 <1 L—1/3
1/3 ОП ГЗ 1 Г
—2/3 1 — 212
—1/3 1J L1 2 3.
III. Матричное уравнение вида АХВ — С. Для решения уравнения
умножим обе его части — слева на а справа на В-1; тогда
получим
А-'АХВВ-1 = А^СВ~\
или
откуда
EXE - А~гСВ-\
X = А~1СВ~\
(5)
Пример 4 Решить матричное уравнение
Ч —3 21 ГЗ 1 Г
3 —4 О .X. 2 1 2
2 — 5 3j L1 2 3_
~ 8 -4 —4“
18 5 10
17 —3 —1
Решение. Находим
’—12
—9
—7
8"
6
5
6
8
Л"1 =
(см. пример 2). Теперь вычисляем
Л“1С =
’—12
—9
—7
8’
6
d Ln
w 8
18
—4
5
—3
—4"
10
—L
'22
12
11
19
13
8
30“
20
13_
—1
—1
—1
Находим В"1:
3
2
1
1
1
2
1
2
3
det В =
4; Вп = -1; В31 = —1;
в31 = 1;
В12— —4; В22 — 8; В32 — —4; Bj3 = 3; В2з = —5; В33 = 1;
-3/4
1/4 —1/4“
—2 1
5/4 —1/4_
По формуле (5) получаем
’22
12
J1
19 301 Г 1/4
13 20 ‘ 1
8 13J L—3/4
1/4 —1/4'
—2 1
5/4 —1/4^
“2 5 6'
1 2 5
1 3 2
П
§ 2.10. Формулы Крамера для решения системы линейных
уравнений
Пусть дана система линейных уравнений (для простоты рассмотрим
систему четвертого порядка)
@11 “Ь «12 ^2 + «13 Х3 «11^4 —
@21 @22 %2 @2 i ^3 ”Ь @24^4 ^2}
@31 %1 “Ь «32 4~ @33 %3 4" «34^4 “ ^3»
«41 *1 + @42 *2 + «43 *3 + «44*4 = *4*
Введем следующие обозначения:
«и
«21
«31
«41
«12 «13
«22 «23
«32 «33
«42 «43
«И «13 «14
«21 ^2 «23 «24
«31 &3 «33 «34
«41 ^4 «43 «41
«11 «12 «13
@21 @22 @23 ^2
«31 «32 «зз
«41 «42 «43 &4
«12 «13 «14
«22 «23 «24
«32 «33 «34
«42 «43 «44
«12 ^1 «14
«22 ^2 «24
«32 &3 «34
«42 &4 @44
Здесь D — определитель системы, a Dlt D3 и D4 — определители,
получающиеся в результате замены столбца коэффициентов при соот-
ветствующем неизвестном столбцом свободных членов.
Если D Ф 0, то система (1) является определенной, т. е.
имеет единственное решение. Это решение можно найти по следующим
формулам:
£>i Z?2 D3
Xi = — > *2 = — , x3 = — , Хл = —,
1 D » 2 D 3 D 4 D >
(2)
которые называются формулами Крамера^
Пример. Еешить по формулам Крамера систему линейных уравнений
2xi — ^2+Хд ф- Зх4 — — 1,
*1+ х2—х3—4х4= 6,
3^1— Х2 4"Хз4~ Х4— 4,
#1—3%2 *фЗх4=—5.
73
Решение Находим определители D, D2i D3 и D& раскладывая ия
на миноры по элементам последней строки, а затем применяя правило треуголь*
ников:
D =
2
1
3
1
+3
—1
1
-1
—3
2
1
3
1
0
—1
1
3
—4
1
3
1
—1
1
(первый и третий определители
столбцы);
Di-
—1
6
4
—5
—1
1
—1
—3
1
—1
1
0
3
—4
1
3
2
+ 3
-1
6
4
-1
1
—1
D2 =
3
1
-1
6
4
-5
1
-1
1
О
3
— 4
1
3
D3 =
+5
2
I
+ 3
2
1
3
— 1
6
4
— 1
1
-1
1
-1
1
3
—4
1
—3
2
1
3
1
—1
1
3
1
= 3.54-3-0 = —15
равны нулю, так как имеют пропорциональные
= 5
1
-1
1
1
1
—1
1
-1
1
—1
1
3
—4
1
—3
—1
6
4
1
—1
1
3
1
-5*0—3.5+3.0- —15;
-1
6
4
1
— 1
1
3
— 4
1
—5
2
1
3
1
— 1
1
3
— 4
1
= —1 . 5-5.54-3 .
10 = 0;
2
1
3
1
— 1
1
— 1
2
1
3
1
-1
1
— 1
-3
-1
6
4
-5
3
— 4
1
3
-1
1
-1
-1
6
4
3
—.4
1
— 3
2
1
3
-1
6
4
3
— 4
1
3
— 4
1
2
4-3
3
-1
1
— 1
1
6
4
= (—1).5 — 3.154-5-( —5)4-3.10=—45;
-1
1
— 1
-3
1
-1
1
о
-1
6
4
—5
-1
1
— 1
1
— 1
1
-1
6
4
-3
2
1
3
1
-1
1
— 1
6
4
5
2
1
3
— 1
1
-1
1
1
1
=(-1) . 0—3 ( — 10)—5
0 = 30.
74
Теперь по формулам Крамера получаем решение системы:
D1 -15
^=-=ZTF = 1!
DS -45
x3=-K=-ziF=3’
О‘2 О
х ---—-----— Q,
2 D —15
D4 30
Xi~ D -_15=“2-
Заметим, что решение системы линейных уравнений по формулам Крамера
очень громоздко. На практике такие системы обычно решают другими методами.
§ 2.11. Решение системы линейных уравнений методом
последовательного исключения неизвестных (методом Гаусса]
Наиболее распространенным методом решения систем линейных
уравнений является метод последовательного исключения неизвест-
ных. Но прежде, чем перейти к объяснению этого метода, необходимо
познакомиться с элементарными преобразованиями систем линейных
уравнений.
Элементарными преобразованиями называются следующие три типа
преобразований систем линейных уравнений:
1) перестановка двух уравнений системы;
2) умножение обеих частей ^равненя системы на любое отличное
от нуля число;
3) прибавление (вычитание) к обеим частям одного уравнения со-
ответствующих частей другого уравнения, умноженных на любое
отличное от нуля число.
Можно доказать, что элементарные преобразования переводят дан-
ную систему линейных уравнений в эквивалентную. Выполнение эле-
ментарных преобразований равносильно выражению одного неизвест-
ного через другие.
Метод последовательного исключения неизвестных (метод Гаусса)
рассмотрим на примере системы четырех уравнений с четырьмя неиз-
вестными. Пусть дана система
' «И *1 + «12 Х2 + «13 Х3 + «14 Х4 = «15>
«21 Х1 «22 Х2 Д* «23 Х1 «24 Х4 ” «*5> М \
«з1 Х1 + «з2 + «33 х3 + а34 х4 = п35, ' }
«41 Х1 + «42 Х2 + «43 Х3 + «44 Х4 = «45-
Будем исключать неизвестное х4 из всех уравнений системы (1),
кроме первого. Назовем ведущим- неизвестным, а коэффициент а41 —
ведущим коэффициентом. Разделив первое уравнение на аи (это воз-
можно, если ап #= 0), получим
£ц аи
„ ^15
Л4 —•
а11 ^11
Обозначим
---- — ^12» — «13>
----~ «14» “ «15
аП--аП
75
и вообще btj = (/> 1). Тогда рассматриваемое уравнение примет
вид
^12-^2 ^13^3 + ^14^4 ” &15» (2)
ИЛИ
fe12x2 Ь13Х3 ^14-^4’
Для исключения неизвестного хх из уравнений системы (1) проведем
следующие преобразования.
1) Из второго уравнения системы (1) вычтем уравнение (2), умно-
женное на а21:
^21-^14'^22 *2 Т а23 х3 + й24 ^4“ ^25
— Г21 Х1 — °21 £12 х2— а21 £13 *3 — ^21 £14 х4 = — ^21 £15
(а22—Й21 £12) *24”(а23—Я21 Ь1$) Х3 4- («24— «21 £н) А = («25— «21 £1б)
Обозначим
^22 ^21 ^12 » #23 #21 ^13 &23*
#24 — #21 Ь14 = a{2l\ а2Ь~ а21 &15 = #$
и перепишем полученное уравнение в виде
<^1 *2 + *з + Ъ = а{&
2) Из третьего уравнения системы (1) вычтем уравнение (2), умно-
женное на а31:
«31 + «32 Х2 + а33 Х3 + «34 *4 = «35
— «31 —«31 £12 Х2— «31 £13 х3— «31 £14 ^4"“ —«31 £Х5
(«32 — «31 Ь\2) х2 + (й33— G31 £13) Х3 "Г (^34 — «ЗХ Х4 — «Зй— «31 &15
Обозначив а33—а31Ь12 = а33— а31Ь13 = «зз1 и т. д., перепишем
полученное уравнение в виде
х2 + а{4 х3 + «V/ xt = «'А’-
3) Из четвертого уравнения системы (1) вычтем уравнение (2),
умноженное на а41. Применив аналогичные обозначения, получим
следующее уравнение:
а(Л’ х2 + а^1 х3 + а<Д> х4 = а^.
В результате проведенных элементарных преобразований имеем
систему трех уравнений с тремя неизвестными, эквивалентную систе-
ме (1):
х3 Н-* ^Уз х3 ~]~ оУ2 ~ ^Уд,
< a^x2 + aMxs + a$x^a^, (И)
а(4У х2 + а») х3 + ау4> х4 = а^,
где коэффициенты atj (i, j 2) вычисляются по формуле а},1’ = а1} -<
~ацЬц (например, = агз — аг1Ь^,
76
Разделив, далее, коэффициенты первого уравнения системы (Г) на
ведущий коэффициент d$ 0, получим первое уравнение системы
в виде
V 4- °*з X -I- а<2*
*а + а(1) Хз +
«22 «22
^4= -¥•
а22
Обозначим
fl(D 23’
“2 2
£11 = £(!)•
a(D °™’
и22
.25
ДО
“2 2
и вообще -щ =: Ь2у (J > 2). Тогда первое уравнение системы (Г) при-
“22
мет вид
х2 + х3 4- х4 = ЬЩ,
ИЛИ
*2 = bw—ьт х3 — х4.
Исключая теперь х2 из всех уравнений системы (Г), кроме первого,
таким же способом, какими мы исключали х19 придем к следующей
системе из двух уравнений с двумя неизвестными:
а$х3 + а$х4=а%, ,
а™х3 + а$х4 = а
где = а},1’ — а^Ь^' (г, j > 3). (Например, йзТ = «зУ — ЯзУ^У-)
Разделив коэффициенты первого уравнения системы (1") на ведущий
коэффициент йзз' у= 0, получим
x3+b$x4 = b™ (2")
где 6^=^g-(j>3), т.е.
“3 3
х3 = 6<2)-6(2)х4.
Исключив теперь х3 аналогичным путем из системы (1"), находим
а^х^аы (1”')
где a'ip =cff — а$ bff (i, j > 4). Отсюда
а(3)
х4 = -^. (2"')
43>
“4 4
Остальные неизвестные системы последовательно определяются из
уравнений (2"), (2') и (2):
x3 = b^ — b^x4,
Х2 = Ь^ — Ь^х4~Ь^х3,
х4 — — b4i х4 Ь43 х3—х2.
77
*1 *2 х8 *4
1 0ц 1 а21 O31 о41 ^011 ои ai2 а22 «32 О42 « °13 ^12 = 0ц 013 с23 Озз О43 < 013 013 = Оц Оц 021 O34 O44 ь -2^ 014 — Оц
| OgV | = 02а — ^21 ^12 а\\} = а31—а31Ь1г а4 1 * = °42 аЛ ^12 . СгР со (« СР । 1“1 | 03 СО чЛ 1 „ _ <ЗСС 1 1111 в" «” И к м 1 <? 1 J ji J1 J । 2F W« гЧм *"£ I _<?Д —СО 1 3 <3 Q 1 1 * S w S | W СО 5 1 « СЗ С м4* |*1‘ '-'«N 1 1 1 1 о о •# «И чф 1 1 04 СО | 3 « Q ~ JI II II 1НтН еНЧЛ 1 _-О1 ч^СО "W*O 4 Q « О
— — — -о I 5s 1 , 1 1 1 Ъ”к 5з 1 11 £ (I I ksl । Ы ° । 1 а о t 1 **Ь9 rfUS 0 1 1Г if 2? . Л £- н 7 7 о I а 1 1 w-'lw— | £>, Г\ Н? * I го*-* coJ-* 1 £ “1 1
— —. — — —— — — — *— — - —.—— 1 й II II SS Лк°, 1 г 1 ~ ~ о 1 R ию 1
1 I 1 1
78
Таблица 2.1
Свободные члены s Разде- лы схемы
01 02^ ^35 0£& * *15 = а11 016 = 0Ц 4“ 012 + 013 + 014 + 015 026 =0214“ 022 “Ь fl23 + 024 + 025 036 = 031 4“ 032 4" 033 4- 034 4" 035 046 = 041 4- 042 4“ 043 4“ 044 4“ 045 *16 = “= 14~* 12 4“ *13 4" *14 4“ *15 011 I Прямой ход
М5 1ft ift j ci со 1 Г-, G ?3 <3 J „Л L_|<n 1 . I 1 — Ci -'M 1 1 1 1 al« Л lO Ю | II ci co ] U « 53 О 1 ii и I 1 5F -ид C?ift Cpft i — Ci — 05 I S3 « e J 1 Яге’ = «26 — «и 6ie = «аг’ + «2з’ + «г1? + «гР яШ = азв— «si 6i6 = a!i12)4-a'P-|-ap4)4-e'P «IV =«46 —«41 61б=«412)+«^13) + «?4> + «р5) 6?e, = E~ = i+6H>+6,H’+6<v 02 2 II
1 й Й | jnN> cjitO СГ 1 1! II — । — eo-'- I СД— й P | । । _ф—. j jj— I - Jjtc, U1W w W — 1 — U».— CO — 1 [ M— 1 tSS— to — 1 cjib4 oil-* «зв’ = Озе’ — «зР бгв’ = «зз’ +«зР + «зР «4в’ = «46J —«Рг’ бгУ =а?3’ + a'iV +«45’ 6^)=£В=1+^’+6Й) а Зо III
1 ? । MCT — 1 — — I CQiftl со1* C I -ft — 1 о 1 ° i 1 11 '3' 1 — 2‘ ! * 1 «43) = «4в’ — «Гз’ Ь£> = аЦ» + а?5’ ^’Ч-В^+б^ 044 IV
<1 = 6‘|> Хз=Ь^ — Ь^> Xi X2 = &25’—*21’ -4 —&23* *3 *1 =615 — bu Xi — bl3 Xg bj2 X2 Х4==6р6> =1+^4 Хз = 6^с’ — 6^X4= 1 +х3 *2= 6-2 в’ — 624’*4 — 6^3> Х3=1 +Х2 Х1 = *16 — *14 ^4 — *13 Х3 *12 Х2 “ 1 4-^1 V Обратный ход 1
79
Таким образом, процесс решения системы линейных уравнений по
методу Гаусса сводится к построению эквивалентной системы уравне-
ний (2), (2'), (2") (2"')* Метод Гаусса применим при том условии, что
все ведущие коэффициенты отличны от нуля.
Для удобства вычисления производятся по схеме, называемой схе-
мой единственного деления. Вычисление элементов Ьц называется пря-
мым ходом, вычисление значений неизвестных — обратным ходом,
так как сначала определяется значение последнего неизвестного.
Схема единственного деления (схема Гаусса) составляется следую-
щим образом.
В раздел I схемы (см. табл. 2.1) записываются коэффициенты при
неизвестных (в столбцах соответствующих неизвестных), свободные
члены и для каждой строки подсчитанные «контрольные суммы»
(столбец S), равные сумме элементов аг; в данной строке (здесь i = 1,
2, 3, 4; / — 1, 2, 3, 4, 5); последняя строка раздела I, состоящая из 1 и
элементов Ьц, получается делением первой строки раздела на ведущий
коэффициент alv
Элементы раздела II схемы равны соответствующим элементам раз-
дела I минус произведение atlbl} (г, 2); например, а$ = а23 —
— ^21^13- Последняя строка раздела II, состоящая из 1 и элементов
получается делением первой строки раздела на ведущий коэф-
фициент а{22}.
Аналогично вычисляются элементы III и IV разделов схемы. 1, II,
III и IV разделы, заканчивающиеся вычислением элементов Ь^[} (t ==
= 1, 2, 3, 4; / = 2, 3, 4, 5) составляют прямой ход вычислений
схемы.
Обратный ход начинается с вычисления последнего неиз-
вестного системы линейных уравнений хх и заканчивается вычислением
первого неизвестного xlt При обратном ходе используются лишь стро-
ки прямого хода, содержащие единицы и соответствующие элементы
btj (назовем эти строки «отмеченными»).
Элемент Ь$ последней «отмеченной» строки и столбца свободных
членов дает значение х4. Далее, остальные неизвестные х3, х2 и
находятся вычитанием из свободного члена «отмеченной» строки суммы
произведений ее коэффициентов на соответствующие значения ранее
найденных неизвестных; например, х3 = Ьз1} — Ь$х^
Значения неизвестных последовательно выписываются в V раздел.
Расставленные там единицы помогают находить для Xj соответствую-
щие коэффициенты в «отмеченных» строках.
Для контроля вычислений используются так называемые контроль-
ные суммы:
5 5
2 ai} (/ = 1, 2, 3, 4) и 6/в = 2^ + 1 (1=1,2, 3,4),
/=1 ;=1
помещенные в столбце S.
Над контрольными суммами в каждой строке проделываются те же
операции, что и над остальными элементами этой строки. При отсут-
ствии ошибок в вычислениях элементы столбца 2 равны суммам эле-
80
ментов соответствующих преобразованных строк. Таким образом, конт-
ролируется прямой ход схемы.
Для контроля обратного хода х4 находится в последней «отмеченной»
строке столбца S, т, е. х4 = &43б\ а остальные неизвестные этого столб-
ца (/ — 3, 2, 1) подсчитываются в тех же строках и по тем же форму-
лам, что и неизвестные х^ только в формулы подставляются соответ-
ствующие хр В итоге числа Xj должны совпадать с числами Xj + 1.
Пример 1. По схеме единственного .еления решить систему
2х4 2x2“” *з 4 х4 == 4,
4" Зх‘2*- х3 4'2х4 —6,
8xi + 5x2—Зх3+4х4 = 12,
Зх ] 3x2 *“ 2х3 4 2х4 === 6»
Решение, В раздел I табл. 2.2 вписываем матрицу системы, ее свободные
члены и контрольные суммы. Затем подсчитываем «отмеченную» строку этого
раздела, разделив первую строку на ап *== 2. Например, Z?i2 = £11 = 1.
2
Таблица 22
*1 X, «8 *4 Свободные члены $ Разделы схемы
Й 2 —1 1 4 8 ।
4 3 —1 2 6 1 4 т
8 5 —3 4 12 26 1
L 3 —2 2 6 12
1 1 —0,5 0,5 1 2 1
IEII 1 0 -2 —2
—3 1 0 —4 —6
0 —0,5 0,5 ; 0 0 II
1 —1 0 2 I 2
Е1 0 2 0
—0,5 0,5 0 0 III
1 1 0 1 0
IM I —0,5 0
1 1 -1 0 IV
1 х4 = — 1 х4 = 0
1 Х3= — 1 х3 = 0 V
1 х2 — 1 х2 == 2
1 X] = 1 Xi~ 2
81
Элементы раздела П вычисляем по следующему правилу: каждый элемент
этого раздела равен соответствующему элементу раздела I минус произве-
дение первого элемента его строки на элемент «отмеченной» строки в его столбце.
Полученный результат записываем на соответствующее место в разделе II. На-
пример, *
а2з’ = а2з—ям &13= —1 —4( —0,5) = 1,
а?з* =а33—а31 &13= —3—8 (—0,5) = 1.
Элементы «отмеченной» строки раздела П получим, разделив его первую строку
на ведущий коэффициент == — 1. Например, ЬА} = ^—= —1 = — К
и22 1
Аналогично вычисляются элементы III и IV разделов. Например:
а'Л = a(il ~ &У2 = 2-3-0,5 = 0,5,
= № - а<42’ = 0—(—0,5) ( — 1) = —0,5.
Для вычисления элементов раздела V, т. е. для нахождения неизвестных,
используем «отмеченные» строки, начиная с последней.
Неизвестное х4 представляет собой свободный член последней «отмеченной^
строки: х$ = = 1, а остальные неизвестные х3, х2 и хх получаются последо-
вательно в результате вычитания из свободных членов «отмеченных» строк сум-
мы произведений соответствующих коэффициентов на ранее найденные
значения неизвестных.
.Контроль осуществляется с помощью столбца 5, над которым производятся
те же действия, что и над остальными столбцами (см табл. 2.1 и 2.2), и в итоге
сумма элементов каждой строки схемы (кроме столбца 2) должна быть равна эле-
менту этой строки из столбца 2. Корни х;, принадлежащие столбцу S, должны
быть равны 1 + Xj для каждой строки раздела V.
В результате получаем xt — 1, х2 — 1, х3 ~ — 1, х4 — — 1.
Пример 2. По схеме единственного деления решить следующую систему ли-
нейных уравнений с точностью до 0,0001:
0,63x^1,00 х2 4-0,71 х3 4-0,34 х4 =2,08,
1,17 Xi 4-0,18 х2 —0,65 х3 + 0,71 х4 = 0,17,
2,71 xi —0,75 х2 + 1,17 х3 —2,35 х4 = 1,28,
3,58 xj 4-0,21 х2 —3,45 х3—1,18 х4 =0,05.
Решение системы приведено в табл. 2.3. Окончательный ответ: xi = 0 4026
х3= 1,5016, х3 = 0,5862, х4 = —0,2678
Если приближенные значения корней, полученные по схеме Гаусса,
достаточно точны, т. е. поправки корней малы по абсолютной величине,
то корни можно не уточнять.
В случае же необходимости уточнения приближенных значений
корней поступают следующим образом:
1) вычисляют для каждого уравнения системы невязки — разности
между правой и левой частями системы, получающиеся после подста-
новки в уравнения приближенных значений корней; если обозначить
приближенные значения корней через x(i°\ хз°\ ...» х«0>, невязки —
через Bi, е2, еп и свободные члены —через Ьъ Ьп, то
82
Т а б л и ц а 2.3
«1 г < г Свободные члены 2
|щбз| 1,17 2,71 3,58 1 1,00 0,18 —0,75 0,21 1,587 0,71 —0,65 1,17 —3,45 1,127 0,34 0,71 —2,35 —1,18 0,539 | 2,08 0,17 1,28 0,05 3,302 4,76 1,58 2,06 —0,79 7,555
— •— — — 1,6768| —5,0508 —5,4715 '"““I —1,9686 —1,8842 —7,4847 1,17402 0,0794 —3,8107 —3,1096 —0,04735 | —3,6933 —7,6684 —11,7712 2,20259 | —7,2593 -18,4141 —27,8370 4,32926
— — — — > | 4,04554 | _ 211*06105 1 О СО , 00 о о jO 1 ~- хг Ю О СО —• 1 И I _ 1 3,45644 0^28027 0,85438 3,45212 —4,14946_ _ | 0,85332
|—4,43085| 1 1,18681 j —0,26785 —3,24404 0,73215
1 1 1 1 *4 =—0,26785 ' х3 = 0,58625 *2 = 1,50164 Х1 = 0,40257 *4 = 0,73215 *3=1,58625 *2 = 2,50164 *j = 1,40257
е1 ~ 2 a ij>
! =i
п
82 = 62 2
1-1
en bn 2j
/ = 1
2) выписывают невязки в/ в отдельный столбец схемы Гаусса
и производят над ними те же операции, что и над другими столбцами
схемы;
3) считая столбец 8 столбцом свободных членов, вычисляют еь
е2, ...» как значения неизвестных;
4) находят уточненные значения неизвестных, прибавляя к при-
ближенным значениям неизвестных соответствующие невязки
Х1 = Аа, + 8ь ^^4G) + 82 = +&п-
83
Пример 3. Решить методом Гаусса с тремя десятичными знаками систему
' 7,09xi+l,17x2—2,23х3 = —4,75,
* 0,43xi+ 1,4 х2—0,62 х3 = —1,05,
3,21 Xi—4,25х2 + 2,13х3 = — 5,06
и уточнить полученные приближенные значения корней до 10~4 .
Р е ш е н и е. По схеме Гаусса вычисляем х^0>, х(20) и с тремя значащими
цифрами (табл. 2.4).
Таблица 2.4
Х1 *3 Свободные члены г е
|7Лй| 1,17 —2,23 —4,75 1,28 0,00097
0,43 1,4 —0,62 —1,05 0,16 0,00087
3,21 —4,25 2,13 5,06 6,15 —0,00295
1 I | 0,1650 -0,3145 —0,6700 0,1805 0,00014
|1,3290| —0,4847 —0,7619 0,0824 0,00081
__=4Д7796 __ 3J395_ Л 2107 5,5706 —0,00340
1 —0,3647 I -0,5733 0,0620 0,00061
|1,3964| 4,4705 5,8669 —0,00048
1 3,2015 4,2015 —0,00035
1 3,2015 4,2015 —0,00035
1 0,5943 1,5943 0,00048
1 0,2388 1,2388 —0,0005
Таким образом, х)0) = 0,239, Хз0) — 0,594, х30) = 3,202.
61
&2
необходимо решить данную систему с той
Чтобы найти невязку 8 =
L ез_
же матрицей
7,09 1,17 — 2,23
0,43 1,4 — 0,62
3,21 —4,25 2,13
и новым свободным членом 8, который подсчитываем следующим образом.
1. Вычисляем значения свободных членов, для чего подставляем в уравнения
данной системы значения х(,°>, х£0>,
7,09*0,239+ 1,17*0,594 — 2,23*3,202 = —4,75097;
0,43*0,239+ 1,4 . 0,594 —0,62*3,202= —1,05087^
3,21*0,239—4,25*0,594—2,13*3,202= 5,06295.
Невязки соответственно равны = — 4,75 + 4,75097 = 0,00097; е2 =
= — 1,05 + 1,05087 = 0,00087; 83 = 5,06—5,06295 = — 0,00295.
Решаем данную систему со свободными членами ег = 0,00097; 82 = 0,00087
и е3 = — 0,00295. Соответственно с точностью до 10 получаются значения
84
8i = — 0,0004; s2 — 0,0005; 8§ = — 0,0001. Теперь находим уточненные не-
известные;
Х! = 40) 4-81 = 0,239 — 0,0004=0,2386,
х2 = х(2°> 4-82 = 0,594 + 0,0005 = 0,5945;
х3 = х^0) -Ье§ = 3,202 —0,0001=3,2019.
§ 2.12. Вычисление определителей с помощью схемы Гаусса
Метод Гаусса может быть использован при вычислении определи-
телей:
• S* С • to J? * со * +> * Э ? иИ -2 2 w ••• rm ,
&П2 ^пп
где ап, аЙ’, «зз1 9 а™ !) — ведущие элементы схемы единственного
деления.
Пример 1. По схеме единственного деления вычислить определитель
d= 112 3 3 _1 _ 1 —2 2 3—1—1 1 2 3—1
Решение приведено в табл. 2.5.
Таблица 2.5
Столбцы 2
1 2 3 1 4
□ 1 2 3 7
3 -1 —1 —2 -1
2 3 -1 —1 3
1 2 3 —1_ _5
I 1 2 3 7
ы —7 —11 —22
1 —5 —7 — 11
Je 4 —2
1 7/4 11/4 22/4
1—27/4| —39/4 —66/4
—3/4 —27/4 _“30/4_
1 13/9 22/9
1-17/3] -17/3
85
Таким
образом, d— L(—4)
— 153.
Пример 2, По схеме единственного деления с точностью до 0,001 вычислить
определитель
1,00 0,42 0,54 0,66
0,42 1,00 0,32 0,44
d — •
0,54 0,32 1,00 0,22
0,66 0,44 0,22 1,00
Решение приведено в табл, 2.6.
Таблица 2.6
Столбцы 2
1 2 3 4
III 0,42 0,54 0,66 2,62
0,42 1,00 0,32 0,44 2,18
0,54 0,32 1,00 0,22 2,08
0д66 0_Л4 0,22 коо_ 2,32
1 0,42 0,54 | 0,66 2,62
|0,823б| 0,0932 0,1628 1,0796
0,0932 0,7084 0,1364 0,6652
0,1628 _^0,_1364_ 0,5644. 0,5908
1 1 0,1135 0,1973 1,3108
|0,697в| —0,1548 0,5430
__ —0,1549 0,5323 0^3774
1 —0,2219 0,7781
|р,4970| 0,4979
Окончательно имеем d = 1 . 0,8236 . 0,6978 - 0,4979 = 0,2861.
§ 2.13 Обращение матрицы с помощью схемы Гаусса
Пусть дана неособенная матрица А = [аг]\ (t, / = 1 ,2, и). Для
нахождения обратной матрицы Л"1 — [хг;] используется основное
соотношение А • Л”1 = Е, где Е — единичная матрица.
Так, для матрицы четвертого порядка, умножив
&п а12 а13 &14 *11 х12 xi3 ~1 0 0 сг
л-л-г= ^21 ^22 ^23 ^24 *21 *22 *2з *24 — 0 10 0
^31 ^32 ^33 ^34 *31 *32 *33 *34 0 0 10
_ $41 $4 2 ^43 ^44 _ __*41 Х42 *43 *44 _ _0 0 0 1_
86
получим 4 системы уравнений относительно 16 неизвестных xt] (i, / =
₽ 1, 2, 3, 4),
В общем случае имеют место соотношения
где
2 Qik'Xkj — У> I — 1>2 ... га),
1
я ( 1, когда i= 1,
( 0, когда i #= /;
6/7- называется символом Кронекера.
Полученные п систем линейных уравнений для / — 1, 2, п
имеют одну и ту же матрицу А и различные свободные члены, состав-
ляющие единичную матрицу, Поэтому эти системы можно решать по
схеме Гаусса.
Решения хо-, найденные по схеме единственного деления, и будут
элементами обратной матрицы А~\
Таблица 27
X1J X2j *8? /=1 / = 2 / -- 3 i
ш 0 1 2 1 0 0 0 5
—1 2 3 1 0 1 0 0 6
4 0 —2 1 0 0 1 0 4
_0_ 2 __1 2 0 0 6
1 0 1 2 1 0 0 0 5
111 4 3 1 1 0 0 11
0 —6 —7 —4 0 1 0 — 16
2 1 2 0 0 0 1 ь ~
1 2 3/2 1/2 1/2 0 ° И/2
13 — / —4 0 1 0 —16
3 —7 —1 __-1 0 1
1 7/6 4/6 0 -1/6 0 16/6
|б/2| 1 —1 -1/2 1 3
1 2/5 —2/5 —1/5 2/5 6/5
[ 1 2/5 —2/5 -1/5 2/5 6/5
1 1/5 7/15 1/15 —7/15 19/15
1 —1/2 1/6 1/6 1/3 7/6
1 0 1/3 1/3 -1/3 4/3
87
Таблица 2.8
х1/ *2.! *3; *4/ Г=1 1-3 / = 4 2
jTTooj 0,47 —0,11 0,55 1 0 0 0 2,91
0,42 1,00 0,35 0,17 0 1 0 0 2,94
—0,25 0,67 1,00 0,36 0 0 1 0 2,78
0,54 —0,32 —0,74 1,00 0 0 0 1 1,48
1 0,47 —0,11 0,55 1 0 0 0 2,91
|0?802б| 0,3962 —0,0610 —0,4200 1 0 0 1,7178
0,7875 0,9725 0,4975 0,2500 0 1 0 3,5075
—0,5738 —0,6806 0,7030 —0,5400 0 0 1 —0,0914
1 0,4936 —0,0760 —0,5233 1,2460 0 0 2,1403
|0,5838| —0,3974 0,5573 0,6594 0,6621 —0,8403 —0,9812 0,7150 1 0 0 1 1,8220 1,1367
1 0,9546 1,1341 —1,6807 1,7129 0 | 3,1209
|1,0388| —0,3896 0,0471 0,6807 1 2,3770
1 1 —0,3750 0,0453 | | 0,6553 0,9626 2,2882
1 = —0,3750 х42 = 0,0453 х4з= 0,6553 xti~ 0,9626 2,2882
1 Х31= 1,4921 х32 = —1,7239 %зз= 1,0873 х34 = — 0,9189 0,9366
1 х21 = —1,2883 х22 = 2,1003 хз3 = —0,4869 хг4 = 0,5268 1,8519
1 хи = 1,9759 х12 = —1,2017 —0,0120 х14 = —0,8781 0,8841
Следовательно,
г 1,9759 —1,2017 —0,0120 —0,8781-1
—1,2883 2,1003 —0,4869 0,5268
1,4921 —1,7239 1,0873 —0,9189
L—0,3750 0,0453 0,6553 0,9626j
л-1-
Пример 1. Обратить по схеме Гаусса матрицу
“10 12'
А_ -1 2 31
- 40—21'
_ 0 2 1 2_
Решение приведено в табл. 2.7 на стр. 87.
Таким образом,
0 1/3 1/3 -1/3 ’
= —1/2 1/6 1/6 1/3
“ 1/5 7/15 1/15 —7/15
2/5 —2/5 —1/5 2/5
Пример 2. Обратить матрицу
1,00 0,47 —0,11 0,55'
_ 0,42 1,00 0,35 0,17
А= —0,25 0,67 1,00 0,36
0,54 —0,32 —0,74 1,00
по схеме Гаусса; все расчеты вести с четырьмя десятичными знаками Ответ ок-
руглить до трех десятичных знаков.
Решение приведено в табл. 2.8 на стр. 88.
§ 2.14. Понятие предела для векторов и матриц
Понятие предела для векторов и матриц необходимо для описания
приближенных (итерационных) методов решения систем линейных
уравнений.
Пусть дана последовательность векторов:
7г->оо
x^-+xlt ..., Хп1} —>хп,
Х^-^Ху Х(2^->Х2,
%2
то вектор X —
называется пределом последовательности век-
X
89
торов Х(,\ Х(2). Х(Д,), а сама последовательность называется
сходящейся к вектору X, т е.
или hmX(A) = X.
k ->30
Аналогично, если имеется последовательность квадратных матриц
aw ... О1Г -of,' of» . а^ ... uin
А(1) = а^агг’ ... с&п , а(2) = С$\ ... й2п > •••
_ап\'' • • №. /7(2) '• • ипп _
а\ 1 Я12 ••• &1п
П(А)
^21 ^22 #2/1
Л(^ -
— 4Znl &п2 ••• —
с элементами а^\ ащ\ где i = 1, 2, и; /== 1, 2, п, то пре-
делом последовательности матриц Л(1\ А^ называется матрица
с элементами = lim а)/, т. е.
А-* ОС’
а'п-^ац; •••; а\Ч-*-ап; ...; 4V-*ann..... a^->flnn,
при условии, что все эти пределы существуют. Сама же последователь-
ность Л(1\ ,,м Л(А) называется сходящейся к Л, т. е.
Л^)->Л, или Jim Л(^==Л.
k —>00
Если A(k> -> Л, то A(k)X -> АХ при любом векторе X и
(Л(*))-1-> л-1.
Из сказанного выше вытекает следующее утверждение (приводим
его без доказательства): если последовательность матриц Л(1\ Л<*>
имеет пределом неособенную матрицу А и векторы В<г\ ..., B<fe> схо-
дятся к В, то решения систем Л(1>Х = В(1\ А^Х = В<*> имеют
предел, являющийся решением системы АХ = В, т, е.
Х^(А^)’1В^-+А~1В.
§2.15. Приближенные методы решения систем линейных уравнений
Приближенные методы решения систем линейных уравнений поз-
воляют получать значения корней системы с заданной точностью в виде
предела последовательности некоторых векторов. Процесс построения
такой последовательности называется итерационным (повторяющимся).
Эффективность применения приближенных методов зависит от удач-
ного выбора начального вектора и быстроты сходимости процесса.
Рассмотрим два приближенных метода: метод последовательных
приближений (метод итерации) и метод Зейделя.
90
Метод последовательных приближений (метод итерации). Пусть
дана система линейных уравнений
^11^1 + ^12^2 + - +<я1пхп=Л,
^21^1 + ^22^2+ — +^2n^n==^
» +г1 ^Т + ^п2 ^2 “Г ••• + &nvi. %п ^п*
Запишем систему (1) в матричном виде:
АХ - В, (2)
выразим через первое уравнение системы, х2 — через второе урав-
нение и т. д, В результате получим систему, эквивалентную систе-
ме (1):
*1
^1 #12 у #13 v а1п у
^2 л3 ••• ЛП>
а11 #11 #11 #11
у — 62 f2! у fl23 у #?71 у
Л2 — Л3 *•* Лп»
#22 #22 #22 #22
(3)
„ #2п #71-1, п
Лп Л1 Л2 ••• ~ Ап—!•
#nn #nn #пм #п/г
7
Обозначим — = рг;---------“ где i = 1, 2, /г; / = 1,2,.. , /г.
#ii #Н
Тогда система (3) запишется таким образом:
31+ «12 ^2 +«13*з+ ••• +«1п*п>'
^2 “ ?2 + «21-^1 +«23^з+ ••• + «2/г
~ Зп + «п1 -^1 + «п2 + •••+^п п-1 -^n-V
Система (3А) называется системой, приведенной к нормальному виду.
Введя обозначения
91
запишем систему (3') в матричной форме:
X = р 4- аХ,
или
(4)
Решим систему (4) методом последовательных приближений. За нуле-
вое приближение примем столбец свободных членов:
—нулевое приближение,
далее, построим матрицы-столбцы
—первое приближение',
—второе приближение
Вообще, любое (k + 1)-е приближение вычисляют по формуле
Х(*+1)==р + аХ(*> (6 = 0, 1, .... «). (5)
Если последовательность приближений Х<°>, XW, ,,,, имеет пре-
дел X = lim Х<*>, то этот предел является решением системы (3),
k^-00
поскольку по свойству предела lim X(fe+1) = р + a lim т. е.
Х-ЮО fe-*0O
X = а + ря.
Пример 1. Методом последовательных приближений решить систему
8xj 4- Xj 4" х3 == 26,
< Xj 5xgXg = 7,
Xi— х24-5х3= 7,
Решение. 1) Приведем данную систему к нормальному видуг
' Xx=s=3,25—0,125 х2 —0,125 х3,
Х2=1,4 —0,2хх 4-0,2х3,
х8=1,4 —0,2X1 4-0,2х21
—0,125 —0,125
а — —0,2
—0,2
0
0,2
0,2
0
3,25
м
1,4
0
92
2) Строим последовательные приближения. Нулевое приближение:
Пер вое пр ибл и же н ие:
3,25” 0 —0,125 —0,125” "3,25” ”2,9 '
r(D х2 1,4 + -0,2 0 0,2 1,4 = 1,03
ЛИ 1,4 -0,2 0,2 0 1,4 1,03
Таким образом, х$ = 2,9935; х2 = 1,0068; х3 — 1,0068 и с точностью до 10"1
получаем хг — 3; х2 — 1; х3 = 1*
Пример 2. Методом итерации решить следующую систему s точностью до 10
7,6x1 + 0,5х2 + 2,4х3 = 1,9,
< 2,2xi+9,1х2 + 4,4х3 —9,7, (*)
—1,3xi+0,2х2 + 5,8х3 =—1,4.
Решение. 1) Приведем данную систему к нормальному виду:
Х1 =
х2 —
х3 =
1,9 0,5 2,4
7,6— 7,6 *2—7,6 Хз’
9,7 2.2 4,4
Хз’ ЙЛИ
-1,4 1,3 0,2
5,8 + 5,8*1 —5,8 *2’
х1 = 0,25 —0,065ха—0,З158х3,
хг= 1,0659 —0,2418X1—0,4847x2,
х3 = —0,2414 +0,2241%1—0, 3448х2;
0 —0,065 —0,3158
а = —0,2418
—0,4847 ;
0,25
-1,0659
0,2241 —0,3448 0
—0,2414
Заметим, что линейную систему можно привести к нормальному виду также
следующим образом: записать коэффициенты при Xj, х2, х3 в соответствующих
уравнениях системы (*) в виде kx, где k — число, близкое к коэффициенту при
соответствующем неизвестном и на которое легко разделить коэффициенты при
неизвестных и свободные члены.
Например.
lOxi — 7,6xi + 2,4xi (в первом уравнении),
10x2 —9,1х2+ 0,9x2 (во втором уравнении),
10х3 = 5,8х3 + 4,2х3 (в третьем уравнении).
93
Перепишем систему (*) таким образом!
10#х = 1»9 4" 2, 4xi— 0, 5х2 — 2, 4х3,
10x2 = 9> 7“ 2,2X14-0,9x2—4,4x3,
Юх3= —1,4 + 1,3x1 — 0,2х2+4,2х3;
Х1 = 0,194-0,24xi — 0,05х2—0,24х3»
х2 = 0,97—0,22xi+9,09х2—0,44xs,
х3= —0,14+0,13х! —0,02х2+0,42х8.
Матрица а и вектор ₽ принимают вид
0,24
—0,22
0,13
—0,05
0,09
—0,02
—0,24
—0,44
0,42
0,19
0,97
—0,14
2) Последовательно
дп"1 0,19' 0,24 —0,05 —0,24' 0,19"
ди л2 — 0,97 + —0,22 0,09 —0,44 0,97 :
до хз J —0,14 0,13 —0,02 0,42_ 0,14
Д2) "1 Х1 0,19" 0,24 —0,05 —0,24" 0,2207
Д2) Л2 — 0,97 + —0,22 0,09 —0,44 1,0771
Д2) Лз J —0,14 0,13 —0,02 0,42 —0,1935
Таю ям образом, С точностью ДО 10“ 3 получаем
Xj = 0,236; х2 == 1,103; х3 = — 0,214.
0,2207
1,0771 ,
0,1935
0,2359
1,1034
—0,2141
а =
§ 2.16. Условия сходимости итерационного процесса
Пусть дана приведенная к нормальному виду система линейных
уравнений А = Н аХ. Итерационный процесс и его сходимость
зависят от величины элементов матрицы а следующим образом: если
сумма модулей элементов строк или сумма модулей элементов столб*
цов меньше единицы, то процесс итерации для данной системы сходит*
ся к единственному решению независимо от выбора начального век*
тора.
Следовательно, условие сходимости можно записать так:
п п
2 I а«/|< 1 (i=l, 2, ... п) или I «//!< 1 (/=1,2,
/=1 z=i
п).
Пример. Для системы
8X14- x2-J- х3 = 26,,
xi4-5x2— х3= 7, или
Xi— х24-5х3 = 7,
Х1 = 3,25—0,125x2—0,125х3,
х2—1,4 —0,2x1 +0,2х3,
х3 ——• 1,4 —0,2X1 4~0,2х2
итерационный процесс сходится, так как
0 —0,125 —0,125'
а= —0,2 0 0,2
0,2 0,2 0
94
I cc ill + | <%2i I + I &3i |=0,2 + 0,2 = 0,4 < 1 j
I aisl 4" \ a22 I _r I аз2 I =0,125 -j- 0,2 = 0,325 < Ц
I a13| + |a23| + | a33 |=0,125+0,2 = 0,325 < I.
Аналогично можно было бы проверить выполнение условия сходимости, взяв
суммы модулей элементов строк.
Процесс итерации заведомо сходится, если элементы матрицы а удовлетво-
ряют неравенству |а^| < 1/п, где п — число неизвестных данной системы.
В нашем примере п = 3 и все элементы < 1/3.
Сходимость итерационного процесса связана с нормами матрицы а
следующими соотношениями. Если выполняется одно из условий'.
п
||a||i = max 2 |aj< 1,
' ! —1
либо
П
|]aj2 = max 2 I|< 1,
1 ' =1
либо
/" п п
DMs = ]/ 2 |aj2 < 1.
то процесс итерации линейной системы сходится к единственному ре-
шению
Так, в рассмотренном выше примере норма
]|а||2 = max (0,4; 0,325; 0,325) = 0,4 < Ц
т. е. итерационный процесс сходится.
§ 2.17. Оценка погрешности приближенного процесса
метода итерации
Если задана допустимая погрешность вычислений 8 и Л\—-вектор
точных значений неизвестных линейной системы, a X\k} есть /г-е
приближение значений неизвестных, вычисленное методом итерации,
то для оценки погрешности)) Хг — X{tk) || е метода применяется фор-
мула
О)
где || а |1 — одна из трех норм матрицы сс, || 0 [| — та же норма вектора
0, a k — число итераций, необходимое для достижения заданной точ-
ности, При этом предполагается, что последовательные приближения
X\t} (где j = 0, 1, k, i = 1, 2, п) вычисляются точно, в них
отсутствуют погрешности округления.
95
Пример. Показать, что для системы
9,9xi— 1,5*2+2,6*3 = 0.
0,4^1 + 13,6*2—4,2х3 = 8,2,
0,7*1+ 0,4*2 + 7,1*3= — 1.3
итерационный процесс сходится, и определить, сколько итераций следует выпол-
нить, чтобы найти корни системы о точностью до 10“+
Решение, 1) Приводим систему к нормальному виду:
10*1= 0,1*1+1,5*2—2,6*3,
20х2== —0,4*1 +0,4х2 + 4,2х3 + 8,2,
Юх3= —0,7*1—0,4х2 4-2,9*з— 1,3,
или
*1= 0,01ti + 0, 15х2—0,26х8п
*2 — —0,02*1 + 0,32*2+0,21*3 + 0,41,
х8=—0,07*1 — 0,04*2+0,29х3 — 0,13,
2) Матрица системы
а
0,01 0,15 —0,26
—0,02 0,32 0,2]
—0,07 —0,04 0,29
Используя норму || а ||2,
Следовательно, итерационный
получим ||<х||2 — max (0,1; 0,51; 0,76) =0,76 < 1,
процесс для данной системы сходится,
0
3) Имеем р= 0,41 , ||₽||2 = 0 + 0,41 +0,13 = 0,54.
—0,13
4) Применяя формулу (1), находим
||Х-Х<&) ||<
1М* + 1 • IIP 112 __ о,76"+'.0,54
1—Il all2 0,46
0,76*+l-0,54 < 10“4-0,46; 0,76*+’ < ----;
54
(/? + !) lg0,76< lg46—lg54—4;
— (fe+ l)-0,1192 < 1,6628—1,7324— 2=—4,0696;
4,0696
& + l> ——=32,91 fe>32,9; й = 33.
0, 192
Теоретическая оценка числа итераций, необходимых для обеспечения заданной
точности, практически оказывается завышенной.
§ 2.18. Метод Зейделя. Условия сходимости процесса Зейделя
Метод Зейделя представляет собой некоторую модификацию ме-
тода последовательных приближений. В методе Зейделя при вычис-
лении (k + 1)-го приближения неизвестного хг учитываются уже
найденные ранее (k + 1)-е приближения неизвестных х1( х2, хг_р
96
Пусть дана линейная система
х1 — 01 + а11-^1 + «12 Х2 4* •••+ а1пХп<
Х2 — 02 + «21 Х1 + а22 х2 4* ••• 4_«2ПЛ'П»
Х3 — 03 4~ «31 Х1 + «32 Х2 + ••• +а3пхп>
(1)
xrr=fin + anixi + anix2+... +аппхп.
Выбираем произвольно начальные приближения корней лс40>,
Х20}, .... Хп' и подставляем в первое уравнение системы (l)j
х<1) = ₽1 + аих(°) + а12х^+ ... +aln4°>j
полученное первое приближение х!1’ подставляем во второе уравнение
системы (1):
4‘ * == 02 + «21 ’ + «22 *(г0> + • - 4- «2П
полученные первые приближения х?’ и Хг1’ подставляем в третье урав-
нение системы (1):
х^ —Рз 4- «314- — 4- «зп х(а0>
и т, д. Наконец,
х" ’ = ₽п 4- «П1 4’ ’ 4- «П2 4” 4- •.. 4- an, 1 j 4- ann x<a°\
Аналогично строим вторые, третьи и т, д, итерации,
Таким образом, предполагая, что k-e приближения корней х®
известны, по методу Зейделя строим (k 4* 1)-е приближения по сле-
дующим формулам:
<+”-014- 3 aux<*>,
Х</+ ') ?=р24-«21 4*+11 + 5а2^44>» (2)
/ = 2
Я— 1
4*+ ° s 0п + 5 ат ’> 4- «пп х^,
i=i
где k — 0, 1, 2, п.
Пример 1, Методом Зейделя решить систему
7,6х1+0,5х2+2,4л3=1,9,
- 2,2 Xf -f- 9t 1 Х2*4*4 >4 9,7(
— b3xi+042x2+5,8xs=;—1,4.
97
Решение. 1) Приведем систему к нормальному виду:
или
10 Xi = 1,9 + 2,4Х]_—0,5 х2—2,4 х3,
< 10x2 = 9,7 — 2f2xi + 0,9x2—4,4х3,
10 Хз =—1,4+1,3 Xj—0,2 х2+4,2 х3,
Х1 = 0,19+0,24 Xi—0,05х2 — 0,24 х3,
х2 = 0,97 —0,22 Xi + 0,09 х2 — 0,44 х3,
х3 s=: —0,14 + 0,13xi “~0,02х2 + 0,42 Хд.
2) За нулевые приближения возьмем соответствующие значения свободных
членов: х|0) — 0,19; х£°> = 0,97; х^0) = — 0,14.
3) Строим итерации по методу Зейделя, Первые приближения:
х(,1) =0,19+0,24-0,19 — 0,05-0,97—0,24. (—0,14) = 0,2207,
41)=0,97—0,22-0,2207 + 0,09-0,97—0,44-(— 0,14) = 1,0703,
/з1^—0,14 + 0,13-0,2207-0,02-1,0703+0,42-(—0,14) = —0,1915.
Вторые приближения:
х<!2) = 0,19 + 0,24-0,2207—0,05-1,0703 — 0,24-(—0,1915) = 0,2354,
42)=0,97 — 0,22-0,2354 + 0,09-1,0703 — 0,44-(—0,1915)= 1,0988,
x!j2,= — 0,14+0,13 0,2354—0,02-1,0988 + 0,42-( —0,1915) = —0,2118
и т. д.
Решение этого примера приведено в табл. 2.11.
Таблица 2 11
Ко итерации х. *3
0 0,19 0,97 — 0,14
1 0,2207 1,0703 — 0,1915
2 0,2354 1,0988 — 0,2118
3 0,2424 1,1088 — 0,2196
4 0,2454 1,1124 — 0,2226
5 0,2467 1,1138 — 0,2237
6 0,2472 1,1143 — 0,2241
7 0,2474 1,1145 -0,2243
8 0,2475 1,1145 —0,2243
Построение итераций заканчивается, когда с заданной степенью точности полу-
чаем одинаковые значения в двух итерациях подряд. В нашем примере это итера-
ции 7 и 8.
Окончательный ответ: хх 0,248; х2 1,114; х3 ~ — 0,224*
Процесс Зейделя для линейной системы X — 0 + аХ так же, как
и процесс последовательных приближений, сходится к единственному
98
решению при любом выборе начального приближения, если какая-нибудь
из норм матрицы а меньше единицы, гги е. если
||а||1 = шах 2 I аа| < 1,
I 7= 1
либо
|]a||2 = tnax 2 |ау|<1,
либо
ll“h=‘[/ Sl<W <1-
Процесс Зейделя сходится к единственному решению быстрее
процесса простой итерации.
Пример 2* Проверить, сходится ли процесс Зейделя для системы, рассмотрев
ной в примере 1.
Решение, 1) После приведения системы к нормальному виду (см» стр» 98)
получаем матрицу
“ 0,24
—0,22
. 0,13
а =
-0,05 —0,24"
0,09 —0,44
—0,02 0,42^
2) Находим
||a|li= max (0>53; 0,75; 0,57) = 0,75 < !•
Следовательно, процесс итерации для данной системы сходится к единственному
решению, несмотря на то, что
|]а )|2= max 2 I ^|=max (0,59; 0,16; 1,1) = 1,1 > L
i — 1
§ 2.19. Оценка погрешности процесса Зейделя
Пусть дана линейная система X = р + аХ. Если Хг — точное
значение корней линейной системы, a Xik} — k-e приближение, вы-
численное по методу Зейделя, то для оценки погрешности этого метода
применяется формула
их—xwiit< цх(1>—x<°>|k.
1-II«Hi
(1)
Пример. Подсчитать, сколько итераций по методу Зейделя необходимо вы-
полнить, чтобы с точностью до 10“"4 найти корни системы
9,9xj— 1,5ха+2,6х3=0,
0,4xj + 13,6x2—4,2х3 = 8,2,
Р, 7x14-0,4х24-7,1 х3= — 1,3.
99
Решение. 1) Приведем систему к нормальному виду (см, стр, 96)1
~0,01хх+0, 15х2—0,26х3,
х2 = 0,41—0,02х1+0,32х5+0,21х8,
х3= —0,13—0,07хх—0,04х2+0»29хз.
2) За нулевые приближения примем столбец свободных членов: х^ “ 0;
Х<о> = 0,41; х£0) = —0,13 и вычислим первые приближения
х^ =0,01.04-0,15.0,41—0,26.(—0,13) =0,0953,
«^>=0,41—0,02.0,0953 + 0,32.0,41 4-0,2Ь(—0,13) = 0,5120»
х(3п = —0,13—0,07-0,0953—0,04*0,5120+0,29(—0,13)=—0,1948.
8) Матрица
0,01
—0,02
-0,07
0,15 —0,26"
0,32 0,21
—0,04 0,29_
Значит, 0а 0 1 “ тах (0,42; 0,55; 0,40) = 0,55. Поскольку
Х<°>«=
" О
0,41
0,13
и Х(1> =
0,0953 ~
0,5120
—0,1948_
имеем
ХП)_Х(0) =
0,0953
0,1120
—0,0648
т. е. 11Х(,’-Х<0)||1=0,1120.
4) По формуле (1) определяем k\
0,55*
И’4 < ~ - «0,1120; 10-<.0,45 < 0,55*.0,1120;
0,45
— 4 1g 10+ 1g 0,45 < k lg 0,55 + lg 0,1120;
4,3468
—4—0,3468 < k (—0,2596—0,9508); k > 2104' = 3>59S * = 4«
Аналогично можно производить оценку метода Зейделя по норме 2.
§ 2.20. Приведение системы линейных уравнений к виду,
удобному для итераций
Процессы последовательных приближений и Зейделя для линейной
системы X = р + аХ сходятся к единственному решению независимо
от выбора начального вектора, если
5 |a0|<l(fel, 2, .... п) или S 2,п).
/=1 ;=1
Таким образом, для сходимости вышеуказанных итерационных
процессов достаточно, чтобы значения элементов ati матрицы а при
i Ф j были небольшими по абсолютной величине. Это равносильно то-
му, что если для линейной системы АХ — В модули диагональных
юо
коэффициентов каждого уравнения системы больше суммы модулей
всех остальных коэффицентов (не считая свободных членов), то ите-
рационные процессы для этой системы сходятся, т. е* если мы имеем
систему 2 auxi = t>t = 1, 2, и), причем | аа | > 2 I I > то
/=1
процессы последовательных приближений и Зейделя для данной си-
стемы сходятся.
Применяя элементарные преобразования, линейную систему
дХ = В можно заменить такой эквивалентной системой X = Р +
+ аХ, для которой условия сходимости будут выполнены,
Пример 1. Привести данную систему линейных уравнений к виду, удобному
для итераций
(0,9%!-Р2,7х2—З,8х3 = 2,4, (А)
<2t5xj-(-5,8x2—0,5х3 = 3,5, (Б)
(4,5X1 — 2,1х2 + 3,2х3=— 1,2. (В)
Решение. 1) Из заданной системы выделяем уравнения с коэффи-
циентами, модули которых больше суммы модулей основных коэффициентов
системы. Каждое выделенное уравнение выписываем в такую строку новой сис-
темы, чтобы наибольший по модулю коэффициент оказался диагональным.
В уравнении (Б) коэффициент при х2 по модулю больше суммы модулей ос-
тальных коэффициентов. Принимаем уравнение (Б) за второе уравнение новой
системы:
2,5xf + 5,8х2 — 0,5х8 — 3,5, (И)
2) Из оставшихся неиспользованных уравнений системы составляем линей-
но независимые между собой комбинации. Так, за первое уравнение новой сис-
темы можно взять линейную комбинацию (2В) + (А), тогда имеем
9,9xj — 1,5х2 + 2,6х3 — 0, (I)
За третье уравнение новой системы можно принять линейную комбинацию
(2А) - (Б), т. е.
0,7x1 + 0,4х2 + 7,1х3 = — 1,3. (Ш)
3) В итоге получаем преобразованную систему линейных уравнений (I),
(II), (III), эквивалентную исходной и удовлетворяющую условиям сходимости
итерационного процесса:
(9,9xj — 1,5х§ -J- 2,бх з = 0,
|2,5xi+5,8x2—0,5х3 = 3,5, (*)
[о, 7xi 4" 0,4х2 4-7, 1х3 «= —1,3«
Приведя систему (*) к нормальному виду, имеем
X} = 0,1X14-0, 1бх2—0,26х3, 0,10 0,15 —0,26 '
х2 = 0,35х1—0,21х24-0,42х34-0,05, а = 0,35 —0,21 0,42
Лз-—0,13X1—0,07х2—0,04х3 4-0,29; 0,13 —0,07 —0,04 _
||а||2=тах (0,58; 0,43; 0,72) = 0,72 < 1.
©стаете я решить систему одним из итерационных методов.
101
§ 2.21. Исправление элементов приближенной обратной матрицы
Пусть дана неособенная матрица А и требуется найти ей обратную
А-1. Предположим, что мы получили приближенное значение обрат-
ной матрицы
Do = Л-Ч
Тогда для улучшения точности воспользуемся методом последователь-
ных приближений следующим образом. За нулевое приближение об-
ратной матрицы А-1 принимаем значение Do, погрешность которого
есть матрица
Fo = Е — AD0,
Дальнейшие последовательные приближения будем строить по фор-
муле
D^Dft-i + D^^.j 2,...) (1)
и соответствующая погрешность
Fk = E- ADh,
Если все элементы матрицы То = [/Д] удовлетворяют неравенству
| А; | < где п — порядок матрицы и 0 < q<Z 1, то процесс итера-
ций заведомо сходится.
Оценка погрешности данного метода имеет вид
||A-i-DftK-15d_^, (2)
где под нормой понимается норма 1 или норма 2,
Процесс уточнения элементов обратной матрицы прекращается,
когда обеспечено неравенство || Dh — || в, где 8 — заданная
точность.
Пример Для матрицы "1,16 0,45 0,32 0,83 - —0,54 0,28 -0,66“ 0,83 1,06
исправить элементы приближенной обратной матрицы G точностью ДО 10"5.
Реше Далее, н и е. 1) Мете Оо= получаем AD0 = 7 (ом Гаусса находим приближу “ 0,495 0,655 —0,205" 0,326 —0,886 0,896 —0,235 0,036 0,768_ 0,99988 0,00066 —0,001С 0,00016 0,99957 —0,0001 0,00058 —0,00032 0,9992 вн; КГ .5 16 /ю обратную матрицу >
102
0,00012
F0 = E — ADQ~ —0,00016
—0,00058
—0,00066
1 0,00043
0,00032
0,00100“
0,00015
0,00064-
Так как „ Fq П i = 0,00178 < 1, то итерационный процесс сходится.
2) Пользуясь формулой (1), находим следующее приближение j
. Имеем
Dq Fq —
0,000164
—0,000339
—0,000479
—0,000111 0,000462“
-0,000309 0,000767
0,000416 0,000262
Dt — Dq Dq Fo =
0,495164
0,325661
—0,235479
0,654889 —0,204538
—0,886309 0,896767
0,036416 0,768262
Г 1,00010501
AD^ 0,00006849
0,00002982
—0,00000021 —0,00000039“
0,99999889 — 0,00000022 ,
—0,00000108 1,00000032J
r—0,00010501 0,00000021
Fi = E—ЛРХ = —0,00006849 0,00000111
L —0,00002982 0,00000108
0,00000039"
0,00000022
—0,00000032-
3) Аналогичным образом получим приближение D2i
-—0,000091
0
0,000001
0,000001 о -
0,000001 о
0,000001 0 -
Z)2 = Di + Di Fi =
Следовательно,
0,495073
0,325661
0,235480
0,654890 —0,204538 -
—0,886308 0,896767
0,036417 0,768262 -
г 0,49507 0,65489
0,32566 —0,88631
L —0,23548 0,03642
—0,20454 -
0,89677
0,76826 _
Упражнения
1. Вычислить ЛВ, если
- 1
3
_ 4
- 1
3
. 2
4"
6 ;
1 -
а)
б)
Л =
А =
—2
—1
—2
—3
—4
—5
Ответы^ а)
-6
9
-8
2
9
9
б)
3 1
2 ;
1 _
2-
1 I
3_
- 1
3
_ 2
' 2
: 1
- 2
-2
1
- 1
-5"|
0 t
-7_
в =
5
10
9
3
2
1
5
2
3
1 -
3
3-
6-
5 ,
2 _
103
2. Вычислить 2(Л + В)(2В—Л), если
О 5 -
1 3 ;
—2 4 .
3. Найти произведение ХУ, если
а) X =
5"
7
—3
2
К = [1 2
-2
31;
б)
х=
“1 ~
2
-3 _
у — [4 5]|
Ответы:
а)
4. Найти
в) Х=[10 17
5
7
-3
2
10
14
—6
4
—10
—14
6
—4
произведение АХ,
~2
а) Л = 7
_3
—1
2
4
8
если
—3
5
1
Ответы:
5. Вычислить определители
—4“
—2
—3
a) d —
1
0
2
3
1
—5
—4
1
3
5 И],
15”
21
—9
6
О
5
—7
4~
2
—1
У =
б)
б)
“12“
7
5
4
_10„
- 4
8
_ 12
Х =
Х =
5п
10
15-
в) 409.
1 -
1
2
3
_ 0_
’—2"
—3
4_
1
7
2
5
1
8
4
6
—2
4
6
8
3
1
—3
—4
104
в) d =
1,6 5,4 —7,7 —3,1
8,2 1,4 —2,3 0,2
5,3 —5,9 2,7 —7,9
0,7 1,9 —8,5 4,8
Ответы, а) 22; б) —26; в) 4279,1.
6. Вычислить Д"1 для следующих
матриц:
Г 2
7 1
2 0
4 2
8 4
4
—1
3
в)
О О
О О
4 О
3 2—13
г—12 —1 8п
Ответы, а) А*1 = —9 —1 6 ;
L —7 —1 5J
б) А"1 =
—4 10 —46 24 " 24 0 0
1 10 —1 67 —36 ... 1 0 12 0
48 —14 —13 7 12 —12 9 6
0 0 -96 48 —28 —5 2
0~
О
О
8
7. Для матриц
' -0,3 L2 —0,2 “ “0,2 0,44 0,81"
Л = —0,1 —0,2 1,6 и В = 0,58 —0,29 0,05
- “1>5 —0,3 0,1 0,05 0,34 0,1
II4|1з«2,55; б) ||В-1,45;
вычислить норму 1, норму 2 и норму 3.
Ответы: а) || A||i = 1,9; || А ||2=1,9;
«1,07; ||В]|з=1,20.
8. Найти АВ, где
" 1 4 1 3 “
0—13 -1
3 10 2 ’
1—2 5 1
“ 1 111“
1 4 2 3
1 10 3 6
6 10 1 4
двумя способами: а) разбив А и
на клетки окаймлением.
В на квадратные клетки; б) разбив А и В
Ответх
24 57 15 31"
—4 16 6 11
16 27 7 14
10 53 13 29_
105
9. Вычислить 4"1, применив разбиение
ние, если:
на квадратные
клегки и окаимле-
а)
4 =
1
2
3
2
2
—1
2
-3
3
—2
—1
2
—2
—3
2
1
б)
Д —
3
2
3
1
-2
1
-1
2
2
1
2
—1
о
-2
1
—1
Ответы^
а) Л-.-=1
б) Л-4
1
2
3
—2
2
—1
—2
—3
3
2
—1
2
2~
—3
2
1
6
— 12
—12
—6
—4
5
11
—5
О
9
9
9
8
— 1
—13
1
10. Матрицы, заданные вупр.
9, разложить на произведение двух треуголы
ных и обратить ихл применяя разложение матриц
вольных,
на
произведение двух треу'
Ответы* a)
Тр1 —
1
2
3
2
О
—5
—4
—7
1
О
О
о
—2
1
О
о
18
1/5
-8/5
1
О
О
О
— 18/5
36/5
2 1
—3
2
1
о
о
о
18
1
О
О
о
2
1
О
О
3
8/5
1
О
О
о
1
2
3
—2
2
-1
—2
-3
—2
— 1/5
—2
1
О
— 1/5
4/18 —5/18
О
О
О
2/5
7/18
—2/18 -3/18 2/18 1/18
3
2
-1
2
2“
-3
2
1
б) Д = /?1/?2 =
3
2
3
1
"1
О
О
О
106
6—4 0 8
1 j —12 5 9 —1
78 -12 11 9 -13
„6—5 9 1
11. Решить матричные уравнения:
0
3
—1
1
а)
X. 2
-1
’ 7 6—3“
-8 3 6 |
11 9 13
Ответы',
б)
7
—8
11
6 —3 1 Г—3 —10 —4 ’
3 6 -Х= 21 14 —10
9 13 48 2 30
" 3
а) Х = О
5
—1 2
О —2
1 2
12. Следующие системы линейных уравнений решить
по формулам Крамера!
—3
2
—1
7
—1
2
1
2
4
3
( 2х4+х2 + 4хз = 7,
а) < 2xi—*2— Зх3 == — 5,
[ 3xi-|-4х2—5х3——14;
Г 11х+3#— г= 15,
6)1 2x4-5#—5г——11,
I х4- #4- г= 1,
Ответы: a) х4 = 0, х2 = — 1, х3 = 2; б) х = 2, у = — 2, z = 1.
АЗ. Решить следующие системы по схеме Гаусса;
*1 —4х2 —х4 = 6,
Xi 4- Х2 4“ 2х3 4- Зх4 = — 1,
2xi + 3х2— х3— х4 =—1,
xi+2x2 + 3x3— х4= 3;
2xi — х3—2х4 =—8,
х2+2х3— х4=— 1,
хх—х2 — х4——6,
—Х|4~ЗХ'2—~ 2х3 == 7,
Ответы: а) хх = 1,
х3 = 0, х4 = 3.
х2— — 1, х3 = 1, х4——1; б) Xi =—1, х2— 2,
14. G точностью до 0,001 решить следующие системы по схеме Гаусса:
а)
1,14xi—2,15х2—5, Их3= 2,05,
0,42x1 —1,13х24-7,05х3= 0,80;
—0,71X1+0,81X2—0,02х3= —1,07;
[ 0,61х+0,71#—0,05г=—0,16,
б) 1,03х—2,05# + 0,87г= 0,50,
[ 2,5х—3,12# + 5,03г = 0,95.
Ответы: а) х4 = 1,120; х2 = — 0,341; х§ — — 0,008; б) х = 0,008; # =а
— 0,231; г = 0,042.
15. Вычислить определители по схеме Гаусса:
a) d =
4
—1
1
—2
1 3
3 —1
0 2
5 1
—1,6 5,4 —7,7 3,1
б) d = 8,2 1,4 —2,3 0,2
5,3 —5,9 2,7 -7,9
0,7 1,9 -8,5 4,8
1
1
Ответы: a) d — 88; б) d = 2111,97.
107
16. Обратить следующие матрицы по схеме Гаусса:
“1 2 2 —Г 0,32 0,52 —0,42 0,23"
а) Л = 2 7 6 —1 ; б) л = 0,44 —0,25 0,36 —0,51 а
0 3 1 4 —1,06 0,74 —0,83 0,48
_0 0 1 -1_ 0,96 0,82 0,55 0,36_
Вычисления вести с тремя десятичными ; знаками, ответ округлить ДО двух деся-
тичных знаков.
10/3 —7/6 1/2 —1/6
Ответы1, а) А'1= —5/3 5/6 -1/2 - -7/6 ;
1 —1/2 1/2 3/2
1 -1/2 1/2 i/2_
1,19 —0,31 —0,82 —о,: 12“
б) = —0,17 1,57 1,23 0,70
—1,75 0,11 0,30 0,87
—0,12 —2,92 —1,09 0,17
17, Решить следующие системы линейных уравнений с точностью до 0,01
методом последовательных приближений, предварительно определив необходи*
мое количество шагов.
8,7xi —3, lx2 + 1,8%з—2,2x4= —9,7,
2,1xi+6,7x2—2,2х3 ==13,1»
а) 3,2xi — 1,8х2—9,5х3—1,9х4 =6,9,
1,2х14-2,8х2 — 1,4х3—9,9х4 —25,1;
б)
6,1х + 0,7г/—0,05г = 6,97»
—1,3х—2,05(/4-0,87z = 0,10,
2,5х—3,12 г/—5,03? = 2,04.
Ответы. а) хг — — 0,72; х2 — 1, 88; х3 = — 0,92; х4 = — 1,94; б) х =
= 1,22; у = — 0,67, г = 0,35.
18. Системы линейных уравнений из у пр. 17 решить методом Зейделя, пред-
варительно определив необходимое количество шагов.
Глава Ш
МЕТОДЫ РЕШЕНИЯ НЕЛИНЕЙНЫХ УРАВНЕНИЙ
§ 3.1. Алгебраические и трансцендентные уравнения
При решении практических задач часто приходится сталкиваться
с решением уравнений. Всякое уравнение с одним неизвестным можно
представить в виде
ф W = g (х), (1)
где <р (х) и g (х) — данные функции, определенные на некотором чис-
ловом множестве X, называемом областью допустимых значений урав-
нения.
103
Уравнение с одним неизвестным можно записать в виде
f « = 0. (2)
Действительно, перенеся g (х) в левую часть уравнения (1), имеем урав-
нение <р(х) —g(x) = 0, равносильное (1). Если обозначить левую
часть последнего уравнения через / (х), то получаем уравне-
ние (2).
Совокупность значений переменной х, при которых уравнение (1)
превращается в тождество, называется решением этого уравнения,
а каждое значение х из этой совокупности называется корнем урав-
нения.
Например, уравнение х2 = 2 — х имеет корни ха — — 2 и х2 = 1»
Подставив — 2 и 1 в заданное уравнение вместо х, получим тождества:
(—2)2 - 2 — (—2), т. е. 4 s 4; I2 - 2 — 1, т. е. 1 = 1.
Решить уравнение — значит найти множество всех корней этого
уравнения. Оно может быть конечным или бесконечным. Так, рассмот-
ренное выше уравнение имеет два корня. Уравнение sin х = 0 имеет
решение х = пп (и —0, ±1, ±2, ...). Придавая п различные значения,
получаем бесконечное множество корней.
Совокупность нескольких уравнений с несколькими неизвестными
называют системой уравнений (неизвестное, обозначенное одной и той
же буквой в каждом из уравнений, должно означать одну и ту же не-
известную величину.
Решением системы уравнений с несколькими неизвестными назы-
вается совокупность значений этих неизвестных, обращающая каждое
уравнение системы в тождество,
Например, система
г x2 + z/ = 5,
I х + //2^=3
имеет решение х — 2, у = 1, так как при этих значениях неизвестных
уравнения системы обращаются в тождества: 4 + 1 s= 5, 2 + 1 3.
Решить систему уравнений — значит найти множество всех ее
решений или показать, что она решений не имеет.
В зависимости от того, какие функции входят в уравнения (1)
или (2), уравнения разделяются на два больших класса: алгебраиче-
ские и трансцендентные.
Функция называется алгебраической, если для получения значения
функции по данному значению х нужно выполнить арифметические опе-
рации и возведение в степень с рациональным показателем. (Опера-
ция извлечения корня может быть представлена как операция возве-
дения в степень с показателем 1/п.)
Алгебраическая функция называется рациональной относительно
переменной х, если над х не производится никаких других действий,
кроме сложения, вычитания, умножения, деления и возведения в це-
лую степень,
109
Например:
Л(х) = йг3+15х2-1200^ + 4; /=2 (х) = -1- + ; •
X— 8 ХД-Э
fa (*) = (X—4) (х + 5); (х) = + -4*±1.
XI оХ О
Если в рациональную функцию переменная х не входит в качестве
делителя или не входит в выражение, являющееся делителем, то такая
функция называется целой рациональной,
Например, следующие функции:
1) у = аохп + агхп~г + ... + ап (п—натуральное число или нуль,
а0, а1г ап — любые действительные числа, причем а0 =/= 0);
2) f(x)= ^-4-^
являются целыми рациональными, Целая рациональная функция оп-
ределена на всей числовой оси.
Если в рациональной функции хотя бы один раз встречается деле-
ние на переменную х или переменная х входит в выражение, являю-
щееся делителем, то такая функция называется дробно-рациональной.
Такова, например, функция
b.x^+h +_fem
а^хп^а1хп-г+
где т— натуральное число или нуль; п — натуральное число;
а0, ^1» •••, Ьъ ... — любые действительные числа (aQ =^= 0, bQ=^ 0).
Дробно-рациональная функция определена на всей числовой оси, за
исключением тех точек, в которых знаменатель обращается в нуль.
Функция называется иррациональной, если для получения значения
функции поданному значению х нужно выполнить, кроме четырех ариф-
метических действий (всех или некоторых), еще и извлечение корня.
При этом функция будет иррациональной лишь тогда, когда аргумент х
стоит под знаком радикала.
Так, ’функция
Зх3—4x4-1^ х —1
у =--------—------
7х —4
является иррациональной, а функция
иррациональной не является, поскольку х не стоит под знакой ради-
кала.
Выше указывалось, что все рациональные и иррациональные функ-
ции относятся к классу алгебраических функций,
Другой большой класс функций — трансцендентные функции,
К ним относятся все неалгебраические функции: показательная а*,
по
логарифмическая loga х, тригонометрические sin x, cos x, tg x, ctg x,
обратные тригонометрические arcsin x, arccos x, arctg x, arcctg x и дрй
Если в запись уравнения входят только алгебраические функции,
то уравнение называется алгабраическим.
Например, уравнения
х5 — 4 — 0, х4 — Зх3 + 5х2 — х + 1 = О
являются алгебраическими.
Алгебраическое уравнение может быть приведено к виду
aoxn + a1xn-i + а2хп~2+ ... +ап_1х + ап = 0. (3)
Поэтому, корда говорят «алгебраическое уравнение», то обычно имеют
в виду уравнение вида (3).
Если уравнение (3) получено преобразованием уравнения, в кото-
рое входила дробная рациональная или иррациональная функция, то
необходимо учитывать, что эти функции определены не на всей число-
вой оси.
Например, уравнение
= з
после освобождения от иррациональности примет вид
4х2 — 16х — 47-0.
Однако первоначальное уравнение определено не на всей числовой
оси, а для х, принадлежащих отрезку [2, 6].
Числа а0> аь ап называются коэффициентами уравнения (3),
они могут быть как действительными, так и комплексными. В дальней-
шем изложении будут рассматриваться алгебраические уравнения ви-
да (3) только с действительными коэффициентами,
Решение уравнения с одним неизвестным заключается в отыскании
корней, т. е. тех значений х, которые обращают уравнение в тождест-
во. Корни уравнения могут быть вещественными и невещественными
(комплексными).
Найти точные значения корней уравнения можно только в исклю-
чительных случаях, обычно, когда есть какая-либо простая формула
для вычисления значения корней, выражающая их через известные ве-
личины.
Так, для нахождения корней квадратного уравнения вида х2 + рх +
+ q = 0 используется формула
(4)
Для решения кубического уравнения вида х3 + рх 4- q = 0 приме-
няется формула
- ГЧ• <5)
111
Однако практическое применение этой формулы весьма затруднительно
и требует использования комплексных чисел.
Для решения уравнения четвертой степени также существует фор-
мула, однако она является настолько сложной, что практически не
применяется, и мы ее рассматривать не будем.
Норвежский математик Абель доказал, что при п 5 не сущест-
вует формулы, выражающей решение алгебраического уравнения (3)
при помощи арифметических операций и извлечения корней. Лишь
для некоторых частных случаев алгебраических уравнений, степень
которых больше четырех, могут существовать формулы решения.
Кроме того, коэффициенты некоторых уравнений являются при-
ближенными числами и, следовательно, вопрос о нахождении точных
корней вообще не может быть поставлен.
Поэтому большое значение приобретают методы приближенного
вычисления корней уравнения f (х) — 0.
При решении многих практических задач точное решение урав-
нения не всегда является необходимым. Задача нахождения корней
считается решенной, если корни вычислены с заданной степенью точ-
ности.
Как же следует понимать утверждение «корень вычислен с заданной
степенью точности»? Пусть £ — корень уравнения, х—его приближен-
ное значение с точностью до е; это означает, что | £ — х | е. Если
установлено, что искомый корень £ заключен между числами а и &,
т. е. а < Е < 6, причем b — а е, то числа а и b — это приближен-
ные значения корня | соответственно с недостатком и с избытком с
точностью до е,так как | g — а | < Ь—е и | £ — b | < b —
За приближенное значение корня £ с точностью до е можно принять
любое число, содержащееся между а и Ь.
Например, если корень g заключен между 3,228 и 3,229 (т. е.
3,228 < g < 3,229), то за приближенное значение корня с точностью
до 0,001 можно принять числа 3,228, 3,229 и любое число, заключенное
между ними.
В настоящей главе мы будем рассматривать способы приближен-
ного решения уравнений и систем уравнений. Некоторые из них оди-
наково применимы к отысканию корней как трансцендентных, так
и алгебраических уравнений. Другие способы применимы только к ал-
гебраическим уравнениям.
§ 3.2. Графические методы решения уравнений и систем
Графические методы решения уравнений. Одним из методов реше-
ния уравнений является графический. Точность такого решения неве-
лика, однако с помощью графика можно разумно выбрать первое при-
ближение, с которого начнется дальнейшее решение уравнения. Су-
ществуют два способа графического решения уравнений.
Первый способ. Все члены уравнения переносят в левую
часть, т. е. представляют его в виде f (х) = 0. После этого строят
график функции у = f (х), где f (х)—левая часть уравнения* Абсци-
112
сы точек пересечения графика функции у = f (%) с осью Ох и явля-
ются корнями уравнения, так как в этих точках у = 0 (рис. 3.1).
Второй способ. Все члены уравнения разбивают на две
группы, одну из них записывают в левой части уравнения, а другую
в правой, т. е. представляют его в виде ф (х) = g (х). После этого стро-
ят графики двух функций у = ф (х) и у == g (х). Абсциссы точек пере-
сечения графиков этих двух функций и служат корнями данного урав-
нения. Пусть точка пересечения графиков имеет абсциссу х0, ординаты
обоих графиков в этой точке равны между собой, т. е. ф (х0) = g (х0).
Из этого равенства следует, что х0 — корень уравнения (рис. 3.2)#
Пример 1. Решить графически уравнение х3 — 2х2 + 2х — 1 = 0.
Решение. Первый способ. Построим график функции у = х3 —
—2х2 + 2х — 1 и определим абсциссы точек пересечения этого графика с осью
Ох. Кривая пересекает ось Ох в точке х = 1, следовательно, уравнение имеет
один корень (рис. 3.3). (Отметим, что алгебраическое уравнение третьей степени
имеет или один действительный корень или три. Так как кривая пересекает ось
абсцисс только в одной точке, то данное уравнение имеет только один действи-
тельный корень. Остальные два корня — комплексные.)
Второй способ. Представим данное уравнение в виде х3 == 2х2 —
—2х + 1 и построим графики функций у — х3 и у = 2х2 — 2х + 1. Найдем аб-
сциссу точки пересечения этих графиков; получим х = 1 (рис. 3.4).
Пример 2. Найти приближенно графическим способом корни уравнения
1g х — Зх + 5 = 0.
Решение. Перепишем уравнение следующим образом:
1g х — Зх — 5.
Функции в левой и в правой части уравнения имеют общую область определения:
интервал 0 < х < + оо. Поэтому будем искать корни именно в этом интер-
вале.
Строим графики функций р = 1g х и I/ — Зх — 5 (рис. 3.5). Прямая у ==
== Зх — 5 пересекает логарифмическую кривую в двух точках с абсциссами
хх 0,00001 и х2 ~ 1,75. На рисунке трудно показать пересечение графиков
этих двух функций в первой точке, однако, учитывая, что нижняя ветвь логариф-
мической кривой неограниченно приближается к оси Оу, можно предполагать,
что пересечение этих двух графиков произойдет вблизи точки пересечения гра-
113
фика функции у = Зх — 5 и оси Оу. Абсцисса точки пересечения приближенно
равна 0,00001. Итак, корни уравнения 0,00001 и х2 ~ 1,75.
Пример 3. Найти графически корни уравнения 2х = 2х
Решение. Строим графики функций у — 2х и у ~ 2х Эти графики пере-
секаются в двух точках, абсциссы которых равны ду = 1 и х2 = 2. Данное урав-
нение имеет два корня хА = 1 и х2 = 2 (рис, 3 6).
Подводя итог вышеизложенному, можно рекомендоватвдля графи-
ческого решения уравнения f (х) = 0, все корни которого лежат
в промежутке [а, Ь], следующую простую схему.
1. Представить указанное уравнение в виде ср (х) = g (х) с таким
расчетом, чтобы функции у = <р (х) и у = g (х) были просты и удобны
для исследования и построения.
2. На миллиметровой бумаге вычертить графики функций у =?
— Ф (х) и у = g (х) в промежутке [а, Ь].
3. Если графики не пересекаются, то корней в данном промежут-
ке нет. Если же графики пересекаются, то нужно определить точки их
пересечения, найти абсциссы этих точек, которые и будут приближен-
ными значениями корней рассматриваемого уравнения.
Графические методы решения систем уравнений. Мы видели, что
решение графическим методом уравнений с одним неизвестным не вы-
зывает особых затруднений. Этого нельзя сказать о решении графи-
ческим методом систем уравнений. Часто даже решение системы двух
уравнений с двумя неизвестными оказывается весьма сложным.
Пусть задана система
( у) = о,
I ?Лх, у) = 0.
Если оба уравнения системы можно разрешить относительно одной
из двух переменных, то решение системы значительно упрощается,
Пусть из первого уравнения системы имеем у = fi (х), а из второго
114
у = (*)• В результате получаем уравнение <р(х) = /у (х) —
— /2 (*) ” которое решаем одним из рассмотренных выше ело
собов.
Пример 4. Найти графически решение системы уравнении
{xi/ + cos х = 0,
ж+у—sin х=0,
считая х > О,
Решение. Разрешаем заданные уравнения относительно yi
cos х
у ~ , y = sinx—X,
X
т е»
COS X
sin X ~х = —----.
X
COS X
Строим графики функций = sin х — х ну = — —-— (рис. 3.7). Абсцисса
и ордината точки пересечения графиков этих функций и дают решение системы;
х 1,22; у « — 0,28.
Пример 5. Найти графически решение системы уравнений
| 2х2 + 3z/2 — 6t/— 4 = 0,
( х2—3//2Д-4х—2 = 0.
Решение. Перепишем заданную систему следующим образом;
| 2х2 + 3(г/—1)2 = 7,
| (х-}-2)2 — Зг/3 = 6.
Первое из преобразованных уравнений определяет эллипс, второе — гиперболу.
Кривые, соответствующие полученным уравнениям, пересекаются в двух точках
Mi (хх; £i) и Л42 (х2; #2) (Рис. 3.8). Если на миллиметровой бумаге сделать более
точный чертеж, то можно определить Xj ~ 0,55; у\~ — 0,46; х2 ~ 1,7; уг ж 1,6.
§ 3.3. Отделение корней
В предыдущем параграфе был рассмотрен вопрос о графическом
решении уравнений и систем уравнений. Однако даже при очень тща-
тельном построении чертежа значения корней можно получить с не-
большой степенью точности, Поэтому чтобы эти значения получить
С любой заданной степенью точности, необходимо применять методы,
которые позволяют «уточнять» найденные значения,
115
Процесс нахождения приближенных значений корней уравнения
разбивается ка два этапа: 1) отделение корней; 2) уточнение корней
до заданной степени точности.
В настоящем параграфе рассматривается первый этап — отде-
ление корней.
Корень £ уравнения f (х) = 0 считается отделенным на отрезке
[а, Ь], если на этом отрезке уравнение / (х) = О не имеет других кор-
ней.
Отделить корни — это значит разбить всю область допустимых
значений на отрезки, в каждом из которых содержится один корень.
Отделение корней можно произвести двумя способами — графиче-
ским и аналитическим.
Графический метод отделения корней. При графическом методе
отделения корней поступают так же, как и при графическом методе ре-
шения уравнений.
Строят график функции у = / (х) для уравнения вида / (х) = О
или представляют уравнение в виде ф (х) — g (х) и строят графики
функций у = ф (х) и у — g (х). Значения действительных корней урав-
нения являются абсциссами точек пересечения графика функции у —
= f (х) с осью Ох или абсциссами точек пересечения графиков функций
у = ф (х) и у = g-(x). Отрезки, в которых заключено только по одному
корню, легко находятся.
Замечание. Пусть график функции у = f (х) имеет вид,
изображенный на рис. 3,9. Кривая трижды пересекает ось абсцисс;
следовательно, уравнение имеет три простых корня.
Если же кривая касается оси абсцисс (рис. 3.10), то уравнение
имеет двукратный корень. Например, уравнение х3 — Зх + 2 = 0
имеет три корня: хх = — 2; х2 = х3 = 1 (рис. 3.11).
Если же уравнение имеет трехкратный действительный корень,
то в месте касания с осью кривая у = f (х) имеет точку перегиба
(рис. 3.12). Например, уравнение х3 — Зх2 + Зх — 1 = 0 имеет трех-
кратный корень, равный единице (рис. 3.13).
Графический метод отделения корней не обладает большой точ-
ностью, Он дает возможность грубо определить интервалы изоляции
116
корня, Далее корни уточняются одним из способов, указанных
ниже,
Аналитический метод отделения корней. Аналитически корни урав-
нения f (х) = 0 можно отделить, используя некоторые свойства функ-
ций, изучаемые в курсе математического анализа.
Сформулируем без доказательства теоремы, знание которых необ-
ходимо при отделении корней.
Теорема 1. Если функция f (х) непрерывна на отрезке {а, Ь} и при-
нимает на концах этого отрезка значения разных знаков, то внутрц
отрезка [а, Ь] существует по крайней мере один корень уравнения
Н%) == °’
Теорема 2. Если функция f(x) непрерывна и монотонна на отрезке
1а, Ь] и принимает на концах отрезка значения разных знаков, то
внутри отрезка [а, Ь] содержится корень уравнения f (х) = 0, и этот
корень единственный.
Теорема 3. Если функция f (х) непрерывна на отрезке [а, Ь] и при-
нимает на концах отрезка значения разных знаков, а производная
f(x) сохраняет постоянный знак внутри отрезка, то внутри отрезка
существует корень уравнения / (х) = О и притом единственный.
Приведем теперь некоторые сведения из математического анализа,
которые понадобятся в дальнейшем.
Если функция f (х) задана аналитически, то областью существо-
вания (областью определения) функции называется совокупность
всех тех действительных значений аргумента, при которых аналити-
ческое выражение, определяющее функцию, не теряет числового смыс-
ла и принимает только действительные значения.
Функция у ~ f (х) называется возрастающей, если с возрастанием
аргумента значение функции увеличивается (рис. 3,14, а и в), и убы-
вающей, если с возрастанием аргумента значение функции умень-
шается ( рис. 3,14, б и г).
117
Функция называется монотонной, если она в заданном промежутке
либо только возрастает, либо только убывает,
Пусть на отрезке [а, функция f (х) непрерывна и принимает на
концах отрезка значения разных знаков, а производная f' (х) сохра-
няет постоянный знак на интервале (а, Ь). Тогда если во всех точках
интервала (а, Ь) первая производная положительна, т. е. f(x) > О,
то функция f (х) в этом интервале возрастает (рис, 3,14х а и е)
?((№, Ю)>0 f(a)>0, f(b)o
fW >0; fv(x)*0 Г(х) ^0, f“(x)*0
Если же во всех точках интервала (а, Ь) первая производная отрица-
тельна, т. е. f (х) < 0, то функция в этом интервале убывает
(рис. 3.14, б и а). Корнем функции служит абсцисса точки пересечения
графика функции f (х) с осью Ох.
Пусть на отрезке [а, Ь] функция f (х) имеет производную второго
порядка, которая сохраняет постоянный знак на всем отрезке. Тогда
если /" (х) > 0, то график функции является выпуклым вниз
(рис. 3.14, а и г); если же /"(х) < 0, то график функции является в ы-
пуклым вверх (рис. 3.14, б и в).
Точки, в которых первая производная функции равна нулю, а так-
же те, в которых она не существует (например, обращается в бесконеч-
на
ность), но функция сохраняет непрерывность, называются крити-
ческими (этот признак является необходимым признаком экстремума).
Если функция f (х) непрерывна на отрезке [а, &], то на этом отрезке
всегда имеются точки, в которых она принимает наибольшее
и наименьшее зн а ч ен и я. Этих значений функция достигает или
в критических точках, или на концах отрезка. Следовательно, чтобы
определить наибольшее и наименьшее значение функции на отрезке,
надо: 1) определить критические точки функции; 2) вычислить значе-
ния функции в критических точках и на концах отрезка [а, Ь}\ 3) на-
ибольшее из значений, найденных в п. 2), будет наибольшим, а наи-
меньшее — наименьшим значением функции на отрезке.
В связи с вышеизложенным можно рекомендовать следующий
порядок действий для отделения корней аналитическим методом.
1. Найти f (я) — первую производную.
2. Составить таблицу знаков функции f (х), полагая х равным:
а) критическим значениям (корням) производной или ближайшим к
ним; б) граничным значениям (исходя из области допустимых значений
неизвестного).
3. Определить интервалы, на концах которых функция принимает
значения противоположных знаков. Внутри этих интервалов содер-
жится по одному и только по одному корню.
Пример. Отделить корни уравнения 2 х — 5х — 3 = 0 аналитическим ме-
тодом.
Решение. Обозначим f (х) = 2х — 5х — 3. Область определения
функции f (х) — вся числовая ось. Найдем первую производную
/' (х) == 2х In 2—5.
Приравниваем эту производную нулю и вычисляем корень:
5
2^1п2 —5=0; 2х In 2 = 5; 2х = —; х 1g2 = Ig5 —lg In 2;
In 2
lg5—lgln2 0,6990+0,1592 0,8582
x = ----------= = 1 = 2,85.
1g 2 0,3010 0,3010
Составляем таблицу знаков функции f (х), полагая х равным: а) критическим
значениям (корням производной) или ближайшим к ним; б) граничным значе-
ниям (исходя из области допустимых значений неизвестного):
X — оо 2 3 + оо
sign £ (х) + — — +
Уравнение имеет два корня, так как происходят две перемены знака функции.
Составим новую таблицу, с более мелкими интервалами изоляции корня:
X —1 0 1 2 3 4 5
sigrUW + — — — — — +
Корни уравнения заключены в промежутках (—1, 0) и (4, 5).
119
§ 3.4. Уточнение корней. Метод проб
Предыдущий параграф был посвящен первому из этапов прибли-
женного решения алгебраических и трансцендентных уравнений —
отделению корней.
Второй этап — уточнение корней, т. е, доведение их до
заданной степени точности.
В настоящем параграфе рассматриваются некоторые способы уточ-
нения корней, применяемые для решения как алгебраических, так и
трансцендентных уравнений. Существуют, однако, приемы, которые
применимы только для решения алгебраических уравнений. Их мы
рассмотрим ниже.
Пусть дано уравнение f (х) = 0, где / (х) — непрерывная функция.
Требуется найти корень этого уравнения £ с точностью до е, где е —
некоторое положительное достаточно малое число.
Будем считать, что корень £ отделен и находится на отрезке [се, б],
т. е. имеет место неравенство а «С S Ь. Числа а и b — приближен-
ные значения корня | соответственно с недостатком и с избытком.
Погрешность этих приближений не превышает длины отрезка b — а.
Если b — а в, то необходимая точность вычислений достигнута,
и за приближенное значение корня | можно принять либо а, либо Ь.
Но если b — а > е, то требуемая точность вычислений не достигнута
и необходимо сузить интервал, в котором находится корень £,
т. е. подобрать такие числа а и Ь, чтобы выполнялись неравенства
a<z < b и b — а<_ Ь — а. При b — в вычисления следует
прекратить и за приближенное значение корня с точностью до е
принять либо а, либо Ь. Следует отметить, что значение корня будет
более точным, когда за приближенное значение корня приняты не кон-
цы отрезка а и б, а середина этого отрезка, т. е. с~ (а + б)/2, Погреш-
ность в этом случае не превышает величины (б — а)/2,
Метод проб. Пусть дано уравнение /(х) = 0 ]/(х) — непрерывная
функция] и корень В отделен на отрезке 1а, б], т. е. f (а) - f (б) < О,
причем б — а > е. Требуется найти значение корня В с точностью до
е (рис. 3.15)
120
На отрезке [а, Ь] выберем произвольным образом точку аь которая
разделит его на два отрезка 1а, nJ и [аь Ь]. Из этих двух отрезков
следует выбрать тот, на концах которого функция принимает значе-
ния, противоположные по знаку. В нашем примере f (а) • f (aj > О,
/ (й1) ’ f (b) < 0; поэтому следует выбрать отрезок [аъ bl. Затем на этом
суженом отрезке опять произвольным образом возьмем точку а2 и най-
дем знаки произведений f (aj • f (a2) и f (a2) • f (b). Так как f (a2)X
X f (b) <Z 0, то выбираем отрезок [a2, bl. Этот процесс продолжаем до
тех пор, пока длина отрезка, на котором находится корень, не станет
меньше е. Корень | получим как среднее арифметическое концов най-
денного отрезка, причем погрешность корня не превышает е/2.
Метод проб в таком виде, как он описан выше, на ЭВМ не приме-
няется. Для составления программ и расчетов на ЭВМ метод проб при-
меняется в виде так называемого метода половинного деления.
Пусть корень | уравнения f (х) = 0 отделен и находится на отрезке
[а, Ь], т. е. / (а) • / (Ь) < 0, причем b — а> е [здесь f (х) — непрерыв-
ная функция]. Как и ранее, возьмем на отрезке [а, Ь] промежуточную
точку, однако не произвольным образом, а так, чтобы она являлась
серединой отрезка (а, Ь], т. е. с = (а + Ь)/2. Тогда отрезок [а, Ь]
точкой с разделится на два равных отрезка [а, с] и [с, Ь], длина которых
равна (Ь — а)/2 (рис. 3.16). Если f (с) = 0, то с — точный корень урав-
нения f (х) = 0. Если же f (с) =# 0, то из двух образовавшихся отрезков
1а, с] и [с, Ь] выберем тот, на концах которого функция f (х) принимает
значения противоположных знаков; обозначим его [ab bj. Затем от-
резок [аг, bj также делим пополам и проводим те же рассуждения.
Получим отрезок [а2, Ь2], длина которого равна (Ь — а)/22. Процесс
деления отрезка пополам производим до тех пор, когда на каком-то
n-м этапе либо середина отрезка будет корнем уравнения (случай,
весьма редко встречающийся на практике), либо будет получен отре-
зок [ап, ЬД такой, что Ьп — ап — (Ь — а)/2п в и ап g Ьп (чис-
ло п указывает на количество проведенных делений). Числа ап и Ьп —
корни уравнения / (х) = 0 с точностью до е. За приближенное значение
корня, как указывалось, выше, следует взять g — (an + bn)/2, при-
чем погрешность не превышает (Ь — a)/2rt+1.
Пример L Методом проб уточнить до 8 = 10~3 меньший корень уравнения
х3 + 3? - 3 = 0.
Решение. Отделим корни этого уравнения аналитически. Функция
f (х) определена на всей числовой оси. Приравняем /' (х) нулю и вычислим корень
производной:
f' (х) = Зх2 + 6х; Зх2 + 6х « 0; х (х + 2) = 0; хх = 0, х2 = — 2.
Составляем таблицу знаков функции:
X ОС —2 —1 0 ]
sign / (х) — + - 1 + +
121
Видим, что первый корень содержится в интервале ( — оо, — 2). Возьмем для
пробы х == -3 и найдем / ( — 3) = — 3:
X 1 -3 —2 -1 0 1 1
sign f (x) 1 “~ + — — 1 +
Следовательно, корни уравнения х3 + Зх2 — 3=0 содержатся в интервалах
( — 35 — 2); ( — 2, — 1); (0, 1).
Уточним меньший корень, лежащий в интервале ( — 3, — 2), методом поло-
винного деления. Для удобства вычислений составим таблицу (см. табл. 3.1).
[Знаки « — » и « + » в верхних индексах ап и Ьп означают, что f (ап) <0 и
f (bn) > 0.]
Таблица 3.1
fl On X —an + bn ™ 2 (n 3^ f(*n>
0 -3 —2 —2,500 —15,625 18,750 0,125
1 -3 —2,500 —2,750 —20,800 22,689 —1,111
2 —2,750 —2,500 —2,625 —17,990 20,670 —0,320
3 —2,625 —2,500 —2,563 -16,840 19,701 —0,139
4 —2,563 —2,500 —2,532 —16,230 19,233 0,003
5 —2,563 —2,532 —2,548 —16,540 19,479 —0,071
6 —2,548 —2,532 —2,540 —16,390 19,356 —0,034
7 —2,540 —2,532 —2,536 —16,310 19,293 —0,014
8 —2,536 -2,532 —2,534 -16,270 19,263 —0,007
9 —2,534 —2,532 —2,533 —16,250 19,248 —0,002
10 —2,533 —2,532
Итак, корень уравнения xj ж — 2,532.
Пример 2. Отделить графически корень уравнения
’ogo.s (* + I) = 1.
Вычислить этот корень методом проб с точностью е = 10~2«
Решение. Представим уравнение в виде
1о8о,5(х+1) = -4-
X3
и построим графики функций у = log0t5 (х + 1) и у = 1/х2. Из рис. 3.17 видно.
что уравнение имеет один корень xt ж
—0,7. Определим знаки функции слева и
справа от xji
’________I
sign f (х) I
—0,8
+
—0,5
Для удобства расчетов перейдем к десятич-
ным логарифмам:
. 3 lg(x + l) Ig(x+1)
12 2
Составим следующую таблицу (табл 3 2).
Таблица 32
п аП Ij 4- Ь п п 2 хп 1g +
0 -0,8 —0,5 —0,65 0,4225 —0,4559 —0,360
1 -0,8 —0,65 —0,73 0,5329 —0,5686 —0,0067
2 —0,73 —0,65 —0,69 0,4761 —0,5086 —0,196
3 —0,73 —0,69 —0,71 0,5041 —0,5376 —0,099
4 —0,73 —0,71 -0,72 0,5184 -0,5528 —0,048
5 —0,73 —0,72
Итак, —0,73.
§ 3.5. Метод хорд
Метод хорд является одним из распространенных методов реше-
ния алгебраических и трансцендентных уравнений. В литературе он
также встречается под названиями «метода ложного положения» (ге-
gula falsi), «метода линейного интерполирования» и «метода пропорци-
ональных частей».
Пусть дано уравнение f (х) = 0, где f (х) — непрерывная функ-
ция, имеющая в интервале (а, Ь) производные первого и второго поряд-
ков. Корень считается отделенным и находится на отрезке fa, b], т. е,
f (a) • f (b) < 0.
Идея метода хорд состоит в том, что на достаточно малом промежут-
ке [а, Ь] дуга кривой у = f (х) заменяется стягивающей ее хордой.
В качестве приближенного значения корня принимается т/зчка пере-
сечения хорды с осью Ох.
Ранее мы рассмотрели четыре случая расположения дуги кривой,
учитывая значения первой и второй производных.
Рассмотрим случаи, когда первая и вторая производные имеют
одинаковые знаки, т, е. [' (х) • [" (х) > 0.
123
Пусть, например, f (а) < 0, f (b) > О, f (х) > О, f (х) > О
(рис. 3.18, а). График функции проходит через точки Ао (a-, f (а)),
В (b: f (&)), Искомый корень уравнения / (х) = О есть абсцисса точки
пересечения графика функции у = / (х) с осью Ох. Эта точка нам не-
известна, но вместо нее мы возьмем точку хх пересечения хорды АпВ
с осью Ох. Это и будет приближенное значение корня.
Уравнение хорды, проходящей через точки Ло и В, имеет вид
У—((а) _ х—а
f(b)-f(a) Ь—а *
Найдем значение х — хх, для которого у = 0:
Эта формула носит название формулы метода хорд. Теперь корень §
находится внутри отрезка [хх, Ь], Если значение корня хх нас
не устраивает, то его можно уточнить, применяя метод хорд к отрезку
[хх, Ь]. Соединим точку Лх (хх; f (хх)) с точкой В (6; [ (&)) и найдем х2 —
точку пересечения хорды АХВ с осью Ох:
хх)
Hb)-f(xA ’
Продолжая этот процесс, находим
v __v f(x2)(&—Хз)
2 ((&)-Нх2)
и вообще
у f(xn)(b—xn)
fW-f(Xn)'
(2)
Процесс продолжается до тех пор, пока мы не получим приближенный
корень с заданной степенью точности,
По приведенным выше формулам вычисляются корни и для случая,
когда f (а) > 0, f (b) < 0, f(x) < 0, f (х) < 0 (рис. 3.18, б).
124
Теперь рассмотрим случаи, когда первая и вторая производные
имеют разные знаки, т. е. f'(x) • f"(x) < 0.
Пусть, например, f (а) > 0, f (b) < 0, f (х) < 0, f (х) > 0
(рис. 3.19, а). Соединим точки А (а; / (а)) и Во (6; / (б)) и запишем урав-
нение хорды, проходящей через А и Во:
у—1(b) х—ь
f (b) — t (а) b — a
Найдем хх как точку пересечения хорды с осью Ох, полагая у = 0:
„ _h l(b)(b-a)
f (b)—f (а)
Корень | теперь заключен внутри отрезка [a, хх].
Применяя метод хорд к отрезку la, xj, получим
„ _ v f(xi)(Xi—a)
Д'9 ---------------------- Д, | гтг“ 1
2 1 /(xf-/(a)
(3)
и вообще
_ __ f(xn)(xn—a)
Xn+i-Xn f (xn)—f (а) •
(4)
По этим же формулам находится приближенное значение кор-
ня и для случая, когда f (а) < 0, f (b) > 0, f (х) > 0, f (х) < 0
(рис. 3.19, б).
Итак, если f (х) • f" (х) > 0, то приближенный корень вычисляет-
ся па формулам (1) и (2); если же f (х) . f"(x) < 0, то — по формулам
(3) и (4).
Однако выбор тех или иных формул можно осуществить, пользуясь
простым правилом: неподвижным концом отрезка является тот,
для которого знак функции совпадает со знаком второй производной.
Если f (Ь) • f" (х) > 0, то неподвижен конец Ь, а все приближения
к корню £ лежат со стороны конца а [формулы (1) и (2)1. Если f (а)Х
X/’ (х) > 0, то неподвижен конец а, а все приближения к корню |
лежат со стороны конца Ь [формулы (3) и (4)1.
При оценке погрешности приближения можно пользоваться фор-
мулой
хп | •< | х„—xn_i |, (5)
где § — точное значение корня, а хп,х и хп — приближения к нему,
полученные на (п — 1)-м и n-м шагах. Однако эта формула справед-
лива лишь на достаточно малых отрезках. Ею можно пользоваться,
если выполнено условие
М < 2 т, (6)
где
М=max 1 f' (х) I, т => min I f* (х) I.
[а.Ы (а.е>)
Пример 1. Методом хорд уточнить до в = 0,001 меньший корень уравнения
л® + Зх2 — 3 = 0. Корни уравнения отделены и меньший корень содержится на
отрезке [ — 3, —2] (см, пример 1 § 3.4).
125
Решение. Проверяем выполнение условия (6):
If' (х)| = |3х2 + бх|;
М~ max | f' (х) 1 = 1 27 —18j = 9; min |f' (х) 1 —112—12 | =0;
[-3,-2] [-3,-2]
М < 2m.
Возьмем середину отрезка [ — 3, —2], т. е. точку х — — 2,5, и выберем
интервал [ — 3; — 2,5]. Проверяем выполнение условия (6):
М = шах |f'(x)| —9; m = min I f'(х) | = 3,75; М < 2т.
[ — 3; — 2,5] [— 3; — 2,5]
Возьмем теперь середину отрезка [ — 3; — 2,5] — точку х = — 2,75;
f ( — 2,75) < 0, f ( — 2,5) >0, f ( — 3) < 0; выбираем отрезок [ — 2,75; 2,5].
Находим
Л4 = max [/' (х)| — 6,189; m = min | f' (х) | = 3,75,
[ — 2,75;-2,5] [—2,75; —2,5]
т. е. в этом случае выполнено условие М < 2 т.
Таким образом, для оценки погрешности корня, лежащего на отрезке
[ — 2,75; —'2,5], можно пользоваться формулой (5):
I £ хп | | Xn Xn_j |,
т. е. процесс последовательного приближения к корню следует продолжать до
тех пор, пока не будет выполнено условие |хп — xn_i| < е.
Определим знак второй производной и установим, по какой формуле надо
производить вычисления. Находим ftr (х) = 6х + 6; на отрезке [ — 2,75; — 2,5]
имеют место неравенства f ( — 2,75) <0, f ( — 2,75) • f" (х) > 0. Значит, за
неподвижный конец отрезка нужно принять х = — 2,75. Тогда вычисления
следует вести по формулам (3) и (4):
f(b)(b — a) f(xn) (хп — а)
Х± b £ / \ * + l с / ч I , \ >
/(&)—/(а) 1(Хп)~ На)
где а = — 2,75 и f (а) — — 1,111. Если последнее выражение представить
в виде
_ f (*п)(Хп—а)
^71+1 ^71 f / \ \ *
f(xn)—f (а)
то сразу же можно будет получать разность между двумя последовательными
приближениями и производить проверку на окончание вычислений, т. е, прове-
рять выполнение неравенства | xn-pi — хп | < в.
Все вычисления удобно производить в следующей таблице;
Таблица 3.3
п хп 2 3^ + СО CJ со * 1 И CQ £2 'Д £ со Й + хп~а К*П> ^п-а)
f (хп) —На)
0 —2,5 —15,625 6,250 18,75 0,125 0,25 —0,025
1 —2,525 —16,098 6,3756 19,1268 0,Q2§8 9,225 —0,00б
2 3 —2,531 —2,5319 —16,213 6,4060 19,2180 0,005б 0,219 —0,0009
Из табл. 3.3 видно, что ] х3 — х21 0,001, поэтому округляя до тысячных
долей, получим £ — 2,532.
Пример 2. Методом хорд уточнить до 8 = 0,001 корень уравнения х —
— sin х = 0,25, заключенный на отрезке [0, л/2].
126
Решение. Запишем уравнение в виде х — sin х — 0,25 = 0 и определим
f' (х) — 1 — cos х. Для проверки выполнения условия (6) составим вспомога-
тельную таблицу, в первых двух столбцах которой указаны начало и конец выб-
ранного интервала изоляции корня.
Таблица 3.4
а ъ Знаки м пг Выполня- ется ли условие м -С 2 т а-\- Ь 2 Знак (а + М Ч 2 )
На) 10)
0,00 1,57 -T 1,00 0 нет 0,785 —
0,785 1,57 — + 1,00 0,29251 нет 1,178 +
0,785 1,178 — + 0,6172 0,2925 нет 0,982
0,982 1,178 — + 0,6172 0,4446 да
Из последней строки табл. 3.4 видно, что на отрезке [0,982; 1,178] условие
М < 2 т выполняется. Следовательно, при оценке погрешности приближенного
значения корня по методу хорд можно воспользоваться неравенством [ хп —
—^п-11 <е. Корень уравнения х — sin х — 0,25 —0 находится на отрезке [0,982;
1,178]. Определим знак второй производной внутри отрезка:
f (к) — 1 — cos х; (х) — sin х > 0.
Если возвратиться к прежним обозначениям, то а ~ 0,982, b ~ 1,178. Знак вто-
рой производной совпадает со знаком функции в точке Ь. Следовательно, этот
конец отрезка является неподвижным, а все приближения к корню лежат со
стороны конца а. Для вычисления корня пользуемся формулами (1) и (2):
а)
Xi — а—--------------;
/(&)-/(«)
/ (хп )(&-хп)
X 77 *4-1 — ХП - ,
/(&)-/(хп)
где b = 1,178, ((b) = 0,00416. Составим следующую таблицу (табл. 3 5):
Таблица 3.5
п хп ~sin хп f(xn) = xn —sin zn — 0,25 b xn fUn) (b-xn) (xn)
0 1 2 0,982 1,171 1,1712 —0,83161 —0,92114 —0,09961 —0,00014 0,196 0,007 0,189 0,0002
Итак, хх 1,171 с точностью до 8 = 0,001.
§ 3.6. Метод Ньютона (метод касательных)
Пусть корень уравнения / (х) = 0 отделен на отрезке [а, &], при-
чем /' (х) и /" (х) непрерывны и сохраняют постоянные знаки на всем
отрезке [а, 6],
Геометрический смысл метода Ньютона состоит в том, что дуга
кривой у = f (х) заменяется касательной к этой кривой (отсюда и вто-
рое название: метод касательных).
127
Первый случай. Пусть f (а) < 0, f (b) > О, f (х) > О,
f"(x) > О (рис. 3.20, а) или f (а) > 0, f (b) < 0, f (х) < 0, f" (х) < О
(рис. 3.20, б). Проведем касательную к кривой у = f (х) в точке
Во (b; f (/>)) и найдем абсциссу точки пересечения касательной с осью
Ох. Известно, что уравнение касательной в точке Во (b\ f (b)) имеет
вид
Полагая у — 0, х = х1г получим
Л1
/• <ы
Теперь корень уравнения находится на отрезке la, xj. Применяя сно-
ва метод Ньютона, проведем касательную к кривой в точке
Bi (хг; f (xj)) и получим
и вообще
V —у f /9)
71+1 П Г (Хп) ‘
Получаем последовательность приближенных значений хь х2,,,,, хп,
каждый последующий член которой ближе к корню чем предыдущий.
Однако все хп остаются больше истинного корня £, т. е, хп — прибли-
женное значение корня £ с избытком,
Второй случай. Пусть f (а) <0, / (Ь) > 0, f (х) > 0,
Г (х) < 0 (рис, 3.21, а) или f (а) > 0, f (b) < 0, f (х) < 0, f" (х) > 0
(рис. 3.21, б). Если снова провести касательную к кривой у == f (х)
в точке В, то она пересечет ось абсцисс в точке, не принадлежащей
отрезку [а, &]. Поэтому проведем касательную в точке Ло (a; [ (а))
и запишем ее. уравнение для данного случая:
У — t (fl) = I' (а) {х — а).
128
Полагая у == 0, х — xlt находим
х1 = а
f(a)
Г (а) ’
(3)
Корень | находится теперь на отрезке |хх, Применяя снова метод
Ньютона, проведем касательную в точке (хг; f (xj) и получим
и вообще
Получаем последовательность приближенных значений хь х2, хп,...»
каждый последующий член которой ближе к истинному корню чем
предыдущий, т* е, хп — приближенное значение корня | с недостат-
ком.
Сравнивая эти формулы с ранее выведенными, замечаем, что они
отличаются друг от друга только выбором начального приближения:
в первом случае за х0 принимался конец b отрезка, во втором — ко-
нец а.
При выборе начального приближения корня необходимо руковод-
ствоваться следующим правилом: за исходную точку следует вы-
бирать тот конец отрезка [а, Ь], в котором знак функции совпадает со
знаком второй производной, В первом случае f (b)f” (х) > 0 и началь-
ная точка Ь = х0, во втором f(a) • f"(x) >0 и в качестве начального
приближения берем а = х0.
Для оценки погрешности можно пользоваться общей формулой
I / Un) |
(5)
где
m = min (х)|
[а.Ь]
(эта формула годится и для метода хорд).
129
В том случае, когда отрезок [а, Ь] настолько мал, что на нем выполз
няется условиеМ2 < 2 тъ где Л12 —max \f" (х) |, a — f (х)|,
[а, ь] [а, Ь]
точность приближения на n-м шаге оценивается следующим образом:
если | хп — | < 8, то | £ — хп | < е2.
Если производная f (х) мало из-
меняется на отрезке 1а, 6], то для
упрощения вычислений можно поль-
зоваться формулой
Хп+1 = хп , , (6)
т. е. значение производной в на-
чальной точке достаточно вычис-
лить только один раз. Геометриче-
ски это означает, что касательные
в точках Вп (xn-,f(xn)) заменяются
прямыми, параллельными каса-
тельной, проведенной к кривой
У= f W В точке Во (х0; f (х0)) (рис.
3.22).
Рис. 3.22 Пример 1. Методом касательных уточ-
нить до £ = 0,001 корень уравнения х3 +
Д-Зх2 —3 = 0, расположенный на отрез-
ке [ — 2,75; — 2,5].
Решение. Ранее было установлено, что f ( — 2,75) • f" (х) > 0 (см.
пример 1 § 3.5). Поэтому, чтобы воспользоваться методом касательных, следует
выбрать х0 — — 2,75. Вычисления будем вести по формуле (6). Находим
/' (х) = Зх2 + 6х; Л (х0) - f ( — 2,75) =6,1875.
Для удобства все вычисления сведем в следующую таблицу:
Таблица 36
п хп
___ 6,1875
0 —2,75 —20,797 7,5625 22,6875 — 1,111 0,179
1 —2,571 — 16,994 6,6100 19,8300 —0,164 0,026
2 —2,545 — 16,484 6,4770 19,431 —0,053 0,008
3 —2,537 — 16,329 6,4364 19,309 0,020 0,003
4 5 -2,534 —2,533 — 16,271 6,4212 19,2636 0,007 0,001
Из табл. 3.6 видно, что |х5 — х4| < 0,001, поэтому § = — 2,533.
Пример 2. Методом касательных уточнить до s = 0,0001 корень уравнения
х —sin х = 0,25, расположенный на отрезке [0,982; 1,178].
Решение. Здесь а = 0,982; b = 1,178. Находим /'(х) — 1 — cos х;
f" (х) = sin х > 0 на [0,982; 1,178]; / (1,178) * f” (х) > 0. Значит, х0 = 1,178.
Вычисления будем вести по формулам (1) и (2) и сведем их в табл. 3.7,
Из табл, 3,7 видно, что [х3 — хй ] <0л0001. Таким образом, | ж 1Д712,
130
Таблица 3.7
п хп — sin Хп — sin хп —0,25 Г 1ЛП>= = 1 — cos Хп -
0 1 3 1,178 1,1715 1,1713 1,17125 —0,92384 —0,92133 —0,92127 0,00416 0,00017 0,00003 0,61723 0,61123 0,61110 —0,0065 —0,0002 —0,00005
§ 3.7. Комбинированный метод хорд и касательных
Методы хорд и касательных дают приближения корня с раз-
ных сторон. Поэтому их часто применяют в сочетании друг с другом,
и уточнение корня происходит быстрее.
Пусть дано уравнение f (х) — 0, корень £ отделен и находится на
отрезке [я, Ы. Применим комбинированный метод хорд и касательных
с учетом типа графика функции.
Если f'(x) * f"(x) > 0, то метод хорд дает приближения корня
с недостатком, а метод касательных — с избытком (рис, 3.23, а и б),
Если же f (х) • f" (х) < 0, то методом хорд получаем значе-
ние корня с избытком, а методом касательных — с недостатком
(рис. 3.24, а и б).
Однако во всех случаях истинный корень заключен между
приближенными корнями, получающимися по методу хорд и_методу
касательных, т. е. выполняется неравенство a <Z хп <Z % <Z хп <; b,
где хп — приближенное значение корня с недостатком, хп — с из-
бытком.
Вычисления следует весги в таком порядке. Если f (х) • f"(x) > О,
то со стороны конца а лежат приближенные значения корня, получен-
131
ные по методу хорд, а со стороны конца Ь — значения, полученные по
методу касательных, и тогда
/(а)(6—а)
f(b)-t(a)
Ьг = Ь
/(6)
Г W •
(1)
Теперь истинный корень находится на интервале [аъ Приме-
няя к этому интервалу комбинированный метод, получаем
f (ai)(6i—щ)
f(6i)-/(ai) ’
f(bi)
Г (61)
и вообще
Qn+l = an
__ f>(an) (Ьп—ап)
t(bn)~t(an) ’
f(bn)
Г (bn)
(см. рис. 3.23, а и 6).
Если же f’(x) • f" (x) < 0, то co стороны конца а лежат приближен-
ные значения корня, полученные по методу касательных, а со стороны
конца b — значения, полученные по методу хорд. Тогда
Г (a) f(b)-f(a)
(3)
Применяя к отрезку [ах, dj комбинированный метод, получаем
а _а k А f (61) (61-М
— W1 • U а — 1/1
Г(М ((б!)-/(01)
и вообще
fln+ls
/(°n) L _______ Ь __ f (6n) (bn — ап)
Г(ап)’ n+1 п f(6n)-f(an)
(4)
Комбинированный метод очень удобен при оценке погрешности вы-
числений. Процесс вычислений прекращается, как только станет вы-
полняться неравенство | X — хп | < е, За приближенное значение
132
корня следует принять
B = yfo + *n). (5)
где хп и Хп — приближенные значения корня соответственно с недо-
статком и с избытком,
Пример. Комбинированным методом хорд и касательных уточнить до 0,001
корни уравнения х3 + Зх2 — 24х + 1 “ 0.
Решение, 1) Отделим корни аналитически. Имеем
f (х) = х3 + Зх2 — 24х + I, f (х) = Зх2 + 6х — 24,
т, е, корни производной = —- 4; х2 = 2. Составим таблицу знаков функции:
X | —оо | —4 | 2 | -|-оо
sign / (х) I — I +1 — I +
Данное уравнение имеет три действительных корня:
Х1$(~оо, —4), х2$(—4, 2), х3£ (2, 4-оо).
Уменьшим промежутки нахождения корней до длины, равной 1:
х j 7 | —6 | —5 [ —4 [ —3 | —2 [ — 1 | 0 | Ь| 2 [ 3
sign f (х) |-|+l+l + l + l + l+ l+ l- l- |-
4
+
Итак Xi С(— 7, —6), х2$(0, 1), х3С(3, 4).
2) Уточним комбинированным методом хорд и касательных корень, лежащий
в интервале ( — 1} — 6). Имеем f( — 7) = — 27 < 0; /( — 6) = 37 > 0 и
f' (Х) = Зх2 + 6х — 24 > 0; /*(х) = 6х + 24 < 0; f' (х) . f (х) < 0.
Для расчетов применяем формулы (4):
f (ап) . . f (bn) (Ьп— ^п)
a7i+i — ап — ‘ р , . > ^п-Н — t \ \ »
/ («») L(bn)~ f(an)
т. е,
bn^ = bn+^bnt где =
an+1 = an+Aczn, где Дап=— ——
f (^п)
f (bn) (Ьп —дп)
t(bn)-f(an)
(ап и Ьп — приближенные значения корня соответственно с недостатком и с из-
бытком). Здесь а0 — а = — 7, bQ = b — — 6.
Вычисления удобно вести в таблице (см. табл. 3.8 на стр. 134).
Следовательно, §1 — 6,639.
3) Определим приближенный корень для интервала (0,1).[Имеем / (0) > О,
f (1) <0 и
f'(x)=3x2 + 6*~24<0j ГМ=6х+6>0; f/(x) • f(x) <0.
Как и в первом случае, воспользуемся формулами (4) при aQ — а — 0;
Ь® = b = 1.
Составляем следующую таблицу (см. табл 3.9 на стр 134).
Таким образом, 0,042.
133
4) Найдем приближенный корень из интервала (3, 4). Имеем f (3) =
= - 17 < 0, / (4) = 17 > 0 и
f (х) = Зх2 + 6х — 24 > 0; f (х) = 6х + 6 > 0; (х) • (х) > 0.
Вычисления будем вести по формулам (2):
т. е.
ап+i — ап
__ / (ап) (^П---ап)
t (&п)------1 (ап)
^п+1 —
f(bn)
Г (Ьп) 9
яп-Н = ап + Дап, где &ап =
f (ап) (Ьп-ап)
t(bn)-f(an)
bn+i = bnгДе &bn —
f(bn)
ff (bn) •
Здесь — a = 3, — b — 4.
Вычисления сводим в таблицу (см, табл. 3,10),
Значит, |3 == 3,596.
Таблица 3.8
п % ап 4 Ч°п) f (ап) Чйп)~ -Чап) д“п an-i 1
Ьп Ьп чм ДЬп bn± 1
0 1 49 —343 —27 81 64 0,333 —6,667
—6 36 —216 37 -0,578 —6,578
1 —6,667 0,089 44,449 —296,34 — 1,985 73,345 6,037 0,027 —6,640
—6,578 43,270 —284,63 4,052 —0,060 —6,638
2 —6,640 0,002 44,090 —292,75 — 1,12
—6,63е 44,063 —292,49 0,011
Таблица 3.9
ri ап '°п ап 4 f (%) >' (ап) f(6n)_ дап ап -f- 1
h п Ьп ЧМ дч ^п~{~ 1
0 0 1 0 0 1 —24 —20 0,040 0,040
1 1 1 —19 —0,95 0,050
1 0,040 0,01 0,0016' 0,00006 0,045 -23,755 —0,147 0,002 0,042
0,050 0,0025 0,00012 —0,102 —0,007 0,043
2 0,042 0,001 0,0016 0,00006 —0;0031
0,043 0,0017 0,00007 0,037
134
Таблица 3 10
п ап Ьп~ап Ч?п) ''(ьп) -f(an) Лап ап 1
Ьп Д*п ^«4* 1
0 3 1 9 27 —17 48 34 0,500 3,500
4 16 64 17 —0,354 3,646 !
1 3,500 0,146 12,250 42,875 —3,375 37,755 5,217 0,092 3,592
3,646 13,293 48,467 1,842 —0,041 3,605
2 3,592 0,013 12,903 46,346 —0,156 36,618 0,477 0,00039 3,5924
3,605 12,996 46,851 0,319 —0,008 3,5963
3 3,5924 0,0039 12,906 46,362 —0,138 36,380 0,142 0,00382 3,59622
3,5963 0,0039 12,934 0,004 —0,0001 3,5962
4 3,59622 3,5962 0,00002
§ 3.8. Метод итерации (метод последовательных приближений]
Пусть задано уравнение / (х) == 0, где f (х) — непрерывная функ-
ция. Требуется определить вещественный корень этого уравнения,
заключенный на отрезке [а, &].
Заменим уравнение / (х) = 0 равносильным ему уравнением
X — ф (х)< (1)
Выберем каким-либо способом х0 £ [а, Ь] и подставим его в правую
часть уравнения (1); тогда получим хх — ф(х0). Затем это значение xt
подставим снова в правую часть уравнения (1) и получим х2 — ф (хх).
Повторяя этот процесс, получаем последовательность чисел хп ==
= Ф (хп_х). Здесь могут встретиться два случая:
1) последовательность х0, хх, хп, сходится, т. е, имеет
предел, и тогда этот предел будет корнем уравнения /(х) — 0;
2) последовательность х0, хь хп, ,,, р а с х о д и т с я, т. е. не
имеет предела.
Приведем без доказательства теорему, выражающую условие, при
котором итерационный процесс сходится.
Теорема. Пусть на отрезке [а, Ь] имеется единственный корень
уравнения х ~ ср (х) и во всех точках этого отрезка производная f (х)
удовлетворяет неравенству | ф' (х) | q < 1. Если при этом выпол-
няется и условие а ф (х) 6, то итерационный процесс сходится,
а за нулевое приближение х0 можно взять либо число из отрезка [а, Ь].
Последнее условие означает, что все приближения х0, хх, хп, ...
также находятся на отрезке [а, 6]. Чем меньше | ф' (х) |, тем лучше
сходимость итерационного процесса.
Рассмотрим вопрос об определении точности вычисленных при-
ближенных значений корня. Пусть £ — точное значение корня
135
уравнения х = ф(х), а число q определяется из соотношения
] <р' (х) | <7 <; 1. Тогда справедливо соотношение
It %П | ^5 j lXn—Xn-ll- (2)
1—9
Если поставить условие, что истинное значение корня £ должно отли-
чаться от приближенного значения на величину е, т. е. | £ — хп |
е, то приближения х0, хп хп надо вычислять до тех пор, пока не
будет выполнено неравенство
—2—|xn—x„_J<e,
1—9
Уравнение f (х) = 0 к виду х = ф (х) можно привести различными
способами, однако для метода итерации следует взять то уравнение
вида х = ф (х), для которого выполняется условие приведенной выше
теоремы.
Геометрическая интерпретация метода итерации. Пусть задано
уравнение /(х) = 0 1/(х) — непрерывная функция]. Приведем это урав-
нение к виду х=ф (х) и построим графики функций у = х и г/ = Ф (х).
Абсцисса точки пересечения графиков этих функций и является
истинным корнем В‘(РИС- 3.25).
Выберем х0 £ [а, Ь\ и определим ф(х0). Условимся последователь-
ность точек, лежащих на кривой у = ф (х), обозначать через
Аг (I — 0, 1, 2, ...), а последовательность точек, лежащих на прямой
у = х, — через Вг (i = 1, 2, 3, ...). Из точки А0(х0; ф(х0)) проведем
прямую, параллельную оси Ох до пересечения с прямой у = х; тогда
получим точку В1(Хь ф(Х0)).
Действительно, А0С0 = ф (х0) = так как А0Вх || ОС0,
BiCdl А0С0. Но OCt — Bfii (А ОС^Вх — прямоугольный и равнобед-
ренный, поскольку прямая у = х есть биссектриса координатного
угла). Следовательно, хг — ф(х0).
Проведем А^В* || ОСХ и, повторяя вышеизложенные рассуждения,
убедимся в том, что ха = ф (хх).
136
На рис, 3.25 изображен сходящийся итерационный процесс. Кри-
вая пересекает биссектрису у = х в точке М с абсциссой g и при
х>§ лежит под биссектрисой, a ф'(х) удовлетворяет условию
0< <р' W<1. Последовательные приближения х0, хъ .... хп, ...
(общие абсциссы точек графиков обеих функций) монотон-
но убывают. Каждое последующее приближение хп ближе
к истинному корню, чем каждое предыдущее хп_г. Ломаная ли-
ния Д0В1Л1В2Д2... имеет вид «лестницы».
На рис. 3.26 производная ф'(х) < 0, но по абсолютной величине
меньше единицы, т. е. | ф'(х) I < 1. Итерационный процесс сходится,
но приближения колеблются около точного значения корня.
Ломаная линия А^А^В^А^.,, имеет вид «спирали».
Итак, если в некоторой окрестности (а, Ь) корня g уравнения
х = ф (х) производная ф' (х) сохраняет постоянный знак и выполнено
неравенство | ф'(х) | q<Z 1, причем ф'(х) > 0, то последовательные
приближения хп = ф (xn-i) (ц = 1, 2, х0 £ [а, 61 сходятся
к корню монотонно. В том же случае, когда ф' (х) < 0, последователь-
ные приближения колеблются около корня
На рис. 3.27 показан расходящийся итерационный процесс. Здесь
ф'(х) > 1. Кривая пересекает биссектрису у = х в точке М и при
х > £ лежит над биссектрисой.
На рис. 3.28 показан расходящийся итерационный процесс для слу-
чая | ф'(х) | > 1. Последовательные «приближения» удаляются от точ-
ного значения корня g.
Рис. 3 27
Рис. 3.28
Пример 1. Методом итерации уточнить до Ю-4 корень уравнения 5х5 —
— 20х + 3=0, заключенный на отрезке [0, 1].
Решение. Данное уравнение следует привести к виду х = <р (х). Это
можно сделать несколькими способами, например:
1) х = х+(5х3—20х+3), тогда <Pi(x) = 5x'— 19х+3;
3 А 20 х—3
тогда ф2(х) =
137
Определим, какой из полученных функций ф (х) следует воспользоваться
для вычисления последовательных приближений. Вспомним, что если <р (х) на
отрезке [я, Ь\ удовлетворяет условию |<р' (х) | < q <; 1, то итерационный процесс
сходится. Находим
| <р[ (х) | = | 15х2—19 I > 1 [на 0,1];
I 15х2 I 3
(Фз Wl = |.-^5-| = —^2< I на [0,1*1.
Следовательно, можно воспользоваться функцией <р3 (х) и искать последова*
тельные приближения методом итерации по формуле
5x^+3
хп —---------.
20
За начальное приближение возьмем max ср' (х) на [0, 1], т. е. x0=0s75. Пользуясь
формулой (3), определим, какой должна быть разность между двумя последова-
тельными приближениями, для того чтобы заданная точность была достигнута!
0,0001 *(1 — 0,75) 0,0001*0,25
- 0175 - 0>75 -0,00003.
Таким образом, когда абсолютная величина разности | хп — xn-i [ не превзойдет
0,00003, итерационный процесс следует прекратить и считать, что заданная
точность достигнута.
Вычисления удобно вести с помощью следующей таблицы:
Таблица 3.11
п хп V3 хп ^ХП>=*ХП+1
0 0,75 0,42188 0,25547
1 0,2555 0,016777 0,154144
2 0,1541 0,005652 0,151413
3 0,1514 0,005443 0,151361
4 0,15136 0,005442 0,151361
На этом итерационный процесс можно остановить и считать £ ж 0,1514.
Пример 2. Вычислить с точностью до s =
= 10~ё корень уравнения ех— х2 — 0.
Решение. Перепишем уравнение в виде
ех — х2 и 0Тделим корни графически. Построим
графики функций у = ех и у — х2 (рис. 3.29).
Из чертежа видно, что уравнение ех — х2 = 0
имеет один действительный корень, который
лежит в интервале [ — 0,8; — 0,7].
Проверим, действительно ли это так. Оп-
ределим f ( — 0,8) и f ( — 0,7): f ( — 0,8) ==
= 0,44933—0,64 = — 0,19067 <0; f ( — 0,7) =
= 0,49659—0,49 = 0,00659 > 0. Так как знаки
Функции f (х) ~ ех — х2 на концах отрезка
— 0,8;—0,7] различны, то внутри этого отрезка
содержится корень уравнения.
133
Попробуем сузить интервал, применив метод проб. Находим f ( —0,75) =:
к= 0t49237—0,56250 < 0, но / ( —0,7) > 0; значит, корень находится на отрезке
I — 0,75; —0,7], Сузим этот отрезок еще раз. Имеем / ( — 0,725) == 0,48432—
— 0,52562 = —0,04130 <0. Но / (—0,7)>0. Следовательно, корень находится
на отрезке [ - 0,725; - 0,7].
Из уравнения ех = х3 определяем, что х = — У?*. (Перед радикалом
берем знак минус, так как нам известно, что корень отрицателен.) Перепишем
ето уравнение в виде х= — ех^2 и проверим, каким будет итерационный процесс:
сходящимся или расходящимся, т. е, выполняется ли неравенство | <р' (х) j < 1.
В нашем примере
Ф(х) =—ех^2, ф' (х)_-i-ez/2,
| ф' (—0,725) |=0,34727; j ф' (_0,7) | = 0,35230.
Поскольку ]<pz (х) 1 < 1, итерационный процесс сходится. Число q в формуле
(3) возьмем равным 0,36. Так как 8 = 10“ё, то
0,00001 (1—0,36) Л
| xn xn„i | —0,000018.
0,36
Таким образом, требуемая точность будет достигнута, если выполняется неравен-
ство | хп — хп-1| < 0,00002. За нулевое приближение можно принять любой
из концов отрезка [ — 0,725; — 0,7] и любую точку внутри его. Примем х0 —
= —0,7.
Вычисления сведем в следующую таблицу:
Таблица 3.12
п хп хп 2 /2 е п'
0 —0,7 —0,35 —0,70460
I —0,70460 —0,35230 —0,70307
2 —0,70307 —0,35154 —0,70360
3 —0,70360 —0,35180 —0,70342
4 —0,70342 —0,35171 —0,70348
5 —0,70348 —0,35174 —0,70346
6 —0,70346
Так как | х6 — х5 ] = | — 0,70348 — ( — 0,70346)\ = 0,00002, то требуемая
точность вычислений достигнута и £ 0,70346.
§ 3.9. Приближенное решение систем уравнений.
Метод Ньютона для системы двух уравнений
В данном параграфе рассматривается решение системы двух нели-
нейных уравнений с двумя неизвестными методом Ньютона. Пусть
дана система
Шх, у) = 0,
I Ч> (х, у) = 0,
где / и <р — непрерывно дифференцируемые функции. Предположим
что известны и-е приближения неизвестных, тогда за более точные их
139
значения можно принять
х “ хп 4* Лл> у “ Уп 4~ kn*
Тогда система (1) запишется в виде
f f Un 4" ^п> Уп 4* &п) ” 0» да
IФ Un 4“ Уп 4* kn) = О*
Разложим функции f и ф в ряд Тейлора по степеням hn и knl
f Un 4~ hn> уп 4* kn) == f Un> yn) 4* hn f% (xny yn) + knfy (xn, //n) 4*
4~О1(ЛП, ^n)>
Ф Un + hn, Уп 4- kn) = ф (xn, yn) 4- hn & (xn, yn) + kn ф' (xn, yn) 4-
4-О2(Лп, £n).
Здесь Oi(/in, £n) и O2Un> &n) содержат члены более высокого порядка
малости, нежели hn и kn. Ограничиваясь в последней системе линей-
ными членами относительно hn и kn, получим
| f (%П> £/п) 4* ^П U Un* Уп) 4~ f& (%п> Уп)^^> (2)
I Ф C^n* Уп) 4“ Ф* (%П> Уп) 4" &п Ф^ Un» Уп) =
ИЛИ
f^nfx(^nt Уп) “1" f & (%п> Уп)~ ~~f Un> Уп)*
t hn Ф* Un» Уп) 4- kn (Ру (хп> yn)=—q> Un» уп)9
откуда
— t(xn, уп) fy(*п> Уп)
Ф (хп > Уп) (хп> Уп) /ел
» (ч)
t'x (Хп, Уп) fу (хп, Уп) Дп V 2
Фх (хп> Уп) <Ру(хп> Уп)
1 fх (хп, Уп) f (хп> Уп)
Ь __ Фх(*п, Уп) — ф(*п, Уп) — (KI
*^п • 1UJ
f'x (хп> Уп) Гу (хп, Уп) Л v 7 ^п
<р'х(хп, Уп) <р'у(хп, Уп)
Таким образом, находим
%п+1 — 4~ hm Уп-hl — Уп 4" &п*
(7)
Исходные значения х0, yQ определяются приближенно, обычно из гра-
фического решения.
Пример. Методом Ньютона решить систему уравнений
( 2х24-3#3—6//—4=0,
( х2--Зг/24- 4х—2 = 0.
Решение. Система имеет два решения. Уточним одно из них, принадле-
жащее области 0,5 < х < 0,6; — 0,48 < у < — 0,44» (Корни ранее были от-
делены графически; см. § 3.2, пример 5.)
140
Таблица 3.13
п хп 4 хп п Цхп* Уп) уп) fp(Xn- Уп) дп A/ln '1п
Уп 34 -4 -31/2-2 V(*n- Уп) (ХП* Уп) 4>'у (хп- Уп) ЛАп kn
0 0,5 0,25 0,50 2,25 —0,1052 2 —8,76 48,32 3,6612 0,0749
—0,46 0,6348 —0,6052 —2,6348 —0,3848 5 2,76 0,2436 0,0050
1 0,5749 0,3306 0,6612 2,6302 0,0222 2,2996 —8,7300 51,2357 ' —0,1409 —0,0027
—0ч4550 0,6210 —0,6490 —2,6210 0,0092 5,1498 2,7300 1,1221 ’ 0,021
2 0,5722 0,3272 : 0,6544 2,6160 —0,1864 2,2888 —8,6040 50,2224 0,0483 0,0009
—0,4340 0 5652 —0,8308 —2,5652 0,0508 5,1444 2,6040 — 1,9751 0,039
3 0,5731 0,3283 0,6566 2,6207 0,1666 2,2924 —8,8380 52,0079 —0,0374 —0,0007
—0,4730 0,6711 —0,4900 —2,6711 —0,0504 5,1462 2,8380 0,9728 0,0180
4 0,5724 0,3272 0,6544 2,6160 0,0054 2,2896 —8,73 51,1647 0,0290 0,0005
—0,4550 0,6210 —0,6490 —2,6210 —0,0050 5,1448 2,73 0,0492 0,0009
5 0,5729 —0,4541
За начальное приближение примем х0 = 0,5; Уъ —0>4б, Далее, находим
/(х, р) —2x2 + 3t/2“6z/—4, ф(х, y)=x2-j-4x—Зу2~21
/я = 4х; ^ = 6^/—6, cp; = 2x+4; ф' = — бу.
Вычисления удобно вести с помощью таблицы (см. табл. 3.13 на стр. 141)*
Окончательный ответ: х ~ 0,573; у ~ — 0,454.
§ ЗЛО. Метод итерации для нелинейной системы уравнений
Пусть задана система уравнений
( F! (х, у) = О, „
I ^2 (X, у) = 0.
Требуется найти действительные решения с заданной степенью точ-
ности.
Перепишем систему (1) в виде
( x=<Pi(x, у), (2)
I г/ = ф2 (х, у).
Пусть х0 и у0 — начальные приближения корней, полученные графи-
чески или каким-либо другим способом. Подставив в правые части
уравнений системы (2) вместо х и у начальные значения х0 и yQ, полу-
чим
^1 = Ф1(^о> Уо)-
У1 = ф2 (*о> &>)•
Аналогично получаем вторые приближения
х2 = Ф1(Х1, г/i),
Уч ~ Фг (^2> Уч)'
В общем случае
*п = Ф1(*п-1> Уп-1)>
</п = Фг(^-1> Уп-1)-
(3)
(4)
(5)
Если функции фх(х, у) и ф2(х, у) непрерывны и последовательности
xlt х2, .... хп, ... и ylt уг, ..., уп, ... сходятся, то пределы их дают ре-
шение системы (2), а следовательно, и системы (1).
Приведем без доказательства теорему об условиях сходимости ите-
рационного процесса.
Теорема. Пусть в некоторой замкнутой окрестности R (а 'С х А,
b :С у В) имеется одно и только одно решение х = х и у = у
системы (2).
Тогда если'.
1) функции ф1(х, у) и ф2(х, у) определены и непрерывно диффереН'
цируемы в Й,
2) начальные приближения х0, у0 и все последующие приближения
Хп, уп (п ~ 11 2, ...) принадлежат 7?;
142
3) e R выполнены неравенства
| ox I I дх I
или неравенства
| дх | | ду |
то процесс последовательных приближений сходится к решению
х х, у = у*
Оценка погрешности n-го приближения определяется неравен-
ством
| X Хп | 4" | у уп | j._(| хп | +1 уп У п-11)» (8)
где М — наибольшее из чисел qt и q2t
входящих в неравенства (6) или (7).
Сходимость метода итер ации счи-
тается хорошей, если М <Z х/2; при
этом 7И/(1 — Л4) < 1. Поэтому если в
двух последовательных приближениях
совпадают, например, три десятичных
знака после запятой, то ошибка послед-
него приближения не превосходит 0,00L
Пример 1 Методом итерации решить си-
стему
f sin (х—0,6)—у~ 1,6,
| Зх—cos у —0,9
с точностью до е = 0,001.
Решение. Приведем систему к виду
1
х=—cos//+0,3 = фх (х, у),
о
// — sin (х—0,6) —1,6 ~ ф2 (х, //).
(Б)
Отделим корни графически (рис. 3.30) Из графика видим, что система (Б) имеет
единственное решение, заключенное в области 0 < х < 0,3, — 2,2 у — 1,8.
Проверим систему (Б) на сходимость итерационного процесса:
1004 | д(р9 I
=0; =[cos(x—0,6)| <|cos0,3] =0,2955<1;
дх I дх \
—+ sin у |<|— 4-sin (-1,8)1 = 0,3246 < 1; 1 = 0.
3113 | ду |
I 3ф1
I ду
143
Следовятрльно,
Условия сходимости выполняются. Последовательные приближения найдем по
формулам
*п+1 =““ cos УпА~ 0 >3,
О
Уп-*г1 =sin (хп —0,6) —1,6.
Выберем х0 = 0,15, у0 — — 2,
Вычисления удобно вести с помощью следующей таблицы:
Таблица 3.14
п *п х„-0,С sin <лгп — 0,6> cos< у cos Уп
0 0,15 —2 * —0,45 —0,4350 —0,4161 —0,1384
1 0,1616 —2,035 —0,4384 —0,4245 —0,4477 —0,1492
2 0,1508 —2,0245 —0,4492 —0,4342 —0,4382 —0,1461
3 0,1539 —2,0342 —0,4461 —0,4313 —0,4470 —0,1490
4 0,1510 —2,0313 —0,4490 —0,4341 —0,4444 —0,1481
5 0,1519 —2,0341 —0,4481 —0,4333 —0,4469 —0,1490
6 0,1510 —2,0333 —0,4490 —0,4341 —0,4461 —0,1487
7 0,1513 —2,0341 —0,4487 —0,4340 —0,4469 —0,1490
8 0,1510 —2,0340
Таким образом, 0,151; у ~—2,034.
§ 3.11. Общие свойства алгебраических уравнений.
Определение числа действительных корней
алгебраического уравнения
Общие свойства алгебраических уравнений. Запишем алгебраи-
ческое уравнение п-й степени
Рп W = + а2хп"2 + ... + ап^ х + ап = 0, (1)
где Рп (х) — многочлен n-й степени, п — наивысшая степень при не-
известном, а0, ...» ап —действительные коэффициенты.
Всякое число обращающее многочлен в нуль, т. е. такое, что
Рп (?) = 0, называется корнем многочлена. Согласно основной теореме
алгебры, многочлен Рп(х) степени а (п 1) с любыми числовыми ко-
эффициентами имеет и корней, если каждый из корней считать столько
раз, какова его кратность.
Число £ является корнем многочлена Рп (х) тогда и только тогда,
когда Рп (х) делится без остатка на х — Ерли при этом Рп (х) делит-
ся без остатка на (х—- (k 1), но уже не делится на (х—то
5 называется k-кратным корнем (или корнем кратности k) многочле-
на Рп(х). Корни кратности k = 1 называются простыми корнями
многочлена,
Н4
Корни алгебраического уравнения (1) могут быть как действитель-
ными, так и комплексными.
Комплексные корни уравнения (1) обладают свойством парной со-
пряженности, т. е. если уравнение (1) имеет комплексный корень
Е = а + ₽/ (где сс и р — действительные числа) кратности /г, то оно
имеет и комплексный корень £ ~ а — р/ также кратности k. Модули
этих корней одинаковы:
IBI = |T|=r^W.
Если уравнение (1) имеет комплексные корни, то их число — четное*
Поэтому всякое алгебраическое уравнение нечетной степени с дей-
ствительными коэффициентами имеет по крайней мере один действи-
тельный корень.
Прежде чем вычислять корни алгебраического уравнения, сначала
необходимо: а) определить число корней, которое имеет данное урав-
нение; б) найти область существования корней (установить верхнюю
и нижнюю границу расположения корней}. После этого можно присту-
пать к отделению корней и их уточнению.
Определение числа действительных корней алгебраических урав-
нений. Определить приближенно число действительных положитель-
ных корней алгебраического уравнения (1)
Рп(х) = аохп + а^-1 + а2хл-2 + ... + ап^х + ап = О
можно с помощью правила Декарта: количество действи-
тельных положительных корней алгебраического уравнения Рп{х) = О
с действительными коэффициентами (подсчитываемых каждый столь-
ко раз, какова его кратность} либо равно числу перемен знака в после-
довательности коэффициентов уравнения Рп(х) — 0, либо на четное
число меньше (равные нулю коэффициенты не учитываются}.
Количество отрицательных корней уравнения равно числу перемен
знака в последовательности коэффициентов Рп(—х) или на четное чис-
ло меньше.
Если уравнение полное, то количество его положительных
корней равно числу перемен знака в последовательности коэффициен-
тов или на четное число меньше, а количество отрицательных корней —
числу постоянств знака или на четное число меньше.
Пример 1. Определить количество положительных и отрицательных корней
уравнения
Х5 _ J7x4 + 12л3 4- 7х2 — х + 1 - 0.
Решение. Согласно основной теореме алгебры это уравнение имеет пять
корней (из них хотя бы один является действительным).
Уравнение является полным, последовательность знаков коэффициентов
уравнения такова: 4~ , — , + , + , — , + . Знак изменяется четыре раза;
значит, положительных корней будет либо 4, либо 2, либо ни одного.
Число постоянств знака равно 1; следовательно, заданное уравнение имеет
один отрицательный корень.
Пример 2, Определить количество действительных положительных и отрица-
тельных корней уравнения
— Зх' д- — 1 = 0.
145
Решение. Данное уравнение имеет шесть корней; последователь-
ность знаков: + , — , + , + , — . Имеет место три перемены знака; сле-
довательно, положительных корней либо 3, либо 1. Далее, для многочлена
Рп ( — X) = X6 — Зх4 — X3 + х2 — 1
последовательность знаков такова: + , — , — , + , — . Здесь также имеем
три перемены знака — поэтому отрицательных корней либо 3, либо 1.
Более точно число корней алгебраического уравнения можно оп-
ределить при помощи правила Штурма, заключающегося
в следующем.
Пусть для данного алгебраического уравнения Рп(х) = 0 каким-
либо способом установлено, что все его действительные корни нахо-
дятся в интервале (а, Ь) (а и b — действительные числа и не являются
корнями уравнения, а < Ь). Найдем первую производную Рп (х) и раз-
делим на нее многочлен Рп(х). Остаток от деления Рп(х) на Рп (х) возь-
мем с противоположным знаком и обозначим его через Ri(x).
Затем точно так же делим Рп (х) на 7?i(x), полученный остаток берем
с противоположным знаком и обозначим через Т?2(х). Разделив R^x)
на R%(x) и снова взяв остаток с противоположным знаком, получим
7?3(х). Процесс деления продолжаем до тех пор, пока не будет полу-
чен остаток, являющийся постоянной величиной. Эту величину также
берем с противоположным знаком.
Получаем последовательность функций
Рп(х), Рп(х), /?!(», т?2(х).... Pm-i(x), Рт = const.
В эту последовательность подставляем вместо х сначала а, затем b
и подсчитываем числа перемен знака в обоих случаях [обозначим по-
лученные числа соответственно через W (а) и IF(6)J. Тогда W (а)
> W(b), и разность W (а) — W (Ь) в точности равна количеству
действительных корней уравнения Рп(х)у заключенных между а и 6*
При помощи правила Штурма можно определить число отрицатель-
ных корней уравнения Рп(х) = 0 [т. е. определить количество действи-
тельных корней уравнения Рп(х) ~ 0 в интервале (—оо, 0)], а также
число положительных корней [в интервале (0, + оо)]. Правило Штур-
ма применяется также для отделения корней. Функции, входящие
в систему Штурма, можно умножать и делить на произвольные поло-
жительные числа. Это значительно упрощает работу, когда произво-
дится деление с остатком.
Пример 3. Определить количество действительных корней уравнения 5х3 —
— 20х + 3 = 0, а также отделить эти корни, пользуясь правилом Штурма.
Решение. Составляем систему функций Штурма. Имеем
рп (х) = 5хз _ 20х + 3, Рп (х) = 15х2 — 20.,
Для определения Rf (х) умножим Рп (х) на 3 и затем разделим на Рп (х):
15х3~60х+9 I 15x2—20
Т15х3±20х I х
— 40х+9
Значит, (х) = 40х — 9 (остаток взяли с противоположным знаком). Умножим
Рп (х) на 8 и разделим это произведение на (х):
146
120х2— 160 I 40х—9
Т120х2±27х j 3x+27
40(27х—160)
40.27х—40-160
Т40-27х±9-27
Поскольку последний остаток является постоянным числом со знаком « — »
(а нас в этом случае интересует именно знак постоянного остатка), меняем его на
противоположный, т. е. на « + ».
Составляем следующую таблицу знаков функций, входящих, в систему
Штурма:
X «2 W(x)
— оо —, + *11 1^ + 3
0 4- + 2
4~ оо + + 4- + 0
Из таблицы видно, что в интервале ( — оо , 4* ) содержатся три дейст-
вительных корня [так как IF ( — оо) — № ( + оо ) = 3—0 = 3]. Из них
один является отрицательным [ IT ( — оо ) — IF (0) — 3—2 — 1], а два — поло-
жительными [IF (0) — IF ( 4- оо) = 2—0 ~ 2],
Отделим корни по правилу Штурма, сократив интервалы до длины, равной 1:
X Рп (X) R-L (X) «2 (X)
— оо + — + 3
— 3 — + — + 3
—2 4- + .— 2
— 1 + + + 2
0 + — + 2
1 — + + 1
2 + + + + 0
Из последней таблицы видно, что корни расположены в интервалах
( - Зр - 2), (0, 1), (1, 2).
§ 3.12. Нахождение области существования корней
алгебраического уравнения
Правило кольца. Пусть дано алгебраическое уравнение
Рп (х) = а0 хп4- аххп~г + а2 хп~г +... + an-iх + ап = 0,
еде а0, alt ап — действительные коэффициенты, и пусть
Л = тах{|а1|, |аа|,В = тах{|а0|, |«i|, | an-i IT
Тогда корни уравнения заключены в круговом кольце г < | х [ < R, где
1 о 1 < А
г = ---------; R — 1 + -—- .
1 В/\ ап\ I so I
147'
При этом г — нижняя, a R — верхняя граница положительных кор-
ней алгебраического уравнения Рп(х) = 0, и —R, —г соответственно
нижняя и верхняя граница отрицательных корней.
Пример 1. Определить границы корней уравнения 5х3 — 20х +3=0,
Решение, Здесь | aQ | = 5, А — 20, | ап | = 3, В = 20, т, е.
Тогда, если действительные корни уравнения бх3—
—20х +3 = 0 существуют (а они обязательно суще-
ствуют, так как уравнение нечетной степени), то они
расположены в интервале ( — 5, 5); при этом отрица-
тельные корни лежат в интервале ( — 5; — 0,013), а
положительные — в интервале (0,013; 5).
При решении уравнений удобно сначала установить границы кор-
ней, а потом уже применять правило Штурма. По правилу кольца эти
границы определяются весьма приближенно.
Укажем прием более точного определения границ действительных
корней алгебраического уравнения Рп(х) ~ 0.
Если Ri — верхняя граница положительных корней Рп(х), —
верхняя граница положительных корней Рп(—х), R3 >> 0 — верхняя
граница положительных корней х/гРп(~-)иТ?4—верхняя граница по-
ложительных корней хпРп [—, то все отличные от нуля действитель-
ные корни уравнения Рп(х) = 0 (если они существуют) лежат внутри
интервалов (——£-) и Ri) *
Для определения верхней границы положительных корней алге-
браического уравнения можно воспользоваться методами Лагранжа
или Ньютона.
Метод Лагранжа. Если коэффициенты многочлена
Рп(х) = aQxn + а^1 + a2xn~* + ... + ап
удовлетворяют условиям aQ > 0, аъ а2, > 0, am<z 0, то верх-
няя граница положительных корней уравнения Рп(х) = 0 находится
по формуле
т / ЁГ
*=,+]/
где В — наибольшая из абсолютных величин отрицательных коэффи-
циентов Рп{х),
148
Пример 2. Методом Лагранжа определить границы положительных и отрица-
тельных корней уравнения 8Х4 — 8х2 — 32х + 1 = 0.
Решение. Здесь а0 = 8 > 0; ai = 0; о2 — — 8 < 0; а3 — — 32, а4 = 1,
= 2 (номер первого из отрицательных коэффициентов), В — 32. Следова-
тельно, 7?! = 1 + 1/32/8 =а 3.
Рассмотрим многочлен
Рл ( — *) = Зх4 — 8х2 + 32х + 1.
Аналогичным образом находим, что для него верхней границей положительных
корней служит Z?2 = 1 + 1/8/8 = 2.
Далее, для многочлена
х4 Рп ( — ) = X4—32х3—8x2 4- 8
\ х /
имеем п0 = 1 > 0, щ ~ — 32 < 0, т» е. т = 1, В = 32, и значит, = 1 +
4- 32 == 33.
Наконец, для многочлена
ж4 Рп Г-|-^=х44-32х8—8x5+8
имеем п0 = I > 0; Oj = 32; а2 = — 8, о3= 0, сц == 8, т. е. т = 2, В = 8. По-
этому /?4= 1 + 1/8'= 1 + 2Д/Т= 3,828.
Следовательно, если уравнение 8Х4 — 8х2 — 32х +1 = 0 имеет действи-
тельные корни, то они обязательно лежат в интервалах ( — 2; — 1/3,828) и
(1/33; 3).
Метод Ньютона. Если при х ~ с многочлен
Рп W = аохП + а1 хп~1 + — + ап
и его производные Рп(%), Рн{х), принимают положительные значе-
ния, то с является верхней границей положительных корней уравне-
ния Рп(х) = 0*
Пример 3. Методом Ньютона определить верхнюю границу положительных
корней уравнения 8Х4 — 8х2 — 32х +1 = 0.
Решение. Находим
Р (х) = 8х4 —8х2 —32х+1; Р' (х) = 32х3 —16х—32;
Р" (х)=96ж2—16; Р'1( (ж) = 192х; PIV (ж) = 192.
Проверке подлежат только значения х > 0. При х = с = Г имеем Р (1) < 0.
ВначиТд проводить далее проверку для х = 1 не следует. Проверим х — с = 2:
Р(2)>0, Р'(2)>0, Р"(2)>0, Р"'(2)>0, PIV>0.
Таким образом, верхней границей положительных корней является число 2,
т. е. R = 2. В качестве нижней границы можно взять число, обратное R, т. е.
г = 1/2.
И9
§ 3.13. Вычисление значений многочлена. Схема Горнера
Вычисление значений многочлена. Пусть дано алгебраическое урав-
нение
Рп (х) = а0 хп + И1 х""1 + а2 хп~2 +... + ап-1 х + ап = 0.
Как известно, корнем уравнения Рп(х) = 0 называется такое значение
неизвестного х, которое обращает многочлен Рп(х) в нуль. Поэтому су-
щественное значение приобретает вопрос о вычислении значения мно-
гочлена. Вычислить значение многочлена Рп(х) при х — £ можно не-
посредственной подстановкой g в многочлен Рп(х), т. е, нужно найти
Рп (I) - а. + at + а, +... + ап^ g + ап.
Если при этом Рп (£) = 0, то g — корень уравнения Рп(х) = 0. Вы-
числение значения многочлена тесно связано с вопросом о делимости
многочлена на линейный двучлен (многочлен первой степени). Если
разделить многочлен Рп[х) на’ линейный двучлен, то остаток будет
либо некоторым многочленом нулевой степени, либо нулем, т. е. не-
которым числом г. Следующая теорема позволяет найти этот остаток,
не выполняя самого деления, когда производится деление на многочлен
вида х —
Теорема Безу. Остаток от деления многочлена Рп(х) на деучлен
х — I равен значению этого многочлена при х =
Доказательство» Пусть
Р„(х) = (х — g) g(x) + г,
где g(x) — многочлен степени на единицу меньшей, чем Рп(х). Найдем
значение Рп(х) при х = %:
рп ш = (!-£) g® + г = г,
что и требовалось доказать.
Следствие. Число I является корнем многочлена Рп(х) тогда
и только тогда, когда этот многочлен без остатка делится на двучлен
х—%.
Если многочлен Рп(х) делится на некоторый многочлен первой сте-
пени ах + Ь, то он делится, очевидно, и на многочлен [% — (—Ь/а)],
т. е. на многочлен вида х — %. Следовательно, разыскание корней
многочлена Рп(х) равносильно разысканию его линейных делителей,
Пример 1. Определить остаток от деления многочлена
Р (х) = х5- + Зх4 — 2х3 + х2 — х + 1
на двучлен х — 3.
Р е ш е н и е, По теореме Безу находим
Р (3) = З5 + 3 > З4 — 2 * З3 + З3 — 3 + 1 =
= ь243 + 243 — 54 + 9—3 + 1 = 439.
Попробуем решить этот пример непосредственным делением на х — 3 Деле-
ние будем производить «углом»;
150
%$4-Зх*—2х3-]-х2—х+1 |__________x—3___________
ух§±3х4 I x44-6x3+ 16x2 4-49x4-146.
6x4—2x3
^FGx^lSxg
16x34“X2
=F 16x3 ± 48x2
49x2 — %
^F49x2 147x
146x 4- 1
T 146x ± 438
' 439 = r
Итак, остаток г — 439, а частное g (x) ~ x4 + бх3 + 16x2 + 49x 4“ 146 есть
многочлен степени на единицу ниже, чем заданный многочлен Рп (х).
Рассмотрим более простой метод деления многочлена Рп(х) на линей-
ный двучлен х —
Схема Горнера. Представим многочлен
Рп (х) = а0 хп + а1хп~1 + а2хп~2+ ... + ап„1х + ап
в виде
Рп(х) = (Х — В) g(x) + Ьп,
где
g (х) = b0 х'1'1 + bx хп~2 + b2 х”~3 +... + bn_y
т. е.
Рп (х) == (х—В) (&0 х^-1 + Ьг хп~2 4- Ь2 хГ1~3 +... + &п-1) + &п-
Раскрывая скобки в последнем равенстве, имеем
а0 хп 4- а, хп~г 4- а2х”-2 4-. •. 4- an-i х 4- ап =
= bQ хп 4- х11"1—Ьо Вл""14-^2 хп~2—Ь} txn~2 4- bs хп~3—b2 txn~3 4- ...
... 4" ^п—1 х Ьп—2 ^х 4- Ьп Ьп.~\ В>
После приведения подобных членов получим
а0 хп 4- ах хп-14- а2 хп~2 4- а3 хп~3 4- • • • 4- х 4- ап
== Ьо хп 4- (Ьх — Ьо В) х"-14- (bi—Ьг В) хп~2 4- (Ь3—Ь2 В) хп~3 4-.„
... 4- 0n-i—bп-г В) х 4- (&n—Vi %)-
В левой и правой частях последнего равенства находятся многочле-
ны от переменной х. Известно, что два многочлена считаются равными,
если равны их коэффициенты при одинаковых степенях неизвестно-
го х. Поэтому:
151
&о
bQ%, Ь^Ь01 + аь
U2 “ ^2 ^1 ^2 ^1 4” ^2»
«з = b3—b21 или &3 = M +
a^b*— b3 E, fe4 = M +
ап-1 — ^п—1 Ьп—2^> an = bn — bn^t, Ьп—1 — 2 В *Г ^п—1> ьп =bn^+an = r=P(l).
Как видно из последних равенств, каждый последующий коэффициент
Ьг получается умножением предыдущего Ь^г на g и прибавлением со-
ответствующего коэффициента ар, так же находится и остаток п
Вычисления удобно располагать по следующей схеме (называемой
схемой Горнера):
«2 а3 ... ап
м ьа Ь31 ... Ьп-1 §
ьо 61 62 63 bi ... 6п-1 6п = Г
В первой строке выписывают коэффициенты многочлена Рп(х) (отри-
цательные коэффициенты со знаком «—», перед положительными коэф-
фициентами знак «+» можно опустить). В третью строку сразу же пе-
реносят ад = 60. Затем каждый коэффициент Ь^ умножают на £ и под-
писывают под следующим коэффициентом а/+1. Числа первой и второй
строки складывают и результат bi+r записывают в третьей строке.
Таким образом, в третьей строке записаны коэффициенты частного,
полученного от деления многочлена Рп(х) на двучлен х — и оста-
ток, численно равный значению этого многочлена при х = 2, т. е*
- РпО) - г.
Пример 2. Пользуясь схемой Горнера, произвести деление многочлена
Рп (х) = + Зх4 — 2х3 4-х2 — х 4~ 1
на двучлен х — 3.
Решение. Составляем схему Горнера для данного многочлена:
1 3 —2 1 — 1 1
3 • 3 18 48 147 438
1 6 16 49 146 439=Р(3)=г
Таким образом,
г = Рп (3) = 439, g (х) = х4 4- бх3 4- 16х2 4- 49х 4- 146
(этот пример ранее мы решали путем деления «углом»). Следовательно,
Рп (х) = (х - 3) (х4 4- бх3 4- 16х2 4“ 49х 4- 146) 4- 439.
152
Пример 3. Определить, является ли £ = 1 корнем уравнения
х3 + 2х2 — 3 = 0.
Решение. Если £ = 1 является корнем уравнения Рп (х) = х3 + 2х2 —
—3 = 0, то многочлен Рп (х) должен без остатка делиться на двучлен х — 1.
Будем решать пример, используя схему Горнера. Учитывая, что в многочле-
не Р (х) = х3 + 2х2 — 3 коэффициент при неизвестном в первой степени равен
нулю, составим следующую схему:
1 2 0 *-3
1 1 3 3
1 3 3 0
Итак, Р (1) == 0 (остаток г — 0) и, значит, 5 1 является корнем заданного
уравнения.
Известно, что всякий многочлен
РП (*) = а0хп + Хп~1 + а2 хп~2 4-... + an_! X 4 ап
с действительными коэффициентами можно представить и притом един-
ственным способом в виде произведения своего старшего коэффициента
и нескольких многочленов степени не выше двух с действительными
коэффициентами. Линейные множители в этом разложении соответ-
ствуют действительным корням уравнения Рп(х) = 0, а квадратич-
ные — парам комплексно-сопряженных корней, т. е.
Pn(x) = a0(x—(х—...
...(x24-p1x + <71)z*(^2 + ^ + ‘72)G — (x2+pmx-]- qm)‘m = 0-
Квадратные трехчлены, входящие в разложение, действительных кор-
ней не имеют и уже не могут быть разложены на линейные множители
с действительными коэффициентами.
Таким образом, зная разложение многочлена на множители, мож-
но свести задачу отыскания корней уравнения Рп(х) = 0 к решению
совсем простых уравнений. Одним из таких методов является выше-
изложенный метод Горнера. Для деления многочлена на квадратный
трехчлен вида х2 + рх + q также имеет ся.очень удобная схема.
§ 3.14. Схема деления многочлена на квадратный трехчлен
Разделим многочлен
Рп(х)=а0 хп + аг хп_1 + й2 xn~2+-.- + an-i* + fln
на трехчлен вида ср(х) = х2 + рх 4- q. Можно записать
с0 хп 4- х""14- аг хп~2 4- ••• + «п-iх + ап =
= (х2 4- рх 4- q) (bQ хп~2 4- хп~3 4- Ьг xn~i 4-... 4- bn_3 х 4~ Ьп_2) 4-
4-bn-ix + ^i-
153
Раскрывая скобки в правой части этого равенства, производя приве-
дение подобных членов и сравнивая коэффициенты при одинаковых
степенях х, получаем
«0 ” ^0» b0 = a0,
а1 = Ьг + рЬ0, b1 = a1—pb0,
ai~b3-\-pbiA-qb3, bi = ai—pb1—qb0,
a^bs + pbi + qby b3 = a3—pb2—qblt
a^bi + pbs + qb^, или ^4 ~ Qb3,
a5 = b.0 + pbt + qb3> Ь5 = а5—рЬь~^Ь3,
—2 ~ ^n—2 P^n—3 “b 4* 2 ” 6^71—2 P^n—3
an^ = bn_r + pbn^ + qbn~3) • ^n—i “ ^n—i pbn—z qbn-&
bn — an qbn~ 2>
Отсюда получаем следующую схему деления многочлена на квадрат-
ный трехчлен*
a, «1 a2 ^3 «4 cin~2 an-l an
—p —pbo —pbi — pbi —pb3 — pbn-2 Р^П~-2
—q —qb0 —qbi ~qb2 —qbn-i —qbn-з —qbn-2
&o bl ^2 Ьз bo ^П~2 bn~i bn
Пример, Разложить на множители многочлен
Рп W = & — 2х4 — 7*3 — ЗЗх2 - 30* - 25,
зная, что одним из сомножителей является квадратный трехчлен g (х) ~ х2 -f*
+ х + 1-
Решение. Многочлен Рп(х) нечетной степени, поэтому он имеет хотя бы
один действительный корень, который обязательно служит делителем свободного
члена. Таким образом, целыми корнями данного многочлена могут быть только
числа — 1 и 1, — 5 и 5, — 25 и 25.
Проверим по схеме Горнера, будет ли х = — 5 корнем многочлена:
1 —2 — 7 —33 —30 —25
—5 — 5 35 — 140 865 —4175
1 — 7 28 173 835 —4200=£0
Так как Р ( — 5) 0, то х = — 5 не является корнем многочлена Рп (х).
Проверим теперь х — 5:
154
1 —2 —7 -33 —30 —25
5 9 • 5 15 40 35 25
1 3 8 : 7 5 0
Итак, Р(5) = 0; следовательно, х = 5 — корень Рп (х). Данный многочлен
можно представить в виде
Рп (х) = (х - 5)(х4 + Зх3 + 8х2 4- 7х + 5).
Один из множителей & (х) == х2 + х + 1 нам известен, поэтому разделим на него
многочлен Q (х) — х? 4- Зх3 + 8х2 4* 7х 4" 5 по схеме деления многочлена на
квадратный трехчлен;
1 3 8 7 5
-1 • — 1 —2 1 ОЛ
— 1 — 1 1 to 1 СП
1 2 5 0 0
Итак, (х) == х2 4“ 2х 4- 5. Следовательно, многочлен Рп (х) можно пред-
ставить в виде произведения сомножителей с действительными коэффициентами
таким образом:
Рп (х) = (х - 5) (X2 4- X + I) (X2 4- 2х 4' 5).
Если потребуется найти корни уравнения Рп (х) = 0, то приравнивая нулю
каждый из сомножителей, легко определим эти корни:
а) х—5 — 0; хх — 5;
— 1±У~4 1 Уз
б) х2Ч-х-Н=0; х2,з=------2------=—Г ± 1 ~2~ 1
в) x24-2x-j-5 —0; Х4Л=—1 ± УТ:г5= —1 ± 2Z.
Здесь сознательно приведен очень простой пример, где многочлен Рп (х)
имеет точный корень, который легко установить, и где заранее известен квадрат-
ный трехчлен, являющийся делителем Рп (х).
Из вышеизложенного следует, что для нахождения корней алге-
браического уравнения Рп(х) = 0 нужно уметь разлагать многочлен
Рп(х) на множители (линейные или квадратичные). При этом сущест-
венную роль играет определение приближенного значения действи-
тельных корней уравнения (для получения линейных множителей),
а также способ построения квадратичного множителя.
Для нахождения приближенного значения действительных корней
алгебраического уравнения можно применять любые из ранее изло-
женных методов (методы проб, хорд, касательных, итерации, комби-
нированные методы).
Квадратичный множитель можно выделить различными способами.
В следующем параграфе мы рассмотрим один из них —способ Хич-
кока.
155
§ 3.15. Выделение квадратного трехчлена по методу Хичкока
Пусть задано алгебраическое уравнение
fn (х) = хп 4- Sj хп~14- а2 х’-8 4-... 4- оп-1* 4- йп = °- 0)
Разделим многочлен fn(x) на трехчлен
g2(x) = х2 4- рх 4- q (2)
с неопределенными коэффициентами; тогда получим тождество
/п(х) = (х2 4- рх 4- <?) L(x) 4- хР(р, q) 4- Q(p,q), (3)
где L(x) — частное от деления Д(х) на g2(x), а Р (р, q) и Q(p, q)—много-
члены от р и q.
Для того чтобы трехчлен g2(x) был делителем /п(х), необходимо и
достаточно, чтобы Р(р, q) = 0 и Q(p, q) = 0.
Если решить систему
Р (р, q) = 0, Q(p, о) а 0, (4)
то тем самым и будут найдены коэффициенты квадратного трехчле-
на (2).
Этот метод выделения квадратного трехчлена и называется ме-
тодом Хичкока. Он по существу является разновидностью метода Нью-
тона для решения систем уравнений, однако здесь не используется яв-
ный вид многочленов Р (р, q) и Q (р, q). Их значения и значения произ-
водных, нужные в методе Ньютона, находятся путем двукратного де-
ления /п(х) на приближенное выражение gz(x).
Разделим многочлен L(x), входящий в соотношение (3), на трех-
член (2) и запишем тождество
1(х) = (х2 4- рх 4- q)Li(x) 4- xR(p, q) 4- S(p, q). (5)
Подставляя Цх) в равенство (3), получим
/4(х) = (х2 4- рх 4- q^Liix) 4* (х2 4- рх 4- q}\.xR(p, q) 4- S(p, q)l 4-
4- xP(p, q) 4- Q(p, q). (6)
Дифференцируя последнее равенство по р и q, имеем
(fn (х))р = 2х (X2 4- рх 4- q) (X) 4- (Lx (х))₽ (х2 4- рх 4- ?)2 4-
_+xiR(p,q) + xS(p,q) + xP'p(j),q) + Qlp(p, q), (7)
(fn (х)Уч = 2 (х2 4- рх 4- q) (х) 4- (Ьх (х)) q (х2 4- рх 4- q? 4-
4-xR (р, q) + S (р, q) 4-xP'q (р, q) 4-Qq (P, q)-
Пусть аг (где i — 1, 2) — корни квадратного трехчлена (2). То?
гда при подстановке аг в выражение (2) получим
£2(аг) = а/ 4- pat 4* q = 0
(корень аг обращает квадратный трехчлен в нуль). Следовательно,
а] — — pcii — q (i = 1, 2). (8)
156
С другой стороны, подставляя аг в равенства (7), имеем
(a* R (р, q) + atS (р, 9) + а, • Рр (р, q) + Q'P (р, q) = О,
R (р, q) + S (р, q) + aiP’q (р, q) ф- Qq (р, q) = 0.
Используя соотношение (8), запишем равенства (9) в виде
[Р₽ (р. ч)+s (р, q)—pR (р, q)]+[Qp (р, <?)—qR <р> <?)] = о, 10)
(а, [Р« (р. 9) + R (Р, 9)1 + [Q? (Р. q)+ s (р, q)] = 0.
Если трехчлен (2) имеет различные корни (ах #= а2), то из соотно-
шений (10) вытекает равенство нулю каждой из квадратных скобок,
т. е.
Рр(Р.9) = рР (рл) —S(p, 9)>
Qp(p,q) = qR(p,q), ,, n
' Р'(Р.9) = -Р(Р.9).
Q? (р. 9) = — S (р, 91-
Таким образом, двукратное деление многочлена fn(x) на трехчлен
g^x) — х2 + рх + q дает возможность получить частные производные
от Р(р, q) и Q(p, q) по р и q и затем решать систему (4) по методу Нью-
тона.
Если уже известно k -е приближение pk и qh, то уточнение коэффи-
циентов делителя g2(x) производится по формулам
Ph+i^Pk + К, где ^=-^,
k (12)
9k+i = 9h + ^- где =
Afe
a Aft, Apft и A(?ft, в свою очередь, определяются так:
д = Pp(Pfe>9s) P?(Pfe>9ft)
к Qp(Pk>4k) QpiPk^h)’
Pq (Р/р 9k) Р (Рк» 9k) (13)
k_____________________________________________Q'4(Ph>qk) Q(p>k’qk)
До = P(Pk’9k) Pp(Pk>9k)
h Q(ph,qh) Q'p(ph<qh)
Значения производных находятся по формулам (11):
P'P(Pk’4k) = PkRk — s.v P'APk’Pk)^— R»
Qp (Pk> Pk)=9k Rk> Qp (pk> Чк) = — Sa.
Величины P(ph, qk) и Q(pk, qk) определяются по формулам (3), a Rh
и Sft — по формулам (5) при подстановке в них р — ph и q = qh.
Расчеты удобно оформлять в виде двух вычислительных схем, од-
на из которых служит для двукратного деления на g% (х), а другая —
для вычисления поправок и tk.
157
Пример/ Решить уравнение
х4 + 4Х3 + 4,8х2 + 16х + I =*0
с точностью до 0,001 при помощи выделения квадратичного множителя.
Решение. Отделим какие-нибудь два корня уравнения, определяя
знаки функции / (х) — х4 + 4х3 + 4,8х2 + 1,6 х + 1 при некоторых значениях
аргумента х:
X 0 1 — 1 —2 —3 —4
sign f (х) — + —. — — +
Один корень лежит в интервале (0, 1), другой — в интервале ( — 4, — 3).
Примем xj ж 0,5; х2?=?—3,5, тогда за начальное приближение квадратичного
делителя многочлена f (х) можно взять
gV0 (Х) == Х2 + ( — 0,5 + 3,5) х — 3,5 . 0,5 = х3 + Зх — 1375,
где pQ = 3, <70 — — 1,75.
Расчеты оформим в виде схем (см. табл. 3.15, 3,16).
Таблица 3.15
k 1 4 4,8 16 1
0 11 ° Тз -О -Q II II II н cl cl Ол Си 1 1 О? 'со со .. 1 1 - 1 1 II 1 CN 1 1 —3 1,75 3,55 1,75 5,30 —So —10,65 1,75 7,1 = Л> 6,2125 5,2125 = Q0
1 —3,9 0,15 —3,9 0,15 1 1 -3,9 0,1 —3,9 - 3,8= —0,39 0,15 4,56 0,15 4,71 =Si —17,784 0,015 —1,769 = 0,684 —0,316=Qi
2 —3,79 0,23 —3,79 0,23 1 1 —3,79 0,21 —3,79 —3,58 = /?2 —0,7959 0,23 4,2341 0,23 4,4641 = S2 — 16,0472 0,0483 0,0011 = Р2 0,9738 —О,О262=(?2
3 —3,7889 0,2361 —3,7889 0,2361 1 1 СТ) —< сг> оо QO — оо г-- ОО —« оо Г''- 1- | СЧ О'- | ю со О оо со 1 1 1 —0,79984 0,2361 4,23626 0,2361 4,47236 —16,05077 0,04984 —0,00093 1,00018 0,00018
4 —3,78885 0,23607 1 —3,78885 0,21115 —0,800016 0,23607 4,236054 —16,04977 0,049846 0,000076 1,000005 0,000005
158
Т а б л и па 3.16
k ph «А ph р'р (.Ph- 4k) p'q (Ph- Ph) ДА Apfe hk
Ч Sh ч Qp (Pk- Ph) Qq (Ph- Ph) Д,?А *k
0 3 —1,75 —2 5,3 7,1 5,2125 —11,3 3,5 2 —5,3 52,89 48,055 83,751 0,9 1,6
1 3,9 —0,15 —3,8 4,71 — 1,769 —0,316 —19,53 0,57 3,8 —4,71 89,82 —9,533 —7,180 —0,11 —0,008
2 3,79 —0,23 —3,58 4,4641 0,0011 —0,0262 — 18,0323 0,8234 3,58 —4,4641 77,55 —0,0889 —0,4715 —0,0011 —0,0061
3 3,7889 —0,2361 —3,5778 4,47236 —0,0093 0,00018 — 18,0283 0,8447 3,5778 —4,47236 77,607 —0,0035^ 0,00246 —0,00005 0,00003
4 3,78885 —0,23607
Следовательно^
f (х) « (ха + 3,78885х — 0,23607)(х2 + 0,21115х + 4,23605) = 0.
Для нахождения искомых корней остается решить два квадратных урав-
нения:
1) х2 + 3,78885х — 0,23607 = 0, откуда
*1,2 = — 1,894425 ± V.3,588846+0,23607 = — 1,894425 ± 1,9557739,
т» е. Xi « — 3,8502; х2 « 0,0613;
2) х2 + 0,21115х + 4,23605 = 0, откуда
х3)4 = —0,105575 ± Уо,01115 — 4,23605 = —0,105575 ± 2,0555*,
т» е. х314 — 0,1056 ± 2,05557.
Таким образом,
хх л? — 3,850; х2 ~ 0,0613; x3j ~ —0,1056 ± 2,05557»
Упражнения
1. Отделить корни аналитически и уточнить их до 0,001 методом проб:
а) х3 — х + 1 ~ 0; 6) х3 + 2х — 4 — 0; в) х4 + 5х — 3 = 0;
г) 2,2х — 2Л = 0; д) 2V — 2х3 — 1 = 0; е) 2х — 4х = О.
Ответы', а)—1,325; б) 1,180; в)—1,876; 0,578; г) 0,781; 2,401; д) 0,0; 0,399j
6,352; е) 0,310; 4,0.
2. Отделить корни графически и уточнить их до 0,001 методом хорд:
а) х3+х—3 = 0; б) х';-|-8х—6--0; в) х3-ф10х—9 — 0; г) х2—cosjix = 0;
д) х2—sinnx = 0; е) 1g х—— = 0.
х2
Ответы*. а) 1,213; б) 0,706; в) 0,841; г) — 0,438; 0,438; д) 0,0;‘0,787; е) 1,897.
3. Методом касательных с точностью до 0,001 найти корни уравнений:
а) х3—6х24-Эх—3 = 0; б) х3—12х—8 = 0; в) х3 + 4х2—6 = 0;
г) 2 1gx—“^“+1—0; Д) х?—20sinx = 0; е) х — cosx = 0.
Ответы: а) —4,071; 0,468; 0,993; б) —0,695; —3,067; 3,757; в) — 3,523;
— 1,567; 1,086; г) 0,398; 4,682; д) 0,0; 2,753; е) 0,739.
4. Комбинированным методом хорд и касательных с точностью до 0Л001
найти корни уравнений:
а) х34~6х—5 = 0; б) х3—2х-р7 = 0; в) х3—2х24-х+1=0;
7
г) 1,8х2 — sin 10х = 0; д) 1gх —---= 0; е) 2х-1пх —1=0
2х+6
Ответы*, а) 0,760; б) — 2,258; в) — 0,465; г) — 0,567; — 0,335; 0,0; д) 3 473;
е) 1,422.
5. Пользуясь методом Штурма, отделить корни уравнений и уточнить их до
0,001 методом итерации:
а) х3 4- 4х — 3 = 0; б) х4 — 2х — 1 = 0;
в) — 5х + 2 = 0; г) х4 + х — 3 = 0.
Ответы*, а) — 0,532; 0.653; 2.879; б) — 0.475; 1.395; в) — 1.582; 0,402;
1,372; г) — 1,453; 1,164. '
160
6, Методом итерации найти корни уравнений с точностью до 0,001:
а) 1пх + О4~1)3“0; б) Д/х + 1—— ; в) х—cosx = 0;
х
г) 31 — cos х —-1 — 0; д) x+lgx = 0,5.
Ответы, а) 0,187; б) 0,755; в) 0,739; г) 0,607; д) 0,672.
7. Решить с помощью метода Ньютона системы двух уравнений, результаты
получить с пятью верными цифрами. Начальное приближение найти графически:
pin (х + у) — 1, 1х — —0,2,
Ь2 + </2-1
б)
pin (% + #) — 1 fix == —0,1,
(x2 + i/2= 1
х > 0, у > 0;
р§(^+0,4) = ха,
В) l0,5x2 + 2i/2 = l
х > 0, у > 0;
х > 0, у > 0;
—ха—у + 1,5,
iU+0»5)2 + z/2 = 1,0.
Ответы: а) 0,99386; у = 0,11065; б) х = 0,67975; у = 0,73344; в) х = 1,1077;
у = 0,43962; г) х = 0,38951; у = 0 45692.
8. Решить системы уравнений методом итерации. Результаты получить
с пятью верными знаками:
(2х?—ху — 5х+1~0, fx2#2—Зх3—6t/3+8 = 0,
а) \ бм
- lx + 3 1g х — г/2 —0; (х4—9// + 2 = 0;
(sin х—у— 1,32,
в) <
tcos у—х~ —0,85.
Ответы: a) xj = 1,4589; у^ — — 1,3968; х2 = 3,4874; у* = 2,2616; б) х^
= — 2,0000; уг — 2,0000; х2 = 1,3508; у2 == 0,59214;" в) х = 1,7913;
у = — 0,34422.
9. Используя метод Хичкока выделения квадратного множителя, найти
с пятью верными цифрами корни уравнений:
а) х3 — Зх2 - 3 = 0; б) х3 — х - 1 = 0; в) х4—бх3 + 11х2 + 2х — 28-0.
Ответы: а) 3,2790; — 0,13951 ± 0,94628 i; 6) 1,3247; — 0,66236 ± 0,56228 г,
в) - 1,2361; 3,2361; 2,0000 ± 1,7321 I.
Глава IV
ИНТЕРПОЛИРОВАНИЕ И ЭКСТРАПОЛИРОВАНИЕ
§ 4.1. Способы задания функций
В практической деятельности постоянно приходится сталкиваться
с необходимостью выявления форм связи в процессах и явлениях
и необходимостью их математического описания.
Остановимся на таких формах связи, для которых некоторая ве-
личина у, характеризующая процесс, зависит от совокупности несвя-
занных между собой величин х2, ...» хп таким образом, что каждому
набору (хх; х2; хп) соответствует единственное значение величины у.
161
Такое однозначное соответствие величины у совокупности независи-
мых переменных х2,...» хп называется функциональной зависимостью,
а сама переменная величина у — функцией переменных величин х15
х2, ЧТО формально записывается в виде
У = f(xi, хг..х„).
Так, выражение у — х\ + 3]/х2 + xix% является функцией трех
переменных.
Если величина у есть функция одной независимой переменной х,
то эту связь можно представить соотношением следующего вида;
у = Кх)-
Например, площадь круга S является функцией независимой пере-
менной — радиуса круга R, т. е. S = f(R); конкретный вид этой функ-
ции S = л/?2. Объем фигуры является уже функцией трех измерений:
V = f(xu х2, х3), и в зависимости от вида фигуры эта функциональная
связь соответственно конкретизируется.
Из курса математического анализа известны три способа задания
функциональных зависимостей: 1) аналитический; 2) графический;
3) табличный.
Наиболее удобным способом задания функциональной зависимости
У “ Кх) является аналитический, так как он прямо указывает дейст-
вия и их последовательность выполнения над независимой переменной
х для получения соответствующего значения величины у.
Так, например, в результате математической обработки можно по-
лучить следующую аналитическую зависимость денежных кредитов
в сельском хозяйстве под товарно-материальные ценности и сезонные
затраты от затрат на крупный рогатый скот:
у - 51,0203 + 0,1059 х,
где у — кредиты под товарно-материальные ценности; х — затраты
ца крупный рогатый скот.
Другой пример аналитической зависимости: связь пути со време-
нем в равноускоренном движении выражается как
Положительным качеством аналитического способа задания яв-
ляется возможность получать значения у для любого фиксированного
аргумента х с любой точностью.
К недостаткам этого способа следует отнести то, что приходится
производить всю последовательность вычислений; кроме того, ана-
литический метод не обладает наглядностью.
Указанные недостатки аналитического способа устраняются в слу-
чае графического задания функции у = Дх).
Графиком данной функции у — Дх) называется геометрическое
место точек плоскости хОу, координаты которых удовлетворяют урав-
нению у ~ Дх).
162 <
Табличный способ задания функций распространен в технике, фи-
зике, экономике, естествознании (и чаще всего возникает в резуль-
тате эксперимента).
Пусть, например, в результате опыта получена зависимость оми-
ческого сопротивления R медного стержня от температуры t° в виде
следующей таблицы:
R 77,80 79,75 80,80 82,35 83,90 85,10
tQ 25,0 30,1 36,0 40,0 45,1 50,0
В этом эксперименте значение омического сопротивления медного
стержня меняется при колебаниях температуры и является зависимой
переменной.
Преимуществом табличного способа задания функции является то,
что для каждого значения независимой переменной, помещенной в таб-
лицу, можно сразу же, без всяких измерений и вычислений, найти со-
ответствующее значение функции.
Недостаток табличного способа состоит в том, что нельзя задать
всю функцию сплошь, т. е. всегда найдутся такие значения независи-
мой переменной, которых нет в таблице,
§ 4.2. Математические таблицы
Среди функций, постоянно встречающихся в математике, много
таких, вычисление которых, несмотря на их простоту, довольно гро-
моздко, В этих случаях вычислительную работу облегчают математи-
ческие таблицы.
Наиболее распространены таблицы функций одной переменной.
К ним относятся таблицы обратных чисел, квадратов и кубов чисел,
квадратных и кубических корней, таблицы логарифмов, таблицы три-
гонометрических функций, таблицы показательной и других элемен-
тарных функций, Составляют таблицы функций двух и большего числа
переменных. Примером таблицы функции двух переменных может слу-
жить таблица произведений двух чисел.
Таблица представляет собой набор значений функции для последо-
вательности значений аргументов х0, хъ х2, ..., хп. Она должна содер-
жать такой набор значений аргумента, чтобы для любых значений ар-
гумента, отличных от х0, хъ х2, ..., хп, можно было получить значение
функции с необходимой степенью точности.
Основными характеристиками таблиц являются: 1) название функ-
ций, значение которых они выражают; 2) объем; 3) шаг; 4) количество
знаков табулируемой функции; 5) количество входов.
Названием функции, численные значения которой собраны в таб-
лице, является аналитическое выражение этой функции, например
sin х, 1g х, ех и т, д,
163
Объем таблицы выражается начальным и конечным значением ар-
гумента. Так, например, объем таблицы у = sin х охватывает значения
аргумента от 0°0' до 89°54'.
Почти для всех табулируемых функций значения аргумента в таб-
лице образуют арифметическую прогрессию, разность которой h на-
зывается шагом таблицы. Таким образом,
h = х^ — Xi ~ const (i = 1,2, ...» и),
или
Xj = Xq + h, x2 = x0 + 2Л, ... .
В качестве иллюстрации рассмотрим фрагмент таблицы перевода
радианов в градусы и градусов в радианы (табл. 4.1).
Таблица 4.1
Радиа- ны Граду- сы Радиа- ны Граду- сы I ра- ДУ сы Ради- аны Гра- дусы Ради- аны Ми- нуты Ради- аны Ми- нуты Радиа- ны
(1) (2) (3) (4) (5) (6) (7) (8) (9) (Ю) (11) (12)
0,20 11,459 0,70 40,107 20 0,34907 70 1,22173 20 0,00582 50 0,01454
21 12,032 71 40,680 21 36652 71 23918 21 00611 51 01484
22 12,605 72 41,253 22 38397 72 25662 22 00640 52 01513
23 13,178 73 41,826 23 40143 73 27409 23 00669 53 01542
24 13,751 74 42,399 24 41888 74 29151 24 00698 54 01571
В первых двух колонках приведенной таблицы в качестве неза-
висимой переменной выступает радианная мера, а градусы рассмат-
риваются как ее функция. То же справедливо и для третьей и четвер-
той колонок. В качестве шага таблицы здесь выбирается h = 0,01
радиана.
Начиная с пятой колонки, рассматривается функция, обратная
данной, где в качестве независимой переменной выбираются градусы
(или минуты), а соответственно радианная мера является функцией
градусов (или минут). Шаг этой части таблицы равен одному градусу
(в пятой и седьмой колонках) и одной минуте (в девятой и одиннадца-
той колонках).
В справочных таблицах используется также и сложный двухуров-
невый шаг. По вертикали откладываются значения аргумента, отличаю-
щиеся на так называемый «грубый» шаг X; = х^ + Я* (i = 1, 2, .... п),
и соответствующие им значения функции уг = f(xt) = f(xt„1 + h*),
а по горизонтальной линии располагаются значения функции в точ-
ках, отстоящих друг от друга на шаг, равный в большинстве случаев
десятой доли «грубого» шага: h ~ 0,1 h*. Так, в табл. 4.2 на стр.
165 приведен фрагмент таблицы кубических корней. Из приведен-
ного фрагмента таблицы нетрудно определить «грубый» шаг по
вертикали, равный Л* = 1, и более точный шаг по горизонтали,
равный h = 0,1.
Обычно шаг таблицы выражается одной единицей какого-либо раз-
ряда (реже двумя или пятью единицами определенного разряда). Так,
в таблицах квадратов, кубов, квадратных, кубических корней, в таб-
161
Таблица 4.2
0 1 2 3 4 5 6 7 8 9
60 8,43433 43901 44369 44836 45303 45769 46235 46700 47165 47629
61 8,48093 48556 49018 49481 49942 50403 50954 51324 51784 52243
62 8,52702 53160 53618 54075 54532 54988 55444 55899 56354 56808
63 8,57262 57715 58168 58620 59072 59524 59975 60425 60875 61325
64 8,61774 62222 62671 63118 63566 ' 64012 64459 64904 65350 65795
Таблица 4.3
0' 6' 12' 18' 24' 30' 36' 42* 48' 54' Г 2' 3' 4' 5'
65° 0,9063 9070 9078 9085 9092 9100 9107 9114 9121 9128 0,9135 24° 1 2 4 5 6
66° 0,9135 9143 9150 9157 9164 9171 9178 9184 9191 9198 0,9205 23° 1 2 3 5 6
67е 0,9205 9212 9219 9225 9232 9239 9245 9252 9259 9265 0,9272 22° 1 2 3 4 6
68° 0,9272 9278 9285 9291 9298 9304 9311 9317 9323 9330 0,9336 21° I 2 3 4 5
69° 0,9336 9342 9348 9354 9361 9367 9373 9379 9385 9391 0,9397 20® 1 2 3 4 5
лицах логарифмов «грубый» шаг Л* = 1, в таблицах натуральных
логарифмов, таблицах обратных чисел «грубый» шаг Л* равен 0,1
(см. табл. 4.2).
Если мы обратимся к таблице синусов (см. табл. 4.3 на стр. 165),
то в ней в качестве «грубого» шага выбирается один градус, более
точный шаг равен шести минутам.
Следующей характеристикой таблиц является количество знаков
табулируемой функции, так как значения функции у = f (х) для та-
булированных значений аргумента в математических таблицах и ре-
зультаты измерений в технических таблицах являются приближенны-
ми величинами.
При ручной отладке программ для ЭВМ расчеты ведут с помощью
таблиц, обладающих повышенной точностью. К ним относятся«Таблицы
семизначных логарифмов» Вега, «Таблицы Барлоу», содержащие квад-
раты, кубы, квадратные и кубические корни, а также обратные вели-
чины.
Для практических ручных расчетов наиболее употребительными
являются «Пятизначные математические таблицы» Б. И. Сегала
и К. А. Семендяева, «Справочник по математике» И. Н. Бронштейна
и К. А. Семендяева и т. д.
В таблицы вносятся только верные знаки числового значения функ-
ции; это означает, что погрешность не превышает пяти единиц первого
отброшенного разряда. При этом значения функции для всех значений
х, приводимых в таблице, определяются с одинаковой абсолютной по-
грешностью. Точность, с которой приведены в таблице значения функ-
ции, называется точностью таблицы. Иногда на разных участках таб-
лицы точность бывает разной.
В некоторых случаях при работе с таблицами необходимо знать
разности соседних приведенных в таблице значений функций. Эти
разности называются табличными разностями и обозначаются через
Аг/:
А^о = У1 “ &У1 = Уъ~ Уъ •••> Ьук = У^1 — Уъ-
Для разностей в таблицах иногда отводят отдельный столбец, а ча-
ще они выписываются в столбце значений функций в промежутке меж-
ду соответствующими ее значениями. Разности записываются в едини-
цах последнего разряда без нулей впереди значащих цифр и без запя-
той. Например, в таблице
х sin х
1,000 0,84147
1,001 0,84201
табличная разность Az/ = 0,84201—0,84147 = 0,00054 напечатана
между соответствующими значениям sin х значащими цифрами
как 54.
Следующей важной характеристикой таблиц является количество
входов в нее. Оно равнозначно числу аргументов функции. Так, таб-
166
липы для функциональных зависпмосчеи у = f{x) явл яснея таблт нами
с одним входом. К ним относятся приведенные выше таблицы 4.1,
4.2 и 4.3.
Табулирование функции двух переменных z = f (х, у) приводит
к таблице с двумя входами. Среди подобных таблиц широкое прак-
тическое применение находят таблицы умножения.
Таблица 4.4
1 2 ' 3 1 1 ’ 5 6 7 8 9
541 1082 1623 2164 2705 3246 3787 4328 4869
542 1084 1626 2168 2710 • 3252 3794 4336 4878
543 1086 1629 2172 2715 3258 3801 4344 4887
544 1088 ' 1632 2176 2720 3260 3808 4352 4896
545 1090 1635 2180 2725 3270 3815 4360 4905
В табл. 4.4 трехразрядное множимое записывается в левый столбец,
одноразрядный множитель — в верхнюю строку таблицы. Шаг обоих
входов в таблицу равен единице. Для получения произведения трех-
значного числа на однозначное достаточно найти строку, в первом столб-
це которой записано множимое, и выбрать тот столбец, в котором рас-
положен множитель. На пересечении найденных строки и столбца
и находится искомое произведение.
Пример 1. Пусть требуется умножить 543 на 8. В табл. 4.4 находим строку,
содержащую 543, и столбец под номером 8. На их пересечении читаем число
4344, что и является искомым произведением.
Для умножения многозначных чисел множимое разбивают на ча-
сти, содержащие не более трех цифр, и к каждой из этих частей при-
меняют указанный способ.
Пример 2. Пусть требуется умножить 541 544 на 37. Разбиваем число
541 544 на две трехразрядные части 541 и 544. Последовательно умножаем каж-
дую часть на 3 десятка и на 7 единиц, полученные частичные произведения
складываем:
541 х 30= 16230
541 X 7 = 3787
20017
544X 30=16320
544 X 7 = 3808
20128
Первое частичное произведение сносим на три разряда влево относительно вто-
рого и складываем:
,20017
20128
20037128
©то и есть искомый результат.
При работе с таблицами следует помнить, что в их расположении
бывают особенности. Поэтому, обращаясь к новому справочнику, не-
обходимо ознакомиться с его описанием.
167
§ 4.3. Математическая постановка задачи интерполирования
В экономике и технике постоянно приходится сталкиваться с не-
обходимостью вычисления значений функции у = Дх) в точках х,
отличных от значений аргумента, фиксированных в таблице. Кроме
того, в некоторых случаях, несмотря на то, что аналитическое выра-
жение функции у = Дх) известно, оно является слишком сложным и
неудобным для дальнейших математических преобразований. Подоб-
ные задачи практики формализуются как математические задачи ин-
терполирования.
Пусть на отрезке [а, Ь\ задана функция у = Дх) своими п + 1 зна-
чениями
Уо = й = /ЬО, .... уп = f (хп)
в точках х0, хь хп, которые назовем узлами интерполяции. Требует-
ся найти аналитическое выражение Г(х) табулированной функции
Уо У1 ••• Уп
Хр | Х1 * * * *п
совпадающей в узлах интерполяции со значениями заданной функции,
т. е.
У о = Ж) = f(x0), уг = Ж) = Ж), уп = F(xn) = f{xn).
Процесс вычисления значений функции в точках х, отличных от
узлов интерполяции, называют интерполированием функции Дх).
Если аргумент х, для которого определяется приближенное зна-
чение функции, принадлежит заданному отрезку [х0, хп], то задача
вычисления приближенного значения функции называется интер-
полированием в узком смысле. Если аргумент х находится за пределами
отрезка интерполирования [х0, хп], то задача определения значения
функции в точке х называется экстраполированием.
Геометрически задача интерполирования для функции одной пе-
ременной у = Дх) означает построение кривой, проходящей через точ-
ки плоскости с координатами (х0; #0), (х^ у^, ..., (хп; уп) (рис. 4.1).
Однако уже из рисунка интуитивно ясно, что через данные точки мож-
но провести бесчисленное множество различных кривых, Таким обра-
зом, задача отыскания функции Дх) по конечному числу ее значений
слишком неопределенна.
Эта задача становится однозначной, если в качестве интерполиру-
ющей функции F(x) для функции у = Дх), заданной п + 1 своими
значениями, выбрать многочлен Fn(x) степени не выше п, такой, что
W = z/o, Рп Ь1) = У1, •••> FnOn) = уп.
Многочлен ГЛ(х), удовлетворяющий этим условиям, называют
интерполяционным многочленом, а соответствующие формулы — ин-
терполяционными формулами^
168
В случае, когда F(x) выбирается
в классе степенных функций, интер-
поляция называется параболической.
Этот способ приближения основы-
вается на том, что на небольших
отрезках функция f(x) может быть
достаточно хорошо аппроксимирова-
на параболой определенного по-
рядка.
Иногда целесообразно использо-
вать другие виды интерполяции.
Если интерполируемая функция f(x)
— периодическая, то в качестве клас-
са {F(x)} выбирают класс тригонометрических функций; в некото-
рых случаях за класс {Е(х)} выбирают рациональные функции.
При интерполировании возникает ряд задач: 1) выбор наиболее
удобного способа построения интерполяционной функции для каждого
конкретного случая; 2) оценка погрешности при замене/(х) интерполи-
рующей функцией F(x) на отрезке [а, Ь], поскольку функции F(x)
и f(x) совпадают только в узлах интерполяции х0, х19 ..., хп; 3) опти-
мальный выбор узлов интерполяции для получения минимальной
погрешности.
§ 4.4. Интерполяционный многочлен Лагранжа
Наиболее общей формулой параболического интерполирования
является интерполяционная формула Лагранжа. Задача параболиче-
ского интерполирования в этом случае формулируется следующим об-
разом: на отрезке [а, 6] в узлах интерполяции х0, хх, хп задается
функция f(x) своими п + 1 значениями
Уо = f(X0), У! = /(%!), .... уп = Дхп);
требуется построить многочлен Цх) так, чтобы в узлах интерполяции
х0, xlt хп его значения совпадали со значениями заданной функ-
ции, т. е.
Ц*о) = = Уъ Цх-п) = Уп>
Следует отметить, что в такой постановке задачи узлы интерполя-
ции х0, хь ..., хп могут произвольно отстоять друг от друга на отрез-
ке [а, 6], иными словами, узлы интерполяции неравноотстоящие,
т. е. h = Xf+1 — Xt #= const (i = 0, 1, ..., n — 1); величина h называ-
ется шагом интерполяции.
Задача имеет решение, если степень многочлена L(x), которым мы
заменяем неизвестную функцию /(х), не выше т
Представим многочлен Цх) в виде
Ln(x) = aQ + агх + а2х2 + ... + апхп,
где at (i = 0, 1, ..., п) —неизвестные постоянные коэффициенты, ко-
торые нам надо найти. Из начальных условий известно, что функция
169
Ln(x) в узлах интерполяции х„, хт....... хп принимает значения
Ln(x0) = Уо, Ln(xi) = уъ .... Ln(xn) = уп. Тогда в узле интерполя-
ции х0 интерполяционный многочлен £л(х) имеет вид
^п(хо) “ яАх0 4~ я2хо 4” я^хо 4~ и. + п^х^,
в узле интерполяции х3 — ви;
Ln(Xi) = Яо + + я2х? + а3х? + + ялх"
и т. д, Наконец, в точке хп интерполяционный многочлен Ln(x)
есть
Ln(xn) = а0 + аххп + а2х„ 4- а3х„ + ... + апхд.
Запишем это в виде системы п + 1 уравнений с п + 1 неизвест-
ными а0, аъ а2, ап\
' a0 + a1x0 + a2x2 + «3x3 + ... + anx^0 = z/0,
a0 + fliX! + a2xf+ а3хЗ + ... + агехп1 = ^,
< а0 + «1 х2 + а2xi + а3 х| 4-... 4- ап хп2 = уг, u
. a0 + aiXn + a2x2n+aax3n + ... + anx" = yn,
где Xi и yt (i —0, 1, п)— табличные значения аргумента и функ-
ции.
' Неизвестные a0, alt ап найдем по формулам Крамера:
где А — определитель системы (1), Если А 0, то система имеет един-
ственное решение. Действительно, определитель этой системы
1 У уЗ уП
1 Ло Ло Ло ... Ло
у2 уЗ ул
AJ "1 '*'1 * * • "1
1 у у2 уЗ yfl
А Л2 Л2 Л2 ... Л2
I хп х\ ... х;
отличен от нуля, если х0, хъ ..., хп различны, Найдя коэффициенты
а0, alt ап, можно представить интерполяционный многочлен в виде
Ln (х) = Д^4-А-х4--^-х24-... + 4гхЛ-
АДА А
Перепишем этот многочлен в другой форме:
(л) “ z/ъ Qu (X) + yi Qx (х) -f- 4-^/nQn (х)< 2)
170
Отсюда следует, что функция Q,(x) должна удовлетворять условиям
, . . (0, если i i;
1, если 1 = !.
Легко проверить, что такой многочлен имеет вид
Q. (х) = • • • (*—*f-i) (x—xi+1) .., (х—хп) .
(Xi— X0)(Xi — Хх) ... (хг — Х;_х) (Xi— Xi+1) ... (Xi— xn)’ ' '
В точках x0, xlt ..., Xj_j, xi+1, .... xn функция Qj(x) обращается
в 0, а в точке xt равна 1.
Окончательно получим для формулы (2) выражение
, , v (X —Хх) (X —ХП) , „ (X —Х0) (X —Х2) ... (X—Хп) ,
ьп Д/о/ ч ч “V У1 . ч z ч < т*"
(ХО“Х1) ... (х0 — хп) (хх—х0) (хх — х2) ... (*1“*п)
... 4-^ (х~"хо) (х—*1) *п-1)
(хп хо) (ХП-Х1) ... (ХП-Хп~1)
Этот многочлен называется интерполяционным многочленом Ла&
ранжси В сокращенном виде его можно записать так:
I у и (Х—Хр) . . (х—Х^1) (Х—Хг+1) ,.. (х—хп)
п А 1 (^^...(^-^(^-^...(Хг-Хп) * W
Пример 1. Построить интерполяционный многочлен^ Лагранжа для функция!
заданной таблично:
1 | 2 | 3 5
1 | 5 | 14 81
Решение. Подставляем исходные данные в формулу (4); степень пол?|
ченного многочлена Лагранжа не выше третьей, так как функция задается зд»
тырьмя значениями:
, (х-2) (х-3) (х-5) . (х-1)(х-3) (х-5)
3U ‘ (1—2) (1—3) (1—5) + ’ (2-1) (2-3) (2-5)
(х-1) (х-2) (х-5) (х-1) (х-2) (х-3)
*4-14* " +81.-------------------
(3—1) (3—2) (3—5)
Пример 2. Функция f (х) задана
2х24~3х— 1.
(5—1) (5—2) (5—3)
таблично:
х
У
0 1 | 2 | 6
— 1 —3 | 3 [ 1187
|Тользуяеь интерполяционным многочленом Лагранжах найти ее значение в точ-
ке х = 4.
171
2
Решение. Подставляя в формулу (4) х = 4, имеем
, ... , (4-1) (4-2) (4-6) 4(4-2) (4-6)
sU ’ (-1)(-2) ( —6) ' 1(1-2) (1-6) +
4(4-1) (4-6) 4 (4-1) (4-2)
2(2 —1)(2 —6) г 6(6—1)(6— 2)
Если в рассмотренном примере добавить к таблице еще одну точку,
то вычисление значения функции при х = 4 придется производить
заново. Кроме того, из самого примера видно, что процесс получения
приближенного значения функции по интерполяционной формуле Лаг-
ранжа связан с большими вычислениями. Это приводит к необходи-
мости упрощения вычислительной работы.
Для удобства вычислений составим вспомогательную таблицу
х —х0 хо—X} х0—х2 ... х0 хп /г0
*1— *0 X — *1 —х2 X] — хп
х2 —х0 Х2—Xj X —х2 V2 —
...
хо *п —*1 хп—х2 X—хп
где xOt xlt х2, хп — узлы интерполяции, ах — значение аргумента,
для которого определяется приближенное значение по интерполяцион-
ной формуле Лагранжа. Обозначим произведение элементов первой
строки через
k0 = (х — х0) (х0 — хг) (х0 — х2) ... (х0 — хп). (6)
В общем виде произведение элементов j-й строки есть
^ = (Xf—Хо) (Xi—xj ...
... (Xi — x^i) (x — xt) (x—xi+1) ... (xt—xn). (7)
Числа k0, kA, ..., kn поместим в крайнем правом столбце таблицы.
Дополнительно вычислим произведение элементов, расположенных
на главной диагонали:
Пп+1 (х) = (х — ха) (х —Xi)... (х—хп). (8)
Тогда интерполяционный многочлен Лагранжа можно переписать
в виде
п
Ln(x) = nn+1(x)V-^. (9)
iTo kl
172
Пользуясь формулой (9), решим снова пример 2 (см. стр. 171). Составим
таблицу
4 — 1 —2 —6 —48
1 4 — 1 1—2 1—6 15
2 —-1 4—2 2—6 -16
6 6—1 6—2 4—6 —240
и найдем П4 (4) =* — 48, Приближенное значение функции в точке х *= 4, т. е.
f (4) ~ L3 (4), определим по формуле
Мх)=П4(х) 2
j=0 ki
ИЛИ
Г —1 —3 3 1187 1
I, (4) _ _48 265.
Интерполяционная формула Лагранжа заметно упрощается, если
узлы интерполяции равноотстоящие, т, е. h = Xj+1 — xt = const, где
h — шаг интерполяции. Введем обозначение q — (х — x0)/h. По фор-
муле (3) имеем
q ______ (х Хо) (X *1) ' * * (х Xj_i) (X Xj-f-j) * (х ХГ1) ,
1 ~ (Xj —Хо) (Xj —Х1) ... (Xj— Xj.j) (Xj—Xi+1) ... (Xj—xn) ’
так как
x—x0 — qh,
x—Xi — qh—h — h(q—1), '
X — Xi = qh—ih = h(q — i),
X—xn — qh—nh — h(q — n),
TO
Q (J) _ ?(?-!)••• И-0-1)] [?-(» +1)1
f ih (i— 1) h ... ft (— ft) ... I — (n — /) h]
Заметим, что часть произведения в знаменателе равна
ih(i — 1) h ... h — t\h\
а другая часть равна
(—h)... | — (n — i)h] = (— — i)! hn-1.
(10)
173
Умножив числитель и знаменатель правой части равенства (10) на
(—1)^~; {q— i), получим
Q (а) = л‘ п) (—_ j ух -1
iW (7_фЦ/г^)1 > q-i П\
(11)
где
С1 = _Л1—
n t! (n—1)! *
Интерполяционный многочлен Лагранжа для равноотстоящих уз-
лов интерполяции теперь можно записать в виде
Ln (х) = Ln (х0 + qh) = V„ 1 y-i А_у.. (12)
И! q—i
х = 0
§ 4.5. Оценка погрешности интерполяционного многочлена
Лагранжа
Интерполяционный многочлен Лагранжа Ln(x) совпадает с функ-
цией f(x) в узлах интерполяции х0, х1У х2, хп.
Чтобы оценить степень приближения интерполяционного много-
члена Лагранжа в точках, отличных от узлов интерполяции, надо сде-
лать дополнительные предположения о поведении функции Дх), задан-
ной таблично. Будем считать, что функция /(л) дифференцируема
п + 1 раз на отрезке la, М.
Представим погрешность в виде функции
R„ х) - f(x) - Ln(x) (1)
и введем вспомогательную функцию
ф(х) = Rn(x) — knn+1 (х), (2)
где
Пл+) (х) = (х — х0) (х — Xt) ,..(х — хп)
есть многочлен, обращающийся в нуль в точках х0, х15 хп. Функция
<р(х) имеет п + 1 корней, т. е. <р(х0) ~ ф(хл) ™ ••• =* ф(*п) = 0> гак как
в узлах интерполяции Rn(xt) ~ 0 (z ™ 0, 1, и) и один из сомножи-
телей функции Пп+1{х) равен нулю.
Подберем теперь коэффициент k таким образом, чтобы функция
Ф(х) имела еще один корень в любой фиксированной точке х отрезка
[а, Ь], но отличной от узлов интерполяции х0, хп> При этом
Пп+1 (х)=/=0> поскольку точка х отлична от узлов интерполяции, Точ-
ка х выбрана таким образом, чтобы qp(x) = 0, т, е.
Rn(x) — k(x — xQ) (х — xj (x — xn) = 0;
174
тогда получим
k W __ ЯЛ) (х)
Пп+1(х) (х Хо) (х ^1) • ♦ • (х Хд)
Определим численное значение коэффициента k. Для этого функцию
ф(х) продифференцируем^ + 1 раз. Так как ф(х) обращается в нуль
на la9 bl в п + 2 точках: х, х0, хь хп, то на основании теоремы Рол-
ля производная от ф(х) обращается в нуль по крайней мере п + 1 раз
на интервале (а9 Ь). Применим снова теорему Ролля к функции ф'(х)<
Вторая производная ф"(х) обращается в нуль не менее п раз на интер-
вале (а, Ь). Продолжая этот процесс, придем к выводу, что производная
(п 4- 1)-го порядка функции ф(х) имеет хотя бы один корень, т. е»
Ф n+D (gj = о. Кроме того, изг соотношений (1) и (2) вытекает, что
ф(х) = f(x) — Ln(x) — Шп+1(х).
Вычислим (и + 1)-е производные для каждого слагаемого вспомо-
гательной функции ф(х); имеем (х) = (п + 1)!, так как (п + 1)-я
производная от многочлена степени п + 1, старший коэффициент ко-
торого равен 1, есть (п + 1)f, a (х) = 0, поскольку (и + 1)-я
производная от многочлена степени п равна нулю. Тогда (п + 1)-Ю
производную от вспомогательной функции ф(х) в точке |сучеюм
сказанного выше запишем следующим образом:
1) (£) —& (/2 н- 1)! = 0,
откуда
. (4)
(л+ п!
Из формул (3) и (4) получим следующее равенство:
f(x) — Ln(x) _
(х — х0)(х —Х1) ... (х—Хп) (л4-1)1
Следовательно,
Ln(x) =,+ , Ч О — ^о) (* — ... (х-хп).
(я+1)’
Точки 5 и х принадлежат отрезку (а, Ы, а х выбрано произвольно.
Так как х — произвольная точка отрезка [а, 6], то можно записать
Rn (x) = f(x) — Ln = (х—х0) (х — хг)... (х — хп).
(л-Н)’
Полагая, что Л4п+1= max \j(n+[)(x)\ получаем оценку погреш-
х £ [а, Ь]
175
ности для интерполяционного многочлена Лагранжа:
Ifln (X) | = I f (х) — Ln (х) | < -~7- ) (х—х0) (х—xj ... (х—хп) I. (5)
Пример, С какой точностью можно вычислить “|/ТТ7 с помощью интерполя-
ционной формулы Лагранжа для функции у *= ~\/х, выбрав узлы интерполя-
ции х0 = 100; xj — 121; х2 *= 144?
1 13
Решение. Найдем у'= —х~ */2, у"~ — — х'“3/2, у'*' == — х“5/2.
8
Отсюда Л43 = тах j у‘"\ ПРИ Ю0<х<144. Ва основании нера-
венства (5) получим
3 1
|Я2| <— * 10-5. —- 1 (115— 100) (115— 121) (115— 140) I 1,6.10-3.
о 3!
§ 4.6. Конечные разности
Табулирование функций в большинстве случаев производится
для равноотстоящих значений аргумента, т, е. х$ = х0 + гд&
i = 0, 1, 2, n, a h — шаг интерполяции.
Для вывода интерполяционных формул для равноотстоящих узлов
интерполяции введем понятие конечной разности.
Поставим следующую задачу: для функции у = /(х), заданной таб-
лично своими значениями
У о = Дх0), у! = /(Xj), .... Уп = f(xn)
в равноотстоящих узлах интерполяции, построить таблицу конечных
разностей.
Назовем конечной разностью первого порядка разность между зна-
чениями функции в соседних узлах интерполяции, Тогда конечные
разности в точках х0, хъ х2, »..,хп_г определяются соответственно как
А Уо ~ Ух Уо ~ f (^i) f (^о) “ A f (%о)>
^У1 — Уч--У1 — } (x2)—f (Xi) = A f (хг),
А Уч = Уз—Уч = / (х8)—f (х3) = A f (х2),
А У п-i — Уп~ У п-i = t (хп) — f (xn_j) = A f (xn_i),
где h = const.
В общем виде первая конечная разность запишется так:
Ай = Уш — У1>
или
Ay ~ Af(x) — f{x + Ах)—f(x). (1)
В математической литературе используются несколько обозначений
конечных разностей:
&У1 ~ У г+х У11 ^У1-\~ 1/2 ” ^/г + 1 У11 X/ 2 “ Z/j-Ы Уь
176
Из конечных разностей первого порядка можно образовать конеч-
ные разности второго порядка:
A2Pi — А#/+1—&Уь 5^2 4-1/2 — 1/2> Н — Л+1/2—
Первая запись второй конечной разности удобна для составления
горизонтальных таблиц конечных разностей (табл. 4.5). Последней
записью пользуются для составления диагональных таблиц конечных
разностей (табл. 4.6). Мы будем пользоваться первым обозначением.
В общем виде конечная разность п-го порядка записывается так:
Д" = Д(Л«-1у). (2)
Таблица 4.5
к У &У ДЛу &3у у дч
*0 Уо куа &Уо №у<1 &*Уо Л5Уо
*1 — 4" А У1 &У1 Л2//1 Ь?У1 Д4У1
%2 == Ху 4~ 2А У? Ь-Уг Л2«/2 Ь3Уг
х3 — х0 4~ 3h Уз &Уз ^Уз
х4 = х04-4А
х5 = х0 -р 5Л Уь
Таблица 4.6
Л У Ьу Къу Д4у
хо Уо
^Уо
Х1=Х0+/1 У1 Д2//о 1 1
^У1 Д3Уо |
Х2 = Х0 + ^ У2 Д2м
^Уг А3У1
хз “ + ЗА Уз Л2(/2
^Уз
Х4 = Хо + 4Л
177
Для составления некоторых интерполяционных формул используют
таблицы центральных разностей^ отличие которых от диагональных
таблиц хорошо видно из сравнения таблиц 4.6 и 4.7.
В таблице центральных разностей (см. табл. 4.7) и Уь располо-
жены в середине столбца.
Таблица 4.7
у &У ДЧ Дчу Д6£/ ДЧ
Ду-з
Д’у-з
Ду-г ’ У
г/-1 Л2 у „о К </-з
Д</-| д У-г у_з,
Уь Л2 Д’у-2 Д6У-3
Дуо Д2 У-1 Д5 У-2
Х1 Д2Уо Д4у-1
Ду! ДЧ
х2 Уъ Д2У1
Д</2
Уь
-
Конечные разности обычно принято записывать в единицах по-
следнего знака соответствующей конечной разности без нулей впереди
(табл. 4,8).
178
Таблица 48
X г/ Д3^
1,70 5,4739 551 4 О
1,71 5,5290 555 7 о о
1,72 1,73 1,74 5,5845 5,6407 5,6973 562 566 4 — j
Рассмотрим некоторые свойства конечных разностей, По опреде-
лению
^Уг= (Xi + ^X) — f(Xi) = yi+1 — yi,
а вторая конечная разность в точке xt есть
Л2 У г = [f (xi+14- Д х)—/ (Xi + Дх)] — [f (хг+1)—f (xJJ
= f (xi+?) — 2f (х;+1) + f (х^ = yi+2—2yi+14- yt.
Выразим третью конечную разность в точке через значения функ-
ции:
Д3 yt = Д (Дг (/.) = [/ (х/+2 4- Дх)—2f (хг+14- Дх) 4- f (xt 4- Дх)]—
-[/ (хг+2)-2f (х/+1) 4- f (xt) = f (xi+s)—3f (хм) +
4- 3f (x/+1) — f(Xi) = yi+3—3yi+2 4- 3yi+1~yt.
Покажем, что общее выражение для конечной разности n-го по-
рядка имеет вид
“ Z/n+j Сп 4- Сп Z/n4-j-2
+ (-1ГС^Уп+^т + ^ + (-1)-У1. (3)
При п = 1, 2, 3 формула (3) справедлива. Предположим, что она
верна для п-й конечной разности, и докажем ее справедливость для
(п + 1)-й конечной разности:
Дп+11/г = Д (Дпyt) = Д« г/г+1—Д" yt=[t/n+i+i—С1п уп+, 4- Q уп+1-1— ... 4*
4- (— V)mCn Уп+i+i-m 4" 4" (— 1)л Уг+i 1 — [Уп+i—Сп Уп+i-i 4"
4- С„ Z/n+f-2 — ... 4- ( — 1 )т Сп Уп+i-m 4~ ... 4- ( — 1)” */{]'
Так как
Ст, I ст 1_______—______I_________2]_______=
Л т\ (п—т)\ (т + 1)! (/г — т — I)!
(п + 1)1
--— -------------- я _1_ 1 .
(т-р 1)1 (п—т)\
то, следовательно,
Дп+i yi _. 1 yn^-f + I 4-
4-(-1 )тС”+, yn+l+l-m 4-... 4-(- l)n+1 yt.
что и требовалось доказать.
179
Отметим следующие свойства конечных разностей.
1. Конечная разность Кпи суммы или разности функций и =
== ср + g есть сумма или разность конечных разностей функций*.
Д'1 Ut = (фг + gi) = Д'1 фг + A" gr
2. При умножении функции на постоянный множитель конечные
разности умножаются на тот же множитель.
3. Конечная разность т-го порядка от конечной разности п-го
порядка равна конечной разности (т + п)-го порядка*.
(Anz/) = Am+nz/.
4. Конечные разности п-го порядка от многочлена степени п по-
стоянны, а конечные разности (п + 1)-го порядка равны нулю.
Следует заметить, что на конечных разностях более высоких поряд-
ков заметно сказываются ошибки округления. Пусть одно из значений
функции содержит ошибку, равную 8. Из табл. 4.9 видно, что влияние
ошибки на конечные разности возрастает с увеличением их порядка.
Таблица 4.9
1 У Д2^ &sy
%П — 2 Vn-2
^Уп — 2
хп — 1 Уп-1 А2
дз Уп-2—Зе
Уп~1
&Уп — А3//п_1 + 3е
I ;/п+1 Л2 Уп + &
А//п-Н
Уп+%
. . . . . .
Пример 1. Составить горизонтальную таблицу конечных разностей функции
у = х3 + Зх3 — х — 1 от начального значения х = 0, приняв шаг h — 1.
Решение. Полагая х0 = 0, хх == 1, х2 = 2, находим соответствующие
значения г/0, гц, у2. ... :
— О, t/0=—1; хх = 1, z/i=2; х2 = 2, t/2=17;
Хз = 3, у3 = 50; х4 = 4, у4 —107; хб = 5, #6=194;... .
180
Найдем конечные разности первого порядка:
&Уо—У1—24~ 1— 3;
17— 2=15;
Аг/2 = ^з—1/2 = 50“ 17 = 33;
Al/з = — i/з = 107— 50 = 57;
Ay4 = r/5 — y4= 194—107 = 87; ... .
Найдем конечные разности второго порядка;
Д2д/0 = Az/x—At/0 = 15— 3=12;
A2z/i=Av2—A^r = 33 —15= 18; j
A 2z/2 —Ays—A//2 = 57—33 — 24;
A2//3 =Az/4 — Az/3 = 87 —57 = 30; ... .
Определяем конечные разности третьего порядка:
А3у0 = А2 г/! —А2у0 =18—12 = 6;
А3!/! =А2г/2 — А2£/х = 24— 18 = 6;
А3№=А2у3-А2^ = ЗО-24 = 6; ... .
Мы видим, что третьи конечные разности A3r/0, Ah/i( A3z/27 •*. постоянны. Это
объясняется тем, что функция f (х) есть многочлен третьей степени. Третью
конечную разность можно вычислить также по формуле
&п Рп (х) — п\ д0 Ъп = const,
т. е. А3Р3 (х) = 3! 1 • I3 =6, а конечные разности четвертого порядка равны
нулю.
Составим таблицу конечных разностей (табл. 4.10):
Таблица 4.10
X У &У Д2г/
0 -1 3 12 6 0
1 2 15 18 6 0
2 17 33 24 6
3 50 57 30
4 107 87
5 194
В дальнейшем при вычислениях целесообразно сразу, же заносить конеч-
ные разности в таблицу.
Пример 2. Найти конечные разности второго порядка для функции, заданной
таблично;
х | 2 | 4 j 6
у | 3,146 I 4,028 I. 4,911
I 8 I ’°
| 5,796 | 6,680
1 81
Решение. Составим таблицу конечных разностей, как и в примере 1;
X У &у ь*у
2 3,146 882 1
4 4,028 883 2
6 4,911 885 1
8 5,796 884
10 6,680
§ 4.7. Первая интерполяционная формула Ньютона
для равноотстоящих узлов интерполяции
Вычисление значений функции для значений аргумента, лежащих
в начале таблицы, удобно проводить, пользуясь первой интерполя-
ционной формулой Ньютона.
Пусть функция f(x) задана значениями
Уо = У1 == ZU1).......Уп = fM
в равноотстоящих узлах интерполяции х0, хг = х0 + h, хп =
“ х0 + nh. Требуется построить интерполяционный многочлен
Рп(х) степени п такой, что
Лг(*о) “ Уо> Рп(^1) “ У& •«*» Рп(Хп) = Уп*
В силу единственности многочлена степени и, построенного по п + 1
значениям функции Дх), многочлен Рп(х) является разновидностью
записи интерполяционного многочлена и в конечном счете совпадает
с многочленом, полученным по формуле Лагранжа.
Будем искать полином в виде
Рп(х) = а0 + ^(х — х0) + а2(х — х0)(х — хг) +
+ а3(х—х0)(х—Xj)(x — х2) + ... + ап(х—х0) (х— хх) <„(х—хп_г). (1)
В этом выражении нам неизвестны коэффициенты а0, , ««•} &п* Для
того чтобы найти а0, положим х = х0. Тогда при подстановке х = х0
в выражение (1) все слагаемые, кроме первого, обратятся в нуль, т. е.
Рп(х0) — а0, а значение функции в точке х0 известно из условия зада-
чи: Рп(х0) — у0. Следовательно, а0 = у0.
Чтобы найти коэффициент alt составим первую конечную разность
для многочлена Рп(х) в точке х. Согласно определению конечной раз-
ности, имеем
ДРп(х) = Рп(х + h) — Рп(х).
Произведя подстановку, получим
182
ДРп (х) — [й0 -f" (X — Xg -р /l) €2^ (X — Xg -pIt) (X — X| It) -|_
4-a3(x — x0 + h) (x — x1 + h)(x—x2 + h) + ...+an (x — x0 + lt) x
X (x — Xi + h)... (x — xn_i + Й)]—[a0 + «i (x —x0) + a2 (x — x0) x
X(x- x1) + a3(x — x0)(x — x,)(x — x2)+ ... +an(x—x0)(x—xj ...
... (x—xn_i)] = aД(X — x0 + h) — (x — x0)J + a2 [(x — x0 + h) (x—xt + h) -
— (x—x0) (x — xj] 4-a3 [(x — x0 + /i) (x — xA + h) (x—x2 + h)—
~(x — x0) (x—xj (x—x2)J + »..+an[(x—x0 + /i)(x—xx + /i) ...
... (x—xn_j + h) — (x—x0) (x—X|)... (x—хп_г)] = hat + 2ha2 (x—x0) +
+ 3ha3(x—x0) (x —xL) +... -'rnhan (x—x0) (x—x5) ... (x—xn_2).
Вычислим первую конечную разность многочлена Рп(х) в точке х0,
Здесь также все члены, кроме первого, обратятся в нуль, и, следо-
вательно, ДРп(х0) = axh, но
АЛЛ^о) = f(*i) — /(*о) = У1 — У о = Д«/о»
откуда Ду0 = a}h и
а - -^2-
Чтобы определить коэффициент a2i составим конечную разность
второго порядка:
№Рп(х) = ДРп(х + Л) — ДРп(х).
После преобразований получим
Д2Рп(х)-2! h2a2 + 2^3-h2a3(х—х0) + ...
... + (п— 1) п№ ап(х—х0)... (X—хп_3).
Полагаем х = х0; тогда все члены, кроме первого, опять обратятся
в нуль и Д2Рп(хи) — Д2#о = 2!Л2а2. Отсюда
А2*/о
(Л л ~ ' ..
2 21/I2
Вычисляя конечные разности более высоких порядков и полагая
х = х0, придем к общей формуле для получения коэффициентов:
а (i = o 1 2, ...,п),
1 c\hl V 7
где будем считать, чтоб! = 1 и Д°у — у. Подставив найденные значения
коэффициентов аг в выражение (1), получим первую интерполяционную
формулу Ньютона
Рп W = уо+ ~~ (*—*о) + (х —хо) (X —XJ + ...
д I ГI л! Д
+^т£“ (Х~хо)---(х~*п-1) (2)
n! hn
На практике часто используют формулу Ньютона в другом виде.
Для этого введем переменную q — (х — x0)//i, где h — шаг интерпо-
183
ляции, a q — число шагов. Тогда первая интерполяционная формула
Ньютона примет следующий вид:
Рп (X) = у о + q&y0 + g(y2~-ir А2 у0 4-... + д^0.
(3)
Формулу (3) удобно использовать для интерполирования в начале
отрезка интерполяции [а, Ь\, где q мало по абсолютной величине.
Если за число узлов интерполяции принять п = 1, то получим фор-
мулу линейного интерполирования
Р(х) = у + ?Az/0.
При п — 2 получим формулу параболического, или квадратич-
ного, интерполирования
Рг (х) = у0 + <7Аг/0 + -q <q~-~
На практике часто бывает необходимо сгустить шаг интерполяции
какой-нибудь таблицы с равноотстоящими аргументами. В таблице
можно считать, что число узлов интерполяции неограничено. Тогда
выбирают п так, чтобы конечная разность была постоянна с за-
данной степенью точности. За начальное значение х0 можно выбирать
любое значение аргумента.
Пример. В табл. 4.11 дань: значения функции
<р (X) = е х2/2 -
Д/2л
Таблица 4.11
X У &у Д27 д3^
2,0 0,0540 — 100 15 —2
2,1 440 —85 13 0
2,2 355 —72 13 -3
2,3 283 — 59 10 — 10
2,4 224 —49 0
2,5 175 — 49
2,6 136
Применяя первую интерполяционную формулу Ньютона, найти <р (2,22).
Решение. Строим конечные разности функции <р (х); ограничимся треть-
ей конечной разностью. За х принимаем число, наиболее близкое к заданному,
т. е. полагаем х — 2,2. Так как шаг h — 0,1, то
2,22—2,20 0,02
—------*—= ——=0,2.
4 0,1 0,1
184
Используя формулу (3), находим
0,2(0,2 — 1)
^ = 0,0355 + 0,2 (—0,0072) +—-----— 0,0013 +
0,2 (0,2—1) (0,2 —2)
+ ----— (—0,0003) = 0,0339.
§ 4.8. Вторая интерполяционная формула Ньютона
Для интерполирования в конце таблицы обычно применяют вторую
интерполяционную формулу Ньютона.
Пусть на отрезке [а, Ь] даны п + 1 различных значений аргумента
х0, Xi, хП9 которым соответствуют значения функции
; Уо = f(x0), Уг = {(Xi), уп = f(xn),
f
а шаг интерполяции постоянен и равен ht т, et Х/+1 — xt + h
(i — 0, 1, 2/ п— 1), Построим интерполяционный многочлен
вида
Рп (х) = а0 + (X—хп) + а2 (х — хп) (х—хп _Д +
+ (х хп) (х хп) (х хп«.2) + • • •
.~ + ап(х—хп)(х — х^-Д... (х — хО. (1)
В этом многочлене неизвестны коэффициенты а0, аи а2) ап. Их надо
подобрать так, чтобы были выполнены равенства
^п(-^о) Уо» №) = У1» ^п(Хп) = Уп*
Для этого необходимо и достаточно, чтобы
= = 1,..., И). (2)
Коэффициент aQ найдем, положив х — хп в равенстве (I):
п(^п) “ Уп ~ ^0»
откуда
” Уп*
Из выражения для первой конечной разности найдем ах:
кРп (х) 2ha2 (х—хп^) + 3/ш3 (х—хп._2) (х—х^) + ...
... + nhan (х—хп^г) (х~хп_2)... (х—Xi).
Отсюда, полагая х = хп~г и учитывая соотношение (2), имеем
A^nUn-i) = ДУп-а =
Следовательно,
^Уп-1
185
Из выражения для второй конечной разности найдем а2:
Ь*Рп (х) = 21 /г2 а2 + 2 • 31? а3 (х - хп_2) + ...
... + п(п - 1)Л2ап(х—Х0... (х—xn_J,
Полагая х = хп_2, получим
- ^Уп-г = 2!Л2я2»
откуда
Методом математической индукции можно доказать, что
(i = 0, 1 2,..., п).
t\hL
Подставив найденные значения коэффициентов в формулу (1), полу-
чим
Рп W -=УпЛ (* —*п) + • (Х~~Хп) (* —*Л-1) +
+ <Л—хп) (х—хп-1) (х—хл.г) + •
’" +A"? - (Х~Х1У (3)
п\ №
Это и есть вторая интерполяционная формула Ньютона,
На практике используют формулу Ньютона в другом виде. Поло-
жим q = (х — хп)!h\ тогда
и формула (3) примет вид
РгАхтУп У^Уп-1 + ~^- ^Уп-г + Д3уп_3+...
,.. + А(? + 1)-- - (?-Н-1.).„ д„ (4)
п\
Первая интерполяционная формула Ньютона используется для
интерполирования в начале отрезка [а, Ь], т, е. для интерполирования
вперед и экстраполирования назад, При интерполировании по первой
формуле Ньютона q = (х — xQ)/h > 0. При экстраполировании назад
также используют первую интерполяционную формулу Ньютона, но
в этом случае q = (% — xQ)/h < 0.
При интерполировании в конце таблицы, т. е. интерполировании
назад, когда шаг интерполяции постоянен, используют вторую фор-
мулу Ньютона, где q = (х — xn)//t < 0. Вторая интерполяционная
формула Ньютона применяется и при экстраполировании вперед,
тогда q = (х — xn)/h > 0.
186
Пример. В табл. 4.12 приведены значения интеграла вероятностей:
Таблица 4.12
х У Ду Д2у Д3у
0,1 0,03983 3943 — 78 —36
0,2 0,07926 3865 — 114 -33
0,3 0,4 0,5 0,6 0,11791 0,15542 0,19146 0,22575 3751 3604 3429 — 147 — 175 —28
Требуется вычислить £/(0,58).
Решение. Здесь шаг интерполяции h ~ 0,1. Отсюда
х—хп 0,58 — 0,6 0,02
q =------— = —--------1—= !---= —0,2.
7 /г 0,1 0,1
Для нахождения у (0,58) воспользуемся второй интерполяционной форму-
лой Ньютона:
Рз (0,58) = 0,22575 + ( — 0,2) 0,03429 + ( — °>2И~°>2+О (__0j00175) +
(—0,2) ( — 0,2+1) (—0,2+2)
+ 2----—------3! м7 (— 0,00028) = 0,21904.
§ 4.9. Оценки погрешностей интерполяционных формул Ньютона
В § 4.5 мы вывели оценку погрешности для интерполяционной
формулы Лагранжа:
I Ю Ю | < ++t | (X — х0) (X—Xj) .. (x—xn)l.
(n+l)l
Если узлы интерполяции равноотстоящие, то введя шаг h —
== %г+1 — xt (i = 0, 1, 2, п —1) и полагая q — (х — x^lh, получим
оценку погрешности для первой интерполяционной формулы Нью-
тона:
R (х) = h*+iq (q~V у •+-П^- + > (В), (1)
(n+1)'
где точка | принадлежит отрезку интерполяции [х0, хп]. В случае
экстраполяции точка £ находится за пределами отрезка xj.
Аналогичным образом для второй интерполяционной форму-
лы Ньютона с равноотстоящими узлами интерполяции, полагая
q = (х — xn)!h, получим оценку погрешности в следующем виде:
Rn (х) = h*+ > 9(?+(-z)+)+'° f(n+!) (t), (2)
где точка £ также принадлежит отрезку интерполяции [х0, хп].
137
В практических расчетах аналитический вид функции не всегда
известен. Тогда для оценки точности составляют таблицу конечных
разностей* и останавливаются на тех, которые можно считать постоян-
ными в пределах заданной точности.
Воспользовавшись предельным переходом
bi) (х) = lim AjLjL
приближенно считают
+1 is
hn+'
Тогда погрешность для первой интерполяционной формулы Ньютона
- А”+1 yQ> 4')
(«4-1)1
а для второй интерполяционной формулы Ньютона
+ <2'>
Пример. Функция у — In х задана таблично:
X \ 2. 1 3 4
У | 0,6931 | 1,0986 0,3863
Построить первый интерполяционный многочлен Ньютона и оценить погрешность
интерполирования в точке х = 2,5.
Решение. Составим таблицу конечных разностей:
К У Ду Дгу
2 0,6931 0,4055 —0,1178
3 1,0986 0,2877
4 1,3863
Учитывая что h = 1, по формуле (2) § 4.7 получим
Л 0,1178
р2 (х) =0,6931+0,40о5 (х —2) — —~-(х—2)(х—3) =
= — 0t0586x2~p0f7000x—0t47l3t
Оценим наибольшее значение третьей производной функции у = In х на отрезке
[2, 4]:
12! I 1
—— = — ,
х3 | 4
Так как h = 1, то q = (2,5—2)//i = 0,5. Вычислим произведение
\q (q—J) (у—2)1 = |0,5.0,5.1,5 ) = 0,375.
По формуле (1) находим
1 0,375
1/?2 (2,5)|<-.-~—^0,0156.
188
§ 4.10. Единственность интерполяционного многочлена
Мы рассмотрели параболическое интерполирование, когда в ка-
честве интерполяционной функции выбирается многочлен степени не
выше и, для функции, заданной п + 1 значениями в узлах интерполя-
ции. Многочлен F(x) степени п есть единственное разложение в классе
степенных функций, так как если бы существовал еще один интерпо-
ляционный многочлен F(x) степени п, принимающий в узлах интер-
поляции заданные значения, то разность этих многочленов обращалась
бы в нуль в п + 1 узлах интерполяции. Но разность F(x) — F(x) яв-
ляется многочленом степени не выше п, следовательно, этот многочлен
тождественно равен нулю.
Итак, если функция Дх) задана п + 1 значениями
Уо = Кхп), Уг = /(лу), уп = f(xn)
в несовпадающих узлах интерполяции, то это означает, что сущест-
вует единственный многочлен F(x) степени и, принимающий в узлах
интерполяции заданные значения
Уо = F(x0), Ух = H*i). .... Уп = F(xn).
Выведенные формулы Ньютона и формула Лагранжа являются
лишь различными формами записи одного и того же многочлена
п-й степени.
§ 4.11. Интерполирование в таблицах
При интерполировании в таблицах обычно пользуются линейной
или квадратичной интерполяцией.
В случае линейной интерполяции значение функции в точке, от-
личной от узлов интерполяции, определяется по двум известным зна-
чениям табулируемой функции yt = f(xi), yi+1 — f(xi+1) в узлах
интерполяции и xf+1, между которыми расположено интересующее
нас значение аргумента xt < х <
Интерполяционная формула Лагранжа для линейной интерполя-
ции примет вид
г i \ X— *1 t X—Ха
Ц (х) = Уо-----— + Ух--------
*0—*1 Х1—Хо
а первая интерполяционная формула Ньютона
Л + Xi),
где Az/£ — — yi — первая конечная разность в точке хг, a h =
«= х<+1 — Xi — шаг интерполяции.
Итак, для получения приближенного значения функции у по фор-
муле Ньютона достаточно к табличному значению уг прибавить по-
правку, равную Az/i(x —
189
Пример 1. Вычислить, сколько градусов содержится в радианной мере
0,222.
Решение. Воспользуемся таблицей
Радианта Г радуста
0,22 23 24 12,605 13,178 13,751
Для линейной интерполяции достаточно рассмотреть данные первых двух ст|эок«
Составим табличную разность
\yt = — yi = 13,178—12,605 = 0,573.
Шаг таблицы h — 0,01, х — хг = 0,222 — 0,220 = 0,002. Подсчитаем поправку
-^i-(X—Хг) = °’573 - . 0,002 = 0,1146
h ' 0,01
и прибавим ев к табличному значению:
г/=12,605 4-0,1146 = 12,7196.
Округляя результат, получим у = 12,720.
Оценим погрешность при замене точного значения функции f (х)
ее приближенным значением, т, е, yt 4- ~ (х — xt). Функция погреш-
сти имеет следующий вид:
Г (X) = / (х) — У1— (X — Xt).
Оценим погрешность на отрезке [хг, хг + 11. Предположим, что вторая
производная функции / (х) на отрезке [xf, хг + ,1 непрерывна и ограни-
чена: | f" (х) | ''1 М2. Дифференцируя функцию г (х), получим
r'(x) — f'(x)---г" (х) = f" (х).
Следовательно, |г" (х) | М2. Кроме того, по условию задачи в узлах
хг и xt +, интерполяционный многочлен совпадает со значениями функ-
ции, значит, г (хг) = г (хг +,) — 0.
В некоторой точке £ интервала (хг, хг +,) функция ошибки г (х)
достигает своего наибольшего значения. Разложим г (х) в ряд Тейлора
в окрестности этой точки. Тогда
г (х)=г &+г' (^) (х- а + (х-в8.
190
Так как в точке £ функция г (х) достигает наибольшего значения, то
производная г' (£) обращается в нуль. Следовательно,
r(x) = r@ + -C>(x-S)3.
В качестве точки к выберем ближайший к ? узел интерполяции
или Xi + р Обозначим эту точку через х. Так как в узле интерполяции
г (х) обращается в нуль, то
0 = г© + -^-^- (х—£)2; или Г(|) = — — g)2.
Так как разность х— g не превышает половины отрезка [хг, хг_х|
(по условию выбора х — ближайший к точке | узел интерполяции),
а | г" (£) | М2 (вторая производная данной функции ограничена), по-
лучаем следующую формулу оценки погрешности для линейной ин-
терполяции:
< M2h2
4 8 '
В силу того, что | г (х) | г (£) на всем отрезке [хг, хг + 11, оконча-
тельно получим оценку погрешности для линейной интерполяции:
В случае квадратичной интерполяции необходимо знать три значе-
ния табулируемой функции yt _ х = f (хг _ х), г/г = / (хг) и #г+1 =
= /(хг + 1) в узлах интерполяции хг_15 хг ихг + 1, Тогда формула
Лагранжа примет вид
L (х) = и- (х~х^ (х—Xi+1) (х—х,--1) (х —хг+1) .
2 i-1 (Xi-1— xt) (Xj-1— Xj+i) 1 (Xf—хг_х) (Xj—Xj+1)
, (X—Xj-1) (X—Xj)
(Xi+1— Xi-1) (Xi+J—Xi)
а первая интерполяционная формула Ньютона
(*) = Vi-i + -1- (х —х,_х) + (х — хг_!) (х—хг).
Пример 2. Построить интерполяционный многочлен Лагранжа для функции
у = In х с узлами интерполяции х — 2, х == 3 и х = 4. Оценить погрешность
интерполирования при х — 2,5<
Решение. Имеем
* 1 2 3 1 4
У 0,6931 1,0986 1,3863
191
Следовательно,
, (х-3)(х-4) (х—2)(х—4)
L2 (х) = 0,6931 \ +1,0986 -1 Ш-.......+
(х—2) (х—3)
4-1,3863 —---~ = —0,0586х3 + 0,7000х—0,4713.
Как и следовало ожидать (в силу единственности интерполяционного много-
члена), мы получили тот же результат, что и при интерполировании с помощью
многочлена Ньютона (ср. с примером в § 4.9),
Оценку погрешности найдем по формуле
, Л43
I ^2 W I < — | (X — Хо) (X — Хх) (х — Х2) |.
о!
Наибольшее значение третьей производной fr"(x) на отрезке [2, 4] достиг^
в точке 2, т, е.
[211
Л43 —max \[ (х)| — max — = —.
2<х< 4 2 х< 4 I х3 I 4
Вычислим
1 (х—х0) (Х-Х1) (X—х2) 1 =? 12,5-2) (2,5—3) (2,5—4) | -0,375.
Тогда
1 0,375
Rl(2,5)< — . — 0,0156.
§ 4.12. Линейное интерполирование по Эйткину
В тех случаях, когда нет необходимости в отыскании приближен-
ного аналитического выражения функции у — f (х), заданной таблич-
но, а требуется лишь определить значение функции в точке, отличной
от узла интерполяции, удобно использовать последовательную линей-
ную интерполяцию по Эйткину.
Интерполяционная схема Эйткина особенно удобна при работе
с таблицами, когда априорно фиксируется погрешность результата.
Вычисление значения функции в точке, отличной от узлов интер-
поляции, начинается с вовлечения в счет двух узлов интерполяции
с последующим включением в схему новых узлов интерполяции.
Процесс счета состоит в следующем. Пусть некоторый интерполя-
ционный многочлен F (х) степени п принимает в узлах интерполяции
х0, х19 х2, хп значения
Уо = Fo (х), у, = F (Xi), уп = F (хп).
Воспользуемся формулой Лагранжа для случая линейной интерполя-
ции. На отрезке [х0, лу] интерполяционное значение функции можно
вычислить по формуле
Уо х0 — х
У1 Xi—х
Ха—Xi ’ ' Х1 — хо “Х^ — Хо
X — Xt . X — Хо
192
на отрезке 1хь х2] — по формуле
^1,2 (X) =£/i
Уч.
X— Xi
%2 '"’“'Xf
£/f Xf — X
02 Х2—X
(2)
и, наконец, на отрезке [х0, х2] — по формуле
I у0 х0—х I
Л>,2 (X) = Уо Х~Х2 + у2 Х~Х° = . (3)
х0 —х2 х2—х0 х2 —х0
Далее, заменим z/0 и z/2 в формуле (3) соответственно на FOjl (х) и
Fx 2 (х) и получим следующее выражение:
Л), 1, 2 W —
Л),1 (х) хо —Х|
Ft, 2 (X) Х2 —х|
Х2 "”Xq
(4)
Раскрывая в последнем выражении определитель, непосредственно
убеждаемся, что Fo, х, 2 (х) — это многочлен второй степени, принимаю-
щий в узлах интерполяции х0, хх, х2 соответствующие табличные зна-
чения:
(х0) = Уо, F (х,) = ylt F (х2) = у2.
HidK, применяя линейную интерполяцию к Fox (х) и FOii (х),
мы получили интерполяционный многочлен второй степени FOiM(x)<
Тот же самый результат можно получить, воспользовавшись двумя
другими формулами:
I W xi—x I | *о—х I
^0 1 2(*) = fo,2(X) *2~* ; Fo I 2(х)=ДД ' (5)
’ ’ Х2 —Xj * *1— Х0
Методом математической индукции можно показать, что интерполя-
ционный многочлен степени п, построенный по п + 1 узлам, получает-
ся посредством линейной интерполяции, примененной к двум различ-
ным интерполяционным полиномам (п — 1)-й степени, каждый из ко-
торых построен по каким-либо п узлам из числа данных.
Пример. Пользуясь схемой Эйткина, вычислить значение sin 0,674 для функ-
ции у — sin х:
Xi х0 = 0,66 Xi = 0,67 х2==0,68
i/j — sin xt 4/0 = 0,61312 у i =0,62099 у 2 = 0,62879
Решение. Согласно формулам (1) и (2) имеем
0,61312 0,66—0,674 I
0,62099 0,67—0,674 |
0,67—0,66
= 0,625730;
FOt х(0,674)-
193
F12(0,674) =
0,62099 0,67—0,674
0,62879 0,68 — 0,674
0,68—0,67
= 0,625643.
Тогда по формуле (4) находим
^о, 1,2 (0,674) =
10,625730 0,66 — 0,674]
I 0,625643 0,68 —0,674 |
0,68—0,66
— 0.625676.
Следовательно, sin 0,676 = 0,62568.
§ 4.13. Разделенные разности
В предыдущих параграфах были рассмотрены формулы Ньютона
для равноотстоящих узлов интерполяции, где коэффициенты много-
члена а±, а2, ап найдены с использованием конечных разностей.
При проведении приближенных вычислений, когда значения функ-
ции задаются в неравноотстоящих узлах интерполяции, вводят поня-
тие разделенной разности, обобщающее понятие конечной разности.
Пусть функция у — f (х) задана своими значениями
y0 = f (*о)> У1 = f Ui). Уп = / Un)
в неравноотстоящих узлах интерполяции х0) х19 хп. Отношения
г v г 1 У1 У 0 г . v 1 _ V2 У\ г ... . 1 _. . У г-Н Уг
[Ло, Ajj — , [Др Л21 '— >•••> Иь Лг+11 —
и х0 Х2—*1 —Xi
назовем разделенными разностями первого порядка.
Определим разделенные разности второго порядка как следующие
отношения:
r г 1 кь ^1 —ко; л!
[Л(), Лр A2J — »
Х2~Х0
|Г . V . г 1 1*2; *з] — [Xi; х2]
х3 —Xi
. v . чл 1 _ кг+ll ^г+г] кН *г-н!
I'M» Лг-Н> Af+2J
Х/4-2 Xi
Зная разделенную разность (k— 1)-го порядка [xf; xf + 1; ...
+ & _ th можно определить разделенную разность k-го порядка
следующим образом:
I у . у . • v 1____kz+i; xi+2,:..: ; xi 44;.«.; Xj+k i ]
Xi+k Xi
Иногда разделенные разности первого порядка обозначают так:
/ Uo! *1). / Uii *2), .... f Ui! xf + i),
разделенную разность второго порядка соответственно
194
тогда для разделенной разности й-го порядка в общем случае исполь-,
дуют выражение
f + Г* •’»» +
Составим диагональную таблицу разделенных разностей (табл. 4.13).
Таблица 4.13
Х1 VI = f(X/ ) [xi- xl+l] [xz; x/+i; xi+2] [Xf, х1+1; х/+2: х<+з] рг;х1-+1;х/+2; Xi+3’ Х!-Н]
Хо 4/о
[«О? *11
Х1 Ух [ад Xjt
[*v -41 [х0; хр х2; х3]
х2 У2 [x£; x2; x3] [х0; xj-. х2; х3; х4]
[X2, X3] [хх; х2; х3; х4]
*3 Уз [x2; x3; xt]
[x8'> Xll
х4 04
Пример. Сое НИЙ X И У'. Решение ные разности пе] Аналогично найд < гтавить таблг X ту разделен ° 1 1 ных раз 5 юностей для 10 следующих значе- находим разделен- 0.
У . Пользуясь эвого порядк [ад ад — Х1- 1/2- [ад х2]- х2- Г 1 [х2; х3] — хз- ;ем разделена , l-ч; «г. х21 — 10 | 20 непосредств< -Уо = 20-1 - Хо 1—С - Ух __ ЮО- - %i 5— - j/2 _ ПОР- -х2 10- ibie разности xd —[хп, хх Л 2 —Xq 100 ;нно ОП| 10 — = 10; 1 •20 £ 1 = - -100 _ -5 “ второгс L _ t 1100 )еделением, Ю - = 20; 4 1000 -201 5 ) порядка: )—10 >—0 ~2,
195
r . x3l —[xi; x2] 200-20 180
xi; x2; x3 =---------------- = ——Г" = — =20.
x3— Xi 10 — 1 9
Разделенная разность третьего порядка
[Xf, х2; х3] — (х0; *1! «21 20—2
[х0; хх; х2; х3] = ---------------- = - =1,8-
— х(| 10
Результаты вычислений сведем в диагональную таблицу разделенных раз-
ностей
X У l-Ч- хг+11 хг+2^ 1*1’ хг+1* хг+2’ xi4-sJ
0 10
10
1 20 2
20 1,8
5 100 20
200
10 1100
§ 4.14. Первая интерполяционная формула Ньютона
для неравноотстоящих узлов интерполяции
Пусть функция f (х) задана значениями
Уо = f (хо), У! = f (хх), уп = f (хп)
в неравноотстоящих узлах интерполяции х0, хь..., хп. Требуется по-
строить интерполяционную формулу Ньютона для неравноегстоящих
узлов интерполяции, так чтобы в узлах интерполяции
Уо = Р (*о), У1 = Р (*1)» •••> Уп = Р (хп).
Построим первую разделенную разность
X—Хо
тогда
Р (х) = Р (х0) + [х; ХО1 (х — х0). (1)
Вторая разделенная разность
X—%!
196
откуда
lx; x0I = [x0; xj 4- tx; х0\ xj (x — x^. (2)
Подставив выражение (2) в (1), получим
Р (х) = Р (х0) + (х0; хг1 (х — х0) + [х; х0; xj (х — х0) (х — xj. (3)
Из определения третьей разделенной разности получим
.. .....Iх; -ад xi!—(х0; хг, х2]
[Л} Лд, A2J —’ ,
Х“Х2
т. е,
[х; х0: xj = [х0; хг; х21 + 1х; х0; хх; х2] (х — х2). (4)
Подставим вторую разделенную разность (4) в выражение (3), тогда,
используя третью разделенную разность, можно представить много-
член Р (х) в следующем виде:
Р (х) = Z5 (х0) + k0; xj (х — х0) + [х0; xj х2] (х — х0) (х — xj +
+ [х; х0: хг; х2] (х — х0) (х — хг) (х — х2). (5)
Продолжая далее этот процесс, получим
Р (X) = Р (х0) 4- [х0; xj(x—Х0) + [Х0; хх; х2] (х—х0) (х—х1)+-
*»* 1^0» Хр %о) (% ху) **' (6)
Эта формула носит название интерполяционного многочлена
Ньютона для неравноотстоящих узлов интерполяции.
Преимущество этой формулы по сравнению с формулой Лагранжа
состоит в том, что добавление новых узлов интерполяции не приводит
к проведению расчетов заново.
§ 4.15. Интерполяционные формулы Гаусса
Введем понятие центральной разности, для которой
kyt = У1 +1 — Уь №yt = &У1 + 1 —&Уь
при Xi == х0 + th (где i — 0, ± 1, ± 2,
Таблица центральных разностей приведена на стр. 198 (см.
табл. 4.14).
При интерполировании в середине таблицы пользуются интерполя-
ционными формулами Гаусса.
Первая интерполяционная формула Гаусса записывается следующим
образом:
Р (*) = Уо + <7 &Уо + ^У-1 +
+ + д4у_г+
(q + rc-1) - (g—п+1) л2п-1,, ,_п (?+»—!) ... (9-п)
(2п —1)1
(2л) I
где A2zz“lz/_ (п- о—центральная разность (2/г — 1)-го порядка
х_ n, a q == (х — x0)//i — число шагов,
A2nZ/-n,
(1)
в точке
J97
Таблица 4.14
X У &У ь2у A3i/ Д*£/ Д5#
Х-3 У-з
^У-з
х_2 У-2 ^2У-з
^У-2 №у-з
Х-1 У-г ^У-2 Л41/-з
Ьу-1 Ь3У- 2 Д^_з
*0 */о ^2У-1 Д‘1/-2
\уа A3V-1 Д61/_2
*1 У1 Л21/о A4V-i
&У1 A3i/o
х2 У1 Д2</1
^У2
*3 Уз
В первой интерполяционной формуле Гаусса используются цент-
ральные разности
Az/0, №у-2, •••>
которые расположены в строке х0 и в следующей за ней строке.
Во второй интерполяционной формуле Гаусса рассматриваются
центральные разности из строки х0 и из строки, расположенной над ней:
Аг/.р А2г/_1( A3z/_2, А4!/..,;,... .
Эта формула имеет вид
Р W - Уа + Ч &У-г + +
+ <l+.1.)«to-1>A,i)_a+ (,+2)(,+ !),(,-!) д,9_з+
(9-f-n—1) ... (g—n—1)
(2га—1)1
^п~1У-п +
—1) (<7—га~Н) д2п ,
п У-п*
(2п)1
(2)
198
Оценки погрешности для формул Гаусса таковы:
(3)
и
^2п-1«^-7(72-12)(72-22) ... ^-(п^1Я(7 + п), (4)
Пример. Для функции у = f (х), заданной таблично, найти значение в точке
а = 4,5:
X 31 4 1 1 5 6
У 91 161 30 72
Решение. Так как требуется определить значение функции в точке#
близкой к середине отрезка интерполяции, то для вычислений следует восполь-
зоваться одной из формул Гаусса. Составим таблицу центральных разностей!
X У Д2^ Д3^
3 9
7
4 16 7
14 21
5 30 28
42
6 72
Пользуясь первой интерполяционной формулой Гаусса, найдем приближен-
ное значение функции в точке х = 4,5:
п, . . . . 7(7 — 1) (? + 1)9(? —1) Л3
Р (*) = i/o+9 Aj/o+ о. Л2Т/-1+ о. &3У-1>
О’
т. е.
0,5 (—0,5)
Р (4,5) = 16 4-0,5-14-j--~ * 7 +
1,5-0,5 (— 0,5)
3!
. 21 ~ 20,81.
§ 4.16. Интерполирование с помощью многочленов Чебышева
В § 4.5 мы вывели оценку погрешности для интерполяционной фор-
мулы Лагранжа
(«4-1)1
199
где величина Л4п + 1 = max |/(л+!) (х)| зависит от свойств функции
/ (х), а сомножитель
П„ + J (х) = (х — х0) (х — Xj) ... (х — хп)
определяется только выбором узлов интерполяции хг.
Поставим следующую задачу: как следует расположить узлы ин-
терполяции, чтобы абсолютная погрешность метода интерполирования
на отрезке [а, Ь] была наименьшей? Будем считать для определенности,
что отрезок интерполирования совпадает с отрезком [ — 1, 1].
Произведем замену переменной х =*
.--р-, —cos 0; функция f (х) становится теперь
Тх. функцией угла 0, т. е. / (cos 0) == ф (0),
/ и преобразуется в периодическую
/ \ функцию от нового аргумента. Так как
/ \ — l^x 1, то можно считать, что угол
/ || 0 изменяется от 0 до л. Замена 0 на
X; х2 х5 л4 л5 —0 оставляет х без изменения. Следова-
тельно, функция ф (0) определена и на
Рис- 4.2 отрезке [ — л, 0]. Кроме того, функция
Ф (0) четная, т. е. ф ( — 0) = ф (0).
Если функция f (х) дифференцируема по х, то и функция ф (0) диф-
ференцируема по 0 в каждой точке промежутка I — л, л], включая
границы,
Функцию ф (0), так же как и f (х), можно разложить в ряд Фурье.
Разложение ф (0) в ряд Фурье имеет вид
1 °°
Ф (0) = — Yo + 2 Va cos kQ-
Вернемся теперь к заданному аргументу, т. е. заменим cos kd
на х. Мы получим так называемые многочлены Чебышева Та (х). Они
представляют попеременно четные и нечетные функции от х и могут
быть получены на основании рекуррентной формулы
тп + 1 (х) = 2хГ„ (х) — Тп _ J (х> (1)
с начальными условиями (х) = 1, 7\ (х) = х. Нетрудно проверить,
что
7\ (х) - 2х2 — 1, Т3 (х) = 4х3 — Зх, 7\ (х) - 8х4 — 8х2 + 1,... .
Тогда разложение f (х) можно представить в виде
f(x) = 2 «А(*). (2)
U0
где
ak = — ф (0) cos kQ dQ.
Л d
200
Возвращаясь к переменной х, имеем
1
- f f(x)Tk (х) —(3)
я J, V1— X»
В результате получаем разложение вида
f W ~ + й1^'1 W + ••• а^п (*) + • (4)
Этот ряд сходится быстрее, чем многочлен Лагранжа.
Узлы интерполяции выбирают следующим образом. Задаются зна-
чениями функции ут в точках 0т = тп!п (т = 0, 1,..., и), т. е. для
переменной х эти точки должны располагаться по закону хт =*
— cos (тя/п). Отсюда видно, что узлы интерполяции располагаются
неравномерно, сгущаясь к концам отрезка [ — 1, 1]; рис. 4.2.
Значения функции в узлах интерполяции таковы:
где т = 0, 1, п.
§ 4.17. Обратное интерполирование
Задача обратного интерполирования заключается в следующем.
Пусть на отрезке [а, 6] заданы точки х0, хъ х2, ..., хп и значения неко-
торой функции f (х) в-этих точках:
Уъ ~ f (*о)» У1 = f (*1)» •••> Уп= f (*nh
Требуется по заданному значению функции f (х) найти соответствующее
значение аргумента х.
Случай неравноотстоящих узлов интерполяции. В случае неравно-
отстоящих узлов интерполяции х0, xlt ..., хп задача легко решается
с помощью интерполяционного многочлена Лагранжа. Для этого дос-
таточно принять у за независимую переменную, а х считать функцией,
т. е.
Х = Х (У~Уп) | х (У—Уо)(У—У2У-ЛУ'-Уп) |
У1)(Уо—(Vo—Уп) 1 (У1—Уо)(У1—У2)... (У1—Уп)
4-д: "• (у—Уп-1)
(Уп—Уа)(Уп У1) ... (Уп Уп-1)
или сокращенно
V х ••• (y—yi-i^y—yi+i) - (У—Уп) 04
1=0 1 (У1—Уо)(У1—У1.) ••• (У1—У!-1)(У«—Уж) ••• (у«—Уп)
Оценка остаточного члена в этом случае такая же, как и при прямом
интерполировании, только производные от данной функции заменяют-
ся производными от обратной функции,
201
Случай равноотстоящих узлов интерполяции Здесь обычно ис-
пользуется метод последовательных приближений. Если задана моно-
тонная функция с равным шагом интерполяции и данное значение
х лежит в начале таблицы на отрезке х0 < х < хъ то можно восполь-
зоваться первой интерполяционной формулой Ньютона (см, §4,7),
Запишем эту формулу в виде
У = Уо+^Я+ - + ^q(q-L) .... (q-n+V). (2)
Формула (2) связывает значение функции у с числом шагов q*
В свою очередь, величина q есть функция аргумента х:
(3)
h
Из этого соотношения, можно определить х, если известно число ша-
гов q:
х- = Xq + qh. (4)
Величина q определяется методом последовательных приолижений
как предел последовательности: q = lim qh где qt == ф О' —
t -> оо
= 1, 2,..).
В уравнении (2) выделим q во втором члене правой части равенства
и получим
Az/0 21 At/0 &Уь
В качестве исходного значения q возьмем = (у — yQ)/&yQ. Тогда
= ^-p-qAq< — О— ••• — — i) - (?0—n + i). (6)
2! At/0 ™ кУо
По найденному значению qr вычислим второе приближение q2 и т. д.
Для г-го приближения имеем
= <7f-i (<7г-1 — 1) — -
21 А у о
- --^^(^-n.-^-i-n+D. (л
/г! &yQ
Количество членов в формуле (7) зависит от числа узлов интерполяции.
На практике процесс итераций продолжают до тех пор, пока не
установятся цифры, соответствующие требуемой точности, причем
полагают q ж qm, где qm — последнее из найденных приближений.
Пользуясь формулой (4), находят искомое значение х, соответствующее
заданному значению у.
Нахождение корней методом обратного интерполирования. Методом
обратного интерполирования можно воспользоваться для нахождения
корней уравнения f (х) = 0. Известно, что функция f (х) имеет по край-
ней мере один корень на отрезке 1а, 6], если она непрерывна и
202
f(a)./(*)<0. Воспользовавшись этим фактом, по заданной таб-
лице находим такой отрезок + J, что f (xj • f (х2 + J < 0, т. е,
ш * yt +1 < 0* Применяя затем прием обратного интерполирования,
1 заданной степенью точности находим значение х, соответствующее
Пример 1. Функция у — f (х) задана таблично:
X * 10 15 | 17 | 20
У 3 7 j 11 j 17
Найти значение аргумента х, для которого у = 10.
Решение. По формуле (1) находим
,1П, ш (10—7)(10—11)(10—17) (10—3)(10—11)(10 —17)
> (3—7^ (3 ——17) (7—3) (7 —11) (7 —17)
' (10—3)(10—7)(10—17) (10—3) (10—7) (10 —11)
* (11 —3) (11—7) (11 — 17) Ф ‘ (17—3) (17—7) (17 —11)
_10 3( —1)(—7) 7( —1)(—7) 17 7<3^(—7)
_4^(—8)(_14) 4(—4)( —10) * 8.4-(—6)
7-3*( — 1) 15 147 17-49 1 1065 1Л „
4-20 • -------= — — 4-—4-------—— =-------=16,64.
14-10.6 32 * 32 64 2 64
+
Пример 2. Функция у = f (х) задана таблично:
X 1,о 1,2 1,4
У 35 55 63
При каком значении х значение у равно 40?
Решение. Составим таблицу конечных разностей:
X У
1 0 35 - 20 — 12
1,2 55 8
1,4 63 !
За начальное значение у принимаем у0 = 35. Отсюда
У—Уо
40—35
20
= 0,25.
Далее, пользуясь методом итерации, найдем
91 = ?о - Яо (<7о-1) = 0,25 - -0,25 (-0,75) = 0,25-0,056= 0,194;
2! Луо 2-20
Л2Уо
21 Д//о
^2 — 7о
91 (^ — 1) =0,25 -0,3-0,194-0,806 = 0,25— 0,047 =0,203;
203
№Уо
9з=9о-5г^;
А24/о
?4 ~<7о--- О| А
2' Af/o
?2 (72 — 1) = 0,25 — 0,3.0,203-0,797 = 0,25 — 0,049 = 0,201?
?3 (<7з — 1) = 0,25—0,3-0,20Ь0,799 = 0,25—0,049 = 0,201.
Теперь по формуле (4) получаем
х = %0 + qh = 1,0 + 0,201 0,2 = 1,04.
Упражнения
1 Функция у — f (х) задана таблично:
X 1,522 1,523 1,524
У 20,477 20 906 21,354
Определить ее значение в точке х = 1,5228 с помощью первой интерполяционной
формулы Ньютона
Ответ 20,819
2. Функция у == I (х) задана таблично:
х | 1,529 | 1,530 | 1,531
у | 23,911 | 24,498 | 25,115
Определить ее значение в точке х = 1,5303, пользуясь второй интерполяционной
формулой Ньютона.
Ответ 24,680.
3 Построить интерполяционный многочлен Лагранжа для функции, задан-
ной таблично;
X —2 — 1 | 2 3
У —12 1 3 5
Ответ Ls (х) — —ygx3 — ggX2 +
4. Построить интерполяционный многочлен Лагранжа для функции f (х) =
= е~х, если узлами интерполяции служат точки Xj = 1, х2 = 2, х3 = 3. Оце-
нить погрешность при х = 1,5.
Ответ L2 (х) = 0,0735х2 — 0,4530х + 0,7474; /?2 (1,5) = 0,23 • 10"1.
5. Составить таблицу конечных разностей для функции, заданной таблично:
6. Составить
таблично.
—2
10
-‘I 0
51 1
1
—15
2 | 3
—50 I —100
разделенных разностей для функции, заданной
таблицу
X —3 1 0 2 3
У —15 —7 1 25 47
х
У
204
7. Для функции у — f (х), заданной таблично*
X 1,03 1,08 1,016 | 1.23 1,26 1,33 1,39
У 2,80107 2,94468 3,18993 | 3,42123 3,52542 3,78104 4,01485
вычислить значение в точке х == 1,21555 с точностью до 10-§, пользуясь
формулой Эйткина
Ответ: 3,37215.
8. Вычислить значение функции в точке х = 1,34627, пользуясь формулой
Гаусса, если функция у — f (х) задана таблично:
X 1,335 1.340 | 1,345 | 1,350 | 1,355 | 1,360
У 4,16206 1 4,25562 | 4,35325 | 4,45522 | 4,56184 | 4,67344
Ответ: 4,379.
9. Для функции, заданной таблично:
х J 1,435
у I 0,892687
1,440 j 1,445
0,893698 I 0,894700
определить значение аргумента, соответствующее значению функции 0,892914.
Ответ 1,43612
10. Методом обратного интерполирования найти в точностью до 10"£ корень
уравнения Д/х +1 —— =0, лежащий в интервале 0,7 < х < 0,8.
Ответ: 0,75487.
11. Расходы государственного бюджета СССР на социально-культурные ме-
роприятия представлены таблицей:
Годы 1940 1950 I960 1970
Расходы на социально- культурные мероприятия (в млрд, руб.) 4.1 11,7 24,9 58
Каковы были расходы государственного бюджета СССР на социально-культур-
ные мероприятия в 1969 г.?
12. Расходы по государственному бюджету СССР на выплату пособий много-
детным и одиноким матерям представлены таблицей:
Годы 1940 1950 1960
Выплата пособий (в млн. руб.) 123 366 496
Обработать математически данную информацию, представив табулированную
функцию интерполяционным многочленом Ньютона.
205
13. Удельный вес электровозной тяги в грузообороте железнодорожного
транспорта (в %) представлен таблицей
Годы 1940 1965 1970 1971
Уд. вес электровозной тяги .... 2,0 39,5 48,7 49,6
Построить интерполяционный многочлен Лагранжа.
14, Оборот внешней торговли развивающихся стран (по годам) задан следую-
щим образом:
Годы 1965 1966 1967 1968 1969 1970
Оборот внешней торговли 74 80 82 90 100 107
Составить таблицу конечных разностей.
15. Численность рабочих и служащих, занятых в электроэнергетике, пред-
ставлена таблицей:
Годы 196t 1967 1968 1969
Численность рабочих и служащих (в тыс. чел.) 581 602 625 635
Методом экстраполяции определить (ориентировочно) численность рабочих и
служащих в электроэнергетике на 1970 г.
16. Производство электротары в СССР в 1966—1968 г. представлено в таб-
лице:
Годы 196b 1968 1969
Производство электротары (в тыс. шт.) . . . . 17 21 23
Обработать математически данную информацию, представив табулированную
зависимость аналитической.
17. Задан по годам выпуск продукции легкой промышленности, товаров
культурно-бытового назначения и хозяйственного обихода:
Годы 1971 1972 1973
Выпуск продукции (в млрд, руб,) 82 89 95
206
Методом экстраполяции определить предварительно выпуск продукции легкой
промышленности на 1974 г.
18. Подобрать аналитическую зависимость, отражающую выпуск специа-
листов высших учебных заведений в СССР (на начало учебного года), если эта
зависимость представлена таблично:
Годы 1966 1967 1968
Число специалистов (в тыс. чел.) 8 12 13
19. Основные показатели развития связи (количество отправленных писем)
представлены таблицей:
Годы 196о 1970 1971
Количество писем (в млрд.) 5,2 8,0 8,3
Определить ориентировочный прирост количества отправленных писем в 1973 г.
по отношению к 1971 г., используя метод экстраполяции
20 Рентабельность промышленных предприятий СССР представлена таб-
лицей:
Годы 19 60 1 965 1970
Прибыль (в млрд, руб.) 14,0 22,5 56,0
Определить рентабельность предприятий в 1968 г., пользуясь схемой Эйткина.
21. Добыча природного газа в Италии за период 1966—1968 г. представлена
таблицей:
Годы 1966 1967 1968
Добыча природного газа (в млрд, м3) .... 8,8 9,3 10,4
Подобрать интерполяционный многочлен, представляющий добычу природного
газа как функцию времени.
22. Добыча природного газа в ФРГ за период 1966—1968 г. представлена
таблицей:
Годы 1966 1967 1968
Добыча природного газа (в млрд, м3) .... 2,8 3,7 5,8
Определить ориентировочно прирост добычи природного газа в 1969 г, по отноше-
нию к 1968 г., пользуясь методом экстраполяции.
207
Глава V
ОПРЕДЕЛЕНИЕ СОБСТВЕННЫХ ЧИСЕЛ И СОБСТВЕННЫХ ВЕКТОРОВ МАТРИЦЫ
§ 5.1. Характеристический многочлен и методы определения
его коэффициентов
Пусть А — [а/;] — квадратная матрица n-го порядка с действи-
тельными элементами и X — некоторое неизвестное. Тогда матрица
А — КЕ, где Е — единичная матрица n-го порядка, называется харак-
теристической матрицей матрицы А, Так как в матрице ХЕ по главной
диагонали стоят X, а все остальные элементы равны нулю, то характе-
ристическая матрица имеет вид
Определитель этой матрицы называется характеристическим оп-
ределителем и равен
det (Л-ХЕ) =
а11— X #12 • • • а1п
#21 #22 • • • #2п
#П1
#п2 • • • ®пп
В развернутом виде det (Л — КЕ) — многочлен п-й степени от X, так
как при вычислении этого определителя произведение элементов глав-
ной диагонали дает многочлен со старшим членом ( — 1)" X", т. е.
det (Л — ХЕ) = (~1Г [Х^ — ^Х^+М""2 —...+( — 1)"рп]. (3)
Многочлен (3) называется характеристическим многочленом матри-
цы Л, а его корни Хъ Х2, Хп, которые могут быть как действительны-
ми, так и комплексными,— характеристическими числами, или соб-
ственными значениями, матрицы Л. Числа р2, ..., рп называются
коэффициентами характеристического многочлена (3).
Ненулевой вектор X = (хь х2, хп) называется собственным
вектором матрицы Л, если эта матрица переводит вектор X в вектор
АХ - XX, (4)
т. е. произведение матрицы Л на вектор X и произведение характеристи-
ческого числа X на вектор X есть один и тот же вектор. Каждому
собственному значению Xz матрицы соответствует свой собственный
вектор Xi (i = 1, 2, п).
Для определения координат собственного вектора составим урав-
нение
(Л — КЕ)Х = 0,
(5)
208
которое называется характеристическим. Переписав его в виде
«11 — «12 «13 • • а1п " *1 - 0“
«21 «22 «23 • • ♦ «2П *2 0
«31 «32 «33 • • • «Зп • *3 0 (5')
_ «П1 «п2 «пЗ • * «пи _ *п _ _ 0_
и выполнив умножение, получим систему линейных однородных
уравнений
(«11—«12*2 + «13*3 + ••• + а1пХп~®*
«21*1 + («22— ^)*2 + «23*3 + - + «2п*п^0,
{ «31*1+ «33*2+ («зз — ^)*з + - + «Зл*п = 0, (5")
«п1*1 + «п2*2 + «п3*3+ •••+(«пп—^)Хп~0»
Определитель системы (5") равен нулю, так как из этого условия
были определены собственные значения матрицы А; следовательно,
система (5") имеет бесчисленное множество решений, ее можно решить
с точностью до постоянного множителя (как систему однородных
уравнений).
Решив эту систему, мы найдем все координаты собственного векто-
ра X. Подставляя в систему (5") поочередно Х2, 1П, получаем
п собственных векторов.
При определении собственных значений и собственных векторов
матриц решается одна из двух задач: 1) определение всех собственных
значений и принадлежащих им собственных векторов матриц или
2) определение одного или нескольких собственных значений и принадле-
жащих им собственных векторов.
Первая задача состоит в развертывании характеристического опре-
делителя в многочлен n-й степени (т. е. в определении коэффициентов
Рь Р2> •••» Рп) с последующим вычислением собственных значений
•••» + и, наконец, в определении координат собственного вектора
X = (%!, х2.... хп).
Вторая задача заключается в определении собственных значений
X (одного или нескольких) итерационными методами без предваритель-
ного развертывания характеристического определителя.
Методы первой задачи являются т о ч н ы м и, т. е. если их приме-
нить для матриц, элементы которых заданы точно (рациональными
числами), и точно проводить вычисления (по правилам действий с обык-
новенными дробями), то в результате будет получено точное значение
коэффициентов характеристического многочлена, и координаты соб-
ственных векторов окажутся выраженными точными формулами через
собственные значения.
Обычно собственные векторы матрицы удается определить, исполь-
зуя промежуточные результаты вычислений, проведенных для опреде-
209
ления коэффициентов характеристического многочлена. Конечно, для
определения собственного вектора, принадлежащего тому или другому
значению, это собственное значение должно быть уже вычислено.
' Методы решения второй задачи — итерационные, здесь
собственные значения получаются как пределы некоторых числовых
последовательностей, так же как и координаты принадлежащих им
собственных векторов. Так как эти методы не требуют вычисления
коэффициентов характеристического многочлена, то они менее трудоем-
ки. Ниже рассматриваются некоторые методы развертывания харак-
теристического определителя и итерационные методы нахождения соб-
ственных значений матрицы.
3 5.2, Метод непосредственного развертывания
Рассмотрим на примере матрицы третьего порядка, как находятся
коэффициенты характеристического многочлена непосредственным раз-
вертыванием характеристического определителя. Пусть
#11 #12 #13 #11 #12 «13
л= #21 #22 #23 , det (Л— ХЕ) = #21 #22 #23 •
#31 #32* #33 #31 #32 #33
Вычислим определитель по правилу треугольников:
#и— А
#21
#31
#12 #13
#22 #23
#32 #33
det А—Х£) =
= (Яц М (#22 М (#33 + #12 #23 #31 #13 #32 #21 ’
#13 #31 (#22 #12 #21 (#33 #23 #32 (#11
= - А?4-Х2(ап + #22 + #з3) —М(#11#22~#12 #21) +
+ (#22 #33 #2 J #32) + (#11 #33 #13 #31)] + (#11 #22 #33 +
+ #12 #23 #31 + #13 #32 #21 #13 #22 #31 # 12 #21 # 3 #23 #32 #11) =
+----(#11 + #22 + # з) +
#11
#31
#13
#33
#11
#21
#31
#12
#22
#32
#11
#21
#12 । #22
#22 #32
#1
#23 >
#33
#23
#33
+
или
def (А — КЕ) = (—I)3 (X3 — М3 + р2Х - р3) = 0.
Здесь коэффициент рг — сумма диагональных элементов матрицы А;
он называется следом матрицы и обозначается Sp А:
Pi = Sp А = ап + а22 + а33;
210
коэффициент р2 — сумма всех диагональных миноров второго порядка
матрицы А:
ап
а21
л12
а22
^22 ^28
^32 +з
ап
аз1
а13
^33
{диагональными минорами второго, третьего, ..., n-го порядка назы-
ваются миноры, элементы главных диагоналей которых являются
элементами главной диагонали определителя det Л); коэффициент
р3 = det А —
^11 ^12 +з
^21 ^22 +з
^31 ^32 +(3
Вообще, если требуется развернуть определитель det (Л — ХЕ)
в многочлен п-й степени:
то коэффициенты plt р2, рп вычисляются по следующим формулам:
п
р± = ан “ Sp А —сумма всех диагональных элементов
матрицы А\
2 Яца
а<(3 Пра
<2аа Пау
Рз= а^с а^у
a <f(< v Пуа ПуЗ Пуу
—сумма всех диагональных миноров вто-
рого порядка матрицы А;
__сумма всех диагональных миноров треть-
его порядка матрицы А;
рп = det А—определитель матрицы А.
Число диагональных миноров &-го порядка матрицы А равно
С* = п(П-1)(п-2)...(п-к + 1) (k==l)2j <<t> n).
/г!
Пример. Методом непосредственного развертывания найти характеристи-
ческий многочлен матрицы
- —4 _3 1 I"
2 0 4 — 1
Л= 1 1 2 —2 •
1 1-1-1
Решение. 1) Находим
, = $Р -А —й11 + а22 + а3з + а44 — —4+0 + 2— 1 = —3.
2) Имеем р2 —
сх <
ааа
Число диагональных миноров второг о по-
211
4 1 3
рядка у матрицы четвертого порядка равно С| = ~ 6. Выписывая все
эти миноры и складывая их, получаем
I —4 _3| 1—411 1—4 II | 0 4 I
Ол = I I -4-1 4-1 I *4* I I 4~
Н2 | 2 0| j 1 2| |1 —1] | 1 2 I
а=1; Н2 а=1; (3=3 а = 1; 0 = 4 а=2; 0=3
а—2; 0=4 а = 3; 3 = 4
2ааа
a<₽<v
ауа
аа0 аау
QYV
Число диагональных миноров треть-
его порядка у матрицы четвертого порядка равно
сз_4~3-2 _
4 1-2-3 41
Следова-
тельно,
а = 2: 3 = 3: у=4
4)
Находим, наконец,
— 4 —3
р4 -- det 4 =
1 1
5) Таким образом, окончательно получаем
D(X)=X4 — рг K3 4-p2 X2 —р3Х4-р4 = Х44-ЗХз —7X2 —24Х—15.
Метод непосредственного развертывния очень трудоемок и приме-
няется при нахождении характеристических многочленов для матриц
невысоких порядков.
§ 5.3. Метод Крылова для развертывания
характеристического определителя
Метод Крылова основан на свойстве квадратной матрицы обращать
в нуль свой характеристический многочлен.
Согласно тождеству Гамильтона — Кел и, всякая
квадратная матрица является корнем своего характеристического
многочлена и, следовательно, обращает его в нуль,
212
Пусть
D(X) = detU — ХЕ) = %я + рД«-’ + р, №-* + ... + рп (1)
— характеристический многочлен матрицы А. Заменяя в равенстве
(1) величину к на А = [ао] (где i ~ 1, 2,..., и; j = 1, 2, п), получим
An + Pi Ля-Ч-р2Ля-2 + ... + рп£ = 0.
Возьмем произвольный ненулевой вектор
ую; =
У[0)
1Л°’
(2)
(3)
и умножим обе части равенства (2) справа на У<0):
д«у(0) + Р1д«-1 У<°> + р2/У-2 У(0)4-... 4-рпУ(0) = 0. (4)
Положим теперь
ду(*-1) = у<*) (Ь1, 2..............п), (5)
т. е.
у<1) — дую»,
У<2> = ЛУ<1> = Л2У«”,
»•••••*«*•
у и = ду(л-1) = Ап У<0).
Равенство (4) принимает тогда следующий вид:
у(«) + лу(«-1) + /72у(п-2) + ,ф> + Рп у(О) = о> (6)
или
У~1 >+р2 У<л - 2> +... + рп У< °> == — У(Ч
т. е.
Pi у^~ ” + Ра Р?-2’ + + Рп У(°} = ~УГ>
Р1 У?- Ь + Pi У(3~2) + — -У Рп y(i} = —РаЛ)»
Р1 У% ~ 1 ’ + Pi У(п ~ 2> + • • • + Рп У^ = — Уп^
213
или, наконец, в матричном виде
^-1) /А"-2' ... У\0) 1 pi г/(") -
^-2) ... ?А0) ' Рг У^
• • —
у(П-1) ^~2) ... ej _Рп_
Векторы Y{iX\ И2), в.., У/п) вычисляются по формулам
/ = 1
1Т- 2 atjY^=AY^9
/=1
Yin}-= i auYT~i}^AY&-V (i = 1,2, n),
/=1
причем координаты начального вектора (3) берутся произвольно. Если
линейная система (7) имеет единственное решение, то ее корни р19
р21 рп являются коэффициентами характеристического многочлена
(1). Это решение может быть найдено по методу Гаусса.
Пример 1. Методом Крылова развернуть характеристический определи-
тель матрицы
“-4 —3 1 I ~
2 0 4 —1
А~ 1 1 2 —2 *
1 1 -1 -1 _
Решение. 1) Выбираем начальный вектор
/(0) =
1
о
о
о
2) Пользуясь формулами (9), определяем
= ду(*-1) (/5=1,2, 3, 4);
координаты векторов =
214
Таблица 5.1
Pl р 'Свободные члены
|—39 20 И 13 1 1 I 1 1 I HI । 5 | 4^ ЬЭСЯ со I 1 — 4 2 1 £ 4/39 1 0 0 0 — 1/39 — 120 47 23 43 40/13 — 150 64 33 53 50/13
—— 15/13 18/13 0 1 —2/39 —5/39 -1/3 —2/45 20/39 11/39 -1/3 4/9 — 189/13 — 141/13 3 —53/5 -168/13 -121/13 3 | -56/5
I —1/15| -1/3 1 -1/3 1/3 5 33/5 3 — 99 31/5 3 -93
— ——— в 1 —30 1 — 15 | —28 — 14
1 1 1 1 ра = —15 р3=—24 Ра=—7 Pi = 3 73 1 ТЗ 1 1 -Q | « “ -’ll II II 1 1 1 1 к—1 № СО 4^
" — 4 — 3 1 1 “—4 ” “12"
2 0 4 -1 2 — 5
у(2) = Лу('> = 1 1 2 —2 1 —2
1 1 1 -1 1 _ — 4
— — —
-4 -3 1 1 " 12 " -39
2 0 4 -1 - 5 20
у(3) = ду(2) = 1 1 2 — 2 - 2 11
1 1 -1 — 1 .. — 4 13 _
— 4 -3 1 1 ~ “-39“ 120 "
2 0 4 — 1 20 — 47
у(4) — 4У<3) = 1 1 2 — 2 11 — - 23
1 1 -1 -1 ~ 13 — 43
215
3) Составляем матричное уравнение
“ -39 12 — 4 1 “ Р1~ 120 ~
20 -5 2 0 Р2 — 47
11 -2 1 0 Рз — 23
13 — 4 1 0 _ _р4_ _ — 43 _
Записываем систему вида (7):
— 39pi4“12p2 — 4рз+Р4 “ — 120,
20pi— 5р2“|-2рз = 47,
llpi— 2р2~Ь Рз = 23,
13pi— 4р2+ рз == 43.
Решаем эту систему по схеме Гаусса (см. табл. 5.1 на стр 215).
Таким образом,
D(X) = det (Л—%£) = V+pi Х34-р2 ^2 + p3X + p4 = X4 + 3V—7^2—24Z —15.
Если же полученная линейная система (7) не имеет единственного
решения, то следует изменить начальный вектор,
Пример 2. Методом Крылова развернуть характеристический определитель
матрицы
—1 —1 2"
3 0—4
1—2—2
1 0 —1
1
1) Возьмем в качестве начального вектора К(0) =
0
у(1)_
1
2
1
1
у(3) — ху(2)
1
4
2
2
тогда получим
216
откуда получаем систему уравнений
>1+Рз+Р4 = Ь
4р14-4р2+2р3= —6,
2Р1— Р2 + Рз = 3,
2Р1 + 2р24~Рз— —3.
Решаем эту систему по схеме единственного деления (см табл. 5.2),
Таблица 5 2
Р1 Pi Рз Pi Свободные члены S
п 4 2 2 1 0 4 — 1 2 0 1 2 1 1 * 1 1 0 0 0 1 1 — 6 3 —3 1 1 4 4 5 2 4
□ — 1 2 1 1 1 1 1111 1 1 1 Tj* OJ СМ 1 -ч 1 1 11 1 1 1 1 1 О LQ 1 со - ||| 1 L 1 2! сою 1 “2 1 1 1 1 1 1 11 1 1 L
— 1,51 0 1 —3 0 2 —2 1 1,333 —6,5 1 4,333
□ 1 1
Так как ведущий элемент равен нулю, то продолжать вычисления по этой
схеме невозможно.
3) Для получения единственного решения меняем начальный вектор,
О
полагая /(0) =
находим
у( 1) — —
—4
—2
-1
/(25 — Ду(1) —
6
— 4
4
— 1
1
2
217
приводит к системе
4Р1+6р2+2рз
4pi—4р2 —4р3
— 4pi4-4p2— 2р3
ч 3р1— р2— РзН“Р4“
= —10,
= —8,
или
= —10,
5,
2pi + Зр2+Рз
Р1- ?2--Рз
—2pt+2p2—p3
3pi— р2 —Рз + Р4 =
= —5,
= —2,
= — 5
5.
которую решаем по схемё единственного деления (см табл, 5.3).
Таблица 5.3
Р1 Рг р8 Р< Свободные члены 2
и 3 1 0 — 5 1
1 — 1 — 1 0 — 2 —3
—2 2 -1 0 —5 —б
3 -1 -1 1 —5 —3
1 1,5 0,5 0 —2,5 0,5
1 —2’5| — 1,5 0 0,5 -3,5
5 0 0 — 10 — 5
-5,5 —2,5 1 2,5 -4,5
1 0,6 0 1 — 0,2 1,4
1-4 0 — 9 — 12
0,8 1 1,4 3,2
1 0 3 4
гп — 1 0
1 Р4 = — 1 р4 = 0
1 Рз — Рз = 4
1 р2= —2 Р2= — 1
1 Р1=—1 Pt = O
Следовательно,
Р(Л)=Л4—Л3—2Р+ЗЛ —L
218
§ 5.4. Вычисление собственных векторов по методу Крылова
Если известны коэффициенты р1г р2,..., рп и корни Alt Л2..
характеристического многочлена, то метод Крылова дает возможность
найти соответствующие собственные векторы по следующей формуле:
Х0) = у(п-1) + ^иу(п-2) + 111 + ^_ь ,Ym (4 = 1,2, (I)
Здесь Y('n~v>, У(п-2>, ..., У(0>— векторы, использованные при на-
хождении коэффициентов plt р2, рп методом Крылова, а коэффи-
циенты дл (j = 1, 2, ..., п — 1; i = 1,2, ..., п) определяются по схеме
Горнера:
= 1; Ян = М; -1. i + Pi- (2)
Пример. Методом Крылова вычислить собственные векторы матрицы
1 —1 —1 —2
2 3 0 —4
А —
1 1-2-2
1 1 0—1
Решение. Характеристический многочлен матрицы А известен1.
det (Л — Х£) = X4 — X3 — 2Ла + 3^ — 1
(см. пример 2 § 5.3), а собственные значения таковы: = 1; = 1; = 0,618;
/Ц= —1,618. Для нахождения собственных векторов воспользуемся формулой (1):
x<‘) = y<3491i Y^+q2i г(1)+9згг<°>.
Здесь' ^Ог — 1, а коэффициенты (/ — 1, 2, 3; t = 1, 2, 3, 4) вычисляем по схе-
ме Горнера (см. табл. 5.4),
Таблица 5.4
Ро~ 1 Р1= — 1 Р2 = — 2 Рз ^=3
К1=1 <7 01 = I <7и=0 721 — 2 <731= 1
%2=1 7 02 — 1 <712 — 0 9 22 ~ 2 9 32 ~ I
К3=0,618 д03= 1 <713=-0,382 | । ^23——4,35 <7зз = 0,312
Ь4= —1 ,618 7о4 — 1 2,618 ^24 1 > 236 <7з4 = 1.09
Воспользуемся выражениями для векторов Г(1), Г(2) и У{3}3 найден-
ными в примере 2 §5.3, и получим
4 6~ 2~ ’О' "О’
4 —4 — 4 0 12
Х(1)=Х<2) = —4 + 0. 4 —2. —2 +1- 0 — 0
3_ —1 _ _ —1 ~ _ 1 _ 6 _
19
Х<3> =
—0,382.
— 4,35.
6
— 4
4
— 1
2
— 4
—2
— 1
4
4
— 4
3_
Метод Данилевского
Две матрицы А и В называются подобными, если одна получается
из другой путем преобразования с помощью некоторой неособенной
матрицы, т» е. выполняется равенство
в = S-MS.
Если матрица В подобна матрице А, то пишут В со А,
В методе Данилевского при построении вычислительной схемы ис-1
пользуется основное свойство подобных матриц: подобные матрицы
имеют одинаковые характеристические многочлены.
Если привести данную матрицу
^2 ^13 “ • &1п
^22 * •• ^2П
А = ^31 ^32 •• &3п
&пЗ •• —
(1)
с помощью преобразований подобия к так называемому виду Фро-
бениуса:
fll /12 fl3 ••• fl, п-1 fin
1 0 0 ...0 0
0 1 0 ...0 0
(2)
_0 0 0 ... 1 0
220
й затем определитель
Ах /12 Г1з •А.п- -1 Ап
1 —X 0 .. ..0 0
det (F- ХЕ) = 0 1 — X . ..0 0 (2)
0 0 0 ... 1 -X
разложить по элементам первой строки, то получим
01X) = det(E-XE) = (A1-X)(-Xr->-A2(-X)'!-2 +
или
D(X) = det (F—ХЕ) =
= (_l)n(X"-p1^-‘-p2X«-2-psX'!-3-...-pJl). (4)
Здесь л = Ai. р2 = Аг. рз = /1з, ..., = Ап — коэффициенты ха-
рактеристического многочлена матрицы F, которые в силу подобия мат-
риц F и А являются и коэффициентами характеристического многоч-
лена данной матрицы А,
Согласно методу Данилевского, переход от матрицы А к подобной
ей матрице Фробениуса F осуществляется с помощью п — 1 преобразо-
ваний подобия, последовательно преобразующих строки матрицы А,
начиная с последней, в соответствующие строки матрицы Р.
Схема преобразования матрицы А в подобную ей матрицу Фробе-
ниуса F. 1) Пусть нам нужно строку ап1ап2... ап, n-i перевести
в строку 0 0... 1 0. Предполагая, что ап> разделим все элементы
(п — 1)-го столбца матрицы А на ant nlv Тогда ее и»я строка примет
вид
«П1 ап2 ••• апп, или anl ап2...1 апп.
-2) Вычтем (л— 1)-й столбец преобразованной матрицы, умножен-
ный соответственно на числа апЪ ап2, апп1 из всех остальных столб-
цов. Для п-й строки получим
ani—ап1 ап2—ап2...1 апп — апп, или 0 0...1 0.
3) В качестве неособенной матрицы берем матрицу полу-
ченную из единичной после таких же преобразований:
-1 о ...о
0 1 ... о
п-1
^п-1,1 ^п—1,2 ••• ^п-1,п-1 ^п-1,п
где
Д) о
Gn,n-1
(5)
221
Произведенные операции равносильны умножению справа матрица
М.п на матрицу А:
В = АМп_1
11 а12 • а1 п-1
21 Й22 • ^2, п-1 а2п
71-1’1 an-lf2 '• • ^П-lfTl-l ап-
_0 0 ... 1 О
"1 0 ... О О
О 1 ... О О
тп-1,1 ^п—1.2 ••• ^n-l,n—1 ^n—l.n
_0 О ... О I
&11 ^12 ••• ^1,п-1 ^1П
^21 ^22 ^2, П-1 ^2п
Ьп-1,1 ^п-1.2 ••• ^п—1,п-1 ^п-1,п
О 0 ... 1 о
Элементы матрицы В вычисляются по формулам
аН “Ь СЦ,п-1 (б)
Однако построенная матрица В — АМп_г не будет подобна матри-
це А.
4) Чтобы получить преобразование подобия, нужно обратную
матрицу Л4„21 слева умножить на матрицу В:
АМ^^Мп^В.
Обратная матрица Л1ПА1 имеет вид
M„li =
"1 О
...о
...о
О 1
О "
о
^П1 ^П2 ^п.п- 1 ®пп
О 0 ...0 1
Полагаем M„-i АМп-г = С; следовательно, С = М„~] В. Умноже-
ние слева матрицы Мп-\ на матрицу В не изменяет преобразованной
строки,последней, и матрица С имеет вид
~1 0 ... О 0 "
О 1 ...о о
X
^п! ^п2 ••• ^п,п-1 ®пп
_0 0 ...0 1
222
^11 &ln
^21 ^22 ••• Ь2п
^n—1,1 ^n-1,2 ••• ^n-l,n-l
0 0 ... 1 0
C11 £12 •**£1,71—1 Cln
£31 £22 £з,п-1 C2n
^n—1,1 ^n->l,2 *•' ^n-l.n—l Cn — L,n
0 0 ... 1
Действительно, перемножая матрицы Mn—t и В, мы меняем только
(п — 1)-ю строку матрицы В, так как = btj для всех остальных
строк. Элементы этой строки находятся по формулам
п
сп-и = 2 anhbhj (/=1,2, ...,п). (7)
А=1
Полученная матрица С подобна матрице А и имеет одну приведенную
строку.
5) Далее, если cn„lf п_2 0, то над матрицей С повторяем ана-
логичные операции, взяв за основную (п—2)-ю строку. Тогда, исполь-
зуя промежуточную матрицу D = СМп _ 2, в результате получим мат-
рицу Е ~ MnE2D == Л1д2_2 СМп_2 с двумя приведенными строками.
Над матрицей Е проделываем те же операции и т. д. до получения мат-
рицы Фробениуса.
Все эти преобразования оформляются в виде вычислительной схемы,
процесс составления которой рассмотрим на конкретном примере.
Пример I. Методом Данилевского, развернуть характеристический определи-
тель матрицы
Г —4 —3 1 1"
. 2 0 4 —1
Л= 112-2
1 1 — 1 —1
третьей строки матрицы Mn-i~ М31
Решение. I э т а п. Матрицу А приводим к виду Фробениуса. Для вы-
числений составляем таблицу (см. табл. 5.5 на стр. 224).
1) В строках 1—4 вычислительной таблицы помещаем элементы йп (/, / == 1,
_ 4 J
3» 4) данной матрицы А и контрольные суммы = X (1 = 1, 2, 3, 4)
/— 1
-—столбец S. Отмечаем элемент а43 — — 1, принадлежащий третьему столбцу
(отмеченный столбец).
2) В строке I записываем элементы
вычисляемые по формулам (5):
«41 1
m3i=---------- ——-= 1;
«43 — 1
/П33 =—1-_____!___1- °44
33 — — — 1, /И34 — —----- =
«43 — 1 а.^
я 42 1 f
/п32= —--= ——
«43 —1
___—1; m35= —-------=—- =0.
— 1 «43 —1
Число 0 должно совпадать с суммой элементов строки I после замены полу-
ценного значения элемента т33 на — 1, но в нашем примере т33 = — 1 (Обычно
для удобства число —1 записывается рядом с элементом т33 и отделяется от
последнего чертой.)
Таблица 5.5
Строки М'1 Столбцы £ S'
1 2 1 3 1 4
1 >2 3 4 —4 2 1 1 —3 0 1 1 1 4 2 El ~ ' СЧ 1 1 1 1 —5 5 2 0
I М-, м, 5 1 —1 — 1 0
5 6 7 8 1 1 —1 —1 —3 6 3 0 —2 4 3 0 —1 —4 —2 1 0 —5 —4 0 —6 1 0 1 —5 5 2 0
7 f 0 El —4 — 1 —6
11 ! м* 0 —1 —4 — 1 —6
9 10 п 12 0 -1 —4 — 1 -3 6 0 0 2 —4 1 0 7 —20 0 1 2 —9 0 0 8 —27 1 1 6 —23 0 0
10' н 0 19 9 22
II! м( 0,167|—i 0 3,167 1,500 | 3,667
13 14 15 16 —6 0 19 9 0,500 1 0 0 2,000 0 1 0 —2,500 0 0 1 -2,500 0 0 0 —2,500 1 1 1 —3 0 0 0
13' —3 7 24 15 43
3) В строках 5—8 в графе Л1-1 выписываем третью строку матрицы MfSi
которая должна совпадать с четвертой строкой исходной матрицы А. |
4) В строках 5—8 в соответствующих столбцах выписываем элементы матри-i
цы В — AM3, вычисляемые по формулам (6) для неотмеченных столбцов.
Первый столбец:
би = + ^з1 ” —4 + 1'1 = —3; b%i = 4" а%з тз1 — 24-4» 1—6;
^31 — «31 4~ ^33 ^31 = 1 2* 1 = 3; &41 — ^41 4- ^43 /?/31 “ 1 + ( 1) ' 1 — 0.
224
Второй столбец:
&12 — a12~j~ «13^32 ~ “~3 1’1 = -2; Z?22 “ а22 + а23 ^32 = О -I- 4 1 =4;
6 32 — «ЗЯ 4“ «33 ^32 = 1 + ^’ 1 = 3; 642 = «42 +«43 ^32 “ 1 + ( — 1) ’ 1 = 0.
Четвертый столбец:
6н — аи4"«1з m34 = 1 +1 •(—1) = 0; Ь24 = «2< + «23 тз4= — 1 +4*(— 1) = —5;
634 = «34+ «33 /Ц34 = 2+ 2‘(— 1) — —4; 644 = «44+ «43 «гз4 =
= —1+(—1)*( —1) = 0.
Преобразованные элементы третьего (отмеченного) столбца получаются
с помощью умножения исходных элементов на т33 — — 1.
"Третий столбец:
61з — «43 тзз= 1 *( — 1) = — 1; 62з — «23 тзз = 4*(— 1) = —4;
бзз — азз тзз — 2-( — 1) = —2; 643 = «4з т33== (—1).(— 1) = 1,
Последняя строка матрицы В должна иметь вид 0 0 10.
Для контроля пополняем матрицу В преобразованными по аналогичным дву-
членным формулам с тзб = 0 соответствующими элементами столбца S':
6is — «is+ «13 Ш35 = —54~ 1*0— —5; бзв — «25+«23 ^35 — 5-|-4*0 — 5;
633 = «зб+ «ззтзъ= 24-2’0 = 2; б4в = «1б+«43 ^з5 = 0 + (—1)»0 = 0.
Полученные результаты записываем в столбце 2' в соответствующих строках.
Прибавив к элементам столбца S' соответствующие элементы третьего (отмечен-
ного) столбца, получим контрольные суммы для строк 5—8 (i = 1, 2, 3, 4).
Столбец S:
61& = 6164~ «is = — 5—-1 = —6; 625— 62е 4"«2з “5—4= 1;
635 ~ 6зе + «зз — 2—2 = 0; 645 = 640+ «43 = 04-1 = 1.
Кроме того, элементы столбца S для контроля вычисляются по формуле 6f5 =
4
= S btj (i = 1, 2, 3, 4):
|=ЗЯ 1 *
615 = 6ц 4“ 6124~ 613 + 614 = —3—2— 14-0= —6; 625 = 6214" 622 + 623 + 624 =
-64-4—4—5=1;
635 = 631 + 632 + 6зз + 634 = 3 + 3—2 — 4 = 0; 645 = 641 + 642 + 643 + 644 =
=0+0+14-0=1.
Матрица В имеет следующий вид:
’—3 —2 —1 0'
6 4—4 —5
3 3 — 2 — 4
_ 0 0 1 р_
5) Преобразование М3 \ произведенное над матрицей В и дающее матрицу
О = изменяет лишь третью строку матрицы В, т. е. седьмую строку
таблицы. Элементы этой преобразованной строки 7' представляют собой суммы
парных произведений элементов столбца находящихся в строках 5—8,
на соответствующие элементы каждого из столбцов матрицы В [см. формулы (7)]:
с = 1 . ( _ 3) + 1 . 6 + ( - 1) • 3 + ( - 1) . 0 = 0;
С32 = 1 • ( — 2) 4- 1 • 4'+ ( — 1) . 3+ ( — 1)-0 = —
= 1 • ( — 1) + 1 • ( — 4) + ( — 1) - ( — 2) + ( — 1) • 1 = - 4;
= 1 • 0 + 1 < ( — 5) + ( — 1) - ( — 4) + ( — 1) • 0 = - 1.
Те же преобразования производим над столбцом S:
с3б = 1 . ( - 6) + 1 . 1 + ( - 1) • 0 + ( - 1) . 1 = ~ 6.
225
В результате получаем матрицу С, состоящую из строк 5, 6, 7', 8 с контроль-
ными суммами в столбце S:
—3
С- 6
О
о
—2 —1 О'
4 —4 —5
|~1 -4 -1
О 1 о
Матрица С подобна матрице А и имеет одну приведенную строку. Этим заканчи-
вается построение первого подобного преобразования С =
II этап. Принимая матрицу С за исходную, выделяем элемент с32 = — 1
(второй столбец) и продолжаем процесс аналогичным образом.
1) Находим элементы матрицы Мп-2 ~ М2 по формулам (5);
Сз1 0 — = ——“ = 0; с32 —1 гзз —4 ^23= — —Г-= —4; — 1 С35 Щ25=-— -= С32 1 1 «22 = — =—7 = —1; с32 —1 £34 —1 < с - -1 - 1; с32 —1 —6 — — ==—6. —1
Просуммируем: 0—1—4 — 1 = — 6 (т22 = — 1; если бы m2S — 1, то нужно
было бы заменить т22 на — 1).
2) В строках 9—12 в графе М"*1 выписываем вторую строку матрицы Alf1,
которая совпадает с третьей строкой матрицы С (см. табл. 5.5). Находим эле-
менты матрицы D = СМ2.
Первый столбец:
du ----- — 3 + ( — 2) 0 — — 3; d21 = 6 + 4 • 0 ~ 6; d31 = 0 + 0 = 0.
Второй столбец (отмеченный) получается умножением соответствующих эле-
менте матрицы С на т22 — — 1:
+12 ” ^12^22 ~ ( — 2) • ( — 1) — 2; ($22 “ С22Ш22 — 4 • ( — 1) = —4}
^32 = ^32^22 “ ( 0 ’ ( 1) ~ 1.
Третий столбец:
^13 ~ Из + ^12^2 <3 ~ 1 + ( 2) *( — 4) — 7; d23 ~ ^гз 4“ ^22^23 =
= - 4 + 4 < ( - 4) = - 20; d33 = с33 + с32т23 = - 4 + ( - 1) ( - 4) = 0.
Четвертый столбец:
d14 = <Д4 + с12ш24 = 0 • 1+( — 2) • ( — 1) = 2; d2± = c2i + c22m24 —
_ 5 + 4 * ( - 1) = - 9; d34 + c32m24 - - 1 + ( - 1) • ( - 1) = 0.
Столбец S'-
die = с15+Г12щ25 =* — 6 + ( — 2) • ( — 6) = 6; rf26 = с25 + c22m25 ==
= 1 + 4 - ( — 6) = — 23; d36 = с35+ es2m25 = — 6 + ( — 1) (— 6) = 0.
Элементы столбца S получаются сложением элементов столбца S' с соответ-
ствующими элементами отмеченного столбца:
^15 = <716 + <712 ~ 6+2=8; г?2б — <726 + d22 = — 23—4 = — 27;
^35 — d36 + d32 = 0 + 1 = 1.
Матрица D имеет вид
3 2 7 2’
D_ б —4 —20 —9
0 10 0
_ о о 1 0_
226
Преобразование Aly1, произведенное над матрицей D и дающее матрицу
Е == МуФ, изменяет лишь вторую строку матрицы Dt т. е. десятую строку таб-
лицы. Элементы этой преобразованной строки 10' представляют собой суммы
парных произведений элементов столбца Aly1, находящихся в строках 9—12:
e2i = 0>(—3)-Н(—0-6 + ( —4)-0+(—1)-0= — 6; е23 = 0-2 + (— 1)• (— 4)+(—4)-1 +
+ (_]).0 = 0; е23 = 0.7+(~1).(-20) + (-4).0 + (-1). 1 = 19; г24=0-2 +
4-( — !)•( —9) + ( —4)-0 + (— 1).0 = 9; е25 = 0-8+(— 1 )• (— 27) + (— 4)-1 +
+ ( — 1)-1 =22; ^=—6+0 + 19+9 = 22.
На этом заканчивается построение второго подобного преобразования
Е = Матрица Е оо С содержит две приведенные строки:
- —3 2 7 2”
|—61 0 19 9
£= 0 1 о о '
_ о О 1 0_
III эта п. Принимаем матрицу Е за исходную. Выделяем в ней элемент
е21 — — 6 (первый столбец) и преобразуем матрицу Е в подобную ей матрицу
Фробениуса F. Продолжая процесс аналогичным образом, по формулам (5) най-
дем элементы матрицы Aln_3 — Adji
1
=-------
*21
т14 =
*24
*21
1 £?nS 0
— = -0,167; /и12=—^-=-—=0;
—6 • e2i —6
£90 19
т13 = —-^-= —-----= 3,167;
е2] -6
— — =1,500; т15=—— = —— = 3,667.
-6 е2. -6
Чтобы получилась сумма S = 3,667, заменяем тц — — 0,167 на — 1:
S = — 1 + 0 + 3,167 + 1,500 = 3,667.
Матрицу Фробениуса F будем записывать в строках 13—16. Сначала строим
Q = ЕМх и затем F = Л4 у1 G. В столбец Му1 выписываем строку 10' матрицы
Е (см. табл. 5.5).
Первый столбец (отмеченный):
= ептц = ( — 3) • ( — 0,167) — 0,500;
£2i *= *21^11 = ( — 6) •( — 0,167) = 1,000.
Второй столбец:
§12 ~ *12 + eiim12 — 2 + ( — 3) • 0 — 2,000;
§22 = *22 + *21^12 = 0 + ( — 6) .0=0.
Третий столбец:
£1з = *1з + *н^1з = 7 + ( - 3) . 3,167 = - 2,500;
§2$ = *23 + *21^13 = 19 + ( — 6) . 3,167 = 0.
Четвертый столбец:
£ii ~ *14 + *11^14 = 2 + ( — 3) • 1,500 = — 2,500;
£24 = *24 + *2i™i4 = 9 + ( - 6) • 1,500 = 0.
Столбец S';
£16 = *15 + *11^15 = 8 + ( — 3) . 3,667 = — 3;
£26 = *25 + *21^15 = 22 + ( — 6) • 3,667 = 0,
227
Столбец S:
£i5 = £ie + £n = - 3 + 0,500 = - 2,500;
£15 = £и + £12 + £1з + £u = 0,500 + 2,000-2,500-2,500 = -'2,500;
£25 = £26 + £21 = 0 + 1 — 1;
£25 = £21 + £22 + £23 + £24 =1 + 0 +0 +0=1.
Элементы преобразованной строки 13' представляют собой суммы парных
произведений столбца Adf1, находящихся в строках 13—16:
fn = ( — 6). 0,500+0* 1+19-0+9^0= —3; /12 = ( — 6).2,000 +
+ 0.0+19*1+9-0 = 7; = (— 6) - (— 2,500) + 0 < 0 + 19.0+9.1 = 24;
f14 = ( —6Н-2,500) + 0.0+ 19.0+9*0= 15; 2 = (-6). (—2,500) +
+04 + 19-1+9-1 =43; 3+7+24 + 15 = 43.
Таким образом, искомая матрица Фробениуса F, подобная 4, имеет вид
"—3 7 24 15"
1000
0 10 0
-00 1 0-
Найдем характеристический определитель матрицы F1
г — 3—X 7 24
D(X)=det (4 — ХЕ) = det (F —ХЕ) =
15"
0
о
0 0 1
Отсюда разложив определитель D (X) по элементам первой строки, получим
—X о
1 -X
0 1
3—X
1
о
7 24 15'
—X о о
1 —X о
О 1 — х_
о
0 +24 -
—X
—X
1
о
о
о
=Х4+ЗХ3—7X2—24Х—15.
Исключительные случаи в методе Данилевского. Этот метод при-
меним без всяких'осложнений, если все выделяемые элементы отличны
от нуля (как в только что рассмотренном примере), Если же при пре-
образовании матрицы А — latjl (с == 1, 2, ом п; / = 1, 2, п) в мат-
рицу Фробениуса F мы пришли к матрице вида
^12 ••• ь-i dlh ••• dr dXn
^21 ^22 •** ^21 ^2, h—1 ••• d2t d2n
D =
dll d[2 *•- . dfl ... d( k~i d[k n-1 ^ln
dki . dht ... ft—1 ^kk n—1 ^kn
0 0 .. . 0 ... 0 1 ... 0 0
_0 0 .. . 0 ... 0 0 ... 1 0 _
223
причем оказалось, что <4, &-i —О, то продолжать преобразования по
методу Данилевского нельзя. Здесь возможны два случая.
Первый случай. Пусть какой-то элемент матрицы D,
стоящий левее нулевого элементаdkt отличен от нуля; например,
где I < k — 1. Тогда этот элемент выдвигаем на место нуле-
вого элемента dkt т. е. переставляем (k — 1)-й и Лй столбцы мат-
рицы D и одновременно переставляем ее (k— 1)-ю и Лю строки. Новая
матрица будет подобна данной и можно продолжать вычисления по
методу Данилевского.
Пример 2. Методом Данилевского развернуть характеристический опреде-
литель матрицы
—2 1 — Г
—2 1 I
—4 2 0
-1 1 1_
Решение. Записываем вычисления в таблицу (см. табл. 5.6).
Таблица 5.6
Строки М"1 Столбцы S S'
1 2 1 3 1 1 *'
1 3 —2 1 —1 1
2 3 —2 1 1 3
3 5 —4 2 0 3
4 -1 —1 | 1 | 1 0
I 1 1 11-1 —1 0
5 -1 4 —1 1 -г 2 1
6 —1 4 -1 1 0 4 3
7 1 7 -2 2 —2 5 3
8 1 0 0 1 0 1 0
7' -1 0 1 0 0
Выделяемый элемент с32 = 0; продолжать вычисления по схеме Данилевского
нельзя. Так как сз1 0, то переставляем второй и первый столбцы, первую и
вторую строки матрицы С и продолжаем вычисления (см. табл. 5.7 на стр. 230).
В результате получаем матрицу Фробениуса
2~
0
0 *
0_
Ч
1
0
_0
—4
0
I
0
2
0
0
1
откуда находим
D (X) = det (Л - IE) = det (F - Х£) = X4 — 4Х3 +4X2 _ 2Х + 2.
229
Таблица 5.7
Строки Л1"1 Столбцы 2 2'
1 2 1 3 1 4
5 —1 —1 4 1 0 4
6 —1 —1 4 1 —2 2
7' 1 0 ЕЛ 1 0 0
8 1 0 0 1 0 1
II 0 —f 1 0 0
9 0 —1 —4 5 0 0 4
10 —1 —1 —4 5 ' —2 —2 2
11 1 0 1 0 0 1 0
12 0 0 0 1 0 1 0
10' ш 5 —5 2 3
III Ml 11-1 —5 5 —2 —3
13 1 —1 1 0 2 2 3
14 5 1 0 0 0 1 0
15 -5 0 1 0 0 1 0
16 2 0 0 1 0 1 0
13' 4 —4 2 2 4
Второй случай. Пусть dkl = 0 (/ = 1, 2, k — 1), т. е.
выделяемый элемент, а также все элементы матрицы, стоящие левее
выделяемого, равны нулю. Тогда матрица D имеет вид
^11 d13 • ^i,k— I 4ft ••• 4, n—1 4n
d31 6?22 • <4, A—1 ••• 4, n-1 4n
<4-1,1 ^k —1, 2 ** • 4—1, k— 1 dk-i, k ••• 4—1, n—1 4—1, n
0 0 . 0 dkk ••• n—1 dhn
0 0 , 0 1 ... 0 0
_0 0 , 0 0 ... 1 0
| ^2
о| D3
230
Разбиваем матрицу D на четыре клетки так, чтобы одна матрица
была нулевой. Тогда характеристический определитель det (D —ХЕ)
распадается на два определителя:
det (D — ХЕ) = det (Dx — ХЕ) • det (D3 — ХЕ),
но матрица D3 уже имеет вид Фробениуса, поэтому остается только
привести к этому виду матрицу Dv
Пример 3. Методом Данилевского развернуть характеристический определи-
тель матрицы
’0 13 2“
я 1 4 5 0
112 1*
_1 1 1 U
Решение. Запишем результаты
вычислений в таблицу (см. табл. 5.8).
Таблица 5.8
Строки Столбцы 2 2'
2 ! 3 | 4
1 2 3 4 0 1 1 1 . 1 4 1 1 3 5 2 ш 2 0 1 1 6 10 5 4
1 —1 — 1 11 —1 —I —4
5 6 7 8 1 1 1 1 СС ^«0 1 1 1 СМ —< -Ч О 1 1 1 3 5 2 1 —I —5 —1 0 —3 —5 —1 1 СО О СО о N 1
Т —8 1~4| 11 —7 —8
II —2 —0,25|—1 2,75 — 1,75 —2
9 10 11 12 °О . —И Гу 1 —2 - 0 0 * 0,5 0,25 1 0 —2,5 2,25 0 1 2,5 —3,25 0 0 1,5 —2,75 1 1 -ЛОО
10' ш 6 4 —7 3 1
Так как'выделяемый элемент равен нулю, то продолжать вычисления по схе-
ме Данилевского нельзя.
231
Матрица D со С имеет вид
1 0,5 —2,5 2,5'
0 6 4 —7
0 1 0 0
' 0 0 1 0
Разбиваем матрицу D на четыре клетки окаймлением и вычисляем D (Х)1
Z>(X) = det (D—IE) =
1—А, 0,5 —2,5 2,5
0 6 — X 4 —7
0 1 —X 0
0 0 1 —X
= (1-Х).
6—X
1
О
4
—к
1
—7
О
—X
= (1-Х)[(6-Х) V+4K-7] = 7V+2X2 + ПК — 7.
§5.6. Вычисление собственных векторов по методу Данилевского
Пусть Y = (уъ у2, уп) — собственный вектор матрицы Фробе-
ниуса F, соответствующий данному значению %. Тогда FY = ХУ, от-
куда (F — XEjY = 0, или
/11 /12 /13 fin
1 —X о ... О
О . 1 —X ... о
О О 0 —X
Произведя умножение, получим систему для определения коорди*
нат уъ у...>уп собственного вектора У:
(/11~Х) +/12#2 + /13*/з + •••
У1 — Х1/2 =0,
У2 — ^Уз =0, (У)
х^п = о.
Эта система линейных уравнений является однородной, так как все ее
свободные члены равны нулю.
С точностью до коэффициента пропорциональности ее решения мож-
но найти следующим образом. Положим уп = 1» тогда последователь-
но получим
Уп-i ” X, уп _2 — Хг/П„х = X2,,,,, уг = Х«’Ч
232
Таким образом, искомый собственный вектор есть
Г
_ 1
Так как матрица F подобна матрице А, то к является также и собствен-
ным значением матрицы А.
Обозначим через X = (хь х2, хп) собственный вектор матрицы
А, соответствующий значению X. Тогда получим
X = (3)
где Мп х, Мп «2,7И1 — преобразованные по методу Данилевского
единичные матрицы.
Например, преобразование Мъ произведенное над У, дает
Следовательно, преобразование Мк изменяет лишь первую коорди-
нату вектора Y, Аналогично преобразование М2 изменит лишь вторую
координату вектора MrY и т, д. Повторив этот процесс п — 1 раз,
получим искомый собственный вектор X матрицы А,
Пример. В примере 1 § 5.5 было показано, что матрица
-3 1 Г
О 4—1
1 2 —2
1 —1 —1-
методом Данилевского приводится к виду Фробениуса
3 7 24 15“
1 О О О
0 10 0*
. 0 О 1 0_
Вычислить собственный вектор Х(1) == х2) х3, х4), если Aj = — 1.
Решение. Воспользуемся формулой (3), т, е. X ==* где
“V~
X
_1 _
“—Г
1
—1
_ 1_
233
а матрицы M3t Л42, берем из табл. 5.5 (см. стр. 224). Последовательно находим
”—0,167
О
о
_ о
Г1
о
о
о
M2M±Y=^
о ;
1
о
о
о
—1
о
о
“1
о
1
_0
3,167
О
1
О
О
—4
1
О
о
1
1
о
1,500'
О
О
1 _
01
—1
О
1J _
о
о
—1
о
О"
о
—1
1_
г
1
—1
- L
—1,5"
1
—1
. 1 _
'—1,5'
2
—1
_ 1 .
’—1,500’
1
—1
. 1 _
'—1,5"
2 .
—1
'—1,5
2
0,5
_ 1
Х^^МзМ^У^
Аналогично можно вычислить собственные векторы и для значений Х2, %3, Х4.
§ 5.7. Метод Леверрье— Фаддеева
Этот метод предложен Леверрье и затем упрощен советским мате-
матиком Фаддеевым. Метод Леверрье основан на формулах Ньютона
для сумм степеней корней алгебраического уравнения и заключается
в следующем. Пусть
det (Л—ZE) —Xn + /?j + + (I)
— характеристический многочлен матрицы Л = [аи] (где i = 1, 2,...
/ = 1, 2, ...,и) и Хр Х2,...,ХП — полная совокупность корней мно-
гочлена (1), Рассмотрим суммы
SA = ^+M+- + ^ Ц=1,2..........п),
т. е.
Si = -р Х2 Л-... 4~ Sp Л,
52-ХН^ + '”+^8рЛ2,
Sn = X? + ^ + ... + ^=Sp Ап
(каждая сумма Sk есть след матрицы Л^). Тогда при k п справедли-
вы формулы Ньютона
+ Pi S+... + Pk-i Sx == — kpk,
откуда получаем
при k = 1 pi — —Sp
При k = 2 p2 = — -Г- (S2 4- Pl Si), (2)
при k = n Pn=----^-(Sn + p1Sn_14-P2^n-2 + "1+/’n-l‘Si).
234
Следовательно, коэффициенты характеристического многочлена
ръ р2,рп можно легко определить,если известны суммы Sx, S2,...,Sn.
Таким образом, схема раскрытия характеристического определи-
теля методом Леверрье состоит в следующем:
1) вычисляют степени Ак = Д*-1 • A (k = 1, 2, п);
2) определяют Sk — суммы элементов главных диагоналей мат-
риц Д*;
3) по формулам (2) находят коэффициенты pt (t = 1, 2, n).
Видоизмененный метод Леверрье, предложенный Фаддеевым, заклю-
чается в вычислении последовательности матриц Дх, Д2, Ап по сле-
дующей схеме:
Д1==Д; 8рДх = дг; В1 = Дг—<7i£;
Д2 = ДВ1; = Вл=А^-даЕ;
— ——2—^ -Дп-1 —
п — 1
ЛП = ДВП_Х; = Bn = An—qnE (Вп — нулевая
п матрица);
“ Р1» Р2» **’’ Рп—1» Рп
Пример. Методом Леверрье — Фаддеева развернуть характеристический
определитель матрицы
"22—2 —Г
л 12-1 2
-10 3 4 ’
- 1 3 1 0_
Решение. Последовательно находим
1) Л1 = Л =
2
1
—1
1
2 —2 —1 '
2-1 2
0 3 4
=24-24-3 = 7;
3 1
2) Л2“Д^1~
2 —2 —Г
—5 -1 2
0—4 4
3 1 —7,
2 —2 -Г
2 —1 2
0 3 4
3 1 0_
“_5 2—2—Г
1 —5 —1 2
—1 0—4 4
_ 1 3 1-7,
-—7 —9 1 Г
0—2 2 15
6 Ю —6 —15
3 —13 —9 9.
1
—1
. 1
235
Г
—15
—15
12-
Sp Л2 —7-2—64-9
B2== A^-q^E —
—4
0
6
—9 1
1 2
10 —3
—13 —9
"0 0 0 0"
Sp44 22+22+22+22 . 0 0 0 0
<?«=—=--------5-----= 2>, В4 = Л-?4Е= o o o o
-0 0 0 0-
5) Таким образом, — — 7, p2 ” — <7s “ 3, p3 — — =
= 55f /?4 — — q4 — — 22 и окончательно находим
D (К) = det (Л - %£) = /Л — 7%3 + 3%2 + 55% - 22.
§ 5.8. Метод интерполяции
Используя интерполирование, можно развернуть характеристи-
ческий определитель
О(Х) = det (Л—ХЕ) = X" + Р1 X"-1 + р2 Х"-2 +... + Pnt
где Л = [агД t = n; j = l,2,..., п, по следующей схеме:
1) выберем равноотстоящие узлы: Хо = 0, X, = 1; Х2 = 2,...,ХП — п
и для определителя D (X) вычислим соответствующие значения D (0),
О (1), О (2),..., D (п\,
236
2) составим горизонтальную таблицу разностей для последователь-
ности чисел Do, Dn D2,..M£>n и обычными приемами находим разности
&D (0) (i = 1, 2, _,п);
3) применяя первую интерполяционную формулу Ньютона, полу-
чим полиномиальное выражение для характеристического определи-
теля
D (X) = D (0) + -А^(0) X + -A^-(0) X (X— 1) 4-
4- -^ДЖх(Х—1)(Х — 2)4-..,4--—^(0-)-Х(Х— 1)... (X—г4-1)
(i=l, 2,..., п).
Например, для определителя четвертого порядка формула (1) при-
мет вид
£>(Х) = £>(0)4-ДГ)(0)-Х4- Да£)(0)-(-Ь X2—^) +
4-Д3О(0). (-Ьх8—+
4-Д4П(0) х4—Lx84--LLx2—L
V 24 4 24 4 '
(2)
£>(0)4-[Д#(0)-~^D(0) 4- -^Д3Г>(0) — ф Д4П(0)]Х4-
+[у д2 D (0) --L дз D (0) 4--Я- Дw (0) ] X2+
4- -Гд3Г)(0) — -Г Д4О(0)^Х34-~ Д4П(0)Х4.
Обозначим в формуле (1) коэффициенты в узлах интерполяции через
cmi, где т = 1, 2, etM n; I = 1, 2, т. Тогда получим интерполя-
ционную формулу Маркова для развертывания характеристического
определителя:
D(X) = D(0)4- 2 Д^Г>(0), (1')
т==*1 ~т
а для определителя четвертого порядка формула Маркова запишется
так:
D (X) = D (0) + [си AD (0) + с12 Д2 D (0) 4- с13 Д» D (0) +
4- еи Д4 D (0)] X 4- (с22 Д2 D (0) 4- с2, Д3 D (0) 4- с24 D (0)] X2 4- (2')
4- [Сзз Д3 D (0) 4- е84 Д3 D ГО)) Xs 4- см Д4 D (0) X4.
Коэффициенты emt постоянные и вычисляются по формуле
2 (1 = 1, 2,...). (3)
237
Так как
JL == х п ^2!_______L а. (%— 1) (х—2) = х2 з_у_х
1! ’ 21 “ 2 2 ’ 31 6 2 ^3’
Х(Л —1)(Х—2)(Х—3) X4 Л" ПХ2 Х
4! 24 4 24 4 ’
то из формулы (3) находим коэффициенты cmi для матрицы четвертого
порядка:
.111
Сп — 1, с12 — — , С13 — з , с14 — — ,
_ 1 _ 1 _ 11
С^~~Т' С*3~ Т' °24~ 24 ’
сзз=~’ С34=-~; С^~^'
Аналогичным образом вычисляются коэффициенты $mi и для мат-
риц любых порядков.
Пример. Методом интерполяции развернуть характеристический опреде-
литель матрицы
2 2 — 2 -1
12—1 2
~ —10 3 4 ’
13 10
Решение» 1) Для узлов интерполяции Хо = 0, = 1; Х2 = 2; Х& 3j
Х4 = 4» Вычисляем соответственно D (0); D (1); D (2), D (3), D (4)j
D(4) =
1
-1
I
2 -2
-2 -1
0 -1
3 1
2) Составляем горизонтальную таблицу разностей и определяем &D (0)
(где i — 1, 2, 3, 4).
238
Таблица 5.9
X О(А.) ДО(М Д2О(К) Д8£)(М д«о<М
0 — 22 52 —22 —6 24
1 30 30 —28 18
2 60 2 — 10
3 62 —8
4 54
3) По формуле Маркова находим!
О (X) = D (0) + [С11ДО (0)+с12 Да D (0)+с1з Да D (0) +си Д4 D (0)] X+
+ [с22 Да D (0) +с23 Л3 D (0)+с24 Д4 D (0)] Ха + [с33 Д3 D (0) +с34 Д4 D (0)] %3+
(- -УУ <-22)+4- <~б)+( - тУ24У+
у z у О у *1 • J
-Гс44Д4О(0)=—22 + 52+
+ [у . (-22) + (- * (~6) + 4г -24] Ьа +
+ Гу . (-6) + f— ’24]^+ -^-•24X4 = V— 7V+3V + 55X—22.
§ 5.9. Определение первого собственного числа матрицы
методом итерации
С помощью итерационных методов можно определить наибольшее
по модулю собственное число матрицы А без раскрытия характеристи-
ческого определителя.
Пусть
det (4 — ХЕ) = 0 (1)
— характеристическое уравнение; Хь Х2,.,., Хл — его корни, являю-
щиеся собственными значениями матрицы А = 1а/;] (где i == 1,2,..,, п;
j = 1, 2,..., п). Предположим, что
I Xj | > | Х21 | Х81 | Хп |,
т. е. Хг — наибольшее по модулю собственное число.
Тогда для нахождения приближенного значения корня исполь-
зуется следующая схема:
1) выбирают произвольно начальный вектор Y\
2) составляют последовательные итерации
У^^ДУ,
YW=A-AY = 42У,
У<3) = 4«Д2У = 43У,
У(т)вД.Д«-»У=вД'»У,
уи+П = Д.Дту = 4т+‘ У;
239
3) выбирают из последовательности два
= АтУ и У(т+^ = Ат+1У; тогда
последних значения
Xi = lim —------, или Xi
r+1)
уГ
(2)
где z/m+n и y\m} —соответствующие координаты векторов У(т+'’ и
(t = 1, 2, и).
Таким образом, взяв достаточно большой номер итерации т, можно
с любой степенью точности вычислить наибольший по модулю корен^
Zi характеристического уравнения матрицы, Для нахождения
этого корня может быть использована любая координата вектора
У<т), в частности .можно взять среднее арифметическое соответст-
вующих отношений для разных координат,
При неудачном выборе начального вектора Y формула (2) может
не дать нужного корня или даже вообще не иметь смысла, т, е. предел
отношения уТ1+1}1у{Г} может не существовать, Последнее легко
заметить по «прыгающим» значениям этого отношения. В таких слу-
чаях следует изменить начальный вектор, В качестве первого собствен-
ного вектора можно взять У(т+1).
Пример, Найти наибольшее по модулю собственное значение матрицы
1 О
2 2
1 1
О
и соответствующий ему собственный вектор.
Решение. 1) Выбираем начальный вектор Y=
2) Составляем т = 10 итераций
У(2> = А2 У,..., Уао> = А10У.
Вычисления помещаем в таблицу (см. табл. 5.10),
Таблица 5.1С
Y ДУ А2У А3 У А4У АбУ А*У А’У А8У А»У А3П
1 4 17 69 274 1075 4 189 16 260 62 973 243 569 941 370
1 5 18 67 253 964 3 693 24 193 54650 210 663 812 585
1 2 17 25 92 345 1309 5002 19195 73 845 284 508
3) Закончив итерации на У(10> = АХоУ, имеем для разных координат
941 370 „ . t/V0) 812 585 п
--------— 3,865; X £2 > » —;---= —-------— = 3 , 857;
243 560 * 1 210 663
284 508
Xf « —(----=-----------=3,853.
1 73 845 *
Xi
У1
У1
240
4) Вычисляем как среднее арифметическое и Ц3):
а Х^>+Л?)+М3) 3,865 + 3,857+3,853
М -----------------= ---------------------= 3,858,
3
5) В качестве первого собственного вектора матрицы А можно взять
941370
вектор Г(Ю> = Л10Г =
812585 4 Нормируя его, т. е. разделив все его коор-
284508
динаты на норму вектора, равную
11 Г < 10 Ч|3 = 1/9413702 4- 812585а 4- 2845082 = 1,28• 100,
получим первый собственный вектор матрицы А, принадлежащий первому соб-
ственному значению = 3,858s
0,74
0,64 0,22
§5.10. Определение последующих собственных чисел
и принадлежащих им собственных векторов
Пусть собственные значения матрицы А таковы, что
I ^-1 I > I ^2 I > I I I 1«
(1)
Тогда для определения \ мы можем воспользоваться так называемыми
к-разностями, используя уже имеющееся значение
Дх, Ат Y s Л";+1 Y—Ат Y, Дм Ат~' Y = Ат Y—1, Ат~1Y,
или
откуда, переходя к координатам векторов, получаем
(i = l,2..n) (3)
Формула (3) дает грубые значения для Х2, так как тоже было опре-
делено приближенно.
Если модули всех собственных значений различны между собой,
ТО при помощи формул, аналогичных формуле (3), можно вычислить
и остальные собственные значения, но последующие результаты будут
еще менее точны.
Номер итерации т при вычислении следует брать меньшим,
чем при вычислении во избежание потери точности при вычитании
близких чисел.
241
Пример. Для матрицы
3
1 О
2 2
1 2
Л = 1
О
найти второе собственное значение Х2 и принадлежащий ему собственный вектор
Л<2). За номер итерации принять т — 8.
Решение. Воспользуемся таблицей значений AmY для т = 7, 8, 9
(см. табл. 5.10 на стр. 240):
Д’У Д8У Д»У
16 260 62 973 243 569
14 193 54 650 210 663
5 002 19 195 73 845
По формуле (2) составляем Л-разности;
Дх> =Г<пг+1>—A.-J (1=1, 2, 3).
Для каждой из строк принимается свое значение Xj!
Хр = 3,865; Х^2> =3,857; Ц3> = 3,853,
Получаем следующую таблицу!
Таблица 5.11
Д8У Кх Д’У Дх/'У Л8 У МД8У Л^Л’У
62 973 62 845 128 243 569 243 390 179
54 650 54 742 — 92 210 663 210 785 — 122
19 195 19 272 — 77 73 845 73 958 -113
3) Для каждой строки по формуле (3) вычисляем X2i
Х(1> „ S/2 = = ],400; Х‘2) « -
128 - Дм®7’
~нз - -
\ y'i
4) Определяем Х3 как среднее арифметическое X£1J, Ц2)
_ Х^'+Х^+Х^3) 1,4004-1,326 + 2,468
Л2 =----------------------------------------
= 1,468.
—77
— 122
-J~ = 1,326;
—92
и X(93h
3 3
5) В качестве второго собственного вектора принимаем
179 ‘
— 122
— 113
= 1,398,
Л<2)=ДМЯ8Г =
242
Нормируя его, имеем
0,73"
—0,50
—0,46
Пля данной матрицы третье собственное значение можно найти, зная след мат-
рицы: так как Xj + Х2 + Х3 — Sp А — 3 4- 2 + 1 = 6, то Х3 ~ 6—3,858 —
L 1,398 = 0.744.
Упражнения
1. Методом непосредственного развертывания найти
многочлены для следующих матриц:
характеристические
2—1 3
J — 3 -1
1 1 1”
1 -1 —1
— 1 1 —1 *
-1 -1 1
Ответыч а) X3 — 2Х2 — 66Х + 1; б) X4 — 4Х§ — 6Х — 41? в) X4 — 4Х8 +
+ 16Х - 16.
2. Методом Крылова развернуть характеристические определители сле-
дующих матриц:
“2 —2 1 3"
4 — 1 —2 —3
б) А =
1 2 —5 4 5
1 — 1 2 —4
1—2 1—2
в) А~
2-1 2—1
1 1—2—2
-2—2 1 1
Ответы} а) X3 + X2 — ЗХ — 7; б) X4 + 8Х3 + 6Х2 + 6Х — 54; в) X4 + X3 —
*-6Х2 - 18Х.
3. Применяя вычислительную схему Данилевского, тические определители следующих матриц: развернуть характер и с-
а) Л = ' 1 1 1 0 2 3 1 б) л= -1 0 2 -1 о Л -2 3 о -3 0 е
_ 0 1 3 О Д 1 -1 А 1 0 -1 _
-1 1 0 1 ~
в) А 3 -2 3 -2 1 1 «
1 1 1 1 _
243
Ответы: а) %3 — 4%2 — % + 4; б) %4 + X3 — 1IX2 + 14% — 16; в) %4 — X3
—5%2 + 5% + 12.
4. Для матрицы из упр. 3 а) вычислить собственные векторы методом'Дани-
левского, если Xj = 4; %2 = 1; %3 = — 1.
5. Методом Леверрье —Фаддеева
лители для следующих матриц:
развернуть характеристические опреде-
а) Л«=
~5
2
1
2
—4
1
1
1
3
—2
1
— 2
—2
4
2
1
3
— 5
3
1
— 3
О
— 1
1
Ответы! а) %4 — 7%3 + 15%2 — 2% — 34; б) %4 — 2%3 — 9%2 — 25% + 17.
6. Методом интерполяции развернуть характеристические определители
для следующих матриц:
а)
Л =
"2
1
1
О
—4 —2 1
1 5 О
2 3—2
1 — 1 — 1
Ответы: а) %4 + %8 + 7%3 — 20% — 54; б) %4 — 6%3 — 9%2 + 55% +61.
7. Методом итерации вычислить первое и второе собственное значение мат-
рицы
Ответ: %г ~ 4,46; %2 ~ 1,59.
Г л a s а VI
МАТЕМАТИЧЕСКАЯ ОБРАБОТКА ДАННЫХ
§ 6.1. Постановка задачи
Анализ экономических и технических процессов приводит к необ-
ходимости выявления существенных факторов, влияющих на исследуе-
мый процесс, а также к выбору формы связи между факторами и к
оценке параметров полученных уравнений связи.
Будем считать, что некоторое явление характеризуется двумя варь-
ируемыми величинами х и у. из которых х выбирается как независи-
мая, а у — как зависимая переменная величина. Предположим, что
между переменными х и у существует однозначное соответствие, т, е*
каждому значению независимой переменной величины х соответствует
с заданной степенью точности одно значение зависимой переменной*
244
Рассмотрим в качестве примера индексы производительности труда
промышленно-производственного персонала в государственной и ко-
оперативной промышленности стран членов СЭВ (табл. 6.1),
Таблица 6.1
Страны 1965 1966 1967 1968 1969 1970 1971
Болгария,. 264 274 295 322 343 467 390
Венгрия... 187 197 207 210 209 222 234
ГДР 184 195 206 217 229 243 256
Польша,... 287 298 309 326 343 367 384
Румыния... 343 372 407 435 456 486 516
СССР Чехослова- 256 269 287 302 316 338 36Д
кия . .... 238 263 263 274 286 309 330
В табл. 6.1 независимой переменной величиной является время. В на-
ших обозначениях это переменная х, Зависимой переменной служит
индекс цен соответствующей страны.
В качестве другого примера рассмотрим изменение производствен-
ных фондов по годам (табл. 6.2).
Таблица 6.2
Годы 1965 1966 1967 1968 1969 1970
Производствен- ные фонды (в млрд. руб.). 420 . 454 494 534 571 625
В табл. 6.2 независимой переменной также является время х, а за-
висимой — производственные фонды у. Таким образом, производст-
венные фонды являются функцией времени: у = f (х), Вид этой функ-
ции пока еще неизвестен.
В качестве третьего примера рассмотрим численность учащихся
средних учебных заведений в расчете на 10 тыс. человек населения
(табл. 6,3).
Таблица 6.3
Годы 1961 1962 1963 1964 1965 1966
Число уча- щихся . 50 71 Q0 по 145 158
245
В табл. 6.3 функциональная зависимость числа учащихся от изме-
нения времени почти очевидна, хотя вид этой связи y = f(x) надо
найти.
Итак, во всех рассмотренных примерах возникает одна и та же за-
дача — выявление формы связи и определение формульной зависимо-
сти, задающей у как функцию f (х).
В общем виде задачу можно сформулировать следующим образом.
Пусть в результате исследования некоторой величины х значениям
хъ х2,..., хп поставлены в соответствие значения уъ у2, уп некоторой
величины у. Требуется, подобрать вид аналитической зависимости
у = f (х), связывающей переменные х и у.
Будем называть аналитические зависимости, полученные в резуль-
тате наблюдений, эмпирическими. Выявление эмпирических зависи-
мостей делится на два основных этапа — выбор эмпиричес-
кой формулы и уточнение коэффициентов выб-
ранной формулы.
Для второго этапа мы рассмотрим три наиболее распространенных
метода определения коэффициентов формульных зависимостей: 1) ме-
тод выбранных точек; 2) метод средних; 3) метод наименьших квад-
ратов,
§ 6.2. Построение эмпирических пинейных зависимостей.
Методы уточнения параметров этих зависимостей
Построение зависимости у —ах. Рассмотрим следующую задачу.
Пусть на некотором предприятии в течение шестичасового рабочего
дня поступают сведения о количестве выпускаемых изделий (табл. 6.4).
Требуется выявить вид эмпирической зависимости и вычислить пара-
метры этой зависимости.
Таблица 64
Текущий чаг 0 1 1,5 2,5 3 4,5 5 6
Количество изделий на хг-й час 0 67 101 168 202 301 334 404
Нанесем точки из табл. 6.4 на график (рис. 6.1), Вид математичес-
кой зависимости количества выпускаемых изделий от времени наглядно
иллюстрируется графиком, Это прямая, проходящая через начало ко-
ординат. Таким образом, искомая зависимость является линейной;
ее математический вид
у = ах.
(1)
Определив вид формы связи между переменными х и у, вычислим
параметр а. Для уточнения параметра а воспользуемся перечисленными
выше тремя методами.
1. Метод выбранных точек. Проведем прямую как
можно ближе к нанесенным на график точкам (рис. 6.1). На этой пря-
мой выбираем произвольную точку М (х*; #*), координаты которой
определим из графика. Пусть х* = 5, 6; отсюда у* — 375 и можно най-
ти параметр а эмпирической формулы
уравнение прямой, проходящей через
начало координат, примет вид у =;
= 66,96 х.
Итак, чтобы вычислить параметр а
для прямой, проходящей через начало
координат, достаточно взять произволь-
ную точку на эмпирической прямой и
поделить ее координаты у и х, т, е,
у
а = —
X
Преимуществом метода выбранных
точек является то, что он обладает хо-
рошей наглядностью, однако выбор ко-
эффициента а существенно зависит от
точности построения чертежа.
Лучшие результаты по сравнению
с методом выбранных точек дает метод
(2)
средних.
2. Метод средних. Каждому табличному значению незави-
симой переменной соответствует определенное значение эмпирической
функции, которое численно можно получить из графика у = ах.
Обозначим значения зависимой переменной, взятые из эмпиричес-
кого графика, через z/*. В тех случаях, когда для соответствующих
^табличные значения yt не совпадают с графическими z/*, имеет место
отклонение экспериментальных данных от выбранной функциональной
эмпирической зависимости:
Уг~У?^ь
(3)
где yt = axi. Определим параметр а из условия минимума средней
ошибки:
2 8; = °, (4)
z=i
или
247
Перепишем выражение (4') в виде
У1— 2 axt=.O,
i = 1 i — 1
откуда
2 У1
----- (5)
2 xi
Z = 1
Таким образом, для линейной функции у — ах, проходящей через
начало координат, параметр а определяется с помощью метода средних
по формуле (5).
Пользуясь этой формулой, найдем численное значение параметра
а для рассматриваемой эмпирической зависимости (см, табл, 6,4):
674-101 + 1684-202 + 301 +334 + 404 _ 1577 g7 j j
1 + 1,5+2,5+3 + 4,5 + 5 + 6 ” 23,5 ” *
Следовательно, искомая зависимость имеет вид у = 67,11 х.
3. Метод наименьших квадратов. Определим зна-
чение параметра а линейной зависимости у = ах из условия минимума
суммы квадратов отклонений табличных значений yt от эмпирических у*:
2 r+ni’H, (6)
I — 1
или
2 (У1~^)2 = min. (6')
Z —- 1
Выразим у? через его значение axt и подставим в соотношение (6');
тогда получим
2 0/г~-О^)2 = 1ШП. (6")
/ — 1
Условие (6"), согласно которому мы будем вычислять параметр а*
включает все табличные значения зависимой и независимой переменных
величин Xt и уh
Минимальное значение суммы квадратов отклонений табличных зна-
чений у* от эмпирических yt при вариации коэффициента а найдем из
248
условия равенства нулю производной по параметру а от функции
F — S (//, — пхг)2. Дифференцируя, имеем
1-1
ЯР Дч
= 2 х;(г/г —ахг) = 0- (7)
1= 1
Раскрывая скобки и представляя сумму разностей как разность сумм,
получим следующее выражение:
2 ХгУ1—а 2 =0’
/=1
откуда параметр а вычисляется как отношение суммы произведений
значений независимой переменной на соответствующие значения за-
висимой переменной yt к сумме квадратов значений независимой
переменной:
п
2 х1У1
« = —---------- (8)
п
2
i = I
Чтобы воспользоваться методом наименьших квадратов для опреде-
ления численного значения параметра а рассматриваемой эмпиричес-
кой зависимости (см. табл. 6.4), составим вспомогательную таблицу,
7 7
откуда находим сумму произведений и сумму квадратов 2%?.
6=1 z«i
Таблица 6.5
Kt и i
1 67,0 67 1
1,5 101,0 151,5 2,25
2,5 168,0 420,0 6,25
3 202,0 606,0 9
4,5 301,0 1354,5 20,25
5 334,0 1670,0 25
6 404,0 2424,0 36
2хг t/j = 6 693,0 2x2=99,75
Теперь, по формуле (8) находим
6693,0 с„ лп
о=-------:— = 67,09.
99,75
249
Подставив найденное значение параметра в линейную функцию
у = ах, получим у — 67,09 х.
Итак, в результате расчетов мы получили три значения параметра
а для функции у = ах, наиболее точным из которых является значение
параметра, полученное по методу
наименьших квадратов; однако на-
глядно убеждаемся в том, что этот
метод требует большего объема вы-
числений.
Построение линейной зависимо-
сти общего типа у=ах-{- Ь. Рас-
смотрим следующую задачу. Подо-
брать. эмпирическую формулу для
роста численности населения в не-
котором городе, пользуясь данными
табл. 6.6.
Нанесем табличные значения на
график (рис. 6.2), из которого вид-
но, что имеет место линейная зави-
симость общего типа. Ее аналити-
ческое выражение
у = ах + Ь. (9)
Таблица 6.6
Годы 1946 1948 1950 1952 1954 1956 1958 I960
Число жителей 50 000 68 500 92 500 110 000 132 500 152 000 175 000 195 000
Для уточнения параметров а и Ь воспользуемся, как и прежде,
тремя различными методами.
1. Метод выбранных точек. Чтобы вычислить парамет-
ры а и Ь, необходимо составить систему двух линейно независимых
уравнений. Выбрав на графике произвольные точки (х*; у'Х) и
М2 (х2; УХ) и подставив численные значения координат этих точек в
уравнение (9), получим систему
( yt = axt + b, 0
( у*2 = ах*2 + b.
Решая ее, находим искомые параметры а и Ь.
Так, для рассматриваемого примера выберем на гафике (рис, 6.2)
точки Mi и М2 с координатами х£ = 4,4; у± = 92,5 • 103; х* = 13,6;
250
//* = 190 • 103. Подставляя координаты этих точек в уравнение (9),
получим систему
| 92,5-103 = 4,4а + Ь,
( 190* 103 - 13,6а + 6,
откуда найдем а = 10 600, 6=45 000. Тогда искомая зависимость при-
мет вид у — 10 600 х + 45 000.
2. Метод средних. Согласно методу средних, лучшим поло-
жением прямой является такое, для которого алгебраическая сумма
всех уклонений вычисленных значений от опытных равна нулю.
'Для определения параметров а и b эмпирической прямой разделим
табличные данные на две группы и для каждой из них запишем:
2 к,1 - (ах} + Ь)] =0,
1=1 (11)
"х [^- НЧь)]=о,
где I и п — I — числа табличных данных соответственно для первой и
второй группы.
Заменим сумму разностей разностью сумм и, сделав преобразова-
ния, получим
^у} = а^х\ + 1Ь, '
„-Г‘ (Н')
2 г/"==а 2 х^ + (п-1)Ь.
Решив эту систему, найдем параметры а и Ь.
Определим теперь параметры а и b с помощью метода средних в рас-
сматриваемом примере. Разобьем данные на две такие совокупности,
для которых суммы yi примерно одинаковы (см, табл, 6,7).
Таблица 6.7
Vi Syi
0 50 000
2 68 500
4 20 92 500 453 500
6 110 000
8 132 500
10 152 000
12 36 175 000 522 000
14 195 000
251
Составим систему вида (1Г):
' 453 500—5Ь—20а = 0,
( 522 000—ЗЬ — 36а = О,
откуда получаем а = 11 500, 6 = 40700. Следовательно, уравнение
прямой запишется так: у = И 500 х + 40700.
3. Метод наименьших квадратов. Согласно методу
наименьших квадратов,
2 axt — 6)2==ш'п. (12)
Используя необходимое условие экстремума функции нескольких
переменных при вариации параметров а и Ь, получим
— 2 (У;—fe)2=°.
да
г”‘ (13)
или
2 2(У1~aXf — Ь)(—хг) = 0,
/=1
2 2(/,г-ах2-6)(-1) = О,
‘ I — 1
откуда
V х^^а 2 Л7 + 6 2 xi'
' 1=1 m
2 ^-=а 2 xi+nb>
Z=1 1 = 1
где и — число наблюдений.
Чтобы вычислить параметры линейной зависимости для нашего
примера, составим вспомогательную таблицу (см. табл. 6.8 на стр.
253).
В результате получаем систему вида (13'):
(8553,5 • 103 = 65а 4-566,
j 965,5-103 = 56а 4- 86,
решая которую, находим а = И 100, 6 = 43 000. Следовательно,
у = 11 100 х 4- 43 000.
252
Таблица 6.8
Годы *1 У1 xi Mi
1946 0 50 000 0 0
1948 2 68 500 137,5-Ю3 4
1950 4 92 500 370-103 16
1952 6 110 000 661,5-103 36 «
1954 8 132 500 1060-103 64 f
1956 10 152 000 1522-103 100
1958 12 175 000 2100-103 144
1960 14 195 000 2702-10s J96
Sxf = 56 Ztji = 965,5-103 2x? = 560
= 8553,5-IO3-
§ 6.3. Выбор эмпирических формул
для нелинейных зависимостей
Выбор вида эмпирической формулы. В предыдущем параграфе мы
рассмотрели эмпирические линейные зависимости, для которых по-
строенный график определял выбор функциональной зависимости*
Для прямой, проходящей через начало координат, аналитическим выра-
жением служит функция у = ах, а для прямой общего положения —
функция у = ах + Ь. Однако графическое построение нелинейной
зависимости не дает ответа на вопрос о том, какой аналитический вад
имеет эта функция, т. е. будет ли эта зависимость степенной, дробно-
рациональной, логарифмической и т. д.
Пусть у есть функция одной переменной с двумя параметрами а и
Ь. В качестве набора функций, из которых будем выбирать эмпиричес-
кую зависимость, рассмотрим:
1) линейную функцию у = ах + Ь;
2) показательную функцию у — ab*\
3) дробно-рациональную функцию у = -%
4) логарифмическую функцию у = а In х + Ь;
5) степенную функцию у — ахь (она определяет параболическую
зависимость, если параметр Ь > 0, и гиперболическую зависимость,
если Ь < 0; если же параметр b => 0, то зависимость вырождается
в линейную);
6) гиперболическую функцию вида у = а +
7) дробно-рациональную функцию вида у = ахХ^_^
Для наилучшего выбора вида аналитической зависимости у =*
*=f(x, а, Ь), соответствующей построенному графику, выполним следую-
щие промежуточные вычисления, На заданном отрезке изменения неза-
253
висимой переменной выберем точки, достаточно надежные и по возмож-
ности далеко отстоящие друг от друга. Для простоты будем считать,
что это точки и хп. Вычислим среднее арифметическое хар~
среднее геометрическое хгеом = Vе х-^ и среднее гармоническое
•^тарм “ '* По вычисленным значениям независимой переменной
найдем из построенного графика соответствующие значения зависимой
переменной
^ар У 1>
•^теом ^/2»
^гарм Уз
для пока еще неизвестной аналитической зависимости у — f (х, а, Ь)<
Выполним вспомогательные вычисления для зависимой переменной.
Вычислим среднее арифметическое крайних значений уар = ,
их среднее геометрическое z/re0M ~ ]/ухуп и среднее гармоническое
Сравним найденные из графика у*, у*, y*s с вычислен-
ными значениями уар, z/re0M, z/rapM и оценим следующие погрешности
результата сравнения:
\У1 I “ ®1’ \У1 Угеом1 = е2> I//1 Угаом!
I Уч /Лзр I “ ^4» 1^2 У1 еом I “ \У j Уа.Х) I £б > I Уз У арм I &7Г
Найдем из этих ошибок минимальную:
е = min {ех, е2, •••, е7}*
1. Если наименьшей среди всех абсолютных ошибок окажется
то в качестве аналитической зависимости для данного графика хорошим
приближением служит линейная функция у — ах +
2. Если наименьшей абсолютной ошибкой является 82, то в качест-
ве эмпирической зависимости следует выбрать показательную функ-
цию у~аЬ^.
3, В том случае, когда наименьшая из абсолютных ошибок есть
е3, искомая эмпирическая зависимость определяется дробно-рацио-
нальной функцией вида у ~
4. Если наименьшая из абсолютных ошибок есть е4, то хорошим
приближением служит логарифмическая функция у = nlnx + b<
5. Для случая, когда наименьшей абсолютной ошибкой является
85, в качестве эмпирической зависимости выбирается степенная функ-
ция у = ахь.
6. Если наименьшей из абсолютных ошибок окажется ев, то за ис-
комую зависимость следует выбрать гиперболическую у — а +
7. Наконец, в том случае, когда наименьшая из абсолютных оши-
бок есть е7, в качестве аналитической зависимости выбирается дробно-
рациональная функция вида у = ах\ь'
254
Пример. Подобрать эмпирическую зависимость для функции, заданной
таблично:
к I а | 2 | 3 4 | 5
у I 521 | 308 1240,5 204 | 183
171
7 | 8 | 9
159 | 152 | 147
6
Решение. 1) Предположим, что в данном примере крайние табличные
значения достаточно надежны. Проведем вспомогательные вычисления и найдем
для крайних значений независимой переменной хх = 1, х9 = 9 среднее арифме-
тическое хар = * —- = 5, среднее геометрическое хгеом == = 3 и
2xtx9
среднее гармоническое хгарм = ~
2) Из графика (рис. 6.3) найдем зна-
чения функции, соответствующие вычис-
ленным значениям аргумента: для хар =
= 5 имеем ух 180; для хгеом = 3 имеем
240; для хгарм ~ 1,8 имеем г/^341.
3) Выполним дополнительные расчеты
для зависимой переменной. Найдем для
крайних значений среднее арифметическое
У1^~Уп 521 +147
Уар =----~2---=-----2----= 334,
среднее геометрическое
Угеом =/521.147 = 274
и среднее гармоническое
2i/i(/n 2-512-147
У га рм — , — =228,
У1+Уп 5124-149
4) Сравним найденные графически значения зависимой переменной с уар,
^геом и (/гарм:
81 = 1^-«/ар 1 = 1 180-3341 = 154, е2 = |//*-(/геом | = | 180-274 | = 106,
8з = |1/;-«/гарМ| = | 180-228| = 48,
е< = I - У ар [ = I 240 - 3341 = 94, е5 = | - Угеом [ = 1240 - 274 | = 34,
е6 = I У*3 - У ар I = 1341 - 334 | = 7, е, = | у*з - Угарм| = | 341 - 228[ = 113.
Поскольку наименьшая из абсолютных ошибок есть es, в качестве аналити-
ческой зависимости следует выбрать гиперболическую зависимость у = a + ~~
(см. рис. 6.3).
Уточнение коэффициентов. Для уточнения коэффициентов выбран-
ной аналитической зависимости у = f (х, а, Ь) воспользуемся, как и
прежде, тремя различными методами.
1. Метод выбранных точек. На построенной кривой
возьмем две произвольные точки М (х*; у\) и N (х*; у*), Составляем
систему
y*-f(x*, a, 6),
= a> b)t
255
разрешаем ее относительно искомых параметров а и b и подставляем
найденные числовые значения параметров в функцию у ~ f (х, а, Ь).
2. Метод средних. В эмпирическую формулу у ~ f (х, а, Ь)
последовательно подставляем табличные значения xt (i = 1, 2, ..ч п).
Полученные значения функции yt = f (xb а, b), вообще говоря, будут
отклоняться от табличных значений: yt — f (xit аъ Ь) = ег*.
Согласно методу средних, за наилучшее положение кривой прини-
мается то, для которого алгебраическая сумма отклонений равна нулю,
т. е.
Для определения параметров а и b по методу средних вся совокуп-
ность ег- (i = 1, 2, п) разбивается на две группы так, чтобы алгеб-
раическая сумма уклонений каждой группы равнялась нулю. Таким
образом, для определения параметров а и b мы получаем следую-
тцую систему двух уравнений:
2 [г/,— а, 6)] = 0,
/ = ’
2 [«/"— ft)] = 0,
где I и п — I — числа табличных данных соответственно для первой и
второй группы.
Заменив сумму разностей разностью сумм в каждом уравнении
системы, получим
?=1 /=1
"2 = *2
Совместное решение этой системы определяет численное значение
двух параметров а и подставив которые в у == f (х, а, Ь), получим ис-
комое эмпирическое соотношение.
3. Метод наименьших квадратов. Согласно методу
наименьших квадратов, наилучшими параметрами а и Ь считаются те,
для которых сумма квадратов уклонений минимальна:
F(a, b) — 2 [У1~ft)]2 = min.
i— 1
Найдем частные производные функции F (a, ft) по варьируемым па-
раметрам а и ft:
-dF^'b}- = -2 2 [yi-f{xha,b)]fa{Xi,a,b),
да ; = i
-1{адь b)- = -2 2 1У1Ч^1,а,Ь)]}^Х1,а,Ь).
256
В силу необходимого условия экстремума функции многих перемен-
ных, наилучшими значениями параметров а и Ъ служат те, при которых
частные производные этой функции по варьируемым параметрам обра-
щаются в нуль:
М (а, Ь)
да
Ь)
дЬ
т. е.
п
У 1уг ~f(xba,b)]f^(Xi,a,b) = O,
п
У, l!/i—f(xt,a, b)]f'b (xt, a, 6) = 0.
/= 1
Решение этой системы относительно а и b и дает искомые наилучшие
значения числовых параметров,
§ 6.4. Преобразование координат
Рассмотрим в системе координат хОу некоторую нелинейную за-
висимость у — f (х, а, Ь), непрерывную и монотонную на замкнутом
отрезке [хь хп]. Перейдем к новым переменным q = ф (х) и z = гр (г/)
так, чтобы в новой системе координат qOz эмпирическая зависимость
стала линейной:
z — aq + b. (1)
Точки 7Уг с координатами (ф (х^); ф (^)) в плоскости qOz практичес-
ки лежат на прямой линии. Обратно, если при построении на плоскости
qOz окажется, что точки лежат на прямой линии, то между переменны-
ми q и z имеет место зависимость
Ф (у) = «ф (х) + Ь, (2)
Покажем, как рассмотренные в § 6.3 нелинейные зависимости пре-
образованием координат можно свести к линейной.
I) Для показательной зависимости вида у — abx, логарифмируя,
имеем 1g у = х 1g b + 1g а. Полагаем lg Ь = В, 1g а = A, 1g у = г,
х = q и в плоскости qOz получим уравнение прямой г = Bq + А.
2) Дробно-линейную зависимость у = ах^_ также можно преоб-
разовать в линейную. Действительно, найдем обратную зависимость
~ = ах + b и введем новые переменные q — х, г = —; тогда получим
у у
зависимость вида z = aq + b.
3) Рассмотрим логарифмическую зависимость у = a lg х + b н
введем новые переменные q = 1g х, г = у. Тогда снова получим ли-
нейную зависимость z — aq + b.
:57
4) Рассмотрим степенную зависимость у = ЬхР, где а> 0, О,
Логарифмируя, находим 1g у = a 1g х-ф 1g b, откуда полагая z=lgy,
q = 1g x, В = 1g b, имеем z = aq + В. Прямую полученного вида удобно
строить, если оси q и z в плоскости qOz взять в логарифмическом
масштабе. Началом координат логарифмической сетки служит точка
q = 0, z = В.
5) В выражении у = а + — произведем замену переменных = q,
у = г. Тем самым заданная гиперболическая зависимость преобразует-
ся в линейную z = а + bq.
6) Рассмотрим дробно-рациональную функцию у = Функ-
1 ь
ция, обратная данной, имеет вид - == а + -. Введя новые координаты
” I А
z = -, q = —, опять получим линейную зависимость z = а + bq>
Пример. Опытные данные занесены в следующую таблицу:
3
х
4 | 5
у | 0,33 0,49 | 0,59 0,65 | 0,71
6 j 7 j 8
0,755 j 0,77 | 0,81
9
0,82
Составить эмпирическую формулу.
Решение. Построим график (рис. 6.4) и определим тип кривой так, как
это было указано в предыдущем параграфе. Аналитическая функция, достаточно
258
корошо соответствующая таблице, есть дробно-рациональная функция вида
X
0 "" ах 4- 6’
1 , ь
Рассмотрим функцию —— а + ™, обратную данной, и введем новые перемен-
у Л
ные 2 = — i q — —, Тогда в плоскости qOz получим линейную зависимость г —
а -f- bq.
Для того чтобы найти коэффициенты q и z, составим таблицу:
1 | 0,5 |0,333 0,25 | 0,2 0,166 0,143 0,125 0,111
Z , 3 1 2 1 1.66 1,54 | 1,41 1,32 1,3 1,24 1,22
Построим в плоскости qOz точки, соответствующие табличным значениям
(рис. 6.5). Мы видим, что эти точки лежат на одной прямой. Следовательно, на-
ши предположения оказались правильными. Остается определить параметры
3—1
а и Ь» а = 1; b = "п~ = 2. Таким образом, эмпирическая формула имеет вид
х
у = 7+2*
§ 6.5. Эмпирические формулы, содержащие три параметра
На практике нелинейную взаимосвязь двух переменных х и у, из
которых одну, например %, считают независимой переменной, а другую
переменную у — зависимой, часто аппроксимируют функцией вида
у — ах2 + Ьх + с,
(1)
где а, Ь и с — параметры, подлежащие определению.
Если количество измерений (хг; yt) равно трем, то численные зна-
чения параметров находятся по методу выбранных точек. Результаты
каждого из трех измерений (хг; у^ (х2; £/г), (*з; Уз) подставим в вы-
ражение (1) и получим систему трех уравнений
у1== axf + Ьх1~\~с,
у2 — ах% + Ьх2 + с,
ys = axl + bx3 + c.
(2)
Решая систему (2) относительно а, b и с, находим численные значения
искомых параметров.
Однако вычисление параметров а, b и с по методу выбранных точек
Дает грубые результаты. Точность можно повысить, если: а) увеличить
число наблюдений; б) воспользоваться дополнительно некоторым кри-
терием оценки точности.
Согласно методу средних, совокупность наблюдений (xf, ^), где
i = 1, 2,..., п, разбивается на три группы, в каждой из которых ал-
гебраическая сумма уклонений равна нулю:
259
V ег = yt-— (ах* + bxt + с) = 0,
'=i
2 г1~У)~ (ax‘i + bxi + c) = °> <3)
/=/+1
2 еь=Ук — (axl+bxh + c)=0.
k = q+t
. Решение системы (3) и дает более точные, чем по методу выбранных
точек, численные значения параметров а, Ь и с.
Лучшие результаты дает метод наименьших квадратов, согласно
которому параметры а, Ь, о вычисляются из критерия минимума
суммы квадратов уклонений
F = 2 е?== 2 (У/ — (axl+bxt +с)]2 == min.
i =1 1
В силу необходимого условия экстремума функции нескольких
переменных получим следующую систему:
~~ =2 2 |уг-(ах?+^г + с)](-х?) = 0,
да
< 2 tyi-laxf + bXi + cM-x^O, (4)
db г±1
-^-=2 2[г/г-(ах? + ^ + с)](-1) = 0,
,-ri
откуда после преобразований получим систему
а 2 xl+b j^xt + c 2 *? =
Z=1 Z = 1 Z=1
i а 2^ + ь 2Х? + С 2*‘= (5)
г=1 Z=1 Z—1 Z=H
а 2 Xt+b 2 xt + cn= 2 У»
'=i i=i r=i
решение которой позволяет найти параметры а, Ь, с,
Пример. Для функции, заданной таблично:
X 2,0 ; I 2,2 | 2,4 2,6 2,8 3,0
У 0,3010 j 0,3424 | 0,3802 0,4150 0,4472 0,4771
подобрать многочлен второй степени у = ах2 + bx + найдя значения парамет-
ров методом наименьших квадратов.
260
Решение. Составим вспомогательную таблицу:
Таблица 6.9
XI У1 2 X' 3 Xi 4 Xi Xi yi 2 Xiyt
2,0 0,3010 4,00 8,000 16,000 0,60200 1,204000
2,2 0,3424 4,84 10,648 23,4256 0,75328 1,657216
2,4 0,3802 5,76 13,824 33,1776 0,91248 2,189952
2,6 0,4150 6,76 17,576 45,6976 1,07900 2,805400
2,8 0,4472 7,84 21,952 61,4656 1,25216 3,506048
3,0 0,4771 9,00 27,000 81,0000 1,43130 4,293900
S 15,0 2,3629 38,20 99,000 260,7664 6,03022 15,656516
Из системы вида (5)
260,7664^+99,000 b + 38,20 с= 15,656516,
99,000 а+38,20 & + 15 с= 6,03022,
38,20 а+15 &+ 6 с= 2,3629
найдем параметры а = — 0,035762; b — 0,354481; с = — 0,26470. Тогда иско-
мый многочлен запишется так:
у = — 0,035762х2 + 0,354481% — 0,26470.
Упражнения
1. Рост производства химического волокна за период 1970—1973 г. пред-
ставлен таблицей:
x (годы) 1970 1971 | 1972 1973
у (тыс. т) 623 676 | 746 829
Подобрать эмпирическую зависимость производства химического волокна-в дан-
ном временном интервале и найти параметры методом наименьших квадратов.
Ответ', у = 69х + 546.
2. Численность рабочих целлюлозно-бумажной промышленности за период
1965—1969 г. составила:
% (годы) 1965 1966
у (тыс. чел.) 212 235
1967 1968 1969
245 252 255
Подобрать эмпирическую зависимость роста численности рабочих по годам.
Ответ', у = а In х + Ь.
3. Подобрать эмпирическую зависимость, отражающую рост внешне-
торгового оборота СССР со странами СЭВ в 1950—1970 г., если известно, что
товарооборот по годам составил:
% (годы) 1955 j 1960 | 1965 1970
у (млрд, руб.) 6 | 11,3 | 22,6 36
Ответ', у — abx.
261
4. Ввод в действие жилых домов с I и по VIII пятилетку составил:
х (пятилетки) I II III IV v V. VII VIII
у (млрд. кв. м.) 56,9 67,3 81,6 200,9 240,5| 474,1 490,6 518,5
Подобрать эмпирическую зависимость, отражающую ввод в действие жилых
домов по годам.
х
Ответ: у —--------.
ax-f- b
5. Функция задана таблично своими значениями:
X 1 2 3 4 5
У 2,9 8,9 19,1 33,2 50,8
Аппроксимировать эту функцию зависимостью у — ах2 4- Ьх + с и найти пара*
метры методом наименьших квадратов.
Ответ: у — 1,936 я2 4- 0,394 х 4* 0,502.
6. Рост парка ЭВМ (в млрд, дол.) в США представлен таблицей:
Годы 1965 1966 1967 1968 1969 1970 1971
Парк ЭВМ 10,1 15,1 19,7 25,3 31,5 37,6 42,7
Построить эмпирическую зависимость роста парка ЭВМ по годам и подобрать
параметры методом наименьших квадратов.
7. Темпы роста общего объема продукции пищевой промышленности за пе*
риод 1965—1970 г. (в % к 1965 г.) представлены в таблице:
Годы 1966 1967 1968 1969 1970 1971
Объем продукции 104 113 119 122 130 137
Построить эмпирическую зависимость, подбирая параметры методом средних.
8. Рост валового общественного продукта по транспорту и связи (в ценах
соответствующих лет в млрд, руб.) представлен в таблице:
Годы 1965 1966 1967 1968 1969 1970
Общественный продукт 18 19 21 22 23 25
Подобрать эмпирическую зависимость, вычисляя параметры методом выбранных
точек.
262
.9. Рост капиталовложений в народное хозяйство СССР (в млрд, руб.) по
годам представлен таблицей:
Годы 1966 1967 1968 1969 1970 1971
Капиталовложе- ния 61,0 66,0 71,2 79,6 82,0 87,7
Представить эту зависимость многочленом второй степени и подобрать коэф-
фициенты по методу наименьших квадратов.
10. Рост алюминиевой промышленности в Италии по годам представлен
таблицей:
Годы 1965 1966 1967 1968 1969 1970
Производство. . 124,1 127,8 127,7 142,3 143,6 146,8
Подобрать двухпараметрическую эмпирическую зависимость.
11. Фонды экономического стимулирования промышленных предприятий
( в млн. руб.) представлены таблицей:
Годы 1967 1968 1969 1970
Фонды экономического стимулирования 3388 5965 8801 10313
Подобрать двухпараметрическую эмпирическую зависимость.
12. Размеры прямого налогообложения частных компаний США представле-
ны таблицей:
Годы I960 1962 1964 1966 1968 1970
Размеры налого- обложения .... 23,0 24,2 27,6 30,0 28,7 37,0
Построить эмпирическую зависимость и подобрать параметры методом средних.
13. Показатели пассажирооборота воздушного транспорта Министерства
гражданской авиации (в млрд, чел.) представлены таблицей:
Годы 1965 1966 1967 1968 1969 1970
Показатели пас- сажирооборота 38,1 45,1 53,5 62,1 71,5 78,2
263
14. Протяженность путей (в км) Московского метрополитена за годы вось-
мой пятилетки соответственно составляла:
Годы 1966 1967 1968 1969 1970
Протяженность путей 335 350 350 383 400
Подобрать двухпараметрическую эмпирическую зависимость и получить чис-
ленное значение параметров методом выбранных точек.
15. Рост занятости женщин в народном хозяйстве по годам (в млн. чел.)
приведен в таблице:
Годы 1940 I960 I960 1970
Число женщин 13,2 19,2 29,3 45,8
Представить рост занятости женщин в народном хозяйстве трехпараметрической
нелинейной зависимостью у = ах2 + Ьх + с и вычислить параметры методом
выбранных точек.
16. Рост числа специалистов, приходящихся на 1000 рабочих в промышлен-
ности СССР, представлен таблицей:
Годы 1950 1960 1965 1970
Число специалистов . . . 101 106 126 142
Представить данную функцию трехпараметрической зависимостью и подоб-
рать коэффициенты методом выбранных точек-.
Глава VII
ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ И ДИФФЕРЕНЦИРОВАНИЕ
§ 7.1. Численное интегрирование. Простейшие квадратурные
формулы
Из курса математического анализа известно, что если функция
Цх) непрерывна на отрезке [а, Ь], то определенный интеграл от этой
функции в пределах от а до b существует и имеет вид
ь
J/(x)dx=F(b)—F(a),
а
где F (х) — первообразная для функции f (х)<
Для большинства элементарных функций первообразную F (х)
не удается выразить через элементарные функции. Кроме того, при
практических расчетах подынтегральная функция задается в виде таб-
лиц. Все это приводит к необходимости замены интегрирования числен-
ными методами.
Задача численного интегрирования состоит в следующем: найти
определенный интеграл на отрезке 1а, Ь], если подынтегральная функ-
ция на отрезке [а, задана таблично.
Формулы приближенного интегрирования называются квадратур-
ными формулами. Рассмотрим простейшие из них.
Метод прямоугольников. Наиболее простым методом приближен-
ного вычисления интеграла является метод прямоугольников, основан-
ный на непосредственном определении интеграла:
£ Л — 1
£/(x)dx = lim V /(Е/)Дхь
/1-1
где S /(£г) Ах^ есть интегральная сумма, соответствующая некоторому
z=o
разбиению отрезка [a, М и некоторому выбору точек |0, на
отрезках разбиения.
ь
Вычисление определенного интеграла 1 =f f (х) dx геометрически
а
сводится к вычислению площади криволинейной трапеции, ограничен-
ной функцией f (х), осью абсцисс и прямыми х = а и х = b (рис, 7.1).
Вычислим приближенное значение интеграла следующим образом. За-
меним криволинейную трапецию DEba прямоугольником АВЬа,
проведя АВ так, чтобы фигуры DAC и СЕВ получились примерно рав-
265
ной площади. Тогда площади криволинейной трапеции, ограниченной
графиком функции у = f (х), и полученного прямоугольника АВЬа
будут примерно равны.
Учитывая, что высота прямоугольника АВЬа есть значение функции
в точке запишем следующее приближенное равенство:
ъ
^f(x)dx^{b--a)f®.
а
Для увеличения точности численного интегрирования можно от.
резок la, ft] разбить на несколько частей и для каждой из них вычис.
лить приближенное значение площади криволинейной трапеции, ос.
нованием которой является отрезок Axt — xt+1— xt (I = 0, 1, ...
..., n— 1), а высотой — число f (g(), т. е. значение функции в точке
£ [хг, хг+11, выбранное из условия минимума ошибки интегриро-
вания. Тогда за приближенное значение интеграла на отрезке [а, Ь1
принимают интегральную сумму:
ь
ty(x)dxnf &) Ахи + f &) Дхг + f (g3) Дх2 +... + f ДхЛ_Р
а
Практически удобно делить отрезок [a, Ь] на равные части, а точки
(i = 0, 1, 2, ..., п — 1) совмещать с левыми (/ (£,) — f (х,)] или
правыми [/ (|г) — f (xi+1)] концами отрезков разбиения.
Если точку |г совместить с левым концом отрезка Дхг, то прибли-
женное значение интеграла геометрически равно площади заштрихо-
ванной ступенчатой фигуры (рис. 7.2), и может быть представлеш
формулой левых прямоугольников'.
р ь—а П-1
/п= \f(x)dxw--------(y0 + yi-i-<..+yn-i) = h 2 Уь (!'
□ й г=о "
где h = (b — а)/п — шаг,
266
Если же в качестве точки выбрать правый конец отрезка Дхь
то приближенное значение интеграла графически равно площади
ступенчатой фигуры, ограниченной сверху пунктирной линией, и вы-
числяется по формуле правых прямоугольников:
Ja^\f(x)dx&—~—(У1 + Уг + — + уп) = h 2 У1' (2)
а /= 1
Пример 6 помощью формул левых и правых прямоугольников вычислить
С А
J - , й , полагая п = 4.
j X ~f* £
Решение. Зная пределы интегрирования а — 1 и b == 9, наводим шаг
й == (ь — а)1п «= 2; тогда точками разбиения служат х0 = 1, xj — 3, х2 — 5,
£3 = 7, ^4 " 9, а значения подынтегральной функции f (х) — в этих точках
таковы:
Уо~1 (*о) = 4"’ = = Уз = ? (хг) = -±-,
О О I
Уз = /(х3) = -~'. 1/4=/(х4) = -~.
Далее найдем чиеленное значение интеграла, пользуясь формулой левых пря-
моугольников: (
/л=й (Уо + У1 + Уз + Уз) =2 (+ 4" + ф + ф ) ж 1,6024.
\ о о / У /
Если же вычисление определенного интеграла производить по формуле пра-
вых прямоугольников, то
/п = й (1/1 + Уз+ Уз+Уь) =2 (4" ^4—4”*^ тг) ~ 1 ’1053,
Метод трапеций. Приближенное значение определенного интеграла
можно вычислить и иным способом. Заменим на отрезке [а, Ь] дугу АВ
графика подынтегральной функции у = f (х) стягивающей ее хордой
(рис. 7.3) и вычислим площадь трапеции АВЬа, Примем значение опре-
деленного интеграла численно равным площади этой трапеции:
J f (х) dxM(b~ а) (3)
а
Это и есть формула трапеций для приближенного вычисления инте-
грала.
Погрешность вычисления
ъ .
R= ^f^dx--— (уй + у^
а
для формулы трапеций оценивается так:
(4)
267
где точка g £ (х0, х0 + /г). В случае, если у" (£)> 0, вычисление по фор-
муле (3) дает значение интеграла с избытком; если у" (£) <. О,
то интеграл вычисляется с недостатком.
Точность вычислений возрастает, если отрезок (а, bl разделить на
несколько частей и применить формулу трапеций к каждому отрезку
Дхг (рис. 7,4). Тогда
Для простоты вычислений удобно делить отрезок [а, Ь} на равные час-
ти, в этом случае длина каждого из отрезков разбиения есть Дхг =
= (& — а)/п. Численное значение интеграла на отрезке Дхг равно
xi+i
J f (х) dx я»
xt
2
а на всем отрезке [а, Ы соответственно
Ь — а Уг+Уг-и
п & 2
/»=о
Так как под знаком суммы величины yt встречаются дважды (от I ==
— 1 до i == п — 1), то последнее равенство запишется следующим
образом:
ь
f/(x)dx« + + + --‘+Уп-1+ тУпГ
.I М \ Л j
а
<5)
z = l
Эта формула называется общей формулой трапеций. Общую формулу
трапеций можно переписать в виде
268
h
^f(x)dx& — (y0 + 2^ + 2z/2 +... 4- 2 z/n_i + yn), (6)
a
рде шар
Пример 1. Пользуясь общей формулой тралений, вычислить f т 2 при п =
о 1“гА;
е=4.
Решение. Здесь f (х) = । по формуле (7) находим h — 0,25
Следовательно, х0 = 0; — 0,25; х2 = 0,5; х$ » 0,75; х& — 1. Тогда по форму*
ле (6) получим
Р dx 0,25 / 2 j 2 г 2 И
J 14-х2 - 2 \1+ 1+0,252 + 1 +0,52‘ 1+0,752 + 2/~°’764?
о
Метод парабол (метод Симпсона). Точность приближенного интег-
рирования заметно возрастет, если подынтегральную функцию у = f (я)
на отрезке [at М заменить квадратичной функцией (рис. 7.5), прини-
мающей в узлах х0 = а, хъ я2 = b значения yQ = f (х0), уА f (xj
И у2 = f (х2).
В качестве интерполяционного многочлена воспользуемся много-
членом Ньютона
Рг(х)-Уо + -^-(х—х0)+ -А^(х —х0) (x — xj.
Тогда
Ъ (х) dx = ( Р2 (х) dx = 2ftу. + . -^1 -
•J #У Г1 tJ
х0
-++ ’ = 2/1Уо + 2h^ + V д2 Уо = -Т + 4л + yj- (8)
Xrl О О
269
Соотношение (8) называется формулой Симпсона. Формула Симп-
сона обладает повышенной точностью и является точной не только для*,
многочленов второй степени, но и третьей*
Погрешность формулы Симпсона
xb + 2h
/?= J f(x)dx—+ +
оценивается следующим образом:
Я = —(9)
где точка ?£ [х0, х0 + 2h]t
Для увеличения точности вычислений отрезок [а, 61 разбивают на
п пар участков 1х2п-2> fyn-u (рис, 7*6) и заменяя подынтеграль-
ную функцию интерполяционным многочленом Ньютона второй
степени, получают приближенное значение интеграла на каждом
участке длины 2h:
Л 4
f f (x) dx « — (г/2 + 4z/s + y4),
•J
X2
Х2П
J / (x)dx^~ (y2n^ + iyZn-i + ^2n).
Г2П-2
Тогда численное значение определенного интеграла на отрезке
[и, Ь\ будет равно сумме интегралов, т. е,
ь
f f(x)dx & — Цу0 + у2п) + 4 + ••• + Уъп-i) + 2 (у2 + ••• + ^2п-2)1*
J и
а
(10)
Соотношение (10) называется общей формулой Симпсона. Ее можно
записать также в виде
ь
J/(x) dx л; —[(«/о +//2п) + 4 (#1 + ••• + #2п-1) + 2 (*/2+ ••• +#2п-2)1>
а
(И)
где
Л=-Ц^-. (12)
2п
270
1
Пример 2. Вычислить по формуле СимпсонаJ
о
Ре ш е н ие. По формуле (10) имеем
1
с dx /
J 1^х2 3 +^2 + 4//з + ^+
о
——при ft = 0,25.
1+ха
Подставляя в подынтегральную функцию / (я) == значения х0 — 0.
g1 = 0,25, ха = 0,5, х8 = 0,75, = 1, получим
dx 0,25 Г 4 2 4 1 1
1+#* = 3 [ + Т+0?252 + 7 + 0,б2 + 14-0,752 + Т] * °’702'
§ 7.2, Обобщенная формула
численного интегрирования Ньютона—Котеса
Пусть некоторая функция f (х) задана в узлах интерполяции хг =*
= Xq+ih (i=l, 2, ft) на отрезке la, 6] таблицей своих значений:
Xq — я | xj | j ... j xn — b
yQ^t (*o) I £/1 —f(xi) I i/s = Z (^2) I • • • I i/n = Z(-^n)
b
Требуется найти значение интеграла f f (x) dx,
a
По заданным значениям подынтегральной функции построим интер-
поляционный многочлен Лагранжа (см. формулу (5) § 4.4]
(х)= У • • • (х~х1-1) (x~xi+i) • (х~хп)
{xi — Xq) ... Xi—i) (Xj — Xj_i) ... (хг Xn)
Для равноотстоящих узлов интерполяционный многочлен Лагранжа
имеет вид
/«= о
/!(я—t)l
?(?—]) (? —») ,,
q — l
(2)
где q = (х — x0)/h— шаг интерполяции [(см. формулу (11) § 4.4].
Далее заменим подынтегральную функцию f (х) интерполяционным
многочленом Лагранжа, тогда
<1 (n — i)l
dx.
9 — 1
(3)
271
Поменяем местами знак суммирования и интеграл и вынесем за
знак интеграла постоянные коэффициенты:
I f (х) dx 2 Уг
( —1)п~( Г ?(? — !)•••(?—») dx.
г!(я —г)1 J q—i
«о
Так как dq = то заменив пределы интегрирования, имеем
а О
...(? —1 + 1)(^ — i—n)dq. * (4)
Для равноотстоящих узлов интерполяции на отрезке!^, Ь} величина
шага определяется как h = {b — а)/п. Подставив это выражение для
h в формулу (4) и вынося b — аза знак суммы, получим
& п
\i(x)dx^(b—a) У ус (~1)П •— f q(q—1) ...
...(q — i+l)(<7—i— 1) ...(q—n) dq. (5)
Положим
n
н i q (q—i) (q—i + ^) (q—i — (q—n) dq, (6)
i!(n — 01 » J
о
где i = 0, 1, 2, tv, числа называются коэффициентами Ньюто-
на ___ Komeca. Эти коэффициенты не зависят от вида f (х), а являются
функцией только п (количества узлов интерполяции). Поэтому коэф-
фициенты Ньютона — Котеса можно вычислить заранее для различ-
ного числа узлов интерполяции и свести в справочную таблицу
(см. табл. 7.1).
Таблица 7.1
п = 1
п-2 Н0 = Нг^\/&, Hi=2/3
п — 3 -tf3=l/8, //i-Z/2-3/8
п — 4 На=Нл = 7/90, /Л = /73= 16/45, 7/а = 2/15
п~Ь HQ = H^ 19/288, = /f4 = 25/96, Н2 = f/3 = 25/144
п~6 Но-Яб = 41/84О, ^ = Я6 = 9/35, Н2 = Н4 = 9/280, Я3-34/105
п = 7 Но = Hi = 751 /17280, Ht = #e = 3577/17280, #2 = #5= 1323/17280, Я3 = Н4 = 2989/17280
272
Окончательно формула (5) примет вид
£ п
\f (х) dx ж (b—a) 2 ytHi'
а ‘=0
(7)
Л/2
f COS X
Пример. Вычислить по формуле Ньютона—Котеса 1 —-—dx> выбрав п=4.
J 1 “Г х
о
Решение. Формула
Ньютона — Котеса для п — 4 имеет вид
от,/2
о
cos х
1+7
. __л_ А
dx — 9 2
z Z = 0
Htyi.
(*)
Определим шаг h — (b — a)/4 0,4. Далее, найдем значения подынтегральной
60S х
функции д = j ц; у в точках х0, xj, х3, x4i
Л cos 0 Л cos 22,5°
*0 = 0; p0 = - -= 1, «1 = 0,4! У1 =— — = 0,659,
1 U 1 -j-U, 4
cos 45® cos 67,5° Л t
х2 = 0,8; у2 = = 0,393, х3 = 1,2; у3 = — —- - = 0,174,
Пользуясь табл. 7.1, находим коэффициенты Ньютона — Котеса:
Яо = Я4 = 7/90; #! = Я8 = 16/45; Я2 = 2/15.
Подставив найденные значения в формулу, (* ) получим
л/2
cos X
14-я
, 31
dx=T
4-(1+°)+ -7Г (0.6594-0,174) + -^.0,393
= 0,670.
Рассмотрим частные случаи формулы Ньютона—Котеса,
Если в формуле (7) положить п == 1, то получим
ъ
J f (х) dx « (b — а) (р0 Яо 4- Р1 ях),
а
где
1 1
/7о= — //i==J<7^=y-
о о
Тогда
ь
J f (х) dx « (р0 + Рх),
а
273
но поскольку b — а — h (ведь n = 1), окончательно имеем
ь
^Hxjdxtt — tyo + yJ. (8)
а
Тем самым в качестве частного случая формулы Ньютона — Котеса
мы получили формулу трапеций.
Положим теперь в формуле (7) п = 2 и найдем коэффициенты Нью>
тона — Котеса [см, соотношение (6)]:
2
Н°= Т’Т J(9-1)(7-2)dq^ т •
о
2
//1==-Т,тЙ(9-2)^=-Г’
о
2
'1=ттК"'!’4-
о
Так как b — а — 2h, то отсюда следует, что
ь
§f(x)dx&-^- (у0 + 4//J + у2). (9)
а
Таким образом, мы получили формулу Симпсона как част-
ный случай формулы Ньютона — Котеса.
Если же в выражении (7) положить п ~ 3, то получаем следующее
равенствоз
ь
[f(x)dx = -^-(y0 + 3y1 + 3y2 + ys) (10)
J о
а
Эта формула называется правилом трех восьмых. Ее погрешность
оценивается соотношением
/?=—(и>
ои
где точка Ь\.
§ 73. Квадратурная формула Чебышева
В § 7.2 была рассмотрена формула Ньютона — Котеса, согласно
которой численное значение интеграла определяется по значениям
функции уг = f (хг) (1 = 1, 2, ..., п) в фиксированных узлах интерпо-
ляции х19 х2, хп. При этом коэффициенты Ньютона — Котеса
Hi (i — 1, 2, п) составляются таким образом, что они не зависят от
значений функции в узлах интерполяции, а являются функцией толь-
ко q и п.
274
п. Л. Чебышев предложил для вычисления определенных интегра-
лов воспользоваться формулой
« п
y(x)dx&(b—а) 2 (1)
a l~ 1
в которой квадратурные коэффициенты ct (i = 1, 2, ..„ п) фиксирова-
ны, а абсциссы xt (i = 1, 2, п) подлежат определению.
Для упрощения вычислений целесообразно выбрать сх = сг = ...
= сп. Рассмотрим сначала частный случай, когда пределы интегри-
рования равны — 1 и 1, Тогда формула (1) примет вид
$ f(x)dx = 2cn[f(x1) + f(x2) + ...+f(xn)], (2)
— 1
где квадратурный коэффициент сп и абсциссы х1г х2, хп подлежат
определению.
Коэффициент сп и узлы интерполяции хъ х2, , хп определим
из условия, что это равенство является точным для случая, когда
(х) — многочлен вида
f(x) = au + a1x + a2x2 + asx3 + ... + anxn. (3)
Подставив многочлен (3) в левую часть равенства (2) и проинтегриро-
вав, получим
£ (a0 + a1x + a2x2 + asxs + ... + anxn)dx = 2 (а0 + + Ь--) .
v \ О О /
— 1
В правую часть равенства (2) подставим значение многочлена (3) в уз-
лах х1г х2, хп:
f (Xi) = а0 + Xj + а2 xf 4- ц8 +... -ф ап х",
f (x2) = a0 + ai x2 + a2xl + a3xs2 + ... + anx1,
f (х3) = а0 + Я1 х3 + аг хз + а3 хЦ-... + ап х«,
f (хп) = а0 + ах хп + а2 х2п + а3 х3п +... + ап_х х".
Тогда равенство (2) примет вид
aQ + ~" 4" ••• ) “ ^сп а1 (*1 + *2 + ••• + ^п) +
\ з о /
Н- &ДХ1 + Х2 + + %п) +#3 (Х? +%2 + ••• + Хд) + ••• (4)
(4+^a + -+^n)J-
275
Полученное равенство должно выполняться при любых значениях
а0, аъ ап, поэтому из сравнения коэффициентов at в правой и левой
частях соотношения (4) находим, что псп = 1, откуда
(5)
и, кроме того,
!%i + + х3 + + хп = О,
+ + + ,
о
х? + Ч- ••• 4~ я? “ О,
•^1 4" #2 + *3 + ~ »
О
х? + х? + х" + . • + ------------- .
( 1 ? ” 2(^+1)
Подставляя найденное для сп выражение в соотношение (2), получим
формулу Чебышева*.
р 9
j f(x) dx к [f (хО + f (х2) + + f (Xn)l, (7)
— i
где точки хъ х2, хп определяются из системы уравнений (6)*
Значения хп х2, хп для различных п вычисляются заранее и
сводятся в таблицу (см. табл. 7.2).
Т а б л и в а 7.2
Число ординат Значения абсцисе
п~2 — x1 = xg = 0,577350
П = 3 — х1=:Хз = 0,707107; х2 = 0
/2 = 4 — Хг = х4 = 0,794654; —Х2 = х3 = 0,187592
/г = 5 — Xj = х5 = 0,832498; — хг = Х4 = 0,374541; х8 = 0
п~6 — Xj — хв = 0,866247; — х2 =* хь = 0,422519; —xs — Х4 = 0,266635
— х1 — х7 =0,883862; — х2 = хб = 0,529657;
— х3 = х5 = 0,323912; Хд = 0
В том случае, когда пределы заданного интеграла отличны от — 1 и
1, формула Чебышева принимает следующий вид:
ь
J f W dx = If (zj + / (z2) 4-... +Ж)], (8)
a
где
(f=l,2.....n), (9)
a Xt имеют указанные в таблице значения*
276
2
Пример, в помощью формулы Чебышева вычислить j sin х dxt полагая
о
а 5.
Решение. Здесь отрезок интегрирования есть [0, л/2]. По формуле (8)
получаем
л/2
Р , л !
I sin х ах — ~'~т- (sin 2i4-sin z24~sin 234~sin z^-J-sin zb)*
-J ZU
0
рде
\ f n \ t/л \ л
гг=Т v+° +т T~° Pi=T(1+r;)-
Пользуясь табл. 7.2, находим:
Zi = 45* (1—0,832498) = 7° 32,26'; sin z1==0,13117;
г$ = 45* (1—0,374541) =28° 8,74'; sin г2 = 0,47171;
г3 —45* (14-0) = 45° 00'; sin zs = 0,70711;
г4 = 45° (14-0,374541) = 61° 51,26'; sin z4 = 0,88176;
г, = 45° (14-0,832498) = 82*27,74'; sin г5 = 0,99136.
Подставляя эти значения в формулу Чебышева, окончательно получим
sin х dx—
—.3,18311= 1,000004.
Так как точное значение интеграла равно I, то погрешность приближенного
значения составляет 0,0004%.
§ 7.4. Квадратурная формула Гаусса
Для получения повышенной точности при численном интегриро-
вании пользуются формулой Гаусса
1
$ f (X) dx^c^f (xj + с2 f (х2) +... 4- сп f (xn),
— 1
(1)
в которой не фиксируются не только узлы интерполяции хг, х2, хп,
но и квадратурные коэффициенты сх, с2, . сп. При этом 2п неиз-
вестных величин хъ х2,..., хп, clt с2, .... сп определяются из условия,
что формула является точной в случае любого многочлена степени
2п — 1.
Таким образом, для любого многочлена (2п — 1)-й степени
f (х) = а0 + at х + at х2 +... + а2п_х х2п~1 (2)
277
должно выполняться точное равенство
jj f(x)dx — c1f(Xi) + ca/(x2) + ... + cnf(xn). (3)
—• 1
Многочлен f (x), степень которого равна 2п — 1, можно представить
в виде
Ж = Р W Q W + R W, (4)
где F (х) — искомый многочлен n-й степени, a Q (х) и R (х) — соот-
ветственно частное от деления f (х) на F (х) и остаток от этого деления;
степени многочленов Q (х) и R (х) не превышают п— 1. Выражение
для F (х) можно записать таким образом:
F (х) = хп + А± хп-1 + Л2 хп~2 +... + Лп == (х—xj (х—х2)... (х—хп);
(5)
здесь величины хь х2, хп— искомые абсциссы формулы Гаусса,
а Аъ Д2,...,ЛП — постоянные.
Так как искомая функция F (х) в узлах хь х2, .*», хп обращается
в нуль, то
f М - R (хг), f (х2) = R (х2), f (xn) = R (хп). (6)
Тогда равенство (3) примет вид
1 1 1
/ (х) dx = F (х) Q (х) dx + R (х) dx = (7)
=c1R(x1) + ciR(xi) + .. -\-cnR(xn).
Но для многочлена R (х) степени не выше п — 1 также должно иметь
место точное равенство
jj R(x)dx = clR(xl) + c2R (x2) + ... + cnR(xn). (8)
•— 1
Вычитая (8) из (7), получим
1
F (х) Q (х) dx = 0. (9)
— 1
Из последнего соотношения можно определить искомую функцию
F (х). Так как равенство (9) справедливо для произвольного много-
члена Q (х) степени п — 1, т. е. для многочлена вида
Q (х) = bQ хп~1 + Ьх хп~2 +... + Ьп„2х + bn_lt (10)
то оно выполняется при любых коэффициентах fe0, следо-
вательно, имеет место следующая система уравнений:
273
I
xn“! F(x)dx = O,
— i
i
(J xn~2 F (x) dx = O,
— i
i
xF (x) dx = 0,
— i
i
,F(x)dx = 0.
— 1
(11)
Подставляя сюда выражение для F (х) из формулы (5) и интегрируя,
получим для определения коэффициентов Alt Л2, Дп систему
п уравнений:
_А_ ц. _А_ ц.... — о,
2п — 1 2/г—3 2/г—5 -
—1----1------------1----------(-.•• = О,
2/г—1 2п—3 2п—5
A I А | Аэ । __ Q (12)
2п—3 2п —5 2п—7
1 1 А । A t Q
2/г—3 2п—5 2и—7
Из этих уравнений видно, что Аг = А 3 = А5 — Л7 = ttl == 0 и, сле-
довательно, искомый многочлен имеет вид
F (х) = х" + Л2хп-2 + Л4хп”4 + Л6х"-6 + .... (13)
Отметим, что при четном п корни уравнения F (х) = 0 попарно равны
по абсолютной величине, но противоположны по знаку, а при нечет-
ном п корнем служит также и х = 0.
Определив из системы (12) коэффициенты Лг (i = 1, 2, и), со-
ставим уравнение F (х) = 0 и найдем его корни хъ х2, хп, т. е. иско-
мые абсциссы формулы Гаусса, а затем вычислим коэффициенты
(/ — 1, 2, л) по формуле
Г (*~*1) ••• (х—ri-i)(х — гг-|х)... (х—xn)dx
1____________________
(Хг—Х1) ... (Xi—Xi-OUj— Xj+1) ... (х< —xn)
279
Пример. Построить квадратурную формулу Гаусса для случая п=2 на отрез-
ке интегрирования [ — 1, 1].
Решение. Общий вид квадратурной формулы Гаусса при п — 2 и задан-
ных пределах интегрирования
1
t(x)dx^c1^(x1)+c2t (х2),
— 1
где подлежат определению квадратурные коэффициенты и а также абсциссы
хг и Х2.
Для определения абсцисс составим многочлен F (х) — х2 + Лхх + Да>
коэффициенты Аг и А2 которого найдем из системы вида (11)3
1
xF (х) dx = 0,
-1
1
$ F(x)dx = 0
k— 1
непосредственной подстановкой многочлена F (х) в систему. Имеем
— + Л2 = 0,
о
т. е. = О, А 2 = — V3. Тогда
F (х)=х2— у = 0,
откуда
1/3 1/3
хх = —= — 0,57735, х2= = 0,57735.
х 3 з
Коэффициенты сг и с2 вычислим по формуле (14):
1 1
С х—х2 , , f X—Xi ,
Ci = I -------dx = 1, cz — 1 -------dx ~ 1.
J Xj — x2 J x2—Xi
— 1 —1
Следовательно,
i
$ t(x)dx = f( —0,57735) + / (0,57735).
— 1
Однако можно подобрать многочлен F (х),‘ удовлетворяющий со-
отношениям (И), без предварительного определения коэффициентов
Л,, ^2, Ап.
Якоби предложил в качестве многочлена F (х) воспользоваться
многочленом Лежандра
F(x)=_L_.^-nn , (15)
nl 2Л dxn
280
для которого справедливы равенства (11), т. е.
J dx'1
— 1
Действительно, интегрируя по частям, находим
,.Г‘ Т _к г
dxn 1 J dxn~l
— 1
(16)
(17)
Первый член правой части равенства (17) обращается в нуль. Отсюда
. (* k < dn~l (х2 — 1)" , ,1ОЧ
sft=—k I xk~x-------—-—— dx. (18)
— i dx
Аналогично получим
C >-i dn~{ (х2—l)n , ,, р h „ dn~2(x2 — If ,
I xk 1-----b----— dx = —(6—1) 1 xk~2--------------- dx,
J dxn~y J dxn~2
P . ЛП—— О / y2 1 yi P fin — k ( 2 1
—У—— 1- C -------------{---— Jx=0,
_J dxn~(A~1> _J dxn~k
Итак, при k < n имеем
P dn~k (x* —
sh = ( —1)4-2.3...^ \ --^^-0.
J dxn k
Таким образом, многочлен Лежандра удовлетворяет системе-уравне-
ний (11).
Можно показать, что всякий другой многочлен, удовлетворяющий
этим условиям, отличается от вышеприведенного лишь постоянным
множителем.
Для вычисления коэффициентов ск используют упрощенную функ-
цию частного вшш. Положим
f (х) = 2Fk (х) F'k (х), (19)
где
Fh (х) = --(х) - = k (х — Xi) (х—*,) • • • (х - х^) (х — xft+1)... (х — хп)
х—хк
(20)
281
(здесь величина k — постоянная). Тогда
С = = —ТТГ^
J (1—*ft)2 (1+хА)2
— 1
__ р2 / j \ _ 4xfe
(1_Х2)2 (1-Х2)2 ’
так как [F ( — I)]2 = IF (I)]2- = 1. Согласно формуле (3)
§ 2Ffe (х) F;. (х) dx = 2ck F (xh) F' (xh),
(21)
(22)
поскольку все остальные члены в формуле (3) обращаются в нуль*
Дифференцируя равенство
(х — xft) Fh (х) = F (х)
дважды по х и полагая х = xfe, получим
Fk (Ч) = F' (xfe), 2F'k (xk) = F" (xfe). (23)
Подставляя (23) в (22) и сравнивая с (21), находим
= —--------------!------. (24)
(1—х|)2 F'(xk)F"(xh) V ’
Так как F (х) удовлетворяет дифференциальному уравнению
(х2 _ р" w + 2xF‘ (х) — п (п + 1)F (х) = О,
то полагая в нем х = хк и замечая, что F (xfe) ~ 0, имеем
(4 — 1) F" (xft) 4- 2xk F' (xft) = О,
откуда
F" (x^=—^-F’(Xh} .
(25)
(26)
Подставляя это выражение в соотношение для коэффициентов ск1 окон-
чательно получаем
=---------=------- (fe~ 1, 2, ..., и).
(1-xl) [Ff (xft)p
2
(27)
ь
Для вычисления интеграла общего вида ]* f (х) dx следует произве-
а
сти замену переменной
«'-‘•з....»).
Тогда формула Гаусса примет вид
ь
(28)
lCl f (*1) + + ••• + cn Ш].
(29)
a
282
Значения квадратурных коэффициентов Гаусса сг (г = 1, 2,
и абсцисс Х( (i = 1, 2, .... п) приведены в табл. 7.3.
Таблица 7.3
п= 1 хх = 0,5 Ci = 2
п=2 —Xi = х2 = 0,577350 сг = с2 “ 1
п = 3 — х1 = х3 = 0,774597 *г = 0 Ci = c3 =0,555555 с2 = 0,888889
и = 4 — хх = х4 = 0,861136 —х2 = х3 = 0,339981 сг=с4=0,347855 с2 = с3 = 0,652145
/г = 5 —Xi = x5 =0,906180 —х2 = х4 =0,538470 х3=0 Ci = с6 = 0,236927 с3 = с4 = 0,478629 с3 = 0,568889
и = 6 — х4 = х6 = 0,932470 — х2 = х5 = 0,661210 —х3 = х4 = 0,238620 d = c6 = 0,171324 с2 = с5 = 0,360761 с3 = с4 = 0,467914
л = 7 — %1 = х7 = 0,949108 —х2 = х6 = 0,741531 — х3 =х х6 = 0,405845 х4 = 0 С,=с, = 0,129485 с2 = св = 0,279705 с3 = с6 = 0,381830 с4 = 0,417960
/г = 8 — Xi — х8 ~ 0,960290 — %2 = х7 = 0,796666 — х3 = %6 = 0,525532 — х4 = х5 = 0,183434 С1 = с8 = 0,101228 с2 = с, = 0,222381 с3 = св = 0,313707 с4 = с3 = 0,362684
Пример. Вычислить интеграл 1 = J Д/х + 1 dx, применяя квадратур-
о
ную формулу Гаусса с четырьмя ординатами.
Решение. Здесь а — 0, b — 1. Согласно формуле (29), имеем
1
J VV+Tdx = [cit(z1) + c2i(^)~[-c3f(23)+cif(z4)].
о
Найдем абсциссы г4, z2, z3 и пользуясь формулой замены переменной (28) и
табл. 7.3:
-у xi = 0,5—0,430568 = 0,069432;
г2 = —д- — х =о,5—0,169991 = 0,330009;
г» = у + 2-х3 = 0,5+0,169991=0,669991;
г4=-|-+ 2-х4 = 0,5 + 0,430568 = 0,930568.
283
Так как квадратурные коэффициенты попарно равны* cj = с4 = 0,347855; с2 ==
=с9=0,652145, то формула Гаусса для рассматриваемого случая принимает вид
I _____ ,
Ух+1 dx = — {Ci [/ (zJ-H (ZJJ4-C2 [/ (z2) + i (zs)]}.
0
Тогда окончательно получаем
i ________________ । ________
1/x+l dx = — {0,347855 [У1,069432+У1,930568 ] -f-
o
4-0,652145 [ У1,330009+V1,669991 ]} = 1,218951.
§ 7.5. Графическое интегрирование
Пусть функция / (х) задана таблично. Требуется определить интег-
рал как функцию верхнего предела:
/ (х) = f (х) dx.
По значениям f (х0), f (л^), f (х2), f (хп) подынтегральной функ-
ции f (х) в узлах х0, хп построим график (рис. 7.7). Найдем из
графика значения f (х0 + + у), f От точки
h,
Й! == х0 + откладываем влево произвольный отрезок М^, которым
воспользуемся в качестве эталона.
Соединим точку /Иг с точкой f (х0 + и из точки х0 проведем
прямую, параллельную МХЬЪ до пересечения с ординатой, проведен-
ной из точки хг (отрезок xJl). Ордината точки /х есть величина опреде-
ленного интеграла:
X 1
ll== ^f(x)dx.
XQ
284
Далее передвинем отрезок Мхах по оси Ох вправо так, чтобы пра-
вый конец его совпал с точкой а2 — хх + у, и получим новый отрезок
Д12а2. Соединив точку М2 с точкой b2 = f (*i+y), из точки проведем
прямую, параллельнуюМ2Ь2, до пересечения с ординатой, проведенной
из точки х2. Тогда
^2 = 5 f(x)dx.
ХО
Далее, сдвигая эталонный отрезок так, чтобы правый конец
h
его совпал сточкой а3=х2 + у , получим отрезок М3а3. Соединим точ-
ки М3 и ba — f[x2 + у) и проведем из точки 12 прямую, параллельную
М3Ь3, до пересечения с ординатой, проведенной из точки х3; тогда
/3 = § fWdx
Хв
И T. Д.
Соединив точки х0 — /0, 1Ъ /2, 73,... плавной линией, получим ин-
тегральную кривую. Точность интеграла, найденного графически, оп-
ределяется точностью формулы трапеций и точностью вычерчивания
графика.
§ 7.6. Численное дифференцирование. Формулы приближенного
дифференцирования, основанные на интерполяционных
формулах Ньютона
При решении задач часто приходится вычислять производную,
однако во многих практических задачах функции задаются таблично и
методы дифференциального исчисления к исследованию таких функций
применить нельзя. В этом случае прибегают к численному дифферен-
цированию.
Задача численного дифференцирования ставится следующим обра-
зом. Пусть функция у = f (х) на отрезке [а, Ь] задана таблично своими
и + 1 значениями. Требуется найти аналитическое выражение произ-
водной.
В качестве аппроксимирующей функции выберем интерполяцион-
ный многочлен. Если узлы интерполяции в исходной задаче равно-
отстоящие, т. е. xl+1 — Xt — h (где i = 0, 1, ..., п), то в этом случае
Для замены функции / (х) можно воспользоваться интерполяционными
формулами Ньютона.
Пусть
/ (-V) « ,Л + Л= а, - Д> й +
г)(,3) д (|)
41
285
где правая часть есть первая интерполяционная формула Ньютона,
выраженная через число шагов; здесь q — (х—xQ)/h и /г = хИ1—
(/ = 0, 1, 2,.,.). Перепишем формулу (1) в следующем виде;
f (*) Л2Уо+ ^3~3^+21?. Д8+
2 о
Заметим, что
df (х) __ df(x) . dq 1 . df (х)
dx dq dx h dx 9
Продифференцировав равенство (Г) и воспользовавшись зависи-
мостью (2), получим
Их)«-Цд</о+-^- A2j/0+—?2~6?+--~ А3% +
h L х 6
+ 2<^^-.3a^o+.J. (3)
Продифференцировав теперь функцию у — fr (х), имеем
г (X) -М АЧ + fr-1) А3 г/0 + +11 А^о +...], (4)
h2 [ 12 J
так как
(Х) = d(f' . Jl
dx dq dx
Таким же образом можно определить и следующие производные
функции f (х).
Формулы приближенного дифференцирования для определения
производных в узлах интерполяции значительно упрощаются. Полагая
<7 = 0, получим
1 / Д _ Ла Уо г Л3Чо А4Г/0 Д5#0 \
h \ 2^3 4~Г5*’7
и
дзУо + 2кд^о_ Ад5//о+„ \ (6)
h \ 12 6 /
Погрешность в определении производной приближенно оценивается
как
R'k (х0) « h^+ ’ ?<?- ') у' у^+О (7)
где точка [а, Ь], но отлична от узлов интерполяции.
286
Чт обы получить значение производной в точке, лежащей в конце
таблицы, следует воспользоваться второй интерполяционной формулой
Ньютона:
/ W к уп + 4- Ж*» Д2 Уп_2 + Д3 yn_s +
+ £(£±1И£±2Н2±з)Д4^_4+/_?
где q — (х — xn)/h. Тогда приближенное значение для производной
есть
Г W « ф [Д^п-1+Д2 Уп-. + А8 уп-ъ+
л L ь
, 2^ + 9^+1^+3 Л4„ , ]
1 У п-4 “г * • • •
(9)
Пример. Функция у = f (х) задана таблично:
1 1 2 3 4
У1 1 4 9 26 61
Методом численного дифференцирования найти первые две производные этой
функции в точке х — 1.
Решение. Составим таблицу конечных разностей:
xi У1 Ду/ д3#г
1 4 5 12 6
2 9 17 18
3 26 35
4 61
Шаг этой таблицы h = 1. Согласно формуле (5)
Г (*о) = 4_(л</о— 4"Л2г/о+ 4" &3Уо 4 Г (1) = 1-
п \ 2 3 /
Вычислим вторую производную в узле интерполяции Xq = 1. По формуле
6) находим
("(Хо)=(Д2^-Д3^); U)=6-
§ 7.7. Формула приближенного дифференцирования,
основанная на интерполяционной формуле Лагранжа
Пусть f (х) — функция, заданная на отрезке 1а, Ь] таблично своими
значениями У1 = f (xt) (где i = 0, 1,..., п) в равноотстоящих узлах
интерполяции, т. е. х/+1 — х2 = h (i = 0, 1,..., п— 1). Построив
287
для данной системы узлов интерполяционный многочлен Лагранжа,
получим
d (п— г)! q — i
где q = (х— x0)/h — шаг интерполяции [см. формулу (11) § 4,4].
Ду
Так как — й, то из соотношения (1) находим
Г у АААА . АГ^-П- <^-п)1 (2)
' V h i (zz-f)! dq [ q — t J v ’
Погрешность, допускаемая при нахождении производной, есть
R'n (х) М~ 1)»~ 1 й» Л ^"+ о (£), (3)
где В — точка отрезка [а, 6], отличная от узлов интерполяции.
Произведем расчет для п = 2 [функция f (х) задана тремя таблич-
ными значениями]. Имеем
ь2 (*) = 0(7—2)—У1<7 (<? — 2) + ~у^д(д — 1).
у' (х) яЦ (х) = 4
h
Отсюда, учитывая, что = й, находим
Уо(2У — 3) — У&Я — 2) + у2 (2q — 1 )j.
В частности, для производных в узлах интерполяции yf (xf) = yt
получим следующие выражения:
уб =— (—3Уо + 4У1—у2)> причем г0= ~^у"’ (|0);
Уо + Уг), причем г1 =--у"' &);
^ = ^Г(У°“4У1 + Зу2)’ ПРИЧеМ r2 = V/l2y,”^2)-
В случае п = 3 [функция f (х) задана четырьмя табличными зна-
чениями] аналогично получаем
У о = -4"(-11 У<> + 181/1- 9^2 + 2«/з) - -7- ylv ©;
УI = ~ (—2 г/о—З^1 + 6г/2 — ys) + у1 v (?);
Ьп 12
У2 = ~ (у0—^У1 + 31/2 + 2у3)-A yiV (g).
Уз = (-2//0 + 9^- 18z/2 + 1 lz/3) + (g).
288
Следует отметить, что формулы численного дифференцирования
являются менее точными по сравнению с интерполяционными, однако
они удобны для проведения практических расчетов.
§ 7.8. Графическое дифференцирование
Пусть функция f (х) задана таблично:
Уо = f (*о)> У1 = f Ui).... Уп= f М.
Нанесем эти точки на график (рис. 7.8) и соединим плавной линией.
Построим для функции f (х) зависимость g (х) = [' (х).
Отложим произвольный от-
резок МО и воспользуемся им
в качестве эталона. Из точки
М проведем прямую, парал-
лельную касательной к кри-
вой f (х) в точке с абсциссой
а; эта прямая пересечет ось
ординат в точке а'. Из точки
а* проведем горизонталь до
пересечения с продолжением
ординаты из точки а. Полу-
чим точку a" = g (a)
В качестве следующей ха-
рактерной точки выберем точ-
ку Ь. Прямая, проведенная
из точки М и параллельная к
с осью Ох. Точка b совпадает с
Определяем наклон касательной к f (х) в точке с абсциссой с и про-
водим прямую параллельно этой касательной до пересечения в
точке с' с осью Оу*, получаем d = g (с) = f (с) и т. д.
Соединив точки a", b\ с\ получим приближенный график
производной g (х) = f (х).
Упражнения
1- Вычислить определенный интеграл j ~\/х + 2 dx, пользуясь формулой
2
левых прямоугольников при п ~ 6.
Ответ: 15,160.
2. Пользуясь формулой правых прямоугольников при п == 8, вычислить
f -dx _
Ь + Г
Ответ: 1,429.
8 dx
3 Пользуясь формулой трапеций при п ~ 8, вычислить J* , у.
п X -f- 1
Ответ: 2,28.
5
4- По формуле трапеции вычислить С —zzzz полная п = 5.
0 V* 1 *
Otnetm: 2,002.
23Э
5. По формуле Симпсона вычислить J 4/9*5 полагая 2п = 10,
Ответ: 0,107250.
6. Вычислить J dx с помощью формулы Симпсона; положить 2п~10.
Ответ: 0,67363.
1 dx
7. Вычислить интеграл j > пользуясь формулой Гаусса при и= 5.
Ответ: 0,6931472.
8. Вычислить тот же интеграл, пользуясь формулой Чебышева при п == 6.
Ответ: 0,6931465.
9, Функция задана таблично:
X 0,525 0,526 0,527 0,528
У 0,50121 0,50208 0,50294 0,50381
Методом численного дифференцирования найти первую производную в точке
х =- 0,525.
Ответ: 0,007.
10. Найти производную первого порядка в точке х = 50 для функции, за-
данной таблично:
X 50 55 60 65
У 1,6990 1,7404 1,7782 1,8129
Ответ: 0,0087.
Г лава VIII
РЯДЫ ФУРЬЕ
§ 8.1. Понятие последовательности и ряда
Напомним некоторые сведения из курса математического анализа,
необходимые для дальнейшего изложения, опуская доказательства
приводимых в тексте утверждений.
Рассмотрим некоторую функцию f (я). В качестве области опреде-
ления этой функции возьмем множество натуральных чисел, т. е. аргу-
мент х принимает значения 1, 2, ,,,, nt Такая функция называется
последовательностью.
Последовательность записывается в виде
от, а* an, или {цп},
причем ап называют общим членом последовательности, ап^ — чле-
ном, предшествующим ап, а ап+1 — членом, следующим за
Приведем примеры последовательностей,
290
I) Последовательность 1, 2, 3,.»,, n,.w, общий член которой ап= щ
называется натуральным рядом чисел.
2) Последовательность аъ а2, ап_ь ап,..., для которой ап —
— ап^ = d, r^ed постоянная величина, называется арифметической
прогрессией. Для задания арифметической прогрессии достаточно знать
ее первый член at и разность прогрессии d. Действительно, общий член
выражается формулой
ап = «1 + d (п — 1).
Так как по приведенной формуле можно найти любой член последова-
тельности, подставив значения и—1, 2, 3, то последовательность
считается заданной.
3) Последовательность Ъх, Ь2,..., Ьп_\, для которой Ьп =
— где q — постоянная величина, называется геометрической
прогрессией. Для задания геометрической прогрессии достаточно знать
ее первый член bY и знаменатель q. Общий член выражается формулой
4) Последовательность q, с3, для которой сп с, где с —•
постоянная величина, называется постоянной последовательностью.
5) Рассмотрим еще один пример последовательности. Будем вы-
числять число е последовательно с одним, двумя, тремя и к д. знаками.
Результаты вычислений можно представить в следующем виде:
2; 2,7; 2,71; 2,718;.,.;
(1); (2); (3); (4);...;
Занумеровав полученные значения числами натурального ряда, как
это показано в скобках, получим последовательность.
Кроме числовых последовательностей мы будем рассматривать и
функциональные последовательности.
Приведем примеры функциональных последовательностей:
1) atx, а2х2„„, ап^хп^1
2) sinx, sin2х; sin3x,,„, sinnx,..,.
Дадим определение предела числовой последовательности, Число
Л называется пределом последовательности {яп}, если для любого
е Д> 0 существует такой номер N, что при всех п > N выполняется не-
равенство | ап — А | < 8» В таком случае пишут Пт ап = А.
П-*ОО
„ Последовательность, имеющая предел, называется сходящейся,
в противном случае — расходящейся.
Пример 1. Показать, что геометрическая прогрессия b, bq, bq%, . .,
♦.. , bqn~1t ,. , при | q | < 1 представляет собой сходящуюся последовательность,
а при lq | > 1 — расходящуюся.
Решение, 1) Сначала рассмотрим случай 1? I < 1. Покажем, что
1 im bqn~l == О,
п
29!
т. е. по заданному 8 > 0 найдем М такое, что при n > М выполняется неравенст-
во | bqn~l — 0 | <8, Для этого разрешим неравенство относительно п. Перепи-
шем его в виде
или kl""1
Прологарифмируем последнее неравенство:
(71—1) ]п|9|<1п—.
|о I
Разделив обе его части на отрицательное число In | <71, получим
1 8 1 Е
тгг
“>1+-Т7|7Г'
Очевидно, в качестве N достаточно взять
= £ 1+----------Lr_L
\ In I?I
где E (x) означает наибольшее целое число, не превосходящее х.
2) Рассмотрим теперь случай q > 1, b > 0. Покажем, что последователь-
ность является расходящейся. Для этого достаточно показать, что для любого
как угодно большого М существует такое М, что при всех ri>N выполняется не-
равенство bq^-^M. Разрешая последнее неравенство относительно п, получим
В качестве Л/ берем
\ q /
Заметим, что при q = 1 последовательность является постоянной и
lim bqn~l — b.
П->оо
Можно показать, что во всех остальных случаях последовательность рас-
ходится.
Пусть имеется последовательность
^1» ^2> •«’> **• •
Выражение вида
Я1 + 02 + '”+ап + '"== 5 °п
а = I
называется рядом’, здесь ап есть п-й член ряда.
Сумма первых п членов ряда называется его п-й частичной суммой:
п
Sn^ 2
1=1
292
Суммой ряда называется предел последовательности его частичных
сумм:
lim Sn = S.
П->эо
Если ряд имеет сумму, то его называют сходящимся, в противном слу-
чае говорят, что ряд расходится.
Приведем примеры сходящихся и расходящихся рядов.
Пример 2. Рассмотрим ряд, получающийся из арифметической прогрессии,
и запишем его n-ю частичную сумму:
О1Ч-ап 2ffj + d(n—1) d 2а,—d
Sn =--------*n =------------- * n=— --------n.
n 2 2 2 2
Очевидно, при стремлении n к бесконечности эта частичная сумма неограниченно
возрастает по абсолютной величине и, следовательно, данный ряд расходится.
Пример 3. Рассмотрим ряд, образованный геометрической прогрессией при
|<71 < 1, и найдем его сумму. Воспользуемся формулой суммы и членов геометри-
ческой прогрессии:
Ранее было доказано (см. пример 1), что litn qn == 0 (|g j < l)j следовательно,
П->ос
S=lim Sn=-A-.
n -*oo 1 — q
Ряды, члены которых являются функциями, называются функцио-
нальными рядами. Таковы, например, ряды
а0 + ахх + а2х2 + + ап^хГ-х +
bQ + Ьг cos х + 62 cos 2х + ••• + ^n-i cos — П* “I* i
Первый из них называют степенным рядом, а второй — тригономет-
рическим.
Рассмотрим функциональный ряд
Щ И + «2 W + — + «п W +
где ип (х) — функции, определенные на замкнутом интервале 1а, 6].
Пусть х0£[а, Ь], тогда ряд •
«1 (х0) + и2 (х0) + + ип (х0) + ...
является числовым рядом и может оказаться сходящимся или расхо-
дящимся.
Совокупность всех значений х£ [а, 61, для которых сходится соот-
ветствующий числовой ряд, называется областью сходимости функ-
ционального ряда.
Очевидно, что
S(x) = lim Sn(x),
П **оо
П
где 5П (х) = (х) зависит от выбора переменной х, т. е. сумма S (х)
Функционального ряда является функцией ючки х.
293
Пусть {Sn {х)} — последовательность частичных сумм функцио-
нального ряда, определенных на одном и том же замкнутом интервале
1а, Ь]. Функциональный ряд называется равномерно сходящимся
к функции S (х), определенной на [а, &], если любому в > 0 можно
поставить в соответствие такой номер N, не зависящий от х£ [а, Ь},
что для любого n > М выполняется неравенство | Sn (х) — S (х) | < е,
Рассмотрим пример, иллюстрирующий различие между понятиями
сходимости и равномерной сходимости ряда,
Пример 4.
д" ря*‘
где 0 х < 1, частичная сумма есть
(1+хр
Покажем, что на рассматриваемом интервале ряд сходится.
Действительно, если х — 0, то Sn (0) — S (0) = 0. Пусть теперь х > 0. Д<
кажем, что в этом случае S (х) — 1, т. е. по заданному 8 > 0 найдем N таксх
чтобы при и > N выполнялось неравенство
(1W
<8.
Решая эю неравенство, получим
с ( |п8 \
Д/ = £ _ ----------- .
\ In (1 4-х) /
Из последнего равенства видно, что N вообще говоря, зависит не только от
е, но и от х, причем для одною и того же е при х, приближающемся к нулю N не-
ограниченно возрастает. Это означает, что по заданному е мы не можем выбрать
одно единственное N для всех х £ [0, 1], другими словами, ряд не яв-
ляется равно мерно сходящимся на указанном интервале.
Приведенный пример показывает, что последовательность непрерыв-
ных на замкнутом интервале частичных сумм может сходиться к раз-
рывной на этом интервале функции. Одна из причин, мотивирующих
введение понятия равномерной сходимости ряда, заключается в том,
чго равномерно сходящийся ряд непрерывных функций имеет своей
суммой также непрерывную функцию.
§ 8.2. Разложение функций в ряд Фурье. Теорема Дирихле
Многие задачи науки и техники связаны с периодическими функ-
циями, отражающими циклические процессы.
Функция / (х) называется периодической с периодом Т > 0, если
она удовлетворяет равенству
/(х) = /(х+Л. (1)
Из практических соображений такие функции удобно представлять
в виде тригонометрического ряда или его частичной суммы с достаточ-
ной степенью точности.
294
Функциональный ряд вида
оо
2 (ancos пх + &n sin пх) (2)
п= 1
называется тригонометрическим, причем ап и Ьп — действительные
числа, не зависящие от х.
Пусть этот ряд сходится для любого х из интервала I — л, л],
тогда он определяет периодическую функцию f (х) с периодом Т = 2л.
Ряд вида (2) называется рядом Фурье для интегрируемой на интер-
вале [ — л, л] функции £ (х), если коэффициенты его вычисляются по
следующим формулам:
л
а0 = — f f (О dx, (3)
и л J
— л
л
ап — ~ ^f(x)cosnxdx (п=1,2,...), (4)
—л
л
Ьп = -Т J f(x)s'mnxdx (п=1, 2,...). (5)
~ Л
Таким образом, мы можем формально рассматривать ряд Фурье
для заданной функции f (х). Однако при этом возникают следующие
вопросы: 1) сходится ли ряд Фурье функции / (х) и 2) если ряд сходится,
то будет ли он иметь своей суммой f (х)? Ответы на поставленные воп-
росы дает теорема Дирихле. Прежде чем перейти к формулировке са-
мой теоремы, напомним некоторые понятия.
Функция f (х) называется монотонной на интервале, если для лю-
бых хг и х2, принадлежащих этому интервалу и таких, что хг < х2,
выполняется только одно из неравенств f (xj / (х3) или f (xj
> f (х2).
Функция f (х) называется кусочно-монотонной на интервале, если
его можно разбить на конечное число открытых интервалов, в каждом
из которых функция монотонна.
Функция f (х) называется кусочно-непрерывной на интервале, если
она имеет на нем конечное число точек разрыва.
Обозначим через / (а + 0) предел функции f (х) при стремлении
х к а справа (правый предел), соответственно, через f (а — 0)
— левый предел.
Теорема Дирихле, Если функция! (х), заданнаяв интервале[-~п, л],
кусочно-монотонна и кусочно-непрерывна, то ряд Фурье этой функции
сходится во всем интервале [ — л, л] и сумма его равна*.
1) / (х) во всех точках непрерывности, принадлежащих ( — л, л);
2)^ I/ (х 0) + / (х + 0)1 во всех, точках разрыва, принадлежа-
щих ( — л, л);
3) ~ I/ ( — л + 0) + Дл + 0)1 на концах интервала, tn, е, в точках
X — — л и X — л.
сю г;
В дальнейшем мы будем писать, что
оо
/и=-у + 2 cos пх+bn sin пх)
П=1
в смысле приведенной выше теоремы Дирихле*
Теорема Дирихле не утверждает равномерной сходимости рядз
Фурье к функции f (х). Однако если усилить свойства, которым должна
удовлетворять функция, т. е* потребовать от нее непрерывности на веек
интервале [ — л, л], кусочной монотонности на нем и выполнения ра-
венства f ( — л) = f (л), то ряд Фурье для такой функции будет равно-
мерно сходиться к функции / (х) на всем интервале I — л, л].
Можно показать, что для четной функции все коэффициента
Ьп равны нулю, а соответствующий ряд Фурье не содержит синусов\
f w=у- + 2 й*cos пх‘ ®
'1=1
где
л
о л
ап =—I f (х) cos пх dx (п = 0, 1, 2,(71
л J
о
Аналогично для нечетной функции все коэффициенты ап ра&
ны нулю и соответствующий ряд Фурье не содержит косинусов:
f(x) = 2 sin п*> (S
а= 1
где
л
Ьп = — J f (х) sin пх dx (п=1,2,...). (9
о
Пример 1. Разложить в ряд Фурье функцию
( —х при —л < х < О,
1(х) = 1 О А
( 2х при 0 <х л.
Решение. Определим коэффициенты Фурье функции / (х). По формула»
(3) и (4) находим коэффициенты а0 и ап:
о л
1 f 1 с 1 л2 1 з
а0 —— | ( — x)dx + — \2xdx=—‘~+ — *л2==-—л;
л J nJ л 2 л 2
—л О
О я
If If
an=— । (—x)cos/wdx+—|2xcosnxdx.
Л J я J
—л 0
296
Интегрируя по частям, получим
3
ЛЛ2 ‘
(1-(-!)“],
t. е,
^ = 0, Ок-1-----1)* ' = 2, 3,...).
Коэффициенты Ьп находим по формуле (5)|
1 ° П
~ J (—х) s*n пх J 2х sfn пх dx=
—л 0
(0 л л
Х I г 1 С < , 2х
—* — cos пх 4- — I cos пх ах+--cos пх —
п I п J п 1
—Л о о
— — f cos пхdx^ = — — Г _ Л (_ 1)л_(_2 — (— l)ftl == ——--
nJ J л [ л ' 1 д ' J ] а
т. е.
&2ft==”"oF* —Г" (£ = Ь 2, 3,...).
Таким образом, ряд Фурье данной функции имеет вид
3 6 I
Цх) = - я__ 2 -2/г_1у-cos (2/г— 1)
1 1
sin (2^ — 1) х— — "V — sin 2fex.
2 -лял k
В интервале ( — л, л) ряд сходится к функции i(x), а в точках х=±л
1 , 3
— К числу —У(—я4-0)+Кл—0)]= — л.
Пример 2. Разложить в ряд Фурье функцию
, ( —sinx при — л < х < 0,
[ (х) == s
I sin х при 0 < х < я.
Решение. Данная функция является четной, следовательно, все коэф-
фициенты t>tt = О, a aR находятся по формуле (7)з
л
2 f
— 1 stn х со* пл dx (п — 0, 1, 2,
л j
297
Отсюда
л
f . . 4
| sm x dx——
J n
0
Далее,
Л Л
I sinxcosnxdx—— I [sin(«4-1)x—sin(n*l)a:]dx=s
J л J
о 0
О при /г —2Л —J,
”=2S <*-*2' 3-->-
Следовательно,
2
А . OO A
£ / К I * I 2 4 1
Отметим, что полученный ряд сходится в функции 1 sin х [ на всем интервале
[ — я, л]
Пример 3. Разложить в ряд Фурье функцию
-1 при —л<х<0,
О при ж—О,
1 при 0 < х < л.
Решение, Данная функция является нечетной, следовательно, все коМь
фициенты <зп= 0, а Ьп находятся по формуле (9)!
от л
2 f 2 | 2
Z?n—— | 1 » sin nx dx =----cos nx —--------[ 1 — (— 1 )Z2J*
nJ ЯЯ I ЛЛ
0 0
Тяким образом, все четные коэффициенты bn равны нулю, а нечетные имеют вид
4
я(2£2Г[)'‘ Следовательно,
4 Vi 1
/М=~ 1 sfn<2^~0-V.
А=1
Очевидно, что сумма ряда в точках х = 0 и х == ± я равна нулю.
Пример 4. Разложить в ряд Фурье функцию
. (х
при
при
0<х<1,
1 <х<2.
Решение, Поскольку функция задана в интервале, отличном от ( — л, л),
х( 4- Я
произведем замену независимой переменной по формуле х = ———> или У —
= л (х — 1). Таким образом, получаем следующую функцию!
— (х'4~Я) при—л<х'<0.
/ ) = < я
, 1 при 0 <; х' л.
298
Так как ©та функция определена на интервале ( — П| я), то для нее можно
записать ряд Фурье» Вычислим коэффициенты этого ряда:
о ft
а0== — \ ---------dx + — \ !• dx = — 9
nJ л я J 2
—л о
о Л
X* +я f 1 f
-------COS ПХ dx +— I 1 • cos ПХ dx =8
я-----я J
-я
^л
1
пяа
0
f sinnx'dx*=»-~- [1 —(—!)«];
J na na
—Л
0 rn
r 1 С x' +я t 4 . , . 1 f. . / , ,
1 --------sin nx dx I 1 • sin nx dx **
nJ л nJ
•—л о
0
1 f f < (-!)•
*=—г l x sin nx dx «r —-----•
Я2 J JWl
Я-Л
Следователь но,
1 VI (“1)п ...........
п==»1
Вычйвлия значения «уммы ряда на концах интервала!
v 1НО+ОЖ (2-0)] =-—« V’
Полученный результат дает возможность найти еумму числового ряда
5= 2 (2Л-1)2 ==1+’з’’+'бг+ •" + (2й—1)« +“* ’
Действительно, на оеаовании теоремы Дирихле при х = 0 или х = 2 имеет место
рааенегьо
-L- —_ 2 у 1
2 ~ 4 я2 (2А-1/ ’
откуда
V 1 "8
(2*-Оа 8 ‘
299
§ 8.3. Интегрирование и дифференцирование рядов Фурье
Пусть I (х) — абсолютно интегрируемая на интервале I — л, л|
а
функция; это означает, что вуществует интеграл J | [ (х) [ dx. Тогда
—л
ряд Фурье для [ (х) имеет вид
00
+ 2 (ап cos пх + Ьп sin пх).
я=1
Рассмотрим функцию
(1)
(2)
Эта функция во всем промежутке I — л, л] разлагается в ряд Фурье,
который сходится к F (х) равномерно:
У (Ancosnx4-Bnsinnx).
х *
П=1
(3)
Определим коэффициенты этого ряда. Имеем
Л
А,>=— С F (х) cos пх dx == ~
Л J ЯП
Г Л
F (х) sin пх | —
L —Л
Л
- J [,w
—— 1 sin nxdx
2 J
Л
----— C f (х) Sin пх dx,
ЯП J
— л
откуда Ап — — bjn. Аналогично находим Вп = ап1п.
А °°
Подставив х==0 в разложение (3), получим O=-y--f- Ап,
откуда • Следовательно,
п= 1
х 1 °° Г А 1
f —2£-|dx = у Г sin пх +(1 —cosnx)],
о L J C=1L J
или
X X ос, X
dx 4- у j (an cos nx 4- bn sin nx) dx. (4
Таким образом, интеграл от функции f (х) получается почленньи
интегрированием соответлтвуютрго ей ряда Фурье.
Следует подчеркнуть то обстоятельство, что от ряда Фурье функци!
/ (х) не требуется сходимости к функции / (х); сама же функция должна
быть абсолютно интегрируемой.
300
Пример. Находя из разложения в ряд Фурье функции
х “ .
£(х) = —= 7, ----------------sinn*
2 -йй п
п® 1
в интервале ( ** га, зт)* получить разложение функции Ф (х) ®» хЧ4 в ряд Фурье
в том же интервале.
Решение. Интегрируй правую и левую чаети разложения в ряд Фурье
функции х/2, получим
— -
4 ” па
П® |
1=^(мм_1)=2 j=lpl+ v
П®1 Л®1
Для нахождения
Яр
величины = 2j
п = 1
----------воспельзуемся равенст-
п2
2 f х3 j лв „ V, (—l)n+1 л8
вом Ло= — I —— ах=» —— . Следовательно. У,----------:----» —- я окон-
я J 4 6 п3 12
О n® I
чательн® разложение функции х2/4 в ряд Фурье имеет вид
х2 я2 г 1 1
1~= ""12—e°s*+^c°s2x- —ees3x-b,..-
Перейдем теперь к почленному дифференцированию рядов Фурье.
Пусть мы имеем непрерывную на интервале I — я, л] функцию f (х),
удовлетворяющую условию f ( — л) = / (л) и имеющую абсолютно
интегрируемую производную ff (х). Запишем ряд Фурье для этой
функции:
f(x)~
~2
(аа cos пх + bn sin nx)t
(5)
Ряд Фурье для f (х) имеет вид
~- + S И» cos пх+Вп sin пх). (6)
2 п=1
Вычислим коэффициенты Ло> Вп1
Ло SS — f t' (х) dx SS О,
л J
—л
1 р 1
= — \ f (х) cos пл dx= —
л J п
— л
/ (х) cos пх | + п f (х) sin nxdx^ nbn,
-*л —л )
301
1 n
Bn=o-a- C f (x)sltinx <?№
ffl J
— Л
if я л i
= — b(x)sin«x I —n \ f (x) cos nx dx\ —nant
Л. I I v |
I — Л J
Следовательно, ряд Фурье функции f'(x) запишется так}
СО
2 (—nan sin пх + nbn cos пх), (7)
Таким образом, ряд Фурье для f(x) получается почленным диф-
ференцированием соответствующего ряда Фурье для функции f (х).
Условие f ( — л) = f (я) является здесь существенным, так как в про-
тивном случае свободный член А 0/2 ряда Фурье (6) не обязан быть рав-
ным нулю и тогда ряд Фурье для f (х) не может получиться из ряда
Фурье для f (х) почленным дифференцированием,
Отметим, что вопрос о сходимости ряда Фурье (7) к производной
f(x) остается открытым. Эту сходимость требуется устанавливать
отдельно, пользуясь теми или иными достаточными признаками, на-
пример, теоремой Дирихле.
§ Е.4 Численный гармонический анализ.
Тригонометрическое интерполирование
Операция представления функции f (х) рядом Фурье называется
гармоническим анализом. При практических же расчетах мы вынужде-
ны ыраничиться только несколькими первыми членами ряда Фурье,
В результате мы получаем лишь приближенное аналитическое выраже-
ние для функции f (х) в виде тригонометрического многочлена Л/-го
порядка
a N
Qa (х) — — + 2 (ап cos пх + s’n пх) (—(1)
2 П=1
Кроме того, формулы (3) — (5) § 8,2 для вычисления коэффициентов
Фурье пригодны лишь в случае аналитического задания функции
На практике, как правило, функция f (х) задается в виде таблиць
пли графика, Поэтому возникает задача приближенного отыскали?
коэффициентов Фурье по конечному числу имеющихся значений
функции.
Обобщая вышесказанное, сформулируем следующую задачу числен-
ного или, как его еще часто называют, практического гармонической
анализа: аппроксимировать на интервале (О, Т) тригонометрическая
многочленом N-го порядка функцию у — f (х), для которой известнь
т ее значений yk — f (xh) при хк « kTlm (k 0, 1, 2, ..., т — 1).
Тригонометрический многочлен для функции, определенной ш
интервале (О, Т), имеет вид
2л'(лг) = -^-4-V fancosn-^-x + bBsinn~x) (0<х<Т). (2)
2 л», \ 1 1 1
1 ' г
302
Коэффициенты ап и Ьп определяются следующими соотношениями:
г
an = -^-\f(x) cos х dx, (3)
7 V 1
О
(и = 0, 1, 2,N).
т
bn = ~^f (х) sin n^-xdx (4)
О
Применяя в соотношениях (3) и (4) формулу прямоугольников
для вычисления интегралов по значениям подынтегральных выраже-
ний в точках xk =; kTlm (k == 0, 1, 2, tn — 1), имеем
„ 2 2л&
«п = — У r/ftCOSH----,
m tn *
^9
(n = 0, 1, 2,..., N)
(5)
(6)
Таким образом, тригонометрический многочлен (2), коэффициенты
ап и Ьп которого находятся по формулам (5) и (6), служит решением
поставленной задачи.
Можно показать, что при m > 2N многочлен (2) дает наилучшее
приближение к функции f (х) в смысле метода наименьших квадратов,
если коэффициенты его вычисляются по формулам (5) и (6). Иными
словами, коэффициенты (5) и (6) минимизируют сумму квадратов от-
клонений
2 [CvfeWd2. (7)
В частном случае при tn — 2N коэффициенты ап и Ьп (п = 0, 1, 2, ...
N—1) определяются соотношениями (5) и (6), а коэффициент aN есть
1 m— I
— ^(-1)^. (8)
m А==0
Сам же многочлен Q/v (х) становится интерполяционным многочленом,
так как в этом случае при любом выполняются соотношения
U/t) = Ук Для всех xk = kT/m (k = 0, 1, 2, tn — 1).
Пример. Исследуем динамику производства сахара из сахарной свеклы.
Это производство носит периодический харакгер, обусловленный периодичностью
выращивания и условиями хранения сырья Поэтому в качестве функции,
аппроксимирующей динамику производства сахара, можно принять тригономет-
рический многочлен (2) при m =12. (Это соответствует числу месяцев в годовом
цикле и позволяет выявить специфическую особенность — сезонность про-
изводства.) Следовательно,
й0 . меч / л л А
<4 (х) = — + У aRcos п ~'Х-уЬа sin п ~ х (0 <х< 11).
2 \ и о j
п— 1 4
303
Таблица 8.1
Месяцы 1 и 11! IV V VI VII VIII IX X XI XII 1 6s
xh 0 I 2 3 4 5 6 7 8 9 10 11
Объем производ- ства в усл. ед. 95 71 55 43 36 31 28 26 25 45 91 102 108
Л COS — хк О 1 0,866 0,5 0 —0,5 —0,866 — 1 —0,866 —0,5 0 0,5 0,866
л sin — xk 6 0 0,5 0,866 1 0,866 0,5 0 —0,5 —0,866 — 1 —0,866 —0,5
л cos — xh о 1 0,5 —0,5 —1 —0,5 0,5 1 0,5 —0,5 — 1 —0,5 0,5
л sin — xh 0 0,866 0,866 0 —0,866 —0,866 0 0,866 0,866 0 —0,866 —0,866
Л COS — хк 1 0 — 1 0 1 0 —1 0 1 0 —1 0
л sin — хк 0 1 0 —1 0 1 0 — 1 0 1 0 —1
2л COS — Хъ о 1 —0,5 —0,5 1 —0,5 —0,5 1 —0,5 —0,5 1 —0,5 —0,5
2л —~xh О 0 0,866 —0,866 0 0,866 —0,866 0 0,866 —0,866 0 0,866 —0,866
Продолжение табл. 8.1
Месяцы 1 И ш IV V VI VIJ VIII IX X XI ХП 1 ’fl2
xk 0 1 2 3 4 5 ( 7 8 9 10 11
Объем производ- ства в уел. ед. 95 71 55 43 36 31 28 26 25 45 91 102 1©8
Л Ук cos ~ (Г У я О 95 61,49 27,5 0 — 18 —26,85 —28 —22,52 — 12,5 0 45,5 88,33 34,99
л УК Sin ~Ук б 0 35,5 47,63 43 31,18 15,5 0 -13 21,65 —45 —78,81 —51 —6,11
л Ук COS ~^Уь 95 35,5 —27,5 —43 — 18 15,5 28 13 — 12,5 —45 —45,5 51 7,75
л Ук Sln 0 61,49 47,63 0 31,18 —26,85 0 22,52 21,65 0 —78,81 —88,33 — 11,98
л Ук cos уУк 95 0 —55 0 36 0 —28 0 25 0 —91 0 —3
л sin 2 0 * 71 0 -43 0 31 0 —26 0 45 0 —102 —4
2л У к cos —уп 95 —35,5 —27,5 43 — 18 — 15,5 28 — 13 — 12,5 45 —45,5 —51 —1,25
2л "й sin — у k о 0 61.49 —47,63 0 31,18 —26,85 0 22,52 —21,65 0 78,81 —88,33 1,59
В экономических исследованиях для хорошей аппроксимации динамического не*
риодического ряда обычно выбирают не более четырех гармоник.
Выражения для коэффициентов ап и Ьп имеют следующий вид;
,11 1 11
I хл л . i я
ап=~г 7, yk cos n—xh, bn = -~ >yhsinn — xh.
b b b b
6=0 A = 0
Вычислим эти коэффициенты для первых четырех гармоник многочлена (х).
Необходимые выкладки оформим в виде таблицы (см. табл. 8.1 на стр. 304, 305).
Из приведенной таблицы получаем, что
й0 ~ 108; йх = 34,99; й2 == 7,75; й3 = — 3; й4 — — 1,25;
= —6,11; _ 11,98; = — 4; = 1,59.
Таким образом, мы имеем следующие четыре математические модели сезон-
ности для производства сахара:
Qi (х) = 54+34,99 cos —х—6,11 sin — x;
6 6
Q2 (х)~ 54 + 34,99 cos — х— 6,11 sin --х+7,75 cos — х—11,98 sin х;
6 6 3 3
Q3 (х) = 54+ 34,99 cos х—6,11 sin — х+7,75 cos х —11,98 sin ~х—
6 6 3 3
л л
— 3cos — х—4 sin — х;
Q4 (х) = 54 + 34,99 cos — х — 6,11 sin —
6 6
л л
2
2
х + 7,75 cos “ х— 11,98 sin — х—
3 3
2л 2л
— 3 cos — х — 4 sin — х— 1,25 cos х + 1,59 sin -у- х,
Сравнение Qj (xfe) с соответствующими значениями показывает, что уже
первая гармоника дает в общем правильную модель динамики производства са*
' хара, отражая ее сезонность.
Вычислим средние квадратические отклонения + = 1/ (хь)— nJ1 2
V *=о
для всех Qi (х); находим 6* = 37,80; 62 = 14,40; 63 = 7,59; 64 = 5,75. Как и
следовало ожидать, значения 6, монотонно убывают с ростом т, причем 64 мало
отличается от 63. Кроме того, сами значения 6g и 64 достаточно малы, так что уже
многочлен (х) является хорошей аппроксимацией ряда, характеризующего
годовую динамику производства
сахара.
§ 8.5. Численные методы определения коэффициентов Фурье
Пусть задан ряд Фурье, сходящийся к периодической функции
/(х):
Й 00
/ (X) =-~ 4- V (ат с°5/о + sin mx), ' (1)
т~ 1
.где
л
ат =— f f (х) cos тх dx (m —0, 1, 2,...), (2)
л J
— л
1 ?
Ьт = — f (х) sin тх dx (т s 1, 2, 3,...). (3)
Л J
— л
306
В предыдущем параграфе мы сформулировали задачу аппроксима-
ции функции f (х) тригонометрическим многочленом Qw (х). Там же при
вычислении коэффициентов ат и Ьт в помощью интегралов мы исполь-
зовали формулу прямоугольников.
В общем случае приближенное вычисление коэффициентов ат и
Ът основано на замене интегралов в формулах (3) и (4) § 8.4 их зна-
чениями, получаемыми по одной из формул приближенного интег-
рирования. В настоящем параграфе мы воспользуемся формулой
трапеций,
Будем предполагать, что функция f (х) является периодической
с периодом 2л. Заметим, что вместо обычных пределов интегрирования
от — л до л при определении коэффициентов ат и Ьт можно рассмат-
ривать любой интервал интегрирования длиной 2л, Для удобства вы-
числений мы возьмем интервал от 0 до 2л, так что
я =—С f (х) cos тх dx (m=sO, 1, 2,...), (4)
01 t)
о
2л
Ьт = —ff(x)sinmxdx (m = 1, 2, 3,...). (5)
л j
в
Разделив интервал [0, 2л] на N равных частей, в результате полу-
чим точки деления 0, 1 * 2 * (N — 1) 2л» Соответствую-
щие значения функции f (х) в точках деления обозначим через уй,
Уъ Уг< •••> Уи-\, Ун = Применяя формулу трапеций, получаем
следующие приближенные формулы для вычисления коэффициентов
Gm>
N
~х~ао~ Уь~ Уь +У1Л--V yN_il (6)
2 4 = 0
V ж-i . 2moi . 1х2тл
V^COS^ — УоН-ЙСОЙ—-+... + ^_1C0S(^-l)--!
Z ДМв /V XV /V
(7)
ТЬст= 2 = ш “дГ + ••• + ^-1 sin(2V —1) — •
(8)
Пусть N — 12, т. е. интервал от 0 до 2л разбит на 12 равных частей,
так что используются значения аргумента 0, им соответ-
ствуют значения функции yQ, уи у2,„„ уи, а величины, на которые
умножаются эти значения, таковы: ± 1; ±sln g = ± 0,5; ± sin —
= ± 0,866. Отсюда, опуская громоздкие выкладки, получим
307
6а0 — Уо 4* У1 + У 2 4" Уз + У 4 4* Уъ 4" У а 4* Уч4" У а 4* Уз + Ум 4* Уи>
6а, = (ys + Z/Io— у4 — у8) sin — + (ft4-fti—ft—ft) Sin 4- (ft—У«),
и О
6ft = (У14- Уъ 4- Уч 4- У11— Уч —ft— Уз—Ум)sin у 4* (ft 4" Уз—Уз—Уз)>
6ft = У о + У 4 4- уа—у 2—у в—Ум>
б-ц = (ft + Уъ—Уч — Утл) -у 4- (ft 4- У4—Уз — Ум) sin 4- (ft— Уз)>
6b2 = (ft 4- Уч 4- Уч 4- Уз — У4—Уъ—Ум—У и) sin v.
6Ь3 = У14- Уъ 4- Уз—Уз—Уч — 2/11
и т. д.
Чтобы свести к минимуму число необходимых арифметических
операций для получения значений ат и Ьт, используют специальную
вычислительную схему —ехему Рунге,
1 ш а г, Выписывают значения функции f (х) в следующем порядке?
У0У1У3 УзУ4УъУв
.2/11 Ум Уз Уз Уч
II ш аг. Подсчитывают суммы и разности каждой пары значений,
стоящих одно под другим. Полученные суммы и разности выписывают
таким образом:
УзУчУч ftftftft
Уп Ум Уз Уз Уч (6)
суммы Uq Ui W8W4
разности
Ilf шаг. Аналогичные операции производят над суммами и раз- ностями (6):
^0 ^2 ^8 Z/g ZZg t>l vi v3 Уъ^4
суммы Cq $1 ^2 с8 ftftft
разности dQ d2 Й1 Ла (7)
[V ni a p, Вычисляют значения am и bm по приближенным формулам
6а„ ==£ е0 4* ®i 4* ®2 4- Og»
6at = d0 4- 0,866^ 4- 0,5dj,
6a2 = (e0—Cg) 4- 0>5 (ex—es),
6flg — d8 d8f
6bx ss 0,5ft 4- 0,866ga 4- g8)
6b, = 0,866(^4-^.
бЬа-ft -ft
(8)
и т. д.
308
Для наглядного сравнения полученных по приближенным форму-
лам коэффициентов и Ьт с точными их значениями приведем при-
мер, в котором функция задана аналитически.
Пример. Рассмотрим периодическую функцию С периодом 2ni
0=4 (*) = • х Л — при 0 < х < л, л 1 при л < х < 2л, 0 при х = 2л*
доставим таблицу
«А 0 л "б я т л Т 2л Т 5л л 7л 4л 3 Зл т 5л з ' Ил 6 2л
УК 0 1 1 1 2 . _5_ 1 1 1 1 1 1 1
6 3 2 3 "б”
Выпишем еогла@но «хеме Рунге значения у^ ц произведем указанные в ней сло-
жения и вычитания [см, формулы E(6)h
О 2 1 1 1 А,
6 3 2 3 6
11111
7
сум МЫ 0 ----
6
4 3 5
3 2 3
разности
5_ __2_ _J_____J______[
6 3 2 3 6
Теперь произведем вычитания и вложения
мам и разностям [см. формулы (7)ji
еу'лмы
по отношению в найденным сум-
разности
11
6
суммы 13 3
2 1
разност. —1 —------—-—*
1 _J_
6 ,3
суммы — 1 1
2 k 1
разности _-- —- —
3 3
Запишем теперь выражения для ат и bmi
6а0 —14- 34-3+ $
6а1==_ 1-4.0,866-0,5.4:
3 О
6а, = ( 1 - -у) +°.5 (3-3)5
6^ = 0,5 ( —1)4-0,866 (-1)-
— 1 —
7 4 3
6 3 2
£ 2 1
6 “ 3 ~ 2
1
6&3 —
309
Отсюда
а0 = l,417j aj = — 0,291} as = —0,083} e§ = —0,111,
bt = -0,311} 62 = — 0,144} 4>8 = —0,083.
Для сравнения приведем течные значения коэффициентов}
at = 1,500} =• — 0,203} аа «= 0,000, eg = — 0,022}
bi=> -0,318} 62=> — 0,159} 6g = —0,106.
Чтобы получить значения коэффициентов по приближенным фор-
мулам е большей точностью, можнд обратиться к схемам с большим
числом ординат.
Следует отметить, что практический гармонический анализ дает
возможность получать аналитические выражения, аппроксимирую-
щие заданные функции с наименьшей средней квадратической ошибкой.
Упражнения '
1. Разложить в ряд Фурье функцию f (х) = xcos х (— л < и < л).
1 °° п
Omeemi xc®sx= — — sinх4-2 ——гЯплл*
2. Разложить в ряд Фурье функцию f (%) «э # sin л (а < х < л).
1 (— 1)п
Omeemi xsinx=l ——cos х—2 У,----------cosnx»
2 i
n=>2
8. Разложить в ряд Фурье п® коеинуеам функцию f (х) а х (я ~ ж)
(0<х <и).
~ ч ла V4 со^ 2/гх
Omeemi х(л—х)~-^-----.
п= 1
4. Разложить в ряд Фурье по винуеам функцию / (х) == х (л — х)
(О < х < л).
Л t 8 х? sin (2/2 — 1) лэ
Ответ! х(л—х) —— У, —-----------;---.
п (2/г—1)2
П во 1
5. Разложить в ряд Фурье функцию
в / ° при — л < х < 0,
1 к при 0 < х < л.
Л tz , п 2 Vcos (2п — 1)х V’(— 1)" .
Отвели i(x)=—-------->, —-------——— >,---------sin пх.
4 л (2п—1)а а
и=1 ' ' 0=»1
310
6. Для функции р =» f (х), определенной на интервале (0, я) и заданной в ви-
де таблицы значений f (xk);
k 0 i 2 3
0 Л T Л 3л 4
№ 1 2 2,4 2,6
сеатавить тригонометрический интерполяционный многочлен.
Ответ- <?2 (х) = 2 — 0,7 cos 2х — 0,3 sin 2х — 0,3 cos 4х + sin 4х.
7. Для функции у = f (х), определенной на интервале (0, 1) и заданной
в виде таблицы значений у%~ f (xh)i
0 t 3 4 5
xk 0 1 6 1 3 1 2 2 3 5 6
Уп 1 0 —2 ~3 0 2
еоставить тригонометрический многочлен не ниже второг® порядка.
7 2
Omeemi Q3(x) = — 1+~соз2лх —$ш'2лх—cos 4лх.
Глаза IX
ПРИБЛИЖЕННОЕ РЕШЕНИЕ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ
УРАВНЕНИЙ
§ 9.1. Понятие о дифференциальном уравнении
Уравнение, в котором неизвестная функция входит под знаком про-
изводной или дифференциала, называется дифференциальным
уравнением*
Например,
Л=2Й-31; ^-<+П
dx di1 дх% dtp
у'==х2\ xdy=syadx.
Если неизвестная функция, входящая в дифференциальное уравне-
ние, зависит только от одной независимой переменной, то дифферен-
циальное уравнение называется обыкновенным.
Таковы, например, дифференциальные уравнения
X2- -- ~ 2; 2s d! = l ds.
dx6
311
Если же неизвестная функция, входящая в дифференциальное урав-
нение, является функцией двух или большего числа независимых
переменных, то дифференциальное уравнение называется уравнением
в частных производных.
Например, дифференциальное уравнение
ду*
есть уравнение в частных производных.
Порядком дифференциального уравнения называется наивысший
порядок производной (или дифференциала), входящей в уравнение.
Так, например, уравнения
\dp дх% ду2
являются уравнениями второго порядка, а уравнения
— *cos^ + sin^== 1; (х2—у*) dx + (х2 + у2) dy
di
— первого порядка.
В настоящей главе рассматриваются только обыкновенные диф-
ференциальные уравнения.
Обыкновенное дифференциальное уравнение n-го порядка в самом
общем случае содержит независимую переменную, неизвестную функ-
цию и ее производные или дифференциалы до n-го порядка включитель-
но и имеет вид
F (х. z/, у', и" //")) = 0. (I)
В этом уравнении х — независимая переменная, у — неизвестная функ-
ция, у\ у\„.> у(п> — производные этой функции.
Если левая часть дифференциального уравнения (1) является мно-
гочленом по отношению к производной максимального порядка от не-
известной функции, то степень этого многочлена называется степенью
дифференциального уравнения.
Например, уравнение
является уравнением второго порядка четвертой степени, а уравнение
{у1 f 4- х* уь ~ {f+я10 = 0
— уравнением первого порядка второй степени.
Дифференциальное уравнение n-го порядка, разрешенное относи-
тельно старшей производной, может быть записано в виде
yw *=1(х,у, у', у"..у(п~1у). (2)
Решением (или интегралом) уравнения (2) называется всякая диф-
ференцируемая функция (х), удовлетворяющая этому уравнению,
т. е. такая, после подстановки которой в уравнение (2) оно обращается
в тождество.
312
График решения обыкновенного дифференциального уравнения на-
зывается интегральной кривой этого уравнения.
Решение дифференциального уравнения, содержащее столько неза-
висимых произвольных постоянных (параметров), каков его порядок,
называется общим решением (или общим интегралом} этого уравнения.
Геометрически общее решение дифференциального уравнения пред-
ставляет собой семейство интегральных кривых этого уравнения.
Частным решением дифференциального уравнения называется вся-
кое решение, которое может быть получено из общего при определенных
числовых значениях произвольных постоянных, входящих в общее
решение.
Произвольные постоянные, входящие в общее решение, определяют-
ся из так называемых начальных условий.
Задача с начальными условиями ставится так: найти решение
у — ф (х) уравнения = f (х, у, у'9 у\ удовлетворяющее
дополнительным условиям, состоящим в том, что решение у — ф (х)
должно принимать вместе со своими производными до (п — 1)-го по-
рядка заданные числовые значения yQt y'o, yl при заданном
числовом значении х = х0 независимой переменной х:
г/==Уо> У' = Уо> y" = yo,-.,y(n-l'l=y^-i} при х = х0. (3)
Условия (3) называются начальными условиями; числа х0, yQ, у‘^
•••» — начальными данными решения, а задача отыскания
решения у = ф (х) дифференциального уравнения (2), удовлетворяю-
щего начальным условиям (3), — задачей с начальными условиями,
или задачей Коши.
В случае уравнения первого порядка, т. е. при п = 1, получаем
задачу Коши для уравнения у* = f (х, у) с начальным условием х = х0,
У
Геометрически задача Коши (для уравнения первого порядка)
состоит в том, что из всего множества интегральных кривых, представ-
ляющих собой общее решение, нужно найти ту интегральную кривую#
которая проходит через точку Л1о с координатами х = х0, у = у0
dy
Пример. Для дифференциального уравнения = 2х о начальным условием
= 2 при х0 = 1 общее решение имеет вид у = х* + С. Оно представляет собой
семейство парабол. Если теперь-в общее решение подставить начальные данные,
то получим 2 — 1 + С, *1. е. С = 1. Следовательно, частное решение, удовлетво-
ряющее указанному начальному условию, есть у = № + 1. I еометрически это
означает, что из всего множества парабол, представляющих общее решение диф-
ференциального уравнения, выбираем одну, проходящую через точку (1, 2)
(рис. 9.1).
Задача Коши имеет единственное решение, удовлетворяющее ус-
ловию у (х0) == г/0> если Функция / (х, у) непрерывна в некоторой об-
ласти ы == {I * — *о| < а» IУ — < Ь} и удовлетворяет в этой
области условию Липшица
I/(*> ~у) I—/(*> у) I < n I*/—у!>
31
2) численные
в виде таблицы.
где N — постоянная Липшица, зависящая от
а и Ь (а и b — границы области).
Методы точного интегрирования диф-
ференциальных уравнений пригодны лишь
для сравнительно небольшой части уравне-
ний, встречающихся на практике.
Поэтому большое значение приобретают
методы приближенного решения дифферен-
циальных уравнений, которые в зависимо-
сти от формы представления решения мож-
но разделить на две группы:
1) аналитические методы,
дающие приближенное решение дифферен-
циального уравнения в виде аналитическо-
го выражения;
методы, дающие приближенное решение
В данной главе для первой группы методов будут рассмотрены ме-
тод последовательных приближений (метод Пикара) и метод интегриро-
вания дифференциальных уравнений с помощью степенных рядов;
для второй группы — метод Эйлера и его модификации, методы Рун-
ге — Кутта и Адамса.
§ 9.2. Метод последовательных приближений (метод Пикара)
Этот метод возник в связи с доказательством теоремы существова-
ния и единственности решения дифференциальных уравнений, Он но-
сит название метода Пикара.
Пусть дано уравнение
у' = f (х, у), (1)
правая часть которого в прямоугольнике {|х—х0| \у — #0[ ^Ь}
непрерывна и имеет непрерывную частную производную по у<
Требуется найти решение уравнения (1), удовлетворяющее начальному
условию
х = х0, у (х0) = у0. (2)
Интегрируя обе части уравнения от х0 до х, получим
У V
dy = f (х, у) dx,
Ув ха
или
У{х) = у0+ у (х, у) dx. (3)
Хо
Уравнение (1) заменяется интегральным уравнением (3), в котором
неизвестная функция у находится под знаком интеграла, Интегральное
314
уравнение (3) удовлетворяет дифференциальному уравнению (1) и
начальному условию (2). Действительно,
У(х0)==у0 + $ [(x,y)dx = y0.
Хо
Заменяя в равенстве (3) функцию у значением у0, получим первое
приближение
Увх) = У0 + § f{x,y0)dx.
Ху
Затем в уравнении (3) заменяем у найденным значением уги получаем
второе приближение
Уг(х) = ^о + f(x>yi)dx.
X,
Продолжая процесс далее, последовательно находим
Уз(*')^Уо+ J f(x,y2)dx,
ха
Уп (х) = у0 + J f (х, уп^) dx.
Хо
Таким образом, составляем последовательность функций
У1 (*)» Уг (Д Уь (Д-, Уп (Д
Справедлива следующая теорема, которую приведем без доказа-
тельства.
Теорема. Пусть в окрестности точки (х0; у0) функция ( (х, у) не*
прерывна и имеет ограниченную частную производную /'у (х, у). Тогда
в некотором интервале, содержащем точку х0, последовательность
{Уг W} сходится к функции у(х), служащей решением дифференциалы
ного уравнения у = f (х, у} и удовлетворяющей условию у (х0) = yQ.
Оценка погрешности метода Пикара определяется по формуле
\У—Уп
(4)
+
где М =* max \f (х, у)\ при (х, у) £R[a, а /V — постоянная Лип-
шица для области/ф равная/V =max Величина h для
определения окрестности [х0 — h х^ х0 4- h] вычисляется по фор-
муле
/i = min|a —); (5)
\ /
а и Ь — границы области
315
Пример. Решить методом Пикара дифференциальное уравнение / » ж2 + 0*
с начальным условием х0 в 0> У (хо) “ Уо О*
Решение. Переходим к интегральному уравнению
У=Уо+$ (x2+y2)dx,
х9
или с учетом начальных условий,
У= / (х2 + </2) Й».
О
Получаем последовательные приближения:
г/1= ^(яг+!/о) dx = [(x2 + <y) dx=~-i
о о
X Х t «У оч
л * п / д'** у дЗ д*7
1/2= \ (Л2+У1)^= \ х2+тИ = -т-+тг!
v v у У / о О._)
О о ' '
А о С ( „ Xs 2х10 Xй \
г/з=$(х2+</22)^=Цх2+—+—+—^л=
О 0 х '
х3 х7 2х13 хг§
~ + "бЗ~ + Т079"+ 59535 *
Оценим погрешность третьего приближения по формуле (4):
У14-1
\У~Уп I < V1 М-------
(л + 1)!
Так как функция / ~ х2 + у2 определена и непрерывна во всей плоскости, то
в качестве а и b можно взять любые числа. Для определенности выберем пря-
моугольник
ХО1 < 0,5, |у — //0|<1},
т е.
р{_0,5<х<0,5, —!<//<!}.
Тогда
Л4 = тах [/ (х, у} [ —max (x3-[-z/2)— 1,25;
// = тах \ffy (х, у) | = тах | 2у | = 2.
Поскольку а = 0,5, Ь/М^0,8, по формуле (5) имеем
/ b \
h— тт а, — =0,5.
\ М J
Решение у будет задано для — 0,5 < х < 0,5. При п = 3 имеем:
, t 1,25*23*0,54 5
Полученная оценка погрешности очень грубая, на самом деле погрешность зна-
чительно меньше.
316
§ 9.3. Интегрирование дифференциальных уравнений
с помощью степенных рядов
Пусть дано дифференциальное уравнение п-го порядка;
У(п) = f yt „ ^(«-1)) (] )
с начальными условиями
х₽ Хо, у (х0) = у0, у' (х0) = Уо.г/(п~(х0) = у%~ (2)
Правая часть этого уравнения есть аналитическая функция в началь-
ной точке /Ио (х0‘> Уо> Уо> .... Представим решение у = у (х)
уравнения (1) в окрестности точки х0 в виде ряда Тейлора:
У = У0 + Уо (х—х0) + (х—х0)2 + (х~х0)3 +(3)
где | х — х0| < h, a h — достаточно малая величина. Для нахождения
коэффициентов ряда (3) уравнение (1) дифференцируют по х нужное
число раз, используя условия (2).
На практике величину |х— х0| берут настолько малой, что при
требуемой степени точности остатком ряда можно пренебречь.
Пример 1. Найти решение дифференциального уравнения у* — у — 4х -ф 3
G начальным условием х0 == 0, yQ — 3.
Решение. Имеем
у = ^ _ 4 = _ 4х — 1, у = д” = д — 4х — у1У = у .
Используя начальное условие, находим
Уз ~Уь — 4x0-}-3 = 3-j-3 —6,
//о ~ Уъ ~~ 4-^0 1—3— 1 — 2,
Подставляя yfQ, д", в ряд Тейлора, получим
У “i/u (Л— А'о) (х— v0)2 + —— (х— *о)3+ ~— (х—х0)4 + ...==
2! 3! 41
= 3+6x+x2+-~ + -j- + ..„
О 1Z
Точное решение заданного уравнения есть функция
у = 2ех + 4х + 1.
Если положить h — 0,1, то можно состав и i ь таблицу значений решения за
данного дифференциального уравнения.
Таблица 91
xi с »J и, У 0,3
Значения, полученные из аналитического реше НИЯ 3 3,6021 4,2428 4,8908
Приближенное решение с помощью степенною ряда . . 3 ^,(103 4,2427 1 8493
317
Пример 2. Найти решение уравнения #' = х2 + у2, удовлетворяющее ус*
ловию х0 — 0, yQ = О.
Решение. Находим
у№ =2x+2t/t/'
/"«2+2
у(л+2)== 2 [у<п) у' +пу(а^1) у* +
+ + <+ •/я-2)/"+... 4- «г/'г/(я)+у,у(п+’)]'
I *
Из последних соотношений и начального условия получим:
у' (Хо)-у'й=О,
У" (*о)=Уо=О,
у"' (х0)=у!)'/=2,
ylV (А>) = УоУ=О,
У \ло/ — у о —и,
У™ (Xo)==J/VH = 8O(
Следовательно, можно записать
80x7
3 63
Ранее этот же пример мы решали методом Пикара и установили, что погрешность
при — 0,5.< х < 0,5 не превосходит 2 • 10~L
Представление искомого решения в виде ряда Тейлора особенно
удобно для небольшого промежутка интегрирования вблизи начальных
значений. Чаще всего такое решение является вспомогательным при
применении других методов приближенного интегрирования дифферен-
циальных уравнений (методов Адамса,'Милна, Штермера).
§ 9.4. Численное интегрирование дифференциальных
уравнений. Метод Эйлера
Решить дифференциальное уравнение у' —f (х,у) численным мето-
дом — это значит для заданной последовательности аргументов х0,
х1( хп и числа у0, не определяя функцию у = F (х), найти такие зна-
чения уъ уг,..., уп, что yt ~ F (Xi) (j = 1, 2, п) и F (х0) = у0.
Таким образом, численные методы позволяют вместо нахождения
функции у = F (х) получить таблицу значений этой функции для за-
данной последовательности аргументов. Величина h = xft — x^-i на-
зывается шагом интегрирования.
Рассмотрим некоторые из численных методов.
Метод Эйлера. Этот метод является сравнительно грубым и приме-
няется в основном для ориентировочных расчетов. Однако идеи, поло-
женные в основу метода Эйлера, являются исходными для ряда других
методов.
318
Пусть дано дифференциальное уравнение первого порядка
У' = t (х, у) (1)
с начальным условием
х = х0, у (х0) = у0. (2)
Требуется найти решение уравнения (1) на отрезке [а, 6],
Разобьем отрезок [а, 6] на п равных частей и получим последова-
тельность х0, х1г х2,..„ хп, где Xi = х0 4- th (t = 0, 1, 2, ,,,, п), а /г =
₽ 0 — а)/п — шаг интегрирования.
Выберем k-й участок хЛ+1] и проинтегрируем уравнение (1):
xk+i xk+i xk+l
J f(x,y)dx==> $ y'dx = y(x) | =z/(W— y(xk) = yh+1—yh,
xh xk
t. e.
Z/A+i = //fe+ $ t(x,y)dx. (3)
xk
Если в последнем интеграле подынтегральную функцию на участке
[xh, лу+1] принять постоянной и равной начальному значению в точке
X — xh, то получим
хк+1 Xk+I
J f(xk,yiddx=f(xh,yb) ‘X I =[(xh, ук)(хк+1—xk)=y'kh.
xh xk
Тогда формула (3) примет вид
Ук+i = Ук + y'kh. (3')
Обозначив у/1+1 — ук = &ук, т. е. y'k h = Дг/Й, получим
№+i = Ук + &Ук. (4)
Продолжая этот процесс и каждый раз принимая подынтегральную
функцию на соответствующем участке постоянной и равной ее значе-
нию в начале участка, получим таблицу решений дифференциального
уравнения на заданном отрезке [а, 6]. Равенство (4) означает, что на
отрезке 1хй, хй+11 интегральная кривая у = у (х) приближенно за-
меняется прямолинейным отрезком, выходящим из точки Mh (хк; yh)
с угловым коэффициентом f (хй, yh). В качестве приближения искомой
интегральной кривой получаем ломаную линию с вершинами в точках
Л40 (х0; Уо)’ (хь Уд< Мп (хп; Уп). Первое звено касается’истинной
интегральной кривой в точке Мо (х0; у0) (рис. 9.2).
Если функция f (х, у) в некотором прямоугольнике
R{\x — х0\ а, \у — у0\<Ъ}
удовлетворяет условию
it^yd—[{хь у2)\^М\У1 — Уг |(/V = const) (5)
319
и, кроме того,
= (M = const), (6)
I dx | I дх ду j 4 9
то имеет место следующая оценка погрешности:
\у ^п)-Уп К ~- [(1 + W-1L
(7)
где у (хп) — значение точного ре.
шения уравнения (1) при х ~ хп, а
уп — приближенное значение, полу-
ченное на n-м шаге.
Формула (7) имеет в основном тео-
ретическое применение, На практи-
ке, как правило, применяют «двой-
ной просчет», Сначала расчет ведет-
ся с шагом 1г, затем шаг дробят и
повторный расчет ведется с шагом
й/2. Погрешность более точного зна-
чения уп оценивается формулой
\Уп~У(Хп)\
~ I Уп Уп !•
(8)
Пример 1. Проинтегрировать методом Эйлера дифференциальное уравнение
у' — у — х с начальным условием х0 == 0, = 1,5 на отрезке [0; 1,5], приняв
h — 0,25. Вычисления вести с четырьмя знаками после запятой.
Решение. Для удобства вычислений составим следующую таблицу
(см. табл. 9.2).
I ш а г. По начальным данным заполняем первую строку в столбцах (2) и (3).
II шаг. Из уравнения у. = у, — х. вычисляем yi (i =з 0,1, 5) в столб-
це (4). 1 i г
III шаг. Содержимое столбца (4) умножаем на h (вычисляем = hy
i — 0, 1, 5) и записываем в столбец (5) этой же строки.
IV ш а г. К содержимому столбца (3) прибавляем содержимое столбца (5)
этой же строки (вычисляем y^t =• у &у$ i = 0, 1, 5) и результат запи-
сываем в столбец (3) следующей строки. Определяем х/4-1 ~ х$ + h и затем шаги
II, III, IV повторяем до тех пор, пока не будет пройден весь отрезок [0; 1,5].
Таблица 9.2
1 xi У1 Д^==
1 .2, j <3) (4) (5)
0 0 1,5000 1,5000 0,3750
1 0,25 1,8750 1,6250 0,4062
2 0,50 2,2812 1,7812 0,4453
3 0,75 2,7265 1,9765 0,4941
4 1,00 3,2206 2,2206 0,5552
5 1,25 3,7758 2,5258 0,6314
6 1,50 4,4072
320
Метод Эйлера может быть применен к решению систем дифферен-
циальных уравнений и дифференциальных уравнений высших поряд-
ков. Однако в последнем случае дифференциальные уравнения должны
быть приведены к системе дифференциальных уравнений первого
порядка.
Пусть задана система двух уравнений первого порядка
| z'=f2(x, у, г)
с начальными условиями
У W = у о, г (х0) = г0. (10)
Приближенные значения у (хг) да yt и г (хг) да zt находятся по форму-
лам
Vi+i = У1 + ^Уь (Н)
г4+1 ~ 2г 4* А2г>
где
&У1 = (xh yt, zt),
(i = o, 1,2, ...). (12)
Дгг = й/а(хъ уi, zt)
Пример 2. Применяя метод Эйлера, решить численно систему дифферен-
циальных уравнений
I У* —
I z' = (z + y)x
с начальными условиями у (0) — 1,0000, г (0) = 1,0000 на отрезке [0; 0,Ы; шаг
h = 0,1. Вычисления вести с одним запасным знаком.
Решение. Для проведения расчетов воспользуемся табл. 9.3. Последо-
вательность действий ясна из таблицы.
Таблица 9.3
xi «г vt = Ч 2/ = = х. Лг4 = = 4 h
0 0 1,0000 0 0 1,0000 0 0
1 0,1 *1,0000 0 0 1,0000 '0,2000 0,0200
2 0,2 1,0000 0,0040 0,0004 1,0200 0,4040 0,0404
3 0,3 1,0004 0,0180 0,0018 1,0604 0,6182 0,0618
4 0,4 1,0022 0,0480 0,0048 1,1222 0,8498 0,0850
5 0,5 1,0070 0,1001 0,0100 1,2072 1,1071 0,1107
6 0,6 1,0170 1,3179
Пример 3. Применяя метод Эйлера, составить на отрезке [1; 1,5] таблицу
значений решения дифференциального уравнения
г/”+-7-+4/=°
с начальными условиями у (1) 0,77; yf (1) = — 0,44 и шагом h = 0,1,
321
Решение. С помощью подстановки у' = г, у- = г' заменим данное урав-
нение системой уравнений
, г
г = - — —у
к
с начальными условиями у (1) = 0,77, г (1) = —0,44. Вычисления проведем
с одним запасным знаком. Для проведения расчетов воспользуемся табл, 9,4.
Таблица 9.4
i *1 »1 ^ = гг йГ 1 И <К> 1 "М II = • h
0 НО 0,77 — 0,44 — 0,044 — 0,44 — 0,33 —0,033
1 1,1 1,2 0,726 — 0,473 — 0,047 — 0,473 —0,296 —0,030
2 0,679 — 0,503 — 0,050 — 0,503 —0,260 —0,026
3 1,3 0,629 — 0,529 — 0,053 — 0,529 -0,222 —0,022
4 1Л 0,576 — 0,551 — 0,055 -0,551 -0,183 —0,018
5 1 ,5 0.521 — 0,569
§ 9.5. Модификации метода Эйлера
Усовершенствованный метод Эйлера. Рассмотрим дифференциаль-
ное уравнение
у' — f (х, у) (1)
с начальным условием
У W = у0. (2)
Требуется найти решение уравнения (1) на отрезке [а, 6],
Разобьем отрезок fa, bl на п равных частей точками хг = х0 + th
(I = 0, 1, 2,..,, и), где h = (b—а)/п—шаг интегрирования. Сущность
усовершенствованного метода Эйлера состоит в следующем: сначала
вычисляют вспомогательные значения искомой функции j/i+i/2 в точ-
ках Xz+1/2 — xt + у с помощью формулы
У1+ 1/2 =«/i+— yl, (3)
затем находят значение правой части уравнения (1) в средней точке
i/;+i/2 = f (X/+I/2, г/м-1/2) и определяют '
У t+i — У1 Л-hyi +1/2. Н)
Замечание. Оценка погрешности в точке хг может быть полу-
чена с помощью «двойного просчета»: расчет повторяют с шагом hi‘2 и
погрешность более точного значения у* (при шаге й/2) оценивают
приближенно следующим образом:
|///-г/(х()|~4-|^-^1, ®
О
322
где у (х) — точное решение дифференциального уравнения. Усовер-
шенствованный метод Эйлера является более точным по сравнению
с методом, рассмотренным в § 9.4.
► Пример 1. Проинтегрировать усовершенствованным методом Эйлера диф-
ференциальное уравнение у' — у — х с начальным условием х0 — 0, у0 == 1,5
на отрезке [0, 1], приняв h — 0,25. Вычисления вести G четырьмя знаками после
запятой.
Решение. Результаты вычислений приведены в табл. 9,5. Она заполняет-
ся следующим образом.
Таблица 95
xi «7= h ~'yi ^+1/2 = » A- = Xf-l г 2 ^'4-1/2== , a * = + — 474-1/2 = = f (*<4-1/2 ^4-1/2) 1 /2
(1) 52) (3) (4) (5) (6) (7) (8) | 0)
0 0 1,5000 1,5000 0,1875 0,125 1,6875 1,5625 0,3906
1 0,25 1,8906 1,6406 0,2051 0,3750 2,0957 1,7207 0,4302
2 0,50 2,3208 1,8208 0,2276 0,6750 2,5484 1,8734 0,4684
3 0,75 2,7892 2,0392 0,2549 0,8750 3,0441 2,1691 0,5423
4 1,00 3,3315 2,3315 0,2914 1,1250 3,6229 2,4974 0,6243
5 6 1,25 1,50 3,9558 4,6856 2,7058 0,3382 1,3750 4,2940 2,9190 0,7298
I шаг. По начальным данным заполняем первую строку в столбцах (2)
0 (3).
II ш а г. Из уравнения у/ = / (хг-, yt) — yt — Xi вычисляем yt для столбца
(4) (/ = 0, 1, 5).
Ill шаг. Содержимое столбца (4) умножаем на п/2 и тем самым определяем
h
"2 • Ув результат записываем в столбец (5).
IV ш а г. Содержимое столбца (6) получаем путем сложения текущего зна-
чения X} и Л/2.
V ш а г. К содержимому столбца (3) прибавляем содержимое столбца (5)
и результат записываем в столбец (7).
VI ш а г. Найденные значения х ь у i [столбцы (6) и (7)] соответствен-
на г + 2
но подставляем в правую часть заданного дифференциального уравнения, опре-
деляем у* х и записываем в столбец (8).
г+ g
VII шаг. Содержимое столбца (8) умножаем на шаг интегрирования h и
определяем [столбец (9).]
VIII шаг. Содержимое столбца (3) прибавляем к содержимому столбца
(9) и полученный результат у ~ уг hyf i (i — 0, 1, 5) записываем
*+ 1 t+г
в столбец (3) следующей строки.
Далее весь процесс вычислений повторяем, начиная со II шага.
Усовершенствованный метод Эйлера — Коши. Сущность метода
Эйлера — Коши состоит в следующем. Сначала определяют вспомога-
тельную величину
^+1==^+М»
(6)
323
затем вычисляют у[^\ = f (xl+li и по формуле
yi-n = yt+h’ У‘ ~^+-
2
(7)
находят соответствующее решение.
Оценка погрешности может быть осуществлена по формуле (5)|
после проведения повторного просчета с шагом й/2.
Пример 2. Пользуясь усовершенствованным методом Эйлера — Коши,|
проинтегрировать дифференциальное уравнение примера 1.
Решение. Результаты вычислений приведены в табл. 9.6. Заполнение
таблицы производится следующим образом.
Таблица 96
1 *1 yi Уь = yt +1“ = + £//4-1 = ”Хг~Н й7<+11 ngi + hyl+\
2
О) (2) 3 (4) (5) (6) (Т (8) (9) Ю)
0 0 1,5000 1,5000 0,3750 0,25 1,8750 1,625 0,4062 0,3906
1 0,25 1,8906 1,6406 0,4102 0,50 2,3008 1,8008 0,4502 0,4302
2 0,50 2,3208 1,8208 0,4552 0,75 2,7760 2,0260 0,5065 0,4808
3 0,75 2,8016 2,0516 0,5129 1,00 3,3145 2,3145 0,5786 0,5458
4 1,00 3,3474 2,3474 0,5868 1,25 3,9342 2,6842 0,6710 0,6289
5 6 1,25 1,50 3,9763 4,7118 2,7263 0,6816 1,50 4,6579 3,1579 0,7895 0,7355
1 ш а г. По начальным данным заполняем столбцы (2) и (3) первой строки.
II шаг. Определяем значение у[ ~ / (jq, yL) — yt — xt (t = 0, I, 5)
для столбца (4).
III шаг. Найденное значение yi из столбца (4) умножаем на шаг интегриро-
вания h и результат записываем в столбец (5).
IV ш а г. Определяем = xt + h (t = 0, I, ... , 5) для столбца Щ).
V ш а г К содержимому столбца (3) прибавляем содержимое столбца (5) и
результат заносим в столбец (7), т. е. определяем уг+г ~ yt + hy'i.
VI ш а г Найденные значения лу+i и yt+i подставляем в правую часть
данного дифференциального уравнения и определяем z/z+1 для столбца (8).
VII шаг. Результат столбца (8) умножаем на шаг интегрирования h и оп-
ределяем h yt+1 [столбец (9)].
VIII шаг. Находим hyi [столбец (10)], для чего определяем полусумму ве-
личин, записанных в столбцах (5) и (9).
IX ш а г. К содержимому столбца (3) прибавляем содержимое столбца (10)
и результат заносим в столбец (3) следующей строки, т. е. определяем —
— z/z +
Затем весь процесс вычислений повторяем, начиная со II шага.
Усовершенствованный метод Эйлера — Коши с последующей ите-
рационной обработкой. Метод Эйлера — Коши с итерационной обра-
боткой является более точным, чем ранее рассмотренный метод Эйле-
ра — Коши, Сущность его заключается в том, что производится итера-
324
дионная обработка каждого найденного значения yt. Вначале выбирает-
ся грубое приближение
y(z°|i =?/«+(8)
затем строится итерационный процесс:
=^ + -^[/(*г,г/г) + Ж+1 <+in]. (9)
Итерации продолжаются до тех пор, пока два последовательных приб-
лижения у$х и не совпадут в интересующих вычислителя зна-
ках. После этого принимается yw & y{iffi\ Если после трех-
четырех итераций при выбранном значении h совпадения нужных
знаков не происходит, то следует уменьшить шаг расчета ht
Пример 3. Применяя метод итерационной обработки, найти в точностью до
четырех совпадающих десятичных знаков решение уравнения #' = £/ — я с на-
чальным условием у (0) « 1. Решение получить на отрезке [0; 1,5], выбрав
Я = 0,25.
Р е ш е и и е, По формуле (8) находим
d0) « Уо + h (I/O - ХО) - 1,5000 + 0,375 = 1,8750.
Далее, применяя итерационный процесс (9), последовательно определяем
'А* ’ = Уо + -у «Уо — *о) + (И0’ — *1)1=
= 1,5000 + 0,125 (1,5000 + 1,875 — 0,25)= 1,89062}
у\2) = уоН-у" *в)+(г/||>—*i)] =
= 1,5000 + 0,125 (1,5000 +1,89062 — 0,25) = 1,89258,
И3> = 1/о + у {(.Уо — хо) (У?У— *1)] —
= 1,5000 + 0,125 (1,5000 +1,89258 — 0,25) = 1,89282}
г/(14) = 1/о+-у [(1/о —*о)+(^3>—*1)1 =
= 1,5000 + 0,125 (1,5000 +1,89282 — 0,25) = 1,89285.
В двух последних приближениях совпадают четыре знака. Поэтому после округ-
ления можно принять yt ~ 1,8929.
Снова пользуясь формулой (8), при I ~ I находим
^20) = У1 + W (xit yt) == 1,8929 + 0,25 (1,8929—0,25) = 2,3036.
По формуле (9) определяем последовательные приближения:
у!1' = 1,8929 + 0,125 [1,6429 + (2,3036—0,50)] = 2,3237;
i/<22> = 1,8929 + 0,125 [1,6429 + (2,3237 —0,50)] =- 2,32622;
у( з> = 1,8929 + 0,125 [1,6429 + (2,32622—0,50)] = 2,32654;
у^ « 1,8929 + 0,125 [1,6429 + (2,32654-0,50)] == 2,32658.
Итерации можно прекратить и принять у2 ~ 2,3266. Применяя далее формулы
(8) ь (9), получим решение данною уравнения, Результаты вычислений помещены
в габл. 9.7 на стр. 326.
325
Таблица 9.7
i xt „(1) viy\ „(2) "Z-j-l „(4) yi+\ ^4- 1
0 0 1,5000 1,875 1,89062 1,89258 1,89282 1,89285 1,8929
1 0,25 1,8929 2,3036 2,3237 2,32622 2,32654 2,32658 2.3266-
2 0,50 2,3266 2,78325 2,80908 2,81231 2,81271 2,81276 2,8128
3 0,75 2,8128 3,3285 3,36171 3,36586 3,3664 3,36645 3,3664
4 1,00 3,3664 3,9580 4,0007 4,00603 4,0067 4,00679 4,0068
5 6 1,25 1,50 4,0068 4,7587 4,6960 4,7509 4,75776 4,75870 4,75872 4,7587
§ 9.6. Метод Рунге — Кутта
Метод Рунге — Кутта является одним из методов повышенной
точности. Он имеет много общего с методом Эйлера.
Пусть на отрезке [а, 6] требуется найти численное решение уравне-
ния
У' = / (х, у) (1)
с начальным условием
у (х0) = Уо> (2)'
Разобьем отрезок 1а, Ь] на п равных частей точками xt = х0 4- ih
(i = 0, 1, ..., п), где h = (b — а)/п — шаг интегрирования. В методе
Рунге — Кутта, так же и в методе Эйлера, последовательные значения
yt искомой функции у определяются по формуле
yi+i = Vi + Ьуь (3)
Если разложить функцию у в ряд Тейлора и ограничиться членами
до /г4 включительно, то приращение функции by можно представить
в виде
ДУ = У (х + Л) — У {х) = hy' (х) + у" (х) + -у у" (х) + -~yv (х),
(4)
где производные у” (х), y,tr (х), у™ (х) определяются последовательным
дифференцированием из уравнения (1).
Вместо непосредственных вычислений по формуле (4) в методе
Рунге — Кутта определяются четыре числа:
k± = hf (х, у).
k2 — hf^x-\-~, у +-|ф,
Ъ = Щ(х + ±.,у + ^-у (5)
К = hf (х + h, у + /?3).
328
Можно доказать, что если числам kb fe2, k3, придать соответствен'
но вес 1/6; 1/3; 1/3; 1/6, то средневзвешенное этих чисел, т, е.
^1 + ~~ k2 + k3 + —- k4 (6)
с точностью до четвертых степеней равно значению Дг/, вычисленному
по формуле (4):
(^ + 2^ + 2^+^.
(7)
Таким образом, для каж-
дой пары текущих значений
Xt и yi по формулам (5) опре-
деляются значения
= (xt, yt),
^ = h^xi + -!L!yi + ^!
. . (8)
ky=M(x^h, yt + k^l
по формуле (7) находится
Дг/; (k? + 2k^ + 2/г</> + Щ>)
и затем
Ft+i = Уг +
Числа kly k2, /?4 имеют простой геометрический смысл. Пусть
кривая MQCMr (рис, 9.3) представляет собой решение дифференциаль-
ного уравнения (1) с начальным условием (2). Точка С этой кривой
лежит на прямой, параллельной оси Оу и делящей отрезок [xb xz+J
пополам, В и G — точки пересечения касательной, проведенной к кри-
вой в точке Л40, с ординатами АС и Л\Л4Р Тогда число с точностью
до множителя h (где h — xf+1 — xi) есть угловой коэффициент каса-
тельной в точке Л40 к интегральной кривой Л1ОС7ИЬ т, е. kt = hy't —
= hf (xh уг).
Точка В имеет координаты х = xt + -%, у ~ yt + Следователь-
но, число /?2 с точностью до множителя h есть угловой коэффициент
касательной, проведенной к интегральной кривой в точке В (BF —
отрезок этой касательной),
Через точку /Ио проведем прямую,, параллельную отрезку BF.
Тогда точка D имеет координаты х = у ~ yt + у и k3 с точ-
ностью до множителя h — угловой коэффициент касательной, прове*
денной к интегральной кривой в точке D (DF\ — отрезок этой каса«
327'
Таблица 9,8
L X У У —] (•*» у} (xt у) &У
(1 (2) (3) | (4) (5) (6)
0 %0 h хо + 2 6 *о+Т Уо 6W У°+ —2~ , Ч0) Уо + -~ Нхо, Уо) / h М 0>Х /1 хо + 2 * 1 h 6(0) \ i Iхо + 2 * + -g- ) f (хо+^» + Ai0' 6(0) 6‘°> б'") 61» 26<» 2б£°> Ч0)
1 xi h h 2 %! Д-Л У1=Уо+^Уо 2 6(1) У1 + -2- У1+Ч1’ / (Х1, У1) / pi + y / h АЮ) \ ЦХ1 + 2 ’ f^i + ^yi+^p) 6U) 6(1) 2 6Л) 3 6U) 4 6(1) 1 26(1) 2 26(1) 3 .6(1) 4
2 *2 У2=Уг№У1
тельной). Наконец, через точку Л10 проведем прямую, параллельную
DR^ которая пересечет продолжение в точке /?2 (хг 4- h\ yt + k3),
Тогда с точностью до множителя h есть угловой коэффициент каса-
тельной, проведенной к интегральной кривой в точке 7?3.
Вычисления по методу Рунге — Кутта удобно располагать по схе-
ме, указанной в табл. 9.8. Эта таблица заполняется следующим образом:
I ш а г. В столбцы (2) и (3) текущей строки записывают нужные
значения х и у. (Если строка первая, то записывают начальные данные
х0 и у^)
II шаг. Значения х и у текущей строки подставляют в правую
часть дифференциального уравнения (I), определяют f (х, у) и записы-
вают в столбец (4) этой же строки.
III ш а г. Полученное значение f (х, у) столбца (4) умножают на шаг
интегрирования h, вычисляют k = hf (х, у) и записывают в столбец
(5) этой же строки.
IV шаг. Найденные значения k умножают на соответствующий
коэффициент (на 1, если это kr или fe4, или на 2, если это k2 или fe3),
результат записывают в столбец (6) текущей строки.
Шаги 1, II, III, IV повторяют для нахождения каждого k в 4-м
решении.
328
Результаты шестой строки суммируют» делят на 6, определяют
&У1 И Уг+\ Уг Н~ fyjl*
Затем все вычисления повторяют, начиная с I шага, до тех пор,
пока не будет пройден весь отрезок [at bl.
Метод Рунге — Кутта имеет порядок точности /г4 на всем отрезке
[а, 6], Оценка точности метода этого очень затруднительна. Грубую
оценку погрешности можно получить с помощью «двойного просчета»
по формуле
О)'
15
где #(%,)— значение точного решения уравнения (1) в точке xh а у, и
^• — приближенные значения, полученные с шагом hJ2 и h.
Если 8 — заданная точность решения, то число п (число делений)
для определения шага интегрирования /г = (Z? — а)/п выбирается та-
ким образом, чтобы
/г4 <8. (10)
Однако шаг расчета можно менять при переходе от одной точки к дру-
гой.
Для оценки правильности выбора шага h используют равенство
где q должно быть равно нескольким сотым, в противном случае
шаг h уменьшают*
Пример 1 Дано дифференциальное уравнение уг — у — х G начальным
условием у (0) = 1,5. Вычислить с точностью до s — 0,01 решение этого уравне-
ния при х — 1,5. Вычисления провести по методу Рунге — Кугта G двумя запас-
ными знаками.
Решение. Выбираем начальный шаг вычислений h из условия Л4 < 0,01.
Тогда h < 0,3. Для удобства вычислений примем h = 0,25. Весь отрезок интег-
рирования [0; 1,5] разобьется на шесть равных частей точками xQ — 0; хл = 0,25;
== 0,50, = 0,75; х$ — 1,00; х5 = 1,25; = 1,50. Из начальных условий
имеем х0 — 0, t/0 = 1,5. Найдем первое приближение щ ~ */0 + где
Лг/о = (fe?' + 24°’ + + О.
Используя формулы (8), получим:
fe<o> = Со — х0) h = 1,5000 • 0,25 = 0,3750;
ь<0)_
ft 2 —
/1 = [(1,50004-0,1875)-0,125] .0,25 = 0,3906;
й = [(1,5000 + 0,1953)—0,125]-0,25 = 0,3926;
/г‘о> = [Со + ^0,)-Со + О] * = [(1,5000 4-0,3926) —0,125]-0,25 = 0,4106.
329
Таблица 9.9
i X У У' — f (x, у) k=hf (x, у) Ду
(1) (2) (3) (4} (5) (б)
0 0 0,125 0,125 0,25 1,5000 1,6875 1,6953 1,8926 1,5000 1,5625 1,5703 1,6426 0,3750 0,3906 0,3926 0,4106 0,3750 0,7812 0,7852 0,4106
0,3920
1 0,25 0,375 0,375 0,50 1,8920 2,0973 2,1073 2,3251 1,6420 1,7223 1,7323 1,8251 0,4105 0,4306 0,4331 0,4562 0,4105 0,8612 0,8662 0,4562
0,4323
2 0,50 0,625 0,625 0,75 2,3243 2,5523 2,5652 2,8093 1,8243 1,9273 1,9402 2,0593 0,4561 0,4818 0,4850 0,5148 0,4561 0,9636 0,9700 0,5148
0,4841
3 0,75 0,875 0,875 1,00 2,8084 3,0657 3,0823 3,3602 2,0584 2,1907 2,2073 2,3602 0,5146 0,5477 0,5518 0,5900 0,5146 1,0954 1,1036 0,5900
0,5506
4 1,00 1,125 1,125 1,25 3,3590 3 6539 3,6751 3,9965 2,3590 2,5289 2,5501 2,7465 0,5898 0,6322 0,6375 0,6866 0,5898 1,2644 1,2750 0,6866
0,6360
5 1,25 1,375 1,375 1,50 3,9950 4,3381 4,3654 4,7426 2,7450 2,9631 2,9904 3,2426 0,6862 0,7408 0,7476 0,8106 0,6862 1,4816 1,4952 0,8106
0,7456
6 1,50 4,7406
330
Следовательно,
Ai/0=— (0,375С 4 2 0,3906+2 0,3926-4 0,4106) = 0,3920
о
и
= 1,5000 + 0,3920 = 1,8920»
Дальнейшее решение уравнения представлено в табл 9 9.
Таким образом, окончательно имеем у (1,5) =4,74
Метод Рунге — Кутта может быть применен и к решению систем
дифференциальных уравнений.
Пусть задана система дифференциальных уравнений первого по-
рядка:
| у' = f (х, у, г),
I z' = g(x, у, г)
с начальными условиями
X = ХО, у (х0) = у0, г (х0) = ?0, (13)
В этом случае параллельно определяются числа и
&yt = + W 4- 2fe« + W),
1 (14)
Az( =+ (/ю + 2/(« + 2/«+
где
= hf (xt, tjb z(),
/w = /zg(x„ yt г,);
/ h A>0*) /(Z) \
few = fe/ (b + T > Ui + , zt + +J;
/ /0) \
/</’ = hg U + -, yt + + , zt + +);
/ h M ,W \ (15)
fe<s= U + — , yi 4- + , Zt 4- + ;
^=hg(Xl+~, yt ++< zt 4- + );
feo==fe/(x,4-/i, yt + k^, г,4-/ф)‘.
W = hg(xt + h, yi + k% Zi + W).
Тогда получим решение системы
У ^У1~\* ^+i —
Пример 2. Задана система дифференциальных уравнений
г'=_2£_
г + х
с начальными условиями я0 — 0,5; #0 — 1; zc = 1. Найти решение системы при
х ~ ОД Вычисления вести G пятью знаками после запятой»
331
Решение. Выберем шаг Л = 0,1 и найдем числа klt /2» 6§»
,1 = /г.2^2 = 011. 2=0^=0>150008
г0 1
l1==h •—^- = 0,1 •— = 0,13333)
го4“хо 1,5
2-1,075—0,55
1,06667
2 1,075
1,06667 + 0,55
= 0,141001
= 0,13299з
2-1,07050—0,55
1,06650
2 1,07050
1,06650 + 0,55
= 0,1
= 0,14918;
= 0,13245)
—h
2(#о + &з)— (*о~Ь^)
S'o "F h
_______2 (X/o ~f~ ^з)____
(го + /з) + (*o+ Л) J
2-1,14918 — 0,6
1, 13245
2-1,14918
1,13245 + 0,6
= 0,14998j
= 0,13266.
Следовательно,
Ai/0 =4- (0,15 + 2-0,14100 + 2-0,14918 + 0,14998) = 0,14672;
6
< Az0 = 4~ (0,13333 + 2-0,13299+2-0,13245 + 0,13266) = 0,13281
6
и окончательно получаем значение искомых функций в точке х ~ 0,6:
^ = 1 + 0,14672 = 1,14672; zt = 1 + 0,13281 - 1,13281.
§ 9.7. Экстраполяционный метод Адамса
При решении дифференциального уравнения методом Рунге —
Кутта необходимо производить много вычислений для нахождения каж-
дого В том случае, когда правая часть уравнения имеет сложное
аналитическое выражение, решение такого уравнения методом Рун-
ге — Кутта вызывает большие трудности. Поэтому на практике при-
меняется метод Адамса, который не требует многократного подсчета
правой части уравнения.
332
Пусть дано дифференциальное уравнение
у' = f (X, у) (1)
с начальным условием
X = х0, у (х0) = у0, (2)
Требуется найти решение этого уравнения на отрезке [а, Я.
Разобьем отрезок 1а, Ь\ на п равных частей точками хг == х0 + th
(j = 0, 1, 2,..., п). Выберем участок [х2, хг+1] и проинтегрируем диф-
ференциальное уравнение (1); тогда получим
yl+i = yt+ $ y'dx,
xt
ИЛИ
*г+1
Ajq = $ У'dx. (3)
Для нахождения производной воспользуемся второй интерполя-
ционной формулой Ньютона (ограничиваясь при этом разностями
третьего порядка):
У' = + ^y‘t-. + ^yl-2 + + у[_3) (4)
21 о.
где t = (х — xt)/ht или
У--у! +лад_, +-^ лад_,лад-,. (4')
Подставляя выражение для у’ из формулы (4') в соотношение (3) и
учитывая, что dx = h dt, имеем
byt = h £ (у', + /А/_ i + ^2. Д2 y-_z + 13 + 3С+21 дз yl_3 1 dt =
v \ 2 о J
О
= hy't 4-4- A (hy!_ 1) + 4 A2 (hyt'_2) + 4 дз (hy'i-i). (5)
2 12 о
Обозначим в дальнейшем
q. = у{ h = f (xh у^ • h (i = 0, 1, 2, ...» n).
Тогда для любой разности имеем А'"^г = Д'71 (гд'/г) и
Аг/г = дг + 4 A?<-i + Т7 А2 9^2 + 4 А8 (6)
2 12 о
По формуле 1/г+1 = yt + &y-i получаем решение уравнения. Формула
(6) носит название экстраполяционной формулы Адамса.
Для начала процесса нужны четыре начальных значения yQ, уъ
Уъ — так называемый начальный отрезок, который может быть най-
ден, исходя из начального условия (2) с использованием одного из
известных методов. Обычно начальный отрезок решения находится
методом Рунге — Кутта.
333
Зная уй, уъ у2, Уз, можно определить
% = ^o = ^(^Z/o); q1 = hy[ = h[(xl, yj;
q2 = Ьу'ъ = hf (xa> й); <7з = hy'3 = hf (x8, Уз).
Далее составляется таблица разностей величины q (табл. 9.10).
Таблица 9.10
i xi У1 ^vt y‘i = i(xi’ »г) Q~hyli
(1) (2) (3) /4) (5) (6) (7) (8) (9)
0 Хо Уо Н*о, Уо) Уо Л?о Д2?0 Дз?0
1 У1 ((*1, У1) У1 Д?1 Д2« ->
2 УЗ, t(x2, Уч) У2 Д<?2
3 Уз Луз Уз) Уз
4 Уъ
5
6
Метод Адамса заключается в продолжении диагональной таблицы
разностей с помощью формулы (6). Используя числа q3, A2qv
Д39о, которые располагаются в таблице по диагонали, по формуле (6),
полагая в ней п = 3 (последнее известное значение у есть получают:
1 А Ч
&Уз ~ Уз + — А?» + — А2 У1 + -т- Уо-
2 12 о
Полученное значение Д#3 вносят в таблицу и находят у} = у3 + Д^3<
Затем, используя х4 и найденное значение t/4, находят / (х4, у4),
&q3, Д272, Д3^, тр е. получается новая диагональ. По этим данным
находят
А#4 — + — &q3 + ~ Ч—г- A3 q^ + &У&
2 12 о
Таким образом, продолжают таблицу решения, вычисляя правую
часть дифференциального уравнения (1) на каждом этапе только один
раз.
Для грубой оценки погрешности применяется принцип Рунге,
который состоит в следующем:
1) находится решение дифференциального уравнения при шаге /г;
2) значение шага h удваивается и находится решение при шаге
И = 2/г;
334
3) вычисляется погрешность метода по формуле
е = (8)
2m—1 v 7
где Уп — значение приближенного вычисления при двойном шаге
Я = 2й, а #2П — значение приближенного вычисления при шаге h.
Замечание* При вычислении с шагом h предполагается, что
на каждом шаге допущена погрешность, пропорциональная
а с шагом 2h — пропорциональная (2Л)'п+\ если порядок точности
метода определен и равен hm*
Отметим, что в экстраполяционной формуле Адамса (6) третьи ко*
печные разности b?q считаются постоянными. Поэтому величину h на*
чального шага вычислений можно определить из неравенства А1 <; е,
где в — заданная точность решения.
На практике следят за ходом третьих конечных разностей, выбирая
h таким, чтобы соседние разности и А3^/+1 отличались между
собой не более чем на одну-две единицы заданного разряда (не считая
запасных знаков).
П ример 1. Вычислить при х — 1,5 в точностью до 0,01 по методу Адамса зна-
чение решения дифференциального уравнения yf = у — х с начальным условием
х0 = 0, — 1,5. Все вычисления веети с двумя запасным! знаками.
Решение. Как и ранее, выбираем h из соотношения ft4 < 0,01, т. е.
h — 0,25. Начальный отрезок gQt yt, у2, У$ возьмем из решения примера 1 § 9.6.
Для решения этого уравнения «оставляем две таблицы: основную (табл. 9.11)
и вспомогательную (табл. 9.12). Назначение их ясно из самих таблиц.
Таблица 9.11
i xi У1 Дг/г Ui = = !(xl. Vl) Д27г д2^
(1) (2> (3) (4) (5) (6) 1 ‘) (81 6J)
0 1 2 3 4 5 5 0 0,25 0,50 0,75 1,00 1,25 1,50 1,5000 1,8920 2,3243 2,8084 3,3588 3,9944 4,7394 0,5504 0,6356 0,7450 1,5000 1,6420 Г, 8243 2,0584 2,3588 2,7444 0,3750 0,4105 0,4561 0,5146 0,5897 0,6861 0,0355 0,0456 0,0585 0,0751 0,0964 0,0101 0,0129 0,0166 0,0213 0,0028 0,0037 0,0047
Таблица 9.12
с —— Д2о. 12 8 1 3 Дуг
3 0,5146 0,0293 0,0054 0,0011 0,5504
4 0,5897 0,0376 0,0069 0,0014 0,6356
5 0,6861 0,0482 0,0089 0,0018 0,7450
Окончательна имеем #(1,5) =4,74. "
335
Метод Адамса применяется также и для решения систем дифферен-
циальных уравнений и дифференциальных уравнений n-го порядка.
Пусть задана система двух уравнений
| / = 1Л г), (д)
1 z'^/2(x, у, г).
Тогда экстраполяционные формулы Адамса для этой системы имеют
вид
^У1 = Р, + ~ + — Д2 Pi-i + "Г А® Pi-»
2 12 8 (1
1 к о 7
4 12 о
где
Pi = hyi = hh (xt, уi, zt), gt = hz'i = hf2 (xt, yt, zj,
и
{/i+i = Pt + tyi, г1+1 =>Zi-i- tet.
Пример 2. -Применяя метод Адамса, решить численно систему дифференци-
альных уравнений
(y‘ = (z — y)x,
[г1~(г-[-у)х
с начальными условиями у (0) = 1,000; г (0) = 1,000 на отрезке [0; 0,6]; шар
h = 0,1.
Решение. Начальный отрезок решения возьмем из табл. 9.3 (ранее мы
решали эту еистему методом Эйлера). Значения функций у (х) иг (х) при
*4 — 0,4; х5 = 0,5 их, — 0,6 будем искать g помощью формул (10), обозначив
Л (х, у, г) « / = (г — у) х и /а (х, у} г) ~ г' = (г + У} Вычисления располо-
жены в табл. 9.13, 9.14 и 9.15 (табл. 9.14 и 9.15 являются вспомогательными)*
Таблица 9.13
1 xi pi
0 0 1,0000 0,0000 0,0000 0,0004 0,0006
1 0,1 1,0000 0,0000 0,0004 0,0010 0,0010
2 0,2 1,0000 0,0004 0,0014 0,0020 0,0004
3 0,3 1,0004 0,0032 0,0018 0,0034 0,0024
4 0,4 1,0036 0,0081 0,0052 0,0058
5 0,5 1,0117 0,0150 0,0110
6 0,6 1,0267
i *i Ч
0 0 1,0000 0,0000 0,0200 0,0004 0,0006
1 0,1 1,0000 0,0200 0,0204 0,0010 0,0013
2 0,2 1,0200 0,0404 0,0214 0,0023 0,0007
3 0,3 1,0604 0,0732 0,0618 0,0237 0,0030
4 0,4 1,1336 0,0987 0,0855 0,0267
5 0,5 1,2323 0,1271 0,1122
6 0,6 1,3594
336
Табл. 9.14 предназначена для определения правых частей данной системы ина-
хождения pi и giy а табл. 9.15 — для определения Д#$ и Дг^ по разностям величин
png, полученным в табл. 9.13.
Таблица 9.14
/ xi zi Vi Pi г1
0 0,0 1,0000 1,0000 0,0000 0,0000 0,0000 0,0000
1 0,1 1,0000 1,0000 0,0000 0,0000 0,2000 0,0200
2 0,2 1,0000 1,0200 0,0040 0,0004 0,4040 0,0404
3 0,3 1,0004 1,0604 0,0180 0,0018 0,6182 0,0618
4 0,4 1,0036 1,1336 0,0520 0,0052 0,8549 0,0855
5 0,5 1,0117 1,2323 0,1103 0,0110 1,1220 0,1122
Таблица 9.15
I pi 4"др'-> — д2рг 12 г"2 T Л3₽‘-’
3 0,0018 0,0007 0,000425 0,000225 0,0032
4 0,0052 0,0017 0,000850 0,000375 0,0081
5 0,0110 0,0029 0,0010 0,00015 0,0150
i 1 д — A«f-i Дгг
3 0,0618 0,0107 0,000425 0,000225 0,0732
4 0,0855 0,0118 0,000958 0,000488 0,0987
5 0,1122 0,0134 0,00125 0,00026 1,1271
Упражнения
1. Используя метод Пикара, найти три последовательных приближения ре-
шения дифференциального уравнения:
а) / = 4г/ (1 + *); начальное условие у (0) » lj
б) уг = х — у\ начальное условие у (0) = 1,
56 4
Ответы: а) Уз = 1 4-8х*ф — + 18х4 * Н-8х^ + — х6^
о о
4 X» X4
б) (/3=1— х + х2— —.
о 24
2. Найти первые семь членов разложения в степенной ряд решения у ~ у (х)
уравнения yfl + 0,1 (/)2 + (1 + 0,1 х) у = 0 е начальными условиями у (0) =
1, / (0) = 2.
Ответ: у(х) = 1 + 2х—OJx2 — 022567х3 + 0,051х4 + 0,00147х3 —0,00101хб.
337
3. Найти решение дифференциального уравнения у" = 4х2г/ + 2е-л; , удов-
летворяющее начальным условиям у (0) = 0, у' (0) — 1. Ограничиться членами
разложения в степенной ряд, содержащими А
2 13
Ответ: у (х) = х —х3+~ х^—— х6.
15 90
4. Полагая h = 0,1, методом Эйлера решить дифференциальные уравнения
при заданных начальных условиях на указанных интервалах:
а) у' = у + Зх; у (0) = — 1; х £ [0; 0,5];
6) / = х - 2г/; у (0) = 0; х^Ю, 1].
Ответы: а) уг — —1,1; У% — —1,18; Уз ~ — 1,238; у$ ~ —1,2718;
Уъ = — 1,2790; б) у± = 0, г/2 = 0,01; у3 == 0,0278; у^ = 0,0524; уь = 0,08192;
i/6 = 0,115536; у? = 0,152429; г/6 = 0,191943; уй = 0,233554; у10 == 0,276844.
5. Применяя усовершенствованный метод Эйлера, найти на отрезке [0, 1]
2х
таблицу решения дифференциального уравнения у' — у — ~ при начальном
условии у (0) — 1, приняв h = 0,2.
Ответ: у0 =1; у± — 1,1836; г/2 = 1,3426; у3 = 1,4850; у^ = 1,6152,
*/5 = 1,7362. *
6. Применяя усовершенствованный метод Эйлера — Коши, решить диф-
ференциальное уравнение из упр. 5.
Ответ: г/0 = 1; yt == 1,1867; г/2 — 1,3484; у3 = 1,4938; г/4 — 1,6272; уь —
= 1,7542.
7. Методом Рунге — Кутта, приняв ft = 0,1, найти решения дифференциаль-
ных уравнений при заданных начальных условиях на указанных интервалах:
а) у' = х + у2; у (1) = 0; х $ [1, 2];
б) у' = х2 — у, у (0) = 2; х £ [0, 1].
Ответы-, а) у3 — 0; у\ = 0,10536; у2 = 0,223136; у3 = 0,356601; yi =
= 0,510424; у6 = 0,691497; у3 = 0,910454; У1 = 1,184648; Уз = 1,544491;
у3 = 2,048721; j/10 = 2,827617; б) у0 = 2,00; У1 = 1,81; у2 = 1,64; у3 = 1,49;
z/4= 1,36, уь= 1,25; у2 = 1,16; у, = 1,09; у3 = 1,04; у, = 1.01.
8. Экстраполяционным методом Адамса решить дифференциальное уравне-
ние у' = 2х — у при начальном условии у (0) = 1 на отрезке [0, 1]. Начальный
отрезок решения задан: у3 — 1, yt — 0,9145; у2 = 0,8562, у3 = 0,8225 (принять
h = 0,1).
Ответ-. у& — 0,8110; у5 = 0,8196; ys = 0,8464; У1 = 0,8898; у3 = 0,9480;
j/e = 1,0197; г/10 = 1,1037.
Глава X
ПРИБЛИЖЕННОЕ РЕШЕНИЕ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
В ЧАСТНЫХ ПРОИЗВОДНЫХ
§ 10.1. Классификация дифференциальных уравнений
в частных производных
Приближенные методы решения наиболее разработаны для диф-
ференциальных уравнений в частных производных второго порядка
с двумя независимыми переменными. Для решения многих практи-
ческих задач необходимо рассматривать так называемые линейные или
338
вполне линейные дифференциальные уравнения в частных производных,
т. е. дифференциальные уравнения первой степени относительно ис-
комой функции и всех ее производных и не содержащие их произведе-
ний. Такие уравнения можно представить в следующем виде:
л / х d%z , D z ч д-z t п i . дгг .
А (х у) — + В(х,у) —— + С (х, у) — +
дх1 дх ду ду*
+ а(х, у) — + Ь(х, у) 4- +с(х, y)z = F(x, у),
дх ду
В уравнении (1) искомой является функция z, а х и у — независи-
мые переменные. Функции А (х, у), В (х, у), С (х, у), а(х, у), b (х, у),
с (*» У) — непрерывные функции от х и у, имеющие непрерывные част-
ные производные.
Проведем классификацию дифференциальных уравнений в частных
производных, основанную на рассмотрении уравнения (1). Введем
обозначения
____ d^z ______ d-z ______ д%г ______ dz ______ dz
Zxx~~d^’ гхУ~~д^’ Zyy~l^’ Zx~HC Zv~lCj
(для удобства записи частных производных «штрихи» опускаются)
и рассмотрим упрощенную форму уравнения (1)*
А (х, у) гхх 4~ В (х, у) zXy + С (х, у) Zyy ~ 0, (2)
соответствующую (1) при a=b = c= F = Q,
Уравнение (2) всегда может быть приведено к одной из трех стан-
дартных канонических форм. Этими формами являются эллиптические,
параболические и гиперболические дифференциальные уравнения
в частных производных. Тип уравнения определяется значением коэф-
фициентов в выражении (2) и связан со знаком дискриминанта А =
— В2(х, у) — 4А (х, у) С (х, у) в выражении (2).
В зависимости от знака дискриминанта имеем:
А < О — эллиптический тип в точке (х, у}\
А = 0 — параболический тип в точке (х, z;);
А > 0 — гиперболический тип в точке (х, у).
Если коэффициенты А, В и С постоянные, не зависящие от х и у, то
канонические уравнения являются полностью эллиптическими, пара-
болическими или гиперболическими.
Чтобы показать, как строятся канонические дифференциальные
уравнения в частных производных, рассмотрим выражение (2) с по-
стоянными А, В и С. Введем две новые переменные
£ = у + агх, и = у + а2х, (3)
где
— В+ У В2-4ДС —В — У В2-4ДС
а. =-----;—v--------, а2 = -----------------•
1 2Л 2 2А
339
Поскольку уравнение (2) линейное относительно производных искомой
функции z (х, у), то решение z (х, у) этого уравнения может быть пред-
ставлено в форме
z (х, у) = f (у + ах). (4)
Рассмотрим функцию г (х, у) как функцию z (В, т]) двух новых пе-
ременных 1 и г). Тогда, учитывая замену переменных (3) и вид искомой
функции (4), получим для частных производных следующие выра-
жения:
= +a2z^; zx!/=-a1z^ + (a1 + a2)z^ + a2zm;
гхх = <*1 а.г zir) + a* znt); zyy = z^ + 2zgn + zw
Используя найденные значения производных, представим уравне-
ние (2) в виде
(Аа% 4- Ваг 4* С) 4~ (2Аа1а2 4- Вах 4* Ва2 4" 2С) 4*
+ (Ла|4* Ва2 + Q ~ 0. (5)
Рассмотрим уравнение
Аа? + Ва> + С = 0 (1 = 1, 2); (6)
оно имеет два корня и а2, которые могут быть действительными и
различными, действительными и равными или комплексно сопряжен-
ными. Тип корней зависит от величины дискриминанта В2 — 4ЛС.
В случае В2 — 4ЛС > 0 корни аг и а2 уравнения (6) действитель-
ны и различны, причем коэффициенты первого и третьего членов вы-
ражения (5) равны нулю. При этом равенство (5) имеет вид канони-
ческой формы гиперболического дифференциального уравнения е частных
производных
= 0, (7)
или
z^=fg& U г, гь zn), (7')
соответствующей выражению (1),
Перейдем к построению канонической формы дифференциального
уравнения эллиптического типа. Если В2 — 4АС = 0, то оба корня
и ^2 уравнения (6) — действительные числа и переменные | и г| яв-
ляются зависимыми. Положим один из корней равным аг == — В/(2Л);
тогда а2 может быть произвольным, причем а± Ф а2. Подставляя и
а2 в соотношение (5), получим
“ 0* (8)
Выражение (8) является канонической формой параболического диф-
ференциального уравнения в частных производных. В общем случае его
можно записать в виде
Zt]T] — fp (£> Т], Z%, ^Т))-
(8')
340
Если В2 — 4АС < 0, то аг и а2 являются комплексно сопряжен-
ными: = bv + t’62, а2 = Ьг — ib2. Тогда р авенство (5) принимает
вид
гп + глл=:::0. (9)
Выражение (9) является канонической формой дифференциального
уравнения эллиптического типа. В общем случае уравнение (9) можно
записать так:
+ Ч 2, Zb 2Л). (9')
Классическими примерами дифференциальных уравнений в част-
ных производных являются уравнение Лапласа
гхх + Zyy = 0 (10)
^имеющее каноническую эллиптическую форму), уравнение тепло-
проводности
?хх “ ?у (11)
(имеющее каноническую параболическую форму) и волновое уравнение
%хх = %уу (12)
(имеющее каноническую гиперболическую форму).
§ 10,2. Конечно-разностные аппроксимации
Конечно-разностные аппроксимации для частных производных яв-
ляются наиболее распространенным подходом к численному интегри-
рованию дифференциальных уравнений в частных производных. Част-
ные производные заменяются со-
ответствующими разностными соот-
ношениями по соответствующим
независимым переменным. В общем
случае размерность области, в ко-
торой необходимо найти решение
дифференциального уравнения в
частных производных, равна чи-
слу независимых переменных. В
случае двух независимых перемен-
ных х и у область является дву-
мерной. 'Метод, используемый для
конечно-разностной аппроксима-
ции, основывается на покрытии
области сетью прямоугольных
клеток шириной h (в направлении оси Ох) и высотой k (в
направлении оси Оу). Величина зависимой переменной z = z(x, у)
устанавливается в любой точке в пределах области. В частности, когда
задана одна точка прямоугольной сети с координатами xr, ys, окру-
жающие ее четыре точки имеют координаты xr+ht ys; xr_h, ys\
x„ ys+h\ x„ ys~k. Геометрический способ покрытия области сеткой пока-
зан на рис. 10.1.
341
Введем следующие операторы: Е — оператор приращения; 6 —
оператор центральных разностей; Д — разностный оператор опере*
жения; D — дифференциальный оператор.
Эти операторы определяются следующими соотношениями:
£/(х) +Л), (1)
Д/ (x)=f(x + h)— f(x), (2)
£>/(х) = -^- = /'(х), (3)
ах
(^+(4)
Представим f (х + h) в виде разложения в ряд Тейлора:
/(х + Л) = /(х) + А f (х) + ^- Г (х) + ... . (5)
Используя оператор D, представим оператор Е в виде
/ /1Л А3 Л2 \
Е/(Х) = (1 + Лт + ^г + -)/М> (6)
или, пользуясь разложением экспоненциальной функции ehD в рЯД
Тейлора, преобразуем выражение (6) так:
£/(х) = ^/(х). (6')
Тогда зависимость оператора Е от D может быть представлена в форме
Е = eflD, (7)
или
hD = 1п£. (8)
Из выражений (1) и (2) получаем следующее соотношение между
операторами £ и Д:
Д/ (х) = £/ (х) — f (х), (9)
или
£ = Д + 1. (10)
Подставляя выражение (10) в формулу (8), получим
hD = In (1 + Д). (11)
Используя разложение логарифмической функции в ряд:
1П(1 + Д) = Д-^ + ^-^ + ^-...( (12)
.получим следующее выражение для оператора D:
D = — (А— — + — — ...У (13)
h \ 2 3 J !
Распространяя изложенный метод на разности второго порядка,
имеем
(/i£)2 = [ln(l 4-А)]2, (И)
342
или
(16)
(17)
(18)
(19)
исполь-
D2= — fzV—Л3+ — A4--------------- A5 + — A8—'...'j. (15)
№ \ 1 12 6 180 J
В формулах (13) и (15) можно ограничиться подходящим числом
членов, чтобы получить конечно-разностное представление для произ-
водной с желаемой точностью. Ограничиваясь в каждом выражении
первой и второй разностью для производных:
dZr 1 / Д А2 | ДЗ \
dx h \ 2 3 J
= — f Д2 —- Л~Ч- — А4-^ .Л
dx* h* \ 12 /*
имеем соответственно
\
= ?г+*~гг 4- О (/г),
dx п
d2 ___ ?г4~1 2гг4~ ^г—1 । q
dx* ” Л2 "Г V /•
Для наглядного представления уравнений вида (18) и (19)
зуют шаблоны, имеющие следующий вид:
dzr _ 1
dx h
В приведенных шаблонах в центре кругов указываются коэффи-
циенты дифференциального уравнения. Круг центральной части шаб-
лона соответствует величине zr. Положительным приращениям по го-
ризонтальным линиям (рис. 10.1) соответствует левый конец, отрица-
тельным — правый конец шаблона.
Аналогичные шаблоны можно получить и в случае использования
оператора 6 центральных разностей. Полагая в соотношении (6) значе-
ния переменной равными х + h/2 и х — h/2, имеем
1 + l.’-4-LgJ + ... 11 2! /(x) = eftD/2/(x), (20)
( h \ ( h\* 1
— — ID — — D2
Ef (х- — \ = \ 2 J 1 + А—A_+L_d +... 1! ‘ 2! f (х)=е~ЛО/2/(л). (20')
343
Поэтому, пользуясь соотношением (4), получаем
6/(х) = (еЛВ/2 —е~ЛО/2Щ*) (21)
или в операторном виде
6 = еЛ£|/2—e_ftD/2 = 2sh(A£>/2), (22)
т. е.
hD = 2 arcsh (6/2). (23)
Разлагая гиперболическую функцию arcsh (6/2) в ряд, имеем
’3\2/‘2*4'5^2/ + "*]
6— J-63+ — 65 + ..Д
24 640 )
Непосредственным возведением в степень получим
о2= — (ба——— „Д
/г2 \ 12 90 )
D* = — (64—— + — 68— ,.Д
Л4 (. 6 240 )
(24)
(25)
(25')
Соотношения для производных, выраженных через центральные
разности, можно записать так:
±r=_L(6— — 6я + A L
dx h \ 24 640 J
dx* № \ 12 90 )
= _L ( 64—— -J. _Z_ fis _ . \ z
dx* h* \ 6 240 '
Ограничиваясь в выражениях для производных первыми и
центральными разностями, находим
, 0 (h2)
dx 2/i '
dzT = —^r+2 4~ 8гг+1— 8gr-x4-zr_2 q ,<
dx \2h Т 1 h
гг гг+1-----2zr4~ | Q (^2)
dx2 hZ
42 z?^r+2 4~ 16zr-f-i —~ 30zr 4~ 1б2г~(/i^)
dx% 12/г2
d* zr _ гг+2 — 4гг+1 + 6г,. —4гг_1 + г,._2 , Q
dx* '* “Г 1 Л
h*
Рассмотрим применение изложенного выше подхода для
разностной аппроксимации частных производных. Для
(26)
вторыми
(2
конечно-
функции
344
z = z (х, у) используем следующее обозначение для значений в узлах
сетки х„ у&\
zr,, = z(xr, ys). (28)
n dt
Поскольку означает производную от z по х при постоянному, полу-
чаем
дх п
(29)
при этом вычислительный шаблон имеет вид
Вычислительный шаблон содержит только горизонтальные элементы,
поскольку s (или у) является постоянной. Аналогично получаем
для производной в направлении s.
Смешанная производная получается аналогично:
Умножением отдельных элементов строки на каждый элемент столб-
ца получим
345
+1
-1
дхду
d2z
4hk
zr,s
Здесь все нулевые члены, за исключением центрального, опущены,
Рассмотрим наиболее часто используемые вычислительные шаб-
лоны (h = k):
346
§ 10.3. Аппроксимация эллиптических дифференциальных
уравнений в частных производных
В качестве иллюстрации численных методов решения уравнений
эллиптического типа рассмотрим двумерное уравнение Лапласа
Это уравнение представляет установившийся режим теплопроводно’
сти через двумерное тело. Предполагается, что уравнение (1) выпол-
няется внутри области /?, окруженной границей В. Задача состоит
в определении г (х, у), причем граничные условия на границе В заданы.
Для упрощения сначала рассмотрим границу В в виде квадрата со
стороной, равной L. Имеются три возможные способа задания величи-
ны г на границе В.
Первый способ:
г = fi (у), х = 0; г = /2 (у), х = L;
z = gi W, У = 0; г = g2 (х), у = L,
где fi, f2, glt g2 — произвольные функции.
Задача нахождения решения уравнения (1) с граничными условиями
(2) называется задачей Дирихле.
Второй способ:
~ = !ЛУ), х = 0; -^ = /2(у), х^Ц
дх дх (3)
~- = gi(x), у = 0; ~^g2{x), y = L.
ду ду
Задача нахождения решения уравнения (1) с граничными условиями
(3) называется задачей Неймана^
Третий способ:
«ij- + «22=a3, Ьх-^- + &2г= b3. (4)
дх ду
Этому способу соответствует смешанный тип граничных условий (4),
которые при специальном выборе значений коэффициентов аи а%, а3 и
blt b2i b3 сводятся к условиям (2) и (3).
Для любого граничного условия, указанного выше, искомая функ-
ция определена на границе В и удовлетворяет уравнению Лапласа
в пределах области, ограниченной границей В. Решение уравнения
Лапласа может быть получено аналитически, однако здесь будут ис-
пользованы только численные методы. Далее рассматриваются обоб-
щения уравнений эллиптического типа, которые не могут быть решены
аналитически, но могут быть решены численно с использованием из-
лагаемых методов решения.
После того как поставлена некоторая краевая задача типа (1) с гра-
ничными условиями одного из трех типов, необходимо, во-первых,
установить систему уравнений, аппроксимирующую дифференциальное
уравнение эллиптического типа и граничное условие, во-вторых,
347
определить метод решения этой систе-
мы и, наконец, определить ошибку
между решением аппроксимирующей
системы уравнений и точным реше-
нием поставленной задачи. Рассмот-
рим способы решения поставленных
вопросов.
На рис. 10.2 показана сеть (h =
— £), покрывающая область R и
включающая границу В, Нижняя
правая точка имеет координаты x0, yQ
и величина 2 равна г (xOt yQ)t или z0.
Величины г в граничных узловых
точках и во внутренних узловых
точках обозначены через zb z2, z24. Для задачи Дирихле вели-
чины z0, zb ..., z14, z15, соответствующие значениям функции на гра-
нице, известны и необходимо вычислить zle, z17, z23, z34 так, чтобы
было удовлетворено уравнение Лапласа.
Имеется значительное число возможных конечно-разностных
представлений для уравнения Лапласа. Наиболее часто используются
шаблоны
В виде уравнения последнее соотношение можно записать следующим
образом:
“ S-р 1 s— 1 2г 4-1. s 1, S — 4zr, §) + 0 (Л2) = 0, (5)
348
§ 10.4. Решение разностных уравнений для эллиптических
дифференциальных уравнений
После того как конечно-разностная аппроксимация для эллиптш
ческого дифференциального уравнения известна [т. е. для уравнения
Лапласа получено соотношение (5) § 10.3], следующей задачей является
эффективное решение аппроксимирующих алгебраических уравнений.
В этом случае для задачи Дирихле имеем такую систему:
+ + —4гг,5 = 0 внутри Я,
zGS = &Gs на границе В.
Здесь Ьг,6 являются известными граничными условиями.
Пусть N — число внутренних узловых точек в строке и N + 1
— число интервалов в строке. Как и прежде, интересующей областью
является квадрат. Простейшим итерационным методом решения сис-
темы уравнений является метод Ричардсона, в котором вычисления
проводятся согласно формулам
1)
$
~ \Zf4-1* s + lt s ~Г s+1 s—[)> Zrt s € K,
> 2r> s £ B.
(2?
Обозначения zj^ и г^п соответствуют п-й и (п + 1)-й аппрокси-
мациям в итерационном процессе. Начиная с допустимых величин
z^J во внутренних узловых точках и известных величин в граничных
точках, выражение (2) используется для сглаживания влияния перво-
начально выбранных точек z^s и для вычисления нового набора точек
Процесс вычислений является итерационным.
Для окончания процесса вычислений требуется выполнение усло-
вия ) г^“1)--г^| < е Для всех г и s, где в — заданная заранее
погрешность вычислений. Когда это условие выполняется, итера-
ционный процесс сходится к решению конечно-разностной аппроксима-
ции уравнения Лапласа с заданными граничными условиями. Это вер-
но для выбранной величины h, использованной для построения сети.
Пример 1. Найти решение уравнения Лапласа для квадрата при граничных
условиях, указанных на рис. 10.3.
Решение. Составим систему конечно-разностных уравнений, используя
вычислительный шаблон (*); см стр. 346. По формулам (2) имеем
2ц = "7“(г21Н“29,34—|-Z12+ 12,38), ?12~ ~~(г22~г26,15—рО,004~2ц),
221 = (38,53 4- 2ц + 222 4" 30,10), 222= ~~ ( 16, 18 4~ 2ц -р 0,00 -|~ 221).
4
Полученная система четырех уравнений с четырьмя неизвестными ги, г13,
г21, г22 может быть записана в виде
Хц—0,25г12—0,25221 == 8,43,
— 0,25гц -у 212 —0,25г22= 6,748,
—0,25гц 4-221—0,25г22= 17,168,
—0,25 г12 - 0,25г21 + г22 = 4,045.
349
0,0
0,0
0,0
16,18 38,53 е 9
0,00 • 9 • 9 50,00
12 • °Z33 °z °z3I • °’0
0,00 • °z oz • 30,10
^22 21 20 ® О Z 22 о ® 0,0 Z 21
0,00 • О о • 12,38
^11 40 ® % °z х 12 о • 0,0 * п
0,00 • • • • 4,31
26,15 29,34 • • •
40 20 12
Рис, 10.3 Рис, 10,4
Решение указанной системы методом последовательных исключений дает
следующие значения неизвестных:
гп = 20,53; г12 = 15,20; z2i *= 29,09; z22 = 14,12.
При применении вычислительного шаблона (*) остались неиспользованными
данные в угловых точках границы квадрата, однако эти значения необходимы при
использовании вычислительных шаблонов других типов.
d2z d2z
Пример 2. Найти решение уравнения Лапласа = 0 при гранич-
ных условиях, указанных на рис. 10.4.
Решение. Вычисление начального приближения проводится путем ин-
терполирования граничных значений на внутренние узлы. При интерполирова
нии предполагается, что значения искомой функции линейно убывают или воз
растают от одной границы до другой. Используются следующие расчетные фор-
мулы:
— гОн + ] (I ~/н)
(для строк) и
•+ К /н)
*К--
(для столбцов). Индексы /н, /н и tK, /к означают начальные и конечные значения
Начальному значению соответствует правый нижний угол таблицы. Для рассмат
риваемого примера /н = 0, /к “ 4. Вычисления начинаем с первой строки сверху
Будем считать, что функция линейно возрастает от г^а = г30 = 0 до =
= z34 — 12. Имеем
12 12 л
г34 —0-J- -—- (4—0)= 12; гзз = °+ 7—“(3—0) =9;
12 12
г32 = 0+— (2-0) = 6; г31=0+—(1-0) = 3.
350
Переходим к правому столбцу: здесь ?гп = ?.и = 0; г,к 7-= 20i — 12; далее
гз1 = 3+т-^(3-3) = 3; г21 = 3 + -Ц (2-3) = 6;
(J —• О v О
9 9
?ii=3+~U~3) = 9: ^1 = 3+—(0-3)=12.
Затем рассматриваем вторую строку, считая, что функция линейно возрастает от
гОн = г21 = 6 до “ г24 = 20. Тогда
14 14
г24 = 6 4- — (4 —1) = 20; г23 = 6 + —у (3— 1) = 15,33;
14 14
г22 = 6 + ^—у (2-1)= 10,66; гм=6+ —(1-1) = 6.
Переходим ко второму столбцу, принимая г/н7- = гг2 = 10,66 и = г02 =
= 20. Имеем
20 — 10,66
г12= 10,66 +------!— (3—2)= 15,33.
4—2
Наконец, находим г18, считая z^B “ zi2 — 15,33 и г^к = гу — 40:
40—15,33
г13= 15,33+---------— (3—2) = 27,67.
4 — 2
После определения указанным способом всех значений во внутренних узлах
процесс построения начального приближения заканчивается.
На следующем этапе в итерационном процессе определения последователь-
ных приближений используются расчетные формулы
г<"+1> = ± + гЙ+0= 7 +*№
г(А+1)= у (г^ + г^ + ^ + гЙ); г(гл2+1,= ^(гй + г'А’ + гй + гЙ);
г?з+1)= у^+г^+АА’+гй); г<2л3+1,= у (г<л> +г® + гЩ + ;<>
г(зл +1 ’ = т (г41 + + г32 + г'з"»);
4
Дп+ 1)____Lf-OO.! /п) । Лп)_ы/«))•
г32 — | \г49 2 Ч^г33
* ,(п+1)____Lf/л) J М 1 (п) 1 (п))
г33 \г4 3 I Ч г3 4 1г3 2/’
Решение примера проведено двумя способами: методом простой итерации и
методом Зейделя. Последовательные приближения по методу простой итерации
приведены в табл. 10.1, а по методу Зейделя — в табл. 10.2 (см, стр 352).
Расчет по методу Зейделя требует шести итераций, что на две итерации меньше,
чем в методе простой итерации. Вычисления заканчиваются, когда значения в по-
следовательных итерациях совпадают с заданной точностью (е = 0,1).
Анализ полученных результатов показывает, что таблицы 10.1 и 10.2 сим-
метричны относительно своих побочных диагоналей из-за специального симмет-
ричного вида граничных условий,
351
Таблица 10.1
Таблица 10.2
§ 10.5. Влияние криволинейных граничных условий
В более общем случае граница В является криволинейной, а не квад-
ратом или прямоугольником. На рис. 10.5 изображена типичная кри-
волинейная граница с квадратной сетью, наложенной на эту границу.
Величины Р^г, P3h, P$h и P3h представляют расстояния от узла Одо
границы или прилежащей точки. Как указано на рис. 10.5, величины
Р5 и Рб меньше 1, а Рг и Р3 равны 1. В последующем изложении вели-
чины Рг и Р3 также могут принимать значения, меньшие чем 1.
Рассмотрим сначала рис. 10.5 с точки зрения решения задачи Ди-
рихле. Здесь z5 и z6 заданы, г2 и z4 — значения функции в фиктивных
(так называемых нерегулярных) узлах за пределами границы.
Разложение функций z (х0 + а, у3) и z (х0, у3 + (3) в ряд Тейлора
в окрестности х0, yQ дает:
Z (^0 У о) = 2 (хо, Уд) Уд) "Т ^хх (^0» У о) +
4"ТГ* ?ххх (*о>
о!
г (х0, у0 + 0) = г (х0, у0) + $zy (х0, у0) + И. гуу (х0, у0) +
+ ТГ zvvv (хо> Уо) + •
Если положим а — Pbh и затем а — — PJi в первом уравнении,
0 = PJi и затем 0 = — Pzh во втором уравнении, то ограничиваясь
в этих уравнениях членами, содержащими вторые производные, с по-
грешностью О (А2) имеем:
г (х0+Р5 h, у0) = г (х0, у0) + Ps hzx (х0, у0) + гхх (х0, УоУ,
г (х0—Р5 h, у0) = г (х0, у0)—Pi hzx (х0, yQ) + zxx (х0, у0),
(^0, У 0 4~ ^6 У о) 4~ hZy (Xq, Уд) “I * Zyy (Хд, Z/q),
(^0> Уп P3h) =Z [Xgj Уд) Pq hZy (Xq, Уд) 4 - Zyy fag, Уд).
352
Из первых двух уравнений (1) величина zx (x0, yQ) может быть ис-
ключена, при этом
(Xj, Уо) ~ 25 —ZO •
Аналогично, используя последние два уравнения (1), получим
Складывая полученные выражения, имеем
В случае Рг — Р3 = 1 выражение (2) приводится к виду
. I 2 Г 1 । , 1 ।
4“ - “1“ ---23 4~ --------^5 г
УУ\ха,У. Й2 L/’s + l Л>+1 ® Р.(Рв+1)
+-----!---гв-^±^г о] + 0(1?) = 0. (3)
Для Р5 = Ре ~ 1 в случае квадратной границы это выражение
приводится к виду
гхх + гп\ = Д-(г1 + г3 + г6-4г0).
1ЛГо,У« Л
Алгебраические преобразования уравнения (3) дают следующее
уравнение;
Р5 Л (Рв + 1) Д 4- Р5 Ра (Р5+ 1) 23 + Рв (Ре +1)20 +
+ Р5 (Рй + 1) 2в - (Р& + 1) (Рв + 1) (Ря + Д6) 20 = 0. [4)
Отметим, что уравнение (2) является уравнением более общим, чем
(4), так как в него включены значения функции на границе и коэф-
353
фициенты Ръ Р3, Р$ и Р&. Теперь процесс решения уравнения Лапласа
состоит в данном случае в использовании уравнения (4) для всех точек,
не прилежащих к границе, и уравнения (2) с соответствующим выбором
величин Р3, Р5 и Р6 для точек, прилежащих к границе* В осталь-
ном решение проводится аналогично решению задачи для случая квад-
ратной границы.
Для задачи Неймана используется подобная, однако более услож-
ненная последовательность действий, В качестве иллюстрации может
быть использован рис. 10.6; здесь на границе задается значение
= f (х, у). Величина является градиентом по нормали от функции
г на границе и имеет наклон 05 к горизонтали* В точке 5 имеем
воряющее
хг + уг =
условию
на окружности
16 (рис. 10.7)
(х, у) = Х2(/2.
д2г , d2z
Пример. Найти приближенное решение уравнения — 0, удовлет-
ду
4
г
о
В
4
В
4о
В
В
О
А
Н
Е
оР
6
6
6
Н
и
6
R
Н
oR
6
6
4о
об
П
оР
ОД
и
В
В
Рис. 10.7
оА
L
В
О
R
е
Н
D
о
Q
е
6
oR
S
и
*2 Г
В
Решение. Пользуясь симметрией заданных граничных условий, рас-
смотрим четверть круга (рис. 10.8). Для применения конечно-разностных методов
необходимо иметь начальное приближение. Построение начального приближения
проводим следующим образом.
Полагаем значения искомой функции в узлах сети, близких к границе,
равными значениям этой функции на границе. Рассмотрим сначала крупную
сеть с шагом h = 2 Для узла А при х = 2 из уравнения окружности имеем у =
= V16 — х3 = V16—4 — 1/12. Ближайшей к узлу А точкой границы является
точка М (2; V12). Из граничного условия находим гА — zM —
— х2и21 /-г- = 48.
Аналогично для узла А' имеем ближайшую точку АГ (1/12; 2) со значением
искомой функции на границе zA, = ?м' = I Х=]/Т2, у=2 = 48* При х °
354
или у = 0 значение функции на границе обращается в нуль, поэтому в узлах
О' (4; 0) и О (0, 4) получаем г0 = z0, == 0.
Для определения значений функции во внутренних узлах (см, рис. 10.7)
имеем систему конечно-разностных уравнений
г5== “(2^ + 2q+2q + 2q)5 ZQ^~ (2o+2s + 2f + 2f),
1
2Л:= ~ (2д + 2з + 2(? + 2д)>
откуда г5 = 24; Zq = 24; zE — 36.
Для повышения точности вычислений уменьшаем шаг до h = 1 и снова рас-
сматриваем четверть круга, учитывая симметрию решений. Начальные значения
искомой функции определяем, зная значения, полученные в узлах крупной сети,
пользуясь симметрией решений и принимая значения в узлах, близких к границе,
равными значениям функции на границе. Находим
гА=гА,=48; zs = zB, = i5; гс = гс,=63.
Для определения значений zD, zG, zpt zR используем уравнения
1 , i
ZD “ ~(2x + 2f + zs + 2c)> 2G“ (г£ + гн+г(? + М>
1 1
гр — 4 (гС>+гр~ЬгЕ~1"гЕ), ZR— 4 (г9 + г$+гн + гн).
Для определения значении искомой функции гн и гЕ используем конечно-разно
стные уравнения в виде
1 1
гН “ 4 (2q + 2q+2f + 2s)> гЕ" 4 (2а + 2о + 2д + 2(?)<
Подставляя числовые значения, имеем систему уравнений
1
tD == 7 (48+ 2^+63+36),
2g = (2^+^//+ 24 + 36),
гр = ~ (ze + ?b+0+24),
Решение системы дает следующие г
г0==28,5; 2d = 43,5; z£ —27;
ZR = 4 (24+24 + гн+гн),
2я - “(24+24+24+36),
гЕ = у (0 + 36 + 48 + 24).
гачения:
2^ = 27; 2р~ 19,5; г^ = 25,5.
Уточним значения искомой функции в граничных узлах В, А и С. Ограничи-
ваясь в разложении Тейлора первой производной, имеем
£ (*о, £о + 6h) == z (х0, (/о) + 6hzy (х0, #0).
Заменяем значения zy(x0, р0) в точках/,, М и N границы их значениями в узлах
Ь А и С:
zb~zl.+ &B__h бв> ^A~zM+ бл,
гд-gjy
гс = гл+ 6С_Л 6с;
355
здесь бв, 6Л, 6С — расстояния от точек границы L, М, N цо ближайших узлов
В, А, С. Получим следующие числовые значения:
бв=| fit | = 4-У-Т5~ 0,13;
= [ AM j = 4—У12 X 0,6;
6с = |СЛГ| = 3—УУдО.35;
гв"|4-5^-“’13 = 12;
гл“48^У °'6 -651
*-63+S-°'35=74'
Составляем таблицу начальных значений и методом простой итерации нахо-
дим значения искомой функции до тех пор, пока значения, полученные в после,
довательных итерациях (см. табл. 10.3), не будут отличаться на величину по-
следнего разряда. В табл. 10.4 приводятся для сравнения значения точного ре-
шения задачи
г(х,у)=х2у2+~-j- [256—(х34-у2)].
О
21 28 47
27 30 38 47
23 29 30 28
28 28 27 21
§ 10.6. Аппроксимация параболических и гиперболических
дифференциальных уравнений в частных производных
Так как основные особенности численного интегрирования диф-
ференциальных уравнений параболического и гиперболического типа
являются сходными, то в настоящем разделе эти дифференциальные
уравнения будут рассмотрены вместе. Классическим параболическим
дифференциальным уравнением в частных производных является од-
номерное уравнение теплопроводности
где г = z (х, О’> а — положительная постоянная; t — время; х — рас-
стояние, причем интервал изменения х является ограниченным. Ог-
раничение изменения х интервалом (0, 1) является условным и может
быть легко обобщено на интервал (а, Ь). Поскольку уравнение (I) яв-
ляется уравнением второго порядка в области пространственной пере-
менной и первого порядка в области временной переменной, необходи-
мо установить два условия для ? в некоторый момент х и одно условие
356
для г в некоторый момент Л Это может быть записано следующим об-
разом:
z (0, t) = fQ (0, х = 0J > О,
2(1, 0 = 0), х= 1,
(2)
г (х, 0) == g$ (х), t — 0, 0 < х < L
(3)
Функции /о (0, fi (0 и g0 (х) являются обыкновенными аналитически-
ми функциями.
Классическим гиперболическим уравнением в частных производ-
ных является волновое уравнение
дгг d2z
дх2 dt2
0<Х<1,
(4)
при том же обозначении перемен-
ных, что и в уравнении (1). По-
скольку (1) является уравнением
второго порядка по обеим незави-
симым переменным, требуется два
граничных и два начальных усло-
вия. Их можно задать следующим
образом:
Рис. 10.9
2 (0, 0 = /о (0, * = О, t > 0;
2 (1, 0 = К (0, * = 1, 0; (5)
2(х, 0)=go(x), /-0, 0<х<1; ~ (х}0) = ^(х), ^0, 0<х<1.
(6)
Условия (5) и (6) можно заменить более общим градиентным условием,
которое имеет форму
ai
дг
дх
х = 0 или х = 1,
(7)
и
^a2z = a2)
и при соответствующем выборе аъ а3 приводится к одному из видов
(5) или (6).
В обоих рассматриваемых классах дифференциальных уравнений
граница определена стрех сторон области (х, I) и неограничена с чет-
вертой стороны. Для постоянных значений /0 (0 и Д (/) и постоянном
g0(x), скажем, равном нулю, область и граница указаны на рис. 10.9.
Задача состоит в определении z (х, t) в области Я при условиях на гра-
нице В, Для применения конечно-разностного метода область покры-
вается прямоугольной сетью с шагом h по направлению х и шагом
k по направлению t. Узловой точке хг, ts соответствует значение функ-
ции
z(xr, ts) = z(rh, sk)-=zrs.
357
Наиболее простое конечно-разностное представление параболиче-
ского дифференциального уравнения в частных производных (1) исполь-
зует формулу центральных разностей для zxx и опережающую разность
для zt. Пользуясь соотношением (<) (см. стр. 346), имеем
гг+1, S-S ?r, s+1 2Г, S_ А
--а/ — Са-----------------------—
хх ‘ /I2 k
ИЛИ
zT, s+ = zr. s + (zr+i, s- 2z,s) + 0 (^) + 0 (k).
Обозначив 0 = а/г//г2, получим
Zr, s+1 = Pzr+1, s + 0 — 20) ZT s + 0Zr-i s, (8)
где 1 r N и s 1. Уравнение (8) имеет вычислительный шаблон
В частном случае, когда 0 = 1/2, уравнение (8) принимает вид
zr, s+1 = (zr+l, S "Г ZT—1, si' (Q)
Соотношение (9) называется формулой Шмидта.
Граничные и начальные условия (2) и (3) принимают следующий
вид:
го, 8 = fo(sk), 8>0,
= S>°> (10)
?r 0 = g0(rh)> ®<г<м.
Способ решения уравнений (8) и (10) следует из вышеизложенного
для уравнений эллиптического типа. Начальные и граничные условия
(10) определяют величины для всех граничных узлов. Уравнение (8)
может быть использовано для вычисления всех s в первой строке по
значениям величины zG0. Это можно легко видеть из вычислительного
шаблона, в котором величина zGs+1 следует из величин функции толь-
ко на уровне з. Как только известна полная строка величина zr^
может быть вычислена с помощью уравнения (8) по известным гранич-
ным условиям и значениям величин Этот процесс может быть про-
358
должен в области времени настолько, насколько это необходимо по
условию задачи. Заметим, что процесс вычисления состоит в простом
вычислении значений уровень за уровнем, с неизвестной г на ($ + 1)-м
уровне, вычисляемой по полученному значению г на предыдущем
s-м уровне. Программа вычислений этого процесса относительно проста
и требования к памяти ограничены. Уравнение (8) называется явным.
Следует отметить, что основная задача состоит в вычислении зна-
чений функции zr>s в первой строке. Разрыв существует в условных
точках z0f0 и 2М,о, поскольку приближение к этим точкам в направле-
нии х и в направлении t ведет к различным величинам. Это обычно ком-
пенсируется использованием средних арифметических значений функ-
ции в условных точках, соответствующих х->0и /->0. В действи-
тельности значение функции в углах не используется в последующих
вычислениях и поэтому не является особенно важным.
д*г dz
Пример. Найти решение уравнения 0 < х < 1» 0 < / < 0,01,
удовлетворяющее условиям
£0(х) = (1,5х1 2+2,2)е+ /0(/) = 2,2; Л(/) = 3,7е^
с заданной точностью 8 = 10-4.
Решение. Воспользуемся явной схемой (8) при р == 1/6. Выберем шаг по
оси х равным h — 0,1. Так как а == 1, Р — 1/6, то по формуле (3 = а/е/А2 находим
шаг по оси t : k = рАа/а = 0,01/6 0,0017.
Записываем в таблицу начальные и граничные значения. Нулевой строке
соответствуют граничные' значения, левому столбцу — начальные условия.
Формула (8) при р = 1/6 принимает вид
1
2r,s+l= 6 (гг+1, s + 4?r, s + 2r-l, s)•
Для первой строки имеем
1
zr> 1 = ~ (^г+1, о4~4гг 0+гг-1, о)-
6 ‘
Подставляя числовые значения, находим
(1,850 + 4-2,004 + 2,2) =2,011;
6
1
z2i =— (1,7304-4.1,850 + 2,004) = 1,856;
6
1
z31 =— (1,636 + 4 1,730 +1,850) = 1,734;
6
z41= —(1,562 +4 -1,636+1,730) =1,639;
6
z51 = — (1,504 + 4-1,562+ 1,636) = 1,564;
6
1
zel= — (1,458 + 4-1,504+1,562) = 1,506;
6
1
г71 = — (1,420 + 4-1,458+ 1,504) = 1,459;
359
Z81 = —(1,388 4-4.1,420 4-1,458) = 1,420;
6
г91=— (3,7e“x+4.1,388 +1,375) = 1,368.
6
Для последующих строк при t = 0,0033; 0,0050; 0,0067 вычисления прово-
дятся аналогично (см. табл. 10.5).
Таблица 10.5
t г17 гз; г5> ze; г1] г8>
0,0067 2,025 1,872 1,748 1,649 1,572 1,512 1,463 1,424 1,391
0,0050 2,021 1,867 1,743 1,646 1,570 1,510 1,462 1,423 1,390
0,0033 2,017 1,861 1,739 1,642 1,567 1,508 1,460 1,422 1,390
0,0017 2,011 1,856 1,734 1,639 1,564 1,506 1,459 1,421 1,389
0,0000 2,004 1,850 1,730 1,636 1,562 1,504 1,457 1,420 1,388
Упражнения
1. Найти приближенное решение уравнения Лапласа
квадрата при указанных граничных условиях:
д2г д2г _
дл-2 + ~ 0 для
0,00 • а) 16,18 38,63 © © © 50,00 6) 17,98 39,02 0,00 • • • • 50,00
0,00 • О О • 30,10 0,00© о О • 30,10
0,00© о 0 • 12,38 0,00© о О < • 12,38
0,00© Ответы: 0,00 • © 26,15 29,3 а) 16,18[38,63| © 4,31 4 50,00 0.00© • 29,05 2 1 0,00 | 17,98 9,63 5) 39,02 • 4,31 50,00
0,00 14,12 26,09 30,10 0,00 | 15,18 36,39 30,10
0,00 15,20 20,53 12,38 0,00 16,37 21,26 12,38
0,00 26,15 29,34 4,31 0,00 29,05 29,63 4,31
2. Найти приближенное решение
_ д2г д2г л
уравнения Лапласа ——-4----------= 0
дх2 ду2
с шагом h=l/6 для квадрата при указанных граничных условиях:
360
9,81 19,78 29,12 40,16 42,31
0,00 X X X X X X X 50,00
0,00 X о о о о о X 40,16
0,00 X о О О о о X 33,11
0,00 X о о О о О X 19,14
0,00 X о о о о о X 13,00
0,00 X о о о о о X 6,98
0,00 X X X X X X X 4,31
17,28 31,96 40,00 30,50 17,28
Ответ:
1 9,81 19,78 29,12 40,16 1 1 42,31
0,00 8,97 17,58 25,36 32,18 36,11 40,16
0,00 8,68 16,00 22,29 26,86 29,69 33,11
0,00 8,36 15,59 20,71 23,05 22,62 19,14
0,00 9,43 17,22 21,71 21,85 18,55 13,00
0,00 12,20 22,09 26,96 24,01 16,70 6,98
17,28 31,96 40,00 30,50 | I 17,28
_ д2г ( д2г
3. Найти приближенное решение уравнения Лапласа 0 с шагом
h = 0,2 в области (С) : х2 Н~ (у +3)~ < 1,6, у > 0 при граничных условиях сле-
дующего вида:
г|у=0=0, г|с = 2//(2хг4-31/).
361
Ответ:
1.0 6,000 6,120 6,480
0,8 5,088 5,184 5,472 5,952 6,624 7,488 8,544
0,6 3,984 4,056 4,272 4,632 5,136 5,784 6,576 7,512 8,592
0,4 2,736 2,784 2,800 3,168 3,504 3,936 4,464 5,088 5,808 6,624 7,536
0,2 1,392 1,416 1,488 1,608 1,776 1,992 2,076 2,568 2,928 3,336 3,792 4,316 4,848
0,0 0,0 ,0,0 0,0 0,0 0,0 0,0 0,0 0,0 0,0 0,0 0,0 0,0 0,0
у / /к 0,0 0,2 0,4 0,6 0,8 1,0 1,2 1.4 1,6 1,8 2,0 2,2
4. Найти приближенное решение уравнения удовлетворяющее
условиям г (х, 0) = g0 (х), г (0, t) = /0 (/), г (1, f) — А (/) для значении
0 < t < Т, взяв по аргументу х шаг h ~ 0,1. Использовать уравнение (8) § 10.6.
a) g0 (х) = (1, 1х2+1,1) sin лх, /0 (/)=А (0=0, Т=0,02, 3 = 1/2;
б) g0(x) = (l,lx24-2,3)a“*; f0 (0=2,3; А (/) = 3,4е-1; Т-0,01; 3 = 1/6.
Ответы:
t ги г27 3J гб; zu г8> г9/
0,020 0,311 0,602 0,855 1,045 1,15 1,145 1,018 0,764 0,412
0,015 0,320 0,621 0,885 1,088 1,206 1,212 1,084 0,824 0,443
0,010 0,328 0,639 0,914 1,131 1,262 1,281 1,162 0,887 0,486
0,005 0,336 0,656 0,943 1,172 1,318 1,351 1,243 0,973 0,531
0,000 0,343 0,672 0,970 1,213 1,375 1,423 1,327 1,062 0,618
t 2и г2/ гз; . гб; г6; г8У г9?
0,0067 2,110 1,939 1,794 1,673 1,572 1,488 1,416 1,355 1,301
0,0050 2,106 1,934 1,789 1,670 1,570 1,486 1,415 1,354 1,300
0,0033 2,102 1,929 1,785 1,666 1,567 1,484 1,413 1,352 1,299
0,0017 2,097 1,924 1,781 Ь,663 1,564 1,482 1,411 1,351 1,798
0,0000 2,091 1,919 1,777 1,660 1,562 1,480 1,410 1,350 1,297
ЛИТЕРАТУРА
1. Г. С. Бараненков, Б. П. Демидович и др. Задачи и упраж-
нения по математическому анализу для втузов. М., «Наука», 1964,
2. И. G. Березин и Н. П. Жидков. Методы вычислений, т. I.
М., Физматгиз, 1959.
3. И. G. Березин и Н. П. Жидков. Методы вычислений, т. II.
М., Физматгиз, 1962.
4. А. А. Гусак, Элементы методов вычислений. Изд-во БГУ
им. В. И. Ленина, Минск, 1974.
5, Р. С. Г у т е р и Б. В. О в ч и н с к и й. Элементы численного ана-
лиза и математической обработки результатов опыта. М., «Наука», 1970.
6. А. Н. Данилова и Г. Н. Семенова. Методическая разработ-
ка для проведения практических занятий по численным методам. Ленинград,
Ленинградский радиополитехникум, 1971.
7. Б. П. Демидович и И. А. Марон. Основы вычислительной
математики. М., «Наука», 1970.
8. Б. П. Демидович, И. А. Марон, Э. 3. Шувалова.
Численные методы анализа. М., «Наука», 1967.
9. И. А. Каплан. Практические занятия по высшей математике, ч. V,
изд-во Харьковского Университета, Харьков, 1972.
10. Н. В. К о п ч е н о в а и И. А. Марон. Вычислительная мате-
матика в примерах и задачах. М., «Наука», 1972.
11. А. Г. К у р о ш. Курс высшей алгебры. М., «Наука», 1965.
12. М и л н В. Э. Численное решение дифференциальных уравнений.
ИЛ, 1955.
13. С. Б. Норкин, Р. Б. Б е р р и, И. А. Ж а б и н, Д. П. По-
лозков, М. И. Розенталь, X. Р. Сулейманова. Элементы
вычислительной математики. М., «Высшая школа», 1966.
14. Г. Н. Положив, Н. А. Пахарева и др. Математичесю и
практикум. М., Физматгиз, 1960.
15. Д. К. Фаддеев и В. Н. Фаддеева. Вычислительные методы
линейной алгебры. М., Физматгиз, 1963.
16. М. П. Черкасова. Сборник задач по методам вычислений и эле-
ментам программирования. Минск, «Высшая школа», 1966.
17. М. П. Ч е р к а с о в а. Сборник задач по численным методам Минск,
«Вышэйшая школа», 1967.
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Абсолютная величина вектора 53
---матрицы 52
— погрешность 10
--- округления 17
--- предельная 11
------алгебраической суммы 20
---, связь с числом верных знаков 18
Абсолютно интегрируемая функция 300
Адамса метод 332—336
— экстраполяционная формула 333
Алгебраическая функция 109
Алгебраическое дополнение 45
— уравнение 111
---, графический метод решения 112, 113
— —, корни 111
---, нахождение корней, см. соотв. ме*
тод
— —, область существования корней 147—
149
---, общие свойства 144, 145
---, определение числа действительных
корней 145, 146
---, отделение корней 115—117, 119
Аналитический метод отделения корней 119
— способ задания функций 162
Аппроксимация уравнений гиперболического
и параболического типов 356—359
-----эллиптического типа 347, 348
Безу теорема 150
Ведущее неизвестное 75
Ведущий коэффициент 75
Вектор 36
Вектор-столбец 36
— неизвестных 69, 70
— свободных членов 69, 70
Вектор-строка 36
Верные значащие цифры в узком смыс*
ле 15
-----------широком смысле 15
Возрастающая функция 117, 118
Волновое уравнение 341, 357
Вычислительные шаблоны 343, 345, 346, 348,
358
Гамильтона — Кели тождество 212
Гаусса интерполяционная формула вторая
198 199
------первая 197, 199
— квадратурная формула 277, 282
— метод 75—77
— схема 78—81
---, использование для вычисления оп*
ределителя 85
--,------обращения матрицы 86, 87
Геометрическая интерпретация метода ите*
рации 136, 137
—-----Рунге — Кутта 327, 328
Гиперболическое дифференциальное урав*
нение 339, 340
------, аппроксимация 357—359
Главная диагональ 37, 41
8S4
Горизонтальная таблица конечных разно*
стей 177
Горнера схема 152
Границы действительных корней алгебраи*
ческого уравнения 147—149
График 162
Графический метод отделения корней 116,
117
-----решения систем уравнений 114, 115
-----уравнений 112—114
— способ задания функций 162
Графическое дифференцирование 289
— интегрирование 284, 285
Данилевского метод для вычисления соб-
ственных векторов 232, 233
------приведения матрицы к виду Фро-
бениуса 220—223, 228—231
Декарта правило 145
Детерминант, см. Определитель
Диагональная матрица 37
— таблица конечных разностей 177
Диагональный минор 64, 211
Дирихле задача 347
— теорема 295
Дискриминант 339
Дифференциальное уравнение 311
---в частных производных 312
— — --------- вполне линейное 339
-----------гиперболического типа 339,
340
-----------параболического типа 339,
340
-----------эллиптического типа 339, 341
---обыкновенное 311
------н-го порядка 312
Дифференцирование графическое 289
— ряда Фурье почленное 301, 302
— численное 285—289
Дробно-рациональная функция 110
Единичная матрица 37
Единственность интерполяционного много-
члена 189
— корня уравнения 117
— решения системы линейных уравне-
ний 73
Задача Дирихле 347
— Коши 313
— Неймана 347
Зейделя метод 96, 97, 99
Значащая цифра 14
Интеграл диффиренциалъного уравнения 312
Интегральная кривая 313
Интегрирование графическое 284, 285
— дифференциальных уравнений с по-
мощью рядов 317, 318
— ряда Фурье почленное 300
— численное 265—283, см. также соотв,
формулы
Интерполирование 168
— в узком смысле 168
Интерполирование вперед 186
— квадратичное 184, 191
— линейное 184, 189—191
----по Эйткину 192, 193
~ назад 186
*— обратное в случае неравноотстоящих
узлов 201
•--------- —* равноотстоящих узлов 202
— параболическое 169, 184, 191
— с помощью многочленов Чебышева 200,
201
— тригонометрическое 302, 303
Интерполяционная формула 168, см. также
соотв. названия
Интерполяционный многочлен 168
----Лагранжа 171, 174
----Ньютона 183, 186
Иррациональная функция НО
Итерационный процесс 90
Квадратичное интерполирование 184, 191
Квадратная матрица 37
Квадратурная формула 265, см. также
соотв. названия
Клеточная матрица 54
Конечно-разностные аппроксимации 341—346
Конечные разности 176
----второго порядка 177
----первого порядка 176
----n-го порядка 177
----, свойства 179, 180
Контрольные суммы 80, 81
Координаты вектора 36
Корень многочлена 144
----кратный 144
— уравнения 109, 111
----отделенный 116
Коши задача 313
Коэффициенты Ньютона — Котеса 272
— системы уравнений 68
уравнения 111
— Фурье 295, 296
Крамера формулы 73
Критические точки 118, 119
Кронекера символ 87
Крылова метод для вычисления собствен-
ных векторов 219
---------развертывания характеристическо-
го определителя 212—214
Кусочно-монотонная функция 295
Кусочно-непрерывная функция 295
Лагранжа интерполяционная формула для
неравноотстоящих узлов 171
---------равноотстоящих узлов 174
— интерполяционный многочлен 171, 174
— метод 148
Лапласа уравнение 341, 347
Леверрье метод 234, 235
Леверрье — Фаддеева метод 235
Лежандра многочлены 280, 281
Линейное интерполирование 184, 189—191
----по Эйткину 192, 193
Липшица постоянная 313, 314
— условие 313
Х-разности 241
Маркова интерполяционная формула 237
Матрица 35
— диагональная 37
— единичная 37
— квадратная 37
— плеточная 54
— неособенная (невырожденная) 49
нулевая 37
»— обратная 49
— окаймленная 56
— особенная (вырожденная) 49
I— противоположная 39
— прямоугольная 36
— симметричная 37
«- системы уравнений 69, 70
Матрица союзная 49
— транспонированная 36
— треугольная 64
— характеристическая 208
Матрица-столбец 36
Матрица-строка 36
Матричная запись системы линейных урав-
нений 69, 70
Матричные уравнения 70—72
Метод Адамса экстраполяционный 332—336
— аналитический, см. Аналитический ме-
тод
— выбранных точек 247, 250, 251, 255, 236
259
— Гаусса 75—77
— графический, см. Графический метод
— Данилевского 220—223, 228—233
— Зейделя 96, 97, 99
— интерполяции для развертывания ха-
рактеристического определителя 236—238
— итерации для линейной системы урав-
нений 90—92, 91, 95
-----нелинейной системы уравнений
142, 143
----- определения собственных чисел
матрицы 239—241
*------уравнения 135—137
-----уточнения элементов приближ< н-
ной обратной матрицы 102
— касательных 127—130
— комбинированный хорд и касательных
131____133
— Крылова 212—214, 219
— Лагранжа 148
— Леверрье 234, 235
— Леверрье — Фаддеева 235
— наименьших квадратов 248, 249, 252,
256, 257, 260
непосредственного развертывания ха-
рактеристического определителя 210, 211
Ньютона нахождения верхней границы
положительных корней 149
*--решения нелинейной системы урав-
нений 139, 140
-----уточнения корней уравнения (ме-
тод касательных) 127—130
— парабол 269, 270
— Пикара 314, 315
•— половинного деления 121
*- последовательного исключения неиз-
вестных (метод Гаусса) 75—77
•— последовательных приближений, см.
Метод итерации, Метод Пикара
— проб 120, 121
— прямоугольников 265—267
— Ричардсона 349
Рунге — Кутта 326—329 , 331
— Симпсона (метод парабол) 269, 270
— средних 247, 248, 251, 252, 256, 259, ZbO
• — трапеций 267—269
е— Хичкока выделения квадратного трех-
члена 156, 157
— хорд 123—125
— Эйлера 318—323
— Эйлера — Коши 323—325
Минор 45 "
Модуль’матрицы 52
Монотонная функция 118, 295
Начальный отрезок 333
Начальные данные 313
— условия 313
Невязка 82
Неизвестные системы уравнений 68
Неймана задача 347
Неопределенная система 69
Неособенная матрица 49
Несовместная (противоречивая) система 69
Норма вектора 53
г- матрицы 52, 53
3G5
Нормальная форма записи приближенного
числа 15
Нормальный вид системы линейных урагв-
нений 91
Нулевая матрица 37
Нумерация 13
Ньютона интерполяционная формула вто-
рая 186—188
-------первая для неравноотстоящих уз*
лов 197
-----------равноотстоящих узлов 183,
184, 187, 188
— интерполяционный многочлен 183, 186
— метод нахождения верхней границы
положительных корней 149
•--решения нелинейной системы урав<
нений 139, 140
— — уточнения корней уравнения 127—130
— формулы для сумм степеней корней
алгебраического уравнения 234
Ньютона — Котеса коэффициенты 272
— формула 273
Область допустимых значений уравнения
108
— существования функции 117
— сходимости функционального ряда 293
Обратная матрица 49
Обратное интерполирование 201—203
Обратный ход 80, 81
Обращение матрицы 49, 50
---окаймлением 59—61
--- разбиением на клетки 57, 58
— — разложением на произведение двух
треугольных матриц 66
---с помощью схемы Гаусса 86, 87
Общее решение дифференциального урав-
нения 313
Окаймление 56
Округление 16, 17
Оператор дифференциальный 342—344
— опережения разностный 342
— приращения 342
— центральных разностей 342, 344
Определенная система 69
Определитель 41
— второго порядка 41
— , вычисление по схеме Гаусса 85
—, свойства 42—44
— системы уравнений 73
— третьего порядка 42
— характеристический 208
Особенная матрица 49
Отделение корней 116, 117, 119
Относительная погрешность 12
•--предельная 12
------ корня 32
------ произведения 25, 28
------ — разности 22, 23
------ степени 31
------суммы 21—23
------частного 29
---, связь с числом верных знаков 19
Оценка погрешности для интерполяционной
формулы Лагранжа 175, 176
-----интерполяционных формул Гаус-
са 199
-----------Ньютона 187, 188
---— метода Адамса 335
------— Зейделя 99
---------итерации в случае линейной
системы уравнений 95
----------------нелинейной системы
уравнений 143
----------------уравнения 136
--------- при уточнении элементов
приближенной обратной матрицы 102
------ — касательных 129, 130
---------комбинированного хорд и ка-
сательных 132, 133
— —------Пикара 315
—-----— рунге — Кутта 329
Оценка погрешности для метода хорд
125 129
---’----Эйлера 319, 320, 322
------правила трех восьмых 274
------формулы линейного интерполиро-
вания 191
------Симпсона 270
------ трапеций 267
Ошибка 10
Пара бол ичеслое дифференциальное урав-
нение 339, 340
--------, аппроксимация 356—359
— интерполирование 169, 184, 191
Периодическая функция 294
Пикара метод 314, 315
Побочная диагональ 41
Погрешность 8, 10
— абсолютная см. Абсолютная погреш-
ность
— исходная 9, 10
— округления 10
— остаточная 10
— относительная, см. Относительная по-
грешность
См. также Оценка погрешности
Подобные матрицы 220
Позиционная система счисления 14
Порядок дифференциального уравнения 312
— матрицы 37
Последовательность 290
Правила округления 16, 17
— подсчета цифр 32, 33
Правило Декарта 145
— кольца 147, 148
— сложения чисел разной точности 20
— треугольников 42
— трех восьмых 274
1— умножения цифр разной точности 26
— четной цифры 17
— Штурма 146
Предел последовательности 291
---векторов 89, 90
---матриц 90
Преобразование нелинейной эмпирической
зависимости в линейную 257, 258
Приближенное число 8, 10
Приведение линейной системы к виду,
удобному для итераций 100, 101
Произведение вектора на число 41
— матрицы на матрицу 39, 40
------ число 38
Противоположная матрица 39
Прямой ход 80, 81
Прямоугольная матрица 36
Равенство матриц 38
Равномерная сходимость функционального
ряда 294
Разбиение матриц на клетки 54
Разделенные разности 194
--- второго порядка 194
--- первого порядка 194
---k-ro порядка 194, 195
Разложение матрицы на произведение двух
треугольных матриц 64, 65
— многочлена на множители 153
— определителя по элементам строки
(столбца) 46
Разность матриц 38
Ранг матрицы 48
Расходящаяся последовательность 291
Расходящийся ряд 293
Рациональная функция 109
Решение алгебраического уравнения 109
— дифференциального уравнения 312
— системы уравнений 69, 109
Ричардсона метод 349
Рунге принцип 334, 335
— схема 308
Рунге — Кутта метод 326—329, 331
366
Ряд 292
— степенной 293
— тригонометрический 293, 295
— Фурье, см. Фурье ряд
Свободные члены системы уравнений 68
Симметричная матрица 37
Симпсона метод 269, 270
— формула 269, 270
— — общая 270
Система линейных уравнений 68, 69
------, матричная запись 69, 70
------, основные понятия 68, 69
, приведение к виду, удобному
для итераций 100, 101
-------»----нормальному виду 91
------, решение методом Гаусса 75—83
------_ Зейделя 96, 97
------> — — итерации 90—92
------, — по формулам Крамера 73
— счисления 13
— уравнений 109
---, решение графическим методом 114,
115
— —, — методом итерации 142, 143
— —,-----Ньютона 139, 140
След матрицы 210
Собственные значения 208
Собственный вектор 208
Совместная система 69
Сомнительная цифра 15
Союзная матрица 49
Степенной ряд 293
Степень дифференциального уравнения 312
— матрицы 41
Сумма векторов 41
— матриц 38
— ряда 293
Схема Горнера 152
— деления многочлена на квадратный
трехчлен 154
•— единственного деления 78—81
— Рунге 308
Сходящаяся последовательность 291
---векторов 89, 90
--- матриц 90
Сходящийся ряд 293
Таблица значений абсцисс для формулы
Чебышева 276
------и квадратурных коэффициентов
для формулы Гаусса 283
— — коэффициентов Ньютона — Котеса
272
— конечных разностей горизонтальная 177
------ диагональная 177
— разделенных разностей 195
— распределения е ошибки в таблице ко-*
нечных разностей 180
— с двумя входами 167
— центральных разностей 178
Табличная разность 166
Табличный способ задания функций 163
Теорема Безу 150
Теоремы о погрешностях 20, 24, 29, 31, 32
---существовании корней уравнения 117
---сходимости итерационного процесса
135, 142, 143, 315
Транспонированная матрица 36
Трансцендентная функция 110, 111
Тригонометрический многочлен 302, 303
— ряд 293, 295
Тригонометрическое интерполирование 302,
303
Треугольная матрица 64
Уравнение волновое 341, 357
— Лапласа 311, 347
— теплопроводности 341, 356, 357
гочнение корней 120
---, полученных по схеме Гаусса 82, 83
— коэффициентов эмпирической зависи-
мости 247—252, 255—257, 259, 260
— элементов приближенной обратной мат-
рицы 102
Формула Адамса 333
— Гаусса интерполяционная вторая 198,
199
------первая 197, 199
---квадратурная 277, 282
— Лагранжа интерполяционная для не-
равноотстоящих узлов 171
---------равноотстоящих узлов 174
— левых прямоугольников 266
— линейного интерполирования 184
— Маркова 237
— Ньютона интерполяционная вторая
186—188
первая для неравноотстоящих
узлов 197
-----------равноотстоящих узлов 183,
184, 187, 188
— Ньютона — Котеса 273
— параболического интерполирования 181
— правых прямоугольников 267
— Симпсона 269, 270
---общая 270
— трапеций 267
---общая 268, 269
— Чебышева 276
— численного дифференцирования, осно-
ванная на интерполяционной формуле
Лагранжа 288
— Шмидта 358
Формулы для нахождения элементов об-
ратной матрицы с помощью окаймле-
ния 60
-------------------разбиения на клет-
ки 57, 58
— Крамера 73
— численного дифференцирования, осно-
ванные на интерполяционных формулах
Ньютона 286, 287
Фробениуса *Вид матрицы 220
Функциональная зависимость 162
— последовательность 291
Функциональный ряд 293
Функция 162, см также соотв. названия
Фурье коэффициенты 295, 296
— ряд 295, 296
•----, почленное интегрирование и диф-
ференцирование 300—302
*--, численное определение коэффициен-
тов 306—308
Характеристическая матрица 208
Характеристические числа 208
Характеристический многочлен 208
— определитель 208
Характеристическое уравнение 208, 209
Хичкока метод 156, 157
Целая рациональная функция ПО
Цена разряда 14
Центральная разность 197
Цифра 13
— значащая 14
— сомнительная 15
Убывающая функция 117, 118
Узлы интерполяции 168
— неравноотстоящие 169
— равноотстоящие 173
Частичная сумма ряда 292
Частное решение дифференциального урав-
нения 313
367
Чебышева многочлены 200
— формула квадратурная 276
Численное дифференцирование 285—289
— интегрирование 265—283
См также соотв формулы
Число верных знаков произведения 27
------ частного 30
— действительных корней ал1ебраическо-
го уравнения 145, 146
Шаг интегрирования 318
— интерполяции 169
— таблицы 164
Шмидта формула 358
Штурма правило 146
Эйлера метод 318—323
Эйлера — Коши метод 323—325
Эйткина интерполяционная схема 192, 193
Эквивалентные системы уравнений 69
Экстраполирование 168
— вперед 186
— назад 186
Элементарные преобразования определите*
ля 42—44
— — системы линейных уравнений 75
Эллиптическое дифференциальное уравне*
ние 339, 341
--------, аппроксимация 347, 348
------, влияние криволинейных гранич-
ных условий 352—354
------, решение разностных уравнений
349
Эмпирическая зависимость 246
---, выбор вида формулы 253, 254
---квадратичная 259, 260
---линейная 246—252
---, преобразование в линейную 257, 258
---. уточнение коэффициентов 255—257
Данилина Нинель Ивановна
Дубровская Нинель Соломоновна
Кваша Ольга Пезровна
Смирнов Георгий Леонидович
Феклисов Геннадий Иванович
ЧИСЛЕННЫЕ МЕТОДЫ
Научный редактор В. М. Савицкий
Редактор А. М. Суходский
Художник А В Исиченко
Художественный редактор В. И, Пономаренко
Технический редактор Н. А. Битюкова
Корректор В. В. К о ж у т к и н а
Сдано в набор 15/IX—75 г. Подп. к печати 9/1V—76 г
Формат 60x90Izi6, Бум тип № 2. Объем 23 печ, л. Усл п л. 23. Уч.-изд. л. 22,46.
Изд. № ФМ-587. Тираж 44 000 экз. Заказ № 449. Цена 84 коп.
План выпуска литературы издательства
«Высшая школа» (вузы и техникумы) на 1976 г. Позиция № 240
Москва, К-51, Неглинная ул., д 29/14,
______________издательство «Высшая школа»________________________
Московская типография № 4 Союзполиграфпрома
при Государственном комитете Совета Министров СССР
по делам издательств, полиграфии и книжной торговли»
Москва, И-41, Б Переяславская, д. 46