Теория околозвуковых течений - Гудерлей К.Г.

Автор: Гудерлей К.Г.

Теги: математика ракетная техника авиатехника

Год: 1960

Похожие

Газовая динамика

Аэродинамика

Теоретическая гидромеханика Ч.2

Сверхзвуковое течение и ударные волны

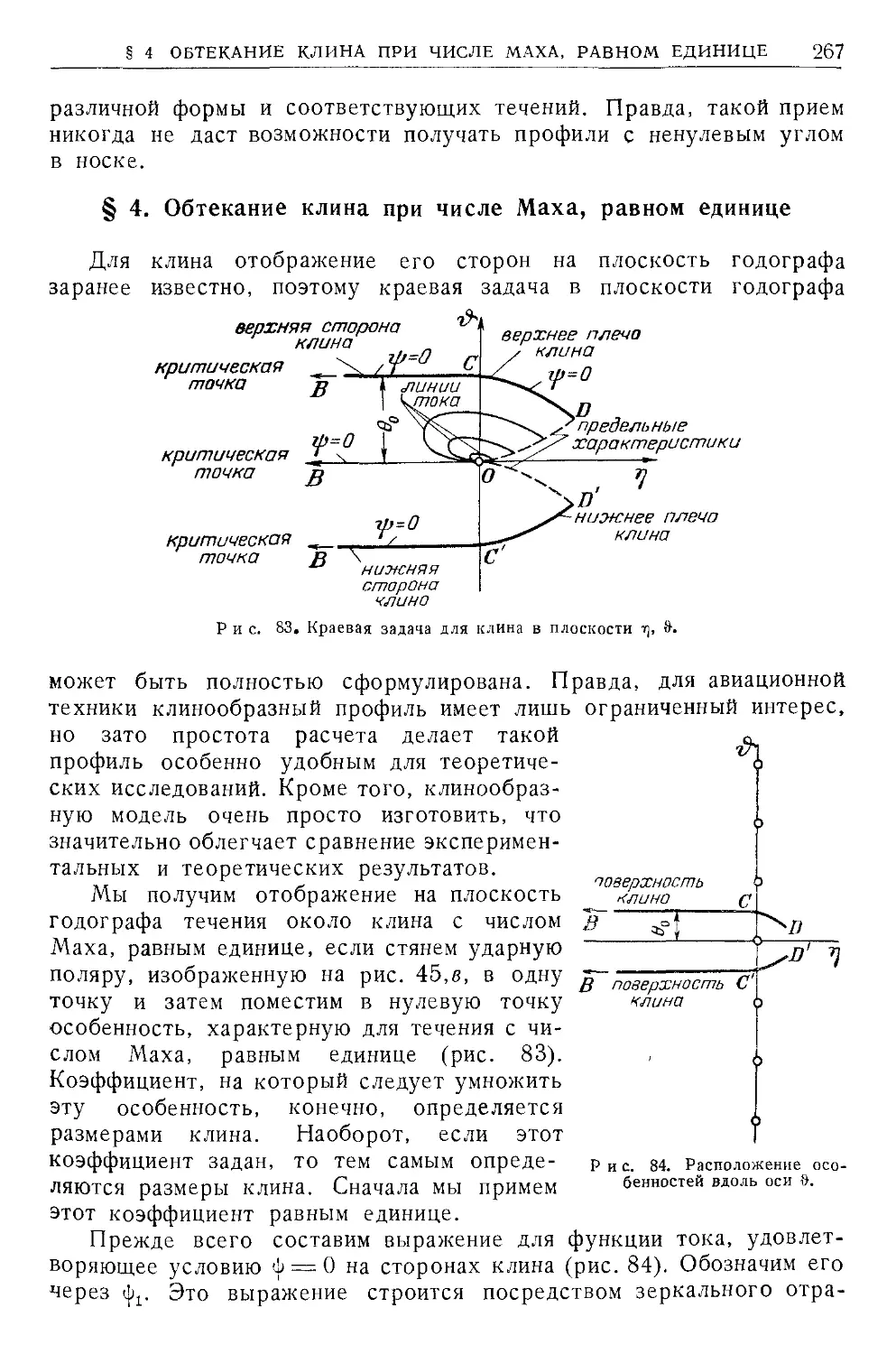
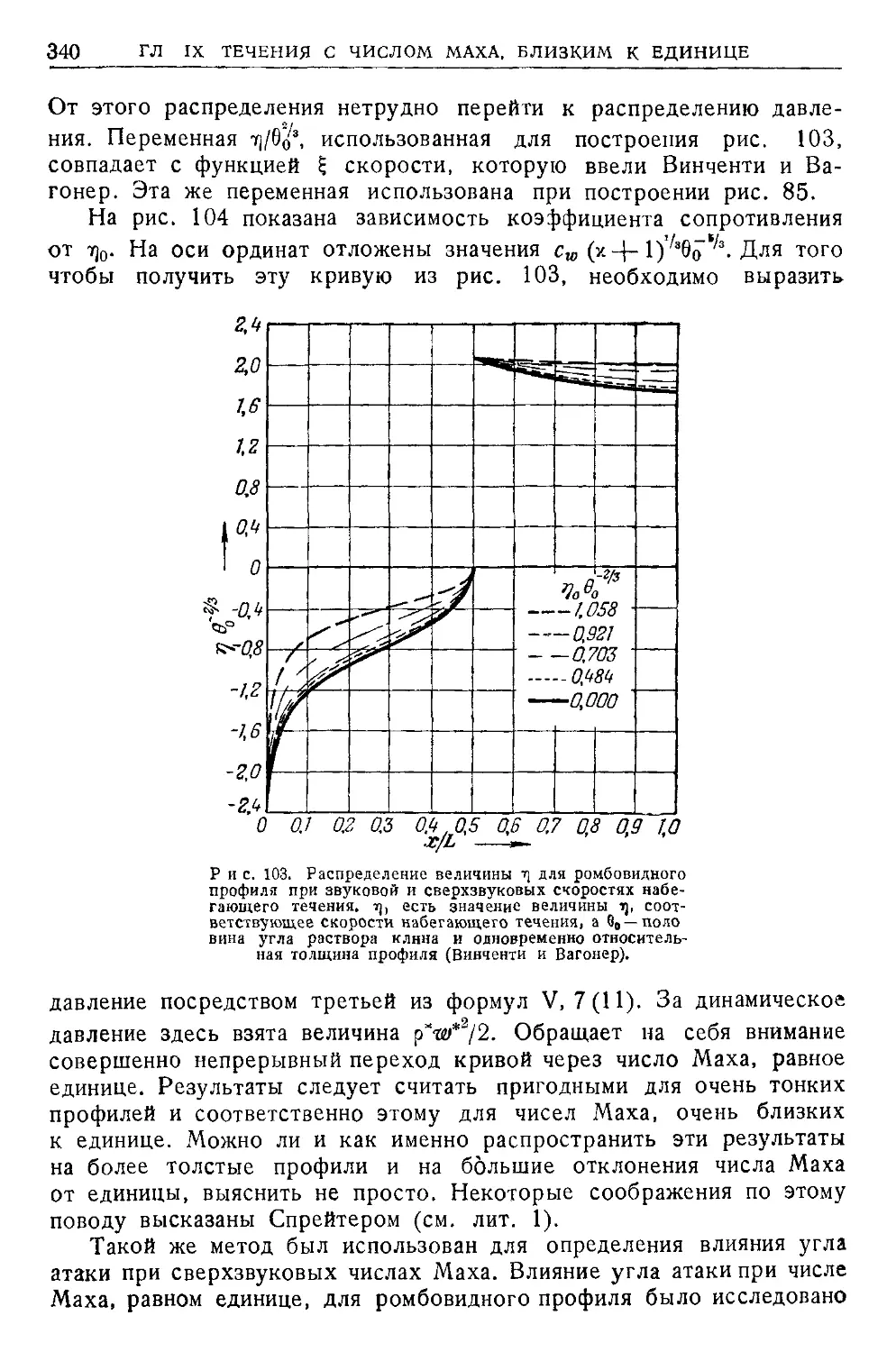
Текст

К. Г. Гудерлей
ТЕОРИЯ
ОКОЛОЗВУКОВЫХ
ТЕЧЕНИЙ
Перевод с немецкого
Г. А. Вольперта
Под редакцией
Л. В. Овсянникова
ИЗДАТЕЛЬСТВО ИНОСТРАННОЙ ЛИТЕРАТУРЫ
Москва, I960

АННОТАЦИЯ
Развитие авиационной и ракетной техники сделало весьма
актуальным вопрос об особенностях течения газа со скоростями,
близкими к скорости звука. Таким течениям и посвящена на-
настоящая книга. Она написана одним из крупнейших в США
специалистов по прикладной газовой динамике и представляет
собой первую в мировой литературе попытку систематического
изложения физических основ и математических методов изучения
околозвуковых течений. Большое количество примеров позволяет
читателю с инженерной подготовкой понять особенности явлений,
происходящих при околозвуковых течениях. В то же время книга
представляет интерес и для математиков, занимающихся урав-
уравнениями в частных производных смешанного типа.
Редакция литературы по математическим наукам

ПРЕДИСЛОВИЕ РЕДАКТОРА
Первые теоретические исследования, относящиеся к околозвуко-
околозвуковым течениям, были выполнены более полувека тому назад. Так,
еще в 1902 г. С. А. Чаплыгин в связи с задачей об истечении до-
дозвуковой струи изучал предельный случай, когда скорость на гра-
границе свободной струи равна скорости звука. Далее, в 1908 г.
Т. Мейер исследовал поведение потока газа, проходящего через
сопло Лаваля, в окрестности точки перехода через скорость звука
на оси сопла. Отдельные работы, появившиеся в последующий пе-
период, не были объединены ни общностью методов, ни преемствен-
преемственностью результатов.
Детальное изучение особенностей околозвуковых течений раз-
развернулось лишь после второй мировой войны, когда развитие авиа-
авиационной техники потребовало решения вопросов, связанных с по-
полетом при околозвуковых и сверхзвуковых скоростях. Наибольшие
успехи были достигнуты в плоской задаче благодаря следующим
двум главным обстоятельствам. Во-первых, основные уравнения пло-
плоскопараллельного установившегося безвихревого течения допускают
линеаризацию посредством перехода на плоскость годографа скоро-
скоростей. Во-вторых, специалисты—механики освоили достаточно хо-
хорошо развитую теорию линейных уравнений смешанного (эллиптико-
гиперболического) типа, разработанную еще в 1923 г. итальянским
математиком Ф. Трикоми.
Эти два момента впервые 5'дачно сочетались в работе Ф. И. Франк-
ля „О задачах С. А. Чаплыгина для смешанных до- и сверхзву-
сверхзвуковых течений", появившейся в 1945 г. Для практического при-
применения теоретических результатов важное значение имел открытый
в 1947 г. Т. Карманом и С. В. Фальковичем закон подобия для
околозвуковых течений. В настоящее время литература по околозву-
околозвуковым течениям насчитывает много сотен работ, и теория около-
околозвуковых течений является теперь полноправной самостоятельной
чаучной дисциплиной.
Автор предлагаемой вниманию читателя книги, К. Г. Гудерлей,
является одним из крупнейших в США специалистов по околозву-
околозвуковым течениям. Его работы в этой области внесли существенный
вклад в теорию, главным образом в ее прикладной части.

ПРЕДИСЛОВИЕ РЕДАКТОРА
Значение и особенности этой книги определяются тем, что она
представляет собой первую в мировой литературе попытку система-
систематического изложения математических методов исследования около-
околозвуковых течений. Здесь нашли свое отражение многие результаты,
полученные в этой области до 1956 г.
Изложение носит конкретный физический характер. Не вдаваясь
Особенно глубоко в тонкости теории уравнений смешанного типа,
Гудерлей все время стремится направить внимание читателя на изу-
изучение явлений, происходящих при околозвуковых течениях. Вся
книга от начала и до конца проникнута духом приложений к прак-
практическим вопросам. Благодаря этому не все стороны- теории полу-
получают одинаковое освещение. Автор подробно останавливается на
таких, например, частных вопросах, как закон подобия, линейная
теория или расчет по Буземану методом характеристик. В то же
время он весьма бегло касается проблем корректности постановки
рассматриваемых краевых задач и применяемых численных методов,
отсылая читателя, когда это возможно, к первоисточникам.
Методика использования математического аппарата, применяемая
Гудерлеем, может быть кратко выражена формулой: „сначала угадай
решение, а затем проверь его". В реализации первой части этой
формулы существенную помощь оказывает метод годографа, кото-
которым автор пользуется с большим мастерством. Что же касается
второй, то здесь не всегда удается получить окончательный резуль-
результат. Это замечание не является упреком автору и сделано только
для того, чтобы подчеркнуть несовершенство теории. И сейчас мы
еще далеки от того, чтобы уметь дать удовлетворительный ответ
на все вопросы об особенностях околозвуковых течений.
Составленная автором обширная библиография охватывает наи-
наиболее важные работы по околозвуковым течениям, в том числе
и работы советских ученых. Она приводится без всяких изменений.
Отдельные дополнительные ссылки даны в подстрочных примечаниях.
В процессе перевода и редактирования в немецком издании книги
было обнаружено большое количество опечаток. В настоящем из-
издании эти опечатки исправлены.
Основная ценность книги К. Г. Гудерлея заключается в том, что
она содержит большой фактический материал. Поэтому она может
быть рекомендована широкому кругу читателей, интересующихся про-
проблемами околозвуковых течений.
Л. В. Овсянников

Посвящается
Адольфу Буземану

ПРЕДИСЛОВИЕ
Околозвуковые течения характерны тем, что в них одновременно
существуют сверхзвуковая и дозвуковая области. Глубокое различие
между сверхзвуковыми и дозвуковыми течениями является причиной
ряда трудностей, возникающих при исследовании околозвуковых те-
течений. До настоящего времени эти трудности не преодолены. Напри-
Например, даже такой, казалось бы, простой вопрос, как распределение
давления вдоль заданного профиля, все еще остается без удовлетво-
удовлетворительного ответа. При таком положении вещей теория "околозвуко-
"околозвуковых течений должна стремиться в первую очередь к тому, чтобы
объяснить главные свойства и особенности околозвуковых течений.
От попыток же точного предсказания деталей теория пока выну-
вынуждена отказываться.
Однако даже при такой ограниченной программе требуется неко-
некоторая осторожность. В самом деле, для дозвуковых и сверхзвуковых
течений могут быть указаны аналогичные физические явления, кото-
которыми можно воспользоваться для придания наглядности пояснениям.
Кроме того, тесное родство между дифференциальными уравнениями
дозвуковых течений и уравнением Лапласа и между дифференциаль-
дифференциальными уравнениями сверхзвуковых течений и волновым уравнением
значительно облегчает исследование тех и других течений. Иное по-
положение мы имеем для околозвуковых течений. Во-первых, почти
не существует других физических явлений, которые были бы анало-
аналогичны смешанным течениям, а, во-вторых, разработанная в настоящее
время теория дифференциальных уравнений смешанного (эллиптико-
гиперболического) типа, как бы она ни была ценна, недостаточна
для получения полного ответа на фундаментальные математические
вопросы.
Таким образом, при исследовании околозвуковых течений едва ли
можно полагаться на физическую интуицию или на соображения
правдоподобности. Однако для автора это вовсе не означает, что
следует итти по чисто формальному пути, так как анализ точных
решений некоторых частных задач и тщательное исследование усло-
условий течения иногда все же позволяют дать наглядное толкование
явлениям околозвуковых течений, что, в свою очередь, дает возмож-
возможность экстраполировать полученные результаты за пределы точно
известного.

10 ПРЕДИСЛОВИЕ
Так или иначе, при исследовании околозвуковых течений во избе-
избежание неправильных заключений необходимо обращаться к основным
положениям чате, чем в теории до- и сверхзвуковых течений. Кроме
того, во многих случаях следует проявлять значительно большую
осторожность в математических умозаключениях. Отсюда становится
понятным, почему в настоящей книге математические рассуждения
занимают значительно больше места, чем в книгах, посвященных до-
и сверхзвуковым течениям.
Автор будет считать свою цель достигнутой, если настоящая
книга поможет специалисту-аэродинамику понять математические ме-
методы и результаты теории околозвуковых течений, а специалисту-
математику покажет те математические вопросы, которые выдвигаются
физическими проблемами околозвуковых течений, и тем самым, быть
может, натолкнет его на желание устранить некоторые пробелы в ма-
математической разработке, упростить ход рассуждений и обогатить
рассматриваемую область новыми методами.
Во избежание чрезмерного увеличения объема книги автором опу-
опущены некоторые вопросы, достаточно освещенные в литературе.
К таким вопросам принадлежат доказательство существования потен-
потенциального течения в сверхзвуковой области, заключенной внутри до-
дозвукового течения, и основы теории крыла в околозвуковой области.
В книге принята следующая система ссылок и обозначений. При
упоминании уравнений, содержащихся в другом параграфе, к но-
номеру уравнения присоединяется спереди номер главы и соответствую-
соответствующего параграфа. Перечень применяемых обозначений дан в конце
книги; в этом перечне указаны также страницы книги, на которых
дается объяснение соответствующего понятия или термина. При ци-
цитировании тех или иных работ упоминаются только фамилии авторов
с добавлением в квадратных скобках номера работы; название же
работы дается под тем же номером в списке литературы в конце
книги. Перечень литературы не претендует на полноту, однако автор
надеется, что основные направления в нем представлены. Личная точка
зрения автора не являлась решающей при выборе этой литературы.
Г. Гудерлей
Дейтон, штат Огайо (США),
сентябрь 1957

Глава I
ОБЩИЕ ОСНОВЫ
§ 1. Основные уравнения для невязких сжимаемых
течений
Свойства околозвуковых течений вытекают из уравнений общей
газовой динамики; вывод этих уравнений можно найти в многочислен-
многочисленных учебниках (см. перечень литературы в конце книги). В этой
главе мы приведем только важнейшие понятия и уравнения с пояс-
пояснениями, показывающими их логическую связь. Более подробно мы
остановимся на понятии характеристик, так как некоторые следствия,
вытекающие из этого понятия, имеют особенно важное значение для
понимания смешанных до- и сверхзвуковых течений. Наконец, мы
покажем формальный способ вывода приближенных уравнений дви-
движения газа. В дальнейшем этот способ в сочетании с законом по-
подобия для околозвуковых течений окажется весьма полезным для
получения важных результатов.
Начнем с вывода основных уравнений для сжимаемых течений.
Здесь и во всех дальнейших исследованиях мы с самого начала бу-
будем пренебрегать трением и теплопроводностью. Это означает, что
в движущемся газе отсутствует механизм для передачи тепла от одних
частиц газа к другим и, кроме того, невозможен переход механи-
механической энергии в теплоту '). Следовательно, энтропия каждой частицы
газа будет постоянной.
Исключение будут составлять скачки уплотнения. С физической
точки зрения такие скачки представляют собой чрезвычайно узкие
зоны, в которых градиент температуры и скорость деформации ча-
частицы принимают столь высокие значения, что увеличение энтропии
возникает даже при ничтожно малых теплопроводности и внутреннем
трении. Если з наших расчетах будут встречаться скачки уплотне-
уплотнения, то мы будем рассматривать занимаемые ими узкие зоны как
общую границу двух областей, в каждой из которых течение про-
происходит без трения и теплопроводности. На этой границе возникают
скачкообразные изменения давления, энтропии и скорости, величина
которых определяется так называемыми условиями перехода через
скачок уплотнения.
Пусть х, у и z суть декартовы координаты пространства,
в котором происходит течение газа, vx, vy и vz — составляющие
1) Имеется в виду невозможность необратимого перехода механической
энергии в теплоту. — Прим. ред.

12 ГЛ. I. ОБЩИЕ ОСНОВЫ
скорости в направлении осей х, у и z, a s — энтропия. Составляющие
скорости и энтропию будем рассматривать как функции координат х,
_у, z и времени t. При принятых обозначениях условием постоянства
энтропии будет уравнение
ds ds . ds , ds , ds л /1Ч
¦dt=-di+dZv" + -5jV"-{-dzVs = 0- A)
Так как силами трения мы пренебрегаем, то единственными си-
силами, действующими на частицы газа, будут силы давления. Приме-
Применив к движущейся частице второй закон Ньютона в проекциях на
направления х, у, z, мы получим уравнения
1 dp , dv.n . dvw , dvx , dvx _ „ (C) .
p ox 'at ' x dx ' ' dy ' z dz '
1 dp dv.. dvv dvv dvu
p dy [ dt l e dx ] v dy * г dz ч '
+ g + Vg)+ + j?. ()
где р есть давление, а о ¦ —плотность. Уравнения B) называются
уравнениями движения Эйлера.
К уравнениям A) и B) необходимо присоединить уравнение, вы-
выражающее условие сохранения массы, которая не может ни вновь
возникать, ни исчезать. Это означает, что количество массы, выхо-
выходящее из неподвижного элемента пространства через его поверхность
и взятое со знаком минус, равно изменению массы, содержащейся
в этом элементе за рассматриваемый промежуток времени. Следова-
Следовательно,
if + JI^^i- «+ат<№> = °- ^
Это уравнение называется уравнением неразрывности.
Уравнения A), B) и C) вместе с термодинамическими соотноше-
соотношениями, выражающими давление газа как функцию энтропии и плот-
плотности, с граничными условиями рассматриваемой задачи и с условиями
перехода через скачки уплотнения (если такие скачки возникают)
дают полное математическое описание течения газа. Никакие другие
физические допущения, вообще говоря, не нужны, и все дальнейшие
исследования должны были бы вестись чисто математическим путем.
Впрочем такой путь исследования отнюдь не исключает целесообраз-
целесообразности привлечения наглядных соображений или физического толко-
толкования результатов, полученных математическим путем. Наоборот,
использование таких методов является важным вспомогательным сред-
средством исследования. Однако результаты можно считать надежными
только тогда, когда их можно вывести из перечисленных выше урав-
уравнений.
Для исследования осесимметричных установившихся течений целе-
целесообразно пользоваться цилиндрическими координатами х, г, со, при-

§ 2. УРАВНЕНИЕ БЕРНУЛЛИ 13
чем ось х следует совместить с осью цилиндра. В такой системе
координат уравнение неразрывности принимает вид
д (?vx)
~дх
где vr есть составляющая скорости в направлении возрастающих зна-
значений г.
§ 2. Уравнение Бернулли
Приняв некоторые дополнительные допущения, мы можем вывести,
сверх указанных в предыдущем параграфе, другие и притом доста-
достаточно общие соотношения. Приведем их здесь без доказательства.
Если скорости не зависят от времени, то либо из первого основ-
основного закона термодинамики, либо—для областей, свободных от скач-
скачков уплотнения,—из уравнений движения Эйлера (путем их инте-
интегрирования) можно вывести соотношение
/ + ^1 = const, A)
где I есть энтальпия, отнесенная к единице массы, a w — абсолют-
абсолютное-значение скорости. Это соотношение называется уравнением
Бернулла. Постоянная в его правой части может быть различной
для разных линий тока; однако во многих случаях, например для
всех течений, обтекающих какое-либо тело так, что до подхода
к телу все линии тока параллельны, эта постоянная одна и та же
на всех линиях тока. Такого рода течения называются азоэнерге-
тическими. Вывод уравнения Бернулли с помощью первого основ-
основного закона термодинамики показывает, что оно применимо также
в тех случаях, когда имеются скачки уплотнения. Напротив, оно не-
неприменимо, если существуют трение и теплопроводность.
Укажем несколько соотношений, которые можно вывести, если
принять, что отношение удельных теплоемкостей остается постоян-
постоянным. Предварительно введем некоторые обозначения. Пусть R есть
газовая постоянная, отнесенная к единице массы, ср и с,. — теплоем-
теплоемкости при постоянном давлении и постоянном объеме, отнесенные
также к единице массы, -/. — отношение cplcv этих теплоемкостей и
Т — абсолютная температура. Тогда уравнение состояния газа будет
иметь вид
|=/?7\ Bа)
Для адиабаты имеет место соотношение
-?= const. B6)

14 ГЛ. I. ОБЩИЕ ОСНОВЫ
Далее, имея в виду, что
-" — х, (За)
Cp — cv = R, C6)
мы получим соотношение
следовательно, энтальпия, отнесенная к единице массы, равна
i==cPT = T=\RT- D)
Введем теперь величину
Ш =;Л, E)
д? Л const Р
причем дифференцирование необходимо выполнять при постоянной
энтропии. Из акустических соображений (см. § 5 гл. III) следует,
что величина а есть не что иное, как скорость звука в газе, хотя
в данном выводе это не очевидно. Внеся величину а в равенство D),
преобразованное в соответствии с уравнением Bа), мы получим
i = -^T. F)
х — 1 v J
Подставив это значение i в уравнение Бернулли A), мы будем иметь
й2 да3 ,_ч
——т-~1—^— = const. G)
То значение скорости w, которое равно соответствующей скорости
звука а, называется критической скоростью. Все величины, вычи-
вычисленные для критической скорости, будем обозначать в дальнейшем
посредством звездочки, поставленной справа от соответствующей
буквы, например w* = a*, p*, р*.
Положив в уравнении G) w = а = w* = а*, мы получим для по-
постоянной, стоящей в правой части уравнения, значение
следовательно,
а — g w г2 w . )
Отношение -да/а называется числом Маха и обозначается буквой М.
При выводе уравнения Бернулли посредством интегрирования
уравнений Эйлера получается — в качестве промежуточного резуль-
результата— для любого закона изменения состояния газа соотношение
= 0, (9)

§ 3. ТЕОРЕМЫ О ВИХРЯХ 15
где дифференциалы следует брать вдоль линии тока. Для изоэнерге-
тического течения, в котором постоянна также энтропия, соотноше-
соотношение (9) применимо во всем поле течения 1).
Наконец, напомним соотношения
(«к»
которые справедливы также при любом законе изменения состояния
газа.
§ 3. Теоремы о вихрях
Пусть v есть вектор скорости. Тогда вектором вихря скорости
будет rot©; он равен удвоенной угловой скорости вращения частицы 2).
Для каждого векторного поля v имеет место соотношение
divrot© = 0. A)
Следовательно, если вектор rot©, вычисленный для определенного
момента времени, рассматривать как вектор скорости в несжимаемом
течении, то тогда на основании соотношения A) уравнение нераз-
неразрывности выполняется автоматически. (Что касается уравнений Эйлера,
то они выполняются только в том случае, когда активные силы
удовлетворяют определенным условиям.)
Проинтегрируем поле направлений, образуемое в определенный
момент времени векторами вихря скорости; мы получим так назы-
называемые вихревые линии, которые соответствуют линиям тока в только
что упомянутом фиктивном несжимаемом течении. Для установив-
установившегося течения можно ввести понятие трубок тока. Эти трубки
образуются линиями тока, исходящими из точек замкнутой кривой,
поэтому поверхность трубки тока состоит всегда из одних и тех же
линий тока. Аналогичным образом можно определить вихревые
трубки. Тогда на основании соотношения A) мы найдем, что поток
вектора вихря скорости через вихревую трубку остается постоянным.
Из этого, в свою очередь, следует, что вихревые трубки, а вместе с ними
и вихревые линии не могут оканчиваться внутри течения. Они могут
быть или замкнутыми, или продолжаться в бесконечность или же
заканчиваться на границах поля течения.
1) В этом случае соотношение (9) представляет собой уравнение в пол-
полных дифференциалах. — Прим. ред.
2) Эта угловая скорость принимается за вектор. Подчеркнем, что поня-
понятие угловой скорости вращения деформируемой частицы требует, вообще
'оворя, особого определения.

16 ГЛ. I. ОБЩИЕ ОСНОВЫ
Допустим, что плотность зависит только от давления; такая
зависимость имеет место, например, в несжимаемых, изотермических
или изэнтропических течениях. Тогда из уравнений Эйлера мы най-
найдем, что интеграл
г = § (Рх dx -4- vy dy -j- v, dz), ¦-
взятый вдоль замкнутой кривой С, движущейся вместе с частицами
газа, т. е. вдоль так называемой жидкой линии, остается постоян-
постоянным во времени. Этот интеграл называется циркуляцией скорости.
На основании интегральной теоремы Стокса он связан с векто-
вектором rot© посредством формулы
Г= Jtotvdf,
в которой интеграл следует взять по поверхности F, опирающейся
на кривую С. Вектор df означает ориентированный элемент поверх-
поверхности, т. е. представляет собой вектор, нормальный к рассматри-
рассматриваемому элементу поверхности. Направление этого вектора опре-
определяется направлением обхода элемента поверхности, а его модуль
равен площади элемента поверхности. Выражение rotorf/, стоящее
под знаком интеграла, есть скалярное произведение обоих векторов.
Согласно сформулированной теореме, циркуляция в течении,
в котором первоначально вихри отсутствовали, остается равной нулю
для всех жидких линий, первоначально бывших замкнутыми и остаю-
остающихся замкнутыми в дальнейшем. Наличие вихревых поверхностей,
образующихся в следе за крылом или срывающихся с острых кро-
кромок обтекаемого тела, не противоречит этой теореме, так как
жидкие линии, проходящие через такие поверхности, в предшествую-
предшествующие моменты времени были не замкнутыми, а оканчивались на поверх-
поверхности рассматриваемого тела.
Если отбросить допущение, что плотность зависит только
от давления, то отсутствие вихрей в начальном состоянии отнюдь
не означает, что течение будет безвихревым и в дальнейшие моменты
времени. Вращение частиц будет возникать, например, в том слу-
случае, когда энтропия внутри поля течения не постоянна.
Для установившихся 1) изоэнергетических течений имеет место
теорема Крокко (Осватич [1], см. лит. 1), выражаемая уравнением
rot v X ч> = Т grad s, C)
где знак X означает векторное умножение. Это уравнение опре-
определяет составляющую вихря в направлении, перпендикулярном к линиям
!) Слово „установившиеся", собственно говоря, излишне, так как опре-
определение изоэнергетического течения уже предусматривает установившийся
характер течения.

§ 4. ПОТЕНЦИАЛ СКОРОСТЕЙ 17
тока. Так как вдоль линии тока энтропия 5 постоянна, то grads
направлен перпендикулярно к линиям тока. Для вычисления каса-
касательной составляющей вектора вихря скорости следует использовать
уравнение A).
В плоских и осесимметричных течениях составляющая вектора
вихря по направлению линий тока вследствие симметрии равна нулю.
Для таких течений вектор вихря скорости определяется на основа-
основании одной только теоремы Крокко.
В дальнейшем теорема Крокко будет использована для того,
чтобы оправдать пренебрежение вихрями в околозвуковых течениях.
§ 4. Потенциал скоростей
Пусть энтропия в течении постоянна, а само течение в началь-
начальном состоянии свободно от вихрей; в таком случае течение остается
свободным от вихрей и в дальнейшие моменты времени, если
не считать вихревых слоев, которые могут возникать на острых
кромках обтекаемого тела. Это означает, что составляющие вектора
вихря скорости обращаются в нуль, т. е. имеют место равенства
dv~ dv,, dv,, dv, dv~ dv.r
* -^ = 0, «—'=0, -,'-—-A- = 0, A)
dy dx dz dy dx dz v '
и поэтому вектор скорости может быть выражен в виде
В координатной записи эта формула распадается на три формулы:
_ дФ дФ дФ
х дх У ду - dz v '
Следовательно, в рассматриваемом случае векторное поле скоростей
описывается скалярной величиной Ф, называемой потенциалом ско-
скоростей.
Если составляющие скорости заданы формулами B), то уравне-
уравнения Эйлера I, 1 B) удовлетворяются автоматически. Смысл, в кото-
котором следует понимать эти слова, поясним для случая установившегося
течения. Пусть Ф есть произвольная дважды дифференцируемая
функция от х, у, z. Имея эту функцию, мы можем определить по-
посредством формул B) скорости vx, vy, vz. Если скорость известна,
то из уравнения Бернулли можно вычислить давление. Подставив
найденное значение давления в уравнения Эйлера, мы увидим, что
последние тождественно удовлетворяются. Следовательно, единствен-
единственным соотношением, которому должна удовлетворять функция Ф,
остается уравнение неразрывности.
В случае изоэнергетического течения, для которого отнюдь не
обязательно допущение о постоянстве энтропии, уравнение неразрыв-
неразрывности I, 1 C) можно выразить через потенциал скоростей Ф сле-
следующим образом. Будем рассматривать при описании термодинами-
2 Зак. 534. К. Г. Гудерлей

18 ГЛ. I. ОБЩИЕ ОСНОВЫ
ческого состояния газа давление и энтропию как независимые пере-
переменные. Выше мы ввели для производной др/др (которая всегда
положительна, так как в противном случае состояние газа было бы
неустойчивым) обозначение 1/а2 [формула I, 2E)]. Величина а,
представляющая собой скорость звука в газе, зависит только or
термодинамического состояния газа, но не от его движения. Мы имеем
dp dp dp , dp ds __ 1 dp , dp ds ,q..
Wx ~др Их* ~5s "die ~cfl ~d~x ' ~ds ~dx ^
для направления x и аналогичные соотношения для других напра-
направлений. Для установившихся течений уравнение неразрывности I, 1 C)
в более развернутой записи принимает следующий вид:
dp dp dp dvx dv,, dvz
Подставив сюда вместо др/дх, dpjdy, dp/dz выражения вида C) иг
исключив производные от р при помощи уравнений Эйлера, а про-
производные от я— при помощи уравнения I, 1A), мы получим
д х \1 а* ) ^ dy \ cfl )^r dz
(дух дуу \ ухуу (дуу dvz\ vyvz / dv
dx I a? V dz "¦" dy J '~cfl~ \ dx ^ dz ) a? ~~0'
D)
Если течение потенциальное, то это уравнение принимает вид
ФТ,Ф,,
Далее, из уравнения Бернулли следует, что
fl2_^_+i ^_ JL--L(ф + J + % (>
Для осесимметричного потенциального течения уравнение E) при-
принимает более простой вид, а именно:
Ф Ф Ф
Упомянем, что для изэнтропических и первоначально безвихре-
безвихревых течений потенциал скоростей существует и в том случае, если
течение неустановившееся, но тогда уравнение Бернулли заменяется
уравнением
^ у-г-Ф*>= const (8)

5. ФУНКЦИЯ ТОКА 19
Уравнения Эйлера по-прежнему интегрируются путем введения потен-
потенциала. Уравнением неразрывности будет
Ф2'
=0. (9)
ФН .r'Pj/ У z ^z^x
Фх Фу Фг
§ 5. Функция тока
Для плоских установившихся течений уравнение неразрывности
имеет вид
д (ovT) d(pvu)
| (~\ A Л
Для осесимметричных течений в системе цилиндрических коорди-
координат х, г и (о уравнение неразрывности принимает вид
- 0. B)
дх ~*~ дг ' '
Уравнение A) интегрируется посредством подстановок
,™,;=|у. (За)
а уравнение B)—-посредством подстановок
rpv^^-^r, . Dа)
r?v' = -KF' Dб)
Функция <!f называется функцией тока, а линии ф— const — линиями
тока. Направление касательной к линии тока совпадает с направле-
направлением вектора скорости.
Так как уравнение неразрывности не связано с каким-либо пред-
предположением относительно постоянства энтропии или относительно
отсутствия вихрей в течении, то функцию тока можно ввести и для
течений с непостоянной энтропией и с наличием вихрей. Вдоль линии
тока энтропия постоянна, поэтому
S = S(<||).
Для потенциальных течений функция тока ty должна быть
Определена так, чтобы вихрь скорости был равен нулю. Однако

20 ГЛ. I. ОБЩИЕ ОСНОВЫ
использование полученного таким путем уравнения несколько затрудни-
затруднительно, так как входящие в него скорость звука и составляющие
скорости течения связаны очень неудобным образом с производными
от функции тока. При линеаризованном рассмотрении дозвуковых
течений эти трудности не играют никакой роли; они отпадают также
при использовании метода годографа. Для исследования течений
в околозвуковой области лучше всего использовать в плоскости
течения потенциал скоростей.
§ 6. Характеристики
Теория характеристик является надежным инструментом для иссле-
исследования сверхзвуковых течений. Так как постановка вопроса, приво-
приводящая к понятию характеристик, играет важную роль также при
рассмотрении свойств течения в околозвуковой области, то напомним
здесь в общих чертах теорию характеристик.
Построение метода характеристик на основе физических пред-
представлений (например, в форме Буземана) позволяет получить полный
аппарат для расчета течений и, кроме того, приводит к очень
наглядной картине процессов, происходящих при течении. Однако
для целей настоящей книги автор предпочитает формальное построе-
построение метода характеристик, так как такое построение лучше подчерки-
подчеркивает основную идею этого метода (см., например, Курант и Гиль-
Гильберт, т. II, лит. 2). Для простоты рассмотрим здесь только случай
плоского потенциального течения. Такое течение определяется урав-
уравнением неразрывности I, 4D)
и условием равенства нулю вектора вихря скорости
dvx dvv
^^ 0
ду дх
B)
Скорость звука в таком течении, согласно формуле I, 2(8), есть
функция модуля скорости w.
Пусть вдоль некоторой кривой С, лежащей в плоскости течения,
заданы векторы скорости. Конечно, эти векторы не всегда не зави-
зависят друг от друга, однако сначала мы примем, что все они образуют
совместимое распределение. В частности, можно просто взять подоб-
подобного рода распределение из какого-нибудь известного поля течения.
Поставим теперь следующий вопрос, пока еще не имеющий прямого
отношения к понятию характеристик: можно ли, имея заданную сово-
совокупность векторов вдоль кривой С, вычислить поле течения хотя бы
вблизи этой кривой?

% 6. ХАРАКТЕРИСТИКИ 21
Если составляющие vx и vy скорости вдоль кривой С заданы,
то тем самым известны также производные от этих величин вдоль С
по х. В самом деле, эти производные могут быть выражены через
частные производные от vx и vy no x и у и через наклон dyjdx
кривой С следующим образом:
C)
D)
Уравнения A)—D) представляют собой линейную систему уравне-
уравнений для четырех частных производных:
dvx dvx dvy dvy
dvx
дх
dVy
дх '
I dvx
1 ду
¦ дуУ
dy
dx
dvx
dx
dvy
dx
~дх~' ~д~у~' ~д~Т* ~<h~'
Если эта система разрешима, то частные производные от составляю-
составляющих скорости vx и vy могут быть определены для каждой точки
кривой С. Путем дифференцирования можно получить аналогичные
уравнения для производных более высоких порядков, причем коэф-
коэффициенты при неизвестных производных в левых частях уравнений
будут оставаться всегда одними и теми же. Следовательно, зная
векторы скорости вдоль кривой С, мы можем определить в каждой
точке этой кривой все производные составляющих скорости vx и vy;
имея же эти производные, мы можем построить поле течения вблизи
кривой С, пользуясь рядом Тэйлора.
Система уравнений A)—D) всегда однозначно разрешима, если
определитель, составленный из коэффициентов при неизвестных в левых
частях уравнений, не равен нулю. Понятие характеристик относится
к тому исключительному случаю, когда указанный определитель
равен нулю. В системе уравнений A)—D) в коэффициенты при
неизвестных, кроме скоростей vx и vy, входит и наклон dyjdx кри-
кривой С, определяющий ее направление в рассматриваемой точке.
Выясним, имеются ли такие направления кривой С, для которых
определитель, составленный из коэффициентов при неизвестных
частных производных, равен нулю. Для этой цели в рассматривае-
рассматриваемой точке Р кривой С лучше всего перейти к такой системе декар-
декартовых координат х', у', в которой ось х' совпадает с направлением
местного вектора скорости. Это можно сделать, не изменяя формы
Уравнений, так как в плоских течениях отсутствует какое-либо
привилегированное направление *). В новой системе координат соста-
составляющей скорости в направлении оси х' будет w, а составляющей
в направлении оси у' — нуль. Приравняв определитель нулю,
х) Уравнения A) и B) инвариантны по отношению к повороту осей коор-
-хП. ред.

22
ГЛ. I. ОБЩИЕ ОСНОВЫ
мы получим
1_ EL
О
1
О
1
dx'
О
О
— 1
О
1 -.
1
О
о
dx'
= 0,
откуда найдем
*?. ._ + лГ
Л v' ~ 1' я-п.9
dx
a?
Для w <C а (или М <_ 1) характеристик не существует. Именно это
обстоятельство и обусловливает существенное различие между до-
дозвуковыми (М < 1) и сверхзвуковыми (М > 1) течениями.
Обычно в только что полученное уравнение вводят так называе-
называемый угол Маха, определяемый равенством
—= arc sin —.
w
E)
Тогда предыдущее уравнение принимает вид
Следовательно, определитель, составленный из коэффициентов при
неизвестных в левых частях рассматриваемой системы уравнений,
обращается в нуль, если кривая С образует с вектором скорости
угол ± а.
Прежде чем перейти к дальнейшему исследованию нашей системы
уравнений, заменим в них составляющие скорости vx и vy их выра-
выражениями через модуль скорости w и через угол ft, образуемый век-
вектором скорости с направлением оси х или х'. Из соотношений
vx =
Vy ~ та sin ft
F)
мы имеем
dvv —-- dw cos 8 — w sin & db,
dv,, —- dw sin Ь -\- w cos ft dft
if
или для специально выбранной системы осей х', у'
dvx~dw, dVy~wdb.
Внеся эти выражения и найденное выше значение dy'/dx' в уравне-

§ 6. ХАРАКТЕРИСТИКИ 23
ния A)—D), мы получим
-S ctg^a + w|» =0 tga
dw d§ „
3-7 W -,• — = 0
dy dx
da» _• dw , dw
dx' ~ dy' ь dx'
db , d» , rfft
¦ш 3—,- ± tiy 3—7 tg a = и/ -7—.
Ctga
Так как определитель, составленный из коэффициентов при частных
производных в левых частях уравнений, равен нулю, то между
этими уравнениями существует линейная зависимость. Множители,
написанные справа, показывают, как получается линейная комбина-
комбинация, тождественно равная нулю. Эти множители можно найти, после-
последовательно исключая неизвестные.
Если полученные уравнения должны удовлетворяться конечными
значениями частых производных
dw dw d& d$
dl7' д~у~" аЗР"' ду''
(а это имеет место в поле течения почти везде), то правые части
должны быть связаны между собой таким же линейным соотноше-
соотношением, как и левые части. Правые части в последних уравнениях
содержат производные в направлении оси х', т. е. в направлении
кривой С. Следовательно, должно соблюдаться соотношение
ElSfL ?!Е х ** — о G)
w dx' + dx' — V- {l)
Это соотношение иногда называется условием совместности для
характеристик. Кривая, для которой, во-первых, определитель,
составленный из коэффициентов при неизвестных в левых частях
уравнений A)—D), равен нулю во всех ее точках и, во-вторых,
удовлетворяется условие совместности между правыми частями тех же
уравнений, называется характеристикой, а в случае течений газа —
волной Маха. Вдоль характеристики дифференциалы изменений со-
состояния связаны друг с другом соотношением G). Это свойство
используется для расчета поля течения.
Частные производные
dw dw d§ db
d~7' ЪУ' дУ Jy~'~
определены для характеристики не однозначно. В самом деле,
поскольку определитель, составленный из коэффициентов при этих
производных в левых частях уравнений A)—D), равен нулю, су-
существует нетривиальное решение однородной системы уравнений,

24 ГЛ. I. ОБЩИЕ ОСНОВЫ
и полное решение системы A)—D) складывается из решения неодно-
неоднородной системы и решения однородной системы, умноженного на
произвольный множитель. Это означает, что производные скорости
в направлениях, не совпадающих с кривой С, на обеих сторонах
кривой могут быть различны, иными словами, поля течения по обе
стороны кривой С могут не переходить одно в другое посредством
аналитического продолжения. Это обстоятельство часто выражают
также следующими словами: вдоль характеристик может распро-
распространяться особенность первых производных скорости.
Аналогичное обстоятельство имеет место и для производных
более высоких порядков. В самом деле, левые части уравнений для
этих производных остаются такими же, как и в системе уравнений
A)—D), и так как эти левые части определяют направления харак-
характеристик, то разрывы производных высших порядков распростра-
распространяются вдоль тех же кривых, вдоль которых распространяются
разрывы первых производных. С другой стороны, в потенциальных
течениях характеристики являются единственными кривыми, вдоль
которых могут возникать разрывы производных скорости.
Возникают ли в поле течения такие разрывы в действительности,
зависит от граничных условий. Если, например, на стенке, ограни-
ограничивающей течение, имеется в какой-либо точке скачкообразное изме-
изменение кривизны, то вдоль характеристики, исходящей из этой точки,
возникает скачкообразное изменение кривизны всех линий тока.
Можно вычислить также величину скачка, однако здесь мы не будем
этого делать, так как это завело бы нас слишком далеко.
В дальнейшем понятие характеристик используется также в связи
с другими уравнениями. В случае уравнения Трикоми
проще всего положить
Тогда мы получим систему уравнений
Вычисления, аналогичные выполненным выше, дадут для определения
направления характеристик уравнение
Условием совместности вдоль характеристик будет
0. (9)

§ 7. УПРОЩЕНИЯ ДЛЯ ПЛОСКИХ ПОТЕНЦИАЛЬНЫХ ТЕЧЕНИЯ 25
Для осесимметричных околозвуковых течений в качестве при-
приближения мы выведем ниже уравнение
— (х +1) фжфжж+фгг+-;- =-- о.
Введя обозначения
мы получим следующую систему дифференциальных уравнений первого
порядка:
"г — vx =-- 0-
Выполнив вновь такие же вычисления, как и выше, мы найдем для
определения направления характеристик уравнение
^-=±(*~МI/'Ф?. (Ю)
Условием совместности будет
_dx d%, ёФг , Фг__п ,1П
'dr dr ~*~ dr ~т~ r'~ к у
В этих уравнениях производные dx/dr, dQJdr и d^>r\dr взяты вдоль
характеристик Z
§ 7. Упрощения для плоских потенциальных течений
В то время как рассуждения предыдущего параграфа, если их
немного видоизменить, могут быть применены также к течениям
более общего вида, например к неизэнтропическим или к осесимме-
тричным, упрощения, которыми мы займемся сейчас, могут быть
выполнены только для плоских потенциальных течений. Эти упро-
упрощения приводят к некоторым понятиям, важным для дальнейшего
изложения.
В потенциальном течении энтропия постоянна и, кроме того,
постоянная в уравнении Бернулли имеет одно и то же значение для
всех линий тока. В таком течении скорость звука определяется
формулой I, 2(8)
а2 = —J- w* н— w ¦
Следовательно, угол Маха [формула I, 6E)] является функцией
только от скорости, и поэтому уравнение I, 6G) можно проинтегри-
проинтегрировать. Введя обозначение
«?Ldw. A)
w*

6 ГЛ. I. ОБЩИЕ ОСНОВЫ
мы получим для характеристик уравнения
J + Ь — const. B)
Верхний знак относится к характеристикам, направление которых по-
получается из направления линий тока поворотом на угол Маха против
направления движения часоиой стрелки, а нижний знак — к харак-
характеристикам другого семейства. Толмин предложил для этих семейств
характеристик название левобегущих и правобегущих волн Маха1).
Уравнение B) показывает, что характеристики плоскости течения
отображаются в такие кривые плоскости w, 8- (т. е. плоскости годо-
годографа скоростей), которые заранее известны. Конечно, эти последние
кривые представляют собой не что иное, как характеристики урав-
уравнения течения в плоскости годографа скоростей. В самом деле,
свойство характеристик, заключающееся в том, что вдоль них могут
распространяться разрывы производных скорости, при отображе-
отображении сохраняется. В методе характеристик, предложенном Бузе-
маном ([2], см. лит. 1), характеристиками в плоскости годографа
являются эпициклоиды.
При пользовании методом Буземана в плоскости течения строятся
только такие характеристики, которые принадлежат к заранее вы-
выбранному семейству, например такие, которые соответствуют харак-
характеристикам в плоскости годографа, получающимся друг из друга
путем поворота на постоянный угол, называемый „тагом" и равный,
например, 1J. Между точками пересечения характеристик направление
характеристик в плоскости течения заменяется их средним значением.
Так как точки пересечения определяются выбором подлежащих
вычерчиванию характеристик, то в плоскости течения могут встре-
встретиться только заранее определенные значения для наклона характе-
характеристик, которые проще всего подготовить заранее в виде таблицы.
Если это сделано, то диаграмма характеристик в плоскости годо-
годографа, положенная в основу построения, становится больше ненужной.
Однако она сохраняет свою ценность как наглядное представление
(Темпл, см. лит. 1).
Буземан вводит следующие обозначения:
X = 400 + ~ (— /-L- 9), C)
QO
[х =600 -+- — (— J— 9). D)
Значения X — const соответствуют левобегущим характеристикам,
а значения tx = const — правобегущим характеристикам. Если X и ;а
*) Нетрудно убедиться, что эти понятия не зависят от] направления,
в котором проходятся линии тока.

§ 8. ПРИМЕРЫ 27
заданы, то ft и J определяются формулами
f /.-u), E)
(). + IA)]. F)
Множитель 90/-^ введен в формулы C) и D) для того, чтобы угол ft
в формуле E) выражался в градусах. Согласно формуле F), вели-
величина J и вместе с нею скорость w, а также все функции, зависящие
от w, выражаются через /.-(-[А. Для этих функций вычислены
таблицы, помещенные, например, в книге Зауэра (см. лит. 2).
Числа 400 и 600 введены в формулы C) и D) исключительно для
того, чтобы легче различать значения /. и \х.
Для того чтобы дать сети характеристик, построенной рассмот-
рассмотренным способом, наглядное толкование, Буземан рассматривает те-
течение внутри каждого четырехугольника, образованного двумя па-
парами характеристик, как параллельное течение, состояние которого
отвечает центру четырехугольника, образованного соответствующими
парами характеристик в плоскости годографа. В таком случае при
переходе от одного четырехугольника к соседнему направление век-
вектора скорости изменяется на величину „шага", т. е. всегда на один
и тот же угол, независимо от того, в каком месте совершается пе-
переход через характеристику. Из сравнения плоскости течения и пло-
плоскости годографа, а также непосредственно из уравнения I, 6G)
видно, что с переменой направления вектора скорости связано
изменение его модуля, причем это изменение для одной и той же
волны Маха имеет всегда один и тот же знак независимо от того,
где, т. е. при какой скорости, совершается переход этой волны.
Волну Маха называют волной сжатая, или волной уплотнения,
если при переходе ее в направлении течения давление возрастает,
и волной расширения, или волной разрежения,—в противном слу-
случае. Обычно волны сжатия вычерчиваются сплошными, а волны
разрежения — штриховыми линиями. При таком соглашении об обо-
обозначениях каждая из вычерченных в плоскости течения волн как бы
изображает изменение состояния в этой плоскости, а вся система
волн позволяет следить за изменением состояния, происходящим
в поле течения ').
§ 8. Примеры
Покажем на примерах практическое применение метода характе-
характеристик. При этом одновременно выяснится, как следует формули-
формулировать краевые задачи и задачи о начальных значениях.
1) При применении метода характеристик к более общим случаям тече-
течения характеристики такими свойствами не обладают и представляют собой
только линии, по которым особенно выгодно вести расчеты.

28
ГЛ. I. ОБЩИЕ ОСНОВЫ
направление
течения
Пусть вдоль кривой АВ, пересекающей каждую характеристику
самое большее один раз (рис. 1), заданы векторы скорости. Опре-
Определив по этим данным значения функций X и и., возьмем затем для
последних в качестве приближения ступенчатые кривые, поскольку
в методе Буземана используются только заранее выбранные значе-
значения X и \ь. Тогда мы будем знать на кривой ЛВ положение тех
точек, в которых X и ji претерпевают разрывы. Из этих точек
исходят характеристики. Для простоты примем, что разрывы X и о.
происходят также в точках А и В, следовательно волны Маха исхо-
исходят и из этих точек. Тогда, исходя
из кривой АВ, можно построить сеть
характеристик в четырехугольнике
ACBD. Для этого надо использо-
использовать то обстоятельство, что X со-
сохраняет постоянное значение вдоль
левобегущих характеристик, a jj. —
вдоль правобегущих. Четырехуголь-
Четырехугольник ACBD есть именно та область
плоскости течения, в которой тече-
течение определяется векторами ско-
скорости, заданными вдоль линии АВ.
Конечно, возможно — и в действи-
действительности очень часто так и бы-
бывает,— что вдоль первоначально
Рис. 1. Применение метода характе- Выбранной КрИВОЙ ВСС ВеКТОры СКО-
ристик- рости параллельны друг другу, т. с.
имеет место параллельное течение.
В этом случае во всем четырехугольнике ACBD, теперь пред-
представляющем собой параллелограмм, происходит также параллельное
течение. Для того чтобы построить следующие части поля течения,
необходимо продолжить линию АВ так, чтобы вся получающаяся
при этом линия пересекала каждую из характеристик не более одного
раза. Вдоль взятого продолжения линии АВ опять следует задать
векторы скорости.
Если заданы границы течения, пересекаемые исходящими из АВ
линиями Маха, то вдоль этих границ должны быть заданы значения
только одного из элементов, определяющих вектор скорости, т. е.
либо направления скоростей, либо их модули.
Часто продолжением линии АВ является стенка или поверхность
профиля; тогда направление скорости должно быть касательно
к стенке или к поверхности профиля. Примем, что вдоль таких
границ встречаются только те значения Ь, которые получаются из
значений X и ji, заранее выбранных для сети характеристик. В таком
случае для определения состояния течения известны либо значения X,
либо значения ji, так как граница достигается либо левобегущими,
либо правобегущими волнами. Значения недостающей величины»

§ 9. МЕТОД ХАРАКТЕРИСТИК ДЛЯ ОКОЛОЗВУКОВЫХ ТЕЧЕНИЙ 29
т. е. либо [х,, либо X, вычисляются с помощью формулы I, 7E) по
заданному направлению скорости. На рис. 1 в точке Я волна Маха
встречает стенку, которая в этой точке не меняет своего направле-
направления. Вниз по течению от точки П распространяется правобегущая
волна Маха; там ;а = 595. Дано & — — 4°, поэтому X == 391.
В точке F значение i> переходит от —2° к 0°. Стенка дости-
достигается левобегущей волной. Выше и ниже по течению от точки F
величина X —397. По заданному значению Ь находим, что ниже по
течению от точки F величина ja = 597.
Другим часто .встречающимся условием бывает постоянство да-
давления вдоль границы. Вдоль такой границы модуль скорости со-
сохраняет постоянное значение, для которого в качестве приближения
лучше всего взять скорость, соответствующую одной из точек пере-
пересечения заранее заданной системы характеристик плоскости годо-
годографа. Дальнейшее построение производится так же, как и в пре-
предыдущем примере.
Волны уплотнения при встрече с плоской стенкой отражаются
¦от нее опять в виде волн уплотнения, а волны разрежения — опять
в виде волн разрежения; при встрече же со свободной поверхностью
или, в более общем случае, с линией постоянного давления, лежа-
лежащей в том же углу между характеристиками, в котором лежат и линии
тока, волны уплотнения переходят в волны разрежения, и наоборот.
Этих замечаний достаточно для того, чтобы понять суть метода
характеристик. Конечно, для быстрого построения поля течения
необходим некоторый практический опыт. За дальнейшими подроб-
подробностями, а также за менее абстрактным изложением отсылаем к учеб-
учебной литературе.
§ 9. Метод характеристик для околозвуковых течений
Для применения метода характеристик к околозвуковым течениям
следует придать ему несколько иную форму. Остановимся на ней,
во-первых, потому, что вблизи числа Маха, равного единице, дей-
действительно необходимо особое исследование для достаточно точного
определения направления характеристик, а, во-вторых, вследствие
того, что эта специальная форма метода характеристик дает особенно
простое пояснение закону подобия для околозвуковых течений.
Введем в качестве новой переменной разность между скоростью
и критической скоростью, т. е. величину
Дда = ге>— а*. A)
Условие совместности характеристик I, 6G), если ^заменить в нем а
его значением из формулы I, 6E), принимает вид
B)
2 w T

30 ГЛ. I. ОБЩИЕ ОСНОВЫ
Выразим разность w2 — а2 через \w, воспользовавшись для этого
равенством I, 2(8); сохранив только члены с Да> в первой степени,
мы получим
В первом приближении а2;—да*2. Внеся эти значения w1 — аг и а2
в условие совместности B), мы будем иметь
w'" wv* ~~ ""
откуда после интегрирования найдем
C)
таким образом, характеристики в плоскости Ди/, Ь являются в пер-
первом приближении полукубическими параболами.
Для определения направления характеристик вспомним, что ра-
радикал в уравнении (За) представляет собой приближенное значение
ctga, т. е.
Это означает, что отклонение угла Маха от тс/2 пропорционально
у Дда. Из уравнения C) следует, что если в начальной точке угол ft
равен нулю, то порядок его величины остается равным (Дге>K/а
во всем поле течения. Направление волн Маха определяется выра-
выражением Ь ± а. При небольших значениях Д-ш доля, вносимая в это
выражение первым слагаемым (&), на основании только что сказан-
сказанного мала по сравнению с долей, обусловленной вторым слагае-
слагаемым (+ а). Таким образом, для определения направления волн Маха
мы имеем уравнение
¦2-=<«+¦>-•(?)-*.
Уравнения C) и D) являются основой метода характеристик для
околозвуковых течений. В остальном этот метод применяется так же,
как и общий метод характеристик.
Из уравнений C) и D) видно, что путем одновременного изме-
изменения масштабов для зависимых и независимых переменных можно
преобразовать известное поле течения в ряд других течений. Так,
например, оставив координату х неизменной и умножив масштаб
для Дда на 1, масштаб для в- — на г?1* и масштаб для у — на т~-'Ч
мы придем к такой же системе уравнений, как и исходная система.

§ 10 ОБЩИЕ СООБРАЖЕНИЯ. СВЯЗАННЫЕ С ПОНЯТИЕМ ХАРАКТЕРИСТИК 31
г только что указанными изменениями масштабов мы подробнее
ознакомимся в § 6 гл. II при изложении закона подобия для около-
околозвуковых течений.
§ 10. Общие соображения, связанные
с понятием характеристик
Вводя понятие характеристик, мы исходили из задачи опреде-
определения поля течения вблизи кривой С в том случае, когда вдоль этой
кривой заданы векторы скорости. Для решения поставленной задачи мы
определили из линейной системы уравнений производные скорости?
для всех точек заданной кривой. В дозвуковой области эта система
уравнений всегда имеет однозначное решение, так как определитель,
составленный из коэффициентов при неизвестных в левых частях:,
уравнений, никогда не равен нулю. Отсюда следует, что в дозву-
дозвуковой области все частные производные скорости непрерывны..
В противоположность этому в сверхзвуковой области возможны
случаи, когда вдоль характеристик возникают разрывы частных
производных скорости.
Как показывает пример, разобранный выше для пояснения метода
характеристик, в сверхзвуковой области скорости вдоль нехарак-
нехарактеристической кривой можно задать произвольно. В дозвуковой
области этого делать нельзя. Мы сразу в этом убедимся, если рас-
рассмотрим уравнение для потенциала несжимаемых течений. Решения
этого уравнения всегда можно представить как вещественную часть
аналитической функции от аргумента x-\-iy. Если аналитическая
функция вместе со всеми своими производными в какой-либо точке
известна, то на основании принципа аналитического продолжения
эта функция известна во всей плоскости х, у. Следовательно, если-
решение уравнения для потенциала известно вдоль бесконечно малой
части кривой С, то тем самым оно известно также вдоль остающейся
части этой кривой. Поэтому если скорости в точках кривой С
заданы произвольно, то в общем случае мы придем к противоречию.
Это верно также и для сжимаемых течений в дозвуковой области.
Это замечание не лишено практического значения. В самом деле,
были случаи, когда для получения примеров сжимаемых течений за-
заранее устанавливалось распределение скоростей вдоль заданной
кривой (например, вдоль оси сопла или вниз по течению от скачка
уплотнения) и на основании этого распределения скоростей строилось
продолжение поля течения. На основании только что сказанного
такой прием в общем случае недопустим. Правда, обычно выбирают
распределение скоростей в виде аналитических функций; тогда в до-
достаточно малой окрестности существует аналитическое продолжение.
Однако неточность расчета может себя проявить так, как если бы
вь'бранные функции были неаналитическими, что приводит к труд-
трудностям, несмотря на сделанное допущение.

432 ГЛ. I. ОБЩИЕ ОСНОВЫ
§11. Некоторые замечания о формулировке краевых
задач в до- и сверхзвуковых течениях
Вопрос о том, как должны быть сформулированы краевые задачи,
¦с точки зрения инженера в общем случае не является особенно важ-
важным, так как исследуемая физическая задача сама по себе достаточно
ясно показывает, какие величины должны быть заданы *). Однако
для околозвуковых течений формулировка краевой задачи все же
требует осторожности, так как для таких течений имеется случай,
когда краевая задача, вытекающая из физических соображений,
может не иметь решения. Этим случаем является дозвуковое течение,
внутри которого содержится сверхзвуковая область. Для правильной
формулировки краевой задачи
задан один из элементов, в околозвуковой области сначала
определяющих вектор сопоставим важнейшие особен-
ft LKUfJUUIIU Ц
а—*-—^ Л ^ *¦ "^^ ности краевых задач в до- и
сверхзвуковой областях.
Задача о сверхзвуковом тече-
течении считается правильно сформу-
лированной в том случае, когда
ее решение может быть найдено
^д^одиниз С $1- посредством метода характери-
элементов,определяющих стик. Один из примеров такого
вектор скорости рода П(жазан нд рис> 2_ Здесь
Рис. 2. Граничные условия для сверхзвуке- Граница СОСТОИТ ИЗ крИВОЙ АВ,
вой области. ВДОЛЬ КОТОрОЙ ВеКТОр СКОрОСТИ
полностью известен, и из двух
других кривых АС и BD, на которых задан только один из элементов,
определяющих вектор скорости. Другая возможность показана на
рис. 3. Здесь заданы векторы скорости вдоль двух характери-
характеристик АВ и АС. Если, кроме того, вдоль этих характеристик вы-
выполняются условия совместности [уравнение I, 6G)], то поле течения
внутри четырехугольника ABDC, ограниченного двумя парами ха-
характеристик, может быть вычислено.
Вообще для сверхзвуковых течений характерно, что граничные
значения никогда не могут быть заданы вдоль замкнутой кривой2).
Для таких течений область, в которой может быть вычислено ре-
решение, частично должна быть ограничена характеристиками, значе-
значения на которых подлежат определению путем расчета.
*) Правда, при этом приходится опираться на физическую интуицию
и заранее нельзя сказать, насколько это может быть подтверждено строгим
математическим исследованием.
2) Это легко понять, если учесть аналогию между сверхзвуковыми те-
течениями и одномерными неустановившимися течениями. Развитие процесса
•не может быть определено условиями, заданными для будущего времени.

§ 11. НЕКОТОРЫЕ ЗАМЕЧАНИЯ О ФОРМУЛИРОВКЕ КРАЕВЫХ ЗАДАЧ 33
В противоположность этому в задачах о дозвуковом течении
граничные условия должны быть заданы вдоль всей границы рассмат-
рассматриваемой области, причем всегда должен быть задан только один
из элементов, определяющих вектор скорости, например либо его
нормальная, либо касательная составляющая (однако разрешимость
задачи в такого рода случаях зависит еще от одного интегрального
условия). Как было показано в предыдущем параграфе, в общем
случае невозможно произвольно за-
у с лать оба элемента, определяющих
л$ /"->. вектор скорости, вдоль какой-либо
<>$/$>/ \^ части контура.
Рис. 3. Граничные условия для
сверхзвуковой области.
Рис. 4. К вопросу о граничных
условиях для дозвуковой области.
Для пояснения разницы между до- и сверхзвуковыми задачами
приведем следующие два примера. Рассмотрим в плоскости х, у
прямоугольную область, стороны которой определяются уравнениями
у = 0, у =т, х = 0, х=-Ь (рис. 4). В качестве дифференциаль-
дифференциального уравнения, типичного для поведения дозвукового течения,
возьмем уравнение Лапласа
?Ф _j_ дЩ __ „
Пусть вдоль прямых у = 0 и у = ж задано значение Ф = 0. Част-
Частными решениями, удовлетворяющими этим граничным условиям,
будут
ф = е;тх Sin ту (т=1, 2, ...)¦>
С практической точки зрения удобнее использовать линейные ком-
комбинации выражений
Ф — sh mx sin my,
ф .= sh m (b — x) sin my.
Далее, пусть задано, что
вдоль х = О Ф = /i (у) @ <у < и),
вдоль х = Ь Ф = /2 (у) @ < у < ~).
3 Зак. 534. К. Г. ГудерлеЙ

34 ГЛ. I. ОБЩИЕ ОСНОВЫ
Общее решение возьмем в виде
со оо
ams]amxsin тУ + У\ bmsh тф — х) sin ту,
причем коэффициенты ат и Ът остаются пока неопределенными.
Внеся это значение Ф в граничные условия вдоль х = 0 и х = Ь,
мы получим
ее
f2(y) = V ат sh mb sin my,
Л (У) = ^ *m sh ^^ sin
Применив правила гармонического анализа, сразу найдем
Сходимость решения обеспечена, так как каждый из членов обеих
сумм принимает свое наивысшее значение вдоль границы х — Ъ или
соответственно л: —0, и суммы на этих границах сходятся — они
представляют здесь функции $х{у) и /2(у) в виде рядов Фурье.
Если граничные условия были бы такими же, как в сверхзвуко-
сверхзвуковой задаче, т. е. если бы вдоль CD не были бы заданы значения Ф,
а вдоль АВ были бы известны значения Ф-.=^/1(у) и дФ/дх =/2(у),
то формальным решением задачи было бы
ф = i 2 | / (^{у) + ~»г-)sin my dy I(sin my)e
|
m-l ' О
со f « j
/(л^~~P)sinmydy'(sinm-v)e~mx
(формальным потому, что вопрос о его сходимости остается откры-
открытым). В общем случае это решение сходится не во всей рассматри-
рассматриваемой области. При стремлении т к бесконечности должны оста-
оставаться ограниченными внутри рассматриваемой области по крайней
мере отдельные члены первой суммы. Это означает, что должны

§ 12. ОБ ОДНОМ СПОСОБЕ ВЫВОДА ПРИБЛИЖЕННЫХ УРАВНЕНИЙ 35
оставаться ограниченными выражения
f/i СУ) •+-—?¦) si" my dy I e
mx
что, безусловно, налагает сильные ограничения на функции fl и /2.
В качестве второго примера рассмотрим сверхзвуковую задачу,
описываемую уравнением
причем за область, в которой надлежит определить течение, возьмем
такой же прямоугольник, как и в первом примере. Если вдоль х ¦— О
заданы значения Ф=/1(_у) и дФ/'дх —f.,(y), то решением будет
со I r" \
Ф —- V I j /1(y) s\n my dy) sin my cos тх ~\-
т- 1 \0 /
, 2 V / f' . . . , \ 1 .
~\~-¦ /Л\ у? (V) sin/rev a v —sin т у sin mx,
т -1 \ о /
в чем нетрудно сразу убедиться простой проверкой. Мы видим, что
в этом случае решения обладают периодичностью в направлении х
с периодом, равным 2~. Если были бы заданы значения Ф при х = О
и -с=2тт и эти значения не совпадали бы между собой, то мы
пришли бы к противоречию. Если же заданные при х — 0 и х = 2~
значения Ф совпадали бы между собой, то решение было бы неопре-
неопределенным. В самом деле, в этом случае существовали бы решения
Ф —0 при х=0 и х = 27г, между тем как вообще решения Ф не
равны нулю. Такого же рода трудности, только менее очевидные,
возникают и на других границах рассматриваемой области.
§ 12. Об одном способе вывода приближенных уравнений
При исследовании околозвуковых течений также целесообразно
Упрощение дифференциальных уравнений движения газа. Оно по-
позволяет, с одной стороны, уменьшить математические трудности
исследования, а с другой стороны, сделать более ясными физически
важные свойства околозвуковых течений. Однако линеаризация урав-
уравнений, известная из теории до- и сверхзвуковых течений, в около-
околозвуковой области часто приводит к физически бессмысленным ре-
результатам. Поэтому в приближенных уравнениях околозвуковых
течений сохраняется один из членов, отбрасываемых при линеариза-
Ции уравнений до- и сверхзвуковых течений как величины вто-
Р°го порядка малости. То обстоятельство, что сохраняется вполне
3*

36 ГЛ. I. ОБЩИЕ ОСНОВЫ
определенный член второго порядка малости, а не другие подобного
рода члены, часто обосновывается физическими соображениями.
Между тем эти соображения убедительны только в том случае, когда
свойства течений уже достаточно хорошо известны *)¦ Хотя подоб-
подобного рода соображения, как правило, служат исходным пунктом для
выполнения упрощений (в дальнейшем и мы будем пользоваться этими
соображениями для выяснения смысла упрощений), тем не менее
весьма полезен и формальный вывод упрощенных уравнений, так
как он, во-первых, очень четко раскрывает сам процесс упрощения,
во-вторых, дает возможность контроля физических соображений и,
наконец, может служить основой для систематического получения
подобного рода упрощений в других случаях.
Очень часто сложные уравнения упрощаются путем линеаризации.
Совершаемый при этом предельный переход можно обобщить, если
одновременно с переходом к малым возмущениям произвести аффин-
аффинное преобразование координат. Рассмотрим семейство полей течения,
зависящих, во-первых, от координат, определяющих положение.
и времени и, во-вторых, от некоторого параметра -:. Каждое поле
этого семейства характеризуется определенным значением параметра т.
Пусть для т = 0 поле течения известно, тогда отклонения других
полей течения от этого поля могут быть представлены в виде раз-
разложений по степеням i. Такой метод исследования представляет собой
приложение вариационного исчисления.
Получаемые решения зависят от параметра ¦:. Вид этой зависи-
зависимости определяет характер приближения. Если, например, коорди-
координаты не изменяются вместе с параметром, то получаются хорошо
известные линеаризованные уравнения. Поясним эту, а также более
сложные возможности на известных примерах из аэродинамики.
Пример 1. Разложение потенциала скоростей течения около про-
профиля по степеням параметра, характеризующего толщину профиля.
Этот пример, как мы сейчас увидим, приводит к тем же линеа-
линеаризованным уравнениям, которые получаются при применении извест-
известного правила Прандтля.
Будем исходить из уравнения для потенциала I, 4E) трехмер-
трехмерного установившегося течения, т. е. из уравнения
_2Фя,*Л-2Ф1Я№-2Фм*^ = 0. A)
Скорость звука а связана с потенциалом Ф уравнением I, 4F):
а* = *+ 1 w*3 - *4р- К + *S + *?)• B)
1) Иными словами, убедительность таких соображений является наимень-
наименьшей в том случае, когда указанные упрощения производятся впервые.

12. ОБ ОДНОМ СПОСОБГ. ВЫВОДА ПРИБЛИЖЕННЫХ УРАВНЕНИЙ 37
Допустим, что потенциал скоростей подлежащих рассмотрению по-
потей течения определяется уравнением 1)
Ф -= xU -U -Л\ (х, у, z) +- О (х2). C)
В этом уравнении координаты не зависят от х. При т = О по-
получается параллельное течен-ие со скоростью набегания U. Конечно,
это параллельное течение является одним из решений дифферен-
дифференциальных уравнений течения. Если мы внесем указанное значение Ф
в уравнения A) и B) и затем выполним предельный переход х -> О,
то получим
причем
Уравнение D) есть не что иное, как известное линеаризованное
уравнение Прандтля — Глауэрта. То обстоятельство, что применен-
примененный способ упрощения привел к нетривиальному приближенному
дифференциальному уравнению, является подтверждением править-
ности допущения, выраженного уравнением D). Далее необходимо
исследовать, как меняются с изменением параметра х границы. Этого
делать здесь мы не будем, так как ниже мы выполним аналогичное
исследование для околозвуковых течений.
Пример 2. Течение через сопло.
Рассмотрим плоское несжимаемое течение через сопло, контур
которого определяется уравнением y.= f(x). В этом примере одна
из координат преобразуется, т. е. делается зависящей от параметра х.
Внутри сопла потенциал скоростей удовлетворяет уравнению
Лапласа
Для того чтобы ввести в решаемую задачу параметр х, будем рас-
рассматривать некоторое число аффинно-нодобных сопел, получающихся
одно из другого изменением масштаба вдоль оси х. Тогда уравне-
уравнение контура сопла примет вид
У=/$). F)
причем
5 = хх. Fа)
) Говорят, что выражение fi(x) имеет порядок величины g(x), если
]¦ h (x)
j копечен. Это записывается в виде h (х) = О (g (x)).

38 ГЛ. I. ОБЩИЕ ОСНОВЫ
Если параметр х мал, то для того, чтобы придать аргументу функ-
функции /(?) значение, равное х, координата х должна быть очень ве-
велика, т. е. коэффициент растяжения в направлении х должен быть
равен -с. Примем, что потенциал скоростей определяется уравнением
Ф^-^М+^оО+'^оО-г- • • •. G)
где g-_t, gi и т. д. суть функции, которые будут найдены в про-
процессе вычислений. Множитель t, входящий в состав первого
члена, необходим для того, чтобы средняя скорость оставалась по-
постоянной при всех значениях т. Как выясняется из вычислений,
члены с четными степенями - в этом случае не нужны. Внеся зна-
значение Ф, определяемое уравнением G), в дифференциальное урав-
уравнение E) и собрав члены с одинаковыми степенями т, мы получим
Эти уравнения имеют общие решения:
g-i = g-i, о (?) -\~yg-i, i(S).
„в
Г20
Функции g, входящие в правые части этих равенств, могут быть
найдены из граничных условий. На оси _у = 0 вертикальные ско-
скорости равны нулю, поэтому члены g..itl, gltl, g3)i и т. д. обра-
обращаются в нуль. Вдоль контура сопла мы имеем
следовательно,
а потому
?-1,0= const • Г
dZ
/W
Дальнейшие функции g"]j0 и т. д. могут быть определены, если
ввести в граничные условия члены более высоких порядков. С фи-
физической точки зрения последнее равенство дает решение задачи

§ 12. ОБ ОДНОМ СПОСОБЕ ВЫВОДА ПРИБЛИЖЕННЫХ УРАВНЕНИЙ 39
в гидравлическом приближении. Следующие члены дают поправки,
учитывающие изменения давления, обусловленные кривизной линий
тока.
Если в решении G) взять не один только первый член, а не-
несколько членов, то в решение войдут производные более высоких
порядков, поэтому очевидно, что решение будет сходиться в общем
случае не для любой функции /. Правильнее будет предполагать,
что решение G) представляет собой асимптотическое решение урав-
уравнения E) для малых значений т. Это означает, что если в реше-
решении G) использовать только определенное число членов и затем
приближать х к нулю, то решение G) будет все более и более прибли-
приближаться к точному решению для рассматриваемого значениям. Для уравне-
уравнений в частных производных доказательство сходимости или дока-
доказательство того, что решение является асимптотическим, обычно
очень затруднительно или даже невозможно. Инженеры, а иногда
и лица, занимающиеся прикладной математикой, часто не придают
особого значения отсутствию этих доказательств, особенно если
получаемые результаты с физической точки зрения приемлемы.
Пример 3.
В § 9 настоящей главы, посвященном вопросу о применении
метода характеристик к околозвуковым течениям, мы нашли такие
преобразования зависимой и независимой переменных, которые пере-
переводят различные околозвуковые течения одно в другое. Решение
уравнения для потенциала, соответствующее этим преобразованиям,
должно иметь вид
Ф = а* [*--H$i (*> г,, С) + О (х2)],
|где
7j — yzl',
Внеся это значение Ф в уравнение для потенциала сжимаемого те-
течения, мы в конце концов получим для околозвуковых течений
следующее приближенное уравнение:
(детали вывода предоставляем читателю). Ниже мы обобщим эти
соображения на случай, когда в поле течения имеются скачки уплот-
уплотнения.
Очевидно, что в изложенном способе вывода приближенных
Уравнений решающую роль играет форма, которая берется для вы-
выражения зависимости предполагаемого решения от рассматриваемого
параметра; эта форма делает по существу ненужными часто приме-
применяемые соображения о порядке отдельных величин, определяющих
Исследуемое явление. Для отыскания правильной формы зависимости

40 ГЛ. I. ОБЩИН ОСНОВЫ
предполагаемого решения от выбранного параметра иногда необхо-
необходимо некоторое число проб. Единственным критерием правильности
выбранной формы является требование о нетривиальности получае-
получаемого дифференциального уравнения1).
В качестве еще одного примера можно было бы рассмотреть те-
течение при чрезвычайно большом числе Маха. При конечных скоро-
скоростях течения очень большие числа Маха получаются в том случае,
когда скорость звука принимает небольшие значения. Возьмем в ка-
качестве исходного параллельное течение с числом Маха, равным беско-
бесконечности (а = 0). В уравнении для потенциала членом, обусловли-
обусловливающим вырождение уравнения, будет Фуи(а2 — Фда)' так как при
применении обычной линеаризации он выпадает, поскольку в исход-
исходном течении а = 0 и Ф^ —0. Следовательно, для выражения откло-
отклонений от исходного течения необходимо найти такую форму, при
которой этот член не выпадал бы для малых значений т. Рассмотре-
Рассмотрение подробностей предоставляем читателю.
*) Этот критерий сомнителен. Обычно зависимость решения от пара-
параметра обусловливается наличием определенных особенностей, которые должны
быть выявлены путем анализа решений точных уравнений. — Прим. ред.

Глава II
УПРОЩЕНИЕ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ ТЕЧЕНИЯ-
ЗАКОН ПОДОБИЯ ДЛЯ ОКОЛОЗВУКОВЫХ ТЕЧЕНИЙ
§ 1. Предварительные замечания
Если отвлечься от тех сжимаемых течений, которые могут быть,
рассчитаны с помощью метода характеристик или для которых точное
решение определяется методом годографа, то все остальные сжимае-
сжимаемые течения могут быть исследованы только путем упрощения диф-
дифференциальных уравнений течения. Для до- и сверхзвуковых течений
такое упрощение достигается линеаризацией уравнений, что приво-
приводит либо к приближенным уравнениям Прандтля — Глауэрта, либо
к приближенным уравнениям Аккерета. Для околозвуковых течений
упрощение уравнений не может быть проведено столь далеко, как
для до- и сверхзвуковых течений, так как тогда решения часто по-
получались бы бессмысленными; во всяком случае при таком упроще-
упрощении из ноля зрения выпадают все явления, возникающие вследствие
существования рядом до- и сверхзвуковых областей. Тем не менее
упрощение уравнений целесообразно и для околозвуковых течений.
В некоторых специальных случаях упрощенные уравнения допускают
точное интегрирование. Кроме того, имеется возможность путем из-
изменения масштабов для зависимых и независимых переменных полу-
получать из известных решений новые решения. Это означает, что най-
найденные таким путем различные течения связаны друг с другом зако-
законом подобия. Существование закона подобия позволяет уменьшить
число параметров, измеряемых при экспериментальных исследованиях.
Закон подобия для околозвуковых течений был установлен почти
одновременно Карманом, Гудерлеем и Осватичем.
§ 2. Члены, отбрасываемые в приближении
Прандтля—Глауэрта
При изложении метода характеристик специально для околозву-
околозвуковых течений (§ 9 гл. I) мы уже ввели то аффинное преобразование
координат, которое приводит к желательному упрощению дифферен-
дифференциальных уравнений течения. Прежде чем приступить к выполнению
этого упрощения, выясним порядок величины членов, отбрасываемых
в приближении Прандтля—Глауэрта, причем остановимся только
на случае потенциального течения. Это даст нам возможность полу-
получить наглядное обоснование для упрощения дифференциальных урав-
уравнений течения.

42 ГЛ. П. ЗАКОН ПОДОБИЯ ДЛЯ ОКОЛОЗВУКОВЫХ ТЕЧЕНИЙ
Рассмотрим уравнение для потенциала скоростей I, 4E) специально
для плоского течения и примем, что искомый потенциал можно пред-
представить в виде
Первое слагаемое в правой части есть потенциал параллельного те-
течения, имеющего в бесконечности скорость U, а второе слагаемое,
т. е. Ф, есть отклонение действительного потенциала Ф от Ux. Для
•определения Ф мы имеем дифференциальное уравнение
= Ф** {04
где о-» есть скорость звука в невозмущенном течении. При обычной
линеаризации правая часть написанного уравнении отбрасывается. Для
того чтобы получить представление о порядке величин отбрасывае-
отбрасываемых членов, выполним одновременно с аффинным преобразованием
Прандтля — Глауэрта разложение решения в ряд по параметру т. Для
этой цели примем, что
Ф = тФ(*, у), A)
где
*•¦=*. Bа)
у = уУТ^Ж. B6)
Мс = — . Bв)
При таком выборе независимых переменных х и у члены, сохраняе-
сохраняемые в приближении Прандтля — Глауэрта, остаются неизменными при
изменении числа Маха. В самом деле, после перехода к перемен-
переменным х и у мы получим
- т=» —
2
* A - му («-1) иФБФг]Ту^^р-A -мУ'ф^-Ь
+ ^^-A-Л!1)Ф~Ф|. C)

§ 2. ЧЛЕНЫ, ОТБРАСЫВАЕМЫЕ В ПРИБЛИЖЕНИИ ПРАНДТЛЯ—ГЛАУЭРТА 43
Как и следовало ожидать, члены в правой части имеют самое мень-
меньшее второй порядок относительно х, в то время как все члены в ле-
левой части имеют первый порядок относительно х. Таким образом,
при фиксированном числе Маха, составленном для скорости U в беско-
бесконечности, можно сколь угодно уменьшить влияние членов правой
части, если выбрать т достаточно малым.
Мы получим меру ошибки, вносимой отбрасыванием правой части,
если сравним важнейшие члены этой части с одним из членов левой
части. Предположим, что число Маха близко к единице; тогда влия-
влияние членов, содержащих множитель 1 —Ж^, будет небольшим. После
отбрасывания этих членов единственным членом, имеющим второй
порядок относительно х, будет
Отношение этого члена к первому члену левой части равно
—гт- ту ¦ D)
Если это отношение мало, то можно пользоваться правилом Прандтля.
Для того чтобы выяснить, что из этого следует, рассмотрим какое-
нибудь определенное решение дифференциального уравнения, упро-
упрощенного посредством правила Прандтля. В таком решении выраже-
выражение Ф- не зависит ни от числа Маха, ни от х. Относительная тол-
X
типа плоского тела пропорциональна Ф^, т. е. пропорциональна
хУ 1 —М":а, поэтому в отношении D) можно выразить х через отно-
относительную толщину. Следовательно, для того, чтобы можно было
пользоваться правилом Прандтля, относительная толщина должна
стремиться к нулю при приближении числа Маха к единице, как ве-
величина (l — О'7'1).
Для трехмерных течений левая часть уравнения, определяющего
потенциал, будет содержать еще член Ф,,. Тогда может случиться,
что член Фд-Фд,;,,, который мы использовали выше для оценки ошибки,
будет мал но сравнению с остальными членами левой части. Следо-
Следовательно, сформулированное нами условие применимости правила
Прандтля является для трехмерных течений достаточным, но не не-
необходимым. В самом деле, те трехмерные задачи, в которых толщина
обтекаемого тела равна нулю, могут быть исследованы на основе
линейной теории также при числе Маха, равном единице (см. стр. 69).
Предыдущие рассуждения приводят к выводу, сходному с
Тем. к которому мы пришли в § 9 гл. I при рассмотрении метода
х) Из анализа автора следует, что для применимости правила Прандтля
Ребуется стремление т к нулю быстрее, чем A — М\\ '. — Прим. ред.

44 ГЛ. П. ЗАКОН ПОДОБИЯ ДЛЯ ОКОЛОЗВУКОВЫХ ТЕЧЕНИИ
характеристик для околозвуковых течений. А именно, при составлении
приближенного уравнения для околозвуковых течений необходимо
сохранить член
т. е. необходимо ввести такое, соотношение между z и 1—
чтобы этот член не выпадал. Можно, например, принять, что
Этот выбор не является единственным; с таким же успехом можно
принять, что
2A — Мсс)~т.
Свободу выбора соотношения между i и 1 — М^ можно попытаться
использовать для того, чтобы при упрощении дифференциальных
уравнений выполнить и другие условия.
§ 3. Упрощение дифференциальных уравнений течения
Перейдем к систематическому выводу упрощенного дифферен-
дифференциального уравнения для определения потенциала скоростей в около-
околозвуковой области, причем в отличие от предыдущих исследований
рассмотрим случай трехмерного течения. Затем в § 4 мы остано-
остановимся на условиях, которые должны выполняться на скачках уплот-
уплотнения, и, наконец, в § 5 рассмотрим вопрос о граничных условиях,
до сих пор остававшийся совсем не затронутым.
.Может показаться чрезмерной осторожностью исследование во-
вопроса о том, следует ли учитывать влияние энтропии в околозвуко-
околозвуковом течении. В самом деле, мы знаем, что в линеаризованных сверх-
сверхзвуковых течениях изменением энтропии всегда пренебрегают. Однако
поступать так же с уверенностью для околозвуковых течений мы не
можем, во-первых, потому, что последние чувствительны к измене-
изменениям поперечного сечения [согласно уравнению I, 2A0а), плотность
потока массы имеет максимум при числе Маха, равном единице),
а во-вторых, вследствие того, что повышение энтропии проявляет
себя именно в увеличении поперечного сечения трубок тока. В конце
концов мы выясним, что изменением энтропии можно пренебрегать,
однако пока мы будем рассматривать энтропию как переменную ве-
величину.
Течение будем считать изоэнергетическим, так как без этого
предположения число Маха в исходном параллельном течении было бы
близко к единице только на отдельных линиях тока.

§ 3 УПРОЩЕНИЕ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ ТЕЧЕНИЯ 45
Будем исходить из уравнения I, 4D), т. е. из уравнения нераз-
неразрывности для установившихся течений
dv» d Я-4-^ (\-^+^(l-^-
dvy\vxvy /dv^ дщ^хци^ (dv* 1 д%><*\ v*v°= _n
ду ' дх J а- \ дг > ду J а1* \ дх ~^~ дг ) а"
(О
и из теоремы Крокко о вихрях
rotvXv = TgxaAs. B)
Введем параметр т и характерную длину х0 и примем, что соста-
составляющие скорости определяются формулами (Гудерлей [1], см. лит. 1)
v =a*-j-%~Vj.(%, щ, Q, \
где
}
= , 7] = Т /» -^-¦ , С = ТV» . C6)
хо хо хо
Из уравнения Бернулли мы имеем
аг —vl = t (*-+-!) aS)B + О (т2);
а2 — ¦Уз=а*2-|-ОA:).
Таким образом, сохранив в уравнении (I) только члены самого низ-
низкого порядка, мы получим
Величина отклонений от критической скорости, возникающих в рас-
рассматриваемом течении, имеет порядок О(х); поэтому на основании
известных формул для скачка уплотнения изменения энтропии имеют
порядок О(т3).
Для того чтобы ввести скорости, определяемые формулами C),
в уравнение B), вычислим вектор скорости v и его вихрь; мы по-
получим
v = i(a*-\-xvx)-f-j~ vy-\-kx"''vz, }
E)

46 ГЛ II ЗАКОН ПОДОБИЯ ДЛЯ ОКОЛОЗВУКОВЫХ ТЕЧЕНИИ
где i, j и k суть единичные векторы по направлениям х, у, z. Огра-
Ограничившись членами самого низкого порядка, мы найдем из уравне-
уравнения B), что
F)
Отсюда следует, что составляющая вектора вихря в направлении,
перпендикулярном к линиям тока невозмущенного течения, равна нулю.
В этом нет ничего удивительного, так как уравнение B) не учиты-
учитывает влияние энтропии и так как линии тока невозмущенного тече-
течения представляют собой приближение линий тока действительного
течения.
Дальнейшие выводы о векторе вихря можно сделать на основа-
основании того обстоятельства, что составляющая скорости, лежащая в ка-
касательной плоскости к скачку уплотнения, одинакова до и после
скачка. Если течение вначале было свободно от вихрей, то из только
что сказанного следует, что вниз по течению от скачка уплотнения
составляющая вектора вихря в направлении нормали к поверхности
скачка уплотнения равна нулю. Так как нормали к поверхности
скачка уплотнения никогда не могут быть перпендикулярны к линиям
тока (иначе линии тока не пересекали бы поверхности скачка) и так
как, согласно равенствам F), направление вектора вихря совпадает
с направлением касательной к линиям тока, то вектор вихря после
первого скачка уплотнения, а потому и после каждого следующего
скачка равен нулю. Таким образом, в рассматриваемом нами прибли-
приближении должен существовать потенциал скоростей. Приняв для него
выражение
Ф = а*хотФ(?, т], С), G)
мы получим для его определения уравнение
Для осесимметричных течений примем, что
Ф = а*хотФ(?, г), (9)
где
7 = —I1'', г — Y~y2^-z2.
В этом случае мы получим для определения потенциала уравнение
= 0. A0)

§ 4 УСЛОВИЯ НА СКАЧКАХ УПЛОТНЕНИЯ 47
§ 4. Условия на скачках уплотнения
В предыдущем параграфе мы исходили из предположения, что
составляющие скорости определяются формулами II, 3 C). Это пред-
предположение привело к нетривиальной форме дифференциального урав-
уравнения течения и тем самым себя оправдало. Теперь остается иссле-
исследовать, как принятое предположение отражается на других соотноше-
соотношениях, определяющих поле течения. Никаких дополнительных
допущении вводить для этой цели не надо. В этом параграфе
мы займемся условиями на скачках уплотнения, в следующем пара-
параграфе— граничными условиями и, наконец, в § 9 — теми формами
уравнения неразрывности и уравнения импульсов, которые эти урав-
уравнения принимают при сделанных допущениях.
Об условии, согласно которому составляющая скорости, каса-
касательная к скачку уплотнения, не изменяется при переходе через
скачок, уже было сказано выше. Это условие удовлетворяется само
собой, если потенциал скоростей при переходе через скачок остает-
остается непрерывным. Таким образом, нам остается исследовать усло-
условия, которым должна удовлетворять составляющая скорости, нор-
нормальная к скачку.
Будем отмечать состояния до и после скачка уплотнения по-
посредством индексов I и II у соответствующих букв. Для обозна-
обозначения составляющих скорости в направлениях, нормальном и ка-
касательном к скачку, будем пользоваться индексами п и t. Тогда
для идеального газа мы будем иметь следующее соотношение,
найденное Прандтлем:
*а х — 1 2 /1ч
C? — ~^jVt. (I)
Для вывода этого соотношения рассмотрим сначала прямой скачок
уплотнения. Уравнение импульсов, уравнение энергии и уравнение
неразрывности имеют для такого скачка следующий вид:
^п (уравнение импульсов), Bа)
а\-\ 2~~ w\ — апН <Г~ wn (уравнение энергии), B6),
Pj^j = pnwn (уравнение неразрывности). Bв)
Для составления уравнения энергии мы использовали уравнение I, 2G)-
В дальнейшем правую часть уравнения энергии будем обозначать
для краткости через
о ип •
Разделив уравнение Bа) на уравнение Bв) и заменив в соответствии
: равенством I, 2 E) хр/р через а2, мы получим
A+Wl=A.+Wll. B>
хда, ' v.wn '

48 ГЛ II ЗАКОН ПОДОБИЯ ДЛЯ ОКОЛОЗВУКОВЫХ ТЕЧЕНИИ
Воспользуемся теперь уравнением B6) и выразим а, через wl и а*п,
.а ап — через wn и а*. Подставив полученные значения в уравне-
уравнение B), мы будем иметь
Это есть квадратное уравнение относительно wv Один из его корней
известен, именно wl — топ. Умножив последнее уравнение на
мы найдем
wiwn=a*n- C)
Для того чтобы из прямого скачка уплотнения получить косой
«качок, следует наложить на поле течения прямого скачка выше и
ниже по течению относительно скачка составляющую скорости, каса-
касательную к последнему. Скорости wl и wu, которыми мы опериро-
оперировали до сих пор, будут тогда составляющими скорости, нормальными
,к скачку; будем обозначать их теперь через vni и х)пц. Пусть ско-
скорость, налагаемая на поле течения, равна vt. Так как, согласно урав-
уравнению Бернулли,
2 I % 1 2 n+l Л
ап -\ — wu = -f- сГ
то
Внеся полученное значение а*^ в равенство C), мы получим соотно-
соотношение A).
Пусть поверхность скачка уплотнения задана уравнением
Преобразование координат, заданное формулами II, 3 C6), деформи-
деформирует эту поверхность. Единичным вектором, нормальным к поверх-
¦ности скачка, в системе координат х, у, z будет
¦Имея в виду, что вектор скорости v определяется первым из
равенств II, 3E)и ограничиваясь величинами первого порядка относи-

§ 4 УСЛОВИЯ НА СКАЧКАХ УПЛОТНЕНИЯ 49
тельно т, мы получаем для составляющей этого вектора, нормальной
к скачку, значение
*» = «*[ ! ~2 (df
В этой формуле надо добавить индекс I или II в зависимости от того,
рассматриваем ли мы составляющую скорости vn выше или ниже по
течению относительно скачка. Касательная составляющая vt равна
модулю векторного произведения единичного вектора нормали на
вектор скорости. Сохранив в этом произведении только величины
первого порядка, мы получим
у = Zl'd'
Внеся полученные значения vn и vt в уравнение A) и ограничившись
величинами самого низкого порядка, мы будем иметь
Примечательно, что в это соотношение входит наклон скачка,
хотя в предельном случае т -> 0 поверхность скачка перпендикулярна
к направлению скорости набегающего потока. Следовательно, условия
на косом скачке отнюдь нельзя приближенно заменить условиями на
прямом скачке. В самом деле, для прямого скачка уплотнения мы
имеем
и поэтому для такого скачка
Изменение скорости в направлении оси х при переходе через
скачок уплотнения будет равно
F)
x+1
Изменения скорости в направлениях у и z можно определить на
основании следующего соображения: так как при переходе через
скачок уплотнения касательная составляющая скорости не изменяется,
4 Зак 534 К Г Гудерлей

50
ГЛ П ЗАКОН ПОДОБИЯ ДЛЯ ОКОЛОЗВУКОВЫХ ТЕЧЕНИЙ
то приращение скорости должно быть направлено по нормали к скачку.
Отсюда, учитывая уравнение D), мы получаем для искомых измене-
изменений формулы
Ga)
г ги 31 ^ут
Ж
С другой стороны, на основании формул II, 3 (За) мы имеем
G6)
откуда с учетом равенства F) найдем
)
Исключив из правой части с помощью соотношения E) величину
мы окончательно будем иметь
__ /"%+! I /'"«i + vxa uxi — vxii
~~ V 2 V a* a1
(8)
Это есть уравнение ударной поляры для околозвуковых течений.
Впервые оно встречается у Ханцше и Вендта (см. лит. 1). Из выра-
выражения D) и уравнений Gа) и G6) следует, что единичный вектор
нормали к скачку равен
§ 5. Граничные условия
Выявление граничных условий на большом удалении от обтекае-
обтекаемого тела не представляет никаких трудностей. Обычно там имеет
место параллельное течение с числом Маха, в общем случае не рав-

5 ГРАНИЧНЫЕ УСЛОВИЯ 51
ным единице. Поэтому там, как это легко видеть, если учесть равен-
равенство II, 3G), соблюдаются условия
Ф5 = const, Ф^^О, Фс = 0.
Если Ф^ также равно нулю, то для всех значений х число Маха
набегающего потока равно единице. В общем случае отклонение числа
Маха набегающего потока от единицы в приближении наинизшего
порядка пропорционально х.
Для исследования граничных условий на обтекаемом теле можно
было бы попытаться предположить, что преобразование координат у
и z, устанавливаемое формулами II, 3C6), распространяется также
на обтекаемое тело. Легко видеть, что такое предположение не
оправдывается. В самом деле, если оно было бы верно, то наклоны
линий тока, определяемые в первом приближении величинами vyla*
и vja*, были бы пропорциональны x~Va. Однако, как сразу показы-
показывают формулы II, 3Cа), этого не может быть
Пусть линия тока в невозмущенном течении задана уравнениями
Уо =
где 7jo= const и ?q= const. Для определения формы этой линии тока
в возмущенном течении необходимо вычислить отклонения коорди-
координат у и z от значений у0 и zQ. Обозначим эти отклонения через у
и z. Тогда из уравнений II, 3C) мы получим
rfx л* _J_ Т7, /¦(• ¦ -1 v-~ " ¦ —1 J/-~^ ^ '
и аналогичное уравнение для dzjdx.
Если величины, входящие в эти уравнения, дифференцируемы
(внутри течения это почти везде имеет место), то "вблизи невозму-
невозмущенных линий тока они могут быть разложены в ряды; ограничив-
ограничившись в разложениях членами с наименьшими степенями х, мы получим
|У = xoxJl*~vy (I т]0, С,,); ^ = хох!'*Ъг (S, тH, Со). B)
Следовательно, деформации линий тока пропорциональны хох"/к Так
как поверхность обтекаемого тела покрывается линиями тока, то
с большой степенью достоверности можно предположить, что форма
этой поверхности характеризуется также отношением х0х3/=, т. е. что
толщина обтекаемого тела пропорциональна х0х3/\
Во всяком случае наклон линий тока относительно оси х при
т->-0 стремится к нулю. Это означает, что при х -> 0 обтекаемое
тело может быть заменено кусками цилиндрической поверхности,
образующие которой параллельны оси х. Если обтекаемое тело пред-
представляет собой V-образное крыло, то заменяющая его цилиндрическая
поверхность будет состоять из плоскостей, параллельных оси х и
4*

52 ГЛ II ЗАКОН ПОДОБИЯ ДЛЯ ОКОЛОЗВУКОВЫХ ТЕЧЕНИЙ
возможно более тесно прилегающих к крылу. Для замены кольцевого
крыла следовало бы взять круглый цилиндр. С целью обоснования
сделанного выше предположения о виде зависимости толщины обте-
обтекаемого тела от -с необходимо допустить, что поле течения может
быть продолжено до указанной цилиндрической поверхности, т. е.
внутрь тела как с верхней, так и с нижней стороны и притом так,
что между цилиндрической поверхностью и контуром тела не по-
появляются особые точки также и при t ^ 0 '). Конечно, продолжения,
полученные сверху и снизу, могут не смыкаться друг с другом вдоль
цилиндрической поверхности. Это означает, что такая цилиндрическая
поверхность может являться поверхностью, на которой скорость пре-
претерпевает разрывы. Таким образом, обтекаемое тело заменяется
цилиндрической поверхностью, несущей на себе особые точки.
Так как решения, определяющие поле течения, получаются в виде
функций переменных ?, tj, С, то от этих же переменных зависит
и положение указанных особых точек. Следовательно, преобразо-
преобразование координат у и z, определяемое величинами т и х0, распро-
распространяется также на цилиндрическую поверхность, несущую осо-
особые точки. Далее, введем для этой поверхности предположение
о существовании производных, один раз уже использованное при
упрощении уравнения A). Тогда, как и ранее, мы найдем, что откло-
отклонения поверхности обтекаемого тела от этой цилиндрической поверх-
поверхности пропорциональны хот"/к Эти отклонения описывают как толщину
обтекаемого тела, так и угол атаки. Еще раз напомним, что форма
аппроксимирующего цилиндра изменяется при преобразовании так же, ¦
как и координаты у и z, т. е. это изменение определяется величи-
величинами т и х0.
В случаях, поддающихся расчету, граничные условия на поверх-
поверхности обтекаемого тела обычно могут быть выявлены непосредственно,
поэтому остановимся только на отыскании граничных условий для
тела произвольной формы. Рассмотрим цилиндрическую поверхность,
заменяющую поверхность обтекаемого тела при х = 0. Обозначим
через еПо единичный вектор, нормальный к цилиндру, через е{| — еди-
единичный вектор, касательный к поверхности цилиндра и лежащий
в плоскости х = const, и через ех — единичный вектор в направле-
направлении х. Пусть отклонение поверхности обтекаемого тела от аппрокси-
аппроксимирующей цилиндрической поверхности при z Ф 0 задано как рас-
расстояние xohiab, измеренное вдоль направления нормали. При таком
определении h не зависит от т и х0. Тогда при z ф 0 единичным
вектором нормали к поверхности тела приближенно будет
з, dh з- dh
en = eno — xi*^ ex — z >x0Tteto,
i) Такое предположение всегда делается при исследовании крыльев малой
толщины, но оно не всегда выполняется; например, оно безусловно не осуще-
осуществляется в тех точках контура, где производные претерпевают разрыв.

§ 5 ГРАНИЧНЫЕ УСЛОВИЯ 53
где х0 ах и dt суть линейные элементы в направлениях ех и е4[1.
Вектор скорости также разложим на три направления ех, еП1 и eta.
Составляющие в направлениях ещ и et0 обозначим через vn и vt. Так
как составляющие vn и vt получаются из составляющих vy и vz, то
они пропорциональны т%, поэтому мы можем положить
и тогда для вектора v получим выражение
v = (а* -(— xvх) ех -\- 1&/*ип(?п0 -\- 1
Составляющая скорости в направлении, нормальном к поверхности
обтекаемого тела, должна быть равна нулю. Следовательно, если
сохранить только члены наименьшего порядка относительно т, гра-
граничное условие примет вид
~ * dh „ „.
Если производная dhjd% достаточно гладкая, то vn можно выразить
через значения vy и vz на аппроксимирующей цилиндрической по-
поверхности. Мы видим, что в последнее уравнение составляющая vt
не входит.
Если отклонения от критической скорости малы, то из уравне-
уравнения I, 2(9) мы получим для разности давлений р—р* выражение
р—р = — -? (У —а*2), D)
которое следует вычислить на поверхности обтекаемого тела. Эта
поверхность отклоняется от поверхности аппроксимирующего ци-
цилиндра на величину порядка т%. Так как производные от скорости
вдоль поверхности обтекаемого тела предполагаются ограниченными,
то для определения давления вдоль этой поверхности в первом
приближении получается формула
р— р* = — xpV8^. E)
В этой формуле функция Ф^ должна вычисляться для аргументов,
взятых на аппроксимирующей цилиндрической поверхности; поэтому
функция Ф^ не зависит от т, и, следовательно, давления на поверх-
поверхности обтекаемого тела в первом приближении пропорциональны т.
Исключением является осесимметричное тело конечной протяженности.
При т = 0 такое тело стягивается в отрезок прямой, лежащей
на оси х.
Так как для дифференциального уравнения II, 3A0), определяю-
определяющего потенциал скоростей осесимметричного течения, все точки- оси
являются особыми вследствие наличия в уравнении члена Ф-/г, то
потенциал скоростей вдоль отрезка оси, лежащего внутри тела,

54 ГЛ II ЗАКОН ПОДОБИЯ ДЛЯ ОКОЛОЗВУКОВЫХ ТЕЧЕНИЙ
не должен быть обязательно регулярной функцией. Легко убедиться,
что первые члены разложения потенциала скоростей в ряд вблизи
оси имеют вид
Ф = a'xo-z^ (&) + a*xQxf2 (?) 1п7= а*хохФ, F)
где
J=JLX4,
х0
(см. стр 46). Такой вид имело бы решение дифференциального
уравнения II, 3A0), если мы пренебрегли бы членом (х-|~1)Ф^Ф^.
Порядок величины поправочных членов, учитывающих влияние отбро-
отброшенного члена уравнения, одинаков с порядком величины г2In2г.
Для определения контура тела необходимо вычислить составляющую
скорости в направлении г. Продифференцировав равенство F), мы
найдем
г 0^ .
дг dr r
Если контур тела задан уравнением
г=7(х), G)
то из условия, что скорость касательна к поверхности тела, мы
получим
dr(x) = Фг(г,х) ^^ /,(S)*o
dx a* 7E)
откуда
~ dr о , ..,
r-di=^xoW-
Положив
г = х'/.Ло7(?), (8)
мы найдем
следовательно, диаметр пропорционален %1*х0. Последнее уравнение
представляет собой граничное условие на обтекаемом теле. Само
тело заменяется отрезком оси х, состоящим из особых точек. Коэф-
Коэффициент /2(?) перед членом In r в решении F) может быть вычислен
с помощью равенств G) — (9).
Для определения давления на поверхности тела следует исходить
из уравнения D); мы получим

i 5 ГРАНИЧНЫЕ УСЛОВИЯ 5 5
В правой части членом v^/2 всегда можно пренебречь по сравнению
с членом a*vx. Подставив в уравнение F) значение г, соответствую-
соответствующее поверхности тела, мы найдем сначала составляющую скорости
„ dfi , » df-y , , = ... s
a затем, использовав равенство (9),—составляющую скорости
г E) di
Следовательно,
Р—Рл= — ?*а*\ Х
Мы видим, что члены правой части этого равенства, обязанные
своим происхождением составляющим vx и vr, имеют величину одного
порядка, за исключением члена
d?
(т)
In x.
Доказательство того, что при вычислении давления необходимо учи-
учитывать долю, вносимую составляющей скорости vr, можно найти
в работе Осватича и Берндта (см. лит. 1). Примечательно, что здесь
мы получили этот результат чисто формальным путем.
Как выбирается масштаб для т, роли не играет; это означает,
что если в каком-либо известном течении произвести аффинное пре-
преобразование координат в соответствии с законом подобия, то не-
независимо от выбора масштаба для х получается всегда один и тот же
результат. Для того чтобы убедиться в этом, сравним два поля
течения, связанные между собой законом подобия. Пусть этим полям
соответствуют давления р и р', параметры т и т' и радиусы г и г'.
В таком случае для вычисления р' необходимо в уравнении A0)
заменить х на х', а затем выразить в уравнении A0) и в уравнении,
полученном из него после замены т на х', член -да-(-н- ) с помощью
равенства (8) в следующем виде.
1 rf2 / pi
2 У 1x1 d? ^ 2
Тогда мы будем иметь
Г
Р— Р +Р« ..„ .,,¦, , 2
=-Р*лр*

56 ГЛ II. ЗАКОН ПОДОБИЯ ДЛЯ ОКОЛОЗВУКОВЫХ ТЕЧЕНИЙ
Исключив из обоих уравнений выражения, стоящие в квадратных
скобках в правых частях, мы получим
т. е. давление р' зависит только от отношения i'jz. Член —^[-гг
определяется формой рассматриваемого тела.
§ 6. Закон подобия
Согласно результатам предыдущего параграфа, для широкого
класса тел, а именно для крыльев (квазицилиндрические тела) и
осесимметричных тел, деформация поверхности тела, происходящая
вследствие аффинного преобразования, и изменения давлений просто
связаны друг с другом. Для тела, форма которого получается из формы
экспериментально исследованного тела путем деформации на основе
выведенных выше правил, можно найти распределение давления
из распределения давления на исходном теле, не прибегая к выявле-
выявлению других свойств поля течения. Соотношения, позволяющие это
сделать, выражают закон подобия для околозвуковых течений1).
Напомним результаты предыдущего параграфа в той мере, в какой
они необходимы для понимания закона подобия.
Соответственными точками в различных полях течения, свя-
связанных друг с другом законом подобия, будем называть такие точки,
для которых значения ?, -ц и С, определяемые формулами II, 3C6),
!) Так как осесимметричное тело конечной протяженности и квазицилин-
квазицилиндрическое тело деформируются при аффинном преобразовании различным
образом, то не существует закона подобия для полей течения, в которых
обтекаемое тело представляет собой комбинацию обеих указанных возмож-
возможностей (примером такой комбинации может служить сочетание фюзеляжа
с крылом). Если для исходного тела было бы известно все поле течения,
то, конечно, можно было бы рассчитать контур нового обтекаемого тела
после аффинного преобразования исходного течения путем введения пара-
параметра т. Следовательно, аффинное преобразование поля течения дает более
широкие возможности, чем закон подобия. Допустимость аффинного преобра-
преобразования поля течения путем введения параметра т можно считать обосно-
обоснованной формулами II, 3 C), позволившими выполнить упрощение дифферен-
дифференциального уравнения течения. Само собой напрашивается мысль о выводе
закона подобия из упрощенного дифференциального уравнения II, 3(8),
однако логически такой вывод был бы неправомерным.

6 ЗАКОН ПОДОБИЯ 57
совпадают. Значения х, у и z, отвечающие значениям ?, i) и ',
изменяются, с одной стороны, вместе с х0, а с другой стороны,—
вместе с т. Первая возможность означает просто изменение масштаба
всего поля течения, а вторая — собственно аффинное преобразование
в соответствии с законом подобия. Если фиксировать значение х0>
то в соответственных точках
х пропорционально т°,
у я z пропорциональны х^1^.
В соответственных точках отклонение составляющей скорости в на-
направлении х от критической скорости пропорционально х, а откло-
отклонения составляющих скорости в направлениях у и z пропорцио-
пропорциональны т3/».
Обтекаемое тело (за исключением тела вращения) заменяется
цилиндрической поверхностью с образующей, параллельной оси х,
причем потенциал и его производная вдоль этой поверхности пре-
претерпевают разрыв. Аппроксимирующая цилиндрическая поверхность
деформируется при аффинном преобразовании так же, как коорди-
координаты. Отклонение поверхности тела от аппроксимирующей цилиндри-
цилиндрической поверхности пропорционально т'^. Тело вращения заменяется
отрезком оси х, состоящим из особых точек; радиус тела вращения
пропорционален лгот'/».
Отклонение давлений от критического давления на поверхности
обтекаемого тела (за исключением тела вращения) пропорционально х.
Для тела вращения, согласно равенствам II, 5A0) и II, 5(8), пара-
параметру х пропорциональна величина
Для графического изображения результатов опытов, связанных
друг с другом законом подобия, лучше всего пользоваться величи-
величинами, не зависящими от т. Тогда кривые, полученные для различных
значений х, совпадут между собой. Прежде всего рассмотрим гео-
геометрические условия, определяющие поле течения. Обтекаемое телр
описывается аппроксимирующей цилиндрической поверхностью и
поперечными отклонениями тела от этой поверхности. Конечно, эти
поперечные отклонения в соответственных точках полей течения
должны быть пропорциональны друг другу. Пусть поперечное откло-
отклонение в некоторой характерной точке равно D; оно пропорцио-
пропорционально х0т3А, где х0 есть характерное расстояние в направлении х.
Тогда мы будем иметь

58 ГЛ II ЗАКОН ПОДОБИЯ ДЛЯ ОКОЛОЗВУКОВЫХ ТЕЧЕНИЙ
Координаты у и z аппроксимирующей цилиндрической поверхности
пропорциональны xQt-1!*. Использовав последнее равенство, мы найдем,
что в полях течения, связанных друг с другом законом подобия,
величины
х0
составленные для аппроксимирующей цилиндрической поверхности,
должны быть инвариантны. Обратим внимание на то, что коорди-
координаты х изменяются по-иному, для них инвариантным является отно-
отношение х/х0. Далее, поле течения определяется скоростью набегающего
потока. Если число Маха, соответствующее этой скорости, равно Мт,
то следующим условием подобия будет инвариантность величины
или, что то же самое, величины
Величины подобного рода называются параметрами подобия.
Если все перечисленные выше условия выполняются, то поля тече-
течения подобны, и выражения
) или
*QI p"w
в соответственных точках совпадают.
Как было упомянуто в § 2, физические величины, принимаемые
пропорциональными х, определяются с точностью только до членов
второго и более высокого порядков. Иными словами, выражения,
выбираемые в качестве параметров подобия, заранее не предопреде-
предопределены. Такую свободу их выбора можно попытаться использовать для
того, чтобы получить более хорошее приближение к точным реше-
решениям. Спрейтер (см. лит. 1) рекомендует в качестве параметра подобия
выражение
xol
Далее, используя коэффициент давления
, - р-р™
Р 1 2
о гсо со

§ 7 ПРИМЕНЕНИЯ ЗАКОНА ПОДОБИЯ 59
он составляет выражение
D
Оба эти выражения содержат отношение ч удельных теплоемкостей
в такой форме, что подобие околозвуковых течений сохраняется
также при изменении ч Таким путем, как показал Спрейтер на одном
примере, удается значительно улучшить совпадение между резуль-
результатами опыта и теорией. Тем не менее к предложению Спрейтера
следует отнестись с осторожностью, так как соображения, приво-
приводящие к предлагаемому им выбору параметра, далеко не убедительны.
Конечно, во всех таких попытках приходится мириться с довольно
грубыми приближениями. Важные соображения, которые необходимо
учитывать в подобного рода исследованиях, приводятся в работе
Осватича [2] (см. лит. 1). Во всяком случае, без значительного ком-
компромисса почти никогда нельзя получить хотя бы до некоторой сте-
степени общие результаты.
§ 7. Применения закона подобия
Применимость закона подобия для околозвуковых течений значи-
значительно более ограничена, чем применимость правила Прандтля — Глау-
эрта, так как закон подобия всегда требует деформации обтекаемого
тела. В случае пространственного обтекания изменяется не только
толщина крыла, но также угол стреловидности (если рассматривается
стреловидное крыло). Соотношения, к которым приводит закон подобия
при его применении к крылу, без труда могут быть выведены
на основе указаний, сделанных в предыдущем параграфе. Здесь мы
остановимся только на некоторых следствиях, также вытекающих
из сказанного в § 6, но не столь очевидных.
1. Пусть течение около плоской пластинки при числе Маха,
равном единице, известно. Согласно закону подобия, выражение
х0
составленное для соответственных точек, инвариантно. В качестве
отношения D/x0 возьмем угол атаки а. пластинки. Следовательно,
местный коэффициент давления и подъемная сила пропорциональны а1'.
Для угла атаки, равного нулю, величина dcjdo. делается бесконечно
большой. Этот результат показывает, что в данном случае линейная
теория неприменима.

60 ГЛ II ЗАКОН ПОДОБИЯ ДЛЯ ОКОЛОЗВУКОВЫХ ТЕЧЕНИИ
2. Подьемная сила профиля с ненулевой толщиной при малом
угле атаки а пропорциональна а также при числе Маха, равном
единице. Пусть для заданного профиля величина dcjda при числе
Маха М — 1 известна. Далее, пусть подъемная сила равна А, а отно-
относительная толщина профиля пусть равна D/x0. Выполним аффинное
преобразование, при котором сохраняется подобие. При таком пре-
преобразовании величины A(D/xo)"lj и «(D/x,,) остаются неизменными.
Подъемную силу можно представить в виде
dcA
da
Отсюда следует, что при аффинном преобразовании, сохраняющем
подобие течений, выражение
deA / D
а потому и выражение
cA / D \'л
)
da V Хо )
остаются инвариантными; поэтому
dcA ( D
da \ Л'о
Таким образом, наклон кривой, изображающей зависимость подъем-
подъемной силы от угла атаки, увеличивается при уменьшении относительной
толщины D/x0. Конечно, диапазон углов атаки, в котором имеет
место такое поведение, пропорционален относительной толщине D/x0;
для тонких профилей этот диапазон может быть весьма малым.
Полученный результат примечателен тем, что показывает резкое
отклонение поведения околозвуковых течений от свойств до- и сверх-
сверхзвуковых течений, для которых величина dcjda при фиксированном
числе Маха не зависит от относительной толщины.
3. Сравним обтекание заданного профиля в блокированной аэро-
аэродинамической трубе1) с обтеканием этого же профиля в неограни-
неограниченном воздушном пространстве при числе Маха, равном единице.
Отклонение друг от друга распределений давления на теле в обоих
случаях характеризует влияние стенок трубы. Подвергнем оба поля
течения одинаковому аффинному преобразованию, при котором соблю-
соблюдается закон подобия. Конечно, при таком преобразовании сохраняется
относительная разница между обоими распределениями давлений. При
аффинном преобразовании толщина профиля изменяется пропорцио-
пропорционально -еЧ отклонение блокирующего числа Маха от единицы — про-
Речь идет о трубе, блокированной скачком уплотнения —Прим. ред.

§ 8 УПРОЩЕНИЕ ОБОЗНАЧЕНИИ И ЗАПИСЕЙ 61
порционально т, а ширина аэродинамической трубы — пропорцио-
пропорционально т^ (в самом деле, стенки трубы деформируются при аффинном
преобразовании так же. как изменяются координаты). Отсюда следует,
что для толстого профиля в узкой аэродинамической трубе относи-
относительное влияние стенок трубы такое же, как для тонкого профиля
(с той же шириной, как у толстого профиля) в широкой аэродина-
аэродинамической трубе. Если сравнить толстый и тонкий профили в трубе
одинаковой ширины, то тогда для толстого профиля относительное
отклонение распределения давления от распределения давления при
числе Маха М — 1 будет меньше, чем для тонкого профиля, хотя
для толстой модели блокирующее число Маха меньше, чем для тонкой
модели. Если желательно охарактеризовать точность измерений в аэро-
аэродинамической трубе посредством блокирующего числа Маха, то это
допустимо только в том случае, когда модели имеют приблизительно
одинаковую ширину и приблизительно одинаковую относительную
толщину.
Применение закона подобия для определения поправок на влияние
стенок аэродинамической трубы в околозвуковой области можно
найти в работе Гудерлея [7] (см. лит. 1).
§ 8. Упрощение обозначений и записей
После того как мы увидели, что приближенные уравнения для
околозвуковых течений могут быть получены путем предельного пере-
перехода, можно без каких-либо опасений за последствия пользоваться
менее точным представлением, а именно считать отклонения иссле-
исследуемого течения и его скорости от параллельного течения и от кри-
критической скорости „достаточно" малыми, а само обтекаемое тело —
„достаточно" тонким. В таком случае можно положить тих0 равными
единице и забыть о том, что уравнения II, 3(8) и II, 3A0) получены
путем предельного перехода; вместо этого следует рассматривать эти
уравнения просто как приближения к точным дифференциальным
уравнениям Тогда мы сумеем несколько упростить необходимые
записи. Пусть х, у, z будут декартовы, а х, г, ш — цилиндрические
координаты пространства, в котором происходит течение, а Ф — потен-
потенциал течения. Допустим, что этот потенциал можно представить
в виде
Ф = а*[х-^Ф(х, у, z)];
тогда Ф будет определять отклонение поля течения от параллельного
течения с критической скоростью а*. Для определения потенциала Ф
мы будем иметь приближенное дифференциальное уравнение
+ Фаг = 0, A)

62 ГЛ II ЗАКОН ПОДОБИЯ ДЛЯ ОКОЛОЗВУКОВЫХ ТЕЧЕНИЙ
которое для осесимметричной задачи заменяется уравнением
— (х+1)Фа!Фа!а, + Фг1.-ЬА. = 0. B)
В уравнениях II, 4F) и II, 4(8), т. е. в условиях на скачке уплот-
уплотнения, следует заменить величины vxb vxll, t\vx, Диу и Дг»г на ФжГ,
Фхц, ДФа,, АФу и ДФг. В выражении II, 4(9) следует отбросить сте-
степени т. Обтекаемое тело по-прежнему описывается аппроксимирующей
цилиндрической поверхностью и отклонением действительной поверх-
поверхности от аппроксимирующей поверхности (это отклонение опреде-
определяется величиной К). Граничным условием на поверхности тела
теперь будет
дФ dh .„.
Для разности давлений мы будем иметь формулу
В случае тела вращения следует по-прежнему расположить на
оси вращения логарифмические особенности. Вблизи оси преобла-
преобладающую роль играют члены /г(х) и /2(хIпг, следовательно,
Пусть г — г (х) есть уравнение поверхности тела вращения; тогда
... ~ dr
Для определения давлений следует воспользоваться либо формулой
/ Ф2\
(вычислив Фх и Ф,. на поверхности тела), либо формулой
§ 9. Уравнение неразрывности и теорема импульсов
для околозвуковых течений
Покажем, какой вид принимают условие неразрывности и урав-
уравнение импульсов, если для определения добавочного потенциала Ф
пользоваться упрощенным дифференциальным уравнением II, 8 A).
Приближенное условие неразрывности и приближенное уравнение
импульсов могут быть использованы с целью отыскания приближенных
решений в тех случаях, когда для рассматриваемой задачи уравнение
неразрывности точно не удовлетворяется.

§ 9 УРАВНЕНИЕ НЕРАЗРЫВНОСТИ И ТЕОРЕМА ИМПУЛЬСОВ 63
Допустим, что внутри поля течения имеются источники общей
мощности p"a"q. Тогда упрощенным уравнением неразрывности будет
дФх дФу дФг
Рассмотрим объем V, ограниченный поверхностью О. Обозначим
через do единичный вектор направленной наружу нормали к эле-
элементу поверхности, через dV — элемент объема и через i,j, k—еди-
k—единичные векторы по направлениям х, у, z. Тогда, применив к урав-
уравнению A) интегральную теорему Гаусса, мы получим
Ф„/-г-Фг*) do = fffqdV.
Если мы использовали бы точное уравнение неразрывности, то левая
часть имела бы вид
pVyj -\~ pvzk) do.
В первом приближении pvx можно заменить на р*а*. При интегри-
интегрировании по замкнутой поверхности этот член, конечно, выпадает.
Учтя это обстоятельство и сравнив оба выражения под знаками двой-
двойного интеграла, мы найдем, что в околозвуковой области имеют
место следующие приближенные соотношения:
Первое уравнение показывает, что связь между плотностью потока
массы р w (которая приближенно равна pvx) и Фх изображается пара-
параболой. Следовательно, максимум плотности потока массы, так же
как и в случае точных дифференциальных уравнений [см. соотно-
соотношение I, 2A Оа)], получается при критической скорости.
Если теорема импульсов применяется для представления сил,
действующих на обтекаемое тело, в виде поверхностного интеграла,
то необходимо проявлять осторожность, так как импульс выражается
членами довольно высокого порядка. Поэтому выведем теорему
импульсов непосредственно из уравнения неразрывности A) для около-
околозвуковых течений. На первый взгляд может показаться, что для этой
цели удобнее воспользоваться уравнениями Эйлера. Однако последние
при введении потенциала автоматически удовлетворяются, даже если
внутри поля течения имеются источники. Конечно, при выводе тео-
теоремы импульсов следует учесть импульсы имеющихся источников,
если только рассматриваемый объем не является бесконечно малым.
Ниже мы ограничимся рассмотрением только составляющей
импульса в направлении х, так как она является наиболее чувстви-
чувствительной.

54 ГЛ II ЗАКОН ПОДОБИЯ ДЛЯ ОКОЛОЗВУКОВЫХ ТЕЧЕНИЙ
Умножим уравнение A) на Фх и представим результат в сле-
следующем виде:
- (v. +1) ф* фжж + А- (Фжфу)+± (ФжФг) -
Применив интегральную теорему Гаусса, мы получим
(
у—21|' + ФАУ+фЛ*|<«о =
///¦
C)
Обращает на себя внимание высокая степень, в которой входит
в левую часть составляющая потенциала Фх. Однако легко убедиться
в том, что если применить аффинное преобразование, при котором
соблюдается закон подобия, то все члены будут содержать т в оди-
одинаковых степенях, правда, при условии учета деформации элементов
поверхности О. Остается выяснить, действительно ли поверхностный
интеграл в равенстве C) дает составляющую в направлении х импульса
сил давления, действующих на поверхность обтекаемого тела.
На обтекаемом теле имеет место граничное условие
[A + Фх) I + Ф„у-Ь «Ml do = 0.
Преобразуем на основании этого соотношения два последних члена
левой части равенства C); тогда для интеграла по поверхности обте-
обтекаемого тела в равенстве C) мы получим выражение
В этом выражении ido есть проекция элемента поверхности на пло-
плоскость, перпендикулярную к направлению х. Более высокими сте-
степенями Фх мы можем пренебречь, так как поверхность тела дефор-
деформируется при аффинном преобразовании по-иному, чем координаты.
В рассматриваемом приближении выражение
есть не что иное, как разность давлений/?—р". Вывод производится
на основании таких же соображений, как и вывод уравнений B).
В общем случае члены Ф^/2 и Ф^/2 малы по сравнению с членом Фх.
С исключением мы познакомились на стр. 54 при исследовании обте-
обтекания осесимметричного тела. Следовательно, этот исключительный
случай содержится в полученной формулировке теоремы импульсов.

Глава III
ЛИНЕАРИЗОВАННОЕ ИССЛЕДОВАНИЕ ОКОЛОЗВУКОВЫХ
ТЕЧЕНИЙ
§ 1. Предварительные замечания
Из предыдущей главы мы знаем, что околозвуковое течение
описывается нелинейным дифференциальным уравнением. Однако это
отнюдь не означает, что этим уравнением следует пользоваться
во всех без исключения случаях. Имеется целый ряд задач, в кото-
которых нелинейный член играет незначительную роль. Это обстоятельство
чрезвычайно важно, так как решение нелинейного дифференциального
уравнения связано со столь большими трудностями, что оно воз-
возможно— без особо большой затраты труда — только в некоторых
специальных случаях. Среди проблем, допускающих исследование
посредством линейной теории, наиболее практически важной является
определение подъемной силы крыла с большим относительным раз-
размахом.
Линеаризованное исследование поля течения представляет интерес
также с теоретической точки зрения. Даже если численные резуль-
результаты, получаемые в результате такого исследования, неудовлетвори-
неудовлетворительны, все же они дают представление о характере трудностей,
которые необходимо преодолеть при введении нелинейного члена.
§ 2. Линеаризованное исследование плоских
и осесимметричных течений
Отбросив в уравнении II, 8A) член —(*+1) Ф^Ф^, мы получим
линеаризованное дифференциальное уравнение околозвукового тече-
течения, которое для двумерного случая принимает вид
Ф„,= 0. A)
Общим решением этого дифференциального уравнения будет
B)
где / и g суть произвольные функции. Мы видим, что для каждой
линии х — const значение Фу, представляющее в нашем приближении
наклон линий тока, остается постоянным. Следовательно, все линии
тока получаются одна из другой параллельным переносом в напра-
направлении оси у.
5 Зак. 634. К. Г. Гудгрлей

66 ГЛ. III. ЛИНЕАРИЗОВАННОЕ ИССЛЕДОВАНИЕ ОКОЛОЗВУКОВЫХ ТЕЧЕНИИ
Попробуем применить этот результат к обтеканию некоторого
профиля. Для описания формы профиля можно задать наклон & линий
тока к профилю как функцию от х, т. е. задать уравнение & —
Тогда функция f(x) будет определена, а именно мы будем иметь
Как определить теперь функцию g(x)? Для того чтобы не прийти
сразу к бессмысленному результату, рассмотрим обтекание нашего
профиля в свободной струе конечной ширины. При линеаризованном
рассмотрении задачи границы струи простираются вдоль линий
у = const = + у0. На этих линиях должно соблюдаться условие,
что давление на них должно быть равно критическому давлению,
а потому здесь, опять в первом приближении, должно быть Фж = 0.
Это условие удовлетворяется соответствующим выбором функции g.
В качестве решения для верхней половины поля течения мы получаем
C)
Поверхность струи имеет в рассматриваемом приближении такую же
форму, как и профиль. В самом деле, все линии тока получаются
одна из другой параллельным переносом в направлении оси у. Выше
и ниже по течению относительно профиля поверхность струи остается
невозмущенной.
Давления на поверхности профиля пропорциональны Ф^,. Мы имеем
Конечно, для того чтобы можно было применить линейную теорию,
давления должны быть малыми. Это означает, что должен оставаться
ограниченным либо наклон профиля, либо поперечный размер (ширина)
струи.
Какой физический смысл имеет найденное решение? В преды-
предыдущей главе мы получили для плотности потока массы в околозву-
околозвуковой области приближенные формулы II, 9B). Если мы отбрасываем
в дифференциальном уравнении околозвукового течения нелинейный
член, то мы должны отбросить нелинейный член и в формулах II, 9B),
следовательно плотность потока массы в околозвуковой области
будет постоянной. В первом приближении это означает, что расстоя-
расстояние между линиями тока в направлении у постоянно. Таким образом,
форма линий тока заранее известна.
То обстоятельство, что плотность потока массы зависит только
от членов второго порядка, показывает, насколько чувствительны
околозвуковые течения к вынужденным изменениям расстояния между
линиями тока; скорость должна значительно измениться, чтобы вызвать
хотя бы небольшое увеличение расстояния между линиями тока.
После того как форма линий тока определена во всем течении,
давления могут быть вычислены путем интегрирования центробежных.

§ 2. ПЛОСКИЕ И ОСЕСИММЕТРИЧНЫЕ ТЕЧЕНИЯ 67
сил. Именно таким путем получается решение C). Если ширина струи
увеличивается до, бесконечности, то давление на профиле возрастает
до бесконечности, положительной или отрицательной в зависимости
от знака кривизны профиля.
Таким образом, трудности линеаризованного рассмотрения нашей
задачи обусловливаются тем, что интегрирование центробежных сил,
допустимое для полосы ограниченной ширины, при неограниченной
ширине приводит к бесконечному значению давления. Следовательно,
к необходимости отказа от линейной теории приводят части поля
течения, удаленные от обтекаемого профиля. В линейной теории
возмущения, вызываемые профилем, остаются ограниченными только
в полосе, ширина которой не превышает ширины профиля. Нелиней-
Нелинейные члены дифференциального уравнения околозвукового течения
обусловливают, с одной стороны, увеличение ширины возмущенной
области, а с другой стороны, такое затухание первоначальных воз-
возмущений по мере удаления в бесконечность, что интегрирование
центробежных сил дает на профиле конечные давления. Именно
поэтому нельзя пренебрегать нелинейными членами даже на большом
расстоянии от профиля. На первый взгляд это обстоятельство может
показаться удивительным, так как на достаточно большом расстоянии
от профиля все возмущения становятся малыми. О такой роли не-
нелинейных членов всегда следует помнить при оценке приближенных
методов, применяемых для расчета околозвуковых течений 1).
Совершенно аналогичным образом исследуются осесимметричные
задачи. Линеаризованное уравнение для потенциала имеет вид
Фгг + ^ = 0, E)
1) Линеаризация обусловливает существенное изменение дифференциаль-
дифференциального уравнения, описывающего течение. А именно, если это уравнение
в своей первоначальной форме принадлежит в зависимости от знака перед Ф^
либо к эллиптическому, либо к гиперболическому типу, то после линеариза-
линеаризации оно становится параболическим. Однако с точки зрения прикладной
математики отсюда вовсе не следует, что линеаризацией нельзя пользоваться.
В самом деле, такого рода упрощение применяется весьма часто и при этом
обычно без каких-либо серьезных последствий; напомним хотя бы о пара-
параболическом уравнении пограничного слоя, получаемом из эллиптических
уравнений Навье — Стокса, или об уравнении сжимаемых невязких течений,
получаемом также из уравнений Навье — Стокса. Трудности, к которым
приводят такие упрощения, обычно проявляются только в небольших областях
поля течения. Эти области либо подлежат исключению из рассмотрения,
либо исследуются особо. Примерами таких областей могут служить погра-
пограничный слой или скачок уплотнения. В пограничном слое частицы движу-
движущегося газа прилипают к поверхности обтекаемого тела, и поэтому здесь
нельзя вводить допущение об отсутствии трения; теория пограничного слоя
по существу вносит поправки в результаты, получаемые на основе допуще-
допущения об отсутствии трения Скачки уплотнения представляют собой такие
чрезвычайно узкие зоны течения, в которых при использовании уравнений
Навье — Стокса получались бы очень высокие градиенты давления, а при
использовании допущения об отсутствии трения возникало бы перекрытие
плоскости течения.

68 ГЛ III ЛИНЕАРИЗОВАННОЕ ИССЛЕДОВАНИЕ ОКОЛОЗВУКОВЫХ ТЕЧЕНИИ
и его решением будет
Ф=/(*)Ш Г
Отсюда мы находим
Эта величина определяет также наклон вектора скорости.
Пусть форма обтекаемого тела задана уравнением г = 7(х). Тогда
граничным условием будет
f{x) __ d?
г dx
или
Функция g(x) по-прежнему должна быть определена из граничных
условий на некотором расстоянии от тела. Если тело обтекается
свободной струей радиуса г0, то решением будет
* = ?-&&№ г —\пг0].
И теперь при увеличении радиуса г свободной струи до бесконеч-
бесконечности давление на теле приближается к бесконечности, однако зна-
значительно медленнее, чем в плоской задаче. Это объясняется тем, что
при возрастании г, т. е. при увеличении поперечного сечения струи,
кривизна линий тока уменьшается, следовательно, центробежные силы
по мере удаления в бесконечность затухают 1).
На основании сказанного можно ожидать, что в осесимметричных
течениях физические особенности околозвуковой области проявляются
в меньшей степени, чем в плоских течениях.
Этот вывод заслуживает особого внимания, так как большая
часть точных решений для околозвуковых течений относится к плоским
задачам. При переносе результатов, полученных для плоских задач,
на осесимметричные задачи следует соблюдать осторожность.
Результаты линейной теории можно рассматривать как первый
член разложения точного решения по параметру, характеризующему
толщину профиля. Однако в неограниченном пространстве первый
член такого разложения все же дает бесконечно большие давления
на профиле. Для пластинки, помещенной в потоке под углом атаки,
мы нашли в предыдущей главе с помощью закона подобия, что
начальная касательная к кривой, изображающей зависимость подъем-
1) Если бы член Фг/г в уравнении (о) был больше единицы, то давле-
давления на профиле оставались бы, как это отметич А. Буземан, конечными
в любом случае, и, следовательно, применениг линейной теории в около-
околозвуковой области не должно было бы вызывать никаких опасений.

S 3. ПРОСТРАНСТВЕННЫЕ ТЕЧЕНИЯ 69
ной силы от угла атаки, действительно вертикальна. В этой задаче
угол атаки играет такую же роль, как толщина профиля. Таким
образом, хотя линейная теория вообще бесполезна, она все же не-
немного проясняет общую картину.
§ 3. Пространственные течения
Для пространственных течений дифференциальное уравнение
II, 8 A) после линеаризации принимает вид
=0. A)
Мы видим, что это уравнение не содержит производных по х, сле-
следовательно, оно может решаться в каждом поперечном сечении х = const
независимо от соседних поперечных сечений. Правда, позади крыла
различные поперечные сечения связаны между собою граничным
условием, которое должно выполняться на вихревом следе.
На основании уравнения II, 8C) граничным условием на поверх-
поверхности тела будет
»„ = §. B)
где vn есть составляющая скорости, лежащая в плоскости х = const
и перпендикулярная к аппроксимирующей цилиндрической поверх-
поверхности (см. § 5 гл. II), a h есть расстояние от поверхности тела
до аппроксимирующей цилиндрической поверхности, измеренное
в направлении vn. Существенно, что в граничное условие B) входит
только составляющая скорости, лежащая в рассматриваемой плоскости
х = const. В каждой такой плоскости приходится решать краевую
задачу второго рода для двумерного уравнения Лапласа.
Следующее граничное условие получается из требования об обра-
обращении в нуль потенциала в бесконечности, так как иначе там имелись бы
дополнительные, не равные нулю скорости. Если плоскость х== const
пересекает поверхность обтекаемого тела по нескольким кривым,
как это имеет место, например, для стреловидного крыла (начиная
с некоторого расстояния от его передней точки), то последнее гра-
граничное условие уже не приводит к однозначному решению. В этом
случае необходимо допустить, что на следе, образующемся за задней
кромкой крыла, потенциал претерпевает разрыв (однако производная
потенциала в направлении, нормальном к поверхности следа, всегда
остается непрерывной). Непосредственно выше и ниже следа потен-
потенциал постоянен вдоль прямых, параллельных оси х. На задней кромке
крыла должно выполняться условие Кутта *): скорость здесь не должна
принимать бесконечно большого значения. Перечисленные условия
!) Это условие известно также под названием условия Жуковского —
Чапльтина.— Прим. ред.

70 ГЛ. Ш ЛИНЕАРИЗОВАННОЕ ИССЛЕДОВАНИЕ ОКОЛОЗВУКОВЫХ ТЕЧЕНИЙ
приводят к интегральному уравнению, определяющему потенциал
в следе и полностью решающему рассматриваемую задачу обтекания.
Для каждого поперечного сечения х = const потенциал Ф опре-
определяется дифференциальным уравнением и граничными условиями
плоского несжимаемого течения. Интеграл Гvnds, взятый вдоль
кривой пересечения обтекаемого тела с плоскостью х = const (при-
(причем ds есть линейный элемент этой кривой), дает для только что
указанного плоского несжимаемого течения количество жидкости,
вытекающей из объема, занимаемого телом. Если это количество
не равно нулю, то в бесконечности потенциалу соответствует источ-
источник, т. е. там в выражении потенциала главную роль играет член,
содержащий In r. Но именно этот член делает невозможным приме-
применение линейной теории к обтеканию осесимметричного тела. Поэтому
необходимо потребовать, чтобы
vnds=O.
Использовав равенство B), мы можем переписать это условие в виде
¦s— ds = 0. (о)
дх
Но величина
^— Г fids
дх J
есть не что иное, как производная от площади поперечного сечения
тела в направлении х, следовательно, уравнение C) выражает собой
требование о постоянстве площадей поперечных сечений тела, лежа-
лежащих в плоскостях х = const. Но площадь начального поперечного
сечения тела конечных размеров (например, крыла) равна нулю, сле-
следовательно, пространственная линейная теория применима только
к телам с нулевой толщиной.
В практически наиболее важном случае, когда обтекаемым телом
является крыло, цилиндрическая поверхность, в которую тело стя-
стягивается при х = 0, является плоской. Крыло может быть поставлено
под углом атаки, может быть изогнутым и даже закрученным.
В каждой плоскости х = const вдоль отрезка, который представляет
пересечение этой плоскости с крылом, например вдоль отрезка оси z,
производная от Ф в направлении нормали задана. На верхней и ниж-
нижней сторонах этого отрезка значения производной в направлении
нормали имеют для бесконечно тонкого крыла противоположены
знаки. Для систематического получения решения следует конформно
отобразить плоскость х = const на другую плоскость так, чтобы
указанный отрезок оси z перешел в окружность, и затем решить
краевую задачу методом Фурье. Иногда рассматриваемая задача фор-
формулируется в виде интегрального уравнения в плоскости у, z, однако
способ решения от этого не меняется.

'§ 3 ПРОСТРАНСТВЕННЫЕ ТЕЧЕНИЯ 71
В качестве примера приведем решение для крыла с постоянным
углом атаки. В этом случае величина h в уравнении B) является
линейной функцией от х, а нормальная составляющая скорости вдоль
отрезков, представляющих крыло в различных плоскостях х = const,
постоянна. Решение можно получить, либо систематически применяя
описанный выше способ, либо путем догадки, если вспомнить, что
в теории крыла Прандтля эллиптическое распределение подъемной
силы дает в бесконечности постоянную нисходящую скорость.
В соответствии с этим примем, что
Ф = const • Re (У*2-т-С2 — С),
где
Постоянную, входящую в правую часть равенства, несколько позже
подберем так, чтобы получился требуемый угол атаки. Если мы разложим
корень в ряд и выберем при этом положительный знак, то увидим,
что потенциал в бесконечности равен нулю. Для скорости в направле-
направлении у мы получим значение
На поверхности пластинки у —0, поэтому C = i2; корень здесь
равен У^Ь2 — z2 и имеет вещественное значение для .z < 6. Поэтому
на поверхности пластинки вещественная часть выражения QY~b2-{-C2
равна нулю, следовательно,
Фу = — const.
В рассматриваемом случае уравнением поверхности пластинки является
у =— ах, где а есть угол атаки. В качестве граничного условия
мы найдем
Ф„ = — а.
Вследствие линеаризации это условие должно выполняться вдоль
оси z, т. е. постоянная в принятом выше выражении для потен-
потенциала Ф должна быть равна а. Предположим, что контур крыла
симметричен относительно оси х и задан уравнением b = b(x), при-
причем функция b по соображениям, о которых будет сказано ниже,
является неубывающей функцией. Тогда потенциал Ф будет равен
Ф = a
Продифференцировав это выражение по х, мы найдем составляющую
скорости в направлении х, а зная последнюю, сумеем вычислить
давления с помощью уравнения Бернулли.

72 ГЛ. III. ЛИНЕАРИЗОВАННОЕ ИССЛЕДОВАНИЕ ОКОЛОЗВУКОВЫХ ТЕЧЕНИЙ
Если b = const, то в рассматриваемом приближении постоянен
в направлении х также потенциал Ф, и поэтому давления на верхней
и нижней поверхностях крыла равны давлению в набегающем потоке.
Следовательно, там, где b — const, поверхность крыла не воспри-
воспринимает никаких сил, вследствие чего соответствующие части крыла
можно отбросить. Тем самым мы нашли решение также для случаев
с постоянным углом атаки, в которых функция Ъ уменьшается. Потен-
Потенциал в том поперечном сечечии, в котором функция b достигает макси-
максимума, остается в других поперечных сечениях, лежащих ниже по тече-
течению, постоянным и соответствует там потенциалу вихревой пелены.
Полная подъемная сила равна
+ъ
max
A = 2p*ai2 ff Фхс1хс1г = 2р*а*\ f Vblax — z* dz=
площ. крыла ~&max
(множитель 2 учитывает вклад нижней и верхней сторон поверхности
крыла). Таким образом, подъемная сила зависит только от угла
атаки и от максимального размаха.
Линеаризация возможна лишь в том случае, если значения Фя
не становятся слишком большими. Это означает, что поперечное
сечение нг должно изменяться слишком быстро. В предельном слу-
случае обтекания прямоугольной пластинки под углом атаки на передней
кромке имеет место скачкообразное изменение значения Ь, и Фх
становится бесконечно большим. Тем не менее возникающая подъем-
подъемная сила А остается конечной (см. последнюю формулу), но она
целиком концентрируется на передней кромке. Конечно, в этом
случае линейная теория неприменима.
Линеаризованному исследованию стреловидного крыла посвящены
работы Манглера, а также Хислета, Ломакса и Спрейтера (см. лит. 1).
Аналогичные исследования для до- и сверхзвукового течений выпол-
выполнены Р. Т. Джонсом (см. лит. 1).
§ 4. Тело с толщиной, не равной нулю
Как мы выяснили в § 2, линеаризованное уравнение для потен-
потенциала не позволяет найти поле течения около осесимметричного
тела при числе Маха М=\, так как интегрирование центробежных
сил приводит к бесконечным давлениям. Такой же отрицательный
результат получается и для тела произвольной формы, если его
поперечные сечения плоскостями х = const имеют толщину, не рав-
равную нулю. Тем не менее можно сравнительно просто рассчитать
поле течения около тела произвольной формы с неравной нулю
толщиной и, кроме того, получить оценку для сопротивления, если

§ 4 ТЕЛО С ТОЛЩИНОЙ, НЕ РАВНОЙ НУЛЮ 73
воспользоваться способом, предложенным Осватичем и Кёйне (см.
лит. 1). В этом способе предполагается, что известно поле течения:
около так называемого эквивалентного тела вращения. Попереч-
Поперечные сечения такого тела плоскостями х = const имеют одинаковую
площадь с соответствующими поперечными сечениями исследуемого
тела. Поле течения около эквивалентного тела вращения должно
быть определено путем использования полного приближенного диф-
дифференциального уравнения околозвуковых течений х). Влияния несов-
несовпадения поперечных сечений исследуемого тела с соответствующими
поперечными сечениями эквивалентного тела вращения учитывается
посредством линеаризованного уравнения
Способ Осватича и Кёйне основан на следующих соображениях.
Дифференциальное уравнение A) следует рассматривать не обяза-
обязательно как результат линеаризации, т. е. как разложение поля тече-
течения по параметру, учитывающему толщину крыла; его можно полу-
получить также иным путем, а именно принять, что обтекаемое тело-
является достаточно тонким, а затем применить метод, рассмотренный
на стр. 37. Следовательно, дифференциальное уравнение A) вполне
совместимо с представлением, что поперечные сечения, получающиеся
в плоскостях х = const, остаются подобными при предельном пере-
переходе, ведущем к упрощению дифференциального уравнения (при
обычной линеаризации эти поперечные сечения изменяются аффинно).
Вообще, используя уравнение A) в соответствии со способом, рас-
рассмотренным на стр. 37 и 38, можно рассчитать обтекание произ-
произвольного достаточно тонкого тела, на которое набегает свободная
струя со скоростью, равной критической.
Конечно, увеличить радиус свободной струи до бесконечности не-
удастся. С другой стороны, не может быть никаких возражений
против ограничения применения уравнения A) в цилиндрической
области, заключающей в себе обтекаемое тело. Тогда вне этой4
области следует применять полное дифференциальное уравнение около-
околозвуковых течений. Покажем, во-первых, как можно построить реше-
решение на основе высказанных соображений и, во-вторых, что неточ-
неточности, возникающие при таком построении, вполне допустимы длж
достаточно тонкого тела.
Пусть поверхность обтекаемого тела задана уравнением
F (х, ~у, z) = О,
где
!) Полным приближенным дифференциальным уравнением автор назы-
называет уравнение II, 8A).— Прим. ред.

74 ГЛ III. ЛИНЕАРИЗОВАННОЕ ИССЛЕДОВАНИЕ ОКОЛОЗВУКОВЫХ ТЕЧЕНИИ
Параметр х учитывает степень тонкости тела. Если х->•(), то для
того, чтобы соблюдались два последних равенства, необходимо соот-
соответственно уменьшать у и z. Площадь поперечных сечений тела
в плоскостях х = const пропорциональна т. Единичным вектором
в направлении нормали к поверхности тела будет
dF . . ,, dF . , ,, dF .
дх ду
Если принять а*=1, то граничным условием на поверхности обте-
обтекаемого тела будет
*?ф +*?<!>, = _*-%*?. B)
ду у dz г дх
Пусть цилиндрическая поверхность, отделяющая внутреннюю об-
область, в которой используется уравнение A), от внешней области,
в которой следует применять полное дифференциальное уравнение,
задана уравнением
_у2_|_22 —const.
Положение этой поверхности не зависит от х. Ниже мы увидим, что
вне этой поверхности поле течения около достаточно тонкого тела
сколь угодно мало отклоняется от осесимметричного поля, следова-
следовательно, там можно рассчитать отклонение от осевой симметрии путем
линеаризации.
Для эквивалентного тела вращения решением уравнения для потен-
потенциала вблизи оси будет
Ф=/{х)\п r + g{x). ' C)
Если исходить из полного дифференциального уравнения околозву-
околозвукового течения, то к указанным членам присоединятся еще члены
порядка г2 (In гJ. В самом деле, член Ф^Ф^а, имеет порядок (In гJ,
и соответствующее слагаемое в выражении потенциала Ф получается
интегрированием по г. Конечно, при изменении х эквивалентное
тело вращения деформируется. Эгу деформацию можно определить
¦при помощи закона подобия для околозвуковых течений [уравне-
[уравнение II, 5 (8)]. Мы получим
Ф = х {/ (х) In (rxV.) -+- g {x) + О [(rx'/,J (in („•/,) J]}. Ca}
Следовательно, дополнительные члены имеют величину порядка х2 (In тJ.
Пусть для тела произвольной формы Ф^. и Фхх ограничены; это усло-
условие означает, что площадь поперечного сечения тела должна меняться
непрерывно. Если это условие соблюдается, то член Фж Фхх будет
иметь один и тот же порядок и для эквивалентного тела вращения
и для тела произвольной формы, а поэтому и ошибка, получающаяся
при определении потенциала, будет иметь в обоих случаях одинако-
одинаковый порядок.

§ 4 ТЕЛО С ТОЛЩИНОЙ, НЕ РАВНОЙ НУЛЮ 75
В качестве решения для внешней области возьмем решение, соот-
соответствующее эквивалентному телу вращения. Правда, трудности, воз-
возникающие при расчете такого поля течения, полностью еще не пре-
преодолены. Вид решения, соответствующий эквивалентному телу вра-
вращения, нам известен вблизи оси вращения [уравнение (За)]. При
достаточно малом г решение (За) применимо вплоть до границы обеих
областей. Функция g(x) определяется полем течения в целом, а функ-
функция f(x) задана распределением площадей поперечных сечений экви-
эквивалентного тела вращения. Следовательно, потенциал на границе обеих
областей, если его вычисление вести из внешней области, будет
с точностью до членов порядка г2(!птJ равен
Для внутренней области решение имеет вид
причем функция h должна быть аналитической в плоскости y-\-iz
и, кроме того, должна быть выбрана так, чтобы удовлетворялось
граничное условие B) на поверхности обтекаемого тела. Именно
этими требованиями объясняется выбор независимых переменных у
и z и появление множителя х в решении. Далее, разложение функ-
функции h при у -f- iz -> со должно содержать, кроме членов, обращаю-
обращающихся в нуль в бесконечности, только член In (_y —j— /^) и никаких
других членов, зависящих от y-\~iz. Так как распределение площа-
площадей поперечных сечений эквивалентного тела вращения совпадает
с таким же распределением для исходного тела, то в обоих случаях
член Re In (y-\-iz) получается одинаковым. Что касается функции gi(x),
то ее определение не связано с граничным условием на профиле;
мы можем выбрать ее одинаковой с функцией g(x) для эквивалент-
эквивалентного тела вращения.
Теперь можно оценить ошибку, содержащуюся в найденном реше-
решении. Частично она объясняется тем, что для получения решения во
внутренней области было использовано неточное дифференциальное
уравнение; порядок величины этой части ошибки уже был определен
выше. Далее, оба решения совпадают друг с другом на граничной
поверхности между обеими областями не вполне точно. Так, напри-
например, во внутренней области при больших значениях y-\-iz для тела,
обтекаемого под некоторым углом атаки, к решению добавляются
члены порядка ^/(y-\-iz), а для тела, обтекаемого под нулевым
углом атаки, — члены порядка x2/(y-\-izJ. Скачкообразное изменение
на граничной поверхности величин Ф и Фг, вызываемое этими чле-
членами, можно компенсировать наложением дальнейших решений во
внутренней и внешней областях. Соответствующая поправка имеет
самое большее такой же порядок, как порядок величины скачка; для

76 ГЛ III. ЛИНЕАРИЗОВАННОЕ ИССЛЕДОВАНИЕ ОКОЛОЗВУКОВЫХ ТЕЧЕНИЙ
тела, обтекаемого под углом атаки, она пропорциональна х"^, а для
тела, установленного в потоке под нулевым углом атаки, она про-
пропорциональна т2. Можно показать, что на поверхности тела, обте-
обтекаемого под углом атаки, эта поправка дает величину порядка т2.
Таким образом, для достаточно тонкого тела ошибкой получен-
полученного решения можно пренебречь. Примечательно, что положение
граничной поверхности между обеими областями совершенно не влияет
на окончательное решение, так как в него от решения для внешней
области входит только функция g(x).
Оценка ошибки для конкретных случаев дана Ландалем (см. лит. 3).
Краевая задача во внутренней области может быть решена для попе-
поперечного сечения с небольшой толщиной путем разложения в ряд по
параметру толщины. Метод расчета разработан Кейне (см. лит. 1).
В указанном разложении члены высшего порядка могут играть роль
для треугольного крыла, у которого отношение его толщины к раз-
размаху в сечениях плоскостями х = const может не быть малым. Для
других профилей следует пользоваться методами теории аналитиче-
аналитических функций.
Лобовое сопротивление и подъемная сила тела с ненулевой толщи-
толщиной определяются проще всего путем применения теоремы импульсов»
причем контрольная поверхность составляется из поверхности обте-
обтекаемого тела и из поверхности, разделяющей внутреннюю и внешнюю
области. Как нетрудно убедиться с помощью уравнения II, 9 C),
члены, входящие в баланс импульсов, получаются на граничной
поверхности между обеими областями одними и теми же независимо
от того, используется ли дифференциальное уравнение' течения с чле-
членом Ф^Ф^а; или без него. Для вычисления лобового сопротивления
при малых значениях т можно использовать составляющие скорости
в том виде, в каком они получаются для внешней области. Но эти
скорости представляют собой не что иное, как скорости поля тече-
течения для эквивалентного тела вращения. Следовательно, лобовое
сопротивление тела с ненулевой толщиной равно с точностью до
величин высшего порядка лобовому сопротивлению эквивалентного
тела вращения. Это впервые было обнаружено Осватичем и Кёйне,
а также Уайткомом (см. лит. 1).
Очевидно, что при заданной относительной толщине тела враще-
вращения наименьшим лобовым сопротивлением обладает та форма, для
которой изменение площадей поперечных сечений изображается глад-
гладкой кривой (это особенно важно для сверхзвуковой области). Отсюда
следует, что можно значительно уменьшить лобовое сопротивление
самолета в околозвуковой области, если в тех поперечных сечениях,
в которых находятся крылья, сделать фюзеляж втянутым.
Как на основании теоремы импульсов определяется подъемная
сила для тонких тел, хорошо известно из до- и сверхзвуковой аэро-,
динамики. При звуковой скорости результаты для до- и сверхзвуко-
сверхзвуковой области гладко переходят один в другой. Изложенные выше

§ 5 НЕУСТАНОВИВШИЕСЯ ОКОЛОЗВУКОВЫЕ ТЕЧЕНИЯ 77
соображения оправдывают применение теоремы импульсов для опре-
определения подъемной силы также в околозвуковой области.
В качестве курьеза упомянем следующее. При сверхзвуковом
обтекании тела вращения линейная теория приводит к формуле лобо-
лобового сопротивления, дающей для последнего конечное значение также
при предельном переходе к числу Маха М=\, хотя при таком М
давления на поверхности тела делаются бесконечно большими. Конечно,
такой результат должен вызывать недоверие, и, действительно, срав-
сравнение с опытом сразу показывает его неправильность. Недопусти-
Недопустимость применения в данном случае такого способа расчета подтверж-
подтверждается и тем, что если попытаться определить лобовое сопротивление
при числе Маха М =1 путем предельного перехода из дозвуковой
области, то на основании парадокса Даламбера оно должно полу-
получиться равным нулю.
§ 5. Линеаризованное исследование
неустановившихся околозвуковых течений
Многие трудности исследования околозвуковых течений отпадают
для неустановившихся течений с не слишком малыми ускорениями.
С такого рода течениями мы сталкиваемся при полете тел, перехо-
переходящих через критическую скорость со значительным ускорением.
В этих случаях для расчета сил, действующих на летящее тело, как
правило, не требуется прибегать к нелинейной теории.
С физической точки зрения исследование неустановившихся тече-
течений представляет интерес в том отношении, что позволяет выяснить,
почему линеаризованное рассмотрение установившихся течений при-
приводит к появлению бесконечных давлений.
Для исследования неустановившегося течения лучше всего поль-
пользоваться системой координат, связанной с окружающим неподвижным
воздухом. В этом случае уравнение I, 4 (9), если ограничиться только
членами первого порядка, принимает известный из акустики вид
"о
где а0 есть скорость звука в неподвижном воздухе. Для сферических
волн это уравнение заменяется уравнением
г а*0
где
г^ = х2-!гу2-\-г2.
Решением для сферических волн будет

78 ГЛ III. ЛИНЕАРИЗОВАННОЕ ИССЛЕДОВАНИЕ ОКОЛОЗВУКОВЫХ ТЕЧЕНИИ
причем положительный знак следует взять для волн, распространяю-
распространяющихся к центру шара, а отрицательный знак—для волн, распро-
распространяющихся наружу. В дальнейшем мы будем рассматривать только
волны второго рода. В частности, решение A) показывает, что
относительно неподвижного воздуха возмущение распространяется
со скоростью а0. Таким образом, исследуемый нами сейчас случай
подтверждает, что та скорость, которую мы обозначали всегда
через а, действительно является скоростью звука.
Приведенное выше уравнение для потенциала выполняется всюду,
за исключением центра сферы. Так как оно выражает собой не что
иное, как условие неразрывности, то его невыполнение в определен-
определенной точке означает, что там имеется либо источник, либо сток. Для
того чтобы вычислить мощность источника, составим выражение
скорости в направлении г и проинтегрируем это выражение по по-
поверхности сферы, близкой к началу координат. Тогда мы получим
для массы, протекающей в единицу времени через сферу, значение
а0
Если мы будем приближать радиус сферы к нулю, то найдем, что»
мощность источника в момент времени t равна
При движении осесимметричного тела источники и стоки, безу-
безусловно, не могут возникать вне тела. Попытаемся представить тече-
течение, вызываемое движущимся телом, посредством распределения
источников, расположенных на оси тела.
Для определения потенциала источника, находящегося в точке хи
у = 0, z = 0 и имеющего в момент времени t мощность q(xlt tj,
воспользуемся уравнением A), предварительно перенеся соответ-
соответствующим образом начало координат; мы получим
где
R = V{x — xtf + 72 Dа)
и
r2==y2JrZ2m D6)
Вторым аргументом функции q является, согласно сделанному выше
определению этой функции, момент времени tlt для которого
в точке х1 необходимо определить мощность источника; мы имеем

S 5. НЕУСТАНОВИВШИЕСЯ ОКОЛОЗВУКОВЫЕ ТЕЧЕНИЯ
79-
Путем наложения таких источников мы получим для потенциала Ф
формулу
Представим теперь движение тела графиком, изображающим зависи-
зависимость пути х от времени t. Пусть линия х = й (t) изображает дви-
движение передней точки тела. Если тело имеет длину L, то движение
крайней задней точки тела изображается линией х = h(t)-\-L (рис. 5).
io
ось тела в рассматриваемый
момент времени
матр
область,
содержащая
источники
гипербола влияния
для точки,лежащей
на поверхности тела
ЛТ
Рис. 5. К расчету течения около тела вращения, которое
внезапно выводится из состояния покоя и сразу приобретает
дозвуковую скорость.
В области плоскости х, t, лежащей между этими линиями (на рис. 5
эта область заштрихована), мощность источника g может быть отлич-
отличной от нуля. Если в момент времени t мы рассмотрим точку про-
пространства с координатами х и г, то на основании формулы E)
вторым аргументом функции q будет
G)
Следовательно, при фиксированных значениях х, г и t связь между-
междупервым и вторым аргументами функции q определяется уравнением
соответствующим гиперболе, асимптоты которой пересекаются в точке
с координатами хх = х и t1-=t. Такая гипербола, называемая
гиперболой влияния, изображена на рис. 5; она соответствует
точке, которая лежит на поверхности обтекаемого тела. Следова-
Следовательно, для вычисления потенциала Ф по формуле F) необходима

SO ГЛ. III. ЛИНЕАРИЗОВАННОЕ ИССЛЕДОВАНИЕ ОКОЛОЗВУКОВЫХ ТЕЧЕНИИ
использовать точки диагратмы х, t, лежащие вдоль построенной
гиперболы влияния. Если г мало, то эксцентриситет этой гипер-
•болы мал, и поэтому путь интегрирования почти целиком совпа-
совпадает с асимптотами.
Конечно, функция g(xv ^1) определяется граничными условиями
яа поверхности тела. Пусть меридианное сечение задано уравнением
причем система координат г, I движется вместе с телом, а ось ?
совпадает с осью х. В таком случае для фиксированной точки тела
мы будем иметь
Нормаль к поверхности тела задается вектором
(J, есть единичный вектор в направлении х, a j—единичный вектор
в направлении г). Скорость относительно движущегося тела опре-
определяется вектором
дх
Так как нормальная составляющая скорости равна нулю, то, приняв
величину
значение
величину дФ/дх малой по сравнению с dhjdt, мы найдем для Ф~
•Следовательно, значения Ф~ предписываются граничными условиями.
Выразив Ф^ через интеграл, мы получим для определения q инте-
интегральное уравнение. Приближенное рзшение можно найти следующим
образом. Внеся в формулу F) значение t из равенства G), мы най-
найдем для фиксированной точки х
i + [ к
т. е. доля, вносимая в Ф~ источниками, быстро убывает с увели-
увеличением расстояния R источника от рассматриваемой точки. Следо-
Следовательно, для определения Ф~ в заданной точке х, г, t играет роль
только часть соответствующей гиперболы влияния, а именно та
часть, которая расположена в непосредственной близости от задан-
заданной точки. Это означает, что составляющая скорости в направле-

§ 5 НЕУСТАНОВИВШИЕСЯ ОКОЛОЗВУКОВЫЕ ТЕЧЕНИЯ 81
нии г в точке, лежащей вблизи оси х, определяется почти исклю-
исключительно мощностью источников, расположенных в рассматриваемый
момент времени на непосредственно прилегающих частях оси. Эф-
Эффект этих источников легко найти из наглядных соображений.
Пусть g(xv tt) есть мощность источника на единицу длины оси.
Эта масса выходит в единицу времени через поверхность цилиндра,
ось которого совпадает с осью х, следовательно, мы имеем
2я7Ф7 =?(*!, tj.
7
Отсюда, использовав равенство (8), мы найдем в первом приближе-
приближении q. Внеся полученное значение в формулу F) мы получим
+ ОО _
Ф(х. г.0 = т / (E)
причем t1 определяется формулой G), а ? и R — формулами
Строгий вывод этого результата имеется в работе Ф. И. Франкля [1]
(см. лит. 1).
Для определения давлений на теле следует воспользоваться
линеаризованным уравнением Бернулли для неустановившегося тече-
течения. Мы найдем
Как нетрудно видеть из формулы, определяющей потенциал для
отдельного источника, производная Ф^ пропорциональна R'1.
Хотя R~x с увеличением расстояния уменьшается, тем не менее
интеграл, взятый по xv с увеличением х1 логарифмически стремится
к бесконечности, следовательно, величина давлений на теле в значи-
значительной мере может быть обусловлена удаленными частями гипер-
гиперболы влияния.
После этих подготовительных соображений можно построить
качественную картину возникновения аэродинамических сил, дей-
действующих на тело при разных состояниях полета. Пусть тело
выведено из состояния покоя, причем в одном случае ему сразу
сообщена некоторая дозвуковая скорость, в другом случае — тоже
сразу звуковая скорость и в третьем случае — опять сразу сверх-
сверхзвуковая скорость. Соответствующие диаграммы х, t построены
на рис. 5, 6 и 7. В заштрихованных областях величина q не равна
нулю, но при этом она является здесь функцией только расстояния %
от передней точки тела, так как в каждом случае скорость полета
постоянна.
6 Зак 534. К. Г. Гудерлей

82 ГЛ. III. ЛИНЕАРИЗОВАННОЕ ИССЛЕДОВАНИЕ ОКОЛОЗВУКОВЫХ ТЕЧЕНИЙ
На рис. 5 — 7 изображены также гиперболы влияния для точки,
расположенной на поверхности обтекаемого тела. Можно счи-
считать, что каждая из этих гипербол движется вместе с телом. Мы
видим, что при дозвуковой и сверхзвуковой скоростях полета на
величину давления влияют только конечные отрезки гипербол. При
ось тела в рассматриваемый
момент времени
гипербола влияния
для точки, лежащей
на поверхности тела
«V*
область, содержащая
источники
Рис. 6. К расчету течения около тела вращения, которое внезапно
выводится из состояния покоя и сразу приобретает звуковую ско-
скорость.
ось тела в рассматриваемый
момент времени
область, содержащая
источники
гипербала влияния с
для точки, лежащей
на поверхности тела
Р и с. 7 К расчету течения около тела вращения, которое
внезапно выводится из состояния покоя и сразу приобретает
сверхзвуковую скорость.
сверхзвуковой скорости полета это влияние обусловлено только
источниками, расположенными впереди рассматриваемой точки относи-
относительно системы координат, движущейся вместе с телом. При этом
каждый из таких источников влияет на давление в рассматриваемой
точке дважды, а именно: один раз, когда волна, исходящая из источ-
источника и движущаяся вниз по течению, проходит через рассматриваемую
точку, и второй раз, когда рассматриваемая точка догоняет волну,
исходящую из того же источника, но движущуюся вверх по течению.

t 5 НЕУСТАНОВИВШИЕСЯ ОКОЛОЗВУКОВЫЕ ТЕЧЕНИЯ 83
При дозвуковой скорости полета на распределение давления
в заданном месте оказывают влияние все точки тела.
При движении тела с звуковой скоростью заштрихованный уча-
участок диаграммы х, t отсекает от гиперболы влияния конечный
отрезок только тогда, когда время, прошедшее с момента начала
движения, конечно, Пусть движение тела начинается в момент
времени t — Q. Чем больше пройдет времени после этого момента,
тем длиннее будет правая ветвь гиперболы в заштрихованной области.
Так как влияние источника на величину давления пропорционально R~xt
т. е. для больших значений t пропорционально (х— х^, то давле-
давления, определяемые интегрированием по xv возрастают при увеличе-
увеличении t пропорционально 1пх или \x\.t. Тело все время движется со-
скоростью вызванных им возмущений, и эти возмущения влекут за
собой все большее и большее возрастание давлений. Конечно, при
сильном изменении давления изменяется также скорость звука, и по-
поэтому первоначальные возмущения отделяются от тела. В результате
возникает установившееся поле течения, но его формирование опре-
определяется и нелинейными членами дифференциального уравнения,
учитывающими изменение скорости распространения звука.
Если тело движется с непостоянной скоростью, то тогда графики,
связывающие время и путь, пройденный передней и задней точками
тела, уже не будут прямыми линиями. Следовательно, при ускорен-
ускоренном движении заштрихованная область отсекает от гиперболы влия-
влияния, построенной для рассматриваемой точки в рассматриваемый
момент времени, конечный отрезок, и поэтому давления получаются
конечными.
Допустим теперь, что ускорение мало, и выясним, насколько
в этом случае давления на теле отклоняются от соответствующих
давлений при установившемся течении. Такая постановка вопроса
возможна для до- и сверхзвуковой скоростей полета. Пример, разо-
разобранный в работе Ф. И. Франкля [1] (см. лит. 1), показывает, что
во всех практически важных случаях долю сопротивления, вносимую
наличием ускорения, можно не учитывать.
Для движения с околозвуковой скоростью сформулированная
выше постановка вопроса невозможна, так как в установившемся
течении, происходящем со скоростью звука, т. е. при ускорении,
равном нулю, давления на теле становятся бесконечно большими.
Теперь можно поставить вопрос только о том минимальном значе-
значении ускорения, при котором отрезок гиперболы влияния получается
столь малым, что возникающие давления можно учитывать на основе
линейной теории. Такое исследование выполнено Дж. Коулом [21
(см. лит. 1); оно показало, что минимальное значение ускорения
хотя и лежит в пределах возможного, но в большей части случаев
не достигается.
Соображения, изложенные выше, могут быть применены также
к плоским течениям и к обтеканию крыльев с конечным размахом.

34 ГЛ III ЛИНЕАРИЗОВАННОЕ ИССЛЕДОВАНИЕ ОКОЛОЗВУКОВЫХ ТЕЧЕНИЙ
И в этих случаях решение строится из пространственных источ-
источников, однако исследование получается более сложным. На рис. 8—13
изображены важнейшие из результатов, полученных Гарднером
и Ладлоффом (см. лит. 1).
16
1»
О
Л
^&=i.
2
0
Г"
-——.
"Г
1 —
1,0 1,1 1,2 1,3
1.5 1,6 1.7 1.3
7
6
5
3
г
i
\
—
=/,з
— —
о 0,005 сою ао/5 о.ого оог5 аозо
"Р[и с. 8. Зависимость коэффициента подъемной
¦силы от числа Маха при различных коэффициен-
коэффициентах ускорения р (по Гарднеру и Ладлоффу).
СА ~ коэффициент подъемной силы; Ь — ускоре-
ускорение; а —скорость звука; I —длина пластинки;
« — угол атаки; C = 2йЛ/а2 — коэффициент уско-
ускорения.
Рис. 9. Зависимость коэффициента да-
давления от коэффициента ускорения для
клина при Af=l и А1=1,3 (по Гарднеру
и Ладлоффу).
ср — коэффициент давления; 8 —угол ра-
раствора клина; х — координата, измеренная
вдоль ребра клина; Ъ — ускорение, р =
= Ibxja? — коэффициент ускорения.
1
-О
ч
4—
Г
го
16
12
О
1,0 1,1 1,2 1,3
м
1,5 16 1,7 1,3
Рис. 10. Зависимость коэффициента сопротив-
сопротивления с от числа Маха для ромбовидного
профиля (по Гарднеру и Ладлоффу).
й —половина угла при вершине ромба; остальные
обозначения такие же, как на рис. 8.
'О
17
15
13
12
\
\
k
\
S
1—,
V
\
Ч.
.
аг о// о,б as ю и
/з—>-
Рис. 11. Зависимость коэффициента
сопротивления с от коэффициента
ускорения 3 при числе Маха, равном
^единице (по Гарднеру и Ладло<{ ' '
Обозначения такие же, как на рис. 8.
Неустановившимся течением другого рода является движение
вокруг движущегося вперед гребного винта, если рассматривать это
движение в системе координат, связанной с окружающим воздухом.
Если концы лопастей винта движутся со сверхзвуковой скоростью,
то точки лопасти, находящиеся на некотором расстоянии от оси,
имеют относительно окружающего воздуха звуковую скорость.

i 6. ПРЕДЕЛЫ ПРИМЕНИМОСТИ ЛИНЕЙНОЙ ТЕОРИИ
85
В работе Буземана [3] (см. лит. 1) показано, что для течений,
в которых относительное набегание со скоростью звука возникает
только в отдельных местах, применение линейной теории не ведет
к каким-либо трудностям.
^удлинение °°
\ i
\\л/длинение 7
01
Рис. 12. Для клина: зависимость коэффициента сопротивления с
от числа Маха при различных относительных размахах; для пла-
пластинки зависимость коэффициента подъемной силы сд от числа
Маха при различных относительных размахах (по Гарднеру и Лад-
лоффу) Обозначения такие же, как на предыдущих рисунках.
/о
^-—
¦
—— '
0=0,01
__ t '¦
C=1,0
5 10 15
удлинение
20
Рис. 13. Зависимость коэффициента сопротивления ст от отно-
относительного размаха для клина при числе Маха, равном единице,
и при различных значениях коэффициента ускорения р (по Гард-
Гарднеру и Ладлоффу), Обозначения такие же, как на предыдущих
рисунках.
§ 6. Пределы применимости линейной теории
Частые попытки использовать результаты линейной теории
Далеко за пределами ее применимости объясняются тем, что резуль-
результаты более точных исследований недостаточны для практических

86 ГЛ III ЛИНЕАРИЗОВАННОЕ ИССЛЕДОВАНИЕ ОКОЛОЗВУКОВЫХ ТЕЧЕНИЙ
потребностей. Дж. Коул [1] (см. лит. 1) вывел критерий, позволяю-
позволяющий судить о применимости линейной теории в том или ином случае.
Он рассчитывает поле течения сначала с помощью линейной теории,
10
0,8
к 0.6
0.2
id
-—
—. —*
_—¦—

f-ож
г ?
/
__—
/
/
у

I
/,
О
7
/
п\Т 1 I I
0,85 0,90 0,95
1,0
Рис. 14. Зависимость параметра X от числа Маха набе-
набегающего параллельного течения для осесимметричного
тела в установившемся потоке (по Гарднеру и Ладлоффу).
Параметр X, равный отношению критических членов в ли-
линеаризованном и нелинеаризованном уравнениях, опре-
определен для места профиля с наибольшей толщиной (по Дж.
Коулу). I — длина тела, rf —максимальная толщина.
1.2
1,0
[Q8
Я6
o,<*
0,2
О
u \
\\
\
\f=0,IO
л
Д
¦—,
0,05 0,10 0,15 OZO 0,25 0,30 0.35
-\lAL
Р и с. 15 Зависимость параметра X от коэффициента уско-
ускорения в момент прохождения осесимметричного тела
через число Маха, равное единице при ускоренном дви-
движении. Параметр X вычислен для места профиля с мак-
максимальной толщиной (по Дж. Коулу [1]). Ь — ускорение;
/ — длина тела, й — максимальная толщина; о —скорость
звука
а-затем*для какой-нибудь характерной точки (например, для точки
того сечения тела, в котором последнее имеет наибольшую толщину),
сравнивает коэффициент при критическом члене в линеаризованном
уравнении с коэффициентом при том же члене в нелинеаризованном

§ 6 ПРЕДЕЛЫ ПРИМЕНИМОСТИ ЛИНЕЙНОЙ ТЕОРИИ 87
уравнении после подстановки в это уравнение результатов линейной
теории. В качестве параметра сравнения принимается частное X от
деления разности коэффициентов, полученных в обоих указанных
случаях, на коэффициент при критическом члене в линеаризованном
уравнении. При Х = 0 нелинейные члены не играют никакой роли,
при Х=1 изменение, вызванное нелинейным членом, равно его
линеаризованному значению. Так как это невыгодное значение пара-
параметра X возникает в общем случае только в отдельных местах
внутри течения, то значение Х=1 можно рассматривать как пре-
предельно допустимое. Для установившихся течений параметр Х=1
означает, что в отдельных местах внутри течения достигается число
Маха, равное единице. Некоторые результаты, полученные Дж. Коу-
лом, изображены на рис. 14 и 15.

Глава IV
ТОЧНЫЕ РЕШЕНИЯ УРАВНЕНИЯ ДЛЯ ПОТЕНЦИАЛА
ОКОЛОЗВУКОВЫХ ТЕЧЕНИЙ
§ 1. Предварительные замечания
В исследованиях предыдущей главы, если не считать задач о не-
неустановившемся течении, разница между до- и сверхзвуковыми тече-
течениями, а также то обстоятельство, что в поле течения могут
существовать рядом до- и сверхзвуковые области, не играли никакой
роли. Поэтому понятно, что изложенный там метод не может дать
объяснения явлений, связанных с переходом дозвукового течения
в сверхзвуковое. В этой и дальнейших главах мы будем заниматься
исследованием уравнения для потенциала с включением члена, учиты-
учитывающего разницу между до- и сверхзвуковыми течениями.
Это означает, что нам придется отказаться от общности изложе-
изложения и ограничиться отдельными примерами, причем эти примеры хотя
и будут освещать физическую сторону явления, но численные ре-
результаты они будут давать не для всякого приложения. Более того,
примеры, на которых нам сначала придется остановиться, не всегда
будут иметь прямое отношение к вопросам, важным с технической
точки зрения. Насколько такое положение вещей может показаться
иногда привлекательным для исследователя, настолько разочаровы-
разочаровывающим оно будет для лиц, желающих применять полученные ре-
результаты к техническим вопросам.
Большая часть исследований будет выполнена методом годографа.
Однако в настоящей главе мы рассмотрим две задачи непосредственно
в плоскости течения. Эти задачи могут быть решены также для
осесимметричного течения. Другие примеры, потребовавшие большой
математической находчивости, рассмотрены Тамадой и Томотикой
(см. лит. 1),
§ 2. Течение через сопло Лаваля
Точное уравнение для потенциала было решено Мейером (см. лит. 1)
для случая течения в самом узком поперечном сечении сопла Лаваля,
причем решение было получено в виде ряда. Сейчас мы увидим, что
первые члены этого ряда дают точное решение уравнения для
потенциала околозвуковых течений.
Примем, следуя Мейеру, что скорость вдоль оси сопла изме-
изменяется линейно. Тогда для у = 0 потенциалом, описывающим откло-
отклонение от параллельного течения с числом Маха, равным единице,

§ 2. ТЕЧЕНИЕ ЧЕРЕЗ СОПЛО ЛАВАЛЯ 89
будет
ф=с^. A)
Дальнейшие члены решения мы найдем, если внесем это значе-
это значение Ф в уравнение для потенциала околозвуковых течений
— (*+1)Фа,Фаи,-г-Фи, = 0 B)
и уточним допущение A) методом итераций. В результате мы полу-
получим следующее точное решение:
^1+1JС3^-. C)
Это решение полностью определяет картину линий тока, поэтому
"вопрос о том, как можно увязать его с другими формами стенок
сопла, остается открытым. Исследование посредством метода годо-
годографа показывает, что решение C) представляет собой ту часть
полного решения, которая является доминирующей вблизи самого
узкого поперечного сечения.
Для того чтобы из решения C) получить дальнейшие результаты,
представим его в виде
Внутри скобок переменные х и у входят только в комбинации х/у2.
Эта же комбинация войдет и в составляющие скорости вдоль осей
х и у. Вычислив эти составляющие, мы будем иметь
D)
т. е. вдоль парабол х/у2— const составляющие скорости пропор-
пропорциональны второй и третьей степеням у или первой и полуторной
степеням х, если выбрать несколько иной вид записи уравне-
уравнения (За).
Для определения звуковой линии, т. е. кривой, на которой
скорость течения и скорость звука одинаковы, следует положить
Фж = 0, и мы получим
Далее, представляет интерес геометрическое место точек, в которых,
вектор скорости горизонтален. На этой кривой Ф^=0, следова-
следовательно, ее уравнением будет

•90 ГЛ IV ТОЧНЫЕ РЕШЕНИЯ УРАВНЕНИЯ ПОТЕНЦИАЛА
Эта кривая определяет положение самого узкого поперечного сече-
сечения сопла, если заТего стенки принять две линии тока, симметрич-
симметричные относительно оси х. Таким образом, звуковая линия располо-
расположена вверх по течению относительно геометрического места точек,
в которых вектор скорости горизонтален. Направление характеристик
определяется уравнением
получающимся из^ уравнения B).
Выясним теперь, могут ли параболы х/_у2 = const быть одно-
одновременно и характеристиками. Пусть
тогда наклоном такой параболы будет
—- = 2С у.
dy ¦*
Если эта парабола является характеристикой, то должно соблюдаться
равенство
или
Внеся сюда значение Фх из равенства D), мы получим
Из этого уравнения у2 выпадает; это означает, что парабола С = const
на всем своем протяжении совпадает с характеристикой. Последнее
уравнение имеет решения
„ х-4- 1 - х4-1
Обе найденные характеристики показаны на рис. 16 сплошными
линиями.
Для определения формы линии тока следует проинтегрировать
ее наклон Ф,, вдоль прямой у — const. Пусть у есть отклонение
линии тока от выбранной прямой у = const. Тогда мы получим
У = -^- ГО- + 1) с2 тт + (* + ! J -7Г -4-1 •
Две линии тока, расположенные по обе стороны от оси х на оди-
одинаковых от нее расстояниях, можно принять за стенки. Если мы
•будем брать такие пары линий тока на различных расстояниях от

§ 2 ТЕЧЕНИЕ ЧЕРЕЗ СОПЛО ЛАВАЛЯ 91
оси х, то «получим семейство сопел Лаваля. Нетрудно убедиться
в том, что % все эти сопла можно получить одно из другого, если
выполнить преобразование координат в соответствии с законом подо-
подобия [при одновременном изменении х0 и х (см. стр. 45)]. Другими
словами, применение для рассматриваемого примера закона подобия
(без 1 изменения х0) равносильно изменению масштаба поля течения.
Если в качестве стенок выбрать две линии тока, расположенные
по i одну и ту же сторону от оси, то получится решение задачи
о переходе через скорость звука в искривленном канале. Такого
рода поля течения встречаются между лопатками осевых турбин
(Якобе, см. лит. 1).
Для понимания в целом смешанных течений, т, е. течений,
содержащих до- и сверхзвуковые области, имеет важное значение
следующее соображение. Выберем две линии тока и будем рассмат-
рассматривать их как стенки. Известно, что в сверхзвуковом поле измене-
изменение направления стенки дает себя знать только вниз по течению
середина струи
направление течения
дозвуковая звуковая
область линия /
линия, на которой вектор '
скорости горизонтален
Рис. 16. Течение через сопло Лаваля.
относительно той волны Маха, которая отходит от стенки в точке
изменения ее направления. То же самое, конечно, имеет место и
в рассматриваемом нами случае при условии, что волна Маха, вдоль
которой распространяется изменение состояния, не достигает зву-
звуковой линии. Следовательно, точка А на рис. 16 является той точ-
точкой, начиная от которой можно изменять направление стенки, не
влияя на дозвуковую область течения.
Таким образом, расчет течения через сопло Лаваля разбивается
на две отдельные задачи, а именно: 1) на расчет дозвукового поля
и той части сверхзвукового, которая влияет на дозвуковое, и
2) на расчет остающейся части сверхзвукового поля. Для расчета
дозвукового поля требуется знать контур стенки только до точки А.
Течение через сопло Лаваля представляет собой пример такой
задачи, для которой интуиция с самого начала подсказывает пра-
правильную формулировку о смешанном — до-и сверхзвуковом — поле
течения. Ниже, исходя из характера течения через сопло Лаваля,
мы получим путем предельного перехода качественную картину
течения с числом Маха, равным единице вдали от обтекаемого тела.
И в этом случае мы увидим, что подразделение поля течения на две

92 ГЛ IV ТОЧНЫЕ РЕШЕНИЯ УРАВНЕНИЯ ПОТЕНЦИАЛА
области имеет существенное значение. В рассмотренном выше при-
примере положение точки А заранее неизвестно; оно может быть найдено
только путем решения краевой задачи (если только такое решение
возможно в общем виде). Во всяком случае, точка А лежит, как мы
это увидим ниже при применении метода годографа, вверх по тече-
течению относительно самого узкого поперечного сечениях).
Волна Маха АО, отделяющая ту часть сверхзвуковой области,
которая влияет на дозвуковую область, от части, не влияющей на
дозвуковую область, называется предельной волной Маха.
Точное решение уравнения для потенциала околозвукового тече-
течения в случае осесимметричного сопла Лаваля имеет вид
л CJK2 , Х+1 „ „ , (х+1JС! ,
^ — 2 ^ 4 У ^ 64 У '
64
Исследование этого решения может быть выполнено таким же путем,
как и для плоской задачи. Для звуковой линии мы получим урав-
уравнение
х (*+1)с
а для геометрического места точек, в которых линии тока горизон-
горизонтальны, — уравнение
_х___ (x-fl)c
уа ~~ 8 "
Наконец, уравнением волн Маха будет
§ 3. Параллельная струя с критической скоростью
Если мы попытаемся применить метод характеристик для постро-
построения сверхзвукового поля, получающегося при расширении перво-
первоначально параллельной струи, движущейся со скоростью звука, то
столкнемся с трудностями, особенно в случае осесимметричной струи.
Эти трудности возникают потому, что первые волны Маха, полу-
1) Сопло Лаваля рассматривалось в литературе столь часто, что о нем
может создаться впечатление как о проблеме особой важности. Со своеоб-
своеобразной точки зрения подошел к соплу Лаваля в одной из своих работ
Дж. И. Тэйлор. Если сопло симметрично относительно самого узкого попе-
поперечного сечения, то при дозвуковых скоростях поле течения в таком сопле
также симметрично. С другой стороны, симметричности поля течения безус-
безусловно не будет, если сопло будет работать именно как сопло Лаваля. Можно
было предполагать, что исследование перехода от одного типа сопла к дру-
другому дало бы возможность получить представление об особенностях око-
околозвуковых течений Однако непосредственное исследование сопел не при-
привело к ожидавшемуся результату.

§ 3 ПАРАЛЛЕЛЬНАЯ СТРУЯ С КРИТИЧЕСКОЙ СКОРОСТЬЮ 93
чающиеся при построении, пересекаются всегда только внутри струи1),
каким бы мы малым ни брали расстояние между ними. Для аналити-
аналитического исследования рассматриваемой задачи следует ввести допу-
допущение, что
Ф = х3/(у) для плоского случая, 1
Ф = х3/(г) для осесимметричного случая J
{Гёртлер, Гудерлей [18], см. лит. 1). Выбор именно этих выраже-
выражений для потенциала основан на следующем. Возьмем сначала произ-
произвольные степени х и сделаем соответствующие подстановки в диф-
дифференциальное уравнение околозвукового течения II, 8A) или
II, 8B). Затем подберем показатели степени при х так, чтобы сте-
степени х выпали из уравнений. Это и приведет нас к формулам A).
Физически возможны и более высокие степени х\ они означают, что
расширение струи происходит более медленно. Приняв допущение A),
мы получим для определения функции / в случае плоской струи
уравнение
0, Bа)
а в случае осесимметричной струи — уравнение
/" + — — 18(x-f 1)/2 = 0. B6)
Если F (») есть решение дифференциального уравнения
-§Г — ^2 = ° (За)
или дифференциального уравнения
причем dFld'-, = 0 при С = 0, то искомыми решениями уравнений Bа)
и B6) будут
и соответственно
Путем надлежащего выбора постоянной Сх можно сделать так,
чтобы решение удовлетворялось при любой ширине струи. Имеются
различные типы функции F. Для того чтобы получить представление
!) Имеется в виду известное свойство характеристик: они не пересекают
прямую звуковую линию на участках, свободных от особых точек. —
Прим. ред.

94 ГЛ. IV. ТОЧНЫЕ РЕШЕНИЯ УРАВНЕНИЯ ПОТЕНЦИАЛА
о смысле этих решений, исследуем подробнее плоскую струю. Для
нее решением уравнения (За) будет
dx
Если мы выберем верхний знак, то функция F будет изменяться
от положительного значения, определяемого из уравнения
/ з \-'/з
х=1=(|с2) F,
до бесконечности; это означает, что у изменяется от нуля до неко-
некоторого конечного значения. Вблизи F = оо полученному решению
соответствует течение Мейера около угла, следовательно, там лежит
внешняя граница струи. В этом решении функция F всегда положи-
положительна, поэтому струя движется, как это видно из равенства A),
со сверхзвуковой скоростью.
Если мы выберем нижний знак, то функция F будет изменяться
от отрицательного значения до нуля и далее — до положительной
бесконечности. Для нас представляет интерес область отрицательных
значений F. Этой части решения соответствует дозвуковая струя,
которая может перейти в струю с критической скоростью. Для
этого достаточно принять одну из линий тока за границу струи.
Если использовать всю область отрицательных значений F до зна-
значения F = 0, то на граничной линии тока давление будет, в преде-
пределах нашего приближения, постоянным и равным критическому дав-
давлению. Тогда полученное решение может быть реализовано в виде
свободной струи с критической скоростью. Таким образом, мы по-
показали, что свободная струя с критической скоростью может двигаться
на протяжении конечного участка как параллельная струя. Анало-
Аналогичные соотношения получаются и для осесимметричной струи. На
рис. 17—20 показаны функции F и F' для плоского и осесиммет-
ричного течений. В случае сверхзвуковой струи аргументу С=1
соответствует точка, в которой начинается течение Мейера, в дру-
других же случаях этому аргументу соответствует свободная поверхность
струи, движущейся с критической скоростью.
Как известно, в дозвуковой области свободная струя может стать
параллельной только в бесконечности (см. также конец § 5 гл. V).
Напротив, в сверхзвуковой области всегда возможно, путем придания
контуру струи надлежащей формы, получить параллельную струю на
конечном расстоянии от отверстия. Последний пример показывает, что
всегда можно получить на конечном расстоянии от отверстия точно
параллельную струю также при звуковой скорости, даже если внутри
струи течение является дозвуковым; для этого необходимо только,

S 3 ПАРАЛЛЕЛЬНАЯ СТРУЯ С КРИТИЧЕСКОЙ СКОРОСТЬЮ
95
0,2 O,U 0,6 0,8 !,О
Рис. 17. Функция F для плоской и осе-
осесимметричной сверхзвуковых струй.
Значение С=0 соответствует середине
струи, ?=1 — краям струи. При At=const
функция F пропорциональна отклонению
составляющей скорости в направлении х
от критической скорости.
10
Рис 18 Функция F' для плоской
и осесимметричной сверхзвуковых
струй. Значение С = 0 соответст-
соответствует середине, С = 1 — краям струи
При jt—const функция Fr пропор-
пропорциональна составляющей скорости,
перпендикулярной к оси сопла
-70
-8
-6
-Ч
-2
—
к
'плоек
'
9VMM
\
6Г '2
0,2
ОА О,6 0,8 1,0
0,8
I,fJ
Рис. 19. функция F для плоской и осе-
осесимметричной дозвуковых струй. Зна-
Значение С = 0 соответствует середине
струи, С = 1 — краям струи. При v=-const
функция F пропорциональна отклонению
составляющей скорости в направлении х
от критической скорости.
Рис. 20. Функция F' для плоской и осесимме-
осесимметричной дозвуковых струй. Значение С = 0 со-
соответствует середине струи, ^ = 1 — краям струи.
При a;=const функция F пропорциональна
составляющей скорости, перпендикулярной к оси
сопла.

96 ГЛ IV ТОЧНЫЕ РЕШЕНИЯ УРАВНЕНИЯ ПОТЕНЦИАЛА
чтобы на поверхности, ограничивающей струю, было постоянное
давление1). Пример такого рода струи показан на рис. 48 (стр. 155).
Решение, полученное для осесимметричной струи, можно распро-
распространить— путем надлежащего выбора постоянных интегрирования —
на струю, выбрасываемую из кольцевой щели. Если мы отодвинем
внешнюю стенку такой щели в бесконечность, то получим парал-
параллельное течение, ограниченное изнутри цилиндром и движущееся
со скоростью звука до крайнего поперечного сечения цилиндра
х —0; за этим сечением начинается область пониженного давления,
I / / сверхзвуковая
. I / область
параллельное | / /
течение с _ ; Ц. расширяющееся
критической ' / течение
скоростью ji/
'' свободная
77777.
'НОРО
цилиндрическое
тело
/поверхность
\
Рис. 21. Расширение параллельного
течения, имеющего критическую ско-
скорость, в конце цилиндрического тела.
вследствие чего струя начинает расширяться, устремляясь во внут-
внутреннее пространство. Такого рода поле течения может установиться,
например, за тупым концом длинного тела, на которое набегает
поток, имеющий звуковую скорость (рис. 21); обтекаемое тело
должно быть настолько длинным, чтобы течение вдоль него вплоть
до его конца можно было рассматривать как параллельное течение
с критической скоростью (Грехэм, см. лит. 1).
Допущения о виде потенциальной функции, использованные в этой
главе для решения обеих рассмотренных в ней задач, является част-
частным случаем более общего допущения, которое будет сделано
в гл. XI при исследовании осесимметричного течения с числом Маха,
равным единице.
1) Эффект выравнивания критической струи на конечном расстоянии от
отверстия доказан в точной постановке Л В Овсянниковым [Прикл. матем.
и мех., т. 13, вып. 5, 1949]. —Прим. ред.

Глава V
ОСНОВЫ МЕТОДА ГОДОГРАФА
§ 1. Уравнения преобразованного потенциала
и функции тока в плоскости годографах)
Если мы примем в дифференциальных уравнениях течения состав-
составляющие скорости за независимые переменные, то придем к пред-
представлению течения в плоскости годографа скоростей. В гидродина-
гидродинамике такое представление течения применяется только в случаях
с простыми граничными условиями. Такие граничные условия имеют
место для плоских течений, на границах которых либо направление
скорости, либо модуль скорости, а следовательно на основании
уравнения Бернулли и давление сохраняют постоянное значение.
В случае околозвуковых течений подобного рода граничные условия
также очень облегчают исследование; граничные же условия более
общего вида влекут за собой большие трудности. Особое значение
метода годографа для околозвуковых течений состоит в том, что
для плоского течения уравнения преобразованного потенциала и функ-
функции тока оказываются в плоскости годографа линейными. Преимуще-
Преимущества, вытекающие из этого обстоятельства, перевешивают трудности,
которые метод годографа вносит в граничные условия.
Для перехода от плоскости течения к плоскости годографа проще
всего исходить из дифференциальных уравнений для составляющих
скорости. Введя для сокращения записи обозначения vx = u, vy = v,
мы приведем уравнения 1,6A) и 1,6B) к виду
ди ( и2\ (да , dv\ uv dv
*L-p. = 0. A6)
ду дх v '
На основании уравнения Бернулли а есть функция от uz-\-v2.
В плоскости течения мы имеем соотношения
а = и{х, у), v = v(x, у).
В плоскости годографа они должны быть заменены соотношениями
х = х(и, v), y = y(u, v).
!) В дальнейшем для этих уравнений как правило сохранено принятое авто-
автором название „уравнения годографа" (Hodographengleichungen). — Прим. ред.
7 Зак 534 К Г. Гудерлей

98 ГЛ V. ОСНОВЫ МЕТОДА ГОДОГРАФА
Из тождества
и = и[х(и, v), у (и, v)]
путем дифференцирования по и и v мы получим
. ди дх , ди ду
дх ди ' ду ди '
« ди дх . ди ду
дх dv ду dv '
откуда следует, что
ду дх
ди _ Jw_ ди_ __ __ "dp" ™
йл: ~ D ' ду ~~ D ' ^;
причем
п__ дх ду ду дх
Аналогичным путем мы найдем
ду дх_
dv ди dv du
dx~ D ' ду~~ D
D)
Если внести значения B) и D) в дифференциальные уравнения тече-
течения A), то D выпадет из уравнения, и мы будем иметь
dv\l ~W)^\dv ^'Ш)~а^^г ди \l~-tf) —U' W
Уравнение E6) удовлетворяется автоматически, если принять, что
_ д<р(и,у) __ д<?(и,у)
где <р(в, и) есть дважды дифференцируемая функция от а и v.
При использовании функции ср уравнение Eа) примет вид
Обычно уравнение G) выводят из уравнения для потенциала
I, 4 E), ограничивая последнее случаем плоского течения и приме-
применяя преобразование Лежандра (Моленбрёк, см. лит. 1)
ср(и, v) = ax-\-vy — Ф(х, у), (8)
где <р есть преобразованный потенциал (или потенциал Лежандра).
Если в этом уравнении рассматривать х и у как функции от к и v,
то, выполнив дифференцирование по к и имея в виду, что

§ 1. УРАВНЕНИЯ ГОДОГРАФА 99
мы получим
"* ' да * ди х да У да '
откуда
Аналогичным образом мы найдем, что
Но это суть не что иное, как равенства F). Дальнейшие вычисле-
вычисления выполняются совершенно так же, как и выше, а именно опре-
определяют тем же способом, который привел к равенствам B) и D),
производные Фхх, Фху и Фуу, после чего получается уравнение G).
Представление течения в плоскости годографа не связано с вы-
выбором какого-либо привилегированного направления. Это проще
всего выразить в полярных координатах. Пусть w есть модуль
скорости, а Ь — угол, образуемый вектором скорости с какой-либо
фиксированной осью, например с осью х; тогда мы будем иметь
= агс^Т' J
и уравнение G) примет вид
. 1
-0. A0)
При представлении течения в плоскости годографа часто за зави-
зависимую переменную принимается функция тока. Выведем соответ-
соответствующее уравнение годографа, следуя Буземану [1] (см. лит. 1).
Из равенств
~^ — " Р'^') ^ -""¦'¦''' Oil у
дх г ду г
дФ дФ
¦ -з— = м, -=—==v,
дх ду
мы имеем
d'^ = — pvdx-\- pu dy,
dФ = udx-\-vdy,
откуда следует, что
7*

100 ГЛ. V ОСНОВЫ МЕТОДА ГОДОГРАФА
Если мы будем рассматривать в этих равенствах х, у, Ф и t|> как
функции от w и &, то из первого равенства получим
дх , . 'дх ,а
dw
дФ
1 Г sin» / di> , . д<1> ,с,\ . ъ(
= — -j-!- rfty + -^-dtf I -f- cos9-
dw
откуда
ода да \ p dw ' дда/ ч
их 1 / sin» д<1> , „ Й\ /них
-rv = ^—{ — --ж—r-cos^-^u-b (Пб)
Аналогичным образом из равенства, определяющего dy, мы найдем
A2а)
A2б)
Имея в виду, »что dzx[dw д$ = d2xjdb dw, мы получим из первой
пары уравнений
\jw ) d<\i , \ да
дФ
о»
и аналогичным образом — из второй пары уравнений
1 / sin» оф , о оФ\
¦— з1-+ cos Э--:s— ) =
w \ р ода ' йда /
\?w ) dfy \"да~/
dw d» ¦ dw d»
Умножим первое из этих уравнений на cos 9, а второе на sin ft и
сложим их; затем умножим первое уравнение на sin 9-, а второе на cos&
и опять их сложим. Мы получим
1 дф 1 дФ
рда dw даа <?» *
w dw dw дЬ
Далее, исключив путем дифференцирования Ф, мы найдем
ода/

§ 1. УРАВНЕНИЯ ГОДОГРАФА
101
откуда, использовав соотношение I, 2 A0а), получим
у-щ \ / 1S3 \ иф 1 / IS) \ У^Ф
¦ - ¦ ¦ —U— I \ — | — —1— 1 \ I n^z (J, A4/
Если мы решим это уравнение, то, подставив найденное значение ф
в уравнения A1) и A2) и заменив в последних Ф его выражением
через ф, мы будем иметь для определения координат плоскости
течения следующие уравнения:
дх
¦з—
aw
1
рда
sin и ¦— cos v
aw
ду 1 „ дф
-^- = I cos w з-1 sin ¦
dw pw \ dw
1 —
sin w
дх 1 / .
-ла- = — — si
^. = _L(cos&-
d'b
cos
w
d<\>
-3
A5)
Тесную связь, существующую между потенциалом Лежандра ср и
функцией тока ф, легко обнаружить следующим путем. Из соотно-
соотношений л: = срм и _у = ср„, принимающих в полярных координатах вид
— — cp& sin
_у = ср^ sin & + — c
мы
dx
dy
имеем
= (?«,«, cos i
= Uww sin 8
—— 1 ^P i
11L
срэ sin & —
> cos 9 — ep,
P8cos& +
¦s-t-
да sin & -
sin
COS
4-
. cos &
sin %—"ir f»cos ь
сраа cos & — — срэ sin
Подставив эти значения dx и сГу в соотношение
,. д<Ь , . 'йф ,„
аф ^ ^г1- aw -\—^- dv = —
и приравняв коэффициенты при йта и
лучим
I
dy
слева и справа, мы по-
A6)

102 ГЛ V ОСНОВЫ МЕТОДА ГОДОГРАФА
Таким образом, если известен преобразованный потенциал <р, то
функцию тока <|> можно определить путем интегрирования.
Следует ли при решении конкретной задачи исходить из уравне-
уравнения для функции тока или из уравнения для потенциала Лежандра,
зависит от характера граничных условий. Для исследования обтека-
обтекания заданного тела и выявления условий на скачках уплотнения
проще применять функцию тока. Для исследования же течений,
отличающихся от уже известного течения столь мало, что изменение
контура в плоскости течения можно учесть путем линеаризации гра-
граничных условий в плоскости годографа, целесообразнее пользоваться
преобразованным потенциалом.
§ 2. Функциональный определитель D
Если координаты х и у плоскости течения рассматривать как
функции от и и v, то соотношения
дх , , дх
Г *' A)
J да ' dv J
представляют собой систему уравнений, в которой du и dv можно
принять за неизвестные, если dx и dy заданы. Коэффициенты дх/ди,
dx/dv, ду/ди и dy/dv при du и dv зависят, конечно, от положения
рассматриваемой точки поля течения. Для возможности однозначного
решения системы уравнений A) необходимо и достаточно, чтобы
определитель
р. дх dy дх dy ,<y\
ди dv dv ди
не был равен нулю. Этот определитель называется функциональным
определителем. Для сокращения записи будем пользоваться обо-
обозначением
д (и, v) '
Если функциональный определитель D равен нулю, то оба уравнения
системы A) линейно зависят друг от друга, и тогда решения для
du и dv можно получить только при условии, что между dx и dy
существует такая же линейная зависимость, как между правыми
частями уравнений A). Но в таком случае каждому выбранному
отношению между du и dv соответствует такое же отношение
между dx и dy; это означает, что если при разложении dx и dy
в ряды ограничиться только линейными членами, как это и сделано
в уравнениях A), то окрестность рассматриваемой точки плоскости""
годографа отображается в некоторую линию плоскости течения.

§ 2 ФУНКЦИОНАЛЬНЫЙ ОПРЕДЕЛИТЕЛЬ D ЮЗ
Функциональный определитель обращается в нуль также в том
случае, когда все члены первого порядка в правых частях уравне-
уравнений A) равны нулю. Это может иметь место для точек разветвления
линий тока в плоскости годографа или плоскости течения. В таком
случае для выяснения характера отображения необходимо использовать
члены следующего, более высокого порядка. Здесь мы не будем зани-
заниматься общим исследованием этого вопроса, однако ниже, при рас-
рассмотрении частных примеров, мы будем по мере надобности на нем
останавливаться.
Из сказанного выше следует, что для однозначного соответствия
между плоскостью годографа и плоскостью течения требуется, чтобы
функциональный определитель не обращался ни в нуль, ни в бес-
бесконечность. Функциональный определитель может сделаться беско-
бесконечно большим, если некоторые члены в правых частях уравнений A)
будут иметь бесконечно большие значения; в этом случае возникает
возможность, при которой для значений dx и dy, не равных нулю,
соответствующие значения da и dv принимают нулевые значения.
Функциональный определитель можно истолковать как отношение
элементарной площадки в плоскости течения к соответствующей
элементарной площадке в плоскости годографа. В самом деле, эле-
элементарный прямоугольник плоскости годографа со сторонами da и dv
переходит при отображении на плоскость течения в параллелограмм,
стороны которого равны соответственно
, дх , . . ду ,
i -д—du-4-j -~- du
ди ] J ди
и
. дх , . . ду ,
i -з— dv -4-7 ~s- dv.
dv ' J dv
Ориентированная элементарная площадка в плоскости годографа
определяется вектором
а ориентированная элементарная площадка в плоскости течения —
вектором
к dy ду дхч
Отсюда и вытекает указанный выше смысл функционального опре-
определителя.
Конечно, вместо указанного отношения элементарных площадок
можно взять отношение этих же площадок в обратной последова-
последовательности, поэтому
дх ду ду дх I ди dv ди dv \-1 ^-o-v
ди dv да dv \ дх ду ду дх)

104 ГЛ V ОСНОВЫ МЕТОДА ГОДОГРАФА
При применении метода годографа поведение функционального
определителя представляет интерес потому, что равенство этого
определителя нулю или бесконечности указывает на наличие особых
точек в отображении. Для построения картины течения в плоскости
годографа имеет важное значение уже то простое обстоятельство,
что функциональный определитель должен быть отрицательным (до-
(доказательство будет дано ниже). Это обстоятельство влечет за собой
значительное ограничение возможного вида картины течения в пло-
плоскости годографа (см. стр. 153). Для вычисления функционального
определителя следует воспользоваться уравнениями V, 1A5); мы
получим
да2
д С*, у) 1 Г/аф\а , Ж /дфУП
d(w, 8) р2да \_\dw) ~* ^ \db ) у
Далее, приняв во внимание равенства
г» = да sin ft,
мы найдем
д (и, v)
д {w, ») ~~
Имея в виду указанный выше смысл функционального определителя
как отношения двух площадей, мы окончательно будем иметь
п_д(х, у) 1 \(Ц \а . 1 ~ Ж / д\ \2
д(и, v) ~ р2щ/2 [\dw) "Г wi \д% } \' к '
Конечно, значение функционального определителя не зависит от вы-
выбора независимых переменных в плоскости годографа. Если исполь-
использовать уравнения V, 1A6) и перейти к преобразованному потенциалу,
то мы получим
Функциональный определитель, будучи суммой двух квадратов с от-
отрицательным коэффициентом, в дозвуковой области всегда либо
отрицателен, либо равен нулю. Нулевое значение он может иметь
только в изолированной точке. Если бы он был равен нулю вдоль
некоторой линии дозвуковой области, то там имели бы место равен-
равенства dtydw = Q и д$/дЬ = О. Тогда, безусловно, было бы возможно
аналитическое продолжение посредством выбора ф = const, причем,
на основании сказанного при изложении метода характеристик, это
было бы единственным возможным продолжением.
В сверхзвуковой области функциональный определитель обра-
обращается в нуль, если
_ + ____ __ о, F)

§ 3 ПРЕДЕЛЬНАЯ ЛИНИЯ 105
причем, конечно, это равенство должно выполняться только для
одного знака перед корнем. Условие F) приводит к понятию пре-
предельной линии.
§ 3. Предельная линия
Прежде чем предпринять аналитическое исследование свойств
предельных линий, рассмотрим пример, иллюстрирующий эти свой-
свойства.
Рассмотрим течение, вызываемое источником. Все линии тока
такого течения имеют из соображений симметрии радиальное на-
направление. На окружностях, центры которых лежат в источнике,
скорость постоянна. Если г есть радиус одной из таких окружно-
окружностей, то условие неразрывности приводит к уравнению
rpw = const. A)
На основании равенства I, 2A0а) плотность потока массы pw имеет
в изэнтропическом течении максимум при скорости, равной скорости
звука. Это означает, что уравнение A) может соблюдаться только
для значений г, больших некоторого минимального значения г0. Для
значений г^>г0 существуют два решения, а именно: одно решение
для дозвукового течения и второе для сверхзвукового течения.
Можно представить себе, что оба эти поля течения находятся в двух
наложенных друг на друга листах, скрепленных между собой вдоль
окружности радиуса г0. Эта окружность радиуса г0 и представляет
собой в данном случае предельную линию. Однако течение, вызы-
вызываемое источником, является слишком специальным и поэтому не мо-
может достаточно полно выявить свойства предельной линии. Необходимо
рассмотреть течение более общего вида. Для получения такого тече-
течения наложим -на годограф только что рассмотренного решения так
называемый потенциальный вихрь. Это можно сделать, так как урав-
уравнения годографов линейны. При наложении решений в плоскости
годографа значения х и у, соответствующие в исходных решениях
одинаковым векторам скорости, складываются, так как уравне-
уравнения V, 1A5), определяющие х и у, линейны (Толмин [1], см.
лит. 1).
Поскольку и в источнике, и в потенциальном вихре не имеется
какого-либо привилегированного направления, такого направления
не имеется и в течении, получающемся в результате наложения
источника и потенциального вихря. Сверхзвуковую область такого
течения можно легко построить методом характеристик. Для этой
цели зададим вдоль окружности векторы скорости, модули которых
имеют одинаковые значения, а направления образуют с касательной
к окружности постоянный угол. Модуль скорости должен быть либо
больше скорости звука, либо равен ей. Исходя из этой окружности,
продолжим поле течения посредством метода характеристик. Именно

106
ГЛ. V. ОСНОВЫ МЕТОДА ГОДОГРАФА
гаким способом выполнено построение на рис. 22, правда, только
для части окружности. Если за исходную окружность мы возьмем
звуковую линию, то увидим, что внутри окружности будут иметь
место сверхзвуковые скорости, а вне окружности — дозвуковые
скорости. Предположим, что течение направлено из дозвуковой
области в сверхзвуковую. Форма линий тока в дозвуковой области
волны
уплотнения
Рис. 22. Предельная линия, образованная расходящимися
волнами расширения.
определена путем аналитического расчета; на рисунке показаны две
боковые линии тока этой области. При построении посредством
метода характеристик волны Маха, изображенные штриховыми ли-
линиями и начинающиеся на звуковой линии, направлены вверх по те-
течению и на некотором расстоянии от звуковой линии пересекаются
вогны сжатия
предельная линия
Рис. 23. Предельная линия, образованная сходящимися
волнами сжатия.
друг с другом так, что образуется огибающая их линия. Эта оги-
огибающая и представляет собой предельную линию. В поле течения,
соответствующем такому построению, штриховые линии были бы
волнами разрежения, исходящими из предельной линии и направлен-
направленными вниз от нее по течению.
Второй лист течения изображен на рис. 23. Он расположен над
первым листом и получается, если построение, выполненное на рис. 22
и доведенное до предельной линии, продолжить, опять применяя
метод характеристик.

§ 3 ПРЕДЕЛЬНАЯ ЛИНИЯ 107
Аналитическим решением уравнения для функции ф в плоскости
годографа для источника с мощностью 2тг будет
ф = ». A)
Для потенциального вихря линиями тока являются линии постоянного
модуля скорости, поэтому
и из уравнения V, 1A3) следует, что
d
или
Нетрудно найти координаты плоскости течения, соответствующие
этим решениям. Конечно, вследствие симметрии относительно нуле-
нулевой точки это достаточно сделать для какой-нибудь одной линии,
например для оси и, т. е. для & = 0. Тогда для источника, на осно-
основании первого уравнения системы V, 1A5), мы получим
W2
дх а*
dw ow^
или, если учесть равенство I, 2A Оа),
_дх_
dw dw ¦ '
откуда
_ 1
fW
Конечно, этот же результат мы могли бы полечить непосредственно.
Далее мы найдем, что
Для потенциального вихря второе уравнение системы V, 1A5) после
подстановки Ь = 0 принимает вид
dw ри/ 'w>
или, так как tyw = p[w,
dy __ 1
dw да2 '
откуда следует, что

108 ГЛ V ОСНОВЫ МЕТОДА ГОДОГРАФА
К этому же результату мы могли бы прийти и непосредственно,
рассмотрев решение для потенциального вихря в плоскости течения.
Наложим теперь оба полученных решения друг на друга, пред-
предварительно умножив первое на постоянную сг а второе на постоян-
постоянную с2 (заметим, что эти постоянные имеют разные размерности).
Тогда для определения радиуса г окружности, на которой скорости
принимают заданное значение w, мы получим формулу
'А
Предельная линия возникает при минимальном значении г, т. е. при
выполнении условия
dr 1 Г—2с?
dw г L (рдаK dw w3
откуда следует, что
с —+ Ч лГ —
Так как выражение
может принимать в сверхзвуковой области все значения от нуля
до бесконечности, то предельная линия получается при любом выборе
значений ct и с2. В том, что функциональный определитель D на
предельной линии действительно равен нулю, легко убедиться, под-
подставив значения <\ь и tyw, определяемые равенствами A) и B) и
умноженные предварительно соответственно на сх и с2, в уравне-
уравнение V, 2D).
Главные свойства предельных линий легко усмотреть из рис. 22
и 23. Предельная линия образуется либо вследствие того, что рас-
расходятся линии разрежения (рис. 22), либо потому, что сходятся
линии уплотнения (рис. 23). Конечно, при этом необходимо иметь
в виду, что интервал между волнами Маха должен стать бесконечно
малым. Тогда предельная линия будет представлять собой огибаю-
огибающую семейства волн Маха и, подобно волне Маха, будет образовы-
образовывать с вектором скорости угол Маха. Так как второе семейство
волн Маха образует с первым семейством угол 2а, то предельная
линия не является огибающей второго семейства. Волны второго
семейства подходят к предельной линии под вполне определенным
углом, а именно под углом 2а, а затем под тем же углом возвра-
возвращаются назад.

§ 3. ПРЕДЕЛЬНАЯ ЛИНИЯ
109
Пересечение двух волн Маха означает, что даже при бесконечно
"малом интервале между двумя последовательными волнами плотность
волн Маха в точке пересечения бесконечно велика. Само собой
разумеется, что это имеет место только для волн Маха, образующих
своим взаимным пересечением предельную линию; плотность же волн
Маха другого семейства конечна. В методе характеристик — в том
его виде, в каком он разработан Буземаном, — каждая волна Маха
означает вполне определенное изменение состояния, поэтому при
приближении к предельной линии под углом, не равным нулю, изме-
изменение состояния (градиент давления и кривизна линий тока) стано-
становится бесконечно большим. Одновременно становится бесконечно
большой также кривизна линий Маха второго семейства, так как
направление этих волн является функцией скорости.
волны Маха второго
семейства
вторая тачка
пересечения
волны Маха и
линии тока
листы плоскости
течения
предельная
линия
одна из волн Маха,
слияние которых
образует предельную
линию
точка пересечения
волны Маха и
линии тока
Рис. 24. Структура поля течения вблизи предельной линии.
На рис. 24 схематически показаны оба листа плоскости течения,
скрепленные между собой вдоль предельной линии. На этих листах
изображены: волна Маха того семейства, для которого предельная
линия является огибающей, волна Маха другого семейства и линия
тока. Волна Маха второго семейства и линия тока подходят к пре-
предельной линии под некоторыми углами и, дойдя до нее, возвращаются
назад. Если такие линии тока и волна Маха пересекаются на одном
листе, то они должны пересекаться также на втором листе; в самом
деле, во-первых, направления линий тока и волн Маха второго се-
семейства на втором листе лишь немного отличаются от тех направле-
направлений, под которыми они подходят к предельной линии на первом
листе; во-вторых, линии тока и волны Маха второго семейства
пересекаются друг с другом под вполне определенным углом, не
равным нулю, а именно под углом Маха. Если мы рассмотрим волну
Маха, пересекающую исследуемую линию тока как раз на предель-
предельной линии, то такая волна имеет с линией тока две общие соседние
точки. У линий тока, получаемых в результате аналитического ре-
решения уравнения годографа, точки заострения в общем случае
отсутствуют. Следовательно, если линия тока имеет с характеристикой

110
ГЛ V. ОСНОВЫ МЕТОДА ГОДОГРАФА
направление
течения
две общие, совпадающие между собой точки, то это означает,
что линия тока касательна к характеристике. Эти рассуждения на-
наглядно показывают, что предельная линия определяется в плоскости
годографа как геометрическое место точек, в которых линии тока
касательны к характеристикам.
Как показывает пример, изображенный на рис. 25, предельная
линия может иметь точку заострения. В этом примере волны Маха
возникают вследствие искривления стенки. При построении поля
течения для простоты было при-
принято, что набегающее течение пер-
первоначально было параллельным,
вследствие чего в поле течения по-
получается только одно семейство
волн Маха. В свою очередь это
приводит к тому, что в годографе
получаются особые точки, а именно
каждая волна Маха плоскости тече-
течения отображается в одну точку пло-
плоскости годографа, а вся плоскость
течения — в одну характеристику.
Однако легко представить себе при-
пример, в котором имелись бы волны
Маха и второго семейства, следовательно плоскость течения ото-
отображалась бы на некоторую область в плоскости годографа, и это
ни в какой мере не влияло бы на возможность существования точки
заострения у предельной линии.
Перейдем к аналитическому выводу свойств предельных линий,
причем будем исходить только из условия возникновения этих ли-
линий, т. е. из равенства нулю функционального определителя. Из
соотношения
Рис. 25. Пример предельной линии, име-
имеющей точку заострения. Предельная ли-
линия является огибающей сходящихся волн
dw
применимого к любой линии тока ф = const, мы получаем для опре-
определения направления этой линии уравнение
dw Фа
Если в рассматриваемой точке функциональный определитель обра-
обращается в нуль, но фю ф 0 и ф& Ф 0, то из уравнения V, 2F) мы
имеем
dw w

l§ 3 ПРЕДЕЛЬНАЯ ЛИНИЯ 111
С другой стороны, из уравнения V, 1A0) или из уравнения V, 1A4)
мы получаем для определения направления характеристик уравнение
dw
— 4-
~7
У
Это означает, что если функциональный определитель равен нулю,
но производные ф^ и фа не равны нулю, то линии тока касательны
к характеристикам в плоскости годографа.
Далее, определим направление предельной линии в плоскости
течения. Линейные элементы dx и dy, характеризующие какую-
либо кривую в плоскости течения, и линейные элементы dw и d&,
характеризующие соответствующую кривую в плоскости годографа,
связаны между собой соотношениями
, dx , , дх ,а
dx = -з— dw -f- -™- d»,
dw ' oft
следовательно, направление рассматриваемой кривой в плоскости
течения определяется уравнением
dy
dx / дх
дх I Ж
dw \ x ~r dx dw
dw
Если функциональный определитель обращается в нуль, то выра-
выражения в скобках в правой части равны друг другу, и мы получаем
EL
dy dw
~dx=~dT'
dw
т. е. направление отображенной кривой не зависит от dw и db.
Вычислим теперь dy/dx. Так как в плоскости годографа не имеется
привилегированного направления, то совместим направление оси х
с направлением вектора скорости. Тогда, использовав уравнения
V, 1A5) и V, 2F), мы найдем
dx

112 ГЛ. V ОСНОВЫ МЕТОДА ГОДОГРАФА
Это и есть тангенс угла между предельной линией и вектором ско-
скорости. С другой стороны, из соотношения
мы имеем
tg a = —-
5 / М
/ — 1
Следовательно, вектор скорости и предельная линия образуют между
собой угол, равный углу Маха, что подтверждает результат, полу-
полученный раньше наглядным путем.
Покажем теперь, что второй лист плоскости течения переги-
перегибается над первым листом вдоль предельной линии. Если передви-
передвигаться в плоскости годографа вдоль линии тока, то вблизи пре-
предельной линии скорость w можно рассматривать как параметр вдоль
линии тока (в самом деле, так как там линии тока приближенно
касательны к характеристикам, то dw вдоль линии тока безусловно
не равно нулю). Вычислим величину
dx дх , дх rfft 1 a? dfy , d'fy db
dw dw db dw рда \ w db dw dw
изменяющуюся при перемещении вдоль линии тока. Как было пока-
показано выше (стр. ПО), вдоль линии тока
dw
поэтому
йх = 1 ?^_ A а ц.в
dw pffi"V& V w wl
Следовательно, на предельной линии величина dxldw обращается
в нуль. Если вторая производная не равна нулю, то х имеет
экстремум, т. е. линия тока продолжается во втором листе, полу-
получающемся из первого листа путем перегиба вдоль предельной линии.
Равенство нулю второй производной наглядно показывает, что
соотношение V, 2F) соблюдается в двух соседних точках линии
тока. С другой стороны, соблюдение самого соотношения V, 2F)
означает, что в плоскости годографа линия тока касательна к ха-
характеристике. Таким образом, из равенства нулю второй производ-
производной следует, что такое касание происходит в двух соседних точках,
иными словами, в плоскости годографа между линией тока и харак-
характеристикой имеет место касание более высокого порядка. Укажем
без доказательства, что при аналитическом решении уравнения
в плоскости годографа это обстоятельство приводит к появлению
в поле течения точки заострения такого же типа, как на рис. 25.

§ 3 ПРЕДЕЛЬНАЯ ЛИНИЯ 113
Далее, можно аналитически показать, что если в плоскости
годографа предельная линия не совпадает с характеристикой, то
выражение dzx/dw2, составленное вдоль линии тока, может обра-
обращаться в нуль вместе с dxjdw только в изолированных точках
плоскости течения. Если какая-либо линия тока совпадает с харак-
характеристикой, то для всех точек dxjdw = 0 и dy/dw = 0 [см. равен-
равенства V, 1A5) и C)], т. е. все точки характеристики плоскости
годографа отображаются в одну точку плоскости течения. Физически
это означает возникновение расширяющегося течения, вторгающегося
в непараллельное течение. При этом на рассматриваемой линии тока
получается угловая точка, которая и вызывает появление волн Маха
расширяющегося течения. Если эти волны таковы, что для них
Х== const [см. формулу I, 7C)], то в угловой точке эта величина
принимает различные значения в зависимости от направления волны
Маха. В общем случае к угловой точке подходит только одна волна
Маха другого семейства (для которого |i, = const). Отсюда, очевидно,
следует, что угловой точке как результату отображения годографа
на плоскость течения соответствует отрезок кривой р. = const.
В чем же состоит физический смысл предельных линий? Прежде
всего сформулируем этот вопрос несколько точнее. Предположим,
что аналитическим путем найдено поле течения, обладающее пре-
предельной линией, и выясним, какие граничные условия необходимы
для того, чтобы такое поле могло быть полностью или частично
осуществлено. Для этой цели удобнее всего построение методом
характеристик, так как оно отчетливо показывает влияние гранич-
граничных условий. В рассматриваемом течении выберем две линии тока
в качестве ограничивающих стенок. Далее, в сверхзвуковой области
отыщем линию, образующую с вектором скорости угол, который
везде больше угла Маха или по крайней мере равен ему. Затем вдоль
этой линии вычислим — на основе имеющегося аналитического реше-
решения— вектор скорости. Граничные линии тока прервем на предель-
предельной линии. Если обратиться к рис. 22, то на нем мы можем при-
принять течение известным, например вдоль волны Маха АВ. Задан-
Заданными граничными линиями тока пусть будут ВС и AD. Однако
этих граничных условий достаточно только для того, чтобы опре-
определить течение до волны Маха DE. Таких граничных условий,
которые приводили бы к тому, что внутри поля течения волны
Маха исходили бы одна из другой, не существует. Это было бы
возможно только при наличии границ, возвращающихся назад. Такие
границы можно было бы осуществить, например, посредством лопа-
гок, установленных внутри течения. Если отвлечься от подобного
эода искусственных возможностей, то предельная линия, предста-
зляющая собой огибающую волн расширения, физически возникнуть
ie может (Гудерлей [17], см. лит. 1).
По-иному обстоит дело на рис. 23. Здесь границы определяют
юле течения вплоть до предельной линии (и даже еще на некотором
8 Зак. 534. К. Г. Гудерлей

114 ГЛ. V ОСНОВЫ МЕТОДА ГОДОГРАФА
куске плоскости течения после ее перегибания). В этом случае
возникает сближение волн сжатия, вследствие чего образуется ска-
скачок уплотнения.
Таким образом, возникновение предельных линий, поскольку оно
определяется граничными условиями, тесно ¦ связано с явлениями,
известными из сверхзвуковой газовой динамики.
Конечно, при формулировке краевых задач в плоскости годо-
годографа необходимо следить за тем, чтобы в плоскости течения не
получались границы, переходящие во второй лист. Именно поэтому
недопустимо, чтобы граничная линия тока пересекала характеристику
более одного раза.
§ 4. Частные решения уравнения годографа,
полученные Чаплыгиным
В последующем изложении решения точного уравнения годографа
не будут играть никакой роли, так как мы всегда будем предпочи-
предпочитать пользоваться упрощенным уравнением, более удобным в мате-
математическом отношении. Однако всегда будет возникать вопрос
о связи между решениями приближенного и точного уравнения годо-
годографа. Для понимания этой связи необходимо некоторое знакомство
с точными решениями.
Так как в уравнение V, 1A0) или в V, 1A4) & явно не входит,
то можно предположить, что решения этих уравнений имеют вид
(costnb,
lsinm&,
причем т есть постоянная. Эти допущения приводят к обыкновен-
обыкновенным дифференциальным уравнениям
-^1-?)*=»• <*>
где
a* = -^-w ^-Ф. C)
В этих уравнениях скорость w может изменяться от нуля до
w*Y(x~\-l)l(x—О- В самом деле, из уравнения Бернулли следует,
что w* У(¦*.-{- 1)/(%—1) есть наивысшая скорость, которая может

§ 4 ЧАСТНЫЕ РЕШЕНИЯ, ПОЛУЧЕННЫЕ ЧАПЛЫГИНЫМ
115
возникнуть в течении. Легко найти, что решения уравнений Bа) и B6)
выражаются в виде рядов
й = ®«5в.а/Ч Dа>
D6)
коэффициенты которых ап и bn можно вычислить посредством ре-
рекуррентных формул. В случае целочисленного т одно из решений,
например gv следует взять в виде
anw2n
m In
E)
причем для определения коэффициентов ап получается опять рекуррент-
рекуррентная формула. В аналогичном виде следует взять решение также для gz.
После того как решения ли-
линейных дифференциальных урав-
уравнений получены, дальнейшие чи-
численные расчеты не представляют
никаких принципиальных труд- i
ностей. На рис. 26 изображены ^
два линейно независимых реше- §
ния для /ге = 3 и /га =10. «Я
Дифференциальные уравне-
уравнения B) легко можно свести
к известному типу. В самом
деле, если мы введем в ка-
качестве новой независимой пере-
переменной величину
/т-3 >
х — ¦
то получим
1 \w
F)
0.5
Рис. 26. Два линейно независимых реше-
решения я, при от = 3 и от = 10 (масштаб по вер-
тикали не играет никакой роли, так как зна-
чения ?! получаются из линейного дифферен-
дифференциального уравнения).
X— 1
Ga)
, = 0. G6)
Эти уравнения имеют три регулярные особые точки, а именно: 0,
1 и со- следовательно, они представляют собой гипергеометрические
дифференциальные уравнения i). Применив обозначения, обычные
1) С некоторыми свойствами гипергеометрических дифференциальных
уравнений мы познакомимся на стр. 197—199.

116 ГЛ V ОСНОВЫ МЕТОДА ГОДОГРАФА
для гипергеометрических рядов, мы сумеем представить решения
уравнений G), за исключением вырожденного случая, решение кото-
которого определяется равенством E), в следующем виде:
(8а)
(86)
Для целых отрицательных m проще всего использовать решение E).
Для вычисления функций часто предпочтительнее вместо разложения
в степенные ряды производить численное интегрирование дифферен-
дифференциальных уравнений.
Первый член полученных выше ря дов дает приближенное реше-
решение для умеренных скоростей, т. е. для несжимаемых течений.
В самом деле, выражения w±msinmft и w^mcosmb, будучи веще-
вещественной и мнимой частями комплексной функции (и — iv)±m, являются
решениями уравнения годографа несжимаемого течения (это уравне-
уравнение тождественно совпадает с уравнением Лапласа). Именно это
обстоятельство и устанавливает связь между частными решениями
для несжимаемых течений и частными решениями для сжимаемых те-
течений. Следовательно, проявляя надлежащую осторожность, можно
получить представление о сжимаемых течениях путем рассмотрения
аналогичных несжимаемых течений. Однако с физической точки зре-
зрения ценность таких расчетов не очень велика. Таблицы для решений
Чаплыгина составили Чжан и О'Брайен, а также Хуккель (см. лит. 1).
§ 5. Решение одной краевой задачи
Покажем на примере одной краевой задачи, как возникают част-
частные решения Чаплыгина. Рассмотрим истечение из отверстия в пред-
предположении, что течение плоское1). На рис. 27,а слева от заштри-
заштрихованной стенки находится неограниченный резервуар. Из отверстия
1) Эта задача впервые рассматривалась Моленбрёком (см. лит. 1), однако
вследствие ошибки в формулировке граничных условий Моленбрёк не полу-
получил удовлетворительного результата. Правильное решение принадлежит
С. А. Чаплыгин

§ 5 РЕШЕНИЕ ОДНОЙ КРАЕВОЙ ЗАДАЧИ
117
с острыми краями вылетает струя с дозвуковой скоростью. Вели-
Величина этой скорости определяется, конечно, внешним давлением.
Прежде всего построим отображение рассматриваемого течения на
плоскость годографа (рис. 27,6). Для придания большей ясности
соответствию между плоскостью течения и плоскостью годографа
на фиг. 27,6 показано отображение только нижней половины тече-
течения. Соответственные точки плоскости течения и плоскости годографа
обозначены одинаковыми буквами. В бесконечности в резервуаре
скорость движения газа равна нулю, поэтому бесконечно удаленная
точка плоскости течения отображается в нулевую точку плоскости
годографа. Вдоль нижней половины стенки вектор скорости напра-
направлен вертикально вверх, следовательно, в верхней половине пло-
плоскости годографа этой стенке соответствует вертикальная линия.
звуковая линия
свободная
^поверхность
-С-
-с-
середина
струи
Рис. 27. Истечение через отверстие,
а —плоскость течения, б —плоскость годографа
Свободная поверхность струи представляет собой линию постоянного
давления, а потому — на основании уравнения Бернулли —также
линию постоянного модуля скорости. Эта линия изображается в пло-
плоскости годографа в виде круговой дуги ВС. Если перемещаться
в плоскости течения вдоль нижней границы струи в направлении
течения, то вектор скорости будет поворачиваться в направлении
вращения часовой стрелки. В свободной струе на достаточно большом
расстоянии от отверстия все линии тока становятся параллельными
(точка С; в плоскости течения она лежит в бесконечности). В каче-
качестве граничных условий мы имеем ф = 0 на оси симметрии и ф =
= const вдоль стенки и на свободной поверхности струи. Примем
эту постоянную равной —тс/2 (ее выбор определяет масштаб построе-
построения).
Искомое решение получается путем наложения частных решений.
Частным решением, равным нулю вдоль АС и имеющим постоянное
значение вдоль АВ, будет
ф = — Ь.

118 ГЛ V ОСНОВЫ МЕТОДА ГОДОГРАФА
Для целочисленного т частные решения вида
ij = gl(w, 2m)%in2m%
дают t|j = 0 вдоль 9=0 и вдоль & = тг/2. Следовательно, выражение
оо
— 8+2 атё\ (w- 2m) sin 2тЬ
m = i
удовлетворяет всем граничным условиям для & = 0 и 9 = тс/2. Остав-
Оставшиеся пока произвольными коэффициенты ат должны быть опреде-
определены так, чтобы были удовлетворены граничные условия вдоль ВС.
Пусть здесь скорость равна wQ. Это приводит к условию
— 0
^ amgl(w0, 2т) sin 2тЬ = — \ (о < 9 < -J-) .
Следовательно, для того чтобы найти постоянные ат, необходимо
представить выражение —тс/2-j-ft в области 0<&<^тс/2 в виде
суммы функций sin 2tn%. В результате получится решение
Щ, 2m)
Имея это решение, можно с помощью формул V, 1A5) рассчитать
поле течения и, в частности, форму границы струи. Мы не будем
заниматься здесь дальнейшими вычислениями, так как с физической
точки зрения исследуемое течение имеет лишь ограниченный интерес.
С качественной стороны картина истечения из сосуда ясна. Рас-
Рассмотренный пример дает первое представление о том, как надо при-
применять метод годографа. Более сложные случаи исследованы, в част-
частности, Лайтхиллом (см. лит. 1).
§ 6. Приближенные представления решений Чаплыгина
Как показывает пример, рассмотренный в предыдущем параграфе,
решение краевых задач в плоскости годографа приводит к беско-
бесконечным рядам, входящим в частные решения Чаплыгина. В связи
с этим целесообразно для членов более высокого порядка таких
рядов найти приближения, которые сделали бы излишним точное
вычисление этих функций. Кроме того, как мы увидим ниже, одно
из этих приближений дает точное решение уравнения в частных про-
производных, приближенно заменяющего уравнение годографа в около-
околозвуковой области. При помощи этого приближения можно перейти
от решений приближенного уравнения к точным решениям уравнения
годографа.

§ 6. ПРИБЛИЖЕННЫЕ ПРЕДСТАВЛЕНИЯ РЕШЕНИЙ ЧАПЛЫГИНА 119
Приближенное представление решений Чаплыгина получается для
больших значений т. Эти приближения можно найти посредством
некоторых проб, выполняя формальное разложение в ряд относи-
относительно \jm. Более систематичен следующий путь. Преобразуем в урав-
уравнении V, 4Bа) зависимую и независимую переменные таким обра-
образом, чтобы, во-первых, член с первой производной исчез и, во-вто-
во-вторых, чтобы член, в который входит т2, имел постоянный коэффициент.
Выполним такого рода попытку сначала в общем виде.
Рассмотрим дифференциальное уравнение
g"-\~p(w)g' + m?q{w)g = O, A)
где рад суть известные непрерывные функции. Допустим, что
решение этого уравнения может быть представлено в виде
g = h(w)z(x), Ba)
где
x — x(w) B6)
(конечно, здесь величины z и х не имеют ничего общего с коорди-
координатами плоскости течения). Из равенства Bа) мы имеем
* dx
dw dw dx dw '
d"g _ cPh dh -dx dz (Pz I dx \2 dz d*x
dw* dw* Z > dw dw dx ' dx* \ dw ) > dx dw* '
Внеся эти значения в дифференциальное уравнение A), мы получим
dx \2 dz Го dh dx . , d*w . . . dx
Для того чтобы член, содержащий т2, имел постоянный коэффи-
коэффициент и одновременно коэффициент при d2z/dx2 был равен ± 1,
должно соблюдаться равенство
I^ C)
Далее, для того чтобы первая производная dzfdx совсем не входила
в дифференциальное уравнение, должно выполняться равенство
о dh dx . , -d*x , , . , dx
21ы,1 + к+{I1
откуда следует, что

120 ГЛ V ОСНОВЫ МЕТОДА ГОДОГРАФА
Окончательно мы получим
¦%r + l±m*-\-r(x)]z = 0. E)
Знак перед т2 следует выбрать в зависимости от знака первона-
первоначальной функции д(х). Функция г (х) содержит члены, свободные
от т2; она выражается через h(x).
Для больших значений т.2 весьма вероятно, что величиной г(х)
можно пренебречь по сравнению с т2. Следовательно, приближен-
приближенными решениями уравнения E) будут
smmx
Fa)
{ cos mx
при знаке плюс перед т? и
г = е±тя> F6)
при знаке минус перед ni1.
Дальнейшие члены в разложении относительно \\т могут быть
определены без каких-либо трудностей. Получение этих членов не
следует рассматривать как доказательство пригодности полученного
приближения. Однако можно показать, что выражения вида D),
дополненные в случае необходимости конечным числом дальнейших
членов, дают приближенное представление соответствующим образом
выбранных точных решений для достаточно больших значений т
с любой точностью. Ряд относительно \\т в общем случае не схо-
сходится, следовательно, при фиксированном значении т точность при-
приближения не может быть сколь угодно сильно повышена путем уве-
увеличения числа членов в разложении.
Остановимся еще на некоторых соображениях, подтверждающих
приемлемость правил, которые следует учитывать при сопоставлении
указанных выше асимптотических решений с точными решениями.
Асимптотические представления z=e±mx [уравнение F6)] возра-
возрастают или уменьшаются в направлении возрастающих или уменьшаю-
уменьшающихся значений х по экспоненциальному закону. Это возрастание
или уменьшение тем сильнее, чем больше значение т. Точное ре-
решение следует выбрать таким образом, чтобы в заданной точке Р оно
само и его производная совпадали с одним из асимптотических
решений и его производной. Тогда можно ожидать, что кривые,
изображающие точное и асимптотическое решения, будут подобны,
т. е. что одно из линейно независимых точных решений будет воз-
возрастать по экспоненциальному закону для возрастающих значений х,
а другое — для уменьшающихся значений х. Предположим, что, уста-
устанавливая в точке Р соответствие между точным и асимптотическим
решениями, мы выбрали то асимптотическое решение, которое воз-
возрастает вправо. В точке Р мы будем иметь точное совпадение.

§ 6. ПРИБЛИЖЕННЫЕ ПРЕДСТАВЛЕНИЯ РЕШЕНИИ ЧАПЛЫГИНА 121
В общем случае выбранное точное решение будет представлять собой-
линейную комбинацию из решения, возрастающего вправо, и из реше-
решения, возрастающего влево. Конечно, в рассматриваемом примере
решение, возрастающее вправо, будет иметь больший коэффициент,
чем решение, возрастающее влево; коэффициент же последнего реше-
решения в общем случае будет отличен от нуля. Однако доля, вносимая
в полное решение решением, возрастающим влево, для больших зна-
значений т быстро увеличивается по мере перемещения влево и может
превысить долю другого решения, быстро уменьшающегося при
перемещении влево. В результате может получиться, что влево or
точки Р точное решение будет значительно отличаться от прибли-
приближенного решения. При перемещении от точки Р вправо этого н&
может случиться, так как там нежела-
нежелательная, возрастающая влево доля точ-
точного решения быстро становится незна-
незначительной. Этим рассуждениям соответ-
соответствует следующая теорема, доказатель-
доказательство которой с некоторыми обобщениями
можно найти в соответствующей лите-
литературе (см., например, Зейферт, лит. 1): \
выражение z — е+тсс или z — е~тх предста-
представляет точное решение уравнения E) асимп-
асимптотически (т. е. для возрастающих зна-
значений т все лучше и лучше), если
в какой-либо точке комплексной пло-
плоскости х оно само и его первая производ-
производная совпадают с точным решением и его
ПерВОЙ ПРОИЗВОДНОЙ; ЭТО асИМПТОТИЧеСКОе Рис. 28. Функции, используемые
r r ' для приближенного представления
Представление имеет место ДЛЯ ЗНЭЧе- решений Чаплыгина.
ний х, к которым в комплексной число-"
вой плоскости можно подойти по такому пути, на котором веще-
вещественная часть величины е+тх или соответственно е~тх не умень-
уменьшается.
Эти приближения могут быть определены только для уравне-
уравнения V, 4 Bа). Интегрирования, необходимые для вычисления к и х,
выполняются в замкнутом виде, но результат получается довольно
сложным. Решения gx берутся в виде
gl = h(w)lW(w)]±m, G>
где
Графики функций h и W изображены на рис. 28.
Из сказанного выше следует, что установление соответствия
между точными решениями уравнения Чаплыгина и приближенными
решениями зависит от выбора знака в равенстве G). Если этот

122 ГЛ V. ОСНОВЫ МЕТОДА ГОДОГРАФА
знак взять положительным, то необходимо, чтобы совпадение точ-
точного и приближенного решений имело место при -да^О. Если же
этот знак взять отрицательным, то можно было бы потребовать
совпадения точного и приближенного решений при высокой до-
дозвуковой скорости, но тогда решение было бы пригодно только
для небольших скоростей. Для того чтобы область применимости
приближенного решения была возможно шире, необходимо выбрать
скорость, при которой требуется совпадение асимптотического и
точного решений, как можно более высокой. Однако при этом
возникает трудность, связанная с тем, что приближенное реше-
решение G) неприменимо для критической скорости [см. кривую h{wl%if)
на рис. 28]. Приближенные решения становятся бесконечно боль-
большими, в то время как точные решения ограничены.
Принятие приближенным решением бесконечно большого значе-
значения объясняется тем, что при преобразовании исходного дифферен-
дифференциального уравнения A) мы заменили переменный коэффициент q(w)
при члене с /те2 постоянным коэффициентом. Между тем при кри-
критической скорости функция q в первоначальном дифференциальном
уравнении обладает нулем, следовательно, вводя условие C), мы
существенно изменяем исходное дифференциальное уравнение.
Для устранения этой трудности необходимо ввести в соответ-
соответствующий член приближенного дифференциального уравнения
в качестве множителя такую функцию, которая при критической
скорости обладала бы нулем. Воспользуемся опять допущением Bа),
но потребуем теперь, чтобы соблюдалось соотношение
Я (w)
\ dw
Тогда мы получим
У х dx = У q dw,
•откуда найдем
*=[т I УЧ dw] . (8)
Что касается функции h(w), то она по-прежнему определяется
уравнением D). В результате преобразованное дифференциальное
уравнение будет иметь вид
^O. (9)
Для получения приближенных решений следует использовать диф-
дифференциальное уравнение

§ 6. ПРИБЛИЖЕННЫЕ ПРЕДСТАВЛЕНИЯ РЕШЕНИИ ЧАПЛЫГИНА
123
Решения этого уравнения выражаются через функции Бесселя
порядка 7з [табулированы Вычислительной лабораторией националь-
национального бюро стандартов США (Computation Laboratory of National
Bureau of Standards), см. лит. 1]; для отрицательных х мы получим
= У\Щ— W-W
а для положительных х
im
х f") +¦ c2e<*/«/_v. (| im | x fA)] , (lla)
=Yx [Cl/V, (I«'') -+- c2/_Vl
A16)
где сх и с2 суть постоянные. Их выбор не совсем произволен.
В самом деле, выражения
гоог
'.75-
/50 -
имеют одно и то же асимптотическое представление, т. е. оба
выражения асимптотически линейно не независимы. Если выбрать
Cj = с2, то члены разложе-
разложения, играющие преобладающую
роль для больших значений т.,
взаимно уничтожатся и по-
получится выражение, асимпто-
асимптотически линейно независимое
от всех других, в которых '
Cj и с2 не равны друг другу; I
асимптотическое представление ^.
этого решения [равенство A1а)]
уменьшается при х—> — оо по
экспоненциальному закону. Все
другие решения при х—>¦—со
возрастают по экспоненциаль-
экспоненциальному закону. Графики функ-
функций h и х, получающихся при -2.5 -2,о -is -ya -o,s о o,s /.a
применении высказанных со- ' *~
ОбражеНИЙ К уравнению V, 4 Bа), Рис. 29 Некоторые функции, вводимые в расчет
нчпбпяшрны на nuc 9Q «о в связи с асимптотическим представлением реше-
поииуатспш па ри,. z,c7, па ний уравнения Трикоми (по Гудерлею [8]).
котором переменная х обозна-
обозначена через tj. Все построенные на рис. 29 величины являются функциями ч\.
Можно действительно доказать, что выражения вида A1), взятые
один раз со значениями е1 = с2=1, а другой раз — в иной линей-
линейной комбинации, сколь угодно точно представляют соответствующие
точные решения gv
И здесь необходимо соблюдать указанные выше условия об
установлении соответствия между точными и асимптотическими
решениями (правда, при этом требуется некоторое изменение форму-
0.75
0,50
0,25
-но
- 0,5
- 0
-0,5
-1,0
-1,5
-?.о
ч
i
А
$
¦
\
/у
/
1,
/
\
\
1
1м
\

124 ГЛ V. ОСНОВЫ МЕТОДА ГОДОГРАФА
лировки, так как ход изменения функций Бесселя сходен с ходом
изменения экспоненциальных функций лишь асимптотически). Реше-
Решение, получаемое для сх = с3 = 1, представляет собой асимптоти-
асимптотическое приближение того точного решения, которое совпадает
с асимптотическим при i\ = — оо, т. е. при <ш = 0. Этот случай
соответствует решению gv определяемому равенством V, 4 Dа) при
положительном значении т. Для других линейных комбинаций не-
необходимо вводить требование о совпадении асимптотических и точ-
точных решений при звуковой и даже при сверхзвуковой скорости.
Тогда в любом случае получится приближенное представление,
пригодное для большого диапазона скоростей. Математическая теория
дана Р. Е. Лангером; см. также работы Ф, И. Франкля [3], Имаи
и Гудерлея [16] (лит. 1).
§ 7. Уравнение Трикоми
В дальнейших исследованиях мы будем всегда пользоваться
упрощенным уравнением годографа. Было бы желательно иметь это
упрощенное уравнение таким, чтобы для него частные решения
Чаплыгина имели вид, определяемый формулами V, 6A1). Это
дало бы возможность просто переходить от решений приближенного
уравнения к решениям точного уравнения годографа. Для достиже-
достижения поставленной цели применим к полному уравнению годографа
преобразование
Trl(w), 9), A)
в точности соответствующее преобразованию V, 6 Bа). Тогда мы
получим уравнение
Й B)
аналогичное уравнению V, 6(9). В соответствии с преобразованием
II, 3C), примененным в гл. II для упрощения (в плоскости течения)
дифференциального уравнения околозвуковых течений, применим
здесь, пользуясь параметром т, преобразование
C)
a — {h-°
Внеся это значение ф в уравнение B) и ограничившись наинизшими
степенями т, мы получим

7 УРАВНЕНИЕ ТРИКОМ.И 125
Решения Чаплыгина этого уравнения являются, очевидно, асимпто-
асимптотическими представлениями решений Чаплыгина полного уравнения
годографа. Упомянутый выше переход от приближенных решений
к точным решениям можно представить себе (в принципе) следую-
следующим образом: решение приближенного дифференциального уравне-
уравнения D), которое не обязательно должно получиться в виде на-
наложения решений Чаплыгина, развертывается в ряд по этим реше-
решениям и затем вводится поправка на несовпадение решений Чаплыгина
и точных решений1). До настоящего времени примеры такого рода
еще не рассчитаны. Если такие расчеты удастся выполнить, то это
даст представление об ошибках, получающихся при использовании
приближенного уравнения.
Уравнение D) называется уравнением Трикоми, так как Трикоми
первый исследовал краевые задачи, приводящие к такому уравнению.
Обычно уравнение Трикоми выводится не из преобразованного
уравнения годографа, а непосредственно из первоначального уравне-
уравнения годографа, но при этом вместо допущения C) вводится другое,
а именно:
E)
w'*"
Внеся это значение ф в уравнение V, 1 A4) и использовав соотно-
соотношение I, 2(8), мы будем иметь
-j- Члены более высокого порядка относительно т = 0.
Ограничившись членами наинизшего порядка относительно х, мы
получим отсюда опять уравнение D).
Кривая на рис. 29, изображающая связь между скоростью и
независимой переменной т), заменяется при использовании допуще-
допущения E) касательной к ней в точке, соответствующей скорости
звука. Более сложный вид связи, получающийся при использовании
допущения A), обусловливается функцией h(w). Эта более сложная
связь проявляет себя прежде всего при исследовании деформации
контура обтекаемого тела, возникающей при применении закона
подобия. Поэтому следует отдать предпочтение второму способу
вывода уравнения Трикоми. Правда, при переходе от решения
t|j (tj, &) , понимаемого в смысле второго способа вывода, к точному
уравнению годографа возникают трудности. Пример, который
1) Такой переход не всегда может быть выполнен столь просто. Труд -
ности возникают особенно в том случае, когда решения, подлежащие раз-
разложению, имеют особые точки в дозвуковой области.

126
ГЛ V ОСНОВЫ МЕТОДА ГОДОГРАФА
рассчитали Винченти, Вагонер и Фишер (см. лит. 1), показывает, что
приближение C) дает вполне приемлемые результаты (рис. 30).
Внеся аналогичные подста-
подстановки в уравнение преобразован-
преобразованного потенциала и выполнив
соответствующее упрощение, мы
опять получим уравнение Три-
коми
7,0
I
о,г
о
т
1
\
\
\
\
\ \
у\
\
\
\
ч
\
0,2 O,if 0,6 Q8 1,0
Рис 30. Распределение давания на поджи-
поджимающей стороне пластинки ширины L, постав-
поставленной под углом атаки 13°. Сплошная
кривая —решение точного уравнения в плос-
плоскости годографа (Винченти, Вагонер и Фи-
Фишер), штриховая кривая — решение при-
приближенного уравнения V, 7 E); штрих-пунк-
штрих-пунктирная кривая — решение приближенного
уравнения V. 7 C).
<р-~ —19»»='
F)
В дальнейшем для упрощения
записей мы будем писать <[*, ср,
7j, 8- вместо ф. ср, т), ¦&, а пара-
параметр т после выполнения разло-
разложения будем полагать равным
единице. Приведем еще некото-
некоторые соотношения, которые полу-
получаются из точных равенств, если
внести в них значение ф, опре-
определяемое допущением E), и за-
затем ограничиться членами с наи-
наименьшей степенью т. Тогда соот-
соотношения V, 1A6), связывающие
потенциал и функцию тока, при-
примут вид
Ф = РЧ- G)
Для определения координат в плоскости течения мы получим
уравнения
дх 1 , , 1 ч7» ., ду 1 ,
дх
1
~~д^~~ p'or
ду 1
(8)
откуда сразу найдем
_У = —Г Ф.
J р w т
(9)
а затем, использовав преобразованный потенциал, получим
X =
A0)

§ 8. ПРИМЕРЫ ПОСТРОЕНИЯ ГОДОГРАФА
12Т
Далее мы найдем
w — ге/* = ¦о/* (к -j-
Ж— 1 = ^(х
Функциональный определитель D будет равен
Заметим, что уравнение Трикоми F) можно получить также
путем применения преобразования Лежандра к приближенному урав-
уравнению околозвукового течения, выведенному для плоскости течения.
Соотношение G) позволит затем перейти к функции тока. Для
сокращения записей целесообразно перейти от переменных <р и <]>
к новым переменным <p[w* и ф/р*?й* (тогда обе переменные будут
иметь размерность длины). Это означает, что в соотношениях G) —
A0) и A2) р* и w* полагаются равными единице. В последующих
вычислениях мы используем это упрощение.
§ 8. Примеры построения годографа
Для лучшего представления о форме, принимаемой полями тече-
течения после их отображения на плоскость годографа, рассмотрим
несколько примеров.
Сначала остановимся на некоторых несжимаемых течениях1)'.
Пусть
1) Одно время думали, что можно обнаружить существенные свойства
околозвуковых течений, если, взяв в основу решение, соответствующее го-
годографу несжимаемого течения, составить затем такое решение уравнения
годографа сжимаемого течения, которое имеет одинаковую структуру с ре-
решением для несжимаемого течения (принцип соответствия). Однако при-
применение такого метода требует большой осторожности. В одном случае,
разобранном Ринглебом, этот метод оказался плодотворным, а именно:
выяснилось, что существуют течения, в которых возможен как непрерыв-
непрерывный переход от дозвуковых скоростей к сверхзвуковым, так и непрерывный
обратный переход от сверхзвуковых к дозвуковым скоростям. Однако при.
исследовании вопроса о возникновении скачков уплотнения в смешанных
течениях, т. е. в течениях с до- и сверхзвуковыми областями, этот метод
привел к неверным заключениям, так как, несмотря на свою большую,
общность, он все же не охватывает все мыслимые поля течения.

128 ГЛ V. ОСНОВЫ МЕТОДА ГОДОГРАФА
Потенциал и функцию тока плоского несжимаемого течения можно
рассматривать как вещественную и мнимую части функции ком-
комплексного переменного z, т. е. положить
Ф(*. у)-\-14?(х, y)=Q(z). B)
Величина 2 называется комплексным потенциалом скоростей.
Если принять х и у за две независимые переменные, то из уравне-
уравнения B) следует, что
дФ , . <ty dQ.
1hc~^~l~dx~~dz'
Так как
дФ di> ,
то предыдущее равенство можно переписать в виде
u — iv = ^-. C)
dz v '
величина
w = и — iv
.называется вектором комплексной скоростих). Если отождествить
плоскость х, у с комплексной плоскостью z, то вектор комплексной
скорости получится из вектора физической скорости путем зеркаль-
,ного отражения относительно оси х. Следовательно, мы имеем
w = ~ = Q'.~< D)
В плоскости годографа функция тока зависит от скорости, поэтому S
следует рассматривать как функцию от w, т. е. исключить из соот-
соотношений B) и D) величину z.
Переход от плоскости течения к плоскости годографа часто
наиболее просто выполняется посредством преобразования Лежандра
<р = — Ф -4- ах -f- vy
[уравнение V, 1 (8)], которому можно придать вид
где w определяется равенством D). Наоборот,
;?= = *• F)
1) В других параграфах буквой w обозначается абсолютное значение
.скорости, однако спутать между собой эти разные понятия вряд ли воз-
возможно.

§ 8 ПРИМЕРЫ ПОСТРОЕНИЯ ГОДОГРАФА
129
Величина со называется комплексным преобразованным потенциа-
потенциалом. Независимой переменной является, конечно, по-прежнему те».
Примеры. Комплексный потенциал течения, создаваемого источ-
источником, равен
2 = In г.
G)
Отсюда
а
та; = 2' = -
следовательно,
Q(w) = — \nw. (8)
Комплексный преобразованный
потенциал равен
ш = 1 —In w. (9)
Выяснение смысла полученных
соотношений предоставляем чи-
читателю (в подобного рода за-
задачах самостоятельный опыт
имеет особенно большое зна-
значение).
Комплексный потенциал те-
течения, создаваемого диполем,
равен
2 = z-i, (Ю)
отсюда
= — Z
-2
— w,
изображение
бесконечности
Р v, с. 31. Течение около полутела (источник
в параллельном течении), а — плоскость течения,
б — плоскость годографа. Область / годографа
соответствует внутренней области полутела, а
область 2 — внешней области полутела.
(И)
A2)
= — - = — 2Q = — 2 y^
Следовательно, годограф представляет собой двулистную рима-
нову поверхность с точкой разветвления в начале координат.
Течение около полутела (рис. 31) определяется уравнением
z, A3)
где U есть скорость набегающего течения. Отсюда мы имеем
w — U
— In (та; — 10.
, = — !-{-In (та; — U).
A4)
A5)
К Г

130 ГЛ. V. ОСНОВЫ МЕТОДА ГОДОГРАФА
Следовательно, точка w — U плоскости годографа является особой
точкой. Это вполне понятно, так как в эту точку отображаются
все бесконечно удаленные точки плоскости течения. При использо-
использовании функции тока налагаются друг на друга два выражения, имею-
имеющие в точке w = U особенности.
В плоскости течения источник и полутело тесно связаны друг
с другом. В плоскости годографа эта связь в значительной мере
утрачивается. Вблизи особой точки w = U преобладающую роль
играет первый член правой части равенства A4), т. е. здесь кар-
картина линий тока такая же, как у диполя. В бесконечно удаленных
точках плоскости годографа преобладающую роль играет второй
член правой части равенства A4), следовательно, здесь картина ли-
линий тока имеет такой же вид, как у источника. Бесконечно удален-
удаленные точки плоскости годографа являются изображениями источника
внутри полутела, следовательно, линии тока плоскости годографа,
исходящие из бесконечности, являются изображениями линий тока
плоскости течения, исходящих из источника и располагающихся
внутри обтекаемого тела. Так как на этих последних линиях ско-
скорость в бесконечности равна U, то все их изображения в плоскости
годографа должны оканчиваться в точке w = 0. В нулевой точке
плоскости годографа течение должно иметь точку разветвления,
соответствующую критической точке плоскости течения. Если в ра-
равенстве A4) умножить член In (w — U) на положительный множи-
множитель — на первый взгляд это может показаться несущественным
изменением, — то точка разветвления линий тока переместится
в другое место, и мы получим совершенно другую картину
течения. В последнем случае использование комплексного преобра-
преобразованного потенциала приводит к значительно более простой кар-
картине.
В связи с последними замечаниями возникает вопрос о смысле
такого решения уравнения годографа, для которого нулевая точка
не является точкой разветвления линий тока. С подобного рода слу-
случаем можно встретиться при построении решения в плоскости годо-
годографа, если не уделить достаточного внимания нулевой точке. Для
того чтобы выявить существенные свойства поля течения вблизи
нулевой точки, разложим Q в ряд Тэйлора и ограничимся рассмо-
рассмотрением только первого члена разложения. Тогда, если не обращать
внимания на несущественную постоянную, мы будем иметь
а==да. A6)
(Если ряд Тэйлора начинается с члена более высокого порядка, то
нулевая точка является точкой разветвления линий тока.) Из опре-
определения вектора комплексной скорости [равенство D)] следует, что

§ 8 ПРИМЕРЫ ПОСТРОЕНИЯ ГОДОГРАФА
131
Для рассматриваемого случая мы имеем
, dw
dz — —,
w
поэтому
Это означает, что нулевая точка плоскости годографа отображается
в бесконечность плоскости течения. Заметим попутно, что то же
самое получается и для сжимаемых течений. Перейдя в плоскость
течения, мы получим
= ег
. A7)
Этим уравнениям соответствует течение между двумя параллельными
прямыми, например между прямыми _у = 0 и _у = тс. Линии тока
изображены на рис. 32. Такое поле течения можно рассматривать
как предельный случай течения внутри
угла при уменьшении этого угла до
нуля. Предельный переход от угла
к двум параллельным прямым показан
на рис. 33.
Рис. 32. Смысл решения (в пло
скости годографа), не имеющего
точки разветвления линий тока
при нулевой скорости.
Рис. 33. Переход от течения в вогнутом углу
к течению между двумя параллельными стен
ками.
После того как решение в плоскости течения известно, можно
вычислить комплексный преобразованный потенциал; мы получим
u>^=zw(\nw—1). A8)
Следовательно, для комплексного преобразованного потенциала ну-
нулевая точка в плоскости годографа, если она не является точкой
разветвления линий тока, представляет собой особую точку. Обычно
из физических соображений необходимо требовать, чтобы нулевая
точка плоскости годографа была точкой разветвления линий тока.
Тогда при применении функции тока необходимо требовать, чтобы
ее разложение в ряд Тэйлора не содержало линейного члена. От
комплексного преобразованного потенциала требуется только регу-
регулярность. Если комплексный преобразованный потенциал равен ш = w,
то решением в плоскости течения на основании соотношения F)

132 ГЛ V. ОСНОВЫ МЕТОДА ГОДОГРАФА
будет z=l. Следовательно, наложение в плоскости годографа вы-
выражения (о = w равносильно увеличению всех координат в плоскости
течения на постоянную величину. При представлении годографа
с помощью функции тока координаты плоскости течения получаются
путем интегрирования. В этом случае параллельное смещение пло-
плоскости течения обусловливается выбором постоянной интегриро-
интегрирования.
Следующим членом разложения комплексного преобразованного
потенциала в ряд Тэйлора будет
A) =
Отсюда
в
-(*)"•1
A9)
Эти уравнения определяют течение около критической точки.
Выявим теперь смысл такой точки разветвления линий тока,
в которой скорость не равна нулю. Пусть, например, мы имеем
Q = (w — of. B0)
Отсюда
, dQ 2(w — a).
dz = — = — dm.
w w
Проинтегрировав и выбрав надлежащим образом постоянную инте-
интегрирования, мы найдем
z = 2(w — а) — 2а In w.
Для дальнейшего исследования разложим правую часть в ряд
в окрестности точки w = а. Положив
— 2а In а = z0,
мы получим
(да —а)а 2 (w — д)в ,
Отсюда
Обратив это соотношение, мы будем иметь
2
о
Таким образом,
dQ. . ,, . v/
¦да = -j-z = a + a I- (z — z0) /«,

§ 8. ПРИМЕРЫ ПОСТРОЕНИЯ ГОДОГРАФА
133
т. е. для вещественного а в первом приближении
или
¦и= 0 при _у==0, х'
v=±a'/*\x — хо\1Ь при у=0, х
Наклон линий тока в первом приближении равен
О при х >¦ х0,
+ а1!* \ х — х0 |V» при х <С х0.
Следовательно, уравнением линий тока будет
у = 0 при х > х0,
~~~ Xq ^а При ^С "С^ JCq»
. Х0'
B2)
Это течение сходно с течением около задней кромки профиля Жу-
Жуковского. Плоскость течения здесь разветвляется и образует дву-
двулистную риманову поверхность. Само течение может происходить,
разветвленная
линия тока
Рис. 34 а— ючка разветвления линий тока (в плоскости
годографа), в которой скорость не равна нулю; б — соответ-
соответствующая двулистная плоскость течения.
конечно, только в одном листе. На рис. 34, б эти листы изобра-
изображены раздельно. Жирными линиями обозначены нулевые линии тока.
Оба листа скреплены друг с другом вдоль линий, обозначенных
одинаковыми буквами. На рис. 34, а показан соответствующий го-
годограф.

134
ГЛ V ОСНОВЫ МЕТОДА ГОДОГРАФА
Течение около окружности определяется комплексным потенциа-
потенциалом
B3)
После перехода на плоскость годографа мы будем иметь
Q = U1l/~T7^ \-YbVU — w. B4)
Применив преобразование Лежандра, мы получим
* B5)
изображение
окружности
нулевая линия тока
j линия разветвления
Следовательно, один лист плоскости течения отображается на два
листа плоскости годографа. Один лист плоскости годографа, соот-
соответствующий верхней половине плоскости
течения, изображен на рис. 35 вместе с ну-
нулевой и двумя другими линиями тока.
Часто полю течения, кажущемуся совсем
простым, соответствует весьма сложный го-
годограф. Для примера укажем на обтекание
окружности с циркуляцией. Проще всего
такие поля течения исследуются при помощи
преобразования Лежандра.
Рассмотренные выше примеры не при-
принадлежат к числу „классических". Один из
классических примеров, а именно истечение
Рис. 35. Отображение на пло- о г- „
скость годографа симметрии- ИЗ СОСуда, МЫ Привели В § 5 настоящей
ного обтекания круга. главы. Другие такие примеры будут разо-
разобраны в следующей главе. В большей части
этих примеров структура годографа весьма проста. Конечно, внося
небольшие изменения в граничные условия на плоскости течения,
можно значительно усложнять структуру годографа.
В качестве последнего примера рассмотрим то течение через
сопло Лаваля, для которого мы уже нашли решение в § 2 предыду-
предыдущей главы. Так как это решение удовлетворяет приближенному урав-
уравнению для потенциала, выведенному для околозвуковой области, то
соответствующее ему решение в плоскости годографа удовлетворяет
уравнению Трикоми. Переменные Фх и Фу [уравнения IV, 2 D) и
IV, 2 E)] определяют отклонение течения через сопло от параллель-
параллельного течения. В обозначениях предыдущего параграфа мы имеем 1)
1) Начиная с этого места, буква w применяется в своем прежнем смысле,
т. е. для обозначения модуля скорости.

§ 8. ПРИМЕРЫ ПОСТРОЕНИЯ ГОДОГРАФА 135
Уравнения IV, 2D) и IV, 2E) принимают теперь следующий вид:
71 = (х + 1Г2/° У2 [с, у, + т] • B6а)
& = (*+l)-V[c» p + i]. B66)
где
с1 = (*+1)с B6в)
В рассматриваемом приближении линия у = const является линией
тока. Исключив х из уравнений B6а) и B66), мы получим
а = (* + 1Г'Чтц>+(х+31)''1ф'8- B7)
При фиксированном значении _у уравнение B7) дает прямую в пло-
плоскости т), д. Эти прямые имеют своими огибающими характеристики,
проходящие через нулевую точку плоскости т), &. Наклон этих пря-
прямых равен
_ = (х + 1) i'c,y
Наклон характеристик на основании равенства I, 6 (8) равен
Следовательно, для прямой у = const, наклон которой при опреде-
определенном значении т]0 одинаков с наклоном характеристики, соблю-
соблюдается соотношение
Использовав это соотношение, мы можем переписать уравнение B7)
в виде
При т) = т]0 мы получим
т. е. рассматриваемая точка прямой лежит одновременно на характе-
характеристике, проходящей через нулевую точку (в самом деле, эта харак-
характеристика определяется последним уравнением).
Все линии поля течения, вычерченные на рис. 16 (стр. 91), опре-
определяются тем или иным поведением вектора скорости и поэтому без
труда могут быть перенесены в плоскость годографа.
Годограф рассмотренного течения изображен на рис. 36. Бро-
Бросается в глаза следующая его особенность: область, которая распо-
расположена между обеими характеристиками, проходящими через нулевую

136
ГЛ. V. ОСНОВЫ МЕТОДА ГОДОГРАФА
точку, перекрыта линиями тока трижды. В самом деле, через каждую
точку этой области проходят три прямые, каждая из которых
касается одной из указанных характеристик. Годограф на рис. 36
построен только для нижней половины поля течения; область AOBFD
перекрыта один раз, а область ВОЕ — два раза. Трехкратное пере-
перекрытие области EOF полу-
получится после отображения на
плоскость годографа верхней
половины поля течения. Та-
Такого расположения линий
в плоскости годографа следо-
/щоактеристика вал<> ожидать также из рас-
смотрения формы линий тока
в плоскости течения.
Если рассматривать тече-
течение через сопло Лаваля с точ-
%Тб°а7щ§я'линий'тока Х^ КИ 3peH™ КрабВ°Й 3аДЗЧИ
>v (рис. 37), то многократное пе-
перекрытие некоторой области
годографа не является чем-то
особенно важным. Выясним,
в соответствии со сказанным
на стр. 91, какая часть стенки
сопла должна быть задана для того, чтобы можно было определить
дозвуковое поле сопла и ту часть сверхзвукового поля, которая
влияет на дозвуковое поле. Очевидно, должна быть задана граница
ось сопла
дозвуковой
область
Рис. 36. Изображение в плоскости годографа
решения, полученного для течения через сопло
Лаваля.
предельная
^Характеристика
а и i
Рис. 37. а —поле течения через сопло Лаваля, б — изображение
в плоскости т], 9.
всей дозвуковой области и та часть границы сверхзвуковой области,
которая простирается от точки пересечения ее с звуковой линией до
точки пересечения с характеристиками, проходящими через нулевую
точку. Эти характеристики являются предельными. (Необходимо обра-
обратить внимание на следующее: если в плоскости течения задан неко-
некоторый контур, то граничные условия в плоскости годографа не могут
быть предписаны вдоль заранее заданного контура; в то же время

S 9 ЛИНИИ РАЗВЕТВЛЕНИЯ В ПЛОСКОСТИ ГОДОГРАФА 137
предельная характеристика предопределена в любом случае, поэтому
должно быть ясно, что условия, которые заданы по другую сторону
предельной характеристики, не могут влиять на дозвуковое поле
течения.) На рис. 36 часть AOBFD поля течения перекрыта один
раз. Продолжение этой части поля течения можно построить с по-
помощью метода характеристик, причем проще выполнить это построе-
построение в плоскости течения. Отобразив это продолженное поле течения
на плоскость годографа, мы увидим, что многократное перекрытие
сверхзвуковой области получается автоматически *).
§ 9* Линии разветвления в плоскости годографа
В последнем из примеров, рассмотренных в предыдущем пара-
параграфе, мы видели, что вдоль характеристики, проходящей через
нулевую точку, скрепляются друг с другом два листа плоскости годо-
годографа, следовательно, если мы будем перемещаться вдоль какой-либо
линии тока, то перейдем с одного листа на другой. Выясним, какие
условия должны выполняться для того, чтобы была возможна такая
структура плоскости годографа.
Пусть С есть та кривая в плоскости годографа, вдоль которой
скреплены оба листа. Изображение этой кривой в плоскости течения
обозначим также буквой С. Вполне возможно, что в плоскости тече-
течения решения, получающиеся с обеих сторон кривой С, не переходят
одно в другое путем аналитического продолжения. Такой случай
будет иметь место только тогда, когда кривая С является характе-
характеристикой как в плоскости течения, так и в плоскости годографа.
Мы исключим из рассмотрения случай подобного рода и предпо-
предположим, что в плоскости течения решение вдоль кривой С аналити-
аналитическое. Выясним, может ли кривая С быть характеристикой при
таком предположении. Мы имеем общие формулы:
, ди , . ди
, dv , . dv ,
dv — з- dx + 3- dy.
dx ' dy ¦*
Если определитель, состоящий из коэффициентов при dx и dy в пра-
правых частях равенств, не равен нулю [этот определитель представ-
представляет собой не что иное, как обратное значение функционального
определителя d(x,y)[d(u,v)], то правые части линейно независимы,
и поэтому между плоскостью годографа и плоскостью течения суще-
существует взаимно-однозначное соответствие. Очевидно, что в том слу-
случае, когда вдоль кривой С скреплены два листа годографа, такого
!) В литературе многократное перекрытие сверхзвуковой области иногда
используется для получения решения в плоскости годографа. С физической
точки зрения такой способ нельзя считать удовлетворительным.

138 ГЛ V. ОСНОВЫ МЕТОДА ГОДОГРАФА
соответствия между плоскостью годографа и плоскостью течения не
может существовать. Следовательно, если вдоль кривой С скреплены
два листа римановой поверхности, то должно иметь место соотно-
соотношение
ди dv dv ди „
дх ду дх ду '
или, если ввести потенциал скоростей Ф,
Ф«.ФТО —Фэд = 0. A)
Для упрощения вычислений положим в основу исследования прибли-
приближенное уравнение околозвукового течения II, 8A), т. е. уравнение
— (х+1)ФжФжж + Фто = 0. B)
Наклон кривой С определяется выражением dy/dx. Взяв от Ф^ и Ф^
производные вдоль кривой С, мы получим
~ я*^ XV dx' \ '
dx ~ я*^ XV dx
d$>,. dy
У = Фти + фы„ 4- ¦
ХУ т vv dx
dx
Внеся в уравнение A) значение Фуу из уравнения B), мы найдем
«—Фед=0. D)
Это равенство показывает, что рассматриваемая возможность скре-
скрепления обоих листов римановой поверхности осуществима только
в сверхзвуковой области (Фх >¦ 0), так как в дозвуковой области
(Фх < 0) левая часть равенства D), будучи отрицательной суммой
двух квадратов, не может быть равна нулю. Если же Фхх и Фху
в дозвуковой области вдоль кривой С равны нулю, то легко пока-
показать, что в этом случае течение является параллельным. Из уравне-
уравнения D) мы находим
Далее, исключив из уравнений C) Фху и Фуу с помощью уравне-
уравнений D) и B), мы получим
Ct X (_ С
Отсюда
d$y q: У"х -4- 1 У Фж ^Фж = О
или

§ 9. ЛИНИИ РАЗВЕТВЛЕНИЯ В ПЛОСКОСТИ ГОДОГРАФА 139
Это есть дифференциальное уравнение характеристик в плоскости ¦»], &.
Следовательно, скрепление обоих листов римановой поверхности
возможно только вдоль характеристики плоскости годографа.
Остается показать, что кривая С является характеристикой также
в плоскости течения. Одно из условий, обязательных для характе-
характеристик, а именно условие совместности, выполняется, так как кри-
кривая С имеет в плоскости годографа своим изображением характери-
характеристику. Следовательно, остается только выяснить, имеет ли кривая С
в плоскости течения направление, совпадающее с направлением ха-
характеристики. Структура годографа не зависит от того, исполь-
используется ли в качестве зависимой переменной функция тока или пре-
преобразованный потенциал. Вдоль характеристики преобразованный
потенциал удовлетворяет уравнению
V-Ц d% ± <% = 0.
В это уравнение входят только те производные, которые должны
быть составлены вдоль характеристистики. Следовательно, оно удо-
удовлетворяется и в том случае, когда производные от dy^ и rfcp& в дру-
других направлениях не существуют, как это имеет место, например,
для сопла Лаваля. Вследствие соотношений V, 7E) и V, 7A0) по-
последнее уравнение принимает вид
т. е. совпадает с уравнением I, 9D), определяющим направление
характеристик в плоскости течения.
Линии разветвления в плоскости годографа являются как бы подо-
подобием предельных линий в плоскости течения. Однако необходимо
иметь в виду, что предельная линия в плоскости течения в общем
случае не является характеристикой, в то время как линия развет-
разветвления в плоскости годографа всегда представляет собой характе-
характеристику. Конечно, последнее обстоятельство связано с линейностью
уравнения годографа.
В примере с соплом Лаваля в линию разветвления в плоскости
годгграфа отображается та характеристика плоскости течения, кото-
которая выходит из точки пересечения звуковой линии с осью сопла и
направлена вниз по течению В нижней половине плоскости течения
этой характеристикой является правобегущая волна Маха. Такого
рода волны Маха в нижней половине плоскости течения предста-
представляют собой волны сжатия, если они исходят от звуковой линии, и
волны расширения, если они исходят от противолежащей стенки
сопла. В этом и лежит причина двойного перекрытия плоскости годо-
годографа; всегда, когда имеет место такая смена волн сжатия на волны
расширения или наоборот, получается многократное перекрытие пло-
плоскости годографа.

140 ГЛ. V. ОСНОВЫ МЕТОДА ГОДОГРАФА
§ 10. Потерянные решения
Выясним теперь, какой вид имеет годограф для течения, разви-
развивающегося из параллельного течения после искривления ограничи-
ограничивающей стенки. В этом случае при построении поля течения посред-
посредством метода характеристик получаются волны Маха только одного
семейства, например левобегущие волны (рис. 38). Поэтому течение
отображается только в одну характе-
//,'/. ристику плоскости годографа, и ка-
/ / / / / ждая волна, вычерчиваемая при по-
II/// строении поля скоростей, изобра-
/ / I / / жается одной точкой этой характери-
II/// стики. Конечно, такие решения в
if/// плоскости годографа не непрерывны;
rffff777777T///''"//////77777777 например, для рассматриваемой ха-
Р „с. 38. Потерянное решение в пло- РЗКТериСТИКИ ГОДОГрафЗ фунКЦИЯ ф
скости течения. изменяется между двумя предельными
значениями, которые определяются ли-
линиями тока, ограничивающими поле течения. Следовательно, такое
решение обладает вырожденным годографом. Подобного родз ре-
решения называют потерянными решениями (Толмин, см. лит. 1).
Для преобразованного потенциала особенность имеет более про-
простой характер [см. уравнение V, 7G)]. Пусть cpt и ср2 суть два раз-
различных аналитических решения уравнения Трикоми для преобразо-
преобразованного потенциала, и пусть эти решения таковы, что вдоль характе-
характеристики С плоскости годографа совпадзют значения самих функций <рх
и <р2, но не значения их внешних производных. Координатами х
и у, соответствующими решениям срх и <р2, пусть будут х1г ух и
х2, уг. Вдоль характеристики С вследствие совпадения значений
функций cpj и ср2 мы имеем
дт\ д$ df] dri ' d$ dt[ '
или
it ч-7» I db . 114-78 i db
откуда
Xl X% (X~l~ Ч (У1 У2/Щ-
Следовательно, точка второго поля течения, соответствующая задан-
заданной точке характеристики С, может лежать только на такой прямой,
которая проходит через соответственную точку первого поля течения
и имеет наклон dx/dy, равный

§ 11 КРАЕВЫЕ ЗАДАЧИ В ПЛОСКОСТИ ГОДОГРАФА
141
(производная dbjd~f\ должна быть вычислена для рассматриваемой
точки характеристики). Имея в виду равенство I, 6 (8) и равен-
равенства V, 7 (8), мы получим
dx , .
dy -t- v i
Такие прямые суть характеристики плоскости течения, причем если С
есть правобегущая характеристика плоскости годографа, то ей соот-
соответствует левобегущая характеристика плоскости течения. Мы
пришли, таким образом, к следую-
следующему результату (рис. 39): два
решения, для которых значения
преобразованного потенциала вдоль
характеристики плоскости годогра-
годографа одинаковы, но в то же время
значения внешних производных это-
этого потенциала не совпадают между
собой, определяют два таких поля
течения, которые могут быть свя-
связаны друг с другом посредством
потерянных решений. Этот результат
дает ВОЗМОЖНОСТЬ аналитического Рис. 39. Соединение двух невырожден-
„ ных решений посредством потерянного
исследования потерянных решений. решения.
-невырожденное поле
течения
характеристика^
§ 11. Краевые задачи в плоскости годографа
Мы видели на нескольких примерах, что в дозвуковой области
краевые задачи формулируются по-иному, чем в сверхзвуковой
области. Отсюда следует, что при формулировке краевых задач
для смешанных областей необходимо проявлять особую осторож-
осторожность. Этот параграф мы посвятим изложению результатов, известных
для таких краевых задач. Доказательств мы не будем приводить,
но зато сделаем попытку пояснить все формулировки с помощью
физических примеров.
Основной результат принадлежит Трикоми (см. лит. 1). Трикоми
рассматривает уравнение
т. е. приближенное уравнение годографа скоростей для околозву-
околозвуковых течений. Пусть на рис. 40 А и В суть две точки звуковой
линии и пусть начало координат лежит в точке А, а границей рас-
рассматриваемой области в дозвуковой части поля течения является
кривая С, соединяющая точки А и В. Относительно этой кривой
делаются допущения, обычные при рассмотрении краевых задач.
Проведем через точки А и В характеристики AD и BD. Они

142
ГЛ V. ОСНОВЫ МЕТОДА ГОДОГРАФА
7b задано-
задано
представляют собой границу рассматриваемой области в сверхзву-
сверхзвуковой части поля течения. Пусть вдоль кривой С и вдоль характери-
характеристики BD заданы значения функции тока Ф. Эта функция является
ограниченной и, кроме того, она должна удовлетворять некоторым
более или менее самоочевидным
допущениям относительно произ-
производных, составленных в направле-
направлении кривых С и BD. От решения
требуется, чтобы внутри рассма-
рассматриваемой области существовали
его вторые производные и чтобы
вдоль звуковой линии величи-
величина ty Ъ°/> была ограниченной. По-
Последнее условие будем называть
условием Трикома. Трикоми до-
доказал, что при сделанных допу-
допущениях существует единственное
х; граничные
условие
не заданы
Рис. 40. контур в краевой задаче
трикоми.
решение дифференциального урав-
нения A), удовлетворяющее задан-
заданным граничным условиям.
Формулировка рассматриваемой краевой задачи содержит в себе
отличительные черты, свойственные, с одной стороны, дозвуковой
задаче, а с другой стороны, сверхзвуковой задаче (с этими отличи-
отличительными чертами мы уже познакомились на стр. 32—33). В самом
деле, контур, вдоль которого заданы значения Ф, в дозвуковой области
В
дозвуковая
Область
°& \р
11 предельная
звуковая I, характеристика
линия -"'
Рис 41. Течение, годограф которого соответствует задаче
Трикоми.
замкнут; наоборот, в сверхзвуковой области значения Ф заданы
только вдоль одной характеристики.
Для придания сказанному наглядности сформулируем в плоскости
течения такую краевую задачу, которая в плоскости годографа
приводит к задаче Трикоми. На рис. 41 показано сопло Лаваля
с прямолинейной стенкой. Рассмотрим только нижнюю половину
поля течения. Ось симметрии сопла и стенка отображаются на пло-

§ 11 КРАЕВЫЕ ЗАДАЧИ В ПЛОСКОСТИ ГОДОГРАФА 143
скость т],9в виде линий ф = const. Примем, что вдоль оси сопла ф = 0г
а вдоль изображения стенки ф = — 1. Далее необходимо сделать
какое-то допущение о значениях ф во входном поперечном сечении.
Можно, например, задать значения ф вдоль прямой 7] = const,
соединяющей линию тока, совпадающую с осью симметрии сопла,
с линией тока, совпадающей со стенкой. Однако проще отодвинуть
входное поперечное сечение в бесконечность как в плоскости тече-
течения, так и в плоскости годографа. Тогда достаточно потребовать,
чтобы там ф увеличивалось монотонно от — 1 до нуля. Далее
в соответствии с формулировкой Трикоми зададим значения ф = — 1
вдоль характеристики DE и, наоборот, не будем задавать каких-
либо значений ф вдоль характеристики ЕА. Если в плоскости годо-
годографа функция тока вдоль какой-либо характеристики сохраняет
постоянное значение, т. е. если характеристика совпадает с линией
тока, то такая характеристика отображается в одну точку плоскости
течения [см. уравнения V, 1A5) и V, 3C)]. Так как вдоль характе-
характеристики DE направление вектора скорости изменяется, то отобра-
отображение этой характеристики в одну единственную точку плоскости
течения означает, что в плоскости течения имеется угловая точка
(точка Des=E). Около этой угловой точки возникает расширяющееся
течение Мейера, известное из сверхзвуковой аэродинамики. Сказан-
Сказанного достаточно для понимания поля течения на рис. 41. Волны
Маха расширяющегося течения соответствуют тем характеристикам
плоскости годографа, которые, начинаясь на DE, направлены к зву-
звуковой линии (например, характеристике GH).
С точки зрения общей картины течения сопло Лаваля, изобра-
изображенное на рис. 41, мало отличается от сопла Лаваля на рис. 16.
В самом деле, изменение контура сопла в дозвуковой области
в общем случае не играет роли. В сверхзвуковой области разница
между обоими соплами состоит в том, что отрезок АВ, порождаю-
порождающий на рис. 16 волны Маха, идущие к звуковой линии, стягивается
на рис. 41 в одну точку (D = ?). Можно предполагать, что гра-
граничная задача для течения, изображенного на рис. 16, также имеет
единственное решение. Выясним, как следует сформулировать анало-
аналогичную граничную задачу в плоскости годографа. В задаче Трикоми
выбор контура дозвуковой области внутри физически оправданных
пределов почти полностью произволен. Совсем по-иному обстоит
дело с выбором контура сверхзвуковой области. На рис. 41 переход
от дозвукового контура к сверхзвуковому в угловой точке, нахо-
находящейся в самом узком поперечном сечении сопла, кажется совер-
совершенно произвольным. Но если в плоскости течения контур сопла
не имел бы угловой точки, то тогда он не отображался бы в одну
характеристику плоскости годографа. Вдоль контура мы имеем
ф = const, поэтому здесь
дф dw .д<\> .
Ш ~dT~T~M ~~ '

144
ГЛ V. ОСНОВЫ МЕТОДА ГОДОГРАФА
откуда
dw
_
Так как в дозвуковой области функциональный определитель отри-
отрицателен, то он должен быть отрицательным и внутри сверхзвуковой
области; в противном случае мы имели бы физически нереализуемое
течение. Поэтому на основании равенства V, 2D) должно быть
У Л1« —:
dw
Следовательно, контур должен иметь в каждой точке наклон | dw[d$ |
не превышающий наклона характеристик1). Таким образом, мы пришли
С характеристика
характеристика
Рис. 42 Контур в обобщенной крае-
краевой задаче Трикоми.
характеристики
Рис. 43. Дальнейшее обобщение задачи
Трикоми.
к краевой задаче, в которой дозвуковой контур столь же произволен,
как и в задаче Трикоми, а сверхзвуковой контур состоит из харак-
характеристики (АВ на рис. 42)и некоторой кривой ВС, наклон которой
\dw[db\ не превышает местного наклона характеристик. Значения ф
заданы вдоль дозвукового контура и вдоль кривой СВ. Эта краевая
задача исследована не столь полно, как краевая задача Трикоми.
Доказательства единственности решения даны Ф. И. Франклем [6],
Кэтлин Моравец [2] и Гудерлеем [5] (см. лит. 1).
Дальнейшее обобщение краевой задачи мы получим, если для
случая, изображенного на рис. 16, включим в поле течения также
верхнюю половину сопла Лаваля или если возьмем для сопла Лаваля
такое поле течения, которое не обладает симметрией. Для такого
рода краевых задач сверхзвуковые контуры в плоскости годографа
1) С математической точки зрения требования о том, чтобы функцио-
функциональный определитель был отрицательным и чтобы вдоль контура имело
место равенство ф = О, являются чуждыми для краевой задачи. Однако при
эвристическом подходе они вполне допустимы, так как приводят к надлежа-
надлежащей формулировке краевой задачи.

§ 11 КРАЕВЫЕ ЗАДАЧИ В ПЛОСКОСТИ ГОДОГРАФА 145
имеют вид, изображенный на рис. 43. Упомянутые выше доказатель-
доказательства единственности применимы и к этим случаям.
Скачки уплотнения, возникающие в параллельном течении, ото-
отображаются на плоскость годографа в виде ударной поляры, т. е.
в виде заранее известной кривой. Вдоль этой кривой имеет место
граничное условие (Франкль [6] и Гудерлей [2], см. лит. 1), которое
мы сейчас выведем. Уравнения ударной поляры для околозвукового
течения мы получили уже в § 4 гл. II [уравнение II, 4(8)]. Теперь
мы имеем
гц= (х + 1Г'иа\, vxn = (х + 1
следовательно, уравнение II, 4 (8) принимает вид
^^-^). B)
В этом уравнении индекс I по-прежнему относится к состоянию
до скачка уплотнения, а индекс II — к состоянию после скачка.
Граничное условие, которое должно выполняться вдоль ударной
поляры, выражает собой следующее: перемещению в плоскости годо-
годографа вдоль ударной поляры должно соответствовать в плоскости
течения перемещение в предписанном направлении, а именно в на-
направлении линии скачка. Последнее определяется только скоростями
до скачка и после него. Так как изменение вектора скорости, про-
происходящее на скачке, направлено по нормали к линии скачка, то
для определения направления этой линии мы имеем уравнение
Для определения направления ударной поляры следует продифферен-
продифференцировать уравнение B); мы получим
^=+[8(% + Ч1)рCЧп + Ч1). D)
Но мы имеем
, дх , , дх .а
Внеся эти значения в уравнение C), заменив затем частные произ-
производные от х и у их значениями из равенств V, 7(8) и использовав,
наконец, уравнение D), мы найдем линейное граничное условие,
которое должно выполняться вдоль ударной поляры,
10 Зак. 534. К. Г. Гудерлей

46
ГЛ V. ОСНОВЫ МЕТОДА ГОДОГРАФА
Его можно истолковать следующим образом. Вдоль линии ф = const
имеет место соотношение
поэтому наклон этой линии равен

drl 'Ь '
Правую часть этого равенства можно вычислить из граничного усло-
условия на ударной поляре; сделав это, мы получим
¦— +
F)
Следовательно, наклон линий тока вдоль ударной поляры задан
заранее.
На рис. 44 изображены ударные поляры для 7]j—1; 0,8; 0,6;
0,4 и 0,2. На ударной поляре для 7^=1 показаны посредством
Рис. 44 Ударные поляры в плоскости ч, 8 с отмеченными направлениями
подхода линий тока (по Гудерлею [2}).
коротких отрезков направления линий тока, подходящих к поляре.
В точках S поляры соблюдается вдоль линий тока равенство tj = const,
а в точках Q (точки Крокко) — равенство 9 = const; в точках R
разность %п—$! имеет для ударной поляры максимальное значение.
На рис. 44 изображены также некоторые характеристики. Вся
характеристика, проходящая через точку 7^=1, &п — {^ = 0, лежит
внутри ударной поляры, проходящей через эту же точку.

§ П. КРАЕВЫЕ ЗАДАЧИ В ПЛОСКОСТИ ГОДОГРАФА
147
расширяющееся
/печение
Простая краевая задача с наличием скачка уплотнения получается
для обтекания клина с такой сверхзвуковой скоростью, при кото-
которой скачок уплотнения еще не прилегает к острию клина. Если
клин симметричен, то скачок уплотнения, конечно, также симмет-
симметричен. На оси симметрии поля течения получается прямой скачок
уплотнения (точка А на рис 45,а). Вдоль оси симметрии скорость
изменяется от значения, соответ-
соответствующего прямому скачку уплот-
уплотнения, до нуля на острие кли-
клина (точка А на рис. 45,6). На
острие клина вектор скорости
принимает направление сторон
клина, следовательно, на пло-
плоскости годографа он изображается
линией Ь = const. На плече клина
C^D скорость становится рав-
равной скорости звука (на стороне
клина звуковая скорость не мо-
может быть достигнута; причина
этого будет объяснена в § 4
гл. VI). Плечо клина отображается
в характеристику CD плоскости
годографа.
На рис. 45,8 годограф пре-
преобразован к системе координат
Т|, &. В этой системе нулевая точ-
точка обычного годографа изобра-
изображается точкой т] = —со. В каче-
качестве граничных условий мы имеем
ф — о вдоль АВ и вдоль BCD и,
кроме того, условие на ударной
поляре АЕ. Так как все гранич-
граничные условия однородны, то, оче-
очевидно, можно присоединить еще
одно условие, которое позволит
определить масштаб плоскости течения. Можно, например, задать
длину стороны клина или значение функции тока в точке Е (с фи-
физической точки зрения эти условия вряд ли представляют какой-
либо интерес). Единственность решения краевой задачи такого рода
доказана Ф. И. Франклем [6] (см. лит. 1).
Еще один тип граничных условий получается из следующих
соображений. Одной из главных задач аэродинамики является опре-
определение течения около заданного профиля. Однако такая краевая
задача практически неразрешима. В качестве некоторого шага на пути
к ее решению можно поставить следующую задачу: пусть известно
решение в плоскости годографа для течения около заданного тела;
В А
сторона клина С
скорость набегающегс
ft течения
плечо клина
Р и с 45 Схема сверхзвукового течения около
клина с неприлегающим скачком уплотнения.
а — плоскость течения, б~ плоскость годо-
годографа; в—плоскость 1), 8.

148 ГЛ V. ОСНОВЫ МЕТОДА ГОДОГРАФА
следует определить граничные условия для случая, когда контур
в плоскости течения претерпевает заданное небольшое изменение.
Граничные условия такого вида имеют важное значение для исследо-
исследования полей течения вблизи числа Маха, равного единице, а также
для принципиального решения вопроса о том, могут ли возникать
скачки уплотнения в смешанных до- и сверхзвуковых полях, если
контур обтекаемого тела заданным образом изменяется.
Небольшее изменение контура, которое должно быть предпринято
в плоскости течения, может быть учтено линеаризацией граничных
условий в плоскости годографа, причем сначала выводятся гранич-
граничные условия для общего уравнения годографа, а уже затем состав-
составляется приближение специально для случая околозвуковых течений.
Для описания контура в плоскости течения можно задать коор-
координаты х и у в виде функций от ft, т. е. положить
Функции ft и /2 связаны соотношением
dy __ /а _
Контур в плоскости годографа пусть задан уравнением
Если воспользоваться преобразованным потенциалом, то для опре-
определения хну мы будем иметь следующие уравнения:
х=/1Ф) = <?и(Щ- »)««»—^срв(«»0, »)sin», Ga)
y = h (») = ?«, (w0. &)sin а 4- ~ ъ («\>. &)cos &- Gб)
Эти уравнения позволяют вычислить значения ср^ и ср9 вдоль контура;
мы получим
») = /з(»). (8а)
В местной системе координат х, у, имеющей общее начало с перво-
первоначальной системой, но повернутой относительно нее так, чтобы
ось х совпадала с направлением местного вектора скорости, функ-
функции /3 и /4 совпадают с функциями Д и /2. При однократном диф-
дифференцировании выбранная таким способом система координат х, у дол-
должна оставаться неизменной. Угол, образуемый скоростью с осью х,
обозначим через &. Конечно, в рассматриваемой точке & = 0. В системе

11 КРАЕВЫЕ ЗАДАЧИ В ПЛОСКОСТИ ГОДОГРАФА
149
координат х, у уравнение G6) принимает вид
В рассматриваемой точке контура у' = 0, поэтому
Таким образом, граничные условия могут быть представлены в сле-
следующем виде:
-^-«РоК. а) = Л(&). (9а)
cpw (w0, 0) = fl (»). (96)
Из сказанного вытекает геометрический смысл функции /4: она
определяет расстояние касательной, проведенной через рассматри-
рассматриваемую точку контура, от на-
начала координат (рис. 46).
Изменим теперь функцию /4
на небольшую величину Ft.
Тогда решение, удовлетворяю-
удовлетворяющее новому граничному усло-
условию, будет отличаться от пер-
первоначального решения ср на
малую величину Ф. Положе-
Положение контура в плоскости годо-
годоРис. 46 Геометрический смысл функции f,
(по Гудерлею [2])
графа также немного изме-
изменится, т. е. функция wo($)
заменится функцией гг>0(&) +
-\-W0($). Таким образом, граничными условиями в новом течении
будут
-4w- to К+^о. ») 4- ф» (wo ¦+¦ w0, ft)] = /4 (») -h ^4 (&).
Если считать величины F4, Wo и Ф малыми, то линеаризация
последних уравнений дает
Шп
Исключив И/о, мы найдем
-Ф„./-^-4-^

150 ГЛ V ОСНОВЫ МЕТОДА ГОДОГРАФА
Если рассматривать исходное течение в системе координат х, у, то
dy = 0, и на основании уравнения G6) мы будем иметь
wl
, 1
Отсюда после использования дифференциального уравнения V, 1A0)
мы найдем
dw0 да0 v>ww (дао> ft)
db ~ (. да2 \ / 1
Следовательно, граничным условием, которое должно выполняться
вдоль первоначального контура в плоскости годографа, будет
w ^г~^^-Ж-~г* ^i^~r*w°4V (Ю)
где F4(&) и wo($) суть известные функции (Гудерлей [1], см.
лит. 1).
На первый взгляд это линейное граничное условие кажется
довольно сложным, однако в действительности это не так. В самом
деле, уравнение A0) связано с уравнением преобразованного потен-
потенциала так же, как производная по нормали с решением уравнения
Лапласа. Имея уравнение Лапласа, мы можем от соотношения
содержащего интеграл по поверхности, перейти к соотношению
(F есть некоторая поверхность, а С — контур, на который опирается
эта поверхность). Выражение под знаком криволинейного интеграла
тесно связано с производной по нормали к контуру С. Аналогичное
соотношение имеет место и в рассматриваемой задаче. Для того
чтобы показать это, воспользуемся соотношением I, 2A0а) и пере-
перепишем дифференциальное уравнение V, 1A0) в следующем виде:
-з —— I 1 тг) %» = 0.
дда ' да \ а2 } т'т

8 11 КРАЕВЫЕ ЗАДАЧИ В ПЛОСКОСТИ ГОДОГРАФА 151
Тогда, перейдя от интеграла по поверхности
к криволинейному интегралу, мы получим
Мда = 0. (И)
§
Выражение под знаком последнего интеграла пропорционально левой
части уравнения A0). Таким образом, рассматриваемая задача анало-
аналогична краевой задаче второго рода теории потенциала, поэтому мы
будем называть ее краевой задачей второго рода.
Для замкнутого контура соотношение A1) вместе с уравне-
уравнением A0) являются условием разрешимости краевой задачи совер-
совершенно аналогично тому, как это имеет место в теории потенциала.
Однако рассматриваемые нами контуры часто не замыкаются в сверх-
сверхзвуковой области, и тогда заранее не ясно, существует ли такое
условие. Некоторые соображения дают основание предполагать, что
и в этих случаях необходимо существование дополнительного усло-
условия (см. стр. 284).
Соответствующее граничное условие для уравнения Трикоми
получается либо непосредственно, либо путем таких же упрощений,
какие были сделаны при выводе самого уравнения Трикоми. Допу-
Допустим, например, что
Ф := Т Ф (TJ, ft),
где т] и 9- определяются равенствами V, 7E). С этим допущением
совместимо допущение, что
Внесем это значение Fi в граничное уравнение A0); ограничившись
членами наинизшего порядка относительно т и заменив Ф и F4 на Ф
и F4, мы получим
Первоначальный контур в плоскости т), 8- задан уравнением
¦4 = "По (8).
Производная dfjdb определяет в соответствии с уравнением (96)
с точностью до множителя (x-j- 1) значения х, отвечающие задан-
заданным значениям %¦ наклона поверхности, а производная dFJdb—
изменение величины dfjdb вследствие деформации контура. Дока-
Доказательство единственности решения такой задачи дано Кэтлин Моравец
[1] (см. лит. 1).

152 ГЛ. V. ОСНОВЫ МЕТОДА ГОДОГРАФА
В большей части последующих приложений граничные условия
однородны, например поверхность обтекаемого тела дается уравне-
уравнением ф = О или вводится требование о том, чтобы при наложении
на заданное течение другого решения поверхность тела оставалась
неизменной, что приводит к условию A2) с правой частью, равной
нулю. Тогда решение в плоскости годографа содержит по крайней
мере одну особую точку. Очень часто эта точка является особой
точкой звуковой линии, следовательно, возникающая здесь особен-
особенность определяется частным решением уравнения Трикоми. В этих
случаях однородные граничные условия удовлетворяются путем нало-
наложения на решение, определяющее заданную особенность, другого
решения уравнения Трикоми, удовлетворяющего условию Трикоми
и дающего вдоль контура рассматриваемой области такие же допол-
дополнительные слагаемые (с точностью до знака) к граничным значениям,
как и особое частное решение. Для краевой задачи первого рода
такое решение единственно, если задано выражение особенности.
Напомним, что в краевой задаче второго рода заданные гранич-
граничные значения, вообще говоря, должны удовлетворять дополнитель-
дополнительному условию. В таком случае необходимо иметь выражения для
двух особенностей. Одно из этих выражений дается заранее, вто-
второе же умножается на подходящий множитель и затем налагается
на первое. Множитель следует выбрать так, чтобы граничные усло-
условия оставшейся неособой части решения удовлетворяли условию
разрешимости.

Глава VI
ИССЛЕДОВАНИЕ ОКОЛОЗВУКОВЫХ ТЕЧЕНИЙ МЕТОДОМ
ГОДОГРАФА
§ 1. Предварительные замечания
Некоторые поля течения допускают непосредственное отображе-
отображение в плоскость годографа. Полученные годографы можно исполь-
использовать для получения представления об общих свойствах полей
течения. Хотя поля течения, допускающие непосредственное отобра-
отображение в плоскость годографа, лишь редко представляют непосред-
непосредственный интерес для авиационных нужд, тем не менее они заслу-
заслуживают внимания, так как позволяют выявить свойства околозвуковых
течений и получить более глубокое представление о краевых зада-
задачах в околозвуковой области. В отдельных случаях годографы дают
возможность физически истолковать теоретические результаты, ко-
которые были получены другим путем и понимание которых ранее
было затруднительно.
Возможность получения нетривиальных выводов из рассмотрения-
годографа объясняется тем, что отображения, в результате которых
получаются годографы, подчиняются некоторым общим правилам.
В предыдущей главе мы вскользь коснулись этих правил. Соберем
их теперь все вместе.
Так как функциональный определитель V, 2D) в дозвуковой об-
области отрицателен, то направление обхода элементарной площадки при
переходе от плоскости течения к плоскости годографа изменяется
на обратное. Из соображений непрерывности, а также вследствие
того, что мы исключаем из рассматриваемых полей течения предель-
предельные линии, такая же перемена направления обхода происходит и
в сверхзвуковой области. Отсюда можно вывести правило знаков для
волн Маха, исходящих из звуковой линии или на ней кончающихся.
Проще всего сформулировать это правило на основе наглядных со-
соображений, высказанных А. Буземаном х). Вдоль заданной волны
Маха изменение состояния вызывается только волнами другого се-
семейства. На волне Маха, оканчивающейся на звуковой линии, напри-
например на волне АВ (рис. 47), давление по мере приближения к зву-
звуковой линии возрастает, так как при таком приближении совер-
совершается переход от сверхзвуковой области к дозвуковой области.
!) Аналогичные соображения можно найти в работе Никольского и
Таганова (см. лит 1).

154 ГЛ. VI. ИССЛЕДОВАНИЕ ТЕЧЕНИЙ МЕТОДОМ ГОДОГРАФА
Следовательно, эта волна пересекается волнами сжатия. Однако по-
последние представляют собой волны, исходящие от звуковой линии, по-
поэтому все волны, исходящие от звуковой линии, являются волнами сжа-
сжатия. Но так как звуковая линия представляет собой линию постоянного
давления, то все подходящие к ней волны являются волнами раз-
разрежения.
Само собой понятно, что плоскость течения может состоять только
из одного листа; напротив, плоскость годографа можег быть много-
листной. С подобного рода примерами мы уже познакомились в пре-
предыдущей главе. В дозвуковой области переход на другой лист со-
совершается путем обхода особой точки. Соединение двух перекры-
перекрывающихся листов в дозвуковой области вдоль линии невозможно,
так как если бы такая линия существовала, то она была бы харак-
характеристикой, между тем как в дозву-
ковой области характеристики не
_В звуковая линия Сущее ГвуЮТ.
\ Х~~(^ В дозвуковой области плоскости
>\ <'\' \ / I /1/1^- годографа имеются точки, в кото-
Кволны рые сходятся несколько линий тока
волны'м А уплотнения или> выражаясь точнее, точки, в ко-
роэрежвния сверхзвуковая торых функция тока принимает раз-
различные значения в зависимости от
Рис 47. Структура сверхзвукового поля, п
прилегающего к дозвуковой области направления ПОДХОДЭ. В ПЛОСКОСТИ
течения этим точкам соответствует
всегда бесконечно удаленная точка. В самом деле, если вдоль
какой-либо линии плоскости течения при дозвуковой скорости
имеет место параллельное течение — а именно в этом случае в од-
одной точке годографа сходятся несколько линий тока,—то анали-
аналитическим продолжением этого течения будет параллельное тече-
течение во всей плоскости течения. В дозвуковой области поле течения
вследствие отсутствия характеристик не может перейти из параллель-
параллельного в непараллельное. Напротив, особой точке плоскости годографа,
получающейся при звуковой скорости, не обязательно должна соот-
соответствовать бесконечно удаленная точка плоскости течения (с таким
примером мы познакомились в § 3 гл. IV). В дозвуковой области
подобного рода особенности не возникают.
Если в плоскости течения какая-либо характеристика пересекает
линию тока более одного раза, то получается предельная линия и
линия тока меняет свое направление на обратное. Такое поведение,
конечно, недопустимо, по крайней мере для граничных линий тока.
Отсюда возникает требование, чтобы линия тока, изображающая в пло-
плоскости годографа границу поля течения, пересекала каждую харак-
характеристику самое большее один раз. Допустимо, чтобы линия тока
в плоскости годографа совпадала с характеристикой; в этом случае
линия тока в плоскости течения имеет угловую точку (см. в связи
с этим рассуждения по поводу рис. 41). Если линия тока в плоскости

2 ИСТЕЧЕНИЕ ИЗ СОСУДА
155
годографа пересекает характеристику и при этом одновременно каса-
тельна к ней, то в плоскости течения такая линия тока имеет точку
с бесконечно большой кривизной.
§ 2. Истечение из сосуда
При гидравлическом рассмотрении истечения из сосуда количество
вытекающей жидкости (расход) зависит от давления лишь до тех пор,
пока внешнее давление обусловливает дозвуковую скорость струи.
Но как только внешнее давление становится ниже так называемого
критического давления, расход перестает зависеть от давления. Это
внезапное изменение закона истечения кажется с физической точки
зрения невероятным. Ниже мы познакомимся с точным объяснением
этого явления.
Задача об истечении струи с дозвуковой скоростью уже была
исследована в § 5 гл. V (рис. 27). Рассмотренный там способ расчета
В
Р и с 48 Истечение из сосуда со звуковой скоростью
(по Гудерчею [2] )
применим до тех пор, пока струя вытекает с дозвуковой или звуковой
скоростью. Если скорость струи дозвуковая, то сечение, в котором
линии тока становятся параллельными, лежит в бесконечности (коор-
(координата л: = оо). Если же струя имеет звуковую скорость, то посред-
посредством асимптотического представления функций Чаплыгина [уравне-
[уравнение V, 6 (Па)] можно показать, что соответствующая координата х
имеет конечное значение (рис. 48). О возможности образования парал-
параллельной звуковой струи на конечном расстоянии от отверстия уже
было сказано в § 3 гл. IV. Только что упомянутые результаты в даль-
дальнейшем будут полезны для понимания процесса перехода дозвуковой
струи в сверхзвуковую.
Граничная задача для сверхзвуковой струи была сформулирована
Гудерлеем [2] и Франклем [4, 6] (см. лит. 1). Как и в случае

156
ГЛ. VI ИССЛЕДОВАНИЕ ТЕЧЕНИЙ МЕТОДОМ ГОДОГРАФА
дозвуковой струи, на свободной поверхности сверхзвуковой струи дав-
давление постоянно, следовательно, постоянна и скорость; этой скорости
соответствует в плоскости годографа окружность. Однако было бы
безусловно неправильным думать, что годо-
годограф скорости сверхзвуковой струи огра-
ограничен таким же контуром, как и годограф
скоростей дозвуковой струи (линия ABCD на
рис. 49). В самом деле, в таком случае ли-
линия тока, близкая к контуру на плоскости
годографа, пересекалась бы одной и той же
характеристикой дважды, что должно бы-
было бы привести к образованию предельной
линии. Зато физически вполне допустимо,
чтобы часть контура на плоскости годографа
совпадала с характеристикой (BD1 на рис. 50).
В таком случае в соответствующей точке
контура струи на плоскости течения возни-
возникает расширяющееся течение, и граничная
линия тока внезапно изменяет свое напра-
направление. Расширение течения приводит к понижению давления в струе
до внешнего давления, т. е. до точки D1 плоскости годографа.
Эта точка определяет угол начальной касательной к свободной
линия тока, близкая
к контуру
Рис. 49 Гипотетическая кар-
картина отображения течения на
плоскость годографа (поГудер-
лею [2] ).
Рис. 50 Истечение из сосуда со сверхзвуковой скоростью
(по Гудерлею [2])
поверхности струи. Волны, исходящие из угловой точки, являются,
конечно, волнами расширения; от звуковой линии они отра-
отражаются в виде волн сжатия. Если внешнее давление близко к кри-
критическому давлению, то волны Маха многократно пробегают взад и

2 ИСТЕЧЕНИЕ ИЗ СОСУДА
157
вперед между звуковой линией и поверхностью струи. На поверх-
поверхности струи волны сжатия, исходящие от звуковой линии, превра-
превращаются в волны разрежения, следовательно, к звуковой линии подхо-
подходят всегда волны разрежения.
Наконец, одна из волн, исходящих от границы струи, достигает
звуковой линии в точке оси сопла (линия D2C на рис. 50). В этом
месте возникают такие же условия, как в самом узком поперечном
сечении сопла Лаваля. Волны Маха, лежащие вниз по течению отно-
относительно характеристики D2C, уже не могут влиять на дозвуковую
область течения. Следовательно, волна Маха D2C представляет собой
границу той части сверхзвуковой области, которая должна рассчи-
рассчитываться одновременно с дозвуковой областью. Конечно, граничные
В-
Рис 51, Истечение из сосуда с очень большой сверхзвуковой скоростью.
условия вдоль этой волны Маха не могут быть заданы, так как эта
волна перемещается поперек струи. Следовательно, рассматриваемая
граничная задача обладает той характерной незамкнутостью контура,
о которой было сказано в связи с рис. 41.
Если понизить внешнее давление, т. е. если повысить скорость
струи, то годограф качественно останется таким же, только зона
расширения будет простираться дальше, а область, в которой волны
Маха многократно отражаются от поверхности струи и звуковой
линии, станет меньше.
Начиная с некоторого определенного внешнего давления, звуко-
звуковой линии достигают только те волны, которые исходят от началь-
начального расширяющегося течения (рис. 51). В этом случае мы имеем
краевую задачу, соответствующую формулировке Трикоми.
До тех пор, пока волны Маха, исходящие от свободной поверх-
поверхности струи, достигают звуковой линии, давление на свободной

158 ГЛ VI ИССЛЕДОВАНИЕ ТЕЧЕНИИ МЕТОДОМ ГОДОГРАФА
поверхности струи, конечно, влияет на дозвуковую область течения.
По этой же причине расход струи зависит от внешнего давления
также при сверхзвуковой скорости. Только когда внешнее давление
становится столь низким, что ни одна из волн Маха, исходящих от
свободной поверхности струи, не достигает звуковой линии, расход
струи перестает зависеть от внешнего давления.
В рассмотренных примерах мы ограничились исследованием только
той части поля течения, которая влияет на дозвуковую область.
Исследование дальнейшего развития струи представляет собой чисто
сверхзвуковую задачу, решаемую проще всего методом характеристик.
При этом получается такое же трехкратное перекрытие некоторой
области плоскости годографа, как и в случае сопла Лаваля.
Совершенно аналогичные картины в плоскости годографа полу-
получаются и в том случае, когда стенки сосуда наклонены друг к другу.
Чем меньше угол, который образуют между собой стенки сосуда,
тем меньше для струи то число Маха, при котором расход не зави-
зависит от внешнего давления. Следовательно, в предельном случае очень
узкого сопла действительно получается результат гидравлической
теории. Примечательно, что при уменьшении угла между стенками
картина течения изменяется непрерывно. Это относится и к форме
звуковой линии. Непрерывное изменение картины течения сохра-
сохраняется и при переходе к критической скорости истечения.
Если мы переместим одну из стенок сосуда параллельно самой
себе на некоторое расстояние, то ее изображение в плоскости годо-
годографа останется, конечно, неизменным. Однако теперь, вследствие
несимметрии течения, при дозвуковой скорости изменяется направле-
направление свободной струи, т. е. смещается положение точки С, а при
сверхзвуковой скорости смещается характеристика CD2, вдоль кото-
которой не могут быть предписаны граничные значения. Мы видим, что
изменение условий в плоскости течения дает себя знать в плоскости
годографа совсем в другом месте. В дальнейшем мы встретимся
с другими аналогичными примерами.
§ 3. Течение около выпуклого угла
В предыдущем параграфе мы рассмотрели поля течения, в кото-
которых в определенном месте возникает расширяющееся течение Мейера.
Проникая в дозвуковое течение, оно вызывает переход к сверхзву-
сверхзвуковой скорости Линия тока в том месте, где возникает расширяю-
расширяющееся течение, имеет угловую точку. В несжимаемом течении в вер-
вершине выпуклого угла возникает, как известно, бесконечно большая
скорость и отрицательное бесконечное давление. На основании этого
можно предполагать, что при обтекании выпуклого угла сжимаемой
жидкостью в вершине угла достигается звуковая скорость, а давле-
давление здесь понижается на величину, зависящую от изменения напра-

§ 4 КЛИН В СВЕРХЗВУКОВОМ ТЕЧЕНИИ 159
вления линии тока и определяемую в соответствии с законами тече-
течения Мейера Однако предугадать дальнейшие детали возникающего
течения не так просто. Если, например, стенка вниз по течению от
вершины угла прямая, то волны уплотнения, исходящие от звуковой
линии, отражаются от стенки опять в виде волн уплотнения. Но так
как на основании сказанного в § 1 настоящей главы эти отражен-
отраженные волны уплотнения не могут достичь звуковой линии, то они
заканчиваются скачком уплотнения, который и ограничивает собой
сверхзвуковую область. Такого рода скачок уплотнения рассчитан
Йосихарой [3] (см. лит. 1). Продолжение течения за вершину угла
возможно только в том случае, если стенка, подобно поверхности
свободной струи в предыдущих примерах, имеет такую кривизну,
что волны уплотнения, исходящие от звуковой линии, превращаются
при отражении в волны разрежения. Течение вблизи выпуклого угла
можно частично исследовать аналитически, используя частные реше-
решения, которые будут рассмотрены в гл. VII (Гудерлей [3], см. лит. 1).
Это исследование показывает, что граничная линия тока, которая
могла бы преобразовать волны уплотнения в волны разрежения,
должна иметь непосредственно в вершине угла бесконечную кри-
кривизну. Такую же кривизну должна иметь здесь и звуковая линия.
Если стенка вниз по течению от вершины угла прямая, то на
вершине угла сразу образуется скачок уплотнения, правда, очень
слабый. Однако непосредственно за скачком давление быстро
нарастает благодаря волнам сжатия, подходящим от звуковой ли-
линии.
В практических условиях эти эффекты получаются размытыми
вследствие влияния пограничного слоя. Может даже получиться, что
течение вскоре после отрыва опять прижмется к стенке. Вверх по
течению от вершины имеет место падение давления с бесконечно
большим градиентом.
Некоторым сходством с только что описанным течением обладает
подсасывающее течение, возникающее при высоких дозвуковых ско-
скоростях вблизи передней кромки крыла, установленного под углом
атаки и имеющего носок с небольшим радиусом.
§ 4. Клин в сверхзвуковом течении
В § 11 предыдущей главы мы видели, что скачки уплотнения,
возникающие в параллельном течении, допускают отображение в пло-
плоскость годографа, и познакомились в связи с этим со сверхзвуковым
обтеканием клина. В этом параграфе мы рассмотрим явления, кото-
которые происходят при сверхзвуковом обтекании клина, если углу рас-
раствора клина придавать различные значения, но при этом сохранять
неизменным число Маха. Мы увидим, как из чисто сверхзвукового
течения, получающегося при малых углах раствора клина, после

160
ГЛ VI ИССЛЕДОВАНИЕ ТЕЧЕНИЙ МЕТОДОМ ГОДОГРАФА
достижения углом раствора определенной величины возникает тече-
течение, изображенное на рис. 45.
Будем обозначать точки годографа, соответствующие параллель-
параллельному сверхзвуковому течению, римскими цифрами. Например, на
рис. 52,а точка, соответствующая скорости набегающего потока,
отмечена цифрой /. Такое же обозначение будем применять и для
обозначения ударных поляр, например будем говорить об ударной
поляре /. Пусть угол раствора клина настолько мал, что скачок
уплотнения прилегает к вершине клина, а скорость после скачка
остается сверхзвуковой (точка // на рис. 52,аI).
Рис. 52 Сверхзвуковое течение около клина с прилегающим скачком
уплотнения, а — плоскость ч], 9; б —поле течения (по Гудерлею [2]).
При увеличении угла раствора клина, но при неизменном числе
Маха набегающего потока точка // перемещается вдоль ударной по-
поляры по направлению к звуковой линии. Если точка // совпадает
с точкой пересечения ударной поляры и звуковой линии, то ниже
по течению от скачка уплотнения возникает параллельное течение
со звуковой скоростью.
При дальнейшем увеличении угла раствора клина точка, которую
мы до сих пор обозначали цифрой II, переходит в дозвуковую об-
область плоскости годографа. Однако параллельное течение с соот-
соответствующей дозвуковой скоростью теперь не может возникнуть,
так как в противном случае на основании принципа аналитического
продолжения параллельное течение должно было бы иметь место во
всей области вниз по течению от скачка уплотнения, между тем как
это несовместимо с соответствующими граничными условиями на
клине. Следовательно, должен возникнуть слегка искривленный ска-
скачок уплотнения. Мы знаем, что сторона клина отображается на пло-
плоскость т), 0 в виде линии постоянного направления, т. е. в виде от-
1) Для большей наглядности соответствия между плэскость-о течения и
плоскостью годографа, мы всегда вычерчиваем только одну половину поля
течения. Кроме того, вместо плоскости годографа мы пользуемся пло-
плоскостью т), &.

§ 4 КЛИН В СВЕРХЗВУКОВОМ ТЕЧЕНИИ
161
резка FD (рис. 53). Угловая точка D = ? на плече клина отобра-
отображается на основании сказанного в предыдущей главе в характери-
характеристику DE. Наконец, границей дозвуковой области будет также отрезок
ударной поляры. Таким образом, дозвуковая область, образующаяся
вдоль стороны клина, будет представлена в плоскости -ц,Ь об-
областью DFB. Переход к сверхзвуковому течению вызывается рас-
расширяющимся течением Мейера, возникающим на плече клина. Зву-
Звуковая линия простирается от плеча клина до скачка уплотнения.
Часть волн расширения, исходящих из плеча клина, заканчивается
на звуковой линии, а остальные, не играющие никакой роли для до-
дозвуковой области, — на скачке уплотнения.
дозвуковая
^область
Рис. 53. Сверхзвуковое течение около клина с прилегающим скачком
уплотнения (по Гудерлею [2] ).
В связи с только что сказанным возникает неизбежный вопрос,
почему звуковая линия начинается на плече клина. Липман (см. лит. 3)
по этому поводу заметил, что если бы звуковая линия начиналась
в какой-либо точке стороны клина, то ни положение этой точки,
ни положение дозвуковой области в целом нельзя было бы опреде-
определить длиной, приемлемой с точки зрения формулировки краевой
задачи, следовательно, была бы утрачена определенность задачи.
Глубже вникая в детали поведения течения, можно дать следующее
объяснение. При перемещении вдоль звуковой линии от клина к скачку
уплотнения линии тока пересекаются под таким углом, что пройден-
пройденный отрезок звуковой линии проектируется на линию тока либо вверх
по течению, либо вниз по течению от точки пересечения (если бы
линии тока пересекались звуковой линией под прямым углом, то
должна была бы возникнуть предельная линия). В первом случае от
звуковой линии должны исходить волны сжатия, направленные к скачку
уплотнения. При встрече со скачком уплотнения они должны уси-
усилить последний. Однако такое предположение противоречит действи-
действительности. В самом деле, при перемещении вдоль скачка уплотнения
в направлении течения после дозвуковой зоны опять возникает сверх-
сверхзвуковая зона. Во втором же случае, т. е. когда пройденный отре-
отрезок звуковой линии проектируется на линию тока вниз по течению
(при перемещении от клина к скачку уплотнения), от звуковой линии

162 ГЛ. VI. ИССЛЕДОВАНИЕ ТЕЧЕНИЙ МЕТОДОМ ГОДОГРАФА
исходят волны сжатия, направленные к сторонам клина. Здесь эти
волны должны вызвать повышение давления, что также противоре-
противоречит действительности, так как при переходе от доэвуковой скорости
к сверхзвуковой давление вдоль стороны клина должно падать 1).
Первый аргумент показывает, что на пути от стороны клина
к скачку уплотнения пройденный отрезок звуковой линии должен
проектироваться на линию тока вниз по течению, а из второго аргу-
аргумента следует, что звуковая линия может начаться только в таком
выпуклом месте контура клина, что несмотря на волны сжатия, ис-
исходящие от звуковой линии, на контуре клина возникает понижение
давления.
При увеличении угла раствора клина структура поля течения
в качественном отношении остается неизменной до тех пор, пока
угол раствора не принимает такого значения, при котором скачок
уплотнения уже не может прилегать к острию клина. После того
как это наступает, открывается выход в новую область плоскости
годографа, содержащую критическую точку. Тогда получается гра-
граничная задача с картиной течения, изображенной на рис. 45.
Таким образом, проведенные рассуждения показывают, что при
увеличении угла раствора клина поле течения изменяется непрерыв-
непрерывно; поэтому можно предполагать, что такое же непрерывное изме-
изменение поля течения должно наблюдаться и при эксперименте.
§ 5. Аналитическое исследование поля течения вблизи острия
клина в случае прилегающего скачка уплотнения
Дополним сказанное в предыдущем параграфе аналитическим ис-
исследованием поля течения вблизи острия клина, т. е. вблизи точки F
на рис. 53, для случая, когда скачок уплотнения прилегает к острию,
клина. В качестве граничных условий мы имеем ф —0 вдоль стороны
клина и, кроме того, условие V, 11E) для ударной поляры. Если
направление линии тока, предписываемое условием V, 11E), откло-
отклоняется от направления линии FD (в общем случае это всегда имеет
место), то точка F будет особой точкой в плоскости годографа.
Найдем первый член разложения, определяющего решение вблизи
этой точки. В § 14 гл. VII мы познакомимся с точными решениями,
обладающими особенностью заданного вида в произвольной точке
плоскости t\, &. Если мы захотели бы продолжить настоящее иссле-
!) Эти заключения, справедливые для потенциального течения, теряют
силу при точном рассмотрении вихревого течения за криволинейным скач-
скачком. Например, недавно О. М. Белоцерковский (Прикл. матем. и мех.,
т. 22, вып. 2, 1958) установил, что здесь может иметь место „эффект сопла",
т. е. такая форма течения, когда звуковая линия ортогонально пересекает
одну из линий тока и от точки пересечения отклоняется в обе стороны
вверх по потоку. — Прим. ред.

б 5 ИССЛЕДОВАНИЕ ПОЛЯ ТЕЧЕНИЯ ВБЛИЗИ ОСТРИЯ КЛИНА
163
дование, то следовало бы предпочесть точные решения. Однако мы
ограничимся здесь приближенным решением, которое вполне приме-
применимо в непосредственной близости от точки F.
Пусть в точке F абсолютное значение величины tj равно ItjJ
а величина Ь имеет значение 9^. Тогда для этой точки уравнение
Трикоми можно представить в виде
ф +||т]^|—Tj—JTj^l j ф8а = 0. A)
Далее, пусть
р|). Bа)
или
4 = —Ы+иИ*Г • Bб)
Наконец, пусть
8—8, = -». C)
Перейдя в дифференциальном уравнении A) к переменным и и v,
мы будем иметь
*¦*¦'¦ -и дЦ_ __ ^
В непосредственной близости от точки F (а = 0, v = 0) членом
и \i\p\~'1* можно пренебречь, и тогда мы получим упрощенное уравне-
уравнение1)
Л„2 Г А,я == "• D)
Его общим решением будет
где
) = \mF (w),
»= « + iv,
E)
a F есть произвольная аналитическая функция от w. Для вычисле-
вычисления значений х воспользуемся уравнением B6); мы получим
,. дх , , дх ,0
dx = -^r— dri -f- -до- d» = -
"du ¦
dv.
Если ф дано уравнением E), то для малых а и v на основании
соотношений V, 7(8) мы будем иметь
dF
— I -г- da ч—;— dt> I.
dw
1) Можно получить уравнение столь же простое, но в то же время при-
пригодное в более широкой области, если воспользоваться преобразованием,
сходным с преобразованием V, 6B).

164
ГЛ VI ИССЛЕДОВАНИЕ ТЕЧЕНИИ МЕТОДОМ ГОДОГРАФА
Отсюда, обозначив через х0 постоянную интегрирования, мы найдем
jC -^0 "
F)
В системе координат и, v точка F является 'началом координат
(рис. 54). Ось и представляет собой отображение стороны клина.
Пусть угол, образуемый касательной к ударной поляре с осью х,
равен vx. Далее пусть направление подхода линий тока к ударной
поляре определяется углом v2. Для того чтобы в рассматриваемой
области координата v была положительна, будем рассматривать точку
ударной поляры, лежащую в нижней половине плоскости годографа
и плоскости течения. Здесь линия скачка уплотнения начинается
касательная к
ударной поляре
направление подхода
•линии тока
Рис. 54. К вычислению особенности в точке F.
слева наверху и продолжается вправо вниз. Для таких скачков
уплотнения угол vt положителен в области, лежащей между точкой
ударной поляры, в которой 0 имеет максимальное значение, и точкой,
соответствующей скорости звука. Знак угла v2 в этой области ме-
меняется. Точка ударной поляры, в которой v2 = 0, называется точкой
Крокко. Между точкой, в которой 0 имеет максимальное значение,
и точкой Крокко угол чг отрицателен, а между точкой Крокко и
точкой, соответствующей скорости звука, этот угол положителен.
В первом приближении ударная поляра может быть заменена ка-
касательной к ней в точке F. Тогда на основании граничных условий,
во-первых, должно быть
Ga)
([) = 0 при v = 0,
а, во-вторых, выражение dvjdu, составленное вдоль линии
должно быть равно
dv
—— = tg v,
du & 2
Пусть
при
w~re%
) = const,
G6)
(8)

§ 5 ИССЛЕДОВАНИЕ ПОЛЯ ТЕЧЕНИЯ ВБЛИЗИ ОСТРИЯ КЛИНА 165
Допустим, что
ф = Im wm; (9)
тогда мы получим
ф = rm Sitl fflv.
При t> = 0 мы имеем v = 0, так что первое условие допущением (9)
удовлетворяется. Далее мы имеем
¦—- — т Im wm~1 = тгт~1 sin (яг — 1) v
-|i = /и Im (/да™-1) = mr»»-1 cos (m — 1) ч,
поэтому для линии ф = const мы получим
it
dw да
Следовательно, линии ф = const образуют с осью и угол —(т — l)v.
Таким образом, на ударной поляре должно выполняться условие
v2 = —(/и —1^,
откуда
т~\ -.
В первом приближении наклон скачка уплотнения в плоскости тече-
течения пропорционален первой степени расстояния рассматриваемой
точки в плоскости годографа от точки F. Это расстояние—также
в первом приближении — пропорционально г. Координата у в пер-
первом приближении пропорциональна ф и, следовательно, вдоль скачка
пропорциональна гт. Таким образом, наклон скачка пропорциона-
пропорционален yllm. Кривизна скачка пропорциональна величине
_L yl/m-l — ^1 W(vi-va)
т ^j — v2 -^
Если точка F лежит между точкой Крокко и точкой, соответ-
соответствующей критической скорости, то на основании сказанного выше
угол ч2 положителен и, как это ясно из рис. 54, меньше угла ¦ч1.
Если у приближается к нулю, т. е. если при перемещении вдоль
скачка уплотнения мы приближаемся к острию клина, то кривизна
скачка уплотнения становится равной нулю. Если точка F совпа-
совпадает с точкой Крокко, в которой \2 = 0, то получается конечная
кривизна скачка уплотнения, хотя сторона клина имеет нулевую

166 ГЛ. VI. ИССЛЕДОВАНИЕ ТЕЧЕНИИ МЕТОДОМ ГОДОГРАФА
кривизну. Для точки F, лежащей между точкой Крокко и точкой
максимума | ft |, углы vx и v2 имеют противоположные знаки;
поэтому степень, в которой у входит в выражение кривизны, от-
отрицательна. Следовательно, кривизна скачка на острие клина беско-
бесконечно велика.
Таким образом, для клина с углом раствора, в точности соот-
соответствующим точке пересечения ударной поляры со звуковой линией,
получается точно прямолинейный скачок уплотнения, и скорость
ниже по течению от скачка равна скорости звука. Если точка F
лежит между точкой, соответствующей критической скорости, и точ-
точкой Крокко, то скачок уплотнения получается хотя и искривленным,
но на острие клина кривизна равна нулю. Если точка F совпадает
с точкой Крокко, то скачок уплотнения имеет конечную и не равную
нулю кривизну также на острие клина. Наконец, если точка F лежит
между точкой Крокко и точкой максимума Ь, то начальная кривизна
скачка уплотнения становится бесконечно большой. Примечательно,
что по-прежнему имеет место непрерывное изменение картины те-
течения при переходе от одного случая к другому.
§ 6. Клин с криволинейными сторонами
Крокко обнаружил точку, названную впоследствии его именем,
исследуя связь между начальной кривизной скачка уплотнения и
кривизной сторон клина. Это исследование привело к выводу, что
при начальном наклоне скачка уплотнения, соответствующем точке
Крокко, конечная кривизна сторон клина обусловливает бесконечно
большую кривизну скачка. При больших углах раствора клина,
но все же таких, при которых скачок уплотнения еще прилегает
к острию клина, кривизна скачка и кривизна сторон имеют противо-
противоположные знаки. Так как такой вывод с физической точки зрения
абсурден, то у Крокко возникло предположение, не начинается ли
отрыв скачка уплотнения от острия клина уже в точке Крокко.
Решению, полученному Крокко, в плоскости годографа соответ-
соответствует уравнение
ф = г sitlD — N2).
Легко убедиться, что для каждой линии ^ = const имеет место
равенство
т. е. условие вдоль ударной поляры выполняется. Граничная линия
тока определяется значением ч = v2- Вдоль этой линии тока наклон
вектора скорости равен
9- = $F -f- r sin v2.

§ 6 КЛИН С КРИВОЛИНЕЙНЫМИ СТОРОНАМИ 167
Так как рассматриваемое решение в точке F регулярно, то длина
граничной линии тока в плоскости течения пропорциональна рас-
расстоянию рассматриваемой точки плоскости годографа от точки F,
т. е. пропорциональна г, следовательно, кривизна граничной линии
тока пропорциональна sin \2, Далее, необходимо знать кривизну
скачка уплотнения. Угол наклона скачка уплотнения в плоскости
течения в первом приближении пропорционален г (измеренному вдоль
ударной поляры). Длина скачка уплотнения, измеренная от острия
клина, пропорциональна у, т. е. пропорциональна гъ\х\(у^ — v2).
Следовательно, отношение кривизны скачка уплотнения к кривизне
граничной линии тока пропорционально величине
(sinvaTMsin^ — v2)]-\ A)
В точке Крокко эта величина принимает бесконечно большое значе-
значение и меняет при этом свой знак. Для этой точки мы уже нашли,
что нулевой кривизне стороны клина соответствует конечная кри-
кривизна скачка уплотнения.
Нетрудно понять смысл полученного решения и в том случае,
когда точка F лежит между точкой, соответствующей критической
скорости, и точкой Крокко. Значительно труднее истолковать реше-
решение Крокко, если точка F расположена между точкой Крокко и
точкой с максимальным значением 0. При движении вдоль граничной
линии тока от точки F к звуковой линии угол наклона граничной
линии тока увеличивается, следовательно, контур должен быть вогну-
вогнутым. При выпуклом контуре можно предполагать, что решение не
очень сильно отличается от решения краевой задачи для клина
с прямолинейными сторонами. В самом деле, можно найти поведение
течения вблизи точки F клина с криволинейными сторонами, исходя
от случая течения около клина с прямолинейными сторонами и учи-
учитывая кривизну сторон путем введения поправочного члена. Соответ-
Соответствующее решение получается в виде разложения по степеням w-V»i.
Если мы ограничимся двумя первыми членами разложения, то полу-
получим (Гудерлей [2], см. лит. 1)
ф = Im Гсда1-W1 — w-ъ^КС Vl"~V2 e*A], B)
т L \ ^1 sin v2 )\ v '
где К и С суть постоянные. Первый член дает течение около клина
с прямолинейными сторонами, а второй учитывает поправку, вноси-
вносимую кривизной сторон. Из уравнения B) мы имеем
ffi.= CIm w^ — wW^KC
да чх L sin -v2
лг Г 1-2
™L =2l—!l CIm г w-^^~w-24^KC
dv va L sinv3

168 ГЛ VI ИССЛЕДОВАНИЕ ТЕЧЕНИИ МЕТОДОМ ГОДОГРАФА
Составим производную вдоль линии тока; использовав равенство
VI, 5(8), мы получим
I /v, \ _ / * vf / v,
— г Va''' I — sin I —^ у I — KCr %/Vl — sin I v, — 1—=- v
( \~>\ 1 sin -v2 V 'h
аи ( \ Mi /sin-v2\ - чг I)
12
cos BL Л _ КСг->^ ^- cos U -
Подставив сюда v = v1> мы найдем
du
dv
sin v2
cosva
1
1
КСг~чф'
1
1
— 2
sin \
2
V2
'2
= tgv0.
sin v2
Следовательно, условие VI, 5G6) на ударной поляре выполняется.
Для того чтобы получить линию ф = 0, следует представить уравне-
уравнение B) в вещественном виде; мы получим
Ограничившись членами наинизшего порядка относительно
мы найдем в первом приближении
v=0.
Следующий шаг итерации дает более точное значение
Таким образом, отклонение направления линии тока от ее направле-
направления в точке F определяется формулой
"l'h'. C)
Длина линии тока, измеренная от точки F, пропорциональна, со-
согласно формуле VI, 5F), вещественной части функции F (w). Огра-
Ограничившись членами наинизшего порядка относительно /—V»i; мы
найдем
х _ xf ~ Сг1- <*/¦>* cos
U1 — -^
Если величина /-~Va/Vi мала, то косинус можно заменить единицей,
и мы получим
х — Хр^Сг1-1^'. D)
Из формул C) и D) следует, что кривизна сторон в точке F
имеет конечное, не равное нулю значение.

§ 7 ПЕРЕХОД К НЕПРИЛЕГАЮЩЕМУ СКАЧКУ УПЛОТНЕНИЯ 169
Решение вида B) неприменимо в промежутке между точкой
Крокко и точкой, соответствующей критической скорости, так как
там величина /-~V2/v> представляет собой отрицательную степень г.
Решение B) не применимо и в точке Крокко. Этот случай также
исследован Гудерлеем [2] (см. лит. 1).
Теперь понятно, почему решение, полученное Крокко, неприме-
неприменимо в промежутке между точкой Крокко и точкой с максимальным
значением Ь. В самом деле, в этом промежутке поправка, вносимая
в решение кривизной сторон клина, очень мала. В промежутке же
между точкой Крокко и точкой, соответствующей критической ско-
скорости, наоборот, преобладающую роль играет поправка, обусловлен-
обусловленная кривизной сторон, поэтому здесь вполне оправдано решение
Крокко, молчаливо предполагающее это обстоятельство.
§ 7. Исследование перехода от прилегающего скачка
уплотнения к неприлегающему скачку
Переход от течения с прилегающим к острию клина скачком
уплотнения к течению с неприлегающим скачком кажется на первый
взгляд таким радикальным изменением поля течения, что вслед за этим
изменением должно обязательно последовать резкое изменение и
свойств течения, например сопротивления. Поэтому исследование
такого перехода должно представлять особый интерес.
Прежде всего найдем приближенное решение уравнения Трикоми,
пригодное в окрестности точки максимума Ь на ударной' поляре.
Примем эту точку за начало координат и и v (между этими пере-
переменными и одноименными переменными в предыдущем параграфе нет
никакой связи). Далее примем, что для скорости вверх по течению'
относительно скачка уплотнения tj — 1; тогда из уравнения V, 11B)
мы найдем для точки максимума Ъ
! 4 (О
' з /27
и координаты и и v будут
" = t] + j. Ba>
v = Ь + —Lr. B6)
Г /27
Вдоль скачка уплотнения величина v есть функция от а, поэтому-
будем обозначать ее через vs (и). Для малых значений и из уравне-
уравнения ударной поляры V, 11 B) мы найдем
vs = + -Ц— и2- C>

170
ГЛ VI ИССЛЕДОВАНИЕ ТЕЧЕНИИ МЕТОДОМ ГОДОГРАФА
Уравнение для ф в плоскости годографа примет теперь вид
я№=0
Граничным условием на ударной поляре будет
„м_33
3
D)
E)
К расчету течения вблизи точки и —0,
0
Пусть угол раствора клина пе-
7] реходит — вдоль ударной поля-
поляры — от максимально возможного
значения Ь к несколько больше-
большему значению 8--)-с. Ограничимся
рассмотрением нижней половины
ударной поляры, потому что
ей соответствуют положительные
значения v. Будем искать решения
уравнения Трикоми, взятого в ви-
виде D), при следующих граничных условиях (см. рис. 55):
ф= О при v = — с,
/27
ди
ии и | у == О
при v~vs = -
Fа)
F6)
Решения, которые будут получены ниже, пригодны для малых зна-
значений с; точнее говоря, с должно быть одного порядка с va и тем
самым одного порядка с и2. Предполагаемый вид решения можно
найти из следующих соображений. Будем брать с все более и более
малым и при этом будем изменять масштаб для координат и и v
таким образом, чтобы в новых координатах расстояние между гра-
граничной линией тока и ударной полярой в точке F сохранялось
неизменным. Тогда мы получим последовательность конфигураций,
для которых расстояние между ударной полярой и изображением
стенки изменяется тем меньше, чем меньше с. Поэтому можно пред-
предполагать, что решение должно иметь большое сходство с решением
для случая постоянного расстояния между обоими контурами. Реше-
Решения, которые удовлетворяют дифференциальному уравнению и гра-
граничным условиям в точке с минимальным расстоянием между ука-
указанными контурами, имеют вид
п) с-ч] sin [«(»
где п есть целое число. Теперь следует попытаться так обоб-
обобщить это предполагаемое решение, чтобы оно было приближенно
пригодно также на некотором расстоянии от самого узкого попереч-
поперечного сечения между обоими контурами. Рассмотрим вместо самого
узкого поперечного сечения другое поперечное сечение. Если бы

(§ 7 ПЕРЕХОД К НЕПРИЛЕГАЮЩЕМУ СКАЧКУ УПЛОТНЕНИЯ 171
в этом поперечном сечении расстояние между обоими контурами
оставалось постоянным, то решение имело бы вид
(jj = ехр [3~'!1it ( (- п\ c~lu sin тг (га -| ) —~— , G)
где
с = с-\ ~ а2.
Величину с следует рассматривать как постоянную; она представляет
собой расстояние между обоими контурами. В действительности оно
изменяется, однако если на отрезке, который отложен в направле-
направлении оси и и на котором показательная функция изменяется на значи-
значительную величину, это изменение мало, то решение не будет очень
сильно отклоняться от указанного выражения. Следовательно, усло-
условием пригодности решений, которые будут указаны ниже, является
da "*¦*
или (8)
V27 п
4 У7
где левая часть представляет собой производную от расстояния
между контурами по и, а правая часть — приближенное выражение
производной показательной функции по а. Для приближенного пред-
представления решения особенно удобно следующее выражение, отли-
отличающееся от выражения G) в основном своим первым множителем:
. (9)
Однако и это выражение еще нельзя рассматривать как окончатель-
окончательное решение. В самом деле, хотя при подстановке этого решения
в дифференциальное уравнение члены наинизшего порядка в разло-
разложении этого уравнения по степеням а выпадают, но то же самое
получилось бы и в случае, если бы мы умножили решение (9) на
произвольную функцию /г (и), например на некоторую степень вели-
величины с. Так как этот множитель при малых и может значительно
изменяться, то решение (9) может не быть правильным даже при-
приближенно. Очевидно, что недостаточно учитывать в дифференциаль-
дифференциальном уравнении только члены наинизшего порядка, даже если в при-
приближенном представлении решения желательно сохранить лишь один
первый член. Этот член будет определен только в том случае,
когда в дифференциальном уравнении учитываются члены следую-
следующего порядка. Для этого необходимо расширить допущение (9).
В связи с другим исследованием (Гудерлей [1], см. лит. 1) было

172 ГЛ VI ИССЛЕДОВАНИЕ ТЕЧЕНИИ МЕТОДОМ ГОДОГРАФА
показано, как это систематически можно выполнить. Для задачи,
аналогичной рассматриваемой, члены следующего порядка удалось
найти Буземану (Буземан и Гудерлей, см. лит. 1). Таким же путем
можно найти необходимые члены и в рассматриваемой задаче, поэтому
приведем здесь расширенное решение без вывода, а затем прове-
проверим его !).
Пусть
) . A06)
Выше мы упомянули, что с — О(и2). Следовательно,
1=0 (и-2). A0в)
При этих обозначениях искомое решение имеет вид
\ .
\du\ {sin v-\- и (а^ cos v-\- a2v2s\n v)}. A1)
Первый член соответствует прежнему допущению о виде решения.
Величина v равна нулю при г> — — с, т. е. вдоль изображения
стенки; вдоль ударной поляры v=\. Величина X обратно пропор-
пропорциональна ширине поперечного сечения. Постоянные т, аг и а2
имеют следующие значения:
т = ~Н~ —
1<^\ A26)
A2в)
Теперь необходимо показать, что выражение A1) удовлетворяет
дифференциальному уравнению и граничным условиям. Прежде всего
!) Можно возразить, что полученное таким путем решение основано
на формальном разложении. Такое возражение вполне оправдано. Однако
с инженерной точки зрения это обстоятельство должно рассматриваться
только как предостережение о необходимости быть осторожным в примене-
применении решения, но не как повод для полного отказа от него.

'§ 7 ПЕРЕХОД К НЕПРИЛЕГАЮЩЕМУ СКАЧКУ УПЛОТНЕНИЯ 173
мы имеем
rfl 9
иЛ- ,.о .
4г—т\> A3а)
Ч)
; A36)
ecu
— = — -т « -г^тт; A3в)
йи 4 / . J_ \ ч
следовательно,
ди
X X {cosi> + м [a1 (cost» — иsin'o)-)-a2BwisinD + t;2cost))]}, A4a)
-r-^- = Xm exp / X da 3X {— sin г/ -f~ и [a^ (— 2 sin г» — г/ cos г/)] -f-
-f- a2 [Фу cos v -4- 2 sin г) — г>2 sin г;]}. A46) _
Для производных по и выпишем только члены двух самых низких
порядков; имея в виду равенство A0в), мы получим
= кт ехр / X du X I sin v -j- u\ a{0 cos v -\- a2v2 sin г» —
9 m . - 9 ^ -I ) .,_ .
•smw — ^— p. cos г» I, A5a)
4n+4J Jj
-j-i- = X™ exp / X da X21 sin v -\- u\ a^v cos v -f- fl2f2 sin и —
9 2m+ 1 . - 9 1 - -T) ,.__
~T~? п^0—4-7 p-г;cost» I. A56)
Чл + т) Чя+т) Jj
Внеся все эти значения в дифференциальное уравнение D), мы прежде
всего увидим, что множитель
к ехр I К аи\,
общий для всех членов, отпадает. Далее сразу выпадут также члены
наинизшего порядка относительно а и, кроме того, некоторые члены
следующего порядка. Останутся только члены
9 2/Я + 1--9 1 - - п
sin г; — -j — — v cos v — 2а! sin v -4-
-|- 4a2w cos w -[- 2а2 sin г; -4- 3 sin v,
но и они взаимно уничтожатся на основании равенств A2).

174 ГЛ VI ИССЛЕДОВАНИЕ ТЕЧЕНИИ МЕТОДОМ ГОДОГРАФА
В том, что решение A1) удовлетворяет также граничному усло-
условию Fа), мы убедимся сразу, так как при v = — с переменная v
равна нулю. Далее, при ¦u = i»s на основании равенств F6) и A0а)
мы имеем
и поэтому
sinw =
Имея в виду это равенство и внеся значения A4а) и A5а) в усло-
условие F6), мы увидим, что члены наинизшего порядка относительно и
сразу выпадут, а члены следующего порядка взаимно уничтожатся
на основании равенств A2).
Члены этих порядков в решении A1) определены не полностью,
так как выражение
I X йи sir
и ехр I к аи sin v
после внесения в дифференциальное уравнение и в граничное усло-
условие обусловливает ошибку, имеющую более высокий порядок, чем
рассмотренная выше ошибка. Поэтому в решении A1) нет никакого
смысла сохранять члены порядка и1. В результате в качестве при-
приближенного решения мы будем иметь
ф = \т ехр Г 'к du sin v
или, если опустить постоянную,
х 3-7(<+^f 4<»H"+^;zfcl- <i6>
В этом решении особо важную роль играет показательная функция.
В зависимости от знака п показатель степени либо положителен,
либо отрицателен, следовательно возможны решения, которые при
увеличении и либо возрастают по экспоненциальному закону, либо,
наоборот, уменьшаются по экспоненциальному закону. Если с = 0,
т. е. если исследуется окрестность точки F (рис. 54) для случая,
когда угол раствора клина равен максимально возможному углу
вдоль ударной поляры, то получаются — с точностью до несуще-

7 ПЕРЕХОД К НЕПРИЛЕГАЮЩЕМУ СКАЧКУ УПЛОТНЕНИЯ
175.
ственной постоянной — следующие частные решения:
ф = и
exp —
Ж
8
A6a)
Так как из физических соображений очевидно, что ф в точке F
не может принять бесконечно большое значение, то возможны
только неотрицательные значения п. Таким образом, при с==0
решение A6а) заменяет частные решения VI, 5(9).
Пусть теперь с не равно нулю. Выясним, как изменяется реше-
решение в плоскости годографа при изменении с. Поскольку реше-
решения не могут быть указаны в явном виде, нельзя избежать сообра-
соображений, до известной степени
абстрактных.
Выберем на рис. 56 два по-
поперечных сечения и = — е и
и = -\-е, настолько близких
к самому узкому поперечному
сечению между ударной поля-
полярой и изображением стенки,
что между ними решение ф
можно построить путем нало-
наложения только что найденных
частных решений. Вдоль ли-
линии м = е решение граничной
задачи при с — 0, безусловно, отличается от нуля. Примем далее, что
решение изменяется при изменении с непрерывно, т. е. при небольших
значениях с решение вдоль линии и = е мало отличается от решения
при с = 0. Попытаемся найти связь между решением при и —е и
решением в области АВСК- Решение в этой области определяется
значениями ф при и = е и известными граничными условиями
в области ECBAKDI. Для выполнения поставленной цели построим
(в принципе) семейство частных решений, удовлетворяющих гранич-
граничным условиям вдоль ECBAKDI и принимающих вдоль и = е при
неотрицательных п значения
sin' ' ' !
Рис. 56. Исследование перехода от неприле-
гающего скачка уплотнения к прилегающему.
Последнее выражение с точностью до множителя совпадает
с частными решениями A6) при н = е. С помощью такой системы
частных решений можно найти полное решение ф в указанной
области, разлагая ф вдоль и = е по этим частным решениям. В том,
что для поставленной цели выбранная система частных решений
всегда достаточна, можно убедиться интуитивно, путем сравнения

176
ГЛ VI ИССЛЕДОВАНИЕ ТЕЧЕНИИ МЕТОДОМ ГОДОГРАФА
с системой
sin
ге -)- -g-
с -\-v
Y7
которая очень похожа на рассматриваемую нами систему и для кото'
рой полнота устанавливается с помощью теории рядов Фурье (или
задачи на собственные значения).
Искомые частные решения можно построить следующим образом.
Буцем исходить из решения фи, которое вместе со своей первой
производной претерпевает разрыв вдоль линии и — —-е. Пусть
в области КСВАК
-а в области — е < и < е
- , У 27
27 ~ -[т+4 ' (га+т)]
8
х
X ехр
Такое i/n с точностью до множителя представляет собой одно из
решений вида A6). Следовательно, скачок функции фп, возникающий
вдоль линии и = — s, равен
Аналогичное выражение получается и для скачка производной от
ло и. Оба эти скачка имеют величину порядка

§ 7 ПЕРЕХОД К НЕПРИЛЕГАЮЩЕМУ СКАЧКУ УПЛОТНЕНИЯ 177
Так как
то при небольших с порядок величины скачка будет равен
/27
lim 2 arctgf —-==- е = it,
о s /8c
На решение <Ьп наложим другое решение <Ьп, удовлетворяющее,
во-первых, граничным условиям вдоль ECBAKI, во-вторых, рав-
равное <Ьп=0 вдоль EI и, в-третьих, имеющее вдоль линии к= — е
такие же скачки (самой функции и ее первой производной), как и
и функция ijin, но с противоположным знаком. Единственность такого
решения может быть доказана способом Франкля. Само решение
можно построить в рассматриваемом случае путем наложения особен-
особенностей вдоль контуров при помощи соответствующего интегрального
уравнения. Важно при этом отметить следующее. Решение пропор-
пропорционально неоднородным величинам, его определяющим. Этими вели-
величинами являются скачок функции фи и скачок ее производной д^п/ди,
входящие в первую часть решения. Следовательно, вторая часть
решения имеет величину порядка
Но в области и <—е вторая часть является единственной в реше-
решении, поэтому там частное решение имеет величину только что ука-
указанного порядка. Представим теперь решение ф вдоль линии и =s
при с = 0 в следующем виде:
Это решение вследствие его непрерывной зависимости от с является
одновременно приближенным решением для малых с. Следовательно,
решение в области ECBAKI имеет вид
При достаточно малых значениях с основную роль играет первый
член суммы, т. е. в этом случае решением в области ECBAKI будет
12 Зак. 534. К. Г. Гудерлей

178
ГЛ VI ИССЛЕДОВАНИЕ ТЕЧЕНИИ МЕТОДОМ ГОДОГРАФА
Изображение отрезка АВ дает расстояние скачка уплотнения от ост-
острия клина. Последнее выражение определяет зависимость порядка
величины этого расстояния от с. При с = 0 соответствующая функ-
функция вместе со всеми своими производными равна нулю. Таким обра-
образом, переход от прилегающего скачка уплотнения к неприлегающему
скачку происходит совершенно непрерывно.
§ 8. Разветвленные скачки уплотнения
Расчеты сверхзвуковых течений, производимые посредством метода
характеристик, показывают, что возможны случаи, когда два скачка
уплотнения сходятся. В таких случаях в точке слияния обоих скач-
скачков образуются либо два новых скачка, либо один новый скачок и
расширяющееся течение. Если вниз по течению относительно точки
Рис. 57. Истечение сверхзвуковой струи в пространство с повышен-
повышенным давлением. Чисто сверхзвуковая задача (по Гудерлею [2]).
слияния скачков течение имеет дозвуковую скорость, то непосред-
непосредственный расчет поля течения хотя и позволяет выявить детали тече-
течения в точке слияния (Вайзе, Эггинк, см. лит. 1), все же не раскры-
раскрывает роли таких скачков в формировании поля течения. Выяснить
эту роль можно только путем представления поля течения в пло-
плоскости годографа.
Типичный случай, при котором может возникнуть дозвуковое поле»
получается при истечении параллельной сверхзвуковой струи в про-
пространство с более высоким давлением. Пусть состоянию перво-
первоначальной струи соответствует точка / годографа (рис. 57). Далее,
пусть внешнему давлению отвечает скорость, соответствующая линии
т] = const, проходящей через точку II. Ударная поляра, проходящая
через точку /, представляет собой геометрическое место точек, изо-
изображающих все те состояния, которые могут возникнуть из состоя-
состояния / вследствие скачка уплотнения. Так как в верхней половине
плоскости течения скачок уплотнения, начинаясь от выступа стенки,
распространяется, очевидно, вниз, то точка, отвечающая состоя-

i 8 РАЗВЕТВЛЕННЫЕ СКАЧКИ УПЛОТНЕНИЯ
179
нию после скачка, лежит в нижней половине плоскости годографа.
Этот скачок уплотнения достигает центральной линии струи, кото-
которую из соображений симметрии можно рассматривать как стенку.
Вдоль этой стенки вектор скорости, очевидно, должен быть гори-
горизонтален. Можно предполагать, что выполнение этого условия дости-
достигается существованием второго скачка уплотнения, ограничивающего —
вниз по течению — область с состоянием //. Геометрическим местом
точек, соответствующих состояниям, которые могут возникнуть из
состояния //, будет ударная поляра, проходящая через точку //.
Если внешнее давление сравнительно мало, то вторая ударная поляра
пересекает ось $ = 0 в точке ///, расположенной в сверхзвуковой
области и определяющей состояние течения после второго скачка
уплотнения. Эту простую сверхзвуковую задачу мы используем
в качестве отправного пункта для последующих рассуждений.
г5>
Рис. 58. Истечение сверхзвуковой струи в пространство с повышенным давле-
давлением. Ниже по течению относительно второго скачка образуется дозвуковая
область (по Гудерлею [2]).
При повышении внешнего давления точки // и /// перемещаются
в направлении меньших скоростей. В принципе течение остается
неизменным до тех пор, пока точка /// не переходит из области
сверхзвуковых скоростей в область дозвуковых скоростей (рис. 58).
После такого перехода уже невозможно, чтобы все поле течения
ниже второго скачка соответствовало состоянию //. В самом деле,
единственным продолжением такого течения может быть параллель-
параллельное течение, но оно не удовлетворяет условиям на границе струи.
На этой границе в любом случае должно возникать расширение,
обусловливающее переход к заданному внешнему давлению, т. е.
к значению т\, соответствующему точке //. Такое расширение на
границе струи возможно в том случае, когда после второго скачка
уплотнения на ней возникает звуковая скорость. Однако до дости-
достижения границы струи такая скорость после второго скачка уплотне-
уплотнения не может возникнуть. Иначе вниз по течению от второго скачка
уплотнения получилась бы звуковая линия, начинающаяся, естественно,

180
ГЛ VI ИССЛЕДОВАНИЕ ТЕЧЕНИИ МЕТОДОМ ГОДОГРАФА
на этом скачке. Волны уплотнения, исходящие из звуковой линии,
оканчивались бы на скачке уплотнения и вызывали бы при этом
повышение давления. Но такое повышение давления противоречит
предположению, что при перемещении вдоль скачка уплотнения вниз
по течению происходит переход от дозвуковой скорости к сверх-
сверхзвуковой скорости.
Волны расширения, исходящие из точки пересечения скачка
уплотнения с границей струи, распространяются в направлении, про-
противоположном скачку. Так как они не распространяются вверх по
течению, то влиять на скачок уплотнения непосредственно они не
могут. Косвенно, конечно, скачок уплотнения определяется расши-
расширяющимся течением, а именно дозвуковой областью, лежащей между
скачком уплотнения и расширяющимся течением.
Сказанное разъясняет физический смысл годографа рассмотрен-
рассмотренной части поля течения (предоставляем читателю самому проверить
\ дозвуковая
область
Рис. 59 Истечение сверхзвуковой струи в пространство с повышенным
давлением. При отражении скачка уплотнения возникает местная дозвуковая
зона (по Гудерлею [2] ).
направление обхода областей в плоскости годографа и в плоскости
течения). Что касается формы скачка уплотнения в точке А (преж-
(прежняя точка ///), то она определяется теми же условиями, как и при
обтекании клина в том случае, когда скачок прилегает к острию
клина. Кривизна скачка в точке А равна нулю, если эта точка лежит
в промежутке между точкой Крокко и точкой, соответствующей кри-
критической скорости; эта кривизна имеет конечное значение в точке
Крокко, и, наконец, она бесконечно велика в промежутке между
точкой Крокко и точкой максимума Ъ на ударной поляре //.
Если ударная поляра // не пересекается с осью 9, то возникает
явление, сходное с тем, с которым мы познакомились при отходе
скачка уплотнения от острия клина, а именно открывается выход
в новую область плоскости годографа (рис. 59).
Выясним, какой вид имеет соответствующее поле течения. При-
Примем сначала, что точка пересечения обеих ударных поляр лежит
в дозвуковой области. В плоскости годографа линия тока, совпадаю-

§ 9 НОВЫЙ ВИД РАЗВЕТВЛЕННОГО СКАЧКА УПЛОТНЕНИЯ 181
щая с осью симметрии струи, начинается в точке Е (рис. 59), т. е.
в наиболее удаленной точке, которую еще достигает прямой скачок
уплотнения, лежащий в области /. При перемещении вдоль ударной
поляры / проходятся все состояния, имеющие место между точками Е
и F поля течения. Начиная с точки F плоскости годографа, грани-
границей дозвуковой области является ударная поляра //. Линия тока,
проходящая через точку F, отделяет линии тока, пересекающие
только скачок уплотнения области /, от линий тока, пересекающих,
кроме этого скачка, также скачок уплотнения области //. Вдоль
этой граничной линии тока направления скоростей и давления
в обоих прилегающих друг к другу полях течения должны совпа-
совпадать. Так как в околозвуковых течениях изменения энтропии не
учитываются, то такое совпадение направлений скорости и давлений
означает непрерывность вектора скорости. Точка F в плоскости
годографа является единственной точкой непосредственно после скачка,
в которой возможно это совпадение. Если мы начнем теперь пере-
перемещаться вдоль ударной поляры //, то в конце концов достигнем
границы струи в точке В. Там имеет место критическая скорость.
Примечательно, что дозвуковая область ограничена отрезком удар-
ударной поляры //, одна часть которого лежит выше, а другая — ниже
оси симметрии ударной поляры. Следовательно, по отношению
к линиям тока скачок уплотнения является частично левобегущим и
частично правобегущим. Это может показаться на первый взгляд
весьма странным, так как в сверхзвуковых течениях возмущения
никогда не распространяются вверх по течению. В рассматриваемом
примере можно было бы принять точку F за исходную точку возмуще-
возмущений. Однако если мы учтем, что вниз по течению относительно скачка
имеет место дозвуковая скорость, то придем к заключению, что при та-
таких обстоятельствах понятие „распространение" возмущений вообще
неприменимо. Наоборот, для возможности отклонения течения вблизи
оси струи должно существовать такое дозвуковое поле (и соответ-
соответствующие ему давления), которое поддерживало бы притекание газа
к скачку уплотнения в сверхзвуковой области. Из этих рассуждений
следует, что при перемещении из точки F к границе струи часть
скачка II распространяется вверх по течению. Наблюдалась ли такая
картина при экспериментах, автору неизвестно. Если для сравнения
с экспериментальными результатами мы захотели бы получить более
точную картину течения в окрестности точки F (например, поже-
пожелали бы определить изменение радиусов кривизны скачков), то должны
были бы развить метод, сходный с изложенным в § 5.
§ 9. Новый вид разветвленного скачка уплотнения
В предыдущем параграфе мы приняли, что точка пересечения
обеих ударных поляр лежит в дозвуковой области. Однако если
число Маха для подходящей к отверстию струи близко к единице,

182
ГЛ VI ИССЛЕДОВАНИЕ ТЕЧЕНИЙ МЕТОДОМ ГОДОГРАФА
то пересечения обеих ударных поляр не получаетсяг). Существуют
и такие случаи, когда точка пересечения лежит в сверхзвуковой
области. При таких условиях поле течения, описанное в предыдущем
параграфе, не может существовать. С другой стороны, было бы
совершенно непонятно, если бы задача истечения сверхзвуковой
струи в пространство с более высоким давлением не имела решения
или если бы решение существовало, но радикально отличалось бы
от поля течения, описанного в предыдущем параграфе.
характеристика
G
г — "j/иирнии поляра П
окрестность точки F
К
J
Рис. 60 Истечение сверхзвуковой струи в пространство с повышен-
повышенным давлением. При отражении скачка уплотнения возникает местная
дозвуковая зона (по Гудерлею [2]).
Остановимся прежде всего на случае, когда обе ударные поляры
не имеют точки пересечения, если не считать точки //. Для того
чтобы понять, что в этом случае может произойти в точке, соот-
соответствующей точке F на рис. 60, примем сначала, что как после
скачка /, так и после скачка // имеет место критическая скорость.
Тогда направления соответствующих векторов скорости, как это
видно из построения в плоскость годографа, не будут совпадать.
Если бы такое несовпадение возникло в сверхзвуковой области, то
оно сразу ликвидировалось бы благодаря образованию расширяю-
расширяющихся течений с обеих сторон линии тока, проходящей через точку F;
*) Если пользоваться уравнением ударной поляры в околозвуковом при-
приближении V, 11>B), то рассматриваемые здесь ударные поляры никогда не
пересекутся —Прим ред.

§9 НОВЫЙ ВИД РАЗВЕТВЛЕННОГО СКАЧКА УПЛОТНЕНИЯ 183
одновременно эти расширяющиеся течения обусловили бы совпадение
давлений на общей границе обоих полей течения. Для области, лежа-
лежащей после скачка уплотнения //, это действительно возможно, так
как скачок направлен здесь так, что он не может быть настигнут
волнами расширяющегося течения. Здесь образуется картина тече-
течения, сходная с картиной, найденной на рис. 58 для окрестности
точки В. В области / расширяющееся течение должно было бы
соединиться со скачком уплотнения, в результате чего вдоль удар-
ударной поляры получились бы сверхзвуковые скорости. Тогда состоя-
состояние течения в точке, расположенной чуть ниже по течению точки F,
определялось бы точкой пересечения ударной поляры / с характе-
характеристикой, проходящей через точку F. В самом деле, эта характе-
характеристика изображает в плоскости годографа расширяющееся течение,
возникающее в точке F плоскости течения. Волны расширяющегося
течения являются, конечно, волнами разрежения; от звуковой линии
они отражаются в виде волн уплотнения. Заканчиваются они на
скачке уплотнения /, вызывая при этом повышение давления, кото-
которое, в свою очередь, вызывает переход к дозвуковой скорости
вдоль ударной поляры /. Понимание такого поля течения не пред-
представляет затруднений.
Область FGK не удовлетворяет требованиям, сформулированным
в § 11 гл. V для смешанной краевой задачи. В самом деле, сейчас
сверхзвуковой контур нигде не прерывается. В задаче Трикоми не-
незамкнутость сверхзвукового контура была необходимым условием
для существования решения, удовлетворяющего условиям непрерыв-
непрерывности. Можно было бы предположить, что граничные условия вдоль
ударной поляры, существенно отличающиеся от граничных условий
в задаче Трикоми, допускают иной характер сверхзвукового контура.
Однако более точное исследование (Гудерлей [2], см. лит. 1) пока-
показывает, что тогда в точке К должна возникнуть особенность, вслед-
вследствие чего и здесь решение в смысле Трикоми становится невоз-
невозможным. Практически вследствие этой особенности структура поля
течения становится значительно более сложной. В целом намеченная
здесь картина течения правильна.
Только что рассмотренная картина течения возникает и в том
случае, когда точка пересечения обеих ударных поляр лежит
в сверхзвуковой области. (До сих пор мы предполагали, что не
существует точки пересечения обеих поляр, если не считать точ-
точки II.) На рис. 61 схематически изображена картина течения
в предположении, что точка пересечения ударных поляр в сверх-
сверхзвуковой области играет такую же роль, как в дозвуко-
дозвуковой области. Построение в плоскости годографа показывает,
что в таком поле течения возникает звуковая линия, пересекающая
обе ударные поляры. На основании картины в плоскости годографа
можно было бы подумать, что вдоль FH возможен переход от зву-
звуковой скорости к сверхзвуковой, однако в действительности это

184 ГЛ. VI ИССЛЕДОВАНИЕ ТЕЧЕНИЙ МЕТОДОМ ГОДОГРАФА
невозможно, так как волны Маха, исходящие от звуковой линии,
являются волнами сжатия.
Тип разветвленного скачка уплотнения зависит на основании
сказанного от того, в какой области лежит точка пересечения обеих
ударных поляр. Случай, когда эта точка лежит в сверхзвуковой
дозвуковая
ч область
. местная
г'сверхзвуковая
fA зона
Рис. 61. Гипотетическая (но невозможная) форма разветвлен-
разветвленного скачка уплотнения (по Гудерлею [2] )
области, не представляет физического интереса. В литературе встре-
встречается классификация скачков уплотнения, учитывающая только
общее число точек разветвления. С физической точки зрения такая
классификация неудовлетворительна.
§ 10. Смысл „второго" решения задачи о сверхзвуковом
обтекании клина
Для расчета сверхзвукового течения около клина с неслишком
большим углом раствора необходимо, как известно, продолжить луч,
проходящий через нулевую точку плоскости годографа и имеющий
направление стороны клина, до пересечения с ударной полярой.
Однако при этом получаются две точки пересечения, которым со-
соответствуют скачки разной интенсивности. В экспериментальных
условиях всегда наблюдается только более слабый скачок. Между
"тем все случаи течения около клина при неприлегающем скачке
уплотнения показывают, что физически возможно и второе решение.
В самом деле, при обтекании клина с неприлегающим скачком
уплотнения вдоль скачка сменяются все состояния, встречающиеся
вдоль ударной поляры. Возникает вопрос, возможен ли все же
такой эксперимент, при котором около клина наблюдался бы более
сильный скачок уплотнения. Буземан высказал предположение, что
для этого необходимо установить позади клина такое препятствие,
которое позволило бы поддерживать ниже по течению относительно
скачка уплотнения более высокое давление. Это предположение на-
наводит на мысль создать в экспериментальных условиях течение,
которое, с одной стороны, удовлетворяло бы поставленным требо-
требованиям, а с другой стороны, допускало бы простое отображение
поля течения на плоскость годографа.

§ 10 СМЫСЛ «ВТОРОГО» РЕШЕНИЯ
185.
Рассмотрим клин, угол раствора которого превышает макси-
максимальный угол отклонения на ударной поляре, поэтому при обте-
обтекании этого клина должен возникнуть скачок уплотнения, не при-
прилегающий к острию клина. Срежем переднюю часть этого клина
и приставим взамен нее второй клин с меньшим углом раствора,
допускающим возникновение прилегающего скачка уплотнения. До-
Допустим, что имеется возможность изменять отношение длин сторон
обоих клиньев. Если тупой клин очень велик, то получится скачок
уплотнения, расположенный далеко впереди острия переднего клина;
если же тупой клин очень мал, то безусловно возникнет скачок
уплотнения, прилегающий к острию переднего клина. Следовательно,,
Рис. 62. Сверхзвуковое течение около двойного клина. Скачок уплотнения возникает
впереди острия переднего клипа (по Гудерлею [2J).
изменяя размеры тупого клипа, мы можем любым образом варьи-
варьировать повышение давления позади острого клина. На рис. 62 по-
показано поле течения для случая неприлегающего скачка уплотнения.
На оси симметрии возникает прямой скачок уплотнения, соответ-
соответствующий ударной поляре / набегающего течения. Начиная отсюда,
нулевая линия тока продолжается к критической точке Е2, совпа-
совпадающей с острием переднего клина. Между точками Е2 и Е1 ско-
скорость течения направлена вдоль стороны переднего клина. Точки Ех
и Е2 являются критическими точками. В промежутке между ними
скорость достигает максимального значения. Следовательно, сторона-
переднего клина отображается на плоскость годографа в виде от-
отрезка E2FEV Положение точки F на плоскости годографа заранее
неизвестно, оно зависит от отношения длин Е2ЕХ и Efi в плоскости
течения. Если длина ЕХС очень велика, то весь передний клин
лежит в области замедленного течения, т. е. длина EJ* в плоскости
годографа мала. Следовательно, EXF есть параметр годографа, опре-
определяющий отношение длин сторон обоих клиньев1). Если мы будем
1) Иногда при формулировке задачи в плоскости годографа можно не-
заметить существования такого параметра. Тогда исчезает возможность.

186
ГЛ VI. ИССЛЕДОВАНИЕ ТЕЧЕНИЙ МЕТОДОМ ГОДОГРАФА
все более и более укорачивать сторону тупого клина, то точка F
в конце концов дойдет до ударной поляры / (рис. 63). Теперь
область AFE получается замкнутой и из нее больше не могут вы-
выходить никакие линии тока. Нулевая линия тока выходит из точки F
и сразу принимает направление стороны переднего клина. Тогда
на острие этого клина действительно возникает более сильный из
.¦возможных скачков уплотнения.
Рис. 63. Сверхзвуковое течение около двойного клина. Скачок уплот-
уплотнения прилегает к острию переднего клина и соответствует второму
из возможных решений (по Гудерлею [2]),
Выясним теперь, как будет изменяться поле течения, если про-
продолжать укорачивать сторону тупого клина. Изменение поля течения
должно обязательно возникнуть, так как годограф однозначно опре-
определяет поле течения вместе со всеми его размерами. Если мы не
будем изменять размеры тупого клина, то полученное выше реше-
решение можно истолковать как возникновение впереди тупого клина
не прилегающего к нему скачка уплотнения. Пусть теперь из ту-
тупого клина начинает выдвигаться острый клин. Он, конечно, не-
несколько изменяет поле течения. Сначала острый клин движется
в области замедленного течения и затем все более и более прибли-
приближается к возникшему перед тупым клином скачку уплотнения. Поле
течения, получающееся при достижении острым клином скачка
уплотнения, изображено на рис. 63. Если продолжать выдвигать
острый клин, то он пройдет своим острием через скачок уплотне-
уплотнения (рис. 64). Тогда на острие выдвинувшегося вперед острого
клина возникнет скачок уплотнения слабой интенсивности. Будем
обозначать состояние после этого скачка цифрой //. Вне области,
лежащей ниже по течению от скачка уплотнения //, сохраняется
по-прежнему скачок уплотнения /. Этот скачок проникает в область //
и достигает здесь стороны острого клина. Продолжение скачка /
в области // отображается на плоскость годографа в виде отрезка
выполнить в плоскости течения все физически заданные условия Это особенно
опасно в тех случаях, когда рассчитывается не все поле течения, а только
некоторые, наиболее важные его участки.

§ 10. СМЫСЛ «ВТОРОГО» РЕШЕНИЯ
187
ударной поляры //. Оба скачка сливаются в точке Н, в которой
затем могут образоваться разветвленные скачки либо первого, либо
второго вида. Переход к этому полю течения от поля течения,
изображенного на рис. 63, осуществляется благодаря тому, что
в плоскости годографа сверхзвуковая часть контура размыкается
в точке К. Скачок уплотнения в области / изображается в плоскости
годографа обеими сторонами ударных поляр JBXK и КВ2. Поло-
Положение точки К определяет теперь отношение длин сторон обоих
клиньев. Продолжая выдвигать далее острый клин, мы будем по-
получать новые и новые картины течения, в которых скачок уплотне-
уплотнения, обусловливающий переход от сверхзвуковых скоростей к до-
дозвуковым, перемещается все дальше и дальше вниз по течению. За
дальнейшими подробностями отсылаем к работе Гудерлея [2]
(см. лит. 1).
Рис. 64 Сверхзвуковое течение око то двойного клина. Скачок уплотнения,
переводящий сверхзвукозое течение в дозвуковое, начинается на стороне перед-
переднего к чина (по Гудерлею [2]).
Возвращаясь еще раз к рассмотренным примерам, мы видим —-
и дальнейшие исследования подтверждают это, — что переход от
начального поля течения к совершенно непохожему на него конеч-
конечному полю течения осуществляется во всех случаях путем непре-
непрерывного изменения. Это обстоятельство заставляет предполагать, что
при околозвуковых скоростях также невозможны какие-либо раз-
разрывные изменения поля течения.
Конечно, многие из рассмотренных вопросов имеют лишь ака-
академический интерес. Тем не менее полученные результаты могут
быть полезны и для практика, так как они позволяют правильно
с физической точки зрения понять некоторые неясные вопросы,
например смысл точки Крокко.
В связи с последним из рассмотренных примеров обратим вни-
внимание на следующее обстоятельство. Иногда путем незначительного
изменения первоначальной постановки вопроса удается сформули-
сформулировать задачу так, что становится возможным ее исследование ме-
методом годографа, что в свою очередь позволяет глубже проникнуть
в некоторые свойства течения.

188 ГЛ VI ИССЛЕДОВАНИЕ ТЕЧЕНИЙ МЕТОДОМ ГОДОГРАФА
Укажем еще на две задачи, исследование которых возможно1
с помощью методов, аналогичных рассмотренным выше.
1. Клин в закрытой аэродинамической трубе при сверхзвуковой
скорости набегающего течения (Гудерлей [2], см. лит. 1). Если
клин велик, то задача не допускает решения, так как набегаю-
набегающее течение не может оттекать в промежутки между клином
и стенками трубы. Если постепенно уменьшать размеры клина,
то ^сначала образуется не прилегающий к клину скачок уплотнения^
идущий от одной стенки трубы к другой. При дальнейшем умень-
уменьшении размеров клина скачок садится на острие клина и возни-
возникает ряд явлений, сходных с рассмотренными в предыдущем
примере.
2. Бипланное крыло Буземана с клинообразными профилями
и переменным расстоянием между обоими крыльями в сверхзвуко-
сверхзвуковом течении (Гудерлей [1], см. лит. 1). Эта задача соответствует
эксперименту Ферри. Если расстояние между обоими крыльями
мало, то образуется общий не прилегающий к крыаьям скачок уплот-
уплотнения. При большем расстоянии между крыльями получаются два
отдельных скачка, прилегающих к кромкам крыльев. Построение
картин такого течения может оказаться полезным для оценки опытов
Ферри. Правда, результаты опытов несколько отклоняются от тео-
теоретической картины вследствие влияния пограничного слоя. Между
прочим, теоретическое исследование показывает, что течение может
стать неустойчивым и даже при постоянной энтропии или отсутствии
трения.

Глава VII
ЧАСТНЫЕ РЕШЕНИЯ УРАВНЕНИЯ ТРИКОМИ
§ 1. Частные решения Чаплыгина
Для более глубокого проникновения в свойства околозвуковых
течений необходимо довести решения краевых задач, сформули-
сформулированных в плоскости годографа, до численных результатов или
по крайней мере детально исследовать методы решения. При этом
существенную помощь могут оказать некоторые семейства частных
решений. Этим семействам мы и посвятим настоящую главу.
Начнем с частных решений Чаплыгина. В § 7 гл. V мы вывели
уравнение Трикоми
Там же мы рассмотрели выражения, соответствующие частным ре-
решениям Чаплыгина полного уравнения годографа. Такие решения
принимаются обычно в тех случаях, когда вдоль линии & = 60 =
= const выполняется граничное условие ф = 0 или вообще условие
ф = ф0. В соответствии с этим примем для ф одно из следую-
следующих выражений:
ф = g G1, т) sin тъ д-, Bа)
«о
^ = g{_i\,m)zosmv:-r, B6)
где т есть произвольная постоянная (обычно принимающая целые
или полуцелые значения). Тогда мы получим для определения g
обыкновенное дифференциальное уравнение
*" + Ч^-* = 0. Bв)
е
ео
Его решением в сверхзвуковой области будет
(^)] (За)
g(tl,m)= VWl [~ <^-"/6 /у. (е"/а ~ ^ | т) |
см., например, Янке и Эмде, лит. 1), а в дозвуковой области
(Зб)

190
ГЛ VII ЧАСТНЫЕ РЕШЕНИЯ УРАВНЕНИЯ ТРИКОМИ
Здесь Л/, и /_1д суть функции Бесселя порядка 1/3 и соответ-
соответственно —V3 (таблицы этих функций составлены, например. Com-
Computation Laboratory, см. лит. 1), а с1 и с2 — произвольные веще-
вещественные постоянные. Нетрудно убедиться, что при т] = 0 оба ре-
решения гладко переходят одно в другое.
Особый интерес представляет случай, когда с1 и с2 принимаются
равными единице, так как тогда решение g в дозвуковой области
при т] —> — оо стремится к нулю [см., например, соотношения
VII, 7F) и VII, 7(9)]. При таком выборе постоянных с1 и с2 мы
будем иметь в дозвуковой области
,•_,, 2 тяте
з е0 ^
"¦)]•
Dа)
или
тгИl3/a) при ^<°¦
а в сверхзвуковой области
2 /иг.
D6)
Решения Dа) и D6) являются приближениями к тем точным реше-
решениям Чаплыгина, для которых разложение в ряд начинается с по-
положительной степени скорости w (см. § 6 гл. V).
Если разложить функции Бесселя в соответствующие ряды, то
вблизи звуковой скорости (т) = 0) решения C) принимают вид
E)
5 '-I qii
,44
С помощью соотношений VII, 7F) и асимптотического представ-
представления VII, 7(9) функций Ханкеля мы получим для функции g, опре-
определяемой равенствами C), следующие приближенные выражения,
пригодные для больших значений величины т~^к
У
Щ
при Tj>0,
Fa)
g~\4\ "-V ^f
I il 2
ПРИ
2, 7)<0; F6)
- ___3^ mx з/j
e 2 6-j ^ при ct = c2 = 1, 7) < 0. Fb)

§ 1 ЧАСТНЫЕ РЕШЕНИЯ ЧАПЛЫГИНА 19Е
Если заданы граничные условия ф = 0 при 8 = 0 и & = 60, то постоян-
постоянную т следует выбрать целочисленной. Тогда посредством метода,
с которым мы вновь встретимся в § 10 настоящей главы, можно
показать, что в области % < -ц < г12, в которой везде удовлетво-
удовлетворяются уравнение Трикоми и только что указанные граничные усло-
условия, решение ф всегда можно представить как наложение частных,
решений вида C). Следовательно, мы будем иметь
2 rrm зЛ , _ г / 2 тт. ,, \1 отя
т. ,, \1 .
7 ^ Л si
при т] > 0 G)
и аналогичное выражение при т\ < 0. В решении G) clm и с2т суть
подходящим образом выбранные постоянные.
Если разложение этого вида и его производная по ~q сходятся,
при скорости звука, то на основании равенства E) следует, что
ряды
VI ,, . тт. Q vi ,, . тел . о
У clmm- /- sin -к- %¦ и У c^m/'sm-^-ft (8)
яг «г
сходятся. Если для сверхзвуковой области мы воспользуемся асимп-
асимптотическим представлением Fа), то увидим, что сходимость разло-
разложения определяется рядами
1/ . Ш% г.
in m
Поэтому если ряды (8) сходятся, то разложение G) безусловно»
сходится в сверхзвуковой области. Это обстоятельство важно в томг
случае, когда в сверхзвуковой области заданы граничные условия.
Тогда они могут быть удовлетворены путем прямого расчета (см.
§ 4 гл. VIII). Из сходимости ряда для производной фч вдоль звуко-
звуковой линии нельзя вывести заключения, что ряд для этой производ-
производной сходится также в сверхзвуковой областих).
Если решение вдоль звуковой линии представляется сходящимся
рядом, членами которого являются выражения, входящие в правые
части равенств D), то оно безусловно сходится во всей дозвуко-
дозвуковой области. Это следует из соотношения Fв).
!) Относительно сходимости ряда по частным решениям Чаплыгина
cmg {f\, m) sin ^r &.
m
где g (t\, m) определены формулами D), имеет место следующий результат;
если ^ (?т < со, то этот ряд сходится абсолютно и равномерно в любой
т
полуплоскости Y) <; tj0 (даже если т]0 > 0) По этому поводу см. Л. В. О в с я и-
ников, Докл. АН СССР, т. 91, № 3, 1953. — Прим. ред.

192 ГЛ VII ЧАСТНЫЕ РЕШЕНИЯ УРАВНЕНИЯ ТРИКОМИ
§ 2. Другой класс частных решений
Покажем, как можно найти другой класс частных решений урав-
уравнения Трикоми. Из структуры уравнения Трикоми следует, что мы
получим новое его решение, если заменим в известном решении т\
на i\z~1, а & — на &х. Это следует из закона подобия. Если мы
введем новую переменную
•-(множитель 9/4 пока не играет никакой роли), то эта переменная при
только что указанном аффинном преобразовании останется неизмен-
неизменной. Множитель х из уравнения Трикоми выпадает. Поэтому если
преобразовать уравнение Трикоми к независимым переменным [ и ij,
то переменная ч] войдет в каждый член уравнения в одинаковой
степени при условии, что при подсчете мы будем учитывать также
дифференцирование по т]. Эти соображения наводят на мысль
(Гудерлей [3], см. лит. 1), что частное решение можно взять в виде
ф = т] | / (С, «). B)
Из сказанного следует, что после подстановки такого выраже-
выражения ф в уравнение Трикоми переменная т\ должна выпасть, и мы
получим для определения функции /(С, п) обыкновенное дифферен-
дифференциальное уравнение1). В самом деле, вычислив производные
di —3!; ас 9 ь о|
\{п — 1)«/—(б« — 12) с/' + э;2/"],
и внеся фЧ11 и i]>№ в уравнение Трикоми, мы получим обыкновенное
^дифференциальное уравнение второго порядка
^^ = o. C)
1) Вместо того, чтобы исходить из уравнения Трикоми, можно преобра-
преобразовать к переменным т) и С точное уравнение годографа либо с помощью
равенств V, 7 C), либо с помощью равенств V, 7 E) (второе преобразование
предпочтительнее) и затем ограничиться наиболее низкими степенями i\.
"Этот способ вывода допущения B) показывает, что оно описывает локаль-
локальное поведение точного решения в плоскости годографа на звуковой линии,
•что, впрочем, можно было предполагать заранее.

§ 2 ДРУГОЙ КЛАСС ЧАСТНЫХ РЕШЕНИИ 193
Точки 0, 1 и go являются для этого линейного однородного урав-
уравнения регулярными особыми точками; следовательно, оно представ-
представляет собой гипергеометрическое дифференциальное уравнение1).
Такое уравнение вместе с совокупностью своих решений опреде-
определяется положением особых точек и показателями уравнения в этих
точках. На этом основано представление совокупности решений
гипергеометрического дифференциального уравнения посредством
Р-функции Римана. Эта функция представляет собой не что иное,
как сопоставление особых точек (в первой строке), соответствую-
соответствующих показателей (jbo второй и третьей строках) и независимой пе-
переменной. Следовательно, для того чтобы найти Р-функцию, необхо-
необходимо определить показатели гипергеометрического уравнения в особых
точках2). Для уравнения C) мы получим
со 0 1
f=P\
n—I J_ 4я+1
3 2 "б
D)
Линии С = const в плоскости т], ft представляют собой полуку-
полукубические параболы. Для С = 0 мы имеем
» = 0,
3 ДЛЯ С = СЮ
следовательно, последняя линия совпадает с звуковой линией. Для
С = 1 мы получаем
т. е. линиями С=1 являются обе характеристики, проходящие
через начало координат [см. уравнение I, 6(8)]. В сверхзвуковой
области величина С положительна, а в дозвуковой отрицательна.
В точках, симметричных относительно оси т), значения С одинаковы.
Из того, что точки С = 0 и С = оо являются для функции /
особыми точками, отнюдь не следует, что решение ф должно иметь
особенности вдоль линий С = 0 и С=оо плоскости т), ft. Напротив,
такое поведение ф было бы совсем невероятным. О поведении <j*
вблизи этих линий можно получить представление путем подстановки
в уравнение B) первого члена разложения функции / в ряд. В самом
деле, этот первый член с точностью до множителя определяется
!) Желающих подробно ознакомиться с теорией гипергеометрических
дифференциальных уравнений отсылаем к специальной математической ли-
литературе.
2) См., например, Уиттекер и Ватсон, Курс современного анализа,
гл. 10.7.

194 ГЛ VII ЧАСТНЫЕ РЕШЕНИЯ УРАВНЕНИЯ ТРИКОМИ
показателем гипергеометрического дифференциального уравнения
в соответствующей особой точке. Выполнив такую подстановку, мы
получим
для С = 0:
показатель 0 ф = т\п -j- . . .,
1
показатель -^ <Ь = %-цп-3^-j- ...;
для С = со:
п - / 1 \-п'3 /3 ,\2n's
показатель ^
a(n-i)
¦ п—1
показатель =—
Эти выражения, очевидно, не имеют особенностей во всех точ-
точках рассматриваемых линий, за исключением начала координат.
Вдоль С=1 отсутствие особенностей имеет место только для одного
из линейно независимых решений, в другие же решения входит
в общем случае дробная степень величины С—1. Такое поведение
решения ф вдоль линии С=1 вполне понятно. В самом деле, мы
знаем, что вдоль характеристики могут распространяться особенности.
Если подобного рода распространение особенности происходит вдоль
характеристики, проходящей через начало координат, то такое яв-
явление описывается соответствующим особым частным решением.
Характер особенности определяется показателями п. Более строгое
исследование будет дано в § 2 гл. X.
Выбрав в качестве независимой переменной величину С и приняв,
что решение уравнения Трикоми имеет вид B), мы ввели в диффе-
дифференциальное уравнение, определяющее /, особенности, чуждые ре-
решению ф. Это обстоятельство является в известной мере недостатком
допущения B). Но зато такой выбор независимой переменной при-
приводит к дифференциальному уравнению известного типа. Кроме того,
физически характерные линии & = 0 и tj = 0 обладают особым смы-
смыслом также для дифференциального уравнения C), что значительно
облегчает исследование решений.
§ 3. Другое допущение о форме решения
Для дальнейшего изложения особую важность имеет следующий
выбор независимых переменных:
p = _1,S + -ift2==1K(C_1), A)
А = Г''*. B)

§ 3 ДРУГОЕ ДОПУЩЕНИЕ О ФОРМЕ РЕШЕНИЯ
195
На рис. 65 изображена плоскость т], ft с линиями 1 = const и
р = const1). Примем, что искомое решение можно представить в виде
ф = р — С Via) + И- О E, [J-). C)
Заменив в этом равенстве р на ifC-,—1), мы заметим его сходство
с равенством VII, 2B). Приравняв правые части обоих равенств,
мы получим
— 1 + 3jj, = «, Da)
G К, [*¦) = I 5 1 ) ' I ? 1— -™1 I - '
Замена параметра « на параметр (д, позволит в дальнейшем значи-
значительно сократить записи. Введение переменной % устраняет особен-
особенность, возникающую на звуковой линии. Особенность на оси & = О
-0,5 n ~ t ^
Рис. 65. Плоскость rj, & с линиями р — const и $=^const.
сохраняется, но она не мешает исследованию, так как решение
можно разложить на симметричную и антисимметричную части (отно-
(относительно этой оси), после чего отпадает необходимость в рассмот-
рассмотрении перехода через Ь = 0.
Вместо непосредственного вывода дифференциального уравнения
для определения функции G преобразуем сначала дифференциальное
уравнение Трикоми к переменным р и \\ мы получим
-—г—^-fe о ^0 — ?3Иё = 9р2ф.о + o"Piv E)
Часто более предпочтительна следующая запись этого уравнения:
1) Начиная отсюда, буква р больше не применяется для обозначения
плотности.

196 ГЛ VII ЧАСТНЫЕ РЕШЕНИЯ УРАВНЕНИЯ ТРИКОМИ
Внеся ф, определяемое равенством C), в преобразованное уравнение
Трикоми, мы получим для определения G обыкновенное дифферен-
дифференциальное уравнение, которое соответствии с уравнениями E)
и Eа) можно представить в двух видах:
5 V dG 96/1
d& 1-6' rf? ^A-?3) J
4 [A - ^3)% Si 4 %r (~~V'H = 0. F6)
rfs L «re j (i e3) /" V144 /
Смысл выбора решения в виде C) заключается в том, что при таком
выборе параметр jj, входит в дифференциальное уравнение, опреде-
определяющее О, только в коэффициенте при самой функции G, но не
в коэффициенте при производной G'. Следовательно, мы получили
дифференциальное уравнение для задачи на собственные значения,
которое позволяет вывести заключение о полноте системы решений,
состоящей из частных решений вида C). Это важно, прежде всего, для
исследования течений вблизи числа Маха, равного единице. Введение
переменной р имеет своим недостатком совпадение линий р = 0 и
1=1. Для исследования решения вблизи характеристики % = 1 лучше
всего вернуться к переменной т).
Для определения в плоскости течения координат х и у, соот-
соответствующих частным решениям C), необходимо воспользоваться
уравнениями V, 7(8) и V, 7(9), причем р* и •до* можно положить
равными единице. Тогда мы сразу найдем, что
у = ф == p-(V..)+^ G (?, (х). G)
Далее легко видеть, что для координаты х следует взять выражение
;х). (8)
Для отыскания функции K(k, ja) внесем значения ф и х, определяе-
определяемые равенствами C) и (8), в уравнения V, 7(8); мы получим
Г 1 . 1
I Тп + Р с
4Н =
~Т2+!А 9 „ 2 6G'
1 О' J •

§ 4 РЕШЕНИЯ G
197
Выразив т] и ft через р и ?, перепишем эти уравнения в виде
Отсюда найдем, что
1
следовательно,
3/С =
§ 4. Решения G
Так как решения О могут быть выражены через решения /,
а последние допускают представление в виде гипергеометрических
рядов, то такое же представление допускают и решения G. Из соот-
соотношений VII, 2D) и VII, 3D) мы сразу «айдем, что совокупность
всех решений G определяется схемой
со 0 1
— (д. + ^ 0 0 ?
8
A)
Для получения решений О в явном виде воспользуемся следующими
общими соотношениями, имеющими место для гипергеометрических
дифференциальных уравнений.
1) Если величины zv at, bx и cv входящие в правую схему,
получаются из соответствующих величин z, a, b и с левой схемы
посредством одного и того же дробно-линейного преобразования,
то
( a b с } [ <ц Ьх ct ]
Р{ а C т г } = р { а р 1 г,\. B)
I «' Р' Т' J I «' Р' 7' J

198 ГЛ VII. ЧАСТНЫЕ РЕШЕНИЯ УРАВНЕНИЯ ТРИКОМИ
Равенство B) показывает, что особые точки а, Ь и с могут быть
перенесены посредством преобразования в любые заданные положе-
положения ах, Ъ^ и с1 и при этом показатели уравнения в особых точках
не изменятся.
2)
( а Ь с \
-Р[ a" k -k-l C I Z]
\ a' + k P' — А — / f' + l j
Смысл этого соотношения следующий: умножение Р-функции в левой
схеме на стоящий перед ней множитель дает новую совокупность
решений, также удовлетворяющую дифференциальному уравнению
второго порядка с особыми точками а, Ь и с, но с показателями,
измененными соответственно множителю
/ z — а \к ( z — с \1
\г-Ь) \7=F) ¦
3) Совокупность решений, заданная схемой
f со 0 1 \
w=P{ а 0 0 z \, Dа)
1 Ь 1 —с c — a — b J
может быть представлена посредством гипергеометрического ряда
w = F (а, Ь, с, z),
где
F (а, Ь, с, z)=l Н ггг~г~ t J-A 9i ^"Ь
+ — Г(с+1)(с + 2K! z3Jr ^4б^
Для доказательства следует составить дифференциальное уравнение,
соответствующее схеме Dа), и внести в него разложение D6).
Радиус сходимости гипергеометрического ряда всегда равен еди-
единице !).
4) Разложения в различных особых точках связаны между собой
следующими так называемыми переходными подстановками:
)Г(а + 6с) __ о-а-Ъ
V(a)T(b) ^~z> X
X F{c — a, c~ b, 1-t-c — a — ft, 1— z) Ea)
!) Кроме тех случаев, когда гипергеометрический ряд вырождается в поли-
полином. — Прим. ред.

§ 4. РЕШЕНИЯ G 199
и
Г(а)Г(Ь)
Г (с)
F(a, b, с, z) =
E6)
Соображения, которые приводят к этим соотношениям, не могут
быть изложены в немногих словах.
Формулы B) и C) позволяют представить любую Я-функцию
в виде схемы Dа), имея которую можно выразить решение в виде
ряда D6). Формулы Eа) и E6) позволяют перейти от ряда D6)
к другим рядам.
Два линейно независимых решения, необходимые для полного
представления решения G, выберем так, чтобы соответствующие
решения ф были либо симметричными, либо антисимметричными
относительно линии & = 0. В первом случае мы снабдим символ G
сверху индексом s, а во втором случае — индексом а. Вслед-
Вследствие наличия особенности в точке ? = 1 решение О не может быть
аналитически продолжено через эту точку, поэтому мы будем ука-
указывать две отдельные составляющие решения, одну для области
1<;?<оо, другую для области —ао<?<^1.
Равенство A) позволяет сразу перейти к гипергеометрическому
ряду
(s) /, t_s\(Vn)-I*/ 1 .51 е_з\ ,„.
GVJ A5 ) F{ V + tJ + S ) F)
Симметрия этого решения относительно оси Ь = 0 вытекает из того,
что входящая в него переменная %~ может быть представлена
в виде 9&2/4т]3. Радиус сходимости ряда F) равен единице, т. е.
решение сходится в области 1 < % < оо. С помощью соотноше-
соотношения Eа) можно представить решение F) в окрестности точки 1=1
в следующем виде:
Если заменить здесь [а на — ц, то первое и второе слагаемые по-
поменяются местами.

200
ГЛ VII ЧАСТНЫЕ РЕШЕНИЯ УРАВНЕНИЯ ТРИКОМИ
Для того чтобы получить из равенства A) решение QW, необ-
необходимо сначала выделить множитель, обусловливающий анти-
антисимметрию. Для этой цели подходит любой из множителей
В первом случае сохраняется показатель уравнения в точке \ = 1,
во втором случае — в точке ?~3—оо. Мы используем только пер-
первую возможность и получим
0 1
_7_
2"
11
t-з
Отсюда
или, после применения преобразования Eа),
,„л_„ .. г(|)гад
X
X
. 7 , 11 о
7
12"
1 е-з\ i (л с—зчСА
, 1—? ] + (!—& )
) + Iх»- — 3/а
X
12~^
12
1-
3
(9)
Частные решения
— S )
.1 . 5 , о , >--з\
t_3\(*/ia)-li е_з/
11
—5 J,
входящие в решения G) и (9), внешне различны. Однако так как
существуют только два линейно независимых решения — и эти ре-
решения уже определены начальными показателями своих разложе-
разложений— и так как оба приведенных решения имеют совпадающие
начальные показатели, то они должны представлять одну и ту же

S 4. РЕШЕНИЯ G
201
функцию. В этом можно убедиться при помощи равенств.
C) и D)i).
Далее, необходимо составить выражение для O^s\ пригодное на
отрицательной оси &(?—> — со). Для этой цели мы можем исполь-
использовать опять равенство A) и в результате получим решение G(s>,
сходящееся в интервале от ?~3 = — оо до ?~8 = — 1. Однако можно
получить лучшую сходимость. Для этого прежде всего выполним
такое преобразование независимой переменной, которое оставляет
точку 0 неизменной, а точки 1 и оо меняет местами. Перепишем
равенство A) в виде
г со 0 1
! ° ° Г
1 1 1 _L
I 3 2 12
и введем в качестве новой переменной
е-з
Тогда мы получим
со 0 1
~-^ О 0!A-?3)
;Зч-1
12 ^г 2
Отсюда с помощью равенства Dа) мы найдем
A0)
При ? = 0 аргумент принимает значение, равное единице. Использо-
Использовав соотношение Eа), мы получим
Г *)Г -L
A 1 2 53
~!Х + Т^> ^ + 12' Т' 1з1Г
г [4г г —
^гХ
1) Проще получить этот результат с помощью формулы преобразования
гипергеометрического ряда
F(a, b, с, г) = (I — z)c-a~b F(с — а, с — Ъ, с, г). —Прим. ред.

202
ГЛ VII. ЧАСТНЫЕ РЕШЕНИЯ УРАВНЕНИЯ ТРИКОМИ
Эта формула пригодна также для положительных значений ?, но
только до значения Sj3/E3—1) = —1, т. е. до $ = 2 . В связи
с этим выполним еще одно преобразование. Выражение
1 , 2 S3
содержится в совокупности решений
( со 0 1
О=Р
I 1
112
3 2
I
Использовав равенство B), мы получим отсюда
со 0 1 \
0 о -L — (д. е3 !
1 j_ j_
Т 2"
со 0 1
-ч о о
7 1 о
Т2-1* Т 2[i
что приводит к соотношению
_i_ 2
12 ' tx^-
A2)
Выполнив аналогичное преобразование для второго слагаемого пра-
правой части равенства A1), мы получим
? Р/ , 5 5 4 Е3
3' 6s_
. !¦
Использовав соотношения A2) и A3), мы можем представить
s следующем виде:
(l—SY^X

§ 4 РЕШЕНИЯ Q
203
(И)
Для того чтобы перейти отсюда к рядам, пригодным вблизи
точки t-=l, необходимо еще раз применить переходную подста-
подстановку Eа). Гипергеометрические ряды, получающиеся из первого и
второго слагаемых равенства A4), внешне имеют различный вид,
однако из соображений, уже приведенных выше по поводу анало-
аналогичного случая, они попарно представляют одни и те же функции.
После выполнения подстановки Eа) мы получим из первого сла-
слагаемого равенства A4) следующее выражение, пригодное в окрест-
окрестности точки ?=1:
¦(!)-
Аналогичным образом из второго слагаемого равенства A4) мы
получим
гФг(-4)
(Vn)-|i у
Первые и вторые члены двух последних выражений могут быть
объединены.

204 ГЛ VII ЧАСТНЫЕ РЕШЕНИЯ УРАВНЕНИЯ ТРИКОМИ
Напомним следующие соотношения из теории гамма-функции,
которые нам понадобятся либо сейчас, либо позже:
ГО)ГA—
-^ при lz ^
при \z ^
A5а)
A56)
> 1, |argz| <тс; A5г)
>1, arg2|<u. A5д)
sin
Г (г + а) а
Г (г) 2
Обозначим временно сумму коэффициентов при первой гипергеоме-
трической функции в выражениях, полученных из равенства A4),
через А. Мы найдем
гШгBц)
х ; X
J 'DL4)
I
Отсюда, использовав соотношения A5), мы получим
Г Ш Г Bц) [ « sin Гя (ц + -1Л] % Sin Г™ L + ^Л]
•*i — : р ^ ; '-, г~ \ ~~ ",
я sin -^- тс sin I
О \
Выражение в фигурных скобках можно переписать в виде
sin т

§ 4 РЕШЕНИЯ G 205
следовательно,
Л = —— г-г—-, т-г- sin I u( ^ + ^г)_|-
Для определения коэффициента при второй гипергеометрической
функции достаточно в выражении коэффициента Л заменить [а на — ;х.
Окончательно мы получим
, ч [ Г B(а) sin \% U + 4"I
G(s) = 2ГЙ / 5ч/ 14 A -*Ш~* X
^-l*.^—^ 1-2^. 1-5') +
Г(-2,)з1п[,(-^ + |)]
( )Ь)
1—?')}• A6)
Формулы A0), A1), A4) и A6) представляют решение О^ (?, (х)
в области —oo<i<;i. Целесообразность использования этих
формул для численного определения функции G зависит от имею-
имеющихся в распоряжении вычислительных средств. При наличии счет-
счетных машин с программным управлением целесообразнее непосред-
непосредственно численно проинтегрировать дифференциальное уравнение,
определяющее функцию G, а выведенные здесь формулы использо-
использовать только для определения начальных значений и для контроля.
Для наших исследований выведенные формулы ценны тем, что они
выражают в общем виде поведение функции О в точках % = — со,
? = 0 и 5=1, имеющих особый физический смысл.
Соответствующие формулы для решения 0^ имеют вид
-^^, ,, + -1, |, A-53)-1); A7а)
гШг(т)
A V in
1

206 ГЛ VII. ЧАСТНЫЕ РЕШЕНИЯ УРАВНЕНИЯ ТРИКОМИ
G(a) {"'rt=тгтщЬ^гщA - *у/1^ х
7\ ' \ ' У
ti' 4- |3); A7в)
"9" Л / 11\/ 7 \ ^ ? ^ -^
г / 1
Xf(^^, P- + J2' 2^ + Ь 1-?)|- A7Г)
Конечно, гипергеометрические функции, входящие в эти формулы,
кроме первой, одинаковы с гипергеометрическими функциями, опре-
определяющими
§ 5. Специальные решения О
Решения в замкнутом виде полезны не только для первой ориен-
ориентировки, но и для приложений. Они могут быть просто и система-
систематически найдены с помощью Р-функции Римана. Согласно равен-
равенству VII, 4D6), гипергеометрический ряд обрывается, если один
из параметров а и Ъ равен отрицательному целому числу. Как по-
показывает схема VII, 4 (а), а и Ъ суть показатели гипергеометриче-
гипергеометрического уравнения в точке со. Для рассматриваемого гипергеометри-
гипергеометрического уравнения характерно, что в обоих других особых точках
один из показателей равен нулю. Так как посредством дробно-
линейного преобразования можно переместить особые точки в любые
другие положения, то для существования замкнутых решений необ-
необходимо, чтобы в одной особой точке один из показателей был
равен отрицательному целому числу, а в каждой из двух других
особых точек один из показателей был равен нулю.

5. СПЕЦИАЛЬНЫЕ РЕШЕНИЯ О
207
В применении к равенству VII, 4 F) это условие сразу дает
A)
_5_
12 '
= Q, 1, 2, ... .
B)
Преобразовав равенство VII, 4 A) так, чтобы стал равен нулю
второй показатель в точке 0, мы получим
Г
0 1
Отсюда
со 0 1
7
21 _ 1
12
12 "
Дальнейшие преобразования подобного рода приводят к тем же
значениям [J-, но с обратным знаком; это легко понять, если вспом-
вспомнить уравнение VII, 3F).
Другая группа замкнутых решений получается следующим обра-
образом. Показатели уравнения в точке ?~ =?^0 равны 0 и У2.
Если мы введем новую переменную С , то эти показатели станут
равными 0 и 1, а сама точка С=0 будет регулярной. Зато осо-
особенность, которая раньше была в точке С=1, теперь вследствие
введенного преобразования распадется на две особенности в точ-
точках С = -)- 1 и С =—1. Особенность в бесконечности сохра-
сохранится, но показатели уравнения там удвоятся. Следовательно, мы
получим опять гипергеометрическое уравнение, причем будет иметь

208
ГЛ VII. ЧАСТНЫЕ РЕШЕНИЯ УРАВНЕНИЯ ТРИКОМИ
место тождество
со 0 1
-Ц-^ 0 0
±
оо
_2д + 4- О
[-*+!
2ц
Однако эта запись равенства VII, 4 A) пока еще не дает возмож-
возможности выявить новые замкнутые решения. Для отыскания этих ре-
решений необходимо, прежде чем устранить особенность в нулевой
точке, выполнить дробно-линейное преобразование, меняющее ме-
местами точки 1 и оо. Мы получим
= A— Zf^
0 1
1
и. _(_ —— —- 2ia
f оо О 1
w " J*+ 12
= A —r)(ViJ
оо —1 1
Последнюю Р-функцию еще раз преобразуем так, чтобы для новой
Р-функции точки 0 и 1 стали особыми. Для этой цели введем новую
переменную
— 1
Это преобразование перемещает точку оо последней Р-функции
в точку 1, точку —1 в точку 0 и точку -\-1 в точку оо.

§ 5 СПЕЦИАЛЬНЫЕ РЕШЕНИЯ G
209
В результате мы получим
о=A - с)A/^ (уг
х
О 1 оо
О 0 — 2|л-+
C)
Отсюда находим, что замкнутые решения возможны также в том
случае, когда
1 . h
Составим сводку полученных замкнутых решений, причем вер-
вернемся к переменным ч\ и Ь.
Решения ф, соответствующие равенству VII, 4 A), можно пред-
представить в виде
оо 0 1
-H + i 0 0
12 "
Следовательно, мы имеем два решения:
оо 0 1
оо 0 1
J_
12
5
0 0 ?,
Таким образом, замкнутыми решениями будут
при 1* = -^- + А
1 1 9
Dа)
14 Зак. 534. К. Г. Гудерлей

210 ГЛ. VII. ЧАСТНЫЕ РЕШЕНИЯ УРАВНЕНИЯ ТРИКОМИ
-*. _м4. i. |f); D6)
при p=~
при [i^-^
Fа>
И
при (a==-^-
'•2'
Gа)
-ev.+») , , 1.3
(Ч \ / 0 Я2\-"("/в+ай) / 1 3 Q ft'\
т^О-Н) р(-^-т-к'1'тЬУ'Gб)
1 , Л
при ji = -+2-
ф = 7i(VJ+(8fc/a) J 1__? I x
T • V «, /a /
--3- L ,* J (8a)
X
XF -ft, -i-A.^-, U± 4r^ • (86)

§7. ПРИБЛИЖЕННЫЕ ПРЕДСТАВЛЕНИЯ ФУНКЦИЙ G ПРИ БОЛЬШИХ | р. 1 211
Очевидно, что решения (8) не обладают свойствами симметрии
относительно оси & = 0; поэтому мы можем разложить их на сим-
симметричную и антисимметричную составляющие. Таким путем мы по-
получим для рассматриваемого значения [J. два линейно независимых
решения. Соответствующие вычисления будут выполнены в § 3
гл. VIII. Для решений D) — G) такой способ отыскания второго
линейно независимого решения (для рассматриваемого значения [х)
невозможен; для этой цели требуется вычисление интеграла.
§ 6. Соотношения между решениями с различными
значениями ;л
Существование соотношений между некоторыми решениями с раз-
различными [х вытекает из следующего: если мы продифференцируем
решение дифференциального уравнения Трикоми по &, то, очевидно,
получим новое решение уравнения Трикоми, так как коэффициенты
последнего не зависят от &. Выполнив это дифференцирование
и использовав равенства VII, 2A) и VII, 2B), мы найдем
/(С »--§-) = cV(C я),
где под / следует понимать соответствующим образом выбран-
выбранные решения гипергеометрического дифференциального уравнения
VII, 2C). Такого рода соотношения известны из теории гипергеомет-
гипергеометрических дифференциальных уравнений. Для решений О получаются
с помощью равенств VII, 4F) и VII, 4(8) следующие соотношения:
= 6 (_ р + ^ (_ р+^ х
Xp-C«+f-c/,)G(e)(l Р—j); @
B)
В показателе величины р и во втором аргументе функции G пара-
параметр ]х следует взять с одинаковым знаком.
§ 7. Приближенные представления функций О
при больших | [i|
Для теоретических исследований (в частности, для исследования
сходимости), а также для вычислительных целей желательно иметь
приближенные представления функций О при больших значениях |[х|.
Их можно вывести из интегральных представлений гипергеометри-
гипергеометрических функций с помощью метода перевала. Однако такой путь
14*

212 ГЛ. VII ЧАСТНЫЕ РЕШЕНИЯ УРАВНЕНИЯ ТРИКОМИ
требует специального исследования вблизи точки ? = 0. Поэтому
следует предпочесть способ, рассмотренный в § 6 гл. V в связи
с дифференциальным уравнением Чаплыгина. Аналогия существует
между следующими величинами:
да и 5; ри-1р?; ? и Aеу.
Переменную, соответствующую прежней величине х, обозначим
через \. Тогда в соответствии с равенством V, 6(8) мы будем
иметь
Т = Г/1. Aа)
где
Как в дозвуковой, так и в сверхзвуковой области следует выбрать
ту ветвь функции X, для которой разложение в точке 5 = 0 начи-
начинается с члена X. Выражение A6) может быть проинтегрировано,
и мы получим
при |>0 Г==^1п1±|-\ Bа)
при |<0 f=*arctg(—?/,), 0<!<у. B6)
Прежнюю величину dx/dw следует заменить величиной dfydX. Для
этой цели вычислим величину
Далее введем величину hv соответствующую прежней величине h.
Для нее мы получим выражение
Допустим теперь, что
ОE) = А1E)ОA, р), C)
причем функция G играет такую же роль, какую функция z играла
в уравнении V, 6 Bа). Допущение C) приводит к дифференциаль-
дифференциальному уравнению
^[9р,Ч + гA)]О = 0. D)

§ 7 ПРИБЛИЖЕННЫЕ ПРЕДСТАВЛЕНИЯ ФУНКЦИИ G ПРИ БОЛЬШИХ | V- | 213
Член г(?) не играет особой роли, так как в области
или, что то же, в области
он ограничен. При больших | [а | им можно пренебречь, и тогда
решения уравнения D) могут быть выражены через функции Бес-
Бесселя порядка 7зх). Это приводит к следующим асимптотическим пред-
представлениям функции G:
при ? <^ 0;
>0,
или, если использовать равенство Aа),
гг 1-е IV. !-?3 1/п
О— х
при
при
При небольших значениях % > 0 из равенства A6) мы имеем
Поэтому, разложив функции Бесселя /+i/3 и
лучим при \ =О
^
/_i/3 в ряды, мы по-
Eа)
»)Ь E6)
Если наложение обоих выражений E) должно представлять ре-
решения G'a' или О , то это должно иметь место также при 1 = 0.
Следовательно, мы выполним необходимое (но не всегда достаточное)
условие, если построим приближенные представления так, чтобы для
больших | [х [ они совпадали — при ? = 0 — с исследуемыми функ-
функциями G или G как в отношении значений самих функций, так;
и в отношении значений их первых производных. Первый член правой
!) Таблицы для этих функций указаны в списке литературы 1 (Compu-
(Computation Laboratory).

214
ГЛ VII ЧАСТНЫЕ РЕШЕНИЯ УРАВНЕНИЯ ТРИКОМИ
части равенства VII, 4A4) совпадает —с точностью до неко-
некоторого множителя — с выражением E6), а второй член — тоже
с точностью до множителя — с выражением Eа). Асимптотическое
представление решения VII, 4A4) можно упростить, если заменить
входящие в это решение коэффициенты их асимптотическими вы-
выражениями. Покажем, как вычислить такое выражение для пер-
первого коэффициента. Прежде всего воспользуемся соотношением
VII, 4A5д), вытекающим из формулы Стирлинга, а затем устраним от-
отрицательный аргумент в функции Г(—р. —(— б/12) посредством фор-
формулы VII, 4A56). Мы получим
Выполнив аналогичные преобразования для второго коэффициента,
мы найдем
Далее, использовав соотношения Eа) и E6), мы получим
X
1 —?3
П (
Ча
V 3 / I 3 j
(С
"A
),.
¦r s
1 —
) +Г (-1) [х% sin [« (у +J1)] X
при
и аналогичное выражение при
Для дальнейших упрощений воспользуемся опять соотноше-
соотношениями VII, 4A5). В результате мы будем иметь
G(SJ~^uA
' /sin fit (u, +-н
I L \ i*,
+ Щ]1>/Л^\Ц)} при ?<0
- sin
/ia {sin [я ((х +
J7C/6 ЧУ"
при

g 7. ПРИБЛИЖЕННЫЕ ПРЕДСТАВЛЕНИЯ ФУНКЦИЙ О ПРИ БОЛЬШИХ | V-1 215
(а)
Выполнив аналогичные вычисления для О , мы получим
при ?<0
1/a {sin [«; (p +1)] к-^/в
при
Для дальнейшего исследования целесообразно перейти от функ-
функций Бесселя к функциям Ханкеля, воспользовавшись для этого со-
соотношениями
1
Fа)
l> (Z) 4- е-™!ъН(?Ц (zj\. F6)
Тогда мы получим
'{sin [я
при
Ga)
G6)
Ma) I i/ _i/
1 ^-WtlJ.-"/,
Для функций Ханкеля Я^ и
ставления:
К "
при &>0. (86)
существуют асимптотические пред-
¦% при — 2тс < arg г <тс; (9а)
i7r при — тг < arg2< 2тс. (96)

216
ГЛ. VII. ЧАСТНЫЕ РЕШЕНИЯ УРАВНЕНИЯ ТРИКОМИ
Из этих формул следует, что функции Н[^ и Н$> при больших
значениях аргумента асимптотически не совпадают (для функций
Бесселя Ь/а и 1_,/г такое совпадение, напротив, имеет место). В са-
самом деле, одна из этих функций Ханкеля при возрастании z стре-
стремится к бесконечности, а другая — к нулю. Это обстоятельство
весьма важно для определения области применимости асимптотиче-
асимптотических представлений.
С помощью формул (9) можно исследовать поведение решений G)
при % = — оо и при ? = 1 для того, чтобы произвести сравнение
с точными решениями. При больших значениях аргумента функции
Ханкеля и при I < 0 формула Gа) после некоторых преобразова-
преобразований приводится к виду
1 М Via г / _ „д-1
14 \п (ъ ,\\ AОа)
Так как, согласно равенству B6), | I [ = тг/2 при % = — оо, то фор-
формула A0а) дает асимптотическое совпадение с первым членом раз-
разложения решения G(s) в ряд [см. равенство VII, 4A0)].
При ? > 0 мы получим из формулы G6)
¦-я- е
" ел-i
или, приняв во внимание равенство Bа),
_?3 Vis
-,(8)
X
X
Если вещественная часть параметра |х положительна, то первый член
правой части формулы A0а) значительно больше второго, за исклю-
исключением тех случаев, когда
т. е. при
=\, 2
В этих исключительных случаях асимптотическим представлением
решения G будет
при
= А — -
A0в)

g 7 ПРИБЛИЖЕННЫЕ ПРЕДСТАВЛЕНИЯ ФУНКЦИЙ О ПРИ БОЛЬШИХ I у-1 217
Если параметр <х мнимый положительный, то асимптотическое пред-
представление A06) принимает вид
О
(8)-
1 —
' cos
B 11*|1 — ^). (Юг)
Если, кроме того, 1—?<^1, то \ ^> 1 и получаются следующие
приближенные представления:
G(s)~sin[ir(l»4-|-)]4ll(l—«3)A/l')~11. V^h — -|, (Па)
G(s> — етс ' ^ ' A — 13УЛа ее
\\ — положительное мнимое. (Ив)
Эти формулы мы можем сравнить с формулой VII, 4A6), в кото-
которой |A.| следует считать большим. При ^фН — 3/4 вторым членом
формулы VII, 4A6) можно пренебречь; тогда, использовав соотно-
соотношения VII, 4A5в) и VII, 4A5д), мы получим
"" 2 ^ при | и,
Таким образом, дари р ф h — 3/4 формулы (Па) и VII, 4A6
действительно совпадают. Аналогичным образом можно показать
совпадение формулы A16) с формулой VII, 4A6) при ]л = /г — 3/4.
При чисто мнимом |л первые и вторые слагаемые в фор-
формуле VII, 4A6) представляют собой сопряженные комплексные
величины, и поэтому достаточно вычислить только их удвоенную
вещественную часть. И в этом случае формула VII, 4 A6) совпадает
с асимптотической формулой (Ив). Следовательно, при Rejx^-0
имеет место асимптотическое совпадение в точках ? = 0, | = — оо
и \ = 1. Но так как
то тем самым охватывается вся область изменения.
Выполненное исследование еще не доказывает, что формулы G)
являются асимптотическим представлением решения G^, однако
полученные результаты дают основу для такого доказательства.

218
ГЛ. VII. ЧАСТНЫЕ РЕШЕНИЯ УРАВНЕНИЯ ТРИКОМИ
Аналогичные формулы для антисимметричных частных решений
имеют вид
р(а) 1
G(a) ~ -L
2,a
1-55
1-53
V» . г / ni/1 + Г/.
sin те и. +-г —!——
L V ' 4/J \ 1—5'/.
1-6»
(-1)"
при
при
A2а)
A26)
¦ = h — 1/i, A2b)
2р.
— 5»
при положительном мнимом [а. A2г)
Пусть Gj есть следующее специальное решение уравнения, опре-
определяющего О:
dft, ji) = A — 53)ОЛа>
, 1-6»). A3)
Равенство VII, 4A6) представляет собой линейную комбинацию
решений G^S, jj.) и G^S, —(а). Мы видим, что
ОгA МФОгв, —V).
Для Gx получается асимптотическое представление
—58
1-53'
A4)
оно применимо во всей комплексной плоскости ji, за исключением
отрицательной вещественной оси.
§ 8. Функциональный определитель частных решений G
В § 7 гл. V мы получили для функционального определителя D
формулу V, 7A2), которая, если положить pW=l, принимает
«ид
D = -(x-|_l)%(<l>' —Т$- A)
В сверхзвуковой области можно принять, что
Bа)

% 8 ФУНКЦИОНАЛЬНЫЙ ОПРЕДЕЛИТЕЛЬ ЧАСТНЫХ РЕШЕНИИ О 219
где
Du = (n'%±^. B6)
Так как Dx и D2 линейны относительно ф, то определение знака
функционального определителя в сверхзвуковой области выполняется
особенно просто. Если ф задано равенством
ф = т)"/С. я),
то мы получим
^-^- ± («/-З;/')}. C)
Если решения налагаются одно на другое, то соответствующее
наложение производится и в выражениях для Dx и D2. Часто бывает
достаточно определить знак функционального определителя вдоль
С=1 (или 1=1).
В дозвуковой области функциональный определитель всегда
отрицателен. Если же вдоль С=1 функциональный определитель
принимает положительное значение, то в промежуточной области
должна иметь место перемена знака, что обычно делает решение
непригодным. В связи с этим мы выведем некоторые критерии,
позволяющие установить знак функционального определителя вдоль
С= 1 вблизи нулевой точки.
Подставив в равенство
вместо р его значение т]3(С—1) [см. равенство VII, 3A)], мы
получим
4» = tj -рл)+8р- <;: — 1 )-с/»>+«ь о a. t*).
Два линейно независимых решения О можно взять, например, из
равенства VII, 4 G). Тогда, введя произвольные коэффициенты ct
и с2, мы получим частное решение в следующем виде:
Если имеется линейная комбинация таких выражений с различ-
различными [*, то при малых значениях т\ и |С—1| среди первых членов
всех взятых выражений вида D) главную роль играет тот, которому
соответствует наименьшее значение (л. То же самое имеет место
и для вторых членов. Отношение же главного первого члена к глав-
главному второму члену зависит от показателя степени A—СJ''' во
втором члене.
В качестве примера рассмотрим случай, когда показатели сте-
степени в главных членах одинаковы. Использовав равенство C), мы

220 ГЛ VII ЧАСТНЫЕ РЕШЕНИЯ УРАВНЕНИЯ ТРИКОМИ
найдем, что в окрестности С = 1
D2 = , -
I
12"
Здесь при [j. >• х/г первые члены значительно больше вторых, по-
поэтому функциональный определитель положителен. При |* < 0 зна-
значительно больше вторые члены, поэтому для С > 1 (или 5 <С 1)
функциональный определитель отрицателен, а для С < 1 (или % > 1)
положителен.
При 0 < [j, < х/г в ?*i главную роль играет первый член,
а в D2 — второй член, поэтому знаком функционального определи-
определителя будет
Если имеется только первый член, то
sgn D = sgn B[л — 1),
если же имеется только второй член, то
sgnD = — sgn (С— 1).
В случае неодинаковых показателей степени главного первого
и главного второго членов знак функционального определителя за-
зависит от того, каким образом tj и 'С — 1 одновременно приближаются
к нулю. Если один из критериев дает для функционального опре-
определителя положительный знак, то рассматриваемое решение подлежит
исключению. За подробностями отсылаем к работе Гудерлея [3J
(см. лит. 1), здесь же ограничимся только сводкой различных кри-
критериев.
Обозначим показатель главного первого члена через \xv а по-
показатель главного второго члена — через [а2.
1. Приближение к нулевой точке плоскости т;, & проходит вдоль
линии |С—1 | = const <^ 1.
При р.2>-1А1
или с2 = 0 sgnD = sgn ((ij — -~\. Eа)
При A2<1*1
или с1 = 0 sgnD = sgn[—[j,2(C—1)]. E6)
При fJ.1 = p.2>72
и ^ФО, с2ф0 D>0. Eв)

§ 9 СИСТЕМЫ ЧАСТНЫХ РЕШЕНИИ ' 221
При 0 < jix = ;х2 < V2
и схфЪ, с2ф0 sguD = sgnc1c2(C — 1)^! — -^у Eг)
При JA1 = ft><0
и С1фО, с2ф0 sgnD = sgn(;— 1). Eд)
2. Другие пути приближения к нулевой точке.
и с^О sgn D = sgn ^4 — ~у Fа)
При 0 < ^2 < i/2
и С!=?0, с2=?0 sgn D = sgn CiC2 (С — 1)^ — -yg-J. F6)
При (i2 < О
и с2=?0 sgnD = sgn(;—1). Fв)
§ 9. Системы частных решений
При исследовании течений возникает вопрос о правильном
выборе частных решений. Часто (например, в случае течений
с числом Маха, равным единице, см. гл. VIII) бывает известно, что
решения и их производные из физических соображений ограничены
вдоль характеристики ? = 1, правда, иногда за исключением начала
координат. В этом случае выбор частных решений производится
следующим образом. Внесем в уравнение VII, 3C) вместо G(S, \x)
его выражение VII, 4A6), т. е. симметричное частное решение
вблизи 5"—1, затем заменим в соответствии с равенством VII, 3A)
р на тK(^—1) и сохраним в каждом из гипергеометрических рядов
только первый член; мы получим
. J Г Bц) sin Г* (,*+!)] (»О|+4У] , |
Для того чтобы решение ф и его производные оставались конечными при
' = 1> коэффициент при втором члене должен быть равен нулю.
(Случай, когда показатель степени во втором члене равен положи-
положительному целому числу, должен быть исключен, так как тогда гипер-
гипергеометрический ряд первого члена вырождается.) Это требование

222 ГЛ VII. ЧАСТНЫЕ РЕШЕНИЯ УРАВНЕНИЯ ТРИКОМИ
приводит к условиям
откуда
u=:J ,h_ I
12 1 3 ' | B>
где /г есть неотрицательное целое число. Аналогичным образом для
антисимметричного решения, определяемого равенством VII, 4A7г),
получаются условия
1 , h
C)
Эти решения в дальнейшем будут играть особую роль, поэтому
введем для них специальное обозначение, а именно будем обозначать
их буквою ф с нижним индексом, указывающим степень, в которой
в решение входит переменная р. Кроме того, иногда для ясности
будем отмечать антисимметричные и симметричные решения посред-
посредством соответствующего верхнего индекса {а или s). Впрочем, не-
необходимости в этом нет, так как для заданного показателя степени р,
например —5/6> при % =1 конечное значение имеет либо только
симметричное, либо только антисимметричное решение (то же самое
относится и к производным этого решения). Все эти решения могут
быть выражены в замкнутом виде [формулы VII, 5C)—VII, 5(8)].
Таким образом, мы имеем следующий набор решений:
Иногда мы будем называть эти решения естественными част-
частными решениями.
Соображения, которые приводят к этому выбору частных реше-
решений, настолько очевидны, что не требуют пояснений. Однако они
ни в коем случае не могут служить доказательством полноты полу-
полученной системы решений. Такое доказательство без труда можно
дать для другой системы решений, связанной с задачей на собствен-
собственные значения. Дифференциальное уравнение VII, 3 F), определяю-
определяющее G, имеет такой же вид, как и соответствующее дифферен-

5 9. СИСТЕМЫ ЧАСТНЫХ РЕШЕНИЙ 223
циальное уравнение в классической задаче на собственные значения,
за исключением того, что коэффициент при G меняет знак. Условие
G = 0, или (—5)~ —5|- = 0,
имеющее место вдоль & = 0 (? = — оо), если ограничиться только
симметричными или антисимметричными частными решениями, тоже
имеет такой же вид, как соответствующее условие в задаче на соб-
собственные значения. Однако граничные условия, используемые нами
при ?=1, не могут быть использованы в задаче на собственные
значения. Для того чтобы выйти из положения, прибегнем к сле-
следующему искусственному приему: введем верхнюю границу ?=с2
(с2 < 1) области, подлежащей рассмотрению, и потребуем, чтобы там
было О = 0, а затем будем приближать с2 к единице.
Сначала исследуем случай, когда с2<1. Положим [j,2 = X.
Пусть Gj и G2 суть два решения дифференциального уравнения для G,
соответствующие двум различным значениям X, которые обозначим
через Xj и Х2. Далее, пусть решения Gt и G2 удовлетворяют усло-
условию, заданному при $ = — сю. Преобразуем интеграл
с3
—^г О, (%) Go (I) dl
путем интегрирования по частям [с использованием уравнения
VII, 3 F6) и с учетом граничного условия при ? = — сю]; мы получим
dGl
16
E)
16

224 ГЛ VII ЧАСТНЫЕ РЕШЕНИЯ УРАВНЕНИЯ ТРИКОМИ
откуда
(с2) ^ (с2)] . F)
Если функции 0t и 02 удовлетворяют граничному условию G = О
при ? = с2, то из равенств D) и E) мы получим следующие соот-
соотношения ортогональности:
5 r, ,ts n ,ts ft^Q ПрИ xt ф \2, Gа)
J
/ A - &3)"'* ^ "^ Л = 0 при Xt ^ Х2. G6)
— со
Будем рассматривать О в формуле F) как функцию от I и к;
пусть эта функция удовлетворяет граничным условиям при % = — оо.
В качестве определения функции О можно взять либо одно из вы-
выражений VII,-4 A0), VII!_4A1), VII, 4A4), VII, 4A6), либо VII, 4A7),
заменив в них |а на У~\. Если мы совместим Xt и Х2, а тем самым Ot
и G2, то формула F) примет вид
<(для краткости мы обозначили левую часть буквой С). Эта формула
играет особо важную роль в том случае, когда О является собст-
собственной функцией. Она встречается у Гудерлея ([5] и [6], см. лит. 1).
Из соотношения ортогональности G6) вытекает, что собствен-
собственные значения Х = ;х2 должны быть вещественными. Доказательство
основано на тех же соображениях, как и в классической теории
задачи на собственные значения, только в настоящем случае ввиду
перемены знака у члена 5/A — ?3) в соотношении Gа) при 5 = 0
нельзя исходить из этого соотношения. Ход доказательства в основ-
основном следующий. Если бы существовало комплексное собственное
значение Х = >.г-)-Дг, то сопряженное комплексное число Х = ХГ —ikt
также было бы собственным значением, так как дифференциальное
уравнение VII, 3F) имеет только вещественные коэффициенты.
¦Соответствующие собственные функции также были бы комплексно

§ 9. СИСТЕМЫ ЧАСТНЫХ РЕШЕНИИ 225
сопряженными. Обозначим их через
G+ = Qr+- iGi и О" = Gr — iGi.
Так как собственные значения >. = Хг —|— iX^ и Х=ХГ— /Х^ не равны
друг другу, то можно применить соотношение ортогональности G6).
Мы получим
Левая часть этого равенства, безусловно, положительна, следовательно,
сделанное предположение о существовании комплексного собствен-
собственного значения неверно.
Полнота системы собственных функций может быть доказана
с помощью гильбертовой теории интегрального уравнения с поляр-
полярным ядром (Гамель, см. лит. 1). Классическая теория (с использо-
использованием интегральных уравнений с положительно определенным ядром)
не приводит к нужному результату вследствие перемены знака
у весовой функции 1/A —?3)'/о в соотношении Gа).
В дальнейшем ? = сх будет означать нижнюю границу рассмат-
рассматриваемого интервала. Пусть там выполняется одно из граничных
условий:
О = 0 или 4!г = 0.
Если ct и с2 лежат в дозвуковой области, то Х = ;а2 безусловно
положительно. В самом деле, из условия, что 0 = 0 при Z = cl
и ? = с2, следует, что между этими точками имеется по крайней
мере один максимум абсолютного значения О. Если G в точке
с максимальным значением положительно, то вторая производная
безусловно отрицательна (первая производная, конечно, равна нулю).
Дифференциальное уравнение VII, 3F), определяющее G, показывает,
что это возможно только при положительном X. Такой же результат
получается и для граничного условия Q' ==0 на концах интервала.
Если сг и сг лежат в сверхзвуковой области, то, как показывают
аналогичные рассуждения, возможны только собственные значе-
значения X < Vi2-
Если Cj лежит в дозвуковой, а с2 — в сверхзвуковой области,
то получаются как положительные, так и отрицательные собствен-
собственные значения X. Если X отрицательное, то |а — мнимое.
15 Зак. 534. К. Г. Гудерлей

226 * ГЛ. VII. ЧАСТНЫЕ РЕШЕНИЯ УРАВНЕНИЯ ТРИКОМИ
Применив формулу (8) к собственной функции и использовав
соотношение D), мы получим
-00 V > —; 9А. —СО
16
Так как интеграл в правой части всегда положителен, то С всегда
имеет такой же знак, как Vie — 9Х..
Будем располагать собственные значения по их величине и обо-
обозначать их следующим образом:
.. .Х_д, . . ., Х_3, Х_2, \_1, Xlt \2, Х3, .. . , kh, . . . ,
причем отрицательные индексы относятся к отрицательным собст-
собственным значениям, а положительные — к положительным собствен-
собственным значениям. Аналогичный способ обозначения при необходи-
необходимости будем применять также для соответствующих значений ц.
Для собственных функций будем пользоваться обозначениями
• • • G-h °-з. G_2, G_v Gt, G2, G3 Gh, ... .
Аналогичным способом будем обозначать и значения С, соответст-
соответствующие собственным функциям G.
Так как система функций G полная, то функция у(?), если она
удовлетворяет определенным условиям непрерывности, может быть
представлена в виде
У (?) = 2 чОь F) + 2 в-дО-ft (О- (»)
ft=l й=1
Коэффициенты а±п можно найти с помощью формулы (8), предва-
предварительно умножив равенство (9) на Шй(?)/A—?3O/", проинтегрировав
по интервалу (— оо, с2) и применив соотношение ортогональ-
ортогональности Gа). Мы получим
1 f
«8)
A0)
§ 10. Представление некоторых решений уравнения Трикоми
в виде наложения частных решений, составленных
из собственных функций
Из полноты системы собственных функций следует, как пока-
показывают приводимые ниже рассуждения, полнота системы частных
решений, составленных из собственных функций. Рассмотрим такое
решение уравнения Трикоми, взятого в виде VII, 3 Eа), которое

§ 11. СОБСТВЕННЫЕ ФУНКЦИИ И СОБСТВЕННЫЕ ЗНАЧЕНИЯ ПРИ сг -> 1 227
вдоль S = с1 и ? — с2 удовлетворяет либо граничному условию ф = О,
либо условию ф5 = 0. Пусть это решение пригодно в области
р! <С р <С р2. где pj и р2 суть подходящим образом выбранные постоян-
постоянные. Тогда, вследствие полноты системы функций О, решение вдоль
линии р = const можно представить в виде наложения этих функций,
т. е. в виде
ft=+oo
Ф= 2 Мр)од(&), A)
Й=— со
где а±д(р) суть некоторые функции от р. Поскольку сделано пред-
предположение, что дифференциальное уравнение VII, 3 Eа) справедливо
в рассматриваемой области везде, должны везде существовать произ-
производные, входящие в это уравнение; их можно вычислить, произведя
дифференцирование под знаком суммы A). Таким путем мы найдем
¦fr4)= 2 Ц
д?
а.[A^Ч] 2 Mp)-
Внеся эти значения в уравнение VII, 3 Eа) и использовав диффе-
дифференциальное уравнение VII, 3 F), определяющее О, мы получим
следующее уравнение для вычисления коэффициентов ah:
Отсюда найдем
где Ам и Апг суть постоянные. Подставив эти значения в уравне-
уравнение A) и приняв во внимание уравнение VII, 3C), мы увидим, что
решение ф получается именно в виде наложения частных решений,
составленных из собственных функций.
§ 11. Собственные функции и собственные значения
в предельном случае с2 ~* 1
Начиная отсюда, будем считать нижней границей рассматривае-
рассматриваемого интервала опять сх = — со. Для того чтобы определить соб-
собственные значения в предельном случае с2 —>¦ 1, будем исходить
из формулы VII, 4A7г). Если \ = с2 лежит вблизи единицы, то
гипергеометрические ряды могут быть заменены их первыми членами,
15*

228
ГЛ VII. ЧАСТНЫЕ РЕШЕНИЯ УРАВНЕНИЯ ТРИКОМИ
и тогда из условия G = О мы найдем
Г B,) .Ш [«(„+!)] ш
ч и-+С/и)
= 0. A)
Так как это равенство не изменяется при замене ц на —^,, то мы
всегда можеЫ считать, что \х положительно. Разделим равенство A)
IS\
4,0
-3,0 -2,5 -2,0 -1,5 -10 -0,5
Рис. 66. Антисимметричные собственные функции б(а)E,
для у. = 3/„ и. = 'Л. V- — "U.
0,5 1,0
— Сч] и затем будем приближать с2 к единице. Тогда
для антисимметричных частных решений мы получим
т.
=1. 2
B)
Аналогичным образом из формулы VII, 4A6) для симметричных
частных решений мы найдем
Рл = --§+*. А=1, 2 .... C)
Первые три из этих собственных функций изображены на рис. 66
для антисимметричных частных решений, а на рис. 67 — для сим-
симметричных частных решений.

§ 11. СОБСТВЕННЫЕ ФУНКЦИИ И СОБСТВЕННЫЕ ЗНАЧЕНИЯ ПРИ с2-> 1 229
Теперь необходимо определить отрицательные собственные зна-
значения. Для мнимого [а оба члена, входящие в формулу VII, 4A7г),
комплексно сопряженные. Опять заменим гипергеометрические ряды
их первыми членами, равными единице, и положим
[А = /V.
Далее, введем обозначение
Г Bц) sin Г* (ц + J-YI
I 2 / / 11
V 'V u + il
— a N)ei
D)
\
>
=^\
\
/
Л
/
/
/
1,5
1,0
35 °
^-0.5
-1,0
-1,5 .
-3.0 -2.5 -2,0 -IS -1,0 -0,5 0 0,5 1,0
Рис 67. Симметричные собственные функции С»3' (Е, р-)
ДЛЯ [Л = Vi, Н- = 5Л» ^ = 74-
где /4(v) и e(v) суть вещественные величины. Тогда мы получим
или
cos [а (V) — -> In (l — cl) = 0.
Собственные значения мы найдем, положив
o(v) — vln(l — ct) = (h—\Y'
E)
где й есть целое число. Если с2->1, то !пA—с|) стремится
к отрицательной бесконечности, и расстояние между соседними соб-
собственными значениями становится бесконечно малым, т. е. полу-
получается непрерывный спектр отрицательных собственных значений.
Для симметричных частных решений получается такой же результат.

230 ГЛ VII ЧАСТНЫЕ РЕШЕНИЯ УРАВНЕНИЯ ТРИКОМИ
Частные решения, которые можно составить из только что най-
найденных собственных функций, обычно не имеют такого вида, какого
можно было бы ожидать на основании физических соображений.
Так, например, частные решения вида
имеют при найденных здесь положительных значениях [а особенность
в производных высшего порядка, распространяющуюся вдоль S=l.
При мнимых же значениях (j, эти частные решения колеблются
вблизи 5=1 с неограниченно возрастающей частотой и стремятся
к бесконечности при р-»¦(). В § 13 настоящей главы мы рассмот-
рассмотрим преобразование, которое позволяет выявить свойства функции <|>>
ожидаемые из физических соображений. Пока же мы можем опе-
оперировать лишь найденным классом частных решений, так как пол-
полнота системы решений доказана только для него.
§ 12. Представление произвольной функции
в предельном случае с2 -*¦ 1
Вследствие непрерывности спектра отрицательных собственных
значений непосредственное использование уравнения VII, 9(9) для
представления произвольной функции невозможно. Выполним необ-
необходимый предельный переход для произвольной функции на примере
антисимметричных частных решений. В конце параграфа приведем
готовый результат также для симметричных частных решений.
Если с2->\, то для произвольной функции на основании урав-
уравнения VII, 9(9) мы найдем
где Сй определяются формулой
-f-^dx. B)
Для вычисления C±h воспользуемся соотношением VII, 9(8). С целью
сокращения записей введем обозначение

§ 12. ПРЕДСТАВЛЕНИЕ ПРОИЗВОЛЬНОЙ ФуНКЦИИ ПРИ с,>1 231
Тогда на основании формулы VII, 4A7г) мы получим для G<°) вблизи
1=1 следующее выражение:
sin
+ В (- ц) sin [u (- tx +1)] A - |з)('/»)+., D)
В качестве подготовительного шага для вычисления Ch найдем про-
производную
= В («О sin [те (, +1)] (- 3) (^ - ,) A - РГ<"/">-" +
+ В (- [х) sin [u (- ;х +1)] (- 3) ( ^ + ц) A - ^-С'АО+и.. E)
Хотя первые члены правых частей равенств D) и E) при значе-
значениях (л, соответствующих собственным значениям, равны нулю, тем
не менее они вносят в производные по ^ большую долю, чем вто-
вторые члены. Отбросив члены более высокого порядка относительно
1 — I3, мы получим из равенств D) и E) при собственных значе-
значениях следующие выражения для производных по \ь:
ф
Наконец, вспомнив, что для собственных значений имеет место
равенство
[это следует из равенства VII, 11C)], мы найдем с помощью соот-
соотношения VII, 9 (8), что
'(— Ы- F)
причем fj. следует взять из равенства VII, 11C), а В(\ъ) — из
равенства C).
Для отрицательных собственных значений опять положим
11.-= Л. G)
Значения ч, соответствующие значениям ph, будем обозначать через vft.
Из равенства G) мы имеем
?- = -1. Gа)
Между функциями В, А и а на основании равенства VII, 11D

232 ГЛ VII ЧАСТНЫЕ РЕШЕНИЯ УРАВНЕНИЯ ТРИКОМИ
существует соотношение
В (Ь) sin Ггс (v> + 1YJ = А (?) е1" W. (8)
Вычислим производные
да дО
д\>. di
для собственного значения, т. е. с одновременным учетом равен-
равенства VII, 11E), причем для некоторых членов выполним предель-
предельный переход с2—>1. Из равенства D) мы получим
G(a) = (l — cl)'/a A (v) cos [a (v) — v In (l — cl)]>
X sin [a (vjO _ vA In (l — d)] (~ Ы — In (l — cty,
sin [a(vft) - vft In
Вследствие равенства VII, 11 E) абсолютное значение входящих
сюда синусов равно единице. При \ — с2 функция О = 0, и из фор-
формулы VII, 9 (8) мы найдем
[^] (9)
Следовательно, С_й стремится к бесконечности, если 1—с| при-
приближается к нулю.
Теперь необходимо учесть, что при выполняемом предельном
переходе отрицательные собственные значения располагаются все
ближе и ближе одно к другому. На основании равенства VII, 11E)
мы имеем
a(vA)—vAln(l—$ = 1г(а—i-). (Ю)
Если h изменяется на единицу, то a(vA) при небольших значениях
1—с| изменяется только на небольшую величину. Обозначив изме-
изменение у^ между двумя последовательными значениями h через Avfe,
мы найдем из равенства A0), что
1 — с| -> о. (П)
Воспользовавшись этим соотношением, перейдем во втором члене
правой части равенства A) от суммирования по А к суммированию

по
§ 12. ПРЕДСТАВЛЕНИЕ ПРОИЗВОЛЬНОЙ ФУНКЦИИ ПРИ С,-> 1 21
AvA. Подставив одновременно С_л из формулы (9), мы найдем
с2
Теперь можно выполнить предельный переход ?2 —> 1. Мы получим1
¦h«
A2)
Заменим в правой части равенства A) второй член его выраже-
выражением A2), подставим вместо Ch его значение F) и выразим А через В
с помощью соотношения (8). Наконец, в равенстве A2) интегриро-
интегрирование по v заменим интегрированием по [i и выполним последнее
вдоль положительной мнимой оси комплексной плоскости jx. В ре-
результате мы получим
X
— - Г
2 J
X
- ,а) sin
1)] sin [я ( - (X + i-
где
Х
¦
J
а(») = А — 4-
"ft 4«
A3а)
Г ТГ
A36)

234
ГЛ. VII. ЧАСТНЫЕ РЕШЕНИЯ УРАВНЕНИЯ ТРИКРМИ
Аналогичная формула для симметричных частных решений имеет вид
X
где
, ft)
fiW GO Z?(s> ( - (x) sin [« (p + I)] sin [„ (- ц +1
Г Bц)
X
A4)
A4a)
4S) = h ¦
'
A46)
§ 13. Разложение решения ф по частным решениям
В начале § 9 мы выбрали систему частных решений, исходя
из требования, чтобы решение ф обладало определенными свой-
свойствами вдоль характеристик, проходящих через нулевую точку.
контур сверхзвуковой
области
характеристики,
вдоль которых
распространяются'
особенности
особенность в одной из производных
высшего порядка от граничных
значений
аница сходимости
— я/я *
е
'я разложения tl/
по степеням /» '
линия ?=con*t, на которой т/> разлагается
1 ряд по степеням р
Рис. 68. Пояснение ограничений, налагаемых на разложение решения ф
по естественным частным решениям.
Однако вопрос о том, пригодна ли эта система для представления
любой функции ф, обладающей этими свойствами, остался откры-
открытым. Между тем возможность отыскания такого представления весьма
заманчива. Обычно нулевая точка плоскости i\, & изображает беско-

§ 13. РАЗЛОЖЕНИЕ РЕШЕНИЯ Ф ПО ЧАСТНЫМ РЕШЕНИЯМ
235
нечность плоскости течения. Выбранные частные решения распола-
располагаются по степеням р, поэтому их использование дало бы особенно
удобное представление искомой функции, в частности решение вдоль
линии \ = const имело бы вид разложения по степеням р. Но именно
последнее обстоятельство ограничивает возможность использования
такого представления, так как оно возможно только в том случае,
когда функция ф вдоль линии 5 = const регулярна, между тем как
в сверхзвуковой области регулярность ф отнюдь не самоочевидна.
В самом деле, если граничные условия заданы посредством функ-
функций, не являющихся регулярными, то вдоль некоторых характе-
характеристик сверхзвуковой области распространяются разрывы производ-
производных от ф более высоких порядков. Даже если такие особенности
очень слабы, например если они имеются только в какой-либо одной
производной высокого порядка, они все же определяют границу
области сходимости искомого представления решения ф (рис. 68).
Вопрос о возможности разложения решения ф по частным решениям,
выбранным в § 9 гл. VII, исследован в работе Гудерлея [14] (см.
лит. 1). Здесь мы приведем только некоторые основные идеи этого
исследования и притом в упрощен-
упрощенной форме. За подробностями отсы-
отсылаем к оригинальной работе.
Пусть в области, имеющей, на-
например, форму, показанную на
рис. 69, задана функция ф, удовле-
удовлетворяющая везде в этой области г
дифференциальному уравнению Три- /
коми, а в нулевой точке — усло-
условию Трикоми (§ 11 гл. V). Далее,
пусть вместе с решением ф заданы,
по крайней мере в принципе, также
производные ф и ф^ вдоль произ-
произвольной кривой С, лежащей внутри
рассматриваемой области. Имея зна-
чения ф и фр вдоль кривой С. Р "^„^Пё.™ it™J. п°
мы можем восстановить — путем
аналитического продолжения — значения функции ф и в других
местах, по крайней мере в дозвуковой области. Следовательно,
желательное представление функции ф мы могли бы получить путем
построения выражения, принимающего вдоль С указанные значения.
Однако если кривая С соответствует условиям теоремы Трикоми,
то для построения функции ф достаточно знать только значения ее
самой (без значений производной фр), поэтому предварительное за-
задание значений ее производной привело бы в общем случае к про-
противоречию. Правда, если мы хотим использовать для представле-
представления решения формулы, выведенные в предыдущем параграфе, то
знания значений только самой функции, к сожалению, недостаточно.

236 ГЛ VII ЧАСТНЫЕ РЕШЕНИЯ УРАВНЕНИЯ ТРИКОМИ
Поэтому несколько видоизменим поставленную задачу, а именно:
будем рассматривать вместо функции ф функцию ф, совпадающую
внутри кривой С с первоначальной функцией ф, а вне этой кривой
всюду тождественно равную нулю (ф = 0). Построенная таким обра-
образом функция ф имеет вдоль кривой С определенный скачок, так же
как и ее производная в направлениях, не совпадающих с направлением
кривой С. В бесконечности функция ф обращается в нуль, а
в начале координат удовлетворяет условию Трикоми. Такая крае-
краевая задача имеет единственное решение. В самом деле, разность
двух решений этой краевой задачи удовлетворяет дифференциаль-
дифференциальному уравнению Трикоми всюду слева от характеристик ОА и ОВ
на рис. 69, следовательно, и вдоль С; далее, эта разность в беско-
бесконечности обращается в нуль, а в начале координат удовлетворяет
условию Трикоми. Такое решение тождественно равно нулю, как
это следует из теоремы Трикоми, если отодвинуть рассматриваемый
в ней контур в бесконечность.
Преимущество этой формулировки состоит в том, что решение
задачи получается даже в том случае, когда значения функции ф
и ее производной ф0 (или значения скачка функции ф и скачка произ-
производной фр) заданы вдоль кривой С совершенно независимо друг от
друга. Если значения функции и ее производной не согласованы
друг с другом, то единственным следствием такого несогласования
будет только то, что решение в области вне кривой С будет отли-
отличаться от нуля. Если же значения функции и ее производной вдоль
кривой С заданы непосредственно, то в общем случае никакого
решения существовать не будет.
Для выполнения вычислений следует разложить решение на сим-
симметричную и антисимметричную части, после чего достаточно рас-
рассмотреть только верхнюю половину плоскости т), &. Ограничимся
вычислением лишь антисимметричной части решения. Для упроще-
упрощения рассуждений выберем в настоящем изложении в качестве кри-
кривой С линию р = const. В дозвуковой области эта линия целиком
лежит внутри рассматриваемой области О. В сверхзвуковой области
это невозможно, если только область G не простирается до беско-
бесконечности. К счастью, внутри области О должна лежать только ха-
характеристика DE (рис. 69), выходящая из точки пересечения кри-
кривой С со звуковой линией. В самом деле, если значения ф на этой
характеристике известны, то можно продолжить решение до перво-
первоначально заданной кривой р — const следующим способом. Зададим
вдоль характеристики ЕА произвольные значения ф, но такие, чтобы
в точке Е имел место непрерывный переход к значению ф в этой
точке. Тогда решение в области DEA можно построить по значе-
значениям ф вдоль DE и ЕА с помощью метода характеристик. Если
затем построить решение, которое вдоль линии DA (р = const), не
являющейся характеристикой, принимает только что вычисленные

13 РАЗЛОЖЕНИЕ РЕШЕНИЯ Ф ПО ЧАСТНЫМ РЕШЕНИЯМ
237
внешняя область
линия, вдоль которой
задан скачок тр
или гр
/ *р
значения функции Ф и ее производной Фр, то в области ADE оно будет
совпадать с -построенным там решением. Тем самым получается
совпадение решений и вдоль характеристики DE, т. е. вместе с усло-
условиями вдоль DA автоматически выполняется и условие для Ф вдоль DE.
Преимущество такого построения состоит в значительном упро-
упрощении вычислительной работы. В то же время это построение
обладает и недостатком, так как применение метода характеристик
вносит в исследование элемент, за которым невозможно проследить
аналитически. В работе Гудерлея этот недостаток устранен. В даль-
дальнейшем мы опять будем поль-
пользоваться обозначением Ф вме-
вместо ф.
Итак, мы должны решить
следующую задачу. Даны две
функции /t($) и /2(?); тре-
требуется найти такое решение Ф
уравнения Трикоми, которое
в бесконечности обращается
те HV7TK R няияпр ь-nrm пинят Р и с. 70. Деление плоскости г], 9 на внутреннюю
в нуль, в начале координат и В11ешнюю области
удовлетворяет условию Три-
Трикоми, а вдоль линии р = р0 претерпевает разрыв, равный /t(?)
для самой функции Ф и /2(?)/р0 для производной Фр (рис. 70).
Кривая С делит плоскость т), & на две области, которые будем
называть внешней областью Gt (p > р0) и внутренней областью
О г (Р < Ро)-
Во внешней области Gx представим решение в виде
(la)
'внутренняя область.
а во внутренней области G2 — в виде
v—o
A6)
Постоянные ah и bh и функцию р ([л) следз^ет вычислить из условий
перехода, заданных вдоль кривой С. От второго члена решения
A6) берется вещественная часть потому, что этот член вследствие
наличия комплексного показателя степени р/р0 представляет собой
комплексную величину. Как показывает вид решения, в бесконеч-
бесконечности оно стремится к нулю. Удовлетворяется ли в нулевой точке
условие Трикоми, из вида решения неясно. Наоборот, вид решения
показывает, что отдельные частные решения, стоящие под знаком инте-
интеграла, в нулевой точке неограниченно вырастают, так как ;х есть

238 ГЛ. VII. ЧАСТНЫЕ РЕШЕНИЯ УРАВНЕНИЯ ТРИКОМИ
мнимая величина. Это свойство решения выявится позже. Условия,
которые должны быть заданы вдоль кривой С, имеют вид
Ы*- Ро) —<М&. Ро) = Л®. Bа)
Ь; р E, Ро) - «W; р E. Ро) = }о/2 ©• B6)
Разложим функции Л и /2 в ряды при помощи формулы.
VII, 12A3) и внесем затем решения Aа) и A6) в условия Bа) и B6)
Приравняв в полученных равенствах коэффициенты при отдельных
функциях, мы найдем
I /
A-T8)'/.
тс J
те J И — T3\7.
-co I1'
, (J.) Sin I Я
1
Л С
~x3O
Отсюда
Cб)
- rt sin [^ + I)] sin [* ( - (х + 1
I)]

§ 13 РАЗЛОЖЕНИЕ РЕШЕНИЯ Ф ПО ЧАСТНЫМ РЕШЕНИЯМ 239
X
= / [Л СО (v + ^) + Л СО] AJt8)V. gW (*¦ tO^ D)
где
i
/ГмЛ= Г If. М (и,-I-}Л-4- /„fVll
A —т8O'
и в соответствии с равенством VII, 12 A3а)
Таким образом, во внешней области решение можно представить
в виде
а во внутренней области — в виде
3
— Rei I /Po/ — =—}. F6)
W («) [ ( I)] [ ( 1)] I
—!*Jm. sin [« ((, + -I)] sin [™ ( - ц + 1
Для последующих вычислений важную роль играют два свойства
функции /(р.), определяемой равенством D), и интеграла в правой
части равенства F6). 1. Функция 1(\х) представляет собой однозначную
аналитическую функцию от р. 2. Если | [а | в первом квадранте ком-
комплексной плоскости [1 стремится к бесконечности, то выражение,
стоящее под знаком интеграла в правой части равенства F6), убы-
убывает в некоторой области плоскости р, ? так, что становится воз-
возможной деформация пути интегрирования вдоль мнимой оси в путь
интегрирования вдоль вещественной оси. (На доказательстве этих
свойств останавливаться здесь не будем.)
Далее введем допущение, что в первом квадранте комплексной
плоскости [х функция /([i) не имеет полюсов. Более подробно об
этом допущении будет сказано ниже.
Рассмотрим второй член правой части равенства F6). При только
что сделанных допущениях особенности выражения, стоящего под
знаком интеграла, определяются особенностями выражения

40 ГЛ. VII. ЧАСТНЫЕ РЕШЕНИЯ УРАВНЕНИЯ ТРИКОМИ
Если исключить из рассмотрения точку S=l, то функция G (i, ;х)
будет регулярной при всех значениях [х. В самом деле, эта функция
определяется линейным дифференциальным уравнением и начальным
условием (при ? = — со), не содержащим jj,, поэтому решение может
иметь особенности только в таких точках, в которых обладает
особенностями само дифференциальное уравнение. Но последнее при
? ф 1 особенностей не имеет. Следовательно, достаточно рассмотреть
полюсы выражения
+1)] sin [u (-JX +\)}~1. G)
) ( )
Некоторые из этих полюсов обнаруживаются сразу; это те полюсы,
которые соответствуют нулям тригонометрических функций. Полюсы,
возникающие вследствие равенства нулю выражения sin (тс (jx -f-1/4)].
получаются при значениях jx^, входящих в первый член правой
части равенства F6), т. е. в сумму. Эти полюсы, рассмотрим от-
отдельно, так как для них сумма в правой части равенства F6) ста-
становится равной нулю. Вычеты в соответствующих точках равны
Для исследования других полюсов воспользуемся выражением
VII, 12A3) функции В , причем преобразуем гамма-функции, входя-
входящие в это выражение, посредством формул VII, 4A5). Мы получим
— _____
- 2,х sin BЛ(х) Г ^ + Щ Г ((х +1
Отсюда, имея в виду выражение G), найдем, что полюсы будут
в точках
1_=1 + |, А = 0, 1, 2, 3.... (8)
Вычеты в этих точках равны
г (!+А
Г

13. РАЗЛОЖЕНИЕ РЕШЕНИЯ ф ПО ЧАСТНЫМ РЕШЕНИЯМ
241
Путь интегрирования после деформации проходит вдоль веществен-
вещественной оси |х, но при этом обходит полюсы, лежащие на этой оси, по
малым полуокружностям, расположенным выше оси (рис. 71). На
вещественной оси выражение, стоящее под знаком интеграла в пра-
правой части равенства F6), очевидно, вещественно. Вследствие нали-
наличия множителя i перед интегралом в равенстве F6) путь интег-
интегрирования вдоль отрезков вещественной оси вносит в вещественную
часть этого интеграла вклад, равный нулю. Напротив, полуокруж-
полуокружности, обходящие полюсы, вносят в интеграл мнимые вклады,
а именно соответствующие вычеты, умноженные на —Ы (знак
минус получается потому, что обход полюсов совершается
в отрицательном направлении). Таким образом, вещественная часть
интеграла равна сумме вычетов, умноженных на и. При этом вычеты
в точках [aW таковы, что сумма в решении F6) выпадает. В резуль-
результате мы получаем
-.(а)
X
Г'^Г
¦f ri-
/ 4 + 4r
(Ю)
Мы видим, что это выражение представляет собой наложение част-
частных решений VII, 9C) (с положительными показателями степени р),
„.. ._ найденных в § 9 настоящей главы.
Однако это выражение не всегда
комплексная
плоскость м
путь интегрирования
г « г
ьещественная ось
Рис. 71. Путь интегрирования в комплексной
плоскости (J-.
К
Рис 72. Об пасть сходимости для разложения
решения ф по,естественным частным решениям.
может служить полным представлением решения ф2. Определение
функции / [равенство D)] показывает, что до тех пор, пока функции
f1 и /2 ограничены (это предполагается всегда) и пока функция О
также ограничена, решение / сходится равномерно и поэтому
является аналитической функцией от ji, не имеющей полюсов в ком-
комплексной плоскости A.. Поведение функции G(x, jj.) при т = — оо
таково, что там не возникает никаких трудностей для ее исследо-
исследования; но зато при т -> 1 функция О в общем случае стремится
к бесконечности [см. асимптотическое представление VII, 7A26)].
16 Зак. 534. К Г. Гудерлей.

242 ГЛ VII ЧАСТНЫЕ РЕШЕНИЯ УРАВНЕНИЯ ТРИКОМИ
Функция /, безусловно, аналитическая, если вблизи т=1, например
при 1Х < т < 1, функции /t и /2 тождественно равны нулю (tx есть
подходящим образом выбранная постоянная).
Вначале мы предположим, что это условие выполняется. Поло-
Положение точки ?t обусловливает границы области, в которой допустимо
выполненное выше преобразование. В самом деле, эта область опре-
определяется требованием, чтобы выражение под знаком интеграла в ра-
равенстве F6) достаточно быстро стремилось к нулю, если в ком-
комплексной плоскости |[j,|—>оо. Но такое поведение подинтегрального
выражения зависит также от /, а вместе с тем и от tx. Более точ-
точное исследование показывает, что представление A0) применимо
в области, заштрихованной на рис. 72. Проведем через точку S = St
контура С характеристику с положительным наклоном, а через
точку О пересечения этой характеристики со звуковой линией —
линию р = const {GK) и характеристику GH с отрицательным на-
наклоном. Обе эти линии являются границами области применимости
представления A0). В общем случае вне этой области решение A0)
не может сходиться. В самом деле, нельзя исключить возможности
того, что вдоль характеристики PG распространяется особенность.
Эта особенность отражается от звуковой линии, после чего возни-
возникает особенность вдоль GH. Выше мы упомянули, что предста-
представление A0) для решения ф2 имеет вдоль линии \ = const вид разло-
разложения по степеням р1^. Именно поэтому область сходимости не
простирается за пределы ближайшей особенности, т. е. за пределы
линии GH. Как это влияет на дозвуковую область, можно выявить
из асимптотического представления функции Q.
Если % приближается к единице, то область сходимости стано-
становится все меньше и меньше, т. е. представление теряет свою цен-
ценность. Однако так кажется только на первый взгляд. Для того
чтобы выявить поведение представления A0) вблизи точки ?=1,
необходимо более точное представление функции /. Во всяком случае,
согласно сказанному выше, функции ft и /2 не должны иметь особен-
особенностей вблизи ? = 1; но в точке 1=1 допустимы особенности про-
производных высшего порядка. Следовательно, вполне естественно
потребовать, чтобы в окрестности точки ? = 1 функции fx и /2 были
аналитическими функциями от ?. Тем самым вблизи точки \ — 1
функции /х и /2 определяются также а комплексной плоскости ?-
В общем случае они будут многозначными функциями, имеющими
в ?—1 точку разветвления. Без подобного предположения совер-
совершенно невозможно определить функцию / для больших значений
вещественной части jx, так как иначе интеграл, определяемый равен-
равенством D), будет расходиться.
Если вдоль линии %=\ распространяется особенность, то это
можно обнаружить из поведения функций f1 и /2 вблизи Ч, — 1,
более того, эту особенность можно полностью выявить. Очевидно,
что решение A0) можно применять только в том случае, если функ-

13 РАЗЛОЖЕНИЕ РЕШЕНИЯ ф ПО ЧАСТНЫМ РЕШЕНИЯМ
243
ции fx и /2 удовлетворяют дополнительному требованию, а именно
требованию о том, чтобы они не обусловливали распространения
особенности вдоль ?=1. Но это предписывает определенную форму
разложения этих функций в степенной ряд в точке ?=1. Если
только что указанное дополнительное требование не выполнено, то
в комплексной плоскости jx получаются дополнительные полюсы,
вследствие чего в решении появляются дополнительные члены, учи-
учитывающие распространение особенностей (см. работу Гудерлея [14],
лит. 1).
Указанное требование является единственным ограничением при-
применимости решения A0). Область сходимости всегда имеет форму,
изображенную на рис. 72. Точная граница этой области зависит от
поведения функций /х и /2 в комплексной плоскости ?; их поведение
при вещественном \ не является достаточным критерием.
В упомянутой работе Гудерлея все эти вопросы исследуются
подробно, причем на выбор контура С налагаются меньшие огра-
ограничения. В большей части случаев этот контур можно совместить
с контуром рассматриваемой области. Результаты, полученные в этой
работе, можно использовать для того, чтобы для заданного численно
решения определить путем интегрирования коэффициенты разло-
разложения A0).
К
Рис 73. Область сходимости дтя разложения решения
по естественным частным решениям.
Аналогичные соображения применимы также к области, контур
которой имеет форму, изображенную на рис. 73. Контуром исходной
области является ABDEFGH. Внутри этой области, в ее дозвуковой
части, выбираются две кривые С и С", представляющие собой ли-
линии р = const. Затем контур С дополняется характеристикой LM.
Если вдоль характеристики МК задать подходящие граничные зна-
значения, то можно продолжить решение в область MKL и взять от-
отсюда значения ф и фр для кривых С (ILK) и С" (NPK). Тогда изло-
изложенный выше способ даст возможность получить решение для
области, лежащей между кривыми С и С". В этой области вклады,
вносимые в решение кривыми С и С", суммируются. При этом
вклад, обусловленный кривой С", выражается формулой Fа), не
требующей никаких дальнейших преобразований. Эта часть решения

244 ГЛ VII ЧАСТНЫЕ РЕШЕНИЯ УРАВНЕНИЯ ТРИКОМИ
сходится не только вне кривой С", но также вне контура NPQ
(для доказательства проще всего воспользоваться асимптотическим
представлением рассматриваемой функции О). Вклад, вносимый
в решение кривой С, преобразуется указанным выше образом. По
поводу границы сходимости можно повторить предыдущие рассуж-
рассуждения, а именно, в дозвуковой области берется линия р = const,
продолжением которой в сверхзвуковой области служит характе-
характеристика с отрицательным наклоном. Если граничные значения
в сверхзвуковой области подобраны надлежащим образом, то эту
границу сходимости можно совместить с линией ILM. Тогда общей
областью сходимости составляющих решения, обусловливаемых кри-
кривыми С и С", будет область, заштрихованная на рис. 73. Если
воспользоваться обозначениями § 9 настоящей главы, то решение
будет состоять из частных решений ф_E/)_й и 6. к кото-
которым в самом общем случае следует присоединить еще симметричные
частные решения ф_{1/зЬЙ и фй/3.
§ 14. Частные решения Тамады и Томотики
Частные решения Тамады и Томотики, а также частные решения
Фальковича, которые будут рассмотрены в следующем параграфе,
имеют особенности в дозвуковой области. Эти решения могут быть
полезны при расчете течений, имеющих в бесконечности число Маха,
меньшее единицы, а также при исследовании отдельных точек полей
течений, рассмотренных в гл. VI.
Основная идея исследований Тамады и Томотики состоит в сле-
следующем. Дифференциальное уравнение Трикоми содержит & только
в производных от ф, но не в коэффициентах. Так получается потому,
что годограф не имеет какого-либо привилегированного направления
для скорости. Отсюда следует, что из какого-либо решения ф можно
найти новые решения, если изменить все значения & на постоянную
величину 9-0, причем не только на вещественную, но и на мнимую,
т. е. на i%-0. Так как дифференциальное уравнение Трикоми имеет
вещественные коэффициенты, то вещественные и мнимые части полу-
получающихся указанным способом решений также являются решениями
уравнения Трикоми.
Применив такой способ к частным решениям
ф = р-Р/..)-Ч? (S, [*), A)
мы получим
Р=— Ч3 + -|(» + ВД Ba)

§ 14. ЧАСТНЫЕ РЕШЕНИЯ ТАМАДЫ И ТОМОТИКИ 245
Функция О определяется линейным дифференциальным уравнением
с особыми точками ?="|/"l и Е = со. В других точках функция О
не имеет особенностей. При ограниченных значениях т] и 9- величина
? никогда не становится бесконечной. Для особой точки \ = ]/Т из
равенства B6) мы имеем
Так как вещественная и мнимая части в отдельности должны быть
равны нулю, то отсюда находим
(
Это есть единственная точка плоскости т\, Ь, где решение может
иметь особенность. Решение G в этой точке получается как нало-
наложение двух линейно независимых решений, которые в соответствии
с формулой VII,4 A6) могут быть взяты в виде
g.,,, ^-^ 1—2^. 1-
Поведение решения в точке & = 0, tj = — B&0/3) 3 определяется
первым членом каждого из этих рядов. Перейдя к переменным t\ и ft,
мы из уравнения A) получим
-1 С/и)-Iх
и соответственно
Для первого из этих решений точка Ь = 0, т\ = — B&0/3)/'! яв-
является регулярной. Второе решение имеет в этой точке особенность,
характер которой зависит от показателя степени 2р.. Например, для
того чтобы получить точку разветвления двулистной римановой по-
поверхности, следует положить [х = х/4. Для определения поля течения
необходимо вычислить функцию G при комплексных значениях аргу-
аргумента. При [л = 1/4 такое вычисление облегчается, так как одно из
решений может быть представлено в замкнутом виде [формула
VII, 5(8а)]. Применение полученных частных решений показано в
работе Тамады и Томотики (см. лит. 1)

246 ГЛ VII ЧАСТНЫЕ РЕШЕНИЯ УРАВНЕНИЯ ТРИКОМИ
§ 15. Частные решения Фальковича
Другой вид частных решений, обладающих особенностями в до-
дозвуковой области, получен С. В Фальковичем. Вывод этих частных
решений также основан на допущении, что решение можно пред-
представить в виде произведения. Однако переменные, входящие в решения
Фальковича, вещественны в плоскости т], &, поэтому соответствующие
функции должны вычисляться только при вещественных значениях
аргумента Покажем, как можно вывести решения Фальковича.
Прежде всего дифференциальное уравнение Трикоми приводится
к виду, возможно более близкому к уравнению Лапласа. Для этого
следует положить
* = ¦§( —Ч)''1 (la)
ft). A6)
Отсюда
Внеся эти значения в дифференциальное уравнение Трикоми, мы
получим
+1 ( 1) - т]Г('« ЧГ8 +
Если положить а — —1/4, то член с производной Ws исчезнет и
уравнение примет вид
Переменная s принимает вещественные значения в дозвуковой
области и мнимые значения в сверхзвуковой области. Об этом
обстоятельстве не следует забывать в тех случаях, когда решение,
полученное в дозвуковой области, желательно продолжить в сверх-
сверхзвуковую область.
Важнейшей идеей, на которой основан вывод частных решений
Фальковича, является введение биполярных координат в плоскости
s, Ь. Необходимые для этой цели преобразования получаются наиболее

§ 15 ЧАСТНЫЕ РЕШЕНИЯ ФАЛЬКОВИЧА 247
простыми при использовании комплексных переменных. Пусть
z^s-^ib, (За)
z=s —/&, C6)
W(s, &) = Ф(г, z), D)
причем z и z следует рассматривать как независимые переменные.
Это равносильно предположению, что рассматриваются не только
вещественные значения s и Ь, но и мнимые. Вычислив производные
Ws = Ws + f j , fa = jf г _ /ф-,
мы приведем уравнение B) к виду
Фг-г4-^-(^ + ^Ф = о. E)
Введем теперь новую независимую переменную С = /г(.г), где h (z)
есть аналитическая функция от z, которая при вещественных зна-
значениях z принимает также вещественные значения. В таком случае
сопряженным комплексным значениям z соответствуют, как это вы-
вытекает из принципа зеркального отражения Шварца, сопряженные
комплексные значения С, т. е. из соотношения
С = h (z) Fa)
следует, что
Z = h(z) F6)
(здесь черточками над буквами обозначены, как и выше, сопряжен-
сопряженные комплексные величины). Далее примем, что
Ф(г.г) = ф'(С,С). Fв)
Тогда мы будем иметь
Wu = yah'(z)h'(z).
и новым дифференциальным уравнением будет
<]Л h'-(z) h' (z) + ^ (z + z) ~У = 0. G)
В этом уравнении функции, зависящие от z и z, следует выразить
через ^ и С. Введение переменных z и z или С и С практически
выгодно потому, что в дифференциальном уравнении остается в каче-
качестве производной высшего порядка только одна вторая смешанная
производная. Функцию h(z) С. В. Фалькович берет в виде
г = А(г) = 1П?±^, (8)

248 ГЛ VII. ЧАСТНЫЕ РЕШЕНИЯ УРАВНЕНИЯ ТРИКОМИ
где s0 есть постоянная. Отсюда
и дифференциальным уравнением для определения <j/* будет
фк- (е^+Ч/2 — е-К +«''2J + ^- f = 0. (9)
Теперь лучше всего вернуться опять к вещественным независимым
переменным. Пусть
_ (Ю)
откуда
«.— 2 .
„_. с —с
Положив
<]>*(?, С) = ф(а, р), A0а)
мы найдем
и дифференциальное уравнение (9) примет вид
причем независимыми переменными будут « и р, которые можно
отделить друг от друга. Тогда мы будем иметь
? = /(«M!П1. A2)
и для определения функции / получится обыкновенное дифферен-
дифференциальное уравнение
(i!lIJi_|./=o. A3)
Коэффициенты этого уравнения примут рациональную форму, если
положить

§ 15. ЧАСТНЫЕ РЕШЕНИЯ ФАЛЬКОВИЧА 249*
Тогда мы получим
s» + iL+± ? = 0
S I I ~ g (^2 \yz
Это дифференциальное уравнение имеет особые точки ? = 0, t = oor
? —-)-1 и ? = —1. Показатели уравнения в точках Ои оо, а также
в точках -j- 1 и — 1 одинаковы. Существенное упрощение, а именно-
уменьшение числа особых точек, получается путем преобразования,
совмещающего особые точки с одинаковыми показателями. Из раз-
различных преобразований, пригодных для этой цели, Фалькович выби-
выбирает следующее:
Это преобразование отображает особые точки ^ = 0 и t = oo в точку
и = оо, а особые точки t = -\~\ и t= — 1 в точку а=1. В точ-
точках, в которых производная du[dt равна нулю, взаимно однозначное
соответствие между плоскостями и и t нарушается, и там могут
появиться новые особые точки. Равенство dujdt нулю имеет место
при ?=±1 и t = + i. Точки t = ± 1 были особыми уже в перво-
первоначальном дифференциальном уравнении, следовательно, нарушение
взаимно однозначного соответствия в этих точках не вносит в пре-
преобразованное дифференциальное уравнение новых особенностей. Но
при t= ± I возникает новая особая точка, а именно и = 0. Таким
образом, дифференциальное уравнение, получающееся в результате
преобразования A4), имеет три особые точки, и нетрудно убедиться,
что все они являются регулярными особыми точками. Положив
g(t) — k(u), A5)
мы получим после некоторых преобразований следующее гипергео-
гипергеометрическое дифференциальное уравнение:
5 1
du? ^ da Ьи- ^ 2 (и — 1)
Ы^+ш^Г^Н- A6>
Решение этого уравнения, если воспользоваться Р-функцией Римана
(см. § 4 настоящей главы), можно представить в виде
со 0 1
т „ 5
2 ° 12 '
-0L I I I
2 12 J
A7)
Теперь необходимо выразить переменную и через первоначальные

250 ГЛ VII ЧАСТНЫЕ РЕШЕНИЯ УРАВНЕНИЯ ТРИКОМ.И
переменные s и &. Из равенств (За), (8а) и A0) мы находим
-а из равенства A7) получаем
Следовательно, при s = s0 и & = 0
и = oo,
а при s = 0
Если при s = 0 координата Ь изменяется от 0 до s0, то \g p изме-
изменяется от 0 до оо; если же Ь изменяется от s0 до со, то tg p
изменяется от —оо до 0, т. е. 8 принимает на верхней половине
звуковой линии значения между 0 и it. В самом деле, кривые C =
= const, если постоянная изменяется от 0 до со, перекрывают всю
верхнюю половину дозвуковой области.
Из предыдущих рассуждений следует, что возможные предста-
представления решения k имеют вид
/и — 1 \'Wl \тр- )
B0)
Конечно, в случае необходимости с помощью преобразования
VII, 4Eа) можно получить представление решений к вблизи звуковой
линии, а имея это представление, можно составить продолжение
решения в сверхзвуковую область.
Таким образом, частные решения Фальковича имеют следующий
окончательный вид:
ф = (т))-'^ k (а) ' B1)
т cos tnp
где и и р необходимо выразить через s и & с помощью равенств A8)

§ 15 ЧАСТНЫЕ РЕШЕНИЯ ФАЛЬКОВИЧА 251
и A9) и при этом иметь в виду, что, согласно введенному в самом
начале условию Aа),
s = |(— T«)'"- B1а)
Выбор параметра т определяется, конечно, характером той особен-
особенности, которую желательно представить В работе С. В. Фальковича
этот параметр принят равным нулю, что дает особенность в несжи-
несжимаемом течении, соответствующую мнимой части логарифма.
Для применения этих частных решений важную роль играет
следующее обстоятельство. Вдоль линии / = const или вдоль линии
а = const решение представляется синусом или косинусом от р. Это
дает простую возможность составить полную систему частных реше-
решений для представления любой функции, имеющей в точке s = s0,
%- = 0 точку разветвления с заданными свойствами.
При приближении s0 к бесконечности линии t = const переходят,
очевидно, в линии т] — const, а линии р = const — в линии 8-== const.
Следовательно, частные решения Фальковича являются обобщением
частных решений Чаплыгина. Этот предельный переход можно про-
проиллюстрировать переходом от гипергеометрического ряда к функции
Бесселя, которая представляет собой не что иное, как конфлюэнт-
ный гипергеометрический ряд.
Число приложений, к которым можно было бы применить такого
рода соображения, в настоящее время невелико, поэтому мы не бу-
будем заниматься дальнейшим развитием этих исследований. Во всяком
случае эти частные решения вследствие своей общности и простоты
в некоторых случаях могут быть очень полезны.

Глава VIII
ТЕЧЕНИЯ С ЧИСЛОМ МАХА, РАВНЫМ ЕДИНИЦЕ
§ 1. Общие соображения
Сначала довольно трудно представить себе течение с числом Маха,
равным единице, около тела с ненулевой толщиной. При числе Маха,
равном единице, плотность потока массы имеет максимум [см. ра-
равенство I, 2 A0а)], т. е. при любом другом числе Маха количество
массы, протекающее в единицу времени через заданное поперечное
сечение, меньше, чем при числе Маха, равном единице. Когда мы
говорим о теле, помещенном в параллельное течение, то всегда
молчаливо предполагаем, что по мере удаления от тела линии тока
все меньше и меньше отклоняются от параллельных прямых. По-
Поэтому вполне естественно предположить, что поперечное сечение
течения в том месте, где расположено обтекаемое тело, недоста-
недостаточно для того, чтобы набегающая масса газа могла протекать
мимо тела.
С другой стороны, нетрудно представить себе мысленные
эксперименты, показывающие, что можно сколь угодно близко по-
подойти к числу Маха, равному единице. Рассмотрим, например,
модель, помещенную в закрытую аэродинамическую трубу, и пусть
продувка этой модели производится при блокирующем числе Маха,
т. е. при наивысшем возможном дозвуковом числе Маха. Путем
зеркального отражения продолжим течение за пределы стенки
трубы; тогда стенки станут лишними и их можно будет отбросить
(рис. 74). Если мы выделим в таком поле течения две линии тока,
состоящие из осей симметрии двух соседних моделей и верхнего
и нижнего обводов этих моделей, то получим не что иное, как
течение через сопло Лаваля. С примером такого течения мы уже
познакомились в § 2 гл. IV (рис. 16) и можем рассматривать этот
пример как типичный.
Следовательно, мы можем ожидать, что в рассматриваемом слу-
случае, как и при течении через сопло Лаваля, должна возникнуть
звуковая линия и притом выше по течению относительно самого
узкого поперечного сечения. Звуковая линия проходит в основном
поперек линий тока, но по мере удаления от модели поворачивается
все больше и больше, отклоняясь в сторону течения. Это происхо-
происходит потому, что волны Маха, исходящие от модели, заканчиваются
на звуковой линии. Вверх по течению относительно звуковой линии
получается дозвуковое, а вниз по течению — сверхзвуковое поле.
Для определения поля течения в дозвуковой области необходимо

§ 1. ОБЩИЕ СООБРАЖЕНИЯ 253
знать контур сопла, т. е. контур обтекаемого профиля также в не-
некоторой части сверхзвукового поля. Для того чтобы более точно
выявить, какой же именно участок контура сопла надо знать
в сверхзвуковом поле, рассмотрим волны Маха, исходящие от
контура сопла. Часть этих волн заканчивается на звуковой линии,
\\\\\\\\\\\\\\У\\У
,\\\\\W\\\\\\\\\\Y
Л\\\\\\\\\\\\\\\
Рис 74 Эквивалентность течений через сото Лаваля, через-
решетку из профилей и в трубе с жесткими стенками.
остальные же, расположенные ниже по течению, заканчиваются на
противолежащей стенке. Очевидно, для определения дозвукового
поля необходимо знать тот участок контура сопла в сверхзвуковом
поле, который посылает волны Маха, заканчивающиеся на звуковой
линии. Последней из этих волн является так называемая предельная
характеристика. Так как для этой характеристики вектор скорости
на звуковой линии направлен горизонтально и так как все волны Маха,
пересекающие эту характеристику, являются волнами сжатия (в самом
деле они все исходят от звуковой линии, см. § 1 гл. VI), то точка
контура сопла (в его нижней половине), в которой начинается пре-
предельная характеристика, расположена на участке контура, имеющем
положительный наклон. Следовательно, эта точка лежит выше по
течению относительно самого узкого поперечного сечения сопла
или, если говорить о профиле, выше по течению относительно се-
сечения с максимальной толщиной профиля.
Если мы будем увеличивать ширину аэродинамической трубы
до бесконечности, сохраняя при этом форму модели неизменной
и, кроме того, продолжая обдувку все время на блокирующем
числе Маха, то общая структура поля течения будет оставаться
неизменной. Блокирующее число Маха и число Маха вдоль стенок
трубы будут все больше и больше приближаться к единице. Таким
путем мы приходим к представлению о поле течения с числом Маха,

254
ГЛ VIII ТЕЧЕНИЯ С ЧИСЛОМ МАХА, РАВНЫМ ЕДИНИЦЕ
равным единице. В какой мере оправдано возражение против су-
существования такого поля течения, упомянутое в начале настоящего
параграфа, будет выяснено в конце следующего параграфа.
§ 2. Годограф течения с числом Маха, равным единице
При решении задач о течениях с числом Маха, равным единице,
методом годографа важную роль играет то обстоятельство, что
в бесконечности плоскости течения имеет место параллельное тече-
течение со скоростью звука. Это означает, что в плоскости годографа
все линии тока выходят из одной и той же точки звуковой линии.
Здесь получается особая точка, к которой можно применить рассу-
рассуждения, проведенные в предыдущей главе.
Каждой характеристике, исходящей от поверхности тела, соот-
соответствует определенная точка звуковой линии, а именно точка
Ъ предельные
N характеристики.
Рис 75. Течение около профиля при числе Маха, равном единице,
и отображение этого течения на плоскоси, г:, Э (по Гудерчею [2] )
пересечения обеих линий, предельной характеристике соответствует,
очевидно, точка звуковой линии, лежащая в бесконечности. Следо-
Следовательно, в плоскости т;, Ь предельная характеристика проходит
через нулевую точку. Как уже упоминалось, предельная характе-
характеристика начинается в точке обтекаемого тела, расположенной выше
по течению относительно точки, соответствующей наибольшей тол-
толщине тела; поэтому отображение этой характеристики, безусловно,
не может оказаться целиком в бесконечности Конечно, можно
представить себе такой случай, когда контур рассматриваемого тела
имеет в точке, в которой начинается предельная характеристика,
особенность (например, разрыв кривизны). Подобные маловероятные
случаи мы исключим из исследования.
Сначала рассмотрим тело, симметричное относительно оси х
(рис. 75). В таком случае функция тока в плоскости годографа

§ 2 ГОДОГРАФ ТЕЧЕНИЯ С ЧИСЛОМ МАХА, РАВНЫМ ЕДИНИЦЕ 255.
будет антисимметрична относительно оси tj. Для того чтобы функ-
функция у в нулевой точке плоскости -ц, & стремилась к бесконечности,
показатель степени множителя р в решении VII, 3C) должен быть
отрицательным. Вблизи предельной характеристики, т. е. вблизи
линии 5=1, антисимметричное частное решение VII, 3C) может
быть представлено в виде VII, 9A). Для того чтобы при отобра-
отображении на плоскость tj, & предельная характеристика не попадала
целиком в бесконечность, коэффициент при втором члене в правой
части равенства VII, 9A) должен быть равен нулю. Эю условие
выражает одновременно требование, чтобы вдоль ?=1 при поло-
положительном \х не распространялась никакая особенность. Таким
образом, для параметра р. возможны значения, определяемые равен-
равенствами VII, 9C), т. е.
1 . h
«* = — Т2--Ь '
[а = — т — h.
Эти частные решения могут быть представлены в замкнутом виде
(см. стр. 209).
Теперь, для того чтобы из бесконечно большого числа найден-
найденных отрицательных значений р, выбрать то значение, которое дает
особенность, характерную для течения с числом Маха, равным еди-
единице, необходимо детально рассмотреть функции G. Графики трех
первых таких функций изображены на рис. 66. Только функция
G(k, 3/4) не обладает нулями в интервале от k = — оо до ?=1;
для каждой следующей получается по одному дополнительному
нулю. Для решения вида VII, 3C) каждая линия 5 = const плоскости
годографа отображается в обобщенную параболу плоскости течения.
В этом легко убедиться, если исключить р из уравнений, определяю-
определяющих х и у. Если плоскость годографа покрывается линиями ?==
=const, то плоскость течения одновременно покрывается соответ-
соответствующими обобщенными параболами. Функциональный определитель,
составленный для рассматриваемых решений, не обращается в нуль
ни в одной точке дозвуковой области. В самом деле, если бы он
в какой-либо точке этой области был равен нулю, то он должен
был бы быть равен нулю вдоль всей линии \ — const, проходящей
через эту точку, но в таком случае можно показать, что рассмат-
рассматриваемое решение тождественно равно нулю. Таким образом, если
линии \ — const ометают плоскость годографа в определенном на-
направлении, то плоскость течения также будет ометаться только
в одном направлении.
Пусть линия ? =— со отображается в отрицательную ось х.
Тогда линия ? = const, соответствующая ближайшему нулю функ-
функции О, отобразится в положительную ось х. Следовательно, об-
область годографа, простирающаяся от ? = — со до первого нуля

256 ГЛ VIII ТЕЧЕНИЯ С ЧИСЛОМ МАХА, РАВНЫМ ЕДИНИЦЕ
функции G, отображается на всю верхнюю половину плоскости тече-
течения; поэтому если бы мы стали увеличивать ? до значений, больших,
чем значение, соответствующее первому нулю, например до единицы,
то плоскость течения перекрылась бы многократно. В частности,
вследствие особого поведения р и 5 при 5=1 линия 5=1 не ото-
отображается в ось х, хотя функция G на ней также обращается в нуль.
Изложенные рассуждения приводят к заключению, что при тече-
течении с числом Маха, равным единице, для представления бесконеч-
бесконечности пригодна только та функция G, которая не имеет нулей между
1 =— оо и 5 = 1. Это означает, что особенность, возникающая
в нулевой точке плоскости т\, &, определяется уравнением
Общий вид годографа исследуемого течения довольно прост
(рис. 75). По-прежнему будем рассматривать симметричный профиль.
При перемещении из бесконечности по направлению к профилю
вдоль линии тока, совпадающей с осью симметрии профиля, ско-
скорость уменьшается. В передней точке профиля скорость равна либо
нулю, либо какому-либо другому значению, меньшему скорости
звука (первый случай имеет место, если угол, образуемый верхней
и нижней сторонами профиля, не равен нулю, а второй,—если
этот угол равен нулю). В передней точке профиля линия тока
разветвляется как в плоскости течения, так и в плоскости годо-
годографа. Направление вектора скорости изменяется, а модуль ско-
скорости при перемещении вдоль контура профиля обычно увеличивается.
Звуковая скорость достигается еще до места с наибольшей толщиной
профиля; дальше скорость становится сверхзвуковой.
Вдоль изображения контура обтекаемого тела функция тока
должна быть равна нулю (или, в более общем случае, постоянному
значению). Поэтому на выражение ф_5, > имеющее особенность в ну-
нулевой точке, необходимо наложить другое выражение, не имеющее
особенности в эгой точке и такое, чтобы вдоль изображения кон-
контура обтекаемого тела в плоскости годографа было о» = 0. Выра-
Выражение ф_5, предварительно следует умножить на постоянную, зави-
зависящую от размеров тела. Если бы контур обтекаемого тела в пло-
плоскости годографа был задан, то для отыскания дополнительного
к ф_5/ выражения можно было бы развить систематический метод.
Однако практическая потребность в таком методе не очень велика,
так как изображение контура обтекаемого тела в плоскости годо-
годографа не может быть определено непосредственно из контура этого
тела в плоскости течения.
Согласно результатам, полученным в § 12 гл. VII, решение
вблизи нулевой точки можно представить как наложение „есте-
„естественных" частных решений. Коэффициенты, на которые следует

§ 2 ГОДОГРАФ ТЕЧЕНИЯ С ЧИСЛОМ МАХА, РАВНЫМ ЕДИНИЦЕ 257
умножить отдельные частные решения, определяются формой (и раз-
размерами) обтекаемого тела.
Поведение решений в бесконечности определяется только выра-
выражением ф . Согласно равенствам VII, 3G) и VII, 3(9), соответ-
соответствующие координаты х и у в плоскости течения равны
* = p-4/'/i©> Ba)
У = Г*иШ, B6)
причем Д(?) и /2(?) могут быть выражены через G(a)(?, 3U). Исклю-
Исключив р, мы получим
Следовательно, линии % =const плоскости годографа действительно
отображаются в обобщенные параболы плоскости течения. Такими
параболами являются также звуковая линия и предельная характе-
характеристика. Очевидно, что взаимное расстояние между ними в напра-
направлении х возрастает по мере увеличения у. Для определения формы
линий тока необходимо вычислить их отклонение от линий у —
= const, представляющих собой линии тока невозмущенного те-
течения, что сводится к вычислению интеграла
у= I &(t)d(x(?)) при _у = const.
Из равенства VII, 3A) мы имеем
откуда
& = PV./4(?) D)
или, если учесть равенство B6),
Далее из уравнения C) следует, что
* = У/'/в(Е).
Таким образом,
Мы видим, что вытеснение линий тока из их первоначального по-
положения увеличивается по мере возрастания у. При у —>¦ со это
вытеснение также становится бесконечно большим. Полученный
17 Зак 534 К Г. Гудерлей

258 ГЛ VIII. ТЕЧЕНИЯ С ЧИСЛОМ МАХА, РАВНЫМ ЕДИНИЦЕ
результат дает ответ на вопрос, каким образом в течении с числом
Маха, равным единице, набегающий поток находит пространство
для прохода мимо обтекаемого тела. Необходимо подчеркнуть, что
с увеличением у течение все более и более приближается к парал-
параллельному течению с критической скоростью. Бесконечно большое
вытеснение линий тока при у —> оо есть следствие интегрирования
наклона линий тока в направлении х. Впервые эти исследования
были выполнены Ф. И. Франклем [5] и Гудерлеем [3] (см. лит. 1).
§ 3. Пример течения с числом Маха,
равным единице
Прежде всего условимся о некоторых обозначениях. Ниже часто
будут встречаться решения, имеющие особенность в нулевой точке
годографа и удовлетворяющие вдоль изображения профиля в пло-
плоскости годографа заданным граничным условиям. Если коэффи-
коэффициент при составляющей решения, имеющей особенность в нулевой
точке годографа, не требуется находить по заданному профилю, то
будем считать его равным единице. Такого рода решения будем
обозначать буквой ч? с верхним индексом, соответствующим индексу
той особенности, которая играет преобладающую роль. Функцию ф»
входящую в такие решения и удовлетворяющую условию Трикоми
в нулевой точке, будем обозначать через § с соответствующим
индексом. Аналогичный способ обозначения будем применять и для
преобразованного потенциала ср.
В качестве первого примера течения с числом Маха, равным
единице, рассмотрим исследованное Гудерлеем [3] (см. лит. 1) те-
течение, которому соответствует решение
^'•¦ = с^% + с^. A)
Выбор постоянных с1 и с2, если не считать их знака, не играет
существенной роли. В самом деле, умножим правую часть равен-
равенства A) на некоторую постоянную; тогда все значения х и у
умножатся на ту же постоянную; следовательно, получится только
изменение масштаба плоскости течения. Если мы применим закон
подобия для околозвуковых течений, то увидим, что координаты Е
останутся неизменными, но каждое р умножится на г3. Так как
в равенстве A) оба члена правой части содержат р в разных сте-
степенях, то множитель х войдет в каждый из этих членов также
в разных степенях.
Для определения формы тела в плоскости течения необходимо
предварительно найти нулевую линию тока и вычислить для нее
координаты х. Тогда форма обтекаемого тела получится путем инте-
интегрирования по х наклона нулевой линии тока.

§ 3 ПРИМЕР ТЕЧЕНИЯ С ЧИСЛОМ МАХА, РАВНЫМ ЕДИНИЦЕ 259
Выполнение расчета в общем виде довольно кропотливо, однако
окончательный результат получается простым. Приведем здесь только
важнейшие этапы этого расчета. Необходимые частные решения ф_5/
и ^1/, получаются из равенства VII, 5 C). В рассматриваемом слу-
слу3/ !4.
чае !^ = 3/4 и (а = !/4. Мы имеем
Bа)
^)/sb -2 (Ус-У^Т)"]. B6)
причем
Выражения Bа) и B6) представляют собой решения уравнения, опре-
определяющего G, а отнюдь не те выражения О , которые нам необхо-
необходимы. Для последних характерно их поведение при больших отри-
отрицательных значениях ij, или, что то же самое, при малых отрица-
отрицательных значениях С. Поэтому умножим выражения Bа) и B6) на
подходящие постоянные, сначала представив их в таком виде, чтобы
при отрицательных С они были вещественны. Мы получим
Вблизи (—С) = 0 мы будем иметь следующие разложения:
ou, 4 ) =
Искомые решения О должны иметь своим первым членом член ]/"— С
этих разложений. Дальнейшие решения мы найдем, заменив У— С
на —У—С, и решения G^ можно будет представить в основном
в виде разности первоначального решения и решения, полученного
из первоначального переменой знака перед у—С. Следовательно,
мы будем иметь
X [(У"=Ч_1ЛГ^С)-1Д-(-/=Т-/Т^С)~1Л], (За)
х [(/ire _ у тзг-С)-% _ 2 (у=ч - У r
- (- У=^с - уг=с)"'/з + 2 (- У11^ - У ь
17*

260
ГЛ VIII ТЕЧЕНИЯ С ЧИСЛОМ МАХА, РАВНЫМ ЕДИНИЦЕ
Введем новую независимую переменную и, связанную с переменной С
соотношением
D)
В таком случае
= 4-(«3 — м-3J,
1—С
du
~Ж
du
— м-3J '
м-3J
3 мб— и-
_
ц (цв _.
E)
Далее из равенства VII, 3 A) мы найдем
F)
Теперь оба рассматриваемых решения ф можно представить в виде
Gа)
„_«/. 3 О4/
или
Gб)
Приняв в равенстве A) постоянные с1 и с2 равными единице, мы
получим
16
а [а — и'1].
(8)
Для определения нулевой линии тока следует положить W 5/в равным
нулю.
Для вычисления координат х используем уравнение VII, 3 (9).
Целесообразно представить координату х в виде
х = т]/(м).

!§ 3. ПРИМЕР ТЕЧЕНИЯ С ЧИСЛОМ МАХА, РАВНЫМ ЕДИНИЦЕ 261
Тогда, имея в виду соотношения E) и F), мы получим
х == (х + l)v°[— Tjp-V.2-"/.(в» + а-3K/з] X
-3M/з
А (И8_ц-3)
х {?'• (-¦^) ж [~ ж 2</зр/в (м3+м)"% ("+а~1K (м
+р1/в ж [- т27зр1/я(и3+и"зг'л {и - а~Х
Так как для нулевой линии тока левая часть равенства (8) равна
нулю, то в последнем уравнении выражения, стоящие в квадратных
скобках и подлежащие дифференцированию по и, равны друг другу
с точностью до знака. Следовательно,
х = (*+ If- [- 4P-V.2-V+ «"«У7'] %tV>p Х
X 2-<А^|=^р'/.(--§.J1у/.(в-4-«-'Г1А(«-«-1) X
или, после простых преобразований,
х = (х + 1I/'|т1. (9)
Форму обтекаемого тела мы найдем, вычислив для нулевой линии
тока интеграл Г & dx. Вследствие пропорциональности т\ и х [урав-
[уравнение (9)] все величины в этом интеграле можно выразить через ч\.
Для этой цели прежде всего используем равенство (8), чтобы выра-
выразить р в виде функции от и; мы получим
1 (и + и-Щ
Р— 4
Далее из равенства VII, 3 A) мы найдем
Р = т1»(С—1).
Использовав второе из соотношений E), мы получим
Р = — -^(а3+и-3J.
Внеся это значение р в равенство A0), мы найдем
^-=-(«2-i+«-2). (И)

262
ГЛ VIII ТЕЧЕНИЯ С ЧИСЛОМ МАХА, РАВНЫМ ЕДИНИЦЕ
Далее, использовав равенство VII, 3B) и третье из соотношений E),
мы получим
» § (O3 /=^ ( )% B +
Наконец, имея в виду соотношения
вытекающие из равенств E), мы найдем
Точка разветвления нулевой линии тока лежит на оси щ. Там С = 0
и в соответствии с равенством D), м = — 1. Следовательно, для
этой точки на основании равенства A1) tj = —1. При определении
контура обтекаемого тела это значение т) служит нижним пределом
интеграла. Использовав полученные выше результаты, мы найдем
Внеся сюда вместо
тельно получим
A3)
его значение из уравнения (9), мы оконча-
оконча(x-\-l)~%f'[27 — 8х(х+1)']. A4)
Мы видим, что у становится равным нулю при следующих значе-
значениях х:
Уравнения A4) и (9) определяют форму профиля и распределение
переменной т\, зная которое мы можем вычислить по второй из фор-
формул V, 7A1) распределение давления. На рис. 76 показана форма
профиля (зависимость у от х), причем на профиле отмечены точки,
в которых начинаются звуковая линия и предельная характеристика.
Расчет поля течения, расположенного ниже по течению относительно
предельной характеристики, представляет собой чисто сверхзвуковую
задачу. Здесь можно изменить контур обтекаемого тела, и это не
окажет никакого влияния на поле течения, расположенное выше по
течению относительно точки, в которой начинается изменение кон-

3 ПРИМЕР ТЕЧЕНИЯ С ЧИСЛОМ МАХА, РАВНЫМ ЕДИНИЦЕ
263
тура. Следовательно, в точке
в которой у становится равным нулю, можно оборвать профиль.
На рис. 77 показано отображение верхней половины плоскости
течения на плоскость т), Ъ. Область, соответствующая плоскости
течения, заштрихована. В кормовой части профиля наклон линий
i'
о
точка, в которой начинается
предельная характеристика
точка, в которой начинается
звуковая линия
-г
)''/3
Рис. 76. Профиль, для которого поле течения при числе Маха,
равном единице, определяется простым анз 1итическим выражением
(по Гудерлею [2]).
тока отрицателен, поэтому изображение профиля в плоскости ц, 9-
опускается ниже оси т). Если мы отобразим на плоскость годографа
также нижнюю половину плоскости течения, то получим двойное
изображение
профиля
характеристика
Рис. 77. Отображение течения при числе Маха, равном
единице, около профиля, показанного на рис. 76, на пло-
плоскость 1], Ь (по Гудерлею [2]),
перекрытие области, лежащей между характеристиками, проходя-
проходящими через нулевую точку. Для расчета дозвукового поля требуется
только та часть контура в плоскости i\, Ь, которая вычерчена сплош-
сплошной линией. Она заканчивается на характеристике, проходящей через
нулевую точку (на предельной характеристике).

264 ГЛ VIII ТЕЧЕНИЯ С ЧИСЛОМ МАХА, РАВНЫМ ЕДИНИЦЕ
Вблизи звуковой линии с помощью формул VII, 4 A76) получается
следующее представление функций G:
G(a)
[Конечно, этот же результат можно получить из формул C) настоя-
настоящего параграфа.] Преобразовав гамма-функции с помощью фор-
формул VII, 4 A5), мы найдем
Внеся эти значения G(a) в формулы VII, 3 G) и VII, 3 (9), мы получим
вдоль звуковой линии
/s , 3 9-Уз/3 о\г/з
" \2 "/ "~г 2 А \2
Вблизи предельной характеристики % = 1 функции G(a' имеют вид
г(|\
6,
откуда вдоль предельной характеристики
/тс \4 У 2/тс U
Ниже по течению относительно предельной характеристики форму
обтекаемого тела можно произвольно изменять при условии, что при
этом не станут возникать волны сжатия, доходящие до звуковой

§ 3 ПРИМЕР ТЕЧЕНИЯ С ЧИСЛОМ МАХА РАВНЫМ ЕДИНИЦЕ
265
линии и, следовательно, влияющие на дозвуковое поле течения.
Например, можно подобрать кормовую часть профиля так, чтобы
при заданной ширине профиля и заданной его передней части сопро-
сопротивление получилось минимальным. Сопротивление возникает в любом
случае; только для полутела, простирающегося до бесконечности,
;
//
расширяющееся
течение
дозвуковая
область
обпасть, в которую
профиль не отра-
отражает волн
ось X заменяет профиль
в плоскости течения
^неизменная передняч
часть профиля
плоскость течения
^ кормовая часть с наимень -
шим сопротивлением
форма профиля
Рис. 78. Построение кормовой части профиля, имеющего при неизменной*
передней части и неизменной ширине минимальное сопротивчение.
.
ю
0,8
0,6
о 0,4
I. °
-0,2
-О,ч
-0,6
-0,8
_ч
, расширяющееся
течение
Рис. 79. Распределение давления на профиле, изображенном на рис. 78.
Рис 80 Профили различной ширины с одинаковой передней частью.
Кормовые части этих профилей дают для каждой ширины минимум сопротивления
(по Гудерлею [3]).
имеется возможность перевести течение в следе без потерь в парал-
параллельное течение со скоростью звука. Построение кормовой части
с минимальным сопротивлением выполнено в работе Гудерлея [3]
(см. лит. 1). Выяснилось, что вниз по течению относительно рас-
расширяющегося течения, которое необходимо предусмотреть в точке

266
ГЛ VIII ТЕЧЕНИЯ С ЧИСЛОМ МАХА, РАВНЫМ ЕДИНИЦЕ
пересечения профиля с предельной характеристикой и протяженность
которого определяет ширину профиля, последний должен иметь форму,
де допускающую отражения волн Маха (рис. 78). В поле течения
при т —э- 0 профиль получается в ви-
виде отрезка прямой у = 0. Поэтому
на рис. 78 форма профиля изображена
отдельно под картиной течения. Соот-
Соответствующее распределение давления
показано на рис. 79. На рис. 80 изо-
изображены четыре профиля, построен-
построенные таким способом.
С помощью закона подобия такие
профили можно преобразовать к оди-
одинаковой относительной толщине. В ре-
результате получаются аффинно-подоб-
ные профили с различным положе-
положением максимальной толщины и с раз-
различными передними частями (рис. 81).
Это дает возможность теоретически
вычислить сопротивление при звуко-
звуковой скорости набегающего течения и
одновременно найти связь между сопротивлением и положением макси-
максимальной толщины. Такая связь показана на рис. 82, на котором
изображена аналогичная кри-
кривая также для
с клинообразной
Рис. 81. Профили с различным поло-
положением максимальной толщины Пе-
Передние части профилей получены одна
из другой путем аффинного преобразо-
преобразования Каждый профиль имеет при
•неизменной передней части минималь-
минимальное сопротивление (по Гудерлею [3]).
0.090
ромбовидный
профиль
профиль с клинообразной
передней частью и с кормо-
k вой частью наименьшего
сопротивления
профиль с передней частью, рассчи-
рассчитанной аналитически, и с кормовой
^частью наименьшего сопротивления
профиля
передней
частью и, кроме того, отме-
отмечено кружочком значение
коэффициента сопротивле- i
ния для ромбовидного про- '
филя. Все результаты по- ^ 0,085
лучены для относительной
толщины, равной 10%. Для
аффинно-подобных профи-
профилей коэффициент сопроти-
сопротивления, согласно закону
подобия, пропорционален
относительной толщине в
степени 6/3.
Метод годографа не
дает возможности рассчи-
рассчитывать течения около произ-
произвольно заданных профи-
профилей. Это наводит на мысль развить только что изложенный
обратный способ посредством введения дальнейших „естествен-
„естественных" частных решений и таким путем составить каталог профилей
0.080
U0
50
положение максимальной
толщины
60%
Рис 82 Зависимость коэффициента сопротивления
от положения максимальной толщины Относитель-
Относительна? толщина профилей равна 10% (по Гудерлею [3]).

§ 4 ОБТЕКАНИЕ КЛИНА ПРИ ЧИСЛЕ МАХА, РАВНОМ ЕДИНИЦЕ
267
различной формы и соответствующих течений. Правда, такой прием
никогда не даст возможности получать профили с ненулевым углом
в носке.
§ 4. Обтекание клина при числе Маха, равном единице
Для клина отображение его сторон на плоскость годографа
заранее известно, поэтому краевая задача в плоскости годографа
верхняя сторона
клина
критическая
точка
критическая
точка
критическая ^_
точка ?}
верхнее плечо
клина
Р
предельные
характеристики
нижнее плеча
клина
Рис. 83. Краевая задача для клина в плоскости г\,
поверхность
«лина
может быть полностью сформулирована. Правда, для авиационной
техники клинообразный профиль имеет лишь ограниченный интерес,
но зато простота расчета делает такой
профиль особенно удобным для теоретиче-
теоретических исследований. Кроме того, клинообраз-
клинообразную модель очень просто изготовить, что
значительно облегчает сравнение эксперимен-
экспериментальных и теоретических результатов.
Мы получим отображение на плоскость
годографа течения около клина с числом в
Маха, равным единице, если стянем ударную
поляру, изображенную на рис. 45,8, в одну g~ noeepxmcmb C\
точку и затем поместим в нулевую точку клина <|>
особенность, характерную для течения с чи-
числом Маха, равным единице (рис. 83).
Коэффициент, на который следует умножить
эту особенность, конечно, определяется
размерами клина. Наоборот, если этот
коэффициент задан, то тем самым опреде-
определяются размеры клина. Сначала мы примем
этот коэффициент равным единице.
Прежде всего составим выражение для функции тока, удовлет-
удовлетворяющее условию <1) = 0 на сторонах клина (рис. 84). Обозначим его
через фх. Это выражение строится посредством зеркального отра-
Р и с. 84. Расположение осо-
особенностей вдоль оси &.

268 ГЛ VIII ТЕЧЕНИЯ С ЧИСЛОМ МАХА, РАВНЫМ ЕДИНИЦЕ
жения решения с особенностью в нулевой точке. Пусть половина
угла раствора клина равна 0О. Введем обозначение
Тогда для tyj мы получим выражение
й=+со
<!>!= 2 ф_5/аС»]> & — 2А90). B)
Решение ф_5/| определяется равенством A); переход от переменных р
и % к т] и & выполняется при помощи соотношений VII, 3A) и
VII, 3B). Для того чтобы удовлетворить граничному условию ф = 0
вдоль характеристики CD, воспользуемся частными решениями Чаплы-
Чаплыгина в виде VII, 1Bа). Мы получим
где функция g(-q, /m/0o) определяется равенством VII, 1Dа). Оче-
Очевидно, что решение ф2 также удовлетворяет граничному условию ф = 0
на сторонах клина. Решение ф2 следует определить так, чтобы на
характеристиках CD и CD' соблюдалось равенство
Следовательно, функция ф2 определяется краевой задачей Трикоми.
Вдоль звуковой линии функция ф2 ограничена, так как ряд в ра-
равенстве B) сходится там по крайней мере в среднем1). Поскольку
ряд, определяющий ф2, сходится на звуковой линии, он на основании
сказанного в конце § 1 гл. VII сходится также в сверхзвуковой
области2). В указанном параграфе был дан ответ и на вопрос
о полноте системы частных решений, использованных для предста-
представления решения <\'2. Конечно, с практической точки зрения реше-
решение C) можно считать удовлетворительным уже тогда, когда расчеты
покажут, что заданные граничные условия выполняются с хорошим
приближением.
После того как сходимость в сверхзвуковой области обеспечена,
можно определить коэффициенты ап, потребовав непосредственного
выполнения граничных условий вдоль характеристики CD, например,
путем непосредственного численного расчета. В работе Маршнера
(см. лит. 1), посвященной аналогичной задаче, для приближенного
выполнения граничных условий использованы 10 членов выражения B).
1) Характер поведения <1ъ вблизи нулевой точки вытекает из исследова-
исследований, выполненных в § 13 гл VII, поэтому ф2 можно представить как наложе-
наложение естественных частных решений ф,/в, фу , ф5/., • ¦ ¦ .
2) См. примечание на стр. 191 —Прим. ред.

§ 4 ОБТЕКАНИЕ КЛИНА ПРИ ЧИСЛЕ МАХА, РАВНОМ ЕДИНИЦЕ 269
Для этой цели в 40 точках вдоль характеристики CD были вычи-
вычислены значения функции, определяемой решениями Чаплыгина, а также
те граничные значения, которые должны иметь место на этой харак-
характеристике, и затем коэффициенты ап были определены так, чтобы
сумма квадратов отклонений приближенных решений от точных гра-
граничных значений была минимальной1).
Решение рассматриваемой нами задачи имеет вид
Это решение представляет интерес в области BCDOD'C на рис. 83
и, наоборот, не представляет интереса в области, лежащей между
характеристиками OD и OD'. Продолжение решения за предельную
характеристику, после того как определено ее положение в пло-
плоскости течения, проще всего осуществляется методом характеристик.
Для перехода от решения в плоскости годографа к решению
в плоскости течения следует воспользоваться формулами V, 7(8) и
V, 7(9). Если требуется определить только распределение давления
вдоль клина, то достаточно вычислить координаты х вдоль сторон
клина. В частности, для решения ф2 [равенство C)] мы найдем на
основании дифференциального уравнения VII, 1Bв), следующую фор-
формулу:
h= 1
Другая возможность для вычисления х, использованная в работе
Гудерлея и Йосихары [1] (см. лит. 1), состоит в том, что с помощью
равенства V, 7G) выполняется переход от ф к т\, а затем х вычи-
вычисляется по формуле V, 7A0).
Для определения положения предельной волны Маха, знание
которой необходимо для расчета течения на кормовой части обте-
обтекаемого тела, достаточно найти только зависимость координаты у
вдоль этой волны от 7). После этого координата х найдется из
соотношения
выполняющегося вдоль характеристики. Исходя от предельной характе-
характеристики, можно рассчитать течение около кормовой части тела ме-
методом характеристик.
Для практического расчета лучше всего выбрать в качестве
независимых переменных
W
*) Сходимость метода наименьших квадратов в рассматриваемой задаче
доказана в работе Л. В. Овсянникова (см примечание на стр 191)—Прим. ред.

270
ГЛ VIII ТЕЧЕНИЯ С ЧИСЛОН МАХА, РАВНЫМ ЕДИНИЦЕ
В равенство C) входят именно эти независимые переменные, в чем
нетрудно убедиться из равенства VII, 1Cа). Далее легко видеть,
что решение
можно представить в виде
Отсюда следует, что множитель 60 "/з должен войти также в реше-
решение ф2, которому теперь можно
2,0
//
//
If
ч
1
-—течение с
числом Маха М=1
_ течение в
ди
нам
{по
г/ческой трубе
Маршнеру)
1
придать вид
15
10
0,5
-0,5
-7,0
-15
-2,0
О 0$ Ofi 0,6 0,8 1,0
x/L—*¦
Рис 85. Распределение величины т] для
ромбовидного профиля в свободном течении
при Моз=\ и в блокированной аэродинами-
аэродинамической трубе. в0 есть половина угла, образо-
образованного сторонами переднего клина и одновре-
одновременно относительная толщина профиля. Для
рассматриваемого примера относительная
толщина профиля равна 10%, а ширина про-
профиля составляет 13% поперечника трубы.
Блокирующее число Маха равно 0,86 (по
Гудерлею и Йосихаре [1] и Маршнеру).
где новые коэффициенты ah не
зависят от 60. Из формул V, 7(8)
и V, 7(9) мы найдем, что соот-
соответствующие значения у про-
пропорциональны QqS/\ а соответ-
соответствующие значения х пропорцио-
пропорциональны 9<7*/з- Вследствие сделан-
сделанного выбора независимых пере-
переменных значения т) и 9 в соот-
соответствующих точках пропорцио-
пропорциональны бо3 и 80.
Распределение давления для
ромбовидного профиля показано
сплошной линией на рис. 85.
Для построения этого распреде-
распределения коэффициенту сопротивле-
сопротивления придан вид
x)' E)
~"/a
где L есть полная длина профиля. Решением ЧГ будет
Обозначение 47 5/в было пояснено в начале предыдущего параграфа.
Наличие множителя 0оэ следует из сделанных выше замечаний. На-

§ 5 СМЫСЛ НЕКОТОРЫХ РЕШЕНИИ ДЛЯ ДРУГИХ ЗНАЧЕНИИ у 271
помним, что коэффициент при члене ф__5 , входящем в состав правой
части равенства F), равен в соответствии с равенством B) еди-
единице. Полученные результаты многократно подтверждены опытом х).
Лиже (см. лит. 1), использовав в плоскости годографа вместо
уравнения Трикоми другое приближенное уравнение, сумел получить-
для задачи об обтекании клина решение в замкнутом виде.
Способ расчета, примененный в этом параграфе с целью опре-
определения ф2, может быть распространен на краевые задачи для сво-
свободных струй, сформулированные в § 2 гл. VI (рис. 50 и 51).
Однако остается под вопросом, стоит ли такое исследование затра-
затраченного на него времени.
§ 5. Смысл некоторых решений для других значений {i
В § 2 настоящей главы мы выяснили, что при течении с числом
Маха, равным единице, в нулевой точке плоскости годографа воз-
возникает особенность ф_5/. Настоящий параграф мы посвятим физи-
физическому истолкованию других антисимметричных частных решений,
также отображающих нулевую точку плоскости годографа в бес-
бесконечность плоскости течения, но содержащих множитель р в сте-
степени, меньшей —5/6. Рассмотрим антисимметричное частное решение
ф = (ГA/»)-|1О(в)(&, [1).
Пусть функция G, входящая в это решение, имеет свой первый
нуль, если считать от s = — оо, в точке ^ = с1. В бесконечности
плоскости течения получается, очевидно, параллельное течение со зву-
звуковой скоростью. Отрицательная ось т\ отображается в отрицатель-
отрицательную ось х. Для последней & = 0. Линия \ = сх отображается в по-
положительную ось х, однако здесь наклон нулевой линии тока не
равен нулю. Имея наклон линии тока, можно определить форму тела,,
соответствующую рассматриваемому течению, путем интегрирования.
Пусть О' есть производная от G по % в точке \ = сх. Точка линии
\ = cv соответствующая заданному значению р, отображается, согласно
формулам VII, 3G) и VII, 3(9), в точку плоскости течения с коор-
координатами
у = 0, Aа)
Ч } 'Р('/„)-Е. A6)
х) Хорошее соответствие теории и опыта в свое время сильно повысило
доверие как к экспериментальным методам, так и к теории.

272 ГЛ VIII ТЕЧЕНИЯ С ЧИСЛОМ МАХА, РАВНЫМ ЕДИНИЦЕ
Для определения соответствующего значения 9 получаем из
равенств VII, 3A) и VII, 3B) формулу
3 A — с А
Исключив отсюда р с помощью равенства A6), мы будем иметь
1 1 15 1
1 1
X (G') ('/„)-2ax(V,)-2p. _
•Следовательно,
l
= Г & rfx = const •
Таким образом, мы получили течение около полутела, имеющего
своим профилем обобщенную параболу. Вдоль контура получается
либо сверхзвуковая, либо дозвуковая скорость, смотря по тому,
положительно или отрицательно число с1. В первом случае звуковая
линия начинается на носке тела. (Конечно, здесь приближенное
уравнение, полученное для плоскости годографа, неприменимо.)
Переход от сверхзвукового течения к дозвуковому происходит при
[i=u/12. В этом случае ct = 0 и
у = л;0'4.
Звуковая линия совпадает с положительной осью х. Такого рода
течения можно толковать как приближение к течению вблизи перед-
передней части профиля. Если профиль достаточно заострен, то на его
передней части имеет место дозвуковая скорость. При у = х0-4 ско-
скорость остается равной скорости звука на протяжении всего профиля.
При меньших показателях степени х сверхзвуковая скорость начи-
начинается— в рассматриваемом приближении — непосредственно на носке
профиля. Но поскольку при таких степенях х носок профиля тупой,
дозвуковая область перед профилем доходит до самого носка. Зву-
Звуковая линия, начинаясь на носке профиля, простирается до беско-
бесконечности.
§ 6. Обтекание несимметричных профилей
при числе Маха, равном единице
В случае несимметричных профилей отображением бесконечности
ллоскости течения на плоскость годографа является, как и в случае
симметричных профилей, особая точка. К решениям, пригодным

§ 6 ОБТЕКАНИЕ НЕСИММЕТРИЧНЫХ ПРОФИЛЕЙ 273
в такого рода точке, предъявляется прежнее требование, а именно,
чтобы волны Маха ? = 1 не отображались в бесконечность и чтобы
вдоль этих волн не распространялись никакие особенности. При этом
условии наряду с решениями, найденными для симметричных про-
профилей, получаются другие решения, для которых значения пара-
параметра ji определяются формулами VII, 9 B). Такими решениями
являются частные решения
Соответствующими выражениями преобразованного потенциала с точ-
точностью до некоторых множителей будут ?Й\+(Й/3) и ?(?/)_/»• ^ак как
вектор, определяющий положение точки в плоскости течения, опре-
определяется градиентом преобразованного потенциала и так как для
указанных выражений ср производная ср^ вдоль отрицательной оси т]
равна нулю, то эта ось отображается в ось у плоскости течения.
Для получаемых таким путем полей течения ось у является осью
симметрии. Следовательно, должны быть симметричны относительно
оси у также характеристики, которые проходят через нулевую
точку, причем эти характеристики должны представлять собой пре-
предельные характеристики течения. Однако это противоречит нашим
представлениям о структуре поля течения. Таким образом, ни одно
из указанных частных решений, взятое само по себе, не может
представлять поле течения для несимметричного тела в бесконечности.
Далее легко видеть, что все частные решения ф(^,„ ,ft, за исклю-
исключением первого, при приближении к нулевой точке стремятся к бес-
бесконечности быстрее, чем частное решение ф(Д,, описывающее пове-
поведение течения в бесконечности для симметричного профиля; поэтому
вблизи нулевой точки в линейной комбинации решений ф(|0„., й и ф(Д,
преобладающую роль играет все же решение ф®.,. ,ft. Следовательно,
поведение решения в нулевой точке можно задать только линейной
комбинацией решений фМ. и фЩ, . Для преобразованного потенциала
соответствующими решениями будут tp^ и <р№. Однако из этих двух
решений особым в смысле доказательства Трикоми можно назвать
только первое.
Если задача решается для заданного профиля, то на указанные
выше решения следует наложить еще решения ф®3 и ф/у|+№/3) или
Т^з и тй\+шз)» удовлетворяющие в нулевой точке условиям Трикоми.
В общем случае область сходимости такого представления не дохо-
доходит до профиля!).
*) В соответствии с результатами § 13 гл. VU. — Прим, ред.
18 Зак 534, К, Г. Гудерлей

274 ГЛ VIII ТЕЧЕНИЯ С ЧИСЛОМ МАХА, РАВНЫМ ЕДИНИЦЕ
§ 7. Обтекание клина под углом атаки
Для симметричных профилей целесообразно исходить от легко
выполнимого решения в плоскости годографа и уже затем опреде-
определять форму профиля в плоскости течения. Наоборот, для профилей,
поставленных под углом атаки, такой способ почти не представляет
интереса. В самом деле, главной целью подобного рода исследова-
исследований является всегда сравнение с результатами, найденными для про-
профиля с нулевым углом атаки, чтобы таким путем получить представле-
представление о подъемной силе. Очевидно, что для достижения этой цели
форма профиля должна сохраняться.
В качестве первого примера профиля, поставленного под углом
атаки, естественно рассмотреть клиновидный профиль. Правда, полу-
получаемое поле течения не является вполне подходящим с точки зрения
верхняя сторона
клина Т верхнее плечо
клина
предельные
'характеристики
нижняя сторона нижнее плечо
клина клина
Рис. 86. Отображение течения около клина под углом
атаки на плоскость т], 9 (по Гудерлею и Йосихаре [3]).
задач, рассматриваемых в этой главе, так как вследствие обте-
обтекания острия клина возникает местная сверхзвуковая зона. В этом
отношении было бы более интересным исследовать профиль с за-
закругленным носком. Однако, как мы увидим ниже, при малых углах
атаки влиянием местной сверхзвуковой зоны вполне можно пренебречь
(Гудерлей и Йосихара [3], см. лит. 1).
Если отвлечься от этой местной сверхзвуковой зоны, то годограф
течения будет иметь вид, изображенный на рис. 86. Оставим на-
направление набегающего течения при повороте клина на выбранный
угол атаки неизменным; тогда положение нулевой точки плоскости т), Ь
останется прежним, стороны же клина сместятся параллельно самим
себе на расстояния, соответствующие углу атаки. Вдоль сторон
клина имеет место граничное условие ф = 0. Решение содержит теперь
две произвольные постоянные, а именно коэффициенты при выражениях
Ф^5/ и ?-ч • имеющих особенности в нулевой точке. Эти коэффициенты
определяются, как и в задаче об обтекании клина с нулевым углом
атаки (в которую, однако, входит только один коэффициент), раз-
размерами сторон клина. Предположим на минуту, что мы произвольно

§ 7 ОБТЕКАНИЕ КЛИНА ПОД УГЛОМ АТАКИ 275
приняли коэффициент при фМ. равным нулю. Тогда вследствие не-
несимметрии ограничивающего контура в плоскости годографа (отно-
(относительно нулевой точки) решение в этой плоскости будет несим-
несимметричным, и поэтому в плоскости течения получится клин со
сторонами неодинаковой длины. Путем подходящего выбора коэф-
коэффициента при фИ, можно сделать обе стороны одинаковыми по
длине.
Как уже было упомянуто, вследствие обтекания острия клина сле-
следует ожидать появления местной сверхзвуковой зоны. В какой мере
годограф, построенный на рис. 86, позволяет заключить о необхо-
необходимости существования такой зоны? В случае симметричного клина
было очевидно, что в критической точке, т. е. при т] -»•— оо, воз-
возникает точка разветвления. Ожидать, что такая точка появится сама
собой и в несимметричном поле, нельзя. Это вытекает из следующих
соображений. При отрицательных значениях т] решение может быть
разложено по частным решениям Чаплыгина. Использовав асимпто-
асимптотические выражения VII, 7 (9а) для функций Ханкеля, мы получим
в качестве частных решений, играющих при tj —э- — со преобладающую
роль, следующие выражения:
|tj|-'/<еЧУзIч|3/WBeo)cos
Первое из этих выражений затухает при ч; ->— оо менее быстро,
чем второе, и поэтому при tj-> — оо всегда значительно больше
второго. Так как между —90 и +90 оно не имеет нулей, то кар-
картина течения в плоскости т), 3- имеет вид, очень сходный с карти-
картиной, изображенной на рис. 32, хотя там в основе построения лежат
совсем другие координаты. Только в том случае, когда коэф-
коэффициент при первом из этих частных решений равен нулю, полу-
получается точка разветвления линий тока при ~ц -> — оо. В общем же
случае следует ожидать, что годограф будет именно таким, каким он
изображен на рис. 86.
Правда, местная сверхзвуковая зона, имеющая, например, вид, по-
показанный на рис. 87, дает возможность изменить изображение течения
в плоскости годографа так, чтобы критическая точка опять стала
точкой разветвления линий тока. Однако практически вряд ли воз-
возможно рассчитать эту зону, и даже если бы такая возможность суще-
существовала, то результат расчета вряд ли совпадал бы с действитель-
действительностью, так как нельзя не считаться со всегда возникающим отрывом
течения.
Такая же сверхзвуковая зона возникает и при обтекании пластинки,
поставленной под углом атаки. Гудерлей и Йосихара учитывали
влияние местной сверхзвуковой области следующим образом. Годограф,
18*

276
ГЛ VIII ТЕЧЕНИЯ С ЧИСЛОМ МАХА, РАВНЫМ ЕДИНИЦЕ
изображенный на рис. 88, соответствует течению около клина,
имеющего на острие щиток. Точка разветвления лежит на переднем
конце этого щитка. Из годографа мы видим, что обе ветви линии
тока после ее разветвления имеют одинаковое направление, но ско-
скорости для каждой из них различны. При нулевой скорости полу-
получается вогнутый угол. При приближении угла атаки к нулю длина
щитка и сила, действующая на него со стороны течения, стремятся
о
Ч
о
/ I
звуковая /: :
линия I предельная
\// / характеристика
/I/
i 11
!// сверхзвуковая
область
критическая'
точка
дозвуковой
область
линия
сверхзвуковая
•j \ ^ область
\ \ \ предельная
j\ \ харак
6\ \о
ti It
" область
отрыва
А Г
передняя—а \ /
кромка
верхнее плечо
• клина
^предельные
' ^характеристики
нижнее плечо
клина
Рис. 87. Обтекание клина под углом атаки; а — поле
течения; б—отображение на плоскость годографа.
к нулю. Вполне правдоподобно предположение, что влияние щитка
на полную подъемную силу по своей величине имеет такой же по-
порядок, как сила, действующая на щиток со стороны течения. Иссле-
Исследование показывает, что эта сила с уменьшением угла атаки стре-
стремится к нулю быстрее, чем подъемная сила; следовательно, при
достаточно малом угле атаки ею можно пренебречь.
В основе расчетов Гудерлея и Йосихары [3] (см. лит. 1) лежат
следующие-соображения. Раньше изменение угла атаки учитывалось

7. ОБТЕКАНИЕ КЛИНА ПОД УГЛОМ АТАКИ
277
точка \
разветвления \
нулевой линии -
шока „
\
параллельным смещением изображения профиля в плоскости годографа
на некоторое расстояние в направлении Ъ. Однако можно поступить
и по-иному, а именно оставить изо-
изображение профиля на месте, но
зато сместить в противоположном
направлении нулевую (особую) точ-
точку. Будем считать это смещение
малым. Течение около тела с ну-
нулевым углом атаки будем называть
основным течением; оно было
рассчитано на стр. 268. Это тече-
течение имеет в нулевой точке особен-
особенность, определяемую выражением
ф_5/. Для задания этой же особен-
особенности в точке т] = О, Ь = а (а есть
угол атаки) следует взять выражение
ф ,, (тп, Ь — а).
Разложив его по степеням а и
использовав соотношение VII, 6B),
мы получим
направление
набегающего
течения
Рис. 88. Толкование аналитического ре-
решения как течения около клина с носо-
носовым щитком (по Гудерлею и Йосихаре [3]).
Следовательно, в первом приближении перемещение особенности ф_5/
из точки т) = 0, 0 = 0 в точку т] = 0, & = а эквивалентно наложению
на первоначальную особенность ф_5, выражения —кC/2)ф_4/ (т]. &)•
Сначала мы не будем учитывать множитель —C/2)а. Тогда к выраже-
выражению <J)_4, (tj, &) следует прибавить еще решение ф, удовлетворяющее
условию Трикоми и выбранное так, чтобы для полученной суммы
удовлетворялось граничное условие ф = 0 вдоль изображения кон-
контура. Это выполняется, как и на стр. 268, путем зеркального отра-
отражения особенности относительно изображений сторон клина и при-
прибавления частных решений Чаплыгина. Полученное таким спо-
способом выражение (включая 4*_</) обозначим через фх. Если мы наложим
теперь течение, соответствующее функции фр на основное течение,
то получим решение, которое в первом приближении эквивалентно
решению, имеющему в точке tj = O, &=a особенность ф_5, и удо-
удовлетворяющему условию ф — 0 вдоль сторон клина.
Следующим шагом является отыскание решения, имеющего
в точке 7j = 0, &=a особенность ф и удовлетворяющего вдоль

278 ГЛ. VIII, ТЕЧЕНИЯ С ЧИСЛОМ МАХА, РАВНЫМ ЕДИНИЦЕ
изображений сторон клина условию <1> = 0. Приближенно можно
заменить эту особенность такой же особенностью в точке т] = 0, & = 0.
Способ расчета остается, конечно, прежним. Обозначим это реше-
решение через фп„ Теперь необходимо найти такую комбинацию
4*i —1— const- фп,
которая не изменяет длины сторон клина. Выполняется это следующим
образом. Найдем для решений фх и фя значения х, соответствующие
плечам клина, причем для острия клина (f} = — оо) примем х = 0.
Тогда множитель перед фп следует выбрать так, чтобы значение х
для решения фп на плече клина было равно соответствующему зна-
значению х для фр но имело обратный знак. Это условие должно быть
выполнено только для одной стороны клина, так как каждое из ре-
решений, полученных для верхней и нижней сторон, вносит в значе-
значение х вклады, одинаковые по величине, но обратные по знаку.
Найденное таким путем решение, оставляющее при наложении на
Основное течение форму клина неизменной, обозначим через ч?~/з-
Таким образом, мы имеем
4T'/s = <!>! + const. фп.
Это решение в принципе можно представить в виде
где a.z'J/1 есть постоянная, а функция ф~4/" удовлетворяет условию
Трикоми. Обозначения соответствуют соглашению, введенному в на-
начале § 3 настоящей главы. Пусть решение для клина с нулевым
углом атаки дано в следующем виде:
где а~% есть постоянная, которая определяется размерами клина и
может быть найдена из равенства VIII, 4 F). Эффект, возникающий
вследствие небольшого угла атаки, можно получить путем прибавле-
прибавления к этому решению выражения
I%ЧГ€/\ B)
где а, как уже упоминалось, есть угол атаки.
Если в плоскости годографа наложить на основное течение дру-
другое решение, то в плоскости течения точка, которой соответствует
определенный вектор скорости, переместится на расстояние, обусло-
обусловленное наложенным решением. В первую очередь нас интересует,
конечно, изменение давления (или изменение величины т]) в задан-
заданной точке. Для отыскания этого изменения требуется линеаризация;
это не налагает какого-либо ограничения, так как выше, при раз-

§ 7. ОБТЕКАНИЕ КЛИНА ПОД УГЛОМ АТАКИ
279
ложении решения ф_5/ (т), & — а) по степеням угла атаки, мы уже
выполнили такую же линеаризацию.
Значения х и у, найденные для основного течения, обозначим через
xo(f], &) и yo(ri, 9-), а соответствующие значения, полученные для
дополнительного решения ф, —через л;(т), &) и _у(т), &). Следовательно,
мы будем иметь
Наложим на основное течение решение ф, изменим одновременно 7)
на Д-rj и 8- на ДЭ- и предположим, что ip имеет первый порядок ма-
малости; тогда х и у получат следующие изменения:
Подберем теперь Дт) и Д9- так, чтобы Дл: и Д_у стали равными нулю.
Тогда значения -г) —f— Attj и ft-f-ДЭ- будут определять собой вектор
скорости, отображающийся при наложении ф в точку, в которой для
основного течения мы нашли значения к] и &. Следовательно, местные
изменения значений т) и 9- будут равны
Cа)
7
Конечно, на поверхности профиля уо = О. Так как стороны клина
представляют собой отображение линий & = const, то на них
дуо[д-ц = О. Далее, на изображении сторон клина J7= 0. Таким обра-
образом, на сторонах клина мы имеем
Отсюда, использовав вторую из формул V, 7A1), мы можем вы-
вычислить изменение давления.
Для отыскания решения ф в сверхзвуковой области следует при-
применить метод характеристик. При этом могут оказаться полезными
следующие соображения. Если решение выражается через преобра-
преобразованный потенциал, то
•* = (*+l)V>v У = <?*>•

280 ГЛ. VIII ТЕЧЕНИЯ С ЧИСЛОМ МАХА, РАВНЫМ ЕДИНИЦЕ
Характеристики уравнения Трикоми, определяемые уравнением
*3— +7]-'/
db — - ^
должны удовлетворять условию совместности
или
dy
Следовательно, условие совместности для характеристик в плоскости
годографа определяет направления характеристик в плоскости тече-
течения. Поэтому построение преобразованного потенциала в плоскости
годографа можно толковать как построение сети характеристик
в плоскости течения. Для основного течения этот результат является
тривиальным. Но этот результат имеет место и для наложенного те-
течения, взятого в отдельности. По поводу граничных условий для
наложенного течения ф можно сказать следующее. Для ромбовидного
профиля вдоль его кормовой части, отображающейся в рассматри-
рассматриваемом приближении в у = 0, соблюдается равенство $ = — $0. По-
Поэтому в плоскости годографа мы имеем в качестве граничного
условия
у = 0 при & = — ид.
Наоборот, при построении в плоскости х, у граничным условием
будет
Ь = — ft0 при у = 0.
Координаты х, у могут быть определены следующим образом. Сна-
Сначала вычислим вдоль предельной характеристики значения х и у,
соответствующие наложенному решению ф, для тех же пар значений
7j и в-, которые были использованы при определении основного
течения. Затем построим в плоскости х, у сеть характеристик
в точности таким же образом, как это делается в плоскости тече-
течения. Граничным условием будет
8- = — &0 при у = 0.
Для определения изменения, вызванного в распределении давления
наложением решения ф, следует поступить так: взять из построен-
построенного поля значения х и у, соответствующие точкам пересечения тех
характеристик плоскости годографа, которые были построены
в основном течении, т. е. для тех же значений г\ и 9, а затем внести
взятые х и у в формулы (За) и C6) или, если требуется опреде-
определить изменение давления вдоль профиля, в формулу D).

7. ОБТЕКАНИЕ КЛИНА ПОД УГЛОМ АТАКИ
281
Результаты этого расчета изображены на рис. 89 в безразмерном
виде. Построенная кривая дает изменение величины Y] на единицу
угла атаки. Это изменение можно сравнить с изменением давления
около клина, возникающим при небольшом изменении угла раствора
клина. Из формулы VIII, 4 E) мы
имеем -3,5
-3,0
Следовательно, при изменении угла i _^5
раствора клина на Д60 величина т\ изме-
изменяется на 5 -2,о
."'4,
Ат, = | в."
Соответствующая кривая изображена
на рис. 89 штрихами. Мы видим, что
эффект изменения угла атаки сравним
по величине с эффектом изменения
угла раствора клина, но значительно
больше последнего.
Путем интегрирования можно опре-
определить величину dcjda. Положив
v. = 1,4, мы получим
-15
-1,0
-0,5
1
1
\
ч
V
0.2
оа
x/L
as as w
Рис. 89. Изменение величины т; для
ромбовидного профиля под углом
атаки (сплошная кривая) и для клина,
угол раствора которого увеличен на а.
(штриховая кривая). Половина угла
раствора переднего клина и относи-
относительная толщина профиля равны б0;
а есть угол атаки (по Гудерлею и
Йосихаре [3]).
Центр давления отстоит от передней точки ромбовидного профиля
на расстоянии, равном 29,4% хорды профиля.
Примечательно, что здесь величина dcjda зависит от относи-
относительной толщины б0. Ни линейная теория дозвуковых течений, ни
линейная теория сверхзвуковых течений не позволили обнаружить
такой зависимости. Другое примечательное явление обнаруживается
из рис. 105 (стр. 341), на котором изображена зависимость dcjda
от числа Маха набегающего течения. Правая часть кривой пока-
показывает изменение величины dcjda при чисто сверхзвуковом тече-
течении; эту часть кривой можно построить, если выполнить известный
расчет сверхзвукового поля с упрощением вблизи числа Маха,
равного единице. Коэффициент подъемной силы в этой области
значительно выше, чем при числе Маха, равном единице (самая ле-
левая часть кривой). Дальнейшие расчеты покажут, что левая часть
кривой при числе Маха, равном единице, т. е. при т\ = 0, имеет
горизонтальную касательную и что там кривизна кривой равна нулю.
Следовательно, в промежутке между течением со скоростью звука
и чисто сверхзвуковым течением должно иметь место весьма

282
ГЛ. VIII ТЕЧЕНИЯ С ЧИСЛОМ МАХА, РАВНЫМ ЕДИНИЦЕ
своеобразное изменение коэффициента подъемной силы. Это обстоя-
обстоятельство было причиной того, что Винченти и Вагонер [2] (см. лит. 1)
исследовали промежуточную область теоретически и эксперимен-
экспериментально. Левая часть кривой проведена через точки, полученные
в этом исследовании. За подробностями отсылаем к первоисточнику.
Задача обтекания клина с прилегающим к его острию скачком
уплотнения была рассмотрена в § 4 гл. VI (рис. 53). Аналитическое
решение этой задачи дано Йосихарой [1] (см. лит. 1). Некоторые
замечания по поводу этого решения (ему соответствует штриховая
часть кривой на рис. 105) будут сделаны на стр. 342.
§ 8. Краевая задача для тела произвольной формы,
поставленного под малым углом атаки, и родственные задачи
Пусть для тела произвольной формы известна картина течения
при числе Маха, равном единице; следовательно, известно и изобра-
изображение этой картины в плоскости годографа (рис. 90). Примем, что
дозвуковая
область
lil
Ю
I
^предельная
I характеристика
11 сверхзвуковая
I1 область
сверхзвуковая
область
_ звуковая
ч линия
\ особенность
набегающего
линия /
Рис. 90. Течение около тела произвольной формы при числе Маха, равном
в бесконечности единице; а — поле течения, б — отображение на плоскость годографа
это решение имеет место при ьулевом угле атаки. Решение в пло-
плоскости годографа обозначим через W~b/\ Попытаемся найти измене-
изменение давления, вызываемое изменением угла атаки на небольшую ве-
величину. Как и в предыдущем параграфе, изменение угла атаки при-
приводит к перемещению точки годографа, в которую отображается
бесконечность плоскости течения. Это перемещение обусловливает,
согласно сказанному в предыдущем параграфе, наложение на исход-
исходное течение W~ решения, имеющего в нулевой точке в качестве
преобладающей составляющей особенность §_,, . Такое решение

§ 8 КРАЕВАЯ ЗАДАЧА ДЛЯ ТЕЛА ПРОИЗВОЛЬНОЙ ФОРМЫ 283
должно удовлетворять граничным условиям, выражающим требование
о неизменности контура тела при указанном наложении. В дальней-
дальнейшем нам понадобятся решения, удовлетворяющие таким же гранич-
граничным условиям, но обладающие в нулевой точке особенностями, за-
заданными функциями ^_,ti\_ihpy Излагаемое ниже исследование учи-
учитывает и эти более общие решения.
Граничные условия на профиле выражаются проще всего через
преобразованный потенциал ср, который также удовлетворяет диффе-
дифференциальному уравнению Трикоми. Согласно сказанному в § 11
гл. V [уравнение A2)], граничным условием, выражающим неизмен-
неизменность контура в плоскости течения, будет
J.(<P) = <P4 + Wlo^!=0. A)
где т) = тH(&) есть уравнение контура исходного течения в плоско-
плоскости годографа. С помощью соотношения ф = сра, выведенного в § 7
гл. V и связывающего функцию тока с преобразованным потенциа-
потенциалом, и уравнений VII, 6A) и VII, 6B) мы найдем, что при исполь-
использовании преобразованного потенциала выражениям
соответствуют выражения
Выражение ф_„, которое, очевидно, не удовлетворяет условию
Трикоми, преобразуется с точностью до множителя в выражение ср >
удовлетворяющее условию Трикоми. Но там, где краевая задача
может быть сформулирована с помощью функции ф, коэффициент
при ф_„ может быть определен (см. стр. 285).
Таким образом, мы должны найти решение ср уравнения Трикоми,
удовлетворяющее вдоль профиля условию A) и имеющего в качестве
преобладающей составляющей решение ср_,5.^_,hm с особенностью
в нулевой точке.
При отыскании этого решения мы должны учитывать следующее.
В случае течения с числом Маха, равным единице, поведение тече-
течения в нулевой точке описывается выражением ср_„, имеющим здесь
особенность и умноженным на некоторый коэффициент, зависящий
от размеров тела. Если тело несимметрично относительно направле-
направления набегающего течения, то необходимо принять, что этот коэф-
коэффициент зависит также от угла атаки (для симметричного тела он —
как следует из соображений симметрии — имеет постоянное значе-
значение). Конечно, мы должны предполагать, что течение является
единственным, т. е. что изменение коэффициента определяется краевой
задачей. Перемещение нулевой точки учитывается наложением реше-

284 ГЛ. VIII ТЕЧЕНИЯ С ЧИСЛОМ МАХА, РАВНЫМ ЕДИНИЦЕ
ния ср_%. Если при этом одновременно изменится коэффициент
при ср_1/з в полном решении, то в наложенном выражении появится
член ср_„ с множителем, зависящим от только что указанного коэф-
коэффициента. Следовательно, решение, которое подлежит наложению,
содержит две составляющие, имеющие особенности в нулевой точке;
несмотря на это, оно должно оставаться единственным. Возникает
вопрос, как математически выразить это свойство краевой задачи.
Исчерпывающего метода решения краевой задачи второго рода пока
еще не существует. Однако с большой степенью достоверности
можно предположить, что для уравнения Трикоми также должно
существовать дополнительное условие, касающееся граничных зна-
значений и сходное с тем дополнительным условием, которое известно
из теории потенциала. В самом деле, если бы такого дополнитель-
дополнительного условия не существовало, то для известного течения с числом
Маха, равным единице, можно было бы найти такое решение урав-
уравнения Трикоми в виде
<Р = ?_./, + ?•
которое, будучи наложено на исходное течение, оставляло бы кон-
контур в плоскости течения неизменным. (Буквой <р мы обозначаем
в соответствии с соглашением в начале § 3 настоящей главы ре-
решение, удовлетворяющее условию Трикоми.) Путем наложения та-
такого выражения на исходное течение мы могли бы получить для
того же профиля и другое течение с числом Маха, равным единице,
а это означает, что течение с числом Маха, равным единице, взятое
за исходное, не является единственным.
Эти соображения приводят одновременно к следующему выводу:
выражение Z-(tp) [равенство A)], составленное для ср_„ с целью вы-
выполнения граничных условий для функции ср в последнем уравнении,
никогда не может удовлетворять дополнительному условию, необ-
необходимому для краевой задачи второго рода. (Такое утверждение
может показаться странным, поскольку упомянутые дополнительные
условия в деталях неизвестны.) Из сказанного, однако, следует, что
можно добиться разрешения краевой задачи второго рода, если
ввести в нее выражение ср, умноженное на подходящий коэффи-
коэффициент.
Таким образом, мы приходим к предположению, что решение
сформулированной выше краевой задачи для функции ср имеет вид
Т_E/в)_(й/2) Iя- 7з т~7з ГТ • KfJ
Вблизи нулевой точки решение Z~W<)-W2) может быть представлено
как наложение естественных частных решений Трм+шв)" Краевая за-
задача для функции щ-Р/еЫА/а), к которой, таким образом, сводится

§ 8. КРАЕВАЯ ЗАДАЧА ДЛЯ ТЕЛА ПРОИЗВОЛЬНОЙ ФОРМЫ 285
поставленная задача, мо^кет быть решена путем надлежащего рас-
распределения особенностей вдоль изображения контура в плоскости
годографа. Если бы течение было несжимаемым, то эти особен-
особенности были бы аналогичны источникам. Тогда выполнение граничных
условий потребовало бы решения некоторого интегрального уравнения.
До настоящего времени попытка такого расчета не сделана.
Если перейти от ср к <|», то решение B) примет вид
+ а1^-(й/а)ф_1/з+ф-(<Л)-ад. C)
Конечно, коэффициенты а в равенствах B) и C) различны. В ре-
решение C) входит член ф_„ (с особенностью в нулевой точке), ко-
который в решении B) включен в выражение ср.
Более наглядно вычисление этих частных решений выполняется
для клина, так как для него граничные условия могут быть сразу ука-
указаны, а именно на изображении его сторон должно быть ф = 0 как для
основного течения, так и для наложенных решений. Решения, удо-
удовлетворяющие этим граничным условиям, требуют в нулевой точке
только одного выражения ф_„ или ф_Eм_№/2) с особенностью в этой
точке. Однако такие решения в общем случае изменяют длину сто-
сторон клина и, следовательно, при наложении на исходное течение
изменяют форму тела. Если решение фантисимметрично (h — четное
число), то изменения длины обоих сторон клина имеют одинаковый
знак, если же решение ф симметрично (й — нечетное число), то одна
из сторон удлиняется, а другая укорачивается, с чем мы уже встре-
встретились при расчете обтекания клина, поставленного под углом атаки.
Для того чтобы получилось решение, оставляющее длину сторон
неизменной, необходимо наложение дальнейших решений. При чет-
четном h используется решение, имеющее в качестве составляющей
с особенностью выражение ty_s,, т. е. решение для числа Маха,
равного единице; при нечетном h используется решение с выраже-
выражением ф_,. в качестве особенности. Следовательно, искомые частные
решения имеют вид
ЧГ-М-» = V%)_ft + «llJW-» Ua + Г™"*- A = 1. 2. ... D)
Uh)h ^U^{%)_h, A = 0. 1.2 E)
Решения D) и E) совпадают с решением C), если не считать
того, что в решениях D) и E) вследствие симметрии рассматри-
рассматриваемой задачи отсутствуют некоторые члены, входящие в решение C).

286
ГЛ VIII ТЕЧЕНИЯ С ЧИСЛОМ МАХА, РАВНЫМ ЕДИНИЦЕ
Звуковая
линия
сверхзвуковая
область
—О
пиния тока, проходящая
через критическую точку
дозвуковая
область
^характеристика
\
звуковая-Щ
линия \(.4
волны \\'Л
разрежения А \
предельная \ \
характеристика^*
-аУ\
§ 9. Обтекание пластинки под углом атаки
при числе Маха, равном единице
Решение задачи об обтекании пластинки под углом атаки при
числе Маха, равном единице, сравнительно просто и поэтому пред-
представляет особый интерес. Такую пластинку можно рассматривать
как предельный случай кли-
оЦ In на. угол атаки которого
велик по сравнению с углом
раствора.
Представление о струк-
структуре поля течения можно
получить из рис. 91. Пред-
Предположим сначала, что пла-
пластинка помещена в аэро-
аэродинамическую трубу и обду-
обдувается на блокирующем
числе Маха. В таких усло-
условиях в течении образуются
два самых узких попереч-
поперечных сечения: одно между
передней кромкой пластин-
пластинки и верхней стенкой тру-
трубы, другое — между задней
кромкой пластинки и ниж-
нижней стенкой трубы. Поэто-
Поэтому следует ожидать, что на
передней кромке пластинки
возникнет звуковая линия,
направленная к верхней
стенке, а на задней кром-
кромке— такая же звуковая ли-
линия, направленная к ниж-
нижней стенке. Вблизи передней
кромки пластинки обра-
образуется, как и всегда при дозвуковом течении, критическая точка.
Направление линий тока, расположенных непосредственно под
линией тока, проходящей через критическую точку, всегда прибли-
приблизительно совпадает с направлением набегающего течения. Напра-
Направление же линий тока, расположенных непосредственно над линией
тока, проходящей через критическую точку, немного позади крити-
критической точки почти противоположно направлению набегающего
течения.
Поэтому при обтекании передней кромки возникает резко
расширяющееся течение. Звуковая линия, выходящая из передней
кромки пластинки, образуется здесь именно вследствие расширения
V
^характеристика
линия I
тока, проходящая через
критическую точку
Рис. 91. Схема течения около пластинки под углом
атаки при числе Маха, равном единице.

§ 9. ОБТЕКАНИЕ ПЛАСТИНКИ ПОД УГЛОМ АТАКИ
287
течения. Сначала она направлена перпендикулярно к пластинке
вниз, а затем меняет свое направление почти на 180° и продол-
продолжается вверх к стенке трубы. Поле течения вблизи задней кромки
пластинки имеет в точности такую же структуру, как около плеча
клина.
При возникновении расширяющегося течения около передней
кромки пластинки здесь теоретически должен образоваться абсо-
абсолютный вакуум, вслед за которым должно произойти повышение
давления вследствие подхода волн сжатия от звуковой линии.
Практически же здесь возникает местный отрыв течения. Наклон
пластинки приводит к тому, что на верхней ее стороне имеет место
чисто сверхзвуковое течение.
Получив представление об обтекании пластинки в аэродинами-
аэродинамической трубе, мы можем перейти к течению с числом Маха, рав-
равным единице, если отодвинем
стенки трубы в бесконечность.
При исследовании обтекания кли-
клина, поставленного под углом
атаки, мы обнаружили, что вбли-
вблизи острия клина возникает ме-
местная сверхзвуковая зона. Теперь,
при обтекании пластинки, такая
сверхзвуковая зона образуется
над всей верхней стороной пла-
/D
характеристики
\ /
г^
в
Рис 92. Отображение течения около пла-
пластинки, поставленной под небольшим углом
атаки, на плоскость -q, 0.
СТИНКИ.
После сказанного о структуре
поля течения годограф течения
(рис. 91) не требует специальных пояснений. Сомнения может
вызвать только вопрос о формулировке граничных условий в области
расширения течения около передней кромки пластинки. Если ограни-
ограничиться малыми углами атаки, то нулевая точка будет расположена
очень близко от изображения нижней стороны пластинки. Теперь
выполним, в соответствии с законом подобия, такое аффинное пре-
преобразование плоскости годографа, которое оставляет положе-
положение нулевой точки неизменным относительно изображения стороны
клина.
Для этого введем новые переменные
Угол атаки также пропорционален z . При предельном переходе
t —> 0 та часть плоскости i\, &, в которой происходит обтекание
острия клина, перемещается в бесконечность. Следовательно, рас-
рассматриваемое граничное условие не играет существенной роли
(рис. 92). От решения необходимо потребовать, чтобы оно удо-
удовлетворяло условию ф = 0 вдоль *АВС и в бесконечности. Особен-

288
ГЛ VIII ТЕЧЕНИЯ С ЧИСЛОМ МАХА, РАВНЫМ ЕДИНИЦЕ
ность в нулевой точке должна получиться в результате наложения
выражений ф и ф_„. В качестве дальнейших условий мы найдем,
что при р —> со должна получиться точка разветвления линий тока
и что решение должно дать для длины пластинки заданное значе-
значение L.
Оба последние условия определяют те параметры задачи,
которые допускают свободный выбор. Такими параметрами являются
коэффициенты частных решений ф_8. и ф_„.
В последующих вычислениях будем писать ч\ и % вместо ч\ и &.
О том, каким должно быть решение, можно догадаться на основа-
основании его вида в точке Вив бесконечности (Гудерлей [12], см.
лит. 1). Выберем точку В за начало координат системы т\, %. Так
как вдоль СВ и В А должно соблюдаться граничное условие ф = О,
то решение вблизи точки В может быть представлено как наложе-
наложение частных решений фЙ\+й- Вдоль линии ВС частные решения
имеют вид
¦&
линия
тока
следовательно, полным решением будет
где Р(р) есть пока еще неизвестный степенной ряд относительно р.
Для выяснения поведения решения в бесконечности поступим сле-
следующим образом. Мысленно продол-
продолжим решение от характеристики OD
к характеристике АЕ. Для этого не-
необходимо использовать значения ф на
характеристика харакТерИСтике OD, а также усло-
условие ф = 0, подлежащее выполнению
в бесконечности. Характеристика АЕ
„_ представляет собой одну из волн Маха
расширяющегося течения, возникаю-
Рис. 93. Типичное расположение ЩеГ0 На передней кромке ПЛаСТИНКИ.
линий тока в плоскосш^, »для реше- Поэтому эта характеристика не должна
отображаться в бесконечность плоско-
плоскости течения. Те частные решения, ко-
которые, во-первых, при р —»• оо стремятся к нулю, во-вторых,
вдоль |= — оо удовлетворяют условию ф = 0 и в-третьих, таковы
что для них характеристика $ = 1 не отображается в бесконечность,
имеют вид
?\ Bа)
/6
у
фЩ,.
М5/.)-»»
А=1, 2 ... .
B6)

§ 9. ОБТЕКАНИЕ ПЛАСТИНКИ ПОД УГЛОМ АТАКИ 28Э
Функция G , соответствующая первому частному решению, не
обладает нулями между ? — — оо и ?=1. Примерный вид линий
тока в плоскости г\, 0 показан на рис. 93; решение не имеет точки
разветвления в бесконечности. Так как это решение содержит
в себе р в наименьшей возможной отрицательной степени, то при
р -> оо оно играет преобладающую роль и, следовательно, опреде-
определяет поведение полного решения. Таким образом, указанное выше
условие, что бесконечность должна представлять собой точку раз-
разветвления линий тока, исключает возможность частного решения Bа).
Из сказанного следует, что при больших значениях р и ? = — оо
решение должно иметь вид
Обозначим через р0 значение, соответствующее вектору скорости
набегающего течения. Если угол атаки равен 80, то
Ро = |бо- C)
Попробуем взять решение вдоль ? = — оо в виде
При р -> оо и при р = 0 это решение во всяком случае обладает
правильным видом. Имея решение D), можно построить все поле
течения путем аналитического продолжения. Необходимо доказать,
что во всем поле течения, за исключением нулевой точки, отсут-
отсутствуют особенности и что особенность, получающаяся в нулевой
точке, имеет требуемый характер. Имея в виду дальнейшие исследо-
исследования, рассмотрим сразу более общее выражение для решения,
а именно
) (?) . E)
где т и п суть целые числа. Составив биномиальные разложения
правой части этого равенства относительно р/р0 и Кр/Ро)~ > мы по"
лучим
_ / 5 . .Л
C/»)+m+h
19 Зак 534 К Г. Гудерлей

290 ГЛ VIII ТЕЧЕНИЯ С ЧИСЛОМ МАХА, РАВНЫМ ЕДИНИЦЕ
откуда в качестве аналитического продолжения решения найдем
X
)(±) Fа)
х
Подставив сюда соответствующие асимптотические выражения для
G(a'(|, ja) (см. стр. 218), мы увидим, что решение Fа) сходится
при р/ро<1, а решение F6) — при р/р0 > 1. Использовав формулу
VII, 4A76), мы получим вдоль звуковой линии
T(i+n+h)T(i+m+h)T{i
— ("/,)+т—п—h
(?) X
7i=0
й-0
G6)

§ 9 ОБТЕКАНИЕ ПЛАСТИНКИ ПОД УГЛОМ АТАКИ 291
Этим формулам можно придать также следующий вид:
.
«/а, Г \ 6" + т) Г \~з) с. / 5 . 7 . 4 . р \
и
Ро
5 . 11
f+». T+»-'»' Т+"-™- (i)"')}- <8б>
Отсюда нетрудно выяснить поведение решения вблизи нулевой
точки (р/ро=1)> являющейся особой точкой. Прежде всего мы
видим, что гипергеометрические функции, входящие в первые сла-
слагаемые формул (8а) и (86), удовлетворяют одному и тому же гипер-
геометрическому дифференциальному уравнению. То же самое отно-
относится и к гипергеометрическим функциям, входящим во вторые
слагаемые. Поэтому при р/ро= 1 формулы (8а) и (86), если их
преобразовать с помощью соотношения VII, 4 Eа), дают линейную
комбинацию одних и тех же гипергеометрических функций.
Следовательно, для того чтобы показать, что в нулевой точке
оба решения [(8а) и (86)] „подходят* одно к другому, достаточно
исследовать коэффициенты при указанных гипергеометрических функ-
функциях. Это исследование приведет одновременно и к разложению реше-
решения в нулевой точке. За подробностями отсылаем к работам Гудерлея
[12, 13] (см. лит. 1). Окончательный результат можно сформулировать
в следующем виде. Пусть р и ? суть значения р и i для того слу-
случая, когда нулевая точка принимается за начало координат tj, &.
19*

292 ГЛ VIII ТЕЧЕНИЯ С ЧИСЛОМ МАХА, РАВНЫМ ЕДИНИЦЕ
Тогда решением вдоль звуковой линии при & <С 60 будет
Первые коэффициенты a®, a,-?
в это решение, имеют значения
™, ?° и &~<7/2)~™ рядов, входящих
ejr(VJ-» = (_1)«2-('«-»3 21/..
A0а)
— К.
A06)
Следующие коэффициенты вычисляются по рекуррентным формулам:
-4)['
— /»)] =0; A1a)
103 . . . 4 . .,)
3^- — 4 (re — m) — -g (re — mf | —
. A16)

§ 9. ОБТЕКАНИЕ ПЛАСТИНКИ ПОД УГЛОМ АТАКИ
293
На основании формулы (9) решения вблизи нулевой точки могут
быть составлены путем наложения частных решений вида
Если показатель степени величины р отрицателен, то соответствующее
частное решение имеет в нулевой точке особенность. Всегда
имеется только конечное число таких членов. Выпишем в явном
виде первые члены разложений ф0>0, ф1-* и ф2-2. Они понадобятся
для дальнейших вычислений. При %¦ < 90 мы получим
¦ 0,0
9/з
Ро
19
12
"+...]
' = ——2
9/3
A2а)
A26)
и= 1 ^[imJ/'_J«(I\-*+ ...1.
9/3 L 63 V р0 / 378 V ро / J
Имея эти выражения, мы можем вычислить коэффициенты при соот-
соответствующих частных решениях (|)_„, ф_5. и т. д., обладающих
особенностями в нулевой точке. Мы найдем
ьо, о = _.
19
27"
A36)
!J, 2 .
128
143-8
Полученных результатов вполне достаточно для описания искомых
решений в плоскости годографа. В частности, ф0'0 с точностью
до множителя, зависящего от длины пластинки L, представляет собой
решение для пластинки, поставленной под углом атаки.
Теперь остается перейти к решению в плоскости течения.
В частности, необходимо найти распределение г\ вдоль пластинки.
Из равенства D) с помощью равенств V, 7(8) мы найдем
=-(*+1г'л!(!борх
X
(И)

294 ГЛ VIII ТЕЧЕНИЯ С ЧИСЛОМ МАХА, РАВНЫМ ЕДИНИЦЕ
где хп'п есть значение х вдоль пластинки, соответствующее реше-
решению i,n'n. Целесообразно ввести новую переменную:
т =—^Цг- A5)
Тогда мы получим
оо
(и есть переменная, по которой производится интегрирование).
Далее введем обозначение
1+и3ГC/а)~иЛл A7)
со
Положив
мы увидим, что интеграл A7) представляет собой не что иное, как
бета-функцию, и мы получим
.», п 1_
гA+«)гШ
В частности,
^o = _|_AiI_iiZ. A8а)
zi,i = ^/o,o_ (]8б)
,а. з П ,о,о /1 о„\
* — 63 * • v '
Таким образом, для течения с числом Маха, равным единице, около
пластинки, поставленной под углом атаки и имеющей длину L,
решение имеет вид
I 6 ) \ 3 )

§ 9. ОБТЕКАНИЕ ПЛАСТИНКИ ПОД УГЛОМ АТАКИ 295
В этом решении коэффициенты при частных решениях ф__5/ и ф_„
равны
[ (Г]|?Т* BОа)
(!L\
19
или, если выразить р0 через 60 на основании формулы C),
B0г)
Зависимость x/L от rt определяется формулой
где
B1)
/.= йа/,A+цзГ/.<*в. B1а)
Обозначение л:~5/« введено для того, чтобы подчеркнуть, что х соот-
соответствует решению Ч7~ . Формула B1) позволяет вычислить распре-
распределение давления на поджимающей стороне пластинки. Величина tj
всегда отрицательна, поэтому нижний предел интеграла в фор-
формуле B1а) всегда положителен.
Распределение давления на подсасывающей стороне пластинки
определяется методом характеристик. При этом опять возникает
вопрос об отрыве течения около передней кромки пластинки. Оче-
Очевидно, что область отрыва при уменьшении угла атаки становится
все меньше и меньше. Следовательно, при малом угле атаки влиянием
отрыва на распределения давления можно пренебречь. Далее, при
малых углах атаки скорость в любой точке течения (за исклю-
исключением области около передней кромки пластинки) мало отличается
от скорости звука; поэтому вполне оправдано, по крайней мере

296
ГЛ VIII ТЕЧЕНИЯ С ЧИСЛОМ МАХА, РАВНЫМ ЕДИНИЦЕ
формально, применение приближенного уравнения околозвуковых
течений. Следовательно, сначала мы должны определить положение
волны Маха OD (или другой линии, положение которой легко вычи-
вычислить на основании полученных результатов) и, исходя из этой волны,
рассчитать поле течения с помощью метода характеристик для около-
околозвуковых течений. Если волны сжатия, исходящие от звуковой линии,
отражаются от поверхности пластинки, то на передней кромке пла-
пластинки возникает скачок упло-
уплотнения. Тем не менее построе-
построение поля течения показывает,
что давление на подсасы-
подсасывающей стороне пластинки
можно достаточно точно
вычислить путем аналити-
г,5
S,o
1.5
1,0
0,5
„-0,5
-15
-гш
¦2,5
-3,0
значение J], достигаемое при рас-
расширяющемся течении Мейера
у* пластинка под
's^- углом атаки в аэро-
аэродинамической трубе
пластинка под углом
атаки при М= 1
ческого продолжения выра-
выражения для давления на под-
поджимающей стороне. Таким
путем для определения коор-
координаты х на подсасывающей
стороне пластинки получается
формула
X
Т
зг||
1
7>1. B2)
Результат вычисления по этой
формуле показан на рис. 94.
Как и для клина, он может
быть представлен в виде
о
0,2
0,ч 0,6
x/L
0,8 1,0
7] =
Рис. 94. Изменение величины -q для пластинки
под углом атаки при числе Маха, равном еди- ИЛИ
нице (сплошная кривая); для пластинки под упом
атаки в блокированной аэродинамической трубе С~ =
(штрих-пунктирная кривая), для клина (штриховая '
кривая). 6П есть угол атаки или половина у1ла рас-
раствора клина. Кривые для пластинки в аэродинами- =-
ческой трубе рассчитаны для угла атаки 0,1 E,7°)
и ширины пластинки, равной */ю поперечника
трубы (по Гудерлею [2]).
B3)
пластинки не одинакова. На рис. 94
коэффициент давления, получающийся
Конечно, функция g(x/L) на
верхней и нижней сторонах
для сравнения показан также
при расширении первоначально

§ 9 ОБТЕКАНИЕ ПЛАСТИНКИ ПОД УГЛОМ АТАКИ 29Т
параллельного течения, имеющего скорость звука, на угол, равный3
углу атаки пластинки. Для пластинки этот коэффициент получился
бы в том случае, если бы течение вдоль нижней стороны пластинки
не оказывало никакого влияния на течение вдоль верхней стороны.
Кроме того, на рис. 94 изображено распределение давления для:
клина с углом раствора, в два раза большим угла атаки пластинки.
Условия на плечах клина такие же, как на задней кромке пластинки.
Следовательно, разница в распределении давления около пластинки
и клина связана с обтеканием передней кромки пластинки. Вычерчен-
Вычерченные кривые показывают, что взаимное влияние нижней и верхней сторон
пластинки не очень велико. Полная подъемная сила немного больше
двойного значения подъемной силы, которая получилась бы при
осуществлении указанного выше расширения первоначально парал-
параллельного течения. Центр давления отстоит от передней кромки пла-
пластинки на расстояние, равное 46% ширины пластинки. О третьей'
кривой, изображенной на рис. 94, будет сказано ниже. Расчет поля'
течения около пластинки на основании точного уравнения в плоскости*
годографа был выполнен Винченти и его сотрудниками (см. рис. 30),
Ниже будут использованы частные решения W~*'s и W~"'' или
более общие частные решения хр~(<у~( >г\ обладающие следующими
свойствами.
1. В нулевой точке преобладающую роль играет особен-
особенность ф /,,) ,й/9,, которая входит с коэффициентом, равным единице.
Кроме этой особенности, в \jr~^ /з)—{ /а) входят только особенности
*-¦/* и +-•/.-
2. На изображении поверхности пластинки выполняется усло-
условие tj> = 0.
3. При р —> со получается точка разветвления линий тока.
4. Вклад этих решений в полную длину пластинки равен нулю-
Подобного рода решения легко могут быть получены из фор-
формул A3) и A8). Представим эти решения в виде
Т"~4/з = р0-'Т4/' B4а>
где
'^'^8^11!^0) B4в>
B4г)
Соответствующие значения х вдоль пластинки будем обозначать
верхним индексом, совпадающим с индексом функции ЧГ. Эти зна-

298
ГЛ VIII ТЕЧЕНИЯ С ЧИСЛОМ МАХА, РАВНЫМ ЕДИНИЦЕ
чения определяются по следующим формулам:
х-
II'- (А
где
1V 3
х-»/. =
X
11
135
X
_2_ (—1
21 1+(-
B5а)
B56)
B5в)
B5г)
Приведем еще следующие очень простые соотношения, которые нам
понадобятся в дальнейшем:
х-1''
d
X
135
А ("ЧУ 1.
21 l+(-^KJ
B6а)
B66)
4
dr.
§ 10. Другие частные решения, получаемые
аналогичными методами
Покажем дальнейшие применения метода определения решений ф,
изложенного в предыдущем параграфе. Полученные результаты будут
использованы в следующей главе.
Рис. 95. Граничные условия для точки разветвления
второго порядка.
Для расчета течения около несимметричного тела в блокированной
аэродинамической трубе необходимо иметь решения, для которых
точка Q на рис. 95 является точкой разветвления второго порядка.

§ 10 ДРУГИЕ ЧАСТНЫЕ РЕШЕНИЯ 299
На первый взгляд может показаться целесообразным применение
решений Фальковича (см. стр. 246). Однако в рассматриваемом
случае они не подходят по следующим причинам. Задачи, приводящие
к решениям с точкой разветвления второго порядка, требуют раз-
разложения поля течения по параметру, определяющему расстояние
точки Q от звуковой линии. Поэтому используемые решения должны
быть пригодны и в том случае, когда точка Q попадает на звуковую
линию. Но это требует, чтобы волны Маха, проходящие через нулевую
точку, не отображались в бесконечность плоскости течения и не
обусловливали особенностей в кривизне линий тока. Решения Фаль-
Фальковича, а также решения Тамады и Томотики не удовлетворяют
этому требованию. В самом деле, значительные трудности возникают
не только при совмещении точки Q с нулевой точкой, но даже при
приближении точки Q к нулевой точке.
Решения, которые мы сейчас выведем, получаются как наложение
естественных частных решений, поэтому только что указанные труд-
трудности отпадают.
Необходимые нам частные решения симметричны относительно
линии ? = — оо и удовлетворяют условию ф = 0 вдоль линии OQ
(рис. 95). Попробуем представить решение вдоль I =— со при
р > pQ в следующем виде:
- ч -V*
Ре.
где k есть целое число. Разложим правую часть в ряд по степеням
(р/Ро)~Х- Взяв это разложение за основу и использовав частные
решения фН,,-,^, мы сумеем продолжить решение в область р/р_ >¦ 1.
Вдоль звуковой линии мы получим
6 3
Легко видеть, что эта функция уже дает продолжение решения
на всю звуковую линию (не только при р ]> р„У Если мы разложим
это решение по частным решения с мнимыми значениями [х, то уви-
увидим, что рассматриваемая функция ф не имеет в дозвуковой области
особенностей нигде, кроме линии %=. — сю. Гипергеометрические
Функции, определяющие функцию ф вдоль звуковой линии, могут

300 ГЛ VIII ТЕЧЕНИЯ С ЧИСЛОМ МАХА, РАВНЫМ ЕДИНИЦЕ
быть представлены в виде рядов относительно р/р0. Эти разложения
являются основой для следующего представления функции ф в обла-
области р<ре:
X/*/- + *. —+ *, -
V2 6 3
р \ Уз; \з/ /о 1 \ — р
Г I — t —, /с, —=
Т I — -i- ь\г I 11 \ 6 6 ,3
7V" Г(*1)ГШ f/7 U 5
Использовав это разложение, а также асимптотическое представле-
представление решения О, можно показать, что при р <^ р„ не получается ни-
никаких особенностей. Степени р, входящие в функцию ф, соответ-
соответствуют антисимметричным естественным частным решениям. Коэффи-
Коэффициенты этих частных решений могут быть вычислены с помощью послед-
последнего уравнения. Вычисления показывают, что при 1 = — оо и Р<Рл
действительно ф = 0.
Представляют интерес также такие частные решения, которые,
имея в точке Q точку разветвления второго порядка и удовлетворяя
условию ф = 0 при \ = — оо и р < р„, стремятся заданным образом
к бесконечности при р —> оо. В этом случае за основу следует взять
функцию
где ф есть значение правой части равенства A) при k = 0, а вели-
величина h произвольна. Подробности исследования этого случая, во мно-

§ 10 ДРУГИЕ ЧАСТНЫЕ РЕШЕНИЯ
301
гом сходного с предыдущим примером, имеются у Гудерлея [13]
(см. лит. 1). Новой и важной деталью является только определение
постоянной интегрирования в равенстве B). Окончательный результат
для области р > р0 имеет вид
:rJH,,ar
6.
¦ir— 3h) , ~
l
T2
VT
'2г7Т
Г(-ЗА)
Ниже мы рассмотрим течение в свободной струе со скоростью
звука, которое приводит к краевой задаче, схематически изображенной
на рис. 96. Плоскость ч), в де-
делится линиями р = const на внеш- ¦&"
нюю и внутренюю области. Во
внутренней области производится p=const
наложение частных решений ¦ ""
и, кроме того, поскольку ф =
=• const при S = 0, решения
b = O{a)U, ±). D)
''характеристика
%°о
Рли с. 96. Краевая задача для свободной
струи, имеющей скорость звука.
Во внешней области производится наложение частных решений
3 ,
При составлении решения во внутренней области вносит затрудне-
затруднение частное решение D). Поэтому сначала вместо решения ф найдем
его производную по р, в которую частное решение D) не вносит
никакого вклада. Введем обозначение
Граничные условия, которым должна удовлетворять функция х> Ука"
заны на рис. 96. При р <С Ро функцию х можно представить как
наложение выражений
р \J

302 ГЛ VIII ТЕЧЕНИЯ С ЧИСЛОМ МАХА, РАВНЫМ ЕДИНИЦЕ
а при р ]> р0, т. е. во внешней области, — как наложение выражений
р 6 G
Решение при \ — — оо попробуем представить в виде
/3(-^Г3/'. E)
Как и раньше, можно показать, что во всей дозвуковой области
особенности отсутствуют. Выполнив вычисления, мы найдем
при р < р0 Fа)
и
при р > р0. F6)
Вдоль звуковой линии мы получим
7") МТ' Т' 2"' ~г) при р<Ро
Ро / V ^ " ^ Ро /
._"/„,
Ро/ \ Р
о ., / п \ ~u/e
° "-Я1 П кI _ _ . _ i_^i I при
Эти результаты позволяют выяснить поведение решения вблизи точки А.
Решение здесь действительно обладает ожидаемыми свойствами.
Остается перейти от -/ к ф. Прежде всего необходимо знать
значение ф на линии ОА. В бесконечности, согласно условиям задачи,
ф = 0. При ? = — оо мы имеем
Отсюда путем интегрирования мы найдем
Ро

§ 10. ДРУГИЕ ЧАСТНЫЕ РЕШЕНИЯ 303.
В нулевой точке интеграл в правой части представляет собой не
что иное, как бета-функцию, следовательно.
Дальнейшие члены разложения ф в нулевой точке получаются по-
почленным интегрированием равенства Fа). Равенство G) определяет
коэффициент при частном решении О (S, 1/12) Использовав фор-
формулу VII, 4A76), мы найдем для звуковой линии
На эту величину следует разделить функцию ф, вычисленную иа
уравнения E), для того чтобы получить решение, удовлетворяющее
граничному условию ф= 1 вдоль отрезка О А на рис. 96. Для даль-
дальнейших приложений нам понадобятся первые члены разложения ^
в бесконечности. Выполнив это разложение, мы найдем

Глава IX
ТЕЧЕНИЯ, ЛИШЬ НЕМНОГО ОТЛИЧАЮЩИЕСЯ ОТ ТЕЧЕНИЙ
С ЧИСЛОМ МАХА, РАВНЫМ ЕДИНИЦЕ
§ 1. Предварительные замечания
В предыдущей главе мы исследовали особенности, пригодные
.для представления в бесконечности поля течения около симметрич-
лого тела, на которое набегает поток с числом Маха, равным еди-
единице. Это исследование привело сначала к бесконечно большому
числу частных решений, а именно к решениям ^_»/»> Ф-"/« и т- д-
Все эти решения удовлетворяют условию, предъявляемому к волнам
Маха, проходящим через нулевую точку. Для получения одного
.единственного решения нам пришлось ввести дополнительное условие,
согласно которому плоскость течения должна перекрываться только
одним листом. Бесконечно большое число полученных частных
решений заставляет предполагать, что путем наложения друг на
.друга таких решений можно построить также такие поля течения,
.которые на большом расстоянии от обтекаемого тела удовлетворяют
другим условиям.
Что следует под этим понимать, поясним путем рассмотрения
.аналогии между источником в комплексной плоскости и околозву-
околозвуковым течением в плоскости т), Э-. Комплексный потенциал источника
в несжимаемом течении в точке z = 1 определяется уравнением
cp=Re!n (г—1),~
тде z = x -\-1у. При больших значениях z правую часть можно
разложить в ряд, и мы получим
= In r — r~* ;os v рт- г"г cos 2v ^-f~3 cos 3v
Z о
где

2 ПРИМЕРЫ ТЕЧЕНИИ 305
В указанной аналогии друг другу соответствуют следующие величины:
комплексная плоскость z плоскость y], ft
г = 0 нулевая точка
г Р
частные решения r~m cos mi частные решения ф_(«/в)_д
особенность в г = 1 особенность в дозвуковой области
В действительности может быть не одна особенность, а больше;
аналитическая функция всегда может быть разложена в ряд Лорана,
независимо от свойств, которыми функция обладает внутри круга
сходимости. Так, например, следует ожидать, что путем наложения
функций ф_E/)_л можно получить такие решения уравнения Трикоми,
которые в области, ограниченной определенной линией р== const
и играющей роль круга сходимости, имеют весьма сложный вид
В частности, внутри линии р = const могут существовать такие же
пустые области, какие получаются в годографе при возникновении
скачков уплотнения.
Правильность только что указанных предположений мы докажем
(Гудерлей [5], см. лит. 1) в следующих параграфах, опираясь на ис-
исследования, выполненные в гл. VII.
§ 2. Примеры течений, немного отличающихся от течений
с числом Маха, равным единице
Говоря о течениях, немного отличающихся от течений с числом
Маха, равным единице, обычно имеют в виду такие случаи, когда
скорость набегающего течения мало отличается от скорости звука.
Однако мы будем смотреть на это понятие шире и будем включать
в него также случаи, когда отклонение от исходного поля течения
(с числом Маха, равным единице) обусловливается граничными усло-
условиями, заданными на большом расстоянии от обтекаемого тела. Среди
подобного рода течений особую ценность представляют те течения,
для которых легко может быть построен годограф. Примерами таких
случаев могут служить: течение в блокированной закрытой аэроди-
аэродинамической трубе, обтекание тела свободной струей с критической
скоростью и течение около тела при сверхзвуковом числе Маха.
Течение при большом дозвуковом числе Маха слишком сложно,
чтобы проследить за всеми его деталями. Качественное описание
его будет дано на стр. 389—391.
С течением при сверхзвуковом числе Маха мы уже познакомились
в § 11 гл. V (рис. 45). Там в качестве обтекаемого тела мы рас-
рассмотрели клин. Сейчас мы опять рассмотрим обтекание клина, но
примем, что число Маха набегающего течения отклоняется от
20 Зак. 534. К. Г. Гудерлей

306
ГЛ IX. ТЕЧЕНИЯ С ЧИСЛОМ МАХА, БЛИЗКИМ К ЕДИНИЦЕ
единицы очень немного, следовательно, ударная поляра лежит в непо-
непосредственной близости от нулевой точки годографа.
При обтекании тела в блокированной аэродинамической трубе
(рис. 97) все линии тока в годографе выходят из точки Р, лежащей
в дозвуковой области и изображающей скорость, соответствующую
блокирующему числу Маха. Верхняя стенка трубы отображается
в отрезок РО, являющийся частью верхней стороны разреза OQ.
Нижняя стенка трубы отображается в полигон PQO, причем PQ лежит
на верхней стороне разреза OQ, a QO — на его нижней стороне.
ЗвуковаяА предельная
линия 11 характеристика
~-р о
звуковая¦ J \ предельная
линия ^характеристика
VW//////////A//////////////%///////////////////
Рис. 97. Несимметричное течение в блокирован-
блокированной аэродинамической трубе (по Гудерлею [5]).
Рис. 98. Несимметричное течение в сво-
свободной струе, имеющей критическую ско-
скорость (по Гудерлею [5]).
Точка Q соответствует минимальному значению скорости вдоль ниж-
нижней стенки трубы. Примечательно, что для несимметричного поля
течения точка Р не должна лежать обязательно на конце отрезка'Оф.
Для симметричного поля течения точки Р и Q, конечно, совпадают.
Вдоль линий РО и PQO для функции тока должны быть заданы
значения, которые она имеет на стенках трубы. Если ширина трубы
равна W и если плотность потока массы fw* принять равной еди-
единице, то i[> = W/2 на РО и i|> = — W/2 на PQO.
При обтекании тела параллельной струей, имеющей критическую
скорость (рис. 98), все линии тока в плоскости годографа выходят
из одной точки, лежащей на звуковой линии (точка О). На линиях
тока, ограничивающих струю, скорость везде равна критической
скорости, ю направление ее меняется. Поэтому эти линии отобра-
отображаются на плоскость годографа в отрезок, расположенный вдоль

§ 3 ГРАНИЧНЫЕ УСЛОВИЯ НА ОБТЕКАЕМОМ ТЕЛЕ 307
звуковой линии. Для несимметричного поля течения изображения ОЕ
и ОЕ' границ струи имеют разную длину. Граничные условия на
обтекаемом теле не требуют дальнейших пояснений.
Обе эти краевые задачи содержат в общем случае по два свобод-
свободных параметра, которые можно выбирать. Так, например, при течении
в блокированной аэродинамической трубе (рис. 97) блокирующее
число Маха и минимальная скорость вдоль стенок трубы, т. е. поло-
положения точек Р и Q, не связаны непосредственно с геометрическими
параметрами поля течения. То же самое имеет место и в отношении
положения точек Е и Е' (рис. 98). Для того чтобы краевая задача,
схематически представленная на рис. 45, имела единственное реше-
решение, необходимо задать значения функции тока ф в точке ? и в точке,
ей симметричной относительно оси i\. Впрочем, для последующих
вычислений целесообразнее выбирать другие параметры, вводимые
менее искусственным путем.
В том, что искомые поля течения получаются только при пра-
правильном выборе указанных параметров, можно убедиться на примере
несимметричного клина. На основании доказательства Трикоми крае-
краевая задача в плоскости годографа, представленная на рис. 97, имеет
единственное решение, если заданы положения точек Р и Q. Это
означает, что размеры сторон клина получатся вполне определен-
определенными. Только при специальном выборе точек Р и Q получится зара-
заранее заданная форма клина. Ниже мы увидим, что эти параметры по-
получаются одновременно с решением краевой задачи также в более
общих случаях.
При исследовании подобного рода задач сначала определяется
семейство решений, удовлетворяющих граничным условиям на про-
профиле, но не учитывающих граничных условий вблизи нулевой точки.
В нулевой точке решения имеют особенность, в остальной же обла-
области плоскости годографа, ограниченной изображением контура тела
и характеристиками, проходящими через нулевую точку, эти решения
везде удовлетворяют дифференциальному уравнению Трикоми. Иско-
Искомое решение для течений вблизи числа Маха, равного единице, всегда
может быть получено путем наложения только что указанных выра-
выражений. Граничные условия, заданные вблизи нулевой точки, дают бес-
бесконечную систему уравнений для коэффициентов решений, налагаемых
друг на друга. Решение этой системы получается в виде разложения
по параметру, определяющему отклонение искомого течения от исход-
исходного течения с числом Маха, равным единице.
§ 3. Решения, удовлетворяющие граничным условиям
на обтекаемом теле
В § 8 гл. VIII в связи с исследованием течения около тела про-
произвольной формы, поставленного под небольшим углом атаки, уже
было показано, как вычисляются решения, удовлетворяющие граничным
20*

308 ГЛ IX ТЕЧЕНИЯ С ЧИСЛОМ МАХА, БЛИЗКИМ К ЕДИНИЦЕ
условиям на обтекаемом теле. Здесь мы сначала напомним вкратце
полученные результаты и принятую систему обозначений, а затем
докажем, что каждое решение, удовлетворяющее граничным условиям
на обтекаемом теле, может быть получено наложением друг на друга
выражений, использованных в § 8 гл. VIII.
Течение с числом Маха, равным единице, будем считать изве-
известным. Согласно результатам предыдущей главы, это течение всегда
определяется функцией
Обозначения, принятые в этом уравнении, были пояснены в начале
§ 3 гл. VIII. Функция ф~5/' в подходящим образом выбранной обла-
области всегда может быть разложена по естественным частным реше-
решениям, т. е. может быть представлена в виде
Коэффициенты а, входящие в правые части равенств Aа) и A6),
определяются формой обтекаемого тела. Верхний индекс при а сов-
совпадает с верхним индексом той функции W, в выражение которой
входит рассматриваемый коэффициент, а нижний индекс совпадает
с индексом того естественного частного решения ф_,., ф„ или <j*ft,e.
к которому относится рассматриваемый коэффициент. Индекс функ-
функции ф совпадает с индексом функции W.
Согласно сказанному в § 8 гл. VIII, частные решения, оставляю-
оставляющие при наложении на исходное течение контур обтекаемого тела
неизменным, имеют вид
^ ~ >-(%)- (й/2) ^К-V. V-5/o ^
+ а:™-(л/а)ф_1/>+ф-('")-{А/в). B)
где функция ф~^'3'~' 's> может быть выражена через естественные
частные решения следующим образом:
Т. -№-№) _ у „-Ы- (ft/2)
Покажем, что все частные решения, которые при наложении на тече-
течение с числом Маха, равным единице, оставляют контур тела в пло-
плоскости течения неизменным, могут быть представлены (в подходящим
образом выбранной области) бесконечным рядом из частных решений
вида Bа). Для этого следует перейти от функции тока к преобра-
преобразованному потенциалу. В соответствии с равенством VIII, 8 B) мы

§ 3 ГРАНИЧНЫЕ УСЛОВИЯ НА ОБТЕКАЕМОМ ТЕЛЕ 309
имеем
Обозначим для исходного течения с числом Маха, равным единице,
изображение профиля в плоскости годографа через К. Область, огра-
ограниченную контуром К и характеристиками, проходящими через нуле-
нулевую точку, обозначим через О. Неизменность профиля в плоскости
течения при наложении некоторого решения ср выражается гранич-
граничными условиями второго рода. Следовательно, применив способ обо-
обозначения, использованный в равенстве VIII, 8A), мы получим
Ш = о. C)
Пусть для такого решения ср уравнение Трикоми выполняется в обла-
области О везде, за исключением окрестности нулевой точки. Эта окрест-
окрестность представляет собой область, в которой должны быть заданы
дополнительные граничные условия (см. рис. 97 и 98). Решение ср
в подходящим образом выбранной части области О может быть раз-
разложено по естественным частным решениям (см. § 13 гл. VII и рис. 73).
Пусть в этом разложении коэффициентами при частных решениях
?_<./,)-(»/») бУдУт P_(Va)-(ft/2)- Рассмотрим ряд
и выясним, в какой области он сходится, т. е. где функция ср дей-
действительно определяется равенством D). Сначала рассмотрим только
первые слагаемые функций ф"^»~>~^2\ т. е. выражение
Это есть та составляющая функции ср (разложенная в ряд в указан-
указанной выше части области О), члены -которой возрастают по мере
приближения к нулевой точке. Согласно сказанному в § 13 гл. VII,
этот ряд сходится в указанной части области G и притом также для
больших значений р (так как в него не входят функции, возрастаю-
возрастающие вместе с р). В частности, этот ряд и его производная сходятся
вдоль изображения профиля К. Следовательно, сходится и ряд
Точнее говоря, частные суммы
N
^ ^*?-т-(А/а))

310 ГЛ IX ТЕЧЕНИЯ С ЧИСЛОМ МАХА, БЛИЗКИМ К ЕДИНИЦЕ
имеют предел при N-+co. Так как, согласно предположению,
то имеет место также равенство
У / (й ф-E«-(А/ал_,
или
iV
Это означает, что выражения
дают решение краевой задачи второго рода, если в качестве гра-
граничных значений заданы правые части уравнений E). Но так как
для правильно сформулированной краевой задачи при изменении гра-
граничных значений решение изменяется непрерывно и так как весьма
правдоподобно, что рассматриваемая краевая задача сформулирована
правильно, то из сходимости правых частей уравнений E) при N —>со
следует сходимость ряда
У 8 (crE/fbW2)<p
йо (Vb)"(ft/a) /з ^-
во всей области G.
После того как мы выяснили, что ряд ср вдоль К сходится, можно
показать, что разность ср — ср вдоль К удовлетворяет граничному
условию
*•(? — 9) = 0. F)
Кроме того, в упомянутой выше части области О функция ср — ср
может быть разложена по естественным частным решениям. Из по-
построения функции ср следует, что это разложение не содержит чле-
членов <р_„.._.А»., поэтому оно сходится вплоть до нулевой точки, если
только не учитывать члена ср_,, .
Следовательно, разность ср — ср представляет собой, в области О
функцию, удовлетворяющую условиям Трикоми и содержащую в ка-
качестве единственной особенности функцию ср_1; . Кроме того, функ-
функция ср — ср удовлетворяет граничному условию F), поэтому на осно-

§ 4 ГРАНИЧНЫЕ УСЛОВИЯ ВБЛИЗИ НУЛЕВОЙ ТОЧКИ 311
вании соображений, изложенных в § 8 гл. VIII, она равна нулю. Это
означает, что выражение ср в виде ряда D) дает искомое предста-
представление функции ср.
§ 4. Граничные условия вблизи нулевой точки
Как показывают примеры из § 2 настоящей главы, граничные
условия, которые должны выполняться вблизи нулевой точки, могут
иметь весьма различный вид. Могут существовать линейные одно-
однородные и неоднородные граничные условия, они могут -зависеть от
параметров, либо предписываемых самой задачей (например, значе-
значения ф вдоль стенок аэродинамической трубы), либо определяемых
только в процессе решения задачи (например, положение точек Р
и Q на рис. 97). Возможны также нелинейные граничные условия.
Общим для всех этих граничных условий свойством является сле-
следующее: они должны давать соотношения между величинами, оставав-
остававшимися раньше неопределенными. Если мы опять перейдем к функции
тока ф и включим в решение также исходное течение, то сможем
представить каждое решение, удовлетворяющее граничным условиям
на профиле, в следующем виде:
оо
Ф^-ъ+Ея-ш-м*-™-™. A)
где функции Ч?" определяются уравнениями IX, 3A а) и IX, 3B),
а постоянные ?_(«/„)-(й/а) заменяют постоянные Р_{!/)_ №/2)> входящие
в уравнения IX, 3D). Следовательно, граничные условия вблизи ну-
нулевой точки должны давать уравнения для определения коэффициен-
коэффициентов ?_(./,)_ (ft/2).
В подходящим образом выбранной части области G решение может
быть разложено по естественным частным решениям; выполнив это
разложение, мы получим
Такой вид решения A) более удобен для выражения граничных усло-
условий вблизи нулевой точки, так как он не зависит от формы обте-
обтекаемого тела. Предположим, что граничные условия вблизи нулевой
точки приводят к системе уравнений
B_m_m) = F-™-W\B_*/e, В_,А, Ло, А/о Ат, ...). C)
Здесь F суть известные, в общем случае нелинейные функции ука-
указанных аргументов. Величины Аь/е, а также В_% и S_ya могут быть
выражены с помощью уравнений A), IX, 3 Aа) и IX, 3 B) через

312 ГЛ IX ТЕЧЕНИЯ С ЧИСЛОМ МАХА, БЛИЗКИМ К ЕДИНИЦЕ
пока неизвестные величины В-^-^щ следующим образом:
- V — -У,
D)
Внеся эти значения в уравнения C), мы получим систему уравнений
для постоянных б_(*/,)_(а/2). Решение этой системы может быть вы-
выполнено методом итераций. В качестве первого приближения мы возь-
возьмем исходное течение с числом Маха, равным единице. Для этого
течения
Затем из уравнений D) мы найдем
р ^ — 5As D гг~5^ Л г* "~%
-7„ ~~ -V.' -Vs~" -Vs1 Л/б"~ яй/б '
Подставив эти значения в уравнения C), мы получим для В следую-
следующие приближенные значения:
Используя эти значения, мы можем продолжать улучшать решение.
Наши примеры показывают, что граничные условия могут содер-
содержать в себе свободные параметры, которые определяются только
в процессе расчета. Система уравнений C) составлена в предполо-
предположении, что эти параметры исключены. Однако с практической точки
зрения обычно целесообразнее оставлять эти параметры в граничных
условиях. Тогда число уравнений увеличится соответственно числу
параметров. Наиболее естественно такие уравнения получаются
для 5_i/, и #_5/„.
Параметры, допускающие выбор, либо связаны с величиной р
(например, положение точек Р и Q на рис. 97 определяется заданием
значений р для этих точек), либо представляют собой значения функ-
функции тока. В соответствии с той или другой возможностью они будут
обозначаться либо через р1 и р2, либо через ф2 и ф2. Далее при фор-
формулировке неоднородных граничных условий могут встретиться такие
величины, которые хотя и определяются полем течения, но которые
целесообразнее включать в качестве параметров в уравнения, выра-
выражающие граничные условия. Эти величины мы будем обозначать
аналогичным способом.

§4 ГРАНИЧНЫЕ УСЛОВИЯ ВБЛИЗИ НУЛЕВОЙ ТОЧКИ
Таким образом, граничные условия вблизи нулевой точки могут
быть выражены, например, следующей системой уравнений:
В-ы-т = *'~111*~т®1- Ь- Pi. Pa. А). Ч- Ач* ¦¦' а*:*- ¦ ¦ ¦)> E)
причем принимается, что из четырех параметров, входящих в эту
систему, два связаны с величиной р, а два — с функцией тока ф. Два
из этих четырех параметров следует рассматривать как известные.
Вследствие структуры уравнения Трикоми и упрощенных условий
на скачке уплотнения решение этого уравнения в плоскости годо-
годографа остается верным как при изменении масштаба р, так и при
умножении решения на постоянную величину. Первое изменение пред-
представляет собой деформацию поля течения в соответствии с законом
подобия, а второе — простое изменение масштаба плоскости течения.
Для того чтобы выяснить, как эти изменения влияют на форму ра-
равенств D), придадим уравнению B) такой вид, который не зависит
от указанных преобразований. Мы получим
S™
где ф0 и р0 означают характерные для рассматриваемой задачи зна-
значения величин ф и р, а а и Ъ суть новые коэффициенты рядов. Срав-
Сравнив уравнение F) с уравнением B), мы найдем
Граничные условия E) принимают теперь вид соотношений между
коэффициентами а и Ь, а именно
±L_ ?2 Pi P2
\ «I'O ' Фо ' РО ' PO
?2 - . _ \
Т~> а0< Й1/«> • • • > ак/6 • • ¦ •
Ро I
Здесь R суть функции, определяемые условиями вблизи нулевой
точки. Подставив найденные значения #_(у3)_(#/а) в первую систему
уравнений G), мы получим следующую уточненную формулировку
граничных условий E):
Pi P2 Ak/6?o
' ?' ^' То' ' Jo'
За характеристические величины ф0 и р0 следует взять, конечно,
такие параметры, которые уже имеются в формулировке граничных
условий, например значения фг и pt. Тогда отпадет зависимость
граничных условий от этих параметров. Оставшиеся параметры

314 ГЛ IX ТЕЧЕНИЯ С ЧИСЛОМ МАХА, БЛИЗКИМ К ЕДИНИЦЕ
лучше всего выбрать так, чтобы в поле течения, антисимметричном
¦относительно ф, они были равны нулю и чтобы разложение функ-
функций R по этим параметрам начиналось с линейного члена. Полу-
Получится ли так в действительности, можно выяснить, конечно, только
лосле исследования граничных условий для конкретного случая.
При течении в закрытой аэродинамической трубе имеется, согласно
сказанному в § 2 настоящей главы, три параметра, а именно: зна-
значение ф на стенке — его следует выбрать за параметр фх— и зна-
значения р в точках Р и Q, которые обозначим через рр и р„. В каче-
качестве параметра рх целесообразно выбрать значение р„. Для того
чтобы в антисимметричном поле течения второй параметр был равен
нулю, возьмем его в виде разности р0 — рр. Ниже мы увидим, что
разложение граничных условий по этому параметру начинается с члена
/р„ — Рр) > поэтому лучше ввести параметр
о Рр
Второй параметр, связанный с р, если только он вообще имеется,
может быть выбран аналогичным образом. На основании сказанного
уравнениям Eа) можно придать следующий упрощенный вид:
Хд
\р1'Р*'Ж "I?"' •••)
Если требуется определить функции R для граничных условий,
заданных вблизи нулевой точки и характеризуемых значениями фх,
ф2. Pi и р2, то следует найти такое решение уравнения Трикоми,
которое удовлетворяет этим граничным условиям и для которого
разложение по естественным частным решениям имеет при положи-
положительных показателях степени р заданный вид
Тогда в этом решении величины B_(ys)-(ft/3) будут коэффициентами
естественных частных решений при отрицательных показателях
•степени р. Перейдя затем посредством уравнений (8) к функциям R,
мы увидим, что последние зависят только от указанных в этом
уравнении аргументов. Следовательно, такой расчет достаточно
выполнить лишь для одного-единственного выбора параметров ^1
р1; например для ^ = 1 и р1=1. Примеры подобного рода иссле-
лований будут даны ниже.

§ 5 ТЕЧЕНИЯ, ДЛЯ КОТОРЫХ ФУНКЦИЯ ТОКА АНТИСИММЕТРИЧНА 315
§ 5. Поля течения, для которых функция тока <|*
антисимметрична относительно оси х
Целью дальнейших исследований является отыскание разложения
решения IX, 4A) по параметру, определяющему отклонение рас-
рассматриваемого поля течения от исходного течения с числом Маха,
равным единице. Ограничимся, как и всегда, определением только
членов наинизшего порядка.
Для антисимметричного поля течения параметры рг и р2 равны
нулю. Кроме того, отсутствуют коэффициенты Ah/B и B_(i/3)_ft. Сле-
Следовательно, уравнения IX, 4(8) принимают более простой вид,
а именно:
Все функции R, с которыми мы будем иметь дело в этом пара-
параграфе, соответствуют антисимметричным частным решениям. Если
отклонение от исходного поля течения мало, то мало также plf
поэтому при уменьшении этого отклонения до нуля аргументы
•функций R также станут равными нулю. Следовательно, разложив
коэффициенты В в ряд и ограничившись каждый раз членом наиниз-
наинизшего порядка, мы получим
Степень, в которой р входит в правую часть, возрастает с увели-
увеличением h. Если в первом из уравнений IX, 4 D) сохранить только
член с наименьшей степенью р, то мы будем иметь
Внеся это значение в уравнение A), мы получим
В этом решении als/jj, R~'" и либо plf либо ^ известны. Следова-
Следовательно, оно устанавливает связь между известными и неизвестными
параметрами.
Из уравнений A) и B) мы имеем
о -А.-У, Я~ш~ь@, 0, ¦¦ ) ,оч
*-> — (Vo) — h !=r Pia—s/« ^j • V"/
Подставив это значение В в уравнение IX, 4 A) и сохранив только
член с наинизшей степенью рх, мы получим
0, 0, ...

316 ГЛ IX. ТЕЧЕНИЯ С ЧИСЛОМ МАХА, БЛИЗКИМ К ЕДИНИЦЕ
Теперь при помощи равенств IX, 4 D) можем убедиться, что коэф-
коэффициенты А действительно имеют величину порядка единицы и что
поэтому аргументы функций R стремятся к нулю вместе с pt. Если
мы захотели бы дополнить уравнение D) членами более высокого
порядка, то должны были бы учесть, что граничные условия для
профиля в свое время были линеаризованы. Исключение составляет
течение около клина.
Функции W зависят только от формы тела, а выражения R и
параметр pt — только от граничных условий вблизи нулевой точки.
Согласно уравнению D), отклонение от исходного течения, опре-
определяемое с точностью до множителя функцией ч7~ , в первом при-
приближении не зависит от граничных условий, заданных вблизи нулевой
точки.
С помощью уравнений VIII, 7C) и VIII, 7D) мы можем перейти
от уравнения D) непосредственно к формулам для изменения давле-
давления или скорости в плоскости течения.
§ 6. Несимметричные поля течения
Несимметрия поля течения может быть вызвана как формой про-
профиля, так и условиями вблизи нулевой точки. В качестве примера,
иллюстрирующего вторую возможность, вообразим течение в аэро-
аэродинамической трубе около тела, расположенного не вполне точно
на оси трубы. Параметр, характеризующий эту несимметрию, можно
рассматривать как заданный. Будем считать его всегда настолько
малым, чтсбы граничные условия можно было разложить в ряд
по его степеням. В течениях, происходящих в неограниченном про-
пространстве, такой параметр, конечно, отсутствует.
Граничные условия вблизи нулевой точки содержат еще один
параметр, обусловливающий несимметрию. На рис. 97 таким пара-
параметром является положение точки Р. Этот параметр определяется
только в процессе отыскания решения и зависит главным образом
от несимметрии профиля.
В дальнейших исследованиях важную роль будут играть неко-
некоторые свойства симметрии функций #~W">~(ft/2). Эти свойства связаны
с тем, что величины /?_(%)_д и ^4(v,)+(ft/s) представляют собой коэф-
коэффициенты антисимметричных частных решений, а величины В_A/а)_д
и Ah/3— коэффициенты симметричных частных решений. Если pt
и р2 равны нулю, то граничные условия являются чисто антисиммет-
антисимметричными.
Для того чтобы выявить свойства симметрии функций /J"A/j'"('l'2)>
рассмотрим два решения, получающиеся одно из другого путем
зеркального отражения относительно оси г\ и одновременного изме-
изменения знака на обратный. В этих решениях коэффициенты антисим-

§ 6 НЕСИММЕТРИЧНЫЕ ПОЛЯ ТЕЧЕНИЯ 317
метричных частных решений ?A/<ылу8) и ?_(%)_л, т. е. А^ ш
и R~(°'"~ будут иметь одинаковые знаки. Коэффициенты Л/,/зи R~('2'~
симметричных частных решений, а также параметры рх и рг, харак-
характеризующие отклонение от чисто антисимметричных частных реше-
решений, будут иметь противоположные знаки. В дальнейшем перемену
знака, производимую при переходе от первого ко второму решению,
будем выполнять всегда во втором решении. При такого рода зер-
зеркальном отражении граничные условия вблизи нулевой точки, выра-
выражаемые посредством функций R, всегда удовлетворяются. На осно-
основании уравнений IX, 4(8) мы получим в первом случае
„ „ Ао Al/J?i° ^fe/sPi
Р*-' "ъ ifT Yi '•"• 4^~ •
,('/,) +(ft/з)
а во втором случае
¦Pi'
\ 'Pi.'
л „/с/3 л »(VJ + (ft/3) \
¦"¦k/Sfl л»/в+№/3) I
• 9 > , j ™ — > , • I '
т1 Y1 /
Отсюда следует
!—(/•)-ft
. ... . A)
Аналогичным образом мы найдем
_._о-е«-»._А1^
B)
Далее, если мы предположим, что функции R дифференцируемы

318 ГЛ. IX ТЕЧЕНИЯ С ЧИСЛОМ МАХА, БЛИЗКИМ К ЕДИНИЦЕ
по своим аргументам, то получим
о о, Лш+т^ , о, ...) = о. (За>
0, 1, 2 k = 0, 1, 2
о, ...J = 0, (Зб>
""'' 0, .... О, ~™+wvr± , О, ...J = 0. (Зв>
Для течений с числом Маха, равным единице, антисимметричное
выражение ф_г/ играет вблизи нулевой точки преобладающую роль
/б
по сравнению с симметричным выражением ф,,; это означает, что
чем дальше мы удаляемся от профиля в плоскости течения или чем
больше мы приближаемся к нулевой точке в плоскости годографа,,
тем более приближается поле течения к виду, антисимметричному от-
относительно ф. Поэтому следует предполагать, что параметр, харак-
характеризующий отклонения граничных условий от их антисимметричной
формы и заранее не определенный, стремится к нулю, когда вели-
величина р! приближается к нулю, т. е. когда отклонение поля течения
от поля исходного течения становится все меньше и меньше.
Вместе с р, приближаются к нулю также все остальные аргу-
аргументы функций R. Определим теперь для коэффициентов B_(i/8)_j»
члены наинизшего порядка относительно р1. Для коэффициентов В_E/с)_^
антисимметричных частных решений мы имеем
~{%)"h@, 0, . ..)• D)
Как следует из равенства (За), коэффициенты Б_A/з)_й симметрич-
симметричных частных решений должны быть разложены в ряды только no-
параметрам рх и рг, так как остальные аргументы представляют
собой малые величины более высокого порядка относительно рх. Вы-
Выполнив разложение, мы получим
X
Далее, из равенства IX, 4D), если ограничиться только членами наи-
наинизшего порядка относительно ри мы найдем

§ 6 НЕСИММЕТРИЧНЫЕ ПОЛЯ ТЕЧЕНИЯ 319
Внеся эти значения в уравнение IX, 4 (8), мы получим
«:?=Ф,р'/бя~5/чо, о,...) (б>
, о. ...>]+* ^[л-'чо. о, ...
Так же, как и для поля течения, антисимметричного относительно фг
из равенств F) и D) мы найдем
п -%я-(%)-л(о, о,.,.)
В-ш-* = PlK-v.->•/.(<), о,...) • (8>
В равенстве G) один из параметров р, например pv следует рас-
рассматривать как известный. Тогда, использовав равенство F), мы
сумеем вычислить второй параметр и найдем для него значение
v,/r'/-(Q,o.-.-)a--/, 1
Уч — Hi -ч. -V. ft .
Использовав это равенство, а также равенство F), мы сумеем при-
привести уравнение E) к виду
, -jL[/r^bft@, 0, ...)]
Ё_
-»(о>0,
Первый член правой части обусловлен несимметрией профиля (вы-
(выражаемой коэффициентом сс~^), а второй член — несимметрией,
вызываемой граничными условиями вблизи нулевой точки (эта несим-
несимметрия выражается параметром р^).
Если не учитывать второго члена, то из уравнения IX, 4A),
ограничившись членами наинизшего порядка относительно plt мы

-320 ГЛ IX ТЕЧЕНИЯ С ЧИСЛОМ МАХА, БЛИЗКИМ К ЕДИНИЦЕ
получим
-з—[/?~'/з@, 0, ...)]
¦[«"'/•(О, 0,...)] j
Это уравнение показывает, что коэффициенты при W~"/<! и ЧГ~4/* имеют
величину одного порядка относительно pt. Если параметр pj непо-
непосредственно не задан, то он может быть вычислен из фх с домощью
равенства F). Обнаружение зависимости поправочных членов от pi
представляет собой важный общий результат выполненных здесь
исследований.
§ 7. Разложение поля течения по отклонению числа
Маха, характерного для течения, от единицы
Оба преобразования, с помощью которых в § 7 гл. V мы пе-
перешли от точного уравнения годографа к уравнению Трикоми, содер-
содержат параметр pt. В первом приближении этот параметр пропорцио-
пропорционален (М—IK, где М есть число Маха, соответствующее значе-
значению рх. Например, для сверхзвукового течения М есть число Маха
в бесконечности, для течения в блокированной аэродинамической
трубе—блокирующее число Маха. Если бы уравнение Трикоми
тождественно совпадало с уравнением годографа, то тогда измене-
изменение поля течения, вызываемое отклонением указанного характерного
числа Маха от единицы, было бы пропорционально (Ж — IK. Однако
так как уравнение Трикоми является только приближением к точ-
точному уравнению годографа, то сначала мы можем считать этот вывод
правильным только при условии, что приближение оправдано, т. е.
при малых значениях х в уравнениях V, 7C), или, другими словами,
в предельном случае тонких тел.
В действительности указанный вывод справедлив и в общем
случае, так как решения уравнения Трикоми могут рассматриваться
как приближенные представления решений точного уравнения годо-
годографа вблизи нулевой точки.
Для более подробного обоснования этого вывода вернемся
к уравнению V, 7B), причем на функцию h{w), содержащуюся
в допущении V, 7A), не будем обращать никакого внимания, так
как она входит в качестве универсального множителя во все част-
частные решения. Точные решения уравнения V, 7 B) должны учитывать
выражение, стоящее в правой части уравнения. Функция г{т\)
является регулярной при всех конечных значениях т\, в том числе

S 7. РАЗЛОЖЕНИЕ ПОЛЯ ТЕЧЕНИЯ ПО М - 1 321
и при т] = 0. Наличие этой функции приводит к появлению в ре-
решениях уравнения Трикоми поправочного члена, с учетом которого
частные решения, соответствующие выражению VII, 3C), будут
иметь вид
Составим опять частные решения уравнения годографа, удовлетво-
удовлетворяющие граничным условиям на поверхности профиля и имеющие
особенность в нулевой точке. Для каждого такого частного реше-
решения член, играющий в нулевой точке преобладающую роль, таков
же, как и в случае уравнения Трикоми. При выводе результатов,
полученных в предыдущем параграфе, мы использовали именно те
члены, которые играли преобладающую роль в нулевой точке.
Следовательно, при разложении решения точного уравнения годо-
годографа в ряд по степеням М — 1 член наинизшего порядка будет также
пропорционален (М—IK.
Если мы перейдем от выражений W в плоскости годографа
к изменениям скорости в плоскости течения, то последние, конечно,
также будут пропорциональны (М—IK при условии, что полное
давление (т. е. постоянная в уравнении Бернулли) остается неиз-
неизменным. То же самое получится и для местных изменений чисел
Маха и местных изменений давления при неизменном полном давле-
давлении. Однако это заключение неприменимо к коэффициенту давления.
При обычном определении мы имеем
где индекс со относится к состоянию в набегающем течении. Здесь
величины, зависящие от состояния в набегающем течении, изменяются
в первом приближении пропорционально первой степени разности
М — 1. Влияние такого изменения этих величин перекрывает изме-
изменение давления. Остановимся на этом обстоятельстве несколько по-
подробнее.
Сформулированный выше результат для местного изменения
давления можно выразить уравнением
?__
где
>—IK]. (la)
Пусть с* есть коэффициент давления, составленный для динамиче-
динамического давления, соответствующего числу Маха, равному единице,
К1А V Г Г\гтт*птт

322 ГЛ IX ТЕЧЕНИЯ С ЧИСЛОМ МАХА, БЛИЗКИМ К ЕДИНИЦЕ
т. е.
Аналогичные обозначения будем применять и для коэффициентов
подъемной силы и сопротивления.
Для числа Маха, не равного единице, коэффициент давления
можно представить в виде
-,* р w Рсо р
Разложив пра&ую часть по степеням Моо—1» мы получим
ср
( 2 51/. -4-1
ср{ + (+)
+ ^(^00- 1) +2(f^y С^се- 1J + О [(Мсо- IK]- C)
В этой формуле от распределения давления на теле зависят только
первый и последний члены. Все остальные члены зависят от изме-
изменения состояния в бесконечности, возникающего вследствие измене-
изменения числа Маха. Они выпадают, если определяются силы, дейст-
действующие на тело, ограниченное замкнутой поверхностью, например
если определяются коэффициенты подъемной силы и лобового со-
сопротивления. Для коэффициента подъемной силы получается формула
D)
Такой же вид имеет и формула для коэффициента сопротивления cw.
Поправочные члены первого и второго порядка в выражении коэф-
коэффициента са. связаны только с формой определения этого коэффи-
коэффициента; лишь поправочный член третьего порядка обусловлен дейст-
действительно физической причиной. Поэтому с физической точки зрения
предпочтительнее оперировать величинами pip*, с* с'А, c*w или мест-
местными числами Маха. Для технических целей, конечно, следует поль-
пользоваться обычными определениями коэффициентов ср, сл и cw.
Иногда указываются коэффициенты сопротивления, относящиеся
только к передней части обтекаемого тела и составленные для да-
давления в бесконечности. В таком случае вблизи числа Маха, рав-
равного единице, наибольшее изменение коэффициента обусловливается

§ 7 РАЗЛОЖЕНИЕ ПОЛЯ ТЕЧЕНИЯ ПО At — 1 323
членом 4 (Жсо—l)/(x-f-l) формулы C). Однако такое представле-
представление коэффициента сопротивления создает впечатление, что для
плоских течений он возрастает при увеличении числа Маха, между
тем как, согласно формуле D), он уменьшается при увеличении
числа Маха.
Найденная здесь слабая зависимость коэффициента сопротивле-
сопротивления от числа Маха имеет место также для тел со срезанной кормо-
кормовой частью, так как донное давление определяется обтеканием са-
моГо тела.
Ниже будет показано, что аналогичные соотношения получаются
и для осесимметричных течений, однако для таких течений влияние
изменения числа Маха значительно сильнее, а именно теперь оно
пропорционально (Жю—1)% :).
Предыдущие рассуждения дают довольно ясное представление
о полях течения вблизи числа Маха, равного единице. Что следует
понимать под близостью к числу Маха, равному единице, зависит
от относительной толщины профиля. Например, если мы будем
исследовать течение при сверхзвуковом числе Маха способами, изло-
изложенными в предыдущих параграфах, то обязательно должны будем
1) В качестве обоснования полученного результата иногда используется
следующий принцип, называемый принципом соответствия: числа Маха до
и после прямого скачка уплотнения отклоняются от единицы в первом при-
приближении на одинаковые значения (знаки отклонений, конечно, различные).
Таким образом, тело, на которое набегает сверхзвуковое течение и впереди
которого имеется неприлегающий к нему скачок уплотнения, лежит как бы
в дозвуковом поле течения. Отсюда делается заключение, что течение со
сверхзвуковой скоростью очень близко к такому дозвуковому течению, для
которого скорость в бесконечности определяется числом Маха, получившимся
после прямого скачка уплотнения. Если, кроме того, принимается — обычно
молчаливо, —что кривая местных давлений при переходе через число Маха,
равное единице, изображает дважды дифференцируемую функцию, то тогда
действительно получается, что кривая, изображающая зависимость мест-
местного числа Маха от скорости набегающего течения, имеет при М = 1 го^
ризонтальную касательную Конечно, считать такую аргументацию обосно-
обоснованной нельзя. Непосредственно после скачка уплотнения получаются все
скорости, начиная от скорости, соответствующей прямому скачку, и кончая
скоростью набегающего течения. Следовательно, скорость, соответствующая
прямому скачку уплотнения, не является какой-то особо характеристической.
Далее мы знаем, что в околозвуковой области возмущения распространяются
главным образом в поперечном направлении, поэтому сомнительно, чтобы
скорость, возникающая вверх по течению относительно модели, определяла
поле течения около тела Кроме того, ударная поляра с отмеченными на
ней направлениями подхода линий тока (рис. 44) не дает оснований прини-
принимать за возможную общую исходную точку линий тока точку, соответ-
соответствующую прямому скачку уплотнения; скорее за такую точку можно было бы
принять точку, лежащую внутри ударной поляры. Наконец, предположение,
что переход через число Маха, равное единице, описывается дважды диф-
дифференцируемой функцией, отнюдь не очевидно заранее. (Напомним в связи
с этим, что еще не так давно оспаривалось существование течений с числом
Маха, равным единице.) В случае осесимметричных течений такое предпо-
предположение безусловно неправильно.

324 ГЛ IX ТЕЧЕНИЯ С ЧИСЛОМ МАХА, БЛИЗКИМ К ЕДИНИЦЕ
считать, что ударная поляра, соответствующая числу Маха набегаю-
набегающего течения, мала по сравнению с остальными размерами изображения
в плоскости годографа. Если при неизменном сверхзвуковом числе
Маха мы будем все более и более уменьшать угол раствора клина,
то в конце концов указанное условие перестает соблюдаться и по-
полученные результаты становятся неприменимыми.
§ 8. Течение около ромбовидного профиля в блокированной
закрытой аэродинамической трубе
Течения, которые будут рассмотрены в этом и следующих па-
параграфах, представляют некоторый технический интерес, так как
они иллюстрируют влияние стенок аэродинамической трубы на ре-
результаты измерений вблизи числа Маха, равного единице. Обтекание
ромбовидного профиля в закрытой аэродинамической трубе и в сво-
свободной струе с числом Маха, равным единице, было рассмотрено
Маршнером (см. лит. 1).
Так как поля течения антисимметричны относительно функции
тока ij>, то на основании сказанного в § 5 настоящей главы для
определения в первом приближении изменения распределения давле-
давления на профиле достаточно знать только функции чТ~"/в и ЧГ~"/п.
Способ расчета для получения такого решения был изложен в § 4,
6 и 8 гл. VIII. Из результатов вычисления функции ч7~5/|> (т. е. те-
течения с числом Маха, равным в бесконечности единице) используем
формулу VIII, 4 F), которая необходима для вычисления коэффи-
коэффициента ccl"/J [см. формулу IX, 5 B)]; мы получим
Кроме того, в соответствии с уравнением IX, 5 D) нам необходимо
знать величины /?~5/в@, 0, ...) и /?"""/в@, 0, . . .). Аргументы этих
функций равны нулю, т. е. вопрос сводится к вычислению тех со-
составляющих этих функций, которые удовлетворяют неоднородным
граничным условиям вблизи нулевой точки и равны нулю в беско-
бесконечности плоскости т], Ь. Как было упомянуто в конце § 4 настоя-
настоящей главы, в этом случае можно положить постоянные tyi и pt рав-
равными единице. Какие именно граничные условия должны выполняться,
можно видеть из рис. 97, а в последующих примерах —из рис. 98
и 45. Так как сейчас мы рассматриваем поле течения, антисимме-
антисимметричное относительно ф, то точки Р и Q на рис. 97 совпадают
и поэтому получаются граничные условия, отмеченные на рис. 99.
Для поля течения, изображенного на рис. 98, краевая задача, вслед-
вследствие требования антисимметрии, имеет вид, изображенный на рис. 96.

Si 8 ТЕЧЕНИЕ ОКОЛО РОМБОВИДНОГО ПРОФИЛЯ В ТРУБЕ
325
Условия на ударной поляре, которые должны быть удовлетворены
в соответствии с рис. 45, не требуют никаких упрощений.
Выведем граничные условия для закрытой аэродинамической
трубы в явном виде. Для этой цели прежде всего разделим рассма-
рассматриваемую область плоскости
т), Ь на две части линией р = 1,
проходящей через точку Q
(рис. 99). Затем выберем функ-
функцию, удовлетворяющую во вну-
внутренней Области ДИффереН- У*Р
циальному уравнению Трикоми
и неоднородным граничным
уСЛОВИЯМ. D качестве таКОИ
ФУНКЦИИ МОЖНО ВЗЯТЬ фуНК-
цию ф= 1, однако целесо-
целесообразнее взять функцию Н (?), удовлетворяющую уравнению VII, 3F6)
при р = 1/12. Это выгоднее потому, что при !•-»• 1 функция Н(%) стре-
стремится к нулю, что облегчает выяснение вопроса о сходимости. По-
Поскольку [A = 1/i2> уравнение VII, 3F6) принимает вид
!Гп— E3V/e—1—О
Рис. 99. Граничные условия при обтекании ром-
6овидного Профиля в блокированной закрытой
аэродинамической трубе.
Функция Н(%) удовлетворяет граничным условиям
Я(— оо)=1,
B)
0. Bа)
Конечно, эта функция представляет собой линейную комбинацию
частных решений G(o)(l Via) и O(s) (I Via)-
В области, внешней относительно линии р=1, искомое решение
представляется только частными решениями <]>_(«/B)_ft. Во внутренней
области к функции Н присоединяется еще выражение, удовлетво-
удовлетворяющее условию Трикоми. Если не учитывать выражения Н(?), то
остающуюся часть функции ф (будем обозначать ее через ф) можно
охарактеризовать следующим образом. Прежде всего ф = 0 при
\=- — оо и в бесконечности плоскости ij, Ь. Далее ф удовлетворяет
в нулевой точке условию Трикоми и имеет вдоль линии р = 1 ска-
скачок, определяемый функцией Н(?). Такого рода задача уже была
исследована в § 13 гл. VII. Теперь мы должны положить в уравне-
уравнении VII, 13B)
Л(?) = ЯE). ЛЮ = 0.
Прежде всего нас интересует решение во внешней области. Там
функция Н(?) равна нулю, а функция ф тождественно совпадает
с i. Решение определяется непосредственно формулой VII, 13 (За),
причем вместо В(а) следует подставить его выражение VII, 12 A36).

326 ГЛ IX. ТЕЧЕНИЯ С ЧИСЛОМ МАХА, БЛИЗКИМ К ЕДИНИЦЕ
Мы получим
а,, =
X
где
Интеграл в правой части этого равенства может быть вычислен пу-
путем интегрирования по частям. Использовав при этом уравнения B)
и VII, 3 F6), мы найдем
н ®
6(й4~!
Внеся это значение в равенство C), мы получим
„ —
т. Y3
Г E/е) Г A/6)
Величина at есть коэффициент при решении ф_5,, а величина а2 —
коэффициент при решении ф_п/ . т. е. эти величины дают искомые
значения функций R. Таким образом,
, 0, . . .) = —^т= = 0,588, Dа)
5я у 3
R-"'\0, 0, . . о^-М^-^Т—0'
" "
При только что рассмртренных граничных условиях функции R не
зависят от коэффициентов ^4(у„)+(й/з)> так как частные решения, имею-
имеющие своими коэффициентами А, ничего не прибавляют к значениям
функции ф вдоль линии \ = — сю, т. е. не изменяют граничных
условий, заданных на этой линии. Поэтому для клина, для которого
не требуется линеаризации граничных условий на изображении про-
профиля, полное решение может быть указано без каких-либо труд-
трудностей, если тольк-б известны функции \р~E'"~л_
Имея только что найденные значения функций R, определим
прежде всего значение pv входящее в равенство IX, 5B). Пара-

S 8. ТЕЧЕНИЕ ОКОЛО РОМБОВИДНОГО ПРОФИЛЯ В ТРУБЕ 327
метр <]>t задан здесь значением функции тока на верхней стенке
аэродинамической трубы. Если ширина трубы равна W, то
следовательно,
Таким образом, все величины, входящие в уравнение IX, 5 D), мо-
могут рассматриваться как известные.
Перейдем теперь к определению изменения распределения давле-
давления вдоль поверхности клина. Обозначим расстояния х, вычислен-
вычисленные вдоль изображения стороны клина и соответствующие реше-
решениям W~'!° и ч?~"/в, через х~*!' и х'1'1'- Эти расстояния являются,
конечно, функциями от т). Путем рассуждений, аналогичных тем,
которые привели к формулам VIII, 7C) и VIII, 7D), мы найдем для
изменения т) в фиксированном месте поверхности клина формулу
° @, 0,...)
R- >' @, 0, ...)
¦'J,v->4,
If
дг, _
профиль
Величина а_«/°, входящая в виде множителя в решение W ,
а похому и в х~Ч«, определяется размерами обтекаемого тела. Она
должна выпасть, если в качестве независимой переменной взять
частное x/L. Выполнив такое преобразование, мы увидим, что al%
действительно выпадает из выражения
_5/. —"/«
Далее, функции W~'° и Ч7~ , а вместе с ними также х~ и х~
зависят от угла раствора клина. Путем таких же рассуждений, как
и в § 4 гл. VIII, мы найдем, что в соответственных точках полей
течения, получаемых одно из другого путем изменения угла б0, зна-
значения х"'/б пропорциональны б^'Ч а значения х~^° пропорцио-
пропорциональны до'а/*. В этих точках величина ij, согласно определению,
пропорциональна 60 , а величина & пропорциональна 80. Следова-
Следовательно, выражение

328
ГЛ. IX. ТЕЧЕНИЯ С ЧИСЛОМ МАХА, БЛИЗКИМ К ЕДИНИЦЕ
пропорционально оо , поэтому мы можем представить его в виде
-V.
График функции F(x/L) изображен на рис. 100. Внеся значение F)
в найденную выше формулу для Дт), мы получим
,_ „ /?-и/°(о,о,...)
Г%@, 0,...) \lJ\2 °
80
-V»
2,5
\ 2,
2,0
as
о
1
Ф)
\
\
\/
У
F(x
/
/
lL)/
/
или, если учесть равенства A)
и E),
^-). (8)
«г
Согласно третьей из формул
V, 7A1), изменение коэффициен-
коэффициенту^ ^ °'8 ''° та давления равно
РИС. 100. ФУНКЦИЯ F(XlL) ДЛЯ рОМбоВИДНОГО д * q г _|_ 1 \-Vs Дт) (Яя\
профиля (по Маршнеру). "Ьр—- ^ v* I L) '!• \oaJ
Для определения блокирующего числа Маха следует воспользоваться
четвертой из формул V, 7A1) и равенствами A) и E). Выполнив
преобразования, мы получим
1 - Ж6лок. =
В частности, при ч=1,4
¦ 0,705.
1Л27.
(9)
Из последнего уравнения мы видим, что блокирующее число Маха
зависит не только от поперечного сечения, остающегося для дви-
движения воздуха в аэродинамической трубе, но также от длины про-
профиля. Наиболее узкое поперечное сечение между клином и стенкой
трубы полностью не используется, так как, во-первых, линии тока не
перпендикулярны к этому сечению и, во-вторых, плотность потока
массы в этом сечении не является максимальной. То обстоятельство,
что L и 90 входят в уравнение (9) не в степени 1/2, показывает, что
в достаточно широкой аэродинамической трубе блокирующее число
Маха определяется не самым узким поперечным сечением.

S 8. ТЕЧЕНИЕ ОКОЛО РОМБОВИДНОГО ПРОФИЛЯ В ТРУБЕ 329
Ниже мы сравним блокирующие числа Маха для ромбовидного
профиля и для пластинки, поставленной под углом атаки. Для этой
цели нам понадобится формула
1 - M6mR = 1,488 (-^) >', (9а)
получающаяся из формулы (9) после замены L на 2Lm., где Ьпл_ есть
длина ромбовидного профиля, измеренная от передней точки до плеча.
Для распределения давления при числе Маха, равном единице,
мы получили в § 4 гл. VIII формулу VIII, 4 E)
Учтя поправку (8), мы найдем следующее распределение давления
в блокированной аэродинамической трубе:
На рис. 85 показаны результаты измерения распределения давления
около клина с относительной толщиной, равной 10%, в блокиро-
блокированной аэродинамической трубе (штриховая кривая) и в неограни-
неограниченном пространстве при течении с числом Маха, равным единице
(сплошная кривая). Мы видим, что обе кривые не совпадают. Ширина
профиля, т. е. его размер в направлении течения, составляет для
этого примера 13% ширины трубы. Блокирующее число Маха
равно 0,86. Как этот результат изменяется при изменении 0О и ширины
трубы, можно подсчитать по формулам (9) и A0). Относительная
ошибка в распределении давления при неизменной ширине профиля
меньше для тела с большей относительной толщиной 90. Качествен-
Качественным путем мы получили этот результат уже в § 7 гл. II как след-
следствие закона подобия.
Исследования показывают, что блокирующее число Маха не
является подходящим критерием для оценки точности измерений.
Изменение этого числа от 0,9 до 0,95 уменьшает отклонение рас-
распределений давления на 1/6. Вообще можно сказать, что результаты
измерений в блокированной аэродинамической трубе не очень сильно
отличаются от результатов измерений в неограниченном пространстве
при числе Маха, равном единице.
При обработке экспериментальных результатов может представить
интерес распределение давления на стенке аэродинамической трубы.
Для получения этого распределения (Гудерлей [11], см. лит. 1)
необходимо вычислить решение в области р<11, показанной на
рис. 99. Для этой цели следует воспользоваться формулой VII, 13 A0),
заменив в ней р0 на рх. Функция / в соответствии с формулой VII, 13 D)
равна

330 ГЛ IX ТЕЧЕНИЯ С ЧИСЛОМ МАХА, БЛИЗКИМ К ЕДИНИЦЕ
Вычислив интеграл в правой части в точности так же, как это было
сделано для равенства C), мы получим
it \ х 1
Формула VII, 13A0) дает решение рассматриваемой там задачи для
случая, когда вдоль линии ? =1 не распространяются никакие осо-
особенности. Имеются или не имеются особенности, можно выяснить
из характера функций fx и /2, которые при наличии особенностей
должны иметь скачкообразное изменение вдоль р = Ро —Pi- В рас-
рассматриваемом случае роль Д и /2 играет функция H(k), которая
действительно такова, что вдоль 5= 1 распространяется особенность;
поэтому соответствующий член появляется также в подлежащей
наложению функции ф и устраняет при этом особенность функции //(?)•
От функции тока, получаемой из формулы VII, 13A0), перейдем
к координате х в плоскости течения. Воспользовавшись форму-
формулой VII, 3 (9), мы получим
JC =
Значение pt соответствует блокирующему числу Маха. На основании
четвертой из формул V, 7A1) мы имеем
1 — М
Введем для суммы, входящей в равенство A1), обозначение
r(—J-—\r(—-L- —
\-м \^ \"з +"FJ \"з + 6
з + з j \з + з
а для обратной функции, взятой со знаком минус, обозначение
\~М М-\
Заменив в равенстве A1) р1/» в соответствии с четвертой из фор-
формул V, 7A1) на
п Д4« У'а(х-(- I)"''3 • 2:/1а,
мы получим

§ 9 ОБТЕКАНИЕ РОМБОВИДНОГО ПРОФИЛЯ СВОБОДНОЙ СТРУЕЙ 331
Соответствующий график изображен на рис. 101. Последнее уравне-
уравнение содержит в качестве параметров ширину аэродинамической трубы
и блокирующее число Маха и в приведенном виде (в случае доста-
т.о
-0.5
-1.0
/
/
1
1
-as
с'/г
0,5
Рис. 101. Распределение давления на
стенке блокированной аэродинамической
трубы (по Гудерлею [11]).
точкой ширины трубы) не зависит от формы обтекаемого тела. Для
ромбовидного профиля блокирующее число Маха связано с шириной
трубы и размерами модели посредством формулы (9).
§ 9. Обтекание ромбовидного профиля
свободной струей с критической скоростью
и неограниченным потоком со сверхзвуковой скоростью
~%/
~n/e
Определение коэффициентов R~%/°@, 0, . . .) и R~n/e@, 0, ....)
для ромбовидного профиля, обтекаемого свободной струей с крити-
критической скоростью, приводит к краевой задаче, уже рассмотренной
в § 10 гл. VIII. Выполнив вычисления, мы найдем для этих коэф-
коэффициентов значения
-n/'
@, 0, ...) = !•
О
@, 0, .. .) =
оо
1 = 0,403,
/зк-1 = — 0,306
и вместо формулы IX, 8 A0) получим

332 ГЛ IX ТЕЧЕНИЯ С ЧИСЛОМ МАХА, БЛИЗКИМ К ЕДИНИЦЕ
Мы видим, что влияние границ струи приблизительно на 14% больше,
чем влияние стенок закрытой трубы, и имеет противоположный знак.
Следовательно, с точки зрения точности измерений свободная струя
не дает преимуществ по сравнению с аэродинамической трубой.
Решение аналогичной задачи для обтекания со сверхзвуковой
скоростью в неограниченном пространстве имеется в работе Гудер-
лея [9] (см. лит. 1). Границей сходимости для бесконечного ряда,
в который разлагаются частные решения ф"~E/в)~'\ является линия
р = const. Ударная поляра располагается не очень далеко от этой
линии. Это наводит на мысль попытаться выполнить граничные условия
вдоль ударной поляры конечным числом членов разложения ф~^'"~ .
Сначала можно было бы подумать, что точность такого приближен-
приближенного выполнения граничных условий не может быть произвольно
повышена путем увеличения числа членов разложения, однако, как
показывают исследования Бергмана (см. лит. 1), это предположение
не оправдывается (правда, исследования Бергмана относятся к гра-
граничным условиям другого вида).
Численные результаты не очень удовлетворительны. Даже при
использовании восьми членов разложения граничные условия на удар-
ударной поляре выполняются отнюдь не хорошо. Однако можно считать
более или менее приемлемыми следующие значения1):
R~'u@, О, . . .) —1,
R~"u@, О, .. .) = — 1,67.
Теперь формула IX, 8 G) принимает вид
Здесь pj есть то значение р, которое скорость набегающего течения
получает благодаря скачку уплотнения. Если tjj есть значение т\ до
скачка уплотнения, то в соответствии с равенством 11,4E) значе-
значение т) после скачка равно —i\v а р1 = т^. Пусть Мг есть число Маха
набегающего течения. Тогда на основании формулы V, 7A1) мы
будем иметь
Д-г) = 8(х+1) \м1— 1L,67 (-|6о) 'F{t)'
Дс^ = — 16(х4-1)~'/з(^1— IK1,67 Г— 80] Зр{т)-
Первое из этих значений может быть задано заранее.

10. ПЛОСКАЯ ПЛАСТИНКА В АЭРОДИНАМИЧЕСКОЙ ТРУБЕ
333
Так как знак поправки Дс* один и тот же и для свободной струи,
имеющей критическую скорость, и для сверхзвукового течения
в неограниченном пространстве, то течение в свободной струе можно
считать в рассматриваемом приближении эквивалентным течению при
сверхзвуковом числе Маха. Однако установить наглядное соответ-
соответствие между обоими полями течения очень трудно. Попытка сделать
это имеется в работе Гудерлея [9] (см. лит. 1). В этой работе приво-
приводится также асимптотическая форма скачка уплотнения для числа
Маха, близкого к единице.
§10. Плоская пластинка в блокированной
'закрытой аэродинамической трубе
Проиллюстрируем влияние стенок блокированной закрытой аэро-
аэродинамической трубы на несимметричное тело на примере плоской
пластинки, поставленной под углом атаки (Гудерлей [13], см. лит. 1).
характеристика
характеристика
ч.
ч
\
s/////////////////////////////////////////.
Л
звуковая II сверхзвуковая
линия "Ч\ область
дозвуковая И в0ЛНы
область
линия тока, проходящая
через критическую точку
дозвуковая
область
волны
1Uразрежения
3BUI
линия
1
///////////77////////7////V///////////S///7,
^характеристики
Рис. 102. Течение около пластинки под углом атаки в блокированной аэродинамической
трубе; а — поле течения, б — отображение на плоскость годографа; в — отображение на пло-
плоскость Т], Ь.
На рис. 102 изображены плоскость течения, плоскость годографа
и схема краевой задачи в плоскости -q, & (для предельного случая
малого угла атаки). Обозначения на рисунке такие же, как в § 9

'334 ГЛ IX ТЕЧЕНИЯ С ЧИСЛОМ МАХА, БЛИЗКИМ К ЕДИНИЦЕ
гл. VIII, т. е., в частности, В есть начало системы координат т(, &,
в которой берутся значения р и t Начало вспомогательной системы
координат расположим в точке О. Значения Ь, измеренные от точки О,
будем обозначать через &, а соответствующие значения р и \ — че-
через р и \.
Согласно уравнению IX, 6A0), для расчета необходимо знать,
кроме исходного течения 47 , также функции W и ЧГ~ . Все
эти функции уже были определены в § 9 гл. VIII [уравнения VIII, 9A9)
и VIII, 9B4)]. В уравнение IX, 6A0) входят постоянные al'/J и alyj,
которые равны [формулы VIII, 9B0)]
lJL_ гЛ
zl_
19
Далее нам необходимо знать величины
и
Они определяются из граничных условий вблизи нулевой точки.
Постоянные /?~"/в@, 0, . . .) и R~~s/°@, 0, . . .) такие же, как в анти-
антисимметричном поле течения, так как параметры, выражающие откло-
отклонение от антисимметрии, равны нулю. Эти постоянные уже были
вычислены в § 8 настоящей главы [формулы IX, 8 D)] в связи с иссле-
исследованием обтекания симметричной модели в блокированной аэродина-
аэродинамической трубе. Они равны
/Г%@, 0, . . .) = т^к
'3
А 1
R~a''@, 0, .. .) = —^- ^ 37 =0,612, B6)
ТГ'1Г
Для вычисления производных dR~'/3/dp2 и dR~'/a/dp2 необходимо
учесть несимметрию граничных условий, вызываемую несовпадением
точек Р и Q на рис. 102,8. Для широкой аэродинамической трубы
это отклонение незначительно и его влияние можно учесть первым
членом разложения.

8 10 ПЛОСКАЯ ПЛАСТИНКА В АЭРОДИНАМИЧЕСКОЙ ТРУБЕ 335
В непосредственной близости от точки Q дифференциальное
уравнение Трикоми можно привести к более простому виду
где t\q есть значение т\ в точке Q. Внутри области, в которой при-
применимо это приближение, для ф получается формула
C)
Здесь ~i\p есть значение i\ в точке Р. Второй корень всегда поло-
положителен, первый корень положителен в области O"PQ рис. 102, в.
Между точками О" и Р логарифм следует взять от положительного
числа, поэтому мнимая часть равна нулю. Если обойти точку Р по
пути, показанному на рис. 102,8, то аргумент выражения, от ко-
которого берется логарифм, изменится на те. Следовательно, мы по-
получим ф=1 вдоль О"Р и ф = —1 вдоль PQ. Хотя после обхода
точки Q знак первого корня меняется, логарифм берется все же
еще от отрицательного числа, поэтому ф и дальше сохраняет свое
значение ф = —1. Разложив правую часть равенства C) по
(\f]Q\ — l7)?!)^. мы получим
Отсюда следует, что на достаточно большом расстоянии от точки Q
правую часть формулы C) можно представить как наложение лога-
логарифмической особенности, характерной для антисимметричных гра-
граничных условий, и выражения, имеющего в Q точку разветвления
второго порядка. Особенность антисимметричных граничных условий
была исследована выше. Для получения решения, имеющего в Q
точку разветвления второго порядка, следует положить k = 0 в уравне-
уравнении VIII, 10A). Перепишем это-решение в следующем виде:
= /JV/. )j_ _ у* _ 3_1/2 /JL _ ! Г* при 5 = о, J- _ 1.
При 9 = 0 и 7]/t)q > 1 третьему члену правой части равенства D)
можно придать вид
-nQ\-\-np
Примем величину

336
ГЛ IX ТЕЧЕНИЯ С ЧИСЛОМ МАХА, БЛИЗКИМ К ЕДИНИЦЕ
за параметр р2, входящий в уравнение IX, 6A0), и положим/^ = 0
(параметр р1 не был бы равен нулю только в том случае, если бы
модель находилась не в середине аэродинамической трубы). Тогда
третьему члену правой части равенства D) будет соответствовать
выражение
кэт-шт-
Разложив его по (p/pQ) * и использовав отдельные члены в качестве
коэффициентов частных решений qr~M-A, мы получим
4
!-«->, о,...)=i.
Dа)
D6)
Параметр фх определяется значением функции i|> вдоль стенки трубы
и равен
_ w
Величине pv входящей в формулу IX, 6A0), здесь соответствует
величина р„
Теперь мы знаем все величины, необходимые для расчета по
формуле IX, 6A0). Согласно формуле IX, 6F), мы имеем
Г
L
(I)
или
5х
9
(Г-
Использовав соотношение VIII, 9C), мы найдем, что блокирующее
число Маха равно
5тс
1 г 3_]7»
2 L2J '
В частности, при ч=1,4 оно равно
1 — Aw=i.
F)

§ 10 ПЛОСКАЯ ПЛАСТИНКА В АЭРОДИНАМИЧЕСКОЙ ТРУБЕ 337
Перейдем теперь от функции ф, определяемой уравнением IX, 6A0),
к координате х вдоль пластинки. Применив формулу VIII, 9B5),
мы получим
Г (-) т(~
7 361^3
Первый член в скобках обусловливается течением в неограниченном
пространстве. Второй член дает влияние стенок трубы. При по-
постоянном х этот член определяет изменение величины т\ или вели-
величины i\, связанной с т) соотношением VIII, 9A5). Это изменение
вычисляется на основании соображений, изложенных в § 7 гл. VIII.
Выполнив вычисления, мы получим
л= ?q ( 8 80= и, 19 = ,,\(Cidx-'/>\-1
Ро V9/3 77 36/3 Л di\ )
Отсюда, имея в виду соотношения VIII, 9B6), мы найдем
~ 30 ^8
При выводе формулы VIII, 9 B3) мы использовали соотношение
поэтому
Таким образом, для распределения т) вдоль пластинки, обдуваемой
в аэродинамической трубе, мы имеем следующую формулу:
(8)
Результаты, полученные для обтекания пластинки при числе Маха,
равном единице, позволяют найти приближенное распределение
давления на подсасывающей стороне пластинки путем аналитического
продолжения. Получается такая же формула, как и формула (8),
причем для функции g{xjL) следует взять ее значение на подса-
подсасывающей стороне пластинки.
Распределение давления на пластинке в блокированной аэроди-
аэродинамической трубе изображено на рис. 94 штрих-пунктирной кривой.
Длина пластинки равна 0,1 ширины трубы, угол атаки равен 0,1 E,7°).
Сравнение с другими кривыми на рис. 94 показывает, что и в этом
случае влияние стенок довольно мало.

338 ГЛ. IX. ТЕЧЕНИЯ С ЧИСЛОМ МАХА, БЛИЗКИМ К ЕДИНИЦЕ
Влияние угла атаки и длины пластинки учитывается в решении
величиной Pq/p0 [формула E)]. Усиление относительного влияния
стенок вследствие увеличения длины пластинки понятно само собой.
Аналогичный эффект вызывается уменьшением угла атаки, что на
первый взгляд кажется неожиданным, но просто объясняется как
следствие закона подобия.
Формула F) для блокирующего числа Маха имеет такой же вид, как
аналогичная формула IX, 8 (9а) для случая ромбовидного профиля
в аэродинамической трубе. Даже коэффициенты в этих формулах
не очень сильно отличаются друг от друга. Граничное условие на
задней кромке пластинки (с поджимающей стороны последней)
совпадает с граничным условием на плече клина. Зато вблизи
острия клина и передней кромки пластинки поля течения имеют
различный вид.
Гудерлей в своей работе [13] (см. лит. 1) показал также, что
смещение пластинки относительно середины аэродинамической трубы
эквивалентно в рассматриваемом приближении изменению угла атаки.
Однако этот эффект очень слабый.
Вообще можно сказать, что влияние граничных условий, имею-
имеющихся на большом расстоянии от обтекаемого тела, проявляется
в единой форме также для несимметричных тел. Это влияние вы-
выражается посредством двух функций, зависящих от формы тела.
Коэффициенты этих функций определяются граничными условиями.
Если мы захотели бы получить одинаковые результаты как при
измерениях в аэродинамической трубе, так и при измерениях
в другом течении, например в течении с большим дозвуковым числом
Маха, то должны были бы обеспечить совпадение указанных коэф-
коэффициентов в обоих полях течения. Одним из параметров, который
можно использовать для дозвукового течения, является число Маха
набегающего течения; вторым параметром является угол атаки. При
этом важно, чтобы решение W~>J" давало эффект изменения
угла атаки также для тела произвольной формы (см. § 8 гл. VIII).
Следовательно, в рассматриваемом приближении измерения в аэро-
аэродинамической трубе будут эквивалентны измерениям в неограни-
неограниченном потоке, если надлежащим образом выбрать число Маха на-
набегающего течения и изменить угол атаки.
Сказанное иллюстрирует влияние возмущений, действующих на
большом расстоянии от обтекаемого тела, в частности влияние
стенок аэродинамической трубы. То обстоятельство, что влияние
стенок трубы в рассмотренном случае мало и что в первом при-
приближении оно не зависит от рода граничных условий, позволяет
сделать заключение, что поправки на влияние стенок трубы могут
вноситься также в результаты измерений, выполненных в около-
околозвуковой области. Этот вывод остается правильным и вблизи бло-
блокирующего числа Маха, а также для аэродинамических труб с пер-

§ И ДРУГИЕ ИССЛЕДОВАНИЯ ПЛОСКИХ ТЕЧЕНИИ 339
форированными стенками. Более подробно эти идеи развиты Гудер-
леем [7] (см. лит. 1). Поправки должны определяться путем систе-
систематических измерений. Они получаются в виде соотношения между
распределением давления на стенке трубы, эффективным числом Маха
и эффективным углом атаки. Количество необходимых измерений
может быть уменьшено путем применения закона подобия. Исполь-
Использование этого закона вполне допустимо, так как в рассматриваемых
условиях форма обтекаемого тела может совсем не учитываться.
§ 11. Другие исследования плоских течений
В конце § 7 настоящей главы мы упомянули, что если угол
раствора клина или, в более общем случае, относительная толщина
обтекаемого тела при неизменном числе Маха набегающего течения
достаточно мала, то результаты предыдущих параграфов становятся
неприменимыми. Однако это не является препятствием к примене-
применению уравнения для потенциала, упрощенного специально для около-
околозвуковых течений.
Винченти и Вагонер дали решения краевой задачи для таких
случаев. Краевая задача для клина уже была сформулирована в § 11
гл. V (рис. 45). Можно было бы попытаться решить эту задачу
аналитически путем определения частных решений, удовлетворяющих
граничным условиям на поверхности клина и имеющих в точках
ударной поляры логарифмическую особенность. Тогда полное ре-
решение можно было бы искать путем распределения таких особен-
особенностей вдоль ударной поляры. Свойства этих особенностей, ве-
вероятно, можно было бы подобрать так, чтобы получить интеграль-
интегральное уравнение второго рода, которое затем можно было бы решить
численным путем.
Винченти и Вагонер [1] (см. лит. 1) использовали прямой чи-
численный метод. Они покрыли плоскость tj, 0 решеткой из точек
и заменили производные, входящие в уравнение Трикоми, разно-
разностями значений функции тока в точках решетки. Так как исходное
дифференциальное уравнение и граничные условия линейны, то такой
метод приводит к системе линейных уравнений. Решение этой си-
системы представляет наибольшую трудность исследования. Винченти
и Вагонер использовали метод релаксации. Мы не будем останав-
останавливаться на деталях выполнения этих вычислений, так как для
практических применений этого способа так или иначе необходимо
ознакомиться с первоисточником. Приведем здесь только получен-
полученные результаты.
На рис. 103 показано распределение величины т]/6о3 вдоль сто-
стороны ромбовидного профиля при различных значениях числа Маха
набегающего течения (это число характеризуется величиной ~ /й '

340
ГЛ IX ТЕЧЕНИЯ С ЧИСЛОМ МАХА, БЛИЗКИМ К ЕДИНИЦЕ
От этого распределения нетрудно перейти к распределению давле-
давления. Переменная tj/90 , использованная для построения рис. 103,
совпадает с функцией ? скорости, которую ввели Винченти и Ва-
гонер. Эта же переменная использована при построении рис. 85.
На рис. 104 показана зависимость коэффициента сопротивления
от тH. На оси ординат отложены значения cw (?.-\- У)^% . Для того
чтобы получить эту кривую из рис. 103, необходимо выразить
2,Ц
2,0
1,6
12
0,8
ОМ
О
-0J
/
'//
1
г ^
a«es
jw0S8 ¦
0.921
0,703 ¦
0,U8k
—a ooo
-1,2
-1,6
-2,0
, _
0 0.1 0.2 пЗ ОМ 0,5 0,5 0,7 0,8 0,9 1,0
JCflj — а^-
Р и с. 103. Распределение величины т\ для ромбовидного
профиля при звуковой и сверхзвуковых скоростях набе-
набегающего течения, ц, есть значение величины ij, соот-
соответствующее скорости набегающего течения, а % — поло
вина угла раствора клина и одновременно относитель-
относительная толщина профиля (Винченти и Вагонер).
давление посредством третьей из формул V, 7A1). За динамическое
давление здесь взята величина pWa/2. Обращает на себя внимание
совершенно непрерывный переход кривой через число Маха, равное
единице. Результаты следует считать пригодными для очень тонких
профилей и соответственно этому для чисел Маха, очень близких
к единице. Можно ли и как именно распространить эти результаты
на более толстые профили и на большие отклонения числа Маха
от единицы, выяснить не просто. Некоторые соображения по этому
поводу высказаны Спрейтером (см. лит. 1).
Такой же метод был использован для определения влияния угла
атаки при сверхзвуковых числах Маха. Влияние угла атаки при числе
Маха, равном единице, для ромбовидного профиля было исследовано

§ 11. ДРУГИЕ ИССЛЕДОВАНИЯ ПЛОСКИХ ТЕЧЕНИЙ
341
уже в § 7 гл. VIII, причем выяснилось, что соответствующее значение
dCjJda намного меньше, чем при чисто сверхзвуковом течении.
\ —X
>
***х«
линейная сверхзв!,
ковая теория
\
:>
-кВинченти и Вагонер
°Гидерлей и Йосихара
упрощенное уравнение ~~~*
околозвуковых течений
смешанное
течение
—*.
чисто сверхзвуковое
течение
0,6
J'5
в'/3
2,0
2.S
3.0
Рис. 104. Зависимость коэффициента сопротивления ромбовидного
профиля от величины vj, при звуковой и сверхзвуковой скорости.
Ч„ есть половина угла раствора переднего клина и одновременно от-
относительная толщина, 7]0 есть значение величины т], соответствующее
скорости набегающего течения (Вивченти и Вагонер).
о Гудерлей и Йосихара
чВинченти и Вагонер
ойосихара
-интерполированные
значения
отход скачка уплотнения от
острия клина
положение
центра
давления
ii| ¦ нижняя
Ml \ граница
сверхзву
L,нового
Гтечения
12 1,4 1,6
0,2 0,ч 0.6 _2,0,8
Рис. 105 Зависимость коэффициента подъемной силы и положения центра
давления ромбовидного профиля от величины 7]q при сверхзвуковой скорости.
90 есть половина угла раствора переднего клина и одновременно относительная
толщина; а —угол атаки, а т]0 — значение величины т\, соответствующее скорости
набегающего течения (Винченти — Вагонер и Йосихара [1]).
Винченти и Вагонер [2] (см. лит. 1) нашли промежуточные точки
для случая неприлегающего скачка уплотнения (рис. 105). Эти зна-
значения проверены также экспериментально при малых углах атаки,
при которых не возникает отрыв течения. Предполагать, что

342
ГЛ IX ТЕЧЕНИЯ С ЧИСЛОМ МАХА, БЛИЗКИМ К ЕДИНИЦЕ
аналогичные неожиданные изменения величины dcjda. получаются и
для других профилей, трудно.
Йосихара [1] (см. лит. 1) исследовал изменение величины
dcAfda для случая, когда скачок уплотнения прилегает к острию
клина, но скорость вниз по течению относительно скачка остается
дозвуковой. В этом случае верхняя и нижняя стороны профиля не
зависят друг от друга и поля течения сверху и снизу профиля за-
зависят только от угла между стороной клина и направлением набегаю-
набегающего течения. Схема соответствующей краевой задачи показана на
рис. 53 и повторена на рис. 106. Йосихара в своем исследовании
(а)
исходит от частного решения
удовлетворяющего граничным
условиям вдоль стороны кли-
клина OF и вдоль характеристи-
ударная
тляРа
ллечо клина ки О А. Затем путем наложения
этих частных решений он при-
приближенно выполняет условия на
скачке уплотнения. Такой метод
вряд ли пригоден для получения
дГобГа„яГоХв^нГгопроф1ясоск СК0ЛЬ УГОДНО ТОЧНЫХ реЗуЛЬТа-
ком уплотнения, прилегающим к острию пе- тов, но для практических целей
реднего клина. QH mQ]im достаточен Диффе.
ренцирование результата по углу
раствора клина дает коэффициент подъемной силы. Полученные зна-
значения этого коэффициента нанесены на рис. 105.
Йосихара [3] (см. лит. 1) рассмотрел также пример течения
с большой дозвуковой скоростью.
Далее, Винченти, Вагонер и Фишер (см. лит. 1) исследовали те-
течение около пластинки, поставленной под углом атаки, при числе
Маха, равном единице, использовав для этого точное уравнение
годографа. Такое исследование позволило выяснить влияние не-
неточностей, возникающих вследствие применения уравнения Три-
коми вместо точного уравнения годографа. Результаты показаны
на рис. 30.
Можно предполагать, что обтекание крыльев с большим отно-
относительным размахом допустимо рассматривать приближенно как
плоское течение В работе Гудерлея [15] (см. лит. 1) исследован
вопрос, как распределение давления в сечении крыла приближается
с увеличением относительного размаха к распределению давления
в плоском течении. Исследование показало, что отклонения от рас-
распределения давления в плоском течении пропорциональны относи-
относительному размаху в степени —1,2. Эти отклонения можно рассмат-
рассматривать как сумму отклонений, вызванных изменением числа Маха,
изменением давления и — для наклоненной пластинки — изменением
угла атаки. Вследствие недостатка места мы не будем останавли-
останавливаться на подробностях этого исследования.

Глава X
НЕКОТОРЫЕ ИССЛЕДОВАНИЯ, ИСПОЛЬЗУЮЩИЕ
ЧАСТНЫЕ РЕШЕНИЯ ВИДА VII, 3C)
§ 1. Решение в невырожденной точке звуковой линии
в плоскости годографа
Частные решения вида VII, 3C) иногда могут быть с успехом
использованы для исследования специальных задач, например для
выяснения аналитических свойств смешанных до- и сверхзвуковых
течений в конкретных частных случаях. Такая возможность предста-
представляет значительный интерес, так как не всегда имеется математи-
математическая теория, позволяющая дать прямой ответ на интересующий
вопрос. Эту главу мы посвятим такого рода исследованиям. Начнем
с рассмотрения решения в плоскости годографа для невырожденной
точки звуковой линии.
К невырожденной точке звуковой линии предъявляются следующие
требования: в ее окрестности плоскость годографа не должна быть
многократно перекрыта, а вдоль характеристики, подходящей к этой
точке, не должны распространяться особенности. Выясним, в каком
виде получается разложение решения в плоскости годографа вблизи
невырожденной точки.
Пусть рассматриваемая невырожденная точка является нулевой
точкой плоскости 7], Ь. В § 9 гл. VII мы поставили задачу отыскания
таких частных решений, которые вдоль характеристик, проходящих
через нулевую точку, не имеют никаких особенностей. В результате
мы пришли к естественным частным решениям фй/6(/г = 0,1, ¦ • •)•
Из них решения <к,2 и ф{1/з)+№/з) представляют собой полиномы отно-
относительно т) и Ь (см. стр. 210). Конечно, эти решения допускают
гладкое продолжение в область, лежащую на рис. 69 между харак-
характеристиками ЕО и НО. В то же время эти решения являются един-
единственными частными решениями, для которых такая возможность
существует. В этом нетрудно убедиться на основании следующих
соображений. Выражения фй/6 либо симметричны, либо антисиммет-
антисимметричны относительно оси i\. To же самое относится и к продолжениям
этих выражений в область, лежащую между характеристиками АО
и ОВ. От этих продолжений необходимо потребовать, чтобы вдоль
характеристики ? = 1 они совпадали с решениями фй/6 (в отношении
значений самих функций). Вернувшись теперь к формулам VII, 4G)
и VII, 4(9), мы увидим, что решения, которые на положительной
оси т] либо симметричны, либо антисимметричны, для значений
{л. = х/4 —у— Л/2 всегда получаются как наложение обоих частных ре-
решений, возможных вдоль ?=1. Но одно из этих решений всегда

344 ГЛ X. НЕКОТОРЫЕ ИССЛЕДОВАНИЯ
имеет особенность. Согласно результатам, полученным в § 13 гл. VII,
каждое решение в области, лежащей внутри кривой С на рис. 69,
может быть представлено в виде наложения выражений фй/5
(/г=;0, 1,2, . . .), если только нулевая точка не является особой
и если вдоль характеристик ЕО и НО не распространяются особен-
особенности. Дополнительное требование о том, чтобы в области между
этими характеристиками решение смыкалось, но при этом вдоль
характеристик не происходило распространения особенностей, исклю-
исключает выражения фпм.^иу и в результате единственно возможными
выражениями остаются ф и ф,„ )+,h!iy
Среди этих частных решений всегда должно иметься решение ф1/3.
Все остальные решения, взятые сами по себе, отображают плоскость
годографа более чем на один лист плоскости течения. В самом деле,
для них у при обходе нулевой точки становится равным нулю более
одного раза. Вблизи нулевой точки преобладающую роль играет ре-
решение с наинизшей степенью р, следовательно, оно определяет здесь
структуру поля течения.
§ 2. Отражение особенности от звуковой линии
Как известно, в сверхзвуковом течении особенности, имеющиеся
в производных высшего порядка функции ф, распространяются вдоль
характеристик. Выясним, что получается, если какая-либо из таких
характеристик достигает звуковой линии. Мы увидим, что особен-
особенность после достижения звуковой линии отражается от нее иногда
по довольно сложному закону, но при этом сохраняет свой характер.
Кроме того, никакая особенность не исчезает на звуковой линии.
Отсюда неизбежно вытекает, что звуковая линия не может быть
и местом возникновения особенностей (см. Гудерлей [3], лит. 1).
В предыдущем параграфе мы исследовали точки звуковой линии,
в которых не возникают особенности. Нельзя ожидать, что появление
особенности в точке звуковой линии должно повлечь за собой суще-
существенное изменение структуры плоскости годографа. Отсюда выте-
вытекает следующий вывод: в том случае, когда в точке звуковой линии
допускается особенность, необходимо найти по-прежнему решение,
один раз полностью покрывающее плоскость tj, %¦ в окрестности
точки, в которой характеристика достигает звуковой линии.
Вдоль линии ?=1 каждое решение G(?, р) может быть пред-
представлено как наложение выражений
A—53)A/'2)~^ F (~пу — ^>-[9 — ^> 1—2^, 1—13\ Aа)
и
. . . / 1 7 \
A6)

§ 2 ОТРАЖЕНИЕ ОСОБЕННОСТИ ОТ ЗВУКОВОЙ ЛИНИИ 345
Такое представление решений пригодно как при ?<[1, так ш
при ?> 1, если переменить знак множителя, стоящего перед гипер-
гипергеометрическими рядами.
Тогда соответствующие частные решения
будут состоять в основном из уже известных выражений VII, 9A)„
а именно из выражений
(I)"U1J+P(l-») Ba>
и
/^\-(/«)+> A_^3)Vp(i_?S)# Bб>
\w
В каждой точке линии 1=1, за исключением начала координат, первое-
выражение регулярно, в то время как второе вследствие наличия*
множителя A — S3J|i имеет особенность (значения \х, равные целому-
числу или половине целого числа, сначала мы исключим из рассмот-
рассмотрения). Следовательно, распространение особенности определяется'
выражением B6). Если jj, отрицательно, то второй множитель стре-
стремится к бесконечности, а исследуемая характеристика отображается
в бесконечность. Этот случай, конечно, не представляет интереса^
При положительном р, вклад, вносимый выражением B6) в значе-
значения х и у, как нетрудно видеть из формул VII, 3G) и VII, 3(8), равеге
нулю. Для того чтобы в плоскости течения решение, получаемое
для области EDFOH на рис. 69, примыкало без разрывов к реше-
решению для области ЕОН, достаточно, чтобы рассматриваемые частные
решения совпадали в обеих областях только в отношении выраже-
выражения Bа), коэффициенты же выражения B6) могут быть произволь-
произвольными и при 5< 1 и ?> 1 могут не совпадать.
Для расчета отражения особенностей от звуковой линии вос-
воспользуемся возможностью разложения каждого решения на симмет-
симметричную и антисимметричную части. Симметричные и антисимметрич-
антисимметричные решения для областей —со < ? < 1 и 1 < ? < со были указаны
в § 4 гл. VII [формулы VII, 4F) —VII, 4A7)]. Для отыскания
выражений, определенных по всей области, необходимо только»
что указанные решения привести в совпадение при ?=1. (Конечно,,
симметричные и антисимметричные частные решения следует рас-
рассматривать отдельно.) На основании сказанного выше для такого»
совпадения достаточно, чтобы коэффициенты тех составляющих:
каждого решения, которые при 5=1 регулярны, были одинаковыми^
в обеих областях.
Тогда в области 1 < % <[ со решением, примыкающим к задан-
заданному при —со < % < 1 решению G(a', будет решение VII, 4(9), умно-
умноженное на 2 sin [тг ([х-(-г/4)]. В самом деле, после такого умножения

346 ГЛ. X НЕКОТОРЫЕ ИССЛЕДОВАНИЯ
коэффициент первого члена формулы VII, 4(9) совпадет с коэф-
коэффициентом первого члена формулы VII, 4A7г). Аналогичным
образом, продолжением в области 1<|<сх> решения G(s\ опреде-
определенного при —оо<?< 1, будет решение VII, 4G), умноженное на
2sinK[x+3/4)].
Пусть коэффициент частного решения, имеющего особенность
вдоль ?=1, равен а в области % <1 и равен р в области ?> 1.
Отношением этих коэффициентов для антисимметричных частных
решений будет
L [( I)] (За)
для симметричных частных решений1)
-E-=_ctg [«(,*-!)]. C6)
Любой другой случай может быть представлен в виде линейной
комбинации только что указанных выражений.
Ту характеристику, вдоль которой происходит приближение
к звуковой линии в направлении, совпадающем с направлением
течения, будем рассматривать как носителя особенности, движущейся
к звуковой линии. Тогда другая характеристика будет носителем
„отраженной" особенности. Можно было бы попытаться так подо-
«брать особенность, приближающуюся к звуковой линии, чтобы отра-
отраженная особенность исчезла. Для такого исчезновения, очевидно,
необходимо, чтобы составляющие симметричных и антисимметрич-
антисимметричных частных решений, имеющих особенности, взаимно уничтожались,
или, другими словами, чтобы оба отношения (За) и C6) для сим-
симметричных и антисимметричных частных решений совпадали. Однако
легко видеть, что свойства котангенса исключают возможность
такого совпадения при вещественном положительном [а. Следова-
Следовательно, особенность никогда не может быть поглощена звуковой
линией и никогда не может здесь самопроизвольно возникнуть.
В предыдущих рассуждениях особенности на обеих сторонах
характеристики имели в общем случае разные коэффициенты. Эти
коэффициенты могут быть определены из поля течения. Для этого
следует разложить ty по 1—?3, например, вдоль линии T] = const.
В соответствии со структурой найденных решений это разложение
будет состоять из степенного ряда относительно 1 — ?3, соответ-
соответствующего выражению Bа) и одинакового на обеих сторонах
характеристики, и из другого степенного ряда, умноженного на
¦{\—?3) а на одной стороне характеристики и на (i-3—1)^— на
1) Точнее говоря, выражение (За) будет справедливо в том случае
когда особенность имеется только в антисимметричном решении, а выра
жение C6) — когда особенность имеется только в симметричном решении.—
Прим. ред.

§ 2 ОТРАЖЕНИЕ ОСОБЕННОСТИ ОТ ЗВУКОВОЙ ЛИНИИ 347
другой стороне; для этой части разложения ф коэффициенты на
обеих сторонах характеристики могут быть различными. Они могут
быть найдены из разложения ф вдоль заданной линии плоскости т\, 8-.
Такой способ не приводит к цели, если (х представляет собой
целое число или половину целого числа, так как тогда на обеих
сторонах характеристики получаются только степенные ряды отно-
относительно 1—I3, причем некоторые члены этих рядов могут не
совпадать друг с другом. Это дает возможность определить только
разность коэффициентов тех решений, которые для других значе-
значений fj. имеют особенности, но не значения самих коэффициентов.
Здесь мы встречаемся с наиболее интересным случаем, а именно
с распространением вдоль характеристики скачка кривизны линий
тока или производных высшего порядка, характеризующих форму
линий тока. Так как третий аргумент в первом из гипергеометри-
гипергеометрических рядов, входящих, например, в формулу VII, 4G), теперь
•есть отрицательное целое число, то возможность представления
решения посредством гипергеометрического ряда в рассматриваемом
случае отпадает. В решение входит второй гипергеометрический ряд,
умноженный на 1пA—?3). Если особенность, распространяющаяся
в сторону звуковой линии, характеризуется лишь скачком в одной
из старших производных, но не содержит логарифмического члена,
то решение при \ < 1 и при \ > 1 может быть представлено только
с помощью выражений
J_ + ^ J_ + ^ j + 2|А> j _
причем коэффициенты этих выражений при 5<A и при ? > 1 полу-
получаются различными. Задана только разность этих коэффициентов.
Решение все же будет полностью определенным, так как в пло-
плоскости течения решение вдоль отраженной характеристики должно
смыкаться.
Тогда вдоль отраженной характеристики появляются логарифмиче-
логарифмические члены, следовательно, при отражении возникает перемена
характера особенности. Дальнейшие отражения не вносят никаких
усложнений.
Необходимым условием пригодности таких решений является
отрицательный знак их функционального определителя во всем поле
течения, включая и характеристику ?=1. Соотношения, выведенные
в § 8 гл. VII, дают критерий для знака функционального определи-
определителя. При [j, > 1/2 функциональный определитель вдоль характеристики
5=1 всегда положителен. Такие решения, взятые сами по себе,
с физической точки зрения не представляют интереса. Наоборот,
они приобретают интерес, если на них наложить решение при
ja = 5/12, т. е. ф = т], которое в нулевой точке регулярно и играет
здесь преобладающую роль по сравнению с решением, имеющим
особенность.

348 ГЛ X. НЕКОТОРЫЕ ИССЛЕДОВАНИЯ
Если [х лежит между 5/12 и 1/2, то после наложения такого реше-
решения на решение ф — tj знак функционального определителя будет за-
зависеть от коэффициентов части решения, имеющей особенность. Конечно,
представляют интерес только такие решения, для которых характе-
характеристики, направленные к звуковой линии, не образуют предельной
линии; в противном случае поле течения физически было бы невоз-
невозможно. Исследования Гудерлея [3] (см. лит. 1) показывают, что даже
при этом ограничении все же возможно образование предельной
линии, на этот раз из отраженных характеристик. Это означает, что
скачок уплотнения в плоскости течения может возникнуть вследствие
отражения от звуковой линии на первый взгляд „безобидной"
особенности.
Возникает вопрос, как рассмотренные здесь особенности про-
проявляют себя в плоскости течения, например как они влияют на
форму линий тока. Согласно предыдущим рассуждениям, решение,
для которого вдоль характеристики 1=1 распространяется особен-
особенность, в основном может быть представлено в виде
<|> =-- const • 7I-f-7)-(v<)+311 X
X [во -h "№ + а^ + .. . + &У 0О + Ь№ + Ь2Мг +•••)]• D)
где
Первый член правой части соответствует решению, не имеющему
особенности и играющему в нулевой точке преобладающую роль.
Остальные члены соответствуют частным решениям, имеющим
особенности. Однако среди них есть один член, не имеющий
особенности при \—\. Главную роль играет вторая часть выраже-
выражения, заключенного внутри квадратных скобок. Если наложить на
решение D) другие „гладкие" решения, то ничего не изменится.
Вдоль линии тока ф = const, поэтому уравнение D) позволяет опре-
определить т\ как функцию от Д? в виде следующего ряда:
Здесь tj0 и cv ca, ..., с'ч, ... суть надлежащим образом опре-
определенные постоянные, причем си с2, ... получаются из частных
решений, не имеющих особенностей, а </, ...—из частных реше-
решений, имеющих особенности; v есть наибольшее целое число, меньшее
чем 2(А.
Выразив 9 с помощью равенства VII, 3 B) через ч\, мы получи»
1(±
з U

§ 2 ОТРАЖЕНИЕ ОСОБЕННОСТИ ОТ ЗВУКОВОЙ ЛИНИИ 349
Определив надлежащим образом постоянные &0, dlt d2 мы мо-
можем представить & в следующем виде:
1ДГ+1Ч-й:+1Д^х+1+ .... E)
Далее, применив формулу VII, 3(9), выразим координату х через Д?.
Введя новые постоянные х0, ev e% ev /,..., мы получим
Решив это уравнение относительно Д?, мы найдем
при v^-1
о 1 I * * * I о v I & у I ' *' (/ av
при v = О
А
.ар-
Равенство G6) имеет место в том случае, если вблизи ? = 1 преоб-
преобладающую роль играет часть решения, обладающая особенностью.
Подставив значения Д? в уравнение E), мы получим
при v^. 1
при v — О
1
& = &о+-4-—-4-*Y-4j +.... (86)
Величина & есть наклон линии тока. Пусть у есть отклонение за-
заданной линии тока от линии у = const. Тогда мы будем иметь
dx
Внеся _у в уравнения (8а) и (86), мы получим
при v ^ 1
.у - ^о +
при v ==0
|44r;w oti^4"--(9б)

350 ГЛ X. НЕКОТОРЫЕ ИССЛЕДОВАНИЯ
В общем случае [а есть не целое число. Члены, содержащие
2J.+ 1
и Дл; ^ ,
показывают, как особенности, имеющиеся в плоскости годографа,
влияют на форму линий тока. В области, в которой применимо
уравнение (9а), при уменьшении \i уменьшается также степень Дл;,
входящая в представление особенности. При (* < х/г следует пользо-
пользоваться уравнением (96); для него с уменьшением ja степень выра-
выражения, представляющего особенность, увеличивается. При p = l/z
степень в обоих уравнениях получается одинаковой, и мы имеем
скачок в кривизне. В этом исключительном случае вдоль отражен-
отраженной характеристики получается, как было упомянуто выше, лога-
логарифмический член. Если мы перейдем теперь в плоскость течения,
то увидим, что наиболее сильной особенностью, которая там может
распространяться вдоль характеристики, является скачок кривизны;
следовательно, наличие логарифмической особенности позволяет
ожидать, что от звуковой линии отходит скачок уплотнения.
Если заранее задать особенность на граничной линии тока,
а тем самым и показатель решения с особенностью, то для пред-
представления решения в плоскости годографа получится два значения \х.
Для того чтобы объяснить эту многозначность, вспомним, как про-
производится построение сверхзвукового течения посредством метода
характеристик (§ 7 гл. I). При таком построении вводятся две ве-
величины 1 и ]л; величина X в рассматриваемом приближении, с точ-
точностью до множителя 180/тс, равна
При малых значениях Д? мы имеем
Х = —1т,'/.Д5
или, после замены Д? его значениями из равенств Gа) и G6),
и соответственно
В таком случае плотность волн Маха на единицу длины линии тока
равна
dl 1 з/

§ 3 ТЕЧЕНИЕ В САМОМ УЗКОМ ПОПЕРЕЧНОМ СЕЧЕНИИ СОПЛА ЛАВАЛЯ 351
и соответственно
В непосредственной близости от характеристики, несущей особен-
особенность, первое выражение имеет конечное и не равное нулю значение,
а второе равно нулю, так как в этом случае р,^1/2-
Таким образом, мы пришли к следующему представлению о свой-
свойствах поля течения. В свое время мы выяснили, что в сверхзвуковой
области, находящейся внутри дозвуковой области, волны Маха, иду-
идущие к звуковой линии, представляют собой волны разрежения,
а волны Маха, идущие от звуковой линии,—волны уплотнения.
Стенка должна иметь такую кривизну, чтобы волны уплотнения, под-
подходящие к ней от звуковой линии, превращались в волны разре-
разрежения. Рассмотрим теперь стенку, для которой направление каса-
касательной и кривизна хотя и изменяются непрерывно, но в некоторой
точке все же имеют разрыв в старших производных. Ограничим
этой стенкой различные поля течения, так что в окрестности особой
точки плотность волн Маха, приходящих от звуковой линии, будет
принимать различные значения. Если плотность подходящих волн
сжатия не слишком велика, то плотность волн разрежения, исходя-
исходящих от стенки, будет отлична от нуля и получится решение, соот-
соответствующее значению jj- > V2- Если же плотность подходящих от
звуковой линии волн уплотнения велика и притом настолько, что
в особой точке плотность отходящих от нее волн разрежения равна
нулю, то в этом случае получится решение, соответствующее зна-
значению ia<V2- Наконец, если плотность подходящих волн Маха
станет еще больше, то от стенки будут отражаться волны сжатия.
Эти волны еще до достижения звуковой линии сливаются и образуют
скачок уплотнения, вследствие чего вблизи звуковой линии решение
описанного здесь типа становится невозможным. Как было упомянуто
выше, образование предельной линии, а вместе с нею и скачка
уплотнения вследствие отражения от звуковой линии возможно уже
при особенностях, для которых (а < ]/2-
§ 3. Течение в самом узком поперечном сечении
сопла Лаваля
В § 2 гл. IV мы уже познакомились с течением в самом узком
сечении сопла Лаваля. Там разложение скорости вдоль оси сопла
начиналось с члена, линейного относительно х. Возникает вопрос,
обоснован ли физически такой выбор распределения скорости1}
(Гудерлей [3], см. лит. 1). Ограничимся рассмотрением сопел,.
1) Этот вопрос был поставлен Толмином.

352 ГЛ X НЕКОТОРЫЕ ИССЛЕДОВАНИЯ
симметричных относительно оси х. Тогда функция тока будет антисим-
антисимметрична относительно Ь = 0 E = — оо), и член наинизшего порядка
¦относительно р будет представлен в плоскости годографа функцией
Очевидно, что функция ф в нулевой точке должна быть конечной, т. е.
должно быть ц, > Vi2- Поведение такого решения вдоль оси х опре-
определятся уравнением
Решение вдоль характеристики ? —1 определяется формулой VII, 4A7).
Применение критерия VII, 8Eг) показывает, что при (а > Vg
решения невозможны. При р. = х/в получается решение, с которым
мы в свое время познакомились. При ja < х/в решения также воз-
возможны, однако для них волны Маха, достигающие звуковой линии
на оси сопла, являются носителями особенности в одной из старших
производных.
Эти результаты могут быть объяснены следующим образом.
При (л > Ve давление вдоль оси сопла падало бы быстрее, чем по
линейному закону, т. е. в точке пересечения оси сопла со звуковой
лянией распределение скоростей имело бы вертикальную касатель-
касательную. Для того чтобы вызвать такое падение давления, необходимо
обеспечить очень сильное расширение течения. Само по себе искрив-
искривление стенок, каким бы сильным оно не было, для этого недоста-
недостаточно. Единственной возможностью было бы образование расходящихся
волн расширения внутри самого течения. В расчете образование
таких волн выражается появлением предельной линии. О подобном
толковании предельной линии уже было сказано в § 3 гл. V. Ко-
Конечно, такие поля течения физически невозможны.
Наоборот, если падение давления вдоль оси сопла происходило
бы медленнее, чем по линейному закону, т. е. если бы в точке
пересечения оси сопла со звуковой линией распределение скоростей
имело горизонтальную касательную, то плотность волн расширения,
идущих к звуковой линии, по мере приближения к предельной
характеристике должна была бы стремиться к нулю. Для обеспечения
такой возможности необходимо было бы придать стенкам сопла
специальную форму. Таким образом, линейное изменение давления
вблизи предельной характеристики является единственным распреде-
распределением, которое устанавливается само собой, без каких-либо искус-
искусственных приемов.
Конечно, на частные решения Ц>»/я, получающиеся, на основании
сказанного, как бы естественным путем, могут быть наложены
частные решения фл/)+(й/з). В том случае, когда вдоль предельной
характеристики не распространяются никакие особенности, такое
наложение приводит, в соответствии с изложенным в § 13 гл. VII,

§ 4 ИССЛЕДОВАНИЕ СПЕЦИАЛЬНЫХ КРАЕВЫХ ЗАДАЧ 353
к полному представлению решения в плоскости годографа вблизи
нулевой точки. Для учета особенностей следует использовать даль-
дальнейшие частные решения <j/ .
Если расчет сопла Лаваля выполняется в плоскости течения на
основе полного уравнения для потенциала (например, посредством
его разложения в ряд), то обычно начинают с линейного распреде-
распределения скоростей вдоль оси. В результате получается решение для
поля течения, соответствующее решению фув в плоскости годографа.
При таком расчете выясняется, что другие параметры, а именно
коэффициенты разложения скорости вдоль оси в ряд Тэйлора, допу-
допускают свободу выбора. Аналогами этих параметров в плоскости
годографа являются коэффициенты частных решений tyn/)+,h/S). От-
Отсюда становится понятным, как в плоскости течения должно про-
производиться выполнение других граничных условий, заданных выше
по течению относительно самого узкого поперечного сечения сопла.
Далее становится понятным, что разложение потенциала в ряд, по-
получаемое на основе предположения о линейном изменении скорости
вдоль оси сопла, приводит к решению, действительно пригодному
вблизи самого узкого поперечного сечения.
В приведенных рассуждениях мы намеренно не касались об-
области, расположенной вниз по течению относительно предельной
характеристики, так как там расчет течения выполняется автомати-
автоматически посредством метода характеристик. Конечно, для выполнения
этого расчета необходимо знать контур сопла ниже по течению. Если
этот контур является аналитическим продолжением части контура,
расположенной вверх по течению относительно предельной харак-
характеристики, то в плоскости годографа можно просто использовать
продолжение частных решений i|>A. ч+(й/3) по другую сторону предельной
характеристики 5=1. Тогда, вследствие свойств частных реше-
решений fyiM+(ft/3v мы автоматически получим ожидаемое трехкратное
перекрытие плоскости годографа.
Исследования подобного рода могут быть выполнены также для
других особенностей, возникающих на звуковой линии. Напомним
хотя бы о точках В и С на рис. 48.
§ 4. Исследование специальных краевых задач
для уравнения Трикоми
Общая теория краевых задач для уравнения Трикоми разработана
пока еще не в такой мере, как это было бы желательно с точки
зрения приложений. Однако специальные краевые задачи допускают
исследование путем использования частных решений. Этим же путем
можно исследовать условия разрешимости, а также свойства реше-
решений таких задач (Гудерлей [5], см. лит, 1). Конечно, такого рода
23 Зак. 534 К Г. Гудерлей

354
ГЛ. X. НЕКОТОРЫЕ ИССЛЕДОВАНИЯ
метод не может заменить доказательств существования решений и их
единственности.
Области, для которых с успехом могут быть использованы рас-
рассмотренные в предыдущих главах частные решения, имеют границы,
образованные линиями i. = const и р = const. В частности, эти обла-
области могут иметь вид треугольников, ограниченных одной линией
р = const — р0 и двумя линиями $ —const = C] и I — const = с2-
Граничные условия могут быть либо условиями первого, либо усло-
условиями второго рода.
Граничные условия первого рода предписывают вдоль контура
значения <)>. Преобразовав граничные условия второго рода [уравне-
[уравнение V, 11A2)] к переменным р и $, мы получим
A _ S3)'/,
В
где через Fb обозначена правая часть уравнения V, 11A2). [Левая
часть уравнения A) получается из уравнения VII, 3 Eа) путем такого же
интегрирования, какое было выполнено при выводе уравнения V, 11 A1)].
Согласно уравнению A), граничные условия второго рода пред-
предписывают значение ф5 вдоль линии 5 = const и значение фр вдоль
линии р = const. Граничные значения вдоль линий \ = сх и ? = с2
могут не быть равны нулю, и
это не внесет никаких принци-
принципиальных затруднений. Однако
здесь для простоты мы будем
принимать эти значения всегда
равными нулю.
Если сх и с2 лежат в до-
дозвуковой области {ct < с2 < О,
рис. 107), то получается чисто
эллиптическая краевая задача.
В зависимости от того, заданы ли
на линиях | = с1 >и ? = с2 гра-
граничные условия первого или вто-
Р н с. 107. Краевая задача для уравнения Три-
коии при дозвуковой скорости (по Гудер-
лею [5]).
рого рода, там принимают либо
G = 0, либо О' = 0. Следовательно, определение системы функции G
приводится к задаче на собственные значения. Так как в рассматри-
рассматриваемом случае знак коэффициента при О в уравнении VII, 3F6)
всегда отрицателен, то получаются только положительные собствен-
собственные значения ja*. Вдоль линии р = const, образующей часть границы
области, можно задать либо значения ф, либо значения typ. Пусть на
линии р = р0 либо

§ 4 ИССЛЕДОВАНИЕ СПЕЦИАЛЬНЫХ КРАЕВЫХ ЗАДАЧ 355»
либо
Использовав обозначения § 9 гл. VII, мы можем представить решение
в следующем виде:
Граничные условия вдоль линии р = ро дают либо
либо
2в* (- 4-+^) ро"("/и)+1/Гл G» да=л ©¦
ft-1
Применим к этим равенствам соотношения ортогональности VII, 9 Gа)
и VII, 9 (8), которые остаются верными также после замены нижнего
предела интеграла на ct вместо — оо. Мы получим
или
Функции ОЛ будут, конечно, различными в зависимости от того,
какие граничные условия заданы вдоль линий k = c1 и ? = с2. Если
вдоль этих линий задано граничное условие dG/dZ — 0, то одним
из собственных значений будет У"\ = г/12 и соответствующей соб-
собственной функцией будет 0=1. Соответствующими частными реше-
решениями будут
Если вдоль линии р = Ро задано значение ф, то никаких трудностей
не возникает. Напротив, если задано значение ф , то частное реше-
решение ф = 1, регулярное в нулевой точке, не дает никакого вклада
в значение ф . Следовательно, в этом случае для выполнения усло-
условий, заданных вдоль линии р = р0, имеется уже не вся ортогональ-
ортогональная система функций — не достает функции О = 1. В связи с этим-
граничные условия второго рода могут быть выполнены только-

356 ГЛ X НЕКОТОРЫЕ ИССЛЕДОВАНИЯ
в том случае, если соблюдается равенство
о.
Это равенство представляет собой другую форму условия V, 11 A1),
выведенного в § 11 гл. V в связи с рассмотрением краевой задачи
второго рода.
Задать вдоль линии р = р0 произвольно и значение ф и значе-
значение <}>р нельзя. Правда, можно было бы предположить, что решение
имеет вид
и затем формально вычислить коэффициенты ah и bh. Однако част-
частные решения _
при приближении к нулевой точке стремятся к бесконечности и
притом тем быстрее, чем больше Хй, поэтому указанный ряд будет
сходиться только в том случае, если
его коэффициенты достаточно быстро
убывают. В общем случае этого нельзя
ожидать (см. стр. 34).
Перейдем к гиперболической краевой
задаче @<с1<с2<1, рис. 108). Такая
краевая задача считается поставленной
корректно, если она допускает реше-
решение посредством метода характеристик.
В рассматриваемом случае такое реше-
решение возможно, если вдоль линии р —ро
заданы как ф, так и фр, т. е.
Рис, 108. Краевая задача для
уравнения Трикоми при сверхзву- и, __ f (t) ф == f (t\
ковой скорости (по Гудерлею [5]). т Л W> тр /2W>
и, кроме того, вдоль линий ^ = с: и Е = с2 задано либо значе-
значение ф = 0, либо значение ф? == 0. И здесь мы приходим к класси-
классической задаче на собственные значения для функций О, образующих
полную ортогональную систему. Согласно сказанному в § 9 гл. VII,
теперь X<l/i2- Приняв, что решение имеет вид
= р-'Л. 2 [ак cos (/=Х^In р) -+¦ bh sin (V=Th In p)] G_h(S). B)
fti
мы используем полную систему частных решений, которые могут
быть, составлены из собственных функций. Так как эти функции

§ 4 ИССЛЕДОВАНИЕ СПЕЦИАЛЬНЫХ КРАЕВЫХ ЗАДАЧ 357
вдоль линии \ = const представляют собой с точностью до множи-
множителя р~д/», тригонометрические функции от In p, то трудности, свя-
связанные с обеспечением сходимости, теперь, в отличие от дозвуковой
краевой задачи, не возникают. Коэффициенты ап и bh могут быть
без особого труда вычислены с помощью соотношений ортогональ-
ортогональности.
В решении B) примечательным является присутствие множи-
множителя р/», входящего в каждое отдельное частное решение. Это
приводит к тому, что все частные решения в нулевой точке стре-
стремятся к бесконечности. Возникает вопрос, не происходит ли то же
самое с полным решением. Для частного случая, когда сумма
в уравнении B) содержит только конечное число членов, это пред-
предположение подтверждается сразу, так как отдельные выражения
в правой части уравнения B) вследствие ортогональности не могут
взаимно уничтожаться.
В правильности сделанного предположения в более общих слу-
случаях можно убедиться следующим образом. Вдоль каждой линии
р = const заданное решение ф может быть представлено в виде
наложения собственных функций. Коэффициенты при этих функ-
функциях определяются с помощью соотношений ортогональности в виде
интегралов, содержащих значения ф вдоль рассматриваемой линии
р = const и по одной из функций О. Если функция ф ограничена,
а с2<!1, то эти интегралы также ограничены, следовательно, огра-
ограничены и коэффициенты собственных функций. Но уравнение B),
которое можно рассматривать как разложение функции ф по О вдоль
любой линии р — const, показывает, что коэффициенты при G в ок-
окрестности р = 0 не ограничены. Отсюда следует, что первоначаль-
первоначальное предположение об ограниченности функции ф вблизи нулевой
точки неверно.
При этом доказательстве мы сделали предположение, что с2
меньше единицы. Случай с2=1 является исключительным, поскольку
для него при построении посредством метода характеристик было бы
неправильным задавать граничное условие вдоль ? = с2=1.
Для более глубокого понимания предельного перехода с2->-1
рассмотрим пример, изображенный на рис. 109. Пусть вдоль зву-
звуковой линии задано значение ф = 0; далее пусть ф задано вдоль
характеристики АС. Имея эти граничные значения, мы можем опре-
определить посредством метода характеристик решение в области ACD.
Если граничные значения ф в точке С не имеют особенности, то
решение в точке D также не имеет особенности, так как точка С
ничем не выделяется среди остальных точек характеристики АС.
Примем теперь для простоты, что ф имеет в точке С значение,
равное нулю. Тогда решение может быть получено также путем
следующего расчета. Выберем на звуковой линии (рис. ПО) ниже
точки D нулевую точку системы т\, 8 и проведем через точку С
линию I = const, а через точку А — линию р = const. Вдоль

358
ГЛ. X. НЕКОТОРЫЕ ИССЛЕДОВАНИЯ
линии ОСВ зададим для ф значение ф = 0. В области ABC мы можем
построить функцию, удовлетворяющую уравнению Трикоми и при-
принимающую вдоль АС заданные значения ф, а вдоль СВ — значе-
значение ф = 0. Эта функция и ее производная по р принимают вдоль АВ
определенные значения, которые обозначим через /х(?) и /2A). По-
Поступим теперь наоборот, а именно способом, указанным в преды-
предыдущем примере, построим решение, которое вдоль АВ дает значе-
значения »ф =/1(^) и фр = /2(?) и удовлетворяет вдоль AD и О В гра-
граничному условию ф = 0. Такое решение, вследствие единственности
решения рассматриваемой краевой задачи, совпадает в области ABC
с решением, полученным выше посредством метода характеристик.
характеристики
Рис. 109. К пояснению
предельного перехода
'С, -У 1.
Р.и с. 110. К пояснению
предельного перехода
1
Следовательно, вдоль АС оно принимает первоначально заданные
значения ф, а вдоль ? = 0 оно удовлетворяет первоначальному гра-
граничному условию ф = 0. Таким образом, оно представляет собой
в области ADC именно то решение, которое определяется усло-
условиями, заданными вдоль AD и АС. Это решение, безусловно, не равно
тождественно нулю вдоль DC, так как иначе, вследствие заданного
вдоль AD граничного условия ф == 0, оно было бы тождественно
равно нулю во всей области ACD.
Ничего не изменится, если мы начнем приближать нулевую точку
к точке D; в частности, решение в области ACD будет оставаться
неизменным. В любом случае значение ф вблизи нулевой точки будет
неограниченно возрастать. Далее в треугольнике DCO будет проис-
происходить уменьшение ф от его значений вдоль DC до нулевого значе-
значения вдоль ОС. Наконец, когда нулевая точка совпадет с точкой D,
произойдет скачкообразное изменение ф, которое можно толковать
как потерянное решение (§ 10 гл. V). Таким образом, граничные
значения, заданные вдоль ? = с2, не влияют в предельном случае с2-> 1
на решение. Действительный характер решения выясняется из пре-
преобразований, рассмотренных в § 13 гл. VII.
После всех этих подготовительных рассуждений мы можем при-
приступить к рассмотрению смешанной краевой задачи. Особенны*

§ 4. ИССЛЕДОВАНИЕ СПЕЦИАЛЬНЫХ КРАЕВЫХ ЗАДАЧ
359
'характеристика
Рис. 111, Смешанная краевая задача (по Гудер-
лею [5]).
интерес представляет случай, когда в противоположность задаче
Трикоми контур в сверхзвуковой области замкнут. Пусть в дозву-
дозвуковой области контур задан линией р = const = р0 и линией ? =
= с1 = — со (рис. 111), а в сверхзвуковой области — линией ? —с2
и одной из характеристик, проходящих через точку пересечения
линии р = Ро со звуковой линией. Пусть вдоль линий % = cl = — со
и % = сг задано значение ф = 0. Далее, пусть заданы значения ij> вдоль
линии ABC. Рассуждения
остаются почти во всех
деталях такими же, как
для краевой задачи второго
рода. Однако формулировка
нашей краевой задачи отли-
отличается от формулировки
задачи Трикоми, так как
теперь контур, ограничи-
ограничивающий рассматриваемую
область, замкнут, в то вре-
время как в задаче Трикоми он обязательно разомкнут. Можно ожи-
ожидать, что поставленная задача имеет решение только в том случае,
если пренебречь некоторыми условиями, налагаемыми на решения
Трикоми. Ниже мы увидим, что необходимо ввести допущение о су-
существовании у решения некоторой особенности в одной из точек
пересечения контура со звуковой линией.
Для того чтобы получить краевую задачу с контуром, состоящим
только из линий | = const и р = const, продолжим линию р==ро
в сверхзвуковую область до пересечения с линией X = с2. Примем,
что в точке С функция <[> равна нулю, а вдоль CD зададим для нее
значение ф = 0. Тогда таким же способом, как и в предыдущем
примере, мы сумеем построить в области BCD функцию ф по ее
значениям, заданным вдоль характеристики ВС и вдоль линии CD.
Граничное условие вдоль характеристики ВС можно заменить зна-
значениями ф и фр вдоль BD, получающимися при этом построении, и
условием <]> = 0 вдоль CD. Допустим, что решение можно взять
в виде
А-1
Такое решение содержит в себе все частные решения, получаю-
получающиеся для отрицательных собственных значений, и те частные ре-
решения для положительных собственных значений, которые в нулевой
точке стремятся к нулю. Если вообще существует такое решение

360 ГЛ X. НЕКОТОРЫЕ ИССЛЕДОВАНИЯ
рассматриваемой краевой задачи, которое в нулевой точке прибли-
приближается к бесконечности не быстрее, чем р~'/»а, то на основании ска-
сказанного в § 10 гл. VII оно должно иметь именно вид C). В самом
деле, частные решения
при р = р0 становятся равными Gh(?) и G-h&', следовательно, для
выполнения граничных условий, заданных для ф при р = р0, мы рас-
располагаем полной ортогональной системой функций. С помощью со-
соотношений ортогональности VII, 9Gа) можно найти явные выраже-
выражения для коэффициентов ап и ch. Что касается коэффициентов bh,
то они должны быть выбраны так, чтобы для <|>р получились именно
те значения, которые были заданы вдоль р = р0 при 0 < % <С с2.
Простой способ для достижения этой цели неизвестен. Можно
было бы попытаться выполнить граничные условия в отдельных
точках или попробовать подобрать коэффициенты bh так, чтобы
средняя ошибка, получающаяся при выполнении граничных условий,
была минимальной. Во всяком случае важно следующее: если коэф-
коэффициенты ch не равны нулю, то независимо от того, какими полу-
получатся коэффициенты bh, решения в нулевой точке стремятся к бес-
бесконечности. Доказательство этого утверждения вытекает из таких же
соображений, как и в сверхзвуковой краевой задаче.
Рассмотренный пример показывает, чего можно ожидать, если
краевая задача поставлена некорректно, т. е. для замкнутого кон-
контура в сверхзвуковой области. Между тем при наличии внутри до-
дозвукового течения сверхзвуковой зоны физическая краевая задача
принимает именно такой „некорректный" математический вид.
В связи с этим изучение такого рода краевых задач приобретает
очень большой теоретический интерес, а по мнению а,втора — даже
решающий интерес. Однако единой точки зрения по этому вопросу
пока не существует. Ряд идей, затрагивающих также физическую
сторону этого вопроса, имеется в работе Гудерлея [10]. Очень
важные соображения высказаны Кэтлин Моравец [1]. На подроб-
подробностях, ввиду отсутствия места, останавливаться не будем (см. также
работу Франкля [2], лит. 1).
Поскольку в рассмотренном примере контур в плоскости годо-
годографа имеет в нулевой точке бесконечную кривизну, можно было бы
считать пример неудачным. Более того, можно было бы даже пред-
предполагать, что решения принимают в нулевой точке бесконечно
большие значения именно вследствие бесконечной кривизны контура.
Поведение частных решений для контура, не обладающего таким
свойством, было исследовано в работе Буземана и Гудерлея, а также
в другой работе Гудерлея [1] (см. лит. 1). Выяснилось, что и
в этом случае возникают аналогичные особенности. Однако до-

§ 4 ИССЛЕДОВАНИЕ СПЕЦИАЛЬНЫХ КРАЕВЫХ ЗАДАЧ 361
казательства сходимости, которое только и делает такие исследо-
исследования законченными, в этих работах не дано.
Если мы начнем приближать с2 к единице, то можно ожидать,
что произойдет переход к задаче Трикоми такой же, как в при-
примере чисто сверхзвукового течения. Однако детали решения такой
задачи трудно проследить, так как решение в области СЕО влияет
на дозвуковое течение, а тем самым косвенно и на решение в об-
области ВСО. При с2=1 особенность в нулевой точке больше не
возникает, несмотря на то, что частные решения для отрицательных
собственных значений стремятся в нулевой точке к бесконечности
так же, как и р~'/™. Этот результат вытекает из исследований, про-
проведенных в § 13 гл. VII.
Единственность течения с числом Маха, равным единице, тре-
требует, чтобы на решение краевой задачи второго рода было нало-
наложено дополнительное условие даже для случая контура такого же
типа, как в задаче Трикоми (см. стр. 284). В работе Гудерлея [5]
(см. лит. 1) сделана попытка выяснить роль этого условия на ряде
примеров.

Глава XI
ОСЕСИММЕТРИЧНЫЕ ТЕЧЕНИЯ
§ 1. Течения с числом Маха, равным единице
Часть исследований, выполненных в предыдущих главах для
плоских течений, может быть распространена на осесимметричные
течения. Это обстоятельство чрезвычайно важно с практической
точки зрения: достаточно вспомнить о снарядах и сверхзвуковых
самолетах, которые более похожи на тела вращения, чем на плоские
тела. Исследование осесимметричных течений представляет интерес
еще в одном отношении. Результаты, полученные для плоских тече-
течений, часто пытаются переносить на обтекание неплоских тел. Между
тем это иногда может приводить к ошибочным выводам. Напомним,
что при линеаризованном рассмотрении околозвуковых течений
выяснилось, что трудности, специфические для околозвуковых
течений, проявляют себя при исследовании осесимметричных тече-
течений значительно слабее, чем при исследовании плоских течений.
Следовательно, имея решения для осесимметричных течений, даже
если эти решения неполные, мы можем предохранить себя от не-
недопустимых заключений по аналогии.
Начнем с рассмотрения течений, происходящих при числе Маха,
равном единице.
Метод годографа, преобразующий для плоских течений нелиней-
нелинейные уравнения в линейные, теряет свои преимущества при исследо-
исследовании осесимметричных течений. Для того чтобы найти для потен-
потенциала скоростей выражение, которое описывало бы поведение тече-
течения в бесконечности, попытаемся использовать в качестве отправной
точки плоское течение, рассмотренное в § 2 гл. VIII. Там мы
получили уравнение VIII, 2C), согласно которому линия $ = const
отображается на плоскость течения в виде обобщенной параболы.
Вдоль такой параболы у пропорционально p-f/«. На основании урав-
уравнений V, 7G) и VIII, 2A) преобразованный потенциал вдоль
линии ? = const пропорционален р-'/«. То же самое имеет место и
для потенциала в плоскости течения. Поэтому для этого потен-
потенциала можно взять выражение
Обобщая это представление, можно искать Ф в виде
О)

& 1. ТЕЧЕНИЯ С ЧИСЛОМ МАХА, РАВНЫМ ЕДИНИЦЕ 363
где
С = (х + 1)-'/'^- Aа)
(Гудерлей и Йосихара [2], см. лит. 1). В уравнении A) т и п
суть постоянные, которые, как выясняется в процессе вычислений,
связаны между собой соотношением
т = Ъп — 2. A6)
Множитель (l-f-*)~'/s введен в правую часть равенства Aа) для
того, чтобы дифференциальное уравнение, определяющее /, не
содержало /. Допущение A) о виде потенциала пригодно также
для осесимметричных течений, если только координату у, т. е.
расстояние от оси х, рассматривать как цилиндрическую координату,
ранее обозначавшуюся через г.
Допущение A) можно обосновать также непосредственно, не
обращаясь к результатам, полученным для плоских течений. Вполне
правдоподобно допустить, что при удалении в бесконечность пло-
плоскости течения потенциал изменяется пропорционально некоторой
степени расстояния. Однако при этом важную роль играет выбор
линии, вдоль которой происходит удаление в бесконечность. Не-
Нетрудно видеть, что если мы возьмем в качестве таких линий прямые,
то получим тривиальные решения. В качестве следующей пробы
следует использовать обобщенные параболы. Этот выбор и приводит
к допущению A). Между прочим, течения, рассмотренные в гл. IV,
принадлежат именно к этому типу.
Допущение A) можно ввести в уравнение II, 8B), т. е. в около-
околозвуковое приближение дифференциального уравнения для потен-
потенциала осесимметричного течения. К такому же результату мы придем
и в том случае, если введем допущение A) в точное уравнение
потенциала и ограничимся наиболее высокими степенями у. Для
того чтобы для определения функции / получилось обыкновенное
дифференциальное уравнение, необходимо выполнение условия A6).
В осесимметричном случае мы будем иметь
(/' — пК2) f -f- Eft — 4) vLf — Cft — 2J / = 0. B)
При заданном п решения этого уравнения могут быть найдены
посредством численного интегрирования. Однако прежде чем перейти
к решению уравнения B), попытаемся получить общее представле-
представление о совокупности его решений. Это тем более необходимо потому,
что уравнение B) содержит нелинейный член, вследствие чего
нельзя заранее выявить особенности его решения. Соображения раз-
размерности показывают, что если умножить масштаб переменной С
на С, а масштаб функции / на С3, то уравнение B) перейдет само
в себя. Это показывает, что при преобразовании поля течения на
основе закона подобия в сочетании с изменением масштаба

364 ГЛ XI. ОСЕСИММЕТРИЧНЫЕ ТЕЧЕНИЯ
плоскости течения поле течения переходит само в себя. Следова-
Следовательно, если функция / = g-(C) представляет собой решение диффе-
дифференциального уравнения B), то функция
) C)
также будет решением этого уравнения.
Если решение дифференциального уравнения обладает таким
свойством, называемым групповым свойством, то порядок уравнения
может быть понижен на единицу. Это понижение выполняется путем
введения таких новых переменных, чтобы постоянная С выпалах).
Итак, введем новые переменные
« = Г3/. Dа)
* = Г7'; D6)
следовательно,
-g- = — 2С3/' + Г2/" = Г1 (- 2t + Г1/"), Eа)
^ f^C'it-Zs). E6)
Отсюда мы найдем
и уравнение B) примет вид
AL — 2t% + C/г ~ 4)nt ~~ (Зп ~~
ds ~~ (n?
Величина С вычисляется из уравнения E6).
Для численного исследования рассматриваемой задачи уравне-
уравнение F) не представляет каких-либо преимуществ по сравнению
с уравнением B); наоборот, выражаемая им связь между перемен-
переменными s и t, с одной стороны, и интересующими нас физическими
величинами, с другой стороны, менее ясна, чем в уравнении B).
Но зато уравнение F), поскольку оно является уравнением первого
порядка, позволяет получить простое представление о виде инте-
интегральных кривых. Эти кривые получаются в плоскости s, t из
поля направлений дифференциального уравнения F). Для того
чтобы охватить также бесконечность плоскости s, t, спроектируем
1) Постоянную С в равенстве C) можно понимать как постоянную инте-
интегрирования, появляющуюся в результате решения уравнения B). Так как
после перехода к новым переменным эта постоянная интегрирования вы-
выпадает, то следует ожидать, что интегрирование преобразованного диф-
дифференциального уравнения даст на одну постоянную интегрирования
меньше, а это означает, что в результате преобразования его порядок по-
понизился на единицу.

§ 1 ТЕЧЕНИЯ С ЧИСЛОМ МАХА, РАВНЫМ ЕДИНИЦЕ
365
эту плоскость на полусферу, причем центр проекций поместим
в центре сферы. В результате вся плоскость s, t изобразится на
северной полусфере, а бесконечность плоскости s, t — на экваторе.
Затем спроектируем полусферу на внутренность круга. Таким
путем получается картина, изображенная на рис. 112. Для нас
представляет интерес только качественное поведение интегральных
кривых.
Как показывают равенства D6) и A), звуковая линия в пло-
плоскости s, t определяется уравнением ? = 0. Далее важную роль
в плоскости s, t играет линия t = п2. На ней коэффициент при /"
Рис. 112. Расположение интегральных кривых уравнения F)
в плоскости s, t при «=4/i- Стрелки указывают направление,
в котором | С | возрастает (по Гудерлею и Йосихаре [2]).
в уравнении B) обращается в нуль. Из уравнения F) в сочетании
с равенством E6) следует, что С имеет экстремум, когда интеграль-
интегральная кривая пересекает линию ? = /г2. Если мы будем передвигаться
вдоль интегральной кривой в подходящем направлении, то С будет
уменьшаться до тех пор, пока интегральная кривая не достигнет
линии t = я2; начиная отсюда, С начнет увеличиваться. Следова-
Следовательно, линии С = const ометают сначала часть плоскости течения
до экстремального значения С, а затем перекрывают эту же область
вторично. Здесь мы сталкиваемся с примером возникновения пре-
предельной линии в осесимметричном течении. В зависимости от того,
какой знак имеет изменение давления на предельной линии, послед-
последняя представляет собой либо результат слияния волн уплотнения,

366 ГЛ. XI. ОСЕСИММЕТРИЧНЫЕ ТЕЧЕНИЯ
обусловленных граничными условиями задачи, либо результат рас-
расхождения волн разрежения. В первом случае возникает скачок
уплотнения, второй случай физически неосуществим.
Далее, важную роль играют те особые точки поля направлений
дифференциального уравнения F), в которых производная dsjdt ста-
становится неопределенной. В таких точках числитель и знаменатель
правой части уравнения F) одновременно равны нулю. В конечной
области плоскости s, t таких точек три, их координаты равны
для точки A: s = 0, ? = 0;
,-, , Ъп — 4 , о
для точки С: s =п3 -^— о,„ , t = re2;
(on — iy
2 2
для точки D: $=-^-, t = ^r ¦
Для выяснения характера решений вблизи этих точек линеаризуем
в правой части уравнения F) числитель и знаменатель в окрестности
каждой из этих точек. В окрестности, например точки С, мы получим
dt_ (Зя — 2J [А^ Gп* — 4я) — As (Зя — 2)^]
ds At Fя<* — 4я2У '
где
. - Ъп — 4
As = s — пд ¦
(Зя —2J '
Так как это уравнение получено путем линеаризации, то оно одно-
однородное (следовательно, обладает групповым свойством) и поэтому
может быть проинтегрировано. Таким путем можно найти интеграль-
интегральные кривые в непосредственной близости особых точек. На по-
подробностях мы не будем останавливаться. Через точку С проходят
только две интегральные кривые, остальные же кривые распола-
располагаются вблизи точки С наподобие гипербол. Направления подхода
к точке С обеих проходящих через нее интегральных кривых опре-
определяются либо путем вычислений, либо непосредственно из равенства
dt _ Ы
ds As
Из равенства D6) следует, что при t = re2
Далее из равенств A) и Aа) мы имеем
Фх = (ч -)- 1 )-1/8 у3™/' (?). G)
Внеся сюда вместо /' только что найденное его значение, мы по-
получим
ф =(х-\- l)~l/' v8n~a«2C2. (8)

S 1. ТЕЧЕНИЯ С ЧИСЛОМ МАХА, РАВНЫМ ЕДИНИЦЕ 367
Наклон линии С = const в общем случае равен
а при t = ti2 равен
На основании равенства I, 6A0) это есть наклон характеристики,
т. е. все линии С = const, соответствующие какой-либо точке
линии t — п2, имеют наклон характеристики.
Второе условие
. 5л—-4 ,п.
8п3 О)
для особой точки С представляет собой не что иное, как условие
совместности I, 6A1) для характеристик, а именно
dx dФ~. . йФ„ , Ф,,
dy dy ' dy
Для того чтобы убедиться в этом, используем равенства G) и (8),
а также равенство
ф —ySn~3 [(Зя 2)/ «С/'].
При С = const мы найдем
^ -3 [(Зя - 2)/-яС/'].
Внеся эти значения в уравнение A0) и учтя равенства D), мы по-
получим условие (9).
Таким образом, линия С = const, соответствующая точке С,
представляет собой характеристику, причем предельную характе-
характеристику, с которой мы уже познакомились при изучении плоских
течений. Так как точки С достигают только специальные интеграль-
интегральные кривые, то при интегрировании дифференциального уравне-
уравнения F), а также уравнения B) целесообразно начать с предельной
характеристики.
Для определения направления подхода интегральных кривых
к точке t — 0, s = 0 положим
dt t
ds 5 '
Тогда мы найдем
t Зга —2

368 ГЛ XI ОСЕСИММЕТРИЧНЫЕ ТЕЧЕНИЯ
Отсюда следует, что для определения интегральных кривых вблизи
точки А целесообразно ввести новую переменную
, Зп — 2
и = t s,
п
откуда
t^u+^s A1)
и
dt da . Зп — 2
ds ds' n '
Тогда, ограничившись в числителе и знаменателе уравнения F)
только величинами первого порядка, мы получим
ds 2s — an'
откуда найдем
s = —?«ln(ClB) A2)
и
« = 0. A2а)
где Сг есть постоянная интегрирования. Из уравнения E6) мы имеем
г г ds п Г d [и In (CjU)] п Г d_
1П,— I т оТ— к I n 9 1а-
и s
n
откуда
С = const- м-»/2. A3)
Далее мы получаем
фу = ysn-s [Cл _ 2)/ — пС/'] =
— 2) s — /г^] = — уш-Кьпа. A4)
Внеся сюда вместо а его значение из равенства A3), мы найдем
Фу = const • у™-згз-B/«)#
Наконец, заменив С его значением Aа), мы окончательно получим
Фу = const • y-lx
т. е. для этого решения вся ось х состоит из особых точек. Ана-
Аналогичным образом вычисляется и Фх.
Интегральная кривая A2а) является исключительной среди всех
других интегральных кривых; она представляет собой физически
особенно интересный случай, в котором ось х не имеет особых
точек. В самом деле, из равенств A2а) и A4) мы имеем

§ 1. ТЕЧЕНИЯ С ЧИСЛОМ МАХА, РАВНЫМ ЕДИНИЦЕ
369
Для полного исследования интегральных кривых необходимо вы-
выяснить их поведение также в бесконечности. За этими подробно-
подробностями отсылаем к работе Гудерлея и Йосихары [2] (см. лит. 1).
Здесь упомянем лишь, что бесконечно удаленная прямая (экватор
при проектировании на полусферу) представляет собой интеграль-
интегральную кривую, вдоль которой также расположено несколько особых
точек. Точки экватора, лежащие на одном и том же диаметре, сле-
следует считать тождественными, следовательно, точки В и В' являются
эквивалентными. Они представляют собой изображение оси у пло-
плоскости течения. В плоскости течения ось у не играет какой-либо
привилегированной роли. То обстоя-
обстоятельство, что соответствующая точка
в плоскости s, t является особой, обу-
обусловливается выбором переменных s и t.
Если мы выразим t через Фх, х
и у, то увидим, что t принимает в точ-
точке В значение, равное нулю. Как ве-
ведет себя интегральная кривая в пло-
плоскости s, t при прохождении через
точку В, можно видеть из равенств D)
в сочетании с равенством Aа). Вели-
Величины Ф и Фх в этой точке, как и
в любой другой, непрерывны, поэтому
в точке В происходит только пере-
перемена Знака VS. Рис. 113. Пояснение расположения
г* „ интегральных кривых вблизи точки В
Структура семейства интегральных иливгна рис. ш.
кривых вблизи точки В объясняется
тем, что в плоскости течения некоторые решения достигают
предельной линии (t = n2) раньше, чем область существова-
существования решения, ометаемая кривыми С = const, доходит до оси у.
Такие решения не достигают точки В. Для других решений
ось у входит в область существования решения и притом дважды;
поэтому и точка В появляется на соответствующей интегральной
кривой два раза. Для пояснения рассмотрим семейство кривых,
изображенное в верхней части рис. 113. Для кривых этого семей-
семейства величина s вдоль прямой, соответствующей линии t — п2, имеет
максимум. В определенном месте, которому на рис. 112 отвечает
точка В или В', сожмем это семейство кривых, не изменяя при
этом взаимного расположения кривых. В результате мы получим
картину, изображенную в нижней части рис. 113. Поведение интег-
интегральных кривых вблизи точек В и В' в точности соответствует
этой схеме. Поле слева от сужения на рис. 113 отвечает полю
около точки В, а поле справа от сужения — полю около точки В'.
Следовательно, структура семейства интегральных кривых вблизи
точки В совсем не такая „странная", как могло бы показаться на
первый взгляд.
24 Зак 534. К. Г. Гудерлей

370 ГЛ. XI ОСЕСИММЕТРИЧНЫЕ ТЕЧЕНИЯ
Теперь мы можем описать в общем виде искомое решение для
течения с числом Маха, равным единице. Точка А соответствует
оси х. Вверх по течению относительно обтекаемого тела следует
ожидать дозвуковой скорости. Источники вдоль оси х не должны
возникать. Поэтому в точке А следует использовать интегральную
кривую, направленную в сторону отрицательных значений t; на-
начальная точка этой интегральной кривой определяется равенством A2а).
Дальнейшее поведение решения зависит от значения п. Все решения рано
или поздно переходят через звуковую линию, а определенный класс этих
решений достигает линии t = n2, т. е. для них возникает предель-
предельная линия. Такие решения непригодны. Для другого класса реше-
решений, т. е. для других значений п, линия t = n2 никогда не дости-
достигается; интегральные кривые на рис. 112 проходят мимо точки С
и оканчиваются в точке А, подходя к ней со сверхзвуковой сто-
стороны. Решения этого рода перекрывают всю плоскость течения от
отрицательной до положительной оси. На положительной оси распреде-
распределяются источники; следовательно, получается течение около полутела
(аналогичное поле течения для плоского случая было рассмотрено в §5
гл. VIII). Переход от одного класса решений к другому происходит при
определенном значении п, для которого интегральная кривая про-
проходит через точку С. Это значение п и дает искомое решение,
обладающее предельной характеристикой.
Для того чтобы найти это решение, необходимо для различных зна-
значений п вычислить решения, начиная как от точки Л, так и от точки С.
Как уже было упомянуто, вычисления необходимо вести поль-
пользуясь уравнением B). Один раз следует решить это уравнение ис-
исходя от оси х, затем еще раз — исходя от предельной характери-
характеристики. Если при обоих расчетах постоянная С, входящая в урав-
уравнение C), совпадет, то это будет, конечно, случайностью. Для
того чтобы проверить, приводят ли оба хода решения к совпадению,'
лучше всего освободиться от постоянной С, перейдя для этого
к переменным s и t, и затем выяснить, при каком значении п оба
решения при заданных s ш t совпадают.
Эти исследования были выполнены Гудерлеем и Йосихарой [21
(см. лит. 1) и недавно очень тщательно проверены Гертрудой Бланш.
Для п получилось с большой точностью значение « = 4/?- Результаты
вычислений даны в таблице 2 (стр. 387) и изображены на рис. 119
(стр. 386). Эти результаты описывают течение в бесконечности
при числе Маха, равном единице, с точностью до масштаба, кото-
который, конечно, зависит от размеров тела. На рис. 119 показано
также изменение некоторых других величин, характерных для тече-
течения; о них будет сказано в § 5 настоящей главы. Для предель-
предельной характеристики всегда можно выбрать значение С= 1. Тогда пер-
первыми членами разложения функции / в точке С= 1 при ге = 4/7 будут
^ + ^С1)+|(С1>2+

§ 2 УТОЧНЕННОЕ ИССЛЕДОВАНИЕ РЕШЕНИЯ В БЕСКОНЕЧНОСТИ 371
Выявление поведения решения в бесконечности является только
первым шагом на пути определения действительного поля течениях).
Для получения результатов, которые хотя бы сколько-нибудь соот-
соответствовали практической постановке вопроса, необходимо рассмо-
рассмотреть поле течения около тела. Задано ли это тело или же оно
получается только в процессе расчета — особой важности не имеет.
Для тела вращения задача получается очень трудной, потому что
дифференциальное уравнение течения нелинейно и не может быть
линеаризовано подобно тому, как это было сделано в плоском случае
посредством перехода к плоскости годографа.
Йосихара [2] (см. лит. 1), использовав метод релаксации, рас-
рассчитал течение около тела, состоящего из комбинации конуса и ци-
цилиндра.
§ 2. Уточненное исследование решения
в бесконечности
В предыдущем параграфе тело, для обтекания которого мы на-
нашли решение, было представлено только особенностью на оси х.
Если имеется тело с неисчезающими размерами, то на полученное
решение необходимо наложить, как и в плоском случае, дополни-
дополнительные решения, учитывающие изменение первоначального решения,
возникающее вследствие влияния конечных размеров тела. Настоящий
параграф мы посвятим исследованию этих дополнительных решений
(Гудерлей [4], см. лит. 1).
Будем считать, что отклонение действительного решения от ре-
решения, полученного в предыдущем параграфе, мало, и поэтому от-
отбросим в дифференциальном уравнении течения более высокие степени
этого отклонения. Примем, что потенциал равен
Ф = Ф0(х, у) + Ф(х, у), A)
где Ф0(х, у) совпадает с потенциалом, определяемым равенством
XI, 1A), а Ф(х, у) есть отклонение от действительного решения,
обусловленное конечными' размерами тела. Внесем это выражение Ф
в дифференциальное уравнение околозвуковых течений. Отбросив
члены более высоких порядков, мы получим для определения Ф
линейное дифференциальное уравнение
ет + ^^О. B)
1) В то же время этот шаг является очень важным. На стр. 67 было
показано, что трудности линейной теории, а именно возникновение беско-
бесконечно больших значений давления на теле, связаны с поведением течения
в бесконечности.

372
ГЛ XI ОСЕСИММЕТРИЧНЫЕ ТЕЧЕНИЯ
Для отыскания частных решений этого уравнения примем, что они
имеют вид
Это допущение приводит к обыкновенному дифференциальному урав-
уравнению
(/' - пК*) g" + If" + Bш - »*) С] g' - *g = 0. D)
Так же как и в случае плоской задачи, возникает вопрос о полноте
системы таких частных решений. К счастью, дифференциальное урав-
звуковая
\лини.
Рис. 114. Система линий p=const и C=const в плоскости х, у
для осесимметричного течения (по Гудерлею [4]).
нение D) также может быть приведено к виду, соответствующему за-
задаче на собственные значения, и поэтому к нему применимы такие же
рассуждения, как и для плоской задачи. В самом деле, введя функцию
(!:, v),
где h определяется дифференциальным уравнением
h' _ nl
/' —
E)
F)
мы получим для определения функций G дифференциальное уравнение
(/' - «2С2) G" + (Г - пК) О' - \ f^nKi G - 0, G)
причем
X = v2-|-/w. Ga)
Самосопряженной формой уравнения G) будет

§ 2 УТОЧНЕННОЕ ИССЛЕДОВАНИЕ РЕШЕНИЯ В БЕСКОНЕЧНОСТИ 373
Использовав равенство E), мы сможем представить допущение C)
в виде
Ф=РЧ}(С, v), (9)
где
P = yh(C). (9a)
Теперь можно отнести эти частные решения к системе координат р, С
(рис. 114).
Особыми точками уравнения (8) являются С = i оо (ось х)
и значения С, для которых/' — пК2 = 0 (предельная характеристика).
Можно принять, что для предельной характеристики ?=1. Опреде-
Определим теперь решения О в точке ?=1. Для этого разложим в урав-
уравнении G) коэффициенты при О', О" и О по С—1, ограничившись
в каждом из них только первым членом; тогда мы получим
^X) O=0,
где /'A) и /"A) суть значения/' и /" при ?=1. Отсюда в каче-
качестве первых членов разложения О в точке С = 1 мы найдем
G=(C
Соответствующие разложения для функции g, определяемой уравне-
уравнением D), будут иметь вид
2
-1) и g- = (C— 1) /"'(i)-2na »- 4 Я(С— 1). A0а)
Учтя равенства XI, 1 A5) и Gа), мы получим вместо уравнения A0)
следующее:
17/ 2 ч
1— 1ч Н—I (\ 1 *\
Q — tf \\ ь-1Ч\^1 ) р(Г \\ К[Ч
или
7
G = (C— l)r°vP(C— 1) (lla)
и
- — — v
—• \^s *¦) -* 1 ъ A ).
Аналогично вместо уравнений A0а) мы получим
g-=P(C— 1) A2а)
—1).
A26)
Следовательно, одно из решений вблизи С=1 регулярно, в то время
как второе дает при отрицательных м распространение особенности

374 ГЛ XI ОСЕСИММЕТРИЧНЫЕ ТЕЧЕНИЯ
вдоль предельной характеристики. При v >—2/7 решение стре-
стремится к бесконечности, что противоречит допущению о малой ве-
величине возмущений. При отрицательных м решение A26) может быть
регулярным, а именно при целочисленных показателях, т. е. при
значениях
v = —I — i-A (A=l, 2,...). A3)
В этом случае в другое решение входит логарифмический член,
а вместе с ним и особенность при С=1, по крайней мере в одной
из производных.
Нижней границей интервала, подлежащего рассмотрению, яв-
является, конечно, ось х. Здесь необходимо потребовать, чтобы состав-
составляющая дополнительной скорости вдоль оси у была равна нулю.
При определении частных решений посредством задачи на соб-
собственные значения за верхнюю границу интервала следует взять
линию С = с2<1, лежащую в сверхзвуковой области, а затем со-
совершить предельный переход сг -*¦ 1.
Получающаяся таким путем система частных решений опять
имеет положительные и отрицательные собственные значения X.
Соответствующими значениями ч будут
. (И)
Собственные значения Х>—/г2/4 дают частные решения
о (С, v), A5а)
собственным же значениям X < ¦— пг\\ соответствуют частные решения
^-т lnpJG(C-v)- A5б)
Форма уравнения (8) и граничные условия позволяют найти соот-
соотношения ортогональности. Посредством таких же соображений,
как и в § 10 гл. VII, можно показать, что каждое решение линеа-
линеаризованного дифференциального уравнения B), удовлетворяющего
граничным условиям, заданным вдоль С = — со и вдоль С = с2, мо-
может быть представлено в виде наложения частных решений A5).
Граничное условие, заданное вдоль линии С = с2, перестает играть
какую-либо роль, если эта линия совпадает с предельной харак-
характеристикой.
И здесь следует иметь в виду разницу между частными реше-
решениями, получаемыми в результате решения задачи на собственные
значения, и естественными частными решениями, определяемыми тре-
требованием ограниченности всех производных вдоль предельной ха-
характеристики (см. стр. 222). Связь между обоими этими типами

§ 2 УТОЧНЕННОЕ ИССЛЕДОВАНИЕ РЕШЕНИЯ В БЕСКОНЕЧНОСТИ 375
частных решений можно установить, по-видимому, посредством ме-
метода, изложенного в § 13 гл. VII.
Первые естественные частные решения можно найти на осно-
основании простых соображений общего характера. Можно, например,
использовать то обстоятельство, что как
Ф = _уЗ»-2/(С), ¦)
так и | A6)
представляют собой решения уравнения для потенциала околозву-
околозвуковых течений. Вторая форма решения получается из первой после
умножения координат х и у на множитель С. Если С близко к еди-
единице, то разность обоих решений представляет собой то возмуще-
возмущение начального поля течения, которое описывается уравнением B).
Для получения решения уравнения B) следует продифференцировать
разность решений A6) по С и затем положить С равным единице.
Мы получим
Сравнив это уравнение с уравнением C) и положив га = 4/7, мы найдем
v = — у, A6а)
A66)
i J
В качестве второго решения возьмем
Ф = у-2А
Выбор такого решения означает смещение особой точки вдоль
оси х. Повторив такие же рассуждения, как и в предыдущем случае,
и продифференцировав по С, мы получим
^ — f> 8 —J Ы-
Следующие два естественных частных решения получаются, согласно
расчетам Гудерлея [4] (см. лит. 1), при v = —9/7 и v = —12/7 (таблица 1).
Эти значения ч найдены путем численного расчета и поэтому не
обязательно должны быть точными значениями1).
1) Хотя значение п = 4/7 было найдено также путем численного расчета,
но оно получено с такой точностью, что не остается никакого сомнения
в возможности выразить его именно этой дробью Это обстоятельство на-
наводит на предположение, что только что 'указанные значения v также яв-
являются точными и что существует общий закон распределения значений ч,
соответствующих естественным частным решениям.

376
ГЛ XI ОСЕСИММЕТРИЧНЫЕ ТЕЧЕНИЯ
Таблица 1
Значения функции g и ее производной при v = — э/7 и v = —13'7
С
1,0
0,9
0,8
0,7
0,6
0,5
0,4
0,3
0,2
0,1
0
-од
— 0,2
— 0,3
— 0,4
— 0,5
— 0,6
— 0,7
— 0,8
— 0,9
— 1,0
— 1,2
— 1,4
— 1,6
— 1,8
— 2,0
— 2,2
-2,4
g
1,0000
1,3973
1,6038
1,6519
1,5738
1,3990
1,1542
0,8634
0,5476
0,2252
— 0,0886
— 0,3815
— 1,6439
—1,8692
—1,0536
—1,1955
—1,2956
—1,3567
— 1,3828
—1,3789
—1,3507
—1,2459
— 1,1047
— 0,9559
— 0,8164
— 0,6939
— 0,5899
— 0,5035
g'
— 5,0624
— 2,9404
— 1,1887
1,2272
1,3352
2,1818
2,7347
3,0821
3,2328
3,2159
3,0606
2,7963
2,4519
2,0549
1,6315
1,2054
0,79724
0,42380
0,09733
— 0,17470
— 0,38945
— 0,65869
— 0,75307
— 0,75494
— 0,65987
— 0,56576
— 0,47335
— 0,39158
с
1,0
0,9
0,8
0,7
0,6
0,5
0,4
0,3
0,2
0,1
0
— 0,1
— 0,2
— 0,3
— 0,4
— 0,5
— 0,6
— 0,7
— 0,8
— 0,9
— 1,0
— 1,2
— 1,4
— 1,6
— 1,8
— 2,0
— 2,2
— 2,4
g
0
— 0,1497
— 0,2165
— 0,2269
— 0,1957
— 0,1403
— 0,0727
0,0036
0,0597
0,1120
0,1505
0,1739
0,1827
0,1787
0,1642
0,1422
0,1158
0,08775
0,06052
0,03592
0,01510
— 0,01380
— 0,02782
— 0,03147
— 0,02957
— 0,02505
— 0,02034
— 0,01618
g'
0
0,00825
0,02713
0,04930
0,07043
0,08722
0,09787
0,10169
0,09888
0,09029
0,07714
0,06095
0,04312
0,02595
0,00790
— 0,00742
— 0,02032
— 0,03030
— 0,03791
— 0,04273
— 0,04528
— 0,04554
— 0,04140
— 0,03549
— 0,02939
— 0,02393
— 0,01939
— 0,01574
Решение, получающееся при м = —12/7, представляет собой не
только естественное частное решение, но — в пределах точности
расчета — также первое частное решение, определяемое задачей на
собственные значения1). Соответствующее положительное собствен-
1) Это обстоятельство весьма примечательно, так как оба вида частных
решений могут совпадать друг с другом при отрицательных ч только при
значении, определяемом равенством A3). В плоской задаче такого совпаде-
совпадения не получается.

§ 3 ПРИЛОЖЕНИЯ
377
ное значение равно v = 8/7. График собственной функции О для этих
значений v изображен на рис. 115.
Включив в уравнение B) член ФЮШ/_У2, мы сумеем распростра-
распространить выполненное исследование на общий пространственный случай.
Указанный член войдет также в линеаризованное уравнение, опре-
определяющее возмущение. Вместо допущения C) о виде решения теперь
следует взять допущение
Ф —.yvif(?> v> m) cos тш, A7)
причем т. обычно есть целое число*). Для определения функции g
мы получим дифференциальное уравнение
(/' — пКг) g" + U" Н- 2«v — пК) g' — (? — m?)g = 0. A8)
Все остальные преобразования
&
1,0
0,5
О
>
\
\
эвунозоя'
линия
\
1
1
/
А
-2,5 -2,0 -15 4,0 -0,5 О 0,5 1,0
Рис.
115. Собственная ' функция G при
7 или ч = а/7 (осесимметричное тече-
течение).
остальные
выполняются так же, как и выше.
В частности, можно опять найти
ортогональную систему функций.
С помощью полученной си-
системы частных решений можно
представить, по крайней мере
в принципе, любые небольшие
отклонения от решения, рассмо- -0,5
тренного в предыдущем пара-
параграфе, причем безразлично, воз- <°
никают ли эти отклонения из-за
изменения формы тела или из-за
установки тела под ненулевым
углом атаки.
Конечно, ценность получен-
полученных решений ограничена тем, что
они основаны на линеаризации в окрестности Фо. Вблизи обте-
обтекаемого тела такая линеаризация безусловно недопустима.
§ 3. Приложения
Гудерлей и Йосихара [2] (см. лит. 1) ввели частные решения, рас-
рассмотренные в предыдущем параграфе, прежде всего для того, чтобы
таким путем рассчитать первый пример обтекания тела вращения
при числе Маха, равном единице в бесконечности. Они наложили
на решение Фо выражение Ф, соответствующее значению v = —9/7^
и затем определили форму тела, получающуюся в результате такого
наложения. При этом они сделали допущение, что линеаризация,
выполненная для уравнения B), допустима даже вблизи тела.
Конечно, было бы правильнее использовать такое представление
течения только на большом расстоянии от обтекаемого тела,
!) Решение задачи обтекания тела, ограниченного в направлении у>
должно быть периодической функцией ш с периодом 2тс — Прим. ред.

-378 ГЛ XI ОСЕСИММЕТРИЧНЫЕ ТЕЧЕНИЯ
в области же, в которой линеаризация недопустима, определять поле
течения путем аналитического продолжения на основе применения
полного дифференциального уравнения II, 8B). Однако до настоя-
настоящего времени такого рода расчеты не проведены.
Частные решения, выведенные в предыдущем параграфе, дают
возможность исследовать осесимметричные поля течения с числом
Маха, мало отличающимся от единицы в бесконечности (Гудерлей [5],
см. лит. 1). Путь исследования примерно такой же, как и в случае
плоского течения. Однако нелинейность дифференциального уравне-
уравнения влечет за собой некоторое усложнение выводов.
Возьмем за основу течение с числом Маха, равным единице.
Необходимо допустить, что изменение граничных условий, наложен-
наложенных на большом расстоянии от обтекаемого тела, влечет за собой
лишь небольшое изменение поля течения вблизи тела даже в том
случае, если вблизи места возникновения возмущений получаются
большие изменения. При таком допущении изменения вблизи тела
могут быть учтены путем линеаризации. В применении к телу вра-
вращения, находящемуся в блокированной аэродинамической трубе,
сказанное означает, что линеаризация поля течения с числом Маха,
равным единице, допустима вблизи тела, но недопустима вблизи
стенок. При увеличении ширины трубы область, в которой допустима
линеаризация, становится больше.
Область, в которой применяется линеаризация, нуждается в даль-
дальнейшем разграничении. Вблизи тела исходное течение довольно сложно
и, конечно, не может быть описано одной только функцией Фо (х, у).
Однако на большом расстоянии от тела, но все еще в области, в ко-
которой при надлежащих условиях допустима линеаризация, выраже-
выражение Фо дает хорошее представление исходного течения. Там для пред-
представления возмущенного поля течения может быть использована си-
система частных решений, найденная в предыдущем параграфе.
Составим в области, допускающей линеаризацию, частные реше-
решения, оставляющие форму тела неизменной. Такие частные решения
па большом расстоянии от тела, безусловно, не могут быть малыми
по сравнению с решением Ф0(х, у), так как в противном случае
наложение решений можно было бы распространить до бесконеч-
бесконечности, и тогда течение с числом Маха, равным единице, было бы
не единственным. Поэтому среди частных решений, оставляющих
форму тела неизменной, должно содержаться по крайней мере одно
из частных решений XI, 2C) с положительными показателями. Сле-
Следовательно, в области, в которой возможно представление течения
посредством такого частного решения, решения, оставляющие форму
тела неизменной, имеют в принципе вид
ф = УЧ(С Vft) + ?ft. A)
Здесь vh есть положительное значение v, соответствующее собствен-
собственному значению Xft, а срл есть решение линеаризованного уравнения,

§ 3 ПРИЛОЖЕНИЯ 379
имеющее в бесконечности порядок, не превышающий порядка вели-
величины Фо, т. е. О(_у~2/')- Изменение поля течения, вызванное гранич-
граничными условиями, наложенными на большом расстоянии от тела,
учитывается путем наложения выражений вида A). Чем меньше воз-
возмущение, возникающее на большом расстоянии от тела, т. е. чем
меньше отклонение рассматриваемого течения от течения с числом
Маха, равным единице, тем меньше коэффициенты, на которые надо
умножить выражения вида A) при их наложении на решение Фо;
но зато тем больше становится расстояние от тела, на котором
отклонения рассматриваемого течения от течения с числом Маха,
равным единице, могут быть представлены путем наложения выра-
выражений A). На большом расстоянии от тела преобладающую роль
в выражениях A) играют их первые члены; следовательно, течение
в целом, т. е. включая Фо, может быть представлено потенциалом
Ф = а0Ф0+2^У^С„ Ч). B)
Функции <ph, входящие в выражение A), определяются формой тела.
Так как они не входят в выражение B), то последнее зависит
от формы тела только через коэффициент при функции Фо.
Остальные коэффициенты, входящие в уравнение B), должны
быть выбраны так, чтобы аналитическое продолжение функции Ф
(с использованием полного уравнения потенциала околозвуковых
течений) на большом расстоянии от тела удовлетворяло заданным
там граничным условиям (например, граничным условиям на стенках
аэродинамической трубы или граничным условиям при сверхзвуковом
числе Маха).
Пусть решение B) определяет поле течения при некотором
числе Маха Мо, например при Мо> 1, и пусть это решение удо-
удовлетворяет определенному типу граничных условий. При этом ah суть
постоянные, зависящие от граничных условий. Для того чтобы
найти соответствующее решение для другого течения, характеризуе-
характеризуемого числом Маха М, необходимо преобразовать поле течения
согласно закону подобия для околозвуковых течений и одновременно
так изменить масштабы, чтобы коэффициент а0 первого члена, зави-
зависящий от размеров тела, остался неизменным. На основании сообра-
соображений, изложенных в § 6 гл. II, мы получим

380 ГЛ XI ОСЕСИММЕТРИЧНЫЕ ТЕЧЕНИЯ
где n = i!1. Для того чтобы первый член остался неизменным, сле-
следует выбрать х0 = т""''3. Расчеты, упомянутые в предыдущем пара-
параграфе, дают в качестве первого собственного значения v = 8/7.
Следовательно, при малых значениях т мы будем иметь
Ф = aoy~^f (С) + a^/I,g (г, 1
Но М — 1 пропорционально т, поэтому мы можем переписать пре-
предыдущее равенство в виде
Ф = аоу-г''Ю + «i (М - 1)W (С у )+•••¦
где постоянная ах имеет теперь несколько иное значение.
Для составления аналитического продолжения этого решения по
направлению к телу необходимо заменить частные решения y4hg (Z,, Vft)
их полными выражениями вида A). Тогда первый член правой части
последнего уравнения будет представлять течение с числом Маха,
равным единице, а остальные члены будут давать поправки, которые
необходимо ввести в это течение (в последнем уравнении оставлена
только поправка наинизшего порядка). Вызванное этими поправками
изменение в распределении давления пропорционально (М—1)!/з.
Отсюда следует, что кривая, изображающая зависимость коэффи-
коэффициента сопротивления (отнесенного к динамическому давлению p*w*3/2)
от числа Маха набегающего течения, хотя и обладает при М = 1
горизонтальной касательной, но в то же время имеет здесь беско-
бесконечную кривизну.
Правда, в экспериментальных результатах это явление не обна-
обнаруживается: наклон кривой, изображающей зависимость коэффициента
сопротивления от числа Маха, получается всегда положительным.
Возможно, что выполненные исследования применимы к настолько
малой области чисел Маха, что полученный вывод перекрывается
неточностью измерений1).
В связи со сказанным добавим еще следующее. Результаты, изло-
изложенные в этом параграфе, применимы не только к осесимметричным
телам, но и ко всем телам ограниченных размеров. Объясняется
это тем, что на большом расстоянии от тела отклонения от осевой
симметрии перестают играть заметную роль. К числу таких тел
можно отнести стреловидное крыло конечного размаха. Если не счи-
считать явлений, возникающих вблизи корневого и концевого сечений
крыла, то определяющим фактором его обтекания является соста-
составляющая скорости в направлении хорды, т. е. для большей части
такого тела переход через число Маха, равное единице, не влечет
!) Последние измерения, выполненные в лаборатории NACA, как будто
все же подтверждают полученный вывод.

§ 4 ТЕЧЕНИЯ СО СКАЧКАМИ УПЛОТНЕНИЯ 381
за собой существенного изменения поля течения. В такого рода
случаях явление, описанное в этом параграфе, может быть заметно
только в очень узкой области чисел Маха, близких к единице.
§ 4. Специальные плоские и осесимметричные течения
со скачками уплотнения
Допущение о виде решения уравнения для потенциала около-
околозвуковых течений, принятое в § 2 настоящей главы, можно приме-
применять также в тех случаях, когда в поле течения имеются скачки
уплотнения, распространяющиеся вдоль линий С = const (Бериш и
Гудерлей, см. лит. 1). Для того чтобы убедиться в этом, рассмотрим
условия перехода через скачок уплотнения. Пусть поле течения до
скачка уплотнения определяется уравнением XI, 1 A). Тогда мы
будем иметь
где /t и /2 суть надлежащие функции от ?. О скачке уплотнения
сделаем предположение, что он распространяется вдоль линии
С = const = Со. В таком случае его наклон определяется равенством
dy __ (х + 1Г'/з
dx ~
Внесем эти величины в условие на скачке II, 4F), причем в соот-
соответствии со сказанным в § 8 гл II положим т = 1 и вместо \, tj, С
напишем х, у, z. Кроме того, учтем, что по смыслу величины /,
входящей в условие II, 4 F), имеет место соотношение
дх)
Тогда для течения за скачком уплотнения мы получим уравнение
Аналогичным образом, использовав равенство II, 4 Gа), мы найдем
Следовательно, скорость после скачка уплотнения также может быть
представлена в виде, согласующемся с допущением XI, 1 A).
Особенно просто условия на скачке могут быть сформулированы
в плоскости s, t. Мы знаем, что в околозвуковой области измене-
изменениями энтропии можно пренебречь и что потенциал скоростей (который

382 ГЛ XI ОСЕСИММЕТРИЧНЫЕ ТЕЧЕНИЯ
можно ввести именно по этой причине) изменяется при переходе
через скачок уплотнения непрерывно. Непрерывность потенциала
выражает собой тот факт, что касательная составляющая скорости
при переходе через скачок уплотнения не изменяется. Величина С
непосредственно выше и ниже по течению относительно скачка имеет,
конечно, одинаковые значения, поэтому величина s, определяемая ра-
равенством XI, 1 Dа) (не смешивать с энтропией!), также не изменяется
при переходе через скачок, т. е. имеет место равенство
(индексы I и II относятся, как и в гл. II, к состояниям выше и ниже
по течению относительно скачка). Далее, введя допущение XI, 1A)
в условие на скачке II, 4F), мы найдем
Это означает, что при переходе через скачок уплотнения мы пере-
перескакиваем от соответствующей точки плоскости s, t к ее зеркаль-
зеркальному отражению относительно линии t — n2. Так как в результате
скачка происходит всегда повышение давления, а потому — умень-
уменьшение скорости, то допустим только прерывный переход от боль-
больших значений t к меньшим. Этот результат применим как к плоским,,
так и к осесимметричным течениям.
Для плоских течений соответствующие соотношения могут быть
получены также в плоскости годографа.
§ 5. Приложения
Выведенные в предыдущем параграфе соотношения были исполь-
использованы Беришем и Гудерлеем (см. лит. 1) для уточнения картины
течения при числе Маха, равном единице. До сих пор мы рассчи-
рассчитывали поле течения в бесконечности только до предельной харак-
характеристики. Теперь мы займемся исследованием поля течения в беско-
бесконечности ниже по течению относительно предельной характеристики.
Непосредственно ниже по течению относительно обтекаемого
тела скорость течения, по крайней мере в плоском случае, больше
скорости звука. В этом можно убедиться следующим образом. Со-
Состояние течения в точке А на рис. 116 определяется тем, что в этой
точке вектор скорости горизонтален и что сама точка А лежит на
одной из характеристик, исходящих от звуковой линии. При этом
принимается, что изменение состояния при переходе через скачок
уплотнения, который при надлежащих условиях может пересечь ха-
характеристику, не слишком сильно отличается от изменений состоя-
состояния, возможных вдоль этой характеристики (см. в связи с этим рис. 44,
на котором изображены ударные поляры и характеристики). Вектор

§ 5 ПРИЛОЖЕНИЯ
383
скорости вдоль звуковой линии отображается на плоскость годо-
годографа в виде отрезка СО; следовательно, исходная точка характе-
характеристики АВ лежит на этом отрезке. Такие характеристики, очевидно,
обязательно пересекаются с линией 0 = 0.
Все волны, подходящие от звуковой линии, представляют собой
волны сжатия. Волны, расположенные ниже по течению относительно
обтекаемого тела, т. е. в следе за телом, также являются волнами
сжатия. Вполне вероятно, что эти волны сливаются друг с другом
дозвуковая
область
звуковая
Линия
JI Но
в-к I
> / сверхзвуковая
область
, ^характеристикаI
I \ скачок
I z ¦
/-предельная
уплотнения.
«L
/предельн
'характериа
ч
в
^изображение
профиля
предельная
характеристика
-характеристика
^и приближение
к ударной
поляре
Рис. 116. К исследованию состояния течения в точке А.
и образуют скачок уплотнения. Займемся исследованием поведения
этого скачка на большом расстоянии от обтекаемого тела.
Если вблизи профиля для этой цели пригоден метод характе-
характеристик, то на больших расстояниях целесообразнее воспользоваться
аналитическим методом. Можно ожидать, что для расчета поля тече-
течения ниже по течению относительно предельной характеристики по-
прежнему пригодно допущение XI, 1 A). В диаграмме s, t (рис. 112}
имеется два продолжения интегральной, кривой, проходящей через
точку С, а именно CD и СА. Оба продолжения физически возможны
и оба они ведут к положительной оси х. Как показывают более
точные расчеты, кривая СА подходит к точке А таким образом, что
вдоль положительной оси получается распределение источников.
Следовательно, это решение соответствует полутелу, простирающе-
простирающемуся в бесконечность и обладающему такой кривизной (выпуклостью),.

384
ГЛ XI. ОСЕСИММЕТРИЧНЫЕ ТЕЧЕНИЯ
что волны, подходящие к нему от звуковой линии, после отражения
не образуют скачка уплотнения.
Решение, соответствующее кривой CD, представляет собой ана-
аналитическое продолжение того решения, которое имеет место вверх
по течению относительно предельной характеристики. Можно было бы
предположить, что это и есть правильное решение. В самом деле,
предельная характеристика выделяется среди других характеристик
только своим поведением в бесконечности, но не внутри поля тече-
течения, и поэтому было бы неожиданным, если бы на предельной харак-
характеристике менялся характер решения. Однако и это решение не удо-
удовлетворяет условию, которое должно быть выполнено на положи-
положительной оси х, а именно условию, что здесь составляющая скорости
в направлении оси у обращается в нуль. Наоборот, в точке D обе
составляющие скорости (и в направлении х и в направлении у) стре-
стремятся к бесконечности, так так здесь С становится бесконечно боль-
большим. Для того чтобы в этом убедиться, требуется несколько более
подробное исследование.
-S
'
_ ¦—
состояние до скачка
уплотнения
геометрическое место А
возможных состояний
после cm
тка уплог
пнения
—положение
скачка
решение,
котором
х отсутс
зооль оси
твушт
-з
-г
Рис. 117. Диаграмма s, t и определение положения скачка уплотнения для
осесимметричного течения при ЛГ—1 (по Беришу и Гудерлею).^
Так как интегральная кривая CD лежит выше линии t==n2, то
в этой части течения может возникнуть скачок уплотнения, распро-
распространяющийся вдоль линии С = const. Вдоль оси х ниже по течению
относительно скачка уплотнения составляющая скорости в направле-
направлении у должна быть равна нулю. Это условие требует, чтобы соот-
соответствующая интегральная кривая определялась в точке А уравне-
уравнением XI, 1A2а). Следовательно, полю течения после скачка уплот-
уплотнения соответствует заранее определенная кривая в диаграмме s, t.
Состояние до скачка уплотнения определяется кривой CD. Зеркально
отразив эту кривую относительно линии t = ri1, мы получим геоме-
геометрическое место состояний, возможных после скачка уплотнения.
Точка пересечения этой кривой с С А дает положение скачка уплотне-
уплотнения. На рис. 117 такое построение выполнено для осесимметричного
случая.

§ 5 ПРИЛОЖЕНИЯ 385
Таким образом, в том месте, где возникает скачок уплотнения,
следует сомкнуть два поля течения, каждое из которых получается
в результате отдельного расчета. При таком смыкании постоянная С,
входящая в формулу XI, 1 C), должна быть определена для одного
из полей так, чтобы для обоих полей в том месте, где возникает
скачок, получились одинаковые значения ^.
Для определения формы линии тока, т. е. отклонения линии тока
от линии _у = const, необходимо проинтегрировать наклон линии тока
вдоль линии у — const = у0, следовательно, необходимо вычислить
интеграл
= fb(y0, x)dx.
Однако проще воспользоваться уравнением неразрывности так, как
мы это сделали в § 8 гл. II. Остановимся сначала на случае пло-
плоского течения. Рассмотрим для произвольной области такого тече-
течения равенство
/ / ] dx dy = °
и выразим интеграл по поверхности через криволинейный интеграл.
Мы получим
Ф2
причем интегрирование следует выполнить вдоль контура в напра-
направлении, обратном направлению движения часовой стрелки. Если мы
выберем в качестве границы рассматриваемой области линии у — О,
у = у0, х — — со и C = const = C0, то после упрощений найдем
Применив уравнение XI, 1A) и приняв п=*/5, мы получим
\)'1зу,
причем
Для осесимметричной задачи аналогичным образом мы найдем

386
ГЛ. XI ОСЕСИММЕТРИЧНЫЕ ТЕЧЕНИЯ
причем
Результаты расчета по этим формулам даны в таблицах 2 и 3 и изо-
изображены в виде графиков на рис. 118 и 119. В обеих таблицах
Рис. 118. Функции /, /' и у для плоского течения (по Беришу
и Гудерлею).
Рис. 119. Функции /, /' и J» для осесимметричного
течения (по Берчшу и Гудерлею).
обращают на себя внимание некруглые значения координаты С ниже
по течению относительно скачка уплотнения. Причина заключается
в том, что эти значения С были определены только после того, как
были выполнены условия на скачке.
Примечательным, но отнюдь не неожиданным является следую-
следующее явление: в плоском случае при неограниченном увеличении у

Таблица 2
Значения функции /(?) и ее про-
производной для осесимметричного
течения выше и ниже по течению
относительно скачка уплотнения
Таблица 3
Значения функции /(?) и ее
производной для плоского течения
выше и ниже по течению
относительно скачка уплотнения
с
— 2,4
— 2,2
— 2,0
— 1,8
— 1,6
14
—1?
— 1,0
— 0,8
— 0,6
— 0,4
-0,2
0
0,2
0,4
0,6
0,8
1,0
1.2
1,4
1,6
1,8
2,0
2,2
2,24
Г
—1,261
— 1,314
—1,373
—1,439
— 1,514
—1,588
—1,693
—1,797
— 1,911
— 2,033
— 2,159
— 2,283
— 2,401
— 2,505
— 2,587
— 2,639
— 2,650
— 2,613
— 2,517
— 2,352
— 2,109
—1,777
— 1,346
— 0,849
— 0,712
Скачок уплотнения
2,24
2,274
2,366
2,554
2,774
3,113
3,795
— 0,712
— 0,710
— 0,691
— 0,669
— 0,641
— 0,605
— 0,547
V
— 0,2493
— 0,2785
— 0,3126
— 0,3519
— 0,3965
— 0,4457
— 0,4975
— 0,5480
— 0,5917
— 0,6218
— 0,6311
— 0,6128
— 0,5612
— 0,4715
— 0,3403
— 0,1648
0,0570
0,3265
0,6451
1,016
1,435
1,906
2,428
3,001
3,119
0,1528
0,1516
0,1390
0,1253
0,1099
0,0916
0,0615
с
— 3,4
-3,2
— 3,0
— 2,8
— 2,6
— 2,4
— 2,2
— 2,0
— 1,8
— 1,6
— 1,4
-1,2
— 1,0
— 0,8
— 0,6
— 0,4
— 0,2
0
0,2
0,4
0,6
0,8
1,0
1,2
1,4
1,6
1,8
2,0
2,03
f
5,531
5,373
5,211
5,044
4,873
4,696
4,515
4,328
4,136
3,939
3,736
3,529
3,319
3,108
2,899
2,697
2,507
2,336
2,194
2,091
2,038
2,048
2,133
2,308
2,587
2,958
3,516
4,196
4,208
Скачок уплотнения
2,03
3,167
4,749
4,208
5,504
6,802
Г
— 0,7801
— 0,8002
— 0,8216
— 0,8442
— 0,8681
— 0,8933
— 0,9195
— 0,9465
— 0,9736
— 0,9999
— 1,0238
—1,0430
— 1,0540
—1,0524
—1,0322
— 0,9866
— 0,9079
— 0,7886
— 0,6214
— 0,3999
— 0,1886
0,2269
0,6400
1,122
1,678
2,308
3,013
3,795
3,807
1,361
0,933
0,732

388
ГЛ XI ОСЕСИММЕТРИЧНЫЕ ТЕЧЕНИЯ
деформация линий тока не стремится к нулю, в осесимметричном же
случае она, наоборот, стремится к нулю.
Укажем еще на одно применение приведенных соображений.
Если тело обтекается с большой дозвуковой скоростью, то возни-
возникает местная сверхзвуковая зона, часто заканчивающаяся скачком
звуковая
линия
сверхзвуковая
область
точка слияния
скачка уплотнения
и звуковой линии '
юзвуковая
область
характери-
характеристика
скачок
уплотнения
Сверхзвуковая
область
скачок
уплотнения.
Рис. 120 Гипотетическая кар-
картина слияния скачка уплотнения
и звуковой линии. Решение такого
вида не удается найти.
Рис. 121. Возможная картина поведения
скачка уплотнения вблизи звуковой линии.
Скачок уплотнения начинается в сверх-
сверхзвуковой области в результате слияния
волн уплотнения. Попытка подыскать по-
подобного рода пример, допускающий ана-
аналитический расчет, до сих пор не пред-
предпринималась.
уплотнения. Можно предполагать, что этот скачок начинается на
звуковой линии, в связи с чем возникает вопрос: можно ли приме-
применять решения указанного здесь вида к окрестности точки, в кото-
которой начинается скачок уплотнения (рис. 120)? Единственным допу-
допущением, лежащим в основе этих решений, является следующее:
в окрестности точки звуковой линии, в которой начинается скачок
уплотнения, потенциал изменяется — при перемещении вдоль некото-
некоторой обобщенной параболы — в первом приближении пропорционально
некоторой степени расстояния от только что указанной точки.
Исследование, выполненное Вальтером Людвигом путем построения
годографа, показало, что на поставленный вопрос следует ответить
отрицательно 1). По-видимому, поле течения в окрестности подоб-
подобного рода точки значительно сложнее. Возможная структура этой
части поля течения показана на рис. 121. Конечно, было бы жела-
желательно выполнить аналитическое исследование какого-нибудь под-
подходящего примера2).
х) Поскольку результат получился отрицательным, работа Людвига не
была опубликована.
2) По этому вопросу см. работы Ф. И. Франкля {Прикл. матем. и мех ,
т. 19, вып. 4, 1955 и т. 21, вып. 1, 1957) и И. Бийбосунова {Прикл. матем.
и мех., т. 22, вып., 3,1958) —Прим. ред

§6. ОПИСАНИЕ ПОЛЕЙ ТЕЧЕНИЯ ПРИ Мт, БЛИЗКОМ К ЕДИНИЦЕ 389
§ 6. Описание полей течения при М^,
близком к единице
Результаты, изложенные в предыдущем параграфе, позволили
прийти к более точному представлению поля течения при числе
Маха, равном в бесконечности единице. Попытаемся теперь выяс-
выяснить, как развивается такое поле течения в процессе приближения
числа Маха в бесконечности к единице снизу. Далее попытаемся
получить картину перехода такого поля течения в хорошо известное
сверхзвуковое поле.
Пусть на симметричное тело набегает течение при различных
числах Маха. Если число Маха набегающего течения мало, то по-
получается чисто дозвуковое течение (при условии, что тело не имеет
выпуклых углов). При некотором более высоком числе Маха, за-
зависящем от формы тела, впервые возникает небольшая местная
сверхзвуковая зона. Большей частью она заканчивается скачком
уплотнения.
При дальнейшем увеличении числа Маха сверхзвуковая зона стано-
становится все больше и больше и в конце концов распространяется до
конца обтекаемого тела. Если сверхзвуковая зона доходит до конца
обтекаемого тела, то она обязательно заканчивается скачком уплот-
уплотнения. В самом деле, теперь волны сжатия, исходящие от звуковой
линии, бол'ьше не перехватываются поверхностью тела и поэтому
доходят до границы сверхзвуковой области. Однако этой границей
не может быть звуковая линия, так как, согласно сказанному в § 1
гл. VI, все волны, заканчивающиеся на звуковой линии, должны быть
волнами расширения. Поэтому границей сверхзвуковой области может
быть только скачок уплотнения. Правда, выпуклая поверхность тела
превращает большую часть достигающих ее волн в волны разрежения.
Однако кормовая часть тела представляет собой вогнутый угол, и
именно здесь и начинается скачок уплотнения. Если задняя кромка
обтекаемого тела заканчивается нулевым углом, т. е. если там имеется
вогнутость, то скачок уплотнения возникает не на самой задней
кромке, а вблизи нее.
Такой скачок уплотнения не обязательно должен уменьшать сверх-
сверхзвуковую скорость до дозвуковой. При своем дальнейшем распро-
распространении он соединяется с волнами уплотнения, проходящими в следе
позади тела, а затем сливается со скачком уплотнения, замыкающим
сверхзвуковую зону.
Когда дозвуковое число Маха набегающего течения приближается
к единице, скачок уплотнения, замыкающий сверхзвуковую область,
отодвигается все дальше и дальше вниз по течению. Скачок уплот-
уплотнения, сходящий с задней кромки, в сочетании с волнами сжатия,
проходящими через след позади тела, принимает на большом рас-
расстоянии от тела форму, рассчитанную в предыдущем параграфе.
26 Зак. 534 К Г. Гудерлей

390
ГЛ. XI. ОСЕСИММЕТРИЧНЫЕ ТЕЧЕНИЯ
На еще большем расстоянии этот
няется от этой формы, а затем
замыкающим сверхзвуковую зону
скачок уплотнения сначала откло-
отклосливается со скачком уплотнения,
(рис. 122).
дозвуковая
область
звуковая
линия
волны I ! I///\
разрежения ] j 11 '
скачки
'уплотнения
Рис. 122. Структура поля течения при
большой дозвуковой скорости (по Беришу
и Гудерлею).
дозвуковая
Область
I II
4
lii//,
Ш
скачок
уплотнения
сверхзвуковая область,
скорость очень близка
к критической, волны
сжатия малой плот-
плотности
Рис 123. Общая структура поля течения
при чисче Маха, равном единице (по Беришу
и Гудерлею).
.11 ,Ч'
'/ ' / / /А скачок
уплотнения
волны
'разрежения
сверхзвуковая область,
состояние в которой
мало отличается от
состояния в набегающем
течении
Рис. 124. Структура сверхзвукового течения
около профиля (по Беришу н Гудерлею).
Так как, согласно расчетам предыдущего параграфа, после
скачка уплотнения получаются скорости, очень близкие к критиче-
критической скорости, особенно в осесимметричном случае, то можно пред-
предполагать, что скачок уплотнения, замыкающий сверхзвуковую область

5 6. ОПИСАНИЕ ПОЛЕЙ ТЕЧЕНИЯ ПРИ М^, БЛИЗКОМ К ЕДИНИЦЕ 391
позади тела, очень слабый. Следовательно, надо думать, что обрат-
обратный переход к дозвуковым скоростям осуществляется всегда по-
посредством скачка уплотнения, сходящего с задней кромки тела.
Так как дозвуковое поле, образующееся ниже по течению отно-
относительно обтекаемого тела, связано с дозвуковым полем впереди
тела, то оба эти поля влияют друг на друга. Исследование действи-
действительного течения с дозвуковым числом Маха должно было бы
учитывать влияние скачка уплотнения, замыкающего сверхзвуковое
поле, на все дозвуковое поле. Такого рода учет представляет собой
в высшей степени трудную задачу. Попытка решения этой задачи
была сделана Йосихарой [3] (см. лит. 1).
Структура поля течения при числе Маха, равном в бесконеч-
бесконечности единице, изображена на рис. 123.
Если число Маха набегающего течения немного больше еди-
единицы, то скачок уплотнения возникает на значительном расстоянии
впереди тела. Звуковая линия, начинающаяся на теле, заканчивается
на скачке уплотнения. Те из волн уплотнения, которые, начинаясь
на звуковой линии, проходят через след позади тела, соединяются
с волнами, исходящими из задней кромки тела, и образуют скачок
уплотнения. С этим скачком уплотнения мы уже познакомились
в предыдущем параграфе. Отклонение от поля течения, рассмотрен-
рассмотренного в предыдущем параграфе, начинается вблизи места соединения
этого скачка со скачком уплотнения, возникшим перед телом
(рис. 124). При больших числах Маха скачок уплотнения, образую-
образующийся впереди тела, все более и более приближается к его перед-
передней кромке. Все меньшее и меньшее количество волн разрежения
достигает звуковой линии и соответственно этому от звуковой линии
исходит все меньшее и меньшее количество волн уплотнения. При
всех сверхзвуковых скоростях часть поля течения, расположенная
позади тела, не оказывает никакого влияния на распределение давле-
давления на теле.
скачок
л уплотнения/
характеристика/
сверхзвуковое
течение
дозвуковая область
Рис. 125. К определению распределения
давления на кормовой части профиля при на-
наличии неприлегающего скачка уплотнения.
Будем перемещаться в поле течения с большим сверхзвуковым
числом Маха вдоль характеристики (например, ABC на рис. 125),
26*

392 ГЛ. XI ОСЕСИММЕТРИЧНЫЕ ТЕЧЕНИЯ
начинающейся в сверхзвуковой области впереди скачка уплотнения
и достигающей, после пересечения со скачком уплотнения, профиля.
В плоскости годографа этому перемещению соответствует с хоро-
хорошим приближением перемещение вдоль характеристики. В самом
деле, разрыву вектора скорости, возникающему при переходе через
скачок уплотнения, в плоскости годографа соответствует с хорошим
приближением разрыв вдоль характеристики. Отсюда следует, что
в плоском течении давление в точках профиля, достигаемых харак-
характеристиками этого вида, такое же, как в чисто сверхзвуковом поле.
С увеличением числа Маха набегающего течения такое распределе-
распределение давления, начавшись на задней кромке тела, распространяется
на все большую часть профиля.

ЛИТЕРАТУРА
1. Цитированные работы
Страницы в квадратных скобках в конце работы указывают те места
книги, в которых рассматриваемая работа упоминается.
В а г i s h David Т. and Gottfried Q u d e r I e у, Asymptotic Forms of Shock
Waves in Flows over Symmetrical Bodies at Mach one, Journal of the
Aeronautical Sciences, 1953, p. 491 [стр. 381, 382, 384, 386, 390].
Busemann Adolf [1], Hodographenmethode der Oasdynamik, Z. angew.
Math. Mech., Bd. 17 A937), S. 73 [стр. 99].
— [2], статья Gasdynamik в Wiens-Harms, Handbuch der Experimental-
physik, Bd. 4, I Teil, Leipzig, 1931 [стр. 26, 27].
— [3], Theory of the Propeller in Compressible Flow, Proceedings of the
Third Midwestern Conference on Fluid Mechanics, The University of
Minnesota, 1953 [стр. 84].
Busemann Adolf u. K. Gottfried G u d e r 1 e y, The Problem of Drag at
High Subsonic Speeds, British Ministry of Aircraft Production, Volkenrode
Rep and Translations № 184 (March 1947) [стр. 172, 360].
Bergmann Stefan, The Kernel Function and Conformal Mapping, American
Mathematical Society, 1950 [стр. 332].
Chang Chien-Chien and Vivian O'B r i e n, Some Exact Solutions of Two-
Dimensional Flows of Compressible Fluid with Hodograph Method, NACA
Tech. Note 2885 A953) [стр. 116].
Христианович С. А., Обтекание тел газом при больших дозвуковых
скоростях, Труды ЦАГИ, вып. 481 A940).
Cole Julian D. [1], Transonic Limits of Linearized Theory, Guggenheim
Aeronautical Laboratory, California Institute of Ttchnology, Office of
Scientific Research, Technical Note 228 A954) [стр. 86, 87].
— [2], Acceleration of Slender Bodies of Revolution through Sonic Velocity,
Guggenheim Aeronautical Laboratory, California Institute of Technology,
Office of Scientific Research, Technical Note 5—55 A954) [стр. 83, 87].
Croc с о Luigi, Singolarita della corrente gassosa iperacustica nell'intorno di
una prora a diedro, Aerotechnica, 17 A937), p. 519 [стр. 146, 164, 166].
Computation Laboratory, National Applied Mathematics Laboratories, National
Bureau of Standards, Tables of Besselfunctions of Fractional Order, Vol I
and II, New York, Columbia University Press, 1948, 1949 [стр. 123, 190, 213].
Eggink H., Uber VerdichtungsstoBe bei abgeloster Stromung, Forschungs-
bericht, 1850 [стр. 178].
Ф а л ь к о в и ч С. В., Об одном классе сопел Лаваля, Прикл. машем, и мех.,
т. 11 A947), стр. 223 [стр. 246 и далее].

394 ЛИТЕРАТУРА
Франк ль Ф. И. [1], О влиянии ускорения на сопротивление при дви-
движении продолговатых тел вращения в газах, Прикл. матем и мех.,
т. 10 A946), стр. 521 [стр. 81, 83].
— [2], К образованию скачков уплотнения в дозвуковых течениях с ме-
местными сверхзвуковыми скоростями, Прикл матем и мех., т. 11 A947),
стр. 19Э [стр 360].
— [3], Асимптотическое разложение функций Чаплыгина, Докл. АН
СССР, т 58 A947), стр. 661 [стр. 124].
— [4], Истечение сверхзвуковой струи из сосуда с плоскими стенками,
Докл. АН. СССР, т. 58 A947), № 3 [стр. 155]
— [5], Исследования по теории крыла бесконечного размаха, движуще-
движущегося со скоростью звука, Докл. АН СССР, т. 57 A947), стр. 661
[стр. 258].
— [6], О задачах С. А. Чаплыгина для смешанных до-и сверхзвуковых
течений, Изв. АН СССР, сер. матем., т. 9 A945) [стр. 5, 144,145, 147, 155J-
Friedrichs К. О., On the Non-Occurrence of a Limiting Line in transonic
flow, Communications of Applied Mathematics A948), p. 287; Applied
Mechanics Review A950), Review 753.
Gardner C. S and H. F. L u d 1 о f f, Influence of Accelerations on Aero-
Aerodynamic Characteristics of Thin Airfoils in Supersonic and Transonic
Flight, Journal of the Aeronautical Sciences, Vol. 17 A950), p. 47;
русский перевод: Гарднер К., Люд лов Г., Влияние ускорения на
аэродинамические характеристики тонких профилей в сверхзвуковом
и трансзвуковом потоке, сб. Механика, № 1 A951), стр. 31—34 [стр. 84
и далее].
Oortler H., Zum Ubergang von Unterschall- zu Oberschallgeschwindigkeiten
in Diisen, Z. angew. Math. Mech., Bd. 19 A939), S. 325 [стр. 93].
Graham E. W., Solution of a Non-Linear Equation for Transonic Flow with
Rotational Symmetry, Douglas Aircraft CO SM-13677 A949) [стр. 96]
Ouderley K. Gottfried [1], On the Transition from a Transonic Potential
Flow to a Flow with Shocks, Tech. Report F-TR-2160 ND, Head
Quarters Air Materiel Command, Wright Field, Dayton, Ohio, ATI
№ 22—278 A947) [стр. 41, 45, 150, 171, 188, 360].
—^[2], Considerations on the Structure of Mixed Subsonic-Supersonic Flow
Patterns, Tech. Repor; F-TR-2168-ND, Head Quarters Air Materiel
Command, Wright Field, Dayton, Ohio A947) [стр. 145, 146, 149, 155,
156, 160, 161, 167, 169, 178—180, 182—188, 263, 296].
— [3], Singularities at the Sonic Velocity, Tech. Report F-TR-1171-ND,
Head Quarters Air Materiel Command, Wright Patterson Air Force Base,
Dayton, Ohio [стр. 159, 192, 220, 258, 265, 266, 344, 348, 351]
— [4], Axial Symmetric Flow Patterns at a Free Stream Mach Number
close to one, US Air Force Tech. Report № 6285 (October 1950) [стр. 371
и далее].
— [5], Two-Dimensional Flow Patterns with a Free Stream Mach Number
Close to one, US Air Force Tech. Report № 6346 (May 1951) [стр. 144,
224, 305, 306, 353, 354, 356, 359, 361, 378].

ЛИТЕРАТУРА 395
Quderley К. Gottfried [6], A Formula for the Normalization Constant in
Eigen Value Problems, Quarterly of Applied Mathematics, Vol X A952),
p. 176 [стр. 224].
— [7], On Wind-Tunnel Corrections in the Lower Transonic Range, Wright
Air Development Center Tech. Report № 53—506 A953) [стр. 61, 339].
— [8], On Transonic Simplifications of the Hodograph Equation, Wright Air
Development Center, Tech. Report № 53—183 A953) [стр. 123].
— [9], Two-Dimensional Bodies at Slightly Supersonic Mach Numbers, Wright
Air Development Center, Tech. Report № 53—454 A953) [стр. 332,
333].
— [10], On the Presence of Shocks in Mixed Subsonic-Supersonic Regions.
Advances in Applied Mechanics, Vol. Ill, New York, Academic Press
Inc. Publishers, 1953; русский перевод: Гудерлей Г., О необходи-
необходимости существования скачков уплотнения в смешанных потоках,
сб. Проблемы механики, Издатинлит A955), стр. 455—488 [стр. 360].
— [И], The Wall Pressure Distribution in a Choked Tunnel, Wright Air
Development Center, Tech. Report № 53—509 A953) [стр. 329, 331].
— [12], The Flow over a Flat Plate with a Small Angle of Attack, Journal
of the Aeronautical Sciences A954), p. 261 [стр. 288, 291].
— [13], The Flat Plate with an Angle of Attack in a Choked Wind Tunnel,
Journal of the Aeronautical Sciences, vol. 22 A955), p. 844 [стр 291,
301, 333, 338].
— [14], On the Development of Solutions of Tricomi's Equation in the
Vicinity of the Origin, Journal of Rational Mechanics and Analysis,
Vol. 5 A956), p. 747 ff. [стр. 235, 243].
— [15], On Transonic Air Foil Theory, Journal of the Aeronautical Scien-
Sciences, Vol. 23 A956), p. 961 [стр. 342].
— [16], Asymptotische Darstellungen fur die Partikularlosungen der Hodo-
graphengleichung, Ministry of Supply 3 E/244 T [стр 124].
— [17], Riickkehrkanten in ebener kompressibler Potentialstromung, Z. an-
gew. Math. Mech., Bd. 22 A942), S. 121 ff [стр. 113].
— [18], Storungen in ebenen und achsensymmetrischen Schall- und Ober-
schallparallelestrahlen, Z. angew Math Mech., Bd. 25/27 A947), S. 190 ff.
[стр. 93].
О u d e r 1 e у К. Gottfried and Hideo Yoshihara [1], The Flow over a Wedge
Profile at Mach Number one, Journal of the Aeronautical Sciences
A950), p. 723; русский перевод: Гудерлей Г., Йосихара X.
Обтекание клинообразного профиля при числе М, равном единице,
сб. Механика, № 3 A951), стр. 7—28 [стр 269, 270].
— [2], An Axial-Symmetric Transonic Flow Pattern, Quarterly of Applied
Mathematics, Vol. VIII, № 4 (Jan 1951) [стр. 363, 365, 369, 370,
377].
— [3], Two-dimensional Unsymmetric Flow Patterns at Mach Number One,
Journ. of the Aeronautical Sciences, Vol. 20 A953), p. 757 [стр. 274, 276,
277,281].
H a m e 1 Georg, Integralgleichungen, 2 Aufl., Berlin, Springer, 1949 [стр. 225].

396 ЛИТЕРАТУРА
Hantzsche W. u. H. W e n d t, Mit Oberschall angeblasene Kegelspitzen,
Jahrbuch der Deutschen Luftfahrtforschung, 1942, nach NACA Tech.
Memorandum № 1157 A947) [стр. 50].
Heaslet Max A., Harvard Lorn ax and John R. S p r e i t e r, Linearized
Compressible Flow Theory for Sonic Flight Speeds, NACA Rep. 956
A950) [стр. 72].
H u с к e 1 Vera, Tables of Hypergeometric Functions for Use in Compressible
Flow Theory, NACA Tech. Note 1716 A948) [стр. 116].
I m a i Isao, Application of the WKB-rnethod to the Flow of a Compressible
Fluid I, II, Journal for Mathematics and Physics, 1949, p. 173; 1950
p. 205 [стр. 124].
Jones Robert Т., Properties of Low Aspect Ratio Pointed Wings at Speeds
below and above the Speed of Sound, NACA Rep. 835 A946) [стр. 72].
Jacobs Willi, Geschwindigkeitsverteilungen in zwei-dimensionalen gekrumm-
ten Laval-Dusen, Jahrbuch der Wissenschaftlichen Gesellschaft fur Luft-
fahrt (WQL), Braunschweig, Vieweg 1954 [стр. 911.
Jahnke u. Emde, TafeJn hoherer Funktionen, Stuugait, B. O. Teubner;
русский перевод: Янке Е. и Эмде Ф., Таблицы функций с фор-
формулами и кривыми, изд. 3., Физматгиз, 1959 [стр. 189].
К а г m a n Theodore, The Similarity Law of Transonic Flow, J. Math. Phys.
Vol. XXVI A947), p. 182; русский перевод: Карман Т., Закон подо-
подобия для трансзвукового потока, сб. Газовая динамика, Издатинлит,
1950 [стр. 41].
Keune Friedrich [1], Low Aspect Ratio Wings with Small Thickness at Zero
Lift in Subsonic and Supersonic Flow, Royal Institute of Technology,
Stockholm, Schweden KTH Aero TN 21 [стр. 76].
— [2], The Influence of Camber and Geometrical Twist on Low Aspect
Ratio Wings of Finite Thickness in Subsonic Transonic and Supersonic
Flow, Royal Institute of Technology, Stockholm, Schweden KTH Aero
TN 29 [стр. 76].
L i g e r Marc, Nouvelles Equations approchees pour l'Etude des ecoulements
subsoniques et transsoniques, Offices National d'Etudes et de Recherches
Aeronautiques, Publ. 64 A953) [стр. 271].
Light hill M. J., The Hodograph Transformation in Transonic Flow, Parts
I _ Ш, proc_ p>oy, Soc, Lond., Ser. A, Vol. 191, № 1026 A947), p. 323
[стр. 118].
L anger R. E., On Asymptotic Solutions of Ordinary Differential Equations
with an Application to Bessel Functions of Large Order, Trans. Amer.
Math. Soc. A931), p. 23 [стр. 124].
Marschner Bernhardt W., The Flow over a Body in a Closed Wind Tunnel
and in a Sonic Free Jet, Journal of the Aeronautical Sciences, 23 A956),
p. 368 [стр. 268, 270, 324 и далее].
Meyer Th., Диссертация, Gottingen, 1908 [стр.88].
Molenbroek P., Ober einige Bewegungen eines Gases mit Annahme eine1
Geschwindigkeitspotentials, Arch. Math.Phys.,9(\&90), S. 157 [стр.98,116]

ЛИТЕРАТУРА 397
Мог a we tz Cathleen S. [1], On the Non-Existence of Continuous Transonic
Flows Past Profiles I, Communications on Pure and Applied Mathe-
Mathematics, Vol. 9 (February 1956) [стр. 151, 360]
— [2], A Uniqueness Theorem for the Frank! Problem, Comm. Pure
Applied Mathematics, Vol. -1 A954), S. 691 ff. (New York University)
[стр. 144].
Mangier K. W., Calculation of the Pressure Distribution over a Wing at
Sonic Speed, RAE-Report № 2439 A951); Aero Research Council, London,
Rep. Mem. 2888 A955) [стр. 72].
Никольский А. А. и Таганов Г. И., Движение газа в местной сверх-
сверхзвуковой зоне и некоторые условия разрушения потенциального тече-
течения, Прикл. матем. и мех., т. 10 A946), стр. 481 [стр. 153].
Oswatitsch К. [1], Zur Ableitung des Croccoschen Wirbelsatzes, Luftfahrt-
forschung, Bd. 20, S. 260 [стр. 16].
— [2], Die Oeschwindigkeitsverteilung bei lokalen Uberschallgebieten an
flachen Profilen, Z. angew. Math. Mech., Bd. 30 A950), S. 17; русский
перевод: О с в а т и ч К., Распределение скоростей на тонких профилях
при наличии местных сверхзвуковых зон, сб. Механика, № 2 A951),
стр. 18—27 [стр. 59].
Oswatitsch К. u. S. В. Berndt, Aerodynamic Similarity of Axisymmetric
Transonic Flow around Slender Bodies, Stockholm, Royal Institute Techn.
1950 (KTH Aero TN 15) [стр. 55].
Oswatitsch К. и. F. Keune, Ein Aquivalenzsatz fur nichtangestellte
Flugel kleiner Spannweite in schallnaher Stromung, KTH Aero Report 155
A954); Z. Flugwissenschaften, III A954) S. 29 ff. [стр. 73, 76].
Spreiter John R., On alternative Forms for the Basic Equations of Transonic
Flow Theory, Journ. Aero. Sciences, Vol. 20 A954), S. 360 [стр. 58, 340].
Seifert Herbert, Zur asymptotischen Integration von Differentialgleichungen,
Math. Z., Bd. 48 A942), S. 173 [стр. 121].
Toll mien W. [1], Zum Obergang von Unterschall- in Oberschallstromungen,
Z. angew. Math. Mech., Bd. 17 A937), S. 117 [стр. 105].
— [2], Orenzlinien adiabatischer Potentialstromungen, Z. angew. Math.
Mech., Bd. 21 A941), S. 140 [стр. 140].
Tomotika S. and К. Т a m a d a, Studies on Two-Dimensional Transonic
Flows of Compressible Fluids, Parts I, II, III, Quarterly of Applied Ma-
Mathematics A950), p. 127, p. 381; A951), p. 129; русский перевод: Тою-
тика С, Тамада К., Двумерное смешанное течение сжимаемой
идеальной жидкости, ч. I, II, III, сб. Механика, № 4 A951), стр. 31—43;.
№ 6 A951), стр. 31—38; № 2 A952), стр. 31—45 [стр. 88, 245].
Чаплыгин С. А., О газовых струях, Москва, 1902, или в Собрании сочи-
сочинений, т. II, Москва, 1948, а также в Избранных трудах по механике
и математике, Москва, 1954 [стр. 116, 118].
Temple О., The Method of Characteristics in Supersonic Flow, ARC Reports
and Memoranda 2091 A944) [стр. 26].
Tricomi F., Sulle equazioni lineari alle derivate parziali di 2° ordine di tipo
misto, Atti delta R. Academla Nazlonale del Lincel, 1923, Serie Quinta

398 ЛИТЕРАТУРА
della Classe di Science Fisiche, Matematiche e Naturali, Vol XIV, p 134
[стр. 125, 141]
Vincenti Walter O. and Cleo B. Wagoner [1], Transonic Flow past
a Wedge Profile with Detached Bow Wave, NACA Rep. 1095 A952)
|стр. 339 и далее]
— [2], Theoretical Study of Transonic Lift of a Double Wedge Profile with
Detached Bow Wave, NACA Rep. 1180 A954) [стр. 282, 339 и далее]
Vincenti Walter О., Cleo В. Wagoner and Newman H. Fisher, Jr.,
Calculations of the Flow over an Inclined Plate at Free-Stream Mach
Number 1, NACA TN 3723 [стр. 126, 342].
Weise A, Theorie des gegabelten VerdichtungsstoBes, Technische Berichte,
Bd. 10 A943), № 12 [стр. 178]
Withcomb Richard T. [1], A Study of the Zero Lift Drag Rise Characteris-
Characteristics of Wing Body Combinations near the Speed of Sound, NACA
RM-L 52 HO 8 A952) [стр. 76].
— [2], Zero Lift Characteristics of Wing-Body Combinations at Transonic
Speeds, Aeronautical Engineering Review (Institute of the Aeronautical
Sciences) 1956 [стр. 76].
Yoshihara Hideo [1], On the Flow over a Wedge in the Upper Transonic
Region, Proceedings of the second National Congress of Applied Mecha-
Mechanics, Ann-i Arbor, Mich., 1954, Published by the American Society of
Mechanical Engineers [стр. 282, 341, 342]
— [2], The Flow over a Cone Cylinder Body at Mach Number One, Wright
Air Development Center, Tech. Report № 52-295 and Third Midwestern
Conference on Fluid Mechanics, University of Minnesota, 1953 [стр 371]
— [3], On the Flow over a Finite Wedge in the Lower Transonic Region,
Wright Air Development Center, Tech. Report 56-268 and Proceedings
of the International Conference in Applied Mathematics, Brussels, 1956
[стр. 159, 342, 391].
2. Учебники
Sauer Robert, Einfiihrung in die thearetische Gisiynam k, 2 Aufi , Berlin,
Springer, 1952, первое издание имеется в русском переводе: 3 а у э р Р.,
Введение в газовую динамику, Москва, 1947.
Oswatitsch Klaus, Qasdynamik, Wien, Springer, 1952.
Liepmann Hans Wolfgang and Allen E Puckett, Introduction to Aero-
Aerodynamics of Compressible Fluid, John Wiley and Sons Inc; 1947; русский
перевод: Липман Г. и Пакет А., Введение в аэродинамику сжи-
сжимаемой жидкости, Москва, 1949.
Sliapiro A H., The Dynamics and Thermodynamics of Compressible Fluid
Flow, Vol. I and II, New York, The Ronald Press, 1953.
Sears W. R. (Editor), General Theory of High Speed Aerodynamics and Jet
Propulsion, Vol. VI, Princeton University Press, 1954; готовится к печати
русский перевод.
Karman Th. and M. В i о t, Mathematical Methods in Engineering
McGraw Hill Book Company, Inc; русский перевод: Карман Т и
Био М., Математические методы в инженерном деле, Москва, 1948.

ЛИТЕРАТУРА 399
С о u r a n t R. u. D. H i 1 b e r t, Methoden der Mathematischen Physik, I und II,
2 Aufl., Berlin, Springer, 1931; русский перевод: Курант Р. и Гиль-
Гильберт Д., Методы математической физики, т. I и II, Москва, 1951.
W h i 11 a k e r E. T. and O. N. Watson, A Course of Modern Analysis, New
York, The McMillan Company; русский перевод: Уиттекер Э. Т.
и Ватсон Г. Н., Курс современного анализа, т. I и II, Москва,
1933 и 1934
Copson E. Т., An Introduction to the Theory of a Complex Variable, Oxford
University Press.
3. Другие работы
Agmon S, Nirenberg and M. H. P г о 11 e r, A Maximum Principle for
a Class of Hyperbolic Equations and Applications to Equations of Mixed
Elliptic-Hyperbolic Type, Communications of Pure and Applied Math
(Nov. 1953), New York University.
Baranoff Alexis, Sur la resistance d'un corps de revolution effile en mou-
vement accelere ou decelere, Comptes Rendues des Seances de VAcade-
mie des Sciences, t. 240 (fevrier 1955).
Barish David Т., Interim Report on a Study of Mach one Wind Tunnels,
Wright Air Development Center, Tech. Report № 52—88 A952)
Bergdolt V. E, Airflow about Cone-Cylinders with Curved Shock Waves,
Journal of the Aeronautical Sciences A953), pp. 751.
Bers Lipman, Results and Conjectures in the Mathematical Theory of Subsonic
and Transonic Qas Flows, Communications on Pure and Applied Mathe-
Mathematics, Vol. VII, № 1 (February 1954), New York University.
Bergman Stefan, Two-dimensional Subsonic Flows of a Compressible Fluid
and their Singularities, Trans. Amer. Math. Soc, 62 A947), pp. 452.
Berndt S В., Similarity Laws for Transonic Flow about Wings of Finite
Aspect Ratio, Stockholm, Schweden Royal Institute of Technology, 1950
(KTH Aero TN 14)
Bryson Arthur and Earl J u n, An Experimental Investigation of Transonic
Flow past Two-Dimensional Wedge and Circular Arc Sections Using
a Mach — Zehnder Interferometer, NACA Rep. 1094 A952).
Busemann Adolf [1],A Review of Analytical Methods for the Treatment of
Flows with Detached Shocks, NACA TN 1858 A949)
— [2], The Drag Problem at High Subsonic Speeds, Journ. Aero. Sciences,
Vol. 16 A949), p. 337.
— [3], Application of Transonic Similarity, NACA TN 2687 A952).
— [4], The Non-Existence of Transonic Potential Flow, „Fluid Mechanics"
Proc. Symp. Applied Math , Vol. IV, New York, McOraw Hill Book Co,
Inc. A953), p. 29.
В i о t M A., Transonic Drag of an Accelerated Body, Quarterly Appl. Math.,
7 A949), p. 101 ff.
Cabannes Henri [1], Determination Theoriques de PEcoulement d'un Fluide
derriere une Onde de Choc Detachee, Note Techn. № 5 A951), Office
National d'Etudes et de Recherches Aeronautiques.

400 ЛИТЕРАТУРА
— [2], Contributions to the Theory of Compressible Fluids, Transonic Flow,.
Shock Waves, Ann. Sci. Ecole Norm. Sup., 9 (Jan. March 1952).
Carrier Q. F. and F. E. E h 1 e r s, On some Singularities of the Tricomi
Equation, Quarterly of Applied Math., 6 A948), p. 331.
Chang Chien-Chien, General Considerations of Problems in Compressible
Flow Using the Hodograph Method, NACA TN 2582 A952).
Chang С. С and В. Т. С h и, Linearized Theory of Subsonic, Transonic and
Supersonic Flow with Assigned Velocity Gradient, July 1951, The John
Hopkins University, Department of Aeronautics.
Cherry Т. М. [1], Uniform Asymptotic Formulae for Functions with Tran-
Transition Point, Trans. Amer. Math. Soc, Vol. 68 (March 1950), p. 224.
— [2], Flow of a Compressiblei.Fluid about a Cylinder, Part I, Proc. Roy
Soc, London, Ser. A, Vol. 192 A947), p. 45; Part II, там же, Vol. 196
A949), p. 1.
Clauser M. U. and F. H. Clanser, New Methods of Solving the Equa-
Equation for the Flow of Compressible Fluids, Doctorate Thesis, Cal. Institute
of Technology, 1937.
Cole Julian D., Drag of a Finite Wedge at High Subsonic Speeds, /. Math.
Phys., Vol. XXX A951), p. 79; русский перевод: Коул Дж. Д.,
Сопротивление конечного клина при больших дозвуковых скоростях,
сб. Механика, № 4 A952), стр. 7—19.
Cole J. D., G. E. Solomon and W. W. W i 11 m a r t h, Transonic Flow
past Simple Bodies, Journ. Aero. Sciences A953)," p. 627; русский пере-
перевод: Коул Дж., Соломон Г., Уилмарс У., Обтекание около-
околозвуковым потоком простейших тел, сб. Механика, № 6 A954),
стр. 56—68.
Craggs J. W, The Breakdown of the Hodograph Transformation for Irrota-
tional Compressible Fluid Flow in two Dimensions, Proc. Cam. phil.
Soc, Vol. 44 A948), p. 360 ff.
Demtschenko В., Sur la relation entre la dynamique des fluides compres-
sibles et celle des fluides incompressible, Publ. Math. Univ. Belgrade,
Bd. 2 A933), p. 85.
Diaz J. B. and G. S. S. Ludford [1], A Transonic Approximation, Univer-
University of Maryland, Institute for Fluid Dynamics and Applied Mathematics,
TN BN-24.
— [2], On two Methods of Generating Solutions of Linear Partial Differen-
Differential Equations by Means of Definite Integrals, University of Maryland,
Institute for Fluid Dynamics and Applied Mathematics, TN BN-26
Drougge G., The Flow around Conical Tips in the Upper Transonic Region,
The Aeronautical Research Institute of Sweden, Report № 25, Stockholm-
Ulvsunda.
E h 1 e r s F. Edward, On some Solutions of the Hodograph Equation which
yield Transonic Flow through a Laval Nozzle, Journal of the Aeronau-
Aeronautical Sciences, 22 A955), № 2.
Фалькович С. В., К теории сопла Лаваля, Прикл машем и мех., т. 10»
A946), стр. 503.

ЛИТЕРАТУРА 401
•Франкль Ф. И. [1], К теории сопел Лаваля, Изв. АН СССР, сер. матем.,
т. 9 A945).
— [2], Об одном семействе частных решений уравнений Дарбу —
Трикоми и его применение к приближенному нахождению кри-
критического течения в заданном сопле Лаваля, Докл. АН СССР, т. 56
A947), стр. 683.
Fischbach Joseph W., Computation of the Transonic Flow over a Wedge
with Detached Shock Wave by the Method of Steepest Descent, Ballistic
Research Laboratory Aberdeen Proving Ground Maryland BRLM 642
(Jan. 1953).
•Garrick I. E. and Carl Kaplan, On the Flow of a Compressible Fluid by
the Hodograph Method, Fundamental Set of Particular Flow Solutions
of the Chapligin Differential Equation, NACA Rep. 790 A944).
Qermain P. et R. Bader [1], Solutions elementaires de certaines Equations
aux derivees partielles du type mixte, Bull. Soc. Math. France,
1953.
— [2], Sur le^probleme de Tricomi, Rend. Clrc. Palermo (II), 2, 1 A953).
— [3], Sur quelques problemes relatifs a l'equation de type mixte de Tricomi,
Publ. Onera № 54 A952).
•Germain P. [1], Remarks on the Theory of Partial Differential Equations of
Mixed Type and Applications to the Study of Transonic Flow, Commu-
Communications of Pure and Applied Math., Vol. VII, № 1, New York Univer-
University, 1954.
— [2], New Applications of Tricomi Solutions to Transonic Flow, Second
National Congress of Applied Mechanics, 1954.
—'[3], An Expression for the Green's Functions for a Particular Tricomi
Problem, Quarterly of Applied Math. (July 1956).
Germain P. et M. L i g e r, LJne nouvelle Approximation pour l'Etude des
EcouJements Subsoniques et Transoniques, Contptes Rendues de VAca-
demie des Sciences, 23441952), p. 1846.
Griffith Wayland, Shock Tube Sudies of Transonic Flow over Wedge
Profiles, -Journ. Aero. Sciences, Vol. 19 A952), p. 265.
Guderley K.-Gottfried [1], Theoretical Considerations concerning the Flow
Pattern in a two-dimensional Diffusor, Tech. Rep. F-TR-II 14 ND Head
Quarters Air Material Command, Wright Field, Dayton, Ohio.
— [2], New Aspects of Transonic Flow Theory, ATI Technical Data Digest,
Wright Field A Nov. 1947).
Gullstrand Tore R. [1], The Flow over Symmetrical Air Foils without Inci-
Incidence in the Lower Transonic Range, Stockholm, Royal Institute of Tech-
Technology, KTH Aero TN 20 A951).
— [2],-The Flow over Symmetrical Airfoils without Incidence at Sonic Speed,
Stockholm, Royal Institute of Technology, KTH Aero TN 24 A952).
— [3], A Theoretical Discussionpf some Properties of Transonic Flow over
Simple Two-Dimensional Air Foils at zero Lift with a Simple Method to
estimate the Flow Properties, Stockholm, Royal Institute of Technology,
KTH Aero TN 25 A952).

402 ЛИТЕРАТУРА
— [4], The Flow over Two-Dimensional Airfoils at Incidence in the Tran-
Transonic Speed Range, Stockholm, Royal Institute of Technology, KTH Aero-
TN 27 A952).
Gullstrand Tore R [5], Transonic Flow past Two-Dimensional Airfoils,
Z. Flugwissensch. A952), S. 38.
Harder Keith C, Transonic Similarity Rules for Lifting Wings, NACA TN
2724 A952).
Hilton John H., Jr., Flow Characteristics of a Lifting Wedge of Finite Aspect
Ratio with Attached and Detached Shock Waves at a Mach Number
1,40, NACA TN 2712 A952).
I m a i Isao, Extension of von Karman's Transonic Similarity Rule, /. Phys. Soc*
(Япония), 9 (Jan, Febr 1954).
Jacob Caius, Etude d'un Jet gazeux, Bulletin Sclentiflqae de Vecole poly-
technlque de Tlmlsoara (Румыния), Bd. 7 A937), H. 1 u. 2.
Johnston O. W., An Investigation of the Flow about Cones at and beyond
the Critical Angle, /. Aeron. ScL, Vol. 20 A953), p. 378 ff; русский
перевод: Джонстон Дж, Исследование обтекания конусов и клиньев
с углом, равным или большим критического, сб. Механика, № 2 A954).
Kaplan Carl [l],On Similarity Rules for Transonic Flow, NACA Rep. 894A948).
— [2], On Transonic Flow past a Wave-Shaped Wall, NACA Tech. Report,
1149 A953).
К arm an Theodore [1], Some Investigations on Transonic and Supersonic Flow,
Sixth International Congress for Applied Mechanics, 1946.
— [2], Supersonic Aerodynamics — Principles and Applications, J. Aeron.
Set., Vol. 14 A947), p. 373 ff.
Kawamura Tohru [1], Contribution of the Change of Entropy to the Directions
of Spines of Shock polar,-/. Phys. 5ос.-(Япония), Vol. 9 A954), p. 396 ff.
— [2], A Trial Calculation on the Analysis of the Flow behind a Curved
Shock with Special Reference to Chaplygin's Approximation, Institute of
Physics, Pure and Domestic Science Division, The Nara Women's Univer-
University, Nara (Япония).
KeuneF. u. Kl. Oswatitsch [1], Nichtangestellte Korper kleiner Spann-
weite in Unter- und Uberschallstromung, Z. Flugwissensch A953), S. 137.
— [2], An Integral Equation Theory for the Transonic Flow around Slender
Bodies of Revolution at zero Incidence, Stockholm, Royal Institute of
Technology (KTH Aero TN 37).
Keune Friedrich [1], On the Subsonic, Transonic and Supersonic Flow around
Low Aspect Ratio Wings with Incidence and Thickness, Stockholm, Royal
Institute of Technology (KTH Aero TN 28).
¦— [2], Bericht uber eine Theorie der Stromung um Rotationskorper ohne
Anstellung bei Mach-Zahl 1, Forschungsbericht des Wirtschafts- und Ver-
kehrsministeriums Nordrhein Westfalen № 218, Koln und Opladen: West-
deutscher Verlag.
— [3], Zusammenfassende Darstellung und Erweiterung des Aquivalenzsatzes
fur schallnahe Stromungen, Deutsche Versuchsanstalt fur Luftfahrt E V.
Bericht № 8.

ЛИТЕРАТУРА 403
Kraft Hans and Charles O. Dibble, Some Two-Dimensional Adiabatic
Compressible Flow Patterns, J. Aeron. Set., Vol. 11 A944), p. 283 ff.
Крючин А. Ф. [1], Обтекание клиновидного профиля с отсоединенной
линией сильного разрыва, Докл. АН СССР, т. 97 A954), стр. 37.
— [2], О сопротивлении ромбовидного профиля при околозвуковых ско-
скоростях, Докл. АН СССР, т. 97 ,A954), стр. 205.
L a i t о п е Е. V., A Study of Transonic Oasdynamics by the Hydraulic Analogy,
J. Aeron. Set., vol. 19 A952), p. 249 ff.
L a n d a h 1 Marten Т., The Flow around Oscillating Low Aspect Ratio Wings
at Transonic Speeds, Stockholm, Royal Institute of Technology (KTH Aero
TN 40).
Levey H. C, Exact Solutions for Transonic Flow past Cusped Air Foils, Aeron.
Research Lab. Melbourne Rep. A 87 (March 1954).
Liepmann H. W. and A. E. В г у s о n, Jr., Transonic Flow past Wedge
Sections, /. Aeron. Set, Vol. 17 A950), p. 745 ff; русский перевод:
Л и п м а н Г., Б р и с о н А., Обтекание клиновидных профилей пото-
потоком газа с околозвуковыми скоростями, сб. Механика, № 3 A951),.
стр. 29—45.
Liepmann H. W., The Interaction between Boundary Layer and Shock
Waves in Transonic Flow, /. Aeron Set, Vol. 13 (Dec 1946), русский
перевод: Липман Г. В, Взаимодействие между пограничным слоем
и ударными волнами в трансзвуковом потоке, сб Газовая динамика*
Издатинлит, 1950.
Loewner С. A., A Transformation Theory of Partial Differential Equations
of Qasdynamics, NACA TN 2065 A950).
Lorn ax Harvard and Max A. H e a s 1 e t, Linearized Lifting Surface Theory
for Swept Back Wings with Slender Plan Forms, NACA TN 1992 A949).
Mangier K. W., Calculation of the Load Distribution over a Wing with Arbi-
Arbitrary Camber and Twist at Sonic Speeds, RAE Report Aeron 2515.
Man well A. R. [1], A Note on the Hodograph Transformation, Quarterly of
Applied Math., X A952), p. 177.
— [2], A new Singularity of Transonic Plane Flows, Quarterlyof Applied
Math. (January 1955); русский перевод; Мануэля А., Новый вид
особенности в околозвуковом плоском течении, сб. Механика, № 5
A955), стр. 64—71.
Mitchell A. R. and D. E. Rutherford, Application of Relaxation
Methods to Compressible Flow past a Double Wedge, Proc. Roy. Soc
Edinburgh, Sec. A, 63, Part II A951), p. 139.
Мог a wet г С. S., Note on a Maximum Principle and a Uniqueness Theorem
for an Elliptic Hyperbolic Equation, Proc. Roy. Soc, vol. 236 A956),
p. 141 ff.
Morawetz С S. and I. I. К о 1 о d n e r, On the Non-Existence of Limiting
Lines in Transonic Flow, Comm. Pure Applied Math., 6 A953), p. 97 ff.
(New York Univ.); русский перевод: Моравец К., КолоднерИ.
Условия отсутствия предельных линий в околозвуковых течениях,,
сб. Механика, № 2 A954), стр. 14—19.

404 ЛИТЕРАТУРА
Oswatitsch К. [1], Die Geschwindigkeitsverteilung an symmetrischen Pro-
filen bei Auftreten lokaler Oberschallgebiete, Ada Physica Austriaca,
IV, 2/3 A950).
— [2], The Effect of Compressibility on the Flow around Slender Bodies
of Revolution, Stockholm, Royal Institute of Technology, KTH Aero TN
12 A950) und Arch, der Math., II, 6 A949/1950).
Oswatitsch К. и. К. Wieghardt, Theoretische Untersuchungen fiber
stationare Potentialstromungen und Qrenzschichten bei hohen Geschwin-
digkeiten, Lilienthalgesellschaft fur Luftfahrtforschung, Bericht S 13/1 d
A942), S. 7 (NACA TN 1189, 1948).
Pack D. С and A. G. M а с к i e [1], Transonic Flow past Finite Wedges,
Proceedings of the Cambridge Philosophical Society, Vol. 48, Part 1
A952), p. 178.
— [2], Transonic Flow past Finite Wedges, Journal of Rational Mechanics
and Analysis, Vol. 4, № 1, Bloomington Ind., Indiana University.
Pack D. C, Investigation of the Flow past a Finite Wedge of 20 degrees
and 40 degrees Apex Angle at Subsonic and Supersonic Speeds using
a Mach-Zehnder Interferometer, R and M, 2321 British ARC A946).
Protter M. H., A Boundary Value Problem for an Equation of Mixed Type,
Trans. Amer. Math. Soc, Vol. 71 A951), p. 416 ff.
Riabouchinski D., Comptes Rendues de VAcademie des Sciences, p. 194,
p. 1215, Paris, 1932.
Ringleb Friedrich [1], Exakte Losungen der Differentialgleichung einer adia-
batischen Gasstromung, Z. angew. Math. Mech., Bd. 20 A940), S. 185.
— [2], Uber die Differentialgleichungen einer -Gasstromung und den Stro-
mungsstofi, Deutsche Mathematik, Bd. 5 A940), S. 377 ff.
S а к u r a i Takeo, The Flow past a Flat Plate accompanied with an Unsym-
metric Dead Air at Mach Number one, /. Phys. Soc. (Япония), Vol. 11
A956), № 6.
Sjrjeix Maurice, Golaz Paul et Pierre Re buffet, Resultats experimen-
taux obtenus aux voisinage de la vitesse du son sur une maquette d'aile
a profile losangique, Comptes Rendues de VAcademie des Sciences,
Tome 235 A952), p. 459 ff.
Solomon G. E., Transonic Flow past Cone Cylinders, NACA TN 3212
A954).
Spreiter John R. [1], On the Application of Transonic Similarity Rules to
Wings of Finite Span, NACA Rep. 1153 A953).
— [2], On the Range of Applicability of the Transonic Area Rule, NACA
TN 3673 A956).
Spreiter John R. and Alberta A 1 к s n e, Theoretical Prediction of Pressure
Distributions of Non-Lifting Airfoils at High Subsonic Speeds, NACA
TN 3096 A954).
S t a;c к John, Experimental Methods for Transonic Research, Proc. Third Anglo-
American Aeron. Conf. Brighton, Sept. 4—7 A951), p. 586.
Tamada K. and Y. S h i b а о к a, On Supersonic Flow past a Finite Wedge
at the Crocco Mach Number, /. Aeron. Set. A955), p. 261.

ЛИТЕРАТУРА 405
Taylor О. I., Recent Work on the Flow of Compressible Fluids, Joarn.
London Math. Society, Vol. 5 A930), p. 224.
Tsien Hsue-Shen and Yung-Huai К u o, Two-Dimensional Irrotational Mixed
Subsonic and Supersonic Flow of a Compressible Fluid and the Upper
Critical Mach Number, NACA TN № 995.
Tim man R., Asymptotic Formulae for Special Solutions of the Hodograph
Equation in Compressible Flow, Nat. Luchtlab. Amsterdam, Rep. № F 46
(April 22, 1949).
V i n с e n t i Walter, Q. Dugan, W. Duane and E. Ray P h e 1 p s, An Experi-
Experimental Study of the Lift and Pressure Distribution on a Double Wedge
Profile at Mach Number near Shock Attachement, NACA TN 3225.
V i n с е n t i Walter G., Measurements of the Effects of Finite Span on the
Pressure Distribution over Double Wedge Wings at Mach Numbers near
Shock Attachment, NACA TN 3522 A955).
Warren С. Н. E., Recent Advances in the Knowledge of Transonic Air Flow,
/. Roy. Aeron. Soe. (April 1956).
Weinstein Alexander, On Tricomi's Equation and Generalized Axially Sym-
Symmetric Potential Theory, Institute for Fluid Dynamics and Applied Mathe-
Mathematics A951), University of Maryland.
Will m art h William W., The Lift of Thin Airfols at High Subsonic Speeds,
Ph. D. Thesis, Cal. Inst. Tech. A953).
Wood George P., Experiments on Transonic Flow around Wedges, NACA
TN 2829 A952).

ОБОЗНАЧЕНИЯ
В настоящем перечне указаны только либо символы, имеющие
общее значение, либо символы, входящие в формулы, на которые
делаются ссылки в других местах книги.
а — скорость звука, см. формулу I, 2E):
а* — критическая скорость, см. § 2 гл. I;
А — подъемная сила;
ah — коэффициенты в уравнении VII, 13A а); их вы-
выражения в явном виде определяются форму-
формулой VII, 13Cа);
Ь{х) — в § 3 гл. III — функция, определяющая контур
бесконечно тонкого крыла;
В_(«/з)_(А/а), й_(«/,)-(й/2) — см. уравнение IX, 4A) и формулы IX, 4G);
В{%), В{%) — си. формулы VII, 12A36) и VII, 12A4а);
bh — коэффициенты в уравнении VII, 13A6); их
выражения в явном виде определяются фор-
формулой VII, 13C6);
ср, cv — удельные теплоемкости при постоянном давле-
давлении и при постоянном объеме;
сл — коэффициент подъемной силы;
cw — коэффициент сопротивления;
ср — коэффициент давления;
с*А, c*w, с*—те же коэффициенты, но отнесенные к дина-
динамическому давлению, составленному для кри-
критической скорости;
q, c2 — нижняя и верхняя границы интервала, в котором
изменяется переменная %\
Сп — нормализирующая постоянная [формула VII, 9(8)];
индекс h указывает на соответствие с собствен-
собственной функцией Gh;

ОБОЗНАЧЕНИЯ 407
D — в § б гл. II — характерная толщина обтекаемого
тела;
D — в § 2 гл. V — функциональный определитель;
Dv D2 — вещественные множители, на которые можно
разложить функциональный определитель D
в сверхзвуковой области;
/(С, п) — для плоских течений, см.1 уравнение VII,2B);
/(С, п) — для осесимметричных течений, см. уравнение
Х1,1A);
/(?, т], С)—в § 4 гл. II — уравнение поверхности скачка
уплотнения;
F(a,b,c,x)—-символ гипергеометрического ряда, см. равен-
равенство VII, 4D6);
gl(T]fiin) — частные решения уравнения Трикоми, соответ-
соответствующие решениям Чаплыгина для уравнения
в плоскости годографа, см. равенства VII, 1B);
G(z, |x) — функция, входящая в произведение, принимаемое
за решение уравнения Трикоми, см. равен-
равенство VII, 3C);
G(s\ G ' — функции О, для которых соответствующие ре-
решения ф симметричны (антисимметричны) отно-
относительно & = 0;
Ох — функция О, определяемая равенством VII, 7A3);
О2, G3, • • •, Gh — функции О, найденные путем решения задачи на
собственные значения, см. § 9, гл. VII;
h — в § 5 гл. II и § 3 гл. III — функция, характе-
характеризующая распределение толщины обтекаемого
тела;
Я}1), H[J> — функции Ханкеля первого и второго рода и по-
порядка 1/а; связаны с функциями Бесселя фор-
формулами VII, 7F);
i — энтальпия, отнесенная к единице массы;
/i/s, /_i/, — функции Бесселя порядка х/з и —11з'<
/((л.) — аналитическая функция, определяемая форму-
формулой VII, 13D);
L (Ф), L (ср) — дифференциальное выражение для граничных
условий второго рода, см. уравнение V, 11A2);

408
ОБОЗНАЧЕНИЯ
vx, vv
vni
., Ьл)у
L — в § 4 и 9 гл. VIII — ширина (или длина) ромбо-
ромбовидного профиля или пластинки;
1т'п—-интегралы, определяемые формулой VIII, 9A7);
М — число Маха;
Мса—число Маха в бесконечности;
Мблок —число Маха набегающего течения в блокирован-
блокированной аэродинамической трубе;
О(х) — символ порядка величины, см. примечание на
стр. 37.
давление;
давление при критической скорости;
давление в бесконечности;
— Р-функция Римана, см. § 2 и 4 гл. VII;
Р (х) — символ степенного ряда относительно х;
R — газовая постоянная, отнесенная к единице массы;
-№.з) — функции, определяющие граничные условия на
большом расстоянии от обтекаемого тела, см.
формулы IX, 4 (8);
5 — энтропия, отнесенная к единице массы;
Т — абсолютная температура;
и — начиная с гл. V—-обычно составляющая ско-
скорости в направлении х для плоских задач;
v — начиная с гл. V — обычно составляющая ско-
скорости в направлении у для плоских задач;
1> — вектор скорости;
vz — составляющие скорости в направлениях х, у, z\
vr — радиальная составляющая скорости в осесим-
метричных задачах;
— составляющие скорости, нормальные к поверх-
поверхности скачка уплотнения, непосредственно выше
и ниже по течению относительно скачка;
vt — составляющая скорости, касательная к поверх-
поверхности скачка уплотнения;
)г—-изменения скорости в направлениях х, у, z, воз-
возникающие при переходе через скачок уплотнения;

ОБОЗНАЧЕНИЯ 409
vn> vt—в § 5 гл. II — составляющие скорости в на-
направлении нормали и касательной к кривой пере-
пересечения плоскости х = const с поверхностью
обтекаемого тела;
w — абсолютное значение скорости;
t»* = fl* — критическая скорость, см. § 2 гл. I;
х0—-характерный размер обтекаемого тела в направ-
направлении х, используемый] при выводе закона
подобия;
У , z — отклонения координат у и z линии тока от
соответствующих координат той же линии тока
в невозмущенном течении;
а — угол Маха;
а — угол атаки;
'fc и т- Д-—-постоянные, входящие в разложение по частным
решениям, см. уравнение VIII, 7A) и замеча-
замечание в связи с уравнением IX, 3A6);
»Р_Р/„)_(й/а) — постоянные, см. уравнение IX, 3D) и пред-
предшествующее ему замечание;
Г — циркуляция, см. стр. 16;
Г — гамма-функция (функция Эйлера второго рода);
С — при решении задач методом годографа — не-
независимая переменная в плоскости годографа,
см. равенство VII, 2A);
С — в осесимметричных течениях — специальная пере-
переменная в плоскости течения, см. равенство
Qj — в § 4 гл. XI—значение величины С для скачка
уплотнения;
7j—переменная, определяющая отклонение модуля
скорости от скорости звука; см. равенства
V.7 E) и замечание после уравнения V.7 F);
& — угол, образуемый вектором скорости с осью х;
60 —угол, характерный для обтекаемого тела, на-
например половина угла раствора клина, угол
атаки плоской пластинки; одновременно отно-
относительная толщина ромбовидного профиля;

410 ОБОЗНАЧЕНИЯ
х — отношение удельной теплоемкости при постоян-
постоянном давлении к удельной теплоемкости при по-
постоянном объеме;
X, [х — обозначения для характеристик в плоскости
годографа при пользовании методом характери-
характеристик Буземана, см. равенства I, 7C) и I, 7D);
X и Хд — собственные значения для частных решений урав-
уравнения Трикоми, см. § 9 гл. VII;
X — собственные значения для дифференциального урав-
уравнения осесимметричных течений, см. уравне-
уравнение XI, 2G) и равенство XI, 2Gа);
[а —в связи с функциями G(?, [л) — постоянная, по-
позволяющая различать частные решения уравнения
Трикоми, см. уравнение VII, 3C);
jijo), jj^)_см. равенства VII, 12 A3а) и VII, 12A46);
vi- V2 —в § 5 и 6 гл. VI — см. рис. 54;
n—в § 5 и 6 гл. VI — см. уравнение VI, 5(8);
v—в § 11 гл. VII — переменная, определяемая не-
непосредственно уравнением VII, 11D);
ч — в § 2 гл. XI — переменная, позволяющая раз-
различать отдельные частные решения g"(C,v), см.
уравнение XI, 2C);
?, к), С — при выводе закона подобия — пространствен-
пространственные координаты, связанные с координатами
х, у, z; см. равенство II, 3C6);
X, р — при решении задач методом годографа — неза-
независимые переменные в плоскости т), &; см. ра-
равенства VII, 3A) и VII, 3B);
%, — вспомогательная переменная для определения
асимптотических представлений, связанная с пере-
переменной %\ см. равенство VII, 7A6);
р — плотность;
р* — плотность при критической скорости;
р, I см. 5, р;
р0—в § 10 гл. VIII —см. рис. 96;
Ро» Фо—в равенствах IX, 4G) — характерные для рас-
рассматриваемой задачи значения величин р и ф;

ОБОЗНАЧЕНИЯ 411
Pi> ?2> 1*1 • Фг — параметры в формулировке граничных условий;
в первый раз вводятся уравнениями IX, 4E);
pj — в § 5 гл. IX — параметр, характеризующий от-
отклонение от течения с числом Маха, равным
единице;
р — в § 2 гл. XI — независимая переменная, опреде-
определяемая равенством XI, 2(9а); см. также рис. 114;
a (v) — см. уравнение VII, 11D);
т — параметр, по которому производится разложе-
разложение; см. § 12 гл. I;
Ф, Ф, Ф—потенциал, возмущающий потенциал или род-
родственные функции в плоскости течения;
Ф(т], г))илиФ('да,&) — изменение преобразованного потенциала, обус-
обусловленное изменением граничных условий в пло-
плоскости течения;
ф-G6)-(/а) ^ p-j — частные решения для преобразованного потен-
потенциала в плоскости $, р (плоскости годографа),
оставляющие профиль в плоскости течения не-
неизменным;
ср(да, &); ср(т], &) или <р(?, р) — функции в плоскости годографа или в пло-
плоскости т), &, получающиеся из потенциала в пло-
плоскости течения посредством преобразования Ле-
жандра (для краткости называются преобразо-
преобразованным потенциалом);
ср, ср, ср — функции, связанные с ср;
9-(Ve)-(ft/a)—естественные частные решения для преобразован-
преобразованного потенциала ср, соответствующие естествен-
естественным частным решениям для функции тока ф;
см. § 9 гл. VII;
ф— функция тока в плоскости течения и в плоскости
годографа;
ф, tyv ф2 и т. д. — функции, связанные с функцией тока;
ф^/з' <]*-!/„ и т. д. — естественные частные решения, определенные
в § 9 гл. VII;
ЧГ~5/«, ф_!д — специальные частные решения, смысл которых
разъяснен в начале § 3 гл. VIII;
27*

412 ОБОЗНАЧЕНИЯ
^) — естественные частные решения <])_«/„> отнесен-
отнесенные к переменным tj, Ь;
^ —в § 7 гл. VIII —см. равенство VIII, 7B);
, п—частное решение, см. равенство VIII, 9E);
2 — в § 8 гл. V — комплексный потенциал, см. ра-
равенство V, 8B);
ш — в § 8 гл. V — комплексный преобразованный
потенциал, во всех других случаях — угол в ци-
цилиндрических координатах.

ИМЕННОЙ УКАЗАТЕЛЬ
Агмон (Agmon S.) 399
Алксне Альберта (Alksne Alberta)
404
Бадер (Bader R.) 401
Баранов (Baranoff A.) 399
Бергдолт (Bergdolt V. E.) 399
Бергман (Bergmann S.) 332, 393, 399
Бериш (Berish D. Т.) 381, 382, 393,
399
Берндт (Berndt S. В.) 55, 397, 399
Берс (Bers L ) 399
Био (Biot M. А.) 398, 399
Бланш Гертруда (Blanche Gertrude)
370
Брайсон (Bryson A. E.) 399, 403
Буземан (Busemann A.) 26, 68, 84, 99,
153, 172, 184, 360, 393, 399
224, 235, 237, 258, 265, 269, 274, 276,
288, 291, 301, 305, 329,333, 338,342,
344, 348, 351, 353, 360, 361,363, 370,
371, 375, 377, 382, 393, 394, 395, 401
Гульстранд (Gullstrand Т. R ) 401, 402
Демченко (Demtshenko) 400
Джонс (Jones R. Т.) 72, 396
Джонстон (Johnston О. W.) 402
Джун (Jun E.) 399
Диас (Diaz J. В.) 400
Дибл (Dibble G.) 403
Драугг (Drougge G.) 400
Дьюан (Duane W.) 405
Дьюган (Dugan G.) 405
Жермен (Germain P.) 401
Вагонер (Wagoner С. В.) 126, 282,
339—342, 398
Вайзе (Weise A.) 178, 398
Вайнштейн (Weinstein A.) 405
Ватсон (Watson G. N ) 193, 399
Вендт (Wendt H.) 50, 396
Вигхардт (Wieghardt К.) 404
Винченти (Vincenti W. G.) 126, 282,
339—342, 398, 405
Вуд (Wood О. Р.) 405
Гамель (Hamel G.) 225, 395
Гарднер (Gardner С. S.) 84—86, 394
Гаррик (Garrick I E ) 401
Гёртлер (Gortler H.) 93, 394
Гильберт (Hilbert D.) 399
Го (Kuo Y. Н) 405
Гола (Golaz P.) 404
Грехэм (Graham E. W.) 96, 394
Гриффите (Griffith W ) 401
Гудерлей (Guderley К. G.) 41, 45, 61,
93, ИЗ, 124, 144, 145, 150, 155, 159,
167, 169, 172, 183, 187, 188, 192, 220,
Зауэр (Sauer R.) 27, 398
Зейферт (Seifert H) 121, 397
Имаи (Imai I.) 124, 396, 402
Йосихара (Yoshihara H) 159,269,274,
276, 342, 363, 370, 371, 377, 381,
391, 395, 398
Кабанн (Cabannes H ) 399
Кавамура (Kawamura Т.) 402
Каплан (Caplan С.) 401, 402
Карман (KarmanTh ) 41, 396, 398, 402
Каррьер (Carrier G. F.) 400
Кейне (Keune F ) 73, 76, 396, 397,402
Клаузер (Clauser M. U.) 400
Клаузер (Clauser F Н.) 400
Колоднер (Colodner I I.) 403
Копсон (Copson E. Т.) 399
Коул (Cole J.) 83, 86, 87, 393, 400
Краггс (Craggs J. W) 400
Крафт (Kraft H.) 403
Крокко (Crocco L.) 166, 169, 393

414
именной указатель
Крючин А. Ф. 403
Курант (Courant R.) 399
Ладлофф (Ludloff H. F.) 84, 394
Ладфорд (Ludford S S.) 400
Лайтхилл (Lighthill M. J.) 118, 396
Лангер (Langer R. Е.) 396
Ландаль (Landahl M. Т.) 76, 403
Леви (Levey H. С.) 403
Левнер (Loewner С. А.) 403
Лейтон (Laitone E. V.) 403
Лиже (Liger M.) 271, 396, 401
Липман (Liepmann H. W.) 161, 398,
403
Ломаке (Lomax H.) 72, 396, 403
Людвиг (Ludwieg W.) 389
Макки (Mackie А О.) 404
Манглер (Mangier К. W.) 72, 397,
403
Мануэлл (Manwell A R.) 403
Маршнер (Marschner В. W ) 268, 324,
395
Мейер (Meyer Th.) 88, 396
Митчелл (Mitcheil A. R.) 403
Моленбрек (Molenbroeck P.) 98, 116,
396
Моравец Кэтлин (Moravetz Cathle-
en S ) 144, 151, 360, 397, 403
Никольский А. А. 153, 397
Ниренберг (Nirenberg) 399
О'Брайен (О' Brien V.) 116, 393
Осватич (Oswatitsch К.) 16, 41, 55,
59, 73, 76, 397, 398, 402, 404
Пак (Pack D С ) 404
Пакет (Puckett A E.) 398
Проттер (Protter M. Н.) 399, 404
Ратерфорд (Rutherford D Е.) 403
Ребюффе (Rebuffet P.) 404
Ринглеб (Ringleb F.) 127, 404
Рябушинский (Riabouchinski D.) 404
Сакураи (Sakurai Т.) 404
Сибаока (Shibaoka Y.) 404
Сире (Sears W. R) 398
Сирьё (Sirieux M ) 404
Соломон (Solomon G. Е.) 400, 404
Спрейтер (Spreiter J. R.) 58, 72, 340,
396, 397, 408
Стак (Stack J.) 404
Таганов Г. И. 153, 397
Тамада (Tamada К.) 88, 244, 397, 404
Темпл (Temple О.) 26, 397
Тимман (Timman R.) 405
Толмин (Tollmien W.) 105, 351, 397
Томотика (Tomotika S.) 88, 244, 397
Трикоми (Tricomi F.) 141, 397
Тэйлор (Teilor О. I.) 92, 405
Уайтком (Withcomb R. Т.) 76, 398
Уилмарт (Willmarth W. W.) 400, 405
Уиттекер (Whittaker E. Т.) 399
Уоррен (Warren С. Н. Е ) 405
Фалькович С. В. 244, 245, 393, 400
Фелпс (Phelps E. R ) 405
Фишбах (Fishbach J. W.) 401
Фишер (Fisher N. Н.) 126, 342, 398
Франкль Ф. И. 81, 83, 124, 144, 145,
147, 155, 258, 360, 394, 401
Фридрихе (Friedrichs К. О.) 394
Ханцше (Hantzsche W.) 50, 396
Хардер Кэйт (Harder Keith С) 402
Хилтон (Hilton J. H.) 402
Хислет (Heaslet M. А.) 72, 396, 403
Христианович С. А. 393
Хуккель Вера (Huckel W.) 116, 396
Чаплыгин С. А. 116, 397
Чжан (Chang С. С.) 116, 393, 400
Чжу (Спи В Т.) 400
Цянь сюэ-сэнь (Tsien H. S ) 405
Шапиро (Shapiro A. H.) 398
Шерри (Sherry Т. М.) 400
Эггинк (Eggink H.) 178, 393
Элерс (Ehlers F. Е.) 400
Эмде (Emde F.) 189, 396
Якоб (Jacob С.) 402
Якобе (Jacobs W.) 91, 396
Янке (Jahnke E ) 189, 396

ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Аккерета уравнение 41
Бернулли уравнение 13,18
Буземана метод 26
Вихрь 15, 105
Волна Маха 23
Волна Маха левобегущая и право-
бегущая 26
¦ предельная 92, 137, 254, 367
— разрежения 27
— расширения 27
•— сжатия 27
— уплотнения 27
Гипербола влияния 79
Задача краевая в плоскости годо-
годографа (ее формулировка) 141, 142
второго рода 151, 282
для дозвуковой области 33
— —для сверхзвуковой области 32
для сверхзвуковой струи 155
для смешанного течения 142
— — для тела произвольной формы
382
— — для течения со скачком уплот-
уплотнения 145
для уравнения Трикоми 353, 357
— на собственные значения для част-
частных решений уравнения Трикоми
22о
Закон подобия 41, 56, 58, 59
Значения граничные для дозвукового
течения 33
для сверхзвукового течения 32
Истечение из сосуда (отверстия) 116,
155, 156
— струи 155, 178, 179, 180, 182
Источник 105
Клин, см. обтекание или течение
Коэффициент давления в околозву-
околозвуковом приближении 127
при переходе через число М = 1
322
— подъемной силы, его связь с от-
относительной толщиной 281
— сопротивления при М = 1 266
Крокко теорема 16, 45
— точка 146, 164, 187
Крыло бипланное Буземана 188
Кутта условие 69
Лаваля сопло 88—92, 134, 142, 351
Лежандра преобразование 98,128
Линия вихревая 15
— жидкая 16
— звуковая 89, 154, 161, 344, 388
— предельная 105, 106, ПО, ИЗ, 154
— разветвления в плоскости годо-
годографа 137
— тока 19
ее точки разветвления 130, 132
Маха волна 23
левобегущая и правобегущая 26
предельная 92, 137, 254, 367
— угол 22
— число 14
Мейера течение расширяющееся 143
Метод Буземана 26
— характеристик 26
для околозвуковых течений 29
его смысл в плоскости годо-
годографа 280
Обтекание выпуклого угла 158
— клина 159
под углом атаки 274
при неприлегающем скачке уп-
уплотнения 147

416
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Обтекание клина при прилегающем
скачке уплотнения 342
при числе Маха М = 1 267
с криволинейными сторонами
166
сверхзвуковое 184
— несимметричного профиля при чи-
числе М = 1 272
— пластинки в блокированной аэро-
аэродинамической трубе 333
— •—под углом атаки при числе
М = \ 286
— ромбовидного профиля 324, 331
Определитель функциональный 102,
144
Отражение волн уплотнения и раз-
разрежения 29
— особенности от звуковой линии
344
Римана Р-функция 193
Ромб, см. обтекание или течение
Свойство групповое обыкновенного
дифференциального уравнения 364
Сила подъемная при М = 1 341
Скачок уплотнения 11
разветвленный 178, 181
сильный 184
— —слабый 184
Скорость звука 14, 78
— критическая 14
Сопло Лаваля 88—92, 134, 142, 351
Соотношения ортогональности 224
Струя свободная 306
— параллельная с критической ско-
скоростью 92
Параметры подобия 58
Пластинка, см. обтекание или тече-
течение
Поляра ударная 50, 145
Потенциал преобразованный (Лежан-
дра) 98, 129
— скоростей 17
комплексный 128
Правило Прандтля — Глауэрта 42,43,
59
Прандтля — Глауэрта приближение
41
Преобразование аффинное 42, 56
— Лежандра 98, 128
Приближение Прандтля — Глауэр-
Глауэрта 41
Принцип соответствия 127, 323
Профиль ромбовидный, см. обтека-
обтекание или течение
Р-функция Римана 193
Разрыв производных скорости 24
Решения асимптотические обыкновен-
обыкновенного дифференциального уравнения
119, 121, 213
— потерянные 140, 358
— частные естественные 222, 375
для осесимметричного течения
372, 377
Тамады и Томотики 244
уравнения Трикоми 189, 244,245
Фальковича 246, 247
Чаплыгина 114, 116, 118, 189
— G 195. 197
— G специальные 206
Тамады и Томотики решения 244
Тело вращения эквивалентное 73
Теорема импульсов 62, 63
— Крокко 16, 45
— Трикоми 142
Теояия линейная 65, 85
для пространственных течений
69
для неустановившихся течений
77
— характеристик 20
Течение в блокированной аэродина-
аэродинамической трубе 306
— вблизи острия клина 162
— дозвуковое, содержащее сверх-
сверхзвуковую область 358
— изоэнергетическое 13, 44
— Мейера (расширяющееся) 143
— несжимаемое через сопло 37
— неустановившееся 77
— около выпуклого угла 158
— около клина при М = 1 267
— около клина с криволинейными
сторонами 166
— около несимметричного профиля
при М = 1 272
— около ромбовидного профиля 324,
331
— осесимметричное 12, 25, 53, 65, 362
— — при числе М = 1 362
— при чрезвычайно большом числе М
40
— расширяющееся, примыкающее к
дозвуковой области 156, 158
— с числом Маха, близким к едини-
единице 305, 320

ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
417
Течение с числом Маха, равным еди-
единице 252
вытеснение линий
тока 257
. — •— около несиммет-
несимметричного профиля 272
около пластинки
под углом атаки 286
около ромбовидно-
ромбовидного профиля 267
около ромбовидно-
ромбовидного профиля под углом атаки 274
¦ около симметрич-
симметричного профиля 266
— особенность в ну-
нулевой точке плоскости i\, Ь 256
— •— -со скачком уплот-
уплотнения 381
— через сопло Лаваля 88—92, 134,
252, 351
Точка невырожденная на звуковой
линии 343
— Крокко 146, 164, 187
— разветвления линии тока в плос-
плоскости годографа 103, 131, 137
Точки соответственные 56
Трикоми уравнение 24, 125, 126, 189
— условие 142
Труба аэродинамическая блокирован-
блокированная 60, 252, 298, 329
Трубка вихревая 15
— тока 15
Угол Маха 22
Уравнение Аккерета 41
— Бернулли 13, 18
— дифференциальное гипергеометри-
гипергеометрическое 115, 193
околозвукового течения линеа-
линеаризованное 65
— для потенциала в плоскости тече-
течения 18, 36, 42
— для преобразованного потенциала
в плоскости годографа 99
Уравнение для функции тока в пло-
плоскости годографа 101
— импульсов приближенное 62
— интегральное с полярным ядром
225
— неразрывности 12, 18, 45
приближенное 62
— Прандтля — Глауэрта 37, 41
— Трикоми 24, 125, 126, 189
Уравнения движения Эйлера 12
Условие Кутта 69
— совместности для характеристик 23-
— Трикоми 142
Условия граничные второго рода 151
на обтекаемом теле 51, 52, 54, 62"
на оси симметричного тела 53
на скачке уплотнения 47
— в плоскости годографа
145
Фальковича решения 246, 247
Ферри эксперимент 188
Функция тока 19, 102
Характеристика 23
— предельная 92, 137, 254, 367
Цилиндр аппроксимирующий 51, 57
Циркуляция скорости 16
Чаплыгина грешения 114, 116, 118,
189
Число Маха 14
блокирующее 252, 328, 336
Эйлера уравнения движения 12
Эксперимент Ферри 188
Энтальпия 13
Энтропия 11, 44

ОГЛАВЛЕНИЕ
Предисловие редактора 5
Предисловие • 9
Глава I. Общие основы И
§ 1. Основные уравнения для невязких сжимаемых течений . . 11
§ 2. Уравнение Бернулли 13
§ 3. Теоремы о вихрях 15
§ 4. Потенциал скоростей . . . . . . ... 17
§ 5 Функция тока . 19
§ 6. Характеристики . . . 20
§ 7. Упрощения для плоских потенциальных течений 25
§ 8. Примеры 27
§ 9. Метод характеристик для околозвуковых течений 29
§ 10. Общие соображения, связанные с понятием характеристик . 31
§ 11. Некоторые замечания о формулировке краевых задач в
до- и сверхзвуковых течениях 32
§ 12. Об одном способе вывода приближенных уравнений .... 35
Глава //.Упрощение дифференциальных уравнений течения.
Закон подобия для околозвуковых течений 41
§ 1. Предварительные замечания 41
§ 2. Члены, отбрасываемые в приближении Прандтля—Глауэрта 41
§ 3. Упрощение дифференциальных уравнений течения 44
§ 4. Условия на скачках уплотнения 47
§ 5. Граничные условия . . . . 50
§ 6. Закон подобия . . ... 56
§ 7. Применения закона подобия ... 59
§ 8. Упрощение обозначений и записей 61
§ 9. Уравнение неразрывности и теорема импульсов для около-
околозвуковых течений 62
Глава III Линеаризованное исследование околозвуковых те-
течений 65
§ 1. Предварительные замечания 65
§ 2. Линеаризованное исследование плоских и осесимметричных
течений 65
§ 3. Пространственные течения . 69
§' 4. Тело с толщиной, не равной нулю .... ... .72

ОГЛАВЛЕНИЕ 419
§ 5. Линеаризованное исследование неустановившихся околозву-
околозвуковых течений 77
§ 6. Пределы применимости линейной теории 85
Глава IV. Точные решения уравнения для потенциала околозву-
околозвуковых течений 88
§ 1. Предварительные замечания ... 88
§ 2. Течение через сопло Лаваля 88
§ 3. Параллельная струя с критической скоростью 92
Глава V. Основы метода годографа 97
§ 1. Уравнения преобразованного потенциала и' функции тока
в плоскости годографа 97
§ 2. Функциональный определитель D . . . . .... 102
§ 3. Предельная линия 105
§ 4. Частные решения уравнения годографа, полученные Чап-
Чаплыгиным 114
§ 5. Решение одной краевой задачи .... 116
§ 6. Приближенные представления решений Чаплыгина .... 118
§ 7. Уравнение Трикоми 124
§ 8. Примеры построения годографа . 127
§ 9. Линии разветвления в плоскости годографа ... . . 137
§ 10. Потерянные решения . . 140
§ 11. Краевые задачи в плоскости годографа 141
Глава VI. Исследование околозвуковых течений методом годо-
годографа 153
§ 1. Предварительные замечания . . 153
§ 2. Истечение из сосуда . . ... 155
§ 3. Течение около выпуклого угла ... . . 158
§ 4. Клин в сверхзвуковом течении 159
§ 5. Аналитическое исследование поля течения вблизи острия
клина в случае прилегающего скачка уплотнения .... 162
§ 6. Клин с криволинейными сторонами .... . . . . ¦ 166
§ 7. Исследование перехода от прилегающего скачка уплотнения
к неприлегающему скачку 169
§ 8. Разветвленные скачки уплотнения . . 178
§ 9. Новый вид разветвленного скачка уплотнения 181
§ 10. Смысл „второго" решения задачи о сверхзвуковом обтекании
клина 184
Глава VII. Частные решения уравнения Трикоми . . ... 189
§ 1. Частные решения Чаплыгина 189
§ 2. Другой класс частных решений . 192
§ 3. Другое допущение о форме решения 194
§ 4. Решения G 197
§ 5. Специальные решения G 206

420 ОГЛАВЛЕНИЕ
§ 6. Соотношения между решениями с различными значениями [* 211
§ 7. Приближенные представления функций G при больших | р | 211
§ 8. Функциональный определитель частных решений G . . . . 218
§ 9. Системы частных решений 221
§ 10. Представление некоторых решений уравнения Трикоми
в виде наложения частных решений, составленных из соб-
собственных функций 226
§ 11. Собственные функции и собственные значения в предельном
случае с2->1 227
§ 12. Представление произвольной функции в предельном случае
са->1 230
§ 13. Разложение решения ф по частным решениям 234
§ 14. Частные решения Тамады и Томотики 244
§ 15. Частные решения Фальковича 246
Глава VIII. Течения с- числом Маха, равным единице 252
§ 1. Общие соображения" 252
§ 2. Годограф течения с числом Маха, равным единице .... 254
§ 3. Пример течения с числом Маха, равным единице 258
§ 4. Обтекание клина при числе Маха, равном единице .... 267
§ 5. Смысл некоторых решений для других -значений [а . . . . 271
§ 6 Обтекание несимметричных профилей при числе Маха,
равном единице 272'
§ 7. Обтекание клина под углом атаки 274
§ 8. Краевая задача для тела произвольной формы, поставлен-
поставленного под малым углом атаки, и родственные задачи . . . 282
§ 9. Обтекание пластинки под углом атаки при числе 'Маха,
равном единице 286
§ 10. Другие частные решения, получаемые аналогичными ме-
методами 298
Глава IX. Течения, лишь немного отличающиеся от течений
с числомтМаха, равным» единице 304
§ 1. Предварительные замечания 304
§ 2. Примеры течений, немного отличающихся от течений с чис-
числом 'Маха, равным единице 305
§ 3. Решения, удовлетворяющие граничным условиям на обте-
обтекаемом теле 307
§ 4. Граничные условия вблизи нулевой точки 311
§ 5 Поля течения, для которых функция тока ф антисимметрична
относительно оси х 315
§ 6. Несимметричные поля течения 316-
§ 7. Разложение поля течения по отклонению числа Маха, харак-
характерного для течения, от единицы 320*
§ 8. Течение около ромбовидного профиля в блокированной
закрытой аэродинамической трубе 324

ОГЛАВЛЕНИЕ 421
§ 9. Обтекание ромбовидного профиля свободной струей с кри-
критической скоростью и неограниченным потоком со сверх-
сверхзвуковой скоростью . . . 331
§ 10. Плоская пластинка в блокированной закрытой аэродинами-
аэродинамической трубе . 333
§ 11. Другие исследования плоских течений 339
Глава X. Некоторые исследования, использующие частные ре-
решения вида VII, 3C) 343
§ 1. Решение в невырожденной точке звуковой линии в пло-
плоскости годографа 343
§ 2. Этражение особенности от звуковой линии 344
§ 3! Течение в самом узком поперечном сечении сопла Лаваля 351
§ 4. Исследование специальных краевых задач для уравнения
Трикоми 353
Глава XI. Осесимметричные течения 362
§ 1. Течения с числом Маха, равным единице 362
§ 2. Уточненное исследование решения в бесконечности .... 371
§ 3. Приложения 377
§ 4. Специальные плоские и осесимметричные течения со скач-
скачками уплотнения 381
§ 5. Приложения 382
§ 6. Описание полей течения при Mm, близком к единице . . . 389
Литература . 393
1. Цитированные работы . 393
2. Учебники .... 398
3. Другие работы . . . . 399
Обозначения 406
Именной указатель ... 413
Предметный указатель 415