MOLECULAR THEORY OF SURFACE TENSION
IN LIQUIDS
by
SYU ONO and SOHEI KONDO
HANDBUCH DER PHYSIK
Herausgegeben
von
S. FLUGGE
Band X
Springer-Verlag
Berlin-Gottingen-Heidelberg
I960

с. оно, с. кондо
МОЛЕКУЛЯРНАЯ ТЕОРИЯ
ПОВЕРХНОСТНОГО
НАТЯЖЕНИЯ В ЖИДКОСТЯХ
ПЕРЕВОД С АНГЛИЙСКОГО
С. И. АНИСИМОВА и Т. Л. ПЕРЕЛЬМАНА
ПОД РЕДАКЦИЕЙ
И. 3. ФИШЕРА
ИЗДАТЕЛЬСТВО ИНОСТРАННОЙ ЛИТЕРАТУРЫ
Москва 196 3

Редакция литературы по физике

ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
Предлагаемая вниманию читателей книга
японских физиков С. Оно и С. Кондо представляет
собой перевод большой обзорной статьи из X тома
второго издания Handbuch der Physik —
физической энциклопедии, выпускаемой в настоящее время
под общей редакцией С. Флюгге. Первый из
авторов—С. Оно —не нуждается в рекомендации. Его
имя хорошо известно по вкладу, внесенному им в
статистическую теорию жидкостей, особенно в теорию
свободного объема и теорию поверхностных явлений.
С. Кондо — также видный специалист по теории
поверхностных явлений и автор многих работ по этому
вопросу. В книге чрезвычайно подробно освещено
современное состояние теории поверхностных
явлений в чистых жидкостях и жидких растворах, в
частности растворах полимеров, а также некоторых
других примыкающих к этой теме вопросов, в том
числе проблемы поверхностных явлений на границе
раздела твердое тело — газ.
Книга состоит из трех частей, в которых один и
тот же круг вопросов последовательно освещается
и анализируется сначала с точки зрения общих
методов термодинамики (I часть), затем с точки
зрения статистической механики (II часть) и, наконец,
с точки зрения модельных теорий жидкого
состояния (III часть). При таком фронтальном подходе к
материалу авторам удалось охватить почти все
сколько-нибудь важные вопросы и методы теории
поверхностных явлений в жидкостях. Поэтому
книга может служить не только хорошим пособием, но
и универсальным справочником по излагаемому

6
Предисловие редактора перевода
предмету. Необходимо отметить, что авторы совсем
не затрагивают феноменологической теории
капиллярности, который в этом же томе Handbuch der
Physik посвящена отдельная статья.
Центральное место в книге как по объему, так
и по значению занимает вторая часть, посвященная
молекулярно-статистической теории поверхностных
явлений. Эта теория является частью общей
статистической теории жидкого состояния вещества,
получившей заметное развитие в последние годы.
Именно этот путь позволяет последовательно вскрыть
молекулярный механизм разнообразных физических
и физико-химических явлений в жидкостях, в
частности поверхностных явлений.
В литературе на русском языке — отечественной
и переводной — молекулярная теория поверхностных
явлений в жидкостх освещена недостаточно. С
другой стороны, нет необходимости доказывать важное
научное и практическое значение физики
поверхностных явлений. Поэтому нам представляется, что
издание настоящей книги принесет большую пользу
работающим в области молекулярной физики,
физической химии и их применений, а также и всем тем,
кто изучает или интересуется физикой
поверхностных явлений.
И. Фишер

Вв едение
Настоящая книга посвящена трактуемому с
молекулярной точки зрения описанию поверхностного натяжения и
физической адсорбции в чистых жидкостях и растворах.
Основу такого описания составляют методы термодинамики
и статистической механики.
Если находящаяся в равновесии система состоит из
двух или более фаз, то промежуточная область между
любыми двумя фазами вносит малый, но заметный вклад в
механическое и термодинамическое поведение всей системы.
Среди многочисленных явлений, связанных с этой
промежуточной областью, наиболее важным является
поверхностное натяжение. Со времен Юнга [1] граница между двумя
деформируемыми средами, скажем между жидкостью и ее
паром, рассматривалась с механической точки зрения, как
если бы это была равномерно натянутая пленка нулевой
толщины. Поверхностное натяжение определялось на
основе макроскопических концепций как сила сцепления т>
действующая поперек каждой единицы длины линии на
этой фиктивной пленке.
Когда две жидкости, находящиеся во взаимном
механическом равновесии, разделены сферической границей
радиуса а, давление на границе жидкости изнутри ра отличается
от давления снаружи рр. Если предположить, что граница
имеет нулевую толщину, то из условия механического
равновесия вытекает простое соотношение между ра и р$\
Р«-Р* =% (0.1)
хорошо известное как соотношение Кельвина [2].
Описанный выше метод рассмотрения поверхностного
натяжения прост, нагляден и полезен, но с молекулярной

8
Введение
точки зрения он является по сути своей приближенным,
поскольку при переходе через действительную границу
структура жидкости испытывает не разрыв, а постепенное
изменение, хотя толщина переходной области, оцененная по
эллиптичности отраженного света, крайне мала.
Основываясь на такой концепции, ван дер Ваальс и его ученики
(см. [3]) предложили выражать поверхностное натяжение
как интеграл, взятый по этой переходной области от
разностей между двумя давлениями, нормальным и
касательным к поверхности раздела, приняв предположение, что
к этому весьма малому количеству неоднородного вещества
применимы законы макроскопической гидродинамики.
В этой книге мы, следуя] Гиббсу [4], рассматриваем
межфазовую зону, относя ее свойства — чтобы избежать
необходимости приписывания ей какой-то толщины — к
некоторой математической поверхности, называемой
разделяющей поверхностью. Мы можем, таким образом, строго
определить поверхностное натяжение относительно этой
разделяющей поверхности. Кроме того, любое другое
свойство межфазовой зоны также можно определить как
величину, отнесенную к разделяющей поверхности и
принимающую определенное значение, как только выбрано
определенное положение разделяющей поверхности. Если
величины в переходной зоне рассматривать таким образом,
то термодинамические уравнения для них принимают
форму, аналогичную той, которую они имеют в однородных
фазах.
Мы начнем с изложения термодинамической теории
поверхностного натяжения и адсорбции, пользуясь методом
разделяющей поверхности, введенным Гиббсом.
Использование понятия разделяющей поверхности или ее
эквивалента неизбежно при рассмотрении искривленной границы
фаз, поскольку в противном случае понятия площади и
кривизны границы нельзя определить точно.
Однако в случае плоской границы введение
разделяющей поверхности не является необходимым. В этом случае
справедлив другой подход, предложенный Гуггенгеймом
[5, 6] и состоящий в том, что межфазовая зона
рассматривается как отдельный слой вещества, имеющий некоторую
определенную толщину и ограниченный двумя
математическими плоскостями. Этому методу, однако, будет уделено

Введение
9
меньшее внимание, поскольку он представляется
второстепенным в свете статистической трактовки межфазовой
области.
Во избежание всякой неясности приводимое здесь
рассмотрение сферической межфазовой границы
базируется не на оригинальном методе Гиббса, а на модификации
этого метода, данной Хиллом [7] и Кондо [8]. Этот
модифицированный метод, однако, неприменим к границам
несферической формы, в настоящей книге не рассматриваемым.
Хотя все соотношения для плоской границы можно
получить из соответствующих соотношений для сферической,
если положить кривизну равной нулю, все же плоский и
сферический случаи рассмотрены отдельно ввиду
практической важности и физической наглядности случая плоской
границы. Термодинамический метод определения
поверхностного натяжения, основанный на втором законе, удобен,
но применение его ограничено случаем систем, находящихся
в термодинамическом равновесии. Так как явление
поверхностного натяжения не ограничено одними лишь
равновесными системами, то будет описан также
гидростатический подход к теории поверхностного натяжения, который
применим и к системам, не находящимся в равновесии.
Кроме того, мы дадим краткое изложение необратимой
термодинамики поверхностных явлений и построим
квазитермодинамическую теорию как переходную форму от
макроскопической теории к молекулярной.
С другой стороны, для поверхностных явлений был
предложен ряд эмпирических формул. Некоторые из них будут
рассмотрены в связи с принципом соответственных
состояний. Принцип соответственных состояний выполняется
весьма точно в применении к поверхностному натяжению
простых молекул. Чрезвычайная полезность его становится
очевидной, когда этот принцип, модифицированный таким
образом, чтобы учесть квантовые эффекты, применяется
к поверхностному натяжению легких веществ. В
дальнейшем будет приведено также его статистико-механическое
развитие.
Общее описание макроскопических явлений с
молекулярной точки зрения дает статистическая механика. В
условиях термодинамического равновесия термодинамические
величины системы в принципе могут быть выражены в тер-

10
Введение
минах статистической термодинамики, основу которой
составляет связь между свободной энергией и
статистической суммой. Мы получим выражение для свободной энергии
в виде функции площади межфазовой границы, откуда
выводятся точные выражения, связывающие поверхностное
натяжение и другие поверхностные величины с
межмолекулярными потенциалами и молекулярными функциями
распределения. Будет изложен также метод большой
статистической суммы, поскольку он особенно удобен при
рассмотрении разбавленных растворов.
В случае поверхностного натяжения можно получить
те же самые результаты методом статистической
гидродинамики, исходя из прямой связи между тензором давления
и функциями распределения. Преимущество этого метода
состоит в том, что он применим к поверхностному
натяжению в системах, не находящихся в равновесии, поскольку
он не основан на условии равновесия. В настоящее
время в статистической механике бинарная функция
распределения в переходной области остается
неизвестной. Мы вынуждены вычислять поверхностное
натяжение на основании некоторых приближений для
функций распределения. Теоретические результаты
сравниваются с экспериментальными данными.
Другим характерным свойством межфазовой области
является физическая адсорбция. Адсорбированное
количество вещества определяется как поверхностная плотность
молекул, относимая к разделяющей поверхности. Эта
величина истолковывается на основе общего статистико-механи-
ческого рассмотрения.
Выражение для поверхностного натяжения, полученное
методами классической статистики, обобщается на случай
квантовой статистики.
Другой метод вычисления поверхностного натяжения
из межмолекулярного потенциала основан на некоторых
моделях жидкостей или растворов. В этой книге для
вычисления поверхностного натяжения использованы модель
свободного объема и дырочная модель. Результаты расчета
сравниваются с экспериментальными данными для чистых
жидкостей, регулярных растворов и атермических
растворов полимеров. Эти модели, однако, неприменимы к случаю
сферической поверхности раздела.

ТЕРМОДИНАМИКА
И КВАЗИТЕРМОДИНАМИКА

Глава I
ТЕРМОДИНАМИКА
§ 1. Термодинамические величины поверхностного слоя
1. Разделяющая поверхность. Рассмотрим систему,
состоящую из двух фаз, соприкасающихся в узкой
переходной зоне, которая может быть плоской или
искривленной. Следуя Гиббсу [4], представим себе
математическую поверхность, называемую разделяющей поверхностью,
фаза р
фаза а
Фиг. 1.
которая построена таким образом, чтобы точно разделить
две основные фазы. На протяжении всей книги мы будем
обозначать эти две фазы как а или (J соответственно, и любая
величина, относящаяся к одной из фаз, будет отличаться
верхним индексом а или (J. Нижний индекс i будет
использоваться для обозначения r-й молекулярной компоненты.
Вообще разделяющая поверхность выбирается таким
образом, чтобы она была нормальной к градиенту плотности
в переходной зоне и, следовательно, в случае плоской
границы она должна быть плоскостью. С чисто математической
точки зрения положение разделяющей поверхности оказы-

14 Часть I. Термодинамика и квазитермодинамика
вается достаточно произвольным, хотя обычно бывает
удобно выбирать ее внутри переходной зоны или очень
близко от нее. Использование разделяющей поверхности
имеет то преимущество, что позволяет нам рассматривать
межфазовый слой, без указаний на его толщину.
В качестве характерного примера рассмотрим
многокомпонентную систему, состоящую из раствора в контакте
с воздухом, в которой некоторые из компонент имеют
тенденцию к большему относительному содержанию в
межфазовой области, чем в объемных фазах. На первый взгляд
может показаться, что можно определить концентрацию
или адсорбированное количество любой из компонент в
переходном слое в точности так же, как в обычной
однородной фазе.
Однако в действительности адсорбированное
количество зависит от выбора двух границ, которые необходимы
для отделения переходного слоя как самостоятельной
подсистемы от двух соседних объемных фаз [5, 6]. Чтобы
снизить произвольность в выборе толщины слоя, можно
ввести вместо двух — только одну математическую
поверхность, т. е. разделяющую поверхность. Полезность ее
станет очевидной в этой книге.
Сделав некоторый определенный выбор разделяющей
поверхности, мы можем разделить весь объем V,
занимаемый системой, на два объема Vх и V^. Если разделяющая
поверхность выбрана, как обычно, лежащей в переходном
слое, то Vх содержит объемную фазу а вместе с частью
вещества переходной зоны, а Кр содержит объемную фазу Р
и остальную часть вещества переходной зоны.
Следуя Гиббсу [4], представим себе гипотетическую
систему, построенную из двух объемных фаз а и Р, которые
остаются строго однородными вплоть до определенной
выше разделяющей поверхности и имеют, следовательно,
объемы V* и Ур соответственно. Пусть Nf и Nf — числа
молекул 1-го сорта в упомянутых гипотетических фазах
аир. Именно, N* равно nf — числу молекул t-го сорта
в единице объема фазы а, умноженному на занимаемый
этой фазой объем Va, а Nf равно соответственно nfv^.
Необходимо отметить, что, вообще говоря, N£ — полное
число молекул i-го сорта в реальной системе — не обяза-

Гл. I. Термодинамика
15
тельно равно числу Nf -\-Nt для вышеупомянутой
гипотетической системы; однако его можно представить в форме
Ni = N? + Nf + Nl (1.1)
где N* можно рассматривать как добавку, связанную с
существованием в реальной системе межфазовой области.
В случае однокомпонентной системы мы можем выбрать
разделяющую поверхность таким образом, чтобы эта
добавка от межфазовой области обратилась в нуль. Эта
особая разделяющая поверхность играет важную роль
в теории поверхностного натяжения и называется
эквимолекулярной разделяющей поверхностью.
Необходимо отметить и подчеркнуть, что N] не всегда
можно называть числом молекул сорта t, адсорбированных
в межфазовой области, поскольку N* зависит от положения
искусственно вводимой разделяющей поверхности. Число
N* и всякую другую аналогичную величину мы будем
называть в этой книге поверхностной величиной и отмечать
верхним индексом s.
2. Вклад межфазового слоя в термодинамические
величины. Аналогично тому, как это было с числом
молекул, любое экстенсивное термодинамическое свойство
всей системы можно рассматривать относительно
произвольно выбранной разделяющей поверхности как сумму
трех вкладов: вклада фазы а, вклада фазы Р и вклада
межфазовой области. Например, свободную энергию Гельм-
гольца для всей системы можно записать как
F=Fa + F^ + Fs. (2.1)
Здесь Fa — свободная энергия объемной фазы а в случае,
когда последняя остается однородной вплоть до
разделяющей поверхности, F^ — аналогичным образом
определенная величина для объемной фазы р. Таким образом, Fa + F^
представляет собой свободную энергию гипотетической
системы, в которой интенсивные физические свойства
скачком изменяются на разделяющей поверхности от значений,
которые они имеют в объемной фазе а, до значений,
которые они принимают в объемной фазе р, a Fs есть вклад

16 Часть I. Термодинамика и квазитермодинамика
переходного слоя в действительную свободную энергию.
Так как полная свободная энергия двухфазной системы
вместе с межфазовой областью есть вполне определенная
величина, соотношение (2.1) можно рассматривать как
определение избыточной свободной энергии Fs.
Аналогичным образом, избыточные внутренняя
энергия Us и энтропия Ss определяются соответственно как
U= U*+U* +Usy (2.2)
S = Sa +S^ + SS. (2.3)
Используя соотношение F = U — TS и приведенные
выше определения, мы получаем
Fs= US-TS\ (2.4)
причем абсолютная температура Т предполагается
постоянной во всех частях системы.
§ 2. Плоская граница раздела]
3. Определение поверхностного натяжения. Пусть
двухфазная система, имеющая плоскую межфазовую
границу с площадью Л, заключена в сосуд, имеющий форму
прямоугольного параллелепипеда, одно ребро которого
направлено по нормали к границе (см. фиг. 1).
| Представим себе теперь, что площадь границы А
увеличилась на величину dA посредством обратимого
изотермического смещения боковых стенок сосуда. Если система
находится в гидростатическом равновесии при давлении р,
то работу, произведенную ею в описанном процессе, можно
подразделить на две части: работу pdV, затраченную на
увеличение объема dVt и избыточную работу, связанную
с увеличением площади границы на dA, которую мы
обозначим— «fdA. Тогда полная работа, совершенная системой
в этом процессе, равна pdV — ^dA. Сдвинем теперь
верхнюю и нижнюю крышки сосуда таким образом, чтобы
вернуть систему к ее первоначальному обт&му. Работа,
совершенная системой в таком процессе, равна — pdV. В конце
этих двух процессов система будет иметь те же давление,

Гл. 1. Термодинамика
17
состав и температуру, которые она имела первоначально.
Единственное изменение сводится к тому, что площадь
границы увеличилась на dA. Это означает, что работа,
совершенная системой, для того чтобы вызвать увеличение
площади границы на dA при постоянных объеме, давлении
и температуре, равна ^dA. Следовательно, у представляет
собой работу, совершаемую системой при единичном
увеличении площади поверхности раздела. Она называется
поверхностным натяжением. Это поверхностное натяжение
эквивалентно кратко рассмотренному во введении понятию,
определенному как сила, действующая поперек единицы
длины произвольной линии, лежащей на межфазовой
границе.
Таким образом, элементарную работу dW, производимую
системой при изменении ее объема и площади границы
соответственно на dV и dAy следует записать как
d\V = pdV — ydA. (3.1)
Это выражение можно рассматривать как определение
поверхностного натяжения у. Из (3.1) можно видеть, что в
случае плоской границы поверхностное натяжение не
зависит от положения разделяющей поверхности, поскольку
в этом случае изменения последней никак не влияют на
площадь границы.
Если бы величина поверхностного натяжения у,
определенная описанным способом, была отрицательной, то
работа, совершаемая системой при увеличении площади
границы раздела, оказалась бы положительной и, следовательно,
площадь поверхности раздела могла бы возрастать
спонтанно. Это означает, что плоская* поверхность раздела
устойчива только при положительных у. Поэтому величина
поверхностного натяжения, определенная выше, не может
быть отрицательной, точно так же, как не может быть
отрицательным давление в жидкости, определенное обычным
образом.
Внутренняя энергия U двухфазной системы также
изменяется с увеличением площади межфазовой границы. Если
количество теплоты, полученное системой в процессе
бесконечно малого возрастания площади границы dA,
обозначить dQ, то первый закон термодинамики записывается

18 Часть I. Термодинамика и квазитермодинамика
в форме
dQ =dU +pdV — ydA. (3.2)
Следует заметить, что равенство (3.2) справедливо и для
неравновесных систем до тех пор, пока они находятся в
механическом равновесии при постоянном давлении.
4. Поверхностная свободная энергия. Если система
находится в термодинамическом равновесии, то количество
тепла dQy поглощаемое в процессе обратимого изменения
состояния, согласно второму закону равно возрастанию
энтропии системы dS, умноженному на температуру Г.
Комбинируя это утверждение с первым законом (3.2),
получаем
dU = TdS — pdV + ydA. (4.1)
Это важное соотношение можно представить в более
удобной форме, используя выражение для свободной энергии
Гельмгольца:
dF = — pdV — SdT + ydA. (4.2)
В открытой системе, которая может обмениваться с
окружающей средой как веществом, так и энергией, число
молекул может изменяться и, следовательно, полный
дифференциал свободной энергии, даваемый выражением (4.2),
должен иметь дополнительный член, связанный с этим
изменением:
X
dF = — PdV — SdT + ydA + 2 fydNi, (4.3)
£=1
где х — число компонент, \i£ — химический потенциал,
рассчитанный на молекулу i-й компоненты, который
должен быть постоянным во всей системе, если она находится
в химическом равновесии. Фундаментальное уравнение
Гиббса (4.3) для двухфазной системы можно рассматривать
как уравнение, определяющее поверхностное натяжение у
в открытой системе.
Если известна свободная энергия F как функция
объема, температуры, площади границы раздела и чисел мо-

Гл. I. Термодинамика
19
лекул, то у можно легко вычислить из соотношения
H^V.v (4-4)
где символ N представляет набор чисел Nl9 N2, . . . , Nx.
Будем увеличивать объем двухфазной системы,
изображенной на фиг. 1, ограничиваясь при этом
термодинамически равновесным случаем и сохраняя температуру,
давление, состав и высоту сосуда неизменными. Тогда
величины F, V, N> А изменяются в одной и той же
пропорции. Таким образом, F есть однородная функция
первой степени переменных V, N и А, и, следовательно, по
теореме Эйлера мы получаем из (4.3)
X
F^^Ni-pV+yA. (4.5)
£=1
Для объемных фаз а и р
X
Fa = %PiN?-pV, (4.6)
^=2^-рКр. (4.7)
1=1
Вычитая (4.6) и (4.7) из (4.5) и используя раЕенстЕа (1.1)
(2.1) и условие аддитивности объемов, получаем
х
Fs= ^Nse + yA. (4.8)
/=1
В противоположность поверхностному натяжению у, такие
избыточные величины, как Fs, Us и N* зависят от
положения разделяющей поверхности. Если выбрать разде-
X
ляющую поверхность таким образом, чтобы сумма 2 Hv^
оказалась равной нулю, то (4.8) сведется к соотношению
Fs = yA. (4.9)

20 Часть I. Термодинамика и квазитермодинамика
В случае однокомпонентной системы выбранная таким
образом разделяющая поверхность становится идентичной
эквимолекулярной разделяющей поверхности, определение
которой мы дали в п. 1. Из (4.8) видно, что поверхностное
натяжение становится равным поверхностной плотности
свободной энергии только при таком специальном выборе
разделяющей поверхности [9, 10]. Следует заметить, что
поверхностное натяжение не есть ни внутренняя
энергия, ни потенциальная энергия единицы площади
поверхности.
Чтобы рассмотреть открытую систему, удобно ввести
полный термодинамический потенциал, определяемый
равенством [11—13]
х
Q = F— 2iVV,. (4.10)
/=i
Из (4.5) получаем тогда
Й = уЛ— pV, (4.11)
а из (4.3)
X
dQ = — 5 dT — pdV -4- ydA — 2 Nfat. (4.12)
Используя обозначение p. = \il9 jli2, . . .
посредственно получаем x
s = -(w) •
( dQ \
A/ . _ (dSl\
,|*K,
из (4.12) не-
(4.13)
(4.14)
(4.15)
Тогда из (4.10) и (4.13) следует соотношение
X
Q
2^Д-(/ = Г^(А). (4.16)
1 Везде в этой книге нижний индекс [i, используется для
указания, что все переменные \iv . . . , fx^, кроме \i£f удерживаются
постоянными.

Гл. I. Термодинамика
21
5. Термодинамические соотношения для плоской
границы. Фундаментальные уравнения Гиббса для объемных
фаз а и Р записываются следующим образом:
X
dF* = — pdVa — SadT +2 Ц/flV?, (5.1)
x
dF* = — pdV* — S^dT + 2 IV^V?. (5.2)
Вычитая (5.1) и (5.2) из (4.3) и используя (1.1), (2.1) и
(2.3), получаем соотношение
х
d/7s = _SS^Г + ydA + 2 iyW/. (5.3)
которое можно рассматривать как фундаментальное
уравнение Гиббса для межфазового слоя. Таким образом, мы
видим, что межфазовые термодинамические величины
связаны друг с другом таким же соотношением, как и в случае
обычной объемной фазы, и, следовательно, их можно
рассматривать так, как если бы они определяли некоторую
третью фазу.
Дифференцируя (4.8) и используя (5.3), мы приходим
к уравнению адсорбции Гиббса в его общей форме для
плоского межфазового слоя
х
Ady + Ss dT +2 ЛГ-ф. = 0. (5.4)
Так как N], Ss и Vs все пропорциональны площади А
границы, то удобно ввести следующие обозначения для
поверхностных плотностей этих величин:
(5.5)
(5.6)
(5.7)
Г/
сз
1)
=
=
=
щ
А
А
Us
А

22 Часть I. Термодинамика и квазитермодинамика
Поверхностные плотности энтропии а и внутренней энергии
v обычно называют поверхностной энтропией и
поверхностной энергией. Соответственно величину Г£ мы будем
называть поверхностной плотностью числа молекул
сорта i. Тогда (5.4) записывается как
dy + odT + 2 Г/ф. = 0, (5.8)
а (4.8) — как
г = г_аГ-2 1>.. (5.9)
Здесь использовано равенство (2.4).
Ограничимся теперь для простоты случаем, когда
каждая из компонент присутствует в заметном количестве
в обеих фазах. Более общий случай будет рассмотрен
позже, в п. 10. Определим молярную долю t-й компоненты как
N£
х< = -^-. (5.10)
i=i
Тогда температуру Т и молярные доли в фазе а х%, . . . ,#*
можно принять за полный набор х независимых
переменных, так как, согласно правилу фаз Гиббса, система,
состоящая из двух фаз и содержащая х компонент, имеет х
степеней свободы. Таким образом, мы можем записать
где sf и vf представляют собой соответственно парциальную
энтропию и парциальный объем на одну молекулу сорта /
в фазе а и определяются соотношениями г
s« = (^\ , *=(■*£-) . (5Л2)
См. примечание 1 на стр. 20.

Гл. I. Термодинамика
23
Используя (5.8) и (5.11), получаем
(*l--e+tr'(f-f(#U- (513)
Из (5.9) и (5.13) имеем
• - 1-Ч&1 + S r,(f, + П? - Tv- (£) ). (5.14)
Можно выбрать разделяющую поверхность так, что сумма
величин Vfti обратится в нуль. Обозначая поверхностную
плотность молекул i-ro сорта по отношению к выбранной
таким образом поверхности Г|и), имеем
х
2»"Г*о> = 0, (5.15)
а уравнение (5.14) в этом случае сводится к
*=y-T[w) +2^ГГ, (5.16)
где hf — парциальная энтальпия на молекулу сорта i
в фазе а.
Представляет особый интерес рассмотреть случай
чистых жидкостей. Если в качестве разделяющей поверхности
выбрана эквимолекулярная поверхность, то (5.13)
сводится к уравнению
w = -o, (5.m
а (5.14) — к уравнению Гиббса — Гельмгольда для
плоской границы
V = v-Tw> <5Л8>
или, в другой форме,
Необходимо подчеркнуть, что хотя Г/, v и а зависят
от выбора разделяющей поверхности, общая форма по-

24 Часть I. Термодинамика и квазитермодинамика
лученных до сих пор термодинамических уравнений, как
будет показано в следующем пункте, остается, за
исключением специальных случаев, таких, как (4.9), (5.16),
инвариантной относительно сдвига разделяющей
поверхности.
6. Адсорбция на плоской поверхности раздела.
Предположим, что фаза а представляет собой слабо летучий
раствор, пар которого образует фазу ($. Мы выберем
разделяющую поверхность таким образом, чтобы на ней
исчезала поверхностная плотность молекул растворителя.
Плотность частиц растворенного вещества в межфазовой
области может, вообще говоря, отличаться от ее значения
внутри каждой из объемных фаз.
Если некоторые из растворенных веществ плохо
растворимы, их концентрации вблизи поверхности будут
гораздо больше, чем внутри каждой из объемных фаз; другими
словами, они будут адсорбироваться на границе.
Очевидно, что тогда Г/ для каждого такого вещества будет
положительной и не малой величиной независимо от
расположения разделяющей поверхности и поэтому ее можно
рассматривать как меру адсорбции молекул *-го сорта. Следует
отметить, однако, что для сильно летучих или хорошо
растворимых веществ величины Г, существенно зависят
от выбора искусственно вводимой разделяющей
поверхности и могут в зависимости от этого выбора даже менять
знак.
Обсудим теперь, исходя из уравнения (5.8), адсорбцию
у плоской границы двух фаз, находящихся в
термодинамическом равновесии.
При постоянной температуре (5.8) сводится к
х
-^=2г,-ф.. (ел)
Это уравнение связывает поверхностное натяжение с
адсорбцией и играет фундаментальную роль в термодинамике
поверхностных слоев.
Поскольку Г/ зависят от выбора разделяющей
поверхности, то возможен и целесообразен такой выбор
последней, при котором поверхностная плотность одной из ком-

Гл. I. Термодинамика
25
понент, скажем первой, обращается в нуль. Мы будем
обозначать поверхностную плотность t-й компоненты,
определенную таким образом, через Г/1* для указания, что
выделенной здесь является компонента 1. Место (6.1) тогда
занимает соотношение
X
-dY = 2 г^ф,, (6.2)
которое хорошо известно как адсорбционная формула Гибб-
са [41.
Если плотность пара столь мала, что пар каждой из
компонент подчиняется закону идеального газа, то
химический потенциал задается соотношением
Ъ=% + кТ\прг (6.3)
где р. — парциальное давление пара i'-й компоненты и
Ф, — функция только температуры. Тогда (6.2) можно
переписать следующим образом:
X
— dy = kT% Tfd\npr (6.4)
z=2
Это уравнение показывает, что Г/х) должны быть
положительными или отрицательными в соответствии с тем,
уменьшается или возрастает наблюдаемое значение у, когда мы
увеличиваем концентрацию i-й компоненты внутри
жидкой фазы, оставляя другие компоненты при их заданных
концентрациях.
Покажем теперь, что правая часть (6.1) остается
неизменной при изменении выбора разделяющей поверхности
1141. Пусть nf и nf— плотности числа молекул сорта i
в объемных фазах аир соответственно. Рассмотрим две
произвольные разделяющие поверхности А и Л'; пусть
разделяющей поверхности А соответствует поверхностная
плотность Г/, а поверхности А' — плотность Г/. Тогда
из определения разделяющей поверхности ясно, что
tf = Г/-(я?-/!?) А', (6.5)

26 Часть I. Термодинамика и квазитермодинамика
где расстояние Д' между поверхностями Л к А'
положительно, если А' расположена ближе к фазе Р, чем А.
С другой стороны, при постоянной температуре для
объемных фаз а и Р имеют место известные уравнения
Гиббса—Дюгема, которые легко можно вывести из (4.6)
и (4.7), рассматривая их совместно с (5.1) и (5.2)
соответственно:
х
— dp + 2 л«ф/ = 0> (6.6)
X
-dp + 2 л?Ф/ = 0. (6.7)
/=i
Так как dp и d\i. в (6.6) должны равняться тем же
величинам в (6.7), когда фазы аир находятся в равновесии,
мы имеем
X
2(л?-л?)4ц,= 0. (6.8)
Используя (6.5) и (6.8), мы можем переписать (6.1) как
х
— <*у = 2Г)Фг (6.9)
Таким образом, инвариантность уравнения (6.1) по
отношению к сдвигу разделяющей поверхности доказана.
Весьма сходным образом можно доказать
инвариантность других соотношений — (5.3), (5.4), (5.9), (5.14) и
подобных им.
Исключая фх из (6.1) с помощью (6.8), мы имеем для
произвольной разделяющей поверхности
- dy = S (г, - г, 1^4) 4v (6.10)
Это выражение также инвариантно по отношению к сдвигу
разделяющей поверхности.
Введем обозначение
r^iv-rj-^jPr. (6-11)

Гл. L Термодинамика
27
Из (6.5) видно, что Г/i остается неизменным при смещении
разделяющей поверхности. Эта инвариантная величина
называется относительной адсорбцией [15]. Гиббс
обозначал эту величину через r[s).
Границу раздела фаз можно, следуя Гуггенгейму [5,6],
рассматривать как отдельный слой вещества конечной
толщины, ограниченный плоскостями К Н' и К"Н\
параллельными разделяющей поверхности КН (фиг. 2). Если
к'
фаза р
фаза <х
И
н"
Фиг. 2.
остальные части системы полностью однородны, так что
пространственное изменение термодинамических величин
ограничено поверхностной фазой, заключенной между К'Н'
и К"Н" и имеющей толщину А, то число молекул i-ro сорта
на единицу площади этой поверхностной фазы дается
соотношением
Г/ = Г, + Дв(л? - nf) + Aaz? , (6.12)
где Аа — расстояние между КН и К"Н\ Мы имеем, далее,
P/i= Г/-
.Г "' я"
«r«?-«i4e
"Г -А.
(6.13)
Если каждая из компонент имеет столь низкую плотность
пара, так, что можно пренебречь я? по сравнению с л?,

28 Часть I. Термодинамика и квазитермодинамика
то (6.13) сводится к
r^IV-f^-IV (6.14)
Отсюда видно, что, хотя 1\ и Г£ не определены точно,
пока не заданы точные положения обеих границ, Гц
практически инвариантно по отношению к их положению и
равно относительной адсорбции, определяемой соотношением
(6.11), до тех пор, пока указанное выше приближение
справедливо. Если фаза ($ подчиняется законам идеального
газа и, следовательно, справедливы приближенные
соотношения (6.3) и (6.14), то (6.10) упрощается:
-dY= ^2 (Г/-f^dlnp.. (6.15)
1=2 \ П1 '
Для двух компонентной системы (6.14) и (6.15)
записываются как
Г21^Г21^Г2-Г1Т^, (6.16)
-dY-Ar(r2-Tir^)dlnp2, (6.17)
где х = п\1(п\ + /г2).
Хотя величина Г,-, имеющая наглядный физический
смысл, более удобна, чем абстрактная величина Г/,
относящаяся к мнимой разделяющей поверхности, этот метод
оказывается неадекватным в применении к случаю
искривленной границы раздела.
Для некоторых целей может оказаться полезной
разделяющая поверхность, выбранная так, чтобы обращалась
в нуль сумма поверхностных плотностей числа частиц.
Мы обозначим поверхностные плотности при таком выборе
разделяющей поверхности через Г/^:
X
S Г^> = 0. (6.18)
i=i
Для системы, состоящей из двух компонент, (6.18) имеет
вид

Гл. I. Термодинамика
29
T[N) = -T{2
(6.19)
Мы уже пользовались величинами rf \ определенными
условием (5.15). Формула (6.18) представляет собой другой
пример конкретного выбора разделяющей поверхности.
§ 3. Сферическая граница раздела
7. Определение поверхностного натяжения. В этом
параграфе мы получим термодинамические соотношения для
сферической
поверхности раздела. Один из
самых известных
примеров сферической
границы — это случай капли
жидкости в
окружающем ее паре.
Рассмотрим
замкнутую систему, состоящую
из двух фаз,
разделенных сферическим
разделяющим слоем, т. е.
случай переходной зоны
постоянной кривизны.
Для удобства мы
рассмотрим ограниченную
часть системы,
заключенную в конический
сосуд, такой, как показано
на фиг. 3, где со и г
обозначают соответственно телесный угол конуса и
радиальную координату, отсчитанную от вершины
конуса О. Сосуд состоит из части конуса, заключенной между
г = #а и г = #э, где /?а < #э. Мы предполагаем, что
система состоит из х независимых компонент, внешние поля
отсутствуют и центр кривизны сферического
поверхностного слоя лежит в точке О. Тогда любое интенсивное
свойство системы может зависеть только от г. Так
называемые внутреннюю и внешнюю фазы мы будем обозначать
соответственно как аир.

30 Часть I. Термодинамика и квазитермодинамика
Выберем в качестве разделяющей поверхности сферу
г =а. Она разделит полный объем V на два объема V* и
К3, равные соответственно
V = 4-®{fl3-(*e)8>, (7.1)
V*= А-© {(/?*)» — а3}- (7.2)
Площадь разделяющей поверхности будет равна
А =ш\ (7.3)
В противоположность случаю плоской границы ра —
давление во внутренней фазе а не может равняться р& —
давлению во внешней фазе р, пока система находится в
механическом равновесии. В этом пункте температура не
предполагается постоянной. Единственное ограничение
состоит в том, что ра и р& постоянны внутри объемных фаз
аир. Надо заметить, однако, что излагаемый метод нельзя
применить к случаю сферических капель, настолько
малых, что однородных свойств невозможно достичь даже
в центре фазы а.
Представим себе, что телесный угол со увеличивается
на dco путем обратимого изотермического смещения боковой
стенки, причем все остальные переменные остаются
неизменными. Работа, производимая системой в этом процессе,
пропорциональна dco и может быть записана как — rjdo).
Так же, как и в плоском случае, эту работу можно
рассматривать как состоящую из двух частей: работы padl/a +
+ рЫУ^, связанной с изменением объемов двух
однородных объемных фаз, и избыточной работы, которую мы
обозначим через —ydA. Таким образом, можно записать,
что
dW = — r\d(D = p«dVa + pW* — ydA. (7.4)
С чисто математической точки зрения можно сказать, что
— ydA представляет собой просто поправочный член,
введенный для того, чтобы сумма давала полную работу dW,
которая является полностью определенной величиной,
содержащей, кроме вкладов от однородных частей в фа-

Гл. I. Термодинамика
Si
зах а и Р, сложные эффекты, возникающие в результате
присутствия поверхностного слоя. Коэффициент у можно
рассматривать, однако, как совершенную над системой
работу, связанную с единичным приращением площади
разделяющей поверхности при данной кривизне. Это
позволяет рассматривать действительную систему как если
бы она состояла из двух однородных фаз, аир,
разделенных сферической пленкой нулевой толщины, с радиусом а
и однородным по всем направлениям натяжением у. Тогда
естественно принять у» определяемое согласно (7.4),
за поверхностное натяжение сферической границы.
Используя (7.1) —(7.3), получаем из (7.4) [8]
где
К = л + 4" (Я3)3 ^ —г(/Г)3 Р*' (7*6)
Величина К не зависит от выбора разделяющей
поверхности. Поэтому, согласно (7.5), поверхностное натяжение,
определяемое (7.4), в отличие от плоского случая, зависит
от выбора разделяющей поверхности.
Используя (7.1) —(7.3) и (7.6), равенство (7.5) можно
переписать в альтернативной форме:
г)со = ГА — paVa — р№. (7.7)
Дифференцируя (7.5) по я, получаем [81
Здесь [ду/да] da есть изменение величины поверхностного
натяжения, связанное с математическим смещением
разделяющей поверхности на da при условии, что все
физические величины внутри системы и внешние условия
остаются неизменными х. Это изменение величины
поверхностного натяжения связано просто с произвольностью в вы-
1 Обозначение [ду/да] следует отличать от производной по
действительной зависимости от радиуса, которая будет записываться как
ду/да.

32 Часть /. Термодинамика и квазитермодинамика
боре разделяющей поверхности, и его не следует смешивать
с изменением у от увеличения радиуса физической
поверхности разрыва. Как мы увидим позже, производная [ду/да]
играет важную роль в термодинамике сферической
поверхности раздела.
Так как произведенная системой работа, связанная
с изменением dRa и dR^, равна —расо (Ra)2dRa +
+ р3о) (R^)2 dR^ , общее выражение для элементарной
работы dW вместо (7.4) должно быть записано в форме
dW = — г]Жо + /Л) (У?3)2 dR* — р* со (7?а)2 d7?a. (7.9)
Каждый из членов в правой части (7.9) не зависит от
выбора разделяющей поверхности. Из формул (7.1) — (7.3)
получаем
dV* - ^ {a3 — Ю3} + <*>a2 da —со (#a)2 dR\ (7.10)
d,4 = a2 dco -f 2coada. (7.12)
Затем, решая эти уравнения относительно dRa, dR и dco,
подставляя результат в (7.9) и используя (7.1) — (7.3) и
(7.7), получаем
dW = padl/a + p^dl/3— ydA — {(pa — pt)— ^J^da.(7.13)
Последний член в правой части этого уравнения играет
важную роль в термодинамике сферической поверхности
раздела.
Используя (7.8), можно переписать (7.13) в более
наглядной форме:
dW = padV* + p*dV* — ydA — [ЩА(1а. (7.14)
Нетрудно показать, что (7.14) остается неизменным
при бесконечно малом нефизическом изменении
dVa = — dl/* = A da, dA = 2Л ^-, (7.15)
возникающем при чисто математическом смещении
положения разделяющей поверхности.

Гл. I. Термодинамика
33
Рассмотрим теперь изменение не только со, Ra и /? ,
но и других переменных состояния. Даже в этом общем
случае уравнение (7.14) остается справедливым. Поэтому,
если обозначить через dQ тепло, полученное системой,
а через dU — изменение ее внутренней энергии в ходе
этого процесса, то выражение первого закона
термодинамики приобретает следующую форму:
dU = dQ—padVa — p^dV^ + rdA+Up*— р^)—^}Ada.
(7.16)
Следует заметить, что это уравнение справедливо
также и для систем, не находящихся в термодинамическом
равновесии, коль скоро значения ра и р& для них
полностью определены.
8. Поверхность натяжения. Как уже отмечалось во
введении, условие механического равновесия системы,
состоящей из двух фаз а и Р, разделенных сферической
мембраной радиуса а и имеющей однородное натяжение у,
приводит к известному соотношению Кельвина (0.1). С
другой стороны, мы имеем соотношение (7.8), которое
применимо к любой системе со сферической межфазовой границей.
Выберем теперь разделяющую поверхность так, чтобы
исчезала производная [ду/да], отмечая величины,
связанные с таким выбором, индексом s. Радиус этой
разделяющей поверхности, as, определяется из соотношения [8]
[£Ц-°- <8Л>
Таким образом выбранная разделяющая поверхность
оказывается одной из наиболее важных, так как только для
такой поверхности из (7.8) следует простая форма
соотношения Кельвина (0.1):
Ра - ** = 1П • <8-2>
us
Согласно Гиббсу [41, эта особая разделяющая поверхность
называется поверхностью натяжения. Согласие между (8.2)
и соотношением Кельвина означает, что механическое

34 Часть I. Термодинамика и квазитермодинамика
действие реальной сферической границы, имеющей
сложную структуру, можно заменить действием простой
гибкой пленки, расположение которой совпадает с
положением поверхности натяжения, имеющей нулевую
толщину и натяжение у, одинаковое по всем направлениям [4, 16].
Подстановка (7.5) в (8.2) приводит к соотношению
Используя его, мы можем исключить К из (7.5) и
получить [8]
Л 2Tsa
г = °# + -357- <8'4>
Так как значения поверхностного натяжения всегда
положительны, то из (8.4) легко видеть, что у достигает
своего минимального значения ys при а = as. Мы можем
заключить поэтому, что до тех пор, пока as велико по
сравнению с толщиной переходного слоя, все значения у,
относящиеся к тем разделяющим поверхностям, которые
находятся внутри или вблизи этого слоя [можно ожидать,
что в нем лежит и поверхность натяжения (см. п. 37, 38)],
почти равны * минимальному значению ys [8]. Это
означает, что с макроскопической точки зрения поверхность
натяжения можно рассматривать как практически
независящую от положения разделяющей поверхности до тех
пор, пока последняя лежит внутри поверхностного слоя
(кроме случая капель и пузырьков, столь малых, что их
радиусы сравнимы с толщиной поверхностного слоя).
Таким образом, физическое поверхностное натяжение в
случае сферической границы можно полностью определить
посредством такого у.
Наконец, мы должны подчеркнуть, что полученные
в этом пункте соотношения справедливы и для систем,
не находящихся в равновесии.
1 Из (8.4) легко видеть, что
( (а — а)3 (а — а s\\

Гл. I. Термодинамика
35
9. Фундаментальные термодинамические уравнения для
сферической границы [7, 8]. Количество тепла dQ,
полученное системой в процессе обратимого превращения,
равно TdS, где dS — возрастание энтропии. Поэтому
уравнение (7.16) приводится к виду
dU = TdS — padVa — pPdV* +rdA +
+ {(p«-pt)-lf\Ada. (9.1)
Тогда изменение свободной энергии Гельмгольца по ее
определению дается следующим выражением:
dF = — PadVa — p*dV* —SdT + rdA +
+ {(Pa-P&)-^\Ada. (9.2)
1 Здесь надо отметить, что в противоположность (7.16)
выражения (9.1) и (9.2) справедливы только для
систем, находящихся в термодинамическом равновесии.
Условие химического равновесия гласит: \if = \if = \ii
(i = 1, 2, 3, . . . , >c, где >c — число независимых
компонент).
В случае открытой системы свободная энергия вместо
(9.2) дается соотношением [7]
dF = — padVa — pPdV* —SdT + rdA +
+ {(Pa - Pp) - Ц] A da + J frdNi. (9.3)
Пользуясь (7.8), можно переписать (9.3) следующим
образом [8]:
dF = — p«dVCL—ptdV('—SdT+ rdA +
+ [*L]Ada+ j^vadNt. (9.4)
/=i
Таким же путем мы получаем фундаментальное
уравнение для изменения внутренней энергии

36 Часть I. Термодинамика и квазитермодинамика
dU = TdS— p«dVa — pW3 + ydA +
+ [*L]Ada+%liidNt. (9-5)
*=1
Подставляя (7.10), (7.11) и (7.12) в (9.3) и используя
(7.6) и (7.8), получаем [7]
dF = T|£fa + paG) (Ra)2 dR« — /Л) (R*)2 dR* —
-SdT+ %]ndNl9 (9.6)
откуда непосредственно находим [7]
Ч = (-?") • (9.7)
Это выражение представляет собой определение величины
т), основанное на втором законе.
Так как F — однородная функция первого порядка
относительно Nlf N2, . . . , NK и о), то из (9.6) по теореме
Эйлера получаем
X
F = 2 Mf/ + г)0). (9.8)
Подстановка (7.7) в (9.8) приводит к соотношению
F = J] |i/tf/ - РаГ - /Wp + г А, (9.9)
г=1
которое можно рассматривать как уравнение,
определяющее поверхностное натяжение у для системы, находящейся
в термодинамическом равновесии.
Из (9.9) мы получаем также
U = 2 yuNt + TS — pal/a — р^И + гА. (9.10)

Гл. I. Термодинамика
37
10. Термодинамические соотношения между
избыточными величинами сферической границы. Так же, как
и в случае плоской поверхности раздела,5 для
объемных фаз а и Р, находящихся в термодинамическом
равновесии, имеют место уравнения
Fa = -paVa+ 2Mff, (ЮЛ)
г=1
F* = _p»V*+2|i/JV?. (Ю-2)
Вычитая эти уравнения из (9.9) и пользуясь (1.1) и (2.1),
мы приходим к следующему соотношению для избыточной
свободной энергии Fs:
Fs= 2^ + тЛ. <10-3)
Если разделяющая поверхность выбрана так, что сумма
х
2 PiN* обращается в нуль, то (10.3) сводится к равенству
г=1
Fs = rA. (10.4)
Отсюда следует, что поверхностное натяжение на
сферической границе равно избыточной свободной энергии,
приходящейся на единицу площади разделяющей поверхности,
если последняя выбрана таким образом, чтобы обращалась
х
в нуль 2 PiN*. Напомним, однако, что в случае любой
другой разделяющей поверхности у уже не равно
избыточной свободной энергии.
Изменения величин Fa и F^ даются соотношениями
dF« = — padVa — SadT + 2 \iidN«, (10.5)
/=i
dF* = — p4v* — S*dT+ 2 pidN*. (10.6)

38 Часть I. Термодинамика и квазитермодинамика
Вычитая оба эти уравнения из (9.4), получаем
х
dFs = — SsdT + г dA + ^ \И<Ш*£+ [|Пл da. (10.7)
Дифференцируя (10.3) и комбинируя с (10.7), мы
приходим к соотношению Гиббса — Дюгема для сферической
границы между фазами:
Adr+SsdT+ ^NidvLi = [^]Ada9 (10.8)
или через поверхностные величины, определяемые
соотношениями (5.5) и (5.6) [8,12]:
dr + odT + 2 Г,ф, = [|I] da. (10.9)
Это выражение представляет собой обобщение
адсорбционной формулы Гиббса; оно отличается от адсорбционного
уравнения (5.8) для плоской поверхности раздела лишь
тем, что в нем появляется член [ду/да] da.
Следуя Кенигу [17], мы теперь разделим все
компоненты на три класса, которые будем называть классами 1,
2 и 3 соответственно, и определим их следующим образом:
класс 1 —компоненты,присутствующие в заметном
количестве в обеих фазах; класс 2 — компоненты,присутствующие
в заметном количестве лишь в фазе а; класс 3 —
компоненты, присутствующие в заметном количестве только в фазе
р. Будем обозначать число компонент в классе 1 через к\
в классе 2 — через х" и в классе 3 — через и'", а число
компонент, присутствующих в заметном количестве в
фазах аир, через >са и *ср соответственно. Тогда имеют место
соотношения
к = к' + х" + х"\ х* = х/ + х% к£ = к' + к". (10.10)
В качестве примера рассмотрим водный раствор
нелетучих солей, находящийся в контакте с воздухом. Здесь
вода принадлежит к классу 1, а соли — к классу 2. Если
бы межфазовая граница в нашей системе удерживалась

Гл. I. Термодинамика
39
плоской, то, согласно обычному правилу фаз, число
степеней свободы было бы равно х. Отступление от этого
ограничения, очевидно, увеличивает число степеней
свободы на единицу. Таким образом, для полного определения
каждой из интенсивных переменных системы необходимо и
достаточно иметь х + 1 независимых интенсивных
переменных [17]. Обозначим молярную долю i-й компоненты
через Хс. Тогда имеют место следующие ограничения:
yOL yt у"
i=i <=i «=i (10.11)
2 4 = 2 *? + 2 x? = i.
/=i /=i /=i
JT1.3 \А,^ , . . . , Л,^, , А,^ , . . . , Л^, , Л^ , . . . , Л^„ ,
x"Q, . . . , л£,'й) можно выбрать большое число
комбинаций х — 1 независимых переменных. Так, мы можем
принять за полный набор независимых переменных (а, Т, ха, ...
. . . , л£а, л^'Р, . . . , •*£,'?,), который будем называть
набором Л. Радиус разделяющей поверхности можно выбрать
за независимую переменную, если условие для
разделяющей поверхности фиксировано. Кроме того, нам
понадобятся три вспомогательных набора независимых
переменных: набор I — (ра, 7\ х% , . . . , *«а, а", . . . , л£„);
набор II — (ра, Г, *j, . . . , х?а) и набор III —(/Л Г, *£,...
. . . , л£р). Частные производные, соответствующие
набору А, мы будем записывать без индексов, а
соответствующие наборам I — III будем отмечать индексами I — III
соответственно. Тогда мы имеем [см. (5.12)]:
фа = _sadT + v«dp* + 2 у— j dXf(i =1,2,..., Х«),
(10.12)
Ф7р = -^ЛГ+^рЗ + 2 (-^г) d*?(*=l,2,...,x''').
(10.13)

40 Часть I. Термодинамика и квазитермодинамика
Таким образом, при заданном составе системы в
переменных набора Л получаем [17]
d\i* = — s« dT + vf dp", (10.14)
ф;э = — s;p dT + \v"!t l^r\ + wmA dp", (10.15)
где
^|Щ„Щ- (10Л6)
Следовательно, мы можем переписать (10.9) в удобной
форме (см. [17]):
dr = (2sa -а) ОТ- 2,a dp- + [-g-] da, (10.17)
(x% , . . . , хГт — постоянные),
где
V /« i ^Л r>" "a
2sa = 2 r<s'e + 2 r'*e + S W, (I0-18)
x" x'"
2.a =
/=1 /=1
H-SW+S^+Srrx
X
{°"э (■^■)I+<"} • (laI9)
Из (10.17) мы можем получить следующее выражение для
температурной зависимости поверхностного натяжения:
S—+si4<--?(£)}+
+1г" {sr$ - [»;• - Щ + <р] (£■)} • (Ю.20)

Гл. I. Термодинамика
41
С другой стороны, из (2.4) и (10.3) легко получаем
Us = 2МЯ +TSs + rAf (10.21)
г=1
или, вводя поверхностные плотности, определенные
согласно (5.5), (5.6) и (5.7),
v = |j [х,Г, + оТ + г- (Ю.22)
Используя (10.20), мы можем исключить о из (10.22) и
в результате получить
« = г -т{&) + 2 г; [к« + г {*;«- er-(^.)}1 +
+ |г;[,;- + г{5;.-0;.(^)}]+
+ s г; [*-.+ t{s7- (^ (£) + <) (£)}].
г=1
(10.23)
Если положить х" = у!" = 0, как в п. 5, то (10.20) и
(10.23) станут по форме идентичными (5.13) и (5.14)
соответственно.
Мы выберем разделяющую поверхность таким образом,
чтобы исчезала 2о(Х, определяемая равенством (10.19),
и обозначим значения величин Гг-, у, а и v, относящиеся
к этой поверхности, через Г/0), fV9 ov и vv соответственно.
Условие, определяющее разделяющую поверхность, имеет
вид
20в=2гГ»?+згГ»;* +
+ | Г?>'" («^ ^ + ар) = 0, (10.24)

42 Часть I. Термодинамика и квазитермодинамика
т. е. представляет собой обобщение условия (5.15). Тогда
(10.20) и (10.23) сводятся соответственно к
^ = - бо + 2 гГ rf" + 2 гГ*' + 2гГ*"э.
/=1 Л=1 »=1
(10.25)
* = т.-г(^)+2г№ +
х" X7'
+ 2 гГА? + 2 Wh?, (10.26)
г=1 г=1
где ht — парциальная энтальпия, рассчитанная на одну
молекулу сорта L
В случае чистых жидкостей, если в качестве
разделяющей выбрать эквимолекулярную поверхность, (10.20) и
(10.23) принимают соответственно вид
%г = - о0 (10.27)
и
vv = -T^[^-). (10.28)
Эти выражения идентичны по форме с (5.17) и (5.19).
11. Зависимость поверхностного натяжения от
кривизны. Рассмотрим специальный случай разделяющей
поверхности, определяемой условием (10.24). В этом случае из
(10.17) легко получить [8]
Подчеркнем, что d^Jdav означает отношение
приращения поверхностного натяжения к приращению
действительного радиуса капли или пузырька. С другой стороны,
введенная в п. 7 величина [ду/да] означает* отношение
1 См. примечание 1 на стр. 31.

Гл. I. Термодинамика
43
изменения поверхностного натяжения к нефизическому
изменению в выборе радиуса разделяющей поверхности.
Таким образом, из (11.1) следует, что только для
разделяющей поверхности, выбранной так, что 2уа = 0, скорость
изменения поверхностного натяжения, соответствующая
действительному изменению радиуса капли или пузырька
(связанному с некоторым изменением ра и рр),
оказывается совпадающей со скоростью изменения, обусловленного
искусственным смещением разделяющей поверхности
(которое не приводит ни к каким изменениям физического
состояния системы).
С другой стороны, дифференцирование (8.4) дает
3
откуда непосредственно следует, что
[
дГЛ = 2 4s(av-as)
да1а=а„ " а* а
vus
(11.3)
dTt, ^ 1 ag + 2ag dys 2 og —ag да, 2 <% — $
да,, 3 а*п да,, + 3 Ts „г „а да,, + 3 Ts „з„
avas "«„ •> а^а$ "«v J a^,as
(11.4)
В согласии с (11.1) мы приравниваем (11.3) и (11.4) и
получаем
as dys 2(asv-ass)
Ts das a3s + 2al
(11.5)
Подставляя (11.3) в (11.1) и учитывая (8.4), можно легко
получить равенство
(и.б)
Ъ„
д%
2 У5(а1-аЬ
3 alas
zyv(4-4)
< + 2al

44 Часть I. Термодинамика и квазитермодинамика
Наконец, комбинируя (11.3) и (11.5) с (11.6), мы приходим
[8] к уравнению Гиббса — Толмена — Кенига — Баффа
[4, 17-19]:
6 1 / 6 \2"
га in г]
\_д In а\а
dlnyv ainTs 2[as JL1 + as + 3 { as ,
д In av d\n as
где
(11.7)
6 = av — as. (11.8)
Если условие выбора разделяющей поверхности
фиксировано, то, как установлено в п. 10, радиус
разделяющей поверхности можно выбрать в качестве
независимой переменной состояния. Таким образом, as или av
в написанных уравнениях следует рассматривать как
переменные состояния [17]. В тех случаях, когда as служит
мерой действительного радиуса капли или пузырька, мы
часто вместо as будем использовать обычный символ R.
Тогда интегрирование (11.7) приводит к искомому
выражению для зависимости поверхностного натяжения от
кривизны [18]:
R 2б L , 8 , 1 / б \21
где Хоо — поверхностное натяжение для плоской
поверхности.
Вполне разумно принять предположение, что и
поверхность натяжения, и разделяющая поверхность, выбранная
согласно (10.24), лежат внутри или очень близко к
межфазовому слою, и, следовательно, б составляет самое
большее величину порядка А-толщины межфазового слоя.
Если ограничиться рассмотрением капель или пузырьков,
радиус которых R велик по сравнению с А, то б можно
приближенно считать постоянной и равной боо-значению
на плоской границе. Тогда интегрирование в (11.9) легко
выполняется, и мы имеем

Гл. I. Термодинамика
45
Ts (Я) = Ц1-^ +.-.)> (НЛО)
а из (11.7) аналогичным образом следует, что
Y„(S-)=Yco(l-^f +■•■). (П.П)
где Rv использовано вместо av. Как легко видеть из (10.24),
Rv соответствует радиусу эквимолекулярной разделяющей
поверхности для случая чистых жидкостей.
Из (11.8) и (11.7) или (11.10) очевидно, что
поверхностное натяжение уменьшается или возрастает с
уменьшением радиуса капли или пузырька соответственно тому,
больше aVf чем as, или меньше, причем относительное
изменение составляет величину порядка 2боо/#.
Относительно знака и величины б = av — as нет
никаких экспериментальных сведений, но основанные на
статистической механике приближенные вычисления для
жидкого аргона (они будут описаны в п. 37, 38) показывают,
что б должна быть величиной порядка 3 А, причем в
случае жидкой капли — положительной. Таким образом,
приняв значение б = 3 А, мы можем ожидать, что
поверхностное натяжение на сферической границе радиусом
в 100 А будет для капли на 6% меньше, а для пузырька —
больше, чем на плоской границе.
Табл. 1 содержит значения у/Тоо» вычисленные из (11.9)
в предположении, что б — постоянная [18].
Таблица 1
Изменение поверхностного натяжения с
радиусом кривизны R поверхности натяжения
(по Толмену [17])
8/R
0,00
0,01
0,02
0,05
0,10
V^co
1,00
0,98
0,96
0,91
0,83
S/R
0,20
0,30
0,40
0,50
0,60
V^oo
0,70
0,60
0,52
0,46
0,41
S/R
0,70
0,80
0,90
1,00
V^oo
0,36
0,33
0,30
0,28

46 Часть I. Термодинамика и квазитермодинамика
12. Давление пара и работа образования капли и
пузырька. Рассмотрим жидкую фазу в равновесии со своей
парообразной фазой. Если эти две фазы разделены
плоской границей, то давление ра фазы а и давление рр фазы
Р оба равны обычному давлению пара, которое мы
обозначим р°°. Однако в случае сферической границы, согласно
соотношению Кельвина (0.1), давления ра и рр не могут
быть одинаковыми, и, следовательно, давление пара
должно зависеть от кривизны границы.
Нам предстоит теперь исследовать эту зависимость
давления пара от кривизны. Из соображений простоты
ограничимся случаем, когда все к компонент присутствуют
в заметном количестве в обеих фазах. При фиксированной
температуре и составе фазы а мы получаем из (10.12)
dpf = vfdp*. (12.1)
Если внутренняя фаза а представляет собой жидкость,
а внешняя фаза (J — пар, который можно считать
идеальным газом, то химический потенциал i-й компоненты
дается выражением
fxf = ср. + kT In pf, (12.2)
где р? — парциальное давление i-й компоненты и ц>. —
функция только температуры.
Так как для системы, находящейся в равновесии,
^а = jxP, мы получаем из (12.1) и (12.2)
dp?
vfdp* = kT-^-. (12.3)
Предполагая, что жидкость несжимаема, можно
проинтегрировать обе части (12.3) по ра и получить
v*{p*_p™) = kT\n^, (12.4)
где pf — парциальное давление i-й компоненты в случае
плоской границы между фазами.

Гл. /. Термодинамика
47
Если исключить ра из (12.4), используя (7.8), то
получим соотношение
^+[£]-tinf-<'e-"">- <12-5»
Так как l/v& значительно меньше, чем l/va, то при
температурах заметно ниже критической можно пренебречь
(kT/vP) In (рР/р°°) в сравнении с (kT/vf) In {p^lpf). Тогда
с помощью равенства v& = kTlp$ можно переписать (12.5)
в виде соотношения
которое идентично формуле Гуггенгейма [20], если не
считать малой поправки [ду/да]. Для чистых жидкостей эта
формула сводится к обобщенной формуле Гиббса — Том-
сона
которая связывает радиус жидкой капли с давлением
насыщенного пара в случае однокомпонентной системы.
Принимая R и Rv за радиусы поверхности натяжения и
разделяющей поверхности, определяемой условием (10.24),
и используя (8.1) и (11.1), мы можем переписать (12.7)
следующим образом [19]:
рЭ 2v«ys v* /2т, dyv\
Таким же путем получаем обобщенную формулу
Гиббса — Томсона в случае пузырьков:
ln ^ = ~wi = -w[r; + Wj (пузырек), (12.9)
где предполагается, что внутренняя фаза а представляет
собой идеальный газ.
Теперь рассмотрим работу образования капли из боль-

48 Часть I. Термодинамика и квазитермодинамика
шого количества пара при данной температуре. Согласно
(9.10), внутренняя энергия двухфазной системы равна
U = |] VL£Ni +TS— раУ* — р^ + уА. (12.10)
Предположим, что вначале рассматриваемая система
состояла из однородной парообразной фазы и имела то же
самое число молекул каждого сорта, объем и энтропию,
что и вся система в конечном состоянии. Тогда внутренняя
энергия исходной системы равна
х
(/° = 2 № + T°s — p°v> (12-1 *)
1=1
где предполагается, что V = Va +V^. В общем случае
химический потенциал fx°, температура Т° и давление р°
могут отличаться от соответствующих величин \ip Т и р&
в парообразной фазе Р, имеющей число молекул Nf,
энтропию 5Э и объем Vp в конечном состоянии.
Если Va достаточно мало по сравнению с V, то можно
пренебречь членами, квадратичными по (Nf—Nj)9 (5Э—S)
и (Кэ—V); тогда получаем
+ (fX. » <S*"S) + (ж)1. „С'-"). (12.13)

Гл. I. Термодинамика
49
где индекс 0 означает, что производные взяты в начальном
состоянии системы х.
С другой стороны, мы имеем термодинамические
соотношения:
\W)v.s.«r^'v.s.^ <12'15)
(^L.„r(S')vv <12лв>
($),...».--($)..»■ (Ш7>
(ж),„= -(*),„■ с2-18»
Так как в однородной фазе fx/, Тир суть однородные
функции нулевой степени по V, Nt и 5, то, используя
(12.15) — (12.18), получаем
2 Ц)„. s, „„"' + [щ)г, s, „/ - (щ)к s, „sv =
= ,|(a^),,„/' + (S),„S + (l'),/=0-'12-19>
-1Щ,,.„*< + (Si, »* + (жк „^ = 0. «2.20)
" i(£),„*<+(*),„Mf),/=
— 2 (ft), , „.MSI »M£), /-°-<'2-21)
Если пренебречь квадратичными членами, то можно, ис-
1 См. примечание 1 на стр. 20.

50 Часть I. Термодинамика и квазитермодинамика
пользуя эти соотношения, переписать (12.11) в виде
[/о = ^ ^ +TS- p*V. (12.22)
Интересно заметить, что сами разностиN.\x.—7У.[а°?
TS—T°S и p°V — p$V могут и не быть пренебрежимо
малыми.
Сравнивая (12.10) с (12.22), мы без труда находим
увеличение внутренней энергии замкнутой системы при
постоянных объеме и энтропии, вызванное образованием
капли:
W = U — UQ = гА — (ра — р3) V*. (12.23)
Можно доказать, что если вместо энтропии постоянной
поддерживать температуру, то работа образования капли
равна приращению свободной энергии. В случае
сферических капель работа их образования, согласно (12.23),
выражается как
W = 4яа2Т — ^ (ра — рр). (12.24)
Используя (7.5) или (7.8), это уравнение можно
переписать в виде
или
W =4п/С, (12.25)
»-*?('-в (,2-2б)
Из (12.25) мы устанавливаем, что константа /С,
определяемая соотношением (7.6), равна работе по образованию
. капли, деленной на 4я.
Если выбрать в качестве разделяющей поверхности
поверхность натяжения с радиусом R, то при учете (8.1)
уравнение (12.26) принимает простую форму:
W = ^ = ^. (12.27)
Работа образования капли играет важную роль в
теории образования центров конденсации в пересыщенном
паре, детали которой выходят за рамки настоящей книги.

Гл. I. Термодинамика
51
Необходимо заметить, однако, что число молекул,
содержащихся в капле чистой жидкости, определяется вместо
4я/?3/3аа выражением 47tRl/3va, где Rv — радиус
эквимолекулярной разделяющей поверхности. Используя (11.1),
можно переписать (12.26) в виде [19]
где д In^Jd \п Rv дается соотношением (11.7).

Глава II
ГИДРОСТАТИЧЕСКИЙ ПОДХОД
13. Механическое определение поверхностного
натяжения в случае плоской границы раздела. Как отмечалось
выше, физическая граница раздела фаз представляет собой
не геометрическую поверхность нулевой толщины, а
переходный слой, толщина которого конечна. Так как
плотность в переходной зоне заметно изменяется в
направлении, нормальном к границе раздела, внутри этой зоны
тензор давления, определенный в гидростатическом
смысле, также может изменяться, обращаясь в изотропное
и постоянное гидростатическое давление внутри каждой
фазы.
Введем прямоугольную систему координат (х, у, z) с
осью г, направленной по нормали к плоской границе
раздела от фазы а к фазе р, и плоскостью ху, лежащей в
межфазовом слое.
Во всякой однородной фазе давление изотропно, т. е.
сила, действующая на единичную площадку, нормальна
к ней и одинакова при всех ориентациях площадки.
Следовательно, внутри каждой из однородных фаз а или Р
тензор давления р сводится к гидростатическому
давлению р, умноженному на единичный тензор 1:
Р = РЬ Рхх = Руу = Ргг = Р>
РХу = Руг = Р2Х = О' (13Л)
Внутри межфазового слоя сила, действующая по
нормали к единичной площадке, не одна и та же во всех
направлениях. Однако из требований симметрии легко
видеть, что в плоском случае даже в межфазовом слое рху,
Руг' Ргх Должны исчезать, а рхх и р должны быть равными
друг другу и не зависеть ни от х ни от у. Удобно поэтому

Гл. II. Гидростатический подход 53
ввести обозначения рТ {г) и pN (z), которые мы будем
называть тангенциальной и нормальной составляющими
тензора давления в точке г\
Р = Рт (z) (*А + VP +pN (z) ezez> Pn (z) = P> (13*2)
где ex, ey и ez — единичные векторы, направленные вдоль
координатных осей. Тангенциальная составляющая рт
может изменяться сложным образом в зависимости от z,
тогда как pN по условию гидростатического равновесия
должно равняться р даже в переходной зоне.
Выберем площадку в форме полоски, имеющей
единичную ширину в ^-направлении и простирающейся от —1/2
до 1/2 в z-направлении. Очевидно, что полное напряжение
AS*, действующее в направлении оси х через эту
площадку, можно записать как
1/2
AZ, = - \ рт (г) dz. (13.3)
-1'2
Если бы величина Д2Л. не содержала вклада от
переходной зоны, она была бы просто равна —pi. Поэтому
избыточное напряжение, обусловленное наличием межфазовой
границы, равно [21]
1/2 1/2
Т = - \ pT(z)dz +pl= ^ {р - рт (z)} dz. (13.4)
-1/2 -//2
Это уравнение показывает, что действительную систему
с плоской границей между фазами можно рассматривать
так, как если бы она состояла из двух однородных фаз,
разделенных плоской мембраной нулевой толщины,
несущей натяжение у, определяемое (13.4). Таким образом,
уравнение (13.4) представляет собой определение
поверхностного натяжения, и мы будем принимать его за
механическое определение у.
Очевидно также, что поверхностное натяжение,
определяемое (13.4), не зависит от / при условии, что / имеет
такую макроскопическую длину, что при z= 1/2 и z = —1/2
Рт (г) становится равным гидростатическому давлению р.
Исходя из этого соображения, мы можем принять, что /

54 Часть I. Термодинамика и квазитермодинамика
бесконечно велико, и переписать (13.4) в общепринятой
форме:
оо
Т = \{Р-РТ (г)} dz. (13.5)
-ОО
Если касательная составляющая давления рт как
функция г известна, то можно рассчитать положение
пленки, которая механически эквивалентна реальному
межфазовому слою в отношении и результирующей силы, и
момента, действующего на площадку. Положение такой
механически эквивалентной пленки дается выражением [7]
00
2s=T \ {р~рт (z)}zdz- (13,6)
-оо
Как будет показано в п. 15, при кривизне, стремящейся
к нулю, поверхность натяжения, рассмотренная в п. 8, в
пределе оказывается разделяющей поверхностью, имеющей
координату zs. Таким образом, если поверхность натяжения
принять за плоскость ху, условие для поверхности
натяжения (13.6) сведется к
оо
\ {р - рт (г)} zdz = 0. (13.7)
-00
Используя тот факт, что pN не зависит от г и равно р,
можно из (13.5) получить уравнение Беккера [3]
оо
Г = \(Pn~Pt) dz- О3-8)
-оо
Необходимо, однако, отметить, что хотя понятие
тангенциального давления оказалось весьма полезным и сыграло
со времени первых работ ван дер Ваальса и его школы [3]
важную роль в теории поверхностного натяжения, в
обычной гидродинамике физические величины на длинах
порядка радиуса действия межмолекулярных сил
предполагаются постоянными, и поэтому рт (z), которое мы исполь-

Гл. II. Гидростатический подход
55
зовали до сих пор, нельзя непосредственно отождествить
с давлением в гидродинамическом смысле.
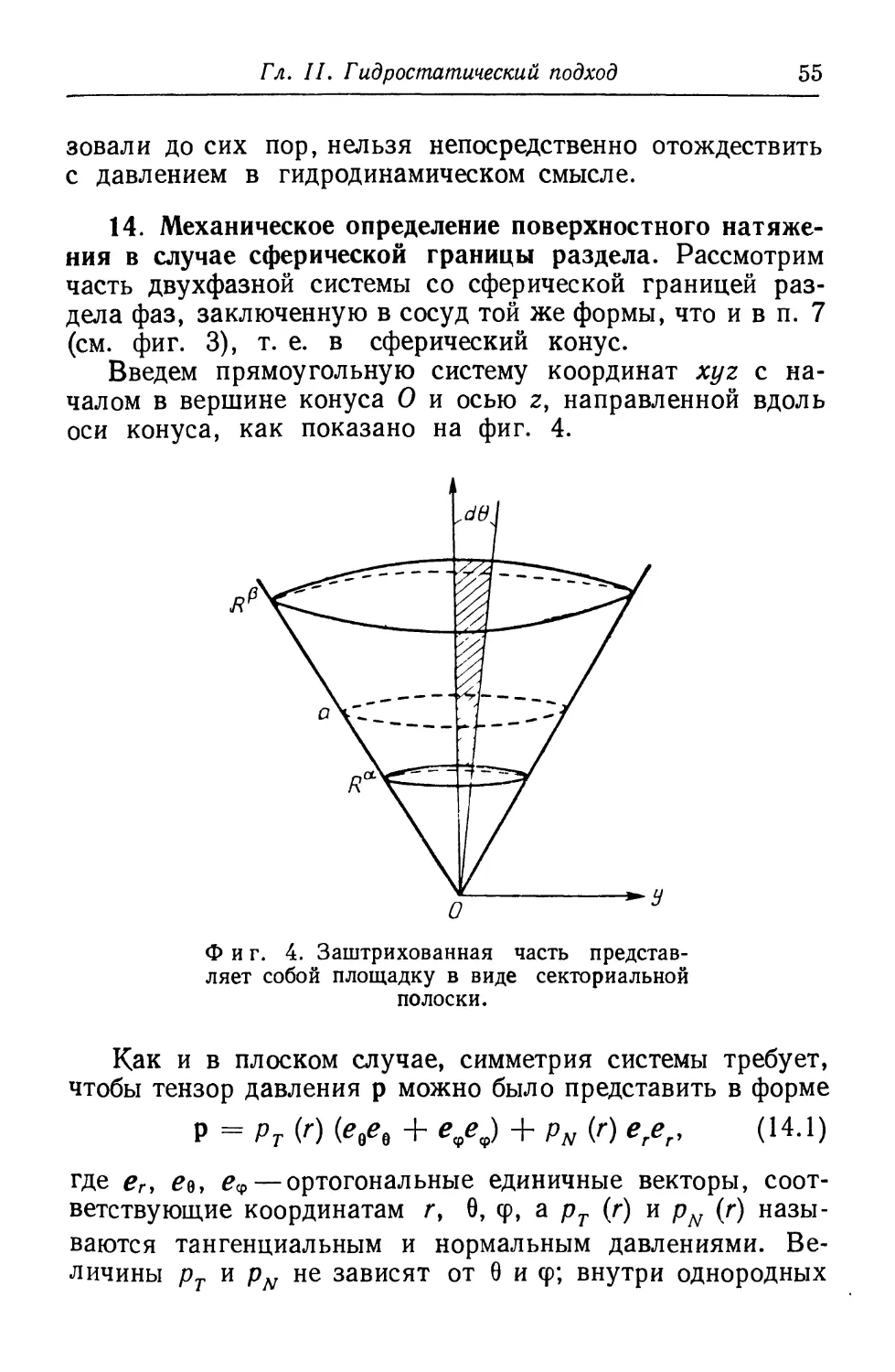
14. Механическое определение поверхностного
натяжения в случае сферической границы раздела. Рассмотрим
часть двухфазной системы со сферической границей
раздела фаз, заключенную в сосуд той же формы, что и в п. 7
(см. фиг. 3), т. е. в сферический конус.
Введем прямоугольную систему координат хуг с
началом в вершине конуса О и осью z, направленной вдоль
оси конуса, как показано на фиг. 4.
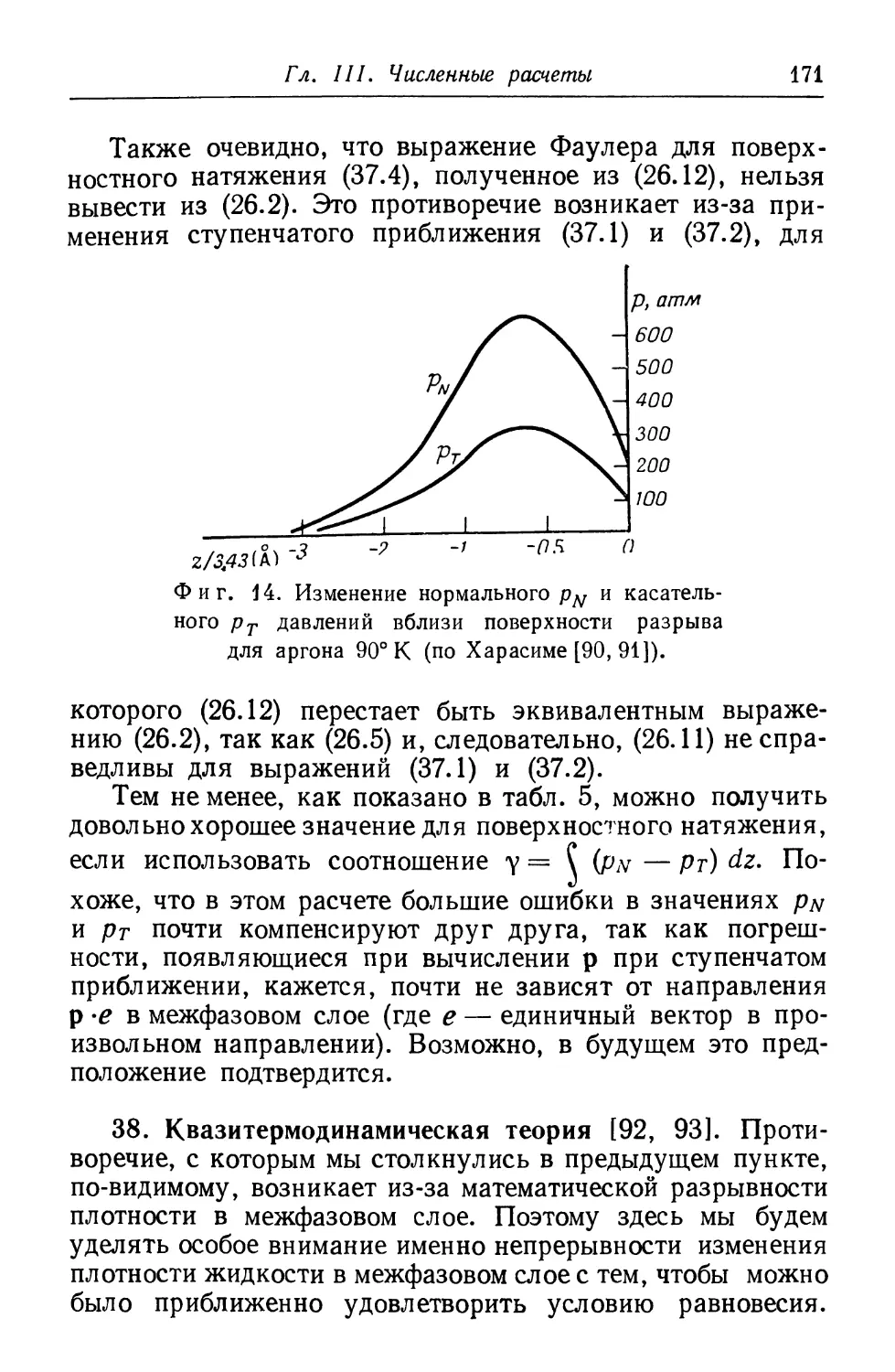
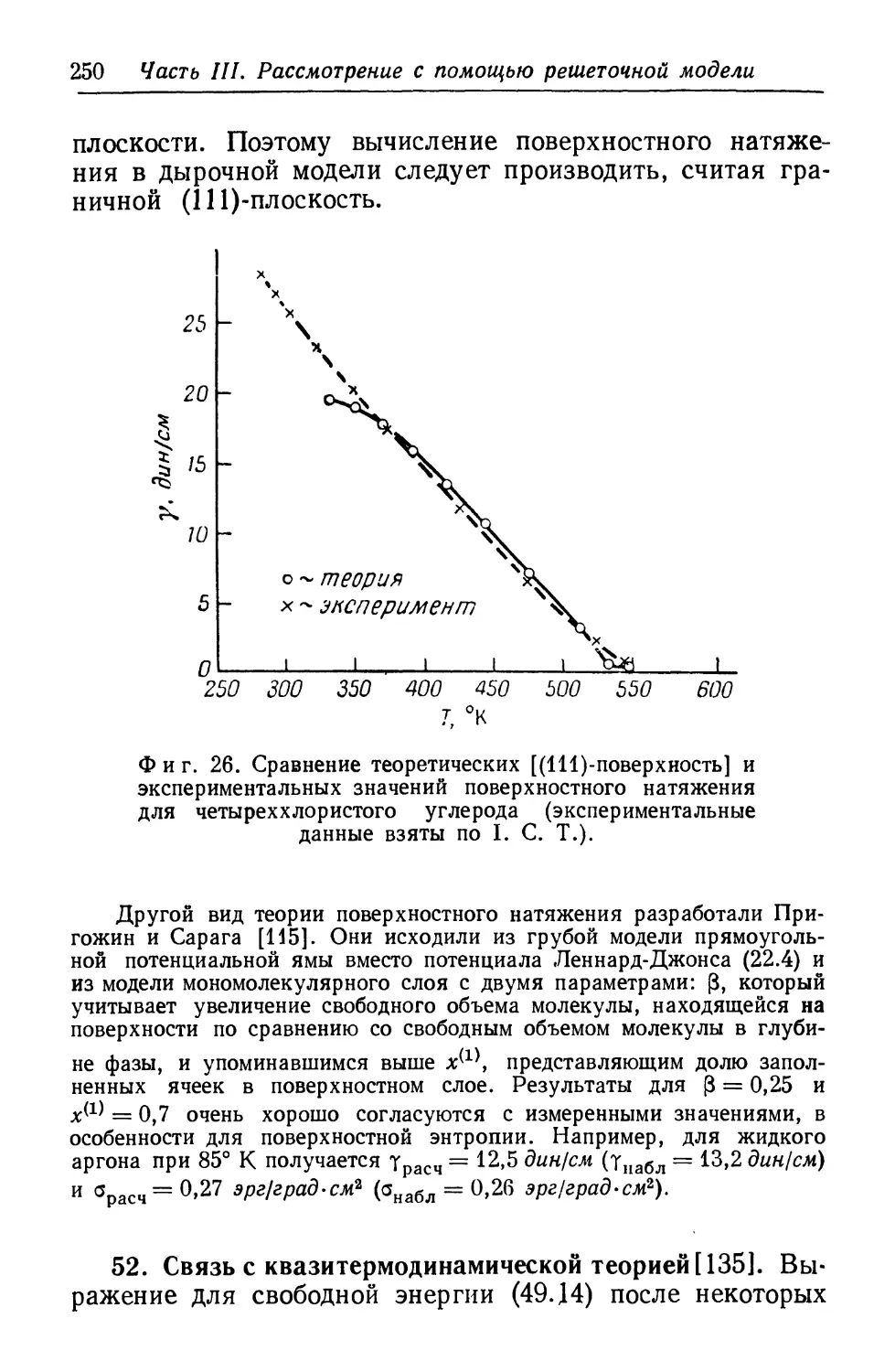
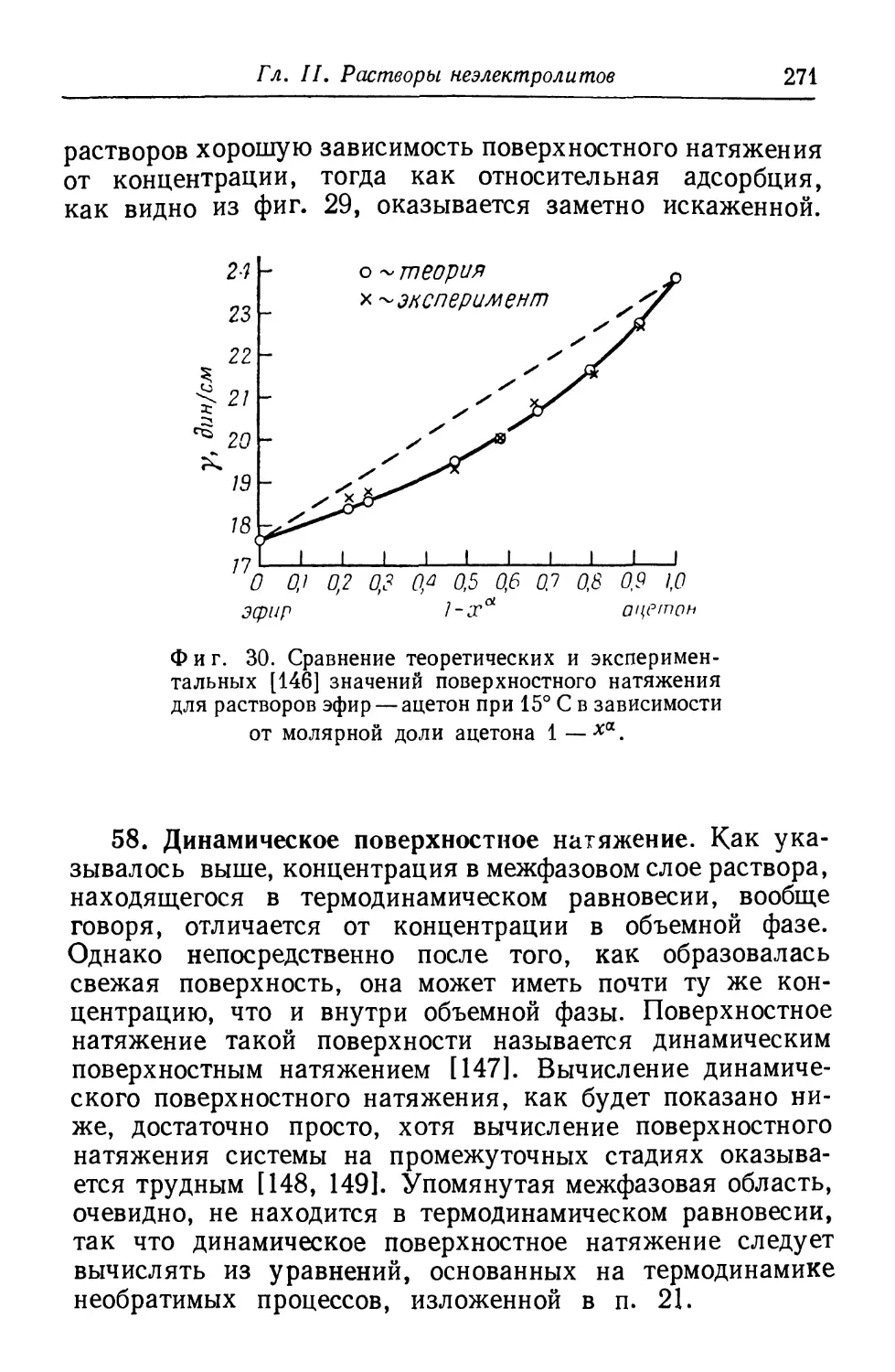
Фиг. 4. Заштрихованная часть
представляет собой площадку в виде секториальной
полоски.
Как и в плоском случае, симметрия системы требует,
чтобы тензор давления р можно было представить в форме
Р = РТ (г) (eQeB + e9ej + pN {г) erer, (14.1)
где ег, £е, £ф—ортогональные единичные векторы,
соответствующие координатам г, 9, ф, а рт (г) и pN (г)
называются тангенциальным и нормальным давлениями.
Величины рт и pN не зависят от 0 и ф; внутри однородных

56 Часть I. Термодинамика и квазитермодинамика
фаз а и Р они равны между собой и переходят в ра и рр
соответственно. В сферическом случае р^ (г) оказывается
уже не константой, а функцией г, которую можно
определить из условия гидростатического равновесия. В
отсутствие внешних полей уравнение гидростатического
равновесия имеет вид
Vp = 0. (14.2)
Из (14.1) и (14.2) мы получаем условие гидростатического
равновесия в следующих эквивалентных формах [21]:
dPN __ 2(Pt — Pn)
ЧГ~ г »
й^Рм) «, , о ч d(r*pN)
—j— = г2 (pN + 2рТ), -^ = рт. (14.3)
Интегрируя последнее из равенств (14.3) по г от /?а
до JRP, получаем интегральную форму условия
гидростатического равновесия:
(R*)V - ЮУ = 2 ^ pTrdr. (14.4)
R«
Возьмем площадку в виде полоски в плоскости yz,
имеющей форму сектора с углом d0 и ограниченной
окружностями г = R* и r = i?p, как показано на фиг. 4.
Чтобы получить механическое определение
поверхностного натяжения для сферической границы способом,
аналогичным тому, которым это было сделано для плоской,
представим себе гипотетическую систему, состоящую из
фаз а и Р, однородных вплоть до разделяющей их
сферической пленки радиуса as, несущей натяжениеys. Мы можем
определить ys и а$ из условия, что гипотетическая система
механически эквивалентна реальной системе как по
результирующей силе, так и по результирующему моменту,
действующему на выбранную секториальную площадку.
Найденное таким образом соотношение для ys можно
принять за механическое определение поверхностного
натяжения в случае сферической границы раздела.

Гл. II. Гидростатический подход
57
Результирующее напряжение dZx, действующее в
направлении оси х нормально к выбранной площадке в
реальной системе, дается выражением
d2x = —d§\pT (г) г dr. (14.5)
С другой стороны, в гипотетической системе напряжение
d2aP, действующее в направлении оси х на нашу секто-
риальную полоску, можно представить в форме г
d^= — dti \ р**г dr + ysasdQ, (14.6)
p«v = p« [l—A (r — a)] + p*A (r — a);
Л (,-*) = >'* Г>\ (14.7)
10, r<aj
Приравнивая (14.5) и (14.6), мы получаем формулу,
определяющую поверхностное натяжение для сферической
границы раздела:
Rt
rs = ^- J (p«t-pT)rdn (14.8)
s я*
Значение as определяется условием равновесия по
отношению к результирующему моменту:
Rt
\ (РаР — РТ) г (г — as) dr = 0. (14.9)
Если бы действительная граница раздела фаз
представляла собой пленку нулевой толщины, несущую
равномерное натяжение у , то соотношение Кельвина (0.1) удовлет-
1 Для pa(i > которое входит в (14.6), (14.8) — (14.10), (14.12) и
(14.13), мы полагаем а = as, но вообще а в (14.7) есть радиус
произвольной разделяющей поверхности.

58 Часть I. Термодинамика и квазитермодинамика
ворялось бы точно как следствие механического
равновесия. Поскольку сферическая пленка, натяжение которой
дается уравнением (14.8), а положение— уравнением (14.9),
механически эквивалентна действительной межфазовой
границе, то нетрудно видеть, что значения as и ts должны
автоматически удовлетворять уравнению Кельвина до тех
пор, пока система находится в механическом равновесии.
Это означает, что разделяющая поверхность,
удовлетворяющая условию (14.9), идентична поверхности натяжения,
которая была определена в п. 8 как разделяющая
поверхность, точно удовлетворяющая уравнению Кельвина.
Другими словами, (14.9) представляет собой условие для
определения радиуса поверхности натяжения as. Предвидя
этот результат, мы использовали обозначения ^s и as-
Используя тот факт, что рТ внутри фаз аир обращается
соответственно в ра и р&, можно переписать (14.9) в виде
оо
\ (P**-PT)(i + ±i) 6*6 = 0, (14.10)
где
Б= г — а8. (14.11)
В предельном случае нулевой кривизны условие (14.10)
сводится к уравнению (13.7), определяющему поверхность
натяжения в плоском случае.
Аналогичным образом, (14.8) записывается в виде
оо
Ys= \ (pO-Pj^ + ^dt. (14.12)
Учитывая (14.10), мы имеем альтернативное
выражение для (14.12):
00
Г3= \ (p**-PT)(l+-^i)%dl- (И.13)
Дадим теперь, исходя из условий гидростатического
равновесия, прямое доказательство того, что
соотношение Кельвина удовлетворяется точно, если разделяющая

Гл. II. Гидростатический подход
59
поверхность определена условием (14.10). Для этой цели
перепишем интегральную форму условия
гидростатического равновесия (14.4) в виде [13]
Ра-Р^=-^ \ (pa* — pT)rdr =
R*
оэ
-ОО
1 = г -а, (14.15)
где через а обозначен радиус произвольной разделяющей
поверхности х и использовано соотношение
R*
^ p^rdr = \ [(/?р)2 // - а2/ + а*ра - (Ray ра], (14.16)
R*
которое легко получить из определения (14.7).
Сопоставление (14.12) и (14.14) при а = as сразу
приводит к соотношению Кельвина. Хотя условие (14.10) и
не было непосредственно использовано при выводе
соотношения Кельвина, следует, однако* отметить, что fs>
определяемое по (14.12), можно отождествить с
поверхностным натяжением только тогда, когда оно относится
к поверхности натяжения, определяемой условием (14.10).
Таким же образом, как и при выводе (14.14), из второго
уравнения (14.3) получаем
со
р« - pt^ ±[2 \ (р«* - pT)(l + ±i) d%+
-ОО
ОО
+ \ (Р8*-/>*)(! + -f5)'d(|- (ИЛ7)
-ОО
Полагая в (14.14) и (14.17) а = as и используя (14.10),
мы можем исключить ра& из (14.13) и прийти к уравнению
1 См. примечание 1 на стр. 57.

60 Часть I. Термодинамика и квазитермодинамика
Беккера:
оо
rs= \(Pn-pt){1 + 4-б)'*5- (14Л8>
-оо
Строгий вывод этого уравнения был впервые выполнен
Баффом [12].
15. Механическое определение поверхностного
натяжения через работу, выполненную системой. В предыдущем
пункте поверхностное натяжение на сферической границе
раздела было однозначно определено с чисто
механической точки зрения. Этот способ определения
поверхностного натяжения, в противоположность
термодинамическому, применим лишь для поверхности натяжения.
Рассмотрим снова двухфазную систему со сферической
границей, подобную использованной в п. 14. Тензор
давления в этом случае определяется выражением (14.1),
и, следовательно, силу, действующую поперек элемента
поверхности конической стенки (см. фиг. 4), заключенного
между г и г -\-dr и между ф и <р + dq>, можно записать
как рТ (г) г sin Qdrdtp. Дадим телесному углу конуса
бесконечно малое приращение dco. Тогда работа по
перемещению стенки дается выражением
dW = dco [ рт (г) r2dr. (15.1)
Сопоставляя с (7.4), получаем
dec J рт (г) тЧг = padVa + p*dV* — 4dA, (15.2)
где теперь dA = a2d(x>, причем а — радиус произвольной
разделяющей поверхности. Согласно (7.1) — (7.3),
приращения объемов V* и И, соответствующие dco, даются

Гл. II. Гидростатический подход
61
выражениями
а
dVa = da> \ r2dr, (15.3)
dl/p = dw ^ г* dr. (15.4)
а
Подстановка (15.3) и (15.4) в (15.2) приводит к формуле
R&
Г = -&-[ (fy*-pT)r*dr, (15.5)
где ра^ определяется выражением (15.7). Выражение (15.5)
можно рассматривать как другой вид механического
определения поверхностного натяжения, справедливый для
йюбой разделяющей поверхности.
Дифференцирование f поав (15.5) дает [8]
Rt
Щ = —Ж \ &* ~ Рт) гЧг + (Р* ~ Р")> (15'6)
R*
где член (р* — р&) появляется в результате
дифференцирования раР. Теперь мы видим, что (15.6) идентично
обобщенному соотношению Кельвина (7.8), и, следовательно,
(15.5) представляет собой искомое выражение,
эквивалентное термодинамическому определению поверхностного
натяжения.
Если ввести переменную £ = г — а, то (15.5) можно
переписать в другой форме:
00
у = ^(paP_pr)(l+JLi)2dS. (15.7)
—оо
Мы находим, таким образом, что условие
гидростатического равновесия (14.4) позволяет свести (14.6) к урав-

62 Часть I. Термодинамика и квазитермодинамика
нению Толмена — Баффа [13; 16J.
оо
ffi—ir\(r>-PT){l + ±l)ldl (15.8)
—ОО
Сравнивая (15.6) с второй формой условия
гидростатического равновесия (14.17), получаем
оо
Ш = ^\^-Р»){1+1ГУ*1. (15.9)
—ОО
Это выражение впервые было получено Баффом [12].
Из уравнения Толмена — Баффа (15.8) следует, что
условие, определяющее радиус поверхности натяжения,
[ду/да] = 0 (см. п. 8), совпадает с условиями (14.9) или
(14.10), полученными из чисто механических соображений.
Из (14.13) и (15.7) ясно, что при а = as определенное
здесь у совпадает с у, определение которого было дано,
в п. 14.

Глава III
КВАЗИТЕРМОДИНАМИКА
16. Вводные замечания. В предыдущих пунктах мы
предполагали, что давление в каждой точке, даже в
микроскопической переходной зоне, можно определить как функцию
этой точки. Этот прием очень полезен при рассмотрении
микроскопической структуры межфазовой границы.
Распространение этого углубленного подхода на все
термодинамические величины дает фундаментальную основу для
квазитермодинамической теории, которая будет развита в
последующих пунктах.
В общем случае локальная формулировка
термодинамики возможна, так же как и в случае термодинамики
необратимых процессов. Но существует непременное требование
к такой локальной формулировке, которое
заключается в том, что пространственные изменения физических
условий внутри любого элемента объема молекулярных
размеров должны быть полностью пренебрежимы. Однако
поверхностный слой, как будет показано в частях II и III,
составляет по толщине всего несколько молекулярных
размеров, и можно предвидеть, что указанные изменения не
будут малыми. Следует ожидать поэтому, что
термодинамические функции, используемые в своей лсжальной форме,
не будут столь же хорошо определены в межфазовой
области, как в объемных фазах. Теория поверхностных слоев,
основанная на локальной формулировке термодинамики,
называется квазитермодинамикой поверхностных слоев.
Таким образом, излагаемая ниже
квазитермодинамическая теория, которая несколько отличается от
разработанной первоначально Толменом [16], не является, строго
говоря, точной, но тем не менее полезна в том отношении,
что обеспечивает физическое исследование структуры
межфазового слоя без использования точных, но более сложных

64 Часть I. Термодинамика и квазитермодинамика
уравнений, основанных на статистической механике. Таким
образом, квазитермодинамика служит как бы мостом между
макроскопической термодинамикой и молекулярной
теорией, основанной на статистической механике.
17. Основной постулат квазитермодинамики в случае
плоской границы раздела. Ограничимся для простоты
случаем однокомпонентной системы. Будем предполагать, что
наша система состоит из двух разделенных плоской
границей фаз, находящихся в равновесии, и заключена из
соображений удобства в сосуд, имеющий форму
прямоугольного параллелепипеда (см. также фиг. 8, стр. 101).
Введем прямоугольную систему координат, плоскость ху
которой лежит в межфазовом слое и является
разделяющей поверхностью, а ось z направлена по нормали к
границе от фазы а к фазе |3. Пусть 1Ъ /2, /3 — длины ребер
сосуда, направленных вдоль координатных осей, и пусть
нижняя и верхняя границы сосуда расположены при
z = — I" и 2 =/р соответственно. Тогда объем сосуда V
равен /1/2/3» а площадь межфазовой границы А равна /х/2.
В случае обычной макроскопической термодинамики
все интенсивные величины определены однозначно как
функции плотности и температуры. Наш основной
постулат квазитермодинамики состоит в том, что любая
интенсивная термодинамическая величина однозначно
определена в каждой точке как функция температуры и плотности
числа молекул в этой же точке \
Пусть п (z), v (z) и / (z) — соответственно число
молекул в единице объема, объем, приходящийся на одну
молекулу, и свободная энергия на одну молекулу. Имеем по
определению:
N = 1г12 ^ п (z) dz, (17.2)
1 По-видимому, учет вклада от производных локальной
плотности был бы улучшением этого постулата [21]; см. также [15] и п. 33.

Гл. III. Квазитермодинамика
65
F = l±l2 \ n(z) f (г) dz. (17.3)
Предположим, далее, что тензор давления р выражается
через тангенциальную рт (z) и нормальную pN (z)
составляющие давления в форме (13.2).
Пусть теперь площадь А увеличивается на
произвольную величину 6Л путем обратимого изотермического
перемещения боковой стенки сосуда. Тогда элементарная
работа, произведенная элементом системы, заключенным
между z и z + dZy в отсутствие внешних полей выражается
равенством
dw =рт (г) bAdz. (17.4
Этот слой может в общем случае и не представлять собой
замкнутой системы, поскольку в процессе расширения
некоторое количество молекул может проникать в него и
выходить из него благодаря изменению в распределении
молекул.
Удобно, однако, рассмотреть виртуальное изменение,
такое, при котором определенная выше бесконечно малая
система является замкнутой, т. е.
АЬп(г) +n(z)6A =0. (17.5)
Мы будем часто использовать символ б для обозначения
изменения в термодинамическом состоянии системы, в
отличие от d, которое означает изменение положения, как
в dz.
Работа, произведенная системой (17.4), должна быть
равна уменьшению свободной энергии в той же точке
— An (z) б/ (z) dz и, следовательно, мы имеем
An (г) б/ (г) = — рт (z) ЪА. (17.6)
Из двух последних уравнений получаем
df(z) Рт(*) М77,
дп(г) (n(z))2* V1'-'/
Используя выражение (17.1) для v (z), можно переписать

66 Часть I. Термодинамика и квазитермодинамика
(17.7) в иной форме:
df(z)
dv(z)
= -Рт (г). (17.8)
18. Условие равновесия для плоской границы раздела.
Согласно нашему постулату, можно написать
f(z,T)=f(n(z,T);T), (18.1)
т. е. при данной температуре свободная энергия F системы
как целого есть функционал от п (г). Поэтому
равновесная форма п (г) должна определяться из условия
минимума F при заданных температуре и объеме.
Вариацию F при постоянных Г, V и N можно получить
из (17.3) с помощью (17.2) и (17.7) в следующей форме:
/3
6F = /XZ2 J (/ (г) + Ц^-) Ьп (г) dz, (18.2)
где предполагается, что на вариацию б/г (г) наложены
ограничивающие условия Ш = 0 и 6V = 0:
hk \ вл (z) dz = 0. (18.3)
-/»
Используя неопределенный множитель Лагранжа [г, легко
получаем из (18.2) и (18.3) квазитермодинамическое
условие равновесия (см. [8, 161):
f(z) +рт (2)^=11. (18.4)
Очевидно, что /х представляет собой общий для объемных
фаз аир химический потенциал, поскольку внутри
объемных фаз рт (г) сводится к обычному гидростатическому
давлению р, и, следовательно, левая часть (18.4) — к
химическому потенциалу. Уравнение (18.4) представляет
собой одно из самых фундаментальных соотношений
квазитермодинамики.

Гл. III. Квазитермодинамика
67
Дифференцирование обеих частей (17.3) по Т при
постоянных V и N дает
-Za
где использовано (18.1) и вариация п (z) подчинена
условию (18.3). Подставляя с учетом (18.4) соотношение (17.7)
в уравнение (18.5) и используя (18.3), приходим к более
наглядному выражению
/3
S - l±l2 [ n(z)s (z) dz, (18.6)
где
s (z) = - ^.. (18.7)
Из (18.6) очевидно, что величина s (z), определяемая
выражением (18.7), представляет собой энтропию на одну
молекулу в точке г. Следовательно, внутренняя энергия
на молекулу в точке z, и (г), дается равенством
и (г) =f(z) +Ts(z). (18.8)
Кроме того, внутренняя энергия и (z) удовлетворяет
соотношению, аналогичному (18.6).
19. Квазитермодинамические соотношения для плоской
границы раздела. Теперь мы можем вывести основные
уравнения квазитермодинамики. Из (18.1) и (17.7) и (18.7)
имеем
6/=-S67'-pr6(4-). (19.1)
Это можно, используя (18.8), переписать в форме (см. [8])
Ьи =T6s — Ргв(4")- О9-2)
Дифференцируя (18.4) и комбинируя результат с (19.1),

68 Часть I. Термодинамика и квазитермодинамика
получаем [81:
— Ьрт + nsdT + nd\i = О, (19.3)
что соответствует уравнению Гиббса — Дюгема.
Умножая обе части (18.4) на п (г) и интегрируя по z,
получаем с учетом (17.2) и (17.3)
— kk \ Prdz =F — iiN. (19.4)
-za
Сопоставляя это с (4.5), мы сразу получаем выражение
для поверхностного натяжения
оо
У - \ (p-pr)dz, (19.5)
идентичное (13.5), выведенному из механического
определения поверхностного натяжения.
Отсюда следует, что можно вывести выражение (13.5)
из квазитермодинамического условия равновесия (18.4).
Этот результат является эмпирическим подтверждением
нашего основного постулата квазитермодинамики, но ничем
больше.
Перепишем термодинамические соотношения,
полученные в п. 5, в квазитермодинамической форме. Для этой
цели введем следующие обозначения [по аналогии с (14.7)1:
х^ = (1 _ A (z)) х- +А (г)х\ (19.6)
Л(г)=| *ПРИ2>°> (19.7)
\ 0 при z < О,
где х может означать произвольную термодинамическую
величину, например плотность числа частиц п.
Из определений (1.1), (2.2) и (2.3) очевидно, что для
поверхностной плотности энтропии a = Ss/A,
поверхностной плотности энергии v = VsIА и поверхностной плот-

Гл. III. Коазитермодинамика
69
ности числа частиц Г = Ns/A мы имеем соответственно
оо
а = [(ns — /i»*s«*) dz, (19.8)
—ОО
ОО
v = ^ (пи — л^и**) dz (19.9)
—ОО
И
оо
Г= \ (n-n^)dz, (19.10)
—ОО
где предполагается, что плоскость ху совпадает с
разделяющей поверхностью, к которой отнесены выписанные
поверхностные величины.
С другой стороны, обычные уравнения Гиббса — Дю-
гема для фаз а и р можно записать в форме
— др+ n**sf*bT + n«td\i = 0. (19.11)
Вычитая отсюда (19.3) и интегрируя результат по z,
получаем
ОО ОО
6(р — рт) dz +&Т[ (ns—n^s^) dz +
—ОО —ОО
ОО
+ бц \(п — п^) dz = 0. (19.12)
—ОО
С помощью (19.5), (19.8), (19.9) и (19.10) можно
непосредственно показать, что (19.12) идентично адсорбционному
уравнению Гиббса (5.8), что является еще одним
эмпирическим подтверждением нашего основного постулата
квазитермодинамики.
20. Квазитермодинамические соотношения для
сферической границы раздела. Рассмотрим ту же систему,
которая рассматривалась в п. 7 и 14; будем пользоваться теми
же обозначениями (см. фиг. 3 и 4). В сферическом случае
интенсивные термодинамические величины являются
функциями только радиуса г. Поэтому, согласно (17.1), (17.2) и

70 Часть I. Термодинамика и квазитермодинамика
(17.3)
N = со \ /г (г) r2dr,
/? = со J л (г) / (r) r2dr.
Тензор давления р принимает вид (14.1), т. е. и
тангенциальное, и нормальное давления зависят только от г.
Точно так же, как и в плоском случае, можно вывести
квазитермодинамическое условие равновесия для
сферической поверхности
f(r)+Pr(r)-~- =|i. (20.4)
Этот результат по форме идентичен с (18.4) для плоской
границы. Если умножить (20.4) на сог2/г и
проинтегрировать по г от Ra до R&, то с помощью (20.2) и (20.3) получим
— со \ рт (г) r2dr= F — \iN. (20.5)
Ra
Подставляя в (20.5) термодинамическое соотношение (9.9),
учитывая (7.1) — (7.3) и переписывая результат с
использованием обозначений раР согласно (14.7), мы легко
получаем следующее выражение для поверхностного
натяжения у относительно произвольной разделяющей
поверхности радиуса а:
R*
У =-&-] {р**-Рт)гЧг, (20.6)
R*
или в обычной форме
оо
V = \ (р«Р - Рг) (1+4" *)' dZ> (20-7)
—ОО
(20.1)
(20.2)
(20.3)

Гл. Ill, Квазитермодинамика
71
что совпадает с выражением (15.7), выведенным из
механического определения поверхностного натяжения.
Для поверхностных плотностей энтропии а, энергии v
и числа частиц Г имеем [16]
оо
а = ^ (ns - n«Ps«P) (l +4" tf d^ (20-8)
—OO
oo
v = ^ (nu — л»Ри«Р) (l +-i- б)* dl, (20.9)
—OO
oo
Г = J (« - я»Р) (1 +4- £)2 rfg, (20.10)
—oo
где использованы обозначения (14.15) и (19.6).
Так как уравнение Гиббса — Дюгема, представленное
в форме (19.11), справедливо для обеих объемных фаз а
и Р независимо от того, какова форма межфазовой области,
плоская или сферическая, то мы получаем из (20.4) *
оо
—оо
оо
+ 67 \ {ns — п<#&?) (l + -i. &)* d% +
—OO
oo
+ 6ц ^ («_««0)(l+J-!)2d£ =0. (20.11)
—oo
С другой стороны, вычисление полною дифференциала
(20.7) дает
оо
ЬУ=\[Ь (р#-рТ)) (1 +4 if dl +[£] Ль (20.12)
—OO
Здесь использовано соотношение, аналогичное (19.1).

72 Часть I. Термодинамика и квазитермодинамика
Подстановка (20.12), (20.8) и (20.10) в (20.11) сразу
приводит к соотношению [8]
6Y + одТ + Гб[х = [|I] da, (20.13)
которое в точности совпадает с обобщенным
адсорбционным уравнением Гиббса (10.9), полученным при помощи
обычной термодинамики.

Глава IV
ПРИМЕНЕНИЕ ТЕРМОДИНАМИКИ НЕОБРАТИМЫХ ПРОЦЕССОВ
21. Граница раздела между двумя фазами, не
находящимися в равновесии [15, 23]. а) Сродство адсорбции.
Рассмотрим систему с плоской межфазовой границей,
разделяющей две фазы а и (3, которые находятся в
механическом и тепловом равновесии, но не в химическом
равновесии. Это означает, что температура Т и давление р одни
и те же во всей системе, но химический потенциал \if в
фазе а не обязательно равен химическому потенциалу jx?
в фазе р. В переходной зоне химический потенциал может
изменяться непрерывным образом вдоль нормали к границе
раздела.
К этой неравновесной системе мы применяем
термодинамику необратимых процессов [24, 25]. Изменение
энтропии dS расщепляется тогда на две части: deS — поток
энтропии, обусловленный взаимодействием с внешней
средой, и d;S — вклад, связанный с необратимыми
процессами внутри системы. Таким образом,
dS =deS +d;S. (21.1)
Если система замкнутая, мы имеем, кроме того:
deS = ^L, (21.2)
где dQ — тепло, полученное системой. Изменение
энтропии в результате внутренних процессов, d/S, согласно
второму закону термодинамики, не может быть
отрицательным.
Мы не будем, ради простоты, рассматривать другие
химические реакции, кроме адсорбции на границе и
переходов частиц между основными фазами аир.

74 Часть I. Термодинамика и квазитермодинамика
Предположим прежде всего, что система замкнутая.
Тогда Nf, Nf и N*, которые теперь становятся
переменными величинами, зависящими от времени, выражаются
через начальные значения N%, N% и N*0 в виде
Nf -N%=- If; Nf- N% = - gf;
W-Nsi0=Z?+Zf, (21.3)
где £? и £? называются степенями развития реакции
адсорбции в фазах а и р соответственно [25].
Написанные уравнения означают, что миграция молекул из
фазы а в фазу [3 представляет собой линейную
комбинацию двух реакций адсорбции: адсорбции из фазы а и
адсорбции из фазы р.
Необратимое возрастание энтропии в процессе
бесконечно малого самопроизвольного изменения величин £?
и if выражается как
X X
TdiS = S *?<*£? +2 А?<*6?, (21.4)
где /С? и /Cf суть сродства адсорбции на границе раздела
для молекул сорта i соответственно из фаз аир. Если
температура Г, объем V и площадь границы раздела А
остаются постоянными, то приращение внутренней
энергии, связанное с таким бесконечно малым изменением,
можно записать в виде
dU =-2 *Td& - 2 r?d$- (21-5)
Согласно первому закону термодинамики, эта величина
равна количеству тепла, полученного системой в
рассматриваемом процессе. Это значит, что rf представляет собой
теплоту адсорбции из фазы а, т. е. теплоту, выделяющуюся
в системе, когда одна молекула сорта i из фазы а
адсорбируется на межфазовой границе.

Гл. IV. Применение термодинамики необратимых процессов 75
Используя (21.2), (21.4) и (21.5), можно переписать
выражение (21.1) в виде
X X
TdS = 2 (*?- г?) dtf + 2 (К?- /?) «f. (21.6)
Из (21.5) и (21.6) следует выражение для приращения
свободной энергии
X X
dF =-S A?dg?-S *?<$• (21.7)
В термодинамике необратимых процессов вообще
предполагается, что энтропия системы задана как функция
макроскопических переменных Т, А, V, Ж, £а, £3 г.
Поэтому из (21.6) получаем непосредственно
Kt = rf + T(^)
/ яс v (21-8)
Kf^rf + Ti98-"
Эти уравнения в принципе позволяют вычислить сродства
адсорбции /С? и Kf по теплоте адсорбции и изменению
энтропии, связанному с процессом адсорбции.
До настоящего момента мы имели дело лишь с
замкнутыми системами. В теории адсорбции, однако, удобнее
рассматривать открытые системы. Предположим, как и в
равновесном случае, что свободная энергия может быть
представлена как функция переменных Г, Уа, У3, Л, Na,
N* и Ns. Тогда
dF=—SdT—pdVa—pdV^ + rdA + 2 №dfff +
+ p!dN? + tidNl), (21-9)
1 Символ £ означает набор из х переменных £г . . . , £х; см.
также примечание 1 на стр. 20.

76 Часть I. Термодинамика и квазитермодинамика
где \i? и [if называются в отличие от обычных химических
потенциалов полными химическими потенциалами и
определяются равенствами
# = (;£=■) • (21Л°)
Vt=(—s) • (21-12)
\dNi > Т. V. A. Nsj, AT», H*
Вспоминая сказанное в п. 2 об избыточных величинах,
положим
!L = f = f (7\ Г1( . . . , Гх, nf, . • • , ni, п? , . . . , nl),
(21.13)
п' - Va . "' - ка •
Тогда с использованием (2.1) и (21.13) нетрудно
переписать выражения (21.10) — (21.12) в другом виде:
где
а
Я
v\ =
1*? =
tf =
= *' + £«?.
р , А р
= |*? + ^в?,
\dNt)T,Va,Nf
JdF>\
WfJT.V^Nf
(21.14)
(21.
.15)
(21.16)
(21.
(21.
.17)
.18)

Гл. IV. Применение термодинамики необратимых процессов 77
'* ~ (*?)
(21.19)
Т. Г. п?лР
«?=Ш . ■ (21.20)
\дп;/т,г,п?,п*
Символами \if и jif обозначены обычные химические
потенциалы, которые в данном случае не обязательно равны
друг другу. Новые величины ef и е& мы будем называть,
следуя Дефею [23], вторичными химическими потенциалами.
С ними связано различие между \if и \if и между \i& и [х?
соответственно. Таким образом, с использованием (21.14)
и (21.15) мы можем переписать (21.9) в виде
dF = — SdT — pdVa — pdV* + rdA +
1=1 Ч V
+ 2 (tf + 4 «f) <№ + 2 i*? ^- (21-21)
i=l ч K 7 1=1
б) Адсорбционная формула Гиббса, обобщенная на
неравновесный случай [15, 23]. Рассмотрим теперь изменение
свободной энергии в простом адсорбционном процессе,
описываемом равенствами (21.3). Сравнивая (21.7) с (21.21)
при учете (21.3), находим
К?=ц--^ + Ае?, (21.22)
Af=^_^ + ^e?. (21.23)
Используя соотношения (21.10)—(21.16), получаем из
(21.22) и (21.23)
\dNi K.V.A.Nf.N^.N5 \dNVT.V.A.N*.N*.Nfi'
(21.24)
Wi'T.V.A.Nf.N*.* \dNi'T.V,A.N*.N*.ltfi
(21.25)

78 Часть I. Термодинамика и квазитермодинамика
Фундаментальные уравнения Гиббса для объемных фаз
а и Р имеют вид
X
dFа = —SadT- pdVa + 2 И? dNf, (21.26)
X
dF* = —S*dT-pdV*+ 2 V>fdN$. (21.27)
Вычитая (21.26) и (21.27) из (21.21) и вспоминая
определения (2.1) и (2.3), получаем
X
dFs = -SsdT + ydA+^^ ef dNf +
£=1 V
X X
+ 2 A ef <W? + S |ij dVj. (21.28)
Поскольку Fs, как легко видеть из (21.28), не зависит от
Г и Ур, мы получаем из (21.13):
T.r.nf.n*
-О, (21.29)
2*? (Я) = °- (21-3°)
/=1 WI'T.T.nf.n*
Сопоставляя эти равенства с (21.19) и (21.20)
соответственно, получаем важные соотношения:
X
2«°е? = 0, (21.31)
X
2 л£в£ = 0. (21.32)
/=i
Так как F — однородная функция первой степени по
переменным Уа, И, А, ЛГа, ЛГЭ, ЛЛ то с помощью теоремы

Гл. IV. Применение термодинамики необратимых процессов 79
Эйлера получаем из (21.21) выражение
р=is (и?+£в-) *?+is {^+^N1+
х
+ 2 tf N] - рУ - рИ + ГЛ. (21.33)
Вычитая из (21.33) интегральные формулы для каждой
х
из объемных фаза и Р, F" = 2 PfN? — pV* и?р =
*=i
X
= 2 |i?tf? — pV*9 и используя (21.31) и (21.32), имеем
х
^=S^/ + T^. (21-34)
или через поверхностные плотности:
х
Г = Г-2и;Гл (21.35)
Эти выражения по форме идентичны выражению (4.8)
для поверхностного натяжения в равновесной системе.
Дифференцируя (21.34), приравнивая результат к (21.28)
и используя (21.31) и (21.32), получаем искомое уравнение
[15, 23]
XXX
-dT = odT + 2 Г,Ф* + 2 nfdef + 2 пЩ,
г= 1 /=i /=i
(21.36)
где о — поверхностная энтропия, даваемая уравнением
(5.6). Уравнение (21.36) является обобщением уравнения
Гиббса (5.8). Оно отличается от (5.8) наличием членов с
вторичными химическими потенциалами. В случае
термодинамического равновесия эти члены исчезают, и (21.36)
сводится к (5.8).

80 Часть I. Термодинамика и квазитермобинамика
Следует заметить, что |х*, ef и ef зависят от положения
разделяющей поверхности, так что (21.36) и любые другие
уравнения, выведенные из (21.4), справедливы только по
отношению к специально выбранным разделяющим
поверхностям, которые, одновременно удовлетворяют
соотношениям (21.31) и (21.32). Это означает, что само
соотношение (21.4) справедливо лишь для таких специальных
разделяющих поверхностей. Подробно условие
инвариантности рассмотрел Дефей в работе [26].
С чисто логической точки зрения представляется,
однако, возможным, что разделяющая поверхность,
удовлетворяющая соотношению (21.31), может, вообще говоря,
отличаться от разделяющей поверхности, удовлетворяющей
условию (21.32), поскольку из излагаемой теории не
вытекает никакой связи между ef и е£. Эта ситуация
подсказывает вывод, что макроскопическая термодинамика
необратимых процессов справедлива лишь в ограниченном ряде
частных случаев, когда она применяется к поверхностному слою,
в котором термодинамические величины изменяются
заметным образом уже на расстояниях порядка молекулярных
размеров. Поэтому дальнейший прогресс в этом
направлении представляется затруднительным без детального
рассмотрения всех происходящих внутри поверхностного
слоя изменений, в точности так же, как это делается
в квазитермодинамической теории *.
1 Как показал Кондо [27], возможно более общее рассмотрение
поверхностного натяжения в неравновесном случае без использования
понятия вторичных химических потенциалов.

Глава V
ЭМПИРИЧЕСКИЕ УРАВНЕНИЯ ЗАВИСИМОСТИ ПОВЕРХНОСТНОГО
НАТЯЖЕНИЯ ОТ ТЕМПЕРАТУРЫ
22. Закон соответственных состояний и эмпирические
формулы для поверхностного натяжения, а) Закон
соответственных состояний. Для описания зависимости между
давлением, объемом и температурой газов и жидкостей
предлагались различные полуколичественные уравнения
состояния, наиболее известным из которых является
уравнение ван дер Ваальса
[p + t%)(V-N0b) = N0kT, (22.1)
где N0 — число Авогадро, V — молярный объем, а а и
Ъ — постоянные ван дер Ваальса на одну молекулу.
Обычно критическая точка определяется как точка,
в которой производные (dpidV)T и (д2р/dV2)T обращаются
в нуль. Значения р, V, Т в этой точке обозначаются
соответственно как рс, Vc, Тс. При температурах ниже
критической изотермы уравнения (22.1) образуют петлю ван
дер Ваальса. В этой области горизонтальные линии,
соединяющие объемы, соответствующие одинаковому давлению
и одной и той же свободной энергии Гиббса на двух
ветвях кривой, для которых (dp/dV)T<iO, рассматриваются
как линии сосуществования жидкой и газообразной фаз.
Введем приведенные переменные
ГС ¥ С 1 С
позволяющие исключить а и Ь из уравнения (22.1). Это
означает, что для всех веществ, подчиняющихся
уравнению ван дер Ваальса, одна из трех величин pr, Vr и Тг
является универсальной функцией двух остальных.

82 Часть I. Термодинамика и квазитермодинамика
Хотя уравнение в приведенных переменных,
полученное из уравнения (22.1), справедливо лишь как
полуколичественное, для некоторых групп близких по свойствам
веществ [28, 29] получено опытное подтверждение того,
что одна из трех приведенных переменных является
универсальной функцией двух остальных. Это и есть закон
соответственных состояний. Согласно этому закону любая
безразмерная величина, например фактор сжимаемости
pVINkT, является универсальной функцией рг и 7V.
Выберем для поверхностного натяжения безразмерную
величину тг = Т^/з (^)_1> которую назовем приведенным
поверхностным натяжением (здесь vc — объем в
критической точке на одну молекулу). Следует ожидать, что
величина тг окажется универсальной функцией Тг для
веществ, подчиняющихся закону соответственных
состояний:
kT / т \
где G — универсальная функция. На фиг. 5 нанесены
значения тг в зависимости от Т/Тс для неона, аргона, азота и
кислорода. Как видно из фиг. 5, закон соответственных
состояний успешно применим к описанию поверхностного
натяжения в аргоне, азоте и кислороде. Для неона имеют
место заметные отклонения от закона соответственных
состояний, которые будут рассмотрены ниже.
Для определения приведенных переменных можно
также использовать постоянные межмолекулярного
взаимодействия. В случае химически насыщенных молекул
потенциальная энергия системы принимается равной сумме
членов, каждый из которых представляет собой энергию
взаимодействия пары молекул. Межмолекулярная
потенциальная энергия 0 (г) пары сферических или почти
сферических молекул зависит только от расстояния между этими
двумя молекулами. Кроме того, разумно предположить,
что межмолекулярный потенциал может быть представлен
в виде 0 (г) = ef(r/D), где / — универсальная функция \
1 На основе статистической механики можно доказать, что в
действительности закон соответственных состояний вытекает из вида
межмолекулярного потенциала 0 (г) = е/ (гID) (ср. п. 26).

Гл. V. Эмпирические уравнения зависимости от температуры 83
а е и D — два масштабных параметра, характеризующие
сорт молекул. В качестве приближенного вида этой
функции часто используется потенциал Леннард-Джонса:
*«-*{®"-(°П-
(22.4)
Фиг. 5. Зависимость поверхностного натяжения от температуры
(в приведенных единицах).
С помощью этого потенциала методами статистической
механики были вычислены многие из свойств газов и
жидкостей. В табл. 2 приведены значения еи'О, рассчитанные
на основе экспериментальных данных о вторых вириальных
коэффициентах; здесь D — расстояние, для которого
0(г) = О, а —б — минимальное значение функции ф(г).
Далее, соответственно формулам (22.2) можно определить
другую систему трех приведенных переменных
Р =*г-
pD3
8
if =
NDS>
/Т1* kT
(22.5)
где N — число молекул в объеме V. Аналогичным образом

84 Часть 1. Термодинамика и квазитермодинамика
Таблица 2
Значения постоянных, входящих в потенциал Леннард-
Джонса
Газ*
Не (кв)
Не (кл)
Н2 (кв)
Н2 (кл)
D2 (кв)
D2 (кл)
e/k, °К
10,22
6,03
37,00
29,2
37,00
31,1
D, А
2,556
2,63
2,93
2,87
2,93
2,87
Газ
Ne
Аг
Кг
Хе
N2
о2
Ф, °к
34,9
119,8
171
221
95,9
118
D, А
2,78
[3,405
3,60
4,10
3,71
3,46
* Для наиболее легких элементов имеется по два набора
входящих в потенциал постоянных. Значения со значком «кв»
определялись из формул квантовой механики, а со значком
«Кл» _ на основе классической теории, которая не является
совершенно точной при очень низких температурах. Квантовые
значения постоянных являются точными, классические лишь
эффективными значениями. Для точных расчетов и
экстраполяции к высоким температурам следует использовать кв-пара-
метры.
приведенное поверхностное натяжение можно представить
как r* = rZ)2/e. Тогда в соответствии с уравнением (22.3)
f = ^ = f(T*), (22.6)
т. е. г* есть универсальная функция Т*. Если для Аг,
N2 и 02 построить график зависимости у* от Т\ то
получается кривая, аналогичная приведенной на фиг. 5 (см.
также фиг. б, стр. 89).
б) Эмпирические уравнения для поверхностного
натяжения. С повышением температуры величины
поверхностного натяжения жидкостей, как правило, уменьшаются.
Одним из наиболее ранних и известных эмпирических
уравнений зависимости поверхностного натяжения от
температуры является уравнение Этвеша [30]:
Т~(^о-7,>' (22-7)
где V* — молярный объем жидкости, а Т0 — температура,
почти равная Тс. Оказалось, однако, что эта формула не-

Гл. V. Эмпирические уравнения зависимости от температуры 85
Г
точна, поэтому были предложены различные ее
модификации, наиболее удовлетворительной из которых оказалась
формула Катаямы 131]:
~!fu{\-Q, (22.8)
уУс = Р_Р (22.9)
где Vc, pa, рр и рс представляют собой соответственно
критический молярный объем, ортобарические плотности
жидкости и пара и критическую плотность. Как показал Катаяма
на примере различных органических соединений, эта
формула весьма существенно улучшает формулу Этвеша.
С другой стороны, Гуггенгейм [29, 6] показал, что
ортобарические плотности простых молекул ра и рр с высокой
точностью удовлетворяют следующей эмпирической формуле:
Hr-il1-^) ' (22-,0)
Подставляя (22.10) в (22.9), мы из формулы (22.8) получим
формулу Катаямы — Гуггенгейма [29, 6]
Т \"/«
То' "
(■-£) '• (22Л1)
Как видно из табл. 3, расчетные данные обнаруживают
очень хорошее согласие с экспериментом.
Из уравнения (22.3) следует, что величина To^TV1
должна принимать общее значение для веществ,
подчиняющихся закону соответственных состояний. Табл. 3
показывает, что это действительно осуществляется.
Мак-Леод [32] предложил для определения
поверхностного натяжения эмпирическое уравнение
Т = const (pa — р^)4. (22.12)
Сагден записал его в виде [33]
Ра-Р3'
(22.13)

86 Часть I. Термодинамика и квазитермодинамика
Таблица 3
( Т \ и/9
Сравнение формулы Катаямы— Гуггенгейма т=То И — f~' с
экспериментальными значениями для простых молекул (по Гуггенгей
му [29])
Ne
Гс = 44,8 °К
Y0 = 15,1 дин/см
т °к
24,8
25,7
26,6
27,4
28,3
Y, дин/см
теор.
5,64
5,33
5,02
4,75
4,45
эксп.
5,61
5,33
4,99
4,69
4,44
V с=41,7 см*/моль
=4,05 эрг/г рад X
X моль*/*
Аг
Гс = 150,7 °К
Y0 = 36,31 дин/см
Т °к
85,0
87,0
90,0
Y, дин/см
теор.
13,16
12,67
11,95
эксп
13,19
12,68
11,91
IV с~1Ь,Зсмг/моль
То ^7? =
=4,3 эрг/град х
X моль1*
N2
Тс = 126,0 °К
Y = 28,4 дин/см
Т °К
70,0
96,0
80,0
85,0
90,0
Y, дин/см
теор.
10,54
9,40
8,29
7,20
6,14
эксп.
10,53
9,39
8,27
7,20
6,16
\V с=90,2 см3/моль
=4,5 эрг/град X
X моль/з
о2
Т с = 154,3 °К
Y0 = 38,4 дин/см
Т°К
70,0
75,0
80,0
85,0
90,0
Y, дин/СМ
теор.
18,34
17,02
15,72
14,44
13,17
эксп.
18,35
17,0
15,73
14,5
13,23
V с=1^,5см3/моль
ToV/'7^ =
=4,4 эрг/г рад X
X моль/з
где М — молекулярный вес. Постоянную Р называют
«парахором». Сравнительное изучение значений парахора
для различных жидкостей подтвердило, что Р постоянно
(точнее, почти постоянно) для любого данного вещества
независимо от изменения Т в широком интервале и что
парахор молекулы приблизительно равен сумме значений
парахора атомов, образующих эту молекулу. Фаулер [9]
сделал попытку вывести уравнение Мак-Леода, исходя из
общих статистических соображений, и получил из
статистической механики выражение для парахора Р.
Однако уравнение Катаямы — Гуггенгейма (22.11) в
сочетании с уравнением (22.10) дает [6, 29]
Г = const (ра — р^)п/з. (22.14)

Гл. V. Эмпирические уравнения зависимости от температуры 87
Для простых молекул это уравнение оказалось в
действительности более точным, нежели уравнение Мак-Леода.
в) Квантовые поправки к закону соответственных
состояний. Поведение неона, как видно из фиг. 5, заметно
отклоняется от предсказываемого законом соответственных
состояний; эти отклонения еще более значительны в
случаях D2, Н2 и Не. Поскольку в жидком состоянии эти
вещества находятся при очень низких температурах, где
существенную роль играют квантовомеханические
эффекты, то можно ожидать, что эти отклонения обусловлены
указанными эффектами.
Бик [34] впервые предложил изменить классический
закон соответственных состояний таким образом, чтобы он
включал в безразмерном виде постоянную Планка h
(которая и позволяет учитывать квантовые эффекты).
Используя молекулярные параметры D и е, можно построить
безразмерную комбинацию
Л* = -£=, (22.15)
D у те
впервые введенную де Буром и его сотрудниками [35—37].
Так как hlYmz—длина волны де Бройля
(соответствующая приведенной массе \i = т/2 и энергии е), то Л
показывает, насколько важны диффракционные эффекты,
обусловленные волновой природой молекул. Следовательно,
можно ожидать, что квантовые отклонения от
классического закона соответственных состояний зависят от
величины параметра Л*.
По аналогии с классическим соотношением (22.6)
приведенное поверхностное натяжение можно представить
в виде
Т* = Г* (Т\ Л*). (22.16)
Это означает, что приведенное поверхностное натяжение
является функцией приведенной температуры, зависящей
от квантовомеханического параметра Л*.
На фиг. 6 даны значения приведенного поверхностного
натяжения у* в зависимости от Т* и Л*. Из нее видно, что
квантовые отклонения более значительны для веществ,
для которых значения Л* больше.

88 Часть I. Термодинамика и квазитермодинамика
Де Бур и Берд [38] записали универсальную функцию
Г* (T*fA*) в формуле (22.16) в явном виде, приняв для
нее следующее выражение:
Т* = р(Л#)(7;-Г*)п/в, (22.17)
что соответствует классическому уравнению Катаямы —
Гуггенгейма(22.11). Обрабатывая данные по
поверхностному натяжению для Н2, Не4, Ne и Аг на основе уравнения
(22.17), можно, как показано на фиг. 7, представить
графически Р как функцию параметра Л*. Путем
экстраполяции де Бур и Берд [38] нашли, что для Не3 |3 = 0,56.
В табл. 4 данные, полученные на основе квантовомехани-
Таблица 4
Поверхностное натяжение Не3
т, °к
у экстрапо.
у экспер.
1,75
0,123
0,102
2,00
0,101
0,086
2,25
0,078
0,070
2,50
0,057
0,054
2,75
0,037
0,039
3,00
0,019
0,022
ческого закона соответственных состояний, сравниваются
с экспериментальными значениями* поверхностного
натяжения для Не3. Экспериментальные данные показывают
хорошее согласие с квантовомеханическим законом
соответственных состояний. Значения поверхностного
натяжения для изотопов водорода HD, НТ, DT и Т2 не измерялись.
г) Пределы применимости и обобщения. Как видно из
фиг. 6, значения поверхностного натяжения для Не4
ниже Я-точки явно не согласуются с уравнением (22.17)
и при стремлении Т к абсолютному нулю т* перестает
зависеть от температуры. Этого следовало ожидать
согласно третьему закону термодинамики, так как при Г—>0
1 Численные значения ТЭКсп рассчитаны по экспериментальной
кривой К. Н. Зиновьевой [39]. См. также [40 — 43].

Гл. V. Эмпирические уравнения зависимости от температуры 89
поверхностная энтропия также стремится к нулю и,
следовательно, при абсолютном нуле dy/dT исчезает.
До сих пор мы ограничивались применением закона
соответственных состояний к простым молекулам. Однако
путем введения дополнительных параметров [44—48] этот
закон можно распространить и на многоатомные и
полярные молекулы. Используя обобщения закона
соответственных состояний, полученные Мейсснером и Сеферяном [44]
\
\
>^ч S? ч \ч > \
Ч Ч \^ ЧЧ
Ч Ч \^
ч \ \ч
*. х s N ч
N Ч \ V ч
ч ч \ч ч\
ч ч ч \NV ЧЧ
ч Ч ч чч ЧЧ
^* ^ ^ ^Ч\ \Ч
Т'^ Г^ i i . -^, % чч^чч
1,0
0,9
0,8
0,7
л 0,6
■? 0,5
to,
0,3
0,2
0,1
О
01 0,2 0,3 0,4 0,5
А 1
Тс Не3 Не*
Фиг. 6. Приведенное поверхностное натяжение как функция
приведенной температуры Г* и квантовомеханического параметра Л*.
Стрелки над атомными и молекулярными символами указывают приведенные
критические температуры соответствующих веществ (согласно де-Буру и
Берду [38]). Экспериментальные значения для D2 и Не'(Х) приведены для
сравнения с теоретическими значениями, вычисленными де-Буром и Бердом.
и Риделем [45], Брок и Берд [49] предложили
модифицированные формулы Катаямы — Гуггенгейма:
Г = (-0,951 +0,432 i)(l-0VV 2с=щ, (22.18)
0,6 0,7 0,8
T=kT/s
0,9
t
Н2
1,0
т
HD
t DT t Ne\
D2 T2 Аг

90 Часть I. Термодинамика и квазитермодинамика
Т \и/»
Г = (— 0,281 + 0,133П) (l — ^) \ Ус
d\npV
d\nT
IS
1,0
0,5
0
i
;
л#
ч.
1 1
2 J
Фиг. 7. Зависимость Р(Л *) от Л *
[по де-Буру и Берду (см. фиг. 6)].
(22.19)
Обе формулы достаточно точны для простых
неорганических веществ и для большого ряда разнообразных
органических соединений.

ЧАСТЬ II
СТАТИСТИЧЕСКАЯ МЕХАНИКА
Только статистическая механика позволяет построить
общее описание макроскопических явлений на основе
молекулярной теории. В этой части книги при описании
поверхностного натяжения через межмолекулярные
потенциалы и молекулярные функции распределения мы будем
использовать строгие положения классической и квантовой
статистической механики. Однако квантовостатистический
анализ поверхностного натяжения будет лишь кратко
изложен в п. 42. Будет дано сравнение экспериментальных
данных с теоретическими результатами, полученными на
основе некоторых приближений классической статистики.

Глава!
МЕТОД СТАТИСТИЧЕСКОЙ ТЕРМОДИНАМИКИ 1
§ 1. Канонический ансамбль
23. Статистическая сумма и поверхностное натяжение.
В статистической термодинамике, в которой
рассматривается лишь вещество, находящееся в состоянии равновесия,
свободную энергию F замкнутой системы обычно выражают
через статистическую сумму Z с помощью соотношения
F = — kTlnZ. (23.1)
Рассмотрим замкнутую систему, состоящую из Nlf..., Nx
молекул 1-го, . . . , х-го сорта соответственно. Обозначим
вектор, указывающий положение центра масс s-й молекулы
(s) (\) (N/)
1-го сорта, через г)}, множество таких векторовг\',..., г/
всех Ni молекул t-ro сорта через {/*/}, а произведение
элементов объема для этих Nt молекул drf'K . . dr i '' через
d{rt}. Тогда классическая статистическая сумма Z имеет
вид
х
Z (ДГ, V,T)= Z(Nlt . . . , Nx, V, Т) = П (ЬТ'/ДЛЛ X
1=1
X Q (Nlt . . . , Nx> V, Т), (23.2)
Q(N,V,T) = Q(Nlt...,NK,V,T) =
= \ .. Лехр [-. w \d{ri).. .d{rx},
(23.3)
1 Общее изложение статистической термодинамики см., например,
в работе [50].

94
Часть П. Статистическая механика
(2nm,.kT)tJ2
^= ; , (23.4)
где Ф ({ri}, . . ., {гх}) — потенциальная энергия, h —
постоянная Планка, т,— масса молекулы /-го сорта,
величина Q называется конфигурационным интегралом, а
величины j. (Г) описывают вклады вращательных и
колебательных степеней свободы молекул i'-го сорта в
статистическую сумму. В данной книге повсюду предполагается,
что колебательные и вращательные степени свободы
отделимы от поступательных, хотя в общем случае
потенциальная энергия системы зависит от координат, описывающих
вращение, столь же существенно, как и от координат
поступательного движения молекул. Наше предположение
кажется несколько смелым для статистической
термодинамики поверхностей раздела, поскольку условия
вращения существенно зависят от агрегатного состояния
вещества. Следовательно, излагаемая ниже теория дает точные
результаты только в случае одноатомных веществ, для
которых ]£ (Т) = 1, и оказывается лишь приближенной в
применении к веществам, состоящим из двухатомных или
многоатомных молекул.
Далее, нам предстоит часто использовать функцию
плотности вероятности Р(Л° ({гх},. . . , {г*}; {р2}, . . .,{р*}),
которая определяется так, что вероятность пребывания
системы в состоянии d {гг}. . A {rx} d {рх}. . А {рх} вблизи
точки фазового пространства {гг}9. . . , {rx}, {pi\y ... , {р*}
равна
РШ) ({Гх}, . . . , {гх}; {Pl}9 . . . , {р.}) х
xdirj . . . d{r*}d{pj . . . d{px},
гДе {pi} означает множество импульсов р^\ . . . ,р{!*1\
pis)— импульс s-й молекулы 1-го сорта, a d {pi} =
= dpV...dpfi\
Функция плотности вероятности P(N) в случае
замкнутой системы, находящейся в равновесном контакте с
тепловым резервуаром, имеющим температуру Г, определяется

Гл. I. Метод статистической термодинамики
95
соотношением
PiN) ({гг} {/\}; {/М {/>*}) =
X
Хехр
u 1=1 L J
Я({Г1>, . . . ,{rx); {ро, . . . , {рх})
(23.5)
где Я — гамильтониан системы
я = S SST 2 W + ф an}. • ■ • . (М). (23-6)
/=1 г s=l
Ансамбль систем, распределение вероятностей в котором
определяется формулой (23.5), называется каноническим
ансамблем.
Если с помощью уравнений (23.2) и (23.3) вычислить
статистическую сумму Z как функцию внешнего
параметра У, то возможно, в принципе, получить все
термодинамические свойства однородной системы из Z. Необходимые
для этой цели основные уравнения можно взять в
следующем виде:
U = kT*(^)vN, (23.7)
S =k\nZ+kT(*^)vN. (23.9)
Если бы в случае двухфазной системы площадь
поверхности раздела А можно было рассматривать как
внешний параметр, то из уравнений (4.4) и (23.1) можно было
бы получить статистическо-механическое выражение для
поверхностного натяжения
*-(£),.,.„■—*»■№■),.,.„• <2310>
Однако площадь поверхности раздела не всегда можно
рассматривать как внешний параметр, так как
термодинамические величины системы зависят не только от площади,
но и от формы и ориентации поверхности раздела. Тогда

96
Часть II. Статистическая механика
площадь поверхности раздела следует принимать за внешний
параметр, выбирая ее в каждом отдельном случае с учетом
дополнительных соображений, как это показано в
нижеследующих примерах.
Рассмотрим двухфазную систему, находящуюся в
сосуде, имеющем форму прямоугольного параллелепипеда.
Если система помещена в однородное гравитационное поле
так, что верхняя и нижняя стенки сосуда находятся в
горизонтальном положении, то с макроскопической точки
зрения можно считать, что площадь поверхности раздела
единственным образом определена через площадь одной из этих
горизонтальных стенок. В этом случае площадь
поверхности раздела можно отождествить с площадью любой из
этих стенок, которая, разумеется, является внешним
параметром. Другими словами, для того, чтобы из статистико-
механического выражения (23.10) получить уравнение для
поверхностного натяжения, необходимо только вычислить
статистическую сумму как функцию площади такой стенки.
Следует заметить, что поскольку влияние гравитации
на поверхностные свойства пренебрежимо мало вследствие
крайне незначительной толщины межфазового слоя, то
плоскую поверхность раздела можно рассматривать, вообще
не вводя явно такого вспомогательного поля,
поддерживающего плоскую форму поверхности раздела.
При изучении поверхностного натяжения в случае
сферической поверхности раздела вместо однородного поля
тяжести вводится вспомогательное поле центральной силы
(см. п. 27).
24. Молекулярные функции распределения. Для
дальнейшего развития статистической теории межфазовых
поверхностей раздела необходимо определить функции
распределения молекул. Эти функции играют важную роль
в молекулярном толковании термодинамических свойств
макроскопических систем. Унарная функция
распределения *■ щ (г) определяет среднее число щ (г) dr молекул
1 Наряду с термином «унарная функция распределения» часто
используется название «одночастичная функция распределения», а
вводимые ниже бинарную и тернарную функции распределения
называют также двухчастичной и трехчастичной функциями распределения
соответственно. — Прим. ред.

Гл. I. Метод статистической термодинамики
97
1-го сорта в элементе объема dr в окрестности точки г.
Бинарная функция распределения пц (г, г') определяется
таким образом, что среднее число пар молекул /-го и /-го
сортов равно tiijdrdr\ причем молекула 1-го сорта
находится в элементе объема dr в окрестности точки г, а
молекула /-го сорта находится в тот же момент времени в
элементе объема dr' в окрестности точки г'*.
Из уравнения (23.5) прямо следует, что для
канонического ансамбля функции распределения щ и пц
определяются соответственно как
"'(r<1))=(n^S---Wr<1,-^)x
Хе~ф//гГ d{ri). . . d{rx}, (24.1)
nuWf»)- £'№^ \...\Ыг«-гГ)х
k
X б (г<2> — г}')) е-ф/*г d {л} ...d {rx}, (24.2)
где Q—конфигурационный интеграл, определенный по
(23.3), а б (г —г') —дельта-функция Дирака 2.
Внутри гомогенной жидкой фазы функция т (г(1)) не
зависит от координаты г(1) и равна средней плотности молекул
1-го сорта Ni/V, а бинарная функция пц (г(1), г(2)) зависит
только от расстояния |г(1)—г(2)|. Однако внутри
межфазового слоя или вблизи его обе эти функции могут
заметно изменяться в зависимости от расположения частиц.
Трудности, имеющиеся в молекулярной теории
поверхностного натяжения, объясняются тем, что физические свой-
1 Из этого определения следует, что бинарные функции
распределения удовлетворяют соотношению пг{г^', И2)) =п„ (г^2\ г(1)),
однако, вообще говоря, пг (г(1\ г(2)) ф Пц (r(2V(1)).
2 Дельта-функция Дирака Ь(г — г1) обладает тем свойством,
что она равна нулю везде, кроме точки \г — г' \ — О, а в этой точке
она столь велика, что интеграл от 6 (/* — г') по всему пространству
равен единице (см., например, [51]).

98
Часть II. Статистическая механика
ства межфазового слоя существенно зависят от
пространственного изменения функций распределения.
В настоящей книге предполагается, что полную
потенциальную энергию системы можно представить в виде
Ф = | 2 2 2 0//(k<«)-r}')|). (24.3)
/, /=1 s=l /=1
Здесь фц(г) — межмолекулярный потенциал двух молекул
1-го и /-го сортов, находящихся на расстоянии г друг от
друга. Соотношение (24.3) имеет место для большинства
встречающихся химически насыщенных сферических или
почти сферических молекул.
Таким образом, -внутреннюю энергию системы можно
записать в следующем виде:
X
+ Т 2 J " ' Wr<V<*>)0/7 (rb*)drWdrM, (24.4)
л /=i
где r(12) = гi — r2. Первый член в правой части уравнения
представляет собой среднюю кинетическую энергию
системы, а второй член — среднюю потенциальную энергию.
Если предположить, что функция потенциальной
энергии имеет вид (24.3), то после дифференцирования
уравнения (24.1) по г(1) получим
I
X v<-s) Фи ('(s/)) е~ф/кТ б (rjs> — r<D) d {гг} ...d {г*}, (24.5)
или, используя уравнение (24.2),
V(i)n/(r(i)) = _^ ^ ^ 0;,(г(»>) л/7 (га), r<«)dr<«, (24.6)
/=ir
где при суммировании необходимо опустить члены,
соответствующие s = / и 1 = /. Уравнение (24.6) представляет
собой обобщение уравнения Борна — Грина — Ивона [52,

Гл. I. Метод статистической термодинамики 99
53,84] для унарной функции распределения на случай
многокомпонентной системы [54] и является одним из основных
уравнений статистической механики поверхностного
натяжения *.
Операции, совершенно аналогичные тем, которые были
выполнены при выводе уравнения (24.6), приводят нас
после дифференцирования уравнения (24.2) относительно
г(1) к обобщению уравнения Борна— Грина — Ивона для
бинарной функции распределения на случай
многокомпонентных систем [54, 56]:
V(1) л// (r(1), r<»>) +zjrnif (/*>, r<*>) v(1) Фи ('(12)) =
= ^-ll\nifk(r^\ r<*\rM№»<pik(r™)dri*\ (24.7)
где rink (r(1), r(2), r(3))— тернарная функция распределения,
определяемая уравнением
Nt {N; — 6,,) (Nk — bik — 6,k)
1 V ' (П Nt\) Q
/
X S ' ' ' \ S (rU) "~ rW S (Г(2) — Г/0) S (r{3> — Г^ X
x^-o/^rd{ri} . . .^{rx}. (24.8)
Поскольку уравнения (24.7) для бинарных функций пц
содержат тернарные функции распределения, необходимо
ввести некоторое приближение для тернарных функций,
выразив их через бинарные с тем, чтобы свести уравнения
(24.7) к замкнутой системе уравнений для пц. В случае
однородной системы часто используется следующее
приближение, введенное Кирквудом и обычно называемое
суперпозиционным приближением [57]:
пи (г(1), r(2W(r<2\ г(8))лл/(г(8), г(1))
(24.9)
1 Наиболее полное и систематическое изучение молекулярных
функций распределения было выполнено Н.Н. Боголюбовым [55],
рассмотревшим не только равновесные, но и кинетические функции
распределения групп молекул. В работе [55] с самого начала
исследуется общий случай многокомпонентной системы. — Прим. ред.

100
Часть II. Статистическая механика
Подставляя последнее выражение в уравнение (24.7),
получаем
Vw In п„ (г<», г<«) + ± V(1V,7(/-(,2)) =
= 1 yrn^rM^n^.W v
kTf) ЯЛГ<1))Я/ (r«))«ft(r«))
В случае однокомпонентной и однородной системы
уравнение (24.10) было решено численными методами для
молекул — твердых шариков [58] и для молекул с
модифицированным потенциалом Леннард-Джонса [59]. В принципе
уравнение (24.10) можно также использовать для решения
задачи двухфазной системы с поверхностью раздела,
однако представляется довольно трудным делом получить
численное решение для такой системы. Нахождение
бинарной функции распределения представляет собой поистине
ключ к проблеме межфазового слоя.
Для однородной жидкости бинарную функцию
распределения часто выражают в виде
пц (г) = тп,-&/ (г), (24.11)
где щ и п/ не зависят от г, a gv7- (/*) называется
корреляционной функцией.
25. Поверхностное натяжение на плоской поверхности
раздела в многокомпонентных системах. Рассмотрим
систему, находящуюся в сосуде, который имеет форму
прямоугольного параллелепипеда с ребрами длиной Zlf /2, /3,
направленными вдоль осей прямоугольной системы
координат х, у, z соответственно; ось z направлена вертикально
вверх — противоположно направлению силы тяжести.
Примем те же обозначения, что и в п. 17 (см. также фиг. 8).
Тогда
V=hl2l3i (25.1)
А = ltl2. (25.2)
Если свободная энергия Гельмгольца двухфазной
системы зависит от Л и V, то получим следующее соотноше-

Гл. I. Метод статистической термодинамики 101
ние:
Xdllll2,l3,T,N \dA>V,T,N \dV>A,TtN '
Но поскольку (dF/dA)v г ^ и — (3F/dV)A г
^соответственно равны поверхностному натяжению у и давлению р, то
мы имеем
т-Л + гвг)ььг.ж- <25-4'
Используя соотношение (dF/dV)A Т N= (l//i/2) X
X (dF/dls)^ h Tt N, можно переписать уравнение (25.3)
в альтернативной форме как
т = 7^4^-Чах)]
(25.5)
Давление системы в терминах молекулярных функций
распределения нельзя получить путем непосредственного
Фиг. 8.
дифференцирования kT In Z по V. Это удается сделать либо
исходя из теоремы вириала, либо с помощью аппарата,
специально разработанного Боголюбовым [55] и Грином
[60]. Выражение для поверхностного натяжения через
функции распределения получено для простой жидкости
с помощью обобщения аппарата Боголюбова — Грина

102
Часть IL Статистическая механика
0
[61, 62, 63]. Как выяснится ниже, при применении этого
аппарата более удобно пользоваться уравнениями (25.4)
или (25.5), нежели уравнением (23.10).
Чтобы продифференцировать статистическую сумму,
введем приведенные переменные (см. фиг. 8):
(25.6)
Тогда конфигурационный интеграл (23.3) можно записать
в виде
П&'аЛ г 1
Qn = -*-= \ ...\ <r^>*<kT П <&>.. • dlNit, (25.7)
i
где Ф* — потенциальная энергия Ф, выраженная в виде
функции приведенных переменных согласно формулам
(25.6). Кроме того, мы имеем
if=к[ ll (lf) ~ l>)f+ll ^ ~~ ^>)2+
+ *з (ds> - tW* (25.8)
и, следовательно [см. (24.3)],
^422^^4<<г>- (25-9)
i,Js,t 4j
Используя приведенные выше соотношения, из уравнений
(23.1), (23.2) и (24.2) немедленно получаем
h (ах) = - 51 Njtr +
\°l1 'h. h, T.N i==1
+ i 2 [\ "// (rw. /-<2>) 0;,. (r<">) (^!!l dr(»dr<2», (25.10)
/ / «-(12)
где #<12> == jcd) — #(2) есть jc-составляющая r<12) = r<L)—
— r(2), вектора взаимного расстояния между точками г(1)
и г(2), направленного из точки г(1) к точке г(2).

Гл. I. Метод статистической термодинамики 103
Если пренебречь краевыми эффектами,
обусловленными стенками сосуда, то nL (г^) будет зависеть только
от zM и ее можно обозначить через nt (г*1*), а пц (г(1), г(2))
будет зависеть только от координат z^ и г(12) и ее можно
обозначить, как пц (г*1*, г(12)). Уравнение (25.10) теперь
приводится к виду
'7 -/а
Аналогично получаем
+ 1-г 2 J ^(1) J щ, (z<«; /■<»>) 0)/ (г'12') (^J-2 dr<»>. (25. J1)
+ ^S ^ dz<i) ^//(га); ro«)0;,(r(»))^^dr(«>. (25.12)
11 -/« Г
Подстановка уравнений (25.11) и (25.12) в уравнение
(25.5) тотчас же приводит к требуемому выражению
для поверхностного натяжения на плоской границе
раздела фаз1 [61—63]
00
х ^ пц (2d); г<»>0',,(/-<»>) (*il2))2-(zil2))2 drm), (25.13)
Из уравнений (25.4) и (25.11) получаем альтернативное
1 Здесь использован тот факт, что величины /а и г можно
заменить на со , если они достаточно велики по сравнению с толщиной
межфазовой зоны.

104
Часть II. Статистическая механика
выражение для у:
Т= \ pdzW- \ [Зя/ЛГ —
—ia —г
-т2$%0;/^ШГ^(12)]^). (25.14)
Если вся система однородна и поверхность раздела
не оказывает на нее влияния, то в уравнении (25.11)
lx (dF/dlJit, /3, т, n равное (dF/dV) = — pV и, следовательно,
/ i. I г
р = У n«kT — ^S^^-^Sr 0;/(^(1',)rfr<")f 1(25.16)
Таким образом, внутри фаз аир соответственно имеем
(л.(12))2
P-S«?*r-jSUf,^0;/(r«»)<(r«». (25.17)
Подставляя последние два уравнения в уравнение (25.14),
получаем
оо оо
Y = w2 5 (nf — m) dzM — i-2 5 d*(1) x
* — оо *"» / — оо
X ^(п-/-л//) 0;.^dr^>, (25.18)
где п*р и njtf определяются как
л«з= /if 11—A (*a>)] +п?А (2(D), (25.19)
nf = nf.il —A (zV)\ + nf, А (2d)). (25.20)
Здесь A (z) — функция единичного скачка, определенная
согласно (19.7).

Гл. I. Метод статистической термодинамики 105
Поверхностная плотность молекул t-ro сорта
определяется как интеграл
оо
Г/ = \ (ъ (z<l>) — nf) d&h (25.21)
— ОО
Мы можем также ввести другую подобную величину —
поверхностную плотность пар молекул i-vo и у-го сортов:
оо
iv (г<">) = \ (пц (г'1'; г<12>) — я«/) rfz<». (25.22)
— ОО
Тогда уравнение (25.18) можно переписать в виде
оо
Г = -kf% Г, +|2 J Г/7 (r<»>) 0;..(r(^)(-^fdr(^. (25.23)
/ i, j -co r
Уравнения (25.13), (25.14) и (25.23) представляют собой
эквивалентные и строгие выражения для поверхностного
натяжения на плоской границе раздела. Они совершенно
не зависят от каких-либо других предположений, кроме
(24.3), так как именно из этого уравнения следует, что
поверхностное натяжение может быть выражено только
через унарные и бинарные функции распределения,
независимо от вида функций распределения высших порядков.
Из уравнения (25.13) видно, что численное значение
поверхностного натяжения можно легко вычислить, если
известна бинарная функция распределения в межфазовой
области. Однако, как уже кратко упоминалось в
предыдущем пункте, на современном этапе развития статистической
механики еще не получено решение приближенного
интегрального уравнения для бинарной функции распределения
в межфазовой области даже для случая однокомпонентной
системы. Чтобы рассчитать значение поверхностного
натяжения методом функций распределения, необходимо ввести
еще более далеко идущие приближения. В п. 37—39 будут
приведены результаты некоторых численных расчетов,
выполненных на основе таких приближений.
В случае однородной жидкости благодаря ее
изотропности имеют место уравнения, которые можно получить

106
Часть II. Статистическая механика
заменой л;(12) в уравнении (25.15) на у{12) или z<12>.
Складывая все три уравнения соответственно с х^12\ #(12) и г(12),
получаем
с»
= 2 л, А71 - ^ 2 п/Л, \ ft, (/<">) 0;у (г) r3dr. (25.24)
/ Л J о
Это уравнение обычно используется в качестве уравнения
состояния.
26. Поверхностное натяжение на плоской границе
раздела между чистой жидкостью и ее паром, а) Общие
соотношения [20]. Обращаясь к случаю однокомпонентной
системы, перепишем уравнения, полученные в
предыдущем пункте, в более удобном для вычислений виде. С этой
целью обозначим унарную функцию распределения через
п (г), а бинарную — через п2 (г, г'). Тогда выражения
(25.13) и (25.23) для поверхностного натяжения
приобретут соответственно следующий вид:
Г = у ^ dzil)\п*(2(1)'. г(12))Ф'(г(12)) (Х{12))~(12){12))2 dril2)>
— оо
(26.1)
г = _ rkT + i $ Г2 (г<«>) 9>' (/-<»>) ^ Л<«>, (26.2)
где Г и Г2 определяются [вместо (25.21) и (25.22)]
соответственно как
оо
Г = [ (п — п*0)йгЫ, (26.3)
Г2 = (г<12>) = \ Ыг (г<»; r«2>) — nf] dz^. (26.4)
— ОО
Обобщенное уравнение Борна — Грина — Ивона (24.6)

Гл. I. Метод статистической термодинамики 107
для унарной функции распределения в случае одноком-
понентной системы сводится к следующему:
d/i(*(1)) 1 С *(12) ^,
1&>
= w\jm Ф'(г{12))п2(гЫ; i*«)dr<»>, (26.5)
где предполагается, что унарная функция
распределения зависит только от z(1).
Определим v-e моменты [п (z) — пар] и [п2 (z; г(12))—п*&]
следующим образом:
оо
[Г]» = J г» [л (г) — п«Ч dz, (26.6)
— ОО
ОО
[Г,]» = ^ z* [«2 (z; r<12>) —nf 1 dr (26.7)
— ОО
Интегрирование уравнения (26.5) по z(1) от — оо до оо
дает
п(* — п* = ^^-ф> (Г(12>) г2(Г(и)) dr<12>. (26.8)
Здесь были использованы следующие соотношения:
lim п(г) =na, lim п (z) =п^9 (26.9)
2-»-—ОО Z-K»
\ 1ST #' (г<12)) n2P dr<12> = °- (26-10)
Аналогичным путем получаем для v-ro момента:
•Г»* = -^ТТТ^ 0'('<12)Hr2]v+1rfra*>. (26.11)
Поскольку [Г]0 равно поверхностной плотности молекул Г,
определенной согласно (26.3), подстановка (26.11) при
v =0 в (26.2) дает для поверхностного натяжения
формулу
Y = $7^0' (гМ^ЩГА + ^ [Г,]0]лк»>, (26.12)

108
Часть II. Статистическая механика
которая представляет собой другую форму выражения
для поверхностного натяжения, полученного
первоначально Кирквудом и Баффом [21].
Теперь рассмотрим статистическое выражение для
избыточной внутренней энергии, которую иногда называют
поверхностной энергией. Из уравнений (2.2) и (24.4)
можно без труда получить следующее выражение:
Us = ^NskT + 4r\\ ln2(z^;r^)—nf) ф (/<">)dr^dz«\
(26.13)
куда в результате интегрирования по *(1) и уМ входит
площадь поверхности раздела А. Используя уравнения
(5.5), (5.7) и (26.4), можно переписать выражение (26.13)
в форме соотношения для поверхностной плотности
энергии:
v =lTkT + ±\Т2(г<12>) ф (r<«>)dr^l (26.14)
Если выбрать в качестве плоскости ху
эквимолекулярную разделяющую поверхность, то выражения (26.2) и
(26.14) приобретут соответственно следующий вид:
У - ^\т'Лг{12))Ф' (r^){-^dr^K (26.15)
v = 1 ^ Г2 (г<12>) ф (/■<">) dr^K (26.16)
б) Закон соответственных состояний. Хотя выражение
(26.1) определяет поверхностное натяжение чистой
жидкости через межмолекулярный потенциал и бинарную
функцию распределения, определить численное значение
его с помощью этого соотношения крайне трудно, не
прибегая к грубым приближениям для функции
распределения. Однако довольно легко удается дать статистическую
интерпретацию закона соответственных состояний для
молекул, межмолекулярный потенциал которых может быть
представлен в виде некоторой универсальной функции /,
содержащей два масштабных параметра D и е, которые

Гл. У. Метод статистической термодинамики 109
характеризуют тип молекул:
0 М = в/(-£-). (26.17)
Потенциал Леннард-Джонса, определенный согласно (22.4),
является известным примером приближенной
универсальной функции, содержащей две постоянные е и D. Как и
в п. 22, определим приведенные переменные:
Используя уравнения (23.3) и (24.2), бинарную
функцию распределения в чистой жидкости можно выразить
как
п2 (г, г') =
W (# - 1) J J 6 (г - г(1)) 6 (г' — г(2))ехр [— Ф/kT] П dr(s)
—^ ,(26.19)
J jexp[— Ф/kT] f[ dris)
N
П
s=l
где Ф — потенциальная энергия системы.
Чтобы представить бинарную функцию распределения
в приведенном виде, используем переменные
e(s) = ^, 6(s'> = 4r, °<s° = 4r- (26-2°)
Для простоты будем рассматривать систему,
заключенную в сосуд, имеющий форму куба с длиной ребра /.
Тогда уравнение (26.19) можно переписать в приведенном
виде *
1 Строго говоря, для сохранения плоской границы раздела
необходимо, как показано в п. 23, ввести вспомогательное внешнее поле,
подобное полю силы тяжести. Однако вводить явно внешнее поле нет
необходимости, так как результаты не зависят от величины этого
вспомогательного поля до тех пор, пока оно по порядку величины близко
к обычному гравитационному полю.

110
Часть II. Статистическая механика
DGn2(D6,D6') =
l/D l/D N
n(n — i) I ... J б(e — e(1))б(6' — e(2))exP[—Ф/kT]П^e(s)
0 0 s=l
~~ l/D l/D N »
j ... J exp [— Ф/kT] П d0(s)
0 0 S=l
(26.21)
Ф-{2 / (0<S°) (26-22)
s,/=l
Легко видеть, что правая часть уравнения (26.21) зависит
только от l/D и e/kT. Следовательно, D6n2 (г, г') является
универсальной функцией приведенного объема v* и
приведенной температуры Т\ определяемых по (26.18), пока число
молекул N остается постоянным.
Используя уравнение (26.22) и приведенные
переменные 6(s) и 6<s/), определяемые по (26.20), можно переписать
(26.1) в следующем виде:
оо
f = 1 ^ de<x) ^D*n2 (DQ?; D6(,2)) x
— ОО
x Г (О (^12))2е72)(6'12))2 dbil2)> (26-23)
где у* — приведенное поверхностное натяжение,
определенное согласно (26.18). Поскольку было доказано, что
D^iD^'yD^) является универсальной функцией Т*,
у*, 02° и 6(12), то у* должно быть универсальной функцией
только Т* и V*.
Если значение N/V взято промежуточным между
значениями плотностей молекул жидкости и пара при орто-
барическом давлении, то плотность объемной фазы с
каждой стороны разделяющей поверхности зависит только
от температуры, но не от значения N/V. Таким образом,
при заданной температуре бинарная функция
распределения п2 (z(1), г(12)) имеет вполне определенную величину
в межфазовой области, так же как и внутри обеих фаз.
Поэтому величина у*, определяемая из уравнения (26.23),

Гл. I. Метод статистической термодинамики 111
не зависит от числа молекул и от объема и формы сосуда.
Следовательно, у* является универсальной функцией лишь
приведенной температуры Т*. Это согласуется с
формулировкой закона соответственных состояний, данной в
соотношении (22.6).
27. Поверхностное натяжение на сферической
поверхности раздела. Чтобы избежать ненужных усложнений,
ограничимся рассмотрением однокомпонентной системы.
Обобщение на многокомпонентную систему не представляет
труда \
При термодинамическом анализе сферической
поверхности раздела фаз удобно рассматривать часть сферы. Хотя
можно использовать ту же часть сферы, которая
рассматривалась в п. 8. [12], для простоты рассмотрим часть
шарового слоя, определяемого неравенствами (фиг. 9)
©i< в< ©2, (27.1
О < Ф < Y,
где г, 0 и ф — полярные координаты, начало которых
совпадает с центром кривизны сферической поверхности
раздела, а соответствующие ортогональные единичные
векторы есть еп е$ и еф [64]. Если краевыми эффектами —
влиянием стенок — можно пренебречь, то для
воспроизведения такой поверхности раздела было бы достаточно
слабого центрального поля с центром сил в начале
выбранной системы координат.
Выберем в качестве разделяющей поверхности
сферическую поверхность г = а и рассмотрим бесконечно малую
вариацию б¥ при постоянных а, /?а, /?3, в1э в2, Т и N.
Тогда, учитывая происходящие одновременно изменения
значений Va, V& и А и постоянство а, а также используя
1 Как можно заключить из результатов, полученных в предыдущих
пунктах вслучае плоской границы раздела фаз,большинство уравнений,
выведенных в настоящем пункте, можно обобщить на случай
многокомпонентной системы просто путем суммирования по этим
компонентам. В п. 36 приводится другой метод вывода уравнений для случая
многокомпонентной системы.

112
Часть II. Статистическая механика
уравнение (9.4), получаем
dF_
— Р"
dV*
дЧ
(27.2)
<puju (X
Фиг. 9.
V
В нашем случае
Уа = {с3 — (#а)3} (cos 6j — cos 02) -^,
Ур = {(/?*)» _ as} (cos 6L — cos 62) -|-,
Л = с2 (cos 6j — cos в,) V.
(27.3)

Гл. I. Метод статистической термодинамики 113
Подставляя последние соотношения в уравнение (27.2),
получаем [см. (14.7)]
Y = Я \ Р^гЧг + coseiicos62 £] • (27.4)
Дифференцирование dF/dW можно выполнить таким же
способом, как и в случае плоской поверхности раздела,
определив приведенные переменные следующим образом:
ф(«) = ¥5(S)> о < ш(*> < 1, (s = 1, . . . , N). (27.5)
Тогда элемент объема для s-й молекулы и расстояние
между s-й и /-й молекулами соответственно записываются
как
dr<s> = (r<s>)2 ¥ sin 0(s)dr(s)d0(sWs) (27.6)
и
г&) = [(r<s>)2 + (r<'>)2 — 2r<s>r«> x
X {sin 0(s) sin 0(O cos (¥ (ю(0 — ©(s))) + cos 0(s) cos e(0}]v\
(27.7)
Отсюда конфигурационный интеграл (23.3) можно
представить в виде
s=l
(27.8)
где переменные интегрирования r{s\ 0(s) и <o(s) изменяются
соответственно от i?a до R , от вх до в2 и от 0 до 1, а
потенциальная энергия Ф* является функцией приведенных
переменных.
Если Ф задана в виде (24.3), то из уравнений (23.1),
(27.7) и (27.8) следует
V 5¥ = _ NkT + MWr(1)' Г(2>) 0/(r(12)) Х
,а)^(Ф<^фа))з1п(Ф(^фа)) sjn e(1)s.n fl(2) ^(1),r(2,
(27.9)

114 Часть II. Статистическая механика
Пренебрегая влиянием границ, мы можем благодаря
симметрии системы записать
п (r<D) = п (r<D), п2 (гМ, г&) = п2 (г»); г<12>). (27.10)
Составляющая вектора г<12) в направлении еф
приобретает следующий вид (здесь е^ соответствует г(1) и г(2) соог-
ветствует е^):
rU2).^) = r(2)sine(2)sin(T(2)-9(1)),
rU2) . ef = r{1) sin в(1) sin (ф(« — ф(1>). (27.11)
Тогда имеем
И1* г<2> (ф(2)_ф(1)) sin (ф<2) — ф(1)) sin ew sin 6<2> =
" С™ • g-))2Sin(^-^>) ~ (r(12> • ^ X
[r<">-(4"-*?>)] .^-^ ■ (27.12)
Подставляя уравнения (27.10) и (27.12) во второй член
правой части уравнения (27.9), получаем
у^П2(г(1)' г{2)) Ф'(г{12)) X
х г<*> г<2> (Ф<2> - ф^>) sin (Ф<2> - yd)) sin № sin 6<2> irn Wi^ =
r(12)
X
ъ\\ъ(г{1)\г™)ф'(г™)
(г<»>-^))а(ф(«-Ф»)) ^ мы ^
у - dr^drW —
Л r<,2>sin(<p<2>-<p<»)
a Of [Г(12) . Ш_в(1))]2
US "^(1>;г(,2)) 0'w—V> х
(ф(« _ ф(1>)
Х ,1п(ф«-фО)) rfr(1,dr(2>' <27ЛЗ)

Гл. I. Метод статистической термодинамики 115
где второй член следует из соотношения
^п2(гЫ,гМ)ф'(г№) х
(г<12>-<>)[г<'2>- (^)-42))](ф(2)-ф(10
Х r^sinfa'2»-?*1')
(г<21> • <2>) [ г<21> • (*<?> - ^>)] ( ф<1> - ф<2>)
dr<D dr*2' =
,(12>Ш1(ф(1>_ф(2))
= ^"2(г(1>,г(2))^'(г(12>)х
[г(12).(еа)_^2))]2(ф(2)_(р(1))
drW dr&
rttWsinfoW-q)*»)
drwdrw. (27.14)
Пусть т — длина порядка радиуса действия
межмолекулярных сил ф' (г<12>). Тогда подынтегральные
выражения в правой части уравнения (27.13) обращаются в нуль
для г(12)^>т. Так как во всем объеме |ф(2)—ф(1)| повсюду
составляет самое большее величину порядка г'12'//-*1), то
(ф(2> _ф(1))/ Sin (<р<2> _ф<1>) =1+0 (T2/(rd>)2) при r<12>^t.
Аналогичным образом | е^ — е$>2> | является величиной
порядка т/г(1). Поэтому, если пренебречь величинами
порядка (т/г*1*)2, то подынтегральное выражение в правой
части уравнения (27.9) можно заменить на пг (г*1*; г<12)) х
X ф' (г<12>) (г<12> • 4))2/'•(12,.
Если радиус поверхности раздела достаточно велик
по сравнению с т, то можно подобрать величины Ra, /?3,
6Х и 62 таким образом, что в уравнении (27.9) можно
будет произвести указанную выше замену для всей области
интегрирования и получить уравнение [64]
г (г(12) . (1))2
X \п2 (/*>, г(«)) 0' (/<»>)- ^f—-dr<i2), (27.15)

116
Часть II. Статистическая механика
которое справедливо для членов до первого порядка по x/R
включительно.
Если в объеме Vй заключена только однородная
объемная фаза а, то влияние поверхности раздела фаз
отсутствует, и тогда по аналогии с равенством (27.4) получаем
а
£\p*(rii))*drv = -4^. (27.16)
Ra
Тогда из (27.15) легко видеть, что
а а
#-\ ра (г*1))2 drW = N*kT — ^2 \ (r(i>)2 d/W X
R* R*
Г /-(12) J*h
Х\п2(г^)ф'(г™уг '* > drw, (27.17)
и аналогично
Д0 R*
£ J pP (rd))2 drV = Л^£Г — ^-2 ^ (r(*>)2 Л*> X
X
с о ( r(12) • e{1)V
\ /i§ (r<">) 0 ' (r<«>) т^-ф-^ dr<12>. (27.18)
Последние два уравнения можно записать совместно в
компактном виде
R& R&
Jpotf (Г(1))2 rf^l) = ^ [nafikT —~\п*
Ra R*
г1
PX
X 0' (г<12))v _(12)ф dr<12>] (/•»>)* dr«>, (27.19)
где обозначения аналогичны введенным в (25.19) и (25.20):
п«(з = я« {1 — Л (/•»> — а)} + >Л4 (rd> — а), (27.20)
nf = п\ { 1 — А (/-<» - а)} + л£л (г*"— а). (27.21)

Гл. I. Метод статистической термодинамики 117
Подставляя (27.15) и (27.19) в (27.4), получаем [64]
Y = - % \ (п - п**) (г*))* dr») +± J (г^У drM X
R* Ra
с п ( г(12) • еа))2
Х\(п2- nf) ф' (/<»>)' -j&r-drw. (27.22)
Если использовать переменную £(1) = г(1) — а,
аналогичную (14.15), то (27.22) перепишется в виде
1 г (г(12)-е(1))2
Y = _ YkT + \ \ Г2 0' (Га«)V -^- dr<»>, (27.23)
где
оо
Г = \(п — л0"3) (l + ^-)2d|(i>, (27.24)
—ОО
оо
Г2 = \ (п%- nf) (1 +^-)2 d|(1)- (27.25)
—ОО
Очевидно, что в пределе а -* со (28.23) должно сводиться
к (26.2), поскольку равенства (27.24) и (27.25) в этом же
пределе сводятся соответственно к (26.3) и (26.4).
Выражение для поверхностной энергии можно вывести
тем же способом, что и в случае плоской границы, в
результате чего получается уравнение, аналогичное
уравнению (26.14)
v = у YkT + у ^ Т2Ф (r<i2>) dr<12>, (27.26)
где Г и Г2 определяются соответственно по (27.24) и (27.25).
§ 2. Большой канонический ансамбль1
28. Большая статистическая сумма и поверхностное
натяжение. До сих пор мы рассматривали только замкну-
1 Общее описание и подробное обсуждение большого
канонического ансамбля можно найти, например, в книгах тер-Хаара [65] и Хил-
ла [50].

118
Часть II. Статистическая механика
тые системы, для которых плотность вероятности
определенного состояния находится из уравнения (23.5).
Чтобы методами статистической термодинамики связать
термодинамические свойства открытой системы, которая может
обмениваться не только энергией, но и массой с
окружающей средой, с межмолекулярными потенциалами
взаимодействия, вводится большая статистическая сумма.
Для незамкнутой системы, имеющей химические
потенциалы |Ц» - - - » И*! температуру Т и объем V, большая
статистическая сумма определяется соотношением
Н totT9V) = E(uLl9... ,VlK9T9V) =
=2-.. ^Z(N9T9V)\[eN^lhT, (28Л)
где Z — статистическая сумма, определяемая по (23.2).
Вероятность того, что открытая система содержит
Nl9 . . . , Ny. молекул соответствующего сорта, задается
формулой
P(N9T9V)=P{Nl9...9NK9T9V) =
X
= Z-4{N,T,V)\\eNinlkT. (28.2)
В классической статистике функция плотности
вероятности для открытой системы, соответствующая в случае
закрытой системы выражению (23.5), имеет вид
Pn ({г±} w,,..., {rx}wx; {Pi}ni9 • • • > {P*}nx) =
хехр[ — ^#*({/!}*„ .. .,{гх}лгх; {Pi}N„ ■ ■., {Рх}дгх)1,(28.3)
где Hn — гамильтониан системы, состоящей из N1
молекул сорта 1, N2 молекул сорта 2 и т. д.:
н„ = 2 _i_2 ^s>>2 + ф" «ri>* <r*>*x)- <28-4>
i=l i s=i

Гл. I. Метод статистической термодинамики 119
Здесь Фы — потенциальная энергия. Набор векторов rf],
указывающих положение N молекул i-ro сорта,
обозначается символом {Г[}ы11)- Интегрирование (28.3) по всему
фазовому пространству дает формулу (28.2). Ансамбль
систем, для которых распределение вероятности задается
формулами (28.2) и (28.3), называется большим
каноническим ансамблем.
Среднее значение динамических переменных
по большому каноническому ансамблю определяется как
оо оо
Х= 2"- S^.^^Xjrrf^if,...
•. • d {р*}м* d {r1)Nx ...d {rx}Nyc. (28.5)
Как и в случае канонического ансамбля, внутренняя
энергия равна осредненному гамильтониану системы:
U =Н, (28.6)
а давление р определяется как
/» = -#■• (28-7>
Макроскопическое значение числа частиц N;, равное числу
молей, умноженному на число Авогадро, задается как
среднее от jV,:
оо оо
Ni (макроскопическое) - Ni = 2 е" 2 N!PW>T>V)- (28«8)
#,=о лгк=о
Используя определения (28.2), (28.3) и (28.5), можно
переписать (28.6) — (28.8) соответственно следующим
образом 2:
"-^(Т)....ч + и,(тг1„. <ад
1 Индекс Ni необходим для определения числа молекул i-ro сорта,
так как число Ni является переменным в случае открытой системы
в противоположность случаю замкнутой системы.
8 См. примечание 1 на стр. 20.

120
Часть II. Статистическая механика
M^srUv <28|!>
Сравнивая (28.9) — (28.11) с уравнениями (4.13) — (4.15),
получаем
Q = — kT\n Н, (28.12)
где постоянная интегрирования определена по предельному
значению в случае бесконечного разрежения. Уравнение
(28.12) является фундаментальным для большого
канонического ансамбля. Оно связывает термодинамические
величины с межмолекулярными силами и соответствует
уравнению (23.1) для канонического ансамбля.
Подстановка (4.11) в уравнение (28.12) приводит к
искомому уравнению
уА = — kT\n Н +pV, (28.13)
которое в случае однородной системы переходит в обычное
соотношение
pV =kT\n Н.
Используя (28.10), можно записать уравнение (28.13)
в другом виде
уЛ =ьм{£($*)}л^. (28.14)
Приведенные выше соотношения основаны на
предположении, что площадь поверхности раздела А является
одним из внешних параметров системы. Но, строго говоря,
это предположение не всегда справедливо, поскольку,
как указано в п. 23, для сосуществования двух фаз
требуется (без всякого исключения—в противоположность
случаю замкнутых систем) наличие небольшого возмущения
типа гравитационного поля. Этот вопрос будет подробно
рассмотрен в следующем пункте.
29. Двухфазная система в большом каноническом
ансамбле. В предыдущем пункте мы ограничились
формальным обзором статистической теории поверхностного натя-

Гл. I. Метод статистической термодинамики 121
жения на основе большого канонического ансамбля. В
большом каноническом ансамбле система характеризуется
набором химических потенциалов взамен набора чисел
молекул различных сортов. Обычно предполагается, что
химический потенциал каждого сорта молекул однороден
вдоль всей системы даже в случае двухфазной системы.
Однако, как будет показано ниже, вероятность найти
систему в таком состоянии, когда одновременно
существуют обе фазы, почти равна нулю.
Исследуем более тщательно условия применимости
метода большой статистической суммы к теории
поверхностного натяжения. Для выяснения сути вопроса рассмотрим
однокомпонентную систему. Тогда, согласно формуле (28.2),
вероятность того, что система состоит из N молекул,
определяется как
Р (N,V,T) = S"1 Z (N, Т, V) eN*jkT. (29.1)
Если выразить большой термодинамический потенциал
Q, определяемый по (4.10), как функцию Л/, Т и V (хотя Q
обычно выражается через (х, Т и У), то можно переписать
равенство (29.1) в виде
Р (N, V, Т) = E-ierW-v *we (29.2)
Обычно считается, что вероятность Р (N, Т, V) при
заданных значениях V и Т имеет лишь один острый
максимум для определенного значения N, скажем для N, за
исключением случая, когда jn принимает определенное
значение \х*, соответствующее условию равновесия пар —
жидкость. Число N является известной функцией
переменных V, Т и |i и соответствует макроскопическому числу
молекул в системе.
Пусть N' — число молекул в системе в состоянии, когда
весь объем заполнен паром, образующим однородную фазу
с химическим потенциалом \i\ a N" — число молекул в
состоянии, в котором объем заполнен однородной жидкой
фазой, имеющей тот же химический потенциал. Тогда
pV не зависит от значений N, заключенных между N' и
ЛГ. Если влияние межфазовой области совершенно не
принимается во внимание, то большой термодинамический
потенциал Q, определяемый согласно (4.11), равен —pV

122
Часть II. Статистическая механика
и, следовательно, из (29.2) получаем вероятность Р (N, I/, Т)
в виде, схематически показанном на фиг. 10.
В реальной системе, состоящей из двух фаз,
необходимо, однако, учитывать вклад межфазовой области и
поэтому, согласно (4.11), следует записать, что Q =уА—pV.
—^ N
Фиг. 10. Зависимость p(N,r V, Т) при у = 0.
Тогда для положительных значений у вероятность
Р (N, V, Т) имеет вид, схематически представленный на
фиг. И. На этой кривой видны два острых максимума
при N' и ЛГ.
При отрицательных значениях y потенциал Q = уА—pV
уменьшался бы при увеличении А таким образом, что,
согласно уравнению (29.2), даже для случая \i = \л*
вероятность P(N,V,T) имела бы при каждом N только
один максимум, для которого | у \ А достигает максимума.
Это значит, что субмикроскопические капли или пузыри
распределялись бы по объему V приблизительно
равномерно, что соответствует видимому разделению вещества на
пар и жидкость ниже критической температуры [65].
Таким образом, можно сделать вывод, что ниже
критической температуры измеряемое поверхностное натяжение
имеет положительное значение, а отрицательное значение
могло бы иметь место только при температуре выше
критической или для двух смешивающихся жидкостей [67].
Кроме того, вероятность Р (N, V, 7), имеющая вид,
схематически представленный на фиг. 11, была
действительно получена Катцурой [68] путем точного вычисления
для конечной системы, состоящей из небольшого числа
молекул. Мы рассматриваем результат Катцуры как под-

Гл. /. Метод статистической термодинамики 123
тверждение существования положительного поверхностного
натяжения. Его результат дает петлю на р — К-диаграмме,
которая, как доказал Хилл [69] 1\ исчезает в пределе N -+ оо
и поэтому не является петлей типа петли ван дер Ваальса.
Из фиг. 11 видно, что вероятность нахождения системы
в состоянии сосуществования обеих фаз ничтожно мала.
Следовательно, для любых поверхностей раздела в случае
Ф[и г. И. Зависимость" p(7V, V, Т) при Т>0.
большого канонического ансамбля особенно необходимо
вводить вспомогательное поле, такое, как поле силы
тяжести для плоской границы в п. 23.
Гравитационная потенциальная энергия молекулы с
массой m в точке с координатой z равна mgz, где
вертикальная ось z направлена вверх, a g обозначает ускорение
силы тяжести. При смещении молекулы из точки zu) в
точку z(2) изменение свободной энергии системы равно
6F = (fx (z<2>) + mgzM) — (\i (zM) + mgz^), (29.3)
где jli (z) — величина химического потенциала в точке z.
Из условия термодинамического равновесия 6F = О
имеем
И*) +Щг =И0). (29.4)
Если при z == 0 величина химического потенциала (х (0)
равна \i* — значению, при котором две фазы существуют
вместе и находятся в равновесии, то, согласно формуле
(29.4), \i (z) при z < 0 принимает значение большее, чем
|х*, и, следовательно, часть жидкости, находящейся ниже
См. также книгу Хилла Г50].

124
Часть II. Статистическая механика
плоскости 2=0, должна быть занята более плотной фазой,
поскольку химический потенциал является неубывающей
функцией плотности жидкости, а верхняя часть будет
занята менее плотной фазой.
Это соответствует большому каноническому ансамблю
систем, непосредственно соединенных при г = 0 с
сосудом, химический потенциал которого точно равен \i*.
Как мы показали, для того, чтобы вещество
существовало в двух фазах, необходимо некоторое вспомогательное
поле, которым, однако, можно пренебречь с
термодинамической точки зрения, поскольку для того, чтобы
существование двух фаз было возможным, достаточно такого
слабого поля, что его прямым влиянием на свойства
поверхности раздела можно пренебречь.
30. Молекулярные функции распределения и
выражение большой статистической суммы в виде ряда. В
классической статистической механике большая
статистическая сумма S ([л, Т, V), определенная формулой (28.1),
может быть переписана с помощью уравнения (23.2) в
следующем виде:
оо оо
s«, т, V) = 2 • • • 2 Q W т, v) & £\ (зол)
Ь = XiWkT, (30.2)
где %i определяются из уравнения (23.4), а // — вклад
вращений и колебаний молекулы i-ro сорта в
статистическую сумму. Величины £,• в дальнейшем будут называться
активностямиХ).
Для смеси газов, которая достаточно разрежена, чтобы
ее можно было считать идеальной, химический потенциал
|х/ приводится к виду [см. (6.3)]
|х? = — kT In {iTjt) + kT In щ. (30.3)
1 Дж. Майер и М. Гепперт-Майер назвали этот параметр
летучестью. Обычно активность обозначается через ziy но в данной работе
использовалось обозначение ££., чтобы ее не смешивать с координатой
z прямоугольной системы координат.

Гл. I. Метод статистической термодинамики 125
Следовательно, из выражения (30.2) получаем
Пт(^Ч= 1. (30.4)
Молекулярные функции распределения в большом
каноническом ансамбле зависят от совокупности активностей
£. Таким образом, можно записать унарную и
бинарную функции распределения соответственно как щ (£; г(1))
и пц (£; г<х), г<2)). Используя уравнения (28.3) и (28.4)',
получаем
со ^.П tf*
Я/(С;Г(1)) = а-1 S ... S Г1 х
/=1
X J ... ^ехрГ— £\ б (г<« - /?>) П ^ fob/. (30.5)
со Л^-б^П tf*
я//(С;г<1),г(«) = 2-1 2 ••• S s———х
/=1
X
X \.. . Jexp [-£] б (/*>-/?>) б (r<«-r}'>) П rf {rj^., (30.6)
где б// — символ Кронекера.
Далее, можно определить молекулярные функции
распределения высшего порядка как г
оо оо 11 £,•
т,...р (С; г<«,..., /■<•>) = S-i 2 • • • S т^1 х
*,=*, Nx=sx Yl (N.-S.)\
х
X J.. . J ехр [~%г] П ^ {гЛ^-s,.. (30.7)
1 С точки зрения согласованности обозначений было бы
желательно использовать обозначение п (£; {rf} S/- •• {г J SJ для функций
распределения высших порядков. Однако для удобства принято
обозначение, приведенное в тексте.

126
Часть II. Статистическая механика
где S/ — число молекул t-ro сорта (i совпадает с одним
х
из индексов **, /,..., р функции распределения) и 2$/=s.
i—l
Дифференцируя уравнение (30.1) по (д/д^У1 . . . (д/д£х) х,
получаем
д£...д&*
= S ••• 2 \П (/i's), fQ(Ar,V,r). (30.8)
Из (23.3) и (30.7) получим
д*3
= E^. ..5/г^..р(?;г^ r^drW... *■<•>. (30.9)
Следовательно, разложение функции E (£) в точке £
в ряд Тейлора имеет вид [49, 69]
оо ОО X •
«1=0 sx=o U=l г ^ ^г ' J
х \... ^...Р(Г; г<»,..., r^)drM... dr*\ (30.10)
где для краткости в аргументах больших статистических
сумм и функций распределения опущены переменные Т
и V. Это разложение большой статистической суммы,
впервые полученное Макмилланом и Майером[71 ], играет
важную роль в теории растворов.
Аналогично тому, как были выведены уравнения
(30.8), (30.9), получим из уравнения (30.5)
д#...а# ...ее? (30.11)
= -i- S ^ ... JЯу...р (С; г«, г<»,..., г'8') <*г")... dг<*>.

Гл. I. Метод статистической термодинамики 127
Поэтому разложение функции S (£) щ (£; г(1)) в ряд
Тейлора имеет вид
S Q гы (С; /*>) -
оо со X * Sy
= 2(о2...2Гт^)П(-^г х
s,=0 sx=oL\ ^' w //=i £/ь/ J
х J...$/»,/..., (Г; гЧ г<2\..., r<*>)dr<2> .. .dr<«>. (30.12)
Подобным же образом имеем для бинарной функции
распределения
- = (П2...2[^^П^| х
Sl=0 sx-o L ^w "" W ^/ — fe/J /=1 s;! s, J
xj...Jn//ik...p(f; г*1*, r<2>, r<»>,..., r<s>)dr(*>... dr<s>.(30.13)
Одним из наиболее полезных приложений
вышеизложенной теории является рассмотрение раствора
нескольких растворенных веществ в растворителе, скажем,
сорта 1. Тогда можно определить стандартное состояние этого
раствора из условия, что все активности растворенных
веществ равны нулю, а активность растворителя Й
такова, что чистая жидкость имеет некоторое давление р°.
Совокупность активностей такого стандартного состояния
обозначим через £°. Далее предположим, что имеется
мембрана, проницаемая для растворителя, но непроницаемая
для растворенных веществ. Пусть этот раствор с
активностью, которую обозначим через £, в состоянии
равновесия граничит через мембрану с раствором, содержащим
только растворитель. Тогда, по определению, разность
давлений на мембране равна осмотическому давлению я:
л =р — р°,
(30.14)

128
Часть II. Статистическая механика
где давление р соответствует активности £. В этом случае
растворитель имеет одинаковую активность £? в двух
состояниях 5 и ?° благодаря проницаемости мембраны для
растворителя. При таком специальном выборе активностей
С и £*, равных £°, в суммы, входящие в уравнения (31.10),
(30.12) и (30.13), вносят вклад лишь члены, которые
описывают только растворенные вещества. Эти условия были
впервые введены Макмилланом и Майером [71] и
называются осмотическими условиями.
Определим теперь потенциалы средних сил, играющих
особенно важную роль в теории растворов Х)
п.. (Г- r(i) r(s)\
W£i^p = -kT\u^^ "••' ', (30.15)
где верхний индекс а относится к фазе а. Ограничимся
рассмотрением потенциалов средних сил, действующих
на молекулы растворенных веществ (т. е. нижние индексы
/, /, . . . , р будут обозначать только растворенные
вещества).
Как и раньше, обозначим жидкую фазу раствора, как
фазу а, а фазу насыщенного пара этого раствора, как фазу
р. Из уравнения (30.15) очевидно, что величина \Рц ,р
точно приводится к ее значению в однородной объемной
фазе а, если все радиус-векторы молекул г(1), . . . , r(s)
оканчиваются внутри фазы а, и принимает с точностью
до аддитивной постоянной значение, характерное для
объемной фазы Р, если все радиус-векторы г<1), . . . , r(s)
оканчиваются внутри фазы р.
Суперпозиционное приближение, определяемое
уравнением (24.9) для тройной функции распределения,
обобщается следующим образом:
/»// р(г(1),.. ■,/•<*>) ^ nij{r^\r^) nik(r^\r^)
/i/(r(1)) «/ (г(2)) • . • пр (r<s)) rij (г*1*) nf (r^) /i. (г*1*) nk (r<s>) ' * •
/»0D(r(f-1,.r(s))
' n0(r^'l))nD (r(s))
(30.16)
1 Обычно потенциалы средних сил определяются аналогичным
образом и для канонического ансамбля. Они играют важную роль
даже в случае чистой жидкости, однако в настоящей книге они будут
использованы только для большого канонического ансамбля.

Гл. 1. Метод статистической термодинамики 129
Последнее соотношение устанавливает, что вероятность
найти совокупность s молекул *', /,..., р-го сортов
соответственно в точках г(1),. . . , r(s) может быть приближенно
выражена в виде произведения независимых вероятностей
для пар молекул. Очевидно, что это приближение можно
переписать с помощью потенциалов средних сил
[уравнение (30.15)] следующим образом:
Wi/...p(rw9..., /•<*>) - Wi(ri») - wj (r<«) — ... — wp (r<s>) =
= (Wi, (гЧ r<2>) — Wi (rM) — Wj (r<2>)) + (Wik (r<«, r<3>) —
— w£(rM) — wk(rM)) + . . .
-.. + (Wop(ri-», rM) — w0(ri-») — wp(rM)), (30.17)
где для удобства вместо Wi используется символ ш/.
С другой стороны, потенциал средней силы Wri (г(1), г(2))
можно выразить в виде
Wif (гЧ г<2>) = w£(rM) + w,(rM) + Wij (гЧ r<2>), (30.18)
где Wij (r(1), r(2))—составляющая потенциала двух
молекул, которая рассматривается как потенциал средней
межмолекулярной силы, действующей между молекулой
1-го сорта, находящейся в точке г(1), и другой молекулой
/-го сорта в точке г(2).
| Подставляя выражение (30.18) в (30.17), получим
другое выражение для суперпозиционного приближения:
№„...р(гЧ . .., r<s>) = Wi{r^) + ... + wp(r&) +
+ w^ (гЧ г<2>)+ю/Л(г(1). г<3>) + ... + wop(r<e-«,r<e>).(30.19)
Поскольку в пределе бесконечно разреженного газа
Щ (/*(1)> **(2)) становится равным межмолекулярному
потенциалу фц (| г(2) — г(1) |), а ш/ (г(1)) -»• 0, то приближение
(30.19) в этом пределе обычно считается столь же точным,
как и соотношение (24.3). Однако приближение (30.19)
для потенциала средних сил гораздо серьезней.
Как частный случай уравнения (30.15) получим
плотность числа молекул щ (г(1)) в виде
т(г<») = nfew'{r{1)),kT. (30.20)
Дифференцируя уравнение (30.12) по г(1) и используя
выражения (30.13) и (30.19) — суперпозиционное прибли-

130
Часть II. Статистическая механика
жение для 1#7/...р, легко получить уравнение Борна —
Грина — Ивона для унарной функции распределения:
— iSf-S C/7.C/ W (Г(1)> r(2))V(1)atf/(/■<«, rM)drW. (30.21)
31. Разность поверхностных натяжений раствора и
чистого растворителя. Как указывалось в предыдущем
пункте, разность давлений между раствором и чистым
растворителем в осмотических условиях равна
осмотическому давлению. В настоящем пункте мы рассмотрим при
тех же условиях разность поверхностных натяжений.
С этой целью рассмотрим большой канонический ансамбль
многокомпонентных систем с совокупностью активностей
С в слабом гравитационном поле. Как и в предыдущем
пункте, обозначим давление через р, поверхностное
натяжение, которое предполагается существующим в этом
состоянии, через у, а соответствующие величины в
произвольном исходном состоянии £* соответственно через р*
и у*. Тогда из уравнения (28.13) получим
ехр[('-^-(Т~Т'М] = #- (ЗЫ)
Далее предположим, что система находится в сосуде,
имеющем форму прямоугольного параллелепипеда со
сторонами длиной 1Ъ /2, /3, направленными вдоль
прямоугольных осей координат, как показано на фиг. 8. Ось г
направлена вверх, противоположно направлению силы тяжести.
Тогда объем системы и площадь поверхности раздела фаз
соответственно равны V = 1г121з и А = hh-
Из выражений (30.10) и (31.1) получаем
(p-P*)V-(r-f)A =
ОО ОО X * S£
-и-ш S...2 1Шс-^)}х
x \...U«/...p(r; г'-1'...., r's>)rfro)...dr&]. (31.2)

Гл. I. Метод статистической термодинамики 131
Как и в случае осмотических условий, будем в
дальнейшем предполагать, что растворитель (назовем его
веществом 1) имеет активность £ь равную £J. Тогда
уравнение (31.2) приводится к виду
(p-p*)V-(y-f)A =
ОО ОО X * S/
= »n.[S...S{ni(bi))x
Ls2=0 sx=0 М=2 ' \ W / ^
Х^... JnJ,.. р(г<«,..., r<«>) d г<*> . .. dr^] , (31.3)
щепц...р (r(1),... ,r(s>) вводится вместо /i//...P(C*,r(1),..., r(s))
и ни один из индексов *', /, . . . р не принимает значения 1,
соответствующего растворителю; следовательно, в рас-
х
сматриваемом случае вместо s = 2 s* следует брать
£=1
s = 2 s'-
/=2
Подставляя Ufy. .„ из уравнения (30.15) в (31.3), имеем
(p-p*)V-(y-f)A =
ОО оо х * s,- *а s,-
-и-in s...s{n(t=^-(f-) }х
L s2=0 sx=0 ^ /=2 ' \ W / J
4--К*1/-"(Г(1) (S,,/"^(1>...dr's»], (31.4)
в котором функции со звездочками относятся к исходному
состоянию £*• Последнее уравнение является основным
для поверхностного натяжения в осмотическом растворе.
Дифференцирование уравнения (31.4) по 1г с учетом
соотношений V = 1г1213 и А = 1Х1% дает следующее:
kT
д
(Р-
ОО
IS-.
s2=0
\-\'
Р*) Уз —
ОО X
• 2{П
sx~° ^=2
-*?/... Ре-(1).
(г
(Сг
.... /
-т*)
- V)'1
*/1
'(s))/ftf
*2 —
-(!
(г(1).
X
dr(s). (31.5)

132
Часть II. Статистическая механика
Если пренебречь краевыми эффектами, то щ (г(1))
является функцией лишь z(1) и может быть обозначено через
Wi (z(1)). Аналогично тц (г(1), г(2)) представляет собой
функцию переменных г(12) = г(2) — г(1) и z(1) (или z(2)). Однако
для удобства ограничимся случаем, когда хюц можно
представить в виде wij (r(12), rffi), где (см. также фиг. 17)
Г<12) = [(*<2) _ ^(1))2 _|_ ^(2) _ у(1)у _|_ (Z(i) + г(2))]У2. (31.6)
Тогда суперпозиционное приближение [выражение (30.19)]
можно записать следующим образом:
Wi,.. р (Г(1), . . . , Г<5>) = Wi (z<») + . . . + wp (z<*>) +
. .. +Wop(r^s)yr(s-l,s)y (31.7)
Как и в п. 25, используя метод Боголюбова — Грина,
основанный на замене переменных (25.6), получим из (31.7)
s2=0 sK=0 U=^2 ' ч W / )
х |.J... ^-П...^1» rish/kTdra> m ^ dr^ =
4S2...s.n^m'
i'=2 s2=0 sx=0 I/=2 ' \ W / )
x\...\e-wb-p'kTdrw...dr{s)-
x x oo oo x , sz *a S,
I*/— ъч I ni
X
1=2 /=2 s2=u sK=oL u=2 ' \ w / ;
X
r(12) dr№)
'//n urim ' J

Гл. I. Метод статистической термодинамики 133
Используя выражение (30.15), (30.12) и (30.13), можно
переписать выражение (31.8) в виде
00 00 , X /fc c*4S; *„ S,-
2-2 П^(£)'х
s2=o sK=0 U=2 ' \ W / J
= | £ 2-M-U (*»)*<»-
(jcW-jc(i))8 <47 (л*2)-**1*)2 <4;
г(12) лг(12) "Г r(12) ^ (12)
X пц(гЫ\ r^)dr^dr^.
x
(31.9)
Подставляя выражение (31.9) в (31.5) и умножая
полученный результат на /1э получаем с учетом V =1г1213 и
(p-p')V-(r-y')A=A^-^j^kT \ n, (*»)<&»—
1=2 -{a
i. /=2 -za
(jg(12) )2 Qw*j
r(12) ^(12)
+
/у(12)ч2 dw*n 1
+ ^ТШГ ~^Ш пч (г(1). **»)* r(12)> (31 л°)
4m
где /a и /0 имеют тот же смысл, что и в п. 26 (см. фиг. 8).
Поскольку /3 = /а + /3, то выражение (31.10) можно
записать в следующем виде:
Г-Т*= \ (р —p*)dz<i> —2 J d2(1) х
—/a '=2 _^a

134
Часть //. Статистическая механика
X
X [Ц^/1,(2(1))^-4-2 ^"^«/"^ х
L w ^ /==2 С/С/
г» f/y(12)\2 to?, /^(12)4 2 to*. \ 1
\ „(12) Лг(12)
Если мы продифференцируем уравнение (31.4) по 13
вместо 1Ъ то точно тем же способом, как и при выводе
выражения (31.10), получим
(р - р*) V = А 2 -Цг-i £Г ^ л, (z<D) dz<» -
/=2 __ /а
-42 (b"g)^"c;) f^x
С/С/
Л/=2 ' ./а
X
/z(12)\2 to*/ (М _1_ z(2)\2 to!, 1
Ы froS'+'H^2-*#-Н,Ш: r"Я)'"■1",•
(31.12)
Вычитая выражение (31.10) из (31.12), получаем
следующее выражение для поверхностного натяжения г:
х
у - y* = - 2 ^ 5г(1) -да-"<(г(1>) «г(1) +
/=2 —оо
+ -1-2 <^-^«/-^ ^гц>х
/,/=2 ' —оо
(*(12))2 _ (г(12))2 dw]j (л:(12))2_(2(1) + г(2))2 to*;
*<«> ' r£f drj«> j
X
X n/,(2(i); r<18>)rfr<12). (31.13)
Используя это выражение и зная унарные и бинарные
функции распределения молекул, а также потенциалы
1 См. примечание на стр. 103.

Гл. I. Метод статистической термодинамики 135
средних сил w. и wijf можно вычислить разность
поверхностного натяжения между двумя состояниями 5 и 5*
при осмотических условиях.
Для однородных объемных фаз а и (J выражение (31.10)
сводится соответственно к виду
х *. е.* О
(р — р*) V* = А 2 ^j^- kT ^ nf (2(D) <fe<i> -
/=2
2 2j 5<£/ J J r<12> <fr<12>
'./=2
_/<х
X
(31.14)
х n?/(r<u>)dr«u>,
(p _ p*) v* = A ^ -^-^- kT J /if (z<«) dz<» —
/=2 0
_A * (Ci-g)«/-Qfd:;mf(^>)'^y „
2 2j g,C/ J J r<12> dr<12> X
*,/=2 0
x n% (№) dr<u>, (31.15)
где тц и o£f являются функциями только г<12).
Вычитая выражения (31.14) и (31.15) из (31.10),
учитывая аддитивность объемов Vх и Ур и используя
обозначение я*/, определяемое соотношением (25.20), а также
обозначение ^/аР, определяемое аналогичным способом,
получаем
/=2
1 ^ (Ь-С/)(С/-С/)
00
5 ЛР» х
—оо
J L г<12' \ <?г<12> " аг<12» л" /+
+ 4-S
/,/=2
ьс,
(*(12))2 dttfy
+ г(12) д (12) Л//
dr<12>,
(31.16)
где мы использовали соотношение (25.21),

136
Часть II. Статистическая механика
Как будет показано ниже, выражения для
поверхностного натяжения (31.11), (31.13) и (31.16) представляют
собой соответственно обобщения выражений (25.14), (25.15)
и (25.23).
Примем исходное состояние £* в качестве стандартного
состояния £°, т. е. положим £ = £?, £2 = • • • Ex = 0.
Тогда выражения (31.11), (31.13) и (31.16) приводятся
соответственно к виду
Y — y° = \ ndzF> — 2 J d*(1) Г/2,- (2(D) kT —
_*/а /=2 _ /а
x °°
Y° = — 2 \ dzV
/=2 —00
dw°.
__Lv [ \( (*(12>>2 dw« (*(12))2 to°/ ^
_ i£—I !Z__L-i£ + z 1 fi_H tinted- r<12)Wr<12)) .
(31.18)
X X °°
/=2 Л/=2 —00
f f (*<12>)° / H to^ «Л ,
' im im }
где разность p — p* заменена осмотическим давлением я
[см. выражение (30.14)1, у0 — поверхностное натяжение
чистого растворителя и Щ., itfjW — потенциалы средних
сил между двумя соответствующими молекулами
растворенных веществ в бесконечно разбавленном растворе,

Гл. I. Метод статистической термодинамики 137
т. е. в чистом растворителе. Последние три уравнения,
основанные на суперпозиционном приближении (31.7),
являются основными для изучения поверхностного
натяжения осмотических растворов. Эти уравнения впервые
были выведены Баффом и Штиллингером [71] другим
методом, основанным на теории растворов Кирквуда — Баф-
фа [72].
В более частном случае, когда звездочка относится к
бесконечно разреженному газу, потенциал средней силы
хюц сводится к межмолекулярному потенциалу, a wt
обращается в нуль, и, следовательно, выражения (31.11),
(31.13) и (31.16) соответственно сводятся к выражениям
(25.14), (25.13) и (25.23) (р* и у* обращаются в нуль).
32. Применение точного разложения в ряд по
активностям к рассмотрению поверхностного слоя. Теория,
приведенная в предыдущем пункте, основана на
суперпозиционном приближении. В настоящем пункте мы
рассмотрим точную, но до некоторой степени формальную теорию
поверхностного натяжения в растворах.
Для простоты введем обозначение
©/=(&-©-£-. (32.1)
Тогда строгое фундаментальное соотношение для
осмотического раствора —уравнение (31.3) —можно переписать
следующим образом:
(р-р*)У-(У-Ч*)А _
kT ~~
ОО ОО X 8л
LS2=0 Sx=0li=2 s.!(rt;«)s* J
x \ • • • \ n'a..JrW> •■■< r<s))drW ■ ■ ■ drM] > (32.2)
где рассматривается та же система, которая
использовалась в связи с уравнением (31.2). Разлагая правую часть

138
Часть II. Статистическая механика
уравнения (32.2) по степеням со*, можно написать
оо *
(/>-Р')У-(Т-т'М ^ V ••• У, Vbt(m2,...,m*)T[mm',
(32.3)
где 6* (т2, . • • , ту) — обобщенный групповой интеграл
[74, 75], отнесенный к £*, а т2\ . . . /ях1 W (/яа. . . • , /ях)
соответствует полуинварианту распределения в
многомерном пространстве в теории вероятностей [76].
С другой стороны, имеем аналогичные соотношения
для однородных объемных фаз а и р, объемы которых
соответственно равны Va и V^:
„ ОО 00 х
{P-£)V = S • • • 2 У***' («•. • • • • ^)П<\ (32.4)
m2=o mx=o г=2
i^H-0 = S • • • S ^**P(«.. • • •. «OIK4- (32-5)
m2=0 mx=o г=2
Введем теперь обозначение Л" (mri, . . . , тх):
АА* (от, от») П (—4г) = W (т2, . . . , Отх) —
1=2 *
-]ГЬ'а (т2, . . . , /я*)- 1/V (т2, . . . , /их), (32.6)
где Г* — поверхностная плотность молекул 1-го сорта
в исходном состоянии £*. Назовем Л* (ш2, . . . , тк)
поверхностным групповым интегралом, отнесенным к £\
Тогда из (32.1),(32.3) — (32.5) и аддитивности объемов
Vх и И получим для разности поверхностных натяжений х:
оо оо
Y — у* = — W 2 • • * S Л* (т* * " ' ' mx) Х
га2=0 171^=0
*П {«.-£>£} • (32-7)
г=2 '
1 См. работу Сайто [77]. Его результат, однако, не является
совершенно эквивалентным уравнению (32.7), поскольку вместо условий
осмотического давления Сайто предполагает, что два состояния
находятся при одинаковом давлении.

Гл. I. Метод статистической термодинамики 139
Покажем, что Л* (тъ . . . , ту) не зависит от площади Л.
Во-первых, для выяснения смысла Л* (т2, . . . , т,у)
рассмотрим небольшие множества чисел /я2, . . . , тх. Для
одного из наименьших множеств (рц = 1 и ?щ = 0 для всех
/ =h i) получим из (32.2) и (32.3)
Vb
п\(гЫ)
■• (0, . . . , 1, . . . , 0) = [ "1\а drw. (32.8)
По определению имеем
Vafc*a(0, ..., 1, . . . ,0)= Va, (32.9)
/3 А*е /п 1 п\ _ т/3 Л1
*з
VP6P(0, ..., 1,...,0)= Г-V- (32.10)
Па
Подставляя выражения (32.8) — (32.10) в (32.6), получаем
А Л* (0,..., 1,..., 0) = JL \ (п!(г(«) - п\**) drv, (32.11)
где гг?з определены соотношением (25.19). Из уравнений
(25.21) и (32.11) находим значение
Л*(0, ..., 1 0) = 1, (32.12)
которое не зависит от А.
Для множества mi = 1, т/ = 1 и тк = 0 при k=f=in k=f=j9
групповой интеграл Ь* (0, ... , 1, . . . , 1,.. ., 0)
выражается с помощью (32.2) и (32.3) следующим образом:
Vb* (0, . . . , 1, . . . , 1, . . . , 0)= ' X
(1 + 6if) п£ nf a
X Ц [п;у (г*1*, г<«) — п) (г*1*) п) (rW)\drM dr™ (32.13)
v
и аналогично
V4'(0, ...,1, ...л, •••,0)= .. , * *я ,. х
X \\ [п;;. (г<12») — n;«nj«]rfr«» dr<2> , (32.14)

140
Часть II. Статистическая механика
v"Vp (о,.... 1,.... 1,..., о)= *.« »- х
(1 + б;/) щл /г;а
X \\Kj4r<12>)— n**n)*)\drWdrW. (32.15)
Подстановка выражений (32.13) — (32.15) в (32.6)
немедленно приводит к результату
"*•«» ' ' 0>=„+4,г;г;х
X \\ {гСп (г*1*, г<2>) — n]f) dr'1» cfr<2> —
- н^Лг-Д к* (r(i))*; с-<2)) - ";ар «;ар)^а) d>-(2,>
d + Vr/r/V (32.16)
где п*/ар определяются следующим образом:
-.Э _ ft (Г(12)) ~nia nY + ПТ П1а" ^ 2(1) < °> П9 17ч
П// ~~К? (^(12)) — п? п? + п? п]** (**>); 2<1>>0. * ;
Следует отметить, что величины я?Р отличаются от г№,
определяемых из (25.20); в противном случае выражение
(32.16) перестает быть справедливым.
С другой стороны, согласно (25.21), имеем
\\ [п] (г<«) п) (г<2>) — rC** re**\drw drw = Л2 Г,* Г7* +
+\\ \п) (г<«) п;^+гг;а^; (г^)—2пГ** п]**\ dr™ dr<»>. (32.18)
Используя приведенные выше соотношения, можем
записать выражение (32.16) в виде1
1 Легко видеть, что уравнение (32.19) соответствует выражению
дли группового интеграла Ъ а (0, . . . , 1 , . . . , 1 , . . . , 0),
определяемого для однородной фазы а как Ъ а (0 , . . . , 1 , . . . , 1 , . . . , 0) =
/4с(12))
(1+6//) )\п{ап^ I

Гл. I Метод статистической термодинамики 141
Л* (0 1 1 0) =
. (32.19)
= TT67)й(l^--1)^(12,^(12,'
где
А/,- = \\ к,- (r<i>, г<») - n)f - «; (г<«) п;«р -
— пУ гС. (г<2>) +2п'«Р пУ\ dzM dz^. (32.20)
Так как бинарная функция распределения п)} (r^l\ г^2))
на расстояниях г<12) = | г(2) — r(1) |, существенно больших
размеров молекул, сводится к произведению унарных
функций распределения п* (г(1)) я!(г(2)), то из выражений
(25.21), (32.16), (32.18) и (32.20) получаем
lim Д*//=г;г;. (32.21)
г(12)-юо
Таким образом, можно сделать вывод, что поверхностный
групповой интеграл (32.19) не зависит от площади
поверхности раздела, если размеры сосуда, в котором находится
система, могут быть взяты достаточно большими по
сравнению с молекулярными размерами. Мэжно получить
аналогичные уравнения для более сложных поверхностных
групповых интегралов, выраженных через поверхностные
плотности высших порядков, и доказать, что результаты
не зависят от площади Л, но мы не будем углубляться
в эти утомительные вычисления.
Дифференцируя уравнение (32.7) по £/ /получаем г
1 Рассматривая коэффициенты при членах правой части
уравнения (32.7), мы находим отдельные члены, которые действительно
зависят от выбора положения разделяющей поверхности, в то время
как поверхностное натяжение, определяемое их суммой, не зависит
от этого выбора. Аналогичным образом дифференциальный
коэффициент, определяемый уравнением (32.23), зависит от выбора
разделяющей поверхности. Однако эта зависимость только кажущаяся, так
как изменения значений величины £/ или \ii не являются
независимыми друг от друга, а ограничены условием (6.8), причем в
осмотическом растворе величина (хх всегда постоянна.

142
Часть П. Статистическая механика
<ь-©Щ. = -иг S ••• S т<х
.ч Г/ Г*
(1 / \"1/
(Ь — CJ) тг) . (32.22)
/=2
Когда £! стремится к £/, последнее уравнение приводится,
согласно (32.12), к виду [76]
Ь (^-) = - Л7Т, (t = 2, ... , х). (32.23)
(^г) = Г< С=2,...,х). (32.24)
Используя (30.2), можно записать уравнение (32.23)
следующим образом:
Тогда из уравнения (32.24) при постоянных Т и \хг
получим [76]
X
— dy =2Г/ф/. (32.25)
/=2
Это уравнение представляет собой адсорбционное уравнение
Гиббса (6.1) при условии, что ^постоянно.
Из уравнений (32.22) и (32.23) получим
*. *•* 00 оо
^~^ г,= 2 • • • 2 т'Л* <от* ■ • •'m*)х
т2=0 тх=о
х , р~ ту
хП(^-Фтг) ■ (32,26)
/=2
Если исходное состояние £* совпадает со стандартным
состоянием 5°, то, полагая £*= Z£ ... = {£ = О,
приведем уравнение (32.26) к виду
оо оо ч *• т.-
г,= 2 • • • 2 т*А° <w»« • • • • ^П Ш ' (32-27)
т$=о тх=о /=2 '

Гл. I. Метод статистической термодинамики 143
Гу= lim %-, (32.28)
где fj можно назвать поверхностным коэффициентом
активности /-го растворенного вещества в бесконечно
разбавленном растворе, а Л° соответствует Л* в бесконечно
разбавленном растворе. Если поверхностное натяжение
чистого растворителя обозначить через у°> то уравнение
(32.7) запишется в виде
оо оо х £. Щ£
T_Yo =_kT ^ ... 2Л°к,•••,/"*)п(т^) •
m2=0 mx=o /=2
(32.29)
что можно рассматривать как результат интегрирования
адсорбционного уравнения Гиббса. Поскольку, согласно
(32.12), поверхностный групповой интеграл Л° для одной
молекулы любого сорта равен единице, то для достаточно
разбавленных растворов имеем
y^f-kT[^ + ...+^]. (32.30)
Так как для однородной объемной фазы а имеем — Qa — р*
V=(p — р*) V, то из уравнения (4.15) находим
п« = (а(р-р,)) (*=2,...,х). (32.31)
Затем с помощью (30.2), (32.1) и (32.4) уравнение (32.31)
можно записать следующим образом:
^L „а = ^ . . . 2 «itb*a (от, , тх) X
m2=0 mK=0 (
х г *<х т. V
/=2 ъ'
Если исходное состояние совпадает с нормальным со-

144
Часть П. Статистическая механика
стоянием £°, то уравнение (32.32) приводится к виду
оо оо х «. m;
nf = 2 • • • 2 «/*°" (/п.. • ■ • . т«)Ц (-^-) , (32.33)
т2=о тк=0 /=2 J
где F/a — обычный коэффициент активности /-го
растворенного вещества, определяемый в предельном случае
чистого растворителя как
FT= Hm \ (/ = 2 х). (32.34)
"Z »?-о я/
В принципе можно получить изотерму адсорбции из
уравнений (32.29) и (32.33) путем исключения £2, . . . , £х
из этих х уравнений.
33. Адсорбция газа на твердой поверхности.
Результаты, полученные в предыдущих пунктах при обсуждении
поверхностного натяжения на плоской поверхности
раздела, могут быть применены к проблеме адсорбции газа
на твердой поверхности. Хотя последующие результаты
можно получить как частный случай соответствующих
результатов предыдущих пунктов, если считать, что одна
из фаз представляет собой твердое адсорбирующее
вещество, мы выведем их другим, более простым методом [49,
77—79].
Рассмотрим газ, находящийся в сосуде, как показано
на фиг. 12. Предположим, что молекулы газа не
взаимодействуют со стенками сосуда, за исключением одной из них,
например /?С, которую можно рассматривать как твердый
адсорбент х. Для определенности положим, что сосуд имеет
объем Vх и индекс а относится к газовой фазе.
Согласно уравнениям (23.3) и (30.1), большая
статистическая сумма для этой системы имеет вид
оо оо х */уг
s<c,7\n= 2 ••• 2 (Пж)х
Nl=0 wK=o /=1
1 В данном случае не обязательно, чтобы твердая поверхность
была плоской.

Гл. I. Метод статистической термодинамики 145
х$.-.$ехр[-
®NUriNl'---'irx}Nx)-.*
kT
х Nt
]Hd{r,}Ni, (33.1)
£—i s=l
„ x ^ Nj
(33.2)
(33.3)
/,/=ls=i /=l
где Фдг — полная межмолекулярная потенциальная энер
гия, определяемая уравнением (24.3), H%(rls)) — потен
Фиг. 12. Газ, адсорбируемый на
поверхности твердого тела.
циальная энергия взаимодействия с адсорбентом i-й
молекулы в точке rfK
Рассмотрим тот же газ, содержащийся втом же сосуде,
но теперь при условии, что ни одна из стенок не
взаимодействует с газом. Напишем большую статистическую сумму
для такой системы
со со х *™£
s-e,r,v)= Е--- 2 (Пib)
X
$...$«р[.
АГ
]П^{^К- (33.4)

146
Часть 11. Статистическая механика
Так же, как при выводе уравнения (32.3), разложим S
по степеням СГ1 • • • £ГК:
1пЗ= ^ • • •
rrii=0
и аналогично
со
1пНа= 2 •
т,=о
где b° (mlf . . .
2 VVimu...
тк=0
со
• • %УЧГ(т1г.
тк=о
, /Их) и 60а (тъ . .
, /я») £?■ • • • £*"> <33-5)
...,/пккГ'• • • С*.
(33.6)
• , #Zx) — групповые ин-
тегралы соответственно при наличии и в отсутствие
адсорбента х.
Поскольку пУ/t,*. стремится к единице при бесконечном
разрежении, то легко видеть из уравнений (31.1), (32.1) и
(32.3), что Ь° (тъ . . . , ту) соответствует Ь* (тъ . . . , тх)
при бесконечном разрежении и что Ьол(тъ . . . , тх)
совпадает с групповым интегралом Майера [81,82] для
газовой смеси.
Среднее число молекул *-го сорта в рассматриваемых
двух случаях, согласно уравнениям (30.2) и (28.11),
составляет соответственно
Л 1 " °° °°
Nt = ti^r = 2 • • • 2 v*m*b0(mi m«№ • • • С".
mi=0 m"=° (33.7)
r_i0t CO CO
N7 = L-^f- = 2 • • • 2v^b°a^<■ ■ • -«£"'• • • Cx.
'"'=0 mx=° (33.8)
Так как число адсорбированных молекул определяется
как средний избыток молекул в объеме V* благодаря
наличию адсорбента, то количество адсорбированного газа
t-ro сорта можно выразить с помощью уравнений (33.7) и
1 Групповые интегралы 6° (mi , . . . , mx), введенные в этом
пункте, являются частными случаями групповых интегралов,
рассмотренных в предыдущем пункте.

Гл. I. Метод статистической термодинамики 147
(33.8) как функцию активностей отдельных газовых
компонент следующим образом:
со со
iv, - Nf = 2 • • • S уа т№ (/"i' — т^-
mt=o mx=o
-60e(«lf ...,тк)}СГ... С- (33-9)
Как и в случае коэффициента Л* (тъ . . . , тх) в
уравнении (32.7), можно показать, что Vх {Ь° (тъ . . . , тх) —
— Ьоа (тъ . . . , /Пх)} пропорциональна площади
поверхности адсорбента.
Мы, однако, проведем детальное рассмотрение лишь
для случая однокомпонентного газа. Тогда уравнения (33.1)
и (33.5) соответственно сводятся к уравнениям
N=0 s, f=l
+ 2 *(r(s))}IdrW■■■driN)> (33.io)
CO
InE = y]VabmC, (33.11)
m=0
в которых опущен индекс, указывающий на сорт молекул,
а групповой интеграл обозначен через Ьт. Если
обозначить через Ьт групповой интеграл для газа без адсорбента,
то уравнение (33.9) можно записать следующим образом:
Г = \-^тф,п-Ьат)С (33.12)
m=i
здесь Г — число адсорбированных молекул на единицу
площади поверхности адсорбента.
Сравнивая соответствующие коэффициенты в
уравнениях (33.10) и (33.11), получим следующие выражения
для групповых интегралов:
Ьх = 1 + —а \ (e-^ril))/kT — 1 )dru>, (33.13)

148 Часть II. Статистическая механика
ы =
.^[(^Л(г(12))/ЛГ_1) +
2Va
+ (е-'^г<12)икГ — 1) (бгф(г(1)>*г — 1) +
+ (е-&1г{12)УкТ — \){e-^ri2))lkT — 1) + (е-(>(г(12)Уьт — 1)х
X(e-*('{1))/kT _ 1) (e-W^)lkr _ i)j drU) dr(2)> (33.14)
Таким же путем для газа без адсорбирующего вещества
получим
Ь1 = 1, (33.15)
6* = "^S(e_i;>(r(12))/"r - !) dr{1)drM. (33.16)
С помощью выражений (33.13) — (33.16) главные члены
разложения (33.12) запишутся в случае разреженного
газа
Г-1((г*с(1))/*г — \)drM + -^ [(е-'><г(12)>/*г — 1)х
X {(£r*<r(1)>/ft7' — 1) + (e-*iri2)vkT — 1) + (e-*<r(2)>/fc7, — 1) X
х (e-4r*hikT _щ drWdr™. (33-17
Так как функция er*WkT — 1 равна нулю, за
исключением того случая, когда точка г находится на расстоянии,
меньшем молекулярных размеров, от адсорбирующей
поверхности, а функция е-0(О/*г — 1 равна нулю, за
исключением случая, когда расстояние г порядка диаметра
молекулы, то Г, определяемое уравнением (33.17),
асимптотически не зависит от А.
Если желательно выразить Г как функцию давления,
то необходимо использовать соотношение
р = ^гГс+^г5^-'3(г(12))/^ ~~ l)dril)dr{2) +• • .1(33.18)
которое легко получить из уравнения pV = kT In Sa
для газа без адсорбента с помощью уравнений (33.15) и

Гл. /. Мепэд спап ten теской термодинамики 149
(33.16). Из уравнений (33.17) и (33.18) получим
Г = ± [^ J (<r*<r<%*7- - 1) dr<« +
+ (йг)* ^ (^(г(12))/*г — 1) {(^с(1))/^ _ 1) (е-чгЩкт _ 1) +
+ ^(в-Ф(г(1))/ЛГ — 1) + |>(в-Ф(г(2))/ЛГ _ l)}dr(l)dr(2) +...].
(33.19)
В конечном итоге мы видим, что уравнение (33.17)
является частным случаем уравнения (32.27) и что согласно
уравнению (33.17) коэффициент поверхностной
активности /0, определяемый (32.28), приводится к виду
/° = ттт^ (33.20)

Глава II
МЕХАНИЧЕСКОЕ ОПРЕДЕЛЕНИЕ ПОВЕРХНОСТНОГО
НАТЯЖЕНИЯ
34. Статистическое выражение для тензора
давления в жидкостях. Функция плотности вероятности
P{N) ({fib ■. -. {/-J; {Pi}, . . . , {/>*}), введенная в п. 23,
может быть определена также и для неравновесных систем.
В таких случаях плотность вероятности, вообще говоря,
изменяется во времени согласно уравнению Лиувилля.
Определение унарной функции распределения л,- (г(1)), бинарной
функции распределения пц (г(1), г(2)) и других функций
распределения высшего порядка для неравновесной системы
остается таким же, как и для равновесной системы.
Цель настоящего параграфа заключается в
установлении выражения для тензора давления в каждой точке
жидкости через функции распределения и межмолекулярные
потенциалы. При этом мы будем следовать методу Ирвинга
и Кирквуда [83].
Пусть dS — элемент поверхности, расположенный в
точке г внутри жидкости. Разделим жидкость на две части
плоскостью, касательной к dS. Назовем часть, внутрь
которой направлен вектор dS, внешней частью жидкости,
а другую часть — внутренней. Ограничимся случаем, когда
полная потенциальная энергия жидкости представляет
собой, согласно предположению (24.3), сумму
двухчастичных потенциалов, каждый из которых является функцией
лишь расстояния между молекулами. Будем говорить,
что сила между двумя молекулами действует через
элемент dS лишь в случае, если прямая линия, соединяющая
центры двух молекул, проходит через dS. Для бесконечно
малого элемента поверхности dS это может случиться
только тогда, когда две молекулы находятся по разные
стороны элемента dS (см. также фиг. 13, а на стр. 157).
Далее, рассмотрим силу, с которой действуют молеку-

Гл. II. Механическое определение поверхностного натяжения 151
лы, находящиеся во внешней части жидкости, на
молекулы внутренней части жидкости. На молекулу t-го сорта
в точке г' во внутренней части жидкости действует со
стороны молекулы /-го сорта, находящейся в точке г' + R
внешней части жидкости, сила (R/R) ф'г (/?). По условию
эта межмолекулярная сила действует через элемент dS
только в том случае, если вектор г' + r\R оканчивается
на dS при некотором значении т], лежащем между 0 и 1.
Если вектор R фиксирован, то элемент объема, для
которого вектор г' + v\R оканчивается на элементе поверхности
dS при значениях т], лежащих между т] и г] -f dr\, равен
dS-Rdv). Среднее число пар молекул, одна из которых
является молекулой i-ro сорта, находящейся в упомянутом
элементе объема, а другая /-го сорта — в другом элементе
объема dR вокруг точки г' + /?, определяется уравнением
пц(г',г' +R)(dS-Rdr])dR =
= пц (г - r]tf,r — г]Я + R) (dS-Rdi)) dR, (34.1)
В последнем уравнении г' + x\R есть произвольная точка
на элементе поверхности dS, а разность между гиг' +v]R —
бесконечно малая величина высшего порядка.
Теперь мы можем вывести выражение для полной силы,
с которой внешние молекулы действуют. на внутренние
через элементе и которую мы обозначим F^ dS. Умножая
уравнение (34.1) на (R/R) ф \ц) (/?), интегрируя затем по всем
/?, для которых скалярное произведение R dS
положительно (т. е. по всей внешней части жидкости), и, наконец,
суммируя результат по сортам молекул i и /, получаем
XX 1
F^dS =d5-S S 5 dR \\^^ij {R) x
X пц (r — v)R, r— v)R + R) dx\ J . (34.2)
Положив £ =1 — т], найдем
i
J 2* 0i, (/?) щ, (r-riR,r-4R +R)dr\ =
0
1
= \ ™ <j>\, (R) n„ (r + tR - R, r + IR) d%. (34.3)
0

152
Часть II. Статистическая механика
Поскольку по определению функция пц (г(1), г(2)) должна
быть равна пц (г(2), г(1)), а функция ф'ц (R) — функции
Фи (Юу уравнение (34.3) можно переписать в виде
^ ^ ф'ц (R) пц (г - лЛ, г - r]R + R) dy] =
О
1
= \ ™ ф'ц (/?) пц (Г + т,Я, г + r]R - R) Л]. (34.4)
О
Поэтому уравнение (34.2) можно записать следующим
образом:
X 1
F^dS =\dS■ 2 \dR { ^^ 0;7(#) Л// X
/,/=1 о
X (г — riR, г — x\R + /?)Ц , (34.5)
где интегрирование по R проводится уже по всему
пространству.
С другой стороны, с макроскопической точки зрения
тензор давления р (г) в жидкости является функцией
пространственных координат; сила, действующая через
элемент поверхности dS, равна dSp (г). Для простоты
ограничимся рассмотрением случая системы в состоянии
покоя в отсутствие внешнего поля. Тензор давления р (г)
состоит при этом из части, появляющейся за счет вклада
межмолекулярных сил р(ф) (г) и части, появляющейся
за счет вклада кинетической энергии р(Л) (г). Если
жидкость находится в состоянии покоя, то произведение
dS-v(k) (г) равно импульсу, переносимому в единицу
времени через площадь dS вследствие теплового движения
к
молекул, и pW(r) находится из выражения &Г2 щ (г)-1,
известного для случая разреженных газов, так как в
покоящейся жидкости исчезают недиагональные члены в
тензоре давления. Межмолекулярные силы дают вклад
— dS-p(cp) (г), т. е. силу, действующую через элемент dS
благодаря взаимодействию молекул на противоположных

[л. //. Механическое определение поверхностного натяжения 153
сторонах поверхности dS. Эта сила определяется согласно
соотношению (34.5). Окончательно, воспользовавшись
приведенными выше соображениями статистической механики,
получаем следующее выражение для тензора давления:
р = р(Л) 4- р«р>, (34.6)
р(*)(г) = ЛГ 2*/(г)1, (34.7)
х 1
р«Р)(г) = _ _L 2 \dR { \f- ф'„{Д) X
X щ, (г - y)R,r - г]Я + R) dx\} . (34.8)
Определенный таким образом тензор давления должен
удовлетворять условию гидростатического равновесия
ур = 0. (34.9)
Унарная и бинарная функции распределения в случае
термодинамического равновесия должны удовлетворять
обобщенным уравнениям Борна — Грина — Ивона (24.6).
Таким образом, тензор давления (34.6) для системы,
находящейся в термодинамическом равновесии,
автоматически удовлетворяет условию гидростатического
равновесия (34.9) [21].
Следует заметить, что сила, действующая через элемент
dS в. точке г, а следовательно, и тензор давления, как
функция пространственных координат г, определяются
с некоторой степенью произвола и возможны другие
определения вместо (34.8). Однако с физической точки зрения
все определения должны приводить к одинаковым
результатам после интегрирования по некоторой области,
большей радиуса действия межмолекулярных сил. Последнее
требование не может быть выполнено в случае капли или
пузырька, настолько малых, что радиус поверхности
раздела не очень велик по сравнению с радиусом молекул.
35. Плоская поверхность раздела. Теперь результаты,
полученные в п. 13 с чисто механической точки зрения,
можно выразить через межмолекулярные силы и молеку-

154
Часть //. Статистическая механика
лярные функции распределения. Как и в п. 13, определим
систему прямоугольных координат (х, у, z), у которой
плоскость (х, у) совпадает с поверхностью раздела, а ось z
направлена перпендикулярно этой плоскости от фазы а
к фазе р. Так как в случае плоской поверхности раздела
любое физическое свойство внутри межфазовой области
зависит только от 2, унарную функцию распределения
t-ro сорта можно, как это сделано в п. 25, представить
в виде /I/ (2(1)), а бинарную функцию распределения —
через пц (2(1); г(12)). Тензор давления р определяется из
уравнения (13.2):
р = рТ (z) (ехех + еуеу) + pN (г) егег, (35.1)
где рт (z) и pn (z) — соответственно нормальная и
тангенциальная составляющие тензора давления. Если
приравнять правую часть уравнения (35.1) статистическому
выражению (34.6), то можно сразу получить
рт (2(D) =kT% n,(*(1)) —
х 1
t,/=l О
(35.2)
X
i=l
1
- 4- s S tSt ф'ч(г<12)) \n» (z(i) - riz<i2); r(i?>)dridr<i2)>
t,i=i о
(35.3)
и альтернативное выражение для рт (2(1)), получаемое
заменой *<12> на #<12> в (35.2). Согласно условию
гидростатического равновесия, нормальная составляющая pN
должна быть равна постоянному гидростатическому давлению р
в объемных фазах аир.
Подстановка уравнений (35.2) и (35.3) в уравнение

Гл. II. Механическое определение поверхностного натяжения 155
(13.8) сразу же дает для поверхностного натяжения
/,/=1 —оо О
х ф'и (г<">) пц (г<1> — Л2<12>; r<12>) А). (35.4)
Можно переписать уравнение (35.4) в более простом виде
(см. [21])
т = 4 2 5 dz<1)$Mz(1); '•(12))0^('-<12,)х
-00
(* L ( ^(l2)> (35-5)
/,/=1 —оо
Х г(12)
если использовать соотношение
оо 1
[ dzM \пц (2<D — Л2(12); Г<12>)Л) =
—оо о
оо
= J пц (2d'; r<12>) dzu, (35.6)
—00
полученное переменой порядка интегрирования по г) и
2(1). Выражение (35.5) совпадает с термодинамическим
выражением (25.13).
Давления в объемных фазах а и р можно записать с
помощью уравнения (35.2) в компактном виде
Р =kTinf-± S \{^Ф,(г{12))п^г^, (35.7)
где п^ и /г?/ определяются соответственно формулами
(25.19) и (25.20). Подстановка уравнений (35.2) и (35.7)
в уравнение (13.5), определяющее поверхностное
натяжение как избыток касательного напряжения, приводит к

156
Часть II. Статистическая механика
соотношению [19]
х °°
у =kT% ^ (nf-ni)dz(»-
X °°
-У 2 \ ^(1)\(^-па)Фи(гш)) {J^drm, (35.8)
/,/=1 —оо
которое идентично уравнению (25.18).
Статистическое определение тензора давлений, как это
уже упоминалось в предыдущем пункте, не является
однозначным. Однако легко показать из (35.5) или
непосредственным вычислением из (35.2) и (35.3), что если функции
щ и пц мало меняются с изменением z^ в области
действия межмолекулярных сил, то вместо (35.2) и (35.3)
можно использовать альтернативные выражения
х
РТ (2<«) =£Г2 ru(zW)-
1=1
X
- 4 2 \ {j^r Ф'ц (га2)) Щ (2d); г<»)) dr^, (35.9)
X
Ры{**) =£Г2 «,(z(1>)-
1=1
Г 2 \(i^J 0^/('-<12))"<7(2<,>; r<»>)rfr'»), (35.10)
или в тензорном виде [83]
х
P(2(D) = £7*2 nt(*V)l —
1=1
л * (. г(12)г(12)
- Х ? J г(ц) 0// ('(12)) пц (z(«; r<«>) *•<">. (35.11)
Последнее выражение часто используется в статистической
механике явлений переноса и является весьма точным
приближением для объемной жидкой фазы [82, 83].

Гл. //. Механическое определение посерхпостного натяжения 157
Рассмотрим более подробно физический смысл
выражения для тангенциальной составляющей тензора
давления (35.9) [19]. Рассмотрим бесконечно узкую полоску,
перпендикулярную оси х9 имеющую единичную ширину
в направлении у и заключенную между z(1) и z(1) + dz(1) в
направлении z. Пусть F^dz^ есть х-компонента силы,
Фиг. 13. Диаграммы, иллюстрирующие различие между двумя
разными определениями касательного давления рТ
а — Для уравнения (45 2); б —для уравнения (35.9).
с которой все молекулы в полубесконечном пространстве
х > О действуют на молекулы в столбе жидкости,
поперечное сечение которого равно определенной выше
полоске и простирающейся перпендикулярно плоскости
(у, z) от х = О до — оо (фиг. 13, б). Составляющая по
оси х средней межмолекулярной силы, с которой действуют
молекулы, находящиеся в элементе объема dr(12) вблизи
точки г(1) + г(12), на молекулы в элементе объема dr^l)
вокруг точки г(1), равна
^ д'>//(г(12))
- 2j *У(1) пц(гМ\ rM)drMdrW. (35.12)
Интегрируя по всем г<1> внутри столба и по всем г(12), та-

158
Часть //. Статистическая механика
ким, что х(2) > 0, получаем в результате
х Чг о
Fx^ (2(1)) dza) = 2 <k(1) \ dyM \ dxi» X
'./=1 —V —оо
оо оо оо
X \ rfz<"> 5 <fc/<12> J ЛхЮпцф'ц -j^r ■ (35.13)
—00 —оо —*(1)
Перемена порядка интегрирования по переменным х{12) и
х(1) после некоторых преобразований с учетом требований
симметрии приводит к
= 4" S 5 (^^/('(иОМг(1);г»«)Л-<*>. (35.Н)
/,/=1 —оо
Последнее соотношение описывает вклад межмолекулярных
сил в компоненту тензора давления рхх (z*1*), т. е. в
тангенциальную составляющую рт (z(1))- Следовательно, скла-
X
дывая кинетический вклад kT 2n<(z(l)) и —F{x\ мы по-
4=1
лучаем выражение (35.9). Таким образом, находим, что
выражение для рт, определяемое уравнением (35.9),
справедливо даже в плоской межфазовой области.
Так как в общем случае определение тангенциальной
составляющей тензора давления, данное в выражении
(35.9), отличается от ранее данного определения в
выражении (35.2) (см. фиг. 13, а и б), то очевидно, что
статистическое определение тензора давления не является
однозначным. Что касается составляющей pN (z(1)), то легко
видеть, что определение, аналогичное данному выше при
использовании полоски, перпендикулярной оси z,
приводит не к выражению (35.10), а к выражению (35.3),
которое основывается на ранее упомянутом определении.
Действительно, определение рм, согласно (35.10), не
справедливо в межфазовой области, хотя выражения (35.3) и
(35.10) дают один и тот же результат, если их
проинтегрировать по некоторой области, достаточно большой по срав-

Гл. II. Механическое определение поверхностного натяжения 159
нению с молекулярными размерами при условии, что
краевыми эффектами можно пренебречь.
Положение поверхности натяжения z определяется
уравнением (13.6). Подстановка (35.7) и (35.9) в уравнение
(13.6) дает
X 00
г.= \[-кТЪ \ {ni-nf)zwdzw +
*=1 —оо
X оо
+ 4" S \d'{n){j^- Ф'^п)) \ {nti-nthz^dz™] . (35.15)
Л/—1 —оо
В случае однокомпонентной системы уравнение (35.15)
с помощью уравнений (26.6), (26.7) и (26.11) можно
записать в виде [19]
Zs=Ь В ~жф'(г(12)) {(х(12))2 [Гг11 +
+ z^)lT2]2}dr^y (35.16)
Это уравнение можно использовать для вычисления
расстояния между поверхностью натяжения и
эквимолекулярной разделяющей поверхностью 6, которое, как
показано в п. 11, имеет большое значение для определения
зависимости поверхностного натяжения от кривизны.
36. Сферическая поверхность раздела. В случае
сферической поверхности раздела тензор давления
определяется уравнением (14.1). Из симметрии системы следует,
что функции щ (гМ) и пц (г*1*; г(12)) можно выразить
соответственно как щ (№) и пц (г(1>; г(12)).
Аналогично плоскому случаю,сравнение уравнений (34.6)
и (14.1) немедленно приводит к
х
рт (г<«)=АГ2 nt(rW) —
1=1
—2" 2 \ ^пР- 0;/(r(u))/i/,(r<i);r<»))rfr(»)f (36.1)

160
Часть II. Статистическая механика
пц (r<D; r<12>) = J пц (| гЫ — г]Г(12> |; r<12>) dr\. (36.2)
о
Здесь обозначение пц (г(1) — г)г(12); г(12)) соответствует
использованному ранее в (34.8) обозначению пц (г(1)— т]г(12),
г(1) — Т]Г(12) + г(12)).
Для двух однородных объемных фаз а и р, разделенных
сферической поверхностью раздела г =а, уравнение (36.1)
приводится к виду
p«t = kT^ nf- -L S \ ~Ш~ Ф№$*гь*\ (36.3)
/=i * /,/=iJ
где
л#> = ^(г(1); г(12)) [1 -Л (г(1) - а)] +
+ ^?/(г(1);г(12))Л(г(1)-а), (36.4)
а определение функции п"э аналогично приведенному
в (27.20).
Подстановка (36.1) и (36.3) в (15.5) дает выражение
для поверхностного натяжения на поверхности раздела
радиуса а (ср. [21])
У- , * /г(12) .о(1)\2
Y = - 2 Г<^+2- 2 \ Г</*« (r<12>) f(U) dr<12>' <36-5>
/=1 /,/=1
где при £ = г — а
00
= J (д,-л,вЭ) (i+-L)*rfg, (36.6)
—оо
Я3
Г//= J Й7-^3)^-^). (36.7)
Покажем теперь, что в случае к = 1 уравнение (36.5)
эквивалентно уравнению (27.23), которое основывается

Гл. II. Механическое определение поверхностного натяжения 161
на термодинамическом определении. Из выражений (34.4),
(36.2), (36.4) и (36.7) имеем
X у. 1 *3
',/=1 *"./=0 0 ^а
— л?/ (| гы - г]Г<12> |; г<">) + пц (| г(« + г]г(12> |; — г<12>) —
— я?/ (| г^ + т|г<12> |; — г<12>)] (^-)2 dri» dr). (36.8)
Если радиус а разделяющей поверхности, которая теперь
предполагается расположенной внутри сферической
межфазовой области, достаточно велик по сравнению с
радиусом действия межмолекулярных сил т, так что отношением
(т/а)2 можно пренебречь по сравнению с единицей, то для
расстояний г(12> — т имеем
\ пц (| г*1* ± г]г<12> |; + r<12>) (r(i>)2 dr<D ж
*3±-ПГ(12)С05ф(1)
~ \ nlf(rM;+rM)(rM +
^а±-Пг(12)со5ф(1)
=F Л^(12) cos ipd))2 rfr^1), (36.9)
г(1).г(12)
С0^(1, = 7а^Г- (36Л0)
Поскольку вне межфазовой области подынтегральное
выражение в (36.8) обращается в нуль, можно, используя
(36.9) и (36.8), переписать второй член в правой части
выражения (36.5) в виде
(Г(12).^(1))2
\ [{ntf{rW; r("))-/i?f(rW;r("')}

162
Часть II. Статистическая механика
(r(D)2 + J_ (r(12)C0S ^(1))2
X 3— +
а2
+ \ {Щ № г<">) - пц (r(D; - r^)} х
X J° ^ JrffW. (36.11)
По определению (см. также примечание на стр. 97) имеем
пц (г^, г*1* — г<12>) = л,/ (И1) — г<12>, г*1*),
а следовательно, как и в случае (36.9),
[ Пц (Г(1); _ Г(12)) r(l)r(12) C0S ,|,(1) ^(1) ~
~ С Л// (Г(1); r(i2)) (r(i) _|_ r(i2) cos ^(D) r(i2) cos ifd) dr*1*.
Таким образом, пренебрегая членами порядка (т/а)2, можно
привести выражение (36.5) к виду
у = -2 TtkT +
+ 4- S \ г'/0// С''"2') лиг- dr(12)> (36-12>
Г/; = 5 (т,- п?р) (1 + ^)2 dg<". (36.13)
—оо
Выражение (36.12) справедливо до величин порядка (т/а)
включительно, и для случая однокомпонентной системы
сводится к (27.23).
Таким образом, можно сделать вывод, что
механическое и термодинамическое выражения для поверхностного
натяжения на сферической поверхности раздела
эквивалентны до тех пор, пока можно пренебречь величинами
порядка (т/а)2.
В п.35 мы видели, что в случае плоской поверхности
раздела для тангенциальной составляющей тензора
давления приемлемы два различных выражения — (35.2) и

Гл. II. Механическое определение поверхностного натяжения!№
(35.9). По аналогии с (35.9) в качестве другого выражения
для составляющей рт, определяемой соотношением (36.1),
примем
х
1=1
~4" ? у г(12) 0//(г<»>)Мг<1>; r(»))rfr(»>. (36.14)
Тогда взамен (36.3) необходимо использовать вместе с
(36.14) следующее выражение:
p^ = kT^ nf —
i=l
-4-ДГ-^-тёг- 0:-/(/*(12))<^12), (36.15)
где
^=^.(г(12))[1-Л(г(1)-а)] +
+ /|?/(г(и))Л(г(1)-а). (36Л6)
Подстановка (36.14) и (36.15)~в (15.5) немедленно приводит
к выражению (36.12). Хотя в противоположность плоскому
случаю физический смысл выражения (36.14) для
сферического случая еще недостаточно очевиден, все же следует
ожидать, что результирующие эффекты, полученные путем
интегрирования по областям, достаточно большим по
сравнению с размерами молекул, эквивалентны как для
выражения (36.14), так и для (36.1).
Таким образом, можно сделать вывод, что статистическое
выражение для тангенциальной составляющей тензора
давления на сферической поверхности раздела можно
считать совпадающим по форме с соответствующим выражением
для плоской поверхности раздела с точностью до членов
порядка (x/R)2 включительно и что до тех пор, пока
рассматривается лишь поверхностное натяжение, унарная
и бинарная функции распределения действительно
описывают зависимость составляющей рт от радиуса, если эта

164
Часть II. Статистическая механика
составляющая существует для значений /?, для которых
величина (х/R)2 пренебрежимо мала по сравнению с
единицей.
Из сказанного можно заключить, что в случае одноком-
понентной системы выражение поверхностного натяжения
(27.23), полученное методами статистической
термодинамики, согласуется с выражением (36.5), полученным из
соображений статистики и гидростатистики, с точностью до
погрешностей порядка (тА/?)2. Это же справедливо и для
случая многокомпонентных систем. В таком случае зависимость
поверхностного натяжения от кривизны можно разделить
на две части. Одна из них связана с геометрией сферической
поверхности раздела, рассмотренной в п. 15, это
коэффициент (1 -f-flf3?)2 в (15.7). Другая часть возникает
вследствие изменения самой величины рг, что происходит
благодаря изменению унарных и бинарных функций
распределения, и вычислить ее невозможно до тех пор, пока не
получено с достаточной точностью некоторое приближенное
решение уравнения Борна — Грина — Ивона в
поверхностном слое.
Если радиус капли или пузырька сравним с радиусом
действия межмолекулярных сил, то может
появиться противоречие между двумя определениями
поверхностного натяжения. Следует, однако, заметить, что для столь
малых систем поверхностное натяжение потеряло бы свой
обычный смысл, так как внутренняя фаза даже в ее центре
не имела бы свойств, присущих объемной фазе. В то же
время методика, использованная в п. 7 и 15 для вывода
термодинамического выражения для поверхностного
натяжения, уже не пригодна из-за краевых эффектов. Одной
из наиболее важных причин, не позволяющих определить
поверхностное натяжение как термодинамическую величину
для таких малых капель или пузырьков, является то, что
площадь поверхности раздела не может быть определена
как внешний параметр. Из-за тепловых флуктуации было
бы невозможно сохранить форму такой капли или
пузырька, используя вспомогательное поле типа слабого
центрального поля, рассмотренного в п. 27. Это означает, что
площадь поверхности раздела уже нельзя рассматривать как
контролируемый внешний параметр в термодинамическом
смысле.

Гл. II. Механическое определение поверхностного натяжения!6Ъ
Наконец,следует заметить и подчеркнуть,что выражения
для поверхностного натяжения, приведенные в п. 35 и 36,
справедливы также и для неравновесных систем, если
системы находятся в состоянии покоя в отсутствие внешнего
поля, а их полные потенциальные энергии выражаются
согласно (24.3). Поэтому можно сделать вывод, что
поверхностное натяжение определяется статистическим
выражением, совпадающим по форме как для равновесного, так
и для неравновесного случаев, и что разница между
поверхностным натяжением в равновесном и неравновесном
состояниях объясняется лишь различием унарных и бинарных
функций распределения в этих состояниях.

Глава III
ЧИСЛЕННЫЕ РАСЧЕТЫ
§ 1. Чистая жидкость
37. Поверхность разрыва. [19]. Нами уже установлено,
что вычисление поверхностного натяжения требует точного
знания унарной функции распределения щ (г(1)) и
бинарной функции распределения пц (г(1), г<2)) в межфазовом
слое. Для случая однородной однокомпонентной жидкости,
находящейся в термодинамическом равновесии, были
выполнены довольно точные вычисления бинарной функции
распределения с помощью уравнения Борна — Грина —
Ивона (24.10), основанного, как упоминалось в п. 24, на
суперпозиционном приближении. Однако аналогичные
вычисления для функций распределения в межфазовом слое
не проводились из-за вычислительных трудностей. Поэтому
ниже будут использованы более грубые приближения и
обсуждение будет ограничено лишь случаем
однокомпонентной системы с плоской поверхностью раздела.
Предположим, что система состоит из однородной
жидкой фазы а с постоянной по всей фазе вплоть до
разделяющей поверхности плотностью, находящейся в
соприкосновении со своим паром —фазой р, настолько разреженной,
что ее можно рассматривать как вакуум. Тогда имеем
п (z<D) =ла, z<« < 0,
(37.1)
п (Щ = 0, zF> > 0,
п2 (гЫ; г<12>) - п (г<1>) п (г^ + г(12)) gi (/*(12)), (37.2)
где g% (г(12)) — корреляционная функция в однородной
жидкой фазе, определяемая уравнением (24.11). Тогда
разделяющая поверхность соответствует эквимолекулярной
разделяющей поверхности, т. е. Г = 0. Подстановка (37.2)

Гл. III. Численные расчеты
167
в (29.7) дает
[ГгЬ J (-i)v+l(^(*«)W*>), *»>о. (37.з)
I 0, z<12><0.
Таким образом, используя уравнение (26.12), получаем
требуемое приближение для поверхностного натяжения
в следующем виде:
оо
у =^\ ф'(г)ё1{гЖг. (37.4)
О
Это выражение было впервые получено Фаулером [9]
на основе такого же приближения для бинарной плотности
п2, но совершенно другим методом.
Подстановка соотношения (37.3) в (26.16) приводит
в принятом выше приближении к следующему выражению
для поверхностной энергии, отнесенной к
эквимолекулярной разделяющей поверхности.
v = - ^\ Ф (г) gt: (г) гЧг. (37.5)
о-
Из выражений (35.16), (37.3) и (37.4) получим
выражение для определения положения поверхности натяжения
боо = — zs = -~ , (37.6)
о
где zs — расстояние до поверхности натяжения, измеренное
от эквимолекулярной разделяющей поверхности в сторону
газовой фазы р. Значение величины б, определяемой
уравнением (11.8), для плоского случая обозначается 6^,.
Гидростатическое давление и молярная энергия
парообразования определяются известными выражениями
оо
р = n'kT - Щ- (п«)2 \ф'(г) gl (г) гЧг, (37.7)

168
Часть II. Статистическая механика
AU0 = - 2nNona \ ф (г) gl (г) гЧг, (37.8)
О
где N0 — число Авогадро. При выводе (37.7) было
использовано (25.24). Выражение (37.8) является прямым
следствием (24.4), если в газовой фазе пренебречь вкладом
межмолекулярных сил.
Теперь из (37.4) — (37.6) соответственно можно легко
вычислить термодинамические величины у» v и ^х>, если
только известен межмолекулярный потенциал ф{г) и
корреляционная функция g2 (г) жидкости. Такие вычисления
для жидкого аргона при температуре 90° К были
выполнены Кирквудом и Баффом [ 191- Они использовали
модифицированный Рашбруком [85] потенциал Леннард-Джонса
, , ч 8,62-10-8 1,Ц.Ю-Ю
Ф М = —^ —fi ■ (37-9)
1ф(г) — в эргах, г — в А] и аналитическое приближение
gt(r)= 1, fli<r
для первого пика на экспериментальной кривой,
определенной из работы Эйзенштейна и Гингрича [85] по
дифракции рентгеновских лучей. Поскольку только первый
пик играет заметную роль в таких вычислениях, то
достаточно аппроксимировать единицей функцию g% (г) на
расстояниях, больших av Параметры ах и t определяются
из экспериментальных данных. Остальные параметры s
и ат подбираются таким образом, чтобы удовлетворить
уравнениям (37.7) и (37.3) при значениях р и AUV,
определенных из эксперимента. Таким способом авторы
работы [19] получили для жидкого аргона при 90° К,
находящегося в равновесии с насыщенным паром,
аг = 4,50 A, t = 14;
(37.11)
am = 3,55 A, s =7,00.

Гл. III. Численные расчеты
169
В табл. 5 приводятся рассчитанные значения х у, v
и бос, а также результаты расчетов Хилла, которые будут
обсуждаться в следующем параграфе, и экспериментальные
данные [86, 87]. Ввиду грубого приближения,
использованного для функций распределения, можно считать, что
теоретические результаты хорошо согласуются с
экспериментальными данными.
Таблица 5
Поверхностное натяжение, поверхностная
энергия и расстояние между поверхностью
натяжения и эквимолекулярной разделяющей
поверхностью аргона при 90° К.
Кирквуд и
Бафф [20]
Хилл [93]

Эксперименты [87, 88]
Y, дин/см
14,9
6,0
11,9
и, дин/см
27,2
19,0
35,0
»оо А
3,63
2,81
Положительное значение величины бсо означает, что
поверхность натяжения находится на расстоянии 3,63 А
от эквимолекулярной разделяющей поверхности в сторону
жидкости и, следовательно, согласно уравнению (11.10),
поверхностное натяжение должно уменьшаться для капли
или увеличиваться для пузырька с уменьшением радиуса
поверхности раздела 2. Толмен [88] на основе
квазитермодинамики оценил боо для других жидкостей и получил
тот же знак и величину.
Теперь вычислим отдельно величины рт (z) и рм (г)
для однокомпонентной системы путем подстановки
выражений (37.1) и (37.2) в (35.9) и (35.3). Тогда получим сле-
1 Согласно частному сообщению д-ра Баффа, расчет основывался
на системе более точных значений а\ = 4,500 A, t= 14,000, am = 3,554А,
s = 7,007. В соотношении (37.11) числа округлялись.
2 Хилл [28] применил ступенчатое приближение (37.1) и (37.2)
к сферическим поверхностям. Однако оказывается, что полученные им
значения для зависимости поверхностного натяжения от радиуса
слишком малы.

170
Часть II. Статистическая механика
дующие выражения:
оо
Рт (г) = F- + -£- (п*У \ф'(г) «J (г) гЧг -
—Z
ОО
__£.(„«)• a* J 0'(r)tf(r)dr +
—Z
ОО
+ -f- (л«)2 z ^ 0' (г) «• (г) Л<Л (37.12)
—Z
ОО
Ра, (2) = Ра + 2-f ("а)2 J ^' W «? if) Л*г -
—2
ОО
_JL(„a)223^ ф'{г)ё1{Г)йг +
—2
ОО
+ я (п«)2 2 ^ 0' (г) g2a (г) Л*г, (37.13)
—Z
где ра — гидростатическое давление внутри жидкой
фазы а.
Используя (37.12) и (37.13), Харасима [90, 91] на основе
тех же приближений, что и в выражениях (37.9) — (37.11),
вычислил значения величин рт и рм как функций г.
Результаты его вычислений приведены на фиг. 14.
Из этой фигуры видно, что нормальное давление pN
существенно меняется в межфазовой области, достигая
при z =2,4 А максимального значения 660 апгм. Это
противоречит условию гидростатического равновесия, согласно
которому рм одинаково вдоль всей системы, и,
следовательно, означает, что поверхность раздела фаз с таким
разрывным изменением плотности, какое дают выражения
(37.1) и (37.2), весьма далека от состояния механического
равновесия. Кроме того, очень большое положительное
значение рт в межфазовой области не может дать
положительного значения поверхностного натяжения, если
воспользоваться определением y = \ (Р — Рт) dz.

Гл. III. Численные расчеты
171
Также очевидно, что выражение Фаулера для
поверхностного натяжения (37.4), полученное из (26.12), нельзя
вывести из (26.2). Это противоречие возникает из-за
применения ступенчатого приближения (37.1) и (37.2), для
\р, атм
600
500
400
300
200
100
Фиг. 14. Изменение нормального pN и
касательного рТ давлений вблизи поверхности разрыва
для аргона 90° К (по Харасиме [90, 91]).
которого (26.12) перестает быть эквивалентным
выражению (26.2), так как (26.5) и, следовательно, (26.11)
несправедливы для выражений (37.1) и (37.2).
Тем не менее, как показано в табл. 5, можно получить
довольно хорошее значение для поверхностного натяжения,
если использовать соотношение у = С (рм — рт) dz.
Похоже, что в этом расчете большие ошибки в значениях рм
и рт почти компенсируют друг друга, так как
погрешности, появляющиеся при вычислении р при ступенчатом
приближении, кажется, почти не зависят от направления
р е в межфазовом слое (где е — единичный вектор в
произвольном направлении). Возможно, в будущем это
предположение подтвердится.
38. Квазитермодинамическая теория [92, 93].
Противоречие, с которым мы столкнулись в предыдущем пункте,
по-видимому, возникает из-за математической разрывности
плотности в межфазовом слое. Поэтому здесь мы будем
уделять особое внимание именно непрерывности изменения
плотности жидкости в межфазовом слое с тем, чтобы можно
было приближенно удовлетворить условию равновесия.

172
Часть II. Статистическая механика
Если давление рт известно как функция z, то
поверхностное натяжение можно непосредственно вычислить из
уравнений (13.5) или (19.5). Чтобы получить рт как
функцию 2, рассмотрим прежде всего с точки зрения
квазитермодинамической теории систему, описанную в п. 17—20.
Из квазитермодинамического соотношения Гиббса —
Дюгема (19.3) получим
дм = j_ (38I)
дрт j т n ч '
Как указывалось в п. 17, в квазитермодинамике
принимают, что рт однозначно определено в каждой точке как
функция Тип. Если функциональная зависимость
рт (п, Т) известна, то с помощью уравнения (38.1)
химический потенциал \i можно выразить через п в каждой точке
и потребовать, чтобы химический потенциал (li в свою
очередь был одинаковым во всех точках всей равновесной
системы.
Так как весьма трудно определить точный вид
зависимости рт от п (z) и Т, даже если предположить, что рт
действительно представимо как функция этих переменных,
вычислим рт, предположив, что оно подчиняется
уравнению состояния, которое обычно используется для
вычисления давления р в объемных фазах, а именно уравнению
состояния ван дер Ваальса для одного моля вещества
[89, 92]
/ Ы2а \
[Р+ -уг~) <У ~ Nob) = N0kT, (38.2)
где V — молярный объем, а и Ь — постоянные ван дер
Ваальса на одну молекулу к N0 — число Авогадро. Это
простое полуэмпирическое уравнение дает довольно
хорошее приближение к наблюдаемой р — V зависимости
даже для объемов, соответствующих жидкой фазе.
Разрешая (38.2) относительно р, получаем
1бг-=1+(»-1г)(тН + -- <38-3>
где [Ь — —) — второй вириальный коэффициент.

Г л* III. Численные расчеты
173
Как известно из статистической механики *, один из
простейших межмолекулярных потенциалов, который
приводит к уравнению (38.3) в пределе низких плотностей и
высоких температур, имеет вид
0(г) = -e(-f)e, г>г0;
ф (г) = + оо г^г0. (38.4)
Молекулы, подчиняющиеся закону взаимодействия (38.4),
ведут себя как твердые сферы радиуса 1/2Го- Показано,
что в этом случае постоянные а и Ь соответственно равны
а = ей, (38.5)
г;
Ь=2я-±. (38.6)
з
Для системы, состоящей из молекул, подчиняющихся
закону для потенциала (38.4), мы используем приближенную
корреляционную функцию
*•(') = К '^'0' (38.7)
П г>г0,
10 r<r0,
которая справедлива в пределе высоких температур.
Далее, предположим, что тангенциальное давление рТ
определяется даже в области раздела фаз уравнением ван дер
Ваальса:
{Рт + п*а)[-±г-Ь)=кТу. (38.8)
где молярный объем V заменен на NJn, а тангенциальное
давление рт может принимать отрицательные значения.
Уравнение (38.8) можно переписать в более удобной
форме:
llL = -l — 02 (38.9)
ит 1-е 2 и' v '
6 = п6, (38.10)
1 См., например, книгу Дж. Майера и М. Гепперт-Майер [94].

174
Часть II. Статистическая механика
« = Жт = Ш> (38Л1>
где последнее выражение в (38.11) следует из (38.5).
Проинтегрируем (38.1) по п, предварительно подставив
в него (38.9). Получаем
ц = ц0 (Т) + kT In р£-) + kTv, (38.12)
v = /(6) — аб, (38.13)
fW=hT=W + T=W> (38Л4)
где постоянная интегрирования \i0 (Т) определена так, что
химический потенциал \i приближается к (6.3) в пределе
бесконечного разбавления и зависит только от 7\
Как видно из (24.4), в однородной объемной фазе
среднюю межмолекулярную потенциальную энергию на одну
молекулу можно выразить в следующем виде:
оо
ы(ф) = 2лп \ g2 (г) ф (г) гЧг. (38.15)
о
Подстановка (38.4) и (38.7) в (38.15) дает
и(ф)= _2jt_Vi# (38.16)
Умножая (38.10) на (38.11), увеличенное в ^- kT раз,
и учитывая (38.6), мы получаем выражение, в точности
совпадающее с правой частью (38.16). Таким образом,
после сравнения с (38.15) имеем
оо
а0£Т = — 4лп \ g2 (г) ф (г) гЧг. (38.17)
о
Отсюда видно, что в (38.12) член —aftkT представляет
собой вклад потенциальной энергии на одну молекулу
в химический потенциал.
Следовательно, уравнение ван дер Ваальса можно
использовать в качестве соотношения, связывающего
тангенциальное давление рт (z) в точке z, лежащей в меж-

Гл. III. Численные расчеты
175
фазовом слое, с плотностью числа молекул п (z) в этой
же точке. С другой стороны, статистико-механическое
соотношение (35.9) показывает, что в межфазовой области
величина рт (г) определяется не одним только значением
п (z) в точке z, но зависит также и от эффектов,
обусловленных изменением плотности числа частиц в окрестности
этой точки. Следовательно, рт (z) не может совпадать с
давлением в объемной фазе при той же плотности числа
молекул п (z).
Для того чтобы более точным образом учесть вклад
пространственного изменения плотности числа молекул
в значение внутренней энергии, Хилл [92, 93] заменил
приведенное выше грубое выражение для
межмолекулярного потенциала —aQkT на
kTW (z(1)) = $ п (z(1) + z(12)) g2 (r(12)) ф (r(12)) dr{12\ (38.18)
которое с точки зрения статистической механики
представляется гораздо более обоснованным. Для системы,
состоящей из молекул, взаимодействующих по закону
(38.4), для которой значение g2 (г) соответствует (38.7),
это уравнение записывается как
г—1
За I С е (s +1) t-*dt +
i
+ [ 6 (s + t) dt + \ 6 (s + t) t-*dt
s = ; t ■■
Го
г'12>
го
0 (s) = bn {zw)
dh
(38.19)
(38.20)
Тогда в выражении (38.12) для \i величина v вместо (38.13)
задается как
v=/(6(s))+Y(s). (38.21)
Согласно квазитермодинамическому условию
равновесия (18.4), этот химический потенциал должен быть
постоянным во всей области изменения s. Таким образом,
(38.12) при учете (38.21) представляет собой нелинейное
интегральное уравнение, определяющее 8 (s). Решая это

176
Часть II. Статистическая механика
интегральное уравнение и используя (38.20), можно
определить п (z) как функцию z.
Дальнейшее развитие вышеизложенного метода было
осуществлено Хиллом [93]. Оно состояло в использовании
более точного уравнения состояния, чем уравнение ван
дер Ваальса. Хилл воспользовался уравнением Тонкса [95]:
РЬ' _ 6 (1 + 2,96196 + 5,483 6») „ _ ,, ,, _ _^о_ m „g*
kT ~ 1 -О,851703- 0,1483 04 ' ~~ ПО ' ° ~ у2 * К°°'^}
которое описывает зависимость p-V-T в случае жидкости,
образованной молекулами в виде жестких сфер (это
значит, что в (38.4) г = 0) с точностью до третьего вириаль-
ного коэффициента. В случае молекул,
взаимодействующих с потенциалом (38.4) и корреляционной функцией
(38.7), уравнение Тонкса можно модифицировать
следующим образом:
рТЬ' 0(1+2,96190 + 5,483 02) <х' g
~W~ = 1—0,8517 03 —0,1483 04 Т 6 ' (38.23)
а' = 2,9619а, (38.24)
где а =2г//гТ согласно (38.11). Второй член в правой
части (38.23), соответствующий члену ^-02 в (38.9),
выражает вклад во внутреннюю энергию, обусловленный
силами притяжения. В случае системы, состоящей из
молекул, притяжение между которыми определяется
потенциалом (38.4), модифицированное уравнение Тонкса (38.23)
не дает точного значения третьего вириального
коэффициента, но его, однако, можно считать более точным,
чем уравнение ван дер Ваальса, поскольку при
критической температуре оно дает величину pcVc/N0kTc = 0,342,
что в случае одноатомных газов лучше согласуется со
средним экспериментальным значением 0,293, чем
величина 0,375, которую дает уравнение ван дер Ваальса.
Подставив (38.23) в (38.1), проинтегрируем результат
по п и заменим — а'8 на статистико-механическое
выражение Y (s), которое можно получить из (38.19), заменяя
а на а', определенное по (38.24).

Гл. III. Численные расчеты
177
Окончательно получим следующие уравнения:
ц = Цо (Г) +kT\n^r + kTV, (38.25)
v' = / (6 (s)) + У (s), 6 = nb', (38.26)
[-1 i
^ 0(5+^)Г4Л+5 6(s+*)# +
-00 -1
оо -■
+ \ e(s + о'~4^»
(38.27)
/(9) =1п
0,99195 In (1 + 0,1730696) +
(1-6)3
+ 1,49597 In (1 + 0,8269316 + 0,85688462) —
— 1,33238 arc tg (1,034626 + 0,49923) +
1 + 2,96196 + 5,483 б2 п эд w m 9R,
+ 1_о,8517е^-о,148зе« - °.38307- (38-28>
Нелинейное интегральное уравнение (38.25) численно
решил
1,0
as
0,6
и/*
0,2
п
Хил л
i i
[93],
1 1
пользуясь э.
1111
'.. _J_. 1 1 1
лектронно-сче
tiii
T/Tc--a,sa 1
■ ■ ■. °^°
0,10 1
480 "|
о,ао Н
""" 0,95 А
_^_^_ ]
0,98 \
1 1 .;_.... 1
'5 ~4
-2 -I
i г
~/'h
Фиг. 15.Кривые изменения плотности в межфазовой области
(по Хиллу [92]).
Для сравнения с результатами теории дырок (см. фиг. 25) ось г
направлена от газовой к жидкой фазе.
машиной. Результаты этих вычислений приведены в табл.
5 и на фиг. 15 и фиг. 16, где Тс — критическая тем-

178
Часть II. Статистическая механика
пература, определяемая соотношением г/кТс = 2,44.
Значение у, полученное этим методом, не дает лучшего
согласия с экспериментальными данными, чем то, которое
/,/
10
0,9
0,8
°fc 0,1
7: о,в
- 0,4
o,s
0,2
0,1
-
-
-
-
4
l
-з
1
-2
Г\г/тс=
1 0,60 \
// 0,70 \
II/ jwOxL
-/ 0 1
z/r0
--0,50
Z
,0,95
3 4
Фиг. 16. Графики изменения касательного давления рт в
межфазовой области и расположение поверхности натяжения (Хилл [93]).
Для сравнения с результатами теории дырок (см. фиг. 27) ось г направлена
от газовой к жидкой фазе.
Кирквуд и Бафф [20] получили, пользуясь радиальной
функцией распределения. Причина этого, возможно,
заключается в грубой приближенности
квазитермодинамических приемов, применявшихся в методе Хилла.
Однако существенно то, что обсуждаемый метод хотя и
содержит некоторые противоречия между предположениями,
принятыми относительно вклада энергии и вклада
энтропии в химический потенциал, но все же дает сравнительно
простой путь расчета изменения плотности в разделяющем
слое. Также существенно, что в отличие от
рассмотренного в предыдущем пункте приближения Кирквуда —
Баффа давление рт> получаемое с помощью этого
метода, принимает отрицательные значения, а это
действительно имеет место в разделяющем слое, как
можно видеть [3, 81 из (13.5) или (19.5) (см. также фиг. 27).

Гл. III. Численные расчеты
179
§ 2. Раствор электролита
39. Поверхностное натяжение разбавленных
растворов сильных электролитов. Потенциал средней силы в очень
разбавленном электролитическом растворе с плоской
границей раздела фаз можно определить с помощью
модифицированной теории Дебая и Хюккеля [96] *.
В этом пункте мы на основе общей теории, развитой
в п.31, получим из потенциала средней силы
приближенное выражение для поверхностного натяжения в растворе
электролита.
а) Однородный раствор электролита. Прежде чем
обратиться к модификации средней силы, действующей
между ионами в растворе, вследствие наличия поверхности
раздела, рассмотрим однородный раствор х — 1 сортов
ионов в растворителе, который мы будем считать
бесструктурной средой, имеющей постоянную
диэлектрическую проницаемость D. Обозначим через R расстояние от
иона сорта *', который мы будем считать точечным зарядом
величиной г.у через p. (R) — среднюю плотность
электростатического заряда на расстоянии R от центрального иона
сорта £, а через ty. (R) — средний электростатический
потенциал на расстоянии R. Тогда p. (R) и я|х (R) связаны
уравнением Пуассона
V2^, (R) = - ^Р,(Я). (39.1)
С другой стороны, среднее число ионов сорта / в единице
объема на расстоянии R от центрального иона i равно
пц (R)/tii, где бинарная функция распределения пц (R)
зависит только от R вследствие сферической симметрии
иона и изотропности однородного раствора. Если
использовать потенциал средней силы (30.15), то
ЛИР- = nf*"i{*vkT, (39.2)
где Wtj (R) — элементарный потенциал средней силы,
определенный в (30.18), a Ws и wj в глубине однородного раствора
можно приравнять нулю. Если использовать элемент арный
1 См. также статью Е. Дармуа в Handbuch der Physik, Bd. XX.

180
Часть II. Статистическая механика
потенциал между растворенными ионами хюц {R), то
плотность заряда p. (R) можно с помощью (39.2) записать как
p^R) = 2niGie~WiJ{R)/kT' <39-3>
С другой стороны, мы предположим, что раствор настолько
разбавленный, что вклады близкодействующих сил
отталкивания и сил ван дер Ваальса между ионами в величину
Wij весьма малы по сравнению с вкладом
электростатических сил. В этом случае можно использовать приближение
wi} (R) = в/% (/?). (39.4)
Подставляя (39.3) в (39.1) и используя (39.4), мы
приходим к уравнению Пуассона — Больцмана:
V4/ (/?) = —£2 n,Bfi-l*W. (39.5)
Дальнейшее приближение, сделанное Дебаем и Хюккелем,
состоит в предположении, что 2 8/% (R)/kT мала по срав-
/=2
нению с единицей для всех существенных значений R.
Тогда экспоненту в (39.5) можно разложить в степенной
ряд, замечая, что первый член исчезает благодаря
условию электронейтральности
х
2 л/е, = 0. (39.6)
/=2
Пренебрегая всеми членами выше второго порядка, мы
получаем приближение, впервые найденное Дебаем и
Хюккелем [96] \
V2% (R) = K^t (#), (39.7)
1 См также R. A. Robinson, R.H.Stokes, Elecfrolite
Solution, London 1955, p. 72—78.

Гл. III. Численные расчеты
181
где К — постоянная экранирования, определяемая как
^-4лЗ/1,^г. (39.8)
/=2
Решение уравнения (39.7), остающееся гконечным на
больших расстояниях от центрального иона, имеет вид г
е e~KR
*/W) = -5~F"- (39'9)
Из уравнения Пуассона получаем, что плотность
заряда pi (R) равна
К*ъ, e~KR
М*)= —-&—*-• (39Л°)
где постоянную экранирования \/К часто называют средней
толщиной ионной атмосферы. Поскольку
электростатический потенциал, создаваемый центральным ионом, равен
Ei/DR, средний потенциал, создаваемый остальными
ионами, равен
*'(*) = т^**-1)- (39Л1)
Электростатическая потенциальная энергия самого
центрального иона выражается в виде произведения его
заряда на7р/ (0)— потенциал (39.11) при R=0:
ел?/(0)=—^-. (39.12)
Но если применять эти соображения к каждому иону, то
каждый ион будет засчитываться дважды, один раз как
центральный и второй раз как входящий в окружение
некоторого другого. Таким образом, обусловленный взаимодействием
1 Обычно в теории Дебая и Хюккеля используется среднее
расстояние сближения а. Расстояние а представляет собой предельное
расстояние, такое, что никакой другой ион не может приблизиться к централь-
8, еКа -KR
ному ближе, чем на а. Тогда (39.9) переходит в г|}{ (R) = — ■ р
где постоянные интегрирования определяются из условия
электронейтральности. Уравнение (39.9) получено как предельный случай при а—О
(см. также [97]).

182
Часть II. Статистическая механика
вклад иона сорта i в энергию составляет
«* =—b-- (39ЛЗ)
Химический потенциал чистого смешивания, т. е.
химический потенциал идеального раствора, имеет вид
ttf + kT In т, и мы, следовательно, получаем 1
|1/==|10 +£74^,-4^, (39.14)
где |л° не зависит от концентрации.
В частном случае одновалентных ионных пар (39.8)
и (39.14) сводятся соответственно к
/С2 = -^-, (39.15)
и
в« <39Л6)
где я — плотность числа положительных или
отрицательных ионов в растворе.
б) Раствор с плоской границей раздела. Рассмотрим
теперь раствор с плоской границей раздела в контакте
с воздухом. Как и в п. 25, мы выберем систему координат
(лс, у у z), приняв разделяющую поверхность за плоскость
ху. Хотя растворитель по предположению и представляет
собой бесструктурную среду с постоянной диэлектрической
проницаемостью D, заполняющую пространство снизу
вплоть до разделяющей поверхности, концентрации ионов
могут меняться в зависимости от z благодаря
существованию поверхностного потенциала. В этом случае средний
электростатический потенциал в точке г, когда ион сорта i
фиксирован в точке г(1), зависит не только от г — г(1), но
1 Е. Шмутцер [97] в своей теории поверхностного натяжения
пользовался улучшенным уравнением, применимым к некоторым
неидеальным растворам.

Гл. III. Численные расчеты
183
также от самого г(1), и, следовательно, может быть
записан как % (г<1}, г). Тогда модификация (39.7) для этого
случая может быть представлена в виде [98, 99, 100]
V2^ (гЧ Г) = К2 (г) % (гЧ г), (39.17)
X
4я2 ti;(z)e2
К2 (г) = i=2DkT , г<0. (39.18)
С другой стороны, предполагается, что давлением ионных
паров можно полностью пренебречь, поэтому
электростатический потенциал г|$(г(1), г) вне ионного раствора
удовлетворяет уравнению Лапласа:
У2г|)° (гЧ г) = 0, z>0. (39.19)
Согласно электростатической теории решения, удовлетво
ряющие этим уравнениям, должны подчиняться условиям
V ду Л=о~ V дУ /2=о ' \ дг /*=о \ дг /2=0'
(39.20)
где D0—диэлектрическая проницаемость воздуха. Хотя
Шмутцер [97] получил точное решение этих уравнений,
используя модифицированные функции Ханкеля, мы примем
следующие два допущения.
Во-первых, заменим диэлектрическую проницаемость
воздуха на
D0 = 0, (39.21)
что впервые сделал Вагнер [98]. Онзагер и Самарас [100]
показали, кроме того, что относительная ошибка,
вносимая в значение потенциала средней силы этим
приближением, меньше, чем 2/(D +D°).
Во-вторых, мы заменим постоянную экранирования
(39.18) ее значением в глубине однородного ионного
раствора
К (г) =К (- оо) = /(, (39.22)

184 Часть //. Статистическая механика
что впервые было принято Ока 199]. С помощью
приближений (39.21) и (39.22) можно разрешить выписанные выше
дифференциальные уравнения (39.17) и (39.19) с условиями
(39.20) и получить простое выражение [100]
_К | r_r(l) , -К 1 r-r(D+2z(l> ez |
^•(Г(1)' Г) = * D|r-rU)l + e'-D|r-r"+*<4) '
(39.23)
где второй член обусловлен поверхностным зарядом.
Поскольку % (г*1*, г) есть средний электростатический
потенциал в точке г, когда ион сорта i фиксирован в точке
г(1), потенциал средней силы между ионом сорта i,
расположенным в точке г(1), и ионом сорта /,
расположенным в точке г(2) (т. е. хюц (г(1); г(2) — г(1))), определяется
как е/% (г(1), г(2)) аналогично (39.4). Поэтому из (39.23)
следует выражение [100]:
- /о(12)
ш, (*«; Г(Ш) = в/в/|1__ + ^г} . (39.24)
где г(12) — расстояние между двумя ионами, а rfm =
= | г<2) —г(1)+ 2гМег\, определенное согласно (31.6), равно
расстоянию между одним из ионов и изображением другого,
как показано на фиг. 17. Обозначим средний
электростатический потенциал в центре иона сорта i, расположенного
в точке г(1), обусловленный остальными ионами и
поверхностным зарядом, через % (г(1)). Вычитая создаваемый
самим ионом / потенциал e£/(D \ г — г(1) |) из (39.23) и
приравнивая г к г(1), получаем
p2/CzU> ед
♦'^"•'г^п—в-* (39'25)
где первый член представляет собой потенциал
электростатического изображения экранированного иона. Средний
электростатический потенциал, обусловленный наведенным
поверхностным зарядом, зависит от расстояния г{ш между
ионом i и изображающей его точкой.

Гл. III. Численные расчеты
185
Следовательно, электростатическая сила,
действующая на этот ион, задается как [100]
е,-
Щ С(1))
№=-2zM
--^е,-
1 л *[>/ (rw)
. (39.26)
Тогда из (39.25) и (39.26) следует, что потенциал средней
силы, действующей на сам ион сорта i со стороны осталь-
Мнилюе изображение
точи и г,
+~У
Фиг. 17. Расположение г(12) и г^'
относительно точечного заряда, помещенного в
точку r(i), и его изображения.
ных ионов, равен [100, 97]
6/в'
,2Кг(1)
-Wz™
(39.27)
где постоянная интегрирования выбрана так, что внутри
раствора wt становится равной нулю. Этот потенциал
называется адсорбционным потенциалом [98, 100].
Используя (30.20), получаем плотность молекул сорта
/ в точке г в виде
Г г2-е2Кг Л
щ (г) = п* ехр {—7-} . * < 0. (39.28)

186
Часть II. Статистическая механика
Эту функцию вычислил Ока *. Кривая ее для раствора
одновалентных ионных пар при температуре 20° С и
концентрации 0,05 моль/л показана на фиг. 18.
Поскольку плотности числа растворенных молекул в
газообразной фазе полагаются равными нулю, подстановка
(39.28) и (25.21) приводит к следующему выражению для
поверхностной плотности числа частиц:
Л- = я? ^ [ехр
dz.
(39.29)
Теперь мы можем вычислить разницу между
поверхностными натяжениями сильно разбавленного электроли-
-// ЧО-9 -8 -7 '6 -5 -4 -3 -2 -1 О
г, А
Фиг. 18. Относительное распределение
плотности в поверхностном слое для
одно-одновалентных электролитов.
тического раствора и чистого растворителя с помощью
(31.17) или (31.18). Поскольку в чистом растворителе эффект
экранирования отсутствует, мы имеем в предельном случае
нулевой концентрации К = 0. Тогда Ш.24) и (39.27)
сводятся соответственно к
wl(rV К») = в/е/ f^ + 7^55) , (39.30)
Dr
DW,
1 Ока [99] пользовался значением адсорбционного потенциала,
вдвое превышающим величину (39.27), так как он не учитывал
множитель 1/2 в правой части (39.26).

Гл. III. Численные расчеты
187
Эти потенциалы обусловлены чисто кулоновской силой и
силой электростатического изображения.
Из (30.15), (30.18) и (30.20) получаем
„,7(Г(1))Г<2>) =
= nWi ехр {- ± (wt (r<i>)+ w,(г<2>) + w„ (г<»; г<«))} =
= Я/ (*») п, (г<« + г»)) е-ш<7(г(1): Г(12>№Г. (39.32)
Поскольку всеми членами второго порядка по тц1кТ мы
в этом расчете пренебрегли, можно вместо (39.32)
использовать линеаризованное соотношение
/ w..(r{l); г(12))\
пц (г(«; г<12>) = л, (r<i>) л/ (r(D + г<12>) (1 ^-^ - J .
(39.33)
Подставляя (39.30) и (39.33) в (31.17) и учитывая условие
электронейтральности (39.6), находим
о
у — то = J (я — яг (2<i>)) dz">, (39.34)
—оо
где
х х —2(!) ОО ОО
ПТ(гЫ) = kT^riiizW)-^. ^ J d2(12) ^ ^(12) ^ ^(12)X
/=2 /, /=2 — oo —oo —со
Я/Я/8,8, ffv(12h2 ^12h2 )
x -"mr-l^r + ^p(г(1,; r(12))- <39-35>
В этом уравнении интегрирование по z(12) ограничено
таким образом, что все учитываемые значения г(2)
соответствуют точкам, лежащим внутри раствора. Поскольку
rffi представляет собой расстояние между г(2) и
изображением точки г(1), которое, как видно из фиг. 17, всегда
расположено вне раствора, можно переписать (39.24) с по-

188
Часть II. Статистическая механика
мощью (39.24) в следующем виде:
X
пТ (z<D) = kT% щ (2d') —
1=2
2/.£j Lie(12))3 («v/x
g-*r<u> Mr<V,(rM)efrM
Х r(i2) D2^r J '
(39.36)
где интегрирование по г(12) распространено на все
пространство.
На больших расстояниях от границы раздела ят, как
видно из (31.14), сводится к осмотическому давлению
/. /=2 J
it = kT 2 л? —
/=2
dr<i2> i^_l_ ^__ y_Ll e (39.37)
(r(12))S
r(12)
DW
Совершенно аналогичным образом из (31.18) получаем
х 00
г - г° = - У, ( dz^ dWi{zl) Щ (2(D) 2(D +
/=2 —oo
+ jj rfz<« [Ядг (Z<« — ЯГ(2<«)],
(39.38)
где
nw(z<i)) = /jr2»((2(1>)-
*'=2
1 2 ^r(i2)[/i£(12))2 i (*(1)+*(2))2
2 . — j
*. /=2 *
2(12))2
r(12)) 3
Cfi?>» /X
-Kr(12)n (г(1)} „/,.(») Л и"!
Xer(12) Д V4r ']• <39-39>

Гл. III. Численные расчеты
189
Обозначения пТ и nN были использованы потому, что
в известном смысле пт и nN можно понимать как меры
тангенциального и нормального осмотических давлений, что
можно было предвидеть, исходя из соображений относительно
рт и pN, высказанных в п.35 [72]. Точные же
механические выражения для тгт и тгм — тангенциального и
нормального осмотических давлений еще не получены.
40. Численный расчет для раствора одновалентных пар
ионов [72, 100]. Мы выполним численный расчет разности
между поверхностными натяжениями раствора
одновалентных пар ионов и чистого растворителя на основе
изложенной выше теории электролитических растворов. Пусть
п (г(1)) будет плотностью числа ионов сорта 2 или 3, а
е — абсолютной величиной электронного заряда. Тогда
(39.36) и (39.39) сводятся соответственно к следующим
выражениям [721:
кт (z(i)) = 2/1 (2(«) КГ - n(Z^W X
х\{У^ + ^ф}^г^, (40.1)
nN (Щ = 2п {*») kT - п^1*К* X
х \ 1 <£^ + (*(1) + z(2))24 e~Krm dr™ (40 2)
где К — постоянная экранирования, определенная по
(39.18), принимает вид
«2= 8Яшг)82 • С40-3)
Согласно приближению (39.22), ее можно считать
независимой от г и, следовательно, равной (39.15). Интегралы
в уравнениях (40.1) и (40.2) можно вычислить, пользуясь
биполярными координатами. В результате имеем:
-и -и -и Л -,
- -sr - V - V}]. <40-4)

190
Часть II. Статистическая механика
_l_ e~U _i_ 2е~" I 2е_"11 /лпеч
+ -IF + T + t}J< (40-5)
и = — 2/С2<». (40.6)
Обозначая приращение поверхностного натяжения
согласно (39.34) через Ду1, а согласно (39.38) через Af", запишем
их следующим образом [72]:
0
о
О
* = w« <40-9>
где w° (г(1)), определенное в (39.31), уже использовалось
в качестве адсорбционного потенциала в (39.38), а п*
представляет собой плотность числа частиц в объемном
растворе. Проделав аналитическую оценку интегралов
такого вида, Бафф и Штиллингер [72] вывели следующие
выражения:
паг2 ni
ЛГ1^-^ (У), (40.10)
FUy)=L(y) + ^^^](AUny + B\)t (40.11)
АГ" =^"(У). (40-12)
F" (у)=Ь(у)+1 я, (Г+ 2)1 <Л " 1п У + *">' <40ЛЗ>
1(»+ 2).

Гл. III. Численные расчеты
191
где
L(0 = -iln0-r + -|, (40.14)
А\ = (я + 1)" ("*~2) - у (5л2 - Зя - 2), (40.15)
В'=£+!£{(,»._ 2) (In (я + 1)+ 1)-
_ л (я + 1) / (я + 1)- (л - 1) (л + 2) / (я + 2) +
+ 2 (я + 1) Н« + 3)} —^{(5«2 — Зя — 2) In я +
+ (5я2 + Зя - 2) + 2 (я + 1) (я + 2) / (я + 1) -
_ 6я2 (/(я) + / (я + 3))}, (40.16)
А)? = (я + l)n+1 (я - 1) - Зя"+2, (40.17)
В" = (п + 1)Л+г {(л - 1) (In (я + 1) + 1 - / (я + 1)) -
- (я + 2) / (я + 2) + 3/ (я + 3)} -
-Зя"+2(1пя+^-/(я)-/(я + 3)), (40.18)
/(«) = -T+2_L. (40.19)
m=l
Г = постоянная Эйлера = 0,5772157 .... (40.20)
Величины F1 (у) и Fu (у) приведены в табл. 6.
Другой способ расчета приращения поверхностного
натяжения состоит в интегрировании адсорбционного
уравнения Гиббса (5.8). Ока [99] пользовался уравнением,
эквивалентным (5.18), а Онзагер и Самарас [100], а также
Шмутцер [97] —эквивалентным уравнению (33.25). В
случае раствора одновалентных ионных пар (32.25)
записывается как
— dT = Г2ф2 + Г3ф3. (40.21)
Из (39.29) имеем
00 г
Г-Г.-Г.-^J „р(_£1-,
du. (40.22)

192
Часть II. Статистическая механика
Рассматривая интеграл в комплексной области и
применяя теорему Лагранжа, Онзагер и Самарас [100]
получили следующее выражение * для Г из (40.22):
оо
г = ж2-Й!г(1пу+&). (40-23)
s=l
S
& = In s + 1 + 2r -2 2 4" , (40.24)
П=1
где у определяется уравнением (40.9), а у—постоянная
Эйлера, приведенная в (40.20).
При постоянной температуре из уравнений (39.15) и
(39.16) имеем
Подстановка уравнений (40.23) и (40.25) в (40.21)
приводит к соотношению
00 I
dr = - "шг S Чпг (2 - у] yS (1п ^ + *•> dK- (4а26)
^ S=l
Интегрируя по К, получаем
ДГШ = ^V" (*/), (40.27)
* S=l
X^Onif-rb + ^-^O^-.^ + ft)}-
(40.28)
Значения функции F111 (#) также приведены в табл. 6.
Экспериментальные значения были определены Баффом и
1 Онзагер и Самарас [100] выполнили интегрирование, разлагая
в степенной ряд экспоненциальную функцию. Шмутцер [97] вычислил
интеграл путем учета расстояния наибольшего сближения двух ионов а,
что позволило ему избежать разложения экспоненты в степенной ряд
в области, где такое разложение бессмысленно.

Гл. III. Численные расчеты
193
Штиллингером так, что кривая проходит через значение,
найденное Швенкером [101].
Таблица 6
Сравнение значений функций Fl(y), Fu(y), FUI (у)
с экспериментальными значениями для
одно-одновалентных электролитов в воде (по Баффу и Штиллингеру ([72])
У7
0,0063
0,0126
0,0189
0,0315
0,0378
0,0630
0,0944
0,1259
0,1574
0,1889
0,2014
0,2266
^ш<*)
1,486
1,325
1,233
1,117
1,077
0,966
0,880
0,819
0,772
0,735
0,722
0,697
F 1 {у)
1,492
1,333
1,242
1,130
1,090
0,981
0,899
0,839
0,794
0,758
0,745
0,722
F П (У)
1,549
1,405
1,323
1,223
1,189
0,095
1,023
0,974
0,937
0,908
0,897
0,879
F(y)
эксп.
1,25
1,22
1,18
1,14
1,12
1,06
1,03
1,02
1,00
С, МОль/л
при 18°С
0,0046
0,0091
0,0137
0,0228
0,0273
0,0456
0,0683
0,0911
0,1138
0,1366
0,1457
0,1639
Примечание. Диэлектрическая постоянная виды
рассчитывалась с помощью уравнения Акерлофа — Ошри (А к е г 1 о f,
О s h г у, Journ. Am. Chem. Soc, 72, 2844 (1950) : D = 5321 -£- +
233,76—0,9297 T +0,001417 Га—0,068292 T3; T =273,l+t.
Для случаев I, II и III имеет место идентичный
предельный закон, который для электролита, содержащего
одновалентные пары, принимает форму [100]:
= -n^(lnw-°'34557)> <40-29>
или [72, 100]
Ar^rln1'130-1;?-18^8, (40.30)

194
Часть II. Статистическая механика
где у — поверхностное натяжение (в дин/см), ас —
концентрация растворенного вещества (в мол/л) х.
В более концентрированных растворах описанная
основная модель перестает быть справедливой. Кроме того,
введение приближенных функций распределения в строгие
формулы для термодинамических переменных приводит
к внутренней противоречивости. Сопоставление
полученных величин служит критерием справедливости
приближений. Например, разница между величинами Ау1 и Ду11
возникает из-за несостоятельности условия
гидростатического равновесия. Как видно из табл. 6, значения Ау11
лучше согласуются с экспериментальными данными.
Аналогичное внутреннее противоречие было отмечено и в
случае ступенчатого приближения, использованного при
вычислении поверхностного натяжения жидкого аргона. В
используемых нами'обозначениях величина у11 соответствует
(Pn — Рг) ^2» а Т1 соответствует \ (р — рт) dz. В этом
случае, как показано в п. 37, величина у11 довольно
хорошо согласуется с экспериментальным значением, тогда как
величина у1 оказывается даже отрицательной.
Хотя адсорбционное уравнение Гиббса само по себе
правильно, но основывающаяся на ней теория Онзагера—Са-
мараса [100] также приводит, как видно из табл. 6, к
некоторым расхождениям. Часть из них обусловлена тем, что
мы пренебрегаем членами высшего порядка в разложении
экспоненциальных функций, а также расстоянием
наибольшего сближения двух ионов. Шмутцер [97] вычислил
разность поверхностных натяжений, учитывая вклад
расстояния наибольшего сближения. Его результаты для
растворов хлористого натрия хорошо согласуются с
экспериментальными данными вплоть до сравнительно
высоких концентраций.
§ 3. Адсорбция газа на твердой поверхности
41. Адсорбция молекул одноатомного газа на твердой
поверхности, а) Общая теория. Число молекул i-ro сорта
в системе, содержащей адсорбент, определяется уравне-
1 Новейшие значения физических постоянных взяты по Дюмонду
и Коэну [102].

Гл. 111. Численные расчеты
195
нием (33.7). В случае однокомпонентной системы это
уравнение сводится к
N = l^ = ^V«mbmtr, (4Ы)
m
где In S определяется согласно (33.11). Если сохранить
лишь члены до второго порядка по N/Va, то из (41.1)
получим
С = -£ 2 ПО*. (41.2)
Подставляя уравнение (41.2) в (33.18), получаем
p = -^Ui ^ЧЛ, (41.3)
c2 = V* (2Ь2 — ЬгЫ)9 (41.4)
где Ъ\ определяется по (33.16).
Разделяющая поверхность определяется как
математическая плоскость, проходящая через центры молекул,
которые образуют поверхность твердого тела. Обозначим
площадь этой поверхности через А, а расстояние
наибольшего сближения молекул газа с молекулам pi, образующими
твердую поверхность,— через D. Периодической
структурой кристалла мы в данном случае пренебрегаем. Тогда
часть объема 1/а, равная AD, является недоступной для
центров молекул газа.
Экспериментальные результаты более удобно выражать
через кажущийся объем системы V*, определяемый
согласно закону идеального газа, чем через число молекул N:
у* = N-. (41.5)
Кроме того, определим избыточный объем
Vex = V* — Va + AD. (41.6)
Так как Va — AD образует объем, доступный центрам
молекул газа, то Vex представляет собой избыточный
кажущийся объем, связанный с присутствием твердого ад-

196
Часть II. Статистическая механика
сорбента и поэтому характеризующий количество
адсорбированного газа.
Подстановка N из уравнения (41.5) в (41.3) дает
kTjV^f кТ(УаЬг)3 ш?.
Р- у*Сг у**Сг • К**-')
Дифференцируя (41.7), получаем следующее выражение
для наклона кривой V* (р):
dV* V**d
dp 2kT (Vabif — kTV* (V*b{f
а/,л»
(41.8)
Из уравнения (33.13) видно, что в предельном случае
нулевого давления
lim&i^ Hm61= 1. (41.9)
р->0 V'a-*oo
Из уравнений (41.3) и (41.5) имеем
Пт -^- = 1. (41.10)
Таким образом, в пределе нулевого давления выражение
(41.8) приобретает вид
dV*
dp
= w- (41Л1)
Используя (33.13) и (33.16), уравнение (33.14) можно
записать следующим образом:
Ь2 = Ь1 + 2(6,-1) Ь\ +^г\\(е-^т^т- 1) х
х (е_Ф(г(1>,/*г _ j} {е-ЧгЩ,ьт _ ,} dr(i)dr(2)_ (4] Л2)
Тогда величину с2 из (41.4) можно выразить как
с2 = V" (« -Ж) + Ц (е-'>(г(12))/^_ 0 (е-ф(г('>)/*г_1) х
х (е-ф(г<г))/*г - 1) dr(1)dri2). (41.13)
Если температура достаточно высока по сравнению
с критической температурой адсорбированного вещества,
а давление газа невелико, то можно не учитывать вклад

Гл. III. Численные расчеты
197
потенциала взаимодействия ф (г) между молекулами газа.
Тогда из (33.13) и (33.14) получаем
bl = ] + £r \ (e-*{ril))/kT - 1) rfru>, (41.14)
b2 = b3 =. . . =0. (41.15)
Таким образом, используя уравнение (33.7), число
молекул N можно выразить в виде
лг = С /v- + $ {e-^))ikT _ 1} rfrd, у (41Лб)
Поскольку для. идеального газа величина £, как видно
из (33.18), равна р/АТ, то уравнение (41.16) можно записать
через кажущийся объем К*, определяемый уравнением
(41.5), следующим образом:
Г = Vе + \ (<Гф(г(1))/*г - 1)dr{l). (41.17)
Тогда избыточный объем (41.16) определяется как
Vex -AD = \ (e-^h/kr _ 1}dr(1)> (4U8)
б) Грубая модель [80, 103]. Пренебрежем сначала
взаимодействием между молекулами газа [103]. Если
потенциал притяжения i|) (г) между молекулой газа и
молекулами твердого вещества соответствует силам Лондона, то имеем
( оо, r<D,
Ф (г)= ^_УД r>D (41Л9)
где Rs — расстояние между молекулой газа и s-й
молекулой кристаллического твердого адсорбента, а
суммирование проводится по всем молекулам твердого вещества. Если
кристалл можно приближенно заменить полубесконечным
бесструктурным твердым телом с плоской поверхностью г,
1 Капиллярные и кристаллические поверхности рассмотрели Стил
и Холсей [104].

198
Часть II. Статистическая механика
то суммирование в последней формуле можно заменить
интегрированием, и мы получим [105]
*(г) = \
°о, r<D,
. D3 ^п (4L20)
nCti
s
+0 = -^-. (41.21)
где ns — число молекул в единице объема твердого тела.
При подстановке формулы (41.20) в (41.18) получаем
оо
^ = ^{exp(fg)-l}dr. (41.22)
D
Разлагая экспоненту в степенной ряд и выполняя
интегрирование, получаем [103]
Значения In (Vex/AD) как функции tyo/kT, вычисленные
из уравнения (41.23), приведены на фиг. 19 (непрерывная
кривая).
Согласно уравнению Кирквуда —Мюллера [106],
постоянная Лондона С в (41.21) определяется как
С = 6mAiQ*s [-~ + -g-)"1, (41.24)
где те2 — масса электрона, умноженная на квадрат
скорости света, а—поляризуемости, % — диамагнитные
восприимчивости, а индексы G и S соответственно относятся
к газообразному и твердому состояниям. Подстановка
(41.24) в (41.21) дает
nsmc2 лал(Хо / ас а5 \-1
ь = w^^ + li) ■ <41-25>
Однако, надо заметить, что плотность числа молекул
вблизи адсорбирующей поверхности не может быть столь
низкой даже когда сам газ при отсутствии такой поверх-

Гл. III. Численные расчеты
199
ности остается существенно идеальным. Поэтому мы учтем
взаимодействия следующего более высокого порядка [80].
Фиг. 19. Зависимость избыточного объема для
газовой сажи от обратной температуры (в
приведенных единицах), вычисленная по уравнению
(41.23) (по Стилу и Холсею [103]).
Если сам газ идеален, то коэффициент б£ пренебрежимо
мал, и, следовательно, можно опустить первый член в
(41.13):
С! = 5(г^%г-1)х
х (е-Ф(г(1))/*Г_1)(е-ф(г(2))/*Г_1Мг(1,£/г<2)> (4L26)
Предполагается, что молекулы газа ведут себя как
твердые непритягивающиеся шары диаметром г0:
р-ф(П/кт « / J> г < го,
~ I 0, г>г0.
(41.27)
Подставляя формулы (41.20) и (41.27) в уравнение

200
Часть II. Статистическая механика
(41.26) и выполняя интегрирования, получаем
^ехр{^(^)3}{1 -&»-<*»)*}Л?, (41.28)
(41.29)
X
D
го
а(2) = -L
где oW изменяется от в до Уа/Аг0, а сг<2> принимает
значения от 6 до orW+1, когда 8 больше а^> — 1, и от а^> — 1
до а*1* + 1 в противном случае.
'4.01
4П 5,0
6,0 W 8,0
ф0/к Т
9,0
Фиг. 20. Вычисленные значения ln(— c2fArl) для
различных значений 6 = D/r0 (по Фримену и Хол-
сею [80]).
Фримен и Холсей [801 вычислили интеграл (41.28)
графически. На фиг. 20 вычисленные значения
In (—с^Аг*) представлены в виде функции от tyJkT для
различных значений параметра 8.
в) Сравнение с экспериментальными данными.
Адсорбцию инертных газов на твердых телах изучали
экспериментально Стал и Холсей [103]. Они замеряли кажущиеся

Гл. III. Численные расчеты
201
объемы сосудов, содержащих порошки с развитой
поверхностью и инертные газы, при различных высоких
температурах 1. Полученные данные обрабатывались с помощью
уравнения (41.23) методом проб и ошибок.
В этих случаях V* равен полному объему сосуда минус
объем содержащихся в нем порошков, тогда как объем
действительно недоступного для газа пространства равен
Va—AD, В пределе высоких температур объем Vex,
согласно уравнению (41.22), обращается в нуль, и тогда
формула (41.6) переходит в
V =V* —AD, (41.30)
которая и определяет значение измеренного кажущегося
объема. В качестве первого пробного значения Va — AD
была использована величина объема недоступного
пространства для гелия при достаточно высокой температуре.
Теоретическое значение In (Vex/AD) было вычислено из
уравнения (41.23) как функция ^kT. Результаты этого
расчета представлены на фиг. 19 в зависимости от ^JkT
(см. непрерывную кривую). Экспериментальные данные
были приведены в соответствие с теоретической кривой
путем подбора масштаба. Экспериментальные значения
AD и % определялись соответственно из значений Vex при
Vex/AD = 1 и из значений 1/Т при г|У#Г = 1, как показано
на фиг. 19. Значения D вычислялись по известному
значению if0 и наблюдавшимся значениям поляризуемости и
восприимчивости с помощью уравнения (41.25). Значения
площади А были рассчитаны по этим значениям D и по
упомянутым выше экспериментальным значениям AD.
Экспериментальные значения ур0 вместе с расчетными
значениями D и А приведены в табл. 7.
Большое значение потенциала i|)0 свидетельствует о том,
что атомы инертных газов сильно взаимодействуют с
твердыми поверхностями. Значения площадей А для
различных газов довольно близки друг к другу, особенно в случае
газовой сажи. Эти значения хорошо согласуются с пло-
1 Интервал температур для гелия составлял 78—303° К, для
неона — 153—492° К, для аргона — 302—492° К и для криптона — 332—
491° К. Все эти температуры достаточно велики по сравнению с
критическими температурами, которые составляют соответственно 5,3; 44;
151 и 2зо° к.:

202
Часть II. Статистическая механика
Таблица 7
Экспериментальные значения параметра я|)0,
определяемого из уравнения (41.23),
расстояния наибольшего сближения D,
вычисленного из уравнения (41.25), и площади
поверхности на грамм-атом, вычисленные
по известным значениям D и
экспериментальным значениям AD (по Стилу и Холсею
[104]).
Адсорбент
Газовая
сажа
Древесный
уголь
Пористое
стекло
Окись
алюминия
Газ
Гелий
Неон
Аргон
Неон
Аргон
Неон
Аргон
Аргон

Криптон
ЛГ0Ф0.
ккал*
0,60
1,36
4,34
1,33
4,14
1,56
3,79
2,80
3,46
D, А
2,47
2,70
2,75
2,72
2,79
1,93
2,21
1,87
1,99
А, мш/г
462
367
262
774
787
101
71
131
141
N* о— число Авогадро.
щадями, полученными методом Бранауэра, Эмметта и
Теллера *. Таким образом, описываемый способ позволяет
также делать оценки площади порошкообразных
адсорбирующих веществ.
Фримен и Холсей [80] сравнили наклон dV*/dp,
вычисленный по уравнению (41.11), с экспериментальными
данными для инертных газов на порошках с развитой
поверхностью. Значения In (—c2/Art), вычисленные для
различных значений параметра 8 =D/r0 из уравнения (41.28),
1 Метод определения площадей с помощью адсорбционной
изотермы [107] (см. также [108]). Этот метод наиболее употребителен для
определения площади поверхности порошка. Однако мы ограничимся
применением общей теории, основанной на статистической механике, и не
будем подробно рассматривать теорию физической адсорбции.

Гл. III. Численные расчеты
203
Таблица 8
Значения параметров, используемых для
вычисления с2у определенного по уравнению
(41.28) (по Фримену и Холсею [80])
Адсорбент
Газовая сажа
Окись
алюминия

Термопластикат S-85
Газ
Аргон
Криптон
^ Аргон
I / Неон
Л^оФо.
ккал
4,34
3,46
3,66
1,28
А, мг/г
262
141
1030
1135
го. А
3,42
3,61
3,41
2,80
D, А
2,75
1,90
2,90
2,55
Таблица 9
Сравнение теоретических и экспериментальных значений
наклонов dV*/dp (по Фримену и Холсею [80])
Адсорбент
Газовая сажа
Окись
алюминия
Термопластикат
S-85
Газ
Аргон
Криптон
\ Аргон
J Неон
t, °с
0,00
27,71
57,85
84,3
0,00
30,2
0,00
5,09
31,0
-195,7
—194,7
—182,1
1 „ (смЛ
Наклон 1 — 1,
1 мм рпг. ст.хЮ*
теор.
62,1
13,1
5,29
2,25
1,51
0,528
34,0
26,4
10,1
806,0
679,0
87,3
эксп.
60,2
16,4
6,82
2,70
2,17
0,528
32,1
24,2
13,6
538,0
645,0
83,4
приведены на фиг. 20. На фиг. 21 проведено сравнение
наблюдаемых величин для аргона, адсорбируемого на
газовой саже, с расчетной прямой, построенной на
основе данных табл. 8, в которой значения г0 вычис-

204
Часть II. Статистическая механика
лены из данных о вязкости, а величины А и D
определены из уравнения (41.23), как показано в табл. 7.
В табл. 9 сравниваются экспериментальные значения
наклонов dVVdp, обработанные по методу наименьших
квадратов, со значениями, вычисленными из уравнения (41.11)
и расчетных значений с2. Если учесть грубость модели и
13
12
V ;/
о
i
J5 9
8
76 0 W 8,0
Ц>0/кТ
Фиг. 21. Сравнение экспериментальных данных
для аргона на газовой саже с теоретической прямой
(по Фримену и Холсею [80]).
отсутствие в теории свободно подбираемого параметра,
то описанное выше согласие между теорией и
экспериментом можно считать вполне удовлетворительным.

Глава IV
КВАНТОВАЯ СТАТИСТИЧЕСКАЯ МЕХАНИКА
42. Квантовые эффекты для поверхностного натяжения
[109]. До сих пор мы рассматривали только системы,
подчиняющиеся законам классической механики. Этого было
достаточно для теоретического анализа свойств
большинства жидкостей. Однако как было установлено при
изучении поверхностного натяжения в наиболее легких
веществах, таких как водород и гелий,1 квантовые эффекты
в этом случае оказываются существенными.
Пивердем теперь точный, но несколько формальный
квантовомеханический анализ поверхностного натяжения.
Рассмотрим систему N одинаковых молекул, помещенных
в сосуд, имеющий форму куба с ребром длиной /
1 Как показали Де-Бур и Берд [381, наблюдаемые значения
поверхностного натяжения этих веществ отклоняются от классического
закона соответственных состояний. Для гелия ниже Я-точки, как видно
из фиг. 6, ситуация особенно отличается от предсказываемой этим
законом.
Чтобы учесть эту своеобразную зависимость поверхностного
натяжения гелия-II от температуры, Аткинс [ПО], следуя классическому
рассмотрению обычного поверхностного натяжения, данному
Френкелем [111], предположил, что этот эффект возникает из тепловой энергии,
связанной с колебательными степенями свободы поверхности, и
применил к последним квантовомеханический подход, напоминающий
методику, разработанную Дебаем в теории твердого тела. Еще до появления
теории Аткинса Борн и Курант [112] впервые выполнили работу,
основанную на теории Дебая, ставившую целью получить квантовомехани-
ческую зависимость поверхностного натяжения от температуры. Лавд-
жой [42] применил теорию Аткинса [ПО] к поверхностному натяжению
в Не3. Котари [113], Трика и др. [114] также сделали попытки
построения теории. Используя метод ячеек Пригожина и Сарага [115], Хараси-
ма и Шимура [91, 116] исследовали квантовые эффекты для
поверхностной энергии. Их результаты довольно хорошо согласуются с
экспериментальными данными, однако мы отсылаем за всеми деталями этих
грубых моделей к цитированной литературе.

206
Часть //. Статистическая механика
(см. фиг. 22). Предположим, что имеются две фазы аир,
соприкасающиеся на плоской поверхности раздела и
находящиеся под действием слабого гравитационного поля,
которое позволяет рассматривать площадь поверхности
раздела как внешний параметр. Обозначим собственные
Фиг. 22. Двухфазная система с плоской
поверхностью раздела в кубическом сосуде.
значения энергии системы в целом через Еъ Е2У ... , Ер,
Тогда квантовомеханическая статистическая сумма
определится как
Z(T,V,A) = %e-EplkT, (42.1)
Р
где суммирование распространяется на все энергетические
состояния. Если же суммирование производить по всем
энергетическим уровням вместо энергетических состояний,
то каждый член суммы следует умножить на кратность
вырождения данного уровня. Поскольку собственное
значение Ер зависит от объема V и площади поверхности
раздела Л, то из определения (42.1) следует, что
статистическая сумма является функцией 7\ V и Л.
Как и в случае классической статистической
механики, вероятность нахождения системы из канониче-

Гл. IV. Квантовая статистическая механика 207
ского ансамбля в состоянии с энергией Е9 равна
ехр (— E9lkT) /2ехР (— Ep/kT). Следовательно, плотность
р
вероятности Р (г(1), . . . , r{N)) в конфигурационном
пространстве определяется как
/>(га) Л =
= Z^ е~Ер/кТГр (r(1) r(">) % (r(1), . . . ,r(">).
(42.2)
Здесь функции Wp образуют полную ортогональную
систему симметризованных или антисимметризованных
собственных функций.
Плотность вероятности соответствует диагональной
части (относительно координат) матрицы плотности,
определяемой формулой (см., например, [65])
Р(г(1\...УЛ°;г'(1\...,г'(Л')) =
= 2 e-E>lkT% (r'(1\ . .., г'(Л") УР (г(1), ..., /•<">). (42.3)
Р
Унарная и бинарная функции распределения
определяются соответственно уравнениями
п(г) =Л^. . .^S(r-r(1))P(r(1),. . .,r('V))dr(1)...drw,
(42.4)
л, (г, О =tf (ЛГ-1)$...$в(г-г(1)) х
X б (г' — г<2>) Р(г(1), . . . , г(Л°) dr(1). . . dr(N), (42.5)
соответствующими классическим уравнениям (24.1) и (24.2).
Как и в случае классической системы, свободная
энергия выражается уравнением (23.1) через статистическую
сумму Z, и поэтому поверхностное натяжение определяется
по (23.10). Таким образом, подставляя (42.1) в (23.10),
получаем

208
Часть II. Статистическая механика
Величину (дЕр (1/, А)/дА)у мы рассчитаем следующим
образом. В общем случае гамильтониан системы Ж
определяется как
^ = -|r2v(s)2+S Ф{^% (42.7)
s=l s<t
где ф (r(st)) — межмолекулярный потенциал.
Стационарное уравнение Шредингера имеет вид
ЖЧ (rb\ . . ., гЩ =ЕЧ (г*1* , . . ., г<">), (42.8)
где Е — собственное значение энергии системы. Волновая
функция W должна обращаться в нуль на стенках сосуда,
т. е. при л: = 0, # = 0, z = 0, х = I, у = I и z = I.
Сместим на расстояние е/ по направлению наружу одну
из вертикальных стенок, перпендикулярную оси ху и в то
же время сдвинем на расстояние е/ внутрь одну из
горизонтальных стенок, перпендикулярную оси z. Тогда
величины £и? претерпят некоторые изменения, зависящие
от 8, и их можно записать, как £ (е) и Т (г(1), . . ., r{N); е).
Граничное условие ¥ (е) =0 теперь задается при jc(s) = 0,
y(s) = 0, Z^ = 0, Х^ = 1(1 + 8), у^ = I И Z<s> = I (1 — 8)
(s =1,2, . . . ,7V).
Так как теперь площадь А (е) = /2 (1 +8), а объем
У (е) =: £3 (1 — 82) = У (0) (1 —е2), то, продифференцировав
Е (е) по е, получим
1 дЕ (0) _ /д£
= (пЪ <42'9»
Г2 д& \ил /^
где (дЯ (е)/де)е=0 условно записано как дЕ (0)/де.
Вводя новые переменные x{s) = *(s)/(l -f е), #<s) = */(s),
2(s) = 2(SV(1 — e), можно записать гамильтониан и
волновую функцию соответственно следующим образом:
^ w ~ 2/л 2i 1ч (1+ е)« d?s>2 + дум* + (1 - е)« a?s>2Ji~
+ 2 ^ ^(S°(£))» («. Ю)

Гл. IV. Квантовая статистическая механика 209
г<«'> (в) = [(1 + е)2 (*<'> — х^)2 + &') — г/(*>)2 +
+ (1 — е)2 &t} — z<s>)2lVt, (42.11)
¥ (в) = ¥ ((1 +£) ^>, 1р\ (1 — в)1Ч . . .
. . ., (1 + в) *<*>, £<"), (1 _ 8) 'гт). (42.12)
Тогда уравнение (42.8) можно переписать в виде
Ж(г)Ч (г) = £(в)¥(в), (42.13)
где граничное условие ¥ (в) = 0 накладывается при х^ = 0,
и, следовательно, функция ^Р (е) имеет те же граничные
условия, что и раньше, независимо от значения е.
Дифференцируя уравнение (42.13) по е и полагая
затем е=0, получаем
где производная д¥ (0)/де имеет смысл, аналогичный
обозначению дЕ (0)/де в (42.9). Умножая затем уравнение
(42.14) на ¥* и интегрируя результат по всему
конфигурационному пространству внутри сосуда, получим
J ¥* (0) Ж (0) ^y°ldrd>. . . drW +
+ ^Т(0)ЩрУ (0) dr<D . . . dr<N> =
= Е (0)\¥* (0)^р-drW . .. drW+ д-^ . (42.15)
Вследствие эрмитовости оператора Ж (0) имеем
\ ¥* (0) Ж (0) д-^р- dr^ . . . dfW) =
= \ (Ж (0) ¥(0))' ^p-drV . . . drW =
(0)$V(0)
^P-dr^. . •>-<">. (42.16)

210
Часть II. Статистическая механика
Следовательно, уравнение (42.15) можно записать в виде
d-l^L = \ Y (0) Щ^ V (0) drM . . . drW. (42.17)
Используя (42.10), можно переписать уравнение (42.17)
в виде
N
дЕ(0) С ~*Г й.2 ^ { д* д2
де
N
~ \ ^ I ~^ ^ V дг^2 — дх^2 ) +
+ ^ (^)2~jp)2 0' (г<">) 1 WrM . . . dr&\ (42.18)
s<t rS -*
так как W (0) есть не что иное, как исходная волновая
функция Y.
Из (42.6), (42.9) и (42.18) получаем следующее
выражение для поверхностного натяжения:
Р s=l
+ 2 (,/} 0' ('(s/)) 14fpdr(1) • • • dr{N)> (42-i9)
s<f
где 4^ — собственная функция, соответствующая
состоянию с энергией £р.
Квантовостатистическое среднее оператора импульса
p(s) s-й молекулы определяется как
l(s)
= Z-1^ е~Ер/*Г ^ Ч'р (-J- V(s)) Vvdri». . . drW. (42.20)
Отсюда, используя (42.5) и (42.20), можно переписать
выражение (42.19) в виде
N /~2 2\ |
+ 2?)Г (i2? 0'(^2))«2(r«), rt^rfr»)^*). (42.21)

Гл. IV. Квантовая статистическая механики 211
В классическом случае второй член в последней формуле
можно записать в виде, идентичном (26.1) г.
Первый член характерен для квантовой статистики и
не обязательно исчезает даже в состоянии равновесия [109,
118], тогда как в классическом пределе он, очевидно,
исчезает благодаря изотропии распределения Максвелла
в импульсном пространстве.
Более того, поскольку бинарная функция распределения
молекул в квантовой статистике, вообще говоря,
отличается от классической бинарной функции распределения,
то квантовые эффекты могут возникнуть также и из-за
второго члена, хотя квантовомеханическую модификацию
бинарной функции распределения молекул еще не удалось
подсчитать.
С помощью матрицы плотности (42.3) выражение (42.19)
можно записать следующим образом [109]:
T = _[2Sp{—-%(^-—)х
s=l
PN (r<D,. . . , r<">; r'd>, .... /•'<">)} (SpM-1 +
+ 4~S(JC<12>)2~ii)<12))2 Ф'{г^)пг{Гт,г^)<1гтг^\. (42.22)
1 Исходя из предположений, аналогичных тем, которые были
приняты Кирквудом и Баффом для жидкого аргона [см. условия (37.1) и
(37.2)] Р. Браут и М. Нейнберг [117] недавно рассчитали численно
поверхностные натяжения для Не4 и Не3. Они пренебрегали первым
членом (42.21) и использовали потенциал Слэтера — Кирквуда между
двумя атомами гелия и приближенную радиальную функцию
распределения, которая была определена из экспериментальных данных,
полученных методом, аналогичным методу Кирквуда — Баффа, описанному
в п. 37. Вычисленные значения довольно хорошо согласуются с
экспериментальными.

ЧАСТЬ 111
РАССМОТРЕНИЕ
С ПОМОЩЬЮ РЕШЕТОЧНОЙ
МОДЕЛИ
Как было показано в ч. II, если известны
межмолекулярные силы, то методы статистической термодинамики
позволяют, в принципе, рассчитать все термодинамические
свойства жидкости с помощью статистической суммы или
молекулярных функций распределения. Но точное
вычисление оказывается трудным, за исключением случая идеальных
газов или столь разреженных реальных газов, что для них
справедливо вириальное разложение. Как кратко
упоминалось в п. 24, для выполнения численных расчетов
термодинамических величин однородной жидкости можно с
успехом использовать основанное на суперпозиционном
приближении уравнение Борна — Грина — Ивона. Однако
решение такого интегро-дифференциального уравнения
в переходной области представляется крайне трудным даже
с помощью быстродействующих электронных
вычислительных машин. Обсуждавшиеся же выше методы функций
распределения, позволяющие провести численный расчет
поверхностного натяжения, основаны на довольно грубых
приближениях, таких, как ступенчатое приближение и
квазитермодинамическая теория.
Для получения в случае жидкостей приближенных
статистических сумм оказались полезными некоторые модели;
эти же модели применимы, конечно, и к расчету
поверхностного натяжения. В этой части мы обсудим применение
к случаю плоской межфазовой границы решеточных теорий,
которые были успешно использованы для расчета
термодинамических свойств чистых жидкостей и растворов
неэлектролитов. Для трактовки искривленной поверхности раздела
решеточные модели представляются, однако,
неподходящими.

Глава I
чистые жидкости
§ 1. Теория свободного объема
43. Метод ячеек для вычисления статистической суммы
[119, 120] х. Мы будем рассматривать классическую одно-
компонентную систему, состоящую из N частиц, которая
принадлежит каноническому ансамблю. Термодинамические
свойства такой системы рассчитываются с помощью
статистической суммы, задаваемой выражением (23.2).
Разделим координатное пространство на L ячеек Дх, . . . , AL.
Предполагается, что эти ячейки имеют одинаковую форму
и одинаковый объем А. Конфигурационный интеграл (23.3)
можно записать тогда как сумму членов, в которых
координаты каждой молекулы заключены в некоторой
определенной ячейке:
QN = (N\)-*% ... 2 \ •••
. . Л ехр/ Ф(г(1),..-,г(Л^)\г^ dr^. (43.1)
Так как молекулы неразличимы, величина каждого члена
остается неизменной при перестановках молекул. Пусть
величины Qm (mlt т2У . . . , mi) суть различные члены
в (43.1), соответствующие случаю, когда т1 молекул
находится в ячейке 1, т2 молекул —в ячейке 2, . . . , mt
молекул — в ячейке L. При фиксированной
последовательности {т} = тъ т2, . . . , mL возможны перестановки
См. также книгу Гиршфельдера, Кертисса и Берда [48].

216 Часть III. Рассмотрение с помощью решеточной модели
N
N молекул и, следовательно, существует^! / П ms\ \ спо-
S=1
собов размещения этих N молекул в L ячейках. Поэтому
конфигурационный интеграл приобретает вид
limJ
Qn = ^ 1 , (43.2)
где суммирование распространено на все наборы {т},
L
подчиняющиеся условию 2 ms = ^т
s=l
В общем случаеL не обязательно должно быть равно N,
но здесь мы ограничимся случаем L =N. Тогда (43.2)
принимает вид
2 Qtf (mb--»'Htf)
Qn = {-^—й , (43.3)
EUS!
s=l
а объем ячейки оказывается равным объему,
приходящемуся на одну молекулу:
* = -£-• (43'4)
При достаточно высоких плотностях все величины
Qm (тъ . . . , mN), кроме QN (1, . . . , 1), обращаются в
нуль, так как значительные силы отталкивания
препятствуют заселению одной ячейки несколькими молекулами.
В таком случае (43.3) сводится к
Qn= Qn(U 1,. . . , 1) = Qjj\ (43.5)
При малых плотностях необходимо учесть члены,
соответствующие парному и множественному заселению.
Таким образом, в общем случае конфигурационный интеграл
можно записать в виде
QN = 4*QW. (43.6)

Гл. I. Чистые жидкости
217
Сравнивая (43.3) с (43.6), мы получаем выражение для ц:
При достаточно высоких плотностях все QN (ть . . . , mN)y
кроме 0$, исчезают, так что
г] = 1 (предел при больших плотностях). (43.8)
Для крайне разреженного газа вклад, обусловленный
взаимодействием между молекулами, практически
отсутствует, так что все члены в правой части (43.1) равны
между собой, а число их равно NM (это соответствует NN
способам размещения N молекул в N ячейках). Поэтому,
применяя формулу Стирлинга для АЛ', находим из (43.1)
и (43.6), что
к] = е (предел при малых плотностях). (43.9)
44. Свободный объем и коллективная энтропия.
Вычислим конфигурационный интеграл Q$\
соответствующий случаю, когда каждая ячейка занята одной и только
одной молекулой. Пусть потенциальная энергия системы
Ф (г(1\ . . . , г(Л°) задается как сумма 5уу (N — 1)
межмолекулярных потенциалов:
Ф (r<D,. .., r<">)= -1-2 0 (гЫ)9 (44.1)
что соответствует выражению (24.3). Если каждая из N
молекул находится в центре своей ячейки, то (44.1)
приобретает вид
Фо=4-2 0(l«(r>:-a(s>|)> (44.2)
где a(s) — вектор, определяющий положение центра s-й
ячейки. Вклад в полную потенциальную энергию,
обусловленный взаимодействием s-й молекулы, находящейся в
точке, радиус-вектор которой относительно центра ячейки
есть /?<s) с остальными N — 1 молекулами, расположен-

218 Часть III. Рассмотрение с помощью решеточной модели
ными в центрах своих ячеек, равен
м
V (#(s)) = S (0 (I «(г) - я(5) - #(s) I) —
— ф(\а^ — а^\)}. (44.3)
В качестве первого приближения для полной
потенциальной энергии (44.1) мы примем
Ф (г<*>, . . . , г<">) = Ф0+ 2 Y (#(s))> (44-4)
s=l
где Ф0 — нулевое приближение (44.2).
Если а(1), . . . , a{N) образуют пространственную
решетку, то Ф0 можно рассматривать как энергию
кристаллической решетки, а У (R{s)) — как увеличение энергии
s-Pl молекулы, обусловленное ее отклонением на /?(s) от
равновесного положения. Это означает, что жидкость
можно рассматривать как несовершенный кристалл с одной
молекулой в каждом узле решетки или вблизи него. С
помощью такого интуитивного подхода впервые разработали
ячеечную теорию жидкости Леннард-Джонс и Девоншайр,
поэтому эту модель обычно называют моделью Леннард-
Джонса и Девоншайра [120].
Если пользоваться приближенным потенциалом (44.4),
то из (43.1) легко получить, что
Q(% =e-^kTvf, (44.5)
где V/ определяется выражением
vf = \e-vwllTdR. (44.6)
Л
Статистическая сумма (44.5) эквивалентна статистической
сумме кристалла в модели Эйнштейна, по которой каждая
молекула свободно движется в объеме vf в поле
постоянного потенциала Ф0. По этой причине vf называют
свободным объемом.
Мы используем в этой работе термин «теория
свободного объема» для обозначения решеточной теории
жидкостей, в которой число ячеек считается равным числу

Гл. /. Чистые жидкости
219
молекул. Эту теорию следует отличать от дырочной теории,
которую мы опишем в п. 49.
Используя (43.6) и (44.5), мы получаем приближенное
выражение для свободной энергии, определяемой по (23.1):
F = — NkT In (Яг8/ (Т)) — NkT In (x\vf) + Ф0. (44.7)
При достаточно низкой плотности, согласно (43.9),
г] = е, Ф0 равно нулю и Vf — объему ячейки v.
Следовательно, в предельном случае малых плотностей (44.7)
сводится к выражению
F = — NkT In (\-*j (Т)) — NkT ln-£- — NkT, (44.8)
которое идентично выражению для свободной энергии
идеального газа.
В этом случае —NkT In rj вносит вклад—NkT в
свободную энергию и, следовательно, вклад Nk — в энтропию.
Эта добавочная энтропия связана со свободным
перемещением молекул по всему объему и поэтому называется
коллективной энтропией. С другой стороны, —NkT\ni\
обращается в нуль в предельном случае высоких
плотностей. Так как свободная энергия является непрерывной
функцией плотности, то существуют основания считать,
что г) — также непрерывная функция плотности. Однако
точный вывод зависимости ч) от плотности представляется
чрезвычайно трудным. В качестве приближения часто
принимают, что коллективная энтропия появляется при
плавлении и что жидкое состояние имеет полную
коллективную энтропию, соответствующую tj = е [122]. С такой
точки зрения можно ожидать, что энтропия плавления
окажется равной 1,98 жал/моль-град. Хотя
экспериментальные значения для большинства одноатомных веществ
удовлетворяют этому условию, проблема коллективной
энтропии, как подчеркнул Райе [123], представляется все
еще открытым вопросом.
45. «Сглаженный» свободный объем. Для вычисления
свободной энергии по уравнению (44.7) необходимо оценить
величину свободного объема vf. Но вычисление точного
свободного объема оказывается очень трудным вследствие
геометрической сложности ячейки и того факта, что по-

220 Часть III. Рассмотрение с помощью решеточной модели
тенциал Y (R) зависит как от величины вектора /?,
так и от его направления.
При вычислении свободного объема обычно используют
«сглаженный» или приведенный к форме сферы свободный
объем. Это достигается заменой в (44.6) зависящего от
углов потенциала ¥ (R) осредненным по углам
потенциалом \у (R), который определяется соотношением
^W) = S4H-\U0(|e(r)-a<«)-J?|)-
- 0 (|a(r) — a^\)}smMMq, (45.1)
где 0 и ф вместе с R образуют сферическую систему
координат. Если все ячейки эквивалентны, то W (R) не зависит
от s.
Пусть имеется с ближайших соседей, удаленных на
расстояние а от некоторой произвольной точки, и с2
вторых соседей, удаленных на расстояние а2. Если пренебречь
эффектами, обусловленными третьими и еще более
удаленными соседями, то выражение для осредненного
потенциала (45.1) принимает вид
^<*> =c[±§0(\a-R\)sinmdq)-<p(a)] +
+ с2 [± \\ 0 (| а2 - R |) sin 6<Ш<р - 0 (аа)] . (45.2)
Подставляя (45.2) в (44.6), получаем выражение для
приведенного к сферической форме, или «сглаженного»
свободного объема Vfi
а/2 _
vf=4n \er-vt*v*TR»dR. (45.3)
0
где а/2 — радиус приведенной к сферической форме
ячейки. Однако выбор верхнего предела интегрирования
оказывается довольно произвольным.
Сглаженный свободный объем для потенциала Леннард-
Джонса (22.4) при учете лишь ближайших соседей дается
формулой
щ =2na3g, (45.4)

Гл. 1. Чистые жидкости
221
О
/ (у) = (1 + 12*/+25,2*/2 + \2у3 + у*) (1 -^-"„^ (45.6)
/" fe) =(1 +y)(l-y)-'-U (45.7)
,=(£)'• («.8)
где v* и Г* представляют собой соответственно
приведенный размер ячейки и приведенную температуру,
определяемые равенствами (26.18).
Если узлы решетки образуют гранецентрированную
решетку с плотнейшей упаковкой, то у0 = (3/4я У~2)%!*.
Расчет можно сделать более точным, если принять во
внимание вторых и более удаленных соседей.
Величину Ф0 в (44.2) можно вычислить из (22.4).
Результат для гранецентрированной кубической решетки
имеет вид [124]:
m 6 NkT /1,0110 2,4090 \ /4-Q.
где дроби 0,0110 и 0,4090, появляющиеся в правой части,
соответствуют вкладам, вносимым не самыми ближайшими
соседями. Подстановка (45.4), (45.9) и ц =е в (44.7)
приводит к искомому точному выражению для свободной
энергии. Используя затем соотношение р = — (dF/dV)r,
мы получаем уравнение состояния. Полученное уравнение
обнаруживает петлю вандерваальсовского типа в области
ниже приведенной температуры \ равной
Т*с = 1,30.
Температура, при которой исчезает петля, обычно
отождествляется с критической температурой и обозначается Тс.
46. Поверхностная энергия. Здесь мы применим теорию
свободного объема к численному расчету поверхностной
1 В оригинальном исследовании Леннард-Джонс и Девоншайр
пренебрегли вкладом в свободный объем от удаленных соседей и получили
Тс * = 1,33. См., например, книгу Фаулера и Гуггенгейма [125].

222 Часть III. Рассмотрение с помощью решеточной модели
энергии жидкостей. Будем считать, что плотность пара
настолько мала, что при вычислении поверхностной энергии
его можно рассматривать как вакуум, аналогично тому,
как было сделано в п. 37. Кроме того, примем, что
жидкость и ее поверхность образуют столб со структурой,
подобной структуре решетки, причем открытой остается
одна из кристаллических плоскостей. Предполагается,
что на плоскости, граничащей с паром, узлы решетки
несколько сдвинуты внутрь жидкости, тогда как на узлы
решетки, лежащие во всех остальных плоскостях,
присутствие поверхности никак не влияет. Мы выберем положение
разделяющей поверхности НК непосредственно над
поверхностным слоем и параллельно ему. Тогда плоскость
НК будет эквимолекулярной разделяющей поверхностью,
если предположить, что газообразная фаза эквивалентна
вакууму. Пусть имеется сг ближайших соседей на
расстоянии аъ с2 вторых соседей на расстоянии а2, с3 третьих
соседей на расстоянии а3 и т. д.
Пренебрегая поверхностными эффектами, мы сначала
предположим, что все N молекул, расположенные ниже
плоскости НК, можно рассматривать как находящиеся
внутри жидкой фазы а.
Согласно (44.2), потенциальная энергия однородной
объемной жидкой фазы, состоящей из N молекул, дается
выражением
N оо
ф0"=2 0(1«<г)-а(5)|) = х^2^0Ю, (46.1)
где замена конечной суммы по всем узлам решетки внутри
жидкости бесконечным рядом допустима ввиду быстрой
сходимости ряда ^стф (ат).
т
С другой стороны, в действительной жидкости,
ограниченной плоской поверхностью, любая молекула в
поверхностном слое или вблизи него имеет меньшее число
соседей. Поверхностный слой, образованный узлами
решетки, лежащими в плоскости, соприкасающейся с паром,
мы будем называть первым слоем, а последовательные
слои узлов решетки, параллельные первому,— вторым,. . .
. . . , /-м, . . . , w-u слоями. Предполагается, что все слои

Гл. I. Чистые жидкости
223
имеют одинаковую площадь Л, толщину d и число узлов
на единицу площади v.
Рассмотрим молекулу, помещенную в узел решетки
в /-м слое; обозначим через с{т] число ее соседей,
находящихся на расстоянии ат. Значение Cm отличается от ст
благодаря наличию поверхности раздела. По аналогии
с (46.1) запишем выражение для потенциальной энергии
решетки, имеющей плоскую поверхность, граничащую
с вакуумом:
W оо
Фо = -Г^2 2 &ФЫ. (46-2)
/=1 т=1
где w — полное число слоев, параллельных поверхности,
а сдвиг первого слоя пока не учтен. Заменяя N в (46.1)
на wAv, получаем
1 °°
Фа0 = -у wAv 2 Стф (ат). (46.3)
т=1
Из (46.2) и (46.3) можно получить поверхностную
плотность потенциальной энергии:
ф фа оо оо
„(*)= JL_-i.=-i-v2 2 («m-<».)0(««)» (46-4)
где верхний предел суммирования по / выбран
бесконечным ввиду того, что с(т — ст быстро стремится к нулю
с возрастанием /.
В гранецентрированной кубической решетке имеются
три главные плоскости. Площадь, приходящаяся на одну
молекулу, для (Ш)-плоскости равна (КЗ/2) а2, а для
(100)-плоскости — а2, причем а = 2'V». Имеем поэтому
v = Ьи~\ (46.5)
b _ f 3—V«2*/s для (Ш)-плоскости,
[2-1/з для (ЮО)-плоскости.
Толщина одного слоя
d =-vv + bv\ (46.7)

224 Часть III. Рассмотрение с помощью решеточной модели
Если пренебречь смещением первого слоя и вкладом,
обусловленным смещением молекул относительно узлов
решетки, то определяемая равенствами (2.2) и (5.7)
поверхностная плотность внутренней энергии v становится
равной (46.4), так как кинетическая энергия не вносит
вклада в поверхностную энергию, пока справедлив
классический закон равнораспределения. При этих
предположениях Харасима [91, 126] получил для поверхностной
плотности энергии чистой жидкости, состоящей из молекул,
взаимодействие которых описывает потенциал Леннард-
Джонса (22.4), помещающихся в узлах гранецентриро-
ванной кубической решетки, следующее выражение:
v =
1,43е / 2,70
o'VaD2
(46.8)
где v — приведенный объем ячейки: v = v/D3.
Вычисления Харасима проведены для случая, когда пограничной
является (Ш)-плоскость. Коэффициенты 2,70 и 1 в (46.8)
получены из довольно грубой оценки. Вычисленные
значения поверхностной энергии приведены в табл. 10 вместе
Таблица 10
Теоретические и экспериментальные значения
поверхностной энергии (по Харасиме
[91,126])*

Вещество
Не
н2
D2
Ne
N2
Ar
\/v*
0,39
0,56
0,66
0,75
0,96
0,86
»ieor>, эрг/см*
0,6
4,4
6,4
9,1
22,4
26,4
иэксгт эрг/см*
0,6
5,4
8,2
15,0
26
35
* В качестве постоянных в потенциале Лен-
нард-Джонса для Не и Н2 использованы кванто-
вомеханические величины, приведенные в табл. 2.
Значения иТСОр вычислены по (47.8).
с экспериментальными значениями, рассчитанными из
наблюдаемой величины поверхностного натяжения с исполь-

Гл. I. Чистые жидкости
225
зованием (5.18). В этих вычислениях величины у*
определяются из экспериментально измеренных плотностей
жидкости в точке плавления.
Ввиду грубости экспериментальных данных Харасима
считал несущественным, какая из кристаллических
плоскостей является пограничной. Однако тщательно
выполненные вычисления Корнера с использованием (46.4)
показывают, что (Ш)-плоскость соответствует наименьшей
потенциальной энергии. Корнер [127] получил численные
значения v^ для пограничной (Ш)-плоскости с
использованием потенциала Леннард-Джонса (22.4),
просуммировав вклады от 428 узлов решетки, удаленных не более
чем на Ъа от данной точки поверхностного слоя, и оценив
вклады от молекул, удаленных более чем на 5а.
Далее, Корнер [127] учел смещение Аг первого слоя
внутрь жидкости и вычислил х (Лг)-потенциальную
энергию молекул, находящихся на поверхности, как функцию
Az в предположении, что в других слоях молекулы
остаются неподвижными. Равновесная величина смещения
первого слоя Az0 определялась так, чтобы % (Az) была
минимальной. Некоторые результаты этих вычислений даны
в табл. 11. Вначале приводятся значения Az0. Далее, даны
Таблица 11
Вклад межмолекулярной потенциальной энергии в
поверхностную энергию (по Корнеру [127])
1
V*2
0,7
0,8
0,9
1,0
Az0*
(aV3~/2)
0,075
0,054
0,036
0,020
X (Az,)
10,6524
11,1648
11,5496
11,8077
х (0)
е
10,1361
10,8585
11,3994
11,7589
(<D0(Az0)-<Do)Z)a
А Г
1,550
1,990
2,377
2,703
D2 _ 1,43
е ~~ д*2/3
/2.70 М **
х [ v*2 V** )
1,778
2,018
2,237
| 2,431
* aVs /2 —расстояние между (Ш)-плоскостями.
** По уравнению (46.8).
потенциальные энергии поверхностной молекулы % (Az0),
когда поверхностный слой смещен на Az0 и когда такое

226 Часть III. Рассмотрение с помощью решеточной модели
смещение отсутствует. Поверхностная плотность
потенциальной энергии, г)(0) = (Ф0 (Az0)— Фо)Л4, соответствует
(46.8), которую Харасима [91] считал равной
поверхностной энергии. В последнем столбце приведены для
сравнения величины v, вычисленные из (46.8).
47. Поверхностное натяжение. Если вместо N для
обозначения полного числа молекул использовать ovlv, то
выражение (44.7) для свободной энергии однородной
объемной жидкой фазы а записывается в виде
F* = wAvkT In (A,8/"1) —wAvkT In (где) + Ф?, (47.1)
где Vf — свободный объем, определяемый равенством (44.6),
a w — число слоев решетки.
Вычислим теперь, исходя из теории свободного объема
[128], свободную энергию жидкости, ограниченной
плоской поверхностью. Избыточная потенциальная энергия
^(R) поверхностной молекулы, связанная с ее
смещением R от положения равновесия, должна из-за разницы
в числе соседей отличаться от 4я (/?) в (44.6), которая
записана для внутренней молекулы жидкости. Предполагая,
что все структурные различия с объемной фазой
сосредоточены лишь в первом слое, запишем потенциальную
энергию (44.4), в виде
Ф(г(1>, ... ,/•<">)= Ф0(Дг0) +
А\> wAv
+ 2Т*(*(0)+ 2 4(8% (47.2)
где Ф0 (Az0) — потенциальная энергия в случае, когда
каждая молекула находится в своем узле решетки и
поверхностный слой смещен на Az0 внутрь жидкости, как
описано в предыдущем пункте, а номера от 1 до Av
относятся к поверхностным молекулам. Изменения в
избыточной потенциальной энергии второго и более далеких слоев
не учитываются.
Если мы используем приближенный потенциал (47.2)
вместо (44.4), то по аналогии с (44.5) получим следующее

Гл. I. Чистые жидкости
227
выражение для Q$}:
Q(l) = в-Фо(Аг0)/^ v'A* Vy-DA^ (47<3)
Здесь v\ — свободный объем молекулы поверхностного слоя,
даваемый выражением
v'f= \e-wU«),kTdR, (47.4)
А'
где А' — любая из ячеек поверхностного слоя.
Поскольку миграция поверхностных молекул может
совершаться легче, чем внутренних, (43.6) можно
преобразовать в данном случае к следующему виду:
QN ^mv^-xmvqU), (475)
причем множитель ц'/ц соответствует вкладу, связанному
с возможным увеличением вероятности множественного
заселения ячеек в поверхностном слое. Из (23.1), (23.2),
(47.3) и (47.5) по аналогии с (47.1) получаем
F = wAvkT In (А,8/-1) — (w — 1) AvkT In (где) —
-i4vln(T|^;) +Ф0(А20). (47.6)
Подстановка (47.1) и (47.6) в (47.9) приводит к следующей
формуле для поверхностного натяжения:
F F* =v((f))_vkTln^_y;kTln^_t (4?/7)
1 A vf т] v 7
Свободный объем Vf можно заменить сглаженным
свободным объемом Vf, согласно равенству (45.3). В случае
гексагональной упаковки IF* (/?) для поверхностных молекул
можно в хорошем приближении заменить функцией,
имеющей не сферическую, а цилиндрическую симметрию. Тогда
Vf можно заменить сглаженным свободным объемом Vf,
вычисленным по (45.3), с использованием вместо ¥* (/?)
осредненного по азимуту потенциала ¥f (J//?2 — z2). Если
пренебречь различием между г\ и х\'у то (47.7) сведется

228 Часть III. Рассмотрение с помощью решеточной модели
к равенству
r =v«*) — vA74n4X, (47.8)
vf
где вклад от молекулярного вращения в случае двух- и
многоатомных молекул был бы более важным, чем вклад,
обусловленный разницей г\ и ц'.
Корнер использовал соотношение (47.8) для
вычисления поверхностного натяжения как функции
температуры. Его результаты для у* = yDVe и In Vf/Vf даны в табл. 12
Таблица 12
Поверхностное натяжение,
вычисленное по теории свободного объема (по
Корнеру [127])
1
V* 2
0,7
0,8
0,9
1,0
г
0,620
0,521
0,421
0,319
1
Т*
1,2495
1,4871
1,8432
2,4280
Vf
In—
vf
0,009
0,153
0,295
0,427
y*=yD2)z
1,545
1,902
2,236
2,542
в зависимости от v* = v/D3. Чтобы получить численные
значения поверхностного натяжения, необходимо еще
установить связь между плотностью и температурой. Корнер
[127] принял следующую зависимость:
Т-етЕ' + хО-тжКхО-^Г]' <47-9>
где v* и Т* — приведенные объем и температура,
определяемые по (26.18). Записанное уравнение получается после
подстановки эмпирических значений kTJe = 1,29 и vJD* =
= 3,05 в эмпирическое уравнение Гуггенгейма для чистых

Гл. I. Чистые жидкости
229
жидкостей [29]
£-'+4('-тг) + т(>ЧГ- <47-10>
где v — объем на одну молекулу и индекс с соответствует
критической точке.
Для жидкого аргона при температуре 90°К Т/Тс= 0,6;
если взять значения е и D из табл. 2, поверхностное
натяжение получается по табл. 12 равным 23,1 дин/сму что
значительно больше экспериментальной величины 11,9 дин/см
[48].
Так как разделяющая поверхность в нашем случае
эквимолекулярная, то из (5.91) следует, что
у =v — To. (47.11)
Если отождествлять и(^) из правой части (47.8) с
поверхностной энергией, как это сделал Харасима [91, 126]
(см. также п. 46), то второй член vkT In (vf/vf) будет
представлять собой поверхностную энтропию, умноженную на Т
в соответствии с (47.11), а значение а будет следовать из
величин In (v'f/Vf)y приведенных в табл. 12. Таким образом,
для поверхностной энтропии жидкого аргона при 90° К
вычисленная величина равна 0,012 эрг/см2-град, что
значительно меньше экспериментального значения а =
= 0,25 эрг/см2-град, полученного из наблюдаемой
величины у и ее температурной зависимости. С другой стороны,
пользуясь (46.5), можно переписать (47.7) в виде
r = ^)_^.(l„i + lnJl). (47.12)
Представляется неоправданным считать здесь г]' =т], как
это сделано в (47,8), поскольку вклад коллективной
энтропии для поверхностных молекул может быть больше, чем
для внутренних, ввиду структурных искажений внутри
межфазового слоя [129], которые будут рассмотрены в
следующих пунктах с точки зрения дырочной теории жидкостей.
Учет этого различия улучшил бы вычисленное значение
поверхностного натяжения. В то же время можно было бы
ожидать более приемлемого значения и для поверхностной
энтропии.

230 Часть III. Рассмотрение с помощью решеточной модели
§ 2. Теория дырок
48. Общий обзор теории дырок для жидкостей [120,
130]. До сих пор мы считали число ячеек L равным числу
молекул N. Можно, однако, выбрать L несколько большим,
чем N, и допустить существование вакантных ячеек.
Предположим, что каждая из ячеек достаточно мала, так что
вероятностью множественного заселения можно пренебречь,
и в то же время достаточно велика, так что взаимодействие
молекул, удаленных друг от друга больше, чем
находящиеся в соседних ячейках, можно рассматривать как малую
поправку. Обоим этим условиям можно одновременно
удовлетворить лишь в случае достаточно
короткодействующих межмолекулярных сил (например, в случае
неполярных нейтральных молекул). Так как L больше N, то
существуют пустые ячейки, которые мы назовем дырками. Тогда
жидкость или газ можно рассматривать, как если бы они
состояли из молекул и дырок, и поэтому решеточную
теорию, в которой число ячеек выбрано большим, чем число
молекул, часто называют теорией дырок, в отличие от
теории свободного объема, рассмотренной в предыдущих
пунктах.
Начнем с конфигурационного интеграла, записанного
в форме (43.1). Хотя сумма содержите членов, что
соответствует числу возможных размещений N молекул в L
ячейках, члены, соответствующие множественному
заселению, должны быть, согласно принятому выше
предположению, опущены. Тогда (43.1) сводится к
«„-as- \ **[-«*• „-'"Ч п*«.
ЛЛ AlN s=i
(48.1)
где суммирование распространяется на все Ll/N\ (L — N)l
размещений, которые нельзя получить одно из другого
перестановками.
Конфигурационный интеграл, записанный в виде (48.1),
верен как для газов, так и для жидкостей. В нашем случае
объем ячейки q отличается от v =V/N:
?=-Г- (48-2)

Гл. I. Чистые жидкости
231
Как и в теории свободного объема, вычисление
интеграла (48.1) зависит от выбора структуры решетки и формы и
ориентации ячеек. Будем рассматривать пространственную
решетку такую, что каждый узел имеет с ближайших
соседей, находящихся на расстоянии а. Обозначим через co(s)
долю ближайших соседних к s-й молекуле ячеек, которые
при данной конфигурации не заполнены. Тогда, если
полное число пар соседних ячеек, одна из которых заполнена,
а другая свободна, равно сХ, то мы имеем
N
х= 2 <°(s)- (48-3)
s=l
Если все молекулы фиксированы в центрах их ячеек, то
потенциальная энергия s-й молекулы равна с(1—(d<s)) ф (а),
а полная потенциальная энергия системы дается
выражением
Ф0=~(М-Х) ф (а), (48.4)
где ф{г) —межмолекулярный потенциал, а вкладами
от вторых и более удаленных соседей пренебрегли. Если
молекулы смещаются относительно центров своих ячеек,
то потенциальную энергию можно аппроксимировать
формулами
N
Ф (г<«, . . . , г<">) =Ф0+ 2 Ys (/?(*>), (48.5)
s=l
N
Ws (/?(s)) = S {0 (I aw - a<s> - /?<*> |) - 0 (| a<'> - a(s) |)}.
(48.6)
Эти два уравнения соответствуют уравнениям (44.4) и
(44.3) из теории свободного объема. Однако Ч^ (/?(s)) в них
зависит не только от /?(s), но также от числа с (1 —co(s))
соседних молекул и их расположения вокруг s-й молекулы.
По аналогии с (45.2) заменим зависящий от углов
потенциал Yg (/?(s)) осредненным по углам потенциалом
W (/?, cd<s>), который дается формулой

232 Часть III. Рассмотрение с помощью решеточной модели
Т (Я, со) =
= с(1-с»)[±-\\ф(\а-Я\) sin е<Ш<р - 0 (а)]. (48.7)
Эта функция зависит не только от вектора положения
молекулы /?, но и от числа ближайших соседей. Для
промежуточных между 0 и 1 значений со потенциал \PS (/?, co^s))
может быть менее строго сферическим.
Если пользоваться осредненным по углам потенциалом
48.7), подстановка (48.5) в (48.1) дает
QN =e-Nc(f>(a)/2kT ^ {Vf (toM)Vf (g><2>) ... vf (©<">)} eXc^^2kT,
(48.8)
где
Vf (о) = J erWRrtikT 4я/?М/?. (48.9)
A
Функция Vf (со) представляет собой обобщенный
свободный объем. Если все соседние ячейки заполнены, т. е.
со равно нулю, Vf (0) становится в точности равным
приведенному к форме сферы свободному объему (45.3). Если
же соседние! ячейки пусты, т. е. со = 1, то Vf (1) точно
равно объему ячейки q. Таким образом,
vf(0)=vh vf(l)=q. (48.10)
Из (48.8) и (48.10) следует предельный вид
конфигурационного интеграла }при малых и больших плотностях:
QN =Ъ?е-"с'!>{а)/2кТ (предел больших (48.11)
плотностей),
п„ - п» *± ж е» Ш" <пРедел МДЛЫХ (48 12)
4N — Ч N\(L — N)\ \ N I ПЛОТНОСТеи). \to.LZ)
Уравнение для предельного случая больших плотностей
идентично приближению Эйнштейна для
конфигурационного интеграла кристалла. Уравнение для предельного
случая малых плотностей точно совпадаете
конфигурационным интегралом идеального газа. Так как множитель eN
появляется в (48.12) как естественное следствие теории,

Гл. I. Чистые жидкости
233
теория дырок оказывается более удовлетворительной, чем
теория свободного объема, поскольку она допускает
непрерывный переход от жидкостей к газам без использования
сомнительной концепции коллективной энтропии.
Ввиду того что Vf (со) зависит от со довольно сложным
образом, для выполнения суммирования в (48.8)
необходимо принять некоторую упрощенную функциональную
зависимость Vf (со). Вычисления были выполнены только
для единственного случая линейной аппроксимации. Из
четырех линейных приближений [120, 130—132] к In Vf (со)
мы используем лишь следующее [1201:
In vf (со) = In Vf (0) + со In Щ-. (48.13)
Подстановка линейной аппроксимации (48.13) в (48.8)
приводит к выражению
QN = е-ксф(а)ыт (Vf (о))" 2 G (N, L, X) е-™*7, (48.14)
X
£ = --£-0 (a)-kT\n^, (48.15)
где G (N9 L, X) — число различных распределений N
молекул в L ячейках для фиксированного X. Значение
G (N, L, X) нельзя вычислить точно, но его приближенное
значение получено при помощи квазихимического
приближения в теории бинарных сплавов \ Приложение
квазихимического метода к однородной фазе оказалось
сравнительно успешным, но его применение к границе фаз —
довольно громоздким 2. Поэтому мы используем при
рассмотрении границы фаз более грубое приближение,
эквивалентное приближению Брэгга — Вильямса.
Вероятность того, что в однородной жидкости ячейка
1 См., например, книгу Фаулера и Гуггенгейма [125].
2 Излагаемая в этой работе теория дырок была в действительности
обобщена Куратой [133] на случай квазихимического приближения.
Разница между результатами, полученными на основе этих двух
приближений, составляет лишь несколько процентов.

234 Часть III. Рассмотрение с помощью решеточной модели
занята молекулой, равна
* = £—*- (48-16)
Определим вероятность того, что одна из двух соседних
ячеек занята молекулой, а вторая пуста. Если смесь из
молекул и дырок совершенно однородна, то эта
вероятность дается выражением х (1 — х). Этим-то
приближением однородной смеси, эквивалентным приближению
Брэгга-Вильямса, мы и воспользуемся. В таком
приближении полное среднее число сХ пар соседних ячеек,
одна из которых заполнена, а вторая пуста, дается
выражением
сХ =cLx(l —х). (48.17)
Заменяя X в (48.14) на X по (48.17), получаем
приближенный конфигурационный интеграл в виде
QN-e <* {vf(i))) m{L_N)l exp| ш J,
(48.18)
где использовано соотношение
%G(N,L,X)= m{?_N)] (48.19)
в соответствии с числом способов, которыми можно
разместить N молекул в L ячейках.
Из (48.18), используя (20.1) и (23.2), сразу же получаем
свободную энергию
F = ^>М — NkT In (^-3/ (Т) vf (0)) +
+ LkT {х In х + (1 — х) In (1-х)} + Lx (1 — х) I. (48.20)
Тогда известные выражения для давления р и химического
потенциала \i записываются соответственно в виде
' — ($),.» ~7Йг),.„. <«'21>

Гл. I. Чистые жидкости
235
Подставляя (48.20) в (48.21), получаем
p=-^{ln(l-*) + r^} =
--тН-Я + УгШ <48-23>
и точно тем же способом
|i = -f ф (а) - kT In (yjvf (0))+ £Г In jJL- + (1 _ 2x) £.
(48.24)
Поскольку объем ячейки q считается постоянной
величиной, (48.23) представляет собой уравнение состояния.
Можно показать, что это уравнение состояния приводит
к изотермам, имеющим перегибы вандерваальсовского типа
при температурах ниже критической температуры Тс,
определяемой соотношением
- !<*(*)
kTc = 2 + m(uf(l)/uf(0)) • (48*25)
Это свойство изотермы можно рассматривать как
указание на то, что две фазы а и р сосуществуют в равновесии
при температурах ниже критической Тс. Введем для
значений х в фазах а и (5 обозначения ха и х& соответственно,
причем большее из них пусть соответствует жидкости,
а меньшее — пару. Так как давления и химические
потенциалы фаз а и р должны быть одинаковыми, когда фазы
находятся во взаимном равновесии, то из (48.23) и (48.24)
следует, что условия равновесия можно записать в виде
_L(2A:a_1)=ln_£?) (48.26)
х* +xt = L (48.27)
49. Свободная энергия двухфазной системы [120].
Развитая в предыдущих пунктах теория дырок будет теперь
распространена на случай неоднородной системы,
состоящей из двух фаз, разделенных плоской границей. Будем
рассматривать систему, заключенную в сосуд, имеющий
форму прямоугольного параллелепипеда и расположенный

236 Часть III. Рассмотрение с помощью решеточной модели
таким образом, что одно из его ребер параллельно
направлению силы тяжести. Предположим, что одна из главных
плоскостей решетки, составляющей нашу систему,
перпендикулярна к направлению силы тяжести. Такие
плоскости мы будем называть эквипотенциальными. Для
краткости одну из эквипотенциальных плоскостей будем счи-
и
-и+1
-/
О
+1
w-i
W
Фиг. 23. Двухфазная система с плоской
поверхностью раздела.
Предполагается, что система состоит из
решетчатых слоев, параллельных поверхности раздела
фаз.
тать нулевым слоем и придадим номера —1, —2, . . . , —и
последовательным слоям, лежащим выше нулевого, а
номера 1, 2, . . . , w слоям, лежащим ниже нулевого (фиг. 23).
Способ, которым выбирается нулевой слой, описан ниже,
в п. 51.
Величины, относящиеся к t-uy слою, будем отмечать
индексом t, например, число молекул в t-м слое будем
обозначать через N{t). Предполагается, что все слои имеют
одинаковые площади. Как и в теории свободного объема,
d и А обозначают соответственно толщину и площадь
каждого из слоев.
фаза /3
фаза а

Гл. I. Чистые жидкости
237
Выражение для конфигурационного интеграла (48.8)
справедливо как для однородной, так и для неоднородной
системы. В последнем случае, однако, оно неудобно, так
как плотность числа молекул в межфазовой области может
заметным образом изменяться в вертикальном
направлении. Запишем конфигурационный интеграл как сумму
членов, которые обозначим через Qm (N{~u), . . . , Л^(_1),
N{0) , . . . , N{w)) в соответствии с заданным набором чисел
N{~u\ . . . , JV(0), . . . , Niw):
Qn= S . . . 2 Qn (N{~u\ . . .., N{0\ . . ., Л/(ш)), (49.1)
Ni—") n(*») w
2 NV) = N, (49.2)
t=-u
где
Q^N™ ..., Nl0\ .... №) =
= e-»'*™*» 2 {v, («(« ...v, (0.W)} eXc'^amT (49.3)
(суммирование проводится по всем конфигурациям,
совместным с данным набором чисел N{~u\ ... , N{0), ..., N{w)).
Подставляя в (49.3) линейное приближение (48.13),
получаем
QN(N{-"\ ... ,#<»>) = (49.4)
= e-Nc'>{a)/2kT (Vf (0)f%g (#<"">, . . . , #<"»; X) «f «"r,
где g (N{-u\ . . . , JV(0), .. . , N{w); X) — число способов,
которыми можно разместить N{~u\ . . . -у N{0\ . . . , N{w)
молекул в соответствующих Av ячейках каждого из слоев
при данном значении X. Если просуммировать функции
g (N{-u\ . . . , 7V(0), . . . , N{w); X) по X, то получим число
указанных выше размещений без ограничения:
2# (ЛГ(-И), .... JV<°\ . . . , #«">; X) =
X
w
-n.U<ffW- <49-5»

238 Часть 111. Рассмотрение с помощью решеточной модеш
что соответствует (48.19). Рассмотрим произвольную
ячейку в /-м слое. Пусть число ячеек, граничащих с ней в
том же слое, равно /с, а число граничащих с ней ячеек в
одном из соседних слоев равно тс. Тогда очевидно, что
полное число ячеек, граничащих с данной центральной,
равно (/ + 2т) с, и мы имеем по определению
I +2т =1. (49.6)
С другой стороны, вероятность того, что произвольная
ячейка в t-u слое занята молекулой, равна
*»-&• (49-7)
Определим полное число ближайших пар,
образованных из дырки и заполненной ячейки каждая. О таких
парах мы будем для краткости говорить в дальнейшем, как о
контактах дырка — молекула. Если предположить, что
конфигурация молекул в каждом слое совершенно случайна,
то среднее число контактов дырка — молекула в t-u слое,
по аналогии с (48.17), можно записать как
cX{t>f) = cAvlxM (1 — *('>). (49.8)
Подобным же образом среднее число cX(t' Ul) контактов
дырка — молекула между (t + 1)-м и t-u слоями дается
выражением
СХ«. *+i) = c*Lm [Х(П (i _ X(t+D) + X(t+D (i _ *(/))]. (49.9)
Тогда для любого данного набора х<~и\ . . . , х<0), . . . , х(ш>
среднее полное число контактов дырка — молекула в
системе определится как
+ mxft+v (1 — *«>) + mxW (1 — *('-!>) + mjte-D (1 — *<*>)},
(49.10)
где мы пренебрегли краевыми эффектами. __
Заменяя, как и в предыдущем пункте, X в (49.4) на X
по (49.10) и используя (49.5), получаем следующее при-

Гл. 1. Чистые жидкости
239
ближение для конфигурационного интеграла (49.3):
QN (*<-«>, ..., *«», ..., xW) =
w
X exp —
t=-U
+ wjcW (1 — x«+1)) + m*('+1> (1 — *«>) + mx<'> (1 — xC-1)) +
+ m^-D (1 — *<«)}]. (49.11)
Число членов, содержащихся в Qw, согласно (49.1),
меньше числа членов (Av)u+W+1 в случае, когда полное число
молекул не ограничено. Таким образом, для наибольшего
члена Qw, входящего в (49.1), имеет место неравенство
О < In QN — In Q*N < (и + w + 1) In (Av). (49.12)
При обычных условиях (и +w + О составляет величину
порядка N1/s и, следовательно, вклад от разности между
In QN и In Q*N в свободную энергию системы составляет
по порядку величины Nl,2kT, что пренебрежимо мало даже
в сравнении с вкладом от поверхности. Поэтому можно
заменить In Q^HalnQ^v, и это будет достаточно хорошим
приближением. Используя (23.1) и (23.2), получаем
таким образом
F = — NkT In (К-*] (Г)) — kT In Q*N. (49.13)
Подставляя (49.11) в (49.13) и используя формулу
Стерлинга, находим
F = Щ- ф (а) - NkT In (Я-3/ (Г) vf (0)) +
W
+ AvkT ^ {*{t) I" *(0 + (1 — *<0)ln (1 — *<'>)} +
t=—u
Avt w
+ 2 S {2/*(0 ^ — X(") + mx(° 0 — JC('+1>) +
t=-u
+ m#i) (1 — tff>) + mx») (1 — *<'-») + /их<'-« (1 — x®)},
(49.14)

240 Часть III. Рассмотрение с помощью решеточной модели
где набор величин (х^и\ . . . , х^\ . . . , xiw)) взят таким,
чтобы сделать максимальной величину Qm (х^и\ . . .
. . . , л:<0), . . . , xW), определяемую соотношением (49.11),
при дополнительном условии:
w
Av ^ x(t) = N- (49.15)
t=-u
Используя формулу Стерлинга для факториалов, получаем
из (49.11) и (49.15) следующее условие максимума:
С {/12 (1 — 2х<'-1>) +1(1— 2х&) + m (1 — 2*№>)} +
(t = — и, . . . , 0, . . . ,w), (49.16
где Л —неопределенный множитель Лагранжа.
Из (49.13) следует, что набор величин х^~и\ . . . , д:(0), ...
. . . , х(ш), определенный согласно (49.16) и (49.15),
минимизирует свободную энергию, которая дается как
функция *<-">, . . . , х(0), . . . , х^ выражением (49.14). Так
как плотность числа молекул в t-м слое равна x{t)/q, то из
сказанного следует, что равновесное распределение
локальной плотности определяется условием минимальности
F при дополнительном ограничении (49.15), точно так же,
как это имело место для условия равновесия в
квазитермодинамике (см. п. 18).
50. Вычисление равновесного распределения
локальной плотности [120]. Равновесное распределение плотности
1 11
— *(""\ . . . , — jc(0), . . . , — x(w) и неопределенный
множитель Л можно в принципе определить из решения
системы и +w + 2 уравнений (49.16) и (49.15). Однако
нет необходимости выполнять действительное вычисление
плотности для всех слоев, так как заранее можно
предвидеть, что все х равны х* или х&, за исключением тех,
которые относятся к межфазовому слою и его окрестности.
С макроскопической точки зрения в системе, состоящей
из жидкой и газообразной фаз слои с достаточно большим
положительным t лежат внутри жидкой фазы а, а слои

Гл. I. Чистые жидкости
241
с достаточно большим отрицательным t — внутри
газообразной фазы Р, т. е.
lim *'> - х*9 lim *<*> = хР. (50.1)
/-►эо t-+—оо
Следовательно, для больших положительных t (49.16)
сводится к соотношению [см. (49.6)]
I (1 -2х«) + kT ln-^Ц. =Л. (50.2)
1 — X
Сравнивая с (48.26), находим непосредственно
Л = 0. (50.3)
Введем следующие обозначения для разностей:
Д*е> = *<'+i>— *«>, Д*х«> = Ах«+Ч — Д*«>. (50.4)
Теперь, используя (49.6) и (50.4), можно переписать (49.16)
в более компактной форме
Л,*('-,) = i (§ '"rS + т:"*т) • <50-5)
которая представляет собой нелинейное разностное
уравнение. Его можно решить численно в точности тем же
способом, которым численно интегрируют обыкновенные
дифференциальные уравнения. Это значит, что можно
получить решение этого разностного уравнения, если заданы
значения х^ и Ax{t) для некоторого определенного t,
например х{1) и Д*(1). Для нашей краевой задачи
граничные условия выражаются соотношением (50.1).
Как и для краевых задач в случае обыкновенных
дифференциальных уравнений, удовлетворить граничным
условиям оказывается возможно только при некоторых
определенных значениях л;<1> и ДлЯ*. Но найти решение,
имеющее подходящие свойства, путем подгонки двух
параметров х{1) и Ах{1) довольно сложно. Однако в нашем случае
можно исключить любой из этих параметров, обращаясь
к свойству симметрии, состоящему в том, что (50.5) остается
инвариантным при замене t на 1]—/ и x{t) на 1 —x{t).
Если x{t) удовлетворяет разностному уравнению (50.5)
вместе с условием (50.1), то это имеет место также для

242 Часть III. Рассмотрение с помощью решеточной модели
х^ == 1 — *(1~~°, так как (50.5) инвариантно относительно
такого преобразования, а граничные условия (50.1)
удовлетворяются в силу (48.27). Если при подходящих
граничных условиях имеется только одно решение, которое
изменяет знак величины x{t) — 72 между нулевым и первым
слоями, то мы имеем
*о-« + *<') = 1. (50.6)
Для / = 1 это сводится к равенству
*<о> +ХМ = 1, (50.7)
откуда получаем непосредственно Ал:(1) = *(1) — *(0) =
= 2х{1) — 1. Следовательно, для того чтобы получить
решение, удовлетворяющее граничным условиям,
необходимо подгонять значение лишь одного параметра л;*1).
Пользуясь свойством симметрии (50.5), легко доказать,
0,9
Q8
Q7
0,6,
/у*
0$\ 1 1 1 1 1 1—
' / Z 3 4 5 6 7
t
Фиг. 24. Пробные решения разностного
уравнения (50.5) (по С. Оно [110]).
Из трех кривых лишь В дает нужное решение, так
как она стремится с ростом t к постоянному
значению ХЛш
что решение, которое удовлетворяет (50.7), всегда
удовлетворяет (50.6).
Предположим для простоты, что решетка представляет
собой гранецентрированную кубическую структуру.
Поведение некоторых решений уравнения (50.5) при 2£77£ =
= 1,05 в случае (ЮО)-плоскости, для которой m = 73,
вычисленных для различных значений х(1), показано на
иг. 24. Из приведенных кривых только кривая В, для

Гл. I. Чистые жидкости
243
которой jttt> = 0,525, удовлетворяет граничным условиям
(50.1). Численное решение уравнения (50.5) было
выполнено Оно [120] и Курата [133] г. Некоторые из этих
результатов приведены в табл. 13 и на фиг. 25.
Таблица 13
Распределение плотности в поверхностном слое для
HkT =5,0
t
1
2
3
4
со
Плоскость (100)
0,836
0,988
0,993
0,993
0,993
Плоскость (111)
0,903
0,991
0,993
0,993
0,993
Плоскость (НО)
0,760
0,970
9,992
0,993
0,993
Примечание. Значения для (100)-плоскости были рассчитаны
Оно [120], а для (111)- и (ИО)-плоскостей— Куратой [133].
В случае (НО)-плоскости было использовано
модифицированное уравнение Курата.
Используя (48.25), можно исключить ф (а) из (48.15)
и получить
2kT
гит т у^ 2 v Tc)luvf(0)j
(50.8)
Исключение £ из (50.8) с использованием (48.26) и (48.27)
дает
Т {2+ln(Pf(l)/Pf(0))}(l-2^
In
1— ATf
+ (l_2**)ln^
(50.9)
vf(0)
Значения ZJkT, приведенные на фиг. 25, вычислены из
(50.8) для заданного значения In vf (l)/vf (0) = 3,55,
выбранного таким образом, чтобы (50.9) соответствовало
1 В случае (ЮО)-плоскости необходима модификация уравнения
(50,5), так как некоторые из ячеек, граничащие с данной, находятся
во втором соседнем слое, тогда как для (Ш)-плоскости нужно просто
положить m = V4.

ho
ХШ
0,6
Ofl
0,2
0
C/kT=S.O T/TC = 0,6S
Q8\- ! ^^^~2^3'i5-T **~T/TC=0,S56
I S ^^ ^ J?'--*-*--<-~T/T=0,982
1 I ±*r4-^ I
-5-4-3-2-101234567
t
Фиг. 25. Изменение плотности около поверхности раздела фаз,
вычисленное по теории дырок; (111)-поверхность.

Гл. I. Чистые жидкости
245
наблюдаемой зависимости ортобарических плотностей х&
почти идеальных жидкостей от температуры [120]. Мы
увидим, что при Т/Тс = 0,65 изменение плотности в
переходной зоне, в сущности, полностью сосредоточено на участке
толщиной в два молекулярных слоя и что толщина
переходной зоны возрастает с приближением Т к критическому
значению.
Далее, можно заметить, что кривые плотности в
зависимости от глубины, приведенные на фиг. 25, сильно
напоминают кривые, показанные на фиг. 15, которые
вычислил Хилл на основе квазитермодинамического анализа г.
Этот вопрос будет снова обсуждаться в п. 52 2.
51. Поверхностное натяжение и поверхностная
энергия. Поместим разделяющую поверхность между нулевым
и первым слоями. Тогда из (50.6) и (49.2) имеем
N =N* + N*9 (51.1)
1 Кан и Хиллард [22] сделали попытку представить локальную
свободную энергию межфазовой области как сумму двух вкладов,
зависящих соответственно от локального состава и его производных.
Расчет зависимости состава от глубины был выполнен для границы между
двумя сосуществующими бинарными регулярными растворами.
Полученные ими кривые напоминают изображенные на фиг. 25. Это сходство
можно объяснить тем, что теория дырок есть теория регулярного
раствора из дырок и молекул. Поскольку их теория более проста (хотя при
этом менее строга), чем теории Оно и Хилла, им удалось показать, что
толщина межфазовой области возрастает с температурой и становится
бесконечной при критической температуре. Ниже критической
температуры, но вблизи нее поверхностное натяжение пропорционально
(Т—ТсУк. Эта теория очень хорошо согласуется с экспериментальными
данными.
2 Решеточные теории, как и квазитермодинамическая, приводят
к плавному изменению плотности с глубиной в переходном слое между
жидкостью и ее паром. Более строгая теория, основанная на изучении
молекулярных функций распределения, показывает, что изменение
плотности жидкости n(z) в переходном слое не является плавным, а
имеет слегка осциллирующий, или, вернее, ступенчатый, характер,
с последующими затухающими осцилляциями вблизи значения па в
жидкой фазе. Пространственный период этих осцилляции примерно равен
среднему межмолекулярному расстоянию, как и в случае хорошо
известных осцилляции радиальной функции распределения в однородной
жидкости. Физическое происхождение этих осцилляции в обоих
случаях одно и то же. Таким образом, более строгая теория приводит к
заключению о частично слоистой структуре переходной зоны между
жидкостью и ее паром. (Более подробно см. книгу Фишера [159]). —
Прим. ред.

246 Часть III. Рассмотрение с помощью решеточной модели
т. е. разделяющая поверхность является эквимолекулярной
и Г = 0. Поэтому в соответствии с (2.1) и (4.8)
поверхностное натяжение у дается формулой
г= д ' (51-2)
где F* и F^ — соответственно свободные энергии объемной
жидкой фазы и объемной газообразной фазы, которые
считаются строго однородными вплоть до разделяющей
поверхности. Согласно (48.20), свободные энергии F* и F^
даются соотношениями
F* = ^ ф (а) — N'kT In (Аг8/ (Г) vf (0)) +
+ L*kT {*« In jk« +(1 — x«) In (1 — jca)} + La*a (1 — x*) £
(51.3)
Fp = ^ 0 (a) - Л^£Г In (^-3/ (T) vf (0)) +
+L*kT{xP In** + (1 — *<>) In (1 — x*3)} +LV(1—**)£, (51.4)
где
La = roAv, L* = (a + 1) Av, (51.5)
L =La + /Л (51.6)
Подстановка (49.14), (51.3) и (51.4) в (51.2) приводит к
следующему выражению для поверхностного натяжения:
t=-u
+ /72*('+1> (1 — *0) + /я*<'> (1 — ^'-D) +
+ m^"1* (1 — *<'>) — 2jca (1 — JCa)} +
+ vkT J {*<» In x<» + (1 — x<») In (1 — *<») — jca ln*« —
w
— (1 — ЛГ«) In (1 — X*)} = V 2 (£*(° (/n^'-D + /*«> +
+ mtf'+D) + AT ln(l - *<'>) — £(*a)2 — Win (!—*«)}, (51.7)

Гл. I. Чистые жидкости
247
где были использованы соотношения (48.27), (49.16), (50.3)
и (48.26).
Заменяя теперь x^~f) на 1 — х^\ согласно (50.6),
можно переписать (51.7) в следующем виде:
00
Т = v£2 К2'*'0 0 — *(") + mx{t) 0 — *"+1)) +
t=i
+ mx<'+1> (1 — *<») + тх^(l—xV-») + тх«-ъ (1 — *<«) —
оо
— 2jca(l — xa)] + 2v&r2 W0 ln^> + (1—*('>) ln(l — *<'>)_
— *a In x* — (1 — xa) In (1 — **)], (51.8)
где верхний предел суммирования заменен бесконечностью,
поскольку члены в обеих суммах быстро стремятся к нулю
при достаточно больших значениях t.
В теории свободного объема число ячеек v на единицу
поверхности каждого слоя дается выражением (46.5);
однако при этом следует заменить v на объем ячейки в теории
дырок q:
v = bqr*l*, (51.9)
где b дается формулой (46.6). Тогда (51.8) можно
переписать в следующем виде, более удобном для практических
расчетов:
Г = 2-V/8-|- Р (Jr) - 2%uq-%l*kTD (J.) , (51.10)
где
у оо
p[w)= 3-2'/з&2 ^°(1 — /**('-1) — /*<0 ~ mx(t+1)) +
+ (1 — х<'>) (mje('-i) + /*<'> + mx('+D) — 2х* (1 — *«)}. (51.11)
оо
D (JL) = 21/з&2 (*(0 I" *(0 + (1 — *(0) 1п (1 — х^) —
t=i
— xa In xa — (1 — хл) In (1 — xa)}. (51.12)
Вычисленные значения P и D в зависимости от £/АГ
представлены в табл. 14. Из (51.7), (49.16) и (50.3) нетрудно

248 Часть III. Рассмотрение с помощью решеточной модели
получить
).
= 0.
(51.13)
Таким же путем, используя (48.26), имеем
{■&),. ,-°- (5Ы4)
Таблица 14
Функции Р ЩИТ) и D (£/&Г) для граничной
(111)-плоскости
WT
6,0
5,5
5,0
4,5
4,0
Р
0,990
1,090
1,148
1,217
1,298
D
0,226
0,281
0,331
0,382
0,441
fy/гГ
3,5
3,0
2,5
2,25
2,1
р
1,360
1,394
1,272
1,100
j 0,753
D
0,480
0,499
0,447
0,380
0,255
Так как в данном случае разделяющая поверхность
эквимолекулярная, поверхностную энергию можно
вычислить из (51.10) и (5.18). Используя (51.13) и (51.14),
нетрудно получить для поверхностной энергии выражение
^2-^'{1-Т§)Р-ШИ. (51.15)
Аналогичным образом из (5.17) и (51.10) получаем
а-_2^(£^-2*ГО(£)). (51.16)
Из (48.15) и (48.10) имеем также
dT
dT
(51.17)
C_ri = -|-c0(a)-^J^. (51.18)
<*г

Гл. I. Чистые жидкости
249
Если мы знаем q/vf как функцию температуры, то, вообще
говоря, можно рассчитать поверхностное натяжение как
функцию Т из (51.10) и (14.8) и табулированных значений
функций PhD (см. табл. 14). Таким же путем можно
вычислить значения поверхностной энергии и поверхностной
энтропии.
Если использовать упоминавшееся в п. 50 эмпирическое
значение \n(q/vf) = 3,55 и пренебречь температурной
зависимостью In {q/vf), то из (51.10) получим для жидкого
аргона с молярным объемом 28,1 см3/моль значение у =
= 11,2 дин/см при 90° К- Это хорошо согласуется с
экспериментальным значением у = 11,9 дин/см. Однако
вычисленная из (51.15) величина поверхностной энергии
25 эрг/см2, плохо согласуется с экспериментальным
значением 35 эрг/см2. Это расхождение возникает, по-видимому,
вследствие пренебрежения тепловым расширением объема
ячейки.
Пренебрегая d In (q/vf)/dT и исключая £ из (51.10)
с помощью (50.8), получаем
.-"/.„-v.*
Y = 2-/3q-,akTc
2 + \п±)Щ*!±
vf I
_£pzmln4-+2D(i)}]. (51.19,
Вычисленная по формуле (51.19) температурная
зависимость поверхностного натяжения для четыреххлористого
углерода вместе с экспериментальными значениями
изображена на фиг. 26. При вычислениях было принято
эмпирическое значение In (q/vf) = 4,0, определенное из
температурной зависимости ортобарической плотности
четыреххлористого углерода, и значение q, вычисленное
при Тс = 556,3° К и молярном объеме 94,18 смУмоль в
точке плавления. Если заметить, что подбираемые
параметры в нашем анализе не фигурировали, то согласие
теоретических и экспериментальных значений
представляется вполне удовлетворительным.
Значения у, вычисленные для случаев граничных (100)-
и (ПО)-плоскостей, оказываются выше, чем для (111)-

250 Часть III. Рассмотрение с помощью решеточной модели
плоскости. Поэтому вычисление поверхностного
натяжения в дырочной модели следует производить, считая
граничной (111)-плоскость.
«8
25
20 Ь
/5
10
5
о «ч, теория
х - эксперимент
л
О
250 300 350 400 450 500 550 600
7, °К
Фиг. 26. Сравнение теоретических [(Ш)-поверхность] и
экспериментальных значений поверхностного натяжения
для четыреххлористого углерода (экспериментальные
данные взяты по I. С. Т.).
Другой вид теории поверхностного натяжения разработали
Пригожий и Сарага [115]. Они исходили из грубой модели
прямоугольной потенциальной ямы вместо потенциала Леннард-Джонса (22.4) и
из модели мономолекулярного слоя с двумя параметрами: (3, который
учитывает увеличение свободного объема молекулы, находящейся на
поверхности по сравнению со свободным объемом молекулы в
глубине фазы, и упоминавшимся выше х^\ представляющим долю
заполненных ячеек в поверхностном слое. Результаты для р = 0,25 и
х^ = 0,7 очень хорошо согласуются с измеренными значениями, в
особенности для поверхностной энтропии. Например, для жидкого
аргона при 85° К получается трасч = 12,5 дин/см (Тиабл = 13»2 дин/см)
и <зрасч = 0,27 эрг/град-см2 (<знабл = 0,26 эрг/град-см2).
52. Связь с квазитермодинамической теорией [135].
Выражение для свободной энергии (49.14) после некоторых

Гл. I. Чистые жидкости
251
преобразований можно переписать в следующем виде:
W
F = Av 2 *(0/(0. (52.1)
t=—и
_ гЛ (п\ h
f(t) --= ±ф (а) - kT \п (X-*j (Г) vf (0)) +
+ C{m (1 — *<'-«) + / (1 — *<*>) + m (1 — tf'+D)}. (52.2)
Так как Avx^f) — число молекул в ^-м слое, /(0 можно
рассматривать как свободную энергию на одну молекулу в
t-м слое, соответствующую величине / (z) в
квазитермодинамической теории, изложенной в п. 17. Тем не менее
необходимо отметить, что однозначного определения /()
дать нельзя. С другой стороны, химический потенциал
одной молекулы в ^-м слое, согласно (49.14), можно
записать как
^ = ;f|£> = "Н (а> ~ *г1п (ь-3/ СП v, (0)) +
+ КГ ln-^r + I {m (1 - 2*'-») +1(1- 2х«>) +
1 — хК1)
+ m (1 — 2*('+i>}. (52.3)
Условие равновесия (49.16) записывается через \lM
следующим образом:
|i<*> = |i, (52.4)
где fx — химический потенциал в объемной фазе. Это
соответствует квазитермодинамическому условию равновесия
(18.4). Кроме того, это условие выведено с помощью
минимизации свободной энергии как функции локальной
плотности, что как раз соответствует основному постулату
квазитермодинамики, обсужденному в п. 17.
Чтобы получить выражение для касательной
составляющей давления, рассмотрим изменение площади плоской
границы. Соответствующее изменение свободной энергии,

252 Часть III. Рассмотрение с помощью решеточной модели
определяемой выражением (49.14), равно
W
{m)n = vkT 2 {*<0 ln *(0 + (1 — *f)) In О — x(t)) +
t=—U
w
+ S 2 {2w« (i — *">) + «*<') (i — *<*+») +
1 t=-u
+ m^'+D (1 — *<'>) + m*« (1 — *«'-«) + «*<'-« (1 — *">)} =
- vkT 2 (*(0 In *(0 + (1 — *<'>) ln (1 — *<'>)} +
t=—u
w
+ v£ 2 (m*(0 (1— *('-1)) + W° (1 — *(0) +
+ mx(0 (i—^+i))}. (52.5)
Второе выражение здесь можно получить, используя тот
факт, что, как и в случае (51.13), изменения величин х^\
обусловленные изменением площади, согласно (49.16) и
(50.3), не вносят вклада.
В то же время из (49.16) и (50.3) получаем
kT In *('> = kT In (1 — *<0) _ i {m (1 — 2*<'-D) +
+ 1(1— 2*W) + m (1 — 2*<'+«)}. (52.6)
Подставляя (52.6) во второе выражение (52.5), имеем
W W
(g) = vkT 2 In (1 - *<'>)+ v£ S *<'> (w*<'-« +
t=—u t=—u
+ Ы*> +mxft+v. (52.7)
С другой стороны, элементарная работа, произведенная
частью системы, заключенной между z и z + dz при
увеличении площади границы на ЬА при постоянной
температуре 7\ дается формулой (47.4). По теории дырок, если
обозначить тангенциальное давление в /-м слое через рф,
работа, совершаемая /-м слоем системы, записывается как
W» = рфШ. (52.8)

Гл. I. Чистые жидкости
253
Таким образом, изменение свободной энергии,
обусловленное изменением площади 6Л, можно выразить как
6F = — 2 8ш<'> - - (6Л) 2 P(r°d- (52-9)
* t
Сравнивая (52.9) с (52.7), получаем выражение для
тангенциального давления г
рф = —-{kT In (1 — *<'>) + W> (/я*(И) +
+ WO + m^+1))}. (52.10)
Внутри объемных фаз (52.10) переходит в обычное
гидростатическое давление, определяемое выражением (48.23).
Из (52.1) — (52.3) и (52.10) легко получить соотношение
ц = ^) = /<'> + ^>^). (52.11)
Так как q-1^ представляет собой плотность числа
молекул в t-ы слое, соотношение (52.11) по форме идентично
квазитермодинамическому условию термодинамического
равновесия (18.4).
Далее, из (48.23), (48.16), (51.7) и (52.10) следует
соотношение
W
Т= 2 (P-P(p)d, (52.12)
t=-U
которое соответствует механическому определению
поверхностного натяжения (13.5) или (19.5).
Таким образом, мы видим, что в дырочной теории
поверхностного натяжения имеют место соотношения, по
форме идентичные соотношениям квазитермодинамики.
Химический потенциал \i<t\ определяемый выражением (52.3),
зависит, однако, не только от х^\ но и от xV+v и х^~гК
В нашей квазитермодинамической теории (см. п. 16—19)
химический потенциал рЮ был функцией *('>, но не
зависел ни от x^+D, ни от х^~1). В соответствии с этим
предположением \i№ можно получить из (48.24), если заме-
1 Определение тангенциального давления не однозначно; см. также
п. 36.

254 Часть III. Рассмотрение с помощью решеточной модели
нить х на х^. Мы видим отсюда, что теория дырок
соответствует скорее не нашей грубой форме
квазитермодинамики, а модификации Хилла [92, 93], рассмотренной
в п. 39 (см. также работу Толмена 116]). Сходство между
Q2
О
^ -0,2
-0,6
'0,8
40
Г ^ г'
U * г
Г' I "
Г v
1—1 1 1 1 1 1-1 1 1 1
-4 -3 -2 -/
О /
С
Фиг. 27. Пространственное изменение тангенциальной
составляющей давления согласно теории дырок (£/КУ=2,0
соответствует критической температуре).
кривыми фиг. 15 и 25, изображающими зависимость
плотности от глубины, представляется нам связанным с этим
фактом.
Изменение тангенциального давления (52.10) внутри
межфазовой области, рассчитанное для (Ш)-плоскости,
показано на фиг. 27. В случае жидкого аргона
минимальная величина тангенциального давления равна —280 шпм
для £/&Г=5,0, что соответствует Т= 104° К.

Глава II
РАСТВОРЫ НЕЭЛЕКТРОЛИТОВ
§ 1. Регулярные растворы
53. Применение метода ячеек к растворам. Рассмотрим
теперь смесь молекул двух сортов А и В и вычислим
статистическую сумму путем разделения пространства на ячейки,
как и в случае чистых жидкостей, рассмотренном в
предыдущих пунктах. Предположим, что размеры молекул сортов
А и В примерно одинаковы (в противном случае необходимо
ввести некоторые изменения в теорию). Размер ячейки
выберем таким, чтобы исключить множественное заселение и
чтобы в то же время взаимодействие молекул,
находящихся за пределами соседних ячеек, можно было рассматривать
как очень малую поправку. Молекулы предполагаются
сферическими или почти сферическими.
Те же приемы метода ячеек, которые обсуждались до сих
пор, в равной мере применимы и к произвольным смесям
жидкостей, однако мы ограничимся более простым анализом
случая бинарных растворов. Пусть число ячеек равно
полному числу молекул. Предположим, во-первых, что
пустых ячеек нет и что молекулы обоих сортов упакованы
так, что их центры образуют гранецентрированную
кубическую решетку. Во-вторых, предположим, что свободные
объемы Via и vib молекул сорта А и сорта В не зависят от
расположения соседних с ними молекул и равны их
свободным объемам в соответствующих чистых жидкостях. Хотя
это ограничение представляется слишком жестким, можно
учесть зависимость свободных объемов от отношения числа
молекул сорта А к числу молекул сорта В в соседних
ячейках без каких бы то ни было существенных изменений,
пользуясь линейным приближением [135], аналогичным (48.13)
в дырочной теории чистых жидкостей. Растворы,
удовлетворяющие перечисленным предположениям вместе с предпо-

256 Часть III. Рассмотрение с помощью решеточной модели
ложением о размере ячейки, мы будем называть
регулярными растворами1.
Обозначим через %АА> хлв, %вв потенциальные
энергии взаимодействия пар молекул А и Л, Л и Ву В и В,
которые располагаются в центрах соседних ячеек и о
которых мы будем говорить далее как об ЛЛ-, А В- и ВВ-кон-
тактах соответственно. Пусть NA и Nb означают полные
числа молекул А и В в системе. Согласно (23.2),
статистическая сумма раствора записывается тогда в виде
Znanb = (Ла1а) (*в/в) Ца Цв Qnanb, (53.1)
Л л = ^ , лв = ^ , (53.2)
где y\AA4BBQ{NANB — конфигурационный интеграл, а г)л,
х\в — множители, соответствующие коллективной
энтропии, определяемой равенством (43.7). Конфигурационный
интеграл Q{nanb соответствует состоянию, в котором
каждая ячейка содержит одну и только одну молекулу любого
сорта [см. (46.3) и (47.14)]:
«»>.- •МТ"* {- '"^г"'^} х
x'2C{NA,N,,X)i-w, (53.3)
X
Х = ХАВ-ХАА?ХВВ, (53,4)
где сХ — полное число Л5-контактов, a G (NAy NBy X) —
число различных размещений при данном значении X.
Как и в случае чистых жидкостей (см. п. 43), мы
выберем для цА и цв их значения в пределе малой плотности
(43.9):
*\А = Чв = е- (53.5)
1 Это определение регулярного раствора несколько отличается от
определения Гильдебранда [136], но по сути дела совпадает с
определением строго регулярного раствора Фаулера и Гуггенгейма (см. [125]).

Гл. II. Растворы неэлектролитов
257
Будем вычислять конфигурационный интеграл, исходя
из приближения случайной смеси [124], как в п. 48 для
чистых жидкостей. Пусть х — молярная доля компоненты
А и N — полное число молекул. Тогда
х = -£9 1-х=-£, (53.6)
N = NA + NB. (53.7)
В предположении о случайной смеси молекул среднее
значение сХ по аналогии с (48.17) выражается как
cX = cNx(l —х). (53.8)
Заменяя теперь X в (53.3) на X и используя соотношение
%G(NAyNB,X) = Nl/NAlNB\, получаем
х
nU> flvn / (nac*aa + MbcXbb)\ „na„nb „
Qnanb = exp | ^ J V% X
NA\ NB\ eXP \ kf ) ' (М'У)
Вспоминая (23.1) и применяя формулу Стирлинга,
получаем из (53.1), (53.5) и (53.9) следующее выражение для
свободной энергии раствора:
F = \{NA1AA + NB%BB} - NA kT In (tfjAevfA) -
— NBkT In (K~B3jBevfB) + NkT {x In x + (1 — x) In (1 — x)} +
+ Ncx(l — x)%. (53.10)
Разность между химическими потенциалами \хд и \iB
молекул сортов А и В дается тогда равенством
^л VB - N [dx j^ TN- 2 ^aa Ъвв> +
+ ^Г1п(^^) + ^Г1п1^- + ^(1-2л:)х. (53.11)
Чтобы получить химические потенциалы \iA и \iB в
отдельности, пренебрежем разностью между свободной энер-

258 Часть III. Рассмотрение с помощью решеточной модели
гией и термодинамическими потенциалами в переменных
р, Т. Это обычно допустимо при таких давлениях, как
ортобарическое. Тогда
V А)р, T,NB \UiyAJp,T,NB
Используя (53.10), сразу же получаем
Ра = т %лл ~ kT ln <№jAevfA) + kTlnx+c(l- х)\,
(53.13)
Рв = у Хвв-кТ 1п (К~в1'веЧв) + kT 1п 0 - *) + ^2Х.
(53.14)
Если система состоит из двух фаз, скажем а и (J, то
в равновесии химические потенциалы \iA и \хв должны быть
одинаковыми в обеих фазах; отсюда вытекает следующее
условие равновесия:
w^-V = lnT=*> (53Л5)
х*+х&= 1, (53.16)
которое соответствует условиям (48.26) и (48.27). Из
написанных условий видно, что две фазы могут
сосуществовать в равновесии, только когда % — положительная
величина.
54. Регулярный раствор с плоской границей раздела.
Рассмотрим регулярный раствор, отделенный плоской
межфазовой областью с площадью А от газообразной фазы.
Для удобства мы рассматриваем систему, заключенную
в сосуд, имеющий форму параллелепипеда, как показано
на фиг. 28. Допустим, что температура столь низка, что
газообразную фазу можно рассматривать как вакуум.
В случае, когда необходимо учитывать конечную
плотность пара, следует учесть наличие дырок в растворе1.
Выберем разделяющую поверхность НК непосредственно
1 Курата [137] применил теорию дырок, изложенную в п. 48—51
к бинарному регулярному раствору, рассматривая его как трехкомпо-
нентную смесь молекул сорта Л, молекул сорта В и дырок.

Гл. II. Растворы неэлектролитов
259
над внешней поверхностью решетки и параллельно ей;
последовательные слои ячеек, параллельные внешней
поверхности, будем называть 1-м, 2-м, . . . , w-м слоями
(см. фиг. 28).
Пусть Na и N{b обозначают, соответственно, числа
молекул сорта А и В в t-м слое. Тогда по аналогии с (49.1)
w
Фиг. 28. Раствор с плоской
поверхностью раздела НК, соприкасающийся
со своей газообразной фазой, которую
можно считать вакуумом.
можно записать конфигурационный интеграл в виде
ли,
(1)
А"В
= 2.л 2 Q(n4\n4\...9nW)9 (54.1)
л)
Aw)
где Q (N{a\ N(a\ . . . , N^) представляет собой член,
отвечающий набору чисел N(a\ N{a\ . . . , N{aK Эти члены
выражаются в виде, аналогичном (49.4), но необходимо учесть
следующие особенности.
Во-первых, мы рассматриваем изменение полного числа
АА -контактов, обусловленное наличием поверхности. Как и
в теории дырок, мы используем обозначения / и т>
принятые в п. 49. Среди cNA ближайших соседей NА молекул
сорта А сХ соседей являются молекулами сорта В, a mcN{A
соседей N{a поверхностных молекул сорта А суть свобод-

260 Часть III. Рассмотрение с помощью решеточной модели
ные ячейки в газообразной фазе. Поскольку число
остающихся пар (cNA — сХ — шсЫ{а) представляет собой
удвоенное число А А -контактов и точно так же (cNb —сХ —
— tticN^b) есть удвоенное число ВВ-контактов, то
сЫд—сХ — тсЫ^
Число АА-контактов = —^ ^ >
cNB-cX-mcN$ (54'2)
Число ВВ-контактов = — г, •
Во-вторык, учтем изменения свободных объемов,
обусловленные присутствием поверхности раздела. Пусть vfA
и vfB — свободные объемы поверхностных молекул сортов
Л и В соответственно. Тогда вместо (49.4) имеем
<4> . АГЦ>
X
х ехр[- Ш{(Млс%ал + Мвсхвв) —
-{^тс1ДА+Ы^тсХвв)}}х
X S В М*\ • • • > №>; X) е-хсттг (54.3)
где g (N{A\ N'a\ • • • »#а°; Я) — число конфигураций при
данном наборе чисел /Уд°, #д\ • • • . ^'КТ и X.
Пусть x[t) — молярная доля компоненты А в /-м слое.
Мы имеем
где, как и в (51.9), v означает число ячеек на единицу
площади каждого слоя. Тогда вероятность нахождения
молекулы сорта А в ячейке (-го слоя равна x{t). Поэтому,
используя предположение о случайном перемешивании,
получаем, совершенно аналогично (4Э.10), следующеевыра-

Гл. If. Растворы неэлектролитов 261
жение для среднего числа ЛБ-контактов:
р W
сХ = 4™\У, {2lxff) (1 — *<") + mxff) (1 — *<'+!>) +
+ mxtf+« (1 — х«>) + mx<'> (1 — ^-D) + m^«-«(l — *«>)} +
+ 2W> (1 — л:'1') + mxW (1 — *<2>) + m*<2> (1 — *<«). (54.5)
Заменяя X в (54.3) на X, получаем
S г №\ лг<?> л#>; X) *-*«/«■ =
ад
В частности, так же как и в п. 49, можно с достаточной
точностью заменить сумму (54.1) ее наибольшим
слагаемым. Подставляя теперь (54.6) в (54.3) и учитывая
(23.1) и (53.1) вместе с (53.5), получаем свободную энергию
регулярного раствора с плоской межфазовой границей
в следующем виде [138]:
F=i (.NaXaa + Nb%bb) -^{хЫ%аа+(1 - хЫ) хвв}-
— NAkT In (KA3jA evfA) — NBkT In (%2jBevfB) —
—AvxWkT\nV-^ — Av (1 — x<i>) kT\nV-IS +
vfA vfB
w
+ AvkT 2 {*(0 In *«> + (1 — *f)) In (I — хЩ +
t=i
2{2W> (1 — №) + mxfn (1 — *<'+«) +
t=2
+ m*('+D (1 — x№) + mx№ (1 — x^-D) + m^-D (1 — *<'>)} +
+ 2lxF> (1 — &■)) + mxW (1 — xW)+mx& (1 — *u>)]. (54.7)
Набор чисел jtf1), #(2\ . . . , л:^ здесь должен быть
выбран так, чтобы величина Q (Na\ . . • , Л^) была
максимальной, т. е. свободная энергия F при данных NА

262 Часть III. Рассмотрение с помощью решеточной модели
и NB была минимальной. Определенный этим условием
набор л:<1), . . . , #(ш) рассматривается как набор
равновесных величин, характеризующих локальный состав.
Условия, определяющие эти величины, имеют следующий вид:
V!A VIB 2 * АА ВВ>
х<1>
+ {/ (1 - 2хМ) + /и (1 - 2хЩ ct+kT\n ^^-^ = ^
(54.8)
{т (1 — 2*»-») + * О — 2*<") + m (1 — 2*»+»)} сх +
1 — JTU
Неопределенный множитель Лагранжа \i* определяется
из ограничивающего условия
w
Av%xW = NA. (54.9)
Так как внутри раствора величины хЮ и х(*> совпадают,
имеет место условие
lim *<'> = *«. (54.10)
f-XX>
В то же время с помощью (49.6) и второго соотношения
(54.8) имеем равенство
сХ (1 - 2*«) + КГ In -^ = fx% (54.11)
1 — лг
из которого удобно определить fx*.
Используя (54.11), (49.6) и обозначения для разностей
(50.4), можно переписать (54.8) следующим образом:
Ах{1) = Ш^(ГА-Гв)+±{1(1- 2*») +
+ т (1 - 2*а>) - (1 - 2^)}+^- (ln-^-ln
дг
2/псх V 1—*(1) 1--*а/
(54.12)

Гл. II. Растворы неэлектролитов
263
где ул и тБ — поверхностные натяжения чистых
жидкостей А п В соответственно, которые определяются
выражениями
Г^-^Хл.-v^lnii, (54.14)
/
rB = -?XBS-v^ln^. (54.15)
Выражения (54.14) и (54.15) соответствуют выражению
(47.8) для поверхностного натяжения чистых жидкостей,
полученному из теории свободного объема. Уравнения
(54.12) и (54.13) впервые были получены и численно решены
Оно [138] \
Некоторые решения уравнений (54.12) и (54.13) для
с% = 450 кал/моль (см. п. 57) показаны на фиг. 29.
55. Поверхностное натяжение и адсорбционная
формула Гиббса [140]. Если внешнюю поверхность решетки
регулярного раствора выбрать в качестве разделяющей
поверхности и пренебречь плотностью пара, то для
поверхностной плотности числа молекул сортов Л и В, согласно
определениям (1.1) и (5.5), получаем из (53.6) и (54.4)
W
Т (55.1)
Гв^З{(1-*°)-(1-*«)>.
1 Оно получил эти уравнения для случая регулярного раствора
в контакте с твердой стенкой, рассматриваемой как адсорбент. Однако
в его расчет не нужно вносить существенных изменений, кроме того,
что твердую стенку следует заменить газообразной фазой,
рассматриваемой практически как вакуум. Оно получил также изотерму
адсорбции, используя метод разностного уравнения [139].

x(t)
W9-
х =1,000 _,^ J>
09 \
Ь-^
0,8
0,7 V-
0,6
0,5
0,4
0,3
0,2
0,1
О
г"=0530
-ч> // -л
<гЧ
>^^
\
•о- //- -Л
-у "^
V). ±zP,WI
. — -Л
. __ зг= 0,088 , .
-//-
Фиг. 29. Изменения относительной концентрации
вблизи поверхности для бинарного раствора с
су = 450 кал/'моль при 15° С.

Гл. II. Растворы неэлектролитов
265
Отсюда непосредственно видно, что
ТА + ТВ= 0. (55.2)
Умножая первое выражение (55.1) на (53.11), где х
положено равным хау и преобразуя результат, приходим
к соотношению
w
<Ра -МГ^ = |2 К*" - *(а)) *аа + W - *(°) -
- (1 - х-)} %вв- (*<" - *а) £Г In (k7jAevIA) -
-{(1 - *«>) - (1 - **)} kT In (Х?/вво/в)] +
+ vkT 2 Ц*0 — *°0 In х« + {(1 — *<'>) —
_ (1-д«)} In (1-**)] +
+ vex 2 (*(0 — *a) (1 — 2*a). (55.3)
*=i
С другой стороны, свободная энергия объемной фазы,
остающейся строго однородной вплоть до разделяющей
поверхности, согласно (53.10), выражается формулой
Fa = \ №%АА +N%Xbb) -N«AkT\n <filjAevfA) -
-N%kT In (KgjBevfв) +
+ NkT{x* In x* + (1 — xa) In (1 — x*)} + Ncx* (1 — *a) x,
(55.4)
где Л^ и N% — полные числа молекул соответственно
сортов Л и В в упомянутой гипотетической объемной фазе а.
Используя (55.2), можно свести выражение (4.8) к
т=^!_(^_^)Гл. (55.5)

266 Часть III. Рассмотрение с помощью решеточной модели
Подстановка (54.7), (55.3) и (55.4) в (55.5) дает
Г = *(1)ГЛ + (1 - *(1)) Гв +
+ vkT J p) ln^ +(1 -*«>) lni-^-J-
_ ™* [21 (*&>—*«)« +m{4(*W— xa)2— (*<2>— *<*>) (1 —2*a>) -f
+ 2*w (1 — *(1>)} + 2 {21 (*<'> — x*f +
+ 4m (*W — X*)2 — m (xP-v +
+ *('+i> — 2**)) (1 — 2*<'>)}Ь (55.6)
где Тл и T5 — поверхностные натяжения чистых
жидкостей А и В соответственно, которые даются выражениями
(54.14) и (54.15).
Локальный молекулярный состав *(1), *<2), . . . , х^\ ...
. . . , x(w) меняется с изменением величин \iA и \iB.
Изменим х{1\ х{2), . . . , *(ny) таким образом, чтобы они
удовлетворяли лишь условиям равновесия (54.8), но не (54.9),
т. е. чтобы число молекул не являлось ограниченным.
Тогда из (54.7) и (55.4) с помощью (53.11) и (54.11)
получаем
^d(F-F*) = <РА ~ ИВ) dTA- (55.7)
Из (55.5), (55.7) и (55.2) находим
- dr = TAd ((хл - цв) = TAdiiA + Гвфв. (55.8)
Это соотношение и есть адсорбционное уравнение Гиб-
бса (6.1). Таким образом, излагаемая теория является
самосогласованной по отношению к термодинамическим
соотношениям на поверхности.
Далее, из (53.11) получаем следующее соотношение:
«*л-М =-2с%+ kT . (55.9)
Сопоставляя с (55.8), получаем уравнение Гильдебран-
да [141], т. е. точную адсорбционную формулу Гиббса для

Гл. II. Растворы неэлектролитов
267
регулярного раствора
—а = а Та а {kT - 2сх* (1 - х*) х}. (55.10)
Для идеального раствора, который представляет собой
регулярный раствор с дополнительным свойством % = 0,
условие равновесия (54.8) с помощью (54.14) и (54.15)
сводится просто к
r^-rs+v^ln^=v^lnT^?i (55.11)
д.(2) = X(s) = т и т = х*ш (55.12)
Отсюда следует, что в случае идеального раствора
концентрация лЯ в t-м слое та же, что и в объемной фазе;
исключение составляет первый слой. Поэтому использованное
в ранних теориях поверхностного натяжения растворов
[142—144] предположение о том, что различие в составе
между поверхностью и объемной фазой ограничено лишь
мономолекулярным слоем, в случае идеального раствора
вполне допустимо.
Из (55.6) легко получается следующее выражение для
поверхностного натяжения идеального раствора:
Т = *(1)Гл + (1 - *<i>) гв -г
Xii) inf_ + (1 — *<*>) In-—М . (55.13)
ха 1 — ха J
Используя (55.11), можно переписать (55.13) в виде
r=rA + vkT]n^ = TB +vkT]n^_z^y (55.14)
что эквивалентно закону смешения Гуггенгейма [144] для
поверхностного натяжения идеальных растворов
е-ч,.кт = Л-,лМг + (1 _ х*) е*в№ш (55л5)
56. Модель однослойной межфазовой области. Как
явствует из (55.11), для идеального раствора однослойная
модель является точной. В этой модели отличие от состава

268 Часть III. Рассмотрение с помощью решеточной модели
объемной фазы имеет место только для одного слоя молекул
в межфазовой области. Более того, из фиг. 29 видно, что
даже в более общем случае регулярного раствора различие
в составе мало для всех слоев, кроме первого. Поэтому
однослойная модель представляется приближенно
правильной и применимой к неидеальным регулярным
растворам [144].
Для однослойной модели, в которой все х^\ кроме я*1),
равны концентрации в объемной фазе (55.6), сводится к
равенству
Г = *{1)ГА + О - *(1)) Гв +
( v(D 1 _ М)\
+ v*T |*u> In*- + (1 - *!>) In L-^J -
— vex {(I + m) (*<*> — *a)2 + mxF> (1 — *<*>). (56.1)
Условие равновесия (54.12) принимает вид
yd)
Г л -Гв+ v{/(l — 2х»>) + m(l-2*)}ca + v*71n_f^ =
= v (1 — 2х*) сх + vkT \п-£—. (56.2)
1 —X
Из этого условия можно определить *(1> в однослойной
модели. Применяя условие равновесия (56.2), можно
переписать (56.1) в следующем виде (Гуггенгейм [144]):
+ vfcx {(1 — *(1))2 — (1 — х*)2} — vmc% (1 — х*)2 =
= ГВ + vkT In 1j^ + vfcx {(xV)2 - (x-)2} -
— vmc% (x*)2. (56.3)
Все же предположение о мономолекулярном
межфазовом слое не является самосогласованным и несовместимо
с адсорбционной формулой Гиббса, как отметили Дефе и
Пригожий [145]. Согласно однослойной модели,
поверхностная плотность (55.1) молекул сорта А дается равен-

Гл. П. Растворы неэлектролитов
269
СТВОМ
Гл = v (*(i> — jca). (56.4)
Из (56.3) и (56.2) получаем
(56.5)
^1 = V (*(*> — *а)
dxa '
kT +2c(l+m)%
ха(1 — ха)
С помощью (56.4) это равенство можно переписать в виде
[kT — 2с(1+ т) х« (1 — х*) х]. (56.6)
dy _ Гл
dxa ха (1 — ха)
Последнее выражение не совпадает с уравнением Гиль-
дебранда (55.10) за исключением случая идеального
раствора, для которого х = 0. Другими словами, однослойная
модель несовместима с адсорбционной формулой Гиббса
для неидеальных регулярных растворов. Это происходит
потому, что такое распределение плотности, когда х^ =
= #(з) = . . . = х*, не удовлетворяет второму условию
(54.8) и, следовательно, не может быть равновесным.
Хотя Дефе и Пригожий [145] показали, что в случае
двухслойной модели отклонения от формулы Гиббса
становятся практически незаметными, все же любая теория,
основанная на конечном числе слоев, в принципе
противоречит формуле Гиббса [140].
57. Сравнение с экспериментом. Существует много
видов растворов, которые можно приближенно
рассматривать как регулярные. Чтобы сравнить значения
расчетных величин, полученные по теории ячеек, с
экспериментальными данными для приближенно регулярных
растворов, необходимо прежде всего оценить энергию
смешения х» определяемую согласно (53.4).
Так как пар, находящийся в равновесии с
регулярным раствором, мы считаем весьма разреженным, его можно
с достаточной точностью рассматривать как смесь
идеальных газов. Химические потенциалы (6.3) тогда равны
Va = Фл + kT ln Ра> Vb = Фв + kT 1п Рв> (57' *)
где рА и рв — парциальные давления компонент А и В
соответственно. Химические потенциалы \х°А и \i°B чистых

270 Часть III. Рассмотрение с помощью решеточной модели
жидкостей, имеющих давления паров р°А и р°в, при одной
и той же температуре равны соответственно
\i°A = Фл + kT In роА и |io = Фб + kT In ро. (57.2)
Из (57.1) и (57.2) получаем следующее соотношение:
- {цв -р%-ЬТ In (1 - х)}. (57.3)
Сравнивая с (53.11), получаем
(1 - 2х) сх = kT In (£L V-*A) . (57.4)
\ Рв xp°A ]
Для системы эфир — ацетон при 288° К величина с%>
вычисленная из давления пара, составляет 450 кал/моль [146].
Из (54.12) и (54.13) мы получаем тогда кривую изменения
концентрации эфира и ацетона вблизи поверхности,
изображенную на фиг. 29. Численный расчет был выполнен
для (Ш)-плоскости в качестве межфазовой границы, т. е.
для I = 72, m = V4, с использованием среднего значения v,
даваемого выражением
где ^л и vB — значения v для чистых жидкостей А и В
соответственно. Изображенная на фиг. 30 кривая для
поверхностного натяжения вычислена из (55.6) с
использованием приведенного выше значения с% и
экспериментальных значений поверхностного натяжения чистых эфира и
ацетона. Рассчитанные Пригожиным и Нарбондом [146]
с помощью однослойной модели и формулы Гуггенгейма
(56.3) величины с% совпадают с приведенными на фиг. 30
с точностью порядка одного процента г. Итак, мы можем
заключить, что однослойная модель дает для регулярных
1 Однако наилучшее согласие было получено в случае простой
кубической решетки, который, по-видимому, едва ли применим к регу-
ярным растворам.

Гл. II. Растворы неэлектролитов
271
растворов хорошую зависимость поверхностного натяжения
от концентрации, тогда как относительная адсорбция,
как видно из фиг. 29, оказывается заметно искаженной.
24
23
22
21
20
19
18{
77
-
.1
У
о ~ теория п
^-^эксперимент ^<у
у &
у /
у /
У JJ
У У*
У ^^*
1 1 1 1 1 1 1 1 1
О 0,1 0,2 0,3 0? 0,5 0,6 01 0,8 09 1,0
эфир l-x* ацетон
Фиг. 30. Сравнение теоретических и
экспериментальных [146] значений поверхностного натяжения
для растворов эфир — ацетон при 15° С в зависимости
от молярной доли ацетона 1 —*а.
58. Динамическое поверхностное натяжение. Как
указывалось выше, концентрация в межфазовом слое раствора,
находящегося в термодинамическом равновесии, вообще
говоря, отличается от концентрации в объемной фазе.
Однако непосредственно после того, как образовалась
свежая поверхность, она может иметь почти ту же
концентрацию, что и внутри объемной фазы. Поверхностное
натяжение такой поверхности называется динамическим
поверхностным натяжением [147]. Вычисление
динамического поверхностного натяжения, как будет показано
ниже, достаточно просто, хотя вычисление поверхностного
натяжения системы на промежуточных стадиях
оказывается трудным [148, 149]. Упомянутая межфазовая область,
очевидно, не находится в термодинамическом равновесии,
так что динамическое поверхностное натяжение следует
вычислять из уравнений, основанных на термодинамике
необратимых процессов, изложенной в п. 21.

272 Часть III. Рассмотрение с помощью решеточной модели
Так как концентрация в только что образовавшейся
межфазовой области считается в точности равной
концентрации в объемной фазе, то поверхностная плотность числа
молекул равна нулю: ТА = ГБ = 0; следовательно, (21.35)
переходит в равенство
г га
Г,= ^-, (58.1)
где, как и ранее, вкладом от газообразной фазы мы
пренебрегаем. В то же время свободная энергия дается
выражением
F = Т {"а%аа + Nb%bb) - *тг l**AA + d - *") W-
- NA kT In (bfjAevfA) - NB kT In (^V V -
-Avx-kT ln^ — A v (1 — **) feTln^ +
vfA VfA
+ NkT {x* In xa + (1 — xa) In (1 — xa)} +
+ Afcjta (1 — x*) % — Avcmx* (1 — *a) ь (58.2)
которое получается из (54.7), если положить все *<*>
равными ха. Подстановка (58.2) и (55.4) в (58.1) приводит к
выражению
Ъ = - иг {**лл + (1 - *а) W - ™а ^ ln ^ -
_ v (1 — х?) kT\r№ — vcmx* (1 — *а) х- (58.3)
С помощью выражений (5.14) и (5.15) для гл и тБ можно
переписать (58.3) в виде [148]
Td = *аГл + (1 — *а) Гв — vcmx<x (1 — *а) Х- (58.4)
Пригожий и Дефе [148] сопоставили вычисленное с
помощью (58.4) динамическое поверхностное натяжение с
экспериментально измеренным статическим поверхностным
натяжением для эфир-ацетоновой системы, упоминавшейся
в п. 57. Результаты приведены на фиг. 31. При расчете было
выбрано m = V6, что соответствует простой кубической

Гл. II. Растворы неэлектролитов
273
решетке. При вычислении теоретических значений авторы
использовали статические поверхностные натяжения ул
и чв для чистых жидкостей, поскольку время релаксации
для установления механического равновесия относительно
мало по сравнению со временем, необходимым для
установления термодинамического равновесия в межфазовой
24
23 \-
22
I
с§
20V-
19 V
18
о ~ теория
г у ~ эксперимент
L
/
'<£
W
L /у
/ / /
/ У /
V / / *
''/У
'S
V's
У/ i i i_.
//7
///
V/
'//
'/У
/ /
/ х
/£
¥
75°;
? |
О 0,2
Эфир
04 0,6
0,8 1,0
оцептн
Фиг. 31. Сравнение теоретического динамического
поверхностного натяжения и экспериментального
статического поверхностного натяжения для
раствора эфир—ацетон в зависимости от молярной доли
ацетона [148].
области в результате диффузии веществ из объемной фазы
к поверхности.
Далее, в случае идеального раствора (58.4) сводится
к соотношению [148]
Yd = x*Ya + 0 _ *а) 7в (идеальный раствор), (58.5)

74 Часть 111. Рассмотрение с помощью решеточной модели
которое очевидным образом отличается от выражения для
статического поверхностного натяжения (55.13).
Вообще говоря, выражение для поверхностного
натяжения имеет одинаковую форму как в равновесном, так и
в неравновесном случае (см. п. 36). Поэтому (58.4)
представляет собой лишь частный случай (55.6), такой, в
котором все х& равны ха.
Пригожий и Дефе [148] вычислили также вторичные
химические потенциалы, определяемые выражениями (21.19)
и (21.20), из значений динамического поверхностного
натяжения с помощью соотношения (21.31), которое в
рассматриваемом случае сводится к
х*е,«А + (1 — х*) е£ = 0. (58.6)
Дефе [26] показал, что это условие действительно
справедливо для динамического поверхностного натяжения,
исходя из допущения, что обмен частицами на свежей
поверхности является чисто гидродинамическим, без
необратимого производства энтропии. Однако авторам это
допущение представляется неубедительным.
§ 2. Растворы полимеров
59. Решеточная теория для атермических растворов
полимеров. Хотя до сих пор применение теории решеток
к растворам ограничивалось случаем растворов,
состоящих из молекул примерно равных размеров, этот метод
применим также к растворам, состоящим из молекул,
размеры которых совершенно различны, например к
растворам полимеров. В настоящей работе мы ограничимся
случаем раствора, состоящего из молекул растворителя Л,
каждая из которых занимает одну ячейку, и молекул типа
жестких стержней х растворенного вещества В, которые
занимают по г ячеек на молекулу. Наша цель будет
состоять в том, чтобы вывести простые точные формулы,
удобные для качественного рассмотрения поверхностного
натяжения растворов полимеров.
1 О более общем случае, когда молекулы полимера (тримера)
являются гибкими, см. [150].

Гл. //. Растворы неэлектролитов
275
Среди сг ячеек, соседних с г ячейками, занятыми
молекулой В, 2 (г—1) ячеек заняты самой центральной
молекулой. Следовательно, число cq соседних ячеек, занятых
другими молекулами вокруг стержнеобразной молекулы
сорта В, удовлетворяет равенству
с (г — q) = 2 (г— 1). (59.1)
Будем теперь рассматривать каждую молекулу сорта В
как разделенную на г сегментов, каждый из которых
занимает в точности одну ячейку. Тогда конфигурационный
интеграл для однородного объемного раствора, состоящего
из N а молекул сорта А и NB молекул сорта В, по
аналогии с (53.3) равен
Qnanb = v"/vfBBexp {- JL (NAc%AA + NcqxBB)} x
X^G{NAjNBjX)e-^y-lkT}
x
% = %ab- ?^ + *™ , (59.2)
где cX и %AB означают число пар «молекула сорта А —
сегмент молекулы сорта 5» и потенциал взаимодействия
в такой паре; %АА и %вв — потенциалы взаимодействия
между двумя молекулами сорта А и между двумя
соседними сегментами, принадлежащими различным молекулам
сорта В; vfA — свободный объем на один сегмент. Число
конфигураций G (NA, NB, X) отличается от той же
величины для регулярных растворов. Когда % обращается
в нуль, раствор называют атермическим раствором
полимера. Такой раствор соответствует идеальному раствору,
рассмотренному в предыдущем пункте в связи с
регулярными растворами.
Сумма величин G {NA, NB, X) по X представляет собой
полное число способов размещения N а молекул сорта А
и NB молекул сорта В. Следуя методу Флори и Хьюгин-
са \ имеем
1 См., например, книгу Миллера [151].

276 Часть III. Рассмотрение с помощью решеточной модели
%G(NA, NB,X) =
х
cNfs 1 {NA + rNR)l
с I к а -г в> ^593^
где множитель 1/2 возникает вследствие симметрии
полимерной молекулы. Таким образом, для атермического
раствора (59.2) сводится к выражению
Лм\ N л rNB Г 1 ж, . ,, ч 1 *
Qnanb = vfB vfB exp |— -j^ NAc%AA + NBcq%BB)} X
с»в j (NA + rNBy.
X {MA + rNB)N^-l) 2NB WW ■ ( >
Тогда, по аналогии с (53.10), для свободной энергии F
объемного атермического раствора получаем следующее
выражение:
- NB kT In (bfjBriBv'fB) -NBkT\n\+{r-\)NBkT-
-NAkT]nN^p^-NBkTlnN-^, (59.5)
где r\B — коллективная энтропия на один сегмент
молекулы 5.
60. Поверхностное натяжение атермических растворов
полимеров [152]. Теперь мы готовы к тому, чтобы
рассмотреть атермический раствор полимера, отделенный от
своего пара плоской границей раздела фаз. В общем случае
молекулы типа жестких стержней, состоящие из г
сегментов каждая, могут принимать различные ориентации
относительно разделяющей поверхности. Вследствие не°б-
ходимости учета всех возможных ориентации этих моле~
кул рассмотрение такой системы весьма сложно.
Ограничимся поэтому упрощенной моделью, в которой
учитывается только такая конфигурация, при которой

Гл. 11. Растворы неэлектролитов
277
стержни расположены параллельно поверхности. Этот
случай рассмотрен Пригожиным и Марешалем [152].
Вычисления в более общих случаях выполнили Пригожий
с сотрудниками [150, 153, 154] и Курата [155].
Рассмотрим атермический раствор полимера,
находящийся в сосуде, имеющем форму прямоугольного
параллелепипеда, и отделенный от своей газообразной фазы
(представляющей собой почти вакуум) разделяющей
поверхностью НК, которая расположена непосредственно над
внешней гранью решетки раствора, как изображено на
фиг. 28. Как и в п. 54, мы обозначим последовательные
слои ячеек, параллельные поверхности раздела, номерами
от 1 до ш и будем пользоваться теми же обозначениями /
и т, что и раньше.
Если выбор ориентации стержнеобразных молекул
ограничен только направлениями, параллельными
разделяющей поверхности, то число конфигураций молекул сортов
А и В 2<3 (NAy NB, X) уменьшается до
х
^G(NA,NB,X) =
х
(lcfB 1_ {NA + rNB)\
(60.1)
Рассмотрим теперь такую гипотетическую систему,
которая вплоть до разделяющей поверхности имеет те же
свойства, что и наш раствор в глубине жидкой фазы. С
помощью (60.1) имеем тогда вместо (59.5) выражение
Fa=j {№кгАА + N%q'%BB) - NAkT In (tfj A4AvfA) -
- N% kT In (XB*jBi{BxffB) - NBkT In (|) +
+ (r-\)NBkT + NAkT\n—II— +N%kT\n Nb
(60.2)
где индекс а относится к объемной жидкой фазе a, a q' —
= lq + 2mr.

278 Часть III. Рассмотрение с помощью решеточной модели
Химические потенциалы \хА и \iB по аналогии с (53.11)
удовлетворяют следующему условию:
1 кТ у (1с\ КГ у К . .„I NA
t*A г ГВ г \2) г N^+rN% ^A+rNB
- kT In Q^!Ar[AvtA) Л-Щ- In №1в№в) +
+ ^{tAA-q7tBB). (60.3)
Пусть числа молекул сортов А и В в t-ы слое реальной
системы равны соответственно. Согласно
принятому предположению, ни одна молекула В не вх^цит
одновременно в два или более слоя. Конфигурационный
интеграл атермического раствора полимера с плоской
межфазовой границей можно по аналогии с (54.1) и (54.5) записать
в виде
<№Л»в= 2 • • • 2 Q Wa, • • • , NT), (60.4)
Q (NlX\ ..., N%>) = rfSffi exp{- -^L- (NAcXAA +
+ NBcq'XBB) + ~r {N<$maAA + N$ пгсг%вв)} X
x т^У^У^пГ м"® 1 ^'+fJVB)'1
(60.5)
Введем сокращения
(ft NA (ft rN<B
*A= N% + rN$' ФВ=<) + г<' (6°-6)
которые выражают объемные доли компонент А и В
соответственно. Мы имеем
Av = #<? + rtfg\ (60.7)
где v — число ячеек на единицу площади и А — площадь
каждого из слоев решетки. Для атермического раствора
полимера (r-мера) из (60.7) получаем вместо (55.2) следую-

Гл. II. Растворы неэлектролитов
279
щее соотношение:
Гл + гТв = 0. (60.8)
Далее, согласно (59.5), получаем из (60.4) и (60.5)
выражение для свободной энергии
F=\ (NaXaa + NBq'lBB) - ^(фа>Хлл +<р$Хвв) -
— NAkT In (K?jAr\Av[A) — NBkT In (№jBibd}B) —
- Av^kT In (fy - A*№ kT In {^j -
-NBkT lng) + 2^v[(r-l) (^-j £Г +Ф<?AT ln<p<? +
+ (^)&Tln(^)]. (60.9)
В этом уравнении ф(д ифд следует определять условием
минимума (60.9) при заданных значениях NA и NB. Это
условие имеет следующий вид:
_S(X^_xM)-ln(£) + ln(i) +
+ (ln,a>_llnf) =
= In^-jlnf =... = lnqu —iln^. (60.10)
Из выписанной системы уравнений следует, что все фх
и фв. кроме фл' и фв\ равны соответственно
JVa, гЛ/1!,
Фл = — , Фв = в . (60.11)
^А N*A + rN% ' ^В N*A + rNaB К }
Это означает, что однослойная модель в случае атерми-
ческого раствора полимера является точной — до тех пор,
пока ориентация стержнеобразных молекул ограничивается
направлениями, параллельными поверхности \
1 Если требуется учитывать ориентацию молекул полимера,
нормальную к поверхности, модель монослоя перестает быть справедливой
даже для атермических растворов, молекулы которых представляют
собой жесткие стержни [150, 153, 155].

280 Часть III. Рассмотрение с помощью решеточной модели
Если воспользоваться соотношением (60.8), то (4.8)
записывается как
Г = ^!-(|хл-|^)Гл. (60.12)
Так как ТА =±l^ N^—NaA\ , то с помощью (60.2),
(60.3), (60.9) и (60.10) получаем из (60.12)
/ cdW cd(1> cd(1)\
Г = <9{frA + Ф(вЧв + vkT (qfl> Ш ^ + Ц- In |-) +
ф8} - Фв
+ vyfe7(r— 1)-^ —, (60.13)
(60.14)
где уЛ и тв — поверхностные натяжения чистых
жидкостей А и В соответственно. Используя условие равновесия
(60.10) с учетом (60.14), можно переписать (60.13) в более
простом виде:
Г = ГА + vkT In Ц. + vkT (г - 1)Тв Тв =
Фл г
= TB + ^ln|+v,T(r_1)^z^. (60.15)
Для г = 1 (60.15) становится идентичным выражению для
поверхностного натяжения идеального раствора (55.14).
Условие равновесия (60.10) можно с помощью (60.14)
переписать в другой форме:
с^внг (Фв)1/Г (Фв"Г

Гл. II. Растворы неэлектролитов
281
Соотношения (60.15) и (60.16) впервые были получены При-
гожиным и Марешалем [152]. Если г достаточно велико
и ни ф^, ни ф^ не равны нулю, то
(Фв)1/г^(ф2>)1/г^1. (60.17)
Тогда с помощью (60.16) и (60.17) можно привести (60.15)
к виду
Ч-ГЛ = -(ЧА- Гв) + rkTr-^-(l - е-^А-гв)^ ^
(60.18)
Далее, если | тл —ув\ / (vkT) <^ 1, то (60.18) упрощается:
Г = ГлФл + ТвФв- (60Л9)
На фиг. 32 приведены значения поверхностного
натяжения дибензилбензола, вычисленные по (60.19) при г = 2,
в зависимости от молярной доли бензола в объемной фазе:
NaA
хА= а А а . (60.20)
Пунктирная кривая отвечает приближенному
уравнению (60.19); для сравнения штриховой линией показано
поверхностное натяжение, вычисленное для идеального
раствора по (55.15). Согласие между теорией и
экспериментальными данными удовлетворительно.
Правило Траубе [155] г. Так как решить уравнение
(60.16) в общем случае трудно, мы ограничимся случаем
разбавленных растворов. Считая, что ф*—малая величина,
запишем (60.16) в виде
<pg>= (e{yA~yB)/vkT)r(faB+члены высших порядков. (60.21)
С другой стороны, из (60.6) и (60.17) имеем Ф^} =
= 1 —<pg> и ф^=1 —<р*. Следовательно, можно
переписать первую формулу (60.15) в виде
ГА -Г = vkT [i fog) - Гв) + S (<)S7(^)S1. (60.22)
L S=2 J
1 Авторы благодарны проф. Курата, который обратил их внимание
на излагаемый ниже вопрос. Правило Шишковского было также
выведено Куратой [155].

282 Часть III. Рассмотрение с помощью решеточной модели
Подставляя (60.21) в (60.22) и пренебрегая членами второго
и более высоких порядков по ф^> и ф*, получаем
Гл-Г=^[(^)Г-1](#). (60.23)
ю
9
8
К
■k5
i
^ 4
3
2
О 0,1 0,2 0,3 0,4 0,3 0,6 0,7 0,8 0,9 10
дибензил хД бензил
Фиг. 32 Сравнение экспериментальных
значений поверхностного натяжения для дибен-
зилбензола со значениями, рассчитанными по
трем различным теоретическим уравнениям.
/—экспериментальные значения [15, 154]; 2 — по
точному уравнению (60.15); 3 — по приближенному
уравнению (60.19); 4 — по уравнению для идеального
раствора (55.15). Вычисления выполнены при г = 2,
v2/a=28,94 А2 [14, 154] и для (11 !)-плоскости, т. е.
v^22/»3~V2 о"2/» [см. (46.6)].
Если адсорбция растворенного вещества В велика, то,
|\^>
Г^4
L \
(—
L_
1—
L.
L
1
г—
L
о ~/
vr ^ ~ 2
Хчч ~з
\Vsx 4
\ X ч
\ X \
\ \ N
4 \ \
4 \ \
4 \ \
4 \ \
\ \ ч
\ \ ^
4 \ N
\ \ х
ч \л
\ я ч
\ Xх*
\\х
\о\
—J 1 1 i i ■ i i\
как видно из (60.21), можно считать, что \е
Тогда (60.23) сводится к
vkT
vkT
г
(60.24)

Гл. II. Растворы неэлектролитов
283
Так как ср*//* при малых ф* практически равно молярной
доле растворенного вещества, то предельное выражение
(60.24) для поверхностного натяжения идентично правилу
Траубе [156]1. Для очень разбавленных растворов
уменьшение поверхностного натяжения, вызываемое
растворенным веществом, пропорционально концентрации
последнего, причем коэффициент пропорциональности
экспоненциально возрастает с увеличением длины растворенных
полимерных молекул 2.
1 Траубе показал, что в гомологическом ряду жирных кислот и
спиртов концентрации, которые дают одинаковое уменьшение
поверхностного натяжения в разбавленном водном растворе, уменьшаются
втрое на каждую дополнительную СНг-группу в углеводородной цепи
(см., например, книгу Адама [67]).
2 Аранов и Виттен [157] отметили недавно, что разница в работе,
совершаемой при перемещении молекулы из глубины на поверхность
воды, для малоновой и янтарной кислот гораздо меньше, чем возрастание
этой работы при добавлении группы СНг в длинных цепочках
углеводородов с одной концевой группой, притягиваемой водой. Так как обе
эти кислоты имеют по два притягивающих конца, их молекулы плотно
связаны с молекулами воды на обоих концах. Авторы пришли к выводу,
что это расхождение связано с вертикальной ориентацией углеводороди-
стых молекул вблизи поверхности воды и что обычное предположение
о параллельном расположении по отношению к поверхности полимерных
молекул в разбавленных растворах является неубедительным. Они
таким образом предложили грубую теорию для объяснения правила
Траубе, основанную на предположении о случайных заторможенных
поворотах поверхностных углеводородных молекул.

ЛИТЕРАТУРА1
1. Young Т., Phil. Trans. Roy. Soc, 95, 65 (1805).
2. Thomson W. (Lord Kelvin), Proc. Roy. Soc, 9, 255 (1858);
Phil. Mag., 17, 61 (1859).
3. Ba к к e г G., Kapillaritat und Oberflachenspannung, Handbuch
der Experimentalphysik, Bd. VI, Leipzig, 1928.
4. G i b b s J. W., Collected Works, Vol. 1, New Haven, 1948. (См.
перевод: Дж. Г и б б с, Теория капиллярности, в книге
Дж. В. Г и б б с, Термодинамические работы, М.— Л., 1950,
стр. 288.)
5. G u g g е n h е i m Е. A., Trans. Faraday Soc, 37, 397 (1940).
6. G u g g е n h е i m E. A., Thermodynamics, Amsterdam, 1950.
7. H i 1 1 T. L., Journ. Phys. Chem., 56, 526 (1952).
8. KondoS., Journ. Chem. Phys., 25, 662 (1956).
9. F о w 1 e r R. H., Proc Roy. Soc, A, 159, 229 (1937).
10. F о w 1 e r R. H., Physica, 5, 39 (1938).
11. Kramers H. A., Proc Kon. Nederl. Akad. Wetensch.,
Amsterdam, 41, 10 (1938).
12. OnoS., Busseiron Kenkyu, No. 23, 10 (1950).
13. В u f f F. P., Journ. Chem. Phys., 3, 419 (1955).
14. G u g g e n h e i m E. A., A d a m N. K., Proc Roy. Soc, A139,
218, 1933.
15. D e f а у R., P r i g о g i n e I., Tension Superficielle et
Adsorption, Liege, 1951.
16. T о 1 m a n R. C, Journ. Chem., Phys., 16, 758 (1948).
17. К о e n i g F. O., Journ. Chem. Phys., 18, 449 (1950).
18. T о 1 m a n R. C.t Journ. Chem. Phys., 17, 333 (1949).
19. В u f f F. P., Journ. Chem. Phys., 19, 1591 (1951).
20. Guggenheim E. A., Modern Thermodynamics by the Methods
of J.W. Gibbs, London, 1933.(См. перевод: Э. А. Гуггенгейм,
Современная термодинамика, изложенная по методу Гиббса,
Госхимиздат, 1941).
21. Kirkwood J. G., В u f f F. P., Journ. Chem. Phys., 17, 338
(1949).
22. С a h n J. W., H i 1 1 i a r d J. E., Journ. Chem. Phys., 28, 258
(1958).
1 Литература со звездочкой добавлена редактором перевода.

Литература
285
23. D е f а у R., Etude Thermodynamique de la Tension Superficielle,
Vol. 1, Paris, 1934; Groupement de Communication a PAcademie
Royale de Belgique (Classe des Sciences), Annees 1929 a 1934.
24. P r i g о g i n I., Etude Thermodynamique des Phenomenes Irrever-
sibles, Liege, 1947. (См. перевод: И. Пригожий, Введение
в термодинамику необратимых процессов, ИЛ, 1960.)
25. D е D о п d е г Т., L'Affinite, Paris, 1927.
26. D е f а у R., Bull. Acad. Roy. Belg., CI. Sci., 41, 138 (1955).
27. KondoS., Busseiron Kenkyu, No 2, 926 (1956).
28. PitzerK. S., Journ. Chem. Phys., 7, 583 (1939).
29. GuggenheimE.A., Journ. Phys., 13, 253 (1945).
30. E б t v 6 s R., Wied. Ann. Phys., 21, 448 (1886).
31. К a t а у a m a M., Sci. Rep. Tohoku Imp. Univ., 4, 373 (1916).
32. M а с L e о d D. В., Trans. Faraday Soc, 19, 38 (1923).
33. SugdenS., The Parachor and Valency, London, 1930.
34. В у k A., Ann. d. Phys., 66, 157 (1921); 69, 161 (1922).
35. De Boer J., Physica, 14, 139 (1948).
36. De Boer J., В 1 aisseB.S., Physica, 14, 149(1948).
37. D e В о e r J., L u n b e с k R. J., Phisica, 14, 520 (1948).
38. De Boer J., Bird R. В., Quantum Theory and Equation of
State, в книге J. О. Hirschfelder, С. F. Curtis s,
R. В. В i r d, Molecular Theory of Gases and Liquids, New York,
1954. (См. перевод: Дж. д e Бур, P. Б. Б e p д, Квантовая
теория уравнения состояния, в книге Дж. Гиршфельдер,
Ч. К е р т и с с, Р. Б е р д, Молекулярная теория газов и
жидкостей, ИЛ, 1961.)
39. 3 и н о в ь е в а К. Н., ЖЭТФ, 29, 899 (1955).
40. Е с е л ь с о н В. Н. и Б е р е з н я к Н. Г., ДАН СССР, 99, 365
(1954).
41. 3 и н о в ь е в а К. Н., ЖЭТФ., 28, 125 (1954).
42. L о v е j о у D. R., Canad. Journ. Phys., 33, 19 (1955).
43. A t k i n s K. R., Liquid Helium, London, 1950, p. 233—234.
44. M e i s s n e r H. P., S e f e r i a n R., Chem. Eng. Progr., 47, 579
(1951).
45. Ridel L., Chem. Ing. Techn., 26 (1954).
46. R о w 1 i n s о n J. S., Trans. Faraday Soc, 50, 647 (1954).
47. P r i g о g i n e I., В e 1 1 e m a n s A., N a a r - С о 1 i n C,
Journ. Chem. Phys., 26, 710, 751 (1957).
48. Hirschfelder J. О., С u r t i s s С F., В i r d R. В.,
Molecular Theory of Gases and Liquids, New York, 1954. (См. перевод:
Д ж. Гиршфельдер, Ч. Кертисс, Р. Берд,
Молекулярная теория газов и жидкостей, ИЛ, 1961.)
49. В г о с k J. R., В i г d R. В., Amer. Inst. Chem. Eng. Journ., 1,
147 (1955).
50. Т. L. H i 1 1, Statistical Mechanics, New York, 1956. (См. перевод:
Т. Л. X и л л, Статистическая механика, ИЛ, 1960.)
51. S с h i f f L. I., Quantum Mechanics, New York, 1949. (См. перевод:
Л. Шифф, Квантовая механика, ИЛ, 1959.)
52. Born М., Green Н. S., Proc. Roy. Soc, А188, 10 (1946).
53. Y v о n J., La theorie statistique des fluides et Tequation d'etat,
Paris, 1935.

286
Литература
54. О п о S., Progr. Theor. Phys., 5, 822 (1950).
55. Боголюбовы. H., Проблемы динамической теории в
статистической физике, М.— Л., 1946.
56. FournetG., Journ. phys. rad., 12, 502 (1951).
57. Kirkwood J.G., Journ. Chem. Phys., 3, 300 (1935).
58. Kirkwood J. G., M a u n E. K., A 1 d e r B. J., Journ. Chem.
Phys., 18, 1040 (1950).
59. Kirkwood J. G., L e w i n s о n N. A., A 1 d e r B. J.,
Journ. Chem., Phys., 20, 929 (1952).
60. G r e e n H. S., Proc. Roy. Soc, A189, 103 (1947).
61. В u f f F. P., Zs. Electrochem., 56, 311 (1952).
62. M с L e 1 1 a n A. G., Proc. Roy. Soc, A213, 274 (1952).
63. H a r a s i m a A., Journ. Phys. Soc. Japan, 8, 343 (1953).
64. К о n d о S., Journ. Phys. Soc. Japan, 10, 381 (1955).
65. T e r H a a r D., Elements of Statistical Mechanics, New York,
1954.
66. R i се О. K., Journ. Chem. Phys., 15, 314 (1947); Critical
Phenomena, в книге Thermodynamics and Physics of Matter., ed. by
Rossini F. D., Princeton, 1955.
67. A d a m N. K., Physics and Chemistry of Surfaces, London, 1941.
(См. перевод: H. К. Адам, Физика и химия поверхностей,
М.—Л., 1947.)
68. К a t s u г a S., Journ. Chem. Phys., 22, 1277 (1954); Progr. Theor.
Phys., 11, 476 (1954).
69. Hill T. L., Journ. Phys. Chem., 57, 324 (1953); Journ. Chem.
Phys., 23, 812 (1955).
70. О n о S., Progr. Theor. Phys., 6, 447 (1951).
71. M с M i 1 1 a n W. G., MayerJ.E., Journ. Chem. Phys., 13, 276
(1945).
72. В u f f F. P., S t i 1 1 i n g e r F. H., Journ. Chem. Phys., 25, 312
(1956).
73. К i r k w о о d J. G., В u f f F. P., Journ. Chem. Phys., 19, 774
(1951).
74. О n о S., Journ. Chem. Phys., 19, 504 (1951); Progr. Theor. Phys.,
8, 1 (1952).
75. К i 1 p a t r i с k J. E., Journ. Chem. Phys., 21, 274 (1953).
76. Cramers H., Mathematical Methods of Statistics, Princeton,
1951. (См. перевод: Г. Крамере, Математические методы
в статистике, ИЛ, 1960.)
77. S a i t 6 N.. Bull. Kobayasi Inst. Phys. Res. Japan, 1, 157 (1951).
78. О n о S., Mem. Fac. Eng. Kyushu Univ., 12, 9 (1950).
79. On о S., Journ. Chem. Phys., 18, 397 (1950); Journ. Phys. Soc.
Japan, 6, 10 (1951).
80. F r e e m a n M. P., HalseyG. DM Journ. Phys. Chem., 59, 181
(1955).
81. M а у e r J. E., Journ. Chem. Phys., 5, 67 (1937).
82. M а у e r J. E., Journ. Phys. Chem., 43, 71 (1939).
83. Irving J. H., Kirkwood J. G., Journ. Chem. Phys., 18,
817 (1950).
84. G r e e n H. S.f The Molecular Theory of Fluids, Amsterdam, 1952.
85. RushbrookeG. S., Proc. Roy. Soc, Edinburgh, 60, 182 (1940).

Литература
287
86. Е i sens t е i n A.,Gi ngr i ch N. S., Phys. Rev., 62, 261 (1942).
87. В a 1 y, D о n n a n, Journ. Chem. Soc, 81, 907, (1902).
88. Rudorf G., Ann. d. Phys., 29, 751 (1909).
89. TolmanR. C, Journ. Chem. Phys., 17, 118 (1949).
90. Harasima A., Proceedings of the International Conference of
Theoretical Physics, Tokyo, 1954.
91. Harasima A., Molecular Theory of Surface Tension, в книге
Advances in Chemical Physics, Vol. I, Nev York, 1958.
92. H i 1 1 T. L., Journ. Chem. Phys., 19, 261 (1951).
93. H i 1 1 T. L., Journ. Chem. Phys., 20, 141 (1952).
94. M а у e r J. E., M а у e r M. J., Statistical Mechanics, New York,
1940, p. 266—269. (См. перевод: Дж. Майер, M. Г е п п е р т-
М а й е р, Статистическая механика, ИЛ, 1952.)
95. Tonks L., Phys. Rev., 50, 955 (1936).
96. D е b у е Р., Н и с k е 1 Е., Phys. Zs., 24, 185 (1923).
97. S с h m u t z е г Е., Zs. phys. Chem., 204, 131 (1955).
98. WagnerC, Phys. Zs., 25, 474 (1924).
99. Oka S., Proc. Phys.- Math. Soc. Japan, 14, 233, 649 (1932).
100. Ons age r L., Samaras N. N.. Journ. Chem. Phys., 2, 528(1934).
101. SchwenkerG., Ann. d. Phys., 11, 525 (1931).
102. DuMond J. W., Cohen E. R., Rev. Mod. Phys., 25, 691
(1953).
103. S t e e 1 e W. A., HalseyG. D., Journ. Chem. Phys., 22, 979
(1954).
104. Steele W.A., HalseyG. D., Journ. Phys. Chem., 59, 57 (1955).
105. H i 1 1 T. L., Journ. Chem. Phys., 16, 181 (1948).
106. M u 1 1 e r A., Proc. Roy. Soc, A154, 624 (1936).
107. BrunauerS., EmmettP. H., Teller E., Journ. Amer.
Chem. Soc, 60, 309 (1938).
108. BrunauerS., Adsorption of Gases and Vapors, Princeton, 1943.
109. T о d a M., Journ. Phys. Soc. Japan., 10, 512 (1955).
110. A t k i ns K. R., Canad. Journ. Phys., 31, 1165 (1953).
111. Френкель Я. И., Кинетическая теория жидкостей, в
Собрании избр. работ, том 3, Изд-во АН СССР, 1959.
112. В ornM., Со ur an t R., Phys. Zs., 14, 731 (1913).
ИЗ. К о t h a r i D. S., AuluckF.C, Nature, 159, 204 (1947).
114. T r i k h a S. K., R и s t g i O. P., Progr. Theor. Phys., 15, 296
(1956); 17, 303 (1957).
115. Prigogine I., SaragaL., Journ. Chim. phys., 49, 399
(1952).
116. H a r a s i m a A., ShimuraY., Journ. Phys. Soc, Japan, 11,
14 (1956).
117. В г о и t R., NauenbergM., Phys. Rev., 112, 1452 (1958).
118. MacLellan, Proc. Roy. Soc, A217, 92 (1953).
119. К i r k w о о d J. G., Journ. Chem. Phys., 18, 380 (1950).
120. О n о S., Mem. Fac. Eng. Kyushu Univ., 10, 195 (1947).
121. L e n n a r d - J о n es J. E., Devonshire A. F., Proc.
Roy. Soc, A163, 53 (1937); A165, 1 (1938),
122. HirschfelderJ. O., Stevenson D. P., EyringH.,
Journ. Chem. Phys., 5, 896 (1937).
123. R i с e О. K., Journ. Chem. Phvs., 6, 476 (1938).

288
Литература
124. W е n t о г f R. Н., В uehler R. J., H irschf el der J. Ом
С u r t i s s С. F., Journ. Chem. Phys., 18, 1484 (1950).
125. FowlerR.H., GuggenheimE. A., Statistical
Thermodynamics, 2nd ed., London, 1949. (См. перевод: P. Ф а у л e p,
Э. Гуггенгейм, Статистическая термодинамика, ИЛ, 1949.)
126. Н а г a s i m a A., Proc. Phys.- Math. Soc. Japan, 22, 825 (1940).
127. Corner J., Trans. Faraday Soc, 44, 1036 (1948).
128. Lennard-Jones J. E., Corner J., Trans. Faraday Soc,
36, 1156 (1940).
129. H a r a s i m a A., Proc Phys.- Math. Soc Japan, 23, 983 (1941).
130. Cernuschi F., Eyring H., Journ. Chem. Phys., 7, 547
(1939).
131. P e e'k H. M., Hill T. L., Journ. Chem. Phys., 18, 1252 (1950).
132. RowlinsonJ. S., CurtissC. F., Journ. Chem. Phys., 19
1519 (1951).
133. К u r a t a M., Busseiron Kenkyu, 39, 77 (1951)
134. О n о S., Nuovo Cimento, Suppl., 9, 166 (1958).
135. On о S., Mem. Fac Eng., Kyushu Univ., 12, 201 (1950).
136. HildebrandJ. H., Journ. Amer. Chem. Soc, 51, 66 (1929).
137. К u r a t a M., Busseiron Kenkyu, 27, 37 (1950).
138. OnoS., Mem. Fac. Eng., Kyushu Univ., 12, 1 (1950).
139. OnoS., Journ. Phys. Soc. Japan, 5, 232 (1950).
140. Murakami Т., OnoS., Tamura M., Kurata M.,
Journ. Phys. Soc. Japan., 6, 309 (1951).
141. HildebrandJ.H., Solubility, New York, 1939. (См. перевод:
ГильдебрандГ., Растворимость неэлектролитов, М.— Л.,
1938.)
142. BeltonJ.W., EvansM. G., Trans. Faraday Soc, 37, 1 (1941);
41, 1 (1945).
143. ЖуховицкийА. А., ЖФХ, 17, 313 (1943).
144. G u g g e n h e i m E. A., Trans. Faraday Soc, 41, 150 (1945).
145. DefayR., Prigogine I., Trans. Faraday Soc, 46, 199
(1950).
146. Prigogine I., NarbondJ., Trans. Faraday Soc, 44, 628
(1948).
147. R i с e О. K., Journ. Phys. Chem., 31, 207 (1927).
148. P r i g о g i n e I., DefayR., Journ. Chim. phys., 46, 367 (1949).
149. DefayR., Journ. Chim. phys., 51, 299 (1954).
150. Prigogine I., Sarolea L, Journ. Chim. phys., 47, 807
(1950).
151. M i 1 1 e r A. R., The Theory of Solutions of High Polimers,
London, 1948.
152. P r i g о g i n e I., MarechalJ., Journ. Coll. Sci., 7, 122 (1952).
153. P r i g о g i n e I., Journ. Chim. phys., 47, 33 (1950).
154. M a г e с h a i J., Trans. Faraday, Soc, 48, 601 (1952).
155. Kurata M., Busseiron Kenkyu, 56, 60 (1952).
156. T r a u b e I., Liebigs Annalen, 265, 27 (1891).
157. А г о n о w R. H., W i t t e n I., Journ. Chem. Phys., 28, 405 (1958).
158.* Русинов А. И., Термодинамика поверхностных явлений,
Л., 1960.
159 *. Ф и ш е р И. 3., Статистическая теория жидкостей, М., 1961.

ОГЛАВЛЕНИЕ
Предисловие редактора перевода . 5
Введение 7
Часть I. Термодинамика и квазитермодинамика 11
Глава I. Термодинамика 13
§ 1. Термодинамические величины поверхностного слоя 13
1. Разделяющая поверхность ( 13 ). 2. Вклад
межфазового слоя в термодинамические величины ( 15 ).
§ 2. Плоская граница раздела 16
3. Определение поверхностного натяжения ( 16 ). 4.
Поверхностная свободная энергия ( 18 ). 5.
Термодинамические соотношения для плоской границы ( 21 ).
6. Адсорбция на плоской поверхности раздела ( 24 ).
§ 3. Сферическая граница раздела 29
7. Определение поверхностного натяжения ( 29 ). 8.
Поверхность натяжения ( 33 ). 9. Фундаментальные
термодинамические уравнения для сферической
границы ( 35 ). 10. Термодинамические соотношения
между избыточными величинами сферической
границы ( 37 ). 11. Зависимость поверхностного
натяжения от кривизны ( 42 ). 12. Давление пара и работа
образования капли и пузырька ( 46 )
Глава II. Гидростатический подход
13. Механическое определение поверхностного
натяжения в случае плоской границы раздела ( 52 ). 14.
Механическое определение поверхностного
натяжения в случае сферической границы раздела ( 55 ).
15. Механическое определение поверхностного
натяжения через работу, выполненную системой ( 60 ).
52
Глава III. Квазитермодинамика
16. Вводные замечания ( 63 ). 17. Основной
постулат квазитермодинамики в случае плоской границы
63

290
Оглавление
раздела ( 64 ). 18. Условие равновесия для плоской
границы раздела ( 66 ). 19. Квазитермодинамические
соотношения для плоской границы раздела ( 67 ).
20. Квазнтермодинамические соотношения для
сферической границы раздела ( 69 ).
Глава IV. Применение термодинамики необратимых процессов. 73
21.Граница раздела между двумя фазами, не
находящимися в равновесии ( 73 ).
Глава V. Эмпирические уравнения зависимости поверхностного
натяжения от температуры 81
22. Закон соответственных состояний и
эмпирические формулы для поверхностного натяжения ( 81 ).
Часть II. Статистическая механика
Глава I. Метод статистической термодинамики 93
§ 1. Канонический ансамбль 93
23. Статистическая сумма и поверхностное
натяжение ( 93 ). 24. Молекулярные функции
распределения ( 96 ). 25. Поверхностное натяжение на плоской
поверхности раздела в многокомпонентных системах
( 100 ). 26. Поверхностное натяжение на плоской
границе раздела между чистой жидкостью и ее паром
( 106 ). 27. Поверхностное натяжение на
сферической поверхности раздела ( 111 ).
§ 2. Большой канонический ансамбль 117
28. Большая статистическая сумма и поверхностное
натяжение ( 117 ). 29. Двухфазная система в большом
каноническом ансамбле ( 120 ).30. Молекулярные
функции распределения и выражение большой
статистической суммы в виде ряда ( 124 ). 31. Разность
поверхностных натяжений раствора и чистого
растворителя ( 130 ). 32. Применение точного разложения в
ряд по активностям к рассмотрению поверхностного
слоя ( 137 ). 33. Адсорбция газа на твердой
поверхности ( 144 ).
Глава II. Механическое определение поверхностного натяжения 150
34. Статистическое выражение для тензора давления
в жидкостях ( 150 ). 35. Плоская поверхность раздела
( 153 ). 36. Сферическая поверхность раздела ( 159 ).

Оглавление 291
Глава III. Численные расчеты 166
§ 1. Чистая жидкость 166
37. Поверхность разрыва ( 166 ). 38.
Квазитермодинамическая теория ( 171 ).
§ 2. Раствор электролита 179
39. Поверхностное натяжение разбавленных
растворов сильных электролитов ( 179 ). 40.
Численный расчет для раствора одновалентных пар ионов
( 189 ).
§ 3. Адсорбция газа на твердой поверхности .... 194
41. Адсорбция молекул одноатомного газа на
твердой поверхности ( 194 ).
Глава IV. Квантовая статистическая механика 205
42. Квантовые эффекты для поверхностного
натяжения ( 205 ).
Часть III. Рассмотрение с помощью решеточной модели
Глава I. Чистые жидкости 215
§ 1. Теория свободного объема 215
43. Метод ячеек для вычисления статистической
суммы ( 215 ). 44. Свободный объем и коллективная
энтропия ( 217 ). 45. «Сглаженный» свободный объем
( 219 ). 46. Поверхностная энергия ( 221 ). 47.
Поверхностное натяжение ( 226 ).
§ 2. Теория дырок 230
48. Общий обзор теории дырок для жидкостей ( 230 ).
49. Свободная энергия двухфазной системы ( 235 ).
50. Вычисление равновесного распределения
локальной плотности ( 240 ). 51. Поверхностное
натяжение и поверхностная энергия ( 245 ). 52. Связь с
квазитермодинамической теорией ( 250 ).
Глава П. Растворы неэлектролитов 255
§ 1. Регулярные растворы 255
53. Применение метода ячеек к растворам ( 255 ).
54. Регулярный раствор с плоской границей
раздела ( 258 ). 55. Поверхностное натяжение и
адсорбционная формула Гиббса ( 263 ). 56. Модель однослойной
межфазовой области ( 267 ). 57. Сравнение с
экспериментом ( 269 ). 58. Динамическое поверхностное
натяжение ( 271 ).
§ 2. Растворы полимеров 274
59. Решеточная теория для атермических растворов
полимеров ( 274 ). 60. Поверхностное натяжение
атермических растворов полимеров ( 276 ).
Литература. . „ . . . . . г 284

С. Оно, С. Кондо
МОЛЕКУЛЯРНАЯ ТЕОРИЯ
ПОВЕРХНОСТНОГО НАТЯЖЕНИЯ
в жидкостях
Редактор В. Захаров
Художник Н. Л. Усачев
Технический редактор А. Д. Хомяков
Сдано в производство 29/1 1963 г.
Подписано к печати 10/V 1963 г.
Бумага 84x1087» =4,6 бум. л.
15,0 печ. л.
Уч.-изд. л. 12,5. Изд. М 2/1657
Цена 1 р. 08 к. Зак. 1800
ИЗДАТЕЛЬСТВО
ИНОСТРАННОЙ ЛИТЕРАТУРЫ
Москва, 1-й Рижский пер., 2
2-я тип. Изд-ва АН СССР,
Москва, Шубинский пер., д. 10