ll—-----Г” —	_
УЧЕБНИК / ДЛЯ ВУЗОВ л
А. М. Андронов
Е. А. Копытов
Л. Я. Гринглаз
ТЕОРИЯ ВЕРОЯТНОСТЕЙ
И МАТЕМАТИЧЕСКАЯ
СТАТИСТИКА
ПИТЕР
Москва  Санкт-Петербург  Нижний Новгород • Воронеж
Ростов-на-Дону • Екатеринбург  Самара • Новосибирск
Киев • Харьков • Минск
2004
ББК 22.17я7
УДК 519.2(075)
К65
Рецензенты:
В. Б. Мелас, доктор физико-математических наук, профессор Санкт-Петербургского
государственного университета.
П. П. Бочаров, доктор технических наук, профессор, зеведующий кафедрой теории
вероятностей и математической статистики Российского университета дружбы народов.
Андронов А. М., Копытов Е. А., Гринглаз Л. Я.
К65 Теория вероятностей и математическая статистика: Учебник для вузов. — СПб.:
Питер, 2004. — 461 с.: ил. — (Серия «Учебник для вузов»),
ISBN 5-94723-615-Х
Перед вами — расширенный учебник по теории вероятностей и математической статистике. Тради-
ционный материал пополнен такими вопросами, как вероятности комбинаций случайных событий, слу-
чайные блуждания, линейные преобразования случайных векторов, численное нахождение нестационар-
ных вероятностей состояний дискретных марковских процессов, применение методов оптимизации для
решения задач математической статистики, регрессионные модели. Главное отличие предлагаемой книги
от известных учебников и монографий по теории вероятностей и математической статистике заключается
в ее ориентации на постоянное использование персонального компьютера при изучении материала. Изло-
жение сопровождается многочисленными примерами решения рассматриваемых задач в среде пакетов
Mathcad и STATISTICA. Книга написана иа основе более чем тридцатилетнего опыта авторов в препода-
вании дисциплин теории вероятностей, математической статистики и теории случайных процессов для
студентов различных специальностей высших учебных заведений.
Представляет практический интерес как для студентов и преподавателей вузов, так и для всех, кто
интересуется применением современных вероятностно-статистических методов.
ББК 22.17я7
УДК 519.2(075)
Все права защищены. Никакая часть данной книги не может быть воспроизведена е какой бы то ни было форме без письменного
разрешения владельцев авторских прав.
Информация, содержащаяся в данной книге, получена из источников, рассматриваемых издательством как надежные. Тем не
менее, имея в виду возможные человеческие или технические ошибки, издательство не может герантировать абсолютную точ-
ность и полноту приводимых сведений и не несет ответственности за возможные ошибки, связанные с использованием книги.
ISBN 5-94723-615-Х
© ЗАО Издательский дом «Питер», 2004
Краткое содержание
Введение ................................................. 8
1.	Пространство элементарных событий....................11
2.	Классическое определение вероятностей
и повторные испытания...................................51
3.	Дискретные случайные величины........................74
4.	Непрерывные случайные величины.......................92
5.	Многомерные дискретные случайные величины...........129
6.	Многомерные непрерывные случайные величины..........151
7.	Суммирование случайных величин и предельные теоремы .... 182
8.	Цепи Маркова........................................209
9.	Дискретные марковские процессы......................245
10.	Задачи математической статистики
и первичная обработка данных...........................278
11.	Точечные оценки параметров распределений...........310
12.	Оценивание с помощью доверительных интервалов......337
13.	Проверка статистических гипотез....................367
14.	Регрессионный и корреляционный анализ..............406
Литература.............................................454
одержание
^едение.................................................................8
Общая характеристика книги..............................................8
Структура книги.........................................................8
Стиль, нумерация и выделения в тексте...................................9
Благодарности.......................................................... 10
От издательства ........................................................10
Пространство элементарных событий.......................................11
1.1.	События и операции над ними........................................11
Компьютерный практикум № 1. Операции над событиями в пакете Mathcad....16
1.2.	Комбинации событий.................................................25
1.3.	Структурная надежность систем......................................29
Компьютерный практикум № 2. Комбинации событий в пакете Mathcad.........31
1.4.	Вероятности на дискретном пространстве элементарных событий........34
1.5.	Вероятность наступления комбинации событий.........................42
Компьютерный практикум № 3. Вероятности событий в пакете Mathcad........45
Задачи..................................................................48
Классическое определение вероятностей и повторные
испытания..............................................................51
2.1.	Различные определения вероятностей................................51
2.2.	Элементы комбинаторики............................................52
2.3	Последовательности испытаний......................................56
2.4.	Случайные блуждания* .............................................59
Компьютерный практикум № 4. Анализ повторных испытаний
и случайных блужданий в пакете Mathcad..............................66
Задачи ................................................................70
. Дискретные случайные величины.........................................74
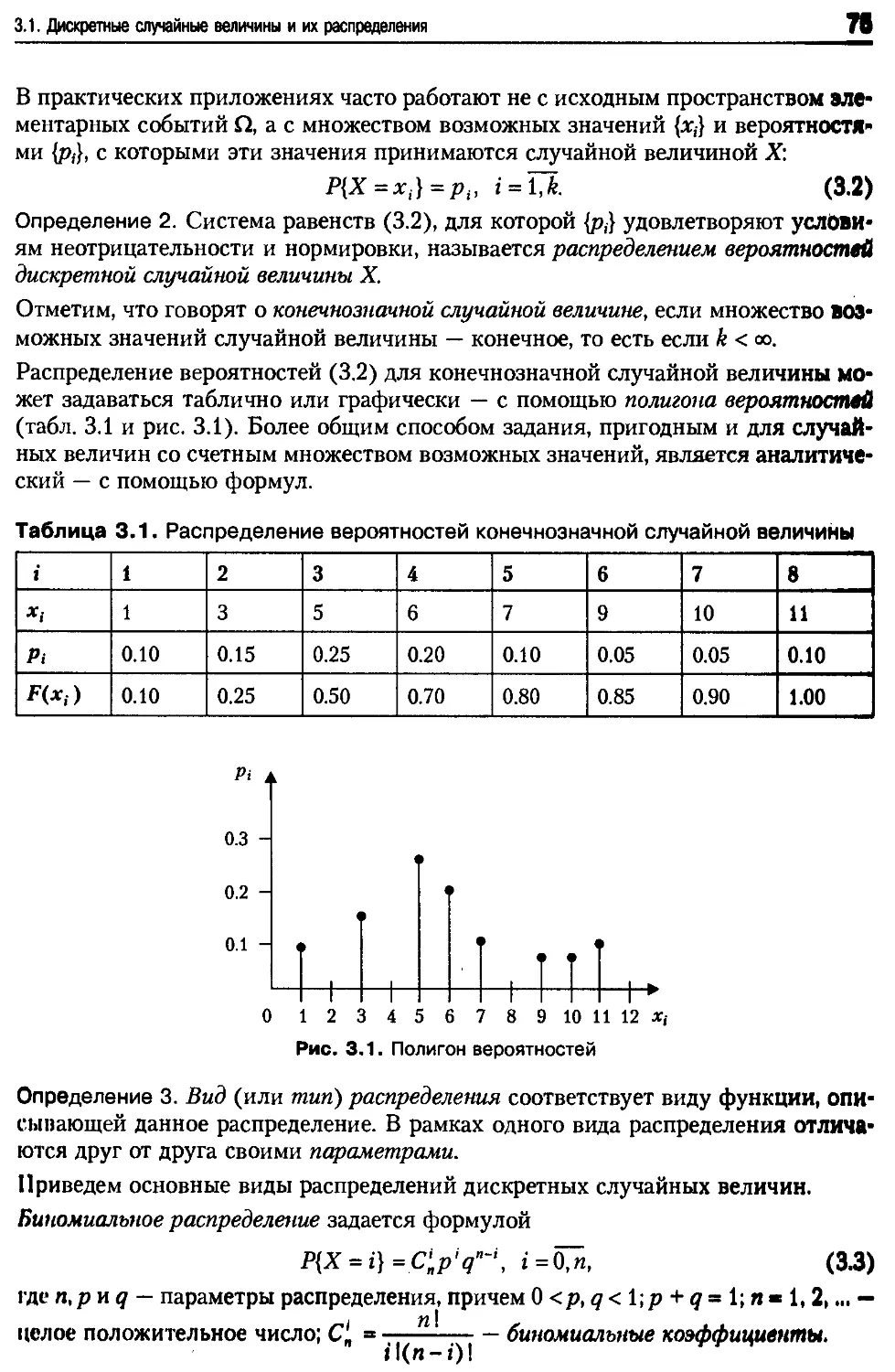
3 1 Дискретные случайные величины и их распределения...................74
3.2 Млтематическое ожидание дискретных случайных величин...............81
3 3 Функции дискретных случайных величин...............................83
Компьютерный практикум Nv 5. Распределения дискретных случайных величин
....................86
Содержание
5
4.	Непрерывные случайные величины .....................................92
4.1.	Распределения непрерывных случайных величин ....................92
4.2.	Математическое ожидание непрерывных случайных величин..........102
4.3.	Функции и моменты непрерывных случайных величин................104
4.4.	Распределения функций непрерывных случайных величин*...........109
4.5.	Неравенства для моментов и вероятностей*.......................114
Компьютерный практикум № 6. Распределения непрерывных случайных величин
в пакете Mathcad..................................................118
Задачи..............................................................126
5.	Многомерные дискретные случайные величины.........................129
5.1.	Распределения многомерных дискретных случайных величин........129
5.2.	Функции многомерных дискретных случайных величин..............135
5.3.	Индикаторы событий*...........................................140
Компьютерный практикум № 7. Многомерные дискретные случайные величины
в пакете Mathcad..................................................142
Задания для самостоятельной работы..................................148
Задачи..............................................................149
6.	Многомерные непрерывные случайные величины........................151
6.1.	Распределения многомерных непрерывных случайных величин........151
6.2.	Функции многомерных непрерывных случайных величин..............157
6.3.	Линейные преобразования случайных векторов*....................159
6.4.	Многомерное нормальное распределение* .........................167
Компьютерный практикум № 8. Двумерное нормальное распределение......171
Компьютерный практикум № 9. Многомерное нормальное распределение...176
Задачи..............................................................180
7.	Суммирование случайных величин
и предельные теоремы ...................................................182
7.1.	Суммирование дискретных случайных величин......................182
7.2.	Суммирование непрерывных случайных величин.....................185
7.3.	Суммирование независимых многомерных случайных величин*........187
7.4.	Центральная предельная теорема.................................194
7.5.	Закон больших чисел............................................196
Компьютерный практикум № 10. Суммирование дискретных случайных величин . . 197
Компьютерный практикум № 11. Суммирование непрерывных случайных величин ..201
Компьютерный практикум № 12.	Предельные теоремы теории вероятностей .... 203
Задания для самостоятельной	работы..................................205
Задачи..............................................................206
8.	Цепи Маркова ......................................................209
8.1.	Основные определения...........................................209
8.2.	Классификация состояний и цепей Маркова........................215
8.3.	Эргодические конечные цепи.....................................218
8.4.	По, летающие цепи Маркова......................................222
Содержание
Компьютерный практикум № 13. Анализ цепей Маркова в пакете Mathcad....237
Задания для самостоятельной работы....................................242
Задачи................................................................242
Дискретные марковские процессы........................................245
9.1.	Определение марковского процесса ................................245
9.2.	Уравнения Колмогорова........................................... 250
9.3.	Пуассоновский процесс............................................252
9.4.	Численное решение уравнений Колмогорова..........................255
9.5.	Стационарное распределение вероятностей состояний................259
9.6.	Процессы размножения и гибели. Процессы массового обслуживания...263
Компьютерный практикум № 14. Анализ дискретных марковских процессов
в пакете Mathcad (часть 1) ..........................................268
Компьютерный практикум № 15. Анализ дискретных марковских процессов
в пакете Mathcad (часть 2) ..........................................272
Задания для самостоятельной работы....................................275
Задачи................................................................276
1 Задачи математической статистики и первичная
обработка данных......................................................278
10.1.	Задачи математической статистики ...............................278
10.2.	Представление статистических данных.............................281
10.3.	Определения и свойства выборочных характеристик.................284
Компьютерный практикум № 16. Решение задач дескриптивной статистики
в пакете STAT1STICA..................................................287
Компьютерный практикум № 17 Работа с распределениями случайных величин
в пакете STATISTICA..................................................299
Задания для самостоятельной работы....................................308
Задачи................................................................308
1. Точечные оценки параметров распределений............................зю
111. Определение и основные свойства точечных оценок...................310
I I 2 Неравенство Рао—Крамера и эффективность*.........................316
11.3. Могод моментов для нахождения оценок параметров распределения....319
1 1.4. Метод максимального правдоподобия...............................322
11.5. Достаточные статистики*..........................................325
Компьютерный практикум № 18. Методы точечного оценивания параметров
распродслений в пакете Mathcad......................................326
Задания для самостоятельной работы.....................................334
Задачи.................................................................334
2. Оценивание с помощью доверительных интервалов . . 337
I2 I Основные определения ...........................................  337
1? 2 I locipooiinn д()1Н1|)иннн>ных интервалов в случае
цсимнмни'н’ми норм.ип.ных оценок................................... 340
12.3. Ochohiii.u р.н 11| ч д'ионии маюмагичоской шагистики............346
19 Л Ihii iihuiiihh И( ни II 111 I < itli.in.tx MIIHHIU.UHMI И (flVHHH МИЛЫХ НЫПОООК
Содержание
7
12.5	. Численный метод построения доверительных интервалов
для параметрической функции*.........................................356
Компьютерный практикум № 19. Построение доверительных интервалов
в пакете Mathcad...................................................361
Задания для самостоятельной работы...................................364
Задачи...............................................................365
13.	Проверка статистических гипотез....................................367
13.1.	Основные понятия ..............................................367
13.2.	Проверка гипотез относительно вероятности......................373
13.3.	Проверка гипотез о математическом ожидании.....................377
13.4.	Проверка гипотез о дисперсии нормальной совокупности...........380
13.5.	Наиболее мощные критерии*......................................382
13.6.	Непараметрические критерии для проверки гипотез
о распределениях случайных величин...................................386
13.7.	Непараметрические критерии сравнения двух совокупностей .......391
Компьютерный практикум № 20. Непараметрическая проверка гипотез
в пакете STATISTICA................................................393
Задания для самостоятельной работы...................................401
Задачи...............................................................402
14.	Регрессионный и корреляционный анализ..............................406
14.1.	Одномерная линейная регрессия .................................406
14.2.	Проверка адекватности модели одномерной линейной регрессии ....412
14.3.	Многомерная линейная регрессия.................................418
14.4.	Проверка адекватности модели многомерной линейной регрессии....426
14.5.	Общая модель регрессии.........................................431
14.6.	Статистическое оценивание корреляционных зависимостей..........435
Компьютерный практикум № 21. Оценка параметров модели линейной регрессии
в пакете STATISTICA................................................436
Задания для самостоятельной работы...................................451
Задачи...............................................................452
Литература..............................................................454
Алфавитный указатель ...................................................455
ведение
щая характеристика книги
шая книга представляет собой расширенный учебник по теории вероятностей
ia'1'ематической статистике, ориентированный на постоянное использование
сональных компьютеров при изучении излагаемого материала. Она предна-
чена для студентов высших учебных заведений, обучающихся по различным
циалыюстям, в их числе: информатика и вычислительная техника, приклад-
। информатика, математика и компьютерные науки, математическое обеспече-
; и администрирование информационных систем и др.
1астоящее время имеется много прекрасных учебников и монографий по тео-
а вероятностей и математической статистике, написанных в классическом
)ле. Однако практически ни в одной из них нет компьютерного сопровожде-
я, когда теоретические результаты реализуются и иллюстрируются с помо-
ю компьютерных программ. На наш взгляд, последнее необходимо по двум
ичпиам. Во-первых, персональные компьютеры в огромной степени расширя-
возможиости рассмотрения численных примеров и экспериментальных рас-
к>1>. Опп позволяют отойти от рассмотрения нарочито упрощенных, учениче-
нх задач и формулировать и решать более приближенные к практике и более
персгпые задачи. Во-вторых, предоставляемая ими визуализация изучаемых
тятиii н закономерностей позволяют быстрее и лучше освоить излагаемый ма-
риал. К этому следует добавить эффект активной формы обучения, когда уча-
ийся самостоятельно выполняет на компьютере разные задания. Этим самым
I приобщается к математике посредством компьютера.
асюящая книга написана на основе более чем тридцатилетнего опыта авторов
преподавании дисциплин теории вероятностей и математической статистики
in студентов различных высших учебных заведений и специальностей. В по-
|едпис годы осуществлялся пересмотр методики преподавания на основе широ-
>к> использования персональных компьютеров.
Структура книги
'одержание мни и делшея на три части. Первая часть (сланы 1 7) содержит
радишн iitiii.ni .м.исрнал ио icopini вероятностен. Изложение не использует тео-
““ ........  ииняегся	nocia io'iiio c i росим. Вторая часть (сланы 8 н 9) дает
Введение
9
ся только процессами с дискретным пространством состояний. Последняя часть
книги (главы 10-14) излагает основы математической статистики.
Главы делятся на разделы. Некоторые из них помечены звездочкой, говорящей
о том, что раздел содержит дополнительный материал и может быть при жела-
нии пропущен.
В конце глав имеются компьютерные практикумы, задания для самостоятельной
работы (на компьютере) и раздел «Задачи».
Компьютерный практикум ставит своей целью реализацию и иллюстрацию на
компьютере соответствующих теоретических положений, а также получение
практических навыков в решении задач. Можно добавить, что попутно студенты
приобретают навыки работы на компьютере, алгоритмизации и программирова-
ния задач. В практикумах используется два компьютерных пакета программ:
Mathcad и STATISTICA. Первый представляет собой язык программирования,
ориентированный на математические вычисления. Запись программы на этом
языке и принятая в математике запись формул и алгоритмов фактически совпа-
дают. Пакет STATISTICA представляет собой мощную интегрированную систе-
му статистического анализа и обработки данных. Для этих целей в состав пакета
включены разнообразные статистические модули. В процессе решения конкрет-
ной задачи в пакете STATISTICA необходимо вызвать требуемый модуль, вве-
сти исходные данные, установить необходимые параметры и выбрать выходную
форму с полученными результатами.
Практикум начинается с изложения необходимого справочного материала, далее
следует описание реализации и выполнения заданий. Основной составляющей
практикума, проводимого на базе системы Mathcad, является компьютерная
программа (или пользовательская функция). Обычно приводится ее текст, со-
держащий необходимые пояснения. Слабо подготовленный по программирова-
нию студент может просто набрать этот текст, а затем провести соответствую-
щие расчеты. Хорошо подготовленному студенту рекомендуется разобраться в
логике работы программы и постараться улучшить ее. При разработке программ
авторы в первую очередь стремились сделать их простыми для понимания, так
ч то здесь имеется большой простор для совершенствования. Авторы будут рады
получить от читателей соответствующие модификации, предложения и заме-
чания.
Задания для самостоятельной работы содержат разного рода задания (от состав-
ления новых программ до проведения расчетов по имеющимся программам), ко-
торые студенты должны выполнить на компьютере.
Предлагаемые задачи позволяют закрепить пройденный материал, а также сде-
лать на его основе дальнейшие обобщения.
Стиль, нумерация и выделения в тексте
Главы имеют сквозную нумерацию, от первой до четырнадцатой. Разделы имеют
двойную нумерацию, состоящую из номера главы и номера раздела внутри гла
вы, например, второй раздел седьмой главы имеет номер 7.2. Аналогичным обра
зом нумеруются формулы, теоремы, примеры, таблицы и рисунки. Если один
Введение
смотрении к его номеру приписывается очередная буква русского алфавита,
рпмер, пример 1.2а.
ределения имеют ординарную нумерацию внутри главы. Имеющиеся доказа-
ьства выделяются словом Доказательство. Окончание доказательства или
смотрения серии примеров указывается символом □.
ексте широко используются выделения с помощью курсива — для вводимых
«•делений, формулировки теорем, привлечения внимания к определенной
си текста.
онце книги имеется алфавитный указатель, к которому следует обращаться,
да встречается незнакомый термин.
1агодарности
.....ыражают глубокую благодарность Ирине Геннадьевне Михневич и Ната-
Львовне Савельевой за прекрасную работу по подготовке книги к изданию.
' издательства
ни замечания, предложения и вопросы отправляйте по адресу электронной
!ты comp@piter.com (издательство «Питер», компьютерная редакция).
i будем рады узнать ваше мнение!
ссты приведенных в книге заданий вы можете найти по адресу:
http://www.piter.com/download.
дробную информацию о наших книгах вы найдете на веб-сайте издательства
x//www. piter.сот.
Пространство элементарных
событий
1.1. События и операции над ними
Теория вероятностей, как и любая другая математическая дисциплина, начинает
е неопределяемых понятий. В теории вероятностей это понятия испытания
(унотребимыми синонимами также являются опыт, эксперимент, наблюдение
и пр.) и элементарного события (элементарный исход).
Под испытанием понимается реализация определенного комплекса условий, в
результате которой наступает ровно одно элементарное событие из общей их со-
вокупности, называемой пространством элементарных событий. Пространство
элементарных событий мы будем обозначать заглавной буквой греческого алфа-
вита Q. Входящие в него элементарные события обозначаются строчными буква-
ми греческого алфавита, при необходимости — с индексами: со, со(, со2, со;),... Про-
странство элементарных событий описывается, как и любое множество —
фигурными скобками, в которых перечисляются входящие в него элементарные
события, например, Q = {со 1( со2, со3, ...}.
В зависимости от числа элементарных событий в пространстве, мы будем разли-
чать конечное, счетное и несчетное пространство элементарных событий. Конеч-
ное пространство содержит конечное число элементарных событий, счетное -
бесконечное число, однако такое, которое можно перенумеровать (говорят так-
же — пересчитать). Наконец, несчетное пространство содержит бесконечное чис-
ло элементарных событий, не поддающихся нумерации (пересчету).
Па базе введенных понятий даются другие определения теории вероятностей.
При их формулировке мы будем давать два определения: теоретико-множест-
вен ное, использующее язык теории множеств, и вероятностное, основанное па
содержательном смысле вводимого определения.
Определение 1. Событием (иначе составным событием) называется некоторое
подмножество пространства элементарных событий. Говорят, что событие на-
ступило в результате испытания, если наступило одно из элементарных собы-
тий, входящих в данное событие.
События мы будем обозначать заглавными буквами латинского алфавита Л, /J,
(', ... Как и ранее для пространства Q, событие А описывается с помо1цыо <|>нгур
пых скобок, внутри которых указываются элементарные события, составляющие
эго событие, например, Л <о4, <o(i, <он}.
2
1. Пространство элементарных событий
л приведенного определения естественно вытекает следующее определение,
цюделение 2. События называются эквивалентными (символ эквивалентности =),
ли они состоят из одних и тех же элементарных событий. Эквивалентные со-
ития наступают или не наступают одновременно.
з всевозможных событий два события занимают особое положение — это не-
ыможиое и достоверное события.
пределение 3. Событие называется невозможным, если оно не содержит ни
(пою элементарного события, иначе — это пустое подмножество Q. Невозмож-
>с событие никогда не происходит, оно обозначается 0. Событие называется
хтоверным, если оно содержит все элементарные события пространства Q,
паче — если оно совпадает с самим пространством. Достоверное событие про-
ходит при каждом испытании, оно обозначается V (или просто Q, хотя это
формально некорректно: U — это подмножество Q).
римеры
ример 1.1. Однократное бросание игральной кости. Игральная кость представ-
ив г собой правильной формы кубик, на шести гранях которого точками изобра-
зим числа 1, 2, 3, 4, 5, 6, на каждой грани по одному числу. После бросания кос-
। фиксируют число, записанное на верхней грани кубика. О нем говорят как о
ыпаншем числе очков.
данном случае элементарным событием является число выпавших очков. Если
ыпало г очков, i = 1, ..., 6, то будем говорить, что произошло событие со,. Следова-
'льно, Q = {соь со2, со3, со4, со5, со6}> пространство содержит шесть элементарных со-
итий и является конечным. Событие «число выпавших очков равно 9» является
(•возможным, а событие «число выпавших очков не более 7» является достоверным,
ели А,,,,, обозначает событие «выпало четное число очков», то Ачет = {со 2, ®4> ®е}-
<3 = {(о |, со2, со3, со4} представляет собой событие «число выпавших очков менее пяти»,
ример 1.2. Двукратное бросание игральной кости. Пусть игральная кость броса-
гся дважды. Эти два бросания образуют одно испытание. Если при первом бро-
ни нн выпало г очков, а при второму очков, то будем этот результат записывать в
идс у и считать это элементарным событием. Следовательно, пространство эле-
1сн гарных событий Q = {11, 12, 13, 14, 15, 16, 21, 22, 23, 24, 25, 26, 31, 32, 33, 34,
5, 36, 41, 42, 43, 44, 45, 46, 51, 52, 53, 54, 55, 56, 61, 62, 63, 64, 65, 66}. Более ком-
актпая запись следующая: Q = {ij: i,j е{1, 2, 3, 4, 5, 6}}. Она означает, что рас-
магриваются все пары ij, где i nj пробегают всевозможные значения от 1 до 6.
дли Л_ - событие «при обоих бросаниях выпало одинаковое число очков», то
L  {11, 22, 33, 44, 55, 66}. Событие А^=10 «сумма выпавших очков равна 10», за-
ш ынаетея гак: А£=10 = {46, 55, 64}.
1римор 1.3. Бросание монеты. В соответствии со старинной русской традицией,
удем одну сторону монеты (вне зависимости от ее достоинства и страны) назы-
агь «гербом», а вторую — «решеткой». Пусть монета подбрасывается до первого
ыпадения герба. Вся последовательность таких подбрасываний составляет одно
и ныганпе. Если результат выпадения герба при одном подбрасывании обозпа-
агь Г, а решетки Р, то пространство элементарных событий записывается в виде
1.1. События и операции над ними
13
11 = {Г, РГ, РРГ, РРРГ, РРРРГ, ...}. Мы видим, что число элементарных событий
пространства бесконечно. Это — пример «счетного» пространства элемен тарных
собы тин.
Событие Л5 — «первый герб выпал при пятом бросании» есть Л5 = {РРРРГ}. ()но
состоит только из одного элементарного события РРРРГ. Событие «потре-
бовалось пе более четырех бросаний» записывается так: As4 = {Г, РГ, РРГ,
РРРГ}. Событие В «герб выпал до седьмого подбрасывания, но при подбрасыва-
нии с четным номером» может быть представлено так: В = {РГ, РРРГ, РРРРРГ).
Чтобы записать событие Ачст «герб выпал при подбрасывании с четным номе-
ром», мы введем следующее обозначение, принятое в формальных языках и
грамматиках: i-я степень символа означает, что этот символ в записи повторяет-
ся г раз. Например, Г5 означает ГГГГГ. Теперь можно записать АЧС| = {Р2' 1 /’,:
1=1,2,...}.
Пример 1.4. Задача о встрече. Два приятеля договорились встретиться между
двенадцатью и часом дня в условленном месте. Сконструируем пространство
элементарных событий, соответствующее данной ситуации. Будем рассматри-
ваемый интервал времени обозначать (0, 1), момент прихода первого приятеля х,
а второго приятеля у. Фиксация этих моментов времени будет соответствовать
элементарному событию (х, у). На числовой плоскости оно обозначается точкой.
Все пространство элементарных событий геометрически представляет собой
квадрат с единичной длиной сторон, расположенный в начале положительного
квадранта плоскости. Аналитически это можно записать в виде Q = (0, 1 )х((), 1)
= {(х, у): х, у е(0, 1)}. Отметим, что это — несчетное пространство элементарных
событий: число его элементарных событий нельзя пересчитать или перенумеро-
вать.
Событие А «оба приятеля пришли до половины первого» записывается в виде
А = {(х, у): х, у е(0, 0.5)}. Предположим, что пришедший первым ждет приятеля
четверть часа и уходит, если тот не придет до этого. Тогда событие В «прия тели
встретятся» есть В = {(х, у): х, у е (0, 1), | х - у | < 0.25}.
Пример 1.5. Случайное блуждание на плоскости. Представим себе шахматную доску
и некоторую гипотетическую фигуру на ней, которая может ходить только на
одну клетку или направо по горизонтали, или вверх по вертикали. Вначале фп
гура стоит в нижнем левом углу доски. Это соответствует клетке (полю, па шах-
матном языке) al, если вертикальные ряды клеток обозначать a, b, с, d, е, f, ц, h,
а горизонтальные ряды 1, 2, 3, 4, 5, 6, 7, 8. Опишем перемещение фигуры за пя ть
ходов.
В данном случае будем понимать под одним испытанием все пять ходов фигуры.
Элементарным событием является отдельная траектория, описывающая дниже
нис фигуры в течение этих пяти ходов. Удобно его записывать в виде пятнмер-
ного булевого вектора, компоненты которого принимают значения 0 и 1. i-я ком
попепта вектора соответствует i-му ходу фигуры, 0 — перемещению фигуры
направо, а 1 — перемещению вверх. Так, элементарное событие 00000 означает,
что фигура все время двигалась направо по горизонтали, 11111 — ч то двигалась
вверх но вертикали, 11100 — что первые три шага сделала вверх, а два послед
них направо. Бели обозначить В {(), 1} множество из двух булевых значении
14
1. Пространство элементарных событий
) и 1, а В5 множество всевозможных булевых векторов с пятью компонентами, то
||>остранство элементарных событий Q = В5.
Событие Л,;4 «после пятого шага фигура находится на клетке с4» записывается
срез элементарные события так: Лс4 = {00111, 01011,01101, OHIO, 10011, 10101,
10110, 11001, 11010, 11100}. Этот пример интересен тем, что элементарному со-
>ытию здесь соответствует некоторая траектория движения фигуры. Данная си-
уация характерна для теории случайных процессов, которая будет рассматри-
>аться далее.	□
Геперь мы рассмотрим операции над событиями, важнейшими из которых явля-
о гся сумма, произведение и разность.
Определение 4. Сумма событий А, ,Д2,...,Д4 — это событие
k	г	___ 1
U At = Д + А2 + ... + Д = <! со:Э i = l,k шеД. >,	(1.1)
i=t	I	J
:остоящее из элементарных событий, входящих в события-слагаемые. Оно на-
гупает тогда, когда наступает хотя бы одно из событий-слагаемых: или Д или
12 и т. д. — принцип «или»-«или».
Определение 5. Произведение событий A1,A2,...,Ai — это событие
k	f	___ 1
ПА = Д A2-...-Ak со: V i = 1, Jfe соеДД	(1.2)
I	J
^стоящее из элементарных событий, входящих во все события-сомножители.
Оно наступает, когда наступают все события-слагаемые: и At, и Д, и т. д. —
рипцип «и»-«и».
Рис. 1.1. Диаграммы Венна
Определение 6. Разность событий А и И — это собы тие
А - в - < cd : <о с А, со </ И},
(13)
1.1. События и операции над ними
16
состоящее из элементарных событий, входящих в А, но не входящих в В. Оно на-
ступает, когда событие А наступает, а событие В не наступает.
Введенные выше понятия могут быть проиллюстрированы геометрически с по-
мощью диаграмм Венна (рис. 1.1). На этом рисунке поясняемые понятия выне-
сены на полочку. Соответствующие им события заштрихованы.
Примеры
Пример 1.1а. Однократное бросание игральной кости. Как и раньше, пусть А,,,., —
событие «число выпавших очков четное», а Л<5 — событие «выпало менее пяти
очков». Тогда сумма этих событий происходит, когда выпало или четное число
очков, или когда это число менее пяти: Ачет + Л<5 ={<»,, со2, со3, со4, со6}. Иными
словами, она происходит всегда, когда число выпавших очков не равно пяти.
Произведение этих событий наступает при двух элементарных исходах: число
выпавших очков должно равняться двум или четырем: АчетА<5 = {со2, со4}. Раз-
ность Л<5 - Ачет означает событие «число выпавших очков меньше пяти и нечет-
ное» : Л<5 -Ачет ={®i, ®3}.
Пример 1.2а. Двукратное бросание игральной кости. Произведение двух событий
А. «число выпавших очков на обоих гранях совпадает» и Az=10 «сумма выпавших
очков равна десяти» есть событие, состоящее из одного элементарного собы тия.
Их разность А. - Az=10 = {И, 22, 33, 44, 66}.
Пример 1.3а. Бросание монеты. Событие «герб выпал до пятого бросания, при-
чем это было бросание с четным номером» можно представить в виде произведе-
ния A4„As4 событий А,1ет и As4. Разность As4 -Ачет ={Г, РРГ} означает событие
«герб выпал до пятого бросания, причем это было событие с нечетным номером».
Пример 1.4а. Задача о встрече. Произведение АВ означает событие «оба прияте-
ля пришли до половины первого и встретились», в то время как разность А В,
что «они пришли до половины первого, но не встретились».	□
Между событиями существуют различные отношения. С одним из них мы уже
познакомились, это отношение эквивалентности событий =. Рассмотрим другие
важные отношения.
Определение 7. События называются противоположными, если каждое из них
содержит те элементарные события, которые не содержит другое событие. Если
А — некоторое событие, то противоположное ему событие обозначается А, при
чем это противоположное для А событие единственно. Если некоторое событие
произошло, то противоположное ему событие не произошло, и наоборот.
Противоположное для А событие можно формально определить так:
А = {со е Q: со g А}. Поскольку одновременное наступление события А и противо-
положного ему события А невозможно, то А-А =0. Из определения следует
также, что одно из этих событий происходит обязательно, поэтому А + A =U.
Понятие противоположного события позволяет выразить разность событий и
виде произведения: А -В = АВ.
Определение 8. События А и В называются несовместными, если они не содер-
жа! общих элементарных событий, то есть одновременно наступить не могут,
I fl______________________________
I. I ipiA«!|JCinVI<KS да1 VN*Vn Ш|Л1ИЛ vw«t>r«r<
Следовательно, их пр<>и hkiu une <<и. невозможное событие; AB = 0. О событиях
At, A.,,... loiiop,n, hi.и nonti/mo несовместны, если никакие два из них не со-
IIMCI TIII.I
Онридвпини» u 11 ни i| »i ।, что событие А влечет событие В, и записывают это как
I  /<. ci мн luirtoior ,iнемец гарное событие из А входит в событие В. Наступление
Пып1>| Л iiiii'Mei наступление события В. Очевидно, А В = А, А + В = В.
'нрндинокпо К) События А,, А2,..„ Ak образуют полную группу событий (ина-
i< pa.ifHieiiiie пространства Q), если они; попарно несовместны; не невозмож-
ны, и < умме дают все пространство элементарных событий, то есть достоверное
событие 12. События полной группы называют гипотезами.
Рисунок 1.2 дает графическое представление полной группы событий.
Рис. 1.2. Полная группа событий
Примеры
Пример 1.1b. Однократное бросание игральной кости. Противоположным собы-
тию Ачст является событие Ачет ={«>t, о>3, о>5} — «число выпавших £чков нечет-
но». Если В = {ш2, со 4} — событие «выпало два или четыре очка», то Ачет и В — не-
совместные события. Ясно также, что событие В влечет событие Ачст. События В,
Л и (oG образуют полную группу событий.
Пример 1.2b. Двукратное бросание игральной кости. События At_5: «сумма вы-
павших очков не больше пяти», А6_9: «сумма выпавших очков составляет от шес-
ти до девяти» и А10_12: «сумма выпавших очков больше девяти» образуют пол-
ную группу событий.	□
Компьютерный практикум № 1.
Операции над событиями в пакете Mathcad
Общие положения
I [астоящий практикум открывает цикл работ, выполняемых на персональном
компьютере (ПК). В первой части книги при решении задач теории вероятно-
стей будем использовать пакет Mathcad, во второй части при решении задач ма-
тематической статистики — пакет STATISTICA. Выбор данного программного
обеспечения не случаен. Оба пакета представляют собой интегрированные мно-
гофункциональные системы, предназначенные для проведения разнообразных
вычислений. Они получили широкое распространение и достаточно хорошо
описаны и отечественной Jinrcpaiуре (см. список литературы н конце киши)
При наложении материала практикумов авторы не ставили своей целью полное
научение данных пакетов, а стремились показать, каким образом задачи теории
вероятностей и математической статистики могут быть решены па ПК. Для ус
пепиюго прохождения компьютерных практикумов не требуется предвари гель
пая подготовка по пакетам программ или программированию для ,')ВМ. 11собхо
дпмые для работы сведения будут излагаться по мере изучения практикумов
Дополнительный справочный материал по пакетам Mathcad и STAT1STICA
можно найти в литературе [1, 6]. Читатель, прошедший все практикумы, не голь
ко закрепит теоретический материал курса и решит разнообразные практические
примеры, но и приобретет умение работать с пакетами Mathcad и STATISTIC’Л,
а говоря более обобщенно — умение программировать. Отметим также, что мало
подготовленный читатель может пользоваться представленными программами,
не особенно разбираясь в логике их работы. Для более подготовленного читате-
ля представляются широкие возможности усовершенствования и развития этих
программ.
Цель и задачи практикума
Целью практикума является компьютерная реализация основных операций над
событиями в среде Mathcad.
Задачами данного практикума являются:
□	задание пространства элементарных событий и отдельных событий;
□	проверка принадлежности данного элементарного события составному собы
тию;
□	выполнение операций суммы, произведения и разности событий.
Необходимый справочный материал
В процессе работы в пакете Mathcad создаются документы, которые могут содер-
жать формулы, программы, комментарии, результаты вычислений и графики.
11ростые вычисления реализуются посредством ввода соответствующих формул,
для организации сложных вычислительных процессов составляются программы.
Формулы могут иметь вид арифметического выражения, которое необходимо
вычислить, или вид определяемой функции. Достоинством пакета является про
с гота представления формул, которые имеют естественную запись. Программы
на Mathcad оформляются в виде программных блоков (см. ниже). При вводе
конструкций Mathcad рекомендуется использовать вызываемые на экран палит
ры инструментов, содержащие множество математических символов, ключевые
слова и др. Рядом с выражениями рекомендуется вводить комментарии, которые
поясняют их назначения. Результаты расчетов также необходимо сопровождав ь
комментариями. Ввод формул, программ и текста производится в любом меги-
рабочего окна. При этом для каждого выражения и фрагмента текста создается
своя рабочая область, ограниченная обычно невидимым прямоугольником (этот
прямоугольник становится видимым при вводе в него курсора и нажатии па ле-
вую кнопку мыши).
Документ в Mathcad образуется из совокупности всех рабочих областей, создан
пых пользователем, при сохранении он получает расширение .med.
IO
1. Пространство элементарных событий
В системе Mathcad использую гея три средства для ввода и редактирования эле-
ментов документа, одно из которых обязательно присутствует на экране. Рас-
смотрим подробнее эти средства.
Крестообразный курсор или визир (красный плюс) используется для размеще-
ния новых выражений, графиков и текстовых областей. Отмечает место в рабо-
чем документе, где должна появиться новая область.
Маркер ввода (вертикальная черта) подобен аналогичному средству в текстовом
редакторе. Он используется для удаления и вставки отдельных символов и эле-
ментов.
выделяющая рамка, по сути, является двумерным маркером ввода (имеет синий
цвет) и предназначена для работы в математической и графической областях.
Выделяющая рамка широко используется при вводе и редактировании матема-
। ических выражений. При этом действует следующее важное правило: то, что за-
ключено в выделяющую рамку, становится операндом следующего вводимого
оператора. Правильное использование выделяющей рамки позволяет избежать
многих ошибок, связанных с неправильным порядком выполнения математиче-
ских операций. Имеется несколько способов заключить часть выражения в выде-
ляющую рамку. Один из них — поставить маркер ввода на требуемое место и на-
жать клавишу «пробел» нужное число раз. Другой способ — отметить мышью
нужное выражение, и используя клавиши, обозначенные стрелками, перемещать
курсор ввода в нужном направлении.
Вид окна Mathcad 2001, содержащего примеры различных объектов языка и ре-
зультаты вычислений, показан на рис. 1.3. Все примеры снабжены текстовыми
комментариями. Окно имеет стандартную для окна приложения MS Windows
cipyicrypy. Верхняя строка окна содержит имя приложения Mathcad Professional
(альтернативным является использование Mathcad 6+, Mathcad 7 и др.), имя
файла, в котором сохраняются результаты работы, (в нашем случае это имя
examples) и справа — размерные кнопки для работы с окном. Вторая строка окна
содержит команды прикладного меню. Это меню имеет набор стандартных для
приложений MS Windows групп команд: File, Edit, View, Format, Windows, Help,
а также две специфичные группы Math (Математика — операции управления
вычислениями) и Symbolics (Символьные вычисления — операции символьной
математики). Следующие три строки содержат панели инструментов. Многие
инструменты должны быть известны читателю, так как они имеются в болыпин-
сгне приложений MS Windows. Среди инструментов, специфичных для Mathcad,
следует указать кнопку f(x), которая открывает список встроенных функций,
а также инструменты панели математических операций, которая в нашем случае
расположена в пятой строке окна. Эта панель содержит кнопки запуска девяти
палитр инструментов, предоставляющих пользователю множество математи-
ческих символов, ключевые слова, шаблоны и многие другие символы, которые
облегчают набор базовых конструкций Mathcad. Для того чтобы узнать название
отдельных палитр, достаточно навести на соответствующую кнопку (иконку)
курсор мыши. Следуя слева направо по группе кнопок, поясним назначение каж-
дой из палитр:
U Calculator Toolbar — панель калькулятора, содержит общие арифметические
операторы;	л
V 1\
Комньюшрный прак1икум № I. Операции над (лИплинми и намни Mathcad
19
□	Graph Toolbar — панель графиков, содержит набор двух- и трехмерных графиков;
□	Vector and Matrix Toolbar — панель матричных и векторных операции;
□	Evaluation Toolbar — панель вычислений, содержит набор знаков, iiciio.in..iye
мых в математических выражениях (равенство, тождество и др.);
□	Calculus Toolbar — панель операций математического анализа (нронзиодныс,
интегралы, пределы, произведение и др.);
□	Boolean Toolbar — панель отношений, содержит знаки операций сравнения;
□	Programming Toolbar — панель программирования, содержит набор базовых
операторов языка Mathcad;
□	Greek Symbol Toolbar — панель греческих букв;
□	Symbolic Keyword Toolbar — панель ключевых слов языка Mathcad.
Отметим, что в отдельных версиях пакета Mathcad часть из перечисленных на
литр вызывается с использованием команды прикладного меню View-Toolbars.
Mathcad Professional г (examples)
Г"‘ ,-| »।Л.
'Й-Н

Примеры использования различных конструкций языка MATHCAD
Пример 4. Программа вычисления факториала числа п
Fact(n) :• f <- 1
Пример 1. Вычисление арифметического выражения
и Р. . /е _ 1 то

Пример 2. Вычисление алгебраического выражения
i2 + b2 - 5
а 3 b := 4
Пример 3. Вычисление таблицы значений функции
2
х-1,2.8 у(х) - а х +Ьх+1
У(х)-
_____8_
21
~~4o'
65
96
133
176
225
for I« In
Пример 5. Построение графика функции у(х)
Факториал числа 6 равен: Fact(6) - 720
Рис. 1.3. Окно Mathcad с примерами вычислений
L*J J
Ргги Fl fa

Под строками инструментов находится окно рабочего документа, в котором рас
полагаются все введенные выражения, операторы и результаты расчетов. Содер
жимое окна документа можно редактировать, форматировать, сохранять и выно
лить на печать. Под текстом «пример 4» можно увидеть крестообразный курсор,
который отмечает место в рабочем документе для ввода нового объекта.
1(цжпяя строка окна приложения называется строкой состояния. Она содержи i
рекомендацию пользователю (Press F1 for help — для получения справки важаи
1. Пространство элементарных событий
клавишу F1); информацию о режиме работы (и пашем случае Auto соответствует
режиму автоматических вычислений); помер текущей страницы рабочего доку-
мента (в пашем случае Раде 1 - первая страница).
/1./1Я выполнения операций над событиями в пакете Mathcad читатель должен
умен, работать со скалярами, векторами и матрицами, которые могут быть по-
стоянными или переменными; использовать функции от одной или нескольких
переменных; составлять программы, реализующие в среде Mathcad типовые вы-
числительные процедуры.
Задание скаляров, векторов и матриц в пакете Mathcad осуществляется с помо-
щью оператора «присвоить», обозначаемого :=. Слева от этого оператора стоит
идентификатор (имя, обозначение) объекта, а справа — определяющее его выра-
жение. Например, п: = 5 означает, что п является постоянной величиной, равной
пяти.
Н программах на Mathcad довольно часто используется оператор внутреннего
локального присваивания, действующий внутри программы и обозначаемый сим-
волом . В этом случае присвоенное значение сохраняется только в теле про-
|раммы. Например, выражение х <— 15 присваивает переменной х значение 15
внутри программы; за пределами тела программы значение переменной х либо
является неопределенным, либо равно значению, которое задано вне программ-
ного блока.
Часто необходимо указать множество значений, которые может принимать ска-
лярная переменная. Если речь идет о переменной г, которая пробегает целые зна-
чения от 0 до п, то это записывается в виде 1 := 0 .. п. Как правило, такое выра-
жение используется для описания области действия целочисленных аргументов
функции, а также индексов векторов, матриц и циклов.
Рассмотренные выше символы := и .. набираются путем нажатия на клавишу
«Ж» и «ж», соответственно. При этом заглавные буквы, как обычно, получаются
пажа гнем па клавишу «Shift». Альтернативным способом является использова-
ние «кал ькулятора».
Для задания вектора или матрицы следует выполнить команду прикладного меню
Insert Matrix... или активизировать соответствующую кнопку (иконку) на палит-
ре инструментов Vector and Matrix Palette. В результате этих действий появляется
окошко Insert Matrix, в котором пользователь должен задать требуемое число
строк и столбцов матрицы. Для вектора-строки указывается одна строка, а для
вектора-столбца — один столбец. После ввода размеров матрицы следует нажать
на кнопку Insert, и в окне редактирования на экране появится шаблон вектора
пли матрицы заказанных размеров с пустыми клеточками.
Следует обратить внимание на то, что нумерация строк и столбцов начинается
< пулевого элемента, так что при размерности вектора, равной п, его последняя
компонента имеет номер п-1. Важно также помнить, что Mathcad оперирует
<• векторами-столбцами. Он выдаст ошибку, если мы попытаемся обратиться к
конкретному элементу вектора-строки. Поэтому перед началом работы с век-
тор-строкой ее следует транспонировать в вектор-столбец. Эта операция осуще-
ствляется или вручную (приписыванием буквы Т сверху справа над вектором
Компьююрный практикум Nt 1. Операции н.щ иЛшинми и h.imhu m.iIIk .kI
или матрицей) или автоматически (вызовом этой буквы с напели нп< грумепгоп
Vector and Matrix Palette).
В пакете Mathcad используется сотни встроенных функций, причем их количсс!
во в новых версиях пакета становится все больше. Функция имеет аргументы.
записываемые в круглых скобках после имени функции. Они могут бы ть число
выми константами, переменными с буквенными обозначениями или математи
ческими выражениями, вычисляющими численные значения. Вызов наиболее
известных элементарных функций может осуществляться непосредственно пу-
тем ввода соответствующих обозначений, например, sm(0.4), co.v(.r), е\р(а),
1п(2.3) и т. д. Для облегчения процедуры ввода встроенных функций рскоменду
ется использовать кнопку/(х) палитры инструментов или команду прикладного
меню Insert—Function... После ввода данной команды открывается окно, содер
жащее список имеющихся функций, из которого необходимо выбрать нужную.
В последних версиях пакета эти функции разбиты на тематические разделы.
Выбор отмеченной курсором функции фиксируется щелчком на кнопке lnsoil
диалогового окна, после этого функция переносится в окно текущею докумен ia.
В настоящем практикуме используются встроенные функции if, rows и cols.
Функция if имеет следующий формат: if(condition, а, Ь). Здесь condition - логи-
ческое условие. Это условие может представлять собой булево выражение пли
записываться с помощью символов «меньше» <, «меньше или равно» <., «боль
ше» >, «больше или равно» >, «равно» =, «не равно» * (все эти символы берутся с
панели инструментов Evaluation and boolean Palette). Слева и справа от символов
записываются сравниваемые скаляры (в виде постоянных или уже определен
пых к этому моменту значений переменных или функций). Далее, а — вы раже
ние, определяющее значение функции в случае, если условие condition выполне-
но; b — выражение, определяющее значение функции в случае, если условие
condition не выполнено.
При работе с векторами разной длины используются функции cols(M) и rows(M),
значения которых равны соответственно числу столбцов и строк матрицы М.
Например, если cols(M) = 6, то это значит, что матрица М имеет шесть столбцов.
В настоящем практикуме используется несколько функций пользователя для ра
боты с событиями, с этой целью были разработаны соответствующие програм
мы. Следует отметить, что Mathcad является постоянно развивающимся пакетом
программ. Каждая новая версия пакета предоставляет пользователю все новые
возможности. Так, в последних версиях (например, Mathcad 2002) имеются
встроенные функции для работы с множествами, а, следовательно, и с собы гни
ми, поскольку последние являются множествами. Ввиду учебного характера дан
ной книги мы рассмотрим ситуацию, когда такая возможность отсутствует и
пользователю необходимо самому создать соответствующие функции н опера ги
ры; при этом для реализации большинства рассматриваемых в книге примерив
достаточно иметь версию пакета не ниже Mathcad 6+.
Программирование в пакете Mathcad заключается в создании программных ми
дулей — блоков, выделенных слева отрезками жирных вертикальных прямых
Доступные элементы языка программирования (операторы) содержатся в напели
Programming, которая открывается при нажатии кнопки (иконки) ProQiamnuiHi
,, • Ifrwifzunwiuv «З/IQNRiniapnDIA UUVDIIMM
toolbar (см. рис. 1.4). /(ля набора в окне редактирования любого из данных опе-
ра горов необходимо щелкнута левой кнопкой мыши по соответствующей кнопке
на панели Programming. В результате откроется окошко, содержащее ключевое
слово и шаблон для ввода требуемых параметров (операнд).
Mathcad Professional - [Untitled:!]
Edit View Insert Formal Math Symbol
| Programming T oolbar]
if	otherwise
for while
break	continue
return	on error
Рис. 1.4. Панель программирования Programming в окне Mathcad
Создание программных модулей предполагает знакомство читателя с основами
программирования, так как любой программный блок сначала необходимо за-
программировать. Создаваемый блок может иметь имя или не иметь такового.
В первом случае нужно набрать имя и в круглых скобках — формальные пара-
метры, если таковые есть. После этого необходимо записать символ присваи-
вания :=. Дальнейшие действия совпадают с действиями для случая, когда имя
программы не задается. Для ввода программного блока необходимо щелкнуть
левой кнопкой мыши по кнопке Add Line на панели Programming. В результате
этого действия в окне редактирования появляется вертикальная черта, справа от
нее высвечивается окошечко, в котором надо начать записывать текст програм-
мы. Повторное нажатие на клавишу Add Line создает дополнительные окошечки.
За первой вертикальной чертой могут следовать другие вертикальные черты,
в этом случае говорят о ступенчатой записи программы. Такая запись делает
прозрачной структуру вычислений.
Отметим, что набор базовых операторов пакета Mathcad ограничен и включает
всего восемь операторов (см. рис. 1.4), из которых мы будем использовать сле-
дующие:
□	<---оператор локального присваивания;
□	while — оператор цикла типа «пока»;
□	for — оператор цикла с фиксированным числом повторений;
□	if — условный оператор;
□	otherwise — оператор альтернативного продолжения (работает с оператором if).
Компышорный пракшкум № 1. ОГКЦМЩИИ ИИД (КОШИИМИ II II.IHIIII M.ltllUM	av
В рассматриваемых в данном практикуме примерах программ кроме oia paiop.i
локального присваивания широко используется оператор цикла for. Для зада
ппя цикла for необходимо указа ть индекс цикла, диапазон изменения его значе
пип, а также описать выражение, многократно вычисляемое в цикле для разных
значений индекса цикла. Если индексом цикла является i, а диапазон изменения
сто значений 0, 1, 2,..., п, то цикл начинается с выражения for i е ()..//, за которым
следует вычисляемое в цикле выражение.
Для повышения наглядности вводимых выражений и программ в пакте
Mathcad мы будем использовать соответствующие комментарии. Наличие ком
ментариев существенно упрощает работу пользователя с ранее набранными и к
стами, а также помогает при работе с полученными результатами.
Реализация задания
Наша задача заключается в формировании нескольких составных событий и вы
полпенни над ними типовых операций. Будем представлять элементарные co6i.it пя
веп1ественными числами, а состоящие из них множества (в том числе прострзп
ство элементарных событий и составные события) — в виде векторов-с трок. Раз
мерность вектора совпадает с числом элементов множества, а значение компо
цент вектора — суть элементы множества, то есть вещественные числа. В пашем
примере рассматривается три составных события С, G и D, записанных в виде:
С = {1, 2, 3, 4, 5, 6, 7}, D = {4, 5, 6, 7, 8, 9, 10, 11} и G = {1, 8, 11, 9}. 11ад этими с<>
бытиями необходимо выполнит), основные операции.
Для реализации типовых операций над составными событиями используюк я
программные модули, тексты которых представлены на рис. 1.5. Каждый модуль
определяет пользовательскую функцию, имя которой вместе со списком фор
мальных аргументов указано в заголовке программы. Если мы хотим невольно
вать данные функции для проведения операций над событиями, то вместо фор
мальных аргументов следует подставить конкретные события, над коюрыми
проводятся операции. Функции пользователя имеют следующее назначение:
□	ProdNum(A, В) вычисляет число элементарных событий, общих для собьпий
А и В, то есть число |А В| элементарных событий произведения А В;
□	SumNum(A, В) вычисляет общее число различных элементарных ......  в
составных событиях Л и В, то есть число элементарных событий суммы A । II,
□	DifNum(A, В) вычисляет число элементарных событий, которые входят и со
бытие Л и не входят в событие В, то есть число элементарных событий разно
сти А - В;
□	Sum(A, В) определяет сумму событий А и В;
□	Prod(A, В) определяет произведение событий А и В;
□	Dif(A, В) определяет разность событий Л и В;
□	Arise(i, А) указывает, произойдет (возвращает значение 1) или нет (возврата
ет значение 0) событие А, если произошло элементарное событие i.
Напомним, что по умолчанию в Mathcad вектор понимается как столбец. Дли
перехода от строки к столбцу нужно транспонировать вектор-строку. (’ друпш
стороны, при выводе результатов мы также пользуемся операцией трат нонн
24
1. ПрОС1|>	янтарных событий
ровапия, поскольку ваши функции дают результаты в виде векторов-столбцов,
которые занимают много места.
При разработке модулей были использованы встроенные функции if, rows и cols,
операторы присваивания := и а также оператор цикла for, рассмотренные
выше. В программах используются вложенные циклы, организуемые по двум
индексам i nj. Наличие в текстах программ соответствующих отступов и верти-
кальных линий позволяет определить тело каждого цикла.
Результаты вычислений
Полученные результаты представлены на рис. 1.6. Вычисления проведены для
трех событий С = (1 23456 7)т, D = (4 5 6 7 8 9 10 11)т и G = (1 8 11 9)т. Все ре-
зультаты снабжены комментариями и не требуют дополнительных пояснений.
Заметим, что наряду с разработанными пользовательскими функциями в вычис-
лениях используется встроенная функция rows, определяющая число элементар-
ных событий соответствующего составного события.
Практикуй Nt 1. Операции над событиями
Пользовательские функции
Число элементарных событий произведения	Произведение событий А и В	
событий А и В		
ProdNum(A.B) := st~ 0	Prod(A.B).«	for IeO. ProdNum(A.B) -
for leO.. rows(A) - 1		qe-0
fe-0		ne-0
for JeO.. rows(B) - 1		for ieO.. rows(A) - 1
f*-.f+If(Ai»Bj,1,0)		f«-0
s <-s + if(f > 0.1,0)		for j < 0. rows(B) - 1
s		f<-f+if(Aj = Bj.1,0)
		if f>0
Число элементарных событий суммы событий А и В		
SumNum(A,B) rows(A) + rows(B) - ProdNum(A.B)		| П П + 1
		C
Число элементарных событий разности событий А и В
DifNum(A,B) := rows (А) - ProdNum(A,B)
Сумма событий А и В
Разность событий А и В
Sum(A,B) ••
for ieO.. row$(A) - 1
Q<-A|
n <- rows(A)
for leO.. rows(B) - 1
fe-0
for Je 0.. rows(A) - 1
f f- f+ if(A] « Bj.1.0)
If f.O
П П + 1
Dif(A.B) -	fo	i e 0 . DifNum(A.B) - 1
	c^o	
	n <-	-0
	fo C	led rows(A) - 1 f«-0 for JeO.. rows(B) - 1 Г«-1+И(Д| = В|.1.0) if fcO |C,.^Ai I n ♦— n + 1
Проверка наступления события A
Arise (i. A) -
f«-0
for j e 0 .. rows (A) - 1
f <-f + lf[i = (A),.1.0]
g lf(f > 0.1.0)
g
Рис. 1.5. Реализация типовых операций над событиями
17.	КОМОИН.ЩИИ (.()1)Ы1ИИ
I’VUJlblVUI 1Ы‘1И1Ли11ИИ
Исходные собьния:	С-(1 2 3 4 Л И //	0 - (4 5 6 7 в	9 1U 11 )l	G -(1 II 11 II)’
1. Число элементарных событий а) е составных событиях: rows(C) - 7 rows(D) - В	rows(G) -	4 cols((1 2 4 9 0))-5
б) в произведении деух событий:	ProdNum'C, D) > 4	ProdNom(G,C) - 1
в) в сумме деух событий:	SumNum(C.D) - 11	SurnNum(C,G) - 10
г) в разности двух событий	DifNum(D.C) - 4	DlfNum(D.G) - 5
2. Проверка принадлежности элементарного события Arlse(4.C)-1	Arise(11 ,С) - 0	Ar Ise(21,(1	34 07 21 22)’) . 1
3.	Операции над событиями а)	произведение:	Prod(C,G)T -(1)	Prod(c,(1 б)	сукна:	Sum(c,(1 7 11)’) .(1234567 в)	разность;	011(0, С)’ -(В 9 10 11)	5 7 И)’ / - (1 5 7) И)
4, Комбинация событий
F - Dlf(D,Sum(C,G)) f’-(W)
Arlse(I.F) - 0	Arise(1, Dif (D ,Sum(C. G))) - 0	Arise(10,F) - 1	1 Arlee(10,Dlf(0,Sum(C.G))) -
Рис. 1.6. Результаты выполнения операций над событиями
Задания для самостоятельной работы
I.	Апробировать приведенные на рис. 1.5 программы для различных (читанных
события А, В, ...
2.	Описать логику работы программных модулей ProdNum(A, В) и Prod(A, /<)
3.	Составить программу, вычисляющую симметрическую разность событий .1 и И,
определяемую как (А - В) + (В - А).
1.2.	Комбинации событий
Введенные выше операции отрицания, суммы, произведения и разности собы i nii
позволяют образовывать новые события из уже имеющихся, то есть осунцчтп
лить комбинации событий. Комбинации событий записываются в виде формул,
содержащих исходные события, а также символы	— операций отри
цаиия, суммы, произведения и разности. Последовательность выполнения one
раций в формулах обычно определяется скобками. Количество скобок можно
сократить, если договориться о приоритете (порядке выполнения) операций
Общепринятой договоренностью является приоритет произведения над суммой,
аналогичный приоритету умножения над сложением в арифметике и алгебре.
'Гак, А + В • С является сокращенной записью А + (В • С). Оно представляет собой
событие, которое наступает только тогда, когда наступает или событие А или оба
события В и С. Далее, F = В • (А + С) представляет собой событие, которое пасту
идет, когда не наступает событие В и наступает или А или С.
Формулы, описывающие комбинации событий, можно преобразовывать, ш ноль
зуя следующие свойства операций суммы и произведения событий:
□	коммутативность-.
А + В = В + А, АВ = В-А;
□	at < оциашнаиш mi>;
(A + B) +С = A+(B + С) = Л + В + C,
(А -В) С = A (B С) = A -В  C;
□	дистрибутивность-.
A(B + C) = AB + AC,
(AB)+C = (A +C)(B + C);
□	идемпотентность-.
A + A = A,
AA = A;
□	поглощение-.
если А с В, то A + В = В, А - В = A.
Справедливость этих свойств следует непосредственно из определений суммы
и произведения событий.
()i мстим, что отрицание А также можно рассматривать как унарную операцию,
применяемому к одному событию А. Для него справедливы следующие свойства:
Х=А, А = В=>А=В, А = В=>А=В.
С от рицанием также связаны свойства, называемые законами де Моргана'.
А + В = АВ, А^В = А+В.	(1.4)
11а эт их формулах мы сейчас проиллюстрируем общий метод доказательства эк-
вивалентности двух событий G и Н, то есть того, что G = Н. Доказательство со-
стоит из двух этапов. Вначале доказывается, что из того, что со е G, следует, что
<о с II. Следовательно, G с Н, то есть событие G влечет событие Н. Потом рас-
сматривается обратное утверждение: из условия со е Н следует, что со е G.
Следовательно, Н с G, то есть в действительности G = Н.
Итак, докажем первое равенство (1.4). Для этого необходимо убедиться в том,
что А + В с: А В, и наоборот, АВ с А + В. Пусть со е А + В. Тогда со g А + В. Но это
значит, что одновременно со g А и со g В. Отсюда следует, что одновременно со е А
и со е В, то есть со е А В. Итак, доказано, что из соеЛ + В следует со е А В, иначе
А + ВсАВ.
/(ля доказательства того, что АВ с А + В, достаточно посмотреть предыдущую
цепочку формул в обратном порядке. Следовательно, первое из равенств (1.4)
доказано.
Для доказательства второго равенства (1.4) подставим в первое равенство А вме-
сто А и В вместо В. Тогда
А+В = АЁ = АВ, А+В = АВ.
Доказательство формул (1.4) закончено.	□
Итак, комбинация событий также является событием. Как и любое событие, это
событие наступает, если наступает некоторое элементарное событие, входящее
в него. Например, если А = {©р со3, со4, со7}, В = {сор со2, со4}, Н = {со3, со5, со6, со7},
то комбинация событии (/ All i li (<°i. <'»2, (0.i> (l,o ">/} наступает, если na< ly
uric г любое из элементарных событий <о,, <о2, (»>:,, <ол, <о7.
Однако в формулах, описывающих комбинации событий, элементарные события
обычно явно пс фигурируют. В этом случае наступила или нет комбинация со
бытии определяется тем, наступили или нет входящие в комбинацию cociэнные
события. Как определить факт наступления комбинации событий на основе ни
формации о том, какие из входящих в него событий наступили, а какие не нэп у
пили? Для этого следует использовать понятия теории булевых функций (иначе
функций алгебры логики или логических функций). Это осуществляется следую
щим образом.
Пусть комбинация включает события Ль Л2, ..., А„. Событию Л,- поставим в кин
ветствие булеву переменную х,, принимающую только два значения: х, = 1, е< ли
событие Л,- наступило, и х,- = 0, если событие Л,- не наступило, то есть наступ и во
событие Лг. Комбинации событий G поставим в соответствие булеву перемен
пую у, равную 1, если комбинация наступила, и равную 0 в противоположном
случае. Переменная у выражается через переменные х, с помощью операций
конъюнкции, дизъюнкции и отрицания. Конъюнкция соответствует пронэнеде
нию событий и описывает логическую связку «и-и». Дизъюнкция соответствуй!
сумме событий и описывает логическую связку «или-или». Отрицание cootuci
ствует противоположному событию и описывает логическое «не». Разность со
бытий Л - В может быть вычислена как ЛД. Обычно операция конъюнкции изо
бражается символом &, операция дизъюнкции v, отрицания —. Таблица I 1
содержит значения этих операций. Мы видим, что значения конъюнкции равны
минимуму из аргументов (может быть, нескольких), а значения дизъюнкции
максимуму. Принято, что конъюнкция имеем приоритет в очередности вы полис
ния перед дизъюнкцией.
Таблица 1.1. Операции конъюнкции, дизъюнкции и отрицания
*1	х2	хх& х2	Хг V х2	*1
0	0	0	0	1
0	1	0	1	1
1	0	0	1	0
1	1	1	1	0
Теперь значение у можно вычислить как значение булевой функции g(xt,x2,.г„),
которая получается, если в выражении для комбинации G заменить Л, па х„ спм
вол произведения_на конъюнкцию, символ суммы на дизъюнкцию. Например,
если G = Л| • Л2 + А, (Л3 + Л4 X то g(xt ,х2,х3,х4 ) = х, &х2 v х{ &(х3 v х4). Так.
если события Л! и Л3 не наступили, а остальные наступили, то xt = 0, х2 = 1, хл О,
х4 = 1 и мы имеем g(0, 1, 0, 1) = 0 & 1 v 0 & (0 v 1) = 1, что соответствует действн
тельности.
Поскольку мы работаем только со значениями 0 и 1, то операции конъюнкции
и произведения тождественны, в связи с чем можно вместо символа конъюнкции
28
1. Пространство элементарных событий
& использовать символ умножения • или вообще опускать его. В этом смысле
дизъюнкцию v с суммированием отождествлять нельзя, однако все-таки можно
использовать суммирование, но результат заменять на единицу, если он больше
нуля. Отрицание х вычисляется как х = 1 - х. В результате вместо булевой функ-
ции g(x\, х2.хп) мы получаем арифметизированную функцию gA(xr х2......х„).
Если последняя больше нуля, то булева функция Дх^х^, •> хп) равна единице:
g(x„x2, ..., хя) = if (gA(xbx2, ..., хя) > О, 1,0).
В частности,
xt v х2 v ... v хп = if (х( + х2 + ... + х„ > 0,1, 0).
Здесь используется оператор Mathcad if, в записи которого первой фигурирует
логическое условие, за которым после запятой следует значение, выдаваемое,
если условие выполняется, далее — значение, выдаваемое, если условие не вы-
полняется.
В случае когда элементарные события явно не фигурируют в комбинации собы-
тий, можно поступать и другим способом. Сейчас мы покажем, как можно по-
строить искусственное пространство элементарных событий на базе событий,
фигурирующих в комбинации. Это позволит нам в дальнейшем рассчитывать ве-
роятности наступления комбинации событий.
Снова рассмотрим комбинацию G, включающую п событий А1; А2, ..., Ап. Как
и ранее, пусть 1 означает наступление события, а 0 — ненаступление события.
Тогда конкретная реализация событий в данном испытании описывается «-мер-
ным булевым вектором (а1; а2, ..., а„). i-я компонента этого вектора я,- относится
к событию А). Иными словами, вектор (яь а2, ..., а„) описывает наступление или
ненаступление всех событий в рассматриваемом испытании. Подчеркнем, что в
отличие от переменной xjt которая может принимать оба значения 0 и 1, значе-
ние я, фиксировано. Мы будем рассматривать вектор (яь а2, ..., а„) как элемен-
тарное событие со, то есть <о= (ait а2, ..., я„): в рассматриваемом «испытании» мы
имеем такие исходы для событий.
С помощью булевого вектора (яь а2,..., а„), или просто а^ а2... ап, можно описать
элементарное событие и другим способом, а именно, как А”1 А“2 ... А“", где
А(, если я, =0,
А,, если ai =1.	|
Например, 0101 означает реализацию события Д А2 А3 А4, в которой события
А2 и А4 наступили, а события Д и А3 — нет.
Очевидно, элементарных событий столько, сколько различных «-мерных буле-
вых векторов. Обычно множество таких векторов обозначается В", где В = {0, 1}:
В” = {(яь а2,..., я„): V я, е{0, 1}}. Следовательно, наше пространство элементарных
событий Q =В". Легко видеть, что число различных «-мерных булевых векторов
равно 2", следовательно, число элементарных событий |Q| = 2".
Теперь можно выразить исходные события Аь А2, ..., А„ через эти элементарные со-
бытия: а именно, событие А, состоит из тех элементарных событий <о= (яь а2,..., я„),
в записи которых на месте буквы я, стоит 1:
А, = {со = («], а2.ап) еQ: я, = 1}.
А“< =
। । i вычурная надежность систем
29
Н । .iK, каждое элементарное событие описывается и-мерным булевым вектором
<п -	а2,	а,,). Оперировать с такими векторами неудобно. Лучше все их перс
нумеровать и присвоить им имена, совпадающие с соответствующими номерами
ho (>удет в точности совпадать с обозначениями элементарных событий, кото
рым и мы пользовались в программах, разработанных ранее для Mathcad.
/1чч десятеричной нумерации булевых (иначе — двоичных) векторов исполину
ин III)(' код (Binary Decimal Code). Этот код хорошо знаком из начальных кур
ши информатики. Булев вектор 010 означает число 2, 0101 — число 5, 1110
чи< ч<> 14 и т. д. Справа располагаются младшие разряды, а слева — старшие,
II < амом младшем (самом правом) разряде указывается число единиц. Во втором
I и।Ына разряде — число двоек, потом число четверок, восьмерок и последующих
• о цепей числа 2. г-й справа разряд (z = 1, 2, ..., п) содержит количество чисел,
равных двум в степени г-1. Следовательно, для булева вектора а = (аь а2, ..., ап)
III )С код есть
BDC(a) = £а;2"-‘.	(15)
м
Примнр 1.6. Пусть имеются три исходных события А(, А2, А3 и две комбинации
нм / Л, • А2 + А:1 и G = А2 •'А3. Итак, событие Fпроисходит, если наступает или
11ifii.i। не А, или событие Аь но не А2. Событие G наступает, если наступают и А2,
н I, Н данном случае п = 3, а пространство элементарных событий выглядит
mi' О {ООО, 001, 010, 011, 100, 101, 110, 111}. В частности, элементарное
' на । ис 011 означает, что событие Aj не наступило (а( = 0), событие А2 наступи
in {а, равно I), событие А3 также наступило (а3 = 1). Десятичный код этого эле
мен ирного события равен 3.
1Ь читные события теперь представляются так:
.1, {001, 011, 101, 111}, Л2 = {010, 011, ПО, 111}, Л, = {100, 101, ПО 111}.
I'iii । m.iiрпнаемые комбинации выражаются через элементарные события сле-
дующим образом: G = {011, 111}, F= {001, 011, 100, 101, 111}.	□
Мы Путем использовать эту систему представления событий и их комбинации в
। и i\ iniiii'M разделе при описании структур логических систем, а также при со
Цйптснии компьютерных программ.
1.3. Структурная надежность систем
II iii'puu надежности рассматриваются системы, состоящие из элементов. Каж
и.hi i h’Mcht может находиться в одном из двух возможных состояний: рабою
< । в и । ю । в >м (исправном) и неработоспособном (состоянии отказа). Система так
«в iimci'i loni.KO дна состояния: работоспособное и состояние отказа. Состояние
linn мы выражается в виде некоторой комбинации состояний составляющих
и mi в и in (обозначим п число элементов системы. Пусть А,- означае т собы тис
ii’mi и । находится в работоспособном состоянии», А, означает пеработоспо
iiitiiiiie ini 1ОЯНИС этого элемента. Для системы аналогичными событиями буду
II раТииогиогобпое состояние, Л неработоспособное состояние.
11рн не,тем ( hi в > 1111 ы с сипы споем, рассматриваемые в теории падежное i н.
30
1. Пространство элементарных событий
Последовательной называется система, в которой отказ любого элемента при-
водит к отказу системы (см. рис. 1.7, а). Иначе говоря, система будет работо-
способна, если работоспособны и первый, и второй, и все другие элементы. Это
соответствует операции умножения событий. Следовательно, условие работо-
способности последовательной системы записывается в виде
в = А-а2....-а„.	(1.6)
Соответствующая булева функция имеет вид:
gs(Xj ,х2,...,х„) = х,&х2&...&х„.	(1.7)
Параллельной называется система, которая остается работоспособной, пока рабо-
тоспособен хотя бы один ее элемент (см. рис. 1.7, б). Иначе говоря, система будет
работоспособна, если работоспособен или первый, или второй, или какой либо
пл последующих ее элементов. Это соответствует операции сложения событий.
Следовательно, условие работоспособности параллельной системы записывается
в виде
B = At +А2 +... + А„.	(1.8)
Соответствующая булева функция имеет вид:
g/,(x1,x2,...,x„) = x1 v х2 v...v х„.	(1.9)
а	б
Рис. 1.7. а — последовательная и б — параллельная системы
В общем случае говорят о последовательно-параллельной системе, если ее можно
разбит ь па последовательные или параллельные подсистемы, которые соедине-
ны между собой также последовательно или параллельно. Условие работоспо-
собности таких систем представляет собой комбинацию вышеприведенных усло-
вий для последовательных и параллельных систем.
Принятая графическая схема последовательно-параллельной системы приведена
па рис. 1.8. Элементы системы изображаются на схеме прямоугольничками. Сис-
тема считается работоспособной, если существует хотя бы один путь, ведущий
от левого конца схемы к правому ее концу и проходящий только через исправ-
ные элементы. Для последовательно-параллельной системы, изображенной на
pin 1.8, событие «система работоспособна» записывается так:
В = (Л, +Л2) А, (Л4 • Л5 +Л,;).
Соогвек твующая булева функция записывается в виде:
g (•' I , Л'2 , х2, Л 4 , Л 5, Хв ) = (Х| V х2 ) & Л ч & ((Х4 & Xj ) V Л о ).
Компьютерный практикум № 2. Комбинации событий в пакете Mathcad
31
Рис. 1.8. Последовательно-параллельная система
Пример 1.7. Система «два-из-трех». Так называется система из трех элементов,
которая является работоспособной, когда работоспособны хотя бы два элемеша
Следовательно, условие работоспособности системы имеет вид:
В =А,А2 + А,А3 +Л2Л3.	(1.10)
Соответствующая булева функция
g(Xj, х2, х3) = (Xj &х2 )v (xt &х3 )v (х2&х3).
Применим технику, изложенную в конце предыдущего раздела, для этого при
мера. В данном случае число исходных событий равно 3. Следовательно, имеем
23 = 8 элементарных событий и следующее пространство элементарных событий:
Q = {ООО, 001, 010, 011, 1007 Ю1, 110, 111}. Исходные события представляю гея
теперь так: Л3 = {001,011,101,111}, Л2 = {010,011,110,111}, Л, = {100,101, 110, 111}
Следовательно, В = {111, 110, 101, 011}.	□
Компьютерный практикум № 2.
Комбинации событий в пакете Mathcad
Цель и задачи практикума
Целью практикума является приобретение практических навыков в описании
различных комбинаций событий и определении факта их наступления или пена
ступления в зависимости от наступления других составных и элементарных со
бытий.
Основной задачей данного практикума является построение искусственного
пространства элементарных событий на базе событий, фигурирующих в комби
нации. В качестве иллюстрации рассматривается исправность системы «два-из
трех».
Необходимый справочный материал
В настоящем практикуме кроме конструкций пакета Mathcad, описанных выше,
используется оператор цикла while. Оператор while служит для организации цнк
ла типа «пока», повторяемого до тех пор, пока выполняется заданное условие
condition. Оператор имеет следующий формат: while condition, где condition ло
гическое условие. Это условие может представлять собой булево выражение пли
записываться с помощью символов «меньше» с, «меньше или равно» < «боль
ше» >, «больше или равно» >, «равно» =, «не равно» слева и справа от епмво
лов записываются сравниваемые скаляры (в виде постоянных или уже опреде
ленных к этому моменту значений переменных или функций).
Реализация задания
Для проведения вычислений нам понадобятся две программы из Иракiикума .N- I.
которые реализую! пользовательские функции Sum(A, В) и Prod(A, В) и определи
32
1. Пространство элементарных событий
ют соответственно сумму событий Л и В и их произведение. Дополнительно оп-
ределим новые функции пользователя, которые позволяют выражать комбинацию
событий через элементарные события, а также определять факт наступления или
ненаступления комбинации событий, если известно наступившее элементарное со-
бытие. Программные модули, реализующие функции пользователя, представлены
на рис. 1.9. Функции имеют следующее назначение.
BDC(a) переводит двоичную запись а = (ait а2, .... ап) в десятеричное число со-
гласно формуле (1.5), a DBC(n, N) производит обратную операцию: десятерич-
ное число N записывается как и-разрядное двоичное число.
Event(n, i) формирует для события А,- вектор-столбец входящих в него элемен-
тарных событий искусственного пространства, построенного для п событий Alt
А2, ..., А„. Сами эти элементарные события представляются в виде BDC кода
(см. формулу 1.15). Например, Event (3, 1) = (4, 5, 6, 7)т. Fam(ri) формирует все
такие вектор-столбцы для всех событий Ль А2, ..., А„.
Ранее рассмотренная функция Arise(i, А) выдает значение 1, если элементарное
событие i (представленное целым десятеричным числом) входит в событие А.
Новая функция Avaliab(a, А) выполняет те же действия для случая, когда эле-
ментарное событие записано в виде бинарного вектора а = (а(, а2,..., а„), соответ-
ствующего искусственному базису.
Практикум Nt 2. Комбинации событий
Пользовательские Функции
Перевод двоичного числа в десятиричное
BDC(a)
Формирование вектора элементарных
событий в BDC-кодах для события AI
for J е 0. п - 1
N<-N+aj2n-1-i
N
Перевод десятиричного числа в двоичное
Event(n.l)
DBC(n,N) -
k<- N
for »e 0., n - 1
If ksz"'1"*
4<- 1
a; <- 0 otherwise
a
Формирование векторов элементарных событий для
всех составных событий набора
Fam(n).»
k<-0
for J в 0 . t-1
|k<- k+ 1
m <- I - 1
kk«- k- 1
h <-0
while m> 0
t < 2n-m
for J e 0 . kk
bn t + bj
k<- k+ 1
m <- m - 1
kk<-k-1
b
A
Проверка наступления события Д
Avallab(а,A) = И (Arlse(BDC(a). A), 1.0)
Определение состояния системы “два из трех"
YTwoThree(x,y,z) := lf(x у+ х z + у г > 0,1,0)
Формирование вектора элементарных событий в BDC-кодах для исправной системы “два из трех"
TwoThree(A1 .А2.АЗ) - Sum(Prod(A1 ,А2) ,Sum(Prod(A!,АЗ) ,Prod(A2,AJ)))
Рис. 1.9. Программные модули, реализующие пользовательские функции
Компьютерный практикум № 2. Комбинации событий в пакете Mathcad
33
YTwoThree(x, у, z) определяет исправность системы «два-из-трех» (1 — да, 0 —
нет) как значение соответствующей булевой функции трех переменных х, у, г.
TwoThree(A], А2, А3), получая описание составных событий Аь А2, А3 в виде век-
торов-столбцов элементарных событий, в качестве результата дает вектор-стол
бец элементарных событий, составляющих событие AtA2 + At А3 + Л2Л3.
Отметим, что при рассмотрении другой комбинации событий следует замени и.
две последние функции.
Результаты вычислений
Результаты проведенных расчетов представлены на рис. 1.10. В первой части
распечатки иллюстрируется работа функций BDC и DBC. Первая функция пере-
водит булев вектор 110 в десятеричное число 6. Вторая реализует обратную опе-
рацию. Далее иллюстрируется работа функции Event(3, 3), которая формирует
для события А3 вектор-столбец входящих в него элементарных событий искусст
венного пространства, построенного для А1: А2, Л3, то есть (1, 3, 5, 7).
Во второй части задания рассматривается система надежности «два-из-трех»
(см. формулу 1.10). Функция YTwoThree(l, 0, 1) возвращает 1, то есть система
«два-из-трех» исправна при исправных 1-ми 3-м элементах. События А,, А2 и А,
означают безотказную работу первого, второго и третьего элемента соотвстет
венно. Они представляются как множества некоторых элементарных собы тий,
описываемых натуральными десятеричными числами с помощью функции
Fam(3). Выдаваемый ею г-й вектор-столбец и следует подставить в качестве ар
гумента А,- при обращении к функции TwoThree(A,, А2, А3). В результате получим
вектор элементарных событий, для исправной системы «два-из-трех», представ
ленный десятеричными числами 6, 7, 5, 3.
Наконец, для конкретного набора 0101, описывающего факты наступления (значе-
ние 1) или ненаступления (значение 0) событий Аь А2, А3, функция Avaliab опреде-
ляет, что система «два-из-трех» исправна, возвращая результат 1.
Результаты вычислений
Преобразование двоичного числа 110 в десятеричное:
Преобразование десятеричного числа 6 в 3-разрядное двоичное:
Формирование вектора элеменУарных событий для
события Аз (исправлен 3-й) в виде BDC-кода:
Проверка исправности системы "два из трех" для (1,0.1):
BDc([1 1 0)Т]-6
DBC(3.6)T-(1 1 0)
YTwoThree(1.0,1) - 1
Определение вектора элементарных событий для исправной системы "два из трех"
Fam(3) -
ТшоТЬгее(рат(э/°\рат(з/1\рат(3)^) -(6 7 5 3)
U 7 7 J
Проверка исправности системы "два из трех" для набора 0101
ЛиаНл1>((1) 1 II 1)’ ,1wotl1i»o(F«m(3)<II>,l ат(3)<1>.Гаш(3)<2>)) - 1
Рис. 1.10. Резу/1ыаты иыполнении задания по работе с комбинациями собыiий
34
1. Пространство элементарных событий
Задания для самостоятельной работы
1.	Испытать составленные программы для различных событий.
2.	Экспериментально проверить справедливость сформулированных выше свойств
операций суммы, произведения и разности событий.
3.	Экспериментально проверить справедливость законов де Моргана (1.4).
4.	Описать логику работы программы Event(n, i), представленную на рис. 1.9.
5.	Составить программу, описывающую состояние «последовательной 2-из-н-сис-
темы» (см. ниже задачу 1.16).
1.4.	Вероятности на дискретном пространстве
элементарных событий
Рассматриваемые нами события являются случайными. Последнее означает, что
в одних испытаниях наступают одни события, в других — другие, причем зара-
нее невозможно предсказать, какое событие наступит. Количественной мерой
возможности наступления конкретного события в одном испытании является
вероятность этого события. Мы не рассматриваем философских аспектов этого
понятия, то есть вопросов о том, является ли вероятность объективным свойст-
вом внешнего мира, или же это мера нашей информированности об этом мире.
Мы даем математическое определение вероятности, ограничиваясь в данной гла-
ве дискретным, пространством элементарных событий — пространством, эле-
ментарные события которого могут быть пересчитаны.
Определение 11. ПустьQ = {tOj, <о2,...} — дискретное пространство элементарных
событий. Говорят, что на этом пространстве определены вероятности, если каж-
дому элементарному событию со, е О поставлено в соответствие число р, = /’{со,},
называемое вероятностью элементарного события со,. Эти числа удовлетворяют
следующим условиям'.
□	неотрицательности: V<a е Q Р{<о} > 0;
□	нормировки: /э{со1} + Р{со2} + ...= 1.
Отсюда следует, что вероятность каждого элементарного события не превосхо-
дит единицы. Вероятность является количественной мерой возможности наступ-
ления данного элементарного события (исхода) при однократном опыте.
Определение 12. Вероятность составного события А с Q определяется как сум-
ма вероятностей элементарных событий, входящих в А:
Р{А}=Хр{^}-	(111)
ix», еА
Очевидно, 0 < Р{А} < 1 для всех А с О. Р{Л} характеризует количественную меру
возможности наступления события А при однократном опыте.
Из определения 12 вытекают следующие свойства вероятностей:
P(A} = i-P{A}:	(1.12)
Р<01=О. /401= 1;	(1.13)
1,4. Вероятности на дискретном пространстве элементарных событий
35
(мп
I >=1 J '=1
Приведенные свойства вытекают из определения вероятности составного собы
тня. Комментарии требуются, быть может, к свойству (1.14): вероятность суммы
событий не больше суммы вероятностей событий. Это действительно так, по
скольку любое элементарное событие представляется в левой части неравенства
(1.14) не более одного раза, в то время как в правой части оно представляется
столько раз, сколько раз оно входит в разные события At, А2, ..., Ак.
Примеры
Пример 1.1с. Однократное бросание игральной кости. Если игральная кость пра
вильной формы, то выпадение всех граней равновероятно. Поскольку всего нме
ется шесть элементарных событий, то из условия нормировки для вероятное гей
следует, что р, = Р{со,} =1/6 для всех i = 1, 2, 3, 4, 5, 6. Вероятность выпадения
четного числа очков Р{ЛЧС,} = Р{Л2} + Р{Л4} + Р{Л6} = 3/6 = 0.5. Вероятность того,
что выпадет менее пяти очков, Р{Л<5} = Р{Л ]} + Р{Л2} + Р{Л3} + Р{Л4} = 4/6.
Пример 1.2с. Двукратное бросание игральной кости. Как и в предыдущем при
мере, здесь все элементарные события равновероятны. Поскольку элементарных
событий 36, то вероятность каждого из них 1/36. Следовательно, вероятность
выпадения на обеих гранях одного и того же числа очков Р{Л.} = 6/36 = 1/6. а не
роятность того, что сумма выпавших очков будет равна 10 — Р{ЛЕ= 10} = 3/36 = 1/12,
Пример 1.3b. Бросание монеты. Каждое бросание с одинаковой вероятностью 0.5
заканчивается или выпадением решетки Р пли герба Г. Интуитивно ясно, чн>
Р(Г} = 0.5, Р{РГ} = 0.52, Р{РРГ} = 0.53и т. д. Вероятность того, что для выпадения
герба потребуется г бросаний Р{Р'”'Г} = 0.5'. Это — частный случай так пазыиае
мого геометрического распределения, которое будет рассмотрено в главе 3.	□
Вероятность является основным понятием теории вероятностей. Сейчас мы рас-
сматриваем вероятность событий, в главах 3 и 4 будем рассматривать вероятно
сгн, связанные со случайными величинами, далее вероятности для случайных
процессов, а вторая часть настоящей книги в основном посвящена проблемам
оценивания вероятностей па основе имеющихся статистических данных. Принс
дем основные теоремы и понятия, связанные с вероятностями событий.
Гоорема 1.1 (Сложения вероятностей событий). Вероятность суммы двух событий
ранка сумме вероятности этих событий минус вероятность произведения собы
1 и и:
Р{А + В} = Р{А} + Р{В} -Р{АВ}.	(1.15)
II частности, вероятность суммы двух несовместных событий равна сумме их н<’
роя I ностей:
Р{А + В} = Р{А} + Р{В}.	(1.16)
Нгроятпоеть ралности событий равна вероятности события-уменьшаемого мп
иг< верой гноен, произведения этих событии:
Р{А II) Р{А}-Р{ЛВ}.	(117)
36
1. Пространство элементарных событий
В частности, если событие В влечет событие А, то вероятность разности событий
А и В равна разности их вероятностей:
Р{А-В} = Р{А}-Р{В}.	(1.18)
Если А1( А2, .... Ак — попарно несовместные события, то есть A, Aj = 0 при i *j, то ве-
роятность их суммы равна сумме вероятностей событий:
Р{Д + А2 +... + Ак} = Р{А1} + Р{А2} + ...+ P{Ak},	(1.19)
где число слагаемых k может быть конечным (k = 1, 2,...) или бесконечным (k = со).
Доказател ьство
Начнем с доказательства формулы (1.16) для несовместных событий А и В. Она
непосредственно следует из определения вероятностей событий:
Р{А + В} = X Л®} = X В{со} + X Р{со} = Р{А} + Р{В}.
теА + В	(оеД	<оеВ
Формула (1.17) следует из того, что любое событие А представимо в виде:
А = (А-В) +А-В, причем события Л-В и Л-В несовместны (см. рис. 1.1). По-
этому согласно только что доказанному равенству (1.16)
Р{А} = Р{(А - В) + А  В} = Р{А - В} + Р{А  В},
что эквивалентно формуле (1.17).
Если событие В влечет событие А, то есть В с. А, то А - В = В, и из формулы
(1.17) вытекает формула (1.18).
Для доказательства формулы (1.15) представим сумму Л + В в виде суммы двух
несовместных событий В и А - В: А + В = В + (А - В). Для несовместных собы-
тий по формуле (1.16)
Р{А + В} = Р{В + (А - В)} = Р{В} + Р{А - В}.
Использование теперь формулы (1.17) приводит к формуле (1.15).
Для конечного числа слагаемых k формула (1.19) доказывается по индукции.
Для двух слагаемых (k = 2) она справедлива, поскольку совпадает с уже доказан-
ной формулой (1.16). Если она верна для k >2, то справедливость ее для k + 1
следует из равенств
Р{А, + ... + Ак + Ai+t} = Р{А, +... + Ак} + Р{Ак+,}= Р{А,} + ... + Р{А,} + Р{АЖ}.
Пусть теперь число слагаемых бесконечно. Нам надо доказать, что
±Р{А,} Р&Л
i=i ',_>х I <=i J
Вероятность суммы бесконечного числа слагаемых с = Р{А] + А2 + ...} понимает-
ся как предел неубывающей последовательности частичных сумм = P{Aj},
с2 = Р{А, + А2}, ..., с„ = Р{А; + А2 + ... + А,,}. Согласно свойству сходящейся число-
вой последовательности, для любого как угодно малого положительного числа
е > 0 найдется такой номер члена последовательности л?(е), что
- Еесоятности на дискретном пространстве элементарных событий
шательно,
Г X I „(С)	( X 1	[ «(С)
р ZA -IM-} =р ZA -/ ХА
< £.
.'пользовалось уже доказанное соотношение (1.17) для конечного числа сла-
ых. Поскольку величина s может быть произвольно малой, отсюда следует,
..ействительно Х^АОимеет пределом	^А,Л.	□
i=i	I1=1 J
"оимеры
*: '.'ер 1.1d. Однократное бросание игральной кости. Найдем вероятности ком-
глий событий, рассмотренных в примере 1.1а: Ачет + А<5, Ачсг А<5 и Л<5 - Ачст.
.-родственное применение определения вероятности составного события по
•vy.ie (1.11) использует явное выражение этих комбинаций через элементар-
тбытия:
Р{А.КТ + А<5} = Р{ыъ со2, со3, ац, со6} =
= P{a,i}+P{a2}+P{(o3}+P{a,l}+P{a,6} = 5/6,
Р{Ачет А<5} = Р{со2, со4} = Р{со2} + Р{со4} = 2/6 = 1/3,
Р{А<3 - Ачст} = Р{Ю1, со3}= РЫ + Р{со3} = 2/6 = 1/3.
-:тности для суммы и разности событий можно получить иначе, путем ис-
 >вания теоремы сложения (1.15) и формулы (1.17) для разности вероятно-
-обытий:
Р{АЧСТ + А<5} = Р{АЧ„} + Р{А<5} - Р{АЧ„ А<5} = 1/2 + 2/3 - 1/3 = 5/6,
Р{А<5 - Ачст} = Р{А<5} - Р{А<5 Ачсг} = 2/3 - 1/3 = 1/3.
': •ер 1.2d. Двукратное бросание игральной кости. Для вычисления вероятно-
лроизведения и разности событий можно применить исходную формулу
Р{А.  Az=10} = Р{55} = 1/36,
- Av=10} = Р{11, 22, 33, 44, 66} = Р{11} + Р{22} + Р{33}+Р{44} + Р{66} = 5/36.
~ пула (1.17) позволяет найти вероятность разности событий, не прибегая
.ментарным событиям:
Р{А_- Av=10} = Р\АА - Р{А. Az=l0} = 6/36 - 1/36 = 5/36.
•.ер 1.3с. Бросание монеты. Найдем вероятность Р{АЧСТ} того, что потребное
 бросаний является четным числом. Очевидно, Ачет = {РГ, Р3Г, Р5Г, Р'Г,...},
Р{АЧСТ} = Р{РГ} + Р{Р3Г} + Р{Р5Г} + Р{Р7Г} + ... =
= 0.52 + 0.54 + 0.56 + 0.58 + ... =
= £0.52' =^0.25' =0.25^0.25' =
1=1	1=1	1=0
= 0.25  1/(1 - 0.25) = 0.25/0.75 - 1/3.
38
1. Пространство элементарных событий
Здесь мы применили формулу для суммы геометрической прогрессии: если аб-
солютное значение числа q меньше единицы: \q\ < 1, то
X?' =i/d-?).
1=0
Вероятность Р{Д|СЧСТ} получения первого герба при бросании с нечетным номе-
ром вычисляется как вероятность противоположного события по формуле (1.12):
Р{Л,,ЧСТ} = 1 - Р{ЛЧС1} = 1 - 1/3 = 2/3.
Пример 1,4b. Задача о встрече. Пространство элементарных событий в этой зада-
че не является дискретными, так что применить изложенные выше подходы
нельзя. Это пространство представляет собой единичный квадрат, изображен-
ный на рис 1.11. Заштрихованная часть его соответствует элементарным событи-
ям, при которых наступает событие «приятели встретились». Интуитивно ясно,
что вероятность последнего события равна отношению заштрихованной площа-
ди ко всей. В этом случае говорят о «геометрических вероятностях». Мы про-
должим рассмотрение этого примера в главе 4.
Рис. 1.11. Пространство элементарных событий в задаче о встрече
Пример 1.5а. Случайное блуждание на плоскости. Будем считать, что перемеще-
ния фигуры в различных ходах осуществляются взаимно независимо, причем
фигура перемещается вверх с одной и той же вероятностью р для всех ходов и
перемещается вправо по горизонтали с противоположной вероятностью q = 1 - р.
Какова вероятность того, что после пятого хода фигура окажется на поле с4, то
ест ь сделает два хода вправо и три хода вверх?
Оказывается, что рассматриваемая задача — это другая формулировка испыта-
ний Бернулли, которые будут рассматриваться в следующей главе. Там будет по-
казано, что искомая вероятность рассчитывается по формуле биномиального рас-
пределения.	□
Рассмотрим некоторое событие А. Часто возникает ситуация, когда поступает
информация о том, что некоторое другое событие В наступило, в то время как о
событии А ничего не известно. Как в этом случае изменится вероятность наступ-
ления события А? Такие вероятности называются условными вероятностями, is
отличие от ранее рассматриваемых безусловных вероятностей Р{Л}. Естествен-
ный ход рассуждений следующий. 1:слн наступило событие В, то это означает,
что наступило одно из элементарных событий, входящих в событие В. Следова-
1.4. Вероятности на дискретном пространстве элементарных событий
39
тельно, событие А может наступить только за счет событий, которые являются
общими для обоих событий, то есть за счет произведения событий А  В. Это при
водит нас к следующему определению.
Определение 13. Пусть В — событие, имеющее ненулевую вероятность: Р{В} / О
Условная вероятность события А при условии, что событие В произошло, опре-
деляется как
(1.20)
Условные вероятности, рассматриваемые при одном и том же условии В, облада
ют всеми свойствами обычных вероятностей (1.12)—(1.17). В частности, для не-
совместных событий At и А2 P{At + А21 В} = Р{Л ( | В} + Р{А21 В} и т. д.
Из определения условной вероятности (1.20) следует формула умножения евро
ятиостей: если Р{В} 0, то
Р{АВ} = Р{В}Р{А | В}.	(1.21)
По индукции доказывается следующая формула, справедливая, если ниже выпи
санные условные вероятности существуют (то есть вероятности условий не ран
ны пулю):
P{Ai А2 ... Ak} = Р{Л J Р{А21 А,} Р{Л31 А, А2} ... P{Ak | А1... Ak_t}. (1.22)
Часто вероятность события А легче рассчитать, рассматривая наряду с ним дру-
гие события (гипотезы), с которыми событие А может наступить. Это приводи i
к следующему результату.
Пусть Яь Я2,..., Нк — полная группа событий, отдельные события которой пазыва
ются гипотезами (см. Определение 10). Имеет место формула полной вероятности
P{A} = fp{Hi}P{A\Hi},	(1.23)
i=i
то есть вероятность события А равна сумме вероятностей гипотез, умноженных
на условные вероятности события А при условии, что соответствующие гппоге
зы произошли.
Доказательство формулы (1.23) простое. Поскольку
А = £1 -А = (Я, + Я2 + ... + Нк)-А = Я1 - А + Н2  А + ... + Нк  А
и из несовместности Н, следует несовместность A-Hjt то, согласно формулам
(1.19) п (1.21),
РИ) = р( £ я,. •	= £ Р{Я; • Л} = £ Р{Я,} • Р{А\Я,}.
I i=i J 1=1	i=i
11 формуле полной вероятности мы вычисляем вероятность события А па oenoiu-
вероятностей различных гипотез. Обратная ситуация возникает, когда нам г га
попптся известно, что событие А произошло, но мы не знаем, с какой нме......
гипотез. В ;>том случае используется формула Байеса.
Условная вероятность гипотезы //,, вычисленная при условии, ч то собы пн- .1
произошло, находится по формуле Байеса (формуле проверки вероятт» теп
гипотез):
40
1. Пространство элементарных событий
Р{Н^=ШШ
Р{А}
(1.24)
Эта формула вытекает из свойства коммутативности умножения: А - Н, =Hi - А:
Р{А • Н;} = Р{А}  Р{Н,\А} = Р{Н,}- Р{А\Н^.
Исходные вероятности гипотез Р{Н,} называются априорными, а пересчитанные
условные вероятности Р{Н,|Л} — апостериорными, поскольку учитывают ин-
формацию, поступившую после испытания.
Определение 14. События А и В называются независимыми, если
Р{АВ} = Р{А}Р{В}.	(1.25)
Если события А и В имеют ненулевые вероятности, то условие независимости
(1.25) равносильно любому из двух эквивалентных условий:
Р{А\В} = Р{А}, Р{В|Л} = Р{В}.	(1.26)
Иными словами, события независимы тогда и только тогда, когда их условные и
безусловные вероятности совпадают. Тем не менее определение (1.25) предпоч-
тительней, поскольку не требует отдельного рассмотрения случая, когда одно из
событий является невозможным: из формулы (1.25) следует, что невозможное
событие и любое другое событие независимы.
Обсудим степени зависимости между случайными событиями. Крайнюю степень
зависимости имеют эквивалентные и противоположные события. Эквивалент-
ные события наступают и не наступают одновременно, а для противоположных
событий наступление или ненаступление одного события влечет ненаступление
или наступление другого события. Более слабую степень зависимости дают не-
совместные события. В этом случае наступление одного события исключает на-
ступление другого события, однако ненаступление одного события не гарантиру-
ет наступление другого события, хотя при этом вероятность наступления
второго события увеличивается. Формально это доказывается так. Поскольку
для двух несовместных событий А и В наступление А влечет наступление не В,
то есть А с В, то АВ = А и поэтому
Р{А\В} =	> Р{А}.
Р{В} Р{В}
Для независимых событий какая-либо зависимость отсутствует, так что факт на-
ступления одного события никак не влияет на наступление другого события.
Если события А и В независимы, то формула (1.15) для вероятности их суммы
уточняется так:
Р{А + В} = Р{А} + Р{В} - Р{А}Р{В}.	(1.27)
Определение 15. Пусть А ь Л2,..., Ак — некоторые события. Говорят, что эти собы-
тия попарно независимы, если любые два из них независимы. Эти события неза-
висимы в совокупности (или взаимно независимы), если для любого подмножест-
ва этих собы тий А, ,Л: , ...,А, , I < k
P{AiAl.i...Ali}^P{A,i}P{Ali}...P{All}.	(1.28)
1.4. Вероятности на дискретном пространстве элементарных событий
41
В частности, если Alt А2, ..., Ак независимы в совокупности, то вероятность их
произведения равна произведению вероятностей (так называемая Теорема умно
жения вероятностей событий):
P{At А2... Ак] = Р{А,}Р{А2}... Р{Ак}.	(1.2'ф
Следующий пример, принадлежащий С. Н. Бернштейну, показывает, что собы
тия могут быть попарно независимыми, но зависимыми в совокупности. IIус и
О ={сор со2, со3, со4} и все элементарные события равновероятны: Р{со, } = 1/4, i 1,4
Рассмотрим события А ={<0], со2}, В ={<0], со3}, С ={со,, со4}. Тогда
Р{А} = Р{В} = Р{С} Л,
Р{А-В} = ?{«,} = 1 = Р{А}-Р{В},
4
P{A-Q = ?{«,} =1 = P{A}-P{Q,
4
Р{С -В} = />,} =1 = P{Q-P{B},
4
то есть события А, В и С попарно независимы.
В то же время
Р{А-В-С} = />,} =1^Р{А}.Р{В}Р{С}=А.1.1 = 1.
4	2 2 2 о
Итак, эти события попарно независимы, но не независимы в совокупности.
Примеры
Пример 1.2d. Двукратное бросание игральной кости. Найдем вероятности собы
тип А. иАЫ0, используя формулу полной вероятности. Рассмотрим следующп
гипотезы: Я, — на первой игральной кости выпало i очков, i = 1, ..., 6. Очевидш
/>{//,} = 1/6, i = 1,..., 6. Далее, Р{А.|Н,} = 1/6; Р^М = Ж=.о|Я2} = Р{А^и\//.,} (
/’{АЬ10|Я4} = Р{А£=10| Я5} = Р{А£=10| Я6} = 1/6. Следовательно,
6	111
Р{А.} ^P{Hi}-P{A.\Hi}=6^^=^,
i=i	6 b 6
= tРШ  P{A^lQ\Hi} = 1 • 3-1 = a
j=i	6	6 12
го есть получены прежние результаты.
11ример 1.8. Урновая схема. Имеется k урн, содержащих, соответственно, п2, .
нк шаров, среди которых белых шаров mt, т2,..., тк. С вероятностью р, выбирав!
ся /'-я урна (р, + р2 + ... + рк = 1) и из нее выбирается наудачу шар. Какова всроя i
йоги, того, что выбранный шар — белый? Если выбран белый шар, то каковы ш
роятностн его выбора из различных урн?
Пусть А означает интересующее пас событие — выбор белого шара, а II, се и. с<
(в.11 иг гипотеза  выбрана урна номер/. 11о условиям задачи Р{11,} - р,, /ф4|//,)
- т, /nt. Следовательно,
42
1. Пространство элементарных событий
Р{А} =р\ тх/щ + р2 т2/п2 + ... + рктк/пк.
Если выбран белый шар, то вероятность его выбора из г’-й урны составит
Р{Я,|А} = Р{Я,.|А} = Р{Я'Л} =—, i = i,2,...,k.	(1.30)
Р{А} М
П: 2-1
.......... ,	,	>1 nj
Пример 1.9. Последовательная проверка гипотез. Рассмотрим две урны, содержа-
щие белые и красные шары. Доля красных шаров в первой урне равна р,, а во
второй урне р 2. Вначале наудачу выбирается урна. Вероятность выбора первой
урны равна р, а второй урны 1 - р. Затем из выбранной урны последовательно
выбирается п шаров с возвращением, так что каждый выбранный шар после
фиксации его цвета возвращается в урну. Пусть все выбранные шары оказались
красными. Какова вероятность того, что они были извлечены из первой урны?
Как эта вероятность зависит от числа извлечений п?
В данном случае имеется две гипотезы: Я, —- первоначально была выбрана пер-
вая урна, Я2 — была выбрана вторая урна. Рассматриваемое нами событие А —
«все п извлечений дали красные шары». Условные вероятности А составляют:
Р{А\Н\} =р", Р{А\Н2} =р2.
Теперь вероятность события А подсчитывается по формуле полной вероятности
(1.23):
Р{А} = Р{Н{}Р{А | Я,} + Р{Н2}Р{А | Я2} =р р” + (1 - р) р''.
Искомую условную вероятность гипотезы Ht подсчитаем по формуле Байеса
(1.24). Вероятность того, что выбрана первая урна и что все шары красные, со-
ставляет:
Р{РЦ} Р{А \ Нг} = р р".
()копчательно получаем формулу
РР"
P-P'i +(1-P)-P2
Пусть р =0.5, pt =0.6, р2 =0.4. В табл. 1.2 приведена зависимость условной ве-
роятности Р{Нх\ А} того, что была выбрана первая урна, от числа извлечений п,
в течение которых все время извлекались красные шары. Мы видим, как растет
наша уверенность в том, что мы имеем дело с первой урной.	□
Таблица 1.2. Условная вероятность Р{Ц| А} как функция числа извлечений п
N	1	2	3	4	5	6	7	10	15	20
РП^Л}	0.556	0.610	0.661	0.709	0.753	0.792	0.827	0.903	0.966	0.989
1.5. Вероятность наступления комбинации событий*
Формулы (1.19) п (1.29) позволяют найти вероятности простейших комбинаций
собы тий суммы несовместных событий и произведения взаимно независимых
событий. В атом разделе мы покажем, как нахо цпь вероятность произвольной
1.5. Вероятность наступления комбинации событий’
43
комбинации событий. Проведем наше изложение в контексте структурной на
дежности систем (см. раздел 1.3).
Состояние каждого элемента системы, фиксируемое в некоторый момент вре-
мени (например, начала работы или обслуживания), является случайным. Пред-
положим, что различные элементы сменяют свои состояния независимо друг
от друга. Иными словами, если А,- это событие «г-й элемент находится в рябого
способном состоянии», то события At, А2, ..., А„ являются взаимно независимы
ми. Будем обозначать вероятности этих событий (иначе — надежности элемен-
тов) р2, рп.
Определение 16. Надежностью системы R называется вероятность ее работоспо-
собности: R = Р{В}, где В — событие «система работоспособна».
Наша задача заключается в том, чтобы выразить надежность системы через на-
дежность ее элементов.
Для последовательной системы (см. формулу (1.6)) из условия взаимной незави-
симости {А;} и формулы (1.29) сразу вытекает, что ее надежность системы
Rs = PlP2-Pn-	(1.31>
Итак, надежность последовательной системы равна произведению надежностей
ее элементов.
Чтобы получить аналогичный результат для параллельной системы, следует и
формуле (1.8) перейти к противоположному событию В. По закону де Моргана
(1.4) получаем
В = At + А2 + ... + Ап = А, • А2 •... • Ап.
Следовательно,
Р{В}=Р{Ах}Р{А2}...Р{Ап}.
Поскольку Р{А,} = 1 - P{Aj} = 1 - pit а надежность параллельной системы /\;, 
= 1 - Р{В}, то
R,, = 1-(1-Р1)(1-р2)...(1-ри).	(1.32)
I Ггак, надежность параллельной системы равна единице минус произведение веро
ятностей ненадежностей элементов.
Практически так же легко выразить надежность последовательно-параллельной
системы. Например, для системы, изображенной на рис. 1.7, имеем:
R4, = Р{В} = Р{(А, + А2) • А3 • (А4 • А5 + А6)}.
Используя формулы (1.15) и (1.29), находим:
Р{А, + А2} = Р{А,} + Р{А2} - Р{А, }Р{А2},
Р{А4 • А5 + Ао} = Р{А4 }Р{А5} + Р{АС} - Р{А4 }P{A5}P{A(i}.
('ледовательпо,
=(Р| +Р2 -Р1Р2)Р.)(Р4Р5 +Ро -Р^РэРв)-
Последний пример показывает, как вычислять надежность последовательно на
раздельной i iktcmh, в записи которой отсутствует повторение одних и тех *<•
событий: следует последовательно применять формулы (1.31) п (1.3'2) д/|я на
дежности последовательной п параллельной спечем.
44
1. Пространство элементарных событий
В том случае, когда в указанной записи некоторые события повторяются, воз-
никают осложнения, как это можно видеть на примере системы «два-из-трех»
(1.10). Здесь мы имеем сумму трех совместных событий At А2,А1  А3 и А2 • А3:
В =	• А2 + А( • А3 + А2 • А3. Мы можем представить ее как сумму несовместных
событий, используя свойство идемпотентности At • А2 • А3 + Д • А2 • А3 = Д • А2 • А3
и тождества 
А(  А2 = Д • Д • Q = Д • А2 • ( Д + Д ) = Д • А2 • А3 + Д • А2 • Д.
Итак,
В = Д • Л2  Д3 + Д • Л2 • Д + Д • Д • Д3 + Д • А2 • Д.	(1.33)
Слагаемые правой части равенства являются несовместными событиями, поэто-
му надежность рассматриваемой системы
Я = Р1Р2Р-з + B1B2U “Вз )+Bi G _В2 )В.з +(1-Р1)Р2Рз-	(1-34)
Отметим, что булева функция, соответствующая выражению (1.33), есть
g(x{ ,х2,х3) =х{ &х2&х3 v х{ &х2&х3 v х{ &х2&х3 v xt &х2&х3. (1.35)
Такое представление булевой функции называется ее дизъюнктивной совершен-
ной нормальной формой.
Теперь мы видим, что представление события В «система работоспособна» в
виде (1.33) и (1.35) в точности совпадает с представлением этого события с по-
мощью искусственного пространства элементарных событий, рассмотренных
выше в примере 1.7 раздела 1.3: В = {111, 110, 101, 011}. Здесь 1 соответствует на-
ступлению события А, а 0 — событию А. Теперь мы можем сформулировать ал-
горитм решения поставленной задачи в общем виде.
Алгоритм вычисления вероятности наступления комбинации независимых событий
Вход : некоторая комбинация независимых событий В; вероятности р, наступле-
ния событий А, , входящих в комбинацию В.
Выход: вероятность Р{В} наступления комбинации В.
Алгоритм
Шаг 1. Выразить комбинацию В через элементарные события искусственного ба-
зиса, как это описано в разделе 1.2.
Шаг 2. Подсчитать вероятности элементарных событий, входящих в В, как веро-
ятности (1.29) произведения взаимно независимых событий. При этом элемен-
тарному событию Af А"2 ... А“" приписывается вероятность
в Г(1 - В,р?V-P2Г”2... в?(1 -в„Га".
где
(А,, если а, =1,
А,°- = _	(1.36)
|Д, если at =0.
Шаг 3. Суммировать полученные вероятности, что дает искомую вероятность со-
бытия В.
Программное* обеспечение этого алгоритма составляют Программы Prod, Sum, Arise,
BDC, Euenl, Aoaliabl, Prob, ProbProd, ProbSum.
Компьютерный практикум № 3. Вероятности событий в пакете Mathcad
45
В заключение отметим изменения, которые необходимо внести в алгоритм в случае
зависимости исходных событий то есть когда отказы элементов системы —
взаимнозависимые. Для этого случая в Шаге 2 алгоритма подсчет вероятности
элементарных событий производЬится не по формуле (1.29) для независимых и
совокупности событий, а по формуле (1.22) для зависимых событий. Соответ < i
вующие условные вероятности должны быть заданы в качестве исходных дан
ных.
Компьютерный практикум № 3.
Вероятности событий в пакете Mathcad
Цель и задачи практикума
Целью практикума является вычисление вероятностей составных событий них
комбинаций в пакете Mathcad.
Задачами данного практикума являются:
□	задание вероятностей элементарных событий;
□	описание составных событий;
□	вычисление вероятностей составных событий и их комбинаций;
□	нахождение условных вероятностей событий;
□	вычисление апостериорных вероятностей гипотез;
□	применение алгоритма вычисления вероятностей наступления комбинаций
независимых событий для расчета надежности системы «два-из-трсх».
Необходимый справочный материал
В настоящем практикуме рассматриваются дискретные пространства элементар
ных событий. Подсчет вероятностей составных событий такого пространства
сводится к суммированию вероятностей элементарных событий, входящих в
пего. Поэтому основным используемым оператором будет операция суммпрова
нпя. В пакете Mathcad имеется два варианта этой операции, доступ к которым
предоставляется после открытия окна Calculus Palette. В первом случае (см.
рис. 1.12) вызывается операция суммирования S, в которой указаны как пнжнис,
гак и верхние пределы суммирования. Необходимо указать эти пределы и ни
деке суммирования. Пределы должны быть целыми числами, причем верхний
предел не меньше нижнего. Индексом суммирования может быть какая-либо бу
ква или слово. В процессе суммирования индекс пробегает все целочисленные
значения, начиная с нижнего и кончая верхним. Справа за знаком суммы запп
t ывается выражение для общего члена суммы. Обычно оно содержит индекс
суммирования, что позволяет суммировать различные слагаемые. Во втором
случае под символом суммирования указывается только индекс суммирования.
Интервал изменения его значений задается ранее путем применения оператора
присвоить :=, например, 1 := 2 .. 10.
Аналогичную структуру в Mathcad имеет и операция произведения II, которая
подобно операции суммирования, используется также в двух вариантах: с указа
пнем верхнего и нижнего пределов индекса п без них. Данная операция шпиль
луегся в практикуме при вычислении вероятностей произведения событий.
46
1. Пространство элементарных событий
Суммирование и произведение могут быть осуществлены также путем использо-
вания оператора цикла for, что также имеет место в одной из программ, пред-
ставленных ниже.
Реализация задания
/(ля проведения вычислений нам понадобятся три функции пользователя из ком-
пьютерного практикума № 1: Sum(A, В), Prod(A, В) и Arise(i, А), и три — из прак-
тикума №2: Fam(n), DBC(n, N) и TwoThree(Au А2, А3). Назначение данных функ-
ций описано ранее в соответствующих практикумах. Дополнительно определим
новые функции пользователя, которые позволяют вычислять вероятности исход-
ных событий и комбинаций. Программные модули, реализующие функции поль-
зователя, представлены на рис. 1.12. Функции имеют следующее назначение.
Практикум №3. Вероятности событий
Пользовательские функции
Вероятность составного события
Prob(A.Pr)
S<-0
for i € 1 cols(prT) - 1
Вероятности всех элементарных событий
искуственного пространства
EIEvPr(Pr)
cols(pj ) - 1
S S + if(Arise(i.A),Prt,O)
Вероятность произведения событий А и В
ProbProd(A,B,Pr) .= Prob(Prod(A,B),Pr)
for («о 2n-1
nel DBC(n,i)
•к- fl (pnrlj-, 6-p>i)VnelJ-’
J = 1
Вероятность сунны событий А и В
ProbSum(A,B ,Рг) - (Prob(A.Pr) + Prob(B ,Рг)) - Prob(Prod(A,B), Рг)
Условная вероятность Р(А/В)
CondProb(A,B,Pr)Iffprob(B.Pr) «0,0, PL0A~0.d(AB^Pr)>|
I.	Prob(B.Pr) J
Формула полной вероятности
cote(H)-1
TotalProb(A.H.Pr).- V Probtll1 ,PrJ CondProb(A,H ,PrJ
Формула Байеса:
ApostProb(H.A.Pr) :=
for i « 1._ cols(H) - 1
, РгоЬРго<|(а,Н(|>.Рг)
bi <---------------------
TotalProb(A,H,Pr)
b
Рис. 1.12. Программные модули, вычисляющие вероятности событий
Основной является функция Prob(A, Рг), вычисляющая по формуле (1.11) веро-
ятность составного события А. Событие А описывается вектором-столбцом, ком-
поненты которого — элементарные события, составляющие событие А. Вероят-
ности элементарных событий задаются вектором-столбцом Рг, причем г-я компо-
нента этого вектора Рц есть вероятность г-го элементарного события со, . Обычно
элементарное событие со() отсутствует, в этом случае необходимо положить Piy = 0.
Функции ProbSum(A, В, Рг) и ProbProd(A, В, Рг) вычисляют вероятности суммы
1'{А t В} и произведения Р{А В) событий А и В. Условная вероятность В}
события А при условии, что событие В произошло, вычисляется функцией
Компьютерный практикум № 3. Вероятности событий в пакете Mathcad
47
CondProb(A, В, Рг). Формула полной вероятности (1.23) реализуется функцией
TotalProb(A, Н, Рг), а формула Байеса (1.24) — функцией ApostProb(H, А, Рг). При
этом отдельные гипотезы Н}, Н2, ... задаются как столбцы матрицы Н (нулевой
столбец Но содержит нулевые значения и не используется). Как и ранее, вероя i
ности элементарных событий задаются вектором-столбцом Рг.
Функция ElEvPr(Pr) вычисляет по формулам (1.29) и (1.36) вероятности всех
элементарных событий искусственного пространства, соответствующие заданным
вероятностям взаимно независимых событий р, = Р{А।}, р2 = Р{Л2}, ..., р„ = /’(/I,,)
Результаты вычислений
Полученные результаты представлены на рис. 1.13. Вычисления осуществляю!
ся на основе одиннадцати вероятностей элементарных событий 1, 2, ..., 11. .')in
вероятности содержатся в векторе Prll. При этом нулевая компонента этого век
тора не используется, поскольку мы начинаем нумерацию элементарных собы
тий с единицы, а компоненты векторов в Mathcad нумеруются с нуля.
Результаты вычислений
Вероятности 11 элементарных событий
Рг11 = (0 02 0.1 0.3 0Л5 0.05 0.14 0Л4 0.02 0.03 0.06 0.01 )Т
Составные события:	С>(1 2 3 4 5 6 7)Т	G:«(1 0 11 9)Т
Вероятности составных событий
Prob((2 5 1 9 4 11)Т .Prill-0.44 Prob(Sum(C,G). Prll) = 0.94 Prob(C.Prll) - 0.88
Вероятность суммы событий С и G:
Вероятность произведения событий С и G:
ProbSum(C,G,Pr!1) - 0.94
ProbProd(C,G,Pr11)  0.2
Условная вероятность P(G/Q:
CondProb(G.C.Prll) - 0.227
Гипотезы
2 3 4 5)Т	н<2>(6 7 8)т	Н<3>.-(9 10 11 )Т
0 16 9
0 2 7 10
Н- 0 3 0 11
0 4 0 0
ч0 5 0 0 ,
Ргоь(н^.Рги) - 0.7
Составное событие ДР:
Вероятность составного события АР:
Условные вероятности события АР):
Соп0Ргоь(ар , Н<2>. Prll) - 0.1
Вероятность составного события АР:
Вероятности гипотез
Prob
(н<2>,Prll) - 0.2	Ргоь(н<3>,Рги) - 0.1
АР - (4 5 0 9)Т
РгоЬ(АР, Prll) - 0.15
CondProb (ар, H^’.Prll)-0.143
СопОРгоь(аР . Н<3>. Prll) - 0.3
То<а1РгоЬ(АР,Н,Рг11) - 0.15
Апостериорные вероятности гипотез
ApostProb(H,AP.Pr11)T - (0 0.667 0.133 0.2)
Расчет надежности для системы “два из трех"
Надежность элементов системы:	RialEI - (0 0.4 0.0 0.5)Т
Вероятности всех элементарных событий для системы “два из трех”
EIEvPr(RlalEI)T - (0.06 0.06 0.24 0.24 0.04 0.04 0.16 0.16)
Вероятность исправности системы “два из трех*’
Piob( Iwo1Iiioo(f агп(з/°> ,Гат(з/^ .1 atn(3)<2>). EIFvPr(RialEI)) - 0.6
Рис. 1.13. Puuy/iKiuiw расчета вероятностей событий
48
1. Пространство элементарных событий
Вначале вычисления проводятся для различных способов заданий составных со-
бытий: путем непосредственного указания множества составных событий, путем
использования имен событий, путем комбинаций событий. Выполняется расчет
вероятностей суммы и произведения событий; условных вероятностей событий.
Далее рассматриваются гипотезы Я(1>, Я(2>, Я(3>, а также событие АР. Опреде-
ляется вероятность события АР непосредственно и с помощью формулы полной
вероятности на базе функции TotalProb. Оба варианта дают одинаковый резуль-
тат 0.15. Затем находятся апостериорные вероятности гипотез {функция ApostProb).
В заключительной части работы рассчитывается надежность системы
«два-из-трех» путем непосредственного использования приведенного в конце
раздела 1.5 алгоритма. Надежности элементов системы были приняты следую-
щими: р, = 0.4, р2 = 0.8, р3 = 0.5. Полученное значение надежности 0.6 (см.
рис. 1.13) совпадает со значением, которое дает формула (1.34).
Задания для самостоятельной работы
1.	Апробировать представленные функции пользователя путем расчета вероят-
ностей различных событий.
2.	Экспериментально проверить правильность вычисления вероятностей по
формулам (1.16), (1.17) и (1.23).
3.	Использовать представленные программы для вычислений при решении ни-
жеприведенных задач 1.11-1.14.
4.	Описать логику работы программы ElEvPr{Pr), приведенной на рис. 1.9.
5.	Разработать программу, производящую необходимые вычисления в задаче 1.13.
6.	Разработать программу, вычисляющую вероятность безотказной работы по-
следовательной «два-из-н» системы (см. задачу 1.16).
Задачи
Задача 1.1. Доказать следующие свойства:
2 =АА = В^>А=В, А = В^>А=В.
Задача 1.2. Доказать формулы:
А-В = АВ, А{В - С) = АВ - АС,
A-В = {А +В)-В = А-АВ.
Задача 1.3. Показать на примере, что разность свойством ассоциативности не об-
ладает:
(А-В)-С* А-(В-С),
в связи с чем выражение А - В - С не определено.
Задача 1.4. Упростить следующие выражения:
А + АВ, (А - С){В - С), (А + В)(В + С),
(А + В)(А + В), {А + В){А + В){А + В).
Задача 1.5. Доказать тождества:
{А + В) - В = А - В = А В, (Л - А В) + В = А + В,
(Л I В) АВ - АВ I АВ.
Задачи
49
Задача 1.6. Пусть А, В, С — три произвольных события. Найти выражения для
событий, состоящих в том, что из А, В, С:
□	произошло А;
□	произошли Я и В, в то время как С не произошло;
□	произошло по крайней мере одно событие;
□	произошло ровно одно событие;
□	произошло ровно два события;
□	ни одно событие не произошло;
□	произошло не более двух событий.
Задача 1.7. Покажите, что если события А и В независимы, то независимы и со-
бытия всех пар А и В, А яВ, А и В.
Задача 1.8. Обобщите предыдущий результат для случая взаимнонезависимых
событий , А2,..., Ak.
Задача 1.9. Два стрелка независимо друг от друга делают по одному выстрелу
в цель. Вероятность поражения цели первым стрелком составляет р,, вторым
стрелком — р2. Найти вероятность того, что цель будет поражена.
Задача 1.10. Среди 25 экзаменационных билетов 5 «хороших» для некоторого
студента. Найти вероятность следующих событий: А — «студент, идя на экзамен
первым, вытащит “хороший” билет» ; В — «студент, идя на экзамен вторым, вы
тащит “хороший” билет, если до него был вытащен также “хороший” билет»; С
«студент, идя на экзамен вторым, вытащит “хороший” билет».
Задача 1.11. В первой урне имеется 1 белый и 9 черных шаров, во второй у pi к
1 черный и 5 белых шаров. Наудачу выбирается урна и из нее извлекается шар
Какова вероятность того, что извлеченный шар — черный? Если извлечен чср
ный шар, то какова вероятность того, что он был извлечен из первой урны?
Задача 1.12. В первой урне имеется 1 белый и 9 черных шаров, во второй урне
1 черный и 5 белых шаров. Из каждой урны случайным образом удалили но од
ному шару. Оставшиеся шары ссыпали в одну урну, после чего из нее извлекли
наудачу шар. Какова вероятность того, что извлеченный шар — белый?
Задача 1.13. Поиск неисправности. На изделии может возникнуть три истирав
пости. За определенный промежуток времени вероятности возникновения ншк
иранностей соответственно составляют 0.2, 0.15, 0.1. После возникновения нерпой
неисправности изделие отказывает с вероятностью 0.8, второй — с вероятностью
0.5 и третьей — с вероятностью 0.9. Найти вероятность отказа изделия, вредно
лагая возникновение неисправностей несовместными событиями. В какой по
следопателыюсти следует искать неисправность, явившуюся причиной отказа?
Задача 1.14. Имеется 5 ури. В первых трех урнах находится по дна белых п ipn
красных шара, в четвертой и пятой — по одному белому и одному красному
шару. Случайно выбирается урна и из нее извлекается шар. Какова условная не
роятпость того, что выбрана четвертая или пятая урны, если извлеченный шар
оказался белым?
Задача 1.15. I loc.'ie<)oeame.’n>H<i>i «<)<ia-n:i-n» система. Система состоит па п эн
меиюн, откалывающих иглавпснмо друг от друга. Элементы системы пропумсро
1. Пространство элементарных событий
ваны числами от 1 до п. Система отказывает, если отказывают не менее двух ря-
дом расположенных элементов, то есть первый и второй, или второй и третий,
или третий и четвертый, и т. д. Написать выражение для события В «система ра-
ботоспособна». С помощью приведенного программного обеспечения рассчитать
надежность системы для выбранных значений числа элементов п и вероятности
безотказной работы элементов {р,}.
2 Классическое определение
вероятностей и повторные
испытания
2.1.	Различные определения вероятностей
При задании вероятностей элементарных событий мы не обсуждали, как эти вс
роятности определяются. Теперь мы рассмотрим этот вопрос. Существую! еле
дующие основные принципы задания вероятностей: классический, геометрический
в статистический.
В ряде практических ситуаций все элементарные события являются равноты
можными, равновероятными. Если общее число равновероятных событий про
странстваИ равно т, то из условий нормировки и неотрицательности следуе!, то
Р{со,} = 1/т, г = 1,т.	(2 1)
Отсюда и из определения (1.11) вероятности составного события А находим, ч го
вероятность события А равна отношению числа тА = | А | элементарных собыt пй.
входящих в А (иногда их называют благоприятствующими событиями), к обще
му числу элементарных событий пространства т = |Q|:
Р{А} = тЛ/т, ЛсП.	(2.2)
Описанный принцип назначения вероятностей элементарных событий пазыва
ется классическим. Из формул (2.1) и (2.2) следует, что он сводится к определи
нню т = |Q| — общего числа элементарных событий пространства Q и тЛ |/1|
числа элементарных событий, входящих в событие А, вероятностью которого мы
интересуемся. Подсчет этих чисел производится обычно комбинаторными мето
бими. В связи с этим ниже излагаются основы комбинаторики.
Мы видим, что классический принцип применим, если число элементарных со
бытии пространства конечно. Если же пространство элементарных собыt ни
пс< четно, то иногда может быть применен принцип, основанный па геомет-
рической трактовке пространства элементарных событий и составных событий
В двумерном случае каждое элементарное событие отмечается па плоско! in
ючкой. Тогда все пространство элемен тарных событий Q изображается па пи»
кости некоторой областью, площадь которой обозначим 5(1. Интересующее ii.ii
составное собы тие /1 также отмечается на плоскости областью с площадью 5 ,
52
2. Классическое определение вероятностей и повторные испытания
Тогда вероятность событий А определяется как отношение соответствующих
площадей:
P{A} = SA/Sn.	(2.3)
Так назначаемые вероятности называются геометрическими вероятностями. Ясно,
что этот подход применим для любой размерности представления пространства
элементарных событий. Важно только, чтобы события, которым соответствуют
равные площади или объемы (в многомерном случае), были бы равновероятны.
Оба изложенных подхода базируются на принципе равновозможности, приме-
ненном для случаев конечного и бесконечного числа элементарных событий
пространства. Это весьма редко встречающаяся иа практике ситуация.
Если элементарные события неравновсроятпы, то их вероятности оцениваются
на основе статистических данных. В этом случае проводится последовательность
испытаний, число которых обозначим п. Если пш и пА есть число испытаний,
в которых было зарегистрировано элементарное событие <о и составное собы-
тие А, соответственно, то вероятности этих событий определяются как
р{®} = «ыА Р{А} = пА/п.
Это — статистическое определение вероятностей. Обоснование такого подхода
дается в законе больших чисел и теории точечных оценок (см. разделы 7.5 и 1.11).
Сейчас только отметим, что точность так назначаемых вероятностей растет с рос-
том числа испытаний п.
2.2.	Элементы комбинаторики
Вернемся к классическому определению вероятностей событий. Уже говори-
лось, что при назначении вероятностей по формулам (2.1) и (2.2) используются
элементы комбинаторики.
В комбинаторике рассматривается некоторая генеральная совокупность W, содер-
жащая конечное число элементов и: п = |1У|. Основополагающим является поня-
тие выборки. Выборкой объема г, или r-выборкой, называется совокупность из г
элементов, каждый из которых — элемент из W. Выборки классифицируются по
двум принципам: возможностью повторения элементов и упорядоченностью
элементов. Если допускается повторение одних и тех же элементов W в выборке,
го говорят о выборке с повторениями, иначе — выборке без повторений. Если две
выборки с одними и теми же элементами считают различными, коль скоро они
отличаются лишь порядком элементов в выборке, то говорят об упорядоченных
выборках. Если же порядок элементов в выборке считается несущественным, то
говорят о неупорядоченных выборках.
Понятие выборки можно интерпретировать следующим образом. Из генераль-
ной совокупности W последовательно извлекается г элементов. При выборке с
повторением каждый извлеченный элемент возвращается в генеральную сово-
купность до того, как будет извлекаться очередной элемент выборки (что и дела-
ет возможным повторение одних и тех же элементов в выборке). В связи с этим
выборки с повторением называют также выборками с возвращением. При выбор-
ке без повторений извлеченные элементы в генеральную совокупность не воз-
вращаю гея. Такие выборки называют также выборками без возвращения.
2.2. Элементы комбинаторики
53
Упорядоченные выборки соответствуют ситуации, когда учитывается очередность
извлечения элементов из генеральной совокупности; неупорядоченные выбор
ки — когда очередность не учитывается. Упорядоченные выборки называются
перестановками, неупорядоченные — сочетаниями. Выборка объема г называй!
ся r-перестановкой или r-сочетанием, судя по тому, является она упорядоченной
или неупорядоченной.
Описанная нами классификация выборок представлена в табл. 2.1.
Таблица 2.1. Классификация выборок
Возможность повторения элементов в выборке	Учет порядка элементов в выборке	
	Упорядоченные выборки	Неупорядоченные выборки
Без повторения	Перестановки без повторения	Сочетания без повторения
С повторением	Перестановки с повторением	Сочетания с повторением
Формулы для числа различных r-выборок из генеральной совокупности с п эле
ментами приведены в табл. 2.2. В этой таблице Сгп — это биномиальные коэффп
циенты, определяемые формулой
с;; =--------, г = 0,1, ..., п.
г\(п-г)\
(2.1)
Таблица 2.2. Число различных r-выборок из генеральной совокупности объема п
Возможность повторения элементов в выборке	Учет порядка элементов в выборке	
	Упорядоченные выборки	Неупорядоченные выборки
Без повторения	п (п - !)...(/? - г + 1)	сг„
С повторением	пг	
Докажем формулы, приведенные в табл. 2.2. Вначале рассмотрим упорядочен
пые выборки. Если объем такой выборки г, то выборка имеет г мест, коюрыс
должны быть заполнены элементами генеральной совокупности W. Число таких
элементов п. В случае выборки с возвращением каждое очередное место можез
быть заполнено п способами, так что общее число вариантов равно пг. Если
выборки без возвращения, то первое место может быть заполнено п способом
второе и-1 способом (элемента, извлеченного первым, уже нет в генерал ыioii со
вокупности), третье п - 2 способами и т. д„ последнее r-е место п - (г - 1) сиосо
бами. Итак, общее число вариантов есть п (п - 1) (п - 2) ... (п - г + 1).
Теперь рассмотрим неупорядоченные выборки. Для выборок без возвращснн>1
применимы следующие рассуждения. Из каждой неупорядоченной выборки бей
возвращения Можно образовать г! упорядоченных выборок без возвращения
Следовательно, вторых в г! раз больше, чем первых. Поскольку вторых выборок
и (и 1) ... (п - г + 1), то первых — п (п - 1) ... (п - г + 1)/г! = С'.
Нам осталось доказать формулу для числа неупорядоченных выборок (сочепг
iinii) с повторениями, будем трактовать /-сочетание как неупорядоченную вы
(юрку с возвращением объема / из генеральной совокупности, содержащей н эле
54
2. Классическое определение вероятностей и повторные испытания
ментов. Каждая такая выборка полностью описывается указанием того, сколько
раз попал в выборку первый элемент генеральной совокупности, второй элемент
и г. д. Схематически это может быть изображено следующим образом. Будем ко-
личеством звездочек указывать число попаданий данного элемента в выборку.
Черточки будут использоваться для различения одних элементов от других. Ко-
личество звездочек между первой и второй черточками — это количество извле-
чений первого элемента, между второй и третьей — количество извлечений вто-
рого элемента и т. д. Например, при г = 8 и п = 6 запись /***/*////****/ означает,
что первый элемент попал в выборку три раза, второй элемент — один раз, тре-
тий, четвертый и пятый — не попали, тестой элемент — попал четыре раза.
Такие записи содержат /'звездочек и п + 1 черточек и всегда начинаются и кон-
чаются черточками, но остальные п - 1 черточек и г звездочек располагаются
произвольным образом, причем каждому расположению соответствует своя вы-
борка. Следовательно, число различных рассматриваемых выборок — это число
способов выбора г мест для звездочек из п + г - 1 мест, то есть Сгп+Г_{.	□
Фигурирующие в табл. 2.2 биномиальные коэффициенты Сгп известны из фор-
мулы разложения бинома Ньютона:
(а + Ь)п =tc;arb-\	(2.5)
г«0
В частности, полагая здесь а = b = 1, находим, что
£С'=2".	(2.6)
г=0
Общая схема применения изложенных результатов для определения вероят-
ностей событий заключается в следующем. Процедура выбора /'элементов гене-
ральной совокупности трактуется как опыт (испытание, наблюдение, экспери-
мент). Мыслимо нерасчленимым исходом этого опыта является выборка. Иначе
говоря, каждой выборке соответствует элементарное событие пространства Q.
Число таких элементарных событий т равно числу различных выборок и задает-
ся табл. 2.2. На основе этого по формуле (2.1) определяется вероятность каждого
элементарного события пространства Q. Отметим, что из условия задачи должно
следовать, какие выборки необходимо рассматривать (упорядоченные или нет,
с возвращением или нет), с тем чтобы все они были равновозможными, и можно
было применить классический принцип назначения вероятностей. Аналогичным
образом реализуется формула (2.2): подсчитывается число тА выборок, удовле-
творяющим условиям, описывающим событие А, и производится деление его
па т.
Примеры
Пример 2.1. Гипергеометрическое распределение. В урне имеется п шаров, прону-
мерованных числами 1, 2, ..., п. Из п шаров щ имеют красный цвет, а остальные
п nt шаров — белый. Из урны наудачу извлекается без возвращения г шаров,
/• <, п. Какова вероятность того, что среди них шаров красного цвета?
Решение
В рассматриваемом случае порядок шаров в выборке значения не имеет, следо-
iiaiсльпо, рассматриваются неупорядоченные выборки без повторения. Число
2.2. Элементы комбинаторики
55
таких выборок, согласно табл. 2.2, составляет С,'. Следовательно, число элемеп
тарных событий пространства т = |Q| = С',. По условию задачи все такие выбор-
ки равновероятны, поэтому согласно формуле (2.1) Р{со} = 1/Сп.
Каждое элементарное событие пространства Q описывается набором (гф г2, .... i,),
где все г) принимают значения от 1 до п, причем порядок роли не играет. Остано
вимся на интересующем нас событии, которое обозначим через А. В собы тие .1
входят те элементарные события, которые содержат ровно номеров шаров,
имеющих красный цвет, и г - номеров шаров, имеющих белый цвет. Из общею
числа П] красных шаров г, шаров можно выбрать С'1 способами (как и рай..•.
без учета порядка выбора шаров). Из общего числа п - и, белых шаров г /1
шаров можно выбрать способами. Следовательно, общее число элементар
ных событий, содержащих ровно rt красных и г - г, белых шаров, тЛ = С\' С'
Окончательно по формуле (2.2) получим
Р{А} =
(2.7)
Это — так называемое гипергеометрическое распределение. Оно широко приме-
няется в выборочном контроле качества продукции. Роль белых шаров здесь иг-
рают годные изделия п, роль красных — бракованные. Известны: общее чиемо
изделий п, объем выборки г и число негодных изделий в выборке г,. На основе
этих данных необходимо оценить число бракованных изделий в партии ()ц< и
кой максимального правдоподобия числа бракованных изделий является закое
значение n]t при котором достигается максимум вероятности (2.7) при даниы
значениях п, г и rt.
Пусть п = 12, ?•= 5 и Г) = 2. Вероятности 7? = Р {А} как значения функции (2.7) от
аргумента щ представлены в табл. 2.3. Из таблицы видно, что наиболее w/кад/
ное (максимально правдоподобное) число бракованных изделий в партии //,	5
Отметим, что приведенные в таблице вероятности не составляют распределение
вероятностей (их сумма не равна единице), поскольку соответствуют' разным
пространствам элементарных событий.
Таблица 2.3. Вероятность Я = Р {А} как функция л,
«1	0	1	2	3	4	5	6	7	8	9
	0	0	0.152	0.318	0.424	0.442	0.379	0.265	0.141	0.045
Пример 2.2. Выборка с повторением. Из генеральной совокупности, содержани и
и элементов, извлекается с возвращением г элементов. Какова вероятность тою,
ч то все элементы выборки различны? Отметим, что к этой задаче сводя тся мин
гпе другие задачи.
Решение
Выборку здесь образуют номера извлеченных с возвращением элсмеи ion /I -ш
того чтобы выборки были равновероятны, необходимо учитывать порядок гк
ментон н выборке. Чпсмо ihkiix выборок равно и1. Выборки, в которых псе > ie
56
2. Классическое определение вероятностей и повторные испытания
менты различны, соответствуют извлечениям без возвращения. Число таких
упорядоченных выборок равно и(и - 1)... (п - г + 1). Следовательно, искомая ве-
роятность составляет
Г 1Y 2^ ( г-Й
(п -1)(« -2)... (п -(г - 1))/и' = 1 — 1 — ... 1-.
( пД п) \ п )
2.3.	Последовательности испытаний
Простейшей схемой последовательности испытаний являются испытания Бер-
нулли. Словесно они описываются следующим образом. Проводится п независи-
мых испытаний. Каждое испытание может закончиться двумя исходами, кото-
рые условно называют «успех» и «неудача» и обозначают соответственно У кН.
Вероятность успеха не меняется от испытания к испытанию и равна р, а вероят-
ность неудачи q - 1 - р, причем р, q > 0. В этих условиях обычно интересуются
вероятностью того, что в п испытаниях успех наступил ровно i раз, i =0,п.
Математическая формулировка испытаний Бернулли следующая. Имеется про-
странство, состоящее из двух элементарных событий: Q = {У, Н}. Вероятности
элементарных событий составляют Р{У} = р и Р{Н} = q = 1 - р. Образуем новое
пространство Q", элементарными событиями которого являются последователь-
ности из п символов, каждый из которых — один из символов элементарного со-
бытия из Q: Q" = {(о | (о = («>| ,со2, ...,со„)}, где Усо,- е {У, 7/}.
Элементарному событию w = (со, ,со2,...,со„) из нового пространства Q'' припи-
шем вероятность, равную произведению, получающемуся в результате замены
компоненты У нового элементарного события w на вероятность р, а компоненты
II - па вероятность
Р{(Ю1, со2 Р{Ю1 №2 }••  Р{со„ }	(2.8)
В результате этого элементарное событие, содержащее i символов У и, следова-
|елыю, п - i символов Н, наделяется вероятностьюр'q"~'. Так определенная ве-
роятность на новом пространстве Q" удовлетворяет условию неотрицательности.
Проверку условия нормировки мы проведем одновременно с аналогичной про-
веркой для формулы (2.9).
Обозначим X число появлений успехов в п испытаниях Бернулли. Вероятность
события {X = i} = «успех наступил i раз» определяется формулой биномиального
распределения
Р{Х = i} =Cinpiq”~i, г=0~п,	(2.9)
.	fl I
где C'tl =-------биномиальные коэффициенты.
i !(п - I)!
/(окажем эту формулу. Интересующее нас событие {X = i} = «успех наступил
ровно ? раз» состоит из тех элементарных событий, которым соответствуют
(в любом порядке) ровно i успехов и п - i неудач. Как уже отмечалось, вероят-
ное гь каждого такого элементарного события равнаp'q"~‘, следовательно, ве]Х>-
я 11кс обытия {У - /} равняется произведению числа входящих в него элемеп-
।аоных событий па Ба"
2.3. Последовательности испытаний
Для вычисления указанного числа элементарных событий заметим, что элемен
тарные события, составляющие событие {X = i}, отличаются друг от друга только
порядком расположения символов У и Н, в то время как количество символов .'
и Н остается неизменным и равным, соответственно, i и п - i. Поскольку выбор /
мест для символа У однозначно определяет места для символа Н, то необходимо
найти число различных способов выбора i мест из п для символа У. Будем :ну
процедуру трактовать как выбор без возвращения из генеральной совокупное i и
чисел 1, 2,..., п. Выборка имеет объем i, порядок элементов в выборке не сущее т
венен. Следовательно, имеет место /-сочетание без возвращения, число которых
С'. Это и доказывает формулу (2.9).	П
Проверим выполнение условия нормировки для биномиального распределения
(2.9). Поскольку/) + <?=!, то па основании формулы (2.5)
£с'//<7"-; =(р+<7)" =1.
i=0
Вероятность появления не более i успехов вычисляется по формуле
Р{Х </} = £Сi=^n-	(2.10)
г=0
Примеры
Пример 2.3. Возвратимся к примеру 1.5 из разделов 1.1 и 1.4. Какова вероятное ! I.
того, что после пяти ходов фигура окажется на поле с4 шахматной доски?
Решение
Будем трактовать испытание как один ход фигуры, успех — как перемещение
вверх, неудачу — как перемещение вправо. Фигура оказывается на поле с4, если
из пяти ходов три будут сделаны вверх, а два — направо, следовательно, искомая
вероятность равна вероятности трех успехов в пяти испытаниях Бернулли. По
скольку по условию задачи вероятность успеха (хода вверх) в одном йены гании
равна р, то ответ дается формулой (2.9) при п = 5 и i = 3. В частности, для /> 0 6
вероятность оказаться на поле с4 составит 0.346. Вероятности других позиции
фигуры после пяти ходов представлены в табл. 2.4. Здесь же даны накопленные
вероятности, рассчитанные по формуле (2.10).
Таблица 2.4. Вероятности различных позиций после пяти ходов
Позиция	Л	е2	</3	с4	65	аб
Число успехов	0	1	2	3	4	5
Вероятность	0.010	0.077	0.230	0.346	0.259	0.078
Накоп. всроят.	0.010	0.087	0.317	0.663	0.922	1.000
Пример 2.4. Найдем вероятность того, что в последовательности пены ганий Бер
пулли а успехов встретятся раньше, чем b неудач.
Решение
Зафиксируем свое внимание на результатах, полученных после испытания с по
мером п - а 1 h 1.1 In гересующее нас собы тие происходит тогда п только ня ла
58
2. Классическое определение вероятностей и повторные испытания
когда в этот момент число зарегистрированных успехов X не менее а. Это собы-
тие противоположно событию «число успехов X не более а - 1». Вероятность
последнего события Р{Х < а - 1} находится по формуле (2.10) при i = а - 1
и и = а + b - 1. Следовательно, искомая вероятность Р{Х > а} = 1 - Р{Х < а - 1}.
В частности, в условиях предыдущей задачи вероятность того, что фигура до-
стигнет четвертой горизонтали раньше, чем четвертой вертикали, получается от-
сюда, если положить здесь а = b = 3. Нужные нам численные значения содержат-
ся в табл. 2.2: Р{Х< 2} = 0.317, Р{Х> 3} = 1 - Р{Х < 2} = 1 - 0.317 = 0.683.	□
Часто испытания Бернулли рассматриваются в другом контексте. Пусть число
испытаний пе фиксировано, и испытания проводятся до получения первого
успеха. В этом случае пространство элементарных событий имеет вид
Q = {У, НУ, ННУ, НИНУ,...}.
Вели вероятность успеха в одном испытании р, а неудачи q = 1 - р, причем р,
q > 0, то элементарному событию НН...НУ, описываемому i символами (из кото-
рых г - 1 первых символов равны Н, а последний символ — У), естественно при-
писать вероятность q'~lp. Так определенные вероятности удовлетворяют услови-
ям нормировки, поскольку
со	оо	4
£ <7<7'~1 = ^7—7 = 1‘
i=i	/=|	1 ~ Q
Обозначим У число испытаний, необходимых для получения первого успеха. Со-
бытие {У = /} соответствует одному элементарному событию НН...НУ из i симво-
лов и имеет вероятность
P{Y = i] = pq'-', г = 1,2,...	(2.11)
Э го — так называемое геометрическое распределение.
Событие {У < i} — «необходимое число испытаний не превосходит г» является
противоположным событию {У > ?} — «все первые г испытаний закончились не-
удачами». Поскольку вероятность последнего события равна q', то
P{Y<i} = l-q', г’= 1,2,...	(2.12)
Г.стествепное обобщение испытаний Бернулли заключается в том, что каждое
испытание может закончиться не двумя, а большим числом исходов. Иными
словами, исходное пространство состоит из конечного числа элементарных со-
бытий: Q = {®|, со,,..., со,,,}. Элементарному событию сп; этого пространства при-
писана вероятность Pj = /’(сп-), причем V;?, > 0,Р\ + р2 + ... + рт = 1.
Элементарное событие пространства Q”, отвечающего п независимым испытани-
ям, описывается последовательностью п символов, каждый из которых — символ
племен гарного события из Q:
со = (со, coJ2... coJn ) е Q", Vco; gQ.	(2.13)
Элементарному событию co = (co;i соу,...со,- ) нового пространства припишем ве-
роятность, равную произведению, получающемуся в результате замены компо-
ненты элементарного собы тия со па вероя тность р f :
2.4. Случайные блуждания*
59
В результате этого элементарное событие, содержащее ij символов , j = 1, in.
будет наделено вероятностью p't’ р'., ... р'"'.
Пусть Xj — число появлений исхода в п испытаниях. Тогда вероятность собы
тия «первый исход появился г( раз, второй исход — г2 раз,..., т-тл исход — г,„ раз»
Р{Х =ij, j = l,m} =——-р;'1 р'*...рЛ it + i2 + ... + im = n. (2.11)
г( !г2 !.../„, !
Это так называемое полиномиальное распределение.
В рассмотренных выше схемах последовательности испытаний предполагалась
независимость результатов отдельных испытаний. Отказ от этого предположи
ния приводит к следующей схеме. Исходным является пространство элеменrap
ных событий Q, содержащее т элементарных событий: Q = {<Bt, <в2,.№»)• 11"
вым пространством элементарных событий является Q".
Элементарному событию нового пространства приписывается вероятность про
изведения событий по формуле для вероятности произведения зависимых собы
тий (1.22):
Р{(Ш7| ш72... ®7л )} = Р{(07| }Р{(0,21 со„ }... Р{(ОЛI о,,... ш7п , },	(2.15)
где Р{<072| <О71 }, •••, P{aj, I	~ заданные числа, трактуемые как условные
вероятности (1.20) и удовлетворяющие условиям
P{fi>7,|fi>7i...fi>7,|}>0, Vco,
УЛ<в, Iсо, со, ...со,-, } = 1, Vco, ,со, ,...,со, еО.
1 Л* J\ J'2	Л-\ *	’	’ 72’	’ 7/-1
G)j j € Q
2.4.	Случайные блуждания*
Задачи, связанные со случайными блужданиями, часто возникают при рассмотри
нии вопросов управления запасами, страхования, рисков, разорения и т. и. Мы
рассмотрим только случай симметричных блужданий, поддающийся анализу
комбинаторными методами раздела 2.2. Излагаемый ниже материал требует по
вышенного внимания, поэтому его можно опустить. Однако освоивший его чи за
тель приобретет навыки в решении некоторых задач теории страхования, разоре
ния и управления запасами.
Рассмотрим блуждание частицы по целочисленным точкам прямой. Па каждом
шаге с номерами 0, 1, 2, ... частица перемещается или в левую или в правую со
седине точки. Траектории такого блуждания удобно изображать на плоскости, в
которой ось абсцисс является осью времени, а ось ординат показывае т положе
вне частицы на прямой в соответствующий момент времени. Каждая такая тра
ектория изображается путем, представляющим собой ломаную с вершинами,
которым соответствуют абсциссы 0, 1, 2,..., а ординаты у0, уь у2,... удовлетворяю!
условию г/, - У)_\ = ± 1, г = 1, 2, ... Путем из начала координат в целочисленную
точку с неотрицательными координатами (х, у) называется путь, для которою
//0 - 0, у, = у. /(липой пути называется число шагов х.
Точка с целочисленными неотрицательными координатами (г,//) може т бы и. со
едниепа путем с началом координат в том и только том случае, если г и у имею!
вид л = а । Ь, у - а Ь, где а и b целые положительные. Чтобы убедшься в
50
2. Классическое определение вероятностей и повторные испытания
ном, достаточно трактовать а как число шагов вправо, а b — как число шагов
влево, так что х = а + b — общее число шагов, у = а - b — заключительное поло-
жение частицы. Если координата у должна быть положительной, то накладыва-
ется дополнительное условие а> Ь.
Многие важные заключения могут быть получены на основании следующих
простых лемм.
Лемма 2.1. Число различных путей из начала координат в точку (х = а + Ь, у = а - Ь)
равно Ся+6 = Сх .
Доказательство следует из того, что пути этой совокупности отличаются один от
другого только а номерами шагов, которые делались направо. Поэтому число
различных путей совпадает с числом сочетаний из а + b по а.	□
Лемма 2.2. Принцип отражения. Пусть А - (Xt; Л2) и В = (В^, В^) — две точки с
целочисленными координатами, причем В{ >	> 0, А2 > 0, В2 > 0. Число путей
из А в В, которые касаются или пересекают ось абсцисс, равно числу всех путей
из А1 в В, где А’ = (Л^ -Л2).
Доказательство
Рассмотрим произвольный путь из А в В, одна или несколько вершин которого
лежат на оси абсцисс (рис. 2.1). Пусть С — первая вершина, лежащая на оси абс-
цисс. Если отразить участок АС симметрично относительно оси абсцисс, то полу-
чим путь А1СВ, ведущий из А1 в В и впервые пересекающий ось абсцисс в точке С.
Таким образом установлено взаимно однозначное соответствие между всеми пу-
тями из А1 в В и путями из Ав В, имеющими точки на оси абсцисс.	□
Рис. 2.1. Иллюстрация принципа отражения
Лемма 2.3. Число путей из начала координат в точку (х, у), где х = а + b > 0,
у = а - b > 0, которые не касаются оси абсцисс, равно — Cjr+!/)/2 = ——-Caa+h. Чис-
х	a + b
ло путей, не пересекающих ось абсцисс (т. е. не касающихся плюс касающихся),
равно С‘1+;,/ + 2>/2 = a~b + i С“++|+1 •'
х + 1	а + b + 1
Доказательство
/(окажем первое утверждение для некасающихся оси абсцисс путей. Каждый из
рассматриваемых путей начинается со скачка вверх, в результате чего он оказы-
вается в точке (1, 1). Теперь остается х - 1 шаг и необходимо сдвинуться еще на
//	1 позиций вверх. Поэтому общее число путей из точки (1, 1) в точку (.г, у)
равно числу сочетаний по (.г - 1 + у- 1)/2 па .г - 1, то есть ’2)/2. Искомое
число путей равно разности двух чисел: этого и числа путей из точки (1, 1) в точ-
2.4. Случайные блуждания*
61
ку (х, у), касающихся или пересекающих ось абсцисс или, что то же самое, па
точки (0, 1) в точку (х - 1, у). Согласно Лемме 2.2, это число равно числу всех
путей из точки (0, -1) в точку (х - 1, у), иначе — из точки (0, 0) в точку (х - 1,
у + 1). Следовательно, это число равно С^р',/2.
Окончательно находим, что искомое число путей
^(.v+»-2)/2 _£(л+у)/2 ___(-г~ ~ 1) !__________
1-1	1-1	(х + У -2) Yx - у Y Гх + у Y (х —у-2 Y
I 2	2 ) ( 2 Л 2 )’
=	(х-1)!___________2 _ 2	= (х -1)! г/ = у_ с<х+!, )/2
(х + у -2Y (х-у-2Y х-у х + у Гх + у) Гх-г/Y х
I 2 J ’ [ 2 ) ’	Л 2~ J' I 2 J ’
Теперь докажем утверждение для путей, непересекающих (некасающихся и ка-
сающихся) оси абсцисс. Число путей из точки (0, 0) в точку (х, у), некасающихся
оси абсцисс, равно числу путей из точки (1, 1) в точку (х, у), непересекающих го
ризонталь, проходящую через точку 1 оси ординат. Последнее число путей сов
падает с числом путей из точки (0, 0) до точки (х - 1, у - 1), непересекающих осп
абсцисс. Следовательно, число путей из точки (0, 0) в точку (х, у) непересекаю
щих оси абсцисс, равно числу путей из точки (0, 0) в точку (х + 1, у + 1) пека
сающихся оси абсцисс. Согласно первому утверждению доказываемой леммы
оно равно ^-^С<1р!/+2>/2-	□
Последняя лемма позволяет достаточно просто находить вероятности некоторых
событий, связанных со случайными блужданиями. Элементарным событием
здесь будет определенный путь блуждания, пространством — вся совокупное и,
возможных путей. Все пути считаются равновероятными, так что имеет место
классическое определение вероятностей (2.2). Следовательно, для нахождения
вероятности некоторого события А необходимо вычислить общее число ну теп т
и число путей тА, соответствующих событию А. Последнее осуществляется час-
то с помощью леммы 23.
Примеры
Пример 2.5. Задача о баллотировке. Два кандидата на выборах набрали cooihci
ственно а и b голосов причем, а> Ь. Используя результаты предыдущей леммы,
покажем, что вероятность того, что первый кандидат был все время впереди, ран
на (а - Ь)/(а + Ь~). Вероятность того, что первый кандидат не отставал от второ
го, составляет (а - Ь +1)/(а +1).
Решение
Ход голосования можно описать путем, начинающимся в начале коордпи.н (О, (I)
и заканчивающимся в точке (а + Ь, а - Ь). Общее число таких ну теп равно
in - Пути, не касающиеся осп абсцисс, составляют событие «первый к.-пi.iи
дат был все время впереди». Согласно лемме 23 число их тА = С"+/,(a l>)/(<i i b)
()i ношение iuA/iii дает первую вероятвость.
Событию «первый кандидат не оюгавал от второго» соответствуют нуги, ш- ш
ресекающне оси абсцисс. Их число, согласно лемме 23, равно
62
2. Классическое определение вероятностей и повторные испытания
C^{a+l-b)/{a + b + l).
11осле деления его на т получаем вторую вероятность.
Пример 2.6. Показать, что среди С^,, путей, соединяющих начало координат с
точкой (2«, 0) на оси абсцисс, существует ровно С2""12/п путей, для которых все
вершины, кроме первой и последней, лежат выше оси абсцисс.
Решение
У всех рассматриваемых путей общим является то, что первый шаг был вверх и
приводил в точку (1, 1), а последний шаг был вниз из точки (2п - 1, 1). Отдель-
ные пути отличаются друг от друга только поведением в течение 2п - 2 шагов.
Можно считать исходную точку (1.1) за начало координат и рассматривать пути,
ведущие из нес и не пересекающие оси абсцисс. Тогда последней точкой будет
(2// - 2, 0), а предпоследней (2/г - 3, 1). Согласно лемме 2.3 число путей длины
2п - 3 из начала координат в точку (2// - 3,1), которые не пересекают оси абс-
цисс, составит С^|'/+2)/2(у + 1)/(х + 1) = С2„_,2/(2/г-2) = С'^/п. Это и есть ис-
комое число.	□
Будем называть d-горизонталью горизонталь, проходящую через точку d на оси
ординат.
Лемма 2.4. Число путей из точки (0, с) в точку (а + Ь, с + а - Ь), которые сверху
касаются или пересекают //-горизонталь, c-b <d < min{c, с + а - Ь}, равно .
Число аналогичных путей, которые сверху пересекают //-горизонталь, равно
/’"Д '/и > c-b+l<d<l+ min {с, с + а- Ь}.
Доказательство
Рассмотрим вначале случай d = 0. Из условий, наложенных на d, следует, что
с > 0, с + а - b > 0, Ъ > с. Лемма 2.2 утверждает, что число путей из точки (0, с)
в гочку (а + Ь, а + с - Ь), которые касаются или пересекают ось абсцисс, равно
числу всех путей из точки (0, -с) в точку (а + Ь, а + с - Ь). Последнее же число
равно числу всех путей из начала координат в точку (а + Ь, а + 2с - Ь) и согласно
и-мме 2.1 составляет С"*};. Итак, случай d = 0 доказан.
Случай d > 0 сводится к рассмотренному, если заменить с на с - d, то есть просто
принять за новую ось абсцисс //-горизонталь, проходящую через точку d на оси
ординат.
Для доказательства второй части леммы заметим, что число путей, сверху пере-
секающих //-горизонталь, равно числу путей, которые касаются или пересекают
(d - 1 )-горизонталь.	□
Лемма 2.4 описывает поведения минимумов случайных блужданий. Поведение
максимумов может быть получено путем использования принципа симметрии-.
каждому пути из точки (0, с) в точку (а + b, с + а - й) однозначно соответствует
путь, симметричный относительно с-горнзонтали. Последний ведет из точки (0,
с) в гочку (а + Ь, с + b - а) и получается заменой на противоположные направле-
ния скачков частицы на отдельных шагах.
Лемма 2.5. Число путей из точки (0, с) в точку (а + Ь, с + а - Ь), которые снизу
касаются или пересекают //-горизонталь, max{c,c + а - h} <h <с + а, равно
Число аналогичных путей, которые cini.iy пересекают //-горизонталь, равно
( л ’'1. max {с, с I а - //} -1 < // S с; + а 1.
2.4. Случайные блуждания*
63
Доказательство
На оси ординат для точки h симметричной относительно точки с является точка
(2с - 7г). Поэтому согласно принципу симметрии искомое число путей равно
числу путей из точки (0, с) в точку (а + b, с + b - а), которые сверху касаются
или пересекают (2с - /г)-горизонталь, следовательно, согласно лемме 2.4 это чис
ло составляет С^~<2с~А) = С'^~с.
Вторая часть леммы следует из того, что пересечь снизу /г-горизонталь это
снизу коснуться или пересечь (h + 1 )-горизонталь.	□
Теорема 2.1. Условные экстремумы случайных блужданий. Рассмотрим пути, па
пинающиеся в точке (0, с) и оканчивающиеся в точке (а + Ь, с + а - Ь). Вер< >
ятность того, что путь сверху коснется или опустится ниже ^-горизонтали,
c-b <d < min{c, с + а - Ь}, вычисляется по формуле
Fmin(rf) =-------’ c-b <d <min{c,c + a-b}.	(2.17)
(а + с -d)! (b-c + d)\
Вероятность того, что путь опустится ниже d-горизонтали, равна Fmin (d -1).
Вероятность того, что путь снизу коснется или поднимется выше /г-горизоитал и,
max {с, с + a-b} <h < с + а, вычисляется по формуле
F„..,Ah) =-------а. b.------- max{c,c + а - b} < h < с + а. (2.18)
(b + h - с)! (а+ с-h)!
Вероятность того, что путь поднимется выше /г-горизонтали, равна F„I;1X (// i I).
Доказательство
Для доказательства формулы (2.17) достаточно применить результаты лемм 2.1
и 2.4. Для доказательства формулы (2.18) следует воспользоваться леммами 2.1
и 2.5.	□
Пример 2.7. Задача о дефиците. В некоторой авиакомпании планируется попав
ка а и расход b авиадвигателей. Поступление и расходование авиадвпгакчкч’1
осуществляется независимо друг от друга и по одному. Какова вероятность от
сутствия дефицита авиадвигателей, если первоначальный запас их с, с < b < а i с?
Решение
Процесс поступления а и расходования b авиадвигателей описывается путем, па
чальной точкой которого является (0, с), а заключительной (а + Ь, а + с - b). J[e
фицит имеет место, если путь пересечет ось абсцисс. Следовательно, необходимо
подсчитать вероятность такого пути.
Согласно теореме 2.1 вероятность того, что путь опустится ниже осп абсцисс
(г/ = 0), составляет F,nil) (-1). Итак, вероятность отсутствия дефицита
0,	b > а + с,
«(< ) = ! “Л..(-D =
I,	с £ Ь.
64
2. Классическое определение вероятностей и повторные испытания
Рассмотрим следующие численные данные. Пусть расход авиадвигателей в два
раза превышает поступление: b = 2а. Вероятности отсутствия дефицита для раз-
личных значений а и первоначального запаса с представлены в табл. 2.5. Из нее,
например, видно, что при а = 4, с = 4 эта вероятность составит 0.556. Если перво-
начальный запас с увеличить до шести, то вероятность отсутствия дефицита воз-
растет до 0.976.	□
Таблица 2.5. Вероятность отсутствия дефицита f?(c)
	с = 1	с = 2	с = 3	с = 4	с = 5	с = 6	с = 7	с = 8	с = 9
а = 1	0.667	1.000	1.000	1.000	1.000	1.000	1.000	1.000	1.000
а = 2	0	0.600	0.933	1.000	1.000	1.000	1.000	1.000	1.000
а - 3	0	0	0.571	0.893	0.988	1.000	1.000	1.000	1.000
а = 4	0	0	0	0.556	0.867	0.976	0.998	1.000	1.000
а = 5	0	0	0	0	0.545	0.848	0.965	0.995	1.000
Весьма полезным является следующий принцип двойственности. Для каждого
пути с ординатами г/0, у{, у2, ..., уь определим обращенный путь с ординатами
у о = г/o' У 'i = Уь ~ Ук-v i=l,k -1, у\ = у^, получающийся изменением порядка вер-
шин на обратный и совмещением крайних вершин прямого пути с крайними
вершинами обратного пути. Тогда каждому утверждению о путях соответствует
утверждение об обращенных путях.
В частности, из леммы 2.3 сразу следует следующая лемма.
Лемма 2.6. Число путей из начала координат (0, 0) в точку А = (а + Ь, а - Ь),
таких что точка А единственная самая высокая, равна ——-С"+ь. Число путей,
а + b
.	а-b + 1 „,.+1
в которых нет точек выше, чем точка А, составляет-----С ‘.
а + b+ 1
Приведенные леммы позволяют находить вероятности различных событий в
схеме случайного блуждания, в которой частица на каждом шаге перемещается
вправо или влево с одинаковой вероятностью 0.5. Отметим, что это — другая
формулировка испытаний Бернулли с равными вероятностями успеха и неудачи
в каждом испытании. Основным здесь является следующий факт: вероятность
любого пути, соответствующего х шагам (испытаниям) равна 2“'. Следователь-
но, дело сводится к подсчету числа различных путей. Это число подсчитывается
с помощью вышеприведенных лемм.
Примеры
Пример 2.8. Пусть на каждом шаге частица, первоначально находящаяся в нача-
ле координат, перемещается вправо и влево с одинаковой вероятностью 1/2. По-
кажем, что вероятность того, что ордината у > 0 будет достигнута впервые в мо-
мент 2п у, равна —-—С2 2"~2", п > у > 0.
2и-г/
2.4. Случайные блуждания*
65
Решение
Рассмотрим момент времени х = 2п - у. Обозначим А событие «ордината точки в
этот момент равна у, причем это самая высокая ордината траектории». Для под-
счета числа таких траекторий применим первое утверждение леммы 2.6. Исполь-
зуя представления х = а + Ь,у = а - Ь, получаем а = (х + у)/2, h = (х - у)/2 и чис-
ло траекторий равно С(х+у'>/2у /х. Вероятность каждой траектории длины л
равна 2~х = 2-<2''"//), что и доказывает утверждение.
Пример 2.9. В условиях предыдущего примера покажем, что вероятность того,
что первое возвращение частицы в начало координат произойдет в момент 2н,
равна
-С”-’22-2", w = 1, 2, ...
п
Решение
Во-первых, вероятность каждого пути длины 2п равна 2’2''. Во вторых, число со-
ответствующих путей, лежащих выше оси абсцисс, подсчитано в примере 2.6. Та-
ково же число путей, лежащих ниже оси абсцисс, так что общее число путей в
два раза больше.
Пример 2.10. Продолжим рассмотрение предыдущего примера. Покажем, что
следующие вероятности одинаковы и равны С?1п2~2”-. а) в момент 2п частица воз-
вращается в начало координат; б) до момента 2п включительно частица ни разу
не возвратилась в начало координат.
Из а) и из результатов предыдущего примера выведем тождество
Сп2л =2Z^C‘-L,) C”-k„_k),n=l, 2, ...
4=1 «
Решение
Рассмотрим пути фиксированной длины 2п, то есть пути, последние точки кото-
рых соответствуют абсциссе 2п. По условию все такие пути равноверояшы.
Поскольку общее число путей длины 2п равно 22", то согласно классическому
принципу каждому пути приписывается вероятность 2~2". Для нахождения веро-
ятности пути, обладающего заданным свойством, необходимо найти число путей
с этим свойством и умножить его на 2“2".
11айдем число путей длины 2п, оканчивающихся на оси абсцисс. Каждый такой
пуп> имеет ровно п единичных скачков вверх и столько же скачков вниз (соот
ветсгвующих перемещениям частицы вправо и влево). Следовательно, число ia
кпх путей равно числу сочетаний из 2п по п, то есть С^п. Итак, вероятность того,
что частица в момент 2п возвратится в начало координат, равна С'^2 J". Зтпм
и доказывается часть а) примера.
Для доказательства части б) примера рассмотрим событие Д24: «первое возвра
щенне частицы в начало координат произойдет в момент 2k». Вероятность этого
собы । ня найдена в предыдущем примере. Иптересующее нас событие «до мо
меша '.’.и включительно час тица нс возвра ти iся в начало координат* обоэпа
ним Н..
66
2. Классическое определение вероятностей и повторные испытания
Очевидно, Л2(А+1) с #24 и #2(4+d = #24 ~ ^2(k+ ij- В предыдущем примере было пока-
зано, что Р{Л24} = — С24122~2/', k = 1, 2,... Покажем по индукции, что P{B2t} = C2t2'2i,
k
k = 1,2,... Для k = 1 это очевидно:
р\в2 =-1 = С22"2.
I 21	2
Пусть это справедливо для k > 1. Тогда
Р{В?\м)} ~ B{B2k Д2(4+1)} — Р{Ви} Д{Дг(*+1)}—
_2k 2k+ 1
2(k +1)
__ х+4 9 -2 k	2 ,-,4 п -2 (4+1) __ Л’4 9-2 4 j ,	9
2к ~kiA2k ~ 2к I/ 2(& + l)J- 2к
_ (2*)1 24_, 2k +1	(2(fe + l))! 1о.2.^ _ м
k\k\ k + 1 (k + !)!(& + 1)! 2	2(к+1)
2-2(4+!)
Следовательно, утверждение справедливо для k + 1, а поэтому и для всех k.
Последнее утверждение леммы обосновывается так. Во-первых, из утвержде-
ния а) рассматриваемой леммы следует, что число путей, возвращающих частицу
в начало координат в момент 2п, равно С2п. Во-вторых, это же число можно по-
лучить следующими рассуждениями. Пусть первое возвращение частицы в нача-
ло координат произошло в момент 2k. Число таких путей равно 2 C2^2/k, по-
скольку оно в два раза больше найденного в примере 2.6 (пути могут находиться
как выше, так и ниже оси абсцисс). После этого, спустя 2(и - k) шагов, частица
очередной раз оказывается в начале координат. Число таких путей длины
2(п - k) определяется утверждением а) рассматриваемой леммы. Значение k мо-
жет быть любым от 1 до и, так что общее число путей получается суммировани-
ем. Это и дает доказываемое тождество.
Компьютерный практикум № 4. Анализ повторных
испытаний и случайных блужданий в пакете Mathcad
Цель и задачи практикума
Целью практикума является приобретение практических навыков в программи-
ровании и решение задач, связанных с повторными испытаниями и случайными
блужданиями.
В данном практикуме нами решаются: задача выборочного контроля качества
изделий, задача последовательных испытаний и задача о дефиците.
Необходимый справочный материал
Вначале мы познакомимся с особенностями просмотра в Mathcad векторов и
матриц, имеющих большое число элементов. Если для просмотра всех элементов
массива размера рабочего окошка недостаточно, в нем показывается только
часть массива. Для просмотра всего множества элементов применяется так назы-
ваемая линейка прокрутки. Для получения линейки прокрутки необходимо
щелкнуть в площади окошка, содержащего часть элементов матрицы (вектора).
Далее, перемещая появившийся ползунок линейки, можно просмотрен, весь
Компьютерный практикум № 4. Анализ повторных испытаний и случайных блужданий в пакете Mathcad
67
Наряду с конструкциями Mathcad, рассмотренными в главе 1, в настоящем прак-
тикуме широко используется операция вычисления факториала целого положи-
тельного числа, обозначаемая знаком I, например, п! является факториалом чис-
ла п.
При вычислении сумм применяется способ, когда в операции суммирования L
указывается только индекс. Этот индекс суммирования необходимо предвари-
тельно определить как целочисленный аргумент. Интервал изменения его значе-
ний задается путем применения оператора присвоить :=, например, г:=0. .5, при
этом суммирование выполняется для каждого значения целочисленного аргу-
мента от 0 до 5.
В последних версиях Mathcad среди встроенных статистических функций име-
ются функции, которые можно использовать в представленных ниже вычисле-
ниях. Перечислим эти функции'.
□	сотЫп(г, п) вычисляет значение биномиальных коэффициентов С' по форму-
ле (2.4);
□	dbinom(i, п, р) дает значение вероятности (2.9) для биномиального распреде-
ления при значении аргумента i и значениях параметров пир;
□	pbinom(i, п,р) дает аналогичное значение для функции распределения (2.10);
□	dgeom(i,p) дает значение вероятности (2.11) для геометрического распределе-
ния при значении аргумента i и значении параметра/?; аналогичное значение
для функции распределения (2.12) дается функцией pgeom(i, р).
Ввиду учебного характера данной книги мы рассмотрим ситуацию, когда эти
функции требуется запрограммировать пользователю. В этом случае читатель
может, как и в предшествующих практикумах, использовать ранние версии паке-
та, но не ниже Mathcad 6+.
Реализация задания
Для проведения вычислений будем использовать функцию сотЫп(п, г), кото-
рая описана выше и фигурирует в списке стандартных функций ряда версий
Mathcad, а также функции пользователя dHyperGeom(n, nl, г, rl), dPolin(n, р. i)
п 1\(а. Ь, с). Программные модули, реализующие эти функции, представлены на
рис. 2.2. Новые функции имеют следующее назначение:
□	dllyperGeom(n, nl, г, rl) вычисляет вероятность (2.7) для гипергеометрпчс-
< кого распределения с параметрами п, гц = nl, г, и = rl;
U dPolin(n, р, i) вычисляет вероятность (2.14) для полиномиального распределе
пня, параметрами функции являются: число испытаний п и вектор-столбец
р (р<>. Рь Рг....pm)T вероятностей наступления отдельных исходов; аргумеп
ты функции задаются в виде вектора-столбца числа различных исходов г = (у>,
б. '2.i,,,)';
U R(a, b, с) вычисляет вероятность отсутствия дефицита (2.19), рассматривав
шуюся в примере 2.7.
1’0 lyai.iaii.i вычислений
11опученные результаты представлены па рис. 2.3. В пункте 1 решается задача
выборочного контроля качества iri/lc'niti 11ыч i lenei i ня iinonniiu гея min iiiiioni >-о
68
2. Классическое определение вероятностей и повторные испытания
метрического распределения, рассмотренного в примере 2.1. Объем партии
п - 12, объем выборки г = 5, в выборке оказалось 2 бракованных изделия (rt = 2).
Если в партии п{ = п! бракованных изделий, то вероятность получения двух бра-
кованных изделий в выборке равна значению dHyperGeom(12, nl, 5, 2). Мы обо-
значили ее defect(nl), с тем чтобы проанализировать изменение этой вероятно-
сти в зависимости от значения nl. Результаты содержатся в векторе-столбце Рг.
После его транспонирования получается вектор-строка Ргт. Последняя выведена
среди результатов: первая строка содержит значения nl, а вторая — соответст-
вующие вероятности. Эти же вероятности были приведены в табл. 2.3. Отметим,
что они не составляют распределение вероятностей — это видно из того, что сум-
ма их не равна единице. Распределение вероятностей будет, если при фиксиро-
ванных п,п1 иг варьировать значение как это должно быть для гипергеомет-
рического распределения (2.7). В этом случае суммирование вероятностей по г{
действительно дает единицу, как это видно на распечатке.
Практикуй №4. Повторные испытания и случайные блуждания
Пользовательские Функции
Биномиальные коэффициенты
combin(n,r) ; If^rS n, 	.о)
Вероятности гипергеонетрического распределения
.	.. и( . х . [. . .т\ combin(n1 ,r1) combln(n-n1,r-r1) Л
dHyperGeom(n,n1 ,r,r1) > Ifl г + n1 - n < Н < mini(n1 r) I.-----------------------.0
\	combin(n.r)	)
Вероятности полиномиального распределения
Вероятность отсутствия дефицита
Рис. 2.2. Программные модули, реализующие пользовательские функции
В пункте 2 рассматриваются последовательные испытания. Вычисления прово-
дятся для полиномиального распределения (2.14). Предполагается, что возмож-
ны три исхода, вероятности которых/?! = 0.5,р2 = 0.3 ир3 = 0.2 содержатся в век-
торе-столбце Prez (нулевой исход игнорируется, и его вероятность принимается
равной нулю). Число испытаний п полагается равным 5. Далее определяются ве-
роятности различных исходов i = (i0,	i2, z3)T. Например, вероятность того, что
первый и второй исходы появятся по два раза, а третий — один раз, равна 0.135.
В заключение проверяется, что сумма таких вероятностей, подсчитанная по всем
возможным исходам в пяти испытаниях, равна 1.
Вычисления, проведенные в пункте 3, связаны с задачей о дефиците (см. при-
мер 2.7~). Приводятся результаты расчета вероятностей отсутствия дефицита (2.19)
с использованием функции R(a, h, с) для случая, когда число расходуемых изде-
лий b в два раза больше, чем число поступающих изделий а, то есть b = 2а. Число
расходуемых изделий а варьирует в диапазоне от 1 до 5, а первоначальный запас
...К1П Н|,1ЧИС)|<>-
Компьютерный практикум № 4. Анализ повторных испытаний и случайных блужданий в пакете Mathcad
69
ний используется матрица MR, строки которой соответствуют значениям а, и
столбцы — значениям с. Иными словами, MRlhC = R(a, 2а, с). Эта матрица распе-
чатана. Ранее эта матрица была представлена в табл. 2.5.
Отметим, что в окне вывода может быть показана только часть матрицы MR,
имеющей 9 столбцов. Аналогичная ситуация может наблюдаться и при выводе
вектора-строки Ргг, содержащего 9 элементов. Тогда для просмотра этих масси
вов целиком следует использовать линейку прокрутки.
Результаты вычислений
1.	Выборочный контроль качества для партии из 12 изделий
Вероятность получения 2-х бракованных изделий в выборке обьеиа 5 при п1 бракованных изделий в партии
dofect(nl)dHyperGeom(l2,n1,5,2)	n1;-0. 12
Проверка на нормировку вероятностей получения г1 бракованных изделий в выборке обьеиа 5 при 5-ти
бракованных изделий в партии
г1.-О 5	dHyperGeom(12,5,5,r1)  1
г1
Вероятность получения 2-х бракованных изделий в выборке обьеиа 5 в зависииости от количества
бракованных изделий в партии л1
for п1 е0 9
R„1 If(n1 <2,0,de(ect(n1))
2.	Последовательные испытания
Вероятности исходов в испытаниях:	Prez - (0 0.5 0.3 02 )Т
Вероятности заданного числа исходов в 5-ти испыганииях
dPolin'5 ,Р<ег .(0 2 2 1)’!- 0.135
dPollnts, Ргег. (0 3 1 1 )Т) - 0.15
Проверка распределения вероятностей
на нормировку:
dPolin(s .Prez.fO 3 2 0)Т). 0.113
dPolinfs, Ргег, (0 3 2 1 )Т) - 0
5	5-11
у1	dPolin(5, Prez, (0 i1
11 - 0 i2 - О
I2 5- 11 - I2)T) - 1
3.	Задача о дефиците
Вероятности отсутствия дефицита
MR -
(or а е 15
(от с « 1 9
MRa.c R(a .2 а ,с)
MR
		1		S'		'W	->	1		9
	0	0	0	0	0	0	0	0	И	
	0	0.667	1	1	1	1	1	1	1	
:2	0	0	Об	0 933	1	1		1	1	1
	0	0	0	0 571	0,693	0 998		1	1	1
	0	0	0	0	0 556	0.867	0.979	0 998	1	1
	0	0	0	0	0	0 545	0 949	0 965	0 995	1
Рис. 2.3. Результаты решения задач, связанных с повторными испытаниями
и случайными блужданиями
Задания для самостоятельной работы
I ( остаипгь программу, вычисляющую вероятности для многомерного гннергео
нетричеекого распределения, рассматривающегося в задаче 2.2.
' Экспериментально проанализируйте описанную в задаче 2.1 сходили» iь in
ncpiсоме)рпчсского распределения к биномиальному распределению.
»ь< нерп,мен in. H.iio нроанализпрона гь описанную н задаче 2.27 сходимгки.
онномпа luioi о распределения к пуассоновскому.
70
2. Классическое определение вероятностей и повторные испытания
Задачи
Задача 2.1. Предельная теорема для гипергеометрического распределения. Пусть
п и п\ неограниченно возрастают, причем так, что пх/ п=р, а объем выборки г ос-
тается постоянным. Показать, что вероятность (2.7) стремится к биномиальному
распределению:
Р{А} = С? pr' (1 - р)г-г', г, = 0~г.
Задача 2.2. Многомерное гипергеометрическое распределение. В урне имеется п
шаров, из которых щ шаров первого типа, и2 шаров второго типа,.... nk шаров k-m
типа, П\ + ... + щ = п. Из урны наудачу без возвращения извлекается г шаров. Ис-
пользуя результаты примера 2.1 и метод математической индукции, показать,
что вероятность того, что из г извлеченных шаров rt шаров г-го типа, г, < и„ равня-
ется
су- с+ г2 +...+rk = г.
П| П2	H/g ' п ' I ±	К
Задача 2.3. На полке в случайном порядке расставлены 40 книг, среди них трех-
томник А. С. Пушкина. Найти вероятность того, что эти тома стоят в порядке
возрастания номеров слева направо (но не обязательно рядом).
Задача 2.4. У человека имеется п ключей, из которых только один подходит к его
двери. Когда ему необходимо открыть эту дверь, он последовательно, без повто-
рения, испытывает ключи. Этот процесс может окончиться при 1, 2,..., п испыта-
ниях. Показать, что каждый из этих исходов имеет вероятность 1/ и.
Задача 2.5. п шаров случайным образом размещаются по п ящикам. Найти веро-
ятность того, что все ящики будут заняты. Обсудить связь с примером 2.2.
Задача 2.6. Лифт. Лифт отправляется с г = 7 пассажирами и останавливается на
п = 10 этажах. Чему равна вероятность того, что никакие два пассажира не вый-
дут на одном и том же этаже? (Предполагается, что способы распределения пас-
сажиров по этажам равновероятны.) Обсудить связь с примером 2.2.
Задача 2.7. Дни рождения. Какова вероятность того, что у г наудачу взятых лю-
дей дни рождения окажутся различными? (Предполагается, что распределение
дней рождения по дням года равновероятно.) Обсудить связь с примером 2.2.
Задача 2.8. Бросаются шесть симметричных игральных костей. Какова вероят-
ность того, что выпадут все грани? Обсудить связь с примером 2.2.
Задача 2.9. В городе в течение недели произошло семь пожаров. Какова вероят-
ность того, что все пожары приходились на разные дни недели? Обсудить связь
с примером 2.2.
Задача 2.10. г шаров случайным образом размещаются по п ящикам. Какова ве-
роятность того, что заданный ящик содержит i шаров, i = 0,г?
Задача 2.11. Один профессор Корнельского университета двенадцать раз штра-
фовался за незаконную ночную стоянку автомашины, причем все двенадцать раз
эго происходило или во вторник или в четверг. Найти вероятность этого события
в предположении, что распределение проверок по дням недели равновероятно.
Задача 2.12. Группа из 2k мальчиков и 2k девочек делится на две равные части.
I lain и вероятность того, что и каждой части депочек и мальчиков одинаковое ко-
Задачи
71
Задача 2.13. Найти вероятность того, что случайно взятое натуральное число из
множества 1, 2,..., п делится на фиксированное натуральное число. Найти предел
этой вероятности при п —> со.
Задача 2.14. Из чисел 1, 2,..., п случайно выбирается число а. Найти вероятность
того, что: а) число а не делится ни на аь ни на а2, где at и а2 — фиксированные
натуральные взаимно простые числа; б) число а не делится ни на какое из фик-
сированных взаимно простых чисел аь а2, ..., ак. Найти при и —> » пределы веро-
ятностей в случаях а) и б).
Задача 2.15. Из тридцати чисел {1, 2, ..., 30} случайно отбираются 10 различных
чисел. Найти вероятности событий: А — «все числа — нечетные»; В — «ровно 5
чисел делится на 3»; С — «5 чисел нечетных и 5 чисел четных, причем ровно
одно делится на 10».
Задача 2.16. Из множества чисел {1, 2, ..„ п} по схеме выбора без возвращения
выбираются два числа. Найти вероятность того, что первое из выбранных чисел
больше второго. При выборе трех чисел найти вероятность того, что второе чис-
ло лежит между первым и третьим.
Задача 2.17. В первом ряду кинотеатра, состоящем из п кресел, сидят г человек.
Найти вероятность того, что а) никакие два человека не сидят рядом; б) каждый
из г человек имеет ровно одного соседа; в) из любых двух кресел, расположен-
ных симметрично относительно середины ряда, хотя бы одно свободное, если
число кресел четно.
Задача 2.18. При передаче сообщения по каналу связи вероятность искажения
одного знака равна 1/10. Какова вероятность того, что сообщение из 10 знаков:
а) не будет искажено; б) содержит ровно 3 искажения; в) содержит не более трех
искажений?
Задача 2.19. Система состоит из п идентичных элементов. Каждый элемент неза-
висимо от других за рассматриваемый период времени отказывает с вероятно
стыо р. Система является работоспособной, если не отказали k элементов или
более. Какова вероятность того, что система будет работоспособна? Найти мини-
мальное п, при котором эта вероятность будет не ниже 0,9, если р = 0,8, k = 4.
Задача 2.20. Найти вероятность того, что в 2п испытаниях Бернулли с вероятпо-
стыо успеха в одном испытании р появится п + т успехов и все испытания с не-
четными номерами закончатся успехом.
Задача 2.21. По каналу связи передаются сообщения из нулей и единиц. Из за
помех вероятность передачи правильного сообщения равна 0,55. Для повышения
вероятности правильной передачи каждый знак сообщения повторяется п раз. За
передаваемый принимают знак, повторяющийся в полученном сообщении пан
большее число раз. Найти вероятность правильной передачи одного знака при
п кратном повторении, если п = 5. Подобрать кратность передачи знака п так,
чтобы эта вероятность была не ниже 0,99.
Задача 2.22. За<)ача о движении городского транспорта. Для описания движения
ipaiicnopra через уличный переход предположим, что каждую секунду hmcci мс
> |о одно испытание Бернулли. Успехом будем называть проезд автомобиля че
pea переход, /(опустим, что пешеход может перейти улицу только при условии,
72
2. Классическое определение вероятностей и повторные испытания
что в последующие три секунды переход будет свободным. Найти вероятность
того, что пешеходу придется ждать г= О, 1, 2, 3, 4 секунд.
Задача 2.23. Используя связь биномиальных коэффициентов с испытаниями
Бернулли, доказать следующее тождество:
и	min(r,/)	__ _________
М=2", X C/C'-j=C', Vi = 0,и,/ = 1,и-1.
/=0	;=0
Задача 2.24. Из множества {1, 2,..., п} случайно и независимо друг от друга выби-
раются два подмножества At иА2. При этом каждый элемент независимо от дру-
гих включается в подмножества At и А2 с вероятностью р. Найти вероятность
того, что эти подмножества не содержат одинаковых элементов.
Задача 2.25. Задача Банаха о спичечных коробках. Некий математик всегда носит
с собой две коробки спичек. Каждый раз, когда ему нужна спичка, он выбирает
наугад одну из коробок. Найти вероятность того, что в момент; когда он впервые
вынет пустую коробку, в другой коробке будет г спичек, г = 0, и, где п — первона-
чальное число спичек в каждой коробке.
Задача 2.26. В условиях предыдущей задачи найти вероятность того, что в мо-
мент, когда впервые одна из коробок окажется пустой, другая коробка содержит
г спичек, г = 0,д (Отметим, что указанный момент не совпадает с моментом,
когда вынута пустая коробка.)
Задача 2.27. Пусть в испытаниях Бернулли вероятность успеха в одном испыта-
нии зависит от числа проводимых испытаний п: р = рп, qn = 1 - р„. Предположим,
что и —> с®, —> 0, причем прп = А, где А — положительная константа. Показать,
что в этом случае биномиальное распределение (2.9) стремится к распределению
Пуассона:
V
P{X = i}=Ci„pt„q”„-i	i = 0,1, 2,...
п-+оо 2 |
Задача 2.28. По каналу связи передается 1000 знаков. Каждый знак может быть
искажен независимо от других с вероятностью 0,005. Найти приближенное зна-
чение вероятности того, что будет искажено не более трех знаков.
Задача 2.29. В таблице случайных чисел цифры сгруппированы по две. Найти
приближенное значение вероятности того, что среди 100 пар пара 09 встретится
не менее двух раз.
Задача 2.30. Используя формулу (2.9) и принцип математической индукции, до-
казать формулу (2.14) для полиномиального распределения.
Задача 2.31. Найти вероятность P{Xj = ij} того, что в полиномиальной схеме (2.13),
(2.14) исход tOj наступит ровно г) раз.
Задача 2.32. В условиях предыдущей задачи найти условную вероятность
Р{Х2 = i2, ...,Хт = г1П/Х1 = /,}, it +i2+... + im =п.
Задача 2.33. Имеется п ящиков, по которым случайным образом размещаются
шары до тех нор, пока какой-нибудь шар не попадет в уже занятый ящик. Какова
........... кио >|1(| ши- шюнесс закончился на >-м шаге, г =2,н+ 1?
Задачи
73
Задача 2.34. По каналу связи передается одна из последовательностей буки
АААА, ББББ, ВВВВ с вероятностями p\,pi мр-$(р\ + р?+ Рз = 1)- Каждая переда
ваемая буква принимается правильно с вероятностью а и с одинаковой вероят-
ностью (1-а)/2 принимается за две другие буквы. Предполагается, что буквы
искажаются независимо друг от друга. Какова вероятность того, что передана по
следовательность АААА, если принята АВБА?
Задача 2.35. Два игрока последовательно извлекают шары из урны, содержащей
2 белых и 4 черных шара. Выигрывает игрок, первым вытащивший белый шар
Какова вероятность выигрыша у игроков, начавших игру первым и вторым?
Если право начать игру разыгрывается вначале путем подбрасывания монеты, ю
какова вероятность выигрыша данного игрока?
Задача 2.36. Движение частицы по целочисленным точкам прямой описывается
схемой Бернулли. Если происходит успех, то частица перемещается в правую со-
седнюю точку, а если неудача, то в левую. Найти вероятность того, что за п ша-
гов частица переместится вправо на 1г точек.
Задача 2.37. Движение частицы по целочисленным точкам плоскости описыка
ется полиномиальной схемой с т = 4. Каждому из четырех возможных исходов
соответствует движение частицы в соседнюю точку, расположенную левее, пра
нее, ниже или выше данной, причем все они равновероятны. Найти вероятность
того, что за п шагов частица, отправляясь из начала координат, окажется в точке
(Л„ Л2).
Задача 2.38. Показать, что среди С'1п путей, соединяющих начало координат
с точкой (2п, 0) на оси абсцисс, существует ровно С"2„/(п + 1) путей, у которых
все промежуточные вершины лежат не ниже оси абсцисс.
3
ретные случайные
величины
3.1.	Дискретные случайные величины
и их распределения
Фактически с дискретными случайными величинами мы уже имели дело. Ранее
рассмотренные примеры их — это число выпавших очков при однократном и
двукратном бросании игральной кости, число успехЬв в испытаниях Бернулли,
необходимое число испытаний до получения первого успеха и т. п. Формальное
определение выглядит так.
Определение 1. Пусть Q — дискретное (конечное или счетное) пространство эле-
ментарных событий: Q = {<»!, со2,..., сога}, где т = <ю для счетного пространства Q.
Дискретной случайной величиной называется действительная функция Х(со), оп-
ределенная на Q: X:Q -> Rlt где 7?t = [0,<ю) — одномерное вещественное про-
странство. Каждому элементарному событию со е Q она ставит в соответствие не-
которое действительное число Х(со). В результате испытания (наблюдения,
эксперимента, опыта) наступает какое-то одно элементарное событие со из Q.
Функцией Х(со) оно трансформируется в вещественное число Х(со), которое и
воспринимается как «случайная величина X» (обозначение со при этом обычно
опускается).
Образ пространства Q, соответствующий функции Х(со), называется множеством
возможных значений случайной величины X, а отдельный элемент этого множе-
ства — возможным значением. Обозначим k число элементов этого множества
(k = оо для счетного случая), а сами элементы, то есть возможные значения слу-
чайной величины X, хь х2,..., xk. Пусть {X = х,} означает составное событие «слу-
чайная величина X приняла значение х". Это событие состоит из тех элементар-
ных событий пространства Q, которые функцией X отображаются в значение х\
{X = х(} = {со: Х(со) = х,, со е Q}.
В соответствии с определением (2.2) вероятность события {X = х,} подсчитывает-
ся по формуле
Р{Х=х,}= £Р{со).	(3.1)
3.1. Дискретные случайные величины и их распределения
те
В практических приложениях часто работают не с исходным пространством але-
ментарных событий Q, а с множеством возможных значений {х,} и вероятностя-
ми {р,}, с которыми эти значения принимаются случайной величиной X:
P{X=xi}=pi, i = lj.	(3.2)
Определение 2. Система равенств (3.2), для которой {р,} удовлетворяют услови-
ям неотрицательности и нормировки, называется распределением вероятностей
дискретной случайной величины X.
Отметим, что говорят о конечнозначной случайной величине, если множество воз-
можных значений случайной величины — конечное, то есть если k < оо.
Распределение вероятностей (3.2) для конечнозначной случайной величины мо-
жет задаваться таблично или графически — с помощью полигона вероятностей
(табл. 3.1 и рис. 3.1). Более общим способом задания, пригодным и для случай-
ных величин со счетным множеством возможных значений, является аналитиче-
ский — с помощью формул.
Таблица 3.1. Распределение вероятностей конечнозначной случайной величины
i	1	2	3	4	5	6	7	8
xi	1	3	5	6	7	9	10	11
Pi	0.10	0.15	0.25	0.20	0.10	0.05	0.05	0.10
F(xt)	0.10	0.25	0.50	0.70	0.80	0.85	0.90	1.00
0.3 -
0.2 -
0.1 -
0 1 2 3 4 5 6 7 8 9 10 И 12 х,-
Рис. 3.1. Полигон вероятностей
Определение 3. Вид (или тип) распределения соответствует виду функции, опи-
сывающей данное распределение. В рамках одного вида распределения отлича-
ются друг от друга своими параметрами.
Приведем основные виды распределений дискретных случайных величин.
Биномиальное распределение задается формулой
P{X = i}=C'p'9n-', i=0^,	(3.3)
где п, р и q — параметры распределения, причем 0<р,9<1;р + ^=1;я«1,2,... —
целое положительное число; С' = ——---------биномиальные коэффициенты.
il(n-i)!
76
3. Дискретные случайные величины
Условие нормировки для биномиального распределения было проверено в раз-
деле 2.3. Случайную величину X, имеющую это распределение, можно тракто-
вать как число успехов в п испытаниях Бернулли с вероятностью успеха в каж-
дом испытании р, а неудачи q.
Геометрическое распределение определяется выражением
Р{Х = i} =p-q"', г = 1,2.	(3.4)
где р и q — параметры распределения, причем 0 <р, q < 1; р + q = 1.
Это распределение уже рассматривалось в разделе 2.3 — оно является распреде-
лением числа испытаний в схеме Бернулли, необходимых для получения перво-
го успеха.
Гипергеометрическое распределение-.
С' С1"'
P{X = i}=——max{0, г + nt -п} < i < min^j, г),	(3.5)
С„
где п, ni и г — параметры распределения, являющиеся неотрицательными целы-
ми числами, причем пх < п, г < п, max{0, г + п{ -п} <i< min{r, nt}.
Как было показано в примере 2.1, оно является распределением числа шаров оп-
ределенного цвета X в выборке объема г из совокупности п шаров, среди которых
И| шаров данного цвета.
Распределение Пуассона'.
P{X = i} = — e-\ 1 = 0,1, 2,...,	(3.6)
i!
где X > 0 — параметр распределения.
Согласно определению экспоненциальной функции
(3.7)
так что условие нормировки для распределения Пуассона выполняется:
£р(Х = i) =	i = 1.	(3.8)
i=0	i=0 I '	i=0 2 1
Наряду с заданием распределения дискретной случайной величины системой ра-
венств (3.2) для этой цели можно также использовать функцию распределения.
Определение 4. Функцией распределения случайной величины X называется
функция F(x) вещественной переменной х, равная в точке х вероятности того,
что случайная величина X не превзойдет значения х:
F(x) = Р{ X < х}, -оо < х < оо.	(3.9)
Итак, значение функции распределения в точке х равно вероятности события
{X < х}. Отметим, что определение 4 справедливо как для дискретных, так и для
непрерывных случайных величин, которые будут рассматриваться далее. Однако
вычисление функций распределения будет осуществляться по-разному.
/1ля дискретной случайной величины распределение вероятностей (3.2) устанав-
ливает вероятность принятия случайной величиной конкретного значения, то
3.1. Дискретные случайные величины и их распределения
77
есть вероятность для точки числовой оси. В связи с этим часто говорят о диффе-
ренциальном законе распределения случайной величины. Функция распределе-
ния устанавливает вероятность принятия значений из интервала, в связи с чем
о ней часто говорят как об интегральном законе распределения.
Для дискретной случайной величины X, принимающей возможные значения Х(
с вероятностями р„ значение функции распределения в точке х вычисляется по
формуле
F(x)= £Р{Х=х,}=£р,..	(3.10)
Xj$X	Xj£X
Можно также использовать рекуррентные вычисления: F(x0) = 0,
F(x,) = F(x;_1)+p„ i=l, 2,...	(3.11)
График функции распределения представляет собой ступенчатообразную линию,
имеющую вертикальные скачки величины р, в точках возможных значений я)
(см. рис. 3.2 и табл. 3.1).
F(x)
Рис. 3.2. График функции распределения
Для биномиального и геометрического распределений функции распределения
были уже получены в формулах (2.10) и (2.12):
F(i) = l-<7', г=1, 2, ...	(3.13)
Сформулируем основные свойства функции распределения, вытекающие из ее
определения:
1.	Функция распределения является неубывающей функцией своего аргумента:
F(x)iF(x') прих^х'.
78
3. Дискретные случайные величины
2.	Значения функции распределения заключены в замкнутом интервале [0, 1],
причем F(x) -> 0 при х -> -со, F(x) -> 1 при х -> <ю.
3.	Функция распределения непрерывна справа, то есть ее значения в точках раз-
рыва (скачках) равны значениям функции немного правей точек разрыва:
F(x) = lim F(x + е).
с-+0. его
Отметим, что непрерывность справа вытекает из определения функции распре-
деления: ее значение в точке х включает вероятность принятия этого значения х.
Функцию распределения удобно использовать для вычисления вероятностей по-
падания случайной величины в те или иные интервалы. Действительно, по-
скольку для а < b выполняется равенство {X < b} = {X < а} + {а < X < Ь} и события
правой части равенства несовместны, то
Р{Х <Ь} = Р{Х <а} + Р{а<Х <Ь}
и, переходя к функциям распределения, окончательно получаем
Р{а < X < b} = F(b)~ F(a), a<b.	(3.14)
При использовании этой формулы необходимо проявлять осторожность в точ-
ках разрыва функции распределения. Например, если возможными значениями
случайной величины являются только целые числа и а и b являются такими чис-
лами, то
Р{а<Х <b} = F(b-\)-F(a),
Р{а < X < b} = F(b -1) - F(a -1),
Р{а<Х <b} = F(b)-F(a-l).
Примеры
Пример 3.1. Пусть X — случайная величина, распределение которой приведено в
табл. 3.1. Вычислим вероятности попадания этой случайной величины в некото-
рые интервалы:
Р{6 < X < 10} = F(10)-F(6) = 0.90-0.70 = 0.20,
Р{6 < X < 10} = Г(9)-Г(6) = 0.85 -0.70 = 0.15,
Р{6 < X < 10} = F(9) - F(5) = 0.85 -0.50 = 0.35,
Р{6 < X < 10} = F(10) - F(5) = 0.90 - 0.50 = 0.40.
Пример 3.2. Расход изделий некоторого типа за рассматриваемый период имеет
распределение Пуассона с параметром X = 9. Первоначальный запас составляет
с = 10 изделий. Какова вероятность того, что этот запас будет достаточным? Ка-
ким должен быть первоначальный запас, чтобы он был достаточным с вероятно-
стью р = 0.95?
Решение
В табл. 3.2 приведены значения функции распределения Пуассона (3.12) для X = 9.
3.1. Дискретные случайные величины и их распределения
те
х
Таблица 3.2. Функция распределение Пуассона F(x) = У — е'х с параметром
X	0	1	2	3	4	5	6	7	8	9	10
F(x)	0	0	0	0.251	0.055	0.116	0.207	0.324	0.456	0.587	0.706
X	И	12	13	14	15	16	17	18	19	20	
F(x)	0.803	0.876	0.926	0.959	0.978	0.989	0.995	0.998	0.999	1	
Из таблицы видно, что Е(10) = 0.706, то есть десять изделий будет достаточно
с вероятностью 0.706. Минимальное значение х, при котором F(x) > 0.95, состав*
ляет 14, поскольку Е(13) = 0.926, Е(14) = 0.959. Итак, 14 изделий будет достаточ-
но с вероятностью 0.959.
Пример 3.3. Задача о дефиците. Продолжим рассмотрение задачи 2.7. Предполо-
жим, что число расходуемых авиадвигателей является случайным и имеет рас-
пределение Пуассона с параметром X. Какова в этом случае вероятность отсутст-
вия дефицита?
Решение
В примере 2.7 была получена вероятность отсутствия дефицита R(c), как функ-
ция первоначального запаса с, запланированного числа поступлений авиадвига-
телей а и числа расходуемых авиадвигателей b (см. формулу (2.19)). В данном
примере b является случайной величиной. Если b < с, то дефицит возникнуть не
может и Я(с) = 1. Если b > с + а, то дефицит обязательно имеет место и Я(с) "0.
Если значение b больше с, но не превосходит с + а, то вероятность R(c) вычисля-
ется согласно выражению (2.19).
Пусть А есть событие «отсутствие дефицита», aHb — гипотеза «расход составил
b авиадвигателей». Тогда, согласно формуле полной вероятности (1.23)
Р{А}=±Р{НЬ}Р{А/НЬ}.
ь=о
В этой формуле вероятность Р{НЬ} расходования b авиадвигателей вычисляется
по формуле Пуассона (3.6), а условная вероятность Р{А/НЬ} отсутствия дефици-
та при условии, что расход составил Ь, есть ранее рассмотренная вероятность
Я(с). Следовательно, безусловная вероятность отсутствия дефицита
с V	с+а yi	с
Р{Л} = е" + £ Т7 e-^R(c) = ^e-^ +
i=0 I I	i=c+l 1 !	М I 1
СЛ“ X'	a!i!
+ у —е \1----------------------) =
(a + c + l)!(i-c-l)i
= f - S х(------------------------е-\
^i!	(а + с + 1)!(г-с-1)!
В табл. 3.3 приведены вероятности отсутствия дефицита РА для А = 2а при раз-
ных значениях а и с, вычисленные функцией Р{Л}(а, X, с) (рис. 3.4). Интересно
их сравнить с соответствующими вероятностями из табл. 2.5, когда расход по-
стоянен и равен 2а.
80
3. Дискретные случайные величины
Таблица 3.3. Вероятность отсутствия дефицита
при случайном расходовании авиадвигателей
	с = 0	с = 1	с = 2	с = 3	с = 4	с = 5	с = 6	с = 7	с = 8	с = 9
а = 0	1	1	1	1	1	1	1	1	1	1
а = 1	0.271	0.586	0.812	0.929	0.977	0.994	0.998	1	1	1
а = 2	0.116	0.311	0.531	0.720	0.852	0.930	0.970	0.989	0.996	0.999
а = 3	0.058	0.174	0.334	0.511	0.672	0.799	0.887	0.942	0.972	0.988
а = 4	0.032	0.101	0.210	0.350	0.501	0.643	0.762	0.852	0.914	0.953
а = 5	0.018	0.060	0.133	0.236	0.361	0.495	0.623	0.735	0.824	0.890
Пример 3.4. Метод Монте-Карло. Этот метод заключается в имитации рассмат-
риваемых случайных величин и процессов. Метод базируется на выработке слу-
чайных величин с заданным распределением. Выработка осуществляется так
называемыми «генераторами или датчиками случайных чисел», которые реали-
зуют определенные численные алгоритмы. Фактически получаются не случай-
ные, а «псевдослучайные» величины, поскольку при запуске датчиков при одних
и тех же начальных условиях будут вырабатываться одни и те же последователь-
ности чисел. Однако основные статистические свойства сохраняются: заданное
распределение вероятностей и независимость.
Покажем, как вырабатываются дискретные случайные величины с заданной функ-
цией распределения F(x). Исходными являются случайные величины R, имею-
щие равномерное распределение в интервале (0, 1). Такие величины являются
непрерывными и будут рассматриваться в следующем разделе. Сейчас же можно
рассматривать их задание с помощью использования геометрических вероятно-
стей: вероятность попадания случайной величины R в интервал (а, Ь), принадле-
жащий интервалу (0, 1), равна длине интервала b - а-
P{Re (a,b)} = b - a, 0<a<b < 1.
Итак, пусть R — равномерно распределенное в интервале (0, 1) число, вырабо-
танное датчиком. Отложим его значение на оси ординат графика функции рас-
пределения F(x) дискретной случайной величины X (см. рис. 3.3). Проведем из
этой точки на оси ординат горизонтальную прямую до пересечения с графиком
и опустим из точки пересечения вертикаль на ось абсцисс. Полученная точка на
оси абсцисс и даст нужную реализацию дискретной случайной величины X.
Покажем, что случайная величина X действительно имеет заданную функцию
распределения F(x). Для этого достаточно показать, что случайная величина X
принимает возможное значение х,с вероятностью р, = F(x,) - F{x^\). Но это сле-
дует из равномерности распределения случайной величины R.
Р{Х =%, }= P{R е (F(xw ),F(x,.)]} = F(xt )-F(x,_> ),
где (о, b] означает интервал, открытый слева (левая граница которого а нс вхо-
дит в интервал) и замкнутый справа (правая граница b входит в интервал).
3.2. Математическое ожидание дискретных случайных величин
81
1 -
R
О
Рис. 3.3. Генерация дискретной случайной величины
X
Проведем небольшой имитационный эксперимент. Согласно описанной методи-
ке выработаем п случайных величин, имеющих представленное в табл. 3.1 и на
рис. 3.2 распределение. Зафиксируем число случаев когда наблюдалось значе*
ние и подсчитаем соответствующую частоту ni /п. В табл. 3.4 показано, как
с ростом числа экспериментов п эти частоты стремятся к истинным вероятно-
стям pit представленным в табл. 3.1. В табл. 3.4 вероятности р, записаны в стро-
ке для п = оо.
Таблица 3.4. Сходимость частот к вероятностям
Число экспери- ментов, п	Частота п, /п							
	х, = 1	х2 = 3	х3 = 5	х4 = 6	х5 = 7	х6= 9	х7 = 10	х,- 11
10	0	0.100	0.200	0.200	0.100	0.200	0	0.200
20	0	0.300	0.200	0.200	0.100	0.150	0	0.050
40	0.100	0.175	0.200	0.325	0.025	0.100	0.050	0.025
80	0.088	0.200	0.188	0.250	0.113	0.050	0.063	0.050
200	0.125	0.110	0.220	0.235	0.130	0.035	0.065	0.080
500	0.091	0.150	0.255	0.196	0.108	0.045	0.048	0.107
1000	0.106	0.149	0.267	0.191	0.081	0.053	0.055	0.098
00	0.10	0.15	0.25	0.20	0.10	0.05	0.05	0.10
3.2.	Математическое ожидание
дискретных случайных величин
Распределение вероятностей дает полную информацию о случайной величине.
Иногда достаточной является более компактная информация, содержащая основ-
ные сведения о случайной величине. Таковыми, в частности, являются числовые
характеристики случайной величины: математическое ожидание, моменты,
дисперсия и др.
82
3. Дискретные случайные величины
Определение 5. Математическое ожидание (среднее значение) конечнозначной
случайной величины X обозначается р или Е(Х) и определяется формулой
р=ад=Хадр{а>}.	(3.15)
Если в правой части выписанного равенства привести подобные члены, или если
непосредственно исходить из задания случайной величины распределением ве-
роятностей (3.2), то эквивалентным будет такое определение математического
ожидания:
р d=E{X} d=XXiP{X = х,} = £х,р(.	(3.16)
i=i	;=1
Для дискретной случайной величины со счетным множеством значений требу-
ется дополнительное условие существования математического ожидания —
абсолютная сходимость суммы:
£|хШР{о>;} = £М^ <оо.	(3.17)
1=1	1=1
Если абсолютной сходимости нет, то говорят, что математического ожидания не
существует. Отметим, что если все возможные значения счетнозначной случай-
ной величины имеют один знак, то проверка сводится к установлению конечно-
сти суммы, то есть конечности математического ожидания. Абсолютная сходи-
мость нужна, чтобы произвольно переставлять и группировать слагаемые
бесконечных сумм.
В табл. 3.5 приведены выражения для математических ожидания основных рас-
пределений дискретных случайных величин.
Таблица 3.5. Числовые характеристики основных распределений
дискретных случайных величин
Наименование распределения	Параметры	Математиче- ское ожидание, И=Е(Х)	Дисперсия, а2 = D(X)	Сред. кв. отклонение, о
Биномиальное	n,p,q	пр	npq	Vw
Геометриче- ское	р<ч	р	Я Р2	4ч р
Пуассона	X	X	X	
Гипергеомет- рическое	п, Пр г	г П1- п	3 з Н 1 з 1^5 И	
				11	п-п< Jntr(n г) п V	п -1
Ниже приведены примеры вывода формул для математических ожиданий слу-
чайных величин, имеющих геометрическое распределение и распределение Пу-
ассона. Аналогичные формулы для биномиального и гипергеометрического рас-
3.3. Функции дискретных случайных величин
м
пределений проще получить с помощью индикаторных функций, так что этот
вывод будет отложен до пятой главы.
Примеры
Пример 3.5. Распределение Пуассона. Согласно формулам (3.6) и (3.16)
ц =Е{Х} =£х,Р{Х} =Xf =^1~ е =£i— е =
>=1	i!	м г!
go	со
= У^-е-х = Х У —----------е-х = Х-1 = Х,
£(i-l)l	£Г(г-1)!
где использовалось условие нормировки (3.8) для распределения Пуассона.
Пример 3.6. Геометрическое распределение. В данном случае нужный результат
проще получить не прямым применением формулы (3.16), а путем составления
уравнения относительно неизвестного математического ожидания ц:
i»l	j=1	i=l	i=l	i=l
= Z(i - i)p?"‘ +1 = tfZO ~ Op?"2 +1=?Ijp?j”1 +1 = яр +1.
j=2	f=2	y=l
где использовалось условие нормировки £ pq'~{ = 1 для геометрического рас-
>=1
пределения.
Итак, имеем следующее уравнение относительно неизвестного математического
ожидания ц:
Ц = QP + 1-
Отсюда находим, что ц = 1/( 1 - q) = 1/р.	□
3.3.	Функции дискретных случайных величин
Определение 6. Пусть у(х) — вещественнозначная функция вещественного аргу-
мента х, а X — дискретная случайная величина с распределением (3.2). Новая
случайная величина У = у(X) называется функцией случайной величины X. Она
может рассматриваться как дискретная случайная величина У = \|/(Х(со)), непо-
средственно заданная на исходном пространстве элементарных событий Л с по-
мощью функции \|/(Х(-)).
Основная задача заключается в нахождении распределения случайной величины
У на основе распределения вероятностей случайной величины X. Ясно, что если
величина X дискретна (в частности, конечнозначна), то и У дискретна (конечно-
значна). Далее, если Vx есть множество возможных значений X, то множеством
Уу возможных значений У является образ Ух при отображении у:
V, ={у/3х( eVv, у, = у(х,)}.
84
3. Дискретные случайные величины
Событие {Y=у}] является составным: оно состоит из тех событий {X = х,}, для ко-
торых значение х,- отображается функцией у в у,. Поэтому на основании опреде-
ления вероятности составного события (2.2)
P{Y=yj}= £Р{Х=х,.} = 2>,J=1,2,...	(3.18)
<: Ч<(^,) = »)
Зная распределение вероятностей (3.18) случайной величины У, можно вычис-
лить ее математическое ожидание по формуле (3.16). Это математическое ожи-
дание может быть вычислено также по формуле (3.15), если рассматривать
Y = у(Х)как новую случайную величину У = у (Х(со)), заданную непосредствен-
но на исходном пространстве элементарных событий Q:
£{у(Х)}=]>>(Х(Ю))Р{Ю}.	(3.19)
Для случайной величины со счетным множеством возможных значений для су-
ществования математического ожидания требуется выполнение условия абсо-
лютной сходимости:
X lvW®>})lP{®(} = i Iv(*,)Ip> <0°-	(3-20)
i=l	i«l
При вычислении математического ожидания случайной величины У по формуле
(3.16) необходимо знать распределение вероятностей У, а по формуле (3.19) —
вероятности элементарных событий со е Q . Следующая полезная теорема позво-
ляет вычислять математическое ожидание функции случайной величины непо-
средственно на основании распределения вероятностей этой случайной вели-
чины.
Теорема 3.1. Пусть дискретная случайная величина X принимает значение х,
с вероятностями р,. Если математическое ожидание случайной величины У=у (X)
существует, то оно может быть вычислено по формуле
Е(Х) = f V(*( )Р\Х = х,} = £ V(x,. )pf.	(3.21)
i=i	>-i
Доказательство
Идея перехода от формулы (3.19) к формуле (3.21) может быть объяснена так.
Предположим, вам необходимо пересчитать горсть монет разного достоинства.
Один способ — пересчитать монеты одну за другой, с учетом их достоинства, по-
следовательно прибавляя к прежней сумме новое значение. Это соответствует
формуле (3.19). Другой способ пересчета — когда вы предварительно группируе-
те монеты по достоинству и затем нужную сумму получаете умножением числа
монет каждого достоинства на их номинал. Математически эти соображения
оформляются так:
Е(у(Х)) = XvW<»))P{«>} = 5 Z V(W{«>} =
<о€П	6=1 (о:Х((о)=.Г|
= Ё'И(Л'-) £Лю} = £у(х,)Р{Х=х,} = ]Гу(х()р(.	□
Ы	n:X(a>)*xf 1*1	/-1
3.3. Функции дискретных случайных величин
U
Важнейшими являются линейная и показательная функции. Рассмотрение пока-
зательной функции \|/(х) =xr, r= 1, 2,... приводит к понятию момента случайной
величины.
Определение 7. Момент r-го порядка, r= 1, 2.определяется формулами
рг = Е{Хг} = ^(Х(ь>)УР{ь>},
(3.22)
./	k
pr = E{Xr} = ^х-pf.
>=i
Для счетнозначной случайной величины для существования момента г-ro поряд-
ка требуется абсолютная сходимость суммы, то есть чтобы
X Ли,} = Ё <0°-
М	i=l
Момент первого порядка р, — это математическое ожиданиер (индекс 1 принято
не писать). Из других моментов наибольшее значение имеет момент второго по-
рядка р 2. С помощью его определяется дисперсия случайной величины.
Определение 8. Дисперсия случайной величины X определяется по формуле
£>(Х)=£((А’-р)2) = р2 -р2.	(3.23)
Для дискретной случайной величины X с распределением вероятностей (3.2)
дисперсия может быть подчитана также по формуле
D(X) = £(x(-p)2pf.	(3,24)
i=l
Действительно,
k	k	k	k
£(*, -ц)2р,	= ^xiPi -2^xiPi +
z=l	/=1	z=l	i=l
k
+	=H2-2p-p + p2 =P2-P =D(xy
i=l
Положительное значение корня квадратного из дисперсии а = y]D{X) называет-
ся средним квадратическим отклонением случайной величины.
В то время как математическое ожидание представляет собой среднее значение
случайной величины, дисперсия представляет меру разброса случайной величи-
ны относительно математического ожидания. Размерность дисперсии случайной
величины равна квадрату размерности этой величины, в то время как размерно-
сти математического ожидания и среднего квадратического отклонения совпада-
ют с ней.
Рассмотрение линейной функции у(х) = а + Ьх позволяет установить важные
свойства математического ожидания и дисперсии.
Теорема 3.2 {Свойства математического ожидания и дисперсии). Если а и Ь —
константы, то
86
3. Дискретные случайные величины
E(a + bX) = a + bE(X), D(a + ЬХ) = b2D(X),	(3.25)
В частности: математическое ожидание постоянной величины равно самой по-
стоянной, а постоянный сомножитель можно вынести за символ математическо-
го ожидания:
Е(а) = а, Е(ЬХ) = ЬЕ(Х):	(3.26)
дисперсия постоянной величины равна нулю, а постоянный сомножитель выно-
сится за символ дисперсии в квадрате:
D(a) = 0, D(bX) = b2 D(X).	(3.27)
Доказательство. Применим формулу (3.21) для функции у (х) = а + Ьх:
Е(а+ЬХ) = ^Г(а +bxt)pt = a^Pj + b'^xipj = а + ЬЕ(Х).
м	м м
Для вычисления дисперсии используем формулу (3.23), заменяя в ней X на а + ЬХ,
а ц — на Е(а + ЬХ):
D(a + bX) = Е((а + ЬХ ~Е(а + ЬХ))2) = Е((а + ЬХ - а - Ьр)2) =
= Е((Ь(Х -ц))2) = Ь2ЕЦХ -ц)2 ) = b2D(X).
Отметим, что при выводе мы использовали перестановку членов суммы, которая
допустима в случае абсолютной сходимости.	□
Компьютерный практикум № 5.
Распределения дискретных случайных величин
в пакете Mathcad
Цель и задачи практикума
Целью практикума является приобретение практических навыков по работе с ди-
скретными случайными величинами в пакете Mathcad.
В настоящем практикуме требуется:
□	рассчитать значения функции распределения для распределения Пуассона
с заданным параметром А;
□	определить вероятности отсутствия дефицита для разных значений первона-
чального уровня запаса с и количества планируемых поступлений а (см. зада-
чу о дефиците из примера 3.3);
□	для конечнозначной случайной величины с заданным распределением веро-
ятностей определить: функцию распределения, математическое ожидание,
второй начальный момент и дисперсию, выработать 200 случайных чисел и
подсчитать частоты различных значений;
□	вычислить распределения вероятностей для функции дискретной случайной
величины \р(X), где X — дискретная случайная величина с заданным распре-
делением вероятностей.
Компьютерный практикум Nt 5. Распределения дискретных случайных величин в пакете Mathcad
87
Необходимый справочный материал
Среди встроенных функций пакета Mathcad имеются функции, соответствую-
щие основным распределениям дискретных случайных величин. При этом мож-
но пользоваться как распределением вероятностей (3.2), так и функцией распре-
деления (3.9). В первом случае название функции начинается с буквы d, а ВО
втором — ср. При обращении к функции задаются параметры распределения
и значения аргументов. Возвращаемое значение функции — это или вероятность
принятия случайной величиной этого значения или вероятность того, что слу-
чайная величина не превысит его. Рассмотренным выше дискретным распреде-
лениям соответствуют следующие функции:
□	dbinom(i, п, р) и pbinom(i, п, р) — значения биномиального распределения
(3.3) и (3.12) с параметрами п и р в точке i;
□	dgeom(i, р) и pgeom(i, р) — значения геометрического распределения (3.4)
и (3.13) с параметром р в точке i;
□	ppois(i, X) и dpois(i, X) — значения распределения Пуассона (3.6) с параметром
X в точке i.
Ряд функций Mathcad предназначен для выработки случайных величин с за-
данными законами распределения. Наименование этих функций начинается с
буквы г. При обращении к соответствующей функции указываются число вы-
рабатываемых случайных величин т и параметры распределения. Функция
возвращает вектор-столбец, содержащий заданное число выработанных случай-
ных величин. Следующие функции соответствуют вышерассмотренным распре-
делениям: rbinom(m, п, р) — биномиальному, rgeom(m, р) — геометрическому,
rpois(m, X) — Пуассона.
Если необходимо получить случайные величины, распределения которых отсут-
ствуют в списке, предлагаемом Mathcad, необходимо реализовать методику, из-
ложенную в примере 3.3. При этом для выработки равномерно распределенных в
интервале (0,1) случайных величин R используется функция md(a), дающая слу-
чайную величину, равномерно распределенную в интервале (0, а).
Реализация задания
Для проведения вычислений определим девять функций пользователя. Про-
граммные модули, реализующие эти функции, представлены на рис. 3.4 и 3.5.
Функции имеют следующее назначение.
FPois(k, а, Ь) для распределения Пуассона с параметром X вычисляет значения
функции распределения в интервале от а до Ь.
yr(Dist, г) по формуле (3.22) вычисляет r-й момент для распределения Dist. По-
следнее задается матрицей из двух столбцов: в первом содержатся возможные
значения {х,} случайной величины, а во втором — соответствующие вероятности
{р4-
Е4(Х, а, с) по формуле из примера 3.3 вычисляет вероятность отсутствия дефи-
цита авиадвигателей, если расход их имеет распределение Пуассона с парамет-
ром X.
Следующие две функции связаны с выработкой п случайных величин, имеющих
заданную функцию распределения F. При этом реализуется процедура, описан-
3. Дискретные случайные величины
.3. Распределение F задается двумя столбцами аналогично выше-
данию распределения Dist.
ная в пр1^меРфабатывает п случайных величин, имеющих распределение F.
описанному BbIpag0TK1I СЛуЧайных величин (как и в функции RandV) подсчи-
RandV(F, и) I принятия различных возможных значений для распределения F.
Fr(F, п) кро!ПрИведенных функций позволяют находить распределение функ-
тывает част(айной величины X. В качестве примера рассматривается функция
Последние использовавшаяся ранее в практикуме № 1 функция Arise(i, А) оп-
ции \у(Х) с-адлежит (значение 1), или нет (значение 0) число i вектору-столб-
= *2-	включает число i в вектор-столбец А. Функция Dom(Dist)
т п:тор-столбец возможных значений функции \j/, если аргументом ее
РеДд фу’пк1йпая величина X с распределением вероятностей Dist. Обратите
ЦУ использование здесь рекурсии при формировании вектора А.
Ф 1 я (Dist) вычисляет искомое распределение вероятностей для функ-
нимание ’ распределение задается аналогично распределению Dist.
функция
ции (X)
Практикум Не 5. Дискретные случайные величины
Пользовательский Функции
1внил функции распределения для	г-й момент для распределения Diet
ределения Пуассона в интервале от а до b
FPois(K,a.b) •
I <- а
while I < b
ppois(i.k)
1<- 1+ 1
^r(Dlst, г)
k<- rows(Dlst) -1
s^o
for j е 1 к
S<- S+ (Dbtj>()r Dlstj ]
S
>оятносп> отсутствия дефицита авиадвигателей
с+а
РД(аА.с) - £
I - I
(с+а
aSO.O.^P
I - с+1
ерацил n случайных величин,
лоции распределение F
Генерацил п случайных величин, имеюцих
распределение F, и расчет чатот их появления
RandV(F.n) .-
fat I« 1.. n
Fr(F.n).- k«-rows(F)-l
R+- rnd(l)
f+-l
while f  1
If RSFj.1
j«-j + l
Y
товерка наступления события A
Arise (I, A)
f<-0
for j e 0 rows (A) - 1
for j e I k
for I « 1 . П
R+- rnd(l)
J«-l
f«-l
while f  1
If RSFj.i
|Sj i«- Sj j+ 1
|f«-0
f +- f + lf(l  Aj ,1.0)
g+-if(f> 0,1.0)
fl
for j e I k
Sj,l«- Sj i n’1
.4. Поогоаммные модули, реализующие пользовательские функции
Компьютерный пректикум № 5. Распределения дискретных случайных величин в пакете Mathcad
Включение I в вектор А
1пс1(1, А):.
Заданная функции У(х)
В«-A If Arias (I, А)
otherwise
к«- rows(A)
for JeO . к - 1
*(х)х‘
. Формирование вектора значений функции у (х)
Dom(Dlst) :•
ш*- row»(Dtet)
А. *- * (0>«в ,в)
for J« 1.. m - 1
А«- |ncl(y(D|stjj) ,А)
А
В
Распределение вероятностей для функции у (X)
YD(Dls)
ш *- rows(Dle)
к rows(Dom(Dle))
for I « 0 . к - 1
|А|(| Dom(0h)|
for -1еО , к - 1
for JeO . m - 1
А]( 1Aj (1 + If (у (Oisj j) • Dom(Dis)| ,DlBj( 1,0)
А
Рис. 3.5. Программные модули, реализующие пользовательские функции (продолжение)
МА-
for аеО. 5
for с в 0. 9
МАа.с *- РА(а,2 а,с)
МА
МА
И S	и	п	а	п	ЮИМЗИЕММЯВ					
	0 271	0 586	0812	0.929	0977	0 994	0.998	1	1	1
	0.116	0.311	0.531	0.72	0.652	0.93	0.97	0.989	0 998	0.198
	0.058	0.174	0.334	0.511	0 672	0.799	0.667	0.942	0.972	0499
	0032	0.101	0 21	0.35	0.501	0.643	0.762	0.852	0.914	0.953
	0.016	0.06	0.133	0.23?	0.361	0 495	0.623	0.735	0.924	0 99
Функция распределения F
Распределение вероятностей Diet
Dtet:-
0 1	3	5	6 7	9
О 0.1 0.15 0J5 0J 0.1 045
10 11
045 0.1
(о 1	3	5 6 7	9 10 11
F:- I
<0 0.1 0.25 05 0.7 ОД 045 04 1
Генерация 200 случайных чисел, имеющих функцию распределения F, и частоты их появления
т /0	1	3	5	6	7	9	10	11
Fr(F,200)' -
<0 049 0.195 0.195 0J5 0.1 048 0445 0455
Математическое ожидание, второй начальный момент и дисперсия для распределения ОШ
дг(01«,1)-5.75	дг(О1в<,2) - 4045 ОХ -дг(0|«,2) - ДГ(01«, 1)'
DX - 7489
у(Х)
Реслредепение вероятностей случайной
величины X;
(-3 -2
Dl«t2 -
<0.1 0Д5
9J О J
1	2 О
OJ 0J 045
Значения функции у(х):
Dom(DlstZ)
0)
Распределение вероятностей функции у (X):
YD(0fa2)
0.19
1 О
04 0J5
Рио. З.в. Результаты решения задач
90
3. Дискретные случайные величины
Результаты вычислений
Результаты расчетов представлены на рис. 3.6. Вначале вычисляются значения
функции распределения для распределения Пуассона с параметром X = 9 для
возможных значений случайной величины от 8 до 20. Аналогичные результаты
приведены также в табл. 3.2.
Матрица МА содержит вероятности отсутствия дефицита (см. пример 33) для
разных значений первоначального уровня запаса с и количества планируемых
поступлений а. Они рассчитываются с помощью функции РА. Перебор рассмат-
риваемых значений с и а осуществляется с помощью вложенных операторов
цикла for.
Далее определяются распределение вероятностей Dist и функция распределе-
ния F, соответствующие табл. 3.1. С помощью функции Fr(F, 200) выработаны
200 случайных чисел, имеющих функцию распределения F, и подсчитаны часто-
ты различных значений. Значения частот для других количеств вырабатываемых
случайных величин были приведены выше в табл. 3.4.
Математическое ожидание и второй начальный момент для распределения Dist
вычисляются с использованием функций pr(Dist, 1) и pr(Dist, 2), данные харак-
теристики используются для вычисления соответствующей дисперсии DX.
В заключение приводятся результаты вычисления распределения вероятностей
для функции \|/(Х) = X2, где X имеет распределение вероятностей Dist2. Вначале
с использованием функции Dom(Dist2) определяется множество возможных зна-
чений, а затем по функции YD(Dist2) — само распределение.
Задания для самостоятельной работы
1.	Проведите имитационной эксперимент, наподобие рассмотренного в приме-
ре 3.4, для биномиального распределения с параметрами п = 9 и р = 0.6.
2.	Вычислите математическое ожидание функции у(Х) для распределения ве-
роятностей Dist2 случайной величины X двумя способами: путем использова-
ния формулы (3.16) и распределения вероятностей YD(Dist2) этой функции;
путем использования формулы (3.21) и распределения вероятностей Dist2
случайной величины X.
3.	Проверьте экспериментально на распределениях вероятностей Dist и Dist2
правильность формул (3.25) и (3.26).
Задачи
Задача 3.1. Двое игроков бросают симметричную игральную кость. При выпаде-
нии нечетного числа очков выигрывает первый игрок, а четного числа — второй.
Найти распределение вероятностей, математическое ожидание и дисперсию вы-
игрыша первого игрока, если ставка игры 1 рубль.
Задача 3.2. В лотерее 100 билетов, из которых выигрышных 30. Стоимость одно-
го билета 30 рублей, выигрыш по одному билету составляет 1000 рублей. Найти
математическое ожидание и дисперсию денежного эффекта от участия в лотерее.
Задача 3.3. В условиях примера 3.2 предположите, что каждое изделие, приобре-
таемое для первоначального запаса, обходится в 200 руб,, а дефицит каждого из-
Задачи
делия приводит к убытку 400 руб. Каким должен быть первоначальный запас с,
при котором математическое ожидание суммарного убытка минимально?
Задача 3.4. Обобщите задачу о дефиците (см. пример 3.3) для случая, когда чис-
ло поступающих авиадвигателей а является случайной величиной, имеющей
распределение Пуассона с параметром v.
4 Непрерывные случайные
величины
4.1.	Распределения непрерывных случайных величин
Рассматривавшиеся в предыдущей главе дискретные случайные величины ха-
рактеризовались тем, что их отдельные возможные значения можно было пере-
числить и выписать в ряд хь х2, ... Это, грубо говоря, означает, что возможные
значения «отделимы» друг от друга, то есть любые два из них находятся на неко-
тором расстоянии друг от друга. В противоположность этому существуют слу-
чайные величины, возможные значения которых занимают «сплошь» некоторый
интервал. Такие случайные величины называются непрерывными. При задании
распределения этих величин возникает трудность, заключающаяся в том, что ве-
роятность принятия непрерывной случайной величиной наперед заданного значе-
ния равна нулю. Тем не менее вероятность принятия этой величиной значения из
заданного интервала (даже как угодно малого, только не нулевой длины) будет
положительной.
Здесь уместно провести аналогию с двумя видами нагрузок в механике — сосре-
доточенной и распределенной нагрузками. Представим себе балку (опору), на
которую воздействует нагрузка. В случае сосредоточенной нагрузки масса (вес)
приложена в некоторых точках хь х2, ... , причем величина массы в этих точ-
ках составляет рь р2, ... Это соответствует дискретной случайной величине
(рис. 4.1, а). В случае распределенной нагрузки на балку насыпано некоторое сы-
пучее вещество, например, песок. Пусть в двумерном изображении на плоскости
(см. рис. 4.1, б) балке соответствует ось абсцисс Ох, а верхняя граница песка опи-
сывается некоторой кривой /(х). Пусть удельная масса песка (приходящаяся
на единицу площади) равна единице. Ясно, что на точку х воздействует нулевая
масса (поскольку площадь над ней равна нулю). На часть балки, соответствую-
щей ненулевому интервалу (а, Ь), воздействует масса, равная площади криволи-
нейной трапеции, простирающейся от этого интервала до кривой /(х). Как бы
мал этот интервал не был, эта площадь будет положительной, если только поло-
жительна функция /(х) на этом интервале. В частности, если в точке х функция
/(х) непрерывна и положительна, то для бесконечно малого (элементарного)
интервала (х, х + Дх) длины Дх>0 эта площадь составит приблизительно
Лх^Дх > 0.
4.1. Распределения непрерывных случайных величин
93
Рис. 4.1. Сосредоточенная а и распределенная б нагрузки
Распределение вероятностей для непрерывных случайных величин конструиру-
ется аналогично рассмотренному случаю распределенной нагрузки в механике.
Фигурирующее здесь понятие массы в нашем случае будет трактоваться как по-
нятие «вероятностной массы». При этом основополагающую роль играет функ-
ция f(x).
Определение 1. Плотностью распределения называется функция вещественной
переменной /(х), которая:
□	определена на всей числовой прямой: -со < х < <ю;
□	неотрицательна: / (х) > 0, Vx;
□	интегрируема и удовлетворяет условию нормировки:
]f{x)dx = l.	(4.1)
Определение 2. Говорят, что задана непрерывная случайная величина X, если эа-
дана плотность распределения / (х), с помощью которой вероятность попадания
случайной величины X в вещественный интервал (а, Ь), где а < Ь, выражается
формулой
ь
Р{а<Х <b} = \f(x)dx.	(4.2)
а
Поскольку определенный интеграл численно равен соответствующей площади
под кривой /(х), то из формулы (4.2) следует, что вероятность принятия слу-
чайной величиной значения из интервала (а, Ь) равно площади криволинейной
трапеции, заключенной между вертикалями, проходящими через точки а и b оси
абсцисс, кривой f(x) и осью абсцисс (рис. 4.2).
Рис. 4.2. Кривая плотности распределения
94
4. Непрерывные случайные величины
Рис. 4.3. Кривая функции распределения
Если в качестве интервала в формуле (4.2) взять (-оо, х), то получим формулу,
выражающую функцию распределения непрерывной случайной величины X че-
рез ее плотность:
F(x) = ]f(y)dy = Р{Х <х}.	(4.3)
Физический смысл функции распределения непрерывной случайной величины
тот же, что и для дискретной случайной величины (см. определение 4 главы 2):
значение этой функции F(x) в точке х есть вероятность того, что случайная ве-
личина X не превзойдет данное значение х. Сохраняются все свойства, приведен-
ные в разделе 3.1 для функции распределения дискретных случайных величин,
однако для непрерывных случайных величин функция распределения является
непрерывной функцией. Типичный график функции распределения приведен на
рис. 4.3. Он представляет собой непрерывную кривую, монотонно возрастающую
от нуля до единицы.
Из формулы (4.3) следует, что
Р{а < X £ b} = F(b) - F(a).	(4.4)
Обратим внимание на следующее обстоятельство. Для дискретной случайной
величины вероятность ее попадания в тот или иной интервал зависела (в общем
случае) от того, включены или нет границы в интервал (см. пример 3.1). В непре-
рывном случае это роли не играет — для всех разновидностей интервалов (от-
крытых и замкнутых с одной стороны или с обеих сторон) эти вероятности сов-
падают. Данное обстоятельство следует как из свойств интегралов, так и из
отмеченного выше факта: вероятность принятия непрерывной случайной вели-
чиной наперед заданного значения (в данном случае — соответствующего грани-
це интервала) равна нулю.
Наряду с функцией распределения F(x) часто используется дополнительная
функция распределения F(x) = 1 -F(x). Ее значение в точке х равно вероятности
того, что случайная величина X превзойдет х:
F(x) = Р{Х > х} = i-F(x).	(4.5)
В теории надежности случайная величина X трактуется как длительность безот-
гаяилД nalviTu ирчглтлплгл ичпрпио Тигля глбытир /X > rl лянячяат бяялткяянчю
96
4. Непрерывные случайные величины
Таблица 4.2. Основные функции распределения непрерывных случайных величин
Наименование распределения	Функция распределения F(x)		Примечание
	Выражение	Область определения1	
Равномерное	х - а Ь - а 1	а < х < b х>Ь	
Экспоненциальное	l-e'^	х>0	
Нормальное	1 0 'Н	 е	—оо < х < оо	Ф(а) — ф. р. стандартного нормального распределения с параметрами ц = 0, а = 1
Эрланга	1=0 ! 1	х> 0	
Наглядное представление о типе распределения дает график соответствующей
плотности. Для названных распределений графики приведены на рис. 4.4. Вид
графика плотности распределения позволяет выдвинуть предположение о кон-
кретном типе распределения. В отличие от этого график функции распределе-
ния не столь наглядно представляет тип распределения (см. рис. 4.3).
Рис. 4.4. Графики кривых плотностей основных распределений: а — равномерного,
б — экспоненциального, в — нормального, г — Эрланга
1 llnu nminunuv uunui.iiuuY пппампинаД гчнячгчшр ПППТ11ПГТИ пярппелопеиия nannn IIVJIIO
4.1. Распределения непрерывных случайных величин
98
работу изделия в течение времени х. Вероятность этого события равна значению
дополнительной функции распределения F(x) в точке х и называется надежно-
стью изделия за время х.
Из математического анализа известно, что если плотность /(х) непрерывна
в точке х, то ее значение в этой точке равно производной от интеграла (4.3):
f(x) = F'(x). Отсюда также следует, что при этом же условии вероятность попа-
дания непрерывной случайной величины X в элементарный (бесконечно малый)
интервал (х, х + Дх)
Р{х < X <х + Дх} = /(х)Дх + о(Дх),	(4,6)
где о(Дх)есть величина бесконечно малая по сравнению с Дх: о(Дх)/Дх -> 0 при
Дх -> 0.
Последняя формула позволяет следующим образом определить физический
смысл плотности распределения f(x): значение плотности распределения f(x) в
точке х, умноженное на бесконечно малое приращение Дх, приблизительно равно
вероятности попадания непрерывной случайной величины X в элементарный ин-
тервал (х, х + Дх).
В инженерной практике выражение (4.5) записывают в виде
Р{а < X <х + Дх} ® /(х)Дх.
В аналитическом выражении для плотности /(х) обычно присутствуют некото-
рые постоянные, называемые параметрами распределения. Говорят (см. опреде-
ление 3 главы 3), что распределение принадлежит одному типу, если плотности
распределения отличаются друг от друга только параметрами.
Основными типами распределений непрерывных случайных величин являются:
равномерное, экспоненциальное, нормальное, Эрланга, логарифмически нормальное
и др. Соответствующие плотности распределения приведены в табл. 4.1, а функ-
ции распределения — в табл. 4.2.
Таблица 4.1. Основные плотности распределения
Наименование распределения	Плотность распределения /(х)		Параметры	Область значений параметров
	Выражение	Область определения1		
Равномерное	1 Ь-а	а <х< b	а, Ь	а< b
Экспоненци- альное		х > 0	X	Х>0
Нормальное	1 _	z> 2 О ск/2л	-00 <Х<00	р,а	а>0, -оо <р <00
Эрланга	—А_(Хг)«е-^ («-1)1	х> 0	Х,1	X >0. 1  1,2,... - целое
Ппи остальных значениях псосменной х значение плотности распределения равно нулю.
4.1. Распределения непрерывных случайных величин
87
Равномерное распределение задается плотностью
1
/(х) = j b -а
0,
х е (а,Ь),
(4.7)
где а и b — параметры распределения, причем а < Ь.
График плотности равномерного в интервале (а, Ь) распределения представляет
собой прямоугольник (рис. 4.4, а).
Функция распределения (4.3) имеет вид:
[0,
х-а
Ь-а’
1,
F(x) =
х е(а,Ь),
х > b.
(4.8)
Равномерное распределение возникает как распределение ошибок при округле-
ниях чисел. Например, если мы проводим вычисления с точностью до первого
знака после запятой, то ошибка такого округления имеет равномерное распреде-
ление в интервале (-0.05, 0.05). Следовательно, если после вычислений мы по-
лучаем число 4.6, то фактическое значение лежит в интервале (4.55, 4.65).
Экспоненциальное распределение имеет плотность и функцию распределения, за-
даваемые формулами:
f(x) =
F(x) =
0,	х <	;0,	
	х :	>0,	(4.9)
0,	х -	<0,	
			(4.Ю)
1-е ,	х :	>0,	
где А. > 0 — параметр распределения.
Условие нормировки для плотности (4.9)
(4.10) равен 1 при х = оо. График экспоненциальной зависимости (рис. 4.4, tf)
описывается кривой, монотонно убывающей от А. при х = 0 до 0 при х = со.
Экспоненциальное распределение возникает как распределение времени ожида-
ния совершенно случайного события. Например, по статистике установлено, что
интервалы времени между падениями метеоритов на Землю, рождениями трой-
ни, отказами радиоэлектронной аппаратуры и т. п. имеют экспоненциальное рас-
пределение. В связи с этим экспоненциальное распределение играет большую
роль в теории случайных процессов (см. главу 9).
Отметим, что экспоненциальное распределение является непрерывным анало-
гом геометрического распределения (2.12). Как мы уже знаем, последнее являет-
ся распределением числа испытаний Бернулли У, необходимых для получения
первого успеха:
выполняется, поскольку интеграл
P{Y >i} =(1-р)', 1 = 1,2, ...
Пусть испытания проводятся через равноотстоящие промежутки времени длины
1/п. Рассмотрим ситуацию, когда скорость проведения испытаний неограничен-
х £ (а,Ь),
98
4. Непрерывные случайные величины
но возрастает (и —> со), однако вероятность успеха в одном испытании убывает
но закону р - к/п, где А > 0. Отметим, что среднее число успехов в единицу вре-
мени будет при этом постоянным и равным пр = nA/и = А.
Покажем, что при сформулированных условиях время до первого успеха
X = Y/n стремится к экспоненциальному распределению:
P{X>t}---------->е~и, t>0.
v 1	п~+<х>
Для этого воспользуемся следующим замечательным пределом:
1--
п

Имеем:
Р{Х >t} = P{Y/n >t} = P{Y > nt} = (1 -рУи = (1 - A/и)"' =
= ((1 - A/и)" )'.>(e-)-)' = e~\
Нормальное распределение имеет следующие плотность и функцию распреде-
ления:

/(*) =
- 00 < х <00,
(4.И)
Д а ) }
Г/ A f 1
J7r-exp
— 00 < x < oo,
(4.12)
где ц и а — параметры распределения, причем о > 0.
График плотности нормального распределения (рис. 4.4, г) является колоколо-
образной кривой, симметричной относительно вертикали х = ц и убывающей до
нуля при х —> ±оо. Влияние параметров ц и о на форму кривых /(г) и F(x) рас-
сматривается в компьютерном практикуме № 6.
Интеграл (4.12) через элементарные функции не выражается, поэтому для его
вычисления используют так называемое стандартное нормальное распределение,
имеющее следующие значения параметров: ц = 0, о = 1. Плотность и функция
распределения для стандартного нормального распределения определяется фор-
мулами:
<p(z) = -Lexpf-^z2\ -со <2 < со.	(4.13)
У2.П	к	4	)
(	1	А
Ф(г)=|-=ехр —у2 \dy, -co<z<co.	(4.14)
i,v2n	к	2	)
Значения <р(х) и Ф(д) табулированы и выдаются соответствующими функция-
ми, имеющимися во всех языках программирования. С помощью их проводятся
необходимые вычисления для нормального распределения с произвольными
значениями параметров ц и о:
/(л-) = -<р
О
(4.15)
4.1. Распределения непрерывных случайных величин
F(x) = Ф —
(4.1в)
Проверка условия нормировки (4.1) для нормальной плотности (4.11) основыва-
ется на интеграле Пуассона
J expf——z2 | г/г = л/2тт.	(4.17)
Используя этот интеграл и подстановку z = (у -р)/о, находим:
Г/ ч г 1	(	fi	Г i 2V <
F(oo) = I ——— exp	-——	dy = -—exp --z \dz = 1.
Дч/2ла	pl о J J Дч/2л	'2 J
Нормальное распределение возникает как распределение суммы большого числа
случайных величин. Поскольку такая ситуация встречается часто, нормальное
распределение имеет большое распространение. Подробнее об этом будет сказа-
но в главе 7.
Распределение Эрланга задается	формулами:	
		0,	х < 0,
/(х) =		.(Хх)'-1 _	(4.18) Л	0	л? > V,
		(/-1)!
	0,	х < 0,	
F(x) = .		а->0.	(419) h И
где Хи/ — параметры распределения, причем X > 0, а I — целое положительное
число 1, 2, ...
Частным случаем распределения Эрланга при 1=1 является экспоненциальное
распределение (4.9). С ростом значения параметра I плотность распределения
Эрланга стремится к плотности нормального распределения (см. главу 7).
Кривая плотности распределения Эрланга представлена па рис. 4.4, г.
Условие нормировки для плотности распределения Эрланга (4.18) можно прове-
рить, применяя метод математической индукции. При 1=1 мы имеем дело с экс-
поненциальным распределением, для которого условие нормировки выполняет-
ся. Предположим теперь, что это условие выполняется для значения параметра
/ 2: 1. Тогда для значения параметра I + 1 имеем, используя правило интегрирова-
ния по частям и предположение индукции:
. г.(Хх)'	,	?(Хх)'_ ь.	(Хх)' _ь. "
F(co) = j ХУ—— в dx = -j У—-de	= -	'-е м +
о / •	о * !	fl	О
+ fx/<^e^.o+fx<^e-^ = i,
где неопределенность была раскрыта но правилу Лопиталя:
100
4. Непрерывные случайные величины
,. ,, и г (W ,.	г Z(W’'
lun(Xx) е	= lim——— = lim-^-------= lim /-— ---=
Л —*00	Л" —>00 g**'	.v->x (I	g*-1
dx
-T^'	nrV-2	1
= I Hm --------= 1(1-1) lim Y = ... = /! lim 4~ = 0.
.V-HG fl	x~»oo	X —>oo
7^
Итак, условие нормировки выполняется для I + 1, а, следовательно, и для всех I.
Распределение Эрланга возникает как распределение суммы I независимых слу-
чайных величин, имеющих одно и то же экспоненциальное распределение с па-
раметром X (см. главу 7). Такая ситуация часто возникает при рассмотрении за-
дач резервирования в теории надежности, управления запасами и пр.
Примеры
Пример 4.1. Длительность X безотказной работы некоторого изделия имеет экс-
поненциальное распределение с параметром Л. = 0.1. Найти вероятность того, что
изделие не откажет в течение установленного ресурса г, равного 5.
Решение
Используя формулы (4.5) и (4.10), находим:
Р{Х > г} = 1-F(r) = l-(1-Yr) = e’Y
Для наших численных данных эта вероятность составит ехр(-0.1 • 5) = 0.607.
Пример 4.2. Рассмотрим стрельбу по цели, представляющей собой отрезок дли-
ны а на оси абсцисс. Пусть отклонение снаряда от центра цели X имеет нормаль-
ное распределение с параметрами ц и о. Найти вероятность поражения цели при
одном выстреле. Какова будет эта вероятность при двух выстрелах?
Решение
Обозначим At событие «поражение цели при первом выстреле». Очевидно,
= {-л/2 < Х< а/2}. Следовательно, согласно формулам (4.4) и (4.16) вероят-
ность поражения цели при одном выстреле
Р{Д} = Р{-а/2 <Х< а/2} = F(a/2) - F(-a/2) = Ф|-^а//2 ~МЯ-Ф|
< о ) V с )
Обозначим А2 событие «поражение цели при втором выстреле». Очевидно, собы-
тие «поражение цели при двух выстрелах» есть сумма событий и А2. Если
считать эти события независимыми, а их вероятности одинаковыми, то для веро-
ятности суммы этих событий по формуле (1.27) находим:
Р{Д + А/= Р{А/+ Р{А2} - Р{А/Р{А.,} =2Р{А/-Р{А,}~.	□
Выше приводились примеры плотностей распределений, так сказать, «в чистом
виде». На их основе возникает множество других, производных от них, плотно-
стей распределений. Остановимся на двух модификациях: усеченных распреде-
лениях и смеси распределений.
4.1. Распределения непрерывных случайных величин
101
Усеченные распределения. В некоторых случаях к имеющейся информации О
плотности распределения случайной величины поступает дополнительная, со-
стоящая в том, что возможные значения случайной величины принадлежат не-
которому заданному интервалу. Например, если установлен общетехнический
срок службы изделия, то момент его отказа не может превышать этот срок. Такая
ситуация приводит к усеченным справа распределениям.
Второй важный пример дает нам теория и практика страхования жизни по воз-
расту. Длительность жизни людей некоторого региона имеет определенное рас-
пределение, обычно хорошо известное из статистики. Но когда в страховую ком-
панию приходит клиент, возраст которого, например, шестьдесят лет, его
страхование осуществляется на основе распределения «остаточной длительно-
сти жизни», рассчитанного при условии, что человек дожил до теперешнего сво-
его возраста. Тут имеет место усечение исходного распределения слева.
Итак, пусть X — непрерывная случайная величина с плотностью распределения
/(х) и функцией распределения Е(х). Предположим, что поступила дополни-
тельная информация о том, что возможные значения X принадлежат интервалу
(а, 6), где а < b. С учетом этого плотность и функция распределения X будут:
/у (х) = f(x)/P{a < X < b}, а<х<Ь,
Fy(х) = F(х)/Р{а <Х <Ь},	а<х <Ь.
Соответствующий численный пример будет рассмотрен в разделе 4.4.
Определение 3. Смесь распределений. Пусть р2, .... Р/ — набор вероятностей,
удовлетворяющих условию нормировки:pt + р2 + ... =pt=X, a/i(x),/2(x), ...,//(х) —
набор плотностей распределений. Тогда смесь распределений задается плотностью
/(х) = Р) /, (х) + р2/2 (х) +... + p,ft (х).
Вероятностная интерпретация смеси распределений следующая. Из имеющихся
I распределений наудачу выбирается одно, причем г-е распределение с вероятно-
стью pj. Если выбрано г-е распределение, то наблюдают случайную величину X/,
имеющую именно это распределение.
Функция распределения смеси выражается через исходные функции распреде-
ления {Е;(х)} аналогичным образом:
Е(х) = р, Г, (х) + p2F2 (х) + ... + PiF,(x).
Пример 4.3. В цехе один из работающих станков (дающий 100р % всей продук-
ции) разладился. После обработки нормально работающим станком некоторый
размер детали имеет нормальное распределение с параметрами ц и <х У разла-
дившегося станка при том же значении параметра ц второй параметр о, > о.
Деталь бракуется, если ее замеренный размер отклоняется по абсолютной вели-
чине от значения ц более чем на 8 > 0. Какова доля бракуемых деталей? Какой бы
она была, если бы разладка не произошла? Далее, пусть деталь оказалась брако-
ванной. Какова вероятность того, что она была обработана на нормально рабо-
тающем станке?
Решение
Обозначим <у вероятность брака, А' - фактический размер детали. По условию
.111/111’11!
102
4. Непрерывные случайные величины
/7 = Р{|Х-ц| >5} =Р{Х-ц >8} + Р{Х-ц <-8} = Р{Х >ц + 8) + Р{Х <ц-8) =
= 1 - Р{Х < ц + 8} + Р{Х < ц - 8}.
Если бы разладки станка не было, то имело бы место нормальное распределе-
ние (4.16) для вероятности брака <у0, поэтому
, . ((ц + 6-цЙ	. .(8^ . f-8^
q(l = 1 - ф ill-1-4 + ф -----'XL = j _ ф _ + ф _ I
( ст )	( ст ) (сту I ст у
В случае разладки станка мы имеем смесь двух нормальных распределений с па-
раметрами: цист (доля 1-р); ц и ст( (доляр). Поэтому вероятность брака q}:
q, =-- 1-(1-Р)ГфГ—^|-фГ—У|-р фГ-АЪфГ—.
Пусть Но означает гипотезу «деталь изготовлена на нормально работающем
станке», Я, — противоположную гипотезу, А — событие «деталь бракованная».
По формуле полной вероятности (1.23) находим:
Р{А} = Р{Н0}Р{А\Н,} + Р{Я, }Р{А\Я,} = (1 -p)q0 + pqt.
Теперь по формуле Байеса (1.24) имеем следующее выражение для вероятности
того, что бракованная деталь изготовлена па нормально работающем станке:
Р{Н0\А} =Р{Н0А}/Р{А} = (1-р)<7о/((1~РИо +p<h )•
В табл. 4.3. приведены численные значения рассмотренных показателей в зави-
симости от значения ст(. Остальные параметры были приняты следующими:
р = 0.2, ст = 0.4, 8 = 1. Вероятность отбраковки детали, обработанной на нормально
работающем станке, <у0 - 0.012. Отметим, что эти данные были рассчитаны про-
граммами q0, ql и РИА, которые будут описаны ниже в компьютерном практи-
куме.
Таблица 4.3. Вероятности q, и Р{Н0 | Д) в задаче отбраковки детали
О|	0.400	0.480	0.576	0.691	0.829	0.995	1.433	1.720	2.064
<7,	0.012	0.017	0.025	0.034	0.043	0.052	0.061	0.069	0.077
Р{Н0\А}	0.800	0.572	0.401	0.296	0.232	0.190	0.163	0.143	0.129
4.2. Математическое ожидание
непрерывных случайных величин
Плотность (или функция) распределения представляет полную информацию о
непрерывной случайной величине. Часто можно обойтись и менее полной ин-
формацией, содержащейся в числовых характеристиках. Как и для дискретного
случая, важнейшим из них являегся математическое ожидание.
Определение 4. Пусть интеграл отл/(х) в полных пределах сходится абсолютно,
то есть
j|х| j\x)dx < оо.
(4.20)
4.2. Математическое ожидание непрерывных случайных величин
103
Тогда говорят, что существует математическое ожидание непрерывной случай-
ной величины. Оно обозначается ц =£(АЛ)и вычисляется по формуле
p=E(X)=]xf(x)dx.	(4.21)
Если абсолютной сходимости нет, то есть интеграл (4.20) принимает бесконеч-
ное значение, то говорят, что математического ожидания не существует.
Если математическое ожидание случайной величины существует, то оно обычно
просто выражается через параметры распределения. В табл. 4.4 приведены соот-
ветствующие выражения для рассматривавшихся типов распределений. В част-
ности, из нее следует, что для нормального распределения параметр р. есть мате-
матическое ожидание, а для экспоненциального распределения параметр X есть
величина, обратная математическому ожиданию. Приведем выводы соответст-
вующих формул.
Примеры
Пример 4.4. Математическое ожидание для равномерного распределения (4.7) на-
ходится совсем просто:
Е(Х) = \xf(x)dx = fx—!— dx = х2 —-—-
Д.	„ “-а	2(Ь-а)
= (^2 -а2)^ТГ—; ^<а + ,А
а	2 (о — (I)	2
Пример 4.5. Для экспоненциального распределения (4.9) применение формулы
(4.21) и использование интегрирования по частям дает:
Е(Х) = ^xf(x)dx =JхХе-’'1 dx = - jxde u =-xe ъ | + Je k' dx =
о	о	0
= 0-- f d(-Xx) = -1]de~kr
A. ()	A ()
где имевшаяся неопределенность была раскрыта по правилу Лопиталя, как это
было сделано выше при проверке условия нормировки для плотности распреде-
ления Эрланга.
Таблица 4.4. Числовые характеристики основных непрерывных распределений
Наименование распределения	Математическое ожидание, ц = Е(Х)	Дисперсия, с2 = D(X)	Среднее кв. отклонение, с	Момент г-го порядка, цг
Равномерное	а + b Т~	(b-af 12	Ь - а ТеГ	1 У*1
				г + 1	1> -а
Эксиооснци- 11ЛЫ1ОС	j_ X	1 X2	2 X	Н хг
Нормальное	Я	•)	а	Формула (4.33)
Эрланга	е X	t X2	V7 X	(, + г-1)1 Хг(Г-1)1
104
4. Непрерывные случайные величины
Пример 4.6. При вычислении математического ожидания для нормального
распределения (4.11) используются замены переменных интегрирования
г = -——, dz = dx/a, v = -z, dv = - dz, свойство нормировки для плотности стан-
су
дартного нормального распределения и следующее свойство определенного ин-
теграла: если нижний и верхний пределы интегрирования меняются местами, то
знак интеграла меняется на противоположный. Имеем:
Е(Х)= Jx/(x) = |х
-со	—со
ехр
if х -ц
2у о
dx =
= Ц
1
>/2лст
Пример 4.7. При рассмотрении распределения Эрланга (4.18) воспользуемся тем,
что (как это было доказано выше) для него при любом значении параметра I вы-
полняется условие нормировки для плотности. Итак,
r/vx f ft х ?	-м- ,	I . I
Я(Л ) = J х/(х) = J ^7,-—г е * = т	e-dx = -A = -.
Д	g(Z-l)!	Xg/1	X Л
4.3. Функции и моменты
непрерывных случайных величин
Определение 5. Пусть X — непрерывная случайная величина с плотностью рас-
пределения /(х), у/(х) — вещественнозначная функция, определенная на всей
действительной прямой и являющаяся непрерывной за исключением, быть мо-
жет, конечного числа точек разрыва. Под функцией случайной величины X пони-
мают случайную величину Y = у(Х), получающуюся подстановкой в функцию
\|/(х) вместо аргументах случайной величины X.
Это определение не является математически строгим, которое будет дано ниже в
разделе 4.4 для определенного класса функции у(х). Этому мы предпошлем ряд
общих результатов.
Математическое ожидание функции непрерывной случайной величины опреде-
ляется аналогично формуле (3.19) для дискретного случая. Пусть выполняются
(формулированные выше условия и, кроме того, произведение ч'(.г)/(.г) абсо-
икнпно iiiiiiie/iiHrH/CMo в бесконечных пределах, то есть
4.3. Функции и моменты непрерывных случайных величин
toe
f I V (*)!/(*) < со.	(4.22)
-оо
Тогда говорят, что математическое ожидание функции непрерывной случайной
величины Y - v(Az) существует и вычисляется по формуле
£(v(X))=jv(x)/(x)&	(4.23)
Если абсолютной интегрируемости нет, то математическое ожидание функции
не существует.
Важными частными случаями функции ц(х) являются линейная функции
у-а + Ьх, модульная функция у = |х| и показательная функция у =хг, г= 1,2,...
Если математическое ожидание непрерывной случайной величины существует
то оно обладает всеми теми свойствами, которые были сформулированы в те0‘
реме 3.2 для дискретной случайной величины. Доказательство этих свойств ана
логично приведенным в теореме 3.2 с заменой сумм на интегралы. Например
используя формулу (4.23), мы имеем для линейной функции следующие свойст
ва математического ожидания: если X — случайная величина, имеющая конвч
ное математическое ожидание Е(Х),аяЬ- константы, то
Е(а + ЬХ) = а + ЬЕ(Х),	(4.24)
в частности, математическое ожидание постоянной равно самой постоянной
Е(а) = а: постоянный множитель выносится за символ математического ожида
ппя: ЕЛЬХ) = ЬЕ(Х). Кроме того, Е(\Х\) > |Е(Х)|.
Определение 6. Пусть X — непрерывная случайная величина с плотностью f(x)
г = 1, 2, ... — натуральное число и произведение x'f(x) абсолютно интегрируема
в бесконечных пределах:
||х'|/(х)Дг < со.	(4.25
-со
Тогда говорят, что момент r-го порядка непрерывной случайной величины X сущи
ствует. Он определяется как математическое ожидание r-й степени случайно!
величины;
= E(Xr) = ]x'f(x)dx.	(4.26
Если абсолютной интегрируемости нет, то момент г-го порядка не существует.
Как н для дискретного случая, момент первого порядка ц, — это просто матеми
шчегкое ожидание ц = Е(Х) случайной величины X. 13 связи с этим индекс
у момента р, опускается.
Следующая лемма справедлива как для непрерывных, так и для дискрет ных еду
чайных величин.
Ломма 4.1. Если момент /-го порядка ц,., существует, г = 2, 3, ..., то существую
и нес моменты ц,. низших порядков, г' < г. При этом имеет место нсравепстш»:
Е(|А'|" ),/(' <(Е(|А'|' ))*".	(4.27
106
4. Непрерывные случайные величины
J(v-р)2/(.г)<1х <со.
Доказательство этой леммы будет проведено в разделе 4.6.
Как и в дискретном случае, математическое ожидание является средним значе-
нием случайной величины. Мерой разброса случайной величины вокруг этого
среднего служит дисперсия и среднее квадратическое отклонение.
Определение 7. Пусть произведение (х-р)2 f(х) интегрируемо в бесконечных
пределах:
(4.28)
Тогда говорят, что существует дисперсия случайной величины, равная матема-
тическому ожиданию квадрата отклонения случайной величины от ее матема-
тического ожидания, и определяемая формулой
о2 = D(X) = £((X-p)2) = |(х-д)2/(т)Де.	(4.29)
-00
При вычислении дисперсии часто предпочитают пользоваться не формулой (4.29),
а следующей формулой, связывающей дисперсию и момент второго порядка р 2:
о2 = р2 -р2.	(4.30)
Эта формула показывает также, что дисперсия и второй момент существуют или
нет одновременно.
Размерность дисперсии (и второго момента) есть квадрат размерности случай-
ной величины. Это представляет некоторое неудобство, в связи с чем часто вме-
сто дисперсии используется положительное значение квадратного корня из нее,
называемое средним квадратическим отклонением о, которое имеет размерность
случайной величины:
о =	= +yjD(X).
Для наиболее важных распределений непрерывных случайных величин выраже-
ния для моментов и дисперсий приведены в табл. 4.4. Докажем некоторые из вы-
ражений для моментов. Напомним, что с помощью момента второго порядка
дисперсия вычисляется по формуле (4.30).
Примеры
Пример 4.8. Момент r-го порядка для равномерного распределения (/1.7) находит-
ся следующим образом:
р= E(Xr) = jx'f(x)dx = jdx = ------------------- = - а--------.
\,Ь-а (г + 1)(6-а)я (г + 1)(й-а)
Пример 4.9. Момент r-го порядка для экспоненциального распределения (4.9)
можно вычислить просто, если воспользоваться условием нормировки для плот-
ности распределения Эрланга с параметрами А и I = г + 1:
рr = Е(Х‘) - Jx'f(x)dx = JхrХе~иdx f аЛ—dx =-;-.
о	А.' о r I	К
4.3. Функции и моменты непрерывных случайных величин
107
Аналогичным образом вычисляется момент r-го порядка для распределения Эр*
лата с параметрами Хи Г. эту проблему решаем, используя свойство нормиров-
ки для плотности распределения Эрланга с параметрами X и I = I + г.
рг = Е(Х' ) = Jxrf(x)dx =	=
= (г + /-1)! Jz (Xr)-M	_(г + /-1)! t = (г + /-1)!
(/-1>!Х о (г + /-1)! (Z — 1)! Хг (/-1)!ХГ
Свойства дисперсии. Если дисперсия непрерывной случайной величины X суще-
ствует, то она имеет свойства, приведенные в теореме 3.2 для дискретной слу-
чайной величины: если а и b — конс!анты, то
О(д + 6Х) = 62Г)(Х),	(4.31)
в частности, дисперсия постоянной равна нулю: D(a) = 0; постоянный сомножи-
тель выносится за символ дисперсии в квадрате: D(bX) = 1УН(Ху
Определение 8. Пусть X — случайная величина, имеющая математическое ожи-
дание р и дисперсию о2. Нормированной случайной величиной называется случай-
ная величина Z -{X -р)/о.
Лемма 4.2. Нормированная случайная величина Z =(Х -ц)/о имеет нулевое ма-
тематическое ожидание и единичную дисперсию. Момент r-го порядка р, слу-
чайной величины X выражается через моменты {о, = E(Z")} соответствующей
нормированной случайной величины Z по формуле (в которой положено о0 = 1)
цг =Е(Х') = £с,'Ар'-',	(4.32)
i--0
в частности,
Ц) = Ц + ОТ, ,
p2 =ц2 +2ОП.Ц + о2п2,
р3 = р3 тЗот^р2 + 3<т2а2р + oJf3.
Доказательство
Используя свойства математического ожидания (4.24) и дисперсии (4.31), полу-
чаем:
£(Z) =	= 1(£(Х)-р) = 1(ц -р) = 0.
V о 7 о	и
D(Z) = d(= J_ D(X) = si = 1.
V о J о	о2
Далее используется разложение бинома Ньютона (2.5):
Е{Х' ) = i'((oZ + р)' ) = Е(Х С‘ (oZy р) =
1x0
= XC'a'/'(Z')p’-'	□
1-0	/-0
108
4. Непрерывные случайные величины
Пример 4.10. Моменты нормального распределения. В следующем разделе будет
показано, что случайную величину X, имеющую нормальное распределение
(4.11) с параметрами цист, можно представить в виде X = ц + ctZ, где Z имеет
стандартное нормальное распределение (4.13) с нулевым средним и единичной
дисперсией, то есть является нормированной случайной величиной для X. По-
этому достаточно найти моменты для нормированной величины Z, поскольку
моменты для X будут определяться по формуле (4.32).
Моменты {уг} случайной величины Z, имеющей стандартное нормальное распре-
деление, выражаются рекуррентно друг через друга, как это показывают следую-
щие выкладки:
00	1	——2^	°°	1	-—2%	1
vr = [zr—=е~2 dz = -	r/(--z2) =
) = -zr-’
= 0 + (r - l)or_2 = (r- l)pr_2,
где неопределенность была раскрыта по правилу Лопиталя.
Итак,
vr = (г - 1)а,._2, г = 2,3, ...
Эго рекуррентное соотношение позволяет выразить моменты любого порядка
через моменты наименьшего порядка в0 и причем той же четности: четные мо-
менты v2r через в0, а нечетные моменты в2,+1 через щ. Значения этих моментов
нам известны: в0 = 1, поскольку это есть интеграл по плотности в полных преде-
лах, равный единице по условию нормировки (4.1); щ = 0, так как это есть мате-
матическое ожидание стандартного нормального распределения, равное нулю,
как это уже было установлено в примере 4.6.
Моменты нечетного порядка равны нулю, поскольку наименьший из них щ ра-
вен нулю:
v3 =(3-1)??! =0, v5 = (5 - 1)и3 =0, ...
Для моментов четного порядка имеет место соотношение:
v2l. = (2r-l)v2(r_t> = (2r - l)(2(r -1) - l)v2(r. 2) =... = П(2: - 1).е0 = П(2г-1).
(=1
Окончательно имеем следующие формулы для моментов стандартного нормаль-
ного распределения:
^2г-1 =°>	v2,. =fl(2z-l), г = 1,2,...
В частности, моменты второго и четвертого порядка составляют:
02 = (2-1) = 1,
v =(2-1-1)(2-2-1) = 3.
Моменты нормального распределения (4.15) с параметрами цист вычисляются
пн (Iwmwviio (Л Я? У
4.4. Распределения функций непрерывных случайных величин*
109
ц 2г = £(Х2г) = ц2’- + X С2^2'Н 2<г-') Г1 (2; -1),	Г = 1,2,...,
'=’	'=’	(4.33)
ц2г+1 = £(X2r+1 ) = ц2,+1 + £С2'+1о2ф2(г-,)+) fl(2;-l), г = 0,1,2.
<=1	) =i
где сумма без слагаемых (когда верхний предел суммирования меньше нижнего)
равна нулю.
В частности,
р2 =ц2 +ст2,
ц:) = р3 + Зст2р,
р4 =р4 +6р2о2 + ЗсД.
Итак, согласно формуле (4.30) ст2 является дисперсией нормально распределен-
ной случайной величины X.
4.4. Распределения функций
непрерывных случайных величин*
Выше мы интересовались только числовыми характеристиками функций непре-
рывных случайных величин. Теперь будет рассмотрена более трудная задача на-
хождения распределения этих функций. Вначале ограничимся только классом
монотонных функций или строго возрастающих, когда у ) < у (,га) при
Л'| < .г2, или строго убывающих, когда приведенное неравенство для функций ме-
няется па противоположное.
Пусть ф(х) — строго возрастающая функция, X — непрерывная случайная вели-
чина с плотностью распределения fix). Рассмотрим случайную величину
У - у(Х). Очевидны следующие тождества для множеств: для любого вещест-
венного у {Y < у} = {у(Х) < у} = {X < у"1 (г/ )}> гДе V 1 (у) ~ функция, обратная к
функции у =
Следовательно,
P{Y <у} =Р{Х < у’1 (г/)}, -оо<г/<оо.	(4.34)
Последнее соотношение является основным для выражения распределения
строго возрастающей функции случайной величины через распределение гний
случайной величины. Сама формула (4.34) выражает функцию распределения
случайной величины У, которую мы обозначим FY(y), через функцию распреде-
ления /'(.т) случайной величины X:
FY(y} = Лч'"' ((/)), -<х><у<ж.	(4.3J5)
Для существования в точке у плотности распределения fY(y) случайной величи-
ны У необходимо и достаточно существование производной пог/ от правой части
формулы (4.35). В свою очередь для этого необходимо и достаточно cyiuccTuoiilt-
iiiK- производной функции v(.r), поскольку, как известно из математического
анализа
(у) = 1 К ?у(хЛ
Лг Л....'on'
110
4. Непрерывные случайные величины
Поскольку функция ц/(х) является строго возрастающей, то эта производная ни-
где не обращается в нуль, так что последнее выражение всегда определено. Ана-
логичным образом рассматривается случай монотонного убывания функции
v|/(x). Результаты могут быть сформулированы в следующем виде.
Теорема 4.3. Пусть X — непрерывная случайная величина с плотностью распре-
деления f (х), у (.г) — строго монотонная (убывающая или возрастающая) функ-
ция. Тогда У = v|/(A7) является непрерывной случайной величиной с плотностью
распределения
AG/) = /«'(*/))
<Э1|/(.г)
дх
(4.36)
Если а и Ь — постоянные и У = а + ЬХ, то
FY(y) =
Ь>0,
(4.37)
(4.38)

Линейное преобразование У = а + ЬХ является важнейшим преобразованием
случайной величины X. Формулы (4.37), (4.38) позволяют находить функцию и
плотность распределения этого преобразования. Ниже будут приведены наибо-
лее важные примеры.
Утверждение 1. Пусть X — случайная величина, имеющая равномерное распреде-
ление в интервале (а, Ь), где а < Ь. Тогда ее линейное преобразование У = с + dX,
где d * 0, имеет равномерное распределение в интервале (с + ad, с + Ь<1).
Утверждение 2. Пусть X — случайная величина, имеющая нормальное распределе-
ние с параметрами Е(Х)-р и £)(А) = о2. Тогда ее линейное преобразование
У = а + ЬХ, где Ь * 0, также имеет нормальное распределение с параметрами
Я(У) = а + 6ц, П(У) = (6о)2.
В частности, если рассмотреть нормированную случайную величину Z = {X -ц)/о,
то в этом случае а = -ц/с, Ь = 1/о. Следовательно, E(Z) = 0, D(Z) = 1 и Z имеет
стандартное нормальное распределение (4.13).
Обратное соотношение X=p+oZ обычно используется при выработке нор-
мально распределенной случайной величины X с произвольными параметрами ц
и о на основании случайной величины Z, имеющей стандартное нормальное рас-
пределение (4.13).
Утверждение 3. Пусть X — случайная величина, имеющая распределение Эрланга
с параметрами I и X. Тогда У = ЬХ, где 6*0, имеет распределение Эрланга с пара-
метрами I и Х/Ь.
Утверждение 4. Пусть X — случайная величина, имеющая экспоненциальное рас-
пределение с параметром X. Тогда У = ЬХ, где 6*0, имеет экспоненциальное рас-
пределение с. параметром Х/6.
4.4. Распределения функций непрерывных случайных величин*
111
Выше было наложено ограничительное условие, касающееся строгой монотОМ*
ности функции \|'(х). От него легко избавиться, если разбить всю числовую ОСЬ
(-со, со) на интервалы, внутри которых функция \|/(х)или строго монотонна ИЛИ
постоянна. Теперь каждый такой интервал следует рассматривать по отдельно-
сти. Если на интервале I функция \|/(х) принимает постоянное значение с, при-
чем Р{Х е 7} = р * 0, то это дает вклад в вероятность P{Y = с} принятия значения
с, равный р. Ясно, что в этом случае случайная величина Y уже не будет непре-
рывной. Если на интервале I функция у(х)строго монотонная, то для нее МОЖНО
вычислить плотность по формуле (4.46). Полученные таким образом плотности
могут перекрываться. Окончательно выражение для плотности Y в точке у полу-
чается суммированием значений в этой точке тех плотностей, которые не равны
нулю.
Примеры
Пример 4.11. Логарифмически нормальное распределение. Говорят, что случайная
величина Y имеет логарифмически нормальное распределение, если ее натураль-
ный логарифм 1пУ имеет нормальное распределение. Показать, что соответст-
вующие плотность и функция распределения имеют вид
/г(у) = -Л-ехр|-(1П^~")2],	у >0,	(4.39)
VZTTSZ/ (	2.5“ J
Ег(г/) = Ф((1п(^)-а)/5),	(4.40)
где 5 > 0 и а — параметры распределения, Ф(г) — функция стандартного нор-
мального распределения (4.14).
Показать, что момент r-го порядка, математическое ожидание и дисперсия для
этого распределения вычисляются по формулам:
р,. = E(Yr) = expf га + -r2s2 |,
1	2 J	(4.41)
E(Y) = expfa + ^x2 j, D(Y) = (e'~ -l)exp(2a + s2).
Решение
Пусть X — случайная величина, имеющая нормальное распределение с парамет-
рами а и s. Тогда рассматриваемую случайную величину можно представить в
виде Y = ехр(Х). Очевидно, что У — строго положительная случайная величина.
Найдем ее плотность распределения, следуя вышеизложенной методике. В каче-
стве функции \|/ мы имеем у(х) = ехр(х), причем это — строго монотонно возрас-
тающая функция. Обратная ей функция у’1{у) = 1п(у), а производная от нее
<Эц/(.г)/йг = схр(х). При значении аргумента х = 1п(г/) значение этой производной
равно у. Подставляя все это в формулу (4.36), мы получаем формулу (4.39).
Формула (4.40) следует из формулы (4.35).
Математическое ожидание £(У) можно найти двумя способами. Во-нсрпых, по
формуле (4.21) как математическое ожидание непрерывной случайной величи-
ны У с плотностью распределения (4.39). Во-вторых, но формуле (4.23) как мя-
112
4. Непрерывные случайные величины
тематическое ожидание функции Y = \р(Х) = ехр(Х) нормально распределенной
случайной величины X с параметрами ц = а и ст = s. Выберем второй путь, как
более простой. Более того, он позволяет сразу найти момент r-го порядка этой
функции. Для него имеем:
£(У') = £((е*У) = j(er )г —X-ехр
л/2л5 I
. z \2 \
If х-а]	.
- ---- ах =
21 5 J

х -а
ехр хг— -------
21 s
dx.
Преобразуем показатель экспоненты, так чтобы использовать условие норми-
ровки для плотности нормального распределения:
=^s*2(2xrs2 -х2 + 2ах-а2) - ~^s~2(x2 -2x(rs2 + а) + а2) =
= ~s'2(x-(rs2 + а))2 -|s"2(a2 -(rs2 + а)2) =
z	2	-.2
11 х - (rs + а)
I 5 >
+ ^r(2a + rs2).
Подставляя это в интеграл, имеем:
£(УГ)= f-^-exp
= ехр( r(2a + rs2
1(х-(rs2 + a)V,	( 1	2^
- ---1------- dx = exp- r(2a + rs )J,
где использовалось условие нормировки для нормальной плотности с парамет-
рами j.l = rs 2 + а и ст = s.
Математическое ожидание находится теперь как момент первого порядка ц(, а
дисперсия — через момент второго порядка ц2 по формуле (4.30).
Пример 4.12. Пусть X — случайная величина, имеющая экспоненциальное рас-
пределение с параметром X. Предположим, что функция \|/(х) имеет вид
у(л-) =
с
-X,
а
2с- — х,
а
0 <х < а,
а <х <2а,
график которой представляет собой равнобедренный треугольник с основанием
на отрезке (0, 2а) вещественной оси. Найдем распределение случайной величи-
ны У = \|/(Х).
Решение
Разобьем вещественную ось (-оо, оо) на несколько интервалов. Первый интервал
(-О1 (й можно не учитывать. поскольку вепоятность попадания в него равна
4.4. Распределения функций непрерывных случайных величин'
11S

егл+—\
с о
нулю. На интервале (0, а) функция у(х) равна сх/а и монотонно возрастает. По-
этому составляющая плотности Y, вносимая этим интервалом, согласно (4.38),
будет — е~аку/с для 0 < у < с. На интервале (а, 2а) функция у(х) равна 2с-—X
с	а
и монотонно убывает. Поэтому составляющая плотности Y, вносимая ЭТИ)<
интервалом, будет — е-А(-2с-у)/с для о < у < с. На интервале (2а, оо) функций
с
у(х) равна нулю. Вероятность попадания случайной величины в этот интервал
равна е’2Л.
Следовательно, окончательное выражение для функции распределения Y имей*
вид:
О,	у <0,
У =0,
-а>.у -яХ(2с-у) ”	-2яХс+аХу -яХу
е с + е с dy = 1 + е с -е с , 0 < у < с,
1,	у>с. П
Возвратимся к формуле (4.35). Важным применением этой формулы является
случай, когда в качестве X берется равномерно распределенная в интервале (0; 1)
случайная величина, а в качестве функции \р(х) — функция, обратная некоторой
функции распределения G(x): у(Х) = G"1 (X).
Тогда в формуле (4.35) F(x) = х, 0 < х < 1,
v-1(z/) = (G-t(z/))-1 = G(y),
и функция распределения случайной величины Y = \|/(Х) = G"1 (X) есть
FY(y) = F(y~'Xy)) = F(G(y)) = G(y), -со<у^со.	(4.42;
Последнее равенство широко используется при имитационном моделировании
Для того чтобы выработать случайную величину, имеющую заданную функции
распределения G(x), достаточно выработать равномерно распределенную в ИМ
тервале (0; 1) случайную величину X и вычислить Y по формуле
Y = (Г1 (X).	(4.43,
В частности, экспоненциально распределенная с параметром X случайная вели
чина Y имеет функцию распределения G(y) = 1 - exp (-Ху). Обратная этой фунК
ции распределения есть функция
G~‘ (х) = —^ln(l-x).
Следовательно, случайная величина Y вырабатывается по формуле
У =--ln(l-X).	(4.44
X
Поскольку X и 1 - X имеют одно и то же равномерное распределение в интерм
ле (0, 1), то предпочтительнее пользоваться формулой
У--у1п(Х).	(4.45
Л
114
4. Непрерывные случайные величины
4.5. Неравенства для моментов и вероятностей*
В настоящем разделе мы собрали важные неравенства для моментов и вероятно-
стей, широко применяемые при установлении факта существования моментов,
вычислении оценок для нижних и верхних границ вероятностей событий, дока-
зательстве предельных теорем теории вероятностей (см. главу 7). Начнем с нера-
венств для моментов. Вначале докажем утверждения леммы 4.1.
Доказательство леммы 4.1
Покажем вначале, чтЬ если существует момент г-го порядка ц г, то существует и
любой момент меньшего порядка ц,., г' <г. Напомним, что существование мо-
мента означает выполнение условия (4.25), то есть абсолютную сходимость соот-
ветствующего интеграла. Рассмотрим следующее разбиение вещественной оси:
(—со, оо) = (-оо, -1) U [-1, 1] U (1, °о). Вне интервала (-1, 1)|х|' < |х|г, так что если
здесь интеграл от | х|г сходится, то сходится интеграл и от}х|г. Интеграл от |х|г’
по интервалу (-1, 1) не превышает 1. Отсюда следует конечность интеграла
(4.25) при г = г'.
Докажем теперь неравенство (4.27), означающее, что (£(|Х|Г )),/г является не-
убывающей функцией от г > 0. Квадратичная функция от переменной и
Е и|Х| 2 +|Х|~
= и2 £(| Х| "-1 ) + 2м£(| Х|") + £(| Х|,,+
).
очевидно, положительна. Следовательно, эта функция с осью абсцисс не пересе-
кается, то есть не имеет корней. Поэтому ее дискриминант отрицателен:
£(|ХГ* )£(|ХГ> )>(£(|%Г))2,
то есть
,(W ))г'(£(|Х|1,+1 ))° >(£(|ХГ ))2".
Полагая v = 1, 2, .... г и перемножая полученные неравенства, находим:
гкшхг-1 )у(адг’+1 ))г =
Р=1
= £(|Х| )П(£|Х|1’ )2"(£|Х|Г+
г,=2
г* садг г
£(И)
£(|ХГ)£(|ХГ )
= П(£(|Х|" ))^1|Й1р!Х > П(£(|Х|» ))2\
1₽1	(£(|Л| ))	,.=1
Итак,
(£(|Х|Г)Г' <(£(ИГ+1 ))’•
□
Лемма 4.3. (Неравенство Шварца.) Если фигурирующие ниже математические
ожидания существуют, то для любых функций 1|/(х) и р(.г)
(£(V(X)p(X)))2 SE(W2(X))E(p'2(X)).	(4.46)
4.5. Неравенства для моментов и вероятностей*
116
Доказательство
Поскольку при замене у if р в (4.46) на ау и рр, где аир— любые постоянные,
получается равносильное неравенство, то достаточно рассмотреть случай £(\|/2(Х)) 
- £(р2(Х)) = 1. Теперь для получения (4.46) достаточно взять математическое
ожидание от обеих частей неравенства
2| V(X)p(X)| < y2(X) + P2(X).	□
Следующее неравенство касается выпуклых функций. Напомним, что функция
ц/(.г), заданная на вещественном замкнутом интервале I, называется выпуклой,
если для каждой точки а этого интервала существует так называемая опорная
прямая L, проходящая через точку {а, у(а)) плоскости и целиком лежащая под
графиком функции ц/(х)на I. Аналитическая запись условия выпуклости такая:
при всех х е I:
у(х) > у(а) + Х(х - а),
где X — тангенс угла наклона прямой L.	>
Лемма 4.4. (Неравенство Иепсепа.) Пусть X — случайная величина, сосредото-
ченная на интервале I, то есть Р{Х е 1} = 1, и имеющая математическое ожидание
Е(Х). Тогда для выпуклой функции ц/(т)
Е(\\1(Х))>у(Е(ХУ).	(4.47)
Доказательство
Используя условие выпуклости для точки а = Е(Х) = ц и свойства математиче-
ского ожидания (4.24), имеем:
Е<У(Х)) > £(у(ц) + Х(Х -ц)) = £(i|/(p)) + Х(£(Х)-ц) = \р(ц) + 0 = \р(ц). □
Математическое ожидание, моменты высших порядков, дисперсия и среднее
квадратическое отклонение являются числовыми характеристиками случайной
величины. Каждая из них характеризует распределение случайной величины
одним числом. Разумеется, такая характеристика не будет полной. Однако она
весьма лаконична и в ряде случаев вполне достаточна.
Моменты позволяют также оценивать вероятности попадания случайной вели-
чины в те пли иные интервалы. Речь здесь идет об оценивании, поскольку ука-
занные вероятности оцениваются посредством неравенств, выраженных только
через моменты случайных величин и границы интервалов.
Чем больше моментов случайной величины известно, тем большей информаци-
ей о распределении случайной величины мы располагаем, тем более точными бу-
дут неравенства для вероятностей. Ниже мы покажем, как даже при минималь-
ной информации, заключающейся в знании одного или двух первых моментов,
можно оцепить распределение вероятностей. Приводимые леммы справедливы
как для непрерывных, так п для дискретных случайных величии. Доказательства
будут проведены только для непрерывного случая.
Лемма 4.5. Пусть X — неотрицательная случайная величина (то есть
Р{Х i 0} - 1), математическое ожидание р которой существует. Тогда для любого
положительного х
Р{Х г х} <; ц/х.
(4.48)
116
4. Непрерывные случайные величины
Доказательство
Согласно определению математического ожидания
00
ц = ^xf(x)dx.
о
Фиксируем некоторое х и разобьем область интегрирования в правой части по-
следней формулы иа интервалы (0, х) и [х, со). Тогда в силу неотрицательности
подынтегрального выражения
М Jyf(.y)dy > х| f(y)dy = хР{Х > х}.	□
В формуле (4.48) задействован только один момент — математическое ожида-
ние. Следующий результат предполагает использование двух моментов.
Лемма 4.6. (Неравенство Чебышева.) Если дисперсия ст2 случайной величины X
существует, то для любого положительного х
Р{\Х-р\> х} < а2/х2.	(4.49)
Доказательство
Запишем неравенство (4.48) для случайной величины Yи переменной х2 в виде:
P{Y > л2} < E(Y)/x2. Если теперь положить Y = (Х -ц)2, то согласно определе-
нию дисперсии (4.29) E(Y) = Е((Х-ц)2) = ст2. Теперь неравенство (4.48) имеет
вид
Р{(Х-ц)2 >х2} <ст2/х2,
который эквивалентен неравенству (4.49).	□
Неравенство Чебышева, названное так по имени впервые получившего его вы-
дающегося русского математика Пафнутия Львовича Чебышева (1821-1894),
играет большую роль в теории вероятностей. Следующее неравенство не столь
известно, однако дает большую информацию о распределении случайной вели-
чины.
Лемма 4.7. (Обобщенное неравенство Чебышева.) Пусть функция у(х) неотрица-
тельна, монотонно возрастает при х > 0 и существует математическое ожидание
Е(у(рф) = т. Тогда при х > О
Р{|Х| > х} < т/\у(х).	(4.50)
Доказательство
Повторяя доказательство неравенства (4.48), получаем для х > 0:
т = j i|/(| z/| )f(y)dy > J у(| z/| )f(y)dy + j V(| z/| )f(y)dy >
-00	.t	-00
00	—,v
^(.x)(^f(y)dy + \f(y)dy) = y(x)P{\X| > x},
x	-x
что эквивалентно неравенству (4.50).	□
доказанное неравенство позволяет получить много других полезных неравенств.
В частности, если момент четного порядка ц2,. существует, то для х > 0:
7->{|Х| 'г х} <,р.1г/х2'.	(4.51)
4.5. Неравенства для моментов и вероятностей’
117
Если момент четвертого порядка ц 4 случайной величины X существует, то для
k > 1
P{|x-Ml >МS—^;g‘	<4ла>
Ц4 + k <5 -2k ст
Пример 4.13. В настоящем примере анализируется точность неравенства Чебы-
шева. С этой целью рассматривается несколько распределений, для которых под-
считываются точные вероятности. Эти вероятности сравниваются с оценкой, да-
ваемой неравенством Чебышева.
Фиксируем значения математического ожидания ц и дисперсии ст2 для рассмат-
риваемых распределений. Используя табл. 4.4, будем параметры распределений
подбирать так, чтобы получались заданные значения цист2. Остановимся на че-
тырех распределениях: равномерном, Эрланга, нормальном и логарифмически
нормальном.
Для равномерного распределения (4.7) для значений параметров а и Ь имеем сис-
тему из двух уравнений:
(а + 0/2 = ц, (Ь-а)2/12 = ст2.
Решая эту систему, находим, а = ц - 2л/3 ст, b = ц + 2V3 О.
Для распределения Эрланга (4.18 ) ц = //X, ст2 = //X2. Отсюда сразу получаем
X = ц /ст2,/ = ц2 / ст2. Значения цист следует подобрать так, чтобы параметр / по-
лучался целым.
Для нормального распределения цист совпадают со значениями соответствующих
параметров.
Для логарифмически нормального распределения (4.39), подставляя в формулы
(4.41) вместо математического ожидания E(Y) и дисперсии D(Y) значения Ц
и ст2, получаем систему уравнений
ц = ехр(а + s2/2), ст2 = ехр(2а + s2 )(ехр($2) -1),
Отсюда находим:
ст2/ц2 =ехр(52)-1,	5 = 71п((ц2 +ст2)/ц2), а = 1п
№ +»
Мы интересуемся вероятностью события {|Х-ц| >х} для некоторого положитель-
ного значения аргумента х. Оценку сверху этой вероятности дает неравенство
Чебышева (4.49). Мы хотим сравнить эту оценку с истинными вероятностями
для различных распределений, подсчитываемыми по их функциям распределе-
ний Е(х):
Р{|Х-ц| >х} = 1-Р{|Х-ц| <х} = 1-Р{-х<Х-ц<х}=	(4М)
= 1-(Г(ц+х)-Г(ц-х)).
Рассматриваемые нами функции распределения даются формулами (4.8), (4.19),
(4.12) и (4.40). Вычисленные значения вероятностей для ц = 1, а = 0.5 и разных X
приведены в табл. 4.5. Они позволяют сравнить истинные вероятности с оцен-
кой, даваемой неравенством Чебышева. Из таблицы видно, что неравенство Че-
бышева дает верхнюю оценку рассматриваемой вероятности. Обычно эта оценка
118
4. Непрерывные случайные величины
оказывается очень грубой. Например, при х = 0.467 в случае логарифмически
нормального распределения истинная вероятность составляет 0.128, в то время
как неравенство Чебышева дает значение 0.51. Далее, при х = 0.667 эта вероят-
ность для равномерного распределения будет нулевой, а неравенство Чебышева
дает 0.250. Однако следует иметь в виду, что неравенство Чебышева является
универсальным: оно пригодно как для дискретных, так и для непрерывных вели-
чин, положительных и отрицательных, имеющих и не имеющих моменты поряд-
ка выше второго и пр.
Кроме того, следующий пример показывает, что неравенство Чебышева не мо-
жет быть улучшено, если только не использовать дополнительную информа-
цию о распределении случайной величины. Этот пример касается дискретной
случайной величины, возможные значения которой есть -1, 0, 1, а соответствую-
щие вероятности их принятия 1/18, 8/9, 1/18: Р{Х = -1} = 1/18, Р{Х = 0} = 8/9,
Р{Х = 1} = 1/18. Легко подсчитать, что для этого распределения ц =0, ст2 = 1/9,
о = 1/3.
Рассмотрим событие {|Х| > 1}. Его точная вероятность
Р{|Х|> 1} = Р{Х = -1} + Р{Х= 1} = 1/18+ 1/18 = 1/9.
Это же значение дает и неравенство Чебышева:
Р{|Х| > 1} =Р{|Х-р| >1}<ст2/12 = 1/9»0.111.
Итак, для данного примера неравенство Чебышева дает точное значение вероят-
ности и поэтому в общем случае не может быть улучшено. Можно сделать также
следующий важный вывод, называемый «правилом трех сигм»: вероятность
того, что случайная величина отклоняется по абсолютному значению от своего
математического ожидания более, чем на три и, не превосходит 1/9. Отметим,
что для нормального распределения эта вероятность составляет 0.003.
Таблица 4.5. Анализ точности неравенства Чебышева
Распределения	х = 0.467	х = 0.533	х = 0.600	х = 0.667	х = 0.733	х = 0.800	х = 0.867
Равномерное	0.192	0.076	0	0	0	0	0
Эрланга	0.147	0.096	0.063	0.041	0.028	0.020	0.014
Нормальное	0.162	0.110	0.072	0.046	0.028	0.016	0.009
Логарифм, нормальное	0.128	0.084	0.058	0.042	0.032	0.024	0.019
Неравенство Чебышева	0.510	0.391	0.309	0.250	0.207	0.174	0.148
Компьютерный практикум № 6. Распределения
непрерывных случайных величин в пакете Mathcad
Цель и задачи практикума
Целью практикума является приобретение практических навыков по работе с не-
прерывными случайными величинами в пакете Mathcad.
Компьютерный практикум № 6. Распределения непрерывных случайных величин в пакете Mathcad
119
Задачами данного практикума являются:
□	построение графиков кривых плотностей для рассмотренных в данной главе
распределений: равномерного, экспоненциального, нормального и Эрланга И
комбинации двух нормальных распределений;
□	вычисление вероятности отбраковки детали (см. пример 4.3);
□	расчет значения функции распределения и графика математического ожида-
ния оставшегося времени жизни для индивида, дожившего до возраста х (см.
пример 4.11);
□	анализ точности неравенства Чебышева (см. пример 4.13).
Необходимый справочный материал
Как и для дискретных случайных величин, в пакете Mathcad имеются встроен-
ные функции для работы с распределениями непрерывных случайных величин.
Функции, имена которых начинаются с букв d пр, вычисляют значения плотно-
сти и функции распределения в заданной точке, а с буквы г -- вырабатывают
заданное число соответствующих случайных величин. Перечислим их для рас-
смотренных выше распределений:
□	dunif(x, а, Ь) и punif(x, а, Ь) выдают значения (4.7) и (4.8) для равномерного
в (й, Ь) распределения;
□	dexp(x, 7) и рехр(х, 7) выдают значения (4.9) и (4.10) для экспоненциального
распределения с параметром 7;
□	dnorm(x, р, а) и рпогт(х, ц, а) выдают значения (4.11) и (4.12) для нормально-
го распределения с параметрами ц и а;
□	dgamma(x, I) и pgamma(x, I) выдают значения (4.18) и (4.19) для распределе-
ния Эрланга с параметрами X = 1 и I;
□	dlnorm(x, a, s) и plnorm(x, a, s) выдают значения (4.39) и (4.40) для логариф-
мически нормального распределения с параметрами а и $;
Фрикции rexp(n, X), morm(n, ц, a), rgamma(n, I) и rlnorm(n, a, s) вырабатывают п
случайных величин с вышерассмотренными распределениями.
Для выработки непрерывных случайных величии с распределениями, которых
нет п Mathcad, следует использовать формулу (4.45). Фигурирующая в ней рав-
номерно распределенная в интервале (0; 1) случайная величина Y вырабатывает-
ся фрикцией rnd(n, х), если положить х = 1 (верхняя граница интервала равна I)
и и = 1 (если вырабатывается только одна случайная величина).
Согласно общей формуле (4.3) функция распределения непрерывной случайной
величины выражается через плотность распределения путем интегрирования по-
следней. В пакете Mathcad имеется оператор, вычисляющий значения определен’
пых интегралов. Для использования его необходимо вызвать шаблон интеграла
и.। палитры математических символов (Calculus Toolbar) или нажать клавишу &.
Шаблон содержит четыре места ввода: для подын тегральной функции (в пашем
случае1 это — плотность распределения); для нижнего предела интегрирования
(наименьшее возможное значение рассматриваемой случайной величины); для
верхнего предела интегрирования (переменная функции распределения ИЛИ се
числовое значение); для переменной интегрирования. Отметим, что интегралы
120
4, Непрерывные случайные величины
(как и суммы и другие операторы) могут входить в сложные математические
формулы. Достигаемая при этом визуализация аналитических выражений — важ-
нейшее достоинство системы Mathcad.
Другим важным достоинством Mathcad является возможность графического
представления функций. Это особенно важно для плотностей распределений, по-
скольку их графики более наглядны, чем графики функций распределения. Для
создания графиков используются шаблоны, перечень которых представлен в
подменю Graph (График) меню Insert (Вставка). Для построения графиков кри-
вых плотностей или функций распределения используется двумерный декартов
график, вызываемый командой X-Y Plot из подменю Graph. По оси абсцисс откла-
дываются значения переменной, а по оси ординат — значения плотности или
функции распределения. После ввода команды на экране появляется пустой
прямоугольник с местами ввода данных в виде маленьких темных прямоуголь-
ничков. В прямоугольничек, расположенный на оси абсцисс, следует ввести имя
переменной (например, х, у и т. п.), а в прямоугольничек на оси ординат — имя
функции. В одном окне можно построить несколько графиков функций. Список
данных функций следует вводить через запятые. Диапазоны изменения значе-
ний переменных и функций (масштаб графика) по умолчанию задаются авто-
матически. При необходимости можно прибегнуть к форматированию. Команда
форматирования позволяет изменять параметры графика и предоставляет поль-
зователю разнообразные возможности по оформлению графиков.
Для вызова окна форматирования текущего графика следует его выделить, щелк-
нув мышью на графике. Далее необходимо выполнить команду прикладного
мелю Format—Graph—X-Y Plot... или дважды щелкнуть мышью по выделенному
графику. В результате откроется окно, представленное на рис. 4.5.
Рис. 4.5. Вид окна форматирования текущего графика
Скво содержит четыре закладки. Первая закладка X-Y Axes предназначена для
оформления осей координат и их масштабирования. Вторая закладка Traces ис-
пользуется для изменения свойств графиков (вида линии, цвета, толщины, типа
и др.). Третья закладка Labels предназначена для оформления графиков (ввода
Компьютерный практикум № 6. Распределения непрерывных случайных величин в пакете Mathcad
121
заголовка, надписей на осях, имен кривых и отображаемых переменных). По-
следняя закладка Defaults обеспечивает возврат установок, назначенных по
умолчанию. Здесь же можно изменить установки, назначаемые по умолчанию.
График можно перемещать по выделенному полю экрана. Для этого необходимо
выделить график, щелкнув по нему мышью. Далее следует подвести указатель
мыши к выделенной границе, так чтобы вместо маленького красного крестика
появился вид ладони руки. Теперь, оставляя нажатой левую кнопку мыши, необ-
ходимо перемещать мышь до нужного места. После отпускания кнопки мыши
новое место графика будет зафиксировано. Перемещение графика можно осуще-
ствить и по-другому. Если при выделенном графике нажать на клавишу F3, то
график пропадет — он окажется в буфере обмена данных. Переместив курсор
в новое место и нажав на клавишу F4, мы размещаем график на этом месте.
Для изменения размера графика следует подвести указатель мыши к маркерам
изменения размера (черным маленьким прямоугольничкам на осях). При этом
указатель приобретет форму двусторонней стрелки. Нажав левую кнопку мыши
и захватив сторону или угол шаблона графика, не опуская кнопки, можно растя-
гивать или сжимать график в горизонтальном, вертикальном или диагональном
направлениях. После отпускания кнопки размер графика изменится.
Реализация задания
Для проведения вычислений нам понадобятся одиннадцать функций пользователя.
Программные модули, реализующие эти функции, представлены на рис. 4.6
и рис. 4.7.
Практикум Ns 6. Непрерывные случайные величины
Пользовательские Функции
Усеченное экспоненциальное распределение
т .г- , , J . , -xxf-ia -хьГ1 п
ТгипкЕхр(х. А , а ,Ь) » if[_a < х < Ь, А е Де -е 1	.0J
Смесь двух нормальных распределений
MixN(x, р ,д1, ai, д2, а2):» р dnormfx ,д1,а1) + (1 - р) dnorm(x,/t2.ff2)
Вероятности отбраковки детали
q0(6 , о) «1- pnorm| — ,0,1 j + pnormf-— ,0,1
( (ь \	( ь \\ (	(6	\	( 6	'
q1(6,p,o ,<Н)1 - (1 - р) рпогт —,0,1 - рпогт -—,0.1 - р рпогт — ,0.1 - рпогт —-,0.1
\	J \ ° JJ X \ff1 7	\ oi
РНА(6 ,р,Р ,g1)
Логарифмически нормальное распределение	( .2s
1	I**—
Подп(у,а,а) - - dnorm(ln(y) ,а,s) Flogn(y,a,s) > рпогт(1п(у) ,a,s) Evlogn(a.s)  e''
V	4	r150
Vlognfa,s) > e^2 a+®2^ (e$2 - 1)	Resud(x a s) ‘ 1 - ! iogn.x. a.s) Jx (У-«)Л«»п(У..,0>-У
Рис. 4.6. Функции пользователя для работы с непрерывными случайными величинами
Функции имеют следующее назначение.
TinnkExp(x, К, а, Ь) вычисляет значение в точке х плотности экспоненциального
распределения (4.9) с параметром X, усеченного интервалом (а, Ь):
ЛЛО ^е х'/(е -е
(4.54)
122
4. Непрерывные случайные величины
MixN(x, р, ц ।, ст।, р 2, а2) вычисляет значение в точке х плотности распределения
смеси двух нормальных распределений (4.11) с параметрамиpt, иц2, о2 и до-
лей первого распределения р:
/(л) - р — ср ---— + (1 - р)— <р —-^-4- , со < х < со. (4.55)
°1	\ СТ1 7	°2	\	°2	/
Функции q0(<5, о), с/1(р, ё, о, Oj )и РНА вычисляют вероятности qc, qt и Р{Н0 | А}
из примера 4.3.
Следующие функции связаны с рассмотренным в примере 4.11 логарифмически
нормальным распределением: flogn(y, a, s') и Flogn(y, a, s) вычисляют в точке у
значения плотности (4.39) и функции (4.40) распределения с параметрами а и s;
Evlogn(a, s) и Vlogn(a, s) находят математическое ожидание и дисперсию по фор-
мулам (4.41); Resud(x, a, s) рассчитывает математическое ожидание остаточного
времени жизни по формуле:
Res(z/) = Д(У - у|У >у) =
1	г х~у ( (1п(х)-а)2>1 ,	(4.56)
=--------;-----------7=^- ехР ..... ..~--о-— \dx-
l-<J>((ln(.y)-<7)/s)J0 V2nsx	2s2	)
Функция Cheb(p, о) вычисляет вероятности (4.53) для рассмотренных в приме-
ре 4.13 распределений, а также оценку, получаемую по неравенству Чебышева
(4.49). Программный модуль, реализующий данную функцию, представлен ниже
на рис. 4.7.
СКеЬ(д , о)
а <— д - о /3
b д + о -/3
_ 2
Кьд а 4
К-/»'2
s^VinLU2+«2)<2J
1
2 f 2	2^
aa 4- ln[ д Ад + а )
for i е 1 7
Пользовательские функции «продолжение).
Неравенство Чебышева
До1.2 <7 + 0.2 о i
А31 t- 1 - рпогпЦд + х.д ,а) + рпопп(д - х,д , о)
Ад 11 - рпогт(1п(д + х) ,aa,s) + И(д > х ,рпогт(1п(д - х) ,aa,s) .0)
Рис. 4.7. Функция пользователя для работы с неравенством Чебышева
На вход подаются математическое ожидание ц и среднее квадратическое откло-
нение а. Для них по формулам, приведенным в примере 4.13, рассчитываются па-
раметры: а и b равномерного распределения; X и I распределения Эрланга; а н л
Компьютерный практикум № 6. Распределения непрерывных случайных величин в пакете Mathcad
tn
логарифмически нормального распределения (в программе используется вво-
значение аа вместо а, чтобы не путать с аналогичным параметром равномерною
распределения).
В программе предусмотрен расчет вероятностей для семи значений аргумента X»
начиная со значения 1.2ос интервалом 0.2о. Эти значения аргумента содержатся
в первой строке выдаваемой программой матрицы. Последующие строки содер-
жат значения вероятностей для рассмотренных распределений: первая строка —
для равномерного, вторая — Эрланга, третья — нормального, четвертая — лога-
рифмически нормального. Последняя строка содержит оценку, даваемую нера-
венством Чебышева.
Результаты вычислений
Результаты выполнения задания представлены на рис. 4.8-4.11. Вначале строятся
графики кривых плотностей для четырех вышерассмотренных распределений:
равномерного, экспоненциального, нормального и Эрланга (рис. 4.8). Графики по-
строены для разных значений параметров, что позволяет проанализировать ИХ
влияние на вид кривых.
х -0,0.1. 8
Равномерное распределение
Экспоненциальное распределение
124
4. Непрерывные случайные величины
Для равномерного распределения (4.7) построены две плотности: для значений
параметров a = 2,Z> = 6na = l,Z> = 7. Как видно из табл. 4.4, математическое ожи-
дание для обоих случаев совпадает и составляет Е(Х) = (а + Ь)/2 = 4. В то же вре-
мя дисперсии D(X) = (b - а)2/12, соответственно, равны 4/3 и 3. Эти значения и
формы кривых плотностей показывают, что дисперсия действительно является
мерой разброса случайной величины.
Для экспоненциального распределения (4.9) также построены две плотности для
значений параметров 1 = 1 и X = 0.5. Обратное значение этого параметра равно
математическому ожиданию случайной величины Е(Х) = 1/Х. Из графика на-
глядно видно, что во втором случае среднее значение действительно больше.
Для нормального распределения (4.11) построены три кривые плотностей для
значений параметров ц = 3, ст -1; ц = 3, ст = 1.5; ц =5, ст = 1. Из представленных
графиков видно, что изменение значения параметра ц (среднего значения) при
постоянном ст (среднем квадратическом отклонении) приводит к эквидистантно-
му сдвигу кривой плотности вдоль оси абсцисс. Если же ц постоянно, то с рос-
том ст кривая становится более плоской.
Для распределения Эрланга (4.18) построены четыре кривые плотностей для зна-
чений параметра I = 1, 2, 4 и 5 при одном и том же значении параметра X = 1. Из
графика видно, что при 1=1 мы имеем экспоненциальное распределение. С ростом
значения этого параметра распределение Эрланга приближается к нормальному.
Далее (рис. 4.9) представлен график кривой плотности обычного (4.9) и усечен-
ного (4.54) экспоненциального распределения с параметром X = 0.8. Во втором слу-
чае распределение усечено только справа значением 2.5, то есть в формуле (4.54)
а = 0, b = 2.5. Проверяется также выполнение условия нормировки для плотно-
сти: интеграл от нее равен единице. На втором графике приведена кривая плот-
ности смеси двух нормальных распределений (4.55) с параметрами р = 0.2, ц, = 1,
ст, =0.5, ц2 - 4, ст2 =1.
Вероятности отбраковки детали, рассматривавшиеся в примере 4.3, были рас-
считаны для следующих исходных данных: р = 0.2, 5 = 1, ст = 0.4 (см. рис. 4.10 и
табл. 4.3). Значения параметра ст, варьировали в виде ст, = zct, где z = 1, 1.1,..., 2.8.
Если z = 1, то ст = ст,, фактически разладки станка нет, и вероятности q0 и сов-
падают и равны 0.012. С ростом ст, вероятность отбраковки увеличивается.
При ст, = 2.8 она почти в семь раз превышает вероятность q(} для случая отсутст-
вия разладки.
Для логарифмически нормального распределения из примера 4.11 были подсчита-
ны значения функции распределения (4.40) и график математического ожида-
ния оставшегося времени жизни для индивида, дожившего до возраста х. В каче-
стве параметров распределения (4.39), (4.40) были приняты следующие: а = 3.9,
$ = 0.43. Подсчитаны также математическое ожидание Evlogn и дисперсия Vlogn
этого распределения.
В заключение рассматривалась точность результатов, получаемых по неравенст-
ву Чебышева. Распечатка результатов работы функции Cheb для значений пара-
метров ц = 1, ст = 0.5 приведена на рис. 4.11. Эти результаты были прокомменти-
рованы в примере 4.13.
Компьютерный практикум № 6. Распределения непрерывных случайных величин в пакете Mathcad
126
TrunkExp (х, 0.8,0,2.5)
dexp(x ,0.8)
Спесь двух нормальных распределений
Проверка плотности
распределения на нормировку
[ TrunkExp(x,1,0.2) dx = 1
J0
Проверка плотносги
распределения на нормировку
Г10
MixN(x.02,1,0.5,4,1) dx* 1
-2
Рис. 4.9. Графики плотностей распределений (продолжение)
Вероятности отбраковки детали
>1,12.3	q0(1,0.4)-0.012
q1(1,0.2,0.4,0.4 г) РНА(1,02,0.4,0.4 z)
Логарифмически нормальное распределение
Функция распределения
w»1. 9
0.012
0.025
0 034
0.043
0.052
0 061
0 069
0.077
0 094
0.091
0.8
0572
0.401
0 296
0.232
0.19
о7бз
0143
0129
0118
о.Тоэ
F1ogn(w. 3.9,0.43)
_____________0_
4.399 10-14
3.636 10-111
2.52 10-®
4 995 10-3
4 722 10-7
2.755Ч 0 -8
1 14910-8
¥748 10^
v - 20,30 120
Flognfv. 3.9,0.43)
0018
0123
0.312
0.511
О 674
"5 zVT
0.869
оэТ?
0.949
О 96?
0.98
Математическое ожидания остаенегося времени жизни
(возраст)
1.. 120
Рис. 4.10. Результаты решения примеров 4.3 и 4.11
Математическое ожидание
Evlogn(3.9,0.43)  54.187
Дисперсия
Vlogn(3.9,0.43) - 596,354
Анализ точности неравенства Чебышева
/о
0.467 0.5J3 0.6 0.667 0.733 0.8	0.867
о
( П 0
Cheb 1,- I -
\ 3/	0
0
ч0
0,192 0Л76
0.147 0.096
0.162 0.11
0.128 0.084
0.51 0.391
0	0
0.063 0.041
0.072 0.046
0.058 0.042
0.309 0.25
0	0
0.028 0.02
0.028 0.016
0.032 0.024
0.207 0.174
О
0.014
9.322 к 10“3
0.019
0,148
Рис. 4.11. Анализ точности неравенства Чебышева
126
4. Непрерывные случайные величины
Задания для самостоятельной работы
1.	Построить графики различных плотностей распределений и с их помощью
проанализировать влияние параметров на вид графиков.
2.	Составить программу, вычисляющую функцию распределения из при-
мера 4.12 и строящую график з гой функции.
3.	Составить программу и с ее помощью экспериментально проверить неравен-
ство Шварца (4.46) для выбранных функций у и р и распределения непре-
рывной случайной величины X.
4.	Составить программу и с ее помощью экспериментально проверить неравен-
ство Йенсена (4.47) для выбранных функции у и распределения непрерыв-
ной случайной величины X.
5.	Проанализировать логику работы функции Cheb(p, о), представленной на
рис. 4.7.
Задачи
Задача 4.1. Пусть X — случайная величина, имеющая равномерное распределение
с параметрами а = N/2, b = 2N, где N — номер студента по групповому журналу.
Построить графики плотности и функции распределения. Найти вероятность
попадания X в следующие множества:
1.	(W;3/21V);
2.	(МЗЛО;
3.	(N/4; N) U (3/2Л1; 3N).
Задача 4.2. Решить задачу 4.1 в предположении, что X — экспоненциально рас-
пределенная с параметром Z.-7/N случайная величина.
Задача 4.3. Решить задачу 4.1 в предположении, что X — нормально распреде-
ленная с параметрами ц = N, о = случайная величина.
Задача 4.4. Решить задачу 4.1 в предположении, что X имеет распределение Эр-
ланга с параметрами к. = 1/N, 1-2.
Задача 4.5. Какой должна быть константа с, чтобы функция
. I с(1 + xYk, х > а,
/(r)= о
[О,	х < а,
где а, 1г > 0, была плотностью распределения?
Задача 4.6. В условиях предыдущей задачи определить, при каких значениях па-
раметра k существует математическое ожидание?
Задача 4.7. Математическое ожидание имеет смысл среднего значения случай-
ной величины. Проиллюстрируйте это на примере нормального распределения с
параметром ст = 1. Постройте и проанализируйте графики плотности этого рас-
пределения при различных ц (например, ц =0, 2, 5).
Задача 4.8. Дисперсия и среднее квадратическое отклонение являются мерой
разброса случайной величины около ее среднего значения. Проиллюстрируйте
Задачи
127
это на примере нормального распределения с параметром ц = 0. Постройте и прв-
анализируйте графики этого распределения при различных о (например, а = 1, 2,5).
Задача 4.9. Моменты какого порядка существуют для плотности, приведенной В
задаче 4.5? Вычислите эти моменты.
Задача 4.10. Распределение Коши. Плотность этого распределения дается форму-
лой
/(х) - 1/(л(1 + х2 )), -оо<х<<ю.	(4.57)
Покажите, что никакие моменты этого распределения (даже математическое
ожидание) не существуют.
Указание. Достаточно показать, что интеграл от х/(х) по интервалу (0, а) стре-
мится к со при а —> оо.
Задача 4.11. Распределение Лапласа. Плотность этого распределения есть
= ^ехр(-|х|), -со<х<оо.	(4.58)
Постройте график этой плотности. Найдите момент порядка г.
Указание. Сведите дело к уже известным результатам для экспоненциального
распределения.
Задача 4.12. Случайная величина X имеет нормальное распределение с парамет-
рами цист2. Покажите, что ее среднее отклонение
£(| X -ц|) = ст^2/я » 0,7979а.
Задача 4.13. Найдите выражение для плотности усеченного распределения Эр-
ланга, сосредоточенного на интервале (а, Ь), где а<Ь. Постройте график плотно-
сти распределения с параметрами X = 1 и I = 3, сосредоточенного в интервале (О,
2). Обсудите случай b -» со.
Задача 4.14. Найдите выражение для плотности усеченного нормального распре-
деления, сосредоточенного на интервале (а, Ь), где а<Ь. Постройте график плот-
ности усеченного нормального распределения с параметрами ц = 1, ст = 2, сосре-
доточенного на интервале (0, 4).
Задача 4.15. Распределение Парето. Плотность этого распределения задается как
/(x) = -f->| , х>а,	(4.59)
аух J
и равна нулю при х < а. Здесь k > 1 — параметр распределения.
Покажите, что математическое ожидание существует и равно ak/(k - 1). При ка-
ких условиях существует момент r-го порядка?
Задача 4.16. В условиях задачи 4.1 найдите точное значение вероятности Р{Х «К N)
и сравните его с оценкой, получаемой по неравенству (4.48).
Задача 4.17. В условиях задачи 4.2 найдите точные значения вероятности
Р{Х г х) при х = N; 2N; 3N и сравните их с опенками, получаемыми по неравенст-
ву (4.48).
128
4. Непрерывные случайные величины
Задача 4.18. В условиях задачи 4.3 найдите точное значение вероятности
Р{ | X -ЛГ| > 2VjV} и сравните его с оценкой, получаемой по неравенству Чебыше-
ва (4.49).
Задача 4.19. В условиях предыдущей задачи оцените эффективность неравенст-
ва (4.51).
Задача 4.20. Рассмотрите пример 4.12 для случая, когда X имеет равномерное
распределение в интервале (0, За).
Задача 4.21. Рассмотрите пример 4.12 для случая, когда X имеет нормальное рас-
пределение с параметрами ц = а и о2.
Задача 4.22. Доказать свойства математического ожидания и дисперсии (4.24)
и (4.31), используя явное выражение (4.38) для плотности линейного преобразо-
вания Y = а + ЬХ.
5 Многомерные дискретные
случайные величины
5.1. Распределения многомерных
дискретных случайных величин
Ранее рассматривались случайные величины, которые принимали только ска-
лярные значения. Теперь мы переходим к изучению случайных величин, являю-
щихся векторно-значными.
Определение 1. Многомерной случайной величиной (случайным вектором) X назы-
вают совокупность одномерных случайных величин Хь Х2,..., Хт, определенных
на одном и том же пространстве элементарных событий Q:
Х(со) = (Xt(со), Х2(со).Хт(и>)).	(5.1)
Как и раньше, обозначение элементарного события со обычно опускают и пишут
Х»(Х„Х2....хм).
Начнем изучение многомерных случайных величин с дискретного случая, когда
все случайные величины Хь Х2, ..., Хт — дискретные.
Определение 2. Распределением вероятностей многомерной дискретной случай-
ной величины X = (Хь Х2,..., Хт) называется система равенств
P{Xt=x«\X2=x?...........Xm=x^}=p.,i2.im,
ij=l,2,	...,т,	(5.2)
где x(tJ) и (Хц\ х.р,..., x<i"‘>) — возможные значения одномерной случайной ве-
личины Xj и многомерной случайной величины X соответственно, kj — число
возможных значений Xj.
Псроятпости р; должны удовлетворять условиям неотрицательности
Рц t I, ^Ои нормировки
*i Д, А.
Z	..,.=!	(5.3)
jj -1
Обычно распределение вероятностей (5.2) многомерной дискретной случайной
величины задается аналитически — с помощью формул. Примером такого зада-
ния является полиномиальное распределение (2.14) с параметрами п и pltpj.
р„, где п - целое положительное число, а вероятности {pj удовлетворяют усло-
вии, нормировки р] + р2 + ... + р,„ = 1. Оно определяет распределение миогомер-
130
5. Многомерные дискретные случайные величины
ной дискретной случайной величины X = (Хь Х2, ..., Хт), компоненты которой
принимают целочисленные неотрицательные значения, такие, что сумма их рав-
няется п:
P{Xj =i j =	— -р'1 р!22...р'т", i, +i2+...+im = п. (5.4)
I. 12«	2 I
Если число компонент равно двум, то говорят о двумерной случайной величине
X = (Xj, Х2). В этом случае распределение вероятностей (5.2) удобно задавать
таблицей (матрицей). Ее строки соответствуют возможным значениям первой
компоненты, а столбцы — значениям второй компоненты. На пересечении их
стоят вероятности соответствующих значений:
PiJ =Р{Х, =х<»,Х2 =х<2>}.	(5.5)
Итак, Ру есть вероятность того, что первая компонента примет свое г-е возмож-
ное значение, а вторая — j-e.
Определение 3. Частное (маргинальное) распределение отдельной компоненты Ху
находится суммированием ,	( по всем индексам, отличным от г). Оно обо-
значается р*> = P{Xj =xt). В частности,
^2
Р{Х. =х<|)} = £ ...Ер(,.(2...(5-6)
Аналогично определяется двумерное распределение компонент Xt и Х2:
Ри =Р{Х. =<О.Х2 = <2)}= £ ...Zp,„,2...........iffl- (5.7)
<3=1	'»а|
Пример 5.1. Рассмотрим распределение вероятностей двумерной случайной ве-
личины X = (Xj, Х2), заданное в табл. 5.1. Первая компонента Х} имеет три воз-
можных значения -1, 0, 1. Число возможных значений второй компоненты Х2
равно четырем — это -2, 1, 2, 5. В таблице приведены вероятности (i = 1, 2, 3;
j = 1, 2, 3, 4) всех двенадцати комбинаций возможных значений обеих компонент.
Например, вероятность того, что первая компонента примет значение ноль, а вто-
рая два, р23 = P{Xt = 0, Х2 = 2} = 0.10. Последние столбец и строка таблицы содер-
жат частные распределения, соответственно, первой и второй компоненты. Так,
P{Xj = 0} = 0.25, Р{Х2 = 2} = 0.25. Сумма элементов последних столбца и строки
равна единице, что говорит о выполнении условия нормировки (5.3).	□
Таблица 5.1. Распределение вероятностей {р, двумерной случайной величины
	х<2) = -2	х<2> = 1	х<2>=2	х<2) = 5	P{Xt = х<‘>}
х}0 = -1	0.05	0.10	0	0.10	0.25
*<'> = 0	0	0.15	0.10	0	0.25
xj’^l	0.10	0.20	0.15	0.05	0.50
Р(Х2 = х<2»}	0.15	0.45	0.25	0.15	1
5.1. Распределения многомерных дискретных случайных величин
131
Математическое ожидание E(Xj), моменты £(XJ ) и дисперсия D(X;) каждой ком-
поненты случайной величины Х;- определяется по формулам (3.16), (3.22) и (3.23)
или (3.24).
Определение 4. Если Р{Х( = х*'*} > 0, то существует условное распределение век-
тора (Х2, Х3 ..., Хт) при условии, что {X, = х,‘|)}:
_ г<2)
'2 ’
Л.=х';>|х,
И X, =л"’,Х,	....Х_ =х‘">
d	1	<1 ’	2 Ч *	’ т «ж
• (5.8)
В частности, условное распределение компонента Х2 при условии, что •! Xt =Хц'
Р jXt =х-’),Х2	>
Р Х2 =х<2>| X, = х<’> I = -1-г---pH. (5.9)
1	J РХ1=х<Ч
Отметим, что в определении 4 в условии может фигурировать любая величина Х(, а
в качестве вектора (Х2, Х3 .... Хт) — любой вектор, не содержащий величину Xt,
Определение 4 было дано для величины Xj с целью упрощения формулировки.
Условные распределения обладают всеми свойствами обычных распределений.
В частности, для них можно определить математическое ожидание, моменты и дис-
персию, если только выполняются обычные условия на их существование. Эти чи-
словые характеристики называются условными.
Определение 5. Пусть р|х( >0. Условным математическим ожиданием
случайной величины Х2 при условии, что случайная величина Xt приняла значение
Х(|, то есть что произошло событие |х, =x(V j-, определяется формулой
£(Х2|Х, = х<'>) = £х<2)Р (х2 =х<2)|Х, = х<‘>|.	(5.10)
1*2 =1	L	J
Если число возможных значений компоненты Х2 бесконечно: k2 = оо, то для су-
ществования условного математического ожидания дополнительно требуется
выполнение абсолютной сходимости суммы членов бесконечного ряда:
2Х”|	=х«>}<».
,,.! I	)
С тем чтобы отличать обычное математическое ожидание от условного, часто пер-
вое называют безусловным. Иногда его удобнее вычислять через условные матема-
тические ожидания, используя следующую теорему.
Теорема 5.1. Если математическое ожидание Е(Хг) существует, то оно может быть
вычислено по формуле
132
5. Многомерные дискретные случайные величины
(	1
Е(Х2 ) = £ Р X, =х<; ’ • Е(Х21X, = х ’).
<1 =1 I	J
(5.11)
Доказательство
Существование математического ожидания £(Х2) означает абсолютную сходимость
суммы членов ряда, что позволяет группировать члены ряда произвольным обра-
зом. Используя это свойство, имеем:
е(х2)=ix^.p[x2 =хМ=ix ’ • х’РЬ	-
1*2 =1	(.	J *2 Й el I	JI	J
=	-p\xi =<>ix, =x<4 =
4=1 I	J <2’1 I	J
k (	1
= 'Lp\Xl =x^\-E(X2\Xi = x<‘>).
t’l “11,	J
Пример 5.2. Вернемся к табл. 5.1. Условное распределение компоненты Х2 при
условии, что компонента Xj приняла значение х^ = 1, приведено в табл. 5.2.
В частности, Р{Х2 = 2 | Xt = 1} = Р{Х{ = 1, Х2 = 2}/Р{Х{ = 1}= 0.15/0.50 = 0.3. Услов-
ное математическое ожидание компоненты Х2 при условии {Xj = 1} вычисляется
по формуле (5.10):
£(Х2| X, = 1)=-2 • Р{Х2 = -21 Xj = 1} + 1 • Р{Х2 = 11 Xj = 1} + 2 • Р{Х2 =2 | X. = 1} +
+ 5-Р{Х2 =5 |Х, = 1} = -2-0.20 +1-0.404-2 0.30 + 5-0.10 = 1.1.
Аналогично вычисляются другие условные математические ожидания компо-
ненты Х2: Е(Х2 | Xj = -1) = 2.0, Е(Х2 | Х( = 0) = 1.4. Это позволяет по формуле
(5.11) вычислить безусловное математическое ожидание Х2:
£(Х2) = Р{Х, =-1}-£(X2|Xj =-1) + Р{Х, =0} -£(Х2| X, =0) +
+P{Xj =1}-£(X2|Xj = 1) = 0.25-2.0+ 0.25 1.4+ 0.50 1.1= 1.4,
где вероятности p|xj =х-1> | взяты из табл. 5.1.
Этот же результат мы получим, если вычислим £(Х2), используя формулу (3.16)
и распределение вероятностей компоненты Х2, представленное в табл. 5.1:
£(Х2) = -2  0.15 + 1  0.45 + 2 • 0.25 + 5 • 0.15 = 1.4.
Аналогичным образом получаем математическое ожидание второй компоненты:
£(Х,) = 0.25.	□
Таблица 5.2. Условные распределения вероятностей и математические ожидания
компоненты Х2
Условие	х’2) =-2	х<2> = 1	х<2) = 2	х<2> = 5	£(Х1Х =0
х =-1	0.20	0.40	0	0.40	2.0
X = о	0	0.60	0.40	0	1.4
X = 1	0.20	0.40	0.30	0.10	1.1
5.1. Распределения многомерных дискретных случайных величин
133
Вернемся к полиномиальному распределению (5.4), которое будет в дальнейшем
неоднократно рассматриваться.
Теорема 5.2. Пусть многомерная случайная величина X = (Xit Х2>..., Хт) имеет по-
линомиальное распределение (5.4). Тогда: 1) распределение (5.4) удовлетворяет ус-
ловию нормировки (5.3); 2) частное распределение компоненты Xj является бино-
миальным (3.3) с параметрами п и р = р-, 3) если компонента Xj приняла значение ij,
то условное распределение остальных компонент является полиномиальным с па-
раметрами п = п - ij и pr = pr/(l - Pj), г = 1, 2, ...,j - l,j + 1,.... т.
Доказательство
Первые два утверждения теоремы доказываются одновременно. Будем их доказы-
вать, используя индукцию по числу компонент т. При т = 2 имеется только два ис-
хода. Будем первый трактовать как «успех», а второй — как «неудачу». Тогда Х1 —
это число успехов в испытаниях Бернулли. Оно имеет биномиальное распределе-
ние с параметрами п, р = р^ и q = 1 - р = р2. Вторая компонента выражается через
первую однозначно: Х2 = п - Х{. Для биномиального распределения выполнение
условия нормировки было доказано в параграфе 2.3. Итак, для т = 2 оба утвержде-
ния теоремы выполняются.
Предположим теперь, что они выполняются для т > 1, и докажем их выполнение
для т + 1. Используя перестановку слагаемых суммы, можно записать;
Z =г;.,; = 1,тп+11 =	“
«1 + =n I	J q + ... Ч 'h ! •••	+ 1 !
£	(n-fW4i)! ( Pt Y‘ ( р2 Y2 ( р„
I'l + ...+im=n-im+l if ! г’2 ! ...im ! 1^1 - Pm+) J	J yl-Pm+t j
В последнем выражении вторая сумма — это сумма вероятностей всех возможных
значений ти-мерной случайной величины (Хь Х2.Х,„), имеющей полиномиальное
распределение с параметрами п - п - im+t и pj = pj/(\ - pm+t). По предположению
индукции условие нормировки выполняется и эта сумма равна единице. Оставшая-
ся теперь первая сумма — это сумма всех вероятностей биномиального распреде-
ления (3.3) с параметрами п, р = pm+t, q=l-p=l- pm+i, так что она тоже равна
единице. Следовательно, условие нормировки выполняется, a Xm+i действительно
Имеет биномиальное распределение с указанными параметрами. Вместо Хт+1 может
фигурировать любая компонента, так что первые два утверждения теоремы дока-
заны.
Справедливость третьего утверждения теоремы следует из определения (5.8) услов-
ного распределения и только что доказанного утверждения о биномиальном рас-
пределении отдельной компоненты. Полагая для упрощения записи./ ® 1, находим;
Р\Х2=х«\..„ X,
о)
134
5. Многомерные дискретные случайные величины
Р Х1=х<‘’,Х2 = х™.... Хт+1
(О
г, !(п-г()!
,	 \ I (	\'2 /	Х'З /	Х'т /	,
I—'dL. [	1	/_Л’_р;(1_р1у
i, li, ill-р, J U-P, ) U-pJ /i,
/	• \ I	(	\'2 /	VS	f
(n-Q!	f	p2 ) f	p3 )	f	pm )
i2 !i3 !... im l^l-p, J U-pJ "Vl-pJ
□
В заключение этого раздела мы рассмотрим процедуру генерирования многомерной
дискретной случайной величины X = (Х(, Х2,..., Хт) с заданным распределением ве-
роятностей (5.2). Она сводится к последовательному генерированию т одномерных
случайных величин Х(, Х2,.... Хт. Каждая из этих величин генерируется по методи-
ке, изложенной в примере 3.4, согласно ее условного распределения, вычисленного
при условии, что ранее сгенерированные величины приняли данные значения. Для
первой величины используется ее безусловное распределение.
Рассмотрим, например, двумерную случайную величину (Xt, Х2) из примера 5.1.
Вначале мы вырабатываем реализацию случайной компоненты Xt согласно ее част-
ного распределения, представленного в последнем столбце табл. 5.1. Предположим,
это было значение 0. Найдем условное распределение второй компоненты Х2 при
условии, что Xt = 0. Это условное распределение представлено в табл. 5.2. Генери-
руем реализацию второй компоненты Х2 согласно этого условного распределения.
Если бы компонент было больше двух, этот процесс надо было бы продолжить.
Алгоритм генерирования многомерной дискретной случайной величины
Вход: Распределение вероятностей (5.2) m-мерной дискретной случайной величины.
Выход: Реализация (Хь Х2,..., Х„) m-мерной дискретной случайной величины.
Алгоритм
Шаг 1: Генерировать случайную величину Х( согласно ее частного распределения
вероятностей (5.6). Положить i = 2.
Шаг i: Найти условное распределение компонент (Х(, Х,+1,.... Хт) при условии, что
для предыдущего шага известно: 1) условное распределение компонент (Х,_ t, Х„ ...,
Хту, 2) зафиксированное значение компоненты Х,_(. Рассчитать частное условное
распределение компоненты X,. Генерировать случайную величину X, на основании
этого условного распределения. Если i = т, то — конец работы алгоритма, иначе по-
ложить i = i + 1 и перейти к шагу i.	□
В компьютерном практикуме этот алгоритм будет реализован функцией RandPol
для выработки многомерных дискретных случайных величин, имеющих полиноми-
альное распределение (5.4). Согласно теореме 5.2 в этом случае условное распре-
деление подмножества компонент будут полиномиальным, а частное распределение
отдельной компоненты — биномиальным. В нижеследующей таблице приведены
результаты имитационного эксперимента, заключающегося в выработке случайных
величин (Xj, Х2, Х3, Х4), имеющих полиномиальное распределение (5.4) с парамет-
оами п и р, = 0.4, Dt = 0.3, = 0.2, р4 = 0.1 (см. ниже пример 5.4). В таблице приведе-
5.2. Функции многомерных дискретных случайных величин
136
ны частоты {Х,/п}, подсчитанные для разного числа п. Из таблицы видно, как
с ростом числа п эти частоты стремятся к истинным вероятностям {р,}. Эти вероят-
ности содержатся в столбце и = оо. Сходимость частот к вероятностям говорит
о корректности алгоритма выработки случайных величин.	□
Таблица 5.3. Сходимость частот к вероятностям
для полиномиального распределения
Частоты Х,/п	п							
	10	50	100	500	1000	5000	10000	оо
Х/п	0.30	0.38	0.33	0.418	0.389	0.404	0.396	0.4
Х2/п	0.50	0.28	0.35	0.314	0.301	0.297	0.300	0.3
Х3/п	0	0.24	0.22	0.170	0.216	0.200	0.200	0.2
Х</п	0.02	0.10	0.10	0.098	0.094	0.098	0.104	0.1
5.2. Функции многомерных дискретных
случайных величин
Определение 6. Пусть х2......х„) — вещественнозначная функция веществен*
пых аргументов г(, х2,..., хт, а X = (Х}, Х2,..., Хт) — многомерная случайная величи*
на с распределением (5.2). Новая случайная величина У = \|/(Х(, Х2,..., Хт) называет*
ся функцией многомерной случайной величины.
Распределение вероятностей функции многомерной дискретной случайной величи-
ны У = v(Xi, Х2.Хт) находится аналогично тому, как это делалось для одномер-
ного случая (см. параграф 3.3). Пусть V — множество возможных значений m-мер-
ной случайной величины X, элементами которого являются m-мерные векторы.
Образ V при отображении чр представляет собой множество Vy возможных значе-
ний новой случайной величины У:
Уу ={у:Э(х,,х2, ...,xm)eV, y(xltx2..хт) = у}.	(5.12)
Вероятность принятия случайной величиной У конкретного возможного значения
У « Уу определяется аналогично формуле (3.18):
P{Y=y}=	£Р{Х,=х,.....Хт =х„}.	(5.13)
Ui..i.):
V('l  = »
Зная распределение вероятностей (5.13) случайной величины У = у(Х), можно по
формуле (3.16) вычислить ее математическое ожидание E(Y). При этом если мно-
жество Уу содержит бесконечное число элементов, то следует проверить условие аб-
солютной сходимости (3.17) — только в этом случае математическое ожидание су-
ществует.
Математическое ожидание £(У) можно вычислить, не находя предварительно рас-
пределения вероятностей для функции У = ц/(Х). Следующая теорема обобщает
теорему 3.1 и может быть доказана индукцией по числу компонент т.
136
5. Многомерные дискретные случайные величины
Теорема 5.3. Если математическое ожидание функции у многомерной дискретной
случайной величины X = (Х1( Х2..Х1П) существует, то оно может быть вычислено
по формуле
E('V(Xl,X2...Х,„))=ХХ	..............<5Л4>
Примеры
Пример 5.3. Найдем распределение функции Y = Х,Х2 случайных величин Х( и
Х2 из табл. 5.1. Вычислим, например, вероятность значения 2. Событие {У = 2}
состоит из двух событий: {Х( = -1, Х2 = -2} и {Xj = 1, Х2 = 2}. Эти события несо-
вместны и имеют вероятности, соответственно, 0.05 и 0.15. Итак,
P{Y = 2} = 0.05 + 0.15 = 0.20. В табл. 5.4 приведено распределение вероятностей
случайной величины У. Это позволяет вычислить ее математическое ожидание:
Е(У) = -5 • 0.10-2  0.10-1 • 0.10 + 0• 0.25 + 1  0.20 + 2  0.20 + 5 • 0.05 = 0.05.
Этот же результат мы получим, если будем использовать для вычисления мате-
матического ожидания формулу (5.14) теоремы 5.3:
Е(У) = (-1)(-2) 0.05 + (-1)-1-0.10 + (-1)-2 0 + (-1)-5-0.10 + 0 +
+ 1 • (-2) • 0.10 + 1 • 1  0.20 + 1  2 • 0.15 + 1 • 5 • 0.05 = 0.05.
Таблица 5.4. Распределение вероятностей функции У = Xj Х2
i	-5	-2	-1	0	1	2	5	S •
P{Y = i}	0.10	0.10	0.10	0.25	0.20	0.20	0.05	1.00
Пример 5.4. На грузоперевалочный пункт ежедневно прибывает пять автомашин
четырех марок. Автомашина первой марки доставляет груз весом 1 т, второй —
2 т, третьей — 3 т, четвертой — 5 т. Вероятности того, что прибывающая машина
окажется первой и т. д. марок (независимо от марок других машин) составляет
0.4, 0.3, 0.2 и 0.1. Каково распределение веса груза, доставляемого всеми автома-
шинами за сутки?
Решение
Обозначим X, — число машин i-й марки, прибывающих за сутки, i = 1, 2, 3, 4. По ус-
ловию задачи многомерная случайная величина (X,, Х2, Х3, Х4) имеет полиноми-
альное распределение (5.4) с параметрами п = 5, р, = 0.4, р2 = 0.3, р3 = 0.2, р4 = 0.1.
Мы интересуемся функцией этой случайной величины У = ц/(Х4, Х2, Х3, Х4) =
= 1 • Х( + 2 • Х2 + 3 • Х3 + 5 • Х4 — суммарным весом груза, поставляемого за
сутки.
Распределение этой случайной величины находится по формулам (5.12) и (5.13).
Соответствующие вычисления были проведены функцией YpolD. описанной
ниже в разделе Компьютерный практикум. Соответствующие результаты приве-
дены в табл. 5.5. Например, вероятность того, что вес поставляемого груза не
превысит 10 т, составляет 1 - 0.024 - 0.009 - 0.006 - 0.001 = 0.96.	□
5.2. Функции многомерных дискретных случайных величин
137
Таблица 5.5. Распределение вероятностей веса груза, поставляемого за сутки
У)	3	4	5	6	7	8	9	10	и	12	13	15
Р{Т = У}	0.064	0.144	0.204	0.171	0.150	0.108	0.083	0.036	0.024	0.009	0.006	0.001
Рассмотрение функций Xj) = (xf - E(Xf))(x} - E(Xj)) и у(хь х}) = x-Xj приводит к
понятиям смешанного момента и ковариации.
Определение 7. Смешанным моментом Е(Х, Xj) и ковариацией C(Xj, Xj) случай-
ных величин Xj и Xj называется
E(XiXj) = xi^x^p[xi=x(vi\Xj = х<4.	(5.15)
v=i <;=i	I	J
C(Xi,XJ ) d= E((Xt - Е(Х, ))(Ху - Е(Х}))) = E(XjXj) - Е(Х, )Е(Х>). (5.16)
Ковариация случайной величины X, сама с собой дает дисперсию D(Xj).
Рели хотя бы одна из компонент X, или Ху имеет бесконечное число возможных
значений, то, как обычно, следует проверить условие абсолютной сходимости.
В данном случае существование смешанного момента и ковариации гарантиру-
ется, если существуют вторые моменты Е(Х,2) и Е(Х?) случайных величин Х( и Xj.
Э го вытекает из неравенства Шварца
(£(Х, Ху ))2 < £(Х2) £(Х2).	(5.17)
Отметим, что отсюда получаем важное неравенство
C(Xf, Ху)2 <ZJ(X,)D(X.),
которое вытекает из формулы (5.17), если в ней заменить Х; и Ху на X, - £(Х<)
и Xj - E(Xj) соответственно.
Определение 8. Пусть X — m-мерная случайная величина, у которой для всех пар
компонент Х„ Ху ковариации С(Х„ А/ существуют. Ковариационной матрицей С(Х)
называется квадратная матрица порядка т, у которой на пересечении i-й строки
и/го столбца стоит ковариация z-й и /й компонент вектора X
С(Х),.у =С(Х,,Ху).	(5.18)
Отметим, что ковариационная матрица является симметрической матрицей и
что ее диагональные элементы равны дисперсиям компонент X.
Ковариация имеет размерность произведения размерностей случайных величин.
Безразмерной характеристикой является коэффициент корреляции.
Определение 9. Если ковариация С(Х„ Ху) существует, то коэффициент корреля-
ции случайных величин X, и Ху определяется формулой:
С(Х;,Х; )
р = —1 "	(5.19)
J ^D(Xj)D(Xj)
Ковариация и коэффициент корреляции являются мерой линейной зависимости
случайных величин. Для случайных величин X, и Ху, связанных линейной.зави-
симостью Xt = а + hXj, где b * 0, коэффициент корреляции равен 1 при b > 0 и -1
при b < 0. Во всех остальных случаях -1 < р, у < 1.
138
5. Многомерные дискретные случайные величины
Определение 10. Случайные величины X, и Xj, для которых ковариация С(Х„ Х;)
равна нулю, называются некоррелированными.
Пример 5.5. Проведем соответствующие вычисления для случайных величин,
распределение которых представлено в табл. 5.1. В примере 5.3 было вычислено,
что E(Xi Х2) = E(Y) = 0.05, а в примере 5.2, что E(Xt) = 0.25, Е(Х2) - 1.4. Теперь по
формуле (5.16) вычисляем ковариацию:
С(Х„Х2) = ВДХ, )-Е(Х, )Е(Х2) = 0.05 -0.25  1.4 = -0.3.
Для вычисления коэффициента корреляции необходимо найти средние квадра-
тические отклонения компонент Х{ и Х2. С этой целью по формуле (3.24) нахо-
дим соответствующие дисперсии:
з С	V	Г
ОД)=£х<1)-£(Х,) РХ1=х,0’
1=1 \ 	)	I
= (-1-0.25 )2 -0.25+(0-0.25 )2 0.25 + (1-0.25)2 0.50=0.688.
4 (	\2	Г
D(X2) = 3 х<2> - Е(Х2)  Р\Х2 = х<2>  =
Л1\	J	I
= (-2-1.4 )2 0.15 + (1-1.4)2 0.45 + (2 -1.4)2 0.25 + (5 -1.4)2 0.15 =3.84.
Теперь по формуле (5.19) вычисляем коэффициент корреляции:
С(Х„Х,)	=	-0.3	_ _0185
'	jD(X,')D(X1) V0.688-3.84
В практических приложениях наибольший интерес представляет сумма случай-
ных величин 5 = Xt + Х2 + ... + Хт.
Теорема 5.4. Если математические ожидания случайных величин существуют, то
математическое ожидание их суммы равно сумме их математических ожиданий:
Е(5) = ад) + ад2) +... + Е(Хт).	(5.20)
Если дисперсии {D(X,)} случайных величин{Х,} существуют, то дисперсия их
суммы D(S) вычисляется по формуле
Я(5) = £ад) + 2§ £ад,ХД	(5.21)
М	i-l ;=>+!
В частности, дисперсия суммы (разности) двух случайных величин равна сумме
их дисперсий плюс (минус) их удвоенная ковариация:
D(X, ±X2) = D(Xi) + D(X2)±2C(Xl,X2).	(5.22)
Для некоррелированных случайных величин дисперсия их суммы равна сумме
дисперсий:
D(5) = D(X{) + D(X2) + ... + D(Xm).	(5.23)
Доказательство
Достаточно рассмотреть только случай двух слагаемых суммы, поскольку случай
произвольного конечного числа слагаемых доказывается по индукции. Исполь-
ivo n rhnnuvnp (И 141 п качргтпе rhvHKituu vi(x.. х-Л cvmmv х, + х->. получаем:
5.2. Функции многомерных дискретных случайных величин
1М
4, k2 (
E(.Xt +X2) = I I х,(,) + х
М 7=1
*1 *г	(
= Z x^xf’.x,
r-1 J-l	I
4,	42 Г
^xf’pX^U
>=1	;=1 I
*1 r	1
= £x<*>P X^x,!1’
^^Х^х^Х, = x<2)| =
.	*1 *2	f
= x<2) +£ Jxf’P X, = x<*>,X2 = x<2>
J	M ;=1	I
1	*2	*1 Г
= z<2’ +£x<2’£p x, = x10),X2 = x<2)
J 7=1	>-l I
+ i><2)p(X2 = x<2)l = £(X, )+ £(X2).
Для доказательства формулы (5.22) учтем, что по только что доказанному
Е(Х\ + Х2) = Е(Х{) + £(Х2). Поэтому на основании определения дисперсии по
формуле (3.23)
£»(Х, + Х2) = £((Х, + Х2 - £(Х, + Х2 ))2 ) = £(((Х, - Е(Х, )) + (Х2 - £(Х2)))’ ) .
= £((Х, - £(Хх ))2 + 2(Х, - £(Хх ))(Х2 - £(Х2 )) + (Х2 - £(Х2 ))2) =
= £((Х, - £(Х, ))2 ) + £(2(Х, - £(Х, ))(Х2 - £(Х2))) + £((Х2 - £(Х2 ))2) =
= D(Xt ) + D(X2) + 2C(Xt, Х2).
Аналогично доказывается формула для дисперсии разности двух случайных ве-
личин.	□
Определение 11. Случайные величины Хь Х2, ..., Хт называются попарно незави-
симыми, если
р|х/=х(,),Ху
= х('Ч = Р]Х/=х°Чр]ху = x0)kvi#)их('!х°! (5.24)
Если Xt и Х2 независимы, то их условные распределения (5.8) совпадают с безус-
ловными.
Определение 12. Случайные величины Хь Х2,..., Хт называются взаимно незави-
симыми, если для любого подмножества их X,, Х„ ..., Xt и всех возможных значе-
ний х^.х?...
p(x7.=z<;’,xs =х<”.xt=z<£)l =
Г	1 Г 1	(5,25)
= р|х; =x<nWx,=x<s)l ...р1х( = х<01.
Для взаимно независимых случайных величин Хь Х2,..., Хт имеет место теорема
умножения математических ожиданий-.
£(Х,Х2 ...Хи) =£(Х,)£(Х2) ... £(Х„).	(5.26)
Отмстим, что из взаимной независимости следует попарная независимость, Ж U9
попарной независимости следует некоррелированность случайных величин.
Пример 5.6. Случайные величины Х{ и Х2 с распределением вероятностей иа
табл. 5.1 являются зависимыми. Это следует из того, что их ковариация и коэф-
фициент корреляции не равны нулю (см. предыдущий пример). Можно также
факт зависимости установить иначе, не вычисляя ковариацию и коэффициент
140
5. Многомерные дискретные случайные величины
корреляции. Действительно, для значений Хх = 1 и Х2 = -2 мы имеем P{Xr = 1,
Х2 = -2} = 0.10, в то время как P{Xt = 1} = 0.50, Р{Х2 - -2} = 0.15, так что
0.10 = Р{Х1 = 1, Х2 = -2} * Р = 1} • Р{Х2 = -2} = 0.50 • 0.15 = 0.075. Следователь-
но, условие независимости (5.25) нарушается.
Вычислим теперь математическое ожидание и дисперсию их суммы Хг + Х2, ис-
пользуя формулы (5.20) и (5.22):
£(Xj + Х2) = ВД) + £(Х2) = 0.25 + 1.4 = 1.65,
D(Xt + Х2 ) = D(X,) + D(X2 ) + 2 • C(Xl, Х2) = 0.688 + 3.84 + 2 • (-0.3) = 3.928.
5.3. Индикаторы событий*
Простейшим примером случайной величины является индикатор 1А фиксиро-
ванного события Л с (1. На исходном пространстве элементарных событий он
определяется так:
Из определения индикатора следует, что он принимает значение 1, если собы-
тие А наступило, и 0 — если не наступило. Распределение вероятностей для ин-
дикатора задается формулой
Р{1 А = 1} = Р{А}, Р{1а = 0} = 1-Р{Л).
Математическое ожидание и второй момент индикатора события А равны веро-
ятности события А:
Е(1а) = Е(1а) = Р{А},	(5.28)
а дисперсия
D(I А) = Р{А}(1-Р{А}).	(5.29)
В практических приложениях интересующую нас случайную величину Y можно
представить в виде суммы индикаторов Д, 12, ..., 1т фиксированных событий
Л|, А2, ..., Ат:
У =/,+/2+... + /„.	(5.30)
Математическое ожидание этой величины будет равняться на основании фор-
мул (5.20) и (5.28) сумме вероятностей событий {Л,}:
E(Y) = P{At} + Р{А2} + ... + Р{Ат}.	(5.31)
Дисперсия суммы на основании формул (5.21), (5.16) и (5.29) вычисляется по
формуле
£»(У) = £р{Л,.}(1-Р{А,}) + 2^ £(Р{ДЛу}-Р{Д}Р{Л?}).	(5.32)
г=1	1=1 7=1+1
Если события А2,..., А/ попарно независимы, то
В(У) = £р{Д}(1-Р{Л(.}).	(5.33)
1=1
Следовательно, для вычисления математического ожидания и дисперсии слу-
чайной величины (5.30) достаточно найти вероятность каждого из событий
5.3. Индикаторы событий’
141
А1г А2, ..., Ат, а также вероятности попарного наступления этих событий А) Aj
при i *j.
Применение индикаторов для нахождения математического ожидания и диспер-
сии случайных величин содержится в задачах 5.2-5.19.
Примеры
Пример 5.7. Пусть X — случайная величина, имеющая биномиальное распределе-
ние (3.3) с параметрами п, р, q = 1 - р. Показать, что ее математическое ожида-
ние и дисперсия определяется по формулам
Е(Х) = пр, D(X) = npq.
Решение
Случайную величину X, имеющую биномиальное распределение (3.3), можно
трактовать как число успехов в п испытаниях Бернулли с вероятностью успеха
в отдельном испытании р. Поэтому X представимо в виде суммы числа успехов
в отдельных испытаниях:
Х = Ц + 72+... + 7„,
где 7, — число успехов в г-м испытании.
Ясно, что 7, является индикатором события А/ - «в i-м испытании имел место ус-
пех». Поскольку вероятность всех таких событий по определению равна р, то из
формулы (5.31) сразу следует
£(Х) = иР{А,} = пр.
Для вычисления дисперсии заметим, что события {Л,} попарно независимы, В
связи с чем можно воспользоваться формулой (5.33):
D(X) = пР{Л,}(1 - Р{Л,}) = npq.
Пример 5.8. Пусть X — случайная величина, имеющая гипергеометрическое рас-
пределение (3.5):
Р{Х = i}
ci.cz,
i = max(0, г + п, -ri),..., min(r, n, ),
где r, n, щ — параметры распределения, являющиеся натуральными числами,
причем П\ < п, г < п.
I (оказать, ч то математическое ожидание и дисперсия X определяются по формулам
E(X) = ni-,D(X) = r^-(i--}^Jh..	(5.34)
п	п\ п) п-1
Решение
Случайную величину X, имеющую гипергеометрическое распределение (3.5),
можно трактовать как число красных шаров, оказавшихся в выборке без возвра-
щения объема г из генеральной совокупности, содержащей я, красных и Я - Я|
белых шаров (см. пример 2.1). Пронумеруем все красные шары, имеющиеся в ге-
неральной совокупности, числами от 1 до я(. Рассмотрим событие А(  <(-й крас-
ный шар генеральной совокупности попал в выборку». Пусть 7( — индикатор со-
142
5. Многомерные дискретные случайные величины
бытия А„ i = l,nt, так что в формулах (5.31), (5.32) т = nt. Очевидно, общее
число красных шаров в выборке равно сумме введенных индикаторов:
X = Ц +12 + ... +1„с
Из постановки задачи ясно, что вероятности извлечения любого красного шара
одинаковы. Следовательно, согласно формуле (5.31) математическое ожидание
X будет равно вероятности отдельного события Л„ умноженной на число крас-
ных шаров Пр
Для нахождения вероятности того, что данный красный шар попадет в выборку,
возвратимся к рассмотрению примера 2.1. Общее число элементарных событий
пространства Q составляет СГП. Интересующее нас событие состоит из тех эле-
ментарных событий (it, i2,..., ir), которые содержат номер нашего красного шара.
Общее число таких событий составит Сг„~\. Следовательно,
РИ(} = С:5/с>-. i =
п
откуда и следует формула (5.34) для математического ожидания.
Перейдем к доказательству формулы для дисперсии. Аналогично предыдущему,
вероятность того, что выборка содержит два зафиксированных красных шара с
номерами i nj,
P{AiAJ}=C^ICrn=^p^-
n(n-l)
Подставляя это в формулу (5.32), находим
D(X) = и, -(1--1 + 2 •"£(«, -:)
п) j=i
r(r-l) J г V
n(n-l)
г(, Н ПГ Г~П ( /	1+П.-1.
= «1 - 1— +2---------- «1(«1 -1)---7.--(«1 -1) =
п) пп(п-1д	2
„ г} ' „ г(г-п) п{	г(<
= п1 - 1— + 2 —-----”1 - 1—
nJ п (п-1) 2	пД
»1 -1
п-1
Компьютерный практикум № 7. Многомерные
дискретные случайные величины в пакете Mathcad
Цель и задачи практикума
Целью практикума является приобретение практических навыков при работе с
многомерными дискретными случайными величинами.
Задачами данного практикума являются: расчет параметров двумерного распре-
деления; выработка случайных величин, имеющих полиномиальное распределе-
ние, и вычисление частоты появления различных исходов; вычисление распреде-
ления вероятностей функции многомерной случайной величины.
Необходимый справочный материал
При работе с многомерными дискретными случайными величинами использу-
ются нее позможности. ппелоставляемые Mathcad пои оаботе с одномеоными
Компьютерный практикум № 7. Многомерные дискретные случайные величины в пакете Mathcad
143
дискретными величинами. Напомним их. Во-первых, это функции, вычисляю-
щие вероятности принятия отдельных значений случайной величины с задан-
ным распределением; названия их начинаются с буквы d: dbinom, dgeom, dpois И
др. Во-вторых, функции, вычисляющие значения функций распределения; на-
звания их начинается с буквы р: pbinom, pgeom, ppois и др. В-третьих, функции,
вырабатывающие случайные величины с заданным распределением; названия ИХ
начинаются с буквы г: rbinom, rgeom, rpois. Как говорилось выше и как будет да-
лее проиллюстрировано, этих функций вполне достаточно для работы с много-
мерными дискретными случайными величинами (для вычисления связанных
с ними вероятностей, их выработки и т. п.).
Эффективным приемом прикладной математики и современных языков про-
граммирования является использование рекурсии. Она заключается в том, что в
процессе вычисления значения функции, зависящей от параметра, происходит об-
ращение к этой же функции, но для другого (для определенности, скажем, мень-
шего значения) параметра. При этом значение функции для начального (в на-
шем случае — минимального) значения параметра — известно. Программа
последовательно обращается к функции с все меньшими и меньшими значения-
ми параметра, пока не дойдет до начального значения. Это так называемый
«прямой ход» вычислений. При начальном значении параметра значение функ-
ции известно. Затем реализуется «обратный ход» вычислений — программа по-
следовательно вычисляет все значения функции в обратном порядке, пока не
дойдет до заданного значения параметра.
Mathcad предоставляет возможность использовать рекурсию, что существенно
упрощает программирование ряда задач. Например, факториал fact(n) числа п
может быть эффективно вычислен без использования встроенной функции nl
Для этого достаточно ввести функцию fact(n).= if(n = 0, 1, п * fact(n-l)).
Ниже использование рекурсии позволит нам весьма просто сформировать все
возможные значения многомерной случайной величины, имеющей полиноми-
альное распределение (5.4).
Реализация задания
Для проведения вычислений нам понадобятся различные функции пользователя.
Программные модули, реализующие эти функции, представлены на рис. 5.1-5.3,
Поясним назначение этих функций.
Функции Arise(i, А) и Incl(i, А) уже использовались нами в компьютерном прак-
тикуме № 5. Arise(i, А) определяет, принадлежит (значение 1) или нет (значение
0) число i вектору-столбцу A. Incl(i А) включает число i в вектор столбец А, если
только первого там нет.
MargD(Tw, k) вычисляет частное распределение k-й компоненты (k = 1, 2) дву-
мерной дискретной случайной величины, распределение которой задано матри-
цей Tw. Возможные значения первой компоненты содержатся в нулевом столб-
це, а второй компоненты — в нулевой строке этой матрицы. На пересечении
ненулевых строки и столбца матрицы Tw стоят вероятности принятия соответ-
ствующих значений. Результат выдается в виде матрицы, содержащей два столб-
ца: в нулевом столбце содержатся возможные значения k-й компоненты, а в пер-
вом столбце — соответствующие вероятности.
144
5. Многомерные дискретные случайные величины
Практикум N« 7. Многомерные дискретные случайные величины
Пользовательские (Ьуншии
Проверка наступления события А
Включение i в вектор A
Arlee(I.A).-
f«-0
for JeO.. rewt(A) - 1
f<-f+lf(I.A),1,O)
9 <- lf(f > 0,1,0)
9
B<-A tf Arlae(I.A)
otherwiae
k ♦- rowa(A)
for J eO.k-1
Bjt-A)
Вц<-1
В
Частное распределение k-й компоненты
двумерной с.в., имеющей распределение Tw
Математическое ожидание k-й компоненты
двумерной с.в., имеющей распределение Tw
MargD(Tw.k)
A<-Tw If k>1
A«-TvJ otherwiae
н <- rows(A)
m <- colt(A)
for I e 1. л - 1
A*,o
m-1
B|,1 *-	**.)
1-1
MergE(Tw.k) *
А<- MargD(Tw.k)
m <- rowa(A)
m-1
**“22 **’0 A*’1
I - 1
Д
Коеериация даумерней с.6., имеющей
распределение Tw
Дисперсия к- й компоненты двумерной с.е.,
имеющей распределение Tw
Cov(Tw) -
п <- rowa(Tw)	MarQV(Tw,k)
m <- cols(Tw)
д1 *- MargEfTw.l)
д2 «- MargE(Tw,1)
Cov«- £ £ (Tw|<0-Ml) (Twoj-m2) Twjj
1-1 )-1
A<- MargD(Tw.k)
m «-* rowa(A)
д «- MargE(Tw.k)
m-1
v«- x (**.«-*) **.i
I -1
V
Cov
Коэффициент корреляции двумерной с.в.,
имеющей распределение Tw
CorrfFw)
<d *- VMargV(Tw.l)
o2 7MargV(Tw,2)
Corr «-
Cov(Tw)
el o2
Рис. 5.1. Пользовательские функции, обеспечивающие работу
с двумерными распределениями
MargE(Tw, k) и MargV(Tw, k) вычисляют математическое ожидание и дисперсию
k-й компоненты двумерной дискретной случайной величины, распределение ко-
торой задано матрицей Tw.
Cot?(Tw) и Coz7*(Tw) находят ковариацию и коэффициент корреляции для дву-
мерной дискретной случайной величины с распределением вероятностей, опи-
сываемым матрицей Tw.
Две следующие функции обеспечивают генерирование случайных величин,
имеющих полиномиальное распределение (5.4). RandPol(n, р) вырабатывает одну
случайную величину, имеющую полиномиальное распределение с параметрами
п и р. Входным параметром функции являются число испытаний п и век-
i'OD-столбец d веооятностей оазличных исходов в одном испытании. Если число
Компьютерный практикум № 7. Многомерные дискретные случайные величины в пакете Mathcad
148
различных исходов равно т, то размерность вектора р составляет т + 1. На 1-М
месте в векторе р стоит вероятность i-го исхода рь г = 1,2, ..., т. Нулевая компо*
нента р0 вектора р не используется. Программа, реализующая функцию, основы*
вается на теореме 5.2 и использует алгоритм генерирования многомерных ДИС-
кретных случайных величин, приведенный в конце раздела 5.1. В программе
используется встроенная функция гЫпот{1, п,р), вырабатывающая одну случай-
ную величину, имеющую биномиальное распределение (3.3) с параметрами пир.
FrPol(n, р), получая от функции RandPol реализации случайной величины, имею-
щей полиномиальное распределение (5.4), вычисляет для нее частоты (доли)
различных исходов Х(/п, Х2/п, ..., Хт/п.
Генерация случайной величины, имеющей поли*
номиальное распределение с параметрами л, р
Частоты различных исходов для с.е., имеющей
полиномиальное распределение с параметрами л, р
RandPol(n.p) :
m <- row»(p) - 1
J*-1
Aq*-D
while j < m
1-1
N<-n- £ A*
l-O
( У1
P^PI 1-£ n
( 1-0 J
Aj«- lf(N «0.0,rblnom(1,N.P)o)
Fr₽ol(n,p) >
A<- RandPol (n.p)
fer ieO. rowe(p) - 1
Вероятность принятия значения I m-мерней с.в.,
ниеющей полнномнальнее распределение с
параметрами л, р
rows(p)-l	.
PolPr(n,p, I):- nl- pl (₽i)j J]
1-1	1
m-1
Am*- n- £ Aj
I - 1
Возможные значения m-мерного вектора, имеющего
полиномиальное распределение с параметром л
Pres(n,m) .<•
Bl.o<-0
в 1.1 ”
otherwise
v<-0
for k « O n
A«- Pres(n - k.m - 1)
s ♦- rowe(A) - 1
for te 1.. 3
for г e 1m - 1
Bv+t,r«- At j
Bv+t.m k
Рис. 5.2. Пользовательские функции, обеспечивающие работу
с полиномиальным распределением
Оставшиеся три функции предназначены для нахождения распределения веро-
ятностей функции \|/ m-мерной случайной величины (Xt, Х2..Х„), имеющей по-
линомиальное распределение (5.4). В качестве функции \|/ взята линейная функ-
ция \|/(i, а) = ifa, + г2а2 + ... + 1„ат. Входом в функцию \|/(i, а) являются (т + 1 ^мер-
ные вектора i и а, нулевые компоненты которых г0 и а0 не используются.
146
5. Многомерные дискретные случайные величины
Pres(n, т) выдает все возможные значения m-мерной случайной величины,
имеющей полиномиальное распределение (5.4) с параметром п. Каждое такое
возможное значение, согласно (5.4), — это m-мерный вектор, компоненты кото-
рого принимают значения 0, 1, ..., п, причем сумма всех компонент равна п. Эти
векторы располагаются в строках матрицы, выдаваемой программой. Нулевые
строка и столбец матрицы не используются. Следовательно, фактическое число
столбцов матрицы равно т + 1. При п = 1, т = 1 функция выдает (без учета нуле-
вых строки и столбца) скаляр п. Далее эффективно используется рекурсия. Если
т> 1, то перебираются все возможные значения k последней m-й Компоненты от
О до п. При фиксированном k на оставшиеся т - 1 компонент приходится п - k
испытаний. Обращение к функции Pres(n-k, т-1) дает все возможные значения
для первых т - 1 компонент. Добавляя к этим векторам в качестве последней
т-й компоненты зафиксированное ранее значение k последней компоненты, мы
получаем m-мерный вектор, как возможное значений m-мерной полиномиальной
случайной величины.
PolPr(n, р, г) рассчитывает вероятность принятия значения i = (0, it, i2, .... im)
m-мерной случайной величиной, имеющей полиномиальное распределение (5.4)
с параметрами п и р = (0, ръ р2, ..., р„). Компоненты векторов i и р с нулевыми
номерами не используются.
rows(a)-1
Заданная функции * (х):	* (I, а)£ ар ij
i- 1
Возможные значения функции t	Распределение вероятностей функции р многомерной
многомерной случайной величины	случайной величины
ОошРоДд, о) - m <- rows(a) - 1
YPoiD(n,p,a)
8 <- Pres(o, m)
*><- ♦[(вТ)<1’.а]
s<~ rowt(B) -1
for i e 1. s
A *-1пс|[р[(вТ) .a],Aj
A
Dorn <- DomPol(n.a)
k<- rows(Dom) - 1
for J « 0 . k
Apo <- Domj
Арк-0
m rowt(a) - 1
8 Pree(n, m)
s<- rows(B) - 1
for JeO k
for lets
И ♦[(вт)<1>.а].A|,o
x <— Ро1Рг[п.р.(вТ )(<
Рис. 5.3. Пользовательские функции, обеспечивающие вычисление распределения функции
многомерной случайной величины
DomPol(n, а) формирует множество возможных значений функции у многомер-
ной случайной величины, возможные значения которой выдаются функцией
Pres(n, т). Она может работать с любой предварительно описанной функцией у
и матрицей, выдаваемой функцией Pres, однако они должны быть согласованы.
В нашем случае размерность вектора а должна быть т + 1, функция у и матрица
Pres были описаны выше.
Компьютерный практикум № 7. Многомерные дискретные случайные величины в пакете Mathcad
147
Наконец, функция YPolDfn, р, а) вычисляет распределение вероятностей функ-
ции \|/ многомерной случайной величины, имеющей полиномиальное распреде-
ление (5.4) с параметрами п и р. Возможные значения многомерной случайной
величины она берет из матрицы, сформированной функцией DomPol, а соответст-
вующие вероятности рассчитываются с помощью функции PolD. Алгоритм рабо-
ты PolD вполне аналогичен алгоритму для функции, рассмотренной в компью-
терном практикуме № 5.
Результаты вычислений
Полученные результаты приведены на рис. 5.4.
Вначале рассматривается двумерное распределение, которое было определено
выше в табл. 5.1, а при вычислениях вводится как матрица Tw. Для него вычис-
ляются частные распределения Marg£)(Tw, 1) первой и A/argD(Tw, 2) второй
компонент, а также их математические ожидания A/azg£(Tw, 1) = 0.25 и
MargE(Tw, 2) = 1.4 и дисперсии MargV(Tw, 1) = 0.688 и Afa;gV(Tw, 2) = 3.84 соот-
ветственно. Затем вычисляются ковариация Cov(Tw) = -0.3 и коэффициент кор-
реляции Corr(Tw) = -0.185.
Результаты еычисланнй
^Распределения двуиериай случайней величины
Распределение вероятностей двунериой случайной ееличииы	Честные распределения коиненент двуиерией случайией веничины
	,	.	<0 8
0-2	1	2	5 '	0	0
	-2 8.15
-1 045 0.10 040 0.10	-1 025
Tw:- 0 0.00 0.15 0.10 0Л0	MbtoD(Tw,1)-	MargD(Tw.2)- 1 845 ° °-25	7 ПИ
1 0.10 020 0.15 045,	L и^э 1 04	ж ж в
	1,5 8.15
Мэтеиетическио ожмдаиля и дисперсии коилеиент диуаерней случайней величины
MargE(Tw.l) - 025 MargE(Tw,2) -1.4 MargV(Tw.l) - 0488
Ковариация и коэффициент корреляции двуиерией случайной величины
Cov(Tw) - -02	Corr(Tw) - -0.185
MaroV(Tw,2) • 344
2. Фуикции аиогоаерней случайией
Вектор, эадаилдий значеиия паранетров (р,)
поиинеииальиого распределенил
р:-(0 0.4 0.3 0.2 0.1 )Т
величины
Вектвр. еписываиндий лиивйиую функцию
*(Х. а)
а:-(0 1 2 3 S)T
Частоты резличиых исхадае при генерации п случайных величин с распределениеи (5.4)
FrP«l(1000,p)T -(0 0.419 0.209 0-201 0.091) FrPlI(10000.р)Т - (0 0.404 0.301 0203 0ЯП)
Ввзножиые знеченил фуикции р(Х, а) ннегонериой случайней величины
DemPe1(3,a)T - |У Ест	! Al
Респрвдеяаиие вероятностей функции р(Х,а)
ТРеГО(3,р.а)Т
г owe (DomPol (3 ,а))-1
Проверка распределения ввролтинстей ио иернироеку:	52	УРоЮ(3, р. я)и - 1
1'0
Рио. 6.4. Результаты вычислений многомерных дискоетных оаспоедалений
148
5. Многомерные дискретные случайные величины
Далее реализуются функции RandPol(n, р) и FrPol(n, р) выработки случайных ве-
личин, имеющих полиномиальное распределение (5.4). Вначале вводится вектор
р = (0, 0.4, 0.3, 0.2, 0.1), задающий значения параметров {/>,-} этого распределения.
Затем вычисляются частоты FrPolln, р) появления различных исходов при числе
испытаний, равном п = 1000 и п = 10 000. Значения частот для более полного
перечня числа испытаний п приведены в табл. 5.3.
В заключение выполняются расчеты для примера 5.4, в котором рассматривает-
ся распределение линейной функции у(Х, а) случайной величины X, имеющей
полиномиальное распределение с параметрами п = 3 и р. Вначале вводится век-
тор а = (0, 1, 2, 3, 5), описывающий линейную функцию. Обращение к функции
Pres(3, 4) дает все возможные значения четырехмерной случайной величины X,
а к функции YPolDlp, а) — распределение вероятностей функции у(Х, а). В за-
ключение проверяется, что последнее распределение удовлетворяет условию
нормировки для вероятностей.
Задания для самостоятельной работы
Используя компьютерные функции MargD, MargE, MargV, Cov и Corr, найдите
маргинальные распределения, математические ожидания, дисперсии, ковариа-
цию и коэффициент корреляции для случайных величин, совместное распреде-
ление которых задано табл. 5.6.
Таблица 5.6. Распределение вероятностей {р,у} двумерной случайной величины
	х<2> = 0	х<2> = 1	х<2> = 4	х<1 2) 3 4=6	х<2> = 7
х<” =-2	0.02	0.07	0.03	0.03	0.05
= -1	0.10	0.05	0.03	0.17	0
х<'> = 1	0.20	0.02	0.08	0.05	0.10
1. Экспериментально, на базе данных табл. 5.6, проверьте правильность теоре-
мы 5.1. и формулы (5.11).
2. Проанализируйте логику работы компьютерных функций DomPol и YPolD.
3. По аналогии с компьютерными функциями DomPol и YPol составьте компью-
терную функцию, которая бы для заданной матрицы Tw, определяющей распре-
деление вероятностей двумерной дискретной случайной величины X = (Хь Х2),
и функции v(ri, х2) вычисляет распределение вероятностей этой функции,
а также ее математическое ожидание и дисперсию. Проверьте правильность
работы функции для распределения из табл. 5.6 и функции \|/(*i, х2) = X] + х2.
4. Рассмотрите функцию y(i, а) = ц  г2 • *з • Ц и случайную величину X - (Хь Х2,
Х2, Хл), имеющую полиномиальное распределение (5.4) с параметрами п = 8,
р\ - 0.2, р2 - 0.1, рл = 0.4, рь = 0.3. Используя компьютерные функции DomPol и
YpolD, вычислите распределение вероятностей этой функции.
Задачи
140
5. Составьте компьютерную функцию, реализующую формулы (5.8) и (5.9) ДЛЯ
вычисления условных распределений многомерной дискретной случайной
величины.
Задачи
Задача 5.1. Случайные величины Хъ Х2, Х3, и Х4 попарно независимы, причем
D(Xi) = a2 Vi. Найдите коэффициент корреляции a) Xt + Х2 и Х2 + Xtf
б) Хг + Х2 + Х3 и Х2 + Х3 + Х4.
Задача 5.2. В условиях примера 2.2 найдите математическое ожидание и диспер*
сию числа различных элементов выборки.
Задача 5.3. В условиях задачи 2.8 найдите математическое ожидание и диспер-
сию числа различных выпавших граней.
Задача 5.4. В условиях задачи 2.10 найдите математическое ожидание и диспер-
сию числа свободных ящиков.
Задача 5.5. В условиях задачи 2.10 найдите математическое ожидание и диспер-
сию числа шаров в данном ящике.
Задача 5.6. В условиях задачи 2.33 найдите математическое ожидание числа ис-
пользованных шаров X.
Задача 5.7. В условиях задачи 2.4 найдите математическое ожидание и диспер-
сию числа попыток X, необходимого для нахождения нужного ключа. Решить за-
дачу прямым методом и с использованием индикаторов.
Задача 5.8. В условиях задачи 2.24 найдите математическое ожидание и диспер-
сию числа различных элементов подмножеств At и А2.
Задача 5.9. В условиях задачи 2.24 найдите коэффициент корреляции числа эле-
ментов подмножеств А} и А2.
Задача 5.10. В условиях задачи 2.25 найдите математическое ожидание числа
спичек X, остающихся во второй коробке.
Задача 5.11. Пусть в условиях задачи 2.35 игрок, выигрывающий при i-й
попытке, г = 1,5, получает от партнера 6-г рублей. Найдите математическое ожи-
дание и дисперсию выигрыша первого и второго игроков.
Задача 5.12. Найдите коэффициент корреляции для чисел :-го X, и j-го Xj исхо-
дов в полиномиальной схеме, описываемой формулой (5.4).
Задача 5.13. В полиномиальной схеме (5.4) найдите: а) математическое ожида-
ние и дисперсию числа не появившихся исходов; б) математическое ожидание
числа исходов, появившихся г раз.
Задача 5.14. Из урны, содержащей щ красных и п - nt белых шаров, последова-
тельно извлекаются все шары. Пусть X, — число шаров, извлеченных до появле-
ния r-го красного шара, i = 1, и,, ХЛ| +1 — число шаров, остающихся в урне после
извлечения последнего красного шара. Найдите математическое ожидание Х(,
i -- I, И| + I.
150
5. Многомерные дискретные случайные величины
Задача 5.15. Видоизмените соответствующим образом формулу (5.31) и (5.32)
если вместо (5.30) имеет место представление
У = с1/1 + с212 + ... + ст1т,
где {с,} — постоянные, {/,} — индикаторы событий {Д}.
Задача 5.16. Из множества чисел {1, 2, ..., 30} случайно выбирается 3 различных
числа. Используя результаты предыдущей задачи, найдите математическое ожи-
дание и дисперсию их суммы.
Задача 5.17. Задача о совпадениях. Имеются две одинаковые колоды карт, со-
стоящие каждая из и различных карт. Карты в колодах располагаются случай-
ным образом, после чего сравнивается расположение карт в колодах. Если ка-
кая-либо карта занимает одно и то же место в двух колодах, то говорят о
совпадении. Найдите математическое ожидание и дисперсию числа совпадений
X.
Задача 5.18. В условиях примера 2.5 предположим, что процесс голосования осу-
ществляется по шагам, причем на каждом шаге подается голос за одного из кан-
дидатов. Найдите математическое ожидание и дисперсию числа шагов, в течение
которых: а) первый кандидат был впереди, б) первый кандидат не отставал от
конкурента.
Задача 5.19. В условиях примеров 2.8-2.10 найдите математическое ожидание
и дисперсию числа возвращений частицы в начало координат за время 2и.
Задача 5.20. Пусть Xit Х2,... — некоррелированные случайные величины с одина-
ковыми дисперсиями о2. Рассмотрим две суммы S' и S”, первая из которых со-
держит п таких величин, а вторая — т, причем i величин у них общие, например,
5'= Xj + Х2 + ...+ Х„, S"= X„_j+) + Х„_,+2 + ... + Покажите, что ковариация
С(5', 5") = io2, а коэффициент корреляциир = i/Фп-т. Если п = т, тор = i/n, то
есть коэффициент корреляции равен доле общих слагаемых. Статистики интер-
претируют это следующим образом: коэффициент корреляции равен доле общих
факторов в совокупном числе равновеликих факторов. В частности, если i = п = т,
то коэффициент корреляции равен 1. Если обе суммы содержат одни и те же
слагаемые, но с разными знаками, то коэффициент корреляции равен -1.
Задача 5.21. Пусть X и Y — независимые случайные величины, имеющие одина-
ковые математическое ожидание и дисперсию. Рассмотрите случайную величи-
ну Z, принимающую значение X с вероятностью р, и значение Y с вероятностью
1 - р. Покажите, что коэффициент корреляции между X и Z равен р.
6 Многомерные непрерывные
случайные величины
6.1.	Распределения многомерных
непрерывных случайных величин
В предыдущей главе многомерная случайная величина X = (X, ,Х2,...,Хп)была
определена как вектор, все компоненты которого — случайные величины. Ранее
рассматривался случай, когда эти величины — дискретные. Теперь будет рас-
смотрен случай непрерывных величин. Фактически будет повторен материал,
изложенный выше для многомерных дискретных случайных величин, с коррек-
тировками для непрерывного случая. Эти корректировки сводятся, в основном,
к замене сумм интегралами, а вероятностей отдельных значений — плотностями
распределения. Как и в одномерном случае, плотность распределения является
основным элементом задания непрерывной случайной величины.
Определение 1. Многомерной плотностью распределения называется веществен-
нозначная функция вещественных аргументов, удовлетворяющая условиям не-
отрицательности: /(х(, х2, .... хп) > О, V х(, х2, .... х„ е (-оо, оо), интегрируемости
и нормировки:
J j	*2....xn)dxidx2...dxn =1.	(6.1)
-«-«I	-00
Определение 2. Говорят о многомерной непрерывной случайной величине
X = (Х(, Х2,.... Х„), если задана ее плотность распределения/(х(, х2 х„), с помо-
щью которой определяется вероятность попадания X в любой многомерный ве-
щественный интервал (ab Z>i) х (а2, />2) х ... х (а„, />„), V а, < Ь;.
Р{а, <Х1 <(>!, а2 <Х2 <Ь2, ...,а„ <Хп <Ь„} =
Ь '-2	(6.2)
= J J ... jf(x1,x2,...,x„')dxidx2...dxn.
О| а2 ап
Как и в одномерном случае, вероятность принятия многомерной случайной ве-
личиной X некоторого значения (х(, х2, ..., х„) равна нулю, поэтому вероятность
(6.2) не зависит от того, включены или нет границы в интервалы. Физический
смысл многомерной плотности распределения определяется соотношением
152
6. Многомерные непрерывные случайные величины
Р{х, <Xt <	+ Дх,, х2 < Х2 < х2 + Ах2,..., хп <Хп < х„ + Ах„} =
= /(х, ,х2..х„)Ах,Ах2...	Ах„ + 0(Ах, -Ах2 - ...-ДХд),
то есть плотность /(х„ х2,	х„) в точке (х,, х2,	х„), умноженная на произведе-
ние бесконечно малых приращений Ах,Ах2 ... Дх„, приблизительно равна веро-
ятности попадания случайной величины X в многомерный интервал
(х,, X! + Дх,) х (х2, х2 + Дх2) х ... х(х„, х„ + Дх„).
Определение 3. Функцией распределения F(x<, х2, ..., х„) многомерной случайной
величины X = (X,, Х2, ..., Х„) называется функция п вещественных аргументов,
равная в точке (х,, х2, ..., х„) вероятности того, что каждая компонента Х; не пре-
взойдет соответствующего значения аргумента х,:
F(x,,x2, ...,х„) = Р{Х, <х,,Х2 <х2,...,Х„ <х„}.	(6.3)
Функция распределения выражается через плотность распределения по формуле:
F(x,,х2, ...,х„) = J j ... |7(г/1-г/2.y„}dyxdy2 ...dyn.	(6.4)
В многомерном случае функция распределения не используется так часто, как в
одномерном случае, что объясняется трудностью работы с многомерными инте-
гралами.
Как получить одномерное распределение отдельной компоненты Х;, зная много-
мерное распределение всего вектора X = (X,, Х2,..., Х„)? В дискретном случае пе-
реход от многомерного к одномерному распределению осуществлялся с помо-
щью операции суммирования, в непрерывном случае — осуществляется с
помощью операции интегрирования.
Определение 4. Частная (маргинальная) плотность распределения fx(x{) ком-
поненты X; находится путем интегрирования f (х,, х2, ..., х„) в бесконечных пре-
делах по всем аргументам за исключением х,. В частности, для компоненты X,
Л, (*i )=/••• \f(xi,x2,...,x„)dx2...dxn, -оо<х, <со. (6.5)
Аналогично определяются двумерные плотности. Например, для двумерной не-
прерывной случайной величины (X,, Х2) ее двумерная плотность распределения
/х„х2(*1>*2) = J... J/(x„x2, ...,xn)dx3...dx„.	(6.6)
Наиболее известной является двумерная нормальная плотность:
/	х2 V
2 х, -р, х2 -р2 + х2 -р2
СТ, Ст2 I СТ2 J
-со < X, ,х2 < СО,
(6.7)
где ц,, ц2, ст,, ст2 и р — параметры распределения, причем ст,, ст2 > 0, -1 < р < 1.
6.1. Распределения многомерных непрерывных случайных величин
iea
Пример 6.1. Частные плотности двумерного нормального распределения.
Найдем частную плотность распределения компоненты X, двумерного нормаль-
ного распределения (6.7). Согласно формуле (6.5) имеем, используя замену пе-
ременной интегрирования z = (х2 -ц2 )/о2, dz = dx2/о2:
00	00	1
Л, (*1 ) = J/Ol Ж = J ---------------------г=у ехр-
-ос	-оо 2л о । о 2 -у 1 р
. (( \2
1 *i -Hi 1
2(1-р2\1 п, J
ехр-
(	с \2 / л2
-----1---- (1-Р2 )|	| +| pfLZhL
2(1-р2)|<	I Ci J	I	a, J
о х < ц <	2 I J 1
-2р—------z + z \\dz=----= ехр-
<J|	J Ojv2n
1
2(1-р2)
(1-р2) £1_Е1
1
—...7-^- ехР
Oj У2п
ехр-
В последнем выражении под интегралом стоит плотность нормального распреде-
ления с параметрами ц = р(х1 -щ )/oj и о = ^l-p2. Поскольку эта плотность
удовлетворяет условию нормировки, данный интеграл равен единице. Итак,
A, (*1 ) =
1
Oj V2n
ехр-
2 | xi р1
2 у CFj
Эта формула показывает, что частное распределение компоненты Х( является
нормальным с параметрами ц = ц j и о = Oj. Аналогичное утверждение справед-
ливо для компоненты Х2, параметры нормального распределения которой ц  ц а
и а = п2. Таким образом установлен физический смысл четырех из пяти пара-
метров двумерного нормального распределения (6.7): ц, является математиче-
ским ожиданием, а о, -- средним квадратическим отклонением компоненты X/,
^1,2.	□
Простым методом получения двумерных распределений является следующий.
Предполагается, чю для данной случайной величины А'| с известной плотностью
154
6. Многомерные непрерывные случайные величины
/й(х() некоторый параметр 6 сам является непрерывной случайной величиной
Х2 с плотностью g(x2). Тогда (Xt, Х2) имеет двумерную плотность
Л„Х2 Ol. Х2 ) = СХ1 )g(*2)-	(6-8)
Этот метод называется рандомизацией параметров распределений. Очевидно, та-
ким способом можно рандомизировать не один, а несколько параметров, получая
тем самым многомерные случайные величины.
Пример 6.2. Пусть Х| является экспоненциально распределенной случайной ве-
личиной с параметром 1 = Х2, имеющим экспоненциальное распределение с па-
раметром ц. Тогда двумерная случайная величина (Хи Х2) имеет следующую
плотность распределения:
Л1.х2(^1>^2) = х2е'12Г'не‘ЙХ2-	хрх2>0.	(6.9)
Определение 5. Непрерывные случайные величины Хь Х2, ..., Х„ называются по-
парно независимыми, если для любых двух случайных величин X, и Xj и всех воз-
можных значений .г, и Xj их совместная плотность распределения в точке (х„ х;)
равна произведению частных плотностей:
fxt.x1(xi<x2) = fXt(xi)fXi(x2), -<*><Xt,X2 <оо.	(6.10)
Определение 6. Непрерывные случайные величины Xit Х2,..., Х„ называются вза-
имно независимыми или независимыми в совокупности, если для любого подмно-
жества Xj, Xs.... Xt этих величин их совместная плотность распределения
fx. х х< равна произведению частных плотностей:
fxj.x,, ...X, (Хр Xs.xt) = fxj (Xj) fxSxs) •••fxl (Xt)-
Ясно, что из взаимной независимости следует попарная независимость случай-
ных величин.
Тривиальным способом получения многомерных случайных величин является
использование в качестве их компонент взаимно независимых случайных вели-
чин. Согласно последнему определению и формуле (6.11) плотность многомер-
ного распределения будет представлять собой произведение одномерных плот-
ностей отдельных компонент.
Примеры
Пример 6.3. Многомерное равномерное распределение и геометрические вероятно-
сти. Пусть Х1( Х2,..., Хп — взаимно независимые случайные величины, имеющие
равномерное распределение, параметры которого а, и 6, для компоненты X,. Мно-
гомерная случайная величина X = (Хь Х2,..., Х„) имеет многомерное равномерное
распределение с параметрами а = (аь а2,..., ап) и b = (Ь{, Ь2,..., Ь„) и плотностью
1
f(Xi,X2’
-<xn) = \(.bl -а^...{Ьп -а„)
О,
при a, <Xj < bit z = 1,2,
в противном случае.
,п,
(6-12)
Рассмотрим двумерную случайную величину X = (Хь Х2), равномерно распреде-
ленную в единичном положительном квадранте плоскости (at = а2 = 0, b{ = b2 = 1).
Пусть А — некоторая область этого квадранта, имеющая площадь SA. Очевидно,
вероятность попадания двумерной случайной величины X в эту область
6.1. Распределения многомерных непрерывных случайных величин
18В
Р{ХеЛ) = JJ 1 dx,dx2 =SA,
(.Г| ,д*2)еЛ
где мы использовали то, что определенный интеграл равен соответствующей
площади.
Итак, искомая вероятность равна площади области, попаданием в которую
мы интересуемся. Мы называли так задаваемые вероятности геометрическими
(см. раздел 2.1). Следовательно, они возникают для равномерных распределе-
ний. Очевидно, если рассматривать не двумерный случай, а трехмерный, то речь
будет идти не о площади, а об объеме и т. д.
Пример 6.4. Многомерное стандартное нормальное распределение. Пусть Z\, Z2...
Z„ — взаимно независимые случайные величины, имеющие стандартное нор-
мальное распределение с плотностью (4.13). Многомерная случайная величина
Z = (Zb Z2.... Z„) имеет многомерное стандартное нормальное распределение
с плотностью
f(Zi,z2...z„) =fj<p(z,.) = (2л) 2 exp -1 Jz,2 =(2л) 2 exp ~-zzT , (6.13)
i=l	k & i=l )	\ J
где z = (zb z2,.... z„).
Далее будет показано, как с помощью линейного преобразования вектора Z мож-
но получить многомерную нормально распределенную случайную величину с
произвольными значениями параметров.	□
Определение 7. Пусть (Х{, Х2) — двумерная непрерывная случайная величина с
плотностью распределения fXl,x2Cxi>x2), причем частное распределение компо-
ненты Х{ имеет строго положительную плотность в точке х{: fX} (.г,) > 0. Услов-
ная плотность распределения компоненты Х2 при условии, что компонента Х\
приняла значение хь определяется формулой
fx2CX2 = Xi) =	'	, ----- ~«><Х2 <0°.	(6.14)
Л, (*1 )
С тем чтобы отличать f(x) от условной плотности, часто ее называют безусловной
плотностью распределения.
В случае независимости Хг и Х2 условные плотности совпадают с безусловными,
как видно из определения независимости (6.10):
=*i) =Л2(*2)- A, (*il*2 = х2> =fx, Ai)- (6.15)
Условные плотности распределения обладают всеми свойствами обычных, без-
условных, плотностей распределений. Для них по известным формулам для од-
номерных непрерывных распределений могут быть подсчитаны условные мате-
матическое ожидание, моменты и дисперсия, если только в соответствующих
выражениях заменить безусловные плотности на условные:
Е(Х21-Х) = *1) =	=xi)dx2,	(6.16)
-00
E(X2\Xt *, )= Jx2/(x2|Xt =xt)dx2,	(6.17)
156
6. Многомерные непрерывные случайные величины
D{X2\X, = х,) = J(x2 -£(Х2|Х,^х,))1 2/^*, =х1)г&2,	(6.18)
при этом для существования соответствующих числовых характеристик должно
выполняться условие абсолютной сходимости интегралов (4.22).
Пример 6.5. Условные распределения для двумерного нормального распределения
(6.7). Найдем условную плотность распределения компоненты Х2, вычисленную
при условии, что компонента Х{ приняла значение х(.
Используя определение условной плотности распределения (6.14) и формулу
(6.7) для плотности двумерного нормального распределения, находим:
1	(х2 Нг _ xi Pi
2(1 -Р2К о2 о, )
1
х/2ло2>/1-р2
Последнее выражение представляет собой плотность нормального распределе-
ния (4.11) с параметрами
ц =ц2 +Р — (*1 -Ц1 Л
О = о2 д/1-р2-
Следовательно, условное распределение компоненты Х2, вычисленное при усло-
вии, что компонента Х{ приняла значение х1( является нормальным с указанны-
ми параметрами. Итак, условные математическое ожидание и дисперсия компо-
ненты Х2 определяются формулами
£(Х21^1 =х1) = Иг +Р —(*1 -Ц1),
Р(Х2|Х, = х,) = о2 (1 — р2).
6.2. Функции многомерных непрерывных случайных величин
157
Аналогичные утверждения имеют место для компоненты Хь следует только по-
менять местами индексы 1 и 2.	□
Как и в дискретном случае, безусловное математическое ожидание Е(Х2) компо-
ненты АЛ2 (если оно существует) может быть вычислено с помощью условных ма-
тематических ожиданий Е(Х2| ~xt У
Е(Х2)= |е(Х2|Х1 =х1)Л1(х,)&1.	(6.19)
6.2.	Функции многомерных
непрерывных случайных величин
Определение 8. Пусть \|/(хь х2, хп) — вещественнозначная функция п вещест-
венных аргументов, а (Хь Х2,..., Хп) «-мерная непрерывная случайная величина.
Новая случайная величина Y = v(^i> ^2 Х„) называется функцией многомерной
непрерывной случайной величины. Если имеет место абсолютная сходимость мно-
гомерного интеграла:
СО СО	СО
J J ••• fl V(^i>x2>	)|/(x, ,х2, ...,х„ )dxidx2 ...dxn < со, (6.20)
—00—СО —со
то говорят, что математическое ожидание функции многомерной непрерывной
случайной величины существует. Оно обозначается E(\|/(Xt, Х2, •••> Ап)) и вычис-
ляется по формуле
E(y(X1,X2,...,X„))=f j... fу(Х',х2,...,х„)/(х},х2..х n)dx^dx 2... dx п. (6.21)
-00—30 -СО
Если в качестве функции у рассмотреть сумму y(xi, х2, ..., х„) = х, + х2 + ... + х„
и предположить, что математическое ожидание E(Xj) каждой компоненты Xj су-
ществует, то из (6.21) получим теорему сложения математических ожиданий,
аналогичную (5.20):
Е(Х, +Х2 +... + Х„) = £(Х1) + £(Х2) + ... + Е(Хл). (6.22)
Для дисперсии суммы остаются в силе формулы (5.21), (5.22). При этом кова-
риация C(AZ„ Xj) и второй момент Е(Х, ХД (если они существуют, то есть если
имеет место абсолютная сходимость (6.20)) вычисляются по формулам:
С(Х,,Х7) = Е((Х, -E(Xf ))(Х; -Е(Х;.))) =
(6.23)
= f f(.r, -Е(Х,))(х} -E(Xj))fXiXj (xj,xj)dxldxj,
-co—co
co co
E(X,X7) = f f x,Xj/x.x. (Xj,Xj )dxidxj.	(6.24)
Ковариацию можно также вычислить по формуле (5.16), справедливой как ДЛЯ
дискретных, так и для непрерывных случайных величин. Коэффициент корреля-
ции между случайными величинами А', и Xj вычисляется по формуле (5.19). Для
него остаются справедливыми все свойства, сформулированные для дискретного
случая.
158
6. Многомерные непрерывные случайные величины
Как и в дискретном случае (см. определение 10 главы 5) некоррелирован-
ность случайных величин означает равенство нулю коэффициента корреляции р
(см. (5.19)). Для таких величин дисперсия суммы равна сумме дисперсий слагае-
мых — см. формулу (5.23).
Если Xlt Х2,..., Х„ взаимно независимы, то из (6.11) вытекает теорема умножения
математических ожиданий (5.26).
Примеры
Пример 6.6. Показать, что ковариация случайных величин Xt и Х2, имеющих
двумерное нормальное распределение (6.7), равна ро1о2. Следовательно, их
коэффициент корреляции равен р. Это устанавливает физический смысл послед-
него из пяти параметров двумерного нормального распределения. Кроме того,
важно отметить, что для двумерного нормального распределения понятия некор-
релированности и независимости совпадают: если коэффициент корреляции р
равен нулю, то совместная плотность (6.7) становится произведением двух част-
ных одномерных плотностей для компонент, что и свидетельствует об их незави-
симости.
Решение
Для двумерного нормального распределения (6.7) ковариация (6.23) вычисляет-
ся так:
оо оо
ОД Л2) = J J(Х1 ~щ)(#2 “"Нг)’*^2yd^\d^2 ~
-00-00
00 00
= /[(*> ~Р1)(*2 -Ц2)--------г=техР‘
2ло1о2у1_Р
, (f	\2
1	*1 -Р1
2(1-р2)[1 о. J
2рХ, -|At х2 -ц2
2 Ц 2
°2
 dxt dx2.
О
После замены переменных Z( =(х(	z2 =(х2 -ц2)/о2 получаем:
1
ОДЛ2)= J JZ1z2—-
< <	О" И _„2
exp-j-----—— (z.2
I 2(l-p2)
_	,2 oo	4	f	4
=J-z2e 2 2 f zt.... ....exp]--------— (zf
i V2^/W I 2(l-p2)V
00 1 00
>1CT2 J-S=z2e 2 2 JZ1 -—-=== exp- -
4V2tc Д 72^/1-P
-2pztz2 +z2)\dzidz2 =
-2pziz2 +p2z2) dzidz2 =
(z, — pz2)2 >dzidz2.
2(l-p2)	J
1
Внутренний интеграл представляет собой формулу для вычисления математиче-
ского ожидания нормального распределения с параметрами ц = pz2 и 0=^1 -р2.
Известно, что это математическое ожидание равно параметру ц, то есть pz2. Если
вынести р за знак интеграла, то внешний интеграл будет представлять собой
формулу для вычисления второго момента стандартного нормального распреде-
6.3. Линейные преобразования случайных векторов’
169
ления. Этот момент равен единице, так что искомая ковариация действительно
равна ptTjCTj.
Пример 6.7. Функции минимума и максимума. Важное практическое и теоретиче*
ское значение имеют функции минимума y„)in = min^, Х2, .... Х„} и максимума
У|пах = тах{Х1( Х2, ..., Хп} независимых случайных величин Xit Х2, .... Хп. Пусть
Fj(x) есть функция распределения случайной величины Х(. Покажем, что функ-
ции распределения случайных величин Утах и Ут,п даются формулами
Л„ах(*) = Ж,ах <X}=F1(X)F2(X)...F„(X),	(6.25)
£min(x) = P{yniin ^x}=l-(l-F1(x))(l-F2(x))...(l-Fn(x)).	(6.26)
Доказательство
Имеет место следующее очевидное представление события {Утах < .г}:
{У1Пах <х} ={тах{Х1,Х2..Хп} <х} = {Xt <х,Х2 <х,...,Х„ £х}. (6.27)
События Xt <х, Х2 < х..Хп < х взаимно независимы, так что вероятность их
произведения равна произведению вероятностей Р{Х( <х }=F1(x),P{X2 Sx)-
= F2(x), .... Р{Х„ < ,r} = F„(.r), что и доказывает формулу (6.25).
Эти же рассуждения применимы для представления события {УП1(П > х}:
{ymin > х} = {Х_ > х, Х2 > х.Х„> х}.	(6.28)
В силу взаимной независимости событий опять имеем
Р{Ут!п >х} =Р{Х, >х}Р{Х2 >х}...Р{Х„ >х} = (1-F1(x))(l-F2(x))...(l-F,(x)).
Переходя к противоположному событию {У,|Ип < .г}, получаем формулу (6.26).
Пример 6.8. Последовательное и параллельное соединение элементов в систему.
Эти соединения рассматривались уже ранее в разделе 1.5. Формулы (1.31) и (1.32)
выражают вероятность безотказной работы системы R как функцию вероятно-
стей безотказной работы ее элементов {р,}. Теперь мы можем конкретизировать
выражения для этих вероятностей. Если F,(.r) — функция распределения време-
ни безотказной работы г-го элемента, a F(x) — функция распределения времени
работы всей системы, то соответствующие зависимости даются формулой (6.25)
для параллельной системы и формулой (6.26) — для последовательной системы.
В частности, если все элементы идентичны и имеют экспоненциально распреде-
ленное время безотказной работы с параметром X, то время безотказной работы
последовательной системы из п элементов имеет экспоненциальное распределе-
ние с параметром rik:
F(x) = P{Ym.m>x}=e-nk\ х >0.	(6.29)
6.3.	Линейные преобразования случайных векторов*
Наиболее часто используемыми функциями многомерных случайных величин
являются линейные функции. Такие функции называются линейными преобра-
зованиями. Для их анализа применяется математический аппарат линейной ал-
гебры. который мы и будем использовать. Согласно принятой в линейной алгеб-
ре терминологии многомерную случайную величину X = (Х„ Х2.Хп) называют
160
6. Многомерные непрерывные случайные величины
случайным вектором. Будем понимать его как вектор-строку. Переход к векто-
ру-столбцу Хт осуществляется с помощью операции транспонирования т.
Ряд математических операций над векторами (умножение на константу, сложе-
ние и вычитание векторов) осуществляется покомпонентно: если с константа,
X = (Хь Х2..Х„) и Y = (Ур У2..Yn) ~ Два вектора одинаковой размерности, то
сХ = (сХ„ сХ2... сХ„), X + Y = (X, + У„ Х2 + У2, ..., Х„ + У„), X - Y = (Х( - У„
Х2 - У2,..., Х„ - Уя). Эти операции распространяются с векторов на матрицы. Как
и вектора, матрицы будут обозначаться заглавными полужирными латинскими
буквами. Если матрица М имеет k строк и п столбцов, то она будет записывать-
ся в виде М = (щ,;7)^хЯ, где — (i, ;)-й элемент матрицы, стоящий на пересече-
нии i-й строки и j-m столбца. 7-й столбец матрицы М обозначается М<7>, то есть
М*'* = (Mjj,m2j mkj )т. Транспонированной к матрице М = (Щ;,у)ья называется
матрица Мт = (/пт,-,^)яхл > строки которой являются столбцами матрицы М, и на-
оборот: тит, у = mj j. Квадратная матрица М называется симметрической, если она
совпадает со своей транспонированной матрицей: М = Мт.
Определение 9. Математическим ожиданием Е(М) матрицы М называется мат-
рица, получаемая из М заменой каждого элемента Мц (понимаемого здесь как
случайная величина) на его математическое ожидание Е(М^):
Е(М) = (Е(М,.;))Ы1.	(6.30)
В частности, математическое ожидание случайного вектора X = (Xt, Х2, ..., Х„)
есть вектор Е(Х), состоящий из математических ожиданий его компонент:
Е(Х) = (ВД), £(Х2),..., Е(Х„)).	(6.31)
Последнее определение позволяет выразить ковариационную матрицу С(Х) век-
тора X (см. определение 8 и формулу (5.18) главы 5) в матричной форме. Для
этого напомним правила умножения двух матриц. Матрицу М можно умножить
(справа) на матрицу L = (/,,), если число ее столбцов равно числу строк матри-
цы L. (г,у)-й элемент rj; произведения R = ML определяется по «правилу умно-
жения строки на столбец»: он равен сумме произведений соответствующих эле-
ментов г-й строки матрицы М и ;-го столбца матрицы L:
Произведение R = М L будет содержать число строк, равное числу строк матри-
цы М и число столбцов, равное числу столбцов матрицы L. В частности, произ-
ведение вектора-строки а = (аь а2, ..., ап) на вектор-столбец Ьт = (Ь\, Ь2, Ь„)Т
дает константу at bt + а2 b2 + ... + а„ Ьп. Обратный порядок умножения (столбца
ат на строку Ь) дает квадратную матрицу, (i, ))-й элемент которой равен а, Ь-.
	'“А а2Ьх	ах Ь2 а2Ь2	ахЬ2 . а263	 «А-i •• Д2^-1	aib„ а1Ьп	
aTb = (а( bj )лхя =	а3Ьх	а3^2	а363	 «:А-1	а3Ьп	(6.32)
	«П-1	а„.гЬ2	«„-А •	йп-А-1	ап-1Ь„	
	,a„bi	а„Ь2	«Л .	•• anbn.l	а„Ьп ,	
6.3. Линейные преобразования случайных векторов’
161
Итак, пусть X = (Хь Х2, .... Х„) — случайный вектор, математическое ожидание
которого обозначим р = (р (, р   р „), где р,. = E(Xt), а ковариационную МВТ’
рицуС(Х) = (С(Х,,Х,))йхя.
Лемма 6.1. Имеет место формула
С(Х) = £((Х-р)т(Х-р)).	(6.33)
Доказательство
Напомним (см. (5.18)), что (г,у)-м элементом ковариационной матрицы С(Х) яв-
ляется ковариация г-й и у-й компонент вектора X. Последнее же, согласно опре-
делению ковариации (5.16) и (6.23), есть E((Xt - р,- )(Х; - р; )). Но это (с учетом
формул (6.30) и (6.32)) как раз и есть (:,у)-й элемент матрицы, представленной
правой частью формулы (6.33).	О
Напомним, что симметрическая матрица М порядка п называется неотрицатель-
но определенной, если для любого n-мерного вектора х = (хь х2,.... хк) квадратич-
ная форма хМхт неотрицательна: хМхт > 0. М положительно определена, если
для любого ненулевого вектора х эта форма строго положительна: хМхт > 0.
Лемма 6.2. Ковариационная матрица С является неотрицательно определенной.
Если матрица С невырождена, то она положительно определена.
Доказательство
В доказательстве первой части леммы используется то, что х(Х - р)т и (X - р)тх
являются одним и тем же скаляром, так что их произведение — это квадрат этого
скаляра. Напомним также, что транспонирование произведения матриц (или
векторов) дает произведение транспонированных матриц, взятых в обратном по-
рядке: (ML)T = LT Мт. Согласно определению ковариационной матрицы (6.33)
и сформулированных ниже свойств математического ожидания (6.35), имеем;
хСхт = хЕ((Х-р)т(Х-р))хт - Е(х(Х-р)т(Х-р)хт) =
= £(х(Х- р)т(х(Х- р)т )т ) = Е
>0.
Вторая часть леммы будет следовать из леммы 6.3.	D
Теперь мы рассмотрим линейное преобразование вектора X = (Хр Х2....X*).
Определение 10. Пусть М = (лг, 7)*х„ — матрица kxn, а = (аь а2,.... а„) — п-мерный
вектор, компонентами которых являются константы. Линейным преобразованием
случайного вектора X = (X!, Х2..X*) называется случайный вектор
У = а+ХМ.	(6.34)
Следующая теорема выражает математическое ожидание и ковариационную
матрицу линейного преобразования Y через математическое ожидание и кова-
риационную матрицу исходного вектора X.
Теорема 6.1. Если р = Е(Х) — математическое ожидание, С(Х) — ковариацион-
ная матрица случайного вектора X, то математическое ожидание £(Y) и ковариа-
ционная матрица C(Y) линейного преобразования (6.34) вычисляются по фор-
мулам
£( Y)  £(а + ХМ) = а + рМ,	(6.35)
162
6. Многомерные непрерывные случайные величины
C(Y) = C(a + XM)=MTC(X)M,	(6.36)
где Мт означает матрицу, транспонированную к М.
Доказательство
i-ая компонента вектора Y линейного преобразования (6.34) У, = at + ^Xvmvi.
V
Беря математическое ожидание и используя свойства (3.25) и (4.24) математиче-
ского ожидания, получаем
ОД) = а, + ^Е(Х„)т^ =а,+
V	V
Это отличается от исходного выражения для У; только тем, что вместо Xj здесь
присутствует р . Следовательно, в векторной записи (6.34) для E(Y) вместо X
должно присутствовать ц. Это и дает формулу (6.35).
Для доказательства формулы (6.36) найдем выражение для ковариации компо-
нент У, =а, + ХХд,( и У, = dj + YX№m№j-
V	w
Cov^.Yj) = £((У; -ОД))(У> -ОД;))) =
= £«,+£ x»m».t - а, - Е И vmv.i °; + Е Xwmw,j	wmw,j =
\ \	v	V J\ w	w	J)
=е ЕХ.Л -иЛЕс**-цг,)(А'а, -pw))mwj =
\ V	w	J v w
= E E Cov(Xv, Xw) mwj.
Итак,
Соу(УрУу )=ZZ^,iCov(X„Xw)?na, . =
VW	VW
где m\v означает (г, г)-й элемент транспонированной матрицы Мт.
Последнее выражение в точности совпадает с (i, j)-m элементом матрицы, стоя-
щей в правой части формулы (6.36).	□
Отметим, что теорема обобщает ранее доказанные свойства математического
ожидания и дисперсии (3.25)-(3.27), (4.24), (4.31), которые являются частным
случаем теоремы при п = 1.
Определение 11. Говорят, что случайный вектор X = (Хь Х2,..., Хп) имеет невыро-
жденное распределение, если его ковариационная матрица С является невырож-
денной, то есть имеет обратную матрицу, которую мы обозначим С"1.
Определение 12. Верхней (нижней) треугольной матрицей называется квадрат-
ная матрица, все элементы которой, расположенные ниже (выше) главной диаго-
нали, равны рулю. Если С — ковариационная матрица, то квадратным корнем
Холесского из нее называется нижняя треугольная матрица С1/2, такая, что
С = С1/2 (С1/2)т.
Следующая лемма имеет большое значение при анализе и моделировании мно-
гомерных случайных величин.
6.3. Линейные преобразования случайных векторов*
1М
Лемма 6.3. Квадратный корень Холесского С1/2 существует и единственен ДЛЯ
любой ковариационной матрицы С. Если ковариационная матрица С невыроЖ'
дена, то невырожден и квадратный корень Холесского, а С — положительно оя-
ределенная матрица. Матрица, обратная к С1/2, обозначается С"1/2. Кроме ТОГО,
(СТГ1/2 = (С-,/2 )т.
Доказательство
Ограничимся доказательством для случая невырожденной матрицы С.
Будем доказывать лемму индукцией по размерности матрицы п. При п = 1 мат-
рица вырождается в неотрицательный скаляр, являющийся дисперсией единст-
венной компоненты. Квадратный корень из этого скаляра будет одновременно и
верхней и нижней треугольной матрицей. Следовательно, при п = 1 лемма верна.
Как будет показано в примере 6.7, она верна также для п = 2.
Пусть лемма верна для п и докажем ее справедливость для п = п + 1. Если С. яв-
ляется невырожденной ковариационной матрицей порядка п + 1, то ее можно
представить в виде:
где С# — невырожденная ковариационная матрица порядка п, соответствующая
п первым компонентам,
с и ст — вектор-строка и вектор-столбец, получающийся транспонированием с,
Ся+|, „+1 — последний диагональный элемент матрицы С.
11о предположению индукции, матрицу С# можно представить в виде произведе-
ния невырожденных нижней С1/2 и верхней (С1/2 )т треугольных матриц, так что
С =
СУ2(С‘/2)Т с
В силу невырожденности матрицы С1/2 она имеет обратную (С1/2)"1, и мы мо-
жем определить матрицу
(6.37)
где d = с ((С1/2 )т )"' и а = д/Сп+1 n+1 - ddT, 0т — «-мерный вектор-столбец из ну-
лей.
Легко проверить, что матрица С представляется в виде: С =С|/2(С|/2 )т, то есть
указанное в лемме представление имеет место и для п + 1.
Покажем теперь, что если матрица С невырождена, то такова же и С1/2, а диаго-
нальные элементы матрицы С1/2 строго положительны.
Если матрица С невырождена, то ее определитель | С| больше нуля: | С| >0. Опре-
делитель произведения матриц равен произведению их определителей:
|С|-|С|/2||(С|/2)т|. Определители нижней С /2 и верхней (С|/2)т треугольных
матриц равны произведению их диагональных элементов. Следовательио, все
164
6.. Многомерные непрерывные случайные величины
эти диагональные элементы — ненулевые. Итак, С,/2 - невырожденная матрица,
то есть ее строки — линейно независимые векторы. Следовательно, для любого
ненулевого вектора х хС1/2 = у = (у{, у2, ...,г/„ ) # 0. Отсюда следует, что
хСхт = хС1/2(С,/2 )тхт = хС1/2(хС1/2 )т =уут = £г/2 >0.
Итак, С — положительно определенная матрица.	'	□
В приведенном доказательстве фактически содержится алгоритм вычисления
матрицы Холесского С1/2. Алгоритм предусматривает последовательное вычис-
ление этой матрицы для все увеличивающейся размерности: вначале для п = 1,
потом для п = 2 и т. д. При этом переход от размерности п к размерности п + 1
осуществляется по формуле (6.37). Обычно можно получить матрицу Холесско-
го путем использования соответствующих компьютерных программ. В пакете
Mathcad таковой является программа cholesky.
Определение 13. Случайный вектор Z = (Zb Z2...Z„) называется нормирован-
ным, если его компоненты некоррелированы и имеют нулевое математическое
ожидание и единичную дисперсию: £(Z) = 0, C(Z) = I, где 0 — вектор с нулевыми
компонентами, I — единичная матрица.
В частности, вектор Z, имеющий стандартное нормальное распределение (6.13),
является нормированным.
Лемма 6.4. Пусть X — случайный вектор, имеющий невырожденное распределе-
ние с математическим ожиданием ц и ковариационной матрицей С. Тогда ли-
нейное преобразование Y = (X - р)(С",/2)т представляет собой нормированный
случайный вектор.
Доказательство
Используя свойства математического ожидания (6.35), доказываем, что £(Y) = 0:
£’(Y) = £’((X-p)(C",/2)T) = (£(X)-p)(C',/2)T =(ц-ц)(С-,/2)т =0.
Равенство ковариационной матрицы единичной матрице I вытекает из выраже-
ния (6.36) для ковариационной матрицы линейного преобразования:
C(Y) = С((Х-ц)(С",/2 )т ) = С*1/2С(Х)(С-'/2 )т =
= С-1/2С(С-,/2)т =С-1/2С,/г(С,/2)т(С-,/2)т =1(С-,/2С'/2)т =1.	□
Примеры
Пример 6.9. Двумерное распределение. Для этого распределения имеем следую-
щую ковариационную матрицу:
Z 2
°1	Р°1°2
2
\Р °t ° 2	° 2
Найдем разложение Холесского С =С1/2(С1/2 )т для этой матрицы. Представим
нижнюю треугольную матрицу С,/2 в виде:
£t/2 =(Х О')
U У)
с =
(6.38)
гид г. и. 2 — поллежашие опоеделению неизвестные.
6.3. Линейные преобразования случайных векторов*
1вв
Эти неизвестные находятся из матричного уравнения С =С1/2(С*/2 )т, которое
в развернутой форме имеет вид:
(	2
Р CTtCT2
<Р СТ1 ст2
X 0И.Г Z
2 У) 1° У
Данное матричное уравнение запишем в виде системы скалярных уравнений:
2	2
X = СТ, ,
гх=рст,ст2,
2	2	2
У 4-Z2 = СТ2.
Решением этой системы является: х = стр у = ст2~р2 > 2 =РСТ2- Итак, квадрат*
ный корень Холесского для матрицы С дается выражением
С1/2
' СТ, 0	'
чра2 ст2-у/1-р2 >
(6.39)
Согласно последней лемме случайный вектор Y = (Х-ц)(С“1/2 )т является нор-
мированным, то есть имеет нулевое матожидание и единичную ковариационную
матрицу. Обратная матрица С-1/2 имеет вид
С'1/2	1 c^Vi-P2 0
СТ, СТ2Л/1 -р2 1-Р<?2	СТ1>
Пример 6.10. Симметричное многомерное распределение. Таковым будем назы-
вать распределение, у которого дисперсии всех компонент Х\, Х2.Хп одинако-
вы и равны ст2, а коэффициент корреляции любых двух разных компонент Х( К Xj
равен р. Ковариационная матрица в этом случае имеет вид:
	'ст2	рст2	рст2 ...	рст2	рст2	рст2>
	рст2	ст2	рст2 ...	рст2	рст2	рст2
	рст2	рст2	ст2	рст2	рст2	рст2
с =	рст2	рст2	рст2 ...	ст2	рст2	рст2
	рст2	рст2	рст2 ...	рст2	ст2	рст2
	крст2	рст2	рст2 ...	рст2	рст2	°2)
Найдем для нее матрицу Холесского С1/2.
Решение
Мы покажем, что в качестве С,/2 выступает нижняя треугольная матрица, у ко-
торой элементы каждого столбца, расположенные ниже диагонали, одинаковы.
Иными словами, матрица вида:
166
6. Многомерные непрерывные случайные величины
с1/2 =	ооо	;	о	о	-q' ооо	:	о	i	i CN	CN	CN ООО	;	i	i	i ’	-5t -5t _ CO	*	CO	CO	CO °	°	:	*51	C	*51 —-s	CN	CN	‘	CM	CM	CM °	.	-S2	-S2	-S2 -sf	:	-sf	-sf
Наша задача — определить значения с.(2 элементов матрицы С1/2 из уравнения
С=С1/2(С,/2 )т.
При этом следует иметь в виду, что элемент с„; матрицы С получается в резуль-
тате скалярного произведения г-й строки матрицы С1/2 на j-й столбец матрицы
(С1/2)т. Поскольку (С1/2)т — матрица, транспонированная к С1/2, то ее столбцы
совпадают со строками С1/2> так что с;j — скалярное произведение i-й и j-й строк
матрицы С1/2.
Для первого элемента с)Л матрицы С имеем выражение
См = <%
Поскольку с, j = ст2, находим, что = ст.
Для любого другого элемента Сц = рст2 первого столбца С имеем выражение
рст2 = dl(c'/2)il.
Следовательно, (с1/2 ),д =рст. Итак, ht = рст.
Теперь предположим, что постулируемая форма матрицы С1/2 верна для строк и
столбцов, номера которых не превышают i, i > 1 Покажем, что тогда она будет
верна и для i + 1. Из этого будет следовать, что она верна для любых i. Для диа-
гонального элемента ci t = ст2 матрицы С имеем соотношение
ст2 = h2 + Л22 + ... + Л2., + d2,
откуда сразу получаем
di = -^ст2 -Л2 -Л2 -...-/г2.,, i = 2, 3.п.
Для любого элемента cjt = рст2 (i < j) i-ro столбца матрицы С, находящегося ниже
диагонального элемента с„, имеем соотношение
рст2 = h2 + h2 + ... + Л2., + rfjC*/;2, i = 2,3.п-1,	j = i + l.п.
Отсюда ясно, что с‘/2 =Л, не зависит otj, кроме того,
= -i-(рст2 - h2 -h} -... - Л2., ), i' = 2,3.п -1.
“i
Полученные соотношения можно записать в рекуррентной форме:
J, =-J</2.| -Л2.!, i=2,3,...,n,
6.4. Многомерное нормальное распределение*
18Т
Aj = ^-(</м -A,_j), i = 2, 3,..., п-1.
dt
В частности, для п = 2 мы получаем di = о, ht = per, d2 - стл/1-р2, что совпадает
с результатом предыдущего примера (6.39) при = ст2 = а Эти соотношения
будут реализованы в компьютерных программах, вычисляющих матрицы Холес-
ского для симметричных многомерных распределений.
6.4.	Многомерное нормальное распределение*
Ниже будет дано определение многомерной нормально распределенной случай-
ной величины. В нем мы отступаем от принятого нами порядка задания непре-
рывной случайной величины через ее плотность распределения. Это объясняет-
ся следующими причинами: 1) возможностью решения ряда задач без
использования плотности распределения; 2) трудностями, возникающими при
работе с многомерными плотностями; 3) удобством использования линейных
преобразований, с которыми связана характеризация нормальных распределений;
4) тем, что предлагаемое определение является конструктивным.
Определение 14. Говорят, что случайный вектор X = (Xt, Х2,..., Хп) имеет много-
мерное нормальное распределение, если его можно представить в виде
X = P + ZM,	(6.40)
где ji = (у. J, у. ..ц,) и М = (w,;7)ixn — вектор и матрица из констант,
Z = (Zb Z2,..., Zk) — ^-мерный случайный вектор, имеющий стандартное нормаль-
ное распределение (6.13).
Из нормированное™ вектора Z и формул (6.35), (6.36) сразу следует, что мате-
матическое ожидание Е(Х) и ковариационная матрица С(Х) вектора X опреде-
ляются формулами
£(Х) = ц, С(Х) = МТМ.	(6.41)
Рассмотрим теперь следующую задачу: как подобрать матрицу М линейного
преобразования (6.40) так, чтобы вектор X имел заданную ковариационную мат-
рицу С? Ответ дается матрицей Холесского: из формулы (6.41) следует, ЧТО
М - (С,/2)т.
Лемма 6.5. Пусть случайный вектор Z = (Zb Z2.Zk) имеет нулевое математиче-
ское ожидание и единичную ковариационную матрицу, а С — произвольная ко-
вариационная матрица. Тогда случайный вектор X = ц + Z(C1/2 )т имеет матема-
тическое ожидание ц и ковариационную матрицу С.
Отметим, что эта лемма используется при генерации нормально распределенных
случайных векторов с произвольными ц и С путем преобразования взаимно не-
зависимых скалярных величин, имеющих стандартное нормальное распределе-
ние (4.13).
Определение 15. Пусть ранг матрицы М равен п, то есть числу столбцов М (а для
этого необходимо, чтобы А 2 л), так что матрица МТМ размера пхп является не-
168
6. Многомерные непрерывные случайные величины
вырожденной. Тогда говорят, что X имеет невырожденное нормальное распреде-
ление.
Для невырожденного нормального распределения существует плотность распре-
деления, вид которой устанавливается теоремой 6.2.
Пример 6.11. Двумерное нормальное распределение. Пусть Z = (Zlt Z2) — двумер-
ный случайный вектор, компоненты которого независимы и имеют стандартное
нормальное распределение p = (pt,p2), С1/2 — матрица, задаваемая формулой
(6.39). Рассмотрим линейное преобразование
X=p+Z(C1/2)T =p+Z
рст2
— Р >
Согласно формулам (6.41), вектор X имеет математическое ожидание ц и кова-
риационную матрицу С, задаваемую формулой (6.38). Позже мы покажем, что
плотность распределения X является двумерной нормальной (6.7).	□
Теорема 6.2. Пусть вектор X = (Х{, Х2, ..., Х„) определяется формулой (6.40)
и имеет невырожденное нормальное распределение с математическим ожидани-
ем р и ковариационной матрицей С. Тогда существует плотность распределения
вектора X, задаваемая формулой
/(х) = - . 1 ... ехр J— (х -р)С’*(х -р)т1.	(6.42)
7(2я)"|С| I 2	J
Верно и обратное утверждение: если (6.42) является плотностью распределения
случайного вектора X = (Хь Х2, ..., Х„), то последний может быть представлен в
виде (6.40). Следовательно, для невырожденных распределений между задания-
ми распределений формулами (6.40) и (6.42) имеется взаимно однозначное соот-
ветствие.
Доказательство
Вначале мы рассмотрим случай, когда размерности векторов Z и X из формулы
(6.40) совпадают, то есть когда п = k. Случай п < k будет рассмотрен в следующей
главе.
Приведем некоторые факты из теории интегрирования функций многих перемен-
ных. Пусть имеется многомерный (кратный) интеграл от функции <p(z(, ...,z„) по
области G переменных zlt z2,..., z„:
1	......2n)r/z,...r/z„.
Рассмотрим преобразование х = y(z):
= Vi Oj....z„) = ^(z),
*2 = V2(Z1....z„)	= v2(z),
=Vn(Z!....z„) = v„(z),
означающее переход от переменных z(,...,z„ к новым переменным х{, ...,х„.
6.4. Многомерное нормальное распределение’
iae
Пусть это преобразование — непрерывно дифференцируемое по всем перемен*
ным в области G и взаимно однозначное, то есть существует обратное преобраэо-
вание z = ф-1(х)
z, = ф	= фГ’(х),
z2 =^2(Х1....Х„) = V2*(X),
zn	....х„) = v;'(x).
Обозначим С образ области G для этого преобразования:
С = {х: х = ф(г), z е G}.
Если осуществить замену переменных в интеграле I, то следует пользоваться
формулой
7 = J „. J v(z,.z„) rfz,... rfz„ = J J ф(ф Г‘ (х),.... у(х)) —1— dxt... dx„,
где
U(x)| =
Jz,
яхл
‘v;1 (»>
есть абсолютное значение функционального определителя преобразования (яко*
биана) в точке z = ф 1 (х).
Если <p(z) = q>(z(.z„) — плотность распределения непрерывной случайной ве-
личины Z = (Z ,,..., Z„), то плотность распределения многомерной случайной ве-
личины Х=(Х 1,...,Х„) = (ф 1(Z),...,v„(Z)) = v(Z) будет
Ж.........х„) = ср( у Г’ (х),.... ф;1 (х))—i-r = ф( ф 4 (х))|-^тг.	(6.43)
U(x)l U(x)l
Рассмотрим теперь невырожденное преобразование
х = ф(г) = р + г(С,/2 )т,
Где ц = (ц(, ...,ц„)— n-мерная вектор-сторока, С1/2 — невырожденная симметри*
ческая матрица размера п.
Тогда
Z = ф-1 (х) = (X - Р)(С’,/2 )т,
U(X)| =|c1/2|.
Если Z — многомерная случайная величина с плотностью	то плот-
ность распределения многомерной случайной величины X = ц + ZCt/2T будет
Ж.......х„) = ф((х - р)(С-1/2 )т )-U	<6.44)
I
В частности, если ф(г) есть п-мсрная плотность нормального распределения
(fl. 13), то
170
6. Многомерные непрерывные случайные величины
Ж......хп ) = (2л)-"/2 —ехр/~(х - И)(С-,/2 )тС’1/2(х -р)т| =
|v | I	J
=<2л)'и/2 ГтЫ ехр|4<х - н)(с,/2 <с‘/2 >Т Э’1 (х - и)т1-
|С | I 2	J
Используя матрицу Холесского из Определения 12, так, что С =С1/2(С1/2 )т, по-
лучаем окончательную формулу для многомерного нормального распределения
с математическим ожиданием ц и ковариационной матрицей С:
/(х) = (2л)’и/2 —ехр | ~ (х - р)С* (х - ц)т
|О | I 2	J
Утверждение, обратное доказанному, гласит, что каждой плотности распределе-
ния (6.42) соответствует случайная величина, представимая в виде (6.40). Чтобы
в этом убедиться, достаточно в преобразовании (6.40) взять М =(С1/2)Т. Теоре-
ма доказана.	□
Доказанная теорема имеет фундаментальное значение. Теперь можно говорить о
невырожденных многомерных нормальных случайных величинах без уточнения
способа их задания (6.40) или (6.42). Тем не менее задание с помощью представ-
ления (6.40) является более общим, поскольку охватывает и вырожденные слу-
чайные величины, для которых ковариационная матрица существует, но является
вырожденной, в связи с чем плотности распределения они не имеют. Из теоремы
вытекают утверждения, содержащиеся в следующей теореме.
Теорема 6.3. В условиях теоремы 6.2 имеют место следующие утверждения:
1.	Если i-й диагональный элемент Су ковариационной матрицы С является по-
ложительным, то частное распределение компоненты X, является нормаль-
ным с математическим ожиданием E(Xj) = ц, и дисперсией D(Xi) = су.
2.	Любое подмножество компонент (Xj, Xj, ..., Х„) вектора X имеет многомерное
нормальное распределение с математическим ожиданием (щ , ц,.....Цг>) и к0’
вариационной матрицей, получающейся из ковариационной матрицы С век-
тора X путем оставления только строк и столбцов с номерами i, j, ..., v,
которые соответствуют компонентам Xi, Xj, ..., X,.
3.	Любое линейное преобразование Y = v + XL вектора X имеет многомерное
нормальное распределение с математическим ожиданием E(Y) = v + pL и ко-
вариационной матрицей C(Y) = LT C(X)L.
Доказательство
1.	Рассмотрим i-ю компоненту X, вектора X = (Хь Х2, ..., Хп). Ее можно пред-
ставить в виде линейного преобразования X, = Хе, вектора X, где е; = (0, 0, ...,
0, 1, 0,..., 0)т — «-мерный вектор-столбец, у которого все компоненты, кроме
i-й, равны нулю, а i-я компонента равна единице. Поэтому доказательство
будет следовать из третьего утверждения леммы, согласно которому имеем
нормальное распределение с параметрами
Е(Х,) = Е(Х)е( = £(Х)(0,0,..,0,1,0.0)т =щ,
D(X<) =е?Се( =(0,0.....0,1,0....0)С(0,0....0,1,0 0)т =см.
Компьютерный практикум № 8. Двумерное нормальное распределение
171
2.	Для простоты записи рассмотрим первые т < п компонента X' = (Xi, Х2,Х«)
вектора X = (Xi, Х2,Х„). Их можно представить в виде линейного преобра-
зования X' = XL, где L представляет собой матрицу с п строками и т столбца-
ми. Последние п - т строк этой матрицы состоят из нулей, обозначим О эту
подматрицу размера (п - т)хт. Первые т строк этой матрицы образуют еди-
ничную матрицу порядка т, обозначим ее I. Тогда L представимо в виде
блочной матрицы L = (I От)т. Теперь доказательство опять будет следовать ИЗ
третьего утверждения леммы. Нормальность оговаривается в нем явно, а ма-
тематическое ожидание и ковариационная матрица даются формулами
£(Х') = £(XL) = £(X)L = £(X)(IOT)т = (ВД ).....Е(Хт)) = (И1...ц„),
С(Х') = C(XL) = LTCL = (Ю)С (Ют )т = (Сц )ихга,
где в конце последней строки записана матрица порядка т, составленная ИЗ
первых т строк и столбцов ковариационной матрицы С.
3.	Согласно определения, вектор X может быть представлен в виде линейного
преобразования (6.40), в котором вектор Z составлен из взаимно независи-
мых компонент, имеющих стандартное нормальное распределение, а матрица
М=(С1/2)Т. Через эти же компоненты может быть выражен и вектор Y,
а именно,
Y = v+XL =v + (p+ZC1/2T)L =(v+ pL) + Z(C1/2TL).
Теперь из Определения 14 следует, что такое представление предопределяет
нужное распределение.	□
Теорема 6.4. Устойчивость семейства нормальных распределений.
Пусть X = (Х„ Х2,.... Х„) — n-мерная случайная величина, имеющая Нормальное
распределение с математическим ожиданием р = (р1,...,ря)и ковариационной
матрицей С, а 1 = (1,1, ...,1)— единичный n-мерный вектор-строка. Если 1С1Т >Ц
то сумма компонент Xt + Х2 + ... + Х„ имеет нормальное распределение с матема-
тическим ожиданием р = ц, +... + р„ и дисперсией о2 = 1С1Т.
Доказательство
Сумму компонент вектора X = (Х1т Х2, ..., Х„) можно представить как линейное
преобразование этого вектора Y = Х1т. Согласно предыдущему следствию, У
имеет нормальное распределение с указанными параметрами.	□
Компьютерный практикум № 8.
Двумерное нормальное распределение
Цель и задачи практикума
Целью практикума является приобретение практических навыков при работе
п пакете Mathcad с двумерным нормальным распределением.
Задачами данного практикума являются:
□	построение графиков поверхностей двумерного нормального распределения;
□	расчет вероятностей попадания соответствующей случайной величины в ин-
тервал и круг;
U генерация случайных величин и подсчет частот их попаданий в подынтервалы.
172
6. Многомерные непрерывные случайные величины
Необходимый справочный материал
Многомерные непрерывные случайные величины задаются своими плотностями
распределений, являющимися функциями многих переменных. Вероятности
принятия этими величинами значений из многомерных областей находятся ин-
тегрированием плотности по этим областям. В связи с этим в практикумах № 8
и № 9 нами будет использоваться операция многократного интегрирования, имею-
щаяся в системе Mathcad. В последних версиях пакета, например в Mathcad 2001,
допускается, чтобы пределы интегрирования во внутренних интегралах явля-
лись функциями других переменных интегрирования. Однако данную операцию
многократного интегрирования следует применять осторожно: в ряде случаев
наблюдается неустойчивая работа пакета. Если же все пределы интегрирования
должны быть постоянными, то для избежания проблем следует в качестве по-
дынтегральной функции использовать оператор if.
В предлагаемом практикуме широко используется такая возможность Mathcad,
как трехмерное представление поверхностей и геометрических тел. Для этого
следует ввести команду прикладного меню Insert—Graph (или щелкнуть по кноп-
ке Graph Toolbar на панели инструментов) и выбрать одну из предлагаемых
опций (рис. 6.1). Нами будут использоваться три из имеющихся опций: Surface
Plot, Contour Plot и 3D Bar Plot. Опция Surface Plot предназначена для построения
трехмерной поверхности, которая описывает функцию двух переменных; в на-
шем случае это будет плотность двумерного распределения. В созданных в по-
следние годы версиях пакета достаточно указать имя этой функции в светящем-
ся окне возникающего на экране шаблона. В более ранних версиях, например
Mathcad 6 Plus, необходимо предварительно построить матрицу аппликат. Гра-
фик строится для конечного множества значений переменных функции. Одной
переменной соответствуют строки матрицы, другой — ее столбцы. Сама матрица
содержит соответствующие значения функции.
Опция Contour Plot предназначена для построения контурных графиков, изобра-
жающих линии уровней поверхности в двумерном пространстве. Для построе-
ния трехмерной гистограммы в виде совокупности столбиков применяется оп-
ция 3D Bar Plot.
Рис. 6.1. Окно команды прикладного меню Insert—Graph
Компьютерный практикум № 8. Двумерное нормальное распределение
ITS
Из стандартных встроенных функций Mathcad в данном практикуме будем ИС*
пользовать функцию cholesky(C), выдающую матрицу Холесского для положи*
тельно определенной матрицы С, и функцию топп(п, ц, ст), которая вырабашм*
ет п случайных величин для нормального распределения с параметрами ц и О,
Реализация задания
Для проведения вычислений нам понадобятся дополнительно функции пользовате*
ля. Программные модули, реализующие данные функции, представлены на рис. &2,
Функции имеют следующее назначение.
Практикум Nt 8. Двумерное нормальное распределение
Пользовательски» Ауикммм
Построение матрицы аппликат поверхности плотности раслрадолоимя:	I.-1.. 40 J 140
С| _ .	fl-20 J-20
.8.8.1.1.8
FI,TwoD, j - f.0.0.1.1 .OS
Вероятность попадания а интервал (а. Ь) ж (с, d)
l(a,b,c.d)- j* j* 1(х1,х2,в.0,1,1,0) dx2dx1
Вероятность попадания в круг радиуса г
Г гУЛх?
Р1ГК(г.дТ.д2,»Т,Л.л)»	F(x2.x1.Mt.M2.xt.«2./)dx2dx1
Вероятность попадания как функция радиуса г
PrFhR(p1.p2,o1.o2,p)>
Матрица Халасского
(О <- 8.5 (д1 + д2)
гД <- 0.1 (al + о2)
for 1е0 20
IAojr-fO + l гД
Ai ,| <- PrFlt(Ao j. д1, д2, al, о2 ,р)
А
Генерирование к случайных векторов
ChTwo(e,p) .
Ао,О<-
*0
Ао,1*-0
Ai,0*-*1 р
А
SlmTwo(k.p .о ,р)»
Проверке овладения в (IJ) 4 интервал
yw(x.l.J) . lf[02 (I - 10) Sx» 5 0.2 (1- 10) «02,11(02 (j - 10) S x, 4 0.2 (j - 1(1) »0.2.1,0].o]
Матрица хастог лмадхнх*:	М(к.д.«.^)>
X«- ShnTwo(k. д. о ,р)
for lei.. 20
far Joi 20
tor v . 1. k
Рио. 8.2. функции пользователя, обеспечивающие работу
о двумерным нормальным распределением
174
6. Многомерные непрерывные случайные величины
Функция /(xl, х2, pl, ц2, ст1, ст2, р) — вычисляет плотность двумерного нор-
мального распределения (6.7) с параметрами pj = pl, ц2 = ц2, Oj = ol, ст2 = ей
и р в точке (xl, х2). Для того чтобы построить график поверхности этой плотно-
сти в условиях использования Mathcad 6 Plus, определяются две матрицы ап-
пликат FigTwoNI и FigTwoND. Первая из этих матриц соответствует независи-
мым компонентам, а вторая — зависимым, с коэффициентом корреляции р = 0.9
При работе с более поздними версиями Mathcad для построения графика можно
использовать саму плотность.
Плотность позволяет рассчитать вероятность попадания соответствующей слу-
чайной величины в двумерный интервал (а, fe)x(c, Ь). Эту вероятность для значе-
ний параметров ц! = ц2 = 0, ст1 = о2 = 1, р = 0 вычисляет функция I(a, b, с, d). Если
взять достаточно большой интервал, то можно проверить выполнение условия
нормировки для плотности: интеграл должен равняться единице.
Функция PrFit(r, ц 1, ц2, ст1, ст2, р) вычисляет вероятность попадания двумерной
нормально распределенной случайной величины с параметрами р.1, ц2, ol, ст2, р
в круг радиуса г с центром в начале координат; PrFitR(yA,\i2, ст1,о2,р) вычисляет
указанную вероятность как функцию радиуса г.
Для генерации двумерных нормально распределенных случайных величин ис-
пользуются функции ChTwo и SimTwo. Функция ChTwo(e, р) вычисляет матрицу
Холесского (6.39). Здесь о = (ст( ,ст2 )т является вектором-столбцом с двумя ком-
понентами Oj и ст2. Это же можно осуществить с помощью стандартной функции
cholesky, имеющейся в большинстве версий Mathcad. Функция SimTwofk, ц, а, р)
генерирует k двумерных случайных величин (в виде векторов-столбцов) с плот-
ностью (6.7). Здесь р = (ц1,ц2)т и в = (ст1,ст2)т представляют собой векто-
ры-столбцы.
Функция yes(x, i,j) определяет, попал ли двумерный вектор-столбец х = (х0, xJT
в двумерный интервал
(0.2(г - 10), 0.2(г - 10) + 0.2)х(0.2(/ - 10), 0.2(/ - 10) + 0.2).
Если попал, то функция принимает значение 1, иначе — 0. Функция M(k, ц, а, р)
подсчитывает число попаданий k двумерных случайных величин, выработанных
функцией SimTwo(k, ц, в, р), в вышеуказанные интервалы для i = 1,..., 20, j = 1,..., 20.
Результаты вычислений
На рис. 6.3 и 6.4 представлены результаты решения заданий практикума. Внача-
ле осуществляется проверка выполнения условия нормировки для плотности
двумерного нормального распределения. С этой целью рассчитана вероятность
попадания соответствующей случайной величины с параметрами ц1 = ц2=0,
ст1 = ст2 = 1, р = 0 в двумерный интервал (-4, 4)х(-4, 4). Значение данной вероят-
ности равно единице. Следовательно, условие нормировки выполнено.
Далее представлены два графика поверхности двумерной нормальной плотности
FigTwoNI и FigTwoND для случая независимых и зависимых компонент. Тут же
представлены графики линий уровней для этих плотностей. Для независимых
компонент (р = 0) линии уровня представляют собой окружности, а для зависи-
мых (для коэффициента корреляции р = 0,9) — эллипсы. Обратите внимание на
то, что графики поверхности и линий уровней на рисунках FigTwoD вытянуты
Компьютерный практикум № 8. Двумерное нормальное распределение
178
в разные стороны, в то время как, естественно, они должны иметь одно направ-
ление. Это объясняется тем, что в разные стороны направлена одна из осей гра-
фиков.
Результаты вычиспанмй
Проверка ппетиеств распределеипя на нормировку:
1(-4.4,-4,4) • 1
Графики поверхностей н лннин уровней плотности распределения
Независимые канпоненты (д-0)
FlgTwol
Сильно каррелпреввнные кампононты (д-0.9)
FlgTwol
FlgTwoD
FlgTwoD
Вероятность попадания в крут как функция радиуса г
PrF ltR(O,O,1,1,0)-
PrFhR(0,1,1,4
Рис. 6.3. Результаты вычислений двумерного нормального распределения
Результаты расчета вероятности попадания двумерной случайной величины в
круг радиуса г выполнены для двух вариантов исходных данных и представлены,
соответственно, двумя таблицами.
Последующая часть распечатки иллюстрирует матрицы Холесского и операции
над ними.
В заключение приводятся результаты генерации двумерных нормально распре-
деленных случайных величин в виде матрицы частот попаданий в подынтер-
валы. Далее приведены трехмерные гистограммы выработанных значений ДЛЯ
случая зависимых и независимых компонент. Нетрудно заметить, что эти гисто-
граммы повторяют характер поверхностей соответствующих плотностей.
176
6. Многомерные непрерывные случайные величины
Матрица Холесскоге
(4 ЗА	(0.333 -0.111
С>	С -
^3 9}	^-0.111 0.148 )
(2 О
Che'“IV(Q4l.5 2.»8
Матрица частот попаданий к случайных аектерое в педмнтервалы
Гистограммы частот попаданий к случайных векторов в падинтереалы
Нвэаеисимыв коипаианты (pH))
Сильно коррелированные конпененты (р-0.9)
Рис. 6.4. Генерация двумерных нормально распределенных случайных величин
Компьютерный практикум № 9.
Многомерное нормальное распределение
Цель и задачи практикума
Целью практикума является приобретение практических навыков при работе
в пакете Mathcad с многомерными непрерывными распределениями.
Задачами данного практикума являются:
□	вычисление плотности многомерного нормального распределения;
□	расчет вероятностей попадания соответствующей случайной величины в ин-
тервал;
□	генерация случайных величин и подсчет частот попаданий.
Компьютерный практикум № 9. Многомерное нормальное распределение
177
Реализация задания
В настоящем практикуме определим семь новых функций пользователя. Про-
граммные модули, реализующие данные функции, представлены на рис. 6.5 и 6.6.
Практикум Mt 9. Многомерное нормальное распределение
Одпыряатстьим функции
Плотность респределения
f(х.I*.Q » -	1	»«р[4 1(х - н)Т С’1 (X - р.)!
V(2 ж)го**СС> .|С| L 2
Симметрическое нормальнее распределение
Матрица Холесского
СЬМ(л,а,р) :
Ао.о«-а
for I с 1.. п - 1
А»,о<-о р
И п>2
for id е-2
A.i *- / (A-ij-i)2(А м?
for j е i + 1.. л - 1
Aj J *-- П - Р) « (А»,!)” 1
W 4—О
Ал-1 ,о-1 *- 1/(Ап-2,n-z) _ (An—1 ,n-z)
А
Вероятность события Х< < Х2 < Х3
Prln(p.,a,p) :
,|i,ChM(3,tx,p) (ChM(3,a,p))T
dx3dx2 dxl
<4 ’’xl 'х2
Генерирование k случайных векторов
SlmM(k,|k,a,p) >
m 4- rowt(p)
C ♦— ChM(m ,a, p)
2*- morm(m-k.OJ)
for Id., k
for j e 0.. m - 1
YJ <- Zjm l-J-D
X
Рис. 6.5. Функции пользователя, обеспечивающие работу
с многомерным нормальным распределением
Функции имеют следующее назначение.
Функция f(x, ц, С) вычисляет значения плотности многомерного нормального
распределения (6.42).
ChM(n, а, р) определяет матрицу Холесского размера я для симметрического
нормального распределения при значениях параметров о и р. Отметим, что ату
Ж* матрицу можно получить также путем использования стандартной функции
еАЫмАу(С). Однако при этом необходимо предварительно сформировать кова-
риационную матрицу С в соответствии с примером 6.10.
178
6. Многомерные непрерывные случайные величины
Подсчет частоты события Хо<Х<<Х2 о к исиытаииях
Проверка иаступлеиия события
УмМ(х): H(xq£ xi.tffxt * Х2,1,0),0)
Подсчот частоты наступления события
FrFhM(k, Иго, р)
m <- rows(p)
Х«- SimM(k,p,o ,р)
S<-0
for i« 1.. к
S«-St Yeiulx*)
Частота как функция числа испытаний к
FrFftKM(p.D.p) -
m <- rowa(p)
for l«1 20
к «-150
AO,!*"*
FrFitM(k.p.0,p)
A
Рис. 6.6. Генерация многомерных нормально распределенных случайных величин
Рг1п(ц, ст, р) вычисляет вероятность события {Х( < Х2 < Х3}, если компоненты
имеют симметрическое нормальное распределение с параметрами о и р и век-
тором-столбцом математических ожиданий ц (напомним, что в пакете Mathcad
векторы представляются столбцами, в то время как у нас в тексте — строками).
SimM(k, ц, ст, р) генерирует k случайных векторов-столбцов, имеющих симметри-
ческое нормальное распределение с параметрами ц, о, р, где р — вектор-столбец
математических ожиданий компонент.
УехМ(х) определяет выполнение неравенства х0 < х{ < х2 для вектора-столбца
х = (х0, Xj, х2)т. Подсчет частоты наступления события (Xt < Х2 < Х3) для случай-
ных величин X = (Хь Х2, Х3), выработанных с помощью функции SimM(k, ц, о, р),
осуществляется функцией FrFitM(k, ц, о, р). Функция FrFitKMiyx ст, р) вычисляет
значения этой частоты при k испытаниях, k = 50г, i = 1, 2,..., 20.
Результаты вычислений
На рис. 6.7 показаны результаты решения задач, выполненные для случая трех-
мерного нормального распределения. Вначале вводится ковариационная матри-
ца С. Далее рассчитывается значение плотности распределения (6.42) с нулевым
математическим ожиданием ц = 0 и единичной ковариационной матрицей в точ-
ке х = (0, 1, 0.5)т. Затем рассчитывается вероятность попадания случайной вели-
чины с этим распределением в трехмерный интервал (-4, 4)х(-4, 4)х(-4, 4). Ра-
венство единице этой вероятности свидетельствует о выполнении условия
нормировки для плотности.
Следующие шаги заключаются в вычислении матрицы Холесского размерности
п = 3 для ст = 1 и р = 0.5 и расчета вероятности наступления события {Xj < Х2 < Х2}
для случаев независимых (р = 0) компонент. Эту вероятность можно сравнить
с частотой события для случайных величин, вырабатываемых функцией SimM(k,
ц, а, р). Зависимость частоты от числа k выработанных случайных величин пред-
ставлена в последней таблице.
Компьютерный практикум № 9. Многомерное нормальное распределение
178
Результаты вычислений
Ковариационная матрица трехмерного
нормального распределения
Значение плотности распределения
' 1 02 0.4'
С - 02 1 0.5
.0.4 0.5 1 t
Вероятность попадания в интервал 0,5) х (-5,5) х (-5,5)
Матрица Холосского
СИ >СЬМ(3.1,0.5)
'10	0
СН- 0.5 0.866	0
0.5 0289 0.016
Вероятность события Xq < Х< < Хг
Частота как функция числа испытаний к
	в	♦	tW	£	»•	ПГ^	«	7		1
	0	50	100	150	200	250	300	350	400	450
й	0	0.16	0.13	0.173	0.165	0.184	0.143	0.166	0.15	0.167
	0		м- •		"’4 -	-S		
%	0	50	100	150	200	250	JOU	350
	0	0	0.02	0.02	0015	0 012	зээю-э	357-10*
Рис. 6.7. Результаты работы с многомерными нормальными распределениями
Задания для самостоятельной работы
1.	Проанализируйте влияние на форму поверхности плотности двумерного нор-
мального распределения (6.7) параметров рг. <*1, <*2 и р.
2.	Запрограммируйте функцию (наподобие функции Prlri), вычисляющую веро-
ятность события {Хг < XJ для случайной величины X = (Xi, Х{), имеющей
двумерное нормальное распределение (6.7).
3.	Запрограммируйте функцию, вычисляющую плотность двумерного равно-
мерного распределения (6.12), и постройте график ее поверхности.
4.	Запрограммируйте функции распределения (6.25) и (6.26) минимума и мак-
симума независимых и одинаково распределенных случайных величин.
5.	Запрограммируйте функцию (наподобие функции PrFit), вычисляющую веро-
ятность попадания трехмерной случайной величины, имеющей симметрич-
ное нормальное распределение, в шар радиуса г с центром в точке (во, at, aj),
в. Разработайте программу, реализующую функцию (наподобие SimTwo и М),
которая осуществляет генерацию трехмерных случайных величин, имеющих
180
6. Многомерные непрерывные случайные величины
симметричное нормальное распределение, и подсчитывает частоты попада-
ний в различные трехмерные интервалы.
Задачи
Задача 6.1. Найдите маргинальные плотности для распределения (6.9).
Задача 6.2. Следуя формуле (6.8), рассмотрите двумерную плотность
1
/(х1,х2) =----х1е‘д,'2,х2 >0,а<Х! < Ь.
Ь-а
Найдите Е(ХГ Х2).
Задача 6.3. В предыдущем примере найдите частные плотности распределения.
Задача 6.4. Пусть X = (Хь Х2,..., Хт) является многомерной целочисленной слу-
чайной величиной с распределением вероятностей
P{X1=i1,X2=i2....X„=im} =/>,,.<2 im, Vij =0,1...
a У,, Y2,..., Ym — взаимно независимые непрерывные случайные величины, не за-
висящие также от X, с плотностями распределений gH| (у), gn2(y), ,gnm(y), за-
висящими от целочисленных параметров nlt п2,..., пт. Тогда
/(^1. г2..гт) =	..(2; )	<6-45)
Vi;	j-l
будет многомерной плотностью распределения.
В частности, Yj может быть суммой nj взаимно независимых непрерывных случай-
ных величин. Рассмотрите случай, когда X имеет полиномиальное распределе-
ние (5.4), а Уь У2,..., Ym — распределение Эрланга (4.18) с параметрами щ, п2.пт
и одним и тем же параметром X. Найдите маргинальные распределения компо-
нент, их математическое ожидание и дисперсию, а также ковариации.
Задача 6.5. Решите предыдущую задачу в предположении, что случайные вели-
чины {1у} имеют нормальное распределение (4.11) с различными параметрами
И Ор
Задача 6.6. Покажите, что запись в скалярной форме плотности двумерного нор-
мального распределения (6.42) приводит к формуле (6.7).
Задача 6.7. Распределение Дирихле. Плотность этого распределения задается
формулой
/(*i...хп) =	(1 -*!-•••-*„ )*"+' ’’.
(kt -1)!...(£п+1 -1)!
Vxf >0, £х; < 1.
1=1
Используя индукцию по п и формулу
fхк' -* (1 -х)*2’1 dx =	~1)!,	(6.46)
о	(^1 + ^2 “1)1
покажите, что приведенное выражение удовлетворяет условию нормировки.
Задачи
181
Задача 6.8. В условиях предыдущей задачи покажите, что частная плотность рас-
пределения компоненты имеет вид
fx (х{ )= —~! д-*1 '*(1 -х, )^+"+*"1 , 0 < х, < 1. (6.47)
Это соответствует бета-распределению (7.30), которое будет рассмотрено далее в
задаче 7.4.
Математическое ожидание и дисперсия компоненты X,- даются формулами
ЗД)=,	, k‘——,
kl+k2+... + k„+l
D(x ) =_________Щ+&2+... + fe„t,-fe,)
{kx + k2 + ... + k„^)2(ki +k2 + ... + kn+i +1)’
Ковариация компонент X,- и X; определяется формулой
ktk.
Cov(X,,X ) =-------------------.
(kt +k2+... + kn+l) (^ +k2+... + kn+l +1)
7 Суммирование случайных
величин и предельные
теоремы
7.1.	Суммирование дискретных случайных величин
В настоящей главе изучаются распределения сумм случайных величин. Опера-
ция суммирования — это частный случай функций многомерных случайных ве-
личин, рассматривавшихся в предыдущих главах: \р(А'), Х2,..., Хп) = Х{ + Х2 + ... + Хп.
Поэтому распределение суммы можно находить с помощью общих подходов,
изложенных в этих главах для нахождения распределения функций. Однако
мы выделяем эту проблему в самостоятельную главу как в силу распростра-
ненности операции суммирования, так и в силу простоты относящихся к этому
результатов. Эта простота отчасти объясняется тем, что сумма обладает свойст-
вом ассоциативности — суммирование нескольких слагаемых можно свести к
последовательному сложению двух слагаемых: + Х2 + Х3 + ... + X„_i + Хп =
= ((((Xi + Х2) + Х3) + - + Х„_1) + Хп). В связи с этим часто достаточно ограни-
читься рассмотрением суммирования двух случайных величин.
Итак, пусть Х{, Х2, ..., Х„ —_случайные величины, сумму которых обозначим 5„,
а среднее арифметическое Хп:
Sn=Xi+X2+... + Xn,	(7.1)
Xn=~Sn.	(7.2)
п
Мы начнем с многомерных дискретных случайных величин. Пусть X = (Хь Х2) —
двумерная дискретная случайная величина. Обозначим и V2 множества воз-
можных значений компонент Х} и Х2, а их совместное распределение вероятно-
стей Pjj = P{Xi = х,, Х2 = Xj}, Xj e Ц, Xj e V2. Пусть V+ есть множество возможных
значений суммы Х{ + Х2:
К = {У-У = xi +Xj,Xj е Ц,Xj е V2}.	(7.3)
Отсюда сразу следует, что распределение вероятностей суммы дается формулой
P{Xi+X2=y} = '^p<Xi=xi,X2=xj)=	(JA)
7.1. Суммирование дискретных случайных величин
1М
где запись £ означает суммирование по всем парам значений (х„ х}), в сумме
дающих у.
Если величины Х{ и Х2 взаимно независимы и имеют распределения вероятно*
стей {р‘} и {рJ} соответственно, то
P{Xt =xir Х2 =Xj} = p]p].	(7.5)
Теперь формула (7.4) приобретает следующий вид для вероятности суммы двух
независимых слагаемых:
Р{Х,+Х2=у} = =xt}P{X2 = Xj} = XPiPr <7-в)
х;+хj -у	х,+хj =у
Формулы приобретают еще более простой вид для целочисленных независимых
случайных величин {Л)}, возможными значениями которых являются целые чис-
ла г = 0, ±1, ±2, ... Обозначим = P{Xj = i} распределение вероятностей слу-
чайной величины Х2. Найдем распределение р," =P{Sn - i}, i = 0, ±1, ±2.суммы
п первых слагаемых S„. Это распределение можно вычислить рекуррентно.
Теорема 7.1. Распределения сумм целочисленных независимых случайных вели-
чин находятся по рекуррентным формулам:
d	00
Р-2 =Р{52 = i} = p*Jv, i = О, ±1, ±2,...,	(7.7)
J	00
Р-"" =P{S„+i = 1} = Ы"Р--Г , * = О, ±1. ±2,...	(7.8)
Если все случайные величины неотрицательны, то последние формулы прини-
мают вид:
Р-г =P{S2 = i} = ±р*> p*_l, i = 0, 1, 2,...,	(7.9)
v=0
Р?"" =P{Sn+l = 1} = tpsv"p*r , i = о, 1, 2,...	(7.10)
v=0
Доказательство
Событие {5п+! = i} состоит из несовместных событий {5„ = О, Х„+, = i), {S„  1,
X„,i = i - 1}, {S„ = 2, Хп+! = г - 2}, ..., {S„ = i, Xn+l - 0}, общий вид которых {5„ = о,
X„4i = i - о}, v = 0, 1,..., г. События {5„ = ц} и {Х„+1 = i - v} по условию независимы,
так что вероятность их произведения равна произведению вероятностей этих со-
бытий:
P{S„ = v, Х,+1 = i-о} = P{S„ =v} • P{Xn+l = i-v} = p*' • pft-.
В силу несовместности событий {S„ = v, X„+1 = i - v} для v = 0, 1.i вероятность
их суммы равна сумме вероятностей, что и дает формулу (7.8). Формула (7.7)
следует из этой формулы поскольку 5! = X,, так что P,s' = Р*'. Формулы (7.9)
и (7.10) следуют из формул (7.7) и (7.8), поскольку отрицательные значения
случайных величин и их сумм невозможны.	□
Определение 1. Пусть {Ре} есть семейство (множество) распределений вероятно-
стей случайных величин, зависящих от параметра 0. Если при суммировании не-
7. Суммирование случайных величин и предельные теоремы
184 учайных величин, имеющих распределения из {Ре}, сумма имеет
-------- t из этого же семейства, то {Рв} называется устойчивым семейством
зависимы ,ределения и отмеченного выше свойства ассоциативности сумми-
распред /ет, что для доказательства того, что рассматриваемое семейство
распрео Г1- является устойчивым, достаточно показать это для двух слагае-
Из данного,, что их СуМма ИМеет распределение из этого семейства,
рования сл
распредели
мых, а им«
Устойчивость семейства распределений Пуассона. Сумма S„ =
п мепь- + %п независимых случайных величин, имеющих распределения
ПР „раметрами Х2,..., Х„, имеет распределение Пуассона с параметром
Пример J + равным сумме параметров для слагаемых:
pf” =P[S„ = i} = Д ^е-\ i = О, 1, 2,...
Пуассон?
к = М + ’
ю
:ь выше, достаточно рассмотреть случай двух слагаемых 52 = X, + Х2,
ат распределения Пуассона с параметрами X, и Х2. На основании
ДоказаТ) имеем;
Какотй	.
который =Р{52 = 1} =	р** =
(JlOpMyJ	V-0
(Xi +х2> и
!(/-»)!
(7.11)
1—JCfe’’'2 =
ISH (i-ц)!
= Де’<Х1+Кг)(Х1 +X2)(, i = 0, 1, 2,
>алась формула бинома Ньютона (2.5).
стойчивость семейства биномиальных распределений с фиксирован-
м параметра р. Пусть Хь Х2..X* — взаимно независимые случай-
где и'а> имеющие биномиальное распределение (3.3) с одним и тем же
ПриМраметра р и, быть может, разными значениями параметра п: щ, п2,
ным ственно. Тогда их сумма Sk имеет биномиальное распределение с
ные р и п = пх + п2 + ... + пк:
знач
...,п	Р{54=1-} = С>’(1-р)я-,1 = 0, 1,2,...,п.	(7.12)
пар;
во
:мое утверждение можно доказать без всяких вычислений путем
ассуждений. Случайную величину Х„ имеющую биномиальное рас-
Д01 параметрами р и и„ можно трактовать как число успехов в nt испы-
Р&/лли с вероятностью успеха в одном испытании р. Если имеется k
СЛн с одним и тем же параметром р и параметрами щ, п2,..., то их
nf2 + ... + Хк можно трактовать как число успехов в п = nt + п2 + ... + пк
Т>с вероятностью успеха в каждом испытании р. Согласно преды-
Т^анию, эта сумма имеет биномиальное распределение с параметра-
□
7.2. Суммирование непрерывных случайных величин
186
7.2.	Суммирование непрерывных случайных величин
Изложение теории суммирования непрерывных случайных величин аналогично
соответствующему изложению для дискретных величин. Пусть две непрерывные
случайные величины Хг и Х2 имеют совместную плотность распределения /(Х|,
х2). Если первая случайная величина Xt приняла значение у, то сумма примет
значение х, если вторая случайная величина Х2 равняется х - у. Поэтому плот*
ность распределения g2(x) суммы S2 = Xt + Х2 этих величин задается формулой
g2(x)= ]f(y, x-y)dy.	(7.13)
Если величины Xt и Х2 независимы и имеют, соответственно, плотности распре-
деления fi(xi) и /2(х2), то f(xit х2) = /i(xi) /2(х2) и плотность распределения сум-
мы будет
g2(*)= ]71(У)/2(*-у)Ф> -<»<х <оо.	(7.14)
Наконец, если суммируемые величины независимы и неотрицательны, то
g2(x) = J/1(y)/2(x-y)Jy, х >0.	(7.15)
о
Эти результаты легко распространяются на сумму произвольного числа взаимно
независимых непрерывных случайных величин X,, Х2,...., Xk, как это устанавли-
вается следующей теоремой.
Теорема 7.2. Пусть Xj является непрерывной случайной величиной с плотностью
распределения fj (х). Плотность распределения gn(x) суммы S„ взаимно незави-
симых случайных величин Xit Х2, ...., Х„ вычисляется рекуррентно: для п  2 по
формуле (7.14) и по формуле
]gn(y)f„+i(x~y)dy, -оо<х<оо,	(7.16)
для п = 2, 3,...
Если все величины неотрицательны, то в дополнение к (7.15) имеет место фор-
мула
Sn+Sx) = \gn<y)fn^x-y)dy, x£0, л =2,3,...	(7.17)
о
Доказательство аналогично доказательству теоремы 7.1.
Примеры
Пример 7.3. Устойчивость семейства распределений Эрланга с фиксированным
значением параметра X. Покажем, что если Хь Х2,..., Х„ — взаимно независимые
случайные величины, имеющие распределение Эрланга (4.18) с одним и тем же
параметром X и, может быть, разными параметрами 4, /2,..., 1„, то их сумма 5Л 
 Х| + Х2 +... + Х„ имеет распределение Эрланга с параметрами X и I  /| + 4 +... + 4<
В частности, сумма п взаимно независимых случайных величин, имеющих одно
186
7. Суммирование случайных величин и предельные теоремы
и то же экспоненциальное распределение с параметром X, имеет распределение
Эрланга с параметрами Хил,
Доказательство
В основу доказательства мы положим следующий, уже отмечавшийся ранее
факт: экспоненциальное распределение (4.9) является частным случаем распре-
деления Эрланга при значении параметра последнего I, равного 1. Рассмотрим
вначале случай двух слагаемых п = 2, когда первое слагаемое имеет распреде-
ление Эрланга с параметрами Хи /, а второе слагаемое Х2 - экспоненциальное
распределение с параметром X. Подставляя в формулу (7.15) плотности распре-
деления Эрланга (4.18) и экспоненциального распределения (4.9), вместо функ-
ций и /2, находим
g2(х) = f Х<^' ‘ е^ \e-4x-y)dy =	х'+* е'** f г/'4 dy = Х^^-	, х > 0.
62 7 Jo (/-1)!	У (/-1)!	У 1\
Мы получили плотность распределения Эрланга с параметрами Хи / + 1. Из это-
го можно сделать важный вывод: если случайная величина S имеет распределение
Эрланга с параметрами Хи I, то ее можно представить как сумму I независимых
случайных величин Xt + Х2 + ... + X,, имеющих одно и то же экспоненциальное
распределение с параметром X. Очевидно и обратное: если Х{, Х2,..., Xt — взаимно
независимые случайные величины, имеющие одно и то же экспоненциальное рас-
пределение с параметром X, то их сумма S/ = Xt + Х2 + ... + Xf имеет распределе-
ние Эрланга с параметрами Хи/. Итак, вторая часть нашего утверждения доказана.
Для доказательства первой части повторим рассуждения, приведенные в приме-
ре 7.2. В условиях рассматриваемого примера случайную величину Х„ имеющую
распределение Эрланга с параметрами X и /;, можно представить в виде суммы /,•
взаимно независимых случайных величин, имеющих одно и то же экспоненциаль-
ное распределение с параметром X. Поэтому сумму Xt + Х2 + ... + Х„ можно предста-
вить как сумму /| + /2 + ... + 1„ взаимно независимых случайных величин, имеющих
экспоненциальное распределение с параметром X. Согласно предыдущему замеча-
нию, эта сумма имеет распределение Эрланга с параметрами X и I = /( + 12 + ... + 1„.
Пример 7.4. Холодное резервирование в теории надежности. Выше в первой главе
рассматривалось параллельное соединение элементов в систему как средство по-
вышения надежности последней. При этом предполагалось, что в любой момент
времени работают все элементы, не отказавшие к данному моменту. Такой спо-
соб резервирования называется «горячим». Альтернативным ему является «хо-
лодное резервирование» или «резервирование замещением». В данном случае
в каждый момент времени работает только один не отказавший элемент, если та-
ковые вообще имеются, при этом один из исправных элементов мгновенно заме-
щает отказавший элемент. Система отказывает в момент, когда очередной рабо-
тающий элемент отказывает, а заменить его нечем.
При таком способе резервирования продолжительность S безотказной работы
системы из п элементов будет, очевидно, равна сумме продолжительностей рабо-
ты составляющих систему элементов Х(, Х2,..., Х„. Следовательно, распределение
времени безотказной работы системы при холодном резервировании находится
^лглагип ппиярлрннмм выше (ЬоПМУЛаМ.
7.3. Суммирование независимых многомерных случайных величин*
187
Пример 7.5. Сумма случайного числа случайных величин. Выше рассматривались
суммы S„ случайных величин Xt, Х2, Х„ в предположении, что число слагав-
мых суммы п является неслучайным. Теперь мы предполагаем, что оно явля*
ется целочисленной случайной величиной N с распределением вероятностей
рп = P{N = п}, п = 1, 2, ... Каково будет распределение соответствующей суммы
SN = Xi + Х2 + ... + XN?
Для нахождения функции распределения суммы Fs(x) = P{SN < х} необходимо
рассмотреть событие {5W < х}. Применим для вычисления его вероятности фор-
мулу полной вероятности (1.23). Событие {SN < х] выступает здесь в роли собы-
тия А. В качестве гипотезы Нп примем событие {N = п} — «сумма состоит из п
слагаемых». Согласно условия задачи P{N= п} =рп и по формуле (1.23) находим
P{SN <x}=^pnP{Sn <х}.
п
(7.18)
В частности, пусть N имеет распределение Пуассона с параметром X, а все {X,}
взаимно независимы и имеют экспоненциальное распределение с параметром ц.
Если N= п, то S„ имеет распределение Эрланга (4.18) с параметрами ц и п, поэтому
P{S <х} = P{N = 0} +	= п} P{Sn < г} =
П=1
= е~к + У — е~х(1-У	) - 1 У у (нх)'
„=1 п!	,=о i!	И=1 п!	i I
(7.19)
Отметим, что с вероятностью е~к сумма принимает нулевое значение. Но если
сумма не равна нулю, то она следует распределению непрерывной случайной ве-
личины. Это — пример смешанной случайной величины, представляющей собой
комбинацию дискретных и непрерывных случайных величин.
7.3.	Суммирование независимых многомерных
случайных величин*
В этом разделе мы собрали некоторые результаты, касающиеся суммирования
независимых многомерных случайных величин. Первый из них говорит о мате-
матическом ожидании и ковариации суммы. Он справедлив как для дискретных,
так и для непрерывных независимых случайных величин, и обобщает аналогич-
ные результаты для суммы скалярных случайных величин (см. теорему 5.4 и
формулы (5.20) и (5.23)).
Теорема 7.3. Пусть Хь Х2.Хт — взаимно независимые многомерные случай-
ные величины одной и той же размерности, имеющие математические ожидания
ff(X|), Е(Х2),..., E(Xm) и ковариационные матрицы C(Xt), С(Х2).С(Х„). Тогда
математическое ожидание суммы этих величин равно сумме их математических
ожиданий, а ковариационная матрица суммы равна сумме ковариационных мат-
риц слагаемых:
ВД + Х2 + ...+ XW) =Е(Х()+ Е(Х,) + ...+ Е(ХЖ),	(7.20)
С(Х, + Х2 + ... + Хв) «QX,) + С(Х2) + ... + С(ХВ).	(7.21)
7.3. Суммирование независимых многомерных случайных величин1
1М
где |1( = (ц/д, щ2,..., щ„) и М( =	— вектор и матрица из констант, /  1, 2,
Zz= (Z/д, Zl<2,	Z/j,) — ^-мерный случайный вектор, имеющий стандартное нор-
мальное распределение (6.13).
Пусть I — единичная матрица порядка п. Рассмотрим блочные векторы X = (Xt Х2),
Z = (Z( Z2) и матрицы
м- м‘ , и. П
tMj (jJ
Теперь сумму можно представить в виде Xj + Х2 = X • II. Далее имеем:
X, +Х2 =X-II=(p1 + Z1M1 |i2 + Z2M2)Pl =
= Н1 + H2 + ZM.
= (p1 + Z) Mt + p2 + Z2 M2) =nt + n2 + (Z1 M( +Z2M2) =
JM,
= pt + p2 + z
2
Итак, сумма X( + X2 представима в виде (6.40), что говорит о нормальности ее
распределения. Параметры распределения даются формулами (7.20), (7.21).	□
Впоследующем будет использован следующий результат теории матриц.
Лемма 7.1. Пусть С — невырожденная квадратная матрица порядка и, а а » (д1(
а2,..., ат) — произвольная вектор-строка того же порядка. Тогда матрица С + ата
является невырожденной. Обратная для нее матрица дается формулой:
(С + ата)_| =С-‘
(7.22)
Доказательство
Умножая матрицу С + ата на матрицу, стоящую в правой части последней фор*
мулы, получаем:
(С + ата) С-1
С-’атаС-'
. = cfc-1 -С~'аТаС~' l + aTafc-1
l + aC-'aTJ t l + aC-'aTJ t
т IaTaC-‘ T г С^аС4
=1--------r-=r + a1 aC 1 - a' a----- -
l + aC-1aT	l + aC’’aT
1 (aTaC'* -aTaC-t -аС_1ататаС'’ +aTaC‘,aTaC'*)
С~|атаС~|
1 + аС'*ат
= 1- “Гт
1 + аС’ ат
= I------(-аС-‘ ататаС-‘ + аС1 ататаС-‘ ) = I.
1 + аС-'ат
Последнее равенство говорит о том, что матрицы в левой и правой частях фор*
мулы (7.22) являются взаимно обратными.	□
Ламма 7.2. Пусть А и D — квадратные матрицы (быть может, разных порядков),
причем матрица А — неособенная. Тогда имеет место следующее выражение ДЛЯ
определителя блочной матрицы:
А С
В D
|A||D-BA-'C|.
7. Суммирование случайных величин и предельные теоремы
в
1Г
оме того, если хотя бы одна из матриц {C(Xj)} является невырожденной, то
Квырожденной является и матрица C(Xt + Х2 + ... + Хт).
не
казательство
Дэрмула (7.20) утверждает, что соответствующие компоненты векторов, стоящих
Срава и слева от знака равенства, совпадают. Но это как раз то, что утверждает-
ci формулой (5.20) теоремы 5.4 для скалярных случайных величин. Итак, фор-
с.ла (7.20) доказана.
Мщ доказательства формулы (7.21) представим ковариацию суммы в виде,
/ваемом формулой (6.33), воспользуемся формулой (7.20), а также тем, что
ясилу независимости X, и X, при i * j E((Xj - £(Х,))Т(Х7 - £(Х7)) =
£(Х, - £(Х,))Т£(Х, - £(Х,)) = 0:
=	z \ (г	\Т/	\\
( т \	( т	т	\ т	т	1
С £Х,. =£ |2х,-2ад)| £х,.-££(Х,.) =
\ i=l J 1Д1=1	1=1	/ V»!	7=1
( т	т	т т
= £ Х(Х, -£(Х,.))ТХ(Х; -£(Хр) =£££((Х; -£(Х;))Т(Х,- -£(Хр)) =
\ i=l	7=1	у i»l 7=1
= ££((Xf -£(Xj))T(Xi -£(Х,))) = £с(ХД
i=l	i=l
усть теперь одна из ковариацонных матриц, например С(Х!), является невыро-
денной. Тогда, согласно лемме 6.2, она положительно определена. Это означает,
го для любого ненулевого вектора х: xC(Xt)xT > 0. Положительно определен-
ий является и ковариационная матрица суммы, поскольку любая ковариацион-
1я матрица по той же лемме является неотрицательно неопределенной, т. е. для
енулевого вектора х:
хС(Х, +Х2 + ... + Хт)хт =хС(Х1)хт +хС(Х2)хт +...+хС(Хт)хт >0. □
I предыдущей главе (см. теорему 6.4) было доказано, что сумма нормально рас-
ределенных скалярных случайных величин имеет нормальное распределение.
Следующая теорема устанавливает аналогичный факт для многомерных случай-
ых величин.
еорема 7.4. Устойчивость семейства многомерных нормальных распределений.
1усть Xb Х2, ..., Xm — взаимно независимые многомерные случайные величины
дней размерности, имеющие нормальное распределение с математическими
жиданиями {£(Х,)} и ковариационными матрицами {С(Х,)}. Если хотя бы одна
13 этих матриц является невырожденной, то сумма Xt + Х2 + ... + Хт имеет невы-
южденное нормальное распределение с математическим ожиданием и ковариа-
[ионной матрицей, определяемыми формулами (7.20) и (7.21).
Доказательство
3 силу ассоциативности суммы достаточно рассмотреть случай двух слагаемых
+ Х2. По условию оба слагаемых имеют нормальное распределение (6.40), так
гго можно записать их в виде
X, =u, + z, М(, Х2 =|i2 + Z2M2,
190
7. Суммирование случайных величин и предельные теоремы
В частности, если С является нулевой матрицей О, то
А О
В D
= | A||D|.
Доказательство
Мы начнем со второго утверждения. Оно непосредственно следует из определе-
ния определителя |М| матрицы М =	:
|М| = £±3/,,	,
1.2.к
где суммирование ведется по всем перестановкам (i1( i2,	4) чисел {1, 2,k} со
знаком плюс, если перестановка четная (число инверсий ij > it при) < I четное) и
со знаком минус — если перестановка нечетная.
Пусть размерность подматрицы А равна т. Тогда в рассматриваемом случае не-
нулевым слагаемым суммы будут соответствовать перестановки, у которых пер-
вые члены (ij, г2,..., г„) образуют перестановку из множества {1, 2,..., т}, а осталь-
ные члены (г„,+1, гт+1, ..., 4) — перестановку из множества {т + 1, т + 2, ..., k}. При
этом четность перестановок остается прежней, поскольку элементы первого мно-
жества меньше элементов второго. В итоге после приведения подобных членов
суммы получаем, что
А О
В D
1,2....т	1,2...к-т
Теперь вернемся к основному равенству. Умножая левую часть этого равенства
слева на определитель, равный единице, и используя правила умножения блоч-
ных матриц и только что доказанное равенство, получаем:
I О А С
-ВА 1 I В D
' I OY А
-BA"1 I В DJ
-BA'A + B -BA'C + D
С
D-BA*C
= |A||D-BA-,C|.
А С
В D
А
О
Лемма 7.3. Пусть С и а те же, что и в лемме 7.1, и, кроме того, С является симмет-
рической матрицей. Тогда определитель невырожденной матрицы С + ата дается
формулой
|С + ата| =|С|(1 + аС’*ат ).
Доказательство
Поскольку матрица С невырожденная, то, согласно лемме 6.3, не вырожден и ее
квадратный корень Холесского С1/2, так что матрица С"1/2 существует. Определим
вектор-строку Ь формулой Ь = а(С’1/2)т. Тогда а = Ь(С1/2)Т, ата = С1/2ЬТЬ(С1/2)Т и
| С + а1а | =| С + С1/2 ЬТЬ(С1/2 )т| =| С1/2 (I + bTb)(C1/2 )т| =| С| 11 + ЬТЬ|.
7.3. Суммирование независимых многомерных случайных величин*
191
Следовательно, дело сводится к вычислению определителя |I + bTb|. Докажем,
используя индукцию по размерности т матрицы I и вектора b = (Ьи b2,Ьт), что
11 + bТЬ| = 1 + bbт. Для т = 1 это выполняется с очевидностью:
|1 + ЬТЬ|=|1 + 6,2| = 1 + Ь? = 1 + bbT.
Для т = 2 имеем аналогичный результат:
|1 + ЬТЬ| =
1 О4! ' b2 blb2>
О + bl ,
1 + Ь2 Ь{ Ь2
bxb2 1 + Ь2
= (l + fe12)(l + fe22)-(fe1fe2)2 = 1 + Z>2 +Ь2 =1+ЬЬт.
Общий случай будем доказывать индукцией по т. Пусть лемма верна для т > 1
и докажем ее для т + 1. Обозначим I и Г единичные матрицы порядка т и т + 1
соответственно, b = (Ьх Ь2... bm), b' = (bt b2... bm bm+i) = (b bm+i). Тогда, используя
результаты двух предыдущих лемм, получаем:
|Г + Ь'ТЬ'|
I 0TV Гьть Йи+1ьт>
о 1J к+1ь J
fl + bTb Л .Ьт^
= |I + bTb||l + fe2+i -6ffl+Ib(I + bTb)-‘b4+1l =
= |I + bTb| 1 + b2m+l -Z>2+1bfl-—-i-ybTb1bT =
< 1 + bb J
-=|I + bTb| |l + bbT +fe2+1(l + bbT)-fetibbT -Z>2+i(bbT)2 +/>2+i(bbT)2|-
1 + bb
= | 1 + bbT + fe2+1| = 1 +b'b'T.
Подставляя теперь в последнюю формулу b' = аС“1/2, окончательно получаем
утверждение леммы.	□
Теперь мы завершим доказательство теоремы 6.1 — основной теоремы предыду-
щей главы. Это доказательство сводится к нахождению распределения суммы
двух многомерных случайных величин, в связи с чем мы и отложили его до на-
стоящей главы. В данном случае мы имеем дело с нормально распределенными
случайными величинами.
Завершение доказательства теоремы 6.1
Итак, нам надо доказать следующее утверждение. Если в преобразовании (6.40)
|№змерность п вектора X меньше, чем размерность k вектора Z, но ранг матрицы
М*,я преобразования равен числу ее столбцов п, то вектор X имеет плотность
|шспрсдсления (6.42) с соответствующими математическим ожиданием и кова-
риационной матрицей.
Посмотрим, что из себя представляет произведение вектора-строки Z на матри-
цу М. Разобьем вектор Z на две части, два подвектора: первый подвектор Z' со-
стоит из первых п компонент, а второй Z" — из оставшихся k - п компонент:
Z  (Z' Z"). Аналогично разобьем матрицу М на две подматрицы: первая М' со-
держит первые п строк матрицы, а вторая М" — оставшиеся k - п строк:
192
7. Суммирование случайных величин и предельные теоремы
Теперь вектор X может быть представлен в виде
X = jiZM = jiZ'M' + Z”M".
Итак, как и утверждалось выше, дело сводится к суммированию двух независи-
мых нормально распределенных многомерных случайных величин.
Если матрица М имеет ранг п, то она содержит п независимых строк. Без ограни-
чения общности будем считать, что независимыми являются первые строки (к это-
му всегда можно прийти путем перестановки строк). Следовательно, квадратная
матрица М' — невырожденная, и поэтому линейное преобразование X' = gZ'M'
является взаимно однозначным. Условия первой части теоремы 6.1 выполняют-
ся и вектор X' имеет нормальную плотность распределения (6.42) с ковариаци-
онной матрицей С.
Теперь дело сводится к суммированию двух независимых нормально распреде-
ленных векторов X' и X", из которых X' имеет невырожденное распределение.
Мы должны показать, что сумма X' + X" имеет невырожденное нормальное рас-
пределение вне зависимости от того, каким является X". Вектор X” представим
в виде суммы: X" = Z” М"(1) + Z"2 М"(2) + ... Z "k.„ где Z"f — i-я компонента
вектора Z", М"(,) — i-я строка матрицы М". Компоненты вектора Z" взаимно не-
зависимы и распределены по стандартному нормальному закону. Поэтому доста-
точно доказать, что сумма X' + Z" М"(1) имеет невырожденное нормальное рас-
пределение. Отсюда по индукции будет вытекать аналогичное утверждение для
суммы X' + X''.
Для сокращения записи будем обозначать вектор-строку	через
а = («1, а2, ..., ап). В первую очередь найдем ковариационную матрицу суммы
X' + Z” а. Обозначим С ковариационную матрицу X'. Далее, согласно формуле
(6.36), ковариационная матрица Z"a равна aTC(Z")a. Z” является скаляром, по-
этому его ковариационная матрица есть дисперсия D(Z"), а последняя равна
единице, поскольку ZJ' а имеет стандартное нормальное распределение. Итак, ко-
вариационная матрица Z" а есть ата. Теперь из формулы (7.21) заключаем, что
ковариационная матрица суммы есть С + ата . Обратная ей матрица (С + ата)-1
вычисляется согласно формуле (7.22).
В отличие от формулы (7.14) в данном случае мы суммируем не две скалярные,
а две векторные случайные величины. Тем не менее все рассуждения, обосновы-
вающие эту формулу, остаются в силе. Найдем теперь выражение для соответст-
вующей плотности распределения.
Пусть случайная величина Z" приняла значение у. Тогда для того чтобы i-я ком-
понента суммы приняла значение xit необходимо и достаточно, чтобы i-я компо-
нента вектора X' приняла значение - уа,. Весь вектор X' должен принять зна-
чение х - ya, где х = (хь х2, .., хп). Если X' имеет невырожденное нормальное
распределение (6.42), a Z\ стандартное нормальное распределение (6.13), то по
аналогии с формулой (7.14) для плотности распределения суммы X' + Z\a име-
ем следующее выражение:
7.3. Суммирование независимых многомерных случайных величин*
183
X
х-Х=ехрГ-|г/2Ъг/=(2л) 2 |С| 2 ехр-М(х-ц)С-‘(х-н)т1 х
-у2тс \ 2 J	I 2	J
Преобразуем последний интеграл, дополнив в нем выражение в фигурных скоб*
ках до полного квадрата, записывая его в форме (6.42) и используя условие нор-
мировки для нормальной плотности:
-|(г/2(1+аС'1ат)-2г/(х-ц)С-‘ат)).^ =
= ехр-
1
2^(1 + аС-‘ат)
£_7Г(х-р)С-1ат
7 1
х —= ехр
iV2^
z/(l +аС~'ат)2 -(1 +аС"‘ат) 2(х-ц)С-1ат
= ехрП----7-гпг«х"Н)С‘‘ат)2|(1 + аС-1ат) 2 х
(2 1 + аС a	J
“г 1	1 г/-(1 + аС-'ат)-1(х-|1)С-1ат
J-----------------Гехр "2	----------  ------------
'°°л/2л(1 +аС"‘ат) 2	[	(1 + аС-'ат)2
= (1 + аС-1аг) 2 ехрЦ-----^-^((х -р)С-'аг )2|.
(2 1 + аС a	J
Подставляя это в исходную формулу и используя утверждения лемм 7.1 и 73,
получаем:
g„+1(x) = (27tp|Crhl + aC-taTpx
((х-ти)С *ат)2
1+ аС-1ат
х ехр^ -- (х - ц)С-‘ (х - ц)т -
-X	£
= (2л)"2 |СГ2 (1 + аС-‘ат)'2 =
= (2л) 2 |С + ата| 2 ехр|-^(х -ц)(С + ата)‘‘(х - р)т
Итак, мы действительно получаем многомерное нормальное распределение. □
194
7. Суммирование случайных величин и предельные теоремы
7.4. Центральная предельная теорема
Если число слагаемых п в сумме 5„ достаточно велико, то при весьма общих ус-
ловиях распределение суммы близко к нормальному. Эти условия конкретизи-
руются в различных вариантах центральной предельной теоремы. Простейший
из этих вариантов следующий.
Теорема 7.5. Центральная предельная теорема для одинаково распределенных
слагаемых. Пусть Х2, .... Х„ — взаимно независимые случайные величины,
имеющие одно и то же распределение с математическим ожиданием ц = E(Xj)
и дисперсией о2 = D(X}),j = 1, 2,... Тогда с ростом п функция распределения нор-
мированной и центрированной суммы
Л = 4= £ (Ху - И ) =	- пр)	(7.23)
CSyln	&Jn
стремится к функции распределения Ф( ) стандартного нормального распреде-
ления:
P{Sn <х} -> Ф(х), -<ю<г < со.	(7.24)
Практическое использование этой теоремы сводится к тому, что вероятность по-
падания суммы 5„ в интервал (а, Ь), а<Ь, приближенно вычисляют по формуле
Р{а <S„ <Ь}*ф(j	(7.25)
у CS-y/n J у gVh J
Мы опускаем доказательство сформулированной теоремы, которое можно най-
ти, например, в [11, 12]. Там же приводятся более общие условия, при выполне-
нии которых распределение суммы случайных величин стремится к нормаль-
ному. В частности, можно отказаться от условий одинакового распределения
и независимости случайных величин. Именно поэтому нормальное распределе-
ние так часто встречается при рассмотрении практических задач.
Примеры
Пример 7.6. Вычисления на некоторой ЭВМ проводятся с точностью до шестого
знака после запятой. Для решения определенной задачи требуется выполнить
десять миллионов арифметических операций, каждая из которых дает в силу ок-
ругления вышеописанную погрешность. В предположении, что эти погрешности
взаимно независимы и суммируются, найти вероятность того, что абсолютная
ошибка превысит 0.001.
Решение
Погрешность округления при выполнении отдельной операции является случай-
ной величиной, имеющей равномерное распределение в интервале (а, Ь) =
= (-0.5-10-6, 0.510-6). Математическое ожидание р. и дисперсия о2 равномерного
распределения приведены в табл. 4.4 и равны для нашего случая, соответствен-
но, нулю и (0.5-10 6 - (-0.5-10“6))2/12 = 10-12/12. Для п = 107 операций диспер-
сия суммарной погрешности составит ио2 = 10710*12/12 = 10~s/12. Следователь-
но, согласно формуле (7.25), вероятность того, что абсолютная погрешность S„
превысит 0.001, составляет
7.4. Центральная предельная теорема
*105
Р{| Sn I > 0.001} = 1 - Р{| 5„| < 0.001} = 1 - Р{ -0.001 < 5„ < 0.001} =
. Л 0.001 Л -0.001
= 1 - ф --------- - ф --------- =
1710'712 } 1710’712 J
= 1-{Ф(7Ё2)-Ф(-л/Ё2)} = 1-{Ф(ТЁ2)-(1-Ф(ТЁ2)} = 2(1-Ф(ТЁ2)).
Для вычисления значения функции стандартного нормального распределения Ф0
в точке a/L2 = 1.095 можно использовать, например, функцию рпогт(х, ц, ст) паМта
Mathcad для х = 1.095, ц = 0, ст = 1. Она дает значение 0.863. Следовательно, вероят-
ность того, что абсолютная ошибка превысит 0.001, составит 2(1 - 0.863) = 0.274.
Пример 7.7. Ежесуточный расход бензина определенной марки в некоторой
транспортной фирме является случайной величиной с математическим ожида-
нием 110 т и средним квадратическим отклонением 30 т. Расходы бензина за
разные дни являются взаимно независимыми. Поставка бензина осуществляется
раз в месяц. Какова вероятность того, что имеющийся вначале запас в 3500 т бу-
дет достаточен на месяц, содержащий 30 дней? Каким должен быть первоначаль-
ный запас, чтобы он был достаточным с вероятностью 0.95?
Решение
Можно считать выполненными условия теоремы 7.5, и поэтому вероятность ТОГО,
что месячный расход 530 не превысит имеющийся запас 3500 т, вычисляется по
формуле (7.25) при а = -оо, b = 3500:
Р{530 < 3500} = ф[35°з°0= ф(1 217) =0.888.
Для определения запаса х095, который будет достаточен с вероятностью 0.95,
можно воспользоваться определением квантиля, которое будет дано в главе 12,
или осуществить последовательный подбор нужного значения. В результате на-
ходим, что искомый уровень запаса х0 95 = 3570.3.	□
Из теоремы 7.5 вытекает следующее важное следствие.
Следствиё 7.1. Теорема Муавра—Лапласа. С ростом числа п испытаний Бернул-
ли, с вероятностью успеха/? в одном испытании, распределение числа успехов 5Я
стремится к нормальному. Формулы (7.24) и (7.25) при этом принимают вид:
3» ~ пр
yjnp(i-p)
<х
*Ф(х), —ОО < X < СО.
(7.26)
(7.27)
Доказательство
Обозначим X/ число успехов, наступивших в i-м испытании Бернулли, i  0,1,..., л.
Очевидно, X/ имеет следующее распределение вероятностей: X,  1 с вероятно-
стью р, Х, « 0 с вероятностью 1 - р. Следовательно, математическое ожидание,
второй момент и дисперсия случайной величины Xt равны:
196
7. Суммирование случайных величин и предельные теоремы
ц = £(*,) = 0(1 -р)+ 1р=р-,
ц2 =ад2) = о2-(1 -Р) + 12-р = р-,
о2 =£)(Х,) = Ц2 -Ц2 = Р~р2=р(Д -р)-
Следовательно, к сумме Sn = Xt + Х2 + ... +Хп можно применить центральную
предельную теорему. После подстановки в формулы (7.24), (7.25) полученных
значений ц и о, мы приходим к формулам (7.26) и (7.27).
Пример 7.8. Проводятся сто испытаний Бернулли с вероятностью успеха в од-
ном испытании р = 0.6. Вычислить значения функции распределения F(x) числа
успехов 5100 для значений аргумента х от х = 40 до х = 80 с шагом 5.
Решение
Функция распределения F(x) — это вероятность того, что рассматриваемая слу-
чайная величина 5100 не превысит х: F(x) = Р{5100 х\ Следовательно, можно
применить теорему Бернулли (7.27) для п = 100 и р = 0.6. Поскольку Ф(-оо) = 0, то
F(x) = P{Si00 <х] =Ф
х-100р
х-100 0.6
^100p(l-p)J
J100-0.6 (1-0.6),
х -60
4.899
= Ф
Подсчитанные с помощью стандартной программы рпогт(х, ц, о) Mathcad значе-
ния функции распределения F(x) приведены в табл. 7.1. Из нее, в частности, вид-
но, что с вероятностью 0.846 число успехов не превысит 65, а с вероятностью
0.999 — значения 75.
Таблица 7.1. Функция распределения числа успехов в ста испытаниях
X	40	45	50	55	60	65	70	75	80
F(x)	0	0.001	0.021	0.154	0.500	0.846	0.979	0.999	1.000
7.5. Закон больших чисел
Другая группа предельных теорем теории вероятностей составляет закон боль-
ших чисел. Его формулировка использует следующее определение.
Определение 2. Говорят, что последовательность случайных величин Хь Х2,..., Х„
сходится по вероятности к постоянной а, если для любого как угодно малого
положительного числа е > 0 числовая последовательность Cj = Р{ - а | > е},
с2 = Р{ |Х2 - а | > е},..., сп = Р{ |Х„ - а | > е},... сходится к нулю. Иначе говоря, веро-
ятность того, что случайная величина Хп отклонится от постоянной а по абсо-
лютной величине более чем на е, стремится к нулю. Последнее, в свою очередь,
означает, что для любого 8 > 0 найдется такой номер N(8), что для всех членов
числовой последовательности {с„} с номерами п, большими чем N(8), будет вы-
полняться неравенство | сп | < 8.
Сходимость Хь Х2, ..„ Х„ по вероятности к а обозначается Хп Д а.
Теорема 7.6. Закон больших чисел в форме Чебышева. Пусть Х2, ..., Хп... — по-
следовательность независимых случайных величин, имеющих одинаковые мате-
матические ожидания ц = Е(Х,) и дисперсии о2 = D(Xj), Vi = 1, 2, ... Их среднее
Компьютерный практикум № 10. Суммирование дискретных случайных величин
197
арифметическое Хп = Sn/n, подсчитанное по п величинам, сходится по вероят-
ности к математическому ожиданию р:
(7.28)
Доказательство
Теорему легко_ доказать, используя неравенство Чебышева (4.49). Ясно, ЧТО
Е(Хп ) = ц, D(Xn )_= <з2/п. Применяя теперь неравенство (4.49), в котором следу*
ет положить X = Хп, ст2 = D(Xn ) = ст2/н, получаем
—	<т2
Р(|Х -ц| >х) <—------->0, Vx>0,
пх2 п-*°
что и доказывает сходимость по вероятности (7.28).	О
Следствие 7.2. Теорема Бернулли. В испытаниях Бернулли с вероятностью успе-
ха в одном испытании р, частота успехов в п испытаниях Хп = — Sn сходится ПО
п
вероятности к значению р:
Хп^р.	(7.29)
Ранее мы неоднократно иллюстрировали закономерности, описываемые Законом
больших чисел, не используя, правда, этого термина. Так, данные табл. 3.4 приме-
ра 3.4 показывают сходимость частот события {X = х,} к соответствующим веро-
ятностям для разных значений аргумента х,- и количества экспериментов Я.
Далее, сходимость частот появления различных исходов для полиномиального
распределения (5.4) к теоретическим вероятностям исходов иллюстрировалась
табл. 5.3.
Другие иллюстрации центральной предельной теоремы и закона больших чисел
содержатся в компьютерном практикуме № 12.
В заключение отметим, что две приведенные формы закона больших чисел
(7.28) и (7.29) дают теоретическое обоснование практическому приему, когда не-
известное математическое ожидание заменяется на среднее арифметическое, а
неизвестная вероятность события — на наблюденную частоту события. Такого
рода процедуры оценивания неизвестных параметров вероятностных моделей
составляют содержание теории точечного оценивания — раздела математиче-
ской статистики, которой будет посвящена вторая часть настоящей книги.
Оценки, которые сходятся по вероятности к истинным значениям параметров,
будут названы там состоятельными.
Компьютерный практикум № 10.
Суммирование дискретных случайных величин
Цель и задачи практикума
Целью практикума является приобретение практических навыков при проведе-
ние вычислений, связанных с нахождением распределений сумм дискретных
случайных величин, в пакете Mathcad.
Задачей данного практикума является вычисление распределений сумм для двух
зиписимых и многих независимых дискретных случайных величин.
198
7. Суммирование случайных величин и предельные теоремы
Реализация задания
Для проведения вычислений нам понадобятся две программы из практику-
мов № 1 и 5, которые реализуют пользовательские функции Arise(i, А) и Incl(i, А).
Первая функция выдает значение 1, если элементарное событие i принадлежит
составному событию А, и 0 — в противном случае. Вторая функция включает
элементарное событие i в составное событие А. Дополнительно определим новые
семь функций пользователя. Программные модули, реализующие функции
пользователя, представлены на рис. 7.1. Функции имеют следующее назначение.
Функция DomSTwofCi, С2) определяет множество значений суммы двух компо-
нент, возможные значения которых задаются векторами-столбцами С1 и С2.
PrSTwofTw) вычисляет распределение вероятностей суммы компонент двумер-
ной случайной величины, заданной своим распределением вероятностей Tw. Ну-
левой столбец матрицы Tw содержит возможные значения первой компоненты,
а нулевая строка —возможные значения второй компоненты. Функция возвра-
щает результат в виде матрицы из двух строк. Первая строка содержит возмож-
ные значения суммы, а вторая — соответствующие вероятности.
Следующие функции рассчитывают распределения суммы независимых дис-
кретных случайных величин.
Dsum(Dl, D2) предназначена для суммирования двух величин, заданных своими
распределениями D1 и D2. Последние представлены матрицами D1 и D2, каж-
дая из двух столбцов. Первый столбец содержит возможные значения случайной
величины, а второй столбец — соответствующие вероятности. Функция Dsum
возвращает распределение суммы исходных величин в виде, аналогичном ре-
зультату работы функции PrSTwo.
DSumM(M) выполняет аналогичную задачу для нескольких слагаемых случай-
ных величин. Распределение этих слагаемых задается матрицей М, в которой ка-
ждому слагаемому соответствуют два столбца. Столбец с четным номером (на-
чиная с нулевого столбца) содержит возможные значения слагаемого, а столбец
с нечетным номером — соответствующие вероятности. Результатом вычислений
является распределение суммы заданных случайных величин. Результат пред-
ставляется в виде, аналогичном для функции PrSTwo.
DsumC(C, п) выполняет аналогичную задачу для суммы п независимых случай-
ных величин, каждая из которых имеет распределение С. Структура С аналогич-
на структуре D1 и D2 из функции Dsum(Dl, D2).
Если распределения независимых слагаемых заданы аналитически, то использу-
ется функция DsumCA(n, т). Предполагается, что все слагаемые являются цело-
численными случайными величинами (с возможными значениями 0, 1, 2, ...) и
имеют одно и то же распределение, предварительно заданное функцией Pr(i).
Эта функция определяет вероятность принятия значений i = 0, 1, ... В представ-
ленном примере используется пуассоновское распределение с параметром 1, за-
данное стандартной функцией dpoisfi, 1). Пользователь может выбрать любое
другое распределение. Функция DsumCA(n, т) находит распределение суммы п
случайных величин с указанным распределением Pr(i), выдавая соответствую-
щие вероятности для т возможных значений суммы.
Компьютерный практикум № 10. Суммирование дискретных случайных величин
1М
Практикум Ма 10. Суммирование дискретных величин
Пользовательские Кмппши
Суммирование компонент двумерных дискретных случайных величии
Arbe(I.A) >
f<-0
for J« 0.. rowe(A) - 1
f 4-f + lf(l a Aj ,1.0)
If(f>0,1.0)
0
Ind(I.A):-
В 4-A If Artee(I.A)
otherwise
k«-rowe(A)
for JeO. k-1
Bk<-i
Возможные значения суммы компонент
Распределение вероятностей суммы
DomSTwo(C1,Q)
А<-С1	PrSTwo(Tw)-
b*-ol
m«- rowe(C2) - 1
k 4-rows(C1) - 1
for leO k
B|4-A( + C20
If m>0
for I e 0.. k
for j e 1. m
в
* т <o>
A 4- Tw
D 4- DomSTwo(A, 0)
nt 4- rowe(D) - 1
for v e 1.. m
S«-0
Fov4-Dv
Fi,v«-0
for I e 1.. rowa(A) - 1
for J e 1.. towb(B) - 1
Sr-S+lffc+Bj.Dv.TwijJl)
Fl ,v ♦- Fl ,v + S
Суммирование независимых дискретных случайных величин
Распределение суммы двух величин
DSunt(D1.D2) •-
F*0’ <- DomSTwolo/0’. D2®)
m <- гош»(р<0>) - 1
for v e 0.. m
S«-B
for leO.. rowe(D1) - 1
for JeO.. rowa(DZ) - 1
S <- S + |((d1<“,)1 + (ог®)]• Fw,o.[o1<<1|I]| [d2<1I)|,o]
Fv,1<-S
Распределение суммы нескольких случайных величин
DSuntM(M) >
n«- cob(M) - 1 Анелитическое задание распределений
F<0><-M<n~1)	Pr(l) > dpola(l.l)
F<”^M<n)
n«- n-2
while n 2 0
DSumCA(n.m) «
DSumC(C,r
FF«-DSum(F,D2)
F^FFT
for leO . m
Fn-Pr(D
If n> 1
for v e 1.. n -1
for l«0 . m
I
G|4-£
1-0
F<-G
f«-0
FT
02<0,-|<<"-1>
D2<1)^MW
M<2 <l-1))
F 4- OSumM(M)
F
Рио. 7.1. Функции пользователя для нахождения распределения суммы
диокретных случайных величин
200
7. Суммирование случайных величин и предельные теоремы
Результаты вычислений
Результаты представлены на рис. 7.2. Вначале вводится матрица Tw, задающая
распределение двумерной случайной величины. Возможные значения первой
компоненты, содержащиеся в нулевом столбце, равны -1, 0, 2, а второй компо-
ненты, содержащиеся в нулевой строке, — 1, 2, 3, 4, 5. Распределение суммы этих
двух компонент представлено матрицей Pr57®o(Tw). Например, сумма равна
нулю с вероятностью 0.1, двум с вероятностью 0.2 и т. д. Обращаем внимание на
форму представления матрицы результатов — матрица представлена с заголов-
ками столбцов и строк, имеющими серый цвет. Такая форма указывает на нали-
чие механизма «прокрутки»: после подвода курсора к нижней границе таблицы
появляются стрелки, указывающие направления просмотра следующих элемен-
тов. Данную форму имеет также ряд матриц, описанных ниже.
Результаты вычислений
1. Суммирование компонент двумерной дискретной случайной величины
'0	12	3	4	5 '
-1	0.1	0.05	0.15	0	0.05
0	0	0.05	0.05	0	0.15
ч2	0.1	0.05	0	02	0.05,
PrSTwo(Tw)
2. Суммирование независимый случайных величин
Распределение суммы двух величин
DSum(C2.C1)-
0-2-12	3	4	1	5	6 >
,0.06 0.01 0.03 0.25 0.11 0.18 0.16 0.16 0.04 J
Рекуррентное использование фуикции DSum
OSum(c2,DSum(C2.C2)T
Свертка распределений
DSumC(C2.3)
Проверка условил нормировки:
3. Суммирование многих случайных величин
£ DSumC(C2.3)1(V-1
у - 0
Аналитическое задание распределений:	DSumCA(1,4) • (0.368 0.368 0.104 0.061 0.015)
DSumCA(2,0) - (о.135 0271 0.271 0.10 0.09 0 Л36 0.012 Э4Э7х10~Э 0.593х 10"4)
DSumCA(4,20) - I | ° V ТА	...j ,|
ЭД 0.016 | 0 05 | 0 078 | 0 093 10.097 | 0.094 [ 0.087 j 0.078 10.068 | 0 059 |
40
Проверка условия нормировки:	у1 (DSumCA(4,40)Т)(- 1
I - 0
Рис. 7.2. Результаты вычисления распределений сумм
диоиратных случайных величин
Компьютерный практикум №11. Суммирование непрерывных случайных величин
201
При суммировании двух независимых случайных величин используются распре*
деления С1 и С2. Распределение их суммы представлено матрицей Dsum(C2, Cl).
Далее иллюстрируется возможность рекуррентного использования функции
Dsum, а именно, находится распределение суммы трех независимых случайны#
величин с одним и тем же распределением С2. Это же распределение можно ПО*
лучить путем применения функции DSumC(C2, 3). Под соответствующей табли-
цей приведена проверка выполнения условия нормировки для полученного рас-
пределения суммы.
Функции вычисления распределения суммы независимых случайных величин
иллюстрируются для трех слагаемых. Распределения слагаемых задаются матри-
цей М. Так, возможные значения первого слагаемого есть -1, 0, 1 и 2, а вероятно-
сти их принятия — 0.5, 0.1, 0.2 и 0.2. Два последующих столбца определяют рас-
пределение второго слагаемого, а два последних столбца — распределение
третьего слагаемого. Распределение суммы этих слагаемых содержится в матри-
це DSumM(M). Так, сумма принимает значение -3 с вероятностью 0.04, значение
-2 с вероятностью 0.078 и т. д.
В случае аналитического задания распределения целочисленных слагаемых сле-
дует пользоваться функцией DSumCA(n, т). В нашем случае ранее аналитически
было задано (как функция Pr(i)) распределение Пуассона с параметром 1. Функ-
ция DsumCAfl, 4) выдает вероятности принятия значений 0, 1, 2, 3, 4 случайной
величиной с этим распределением. DsumCA(2, 8) выдает соответствующие веро-
ятности для суммы двух величин, кончая значением суммы, равным восьми.
I)sumCA(A, 20) описывает распределение четырех слагаемых и рассматривает воз-
можные значения суммы до двадцати включительно. Для просмотра всех элемен-
тов матрицы необходимо использовать линию прокрутки, о чем говорилось выше.
Компьютерный практикум №11.
Суммирование непрерывных случайных величин
Цель и задачи практикума
Цмъю практикума является приобретение практических навыков в расчетах с
использованием пакета Mathcad для нахождения распределения суммы непре-
рывных случайных величин.
Задачами данного практикума являются:
Q расчет плотностей распределений сумм двух зависимых и многих независи-
мых непрерывных случайных величин;
Q построение графиков кривых соответствующих плотностей распределений.
Реализация задания
На рис. 7.3. представлены модули, реализующие пользовательские функции.
Вначале задается плотность распределения fexp(z, у) непрерывной двумерной
случайной величины, соответствующая распределению (6.9) с параметром 0.6.
Функция fSumTwo(x) вычисляет для точки х плотность распределения суммы
Компонент этой двумерной величины, а функция Рг1(а, Ь) — вероятность того,
Что дни пая сумма попадет в интервал (а, Ь).
202
7. Суммирование случайных величин и предельные теоремы
Далее находится распределение суммы двух независимых случайных величин.
Плотности распределения этих величин задаются функциями /1(г/) и /2(z).
В рассматриваемом случае они соответствуют экспоненциальному распределе-
нию (4.9) с параметрами 0.5 и 1.5. Пользователь может менять эти функции по
своему усмотрению. Функция fSutnC(x) вычисляет в точке х значение плотности
распределения суммы указанных величин. Функция РгС1(а, Ь) вычисляет веро-
ятность попадания указанной суммы в интервал {а, Ь).
Практикум На 11. Суммирование нвирерывных величин
Пользовательские Функции
Суммирование ки п е и е ит двумерной иеотрицательией случайией
величины с полотиестью ра сиредел о и и л
fexp(z ,у) > lf(z > 0, If (у > □ .0.6	* у *1 .о) .о)
Плотность распределения суммы
f г” )
fSumTwo(x)»If и > 0, fexp(x- z,z) dz.O
V •’о	)
Вероятность поиадаиия суммы в интервал (а, Ь)
Prl(a.b)If^a < b.f fSumTwo(x) dx.O^
Суммирование независимых неотрицательных случайных величии
Сумма двух ееллчин с полетностями распределений
Л (у):- и[у>О.М«‘М,,о) e(z):-lf(z >0,1.5 .’«‘.о)
Плотность распределения суммы
fSumC(x)  If I к > 0, [ fl(y) Q(x - у) dy.O |
\ J0	)
Вероятность попеделил суммы в интервал (а, Ь)
РгО(а.Ь) < b.j^ ISumC(x) dx.O^
Распределение суммы п независимых неотрицательных случайных величин с общей плетнестью
Г(х) . |г(х>О.1.5 е’1Л ,.о)
9(п.х):-
Ь«- Г(х)
h *-[ g(n - 1 ,z) f(x - z) dz If n > 1
h
h(x) :•
•X
1(1) I f(y)f(x-z-y)dydz
Ja
a
Рис. 7.3. Функции пользователя для нахождения распределения сумм
непрерывных случайных величин
Функция g(n, х) вычисляет в точке х значение плотности распределения суммы п
независимых случайных величин, имеющих плотность распределения /(х).
В данном случае используется плотность экспоненциального распределения (4.9)
с параметром А = 1.5. В процессе своей работы процедура, реализующая функ-
цию g(n, х), использует рекурсию', она обращается к самой себе при меньшем зна-
чении аргумента п. Менее универсальной является функция Л(х), решающая ту
же задачу для трех слагаемых, то есть для п = 3.
Компьютерный практикум № 12. Предельные теоремы теории вероятностей
203
Результаты вычислений
Вначале на рис. 7.4 представлены графики плотности распределения суммы двух
случайных величин. Левый график соответствует зависимым величинам, СОВМв»
стное распределение которых задается плотностью fexp(z, у), а правый — незави-
симым случайным величинам с плотностями распределения /1 и /2. Для первогр
случая подсчитаны вероятности попадания суммы в интервалы (0, 40) и (0, 9).
Результаты вычислений
Графики кривых полотностей распределений сумм
Вероятности попаданий в интервал (а. Ь)
Рг1(0,40) - 0.985	PH(0,9) - 0.931
Графики кривых полотностей суми с общим распределением независимых слагаемых
у>0,02 7
Рио. 7.4. Г рафики плотности распределения суммы двух непрерывных случайных величии
На последнем графике представлены кривые плотностей для двух распределе-
ний: экспоненциального f(y) и суммы трех экспоненциально распределенных
независимых случайных величин, вычисленные по функциям h(y) и g(3, у). Как
И следовало ожидать, две последние функции дают одинаковые результаты, ТО
есть на рисунке совпали графики, построенные сплошной и пунктирной (длин-
ной) линиями.
Компьютерный практикум № 12.
Продельные теоремы теории вероятностей
Цель и задачи практикума
Цмъю практикума является иллюстрация закономерностей, формулируемых
Предельными теоремами теории вероятностей, а также их применение при про-
ведении различных вычислений в среде пакета Mathcad.
204
7. Суммирование случайных величин и предельные теоремы
Задачей данного практикума является иллюстрация сходимости по вероятности
средних арифметических к математическим ожиданиям и сходимости распреде-
ления суммы большого числа случайных величин к нормальному.
Реализация задания
На рис. 7.5 представлены модули, реализующие пользовательские функции.
Первая часть практикума посвящена иллюстрации закона больших чисел. Этот
Закон утверждает, что среднее арифметическое случайных величин сходится по
вероятности к математическому ожиданию этих величин. С этой целью выраба-
тываются две последовательности случайных величин X и Y. Первая содержит
7501 выработанных значений для равномерного в интервале (0, 2) распределе-
ния, а вторая — такое же количество для экспоненциального распределения с па-
раметром X = 1. Следовательно, в обоих случаях математическое ожидание ц рав-
но 1. Последовательности формируются в результате обращения к стандартным
функциям runif и гехр, выполняющим роль генераторов (датчиков) случайных
величин. На основании этих последовательностей вычисляются средние ариф-
метические avr(i) и evr(i), подсчитанные по все увеличивающемуся числу вели-
чин 25хг, г = 1, ..., 100. Реализуется по три последовательности средних арифме-
тических (avr, avrl, avr2 и evr, earl, evr2), с тем чтобы показать, что сходимость
является случайной, а не детерминированной.
Практикуя На 12. Предельные теоремы теории вероятностей
Пплыоватвльскме функции
Сходимость по вероятности средних к математическим ожиданиям
X - runif(7501,0,2)	1- 1 100	Y гехр(7501,1)
125	+	125	125
aVr(i) " Тте У xv	У Х2500+»	у Xsooo+v
125 Y-»	125 6-»	251 Y-»
v - 1	v - 1	v - 1
125	.	125	125
У V» “»Л(1) + — У Y2500+V>w2(i) > TZ7 У *5000+»
i-25 Y-*	IZ5 Y—t	125 Y-*
v  1	v  1	v - 1
Сходимость pа сиpeдeлeния сумм к нормальному распределению
Суммы экспоненциально распределенных случайных величин
хп-1
fexp(n,x)——— ехр(-х)	х - 0,0.2 10
Суммы равномерно распределенных в интервале |0*Ь) случайных величин
»-0.0.2 6	у (_n* _^__ tr[yav |,F(y_w
v - 0
Рис. 7.5. Пользовательские функции, иллюстрирующие предельные теоремы
Вторая часть практикума посвящена иллюстрации центральной предельной тео-
ремы. Функция fexp(n, х) вычисляет значение в точке х плотности распределе-
ния суммы п независимых случайных величин, имеющих экспоненциальное рас-
пределение (4.9) с параметром X = 1. Фактически это есть распределение
Эрланга (4.18) с параметрами X = 1 и п. Функция fun(b, п, у) вычисляет значение
в точке у плотности распределения (7.32) суммы п взаимно независимых слу-
чайных величин, каждая из которых имеет равномерное в интервале (0, Ь) рас-
пределение.
Задания для самостоятельной работы
208
Результаты вычислений
Полученные результаты представлены на рис, 7.6. Первые два графика иллюст-
рируют сходимость по вероятности средних арифметических к математическому
ожиданию. На каждом графике представлены по три траектории средних ариф-
метических. Видно, что траектории ведут себя случайным образом, но в конце
концов все они сходятся к истинному математическому ожиданию, равному 1.
Разультаты вычислений
1. Сходимость по вероятности средних арифметических
Равномерное распределение
2. Сходимость к нормальному распределению
Эспоивнцизльное распределение
Суммы экспоненциально распределенных слагаемых
Суммы равномерно распределенных слагаемых
Рис. 7.6. Результаты вычислений, иллюстрирующие предельные теоремы
На последующих двух графиках иллюстрируется сходимость распределения
сумм к нормальному распределению. На каждом графике представлены по три
Кривые плотности распределения, соответствующие одному, трем и пяти слагае-
мым суммы. Для одного слагаемого — это кривая плотности исходного распреде-
ления (экспоненциального или равномерного). Нетрудно заметить, что уже при
ПЯТИ (т. е. достаточно малом числе) слагаемых суммы хорошо просматривается
ИНД кривой плотности нормального распределения.
Задания для самостоятельной работы
I,	Используя компьютерную функцию PrCTwo, найдите распределение суммы
компонент двумерной случайной величины, заданной в табл. 5.1.
2,	Проанализируйте логику работы компьютерной функции DsumCA.
3.	Используя компьютерную функцию DsumCA, найдите распределение вероят-
ностей суммы п = 2 взаимно независимых случайных величин, имеющих гео-
метрическое распределение (3.4) с одним и тем же параметром р  0.5.
206
7. Суммирование случайных величин и предельные теоремы
Проанализируйте сходимость распределения суммы к нормальному распре-
делению с ростом числа слагаемых п.
4.	Используя компьютерную функцию DSum, найдите распределение суммы двух
независимых случайных величин, имеющих биномиальное распределение (3.3)
с параметрами п = 4, р = 0.3 и п = 3, р = 0.6.
5.	Двумя способами, используя компьютерные функции g и Л, найдите плот-
ность распределения суммы трех взаимно независимых случайных величин,
имеющих равномерное распределение (4.7) с параметрами а = 0 и b = 2.
6.	Запрограммируйте формулу (7.32), определяющую плотность распределения
суммы п взаимно независимых случайных величин, имеющих равномерное
распределение (4.7) в интервале (0, Ь). Проведите численное сравнение с ре-
зультатами предыдущего задания.
7.	Составьте программу на Mathcad, которая, используя датчик случайных чи-
сел, иллюстрирует сходимости по вероятности (7.28) и (7.29).
8.	Составьте программу на Mathcad, которая, используя датчик случайных чи-
сел, иллюстрирует сходимость (7.25) и (7.27) суммы Sn к нормальному рас-
пределению.	ь
9.	Определенный интеграл g =jf(x)dx для ограниченной функции /(х) < с
а
можно вычислить следующим образом, используя метод Монте-Карло. Выра-
батываются п пар независимых случайных величин (Xt, Yj), где X, имеет рав-
номерное распределение в интервале (а, Ь), а - равномерное распределе-
ние в интервале (0, с). Для каждой пары вычисляют значение булевой
переменной Z,:
z _ fl, если Г( </(%,),
'	[0, в противном случае.
В качестве оценки интеграла принимается
g*=lC(&-a)£zf.
п ,=1
Дайте теоретическое обоснование такого подхода, основываясь на законе боль-
ших чисел в форме Чебышева.
Выберите некоторую простую геометрическую фигуру, площадь которой хоро-
шо известна (например, квадрат, прямоугольник, треугольник или круг). Прове-
дите имитационный эксперимент и посмотрите, как с ростом числа п оценка g*
приближается к истинному значению площади g.
Задачи
Задача 7.1. Пусть Хъ Х2.Хт — взаимно независимые случайные величины,
имеющие распределение Пуассона с параметрами Х2, ..., соответственно,
a Sm = Xi + Х2 + ... + Хт — их сумма, имеющая, согласно примеру 7.1, распределе-
ние Пуассона с параметром X =	+ Х2 + ... + Хт. Покажите, что условное распре-
деление случайной величины X/ при условии Sm = п является биномиальным
с параметрами п и р = X/ / X.
Задачи
207
Задача 7.2. Пусть Xlt Х2, ..., Хт — взаимно независимые случайные величины,
имеющие биномиальное распределение, у которых параметр р одинаков, а вто-
рой параметр равен иь п2, ..., пт соответственно. Их сумма Sm, согласно приме-
ру 7.2, имеет биномиальное распределение с параметрами р и п = щ + п2 + ... + ГЦ,.
Покажите, что условное распределение X, при условии Sm = s является гипергео-
метрическим (2.7), (3.5).
Задача 7.3. Пусть S„ — число успехов в п испытаниях Бернулли с вероятностью
успеха в одном испытании р, a N — независимая от S„ случайная величина,
имеющая распределение Пуассона с параметром X. Докажите, что SN, то есть чис-
ло успехов при случайном числе испытаний Бернулли, имеет распределение Пу-
ассона с параметром кр.
Задача 7.4. Пусть X и Y — независимые случайные величины, имеющие распре-
деление Эрланга с одним и тем же параметром X и параметрами Ц и 12 соответст-
венно. Тогда условная плотность распределения X при условии, что сумма
X + Y = z, есть
/А.(х|Х + У =2) = Я^Г ‘fl--!'2 1 (/) +	о<х^2. (7,30)
AzJ I z) -1)!(/2 -1)!
Это — плотность так называемого бета-распределения с параметрами z, li и 12.
Задача 7.5. Пусть X и Y — независимые случайные величины, имеющие экспо-
ненциальные распределения с параметрами Z и ц соответственно. Тогда плот-
ность распределения суммы X + Y есть
fx+v(x) = ^-(e^ -е^),	х>0.	(7.31)
ц - л
Задача 7.6. В условиях предыдущей задачи найдите условную плотность распре-
деления X при условии X + Y - z.
Задача 7.7. Пусть X и Y — независимые случайные величины, имеющие нор-
мальное распределение с параметрами ц х, <тА., и ц Y, оу соответственно. Исполь-
зуя формулу (7.14), покажите, что их сумма распределена нормально с парамет-
рами ц Л. + ц у,	+ Оу. Обобщите этот факт на произвольное число слагаемых.
Задача 7.8. Пусть Xif Х2,... — взаимно независимые случайные величины, имею-
щие равномерное распределение (4.7) в интервале (0, Ь). Используя метод мате-
матической индукции, покажите, что плотность распределения их суммы
 Х\ + Х2 + ... + Хп дается формулой
=	У*Ь (7.32)
(п -1)! у_о
где |Х|, = 1, если 0 и [Х.]+ = 0, если 0.
Задача 7.9. Покажите, что сумма Х{ + Х2 + ... + Хп случайных величин, имеющих
распределение Дирихле из задачи 6.7, имеет бета-распределение (7.30) с пара-
метрами z  1, /| * k\ + k2 +...+ k„ и /| = k„ +1.
208
7. Суммирование случайных величин и предельные теоремы
Задача 7.10. Театр, вмещающий 1000 зрителей, имеет два гардероба по 500 мест.
В предположении, что зрители приходят по одиночке и с равной вероятностью
0.5 выбирают любой из гардеробов, найдите вероятность того, что число зрите-
лей, обратившихся в разные гардеробы, будет отличаться более чем на 20, если
все места в театре были заняты.
8 Цепи Маркова
8.1. Основные определения
В предыдущих главах рассматривались случайные величины и их последова-
тельности. Так, во второй главе рассматривались последовательности независи-
мых случайных величин Xit Х2,	Х„. Они соответствовали результатам повтор-
ных независимых испытаний. Индекс п случайной величины Хп соответствовал
моменту времени проведения испытания.
Многомерную случайную величину X = (Хь Х2, ..., Х„) также можно рассматри-
вать как последовательность случайных величин. Если номер п случайной вели-
чины Х„ трактовать как время, то говорят о случайном процессе с дискретным
временем п = 0, 1, 2, ... Рассматриваемый момент времени п называется шагом,
а принимаемые возможные значения х — состоянием процесса. Обозначим Е
множество возможных значений случайных величин, обычно оно называется
пространством состояний. Последовательность состояний xit, х,2.x/(t, при-
нимаемых случайным процессом Хь Х2,..., Хп, называется траекторией процесса.
Если п является текущим моментом времени, то х, называется текущим со-
стоянием процесса, а отрезок последовательности х,(, х, .х,п ( до текущего
Момента п называется предысторией процесса.
Основной задачей теории случайных процессов является прогнозирование со-
стояния процесса для будущего момента времени п' > п на основании зарегист-
рированной траектории х(| ,xi2, ...,xiti до момента п. В случае последовательно-
сти независимых испытаний будущее значение Хп, не зависит ни от текущего
состояния х,п, ни от предыстории х(| ,х,- ,...,х(п (. В общем случае Хп> зависти и
от того, и от другого. Важным является частный случай, когда будущее значение
не зависит от предыстории, если фиксировано текущее состояние х„. В этом
случае говорят о цепях Маркова.
Определение 1. Последовательность случайных величин Xt, Х2, ..., Х„ с множест-
вом возможных значений Е называется цепью Маркова, если при фиксированном
значении х( случайной величины Х„ для текущего момента п значение случай-
ной величины Х„, для будущего момента п' > п не зависит от предыстории
........X !„.,
Р{Х„. =xJXt =х(|, Х2 =х,2....Х„ =Xiii}=P{X„. =х1н.\Хп =xj, (81)
п, п' =0,1,2,..,; п' > п; Х'.х,.х^.х, сЕ.
210
8. Цепи Маркова
В дальнейшем мы будем использовать для цепей Маркова введенную выше тер-
минологию, то есть говорить о пространстве состояний Е, п-м шаге, предысто-
рии и т. п. При этом согласно принятой в теории цепей Маркова практике под
состоянием мы будем понимать номер i возможного значения случайной вели-
чины X,, а не само это возможное значение х,. Следовательно, £={1,2,...} или
£ = {0, 1, 2,...}. Далее Хп = in, in g £, означает событие «на п-м шаге цепь Маркова
находится в состоянии гп».
Итак, формула (8.1) означает, что для предсказания поведения цепи Маркова в
будущем неважно, каким образом попала цепь в данное состояние in в настоящий
момент времени п, важно только само это состояние. В математической литера-
туре это называют марковским свойством.
Определение 2. Цепь Маркова называется конечной, если пространство ее со-
стояний £ конечно, и счетной, если £ счетно.
Основные понятия теории конечных цепей Маркова были введены в 1907 г. вы-
дающимся русским математиком А. А. Марковым. В 1936 г. А. Н. Колмогоров
развил эту теорию на случай бесконечных цепей.
Из определения цепи Маркова и формулы (8.1) следует, что цепь Маркова мо-
жет быть задана распределением вероятностей перехода за один шаг. Пусть, как
и ранее, возможные значения цепи обозначаются i = 1, 2, ..., так что £ = {1, 2, ...}.
Определение 3. Вероятностью перехода р^ за один шаг называется вероятность
того, что цепь Маркова, находясь на данном шаге в состоянии i, на следующем
шаге окажется в состоянии j:
Ptj =P{Xn+i =j\Xn =i},	(8.2)
Данная формула подразумевает, что вероятности перехода не зависят от номера
шага п. Такие цепи Маркова называются однородными. В противном случае гово-
рят о неоднородных цепях Маркова. Мы будем рассматривать только однород-
ные цепи Маркова.
Если цепь Маркова конечна, то переходные вероятности (8.2) удобно задавать
с помощью так называемых стохастических матриц.
Определение 4. Квадратная матрица называется стохастической, если ее элемен-
ты неотрицательны и сумма элементов любой строки равна единице.
Определение 5. Матрицей переходных вероятностей Р = {р,-,} цепи Маркова
с конечным числом состояний k называется стохастическая матрица порядка k,
в которой строки соответствуют текущему состоянию цепи, столбцы — состоя-
нию на следующем шаге, а на пересечении i-й строки и j-ro столбца стоит вероят-
ность Pij соответствующего перехода:			Pl,k-l P 2,6-1	Pl,k P2.k	(8.3)
Р =	Pi.i £2,1	Р1.2 Pl,2			
	Рид	Pk-1.2	Pk-l,k-l	Pk-U	
	< PkS	Pt.2	Pk.t-l	Pk.k ,	
где, согласно условию нормировки для вероятностей,					
8.1. Основные определения
211
Pi,\ + Pi,2 + ••• + Pi,k = 1> i = l,2,...,&.	(8.4)
Часто также задаются вероятности состояний цепи Маркова на начальном, нуле*
вом шаге:
= Р{Х0 = i}.	(8.5)
На вероятности {а;-0)} накладываются обычные условия неотрицательности
Vi а?0> > 0 и нормировки:
i<=i.	(8.6)
2=1
Теперь можно вычислить по формулам (8.1), (8.2) вероятность любой конкрет-
ной траектории i0, ib ..., i„_i, i„ цепи Маркова:
Р{Х0 =i0,X, =i{... Хп =in}=a™Pi^ Р.,2-Р^'.	(8.7)
Легко показать, что формула (8.7) задает вероятности на пространстве £и+| всех
траекторий длины п +1 В частности, выполняется условие нормировки для ве-
роятностей:
k k k
ZZ-Z^o =io.-X'1 = i,........................Xn =i„} = l.	(8.8)
'0 =1'1=1	/,,=!
Обычно для наглядности конечные цепи изображают в виде ориентированного
графа. Узлы графа соответствуют состояниям цепи, а дуги указывают на воз-
можные переходы между состояниями за шаг. Над каждой дугой записывается
вероятность осуществления соответствующего перехода. Пример такого изобра-
жения цепи Маркова представлен на рис. 8.1.
Примеры
Пример 8.1. Задача о разорении игрока-, случайное блуждание по целочисленным
точкам отрезка [0, /] с поглощающими концами (экранами).
Состояниями цепи Маркова здесь являются Е = {0, 1, 2,..., /}. Попав в состояние
0 или /, цепь Маркова остается там навсегда. Во всех других состояниях она пе-
реходит за шаг в ближайшее правое состояние с вероятностью р и в ближайшее
левое состояние с вероятностью q = .1 - р. В данном случае
Ры =0 при i*0, Ро,о=1-
Ри =0 при i * /, рц = 1,
Р,.м = Р> Pi.i-x =l-p=q при i = 1,1-1,
ptj =0 при i = 1, 2. l-l,	;*i-l, i + 1.
Соответствующий граф переходов между состояниями и матрица переходных
вероятностей изображены на рис. 8.1.
Часто используемой интерпретацией этой модели является следующая. Два иг-
|ЮКа разыгрывают несколько партий, каждая из которых завершается выигры-
шем одного и проигрышем другого игрока. Проигравший игрок выплачивает
партнеру одну денежную единицу. Пусть первоначальный капитал первого игро-
ка составляет а денежных единиц, а второго игрока / - а единиц. Вероятность вы-
игрыша первого игрока равнар, а второго q = 1 - р. Игра закапчивается, как толь-
ко один нз игроков останется без денег.
212
8. Цепи Маркова
В данном случае розыгрыш одной партии соответствует одному шагу цепи Мар-
кова, состояние цепи Хп — это количество денег первого игрока после п партий.
Начальное состояние цепиХ0 = а. Интерес представляют вероятности выигрыша
первого и второго игроков.
<7
О о
О р
о о
о о
о о о'
ООО
q о р
оо 1 у
Р =
1
О
О
Пример 8.2. Случайное блуждание по целочисленным точкам отрезка [0,7] с отра-
жающими концами (экранами). В отличие от предыдущего примера здесь на оче-
редном шаге цепь Маркова переходит из состояния 0 в состояние 1 и из состоя-
ния I в состояние /-1с вероятностью 1 (рис. 8.2).	□
Рис. 8.1. Случайное блуждание по целочисленным точкам отрезка [0, /]
с поглощающими концами (экранами)
Рис. 8.2. Случайное блуждание по целочисленным точкам отрезка [О,/]
с отражающими концами (экранами)
При задании цепи Маркова определяются вероятности ее переходов за один шаг.
Как рассчитать вероятности переходов за п шагов? Обозначим р^ вероятность
перехода цепи Маркова из состояния i в состояние у ровно за п шагов:
ptf =Р{Х„ =j/X0 =i}, n = l,2,...	(8.9)
Положим = 1, р^ = 0 при i * j. Имеем:
= р,Р р$ =tp,vPvJ = ±Р,,Р^	(8.10)
V=1	V = 1
и по индукции получаем рекуррентную формулу
п = 2-3,...	(8.11)
v»l
8.1. Основные определения
213
Дальнейшая индукция по т приводит к основному тождеству
к
р<п+т'> -^р^т^
’J v=l	V<J
(8.12)
Это — частный случай уравнения Колмогорова—Чепмена. Он отражает простой
факт: переход за (п + т) шагов из состояния i в состояние у осуществляется через
какое-то промежуточное состояние v на т-м шаге.
Приведенные формулы приобретают более компактный вид, если использовать
векторно-матричные обозначения. Пусть Р<") = (/?*"’) есть матрица переходных
вероятностей за п шагов. Тогда система скалярных равенств (8.11) и (8.12) мо-
жет быть записана в матричной форме следующим образом:
р(") — ppi»-1)
p(n+m) _p(n)p(m) _ р
(8.13)
(8.14)
Повторное использование формулы (8.13) позволяет сформулировать лемму,
позволяющую вычислять вероятности переходов за п шагов.
Лемма 8.1. Матрица вероятностей переходов цепи Маркова за п шагов равна п-Й
степени матрицы вероятностей переходов за 1 шаг:
Р(п) =Р".	(8.15)
В связи с последними формулами отметим, что если Р и Q стохастические мат-
рицы, то их произведение Р Q также является стохастической матрицей.
Итак, формулы (8.13) и (8.15) позволяют найти вероятности переходов цепи
Маркова за п шагов, зная вероятности перехода за шаг, задаваемые матрицей Р.
Пример 8.3. Рассмотрим независимые испытания с k исходами и,, со2,..., со* и
вероятностями этих исходов при одном испытании =Р{со1}, р2 = Р{со2), ....
Р* = P{®k}- Если р = (pi, р2.рк), то
что соответствует условию независимости исходов испытаний.	□
Итак, мы научились находить вероятности переходов между состояниями за
произвольное число шагов п. Теперь рассмотрим ситуацию, когда исходное со-
стояние цепи Маркова является случайным, причем состояние i имеет место с
вероятностью а*0).
Лемма 8.2. Безусловная вероятность переходов между состояниями. Пусть а*0) —
вероятность состояния i на нулевом шаге, а*л) — вероятность состояния j на п-м
шаге:
< = Р{Х0 = i}, а^ = Р{Х„ = Д п = 1, 2, ...
Тогда вероятность того, что в момент времени п цепь Маркова будет находиться
и состоянии j, вычисляется по формуле
214
8. Цепи Маркова
а(п) = £ а,(0) р,(7, п = 1, 2, ...	(8.16)
1=1
Эту же формулу можно записать в матричном виде. Если обозначить а(п) = (а^,
а2п>..a^n)) вектор-строку вероятностей состояний на n-м шаге, то
а(”> =а<0> Р(п>.	(8.17)
В примере 3.4 была изложена процедура выработки дискретных случайных вели-
чин с заданной функцией распределения F(x). Обобщим ее для случая цепей
Маркова.
Алгоритм моделирования цепи Маркова
Вход:
k — число состояний цепи Маркова,
Р — матрица переходных вероятностей за шаг,
а(0) — вектор вероятностей состояний а2(0), •••> а/0) на начальном шаге п = О,
п — число рассматриваемых шагов.
Выход:
X = (Хо, Xt.Х„) — траектория цепи Маркова до n-го шага включительно.
Алгоритм
Шаг 0. Выработать равномерно распределенное в интервале (0, 1) случайное
число R и определить начальное состояние цепи Маркова Хо в момент времени 0:
Хо = min{z = 1,2.................k: R < af0) + a*0' +... + a-0)}.
Положить i -- XQ, t = 1.
Шаг t = 1, 2.n. Выработать равномерно распределенное в интервале (0, 1) слу-
чайное число R и определить состояние цепи Маркова Xt на t-м шаге:
Xt = min{; = 1,2, ...,k: R < p( ) + pj2 + ... + pi; }.
Положить i = Xt, t - t + 1. Перейти к шагу t.
Данный алгоритм реализован в компьютерной программе MChFr(P, а, п), кото-
рая будет описана ниже в компьютерном практикуме.
Пример 8.4. Моделирование цепи Маркова. Рассмотрим цепь Маркова с четырьмя
состояниями и следующей матрицей вероятностей переходов за шаг:
'0.4	0.6	0	О'
0.8	0.2	0	0
"о	0	1	О’
k 0 0.2 0.1 0.7,
Предположим, что первоначально цепь находится в четвертом состоянии, так
что вектор вероятностей состояний на нулевом шаге а(0) = (0, 0, 0, 1). В табл. 8.1
представлены результаты тысячекратного моделирования данной цепи Маркова,
осуществленного согласно приведенному алгоритму программой ImModCh. Мат-
рица содержит частоты {а/"'*} различных состояний в зависимости от номера
8.2. Классификация состояний и цепей Маркова
216
шага п, а также истинные вероятности состояний {а/п)}, подсчитанные по форму-
лам (8.17) программой StPr. Были также рассчитаны значения истинных вероят-
ностей при все увеличивающимся количестве шагов п. Оказывается, что при п,
стремящимся к бесконечности, вероятности состояний 1, 2 и 3 стремятся к неко-
торым положительным константам, а состояния 4 — к нулю. Эти константы
называются стационарными вероятностями состояний. Они приведены в по-
следнем столбце таблицы, в шапке которого записано п = оо. Мы вернемся к об-
суждению этих результатов после классификации состояний цепей Маркова,
Таблица 8.1. Распределение вероятностей и частот состояний
	n = 0	n = 1	n = 2	n = 3	n = 4	я = 5	Я = 00
fl,("r	0	0	0.191	0.204	0.278	0.299	-
fl/”	0	0	0.160	0.208	0.267	0.298	0.381
fl2<”’	0	0.230	0.160	0.250	0.240	0.260	-
fl2(”	0	0.200	0.180	0.230	0.239	0.257	0.286
fl/”'	0	0.092	0.158	0.210	0.235	0.262	-
fl/”	0	0.100	0.170	0.219	0.253	0.277	0.333
fl/”’	1	0.678	0.491	0.336	0.247	0.179	-
fl4<”	1	0.700	0.490	0.343	0.241	0.168	0
8.2.	Классификация состояний
и цепей Маркова
Нашей конечной задачей является определение различных характеристик рас-
пределения вероятностей состояний цепей Маркова, таких как стационарные ве-
роятности состояний, вероятности поглощения и т. п. Эти характеристики будут
зависеть от того, к какому классу принадлежит рассматриваемая цепь. В связи с
этим вначале следует дать классификацию цепей Маркова.
Определение 6. Говорят, что состояние у достижимо из состояния i, если сущест-
вует такое число шагов п, что р^ >0, то есть с положительной вероятностью
цепь Маркова за п шагов переходит из состояния i в состояние/
Определение 7. Множество состояний С с Е называется замкнутым, если ника-
кое состояние вне С недостижимо ни из какого состояния из С. Для произволь-
ного множества состояний М замыканием М называется наименьшее замкнутое
множество, содержащее М. Если одно состояние i образует замкнутое множест-
во, то оно называется поглощающим состоянием.
Пример 8.5 [11,399]. Предположим, что цепь Маркова имеет k = 9 состояний, так
что ее множество состояний Е = (1,2,9}. Возможные переходы между состоя-
ниями указаны в матрице Р, в которой звездочка * означает положительную ве-
роятность перехода за шаг, а ноль — отсутствие возможности перехода:
216
8. Цепи Маркова
II &	'0 0 0 * 0 0 0 * * 0 * 0 0 0 0 0 0 0 * 0 0 0 0 0 0 0 0 0 *0 0 * 0 0 0 0 0 * 0 0 0 * 0 0 * 0 0 0 0 0 0 * 0 0
0 0*'
0*0
0*0
ООО
ООО
ООО
*00
ООО
0 0*,
Замкнутыми множествами здесь будут {1, 4, 9}, {3, 8} и {5}. При этом состояние 5
является поглощающим. Замыканием множества состояний М = {1, 9} являет-
ся М = {1, 4, 9}. Замыканием состояния 2 является (2, 3, 5, 8). Замыканием мно-
жества {6, 7}, включающего состояния 6 и 7, является все пространство состоя-
ний Е.	□
Определение 8. Цепь Маркова называется неприводимой, если не существует
замкнутых множеств состояний, отличных от множества Е всех состояний.
Теорема 8.1. Если вычеркнуть в матрице переходных вероятностей Р все строки
и столбцы, не принадлежащие замкнутому множеству состояний С, то оста-
нется стохастическая матрица, для которой также справедливы соотношения
(8.11)—(8.15).
Теорема говорит о том, что отдельное рассмотрение состояний, входящих в
замкнутое множество, опять приводит к цепи Маркова, которую можно изучать
независимо.
Неприводимость цепи Маркова может быть установлена с помощью следующего
критерия.
Критерий неприводимости цепи Маркова. Цепь Маркова неприводима тогда и
только тогда, когда все ее состояния достижимы друг из друга.
Доказательство
Пусть цепь Маркова неприводима. Согласно определению 8, такая цепь не содер-
жит собственных замкнутых подмножеств. Рассмотрим два ее состояния г и j,
а также замыкание состояния i. Если состояние; недостижимо из i, то замыкание
состояния i не включает / и поэтому является собственным замкнутым подмно-
жеством Е. Это невозможно, поэтому j достижимо из i. Наоборот, если все
состояния достижимы друг из друга, то не существует замкнутого множества,
отличного от множества всех состояний.	□
Определение 9. Говорят, что состояние i имеет период t > 1, если р."у = 0, когда п
не является кратным t, и t — наибольшее число с таким свойством. Состояние i
называется непериодическим, если такого t > 1 не существует.
Примеры
Пример 8.6. Пусть цепь Маркова с двумя состояниями 1 и 2 имеет следующую
матрицу переходных вероятностей:
8.2. Классификация состояний и цепей Маркова
217
1
0 )
Нетрудно видеть, что эта цепь на каждом шаге меняет свое состояние на противо-
положное. Итак, оба состояния являются периодическими с периодом t, равным 2.
Пример 8.7. Рассмотрим цепь Маркова с тремя состояниями и матрицей пере-
ходных вероятностей
Г 0 1 (Г
Р= 0 0 1 .
J 0 oj
Мы видим, что состояния периодически сменяют друг друга в последователь-
ности 1->2->3->1ит. д. Следовательно, состояния имеют период, равный
трем.	□
В дальнейшем будем применять следующие обозначения:
□	/Д!0 — вероятность того, что начиная с состояния z, цепь Маркова впервые
достигнет состояния; на п-м шаге; //0) =0, i *j;
□	fjj — вероятность того, что начиная с состояния г, цепь Маркова когда-нибудь
попадет в состояние;;
□	ц, — среднее число шагов до возвращения цепи Маркова в состояние i, назы-
ваемое средним временем возвращения в состояние г.
Имеют место следующие очевидные соотношения:
Л; =£/,7’>	<8Л8>
(8.19)
И=1
Отметим, что вероятности могут быть вычислены через вероятности pff
в результате рекуррентного применения следующих формул:
Pij = tf^Pj7)’ n = l,2,...
и=1
Определение 10. Состояние i называется возвратным, если вероятность возвра-
щения для него равна единице: /, = 1, и невозвратным, если эта вероятность
меньше единицы: /, < 1.
Следующая теорема дает характеризацию возвратных и невозвратных состояний
цепи Маркова.
Теорема 8.2. Состояние цепи Маркова является возвратным тогда и только то-
гда, когда среднее число возвращений в него бесконечно. Из любого возвратного
состояния нельзя достичь никакого невозвратного состояния.
Доказательство
Пусть i является возвратным состоянием. Тогда с вероятностью 1 будет иметь
место первое, второе и т. д. возвращение в это состояние. Следовательно, среднее
число возвращений и это состояние бесконечно.
218
8. Цепи Маркова
Пусть теперь j — невозвратное состояние, так что вероятность возвращения в
него fjj строго меньше 1. Обозначим Y случайную величину, равную числу воз-
вращений в состояние/ Будем называть «неудачей» каждое возвращение в со-
стояние} и «успехом», если возвращения не было. Тогда X = Y + 1 — это число
испытаний Бернулли, потребных для получения первого успеха. Следовательно,
для X имеет место геометрическое распределение (3.4) с параметрами q=fjj<\.,
р = 1 - q > 0. Математическое ожидание для этого распределения (см. табл. 3.5)
Е(Х) = i/p конечно. Поскольку E(Y) = Е(Х) - 1, то первая часть теоремы доказана.
Для доказательства второй части теоремы предположим, что существует поло-
жительная вероятность fi j > 0 попадания из возвратного состояния i в невоз-
вратное состояние j. Поскольку i является возвратным состоянием, то среднее
число возвращений в него бесконечно, и после каждого возвращения цепь Мар-
кова переходит в состояние j с вероятностью fitj > 0. Следовательно, среднее чис-
ло возвращений в состояние} тоже бесконечно. Это противоречит тому, что для
невозвратного состояния оно должно быть конечным. Следовательно, вероят-
ность попадания из i ej должна равняться нулю.	□
Пример 8.4а. Рассмотрим цепь Маркова, приведенную в примере 8.4. Здесь име-
ется четыре состояния. Состояния 1, 2 и 3 являются возвратными, причем со-
стояния 1 и 2 образуют замкнутый класс, а состояние 3 является поглощающим.
Первоначально цепь находится в состоянии 4. Из матрицы переходных вероят-
ностей Р видно, что из возвратных состояний 1, 2 и 3 попасть в невозвратное со-
стояние 4 нельзя. Поскольку вероятность перехода из состояния 4 в возвратные
состояния положительна, то рано или поздно цепь Маркова покинет это состоя-
ние и более в него не возвратится, так что вероятность этого состояния стремит-
ся к нулю с ростом числа шагов п. Это видно из последнего столбца табл. 8.1,
отвечающего числу шагов п = оо. С вероятностью 1/3 » 0.333 цепь перейдет в по-
глощающее состояние 3 и останется там навсегда, и с противоположной вероят-
ностью 1 - 1/3 » 0.667 она перейдет в замкнутое множество из двух состояний
1 и 2.	□
Следующее определение относится только к конечным цепям Маркова. Случай
счетных цепей будет рассмотрен в разделе 8.5.
Определение 11. В конечной цепи Маркова непериодическое возвратное состоя-
ние i называется эргодическим. Цепь Маркова называется эргодической, если она
неприводима и все ее состояния эргодические.
Другие свойства конечных цепей Маркова будут рассмотрены в разделе 8.5
одновременно со свойствами счетных цепей, которые являются обобщением
первых.
8.3.	Эргодические конечные цепи
В настоящем разделе рассматривается поведение вероятностей переходов между
состояниями за большое количество шагов п для случая эргодической конечной
цепи Маркова. Следующая теорема дается без доказательства, которое можно
найти, например, в книге В. Феллера [11].
8.3. Эргодические конечные цепи
218
Теорема 8.3. Если Р — матрица переходных вероятностей эргодической конеч*
ной цепи Маркова, то:
1) степени Р" при и -> оо стремятся к стохастической матрице А;
2) каждая строка матрицы А является одним и тем же вероятностным вектором
а = (аь а2...ak), то есть А = 1та, где 1 = (1, 1,..., 1) — A-мерная вектор-строка
из единиц.
Теорема утверждает, что вероятность состояния у спустя большое число шагов Я
не зависит от исходного состояния i в момент времени ноль и равна ;-й компо-
ненте вектора а. В этом случае говорят, что момент времени п относится к ста-
ционарному режиму, вектор а называют стационарным распределением вероят-
ностей состояний, а вероятности alt а2 .... а* — стационарными вероятностями
состояний цепи Маркова. Физический смысл этих вероятностей следующий: ве-
роятность а; состояния у есть средняя доля времени пребывания цепи Маркова в
состоянии j для стационарного режима ее функционирования. Следующая тео-
рема устанавливает свойства вектора стационарных вероятностей а, а также ме-
тод его определения.
Теорема 8.4. Если Р — матрица переходных вероятностей эргодической конеч-
ной цепи Маркова, а А и а — то же, что и в предыдущей теореме, то:
1)	для любого вероятностного вектора х последовательность векторов хР" схо-
дится к вектору а при п —> оо;
2)	РА = АР = А;
3)	вектор а — единственный вероятностный вектор, удовлетворяющий системе
линейных алгебраических уравнений
zP = Z.	(8.20)
Доказательство
Если х — вероятностный вектор, то xlT = 1 и поэтому хА = х1та = 1а = а. Соглас-
но первому утверждению теоремы 83, Р” -> А, следовательно,
хР" ->хА = а.
Итак, первое утверждение теоремы доказано.
Доказательство второго утверждения следует из равенств:
А = limP" = PlimP"~' =РА,
п-юо	П-»®
А = limP" = limP"-1P = AP.
Докажем третье утверждение теоремы. Во-первых, из только что доказанного ут-
верждения следует, что аР = а, то есть вектор а удовлетворяет системе уравне-
ний (8.20). Покажем теперь, что вектор а — единственный вероятностный век-
тор, удовлетворяющий этому уравнению. Пусть вероятностная вектор-строка Ь
также удовлетворяет уравнению (8.20), то есть ЬР = Ь. Последовательной под-
становкой получаем ЬР"  Ь. Согласно первого утверждения доказываемой тео-
оемы. ЬР” сходится к а. Следовательно, а » Ь.	□
220
8. Цепи Маркова
Итак, для нахождения вектора стационарных вероятностей состояний а = (а(, а2,
.... ак) необходимо решить систему линейных алгебраических уравнений (8.20)
с дополнительным условием на нормировку вероятностей:
а  1Т = й] + а2 +... + ак = 1.
(8.21)
Пример 8.8. Рассмотрим матрицу переходных вероятностей
'1/3
Р = 1/4
J/5
1/3 1/3"
0 3/4
3/5 1/5,
Все три состояния соответствующей цепи Маркова непериодические и достижи-
мы друг из друга, так что цепь является неприводимой. Поскольку все состоя-
ния, кроме того, возвратны, то цепь эргодическая и поэтому имеет стационарное
распределение вероятностей состояний а. Для нахождения вектора а = (аь а2, а3)
имеем систему линейных алгебраических уравнений, первым их которых явля-
ется уравнение нормировки:
1 = at + а2 +а3 ,
= l/За] +1/4а2 + 1/5<г3,
а2 = 1/За, +3/5 д3,
а3 = 1/Зй! + 3/4а2 + 1/5гг3.
Единственное вероятностное решение этой системы есть а = (0.250, 0.333, 0.417).
Сходимость к предельной матрице А достаточно быстрая. Например,
	<0.261 0.311 0.428 '		'0.250 0.337 0.413"	
р2 =	0.233 0.533 0.233	,Р5 =	0.253 0.294 0.453	
	0.257 0.187 0.557,		ч 0.248 0.362 0.390,	
	'0.250 0.333 0.417"		'0.250 0.333 0.417 "	
р10 =	0.260 0.336 0.414	,р15 =	0.250 0.333 0.417	□
	0.250 0.331 0.418;		0.250 0.333 0.417	
Итак, нахождение вектора стационарных вероятностей а = (ait а2,..„ ак) сводится
к нахождению решения системы уравнений
k	___
j = ^k,	(8.22)
1=1
удовлетворяющего условиям неотрицательности Zj > 0,j = 1, 2,..., k и нормировки:
1^=1.	(8.23)
;=i
Отметим, что система уравнений (8.22) имеет простой физический смысл, сфор-
мулированный в следующем принципе.
Принцип баланса. В стационарном режиме для каждого состояния среднее число
входов в состояние за шаг и среднее число выходов из него совпадают.
8.3. Эргодические конечные цепи
221
Применим этот принцип к некоторому состоянию j. Сколько в среднем раз цепь
Маркова выходит из него за шаг? Чтобы из состояния выйти, необходимо в нем
находиться. Вероятность пребывания в состоянии j есть Zj (так мы обозначаем
неизвестное нам значение а,, то есть это доля шагов, в течение которых цепь на-
ходится в состоянии j). После входа в состояние цепь выходит из него, так ЧТО
среднее число выходов из у за шаг равно Zj — правой части уравнения (8.22). Те-
перь подсчитаем среднее число входов в состояние у. Это число равно сумме чис-
ла входов из разных состояний. В частности, из состояния i за шаг цепь выходит
в среднем z, раз, причем с частотой р,-7 она попадает после этого в состояние/
Следовательно, среднее число входов в состояние j из состояния г за шаг равно
z,p,j. Суммируя это по всем состояниям, получаем левую часть равенства (8.22).
Система (8.22) является однородной, то есть определяет решение с точностью ДО
постоянного сомножителя. Эта неопределенность устраняется условием норми-
ровки (8.23). Обычно одно из уравнений системы (8.22) отбрасывается как из-
быточное, и вместо него используется уравнение (8.23):
k	___
~zj =0- J =2,^,
«	(8.24)
Такая система (в которой отброшено первое уравнение из (8.22)) является уже
неоднородной и имеет единственное решение, которое и дает а.
Для получения явных выражений перейдем к векторно-матричным обозначе-
ниям. Представим матрицу Р в блочном виде:
О / Ч	Г ^>-1 р")
р = (Pij )ы =	_ -
I г Q.J
где р = (р12, Р1,з.Pi.k),
	>2,2	Р2,3	••	P2,k'		>2,1 '
Q =	Рз,2	Рз.з	 Рз,к	, Г =	Рзд
	^Pk.2	Pk,3 •	•• Pk,k)		
Матричная запись системы (8.22) такова:
zP = Z.
Матричная запись системы (8.24) следующая
= z*,	(8.25)
zlT=l,	(8.26)
где 1 « (1, 1.1), z* = (z2, z3.zt), так что z = (zb z*).
Равенство (8.25) перепишем в виде
Z| p + z* Q = z*,
позволяющем выразить 1* через вероятность первого состояния Zp
222
8. Цепи Маркова
z*(i-Q) = *.p-
z* = z1P(I-Q)-1.	(8.27)
Отметим, что существование обратной матрицы (I -Q)'1 доказывается в следую-
щем разделе.
Используя условие нормировки (8.26) в виде
Z* 1Т =1-Zp
находим выражение для Z\.
z, + z1p(I-Q)~1lT =1,
z, =l/(l+p(I-Q)-,lT).	(8.28)
Итак, формулы (8.27) и (8.28) позволяют вычислить вектор стационарных веро-
ятностей состояний.
Пример 8.8а. Для разложения матрицы переходных вероятностей Р из предыду-
щего примера имеем такие выражения: р= (1/3 1/3),
О
3/5
3/4^
1/5/
Вычисления согласно приведенным формулам дают следующие результаты:
J_o=f 1	°	3/4>=Г 1	-3/4Л
U [ 0 1J [з/5 1/5 J [-3/5 4/5 J’
и-or1 =P86 2,1431
[1.714 2.857)’
21 =(i+P(i-Q)-i-)- =fi+(i/3 i/3)f2,286 2,143Y4
1	’	[	7	7 [ 1.714 2.857 J[ 1J
l + (4/3 5/3)
Y1
= (1 + 9/3)-’ =0.25,
7
z* =z1P(I-Q)-’ =0.25(1/3 l/3)f 2’286 2 143
1H	V	[1.714 2.857
= 0.25(4/3 5/3) = (0.333 0.417).
Итак, получены прежние результаты.
8.4. Поглощающие цепи Маркова
Рассмотрим конечную цепь Маркова, имеющую невозвратные состояния. Такую
цепь Маркова будем называть поглощающей. Перенумеруем ее состояния так,
чтобы невозвратные состояния были последними. Согласно теореме 8.2, матри-
ца переходных вероятностей примет следующий блочный вид:
(SO)
IR Q/
(8.29)
8.4. Поглощающие цели Маркова
223
Здесь подматрица S содержит вероятности переходов между возвратными СО*
стояниями, подматрица Q — между невозвратными состояниями, подматрица R
описывает переходы из невозвратных в возвратные состояния, подматрица О СО*
стоит из нулей. Если т и I = k - т число возвратных и невозвратных состояний)
то S имеет порядок тихти, Q — порядок / х/, R — порядок I -хт, О — порядок П»х/.
Поскольку вероятность возвращения в любое невозвратное состояние./ строго
меньше 1, то это означает, что существует такое замкнутое множество состояний
Cj, не содержащее невозвратных состояний, что с некоторой положительной ве*
роятностыо Р7- за конечное число шагов цепь Маркова из состояния j достигнет
множество Cj и более не покинет его. Поскольку рассматривается конечная цепь
Маркова, число невозвратных состояний конечно. Пусть С = U, Cj есть объеди*
нение Cj для всех невозвратных состояний. Существует конечное число шагов N,
не более чем за которое с положительными вероятностями из любого невозврат-
ного состояния можно достичь С (для этого достаточно взять просто наиболь-
шее из этих чисел для отдельных невозвратных состояний). Поскольку для всех
невозвратных состояний {j} эти вероятности {} строго положительны, то наи-
меньшая из них р будет тоже строго положительной. Тогда из любого невозврат-
ного состояния цепь Маркова достигает С не более чем за N шагов с вероятно-
стью, не меньшей чем р. Тогда вероятность не достигнуть С не более чем за nN
шагов из любого невозвратного состояния не превосходит (1 -р)я. Последняя ве-
роятность стремится к 0 при п -> оо. Итак, нами доказана следующая теорема.
Теорема 8.5. В любой конечной цепи Маркова вероятность покинуть множество
невозвратных состояний за п шагов стремится к 1 при п -> оо, каково бы ни было
исходное состояние цепи Маркова.
Рассмотрим матричную интерпретацию этой теоремы, в которой точка на месте
некоторой подматрицы означает, что соответствующее значение роли не играет.
Согласно (8.29), матрица вероятностей переходов за п шагов будет
Р
п
о '
Q",
(8.30)
Из приведенной теоремы следует, что степени матрицы Q стремятся к нулевой
матрице О:
Оя------------->0.
п->=о
(8.31)
Итак,
(8.32)
Важно также отметь, что матрица Q является субстохастической: все ее элемен-
ты неотрицательны и сумма элементов любой строки не больше 1:
Q1T £1т.
При исследовании свойств поглощающих цепей Маркова основное значение
имеет так называемая фундаментальная матрица.
224
8. Цепи Маркова
Определение 12. Для поглощающей цепи Маркова с матрицей переходных веро-
ятностей (8.29), где Q соответствует невозвратным состояниям, фундаменталь-
ной называется матрица (I - Q)"1.
Теорема 8.6. Для конечной цепи Маркова с невозвратными состояниями матри-
ца (I - Q) невырождена (обратима) и
(I-Q)-1 =I + Q + Q2 +...= £q”.	(8.33)
n=0
Доказательство прямо следует из следующей леммы, относящийся к теории мат-
риц.
Лемма 8.3. Если матрицы Q" стремятся к нулевой матрице при п -> оо, то матри-
ца I - Q имеет обратную, причем
(I-Q)1 =EQ".
п=0
Доказательство
Рассмотрим тождество
(I-Q)(I + Q + Q2 +... + Q"'1 ) = I-Q",
которое легко проверить, раскрывая скобки в левой части равенства. По предпо-
ложению, правая часть стремится к единичной матрице I. Отсюда следует, что
предел матриц I + Q + Q2 + ... + Q" при п —> оо существует. Матрица I имеет опре-
делитель, равный 1. Если последовательность матриц имеет предел, то, очевид-
но, имеет предел и последовательность соответствующих определителей (являю-
щихся непрерывными функциями элементов матрицы). Из свойства пределов
вытекает, что при достаточно больших п определитель I-Q” строго положите-
лен. Следовательно, при таких п строго положителен и определитель произведе-
ния матриц, стоящих в левой части (8.34). Поскольку определитель произведе-
ния матриц равен произведению определителей, то определитель I - Q отличен
от нуля, что и доказывает невырожденность I - Q.	□
Фундаментальная матрица (I - Q)1 имеет простой физический смысл. Пусть i и
j — два невозвратных состояния, а ц,• — среднее число шагов, проводимых це-
пью Маркова в состоянии j до выхода из множества невозвратных состояний,
если первоначально цепь находится в состоянии г.
Теорема 8.7. Элементы фундаментальной матрицы равны среднему числу шагов,
в течение которых цепь пребывает в невозвратных состояниях:
(I Q)1 =(^,)/х/.	(8-34)
Доказательство
Вспомним формулу (5.11) для вычисления математического ожидания через ус-
ловные математические ожидания: если X и Y две целочисленные случайные ве-
личины, математическое ожидание которых существует, то
Е(У) = ^Р{Х=ц}Е(У|Х=ц),	(8.35)
где Е(У|Х = v) — условное математическое ожидание У, вычисленное при усло-
вии, что случайная величина X приняла значение V.
8.4. Поглощающие цепи Маркова
228
Обозначим М, j число шагов, в течение которых цепь Маркова пребывает в со-
стоянии j, если начальным является состояние г. Тогда = Е(М^). Примем
в формуле (8.35) в качестве Y число шагов Mtij, а в качестве X — номер состоя-
ния, в которое попадает цепь Маркова из состояния i после первого шага. Цепь
Маркова за один шаг переходит из состояния i в состояние v с вероятностью р^,.
Попав в состояние V, цепь Маркова проводит в состоянии} (по определению) В
среднем ц vj шагов. Кроме того, в силу марковского свойства на будущее влияет
только текущее состояние V, а не предыдущее состояние г, так ЧТО
Е( Y | X = v) = E(Mi j | X = v) = E(MVJ) = ц vf. Таким образом, в силу формулы (8.35)
для i * j
Hi,/ “ S Рi,v И v,j •
V
Если i = j, то необходимо еще учесть, что на начальном шаге цепь Маркова пре-
бывала в состоянии j, поэтому
Ни =1 + ЕРиНи-
V
Две последние формулы можно объединить в одну, если использовать символ
Кронекера
[1,	при i = j,
о( . = <
[О,	при i * j.
Тогда
Hij =8м + EPuHbj-	(8.36)
V
Перейдем к матричной записи этой системы уравненишВо-первых, отметим, ЧТО
матрица (8у), соответствующая всем состояниям i, j = i,k есть единичная матри-
ца I. Во-вторых, обозначим М = (ц,у)/х/. Тогда матричная запись уравнения
(8.36) будет иметь вид
M=I + QM.
В силу невырожденности матрицы из теоремы 8.6, мы можем записать явное
выражение для решения последнего матричного уравнения:
M = (I-Q)-1.
Итак, теорема доказана.	□
Следствие 8.1. Среднее число шагов, которое проводит цепь Маркова в невоз-
вратных состояниях, если исходным является невозвратное состояние i, будет
Можно записать вектор-строку средних времен пребывания в множестве невоз-
вратных состояний в виде
и=(И . М .......И;)=«I - Q)-' iT )т-	(8.37)
Следствие 8.2. Если первоначально цепь Маркова находится в невозвратном со-
стоянии i с вероятностью так что начальное распределение вероятностей не-
226
8. Цепи Маркова
возвратных состояний цепи Маркова задается вектором я =(лга+1, лга+2, •••>
то среднее число шагов до поглощения
т = яцт = я(1-Q)"11Т.	(8.38)
Рассмотрим теперь вопрос, в какое состояние замкнутого множества С попадает
цепь Маркова после того, как покинет множество невозвратных состояний. Обо-
значим bj j вероятность того, что цепь Маркова, исходя из невозвратного состоя-
ния i, после выхода из множества невозвратных состояний попадает в возврат-
ное состояние; множества С. Обозначим В матрицу порядка 1хт, составленную
из вероятностей (&;,Д
Теорема 8.8. Имеет место формула
B=(I-Q)-1R.	(8.39)
Доказате л ьство
Рассмотрим возможные переходы цепи Маркова из состояния i £ С в состояние
j е С. Вероятность непосредственного перехода из i в j равна (по определению)
Pi j. Если после первого шага цепь Маркова попадает в невозвратное состояние v
(вероятность этого pi v), то вероятность последующего попадания в состояние j
есть bvj Эта возможность имеется для всех невозвратных состояний v, так что
вероятности pi v bvj следует просуммировать по v согласно формуле полной веро-
ятности. Если за шаг цепь Маркова попадает в состояние из С, отличное от у, то
она первоначально не попадает в состояние j, и вероятность рассматриваемого
события равна нулю. Итак, окончательно имеем соотношение
ьы = Ptj + Zp,Aj-
V
Матричная запись этой системы уравнения такая:
B=R + QB.
Поскольку матрица I - Q невырождена, то можно записать явное выражение
(8.39) для решения последнего матричного уравнения.	□
Примеры
Пример 8.1а. Задача о разорении игрока: случайное блуждание с поглощающими
экранами. Граф переходов цепи Маркова имеет вид, изображенный на рис. 8.1.
Состояния здесь нумеруются, начиная с нулевого: Е =0, 1. /.	Рассмотрим
случай пяти состояний (/ = 4).
Для получения канонической формы (8.30) матрицы переходных вероятностей
Р перенумеруем состояния, оставив нулевое состояние нулевым, и сделав чет-
вертое состояние первым, первое состояние — вторым и т. д.
Тогда
ч
о
<7
0
0
о о
1 о
о о
0 <7
Р 0
Р =
0 О'
о о
р о
О р
<7
8.4. Поглощающие цепи Маркова
227
Сопоставление с канонической формой (8.30) показывает, что
Фундаментальная матрица (I - Q) 1 имеет вид (как легко убедиться перемноже-
нием):
(I-Q)’1
1
р2 +q2
p + q2
q
q2
i р
q q+p\
Следовательно, среднее число шагов, в течение которых цепь Маркова отправ-
ляясь, например, из третьего состояния, пребывает в четвертом состоянии, есть
Р / (р2 + q\
Вектор вероятностей поглощения в первом и втором состояниях будет
(I-Q)-‘R=-^_
р +q
?(р + ?2)	р3
2	2
q	р
q3 p(q + p2)
2
Дадим игровую интерпретацию полученных результатов. Суммарный капитал
обоих игроков равен 4. Пусть каждый игрок вначале имел по 2 денежные едини-
цы. Это соответствует второй строке последней матрицы. Вероятность того, ЧТО
первый игрок выиграет (он получает всю сумму денег) — это второй элемент
этой строки, то есть р2/(р2 + q2 ).
Пример 8.9. Потоки в сетях. Математической моделью разного рода сетей (ин-
формационно-вычислительных, телекоммуникационных, транспортных И др.)
является следующая. Имеется поступающий извне поток требований (заявок,
сообщений и пр.). Интенсивность потока (среднее число требований в единицу
времени) не зависит от предыдущих поступлений, постоянна и равна X. Сеть со-
стоит из узлов, между которыми циркулируют поступившие требования ВПЛОТЬ
до выхода их из сети. Она описывается ориентированным графом с k вершинами
(узлами) и ориентированными дугами, ведущими от вершины к вершине (быть
может, той же самой). Наличие дуги указывает на возможность перехода требо*
ПИНИЙ между соответствующими узлами. Дуге (i,j), ведущей из вершины i в вер-
шину j, приписывается число pi|Z, равное вероятности того, что покинувшее узел i
требование перейдет в узел у. Все эти вероятности записываются в виде матрицы
переходных вероятностей Р = (pjy )ы. Вершине (узлу) с номером i соответству-
ет i-я строка матрицы. Сумма элементов этой строки может быть меньше еди-
ницы, так что матрица является субстохастической. «Дефект» i-й строки
l(i  I ~(р1А + pi2 +---+Pt.k)равен вероятности того, что, выйдя из t-ro узла, требо-
вание покинет сеть. Заданы также вероятности л, того, что для поступившего в
сеть требования первым будет узел i. Необходимо рассчитать интенсивность по-
токи требований {ХД проходящих через каждый узел.
228
8. Цели Маркова
Фиксируем некоторое требование и проследим его перемещения по сети (такое
требование называется «меченным»). Эти перемещения описываются цепью
Маркова с k состояниями и матрицей переходных вероятностей Р. Состояния
цепи соответствуют узлам (вершинам), в которых находится наше требование.
Поскольку каждое требование рано или поздно покидает сеть, то все состояния
цепи — невозвратные. Среднее число посещений требованием узла у, если пер-
воначальным был узел i, — это среднее число р  визитов цепи в состояние у,
рассчитываемое по формуле (8.34). Поскольку узел г является для требова-
ния первым с вероятностью то среднее число посещений узла у составит
+ л2р2; +...+ л4р4>. В единицу времени поступает Z идентичных требова-
ний, так что интенсивность потока через у-й узел
=к(Л1Ц1,;. + л2р2у +... + ntpt>).	□
Применение к исследованию эргодических цепей Маркова. Как мы знаем, состоя-
ния такой цепи образуют неприводимое множество: из каждого состояния мож-
но попасть в любое другое с положительной вероятностью за конечное число
шагов. Вычислим среднее число шагов до возвращения цепи Маркова в состоя-
ние г. Без ограничения общности положим, что в качестве i рассматривается пер-
вое состояние (благодаря этому нет необходимости перенумеровывать состоя-
ния для приведения матрицы переходных вероятностей к каноническому виду).
Если рассматривать цепь Маркова только до попадания в первое состояние, то
этому соответствуют состояния 2, 3, ..., k. Для наших целей можно рассмотреть
цепь Маркова, состоящую из одного замкнутого множества С, включающего
лишь одно состояние 1, и множества С = {2, 3,..., k} остальных состояний как не-
возвратных. Таким образом, блочная структура матрицы переходных вероятно-
стей имеет вид
уже встречавшийся в предыдущем разделе.
Среднее число шагов до попадания в состояние 1 из невозвратных состояний 2,
3, .... k дается (как мы знаем из следствия 8.1) формулой (8.37):
(I-Q)-1 1т.
С другой стороны, исходя из первого состояния, цепь Маркова на следующем
шаге оказывается в состоянии у, у > 2, с вероятностью р1;. Поэтому по формуле
(5.11) для вычисления математического ожидания находим, что среднее число
шагов до возвращения в первое состояние будет p(I - Q)"1 1т. Здесь еще необхо-
димо учесть первый шаг. Итак, среднее время возвращения в первое состояние
И1 = 1 + p(I-Q) 1 Г.
Сопоставление с формулой (8.28) показывает справедливость следующей теоремы.
Теорема 8.9. В эргодической конечной цепи Маркова стационарная вероятность
а, состояния i есть величина, обратная среднему времени ц, до возвращения
в это состояние.
8.5. Дальнейшие результаты по цепям Маркова*
ап
Комментарий
Теорема имеет простой физический смысл. Вероятность состояния i — это Сред-
няя доля времени, проводимого цепью Маркова в этом состоянии. Если среднее
время возвращения в состояние i есть р.,, то в среднем из р г шагов цепь Маркова
будет находиться в состоянии i в течение одного шага. Отсюда и следует, что ве-
роятность состояния i есть 1/р,.
8.5. Дальнейшие результаты по цепям Маркова*
Определение 13. Цепь Маркова называется счетной, если множество ее состоя-
ний счетно.
Основные понятия конечных цепей Маркова без изменений переносятся на
счетный случай: возвратность и периодичность состояний, замкнутость и непри-
водимость множества состояний и т. п. Тем не менее в этом случае возникает
много осложнений, связанных с бесконечным числом состояний. Первое из Них
заключается в том, что состояние i может быть возвратным (для него вероят-
ность возвращения / , = 1), однако среднее время до возвращения р, бесконечно.
Определение 14. Возвратное состояние i называется нулевым, если среднее время
возвращения в него бесконечно (р t = оо), и ненулевым, если конечно (р ( < оо). Не-
периодическое состояние г, являющееся возвратным ненулевым, называется эр-
еодическим. Неприводимая цепь Маркова называется эргодической, если все ев
состояния эргодические.
Отметим, что для конечной цепи Маркова любое возвратное состояние является
ненулевым (см. теорему 8.13).
Без доказательства приведем несколько теорем, утверждения которых были уЖе
доказаны или могут быть доказаны простыми средствами [11].
Теорема 8.10.
1.	Состояние j является невозвратным состоянием тогда и только тогда, когда
среднее число возвращений в него конечно:
%Р^<ъ	(8.40)
м=0
В этом случае при всех i
и=0
2.	Состояние j является возвратным нулевым тогда и только тогда, когда сред-
нее число возвращений в него бесконечно, однако вероятность возвращения
на п-м шаге стремится при п -> оо к нулю:
(841)
п-0
В этом случае при всех i
Ри -77Г->0-
230
8. Цепи Маркова
3.	Непериодическое (возвратное) состояние j является эргодическим тогда и
только тогда, когда р7- < оо. В этом случае для всех i при п -> оо
Р<?	(8.42)
Следствие 8.3. Если j — непериодическое состояние, то pff стремится либо
К НуЛЮ, Либо К fij/Pj 
Определение 15. Будем называть два состояний однотипными, если они одина-
ково характеризуются по признакам периодичности, возвратности и конечности
времени возвращения.
Теорема 8.11. В неприводимой цепи Маркова все состояния однотипны.
Доказательство
Пусть; и k — два произвольных состояния неприводимой цепи Маркова. В силу
сформулированного выше критерия каждое из состояний достижимо из другого.
Поэтому существует два таких натуральных числа г и s, и положительное число
р, что pjr£ > р >0 и р(к) > р >0. Очевидно,
'	(8.43)
Здесь;, k, s и г фиксированы, тогда как п произвольно. Если; невозвратно, то со-
гласно утверждению 1) теоремы 8.10, pj”} является членом сходящегося ряда.
Согласно неравенству (8.43) это же справедливо для р^, так что состояние k
является также невозвратным. Более того, если pfj -> 0, то и р(кк -> 0, то есть
если; является нулевым состоянием, то такое же и k. Аналогичные утверждения
будут иметь место, если поменять местами k и ;. Поэтому состояния j и k одно-
временно или возвратны или нет. Аналогичные рассуждения и применение ут-
верждения 2) теоремы 8.10 показывают, что состояния; и k одновременно или
нулевые или ненулевые.
Пусть теперь; имеет период t. Так как р^ = 1, то при п = 0 правая часть неравен-
ства (8.43) положительна и, следовательно, r + s кратно t. Но тогда левая часть
(8.43) при п, не кратном t, будет обращаться в ноль. Поэтому состояние k имеет
период, кратный t. Меняя ролями; и k, мы видим, что эти состояния имеют оди-
наковый период.	□
Пример 8.10. Рассмотрим случайное блуждание точки по целочисленным коор-
динатам положительной вещественной прямой R+ = [0, оо) с отражающим экра-
ном в точке 0. На каждом шаге точка переходит в соседнее правое состояние
с вероятностью р и левое соседнее состояние — с вероятностью q = 1 - р. Исклю-
чение составляет только состояние 0, из которого всегда имеет место переход
в состояние 1.
Легко видеть, что цепь является неприводимой, так как все ее состояния дости-
жимы друг из друга. Поэтому достаточно проанализировать только одно состоя-
ние — в силу теоремы 8.11 все ее состояния будут иметь этот же тип. Вначале
найдем вероятность /о,о и среднее время ц0 возвращения точки в начало коор-
динат.
Итак, цепь Маркова первоначально находится в состоянии 0. После первого шага
она неизбежно попадает в состояние 1. Следовательно, искомая вероятность /00
совпадает с вероятностью того, что цепь Маркова из состояния 1 когда-нибудь
8.5. Дальнейшие результаты по цепям Маркова’
231
достигнет состояния 0. Отметим, что (в силу постоянства вероятностей р и q ДЛЯ
всех состояний цепи Маркова) этому же значению f00 равна вероятность Уд.|
того, что цепь Маркова из любого состояния i достигнет ближайшего левого
состояния i -1, i = 1, 2,... Из состояния 1 цепь Маркова за шаг с вероятностью q
переходит в ближайшее левое состояние, в результате чего происходит возвра-
щение в состояние 0. С противоположной вероятностью р цепь Маркова оказы-
вается в состоянии 2. Как уже отмечалось, вероятность /2,1 достижения ИЗ Со-
стояния 2 состояния 1 равна /0 0. Если эта возможность осуществится, то переход
из состояния 1 в состояние 0 происходит с той же вероятностью /о,о-
Итак, по формуле полной вероятности получаем такое соотношение:
J о.о ~ ч т Р J о.о J о.о •
Корнями этого квадратного уравнения являются
l + Jl-4pq
/о'° 2р
Заметив, что 1 - 4pq -(р- q)2, запишем корни в виде
f _i + \p-q\
Jo.o ~ о
2р
Проанализируем полученное выражение для различных значений р и q.
Случай q>p. Поскольку | р - q | = q - р, то
f - х±(р~ч)
/о° 2р
(8.44)
Следовательно, два корня такие:
yd) _! + (?-?)_,. /-(2)	_п /п
/о° 2р ’/о° " 2р ~Ч/Р'
Корень должен быть отброшен, как не имеющий вероятностного смысла:
/о о* = Ч/Р > 1- Итак, в случае q>p вероятность возвращения в 0 равна 1. Следо-
вательно, состояние 0, а с ним, согласно теореме 8.10, и все состояния цепи яв-
ляются возвратными.
Случай q =р. Согласно формуле (8.44) в этом случае f00 = 1, то есть состояния О
И все другие состояния цепи Маркова являются возвратными.
Случай q <р. Поскольку | р - q | = р - q, то по формуле (8.44)
_1±(р-<7)
Joo _ г,
2р
Следовательно, корнями являются:
7 °,°	2р - /о.о 2р Ч/Р-
Из двух корней необходимо выбрать один, который соответствует искомой веро-
ятности /о,о возвращения в ноль. Отметим, что при р = 1 цепь Маркова на каж-
дом шаге детерминированно переходит в соседнее правое состояние, так что
232
8. Цепи Маркова
/оо = 0. Этому условию отвечает корень fffl, так что /00 =	= q/p < 1. Следо-
вательно, в рассматриваемом случае все состояния цепи являются невозвратными.
Приведенные рассуждения применимы также для нахождения числа шагов Цо,
потребных для возвращения в состояние 0. Обозначим х среднее число шагов,
потребных для попадания из состояния z, z = 1, 2,... в ближайшее левое состояние
г - 1. Из состояния 0 цепь Маркова всегда переходит в состояние 1, поэтому
ц 0 = 1 + х. Из состояния 1 цепь Маркова всегда осуществляет шаг. Если в ре-
зультате его она попадает в состояние 0, то все на этом заканчивается. В состоя-
ние 2 цепь Маркова попадает с вероятностью р. В этом случае ей потребуется в
среднем х шагов, чтобы вернуться в состояние 1, и еще х шагов, чтобы из состоя-
ния 1 попасть в состояние 0. Поэтому имеем соотношение х = 1 + р • 2г, откуда
находим х = 1/(<? - р ). Поскольку ц 0 = 1 + х, то среднее время возвращения в на-
чало координат
Но=—•	(8.45)
Я-Р
Случай q > р. Среднее время возвращения в ноль ц0 =2<7/(<?-р) конечно. Сле-
довательно, состояние 0 являются возвратным ненулевым, более того — эргодиче-
ским. В этом случае цепь Маркова — эргодическая.
Случай q = p = 0.5. Среднее время возвращения здесь бесконечно, так что состоя-
ние 0 является возвратным нулевым.
Случай q < р. Среднее время ц0 = 2q/(q-p)B этом случае оказывается отрица-
тельным. Все наши рассуждения, приведшие к формуле (8.45), были корректны-
ми. Ошибка могла только быть при приведении подобных членов, содержащих х:
так нельзя поступать, если х = оо. Следовательно, в этом случае средние времена
бесконечны. Этот результат можно было сразу получить из того, что состояние 0
невозвратное, так что с положительной вероятностью время возвращения в ноль
бесконечно.	□
Вышеприведенные результаты могут быть резюмированы следующим образом.
Теорема 8.12. Для любого возвратного состояния) существует единственное не-
приводимое замкнутое множество Cv, содержащее/ и такое, что для любой пары
состояния z и k из Cv fiJt = 1, fkj = 1. Все состояния цепи Маркова единственным
образом могут быть разбиты на непересекающиеся множества Т, Ct, С2,..., такие
что: 1) множество Т состоит из всех невозвратных состояний; 2) если) принадле-
жит Cv, то /д, = 1 для всех k, принадлежащих Cv, и наоборот, f]:k = Для всех k,
не принадлежащих Cv.
Метод разбиения (декомпозиции) пространства состояний конечной цепи Мар-
кова на множество Т невозвратных состояний и на замкнутые классы С1; С2, —
возвратных состояний.
Вход: матрица переходных вероятностей Р конечной цепи Маркова.
Выход: матрица Асе достижимости: Асс^ = 1, если состояние j достижимо из со-
стояния I, и 0 - иначе; вектор Dec принадлежности состояний к классам: если
Dect = ), то состояние i принадлежит классу/ где) = 0 соответствует классу невоз-
вратных состояний Т, j = 1, 2,... — замкнутым классам С,, С2,...
8.5. Дальнейшие результаты по цепям Маркова'
231
Метод: Рассматриваемые задачи — это классические задачи теории графов. Из-
вестно много красивых алгоритмов их решения. Мы выберем алгоритм, бази-
рующийся на ранее сформулированных результатах. А именно, в матрице пере-
ходных вероятностей Р заменим все положительные вероятности на единицы,
Теперь Pf j = 1 будет означать возможность перехода из состояния i в состояние,/
за шаг, a Р(". = 1 — за п шагов. Тогда /С + Р?} +.. ,+Р,” > 0 означает, что состояние/
достижимо из состояния i не более чем за п шагов. Обозначим соответствующую
матрицу достижимости АО = Р + Р2 + ... + Р". Для следующего шага к указанной
сумме следует прибавить значение Р"}+1, вычисляемое по формуле (8.15) как эле-
мент матрицы Р"+1 = Р”Р. Будем применять суммирование по модулю 2, то есть
фактически использовать дизъюнкцию. Тогда матрица достижимости для п + 1
шага AN = АО + Р"Р = AO(I + Р), при этом всюду положительные значения
элементов матриц заменяются на единицы. Если на очередном шаге оказывается,
что матрицы достижимости па данном AN и предыдущем АО шагах совпали, то
это и есть искомая матрица, и вычисления заканчиваются. Соответствующая
программа Лсс(Р) приведена ниже в компьютерном практикуме.
По полученной матрице достижимости А состояния можно разбить на классы,
руководствуясь последней теоремой (или критерием неприводимости из разде-
ла 8.2). Согласно ей, состояние i возвратно, если не существует состояния j, в ко-
торое можно попасть из г, но из которого нельзя попасть в г. Это легко прове-
ряется по матрице А: каждый элемент z-й строки не должен быть больше
соответствующего элемента z-го столбца. Далее, в один замкнутый класс С попа-
дают возвратные состояния, для которых строки матрицы достижимости А сов-
падают. Состояния, не попавшие ни в один из замкнутых классов, образуют
множество невозвратных состояний Т. Все эти вычисления производятся про-
граммой Dec(P).
Теорема 8.13. В конечной цепи Маркова все состояния не могут быть невозврат-
ными, и в ней нет нулевых возвратных состояний.
Доказательство
Для каждой строки матрицы Р” = (р^ ) сумма ее элементов равна единице^ при-
чем число элементов конечно. Поэтому невозможно, чтобы при заданном J
/** д’ -->0 при всех k. Следовательно, найдется индекс k, для которого сумма
неограниченно возрастает при п -> со. Теперь из части 1) теоремы 8.10
(‘I
следует, что k — возвратное состояние. Более того, из части 2) теоремы 8.10 сле-
дует, что k — ненулевое возвратное состояние. Следовательно, не все состояния
цепи невозвратные, так что первое утверждение доказано.
Далее, каждое возвратное состояние принадлежит некоторому неприводимому
множеству С, все состояния которого однотипны. Если ограничиться только со-
стояниями из С, то мы имеем неприводимую конечную цепь Маркова. По только
что доказанному, в ней существует ненулевое возвратное состояние. Поскольку
согласно теореме 8.11 все состояния С однотипные, то все они — ненулевые воз-
арагпыс.	□
234
8. Цепи Маркова
Следующая теорема обобщает теорему 83 на случай счетных цепей Маркова.
Теорема 8.14. В неприводимой эргодической цепи Маркова существуют не зави-
сящие от начального состояния i пределы {я,}:
я = limply.	(8.46)
Эти пределы строго положительны (я, > О V j е Е) и удовлетворяют условию
нормировки Я) + я2 + ... = 1, а также системе линейных алгебраических уравнений
7 = 1,2,...	(8.47)
i=i
Обратно, если неприводимая цепь Маркова непериодическая и существуют чис-
ла Oj > 0, удовлетворяющие системе (8.47) и условию нормировки, то цепь эрго-
дическая, и для {dj} справедливы соотношения (8.46) и неравенство
я, =—— >0,	(8.48)
Ну
где ц; — среднее время возвращения в состояние/
Определение 16. Распределение вероятностей {я,}, удовлетворяющее условию
(8.47), называется инвариантным или стационарным для данной цепи Маркова.
Смысл инвариантности заключается в том, что если на начальном шаге состоя-
ния имеют инвариантное распределение, то оно будет таким же и на следующем
шаге и так далее, то есть оно «увековечивается» на все времена.
Основная часть теоремы 8.14 теперь может быть сформулирована так: неприво-
димая непериодическая цепь Маркова обладает инвариантным распределением
тогда и только тогда, когда она эргодична. В этом случае все яу > 0 и вероятно-
сти состояния j на п-м шаге а\п) стремятся к яу независимо от начального рас-
пределения вероятностей состояний.
Критерий. Если цепь обладает инвариантным распределением вероятностей {яД,
то я;. = 0 для каждого j, являющегося либо возвратным нулевым, либо невозврат-
ным.
Доказательство
Пусть {я,} — стационарное распределение, удовлетворяющее (8.47). Тогда
1=1	f=l V=1	r=l 1=1	п=1
и по индукции получаем, что {я,} удовлетворяет и системе
ai =Ха.Р^-
Если j — невозвратное или возвратное нулевое, то согласно теореме 8.10, р.^ -> О
и поэтому, как и утверждалось, я; = 0.	□
Примеры
Пример 8.11. Цепь Маркова ^размножения и гибели*. Рассмотрим обобщение
цепи Маркова, изучавшейся в примере 8.10. Допустим, что вероятности перехода
цепи Маркова за шаг зависят от текущего состояния цепи. Итак, рассматривает-
8.5. Дальнейшие результаты по цепям Маркова'
ш
ся случайное блуждание точки по целочисленным точкам неотрицательной ПО*
луоси R = {0, 1, 2,...}. Находясь в состоянии г, г > 1, точка с вероятностью pt пере*
мещается на следующем шаге в соседнее справа состояние г + 1; с вероятностью
q, перемещается влево в состояние i - 1; с вероятностью 1 - р, - qt остается НЯ
месте в состоянии г. Из состояния 0 перемещение влево невозможно, так ЧТО
q0 = 0. Система уравнений (8.47) примет в данном случае вид
ао = (1_ Ро )ао + <7i ai -	(8.49)
а< = (1 - Р, - <7, )«, + qi+t ai+l + p^ aiA, i = 1,2,...
В предположении, что для всех i = 1, 2,... q, * 0 эти уравнения могут быть после*
довательно разрешены относительно а0;
Щ = — а0, а2=^а0, а3=™^а0, ...
<71	<71 <?2	<71<?2<?3
Общая формула имеет вид
а; = р°р'-р<-' а0, i = 1,2, ...	(8.50)
<71<?2--<7i
Способ получения равенств (8.50) показывает, что это — единственное решение сис-
темы (8.47). Вероятность а0 находится из условия нормировки £ а, = 1. Если ряд

(8.51)
конечен, то значение ад определяется по формуле
ао=Г1 + Х^Р,---М‘.	(8.52)
\ i=l <71<?2’"<7i >
Итак, конечность суммы (8.51) является необходимым и достаточным условием
существования инвариантного распределения. Если сумма бесконечна, то все со-
стояния невозвратные или возвратные нулевые. Случай р, = р, «у, = q, р < q дает
вргодичную цепь Маркова, поскольку сумма геометрической прогрессии со зна-
менателем p/q меньше единицы.
Пример 8.12. Процесс обслуживания в дискретном времени. В данном случае вре-
мя измеряется в тактах. Рассмотрим систему, состоящую из s обслуживающих
аппаратов, каждый из которых одновременно может обслуживать одно требова-
ние. Требования поступают в систему извне, обслуживаются в ней и затем поки-
дают систему. Если в момент поступления требования свободных аппаратов нет,
то требование ожидает начала обслуживания. В момент освобождения аппарата
из очереди (если таковая имеется) на обслуживание принимается очередное тре-
бование. (Дисциплина очереди, то есть порядок выбора требований, в данном
случае роли не играет.)
Формально процесс обслуживания представляет собой счетную цепь Маркова с
пространством состояний Е= {0,1,...}. Такты процесса обслуживания соответст-
вую)' шагам цепи Маркова. Состояние i еЕ означает наличие i требований в сис-
теме. За каждый такт с вероятностью а поступает новое требование в систему,
и с вероятностью qt -р завершается обслуживание требования, где
236
8. Цепи Маркова
р > 0 — интенсивность обслуживания одним аппаратом, i — состояние системы
(X
(число требований в ней). Предполагается, что a + ps < 1, р =— <1. Проведем
анализ описанного процесса обслуживания.
Мы имеем дело с цепью Маркова размножения и гибели: на каждом шаге цепь
или остается в том же состоянии г, или переходит в соседние состояния г + 1 или
i - 1. Поэтому справедливы вышеприведенные формулы для стационарных ве-
роятностей состояний {а,}, в которых следует положить для всех г е Е р, = а.
Проверим условие конечности суммы (8.51), обеспечивающее существование
стационарного режима. Имеем:
для 1=1,2, ..., $:
PoPi-Pm = а/ 1	= -f-T;
?192...9,	р-2р-...-1р l!<pj’
для i = s +1, s + 2,...:
P^-::PEL=aj______________I__________=lsy.
4\42---4i Ц-2p •...•($-l)p • sp ...sp s'apJ s!
Следовательно,
у1 PoPi Pi-i = V A
<=i ?i?2---?/ wi!
a A 1 j 1Гсс^ 1 a p
— + — s Ур = 5 — — +----------------------—,
^P J s! ,=J+i	/-it! ^p)	s!^p; 1-p
если p < 1. Итак, при p < 1 сумма конечна. Отметим, что если бы условие р < 1 не
выполнялось, то сумма р + р2+р3 + ...не была бы конечной, и поэтому стацио-
нарного режима не существовало. Обычно р называют коэффициентом загрузки
обслуживающих аппаратов.
Из приведенных соотношений и формул (8.52) и (8.50) получаем явные выраже-
ния для вероятностей состояний:
«о
, № Y1
1 | а 1 р
$KpJ 1-р,
а,
1 („
— — а0, г = 1, 2, ..., $,
г^р J
i a I	. Л
— — Is	6Zq, I — S + 1, S + 2, ...
s !<p J
Эти формулы позволяют вычислить различные показатели эффективности про-
цесса обслуживания, такие как средняя длина очереди, среднее число требова-
ний в системе и т. д.
Рассмотрим численный пример. Пусть $ = 3, a =0.21, р =0.1. Коэффициент за-
грузки аппаратов р = 0.21/(3-0.1) = 0.7, то есть меньше единицы.
Следовательно, стационарный режим существует. Распределение вероятностей
числа требований в системе представлено в табл. 8.2.
Компьютерный практикум № 13. Анализ цепей Маркова в пакете Mathcad
237
Таблица 8.2. Распределение числа требований в системе
i	0	1	2	3	4	5	6	7
ai	0.096	0.201	0.211	0.148	0.103	0.072	0.051	0.035
i	8	9	10	И	12	13	14	15
а.	0.025	0.017	0.012	0.009	0.006	0.004	0.003	0.002
Компьютерный практикум № 13.
Анализ цепей Маркова в пакете Mathcad
Цель и задачи практикума
Целью практикума является освоение методов представления и анализа цепей
Маркова в пакете Mathcad.
Задачами данного практикума являются:
□	задание матрицы переходных вероятностей для цепи Маркова;
□	моделирование цепи в течение заданного количества шагов;
□	нахождение нестационарного и стационарного распределения вероятностей
состояний для эргодической цепи;
□	вычисление средних времен пребывания в невозвратных состояниях погло-
щающей цепи;
□	определение замкнутых классов состояний.
Необходимый справочный материал
Как и ранее, будут использованы стандартные функции, предоставляемые паке-
том, в частности, для работы с матрицами. Назначение этих функций описано
памп в предыдущих практикумах. Из новых отметим функцию identity(n), кото-
рая формирует единичную матрицу размера п (все диагональные элементы рав-
ны единице, а недиагональные — нулю).
Реализация задания
Для проведения вычислений нам понадобится ряд функций пользователя. Про-
граммные модули, реализующие эти функции, представлены на рис. 8.3 и 8.4.
Функция ТгРг(Р. п) вычисляет по формуле (8.15) матрицу переходных вероят-
ностей состояний цепи Маркова за п шагов, если матрица переходных вероятно-
стей за шаг есть Р. Безусловные вероятности (8.16) состояний цепи Маркова на
п-м шаге вычисляются функцией UnTrPr(a, Р, п), где а — это вектор вероятно-
стей состояний на нулевом шаге. Функция StPr(a, Р, п) вычисляет вероятности
состояний для всех п шагов, в предположении, что на нулевом шаге распределе-
ние вероятностей состояний есть а.
('ледующая группа функций обеспечивает моделирование цепей Маркова, реа-
и । ту я алгоритм, изложенный в конце раздела 8.1. Функция Def(z, х) определяет
помер интервала /, в котором содержится число х. Длины интервалов а0, а(,... со-
держатся в пек торе-столбце а. Функция ModMCh(&, Р, п, RN) осуществляет де-
К’рмнннроваппос моделирование цени Маркова в течение п шагов, выдавая одну
траекторию для заданного вектора RN. В качестве входных переменных исполь-
зуются: вектор а, определяющий начальное распределение вероятностей состоя-
238
8. Цепи Маркова
ний цепи; матрица Р вероятностей переходов между состояниями за шаг; век-
тор RN, содержащий п + 1 компоненту RNit RN, < 0 < 1, которые используются
при определении состояний цепи Маркова на различных шагах (компонента RN0
используется для выработки начального состояния цепи согласно распределе-
нию а, остальные компоненты — для выработки состояний на шагах 1, 2,	и).
Эта функция используется в модуле, реализующем основную функцию
ImModMCh(a, Р, п, т), которая сама генерирует значение вектора RN. Данный
модуль осуществляет имитационное моделирование цепи Маркова в течение п ша-
гов. Здесь а, Р, п те же, что и в предыдущей программе, а т — число моделируемых
траекторий. Функция ImModMCh в качестве результата возвращает матрицу, стро-
ки которой соответствуют номеру шага, а столбцы — номеру реализации. На их пе-
ресечении стоит номер состояния на данном шаге в соответствующей реализации.
Практикум Ме 13. Цепи Маркова
>схие Функции
Переходные вероятности состояний
цепи Маркова за п шагов
ТгРг(Р.п) :-Р"
Безусловные вероятности состояний
цепи Маркова на n-м шаге
UaTtPr(a.P.n)аТ р"
Вероятности состояний в течение п шагав ири
начальных вероятностях состояний а
Номер интерваиа, содержащеге числе х
StPr(e,P,n) >
k<- rows(P)
for id . k
far te I n + 1
for i d.. k
Детерминированное модеииреванне цепи Маркова Имитационное моделирование цепи Маркова
MedMCh(a.P.n.RH)
i«- Def(a .RNq)
ImMadMCh(a.P.n.m) >
Xo<-I
пвт«- (и + 1) m
RR«- гииИ(иит,0,1)
for re0.. т- 1
to г (п + 1)
for tcO . n
X4’ MadMCh(a.P.n.RN)
Частоты различных сестоииий при имитациеннеи моделировании
FrModMCh(a, Р, я, т)»
X*-imModMCh(a.P,n.m)
k<-rowo(P)
for teO . я
far ieO . k-1
Fr(J<-0
far r e 0.. m - 1
+ -J-
m
fJ
Рио. 8.3. Пользовательски* функции для моделирования цепей Маркова
Компьютерный практикум № 13. Анализ цепей Маркова в пакете Mathcad
238
Функция FrModMChla, Р, п, т) подсчитывает частоты различных состояний в m
траекториях цепи Маркова, каждая из которых содержит п шагов. Строки соот-
ветствует состояниям, а столбцы — номеру шага. На их пересечении стоит час-
тота данного состояния на этом шаге.
Следующие функции проводят аналитический расчет цепи Маркова (см. рис. 8.4).
Стационарные вероятности состояний эргодической цепи Маркова, имеющей
матрицу Переходных вероятностей Р, рассчитываются функцией StStPrMc^P)
согласно формулам (8.27), (8.28). Структура выдаваемой матрицы такая же, что
и для предыдущей функции.
Эргодические цепи Маркова
Стационарные вероятности состояний
StStPr(P)	k<-	rowe(P)
	fo	Je 1.. k- 1 hj-1 ♦-1 for lei.. k-1
	b*	-/ (Identltyfk - 1) - 0)” 1
	>0	-(1+ |ьь|)-’
	fo	lei., k- 1
	a	<- (bT ' ao
Поглоцаюцио цеии Маркова
Сродное число визите» в невозервтные состояния
MeanV(P.m)	k <- rows(P)
	fer 1 e 0.. k - m - 1
	for jeO.. k-m-1
	Qi J
	A <- (ldenthy(k - m) - Q)~
	A
Вероятности поглощения
AbPr(P.m) :
к«- rows(P)
for I е 0.. к- m- 1
for jеO k- m- 1
QiJ*- Pm+i.m+j
for j e 0.. m - 1
B| J*~ pm+l J
R*-(ldentMy(k-m)-Q)"1B
R
Асс(Р)>
к»-г««(Р)	Матриц.
ANР + identhy(k) дестиживости
j ( 1	состояний
while f в 1
f<-0
АО*- AN
АН<-Р АО
for IeO.. к-1
for jeO к- 1
I ANi j «- lf(AN|,j > 0,1,0)
|f «- f + Jf(AN| j - AO, ( .0.1)
Dec(P)
AH
к <- rowe(P)
A <- Acc(P)	Зеикнутыо классы
.	. л , л состояний
fer ieO k- 1
|Coj*-l
C1*-D
for ieO k- 1
if Cfj-0
f*-0
for jeO ..k-1
f«-f+lf(Aij$ Ajj.O.I)
If f>0
Cl Cl + 1
Cl,|*-C1
fer j< I k-1
for miO. k- 1
• |Aj,m-A|,m|
Cjjt-CI И веО
Рио. 8.4. Пользовательские функции для анализа цепей Марково
240
8. Цепи Маркова
Группа функций используется для анализа поглощающих цепей Маркова.
Функция Mean V(P, т) вычисляет по формуле (8.34) среднее число визитов в не-
возвратные состояния вплоть до выхода цепи Маркова из множества невозврат-
пых состояний. Здесь Р — матрица переходных вероятностей, представленная в
виде (8.29), т — число возвратных состояний. Напомним, что вначале? нумеру-
ются возвратные состояния, так что первые т строк и столбцов матрицы Р свя-
заны с возвратными состояниями. Последцие строки и столбцы описывают ве-
роятности переходов между невозвратными состояниями, число которых k - т,
где k — общее число состояний цепи. Им соответствует квадратная матрица Q
размера k - т. Вышеупомянутое число т находится с помощью функции £>ес(Р),
которая описывается ниже.
Функция АЬРг(Р, т) рассчитывает вероятности поглощения в различные воз-
вратные состояния, если на начальном шаге цепь Маркова находится в опреде-
ленном невозвратном состоянии (см. формулу (8.39)). В функции используется
матрица R, являющаяся подматрицей Р. Столбцы матрицы R соответствуют
возвратным, а строки — невозвратным состояниям цепи Маркова, так что эта
матрица дает вероятности переходов за шаг из каждого невозвратного в возврат-
ное состояние. Результатом работы функции АЬРг(Р, т) является матрица,
столбцы которой соответствуют т возвратным состояниям, а строки — k - т не-
возвратным состояниям. На их пересечении стоит вероятность того, что для
цепи Маркова, выходящей из рассматриваемого невозвратного состояния, пер-
вым возвратным будет данное состояние.
Заключительные две функции позволяют определять замкнутые классы воз-
вратных и класс невозвратных состояний цепи Маркова. Функция Асс(Р) рас-
считывает матрицу достижимости для состояний согласно методу, приведенно-
му в разделе 8.5. Строки и столбцы этой матрицы соответствуют состояниям
цепи Маркова. На пересечении i-й строки иу-го столбца стоит 1, если состояние j
достижимо из состояния г, и 0 — иначе.
Функция £>ес(Р) для каждого состояния определяет номер замкнутого класса, к
которому состояние принадлежит. Исключением здесь являются состояния, ко-
торым соответствует нулевой номер класса: эти состояния являются невозврат-
ными. Нулевая строка выводимой матрицы содержит номера состояний, а сле-
дующая строка — номера классов, к которым принадлежат эти состояния.
Результаты вычислений
Результаты выполнения задания представлены на рис. 8.5. Вначале задаются:
матрица вероятностей переходов за шаг Р и вектор вероятностей состояний на
нулевом шаге а. Обращение к функции StPr(a, Р, 5) дает вероятности состояний
цепи Маркова в течение пяти шагов. Результатом данной функции является
матрица, столбцы которой соответствуют номерам шагов (эти номера указаны в
нулевой строке), а строки — номерам состояний (эти номера указаны в нулевом
столбце). Например, на втором шаге вероятности состояний составляют: первого
0.16, второго 0.18, третьего 0.17 и четвертого 0.49. Эти вероятности можно срав-
нить с частотами состояний, полученными функцией имитационного моделиро-
вания ImModMCh(a, Р, 5, 10000) и обсчитанными в ModMCh{a, Р, п, RN).
Стационарные вероятности состояний подсчитываются для матрицы переход-
ных вероятностей Р2 с помощью функции StStPr(P2).
Компьютерный практикум № 13. Анализ цепей Маркова в пакете Mathcad
241
Результаты вычислений
Матрица аеродтнастм лерехадое за шаг
Вектор вероятностей состояний на
(Ы 0.6 О О
0.8 02 О О
0 0	10
нулевой шага
О 0.2 0.1 0.7/
г0'
О
О
Л,
Вероятности состояний цели Маркова в течение 5-ти шагов
	0 0 1	2	3	4	5
	1 0 0	0.16	0.20В	0.267	0298
StPr(a.P,5) -	2 0 02	0.10	023	0239	0256
	3 0 0.1	0.17	0219	0253	0277
	ч4 1 0.7	0.49	0.343	024	0.168
0
О
Имитационное моделирование цепи Маркова. Частоты состояний
0	0.171	0206	0.273	03 '
0.21	0.175	0238	0239	026
0.095	0.163	0213	0245	0.266
0.695	0.491	0243	0242	0.172 ,
FrModMCh(a. Р.5.10000)-
Стационарные вероятности состояний для зргодической матрицы Р2
1 1 Г
3 3 3
13 1
<5 5 5,
025 '
StStPr(P2) - 0.333
<0.417,
Поглощающая цепь Маркова РЗ
' 1	О О	О	О'
0	10	8	0
РЗ - 0 02 02 0.3 0.3
Среднее число визитов в невозвратные
состояния
О 0 0.5 02 02
<0.1 0 0.4 0.4 0.1
MeanV(P3,2)
3.922
3.725
<3399
2249
3222
2.В76
2.157
2.549
3.203
Вероятности поглощения о различные возвратные состояния
f0216 0.784
АЬРг(Р3.2) - I 0255 0.745
10.32 0.66
Матрицы достижимости состояний цепи
	10000' 0 10 0 0
Асс(РЗ) -	11111
	11111
	<11111,
Принадлежность состояний цепи
к различным классам
(0 1 2 3 4^
Dec(P3) -
<1 2 0 0 0/
Рис. в.5. Результаты вычислений для цепей Маркова
Дилер рассматривается поглощающая цепь Маркова с матрицей вероятностей
переходов за шаг РЗ. Функция A/eanV(P3, 2) выдает среднее число визитов в не-
возвратные состояния. Невозвратные состояния соответствуют строкам (для на-
чальных состояний) и столбцам (для посещаемых состояний) распечатываемой
матрицы. Например, при выходе из первого невозвратного состояния цепь Мар-
242
8. Цели Маркова
/
кова посетит в среднем 3.922 раз это же состояние, 2.549 — второе и 2-157 —
третье невозвратные состояния.	/'
Функция АЬРг(РЗ, 2) дает вероятность поглощения в различные возвратные со-
стояния. В первое состояние цепь Маркова попадает из невозвратных состояний
с вероятностями 0.216, 0.255 и 0.320. С противоположными вероятностйми 0.784,
0.745 и 0.680 цепь после выхода из невозвратных состояний оказывается во вто-
ром возвратном состоянии.
Функция Лсс(РЗ) рассчитывает матрицу достижимости для состояний цепи
Маркова с матрицей РЗ. Цепь Маркова не может выйти из каждого возвратного
состояния (две первые строки матрицы), так что эти состояния являются погло-
щающими. А из каждого невозвратного состояния можно попасть в любое со-
стояние цепи (три последние строки матрицы). Функция Оес(РЗ) описывает
принадлежность состояний к различным классам. Например, каждое из двух
первых состояний образует замкнутые классы с номерами 1 и 2. Остальные три
состояния попадают в нулевой класс, то есть они являются невозвратными.
Задания для самостоятельной работы
1.	Используйте представленные выше функции пользователя для вычислений
при решении нижеприведенных задач 8.1 и 8.2.
2.	Используя функцию Dec, разбейте множество состояний цепи Маркова, рас-
смотренной в примере 8.5, на замкнутые классы.
3.	Проанализируйте логику работы программы, реализующей функцию StPr.
4.	С помощью функций MeanV и АЬРг вычислите средние времена пребывания
в невозвратных состояниях до поглощения и вероятности поглощения в раз-
личные возвратные состояния для матрицы переходных вероятностей Р2 из
задачи 8.1.
5.	Разработайте программу, вычисляющую стационарное распределение вероят-
ностей состояний для цепи Маркова типа «размножения и гибели» (см. при-
мер 8.11).
6.	Составьте программы, выполняющие необходимые вычисления в задачах 8.4
и 8.5.
7.	Составьте программу, вычисляющую матрицу переходных вероятностей за шаг
для обращенной цепи Маркова, описанной ниже в задаче 8.9.
Задачи
Задача 8.1. Дайте классификацию состояний цепей Маркова со следующими
матрицами переходных вероятностей за шаг:
	' 0	0	0	1 '		'1/4 1/4 0 1/4 1/4"
			1	0	0	0	0
Р1 =	0 1/2 1/2 0 0	10	0	, Р2 =	0	0 2/3 1/3 0
	10	0	0		0	0 2/5 2/5 0
			ч 1/8 1/4 1/8 0 1/2,
Задачи
243
Задача 8.2. Пусть начальное распределение вероятностей состояний цепи Мар*
кова задается вектором а(0) = (1, 0, 0) и пусть матрица переходных вероятностей
есть
( 0.2 0.6 0.2'
Р= 0.3 0.2 0.5 .
^0.7 0.1 0.2,
Найдите распределение вероятностей состояний цепи за п = 1, 2, 3 шага, а также
ее стационарное распределение.
Задача 8.3. Пусть Уь У2, ••• — независимые целочисленные случайные величины
с одним и тем же распределением вероятностей р, - Р{У = г}, i = 0, 1, ... Пусть
Sn = У] + У2 + ... + У„ — сумма первых п таких величин. Покажите, что последова-
тельность S2.....Sn образует цепь Маркова. Какой будет матрица переходных
вероятностей для этой цепи?
Задача 8.4. Модель запасов. Недельный спрос на некоторую продукцию, храня-
щуюся на складе, является целочисленной случайной величиной У, имеющей
распределение вероятностей Р{У = i} = pjt i - 0, 1, ... Спрос за разные недели —
взаимно независимые случайные величины. Пополнение запаса продукции про-
исходит раз в неделю по стратегии (s, S): если в начале недели объем хранящейся
продукции больше уровня s, то заказ на поставку продукции не делается и ее
объем остается прежним. Если же объем имеющейся продукции меньше или ра-
вен s, то этот объем пополняется до уровня S.
Рассмотрим моменты времени, соответствующие началу недели. Пусть Хя —
объем продукции сразу после ее пополнения в начале и-й недели. Тогда {Х„} —
цепь Маркова, для которой под шагом понимается неделя, а под состоянием —
уровень запаса продукции. Выпишите для этой цепи выражения для вероятно-
стей переходов между состояниями за шаг.
Задача 8.5. Вероятность разорения страховой компании. Первоначальный капи-
тал страховой компании составляет с условных единиц. Ежемесячно этот капи-
тал увеличивается на 8. В течение месяца поступают иски застрахованных кли-
ентов, которые необходимо оплачивать. Количество исков за месяц имеет
распределение Пуассона с параметром X. Иски за различные месяцы — взаимно
Независимые случайные величины. Выплачиваемая по иску сумма равна одной
условной единице. Компания оказывается разоренной, если в конце месяца ока-
жется, что ей нечем оплачивать поступившие за последний месяц иски.
Пусть Xt — фактический капитал компании в начале г-го месяца. Последователь-
ность Хи, Хь Х2, ... является цепью Маркова, шаг которой соответствует месяцу.
Выпишите вероятности переходов между состояниями этой цепи за шаг. Найди-
те вероятность разорения компании за п месяцев. Проведите численные расчеты
для с  5, 8 = 2, X = 2, п = 1,2, 3, 4.
Задача 8.6. Дважды стохастическая матрица. Квадратная матрица из неотрица-
тельных элементов называется дважды стохастической, если сумма элементон
каждого столбца и каждой строки равна единице. Покажите, что если цепь Мар-
кова обладает дважды стохастической матрицей переходных вероятностей, то
244
8. Цепи Маркова
стационарное распределение вероятностей ее состояний будет равновероятным:
каждое из k состояний имеет вероятность 1/k.
Задача 8.7. Пусть цепь Маркова со счетным множеством состояний задается сле-
дующей матрицей переходных вероятностей:
f<7o	Ро	°	0
?!	?!	Pt	0	•••
?2	?2	?2	Pi
V	:	:	:	)
где Pi q,> 0 и pt + (i + l)g, = 1, i = 0, 1, ...
Действуя так, как в примере 8.11, найдите условие эргодичности цепи и выпиши-
те стационарное распределение вероятностей ее состояний.
Задача 8.8. В условиях примера 8.12 выведите явные формулы для математиче-
ского ожидания числа требований в очереди и в системе.
Задача 8.9. Обращенные цепи Маркова. Пусть Р — матрица переходных вероят-
ностей за шаг эргодической цепи Маркова и а — ее стационарное распределение
вероятностей состояний. Напомним, что (г, у)-й элемент ptj матрицы Р есть веро-
ятность оказаться на следующем шаге в состоянии j, если текущее состояние
есть i. А какова вероятность того, что предыдущим было состояние j, если теку-
щим является i и рассматривается стационарный режим цепи? Обозначим эту
вероятность р.ti.
Вероятность р •, может быть найдена из следующего простого замечания: веро-
ятность события «на двух последовательных шагах состояние i сменилось со-
стоянием j » можно подсчитать двумя способами, что приводит к уравнению
a,Pi,j =Oj Pji-
Откуда находим, что р.= a;pj;/ap Так определенные значения р;, неотрица-
тельны и удовлетворяют условию нормировки, поскольку из условия (8.22) для
стационарных вероятностей следует, что
ILPj.i =YaiPij/aj = aj/aj =1 V>-
i	i
Покажите, что стационарные распределения вероятностей состояний для исход-
ной и обращенной цепей Маркова совпадают.
Отметим, что если исходная цепь Маркова позволяет прогнозировать будущее,
основываясь на настоящем, то обращенная цепь позволяет анализировать про-
шлое, основываясь на настоящем.
9 Дискретные марковские
процессы
9.1.	Определение марковского процесса
В цепях Маркова предполагается, что состояния случайного процесса рассмат-
риваются в равноотстоящие моменты времени п = 0, 1,2, ... Можно считать, что
между этими моментами состояние процесса не меняется (рис. 9.1, а). Итак, вре-
мя «сидения» в каждом состоянии кратно шагу. Предположим теперь, что время
пребывания в состоянии i имеет экспоненциальное распределение с параметром
то есть средним 1/1,-. Тогда та же траектория может выглядеть так, как ЭТО
показано на рис. 9.1, б.
t0	t| tj	t3 t4	tj
6
Рис. 9.1. Тоаектооии a — цепи Маокова ив - маоковг.кпгп пппнаг.г.в
246
9. Дискретные марковские процессы
Определение 1. Дискретным марковским процессом (МП) с непрерывным време-
нем X(t) называется процесс, который:
□	имеет дискретное множество состояний Е = {0, 1, 2, ...};
□	длительность непрерывного нахождения процесса в состоянии i имеет экспо-
ненциальное распределение с параметром (интенсивностью выхода из со-
стояния) X, > 0, i = 0, 1,2, ...;
□	по истечении времени пребывания в состоянии i процесс мгновенно (скач-
ком) переходит в состояние j в соответствии с вероятностями переходов phJ
(не исключено, что i = j);
□	длительности пребывания в состояниях являются взаимно независимыми
случайными величинами, не зависящими также от переходов процесса между
состояниями;
□	переходы процесса между состояниями осуществляются в соответствии с
правилами для цепей Маркова, имеющих матрицу переходных вероятностей
Р = (Pi.j)-
Приведенное определение носит конструктивный характер, поскольку позволяет
построить соответствующий марковский процесс. Действительно, пусть марков-
ский процесс находится в состоянии г. С помощью датчика случайных чисел вы-
рабатываем случайную величину, имеющую экспоненциальное распределение
с параметром Х;. Примем ее за время пребывания марковского процесса в со-
стоянии г. По истечении этого времени в соответствии с вероятностями р1Д,р,2,...
вырабатываем следующее состояние, в которое переходит марковский процесс.
Далее описанная процедура повторяется. Изложим соответствующий алгоритм
моделирования марковского процесса.
Алгоритм базируется на соответствующем алгоритме для цепей Маркова, приве-
денном в разделе 8.1. Отличие заключается в том, что кроме последовательности
состояний, в которые переходит марковский процесс, необходимо указывать и
длительности пребывания в состояниях. С этой целью мы рассматриваем скачки
марковского процесса (т. е. цепь Маркова) и фиксируем состояние Хп после и-го
скачка и момент времени Тп следующего (п + 1)-го скачка. Пару X = (Хо, Xit ...),
Т = (Та, 1\,...) будем называть протоколом марковского процесса. Фактическое со-
стояние марковского процесса X(t) в момент времени t определяется на основа-
нии протокола (X, Т) по формуле
Х(О = Х„, Тп_, <t<T„.
Алгоритм моделирования протокола марковского процесса
Вход:
k — число состояний марковского процесса,
Р — матрица переходных вероятностей за шаг,
X — вектор интенсивностей выходов из состояний Хо, X,,...,	,
а<0) — вектор вероятностей состояний а(0°\ а[0>. а$ в начальный момент
времени t = О,
п — количество скачков процесса, в течение которых осуществляется модели-
рование.
9.1. Определение марковского процесса
247
Выход:
X = (Хо, ...Хп) — состояния цепи Маркова до n-го скачка (шага) включи-
тельно,
Т = (Го, Ti,Тп) — моменты скачков процесса.
Алгоритм
Шаг 0. Выработать равномерно распределенное в интервале (0, 1) случайное
число R и определить начальное состояние марковского процесса Хо на нулевом
шаге, то есть в момент времени 0:
Хо = шт{г=0,1,...,£-1:Я<а<0>+ а‘0) + ... + а,(0>}.
Положить i = Хо. Выработать случайную величину И7, имеющую экспоненциаль-
ное распределение с параметром X,.. Положить То= W, I = 1.
Шаг 1= 1, 2..п. Выработать равномерно распределенное в интервале (0, 1) слу-
чайное число R и определить состояние цепи Маркова X, на /-м шаге:
X, = min{j=0, -1: R<pia +р„ + ... + р^}.
Положить i = X/. Выработать случайную величину И7, имеющую экспоненциаль-
ное распределение с параметром X,-. Положить 7}= 7)_| + W. Перейти к шагу I + 1.
Данный алгоритм реализован в компьютерных функциях ModMpfa, Р, X, R),
lmPMP(a, Р, X, п, т) и Y(a, Р, X, п, 8/ которые описаны ниже в компьютерном
практикуме.
Пример 9.1. Моделирование марковского процесса. Рассмотрим марковский про-
цесс с четырьмя состояниями (k = 4) и следующими матрицей вероятностей пе-
реходов за шаг и вектором интенсивностей выходов из состояний:
0 0.1 0.5 0.4^		'0.5
0.2 0.1 0.2 0.5		1
	, X =	
0.3 0.2 0.2 0.3		0.75
0.1 0.3 0.6 0 ,		1 2
Предположим, что первоначально марковский процесс находится в третьем со-
стоянии (i = 3), так что вектор состояний на нулевом шаге а(0) = (0, 0, 0, 1).
В табл. 9.1 представлен протокол однократного моделирования данного марков-
ского процесса в течение семнадцати скачков (п = 17). Этот протокол был полу-
чен функцией ImPMP. В табл. 9.2 приведена соответствующая траектория про-
цесса, полученная функцией 5.
Таблица 9.1. Протокол однократного моделирования марковского процесса
Номер скачка, 1	0	1	2	3	4	5	6	7	8
Состояние процесса, X,	3	2	3	1	3	2	0	2	2
Момент след, скачка, Т(	0.78	1.57	2.66	2.94	3.24	4.35	5.07	6.18	6.91
Номер скачка, 1	9	10	11	12	13	14	15	16	17
Состояние процесса, X,	3	2	3	1	2	0	2	3	2
Момент след, скачка, Т,	7.14	8.06	8.24	9.90	12.20	13.76	16.86	18.14	18.36
248
9. Дискретные марковские процессы
Таблица 9.2. Траектория однократного моделирования марковского процесса
Момент времени, t	0	1	2	3	4	5	6	7	8
Состояние процесса, X(t)	3	2	3	3	2	0	2	3	2
Момент времени, t	9	10	И	12	13	14	15	16	17
Состояние процесса, X{t)	1	2	2	2	0	2	2	2	3
В табл. 9.3 приведены частоты различных состояний для равноотстоящих с ша-
гом 8=1 моментов времени. Они были получены функциями У(а, Р, v, п, 8)
и FrModMP{a, Р, v, $ п, т) в результате стократного моделирования данного мар-
ковского процесса, осуществленного согласно приведенному алгоритму.
Таблица содержит частоты {рз/t)*} различных состояний в зависимости от мо-
мента времени t, а также истинные вероятности состояний {p3j{t)}, подсчитанные
по формулам (9.10) и (9.15). При t, стремящемся к бесконечности, вероятности
состояний стремятся к некоторым положительным константам. Эти константы
называются стационарными вероятностями состояний. Они приведены в по-
следнем столбце таблицы, в шапке которого записано t = со. Мы вернемся к обсу-
ждению этих результатов в разделе 9.4.	□
Таблица 9.3. Распределение вероятностей и частот состояний
	t = 0	t= i	t = 2	t = 3	t = 5	t = 10	t = co
А,«(О*	0	0.159	0. 211	0.246	0.274	0.309	
А,о(0	0	0.150	0.226	0.264	0.292	0.300	0.301
А..(0‘	0	0.192	0.191	0.176	0.158	0.167	
Рз.|(О	0	0.201	0.194	0.180	0.169	0.165	0.165
Рз.з(О*	0	0.438	0.461	0.462	0.472	0.418	
Рз.зЮ	0	0.433	0.446	0.433	0.421	0.417	0.416
Рз,з(О*	1	0.211	0.137	0.121	0.096	0.106	
Рз.з(О	1	0.216	0.133	0.122	0.119	0.118	0.118
Отметим два свойства марковского процесса. 1) Если рассматривать только мо-
менты скачков процесса, то имеет место обычная цепь Маркова. О ней говорят
как о вложенной цепи Маркова. 2) Информация о том, сколько времени уже на-
ходится процесс в состоянии г, не влияет на длительность остающегося времени
пребывания в этом состоянии. Это свойство экспоненциального распределения
называется отсутствием памяти и вытекает из следующей леммы.
Лемма 9.1. {Отсутствие памяти экспоненциального распределения). Пусть W —
случайная величина, имеющая экспоненциальное распределение с параметром
X. > 0. Тогда для х, у > 0
P{W>x + y | W>y}=P{W>x}.	(9.1)
9.1. Определение марковского процесса
240
Доказательство
Для экспоненциального распределения (4.10) дополнительная функция распре*
деления случайной величины IV дается формулой
P\W>x} = е~1х,х> 0.	(9.2)
Поскольку в силу положительности х и у событие {IV > х + у} влечет событие
{W>y}, то
{W >х + у, W > у} = {W > х + у}.
Следовательно, для условной вероятности события {IV > х + у} при условии, ЧТО
событие {IV > у} произошло, имеем выражение
пптл I irz i >х +У> W > у} P{W >х + у}
P{W > х + y\W > у} = —------—------— = -1-------— =
P{W>y}	P{W>y}
= ^— = е-^ = P{W>x}.
□
Отмеченные выше свойства говорят о том, что в каждый момент времени мар-
ковский процесс полностью описывается состоянием, в котором он находится:
ни время пребывания в этом состоянии, ни то, как он сюда попал, роли не играет
(по свойствам экспоненциального распределения и цепей Маркова). Это свойст-
во, как и для цепи Маркова, называется марковским и означает «зависимость бу-
дущего только от настоящего, но не от прошлого».
При исследовании марковских процессов мы часто будем применять следующее
их свойство, сформулированное ниже.
Лемма 9.2. Пусть марковский процесс находится в состоянии i, в течение време-
ни х. Тогда вероятность того, что в течение ближайшего элементарного интерва-
ла времени длиной A t будет иметь место скачок процесса, равна Х; A t + о(Д t).
Доказательство
Пусть IV есть полное время пребывания процесса в данном состоянии. Событие
(х < IV <, х + АГ} можно представить в виде разницы событий {IV > х} и {IV > х + At}.
Теперь на основании леммы 9.1 имеем соотношения для малых At:
Р{х <W < х + A t| IV >х}= P{W >х|IV >х} -P{W >x + At|IV >x} =
= 1 - P{IV > At} = 1 - e~>/AZ = 1-(1-X, At + o(At)) = X,At + o(At). □
Лемма 9.3. Пусть IV и V — две взаимно независимые случайные величины, имею-
щие экспоненциальное распределение с параметрами X и р. Тогда случайная
иеличипа Z = min{IV, V} имеет экспоненциальное распределение с параметром
а  X. + р. Кроме того, P{IV < V} = Х/(Х + р).
Доказательство
Дополнительная функция распределения случайной величины Z имеет вид
P{Z >z} = P{W >z,V >2} = P{W > z} P{V > z} = e'>Je^ =	”.
Следовательно, Z имеет экспоненциальное распределение с параметром а  Х + р.
Рассмотрим теперь событие {IV S V). Случайная величина IV принимает значе-
ние ил пптсрвала (х, х + dx) с вероятностью X exp (-Хх)<7х + o(dx). Рассматри-
250
9. Дискретные марковские процессы
ваемое событие наступает, если V превышает значение х, вероятность чего
ехр(-цл) + o(dx). Интегрируя это по значениям х, окончательно получаем:
P{W <V} = \e-vxXe-yxdx = -^~.	□
о	^- + Ц
Приведенные леммы будут интенсивно использоваться при исследовании мар-
ковских процессов.
9.2.	Уравнения Колмогорова
Как и для цепи Маркова, при изучении марковского процесса основной интерес
представляют вероятности переходов между состояниями за заданное время.
Пусть означает вероятность перехода процесса из состояния i в состояние j
за время t:
Эти вероятности необходимо выразить через величины {X,} и {Р;Д, определяю-
щие марковский процесс. С этой целью рассмотрим первый скачок процесса по-
сле момента 0. Возможны два случая. Во-первых, этот скачок может произойти
после момента времени t, вероятность этого ехр(-\£)- В этом случае в момент t
процесс будет иметь исходное состояние I. Во-вторых, первый скачок может про-
изойти до момента t, в некотором интервале {и,и + Aw), вероятность этого
X; exp(-X,w)</w. После этого процесс скачком переходит в некоторое промежу-
точное состояние v, вероятность чего есть piv. Наконец, за оставшееся время
t - и процесс переходит из состояния v в состояние j, вероятность этого есть
p„ j (t - и). Поскольку в качестве и может фигурировать любой момент времени
от 0 до i, а в качестве промежуточного состояния v любое состояние, то справед-
ливо уравнение
р, у(Г) = 8.;е"х'' + e~Ku YPi.vPv.j(t-u)du,
0	V
где
[1 при i = j,
о,-  = <
[0 при i * j.
Умножая обе части этого уравнения на ех,‘ и производя в интеграле замену пере-
менных у = t - и, находим, что
‘Pi.jCt') = 8,.j + К j v Z PiyPyj (y>dy-
0	V
Дифференцируя no t обе части этого равенства, получаем
(t) + ex’‘pitj (t) =
V
После сокращения на exp(X,t) окончательно приходим к формуле
=	Pijtt), ViJ, t^O. (9.3)
9.2. Уравнения Колмогорова
281
К этому необходимо добавить начальные условия
Р,.,(0) = 1> Pi,;(0) = 0 при i*j.	(9.4)
Формула (9.3) описывает так называемые обратные дифференциальные уравне-
ния Колмогорова. При каждом фиксированному они представляют собой систему
обыкновенных дифференциальных уравнений. Решая эту систему, находим ве-
роятности того, что цепь Маркова будет находиться в момент времени I
в состоянии у, если в первоначальный момент времени она находится в состоя-
нии i. Мы видим, что система (9.3) дает ответ на тот же вопрос, что и формула
(8.15) для случая цепей Маркова.
При выводе обратных уравнений Колмогорова все рассуждения проводились на
основе рассмотрения первого скачка марковского процесса. Рассмотрим теперь
не первый, а последний до момента времени t скачок марковского процесса.
Пусть процесс исходит из состояния i в момент времени 0. В момент t он окажет-
ся в состоянии у, если в момент и процесс находился в некотором промежуточ-
ном состоянии v (вероятность этого piy (и)), в интервале (и,и + du) произошел
скачок (вероятность этого равна Ju), причем последующим оказалось состоя-
ние у (вероятность pvj) и после этого скачков не было вплоть до момента време-
ни t (вероятность этого равна ехр{-Х; (t-и)}). Учитывая, что в качестве проме-
жуточного может фигурировать любое состояние, а момент и может быть любым
в интервале (0, t), получаем соотношение (с естественной спецификой случая
Р,.;(О = +JXPi.v(w)^v p^e^’^du, ViJ, г SO.
о v
Умножая обе части полученного уравнения на ехр(Х^) и дифференцируя по t,
приходим к уравнению
Pi.}(t) + e >lpitjCty^YPiAOKP^j е'1'.
V
Итак, окончательно получаем систему, называемую прямыми дифференциальны-
ми уравнениями Колмогорова-.
Pi.j(O=XPMK,Pv.j-\Pi.j(t), Vi,j, i>0.	(9.5)
V
Сюда следует добавить начальные условия (9.4).
В «включение обсудим следующий вопрос: когда следует применять прямые
у|№внгния Колмогорова, а когда — обратные? Обратим внимание на то, что в
прямых уравнениях (9.5) в неизвестных вероятностях фиксировано исходное со-
стояние i, а в обратных уравнениях (9.3) — заключительное состояние у. Поэтому
Прямые уравнения применяются, когда исходное состояние i (в нулевой момент
Времени) известно, и мы интересуемся распределением вероятностей различных
Мстояний в момент времени t.
Обратные уравнения используются, когда имеет место противоположная карта-
ЮТ исходное состояние i является случайным, и мы интересуемся вероятностью
Конкретного СОСТОЯНИЯ / В момент племени /
252
9. Дискретные марковские процессы
Системы обыкновенных дифференциальных уравнений (9.3) и (9.5), как прави-
ло, решаются численными методами. Только в отдельных частных случаях уда-
ется получить аналитическое решение этой системы. Таковым, в частности, яв-
ляется пуассоновский процесс.
9.3. Пуассоновский процесс
Пуассоновский процесс задается условиями:
Е = 0,1,2,..., X, =Х,р..+ 1 =l,i = 0, 1, 2, ...
Следовательно, процесс каждый раз переходит в следующее состояние с боль-
шим номером, причем продолжительность пребывания в каждом состоянии име-
ет экспоненциальное распределение с одним и тем же параметром X для всех со-
стояний.
Однако обычно пуассоновский процесс описывается другим способом. Рассмат-
ривается поток однородных событий. Интервалы времени между событиями яв-
ляются взаимно независимыми случайными величинами, имеющими экспонен-
циальное распределение с параметром X. Мы интересуемся числом событий X(t),
наступивших до момента времени t. Чаще такой процесс называют пуассонов-
ским потоком. Далее мы будем использовать этот термин.
В обоих случаях задача заключается в определении переходных вероятностей
Pij(t) = P{X(t) = j | X(0) = i}. Мы решим эту задачу двумя способами, соответст-
вующими двум приведенным определениям пуассоновского потока. Начнем с
первого определения и применим для решения обратные уравнения Колмогоро-
ва (9.3).
Ясно, что Pjj (i) = 0 при j < i и поэтому (9.3) принимает вид
piJ(O = ^i+i,7(O-^u(O>	*>0-
При i = j получаем
=	£>0,
откуда находим, что
= exp(-Xi), t > 0.
Отметим, что начальные условия (9.4) для данного случая выполняются.
Для i < j умножим исходное уравнение на еи и сделаем следующие преобразова-
ния:
eXtpM(0 + XeuPiJ(0 = Xeupi+u(0,
^(^А,;(О) = ^ pi+lj(t).
Мы имеем дифференциальное уравнение с разделяющими переменными. После
его интегрирования получаем:
= pM j(u)du,
о
9.3. Пуассоновский процесс
26Э
р1: j(t) = е и J Хех“ рм j(u)du, i<j, t>0.
о
Это соотношение позволят находить вероятности Pij(t) рекуррентно. Для
i = j -1, t > 0, находим:
(0 = е>Л J	(и) du = e~U J Хе’'“е“’'“du = Xt е~и.
о	о
При i = j - 2, t > 0 аналогично получаем:
Pj-2,j (0 = e"XtJ ^eK“Pj-\.j (u)du =e*x'J Xex“Xw e~'udu =	e~u.
Общая формула имеет вид:
Рм(г>=^57е'Х£-	^°-	о-в)
Итак, приращение пуассоновского потока за время t имеет распределение Пуассо-
на с параметром Xt.
Этот же результат при втором подходе получается так. Здесь предполагается,
ч,то i = 0, так что X(t) — число событий (скачков потока), наступивших до момен-
та t. Обозначим Sn момент времени наступления n-го события. Поскольку интер-
валы времени между событиями взаимно независимы и имеют одно и то же экс-
поненциальное распределение с параметром X, то согласно примеру 7.3, S„ имеет
распределение Эрланга (4.19) с параметрами Хи п:
P{Sn<t} = l-"£^-e~Kt, t>0.
1=0 11
(Иметим теперь соотношение
{X(t) = n}={Sn <t}-{S„+l <t},
фиксирующее очевидный факт: за время t наступило ровно п событий тогда и
только тогда, когда n-е событие наступает до момента t, а (и + 1)-е событие — не
наступило.
Приведенное соотношение позволяет нам выразить вероятность события
(А'(0 = п} через вероятности событий {5И < t} и {5и+1 < t}. Поскольку событие
। £ 1} влечет событие {5„ < t}, то применяя формулу (1.18), получаем преж-
ний результат:
P{X(t) = n}=P{Sn <t}-P{S„+l <t} =
= 1 _ v	i + v g-’ac _ (*-0л
to i!	h г!	n\
Учитывая отсутствие памяти экспоненциального распределения (9.1), можно
сформулировать следующее основное свойство пуассоновского потока', число со-
бытий, наступающих за непсресекающиеся интервалы времени, являются взаим-
но независимыми случайными величинами, причем частное распределение для
интервала длиной / является пуассоновским с параметром Xt.
254
9. Дискретные марковские процессы
Рассмотрим теперь два независимых пуассоновских потока Х[(Г) и Х2(Г) с интен-
сивностями X и р. Из лемм 9.1 и 9.3 следует, что интервалы времени между собы-
тиями объединенного потока являются взаимно независимыми случайными ве-
личинами, имеющими экспоненциальное распределение с параметром Х + ц.
Следовательно, объединенный поток является пуассоновским.
Вероятность того, что за время t наступило i событий первого потока и п - i со-
бытий второго потока, в силу независимости потоков равна
Р{Х, (0 = i, Х2(0 = п - i} =	е-»
Вероятность того, что за время t наступит п событий объединенного потока, вы-
числяется по формуле
Р{Х{ (0 + Х2 (0 = п} =	+ ечх+м )l.
п!
Условная вероятность того, что за время t наступило i событий первого потока,
вычисленная при условии, что имели место п событий объединенного потока, со-
ставляет
Ж, (0 = z IX, (О + Х2 (0 = п} =
-	У ( р
i!(n-i)’.\X + pJ уХ + ц,
Итак, рассматриваемое условное распределение является биномиальным (3.3) с
параметрами р = Х/(Х + р) и п и не зависит от времени t.
Будем теперь рассматривать моменты наступления событий объединенного по-
тока, которые будем называть шагами и обозначать п = 0, 1,... Пусть Y„ есть раз-
ность между количеством событий первого и второго потоков, наступивших до
п-го шага. Следовательно, на каждом шаге Yn увеличивается на единицу с веро-
ятностью р = Х/(Х + ц) и уменьшается с противоположной вероятностью
q = р/(Х + р). Итак, мы имеем случайное блуждание, рассматривавшееся в разде-
ле 2.4.
Как и ранее, конкретную траекторию (0, Уь У2, -> Yn) можно описать последова-
тельностью приращений ДУ,- = Y}~ Y^t, то есть как (О, ДУЬ ДУ2.. ДУ„), где
XYj = +1 означает скачок первого потока, a AYj = -1 — второго потока. Вероят-
ность любой траектории, содержащей i скачков первого потока и п - i скачков
второго потока, равна, очевидно, Х'ц"~'(Х +ц)~". Следовательно, условная веро-
ятность того, что имеет место данная траектория, вычисленная при условии, что
зафиксировано i скачков первого потока и п - i скачков второго потока, равняется
^"-'(X + p)-"	1	1
।	/ , V(	п\	с1	'
п! I X [ [ ц	।	 —___
i!(n-j)!VX + pJ уХ + ц) i!(n-i)l
9.4. Численное решение уравнений Колмогорова
266
Отсюда следует, что все рассматриваемые траектории равновероятны. Ранее (см.
пример 2.5, задача о баллотировке) это предполагалось априори верным. Следо-
вательно, в случае независимых пуассоновских потоков это действительно так.
Пример 9.2. Задача о баллотировке. Продолжим рассмотрение примера 2.5. Пусть
количество голосов, подаваемых за первого и второго кандидатов, описывается
двумя независимыми пуассоновскими потоками с интенсивностями X и ц соот-
ветственно, на интервале времени (0, 1). Найдем вероятность того, что первый
кандидат был все время впереди.
Обозначим А интересующее нас событие, НаЬ — гипотезу «первый кандидат на-
брал а, а второй b голосов». Условная вероятность события А, вычисленная при
условии, что гипотеза НаЬ произошла, была найдена в примере 2.5 и составляет
(а - Ь)/(а + Ь). Вероятность гипотезы НаЬ находится из условия независимости
потоков по формуле (9.6). Теперь по формуле полной вероятности (1.23) полу-
чаем:
Приведенный пример показывает, как можно использовать ранее полученные
результаты относительно экстремумов случайных блужданий (теорема 2.1), ве-
роятности дефицита (пример 2.7) и пр. в случае пуассоновских процессов.
9.4. Численное решение уравнений Колмогорова
Уравнения Колмогорова (9.3) и (9.5) представляют собой систему линейных
дифференциальных уравнений. Стандартная форма представления последних
следующая:
х = х-А,	(9.7)
где х = (x0(i), х, (t),..., хкЛ (t)) — вектор-строка, компонентами которой являют-
(d.	d	d
СМ неизвестные (искомые) функции; х= —x0(i),—x,(i)...—xt_t(t) — век-
V dt	dt	dt	)
Top производных функций (градиент); A = (a;j )м — квадратная матрица из по-
стоянных коэффициентов.
Решение системы (9.7) выражается через собственные числа и собственные век-
торы матрицы Ат. В связи с этим напомним соответствующие определения. Ц
называется собственным числом матрицы Ат, если оно является решением отно-
сительно v уравнения
|Ат-ц1| = 0,	(9.8)
ГД® |М| — определитель квадратной матрицы М; I — единичная матрица размера k.
Для квадратной матрицы Ат порядка k существует k собственных чисел (с уче-
том ИХ кратности) ц0, t>t,..., vk.t. Мы будем рассматривать случай, когда все собст-
венные числа — различные.
Для каждого собственного числа vt существует ненулевой вектор-столбец z,h,
являющийся решением системы линейных алгебраических уравнений относи-
тельно г
256
9. Дискретные марковские процессы
Атг=ц,г.	(9.9)
Теперь решение системы (9.7) можно представить в виде:
x(O = 2>,e'',£(z<'))T>	(9.Ю)
;=0
где bQ, Ь{, ..., Ьк_! — константы, подбираемые из начальных условий (9.4).
То, что формула (9.10) дает решение системы (9.7), проверяется легко. Во-пер-
вых, отметим, что производная по t от функции x(t), задаваемой формулой (9.10),
есть
x = £6.e!'-'a.(z<i>)T.	(9.И)
1=0
Подставляя выражение (9.10) для х в правую часть формулы (9.7), находим
с учетом соотношений (9.9) и (9.11):
х A = £bie''*t(z<i>)TA = £biev‘t(ATz<i) )Т = '^bieVitvi(zt'r> )т = х.
1=0	i=0	i=0
Итак, действительно, формула (9.10) дает решение системы линейных диффе-
ренциальных уравнений (9.7).
Приведем теперь систему уравнений Колмогорова (9.5) к стандартной форме
(9.7). Будем считать, что начальное состояние i марковского процесса фиксиро-
вано (Р{Х(0) = i} = 1), и положим Xj (f) = Pij (t). Выразим матрицу А через матри-
цу P и вектор X:
X, •»,,, если / * j,
а,,	,	(9.12)
-Pjj -Xj, если I = j.
Матричный вид этого соотношения следующий:
A=D(P-I),	(9.13)
где D = diag(X) — диагональная матрица, на диагонали которой стоят компоненты
Теперь уравнения Колмогорова (9.5) представлены в стандартной форме (9.7).
Как указывалось, решение дается формулой (9.10). Фигурирующие в ней неиз-
вестные коэффициенты {6,} находятся из начальных условий: в нулевой момент
времени t = 0 система находилась в состоянии i:
х, (0) = 1; Xj (0) = 0, j * i.	(9.14)
Пусть е(,) = (0, 0.0,1, 0,... 0) — вектор-строка размерности k, у которой единст-
венная ненулевая компонента стоит на г-м месте и равна единице, Z = (z<0>, z<b,....
z(*'”) — матрица, столбцами которой являются собственные векторы Ат. Тогда
условие (9.14) требует, чтобы х(0) = е(,), и вектор неизвестных коэффициентов
b = (b0, Ьь ..., находится из формулы (9.10):
9.4. Численное решение уравнений Колмогорова	___________________________25Т^
1
х(0) = 2б|.(2<0 )т =bZT, х(0) = е(,) = bZT.
b = e<i)(ZT)-1.	(9.15)
Итак, последовательность вычислений по формуле (9.10) следующая.
1.	Формируем матрицу А согласно формуле (9.13).	I <
2.	Находим собственные числа Vq, Vi....... v^-i и собственные векторы z***,
гЛ ..., z<i4> матрицы Ат. В частности, это можно сделать с помощью стан-
дартных функций eigenval и eigenvec пакета Mathcad.
3.	Составляем матрицу Z, столбцами которой являются собственные векторы
_<0> _<1>
Z , Z , Z
4.	Формируем вектор-строку е0) = (0, 0, ...,0, 1, 0,..., 0) с единственной единицей
на г-м месте и вычисляем вектор b = (6о, Ь\, ..., bk-i) по формуле (9.15).
5.	Вычисляем вектор-строку x(t) = (p,.o(t)> P<,i(0> •••> Р»Л-1(О) по формуле (9.10).
Пример 9.3. Рассмотрим следующую матрицу переходных вероятностей за шаг Р
и вектор интенсивностей выходов из состояний X:
Р =
0	0.1	0.5	0.4
0.2	0.1	0.2	0.5
0.3	0.2	0.2	0.3
0.1	0.3	0.6	0
, Х =
' 0.5 '
1
0.75
. 2 .
Матрица А, вычисляемая по формуле (9.13), имеет вид
A = D(P-I) =
'0.5	0	0	О'	'-1	0.1	0.5	0.4'		' -0.5	0.05	0.25	0.2 '
0	1	0	0	0.2	-0.9	0.2	0.5		0.2	-0.9	0.2	0.5
0	0	0.75	0	0.3	0.2	-0.8	0.3		0.225	0.15	-0.6	0.225
<0	0	0	2,	<0-1	0.3	0.6			< °-2	0.6	1.2	-2 ,
Вектор-столбец собственных чисел матрицы Ат, вычисленный функцией
e(ge«t>a/(AT) пакета Mathcad, таков:
v = vt v2 v3 )т = (-2.322 0 -0.712 -0.966)т.
Этим числам соответствуют следующие собственные векторы, вычисленные
функцией eigenvec(A.\ v,):
1<п> =(0.008 -0.283 -0.527 0.802)т, z"1" =(0.554 0.299 0.754 0.214)т,
1,а> «(-0.838 0.352 0.409 0.078)т, z<3> =(-0.075 -0.591 0.793 -0.128)т.
Легко проверить, что эти векторы действительно удовлетворяют уравнению (9.9).
Например, для первого собственного числа ц0 = -2.322 и собственного вектора
I’9, -(0.008 -0.283 -0.527 0.802)т имеем
258
9. Дискретные марковские процессы
	'-0.5	0.2	0.225	0.2'	( 0.008 )		'-0.019'		( 0.008 )	
Arz<0> =	0.05	-0.9	0.15	0.6	-0.283			0.657	= -2.322	-0.283	= Ц02<°>
	0.25	0.2	-0.6	1.2	-0.527		1.223		-0.527	
	,0.2	0.5	0.225	"2>	, 0.802 ,		,-1.861,		, 0.802 ,	
Вектор постоянных коэффициентов Ь, вычисляемый по формуле (9.15) в пред-
положении, что в начальный момент времени t = 0 процесс находился в нулевом
состоянии, имеет вид
		' 0.008	0.544	-0.838	-0.075^		-1
b = e(0)(ZT)-* =(1 0 0 0)		-0.283 -0.527	0.299 0.754	0.352 0.409	-0.591 0.793		
		, 0.802	0.214	0.078	-0.128,		
Г-0.094 0.552 0.820 -0.165)
= (1 ООО)
-0.347
-0.096
0.552
0.552
-0.443 -0.984
-0.312 0.511
= (-0.094 0.552
0.820 - 0.165).
1.063 0.552 0.370 -0.011J
Теперь у нас имеются все составляющие, с тем чтобы применить формулу (9.10)
для вычисления нестационарных вероятностей состояний =Xj(t):
	>о.о (OV	' 0.008 '	т	(0.544'	т
х(0 =	Р 0,1(0 Ро,г(0 кРо,з(0,	0.094 е~2322' -0‘283 -0.527 , 0.802 } Г-0.838)Т	+ 0.552 °2" 0.754 1,0.214; Г-0.075Лт	
+ 0.820 e"°’712t		0,352	-0.165 e-°966t	0,591 . 0.409	0.793 , 0.078 J	1,-0.128,		
Соответствующие вероятности приведены в табл. 9.4.
Таблица 9.4. Нестационарные вероятности состояний {рьДО)
t	0	0.2	0.5	1	2	4	7	10
А о	1	0.907	0.790	0.643	0.468	0.341	0.305	0.301
J=1	0	0.011	0.031	0.063	0.110	0.150	0.163	0.165
J-2	0	0.049	0.116	0.207	0.317	0.394	0.414	0.416
J = 3	0	0.033	0.063	0.087	0.105	0.115	0.118	0.118
9.5. Стационарное распределение вероятностей состояний
2М
Из приведенной формулы видно, что при t, стремящемся к бесконечности, все
Мы получили так называемые стационарные вероятности состояний, о которых
будет идти речь в следующем разделе.
9.5. Стационарное распределение
вероятностей состояний
При изучении цепей Маркова, то есть марковских процессов с дискретным вре-
менем, было показано, что для эргодических цепей имеет место предельное рас-
пределение вероятностей состояний, когда число сделанных шагов стремится К
бесконечности. Аналогичную картину естественно ожидать и в случае непрерыв-
ного времени. Соответствующую теорему приведем без доказательства.
Теорема 9.1. Пусть для рассматриваемого дискретного марковского процесса вы-
полняются следующие условия. 1) Матрица переходных вероятностей Р соот-
ветствует эргодической цепи Маркова. 2) Параметры X, , характеризующие време-
на пребывания в состояниях, строго положительны и ограничены сверху. Тогда
существуют пределы
limp,.J(0 = n., Vi,j,
t-MO J	J
не зависящие от начального состояния i и определяющие стационарное (инвари-
антное) распределение вероятностей состояний.
Физически предел л; означает долю времени, в течение которого марковский
процесс находится в состоянии j, если рассматривать установившийся, стацио-
нарный режим функционирования. Следующая задача заключается в нахожде-
нии этих стационарных вероятностей. При этом следует иметь в виду, ЧТО
p(J (О——>0. Попытка использовать для этого обратные уравнения Колмо-
горова (9.3) успеха не дает, поскольку они приводят к тождествам л^ = Пр V/.
Обратимся теперь к системе прямых уравнений Колмогорова (9.5). Для стацио-
нарного режима ptJ (i) -> л7, ptj (i) ->0, поэтому из (9.5) получаем систему ли*
йейных алгебраических уравнений относительно стационарных вероятностей
состояний nj:
=EMVPVJ- 7=0,1.......	(9.16)
V
дополняемую условиями неотрицательности (л, > 0 V)) и нормировки для ве-
роятностей
£я>-1.	(9.17)
j
260
9. Дискретные марковские процессы
Уравнения (9.16) имеют простой вероятностный смысл, формулируемый обыч-
но как принцип баланса (см. раздел 8.3): в стационарном, установившемся режи-
ме за единицу времени среднее число выходов из любого состояния j равно сред-
нему числу входов в это же состояние. Среднее число выходов в единицу
времени равно доле времени, в течение которого процесс находится в состоянии
j, умноженном на интенсивность выходов процесса из этого состояния, то есть
itj kj. Подсчитаем теперь среднее число входов в состояние/ Если процесс нахо-
дится В СОСТОЯНИИ V, ТО ДОЛЯ pvj всех скачков из этого состояния приводит к со-
стоянию j, то есть среднее в единицу времени число переходов из v в j равно
Следовательно, среднее число входов в единицу времени в состояние j
равно сумме этих произведений по всевозможным состояниям v. Уравнение (9.16)
и указывает на равенство в среднем чисел входов и выходов для состояния/
Подчеркнем, что приведенный принцип баланса применяется в инженерной
практике для вывода уравнения для стационарных вероятностей состояний без
предварительной записи прямых уравнений Колмогорова.
Теорема 9.2. При сформулированных в теореме 9.1 условиях система линейных
уравнений (9.16) имеет единственное вероятностное решение
а.
itj =---J---, j = 0,1,2.	(9.18)
; v Xv
где (й|, а2,...) — стационарное распределение вероятностей состояний для соот-
ветствующей вложенной цепи Маркова.
Напомним, что ait а2,... является единственным вероятностным решением систе-
мы линейных алгебраических уравнений
*>= IX 7=0,1............	(9.19)
дополненной условием нормировки (9.17). Это решение дается формулами (8.27)
и (8.28).
Доказательство
В разделе 8.3 было показано, что система уравнений (9.19) (там она фигурирова-
ла под номером (8.22)) имеет единственное с точностью до константы с решение
calt са2, ... Система (9.16) преобразуется в систему (9.19), если положить ь ней
Х„я„ = zv. Отсюда следует, что вероятностное решение системы уравнений (9.16)
с необходимостью имеет вид са} =	, то есть я; = caj / к.. Константа с нахо-
дится из условия нормировки (9.17), что и дает (9.18) в качестве единственного
решения системы (9.16).	□
Формула (9.18) для стационарных вероятностей состояний имеет простой физи-
ческий смысл. За большое число скачков У процесс окажется в состоянии j при-
мерно Naj раз. При каждом попадании в состояние./ процесс остается там в сред-
нем на время 1/Х; . Следовательно, за N скачков процесс будет пребывать в
состоянии j в среднем время Na^/kj. Итак, вероятность состояния / как доля
времени пребывания процесса в этом состоянии, пропорциональна Коэф-
фициент пропорциональности находится из условия нормировки вероятностей.
9.5. Стационарное распределение вероятностей состояний
очевидно, он равен	Это и дает формулу (9.18) для стационарной веро-
ятности Ttj состояния j.
Пример 9.4. Продолжим рассмотрение предыдущего примера. Найдем стацио-
нарное распределение вероятностей состояний для него я =(7г0,7г1,л2,л3).
Элементы разложения матрицы переходных вероятностей Р, используемого в
формулах (8.25)-(8.28), имеют вид:
р = (0.1
ГОД 0.2
0.5 0.4), Q = 0.2
^0.3
0.2
0.6
0.5'
0.3
0J
Далее находим:
	' 0.9 -0.2	-0.5'		4.937	1.563	1.438'
i-Q =	-0.2 0.8	-0.3	, (I-Q)1 =	0.906	2.344	1.156
	-0.3 -0.6	1 J		ч1.125	1.875	2.125,
а0 =(l + p(I-Q)-tl)-1 =0.174,
(а, а2 a3) = aop(I-Q)’* =(0.191 0.362 0.273).
Применяя теперь формулу (9.18), окончательно получаем стационарное распре-
деление вероятностей состояний я =(0.301 0.165 0.416 0.118).	□
Важным обобщением марковских процессов являются полумарковские процессы
(ПМП). Они отличаются от дискретных марковских процессов тем, что время
пребывания в каждом состоянии имеет не экспоненциальное, а произвольное
распределение (см. определение 1). Обозначим т] среднее значение этого време-
ни для состояния j.
Стационарные вероятности состояний полумарковского процесса я^ могут быть
получены так же просто, как и для марковских процессов. А именно, для вероят-
ности состояния j имеем формулу, аналогичную формуле (9.18):
а.Ш:
у=0, !,...,&-1.	(9.20)
ХХч
v=0
Отметим, что формула (9.18) является частным случаем этой формулы, посколь-
ку для экспоненциального распределения ?п;. = 1/Х,-.
Эвристическое доказательство формулы (9.20) полностью совпадает с только
ЧТО приведенным доказательством для формулы (9.18).
Рассмотрим несколько частных случаев полумарковских процессов.
Примеры
Пример 9.5. Циклический процесс. Процесс имеет k состояний, которые меняются
последовательно: после нулевого состояния — первое, затем второе и т. д. до
(А - 1)-го, после чего опять следует пулевое состояние и т. д. (см. рис. 9.2).
262
9. Дискретные марковские процессы
Рис. 9.2. Граф переходов между состояниями циклического процесса
Если продолжительности пребывания процесса в различных состояниях — вза-
имно независимые случайные величины, то это частный случай полумарковско-
го процесса. Вложенная цепь Маркова для этого процесса имеет k состояний,
которые последовательно сменяют друг друга в циклическом порядке. Хотя эта
цепь — периодическая (с периодом, равным k), доля времени, в течение которого
цепь Маркова проводит в каждом состоянии, равна 1/k. Поэтому для стационар-
ной вероятности состояния j полумарковского процесса по формуле (9.20) полу-
чаем
т,
^=тг~’ >=о,1......k-i-	<9-21)
v-0
Пример 9.6. Звездообразный процесс. Так называется процесс, в котором выде-
лено «центральное» состояние 0, из которого можно попасть в любое другое
состояние 1, 2,..., k - 1, в то время как из других состояний можно попасть непо-
средственно только в состояние 0. Соответствующий граф переходов между
состояниями изображен на рис. 9.3.
Рис. 9.3. Граф переходов между состояниями звездообразного процесса
Пусть р? — вероятность непосредственного перехода из состояния 0 в состояние
j, так что р, + р2 +...+P4-J = 1, Pj > 0. Как и прежде обозначим среднее время
однообразного пребывания в состоянии j, j =0,1, ..., k -1.
Стационарные вероятности состояний для вложенной цепи Маркова находят-
ся как решение системы уравнений (9.19). В данном случае эта система имеет
вид
Zj; =PjZ0, j = l,2, .... k-1,
Z0 +Zt + ...+Zw =1.
Единственным вероятностным решением данной системы является
9.6. Процессы размножения и гибели. Процессы массового обслуживания
а0 = 1/2,	= Pj /2, j = 1,2..k -1.
Следовательно, согласно формуле (9.20), стационарные вероятности состояний
полумарковского процесса есть
«о
я0-------м
то + YlPvmv
Р, т;
-----ГГ----• > =	..‘-1-
m, +£р.т.
(9.22)
9.6. Процессы размножения и гибели.
Процессы массового обслуживания
Важным частным случаем марковских процессов являются процессы размно-
жения и гибели. Они характеризуются тем, что для любого состояния i = 1, 2, ...
возможны переходы только в соседние состояния i -1 и i +1, а из состояния 0 —
только в состояние 1. Обозначим для состояния i вероятности переходов вправо
и влево, соответственно, р, и qb pt + qt < 1, а параметр экспоненциального рас-
пределения времени пребывания в состоянии X,.
Часто процесс размножения и гибели задается другим способом. Для каждого
состояния i=l,2, ... разыгрываются две независимые величины: Xt nYt, имею-
щие экспоненциальные распределения с параметрами а, и0Р Процесс пребыва-
ет в состоянии i время, равное минимуму из этих двух случайных величин. По-
сле этого процесс переходит в левое соседнее состояние, если меньшей оказалась
первая случайная величина, и в правое — если вторая. Доказанная выше лем-
ма 93 показывает, что оба определения процесса размножения и гибели эквива-
лентны, причем их параметры связаны следующим образом:
Х,=а.+Р(, О; =———, 1 = 1,2,...
а;+0,
Говорят о процессе чистого размножения, если р, = 1, то есть 0, = 0 Vi, и о яро-
цессе чистой гибели, если р, = 0, то есть а, = 0. В частности, пуассоновский про-
цесс является процессом чистого размножения.
Уравнения Колмогорова (9.3) и (9.5) предыдущего раздела для процесса размно-
жения и гибели принимают вид при £ > 0:
Pij (О =	(0 + KPiP.+ij (О ~ KPi.j &)•
Pij(t) = Pi,j-i(t)^j-iP]-l +Pf,/+1(O^+i ?у+1 -Xyp^(t).
Проиллюстрируем их применение на следующем примере.
Пример 9.7. Процесс Юла. Рассмотрим популяцию некоторых частиц, каждая ИВ
которых может делиться и образовывать две новые частицы. Время, необходи-
мое для такого деления, имеет экспоненциальное распределение с параметром а
Иными словами, вероятность того, что данная частица разделится в ближайшем
после t интервале времени (t,t + dt), равна adt + o(dt). Вновь образованные час-
(9.23)
(9.24)
(9.25)
264
9. Дискретные марковские процессы
тицы также подвержены делению и т. д. Предполагается, что каждая частица де-
лится независимо от других.
Будем говорить, что система находится в состоянии i, если в данный момент
в ней имеется i частиц. Найдем вероятность pi; (t) того, что в момент времени t
будет иметься j частиц, если в начальный момент времени их было г.
Очевидно, мы имеем процесс чистого размножения со следующими характери-
стиками:
X, =а, = аг, р, =1, q{ =0, Vi.
Обратные и прямые дифференциальные уравнения Колмогорова имеют вид для
рассматриваемого случая: при t > 0, j > i
Pij (О = ai pMJ (t) - ai pQ (t).
Pi,j (0 = a G “ VPij-i (O " aJ Pij (0-
Подстановкой легко проверить, что решением этих уравнений является
р. . (t) = С/;' e~iat(1 - e'at у-, t > 0, j > i.
Этот процесс впервые исследовал Юл Д. в 1924 г. Он использовал его как мате-
матическую модель эволюции популяции.	□
Возвратимся к общему виду процесса размножения и гибели. Будем интересо-
ваться стационарным распределением вероятностей состояний процесса, опреде-
ляемым как единственное решение систем уравнений (9.16) предыдущего разде-
ла. В нашем случае эта система принимает вид:
Хо ло = Qi,
=А.Л17СЛ1РЛ1 +Х>+1лЛ1^+1, 7 = 1,2,...	(9.26)
После подстановки =а, +Р;, р, =а,/(а, +Р;), <7, = 1-р, = Р;/(а, +£,) эту
систему можно привести к виду:
а0Л0 =Р17С1>
(Р; +a.j)nj =аЛ1лЛ1 +Эу+1лЛ1, j = 1,2,...
Подобная система уравнений встречалась нам при нахождении стационарных
вероятностей для цепи Маркова (см. пример 8.11 и формулу (8.49)). Как и там,
эту систему можно решать последовательной подстановкой, в результате чего
получаем
= aoai-a^ у = i 2,...	(9.27)
1
Вероятность л0 состояния 0 можно найти из условия нормировки
=i.
г-О
Поскольку любое решение системы (9.26) имеет вид (9.27), то конечность суммы
(9.28)
У-1 М Р/*|
9.6. Процессы размножения и гибели. Процессы массового обслуживания
ш
свидетельствует о наличии нетривиального (ненулевого) решения, а бесконеч-
ность — о его отсутствии. В связи с этим получена следующая теорема.
Теорема 9.3. В процессе размножения и гибели стационарное распределение
вероятностей существует тогда и только тогда, когда сумма (9.28) конечна.
В этом случае распределение задается формулой (9.27), где
".	(в-»)
\	7-1 /=0 Р/+1 J
причем это распределение является единственным вероятностным решением
системы линейных уравнений (9.26).
В общем процессе размножения и гибели предполагалось, что параметры а( и
зависят от номера состояния i. На практике часто встречается случай, когда ДЛЖ
состояний с номером, большим k, значения а, и р, остаются постоянными и рав-
ными, соответственно, ak и pt:
Р, = Pt- » к.
Предположим, что отношение а*/р4 < 1. Для этого случая бесконечная сумма
в формуле (9.29) преобразуется следующим образом:
Теперь вышеприведенные формулы для вероятностей состояний принимают вид:
1
£Up/+1
1 at z=o P/+i
Pt
(9.30)
<x»a1...a.
Л ; = ------"
1	P^-P,
ЛО,
j = 1,2..k-1,
(9.31)
л,-
a-k
I Pt
Hr Л°’
i-o P/+1
j = k, k + i, ...
(9.32)
*0 =
Приведенные формулы упрощаются, если число состояний конечно. Пусть чис-
ло состояний равно k +1, причем последнее возможное состояние имеет номер А.
Тогда в приведенных формулах следует положить ак = 0. В этом случае сумма
(9.28) содержит k +1 слагаемое (последнее с номером j = k) и поэтому всегда ко-
нечна.
В качестве важного примера процессов размножения и гибели обычно рассмат-
ривают процессы массового обслуживания (иначе — процессы очередей). Рассмот-
266
9. Дискретные марковские процессы
рим пуассоновский поток требований (сообщений, заявок, клиентов, вызовов
и пр.), поступающий на систему обслуживания. Последняя представляет собой
совокупность з идентичных обслуживающих аппаратов (приборов). Каждый ап-
парат одновременно может обслуживать только одно требование, причем дли-
тельность обслуживания имеет экспоненциальное распределение с параметром
0>О. Интенсивность пуассоновского потока требований равна а. Если при
поступлении требования хотя бы один аппарат свободен, то требование немед-
ленно принимается им на обслуживание. В противном случае оно ставится в
очередь. Из очереди требования принимаются на обслуживание в порядке их
поступления в моменты окончания обслуживаний. Обслуженные требования
покидают систему. Такая система называется эрланговской системой массового
обслуживания с ожиданием.
Основной интерес представляют стационарные вероятности } того, что в сис-
теме находится j требований, j = 0, 1,...
Очевидно, что здесь имеет место процесс размножения и гибели. Будем гово-
рить, что система (процесс) пребывает в состоянии j, если в ней находится j тре-
бований. Переход системы из состояния j в состояние j + 1 происходит при по-
ступлении нового требования. Поскольку поток поступающих требований
пуассоновский и не зависит от состояния системы, то а, = а. Система переходит
из состояния j в состояние j -1 при окончании обслуживания требования и по-
кидании им системы. Если число требований в системе j не превышает имеюще-
гося количества аппаратов з, то одновременно обслуживаются все j требования.
Поскольку интенсивность обслуживания одного требования составляет 0, то на
основании леммы 93 получаем, что общая интенсивность обслуживания соста-
вит J0. Если же число требований j превышает число аппаратов з, то обслужива-
ется только з требований, при этом суммарная интенсивность обслуживания
равна S0. Следовательно, 07 = j'P при j < з и р^ = sp при j £ s. Итак, значения па-
раметров и Pj не изменяются при у > s, то есть имеет место вышерассмотрен-
ный случай при k = s, ak = а и р* = sp.
Условие at/pt < 1 эквивалентно условию a < sp. Иначе говоря, интенсивность
потока требований а должна быть строго меньше общей интенсивности обслу-
живания всеми аппаратами sp, то есть пропускной способности системы. Вели-
чина р =a/(sp) называется коэффициентом загрузки системы. Формула (9.30)
преобразуется к виду
1+2й?-+—Й^-
— +
*о =
у-1 /=0 Р/+1	| at /=0 Р/+1
<	Pt >
Итак, в случае р = a/(sp) < 1 по формулам (9.30)-(9.32) окончательно имеем:
*о =
(9.33)
9.6. Процессы размножения и гибели. Процессы массового обслуживания
“| 1
s!
j = 1, 2, ..., s,
j = S + l, 5 + 2, ...
(9.34)
Наибольший интерес для практики представляют такие показатели эффехти**
ности системы обслуживания, как среднее число требований в системе и и в оче-
реди v, среднее время пребывания требования в системе г и в очереди w.
Найдем вначале среднее число требований в очереди v. Если учесть, что при на-
личии в системе j > s требований j - s из них ожидают, то средняя длина очереди
требований составит
00	00	( п '	4	4 (п \5	00
v =	= £ (j-s) £ -——-л0 =— - TtopjTip'-1.
t Р J s I s' 5 s! p J M
Если домножить последнюю сумму на 1 -р, то она будет определять математиче-
ское ожидание для геометрического распределения (3.4) с параметром q  р. По-
скольку указанное математические ожидание, согласно табл. 3.5, равно 1/(1-р),
то сумма составляет (1 - р)"2. Окончательно получаем такое выражение для сред-
него числа требований в очереди:
1 Га
v =— —
•s’lpj (1-р)
—-2-Ло-
(9.35)
Число требований в системе складывается из требований в очереди плюс требо-
ваний, находящихся на обслуживании. Последних столько, сколько аппаратов
занято. Но среднее число занятых аппаратов равно числу аппаратов s, умножен-
ному на коэффициент загрузки р. Следовательно, среднее число требований в
системе и находится по формуле
1 Г а
и = v + sp =  —
slip; (i-p)
р а
—+ —.
2 ° р
(9.36)
Найдем теперь среднее время ожидания требованием начала обслуживания w,
Требование ожидает, если при его поступлении в систему все аппараты оказыва-
ются занятыми. Если все обслуживающие аппараты работают, то общая интен-
сивность обслуживания составляет $р. Следовательно, согласно лемме 9.2, сред-
нее время до окончания очередного обслуживания составляет 1/sp. Пусть
требование застает в системе j > s требования (вероятность этого Лу вычисляется
по формуле (9.34)). В этом случае требование будет ожидать j - $ +1 окончаний
обслуживания, то есть в среднем время(j-s + 1)/$р. Осредняя это по количест-
ву требований}, получаем:
268
9. Дискретные марковские процессы
Повторяя соображения, ранее использованные при выводе формулы (9.35), по-
лучаем следующее выражение для среднего времени ожидания требованием на-
чала обслуживания:
№ =
1
“Т-Я0
5! а
Р
(1-Р)2’
(9.37)
Наконец, среднее время пребывания требования в системе г складывается из
времени ожидания ® и времени обслуживания 1/0, так что
1 faY 1 р 1
0	51a ° (1-р)2 0
(9.38)
Аналогичным образом могут быть найдены и другие характеристики длины оче-
реди (дисперсия, среднее квадратическое отклонение), а также распределение
времени ожидания начала обслуживания и т. п.
Отметим, что процессы массового обслуживания являются наиболее употребляе-
мыми вероятностными моделями при описании различных технических и эко-
номических систем.
Пример 9.8. Пусть система состоит из четырех обслуживающих аппаратов
(s = 4). Интенсивность обслуживания аппаратом требования 0 = 1. Проанализи-
руем влияние интенсивности поступающего потока требований а на показатели
эффективности обслуживания р = a/(sp), и, v, г и w.
Соответствующие вычисления проводились по формулам (9.33), (9.35)-(9.38)
функцией Queue(a, 0, х). Результаты представлены в табл. 9.5. Они показывают,
что при приближении коэффициента загрузки к единице резко возрастает мате-
матическое ожидание числа требований и времени пребывания требований в
очереди и в системе.
Таблица 9.5. Показатели эффективности системы массового обслуживания
	а = 2.2	а = 2.4	а = 2.6	а = 2.8	а = 3.0	а =3.2	а = 3.4	а = 3.6	а= 3.8
р	0.55	0.60	0.65	0.70	0.75	0.80	0.85	0.90	0.95
я,	0.105	0.083	0.065	0.050	0.038	0.027	0.019	0.011	0.005
V	0.277	0.431	0.658	1.000	1.528	2.386	3.906	7.090	16.94
и	2.477	2.831	3.258	3.800	4.528	5.586	7.306	10.69	20.74
W	0.126	0.179	0.253	0.357	0.509	0.746	1.149	1.970	4.457
г	1.126	1.179	1.253	1.357	1.509	1.746	2.149	2.970	5.457
Компьютерный практикум № 14.
Анализ дискретных марковских процессов
в пакете Mathcad (часть 1)
Цель и задачи практикума
Целью практикума является приобретение навыков описания и анализа марков-
ских процессов с непрерывным временем в пакете Mathcad.
Компьютерный практикум Ns 14. Анализ дискретных марковских процессов в пакете Matbead (часть 1)
268
Задачами данного практикума являются задание и моделирование дискретного
марковского процесса.
Необходимый справочный материал
При моделировании процесса используются уже ранее применявшиеся стан-
дартные функции, вырабатывающие случайные величины с заданными распре-
делениями: runif, гехр и др.
Реализация задания
Для проведения вычислений нам понадобятся шесть функций пользователя.
Программные модули, реализующие эти функции, представлены на рис. 9.4 И
рис. 9.5. Функция пользователя Def(&, х) уже встречалась ранее в компьютерном
практикуме № 13. Она вычисляет номер интервала i, в котором содержится чис-
ло х. Длины интервалов содержатся в векторе а.
Проктитам Me 14. Дисфмтмым шимокми процессы (часть 1)
Пажапаам
Номер интервала, содвржатцвго жечонив к
Def (а, х) > в ♦- Bq
1*-0
шМа а<х
марковского процесса м ряд переходов
|4-ОоГ(о,Яо|0)
МоОМР(е.РД.Я) :•
Имытаиноннов моделирование протокола мармоссяого процесса
1тРМР(а ,Р,% ,п,т) >
RN^+-runif (N, 0,1)
RN^wexpCN.I)
to+-r(n*1)
for teO.n
I^t. 0 «- RNfeH, 0
Y«-ModMP(o,P A.R)
/i г) у<о>
y(5)
Состалниа траектории процесса о момент времени 1
S(t,X,v)> n*-rows(X)
u«- v
wMo uin-l
r UXuj
Vl*-Ku,0
Y0*-u
u*-n
other wIbo
IK ♦- U* 1
Y+-i(t.X,u)
Y
Xo,i*-r4<
n*-rows(R)-l
for tel.n
Имитационное модолирааониа
марковскаго процессе
У(е,рд,п.» :•
Xt-lmPM₽(o,p,*,n,l)
Jo<-0
tar I.O.N
Y

Xt,0*-<
**t,i*"’***t-i,i
к
Рио. 0.4. Функции пользователя для моделирования марковского процесса
Функция ModMP(e, Р, X, R) осуществляет детерминированное моделирование
марковского процесса. Входными параметрами функции являются: вектор-стол-
270
9. ДискреВе» марковские процессы
бец начальных вероятностей состояний а; матрица переходных вероятностей за
шаг Р; вектор интенсивностей выходов из состояний X; матрица случайных ве-
личин R, используемых при моделировании. Матрица R состоит из двух столб-
цов. Первый столбец содержит равномерно распределенные в интервале (0, 1)
случайные величины; второй столбец — случайные величины, имеющие экспо-
ненциальное распределение с параметром 1. При моделировании первые величи-
ны используются для розыгрыша нового состояния марковского процесса, а вто-
рые — времени пребывания в нем. Число столбцов матрицы R (число указанных
пар величин) определяет длительность моделирования. Такое моделирование
является детерминированным, поскольку значения случайных величин в матри-
це R не вырабатываются, а являются заданными. В качестве результата функция
возвращает матрицу, состоящую из двух столбцов. Номер строки матрицы соот-
ветствует порядковому номеру скачка. В первом столбце указывается состоя-
ние процесса после соответствующего скачка, а во втором — время наступления
следующего скачка. Иными словами, эта матрица выдает протокол марковского
процесса.
Часюпн сосгалмий марковского процесса при пмфвтом моделировании
FrModMP(a.P Д Д ,п,т)
k<- rows (Р)
Х<-кпРМР(а,РД ,п,т)
for 1е0..т-1
ь,<-(хЬи,))п
b«-sort(b)
тТ«-floor (IL5m)
Т*-ЬтТ
пт«- floor ф
for tet.nT
*0.t«-О"*) *
пипцг- 0
for Je1..k
|FrJi0«-j-1
|FrJit«-0
numo«-0
for r e 0.. m -1
S T .Ноогф ,nlj -1
v«-0
for teO.mm
Y«-S(t*,XJ,v)
w«-Y0
l*-Yi
num, <- num, +1
for teO..nT-1
tor jeO..k-1
(num,)
Рио. 9.8. Функция пользователя, вычисляющая частоты состояний при моделировании
Компьютерный практикум Ns 14. Анализ дискретных марковских процессов в пакете Mathcad (часть 1)
271
Функция ImPMP(&, Р, X, п, т) осуществляет многократное имитационное моде-
лирование протокола марковского процесса (см. раздел 9.1). Входные параметры
а, Р и X — те же, что и в функции ModMP. Целое число т определяет кратность
моделирования, то есть число прогонов (траекторий, реализаций, протоколов)
процесса. В каждом прогоне моделируется п скачков процесса. Результатом ра-
боты функции является матрица ImPMP, состоящая из п + 1 строки и 2т столб-
цов. Строки соответствуют номерам скачков — от начального момента 0 до по-
следнего n-го скачка. Первый, третий, пятый и остальные столбцы с нечетными
номерами содержат номера состояний, в которых оказывался процесс после со-
ответствующего скачка. Второй, четвертый и остальные столбцы с четными но-
мерами — последний момент времени пребывания в состоянии. В итоге выдается
т протоколов моделирования марковского процесса в течение п скачков. Работа
программы, реализующей функцию, осуществляется согласно описанному в раз-
деле 9.1 алгоритму.
Функция S(t, X, Г) определяет состояние марковского процесса в момент време-
ни t. Входными параметрами функции являются: момент времени t\ протокол
однократного моделирования процесса X, полученный, например, функцией
ImPMP', и вспомогательный параметр I — номер скачка процесса, после которого
следует искать в протоколе момент времени t. При первом обращении к функ-
ции следует положить I = 0. Сам этот параметр был введен для удобства про-
граммирования — он позволяет значительно сократить программу, реализую-
щую функцию, за счет использования рекурсии. В качестве результата функция
возвращает двумерный вектор, нулевая компонента которого — номер скачка, а
первая компонента — состояние марковского процесса в момент времени t.
Функция У(а, Р, X, п, 8) обеспечивает имитационное моделирование марковского
процесса. Входными параметрами функции являются: а, Р, X, п и 8. Параметры а,
Р и X — те же, что и ранее. Целое число п указывает количество скачков процес-
са, в течение которых осуществляется моделирование. Значение 8 определяет ве-
личину шага, с которым выдаются результаты — состояния процесса X(J 5) в мо-
менты времени j S,j = O, 1,...
Функция FrModMP(&, Р, X, 8, п, т) с шагом 8 подсчитывает частоты различных
состояний в т траекториях марковского процесса, в каждой из которых имеется
п скачков. В разных траекториях время последнего скачка различное. Поэтому
программа обрабатывает данные только до тех пор, пока еще не закончилась по-
ловина (0.5) всех траекторий.
Результаты вычислений
Результаты расчетов представлены на рис. 9.6. Вначале вводятся исходные дан-
ные: матрица переходных вероятностей Р, вектор интенсивности выходов ИЗ СО-
СТОЯНИЙ X и вектор начальных вероятностей а. Далее представлен протокол од-
нократного (m = 1) имитационного моделирования рассматриваемого марковского
Процесса в течение п = 17 шагов. В матрице результатов ImPMP нулевая строк*
содержит номер состояния, а первая строка — момент времени перехода в сле-
дующее состояние. Например, после четвертого скачка имело место состояние 2,
В котором процесс находился в течение периода с 7.193 до 7.453. Фактические
состояния процесса в моменты времени 0 и 6 выдаются функцией S.
272
9. Дискретные марковские процессы
Рмультдты «ЫЧ»И1«Н»>
Матрица вероятностей порокодов
Интенсивности Начальное распределение
'О 0.1 04 0.4'
02 0.1 04 0.5
04 04 04 0.3
Д1 04 04 0 ,
Имнтационноо ноделировенио протокола марковского процесса
кпРМР(а,Рд ,17,1)т
Состояние вроцосса в нонвнт врвнвнв t
8(О,1т₽МР(о,РД .17,1),0)
6(6,knPMP(o,P,i,17,1),0)
Инитацооннов педалирование марковского процесса
Частоты состояний лрн тлелчокротнвм моделировании мврквоского лрвцесса
FrModMP (в ,Р Д, 1,20,1000)
н	0	1	2	3	4	б	6	7	8
гз	0	0.153	0.231	0,263	0.287	0,284	0.283	0.283	0.28
	0	0.213	0.21	0.178	0.183	0.186	0.186	0.158	0.178
гз	0	0.437	0.422	0.428	0.411	0.404	0.41	0.441	0.418
о	1	0.187	0,137	0.13	0.118	0.136	0.131	0.11	0.116
Рис. 0.6. Результаты моделирования марковского процесса
Далее представлены результаты однократного имитационного моделирования в
течение 20 скачков, выдаваемые с шагом 8 = 1 функцией У. Здесь нулевая строка
матрицы содержит моменты времени, а первая строка — номера соответствую-
щих состояний. Наконец, функция FrModMP выдает частоты состояний при ты-
сячекратном моделировании процесса в виде матрицы FrModMP.
Компьютерный практикум № 15. Анализ дискретных
марковских процессов в пакете Mathcad (часть 2)
Цель и задачи практикума
Целью практикума является закрепление навыков описания и анализа марков-
ских процессов с непрерывным временем в пакете Mathcad.
Задачами данного практикума являются:
□	аналитическое вычисление нестационарных и стационарных вероятностей
состояний марковского процесса;
□	вычисление стационарных вероятностей состояний процесса размножения и
гибели;
□	расчет показателей эффективности эрланговской системы массового обслу-
живания.
Компьютерный практикум Ns 15. Анализ дискретных марковских процессов в пакете Mathcad (часть 2)
273
Необходимый справочный материал
Для рычисления нестационарных распределений вероятностей состояний исполь-
зуются стандартные функции пакета Mathcad, предназначенные для нахождения
собственных чисел и векторов квадратных матриц. Функция eigenval (М) выдает
вектор-столбец, содержащий все собственные числа матрицы М. Размерность век*
тора совпадает с размерностью квадратной матрицы М. Функция eigenvec(M, р)
вычисляет собственный вектор-столбец матрицы М, отвечающий собственному
числу V.
Реализация задания
Будем использовать четыре функции пользователя, представленные на рис. 9.7.
Первые две функции вычисляют нестационарное и стационарное распределение
вероятностей состояний марковского процесса по аналитическим формулам.
Функция Pr(P, k, t, г) реализует алгоритм вычисления нестационарного распре-
деления, приведенный в конце раздела 9.4. Входными параметрами функции яв-
ляются: Р — матрица вероятностей переходов между состояниями за шаг; X —
вектор интенсивностей выходов из состояний; t — момент времени, для которого
определяется распределение вероятностей состояний; i — номер состояния, в ко-
тором первоначально (в момент t = 0) находился марковский процесс.
Функция PrSt(P, X) вычисляет стационарное распределение вероятностей со-
стояний марковского процесса. Входными параметрами являются Р и X, имею-
щие то же содержание, что и в предыдущем случае.
Функция л(а, 0, п) вычисляет по формулам (9.30)-(9.32) стационарное распре-
деление вероятностей состояний процесса размножения и гибели для п + 1 пер-
вых состояний. Входом является число п и два вектора-столбца аир, содержа-
щие параметры {a f} и{0(} из формулы (9.23): а = (а0 at...aA)T, 0 = (0О 0р.. р4)т.
Напомним, что для i > k а( = аА, 0( = 0*,. В качестве результата функция выдает
вектор стационарных вероятностей я = (л0 nt ... л„)т.
Функция QSys(af, 0s, s) рассчитывает показатели эффективности эрланговской
системы массового обслуживания по формулам (9.33), (9.35)-(9.38). Входными
данными являются интенсивность входящего пуассоновского потока требований
а/, интенсивность обслуживания требований 0s и число обслуживающих аппа-
ратов s. Функция выдает вектор-столбец (р л0 v и w г)т, содержащий коэф-
фициент загрузки системы р, вероятность отсутствия требований в системе Я01
среднее число требований в очереди v и в системе и, а также среднее время пре-
бывания требования в очереди to и в системе г.
Результаты вычислений
Соответствующие результаты представлены на рис. 9.8. Вначале вводятся мат-
рица переходных вероятностей за шаг Р1 и вектор-столбец интенсивности выхо-
дов из состояний XI. Функция Рг выдает распределение состояний процесса ДЛИ
моментов времени t  2 и t  5 при условии, что в момент времени t  0 процесс
находился в третьем состоянии (i  3). Стационарное распределение вероятно-
стей состояний выдается функцией PrSt.
274
9. Дискретные марковские процессы
Практикум И» 15. Дискретные марковские процессы (часть 2)
П»л>1а»«ил>йИ1 функции
Распределение вероятностей состояний
марковского процесса в нопекН
Pr(P.A,tJ)>	k 4- TOWB(P)
	D <- dlag(A)
	A«-(D(P-ldaH(lty(k))]T
	A <r- eleeHvah(A)
	fer JeQk-1
	4- alganvec(Ar Aj)
	for JeO k-1
	elj«-0
	elj*-l
	1 el
	k-1
	b| •xp(AJ-t) V*>
	J-»
Стацевиариво расяределвиио вараятивстей
состояний нпрковского процесса
PrSt(P.A)	k«-rowB(P)
	for 1 e 1.. k -1 for J«1 k-1
	• «-[/ (Id.ntlMk-D-PP)'1]' . *-•
	T ri- EM J-
	1 rr a A|
	for 1 e 1.. k - 1
	1 an — 8 A| *8
Стационарное распределение вероятностей состояний процесса рааннопкеимя а гибели
я(а,0,п)>
k <r- rowo(a) - 1
\ J  1 I • I	I “ I
for j« 1.. л
Сметена массового обслуживания
QSya(af,0e,S)»
of
3oS
x3 xj + S и*
X2
af
*4
1
X5*-X4 +
Рис, 9.7. Функции пользователя, реализующие аналитические вычисления
Функция л рассчитывает стационарное распределение вероятностей состояний
для процесса размножения и гибели со следующими характеристиками: Vi a, = 2.6,
Pi = i, i = О, 1.4, P5 = 4. При этом рассматриваются состояния до пятого вклю-
чительно (я = 5). Результатом являются стационарные вероятности этих состоя-
ний: я0 =0.065,	=0.169, л2 =0.22, я, =0.191, я4 =0.124, я3 =0.081.
Задания для самостоятельной работы
278
Р* ияьшы ютислтеий
Матрица переходных вероятностей
'О 01 05 04'
02 0.1 02 04
Р1-
03 02 02 03
Интонсавиостм выходов из состояний
,0.1 03 04 О
Распределение вероятностей состояний марковского процесса
а) в попоит вровоии 2	б) в момент вроиеии 5
Р<(Р1>1,2.3)Т -(0226 0294 0446 0133)	Рс(Р1 ,М,5,3)Т - (0292 0169 0421 0119)
Стационарное распределение вероятностей состояний
PrSt(P1.M)T - (0301 0.165 0416 ОНО)
Стационарное распределение вероятностей состояний процесса раэиноження и гибели
я((24 24 24 24 24 24)T ,(0 1 2 3 4 4)T ,s) - (0465 0169 022 0191 0.124 0481)
Показатели эффективности систвиы поссовете обслуживания
QSys(26,l ,4/ - (045 0465 0458 3258 0253 1253)
Рис. 9.8. Результаты аналитических вычислений
В заключение рассматривается система массового обслуживания из четырех
аппаратов, на которую поступает пуассоновский поток требований с интенсив-
ностью а/ = 2.6. Интенсивность обслуживания одним аппаратом составляет 0s - 1,
Из выдаваемых функцией результатов видно, что р = 0.65, л0 = 0.065, v - 0.658,
u = 3.258, w = 0.253, r= 1.253.
Задания для самостоятельной работы
1.	Используйте представленные выше функции пользователя для решения ни-
жеприведенных задач 9.8 и 9.9.
2.	Проанализируйте логику работы программ, реализующих функции ModMP
и ImPMP.
3.	Составьте компьютерную программу для имитационного моделирования про-
цесса Юла, описанного в примере 9.7. Приведите моделирование для значе-
ния параметра а = 1 и сравните полученные результаты с теоретическими.
4.	Составьте компьютерную программу для имитационного моделирования по-
тока автомашин, описанного в нижеприведенной задаче 9.6. По результатам
моделирования оцените искомое в задаче распределение.
5.	Составьте программу и проведите численные расчеты для примера 9.4.
6.	Проанализируйте логику работы программ, реализующих функции Рг и PrSt.
7.	С помощью пакета Mathcad проверьте правильность вычислений, приведен-
ных в примере 9.8.
8.	С помощью пакета Mathcad постройте графики зависимости вероятностей
Ро./(0, i = 0. 1, 2, 3, найденных в примере 9.3, от времени t. Проанализируйте
скорость сходимости к стационарным вероятностям.
9.	Составьте компьютерную программу, выполняющую вычисления для зада-
чи 9.10 останки и рабочие*.
276
9. Дискретные марковские процессы
Задачи
Задача 9.1. В чем состоит смысл отсутствия последействия экспоненциального
распределения и марковского процесса?
Задача 9.2. Обсудите физические предпосылки, приводящие к прямым и обрат-
ным уравнениям Колмогорова.
Задача 9.3. Во что превращается формула (9.20), когда полумарковкий процесс
является цепью Маркова?
Задача 9.4. Пусть X(t) — пуассоновский поток событий с интенсивностью X,
а Т — не зависящая от него неотрицательная случайная величина. Найдите рас-
пределение, математическое ожидание и дисперсию случайной величины Х(Т) —
числа событий потока за случайное время.
Задача 9.5. Рассмотрите пуассоновский поток событий с интенсивностью X. Пусть
каждое из событий, независимо от других событий, с вероятностью р, относится
к i-му из возможных k классов, pj + р2 + ... + рА =1. Пусть Xj(t) означает число
событий пуассоновского потока в интервале (0, t), отнесенных к i-му классу. По-
кажите, что X,(t) — пуассоновский поток с интенсивностью Х( = Хр , i = 1, 2.k.
Задача 9.6. (Sh. М. Ross). Пусть автомашины появляются на одностороннем шоссе
согласно пуассоновскому потоку с интенсивностью X. Каждая автомашина неза-
висимо от других машин выбирает скорость движения V и движется с этой ско-
ростью. Предполагается, что скорости различных машин являются взаимно
независимыми случайными величинами с общей функцией распределения G(v).
Предполагается также, что при обгоне других автомашин скорость не изменяет-
ся. Используя предыдущую задачу, найдите распределение числа машин, пре-
одолевших по шоссе к моменту t путь, длина которого превышает d.
Задача 9.7. Сложный пуассоновский процесс. Пусть X(t) — пуассоновский поток
событий с параметром X. Каждому событию соответствует случайная величина
(«вклад» события), обозначим ее для i-ro события У;, с общей функцией распре-
деления G(y). Эти величины являются взаимно независимыми для разных собы-
тий и суммируются. Накопленную сумму к моменту времени t
^(0 = ^1 +^2 + -- + Гх(о
называют сложным пуассоновским процессом.
Повторяя рассуждения, использованные в примере 7.5, покажите, что функция
распределения процесса Z(t) дается формулой
P{Z(t)^z} = £^e^G„(2),
Zo п!
где G„(z) — функция распределения суммы п случайных величин У[ + У2+ - + Уя>
G0(z) = 1, г £ 0.
Найдите математическое ожидание и дисперсию Z(t). Отдельно рассмотрите
случаи, когда У имеет экспоненциальное и нормальное распределения.
Отметим, что сложный пуассоновский процесс часто применяется в задачах
о разорении страховых компаний, надежности, управления запасами и пр.
Задачи
Задача 9.8. Альтернирующий процесс. Таковым называется марковский процесс
с двумя состояниями 0 и 1, которые сменяют друг друга. Точнее говоря, вероят-
ности перехода за шагрод = 1- Pi,о = 1- Пусть, как обычно, Хо и / — интенсивно-
сти выхода из состояний.
Составьте уравнения Колмогорова для этого процесса. Покажите, что вероятно-
сти Ро,о(0 и Po,i(0 состояний 0 и 1 в момент времени t, если в начальный момент
процесс был в состоянии 0, даются формулами: p01(i) = 1 -ро,о(О>
т Л>।
Выпишите выражения для стационарных вероятностей состояний л0 и л(.
Задача 9.9. Рассмотрите марковский процесс с тремя состояниями, для которого
	' 0	1	0 '		т
р =	0.5	0	0.5		2
	0.5	0.5			ll
Используя технику вычислений раздела 9.4, покажите, что v0 = 0, = -2, v2 - -3,
А =	'-1 1	0 > 1 -2 1 Ь 1-2,	, z =	'11 1 > 1 -1 -2 <1-1 1,	, z1 =	'1/2 1/3 1/6' 1/2	0	-1/2 k 0 -1/3 1/3 /
На основании этого найдите выражения для распределения вероятностей со-
стояний {Pij(t)}.
Задача 9.10. Задача «станки и рабочие». Имеется т станков, которые обслужива-
ются s рабочими, s < т. Станки время от времени выходят из строя. Время безот-
казной работы станка имеет экспоненциальное распределение с параметром а.
Для различных станков это время — взаимно независимые случайные величины.
Один рабочий одновременно может ремонтировать только один станок. Длитель-
ности ремонтов — взаимно независимые случайные величины, имеющие экспо-
ненциальное распределение с параметром р.
Найдите стационарное распределение вероятностей для числа неработающих стан-
ков, а также такие показатели эффективности рассматриваемой системы, как ко-
эффициент загрузки рабочих, коэффициент использования станков, средине
число простаивающих станков и пр.
10	Задачи математической
статистики и первичная
обработка данных
10.1.	Задачи математической статистики
В предыдущих главах, посвященных изложению теории вероятностей, о вероят-
ностях случайных событий и распределениях случайных величин говорилось как
о чем-то заранее известном. Например, если в последовательности испытаний
Бернулли мы интересовались числом успехов, то вероятность успеха в каждом
испытании считалась заданной. Далее, если необходимо было найти вероятность
того, что данная случайная величина превзойдет некоторое значение, то распре-
деление этой случайной величины предполагалось известным. Обычно такой
информацией не располагают, а все необходимые вероятностные характеристи-
ки случайных событий и величин оцениваются на основе проводимых экспери-
ментов или наблюдений. При этом типичными являются следующие задачи.
1.	Как оценивать неизвестную вероятность случайного события по данным на-
блюдений?
2.	Как оценивать параметры или функцию распределения случайной величины
на основе ее зарегистрированных значений?
3.	Как по статистическим данным проверить гипотезу о том, что две случайные
величины взаимно независимы или имеют одинаковое распределение?
Перечисленные и аналогичные им задачи составляют предмет математической
статистики. В первом приближении задачи математической статистики могут
быть классифицированы на три класса.
1.	Задачи оценки неизвестных параметров распределения. Очень часто тип рас-
пределения случайной величины известен, а неизвестны только параметры
распределения. Например, если данная случайная величина является суммой
большого числа случайных слагаемых, то на основании центральной предельной
теоремы (см. теорему 75) можно ожидать, что она распределена нормально.
Таким образом, в данном случае тип распределения мы устанавливаем из фи-
зических, качественных соображений.
Другой пример такого же характера можно получить, рассматривая распреде-
ление числа успехов в последовательности испытаний Бернулли. Здесь также
10.1. Задачи математической статистики
279
достоверно известен тип распределения — это биномиальное распределение.
Однако параметр р этого распределения (т. е. вероятность успеха в одном ис-
пытании) может быть неизвестен, и его следует определить, исходя из наблю-
даемого числа успехов.
2.	Задачи проверки статистических гипотез. Относящиеся сюда задачи имеют
несколько разновидностей. Одной из важнейших является задача проверки
гипотезы о законе распределения случайной величины. Предположим, что
некоторые физические, качественные соображения позволяют полагать, ЧТО
рассматриваемая случайная величина имеет определенный тип распреде-
ления. Однако у нас нет в этом стопроцентной уверенности. Поэтому на осно-
вании наблюдаемых значений случайной величины необходимо оценить
параметры распределения и проверить, насколько хорошо наблюдаемые зна-
чения соответствуют гипотезе об этом законе распределения,
Аналогичным образом формулируются задачи и в других случаях, когда тре-
буется проверить некоторые гипотезы, касающиеся распределения одной или
нескольких случайных величин. Так, например, можно интересоваться гипо-
тезой о том, что две случайные величины независимы, что с течением време-
ни вероятность некоторого случайного события (например, получения брако-
ванного изделия) не увеличивается и т. д.
3.	Задачи классификации. Классификацией называется разбиение рассматриваемого
множества объектов на однородные, в некотором смысле, классы. При этом
каждый объект описывается многомерным вектором, элементы которого —
значения определенных признаков. Различные постановки задач классифи-
кации предполагают разные условия: наличие информации о распределении
значений признаков для каждого класса или отсутствие таковой, в последнем
случае — наличие разного рода «обучающих» выборок и т. д.
Приведенные три класса задач математической статистики относятся к этапу
статистического анализа данных. Этому этапу обычно предшествует этап описа-
ния (представления) собранных данных. Раздел статистики, занимающийся опи-
санием методов сбора и обработки информации, называется дескриптивной, или
описательной, статистикой. Различные способы описания экспериментальных
данных будут освещены нами несколько позже, а сейчас введем основные поня-
тия и определения математической статистики. В дальнейшем будем говорить
только о случайных величинах, так как каждое случайное событие может быть
представлено как индикаторная случайная величина (см. параграф 5.3).
Исходным «сырьем» для статистического исследования является совокупность
результатов наблюдений (опытов, испытаний или экспериментов) xf, х'г..х*.
Эти результаты представляют собой значения случайной величины X, распреде-
ление которой хотя бы отчасти неизвестно и его требуется определить на основа-
нии этих результатов.
Определение 1. Совокупность результатов наблюдений xj, xj, .... xj называют
выборкой (выборочной совокупностью). В большинстве статистических задач она
может быть интерпретирована как выборка из некоторой генеральной совокупно-
сти, в которой интересующий нас количественный признак распределен среди
элементов так же, как распределена случайная величина X. Число ланнму п »....
280
10. Задачи математической статистики и первичная обработка данных
борке п называется объемом выборки. Если выборка рассматривается до ее фак-
тического получения, то она представляется последовательностью независимых
одинаково распределенных случайных величин Х,, Х2,Х„, являющихся «веро-
ятностными копиями» X.
Отметим, что если это не вызывает недоразумений, звездочки в обозначениях
элементов выборки х*, х2, ..., х* можно опускать и просто писать х1г х2, ..., х„.
Это всегда можно делать для непрерывных случайных величин. Однако для дис-
кретных случайных величин xit х2, ..., х„ означают возможные значения случай-
ной величины, так что здесь надо проявлять осторожность.
Примеры
Пример 10.1. Предположим, что имеется партия деталей в 10 000 штук. Из этих
деталей 9000 годных, а 1000 представляют собой брак. В действительности число
годных и негодных деталей неизвестно. Для того чтобы можно было судить хотя
бы приблизительно об относительной доле брака, отбирают и контролируют сто
деталей. В этом примере генеральной совокупностью является исходная партия
деталей в 10 000 штук. Выборкой является множество деталей, изъятых из гене-
ральной совокупности для контроля. Отметим, что описанная процедура назы-
вается выборочным контролем качества продукции.
Пример 10.2. Из партии товара случайным образом выбраны 25 изделий. Их вес
(в граммах) оказался следующим: 54; 51; 54; 47; 49; 47; 49; 54; 51; 48; 49; 54; 54;
47; 49; 48; 51; 51; 54; 53; 49; 49; 48; 49; 51.
После упорядочивания эти данные выглядят так: 47; 47; 47; 48; 48; 48; 49; 49; 49;
49; 49; 49; 49; 51; 51; 51; 51; 51; 53; 54; 54; 54; 54; 54; 54.
Видно, что различных значений только шесть: 47; 48; 49; 51; 53; 54; значение 47
встречается 3 раза, значение 48 — 3 раза и т. д.	□
Выбор элементов генеральной совокупности можно организовать двояким спо-
собом (см. табл. 2.1): выбор без повторений (без возвращения) и выбор с повторе-
ниями (с возвращением). В первом случае отбор элементов производится одно-
временно. Во втором случае отбор элементов производится поочередно, причем
каждый выбранный элемент обследуется и возвращается в генеральную сово-
купность, после чего производится отбор следующего элемента. Заметим, что
если объем выборочной совокупности значительно меньше объема генеральной
совокупности, то различие между двумя видами выборок практически исчезает.
Определение 2. Если выборка дает возможность достаточно уверенно судить об
интересующем нас признаке генеральной совокупности, то выборка называется
репрезентативной (представительной). Метод исследования свойств генераль-
ной совокупности по данным выборки называется выборочным методом.
Необходимым условием репрезентативности выборки является ее случайность.
Выборка называется случайной, если любой объект генеральной совокупности с
одинаковой вероятностью может попасть в эту выборку.
Если объем в генеральной совокупности конечен, то для обеспечения равной
возможности попадания объектов в выборку применяют различные приемы,
в частности, используют генераторы случайных величин (случайные числа). До-
10.2. Представление статистических данных
281
пустим, что генеральная совокупность содержит У объектов, а в выборке ДОЛЖНО
быть п элементов. Объекты генеральной совокупности нумеруют от 1 до N. За-
тем вырабатывают п случайных чисел, принимающих с равными вероятностями
значения от 1 до N. Так как случайные числа могут повторяться, то выборка по-
лучается с повторениями. Если выборка должна быть без повторений, повторяю-
щиеся номера не учитывают.
ОТСТУПЛЕНИЕ --------------------------------------------------------------
Термин «статистика» может употребляться в различных значениях.
Статистика — это совокупность данных о множестве однородных объектов. Например,
это совокупность данных о количестве пассажиров каждого авиарейса «Рига-Москва» М
июнь-август одного года.
Статистика — это совокупность методов обработки данных. Весьма часто первичная ин-
формация неупорядочена и трудна для понимания. Речь идет о методах преобразования
и описания данных, делающих эту информацию более наглядной и понятной.
Статистика — это некоторая функция выборочных данных, например, сумма наблюден-
ных значений, число данных, превышающих заданную величину, и т. п.
Наконец, статистика — это раздел математики, посвященный методам анализа статисти-
ческих данных. Именно этому направлению будет посвящено в основном дальнейшее
изложение.
10.2.	Представление статистических данных
Определение 3. Исходные данные, записанные в порядке неубывания наблюден-
ных значений, называются вариационным рядом х(1), х(2).х(п),	где
Х(1) -Х(2) -••• -Х(пУ
В некоторых случаях в результате наблюдений сразу получается вариационный
ряд. Если, например, на испытательном стенде исследуется продолжительность
работы некоторых образцов до отказа, то моменты отказа образцов сразу образу-
ют вариационный ряд.
Остановимся вначале на представлении выборки, соответствующей дискретной
случайной величине. Будем в дальнейшим обозначать #{А} число элементов вы-
борки, удовлетворяющих условию А. Например, #{Х = х(;)} есть число данных
выборки, равных х(1).
Для дискретных случайных величин повторяющиеся значения указываются толь-
ко один раз вместе с числом повторений и, для значения x(j).
Определение 4. Пусть дискретная случайная величина X значение х(1) приняла Я|
раз, значение х(2) — п2 раза и т. д., то есть п, = #{Х = х(/)}, 1=1,2,.... k. Частотой Со-
бытия X = х(0 называется отношение
(юл)
п
где п = И| + п3 + ... — общее число наблюдений (объем выборки).
В табличной форме это может быть представлено, как показано в табл. 10.1.
282
10. Задачи математической статистки и первичная обработка данных
Таблица 10.1. Табличное представление наблюдений над дискретной
случайной величиной
Х<1>	хт				*(*)
п,	п2		п1		пк
Pt	р'ъ		Pi		Pk
Рассмотрим графическое изображение данных (рис. 10.1). Данные (х(1), «0,
(х(2), «г). •••> (x(k)> nk) изображаются точками на плоскости. Эти точки соединяют-
ся отрезками прямой. Получается ломаная линия, которая называется полигоном
частот.
Определение 5. Под группировкой данных понимают разбиение интервала, содер-
жащего п наблюдений xj, xj.xj, на некоторое число интервалов т и под-
счет числа наблюдений, попавших в каждый из образованных интервалов. Будем
обозначать длины интервалов Д£(, Д£2.Д£т, а середины интервалов группиро-
вания	Тогда число наблюдений а,, попавших в j-й интервал (или
просто — число наблюдений в j-м интервале) есть число наблюдений х, удовле-
творяющих неравенству
дг,- дл
t.—(10.2)
1	2	1	2
или
i'4<x<ij.,	(10.3)
дг,
где £' =tj +—-— правый конец у-го интервала группирования, у = 1, 2, ..., т,
2
01	2 '
Определение 6. Частотой наблюдений hj в j-м интервале группирования называ-
ется отношение числа наблюдений, попавших в j-й интервал, at =	< х S }
к обшему числу наблюдений и:
10.2. Представление статистических данных
288
Л,	(10.4)
п
Относительной частотой называется величина
л;=А_.	(Ю.5)
Определение 7. Накопленной частотой Нг соответствующей j-му интервалу, на*
зывается сумма наблюдений в первом, втором..j-м интервалах. Иными слова-
ми, это частота наблюдений, не превосходящих верхней границы j-го интервала
At,
группирования t? +
И,-th,.	(10.6)
1=4
Определение 8. Гистограммой относительных частот называется графическое
изображение функции
Л,	At;	At,
/•(t) = ft; = -+- при tj	+	(10.7)
ZAv j	Л	Л
Результат группирования можно представить графически в системе координат
(t,h/ At). По оси абсцисс откладываются интервалы группирования. На каждом
из интервалов строят прямоугольник, площадь которого равна частоте в интер-
вале. Для этого в качестве высоты прямоугольника берется относительная часто-
та. На рис. 10.2 представлена гистограмма относительных частот.
Рис. 10.2. Гистограмма относительных частот
Пример 10.3. Время, за которое пассажир прибывает в аэропорт до вылета, слу-
чайно, так как зависит от многих факторов. В следующей таблице приведены
(в сгруппированном виде) результаты двухсот наблюдений, проведенных в неко-
тором аэропорту. Здесь же приведены результаты вычислений по формулам
(10.4)-(10.6) соответствующих частот, относительных частот и накопленных
частот.
10. Задачи математической статистики и первичная обработка данных
284
ждения улетающих пассажиров в аэропорту
Таблица 10.2. Врем Интервалы вре- меня, мин t)_i - tj Число данных в интервале, Частота в интервале, hj	 Накопленная частота, Hj Относительная^ частота, hj  10	я паю 0- 22—- 17 0.085	20- 40	40- 60	60- 80	80- 100	100- 120	120- 140	140- 160	160- 180
		30	27	43	34	29	9	8	3
		0.150	0.135	0.215	0.170	0.145	0.045	0.040	0.015
		0.235	0.370	0.585	0.755	0.900	0.945	0.985	1.000
	0.42!	0.750	0.675	1.075	0.850	0.725	0.225	0.200	0.075
									
। и свойства выборочных
10.3.	Определен»
характеристик
я совокупность, на основании которой следует сделать
И имеется выбор041 генеральной совокупности. Разумеется, эти выводы
ыводы о распределен больше объем выборочной совокупности. В предель-
б тем достоверней 'званию подвергаются все элементы генеральной сово-
У случае (когда обсЛ'лборочная совокупность совпадает с генеральной) эти
Н°М сти то есть когда точными. Однако обычно мы не можем обследовать
КУ т абсолютность. В одних случаях это вызвано тем, что объем
выводы оудут aucuj	j
генеральную c°0OIt бесконечен, в других — тем, что обследование каждо-
ВСЮ пальной совокупн°'еделенными затратами времени и средств (например,
го элемента связано с Оюгут привести к разрушению испытуемых образцов),
испытания на прочностей выборки случаен, то выводы и оценки, основан-
Ясно что так как сост^ь приблизительными оценками и выводами, имеющи-
ные на ней, .-- ,	,
еооятностныЙ харособом использовать имеющуюся информацию и ука-
ХГИ Р ~	.1	.. ...	ППТТГ.Ч ТТТТТ IV ...,1.1	.... П..... ,,..1. ЛИ-
ТОМ, ч--------,
зать степень достОверЬиале.
ном <------
В первую очер*Д*
ной совокуп
сти. Каждая
ной, и для И
Определяй
чины X. С
значений I
Припиши
ность,
сл
___й являют0* Гер. Задача математической статистики заключается в
чтобы наилучШИ^и оценок и выводов, основанных лишь на ограничен-
степень достоаерЬиале.
статистическом * для каждой характеристики распределения генераль-
ЩЯствующую ей характеристику выборочной совокупно-
СОЙзристика будет называться эмпирической или выбороч-
будет использоваться значок «*».
•Jim множество наблюденных значений случайной вели-
гут быть и одинаковые, как пространство возможных
ой случайной величины X': Q ={х(1),х(2),..., х(п)}.
ентарному событию {X'=x(i)}, i=l,2,...,ra, вероят-
отетические характеристики, полученные для данного
эмпирическими характеристиками исследуемой слу-
(1),х(2).х(п) есть вариационный ряд, соответству-
совокупности. Эмпирической (Ъинкиией оаспрелеления
10.3. Определения и свойства выборочных характеристик
288
называется функция, которая при каждом значении х равна наблюденному числу
значений случайной величины, не превосходящих х, деленному на общее число
наблюдений:

0	при
—#{Х <х} при
п
при
х<х(1);
*(1)
x^xw.
(10.8)
Для уяснения физического смысла функции F'„ (х) рассмотрим событие X Их.
Если функция распределения случайной величины X есть Ё(х), то вероятность
этого события равна Е(х). В результате п независимых наблюдений это событие
появилось #{Х < х} раз, то есть наблюденная частота составила #{Х < х}/п. По
теореме Бернулли (см. следствие 7.2) при п -> оо частота события #{Х <, х}/п бу-
дет стремиться по вероятности к истинной вероятности Е(х), то есть в каждой
точке х
ЕДх) = А#{Х<х}-^->Е(х).
п
(10.9)
Таким образом, эмпирическая функция распределения является эмпирическим
(или выборочным) аналогом функции распределения генеральной совокупности.
Нетрудно проверить, что эмпирическая функция распределения обладает всеми
свойствами функции распределения (она не убывает, на минус бесконечности
равна 0, а на плюс бесконечности — единице, непрерывная справа). Поэтому
эмпирическая функция является приемлемой оценкой функции распределения
F(x). Это подтверждается следующей теоремой, устанавливающей соответствие
между обеими функциями распределения.
Теорема 10.1 (Гливенко). Пусть F(x) — функция распределения случайной вели-
чины X, а Е„*(х) — эмпирическая функция распределения выборочной совокуп-
ности объема п. Тогда
sup |Ея’(х)-Е(х)|—>ol = 1.
(10.10)
Итак, максимальное расхождение между F’(x) и F(x) с ростом п стремится к
нулю. Графическое представление эмпирической функции распределения имеет
вид, изображенный на рис. 10.3.
Это есть ступенчатая кривая, возрастающая от 0 до 1 и имеющая «скачки» в точ-
ках х(1), х(2),.... х(п). Величина скачка в точке х(1) равна и,/и, если наблюдено п< зна-
чений х(|), в частности, 1/п, если наблюдено одно значение. Если x(j) # х(/+1), то
между точками оси абсцисс х(1) и х(1+1) эмпирическая функция распределения
сохраняет постоянное значение.
Выше уже отмечалось, что частота любого события с увеличением объема выбо-
рочной совокупности, то есть увеличением числа наблюдений, стремится к веро-
ятности этого события. Следовательно, эмпирическим (выборочным) аналогом
вероятности события является наблюденная частота этого события. Например,
для дискретной величины вероятность Р{Х =х(П) оценивается частотой nt/n,
286
10. Задачи математической статистики и первичная обработка данных
где п, равно числу наблюдений, в результате которых было зафиксировано зна-
чение х(1). Вероятность Р{Х < х} = F(x) оценивается, как мы уже знаем, частотой
-#{Х <х}. В случае группировки данных вероятность попадания случайной
п
величины в j-й интервал группирования, то есть P{tj -0.5ДГ, <Х <tj + 0.5^},
оценивается частотой Л, = —. Следовательно, если объем выборки достаточно
п
велик, то по наблюденным частотам можно судить о законе распределения. Так,
внешний вид гистограммы должен напоминать кривую плотности соответствую-
щего распределения. Этими соображениями мы воспользуемся, когда будем по
данным выборки исследовать закон распределения случайной величины.

0,8
0,6
0,4
0,2
о -------------------1--------1--------1--------1-------1-----►
47	48	49	50	51	52 х
Рис. 10.3. График эмпирической функции распределения
Итак, мы рассмотрели эмпирические аналоги вероятности событий и функции
распределения. Рассмотрим теперь эмпирические аналоги числовых характери-
стик генеральной совокупности — математического ожидания, дисперсии и дру-
гих моментов.
Определение 11. Эмпирический момент r-го порядка задается формулой:
n:=-i(x(0)r.	(io.li)
И ,=1
В частности, эмпирическое математическое ожидание — это эмпирический мо-
мент первого порядка, называемый также средним арифметическим Хп:
Н* -Hi
П 1.1
Компьютерный практикум № 16. Решение задач дескриптивной статистики в пакете STATISTICA
287
Эмпирическая дисперсия определяется формулой
ст2’=-£(х(1)-ц’)2.	(10.12)
П
Как и для истинной дисперсии, имеет место также следующее соотношение для
эмпирической дисперсии:
ст2’=ц;-(м’)2.	(Ю.13)
В случае повторяющихся данных формулы (10.11) и (10.12) эквивалентны сле-
дующим выражениям, которые обычно применяют для нахождения эмпириче-
ских моментов и дисперсии дискретных случайных величин:
1 * м’ =- Zn>x<0-	(10.14)
П ,=1	
о2, = - 2«,(х<() -ц’)2, Л М	(10.15)
Иг’ =-Е«>(Х(»)Г- П ы	(10.16)
где суммирование ведется только по различным значениям вариационного ряда.
Определение 12. В случае сгруппированных данных эмпирические характери-
стики подсчитываются по формулам:
”j-l	?-1
о2’ =-£о?(«у -ц’)2 = £лу(гу -ц’)2,	(10.18)
«7=1	j-1
Для вычисления по сгруппированным данным эмпирической дисперсии может
быть использована также формула (10.13).
Компьютерный практикум № 16.
Решение задач дескриптивной статистики
в пакете STATISTICA
Общие положения
Настоящий практикум открывает цикл работ, выполняемых в пакете STATISTICA.
Пакет STATISTICA представляет собой интегрированную систему статистиче-
ского анализа и обработки данных. Производитель пакета — фирма StatSoft Inc.
(США) — выпустила первую версию STATISTICA/DOS в 1991 г. С 1994 г. на-
чат выпуск пакета STATISTICA под Windows. Версия STATISTICA 4.5 в 1995 г.
включена в число 100 лучших программных продуктов для персональных ком-
пьютеров (ПК). В настоящей книге мы ориентируемся на версию пакета
STATISTICA 5.5, однако технология решения рассматриваемых нами примеров
практически не меняется при переходе к другим версиям.
288
10. Задачи математической статистики и первичная обработка данных
Цель и задачи практикума
Целью практикума является приобретение практических навыков первичной об-
работки данных в пакете STATISTIC А.
Задачами практикума являются вычисление основных числовых характеристик
выборки и графическое изображение соответствующих результатов.
Необходимый справочный материал
Для анализа и обработки данных в пакете используются статистические модули,
в которых объединены группы логически связанных статистических процедур.
Перечень основных модулей пакета STATISTICA представлен в табл. 10.3.
В данном практикуме нам понадобится модуль Basic Statistics and Tables, в после-
дующих практикумах используются также модули Multiple Regression и Nonpa-
rametrics/Distribution. Для ознакомления с остальными модулями рекомендуется
обратиться к [1].
Таблица 10.3. Основные статистические модули пакета STATISTICA
Наименование модуля	Назначение
ANOVA/MANOVA	Одномерный и многомерный дисперсионный и ковариационный анализ
Basic Statistics and Tables	Описательные статистики, группировка, вычисление корреляции, t-критерий для групповых различий, таблицы частот
Canonical Analysis	Канонический корреляционный анализ
Cluster Analisys	Кластерный анализ
Discriminant Analysis	Дискриминантный анализ
Factor Analysis	Факторный анализ
Log-Linear Analysis	Лог-линейный анализ (анализ сложных многоуровневых таблиц)
Multidimensional Scaling	Многомерное шкалирование
Multiple Regression	Линейный регрессионный анализ
Nonlinear Estimation	Нелинейное оценивание
Nonparametrics/ Distribution	Непараметрическая статистика, подгонка эмпирического распределения к теоретическому
Reliability /Item Analysis	Анализ надежности
SEPATH	Моделирование структурных уравнений (многомерный статистический анализ)
Survival Analysis	Анализ длительностей жизни
Times Series/Forecasting	Анализ и прогнозирование временных рядов
При запуске пакета автоматически открывается окно переключателя модулей
STATISTICA Module Switcher, представленное на рис. 10.4. После выбора из пред-
ложенного списка нужного модуля нажмите курсором мыши на кнопку Switch to
Компьютерный практикум № 16. Решение задач дескриптивной статистики в пакете STATISTICA
288
(Переключить). В результате откроется прикладное окно модуля, содержащее
таблицу с исходными данными, с которыми работали в предыдущем сеансе. От*
метим, что в процессе работы в пакете окно переключателя модулей может быть
вызвано командой прикладного меню Analysis—Other Statistics.
S1AIISTICA Module Switcher
Nonparametrics/Distrib
fUg ANOVA/MANOVA
 
W Multiple Regression

Nonlinear Estimation
Time Series/Forecasting
p Cluster Analysis
Ц1.Ц Data Management/MI M
Factor Analysis
Дрфсйммамй*» * *
Ьэдк&эд tabSH'»'z' , f«
latUn,
симМЬиМЬм&йЬ
tftpri fafjfrtaX лисим,
сймйэддоисямиг '
;
ВДйепшйМ&Х'
сасдМэг
мечЬЫа*ог1а4
• *
Рис. 10.4. Окно переключателя модулей пакета STATISTICA
Прикладное окно пакета STATISTICA представлено на рис. 10.5, оно имеет
стандартную для окна приложения MS Windows структуру. Верхняя строка яв-
ляется заголовком окна и содержит имя приложения — STATISTICA и имя актив-
ного модуля — Basic Statistics and Tables, справа расположены кнопки для изме-
нения размеров окна. Вторая строка содержит команды прикладного меню. Это
меню включает набор стандартных для приложения MS Windows групп команд:
File, Edit, View, Options, Window, Help, а также две специфичные группы Analysis
(команды для управления вычислениями) и Graphs (команды для работы с гра-
фиками).
Рио. 10.В. Окно пакета STATISTICA
290
10. Задачи математической статистики и первичная обработка данных
Гретья и четвертая строки образуют панель инструментов (Toolbar), содержащую
снопки быстрого вызова команд меню. Для настройки панели инструментов ис-
юльзуется команда прикладного меню View—Toolbar. Последняя запись означа-
ет, что вначале выполняется команда View, после чего из появившегося списка
1ыбирается опция Toolbar. Чтобы узнать название отдельной кнопки (иконки),
достаточно навести на нее курсор мыши. Многие кнопки (увеличения и умень-
шения изображения, копирования, вставки, сохранения и т. п.) имеются в боль-
шинстве приложений MS Windows, и они хорошо известны читателю. Среди ин-
лрументов, специфичных для пакета STATISTICA, следует указать кнопки
построения графиков, которые открывают окна, предназначенные для работы с
различными типами графиков. Здесь же находится кнопка Quick Basic Stats (бы-
стрых основных статистик), которая вызывает меню, предназначенное для рас-
<ета основных статистик для одной или нескольких переменных. Необходимо
подчеркнуть, что вид панели инструментов зависит от настроек окна и типа ис-
пользуемого документа. Например, при работе с таблицей исходных данных до-
ступны кнопки с названиями Var и Cases, которые позволяют изменить размеры
таблицы, а также свойства ее столбцов и строк, что будем показано ниже.
Нижняя строка окна является строкой состояния (Status Ваг), в ней указаны ре-
жимы работы системы. В представленном примере система готова к работе (со-
стояние READY).
Основную (центральную) часть окна приложения занимает рабочее окно, в кото-
ром вводятся исходные данные и выводятся результаты их статистической обра-
ботки, представляемые в табличном или графическом виде. В приведенном на
рис. 10.5 примере показан вид рабочего окна на этапе ввода исходных данных.
Ввод данных производится в клетки таблицы с заголовком DATA: NEW.STA
10v*10c. Здесь DATA определяет тип таблицы — таблица с исходными данными;
NEW — имя файла с исходными данными (назначается по умолчанию и может
быть изменено пользователем при сохранении файла); STA — стандартное
расширение для файла с исходными данными в пакете STATISTICA; 10v*10c —
размер таблицы NEW.STA, то есть 10 столбцов для размещения переменных
(Variables) и 10 строк — для наблюдений или случаев (Cases). По умолчанию
таблица с исходными данными, называемая часто Spreadsheet, имеет размер-
ность 10x10, то есть 10 строк на 10 столбцов. Для увеличения количества строк
необходимо ввести команду Cases—Add и далее указать место и количество до-
бавляемых строк. Аналогичным образом по команде Vars—Add добавляется нуж-
ное количество столбцов (Variables). С помощью кнопок Cases и Vars можно вы-
полнить также другие преобразования исходной таблицы, например, уменьшить
ее размеры, переименовать строки и столбцы и многое другое.
Заголовки столбцов таблицы содержат имена переменных. В нашем примере ис-
пользуются имена переменных VARI, VAR2,..., VAR10, которые назначены сис-
темой по умолчанию. Для их переименования надо ввести команду Vars—Current
Spec или дважды щелкнуть курсором мыши на соответствующем имени столб-
ца. Далее в открывшемся окне (рис. 10.6) в поле Name вместо исходного имени
ввести новое имя переменной. В этом окне можно изменить и другие специ-
фикации столбца, например формат исходных данных для выбранного столбца.
Для этого необходимо выбрать нужную категорию (Category), представление
Компьютерный практикум № 16. Решение задач дескриптивной статистики в пакете STATISTICA
291
(Representation) и количество используемых символов (Column width). По умол-
чанию все данные имеют числовой формат 8.3, что означает: общая длина поля —
8 символов, из которых три приходятся на десятичную часть числа.
Если электронная таблица, называемая Spreadsheet, имеет большие размеры, она
может быть разделена на части до четырех секций перемещением специальной
метки разделения (черный прямоугольник на линиях прокрутки). Система по-
зволяет работать как с числами, так и с текстовыми данными, что очень важно ВО
многих статистических исследованиях; например, при обработке анкетных данных.
Пакет STATISTICA поддерживает разнообразные способы ввода исходных дан-
ных в электронную таблицу: ввод данных с клавиатуры; копирование данных на
других приложений через буфер обмена (команды Edit—Copy, Edit—Paste), расчет
по формулам новых данных на основе ранее введенных; импорт данных из дру-
гих приложений (команда прикладного меню File—Import Data) и др.
Variable I
Данг |2ЕНП	но cod*-1 9999 Щ
Diiplqp Fonoat-
СЫиипдаЛК |5 Щ ДвсявЫ» [5 §
Category Hnpfswitalion
Number
Date
Tune
Scientific
Currency
Percentage
1000 000; 100U00U
1 000.000; -1 000 000
1000.000: (1000 0001
1 000.000: (1 000 000)
Long name (label, link, or foiwila with Eunctione |)
Ж
J
d
Exum*»: Lebet Grow reoraeir>193T ' - , ' Formyl®:'*И »v2;comment
link.'	-(v1>0FASE*»3
Рис. 10.6. Окно для задания спецификаций столбца
Результаты статистического анализа выводятся в виде специальной электрон-
ной таблицы, называемой Scrollsheet. Данная таблица может быть сохранена в
файле с расширением .scr (таблица с результатами), а также в файле исходных
данных с расширением .sta или текстовом файле формата .txt.
Пакет предоставляет пользователю широкий набор различных графиков, кото-
рые могут строиться на плоскости (2D) и в пространстве (3D). Графики подраз-
деляются на две категории: специализированные статистические графики
(STATS Graphs) и пользовательские графики (Customs Graphs). Графики можно
сохранять в файлах с расширением .stg.
При наличии большого количества выходных документов в пакете STATISTICA
предусмотрена возможность создания сводного отчета в формате .txt или .rtf,
включающего как таблицы результатов, так и построенные графики. Естествен-
но, не исключается возможность переноса результатов анализа в документы дру-
гих приложений (например, MS Word, MS Excel и др.) через буфер обмена (ко-
манды Edit—Copy, Edit—Paste). С целью сохранения наглядности представления
результатов в документах MS Word их рекомендуется переносить в виде твер-
дых копий экрана, которые получаются путем нажатия клавиши Print Screen.
292
10. Задачи математической статистики и пераичная обработка данных
Реализация и результаты выполнения задания
Выполним первичную обработку статистических данных, характеризующих ме-
теоусловия аэропортов в зимний период. В качестве исходных данных будем ис-
пользовать выборку из 30 аэропортов, для которых известно среднее количество
дней в году с твердыми осадками, то есть со снегом (см. ниже).
Для решения задач описательной статистики будем использовать модуль Basic
Statistics and Tables. Для его запуска выделим строку Basic Statistics в окне пере-
ключателя модулей STATISTICA Module Switcher и нажмем кнопку Switch to. В ре-
зультате откроются окно с таблицей исходных данных и стартовая панель моду-
ля, содержащая список процедур, которые доступны в данном модуле (рис. 10.7).
Назначение этих процедур следующее: Descriptive statistics — расчет описатель-
ных статистик; Correlation matrices — вычисление и анализ корреляционной мат-
рицы; t-test for independent samples и t-test for dependent samples — i-тесты для
проверки гипотез в случае независимых и зависимых выборок соответственно;
Breakdown & one-way Anova — классификация и однофакторный дисперсионный
анализ; Frequency tables — построение таблиц частот; Tables and banners — табли-
цы и заголовки (дополнительные средства работы с таблицами, например, по-
строение и обработка перекрестных (кросс-) таблиц); Probability calculator —
калькулятор вероятностных распределений; Other significance tests — другие кри-
терии значимости, используемые для проверки гипотез; например, для проверки
различий между двумя средними для нормальной совокупности. Для решения
задач данного практикума используются процедуры Descriptive statistics и Fre-
quency tables. Ряд других процедур рассматривается нами в практикумах, пред-
ставленных в последующих главах.
£gg Correlation matrices
H£j t-tett for independent templet
t-tett for dependent samples
к Breakdown I one-way ANOVA
ЙЯЗ Frequency tablet
T ablet and banners
lift Probability calculator
Other tignificanca tests

to Basic Statistics and Tables
E Disruptive statistics
Рис. 10.7. Стартовая панель модуля Basic Statistics and Tables

Первым этапом работы является создание таблицы исходных данных. Если в ра-
бочем окне (см. рис. 10.5) таблица с исходными данными является пустой, то бу-
дем использовать ее; в противном случае с помощью команды File—New Data от-
кроем новую таблицу и сохраним ее на диске с именем airports.sta. С помощью
команды Cases—Add добавим в таблицу 20 новых строк, увеличив общее их ко-
личество до 30.
Для удобства работы переименуем заголовки строк таблицы, заменив их на на-
звания аэропортов, и заголовок второго столбца, заменив стандартное имя VAR1
на СНЕГ. Для этого выполним следующие действия. Отметим первый столбец
таблицы, который содержит номера случаев, и введем команду Cases—Nemes (или
Компьютерный практикум Ns 16. Решение задач дескриптивной статистики в пакете STATISTICA
выполним двойной щелчок по заголовку столбца). В результате последователь-
но откроются диалоговое окно для задания ширины столба (рис. 10.8, а) и окно
для ввода в первый столбец наименований строк таблицы (рис. 10.8, б). Исполь-
зуя первый вариант окна Case Name Manager, установим ширину столбца и на-
жмем кнопку Yes. Появится второй вариант окна Case Name Manager, с помощью
которого введем построчно наименования аэропортов. Отметим второй столбец
с именем VAR1 и введем команду Vars—Current Spec. В открывшемся окне спе-
цификаций столбца (см. рис. 10.6) в поле Name введем новое имя столбца СНЕГ.
Кроме того, в поле Decimals установим 0 цифр в дробной части числа, так как
переменная СНЕГ определяет количество дней с твердыми осадками в году и
должна иметь целый тип.
Далее в столбец СНЕГ введем статистические данные, как это показано на
рис. 10.9. На этом ввод данных закончен.
Рис. 10.8. Окна, используемые для ввода заголовков строк
NUMERIC
VALUES
НдахДНсх,;
ИИ
Сахара '
Волгоград,
Тбилиси
ЁрабаН
Окск
Ллма-Лаа____
Taiintem
aiih-ii

60;
iob!
' so]
"is!
4S]
40i
4 Si
..bb!
' bb!
40
20;
60
20,
ibj
6;
..ib!
’ 6 bi
20
..is!
80]
60:
bb!
bb!
60!
35
100]
40
' 20'
60]
—1
Рио. 10.8. Таблица с исходными данными
294
10. Задачи математической статистики и первичная обработка данных
Для решения задач практикума запустим процедуру Descriptive statistics. Для этого
на стартовой панели модуля (см. рис. 10.7) выберем задачу Descriptive statistics и
нажмем кнопку ОК. Имеется и другая возможность запуска процедуры — из окна
пакета (см. рис. 10.5) с помощью команды Analysis—Descriptive statistics.
В открывшемся окне Descriptive Statistics (рис. 10.10) нажмем на кнопку Variables,
в результате откроется окно Select the varibles for analisys, представленное на
рис. 10.11. В предлагаемом списке переменных выделим переменную, для которой
требуется выполнить первичную обработку. В нашем случае это будет перемен-
ная номер 1, или СНЕГ. Нажав кнопку ОК, вернемся в окно Descriptive Statistics.
Рис. 10.10. Окно процедуры Descriptive Statistics
Рис. 10.11. Окно для выбора переменных
Первой задачей обработки является вычисление числовых характеристик выборки.
1 открывшемся окне Descriptive Statistics нажмем на кнопку More statistics, в ре-
ультате появится окно Statistics, содержащее список показателей, которые тре-
буется вычислить (рис. 10.12). В нашем случае отметим следующие показатели:
Компьютерный практикум № 16. Решение задач дескриптивной статистики в пакете STATISTICA
2М
Valid N (объем выборки), Mean (среднее), Median (медиана), Standart Deviation
(среднее квадратическое отклонение), Variance (дисперсия), Minimum & maximum
(минимум и максимум), Range (размах варьирования), Quartile range (размах
квартилей) и активизируем кнопку ОК.
Рис. 10.12. Выбор числовых характеристик выборки
Для получения ответа нажмем на кнопку Detail descriptive statistics в окне Descriptive
Statistics (см. рис. 10.10). После этого откроется таблица результатов, представ-
ленная на (рис. 10.13). Для просмотра всех результатов необходимо использовать
линию прокрутки. Соответственно на рис. 10.13, а представлена первая часть таб-
лицы результатов, на рис. 10.13, б — ее вторая часть, полученная после прокрутки.
Continue.. J
ИНЕЯ
'ggDescnpUve Statistics (anpoits.sta)
94.00000 ; 40.00000 741.5966	27.23227
б
Рис. 10.13. Результаты расчета числовых характеристик выборки
Следующей задачей обработки является построение таблицы и графиков частот.
Для этого нажмем на кнопку Continue и вернемся в окно Descriptive Statistics. Да-
лее нажмем на кнопку Frequency tables, в результате получим таблицу частот,
представленную на рис. 10.14. В первом столбце таблицы заданы интервалы для
переменной х (количество дней со снегом), причем последняя строка содержит
пропущенные (Missing) значения. Втоллй rm«/»n --------------------“ --
296
10. Задачи математической статистики и первичная обработка данных
ременной в интервалы {Count), третий столбец — кумулятивное число попада-
ний {Cumul. Count), четвертый и шестой столбцы — частоты в процентах соот-
ветственно для имеющихся в наличии (не пропущенных) наблюдений {Percent
of Valid) и для всех наблюдений (% of all Cases), пятый и седьмой столбцы — куму-
лятивные частоты в процентах, соответственно для имеющихся в наличии (не пропу-
щенных) наблюдений {CumuL % of Valid) и для всех наблюдений {Сити! % of All).
11
I laiipoils std)
lilimimmuiu мш
!| \ч .Ml
0
9
30
43
80
...........
iob
11
4
2
~“o
0000
3333
0000
3333
dodo
30
13'
36
13
.......
30
43
.........
ibb
о
•g
.....
24
.....
30
’30
; 30
f'i'3"
>""13
...6.	.
T” Tboow
0.00000
boob'd?
33333
66667 :
33333 ’
66667 :
0.0000
..bbdd
3333
dodo
3333
dodo
0.0000 • 0.00000
..dbbbb'
33333
66667'
33333
. .66667
“djjoooo'
Рис. 10.14. Таблица частот
O.W.jJU?
Для построения графиков частот и кумулятивных частот выделим столбцы
Percent of Valid и CumuL % of Valid и выполним команду меню Graphs—Custom
Graphs—2D Graphs. В открывшемся окне (рис. 10.15) выберем тип графика Line
Plot и нажмем кнопку ОК.
В результате получим графики, представленные на рис. 10.16.
Рис. 10.15. Окно выбора вида графика
(Tjbi.ipM 71) Uiaph
Рис. 10.18. Графики частот и кумулятивных частот
Компьютерный практикум № 16. Решение задач дескриптивной статистики в пакете STATISTICA
297
Для построения гистограммы частот через кнопку Continue... вернемся в окно
Descriptive Statistics. С помощью функциональной кнопки Histograms (см. рис. 10.10)
получим гистограмму, представленную на рис. 10.17. Кроме гистограммы частот
на рисунке показана теоретическая кривая плотности распределения наблюдае-
мой случайной величины в случае нормального закона.
Рис.10.17. Гистограмма частот
В пакете имеется возможность построить диаграмму размаха варьирования слу-
чайной величины х. Для этого в окне Descriptive Statistics (см. рис. 10.10) необхо-
димо нажать на кнопку Box & Wisker plot for all variables. В результате откроется
окно выбора списка выводимых параметров, представленное на (рис. 10.18).
В нашем случае выберем первую строку, задающую следующие параметры выво-
да: медиану, квартиль и разброс.
Box Whiskei Type:

lis
в>::
ЙЕ
j fl*
ЗЗеЛО.	- .
eflnCOl
*.,. z 
ixiu inf wHiiiA
Рис. 10.18. Окно выбора списка выводимых параметров
После нажатия кнопки ОК получим диаграмму размаха, представленную на
рис. 10.19. Диаграмма показывает, как распределены дни со снегопадами для
совокупности аэропортов. В частности 50% случаев приходится на диапазон
от 20 до 60 дней. Медиана равна 45, минимум — 5, максимум — 100 дней.
В заключение отметим, что решение рассмотренных задач практикума можно
выполнить также с помощью процедуры Frequency tables, входящей в состав
модуля Basic Statistics/Tables. После запуска процедуры Frequency tables
откроется окно, представленное на рис. 10.20. Для решения рассмотренных
выше задач практикума необходимо воспользоваться соответственно кнопка-
298
10. Задачи математической статистики и первичная обработка данных
ми Descriptive statistics, Frequency tables, Histograms и Box & Wisker plot for all
variables.
Рис. 10.19. Диаграмма размаха варьирования случайной величины
Рис. 10.20. Окно процедуры Frequency tables
Говоря об основных различиях между процедурами Descriptive statistics и Fre-
quency tables, необходимо подчеркнуть, что последняя предоставляет больше
возможностей при работе с таблицами и графиками частот, однако проигрывает
первой при расчете числовых характеристик выборки, так как вычисляет только
выборочное среднее, среднее квадратическое отклонение, минимальное и макси-
мальное значения.
Компьютерный практикум № 17 Работа с распределениями случайных величин в пакете STATISTICA	2М
Компьютерный практикум № 17
Работа с распределениями случайных величин
в пакете STATISTICA
Цель и задачи практикума
Целью практикума является приобретение практических навыков по работе с
различными распределениями случайных величин в пакете STATISTICA.
Задачами данного практикума являются: построение графиков плотностей И
функций распределения для используемых в задачах статистического анализа
непрерывных распределений (нормального, %2, Фишера и Стьюдента); нахожде-
ние соответствующих квантилей для заданных вероятностей; расчет вероятно-
стей и построение полигона вероятностей и графика функции распределения ДЛЯ
дискретных случайных величин (на примере биномиального распределения).
Необходимый справочный материал
Для решения разнообразных задач статистического анализа необходимо знать
значения функций распределения случайных величин и соответствующих кван-
тилей. Данные задачи можно сформулировать следующим образом: определить
вероятность того, что случайная величина не превысит фиксированного значе-
ния; найти значение случайной величины, для которого функция распределения
равна заданному значению р. Искомое значение случайной величины называет-
ся квантилью, соответствующей вероятности р (подробно это понятие будет рас-
смотрено в параграфе 12.1). В классических учебниках по математической ста-
тистике для этих целей, как правило, используются специальные справочные
таблицы, которые авторы включают в основной текст или в соответствующие
приложения. В настоящей книге справочные таблицы не приводятся — все пока-
затели рассчитываются на персональном компьютере.
Для работы с распределениями непрерывных случайных величин в пакете
STATISTICA используется специальное средство — калькулятор вероятностных
распределений. Для его вызова выполняется процедура Probability calculator, ко-
торая входит в состав модуля Basic Statistics and Tables. С помощью вероятност-
ного калькулятора могут решаться разнообразные элементарные вероятностные
задачи, среди них назовем построение графиков плотностей и функции распре-
деления, определение квантили для заданной вероятности и др.
При запуске процедуры Probability calculator открывается окно калькулятора Pro-
bability Distribution Calculator, представленное на рис. 10.21. В левой части данного
окна дается список распределений непрерывных случайных величин, доступных
пользователю. В средней части в строке р содержится вероятность Р{Х Sx) = F(x),
в строке X — значение случайной величины или квантиль, соответствующая ЭТОЙ
вероятности. Далее содержатся поля для ввода параметров распределения (в на-
шем случае рассматривается нормальное распределение, для которого таких па-
раметров два — математическое ожидание и среднее квадратическое отклонение).
В верхней части окна содержатся опции, предназначенные для настройки режи-
мов работы процедуры. Назначение данных опций следующее: Inverse — работа с
обратной функцией распределения (используется при вычислении квантили);
Two-tailed — построение двустороннего интервала для плотности распределения;
1-Cumulative р — использование вместо вероятности р вероятности 1 - р‘, Create
300
10. Задачи математической статистики и, первичная обработка данных
□raph — создание графика; Print — вывод результатов на печать. Пользователь
чожет выбрать закон распределения и для заданного значения случайной вели-
шны х вычислить значение функции распределения Д(х) или решить обратную
задачу — задать вероятность р и определить соответствующую ей квантиль F-1(x).
Во втором случае следует переключить опцию Inverse.
В нижней части окна выводятся эскизы графиков плотности и функции распре-
деления для выбранного примера. Для построения этих графиков в полном объ-
гме необходимо отметить опцию Create Graph и далее нажать кнопку Compute.
Рг«Ь<*ЬйПу DibtriLuticHi Calculator
Bjrtibution____
I Beta
£ Cauchy
I Chi I
& Exponential
* Extreme value
3 F
a Gamma
» Laplace
Log-Normal
•g Logistic
й Pareto
& Rayleigh
* t (Student)
* Weibull________
ЯСОЕ&ЛНМК
P Fued Scetaig
Рис. 10.21. Окно калькулятора вероятностного распределения
В случае работы с дискретными распределениями для расчета вероятностей и
функций распределения будем применять соответствующие встроенные функ-
ции. Например, для биномиального распределения имеется две встроенные
функции: Binom(x, р, п) и IBinom(x, р, п), вычисляющие соответственно вероят-
ность принятия значения х = i и значение функции распределения в точке х для
биномиального распределения (3.3) и (3.12) с параметрами р и п. В пакете
STATISTICA имеются встроенные функции для всех популярных распределе-
ний, причем функции, у которых имена начинаются с буквы I, вычисляют значе-
ния функций распределения.
Для вычисления встроенной функции в пакете STATISTICA следует отметить
незаполненный столбец таблицы исходных данных Spreadsheet и затем выпол-
нить команду Vars—Current Spec, которая была рассмотрена выше в компьютер-
ном практикуме № 16. Пример ввода встроенной функции с использованием
конструктора Function Wizard показан на рис. 10.22. В открывшемся окне специ-
фикаций переменной, в нижней его части имеется рабочая область Long name
(label, link or formula with Function), которая предназначена для ввода выражений
и комментариев. Набор формулы следует производить здесь, начиная ввод со
знака равно. Далее можно набирать требуемую функцию самому или обратиться
к конструктору, щелкнув мышью по кнопке Function. В последнем случае откро-
ется окно Spreadsheet Formulas, в котором содержится список встроенных функ-
ций. После выбора из списка нужной функции необходимо нажать на кнопку
Insert. В результате после знака равно будет введено выражение, содержащее
нужную функцию с формальными параметрами. Для получения результата
необходимо заменить формальные параметры на фактические, в нашем случае
Компьютерный практикум № 17 Работа с распределениями случайных величин в пакете STATISTICA
301
необходимо задать параметры распределения и значение аргумента. В списке
аргументов функции могут использоваться имена переменных (имена столбцов)
или константы.
Рис. 10.22. Порядок ввода встроенной функции с использованием конструктора
Function Wizard
Реализация и результаты выполнения задания
В первой части практикума выполняются задания для непрерывных распределе-
ний: нормального, х2, Фишера и Стьюдента, во второй осуществляется работа
с биномиальным распределением.
Запустим процедуру Probability calculator, для чего в окне переключателя моду-
лей STATISTICA Module Switcher выберем модуль Basic Statistics и нажмем
кнопку Switch to. В открывшемся окне Basic Statistics and Tables (см. рис. 10.4) из
списка процедур выберем Probability calculator и нажмем кнопку ОК. В результате
откроется окно калькулятора Probability Distribution Calculator, рассмотренное выше
(см. рис. 10.21).
Сначала выполним расчеты для нормального распределения со средним значе-
нием ц = 0.5 и средним квадратическим отклонением а = 1. Первая задача будет
заключаться в поиске квантили для вероятности р = 0.8 и построении графиков
плотности и функции распределения. В окне калькулятора в соответствующие
поля (рис. 10.23) введем параметры распределения, вероятность р и отметим оп-
ции Inverse и Create Graph.
После нажатия кнопки Compute получим окна с результатами, представленные
на рис. 10.24 и рис. 10.25. Значение квантили для заданной вероятности равно
1.341612.
02
10. Задачи математической статистики и первичная обработка данных
Pt obabdity Distribution Calculator

distribution
Bela
a Cauchy
Chit
Exponential
.3 Extreme value
> F
% Gamma
•a Laplace
Log-Normal
й Logistic
£ Pareto
?. Rayleigh
t (Student)
WeibuB___________
«BKConssnHK
PHwnt Seeing
Рис.10.23. Окно с исходными данными для расчета квантили
Probability Distribution Cali ul«t» if

Distribution
Bete
Cauchy
Chi I
Exponential
Extreme value
F
Gamma
Laplace
Log-Normal
Logistic
Pareto
Rayleigh
t (Student)
Weibull
[Normal!
P Fined Scaling
Рис. 10.24. Результаты расчета квантили для нормального распределения
Рис. 10.25. Графики плотности и функции распределения
для нормального распределения
Компьютерный практикум № 17 Работа с распределениями случайных величин в пакете STATISTICA
308
Следующая задача заключается в определении значения функции распределе-
ния для заданного значения случайной величины х= 1. Введя в поле X значение^
равное 1, и нажав кнопку Compute, в поле р получим значение функции распре-
деления, равное 0.691462 (рис. 10.26).
Аналогичные действия выполним для распределений х2. Фишера и Стьюдента.
Результаты проведенных расчетов представлены ниже.
Для х2 -распределения с числом степеней свободы df = 6 и вероятности р = 0.8
определена квантиль Chi_l = 8.558060 (рис. 10.27) и построены графики плотно-
сти и функции распределения (рис. 10.28).
Qislrdwtion
Beta
Г auchy
Г»н I
? Exponential
' Extreme value
F
Gamma
Laplace
:: Log-Normal
Logistic
Paieto
Rayleigh
t (Student)
; Weibutl________
PfmedScahng
Probobilit у Ofstnbut ion Cek id it or
Exponential
Extreme value
Gamma
Laplace
Log-Normal
Logistic
Paieto
Rayleigh
t (Student)
WeibuM
Z INoimal)
PFmed Seeing
Chi I; [esseoto g
-Ф—§
Рис. 10.27. Результаты расчета квантили
для х2-распределения
pjslrdMJbon
Beta
QMjiFaamJ
Рис. 10.26. Результаты расчета функции
распределения для х = 1
Рис. 10.28. Графики плотности и функции распределения для ^-распределения
Для распределения Фишера со степенями свободы т = 4 и п = 15 результаты рас-
четов представлены на рис. 10.29. В поля dfl и dfl введены соответственно зна-
чения т и п, Квантиль этого распределения, соответствующая вероятности
304
10. Задачи математической статистики и первичная обработка данных
р = 0.95, равна F= 3.055568. Графики плотности и функции распределения пред-
ставлены на рис. 10.30.

Probability Distribution Calculator
Рис. 10.29. Результаты расчета квантили для распределения Фишера
pjGrapbl
Probability Density Function
y=F(x;4;15)
Рис. 10.30. Г рафики плотности и функции распределения для распределения Фишера
Probability Distribution Function
p=iF(x;4;15)
Для распределения Стпъюдента с числом степеней свободы df = 10 результаты
расчетов представлены на рис. 10.31. Квантиль этого распределения, соответст-
вующая вероятности р = 0.95, равна t - 1.812461. Графики плотности и функции
распределения представлены на рис. 10.32.
В заключительной части данного практикума рассматривается биномиальное
распределение.
Выполним расчеты для биномиального распределения с параметрами п = 10 и
р = 0.7 в точке х = 9. Введем в таблицу с исходными данными Spreadsheet задан-
ные значения, как это показано на рис. 10.33.
Компьютерный практикум № 17 Работа с распределениями случайных величин в пакете STATISTICA
зов
Рис. 10.31. Результаты расчета квантили для распределения Стьюдента
Probability Density Function
y=student(x;10)
Probability Distribution Function
p=istudent(x;tO)
И'тнрЬЗ

Рис. 10.32. Графики плотности и функции распределения для распределения Стьюдента
Рис. 10.33. Таблица с исходными данными
Далее в окне спецификации четвертого столбца, названного нами Р_Х, в поле
Long name введем формулу для биномиального распределения, как это показано
на рис. 10.34.
Аналогичным образом в окне спецификации для пятого столбца, названного
нами F_X, введем формулу для функции распределения биномиального распре-
деления вида:  IBinom(x, р, п)
306
10. Задачи математической статистики и первичная обработка данных
Рис. 10.34. Окно для ввода функции биномиального распределения
В результате получим следующие ответы: Р{Х = 9} = 0.121 и F(9) = 0.972 (см.
рис. 10.35).
Data Ыпот STA 1flv ж Юс
Рис. 10.35. Таблица с исходными данными и результатами расчета
Далее для биномиального распределения с параметрами п = 10 и р = 0.7 рассчи-
таем распределение вероятностей и функцию распределения. С этой целью вы-
шерассмотренный пример выполним для множества точек х = 0, 1,2.10 путем
формирования 11 строк таблицы. Тогда таблица с исходными данными и полу-
ченными результатами будет иметь вид, представленный на рис. 10.36. Для на-
глядности мы увеличили до пяти знаков длину дробной части чисел четвертого
и пятого столбцов.
binon		> S 1А 10v *	11c	1
NUf|			
		счП. Igglil	у «wfay 4	s X 1 ПСХ	FJK
Г  ж	10 	10 16 10 10 16 16 10 10 10	.70;	0	.00001	.00001 	,7bl	 1	.00014	.00014: .701	 2	.00145:	.00159: 701 		 3:	00900:	.01059: .701	4	.03676;	.04735: 	,70Г	 5	.10292:	.150271 	?70;	 6	.20012;	.35039; 	.’701	 7	.26683:	.61722 70:	8.	.23347:	.85069 . 70l	9	.12106	.97175	
ffl		 ...И	.70;	10	.02825 1 00000	
Рио. 10.38. Таблица с исходными данными и результаты расчета полигона вероятностей
и функции распределения
Компьютерный практикум № 17 Работа с распределениями случайных величин в пакете STATISTICA
307
Используя полученную таблицу с результатами, построим полигон вероятностей
и функцию распределения для заданного биномиального распределения. Для
построения соответствующих графиков необходимо: выделить столбцы Р_Х И
F_X; выполнить команду меню Graphs—Custom Graphs—2D Graphs; в открывшем-
ся окне Custom 2D Graphs (рис. 10.37) выбрать тип графика для столбца Р_Х —
Line Plot (линейный график), для столбца F_X — Step Plot (ступенчатый график)
и задать имя переменной по оси абсцисс — X.
Рис. 10.37. Окно выбора типа графика
После нажатия кнопки ОК получим полигон вероятностей (Р_Х) и график функ-
ции распределения (F_X), представленные на рис. 10.38.
Г1 J
^GraphG: 2D Graph
— p_x
— F_X
Рис. 10.38. Полигон вероятностей и график функции распределения
для биномиального распределения с параметрами п - 10 ио  0.7
308
10. Задачи математической статистики и первичная обработка данных
Задания для самостоятельной работы
1.	Используя пакет STATISTICA, сгенерируйте выборку объема п = 100, соот-
ветствующую экспоненциальному распределению с параметром X = 2. Прове-
дите первичный статистический анализ выборки, как это было сделано выше
в компьютерном практикуме № 16.
Указание. Для генерации п случайных величин, соответствующих заданному
закону распределения, необходимо выбрать один из столбцов таблицы исход-
ных данных, состоящей из п строк. В окне его спецификаций (как это было
показано в компьютерном практикуме № 17) следует ввести формулу, со-
гласно которой вырабатываются необходимые случайные величины. Послед-
ние будут записываться в клетках выбранного столбца.
В частности, для экспоненциального распределения с параметром X, рассмат-
риваемого в настоящем задании, эта формула будет иметь вид:
=VExpon(Rnd(i), X),
здесь — встроенная функция, вырабатывающая случайные величины,
равномерно распределенные в интервале от 0 до 1;
VExpon(y, X) — вычисляет значение обратной функции в точке у для функции
экспоненциального распределения с параметром X.
Для случая нормального распределения, которое будет рассмотрено ниже во
втором задании, аналогичная формула имеет вид:
-VNormal(y, ц; а),
где VNormal(Rnd(\), ц, а) — вычисляет значение обратной функции в точке у
для функции нормального распределения с параметрами ц и а.
2.	Выполните предыдущее задание для выборки из нормального распределения
с параметрами ц = 2 и о = 1.5.
3.	С помощью пакета STATISTICA проанализируйте влияние параметров рас-
пределения на форму кривых плотностей для следующих непрерывных рас-
пределений: экспоненциального, нормального, Фишера, Стьюдента, х2-
4.	С помощью пакета STATISTICA проанализируйте влияние параметров рас-
пределения на форму полигона вероятностей для следующих дискретных
распределений: биномиального, геометрического, Пуассона.
Задачи
Задача 10.1. Число отказов прибора в течение пяти лет гарантийного срока
службы есть случайная величина. Для 50 выбранных приборов число указанных
отказов было следующим: 1, 0,0,1,2, 0,1, 0, 0,0,3,0,1,1, 2,0,0,0, 0,3, 2,1, 1, 0,1,
0, 0, 0, 1, 0, 1, 0, 0, 1, 4, 3, 0, 0, 1, 0, 0, 1, 1, 0, 0, 2, 0, 2, 1, 0.
Требуется: а) построить вариационный ряд исходных данных, рассчитать часто-
ты, построить полигон частот и график эмпирической функции; б) рассчитать
числовые характеристики выборки.
Задачи
Задача 10.2. Размеры дневной выручки магазина (в тысячах рублей) в течение
месяца были следующими: 220, 241,223, 228,190, 184, 205, 228,272, 196, 225, 238,
202,245,184, 230, 188, 204,209,238,247, 264, 216, 207, 232, 224,210, 221, 208, 239.
Для приведенных данных выполнить задание задачи 10.1.
Задача 10.3. Ниже приведены результаты вступительных экзаменов (по
10-балльной системе) по математике 40 случайно выбранных абитуриентов: 8, 7,
8, 8,9,10, 8, 7, 7, 8, 4, 8, 5, 6, 3, 3, 2, 8, 9, 4,10, 3, 9, 8, 6,10, 3, 9, 6, 5, 4, 8, 7,4,9, 8,4,
3, 2, 8, 9, 9.
Для приведенных данных выполните задания задачи 10.1.
Задача 10.4. Для приведенных ниже сгруппированных данных определите сред-
нее арифметическое, эмпирическую дисперсию и среднее квадратическое откло-
нение.
Интервалы изменения данных	7-10	10-13	13-16	16-19	19-22	22-25	25-28
Число данных в интервале	4	8	12	22	3	15	9
11 Точечные оценки параметров
распределений
11.1. Определение и основные свойства
точечных оценок
Первой задачей математической статистики является задача оценки неизвестных
параметров распределений. В этом случае тип распределения известен, а неиз-
вестны только параметры распределения. Например, может быть заранее извест-
но, что случайная величина X имеет нормальное распределение, о параметрах ц
и о которого ничего не известно. Эти параметры и следует оценить по наблю-
цаемым значениям случайной величины.
Пусть Дв(х)есть функция распределения случайной величины X, а 0 — неизвест-
ный параметр (0 может быть вектором). Предполагается, что общий вид функ-
ции Fe(x) задан, так что если бы параметр 0был известен, то распределение слу-
чайной величины было бы определено полностью. Известно также, что значение
параметра 0 принадлежит фиксированному множеству ©, называемому пара-
метрическим пространством. Оценка параметра производится на основании вы-
борки х,’, xj, ..., xj, взятой из генеральной совокупности с функцией распреде-
ления Fe(x), 0 е 0. Выше уже отмечалось, что выборочные значения случайны,
так что в общем случае будем вместо xj, xj, ..., xj описывать выборку как Хь
Х2..ХП.
Определение 1. Точечной оценкой параметра 0 называется любая функция вы-
борки 0(ХР Х2, ...,Х„), подсчитанное значение которой принимается за 0.
Итак, точечная оценка является функцией случайных величин и поэтому сама
является случайной величиной.
В качестве оценки параметра 0 может быть предложено большое число функций
0(-Х\, Х2, ..., Хп). Какие же из этих функций будут действительно наилучши-
ми оценками параметра 0? Оказывается те, которые обладают свойствами несме-
щенности, эффективности и состоятельности. Для уяснения физического
смысла этих свойств еще раз подчеркнем, что оценка 0 является случайной вели-
чиной 0(Xi, Х2,.... Хп), значение которой однозначно определяется тем, какие зна-
чения в выборке приняли независимые и одинаково распределенные случайные
величины Х|, Х2, ..., Х„.
11.1. Определение и основные свойства точечных оценок
311
Остановимся вначале на понятии несмещенности. Так как оценка 0 является
случайной величиной, то при каждой выборке она может принимать новые зна-
чения. Пусть сделано большое число выборок, и подсчитанные значения 0 ока-
зывались равными 01,02,... Поскольку оценку 0 принимают в качестве неизвест-
ного параметра 0, то желательно, чтобы в среднем значение 0 совпадало с 0.
Оценки с такими свойствами и называются несмещенными.
Определение 2. Оценка 0 называется несмещенной, если ее математическое ожи-
дание равно истинному значению оцениваемого параметра 0:
£(О) = 0, 0 е 0.	(11.1)
Примеры
Пример 11.1. Пусть в п испытаниях Бернулли событие У («Успех») наступило
X раз. В качестве оценки р вероятности события У принимается наблюдаемая
частота успехов Х/п. В данном случае 0 = р, 0 = Х/п. Так как X имеет биноми-
нальное распределение с математическим ожиданием, равным пр, то
£(0) = Е\ — | = 1 Е(Х) = - пр = р.
\п) п п
Таким образом, частота события является несмещенной оценкой вероятности
этого события.
Пример 11.2. В качестве оценки математического ожидания ц = Е(Х) случайной
величины X естественно взять эмпирическое математическое ожидание (среднее
арифметическое) ц*, подсчитанное по выборке Х{, Х2,..., Х„ объема п. Таким об-
разом, здесь 0 = ц и
0(Х1,Х2,...,Хя) = ц* =А£хр
п ,.1
Определим математическое ожидание 0, используя свойства математического
ожидания (3.26) и (5.20):
£(9) = Б(ц*)=:£р£Х,Х1£ад) = 1Х^=^.
п ,=1 J п	п
так как математическое ожидание каждой из случайных величин {XJ равно ц.
Итак, эмпирическое математическое ожидание (среднее арифметическое) явля-
ется несмещенной оценкой математического ожидания. Если случайная величи-
на X имеет дисперсию D(X) = о, то для эмпирического математического ожида-
ния ц ’ дисперсия
D(p) = o2/n.	(11.2)
Пример 11.3. Оценим дисперсию D(X) = а2 случайной величины X на основании
выборки объема п. Возьмем п качестве оценки дисперсии эмпирическую диспер-
сию а2’, рассчитываемую по формуле (10.12). Имеем: 0 = о2 и
М2
11. Точечные оценки параметров распределений
Q(XltX2, ...,Х„)=а2’ = 1£(Х,-ц’)2 =-Y(Xi -и + ц-ц')2 =
Пн	«м
=-£(х, -ц)2 +2А(ц_ц’)£(х. -ц)+1 £(ц-ц-)2 =
П ,-.1	П	П ,ж1
= -£(Х, -ц)2 -(ц-ц')2-
п Ы
1 ”
ПОСКОЛЬКУ - У (Xj - Ц ) = ц ’ - ц.
«м
По определению дисперсии (3.23)
D(p-) = £((p’-p)2), £((Х;-ц)2)= о2.
На основании свойств (3.27) и (5.23) имеем
£(ц--ц)2 =Р(ц-) = п(А£х(К41>(*>) = — 
) П1 (.1	п
Поэтому
£(6) = 4-i(X,.-ц)2-(ц-ц')2Ка2-—= —а2.
\ П j=i	)	П П
Следовательно, эмпирическая дисперсия является смещенной оценкой истинной
дисперсии. При больших объемах выборки п (например, п > 30) расхождение не-
существенно, ибо величина -— будет близка к 1.
п
Для получения несмещенной оценки дисперсии о2 достаточно эмпирическую
дисперсию умножить на ——. Итак, несмещенной оценкой дисперсии D(X) слу-
п-1
чайной величины X является
52 =-J-X(Xj-p’)2.	(11.3)
п -1 м
Результаты примера 11.2 являются частным случаем следующей теоремы.
Теорема 11.1. Эмпирические начальные моменты {ц*} являются несмещенными
оценками соответствующих моментов генеральной совокупности {цг} при усло-
вии, что последние существуют.
Доказательство
Напомним, что момент r-го порядка случайной величины X определяется по
формуле (3.22) как цг = Е(ХГ). Для математического ожидания эмпирического
момента r-го порядка (10.11) на основании теоремы сложения математических
ожиданий (теорема 5.4) имеем
(in	1л
ВД) = £ -£х,г =-££(Х,г) = ^£цг=ц,	□
V п i.!	) п ;.1	п ,-.1
Перейдем к понятию эффективности оценок. Пусть, как и прежде, 61,62,... есть
значения, принятые оценкой 0 в различных выборках. Очевидно, из всех воз-
11.1. Определение и основные свойства точечных оценок	311
можных оценок параметра 6 наилучшей будет та, при которой значения 01, ё»,...
плотнее группируются около значения параметра 6, то есть разброс которой
меньше. Действительно, так как параметр 0 оценивается по одной выборке, то в
этом случае более вероятно, что он будет точнее оценен. Поскольку мерой раз-
броса является дисперсия, то естественно несмещенную оценку 0 считать луч-
шей, чем несмещенная оценка 0', если
D(0)<D(0').
Определение 3. Несмещенная оценка 0 эффективнее, чем несмещенная оценка
0', если ее дисперсия меньше. Несмещенная оценка 0 называется эффективной,
если из всех несмещенных оценок, удовлетворяющих некоторым общим ограни-
чениям, она имеет наименьшую дисперсию.
Физический смысл понятия эффективности можно уяснить с помощью
рис. 11.1. Предположим, что имеется два метода оценки параметра, истинное
значений которого равно 0. Пусть далее мы располагаем двенадцатью выборка-
ми. Будем по данным каждой выборки вычислять оценку 0 по первому методу и
оценку 0' — по второму и отмечать полученные результаты точками на числовой
оси. На рис. 11.1 изображено примерное расположение двенадцати полученных
точек, если оценка 0 более эффективная, чем 0'.
9
-----------.---.-------।....— .--------------
е
0
Рис. 11.1. Сравнение эффективности оценок
Примером эффективной оценки является среднее арифметическое значение ц*
как оценка математического ожидания в случае нормального распределения.
Отношение дисперсий двух оценок D(0')/D(0) показывает, во сколько раз необ-
ходимо провести больше наблюдений для достижения одной и той же точности,
если пользоваться оценкой 0', а не оценкой 0.
Рассмотрим теперь понятие состоятельности. Естественно потребовать, чтобы
с увеличением объема выборки оценка 0 сходилась по вероятности (см. опреде-
ление 7.2) к истинному значению параметра 0. Именно этим соображением мы
руководствовались, когда подбирали эмпирические аналоги для характеристик
генеральной совокупности.
Определение 4. Оценка 0(ХЬ Х2, ..., Х„) параметра 0 называется состоятельной,
если она сходится по вероятности к оцениваемому параметру 0, то есть если для
любого е > О
314
11. Точечные оценки параметров распределений
Следовательно, для любых £ > 0 и 3 > 0 можно подобрать объем выборки п так,
1ТО
w 0(Xt, х2,.... х„)-е >£ <3.
Лемма 11.1. Предположим, что 0(Xi, Х2,.... Х„) — несмещенная оценка параметра
Э при любом п. Тогда необходимым и достаточным условием состоятельности
оценки 0 является сходимость дисперсии оценки Л(0) с увеличением п к нулю.
Доказательство этой леммы аналогично доказательству неравенства Чебышева,
и мы его опускаем.
На практике доказательство состоятельности оценки 0 производится с помощью
> гой леммы. А именно, находят дисперсию оценки £>(0), и смотря по тому, стре-
мится ли при п -> оо она к нулю или нет, судят о состоятельности оценки.
Пример 11.4. Продолжим рассмотрение примера 11.1. В данном случае 0 = р,
0 = Х/п. Согласно примеру 5.7, дисперсия числа успехов D(X) = npq. Поэтому
D(0) = d( А = 4 D(X) = - pq.
\п J п	п
Следовательно, при и —> оо 0(0) —> 0, так что частота является состоятельной
оценкой вероятности события.	□
Часто состоятельность той или иной оценки устанавливается на основании зако-
на больших чисел. Так, из следствий теоремы Чебышева вытекало, что среднее
арифметическое сходится по вероятности к математическому ожиданию случай-
ной величины, а частота события — к вероятности. Поэтому отсюда можно сразу
заключить, что среднее арифметическое является состоятельной оценкой мате-
матического ожидания, а частота — вероятности.
Теорема 11.2. Если существует момент р2г порядка 2г, то эмпирический момент
r-го порядка ц’ является состоятельной оценкой момента r-го порядка рг.
Доказательство
Имеем
pr=E(X[), i = l,2,...,n;	=1£(Х,.)Г.
п „1
По теореме 11.1
Далее, согласно определению дисперсии
П(Г) = Е(Г2)-(Е(Г))2
имеем:
)=42<ад2г)-(ВД))2} =
= 4z-(ц,)2} =-[Н2,-(Цг)21-
п1 (.1	п
11.1. Определение и основные свойства точечных оценок
310
Так как это выражение при п оо стремится к нулю и так как эмпирический мо-
мент ц* является несмещенной оценкой цг, то используя лемму 11.1, получаем
доказательство теоремы.	□
Из доказанной теоремы вытекает, что эмпирическое среднее является состоя-
тельной оценкой математического ожидания. Мы видели, что эта оценка несме-
щенная. Можно показать, что в случае нормальной совокупности она является
также эффективной. Поэтому она является наилучшей оценкой для математиче-
ского ожидания нормальной совокупности. Следовательно, если необходимо
оценить только математическое ожидание нормального распределения, то лучше
всего подсчитать среднее арифметическое наблюденных значений в выборке и
приравнять ему неизвестное математическое ожидание.
Пример 11.5. Для иллюстрации понятий несмещенности и состоятельности про-
ведем следующий эксперимент. Пусть в нашем распоряжении имеется генераль-
ная совокупность, распределение которой в точности известно. В качестве такой
совокупности возьмем таблицу случайных чисел, имеющих стандартное нор-
мальное распределение с математическим ожиданием 0 и дисперсией 1. Будем
рассматривать выборки объема 5 из этой нормальной совокупности. Для каждой
выборки найдем две оценки дисперсии а2’ и S2, рассчитываемые по формулам
(10.12) и (11.3). Полученные значения оценок а2* и S2 будем отмечать точками
на числовой оси. Для того чтобы точки не сливались, будем наносить их в не-
сколько рядов. Результаты подсчетов по 20 выборкам (пятеркам) изображены на
рис. 11.2. Так как истинное значение дисперсии равно 1, то из рис. 11.2 видно,
что оценка а2’ является смещенной.
0,5
1,5
0
1,0
2
Рис. 11.2. Смещенная и несмещенная оценки дисперсии
Проиллюстрируем теперь понятие состоятельности. Рассмотрим для этого сред-
нее арифметическое ц " как оценку математического ожидания, равного в нашем
случае нулю. Обозначим ц * (У) значение среднего арифметического, подсчитан-
ного по данным j первых пятерок, то есть по 5j случайным величинам. Зависи-
мость ц’(У)от числа пятерокj изображена на рис. 11.3.
В частности, среднее арифметическое, подсчитанное по первой пятерке чисел
(ц*(1)), равно 0.91, подсчитанное по двум пятеркам (ц’(2)) — равно 0.54 и т. Д.
При увеличении у, то есть числа данных, оценка стремится к истинному значе-
нию параметра, равного 0. В этом и сказывается состоятельность среднего ариф-
метического как оценки математического ожидания.
316
11. Точечные оценки параметров распределений
ц*(Л
1ф
0.5--
-------F
0	4
н—।—।—। ’ * i * * i • • • г >
8	12	16	20	24	28	32	36
Рис. 11.3. Иллюстрация состоятельности оценки
11.2. Неравенство Рао—Крамера и эффективность*
В настоящем параграфе будут рассматриваться только несмещенные оценки.
Оказывается, что любая из возможных несмещенных оценок 0 (Х(, Х2,..., Хп) па-
раметра 0 не может иметь дисперсию меньше определенной величины. А именно,
при соблюдении некоторых общих условий (см. [2, 8, 9]) справедливо так назы-
ваемое неравенство Рао—Крамера. В случае непрерывной величины X с плотно-
стью распределения f(x, 0), зависящей от параметра 0,
Л(0)^
пЕ И1п/(Х;0)
(И.5)
В случае дискретной величины X с вероятностью рд(0) принятия значения х
Л(0)^
ПЕ
(П-6)
Отметим, что в отличие от прежних обозначений f(x) и рх, здесь применены обо-
значения /(х; 0) и рд(0), которые подчеркивают зависимость от параметра 0.
Итак, приведенное неравенство дает нижнюю границу для дисперсии оценки.
Математические ожидания, фигурирующие в приведенных формулах, вычисля-
ются так:
((	уд
Е
z	\2	г	
= [( — 1п/(х;0)| /(х;0)о!х = f—-— —/(х;0)
Д(30 J	Д/(х;0)[ЗО
(П-7)
/	\2 ।	/	\2	г п2
г И1пРх(е) =еИ1пРл.(0) Рд0) = £Ц-APjr(0) . (U.S)
1(90	) I х (30	) х р,(0)[30 J
Определение 5. Несмещенная оценка б параметра 0, дисперсия которой в точно-
сти равняется правой части неравенства Рао—Крамера, называется эффек-
11.2. Неравенство Рао-Крамера и эффективность’
817
тивной. Эффективностью оценки называется отношение дисперсии оценки
к нижней границе дисперсии, определяемой неравенством Рао—Крамера.
Отметим, что эффективной оценки для параметра 0 (оценки с дисперсией, опре-
деляемой правой частью неравенств (11.5) или (11.6)), может не существовать.
Рассмотрим примеры вычисления нижней границы дисперсии несмещенной оцен-
ки, одновременно мы докажем эффективность некоторых из получаемых оценок.
При этом мы будем пользоваться тем, что, согласно формуле (11.2), дисперсия
эмпирического математического ожидания, подсчитанная по п наблюдениям над
ими	м ')	9
случайной величиной с дисперсией о , в п раз меньше дисперсии о .
Примеры
Пример 11.6. Испытания Бернулли. Пусть событие У появилось в п испытаниях х
раз. Найдем нижнюю границу для дисперсии оценки р вероятности р, предпола-
гая значение п известным.
Рассмотрим случайную величину X, равную числу появления события У. Тогда
результаты п испытаний представляют собой одно наблюдение над случайной
величиной X, имеющей биномиальное распределение
Рх =Р{Х=х} = Сх„рх(1-р)п-х, х=0, 1...... п.
Итак, в данном случае 0 = р и рх (0) равно приведенному выражению. Поэтому
д -	/п. х п-х	х-пр
— 1пр, (0) =--------------—,
ар	р i-р р(1-р)
(г	\2>1 (г v \2 А (	< л2
Е\ — 1прх(0)| =£|А_”Р_| =1-----------*--| D(X) =---------,
1^30 'J J [Ip(1-p)J ) Ip(1-p)J р(1-р)
так как
Е(Х) = пр,
£((X-np)2) = D(X) = np(l-p).
Одно наблюдение над X означает, что в формуле (11.6) следует положить п  1,
так что
D(p)>lp(l-p).	(11,9)
п
Из примера 11.4 известно, что частота успехов Х/п является несмещенной оцен-
кой вероятности, причем дисперсия ее равняется правой части последнего нера-
венства. Итак, частота — эффективная оценка вероятности события.
Пример 11.7. Распределение Пуассона. В данном случае 0 = X и
Рх(*) = ^те’Х. *=0,1,...,
х!
А1прД.(Х)-^-1,
Ок	Л
18
11. Точечные оценки параметров распределений
(f а	\
— 1прх(Х)
Ках 'J
Е
= Х2Е((Х - X)2) = Х”2О(Х) = Х”2Х = X”1,
ак как, согласно табл. 3.5, для распределения Пуассона математическое ожида-
:ие и дисперсия равны X.
'ледовательно,
т
О(Х)>-.	(11.10)
п
хли в качестве оценки X взять эмпирическое математическое ожидание ц‘, то
огласно формуле (11.2), О(Х) = О(ц*) = ст2/п = Х/п. Следовательно, ц* — эф-
фективная оценка параметра Xраспределения Пуассона.
1ример 11.8. Экспоненциальное распределение. Имеем 0 = X, f(x; X) = X ехр(-Хх),
>0,
In f(x; X) = 1пХ-Хх,
— In f(x\ X) = — - х,
5Х	X
Е
41п/(Х;Х)
2
/
= Е
Л
ак как (см. табл. 4.4) для экспоненциального распределения математическое ожи-
1	1 тл
1ание равно -, а дисперсия —. Итак,
X	X
D(X)> —X2.
и
1ример 11.9. Нормальное распределение. В данном случае логарифмирование
1лотности распределения (4.11) дает:
(11.11)
1 Z _	\2
1п/(х) = -1пТ2л -1по-- -—-
21 ст )
Рассмотрим вначале случай, когда неизвестным параметром является математи-
еское ожидание ц:
5 . , х-ц
— 1п/(х;ц) = —/s
5ц	ст
Е
( я \2
) )
= о 4Е((Х -ц)2 ) = ст”4ст2 = а’2,
гак как дисперсия X равна о2. Следовательно, нижняя граница дисперсии несме-
ценной оценки математического ожидания ц нормального распределения есть
Г1 о2, но это как раз есть дисперсия эмпирического математического ожидания
' 11.2). Следовательно, ц* — эффективная оценка математического ожидания ц
юрмального распределения.
11.3. Метод моментов для нахождения оценок параметров распределения
319
Рассмотрим теперь оценку среднего квадратического отклонения:
1п/(х; о) = -- - (х - р )2 (—2ст~3) = -- + ст~3 (х - р )2;
он	а 2	о
(( .
Е И.1п/(Х;о)
—	9 —-4	। —.-6 О —4 _с\ -2
=О -ZQ а +Q ЭО =2о ,
-2 -2с'4(Х-р)2 + о’6(Х-р)4) =
так как в примере 4.10 было показано, что
£((Х-р)4) = Зо4.
Поэтому
2
Я(а)>^-.
2.П
Аналогично можно показать, что дисперсия оценки дисперсии о2 удовлетворяет
неравенству Л(о2) > 2о4/я
11.3. Метод моментов для нахождения оценок
параметров распределения
Метод моментов является самым простым общим методом нахождения оценок
параметров. Этот метод был предложен К. Пирсоном. Он заключается в прирав-
нивании эмпирических моментов р’ моментам генеральной совокупности цг.
Последние зависят от неизвестных параметров распределений 0t, 02,.... 0*:
рг = рг(01( 02,..., 0*). Взяв необходимое число эмпирических моментов (в на-
ших обозначениях это k) и приравняв их теоретическим моментам, получаем
систему уравнений относительно оценок параметров 01, 02,..., 0*:
pr(0i,02 0*) = Нг. г = 1,2,...Л	(11.12)
Определение 6. Оценками метода моментов неизвестных параметров называется
решение 01,02,..., Qk системы уравнений (11.12).
Эмпирические моменты, как указывалось выше (теорема 11.2), есть состоятель-
ные оценки моментов генеральной совокупности. Благодаря этому оказывается,
что при довольно общих условиях оценки, полученные методом моментов, являют-
ся состоятельными (см. [2, 8, 9]). Эти оценки за счет простых поправок часто
можно сделать также несмещенными.
Примеры
Пример 11.10. Оценим методом моментов параметры цис нормального распре-
деления (4.11). В данном случае неизвестны два параметра: 0t = р, 02 = о, оцен-
ки которых обозначим 01 = р, 02 = о. Эмпирическое математическое ожидание
и дисперсия находятся по формулам
320
11. Точечные оценки параметров распределений
а” =-£(*,	-о.-)’.
П ;.1
Так как для нормального распределения параметр ц есть математическое ожида-
2	2
ние, о — среднее квадратическое отклонение, а ст =ц2-ц — дисперсия, то
2	2
ц2 = о +ц , и метод моментов дает уравнения:
-	•	-2 , - 2	•
ц =ц , ст +р =ц2.
Следовательно, оценками метода моментов параметров нормального распределе-
ния будут
ц =ц’,5 = 7^2 ~Й2 •	(11.13)
Выше мы видели, что оценка дисперсии б2 = о2’ является смещенной. Смеще-
п
ние легко устраняется умножением на-, так что
п-1
52 =-к£(Х,-ц-)2	(11.14)
есть несмещенная оценка о2. Оказывается, что эта оценка также эффективна.
Пример 11.11. Оценка параметра р биномиального распределения (3.3). Пусть
X — случайная величина, имеющая биномиальное распределение
Р{Х = х} = Схорх qn°'x, х=0,1.п0,
с известным параметром и0. Так как требуется оценить только один параметр
0 = р, то достаточно подсчитать эмпирическое математическое ожидание:
1 п
И ,ж!
где и — число наблюденных значений X.
Так как в случае биномиального распределения математическое ожидание равно
пор, то метод моментов приводит к уравнению
п0 р = ц*.
Отсюда находим, что
Р= —н’= —(11.15)
Ио ПП0 1=1
Выше было показано, что это — состоятельная, несмещенная и эффективная
оценка вероятности.
Пример 11.12. Оценка параметра распределения Пуассона. В случае распреде-
ления Пуассона математическое ожидание равно параметру X. Следовательно,
оценкой метода моментов параметра X является эмпирическое математическое
ожидание:
X = ц*.
(11.16)
11.3. Метод моментов для нахождения оценок параметров распределения
ш
Пример 11.13. Распределение Эрланга (4.18). Математическое ожидание и второй
начальный момент распределения Эрланга с параметрами X и I будут (см. табл. 4.4);
поэтому
7/X = p*, 7/Х2 + (7/Х)2 =pj.	(11.17)
Возведя первое уравнение из (11.17) в квадрат и вычитая его из второго, находим
7/Р =ц;-(Ц-)2 =о2-.	(11.18)
Поделив первое уравнение из (11.17) на (11.18), получаем оценку для X:
Х = ц" /а2’.
Теперь из первого уравнения формулы (11.17) находим оценку /:
7 = (ц‘)2/а2*.
Параметр I распределения Эрланга (4.18) должен быть целым положительным
числом. Поэтому следует округлить полученную оценку до целого положитель-
ного числа, после чего пересчитать оценку X по формуле X = //ц’.	□
Метод моментов обычно применятся в случае больших выборок. При больших
выборках естественно требовать состоятельность оценок, так как в этом случае
вероятность существенного отклонения оценки от истинного значения парамет-
ра мала. Оценки же, получаемые по методу моментов, как уже отмечалось, явля-
ются состоятельными.
Несмотря на отмеченные достоинства, в некоторых случаях метод моментов
приводит к малоэффективным оценкам. Дисперсия этих оценок больше диспер-
сии оценок, получаемых, например, методом максимального правдоподобия. Это
ощутимо при использовании высоких моментов. Однако в рассматриваемых
нами примерах 11.10-11.12 оба метода приводят к одним и тем же оценкам, ко-
торые являются эффективными.
Примеры
Пример 11.14. Предположим, что распределение числа отказов и неисправностей
шасси самолета, обнаруживаемых при одном обслуживании, является пуассо-
новским, и пусть при рассмотрении 100 обслуживаний эмпирическое математи-
ческое ожидание числа отказов оказалось равным 1.82. Тогда оценка параметра X
распределения равна
Х = ц* =1.82.
Пример 11.15. Будем считать, что продолжительность технического обслу-
живания самолета определенного типа после 50 часов налета имеет распределе-
ние Эрланга. При замерах длительностей обслуживания нескольких самолетов
были получены следующие значения: эмпипичеекл* мат»мптми№лл n«u..uu«
322
11. Точечные оценки параметров распределений
ц ’ = 422.8 мин и эмпирическая дисперсия D' = 28590.3 мин2. Оценки парамет-
ров этого распределения находятся по формулам
X = ц‘/о2’ = 422.8/28590.3 = 0.0142 мин'1,
/=(ц‘)2/а2* = (422.8)2/28590.3 = 6.
11.4. Метод максимального правдоподобия
Этот метод был предложен в 1912 г. Р. Фишером. Проиллюстрируем идею этого
метода в случае, когда величина X является дискретной, вид распределения X
известен, а неизвестным является лишь один параметр 0. Иными словами, пред-
полагается известной (кроме параметра 0) функция р/0), задающая вероятность
принятия случайной величиной X каждого из возможных значений х.
Р{Х =х} = px(Q),
так что если бы значение 0 было известно, то распределение случайной величи-
ны X было бы задано полностью.
Предложим, что в результате п независимых наблюдений дискретная случайная
величина X приняла значение xt ровно раз, значение х2 ровно п2 раз и т. д.,
значение хк ровно пк раз. Вероятность такого исхода есть
1(0) = [р„ (0)]"* [Рхг (0)Г... {pXi (0)Г‘ = П [Рх,. (0)Г •	(11.19)
1=1
Естественно теперь в качестве оценки 0 неизвестного параметра 0 принять вели-
чину, максимизирующую вероятность наблюденного исхода. Для этого, очевид-
но, необходимо взять производную от выражения (11.19), приравнять ее нулю и
решить полученное уравнение относительно 0.
Для упрощения расчетов обычно вместо функции 1(0) берут логарифм от нее
In Z(0). Это возможно потому, что 1(0) и In Z(0) достигают экстремума при од-
них и тех же значениях 0, так как логарифмирование является монотонным пре-
образованием и поэтому следующие три уравнения эквивалентны:
^z(0)=o, l^i(e)=o,	^ini(0)=o.
30	L 30	30
Изложенное позволяет сформулировать следующее определение.
Определение 7. Функцией правдоподобия называется функция, зависящая от на-
блюденных значений х1( х2, ... случайной величины X и неизвестного парамет-
ра 0, которая определяется:
1) в дискретном случае по формуле (11.19), где и, — число наблюдений значений
xh i = 1, 2,..., k; рх. (0) — вероятность принятия случайной величиной Xзначе-
ния X/, рассматриваемая как функция неизвестного параметра 0;
2) в непрерывном случае по формуле
Z(0)=/(xi:0)/(x2;0)... /(x*;0) = I4I/(xi:0),	(11.20)
<1
11.4. Метод максимального правдоподобия
32S
где f(Xj, 0) — плотность распределения в точке х„ рассматриваемая как функция
параметра 0.
Определение 8. Оценкой максимального правдоподобия называется решение ура»'
нения правдоподобия
AlnZ(0) = O,	(11,21)
50
обращающее в максимум функцию правдоподобия 1(0).
Для дискретного (11.19) и непрерывного (11.20) случаев уравнение правдоподо-
бия (11.21) уточняется следующим образом:
i,ni---------Рх (0)=0>
м Р,,.(0) 50А'
*	1	й
У—---------f(xi>Q)=0.
м/(Хр0) 50yV
Ясно, что если число неизвестных параметров равно г, то следует рассмотреть г
уравнений правдоподобия (11.21) и решить полученную систему уравнений.
В частности, если неизвестны два параметра 0! и 02, то это приводит к системе
двух уравнений:
— lnZ(0t,02) = O, — lnZ(0i, 02 ) = 0.
50i	502
Примеры
Пример 11.16. Биномиальное распределение. Предположим, что событие У в я ис-
пытаниях появилось х раз. Найдем выражение для оценки максимального прав-
доподобия неизвестной вероятности р наступления события У в одном испыта-
нии. Число появлений событий У в п испытаниях имеет биномиальное
распределение
РЛР}-^пР\1-РГх. х=0, 1, ..., п.	(11.22)
Поэтому результаты п испытаний можно рассматривать как результат одного на-
блюдения над случайной величиной X с распределением (11.22), то есть функ-
ция правдоподобия есть
ад=Рх(р)=^рл(1-Ргг.
Уравнение правдоподобия будет
0 =-^-1п£(р) = -^(1пС* + х 1пр+ (и -х)1п(1 - р)) = - -—*.
др	др	р 1-р
Отсюда находим, что искомая оценка р есть
р=-.	(11.23)
п
Итак, оценкой максимального правдоподобия неизвестной вероятности события яв-
ляется частота. Такую же оценку дает метод моментов. В примерах 11.1, 11.4 и 11.6
было показано, что это - несмещенная, состоятельная и эффективная оценка.
324
11. Точечные оценки параметров распределений
Пример 11.17. Распределение Пуассона. Пусть случайная величина X, имеющая
распределение Пуассона с неизвестным параметром X, приняла значение xt ров-
но и; раз, i = 1,2,..., k, £ nf = и. Тогда
ух
Рх(^)=—.е'к< х=°-	•••;
X I
— 1п!(Х) = -п + х-Ух-п,. =0;
ах	Хм
i = -ixini.	(11.24)
n.-i
Эта оценка совпадает с оценкой метода моментов и является несмещенной, со-
стоятельной и эффективной (см. примеры 11.7 и 11.12).
Пример 11.18. Экспоненциальное распределение. Если случайная величина X,
имеющая плотность распределения
/(х;Х) = Хе"Хх,
в результате п наблюдений приняла значения xt, х2,..., х„, то
1(Х) = П^е ' = Х”е ,
/-1
— InL(X) = - И - X;,
ах X «
X = f-fx(>| =—.	(11.25)
J Ц*
Это опять совпадает с оценкой метода моментов.	□
Из примеров этого и предыдущего параграфов видно, что оценки параметров р
биномиального распределения, X экспоненциального распределения и распреде-
ления Пуассона, цис2 нормального распределения, получаемые методом мо-
ментов и максимального правдоподобия, совпадают. Однако при использовании
для оценки параметров эмпирических моментов порядка выше второго метод мак-
симального правдоподобия оказывается лучшим. Значение этого метода уста-
навливается следующей теоремой, характеризующей асимптотические (т. е. имею-
щие место при больших объемах выборки п) свойства оценок (см. [2, 8, 9]).
Теорема 11.3. Если для параметра 0 существует эффективная оценка 0, то урав-
нение правдоподобия имеет единственное решение, дающее эту оценку. При
выполнении общих условий относительно функции правдоподобия L(0) оценка
максимального правдоподобия является состоятельной, асимптотически нор-
мальной и асимптотически эффективной, то есть дисперсия D(0) стремится при
и -* оо к ппавой части непавенств (11.51 или (11.61
11.5. Достаточные статистики’
Э28
11.5. Достаточные статистики*
Во всех ранее рассмотренных случаях оценки неизвестных параметров зависели
не от отдельных элементов выборки, а от некоторых функций от них, таких как
сумма выборочных значений или сумма их квадратов. Следовательно, в данном
случае при фиксированном значении этих функций конкретные значения эле-
ментов выборки роли не играли. Это приводит к понятию достаточной оценки.
Определение 9. Пусть Р = {Р0: 0 е 0} — семейство (класс, множество) распределе-
ний, зависящее от параметра 0 (быть может, векторного), принимающего значе-
ния из параметрического пространства 0. Обозначим X = (Хь Х2> •••> -^и) выборку,
соответствующую распределению для некоторого неизвестного нам параметра 0.
Статистикой Т называется некоторая функция (быть может, векторная) выбор-
ки Т = T(Xlt Х2, ..., Х„) = Т(Х). Статистика называется достаточной, если
условное распределение выборки X = (Xlt Х2, ..., Хп), вычисленное при условии,
что статистика Т приняла данное значение t, не зависит от параметра 0.
Достаточные статистики позволяют уменьшить объем статистических данных без
потери информации об интересующем нас параметре. Фактически мы уже име-
ли дело с достаточными статистиками в задачах 7.2 и 7.4. Однако достаточность
статистики проще доказывать не прямыми вычислениями, которые применялись
в указанных задачах, а с помощью нижеприведенного критерия факторизации
(см. [2, 7, 8, 9]). Далее мы ограничимся лишь непрерывными случайными вели-
чинами.
Критерий факторизации. Пусть /0(х) ~ плотность распределения случайной
величины X, Т= T(xi, х2.хп) — статистика, рассчитанная по наблюденной вы-
борке х = (хь х2, .... х„). Статистика Т достаточна тогда и только тогда, когда
плотность распределения выборки может быть записана в виде
П/еО.) = £е(Л*1 »х2....Хп y)h(Xi ,Х2.х„).	(11.26)
Итак, критерий устанавливает, что плотность распределения выборки может
быть представлена в виде произведения двух сомножителей, один из которых
(Ji) не зависит от параметра 0, а другой (g) зависит, но не непосредственно ОТ
элементов выборки xt, х2,.... х„, а только через статистику Т.
Примеры
Пример 11.19. Экспоненциальное распределение. В данном случае 0 = Х, а плот-
ность распределения выборки может быть представлена в виде
t-i	i>i
Следовательно, достаточной статистикой Т для параметра X является сумм*
Xi + х2 +... + хп.
Пример 11.20. Нормальное распределение. В данном случае неизвестный пара-
метр 0 является двумерным вектором 0  (ц, а). Согласно формуле (4.11), имеем
такое представление для плотности распределения выборки:
>26
11. Точечные оценки параметров распределений
ПАЖ) = П-/=^ехР
м	1-1 >/2ла
1
чл/2ла
t 1 ( п	п
ехр —Г Xх.2 -2р£х, +пц2
12а Vi.i	;-1
Итак, достаточная статистика для пары (ц, а) представляет собой двумерный
зектор
г=(£хр£хЛ
\ /-1 /
Отметим, что использованные нами выше оценка ц * = £ Х,/и математического
эжидания ц и оценка (11.3) дисперсии а2 были функциями данной достаточной
статистики.	□
Важность достаточных статистик состоит не только в редукции объема данных
без потери информации, а также в том, что оптимальные статистические выводы
базируются только на достаточных статистиках (если только последние сущест-
вуют). Интересный пример здесь дает моделирование. Предположим, мы хотим
сгенерировать некоторую случайную величину X. Для этого мы можем посту-
пать таким образом. Вначале генерируем соответствующую достаточную стати-
стику Т, а потом случайную величину X, используя условную плотность распре-
деления X при данном Т = t. Оказывается, эта процедура эффективна, когда мы
хотим сгенерировать большое число случайных величин X на основании имею-
щейся выборки этих величин и известного условного распределения X при дан-
ном t (которое не будет зависеть от неизвестных параметров). Для этого доста-
точно подсчитать по выборке значение достаточной статистики t и генерировать
произвольное число X согласно условному распределению X для данного t.
Это — так называемый метод достаточного эмпирического усреднения (Е. В. Че-
пурин).
Компьютерный практикум № 18.
Методы точечного оценивания параметров
распределений в пакете Mathcad
Цель и задачи практикума
Целью практикума является компьютерная реализация методов точечного оце-
нивания неизвестных параметров распределений.
Задачами практикума являются: разработка и применение компьютерных про-
грамм, реализующих методы моментов и максимального правдоподобия для оце-
нивания неизвестных параметров распределений.
Необходимый справочный материал
При применении методов моментов и максимального правдоподобия необхо-
димо решать одно уравнение или систему уравнений относительно неизвестных
параметров. Получаемые решения и принимаются за соответствующие оценки
(метода моментов или метода максимального правдоподобия) неизвестных
папаметплн. Пакет Mathcad располагает возможностями численного решения
Компьютерный практикум № 18. Методы точечного оценивания параметров распределений в пакете Mathcad 327
систем уравнений. В случае одного уравнения можно использовать встроенную
функцию root(expr, var). Эта функция выдает значение переменной var, при кото*
ром значение функции ехрг равно нулю. Таким образом, функция root(expr, var)
может быть использована для оценивания одного параметра распределения.
Функция осуществляет поиск корня уравнения итерационным методом, при ЭТОМ
перед ее применением необходимо задать начальное значение переменной var.
В случае необходимости решения системы уравнений следует использовать спе*
циальный вычислительный блок, отличительной особенностью которого являет*
ся наличие директивы Given. В версиях Mathcad 2001 и выше в рамках этого
блока можно также решать задачи одномерной и многомерной оптимизации,
причем структура описания блока во всех случаях остается одной и той же. Эта
структура следующая:
□	Задание начальных значений для переменных.
□	Given.
□	Описание уравнений, содержащих переменные.
□	Описание ограничений, накладываемых на переменные.
□	Формулировка задачи: решение системы уравнений (путем использования
, функции Find) или оптимизация (путем использования функций Maximm
или Minimize).
Поясним отдельные элементы представленной структуры.
Начальные значения для переменных задаются обычным оператором присваива-
ния ’ Например, var := 25. Если переменных несколько, то используется век-
торное представление данных.
Уравнения содержат левую expr-left и правую expr-right части, а также соединяю-
щий их знак логического равенства. Последний вызывается из палитры логиче-
ских операций и выглядит как «жирный знак равенства». Например,
expr-left(varl, var2,...) = expr-right(varl, var2,...).
Ограничения, накладываемые на переменные, записываются с помощью знаков
логического равенства, больше и меньше, берущихся из палитры логических опе-
раций. Например, varl > 0, varQ. < 0, varl < var3.
Для решения системы уравнений используется встроенная функция Find(varl,
vaf2, ...). Например, vector := Find(varl, var2, ...). Здесь vector — вектор-столбец,
содержащий столько компонент, сколько указано переменных в функции Find.
Последняя выдает значения переменных, удовлетворяющих всем уравнениям и
ограничениям, записанным под директивой Given. Эти значения и присваивают-
ся компонентам вектора vector.
Для решения задачи оптимизации используются встроенные функции Maxi-
mize(f, varl, var2,...) и Minimize(f, varl, var2,...). Здесь f — функция, подлежащая
максимизации или минимизации по переменным varl, var2,... Описание функ-
ции / приводится до Задания начальных условий. Функции Maximize и Minimize
выдают значения переменных, соответствующих оптимальному значению функ-
ции /и удовлетворяющих всем вышеприведенным уравнениям и ограничениям.
328
11. Точечные оц енки параметров распределений
Например, vector := Maxtmize(var\, var2, ...), где структура вектора vector та же,
что и ранее.
Успешность решения в пакете Mathcad рассматриваемых задач во многом зави-
сит от задаваемых пользователем начальных значений переменных. В связи с
этим рекомендуется экспериментировать с этими значениями, а также проверять
правильность полученных решений путем прямых вычислений.
Реализация задания и результаты вычислений
Результаты выполнения задания представлены на рис. 11.4—11.7. Рассмотренные
задачи иллюстрируют применение методов моментов и максимального правдо-
подобия для оценки неизвестных параметров распределений.
Первая часть практикума посвящена методу моментов (см. рис. 11.4). Первая
рассмотренная задача заключается в оценивании параметров а и b равномерного
распределения (4.7) на основании двух эмпирических моментов, точнее, первого
момента ц*, равного 9, и эмпирической дисперсии а2’, равной 3. Соответствую-
щие теоретические характеристики являются функциями неизвестных парамет-
ров а и Ь (см. табл. 4.4): ц = (а + Ь)/2 и а2 = (Ь - а)2 /12. Приравнивая их эмпи-
рическим значениям ц* и а2*, получаем систему из двух уравнений, записанную
под директивой Given. Здесь же записано дополнительное условие а < Ь. В выпи-
санных уравнениях вместо параметров а и Ь фигурируют их оценки ае и be
(Estimation — оценка). Непосредственно перед этой директивой Given указаны
начальные значения оценок параметров ае = 0.5 и be = 0.5, с которых начинается
поиск решения уравнений.
Ниже системы уравнений записана функция Find, позволяющая найти решение
системы уравнений. В рассматриваемом случае мы получаем оценки а = ав = 6
и Ъ = be = 12. В заключение проводится проверка правильности полученного ре-
шения.
Рассмотренный пример является тривиальным. Однако мы начали с него, чтобы
избежать часто возникающих трудностей, вызванных отсутствием сходимости:
в этом случае на экране появляется красная запись «do not convergence».
Вторая задача связана с нахождением оценок метода моментов для параметров
а и s логарифмически нормального распределения (4.39). Предполагается, что
подсчитанные по выборке эмпирические математическое ожидание и дисперсия
равны соответственно ц* = 10 и а2’ = 145. Как и ранее, оценки параметров обо-
значаются ае и se, причем в качестве начальных приняты значения ае = 2 и se = 1.
Ниже директивы Given выписаны два уравнения, левые части которых — выра-
жения для теоретических характеристик р и а2 (см. пример 4.11), а правые час-
ти — ц’ и а2’. Здесь же записаны условия неотрицательности параметров и их
оценок: ае > 0 и se > 0. Последующая часть примера полностью аналогична ранее
рассмотренному примеру.
Отметим, что проверка правильности полученного решения проводилась двумя
способами: путем подстановки в соответствующие выражения буквенных обо-
значений оценок ае и se и их вычисленных значений, соответственно 1.855 и
0.947. Разница в ответах показывает, каков порядок ошибки, вызванной округле-
нием чисел до т х знаков после запятой.
Компьютерный практикум № 18- Методы точечного оценивания параметров распределений в пакете Mathcad ЗМ
Практикуя Nt 19. Точечное вценивание пвраветроо распределений
Часть 1. Метод вовоитоа
1.	Оцоииоаино параватроо в в b разноверного распределения (4*7) ио основе зилнричоских
среднего 9 в деслорсии 3
Начальные значения оценок параватроо:	ао^ОД Ье»0Д
Given
i-(ae + bo)  9	~-(Ьо»ао)2аЗ	ве<Ье
Проворна правильности рования:	|(б+12)-9 и ~(12-6)2-3
2.	Оценивание параветров айв иогарифвически нереального распределения (4 J9) на осиооо
эвлиричоских ватопатического ожидания 10 в дисперсии 145
Начальные значения оценок парввотров:	ао> 2 во :• 1	+
Given
охрана + 1 ее2)  10 (охр(м2) - ll-oxpG-aa + во2)  145 ао>0 м>0
С)-*-»- СИЗ
Проворна правильности рования
хр^ах ♦ —хх2) - 10	(xxplxx2) - 1)ххр(1хх ♦ хх2) * 145
ххр^1155 * 1 0Л472) - 10Ш0 (pxptoMT2) - 1) охрЬ1055 ♦ М472) - 145415
3.	Оценивание оаролетроо X, р и р сваей зкелоиеицеальиых распределений по трав
евлиричоскив воаептаа ц1, р2 и рЭ
Получение неладной аыйорки X объева п и подсчет зваиричоских вовеитоа ц1, р2 в рЭ
Х(пД,и,р)>
Ro <- roKp(n.l)
R«- гапК(л.0,1)
for 1 е 0.. n * 1
Х|<-и(ц<р 1ячД Кч'1
к 1 и >
X
р.^ОД Y-X(n.l.p.p)
pa.l.g (¥|)2
i-e
|d-lJ83	p2-3*475	рЭ-19ДО1
Проворна правильности рования:
ро~ ♦ (1 - р«)	- ад»
1ох	рех
.«^.(i-mid-L-.u,
ро -L ♦ (1 . рх) — . 1JS3
1а	ре
pp.-L ♦ (1 - р«)~ . 19521
14	Р*3
0412—Ц ♦ (1 - 1412) —Ц  21М2
1J01*	0ЛГГ
Рио. 11.4. Оценимнио нвизмстных параметров распределений по методу моментов
330
11. Точечные оценки параметров распределений
В третьей задаче рассматривается оценивание параметров А., ц и р смеси двух
экспоненциальных распределений с параметрами А. и ц, в которой распределение
с параметром А. имеет долю р. Плотность этого распределения, а также теорети-
ческие моменты даются формулами (см. пример 4.9):
f(x) =	+ (1 - р)ре'цг, х > 0,
Е(Хг) = г\(рк~г +(1-р)ц-г), г = 1,2,...
Оценивание параметров осуществляется на основании первых трех эмпириче-
ских моментовци Из* которые в программе обозначены pl, ц2 и цЗ. Эти эм-
пирические моменты вычисляются на основе выборки объема п, сгенерирован-
ной функцией пользователя Х(п, А., ц, р). Генерируется выборка объема п = 100
для следующих значений параметров: А. = 1, ц = 0.5 и р = 0.8. Сгенерированная
выборка представляется вектором-столбцом Y. Приводимые далее формулы для
подсчета эмпирических моментов получены из формулы (10.11) для r= 1, 2, 3.
Ниже распечатываются вычисленные по выборке Y значения р.1, р2, и цЗ.
Поиск оценок параметров начинается со значений ке = 1.2, ре = 0.4 и ре = 0.6. Под
директивой Given выписаны три уравнения, каждое из которых приравнивает
теоретические и эмпирические моменты. Здесь же фигурируют условия неотри-
цательности для параметров. Завершение задачи вполне аналогично ранее рас-
смотренным задачам.
Вторая часть практикума посвящена методу максимального правдоподобия.
Согласно этому методу в качестве оценок неизвестных параметров принимаются
значения, максимизирующие функцию правдоподобия (11.19) или (11.20). Для
облегчения задачи поиска максимума рассматривают не функцию правдоподо-
бия £(0), а логарифм от нее 1п(£(0)): это допустимо, поскольку обе функции име-
ют максимум в одной и той же точке. Для поиска максимума можно использо-
вать встроенную функцию Maximize, как это было описано выше в разделе
Необходимый справочный материал. Следует отметить, что процедура использо-
вания этой функции вполне аналогична использованию встроенной функции Find.
Однако мы не будем здесь использовать функцию Maximize по двум причинам.
Во-первых, она отсутствует в более ранних версиях Mathcad, таких как Math-
cad 6+ или Mathcad 7. Во-вторых, работа этой функции весьма неустойчива. Мы
воспользуемся возможностью сведения задачи максимизиции к ранее рассмот-
ренной задаче решения системы уравнений. Каждое такое уравнение получается
приравниванием нулю частной производной по неизвестному параметру от лога-
рифма функции правдоподобия.
Первой рассматривается задача оценивания параметра А. экспоненциального рас-
пределения (4.9) по выборке X объема п (рис. 11.5). Вначале генерируется вы-
борка X случайных величин, имеющих экспоненциальное распределение с пара-
метром А. = 2. Затем выписываются функция правдоподобия £(Х, ке) и ниже —
логарифм от нее ££(Х, ке), а также производная от функции правдоподобия
£££(Х, ке). Как и ранее, добавление буквы е указывает на то, что речь идет об
оценке параметра. Это позволяет избежать путаницы с истинным значением па-
раметра к, которое задается нами, но считается неизвестным и используется для
имитации получения выборки. График зависимости функции правдоподобия
Компьютерный практикум Ns 18. Методы точечного оценивания параметров распределений в пакете Mathcad U1
1(Х, Хе) от значения оценки параметра Хе позволяет наглядно пояснить смысл
метода максимального правдоподобия. Поскольку неизвестным является один
параметр, то мы имеем одно уравнение правдоподобия (11.21). Следовательно,
для нахождения корня этого уравнения можно применить встроенную функцию
root, что и сделано в данном случае. Из графика видно, что максимум функции
правдоподобия действительно достигается около найденного значения корня
Хе = 1.849.
Практикуя И> 18. Точечное оценивание параиетров распределений
Честь 2. Метод иаксинельиего правдоподобия
1.	Оценивание парвпетра X акспененциальиего распределения (4.9) ле
выборке X ебьенап
Получение выборки X обьепв л:-М
из генеральной совокупности с параиетров X > 2
X- гехр(п.Х)
п-1 -хак
функция правдоподобия:	L(X,Xe):*pj Хе е 4
I • В
График аависивести функции прадеподобия от значения иараветра	Хе:- 03.04.. 4
LL(X.Xe) - и In (Хе) - Хе
1-1
Легврифн функции правдоподобия:
*
л-1
Преитаодная логарифм функции правдоподобия:	LLL(X.Xe):-----V X.
Хе
Начальной значение ларанетра:	Хе :• 1	* * *
Xe»roet(LLL(X,Xe),Xe)	Хе-1349
Проверка правильности решения
LLL(X.Xe) -2Л15х 10'*	LLL(X,1349) --3931 х W3
Рис. 11.5. Оценивание параметра А. экспоненциального распределения по методу
максимального правдоподобия
Второй является уже рассмотренная в первой части практикума задача оценива-
ния параметров X, р и р смеси двух экспоненциальных распределений. Оценива-
ние осуществляется на основе выборки объема п (рис. 11.6). Для генерации вы-
борки используется ранее созданная функция пользователя Х(п, X, р, р).
Полученная выборка объема п = 200 для значений параметров X = 1, р = 0.5, р  0.8
представлена в виде вектора-столбца Y. Ниже представлены функция правдопо-
добия £(Y, Хе, ре, ре) и графики ее зависимости от оценок параметров Хе; ре, ре.
При этом каждый раз варьирует только одна оценка, остальные две имеют задан-
ные начальные значения.
332
11. Точечные оценки параметров распределений
2.	Оценивание параметров X, рн р смеси экспоненциальных распределений по
выборке X объема п
Получение исходной выборки X объема п
Х(п,1,р,р)»
n-200
Re <- гохр(п,1)
R<- runtf(n,0,1)
for ieO n- I
xi^^r)<p1r4.1r4'
X
X : I |i:-0J p-OA	Y * X(n,l,p,p)
Функция правдоподобия
HY.Xo.po.pe)[pe la a-*" Y‘ + (1 - po) po e~** **]
i-l
Графики зависимости функции прадопвдобия от значений оцеиок параметров
Ха- 03,035.. 1Д
рв« 03,035.. 10
рв:-03,035. 03
Частные производные логарифма функции правдоподобия
LLp(Y,Xa,pB,pe) - (хв в ** V| - ца е ** Y‘) [ре Хв а ** Y| + (1 - ре)-рв-в
1-0
Начальные значения оценок параметров; Хв13 рв - 0.4 ре - 03
Ghren
LLX(Y,Xa,pB ,ре) в 0 LLp4Y,XB,po,pe) в 0	LLp(Y,Хв.рв.ре) * О
ре > 0	Хв > ре	ре > 0	ре<1
Проверка правильности решения:
11Л(У,Ха.р>,р*)-1.7|хЮ~и Llp4Y.la.pa.pa) >0 Llp(Y.lB.pB.pB) - -1JM к 10' М
Рио. 11.6. Оценивание параметров X, ц и р смеси двух экспоненциальных распределений
по методу максимального правдоподобия
Компьютерный практикум Ns 18. Методы точечного оценивания параметров распределений в пакете Mathcad ЗМ
Далее записывается логарифм функции правдоподобия £.£.(¥, Хе, ре, ре), а тахйсе
частные производные от него по рассматриваемым оценкам параметров: LLk (Y>
Хе, ре, ре) по оценке Хе, ZZp (Y, Хе, ре, ре) по оценке реи LLp (Y, Хе, ре,ре) ПО
оценке ре. Приравнивание нулю этих частных производных дает три уравнения
правдоподобия, которые записаны под директивой Given. Выше этой директивы
заданы исходные значения оценок, с которых начинается поиск решения систе-
мы уравнений. Остальная часть задачи аналогична ранее рассмотренным примерам.
Третья задача практикума имеет дело с распределением целочисленной случай-
ной величины, которое возникает следующим образом. Пусть X — случайная ве-
личина, имеющая экспоненциальное распределение (4.9) с параметром X, Y — це-
лая часть X, то есть наибольшее целое число, не превышающее X. Очевидно, У ~
целочисленная случайная величина со следующим распределением:
р. = P{Y =:} = P{i <, X < i +1} = F(i +1) -F(i) = e'u - eK(f+1), i = 0, 1,...
Наша задача заключается в оценивании параметра Хна основе выборки У  (Yj,
У2..У„)т объема п. В данном случае функция правдоподобия имеет вид
WAJ-ftp,, -ЙО-* -г"'"').
г-0	J-0
Дальнейшие действия аналогичны ранее описанным и отражены на рис. 11.7.
3.	Оценивание параметра 1 распределения целочисленно* случайно* величины по выборке Y
объемап
Получение выверки Y ебьеев п не генеральной совокупности е параметром 1
YW(n,l)>
Хь-гохр(пД)
for I е 0.. п - 1
Y| *- floor(X|)
Y
1-04
Y:- YW(h,1)
Функция аравдонодобил:
График зависимости функции предомдобия от вначанмя оценки параметра 1а : 0J ,03. 1
Логарифм функции правдоподобия:	LL(Y,lo).-^ 1н[е"М Yi - •’М
1-1
Производная логарифма функции правдоподобия
LLL(Y.U);. £ [(Y,* 1)	“ (Yi+1)
l-l
Начальное значение параметра:
lo>raot(LLL(Y.lo),U)
Приварка нраапяьиостм ремоиия
LLL(Y.	10" 4
U-0M1
LLL(Y.0Ml)-IMf « I.*1
Рио. 11.7. Оценивания параметра А. распределения целочисленной случайной величины
по методу максимального правдоподобия
334
11. Точечные оценки параметров распределений
Задания для самостоятельной работы
1.	Проанализируйте логику работы компьютерной функции Х(п, X, ц, р), пред-
назначенной для генерации выборки в задаче нахождения оценок максималь-
ного правдоподобия для параметров смеси экспоненциальных распределений
(см. вторую задачу второй части практикума).
2.	Проанализируйте влияние начальных значений оценок параметров на резуль-
таты работы программ в случаях применения методов моментов и максималь-
ного правдоподобия для оценивания параметров смеси экспоненциальных
распределений.
3.	В условиях предыдущего задания, увеличивая объем выборки п, проиллюст-
рируйте состоятельность оценок, получаемых методами моментов и макси-
мального правдоподобия.
4.	В условиях второго задания проведите сравнительный анализ точности оце-
нок, получаемых методами моментов и максимального правдоподобия.
5.	Разработайте компьютерные программы, вычисляющие оценки методов мо-
ментов и максимального правдоподобия для параметров а и k распределения
Парето (4.59).
6.	Разработайте компьютерные программы, вычисляющие оценки методов мо-
ментов и максимального правдоподобия для параметров ц2, Ор о2 и р
смеси (4.55) двух нормальных распределений.
7.	Разработайте компьютерные программы, вычисляющие оценки методов мо-
ментов и максимального правдоподобия для параметров X и ц распределения
(7.31).
8.	Составьте функцию правдоподобия для выборки (Хь У]), (Х2, Уг), •••> (Х„, У>)
из двумерной нормальной совокупности с плотностью распределения (6.7).
Используя встроенную функцию Maximize, разработайте компьютерную про-
грамму, максимизирующую функцию правдоподобия и вычисляющую оцен-
ки параметров ць ц2, оь о2 и р по методу максимального правдоподобия.
Задачи
Задача 11.1. По результатам следующей выборки {7,8,7,7,18,8,17,10,11,13,28,
9, 20,6,10, 6,13,17,33,12,17, 8,18,12, 20,38, 20, 7, 21,23,16,18, 25,10,30, 27,15,
20, И, 25,15, 20, 24, 6,32, 23,19,30,28, 20,6,15,16, 21, 25,15,12,14,18,15,7,17, 22}
оцените методом моментов параметры, предполагая, что имеет место а) нормаль-
ное распределение, б) распределение Эрланга.
Задача 11.2. Двойное распределение Пуассона задается формулой
Р{Х =х} =- — e~Kl +-~е~к‘1, х=0,1....
2х!	2х!
где Х| и Х2 — параметры распределения (X!, Х2 > 0). Методом моментов оцените
Х( и Х2.
Задача 11.3. Из генеральной совокупности, имеющей функцию распределения
Г(х) = (1-в'“‘)", 0<х<оо,
Задачи
8»
где а>Оит= 1, 2,	— параметры, производится выборка объема п. Методом
моментов оцените параметр а, считая значение т известным.
Задача 11.4. Покажите, что метод максимального правдоподобия приводит к
оценкам (11.13) параметров ц и о2 нормального распределения.
Задача 11.5. Используя результаты примеров 4.10 и 11.9, покажите, что оценка S3
дисперсии о2 нормального распределения (4.11) является эффективной.
Задача 11.6. Из генеральной совокупности, имеющей геометрическое распреде-
ление (3.4) с параметром р, производится выборка объема п.
а) Покажите, что оценки параметра р, получаемые методом максимального прав-
доподобия и методом моментов, совпадают; б) проверьте, является ли эта оценка
эффективной.
Задача 11.7. Эффективность оценок математического ожидания экспоненциаль-
ного распределения. Рассмотрим выборку объема п из генеральной совокупности,
имеющей экспоненциальное распределение (4.9). В качестве оценки математиче-
ского ожидания ц =1/Х можно предложить величину Ji = nXmin, где Xm|n 
= min {Xb X2,..., Xn} — наименьшее из наблюденных значений.
Используя результаты примеров 6.7 и 6.8, покажите, что распределение оценки ц
совпадает с исходным распределением (4.9) случайной величины X. Отсюда сле-
дует, что увеличение числа наблюдений п не повышает точности оценивания.
Оценка р. является, таким образом, примером несмещенной и несостоятельной
оценки. Проанализируйте эффективность этой оценки как функцию числа дан-
ных п.
Задача 11.8. Оценки параметра равномерного распределения. Рассмотрим зада-
чу оценки параметра р равномерного распределения в интервале (О, Р). Если
Х(, Х2, ..., Х„ — наблюденные значения случайной величины, то обозначим
Хтах =тах{Х1,Х2.....Хп} наибольшее из этих значений. Эту величину естест-
венно взять в качестве оценки параметра р. Покажите, что плотность распределе-
ния этой оценки есть
О,	х < 0 или х > р.
r-й момент вычисляется по формуле
Е(ХГтш ) = J*' К К	dx^]x^-'dx =-^~р\
о PIPJ Р о п + г
Поэтому эта оценка является смещенной. Несмещенной оценкой параметра р
является
^(n+l^X^.
Покажите, что дисперсия этой оценки есть
д<Р)-(—Т(Е(х^)-ад,и^2)=р2[«(«*2)г'.
\ И J	\ И J
11. Точечные оценки параметров распределений
Если руководствоваться методом моментов, то в качестве оценки параметра 0
следует взять удвоенное значение эмпирического среднего:
-	9 п
₽'=2ц-=-Х\-
П i.i
Покажите, что дисперсия этой оценки Z?(0') = 02/(3n), так что оценка 0 более
эффективна. Следовательно, при больших объемах выборки п метод моментов
приводит здесь к малоэффективным оценкам.
12 Оценивание с помощью
доверительных интервалов
12.1. Основные определения
Суть точечной оценки состоит в следующем. За неизвестный параметр 0 по дан-
ным выборки принимается некоторое число 0, изображаемое геометрически на
числовой прямой одной точкой. Это число является случайной величиной, ме-
няющейся ’от выборки к выборке. Поэтому оценка 0 всегда будет давать зани-
женные или завышенные по сравнению с 0 результаты. Следовательно, интерес-
но знать, каково возможное отклонение 0 от 0, то есть какова возможная ошибка,
какова точность оценки. Кроме того, в некоторых случаях не столько важно ука-
зать точное значение 0, как указать пределы (допуски), в которых 0 может нахо-
диться. Например, иногда не так существенно, равна ли вероятность брака 0,0095
или 0,0090, как то, что эта вероятность не больше 0,01.
Эти рассуждения приводят к понятию оценки параметров с помощью довери-
тельных интервалов. В этом случае на основании значений выборочной совокуп-
ности указывается интервал (0', 0"), который с наперед заданной вероятностью у
покрывает неизвестное истинное значение параметра 0. Интервал (0', 0") назы-
вается доверительным интервалом, а число у — доверительной вероятностью,
или коэффициентом доверия. Более точно это может быть сформулировано сле-
дующим образом.
Определение 1. Пусть выбрано некоторое число 0 <у< 1, называемое коэффици-
ентом доверия. Если указаны две функции 0'(х1’,х2‘,,..,х*)и 0"(x1’,X2,...,xJ )от
выборочной совокупности (х*, х?,..., х’), такие, что вероятность покрытия неиз-
вестного параметра 0 случайным интервалом (0', 0") равна у, то есть
Р{0' < 0 < 0"} = у,
то интервал (0', 0") называется доверительным интервалом, соответствующим
данному значению у. Если одна из границ доверительного интервала (0', 0*)
априори задается равной бесконечности или предельным значениям параметра
(например, 0 или 1 для вероятности), то доверительный интервал называется од-
носторонним. В частности, (-<», 0") (или (0, 0") для вероятности) называется
нижним доверительным интервалом, а (0', <ю) (или (О', 1)) — верхним доверитель-
338
12. Оценивание с помощью доверительных интервалов
ным интервалом. В этом контексте ранее определенный интервал будем назы-
вать двусторонним.
Отметим, что при построении доверительного интервала иногда оказывается не-
возможным обеспечить точное значение доверительной вероятности у. В этом
случае требуется, чтобы вероятность накрытия доверительным интервалом ис-
тинного значения параметра 0 была не меньше у:
Р{0'S 0 < 0"} > у.
Сделаем несколько замечаний к этому определению. Интервал (0', 0) является
случайным, поскольку концы его 0'(ХЬ Х2, ..., Хп) и 0"(ХЬ Х2, .... Хп) являются
случайными величинами (как и точечная оценка параметра 0(Х], Х2,..., Хп)). По-
этому может случиться, что интервал (0', 0") не накроет истинного значения па-
раметра 0. Однако вероятность таких случаев равна 1 - у.
Таким образом, если у взять близким к 1, то риск ошибки мал. Отсюда и назва-
ние у как количественного показателя «доверия» к данному интервалу. Можно
сказать также, что у — это надежность получаемой оценки. Величину у задают
при постановке задачи. Обычно принимают коэффициент у равным 0.95, 0.99
или 0.999.
Соблазнительно взять у как можно ближе к единице. Однако с увеличением у
растет длина интервала (0', 0"), то есть теряется точность. Длина интервала яв-
ляется мерой точности оценки параметра 0, в то время как у — мерой доверия к
оценке. Для того чтобы при данном у увеличить точность оценки, то есть умень-
шить длину интервала (0', 0"), необходимо увеличить объем выборочной сово-
купности п.
При построении доверительных интервалов важнейшую роль играют квантили,
определяемые следующим образом.
Определение 2. Квантилью распределения случайной величины X, отвечающей
вероятности р, называется такое значение хр, которое случайная величина X не
превосходит с вероятностью р:
Р{Х<хр} = р.
Вспоминая определение 4 главы 3 для функции распределения F(x) = Р{Х < х},
можно определить квантиль хр формулой
Г(х„) = р.	(12.1)
Следовательно, квантиль — это функция, обратная функции распределения.
В связи с этим квантиль, отвечающую вероятности р, обозначают F -1(р). Под-
черкнем, что аргументом функции распределения является возможное значе-
ние х, а квантили — вероятность р, в то время как их значение, наоборот, р и х.
Рисунок 12.1 иллюстрирует соотношение между функцией распределения и кван-
тилью.
Для стандартного нормального распределения (4.14) квантиль обозначается
Ф"‘(р). Квантиль F~\p) для произвольного нормального распределения (4.12)
с параметрами ц и о может быть вычислена через Ф“’(р) по формуле
/",(р)-ц + стФ‘1(Р)-
12.1. Основные определения
зм
Проиллюстрируем на простом примере, как можно построить доверительный
интервал. Оказывается, используя неравенство (4.48), можно получить верхний
доверительный интервал (9',<ю) для математического ожидания р. неотрицатель-
ной случайной величины X, соответствующий доверительной вероятности у.
При этом удивительно следующее обстоятельство: для этого достаточно иметь
только одно наблюдение над случайной величиной X, то есть достаточна выборка
объема один!
Неравенство (4.48) справедливо для любого положительного х > 0. Поэтому по-
ложив х = |i/(l - у), получаем неравенство
pj X >-t-l <1-у.
I i-Yj
Следовательно,
Р{Х(Д - у) < ц} = 1 - Р{Х(Д - у) > ц) = 1 - (1 - у) > у.
Итак, (Х(1-у),оо) является верхним доверительным интервалом для математи-
ческого ожидания ц неотрицательной случайной величины X, отвечающим веро-
ятности у.
Полученный результат можно использовать для построения верхнего довери-
тельного интервала для вероятности р некоторого события А. Пусть в результате
п испытаний событие А наступило S„ раз. Рассмотрим в качестве случайной ве-
личины X частоту события X = S„/n. Число наступления события Sn имеет бино-
миальное распределение с параметрами ппр. Математическое ожидание £(5Я)  пр
(см. табл. 3.5 и пример 5.7), так что Е(Х) = р. Итак, интервал (5„( 1 - у)/п, 1) явля-
ется доверительным интервалом для вероятности р, отвечающим доверительной
вероятности у.
Выше все время речь шла о доверительных интервалах для параметров распреде-
лений. Однако в практических ситуациях основной интерес представляют не па-
раметры, а некоторые функции от их. Пусть, например, мы интересуемся
надежностью (вероятностью безотказной работы) изделия за установленный ре-
сурс т. В нашем распоряжении есть данные о моментах отказов изделий, и мы
хотим на их основании построить доверительный интервал для указанной на-
10
12. Оценивание с помощью доверительных интервалов
гжности. Предположим, что вид распределения длительности безотказной
1боты известен, пусть это будет экспоненциальное распределение (4.9) с неиз-
хтным параметром X. Следовательно, нам необходимо построить доверитель-
ый интервал для надежности 7? = ехр (-Хт). В данном случае интересующая нас
ункция монотонно зависит от параметра. Поэтому если (X', X") есть довери-
зльный интервал для X, то соответствующим доверительным интервалом для 7?
удет (ехр (-Х"т), ехр (-Х'т)).
общем случае рассматривается параметрическая функция g(0) от неизвестного
араметра 0 е 8. Пусть (0', 0") является доверительным интервалом для 0, соот-
етствующим коэффициенту доверия 0. Найдем минимальное g' и максималь-
ое g" значения функции g(0) относительно значений параметра 0, принад-
ежащих этому доверительному интервалу: 0 е(0', 0"). Тогда (g',g"), (-», g”) и
jоо) будут, соответственно, двусторонним, нижним и верхним доверительны-
:и интервалами для параметрической функции g(0), отвечающими доверитель-
ой вероятности у. Действительно, используя определение минимума и макси-
ума функции, имеем (например, для двустороннего интервала):
P{g' ^g(0)^g"}SP{0' ^0^0"} Sy.
(елью данной главы является системное изложение методов построения дове-
ительных интервалов всех видов — двусторонних, верхних и нижних. При этом
удут рассмотрены два основных случая — случай выборки большого объема,
огда используются асимптотическая нормальность, и случай выборки из нор-
[альной генеральной совокупности.
12.2. Построение доверительных интервалов
। случае асимптотически нормальных оценок
3 данном разделе мы будем предполагать, что объем выборки достаточно велик,
(оверительный интервал для неизвестного параметра 0 часто может быть по-
строен, исходя из распределения случайной величины 0 — точечной оценки па-
>аметра 0. В настоящем разделе будет рассмотрено построение доверительных
штервалов в случае, когда 0 имеет нормальное или приблизительно нормальное
^определение. Этот случай встречается особенно часто. А именно, справедливо
:ледующее утверждение, доказываемое с помощью центральной предельной тео-
ремы (7.5): при довольно общих условиях распределение оценок, получаемых мето-
дам моментов и методом максимального правдоподобия, асимптотически нор-
мально, то есть это распределение с увеличением объема выборки п стремится
< нормальному. Так, эмпирическое математическое ожидание асимптотически
нормально.
Изложим общее правило построения доверительных интервалов для параметра 0
з случае нормальной (асимптотически нормальной) оценки 0. Будем считать,
что 0 есть несмещенная оценка 0, то есть £(0) = 0. Начнем с построения двусто-
ронних доверительных интервалов, симметричных относительно оценки 0, то
есть интервалов вида (0-3, 0+8), где 8 > 0. По условию задачи необходимо для
12.2. Построение доверительных интервалов в случае асимптотически нормальных оценок
841
заданного у и полученной по выборке оценке 0 найти такое 5, чтобы выполнялось
условие
р(е-8<0<0 +б) = у	(12.2)
или, что равносильно,
р{ 10— 0)< sj> =у.
Покажем, что для нормально распределенной случайной величины X с парамет-
рами ц и о имеет место равенство
Р{|Х-|л|<8} =20>f-1-1,	(12.3)
koj
где Ф(г) — функция стандартного нормального распределения (4.14).
Действительно, используя соотношение (4.4) и (4.16), имеем:
Р{|Х-|л|<8} = Р{ц-8<Х<|л + 8} =
fp + 8-ц^ fp-8-ц^	(3^1	( 8^
— ф £_----!_ _ ф £2--£2. = ф — — ф-----
О ) V ° J	\°J	\ oj
В силу симметричности относительно начала координат графика плотности
стандартного нормального распределения (см. рис. 4.4) для значения 2 > 0 имеем
соотношение
Ф(-г) = 1 - Ф(-з).
Поэтому
Р{| X -ц | < 8} = ф(-1 - ф(--1 = ф(-1 -[ 1 - фГ-11 = 2ф(-1 -1,
\GJ к с) ко J к ko/J ко J
что и требовалось доказать.
Отметим теперь, что следующие события эквивалентны:
10-8<0<0+81=1-0-8<-0<-0 + 8)=(0-8<0<0 + б1.
Так как 0 имеет нормальное распределение с математическим ожиданием 0 (ведь
0 — несмещенная оценка!) и дисперсией Д(0), то с учетом предыдущих равенств
и формул (12.2) и (12.3), имеем
у = р] 0-8 < 0 < 0 + 8к =2Ф
8
о(0)
-1,
8
о(0)
_ 1 + у
~~2~’
Ф
где о(0) = 7°(6)-
42
12. Оценивание с помощью доверительных интервалов
вспоминая определение квантили (12.1), заключаем, что 8/о(0) — это квантиль
гандартного нормального распределения, отвечающая вероятности (1 + у )/2:
8	1 + уА
о(0) I 2 J
)тсюда вытекает, что
8 = ф-^^о(0).	(12.4)
1оскольку доверительная вероятность у задана, то подсчитав (1 + у)/2, можно
А-1 (1 + у')	<•
1айти значение Ф 1 —1. Следовательно, для вычисления 6 осталось опреде-
тить дисперсию D(0), которая может быть неизвестна. Однако вместо D(0) есте-
ственно взять ее состоятельную оценку D(0), подсчитанную по результатам вы-
5орки. Поскольку объем выборки п велик, то оценка D(0) будет близка к
истинной дисперсии D(0). Итак, получено следующее правило построения дву-
стороннего доверительного интервала (0-8; 0 + 8) с коэффициентом доверия у
для параметра 0 в случае нормальной (асимптотически нормальной) и несмещен-
ной оценки 0.
По данным выборочной совокупности вычисляются оценка 0 и состоятельная
оценка D(0) дисперсии оценки В(0). Затем находится квантиль нормального
\( 1 + У
распределения Ф I I, отвечающая вероятности (1 + у)/2. В частности, при у,
f I + у Л
равном 0.95 и 0.99, Ф I —1 составит, соответственно, 1.96 и 2.58. Далее вычис-
ляется 8 по формуле (12.4), в которой в качестве о(0) принимается -\j D(0).
Тогда интервал (0 - 8; 0 + 8)будет двусторонним доверительным интервалом для
параметра 0 с коэффициентом доверия у.
Намного проще вывод формул для построения односторонних доверительных
интервалов. Приведем окончательные результаты.
Нижним (-оо, 0") и верхним (0', оо) доверительными интервалами для параметра
0 с коэффициентом доверия у в случае нормальной (асимптотически нормальной)
и несмещенной оценки 0 являются интервалы:
(-00, 0") = [ -ОО, 0 + ф-'(7)ТВ(0)
НМГПРПГии Л/ЙУоценки 0.
12.2. Построение доверительных интервалов в случав асимптотически нормальных оценок
ш
Проиллюстрируем сформулированное правило на примерах построения довери-
тельных интервалов для вероятности и математического ожидания. Начнем с ве-
роятности.
Предположим, что требуется построить доверительный интервал для неизвест-
ной вероятности р появления события А. Пусть в результате п наблюдений (где
п достаточно велико) событие А появилось 5„ раз. Мы знаем (см. примеры 11.1
и 11.4), что частота — 5„ является несмещенной и состоятельной оценкой р, при-
п
чем ее дисперсия D{S„/n) = р(1 - р)/п. Как следует из теоремы Муавра—Лапла-
са (7.26), эта оценка асимптотически нормальна. Здесь 0 = р, 0 = — S„. Далее,
п
D(0) = —. Поскольку р неизвестно, то вместо 0(0) следует использовать состоя-
п
тельную оценку 0(0). Так как состоятельной оценкой р является частота -5.,
п
а для q =1 - р такой оценкой будет 1 — 5„, то состоятельной оценкой 0(0) будет
п
o(0)=4\fi--O
п < п )
Теперь по формуле (12.4) находим
8 = Ф'1 f I-I5J.
< 2 J\n2 \ п J
Следовательно, двусторонний доверительный интервал для вероятности будет
иметь вид
[15„	(12>5)
V” V 2 )\п	< п J п \ 2 )\п	\ п )
Нижний и верхний доверительные интервалы для вероятности имеют вид:
Г	1	1 I	7	i	a'I
(0,0)= О, 25я+ф-*(у)± 5И 1--5я ,
k	п	п\	\	п	)
(0', l)=f-5„ -Ф-’(У)-	1 .
n	п\ V п ) t
Пример 12.1. Для оценки вероятности безотказной работы агрегатов определен-
ного типа была отобрана выборочная совокупность в 200 агрегатов. В результате
стендовых испытаний отказало 10 агрегатов. Найти двусторонний доверитель-
ный интервал для вероятности безотказной работы р, соответствующий довери-
тельной вероятности 0.99.
if” 1 + V
Так как у = 0.99, то Ф I 1 = 2.58. Далее, в нашем случае п = 200 и не отказало
190 агрегатов, то есть S„ » 190. Следовательно,
44
12. Оценивание с помощью доверительных интервалов
-S„ =0.95,
п
Н 1 5 fl-IsJ =2.58,1—0.05 «0.0398.
V 2 )\п2 I п nJ V 200
[скомый доверительный интервал есть (0.95 - 0.0398; 0.95 + 0.0398), иначе
J.9102; 0.9898).	□
еперь рассмотрим задачу построения доверительных интервалов для математи-
еского ожидания. Пусть (х^.х^.-.-.х*) — наблюденная выборка для случайной
еличины X, распределенной по произвольному закону с неизвестными матема-
ическим ожиданием ц и дисперсией о2. По этим данным необходимо построить
вусторонний доверительный интервал для математического ожидания ц, отве-
ающий коэффициенту доверия у. Как известно из примера 11.2, несмещенной
ценкой математического ожидания является эмпирическое математическое
1 п
жидание ц* = -Ух‘, которое асимптотически нормально. Дисперсия этой
«i-i
ценки равна В(ц*) = о2/п. Дисперсия о2 случайной величины X неизвестна.
)днако вместо нее можно взять эмпирическую дисперсию
о2’ =-£(*; -ц*)2.	(12.6)
«.и
V	V	2
оторая является состоятельной оценкой дисперсии о .
Следовательно, доверительным интервалом для математического ожидания ц
коэффициентом доверия у будет интервал
1ижним и верхним доверительными интервалами для математического ожида-
1ия будут интервалы:
^-оо; ц ’ + Ф-* (у)7о2*/«^>
* -Ф'1 (y\jcs2'/n; ooj.
5 заключение рассмотрим задачу определения необходимого объема выборки.
5ыше предполагалось, что объем выборочной совокупности фиксирован. В ста-
истических исследованиях часто бывает наоборот: объем выборки подбирается
ак, чтобы добиться заранее установленных точности и надежности оценки.
Сели интервал соответствует доверительной вероятности у, то это значит, что
бсолютное отклонение оценки 0 от истинного значения параметра 0 будет мень-
ие 8 с вероятностью у, то есть
р{| 0-0| < з} = у.
Следовательно, с вероятностью у абсолютная ошибка не превышает 6. При сде-
анных нами предположениях имеем (см. (12.4)) следующее выражение для 8:
12.2. Построение доверительных интервалов в случае асимптотически нормальных оценок
346
мвммив
8 = Ф
(12.8)
где В(0) = (ст(0))2 — дисперсия оценки 0.
Если 0 — состоятельная оценка для 0, то дисперсия В(0) с ростом объема выбор*
ки п стремится к нулю. Поэтому при фиксированном коэффициенте доверия у
значение 5 будет уменьшаться. Каков же минимальный объем выборки я, при
котором абсолютная ошибка 5 с вероятностью у не превысит заданного уровня?
Очевидно, для ответа на этот вопрос необходимо подставить в качестве 8 задан*
ную величину и решить полученное уравнение относительно п.
Определим вначале необходимый объем выборки в случае оценки вероятности р.
Так как в этом случае D(0) = pq/n, то
б = ф-*Г1±1\ЙЕ£)
I 2 Д п
откуда
/>(!-/>)•
(12.9)
В этом выражении неизвестно р. Часто поступают так: предварительно берут не-
большую «пробную» выборку объема пй и по ее данным делают приближённую
оценку р. Если 5о/по — частота события в пробной выборке, то необходимый
объем равен
”о I «О ,
(12.10)
Заметим, что при любом р, заключенном между 0 и 1, р(1-р)£1/4, причем
знак равенства достигается только при р = 0,5. Поэтому в любом случае
//
п £ Ф'1
Л
_1
4
Рассмотрим теперь случай оценки математического ожидания ц. Так как здесь
D(0) = ст2/п, то формула (12.8) дает уравнение
8 = Ф"1 f ^-^Ъст2/п.
I 2 Г
Для оценки а2 поступают, как и раньше: делают пробную выборку объема Яд
и вычисляют по формуле (12.6) соответствующую ей эмпирическую дисперсию
о2*. Подставляя ее в последнюю формулу, находим
°2’- (12л1>
Пример 12.2. Производится оценка среднемесячного дохода семьи в некотором
регионе. Каков должен быть объем выбооки я. если заоанее ппинято. что оомпи.
16
12. Оценивание с помощью доверительных интервалов
явный коэффициент у равен 0.95, а допустимая абсолютная ошибка не должна
эевышать 50 евро?
редположим, что в результате пробной выборки было установлено, что о2’ = 2 • 104.
огда, поскольку при у = 0.95	= 1.96, то п = (1.96/50)2-2-104 =62. □
2.3. Основные распределения
1атематической статистики
ыше была изложена методика построения доверительных интервалов при боль-
их объемах выборочной совокупности, когда оценка интересующего нас пара-
етра распределена приблизительно нормально. Однако особое значение метод
^верительных интервалов имеет в случае выборочных совокупностей малого
5ъема. Действительно, так как оценка параметра обычно состоятельна, то при
эльших выборках она близка к истинному значению параметра. Следовательно,
ринимая в качестве параметра его оценку, мы совершаем, как правило, неболь-
:ую ошибку. Этого нельзя сказать в случае малых выборок, когда оценки имеют
элыпой разброс (дисперсию) около истинного значения параметра. Поэтому
1есь замена параметра его оценкой часто приводит к существенной ошибке,
этом случае особенно важно указать границы интервала, который с наперед
данной вероятностью содержит интересующее нас значение параметра.
[спользуемый здесь метод построения доверительных интервалов основан на рас-
ределении оценок параметра. При больших выборках рассматриваемые оценки
мели приблизительно нормальное распределение. При малых выборках это не
1к. Следовательно, необходимо знать точное (а не асимптотическое) распреде-
ение оценок параметров. Мы ограничимся случаем нормальной генеральной
эвокупности. Оценки параметров нормальной совокупности имеют /2-распре-
еление или ^-распределение Стьюдента.
пределение 2. у? -распределение (читать: хи-квадрат распределение) задается
педующей плотностью:
[ 0	при х < 0,
f(X)=[(2l/2r(l/2))-'xW2i-le-x/2	при х>0,
це1 — параметр распределения, называемый числом степеней свободы, 1=1,2,...,
(а) — гамма-функция:.
Г(а) = ]уа-'е-Чу.	(12.13)
о
[ри / £ 2 кривая плотности этого распределения постоянно убывает для х > 0,
при I > 2 имеет единственный максимум в точке х = I - 2. Соответствующие
рафики для некоторых значений I изображены на рис. 12.2. Момент r-го поряд-
а х2 -распределения задается формулой
цг =/(/ + 2)(/ + 4)...(/ + 2г-2).
)тсюда, в частности, следует, что
£(%) = /, ц2-/2+2/, £>(%) = 21.	(12.14)
12.3. Основные распределения математической статистики
Э47
/(*) ♦ 4
0.5  j
0	2	4	6	8	10
Рис. 12.2. Кривые плотности х2-распределения
Эти формулы могут быть выведены на основании следующего функциональною
уравнения для гамма-функции:
Г(а + 1) = аГ(а), а>0.	(12.15)
В частности, Г(п + 1) = п! для целого положительного п. Хорошо известны так-
же следующие формулы:
(12.16)
Напомним, что квантиль, отвечающая вероятности р, есть число, удовлетворяю-
щее условию: вероятность случайной величины не превзойти его равна р. В слу-
чае х2-распределения с I степенями свободы квантиль, отвечающая вероятности р,
обозначается х2 (О» то есть х2 (О есть решение уравнения
х?,(О
Р=ЛХ2(О)= \f(x)dx,
о
где /(х) определяется формулой (12.12).
Квантили х2-распределения с различным числом степеней свободы могут быть
определены из соответствующих таблиц или, например, с помощью модуля Pro-
bability Calculator пакета STATISTICA или путем использования встроенных
функций пакета Mathcad.
Примечательным свойством х2-распределения является то, что сумма независи-
мых случайных величин, имеющих это распределение, также имеет х2-распреде-
ление.
348
12. Оценивание с помощью доверительных интервалов
Теорема 12.1. Пусть Уь У2..У* есть последовательность взаимно независимых
случайных величин, имеющих х2 -распределение с lt, 12, ..., 4 степенями свободы
соответственно. Тогда сумма У] + У2 + ... + Yk имеет х2 -распределение с
Д + 12 + ... + 4 степенями свободы.
Доказательство
Из свойства ассоциативности для операции суммирования и принципа индук-
ции следует, что достаточно ограничиться случаем двух слагаемых У] и У2. По-
скольку У, и У2 неотрицательны, то неотрицательной будет и их сумма. Если обо-
значить _/\(у) плотность распределения У], а /2(г/) — плотность распределения У2,
то плотность распределения У] + У2, согласно формуле (7.15), будет
/(У) = f/i(^)/2(z/-z)dzr, y>0.
0
Подставляя вместо j\ и/2 выражение (12.12) при /, равном соответственно Ц и /2»
находим, что при у > О
У
f(y) = }(2Z| /2 Г(4/2))’1 z(Z1 /2Н е~г/2 (2'2/2 Г(/2 /2))~‘ (у - z)('2/2H е'(у ~2>/2dz =
О
у
= (2(Z| +'2)/2 ^/2)^/2))-' е~у/2 f z<Z|/2Н (у - z)(Z2/2)-‘ dz. (12.17)
о
Произведем в последнем интеграле замену переменной z = yv, dz = ydv Тогда
v = z/y и пределы интегрирования по переменной v будут 0 и 1:
у	I
jz(,< /2)-‘ (у - z)(/2/2H dz = у «'< +'2)/2>-’ р(/' /2’-‘ (1 -^)<Z2/2)-‘ dv.
о	о
Из таблиц определенных интегралов находим, что
Jv« /=>-> (1	dv = Г(/1/2)Г(4/2)(Г((/1 + /2 )/2))-‘.
О
Подставляя эти результаты в (12.17), получаем плотность х2 -распределения
с /, + /2 степенями свободы.	□
Условия, при которых возникает х2 -распределение, определяет следующая тео-
рема.
Теорема 12.2. Если Уь У2, ..., У/ взаимно независимые случайные величины,
имеющие одно и то же стандартное нормальное распределение (4.13), то сумма
их квадратов Y2+Y2+ ... +Y2 имеет х2 -распределение с / степенями свободы.
Доказательство
Покажем, что если У имеет стандартное нормальное распределение (4.13), то
квадрат У2 имеет х2 -распределение с одной степенью свободы. Отсюда и из пре-
дыдущей теоремы, полагая в ней k = I и lt> = 1, i = 1, 2,..., k, получим требуемое до-
казательство.
Распределение У2 можно легко получить, используя теорему 4.3 для функции
у(х)  х2. Однако мы приведем прямое доказательство, не опирающееся на эту
ТАППАМи
12.3. Основные распределения математической статистики
Согласно формулам (4.13) и (4.14), плотность распределения Y есть
Ф(г/) = -^=е‘!'2/2,
у/2п
а функция распределения — Ф(у).
Случайная величина Y2 не превосходит значения у > 0 тогда и только тогда, ко-
гда Y не превосходит по абсолютной величине у[у. Поэтому
P{Y2 <>y} = P{-Jy <,Y ^} = Ф(^)-Ф(-^) =
Л
= 2O(7F)-l = 2j<p(z)^-l,
о
так как Ф(-а) = 1 - Ф(а) для а > 0.
Дифференцируя это выражение по переменной у, находим, что плотность рас-
пределения случайной величины У2 есть
-^(2®(^)-l) = 2-^=e-v/2^-1/2 = -^=у~'/ге~у/1.
ay	V2n 2 V2tc
Это совпадает с формулой (12.12) при /= 1, поскольку, согласно формуле (12.16),
Г(1/2) = Тл.	□
Доказанная теорема показывает, что случайную величину, имеющую х2'Распре-
деление с / степенями свободы, можно интерпретировать как сумму квадратов /
взаимно независимых случайных величин, имеющих стандартное нормальное
распределение. Такая интерпретация, а также центральная предельная теорема,
позволяют установить, что при /->оо х2 -распределение приближается к нор-
мальному. В частности, при больших I (I > 30) квантиль этого распределения, от-
вечающая вероятности р, может быть вычислена по формуле
ер(1)«1 + ^21ф-'(р),	(12.18)
где Ф-1(р) — квантиль стандартного нормального распределения.
Оказывается, однако, что большую точность обеспечивает другая формула, пред-
ложенная Р. Фишером:
х2(/)^(72Л^+ф-*(р))2.	(12.19)
Она основана на том, что распределение функции -^2х2 --J21-1 от х2 стремится
при /->» к стандартному нормальному быстрее, чем само х2 -распределение.
Теперь мы перейдем ко второму основному распределению математической ста-
тистики.
Определение 3. Случайная величина Т имеет t-распределение Стьюдвнта с / сте-
пенями свободы, если ее плотность распределения задается формулой
где I — пяпяметп. МЛЯМПЯЯМЫЙ Utirnnu гтапаиаЛ галАлАы I _ 1 О
50
12. Оценивание с помощью доверительных интервалов
ривая плотности ^-распределения одновершинна и симметрична относительно
>чки t = 0 (рис. 12.3). Последнее означает, что
(12.21)
Р{Т <-t} = \-Р{Т <t}	при£>0.
Рис. 12.3. Кривые плотности t-распределения при / = 3
и стандартного нормального распределения
Io сравнению с кривой плотности нормального распределения при одних и тех
се значениях математического ожидания и дисперсии кривая t-распределения
юнее крутая, то есть вероятность больших отклонений от математического ожи-
,ания для t-распределения больше. При I -> »t-распределение стремится к стан-
артному нормальному распределению (4.13).
(ля t-распределения существуют все моменты, порядок которых меньше числа
тепени свободы I. Вследствие симметричности распределения все существую-
цие моменты нечетного порядка (в частности, математическое ожидание) равны
[улю. Существующие моменты четного порядка определяются по формуле
И 2г
при 2г < /.
3 частности, используя формулы (12.15) и (12.16), получаем ц2 = о2 = //(/-2).
Квантиль t-распределения Стьюдента с I степенями свободы, отвечающая веро-
1ТН0СТИ р, обозначается tp(l). Значения квантилей t,,(Z) для разных вероятно-
:тей р и числа степеней свободы Z можно определить с помощью модуля Proba-
bility Calculator пакета STATISTICA или встроенных функций пакета Mathcad.
Гак как при увеличении числа степеней свободы I t-распределение стремится
< стандартному нормальному (4.13), то и квантиль tp(l) стремится к квантили
Г‘(р). Оказывается, что уже при Z > 30 и 0.01 < р < 0.99 можно пользоваться
формулой
«.(/)-Ф"'(Р).
12.3. Основные распределения математической статистики
351
Пример 12.3. Найдем квантили ^-распределения с двумя степенями свободы, от-
вечающие вероятности 0.9 и 0.3. С помощью модуля Probability Calculator пакета
STATISTICA находим, что £0.э(2) = 1.886, t03(2) = -1.061.	□
Применение распределения Стьюдента в статистике основывается на следую-
щей теореме.
Теорема 12.3. Пусть X и Y являются взаимно независимыми случайными вели-
чинами, причем X имеет стандартное нормальное распределение (4.13), a Y име-
ет х2-распределение с I степенями свободы (12.12). Тогда величина
т = ^1^	(12.22)
имеет распределение Стьюдента с I степенями свободы.
Доказательство
Если случайная величина Y приняла значение у, то для выполнения неравенства
Т< t необходимо и достаточно, чтобы X < t-Jy I “1/2. Так как X имеет стандартное
нормальное распределение (4.13), то условная вероятность интересующего нас
события {Т < t} при условии Y- у составляет
с _	1	X J. г2
Р{Т < t\Y = у} = Р\х<tjy Г42 \ = J -т=е 2 dz.
I	J V2n
Поскольку значение у может быть произвольным, а случайная величина Y имеет
X2 -распределение (12.12)с / степенями свободы, то усредняя по значениям у, на-
ходим
1-1
у2 e~y/2dy =
«otJ7r(l/2) 1	1,2 ( £ г/\Т' 11
J J -±=е 2 dz 22Г - у2 e~y/2dy.
о	л/2л
Для получения плотности распределения случайной величины Т это выражение
надо продифференцировать по t:
<2у г~С £ г L 1 t
21V 22ГШ у2 е 2dy"
После подстановки
1
2
< t2 ,
1 + — у, dv =
(	t2}
k • J
1
2
последний интегпал будет папен
352
12. Оценивание с помощью доверительных интервалов
ОО м
J v 2 e~vdv =
о
так как по определению гамма-функции (12.13)
00 —-	00	1 1	f / 1 1 \
|v 2 e~vdv =	2 e~ldv = Г ---- .
о	о	\ 2 у
Следовательно, искомая плотность распределения случайной величины Т равна
^-P{T<t}= \ 2 J
dt r[-W
V2J
что соответствует распределению Стьюдента с / степенями свободы.
12.4. Построение доверительных интервалов в случае
малых выборок из нормальной совокупности
Изложенный выше материал позволяет сформулировать следующую важную
теорему, впервые строго доказанную Р. Фишером [2, 3, 9, 10].
Теорема 12.4. Пусть Хь Х2,..., Х„ — выборка объема п из генеральной совокупно-
сти, имеющей нормальное распределение (4.11) с параметрами ц и а. Тогда эм-
пирическое математическое ожидание ц" и эмпирическая дисперсия а2’ взаимно
независимы, причем ц ’ имеет нормальное распределение с математическим ожи-
данием ц и дисперсией а2/и, а пи2'/ст2 имеет х2 -распределение с п - 1 степенью
свободы.	□
Эта теорема будет использована в дальнейшем при построении доверительных
интервалов для дисперсии а2. Доверительный интервал для математического
ожидания ц по этой теореме построить нельзя, так как распределение оценки ц ’
зависит, кроме ц, еще и от неизвестного параметра а. Построение такого интер-
вала основывается на следующей теореме.
Теорема 12.5. В условиях предыдущей теоремы величина (ц’ -p)V«-l/Vo2*
имеет t-распределение Стьюдента с п - 1 степенью свободы.
Доказательство
По теореме 12.4 случайные величины (ц’ -ц)л/й/ст и ист2’/а2 взаимно неза-
висимы, причем первая из них имеет стандартное нормальное распределение,
а вторая — х2 -распределение с (и - 1) степенью свободы. Поэтому доказательст-
во следует из теоремы 12.3.	□
Применим полученные результаты для построения доверительных интервалов
для математического ожидания и дисперсии нормальной генеральной совокуп-
ности. Начнем с двустороннего доверительного интервала для математического
ожидания.
12.4. Построение доверительных интервалов в случае малых выборок из нормальной совокупности	ЭМ
Будем искать симметричный относительно наблюденного значения ц* довери-
тельный интервал, то есть интервал вида (ц’ -8>/о2*, ц* + sVo2* ), где б>О
должно быть подобрано так, чтобы
Р{ц * - 8л/а2’ < ц < ц * + 8л/о2’} = у.
Легко показать, что следующие три неравенства эквиваленты:
ц ’ - 8л/а2’ < р. < (1 * + 8л/а2’,
-5л/а2’ < ц - ц * < 8л/а2’,

/„2-
Соответственно, вероятности этих двойных неравенств равны
По теореме 12.5 величина
(12.24)
имеет t-распределение Стьюдента с п - 1 степенью свободы.
Теперь из формул (12.23) и (12.21) получаем
у = Р{-б7пЛ < Т < sVn^i} =
= Р{Т < SVn^i} -Р{Т <	= 2Р{Т < sVn^i} -1.
Отсюда выводим, что
P{T<sVn^i}=^.
Следовательно,
8л/п — 1 = t1+T (п -1) и 8 =
л/и-1 ~
Таким образом, двусторонний доверительный интервал для математическою
ожидания ц, отвечающий коэффициенту доверия у, имеет вид:
ц’	(n-l)To27;
Vn-1 ~
ц’ + -=L=ty(n-l)To27
Jn-1 —
(12.25)
где jj. * и о2* — эмпирические значения математического ожидания и дисперсии,
вычисляемые по формулам (10.11) и (12.6); tp(n - 1) — квантиль t-распределе-
ния Стьюдента с п - 1 степенью свободы, отвечающая вероятности р.
Нижним и верхним доверительными интервалами для математического ожида-
ния нормальной генеральной совокупности будут интервалы:
-<»; u + -==t,(n-l)vo ,
I	г )
354
12. Оценивание с помощью доверительных интервалов
Пример 12.4. Суточный расход авиационного топлива (в т) по данным 10 дней
составил 220; 200; 240; 190; 160; 260; 210; 200; 170; 150. Предполагая, что суточ-
ный расход имеет нормальное распределение, построим двусторонний довери-
тельный интервал для математического ожидания суточного расхода, отвечаю-
щий коэффициенту доверия у = 0.9.
В первую очередь вычислим эмпирические математическое ожидание и диспер-
сию:
ц' = 200; о2* = 1080.
Учитывая, что п = 10, а число степеней свободы равно п - 1 = 9, находим
^14-0.9 (^) = ^0.95(9) = 1-833.
2
Поэтому искомый доверительный интервал есть (в т)
[ 200—Д—1.833V1080; 200 +  1	1.833Л089 | = (179.92; 220.08). □
I л/ЙПЙ	л/ПГЛ )
Теперь рассмотрим построение двустороннего доверительного интервала для
дисперсии нормальной совокупности. А именно, требуется найти случайный ин-
тервал (О', 9"), с заданной вероятностью у накрывающий неизвестную дисперсию
о2 нормальной совокупности, то есть такой, что
Р{9'< о2 < 9"} = у.	(12.26)
Будем искать границы интервала в виде 9' = 8(о2*, 9" = S2o2*, 8t,82 >0, о2* — эм-
пирическая дисперсия, подсчитанная по выборке объема п. Теперь неравенство
9' < о2 < 9" превращается в неравенство 8( о2* < о2 < 82о2‘, которое равносильно
неравенству
п	па2‘	п
-- <---л— <--•
82 о2	8(
Следовательно, вероятности этих двойных неравенств равны, и поэтому
(12.27)
[ 82 о2 8t
В соответствии с теоремой 12.4, случайная величина
имеет х2 -распределение с п - 1 степенью свободы.
Случайный интервал (9', 9"), с вероятностью у накрывающий о2, определяется
неоднозначно. Остановимся на таком выборе интервала (9', 9"), при котором ве-
роятности выхода за пределы этого интервала влево или вправо одинаковы.
Иными словами, мы накладываем дополнительное условие
Р{о2 < 9'} = Р{о2 > 9"} =	(12.28)
12.4. Построение доверительных интервалов в случае малых выборок из нормальной совокупности
зм
Это условие равносильно следующему:
„[ио2* и| „|ио2* и] 1-Y
р<-----> — > = р<-----< — > =----.
[о2	8) J [о2	32 J 2
В терминах случайной величины х2 = ио2’/о2 это запишется так (рис. 12.4):
4х2	=р1*2 <Т-] =	(12.29)
I J L *	“
Рис. 12.4. Доверительный интервал для дисперсии
. Из формулы (12.29) и определения квантили следует, что и/32 = X<i-z>/2(n —1)>
и поэтому
Х(1-г)/2 (W ~ 1)
(12.30)
где Х(1-Т)/2(и _ О — квантиль х2 -распределения с п - 1 степенью свободы, соот-
1-у
ветствующая вероятности —
Аналогично этому из формулы (12.29) далее получаем
Р х2
_11=1_рЕг ? п] -j 1-у _ 1 + Y
8J I 8, J 2	2 ’
откуда находим, что п/&{ = X (i+T>/2 (” —1)> и поэтому
X(i+y>/2(w О
(12.31)
Таким образом, получаем двусторонний доверительный интервал для диспер-
сии о2, соответствующий доверительной вероятности у и дополнительному ус-
ловию (12.28):
п _2._ п _2.
   I .— II 0 t	-	0
<X<uT)/j(n_0	(п ~ О
(12.32)
356
12. Оценивание с помощью доверительных интервалов
Длина построенного доверительного интервала равна, очевидно,
О Х(1+У)/2(и О,
Попробуем уменьшить эту длину, отказавшись от условия (12.28) одинаковой
вероятности выхода истинного значения дисперсии за пределы этого интервала
вправо и влево. Пусть а — искомая вероятность того, что значение диспер-
сии окажется левее доверительного интервала (ранее директивно полагалось
а = (1-у)/2). Тогда (1-у-а) — аналогичная вероятность оказаться правее:
Р{о2<0'}=а, Р{о2 >0"} = 1-у-а.
Теперь вместо (12.29) имеем соотношение:
Р\ *2 <Т’Г
I 82 J
Значения и 32, определяющие левую и правую границы интервала, выражают-
ся через значение а следующим образом:
5	п	§	п
Х?-а(«-1)’	2	Х?-т-а(«-1)‘
Очевидно, длина интервала составляет (32 -81 )о2’.
В результате мы имеем следующую задачу нелинейной оптимизации:
Минимизировать функцию
G(a) = 82-8j=—-----
Х!-у-а(«-1) Х1-а(«-1)
8,
(12.33)
(12.34)
(12.35)
1
по переменной а >0, удовлетворяющей условию а < 1-у.
Сформулированная задача оптимизации по одной переменной является весьма
простой. Она без труда решается в пакете Mathcad путем использования встро-
енной функции Minimize.
Пример 12.5. Продолжим рассмотрение предыдущего примера. Построим крат-
чайший двусторонний доверительный интервал для дисперсии нормального рас-
пределения, если объем выборки п = 10, значение эмпирической’ дисперсии
о2’ = 1080, коэффициент доверия у =0.6.
Вычисления в пакете Mathcad показывают, что кратчайший доверительный
интервал для дисперсии есть (650.4; 1582). Длина интервала составляет
1582 - 650.4 = 931.6. Для сравнения укажем, что симметричным доверительным
интервалом (12.32) будет интервал (882.2; 2007), длина которого, равная 1124.8,
существенно больше.
12.5. Численный метод построения доверительных
интервалов для параметрической функции*
Ниже будет изложен общий метод построения доверительных интервалов для
параметрической функции, сформулированный Ю. К. Беляевым. Пусть интере-
сующий нас показатель описывается функцией g(0), называемой параметриче-
12.5. Численный метод построения доверительных интервалов для параметрической функции*	367
ской, от вектора неизвестных параметров 0 = (0И 02,..., 0т), значения которого
принадлежат параметрическому пространству 0. В нашем распоряжении имеет-
ся выборка X = (Х1Г Х2, ..., Х„), каждый элемент которой X, является случайной
величиной (или случайным вектором), распределение которой полностью опре-
деляется параметром 0 е 0. Необходимо построить доверительный интервал
(g'(X), g"(X)) для параметрической функции g(0), отвечающий доверительной
вероятности у:
P{g'(X)<g(0)<g"(X)}>y,	V0G0.	(12.36)
В дальнейшем будет использоваться следующее определение.
Определение 4. Выборочным пространством Т называется подмножество «-мер-
ного вещественного пространства, точки которого х = (xt, х2.хП) соответству-
ют возможным значениям выборки X = (Хь Х2................Хя).
Построение доверительного интервала осуществляется в три этапа.
Этап 1. Каждому 0 g 0 ставится в соответствие некоторое множество Тв с. Ч* вы-
борочного пространства Т такое, что если истинное значение параметра есть 0, то
выборка X попадает в это подмножество с вероятностью, не меньшей, чем у:
Р0{Хб'Р0}>у.
В результате имеем семейство множеств
{Те, 0 G 0}.
Этап 2. Исходя из семейства множеств выборочного пространства {То, 0 6 ©},
определяется семейство {0Х, х g Т} множеств параметрического пространства 0
следующим образом: для каждой точки х выборочного пространства Т опреде-
ляется множество 0Х параметрического пространства, состоящее из таких значе-
ний 0, при которых х g Т0:
0Х ={0 G0: х gT0}, xgT.
Отметим, что оба рассмотренных семейства однозначно определяют друг друга.
Случайное событие {X g Т0} имеет теперь эквивалентную форму записи {0 б €>х )•
Следовательно,
Р0{0 G 0Х} = Р0{Х G%}	(12.37)
Определение 5. Семейство множеств {0Х: х gT} параметрического пространст-
ва 0, удовлетворяющее условию (12.37), называется семейством у-доввритвлЪ’
ных множеств для параметра 0 g 0. Если нижняя грань
inf {Р0{0 g 0Х}} = у,	(12.38)
8« ©
то у называется коэффициентом доверия для семейства {0Х: х е Т}.
Отметим, что оба вышеописанных этапа осуществлялись без использования
фактических данных о выборке х.
Этап 3. Фиксируется полученная выборка X = х. Формулируются и решаются
две оптимизационные задачи: найти иифимум и супремум параметрической
функции g(0) на множестве 0Х значений параметра 0:
358
12. Оценивание с помощью доверительных интервалов
g'(x)= infg(0),	(12.39)
0€0Х
g"(x) = sup g(0).	(12.40)
0€0X
Тогда интервал (g'(X), g"(X)) является двусторонним доверительным интер-
валом для параметрической функции g(0), отвечающим коэффициенту доверия у.
Справедливость последнего утверждения следует из того, что множество {0 е 0Х}
содержится во множествах
/ inf g(0)<g(0)l ={g'(x)<g(0)}H|g(0)< supg(0)l ={g(0)<g(x)}.
[вг®«	J	[	0€0, J
Следовательно, для любого 0 е 0
у < Рв{0 е 0Х} < Pe{g '(X) < g(0) < g "(X)},
Итак, (g'(X), g"(X)) является искомым двусторонним доверительным интерва-
лом. Для получения одностороннего интервала достаточно просто не учитывать
один из концов g' или g".
Основными элементами вышеописанной процедуры являются: 1) подбор семей-
ства множеств {чРе: 0 е 0} и 2) решение задач оптимизации (12.39) и (12.40).
Решение задач оптимизации мы переадресуем к соответствующим компьютер-
ным пакетам программ (см. ниже компьютерный практикум № 19). Более акту-
альной для статистиков является успешное решение первой задачи, отчего зави-
сит точность оценивания.
Определение 6. Доверительный интервал для параметрической функции называ-
ется точным, если не существует другого доверительного интервала с тем же ко-
эффициентом доверия и более узкими границами.
Иначе говоря, точный двусторонний доверительный интервал имеет самую ма-
ленькую длину, нижний доверительный интервал — наименьшую верхнюю гра-
ницу, верхний — наибольшую нижнюю границу.
Как отмечает Ю. К. Беляев, «...наиболее точные доверительные оценки удается
построить в исключительно редких задачах». В этих редких задачах такое по-
строение опирается на сведение их к задачам проверки статистических гипотез,
в частности, путем использования фундаментальной леммы Неймана—Пирсона
(см. теорему 13.1).
Примеры
Пример 12.6. Рассмотрим задачу построения доверительного интервала для
вероятности того, что случайная величина X, имеющая нормальное распределе-
ние, попадет в интервал (а, Ь), а<Ь. Предполагается, что параметр а нормально-
го распределения (4.11) известен, а параметр ц — нет. При этом в распоряжении
имеется выборка X = (Хь Х2..Хп) объема п, соответствующая этому распреде-
лению.
В данном случае неизвестен один параметр, а параметрическим и выборочным
пространством будет вещественная ось: 0 = ц, 0 = (-оо, оо), Ч* = (-оо, оо). Парамет-
рическая функция имеет вид:
12.5. Численный метод построения доверительных интервалов для параметрической функции'
358
g(n) =	{а < X < Ь} = ф[ - ф[
I о у I о
(12.41)
Применим для построения доверительного интервала изложенную методику.
Этап 1. Каждому элементу выборки X, поставим в соответствие нормированную
величину Z, = (Х, -ц)/о (см. определение 8 главы 4). Согласно утверждению 2
той же главы, Z, имеет стандартное нормальное распределение (4.13). Квадрат
этой величины Z,2 имеет х2 -распределение с одной степенью свободы (теоре-
ма 12.2). Случайные величины Хь Х2,.... Хп, нормированные величины Zu Z2,....
Z„ и их квадраты Zt2, Z22.Z„2 взаимно независимы, поэтому согласно теоре-
ме 12.1, сумма квадратов Z2 + Z2 + ... + Z2 имеетх2-распределения с п степеня-
ми свободы. Пусть х^(я)~ квантиль х2 -распределения с п степеням свободы, от-
вечающая вероятности у.
Для каждого 0 = ц в качестве множества возьмем
п /	_ \2
= < х =(х,,х2, ...,х„ ): J Н
i=l к О J

Итак, если истинное значение параметра есть ц, то выборка X - (Хь Х2.Х„) по-
падает в эту область с вероятностью у.
Этап 2. Для каждого значения х = (хь х2,..., х„) определяем множество
®х
ре©:	<%2(п)
>=1 \ V )
Семейство {0Х, х g Ч7} является семейством у-доверительных множеств для пара-
метра |i.
Этап 3. Для фиксированной выборки х = (хь х2,..., хп) решаем следующую зада-
чу нелинейной оптимизации:
Найти минимальное g' и максимальное g" значения функции (12.41) на множест-
ве 0Х значений ц.
Интервал (g', g") является искомым доверительным интервалом: с вероятно-
стью у он накрывает вероятность того, что рассматриваемая случайная величина
попадет в интервал (а, Ь).
В представленном ниже компьютерном практикуме № 19 приведена программа
на Mathcad, предназначенная для решения этой задачи.
В качестве численных данных возьмем такие: а = 2, b = 5, о = 1.5, у =0.9, п = 10,
X = (1.3, 2.1, 5.2, 3.4, 6.1, 4.0, 1.9, 5.1, 3.7, 3.0). Программа выдает следующие ре-
зультаты: |imin = 4.76, |imax = 3.5, (g', g") = (0.531, 0.683). Итак, с вероятностью 0.9
интервал (0.531, 0.683) содержит истинную вероятность попадания случайной
величины в интервал (2, 5).
Пример 12.7. Интервальное оценивание структурной надежности системы. Вер-
немся к рассмотрению структурной надежности систем (разделы 1.3 и 1.5).
Пусть система состоит из т элементов. Предполагается, что в начальный момент
времени все элементы исправны. Длительности безотказной работы элементов —
360
12. Оценивание с помощью доверительных интервалов
взаимно независимые случайные величины, имеющие экспоненциальное распре-
деление (4.9) с параметром Х; для г-го элемента. После отказа элемент не восста-
навливается. Надежность системы описывается структурной функцией (см. раз-
дел 1.3). Мы интересуемся надежностью системы в момент времени t > 0.
Вероятность безотказной работы (надежность) i-го элемента в момент времени t
есть р, = exp(-X,i), t > 0. Вероятность безотказной работы (надежность) систе-
мы в момент времени t вычисляется через структурную функцию и значения
{р,} так, как это было описано в разделе 1.5. Обозначим надежность систе-
мы g(Xj, Х2,..., Xm). Здесь использование в качестве аргументов Xj, Х2,..., Хт
подчеркивают зависимость надежности от значений этих параметров.
В действительности эти параметры неизвестны, однако для каждого i-ro элемен-
та известна выборка объема nif содержащая данные о длительностях безотказной
работы i-x элементов. Обозначим их суммарную длительность безотказной рабо-
ты Xj (в действительности это есть достаточная статистика для параметра X,- —
см. раздел 11.5). Эти значения для всех элементов представим как вектор
X = (х„ х2..Хт).
Наша задача заключается в том, чтобы построить доверительный интервал для
надежности системы g(Xf, Х2..Хт ), отвечающий доверительной вероятности у.
Решение этой задачи вполне аналогично предыдущей.
Неизвестным параметром здесь будет m-мерный вектор 0 = X = (Xt, Х2,..., Хт),
каждая компонента которого принимает положительные значения. Выборочным
пространством является m-мерное положительное вещественное пространство:
Т = (0,oo)ffl. Параметрическая функция есть g(Xj, Х2,..., Хт).
Этап 1. Каждому элементу выборки X, поставим в соответствие нормированную
величину Zj = ХД,-. Отметим, что из примера 7.3 следует, что X,- имеет распределе-
ние Эрланга (4.18) с параметрами X = X, и Z = Согласно утверждению 3 главы 4,
Zj имеет распределение Эрланга (4.18) с параметрами X = 1 и / = и,-. Сумма этих
величин имеет распределение Эрланга с параметрами X = 1 и I = п{ + п2 + ... + пт
(пример 7.3). Поскольку Z обычно велико, то согласно Центральной предельной
теореме (теорема 7.5), распределение Эрланга можно аппроксимировать нор-
мальным распределением с тем же математическим ожиданием ц = / и дисперси-
ей о2 = /. Если Ф'1 (у) есть квантиль стандартного нормального распределения,
отвечающая вероятности у, то соответствующая квантиль для данного распреде-
ления будет 1 +41 Ф'1 (у). Определим для каждого X = (ХР Х2,..., Хш) множество
=]х =(*!, х2....хт): Vxf >0, £х,Х,- £ / + 77 Ф’1 (у) I.
I	i-1	J
Этап 2. Для каждого значения х = (xt, х2,..., хт) определяем множество
0Х = j X = (Xt, Х2.. Хш): vx,. >0, £x(Xf ^Z + 7Z®-1(y)
I	1=1
Эти множества образуют семейство у-доверительных множеств для параметров
X = (Xj, Х2..Хш).
Этап 3. Решаем задачи нелинейной оптимизации:
Компьютерный практикум № 19. Построение доверительных интервалов в пакете Mathcad
3в1
Найти минимальное g' и максимальное g " значения надежности системы
g(Xt, Х2,Хт) на множестве 0К параметров X,, Х2,Хт.
Оптимальные значения g' ng" дают доверительный интервал (g', g") для на-
дежности системы g(X,, Х2.Хт), отвечающий доверительной вероятности у.
В компьютерном практикуме №19 рассмотрены следующие численные дан-
ные: число элементов т = 3; первые два элемента соединены параллельно, а тре-
тий — последовательно, так что надежность системы для момента времени t:
^(Xj, Х2, Х3) = exp(-X3t)(exp(-Xjt)+exp(-X2t)-exp(-(X1 +X2)t)); момент вре-
мени t = 3; имеющаяся выборка X = (Хь Х2, Х3) = (4.5, 58, 92); общее число
испытанных элементов / = 20; коэффициент доверия у = 0.6.
Минимальное значение надежности достигается при Xlmin =0.977, X2mjn = 0.28$
X3rain = 0. Сама минимальная надежность g' = 0.452.
Максимальное значение надежности получается равным 1 при нулевых значени-
ях параметров. Итак, доверительный интервал этой надежности (0.452, 1).
Компьютерный практикум № 19.
Построение доверительных интервалов
в пакете Mathcad
Цель и задачи практикума
Целью практикума является приобретение необходимых навыков по реализации
в пакете Mathcad методов построения доверительных интервалов, изложенных в
настоящей главе.
Задачей практикума является вычисление доверительных интервалов, рассмот-
ренных в примерах 12.5, 12.6 и 12.7.
Необходимый справочный материал
При построении доверительных интервалов в полной мере используются воз-
можности, предоставляемые пакетом Mathcad для решения задач оптимизации.
Основными здесь являются встроенные функции Minimize, Maximize и директи-
ва Given. Технология их использования была достаточно полно описана в преды-
дущем компьютерном практикуме.
Построение некоторых стандартных доверительных интервалов для параметров
нормального распределения обеспечивает пакет STATISTICA, к которому и ад-
ресуется заинтересованный читатель.
Реализация и результаты выполнения заданий
На рис. 12.5-12.7 представлены результаты вычисления в Mathcad задач, рас-
смотренных в примерах 12.5, 12.6 и 12.7.
Первой решается задача построения кратчайшего доверительного интервала для
дисперсии (рис. 12.5), рассмотренная в примере 12.5. Для сравнения проводятся
также вычисления по формуле (12.32) для симметричного доверительного ин-
тервала, длина которого оказывается, естественно, больше кратчайшей длины.
Оптимизация достигается за счет минимизации длины интервала (12.35).
362
12. Оценивание с помощью доверительных интервалов
Практикум 19. Методы интервального оценивания
1.	Построение доверительных интервалов для дисперсии нормального распределения
при следующих исходных данных:
доверитеяьиая вероятность:	у	ОД
обьбм выборки:	п10
значение эмпирической диспрсии:	DE1080
1.1.	Нахождение симметричногодоверительного интервале
( 882.198
CIVS-	,
1.2807 х 10J
Длина интервала:	CIVSj - CtVSj - 1J25 х 10Э
U. Кратчайший доверительный интервал для дисперсии
G(a)----------------------------------------------
qchisq(l - у - а,п-1) qchisqfl - а,л- 1)
Начальное значение пареметра:	а ~ *
Given
а > О	а < 1 - у
aopt- Mlnlmlze(G.a)
Оптимальное значение a:	aopt- 0855
Доверительный интервал для дисперсии
[ 650418
CIVC-1	,
11382 х 10J
Длина интервала:	OVCj - CIVC| - 931876
Рис. 12.5. Построение доверительных интервалов для дисперсии
нормального закона распределения
Второй является задача построения доверительного интервала для вероятности
попадания нормально распределенной случайной величины в заданный интер-
вал (см. пример 12.6), представленная на рис. 12.6. Вероятность попадания рас-
считывается по формуле (12.41). Доверительные границы для этой вероятности
получаются путем поиска минимума и максимума данной вероятности на соот-
ветствующем множестве параметров распределения.
Третья задача (пример 12.7) посвящена построению доверительного интервала
для надежности системы. Результаты ее решения представлены на рис. 12.7.
Система состоит из трех элементов, два первых из которых соединены парал-
лельно, а третий — последовательно. Интенсивности отказов элементов обозна-
чены Xl, Х2, ХЗ — это параметры экспоненциального распределения времени
работы элементов до отказа. Надежность системы в момент времени t = 3 есть
Компьютерный практикум № 19. Построение доверительных интервалов в пакете Mathcad
MS
функция этих параметров /?(Х1, Х2, ХЗ). Границы доверительного интервала ПО«
лучаются в результате оптимизации этой функции по соответствующему множе-
ству параметров XI, Х2, ХЗ.
2.	Построение доверительного интервале для вероятности попедения в интервал (в, Ь)
при следующих исходных данных:
а :-2	Ь:-5 а-13 у-09	X:-(I3 2.1 52 ЗА 6.1 4Л 10 5.1 3.7 30 )Т
пrows(X)	п - 10
д(р) :• рпогт(Ь,р , о) - рпогт(а,р ,о)
Начальное значение параиетра:
Given
д 3 3
6 qchisq(y ,п)
pmln - Minimize(д.д)
pmln - 4.76
ртах:- Maxlmlze(g.p)
ртах - 33
Доверительный интераал для вероятности
gtpmln) >
g(pmex) J
Рис. 12.6. Построение доверительного интервала для вероятности попадания
нормально распределенной случайной величины
в заданный интервал
3.	Построение доверительного интервала для надёжности систеиы при следуюацгх
исходных данных:
период вреиени	t3	число злеиентов	т - 3
ииеющаяся статистика	X - (43 58 92 /
по общему числу злеиентов	Г-20	коэффициент доверия	у-03
надежность систеиы
R(X1, Х2, КЗ)ехр(-ХЗ t) [ ехр(-Х1 t) + ехр(-Х2 t) - exp[-t (Х1 + Х2)))
Начвпьные значения параиетров XII Х2I КЗI
Given
XI > О	Х2 > О	ХЗ > О
XI Xg + Х2 • Xj + ХЗ XjS I +	• qnormfy ,0,1)
fXImlnA
X1max'
X2min - Minimize(R,X1 ,X2,X3)
X2max Maximize(R,X1 .X2.X3)
4X3min,
4X3max,
Xlmin'j ^0977'
X2min - 0289
X3mln J \ 0 ,
X1max'
X2max -
^ХЗтах,
O'
0
Доверительный интервал для надёжности
dR ( R(X1mln,X2mln,X3mln)
k.R(X1max, X2mex, X3max)
Рио. 12.7. Построение доверительного интервала
для надежности системы
364
12. Оценивание с помощью доверительных интервалов
Задания для самостоятельной работы
1.	С помощью датчика случайных чисел пакетов STATISTICA или Mathcad
сгенерируйте выборку объема п = 100, соответствующую экспоненциальному
распределению с параметром А.= 2 (см. указание к первому заданию для само-
стоятельной работы главы 10). Проведите экспериментальный анализ влия-
ния на длину доверительного интервала таких факторов, как:
О доверительная вероятность у (у =0.8,0.9,0.95);
О объем выборки п (п = 20, 50, 100, 200).
2.	Выполните предыдущее задание для выборки из нормального распределения
с параметрами ц = 2 и о = 1.5.
3.	Составьте программу на Mathcad, реализующую приведенный в разделе 12.2
алгоритм построения доверительных интервалов. В качестве исходных дан-
ных принять доверительную вероятность у, значение точечной оценки 0,
оценку дисперсии D(Q) точечной оценки 0.
4.	Реализуйте на Mathcad изложенные в разделе 12.4 процедуры построения до-
верительных интервалов для параметров нормального распределения.
5.	Расход некоторых изделий описывается пуассоновским процессом с парамет-
ром к > 0, то есть за время t > 0 расход равен i с вероятностью
Q*Le-u,i = 0, 1,...
i!
Параметр к неизвестен, однако имеется выборка Хь Х2.Х„ интервалов вре-
мени между поступлениями запросов на очередное изделие (имеющих экспо-
ненциальное распределение с параметром X).
Первоначальный запас изделий составляет с. Для коэффициента доверия у
постройте верхний доверительный интервал (P(t)', 1) для вероятности P(t)
того, что запаса будет достаточно в течение времени t:
p(t) = ±^Le-u, t>0.
/-о i!
Составьте программу на Mathcad, реализующую необходимые вычисления.
Указание. Сначала следует найти нижний доверительный интервал (ОД") для
параметра X Сумма 5 = X, + Х2 +.. ,+Х„ является достаточной статистикой
для А. и имеет распределение Эрланга с параметрами / = п и А.. Поэтому для
коэффициента доверия у верхняя граница А." интервала (0, А.") находится как
решение относительно А. уравнения
1=0	1 1
Теперь нижняя граница P(t)' находится как значение P(t), получающееся
в результате использования А." вместо А..
Задачи	ЭМ
Задачи
Задача 12.1. За багаж весом свыше 30 кг с пассажира международного автобуса
взимается дополнительная плата. Случайным образом выбраны 225 пассажиров.
Оказалось, что 25 из них доплачивали за багаж. Найдите доверительный интер-
вал для вероятности того, что вес багажа пассажира превысит 30 кг, при коэффи-
циенте доверия у = 0.95.
Задача 12.2. Фирма продает системы, которые в течение первых двух лет экс-
плуатации должны каждые полгода проходить техническое обслуживание в этой
фирме. Вследствие различных причин очередное обслуживание может быть на-
чато либо несколько раньше планового срока, либо позже. Было проверено 100
случайно выбранных систем. Из них на первое обслуживание системы посту-
пали раньше срока в 22 случаях, ровно в срок — в 47 случаях, позже срока —
в 31 случае. С надежностью 0.9 постройте следующие доверительные интервалы:
□ нижний доверительный интервал для вероятности того, что изделие поступит
раньше срока;
□	верхний доверительный интервал для вероятности того, что изделие посту-
пит ровно в срок;
□	двусторонний доверительный интервал для вероятности того, что изделие по-
ступит позже срока.
Задача 12.3. Продолжительность технического обслуживания самолетов между
рейсами является случайной величиной. Администрация компании междуна-
родных перевозок случайным образом выбрала 34 самолета, продолжительность
обслуживания которых (в минутах) оказалась следующей: 100, 110, 160, 30, 35,
40, 45, 110, 160, 100, 40, 45, 40, 35, 50, 55, 85, 100, 45, 30, 60, 30, 35, 40, 50, 45, 40,
50, 80, 30, 35, 50, 55, 105.
Постройте нижний доверительный интервал для математического ожидания вре-
мени обслуживания при коэффициенте доверия 0.9.
Задача 12.4. Каков должен быть объем выборки п при оценивании математиче-
ского ожидания времени заправки самолета топливом, если допустимая ошибка
8 равна 10 мин, доверительная вероятность у = 0.95, а пробная выборка дала зна-
чения 13, 27, 25, 18, 38 мин?
Задача 12.5. Для проверки надежности агрегатов их испытывают на стенде.
Предварительное испытание 20 агрегатов, которые можно рассматривать как
предварительную выборку, привело к отказу 2 агрегатов. Сколько агрегатов не-
обходимо испытать, чтобы с вероятностью 0.99 ошибка в определении вероятно-
сти безотказной работы не превышала 0.01?
Задача 12.6. Измерение положения некоторого объекта, рассматриваемого как
точка в трехмерном пространстве, происходит с ошибкой. Ошибки по каждому
из трех измерений представляют собой взаимно независимые случайные вели-
чины, имеющие стандартное нормальное распределение (4.13). Найдите распре-
деление квадрата абсолютной ошибки. Постройте график функции распределе-
ния.
Задача 12.7. По цели, находящейся в трехмерном пространстве, производится
выстрел. Отклонения снаряда от центра цели по каждой из трех координат явля-
366
12. Оценивание с помощью доверительных интервалов
ются взаимно независимыми случайными величинами, имеющими стандартное
нормальное распределение (4.13). Найдите вероятность попадания в цель, если
радиус ее равен 1.2; 1.9; 4.
Задача 12.8. Продолжительность безотказной работы агрегата имеет £2-распре-
деление с 10 степенями свободы. Постройте график функции распределения
времени безотказной работы агрегата. Какой ресурс следует назначить агрегату,
чтобы в течение ресурса вероятность отказа не превышала 0.1?
Задача 12.9. Каким должен быть объем выборки при определении доли брака
в большой партии товаров, если доверительная вероятность равна 0.9, а доля
бракованных изделий в Выборке не должна отличаться от соответствующей доли
в генеральной совокупности более чем на 0.01? Пробные выборки дали оценку
доли брака, равную 0.01.
Задача 12.10. Для данных задачи 12.3 найдите доверительный интервал для дис-
персии нормальной совокупности, соответствующий доверительной вероятно-
сти 0.8.
13 Проверка статистических
гипотез
13.1.	Основные понятия
Определение 1. Статистическими гипотезами называются различного рода пред*
положения о распределениях случайных величин, которые необходимо прове-
рить по данным выборочной совокупности. Обычно эти предположения касают-
ся параметров или типа распределений рассматриваемых случайных величин.
Примером статистической гипотезы является утверждение о том, что математи-
ческое ожидание числа занятых мест на авиарейсах Москва—Сочи не менее 140.
Действительно, это утверждение касается некоторого параметра распределения
случайной величины — математического ожидания числа занятых мест, и его
можно проверить, произведя выборочное обследование пассажирской загрузки
нескольких рейсов. Статистической является также гипотеза о том, что откло-
нение от расписания моментов прилета самолетов, совершающих данный рейс,
имеет нормальное распределение с заданными значениями математического
ожидания и дисперсии. Регистрируя в течение нескольких суток моменты при-
лета, можно проверить, насколько хорошо согласуются собранные данные с ука-
занным распределением.
С другой стороны, не будет статистической, например, гипотеза о возникнове-
нии Земли, так как здесь не идет речь ни о каком законе распределения и так как
она не может быть проверена выборочным методом.
При формулировке задачи проверки статистических гипотез кроме гипотезы,
называемой часто нулевой гипотезой, указывается также альтернативное (конку-
рирующее) предположение. Это последнее называется альтернативной гипо-
тезой, или просто альтернативой. На основании выборочных данных следует
отдать предпочтение или гипотезе, или альтернативе, то есть одну из них при-
нять, а другую — отвергнуть.
Предположим, например, что некоторое мероприятие позволяет уменьшить ве-
роятность отказа рассматриваемой системы. Осуществление этого мероприятия
требует некоторых затрат и расчеты показывают, что оно экономически эффек-
тивно в том случае, если вероятность отказа станет не более 0.008. Так как нас
интересует, в конечном счете, получение положительного экономического эф-
фекта, то задача может быть сформулирована так: проверить гипотезу о том, что
368
13. Проверка статистических гипотез
вероятность отказа системы не более 0.008 при альтернативе, что эта вероят-
ность больше 0.008. Следовательно, если организовать в течение некоторого вре-
мени экспериментальное внедрение этого мероприятия и по опытным данным
обнаружить, что гипотеза подтверждается, то это будет означать, что предла-
гаемое мероприятие следует признать экономически эффективным и рекомен-
довать его к внедрению.
Если при формулировке задачи альтернатива явно не указана, то это значит, что
она состоит из всех возможностей, исключающих нулевую гипотезу. Так, в пер-
вом из рассмотренных выше примеров альтернатива заключается в том, что ма-
тематическое ожидание числа занятых мест не равно 140, а во втором — в том,
что не выполняется хотя бы одно из перечисленных условий: нормальное рас-
пределение, заданные значения математического ожидания и дисперсии.
Иногда альтернатива состоит не из всех, а только из части возможностей, исклю-
чающих гипотезу. В этом случае при описании альтернативы все эти возможно-
сти перечисляются.
Формальные определения выглядят следующим образом.
Определение 2. Пусть Р = {Рв: 9 е 0} — семейство распределений, зависящее от
параметра 9, принадлежащего параметрическому пространству 0. Предполагает-
ся, что значение 9 (может быть, векторное) однозначно определяет, верна ли
гипотеза Н или альтернатива А. Иными словами, пространство 0 разбивается на
два подмножества: для одного из них, которое обозначим 0Я, верна гипотеза,
а для второго, которое обозначим 0Л, — альтернатива, так что 0Я +&А =&. Ги-
потеза, или альтернатива, называется простой, если ей соответствует только
одно значение параметра 9, то есть множество 0Я или 0Л состоит только из од-
ного элемента. В противном случае она называется сложной.
Основными элементами процедуры проверки гипотезы являются следующие:
гипотеза и альтернатива, критерий проверки гипотезы, область принятия гипо-
тезы и критическая область, ошибки первого и второго рода, уровень значимо-
сти, функция мощности критерия.
При проверке статистической гипотезы начинают с предположения о том, что
нулевая гипотеза верна. Из этого предположения делают некоторые выводы и
определяют, насколько они подтверждаются имеющимися в распоряжении вы-
борочными данными. С этой целью устанавливают меру расхождения между
этими данными и выводами. Обычно меру расхождения называют критерием
проверки гипотезы.
Определение 3. Критерием проверки гипотезы называется некоторая функция
выборки (Хь Х2,.., Хп), характеризующая степень соответствия выборочных дан-
ных статистической гипотезе. Будем критерий обозначать R(Xx, Х2, .., Х„) или
просто R. Область значений критерия разбивают на два подмножества: область
принятия гипотезы [7?', /?"] и критическую область. При попадании значения
критерия R, подсчитанного по выборке, в область принятия, гипотеза принима-
ется, в противном случае — отклоняется, то есть принимается альтернатива. Об-
ласть принятия является замкнутым интервалом вещественной оси [Л', Л"], в то
время как критическая область содержит все точки этой оси, не входящие в об-
ласть принятия, то есть состоит из двух интервалов (-оо, Л") и (7?', оо). В этом
13.1. Основные понятия
случае говорят о двусторонней альтернативе. Если критическая область состоит
только из одного интервала, то говорят об односторонней альтернативе: лево-
сторонней или правосторонней.
Расположение критической области и области принятия гипотезы в случае дву-
сторонней альтернативы изображено на рис. 13.1.
Как правило, в качестве критерия принимают величину отклонения некоторой
эмпирической характеристики от ее теоретического аналога. Так как критерий
(мера расхождения) подсчитывается по данным выборочной совокупности, ко-
торая случайна, то и сам критерий является случайной величиной. Следователь-
но, не исключена возможность, что извлечена «неудачная» выборочная совокуп-
ность, не дающая адекватной информации о генеральной совокупности. При
этом может оказаться, что руководствуясь наблюденным значением критерия и
данной критической областью, мы отвергаем гипотезу, в то время как она верна,
или, наоборот, принимаем, когда она неверна.
Критическая область
Рис. 13.1. Область принятия гипотезы и критическая область
Определение 4. Ошибкой первого рода называется отклонение верной гипотезы.
Ошибка второго рода заключается в принятии неверной гипотезы. При проверке
гипотезы предварительно задается максимально допустимая вероятность ошиб-
ки первого рода. Последняя называется уровнем значимости и обозначается а
(иногда а дается в процентах). Заданный уровень значимости а обеспечивается
за счет выбора критической области и области принятия гипотезы:
Рн {/?£[/?',/?"]}< а,	(13.1)
где индекс Н означает, что вероятность рассчитывается для гипотезы Н.
При этом если гипотеза является сложной, то расчет ведется для наименее благо-
приятного распределения (наименее благоприятной простой гипотезы). Послед-
нее характеризуется тем, что если неравенство (13.1) выполняется для него, то
оно выполняется и для всех других распределений, охватываемых сложной
гипотезой.
Если вероятность ошибки первого рода равна 0.05, то физически это означает,
что при многократном применении данного критерия относительное число слу-
чаев, когда гипотеза будет неправильно отвергнута, близко к 0.05. Наиболее
употребительными уровнями значимости являются 0.1; 0.05; 0.01 и 0.001. Выбор
того или иного уровня значимости определяется теми последствиями, к которым
может привести неправильное отклонение гипотезы. Например, при проверке
гипотезы о том, что некоторый самолетный агрегат не обладает достаточной
(70
13. Проверка статистических гипотез
вдежностью, вероятность неправильного отклонения гипотезы должна быть
>чень малой.
4з изложенного следует, что границы критической области необходимо подо-
(рать таким образом, чтобы обеспечить заданный уровень значимости а. Иными
:ловами, необходимо определить R и R" так, чтобы вероятность попадания слу-
1айной величины (критерия) R в интервал [/?', Я"] при условии, что гипотеза
>ерна, была не меньше 1 - а:
РИ{Х <R<R"} >1-а.	(13.2)
Очевидно, для вычисления этой вероятности необходимо знать распределение
«личины R. Если R имеет непрерывное распределение, то границы Я' и R" могут
>ыть подобраны так, чтобы вероятность ошибки первого рода в точности равня-
юсь заданному уровню значимости а:
PH{R' <К<Я"} = 1-а.	(13.3)
Предположим теперь, что в результате однократной выборки подсчитанное зна-
1ение критерия попало в критическую область. Если гипотеза верна, то вероят-
юсть этого события по определению не больше уровня значимости а. Так как а
1ыбрано достаточно малым, то это событие маловероятно. Следовательно, более
естественно отнести появление этого события за счет того, что гипотеза неверна,
1 отвергнуть гипотезу.
3 некоторых случаях уровень значимости предварительно не задается, а по
чмеющейся выборке рассчитывается значение критерия. Затем определяется тот
максимальный уровень значимости, при котором критерий еще попадает в об-
1асть принятия гипотезы. Этот максимальный уровень значимости, при котором
ипотеза принимается, называется критическим уровнем значимости. Отметим,
1то в пакете STATISTICA выдается именно критический уровень значимости,
дод названием p-level. Если критический уровень ниже заданного уровня значи-
мости а, то гипотеза отклоняется.
Конечно, как критерий (мера расхождения), так и критическая область могут
5ыть выбраны многими способами. Предпочтение следует отдать тому способу,
который при том же самом уровне значимости обеспечивает меньшую вероят-
чость ошибки второго рода. При этом неверная нулевая гипотеза отвергается
: наибольшей вероятностью.
Определение 5. Функцией мощности критерия р(0) называется вероятность от-
члонения гипотезы, вычисленная при условии, что истинное значение параметра
есть 0:
р(0) = Рв{Яй [Я', /?"]}, 0 е 0,	(13.4)
•де Ро{...} означает, что вероятность рассчитывается для данного значения пара-
метра 0.
Итак, областью определения функции мощности является параметрическое про-
странство 0, а областью значений — интервал (0, 1). Из условия (13.1) следует,
что для значений параметра 0 е 0Я, при которых верна гипотеза, функция мощ-
ности не должна превышать уровня значимости а:
Р(0) S а, 0 е 0Я.
(13.5)
13.1. Основные понятия
371
Определение 6. Пусть и R2 — два различных критерия для проверки одной И
той же гипотезы, соответствующие уровню значимости а, , R" ] и [Л2, Я2 | —
их области принятия, а pt (0) = РДЯ, £ [Я'[,/?"]} и р2 (0) = Pe{R2 £ [Я2, R2 ]} — ИХ
функции мощности. Критерий Rt называется равномерно более мощным по срав-
нению с критерием Р2, если он отклоняет неверную гипотезу с не меньшей веро-
ятностью, чем критерий Р2:
₽1(0)>₽2(0),0е0л,	(13.6)
причем существует альтернатива (т. е. значение параметра 0 е 0Л ), при которой
эта вероятность строго больше.
На рис. 13.2 представлены графики функций мощности двух критериев. Функ-
ция мощности (0) соответствует равномерно более мощному критерию. Отме-
тим, что для значений параметра 0, соответствующих гипотезе, для обоих крите-
риев выполняется условие (13.5), обеспечивающее заданный уровень значимости а.
Рис. 13.2. Функции мощности критериев
Обсудим теперь исключительно важный для практических применений вопрос:
из двух взаимоисключающих предположений которое принять за гипотезу, а ко-
торое за альтернативу? Ответ состоит в следующем: за гипотезу следует прини-
мать то предположение, неверное отклонение которого приводит к более опас-
ным последствиям. Действительно, назначая уровень значимости а, мы тем
самым можем контролировать частоту этих последствий.
Пусть, например, предлагается новое лекарство, которое может вызывать побоч-
ный отрицательный эффект. В качестве гипотезы можно взять как предполо-
жение о том, что «лекарство безвредно», так и предположение «лекарство дает
недопустимый побочный эффект». Если в качестве гипотезы взять первое, то
безвредное лекарство будет отклоняться с заданной частотой а. При этом ника-
кого контроля за частотой поступления вредных лекарств не будет. Следова-
тельно, в качестве гипотезы здесь следует взять предположение «лекарство дает
недопустимый побочный эффект». Выбирая подходящий уровень значимости а,
мы контролируем частоту этого события. Более легальный анализ такого рода
производится на основе функции мощности критерия.
2
13. Проверка статистических гипотез
гак, для проверки статистической гипотезы необходимо выполнить следующие
1ПЫ.
Определить нулевую и альтернативную гипотезы.
Задать уровень значимости а (допустимую вероятность ошибки первого рода).
Выбрать критерий проверки (меру расхождения).
Определить критическую область.
По результатам эксперимента вычислить фактическое значение критерия.
Если наблюденное значение критерия принадлежит критической области, то
отклонить гипотезу, иначе — принять.
1жно отметить, что попадание критерия в область допустимых значений не оз-
чает строгого доказательства гипотезы. Оно лишь указывает, что между гипо-
зой и результатами выборки нет значимого расхождения.
»имер 13.1. Для проведения зачета по некоторому курсу было подготовлено
О вопросов. Если студент знает не менее шестидесяти вопросов, то считается,
о он усвоил курс, и ему может быть поставлен зачет. Разумеется, опрашивать
ждого студента по всем ста вопросам было бы слишком утомительно. Поэтому
ждому студенту предлагается только пять вопросов. Студент получает зачет,
ли ответит не менее чем на три вопроса.
данном случае генеральную совокупность образуют сто вопросов. Выборочной
вокупностью являются пять вопросов, достающихся студенту. Гипотеза, кото-
ю должен проверить преподаватель в результате зачета, состоит, например,
гом, что «студент курса не усвоил». Критерием для проверки служит число
авильных ответов. Областью принятия гипотезы здесь является совокупность
сел 0, 1 и 2, а критической областью 3, 4 и 5.
осмотрим теперь двух студентов: «хорошего» и «плохого». Хороший студент
ает 70 вопросов из 100 и объективно должен получить зачет. Таким образом, в
ином случае гипотеза «студент курса не усвоил» неверна. Однако вполне воз-
>жно, что из пяти попавших вопросов число известных студенту вопросов бу-
т меньше трех. В таком случае преподаватель не поставит зачет студенту, кото-
й объективно его заслуживает, и произойдет ошибка второго рода.
эедположим далее, что плохой студент знает только тридцать вопросов, то есть
о гипотеза справедлива. Разумеется, может статься, что из пяти полученных
просов студент знает три или более. В этом случае будет отвергнута правиль-
я гипотеза, и произойдет ошибка первого рода.
заключение проанализируем возможности уменьшения вероятностей ошибок
рвого и второго рода. Если количество предлагаемых студенту вопросов, то
ть объем выборки, равный пяти, фиксирован, то уменьшить возможность
1ибки первого рода можно путем сужения критической области (например,
ли ставить зачет за четыре и более правильных ответов). Однако возможность
либки второго рода будет при этом возрастать. Аналогичным образом стремле-
ie уменьшить вероятность ошибки второго рода приводит к росту вероятности
либки первого рода. Отсюда ясно, что одновременное уменьшение вероятно-
ей ошибок первого и второго рода возможно только за счет увеличения объема
борки, то есть числа предлагаемых вопросов.	□
13.2. Проверка гипотез относительно вероятности
371
Приступим к рассмотрению некоторых типичных гипотез и правил их проверки.
Вначале будут рассмотрены процедуры проверки гипотез относительно вероят-
ности события, а также математического ожидания и дисперсии случайной вели-
чины. Далее рассматриваются гипотезы о распределении случайной величины
и о сравнении двух выборочных совокупностей.
13.2.	Проверка гипотез относительно вероятности
Рассмотрим вначале один из самых простых и важных в практическом отноше-
нии случаев: проверка гипотезы о том, что вероятность р некоторого события А
равна рй при односторонней альтернативе, что эта вероятность больше Pq.
Гипотеза должна быть проверена на основании выборочных данных, согласно
которым в результате проведения п независимых испытаний интересующее нас
событие А произошло 5„ раз. Ниже будет показано, что проверка этой гипотезы
при указанной альтернативе равносильна проверке гипотезы о том, что р Ро
при альтернативе р > р0.
В этом случае параметрическим пространством 0 является единичный интервал
[О, 1]: 0 = [0, 1]. Гипотезе отвечает подмножество QH - [р0] или 0Д = [0, /?©],
а альтернативе — 0Л = (р0, 1]. Напомним, что круглые скобки применяются, если
соответствующая граница не включена в интервал (открытый с этой стороны ин-
тервал), а квадратные — если включена (замкнутый с этой стороны интервал).
Пример 13.2. К сформулированной выше задаче приводит следующая ситуация.
Имеется большая партия изделий. Эта партия считается годной (качественной),
если доля бракованных изделий в ней не превышает р0. Иными словами, вероят-
ность того, что наудачу выбранное изделие будет бракованным (событие Л), не
должно превышать р0. В противном случае вся партия должна быть забракована.
Для проверки гипотезы о качестве партии организуется выборочный контроль П
изделий. Пусть из этих изделий S„ оказались бракованными (т. е. событие А про-
изошло 5„ раз). На основании этих данных следует принять или отклонить нуле-
вую гипотезу Н: р < рй. Принятие этой гипотезы влечет за собой признание пар-
тии изделий качественной, и наоборот.	□
Итак, гипотеза и альтернатива установлены. Выберем теперь критерий провер-
ки — меру расхождения. Так как эмпирическим аналогом вероятности является
частота, которая, в свою очередь, при заданном объеме выборки п определяется
числом Sn наступления события А, то в качестве критерия естественно взять на-
блюденное число наступления события А:
R = Sn.
С ростом вероятности р события А наблюденное число Sn наступления события
А имеет тенденцию к увеличению. Поэтому большое значение критерия R гово-
рит в пользу альтернативы и противоречит нулевой гипотезе. Следовательно,
критическая область для проверки гипотезы р = р0 при односторонней альтерна-
тиве р > р0 имеет вид (R", оо). Поскольку число S„ не может превышать числа ис-
пытаний п, то в действительности критическая область есть (Я", и].
Если а есть выбранный уровень значимости, то Я*. согласно (13.1), должно быть
подобрано так, чтобы
4
13. Проверка статистических гипотез
P^R" <R<n}< а,	(13.7)
> индекс р0 указывает, что вероятность подсчитывается для значения парамет-
р, равного р0.
к как число S„ наступления события А может трактоваться как число успехов
7 испытаниях Бернулли с вероятностью р0 успеха в одном испытании, то S„
дчиняется биномиальному распределению (3.3), и формула (13.7) принимает
Д
tcMl-Po)"-1 <а.
i=R’+t
(13.8)
вращаясь к таблицам или компьютерным программам для вычисления бино-
тального распределения, можно подобрать такое минимальное значение R",
и котором это неравенство выполняется. Тогда искомой критической обла-
ью будет замкнутый интервал [/?" + 1, и].
(имер 13.3. Пусть в условиях примера 13.2 п = 20, р0 = 0.1, а = 0.05, S„ = 3. По таб-
цам дополнительного биномиального распределения или соответствующим ком-
ютерным программам находим, что R" + 1 равно 5. Следовательно, критической
ластью является замкнутый интервал [5, 20]. Так как наблюденное значение кри-
рия R, равное 3, не принадлежит этому интервалу, то гипотеза принимается. □
эи больших объемах выборки п, согласно теореме Муавра-Лапласа (см. след-
1вие 7.1), для определения значения R” вместо биномиального распределения
3.8) может быть использовано его нормальное приближение. Так как число R
.ступлений события А имеет математическое ожидание пр0 и дисперсию
'о( 1 _ Pah то в этом случае 7?" определяется из условия
а = Рро {R” < R < х} = Рра {R > R"} = 1 - Ф
Ф
R"-nPo
^np^l-p^
1 - а.
R” - пр о
Jnp0(l-p0)
тсюда, используя квантиль Ф"*(1-а) стандартного нормального распределе-
!я, отвечающую вероятности 1 - а, получаем:
/•-"У.
ледовательно, искомая критическая область есть (с учетом того, что R = Sn < п):
(пр0 + Ф'1 (1-а)л/пр0(1-/?0); п].	(13.9)
эимер 13.4. В условиях примера 13.3 находим, что
Ф~‘(1-а) = Ф'’ (0.95) = 1.64.
оэтому критическая область будет
(20 0.1 + 1.64-720 0.1-0.9; и] = (4.2; и].
ак как значение критерия R не может быть дробным, то в рассматриваемом
1учае критические области, построенные по точной (см. пример 13.3) и прибли-
енной формулам, совпадают.	□
13.2. Проверка гипотез относительно вероятности
375
Итак, выше были установлены критические области для проверки гипотезы
р = Ро при альтернативе р > р0. Рассмотрим теперь гипотезу р < р0 при той же
альтернативе р > р0. Покажем, что критические области для проверки этих двух
гипотез совпадают, иными словами, что при определенном результате наблюде-
ния гипотезы р = р0 и р < р0 одновременно или отвергаются или принимаются.
Для того чтобы убедиться в правильности высказанного утверждения, заметим,
что чем меньше значение истинной вероятности р, тем менее вероятно большое
число 5„ наступления события А, то есть большое значение критерия R. Поэтому
если при данном числе S„ гипотеза р = р0 отвергается, то тем более следует от-
вергнуть гипотезу/? = р' для всех/»', меньшихр0. Итак, гипотезар =р0 соответст-
вует наименее благоприятному распределению из определения 4.
Гипотезы р = р0 и р > р0 при односторонней альтернативе р < рй отвергаются в
тех случаях, когда число Sn слишком мало. Поэтому критическая область имеет
вид [О, R"). Этот случай рассматривается аналогично предыдущему. R' должно
быть наибольшим числом, удовлетворяющим неравенству
Я-1
2ад(1-Ро)"" ^а.	(13.10)
При большом объеме выборки п используется нормальное распределение. При
этом различие между открытыми и замкнутыми интервалами, а также между R! ± 1
становится несущественным. Это дает вместо последней формулы уравнение
\^прй(\-рй))
откуда получаем R' = пр0 + Ф"1 (а)^пр0(1-р0).
Критическая область в этом случае будет
[0; пр0 + ф-,(а)А/пр0(1-р())).	(13.11)
В заключение остановимся на проверке гипотезы р = р0 при двусторонней аль-
тернативе р р0, ограничившись случаем больших выборок, когда можно при-
менять нормальное распределение. Гипотеза здесь отвергается как при очень
больших, так и при очень малых значениях S„. Если Sn мало, то гипотеза отверга-
ется, так как предпочтение отдается альтернативе р < р0, содержащейся в альтер-
нативе р * р0. Если S„ велико, то гипотеза также отвергается, так как предпочте-
ние отдается альтернативе р > р0, входящей в альтернативу р * р0.
Естественно поэтому построить область принятия гипотезы, являющуюся сим-
метричной относительно математического ожидания пр0:
[7?о,^] = [пр0 - б, пр0 + 8],
где 8 > 0 — подлежащая определению из условия (13.3) величина.
Считая, что R имеет нормальное распределение (4.11) с параметрами р ® пр0
и и = yjnpo(l-р0 ), находим:
1-а = Р{пр0 -8£ Rz пр0 + 8} =
иРо + 8-пр0
V»Po(l-Po)
»Ро -8-пр о
>/«Po(l-Po)
 2Ф
к
7«Ро(1-Ро\
13. Проверка сгатастических гипотез
как для р > 0 Ф(-р) = 1 - Ф(р). Поэтому
Ф
5
Jnp0(l-p0)
= 1-а/2;
5 = Ф'1 (1 - а/2)Л/пр0(1-р0).
гдовательно, область принятия гипотезы р = р0 при двусторонней альтернати-
э * Ро будет
[пр0 -Ф’1 (1 -а/2)л/пр0(1 “/’о): пРо + Ф'1(1-а/2)л/иРо(1-Ро)]- (13.12)
1мер 13.5. Вероятность безотказной работы прибора р в течение гарантийного
жа службы должна быть не менее 0.99. В процессе эксплуатации 1000 прибо-
। обнаружилось, что 20 из них отказали в пределах этого срока. Используя
'а уровень значимости, проверим гипотезу о том, что вероятность безотказной
юты приборов в течение гарантийного срока отвечает установленному норма-
>У-
1000 рассмотренных приборов безотказная работа имела место в 980 случаях,
есть п ~ 1000, R ~ 980. На основании этих данных необходимо проверить гипо-
у р 0.99 при альтернативе р < 0.99. Согласно формуле (13.11) область при-
гия гипотезы есть
[про +Ф'1(а)л/иРо(1-Ро); 4
к как Ф“’(0.10) = -1.28, то область принятия будет
[1000  0.99-1.28 V1000  0.99-0.01; 1000] = [986; 1000].
блюденное значение критерия R, равное 980, не попадает в область принятия,
этому гипотеза должна быть отвергнута.	□
зультаты этого раздела сведем в табл. 13.1. В ней указаны области принятия
5личных гипотез относительно вероятности р при больших объемах выборки и
я критерия R, равного числу наступления события 5„, и уровня значимости а.
блица 13.1. Области принятия гипотез относительно вероятности
ипотеза	Альтернатива	Область принятия
Sp»	Р>Р«	[0; пр0 + Ф’’(1 - a)^np0(l - ро)]
*Рч	Р<Р»	[про + Ф-1(а)^/пр0(1 - р0); л]
хРа	Р*Р»	„Ро “ ф’’ ~ у) VnPo(l - Ро)-' ”Ро + ф “ у) >/”Ро(1 - Ро)
эедположим теперь, что по данным выборки область принятия гипотезы
', /?"] построена. Вычислим для нее функцию мощности (13.4), где в качестве
13.3. Проверка гипотез о математическом ожидании
параметра 0 фигурирует вероятность события р. Точная и асимптотическая (при
больших объемах выборки п) формулы имеют для 0 < р < 1 вид:
R-
₽(р) = 1-£с’р'(1-р)я’',
i=K
Р(р) = 1- Ф
R“-np
4пр(\-р)
-Ф
R' - пр

Для односторонних альтернатив в этой формуле следует положить R! = О ИЛИ
7?" = п. Отметим, что приведенные формулы соответствуют условным функциям
мощности, вычисленным при условии, что область принятия гипотезы [Д', Я")
фиксирована. Для вычисления безусловных функций необходимо произвести
усреднение по распределению интервала [Д', Я"].
13.3.	Проверка гипотез о математическом ожидании
Ситуация, в которой возникает необходимость проверки гипотезы относительно
математического ожидания, может быть проиллюстрирована следующим приме*
ром.
Пример 13.6. Эксплуатируемое на ряде заводов оборудование определенного
типа должно ежемесячно проходить техническое обслуживание. При сущест*
вующей технологии продолжительность технического обслуживания является
случайной величиной, имеющей математическое ожидание 20 час. С целью со-
кращения простоя оборудования была предложена новая технология обслужива-
ния. Для оценки ее эффективности по сравнению со старой технологией в опыт-
ном порядке на нескольких заводах было произведено обслуживание по новой
технологии. Средняя длительность обслуживания на этих заводах оказалась рав-
ной 19.5 час, то есть уменьшилась на 0.5 час. Спрашивается, чем вызвано такое
сокращение длительности обслуживания: большей эффективностью новой тех-
нологии или случайными факторами, сопровождающими процесс обслужива-
ния? Поэтому возникает следующая задача: проверить гипотезу о том, что мате-
матическое ожидание ц (соответствующее новой технологии) равно ц 0 = 20 час
при альтернативе ц < ц 0. Если гипотеза подтвердится, то нет оснований считать,
что новая технология предпочтительней старой, и наоборот.	□
Вначале рассмотрим случай, когда исходная генеральная совокупность является
нормальной (4.11), о параметрах цист которой ничего не известно. Для проверки
гипотезы в нашем распоряжении имеются результаты п наблюдений Х\, Xi.
Хп. Пусть, как обычно, ц* и а2’ обозначают эмпирические математическое ожи-
дание и дисперсию этой выборки. В качестве критерия возьмем величину
(13.13)
где р о — предполагаемое значение математического ожидания.
Такой выбор критерия обусловлен тем, что если истинное значение математи-
ческого ожидания ц равно ц0, то критерий (13.13), согласно теореме 12.5, имеет

13. Проверка статистических гипотез
аспределение Стьюдента (12.20) с п - 1 степенью свободы. Это позволяет,
юльзуя заданный уровень значимости а и условие (13.3), построить критиче-
по область и область принятия гипотезы.
хмотрим методику проверки гипотезы ц = ц 0 при альтернативе ц > ц 0. В слу-
* справедливости гипотезы значение эмпирического математического ожида-
я ц*, а следовательно, и критерия R будет преимущественно меньшим, чем
лучае, когда справедлива альтернатива. Поэтому критическая область должна
еть вид (R", оо), а область принятия (-оо, /?"]. Граничная точка R” определяет-
из условия (13.3):
P{R<R”} = 1-а.
к как в случае справедливости гипотезы критерий R имеет ^распределение
ьюдента с п - 1 степенью свободы, то отсюда следует, что
7?"=t1.o(n-l),
- ^i-o(ra-i) — квантиль i-распределения Стьюдента (12.20) с п - 1 степенью
)боды, отвечающая вероятности 1 - а.
же гипотеза ц = ц 0 при альтернативе ц < ц 0 отвергается при малых значени-
критерия R. Этот случай диаметрально противоположен предыдущему, и об-
стью принятия здесь является интервал
(Га(п-1), оо) =	(и-1), оо).
1коисц, в случае двусторонней альтернативы ц * ц 0 гипотеза ц = ц 0 отверга-
ли как при очень больших, так и при очень малых значениях критерия R. Бу-
м поэтому искать область принятия [7?', 7?"] в виде интервала [-5; 8], симмет-
чного относительно начала координат. Величина 8 > 0 определяется из
ловия (13.3):
1-а =Р{-8< R <8} = Р{7?< 8}-Р{7?< -8} =2Р{7?<8}-1,
котором было использовано свойство (12.21) 7-распределения Стьюдента.
гсюда следует, что
Р{Р < 8} = 1-а/2, 8 = 71_а/2(и-1).
гметим, что этот же результат мог быть получен путем суммирования критиче-
:их областей для проверки гипотезы ц * ц 0 ПРИ рассмотренных выше двух аль-
рпативах ц >ц0 и ц <ц0. При этом, чтобы обеспечить заданный уровень зна-
(мости а, каждую из двух критических областей следовало взять для уровня
1ачимости а/2.
ак и в случае проверки гипотез о вероятности, ясно, что критерий для проверки
потезы ц < ц 0 при альтернативе ц > ц 0 будет совпадать с критерием проверки
шотезы ц =ц0 при той же альтернативе. Это же справедливо для гипотезы
£ц() при альтернативе ц <ц0. Иными словами, случай ц =ц0 соответствует
шменее благоприятному распределению в определении 4. Полученные результа-
I сведены в табл. 13.2. В ней указаны области принятия гипотез о математиче-
:ом ожидании ц нормально распределенной случайной величины при уровне
шчимости а и критерии проверки R = Vn- 1(ц* -p0)/Vo2*.
13.3. Проверка гипотез о математическом ожидании
370
Таблица 13.2. Области принятия гипотез о математическом ожидании ц
нормально распределенной случайной величины
Гипотеза	Альтернатива	Область принятия
И -Ро	И >Ро	(-со; ^а(п-1)]
И 2=Ро	И <Ро	°0)
И = Ро	И *Ро	Н-а/2(” "	“ 0]
Здесь tp(n - 1) — квантиль i-распределения Стьюдента с п - 1 степенью свободы,
отвечающая вероятности р.
Пример 13.7. Продолжим рассмотрение примера 13.6. Предположим, что: 1) дли-
тельность обслуживания имеет нормальное распределение; 2) по результатам
п = 5 наблюдений подсчитанное значение эмпирического среднего квадратиче-
ского отклонения Vo2’ составило 1 час; 3) выбранный уровень значимости а
равняется 0.05.
Вычислим, во-первых, значение критерия (13.13):
1
Так как квантиль распределения Стьюдента при п - 1 = 4 степенях свободы
^-o.os(n _ 0равна 2.13, то область принятия гипотезы ц = 20 час при альтернативе
|1 < 20 час есть [-2.13, оо). Поскольку наблюденное значение критерия попадает в
эту область, то гипотеза принимается. Это говорит о том, что имеющихся данных
недостаточно, чтобы с большой степенью уверенности считать новую техноло-
гию обслуживания лучше старой.
Отметим, что если бы наблюденные значения ц* и о2’ были подсчитаны по
26 данным, то критерий равнялся бы -2.5, число степеней свободы составило
бы п - 1 = 25, а область принятия была бы (-1.71, оо). В этом случае гипотеза
ц = 20 час отвергается и мы отдаем предпочтение новому способу организации,
рискуя ошибиться только в пяти случаях из ста (а = 0.05).	□
Критерий (13.13) проверки гипотез относительно математического ожидания ц
обладает замечательным свойством: при большом объеме выборки п он является
устойчивым относительно вида распределения генеральной совокупности. Ины-
ми словами, этот критерий при больших п может применяться для проверки ги-
потез относительно математического ожидания ц любой генеральной совокупно'
сти, так как и в этом случае он имеет t-распределеиие Стьюдента. Поскольку
t-распределение при большом числе степеней свободы I = п - 1 близко к нор-
мальному распределению, то при больших п критерий (13.13) имеет стандартное
нормальное распределение (4.13). Это подтверждается следующими соображе-
ниями. При больших п эмпирическое математическое ожидание ц ’ имеет при-
близительно нормальное распределение (4.11) с математическим ожиданием р и
дисперсией а2/п, где рис2 — истинные значения математического ожидания и
дисперсии. Так как эмпирическая диспепсия в2’ является спстсотеякилВ
ю
13. Проверка статистических гипотез
>й дисперсии о2, то при больших п она близка к дисперсии о2. Поэтому с боль-
ой степенью точности
ik что если истинное математическое ожидание есть ц, то R имеет приблизи-
льно стандартное нормальное распределение.
з изложенного следует, что в случае выборок большого объема для построения
мастей принятия при проверке гипотез относительно математического ожида-
ли произвольных распределений в табл. 13.2 можно квантиль tp заменить на
~*(р). Соответствующие результаты приведены в табл. 13.3, в которой даны об-
1сти принятия при уровне значимости а и критерии R = ->/« -1 - 	0 
V о2
аблица 13.3. Области принятия гипотез о математическом ожидании
случае выборок большого объема
Гипотеза	Альтернатива	Область принятия
	Ц >Мо	(-СО; ф-\1-а)]
	М <Мо	[-ф-‘(1-а); оо)
‘ =Мо		а)	а)! -Ф 1	; Ф 1	 1 2/	1 2JJ
редположим теперь, что по данным выборки область принятия гипотезы
7?"] построена. Вычислим для нее функцию мощности (13.4), где в качестве
араметра 0 фигурирует математическое ожидание ц. В случае выборок болыпо-
) объема имеем:
₽(ц) = 1 -Рц {/?' < R < R"} = 1-Рц Я' <
= 1--Рм1Но
[ля односторонних альтернатив следует положить или R' = -оо или R" = оо. В за-
лючение можно повторить все то, что было сказано по поводу безусловных
условных функций мощности в конце предыдущего раздела.
13.4.	Проверка гипотез о дисперсии
юрмальной совокупности
1роверка гипотезы о дисперсии имеет важное практическое значение. Обычно
)акт разладки некоторого механизма, станка, оружейного прицела и т. п. сказы-
13.4. Проверка гипотез о дисперсии нормальной совокупности
381
вается в увеличении разброса значений определенного количественного показа-
теля (размера изготовленной детали, отклонения от центра цели и т. п.). При
этом среднее значение показателя может оставаться прежним. По замерам пока-
зателя и вычисленной на их основе эмпирической дисперсии следует решить,
была или нет разладка.
В качестве критерия проверки гипотез о дисперсии о2 нормального распределе-
ния (4.11) служит величина
Н = ('П-^2\	(13.14)
Сто
где п — объем выборки, о2’ — эмпирическая дисперсия, а2а — предполагаемое
значение истинной дисперсии о2.
Из теоремы 12.4 следует, что если истинная дисперсия равна Од, то критерий
(13.14) имеет х2 -распределение с п - 1 степенью свободы. Это обстоятельство
совместно с условием (13.3) позволяет находить критические области и области
принятия, соответствующие заданному уровню значимости а.
Рассмотрим гипотезу а2 > при альтернативе о2 < Оц. Очевидно, наиболее
трудно различить гипотезу и альтернативу, когда о2 = (наименее благоприят-
ное распределение из определения 4). Поэтому критическая область и область
принятия гипотезы должны быть построены для этого случая. Если значение а?
фиксировано, то большим значениям истинной дисперсии будут обычно соот-
ветствовать большие значения эмпирической дисперсии о2* и, следовательно,
критерия (13.14). Поэтому областью принятия гипотезы о2 = о2 (или а2 £ сг£)
при альтернативе о2 < а2 должен быть интервал [/?', оо). Критическая область
представляет собой интервал [0, /?'). Значение R' определяется из условия (13.1):
P{R < R'} = а. Так как при о2 = Оц критерий R имеет х2-распределение с л - 1
степенью свободы, то
Л'=Х2(п-1).
где 12(п-1)— квантиль х2-распределения (12.12) с л - 1 степенью свободы, от-
вечающая вероятности а.
Рассуждая аналогично, находим, что областью принятия гипотезы a2 S с2 при
альтернативе а2 > ojj есть интервал [0, /?"]. Значение R" определяется из усло-
вия P{R > R"} = а или
P(R<R"} = 1-а, /? = х12-о(п-1)-
В качестве области принятия гипотезы а2 = при двусторонней альтернативе
о2 *о2 целесообразно взять интервал [Ха/2(И“О> Хь-а/гС”-!)]- Во-первых, эта
область соответствует здравому смыслу: как слишком большие, так и слишком
малые значения критерия R не согласуются с гипотезой, чему отвечает попада-
ние критерия в критическую область. Во-вторых, она обеспечивает заданный
уровень значимости а:
ЛХа/2(«-1)^Л^Х?-а/2(«-1)> =
- P{R * X ?-../»<« - D) - P{R S Х2/2(« -1)) - 1 -(а/2) -(а/2) - 1 - а.
2
13. Проверка статистических гипотез
зультаты этого раздела сведены в табл. 13.4, в которой даны области принятия
потез о дисперсии нормального распределения ст2 при уровне значимости а
критерии проверки R = (и - 1)ст^2ст2’.
блица 13.4. Области принятия гипотез о дисперсии нормального
определения о2
ипотеза	Альтернатива	Область принятия
2 Sag	a2 <ag	[Xa(« -1)> °0)
2 ^ag	a2>ag	[0, X?.o(n-1)]
2 =ag	a2 *ag	[Xa/2(n "	Xl2-a/2(” ~ 0]
1есь Х;,(и -1) — квантиль х2 -распределения с п - 1 степенью свободы, отвечаю-
1я вероятности р.
)имер 13.8. Из таблицы случайных чисел, имеющих нормальное распределе-
ic, извлечено пять чисел: 0.596, 0.888, 1.360, 0.396, 1.400. При уровне значимо-
и 0.2 проверим гипотезу о том, что дисперсия ст2 = 1 при альтернативе ст2 * 1.
'шение
□скольку число степеней свободы равно п-1=5-1 = 4, то
Ха/2 (4) = Ход (4) = 1.06; х?-а/2(4) =	(4) = 7.78.
□этому область принятия гипотезы будет [1.06, 7.78]. Вычисления показывают,
о числовые характеристики выборки есть
ц* =0.928, ст2’ =0.161.
□дочитанное значение критерия
R = (и -1) ой2 ст2’ = (5 -1) • 1 • 0.161 = 0.644.
ледовательно, гипотеза отвергается.
3.5. Наиболее мощные критерии*
ыше при описании процедуры проверки гипотезы рассматривался только один
ранее фиксированный критерий проверки R. Теперь мы поставим задачу выбора
шболее мощного критерия среди критериев, обеспечивающих заданный уро-
м 1Ь значимости а (см. определение 6). В такой постановке мы будем работать не
пространством значений критерия (он ведь еще даже не определен), а с исход-
ам выборочным пространством (см. определение 4 главы 12).
усть Н и А - простые гипотеза и альтернатива. Рассмотрим два критерия про-
?рки Rt и /?2, соответствующие уровню значимости а. Пусть 'Р) и Т2 — крити-
юкие области этих критериев в выборочном пространстве 'Р. Иными словами,
ли х = (хь х2.х„) еЧ*,, г = 1, 2, то /?,(хь х2.хп) принадлежит критической
власти критерия Rt.
еперь условие (13.1) может быть записано в следующем виде: если X — выбор-
то для обоих критериев
PJXe'FjSa, PJXeTJ-Ja.	(13.15)
13.5. Наиболее мощные критерии*
ЭМ
Напомним, что критерий Rx называется более мощным, чем критерий R2, если
для него вероятность отклонения неверной гипотезы (т. е. когда верна альтерна-
тива) больше, чем у критерия R2:
Рл{Хе'Р1}>Рл{Хе'Р2}.	(13.16)
Ясно, что при одном и том же уровне значимости предпочтение следует отдавать
более мощным критериям. Мы будем решать эту задачу в предположении, что
имеем дело с непрерывными случайными величинами (дискретный случай бу-
дет оговорен в конце раздела). Обозначим/0(х) и/((х) плотности распределения
выборки в точке х = (хь х2,..., х„) для случаев, когда верна, соответственно, гипо-
теза и альтернатива. Теперь условия (13.15) записываются в виде
f/0(r)d!r = \f0(x)dx = а.	(13.17)
Наша задача состоит в том, чтобы найти такую критическую область %, что
\fQ(x)dx = а,	(13.18)
J (г)dx -> max	(13.19)
по всем критическим областям с ^с условием (13.18).
Решение задачи дается приводимой ниже теоремой и заключается в следующем:
'Р, состоит из таких точек х = (xit х2.х„) выборочного пространства Т, для ко-
торых: /((х) > kf0(x), причем k подбирается из условия (13.18).
Следовательно, в терминах случайной выборки X оптимальный критерий
можно записать так:
*.=4©	(13.20)
/о )
Критическая область для этого критерия есть (/?', оо) = (k, оо). Константа k нахо-
дится из условия (13.18):
PH{Ri>k} = a.	(13.il)
Если при гипотезе Н распределение критерия R{ известно, то константа k может
быть вычислена, по крайней мере, численным методом.
Критерий (13.20) называется критерием отношения правдоподобия. Можно
предложить следующую интерпретацию этого критерия: необходимо на а дол-
ларов купить товара с максимальной полезностью. Точка выборочного простран-
ства х трактуется как определенный товар, /0(х) — его стоимость в долларах,
/](х) — «полезность». Тогда товары для покупки отбираются так, чтобы макси-
мизировать отношение /|(х)//0(х), равное полезности в расчете на единицу
стоимости.
Нам осталось только обосновать изложенную методику.
Теорема 13.1. (Фундаментальная лемма Неймана—Пирсона). Пусть/0(х) и/|(х) —
две плотности распределения, соответствующие гипотезе Н и альтернативе Л,
и а — заданный уровень значимости. Если 4*1 и S', — дна подмножества области
определения/((х) и /о(х), для которых выполняется условие П.З 1R1 и
384
13. Проверка статистических гипотез
/i(x)>Vo(x) ПРИ xe'f'i-
/1(х)<А/()(х) при хеЧ'-Ч',
\fx{x)dx > |Л(х)dx,	(13.22)
*F,	Ч>2
так что критическая область	соответствует более мощному критерию, чем Ч/2.
Доказательство
Обозначим %2 = Ч\ П Ч^ общую часть Ч7, и Ч/2. Тогда
\fx(x)dx = j/1(x)d!r+ \fx(x)dx>\fx(x)dx + \kf0(x)dx =
*1	*|2	*1 -*j2	*12	*i -4>12
= j/jOOdk + AU \f0(x)dx- J/0(r)d!J =
|/0(х)б/г
,*2-*12
= |,/;(х)й!г + ^ \f0(x)dx- \fQ(x)dx  = \fx(x)dx + k-
*12	1*2	*12	J *12
J7i(*)^ + ] J/iCO^Q = \fx(x)dx.
*12	l*2-*12	*2
Итак, неравенство (13.22) доказано.	□
Теорема позволяет сформулировать следующее правило построения наиболее
мощного критерия для непрерывной случайной величины.
1.	Найти распределение критерия отношений правдоподобия (13.20).
2.	Определить константу k из условия (13.21).
3.	Построить критическую область (/?', <ю) = (k, оо).
Для ДСВ с распределением вероятностей pXi и pOi следует выше заменить f на р.
Примеры
Пример 13.9. Гипотеза о параметре экспоненциального распределения. Рассмот-
рим простую гипотезу о параметре экспоненциального распределения (4.9) Н:
X = Хо при простой альтернативе А: X = Хх > Хо. В данном случае плотность рас-
пределения выборки X для гипотезы (р = 0) и альтернативы (р = 1) в точке
х = (хх, х2.хп) есть
Л(х) = Пх»е х'*'> х>0, и=0, 1.
Следовательно, критерий отношения правдоподобия (13.20)
" 1 р~^х<
1=1 лое
т. Y
Л1 I р-Оч -Х0)5,
м
где 5„ = Хх + Х2 + ... + Х„ — сумма элементов выборки.
Критическая область для этого критерия есть (/?', оо) = (Л, оо). Константа k нахо-
дится из условия (13.21). Мы можем, однако, упростить себе задачу, если заме-
13.5. Наиболее мощные критерии'
зм
тим, что между R\ и 5„ существует детерминированная обратная зависимость:
большим значениям соответствуют меньшие значения 5„. Поэтому если пе-
рейти от критерия к эквивалентному ему критерию S„, то критической обла-
стью будет (0, k'). Если гипотеза Н верна, то сумма S„ имеет распределение Эр-
ланга (4.19) с параметрами Хо и I = п (см. пример 7.3) и поэтому условие (13.21)
дает:
PH{Sn<k'}=a,	(13.23)
то есть k' есть квантиль указанного распределения Эрланга, отвечающая вероят-
ности а. Согласно формуле (4.19), она находится как решение относительйо X
уравнения
l-g^(M)'^=-	(13.24)
i=o 11
Пример 13.10. Гипотеза о математическом ожидании ц нормального распре-
деления (4.11) при известной дисперсии а2. Гипотеза и альтернатива имеют вид:
Н: ц = ц0, А: ц =щ >ц0- Плотность распределения выборки X для гипотезы
(v = 0) и альтернативы (v = 1) в точке х = (xit х2,..., хп) есть
А(х) = П-/==-е 2 ° - Vx,p = 0,l.
1=1 у2ло
Следовательно, критерий отношения правдоподобия (13.20)
п 'гт	1 (Xj — ц j
/?! =ПеХР
t=l	Z \ G
2	( v \2
| Xj -Ро |
= Сехрf H-L-Ho £XJ = Сехрs„ |,
I а ,=1 J I о J
где С — положительная константа, S„ =	+ Х2 + ... + Х„.
Как и в предыдущем примере, целесообразно перейти от R{ к эквивалентному
ему критерию 5„. Поскольку щ > ц0, то увеличение приводит к увеличению 5Я,
и критическая область для критерия 5„ будет (k', оо). Если гипотеза верна, то
сумма 5„ имеет (см. теорему 6.4) нормальное распределение (4.11) с математи-
ческим ожиданием пц0 и дисперсией по2. Неизвестная величина k' находится
из условия (13.21):
a=PH{Sn Zk'} = l-PH{Sn
PH{Sn <&'} = l-a.
Следовательно, k' есть квантиль указанного нормального распределения, отве-
чающая вероятности 1-а. Отсюда находим, что k' = дц0 + Ф’1(1-а)сн/я, где
Ф-1 (1 -а) — квантиль стандартного нормального распределения, отвечающая ве-
роятности 1-а.	□
В рассмотренных примерах критическая область не зависела от конкретной аль-
тернативы. Но для каждой конкретной простой альтернативы построенная кри-
тическая область определяла наиболее мощный критерий. Следовательно, он
386
13. Проверка статистических гипотез
остается таковым и для сложной альтернативы. Все это приводит к следующим
выводам.
Определение 7. Равномерно наиболее мощным называется критерий, который
является более мощным для любой простой альтернативы, входящей в сложную
альтернативу. Достаточным условием того, что критерий является равномерно
более мощным, является независимость его критической области от конкретной
альтернативы.
13.6. Непараметрические критерии для проверки
гипотез о распределениях случайных величин
Любой критерий R, служащий для проверки некоторой гипотезы относительно
распределения случайной величины X, является функцией от наблюдаемых зна-
чений этой величины. Поэтому вид распределения критерия R обычно зависит
от распределения величины X. Так, распределение критериев (13.13) и (13.14),
рассмотренных в разделе 13.4, было выведено в предположении нормальной ге-
неральной совокупности. С другой стороны, имеются критерии, вид распределе-
ния которых не зависит от распределения генеральной совокупности X. Ранее
это был критерий (13.13) при больших объемах выборки п. Такие критерии на-
зываются непараметрическими. В настоящем разделе будут рассмотрены наибо-
лее важные из таких критериев.
В первую очередь остановимся на критериях проверки гипотез о распределениях
случайных величин, называемых также критериями согласия. К необходимости
проверки таких гипотез приводит следующая ситуация. Имеются выборочные
данные случайной величины X, функция распределения которой неизвестна.
Однако некоторые соображения дают основание полагать, что величина X имеет
определенный вид распределения (например, нормальный). Так, о распределе-
нии можно судить по внешнему виду гистограммы или полигона частот, на осно-
вании физических предпосылок и т. п. Поэтому следует проверить гипотезу о
том, что случайная величина X имеет данное распределение. При этом обычно
параметры распределения оказываются также неизвестными, и их следует оце-
нить по данным выборки в первую очередь. Обозначим г число параметров рас-
пределения, оцениваемых по выборке. Если г = 0, то это означает, что все пара-
метры распределения известны.
Оказывается, что два рассмотренных случая (г = 0 и г > 0) имеют принципиаль-
ное различие. Если распределение, описываемой гипотезой, определено полно-
стью (г= 0), то в этом случае будем говорить о проверке гипотезы относительно
(конкретного) распределения случайной величины. Если же гипотеза определяет
распределение лишь с точностью до параметров (г > 0), то будем говорить о про-
верке гипотезы относительно вида распределения. В первом случае применяется
критерий Колмогорова, во втором случае — %2-критерий Пирсона.
Начнем с рассмотрения первого случая, а именно, с проверки гипотезы о том,
что имеющаяся выборка взята с генеральной совокупности непрерывных случай-
ных величин с данной непрерывной функцией распределения Fq(x). Все осталь-
ные распределения составляют альтернативу. Итак, в данном случае гипотеза Я:
F(r\ - F„(x\. я альтрпнатива A: F(x) И Fn(xY
13.6. Непараметрические критерии для проверки гипотез о распределениях случайных величин

Критерий проверки данной гипотезы основан на сравнении теоретической Дж)
и эмпирической F*(x) функций распределения. Определяется наибольшая ПО аб-
солютной величине разница между этими функциями (рис. 13.3):
= sup |F(x)-F*(x)|.
-оо <х <00
(13.25)
Рис. 13.3. Теоретическая F(x) и эмпирическая F*(x) функции распределения
Символ sup означает «супремум», то есть точную верхнюю границу. Она имеет
смысл максимума и используется потому, что всегда существует, в то время как
максимум может и не существовать. Супремум ищется по всевозможным значе*
ниям аргумента х, то есть для -оо < х < оо. Индекс п в обозначении величины
подчеркивает, что ее значение подсчитывается по выборке объема п. Оказывает-
ся, что распределение Dn не зависит от распределения F(x) для любого объема
выборки п, то есть основанный на нем критерий будет непараметрическим. Со-
ответствующее асимптотическое распределение (при и > оо) устанавливается
следующей теоремой (см. [2]).
Теорема 13.2. (А. Н. Колмогоров). Если F(x) является непрерывной функцией)
то для любого значения х существует предел
limP{ViiZ) <х}=К(х).
Функцию К(х) можно выписать в явном виде:
К(х) = £(-l№^2.	(13.26)
Эта формула определяет функцию распределения Колмогорова. Интересно отме-
тить, что данное распределение параметров не имеет. Значения функции распре-
деления К(х), а также квантилей К~х(р) можно получить, используя статистиче-
ские таблицы или компьютерные пакеты программ.
ш
13. Проверка статистических гипотез
ледовательно, в качестве критерия целесообразно взять величину R = 4nDn.
эльшие значения критерия говорят в пользу альтернативы, поэтому область
шнятия гипотезы F(x) = F0(x) о распределении непрерывной случайной величи-
л имеет вид [0, /?'] = [О, К-1(1 - а)]. Здесь К“*(1 - а) — квантиль распределе-
ля Колмогорова (13.26), отвечающая вероятности 1 - а.
рименение критерия Колмогорова для проверки гипотезы о распределении не-
эерывной случайной величины будет проиллюстрировано в компьютерном
эактикуме.
ерейдем теперь к рассмотрению второго случая, когда г > 0, то есть когда неиз-
!стны г параметров распределения и проверяется гипотеза о виде распределе-
гя. При этом попутно решается задача оценивания г неизвестных параметров,
данном случае наиболее часто используется критерий х2 -критерий Пирсона.
роцедура его применения состоит в следующем.
ся область возможных значений случайной величины X разбивается на конеч-
эе число т непересекающихся множеств Alt Д2..Дт. В случае несгруппиро-
шных данных дискретной случайной величины X этими множествами будут
1но или несколько возможных значений X, а в случае непрерывной случайной
.‘личины или сгруппированных данных — интервалы. Обозначим а, число
аблюденных в выборке значений X, принадлежащих i-му множеству Д,-:
= #{Х еД,}. Пусть, далее, р, есть вероятность того, что случайная величина,
меющая определяемое гипотезой распределение, примет значение из множест-
1 Д(: Pj =PtI{X е Д, }. Тогда пр, есть математическое ожидание числа наблюде-
ий выборки Хх, Х2, ..., Хп, попавших во множество Д,- при условии, что гипотеза
;рна и объем выборки равен п = а{ + а2 + ...+ ат. Сопоставление чисел а, и пр,
ает основание отвергнуть или принять гипотезу. Если расхождение между на-
дюденными значениями {а,} и их гипотетическими аналогами {пр,} велико, то
>актические данные противоречат гипотезе, а если мало — то подтверждают ее.
.нглийский статистик Карл Пирсон в качестве меры расхождения предложил
зять следующую величину, которую обычно обозначают х2 и называют 12-кри-
\ерием Пирсона:
(13.27)
аметим, что если не все параметры распределения случайной величины X из-
естны (в этом случае будем записывать функцию распределения как Fe(.r)), то
сть если г * 0, то и истинные значения вероятностей {pj неизвестны. Однако
ценив параметры 0 по выборочным данным, можно оценить и вероятности {р,}.
[ля этого достаточно подставить в функцию распределения оценки параметров
, получить таким образом оценку функции распределения F.(r) и оценить
скомые вероятности р,.. Например, если множества {Д,} являются интервалами
: левый и правый концы i-ro интервала Д, есть tt_t и t,, то вероятность р, оцени-
ается по формуле
Pi ~	) fa^-i
(13.28)
13.6. Непараметрические критерии для проверки гипотез о распределениях случайных величин
ЭК
Тогда формула (13.27) для подсчета критерия принимает вид
Я =	(13.29)
1=1 npi
Р. Фишером была доказана следующая важная теорема (см. [2, 7, 9]).
Теорема 13.3. Если проверяемая гипотеза о виде распределения верна, то при
большом объеме выборки п критерий (13.29) имеет приблизительно х2 -распре-
деление с т - г - 1 степенью свободы, где т — число множеств {А,}, г — ЧИСЛО
оцениваемых параметров распределения.
Чем ближе к нулю величина критерия R = х2, тем правдоподобнее кажется гипо-
теза. Наоборот, большие значения критерия указывают на расхождение между
гипотезой и наблюденными статистическими данными. Поэтому в качестве кри-
тической области следует взять интервал (/?", <ю). Как обычно, значение R” вы-
бирается так, чтобы вероятность попадания критерия R в критическую область
(R", оо), когда гипотеза верна, равнялась заданному уровню значимости а. Ины-
ми словами, если гипотеза верна, то R” должно быть таким, чтобы вероятность
наблюденному значению R не превысить R" равнялась (1 - а). Так как в случае
справедливости гипотезы критерий R имеет х2 -распределение с т - г - 1 степе-
нью свободы, то в качестве R" следует взять квантиль этого распределения, отве-
чающую вероятности (1 - a): R" = Xt-a(.m~r_1)-
Вышеизложенное позволяет сформулировать следующее правило проверки гипо-
тезы о виде распределения. Во-первых, если это необходимо, оцениваются не-
известные параметры распределения. Число оцениваемых параметров обознача-
лось г. Затем по данным выборки подсчитывается значение критерия (13.27) или
(13.29). Областью принятия гипотезы для уровня значимости а является интер*
вал
[О, xL(rc-r-l)l,	(13.30)
где X La (?и - г -1) — квантиль х2 -распределения с т - г - 1 степенью свободы, от-
вечающая вероятности (1 - а).
В теореме указывалось, что критерий (13.29) имеет х2 -распределение только при
больших объемах выборки п. Поэтому в каждом из множеств А,- должно насчи-
тываться не менее 5-10 наблюдений. В противном случае соседние множества
следует объединить.
Пример 13.11. Проверка гипотезы о законе распределения дискретной случайной
величины при несгруппированных данных. Используя уровень значимости 0.1,
проверим гипотезу о том, что следующие данные являются выборкой объема 100
из генеральной совокупности, имеющей распределение Пуассона: 1, 0, 3, 1,0, 2, 3,
4, 2, 1, 5,4, 2, 1, 0, 2, 2, 1, 3, 3,1, 3, 2,1, 3, 2,1, 2, 0,0, 0, 2, 3, 2, 2, 2,3,4, 2, 2, 2,0, 1, 2,
2,1, 2, 1,0, 2, 6,2, 3, 0, 2, 0, 4, 3, 2, 2, 1,1,1, 2, 3, 2, 2,1, 0,3, 2,1,0, 0,1, 1,1,1,2,2,4,
3, 5, 0, 4, 1, 1, 2, 2, 3, 2, 1, 0, 3, 3, 2, 2, 0, 1, 2.
В табл. 13.5 в первых двух столбцах приведены наблюденные значения i  0, 1,...
и число наблюдений at. В данном случае имеется один неизвестный параметр
распределения (r« 1) - параметр X. Согласно результату примера 11.7, хорошей
190
13. Проверка статистических гипотез
•ценкой Xявляется эмпирическое математическое ожидание ц’. Для рассматри-
1аемой выборки оно равно 1.82. Следовательно, X = ц ’ =1.82.
Зайдем оценки вероятностей по формуле
—	X	1.82' -182 • л ,
р, = — е =-------е , 1=0,1,...
'	Н Н
)ти вероятности записаны в третьем столбце табл. 13.5. На рис. 13.4 представле-
на полигоны частот р* = 0.01а,- и оценок вероятностей р(.
1 четвертом столбце этой таблицы приведены значения оценки функции распре-
[еления
Л'
:оторая в точке i равна сумме р; по всем j, не превосходящим i. Эти значения
югут быть использованы для сопоставления оцененной (/)и эмпирической (F*)
эункций распределения.
J столбце 5 приведены оценки пр, математического ожидания числа данных, по-
евших в i-й интервал. Взвешенные квадраты уклонений записаны в столбце 6.
’ак, для первого значения i = 0 имеем:
(«> -пр,)2 _(15-16.2)2
—	-	— и.мОл
пр, ^-2
аблица 13.5. Проверка гипотезы о распределении
декретной случайной величины
Значение переменной, i	Число наблюдений, а,.	Оценка вероятности, Pi	Оценка функции распределения, F(i)	Оценка математ. ожидания, иД.	(а, - пр,)2 npi
1	2	3	4	5	6
0	15	0.162	0.162	16.2	0.089
1	25	0.295	0.457	29.5	0.686
2	35	0.268	0.725	26.8	2.509
3	16	0.163	0.888	16.3	0.006
4	6	0074	0.962	7.4	0.265
5	2	0.027	0.989	2.7	0.181
5	1	0.008	0.997	0.8	0.050
7	0	0.002	0.999	0.2	0.200
Сумма	100	0.999	-	99.9	3.986
13.7. Непараметрические критерии сравнения двух совокупностей
391
Сумма взвешенных квадратов уклонений дает значение критерия х2. В рассмат-
риваемом случае х2 = 3.986. Так как по данным выборки был оценен один пара-
метр (г = 1) и имеется восемь множеств (т = 8), то число степеней свободы равно
/п-г-1=8-1-1=6.
Находим квантиль х2 -распределения с шестью степенями свободы, отвечающую
вероятности 0.9. Она равна 10.6. Поэтому область принятия гипотезы есть ин-
тервал [0, 10.6]. Так как значение критерия принадлежит этому интервалу, то ги-
потеза о распределении Пуассона принимается.
Отметим, что мы не производили объединение интервалов, так как и без этого
гипотеза принимается.
13.7. Непараметрические критерии сравнения
двух совокупностей
Предположим, что имеются две генеральные совокупности, соответствующие
непрерывным случайным величинам X и Y. Обозначим их функции распределе-
ния F(x) = Р{Х < х} и G(у) = P{Y< у}. Необходимо проверить гипотезу о том, ЧТО
X и Y имеют одно и то же распределение, то есть гипотезу И: F(x) = G(x) V х.
В качестве альтернатив рассматриваются двусторонняя альтернатива A: F * С
или односторонние альтернативы Л: F(x) < G(x) или A: F(x) > G(x), где неравен-
ство F(x) < G(x), например, означает, что F(x) i G(x) V х, и найдется по крайней
мере одно значение х, при котором имеет место строгое неравенство: F(x) < G(x),
Проверка производится по двум независимым выборкам разного объема их этих
592
13. Проверка статистических гипотез
:овокупностей: выборке Хи Х2, ..., Хт объема т из первой генеральной совокуп-
тости и выборке Y{, Y2, Yn объема п — из второй.
эудут рассмотрены несколько непараметрических критериев'. Вилкоксона, Ман-
ia—Уитни и знаков. Выбор именно этих критериев обусловлен тем, что все они
реализованы в используемом нами компьютерном пакете STATISTICA, в моду-
ie «Nonparametric Statistics». Эти критерии примеряются для проверки и других
родственных статистических гипотез.
Рассмотрим вначале критерий Вилкоксона. Этот критерий является ранговым.
сритерием. Поясним, что это такое. Элементы имеющейся выборки ранжируют-
:я, то есть располагаются в порядке неубывания. Рангом элемента выборки назы-
рается ее порядковый номер в полученной ранжированной последовательности.
1сли встречаются одинаковые элементы, то каждому из них приписывается
:редний ранг. Например, если одинаковые элементы стоят на седьмом и восьмом
лестах, то им обоим приписывается ранг 7.5. Отметим, что в нашей ситуации
рдинаковых элементов быть не должно, поскольку рассматриваются непрерыв-
1ые случайные величины. Здесь одинаковые значения могут появиться только
ia счет округления. Критерии, основанные на рангах элементов (а не самих зна-
1ениях элементов) и называются ранговыми.
Итак, имеются две выборки Хь Х2,..., Хт и Yit Y2,..., Y„. Объединим их в одну по-
:ледовательность из т + п элементов и ранжируем ее. Подсчитаем сумму рангов
>лементов первой выборки Хь Х2, ..., Хт в объединенной последовательности и
рбозначим ее IT. Это и есть критерий Вилкоксона. Очевидно, сумма рангов всех
шементов двух выборок равна 1+2 + ... + п + т = (п + т)(п + т + 1)/2. Исполь-
|уя технику применения индикаторных случайных величин раздела 5.3, легко
юказать, что если гипотеза Н: F(x) = G(x) V х верна, то для критерия IT матема-
•ическое ожидание E(W) = т(п + т + 1)/2, а дисперсия D(W) = пт(п + т + 1)/12.
<роме того, с ростом т и п распределение IT стремится к нормальному (4.11)
: указанными параметрами. Следовательно, критерий
r_W -т(п + т + 1)/2
^jnm(n+ т + 1)/12
юимптотически имеет стандартное нормальное распределение (4.13) и поэтому
логут быть применены процедуры проверки гипотез о математическом ожида-
«ии для ц0 = £(W) = т(п + т + 1)/2, приведенные в табл. 13.3. В частности, при
щусторонней альтернативе F * G область принятия гипотезы выписана в по-
бедней строке табл. 13.3.
Рассматриваемую гипотезу об одинаковом распределении двух генеральных со-
юкупностей можно проверять также с помощью критерия Манна-Уитни. Этот
сритерий тесно связан с критерием Вилкоксона и определяется следующим об-
)азом. Рассмотрим всевозможные пары (Xt, Yj), i = 1, 2,..., m,j = 1, 2,..., n, где Xj —
-й элемент первой выборки, a Yj -j-n элемент второй выборки. Подсчитаем чис-
ю пар, для которых X, < Yj, и обозначим его U. Это и есть критерий Ман-
ia-Уитни.
Между обоими критериями существует следующее детерминированное соотно-
иение:
Компьютерный практикум № 20. Непараметрическая проверка гипотез в пакете STATISTICA
IT + U = тп + т(т +1)/2.
Это говорит о том, что оба критерия эквиваленты. В частности, математическое
ожидание критерия Манна—Уитни находится как E(U) = тп + т(т + 1 )/2 - £( W) 
= пт/2. В силу линейной зависимости IT и U их дисперсии совпадают, так что
D(U) = D(W) = пт(п + т + 1)/12. Как и раньше, с ростом тип распределение
критерия U стремится нормальному. В связи с этим все остальное совпадает С
процедурой использования критерия Вилкоксона за исключением того, ЧТО
E(W) = т(п + т + 1 )/2 следует заменить на E(U) = пт/2.
В заключении остановимся на критерии знаков. Он применяется в случае, К0ГД8
обе выборки имеют одинаковый объем (п = т) и происходит попарное сравнение
элементов выборок: (Xb Y/), (Х2, У2), (Хп, Y„). Фактически здесь имеет место
выборка для двумерной случайной величины (X, Y). Пары (Xb Yj), i = 1, 2.ft
являются взаимно независимыми, но компоненты внутри одной пары могут за*
висеть друг от друга. Такая ситуация возникает, например, при анализе эффек-
тивности некоторого мероприятия. Для группы объектов измеряется некоторый
показатель до и после внедрения данного мероприятия. Результаты измерений
для различных объектов можно считать независимыми, но для одного объекта
измерения будут, очевидно, зависимыми случайными величинами.
Итак, проверяемая гипотеза состоит в том, что компоненты Xj и Yj распределены
одинаково, точнее, что
Р{Х<У}=Р{Х>У}=|
Рассмотрим для каждого i разницу Zt = X, - Yt и в общем случае Z = X - У. Тогда
рассматриваемая гипотеза эквивалента гипотезе
P{Z<0}=P{Z>0}=|
Следовательно, с равной вероятностью 1 /2 знак любого элемента последователь-
ности Zb Z2.Z„ может быть и положительным и отрицательным. Критерием R
здесь является число положительных знаков. Этим и объясняется название дан-
ного критерия. Очевидно, если гипотеза верна, то R имеет биномиальное распре-
деление (3.3) с параметрами п и р = 1/2. Следовательно, можно применять про-
цедуры проверки гипотезы о вероятности события р0 = 1/2, изложенные В
разделе 13.2.
Вышеприведенные гипотезы можно проверять, используя модуль «Nonparametric
Statistics» пакета STATISTICA.
I
Компьютерный практикум № 20.
Непараметрическая проверка гипотез
в пакете STATISTICA
Цель и задачи практикума
Целью практикума является приобретение навыков по проверке статистических
гипотез в пакете STATISTICA.
и
13. Проверка статистических гипотез
гдачами данного практикума являются: проверка гипотез о нормальном распре-
:лении случайных величин с использованием критерия Колмогорова—Смирно-
i и о виде распределения случайных величин (для нормального, логнормально^
। и гамма-распределений) с использованием критерия Пирсона (%2-критерий).
эобходимый справочный материал
ля проверки гипотезы о нормальном распределении случайных величин в па-
.•те STATISTICA используется модуль Descriptive Statistics (Описательные ста-
истики). При этом используется критерий согласия Колмогорова—Смирнова,
тгорый предполагает, что известны параметры нормального закона распределе-
ия случайной величины. В пакете STATISTICA эти параметры, однако, оцени-
1ются. Процедура проверки выполняется следующим образом: сначала по дан-
ым выборки оцениваются среднее значение ц и дисперсия о2 и далее для
элученных параметров проверяется гипотеза о том, что наблюдаемые величины
определены нормально. Естественно, что для небольших выборок найденные
денки параметров могут существенно отличаться от истинных, что может при-
юти к не вполне корректным результатам проверки гипотезы.
роверка гипотез о виде распределения случайных величин для различных
ikohob распределения выполняется в модуле Nonparametric Statistics (Непара-
етрическая статистика), для чего используется процедура Distributing Fitting
МвйМНщКш (Подгонка распределения). На выбор предлагаются следующие
непрерывные распределения: нормальное (Normal), равно-
UMCRC
ALUE8
я,мерное (Rectangular), экспоненциальное (Exponential), гамма
(Gamma), логнормальное (Log-normal), %2 (Chi-square). Име-
175; ется возможность выбора и других законов (опция Others).
х’2 Список рассматриваемых дискретных распределений вклю-
юо чает: биномиальное (Binomial), пуассоновское (Poisson), гео-
метрическое (Geometric) и Бернулли (Bernoulli).
Читателю может быть полезна и вторая процедура Nonpara-
. Z''53j metric Stats, входящая в состав модуля Nonparametric Statistics.
145 В частности, ею можно воспользоваться при решении ряда за-
.....2’. дач, приведенных в конце настоящей главы. Эта процедура
ел: позволяет выполнять сравнение двух совокупностей с исполь-
зованием различных непараметрических критериев: Манна—
I зэ! Уитни, Вилкоксона, критерия знаков, двухвыборочного кри-
| Ч* терия Колмогорова—Смирнова и др.
12$ Реализация и результаты выполнения задания
ио. Задача практикума заключается в проверке гипотезы о зако-
174i не распределения случайной величины, определяющей коли-
|....чество миллиметров снега, выпадающего в течение зимнего
135; периода в аэропортах СНГ и Балтии.
Введем в таблицу исходных данных выборку из 30-ти наблю-
дений, как это показано на рис. 13.5. Технология ввода неход-
кие. 13.S. Исходная
выборка
наблюдений
ных данных была рассмотрена нами в компьютерном прак-
тикуме №16.
Компьютерный практикум № 20. Непараметрическая проверка гипотез в пакете STATISTICA
396
Задача проверки гипотезы о нормальном распределении
Сначала проверим гипотезу о нормальном законе распределения случайной ве-
личины. Для этих целей используется критерий Колмогорова—Смирнова. Рабо-
та производится в модуле Basic Statistics/Tables, вызываемом в окне переключа-
теля модулей STATISTICA Module Switcher.
Проверка гипотезы о нормальном законе распределения случайной величины
включает следующие действия:
1)	выполним команду прикладного меню Analysis—Frequency tables;
2)	в открывшемся окне Frequency Tables (рис. 13.6) нажмем на кнопку Variables,
в результате откроется окно Select the variables for analysis (рис. 13.7);
Рис. 13.6. Окно процедуры Frequency Tables
1 SNOW ММ
f 2-VAR2
PVAR3
J4VAR4
5-VAR5
6-VARG
S7-VAR7
I B-VAR8
| 9-VAR9
* 10VAR10
SeWd гаиЫк:
Рис.13.7. Окно выбора переменных
3)	в списке переменных окна выделим переменную SNOW MM и нажмем кноп-
ку ОК;
196
13. Проверка статистических гипотез
i) в секции Tests of normality (см. рис. 13.6) установим флажок K-S test, mean/std.
dv known, который задает режим проверки нормального закона по критерию
Колмогорова—Смирнова;
i) нажмем кнопку Tests of normality, получим таблицу с результатами проверки
гипотезы, представленную на рис. 13.8.
iv-Smimov Test (airports.sta)
£0iltinue & standard deviation known)
117045
ms
—:------1
p > .20 I
Рис. 13.8. Результаты проверки нормального закона распределения случайной величины
Гак как значение критического уровня значимости большое (р > 0.2), то можно
утверждать, что распределение генеральной совокупности является нормальным.
Лроцедура Frequency tables позволяет проверить гипотезу о нормальном законе
распределения случайной величины с использованием графических средств. Для
•того построим графики гистограммы частот и теоретической плотности нор-
лального распределения и график исходных данных на нормальной вероятност-
юй бумаге.
1ля построения гистограммы относительных частот в окне Frequency Tables от-
летим переключатель No. of exact intervals и в соответствующем ему поле введем
соличество интервалов — в нашем случае оно равно 6. Нажмем кнопку Histogram
л получим гистограмму частот и график теоретической плотности нормального
распределения, представленные на рис. 13.9.
Рис. 13.9. Гистограмма частот и кривая плотности нормального распределения
Компьютерный практикум № 20. Непараметрическая проверка гипотез в пакете STATISTICA
397
Для построения графика на нормальной бумаге в окне Frequency Tables активизм*
руем кнопку Normal probability plots. В результате выводится график, показанный
на рис. 13.10.
Noiinal РюЬйЬгЫу Plot	I
Рис. 13.10. График на нормальной вероятностной бумаге
Полученные результаты — внешний вид графиков на рис. 13.9 и 13.10 — под-
тверждают гипотезу о нормальном распределении генеральной совокупности.
Задача проверки гипотезы о виде распределения
Нельзя однозначно утверждать, что нормальный закон наилучшим образом со-
ответствует распределению случайной величины исследуемой совокупности.
Внешний вид гистограммы частот (рис. 13.9) позволяет выдвинуть и другие ги-
потезы о законе распределения, например, о логнормальном и гамма-распределе-
ниях. Для проверки этих гипотез воспользуемся процедурами пакета, входящи-
ми в состав модуля Nonparametrics/Distribution. Проверку будем выполнять по
X2-критерию Пирсона.
В окне переключателя модулей STATISTICA Module Switcher выберем строку Non-
parametrics/Distrib и нажмем кнопку Switch to. В результате откроется стартовое
окно модуля, вид которого зависит от установки переключателя режимов Nonpa-
rametric stats {Непараметрическая статистика) и Distribution fitting (Подгонка
эмпирического распределения к теоретическому). В нашем случае переключатель
должен соответствовать режиму Distribution fitting, при этом окно будет иметь
вид, представленный на рис. 13.11. В левой части окна в списке непрерывных за-
конов распределения (Continuous Distributions) необходимо выбрать тот, который
соответствует проверяемой гипотезе.
Сначала проверим гипотезу о нормальном законе распределения случайной вели-
чины. Для этого выделим строку Normal и нажмем кнопку ОК. В открывшемся
598
13. Проверка статистических гипотез
жне Fitting Continuous Distributions (рис. 13.12) нажмем на кнопку Variables и далее
т окне Select the varibles for analisys (рис. 13.7) в списке переменных окна выде-
лим переменную SNOW_MM и нажмем кнопку ОК. В результате будут рассчита-
на и выведены в полях Mean и Variance параметры теоретического распределе-
ния соответственно: среднее значение ц = 101.83333 и дисперсия о2 =2409.4536.
Установим переключатели в нижней части окна, как это показано на рис. 13.12.
В нашем примере переключатель Kolmogorov-Smirnov test установлен на No, это
тзначает, что проверка гипотезы производится только по %2-критерию Пирсона.
После нажатия на кнопку Graph получим гистограмму частот, показывающую
[юзультаты подгонки эмпирического распределения к теоретическому (рис. 13.13).
Непосредственно над графиком показаны результаты проверки гипотезы по
критерию Пирсона, который имеет значение %2 = 1.217916, ему соответствует
критический уровень значимости 0.2697783. Так как он имеет достаточно боль-
шое значение (> 0.2), то можно утверждать, что распределение генеральной со-
вокупности является нормальным.
Рис. 13.11. Стартовое окно подгонки эмпирического распределения к теоретическому
Рис. 13.12. Окно проверки гипотезы о нормальном законе распределения
Компьютерный практикум № 20. Непараметрическая проверка гипотез в пакете STATISTICA
ЭМ
Рис. 13.13. Результаты проверки гипотезы о нормальном законе распределения
Повторим рассмотренную процедуру проверки последовательно для гипотез о
логнормальном и гамма-распределениях (см. рис. 13.11). Полученные результа-
ты сравним с результатами проверки гипотезы о нормальном законе.
Результаты проверки гипотезы о логнормальном законе представлены на рис. 13.14
и рис. 13.15. В данном случае критерий Пирсона значительно больше %2 = 2.4598
и ему соответствует меньшее значение критического уровня значимости 0.1168.
Таким образом, преимущество остается за гипотезой о нормальном законе рас-
пределения.
Рио. 13.14. Окно проверки гипотезы о логнормальном закона распрадалания
400
13. Проверка статистических гипотез
.jHGiapW’j Vdoable ^NOW ММ . UnUtbutiiHi I.uqnonnal	Г"> РП IT?:'
Variable SNOW_MM; distribution; Lognormal
Chi-Squ are. 2.459812, df = 1, p = . 1168027 (df adjusted)
Рис. 13.15. Результаты проверки гипотезы о логнормальном законе распределения
Результаты проверки гипотезы о гамма-распределении случайной величины пред-
ставлены на рис. 13.16 и рис. 13.17. В данном случае критерий Пирсона имеет
наименьшее из трех проверок значение у2 = 0.932749 и ему соответствует самое
большое значение критического уровня значимости 0.334156. Таким образом,
в окончательном варианте следует принять гипотезу о гамма-распределении гене-
ральной совокупности.
Рис. 13.16. Окно проверки гипотезы о гамма-распределении
случайной величины
Задания для самостоятельной работы
401
Рис.13.17. Результаты проверки гипотезы о гамма-распределении случайной величины
Задания для самостоятельной работы
1.	С помощью датчика случайных чисел пакета Mathcad выработайте выборку
объема п = 10 для нормального распределения с параметрамиц = 3иа» 1.5.
Для уровня значимости а = 0.05 проверьте следующие гипотезы:
Но: ц = 3 при следующих альтернативах: Hf. ц * 3; Hf. ц > 3; Нс ц < 3.
Но'. о2= 2.25 при альтернативе Нс о2> 2.25.
Но: имеет место нормальное распределение с параметрами ц = 3 и а = 1.5.
2.	С помощью датчика случайных чисел пакета Mathcad выработайте выборку
объема п = 50 случайных величин, имеющих экспоненциальное распределе*
ние с параметром 1=2. Для уровня значимости а = 0.05 проверьте гипотезы:
Но: 1= 2 при альтернативах: Нс 1* 2; Hf 1> 2; Hi: К 2.
Но: имеет место экспоненциальный вид распределения.
3.	С помощью пакета Mathcad составьте программу, реализующую проверку
простой гипотезы при простой альтернативе на основе использования фунда*
ментальной леммы Неймана—Пирсона (см. теорему 13.1). Апробируйте эту
программу для случая двух экспоненциальных распределений с параметрами
10 и 1Р где 10 < X,.
402
13. Проверка статистических гипотез
Задачи
Задача 13.1. По данным задачи 12.1 для уровня значимости 0.05 проверьте гипо-
тезу о том, что доля р пассажиров, имеющих багаж весом свыше 30 кг, не превы-
шает 0.1.
Задача 13.2. В условиях задачи 12.2 проверьте гипотезу о том, что вероятность
поступления системы на обслуживание позже установленного срока не превы-
шает 0.25. Уровень значимости принять равным 0.1.
Задача 13.3. Известны результаты выборки из некоторой генеральной совокуп-
ности: 7, 8, 7, 7, 18, 8, 17, 10, 11, 13, 28, 9, 20, 6, 10, 6, 13, 17, 33, 12, 17, 8, 18, 12, 20,
38, 20, 7, 21, 23, 16, 18, 25,10, 30, 27, 15, 20, 11, 25,15, 20, 24, 6, 32, 23, 19, 30, 28, 20,
6, 15, 16, 21, 25, 15, 12, 14, 18, 15, 7, 17, 22.
Считая распределение нормальным, проверьте следующие гипотезы при уровне
значимости 0.2: а) ц > 15 при альтернативе ц < 15; б) о2 > 200 при альтернативе
о2 <200.
Задача 13.4. Согласно стандарту вес изделия должен составлять 17 г. В действи-
тельности этот вес есть случайная величина. В результате проверки 60 случайно
выбранных изделий оказалось, что средний вес этих изделий равен 16.8 г, а эм-
пирическая дисперсия о2* =0.25 г2. Можно ли при уровне значимости 0.1 счи-
тать, что вес изделия а) ниже требуемого; б) отличен от требуемого стандартом.
Задача 13.5. Следует ли пересмотреть решение предыдущей задачи, если уровень
значимости изменился и стал равным а) 0.2; б) 0.05?
Задача 13.6. Поставщик утверждает, что доля брака в партии товара не превыша-
ет 4%. Для проверки случайным образом выбрано 100 изделий. Из них 5 оказа-
лись бракованными. Начиная с какого уровня значимости нельзя отвергнуть ут-
верждение поставщика?
Задача 13.7. В следующей таблице приведены данные о количестве вызовов де-
журного мастера в течение суток, которое фиксировалось в течение 100 дней.
В частности ни одного вызова не было в течение 13 суток, один вызов в сутки
наблюдался 24 раза и т. д.
Количество вызовов в сутки, i	0	1	2	3	4	5	6	7 и более
Число наблюдений значения i, а.	13	24	31	20	6	5	1	0
Используя критерий Пирсона, проверьте при уровне значимости 0.05 гипотезу
о том, что количество вызовов в сутки имеет распределение Пуассона.
Задача 13.8. В знаменитом опыте Резерфорда, Чедвика и Эллиса радиоактивное
вещество наблюдалось в течение п = 2608 промежутков времени, каждый длиной
в 7.5 с. Для каждого промежутка регистрировалось число частиц, достигших
счетчика. Известны данные о числе п, промежутков времени, в течение которых
наблюдалось ровно i частиц.
i	0	1	2	3	4	5	6	7	8	9	10	Всего
",	57	203	383	525	532	408	273	139	45	27	16	2608
Задачи
4М
Общее число зарегистрированных частиц оказалось равным 2Х = 10094, а эмпи-
рическое математическое ожидание
И* =1У п. =3.87.
п j
Используя критерий %2-Пирсона и 5% уровень значимости, проверьте гипотезу
о пуассоновском распределении с параметром X = 3.87.
Задача 13.9. Известны данные о продолжительности X (в часах) ежегодного про-
филактического обслуживания агрегата: 86, 74,18, 26,37,41,49,60,66,71,62,31»
19, 29, 37,46, 51, 40, 29, 65, 78, 78, 31,38, 43, 49, 23, 31, 40, 38, 29,45, 51, 58,47, 25,
40, 61, 69,92, 80,49, 29, 44, 37, 60, 72, 68, 34, 54, 45, 56, 38, 27,48, 57,60,35,66, 75,
28, 54, 61, 64, 34, 55, 57, 48, 34, 29, 36, 55, 69, 80, 86.
Сгруппируйте эти данные. Найдите оценки математического ожидания и дис-
персии. Для уровня значимости 0.05 проверьте гипотезы о нормальном распре-
делении и распределении Эрланга. Постройте гистограмму и графики накоплен-
ной частоты и теоретических плотности и функции распределения.
Задача 13.10. Для сравнения двух способов обработки сельскохозяйственных
угодий выделено 40 эквивалентных участков. На первых 20 участках обработка
велась по одному способу, а на 20 других — по второму. Урожаи с первых 20 уча-
стков составили (в условных единицах): 23,25,14, 21, 27, 16,22,12, 21, 26,15,11,
21, 14, 16, 13, 19, 32, 21, 19. Урожаи с 20 других участков оказались равными: 16,
13, 12, 9, 14, 13, 19, 16, 23, 14, 15, 10, 16, 12, 16, 18, 29, 16, 19, 17.
Используя непараметрические критерии и уровень значимости 0.2, проверьте
гипотезу об отсутствии различия в способах обработки.
Задача 13.11.
1.	При исследовании потока грузов, поступающих на оптовый склад, было уста-
новлено, что этот поток имеет постоянную интенсивность с 10 до 15 часов,
Используя следующие фактические данные о моментах поступления машин
на склад в течение 6 дней, проверьте при уровне значимости 0.01 гипотезу о
пуассоновском потоке автомашин.
Часы	Дни											
	2/VI		3/VI		4/VI		5/VI		6/VI		7/V1	
	Минуты	Кол-во	1 поступлений	Минуты	„	1 Кол-во поступлений	Минуты	Кол-во поступлений	Минуты	Кол-во поступлений	Минуты	Кол-во поступлений	Минуты	Кол-во ociyiuemul
10	24,38, 43, 54	4	49, 50, 54	3	0, 1, 7, 49, 50	5	и, 45, 51	3	7,29, 48	3	26	1
11	17, 24, 56	3	5, 17, 36, 50	4	4, 16, 50	3	5, 8, 26,41	4	3, 9, 29,39	4	11,20, 29, 52	4
12	0, 2, 37,51	4	и,зо, 42	3	1, 16, 50,54, 56	5	6, 14	2	15,17, 26, 38	4	2, 13	2
404
13. Проверка статистических гипотез
Часы	Дни											
	2/VI		3/VI		4/VI		5/VI		6/VI		7/VI	
	Минуты	Кол-во поступлений	Минуты	Кол-во поступлений	Минуты	Кол-во поступлений	Минуты	Кол-во поступлений	Минуты	Кол-во поступлений	Минуты	Кол-во поступлений
13	28,32, 55	3	19, 23, 38,39	4	7, 15, 29,36	4	5, 43	2	13	1	35, 44	2
14	13,22, 32,51	4	7,31, 48, 50	4	10,20, 38, 47	4	29,38, 53	3	6,20, 48	3	37,48, 57	3
15	24	1	26	1			12	1	18, 27, 37	3	17,33, 42,45, 47	5
2.	Число мест груза X, содержащегося в одной партии, является случайной ве-
личиной. Известны данные о фактическом числе мест груза по результатам
обследования п = 2220 партий:
Число мест в партии, х	1	2	3	4	5	6	7	8	9	10	И
Число наблюдений, пх	924	295	141	114	83	73	43	38	32	37	25
Число мест в партии, х	12	13	14	15	16	17	18	19	20	21	22
Число наблюдений, пх	21	26	14	40	18	23	20	7	42	15	5
Число мест в партии, х	23	24	25	26	27	28	29	30	31	32 и более	
Число наблюдений, пх	8	13	57	5	12	6	7	16	9	51	
Попробуйте подобрать теоретическое распределение, хорошо сглаживающее
эти данные.
3.	Распределение веса одного места груза зависит от числа мест в партии. Из-
вестны сгруппированные данные о весе одного места груза для 500 партий,
содержащих одно место груза:
Вес места, кг	0-4	4-8	8-12	12-16	16-20	20-24
Число наблюдений	2	227	48	73	56	38
Вес места, кг	24-28	28-32	32-36	36-40	40-52	52-92
Число наблюдений	16	6	6	8	14	6
Вычислите эмпирическое среднее и дисперсию. Сравните эти результаты со зна-
чениями и’ * 13.6 кг и D*  129 кг2, полученными по несгруппированным дан-
Задачи
ным. Рассмотрите вопрос о возможности использования для практических рас*
четов усеченного экспоненциального распределения

при х £ 4,
при х к 4.
14 Регрессионный
и корреляционный анализ
14.1. Одномерная линейная регрессия
В настоящей главе изучаются зависимости между случайными величинами. За-
дание совместного распределения дискретных и непрерывных случайных вели-
чин рассматривалось в главах 5 и 6. Если одна из величин является «случайной
функцией» от других величин, то это соответствует материалу разделов 5.2 и 6.2.
Относящиеся сюда статистические задачи составляют содержание регрессионно-
го анализа. Мы ограничимся рассмотрением линейных моделей регрессии, чему
будут посвящены первые три раздела главы. Последний раздел содержит введе-
ние в корреляционный анализ, заключающийся в статистическом исследовании
корреляционных зависимостей между случайными величинами. Примененное
нами прилагательное статистические означает, что анализ проводится на осно-
ве имеющихся выборочных данных.
Мы начинаем с рассмотрения случая одномерной линейной регрессии, что по-
зволит усвоить основные концепции перед их применением для более сложного
многомерного случая. Пусть интерес представляет некоторый показатель Y,
линейно зависящий от определенного фактора t. Кроме того, на эту зависимость
накладывается дополнительный случайный фактор, который мы представим в
виде случайной величины Z. Наша цель заключается в предсказании величины Y
на основе имеющейся информации о величине t. В связи с этим будем называть
Y зависимой переменной {откликом), t — предикторной переменной {фактором),
aZ — случайной составляющей.
Формально постулируемая структура связи между введенными величинами
имеет вид:
y=P0+P,£ + Z,	(14.1)
где Ро и pf — неизвестные параметры модели (постоянные величины);
t — известное и неслучайное значение предикторной переменной;
Z — случайная величина, сопутствующая наблюдению.
Подчеркнем еще раз, что в результате наблюдения регистрируется не истинное
значение Ро + р( t, а его сумма со случайной составляющей Z. В практических
исследованиях наличие составляющей Z может быть вызвано двумя основными
nnuuuuauu rvntPCTnnnaHuPM сЬактопов (поеликтооных переменных), ие учиты-
14.1. Одномерная линейная регрессия
407
ваемых в модели; существованием случайных отклонений от основной тенден-
ции, отражаемой выражением ро + Pj t.
Обычно имеется несколько реализаций (наблюдений) модели (14.1), каждой из
которых соответствуют свои значения У, t и Z. Для указания конкретной реали-
зации будем снабжать эти величины индексом i = 1, 2, ..., п, где п — количество
реализаций. В связи с этим формула (14.1) может быть переписана в виде
У,. =Р0+Pti,+Z,, г = 1,2..п.	(14.2)
Определение 1. Моделью одномерной линейной регрессией называется зависи-
мость (14.2) случайной величины У от неслучайной переменной t, где Zt, Z2, ....
Z„ — взаимно независимые случайные величины, имеющие нулевое математиче-
ское ожидание и одинаковую (быть может, неизвестную) дисперсию:
E(Z,) = 0, £»(Z,) = o2, i = l,2.п.	(14.3)
Задачей регрессии является нахождение оценок PJ и Р, неизвестных коэффици-
ентов (параметров) р0 и Pt на основе наблюденных значений (ib yj, (i2, У2), ...,
<t„, У„).
Формулы (14.2), (14.3) полностью описывают рассматриваемую модель. Мате-
матическое ожидание и дисперсия зависимой переменной согласно этой модели
равны:
E(Yt) = Ро + РЛ, £»(У;) = О2, 1=1,2.п.	(14.4)
Очевидно, случайные величины {У^-} взаимно независимы. Согласно формуле
(14:2), их значения формируются в основном за счет суммы р0 +Р^( (основная
тенденция). На эту сумму накладывается случайная составляющая Zit имеющая
характер или неучтенных факторов или случайных помех. Соотношения (14.3)
постулируют, что эта составляющая не может быть предсказана, если о * Q но
систематическая ошибка в модели отсутствует. Если E(Zj) * 0, то говорят о нали-
чии систематической ошибки.
Итак, задача заключается в нахождении оценок параметров pj и pf. Зная эти
оценки, можно оценить значение зависимой переменной Y, по формуле
УЖ+Р.Ч.	(14.5)
Соответствующий график называется графиком линейной регрессии.
Определение 2. PJ и pjназываются оценками метода наименьших квадратов, если
они минимизируют сумму квадратов отклонений
Ro =t(Y, -У,’)2 = £(У, -(р0 +РЛ))2-	(14.6)
1=1	1=1
Физический смысл этого критерия заключается в том, что он дает прямую
У* = PJ + Р|*Г, относительно которой разброс точек (Г, У) минимален (рис. 14.1).
Для минимизации выражения (14.6) поступаем обычным способом: берем про-
изводные по р0 и р| и приравниваем их нулю. В результате получаем так назы-
ваемую систвми ноомалъных ипаяшпплг
408
14. Регрессионный и корреляционный анализ
2£(rj-(Po+p1t1.)) = O,
м
21Ж-(Ро+М()) = О.
Решая ее, находим следующие оценки метода наименьших квадратов'.
р; = —-—-m -о- Ро =f-p^>	(14-7)
м
гдеУ=-£г(, Г=-£г,.
п м	п ,.1
Рис. 14.1. Г рафик линейной регрессии
Если соотношения (14.1) и (14.3) справедливы, то имеют место следующие ос-
новные свойства оценок метода наименьших квадратов.
1.	Оценки PJ и р‘, вычисляемые по формуле (14.7), являются несмещенными
оценками параметров р0 и Р(:
Ж) = Р0,£(Р1’) = Р1.
2.	Эти оценки имеют наименьшую дисперсию среди всех несмещенных оценок,
являющихся линейными функциями результатов наблюдений Уь Y2,..., Yn.
3.	Несмещенной оценкой неизвестной дисперсии о2 является
°2’ =Ат£р'.-(р;+р;г,)]2.	(14.8)
П — 2 м
В качестве оценки среднего квадратического отклонения будем пользоваться
величиной о* = Vo2’.
Прогноз, рассчитываемый для значения сопутствующей переменной t* (в ча-
стности, для k > и) по формуле
у;-р;+р,7*.	(14.9)
14.1. Одномерная линейная регрессия
является несмещенной оценкой истинного математического ожидания
Ро + Р] tk, причем дисперсия этой оценки минимальна и равна
(14.10)
Необходимо помнить, что все это справедливо, если модель верна, то есть
если соотношения (14.2) и (14.3) действительно имеют место.
Формулу (14.10) можно применять, если дисперсия о2 известна. В против*
ном случае следует пользоваться оценкой дисперсии DIY*), которая полу-
чается в результате подстановки в (14.10) вместо истинной дисперсии аа ее
оценки о2*:
(14.11)
Выше не делалось никаких предположений относительно распределения слу-
чайной составляющей Z. Обычно предполагают, что она имеет нормальное
распределение (4.11) с параметрами (14.3). В этом случае дополнительно
справедливы следующие утверждения.
4.	Оценки Ро и р’ обладают наименьшими дисперсиями среди всех несмещен-
ных оценок ро и Р|.
5.	Отношение (п-2)о2*/о2, где о2 — дисперсия, а о2‘ — вычисляемая по фор-
муле (14.8) оценка ее, имеет х2-распределения с (и - 2) степенями свободы.
(Отметим попутно, что это позволяет на основании результатов главы 12 по-
строить доверительные интервалы для дисперсии о2, отвечающие довери*
тельной вероятности у).
6.	Доверительным интервалом для математического ожидания E(Yk) ро + ptlt,
соответствующего значению предикторной переменной г* и доверительной
вероятности у, является интервал
г; ±^(П-2^п(уБ
<	2	>
(14.12)
где £1+т (и - 2) — квантиль распределения Стьюдента (12.20) с и - 2 степенями
свободы, отвечающая вероятности
7.	При доверительной вероятности у доверительным интервалом для зависимой
переменной У*  0О + Pi h + будет интервал
410
14. Регрессионный и корреляционный анализ
у;±^(И-2)7ду;)+а2-
<	2	>
(14.13)
Отметим, что этот интервал шире, чем интервал (14.12), поскольку он должен
накрывать не постоянную (но неизвестную нам) величину 0О + 0] tk, а случайную
величину 0О + 0(^ + Zk.
Именно формулой (14.13) необходимо пользоваться, если мы при прогнозирова-
нии хотим построить доверительный интервал для фактического значения пока-
зателя (а не его математического ожидания).
Основными постулатами сформулированной выше модели были следующие для
случайных добавляющих Z, предполагалось равенство нулю математических
ожиданий и равенство дисперсий (см. формулу (14.3)). Второе предположение
может быть несколько ослаблено. Можно считать, что дисперсии неодинаковы,
но известны нам с точностью до постоянного сомножителя о2. В этом случае ус-
ловие (14.3) заменяется на следующее:
E(Z,) = 0, D(Zf) = — о2, i = l, 2,..., я,	(14.14)
wi
где Wj — известные постоянные, i = 1, 2,..., я; о2 — неизвестная постоянная.
В данном случае критерий, подлежащий минимизации, имеет вид:
Ro = 1>(У,. -Y’)2 = £^(Г, "(Ро +РЛ))2-	(14.15)
>=i	«=1
Оценки параметров 0О и 0; вычисляются по формулам:
р;
Ywi{iYwiYi	YwiYi -р’Е^л
i=l t=l i=l >=1	/	p* _ t=i
dwiti')2	1Lwi
i=l	1=1	/*1	1=1
(14.16)
а прогноз рассчитывается по той же формуле (14.9).
Из формул (14.14) и (14.15) следует, что наблюдения берутся с весами, обратно
пропорциональными соответствующим дисперсиям D(Zi'). При таком выборе кри-
терия оптимальные свойства оценок наименьших квадратов, сформулированных
выше, сохраняются.
Как будет следовать из результатов следующего раздела, формулы (14.8), (14.10),
(14.12), (14.13) принимают вид:
°2'	-(р; +Р.Ч))2-
П — L
п(г;) = 02
14.1. Одномерная линейная регрессия
411
[(₽; +р^)±^(п-2)7р(г;)1
V	2	У
г---------
(р- +р;^)± ti+y(n-2) р(у;)+о2* —
т V	wk)
где D(Yk) — оценка дисперсии D(Yk" ), получаемая из формулы для D(Yk ) путем
2	2*
замены о на о ;
о2 — — дисперсия случайной составляющей для k-ro наблюдения, для которого
величина считается известной.
Примеры
Пример 14.1. Рассмотрим регрессионную зависимость оборота розничной тор-
говли (млн. рублей) от численности населения (тыс. человек) 20 областей Рос-
сии (за январь-сентябрь 1990 года). Соответствующие статистические данные
приведены в табл. 14.1.
Таблица 14.1. Статистические данные за январь-сентябрь 1990 г. по
численности населения (t) и обороту розничной торговли (У), млн руб.
i	Область	ti	у	i	Область	t.	У,
1	Архангельская	1492	7550.7	и	Костромская	797	3723.8
2	Вологодская	1339	6914.6	12	Московская	6564	32 157.7
3	Мурманская	1017	11208.2	13	Орловская	907	5613.8
4	Ленинградская	1682	8952.8	14	Рязанская	1307	5911.0
5	Новгородская	738	4891.7	15	Смоленская	1157	7747.5
6	Псковская	820	3598.3	16	Тверская	1633	5565.7
7	Брянская	1465	5574.5	17	Тульская	1786	8654.1
8	Владимирская	1631	7218.2	18	Ярославская	1436	8419.4
9	Ивановская	1246	3969.2	19	Кировская	1613	8034.1
10	Калужская	1094	4842.0	20	Нижегородская	3697	19539.4
Оценка линейной регрессии (14.5) имеет вид:
У’ =444.73 +4.8231Т.
Соответствующий график представлен на рис. 14.2. На нем точками указаны
фактические статистические данные.
Остаточная сумма квадратов отклонений (14.6)	 6291.61 • 104, а оценка дис-
Персии (14.8) о2’  349.5 • 104.
412
14. Регрессионный и корреляционный анализ
Рис. 14.2. График линейной регрессии Y* - 444.73 + 4.82311
14.2. Проверка адекватности модели
одномерной линейной регрессии
Далее мы обсудим методы анализа точности описания имеющихся данных пред-
ложенной моделью (14.2), (14.3). Рассмотрим величину (У; -У) — отклонение
i-ro наблюдения от среднего наблюденных значений У. Сумма квадратов этих ве-
личин 22 (I7, - У )2, взятая по всем i от 1 до п, обозначается R%, называется полной
суммой квадратов отклонений относительно среднего и является мерой разброса
наблюденных значений Yj. Эту сумму можно разбить на две составляющие, со-
гласно формуле
ъ=i<Xi -n2 +iov -y)2-	(i417)
i«l
Здесь Yj - Yj" — это отклонение i-ro наблюденного значения от значения У/, вы-
числяемого согласно предлагаемой модели (14.5). Следовательно, квадрат этой
величины (У; - У,’)2 может служить мерой расхождения фактического и пред-
сказанного значений для i-ro наблюдения. Сумма этих квадратов по всем i, то
есть 22 (^ является мерой расхождения всех наблюденных значений от
уравнения регрессии (14.5). Она называется остаточной суммой квадратов от-
клонений или суммой квадратов отклонений относительно регрессии и обознача-
ется Rq:
Ro=£<Yj-Y;)2.	(14.18)
i-1
Величина (У/ -У) — это отклонение i-ro предсказанного значения от среднего F.
Сумма квадратов этих отклонений по всем i есть та составляющая общей суммы
14.2. Проверка адекватности модели одномерной линейной регрессии
41S
(14.17), которая объясняется регрессией (14.5). Она обозначается Rp и называет*
ся суммой квадратов отклонений, обусловленной регрессией'.
RP =t(Y:-Y)2 = tiY,-)2 -n(Y)2.	(14.19)
/-1	i-i
Таким образом, уравнение (14.17) может быть записано в следующей словесной
формулировке: полная сумма квадратов относительно среднего равна остаточ-
ной сумме квадратов (сумме квадратов относительно регрессий) плюс сумма
квадратов, обусловленная регрессией:
Ri-Rt+R,.	(14.20)
Отношение
Т?2=—= 1- —	(14.21)
называется множественным коэффициентом детерминации, a R — множествен-
ным коэффициентом корреляции. Они могут служить для оценки степени точно-
сти описания имеющихся данных уравнением регрессии (14.5), поскольку пока-
зывают долю разброса наблюдений около среднего значения F, которая
объясняется регрессией. Величина R2 принимает значение между 0 и 1. Если
уравнение регрессии идеально описывает данные, то У/ равно Y, для всех i и по-
этому Rq = 0, R2 = 1. Если р( = 0, то есть регрессия У на t отсутствует, то Y* равно
У для всех i и поэтому Rp = 0, R2 = 0.
Следующим важным анализом является графическое исследование остатков.
Остаток, соответствующий i-му наблюдению, определяется как разность
У; -У,*наблюденного и предсказываемого значений зависимой переменной. Так
как Z, = У; - (Ро + Р, t,), а У/ =PJ +P’f,, то остаток У, -У,* служит оценкой слу-
чайной составляющей Zf, имевшей место при i-м наблюдении. Если постулируе-
мая модель (14.2) верна, то остаток является несмещенной оценкой среднего
значения E(Zj), а квадрат его (У, -У,')2 — несмещенной оценкой дисперсии
D(Zj). Согласно постулируемой модели (14.3), математическое ожидание
E(Zt) = 0, а дисперсия D(Zd = о2 независимо от значения номера наблюдений i
и величины сопутствующей переменной t. Поэтому среднее значение остатка
Е(У, -Y*), вычисленное при условии, что зафиксировано данное значение Y*,
также равно 0. Следовательно, если построить график зависимости остатков
У, -У/ как функцию любого из перечисленных аргументов (i, t, Y’), то этот гра-
фик:
□	должен быть симметричным относительно оси абсцисс (условие E(Zi)  0);
□	должен иметь примерно постоянный разброс точек вдоль оси абсцисс (усло-
вие D(Zi) = о2).
Если это не так, то постулируемая модель (14.3) неверна и должна быть пере-
смотрена. Типичные ситуации, которые могут встретиться при анализе графика
остатков, изображены на рис. 14.3. Здесь по вертикальной оси откладываются
значения остатков, а по горизонтальной — значений какого-либо из следующих
аргументов: номера наблюдений i; предикторной переменной Г; прогнозируемой
переменной У/.
414
14. Регрессионный и корреляционный анализ
На графике области разброса остатков для наглядности заштрихованы. В случае
а) отклонений от постулированной модели не наблюдается. Остальные случаи
свидетельствуют о некорректности модели. Случай б) указывает на то, что дис-
персия случайной составляющей зависит от значений аргумента, то есть что
предположение D(Z,) = а2 нарушено. В случае в) остатки несимметричны отно-
сительно оси t, то есть пропущен линейный член модели. Случай г) свидетельст-
вует об отсутствии нелинейных членов модели (например, t2).
У - У* f
Рис. 14.3. Графики остатков
Последней процедурой проверки адекватности модели является проверка гипо-
тезы о незначимости регрессии, то есть об отсутствии линейной зависимости пе-
ременной У от предикторной переменной t. Точная формулировка задачи сле-
дующая: проверить гипотезу Н: У = ро + Z при альтернативе А: У = ро + t + Z,
Pi >0. Основой для проверки гипотезы является сумма квадратов Rp, обу-
словленная регрессией, и остаточная сумма квадратов /?0 относительно ре-
грессии. Критерием проверки служит отношение
Г=(я-2)-2-.	(14.22)
*Ч)
Малые значения критерия указывают на справедливость гипотезы, а большие
значения противоречат ей. Если гипотеза верна, то критерий имеет Е-распреде-
ление с 1 и п - 2 степенями свободы.
Определение 3. Плотность Е-распределения с Ц и 12 степенями свободы опреде-
ляется формулой
1	</ +1 > k !i /м	Jutk
/(*) = И < а Аг Ч-1	(4х + /2) 2 , Х>0, (14.23)
Г| — I Г1 — I
и; (2 J
где и 12 — параметры распределения, /(, /2 = 1, 2,...; Г(а) — гамма-функция (12.13).
14.2. Проверка адекватности модели одномерной линейной регрессии
418
Итак, областью принятия гипотезы для уровня значимости а является интерМЛ
[0;F-‘(l-a, 1,п-2)],	(14.24)
где F'1 (1 - a, 1, п - 2) — квантиль F-распределения с 1 и п - 2 степенями свобо-
ды, отвечающая вероятности 1 - а.
Если подсчитанное значение критерия (14.22) не попадает в области принятие,
то гипотеза отвергается. При этом, пользуясь длительное время этой критиче-
ской областью, примерно в 100(1 - а)% случаев будем принимать верную гипоте-
зу. Отклонение гипотезы свидетельствует о том, что член pt в модели отбрасы-
вать не следует, а принятие гипотезы — что этот член может быть отброшен.
Приведем условия, при которых возникает F-распределение. Пусть и Х2 — не-
зависимые случайные величины, имеющие х2 -распределения с Ц и 12 степенями
свободы. Тогда случайная величина
4 х2
имеет F-распределение с /( и 12 степенями свободы. Оказывается, что в рассмат-
риваемом случае (14.22) Rp и Rq взаимно независимы и имеют х2-распределение
с/| = 1и/2 = я- 2 степенями свободы.
Методы, применяемые для проверки адекватности модели, могут быть значи-
тельно усилены, если для одних и тех же значений предикторной переменной С/
проведено несколько (например, и,) наблюдений. Для каждого значения tlt кото-
рому соответствует несколько наблюдений, вычисляется величина
1 ("I У
sx 4	,
где Yij — значение зависимой переменной, соответствующей ;-му наблюдению
при данном фиксированном i,.
Затем определяется сумма таких величин
к-11*1-±(1?,.,
i=l /=1	\ /=1
«О
(14.25)
которая называется чистой ошибкой. Здесь и0 — число различных значений, при*
нимаемых предикторной переменной.
Название Re обусловлено тем, что различия в повторных испытаниях при одних
и тех же значениях предикторной переменной определяется целиком разбросом
(дисперсией) случайной составляющей Z.
Обозначим
«о
«е =ЕЯ- ~П0 =П'Пй,
где Zn, = п — общее число наблюдений.
Тогда, если для всех наблюдений дисперсия случайных составляющих одна и та
же (D(Zt) = а2), то отношение
(14.26)
416
14. Регрессионный и корреляционный анализ
является несмещенной оценкой дисперсии о2. Эта оценка несмещенная, если
даже математическое ожидание i-го наблюдения £(У;) не равно Ро + Pj i,, то есть
если модель некорректна. Теперь сумму квадратов относительно регрессии Ro
можно разложить на два слагаемых:
R0=R'+(R0-Re).	(14.27)
Второе слагаемое называется суммой квадратов, обусловленной неадекватно-
стью модели. Ее значение находится вычитанием Re из Ro и служит критерием
соответствия модели имеющимся данным.
Разбиение суммы квадратов относительно общего среднего на отдельные состав-
ляющие может быть оформлено в виде так называемой таблицы дисперсионного
анализа (табл. 14.2).
Таблица 14.2. Дисперсионный анализ в случае одномерной регрессии
Источник	Сумма квадратов	Число степеней свободы	Средний квадрат
Регрессия Отклонение от регрессии	of of	1 п-2	Д)/(п-2)|
в том числе: чистая ошибка неадекватность	of i of af	п, п - 2 - пг	(Д,-/%,)/(«-2-ne)J
Отклонение от среднего		п — 1	
Значение средних квадратов в таблице определяется в результате деления сумм
квадратов на число степеней свободы. Фигурные скобки показывают те средние
квадраты, отношение которых следует взять для проверки различных гипотез
(см. формулы (14.22) и (14.28)).
Если имеет место нормальное распределение и справедлива постулируемая мо-
дель (14.2), (14.3), то Re и Ro - Re взаимно независимы, причем обе имеют
X2-распределение: первая с пе степенями свободы, а вторая с (п - пе - 2) степеня-
ми свободы.
Следовательно, отношение соответствующих средних квадратов
f n„(£0 -Re)
(п-пе -2)Де’
имеет ^-распределение (14.23) с Ц = п - пе - 2 и /2 = пе степенями свободы. По-
этому при уровне значимости а областью принятия гипотезы о корректности мо-
дели является интервал
[0;£-1 (1-а; п-пе -2, пе)],
где £"' (р; п - пе -2, nf) — квантиль F-распределения с п - пе - 2 и nf степенями
свободы, отвечающая вероятности 1-а.
Выше был рассмотрен случай равных дисперсий. Если дисперсия для t-ro на-
блюдения равна а2/и>(, где а2 предполагается неизвестной, a wt — известной ве-
14.2. Проверка адекватности модели одномерной линейной регрессии
417
личиной, то для применения изложенных проверок необходимо сделать замену
переменных У,- на . Это вызывает замену
У,’ на .ДУ,* =7®Г(Ро +Р1Ч),
где коэффициенты и pj вычисляются по формулам (14.16). После такой за-
мене новые случайные величины будут иметь одинаковые дисперсии. Поэтому
для них остаются справедливыми все описанные выше процедуры проверки аде-
кватности модели.
Пример 14.1а. Продолжим рассмотрение нашего примера. Рассчитанные суммы
квадратов отклонений составляют: полная (14.17) R% = 820.935 • 10е, остаточная
(14.18) Ro = 62.916 • 106, обусловленная регрессией (14.19) Rp = 758.019 • 10е.
Множественный коэффициент детерминации (14.21) R2 = 0.9234, а множествен-
ный коэффициент корреляции R = 0.9609. Близость последнего к единице гово-
рит о значимости регрессии.
Проанализируем теперь график остатков в зависимости от населения области
(значения предикторной переменной) t. В табл. 14.3 представлены значения за-
висимой переменной фактические Yf и рассчитанные Y’, а также остатки Yt -Y*.
График остатков в зависимости от численности населения t представлен на
рис. 14.4. График выдан пакетом STATISTICA. Его вид свидетельствует о том,
что в первом приближении модель можно считать корректной.
Таблица 14.3. Анализ остатков
i	Область		X	х*	х-х‘
1	Архангельская	1492	7550.7	7640.76	-90.06
2	Вологодская	1339	6914.6	6902.83	11.77
3	Мурманская	1017	И 208.2	5349.80	5858.40
4	Ленинградская	1682	8952.8	8557.15	395.65
5	Новгородская	738	4891.7	4004.16	887.54
6	Псковская	820	3598.3	4399.65	-801.35
7	Брянская	1465	5574.5	7510.54	-1936.04
8	Владимирская	1631	7218.2	8311.17	-1092.97
9	Ивановская	1246	3969.2	6454.29	-2485.09
10	Калужская	1094	4842.0	5721.18	-879.18
И	Костромская	797	3723.8	4288.72	-564.92
12	Московская	6564	32 157.7	32 103.41	54.29
13	Орловская	907	5613.8	4819.26	794.54
14	Рязанская	1307	5911.0	6748.49	-837.49
15	Смоленская	1157	7747.5	6025.03	1722.47
16	Тверская	1633	5565.7	8320.82	-2755.12
17	Тульская	1786	8654.1	9058.75	-404.85
418
14. Регрессионный и корреляционный анализ
i	Область	t,	Y|	К	Yi-Yf
18	Ярославская	1436	8419.4	7370.67	1048.73
19	Кировская	1613	8034.1	8224.36	-190.26
20	Нижегородская	3697	19 539.4	18 275.65	1263.75
	Среднее		8504.3	8504.30	0
Нам осталось проверить гипотезу о незначимости регрессии, то есть о том, что
3( = 0. Примем уровень значимости а = 0.05. В нашем случае число данных п
равно 20. Поэтому квантиль F-распределения
F-1 (1-а; 1, n-2)= F"1 (0.95; 1,18)= 4.41.
Следовательно, область принятия гипотезы (14.24) [0; F"1 (1 - а; 1, и -2)] = [0; 4.41].
Подсчитаем значение критерия Фишера (14.22):
F= (и - 2) Rp/Ro = 18 • 758.019 • 106/62.916 • 106 = 216.87.
Поскольку значение критерия не попадает в область принятия, то гипотеза о
«значимости регрессии отклоняется.

Raw residuals vs. NASELEN
Raw residuals = .00033 - .0000 * NASELEN
Correlation: r = -.0000
i
I
I
8000
6000
4000
2000
0
-2000
-4000
0	1000	2000	3000	4000	5000	6000	7000
"’x. Regression
95% confld.
NASELEN
Рис. 14.4. График остатков для одномерной регрессии
I4.3. Многомерная линейная регрессия
1 общем случае имеется не одна, а несколько предикторных переменных (фак-
оров). Однако если пользоваться матричными обозначениями, то все формулы
жктически остаются теми же, что и для случая одной сопутствующей пере-
1енной.
14.3. Многомерная линейная регрессия
411
Обозначим число предикторных переменных т, а саму предикторную перемен-
ную tjj, где первый индекс i относится к номеру наблюдения (i = 1, 2,я), а это*
рой индекс j — к номеру предикторной переменной (J = 0,1,..., т), причем  1,
Прогнозирование значения зависимой переменной У на момент времени i  А
при значениях первой предикторной переменной второй tk2 и т. д. осуществ-
ляется по формуле
= Ро + Pi^.i +Рг^,2 +---+Ри^.и’	(14.29)
где Pg, Pi,... — оценки неизвестных параметров (коэффициентов).
Для нахождения оценок Ро....Р^ имеются данные п наблюдений. Для каждого
наблюдения известны значения предикторных переменных и зарегистрирован-
ное значение зависимой переменной. Обозначим их так:
□	У — значение зависимой переменной для i-ro наблюдения;
□	— значения 1-й, 2-й..............m-й предикторных переменных для <-Г0
наблюдения.
Кроме того, с каждым наблюдением связана случайная составляющая, величина
которой неизвестна. Пусть Z, есть неизвестная случайная составляющая для i-ro
наблюдения. Также неизвестными (но неслучайными) являются параметры (ко-
эффициенты) Pj, р2,..., Рт.
Используя введенные обозначения, можно так записать математическую модель
формирования значений зависимых переменных У(, У2,..., У„ в соответствующих
наблюдениях:
=Ро +РА1 + Р 2^1.2 + + РяЛ.и +
^2 =Ро +Р1^2,1 + РгГ2,2 +”’ + Ри^,т + ^2 •	(14.30)
УП = Ро +РЛ.1 +Р2^,2 + - + Р,Л.™ +Zn-
Здесь предполагается, что случайные величины Zb Z2,..., Z„ имеют нулевые мате-
2
матические ожидания, одну и ту же дисперсию о и некоррелированы:
£(Z,) = 0, О(У) = с2 i = 1,2, ...,н; C^Z^ ) = 0при i* j, (14.31)
где C(Z„ Zj) — ковариация (5.16) случайных величин Z( и Zj.
Перепишем условия (14.30) и (14.31) в матричном виде. Для этого введем сле-
дующие обозначения:
□	Y = (У, У2, ...,У„)Т — вектор-столбец порядка п зависимых переменных, i-й эле-
мент которого есть зависимая переменная У для i-ro наблюдения;
□	₽ = (Р0, р.,..., р„ )т — вектор-столбец неизвестных параметров (ковффицивН"
тов) порядка т + 1, J-й элемент которого Р; есть коэффициент при J-й пре-
дикторной переменной (для J = 0 полагают 6=1);
□	Z = (Zj, Z2, ..., Z„)T — вектор-столбец порядка п случайных составляющих, i-й
элемент которого есть случайная составляющая Z, в i-м наблюдении.
Кроме того, рассмотрим матрицу Т предикторных переменных порядка
п*(т +1), состоящую из п строк и т + 1 столбцов. Строки этой матрицы соот-
ветствуют различным наблюдениям, а столбцы — различным предикторным
20
14. Регрессионный и корреляционный анализ
еременным. Первая строка содержит значения предикторных переменных для
-го наблюдения, вторая — для 2-го наблюдения и т. д. Первый столбец матрицы
эстоит из единиц. Второй столбец состоит из значений первой предикторной
еременной в различных наблюдениях, третий — из значений второй предиктор-
ой переменной и т. п.
истема равенств (14.30) может быть теперь записана в матричных обозначени-
( следующим образом:
Y=Tp+Z.	(14.33)
словия (14.31) переписывается так:
£(Z) = 0, C(Z) = o2I,	(14.34)
ie C(Z) — ковариационная матрица (5.18) случайного вектора Z,
— единичная матрица порядка п.
пределение 4. Формулы (14.33) и (14.34) определяют модель многомерной ли-
’йной регрессии.
ажно подчеркнуть, что слово ««линейная» относится к параметрам {р,}. Предик-
фные переменные могут быть любыми нелинейными функциями известных фак-
иров. Например, если i — номер наблюдения, то t,(il = i, t/i2 = i2, = 1 /i, = sin(i),
i = ехр(-г) и т. д.
бозначим p вектор-столбец оценок неизвестных параметров, a Aj — век-
ip-строку (порядка т + 1) значений предикторных переменных для k-vo наблю-
ния:
р,т=(р;,р;,...,р;), Al=(i,tM...tk„).
тметим, что AtT, Aj, ..., А^ являются строками матрицы Т.
ормула (14.29) для прогнозирования значения зависимой переменной У*, соот-
тствующего вектору предикторных переменных AJ, принимает теперь вид
у;=а!р’.	(14.35)
iK и раньше, задача заключается в нахождении оценок коэффициентов р*, ко-
рые минимизируют остаточную сумму квадратов отклонений (14.18):
R. = £(Х< -Г)2	-А^Р’)2 = (Y-Tp*)T(Y-Тр*).	(14.36)
i*t	/«1
1алогично случаю одной предикторной переменной, для нахождения оценок
обходимо продифференцировать выражение (14.36) по pj, Р‘,.... PJ, и при-
внять производные нулю. Получающаяся система уравнений называется нор-
тьной. Используя правила векторного дифференцирования, находим, что она
1вет вид
14.3. Многомерная линейная регрессия
4S1
ТтТр’=ТтУ.	(14.37)
Предположим, что матрица ТтТ является невырожденной, то есть имеет обрат*
ную матрицу (ТтТ)-1. Умножая левую и правую части равенства (14.37) HI
(ТтТ)-1, получаем явное выражение для вектора р*:
р, = (ТтТ)1ТтУ.	(14.38)
Оценки, вычисляемые по этой формуле, называются оценками наименьших Квад’
ратов. Для получения их, следовательно, необходимо:
1)	найти произведение TTY;
2)	найти произведение матриц ТтТ;
3)	найти обратную матрицу (ТтТ)-1;
4)	вычислить произведение (ТГТ)”' TTY.
Наибольшую трудность вызывает нахождение обратной матрицы (ТтТ)'’. Отме-
тим, что обратные матрицы высоких порядков находятся обычно с помощью
специальных компьютерных программ.
Если математическая модель (14.33) и (14.34) действительно имеет место, то,
как и в случае одной предикторной переменной (опираясь на результаты шестой
и седьмой глав), можно доказать следующие свойства оценки наименьших квад-
ратов (14.38).
1.	Вектор р’ является несмещенной оценкой истинного вектора неизвестных па-
раметров р:
£(р’) = р.	(14.39)
2.	Оценки наименьших квадратов имеют наименьшую дисперсию среди всех не-
смещенных оценок неизвестных параметров, являющихся линейными функ-
циями наблюдений Уь У2,	У»-
3.	Несмещенной оценкой неизвестной дисперсии а2 является
о2* =--1—£(У дТр*)*,	(14.40)
п - т -1 ,=1
где Л/ - i-я строка матрицы Т.
Оценкой среднего квадратического отклонения служит а* = Ver2*.
4.	Ковариационная матрица вектора оценок р’ имеет вид:
С(р’) = о2(ТтТ)-*.	(14.41)
Напомним, что у-й диагональный элемент этой матрицы С равен дисперсии
О(Р* )оценки параметра р*,j = 0, 1,..., т. Для получения оценкиС(Р*)ковариаци-
онной матрицы С(р‘) необходимо в эту формулу вместо неизвестной дисперсии
ст2 подставить ее оценку а2', вычисляемую по формуле (14.40).
Прогноз, рассчитываемый по формуле (14.35), является несмещенной оценкой
истинного математического ожидания E(Yk) = Д^ р и имеет дисперсию
ДУ;) = а2л;'(ТтТ)-'д;.	(14.42)
которая является наименьшей среди всех дисперсий линейных прогнозов.
22
14. Регрессионный и корреляционный анализ
[одставляя ст2' вместо ст2, находим оценку D(Yk') этой дисперсии.
Свойства 1-4 имеют место при любых распределениях случайных составляю-
1их Zb Z2,	Z„. Если кроме того эти составляющие имеют стандартное тр-
альное распределение (4.13), то оценки метода наименьших квадратов совпада-
ет с оценками максимального правдоподобия, получаемыми на основе
лотности (6.42) при ц = Дт р, С = ст21. В этом случае дополнительно справедли-
ы следующие утверждения.
. Вектор оценок р* обладает наименьшими дисперсиями компонент среди всех
(линейных и нелинейных) несмещенных оценок вектора параметров р.
. Отношение ст2‘/ст2, где ст2 — неизвестная дисперсия, ст2' — ее оценка, вычис-
ляемая по формуле (14.40), имеет х2 -распределение (12.12) с п - т - 1 степе-
нями свободы. Доверительный интервал для неизвестной дисперсии ст2 при
доверительной вероятности у имеет вид:
^0; (п-тп-1)ст2’(х?_т(я-»г-1)Г1 J	(14.43)
где x(2_7(h-»2-1)— квантиль х2 -распределения с п - т - 1 степенями свобо-
ды, отвечающая вероятности 1 - у.
При доверительной вероятности у доверительным интервалом для матема-
тического ожидания Е(У4) = дТр зависимой переменной У*, соответствую-
щей вектору-строке значений предикторных переменных (1 tki ... tkm),
будет
(
А Д[р*±Г1±х(п-т-1)ст'(Л^(ТтТ)-1 Д4)2 .	(14.44)
При доверительной вероятности у доверительным интервалом для значения
зависимой переменной Yk - р + Zk, соответствующим вектору-строке пре-
дикторных переменных A* = (l tki ... tkm), будет
' -
AiTp'±r1±I(n-m-l)CT'(Aj'(TTT)-1At+l)2 .	(14.45)
<	2	J
ущественным условием рассматриваемой математической модели (14.33),
4.34) является равенство дисперсий и некоррелированность случайных состав-
1ющих Z, соответствующих различным наблюдениям. Это условие, как и слу-
1Й одной предикторной переменной, может быть ослаблено. Можно предполо-
ить, что ковариацио иная матрица вектора случайных составляющих является
гагональной и известна с точностью до постоянного сомножителя ст2. При этом
:ловия (14.34) заменяются на следующие:
£(Z) = 0; C(Z) = ct2W,	(14.46)
е постоянная ст2 предполагается неизвестной, а матрица W — известной и диа-
нальной:
14.3. Многомерная линейная регрессия

а»,1 о	...	О
О	гг>2*	•••	О
< о о -
(14.47)
В рамках этого условия случайные составляющие могут иметь различные ДИС-
Персии.
Оказывается, что рассматриваемый случай может быть сведен к ранее рассмот-
ренному, когда W = I. Для этого необходимо использовать матрицу
1 w"2 =	/ 1— 0	0	..	. 0 . 0	(14.48)
	< о	0	..		£
Если умножить теперь обе части выражения (14.33) на матрицу W 2, то полу-
чим
_1 _1 -1
W 2Y = W 2Тр+W 2Z.
Новая случайная составляющая W 2Z имеет, согласно формулам (6.36) И
(14.46), ковариационную матрицу
_1 _1 _1 1
C(W'2Z) = W'2C(Z)(W-2)T = W2a2WW'2 = o2I.
Следовательно, если вместо вектора наблюдений Y рассматривать вектор
(14.49)
а вместо матрицы предикторных переменных Т рассматривать W 2 Т, получаю-
щуюся из Т путем умножений г-й строки на
(14.50)
то приходим к прежней модели с постоянными дисперсиями. Для этой модели
справедливы все ранее выведенные формулы после замены в них, конечно, Y и Т
на (14.49) и (14.50). Если возвратиться к первоначальному вектору ¥, то форму*
лы (14.36), (14. 38), (14.40), (14.41), (14.42), (14.44) и (14.45) должны быть пере-
писаны соответственно в виде
!4
14. Регрессионный и корреляционный анализ
Ко =E^(y>-^₽*)2 =(Y-Tp-)TW-‘(Y-Тр’),	(14.51)
i=l
P, = (TtW-1T)-1TtW’1Y,	(14.52)
п2*=----2>,(У,-Д;ГР,)2>	(14.53)
n - m -1 ,=i
	C(P’) = g2(TtW“1T)-‘,		(14.54)
	D(y;) = o2Al(TTW-’Tr1Ap Ajp-±^(n-/n-l)o<(Aj'(TTW-1T)-1Ak)2 I	2	>		(14.55) (14.56)
с	1 > P^t^n-m-OoXA^rW-'Ty^+l/®*)2 2	>		(14.57)
j a2/wk — дисперсия k-го наблюдения, для которой значение wk считается
вестным.
>рмула (14.43) остается прежней.
качестве примера найдем выражения (14.52) и (14.55) для случая одной пре-
кторной переменной. Имеем:
...	.	_ — —	( V w- У tw,
T'w ‘T = TtW 2w 2T= J? ’	,
IE^®- E^®J
едовательно,
(T^^W’T)-1 =____________ E^®>
Е®-Е^ЧЕ^)Ч-Е^ E®<- )
P*=(TrW’T) 1 ttw*‘y =
=___________i__________f E y<® / E w< - E fiwi E Yiwi '
Еда.Е^Ч ЧЕ^.)21 E^Ey,®/.- -Е^®-Еу.®.- >
i соответствует ранее приведенным скалярным формулам (14.16).
iee, согласно формуле (14.55)
14.3. Многомерная линейная регрессия
426
= °2 V—V.2 1 zvl—~2tk£t>Wi +t^w>^
Ci	У'
Ywi -h
= _2	1	.	)
X wi	S wi S t?wi	- (X	)2
<	7
Последнее выражение также совпадает с приведенной ранее формулой для D(Yj ).
Пример 14.2. Продолжим рассмотрение примера 14.1, приняв в качестве зави*
симой переменной объем платных услуг населению (млн руб.), а в качестве пре-
дикторных переменных:
□	денежные доходы в месяц (за июнь) на душу населения t\ (рублей);
□	прожиточный минимум в месяц (рублей);
□	численность населения области к (тыс. человек).
В табл. 14.4. представлены соответствующие статистические данные.
Таблица 14.4. Статистические данные по 20 областям России
за январь-сентябрь 1990 г.
i	Область		^,2	1i.3	У,
1	Архангельская	1224.8	1111	1492	1769.6
2	Вологодская	1229.3	929	1339	2130.1
3	Мурманская	2411.7	1190	1017	2506.9
4	Ленинградская	1010.2	929	1682	1633.0
5	Новгородская	1209.5	822	738	1116.9
6	Псковская	880.4	729	820	792.9
7	Брянская	840.0	701	1465	1847.7
8	Владимирская	908.1	784	1631	1482.1
9	Ивановская	668.3	722	1246	1618.0
10	Калужская	897.3	776	1094	1207.8
11	Костромская	939.3	744	797	595.4
12	Московская	1058.5	884	6564	13 674.9
13	Орловская	1035.9	755	907	820.6
14	Рязанская	891.8	815	1307	1131.7
15	Смоленская	1198.0	754	1157	1257.7
16	Тверская	706.4	820	1633	1392.2
17	Тульская	1070.2	797	1786	1776.6
18	Ярославская	1259.7	770	1436	1988.8
26	14. Регрессионный и корреляционный анализ
i	Область		Аз	А>	у
9	Кировская	872.9	941	1613	1989.8
0	Нижегородская	890.3	739	3697	4720.3
счисления в пакете STATISTICA показали, что оценка линейной регрессии
4.29) имеет вид:
У* = -2236.32 + 1.38^ -0.59^2 + 2.12Г3.
статочная сумма квадратов отклонений (14.36) 7?0 = 6.885 • 106, а оценка дис-
рсии (14.40) а2* = 43.03-104.
4.4. Проверка адекватности модели
ногомерной линейной регрессии
роверка степени соответствия имеющихся данных постулируемой модели
4.33) и (14.34) для общего случая проводится так же, как для случая одной
«дикторной переменной (см. раздел 14.1). В частности, имеют место формулы
4.17)—(14.20), представляющие полную сумму квадратов отклонений относи-
льно среднего = Х(У; -Y )2 в виде двух составляющих: Rp = Y,(Yi -Y )2 —
чма квадратов отклонений, обусловленная регрессией, Ro = ^(Yt -У,*)2 — ос-
точная сумма квадратов (сумма квадратов относительно регрессии). Конечно,
я вычисления оценок У,* в общем случае необходимо пользоваться формулой
4.35). Отношение R2, вычисляемое по формуле (14.21), служит количествен-
й мерой точности регрессионной модели. Чем ближе оно к 1, тем модель точ-
е. Величина R называется множественным коэффициентом корреляции.
j графических проверок наибольшее значение имеет исследование остатков
у. -у; =у. -д7₽\	(14.58)
е 4} — г-я строка матрицы Т.
афик остатков может быть построен в зависимости от любого из следующих
гументов: номера наблюдения i, значения прогнозируемой переменной У,*, зна-
ния каждой предикторной переменной tj.
ли дисперсии всех наблюдений постоянны, как это следует из модели (14.34),
график остатков не должен иметь тенденции к изменению в зависимости от
)бого из перечисленных аргументов. Различные случаи, которые могут встре-
ться, были изображены на рис. 14.3 и рассмотрены в разделе 14.1.
сьма важно проверить гипотезу о незначимости регрессии Н.$} =0 V j = 1, ...,
то есть о равенстве нулю всех коэффициентов Pi, Р2, • • • > Р„ • Критерием про-
ржи является отношение
R„
F =(п-т-1)—^~,	(14.59)
R^m
областью принятия — интервал
[0,£-'(!-а, т п-т-1)],	(14.60)
14.4. Проверка адекватности модели многомерной линейной регрессии
427
где а — уровень значимости, F ‘(1-а, т, п-т-Г)— квантиль /-распределения
стип-ш-1 степенями свободы, отвечающая вероятности 1-а.
Предположим, что проведенные проверки не выявляли расхождения между
имеющимися данными и моделью. Может возникнуть сомнение в том, ЧТО ВСв
т + 1 коэффициентов р,, р2..Ря являются значимыми, то есть необходимыми
для предсказания значения зависимой переменной Y. Это очень важно, ПОСКОЛЪ*
ку введение каждой дополнительной предикторной переменной в модель вызы-
вает дополнительные затраты, связанные со сбором статистических данных ДЛЯ
оценки соответствующих параметров и с получением значений этой переменной
для прогнозируемой ситуации. Проверим, например, гипотезу о том, что  О,
то есть что т-я предикторная переменная не оказывает значимого влияния на за-
висимую переменную (незначима). Отметим, что т-я переменная выбрана ЛИШЬ
для простоты обозначений (путем перенумерации можно сделать любую пере-
менную последней).
Гипотеза Н: рт = 0 может быть проверена двумя способами. При первом способе
поступают так. Для параметра ря находят оценку и оценку дисперсии D(pJ,),
равную Z)(P’ ) = cm+i, т+1 . Здесь с m+t, m+i элемент ковариационной матрицы С,
стоящий на пересечении последней (т + 1)-й строки и последнего (т + 1)-ГО
столбца (см. формулу (14.41), где вместо неизвестной величины о2 следует под-
ставлять о2*, вычисляемую по формуле (14.40)). В случае справедливости гипо-
тезы Н: р„ =0 отношение (р;„ )2/5(р^) = (Р„ )2/cro+i. га+) имеет распределение
Фишера с одной и п - т - 1 степенями свободы. Для уровня значимости а обла-
стью принятия гипотезы является интервал
[0,Е"’(1-а, 1, п-т-1)1	(14.61)
где /"’ (1 - a, 1, п - т-1) — квантиль F-распределения с 1 ия - и - 1 степенями
свободы, отвечающая вероятности 1-а.
Второй способ проверки гипотезы Н: ри =0 является более общим и применяет-
ся во многих случаях. Гипотеза проверяется в два этапа. Вначале рассматривает-
ся модель регрессии, включающая все т предикторных переменных. Для ЭТОЙ
модели находится сумма квадратов отклонений относительно регрессии
Ro = £(У,। - Y’)2. На втором этапе рассматривается та же модель с условием
р,„ = 0, то есть при наличии только (т - 1 )-й предикторной переменной. Для но-
вой модели также находится сумма квадратов отклонений относительно регрес-
сии, которую обозначим через R'o. Критерием проверки гипотезы является отно-
шение Фишера
/ = А(п-т-1)(Я'о -Яо).	(14.62)
Ко
Если гипотеза верна, то этот критерий имеет /-распределение с1ип-т-1 сте-
пенями свободы. Областью принятия гипотезы при уровне значимости а будет
интервал (14.61).
Может случиться, что следует проверить гипотезу о незначимости сразу не-
скольких предикторных переменных. Для определенности положим, что тако-
выми являются / последних переменных ........Р„.	Как и прежде, гипотезу
128
14. Регрессионный и корреляционный анализ
доверяем в два этапа. Вначале вычисляем сумму квадратов отклонений от ре-
рессии 7?0 для полной модели с т предикторными переменными. Затем вычи-
:ляем эту же сумму для новой модели, содержащей только т - I предикторных
временных. Обозначим последнюю сумму R'rj. Критерием проверки гипотезы Н:
'т./+1 = 0,..., Р,„ =0 при альтернативе отсутствия этих ограничений служит отно-
цение Фишера
F = -L(w_m_i)(7?' -Ro).	(14.63)
/л0
£сли гипотеза верна, то это отношение имеет /’-распределение с/ип-ти-1 сте-
рнями свободы. Областью принятия гипотезы при уровне значимости а будет
[нтервал
[0,/"‘(1-а, /, п-т-1)].	(14.64)
’ассмотренная гипотеза является частным случаем более общей линейной гипо-
езы. Последняя предполагает наличие / линейных соотношений между неиз-
вестными параметрами модели Ро, Р(, Р2, •••> ₽„ и описывается следующим обра-
ом. Пусть Н — известная матрица порядка 1х(т +1). Предполагается, что
[атрица НТН является невырожденной, и условие (14.34) выполнено. Необхо-
,имо проверить гипотезу Н: Y = Тр + Z при ограничениях Нр = 0 при альтерна-
иве A'. Y = Тр + Z без всяких ограничений на параметры.
1оследовательность проверки этой гипотезы такая же, как и прежде. Вначале
досматривается альтернатива и вычисляется остаточная сумма квадратов от-
лонений от регрессии 7?0 = £(У, - У,*)2, затем рассматривается гипотеза. Ограни-
ение нр=о накладывает I независимых связей на неизвестные коэффициенты
0, Р1,..., Ря. Используя их, можно выразить одни коэффициенты через другие и
результате вместо т + 1 получить т + 1 - I неизвестных коэффициентов. Соот-
етственно этому вместо т будет т - / предикторных переменных, а вместо мат-
ицы Т порядка пх(т +1) будет фигурировать некоторая другая матрица поряд-
а пх(т + 1 - /). Решая теперь задачу наименьших квадратов для этих новых
l + 1 - / неизвестных параметров, найдем остаточную сумму квадратов отклоне-
ия от регрессии, которую обозначим Ro. Составим соотношение (14.63). Если
ипотеза верна, то отношение имеет ./-распределение с / и п - т + 1 степенями
вободы. Областью принятия гипотезы является интервал (14.64).
[ак и в одномерном случае, для проверки гипотезы об адекватности модели мо-
ут использоваться более сильные методы, если имеются повторяющиеся наблю-
ения. Повторяющимися считаются наблюдения, характеризующиеся одина-
овыми значениями всех предикторных переменных, то есть те, для которых
троки А Г матрицы Т совпадают. В этом случае сумму квадратов относительно
егрессии 7?0 можно представить в виде двух составляющих: обусловленных чис-
ой ошибкой Re и неадекватностью модели 7?0 - Re. Дисперсионный анализ прово-
ится, как это показано в табл. 14.5, аналогичной табл. 14.2 (последняя получается
з нее при т = 1). При этом остаются справедливыми формулы (14.25)-( 14.27),
риведенные для одномерного случая. Гипотеза об адекватности модели прове-
яется аналогично предыдущему для критерия Фишера
F = ,n^~R^ ,	(! 4,65)
(п-т-п, -1)7?,
14.4. Проверка адекватности модели многомерной линейной регрессии
42»
при области принятия гипотезы
[0,F-l(l-a,n-m-n, -1) пе].	(14.66)
При попадании критерия (14.65) в интервал (14.66) гипотеза принимается. При*
мер изложенного дисперсионного анализа приведен ниже.
Таблица 14.5. Дисперсионный анализ в случае многомерной регрессии
Источник	Сумма квадратов	Число степеней свободы	Средний квадрат	
Регрессия Отклонение от регрессии		т п - т - i	Д)/(л - т -1)	
в том числе: чистая ошибка неадекватность	о:' I а$ а?	п, п - т - 1 - пг	V".	
			п - т -1 - п.	
Отклонение от среднего		п - 1		
Выше рассматривается случай одинаковых дисперсий, соответствующий модели
(14.34). Предположим теперь, что эта модель заменяется на модель (14.46). Для
того чтобы воспользоваться полученными результатами, необходимо провести
следующие преобразования:
У, -> (то есть Y -> W 2 Y),
(то есть Т -> W 2Т).
Теперь для этих новых переменных остается справедливым все сказанное в на-
стоящем разделе.
Пример 14.2а. Продолжим рассмотрение примера 14.2. Рассчитанные суммы
квадратов отклонений составляют: полная (14.17)	= 151.068 • 106, остаточная
(14.18) 7?о = 6.885 • 106, обусловленная регрессией (14.19) Rp = 144.183 • 10е. Мно-
жественный коэффициент детерминации (14.21) R2 = 0.95422, а множественный
коэффициент корреляции R = 0.97695. Близость последнего к единице говорит о
значимости регрессии.
Проанализируем теперь остатки. В табл. 14.6 представлены значения зависимой
переменной — фактические Y{ и рассчитанные У,*, а также остатки Yt - Y*. Гра-
фик остатков в зависимости от номера наблюдения i представлен на рис. 14.5.
Его вид не противоречит постулированной модели.
Таблица 14.6. Анализ остатков для модели многомерной регрессии
i	Область	у	к	у-У
1	Архангельская	1769.6	2096.7	-327.1
2	Вологодская	2130.1	1779.4	350.7
3	Мурманская	2506.9	2549.5	-42.7
4	Ленинградская	1633.0	2234.5	-601.5
эо
14. Регрессионный и корреляционный анализ
	Область	Y-	Y-	Y, -Yt
5	Новгородская	1116.9	487.0	629.9
6	Псковская	792.9	256.6	536.3
7	Брянская	1847.7	1568.0	279.7
8	Владимирская	1482.1	2001.8	-519.7
9	Ивановская	1618.0	895.5	722.5
I0	Калужская	1207.8	855.5	352.3
.1	Костромская	595.4	280.3	315.1
2	Московская	13 674.9	12 594.7	1080.2
3	Орловская	820.6	630.8	189.8
4	Рязанская	1131.7	1298.2	-166.5
5	Смоленская	1257.7	1357.0	-99.3
6	Тверская	1392.2	1758.7	-366.5
7	Тульская	1776.6	2527.5	-750.9
8	Ярославская	1988.8	2021.4	-32.6
9	Кировская	1989.8	1920.6	69.2
0	Нижегородская	4720.3	6339.2	-1618.9
	Среднее	2272.7	2272.7	0
From: Predicted & Residual Values (zad1 .sta)
Dependent variable. Y
8000
еооо
4000
5 2000
8
а
о
-2000
-4000
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
Рис. 14.S. График остатков для многомерной регрессии
14.5. Общая модель регрессии
4>1
Нам осталось проверить гипотезу о незначимости регрессии с помощью крите-
рия Фишера (14.59). Примем уровень значимости а = 0.05. В нашем случае число
данных п равно 20, а число предикторных переменных в модели т = 3. Поэтому
квантиль F-распределения £'*(1-а; щ п-т~1)= F~l(0.95; 3, 16) = 3.24. Следом-
тельно, область принятия гипотезы (14.60) [0; F'1 (1-a; т, п - т -1)] = = [0; 3.24].
Подсчитаем значение критерия Фишера (14.59):
F= (п - т - 1) Rp/(m • R^ = 16 • 144.183 • 106/(3 • 6.885 • 106) = 111.68.
Поскольку значение критерия не попадает в область принятия, то гипотеза О не-
значимости регрессии отклоняется.
Оказывается, что вторая предикторная переменная t2 (прожиточный минимум в
месяц) является незначимой. После ее устранения окончательная модель линей-
ной регрессии имеет вид:
У* =-2552.88 +1.231, + 2.11t3.
В этой модели обе предикторные переменные высоко значимы.
Более подробный анализ линейных регрессионных моделей приведен в камлью-
терном практикуме №21.
14.5. Общая модель регрессии
Как и ранее, мы будем интересоваться предсказанием значения зависимой пере-
менной У. Однако теперь будет предполагаться, что: 1) предикторные перемен-
ные являются случайными величинами, которые будем обозначать Xit Х2,.... Х„',
2) зависимость У от Хь Х2,..., Хт в общем случае не является линейной; 3) кроме
случайных величин Хь Х2,..., Хт на У могут влиять и другие случайные величи-
ны, значения которых не фиксируются и которые называются случайными со-
ставляющими. Задача заключается в том, чтобы найти такую функцию
g(Xit Х2,..., Х,„), называемую предиктором, которая обеспечивает минимум сред-
неквадратической ошибки
£((У-£(Х„Х2...X,,,))2).	(14.67)
Следовательно, зафиксировав значения предикторных переменных Х\, Х2,..., Хя,
прогноз значения зависимой переменной будет осуществляться по формуле
Y* =g(Xt,X2....Х,„).	(14.68)
Теорема 14.1. Пусть X = (Хь Х2,..., Хт)Т, х = (хь х2.хп)г и М(х) = E(Y| X = х) —
условное математическое ожидание У при зафиксированном значении х вектора
предикторных переменных X. Тогда минимальное значение критерия (14.67)
достигается для функции
g(x) = M(x) = £(K|X = x).	(14.69)
Доказательство
Во-первых, используя свойства математического ожидания, установим следую-
щие тождества:
£((У - M(X))(g(X)- М(Х))) = £(£((У - M(X))(g(X) -М(Х))| X - х)) -
= £((g(X) - А/(Х))£((У - Л/(Х))| X = х)) = £((g(X)- Л/(Х))(Л/(Х) - Л/(Х))) -0.
Теперь для критерия (14.67) сделаем следующие преобразования:
432
14. Регрессионный и корреляционный анализ
E((Y -g(X))2) = £((У -М(Х) + M(X)-g(X))2) =
= E((Y - М(Х))2 -2(Y - M(X))(g(X) - М(Х)) + (g(X)- М(Х))2) =
= E((Y - М(Х))2)+ £((g(X)- М(Х))2) £ E((Y -М(Х))2).
Следовательно, нижняя грань для E((Y - g(X))2) достигается для функции
g(X) = M(X).	□
Определение 5. Условное математическое ожидание М(х) = E(Y| X = х) зависи-
мой переменной У, рассматриваемое как функция предикторных переменных
х = (хь х2.хт), называется функцией регрессии У на X.
Итак, наилучшим предиктором (14.68) в случае критерия (14.67) является функ-
ция регрессии М(х).
Отметим, что согласно формуле (6.19)
£(У) = £(М(Х)).	(14.70)
Поэтому зависимую переменную У можно представить в виде
Y =Y'+ Z = М(Х)+Z,	(14.71)
где Z — случайная составляющая, имеющая нулевое математическое ожидание:
£(Z) = 0.
Определение 6. Говорят о линейной регрессии У на X, если функция регрессии яв-
ляется линейной относительно предикторных переменных х = (xit х2,..., х,„)т:
М(х) = р0 +р!х1 +р2х2 + ...+рихи.	(14.72)
В противном случае регрессия называется нелинейной.
Определение 7. Условной дисперсией случайной величины У при условии, что X = х,
называется
£>(У| X = х) = £((У - М(Х))21X = х).
Внутригрупповой дисперсией зависимой переменной У называется математиче-
ское ожидание ее условной дисперсии:
о2.х = £(£>(У| X)) = £((У - ЛГ(Х))2).	(14.73)
Межгрупповой дисперсией называется дисперсия случайной величины Л/(Х):
= £((М(Х) - £(М(Х)))2).	(14.74)
Имеет место следующее разложение дисперсии зависимой переменной У:
£>(У) = £((У - £(У ))2) = £((У - М(Х) + М(Х) - £(У ))2) =
= £((У-М(Х))2) + £((М(Х)-£(М(Х)))2) = о2,х	(14.75)
Определение 8. Корреляционным отношением называется
ц2.х = <s2M/D(Y ) = 1 - ст2 Х/П(У).	(14.76)
По определению 0 <г]2х < 1. Из разложения (14.75) следует, что дисперсия за-
висимой переменной D( У) складывается из отклонений относительно регрессии
ст2 х и отклонений а2м, обусловленных регрессией. Если прогноз зависимой пе-
ременной точный, то Оу х = 0 и корреляционное отношение равно единице. Если
наоборот, информация о значениях предикторных переменных ничего не дает, то
Л/(х) = £(У| X = х) = £(У), Оу х = £>(У)и корреляционное отношение равно нулю.
14.5. Общая модель регрессии
433
Таким образом, корреляционное отношение представляет собой меру связи меж-
ду зависимой и предикторными переменными, или меру точности прогноза.
Важным частным случаем является линейная регрессия (14.72). Так как критерий
(14.67) минимален, когда g(x) — функция регрессии, то последнюю можно искать
путем рассмотрения общей линейной функции
g(x1,x2,...,xm) = p0 + p1x1 + р2х2 +... + рихи
и определять параметры {0Д путем минимизации (14.67).
Введем для дальнейшего следующие обозначения:
□	С — ковариационная матрица предикторных переменных X = (Xj, Х2,..., Х„)г,
предполагаемая невырожденной, так что обратная ей матрица С-1 существует;
□	©о — вектор-'столбец ковариаций между Y и X = (Хь Х2.Хт)т;
□	₽ = (Р1.Р2.МТ — вектор-столбец оптимальных значений параметров
Pi> Р2,..., Рт.
Преобразуем теперь критерий (14.67), используя равенства (14.72), £(У) = р0+рт£(Х)
и (рт(Х-£(Х)))2 = рт(Х-£(Х))(Х-£(Х))тр:
E((Y - М(Х))2 ) = £((У -(Ро + ptX, + ₽2Х2 + ... + ртХи ))2) =
= £((У - р0 - Рт X)2 ) = £((У - £(У ) - рт(Х - £(Х)))2 ) =
= £((У -£(У))2 -2(У -£(У))рт(Х-£(Х)) + (рт(Х -£(Х)))2 ) =
= £((У-£(У ))2) -2 рт£((У-£(У ))(Х- £(Х))) + рт(£((Х - £(Х))(Х -£(Х))Т ))р -
= £>(У)-2рто2+ ртСр.
Итак, подлежащий минимизации критерий имеет вид
£((У -М(Х))2) = £>(У)-2рто2 + ртСр.
Взяв векторную производную по р = (р0, Pt,..., Р„, )т и приравняв ее нулю, полу-
чаем следующую систему нормальных уравнений в матричном форме:
-2о2 + 2Ср=0.
Предполагая, что ковариационная матрица С является невырожденной, то есть
имеющей обратную матрицу С-1, находим выражение для вектора параметров
линейной регрессии Р = (Ро, Pt.Pm):
P = C1g2.	(14.77)
Последний неизвестный параметр Ро находится из условия (14.70):
р0 = £(У)-рт£(Х).	(14.78)
Итак, в случае линейной регрессии имеем выражение:
М(Х) - £(У) + (о2 )ТС’* (X- £(Х)).	(14.79)
Пример 14.3. Рассмотрим случай одной предикторной переменой (т = 1). Обо-
значим £>(Х) и ах дисперсию и среднее квадратическое отклонение единствен-
ной предикторной переменной X; =y]D(Y) среднее квадратическое отклонение
Ю4
14. Регрессионный и корреляционный анализ
1ависимой переменной Y; С(Х, У) и р ковариацию и коэффициент корреляции
лежду предикторной и зависимой переменными X и Y. В данном случае:
Х = (Х), ₽ = (&)• C = (D(X)), С'1 =(D(X))-1, о?=С(Х,У)
4 ПОЭТОМУ
р, = С(Х, У)/Л(Х), р0 = E(Y )-С(Х, У)£(Х)/О(Х).
Следовательно, в случае линейной регрессии прогноз зависимой переменной
эсуществляется по формуле
У’ = £(У) + р-^(Х-£(Х)).	(14.80)
Из последней формулы видно, что если коэффициент корреляции р положите-
лен, то в среднем большим значениям предикторной переменной X отвечают
большие значения зависимой переменной Y, и наоборот. В связи с этим говорят
о положительной (а при р < 0 — об отрицательной) корреляции между случай-
ными величинами У и X.	□
Формула (14.80) позволяет дать важную интерпретацию коэффициенту корре-
ляции р. Найдем дисперсию Д(У’) наилучшего линейного предиктора У’ зави-
симой переменной У, определяемого формулой (14.80), и сравним ее с диспер-
сией У. Согласно формуле (14.80), имеем:
/	ч Z	ч / ч2
D(Y')=D £(У) + р-^(Х-£(Х)) =£> р —X = р— D(X) = р2О(У ).
\	°Х	J к °х J к /
Следовательно, р2 = D(Y*)/D(Y), то есть квадрат коэффициента корреляции
равен доле дисперсии зависимой переменной У, приходящейся на линейный
предиктор У*.
Теперь найдем корреляционное отношение (14.76) в случае одномерной линей-
ной регрессии (14.72): М(х) = Ро + PjX. Согласно формуле (14.74), имеем:
о2м =£((М(Х)-£(М(Х)))2) = £((Ро +pfX-Po ~Р,£(Х))2) =
= р2О(Х) = (С(Х,У))2/О(Х).
Итак,
, _ at _(ЭДУ))2 _р2Р(Х)Р(У)	2
D(Y) D(X)D(Y) D(X)D(Y) Р ’
Итак, в случае линейной регрессии корреляционное отношение равно квадрату
коэффициента корреляции.
Оказывается, что такую же форму (14.80) будет иметь оптимальный (в смысле
критерия (14.67)) линейный предиктор при любой форме регрессионной зависи-
мости У от X.
В заключение этого раздела отметим, что изложенные методы предсказания при-
менимы, когда известны теоретические математические ожидания, дисперсии
и ковариации, то есть изложенные подходы имеют вероятностный характер.
В противном случае мы имеем дело со статистическими задачами. Здесь можно
применять результаты первых четырех разделов, а также материал следующего
пя'гяйпа.
14.6. Статистическое оценивание корреляционных зависимостей
4U
14.6.	Статистическое оценивание корреляционных
зависимостей
В десятой и последующих главах рассматривались статистические задачи, СМ*
занные с одномерными случайными величинами. В настоящем разделе будут
рассмотрены методы обработки статистических данных о двумерных случайных
величинах. При этом основное внимание уделяется ковариации и коэффициенту
корреляции. Излагаемые методы применимы и для многомерных случайных ве-
личин, поскольку позволяют оценивать ковариацию и коэффициент корреляции
для любой пары компонент этих величин.
Итак, пусть (X, У) — двумерная случайная величина и (xit yi), (х2, у2),..., (хЯ1 ул) —
зарегистрированные ее значения в п наблюдениях. На основании этих данных
математическое ожидание, моменты и дисперсия компонент X и У оцениваются
по формулам (11.11) и (11.13). Оценивание характеристик двумерного распреде-
ления для (X, У) производится по формулам главы 5. При этом зарегистрирован-
ные значения трактуются как возможные значения (х,, у}) двумерной случайной
величины (X, У) и каждому такому значению приписывается вероятность 1/п.
В частности, смешанный момент (5.15) и ковариация (5.16) оцениваются по фор-
мулам:
Е’(ХУ) = - У Х,У„ С’(Х, У) = E’(XY)- E‘(X)E'(Y),	(14.81)
п ,=1
_	1 «	- 1А
где £*(Х) = Х = — УХ,, E‘(Y) = Y =-УУ( — оценки математического ожида-
П 1=1	п ,=1
ния компонент X и У.
Вычисленная по приведенным формулам оценка С*(Х, У) является смещенной.
Как показывает следующая теорема, смещение можно легко устранить.
Теорема 14.2. Несмещенной оценкой смешанного момента £(ХУ) является оцен-
ка Е’(ХУ), вычисляемая по формуле (14.81). Несмещенной оценкой ковариации
С(Х, У) является
С(Х,У) = Г(ХУ)-—1_£х,.£Уг	(14.82)
и(и-1)м , j?i
Доказательство
Несмещенность первой оценки устанавливается легко:
£(£'(ХУ )) = е(- У Х,У, 1 = - У Е(Х^ ) = - У E(XY ) = E(XY )
V п 1=1	) п ,=!	п ы
Оказывается, что С*(Х, У) является смещенной оценкой ковариации. Смещение
вызвано тем, что математическое ожидание произведения оценок £*(Х)Е‘(У) не
равно произведению их математических ожиданий:
£(£*(Х)£,(У)) = £|[1УХ,
«И.-1
=44£fz*^+*<i'<T|-
к”	})
= 4ЯЕE{XiYj)+ £(Х,У,)] = 4 tflE(X)E(Y) + Е(ХУ)1 -
п 1-1 к/) п
136
14. Регрессионный и корреляционный анализ
= — E(X)E(Y) + -E(XY)^E(X)E(Y).
п	п
3 отличие от этого в формуле (14.82) произведение X,- У, с одинаковыми индек-
:ами i не встречается, поэтому для математического ожидания имеем:
4-Лгч ££ s £(Х'У> >=
1)1=1	J Tl(ri 1) i=l y*t
=	£ I E(X)E{Y) = E(X)E(Y).
я(я-1)">»>
Следовательно, формула (14.82) дает несмещенную оценку ковариации. □
Этметим, что часто для оценки ковариации используют формулу, эквивалент-
ную (14.82):
С(Х,У) = ^-£(Х;-Х)(У;-У),	(14.83)
п -1 ,=|
гдеХ=А^Х,,У
п	п м
Коэффициент корреляции (5.19) оценивается по формуле
р-=С(ХУ),	(14.84)
где S2X,S2 — оценки (11.3) дисперсии компонент X и Y:
Я =-Ц£(Х,-Х)2.5?	-п!.
п -1 ,=1	п -1 i.1
Имея оценки X, Y, Sx, Sy, р* неизвестных параметров Е(Х), E(Y), ах, Сту, р од-
номерной модели линейной регрессии (14.80), можно подставить их вместо по-
следних. В результате получаем эмпирическую (выборочную) линию регрессии-.
.	J(X, -X)(Yt -У)
У’ =Y +p'^-(X-X) = Y +	---- ------(Х-Х).	(14.85)
°*	£(х,. -*)2
i=i
Это в точности совпадает с оценками (14.7), которые дает метод наименьших
квадратов для одномерной линейной регрессии.
Компьютерный практикум № 21. Оценка параметров
модели линейной регрессии в пакете STATISTICA
Цель и задачи практикума
Целью практикума является приобретение практических навыков по оценке па-
раметров модели линейной регрессии в пакете STATISTICA.
Задачами практикума являются расчет параметров и оценка качества моделей
одномеоной и многомерной линейной регрессии.
Компьютерный практикум №21. Оценка параметров модели линейной регрессии в пакете STATISTICA
437
Необходимый справочный материал
В пакете STATISTICA представлены различные методы регрессионного ана-
лиза, включая многомерную линейную и нелинейную регрессии. Расчет линей-
ной регрессионной модели в пакете STATISTICA выполняется в модуле Multiple
Regression. Оценка параметров нелинейной регрессии в пакете STATISTICA
производится в модуле Nonlinear Estimation. Запуск нужного модуля осуществля-
ется в окне переключателя модулей STATISTICA Module Switcher.
Реализация и результаты выполнения задания
В настоящем практикуме решаются две задачи: расчет модели одномерной ли-
нейной регрессии и расчет модели многомерной линейной регрессии. При этом
будем использовать отчетные данные по 31 области Европейской части России
за январь-сентябрь 1999 г., представленные в табл. 14.7. Данные получены из ста-
тистического сборника «Социально-экономическое положение России: январь-
сентябрь 1999 года. — М.: Российское статистическое агентство, 1999». Данные
последнего столбца таблицы (инвестиции в основной капитал) взяты за 1998 г.
(см. Российский статистический ежегодник: Стат. сб. / Госкомстат России. — М.,
1998).
Таблица 14.7. Социально-экономические показатели России в период
январь-сентябрь 1999 г.
№	Область	Численность населения, тыс. чел.	Число предприятий и организаций	Оборот розничной торговли, млн руб.	Поступление налогов и сборов в бюджет, млн руб.	Объем промышленного производства, млн руб.	Инвестиц ии в основной капитал, млн руб.
1	Архангельская	1492	17 636	7550.7	3395.6	19 609	2508
2	Вологодская	1339	19 023	6914.6	4803.2	36 594	2837
3	Мурманская	1017	15 736	И 208.2	4508.4	24 926	2154
4	Ленинградская	1682	25 814	8952.8	4410.3	23 011	4437
5	Новгородская	738	13 000	4891.7	1567.3	10 247	1079
6	Псковская	820	13 014	3598.3	1134.7	3596	868
7	Брянская	1465	15 926	5574.5	1780.4.	6785	948
8	Владимирская	1631	20 974	7218.2	2802.1	16 161	2220
9	Ивановская	1246	17 082	3969.2	1250.5	6758	879
10	Калужская	1094	18 486	4842.0	1894.2	7988	1691
И	Костромская	797	12 952	3723.8	1299.6	6418	1255
12	Московская	(>564	104 392	32 157.7	20 054.9	56 443	13 363
138
14. Регрессионный и корреляционный анализ
№	Область	Численность населения, тыс. чел.	Число предприятий и организаций	Оборот розничной торговли, млн руб.	Поступление налогов и сборов в бюджет, млн руб.	Объем промышленного производства, млн руб.	Инвестиции в основной капитал, млн руб.
13	Орловская	907	11 728	5613.8	2464.3	6844	1215
14	Рязанская	1307	21 628	5911.0	2365.5	И 245	1721
15	Смоленская	1157	16 874	7747.5	1703.3	13 172	1056
16	Тверская	1633	28 230	5565.7	2426.9	12 881	2293
17	Тульская	1786	23 165	8654.1	3051.4	19 461	2342
18	Ярославская	1436	24 121	8419.4	4346.7	22 636	2382
19	Кировская	1613	24 392	8034.1	2844.1	16 126	1623
20	Нижегородская	3697	49 246	19 539.4	9418.4	50 927	7620
21	Белгородская	1484	21 689	9124.9	3195.8	21 893	3683
22	Воронежская	2486	31 617	14 056.6	3441.8	16 532	3133
23	Курская	1336	17 523	7471.7	2219.3	13 676	2586
24	Липецкая	1248	13 982	8120.1	2864.6	27 638	2497
25	Тамбовская	1292	16 120	7082.4	1538.1	6234	1181
26	Астраханская	1029	14 385	5269.3	1874.1	6701	1912
27	Волгоградская	2701	51 174	И 824.9	5087.2	28 284	5068
28	Пензенская	1549	17 989	5791.8	1997.1	9199	1960
29	Самарская	3309	61 549	48 848.4	14 961.1	76 228	8930
30	Саратовская	2724	44 602	И 799.1	5012.3	21 215	5314
31	Ульяновская	1483	17 323	7344.4	2556.4	14 552	1996
Задача № 1: Одномерная регрессия
Первая задача практикума заключается в расчете модели одномерной линейной
регрессии (14.5), характеризующей зависимость числа предприятий и организа-
ций области (У) от численности населения (Г).
Расчеты будем выполнять в модуле Multiple Regression. Для запуска данного мо-
дуля в окне переключателя модулей STATISTICA Module Switcher (рис.10.4) отме-
тим строку Multiple Regression и нажмем кнопку Switch to. В результате откроется
стартовое окно модуля, представленное на рис. 14.6.
Компьютерный практикум № 21. Оценка параметров модели линейной регрессии в пакете STATISTICA	4N
Рис. 14.6. Стартовое окно модуля Multiple Regression
Ввод исходных данных
Ввод данных выполним в следующей последовательности:
1)	закроем стартовое окно Multiple Regression кнопкой Cancel;
2)	с помощью команды прикладного меню File—New Data откроем новую табли-
цу и сохраним ее на диске с именем Prim_Reg.sta;
3)	с помощью команды Cases—Add добавим в таблицу 21 новую строку, увели-
чив общее их количество до 31;
4)	для удобства работы переименуем заголовки строк таблицы, заменив их на
названия областей, используя технологию, описанную в компьютерном прак-
тикуме № 16;
Рис. 14.7. Таблица исходных данных
МО
14. Регрессионный и корреляционный анализ
5)	переименуем заголовки столбцов VAR1 и VAR2, заменив стандартные имена
переменных на Т и Y (см. компьютерный практикум № 16);
6)	в столбец таблицы Т введем численность населения областей, в столбец Y —
число предприятий и организаций (исходные данные выбираются из табл. 14.7).
Результаты ввода представлены на рис. 14.7. Просмотр исходных данных выпол-
нен с использованием линии прокрутки (на рисунке соответственно показаны
две части таблицы).
Оценка линейной регрессии
Используя значения показателей в столбцах таблицы Т и Y, построим график за-
висимости У от Г (тип используемого графика — Scatterplots), который позволяет
наглядно оценить наличие зависимости между показателями. Технология по-
строения графика включает следующие шаги:
1)	выполнить команду меню Graphs—Stats 2D Graphs—Scatterplots;
2)	в открывшемся окне 2D Scatterplots (двумерные графики рассеивания) выбе-
рем тип графика Regular (обычный) и Linear (линейный), далее с помощью
кнопки Variables зададим по оси абсцисс ( Var X) — независимый фактор Т, по
оси ординат (Var У) — зависимую переменную У; в результате получим вид
окна, представленный на рис. 14.8;
Рис. 14.8. Окно для построения графика зависимости Y от Т
3)	после нажатия на кнопку ОК получим графики, представленные на рис. 14.9.
На этом рисунке точки (°) соответствуют фактическим наблюдениям (I}, Yt),
где i — номер области. Линия является графиком оцененной линейной зави-
симости (14.5).
Полученные графики показывают, что между числом предприятий и организа-
ций в областях и численностью их населения наблюдается сильная зависимость,
то есть можно использовать модель линейной регрессии. Над графиком дается
само вычисленное уравнение линейной регрессии (14.2), где случайная состав-
Компьютерный практикум № 21. Оценка параметров модели линейной регрессии в пакете STATISTICA
441
ляющая обозначена eps вместо г, а предикторная переменная х вместо t, как в МО*
дели (14.2).
i ИЙИЙя	Seittoplat (P(im_R«aSTA
V-202S.007*ie.32S‘x*«p«
Рис. 14.9. Графики зависимости числа предприятий и организаций
от численности населения областей
Анализ значимости модели и ее компонентов
Для получения оценок качества модели необходимо выполнить расчет модели
в полном объеме. Это делается следующим образом.
1)	выполним команду меню Analysis-Resume Analysis;
2)	в открывшемся окне Multiple Regression (см. рис. 14.6) нажмем кнопку Variables,
в результате откроется окно Select dependent and independent variable list (выбор
списка зависимых и независимых переменных), представленное на рис. 14.10;
Select dependent and independent variable feste:

3VAR3
4-VAR4
5-VAR 5
6 VARG
7-VAR7
В-VAR 8
< 9-VAR 9
10-VAR10
3-VAR3
4-VAR4
5-VAR5
Б-VARG
7VAR7
8-VAR8
9-VAR 9
10-VAR10

SgtoctAll[ Spread | Zoo» | Select AH| Spread j jZopiw -1!
Dependant var. M far batch): Independent variable Met
Рис. 14.10. Выбор списка зависимых и независимых переменных
3)	в левом списке переменных окна выделим зависимую переменную У (пере*
менная номер 3), в правом списке — независимую переменную Т(переменная
номер 1) и нажмем кнопку ОК;
142
14. Регрессионный и корреляционный анализ
1) в окне Multiple Regression нажмем кнопку ОК; откроется окно результатов ана-
лиза Multiple Regression Results (рис. 14.11), имеющее следующую структуру:
верхняя часть окна является информационной и показывает результаты ана-
лиза; нижняя часть — функциональная, она содержит кнопки, предназначен-
ные для выполнения детализированных расчетов (с представлением резуль-
татов в числовом или графическом виде).
Multiple Repression Results

Multiple Regression Results
Dep. Vat. : Y	Multiple R : .97567147
R*: .95193482
Mo. of cases: 31 adjusted R1: .95027740
Standard error of estiaate: 4247.8155734
Intercept: -2625.007415 Std.Error: 1412.044 t(
r • 574.3474
df -	1,29
p . .000000
29) - -1.859 p < .0732
T beta-.976
(significant beta's are highlighted)
Рис. 14.11. Окно результатов регрессионного анализа
Поясним назначения выводимых характеристик.
□	Dep. Var. — имя зависимой переменной, в примере — Y.
□	Multiple R — множественный коэффициент корреляции (14.21); в нашем слу-
чае равен 0.97567147.
□	F — значение критерия Фишера (14.22), F = 574.3474.
□	Я2 — множественный коэффициент детерминации (14.21), R2 = 0.95193482.
□	df — число степеней свободы ^критерия (1,29).
□	No. of cases — количество наблюдений, п = 31.
□	adjusted R2 — скорректированный коэффициент детерминации, определяемый
по формуле 1 -(1 - R2 )—, R2 = 0.95027740.
/I — 2
□	р — критический уровень значимости модели, в нашем примере р = 0.000000
показывает, что зависимость У от Г очень значима.
□	Standard error of estimate — среднеквадратическая ошибка (14.8),
o’ = 4247.8155734.
□	Intercept — оценка свободного члена модели регрессии, PJ = -2625.007415.
□	Std.Error — стандартная ошибка оценки PJ, ^D’(Pq>= 14.12044.
□	t(29)  -1.859 ир < 0.0732 — значения ^-критерия и критического уровня зна-
чимости, используемые для проверки гипотезы о равенстве нулю свободного
Компьютерный практикум № 21. Оценка параметров модели линейной регрессии в пакете STATISTICA
441
члена регрессии. В нашем случае гипотеза должна быть принята, если уро»
вень значимости равен 0.0732 или ниже. Примем уровень значимости а  0.10,
тогда гипотеза о равенстве нулю свободного члена регрессии отклоняется.
Для вывода оценок всех коэффициентов модели регрессии и результатов про»
верки их значимости нажмем на кнопку Regression Summary и получим таблицу,
представленную на рис. 14.12.
Рис. 14.12. Результаты расчетов регрессионной модели
В верхней части окна (непосредственно под его заголовком) выводятся резуль-
таты оценки качества модели, которые нами уже пояснялись выше. Рассмотрим
назначение отдельных столбцов таблицы:
□	в четвертом столбце В содержатся оценки параметров модели регрессии
=-2625.01 и р; =16.33;
□	в пятом столбце St. Err. of В — значения стандартной ошибки параметров мо-
дели регрессии, соответственно д/ДЧр;) = 1412.044 и ^’(РГ) =0.681;
□	в шестом и седьмом столбцах £(29) и p-level — значения i-критерия и минималь-
ного уровня значимости, используемые для проверки гипотез о равенстве нулю
коэффициентов регрессии, то есть гипотез ро = 0 и р, =0 соответственно. В дан-
ном примере p-значения близки к нулю, то есть оба параметра модели значимы.
Анализ остатков
Для получения расчетных значений У,* числа предприятий и организаций облас-
ти и отклонений фактических данных от этих значений Yf - Y‘ вернемся в ис-
ходное окно, нажав кнопку Continue... Далее нажмем кнопку Residual analysis
(Анализ остатков) и попадем в одноименное окно, представленное на рис. 14.13.
Инициализируем кнопку Display residuals & pred. (Вывести остатки и предска-
занные значения), в результате получим таблицу, из которой нами будут ИСПОЛЬ-
зоваться только четыре представленных на рис. 14.14 столбца. Они определяют:
номера наблюдений (названия областей), фактические (Observed Value) и рас-
четные (Predicted Value) значения количества предприятий и организаций, От-
клонения фактических данных от расчетных (Residual). Четыре последние стро-
ки таблицы содержат минимальное, максимальное, среднее и медианное
значения показателей. Равенство нулю среднего значения остатков свидетельст-
вует о корректности расчетов.
Для построения графика остатков достаточно выделить столбец Residual (91 ис-
ключением четырех последних строк), выполнить команду меню Qraphs-Custom
Graphs-2D Graphs и выбрать тип графика Bar Dev. Полученный график представ-
лен на рис. 14.15. Из графика видно, что выполняются все требования, сформу-
лированные для такого рода графиков в случае коооектности модели
444
14. Регрессионный и корреляционный анализ
Построение доверительных интервалов
Вернувшись через кнопку Continue... в окно Residual Analysis, с помощью функ-
циональных кнопок можно просмотреть разнообразные стандартные графики,
характеризующие проведенные расчеты.
Для построения графика доверительных интервалов (14.12) для математическо-
го ожидания числа предприятий и организаций в зависимости от численности
населения области, отвечающих доверительной вероятности у = 0.95, инициали-
зируем кнопку Bivariate correlation в группе Bivariate Scatterplots. На экране полу-
чим график, представленный на рис. 14.16.
Residual Analysis
Dep. Vac. : Y
Multiple R :
R1:
adjusted R1:
Standard error of estiaate:
Intercept: -2625.007415 Std.Error:
No. of cases: 31
.97567147
.95193482
.95027740
4247.8155734
1412.044 t(
F • 574.3474
df -
P -
1,29
.000000
29)
• -1.859
.0732
Statistics
Я
jffl РиЫп-У/ЫмпДЫШ |
E3 Pied. 1 obsarvad (£J 11
ЕЗ 0Ы? t (Щ |
РкШмЙгЯЫа
Г71 Hoteal ptat of residt (Ml j
С7, Halbnormal р1Ы ЦЦ I
ГЛ Detrended nonaal ptot (E) j
Casewue Plots
t/lli Plot.ol outlwii. ffi) 'I
LZflt Plata of predicted (Q 1
HtttogtaM
Д Staph of oUarved Ц) |
И Gl«ph Ы piedicUd ЦЦ I
Д Siach o( шидиЫ» (Ц |
Bivariate Scattecpfot*
CZJ Bivariate cwrelafipn fDl |
[Д] ЯмИ» I Indy v». |flj |
E3 Had, К iodM> »« (SJ |
Рис. 14>13. Окно Анализ остатков (Residuals Analysis)
I и р» .- In 1 <-d Г Kestdcal Vdkres		ЛГ?Г?1
		3
Observed ! Case No.	Value	ВЯ		a
1763 6.0 ИИИКм.. аба.	19023.0 МмЫЙвЙьфв»?	 15736.0 ЙМЙЫММИГНаЯ ofa		2 5814.0 13000.0 ЯВБКмМММИ№«£*^ 13014.0 ^ИИДЖг? '7. T'u *®92 6 • ° ? vJ 2 0974.0 ИИмВЗ£яЙ*»х. -1 17082.0 	j 18486.0 12952.0 ДМИВИМ.^ < *	104392.0 Д^ИЙИЙЬЫ^*' *дШ 11728.0 2162 8 * ° 16874.0 Я^Д||^ВНВЯИ|Я 28230.0 '23165.6' ЯВИННВНИ| 24121.0 ISWiii- 5,1-	21737.0	-4101.00 19238.8	.	-215.75 13981.0	:	1755.00	* 24839.4	974.60 9425.4	3574.63 10764.3	2249.70 21296.1	-5370.13 2400677	-3032.65 17720.2	:	-638.21	1 1523е7з"’Г" 3247.71 1038B.7	2563.25 104554.8	-162.77 12184.9	-456.87 18716.2	2911.76 16267.0	607.02 24039.3	:	4190.69	| 26537.6	•	-3372.56	.J 20822.6	3298.39	: jgj	
К Predated л Reudiwd Values tprim^reg.stj)
£ortnue..
Dependent variable: Y
: -8495.18
82.53
: -6350.45 '
' -1666.77
"Г-3770.87 i
I -2351.32
[	208.06
9695.94
' -4678.72
: 10143.25
2748.38
 -4267.04
Г-8495.18 **
i 10143.25
ai
82.63
_________M
Рио. 14.14. Фактические и расчетные значения зависимой переменной и остатки
Компьютерный практикум № 21. Оценка параметров модели линейной регрессии в пакете STATISTICA
440
From: Predicted & Residual Values (prim_reg.sta)
Dependent vanable: Y
Рис. 14.15. График остатков
Correlation г = ,97567
''о. Rtgrtinon
95% confid
Рис. 14.16. Доверительные интервалы для зависимой переменной
Задача № 2. Многомерная регрессия
Рассмотренная выше технология расчета модели одномерной линейной регрес-
сии в пакете STATISTICA переносится для решения задач многомерного регрес-
сионного анализа. Покажем это на примере расчета модели многомепной nernw-
46
14. Регрессионный и корреляционный анализ
ни, характеризующей зависимость инвестиций в основной капитал областей
'осени (У) от следующих четырех факторов:
) ti — численность населения области, тыс. чел.;
1 ti — оборот розничной торговли, млн руб.;
1 t3 — поступление налогов и сборов в бюджет, млн руб.;
)	— объем промышленного производства, млн руб.
J расчетах будем использовать статистические данные, представленные в табл. 14.7.
’аботу в пакете STATISTICA начнем с запуска в окне STATISTICA Module Switcher
юдуля Multiple Regression и ввода исходных данных. Вид окна Data, содержаще-
о таблицу исходных данных, представлен на рис. 14.17. Здесь имена столбцов
7, Т2 ТЗ, Т4 соответствуют именам переменным ib t2, t3, Ц.
Рио. 14.17. Таблица с исходными данными
Компьютерный практикум № 21. Оценка параметров модели линейной регрессии в пакете STATISTICA
447
Для проведения расчетов модели выполним действия, рассмотренные выше.
Результаты регрессионного анализа получим в информационной части окна Mul-
tiple Regression Results в виде, представленном на рис. 14.18.
Г1
Multiple Regression Results
Pep. Var. : Y	Multiple R : R*:	.98144504 .96323437	F - 170.2956	
			df -	4,26
No. of cases: 31	adjusted R*:	.95757812	P -	.000000
Standard	error of estimate:	555.47495311		
Intercept: -559.9493523 Std.Errors		269.2668 t(	26)	- -2.080 p < .0476
Т1 beta-,488 Т2 beta—.06 ТЗ beta-.376 Т4 beta-.222
Рис. 14.18. Результаты регрессионного анализа для модели линейной регрессии
(случай четырех предикторных переменных)
Нетрудно заметить, что для модели получен высокий коэффициент детерми-
нации (14.21) Я2 = 0.96323437, который показывает, что зависимая переменная
(инвестиции) линейно зависит от предикторных переменных (факторов). Фак-
тическое значение критерия Фишера (14.59) F= 170.2956 значительно превы-
шает его критическое значение FKp = 2.742594, определенное с использованием
вероятностного калькулятора (см. компьютерный практикум №17) для уровня
значимости а =0.05 с т = 4 и (п - 5) = 26 степенями свободы (рис. 14.19). Кри-
тический уровень значимости модели р с точностью до шестого знака после за-
пятой равен нулю. Следовательно, полученная регрессионная зависимость высо-
ко значима. Вместе с тем (к сожалению, это не видно в черно-белом варианте
распечатки) вторая предикторная переменная Т2 в отличие от остальных пере-
менных выделена синим цветом, который указывает на ее незначимость.
Рис. 14.19. Расчет критического значения критерия Фишера
Для вывода оценок всех коэффициентов модели регрессии и результатов про-
верки их значимости в функциональной части окна Multiple Regression Results
активизируем кнопку Regression summary. В результате получим таблицу, пред-
ставленную на рис. 14.20. Как видно из последнего столбца p-level, критиче-
ский уровень значимости для второй предикторной переменной Т2 очень высок:
n-level = 0.536805.
448
14. Регрессионный и корреляционный анализ

Continue...
jg Regression Swnmory for Dependent Vdnuble; Y
R- .98144504 Rl- .96323437 Adjusted Rl- .95757812
F(4,26)-170.30 p<.00000 Std.Error ol estimate: 555.47
. N-31	BETA [	fitt'. trt. ЦП	3	St, 1st. at В
	i -559.949	269.2668
.488190 i	.102863 i	1.157	.2437
-.064464 i	.102986 i	-.019	.0306
.375813 i	.167905 j	.251	. 1123
0174
104346
037
.222432
-2.079S3 ’	.047570
4.74603	.000066 jj
-.62595 |	 53 680S~|
2.23825
2.13168
03 3 986
042649 И

Рис. 14.20. Результаты расчетов регрессионной модели (случай четырех предикторных
переменных)
Таким образом, переменную Т2 исключим из модели и повторим расчеты для
трех предикторных переменных Т1, ТЗ и Т4. Результаты этих расчетов приведе-
ны на рис. 14.21 и 14.22. Они свидетельствуют о значимости модели и всех трех
оставшихся предикторных переменных.
Multiple Regression Results
Multiple Regression Results
Dep. Var. : Y	Multiple R : .98116274	F - 232.1596
R‘; .96268032 df -	3,27
No. of cases: 31	adjusted R*s .95853369	p  .000000
Standard error of estinate: 549.18315906
Intercept: -590.5981297 Std.Error: 261.7785 t( 27) • -2.256 p < .0324
T1 beta».500 T3 beta*. 333 T4 beta*.194
Рис. 14.21. Результаты регрессионного анализа для модели линейной регрессии
(случай трех предикторных переменных)
i jg Regression Summary for Dependent Variable: Y

Continue.
R" .98116274 Rl- .96268032 Adjusted Rl" .95853369
F (3,27)-232.16 p<.00000 Std.Error of estimate: 549.18
I St. tor.' 	1-St/fcK. i ' »	L_k»_	tl27)	
i N-31
.U3ZJ7U
i -590.598
261.7785
-2.25610
T1	.500024 i	.099965 :	1.185 	.2368 :	5.00198 :	.000030
73	.332583 :	.151310 ;	.222 i	.1012 \	2.19802	.036703
74	. 193890 i	.092793 :	.032 i	.0154 \	2.08950 '	.046217
П					 _ _				
Рис. 14.22. Результаты расчетов регрессионной модели (случай трех предикторных
переменных)
В четвертом столбце таблицы результатов, приведенной на рис. 14.22, содержат-
ся оценки параметров модели регрессии: pj =-590.598; pj =1.185; pj =0.222 и
PJ = 0.032. Значения ^-критерия и минимального уровня значимости (p-level) в пя-
том и шестом столбцах свидетельствуют, что все коэффициенты модели значимы.
Таким образом, оценена модель многомерной линейной регрессии, характеризую-
щая зависимость инвестиций в основной капитал области России (У) от числен-
ности населения области, поступления налогов и сборов в бюджет и объема про-
мышленного производства:
У = -590.598 + 1.185ft + 0.22213 + 0.032^.
Компьютерный практикум № 21. Оценка параметров модели линейной регрессии в пакете STATISTICA
440
Как видно из полученной формулы, инвестиции увеличиваются с ростом КАЖДОГО
из факторов. Качество полученной модели можно оценить, сравнив фактические
и рассчитанные по модели значения инвестиций и вычислив величины ОСТМ|01,
Для этого в функциональной части окна Multiple Regression Results нажмем кнопку
Residual analysis и попадем в одноименное окно. Инициализируем кнопку Dliplay
residuals & pred.; в результате получим таблицу, первые четыре столбца которой
определяют: наименования областей, фактические (Observed Value) и расчетные
(Predicted Value) значения инвестиций и остатки (Residual) (рис. 14.23).
I’^l'reilKtedCrResiduaJVedues (print				
Continue...	Dependent vactable:			
Case No.	I Value	I fradietd ; I vale* .	Re»M£M2	
	2508.00	j 2565.06	-57.059	
	2837.00	3244.99	-407.992	
	2154.00	2421.42	-267.422	
JtemwMuieitu as«. ;	4437.00	3125.64	1311.362	
		1079.00	963.00	115.996	
	866.00	749.30	116.698	
SjmMMX м».	948.00	1759.97	-811.973	
	2220.00	2486.45	-266.484	
>WWU oS«.	879.00	1381.78	-502.782	
a**»®* ce«-		1691.00	1384.58	306.422	
«Mt ...	1255.00	849.80	405.203	
	13363.00	i 13468.12	-105.122	
	1215.00	1252.93	-37.931	
	1721.00	1846.86	-125.886	I-::''
.йммпияК'ъ .	1056.00	1584.04	-528.037	
	2293.00	2299.52	-6.522	
jsrja=«e Ля-..	2342.00	2832.03	-490.026	
	2382.00	2807.95	-425.951	
JUO_					
at Pn'tlii t rd К	Values (pnm rulpnrj st»)
Рис. 14.23. Фактические и расчетные значения зависимой переменной, остатки
From: Predicted & Residual Values (prim_mlpreg sta)
Pm. 14.24. График остатков для многомерной линейной регрессии
€0
14. Регрессионный и корреляционный анализ
Variables currently in the t-quatton;OV: vl
Continue~ ЦН|НЦ|
7500024J
.332583 
.193890 ;
.693518 ;
.389587 3
.373089
Рис. 14.25. Эмпирические
коэффициенты корреляции
между зависимой
и предикторными
переменными
Используя данные столбца Residual, построим график
остатков, представленный на рис. 14.24. График удов-
летворяет всем требованиям, сформулированным для
такого рода графиков в случае корректности модели.
Зависимость уровня инвестиций от отдельных факто-
ров можно оценить, рассчитав коэффициенты частной
корреляции и построив соответствующие графики. Для
расчета этих коэффициентов в функциональной части
окна Multiple Regression Results активизируем кнопку
Partial correlations (Частные корреляции). В результа-
те получим таблицу, представленную на рис. 14.25.
£ш>Йт»е— |
pjt.raph/: 11 vs*
96» oonfid
Рис. 14.26. Зависимость переменной Y от численности населения области
Hf>raph9: T3vs. Y
Regrearlon
И* oonftd
Рио. 14.27. Зависимость переменной Y от поступления налогов и сборов в бюджет
Задания для самостоятельной работы
451
Перейдя в окно Residual Analysis и активизировав кнопку Bivariate correlation,
в окне Select the two variables for scatter plot (Выбрать две переменные для HO-
строения графика зависимости) отметим переменные, откладываемые по оси
абсцисс и ординат. После нажатия кнопки ОК получим графики, характеризую-
щие зависимость переменной Y от каждого из факторов: численности населения
области, поступления налогов и сборов в бюджет и объема промышленного про-
изводства — представленные соответственно на рис. 14.26-14.28.
jgontthUc.^ I
ПЬгарЫС: 14уу. V
' 138.40 ♦ .14417 " Т4
Correlation: г« .88827
Рис. 14.28. Зависимость переменной Y от объема промышленного производстве
Задания для самостоятельной работы
1.	Попробуйте усовершенствовать регрессионные модели, рассмотренные в нрм-
мерах 14.1, 14.2 и компьютерном практикуме №21. Замените используемые
в моделе предикторные переменные на некоторые функции от них, которые,
на ваш взгляд, могли бы более точно описать их влияние на зависимую пере-
менную. Например, вместо численности населения можно взять корень квад-
ратный из нее.
В качестве критерия качества регрессионной модели принять остаточную сумму
квадратов отклонений Ra.
2.	В регрессионных моделях примеров 14.1, 14.2 и компьютерного практикума
№21 дисперсия случайных составляющих предполагалась постоянной, то есть
не зависящей, в частности, от такого фактора, как численность населения об-
ласти. Это, по-видимому, не так. В связи с этим предположите, что дисперсия
i-ro наблюдения пропорциональна численности населения, то есть положите
значения wt из формул (14.14) и (14.47), равными численности населения.
Проанализируйте графики остатков в зависимости от значения численности
населения, и сделайте вывод о том, стала ли регрессионная модель более аде-
кватной.
3.	Реализуйте в пакете Mathcad формулы (14.38) и (14.52) для оценивания мо-
дели многомерной линейной регрессии, рассмотренной в разделе 14.3.
452
14. Регрессионный и корреляционный анализ
4.	Реализуйте в пакете Mathcad процедуры верификации модели многомерной
линейной регрессии, описанные в разделе 14.4.
Задачи
Задача 14.1. Исследуется зависимость производительности труда рабочих от их
стажа работы. Случайным образом выбраны 50 человек со стажем работы от од-
ного года до пяти лет, выполняющих однотипную работу. Результаты обследова-
ния приведены в табл. 14.8.
Таблица 14.8. Данные наблюдений над производительностью труда
Стаж работы (полных лет), X	Объем продукции, Y					
	.¥, = 20	у, = 25	»5 = 30	у4 = 35	»s = 40	nt
1	3	4	1	-	-	8
2	1	6	4	1	-	12
3	-	2	6	4	3	15
4	-	1	2	8	4	15
V	4	13	13	13	7	п = 50
Здесь через X обозначен стаж работы, а через У — объем продукции, произведен-
ной рабочим за смену. Число, стоящее на пересечении г-й строки и j-ro столбца,
это количество рабочих со стажем i лет, выпустивших за смену г/, единиц продук-
ции (z/j = 20, у2 = 25,..., у5 = 40). Например, число 4, стоящее на пересечении вто-
рой строки и третьего столбца, это число рабочих со стажем работы 2 года, каж-
дый из которых выпустил за смену 30 единиц продукции; п, — число
обследованных рабочих, имеющих стаж работы i лет.
Оцените модель одномерной регрессии (14.2) зависимости У от X. Проведите дис-
персионный анализ согласно табл. 14.1.
Задача 14.2. Следующие данные отражают ежемесячные затраты (в условных
единицах) фирмы на рекламу и объемы ее ежемесячных продаж.
Затраты на рекламу	7	7.3	7	7.4	7.7	8	7.5	8	7.4
Объемы продаж	48	50	50	51	53	55	57	54	50
Оцените линейную регрессию объемов на затраты и коэффициент корреляции.
Проверьте гипотезы о незначимое™ регрессии и влияния затрат на объемы про-
даж. Используя графики остатков, проверьте адекватность модели.
Задача 14.3. Используя модель линейной регрессии, полученную в задаче 14.2,
спрогнозируйте значение объема реализации, если затраты на рекламу составят
J условных единиц. Для коэффициента доверия у = 0.6 найдите доверительный
чнтервал для математического ожидания объема реализации, соответствующего
1 условным единицам рекламных затрат.
Задачи
4М
Задача 14.4. Исследуется зависимость заработной платы специалистов опреде*
ленной профессии от возраста, образования (числа лет обучения), стажа работы
по данной специальности. Случайным образом выбраны 25 специалистов. Ре-
зультаты обследования приведены в следующей таблице, где Y — заработная
плата (в условных единицах), — число лет обучения, t2 — возраст и t3 — стаж
работы по данной специальности.
i	Y	t.	^2	
1	126	4	27	14
2	160	6	30	16
3	104	4	42	10
4	162	7	32	17
5	212	14	44	16
6	130	2	25	16
7	102	0	21	13
8	245	27	53	20
9	183	21	47	16
10	149	3	34	12
И	116	2	27	10
12	158	4	29	18
13	178	15	49	16
14	196	7	54	12
15	142	4	32	16
16	156	10	39	18
17	171	8	49	16
18	140	3	26	14
19	156	7	34	12
20	115	3	28	15
21	142	9	35	12
22	134	3	29	14
23	147	6	36	16
24	173	15	41	16
25	144	3	30	18
Оцените модель линейной регрессии У на предикторные переменные tt, tj и fj.
Проверьте гипотезы о незначимое™ регрессии и каждой из предикторных пере-
менных. Используя графики остатков, проверьте адекватность модели.
Литература
. Боровиков В. П. STATISTICA: искусство анализа данных на компьютере. Для
профессионалов. — СПб.: Питер, 2001.
. Боровков А. А. Математическая статистика. — М.: Наука, 1984.
. Бочаров П. П., Печинкин А. В. Теория вероятностей и математическая стати-
стика. — М.: Гардарика, 1998.
. Гнеденко Б. В. Теория вероятностей. — М.: Наука, 1988.
. Дрейпер Н., Смит Г. Прикладной регрессионный анализ. — М.: Статистика,
1973.
. Дьяконов В. Mathcad 2001: учебный курс. — СПб.: Питер, 2002.
. Леман Э. Проверка статистических гипотез. — М.: Наука, 1979.
. Леман Э. Теория точечного оценивания. — М.: Наука, 1991.
. Рао С. Р. Линейные статистические методы и их приложения. — М.: Наука,
1968.
. Себер Дж. Линейный регрессионный анализ. — М.: Мир, 1980.
. Феллер В. Введение в теорию вероятностей и ее приложения. Том 1. — М.:
Мир, 1984.
. Феллер В. Введение в теорию вероятностей и ее приложения. Том 2. — М.:
Мир, 1984.
. Чистяков В. П. Курс теории вероятностей. — М.: Наука, 1982.
Алфавитный указатель
(/-горизонталь, 59
А
Абсолютная сходимость, 79, 81, 134, 154
Альтернатива, 364
двусторонняя, 366
односторонняя, 366
простая, 365
сложная, 365
Б
Биномиальные коэффициенты, 53, 72
В
Вариационный ряд, 278
Вероятности переходов
безусловные, 210
за шаг, 207
матрица, 207
Вероятности состояний
стационарные, 212, 216, 245
Вероятность
апостериорная, 37
априорная, 37
геометрическая, 35, 49
полигон, 72
произвольной комбинации событий, 40
разности событий, 32
свойства, 31
события, 31
составного события, 31
статистическая, 49
суммы двух событий, 32
условие
неотрицательности, 31
нормировки, 31
условная, 36
элементарного события, 31
Выбор
без повторений, 277
с повторениями, 277
Выборка, 49, 276
без возвращения, 49
без повторений, 49
неупорядоченная, 49
объем, 277
репрезентативная, 277
с возвращением, 49
с повторениями, 49
случайная, 277
упорядоченная, 49
Выборочное пространство, 354
Г
Гамма-функция, 343
Генеральная совокупность, 49, 307
Генераторы случайных величин, 277
Гипотеза, 13, 36, 364
альтернативная, 364
критерий проверки, 365
критическая область, 365
пулевая, 364
о виде распределения, 386
о незначимости регрессии, 411, 423
область принятия, 365
последовательная проверка, 39
простая, 365
сложная, 365
статистическая, 364
Гистограмма относительных частот, 280
д
Дизъюнктивная совершенная
нормальная форма, 41
Дисперсионный анализ, 413
Дисперсия, 78, 82
ннутригрунноная, 429
456
Алфавитный указатель
Дисперсия {продолжение)
межгрупповая, 429
свойства, 82, 104
суммы случайных величин, 135
условная, 152, 429
эмпирическая, 284
Доверительная вероятность, 334
Доверительный интервал, 334
3
Задача
Банаха о спичечных коробках, 69
о баллотировке, 252
о встрече, 10, 12, 35
о движении городского транспорта, 68
о дефиците, 76
о разорении игрока, 208, 223
о совпадениях, 147
станки и рабочие, 274
Закон больших чисел, 193
Законы де Моргана, 23
И
Имитационное моделирование, 110
Индикатор, 137
Интеграл
абсолютная сходимость, 99
Пуассона, 96
Интервал
замкнутый, 77
открытый, 77
Испытание, 8
Испытания Бернулли, 35, 53, 314
К
Квадратный корень Холесского, 159
Квантиль, 192, 335
Комбинаторный метод, 48
Корреляционное отношение, 429
Корреляция
отрицательная, 431
положительная, 431
Коэффициент
доверия, 334
загрузки, 233
загрузки системы, 263
Коэффициент корреляции, 134
множественный, 423
Критерий
более мощный, 368
Вилкоксопа, 389
знаков, 390
Критерий {продолжение)
Манна—Уитни, 389
непараметрический, 383, 389
отношения правдоподобия, 380
Пирсона (хи-квадрат-критерий), 385
равномерно наиболее мощный, 383
ранговый, 389
согласия, 383
факторизации, 322
Л
Лемма
Неймана—Пирсона, 380
Линейка прокрутки, 63
Линия регрессии
эмпирическая (выборочная), 433
м
Максимальное правдоподобие, 52
Марковское свойство, 207
Математическое ожидание, 78-79, 81, 99,
102, 132
безусловное, 128
свойства, 82, 102
суммы случайных величин, 135
условное, 128, 152
Матрица
дважды стохастическая, 240
ковариационная, 134, 157
математическое ожидание, 157
неотрицательно определенная, 158
положительно определенная, 160
предикторных переменных, 416
симметрическая, 134, 157
стохастическая, 207
субстохастическая, 224
транспонированная, 157
треугольная,
верхняя (нижняя), 159
фундаментальная, 221
Холесского, 160
Мера разброса, 82
Метод
выборочный, 277
Метод Монте-Карло, 77
Множественный коэффициент
детерминации, 410
корреляции, 410
Множество возможных значений, 71
Множество состояний
цепи Маркова
замкнутое, 212
Алфавитный указатель
407
Модель запасов, 240
Момент, 78
r-го порядка, 81, 102
r-го порядка
эмпирический, 283
второго порядка, 82, 103
нормального распределения, 104
первого порядка, 82, 102
условный, 152
н
Надежность, 92
параллельной системы, 40
последовательной системы, 40
Неравенство
Йенсена, 112
Рао—Крамера, 313
Чебышева, 113
обобщенное, ИЗ
Шварца, 111, 134
О
Остаток, 410
Оценка
несмещенная, 308
состоятельная, 310
эффективная, 314
Оценки
метода наименьших
квадратов, 404
свойства, 405
наименьших квадратов, 418
Очереди, 262
Ошибка
второго рода, 366
первого рода, 366
п
Переменная
зависимая, 403
предикторная, 403
Перестановки, 50
Плотность распределения
безусловная, 152
двумерная, 149
двумерная нормальная, 149
многомерная, 148
условная, 152
частная
двумерного нормального
распределения, 150
частная (маргинальная), 149
Полигон частот, 279
Поток
в сетях, 224
пуассоновский, 249
свойство, 250
требований, 224
Предиктор, 428
линейный, 431
Преобразование, 165
линейное, 156
якобиан, 166
Принцип
баланса, 217, 257
двойственности, 61
отражения, 57
симметрии, 59
Принцип задания вероятностей
геометрический, 48
классический, 48
статистический, 48
Пространство
состояний, 206
элементарных событий, 8
дискретное, 31
искусственное, 25
конечное, 8
несчетное, 8
счетное, 8
Процесс
альтернирующий, 274
звездообразный, 259
марковский, 243
алгоритм моделирования, 243
протокол, 243
стационарное распределение
вероятностей состояний, 256
массового обслуживания, 262
полумарковский, 258
предыстория, 206
пуассоновский, 249
сложный, 273
размножения и гибели, 260
стационарное
распределение, 262
случайный, 206
состояние, 206
траектория, 206
циклический, 258
чистого размножения, 260
чистой гибели, 260
Юла, 260
Путь, 56
458
Алфавитный указатель
Р
Ранг, 389
Рандомизация параметров
распределений, 151
Распределение
бета-распределение, 204
биномиальное, 35, 53, 72, 74, 320
вероятностей
инвариантное, 231
вероятностей дискретной случайной
величины, 72
вид, 72
геометрическое, 32, 55, 73-74, 80
гипергеометрическое, 52, 73
двумерное, 161
двумерное нормальное, 165
дифференциальный закон, 74
интегральный закон, 74
Колмогорова, 384
Коши, 124
Лапласа, 124
логарифмически нормальное, 108, 114
многомерное
Дирихле, 177
невырожденное нормальное, 165
нормальное, 164
равномерное, 151
симметричное, 162
стандартное нормальное, 152
многомерное гипергеометрическое, 67
наименее благоприятное, 366
невырожденное, 159
нормальное, 95, 101, 107, 114, 315
параметры, 72, 92
Парето, 124
плотность, 90
полиномиальное, 56
Пуассона, 69, 73, 80, 314, 321
равномерное, 94, 100, 103, 107, 114
стандартное нормальное, 95
Стьюдента (t-распределение), 346
тип, 92
усеченное, 98
усеченное слева, 98
усеченное справа, 98
Фишера-Снедекора, 411
Х-квадрат, 343
экспоненциальное, 94, 100, 103, 107,
249, 315, 321
свойство отсутствия
памяти, 245
Эрланга, 96, 104, 107, 114, 318
Распределение вероятностей
двумерное, 127
многомерное, 126
условное, 128
частное (маргинальное), 127
Распределения
смесь, 98
Регрессия
линейная, 429
многомерная, 417
одномерная, 404
нелинейная, 429
Резервирование
холодное, 183
С
Свойство
марковское, 246
отсутствия памяти, 245
Система
два-из-трех, 28, 30
надежность, 40
параллельная, 27, 40, 156
последовательная, 27, 40, 156
последовательно-параллельная, 27
Система нормальных
уравнений, 404, 417, 430
Система обслуживания
эрланговская, 263
Случайная величина
возможное значение, 71
двумерная, 127
двумерная непрерывная, 149
дискретная, 71
ковариация, 134
конечнозначная, 72
многомерная, 126
многомерная непрерывная, 148
некоррелированная, 135
непрерывная, 89 - 90, 101
нормированная, 104
смешанный момент, 134
Случайная составляющая, 403
Случайное блуждание, 251
с отражающими экранами, 209
па плоскости, 10, 35
с поглощающими экранами, 208, 223
Случайные блуждания, 56
условные экстремумы, 60
Случайные величины
взаимно независимые, 136, 151
некоррелированные, 155
Алфавитный указатель
409
Случайные величины (продолжение)
попарно независимые, 136, 151
сумма случайного числа, 184
Случайный вектор, 126
линейное преобразование, 157-158
нормированный, 161
Собственные
вектора, 252
числа, 252
Событие
благоприятствующее, 48
влечет событие, 13
достоверное, 9
невозможное, 9
случайное, 31
составное, 8
элементарное, 8
События
комбинации, 22
независимые, 37
в совокупности, 37
несовместные, 12
полная группа, 13
попарно независимые, 37
попарно несовместные, 13
произведение, И
противоположные, 12
равновероятные, 48
равновозможные, 48
разность, И
свойства, 22
сумма, 11
эквивалентные, 9
Состояние
цепи Маркова
возвратное, 214
возвратное нулевое, 226
достижимое, 212
невозвратное, 214, 220, 226
ненулевое, 226
непериодическое, 213
нулевое, 226
поглощающее, 212
среднее время возвращения, 214
эргодическое, 215, 226
Состояния цепи Маркова однотипные, 227
Сочетания, 50
Среднее арифметическое, 283
Среднее квадратическое
отклонение, 82, 103
Статистика, 322
достаточная, 322
Статистические данные, 49
Сумма квадратов отклонений
обусловленная регрессией, 410
остаточная, 417
остаточная (относительно
регрессии), 409
полная, 409
Сходимость
абсолютная, 128
по вероятности, 193
среднего арифметического, 194
частоты, 194
Счетное множество, 79
Теорема
Бернулли, 194
Муавра—Лапласа, 192
предельная для гипергеометрического
распределения, 67
сложения
вероятностей событий, 32
математических ожиданий, 154
умножения
вероятностей событий, 38
математических ожиданий, 138,
155
центральная предельная, 191
У
Уравнение
Колмогорова—Чепмена, 210
правдоподобия, 320
Уравнения
Колмогорова
обратные дифференциальные, 248
прямые дифференциальные, 248
численное решение, 252
Уровень значимости, 366
критический, 367
Условие
неотрицательности, 126
нормировки, 126
Устойчивое семейство, 181
биномиальных распределений, 181
многомерных нормальных
распределений, 185
распределений
Пуассона, 181
Эрланга, 182
Устойчивость семейства
нормальных распределений, 188
160
Алфавитный указатель
Ф
Формула
Байеса, 36
полной вероятности, 36
умножения вероятностей, 36
Функции
булевые, 24
встроенные, 18
пользователя, 20
Функция
выпуклая, 112
линейная, 81-82, 102
максимума, 156
минимума, 156
непрерывная, 91
параметрическая, 337, 354
показательная, 81, 102
пользователя, 84
правдоподобия, 319
распределения, 73, 91, 149
дополнительная, 91
непрерывная справа, 75
неубывающая, 74
свойства, 74
эмпирическая, 281
регрессии, 429
случайной величины, 80, 101
математическое ожидание, 154
многомерной, 132, 154
строго возрастающая, 106
строго убывающая, 106
Функция мощности критерия, 367
ц
Цепь Маркова, 206
алгоритм
моделирования, 211
вложенная, 245
конечная, 207, 215
моделирование, 211
неоднородная, 207
неприводимая, 213, 226, 230
критерий, 213
обращенная, 241
однородная, 207
поглощающая, 219
размножения и гибели, 231
счетная, 207, 226
эргодическая, 215
конечная, 215
ч
Частота
наблюдений, 279
накопленная, 280
относительная, 280
события, 278
Число степеней свободы, 343, 346
Числовые
характеристики, 78, 99, 112
условные, 128
э
Эмпирическая
характеристика, 281
Андронов А. М., Копытов Е. А., Гринглаз Л. Я.
Теория вероятностей и математическая статистика
Учебник для вузов
Главный редактор Заведующий редакцией Руководитель проекта Научный редактор Художник Корректор Верстка	Е. Строганова И. Корнеев А. Крузенштерн К Кноп Н. Биржаков Н. Солнцева Ю. Сергиенко
Лицензия ИД № 05784 от 07.09.01.
Подписано в печать 06.07.04. Формат70X100	Усл. п. л. 37.41. Тираж 4000 экз. Заказ№ 2917.
ООО «Питер Принт». 196105. Санкт-Петербург, ул. Благодатная, д. 67в.
Налоговая льгота — общероссийский классификатор продукции ОК 005-93, том 2; 953005 литература учабнаа.
Отпечатано с готовых диапозитивов в ФГУП «Печатный двор» им. А. М. Горького Министерства РФ
по лелвм печати, телерадиовещания и средств массовых коммуникаций
197110, Саикт-Петербург. Чкаловский пр.. 15.
А. М. Андронов
Е. А. Копытов
Л. Я. Гринглаз
С^ППТЕР \
ТЕОРИЯ ВЕРОЯТНОСТЕЙ
И МАТЕМАТИЧЕСКАЯ
СТАТИСТИКА
У Ч Е Б Н И К / ДЛЯ ВУЗОВ
•	компьютерный
курс: решение
рассматриваемых
задач в среде
пакетов Mathcad
и STATISTICA
•	активное изучение
современных
вероятностно-
статистических
методов
•	для студентов,
преподавателей
и научных
работников
A. M. Андронов
Е. А. Копытов
Л. Я. Гринглаз
ТЕОРИЯ ВЕРОЯТНОСТЕЙ
И МАТЕМАТИЧЕСКАЯ
СТАТИСТИКА
УЧЕБНИК / ДЛЯ ВУЗОВ
В бизнесе и экономике, страховании
и инвестициях, задачах надежности систем
и управления запасами, медицине и биологии,
проектировании и эксплуатации компьютерных
систем и сетей основополагающую роль
играют вероятностно-статистические расчеты.
Программное обеспечение современных
компьютеров делает эти расчеты легко-
реализуемыми, всесторонними и наглядными.
Освоив эту книгу, вы станете хорошо
подготовленным специалистом в области
разработки и компьютерной реализации
вероятностно-статистических методов.
Книга является базовым курсом для студентов
высших учебных заведений, обучающихся
по различным специальностям в области
информатики, вычислительной техники
и ее приложений.
Отличительной особенностью издания является
его ориентация на постоянное использование
персонального компьютера при изучении
материала.
ISBN 5-94723-615-Х
СЕЛИГЕР
WWW.PITER.COM
К технических наук, профессор. |
т премии Совета министров СССя
заслуженный деятель науки, член |
Американской статистической ассоциаа
Член редколлегии журнала Automatic j
Control and Computer Science.	I
Автор более 200 работ. 10 монографий!
и учебников. Подготовил более 1
30 докторов и кандидатов наук. 1
Специализируется в области теории I
вероятностей, математической статистя
и математических методов.	1
в Евгений Александрович —
доктор технических наук, профессор. Я|
Академик Международной академии свяэт
и Балтийской академии информатизации.
Член редколлегии журнала Computer
Modelling and New Technologies. Автор
150 работ. 20 монографий и учебнико!
Подготовил 5 докторов наук. Область
научных и педагогических интересов:
применение математических методов i
вычислительной техники, информацио!
технологии, базы и банки данных.
аал
физико-математических наук, професа
Академик Балтийской академии
информатизации. Автор более 50 рабо:
8 монографий и учебников. Область
научных и педагогических интересов:
математическая статистика и
математические методы экономики^л
алгебраическая теория автоматое^^Л
г
Посетите наш web-магазин: http:/www.piter.com