Текст
Г-*’*-.
я
ОГЛАВЛЕНИЕ
Предисловие ...............................................в
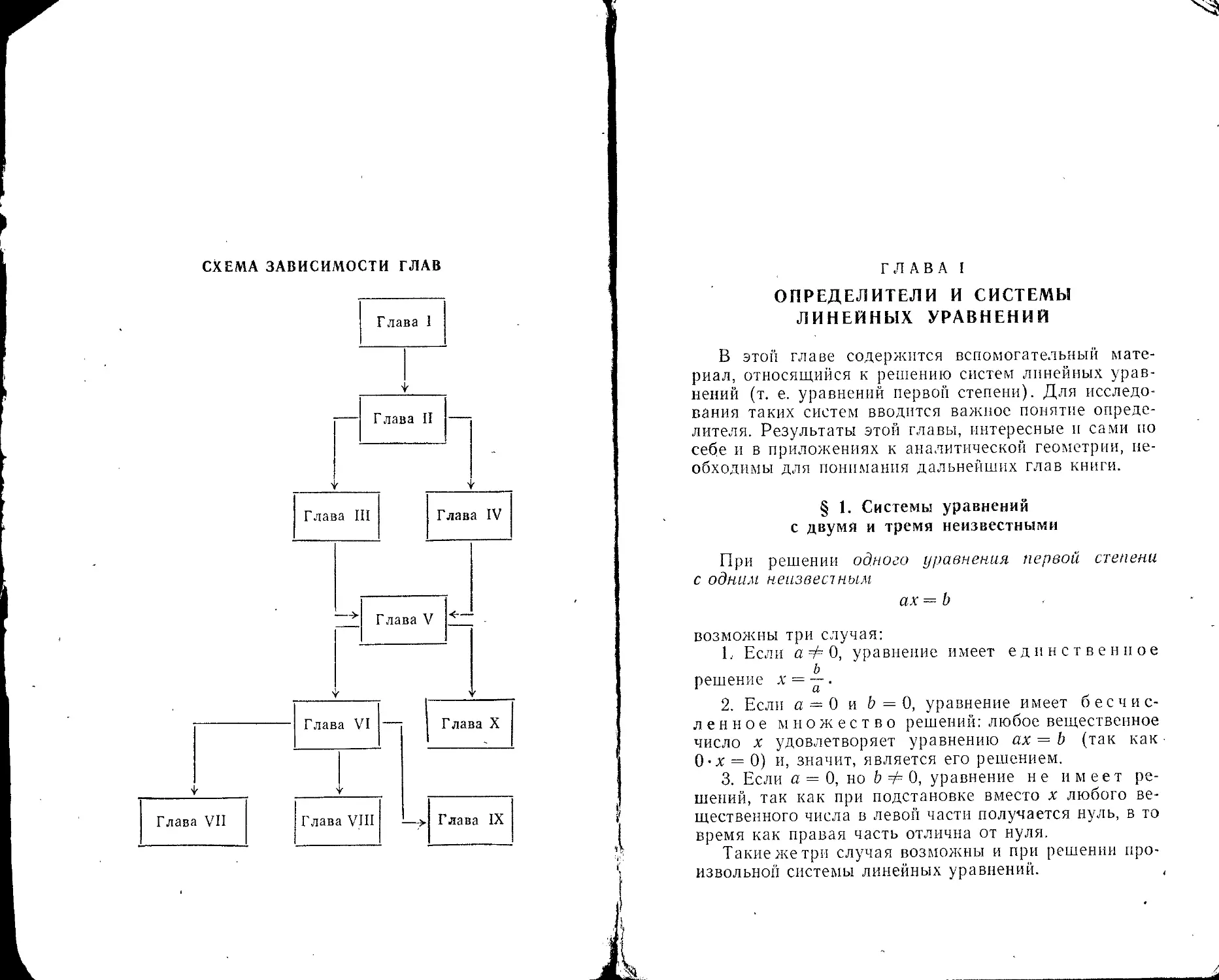
Схема зависимости глав.............•.......................8
Г л а в а I
Определители и системы линейных уравнений
§ 1. Системы уравнений с двумя и тремя неизвестными . . 9
§ 2. Перестановки и транспозиции. Определитель я-го по-
рядка ...................................................}8
§ 3. Свойства определителей............................21
| 4. Миноры и алгебраические дополнения................28
§ 5. Разложение определителя по элементам строки или
столбца..................................................32
. § 8,. Системы п линейных уравнений с п неизвестными . . 35
§ 7- Фанг матрицы.................................... 36
| 8. Понятие о линейной зависимости....................41
| 9. Произвольные системы линейных уравнений...........44
Ь § 16. Однородные системы .................................48
4 у 11. .Метод Гаусса.......................................54
Sfe. Глава II
п-мериое пространство . .
€ 1. Определение векторного пространства....................60
S 2. Раз.мерность и базис...................................64
| 3. Изоморфизм линейных, пространств ........ 71
§ 4. Переход к новому базису................................73
х § 5. Подпространства линейного пространства......................75
16. Пересечение и сумма подпространств.....................78
7.' Определение аффинного пространства...................82
8. Введение координат в аффинном пространстве .... 83
9. Переход к новой системе координат; ’.................85
10. Линейные многообразия '............-.................87
11. й-мерные плоскости в аффинном пространстве ... 89
12. Выпуклые множества в аффинном «-пространстве . . 92
Г л а в а III . .
Линейные преобразования
1 ; /
tl. Определение и примеры........................
2. О перации над линейными преобразованиями . .
. . 96
. . 104
4
ОГЛАВЛЕНИЕ
§ 3. Переход- к новому базису . .........................114
§ 4. Прямоугольные матрицы................................Н5
§ 5. ианг и дефект линейного преобразования..............119
S 6. Невырожденное линейное преобразование .............121
§ 7. Инвариантные подпространства. Собственные векторы и
собственные значения линейного преобразования . . . 122
Глава IV
Евклидово пространство
§ 1. Скалярное произведение ...........................135
§ 2. Ортонормированнып базис...........................138
§ 3. Ортогональное дополнение..........................144
§ 4. Евклидово (точечно-векторное) пространство........147
Глава V
Линейные преобразования в евклидовом пространстве
§ 1. Преобразование, сопряженное к данному ... ... 150
§ 2.. Самосопряженное преобразование . ...............152
§ 3. Ортогональное преобразование......................156
§ 4. Произвольное невырожденное линейное преобразование 165
§ 5. Комплексное линейное пространство.................168
Глава VI
Билинейные и квадратичные формы
§ 1. Линейная функция и линейная форма..............171
§ 2. Билинейная функция. Билинейная и квадратичная формы 172
§ 3. Приведение квадратичной формы к сумме квадратов . . 175
§ 4. Закон инерции квадратичных форм................178
§ 5. Определенные формы..................... 179
6. Билинейные и квадратичные формы в евклидовом про-
странстве ..........................................183
Г л а в а VII
Исследование кривых и поверхностей второго порядка
§ 1. Приведение общего уравнения кривой второго порядка
к каноническому виду...................................186
§ 2. Инварианты кривой второго порядка...................190
§ 3. Определение центра и главных осей центральной кри-
вой. Отыскание црршины и оси параболы................199
§ 4. Исследование общего уравнения поверхности второго
порядка.............................................. 205
Глава VIII
Основные понятия специальной теории относительности
§ 1. Двумерные пространства со скалярным произведением 209
§ 2. Полуевклидова плоскость.......................... 210
оглавление:
5
§ 3. Псевдоевклидова плоскость.........................215
§ 4. Псевдоортогональные преобразования................218
§ 5. Пространство событий. Принцип относительности Гали-
§' 6 . Принцип относительности Эйнштейна ... .... 224
§ 7. Преобразования Лоренца............................227
§ 8. Некоторые следствия из формул Лоренца.............231
Глава IX
Понятие о тензорах
§ 1. Примеры тензоров............................... 239
§ 2. Определение и простейшие свойства тензора.........244
§ 3. Операции над тензорами............................248
§ 4. Тензоры в евклидовом пространстве.................253
Глава X
Основные понятия теории групп
§ 1. Примеры групп. Определение группы.................257
§ 2. Группы преобразований.............................261
§ 3. Подгруппа . ......................................265
§ 4. Изоморфизм групп..................................266
§ 5. Группы преобразований плоскости ..................268
§ 6. Разложение группы по подгруппе....................274
§ 7. Нормальный делитель.............................. 278
§ 8. Фактор-группа ....................................280
§ 9. Нормальные делители группы преобразований евклидо-
вой плоскости и соответствующие им фактор-группы . . 282
Дополнительная литература..............................286
Предметный указатель ..................................287
ПРЕДИСЛОВИЕ
Эта книга представляет собой учебное пособие по
линейной алгебре, рассчитанное на студентов втузов и
естественно-научных факультетов университетов. Она
может быть полезной и читателю, желающему само-
стоятельно познакомиться с основными понятиями ли-
нейной алгебры по источнику, не требующему почти
никаких предварительных сведений из высшей мате-
матики. Предполагается лишь, что, помимо школьного
.курса математики, читатель знаком с элементами ана-
литической геометрии. Используемые в книге понятия
математического анализа (производная, интеграл)
встречаются только в примерах, которые при чтении
книги могут быть опущены без ущерба для ее пони-
мания.
Глава 1 является вводной; она содержит все необ-
ходимые для дальнейшего сведения из теории опреде-
лителей и систем линейных уравнений. Основными
в книге являются главы II—VI, в которых излагается
краткий курс собственно линейной алгебры.
Последние четыре главы, по существу, не относятся
к линейной алгебре, но их результаты основаны на
предыдущем материале («‘..некоторые ее приложе-
ния»). Они независимы друг от друга и могут читаться
в любом порядке (см. ниже схему зависимости глав).
Глава VII посвящена общей теории кривых и по-
верхностей второго порядка; она имеет целью допол-
нить и углубить соответствующую часть курса анали-
тической геометрии, не претендуя на ее замену.
Несколько необычной для учебника линейной ал-
гебры является глава VIII, посвященная специальной
теории относительности. Ее содержание в значитель-
ПРЕДИСЛОВИЕ
7
пой степени навеяно курсом лекций Петра Константи-
новича Рашевского, прочитанным им в Московском
университете задолго до появления его книги [8] (см.
список литературы па стр. 286). При изучении линей-
ной алгебры эта глава может быть и опущена, но
опыт преподавания показывает, что обычно она вызы-
вает у слушателей большой интерес.
Глава IX посвящена основным понятиям тензорной
алгебры. Она является довольно конспективной и мо-
жет служить введением в более обстоятельные изло-
жения той же темы, из числа которых назовем, напри-
мер, указанные в списке литературы книги [9] и [10].
Последняя глава содержит лишь самые общие све-
дения из теории групп, знакомство с которыми сегодня
является обязательным не только для математика, ио
и для инженера. Однако теория групп отнюдь не
является частью линейной алгебры; поэтому для
сколько-нибудь подробного ее изучения читателю сле-
дует обратиться к специальной литературе.
Содержание настоящей книги составляет слегка
расширенный курс лекций, неоднократно читавшийся
автором на отделении физхимии химического фа-
культета МГУ. Помимо уже упомянутой книги [8],
в ней использованы указанные в списке литературы
книги [1]—[3], [10], [11]. ‘
В заключение мне приятно выразить сердечную
благодарность Исааку Моисеевичу Яглому за друже-
скую критику и советы по улучшению книги. Из книги
Яглома («Принцип относительности Галилея и не-
евклидова геометрия», М„ «Наука», 1969) заимство-
вана, в частности, идея интерпретации пространства
событий классической механики на полуевклидовой
плоскости.
Я очень признательна также Д. В. Беклемишеву,
многие замечания которого, сделанные им в обстоя-
тельной рецензии, учтены мною в работе над руко-
писью, а также за ряд полезных советов — моему сыну
Ю. Головину.
Л. И. Головина
СХЕМА ЗАВИСИМОСТИ ГЛАВ
ГЛАВА I
ОПРЕДЕЛИТЕЛИ И СИСТЕМЫ
ЛИНЕЙНЫХ УРАВНЕНИЙ
В этой главе содержится вспомогательный мате-
риал, относящийся к решению систем линейных урав-
нений (т. е. уравнений первой степени). Для исследо-
вания таких систем вводится важное понятие опреде-
лителя. Результаты этой главы, интересные и сами по
себе и в приложениях к аналитической геометрии, не-
обходимы для понимания дальнейших глав книги.
§ 1. Системы уравнений
с двумя и тремя неизвестными
При решении одного уравнения первой степени
с одним неизвестным
ах = b
возможны три случая:
1, Если а ¥= 0, уравнение имеет единственное
Ь
решение х = —.
2. Если а = 0 и b = 0, уравнение имеет бесчис-
ленное множество решений: любое вещественное
число х удовлетворяет уравнению ах = b (так как
0-х = 0) и, значит, является его решением.
3. Если а = 0, но b ¥= 0, уравнение не имеет ре-
шений, так как при подстановке вместо х любого ве-
щественного числа в левой части получается нуль, в то
время как правая часть отлична от нуля.
Такие же три случая возможны и при решении про-
извольной системы линейных уравнений.
10
ОПРЕДЕЛИТЕЛИ И СИСТЕМЫ УРАВНЕНИЙ
[ГЛ. I
Рассмотрим систему двух уравнений с двумя неиз-
вестными:
| arx + Ьру ~ С[.
1 а2х + Ь2у = с2. ' '
Решением такой системы называется каждая пара
значений х = а, у = р, подстановка которых вместо х
и у обращает оба уравнения в тождества. Чтобы ре-
шить эту систему, умножим первое уравнение на Ь2,
второе на — bi и сложим их; мы получим
x(a}b2 — a2bi)= C\b2 — c2bh
Отсюда, если atb2 — a2bi 0, будем иметь
х = (2)
Аналогично находим, что
Таким образом, в случае, когда- ахЬ2— а2Ь1^Р0, си-
стема (1) имеет единственное решение.
Выраженйя, стоящие в числителях и знаменателях
правых частей равенств (2) и (3), устроены одина-
ково. А именно, рассмотрим квадратную таблицу чисел
4-Р' ?' -
а2 Ь2 _
Такие таблицы называются матрицами. Горизонталь-
ные ряды образующих матрицу чисел называются
ее строками, вертикальные — столбцами. Числа at, bi,
a2, b2, составляющие матрицу, называются ее элемен-
тами. В нашем примере мы имеем квадратную мат-
рицу второго порядка. Диагональ, идущая из
левого верхнего угла матрицы в правый нижний, на-
зывается ее главной диагональю. Знаменатели дробей,
стоящих в правых частях равенств (2) и (3), устроены
следующим образом: из произведения элементов, стоя-
щих по главной диагонали матрицы А, вычитает-
ся произведение элементов, стоящих по второй, или
§ 1]
СИСТЕМЫ С ДВУМЯ И ТРЕМЯ НЕИЗВЕСТНЫМИ
11
побочной, ее диагонали:
Полученное выражение называется определителем
матрицы А (определителем второго порядка) и обо-
значается так:
а2 Ь2
Таким образом, по определению
Я]
а2
bi
ь2
— d{b2 — а2Ь\.
В этих обозначениях числитель дроби, стоящей в пра-
вой части равенства (2), представляет собой опреде-
литель
получающийся из знаменателя заменой первого столб-
ца столбцом свободных членов, а числитель дроби,
стоящей в правой части равенства (3), — определи-
тель
Я1 с1
^*2
получающийся из знаменателя заменой второго столб-
ца столбцом свободных членов уравнений системы (1).
Итак, мы нашли, что
х =
С1
01
G-2
bl
Ьг
bi
bi
С1
С2
Ь1
bi
У =
«1
«I
Это — формулы Крамера для решения систе-
мы двух уравнений с двумя неизвестными.
Пример 1, Пользуясь формулами Крамера, решить систему
уравнений
[ 2х + 5у — 8,
1 Зх 4- у = - 1.
12 1 ОПРЕДЕЛИТЕЛИ И СИСТЕМЫ УРАВНЕНИИ [ГЛ. I
Решение.
I 8 5| 12 81
-11 8 + 5 , 3-1 -2-24 _
х = 72-5Г = ГГТ5=-1; = —ГТз- = 2-
13 1 I
Рассмотрим теперь случай, когда
а> = ахЬ2 — а2Ь} = 0. (4)
£?2 Ь‘2
Равенство (4) можно переписать так *):
Д1 _• ь,
<12 ' Ь2 '
т. е. в этом случае коэффициенты при неизвестных
пропорциональны. Если, кроме того, и
С| ?’ =0, т. е. -- = 4>
6*2 Ь% ^'2
то и свободные члены пропорциональны коэффициен-
там при неизвестных, и мы имеем на самом деле одно
уравнение с двумя неизвестными — оно допускает
бесчисленное множество решений.
Наконец, если
т. е. если
Qi Ь} , с।
«2 Й2 с2 '
то уравнения, очевидно, противоречат друг другу, и
система не имеет ни одного решения.
Решение х = а, у = |3 системы уравнений (1) опре-
деляет точку пересечения прямых
а{х + bly = cl и а2х + Ь2у = с2.
Если
«1
а2
это — две
различные, не парал-
лельные прямые, и значит, они имеют единствен-
*) Здесь и дальше
нуля; случай, когда это
мы считаем, что знаменатели отличны от
не так, рассмотрите сами.
§ 1] СИСТЕМЫ С ДВУМЯ И ТРЕМЯ НЕИЗВЕСТНЫМИ 13
ную общую точку. В случае, когда
прямые параллельны и, значит, не имеют ни одной
общей точки. Наконец, если ~ , оба урав-
нения определяют одну и ту же прямую, все точки
которой и будут «точками пересечения» данных
прямых.
Рассмотрим теперь систему трех линейных уравне-
ний с тремя неизвестными:
агх + bty + c{z = dt,
а2х + b2y + c2z = d2, (5)
агх + Ь,у + cyz = d3.
Решением этой системы называется каждая такая
тройка чисел х = а, у = Р, 2 = у, при подстановке ко-
торых все три уравнения обращаются
О
О
= Ьмц - Ь,ся,
в тождества.
множив первое уравнение на
bi
Ьз сз
= Ь(С2 — b2Ci и сложив их все, мы
= Ь2с3 - Ь3с2,
третье — на
второе — на
bi Ct
b2 с2
x(atb2c3 — albic2 + а2Ьур — a2b{c3 + a3b{c2 — a^b^Ci) =
= dtb2c3- dtbyc2 + d2b3ci - d2biC3 + d3b{c2 - d3Z>2c(
получим
(коэффициенты при у и г, как легко видеть, будут
равны нулю). Отсюда, если коэффициент при х отли-
чен от нуля, получаем
^!&2Сз — й\Ьгсг + d^b-jCt — d2b1c,l + d3bjC2 — rf3Z>aCi
«1&2сз — aib3c2 + a2bjCi — a2bic3 + a3&ic2 — a3b2Ci
(6)
Посмотрим, как устроено выражение, стоящее
в знаменателе правой части равенства (6). Для этого
рассмотрим квадратную таблицу {матрицу третьего
порядка)
~ Я] bi Ci"
А = а2 Ь2 с2
а3 ЬЛ с3
14
ОПРЕДЕЛИТЕЛИ И СИСТЕМЫ УРАВНЕНИЙ
[ГЛ. I
Знаменатель в формуле (6) представляет собой
алгебраическую сумму шести членов, каждый из кото-
рых является произведением трех элементов, взятых
по одному из каждой строки и каждого столбца мат-
рицы А, причем знак .плюс имеет произведение эле-
ментов, принадлежащих главной диагонали, и два
произведения элементов, образующих в матрице (рав-
нобедренные) треугольники с основаниями,параллель-
ными главной диагонали:
а знак минус имеет произведение элементов, при-
надлежащих побочной диагонали, и два произведения
элементов, образующих треугольники с основаниями,
параллельными побочной диагонали:
I
§ 1] СИСТЕМЫ С ДВУМЯ И ТРЕМЯ НЕИЗВЕСТНЫМИ 15
Такое выражение называется определителем, со-
ставленным из матрицы А (определителем третьего
порядка), и обозначается так:
Hi b\
0,2 Ь3 С3
ai Ь3 с3
Таким образом, по определению
ai
а2
а3
bi ot
bi С3
— Ulb2C3 + Н2^3С1 + U3biC2
— a3b2Ci — a2b[C3 — aib3c2-
Выражение, стоящее в числителе правой части фор-
мулы (6), получается из знаменателя, если, каждую
букву а заменить буквой d с тем же номером, т. е.
bi Cl
bi с2
d3 Ьз с3
ai bl Cl
а2 b3 Ci
а3 Ьз с3
(6а)
Аналогично можно показать, что при D ¥= 0 из си-
стемы (5) следуют равенства
D> D3
У = ~О’ Z-~D>
(7)
D =
где Di, i= 1, 2, 3, — определитель, получающийся из
определителя D заменой i-ro столбца столбцом свобод-
ных членов. Это — формулы Крамера для систе-
мы трех уравнений с тремя неизвестными.
Пример 2. Решить по формулам Крамера систему урав-
нений
х + 2у + Зг = 7,
х — Зу + 2г = 5,
х + у + г = 3.
16
ОПРЕДЕЛИТЕЛИ II СИСТЕМЫ УРАВНЕНИЙ
[ГЛ. I
Решем е.
2
-3
1
= - 3 + 3 +4+ 9-2-2= 9^0;
2 3
-3 2 =- 21 + 15+12 + 27- 10-14 = 9,
7 3
5 2
3 1
2 7
-3 5
1 3
= 5+ 14 + 9-15-7-6 = 0,
= - 9 + 7+ 10 + 21 - 6-5 = 18.
Следовательно,
Х D
D ’ D
0 =
1
1
1
3
2
1 1
Для того чтобы сформулировать, что такое опреде-
литель п-го порядка, рассмотрим снова определители
второго и третьего порядков:
и
«1 bi
а2 Ь2
= asb2 — а2Ь
(&)
а2
аз
Ь2
Ьз
С1
= aib2c3 + a2b:iCi + a3b1c2 - a3b2Ci —
- a2btc3 — atb3c2. (9)
Мы видим, что определитель есть алгебраическая
сумма всевозможных произведений его элементов, взя-
тых по одному из каждой строки и каждого столбца.
Каждое такое произведение называется членом опре-
делителя. В каждом члене определителя второго по-
рядка расположим множители в порядке следования
столбцов определителя:
а^Ь2 а2Ь[.
Рассмотрим соответствующие расположения (переста-
новки) нижних индексов (указывающих номера строк):
1, 2 п 2, 1.
СИСТЕМЫ С ДВУМЯ И ТРЕМЯ НЕИЗВЕСТНЫМИ
17
В первом произведении эти индексы расположены по
возрастанию, и соответствующее произведение входит
в определитель со знаком плюс; во втором они, как
говорят, образуют беспорядок, или инверсию 2, 1, и
соответствующий член входит в определитель со .зна-
ком мину с.
В определителе третьего порядка шесть членов.
Если в каждом из них расположить множители в по-
рядке следования столбцов, то в членах, входящих со
знаком плюс, нижние индексы образуют перестановки
1, 2, 3; 2, 3, 1; 3, 1, 2.
Рассмотрим три пары индексов 1, 2; 1, 3 и 2, 3 из
первой перестановки 1, 2, 3; числа каждой пары рас-
положены по возрастанию—в этой перестановке
нуль инверсий. Во второй перестановке 2, 3, 1 три
пары индексов: 2, 3; 2, 1 и 3, 1, две из которых —
2, 1 и 3, 1 образуют инверсии. В третьей перестановке
3, 1, 2 — три пары индексов 3, 1; 1, 2 и 3, 2, из которых
две, 3, 1 и 3, 2, образуют инверсии.
Произведениям, входящим со знаком минус, соот-
ветствуют три перестановки нижних индексов:
3, 2, 1; 2, 1, 3 и 1, 3, 2,
причем в первой, как нетрудно видеть, три инверсии:
3, 2; 3, 1 и 2, 1, а во второй и третьей — по одной: соот-
ветственно, 2, 1 и 3, 2. Таким образом, со знаком плюс
входят те члены, у которых в перестановке нижних
индексов четное число инверсий, а со знаком ми-
нус— те, у которых это число нечетно.
Для дальнейшего нам будет удобнее ввести для
определителей второго и третьего порядков новые обо-
значения:
а11 а12
а2| а22
all at2 а13
°21 а22 а23
«31 «32 «33
где все элементы определителя обозначены одной и той
же буквой а с двумя индексами, первый из которых
указывает номер строки, а второй — номер столбца.
18
ОПРЕДЕЛИТЕЛИ И СИСТЕМЫ УРАВНЕНИЙ
[ГЛ. I
Тогда аИ а12 6?21 ^22 — ЯцЯ22 — «21«12
И
«и «12 «13
а21 «22 «23 = ± «ПЩ/ггй/зЗ
«31 «32 «33
где знак плюс стоит перед теми произведениями, в
которых перестановка ilt i2, i3 четная (т. е. имеет
четное число инверсий), и знак минус — перед теми,
где она нечетна. Это можно записать еще и так:
«11 «12 «13
«21 «22 «23 = 1)а «i,l«z22«i33,
«31 «32 «33
где а есть число инверсий в перестановке первых
индексов, й, 12, й (вторые индексы расположены
в естественном порядке), а суммирование распростра-
няется на все шесть перестановок й, к, й из трех
чисел 1, 2, 3.
§ 2. Перестановки и транспозиции.
Определитель п-го порядка
Пусть даны п элементов сц, а2, .... ап (напри-
мер, это могут быть числа 1, 2, 3, ..., п). Как из-
вестно, всевозможные расположения этих элементов
называются перестановками из п элементов. Всего
из п элементов, можно составить п\ перестановок (до-
кажите это).
Если какая-нибудь лара ait а^ элементов пере-
становки расположена в ней так, что элемент с боль-
шим номером стоит раньше элемента с меньшим но-
мером, то говорят, что эти элементы образуют
инверсию. Пусть нам надо сосчитать число инверсий
в какой-то перестановке, образованной числами 1, 2,
3, ..., п (это могут быть номера элементов ai, а2, ...
..., ап). Сделать это можно следующим образом.
Сосчитаем сначала число элементов, стоящих в п е-
§ 2] ПЕРЕСТАНОВКИ И ТРАНСПОЗИЦИИ 19
реди единицы — все эти элементы и только они
образуют инверсии с единицей. Вычеркнем затем
единицу и сосчитаем число элементов, стоящих впе-
реди двойки, — это будут все те элементы, кото<
рые образуют инверсии с двойкой (не считая уже
вычеркнутой единицы, которая тоже может образо-
вывать инверсию с двойкой, но в таком случае эту
инверсию мы уже учли раньше). Затем вычеркнем
двойку и сосчитаем число элементов, стоящих впе-
реди тройки, ит. д. Все полученные числа сло-
жим— эта сумма и будет равна общему числу ин-
версий. Число инверсий в перестановке i2, .... in
обозначается так: [t'i, iz, ..., in]. Например,
[2, 5, 1, 4, 7, 3, 6] = 2 + 0 + 3 + 1 + 0 + 1 = 7.
Перестановки с четным числом инверсий назы-
ваются четными, перестановки с нечетным чис-
лом инверсий — нечетными перестановками.
Пусть дана перестановка из п элементов Я1, az, ...
..., a-i, ...., ah, ..., ап. Поменяем местами два ее
элемента я, и ah; при этом мы получим перестановку
Я], я2, ..., яй, ...,.а{, ..., ап. Такая операция пере-
мещения. двух элементов перестановки называется
транспозицией.
Теорема 1. От одной транспозиции четность
перестановки меняется (т. е. четная перестановка
становится нечетной, а нечетная — четной).
Доказательство. Рассмотрим сначала слу-
чай, когда меняются местами два соседних эле-
мента аир перестановки
ЯЩ2, ..., яг, а, р, Ь\, Ь2, ..., bm. (10)
После транспозиции элементов аир получим пе-
рестановку
Я], я2, .... яг, р, a, Ьг, b2, ..., bm. (11)
Так как перестановки (10) и (11) отличаются друг
от друга только взаимным расположением элемен-
тов а и р (а взаимное расположение каждого из этих
20 ОПРЕДЕЛИТЕЛИ II СИСТЕМЫ УРАВНЕНИИ [ГЛ. I
элементов и какого-то другого, так же как и взаим-
ное расположение любых двух из остальных элемен-
тов, осталось прежним), то число инверсий в пере-
становке (11) на единицу больше или меньше числа
инверсий в перестановке (10), и значит, одна из этих
перестановок четная, а другая — нечетная.
Рассмотрим теперь общий случай. Пусть меняются
местами элементы а и |3 перестановки щ, .... щ, а,
Ci, ..., С)>„ р, Ьт, между которыми стоят
еще k элементов С], с2, ..., ch. Мы можем выполнить
транспозицию элементов аир посредством несколь-
ких транспозиций рядом стоящих элементов: поме-
няем местами а сначала с щ, затем с с2, и т. д., на-
конец, с (при этом мы сделаем k транспозиций
рядом стоящих элементов); затем поменяем места-
ми аир (еще одна транспозиция) и, наконец, по-
меняем местами р последовательно с ch, с с.ь._1, и т. д.
до С[ (еще k транспозиций рядом стоящих элементов).
В конечном счете р станет на место а (и наоборот).
При каждой такой транспозиции четность переста-
новки, как мы уже видели, меняется. А так как она
изменится 2k + 1, т. е. нечетное число раз, то оконча-
тельно нечетная перестановка сделается четной, а
четная — нечетной.
Следствие. Число нечетных перестановок из п
элементов равно числу четных перестановок (и равно,
следовательно, п!/2).
Доказательство. Пусть из п! перестановок
из п элементов р перестановок четны и q нечетны.
Сделаем в каждой четной перестановке одну и ту же
транспозицию, например, поменяем местами первые
два элемента. Тогда каждая четная перестановка пре-
вратится в нечетную, причем ясно, что все р полу-
ченных при этом нечетных перестановок будут раз-
ными. А так как общее число нечетных перестановок
из п элементов, по предположению, равно q, то p^q.
Точно так же можно убедиться в том, что, наоборот,
q^p. Следовательно, р = q.
Дадим теперь общее определение определителя.
Пусть имеется квадратная таблица (матрица п-го
§ 31
СВОЙСТВА ОПРЕДЕЛИТЕЛЕЙ
2i
порядка)
ап а!2 . •
А = ац а22 а2п
&п1 @п2 • • ^ttri _
Числа ац, называются ее элементами, горизонтальные
ряды элементов матрицы называются ее строками,
вертикальные — столбцами. Определителем, составлен-
ным из этой матрицы (определителем п-го порядка),
называется алгебраическая сумма всевозможных про-
изведений элементов, взятых по одному из каждого
столбца и каждой строки матрицы А. Если в каждом
таком произведении {члене определителя) множители
расположены в порядке следования столбцов, то со
знаком плюс берутся те произведения, у которых пе-
рестановка нижних индексов четная, и со знаком
минус — те, у которых она нечетная. Короче:
°11 а12 • • • а1п
а<21 022 . . . а2п
= V (- z2.....
'"1 a^ia^ ... а^,
&П1 @п2 • • &пп
где суммирование распространяется на всевозмож-
ные перестановки и, t2, in из п чисел 1, 2, 3, ...
..., п. Так как число перестановок из п элементов
равно п\, то определитель п-го порядка состоит из п!
членов. Ввиду следствия из теоремы 1 ровно воло-
вина из них, т. е. и!/2, входит в определитель со зна-
ком плюс и столько же — со знаком минус. ж
§ 3. Свойства определителей
С увеличением порядка определителя число его
членов очень быстро растет. Так, определитель чет-
вертого порядка состоит из 24 членов, определитель
пятого порядка—из 120, определитель шестого по-
рядка — из 720 членов, и т. д. Поэтому вычислять опре-
делители порядка выше трех, пользуясь только опре-
делением, практически невозможно. Для того, чтобы
22
ОПРЕДЕЛИТЕЛИ И СИСТЕМЫ УРАВНЕНИИ
[ГЛ. I
вычислять такие определители, нам придется изучить
их свойства. Прежде всего мы докажем одно вспомо-
гательное предложение.
Лемма (о знаке члена определителя). Произве-
дение а^а^ . ^inkn входит в определитель п-го
порядка со знаком, определяемым выражением
(-1)Рг‘'2. ln]+lkVk2....М;
мы будем говорить в таком случае короче: входит со
знаком
(_ 1)(г1 -Ч.У+Р1Л.......М.
Доказательство. Заметим прежде всего, что
если поменять местами два множителя произведения
• • aitlkn’ т0 как в первых, так и во вторых
его индексах, произойдет по одной транспозиции,
и значит, четность каждого из чисел
Ul, Z2, . . ., Z„] и [/?!, k2, . . ., kn]
изменится, а четность их суммы [й, i2,..., Д] +.
+ [fet, fe2, ..., fen] останется без изменения.
Пусть нам дано произведение aiik . ainkn.
С помощью нескольких транспозиций этих множите-
лей расположим их так, чтобы вторые индексы шли
в нормальном порядке. Для этого сначала сделаем
транспозицию, при которой на первое место станет
элемент из первого столбца, затем такую, чтобы на
второе место попал элемент из второго столбца, и т. д.
(Так, например, произведение а^ЯмЯзгаг^зз последо-
вательно преобразуется в а21«14Й52«45«зз, затем в
«21а52«14а45«зз, в a2ia52a?,3a45ai4 и, наконец, в
«21а52«зза14Й45-) Если в конечном счете, когда вторые
индексы расположатся по возрастанию, первые обра-
зуют перестановку [ть ш2,..., отп], то рассматривае-
мый член, по определению, входит в определитель со
знаком (—•••’"’«]. Но так как чётность суммы
h’i,i2,+ [fei,fe2,..., fen] числа инверсий в первых
и числа инверсий во вторых индексах при транспози-
циях множителей не менялась, то четность этой сум-
мы в первоначальном расположении множителей
s 3] СВОЙСТВА ОПРЕДЕЛИТЕЛЕЙ
23
совпадает с четностью числа [mi, m2, ..., m„]—числа
инверсий в перестановке первых индексов окончатель-
ного расположения: в нем вторые индексы образуют
нуль инверсий. Следовательно,
(_ 1)[тГ т2- = (_ l)['r 12.... У + [‘|’ k2.М ,
что и доказывает наше утверждение.
Пример 3. Найти, с каким знаком произведение
432^,3051016024 входит в определи!ель пятого порядка
Решение.
Оц 012 ‘013 014 «15
021 °22 О2з °24 «25
0з1 032 Озз 034 035
041 ° 42 «43 а44 045
0-J а52 а53 а55
[3, 4, 5, 1, 2] = 3+3 = 6,
[2, 3, 1, 5, 4] = 2+ 1 = 3;
(_ 1)6+3 = (_1)9=;_ ]
(12)
Рассматриваемое произведение входит в определитель (12) со
знаком минус.
Свойство 1 («равноправие» строк и столбцов
определителя). Значение определителя не меняется
при его транспонировании, т. е. при замене
каждой его'строки столбцом с тем же номером.
Доказательство. Рассмотрим определители
и
«11 «12 «in
D = «21 «22 • • «2л
«л! ««2 •
«п «21 • • «л!
D'= «12 «22 • • «л2
«1Л .«2л •• * &пп
Надо показать, что D' — D.
24
ОПРЕДЕЛИТЕЛИ II СИСТЕМЫ УРАВНЕНИЙ
[ГЛ. I
Каждый член определителя D является членом и
определителя D', так как его множители и в опреде-
лителе D' находятся в разных строках и разных
столбцах; обратно, каждый член определителя D'
будет членом и определителя D. Таким образом, оба
определителя представляют собой «алгебраическую
сумму» (т. е. сумму, в которой некоторые слагаемые
берутся со знаком минус) одних и тех же членов
вида . ainkn- Различие заключается только
в том, что в определителе D первые индексы — это
номера строк, а вторые — номера столбцов, а в опре-
делителе D' — наоборот. Но так как по лемме о знаке
члена определителя знак такого произведения как
в первом, так и во втором определителе будет одним
и тем же':
(_ 12.У+Рг ......knli
то D’ = D.
Свойство 2. Если поменять местами две строки
или два столбца определителя, то определитель изме-
нит только знак, а по абсолютной величине не изме-
нится.
Докажем это утверждение, например, для столб-
цов. Поменяв в определителе
О.
«и «12 • • «1р • .. alq . .
«21 «22 • • &2р • a2q
«П1 &п2 • ^пр anq • •
местами р-й и </-й столбцы, мы получим определитель
а{1 а12 . .. . . а1р . . . ain
ап а22 • • a2q ... а2р ... а2п
^п\ ^п‘2 • • «пр • • * «яр • • • &пп
Каждый член определителя будет членом
и определителя D2, так как его множители рас-
положены и в £)2 в разных строках и разных
столбцах, и обратно. Возьмем какой-нибудь член
§ 3]
СВОЙСТВА ОГIРЕДЕЛИТЬ’ЛСИ
25
определителя Dr.
d; id; 9 . . . Q; .) . . . d; a . . . d; n.
П1 l'p<} lnn
Так как его множители расположены в порядке сле-
дования столбцов в D\, то он входит в определи-
тель £>i со знаком (— 1)1*1' Ч1 ‘р• ‘и!. для
того чтобы найти знак этого члена в определителе
£>2, расположим его множители в порядке следова-
ния .столбцов в D2:
d ;i(7; 9 ... d; a ... d ; 9 ... di n
Ijl l2- l;[4 lfln
(элемент содержится в р-м столбце определи-
теля £>2, а элемент aij)P — в 9-м). Первые индексы
в определителе О2, так же как и в определителе Dt.
указывают номера строк; поэтому в определитель £)2
рассматриваемое произведение войдет со знаком
(— 1)[*1' 12.••••’/?..‘«J. Но перестановка £, i2, ...
iq, iP, in получается из перестановки
ii, i2, ip, iq, in, посредством одной
транспозиции, а значит, числа
[£, i2, . . . , ip, . . . , iq, . . . , In] И [11, <2, . . . , iq, . . . , ip, . , in]
разной четности. Таким образом, каждый член опре-
делителя Di в определитель D2 входит с противопо-
ложным знаком, и значит, £)2 = —£>ь
Для того чтобы доказать соответствующее предло:
жение для строк, перейдем к транспонированным
определителям £\ (транспонированный определи-
тель £>i) и £)2 (транспонированный определитель О2).
Если определитель D2 получается из £)( перестанов-
кой р-й и <?-й строк, то D> получается из £), переста-
новкой p-то и 9-го столбцов, и значит, D2~ ~D\.
Но D'i = Di и £)2 = £>2> а потому £)2 =—£)>.
Следствие. Определитель с двумя одинаковыми
строками или с двумя одинаковыми столбцами равен
нулю.
Для доказательства поменяем местами одинако-
вые строки (или столбцы) определителя О; от этого
он, конечно, не изменится. А так как, по свойству 2,
26
ОПРЕДЕЛИТЕЛИ II СИСТЕМЫ УРАВНЕНИЙ
[ГЛ. I
он должен при этом изменить знак, то D = —D, от-
куда D = 0.
Свойство 3. Если все элементы строки или
столбца определителя умножить на одно и то же
число, то значение определителя умножится на то же
число.
Доказательство проведем, например, для столб-
цов. Если все элементы й-го стол’бца определителя
D =
а12 . .. а^ . . . ain
Ц21 ^22 • • • a2k • • а2п
O-nl ап2 • • • ank • • • ^пп
умножить на с, мы получим определитель
D.=
аи а12 ... са^ ... а1п
a2i а22 . . . ca2fe . . а2п
&п\ &п2 • • • • • • ^nn
равный
2(~ ‘2’-- . (caikk) • • ainn —
= с 2 (- I)1’1’ ‘2.....l^ai^ai22 . aikk ... ain?l = cD.
Соответствующее свойство для строк легко дока-
зывается переходом к транспонированным определи-
телям.
Таким образом, общий множитель всех элементов
строки или столбца определителя можно выносить за
знак определителя.
Следствие. Определитель с двумя пропорцио-
нальными строками или столбцами равен нулю.
В самом деле, вынося «множитель пропорциональ-
ности» строки или столбца за знак определителя, мы
придем к определителю с”двумя одинаковыми стро-
ками или столбцами, который равен нулю ввиду след-
ствия из свойства 2.
Свойство 4. Если каждый элемент k-го столб-
ца определителя представлен в виде суммы двух.
§ 31 СВОЙСТВА ОПРЕДЕЛИТЕЛЕЙ * 27
слагаемых: aik ~ bik + с,;., т. е. если
«11'012 ... blk + с1й ... а1п
jy _ «21 «22 b2ll + с2к ... а2п
ап1 ап2 • • • Ьпк + спк • • • ®пп
то D можно следующим образом представить в виде
суммы двух определителей:
аи «12 • • blk • • а1п
а21 ^22 * • ь2к . а2п
^nl «л2 • • Ьпк . • ^пп
«11 «12 • • • clfe
«21 «22 • • • с26
«1Я
«2п
= D{ + D2.
«л| «л2 • • Cnk • • • «лл
Аналогичное утверждение справедливо и для строк.
Доказательство вытекает из равенства:
Д==2(_ 0^' 2 ^aitiaiz2 • • • С1кк) • • • ainn =
= 2 (— i)f >’2 n^atpai22 • • bikk • • • ainn +
+ 2 (— l)f 1 2' n^ailiai22 • • • Ci/!k • • • ainti = ^1 + ^2"
Замечание. Легко видеть, что справедливо и
следующее, более общее утверждение: Если каждый
элемент k-го столбца определителя D представлен в
виде суммы р слагаемых: ацг = «к + а«+ ••• + ««,
то определитель D можно представить в виде сум-
мы р определителей:
D- 2
7—1, 2, .
Й11 й12 ’ ' 1 a{k 1 • й1гг
Й21 «щ ... «^ ... «2п
ап1 й«2 ••• а'пк ••• апп
28
ОПРЕДЕЛИТЕЛИ И СИСТЕМЫ УРАВНЕНИИ
[ГЛ. I
Следствие. Определитель не меняет своего
значения, если ко всем элементам какой-либо его
строки или какого-либо столбца прибавить соответ-
ствующие элементы параллельного ряда, умножен-
ные на одно и то же число.
Действительно, пусть дан определитель
flj] Я]2 . . . й|р . . . й]р • • • Я]п
__ Я21 fl22 • • • @2р . . . Cl2q . . • Й2гс
@п\ @п2 • • . C^nq • • • @пп
Прибавив ко всем элементам его р-го столбца соот-
ветствующие элементы q-vo столбца, умноженные на
одно и то же число с, мы получим определитель
@и @12 • • сцр “Ь ca\q ... fljp . . а-.,,
^21 @22 • • • @2р "4" @@2q . . . @2q • - • @2п
D] =
@nl @п2 • • • @пр “Ь c@nq . . . @ ng • • @пп
Ввиду свойства 4 определитель О) равен
fl]] fl|2 • , . fljp • • • @}q . . . fl]rt
Я21 Я22 • • • Opp ... a2q ... a2„
@nl @n2 * • • @np * • @nq • • • @nn
flj] fl,2 . . . Cfl]p . . . flip . . . fl]rt
fl-21 fl22 • ca2q . .. a2q . . . a2n
j
@ni @n'2 • • * C@nq • • @nq • * @nn
(второе слагаемое равно нулю как определитель
с двумя пропорциональными столбцами).
§ 4. Миноры и алгебраические дополнения
Минором Mih элемента aik определителя D п-го
порядка называется определитель (п—1)-го порядка,
получающийся из D вычеркиванием i-й строки и
k-ro столбца.
§ 4] МИНОРЫ И АЛГЕБРАИЧЕСКИЕ ДОПОЛНЕНИЯ 29
Алгебраическим дополнением АЛ элемента на-
зывается его минор, взятый со знаком (—
Alk = (—i)l+k Mik
Теорема 2. Если в определителе D п-го поряд-
ка все элементы k-го столбца (строки), Кроме одного,
равны нулю, то определитель равен произведению
этого, не равного нулю элемента на его алгебраиче-
ское дополнение.
Доказательство. Рассмотрим сначала част-
ный случай, когда в определителе D все элементы
первого столбца, кроме йц, равны нулю:
ЙЦ аГ2 • • а1п
О П22 • • й2п
О ап2 • апп
В каждый член определителя D входит в точности
по одному элементу из первого столбца; но так как
все эти элементы, кроме ац> равны нулю, то в опре-
делителе D все те члены, в которые из первого столб-
ца входит не йп, а какой-либо другой элемент, обра-
щаются в нуль. Следовательно,
р = 2(_1)[1’!г-У
где 12, .... in принимают значения 2, 3, ..., п. Эту
запись можно сократить: так как единица, стоящая
на первом месте, не образует ни одной инверсии, то
[I, i2, ..., /п] = [»2, <п]. И значит,
O = anl](-l)[1'2'””!n]aZ22 а1пП,
где суммирование распространяется на всевозмож-
ные перестановки i2, 13, • • •, in чисел 2, 3, ..., п. А так
как сумма
^(-1)^--‘п]а^ ... а^
равна определителю (п — 1)-го порядка, получающе-
муся из D вычеркиванием первой строки и первого
30
ОПРЕДЕЛИТЕЛИ И СИСТЕМЫ УРАВНЕНИИ
[ГЛ. I
столбца, т. е. равна Л1ц, и Ап = (—1) ,+1Afn = Ми, то
D = ЯцМ и = ОцЛц.
Рассмотрим теперь общий случай, когда все эле-
менты fe-ro столбца определителя D, кроме aih, рав-
ны нулю, т. е. когда определитель имеет вид
аи «21 «12 «22 ... 0 . ... 0 . • аы • «2га
D =
ац (2 alk . • «ira
ап2 ... 0 . • «гага
Переместим i-ю строку определителя D на первое
место, последовательно меняя ее местами с (г—1)-й,
(г — 2)-й, и т. д., наконец, с первой строкой. На это
потребуется I — 1 транспозиций строк, при каждой из
которых знак определителя меняется. Затем' мы пере-
местим fe-й столбец определителя D на первое место,
последовательно меняя его местами с (/г—1)-ым,
(k— 2)-ым и т. д., наконец, с первым столбцом. Для
этого потребуется k—1 транспозиций столбцов, при
каждой из которых знак определителя тоже меняется.
В конечном счете, мы получим определитель
aik аа .. . ain
0 ап . .. аХп
0 ctn[ . .. ипп
отличающийся от определителя D знаком (—l);+ft. Но,
как мы только что видели, определитель Di равен
произведению на определитель (п — 1)-го поряд-
ка, получающийся из D\ вычеркиванием первого
столбца и первой строки, или, что то же самое, полу-
чающийся из D вычеркиванием fe-ro столбца и i-й
строки, т. е.
£>i = aikMih
и, следовательно,
D = (- \)i+kDl = (- V)i+kaikMik = aikAih.
§ 4] МИНОРЫ И АЛГЕБРАИЧЕСКИЕ ДОПОЛНЕНИЯ 31
Доказанная теорема дает возможность, используя
еще следствие из свойства 4, вычислить определитель
какого угодно порядка.
Пример 4. Вычислить определитель пятого порядка-.
2
-1
1
2
1
О
1
4
1
2
D =
1.31
2 2 3
0-15
3 1 2
-1 3 1
Решение. Вычитая из первого столбца определителя D
удвоенный третий, из четвертого — утроенный третий*и из пято-
го — третий столбец, получим
0 0
-5 1
£>= 14
-4 1
1
2
0
3
-1
0 0
-4 - 1
-1 5 =
-8 -1
6 2
= а13Л13 = 1 • (—1)1+3
-5 1
1 4
—4 1
3 2
-4 1
-Г 5
-8 -1
6 2
3 2
В полученном определителе четвертого порядка будем таким
же образом «делать нули»; прибавим к первому столбцу чет-
вертый, умноженный на 5, от второго отнимем четвертый и к
третьему прибавим четвертый, умноженный на 4:
0
26
-9
13
о о
-1 19
2 -12
0 14
1
5
-1
2
= й] .(Ли — 1 • (— 1)'+<<
26
-9
13
-1 19
2 -12
0 14
Мы пришли к определителю третьего порядка, который уже
можно вычислить непосредственно или сведя его к определителю
второго порядка: прибавив ко второй строке удвоенную первую,
получим
26 -1 19
43 0 26
13 0 14
= а12Л12-(-1)(-1)’+2| f|
= 2И? *3 |-2(301-169) =264,
| 1 о I |
значит, определитель D = —264.
32 ОПРЕДЕЛИТЕЛИ И СИСТЕМЫ УРАВНЕНИИ [ГЛ. I
§ 5. Разложение определителя* по элементам строки
или столбца
Теорема 3. Каждый определитель равен сумме
произведений элементов любой его строки (столбца)
на их алгебраические дополнения.
Мы докажем, что при всех I, k
«н сцз • • • а1п
«21 «22 • • «2п
= ацАц + а12А12 + ... + «ьгЛ;„
«п! «м2 * • «пп
(разложение по элементам i-й строки) и
D = + a2kA2k + + ankAnk
(разложение по элементам k-vo столбца).
Для доказательства заметим прежде всего,
что если два определителя отличаются друг от друга
только элементами одного столбца (строки), то алге-
браические дополнения элементов этих столбцов
(строк) в обоих определителях одинаковы, так как
при вычислении этих дополнений столбцы (строки),
которыми отличаются определители, вычерки-
ваются.
Докажем теперь для определителя D справедли-
вость, например, разложения по k-ыу столбцу. Для
этого представим его в следующем виде:
Пц а12 • • • axk + 0 + ... + О ...
Й21 «22 • • • 0 + a2k + . . . + 0 ... а2п
@ni &п2' • • • 0 4* О -Ь ... -Ь апь . •. аггп
(здесь каждый элемент &-го столбца представлен в
виде суммы п слагаемых, п — 1 из которых равны
нулю). По свойству А (см. замечание на стр. 27)
имеем
D — Dj + D2 + ... + Dn,
§5] РАЗЛОЖЕНИЕ ПО ЭЛЕМЕНТАМ СТРОКИ ИЛИ СТОЛБЦА 33
где
«1! «12 • • • «1ft • «1п
«21 «22 • • 0 • • • «2п
«п1 «п2 • • • 0 • • • ®пп
D2 =
«и
«21
«п1
«ц • • 0 . . . ain
«22 • • • «2ft • • «2п
«п2 • • • 0 • • «пп
.... Dn^
«11 «12 • • • 0 . . . «In
«21 «22 • • • 0 • • «2п
«п1 «п2 • • «nft • • «пп
Определитель Di равен произведению элемента ац
на его алгебраическое дополнение в этом определи-
теле. Однако, так как определитель £>i лишь k-M
столбцом отличается от определителя D, это алгеб-
раическое дополнение совпадает с алгебраическим
дополнением элемента aitl в определителе D:
£>i — а1кА1к.
Аналогично,
^2 «2ft-^2fej • • j Dn ^п'с^пЛ'
Мы доказали, что
D = а1кА1к +а2кА2к + + апкАпк.
Эту теорему тоже можно использовать для вычис-
ления определителей, сводя их к определителям низ-
ших порядков.
Пример 5. Вычислить определитель четвертого порядка
-51-4 1
14—15
D~ -4 1 -8 -1 •
3 2 6 2
2 Л. И. Головина
34
ОПРЕДЕЛИТЕЛИ И СИСТЕМЫ УРАВНЕНИЙ
[ГЛ. I
Решение. Разложим определитель, например, по элемен*
там первой строки:
4-1 5
О-(-5) (-!)»+> 1 -8 -1 +
2 6 2
1 -1 5 1 4 5
+ 1 (~1)1+2 —4 -8 - + (_4) (_1)1+з -4 1 -1 +
3 6 2 3 2 2
1 4 -1
+ 1 (-1)1+4 — 4 1 -8 -5.74-(-15) — 4(—31)-33 аж
3 2 6
= -370+ 15+ 124 - 33= -264.
Теорема 4. Сумма произведений элементов лю-
бой строки (или столбца) определителя на алгебраи-
ческие дополнения соответствующих элементов парал-
лельного ряда равна нулю.
Доказательство. Пусть дан определитель
аи aj2 .. • an ... «ife ... ain
q _ «21 a22 • • a2t ... a2k • • u2n
@nl ^n.2 • • • ®ni • • ank • • • ann
Рассмотрим другой определитель, Dit отличаю-
щийся от D лишь тем, что в fe-м его столбце повторен
i-й столбец: ,
ан а12 ... а1г ... а1г ... а1п
& _ а21 а22 ... а2/ • • • аа • • а2п
®п\ ®п2 • • • • • •_ @nl • • • ®пп
Определительравен нулю'(следствие из свойства 2).
Разложим его по элементам fe-ro столбца; получим
D\ = + a2iA2k + ... +an{Ank,
где Ajh — алгебраические дополнения элементов fe-ro
столбца определителя De, но так как определитель Di
лишь k-м столбцом отличается от D, то они же будут
и алгебраическими дополнениями элементов k-ro
столбца определителя D. Таким образом, при всех I
§ 6] СИСТЕМЫ П УРАВНЕНИЙ С П НЕИЗВЕСТНЫМИ 35
и k =# I
«нАй + «2/A2fe + + «n/A„fc = O.
Аналогично, при всех i и k =1= i,
UnAki + ai2Ak2 + ... + a(-rtAto = 0.
§ 6. Системы п линейных уравнений
с п неизвестными
Рассмотрим систему п линейных уравнений с п не-
известными: '
«пМ + а12х2 + +altlxn = bl,
a2ixl + a22x2+ ... + a2nxn=b2,
«юМ + ап2х2 + . . . + аппхп bn.
Решением системы (13) называется любая совокуп-
ность значений неизвестных xj = ом, х2 = а2, ...
..., хп — ап, при подстановке которых все уравнения
системы обращаются в тождества. Предположим, что
определитель, составленный из коэффициентов при не-
известных системы (13), отличен от нуля:
«п а12 ... а1п
«21
«22 • а2п
=7^= 0.
«Л1 «/г2 • • • «пгг
Умножим первое уравнение системы на Ап, второе —
на A2i, и т. д., последнее на Ani, и сложим их все. Мы
получим уравнение
Х1 («1Мн + «2И21 + +«пИ«1) +
+ х2 (а^Ац + «22^21 + . • + ип2Ап1) + ...
• •• + xn(alflAti + а2пА21 + ... + аппАп1) =
= ЬгАц + Ь2А21 + ... + ЬпАп1, (14)
или
XiD = blAll + b2A2lA- ... + bnAnl, (15)
так как заключенные в скобки коэффициенты при не-
известных х2, xs, хп в уравнении (14) по теореме 4
2!
36
ОПРЕДЕЛИТЕЛИ И СИСТЕМЫ УРАВНЕНИЯ
[ГЛ. I
равны нулю, а коэффициент при xit ввиду теоремы 3,
равен D. При этом правая часть
&1Лц + &2Л21 + • • + ЬпА^ — D{,
где Dt — определитель, получающийся из D при за-
мене первого столбца столбцом свободных членов.
(В правой части равенства (15) стоит разложение
определителя Dt по первому столбцу.) Аналогично
уравнению (15), получаем
x2D = D2, ..., xnD = D„, (15а)
где D{ есть определитель, получающийся из D заменой
1-го столбца столбцом свободных членов.
Система (15)—(15а) является следствием системы
(13). Таким образом, мы доказали, что если система
(13) имеет решение, то оно будет решением и системы
(15)—(15а), и значит,
П = 4> ^2= -§-.•••> = (16)
Формулы (16) называются формулами Крамера.
Непосредственной подстановкой этих значений не-
известных во все уравнения системы (13) можно убе-
диться, что они действительно образуют ее решение:
Теорема 5. В случае, когда D =# О, система (13)
имеет единственное решение, определяемое по
формулам Крамера.
§ 7. Ранг матрицы
Снова будем рассматривать таблицы чисел (мат-
рицы), не требуя, теперь, чтобы число строк матрицы
совпадало с числом ее столбцов. Для таких (прямо-
угольных) матриц мы введем важное понятие ранга.
Рассмотрим прямоугольную матрицу, состоящую
из m строк и п столбцов ([m X п]-матрицу). Пусть
/г sC tn и k п. Выделим в этой матрице какие-нибудь
k строк и k столбцов. Из элементов, стоящих на пере-
сечении выделенных строк и столбцов, составим оп-
ределитель &-го порядка. Все такие определители
называются минорами этой матрицы. Ясно, что из
§ 7]
РАНГ МАТРИЦЫ
37
[т х «]-матрицы можно составить Ст Сп МИНОрОВ
«-го порядка. Так, например, из матрицы
”32 12“
Л = 2 0-11
_04 5 1_
можно составить С1-Сз=12 миноров первого по-
рядка—это сами элементы матрицы А, С\ • Сз =
= 6-3=18 миноров второго порядка:
2 2
О 1
1 -1 2 2 4 1 2 1 1 1 11 1 5 0 4 3 0 2 1 -1 5 2 4 2 0 3 0 0 4 0 1 4 1 1 5 I ’ 2 0 3 2 0 1 -1 5 -1 1 5 1
и С4-Сз = 4 миноров третьего порядка:
2 1
4 5
2 1
О 1
3 2 2
2 0 1
О 4 1
3 2 1
2 0-1
0 4 5
3 1 2
2-11
0 5 1
2 1 2
0 -1 1
4 5 1
Нетрудно проверить, что все миноры третьего по-
рядка матрицы А равны нулю, а миноры второго по-
рядка во всяком случае не все равны нулю (отличен
от нуля уже первый из выписанных выше миноров
второго порядка). В этом случае мы будем говорить,
что ранг матрицы Д равен 2.
Рангом матрицы называется наивысший порядок
отличных от нуля миноров этой матрицы.
Таким образом, если ранг матрицы равен г, то
среди миноров этой матрицы есть по крайней мере
один минор г-го порядка, отличный от нуля, в то время
как все ее миноры порядка г + 1 и выше равны нулю.
Ранг матрицы А мы будем обозначать через г(-Д).
Элементарными преобразованиями матрицы назы-
ваются следующие ее преобразования:
38
ОПРЕДЕЛИТЕЛИ И СИСТЕМЫ УРАВНЕНИИ
(ГЛ I
1. Транспонирование, т. е. замена каждой строки
столбцом с тем же номером, и наоборот.
2. Перестановка двух строк или двух столбцов.
3. Умножение всех элементов строки или столбца
на любое число с, отличное от нуля.
4. Прибавление ко всем элементам строки или
столбца соответствующих элементов параллельного
ряда, умноженных на одно и то же число.
Теорема 6 (об элементарных преобразованиях).
При элементарных преобразованиях матрицы ее ранг
не меняется.
Доказательство. Рассмотрим каждое преоб-
разование отдельно. В первых трех случаях наше ут-
верждение почти очевидно:
1. По свойству 1 определителей каждый минор
транспонированной матрицы равен некоторому минору
данной матрицы, и обратно.
2. После перестановки двух строк или двух столб-
цов матрицы А мы приходим к новой матрице, каждый
минор которой либо равен некоторому минору матри-
цы А, либо отличается от некоторого минора матри-
цы А только знаком.
3. При умножении всех элементов строки или
столбца матрицы на число с одни ее миноры не изме-
няются., а другие умножаются на с; но так как с ¥= О,
то наивысший порядок отличного от нуля минора этой
матрицы не изменится.
4. Рассмотрим матрицу В, получающуюся из мат-
рицы А прибавлением ко всем элементам ее i-ro столб-
ца соответствующих элементов й-го столбца, умножен-
ных на с:
ап а12 ... а! { ... а}'к ... а1я
а21 а22 • • • а21 • • a2fc • • • а2п
>
_ ^m2 • • @ml • • ®tnk • • • ^mn -
all al2 • • • aH + falk • aik • • • aln '
aH a22 • • • @21 + c@2k • • • @2k • • • @2n
_ @ml @m2 • • • @mi 4" @@mk • • • @mk • • • @mn _
§ 7]
РАНГ МАТРИЦЫ
39
Пусть ранг г(А) матрицы А равен г. Покажем, что
ранг матрицы В не больше чем г. Для этого доста-
точно показать, что каждый минор матрицы В по-
рядка выше г равен 0. Пусть D будет минор порядка
выше г матрицы. В. Если D не содержит i-го столбца,
то он в точности равен .соответствующему минору мат-
рицы А и, значит, равен 0, как минор Порядка выше г,
составленный из матрицы ранга г.
Если D содержит и i-й и fe-й столбцы матрицы В,
то по свойству 4 он тоже равен соответствующему ми-
нору матрицы А и, значит, равен 0.
Наконец, если определитель D содержит i-й, но не
содержит fe-ro столбца матрицы В, то по свойству 4
его можно представить в виде суммы двух определи-
телей: D = 'Dt + £>2, один из которых равен соответ-
ствующему минору матрицы А, а другой отличается от
некоторого минора матрицы А множителем ±с. (Знак
минус здесь получается из-за того, что столбец с эле-
ментами ал может оказаться «не на своем месте».)
Так, например,.
«21
«41
«51
«22 + ««24 «23
«42 CU4i «43
«52 + ««54 «53
«21 «22 «23 «21 ««24 «23
«41 «42 «43 + «41 ««44 «43
«51 «52 «53 «51 ««54 «53
Следовательно, каждый из определителей и D2 ра-
вен 0, и
Д = 0.
Таким образом, каждый минор матрицы В порядка
выше чем г равен нулю, а следовательно,
г(В)<г(Д).
Но матрица А, в свою очередь, получается из мат-
рицы В с помощью элементарного преобразования
четвертого типа: чтобы получить матрицу А, надо
к i-му столбцу матрицы В прибавить ее k-й столбец,
г
40 ОПРЕДЕЛИТЕЛИ .И СИСТЕМЫ УРАВНЕНИЙ [ГЛ. I
умноженный на —с. По доказанному, ранг матрицы
при этом не увеличивается, т. е.
г.(Л)<г(В).
Следовательно,
г(Л) = г(В).
Нетрудно убедиться в том, что с помощью элемен-
тарных преобразований любую матрицу можно при-
вести к виду
"1 0 0 ... 0 0 ... О-
0 1 0...0 0 ... О
0 0 0 ... 1 о ... О
о о о ... о о ... о
О 0 0...0 о ... 0_
где на «главной диагонали» стоят г единиц, а все
остальные элементы матрицы равны нулю. Ясно, что
ранг такой матрицы, а значит, и исходной матрицы,
равен г.
Пример 6. С помощью
числить ранг матрицы
элементарных преобразований вы-
„О
2 12’
О -1 1
4 5 1
3
А= 2
(рассматривавшейся в начале параграфа).
Решение. Вычитая из третьей строки удвоенную первую,
сокращая второй столбец на 2 и вычитая после этого из первого
столбца утроенный второй, из третьего — второй и из четверто-
го—удвоенный второй, последовательно получим
А
3 2
2 0
-6 0
1 2 Л Г 3 1
-1 1
3 -3
1 21
-1 ’ 1 ~
3 -з.
' 0 1
~ 2 0
. -6 0
0 0’
-1 1
3 -3
где. знак ~ указывает, что соединяемые им матрицы получаются
одна из другой элементарными преобразованиями, и значит,
имеют один и тот же ранг.
§ 8]
ПОНЯТИЕ О ЛИНЕЙНОЙ ЗАВИСИМОСТИ
41
Прибавляя далее к третьей строке утроенную вторую, со-
кращая первый столбец на 2, прибавляя его к третьему и вычи-
тая из четвертого и, поменяв, наконец, местами первые два
столбца, будем иметь
О 1
л~
О
-1
О
2 О
О О
01 ГО 1001 Г I 0 0 О'
1 ~ 1 О О О ~ 0 1 0 0 -
oj L0 о о о_ L0 о о 0.
Мы снова находим, чго ранг матрицы А равен 2.
§ 8. Понятие о линейной зависимости
Если обозначить строки матрицы А (см. § 7) через
et = (3, 2, 1, 2), е2 = (2, 0, — 1, 1), е3 = (0, 4, 5, 1),
то очевидно, что имеет место равенство
е2 — 2i?|
понимаемое в смысле поэлементного сложения: каж-
дый элемент строки е3 равен соответствующему эле-
менту строки еь умноженному на 2, без соответствую-
щего элемента строки е2, умноженного на 3.
Вообще, если е^ е2, ет — строки какой-то мат-
рицы А и, например,
= ад + а,е2 + +ат^1ет-1, (17)
где ой, од, , a.m-i — какие-то числа, мы будем гово-
рить, что т-я строка этой матрицы линейно выражает-
ся через первые т — 1 ее строк, или что ет является
линейной комбинацией строк eit е2, е1П-ь Из равен-
ства (17) вытекает, что
1- • . . Н- - ^ет_ 1 • ет 0,
где нуль в правой части понимается как нулевая
строка (т. е. как строка, состоящая из п нулей).
Мы будем говорить, что строки е2, ..., ет мат-
рицы А линейно зависимы, если можно подобрать та-
кие числа у1, у2, • • •, Ут, не равные нулю одновременно,
что
yiet + y2e2+ . . . +ymem = Q. (18)
Если таких чисел уч не существует, т. е. если равен-
ство (18) имеет место только в том случае, когда все
42
ОПРЕДЕЛИТЕЛИ II СИСТЕМЫ УРАВНЕНИИ
[ГЛ. I
у, — 0, то говорят, что строки е1г е2, ..., ет линейно
независимы.
Ясно, что если одна из строк матрицы линейно вы-
ражается через остальные, то строки этой матрицы
между собой линейно зависимы. Обратно, пусть между
строками матрицы А имеется линейная зависимость
(18). Так как хотя бы одно из чисел у,-, например, ут,
. отлично от нуля, то
_______Vi_p _ Y'n-i Р
Cm „ ,, ^2 • • • ,,
Ym Ym Yin
т. e. в этом случае по крайней мере одна из строк мат-
рицы линейно’выражается через остальные.
Аналогичное понятие линейной зависимости можно
ввести и для столбцов матрицы.
Теорема 7 (о ранге матрицы). Если ранг мат-
рицы рйвен г, то в этой матрице можно найти г ли-
нейно независимых между собой строк (столбцов),
через которые линейно выражаются все остальные ее
строки (столбцы).
Доказательство. Пусть дана [m X п]-матрица
ранга г. Предположим, для определенности, что отлич-
ный от нуля минор г-го порядка этой матрицы распо-
ложен в левом верхнем углу, т. е. что
ап а!2 ... ai„
a2i а22 ... а2п
_^ml от2 . . . а,пп_
Hjl <2l2 • • • air
a2l a22 • • • a2r
ori ar2 ... arr
¥=0.
D =
Докажем, что toy цгт первые г строк этой матрицы
будут линейно независимы. (Если отличен от нуля не
этот, а какой-нибудь другой минор r-го порядка
матрицы А, то линейно независимыми будут именно
те строки, которые образуют этот минор.) Предполо-
жим, что, наоборот, эти строки линейно зависимы;
тогда одна из них, пусть, для определенности, ег, ли-
нейно выражается через остальные:
er = aieid-a2e2A- ... + ar_]er_[.
Вычтем из г-н строки матрицы А первую строку,
умноженную на он, вторую, умноженную на а2, и т. д.,
ПОНЯТИЕ О ЛИНЕЙНОЙ ЗАВИСИМОСТИ
43
наконец, (г — 1)-ю, умноженную на ar-i. После таких
преобразований z-я строка матрицы А окажется со-
стоящей из одних нулей. При этом определитель D,
который ввиду следствия из свойства 4 не должен был
бы меняться, станет равным нулю. Полученное проти-
воречие и доказывает линейную независимость пер-
вых г строк матрицы А.
Докажем теперь вторую часть теоремы — о том,
что все остальные строки матрицы А линейно выра-
жаются через первые г ее строк. Пусть г < k sC m и
1 п; рассмотрим определитель (г+1)-го по-
рядка
а11 ^12 • • й1г а\1
а21 й22 • • а2г а21
Д =
^1 ^г2 • • • ®гг ®rt
&kl ^А2 • ' • @kr ^kl
Он равен нулю при всех k и I: если I г, то у него
два одинаковых столбца, если же / > г, то это минор
(г + 1)-го порядка матрицы ранга г.
Разложим определитель Д по элементам послед-
него столбца:
Д = + а2[А2 + ... + ariAr + a/Z[Ar+1 = 0. (19)
Алгебраические дополнения Ai, А2......Ar, Аг+1 эле-
ментов последнего столбца зависят от k, но не зависят
от /, так как при их вычислении последний столбец
вычеркивается. Кроме того, Ar+i = Z) =# б, и значит,
равенство (19) можно разделить на Аг+1; это дает
akl ~ alall + «2а2/ + • • • 4* Ufarl>
где коэффициенты а, = — — не зависят от I. Под-
ставляя I = 1, 2, ..., п, будем иметь
akl — а1а11 + а2^21 + •••
ak2 ~ а1а12 + а2а22 + • • • + arar2,
akn — al^ln + ^2n + ••• +ararn'
44
ОПРЕДЕЛИТЕЛИ И СИСТЕМЫ УРАВНЕНИЙ
[ГЛ. I
Но это значит, что /г-я строка матрицы А-линейно вы-
ражается через первые г ее строк:
ek ~ а1е1 + а2^2 + ••• -\-О-гег‘
Следствие 1. Максимальное число линейно не-
зависимых столбцов матрицы равно максимальному
числу линейно независимых строк, так как при транс-
понировании матрицы ее строки становятся столб-
цами, а ранг матрицы не меняется.
Следствие 2. Для того чтобы определитель был
равен нулю, необходимо и достаточно, чтобы его стро-
ки (столбцы) были линейно зависимы.
§ 9. Произвольные системы линейных уравнений
Рассмотрим теперь систему пг линейных уравнений
с п неизвестными:
( ПЦ.Г] + 6112-^2 + . . . + а\цХп = Ь[,
| Й21Х1 + а22Х2 + . . + U2nXn = b2,
I + ®1п2х2 . . . + атпХп — Ьт,
где число неизвестных не предполагается рав-
ным числу уравнений.
Решением системы (20) называется совокупность п
значений неизвестных Xi = ои, х2 = «2, • , хп — а,п,
при подстановке которых все уравнения системы обра-
щаются в тождества. Система, имеющая хотя бы одно
решение, называется совместной, система, не имеющая
ни одного решения — несовместной. Система, имеющая
единственное решение, называется определенной-,
система, имеющая более одного решения — неопреде-
ленной.
Рассмотрим две матрицы: матрицу А, составлен-
ную из коэффициентов при неизвестных системы (20),
и матрицу _ . _
а1| <212 • • а1п
g _ «21 Я22 •. • а2п Ь2
_ ^m2 • • • Отп Ьт _
§ 91
СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ
45
получаемую из А добавлением столбца свободных чле-
нов и называемую расширенной матрицей. Ясно, что
r(S) ^г(Л), так как каждый минор матрицы Л .бу-
дет минором и матрицы В, но не наоборот.
Теорема 8 (критерий совместности системы ли-
нейных уравнений). Для совместности системы (20)
необходимо и достаточно, чтобы ранг расширенной
матрицы В был равен рангу матрицы коэффициентов.
Доказательство необходимости. Пред-
положим, что система (20) совместна, т. е. что суще-
ствуют такие числа Xi = ои, х2 = а2, хп = ап, что
йпа1 + aI2a2 + ... + ainan —blt
a2[a[ + a22a2 + ... + a2nan = b2,
+ amM2 "T • * • 4" bl2.
Вычитая из последнего столбца матрицы В первый
ее столбец, умноженный на а(, второй, умноженный на
а2, и т. д., наконец, п-й, умноженный на а„, мы полу-
чим матрицу
йп а12 ... и । 0 I
в а21 а22 ... а2п 0
- ®m2 • • • _
ранг которой, по теореме об элементарных преобразо-
ваниях,' равен рангу матрицы В:
r(Bi) = r(B).
Но ясно также, что r(Si) = г(Л), так как все нену-
левые миноры матрицы Bt равны соответствующим
минорам матрицы А, и обратно. Следовательно,
г(В)=г(Д).
Доказательство достаточности. Пусть
г(В) = г(Л) = г
и предположим, для определенности, что отличный от
нуля определительг-го порядка матрицы А расположен
46
ОПРЕДЕЛИТЕЛИ И СИСТЕМЫ УРАВНЕНИЙ
[ГЛ. I
в левом верхнем ее углу:
«11 «12 • • «1г
D = «21 «22 «2г Ф о.
Ctrl «г2 • • Ягг
Тогда первые г строк матрицы В линейно незави-
симы, а так как ранг ее в точности раве'н г, то осталь-
ные строки матрицы В линейно выражаются через
первые г ее строк. Но это означает, что первые г урав-
нений системы (20) независимы, а остальные m — г ее
уравнений «являются их линейными комбинациями»,
т. е. просто являются их следствиями. В этом случае
система на самом деле состоит лишь из г независи-
мых уравнений. Нам достаточно поэтому решить пер-
вые г уравнений системы; их решения автоматически
будут удовлетворять и остальным пг — г уравнениям.
Далее возможны два случая.
1. г = п. Тогда систему, состоящую из первых г
уравнений системы (20):
+ «12х2 + • • • + atrxr = b{,
^21-^1 4“ «22-^2 4“ • . . Ч- а2гХг =
аг\Х\ -Г Ч- • • • 4- аггхг — ЬГ,
можно решить, например, по формулам Крамера.
В этом случае система имеет единственное реше-
ние. Она — совместная и определенная.
2. г < п. Возьмем первые г уравнений системы и,
оставив в левых частях первые г неизвестных, осталь-
ные перенесем в правые части:
Т" 6Z|2-^2 Ч- ...~j~aifXr b\ а^г^.\Хг^.\ ... «in-^n»
«21-^14" «22-^2 Ч-. • • Ч- a2rxr — b2 а2< г+\ХГ+1 — а2цХп,
«нх1 Ч~ «г2-^2 Ч". • • Ч" arrxr — br аг, г+1^4-1 ... агпхп.
«Свободным неизвестным» xr+i, хг+2, ..., хп можно
придавать какие угодно значения, получая при
этом соответствующие значения неизвестных Xi, х2, ...
§ 9]
СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ
47
.хг из системы (21). Это — случай совместной, но
не определенной системы. Общие формулы решения
можно получить, если разрешить систему (21) относи-
тельно Xi, Хг, .... хг, например, по формулам Крамера.
Теперь мы в состоянии ответить на вопрос, оста-
вавшийся пока открытым: что можно сказать о си-
стеме п уравнений с п неизвестными, определитель ко-
торой равен нулю. Для такой системы ранг мат-
рицы коэффициентов г < п, так как единственный
минор п-го порядка этой матрицы, по условию, равен
нулю. Если ранг расширенной матрицы В такой си-
стемы тоже равен г, то система будет совместной, но,
поскольку г < п, неопределенной; если же ранг мат-
рицы В больше г, то система несовместна.
Пример 7. Решить следующие системы уравнений-.
1. ( xt + 2х2 + Зх3 «= 2,
Х( — х2 + х3 = О,
Х| + Зх2 — х3 = — 2,
• 3x1 + 4х2 + Зх3 = 0.
2. X] + 2х2 + Зх3 — х4 = 0,
X] — х2 + х3 + 2х4 = 4,
X] + 5х2 + 5х3 — 4х4 = — 4,
X] + 8х2 + 7х3 — 7х4 = — 8.
3. X] + 2х2 + Зх3 — х4 = 0,
Xi — х2 + х3 + 2х4 = 4,
X! + 5х2 + 5х3 — 4х4 = — 4,
х, + 8х2 + 7х3 — 7х4 = 6.
Решение.
1. Здесь г(Л) = 3, г (В) = 3; система совместная, определен-
ная. Так как
1 2 3 •
1-1.1 - 14 =#= 0,
1 3 -1
то из первых трех уравнений системы, например, по формулам
Крамера, находим
X! = — 1, Х2 = 0, Х3 = 1.
2. Здесь г(Л)‘ — 2, г(В) — 2; система совместная, ио не опре-
деленная. Определитель
и из первых двух уравнений системы
( хЛ + 2х2 «• — Зх3 + х4,
I Xi — х2 = 4-х3 — 2х4
48 ОПРЕДЕЛИТЕЛИ И СИСТЕМЫ УРАВНЕНИЙ {ГЛ. I
находим:
. где неизвестным х3 и лч можно придавать любые значения.
3. Здесь г(Д) = 2, г(В) = 3, и система несовместна.
§ 10. Однородные системы
Однородные линейные уравнения — это уравне-
ния, у которых правые части равны нулю:
anxi + ai2x2 + • •. + й\,пап — 0,
а21х1 + а22х2 + ... + а2пхп = 0,
( &m\x\ 4“ ^m2x2 "Ь ••• 4“ 0.
Такая система всегда совместна, так как имеет, на-
пример, нулевое решение:
Xi = 0, х2 = 0, ..., х,г = 0
(т. е. решение, в которой значения всех неизвестных
равны нулю).
Важно выяснить, при каком условии однородная
система (22) имеет и ненулевые решения. Ответ
на этот вопрос дает следующая
Теорема 9. Для того чтобы система (22) имела
ненулевые решения, необходимо и достаточно, чтобы
ранг г ее матрицы коэффициентов был меньше п.
Действительно, если г = п, то, как видно из доказа-
тельства теоремы 8, система (22) имеет единствен-
ное и, значит, только нулевое решение:
Х1 = хг = • • • = хп = 0.
Если же г < п, то система (22) является неопреде-
ленной (ведь несовместной она быть не может), и
значит, она имеет бесчисленное множество
решений, в том числе и бесчисленное множество нену-
левых решений.
Из доказанной теоремы непосредственно вытекает
Теорема 10. Для того чтобы однородная систе-
ма п линейных уравнений с п неизвестными обладала
ненулевыми решениями, необходимо и достаточно,
чтобы ее определитель D был равен нулю.
5 ю]
ОДНОРОДНЫЕ СИСТЕМЫ
49
Доказательство. Условие
D = О
здесь необходимо, так как если D 0, то система
имеет единственное и, значит, только нулевое решение.
Это условие также и достаточно, так как если
П = 0, то ранг матрицы коэффициентов системы г < п,
и система имеет бесчисленное множество (ненулевых)
решений.
Пример 8. Найти условие, при котором две прямые в про-
странстве
X — 01 _ у — Ь, _ 2 — С\
/j mi ns
и
х — а2 _ у — b2 _ z — с2
l2 т2 п2
лежат в одной плоскости (система координат прямоугольная).
Решение. Предположим, что эти прямые лежат в плоско-
сти
Ах + By 4- Cz + D ~ 0. (23)
Тогда вектор (А, В, С) ортогонален этой плоскости и, значит, он
ортогонален вектору (а2— at, b2— bi, с2— <j), лежащему в ней,
т. е.
А (о2 — aj + В (b2 — bi) + С (с2 — с,) = 0. (24а)
Кроме того, обе наши прямые ортогональны вектору (Л, В, С) и,
значит,
Л/i + Bmt + Czi, = О,
А1г + Вш2 + Сп2 = 0.
Мы получили систему (24а) — (246) трех линейных уравнений с
тремя неизвестными А, В, С. Для того чтобы- она имела нену-
левые решения, т. е. для того, чтобы существовала Плоскость
(23), содержащая обе заданные прямые, необходимо и доста-
точно, чтобы определитель этой системы был равен нулю:
^2
Z2
b2 — bi с2 Ci
nil ni
m2 п2
= 0.
Это и есть условие, которое мы хотели получить.
Пусть
Xj = О], х2 = а2, ..., хп = ап
какое-нибудь ненулевое решение однородной системы
(22). Это решение можно рассматривать как строку
50
ОПРЕДЕЛИТЕЛИ И СИСТЕМЫ УРАВНЕНИИ
[ГЛ. I
et = (cti, а.2, .... а»), состоящую из п элементов.
Тогда строка
cex = {cai, са2, сап)
тоже, очевидно, будет решением системы (22). Далее,
если
е2 = (Pi > Рг, • • • > Рл)
— какое-то другое решение системы (22), то при лю-
бых Ct и с2 линейная комбинация
+ с2е2 — (CjCtj + С2Р1, С1О2 + С2Р2, • ••> ^ian + сгРл)
этих решений тоже будет решением системы, так как
если
aZlal + а12®2 + ••• + а1лал = 0>
flilPl + Й/0Р2 + ... +й/мРл —0,
то и
аи (ciai + сгР1) + аа (cia2 + С2Р2) + ••• + аы (<дап + сгРл) — 0-
Итак, любая линейная комбинация решений однород-
ной системы (22) тоже будет ее решением. Интересно
поэтому найти такие линейно независимые решения
системы (22), через которые линейно выражались бы
все остальные ее решения.
' Линейно независимая система решений ei, е2, .... е^
уравнений (22) называется фундаментальной, если
каждое решение системы (22) является линейной ком-
бинацией решений ₽i, е2, ек.
Теорема 11 (о существовании фундаментальной
системы решений). Если ранг г матрицы коэффициен-
тов системы уравнений (22) меньше п, то эта система
обладает фундаментальными системами решений.
Доказательство. Пусть ранг г матрицы коэф-
фициентов системы (22) меньше п, и пусть, для опре-
деленности, минор D, стоящий в левом верхнем
углу матрицы А, отличен от нуля:
all а12 din
а21 а22 .. . а2п
— &т\ @т2 • • • &тп —
Яц Ц|2 .. . alr
Я21 а22 .. . а2г
&Г2 * * * ^rr
¥=0.
§ 10] ОДНОРОДНЫЕ СИСТЕМЫ 51
Перенеся свободные неизвестные хг+1, хп пер-
вых г уравнений системы (22) в правые части, полу-
чим систему
йцХ1 4- и^х^ 4* ••• 4* ci\rxr = а.\' г-|_1Хг-^1 ... а,\пхп,
^21^1 + ^22-^2 4“ ••• 4~ ^2r^r = ^2,г+.1^-г + 1 ••• ^2n-'-'n> (25)
4“ а?2-^2 4” • • • 4~ dffXf — drt rjxy_j_i ... arnxn.
Придавая свободным неизвестным значения
xr+1 = 1, xr+2 = 0, .. ., х,г = 0,
получим соответствующие значения Xi = ai, x2 = az, ...
..., xr = ar первых г неизвестных. Это дает нам стро-
ку — решение
(ан а2, . .., ar, 1, 0...0).
Аналогично, придавая свободным неизвестным значе-
ния
хг+1 = 0, хг+2= 1......хп = 0,
и вычисляя соответствующие значения неизвестных
Xi = Pi, х2 = Рг, ..., хг = рг, получим строку
(Pi, р2, .... рг, 0, 1, ..., 0),
и т. д. Так мы получим всего k = n — г решений си-
стемы (25):
e1 = (ai>, ...ar, 1, 0, . .., 0),
е2 — (Pi> Рг, Pr> 0, 1, •••> 0), (gg)
^ = (^.,£2, ...Лг, 0, 0, ..., 1).
Эти k строк между собой линейно независимы,
ибо ранг образованной ими матрицы
- otj a2 ... ar 1 0...0-
Pl P2 ••• Pr 0 1 ... 0
_ ... lr 0 0 . .. 1 _
в точности равен k. (В этой матрице есть минор k-ro
порядка, например, содержащий последние k столб-
цов, отличный от нуля.)
52 ОПРЕДЕЛИТЕЛИ И СИСТЕМЫ УРАВНЕНИЯ [ГЛ. I
Покажем теперь, что решения щ, е2, . -., еь (26)
действительно образуют фундаментальную си-
стему. Для этого достаточно показать, что каждое ре-
шение системы (22) линейно выражается через elt
е-2, ..., eh. Итак, пусть
e = (^i, ...^+1, • • •>
— произвольное решение системы (22). Рассмотрим
строку
е0 = ^-^+А-^+2е2~
Легко видеть, что все элементы, стоящие на послед- 1
них k местах в этой строке, равны нулю, т. е.
e0 = (Pi, Рз, • рг, 0, 0, . .., 0).
Будучи линейной комбинацией решений, строка е9
самд будет решением системы (22). А так как значе-
ния всех свободных неизвестных в е0 равны нулю, то
из однородной в этом случае системы (25), определи-
тель которой отличен от нуля, получаем, что и значе-
ния "всех остальных неизвестных в е0 должны быть
равны нулю, т. е. что е0 есть нулевая строка:
e0 = e-^r+le1-^r+2e2- ... - = (0, 0,..., 0),
и
что и требовалось доказать.
Заметим, что для того, чтобы получить фундамен-
тальную систему решений, мы могли бы придавать
свободным неизвестным и какие-угодно другие значе-
ния, лишь бы соответствующий определитель, fe-ro по-
рядка был отличен от нуля. Так мы нашли бы сколько
угодно других фундаментальных систем решений,
каждая из которых состояла бы из k = п— г строк. I
Можно показать, что любая фундаментальная система
решений уравнений (22) состоит в точности из л — г
элементов (это будет вытекать из результатов следую-
щей главы).
Таким образом, можно сказать, что общее решение
системы (22) линейных однородных уравнений имеет
вид ’
+ а,е2 + ... + алеь
L
§ 10]
ОДНОРОДНЫЕ СИСТЕМЫ
53
где ei, 62, ..., £k — любая, фундаментальная система
решений, a ai, «2, , a&— произвольные числа.
Сделаем еще одно, важное для дальнейшего,
Замечание. Рассмотрим систему уравнений
( anxs + а12х2 + ...
I a2i*'i + а22х2 + ...
+ alzi.rn =&(,
+ а2пхп = Ь2,
4~ п Ьт
(27)
I + ат2х2 + . . .
и соответствующую ей систему однородных уравнений
«их, +а!2х2 + ... +alnxn = 0,
fl2i*i + ci22x2 + . .. + а2пхп = 0,
Chn\xl 4" 4~ • • • 4~ Сктп^п 0.
(28)
Пусть = (ai, a2, ..., an)— какое-то определенное
решение системы (27) и е2 = (0Ь 02, • • •, ₽п) — любое
другое ее решение. Тогда разность
e1-e2 = (ai-Pi, а2-р2, •••. an-p„)
будет решением системы (28): если
azi«i + аг2а2 + ... + ainan = Ьг
и
+ Й/2₽2 + • • • + О/,гР,г = Ь it
ТО »
(®i Pi) Т" cii2 (а2 р2) 4" .. • + ciin (an Pn) bi bi 0.
Наоборот, если e3 = (yi, y2, • • •, Yn) — произвольное
решение однородной системы (28), то строка + е3 =
= (ai + Yb a2 + Y2. • • > ап + у«) будет удовлетворять
системе (27): если
aziai+ai2a2+ ... +ainan = bi
и
fliiYi + a,-2Y2 + • • + ainyn = 0,
то
cin («1 + Yi) + Я/2 («2 + Y2) + ••• + ain (a„ + Yn) = bt + 0 = b^
Отсюда следует, что все решения системы (27) можно
получить, прибавляя к одному какому-нибудь ее
54
ОПРЕДЕЛИТЕЛИ И СИСТЕМЫ УРАВНЕНИЙ
[ГЛ. I
решению всевозможные решения однородной системы
(28). Иными словами, общее решение системы (27)
равно сумме общего решения системы (28) и произ-
вольного, но фиксированного решения системы (27).
§ 11. Метод Гаусса
, Формулы Крамера, представляющие большой тео-
ретический интерес, серьезного практического значе-
ния, однако, не имеют, так как их применение приво-
дит к слишком громоздким вычислениям. Практически
для решения систем линейных уравнений чаще всего
применяется метод Гаусса, состоящий в последо-
вательном исключении неизвестных по следующей
схеме. Для того чтобы решить систему уравнений
( йцХ] + а 12^2 + . . . + й\пХп = Ь1,
I Й21Х1 + а22Х2 + • . . + О-2пХп = Ь2, ^20)
I ftmixl ”1” ftm2x2 4" • • • 4" втпХп = Ьт,
выписывают расширенную матрицу этой системы:
йц п12 ... ain b[
Й21 й22 • • • а<2п Ь2
_arni ат2 ... атп Ьт
где чертой отделен столбец свободных членов, затем
над строками матрицы В производят элементар-
ные преобразования: разрешается' изменять порядок
строк (что соответствует изменению порядка уравне-
ний), умножать строки на любые отличные от нуля
числа (что отвечает умножению соответствующих
уравнений на эти числа) и прибавлять к любой строке
матрицы В любую другую ее строку, умноженную на
любое число (что соответствует прибавлению к одному
из уравнений системы другого уравнения, умножен-
ного на это число). С помощью таких преобразований
каждый раз получается расширенная матрица новой
системы, равносильной исходной. При этом
стараются привести матрицу В к возможно более про-
§ и]
МЕТОД ГАУССА
55
стому виду, из которого решение системы видно непо-
средственно.
Рассмотрим подробнее метод Гаусса в применении
к системам 1, 2 и 3 из примера 7.
1. И- 2х2 4~ Зх3 —- 2,
— 0, Xi + 3x2- -2, v ' 3-Vj 4~ 4х2 4- Зх3 = 0.
Расширенная матрица этой системы имеет вид
~1 2 3 2“
1-1 1 0
1 3 -1 — 2 •
.3 4 3 0_
Вычитая первую строку из второй и из третьей и
утроенную первую из четвертой, получим матрицу
1 2 3 2
0 -3 — 2 — 2
0 1 — 4 — 4
0 -2 -6 -6
Эта матрица — расширенная матрица системы
X] + 2х2 + Зх3 = 2,
— Зх2 — 2х3 = — 2,
х2 - 4х3 = - 4,
— 2х2 — 6х3 = — 6,
(31)
которая получается из заданной системы 7(30), если
первое уравнение вычесть из второго и третьего, а
утроенное первое вычесть из четвертого. Поэтому си-
стема (31) является следствием системы (30)—каж-
дое решение системы (30) будет удовлетворять и си-
стеме (31). Но и обратно, система (30) может быть
получена из системы (31) посредством аналогичных
53
ОПРЕДЕЛИТЕЛИ И СИСТЕМЫ УРАВНЕНИИ
[ГЛ. I
преобразований: первое уравнение прибавляется ко
второму и третьему, а утроенное первое — к четвер-
тому. Поэтому система (30) будет в свою очередь след-
ствием системы (31), и значит, обе системы р а в н о-
сильны — они имеют одни и те же решения.
Далее, прибавив утроенную третью строку ко вто-
рой и удвоенную третью к четвертой, получим
~1 2
0 0
0 1
_о о
3
-14
— 4
-14
2~
-14
-4
-14
Вычитая вторую строку из четвертой и сокращая ее
на —14, будем, иметь
“12 3 0 0 1 0 1 —4 _0 0 0 2“ 1 — 4 0_
Но это — расширенная матрица системы
Х[ 4- 2а?2 + Зх3 ~= 2,
х3 = 1,
х2 — 4х3 = — 4,
равносильной заданной системе (30), и значит, реше-
нием системы (30) будет
х3 = 1, х2 = — 4 + 4л'з = 0, %! = 2 — 2.г2— Зх3 = 2 — 3 = — 1.
В этом случае ранг расширенной матрицы равен рангу
матрицы коэффициентов и равен, очевидно, трем.
2.
лр 4- 2х2 4- 3.V3 х4 = 0,
xi — Х9 4~ х3 4- 2л’3 = 4,
х^ 4- 5х2 &х3 4х3 = 4,
4- 8х2 4- 7х3 — 7х4 = — 8.
L
§ 111
МЕТОД ГАУССА
57
Выписав расширенну! о матрицу этой системы, пос-
ле очевидных преобразовании получим:
"1 23-1 0“ ”1 2 3-1 О'
1-11 2 4 0-3-2 3 4
1 55 -4-4 ~ 0 3 2 — 3 —4 ~
_1 8 7 —7 -8_ _0 6 4-6 -8J
"1 2 3-1 0~
0-3-2 3 4
~ 0 0 0 0 0 ’
- _0 0 0 0 0_
откуда следует, что наша система равносильна еле-
дующей:
Xj + 2х, + Зх3 — х4 = 0,
— Зх2 - - 2х3 + Зх4 — 4,
и значит,
4 2
Хо = 5- 5- X; “ и и + х4,
X; — — 2х2 Зх3 + х4 — з 3X3 х4.
Здесь ранг расширенной матрицы равен рангу мат-
рицы коэффициентов и равен, очевидно, двум.
3.
Xj 4- 2х2 4~ Зх3 х4 — 6,
— х2 + Д'з + 2х4 = 4,
Х[ + 5х2 + 5х3 — 4х4 = — 4,
xt + 8х2 + 7х3 — 7xi = 6.
Имеем, очевидно,
- 1 2 3 -1
1 - 1 1 2
1 5 5 — 4
_1 8 7 — 7
0~ “ 1 2 3 -1 о-
4 0 -3 — 2 3 4
— 4 0 3 2 -3 -4
6 _ _0 6 4 — 6 6 __
1 2 3 - 1 0"
0 -3 — 2 3 4
0 0 0 0 0
О
О
О 0 14
58
ОПРЕДЕЛИТЕЛИ И СИСТЕМЫ УРАВНЕНИЙ
[ГЛ. I
и значит, система несовместна, так как равносильная
ей система содержит уравнение
О • Xi + 0 х2 + 0 • *з + 0 • х4 = 14 (последняя строка).
Здесь ранг матрицы коэффициентов равен, как легко
видеть, двум, а ранг расширенной матрицы равен
трем.
Пример 9. Методом Гаусса решить однородную систему
уравнений
xt + 2х2 + Зх3 + 4х4 + 5х, = О,
2xt + Зх2 + 4х3 + 5х, + х5 = О,
Зх, + 4х2 + 5х3 + х4 + 2х5 = О,
х4 + Зх2 + 5х3 + 12х4 + 9х, — О,
. 4xt + 5х2 + 6х3 — Зх4 + Зх5 = О
и найти ее фундаментальную систему решений.
Решение. Выпишем расширенную матрицу системы (при
этом нулевой столбец можно, конечно, не писать). После по-
нятных преобразований будем иметь
' 1 2 3 4 5 1 1 2 3 4 5 '
2 3 4 5 1 0 -1 -2 -3 -9
3 4 5 1 2 0 —2 -4 -11 — 13
1 3 5 2 9 0 1 2 8 4
_ 4 5 6 - 3 3 _ _ 0 -3 -6 -19 — 17 _
" 1 2 3 4 5 ’ ’ 1 2 3 4 5 '
0 1 —2 -3 -9 0 1 2 3 9
0 0 0 -5 5 0 0 0 -1 1
0 0 0 5 -5 0 0 0 0 0
. 0 0 0 -10 ю . . 0 0 0 0 0 .
т. е. заданная система равносильна следующей:
х, + 2х2 + Зх3 + 4х4 + 5х6 = О,
х2 + 2х3 + Зх4 + 9х5 = О,
— х4 + х5 = 0.
Здесь г — 3, и три неизвестных можно выразить через осталь-
ные, например, так:
х4 = х5,
х2 = — 2х3 — Зх4 — 9х5 = — 2х3 — 12х3,
х4 = — 2х2 — Зх3 — 4х4 — 5х5 = х3 + 15х3.
$ IIJ
МЕТОД ГАУССА
Фундаментальную систему можно получить, если свободным
неизвестным х3, х» придавать значения хз = 1, х5 = 0 (тогда
х, = 1, х» = —2, х4 = 0) и значения х3 = 0, х5 = 1 (тогда X] = 15,
х2 =—12, х4 = 1). Это дает фундаментальную систему решений:
е! = (1, -2, 1,0, 0),
е2«=(15, -12, 0, 1, 1).
Общее решение системы имеет вид
е = ctei + с2е2 = (с2 + 15с2, — 2ct — 12сг, с1; с2, с2),
где ci и с2 — произвольные числа.
ГЛАВА II
«МЕРНОЕ ПРОСТРАНСТВО
§ 1. Определение векторного пространства
Мы начнем с примера, хорошо известного чита-
телю. В геометрии важную роль играет понятие век-
тора, или направленного отрезка. Векторы можно
складывать между собой и умножать на числа. Сум-
ма ОС векторов ОА и ОВ определяется как диаго-
наль параллелограмма ОАСВ (рис. 1, а; это опреде-
ление можно распространить и на тот случай, когда
прямые О А и ОВ совпадают), а произведение OD
вектора ОА на число а определяется из условий:
OD = |а|-ОА и векторы OD и ОА направлены в одну
сторону, если а > 0, и в противоположные стороны,
если а <0 (рис. 1,6).
Но совокупность всех плоских или всех простран-
ственных векторов — это только примеры (хотя и
очень важные примеры) векторных пространств.
§ i] ОПРЕДЕЛЕНИЕ ВЕКТОРНОГО ПРОСТРАНСТВА 61
В главе I мы видели, что если имеются два р е-
ш е и и я
«?1 = (аь а,, . . а„) и е2 = (Pi, ₽2, • • • > ₽»)
некоторой системы линейных однородных уравнений,
то их сумма
е{ + е2 = (а.! + а2 + • • •, ап + Рп)
и произведение любого из них, например, е\, на про-
извольное число с
се{ = (саь са2, .... сап)
тоже будут решениями той же системы. Аналогичная
ситуация, когда имеется множество каких-то элемен-
тов, которые можно складывать между собой и умно-
жать на числа, получая в результате элементы того
же самого множества, встречается в математике очень
часто. Так, например, складывать между собой и
умножать- на вещественные числа можно много-
члены от t с вещественными коэффициентами —
в результате получаются такие же многочлены. Если
складываются и умножаются на числа многочлены,
степени которых не превосходят данного
числа п, то и полученные при этом многочлены
будут степени не выше п. Складывать между собой
и умножать на вещественные числа можно произволь-
ные функции от t — в результате снова полу-
чаются функции от I. Если функции, к которым при-
меняются эти операции, непрерывны на каком-то
отрезке [а,Ь] (или на всей числовой прямой), то и
полученные в результате функции обладают тем же
свойством.
Наконец, разумеется, и сами числа можно скла-
дывать между собой и умножать на числа; более
того, вместо одного числа можно рассматривать пары,
тройки и вообще упорядоченные наборы
(строки), состоящие из п чисел:
(х,, Х2, .... Х„)
(такие строки выше служили решениями данной
системы линейных уравнений, теперь же от них не
G2
П-МЕРПОЕ ПРОСТРАНСТВО
[ГЛ II
требуется ничего!). Строки можно складывать между
собой:
(*1> *2..Хп) + (У1, у2, . . ., Уп)~
= (:Х1 + уъ х2 + у2, • • •, Хп + уп)
и умножать на числа:
c(xh х2, хп) = (сх1, сх2, схп),
получая всякий раз такую-же строку.
Все это — различные примеры векторных про-
странств (причем последний пример особенно ва-
жен для дальнейшего). Для того чтобы охватить все
эти и другие возможные случаи, введем такое
Определение 1. Множество R элементов х,
у, z, ... называется линейным, или векторным, про-
странством, если для любых двух его элементов х, у
определена сумма x + y^R*) и для каждого эле-
мента х се R и каждого вещественного числа а опре-
делено произведение ах е R так, что выполнены сле-
дующие условия:
1. х + у = у + х для всех х, у <ес R.
2. (х + у) + z = х + (у + z) для всех х, у, z се R.
3. Существует такой (нулевой) элемент Oi=R,
что х + 0 = х для всех элементов х е R.
4. Для каждого элемента х се R существует такой
элемент—х (называемый противоположным
к х), что х + (—х) = 0.
5. 1 • х = х.
6. а(р%) = (ар)х **).
7. (а + р)х = ах + р%.
8. а(х + у) = ах + ау.
*) Символы е, =, cz называются знаками включения. За-
пись а е А означает, что а является элементом множества А.
Запись A £= В означает, что множество А является частью
множества В (т. е. что каждый элемент а из А принадлежит
также и В): запись А а В означает, что множество А является
правильной частью множества В, т. е. что А содержится
в В, с -ним не совпадая.
**) Чтобы не путать векторы с числами, мы, в тех случаях,
где может возникнуть недоразумение, условимся обозначать чис-
ла греческими, а векторы — латинскими буквами.
§ 1] ОПРЕДЕЛЕНИЕ ВЕКТОРНОГО ПРОСТРАНСТВА 63
Элементы векторного пространства называются
векторами.
Примеры. Можно говорить о векторном про-
странстве Рп многочленов степени не выше п с веще-
ственными коэффициентами, о векторном простран-
стве С функций, непрерывных на данном отрезке
[а, 6], о векторном пространстве решений данной си-
стемы линейных однородных уравнений, наконец, про-
сто о векторном пространстве строк, состоящих из п
элементов.
Поскольку в пространстве R определено умноже-
ние его элементов на вещественные числа, то R назы-
вается вещественным (векторным, или линейным)
пространством. Если элементы из R можно умножать
на комплексные числа, получится комплексное век-
торное пространство. Примером такого пространства
может служить совокупность всех строк, составлен-
ных из п комплексных чисел, или всех многочленов
с комплексными коэффициентами (подробнее об этом
см. § 5 главы V).
Ввиду условия 2 можно говорить о сумме трех
х + г/ + г = (х + у)+г (или, что то же самое, х +
+ (у + г)) и большего числа элементов из R.
Разностью х — у векторов х и у называется такой
вектор г, что х = у 4- г. Легко видеть, что х — у =
= х + (—у).
Действительно,
У + [х + (- у)] = (у + х) + (- у) =.(- у) + (у + х) =
= [(“ У) + У\ + х = 0 + х = х.
Далее, из определения 1 непосредственно выте-
кают следующие предложения.
1. Единственность нуля. Предположим, что
в пространстве R имеются два нулевых элемента,
01 и 02. Тогда, так как для любого х из R суммы
х + 01 = X и х + 0г = х, то, в частности, 02 + 01 = 0г
и 0t + О2 = О,, откуда, ввиду равенства 0i + О2 =
= О2 +.01, получаем
0, = 02.
64
Л-МЕРНОЕ ПРОСТРАНСТВО
(ГЛ. II
2. Единственность противоположного
элемента. Предположим, что у элемента х име-
ются два противоположных элемента, у и г; тогда
х + у = О и х z — 0. Следовательно,
y + x + z = y + (x + z) = y + O = y
и
y + x + z — (у + х) + z = 0 + z = z,
откуда
У = z.
3. Для каждого элемента х е R произведение
0х = 0*). В самом деле, для каждого х имеем Ох =
= (0 4- 0)х = Ох + Ох. Прибавляя к левой и правой
частям последнего равенства —Ох, получим
0 = Ох.
4. Для любого вещественного числа а и 0 е R
произведение а0 = 0. Действительно, а0 — а(0 + 0) =
— а0 + ссО. Прибавляя к левой и правой частям ра-
венства —а0, получим
0 — а0.
5. Если произведение ах = 0, то либо а = 0, либо
х — 0. В самом деле, пусть а 0; тогда
х = 1 • х = (— а')х = — (ах) = — 0 = 0.
\а ) а ' ' а
6. Для каждого х элемент (—1)х является проти-
воположным к х. Действительно,
х + (— 1) х = 1 • х + (— 1) х = [ 1 + (— 1)] х = 0 • х = 0,
и значит,
(— 1) х = — х.
§ 2. Размерность и базис
Определение 2. Векторы Я;, я2, •••> «д линей-
ного пространства R называются линейно зави-
*) Один и тот же символ 0 употреблен здесь и как число
(слева) и как вектор (в правой части). Здесь и дальше из кон-
текста всегда будет ясно, что означает символ 0 — число нуль
или нулевой вектор.
РАЗМЕРНОСТЬ-И БАЗИС
65
§ 2]
самыми, если существуют такие числа oti, «2 •••> ал,
не равные одновременно нулю, что
cqai + а2а2 + • • • + a,kak = 0.
Векторы, не являющиеся линейно зависимыми, на-
зываются линейно независимыми.
Если векторы а2, ..., ah линейно зависимы:
ща] + <x24Z2 4- • • • 4- ща^ = 0,
и например, ан ¥=0, то
или
ak — 11^1 + ^2«2 + ••• (1)
а,
где g,=------. Если имеет место равенство (1), го-
ak
ворят, что вектор ak является линейной комбинацией
векторов ai, а2, ..., а^, а также, что вектор аь ли-
нейно1 выражается через ai, а2, ak~\. Таким об-
разом, если векторы а2, ..., а!с линейно зависимы,
то по крайней мере один из них линейно выражается
через остальные. Ясно, что верно и обратное, т. е.
что если один из векторов линейно выражается через
остальные, то все эти векторы в совокупности линей-
но зависимы.
Примеры. На плоскости можно найти сколько
угодно пар линейно независимых векторов — линейно
независимы любые два неколлинеарных, т. е. не па-
раллельных одной прямой вектора. Но любые три
вектора плоскости линейно зависимы.
В пространстве любые три некомпланарных (т. е.
не параллельных одной плоскости) вектора а, Ь, с
линейно независимы (так как если а,а + $Ь + ус — 0
. л Ct 6 <
и, например, у 0, то с= и вектор с
компланарен векторам а и Ь). Однако любые четыре
пространственных вектора a, b, с, d будут линейно
зависимыми. В самом деле, если а = ОА, b = ОВ,
с = ОС — некомпланарные векторы и d =. OD —
3 Л. И. Головина
66
«-МЕРНОЕ ПРОСТРАНСТВО
[ГЛ. II
любой четвертый вектор, то, проведя DD^OC (рис. 2;
точка О/ принадлежит плоскости АОВ) и разложив
вектор ODit компланарный саиб, по этим -векто-
рам, получим, очевидно:
ODi = аа + ^Ь,
OD = ODl + D^D
и
DtD = ус,
а значит,
d = аа + р/? + ус,
откуда
d — аа — pb т=-ус — 0.
Рис- 2-' (Если же векторы а, Ь, с
' компланарны, то найдут-
ся такиеэне равные одновременно нулю числа а, р, у,
что
аа + р& + ус = 0,
а тогда и
аа.+ рб + ус + 0 • d = 0,
.— и все четыре вектора тоже линейно зависимы.)
Определение 3. Линейное пространство R на-
зывается п-мерным, если в нем можно найти п ли-
нейно независимых векторов, но больше чем п линей-
но независимых векторов оно не содержит.
Таким о.бразом, размерность простран-
ства— это максимальное число содержащихся в
нем линейно независимых векторов. Размерность
пространства R мы условимся обозначать через
d(R).
Так, размерность множества всех плоских векто-
ров равна двум, размерность множества Лфостран-
ственных векторов — трем.
Пространства, имеющие конечную размерность,
называются конечномерными. Пространство, в кото-
ром можно найти сколь угодно много линейно неза-
висимых векторов, называется бесконечномерным.
§ 2]
РАЗМЕРНОСТЬ И БАЗИС
67
Примером бесконечномерного пространства может
служить множество Р всевозможных многочленов
от t с вещественными коэффициентами или множе-
ство С всех функций от t, непрерывных на данном
отрезке [о, 6] (или' непрерывных на всей числовой
прямой).
Определение 4. Совокупность п линейно не-
зависимых векторов п-мерного пространства R назы-
вается его базисом.
Теорема 1. Каждый вектор х линейного п-мер-
ного пространства R можно представить, и притом
единственным способом, в виде линейной комбинации
векторов базиса.
Д о к а з а т е л ь с т в о. . Пусть е\, е2, ..., еп — про-
извольный базис n-мерного пространства R и хе/?.
Так как каждые п + 1 векторов (n-мерного!) про-
странства R линейно зависимы, то зависимы, в част-
ности, и векторы ei, е2, ..., еп,’ х, т. е. существуют
такие не равные одновременно нулю числа оц, а2, .
..., ап, а, что
«1^1 + а2ех + • • + а„еп + ах = 0.
При этом а =#0, ибо в противном случае одно из чи-
сел at,..., ап было бы отлично от нуля, и значит,
векторы б[, р2, ..., еп- были бы линейно зависимы. .
Следовательно,
ai а2 а„
х -----L е,----- е2 — ...--- еп.
а 1 а z а
а.
Полагая—^~ = хь будем иметь
х = x^t + х2е2 . + хпеп.
Это представление х через еь е2, ..., еп един-
ственно, так как если х = xiei + х2е2 + ... + хпеа
и х = yi£i + у2е2 + . •. + упеп, то
(.У1 — xi)ei +-(у2-Х2)е2+ ... + (уп~ хп) е„ = 0,
и ввиду линейной независимости векторов et, е2, ...
.... еп
У1 = Х1, у2 = Х2, ..., уа=* хп.
3’
68 П-МЕРНОЕ ПРОСТРАНСТВО [ГЛ. п
Числа хх, х2, ..., хп называются координатами
вектора х в базисе ёь е2, еп. Таким образом,
теорема 1 утверждает, что если задан базис «-мер-
ного векторного пространства R, то каждый вектор
нз R имеет (единственным образом определенные) .
координаты в этом базисе. При йтом ясно, что если,
координаты двух векторов х и у совпадают, то эти
векторы одинаковы, так как тогда
х = ххех + х2е2 + ... + хпеп = у.
Поэтому задавать вектор можно, просто называя его
координаты Xi, х2, ..., хп. При этом так и говорят:
вектор х = (jj, х2, ..хп).
Пусть мы имеем два вектора, заданные своими
координатами в некотором базисе. Тогда при сложе-
нии этих векторов их соответственные координаты
складываются: если
х = X1BJ-+ х2е2 + ... + х„е,, и у = + у2е2 + ... + упеа
то
x + y = (%i+ г/1)е1 + (х2 + у2)«?2+ ••• + (х„ + уп) еп. -
При умножении вектора на число все его координаты
умножаются на это число: если
х = ххех + х2е2 + ... + хпеп,
то
ах = (аХ]) ех + (ах2) е2 + ... + (ах„) еп.
У нулевого вектора все координаты равны нулю,
так как из равенства aiCj + а2е2 + ... + апеп = О,
ввиду линейной независимости векторов ех, е2, е„,
вытекает, что все а, = 0. Вектор, противоположный
к х = (хь х2, ..., хп) равен (—Xi,—х2, ...,—хп), гтак
как
л-1, Х2...х„) + (- х1У - х2, . . ., - х„) =
= (0,0......0) = 0.
Теорема 2. Если ех, е2, ..., еп — линейно неза-
висимые векторы пространства R, и каждый вектор
х Ze R линейно выражается через elt е2, ..., еп, то
эти векторы образуют базис в R.
§ 2]
РАЗМЕРНОСТЬ И БАЗИС
69
Доказательство. Векторы в\, е2, еп, по
условию, линейно независимы. Остается доказать, что
в пространстве R нет больше чем п линейно незави-
симых векторов. Црзьмем произвольные т > п векто-
ров из R\ 01, йг, • •, ат. По условию, каждый из них
можно линейно выразить через е2, ..., еп:
«1 = «11^1 + «21<?2 + • • + anien,
а2 ~ «12е 1 + «22е2 + • • • + 0-п2еп>
ат «1те| "Ь ^2т^2 “Ь • * *
Рассмотрим матрицу
«11 «12 • . • «ют
«21 «22 • • • «2т
• • 'J' ' ' •
_«nl «п2 • • • «пт _
Так как число строк этой матрицы равно п, то ее
ранг не больше чем п, и значит, среди ее столбцов
имеется не более чем п линейно независимых. Но так
как т > п, то т столбцов этой матрицы между собой
линейно зависимы. А это значит, тго линейно зави-
симы и векторы fli, 02, ..., ат. Мы нашли, что про-
странство R n-мерно, и Ci, е2, еп — его базис.
Из теоремы 2 вытекает, что пространство Rn упо-
рядоченных строк из гг чисел п-мерно. Действительно,
п строк
е, =(1, 0, ..., 0),
е2 = (О, 1, .... 0),
е„М0, 0, .... 1)
линейно независимы, так как из равенства
«1^1 + а2е2 + ... + апеп = (аь а2, ..., а„) = (0, 0, . .., 0) ,
вытекало бы, что ai = а2 = ... = ап = 0. С другой
стороны, каждая строка е= (Jji, g2, •••; £п) линейно
выражается через ei, ег, ..., еп:
е = £iei + Ье2 + • • + Zneif
СР
70
П-МЕРНОЕ ПРОСТРАНСТВО
[ГЛ. 11
Строки в2, еп образуют, следовательно, базис
пространства Rn.
Пространство Рп многочленов степени не выше п
имеет размерность п+ 1. В самом деле, многочлены
1, t, /2, .... Г
между собой линейно независимы, и каждый много-
член от t степени не выше п через них выражается
очевидным образом.
Теорема 3. В линейном конечномерном про-
странстве каждое множество линейно независимых
векторов можно включить в некоторый базис.
Доказательство. Пусть векторы ei, ег, ...
..., 6А пространства 7? линейно независимы. Если
каждый из остальных векторов из R линейно выра-
жается через еь е2, ..., еь, то, по теореме 2, это уже
базис. Если же найдется вектор еи+\, линейно не вы-
ражающийся через е1( е2, ,еА, то k + 1 векторов
е2, ..., eh, еь+\ линейно независимы. Действитель-
но, если бы имело место равенство
а1е1 + а2е2 + ... + akek + аеН1 = 0,
то а ¥= 0 ввиду линейной независимости векторов
6], е2, ..., eh, и лёктор 6а+1 линейно выражался бы
через 61,-е2, ..., еА.
Присоединим вектор еА+1 к 6Ь б2, ..., 6А. Если
все векторы пространства R линейно выражаются че-
рез 61, е2, ..., ?А, ед-ы, то это уже базис. Если же най-
дется вектор еА+2, не выражающийся линейно через
6], е2, ..., в/,, eA+i, присоединим его к ним; новая си-
стема векторов 61, е2, ...,.еь, eA+i, еА+2 будет линейно
независимой, ц т. д.
. Этот процесс не может продолжаться до бесконеч-
ности, так как пространство R* по условию, конечно-
мерно, и, следовательно, в нем не может быть беско-
йечного множества 6., е2, е3, ... линейно независимых
векторов. Поэтому, в конце концов, мы получим такую
линейно независимую систему векторов еь е2, ..., еА,
бА+), ..., еп, через которую уже будут линейно выра-
жаться все остальные векторы из R. Ввиду теоремы 2
это и будет базис пространства R, содержащий задан-
ные векторы 6.1, е2, ..., 6А.
§ 3] - ИЗОМОРФИЗМ ЛИНЕЙНЫХ ПРОСТРАНСТВ 71
§ 3. Изоморфизм линейных пространств
Пусть R— линейное n-мерное пространство и
вь е2, еп — некоторый fero базис. По теореме 1
каждый вектор хе R однозначно представляется в
виде
х = х{е{ + х2е2 + ... + хпеп.
Если вектору х поставить в соответствие строку
(хь х2,..., х„) то, как мы видели в § 2, при сложенйи
векторов соответствующие им строки тоже склады-
ваются, д при умножении вектора на число соответ-
ствующая ему строка умножается на то же число.
Таким образом, отправляясь от самого общего
определения n-мерного векторного пространства, мы
пришли к тому, что это пространство устроено в не-
котором смысле так же, как пространство всевозмож-
ных строк из п чисел. Значит, все п-мерные вектор-
ные. пространства устроены одинаково; они, как при-
нято говорить, изоморфны между собой. Точный
смысл этого термина дан в следующем определении.
Определение 5. Векторные пространства R
и R' называются-изо мо р ф ными, если между их
элементами можно установить взаимно однозначное
соответствие такое, что если х х' ( г соответст-
вует х') и у’, где х, у ^R, х', у' <= R', то
х + у х' + у'
и при любом а -
ах «—> ах'
(или, короче, (х + у)' = х' + у' и {ах)' = ах').
Имеет место следующая
Теорема 4. Для того чтобы два векторных про-
странства были изоморфны, необходимо и достаточ-
но, чтобы они имели одинаковые размерности.
Доказательство достаточности. Пусть даны два
линейных n-мерных пространства и А?'. Выберем в каждом
из них по базису:
ер е2, .... еп в R и е{, е2, ..., еп — в ft'.
Вектору х, имеющему в базисе £i, е2, ...,«п координаты
Xi, х2, ..., хп, поставим в соответствие вектор х' из /?', имеющий
72 П-МЕРНОЕ ПРОСТРАНСТВО [ГЛ. II
те же самые координаты в базисе ер е2,..., еп. Тогда,
поскольку при сложении векторов их соответственные координаты
складываются, а при умножении на число — умножаются на, то
же число, будем иметь: если
X х', у <-> у',
то
х + У х' + У1
и для любого а
ах *-* ах'.
Следовательно, R' изоморфно R.
Доказательство необходимости. Для того чтобы
доказать, что линейные пространства R и R' разных размерно-
стей не изоморфны между собой, заметим прежде, что при «изо-
морфном» соответствии между двумя пространствами нулевому
вектору одного пространства соответствует, нулевой вектор дру-
гого. Действительно, пусть 0 — нулевой вектор из R и 0' — соот-
ветствующий ему вектор из R', х' — произвольный вектор из R'
и х ч—> х', где х е R. Тогда сумма
О + х 0' + х'.
Но 0 + х = х, причем- х -е—>- л*'; а так как Соответствие между
R и R' взаимно однозначное, то
О' + х' = х',
т. е. О' — нулевой вектор из R'.
Если пространства R и R' изоморфны, и векторам «и, а2, ...
..., ah из R соответствуют векторы ар а2, ..., а'к простран-
ства R', то из линейной зависимости векторов ai, а2, ...,
вытекает, что и векторы ар. а2, ..., ak тоже линейно зависимы,
и обратно. Действительно, пусть, например, сив! + а2а2+ ...
...+aftaft = 0. Тогда вектору atat + а2а2 + ... + ацак простран-
ства R, равному 0 е R, в пространстве R' соответствует вектор
а.а1 + а2а2+ ••• +акак, и, значит,
а1а' + а2в2+ +akak = 0'-
Следовательно, максимальное число линейно независимых
векторов в изоморфных пространствах должно быть одинаковым,
а значит, размерности этих пространств — равные.
В силу теоремы 4 единственной характеристикой
конечномерного векторного пространства является
его размерность. По своей алгебраической структуре
все п-мерные векторные пространства совершенно
одинаковы. Можно, следовательно, сказать, что «-мер-
ное векторное пространство — это пространство всевоз-
§.41
ПЕРЕХОД К НОВОМУ БАЗИСУ
' 73
можных строк из п чисел. Поэтому «-мерное вектор-
ное пространство можно обозначать просто через Rn:
одно обозначение для всех «-мерных векторных про-
странств законно, потому что все «-мерные векторные
пространства одинаковы (изоморфны).
§ 4. Переход к новому базису
Пусть в пространстве Rn имеются два базиса,
elt е2, ..., еп и ef, е'2, . . ., е'п.
Первый условимся называть старым базисом, вто-
рой— новым. Каждый из элементов нового базиса,
по теореме 1, можно линейно выразить через векторы
старого базиса:
e'l = «цб] + «2162 + ••• +
е'ч, = «1261 + «22б2 + . . . + Пга2б(1, (2)
е'п = + «2мб2 + ... + аппеп.
Можно сказать, что новые координатные векторы по-
лучаются из старых с помощью матрицы
«ц «|2 • • «1ге
«21 «22 • а2п
_ &п2 • • • @-пп — $
(причем коэффициенты их разложений по старым ба-
зисным векторам образуют столбцы этой мат-
рицы). Матрица А называется матрицей перехода от
базиса «1, е2, ..., еп к базису е), е2, ..., е'п.
Определитель матрицы А не равен нулю, так как
в противном случае ее столбцы, а следовательно, и
векторы e'i, е2, ..., е,(, были бы линейно зависимы.
Обратно, если определитель матрицы А отличен
от нуля, то столбцы ее линейно независимы, и значит,
векторы e'i, е2, . .., е'п, получающиеся из базисных
векторов 61, е2, ..., еп с помощью матрицы А, ли-
нейно независимы, т. е. образуют некоторый базис.
Значит, матрицей перехода может служить любая
74
11-МЕРНОЕ ПРОСТРАНСТВО
[ГЛ. II
квадратная матрица порядка п с отличным от нуля
определителем.
Посмотрим теперь, как связаны между собой ко- .
ординалы одного и того же вектора в старом и новом
базисах. Пусть
х = x^t + х2е2 + ... + хпеп
и в то же время
х = x'te't + х2е2 + . .. + х'пе'п.
Подставляя вместо e's, е2, е'п. их выражения (2)
через еь е2, ..., еп, получим
х = x'l (ацб1 + а21е2 + ••• + anlen) + х^а^ + а22е2 + ...
« . . -(- Оп2Оп) "Ь • • • "Ь Хп (<21^61 + О2пв2 "Ь • • • =
= (ан%1 + а;2х2 + . .. '+ ainx'n) в] + (021X1 + 022X2 + . ..
. • • + О2пХ'п) 62 + ... + (aniX'i + Оп2Х2 + . . . + Опг+'п) вп,
и ввиду единственности разложения вектора х по ба-
зису еь е.2, ..., еп, отсюда сле-
дует, что
Xj =aHxJ+ а12х2 + ... +ainx'n,
х2 = a2ixj + 022X2 + ... + а2пХп,
Хп = ап\х\ + Оп2Х2 + ... +'аппх'п.
Таким образом, старые коор-
динаты вектора х получаются
из новых с помощью той же
матрицы А, только коэффи-
циенты соответствующих разложений образуют
строки этой матрицы.
Пример. Пусть 61, е2 — единичные векторы, на-
правленные по осям прямоугольной декартовой си-
стемы координат. Повернем оси координат на угол ср
против часовой стрелки, и пусть е{, б2 —новые бази-
сные векторы. Углы, образуемые вектором e'i с век-
ах
торами 6] и е2, равны соответственно ср и ср —у
(рис. 3). Поэтому координаты этого вектора в базисе
§ 5]
ЛИНЕЙНЫЕ ПОДПРОСТРАНСТВА
75
! л \ /
eit е2 равны cosq> и cos I <р — yl = sin <р, значит, ej =
= cos ср в! + sin ф • е2. Аналогично, углы вектора
с векторами в] и е2 равны соответственно у + фИф,
координаты его в базисе elt е2 равны соз^у+,ф^ =
= — sin ср и созф и, значит, е2 = — sin ф • et +.cos ф • е2.
Таким образом, ' матрица перехода здесь будет
такая:
, Г СОЭф — ЭШф'
А = . ,
ЗШф COS ф
а выражения старых координат через новые имеют
вид
Xi = COS ф • х'1 — sin ф • Х2,
Х2 — sin ф • x'l + COS ф • Х2-
§ 5. Подпространства линейного пространства
Определение 6. Подпространством векторного
пространства R называется совокупность R\ его эле-
ментов, саму являющаяся векторным пространством'
'относительно введенных р R операций сложения и
умножения на число.
Для того чтобы убедиться в том, что множество
Z?i элементов линейного пространства R является его
подпространством, необходимо проверить, что для-лю-
бых двух векторов х и у из /?1 их сумма х + у тоже
принадлежит Ri и что для каждого вектора х из Ri
и произвольного вещественного числа а произведение
ах,тоже принадлежит /?!. Покажем, что этого и доста-
точно. Действительно, аксиомы 1, 2 и 5—8 векторного
пространства, справедливые в R, будут выполняться,
> в частности, и для элементов из Ri. Надо показать
еще, что нулевой вектор принадлежит Ri и что для
каждого х из Ri вектор —х тоже принадлежит Ri.
Но если какое-то xe/?j, то и произведения 0-х = О
и X—1)х = —х тоже принадлежат Ri.
• Размерность любого подпространства векторного,
пространства не превосходит размерности самого
76 «-МЕРНОЕ ПРОСТРАНСТВО [ГЛ. IJ
пространства: ведь линейно независимые векторы под-
пространства Ri будут независимыми и во всем про-
странстве, а значит, максимальное число линейно не-
зависимых векторов подпространства не превосходит
размерности всего пространства.
Примеры. В обычном трехмерном пространстве
(рассматриваемом как множество принадлежащих
ему векторов) подпространствами будут все плоско-
сти и все прямые, проходящие через начало коорди-
нат. Подпространствами любого пространства будут
само пространство R и множество, состоящее из од-
ного нуля. В пространстве Рп многочленов степени
не выше п прдпространствами будут, например, все
Ph при /г < н (складывая и умножая на числа много-
члены степени не выше k, мы будем получать снова
такие же многочлены). (Многочлены, степень кото-
рых в точности равна п, не образуют подпро-
странства, так как при сложении таких многочленов
можно получить многочлен и более низкой степени,
за счет того, что старшие коэффициенты этих много-
членов могут взаимно уничтожиться.)
•С /фугой стороны, каждое из пространств Рп со-
держится в качестве подпространства в пространстве
Р всех многочленов с вещественными коэффициен-
тами, а это последнее является подпространством
пространства С непрерывных функций (так
как многочлены являются непрерывными функциями,
и при сложении их и умножении на число получаются
снова многочлены).
Рассмотрим систему линейных однородных урав-
нений, ранг матрицы коэффициентов которой равен г:
ЦцХ'! + ^12^2 + ••• + #lzA ~ 0>
^21-^1 "Е ^22-^2 + • • . + ^2п-^п = О,
(3)
"Ь &т2%2 ~Е ........+ С11ПпХп 3,
н пусть в линейном пространстве Rn зафиксирован ка-
кой-то базис. Если каждое решение (ai, «2, • • , ап)
системы (3) рассматривать как вектор пространства
Rn, то из результатов § 10 главы I вытекает, что со-
§ 51
ЛИНЕЙНЫЕ ПОДПРОСТРАНСТВА
вокупность всех, решений системы (3) является ли-
нейным k-мерным подпространством (где k = n — г)
в Rn, базисом которого служит любая фундаменталь-
ная система решений.
Покажем, что и, обратно, каждое, подпространство
векторного пространства определяется некоторой си-
стемой линейных однородных уравнений. Пусть
/?1 — ^-мерное подпространство в Rn и
(%11, %12, х1п), (х21, Х22, ...,'Х2п), ...
. .., (xftI, хк2, ..., йАп), (4)
его базис. Рассмотрим систему уравнений
( х^а, + х12а2 + ... + xtnan = О,
। Х21Я1 + х22а2 + . . . + х2пап — О,
I xktai + xk2a2 + ... + xknan = О
с неизвестными аь а2, ..., ап. Ранг матрицы
Xji х12 .. .
х21 х22 ... х2п ,
Xkl Xk2 • • • Xktl -
составленной из коэффициентов этой системы, ввиду
линейной независимости векторов (4), равен k и, зна-
чит, эта система имеет г — п — k линейно независи-
мых решений:
(цц, ^12, •••> airJ> (и2\, а22, ..., а2п), ...
• (аг1, аг2, ..., агп).
Таким образом, при всех р = 1,2,..., г и q = 1,2,..k
f ^pixq\ 4~ Пр2х^2 4- •. • 4- врПХдП 0. (о)
Рассмотрим теперь систему уравнений
йцх1 + а12х2+ ... +а1ге.г„ = 0,
a2i^i + а22х2 + . . . + а2пхп — 0,
. аг1х1 + аг2х2 + ... ± агпхп = 0
/
78
П-МЕРНОЕ ПРОСТРАНСТВО
[ГЛ. II
с неизвестными Xi, Х2, .хп и покажем, что опреде-
ляемое ею подпространство R2 совпадает с Ri. Дей-
ствительно, векторы (4) ввиду равенства (5) являются
решениями системы (6), они линейно независимы и
число их k равно п— г, где г — ранг матрицы коэффи-
циентов системы (6). Следовательно, они образуют
фундаментальную систему решений для (6), т. е. каж-
. дый вектор из Rz линейно выражается через векторы
(4), а значит, принадлежит Ri. Обратное очевидно:
каждый вектор из Ri является линейной комбинацией
векторов (4), и значит, так же как и они, удовлетво-
ряет системе (6), т. е. принадлежит Rz-
§ 6. Пересечение и сумма подпространств
Определение 7. Пусть в векторном простран-
стве R имеются два подпространства Ri и Rz- Их пере-
сечением Rz = Ri П Rz 'называется, множество всевоз-
- можных векторов из R, принадлежащих одновременно
и Ri, и Rz.
Легко видеть, что пересечение двух подпространств
Ri и Rz является подпространством (содержащимся и
в Ri, и в Rz).
Определение 8. Если Ri и /^ — подпростран-
ства линейного пространства R, то их суммой Ri =
= Ri + Rz называется множество всех векторов вида
и + v, где и^ Rt и v е Rz.
Сумма двух подпространств является подпростран-
ством (возможно, совпадающим с R). Действительно,
если х, у е Rt и а —-любое число, то
х = «i + nI, y = u2 + v2, где щ, и2<= R{ и щ, v2^R2.
Но тогда
X + у = («1 + и2) + (Vj + О2)>
г где Ui + uz е Ri и щ + v2 е R2 и, следовательно,
х + у е Rt.
Далее, ах = ащ + avlt где a«i е Ri, aVi е R2 и,
следовательно, ах е Ri-
Подпространство Ri (так же, как и Rz) содержится
в Rt, ибо каждый элемент х е Ri можно представить
в виде суммы х + 0, где х е Ri, а 0 е Rz-
§6] ПЕРЕСЕЧЕНИЕ И СУММА ПОДПРОСТРАНСТВ 79
Теорема 5. Если Ri и R2— подпространства ли-
нейного пространства R и R3 = Ri d R2, a Ri = Rt +
+ Rz, то
сЦ/Ш<Ш2) = <Жз) + <Ж). (7)
Доказательство. В подпространстве R3 выбе-
рем какой-нибудь базис
е1, е2, е3, ек. (8)
Дополним множество (8) векторов, принадлежащих
одновременно и Ri и R2, до базиса Ri:
Ci> б2, .. ек, fk-j-i, . • •> fр, - (9)
с одной стороны, и до базиса Rz'-
. ei, е2, .. ., ek, gk+l, . . ., gq (10)
/
— с другой (теорема 3). Покажем, что векторы
61, б2, ek, fk+l, fp, gk+l, gq (11)
линейно независимы. Тогда, по теореме 2, они обра-
зуют базис в /?4, ибо, если вектор z е /?,, то z == х + у,
где х е Rit у е Rz, и значит х, линейно выражается
через векторы (9), а у — через векторы (10). Но тогда
вектор z линейно выражается через векторы (11).
Допустим, что векторы (11) линейно Зависимы:
а1е1+а2е2+ ... + akek + fik+ifk+i + ••• + ₽pfp +
+ Yfc+igfc+i + ... + Y9g9 = 0; (12)
Тогда вектор ,
а = а1е1 + а2е2+ .;. + akek + [Зй-ыГйч-! + ... +₽PfP,
равный — (ул+1^й+1 + • • + Vqgq), принадлежит одно-
временно и Ri, и R2, а значит, и их пересечению R3. Но
в таком случае он должен линейно выражаться через
базисные векторы (8) подпространства /?3; пусть -
а = <?!&! + о2с2 + ... + <Jkek.
Отсюда, ввиду единственности разложения вектора а
по базису пространства Ri,
Oi = ah i=l, 2......... k и pA+1 = pft+2 ==" • • • =₽p = 0,
80
71-МЕРНОЕ ПРОСТРАНСТВО
[ГЛ, II
а тогда из равенства (12) следует, что
aiel + a2e2+ ... + akek + Ya+i^+i-+ ... + yqgq = 0,
и ввиду линейной независимости векторов (10)
«1 = 0, /=1, 2, ..., k и Yft+i = Ya+2= ••• =Y9 = 0.
Таким образом, векторы (11) образуют базис прост-
ранства /?4, и значит, его размерность равна числу
этих векторов:
k + (р - k) + (q - k) = р + q - k.
Ho d(Ri) = p, d^Rz) = q и d{R3) = k. Мы доказали,
что сумма размерностей двух подпространств равна
размерности их суммы, сложенной с размерностью пе-
ресечения.
Так, в четырехмерпом пространстве У?4 два двумерных
подпространства и R2 могут пересекаться по нулевому рек-
тору, и тогда их сумма совпадает со всем пространством; в этом
Случае равенство (7) превращается в 24-2 = 0 + 4. Они могут
пересекаться по прямой (одномерному подпространству), и тогда
их сумма трехмерна; это соответствует равенству 2 + 2 — 1 + 3.
Наконец, Aj и R2 могут совпадать, тогда их пересечение и сум-
ма тоже двумерны, и равенство (7) дает 2 + 2 = 2 + 2.
Два трехмерных подпространства в Ri . либо пересе-
ваются по плоскости (двумерному подпространству) и тогда
3 + 3 = 2 + 4, либо совпадают: 3 + 3 = 3 + 3. (Другие случаи
здесь невозможны, так как сумма этих подпространств не более
чем четырехмерпа.)
Если Ri — двумерное, a Ri — тре хим е р п о е подпро-
странства в /?4. то они либо пересекаются по прямой: 2 + 3 =
= 1 + 4, либо Ri содержится в R2: 24-3 = 2 + 3.
Определение 9. Если пространство R является
суммой своих подпространств Rt и R2, пересечение R3
которых состоит лишь из нулевого вектора, то говорят,
что Ri есть прямая сумма подпространств R^ и Rz,
и пишут
R = Ri Ф %2-
Если R = А1ф Rz, то очевидно, что
d(/?) = d(Ai) + c?(A2).
§ 6]
ПЕРЕСЕЧЕНИЕ II СУММА ПОДПРОСТРАНСТВ
81
Теорема 6. Если R = д ф R2, то каждый вектор
из R единственным способом представляется
в виде и + v, где и Rit v R2.
Доказательство. Каждый вектор из R, по опре-
делению суммы подпространств, представляется в виде
и + v, где и е Ru v е /?2- Предположим, что какой-то
вектор х из R разложен в такую сумму-двумя спосо-
бами:
X = М] + О) = и2 + 02.
Тогда вектор щ — и2 = v2 — щ принадлежит одно-
временно и Rt, и R2, т. е. он принадлежит Rs и, значит,
равен нулю, откуда Ui = и2 и v2 = vh
Так, обычное трехмерное пространство Rs будет"
прямой суммой любой (проходящей через начало ко-
ординат) плоскости л и любой не лежащей в этой
плоскости (но проходящей через начало) прямой / —
ведь каждый вектор ОА из R3 можно представить
в виде суммы векто-
ра, коллинеарного I, и
вектора, компланарно-
го плоскости л (см.
рис. 4, где AAi ||/), при-
чем пересечение л ПI
состоит только из ну-
левого вектора. Прост-
ранство R3 распадается
также и на сумму лю-.
бых двух своих несов-
падающих (проходя-
щих через начало) плоскостей; однако эта сумма не
будет прямой.
Пусть R — какое-то векторное пространство и,
«1, а2, ., аь е R. Совокупность всевозможных линей-
ных комбинаций этих векторов
+ а2а2 + . . . +
является, очевидно, подпространством в R. Мы будем
говорить, что это подпространство порождается век-
торами (ц, а2, ..., Uk- Его называют также линейкой
оболочкой векторов ai, а2, .... ah.
82 П-МЕРНОЕ ПРОСТРАНСТВО [ГЛ. и
§ 7. Определение аффинного пространства
Выше мы неоднократно иллюстрировали общее по-
нятие векторного пространства на примере (обычной)
плоскости или (обычного трехмерного) пространства.
Однако эти иллюстрации были, строго говоря, не сов-
сем точными — ведь основным понятием той геомет-
рии, которая изучается в средней школе, является
точка,~ и все геометрические образы можно понимать
как множества точек, в то время как в определении
векторного пространства точки вообще не фигурируют.
В, школьном курсе геометрии понятие вектора
появляется позже понятия точки: вектором там назы-
вают-упорядоченную пару точек (направленный отре-
зок) АВ, определяя далее условия равенства векторов
и правила их сложения и умножения на число.
Нам сейчас придется поступить иначе. РаспЪла-
гая уже. определением векторного пространства, мы
дополни^ его, введя в рассмотрение еще и точки. По-
лученное таким образом множество (векторов и то-
чек)— его называют то ч е ч н о - в е.кт о р н ы м, йли
аффинным пространством, — будет уже ближе
к тому пространству, которое изучается в курсе эле-
ментарной геометрии,'хотя и не будет еще полностью
с ним совпадать. Дело в том, что само понятие «аф-
финного» пространства предполагает, что это прост-
ранство лишено метрики, т. е. способа измерения
длин и углов. Оно станет вполне идентичным (во вся-
ком случае для двух- и трехмерного случаев) обыч-
ному пространству лишь после введения в нем соот-
ветствующей метрики (см-, ниже, глава IV).
Определение 10. Пусть имеется векторное про-
странство R (элементы его по-прежнему обозначаются
строчными латинскими буквами) и, кроме того, мно-
жество элементов, которые мы будем называть точ-
ками и обозначать прописными латинским-и буквами,
причем ' каждой упорядоченной паре точек М, N по-
ставлен в соответствие один и только один вектор х
из R (хотя разным парам точек может быть поставлен
в соответствие один и тот же вектор); мы будем пи-
сать в этом случае MN = х. Будем предполагать, что
§8]
КООРДИНАТЫ В АФФИННОМ ПРОСТРАНСТВЕ
83
это соответствие между точками и векторами обладает
следующими свойствами:
1, Для каждой точки М и каждого вектора х най-
дется одна и только одна такая точка N, что MN = х.
2. Для любых трёх точек М, N, Р
mn + np^mF.
' Все точки и все векторы вместе образуют тогда
аффинное пространство.
Аффинное пространство называется п-мерным, если
n-мерно соответствующее ему векторное простран-
ство R.
Итак, аффинное пространство А — это множество
элементов двух родов: точек и векторов, связь между
которыми задается с помощью операции откладывания
векторов. Произвольный вектор х можно отложить от
любой точки М, получив при этом определенную точ-
ку N, и тогда MN — х. Точка М называется нача-
лом, а точка N— концом вектора MN.
Далее, почти очевидны следующие предложения.
1. Если MN = QP; то MQ = NP. Это вытекает из
равенства
. RIN+ NT = МР = MQ + QP.
В частностй, так как
MN + W = MN = ММ + MN,
то ММ = NN, т. е. все векторы, у которых начало и
конец совпадают, равны между собой.
2. Вектор, у которого начало и конец совпадают,
является нулевым, потому что из равенства MN +
+ NN = MN следует, что NN = 0.
3. Вектор NM является противоположным к MN,
так как MN + NM = ММ = 0, и, значит NM — —MN.
§ 8. Введение координат в аффинном пространстве
В n-мерном аффинном пространстве А коорди-
наты точек можно ввести следующим образом.
Выберем какую-нибудь точку О в качестве начала
84
’ «-МЕРНОЕ ПРОСТРАНСТВО
(ГЛ. II
координат. Тогда для каждого вектора х ввиду усло-
вия 1 определения 10 найдется и притом только одна
такая точка X, что ОХ=х. Такбудет установлено вза-
имнооднозначное соответствие между всеми точками и
всеми векторами из А: точке X ставится в соответствие
вектор х = ОХ, концом которого она является (в обыч-
ном трехмерном пространстве это — откладывание
.всех векторов пространства от начала координат).
Далее, в соответствующем А векторном простран-
стве R выберем какой-нибудь базис elt е2, .... еп.
Тогда каждый вектор х из А будет определяться стро-
кой своих координат: х = (хь х2, • • •, хп)- Эти же коор-
динаты мы отнесем и соответствующей вектору х точке
X; будем писать в.этом случае: Х(х1г х2,..., хп).
Таким образом, если в n-мерном аффинном про-
странстве А выбрана система координат (т. е.
точка О как начало отсчета и базис е\, е2, ..., еп в со-
ответствующем А векторном пространстве /?), то каж-
дой точке из А будет однозначно сопоставлена строка
из п чисел — ее координат. У точки О все координаты
будут равны нулю, так как ей соответствует, очевидно,
нулевой вектор 0.
Если X(xlt х2, ...,хп) и У(уь У2,..., Уп) — две точки
аффинного пространства А, то ввиду равенства
ОХ+ХУ=ОУ
имеем
XY = OY-OX,
т. е. координаты вектора XY равны разностям коорди-
нат его конца и его начала.
Можно показать, что, подобно векторным про-
странствам, все аффинные пространства одной и той
же размерности тоже устроены в некотором смысле
одинаково.
Пусть А и А'— два аффинных пространства, имеющих одну
и ту же размерность п. Выберем в каждом из них систему коор-
динат и поставим в соответствие каждой точке- из А точку из А',
имеющую те же самые координаты, п каждому вектору из А —
вектор из А' с теми же самыми координатами. Тогда, если
X *-> X', Y гдеХ(х1дХ2,*п), Y(yi, уг, .., Уп) и X,
Y <= А, X', Y' е А', то вектор ХУ = (yi — Xi, yt —- х2, .,,, уп— хп)
5 91 ПЕРЕХОД к НОВОЙ СИСТЕМЕ КООРДИНАТ 85
будет соответствовать вектору Х'У' е А' (так как их координаты
одинаковы), причем это соответствие между векторными про-
странствами R и А!' (отвечающими А и А') будет, очевидно,
изоморфным.
Определение 11. Два аффинных пространства А и А'
называются изоморфными, если между их элементами мож-
но установить такое взаимно однозначное соответствие, сопостав-
ляющее точкам первого пространства точки второго ц векторам
первого — векторы второго, что:
1. Если Х-^ X' и У *-> У', то ХУ *-> ХЁУ.
2. Установленное при этом соответствие между векторными
пространствами R и R' (отвечающими А и А') является изоморф-
ным (в смысле определения 5).
Теорема 7. Для того чтобы два аффинных пространства Л
и А' были изоморфны, необходимо и достаточно, чтобы их раз-
мерности были одинаковы.
Мы уже доказали, что два аффинных пространства одной и
той же размерности изоморфны. Обратное очевидно, так как
если векторные пространства R и R' изоморфны, то по теореме 4
они имеют одну и ту же размерность п. Ту же размерность име-
ют, по определению, и соответствующие аффинные пространства
А и Д'.
Итак, все аффинные пространства одной и той же
размерности одинаковы, и размерность аффинного
пространства является его единственной харак-
теристикой. Поэтому n-мерное аффинное пространство
мы можем обозначать далее просто через А".
§ 9. Переход к новой системе координат
Посмотрим, как преобразуются координаты точки
аффинного пространства Ап при переходе к новой си-
стеме координат.
Пусть сперва изменяется только начало координат.
Предположим, что новое начало помещено в *очку О',
координаты которой в старой системе пусть будут
(ai, аг, ..., ап).
Для любой точки X из Ап имеем
oa+W = дх. (15)
Координаты вектора ОХ — (хь х2,..., хп) — это коор-
динаты точки X в старой системе координат; коорди-
наты вектора O'X = (x'i, х2, ,г„) — координаты
точки X в новой системе; координаты вектора 00' —
86
«-МЕРНОЕ ПРОСТРАНСТВО
[ГЛ II
это координаты, точки О' в старой системе, т. -е.
(ся, аг, .... ап). Из равенства (13) получаем
07Х = 0Х-007,
илр, в координатах,
(х$, хг,__ х£) = (хь х2, ..., хп)-(аь а2, а,г), .
и
x't — Xi — ai,’ t = l, 2, п,
т.е. новые координаты точки получаются, если из ста-
рых ее координат вычесть координаты нового начала
в старой системе координат.
Пусть теперь начало координат не меняется, но
в векторном пространстве /?, соответствующем А, вы-
бирается новый базис с матрицей перехода
ан а12 ... а1п
а2\ а22 .. . а2п (14)
— ^п\ &п2 • • • ^пп -
т. е. старый базис, образованный векторами ei, е?, ...
..., еп заменяется новым, составленным из векторов
е\, е'2, ..., е'п, где
e'i = +аце2+ ... + anien, г=1, 2, к.., п.
Так как координаты точки X — это, но определению,
координаты вектора х = ОХ, то, как показано в1 § 4,
старые координаты точки будут выражаться через но-
вые ее координаты по формулам
Xi = aux'i + ai2x2 + ... +ainXn, где г= 1, 2, ..., п.
. В общем случае, когда и начало координат О пере-
носится в точку O'(ai, аг,..., ап), и базис е1у е2, .. еп
с помощью матрицы перехода (14) заменяется новым,
старые координаты хь х2, ..., хп произвольной точ-
ки X и новые ее координаты x'i, х2, ...» Хп связаны
§ 101
ЛИНЕЙНЫЕ МНОГООБРАЗИЯ
соотношениями:
Xi = апх' + G12X2 + ... + а\пХп + а,,
*2 = «21*1 + «22*2 + . . . + Cl2nXn + 0-2,
Хп — Onix'i + ап2Х2 + . . . + dnnx'n + <ХГ1.
§ 10. Линейные многообразия
Пусть дано векторное пространство Rn, в котором
выбран некоторый базис.
Рассмотрим (совместную) систему линейных, eq-
обще говоря, неоднородных уравнений: ,
On*i "1" ^12X2 + ... + О\пхп = Ь[,
<221*1 + Cl22x2 + . . . + О2ПХП — Ь2,
. OmiXj + От2Х2 + • . • + ОтпХп — Ьп1г
ранг матрицы коэффициентов которой равен г, и пусть
k. = п — г.
Определение 12. Совокупность векторов про-
странства Rn, координаты которых;удовлетворяют си-
' стеме линейных уравнений (15), называется линей-
ным многообразием.
Согласно замечанию, сделанному.в конце § 10 гла-
вы I, общее" решение х системы (15) равно сумме об>-
щёго решения %о соответствующей (т. е. с теми же ко-
эффициентами при неизвестных) однородной системы
• ’«и*! + «12х2 + +й1Л = 0,
«21*1 + «22*2 + ••• + а2пХп — 0>
«т!*1 + «/«2*2 4" . . . + «mn*n 0
и произвольного, но фиксированного решения а =
= (<2i, 02, ..., ап) системы (15). Таким образом, линей-
ное многообразие решений системы (15) получается,
если к каждому вектору из подпространства решений
соответствующей однородной системы (16) прибавить
один и тот же вектор а (см. рис. 5, а, где концы вектО;
ров, образующих линейное многообразие, принадлежат
88
«-МЕРНОЕ ПРОСТРАНСТВО
{ГЛ И
плоскости л„ получающейся из подпространства л0 па-
раллельным переносом на вектор а).
Покажем, что и, обратно, если к каждому вектору
подпространства Rt прибавить один и тот же вектор а,
то получится линейное многообразие. Пусть подпро-
странство Ri определяется- системой линейных одно-
родных уравнений (16) и а = (щ, а2,..., ап). Положим
ДиЛ; + ’а12а2 + ... +a;nan = bi,
^21^1 "Ь ^22^2 + ... + й2пап — Ь2,
Ят1^1 4“ ^т2^2 4“ ... 4" Clmn^n ^т’
и рассмотрим систему уравнений
апх1 4- а12х2 4- ... + a!nxn — bt,
o2i^t 4” а22х2 4" ... 4- С12!гх!г = Ь2,
4~ ^т2^2 4* ... 4“ ятйуп Ьт,
§ 111^
ПЛОСКОСТИ В АФФИННОМ ПРОСТРАНСТВЕ
89
Вектор а является одним из решений этой (вооб-
ще говоря, неоднородной) системы. Следовательно,
линейное многообразие, определяемое системой (17),
совпадает с заданным множеством Ri + а векторов.
Линейное многообразие (15) называется ft-мер-
ным, если ft-мерно соответствующее ему подпростран-
ство (16).
§ 11. ft-мерные плоскости в аффинном пространстве
Пусть в аффинном пространстве Ап установлена
система координат. Рассмотрим снова систему урав-
нений (15). „
Определение 13. Множество всех точек из Ап,
координаты которых удовлетворяют системе уравне-
ний (15), называется k-мерной плоскостью; одномер-
ные плоскости называются также прямыми, а (п—1)-
мерные плоскости — гиперплоскостями.
Понятно, что каждую гиперплоскость' (для кото-
рой r= 1) можно задать всего одним линейным
уравнением:
ар^ -|- 02X2 4- «. И- апхп == Ь.
В трехмерном пространстве гиперплоскости — это
обычные плоскости, а на обычной плоскости — это
просто прямые.
Можно показать, что при переходе к новой системе
координат в Ап точки, удовлетворяющие системе ура-
внений (15), будут удовлетворять некоторой новой
системе линейных уравнений, ранг матрицы коэффи-
циентов которой тоже равен г.
Пусть л будет ft-мерная’плоскость, определяемая
системой уравнений (15). Соответствующая система
(16) линейных однородных уравнений тоже опреде-
ляет некоторую ft-мерную плоскость По, «проходящую
через начало координат». Если все векторы отложены
от начала координат, то те векторы, концы которых
принадлежат Ло, образуют подпространство, а век-
торы, концы которых принадлежат л, образуют ft-мер-
ное линейное многообразие. Это многообразие полу-
чается, если ко всем векторам подпространства лц
90
«-МЕРНОЕ/ ПРОСТРАНСТВО
[1*Я. II
прибавить один и тот же вектор а. Можно сказать
поэтому, что k-мерная плоскость л получается из по
параллельным переносом на вектор а.
Это дает основание для следующего определения.
Определение 14. Две k-мерньЩ плоскости
параллельны, если определяющие их системы та-
ковы, что соответствующие однородные системы рав-
носильны (имеют одни и те же решения), k-ме'рная
плоскость Л1 и l-мерная плоскость л2 параллельны
(при l>k), если trti параллельна какой-нибудь k-мер-
ной плоскости, содержащейся в л2 (в этом случае
определяющие ni и л2 системы таковы, что однород-
ная система, соответствующая л2, является след-
ствием однородной системы, соответствующей Л1).
Пусть снова л—^-мерная плоскость, определяе-
мая системой уравнений (15). Общее решение си-
стемы (15) в векторной форме имеет вид
х = а1с1 + а2с2+ ... +айС£ + а, ' (18)
где
х0 = + а2с2 + ... + сцщ
— общее решение соответствующей однородной си-
стемы (16) и а — некоторый фиксированный вектор
(одно из решений системы (15)). Если щ =
= (^п, Сг2, , cin} при i = 1, 2, ...0 k и а —
= (alt а2, .ап), то, записывая равенство (18) в ко-
ординатах, получим параметрические уравнения k-
мерной плоскости-.
X/ ~ щец + а2с2/- + ... + апсп] + aj, j=l, 2, ..., п.
Если ранг матрицы коэффициентов системы (15) ра-
вен п—1, соответствующую (одномерную) плоскость
мы назвали прямой. В этом случае общее решение
системы (15) в векторной форме имеет вид
х = ас + а, (19)
где х0 — ас — общее решение соответствующей одно-
родной системы и а = (ai, а2, . . ., ап) — некоторый
фиксированный вектор (рис. 5,6). Если с ~
— (ci,c2, ..., сп) и х = (ху,х2, ... , хп), то, записы-
, вая уравнение (19) в координатах, получим парамет-
ПЛОСКОСТИ В АФФИННОМ ПРОСТРАНСТВЕ
9'1
§ и]
рические уравнения прямой-.
X] = аС] + а1г
%2 “ Щ?2 ^2>
%п ОС„ "Ь ^П>
которые, .исключая параметр а, можно переписать
в виде
Х[ “ _* Х2“(22 _ . хП —
С[ .С2 ’ * ’ Сп
(Это — канонические уравнения прямой. Они имеют
смысл и в том случае, если некоторые из знаменате-
лей обращаются в нуль — тогда равны нулю и соот-
ветствующие числители.)
Если в пространстве Ап даны две .точки
А (<2|, а2, . . ., ап) и В (&ь Ь2, . . ., Ьп), то_ проходящая
через них прямая АВ определяется, очевидно, урав-
нениями
xi ____ х2 „ ___ хп.
bl-ai - b2 — a2 ~ ••• ~ bn-an •
Обозначив равные отношения .(20) через 0, получим
параметрические уравнения прямой АВ в виде
хг = а( + Р(&{-а;),
или
хг = (1 — Р)аг + Р&(-, i = 1, 2, ..., п.
Полагая 1 —0 = а, будем иметь
хг = аа( + рбг, гдеа + 0-=1. (21)
Если 0 а, 0 1, говорят, что соответствующая точ-
ка X принадлежит отрезку АВ. <
Если ранг матрицы коэффициентов системы (15)
равен п — 2, то определяемая ею плоскость двумер-
на, и общее решение этой системы в векторной фор-
ме имеет вид
х = ахС\ + а2с2 + а,
где Хо = aiC] + а2с2 — общее решение соответствую-*
щей однородной системы, а а = (щ, а2у-..., ап) — не-
который фиксированный вектор. Если -»
92
Л-МЕРНОЕ ПРОСТРАНСТВО
[ГЛ. II
= (cn, ct2, •••, Cin), i=l, 2, то координаты точек
X = (хь х2, ..., хп) этой плоскости определяются
формулами
xk = «iCife 4- a2c2k 4- ак, k=l, 2, ...,n
(параметрические уравнения двумерной плоскости).
Пусть в аффинном пространстве А" даны две пло-
скости: ^-мерная плоскость л, определяемая системой
уравнений (15), и /-мерная плоскость л', определяе-
мая системой уравнений
I 01-^1 4- с12х2 + ... + ctnxn == (/],
I c21Xj + с22х2 4- ... 4- с2пхп = d2, (22)
| csl-«l ”1” 0'2-^2 4" • • • 4” ^s*
Тогда их пересечение (т. е. множество точек, принад-
лежащих одновременно и л, и л') будет определяться
системой, состоящей из всех уравнений системы (15)
и всех уравнений системы (22) и, значит, вообще го-
воря, тоже будет некоторой плоскостью (которая, в
частности, может состоять из одной точки или даже
вообще не иметь ни одной точки, если объединенная
система окажется несовместной). Легко видеть, что
каждая k-мерная плоскость является пересечением
некоторых г = п — k гиперплоскостей.
§ 12. Выпуклые множества
в аффинном пространстве
Определение 15. Множество точек аффинно-
го пространства называется выпуклым, если вместе
с каждыми двумя своими точками А и В оно содер-
жит и все точки отрезка АВ.
Легко видеть, что пересечение любого числа вы-
пуклых множеств выпукло.
Определение 16. Множество точек аффинно-
го пространства называется ограниченным,
если координаты всех его точек в некоторой системе
координат ограничены (легко видеть, что тогда они
§ 12] ВЫПУКЛЫЕ МНОЖЕСТВА 93
«
будут ограничены и во всех системах коорди-
нат).
Пусть в аффинном пространстве Ап задана гипер-
плоскость
ajX] 4- а2х2 + ... 4- апхп = Ь. (23)
Этой гиперплоскостью все точки из Ап разбиваются
на два полупространства-, А\ — множество точек, для
которых apci + а2х2 + ... + апхп Ь, и А2 — множе-
ство точек, для которых ал 4- «2*2 4- ... 4- апхп -гС Ь.
Полупространства At и пересекаются по самой ги-
перплоскости (23).
Теорема 8. Каждое полупространство аффин-
ного пространства Ап является выпуклым множе-
ством.
Доказательство. Пусть точки P(pt, р2,.... рп)
и Q = (q\, q2, ..., 7и) из Ап принадлежат, например,
полупространству /Ij; тогда
а1р14-едг+ •• +апрп>Ь
и
а1<?1 4-п2^24- ... + anqn^b.
Если X(xt,x2, ..., хп)—произвольная точка отрезка
PQ, то по формулам (21)
х(-= ар, 4- fiqi’ I=l> 2,..., п,
где а, р>0иа4-р=1. Для этой точки X имеем
«[Xj 4- g2x2‘4- ... 4- апхп = а, (ар, 4-0?,) 4-
4- а2 (ар2 4- ₽?2) + • • • + ап (арп 4- 0р„) =
= а (й|Р| 4- а2р2 4- ... 4- апр^ +
4-0 («Н71 4- a2q2+ ... 4-ап<7„) > аб 4-06'= (а 4-0)6 = 6,
т. е. произвольная точка X отрезка PQ принадле-
жит At.
Гиперплоскость (23), как пересечение выпуклых
множеств At и Л2, является выпуклым множеством.
Каждая k-мерная плоскость в Ап, как пересечение не-
скольких гиперплоскостей, выпукла.
94
«-МЕРНОЕ ПРОСТРАНСТВО
[ГЛ. II
Пусть в Ап даны т полупространств, определяе-
мых неравенствами
011*1 + «12-^2 + ...
' Й21*1 4~ 1^22*2 4“ • * • 4” ^2/г-^п ^2» (24)
. ^ml^l 4“ ^m2^"2 4" ... 4"
(Все знаки неравенств здесь одного смысла, так как
этого всегда можно достичь,-умножая в случае необ-
ходимости обе части неравенства на —1.) Пересече-
ние этих полупространств, называемое выпуклой мно-
гогранной областью, определяет множество решений
системы линейных неравенств (24). Если это пересе-
чение ограничено, оно называется (выпуклым) много-
гранником.
§ 12]
ВЫПУКЛЫЕ МНОЖЕСТВА
95.
Так, на (двумерной) плоскости система неравенств
X + у 5^9,
5х + у 5,
(25)
определяет (выпуклый) четырехугольник ABCD
(рис. 6). Система неравенств
' х + у^9, '
5х + у^ 5,
, 2х — у 6,
2у — х 6
[все неравенства системы (25) изменили знак] — пу-
стое множество точек. Система неравенств
х + у 9,
5х + г/ >5,
. 2х — у «С 6
определяет треугольную область АВЕ, а система не-
равенств
х 4- у 9,
5x + z/^5,
. 2у — х*^ 6
— неограниченную треугольную область.
ГЛАВА III
ЛИНЕЙНЫЕ ПРЕОБРАЗОВАНИЯ
§ 1. Определение и примеры
Определение 1. Говорят, что в линейном про-
странстве R задано преобразование si, если каждому
вектору xeR поставлен в соответствие определенный
вектор si{x), или, как мы чаще будем писать six.
Преобразование si называется линейным, если для
любых двух векторов х и у из R и произвольного ве-
щественного числа а
1. si(x + у) = six + siy,
2. .s^(ax) = asix.
Вектор Ах называется образом вектора х.
Выберем в пространстве R базис в\, е2, • •, еп.
Тогда, если х = х^ + х#е2 + ... + хпеп, то в силу ли-
нейности преобразования si имеем
six = x^siex + x2sie2 + ... + хп^п.
Но так как (где i = 1, 2, 3, ..., п) — это тоже
вектор из R, то .sic, можно разложить по базису
61, е2, ..., еп; пусть
sie{ = atiet + a2ie2 + ... +anien.
Тогда
six = Xj (йцб! + «21^2 + + anien) +
+ x2 (a126, + a22e2 + ... + an2en) + ...
... + xn (aInei + a2ne2 + ... + annen] =
= (a^Xt + al2x2+ ... +alnxn)el +
+ (a2iX] + a22x2 + ... + a2nxn) e2-\- • • •
.. • + + an2x2 + ... + annx^ en.
§ И
ОПРЕДЕЛЕНИЕ И ПРИМЕРЫ
97
Если х'1, Хг, х'п — координаты (преобразованно-
го) вектора six в том же базисе в], е2, .. ., еп, т. е.
если
six = х'е. + х'е2 + .. . + х'е,
11 L X. П П
то ввиду единственности разложения вектора по ба-
зису имеем
x'l = auxl + ai2x2 + ... +atnxn,
х2 = a2iXy + а22х.2+ ... + а2пхп, (1)
х'п = ап\х\ + ап2хг + • • • + апп*п-
Таким образом, каждому линейному преобразова-
нию si в заданном базисе eh е2, .. . , еп отвечает
матрица
«и а12 . .. а1п
д _ Ц21 Й22 • • • а‘2п
— @-п\ @п2 • • • Ct-nn -
При этом i-й столбец матрицы А образован коэффи-
циентами разложения вектора по базису
ei, е2, еп, а коэффициенты разложений (1) коор-
динат вектора six по координатам вектора х обра-
зуют строки матрицы А.
Если в n-мерном пространстве R задан базис, то
не только каждому линейному преобразованию si от-
вечает определенная матрица А, но и обратно, каж-
дая квадратная матрица А порядка п может рассмат-
риваться как матрица некоторого линейного преобра-
зования. Действительно; пусть щ, е2, ..., еп — базис
пространства R, я пусть дана матрица
«11 g12 • • • Gln
д _ а21 а22 • • а2п
- @nl Оп> * • • —
(мы будем писать короче: = Обозначим че-
рез si преобразование, переводящее произвольный
4 Л. И. Головина
98
ЛИНЕЙНЫЕ преобразования
[ГЛ. III
вектор
х = ххех + х2е2 + ... + хпеп
в вектор
stx — х'.е. + х'е2 + ... + х'е ,
где
x'l = atxxl + ai2x2 + ... +ainxn при i = 1, 2, ..., п.
Покажем, что это преобразование — л и и е й и о е.
'В самом деле, произвольный другой вектор
У = У + У^2 + + Упеп
наше преобразование переводит в
Жу = у'хех + у'2е2+ ... +у'пеп,
где
У^ а1\У1 + а,2У‘2+ ••• +а1пУп’
а вектор
х + у — (xi + ух) ех + (х2 + г/2) е2 + ... + (х„ + у„) еп
— в вектор
<5^ (х + у) = zxex + z2e2 + ... + znen,
где
zt = aiX (Xi + yx)+al2(х2+у2) + ... + а1п (х„ + уп) = х' + у'.
Поэтому
(х Ч~ у) — $Фх 4" <^у•
Далее, для любого а
ах = (ах^в! + (ах2)е2+ ... +(ах„)еге
и
(ах) = txex + /2е2 + ... + tnen,
где
/г = Ян(ах1) + а/2(ах2)+ ... + ain(axn) = ах'г
Следовательно,
3^ (ах) = aj/x,
и — линейное преобразование.
Таким образом, если в векторном пространстве R:i
задан базис, то каждому линейному преобразованию
§ 1]
ОПРЕДЕЛЕНИЕ И ПРИМЕРЫ
99
отвечает определенная квадратная матрица порядка
п и, обратно, каждой такой матрице отвечает опреде-
ленное линейное преобразование. Поэтому линейное
преобразование и соответствующую ему (в данном
базисе) матрицу мы будем обозначать одной и той
же буквой: .5^, ...— Линейные преобразования,
А, В, С, ... — соответствующие им матрицы. Матри-
ца А называется матрицей линейного преобразова-
ния 54.
Легко видеть, что для произвольного линейного
преобразования ^4
= 0.
При этом, если преобразование таково, что л4х — 0
только при А'= 0, то оно называется невырожден-
ным; в противном случае преобразование — вырож-
денное.
Пусть А = [«;/.] — матрица линейного преобразова-
ния А. Рассмотрим систему линейных однородных
уравнений »
апхх + ц12х2 + ... + аЛпх„ = 0,
а21х1 + ц22х2 + ... + а2пхп = 0,
+ лп2*2 + • + аппхп — 0.
Ввиду теоремы 10 из главы I, для существования не-
нулевого решения этой системы (и значит, для суще-
ствования ненулевого вектора х = х^ + х2е2 + ...
. . . + хпеп такого, что s4x = 0) необходимо и доста-
точно, чтобы определитель матрицы А (обозначим его
через | А |) был равен нулю. Следовательно, для того,
чтобы преобразование .'Л- было невырожденным, необ-
ходимо и достаточно, чтобы определитель матрицы
А этого преобразования (при любом выборе ба-
зиса) был отличен от нуля. Матрица, определитель
которой бтличен от нуля, называется невырожденной
матрицей.
Рассмотрим несколько примеров.
1. Пусть — поворот всех векторов ОХ плоско-
сти хОу (короче — поворот плоскости хОу) вокруг на-
чала координат на угол ф против часовой стрелки.
4!
100
ЛИНЕЙНЫЕ ПРЕОБРАЗОВАНИЯ
[ГЛ. III
Это преобразование линейно, ибо безразлично, сна-
чала ли сложить векторы а и Ь, а потом повернуть их
сумму на угол ф, или сначала повернуть векторы,
а потом их сложить (рис. 7, а); так же будет безраз-
лично, умножить ли сначала вектор а на число а,
б)
Рис. 7.
а затем повернуть его на угол ср, или сделать это в
обратном порядке (рис. 7,6).
Предположим, что базисные векторы — единичные
и взаимно ортогональные. Вектор збех — единичный,
образующий с щ угол <р и с <?2 — угол ф — . Следо-
вательно,
= cos ф • et + sin ф • е>.
Единичный вектор збе2 образует с е\ угол у+ф,
а с С2 — угол ф. Следовательно,
s6e2 = — sin ф • б! + cos ф • е2.
Таким образом,
’ cos ф — sin ф
~ sin ф COS ф
§ 1]
ОПРЕДЕЛЕНИЕ И ПРИМЕРЫ
101
2. Пусть — поворот обычного трехмерного про-
странства на угол ср вокруг оси Oz. Если рь е2, е3—•
единичные векторы прямоугольной декартовой систе-
мы координат, то
s4-ex = cos ф • + sin ф • р2,
.?/-р2 = — sin ф • Pj 4- cos ф • р2,
$/р3 = е3,
и значит, матрица этого преобразования:
А =
cos ф — sin ф 0
sintp СОЗф 0
0 0 1
3. В обычном трехмерном пространстве пусть л&а
будет ортогональной проекцией вектора а на пло-
скость хОу. Линейность этого преобразования
вытекает из того, что проекция суммы векторов равна
сумме проекций слагаемых и что проекция произве-
дения вектора на число равна произведению проекции
вектора на это число. Если базис выбран так, как в
примере 2, то очевидно, что
.я£р1 = <?1, <я£р2 = р2, ^р3=0,
и следовательно,
Л= 0
о
О (Г
1 о
о о
4. В обычном трехмерном пространстве пусть .й/а
будет вектор, симметричный с вектором а относитель-
но плоскости хОу. Линейность этого преобразования
очевидна. При этом
$Фех = ех/ -Ле^ = р2, .?Zp3 = — р3,
и матрица этого преобразования —
А =
'10 0"
0 1 0 .
0 0 -1_
102
ЛИНЕЙНЫЕ ПРЕОБРАЗОВАНИЯ
[ГЛ. ш
5. В пространстве Рп многочленов от t степени
не выше п положим
А (х (/)) = х' (t).
Линейность этого «преобразования дифференцирова-
ния» вытекает из основных правил дифференциаль-
ного исчисления. Чтобы найти матрицу этого преоб-
разования, выберем в качестве базиса, например,
векторы
/3 tn
= 1, <?i Л Ё2~ 'qT , . . •, en .
Тогда
^ео = О, s4-e{—e0, s4-e2 = elt ..., ^e„ = e„_b
и
~0 1 о ... о
0 0 1 ... о
о о о ... о
Z1 — •
0 0 0 ... 1
-0 0 о ... 0„
6. Обозначим через S так называемое тожде-
ственное преобразование линейного про-
странства /?, определяемое равенством: <Sx — х для
любого х^Р. Тогда Sei = вг для всех 1=1, 2, ...
..., п и, следовательно, матрица преобразования <S
в любом базисе имеет вид .
'1 о о ... о
„ 0 1 о ... о
_0 0 О ... 1_
7. Обозначим через О так называемое нулевое
преобразование линейного пространства R, оп-
ределяемое равенством Ох = 0 для всех х е R. Мат-
рица этого преобразования
“0 0 ... 0“
О = ° °:-.’ °
_0' о ... 0_,
состоит из одних нулей.
§ 1]
ОПРЕДЕЛЕНИЕ И ПРИМЕРЫ
103
Ясно, что преобразования 1, 2, 4 и 6 невырожден-
ные, а преобразования 3, 5 и 7 — вырожденные.
Теорема 1. При линейном преобразовании век-
торного пространства каждое подпространство пере-
ходит в подпространство.
Доказательство. Пусть Rt— подпростран-
ство векторного пространства Rn. Обозначим через
s£Ri совокупность всех векторов, являющихся обра-
зами векторов из R\ при линейном преобразовании
Нам надо доказать, что s^R\ — подпространство.
Пусть векторы хну принадлежат styty Это значит,
что х — si-x' и у — sty', где х' е Ri и у' е R\. Но то-
гда х + у = st-x' + sty' = (х' + у') е s£Ri, так как
х' + у'<= Ri, и при любом а ах = as£x'= s^(ax') ^s/Ri,
так как ах'е7?ь Таким образом, s£R\— подпро-
странство.
(Легко понять, что размерность s&R\ не превышает
размерности Ri.)
Теорема 2. При линейном преобразовании век-
торного пространства каждое линейное многообразие
переходит в линейное многообразие.
Доказательство. Пусть М — линейное много-
образие в Rn. Тогда существует такое подпростран-
ство R\ и такой вектор а, что М = R\ + а (см. выше
стр. 87). Если «9/ —линейное преобразование, то
styA = s^-Ri + sty. Ввиду теоремы 1, sty^ является ли-
нейным подпространством и, значит, — линейное
многообразие (см. стр. 88).
Пусть Ап — «-мерное аффинное пространство и
Rn — соответствующее ему векторное пространство,
в котором задано линейное преобразование s£. Это
преобразование можно следующим образом распро-
странить и на точки из Ап. Предположим, что в Ап
выбрана система координат. Тогда, если вектор
х = хщ! + х2С2 +'...'+ хпеп при преобразовании S& пе-
реходит в six = x'et + х'е2 + ... + х'пеп, по определе-
нию, точка X(xi, х2, .... х„) (конец вектора ОХ=х)
переходит в точку X'(х{, х'2, .... х') (конец вектора
ОХ' = six).
101
ЛИНЕЙНЫЕ ПРЕОБРАЗОВАНИЯ
[ГЛ. Ш
Из теоремы 2 непосредственно вытекает, что при
линейном преобразовании аффинного пространства
k-мерные плоскости переходят в плоскости (не боль-
шей размерности). В частности, прямые переходят
в прямые или в точки.
Взаимно однозначное отображение *) множества точек «-мер-
ного аффинного пространства па себя, такое, при котором каж-
дая прямая переходит в прямую, называется аффинным преобра-
зованием. Из теоремы 2 следует, что каждое невырожденное ли-
нейное преобразование аффинного пространства является аффин-
ным преобразованием. Можно показать, что каждое аффинное
преобразование сводится к (невырожденному) линейному преоб-
разованию, сопровождаемому еще, быть может, параллельным
переносом (см. ниже стр. 274).
§ 2. Операции над линейными преобразованиями
А. Сложение линейных преобразований
Если и — два линейных преобразования ли-
нейного пространства R, то суммой ,$ф + назы-
вается такое преобразование 43, что для любого х е R
+ Ях.
Легко видеть, что сумма линейных преобразований
тоже будет линейным преобразованием. Если ли-
нейные .преобразования .5^ и & имеют (в некотором
базисе) соответственно матрицы A=[u1?£] и B = [bih\, то
матрицей преобразования будет С —
где
Cik = citk + blk.
Матрица С называется суммой матриц А и В. Таким
образом, по определению,
[azi] -) = [ai!c +
(Разумеется, складывать можно лишь матрицы од-
ного и того же порядка.)
*) Говорят, что задано взаимно однозначное отображение
множества М на множество N (в частности, М на Л4), если
каждому элементу а е= М поставлен в соответствие определен-
ный элемент beN, причем каждый элемент b е N поставлен
в соответствие определенному элементу а е М. В этом случае
говорят также, что между множествами А н В установлено
взаимно однозначное соответствие (ср. выше стр. 71 и 85).
§ 2]
ОПЕРАЦИИ НАД ПРЕОБРАЗОВАНИЯМИ
105
Сложение линейных преобразований (и сложение
матриц) обладают, очевидно, следующими свойствами:
1. з/+ $ = $ + з/.
2. (з/+ /?) += ./ + (/? +ГС).
3. $4- + С = для любого s4.
4. Если через —обозначить преобразование, оп-
ределяемое тем, что (—з/)х =—.s4x для всех хе/?,
то —будет линейным преобразованием и
(-з/) + з/ = С.
Матрицу преобразования —^4 обозначим через —А;
тогда ясно, что если А = [я«], то —А — [—а,л].
Б. Умножение линейного
преобразования на число
Если s4—линейное преобразование пространства
Rua — число, то произведением s4 на а назы-
вается такое преобразование аи4, что для каждого
вектора х е R
(аз/) х = ас4х.
Ясно, что аз/ — тоже линейное преобразование и
что его матрица аА получается из матрицы А преоб-
разования з/ умножением каждого ее элемента на а:
а [«zd = [а«nJ-
Матрица аЛ называется произведением матрицы А
на число а.
Для умножения линейного преобразования на чис-
ло справедливы, очевидно, следующие тождества:'
1. 1 -з/-=з/.
2. а (рз/) = (ар) з/.
3. (а + р) з/= аз/+ рз/.
4. а (з/ + 31) = аз/ + айв.
Аналогичные тождества справедливы и для умноже-
ния матрицы на число.
В. Умножение линейных преобразований
Произведением преобразований st и $ назы-
вается такое преобразование 43, что для каждого век-
тора x^R
4?х = ,s4 (Six).
106
ЛИНЕЙНЫЕ ПРЕОБРАЗОВАНИЯ
[ГЛ. III
Таким образом, перемножение преобразований со-
стоит в последовательном их выполнении одного за
другим; при этом сначала производится преобразо-
вание ffi, а затем уже полученный вектор ffix подвер-
гается преобразованию
Так, если есть поворот плоскости против часо-
вой стрелки на угол ср, а ffi— поворот (в том же на-
правлении) на угол 1|у то л/Д = будет поворотом
Ра угол ср + ф. Если — симметрия плоскости хОу
относительно оси Ох, а ffi— симметрия относительно
Оу, то = ffi:1 = <S — тождественное преобразование,
a xlffi = ffist- = ffi— симметрия относительно начала
координат. Если si-—ортогональное проектирование
пространства на плоскость или на прямую, то .5-Д =
= 5/. Если ^ — дифференцирование в пространстве
многочленов, то преобразование si-—это взятие вто-
рой производной.
П роизведение линейных преобразований тоже бу-
дет линейным преобразованием.
Действительно,
1. (.$О) (.г + у) = si (ffi (х + у)) = s4- (ffix + ffiy) =
= si (ffix) + .Д ($у) = (.?/$) х + (siffi) у.
2. (siffi) (ах) = si (ffi (ах)) = (affix) =
= asi (ffix) = а (siffi) х.
Найдем, как выражается матрица С линейного
преобразования <F = siffi через матрицы А = [аг)1] и
В = Имеем
(ffiek) = si (blkel + b2ke2 + ... + bnken) =
= biil..y'/e-, + У2/,^/е2 + • • • + bnksien =
= Ь1к (a11eI + a2Ie2 + +onien) +
+ Ь2к (П|2<?1 + «22е2 + ••• + an2en) + •••
••• + bnk (<Wi + а2пе2 + ••• +аппеп) =
= (a!tblk + ai2b2k + +ctinbnk)e1 +
+ (а21Ь1к + а22Ь2к + ... + а2пЬпк) е2 + ...
.. . -р (a^}b\k + ап2Ь2к + .. . + antlbnk) еп,
значит, если 'S’ej. = clkel + c2ke2 + ... + cnken, то
ctk ~ at\b\k + ai2.b2k + ... + ainbnk.
§ 2]
ОПЕРАЦИЙ НАД ПРЕОБРАЗОВАНИЯМИ
107
Мы видим, что для того, чтобы получить элемент
матрицы С, стоящий в пересечении ее i-й строки и
k-го столбца, надо каждый элемент i-й строки матри-
цы А умножить на соответствующий элемент k-го
столбца матрицы В и все полученные произведения
сложить. Матрица С называется произведением
матриц А и В.
Пример ы.
1. 12 3
— 1 1 2
3 2—1
4 1 2
0 —1 1
1 2 1
7 5 7
—2 2 1
11 —1 7
1-4 + 2-0 + 3-1 Ы + 2(-1) + 3-2 1-2 4-2-14-3-1
-1-4 + 1-0 + 2-1 -1-1 + 1 (-1) + 2-2 -1-2+1.1 + 2-1
3-4 + 2-0 + (-1).1 3-1 +2(-l) + (-I)-2 3-2 + 2-1+ (-!)•! .
Произведение тех же
матриц в обратном порядке
равно
"4 1 2" " 1 2 3" "9 13 12"
0 -1 1 -1 1 2 = 4 1 -3
_ 1 2 1 _ 3 2 — 1 _ о 6 6.
Мы видим, что умножение матриц (вообще
говоря) не коммутативно (не подчиняется пере-
местительному закону).
2. Г cos ср — sin ср] Г cos ф
— sin
sin ф cos ф J L sin -ф
COS
cos ф cos ф — sin ф sin ф — cos ф sin — sin ф cosi|)
sin ф cos з|з + cos ф sin — sin ф sin + cos ф cos
cos (ф + Ф) ~ sin (ф + -ф)
sin (ф +ф) cos (ф + ф)
Геометрический смысл второго примера: последова-
тельное выполнение двух поворотов плоскости на уг-
лы ф и ф равносильно одному повороту на угол ф+'фс
Рассмотрим свойства умножения линейных пре-
образований и умножения матриц.
108
ЛИНЕЙНЫЕ ПРЕОБРАЗОВАНИЯ
[ГЛ. III
1. Если st, <%, — линейные преобразования про-
странства R, то
(st$)<& = (W).
Действительно, для любого вектора х R имеем
[(^) х = (^) (&х) = ($ (&х))
и
(Ж)] х = st [(W) х] = ^ ($ (^х));
таким образом, умножение линейных преобразований
(а следовательно, и матриц) подчиняется сочетатель-
ному закону (ассоциативно).
2. Для любого линейного преобразования st
st<S = <5 st = st-.
Матрица Е тождественного преобразования <8 (см.
выше, стр. 102) называется единичной матрицей. Для
любой матрицы А (того же порядка, что и Е)
АЕ = ЕА = А.
3. Умножение и сложение линейных преобразова-
ний связаны распределительными законами-.
(st + $)<& = st<& + &&
и
^ (^ + ^) = w+га,
так как для любого вектора хе/?
((st + $) ^) х = (st + (&х) = st (&х) + $ (&х) =
= (st<8) х + (W) х = (W + W) х
и
(*F (st + $)) X = ((st + $) х) = (stx + ^х) =
= 'F (stx) + % (^х) = (^st) х + (га) х = (% st + га) х.
Аналогичные равенства справедливы и для мат-
риц.
Вспомним основные законЬ! сложения и умноже-
ния чисел.
§ 2] ОПЕРАЦИИ НАД ПРЕОБРАЗОВАНИЯМИ П»
Законы сложения
1. Сложение коммутативно: для любых двух чи-
сел а, b
а + b = b + а.
2. Сложение ассоциативно: для любых трех чисел
а, Ь, с
а + (Ь'+ с) = (а + Ь) + с.
3. Существует такое число 0, что для любого а
а + 0 = а.
4. Для каждого числа а существует такое число
—а, что
а 4- (— а) = 0.
Законы умножения
1. Умножение коммутативно: для любых двух чи-
сел а, b
ab = Ьа.
2. Умножение ассоциативно: для любых трех чи-
сел а, Ь, с
a (be) — (ab) с.
3. Существует такое число 1, что для любого а
а • 1 = а.
4. Для каждого числа а =# 0 существует такое
1
число — = а *, что
а
а • a~l ~ 1.
Кроме того, имеет место дистрибутивный (рас-
пределительный) закон, связывающий сложение с ум-
ножением:
Для любых трех чисел а, Ь, с
а(Ь + с) = ab + ас.
Для сложения и умножения линейных преобразо-
ваний и матриц мы доказали справедливость всех'
этих законов, кроме первого и четвертого законов
по
ЛИНЕЙНЫЕ ПРЕОБРАЗОВАНИЯ
[ГЛ. III
для умножения. Оказывается, что умножение матриц
(см. выше пример 1), а значит, и умножение линей-
ных преобразований, вообще говоря, не коммута-
тивно.
Что же касается существования обратного линей-
ного преобразования (обратной матрицы), то спра-
ведливо следующее предложение. Для каждого не-
вырожденного линейного преобразования л/
существует такое (обратное к линейное пре-
образование что
(и соответственно, для каждой матрицы А, опреде-
литель которой отличен от нуля, существует такая
обратная к Л матрица А-1, что А А-1 = А-1 А = Е),
Докажем это. Пусть дано невырожденное линей-
ное преобразование имеющее в некотором базисе
е\, е2, ..., еп матрицу А. Мы докажем сначала су-
ществование обратной кА матрицы, т. е. такой
матрицы, А"1, что
АА~' = А~'А = Е;
тогда линейное преобразование с матрицей А-1
в том же базисе ei, е2, ..., еп будет обратным к
ибо последовательное, выполнение преобразований
и одного за другим будет линейным преобра-
зованием с единичной матрицей, т. е. тождественным
преобразованием.
Итак, пусть дана матрица А, определитель кото-
рой отличен от нуля. Рассмотрим матрицу, составлен-
ную из алгебраических дополнений соответствующих
элементов матрицы А:
Ац А[2 . •. А1п
Аг1 А22 • • А2п
...........♦ • •
^П1 • * • -Ann -
§ 2]
ОПЕРАЦИИ Н,\Д ПРЕОБРАЗОВАНИЯМИ
Н1
При транспонировании ее получается матрица А*,
называемая присоединенной к матрице А:
Ап Д21 ... Ап\
А12 Ащ ... Ап2
^1п А>п • • • ^пп
Перемножая матрицы А и А*, получим
"Ml 0 ... О '
аа, = а,а= 0 'л| ••• 0
О 0 ... | А |
(теоремы 3 и 4 главы I). А следовательно, матрица
А~
будет обратной кА.
Пример. Найти матрицу, обратную к
А =
1 2
3 2
-1 О
3
-1
1
Решение. Определитель матрицы А равен 4. Алгебраиче-
ские дополнения ее элементов: Ап —2, Лц = —2, А;з = 2,
Asi — —2, А22 = 4, А23 = —2, Аз1 = —8, А32 — 10, А33 = -—-4, и,
значит,
А”1
_1_
4
—2 -8'
4 10
— 2 — 4
1—1—4
-1 2 5
1-1-2
2
— 2
2
Заметим, что если преобразования и невы-
рожденные, то таким же будет и их произведение
(так как нз равенства = s£-(@x) = 0 вытекает,
что &х = 0 и, значит, х = 0), причем
даГ’да-1^1
(а для матриц (АВ)-1 = В-1А-1), так как
да.) (Х1^"’) = ==
112
ЛИНЕЙНЫЕ ПРЕОБРАЗОВАНИЯ
[ГЛ. Ш
Теорема 3. Определитель произведения двух
матриц равен произведению определителей сомножи-
телей'. если АВ = С, то
Доказательство. Пусть
АВ =
ап а12 ... а]п
«21 U-22 • •
~ ®nl &п2 • • • ®пп -
bn Ь12 ... bin
b2i b22 ... b2n
_ bnl bfl9 ... bnn
cH c12 ... cin
C21 c22 • • • c2n
Oil O'.2. • • • Cnn —
Тогда, как известно,
n
cik — o-i\bik + ui2b2k + ... -Y ainbnk—atlbik.
i-ю
Определитель матрицы С равен
п п п
|C| = 2 ii=l .2 S aH2bI22 • )2“1 2 n JS Ct2i2bi22 • •• .2 Qi/A" 'n 1 n ;n 1
n n n
3 anj. bjp 3 anj2bj22 • ^2“' ^i1an<nbinn
По четвертому свойству определителей его можно
представить в виде суммы
“'"'А2 ••• а^пЬ1пп
А'Лр ••• a2lnbinn
h‘ h...in.....................м ' ' ’
“«Л? a4,bv ' a4.bv
§ 2]
ОПЕРАЦИИ НАД ПРЕОБРАЗОВАНИЯМИ
где индексы /1, /2, . . ., /п независимо друг от друга
пробегают все значения 1, 2, 3, . . . , п (всего в «той
сумме пп слагаемых). Однако можно считать, что в
определителе, стоящем под знаком суммы, все индек-
сы /1, /г, .... /п различи ы, так как те определители,
у которых имеются одинаковые индексы /&, равны нулю
как определители с пропорциональными столбцами.
Таким образом, в этой сумме остаются только п! сла-
гаемых, отвечающих разным наборам /1, /2, ..., /п.
Вынося теперь за знак определителя общий множи-
тель элементов каждого столбца, получим
% °i/2 ••• %
(2)
где суммирование ведется по всевозможным пере-
становкам /1, /2, . .. , jn чисел 1,2, . . ., п.
В определителе, стоящем под знаком (последней)
суммы, переставим столбцы так, чтобы вторые ин-
дексы их элементов расположились в порядке возра-
стания. Это можно сделать посредством нескольких
транспозиций столбцов. Так как при переходе от од-
ной перестановки к другой той же четности требуется
четное число транспозиций, а при переходе к пере-
становке другой четности — нечетное число транспо-
зиций (а перестановка 1, 2, ..., п — четная), то оп-
ределитель в правой части равенства (2) равен
(— 1)^г '2.А |. Таким образом, получаем
ici= 2 (-1)^...........^-,6^ ••• \ПИ =
Л’ h..In
= |Д||5|.
Пример. В примере
1 на стр. 107 перемножались матрицы
и
1 2"
-1 1
2 1
При этом |Л| = —10, |В| = —9 и = 1В4| = 90 = |Д| • |В|.
114
ЛИНЕЙНЫЕ ПРЕОБРАЗОВАНИЯ
[ГЛ. III
§ 3. Переход к новому базису
Пусть линейное преобразование si в базисе
61, е2, .. . , еп имеет матрицу А = [а^], а в базисе
е[, е', е'п, вообще говоря, другую матрицу
Л' = [аЦ. Найдем, как связаны между собой мат-
рицы А и А'.
Обозначим через С — [c,ft] матрицу перехода от
базиса ei, ег, ..., еп к базису е\, е', ..., е'. Тогда
< = + ••• +С«А-
Будем матрицу С рассматривать как матрицу линей-
ного преобразования ‘g’ в базисе ei, е2, . . ., еп. Тогда
очевидно, что
= Cliei + C2ie2+ ••• +Cnien = ei’
и значит, линейное преобразование & переводит век-
торы ei, бг, ..., еп соответственно в векторы
е[, е', ..., е'.
Определитель матрицы З7 отличен от нуля (§ 4
главы II), а значит, для существует обратное пре-
образование При котором <F-lei = 61, <g’~162 =
= е2, . .., ^~1е'п = еп- По условию,
sie' = а'е' + а' е' + ... + а'е'п.
Применяя к обеим частям этого равенства преобра-
зование 'З’-1, получим
^~Xsiei = a'net + + ... + a'nien-
Подставляя в левую часть последнего равенства*
e^—^et, будем иметь
+ ... + a'nien,
т. е. матрицей преобразования в базисе
‘61, е2, ..., еп является матрица А’. Но, с другой
стороны, матрица этого преобразования равна про-
изведению матриц преобразований З7-1, si и в ба-
§ 4]
ПРЯМОУГОЛЬНЫЕ МАТРИЦЫ
115
зисе ei, 62, ..., еп, т. е.
А^С^АС.
Отсюда, в частности, следует, что определитель
матрицы линейного преобразования не зависит от
базиса-.
= |С“‘ЛС I = I С~' 11 Л 11С | = I С"111 С |! А | =
= ] С-,С 11 Л | == I £• 11 Л I = [ Л1.
~1б -1
Пример. В базисе еь е2 преобразование А имеет матрицу
], Написать матрицу этого преобразования в базисе
j
е j = et + 2е2, е2 = 2е2 + Зе3. -
Г 1 21
Решение, Матрица перехода здесь С = 3 ’ а °®Рат'
г —3 2Т
пая к ней матрица С = _] • Следовательно,
.,_Г-3 2] Гб -2] Г1 21 Г-3 21Г 2 61
2 — 1]’[б —1J‘L2 3j L 2 -111.4 9 J
Г2 °1-
= Lo з!
§ 4. Прямоугольные матрицы
Матрица, состоящая из m строк и п столбцов, на-
зывается [in X п]-матрицей. Можно определить сло-
жение [m X н]-м атриц, полагая
«11 «1-2 • * * &1п
«21 «22 • • а2п
— 61 ml «m2 • • • 61тп
Ьц Ь12 ... Ь1п
Ь2\ Ь22 ... b2tl
^т\ Ьт2 • • Ьтп _
«11 + Ьц al2 + bl2 ... «in + bin
«21 + b2[ а22 + b22 ... а2п + Ь2п
— ct-mi А- Ьт\ ат2 + Ьт2 ... атп + Ьтп..
116
ЛИНЕЙНЫЕ ПРЕОБРАЗОВАНИЯ
[ГЛ. III
и умножение [т X л]-м атрицы на число
а — равенством
ан й|2 ... ain
а21 ^22 • • а2п
_ Umi ®т2 • • • —
ад,, аа|2 . .. ая1п
аа21 а«22 • • •
СП7/гг; dClm2 * • •
Прямоугольные матрицы можно рассматривать
как матрицы линейных отображений одного вектор-
ного пространства в другое. А именно, пусть имеются
два линейных пространства, вообще говоря, разных
размерностей Rn и Rm, и каждому вектору те Rn по-
ставлен в соответствие вектор s&x е Rm так, что вы-
полнены следующие условия:
1. + у) = 4- з£у.
2. s^(ax) = аз£х.
Выберем в пространстве Rn базис ei, е2, .. ., е„,
а в пространстве Rm базис ft, f2, .... fm. Вектор з£е(
принадлежит R"1, и следовательно, его можно разло-
жить по базису ft, f2, , fm', пусть
— allfl + a2lf2 + •••
&e2 = al2ft + 022/2 + •••
Ty^en — altlf । + a2nf2 4- . • . 4~ amnfm.
Таким образом, линейному отображению д/ простран-
ства Rn в Rm соответствует прямоугольная матрица
Ял a J? ••• flu
Й21 а22 • • а’п
Anil @m2 ’ • • ‘ ^тп ____
Легко видеть, что [т X п]-матрицы (в частности,
квадратные матрицы порядка и) образуют линейное
пространство R. Обозначим через е^ [tn X и]-матрицу,
у которой fli/j = 1, а все остальные элементы — нули.
Тогда ясно, что все эти матрицы между собой ли-
нейно независимы, и что каждая [in Х«]-матрица яв-
ляется их линейной комбинацией. Следовательно,
§ <i
ПРЯМОУГОЛЬНЫЕ МАТРИЦЫ
117
размерность пространства R равна шп. В частности,
пространство всех квадратных матриц порядка п
имеет размерность п2.
По аналогии с умножением квадратных матриц
можно определить и умножение прямоуголь-
ных матриц. Такое умножение выполнимо только
в том случае, если длина строки левого множителя
равна длине столбца правого, т. е. когда число столб-
цов левого множителя равно числу строк правого.
Произведение [т X п]-матрицы на [и X р]-матрицу бу-
дет, очевидно, [т X р]-матрицей. В частности, произ-
ведение [т X п]-матрицы на [п X 1]-матрицу, т. е. на
столбец, будет [тХ 1]-матрицей, т. е. столбцом, а про-
изведение [1 X/ti]-mатрицы, т. е. строки, на [тХ«]-мат-
рицу будет [1 Х«]-матрицей, т. е. снова строкой.
Примеры.
г 1 2 0-
Г-1 3 2013 01
L 1 0 -1 2 J 1 12
.1 -3 3.
10 0 7 1
2 -5 4 ]’
Г 1'
Г 1 2 3 0 1 -1
2' L 2 3 1 2 J 2
_ 1.
3. [1
= [14 20].
Нетрудно понять смысл операции умножения пря-
моугольных матриц. Пусть имеются три линейных
пространства, вообще говоря, разных размерностей:
Rn, Rm, Rp, и пусть даны два линейных отображения:
отображающее Rm в Rp, и М отображающее Rn
в Rm. Отображение • <%, ставящее в соответствие
каждому вектору х Rn вектор пространства
Rp, называется произведением отображений .91 и
Легко видеть, что <20 является линейным отображе-
нием Rn в Rp и что если отображению отвечает
[р Х»г]-матрица А, а отображению &— [т X «J-мат-
рица В, то матрицей отображения будет [pX«J-
матрица АВ.
ЛИНЕЙНЫЕ ПРЕОБРАЗОВАНИЯ
[ГЛ. Ш
118
Для сложения и умножения прямоугольных матриц легко
доказываются следующие соотношения:
1. А 4- В = В 4- А.
2. (А 4- В) 4- С = А 4- (В 4- С).
3. А 4- 0 = А, где 0 — прямоугольная (нулевая) матрица, все
элементы которой равны нулю,
4. А 4- (—Л) = 0, где —А — матрица, все элементы которой
противоположны соответствующим элементам матрицы А.
5. 4 (ВС) = (4В)С.
6. (4 4- В)С = АС 4- ВС.
7. С(А + В) =СА +СВ,
разумеется, если матрицы таковы, что все эти действия над ними
выполнимы. Кроме того, если А — произвольная [т X nJ-ма-
трица, то
АЕп = А и ЕтА = А,
где Еп— единичная матрица порядка п, а Ет— единичная ма-
трица порядка т.
Если £ф — линейное преобразование пространства
/?, то равенству з&х = у, где х, у е R, в каждом ба-
зисе соответствует матричное равенство
AX = Y,
где А — матрица преобразования X — столбец, со-
ставленный из координат вектора х, и Y — столбец,
составленный из координат вектора у.
Рассмотрим систему линейных уравнений
aIIXl + ai2X2 + . . . + ClinXn — Ь ir
а2|х1 + a22x2 + ••• +О2пХп = Ь2, ,~
@mlxl "Ь ®rrt2x2 "I" • • • + ®mnxn
Обозначим через А матрицу из коэффициентов при
неизвестных этой системы, через X — столбец, состав-
ленный из неизвестных, и через В—столбец, состав-
ленный из правых частей. Тогда систему (3) можно
записать в виде одного матричного уравнения
' АХ = В.
Если матрица Л квадратная, и ее определитель
отличен от нуля, то существует обратная к ней мат-
рица А~1. Умножая обе части последнего равенства
РАНГ И ДЕФЕКТ
119
§ 5]
слева на Л-1, получим
/Г1 (АХ) = А~'В, откуда X = А~'в.
В более подробной записи это — формулы Кра-
мера (ср. выше стр. 36).
§ 5. Ранг и дефект линейного преобразования
Определение 2. Пусть si-— линейное преобра-
зование пространства R. Совокупность D всевозмож-
ных векторов .вида six, где х е R, называется
областью значений преобразования si, а со-
вокупность Л1 всевозможных векторов х, для которые
six = О, называется его ядром.
Покажем, что область значений и ядро линейного
преобразования si являются подпространствами в R.
Действительно, если х, у ^D, то х = ^Zxi, y=siyt,
где xb z/i е R, а тогда
х + у = зФх\ + sly-y — si (ху + z/i),
где Xi + г/i <= Д, и значит, х + у е D; кроме того,
ах = asix, = si (axt),
где axi s /?, и значит, ax е D.
С другой стороны, если х, т. е. если j^x=0
и si у — 0, то и
si (х + у) = six + siy = О
и
si (ax) = asix = О,
т. е. х + у е М и ахеМ.
Размерность области значений преобразования si
совпадает с рангом матрицы А (и называется ран-
гом преобразования si). Действительно, под-
пространство D порождается векторами
sie{, sie2, ..., sien, (4)
где еь е2, ..., еп — любой базис пространства R и,
значит, размерность D равна максимальному числу
линейно независимых векторов (4), т. е. максималь-
120
ЛИНЕЙНЫЕ ПРЕОБРАЗОВАНИЯ
[ГЛ. HI
ному числу линейно независимых столбцов матрицы
А (см. стр. 42).
Размерность ядра М называется дефектом ли-
нейного преобразования $4.
Теорема 4. Сумма ранга и дефекта линейного
преобразования $4 равна размерности п простран-
ства.
Доказательство. Пусть ранг линейного пре-
образования s4 равен г. Тогда среди векторов
.‘/ei, лг/ег, .. ., s4en найдутся г линейно независимых,
через которые линейно выражаются все остальные.
Пусть это будут s4e2, . . ., s4er.
Обозначим через L подпространство, порожденное
в R векторами ei, е2...ег, и покажем, что (г-мср-
ное) подпространство L и ядро М пересекаются толь-
ко по нулевому вектору. Действительно, если
х е L Л М, то х е L, т. е.
х = а^1 + а2е2 + ... + агег,
и х е Л1, т. е.
$4х = + a2s4e2 + .. . + ars4er = 0.
Но так как векторы s4e{, s4e2, . . ., s4er линейно не-
зависимы, то ai = а2 = ... = аг = 0, и х — 0.
Покажем теперь, что подпространства L и М по-
рождают все R (т, е. что их сумма совпадает с R).
Пусть х— произвольный вектор из R. Тогда s4x е D,
и следовательно,
s4x = fiiS/et 4-р^е, + ... + pr^/er.
Вектор у = piSj + р2бг + . . + Р,ег принадлежит, оче-
видно, L, а разность z = х— iietM, так как
з4г = (х — у) ~ р4х — s4y = 0.
Мы нашли, что х = у + г, где у Д, a z е М.
Таким образом, пространство R равно прямой
сумме подпространств L и М, а значит, его раз-
мерность п равна сумме размерностей этих подпро-
странств (ср. выше стр. 80).
§ 6] НЕВЫРОЖДЕННОЕ ЛИНЕЙНОЕ ПРЕОБРАЗОВАНИЕ 121
§ 6. Невырожденное линейное преобразование
Линейное преобразование мы назвали невы-
рожденным, если из равенства si-x = 0 вытекает,
что х = 0 (§ 1). Далее (§ 2) было показано, что мат-
рица невырожденного линейного преобразования
в любом базисе имеет отличный от нуля определи-
тель, и что для всякого невырожденного линейного
преобразования .& существует обратное линейное
преобразование s&~x. Наоборот, если для линейного
преобразования существует обратное преобразо-
вание л^-1, то это преобразование невырожденное,
так как из равенства s4-x =0, применяя к обеим его
частям преобразование получаем
(з4-х) = = 0, но <9/~' (^/х) = (^/-1^)х = х
и, значит, х — 0.
Ранг невырожденного линейного преобразования
пространства R” R равен п, так как определитель
его матрицы отличен от нуля; дефект невырожденного
линейного преобразования равен нулю. Обратно, вся-
кое линейное преобразование пространства R ранга п
будет, очевидно, невырожденным. Область значений
невырожденного линейного преобразования zr-мерна и,
значит, совпадает совсем R'. невырожденное линейное
преобразование отображает R на все R. Ядро не-
вырожденного линейного преобразования состоит
лишь из нулевого вектора. Невырожденное линейное
преобразование взаимно однозначно, так как из ра-
венства з4-х = з£у вытекает, что — у) = 0, и зна-
чит, х — у = 0, т. е. х = у.
При невырожденном линейном преобразовании ли-
нейно независимые векторы переходят в линейно не-
зависимые. Действительно, если векторы ei, е2, . . . , ек
линейно независимы и
4- о2^4-е2 4- •.. 4- а.ксИ-ек =
= ^(а1е1 + а2е2 + ... 4-akek) = 0,
то
«А + а2е2 + ... + akek = 0 и а, = а2 = ... = ак = 0.
122 ЛИНЕЙНЫЕ ПРЕОБРАЗОВАНИЯ [ГЛ. 1П
Покажем, что если S&— линейное преобразование
ранга г, а ^ — невырожденное линейное преобразова-
ние, то оба преобразования и So.&l будут ранга г
(а значит, произведение матрицы ранга г на 'матрицу
с отличным от нуля определителем будет матрицей
ранга г).
Действительно, область значений (невырожденно--
го) линейного преобразования $ совпадает со всем
пространством и, следовательно, область значений
преобразования r-мерна, т. е. ранг преобразова-
ния равен г.
С,другой стороны, область значений преобразова-
ния S& r-мерна, а так как преобразование & невырож-
денное, то оно переводит линейно независимые век-
торы в линейно независимые и, значит, область
значений преобразования тоже r-мерна, т. е.
ранг преобразования равен г.
§ 7. Инвариантные подпространства.
Собственные векторы и собственные значения
линейного преобразования
Пусть — подпространство линейного простран-
ства R и — линейное преобразование/?. Образ
s&x вектора х из /?1, вообще говоря, не обязан при-
надлежать /?ь Особый интерес представляют такие
подпространства, векторы которых преобразованием
не выводятся из этих подпространств.
Определение 3. Подпространство RA про-
странства R называется инвариантным относительно
линейного преобразования если образ s&x каждого
вектора х из Ri принадлежит Ri.
Примеры. 1. Пусть ^Z— поворот вокруг оси
Oz обычногр трехмерного пространства. Инвариант-
ными подпространствами будут, например, плоскость
хОу и ось Oz.
2. Если ^Z— ортогональное проектирование того
же пространства R3 на плоскость хОу, то инвариант-
ными подпространствами будут: плоскость хОу, все
плоскости, проходящие через ось Oz, сама ось Oz и
§ 7] ИНВАРИАНТНЫЕ ПОДПРОСТРАНСТВА 123
все прямые плоскости хОу, проходящие через начало
координат.
3. В пространстве Рп многочленов степени не
выше п подпространства Рь при всех k, Q^~k*Cn,
инвариантны относительно дифференцирования.
4. В любом пространстве каждое подпростран-
ство инвариантно относительно тождественного и ну-
левого преобразований.
5. В любом пространстве при любом линейном
преобразовании само пространство R и его подпро-
странство, состоящее из одного нулевого вектора, ин-
вариантны.
Покажем, что пересечение и сумма подпространств,
инвариантных относительно линейного преобразова-
ния инвариантны относительно s4-.
Действительно, если подпространства и R2
инвариантны относительно и ,г е ₽| Г| то x^R\
и х е R2, а значит, s^xEERt и s&x е R2, т. е.
с4-х (= Ri П R2.
С другой стороны, если х е Ri + R2, то х = и + v,
где и е R], v е R2. Но тогда siu е Rit s&v е R2 и
= .sZw + EE. R1 -f- R2.
Особый интерес представляют одномерные
инвариантные подпространства. Если Ri — такое под-
пространство и то и s^-x^Ri, и, значит, s^x =
=Хх. Если у — любой другой вектор из Ri, то г/=ахи
S&y = ^Z (ах) = a^Zx = а (Л,х) = % (ах) = Ху.
Определение 4. Вектор х =р 0 называется
собственным вектором линейного преобразования .$&,
если найдется такое число X, что s&x = Хх; это X назы-
вается соответствующим вектору х собственным зна-
чением преобразования (матрицы А).
Как мы только что установили, если Ri — одно-
мерное инвариантное подпространство в R, то каждый
вектор из Ri является собственным вектором преоб-
разования ^Z и притом с одним и тем же собствен-
ным значением. Обратно, если х—собственный вектор
преобразования s/, то порожденное им одномерное
подпространство Ri (состоящее из всех векторов вида
ах) будет, очевидно, инвариантным относительно ,eZ.
124
ЛИНЕИПЫЕ преобразования
[ГЛ. III
Предположим, что линейное преобразование si
имеет п линейно независимых собственных векторов
еь е2, ..., еп с собственными значениями соответ-
ственно Ль Л2, ..., Лп. Если векторы в), е2, ..ел
принять за базисные, то ввиду равенств
^/б2 = Л262,
Sien
матрица преобразования будет иметь вид
"%! О ... 0~
л = О Л2 ... О
О 0 ... Л„_
(такая матрица называется диагональной). Ясно, что
верно и обратное: если матрица А преобразования si
в некотором базисе является диагональной, то все
векторы этого базиса будут собственными векторами
преобразования si. Однако далеко не каждое линей-
ное преобразование п-мерного пространства имеет п
линейно независимых собственных векторов.
Теорема 5. Собственные векторы преобразова-
ния si, отвечающие попарно различным собственным
значениям, линейно независимы.
Доказательство проведем индукцией по числу рас-
сматриваемых собственных векторов. Для одного век-
тора х это ясно, так как, по определению собствен-
ного вектора, он отличен от нуля (и значит, из равен-
ства ах = 0 вытекает, что а = 0).
Пубть наше утверждение справедливо для k—1
векторов Х|, х2, .. ., Хй-1, и предположим, что k соб-
ственных векторов Xi, х2, ..., xh, отвечающих попар-
но различным собственным значениям Ль Л2, .... Л;;,
линейно зависимы:
ajXj + а2х2 + ... + akxk = 0.
(5)
§ 7] ИНВАРИАНТНЫЕ ПОДПРОСТРАНСТВА 125
Применяя к обеим частям этого равенства преобра-
зование мы получим
+ а2.т/х2 4- ... + aks^xk = О,
или
a^Xi 4- аД2х2 + • • • + «Лй = 0- (6)
С другой стороны, умножая равенство (5) на %ft> бу-
дем иметь
аД&Х] + аД&х2 4- ... 4- оцД^х^ — 0. (7)
Вычитая равенство (7) из равенства (6), получим
cti (%i — %&) хг 4- сс2 Д2 — Хк) х2 4~ ...
... -4-а*—1 (Л,*—1 — X*) xfc_ j — 0;
а так как, по условию, все различны и в силу пред-
положения индукции векторы хь х2, .... хк^ линейно
независимы, то
cq = a2 = ... = aj. _ । = 0,
и тогда из равенства (5) имеем
акхк = 0, и а,/. = 0.
Z
Как найти собственные значения и собственные
векторы линейного преобразования'? Предположим,
что х — собственный вектор, а ). — соответствующее
ему собственное значение линейного преобразования
Тогда s&x = 7.x. Выберем в пространстве R какой-
нибудь базис еь е2, .. ., еп, и пусть
х — Xj6[ 4“ х2б2 4- ... 4~ хпбп,
а матрица преобразования «й/ в этом базисе А=[агк}-
Тогда (см. § 1 главы 111)
s&x = (anX! 4- Ц12х2 + ... +а1пхп)е1 +
4- (a2iXt 4- a22x2 4- 4- а2пхп) е2+ ...
• + (anixi + ап2х2+ ... +аппх„)еп —
= % (a'j ej 4- х2е2 4- ... 4- х„е„),
126
ЛИНЕЙНЫЕ ПРЕОБРАЗОВАНИЯ
[ГЛ. III
откуда ввиду линейной
et, е2, .. ., ёп,
независимости векторов
(<?и — X) Х[ + й12х2 + + а[пхп — О,
+ (а22 ~ х2 + • • • + а2пХп ~ 0, (g)
. ®nlXi + ап2Х2 + • • + (otnn — Z) xn — 0.
Для существования ненулевого решения этой
(однородной) системы необходимо и достаточно,
чтобы ее определитель был равен нулю:
Яц Л й|2 • . . din
a2i а22 — К ... а2п
Ctfl\ ап2 . . . апп Л
(теорема 10 из главы I). Левая часть последнего
равенства представляет собой многочлен относитель-
но Л степени п, который называется характери-
стическим многочленом преобразования <я£
в базисе е\, е2, , еп. Это — определитель матрицы
А — 1JE. Ниже (теорема 6) будет показано, что этот
многочлен на самом деле не зависит от выбора
базиса, и поэтому его можно назвать характеристи-
ческим многочленом преобразования
Мы доказали, что каждое собственное значение
преобразования является корнем его характеристи-
ческого многочлена. Обратно, каждый корень харак-
теристического многочлена преобразования лФ будет
его собственным значением — соответствующие соб-
ственные векторы находятся из системы (8), которая
в этом случае обязательно имеет ненулевые решения,
так как ее определитель равен нулю.
Теорема 6. Характеристический многочлен ли-
нейного преобразования не зависит от выбора базиса.
Доказательство. Характеристический много-
член преобразования в базисе et, е2, ..., еп пусть
будет <ре(Х) — |Д — предположим, что новый ба-
зис е\, е2, ..., е'п получается из старого с помощью
матрицы С. Тогда характеристический многочлен пре-
§ Л
ИНВАРИАНТНЫЕ ПОДПРОСТРАНСТВА
127
образования S& в базисе е{, £Д..е'п
(Ге'(Л) = [ А/-Л£(=(С'1АС-^£| = |С_!АС-С-1л£С| =
= |С”'! (А — Л£)С | = |С~! || А — Л£ || С | =
= | А - Л£ | = ф,, U).
Пусть характеристический многочлен преобразо-
вания s& будет
<р (Л.) — (~ l)nV + (—!)" 1 ct|Z" 1 + ... + ап.
Легко видеть, что ai равно сумме «и + «22 + ... + апп
диагональных элементов матрицы А (это сумма на-
зывается следом матрицы А). С другой стороны,
ап = ф(0) есть определитель матрицы А; поэтому для
того, чтобы преобразование было невырожденным,
необходимо и достаточно, чтобы ф(0) было отлично
от нуля, т. е. чтобы сЛ не имело нулевых собственных
значений.
Примеры. 1. Найти собственные значения и собственнее
векторы линейного преобразования .у!- с матрицей
Решение. Характеристический многочлен преобразова-
ния
<PW = |15X 4-А | = V~5^"6-
Его корни Xi =6, = —1. Собственные векторы находятся из
двух систем уравнений,
(. (1 -X.)Хг 4- 2х2 = О,
[ 5Xj + (4 — Л(.) х2 = О,
(< = 1, 2), каждая из которых, поскольку ее определитель равен
нулю, сводится к одному уравнению.
При Л == 6 это — уравнение 5xi,— 2ха = 0,. из. которого нахо-
дим: Xi : х2 = 2 : 5, и в качестве собственного вектора, соответ-
ствующего Л = 6,. можно взять ш, = (2,.5) (или любой, вектор,
кратный а,).
При К '= —1 имеем уравнение x.i + х2 — 0, из которого
Xi : х2 = —1, и соответствующий собственный вектор а2 = (1, —1)
(или любой вектор, кратный ему).
128
ЛИНЕЙНЫЕ ПРЕОБРАЗОВАНИЯ
[ГЛ. III
Для тождественного преобразования все нену-
левые векторы пространства являются, очевидно, соб-
ственными с собственным значением, равным еди-
нице.
Для нулевого преобразования все ненулевые век-
торы пространства являются собственными с соб-
ственным значением, равным нулю.
Найдем еще собственные значения и собственные векторы
.для преобразований 1—5 из § 1.
1. Поворот плоскости на угол ф.
Характеристический многочлен
... I cos <р — К — sin ф I _
Ф (л) = . , = А2 — 2 cos ф • А + 1.
ч - ' | sin ф cos ф — К 1 *
Его корни Ai,2 = cos ф ± i sin ф комплексны. Значит, вообще го-
воря (если ф не кратно л), это преобразование не имеет (веще-
ственных) собственных значений.
Если ф = 2л/г, преобразование является тождественным, и
каждый вектор — собственный (при X = 1).
Если ф = (2k + 1)л, преобразование является центральной
симметрией, и каждый вектор плоскости будет очевидно, соб-
ственным с собственным значением, равным —1.
2. Поворот трехмерного пространства вокруг оси Oz на
угол ф. Характеристический многочлен
Ф(М =
cos ф — А — sin ф
sin ф cos ф — А
О О
О
= (1 — А) (А2 — 2 cos ф • А + 1).
О
1 - А
Его корни А, = 1, Аг, з = cos ф ± i sin ф.
Пусть ф не кратно 2л. Собственные векторы, соответствую-
щие собственному значению А = 1, находятся из системы урав-
нений
( (cos ф — 1) X] — sin ф- х2 = О,
( sin ф • Х1 + (cos ф — 1) х2 = О,
Так как определитель этой (однородной) системы
I cos ф — 1 — sin ф I , „ , , . . , ф
, = 1 — 2 cos ф + 1 = 4 sin2 -%
I sin ф cos ф — 1 I т 2
отличен от нуля, то ее решение: xi = х2 = 0; при этом х3 произ-
вольно, и собственным вектором будет, например, е3 = (0,0,1)
(и все векторы, кратные ему).
При ф = 2л/г преобразование — тождественное.
При ф= (2k + 1)л преобразование является симметрией от-
носительно оси Oz. Собственному значению А = 1 по-прежнему
отвечает собственный вектор е3 = (0,0, 1). Собственные векторы,
отвечающие собственному значению Аг, з = —1> находятся из си-
ИНВАРИАНТНЫЕ ПОДПРОСТРАНСТВА
129
§ ?!
стемы уравнений
г (cps л + 1) Ari — sin л • х2 = О,
sin я • Xj + (cos л + I) х2 = О,
2х3 = 0>
сводящейся к одному уравнению х3 = 0; значит, собственными
векторами для к — —1 будут все векторы вида aei + |3ег-
3. Проектирование трехмерного пространства на плоскость
хОу. Характеристический многочлен
<р (Л) = - Г(1 - Л)2.
Его корни Xj = 0, /.2, з = 1. При к = 0 собственные векторы на-
ходятся из системы: xj =0, х? = 0. Эго — векторы, кратные е3.
При к => 1 система сводится к уравнению л’3 = 0, и собственными
являются все векторы, вида оим -г- fie?.
4. Симметрия трехмерного пространства относительно , пло-
скости хОу. Характеристический многочлен
Ф(М = -(1 + М(1-М2.
Его корни Л1 = —1, Z3, з=1. Для Л = —1 получается система
Xi = 0, х3 — 0, и собственными являются векторы, кратные е,.
При к = 1 система сводится к уравнению Л'з = 0, и собствен-
ными являются все векторы плоскости хОу.
5. Дифференцирование в пространстве многочленов Pa-i-
Характеристический многочлен Ф(>.) = (— 1) пкп. Его корни*
%1,2,..., п — 0. Соответствующие собственные векторы нахо-
дятся из системы
, х2 = 0, х3 = 0..хп = 0,
и значит, все собственные векторы кратны ей (это — многочлены
нулевой степени).
Вернемся к первому примеру — линейному преобразованию
Г 1 2 1
с матрицей А= g . Его характеристический многочлен, как
мы видели, ф(Х) = кг — 57— 6. Квадрат матрицы А равен
Д2 = Г’ 2]. Г1 ПЛ11 -]01
1.5 4] L5 4j L 25 26 _]•
«Подставив» в <р(Л) вместо к матрицу А получим
Л2 еЛ а я Г11 101 Л1 21 «Г1 °Т_Г°
Ф(А) = Л 5А 6Е j 25 26 J 5^5 4J 6| 0 J [q oj,
т. e. нулевую матрицу. Мы видим, что матрица .4 является «кор-
нем» своего характеристического многочлена. Это верно и для
любой квадратной матрицы.
Теорема 7 (Гамильтона — Кэли). Каждая квадратная
матрица является корнем своего характеристического многочлена.
5 Л. И. Головина
130
ЛИНЕЙНЫЕ ПРЕОБРАЗОВАНИЯ
[ГЛ. III
Доказательство. Рассмотрим многочлен ip (Z) =
='| — Л |, который лишь знаком (—1)" отличается от харак-
теристического многочлена <р(Л) матрицы А, и докажем, что
1Р(Л) = О.
Обозначим через В матрицу, присоединенную к %Е — А -(§2
главы III). Тогда, тождественно относительно Л,
(ЛД-Л)В = |Ь£~Л|£.
Элементы матрицы В — многочлены от X степени не выше п— 1.
Пусть
в-
ь° +ь'а+ ... +г>?гЧп_1 &°+ь!2;
11 11 11 1 £ 1“
, 0 , ,1 л , . г.0 t г, 1 '
г>21 + г>21*.+ ... +ь21 h ь22 + ь22‘
п-Кп-1
12 К
П — 1.П —1
22 К
, 0 . 11 А 1 L 1Л 1 1 ~ 1 L 1 1 , , 1 Я **** 1 0, Д 1
%1 + г,п1Х+ ••• +Ьт К Ьп2 + Ьп2К+ +Ьп2 К
-• b2n+b2^+ - +Ь2п'кП~1
- Ьпп + Ьпп>- + - +Ьпп^П~1
= в1),-+кв1 +к2в2+ ... +V1 1вп_1;гдеВй =
^1
bk
°21
hk hk
°12
р,Ь-
°22 ‘• °2п
, hk
J>n\
rk tfe
°п2 • ’ • °пп^
Если ф (Л) = Я/1 + aiV1 ... мы имеем
(ЛЕ — Л) (jE?o "Ь Л^1 + + • • - + Лп 1 Bn—i) “
“ ф (Л) Е = Н- ctjA/1 1 . + ctft) Е.
Так как это тождество относительно Л, то коэффициенты
при одинаковых степенях Л в обеих частях равенства одинаковы:
Bn_] = Е,
В/г—2 ЛВП_i~ct|E,
Btt_3— АВп-2==^'2^>
В\ — АВ2 — ctfi—гВ,
Во — АВ[ = an_ jE,
АВ о — CLftEt-
§ 7J
ИНВАРИАНТНЫЕ ПОДПРОСТРАНСТВА
Умножая эти равенства слева соответственно на Ап, А ...
..., А, Е и складывая их, в левой части получим нулевую
матрицу, а в правой А " + aiAП-1 + ... +апЕ = -ф(Л), откуда
и следует, что ip (.4) = 0.
Как мы видели выше (пример 1 на стр. 128), не
всякое линейное преобразование имеет хотя бы один
собственный вектор и, значит, одномерное инвариант-
ное подпространство. В то же время имеет место сле-
дующая
Теорема 8. Всякое линейное преобразование
имеет или одномерное или двумерное инвариантное
подпространство. 4 ... ,
Доказательство. Если характеристический
многочлен преобразования имеет хотя бы один ве-
щественный корень, то это преобразование имеет соб-
ственный вектор и, значит, одномерное инвариантное
подпространство. Предположим теперь, ч.тб все кор-
ни характеристического многочлена преобразова-
ния комплексны, и пусть % = сс + будет один
из них. Решая для этого % систему уравнений (8),
мы найдем соответствующие (комплексные) решения:
= %1 4” Zyi, ^2 — у 1уг, ..., zn — хп 4” iyn, и зна-
чит, будут справедливы равенства
«и (xi 4- /у() 4- а12(х2 4- iy2) 4- ... + aln(xn + iyn) =
= (а 4- ф) (xj 4- iyi),
a2l(xl + iyl) + a22(x2 + iy2) + ••• 4г а2п (хп 4- I уп) =
= (а 4- ф) (х2 4- iy2),
Oni Ui 4- (yi) 4- ^rl'2 (х2 4- iy2) 4- ... 4- &пп (xn + iyn) =
= (а 4- /р) (хп 4- iyn).
Приравнивая действительные и мнимые части, полу-
чим две системы равенств:
ЯцХ] 4-<^12^2 4” ••• ainxn = axi — $У1,
. a2iXt + а22х2 + ... А-а2пхп = ах2 — fiy2,
( an[Xj 4- ®п2Х2 4- ... 4- ctnnxn ахп ^>Уц
5:
132
ЛИНЕЙНЫЕ ПРЕОБРАЗОВАНИЯ
[ГЛ. III
и
«ni/i + йигУг + ••• + а\пУп — аУ[ + Рхь
a2ii/i + fl22i/2 + ••• + й2пУп =7 аУ-2 + ₽х2> (Ю)
ап\У1 + ап2у2-+ ... + аппуп = ауп + ₽х„.
Рассмотрим два (вещественных) вектора
и = Xi6[ + х^е2 + . • • + хпеп
и
v — У1е1 + У'2^2 + . . . + Упеп-
Равенства (9) показывают, что siu = аи— рУ, а ра-
венства (10) — что siv = av + р«. Но тргда подпро-
странство Ri, порожденное векторами и и V, инвари-
антно относительно ^Z, так как если т. с.
X — Z.U + Т]V, то и
six — tsiu + T\siv = |(аи — 0и) + т] (аи + рн) =г
= (а| + рп)« + (аП-₽^)»
принадлежит R\. Это подпространство двумерно, так
как если бы векторы и и v были линейно зависимыми:
v = ум, то мы имели бы
siu = аи — ри = (а — Ру) и,
п вектор и был бы собственным -вектором преобразо-
вания si с вещественным собственным значением
а — Ру.
Теорема 9. Если si — невырожденное линей-
ное преобразование и Ri — подпространство, инвари-
антное относительно si, то. R, инвариантно и относи-
тельно si~\
Доказательство. Пусть в\, ег, ..., ег—ба-
зис подпространства R\. Тогда векторы Aei, Ае2, ...
..., Аег, тоже принадлежащие 'R\ (ввиду инвариант-
ности R\}, линейно независимы (см. § 6) и, значит,
они тоже образуют базис Ri, т. е. произвольный век-
тор хе Ri представляется в виде
х — ct^siei Т” ct2v^C2 -f- ... -Г ursieT.
§ 7]
ИНВАРИАНТНЫЕ ПОДПРОСТРАНСТВА
133
Но тогда и
X = 0(6] + Я2«2 4" • • • + У-г^г
Сделаем, наконец, еще одно полезное для даль-
нейшего
Замечание. Пусть — произвольное линейное
преобразование в «-мерном пространстве R, распа-
дающемся в прямую сумму Л =ф/?2, своих
подпространств Ri и /?г, инвариантных относитель-
но st--, е1; е2, ..., ег — базис Rt и ег+1, ег+2, .... еп —
базис /?2. Ввиду инвариантности подпространств Ri и
Rz имеют место равенства
«Ze, = ацб] + а21е2 + ••• + arler,
^Ze2 = «12^1 + «22е2 + • • • + ar2er,
c^er —r «irCj -|- а2ге2 4- ... 4- arrer,
^-er + i «г + 1, r + l^r + 1 3” @r + 2, r + ll-r+2 3- • • • an,
^en «г+i, n^++i 3* «r+2, n^r+2 4- ... 4- annen
(так как ^Zefee Ri при k = 1, 2, ..., г и ^Zefte R2 при
k ~ r 4- 1, r + 2, ..., «). Тогда матрица преобразо-
вания ._«Z в базисе «i, е2, ..., еп всего пространства
имеет вид
аИ а12 ... а1г О
«21 «22
. а2г О
О ' ... О
О ... О
А =
аг1 аг2 ... агг 0 0 ... О
О 0 ... О «г+1,г + 1 «г + 1, г + 2 •- «r+l,Jf
, _ О О ...0 «/г,г + 1 «/г,г+2 •••«/in _
Можно сказать, что матрица А распадается на
«клетки»:
М = Mi 0 1
л [О А]’
134 ЛИНЕЙНЫЕ ПРЕОБРАЗОВАНИЯ (ГЛ. Ш
где А] — матрица преобразования в подпростран-
стве Ri, Аг — матрица преобразования в подпро-
странстве /?2, а .прямоугольные матрицы в левом
нижнем 'и правом верхнем углах состоят из одних
нулей.
Таким образом, зная матрицы Aj и Л2 преобразова-
ния в подпространствах Ri и R^, мы можем соста-
вить из них матрицу преобразования & во всем про-
странстве R.
ГЛАВА IV
ЕВКЛИДОВО ПРОСТРАНСТВО
§ 1. Скалярное произведение
Мы определили линейное пространство, в котором
можно складывать векторы и умножать их на числа,
ввели понятия размерности, базиса, линейного преоб-
разования, а теперь в этом пространстве мы введем
метрику, т. е. способ измерять длины и углы. Мет-
рику в линейном пространстве можно определять по
разному. Мы это сделаем, используя понятие ска-
лярного произведения. В обычном трехмер-
ном пространстве скалярным произведением двух
векторов называется произведение их длин, умножен-
ное на косинус, угла между ними. Таким образом,
скалярное произведение (х, у) векторов х и у — это
функция двух переменных (векторов), обладающая,
как известно, следующими свойствами:
1. Для любых двух векторов х и у
(х, у) = {у, х) '
(коммутативность скалярного умножения),
2. Для каждого вектора х и любого вещественно-
го числа а -
(ах, у) = а (х, у)
(ассоциативность скалярного умножения отно-
сительно умножения вектора на число).
3. Для любых tpex векторов х, у, z
(х + у, z) = (х, г) + {у, г)
(дистрибутивность скалярного умножения от-,
носительно сложения векторов).
136
ЕВКЛИДОВО ПРОСТРАНСТВО
[ГЛ. IV
4. Для, любого вектора х скалярный квадрат
'(х, х) >0, и из равенства (х, х)=0 вытекает, что х=0
(положительность скалярного квадрата).
В общем линейном пространстве у нас нет понятия
длины и угла, и мы введем скалярное произведение
аксиоматически.
Определение 1. Говорят, что в линейном про-
странстве R задано скалярное произведение, если ка-
ждой паре- векторов х, у из R поставлено в соответ-
ствие число (х, у) так, что выполнены условия 1—3.
(Эти условия можно назвать аксиомами скаляр-
ного произведения.)
Векторное пространство, в котором задано скаляр-
ное произведение, удовлетворяющее, кроме условий
1—3, еще и условию 4, называется евклидовым вектор-
ным пространством.
Из равенств 1—3 легко получаются также и сле-
дующие соотношения:
2'. (х, ау) = {ау, х) = а (у, х) = а (х, у).
3' . (z, х + у) = (х + у, z) = (x,z) + (у, z) = (z, х) + (г, у).
Примеры.
1. Пусть в «-мерном векторном пространстве зафиксирован
определенный базис; тогда скалярное произведение векторов
Х = (хь Х2..Хп) И У = (У1, у.....Уп) .
можно определить равенством
(х, y)=xlyt+x2y2 + ... +хпуп (1)
(справедливость условий 1—4 проверяется непосредственно).
2. В пространстве Р многочленов от /ив пространстве С
функций, непрерывных на отрезке [а, &], скалярное произведение
можно определить равенством
ь
(х, у) = [ х (/) у (t) dt (2)
а
(справедливость условий 1—3 очевидна, а 4-е следует из того,
что непрерывная неотрицательная функция, интеграл от которой
равен нулю, тождественно равна нулю).
Определение 2. Длиной, или модулем,
вектора х в евклидовом пространстве называется ко-
§ I] СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ
137
рень квадратный из его скалярного квадрата-.
I х | = ]/(х, х).
Угол <р между векторами х и у определяется равен-
ством
cos ф = Т7ЖГ ’
Покажем, что в любом евклидовом пространстве
так определить угол можно, т. е. что введенный фор-
мулой (3) косинус угла между векторами по модулю
не превосходит единицы.
Нам надо установить, что
_ 1 <' <-1
I х 11 у | •
Для этого достаточно доказать так называемое н е-
равенство Коши — Б у н яковского: в евклидо-
вом пространстве R при всех х и у
(х, у)2 < I X I2 I у I2.
Доказательство. Если а — произвольное ве-
щественное число, то для вектора х — ау, ввиду усло-
вия 4,
(х — ау, х — ау) О,
откуда в силу условий 1—3 получаем
(х, х) - 2а (х, у) + а2 (у, у) > 0.
Это — квадратный трехчлен относительно а. Так как
он должен быть неотрицательным при всех значе-
ниях а, то он не может иметь двух различных веще-
ственных корней и, значит, его дискриминант неполо-
жителен:
(х, у)2-\х\2\у\2^0,
что и требовалось доказать.
Легко видеть, что равенство (х, у)2= |х|2|z/|2 до-
стигается в том и только в том случае, если для неко-
торого числа а имеем х — ау = 0, т. е. если векторы х
и у пропорциональны:
х = ау.
138
ЕВКЛИДОВО ПРОСТРАНСТВО
[ГЛ. IV
Из неравенства Коши — Буняковского, если применить его
к пространству со скалярным произведением (1), получается «не-
равенство Коши»:
(ai6I+a262+ ••• +an6n)2<
<(al + «2+'--- +an)(6? + 62+ +6n)’
справедливое для всех чисел a;, bi, а для пространства С со
скалярным произведением (2) — «неравенство Буняковского»:
ь -12 ь ъ
J х (/) у (2) dt < J [х (/)]’ dt • | [у (О]2 dt,
_ a J а а
справедливое для любых двух непрерывных функций х(/) и y(t).
В евклидовом пространстве выполняется также и
так называемое неравенство треугольника'.
|х + у[<|х| + |у|.
Доказательство. Пользуясь неравенством
Коши — Буняковского, получаем
| х + у |2 = (х + у, х + у) = (х, х) + 2 (х, у} + (у, у) =
=| х |2+2 (х, у)+| у |2 <1 х |2 + 21 х 11 у | + ] у |2 = (| х 1+| у I)2,
откуда
| х + у [ <[ х | + | у [.
Векторы х и у, скалярное произведение (х, у) ко-
торых равно нулю, называются ортогональны ми.
В любом евклидовом пространстве верна «т е о р е-
ма Пифагора»: если векторы х и у ортогональны,
то .
|х'+у|2 = |х|2 + |у|2.
Действительно, если (х, у) = 0, то
| х + у I2 = | х |2 + 2 (х, у) +1 у |2 = | х I2 +1 у |2.
§ 2. Ортонормированный базис
Определение 3. Базис Si, е2,..., еп евклидова
пространства называется ортогонал ъ н ым, если
(е^ eft) = 0 при i k.
ОРТОНОРМИРОВАННЫИ БАЗИС
139
§ 2]
Если, кроме того,
16/1= 1 при t=l, 2, ..п,
то базис называется ортонормированным.
Лемма. Попарно ортогональные и отличные oi
нуля векторы линейно независимы.
Доказательство. Пусть векторы Xi,x2,..., хт
попарно ортогональны: (X/, Ха) = 0 при i =# k, и все от-
личны от нуля. Предположим, что
+ а2х2 + ,. . . + атхт = 0.
Умножая обе части этого равенства скалярно ’на Х{,
i = 1,2...т, будем иметь
О/ Ul. xi) + «2 (хг, xl)'+ • • • + ат (Хт, xi) = 0,
откуда, поскольку (хг-, xh) = 0 при i k и (xf, xt)'=A0
при всех i — 1, 2, ..., т, вытекает, что а/= 0 при
всех i = 1, 2, ..., т.
Теорема 1. Во всяком евклидовом проетран-
стве R имеются ортонормированные базисы.
Доказательство. Пусть gi, g2, • • •, gn — произ-
вольный базис пространства R. Положим fi — gi и
= g2 + afi, причем а подберем так, чтобы векторы
fi и были ортогональны:
(g2 + a/i, fi) = (gz, fi) + a(fi, fi) = 0,
откуда
Так как fi ¥= 0, то знаменатель (Л, fi) последней дроби
отличен.от нуля. Ввиду линейной независимости век*
торов gt и g2, полученный вектор f2—ненулевой.
Предположим теперь, что попарно ортогональные
и отличные от нуля векторы fь/2,..., ffc-i уже найде-
ны. Положим
' fk = gk + ^ifi + М2 + ... + Xh-ifk~i
и подберем числа Xi, Х2,..., Хд-i так, чтобы вектор Д
был ортогонален‘ к_/1,/2, ,.Д Д-i. Для этого нужно,
чтобы выполнялись равенства
</ь ft) = (gk, fi) + ^i(fi> fi) = 0 при /=1, 2...Л-1,
140
ЕВКЛИДОВО ПРОСТРАНСТВО
[ГЛ. IV
откуда
1 = _ fa’
1 (fi, fl)
Знаменатель (Д, /у) здесь отличен от нуля, так как все
векторы fi при i=l,2, —1, по предположе-
нию, — ненулевые. Так как векторы gy, g2, • •, gk ли-
нейно независимы, то и полученный вектор fk тоже
будет ненулевым.
Это построение мы будем продолжать до тех пор,
пока не найдем последнего (ненулевого) вектора
fn = gn + ё(А + Wa + ••• +5n-if«-i>
ортогонального ко ' всем предыдущим векторам
fi, fi, • •., fn-i- В силу последней леммы векторы
ft, fi, , 'fn линейно независимы и, значит, образуют
(ортогональный) базис. Если тепёрь каждый из векто-
ров fi поделить на его модуль, то получится орто-
нормированный базис, образованный векторами
е, = —! е =
1 И, I ’ 2 I (21 ’ ’ • ‘ ’ п \fn\ ’
/Легко видеть, что если базис g\, gz, .. . , gn был
ортогональным, то ft = gt, f-z = gi, , fn = gn, а если
он был ортонормированным, то в\ = gu e2—g2,...
• • •, en = gn.
Примененный здесь способ получения ортонорми-
рованной системы векторов из заданной линейно не-
зависимой системы носит название процесса орто-
гонализации.
3 а м е ч а н и е. Если Rt — подпространство R и
ej, е2,..., ек — ортонормированный базис R\, то векто-
ры еь е2,... ,eh можно включить в ортонормированный
базис всего пространства. Для доказательства доста-
точно дополнить ei, б2,. .., eh до базиса простран-
ства R и произвести ортогонализацию полученного
множества векторов, начиная с в], е2,..eh.
Пример. Найти ортогональный базис в пространстве мно-
гочленов степени не выше 4, определенных на отрезке [—1, 1].
Решение. В качестве исходного базиса возьмем
go=l, g\ = t, gs = t3, gi = t\
ОРТОНОРМИРОВАННЫЙ БАЗИС
141
§ 2]
Положим
fo = So = 1
1
H.fi=gi+«fo- Так как (gb f0) = J / Л = 0, то а = 0 и
-1 »
fi = Si -1-
Далее, положим f2 = gt + ₽f0 + yft. Имеем (g2, f0) =»
I 1
= ip2rfz = '|’ = откуда р = - у и (g2, fi) =»
-1 -1
1
= J t3 dt = 0, и, значит, у = 0. Следовательно,
-1
f2 = /2-l
1
Пусть f3 = g3 + Kfo + jxfi + vf2. Имеем (g3, f0) = j t3 dt = 0,
-1
1 1
откуда Л = 0; (g3, f]) = J t*dt = ~, (fv = J t2dt = у, значит,
-I -1
1
M==— у, И (g3, f2)= /5-y Z3) = О, t. e. v==0. Следо-
-1
3
вательно, f3 = /3 —yt
Положим, наконец, f4 = g-4 + gf0 + + gf2 + pf3. Тогда, no-
Г 2 1
скольку (gt, f0)= J l4rf/ = y, a (fo, fo)_=2, to g = -y; далее,
-1
1
(gi> fi) = |z5ttf = O, значит, т]=0. Затем имеем
-1
(г.Ы-
и
Я*4'’+-9л-Ы4-тг
-1
142 ЕВКЛИДОВО ПРОСТРАНСТВО [ГЛ. IV
1
откуда £ = наконец, (git f3) = д (t3— t] dt = 0,
t - v \ & /
— 1
t. e. p = 0, Следовательно,
Полученные многочлены
fo, fi> /з, Л
—это (с точностью до множителей) первые пять рз так пазы-,
ваемых многочленов Лежандра, играющих' важную роль
в разных разделах математической физики. ...
Найдем выражение скалярного произведения в ко-
ординатах. Пусть elt е2,... ,еп — произвольный базис
пространства R со скалярным произведением, и
х = х{е{ + х2с2 + • • • + хпеп< У = у^ + у^ + ... +
Тогда
(х, у) — 2 x^kiet, ek) = 2gikXiyk,
i, k i, k
где gik = (e,, eh). Если пространство R— евклидово, a
^2,..., en — ортонормированный базис, то (<?;, ek) =0
при i =A k, (e,, e{) — 1 при всех i = 1, 2,..., n и, значит,
(x, у) = Xjt/i + x2y2 + ... + xnyn.
• Легко видеть, что и обратно, если в базисе elt е2,...
-г..,еп скалярное произведение векторов
х = XjCi + х2е2 + ... + хпеп и у = г/1е1 + у2е2 Упеп
равно
Х\У1 + х2у2 + ... + хпуп,
то этот базис ортонормированный, так как в
этом случае (е{, е,) = 1 и (е;, eh) = 0 при i k. Более
того, если в некотором базисе скалярный квадрат про-
извольного вектора х = x^i + х2е2 + ... + хпеп равен
(х, х) = х* + х^+ ... + х^, то этот базис ортонорми-
рованный, так как ei) = 1 при всех i и при i =# k
§ 2]
ОРТОНОРМИРОВАННЫЙ базис
143
имеем
(ez + ek, et + ek) =
= (P + О2 + ... + I2 + О2 + ... + I2 + О2 + ... + О2 = 2
(единицы стоят на г-м й k-м местах) и
(е; + еА, ег + ^) = (е;, e(-) + 2(ez, ek) + (ek, ek)=2 + 2(eb ek),
откуда (e,, eh) = 0.
Пусть 6i, е2, ..., еп— ортонормированный базис и
х = Xi6i + х2е2 + ... + хпеп. Умножив обе части по-
следнего равенства скалярно на ег-, получим (х, е,) —
= xit т. е. i-я координата вектора х в ортонормирован-
ием базисе равна скалярному произведению х на еди-
ничный вектор 6j. (Это скалярное произведение можно
назвать проекцией вектора х на вектор ег-. Та-
ким образом, координаты вектора в ортонормирован-
ием базисе — это его проекции на.базисные векторы.)
О-пределениё 4. Два пространства R и R' со
скалярным произведением называются изоморфными,
если между их элементами можно установить взаимно
однозначное соответствие такое, что если х х',
у «-> у’, где х,у eR, х', у' i= R', то не только х + у <—>
х' + у' и ах ах', но и (х, у) = (х', у').
Теорема 2. Все п-мерные (векторные) евклидовы
пространства изоморфны между' собой.
Доказательство. Пусть R и R' — два n-мерных евкли-
дова пространства. Если в каждом из них выбрать ортонорми-
рованный базис'-(ei, ег, .... еп в R и elt е2, ..., еп— в R'} и
поставить в соответствие каждому элементу из элемент из R'
с теми же координатами, то, как известно (см. § 3
главы II), сумме элементов из R будет отвечать сумма соответ-
ствующих элементов из R' и произведению элемента нз R на
число — произведение соответствующего элемента из R' на то
же число. При этом, если
х = х1е} + х2ег + ... +хпеп, у = у1е1+у2е2 + ... + упгп
(и значит, х =х1е[ + х2е2+ ••• +хпе'п, у =7yle'i+y2e'2 + ... + г/„е'),
то скалярное произведение
(х, у) = xtyt + х2у2 + ... + хпуп = (х', у').
Таким образом, пространства R и R' устроены одинаково:
соответствующие векторы их имеют одинаковые длины
144
ЕВКЛИДОВО ПРОСТРАНСТВО
[ГЛ. IV
( | х | = | ' (х, х) = У(х', х') = | х' |), и углы между парами соот-
ветствующих друг другу векторов равны между собой
I (х, у) (х', у') . 'Д'
\ 1*111/1 1*11/1 )
§ 3. Ортогональное дополнение
Определение 5. Два подпространства и Rz
евклидова пространства R называются взаимно ор-
тогональными, если каждый вектор из R\ ортого-
нален каждому вектору из R2 (мы будем писать в
этом случае Afi ± R2).
Рис. 8.
Так, в обычном трехмерном пространстве проходя-
щая через начало координат плоскость л (понимаемая
как множество принадлежащих л векторов) и перпен-
дикулярная к ней (и тоже проходящая через начало)
прямая I ортогональны (рис. 8,а). Наоборот, две вза-
имно Перпендикулярные в смысле элементарной гео-
метрии плоскости Л1 и лг (рис. 8, б) не будут ортого-
нальными подпространствами в смысле этого опреде-
ления: ведь из того, что а> е ni, а й? е яг, еще не
следует, что а{ ± а2.
Для того чтобы подпространства R{ и R2 были
взаимно ортогональными, необходимо и достаточно,
чтобы все базисные векторы одного были ортогональ-
ны всем базисным векторам другого. Необходимость
§ 31 ОРТОГОНАЛЬНОЕ ДОПОЛНЕНИЕ 145
этого следует из определения 5, а для доказательства
достаточности предположим, что eh е2,ек — базис
Rx И fl ,[2,... ,fm— базис R2, причем (eh fj) = 0 для
всех i 1,2,... ,k, j = 1, 2,. . ., m; тогда для каждого
х = Xtet + х2е2 + ... + xheh и каждого у = г/jfi +
+ yih + ... + t/mfm скалярное произведение
(х, г/)= 2 xiy^et, f/) = 0,
i. i ' .
и значит, эти векторы ортогональны.
Покажем, что два взаимно ортогональных подпро-
странства пересекаются по нулевому вектору.
Действительно, пусть R\ и R2— взаимно ортого,-
нальные подпространства R. Если вектор
то х е Ri hxe.R^. но тогда (х, х) = 0 и, значит, х = 0.
Пусть Ri — произвольное подпространство евклидо-
ва пространства R. Выберем в Rx ортонормированный
базис <?1,е2,.. ., ег и дополним его до ортонормирован-
ного базиса е2,..., er, ег+1,.., еп всего пространства.
Векторы е,+1,...,е„ порождают (и — г)-мерное под-
пространство R2, очевидно, ортогональное Ri.
Покажем, что каждый вектор х из R, ортогональ-
ный Rs, принадлежит R2. Действительно, если вектор
х = XjCt + х2е2 + . .. + хпеп
ортогонален Rx, то
(х, е,) = Xi = 0 при i = 1, 2, . .., г,
и значит,
х = хг+1ег+1 + +xnen^R2.
Определение 6. Подпространство R2, образо-
ванное всевозможными векторами из R, ортогональ-
ными ко всем векторам из Rx, называется ортого-
нальным дополнением Rp, это подпростран-
ство R2 мы будем обозначать через. Rx\
Легко видеть, что ортогональное дополнение /--мер-
ного подпространства («— г)-мерно, и что ортогональ-
ное дополнение к Д;1 совпадает с Rx, т. е. что
ЕВКЛИДОВО ПРОСТРАНСТВО
[ГЛ. IV
W
Подпространства Ri и 2?^ порождают все R и пе-
ресекаются по нулевому вектору. Следовательно, ёв-
клидово пространство R является прямой суммой лю-
бого своего подпространства и его ортогонального до-
полнения:
R = Rt®R^
Поэтому каждый вектор х из R однозначно предста-
вляется в виде суммы к = у + г, где y^Ri, z^Rt'
(теорема 6 главы II). Вектор у можно назвать орто-
гональной проекцией вектора х на подпространство
R\. Угол между вектором х и подпро-
странством Ri считается равным углу между век-
тором х и его проекцией у на Ri, а значит, косинус
этого угла равен
(х, у) _ (у + z, у) _ {у, у) = Щ2 I У |
I х || у | МЫ 1*11у\ 1*11уI 1*Г
Рассмотрим снова систему линейных однородных
уравнений:
«11*1 + 012*2 + ••• +аыхп <=(),
«21*1 + «22*2 + • • • + а2пхп ~ 0, 0)
®mixi "Ь ат2х2 "Ь • •. + атпхп = 0.
Этой системе можно дать следующую геометриче-
скую интерпретацию. В евклидовом пространстве
Rn (в ортонормированием базисе) задано пг векторов
«1 = («н, «12, •.., «in), [ = 1,2, Задача состоит
в том, чтобы найти все векторы х = (Х), хг,хп),
ортогональные каждому из векторов ah а2,..., ат.
Пусть ранг матрицы А = равен г. Если век-
top х ортогонален ко всем векторам at, то он ортогона-
лен и к порождаемому ими r-мерному подпростран-
ству Рь Таким образом, векторы-решения х образуют
ортогональноедополнение Ri~ подпростран-
ства Ri. Размерность Ri~ (т. е.' максимальное число
I 41 ТОЧЕЧНО-ВЕКТОРНОЕ ПРОСТРАНСТВО Ц7
линейно независимых решений системы (4)) равна,
как мы видели, п—г. Каждая фундаментальная систе-
ма решений "уравнений (4) —это базис подпростран-
ства
§ 4. Евклидово (точечно-векторное) пространство
Пусть Ап— n-мерное аффинное пространство и
Rn— соответствующее ему векторное пространство, в
котором введена евклидова метрика (т. е. задано ска-
лярное произведение, удовлетворяющее условиям 1—4
из § 1), В пространстве Ап можно определить рас-
стояние между любыми двумя его точками, Л4 и N,
полагая его равным модулю вектора MN, и угол MPN,
считая его равным углу между вектор-ами РМ и PN.
Пространство Ап с введенной в нем таким образом
метрикой называется просто евклидовым простран-
ством (в отличие от введенного выше евклидова век-
торного пространства).
Таким образом, n-мерное евклидово пространство
может быть определено с помощью следующих пяти
групп аксиом:
I. Аксиомы сложения векторов (1—4
на стр/62);
П. Аксиомы умножения вектора на
число (5—8 на стр. 62);
III. Аксиома размерности: существуют п ли-
нейно независимых векторов, но нет больше чем п ли-
нейно независимых векторов (стр. 66);
IV. Аксиомы, связывающие векторы и
точки (1—2 на стр. 83);
V. Аксиомы скалярного ум iro ж е'н и я
(1—4 на стр. 135—136).
Можно показать, что все n-мерные евклидовы про-
странства тоже «устроены одинаково» (изоморфны
между собой). В частности, при п = 2 это — обычная
плоскость, при п = 3 — обычное трехмерное простран-
ство.
Пусть в пространстве Ап задана й-мерная пло-
скость . Ri, проходящая .через начало
148
ЕВКЛИДОВО ПРОСТРАНСТВО
(ГЛ. IV
координат:
ацХ1 + а 12л'2 + ... + а{пхп = О,
#21Х1 + #22*2 + • • + йчпхп. ~ 0.
. #ml*l 4~ #m2*2 4" . + &тпхп ~ 0
(5)
'(/г-мерное подпространство) и точка Х(£ь g2,. •., |п)«
Тогда вектор х — ОХ можно представить в виде х —
= у + z, где y^R\ и z е/?!* (рис. 9, а). Длина век-
тора z называется расстоянием точки X от
подпространства Д1.
Рис. 9.
Пусть теперь в А"
^-мерная плоскость л:
задана произвольная
#11^1 + #12^2 + ••• + а{пхп =Ь{,
а21х, + а22^2 + • • • + а2пхп = Ь2,
I ®mlx) 4" #m2*2 + ... + отпхп Ьт
и точка X(gi,g2,..., |п). Плоскость л получается из
соответствующего ей подпространства R\, определяе-
мого системой уравнений (5) параллельным переносом
на некоторый вектор а. При этом точка X получается
переносом на тот же вектор а из некоторой точки Хо
§ 4]
ТОЧЕЧНО-ВЕКТОРНОЕ ПРОСТРАНСТВО
149
(и значит, ОХ = ОХ0 + а-, см. рис. 9,6). Расстоя-
ние точки Хот й-мерной плоскости л счи-
тается равным расстоянию точки
Хо от подпространства й-мер-
ная плоскость Л1 и /-мерная пло-
скость яг ортогональны, если
ортогональны / соответствующие
им подпространства л° и л°-
В этом случае каждый вектор МА/,
где тОчки XI, N е л1; ортогонален
каждому вектору PQ, rpeP,
(рис. 10).
Гиперсферой в евклидовом
пространстве Ап называется сово-
купность всех точек, отстоящих
Д
Р .
Рис. 10.
на одно и то же расстояние г
(радиус гиперсферы) от некоторой фиксированной
точки Q (центра). Уравнением гиперсферы радиуса
г с .центром в точке Q (ось «г, • • • , осп) в системе
координат с ортонормированный базисом будет, оче-
видно,
(%!-а1)2 + (х2-а2)2 + ... + (хп - а„)2 = г2.
ГЛАВА V
ЛИНЕЙНЫЕ ПРЕОБРАЗОВАНИЯ
В ЕВКЛИДОВОМ ПРОСТРАНСТВЕ
§ 1. Преобразование, сопряженное к данному
Определение 1. Пусть & — линейное преобра-
зование евклидова пространства R. Линейное преоб-
разование такое, что
№х, у) =='(х, tf'y)
при всех х,уе= R, называется сопряженным к .j/.
Для каждого линейного преобразования st- суще-
ствует не более одного сопряженного к нему преобра-
зования сЛ*. Это вытекает из того, что справедлива
следующая
j Лемма. Если $ и — линейные преобразования
пространства R и
(х, ®у) = (х, <&у)
при всех х, у из R; то ='S’.
Доказательство. Из равенства (х,^у) =
— (х,фу) вытекает, что
“(х>‘8у) — (х,'ё‘у) = (х,@у — е&у) = <б
и, значит, (х, — '?’)?/) = О при всех х и у.
Подставляя, в частности, х = (й?— {&)У, получим
((^-<F)z/, ($-<?’) г/)-О
и. значит, по свойству 4 скалярного умножения,
(33— (ё’)у = 0, т. е. ^у = Ъу при всех y^R. Но это
п значит, что & —
Покажем теперь, что для каждого линейного пре--
образования существует сопряженное ему пре-
§ И
ПРЕОБРАЗОВАНИЕ, СОПРЯЖЕННОЕ К ДАННОМУ
151
образование <&*. Пусть А = [а,л]—матрица линейного
преобразования в о р тон о р м и р о в а н н о м ба-
зисе 61, е2, ..., еп, А'— матрица, транспонированная
к Л и — линейное преобразование с матрицей А'
в том же базисе. Тогда, очевидно, '
(*^6^, е^) (^l^i 4~ P'2i^2 4- ... 4" anieni е^ aki
и
(е{, (е{, a^Y 4- ak2e2 + ... 4- акпеп) — aki,
т. e. (л^бг, 6й) = (<?/, ЖеА) при всех Е k- А тогда, если:
л п
X = 2 хгб/ И у = s г/^fe, то
i==l k=\
(п п \
Ж 2 хрь 2 y^k]= S Х1ук№еь ек)
i — l k~ 1 / i, k
И -
/ rt fl \
(x, sTy) = s Xiei, & 2 ykek = 2 xpjk (et, O*ek) =
\>=i fe=i / i. k , ,,
= 2 Xitjk (s4-et, ek) = (^x, y\
i, ii
t. e. преобразование <й£* является сопряжея-
н Ы М К «5$.
Мы показали, что для каждого линейного преобра-
зования евклидова пространства существует и
притом только одно сопряженное к нему преобразова-
ние матрица которого в любом ортонормировац-
ном базисе является транспонированной к матрице
преобразования s&.
Пусть и — произвольные линейные преобра-
зования евклидова пространства*' R и — тожде-
ственное преобразование. Тогда:
1. <?* = S, так как
(х, %*у} = (^х, у) = (х, у).= (х, Sу)
(или —матрица преобразования «У в любом базисе
совпадает со своей транспонированной: Е' = Е).
2. = ^4-, так как, обозначая (А*)* просто че-
рез А**, имеем
(^х, у) = (х,' ^у) = (^*у, х) = (у, ^*Х) = (^-’х, у) s
152
ЛИЛЕЙНЫЕ ПРЕОБРАЗОВАНИЯ
[ГЛ. V
(или — двукратное транспонирование не изменяет
матрицу: (А')' = А).
3. (<s/4-$)* = <9/* + $‘, так как
(х, + $)* у) = (+ $) х, у) = (^/х + $х, у) =
= (.9/-х, у) + (^х, у) = (х, мСу) + (х, ^у) =
= (х, sPy + №у) = (х, (^‘ + Г) у)
(или — матрица, транспонированная к сумме, равна
сумме матриц транспонированных к слагаемым:
(А + В)' = А! + В').
4. (.9/$)* = SSTsP, так как
(х, (.9/J?)* у) = ( х, у) = ($х), у) = ($х, &*у) =
= (х, 9? (sTy)) = (х, (О‘) у)
(и значит, для матриц имеет место равенство
(АВ)' = В'А').
5. Если .s/-1 существует, то С^"1) =(^) , так как
из равенства = и пп. 4 и 1-вытекает, что
= <S =<о, т. е. что (.а/-1) =(^) '
и значит, для/матриц (/Г’1) =(а') ).
§ 2. Самосопряженное преобразование
Определение 2. Преобразование, совпадаю-
щее со своим сопряженным, называется самосо-
пряженным, или симметрическим.
Если — самосопряженное преобразование, то
тождественно при всех х, у из R выполняется равен-
ство
(^х, у) = (х, sty).
Пусть А = [ai/t] — матрица самосопряженного пре-
образования в ортонор мированном "бази-
се; тогда А' = А, т. е. afk = а^. Такая матрица назы-
вается симметрической.
Тождественное преобразование является самосо-
пряженным, так как ё* = <S.
Сумма самосопряженных преобразований является
самосопряженным преобразованием, так как если
§ 2] САМОСОПРЯЖЕННОЕ ПРЕОБРАЗОВАНИЕ 153
= 34 И 99 = й?, ТО
< = Ж + Я* = зФ +
Преобразование, обратное к невырожденному са-
мосопряженному преобразованию, является самосо-
пряженным преобразованием, так как если з£* = з4,
то
О~')*=№ =
Для того чтобы произведение самосопряженных
преобразований было, самосопряженным, необходимо
и достаточно, чтобы эти преобразования были пере-
становочны между собой. Действительно, если з4* = з&
и = 91, то (^^)* = 91* з4* — 91з4, что равно 3'191
в том и только в том случае, если преобразования з4
и 9 коммутируют между собой, т. е. если з491 = 9-4.
Теорема 1. Если подпространство R[ инвари-
антно относительно линейного преобразования з4, то
его ортогональное дополнение Rf инвариантно отно-
сительно сопряженного к з4 преобразования з4*.
Доказательство. Пусть х— произвольный
вектор из R\ , у — произвольный вектор из R\. Тогда
у) = (х, sty) = О,
так как 34y<^R\ и, значит, х ± з4у. Следовательно,
вектор s4-x^R\, и R^ инвариантно относитель-
но
Следствие. Если з4— самосопряженное преоб-
разование и Rt подпространство, инвариантное отно-
сительно з4, то и R\ инвариантно. относительно з4.
Действительно, по теореме 1, Rf- инвариантно от-
носительно з4*, но з4* = з4, следовательно Д11 инва-
риантно относительно з4.
Т ео р е м а 2. Все корни характеристического мно-
гочлена самосопряженного преобразования з4 веще-
ственны.
Доказательство. Пусть а + ф— комплекс-
ный корень характеристического многочлена самосо-
пряженного преобразования Тогда, как видно из
доказательства теоремы 8 главы III, в пространстве
154
линейные преобразования
[ГЛ. V
/? имеется двумерное подпространство, порожденное
векторами и и V} такое, что
S&U — аи — ри,
s4-v = pu + av,
(1)
где р ¥= 0 и векторы и и v н^ равны нулю одновре-
менно. (Если само пространство R двумерно и в нем
нет собственных векторов, это подпространство совпа-
дает с R.) Умножая скалярпо первое из равенств (1)
на v, второе —на и, получим
(^«, а) = а(и, а) —р(у, v)
и
(и, ^о) = р(п, и) + а(и, о).
Но так как о) = (м, «я£о), то р(|и|2 + |о|2) = 0, и
р = 0, что противоречит предположению.
Теорема 3.. Матрица самосопряженного преоб-
разования в некотором ортонормированном базисе
приводится к диагональному виду. ч
Доказательство. Пусть Xi— одно из соб-
ственных значений самосопряженного преобразова-
ния «яА По теореме 2, Xi вещественно. Соответствую-
щий Xi собственный вектор обозначим через ер, тогда
.&ei — Xi^i. Вектор можно считать единичным, так
как в противном случае его можно было бы заме-
нить вектором -рЧ- — единичным собственным векто-
I I ,
ром с тем же собственным значением Хь
Обозначим через R\ одномерное подпространство,
порожденное вектором вь Его ортогональное допол*
нение будет инвариантно относительно «5$, и в
нем преобразование stf- остается, конечно, самосопря-
женным. Пусть Х2 (вещественное) собственное значе-
ние преобразования .J// в подпространстве Rj'; соот-
ветствующий (единичный), собственный вектор обо-.
значим.через е2; тогда
<$^2 ^-2е2-
Пусть R2 будет (инвариантное) подпространство,
порожденное векторами и е2; тогда подпростран-
§ 2]
САМОСОПРЯЖЕННОЕ ПРЕОБРАЗОВАНИЕ
155
ство Rz тоже инвариантно относительно Продол-
жая это построение, мы найдем п попарно ортого-
нальных (и значит, линейно независимых) единичных
собственных векторов преобразования st-. В базисе,
состоящем из этих векторов, матрица приводится
к диагональному виду:
' Ь1 0 .. . О
О Х2 ... О
о 0 ... _
Геометрический смысл самосопряженного преобра-
зования виден из последней теоремы: если
х. = xifij + х2е2 + ... + xnert
—произвольный вектор из 7?, то
Ах = 4- х2Х2<?2 + ... +
Таким образом, при соответствующем преобразова-
нии точек точка Х(х\, х2,..., хп) переходит в точку
A"(XiXi, А,2Х2, .... А,пХп) и, значит, в базисе, состоящем
из собственных векторов преобразования j/, оно сво-
дится к п растяжениям вдоль координатных осей с
156 ЛИНЕЙНЫЕ ПРЕОБРАЗОВАНИЯ [ГЛ. V
коэффициентами, соответственно равными Ai, Х2, ...
/.„ (см. рис. 11, на котором изображено действие
на фигуру евклидовой плоскости самосопряженного
преобразования с собственными значениями и
Х2 = 2).
§ 3. Ортогональное преобразование
f
Определение 3. Линейное преобразование рФ
евклидова пространства R называется ортого-
нальным, если
(^.г, .й^/) = (*, У)
для всех х и у из R.
Таким образом, ортогональное преобразование со-
храняет скалярное» произведение, а значит, оно сохра-
няет длины векторов и углы между ними.
Впрочем, достаточно потребовать, чтобы линейное
преобразование сохраняло длины векторов, и
тогда оно уже будет ортогональным. Действительно,
предположим, что для в с е х х
I &х | =1 х |.
Тогда
|^(х + г/)| = |* + г/1.
Но
I (* + У) I2 = (х + у), (х + г/)) =
~-(^х + Лу, Лх + s&y) ~
—[рфх, Лх) + 2 (j^x, г-’/r/) + (sty, sty} =
= I ,>/x I2 + 2 (,>/x, sty} +1 sty |2
и
I X + у J2 = (x + IJ, X + y) =
= (x, x) + 2 (x, у) + (у, у) = I x |2 + 2 (x, y) +1 у |2,
откуда ввиду равенств | j^x | = | x |, |^г/| = |г/| и
| Л- (х + у) I = | х + у | находим, что
W, sty) = (х, у).
§ 3]
ОРТОГОНАЛЬНОЕ ПРЕОБРАЗОВАНИЕ
157
Ясно, что ортогональное преобразование перево-
дит любой ортонормированный базис в ортонормиро-
ванный. Покажем, что верно и обратное: линейное
преобразование £4, переводящее хотя бы один орто-
нормированный базис в ортонормированный, ортого-
нально. Действительно, пусть ортонормированный ба-
зис ei, ег, ..., еп при преобразовании переходит
в ортонормированный базис е{, е', е'п. Тогда,
если
х = xtei + х2е2 + ... + хпеп и у = у{е{ + у2е2 + ... + г/гее„,
то
£4х = х.е' + х2е' + ... + хе'
= уге\ + у/' + ... + упе'п
и
(^х, £&у) = Х{у{ + х2у2 + ... + Хпуп = (х, у).
Если — ортогональное преобразование и Ж*—
сопряженное к нему преобразование, то
(х, у) = (<$/х, s4y) = (х, £4* (s4y)) = (х, у)
для всех х, у из А*. Следовательно, = & (лемма
из § 1), или
£4* = £4~\
При этом равенство £4-*£4 = <$, или .j/* = £4~\ яв-
ляется необходимым и достаточным усло-
вием для того, чтобы линейное преобразование^ было
ортогональным. Отсюда, в частности, видно, что орто-
гональное преобразование всегда невырожденное.
Преобразование, обратное к ортогональному, тоже
является ортогональным, так как если £4* = £4~1, то
(^~l)’ = (^’)_1 = (^_1)_1
(или, иначе, ортогональное преобразование — это со-
храняющее длины векторов взаимно однозначное ото-
бражение пространства R на себя; но тогда и обрат-
ное преобразование обладает тем же свойством).
Сумма ортогональных преобразований, вообще
говоря, не будет ортогональным преобразованием.
158
ЛИНЕЙНЫЕ ПРЕОБРАЗОВАНИЯ
[ГЛ. V
Произведение же ортогональных преобразований со-
храняет длины векторов и, значит, тоже является ор-
тогональными Иначе,
(^)* = ЗШ' =
Если А — kJ — матрица ортогонального преобра-
зования в ортонорм ированном базисе
fei, ег, ..., еп, то, поскольку — ё>, имеем
А'А = Е,
или
Й11 Й21 • • • ап\ 1 <212 •• • <2*1п
а12 а22 ... «n2 Й21 а22 а2п =
— ^2п • • • ^пп~. - —
~ 1 О 0 ... О
О 1 0 ... О
_0 0 0 ... 1_
Отсюда следует, что при i =# k
U\ia\k + а21^2к + •••
и для каждого i = 1, 2, ..., п
^- + «1-+ ••• + <&=!,
т. е. столбцы матрицы А, если их рассматривать как
векторы, сами образуют ортонормированную систему.
(Это, впрочем, видно и из того, что, поскольку при
ортогональном преобразований ортонормированный
базис переходит в ортонормированный, то образы
з4е2, ..., з4еп базисных векторов еь е2, ..., еа
сами образуют ортонормированный базис. А значит,
(з4е{, 34ek) =alialh + a2ia2k + ... + aniank = <6 при i=Ek
и s4e^ = a2u + <% + ... + a2ni = 1.)
Если — ортогональное преобразование, то пре*
образование — тоже ортогональное-, зна-
чит, столбцы, матрицы А', т. е. строки матрицы А,
тоже образуют ортонормированную систему.
4* "Ь ... "И ainakn О
§ 3] ОРТОГОНАЛЬНОЕ ПРЕОБРАЗОВАНИЕ 159
при 1 k И
4 + а?2+ ... +<=1.
Матрица Л, для которой
Л'=Л~‘, < ~
называется ортогональной матрицей. Таким образом,
матрица ортогонального преобразования в любом
ортонормированном базисе является ортогональной;
обратно, если в каком-то ортонормированном базисе
матрица преобразования £& ортогональна: Л-1 = А',
то и преобразование тоже является ор-
тогональным.
Определитель ортогональной матрицы равен ±1.
Действительно,-из равенства ЛЛ' = Д.следует
|ЛЛ'| = | Л|| Л'| = |£1=1<
Но так как| А'{ = |Л |, то
|Л|2=1, и |Л|=±1. .
Теорема 4. Собственные значения ортогональ-
ного преобразования равны ±1.
Доказательство. Пусть х— собственный
вектор и А. — соответствующее ему собственное зна-
чение ортогонального преобразования Тогда
(х, x) — {s£x, о£х) = (пх, Ах) = А2(х, х),
откуда получаем (поскольку (х, х)¥=0):
А2=1, и А=±1.
Теорема 5. Если подпространство R^ инвариант-
но относительно ортогонального преобразования st-,
то его ортогональное дополнение тоже инвариант-
но относительно _
Доказательство. Так как £4- — ортогональ-
ное преобразование, то = л£*. По теореме 1 под-
пространство /?/ инвариантно относительно преобра-
зования л-/* = но в ’’’гаком случае в силу тео-
ремы 9 главы III оно инвариантно и относительно
Cs/-1)"1 = ^. •
160
ЛИНЕЙНЫЕ ПРЕОБРАЗОВАНИЯ
(ГЛ. V
Выясним, что собой представляет произвольное
ортогональное преобразование. Пусть сначала st —
ортогональное преобразование прямой /?* и ее/?1.
Тогда Ле/?1 и, значит, ste = Ке, где л= ±1, т. е.
ste ±е, и st — либо тождественное преобразование,
либо центральная симметрия.
Пусть теперь st—ортогональное преобразование
п л о с к о с т и, и
д _ ЙЦ «12
L «21 а-22.
— его матрица в некотором ортонормированием ба-
зисе. Тогда, как мы знаем,
Й11 + Й21 ~
й12 + й22 1,
П; jtZj2 + Й21а22 =
Вейлу первых двух равенств найдутся такие фиф, что
an = cosqp, a2i=,sin<p и а12 = созф, а>> = sin ф.
Но тогда третье равенство дает
cos <р • cos ф + sin ф • sin ф = cos (ф — ф) = О,
откуда следует, что
, л Зл
ф — ф = или * g1-.
В первом случае «12 = соэф = —sinq>, а22 = зшф —
= cos ф, и мы имеем
д _ Г cos ф - sin ф ’
sin Ф cos фу
т. е. преобразование st — это поворот на угол ф во-
круг начала координат. (В частности, при ф = 0 это —
тождественное преобразование, а при <р= л — сим-
метрия относительно начала координат.)
Во втором случае а\2 = sin ф, а22 = —cos ф, и
_ cos ф sin ф
[sirup — СОЭф]'
Эта матрица — симметрическая, значит, ортогональ-
§ 3]
ОРТОГОНАЛЬНОЕ ПРЕОБРАЗОВАНИЕ
161
ное преобразование st- является и самосопряжен-
ным, т. е. в некотором (вообще говоря, новом) орто-
нормированием базисе его матрица приводится к диа-
гональному виду:
д = ГХ‘ 0
д [0 Х2 ’
где Хг=±1. Определитель этой матрицы, равный
Z1Z2, с другой стороны, должен быть равен
cos<p sin qj
sin ф — соэф
а значит, одно из А, равно +1, другое —1, и мат-
рица преобразования st приводится к виду
1 О
О -1
Произвольный вектор х,
Х161 + х2е2, преобразуется
симметрия относительно
прямой, определяемой
вектором 61 — первым ба-
зисным вектором нового
базиса (рис. 12).
Таким образом, орто-
гональное преобразование
плоскости — это либо п о-
ворот вокруг нача-
ла координат на некото-
рый угол ф (в частности,
тождественное пре-
образование или
центральная сим-
метрия; определитель такого преобразования ра-
вен + 1) либо — осевая симметрия (с определи-
телем, равным —1).
Из доказанного, в частности, вытекают две теоремы
(плоской) элементарной геометрии:
1. Произведение двух осевых симметрий является
поворотом вокруг точки пересечения осей симметрии
в новом базисе равный
в х' = XiCi — х2е2. Это —
6 Л- И. Головина
162
ЛИНЕЙНЫЕ ПРЕОБРАЗОВАНИЯ
[ГЛ. V
(так как это — ортогональное преобразование с опре-
делителем, равным +1). '
2. Произведение поворота и симметрии, ось ко-
торой проходит через центр поворота, является
симметрией относительно некоторой новой оси,
проходящей через ту же точку (так как это — орто-
гональное преобразование с определителем, рав-
ным ~1).
Перейдем теперь к общему случаю ортогональ-
ного преобразования «-мерного пространства.
Теорема 6. Матрица ортогонального преобра-
зования в некотором ортонормированном базисе при-
водится к виду
1
-1
-1
cos Ф1 — sin ф,
sin ф, cos ф,
COS ф, — sin ф.
Sin фз COS ф.
cos ф^ — sin Ф^
Sin ф^ СО5ф£ _
(3)
(Все остальные элементы этой матрицы равны
нулю.)
Доказательство проведём методом матема-
тической индукции. Мы уже установили справедли-
вость этой теоремы при п= 1 и п = 2. Предположим,
что теорема верна для всех пространств, размерность
которых меньше п, и пусть R — п-ммуное евклидово
пространство и st— ортогональное преобразование.
Возможны два случая.
1. Преобразование st имеет вещественное соб-
ственное значение (это обязательно будет так, если,
§ 3]
ОРТОГОНАЛЬНОЕ ПРЕОБРАЗОВАНИЕ
163
например, и нечетно): Х=±1. Пусть et— соответ-
ствующий (единичный) собственный вектор (тогда
s4-e\ = ±6i), и Д1— порожденное вектором ei одно-
мерное подпространство. В силу теоремы 5, (п—1)-
мерное подпространство инвариантно относи-
тельно зФ. Ясно, что и в нем будет ортогональным
преобразованием. По индуктивному предположению,
в можно найти ортонормированный базис 6г, 63,...
..., еп, в котором матрица преобразования приве-
дется к виду (3). Учитывая замечание, сделанное в
§ 7 главы III, получаем, что (возможно, после соот-
ветствующего изменения нумерации базисных векто-
ров) матрица преобразования всего простран-
ства R в некотором ортонормированием базисе при-
ведется к виду (3).
2. Преобразование не имеет вещественных
собственных значений. По теореме 8 из главы III
в R найдется двумерное инвариантное подпростран-
ство Ri. По доказанному выше, в плоскости Ri можно
найти ортонормированный базис 6i, 62, в котором мат-
рица преобразования приведется к виду (2). (Дру-
гой случай:
Г1 01
ф невозможен, так как, по предпо-
ложению, преобразование не имеет вещественных
собственных значений.)
Подпространство инвариантно относительно
st, и в нем зФ, разумеется, ортогонально. По предпо-
ложению индукции, в R\ можно найти такой орто-
нормированный базис ег, 63, ..., еп, в котором мат-
рица преобразования з£ приведется к виду (3).
(В этом случае п обязательно четно, и на главной
диагонали этой матрицы .совсем не будет единиц.)
Ввиду замечания из § 7 главы III матрица пре-
образования з£ всего пространства R в орто-
нормированием базисе 6], 6г, ..., еп приведется к
виду (3).
Геометрический смысл ортогонального преобра-
зования виден из последней теоремы. Так как каж-
дая матрица вида (3) является произведением
’6*
164
ЛИНЕЙНЫЕ ПРЕОБРАЗОВАНИЯ
[ГЛ. V
нескольких матриц вида
" 1
1
1
-1
и нескольких матриц вида
cosqp — sin <р
sin(p СОЗф
1
(4)
(5)
•. 1_
то ортогональное преобразование можно осуще-
ствить, произведя Последовательно несколько сим-
метрий относительно «координатных гиперплоско-
стей» (матрица каждого такого преобразования имеет
вид (4)) и несколько поворотов вокруг «(и— 2) -мер-
ных осей» (каждый из которых имеет матрицу вида
(5)) — это преобразование представляет собой оди-
наковый поворот, осуществляемый одновременно во
всех двумерных плоскостях, перпендикулярных к
(« — 2)-мерной «оси» поворота.
§ 41
НЕВЫРОЖДЕННОЕ ЛИНЕЙНОЕ ПРЕОБРАЗОВАНИЕ
165
Объединяя в матрице (3)
— 1 в «клетки»
две соседние +1 или
О
1 О’
о 1.
cos 0 —sin 01 Г — 1
И
sin 0 cos О J [О
cos л —sin л
— 1 J sin л cos л
(возможно, после изменения нумерации базисных
векторов) получим четыре типа ортогональных матриц
(заштрихованы «клетки» вида
в частности, может равняться нулю
мы
COS ф
sin <р
— sin ф
СОЭф
или л).
, где ф,
Для нечетного
§ 4. Произвольное невырожденное линейное
преобразование
Лемма. Если — произвольное невырожденное
линейное преобразование евклидова пространства,
то преобразование Ж*Л (так же как и .я^*) яв-
ляется самосопряженным преобразованием, все соб-
ственные значения которого положительны.
166
ЛИНЕЙНЫЕ ПРЕОБРАЗОВАНИЯ
[ГЛ. V
'Доказательство. Преобразование
самосопряженное, так как
& = (^W)’ = = № - Я.
Пусть теперь еь е2, еп— ортонормированный
базис, в котором матрица самосопряженного преоб-
разования 91 приводится к диагональному виду:
“%! О ... О "
п_ О Л2 ... О
_0 0 ... Л„-
В этом базисе 9tei = Х^е{. Поэтому, если х = XiCi+]
[+ х2е2 + ... +^хпеп — произвольный вектор из /?, то
(@х, х) =
= (x^et + x29Se2 + ... + xn9ten, х1е1 + х2<?2 + ... + х„еп) =
= (хД^+ х2Х2е2+ . .. +хпкпе„, xtei + х2е2+ ... + хпеп) =
== Z..X? + ^2xi + . . . + A.„x2.
11 if i Uli
Но, с другой стороны,
($x, x) == (j/’Л, x) = (^/x, six') 0,
значит, ZjX^ + ZgX^-P ... +Arax^^0 при ,любых
Xi, x2, ..., xn. А тогда все Zi 5? 0, ^гак как если
хотя бы один из этих коэффициентов, например, кь,
был отрицательным, то для вектора х = ek мы имели
бы ($х, х) = Ха < 0, что невозможно.
Далее, если бы какое-то было равно нулю, то
и определитель преобразования был бы равен нулю.
А так как
|В| = | А'Д| = | А'|| А| = | А12,
до и определитель |Л [, вопреки условию, был бы ра-
вен нулю. Мы доказали, что все > 0.
Теорема 6. Невырожденное линейное преобра-
зование зф евклидова пространства можно предста~
I
§ 4]
НЕВЫРОЖДЕННОЕ ЛИНЕЙНОЕ ПРЕОБРАЗОВАНИЕ 16/
вить в виде произведения
где ft— самосопряженное, а Ж— ортогональное пре~
образования.
Доказательство. Возьмем в качестве базиса
пространства R тот, в котором матрица (самосопря*,
женного) преобразования 3S = приводится к
диагональному виду:
“Х1 о ... О ~
£} _ о х2 ... о *
_о о .'.,\п_
где все Z, > О, и обозначим через 'F преобразование,
матрица которого в том же базисе имеет вид
“ Ум 0 ... О
£ __ о Ум • • • о
_о о ... Ум.
Ясно, что — невырожденное самосопряженное
преобразование и что SF2 = $>. Если теперь st =
то Ж = уМсЗМ, и нам остается только показать, что '
преобразование Ж ортогонально. Но это вытекает из
равенства
= = ^~ W"1 = 3*
-—и теорема доказана.
Точно так же можно было бы доказать, что пре-
образование представимо и в виде <s$ =
где 'g’l — самосопряженное, а Ж>\— ортогональное
преобразования. Таким образом, каждое невырожден-:
ное линейное преобразование сводится к нескольким
симметриям относительно гиперплоскостей, несколь-»
ким поворотом около (я — 2)-мерных «осей» и
нескольким растяжениям вдоль взаимно ортогональ-.
ных прямых.
168
ЛИНЕЙНЫЕ ПРЕОБРАЗОВАНИЯ
[ГЛ. V
§ 5. Комплексное линейное пространство
Все, что рассказано до сих пор, относилось к вещественному
линейному пространству. Комплексное линейное пространство —
это совокупность элементов, для которых определены две опера-
ции: сложение и умножение на комплексные числа так, что
выполнены условия 1—8 из § 1 главы II. Комплексное евкли-
дово пространство — это комплексное линейное пространство, в
котором для любых двух векторов х, у определено их (вообще
говоря, комплексное) скалярное произведение (х, у) так, что вы-
полнены следующие условия*):
1. (х,у) = (^Д) **);
2. (ах, у) = а(х, у);
3. (х + у, г) = (х, г) + (г/, г);
4. (х, х) есть неотрицательное число, и из равенства (х, х) = О
вытекает, что х = 0 ***).
Из условий 1—3 получаем:
2'. (х, ау} = (ау, х) — а(у, х) = а (у, х) = а (х, у) и
3'. (г, х + у) = (х + у, г) = (х, г) + (у, г) = (х, г) + (у, г) =
= (z, х) + (г,у).
Длина вектора х по-прежнему определяется как ]^(х, х)
Два вектора, х и у, считаются ортогональными, если (х, у) = 0.
Ортонормированный базис определяется так же, как выше, и
так же как там, можно показать, что всякий базис можно пре-
вратить в ортонормированный. Так же как в вещественном про-
странстве, определяется линейное преобразование, его матрица в
данном базисе и умножение линейных преобразований и матриц.
Так же как выше, вводится понятие инвариантного подпростран-
ства, собственного вектора и собственного значения линейного
преобразования. Первая новая теорема гласит:
В комплексном линейном пространстве каждое линейное пре-
образование имеет хотя бы один собственный вектор.
Это вытекает из так называемой «основной теоремы алгеб-
ры», по которой каждое уравнение с комплексными коэффициен-
тами имеет хотя бы один (вообще говоря, комплексный) корень.
Самосопряженное преобразование комплексного евклидова
пространства определяется тем, что (л^х, у) = (х, s&y} при всех
х, у. Матрица самосопряженного преобразования в любом орто-
нормированном базисе удовлетворяет условию: А = А!, где А —
*) В научной литературе такие пространства называются
унитарными, а термин «комплексное евклидово пространство»
употребляется в несколько ином смысле.
**) Через а обозначается число, комплексно сопряжен-
ное к а.
***) Заметим, что из условия 1, примененного к двум оди-
наковым векторам, (х, х) = (х, х), следует, что скалярный квадрат
(х, х) любого вектора должен быть вещественным.
§ 5]
КОМПЛЕКСНОЕ ЛИНЕЙНОЕ ПРОСТРАНСТВО
169
это матрица, все элементы которой комплексно сопряжены соот-
ветствующим элементам матрицы А.
Докажем снова,- что все собственные значения самосопря-
женного преобразования вещественны. Пусть х — собственный
вектор и X — соответствующее ему собственное значение само-
сопряженного преобразования тогда
(six, х) = (х, six),
или
(Хх, х) = (х, Хх),
откуда
X (х, х) = X (х, х),
и так как (х, х) =^0, то X = X, т. е. К вещественно.
Линейное преобразование комплексного евклидова простран-
ства называется унитарным, если (six, siy} = (х, у) для всех
't.yeR. Если А = — матрица унитарного преобразования в
ортонормированном базисе, то ’
АА' = А'А = Е,
т. е. анан + ацй;2 + •.. +српсцп = 1 и aita-„i + .
...+а;лакп=0 при i=/=k. Такая матрица называется уни-
тарной.
Докажем, что в комплексном евклидовом пространстве все
собственные значения унитарного преобразования по модулю рав-
ны единице. Пусть si— унитарное преобразование, х — его соб-
ственный вектор и X — соответствующее собственное значение.
Тогда
(х, х) = (six, six) = (Хх, Хх) = XX (х, х).
Но так как (х, х)цА0, то XX = 1, или |Х| = 1.
ДТожно доказать, что в комплексном евклидовом простран-
стве матрица унитарного преобразования приводится к диаго-
нальному виду:
— Х1 0 ... О ~
О Х2 .;. О
_0 0 ... Хя_
где все собственные значения Xi по модулю равны единице.
Собственные значения самосопряженного преобразования ве-
щественны; собственные значения унитарного преобразования по
модулю равны единице. Самосопряженные преобразования среди
всех линейных преобразований комплексного евклидова простран-
ства играют в некотором смысле такую же роль, какую играют
вещественные числа в множестве всех комплексных чисел, при-
чём такие самосопряженные преобразования, все собственные
значения которых положительны (они называются положительно
определенными преобразованиями), играют роль положительных
вещественных чисел, а унитарные преобразования играют роль
170 ЛИНЕЙНЫЕ ПРЕОБРАЗОВАНИЯ [ГЛ. V
чисел (комплексных), модуль которых равен единице. Так, не-
трудно показать, что прбизвольное линейное преобразование &!•
комплексного евклидова пространства можно представить в виде
= 9S + 'S’i, где $ и — самосопряженные преобразования, а
1 = У—Л. Более содержательна другая теорема, аналогичная
теореме о представлении произвольного комплексного числа в
виде произведения положительного вещественного числа и числа,
по модулю равного единице («тригонометрическая форма» ком-
плексного числа):
Произвольное невырожденное линейное преобразование
комплексного евклидова пространства можно представить в виде
= %'f?, где — положительно определенное, а Ж — унитар-
ное преобразование.
Соответствующая теорема для вещественного евклидова про-
странства была доказана выше. В случае комплексного про-
странства она доказывается аналогично.
ГЛАВА VI
БИЛИНЕЙНЫЕ И КВАДРАТИЧНЫЕ ФОРМЫ
Результаты первых пяти параграфов этой главы
относятся к произвольному линейному простран-
ству. Метрика (евклидова) используется только в по-
следнем, шестом параграфе.
§ 1. Линейная функция и линейная форма
Определение 1. Говорят, что в векторном •,
пространстве R задана линейная функция
f(x), если каждому вектору x^R постувлено в со-
ответствие число f(x) так, что выполнены следующие
условия:
1- Н* + у) = f(x) + f(y),
2. f(ax) = af (х),
где х, у — произвольные векторы из R, а а — любое
вещественное число.
Для того чтобы найти выражение линейной функ-
ции в координатах, выберем в пространстве R базис
ei, е2, еп. Если х = х^ +.х2е2 + ...+_хпеп— про-
извольный вектор из R, то
f (х) = f (x^i + х2е2 + ... + хпеп) =
= хф (et) + x2f (е2) + ... + xnf (е„)
Таким образом, при фиксированном базисе линей-
ная функция f(x) представляется линейной фор-
мой _
f{x) = а{Х1 + а2х2 + ... +апх„,
где X], х2, .... хп — координаты вектора х, а а{ =
= f(et) — коэффициенты, не зависящие от х.
172
БИЛИНЕЙНЫЕ И КВАДРАТИЧНЫЕ ФОРМЫ
[ГЛ. VI
Пример. Пусть в евклидовом пространстве /?
задан вектор а = (аь az,..., ап) и для каждого х
пусть f(x) = (а, х). Тогда f(x)— линейная функция,
так как
\
/ (х + у) = (а, х + у) = (а, х) + (я, у) = f (х) + f (у)
и
f (ах) = (а, ах) = а (а, х) — af (х).
(Для евклидовых пространств этот пример является
-общим: если в R выбрать ортонормированный базис
et, е2, е„, то для каждой линейной функции f(x)
можно найти такой вектор а, что для всякого х име-
ем f(x) = (а, х).)
§ 2. Билинейная функция.
Билинейная и квадратичная формы
Определение 2. Заданная в линейном( про-
странстве R функция двух переменных А (х, у) назы-
вается билинейной, если при фиксированном х
она линейна по у, а при фиксированном у — линейна
по х.
Таким образом-, если А(х, у)—билинейная функ-
ция, то при всех X, у, z^ R и произвольном веще-
ственном а
А(х + у, z) = А (х, z) + А (у, г);
А (ах, у) = аА (х, у);
A(z, х + у) — A (z, х) + A (z, у);
А(х, ау) — аА(х, у).
Примером, билинейной функции может служить
скалярное произведение (х, у).
Найдем выражение билинейной функции в коор-
динатах. Пусть в пространстве R задан базис е2,...
...,еп и пусть
х = хгег + х2е2 + ... + хпеп, у = У\вх + у2е2 + ... + упеп.
БИЛИНЕЙНАЯ ФУНКЦИЯ
173
§2)
Тогда
А(х, у) =
= А (х1е1 + х2е2 + ... + x„en, у1е1 + у2е2 + ... + упеп) =
= 2 XiykA (ei; ek) = 2 ai^iyk,
i, k i, s
где коэффициенты «« — A (et, ек) зависят только от
базиса и не зависят от х и у. Таким образом, в за-
данном базисе билинейная функция представляется
билинейной формой, т. е. выражением вида
Матрица „Л = [а/А] называется м а т р и-
i, k
ц е й этой билинейной формы. В частности,
скалярное произведение (х, у) представляется били-
нейной формой
2 gikXcUk, где gik = (ei, ek).
i,
Найдем, как изменяется матрица билинейной фор-
мы при переходе к новому базису. Пусть в базисе
» С1, е2> • • •, Сп
А (х, у) = S a^x^k, где alk = A (eh ek),
k
и пусть е', е'2, ц'—новый базис, в котором
А (х, у) = 2 b„ х'у', где b = А(е' сП.
pq Р’q р3q pq ' р q‘
Положим А = [aift], В = [6!Й] и обозначим через
С = [с»*] матрицу перехода от старого базиса к но-
вому; тогда
ер = cipei + с2ре2 + • • • + спреп,
< = с1/1 + с2А+•••+СпА
и
bPq~A(.e'P’ О-
A (CjpCj 4- с2ре2 + ... + cnpen, Г1ре1-^-с2^е2-}~ • 4~^nq^n)~
= S (в{, ек) = 2 Г!IрСhцй№ 2 Г1ра^ск„.
i, й I, k i, ft
174
БИЛИНЕЙНЫЕ И КВАДРАТИЧНЫЕ ФОРМЫ
[ГЛ. VI
Обозначив cip через dpi, получим
Ьрр ~ 2 dpi&ikCkq-
i, k
Матрица [dpi] — С' является транспонированной к ма-
трице С = [с;р]. Далее, так как ^iaikck4 есть элемент,
ft
стоящий в f-й строке и q-м столбце матрицы АС, то
2 dpjCLikCkq = 2 dpi f2 ^ik^kq\
i, k i \ k /
— это элемент, стоящий в р-й строке и q-м столбце
матрицы С'АС. Таким образом,
В = С'АС.
Заметим, что так как матрица перехода С (а зна-
чит, и С') является невырожденной (т. е. имеет
ранг п), то ранг матрицы В равен рангу матрицы А
(см. § 6 главы III). Таким образом, ранг матрицы би-
линейной формы не зависит от выбора базиса и мо-
жет быть назван поэтому рангом билинейной формы.
Билинейная функция А (х, у) называется с и м м е т-
рической, если для всех х и у из R
А(х, у)—А (у, х).
В этом случае aik = ahi, т. е. матрица соот-
ветствующей билинейной формы (в любом базисе)
будет симметрической. Примером симметриче-
ской билинейной функции может служить скалярное
произведение. Последний пример является вполне об-
щим, так как и, обратно, каждая симметрическая би-
линейная функция А (х, у) удовлетворяет, очевидно,
условиям 1—3 из § 1 главы IV и, значит, может быть
принята за скалярное произведение.
Если в симметрической билинейной форме А (х, у)
положить у = х, то получится квадратичная
форма Д(х, х). По квадратичной форме однознач-
но определяется и породившая ее симметрическая
билинейная форма. Действительно, пусть Л(у, х) =
е= А(х,у) при всех х и у. Тогда
А (х + У, х + у) = А (х, х) + 2А (х, у) + А (у, у),
§ 3] ПРИВЕДЕНИЕ к СУММЕ КВАДРАТОВ 175
откуда
А (х, у) = -~ [Л (х + у, X + у) - А (х, х) - А (у, «/)].
Билинейная функция А(х, у) называется кососим-
метрической, если
Л (х, у) = - А (у, х)
при всех х, tj'eR. В заданном базисе кососимметри-
ческая функция представляется кососимметрической
формой
(х, у) = 2 аирс^к,
i, а=1
где, как легко видеть, = —ам при всех i, k, в
частности, аа = 0 при всех i. Так, в трехмерном про-
странстве кососимметрическая форма имеет вид
а (Х1у2 - x2yr) + р(х,z/а - ХзуО + у (х2у3 ~ *з«/г)-
Пусть Д(х, у)—произвольная билинейная функ-
ция. Тогда В (х, у) = А (х, у) + А (у, х) является, оче-
видно, симметрической, а С(х, у) = А (х, у) — А(у,х) —
кососимметрической функциями. Но
А (х, у) = у (В (х, у) + С (х, уУ);
следовательно, каждая билинейная функция может
быть представлена в виде суммы симметрической и
кососимметрической функций.
§ 3. Приведение квадратичной формы
'к сумме квадратор
Теорема 1. Пусть А (х, х) — произвольная квад-
ратичная форма в п-мерном векторном пространстве*
Тогда найдется такой базис, в котором эта форма
приводится к сумме квадратов (т. е. в котором все
коэффициенты при попарных произведениях коорди-
нат- вектора х равны нулю).
Доказательство проведем индукцией по чис-
лу входящих в форму переменных. Если в А(х, х)
176
БИЛИНЕЙНЫЕ И КВАДРАТИЧНЫЕ ФОРМЫ
[ГЛ. VI
входит лишь одна координата, то
А (х, х) = апх2,
и наше утверждение очевидно. Предположим, что оно
справедливо для всех квадратичных форм, зависящих
от т— 1 координат, и рассмотрим
А(х, x) = allx2 + 2al2xIx2 + a22x2 + ... + аттх2т.
Если здесь есть хотя бы один квадрат с отличным
от нуля коэффициентом, например, если атт ¥= 0, то
соберем все члены, содержащие хт:
+ 2ат-1,тХт-1Хт + аттХт
и «выделим полный квадрат»:
2aimXlXm + 2а2тХ2Хт + + 2ат-1, rnXm-lXm +
— + <12/71^2 "Ь • • • "Ь ^т-\, тхт—\ "Ь ^ттхт)
и-тт
---~--{а\тх\ + а2тХ2 + ••• + ^m-1, mvm-i)2.
итт
Тогда
А (х, х) = --+ ^2тх2 + • . • + ammxmf + В (х, х),
и?пт
где квадратичная форма В (х, х) содержит уже только
т — I координат х1( х2, ..., хт_Р Положим
У\ = х1> У2~ x2t •••> Ут~\ = хт-1>
Ут = ^1тх1 + &2тх2 + . • • + Оттхт>
Ут+1 = Хт + Ь • • • > Уп = хп'
Так как определитель
1 0 .0 ... 0 ... 0
0 1 -0 ... 0 ... 0
п ~ атт 0’ (1)
П-lm 42m Qzm • • • “mm • • • u
0 0 0 ... 0 ... 1
§ 3]
ПРИВЕДЕНИЕ К СУММЕ КВАДРАТОВ
177
то этот переход к новым координатам вызывается
переходом к некоторому новому базису (с матрицей
перехода, обратной матрице определителя (1)).
По предположению индукции, форму В(х, х),
зависящую от»!--] переменных хь х2, ..., хт^, по-
средством перехода к новому базису можно привести
к сумме квадратов. При этом окончательно приве-
дется к сумме квадратов и форма А (х, х) .
Мы предполагали, что хотя бы один из квадратов
входит в форму А(х, х) с ненулевым коэффициентом.
Если это не так," т. е. если все 0ц = 0, то допустим,
что например, aj2 =£ 0, и положим
*1 = */1 + У‘2,
Х2 = У1~ У‘2,
хз — Уз,
хп Уп
— это соответствует переходу к новому базису
< = + е2,
С] е2,
ез = ез>
< = еп
с матрицей перехода
"1 1 0 0“
1 -1 о ...... б
0 0 1 ...... о
,_0 0 0 .... 1 _
(определитель этой матрицы равен — 2=£0). При
этом произведение Xi%2 обратится в у\ —у2, й мы при-
дем к первому случаю.
Мы доказали, что если в «-мерном векторном
пространстве В задана произвольная квадратичная
178
БИЛИНЕЙНЫЕ И КВАДРАТИЧНЫЕ ФОРМЫ
[ГЛ. VI
~ форма, то в Я можно найти такой базис, в котором
эта форма приведется к сумме квадратов:
А (х, х) = а^'2 + а2х2 + ... + апх'*, (2)
где Хр х2, х'п — координаты вектора х в новом
базисе. Коэффициенты а, могут быть и положитель-
ными и отрицательными; некоторые из них могут
быть равными нулю. Если сделать еще подстановку
У|пг| x' = Zp то квадратичная форма А(х, х) приве-
дется к виду
А (х, х) = ± z\ ± z2 ± ... ± z2m,
где коэффициент перед каждым неизвестным Zj, z2, .
..., zm равен +1, или —1, или, после изменения ну-
мерации базисных векторов, — к виду
А(х, x) = 4 + z2+ ... + z2-z2p+l- ... -z2+,.
Пример 1. Квадратичную форму х\ + 2Х[Х2 + Зх2 + 4х1х3+
4- 6х2х3 + 5х2 привести к сумме квадратов.
Решение.
Я (х, x) = (xj+х2 + 2х3)2 + 2х2 + 2х2х3 + х3 =
= (Xj + х2 4- 2х3)2 + (х2 + х3)2 + х|.
§ 4. Закон инерции квадратичных форм
Приводя квадратичную форму Л(х, х) к сумме
квадратов разными способами, мы можем получить
в формуле (2) разные коэффициенты. Однако имеет
место следующее важное обстоятельство:
Теорема 2 (закон инерции квадратичных форм).
Если квадратичная форма в двух разных базисах
приводится к сумме квадратов, то число положитель-
ных квадратов, так же как и число отрицательных
квадратов, в обоих случаях одно и то же.
Доказательство (от противного). Предполо-
жим, что в базисе eb е2, ..., еп квадратичная форма
А (х, х) имеет вид
А(х, х) = х2 + х2+ ... + х2-х2+1- ... -х2р+ч, (3)
ОПРЕДЕЛЕННЫЕ ФОРМЫ
179
§ 5]
где Xi — координаты вектора х в этом базисе; и пусть
в другом базисе е{, е2, ..., е'
Л(х, x) = xf+ х'2+ ... +<2-х'2+1- ... -<+т, (4)
где х\ — координаты вектора х в новом базисе. Пред-
положим, что, например, р > k. Рассмотрим в про-
странстве R подпространство R\, порожденное векто-
рами еь ег, ..., ер, и подпространство Rz, порожден-
ное векторами е'А+!, e'k+2, .... е'п. Так как сумма их
размерностей, равная р + (п— k), больше п, то их пе-
ресечение имеет ненулевую размерность (теорема 5
из § 6 главы II), т. е. существует вектор х#=0, при-
надлежащий Ri П Rz. Этот вектор можно представить
как в виде
х = сцб! + а2е2 + ... -Тарвр,
так и в виде
Х = Pfe+ Iе k+1 + $k+2ek+2 + • • • +
Для вектора х по формуле (3)
А (х, х) = оф + а2 + ... + а?р > О,
так как хотя бы одно из а^=#0; в то же время по
формуле (4)
А (х, х) = — р|+1 — р|+2 — ... —
Мы пришли к противоречию, устанавливающему,
что р k. Аналогично доказывается и невозможность
неравенства р < k. Следовательно, р = k. Так же до-
казывается, что q = т.
Легко видеть, что сумма р+’.q равна рангу г
квадратичной формы А(х, х).
§ 5. Определенные формы
Определение 3. Квадратичная форма А(х, х)
называется положительно (отрицательно)
определенной, если А(х, х) > 0 (А(х,х) < 0) при
всех х#=0, и положительно. (Отрицательно)
по л у on р е.д е л енно й, если А (х, х)<>0 (А (х, х)<Л)
при всех х._
180
БИЛИНЕЙНЫЕ И КВАДРАТИЧНЫЕ ФОРМЫ
[ГЛ. VI
Так, если А (х, у) = (х, у)— скалярное произведение
в евклидовом пространстве, то соответствующая ква-
дратичная форма А (х, х) — (х, х) (скалярный квадрат
вектора х) является положительно опреде-
ленно й.
Ясно, что положительно определенная квадратич-
ная форма приводится к сумме квадратов с положи-
тельными коэффициентами, а положительно полуопре-
деленная форма — с неотрицательными коэффициен-
тами (некоторые из которых могут равняться нулю).
Важным условием положительной определенности
формы является следующая
ТеоремаЗ (критерий Сильвестра). Для того что-
бы квадратичная форма А (х, х) была положительно
определенной, необходимо и достаточно, чтобы все
«угловые миноры» матрицы А = [а^], т. е.
Ai = ап,
«11 «12 «13
д 1 0,1 Й12 , Аз ~ «12 «22 «23 , д„ = 1 А
1 «12 «22
«13 «23 «33
были положительны.
Доказательство проведем индукцией по числу входя-
щих в форму переменных.
Для квадратичных форм, зависящих от одной переменной,
А(х, x) = aHXp и наше утверждение очевидно. Предположим, что
оно справедливо для всех квадратичных форм, зависящих от
in — 1 переменных, и рассмотрим квадратичную форму А (х, х) =
m
= aikx-xk от m переменных ,лг1г х2, ..., хт.
a fe=l ,
1. Доказательство необходи м о с т и. Если предста-
вить положительно определенную форму А (х, х) в виде
т-1 т-1
А (х, х) = аг!гхгхй+2 oirnxixm + аттхп,
1,*=1
т—1
то квадратичная форма В (х', х') = aikxixk’ зависящая от
i. k=t
т — 1 переменных х1г х2, . .., xm-i, будет положительно опреде-
ленной, так как если В(х', х') 0 при х' = (Xi, х2, • • •, xm_j), -
то при x = (xlt хг, ..., хот_л, 0) мы имели бы А (х, х) 0.
§ 5]
ОПРЕДЕЛЕННЫЕ ФОРМЫ
181
По индуктивному предположению, все угловые миноры, ма-
трицы квадратичной формы В (х', х') положительны, т. е.
Д1 = «и>0, Д2 = |а11 а’2|>0, ...
I а12 а22I
ап а12 • • • пг—1 '
«12 «22 • • • «2, т— 1
................................ .
«1, т—I «2, т— I ••• «т—1. т—1
Остается доказать, что и Дш = | А | > 0.
Мы знаем, что положительно определенная квадратичная
форма А (х, х) в некотором базисе ер е2.......ет приводится к
сумме квадратов:
- Z2 г2 г2
А (х, х) = Xj + х2 + ... + хт.
В этом новом базисе определитель ее матрицы равен 1 и, значит,
он больше нуля. Однако при переходе к новому базису матрица
билинейной формы преобразуется по формуле (стр. 174)
В = С'АС,
где А — матрица ее в старом базисе, В — в новом, и С — матри-
ца перехода от старого базиса к новому. Следовательно,
| В | = | С 11 А ] | С | = | Л 11 С I2.
Таким образом, знак определителя матрицы билинейной формы
не зависит от базиса; поэтому и в старом базисе
|Л| = Дт>0.
2. Доказательство достаточности. Предположим,
что все угловые миноры матрицы квадратичной формы А(х, х)
положительны:
Д1 > 0, Д2 > 0, ..., Д/п—1 > 0, Ат = ] Л | > 0,
и докажем, что квадратичная форма А(х, х) положительно опре-
деленная. Из предположения индукции вытекает прежде всего
положительная определенность квадратичной формы
т-1
В(х',х’)— 2 aikxixk от т — 1 переменных. Следовательно,
(.fell
,В(х',х') в некотором новом базисе приводится к сумме квад-
182 БИЛИНЕЙНЫЕ И КВАДРАТИЧНЫЕ ФОРМЫ [ГЛ, VT
Сделав соответствующую замену переменных Xi, хг, ..., xm-i и
положив, кроме того, хт — хт, мы получим
,2 z2 Z2
А(х, х) = х1 + х2 + ... +хт_1 +
' Z Z Z Z Z г /\ f2
+ ^2tnx2xm + ”• /п-1, тхт—1хт) + аттхт>
где bim — какие-то новые коэффициенты. Далее имеем
Л (х, х)=.(х^ + 61шх^)2 +
+ (х2 + 1>2тхт) + ••• "* (х/п-1 + ^т—1, тхт) ^хт’
где, очевидно, b = атт - b2iin - b22tn - ... - Ь2т_к т, и, полагая
xi + bimxm ~ Уi> хпг = Ут
(что соответствует переходу к новому базису, с матрицей, опре-
делитель которой равен единице), получим
а(х, х) = у2 + pg + +г/т-1 + &г/т-
Определитель матрицы этой квадратичной формы равен Ь,
а так как знак .его, как показано в п. 1, совпадает со знаком Дга,
то b > 0, и значит, квадратичная форма А(х, х)—положительно
определенная. Теорема доказана.
Теперь нетрудно найти и условия отрицательной
определенности квадратичной формы А(х, х) =
п
= 2 aikxixk- Для того чтобы квадратичная форма
I, fe=i
А (х, х) была отрицательно определенной, необходимо
и достаточно, чтобы квадратичная форма
-А(х, х)= 2 (—а^хр^
i,
была положительно определенной, а значит, чтобы
все угловые миноры матрицы
— йц — 012 • • • ~ а\п
— «12 — й22 • • • ~ а2п
- ^2п • • • ^пп -
4
§ €1
ФОРМЫ В ЕВКЛИДОВОМ ПРОСТРАНСТВЕ
183
т. е.
-«и,
~ «11 —«12
— «12
— «ц - «12 ... — «щ
— «12 — «22 — «2п
«1п «2п «пп
были положительны. Но это означает, что
Д;— «п <01 Аг—
«11 «12
«12 «22
>0,
«11 «12 «13
Д3 — «12 «22 «23 <о,
«13 «23 «33
т. е. что знаки угловых миноров матрицы А чередуют-
ся, начиная со знака минус. -
Пример 2. При исследовании на экстремум функции
F (х, у, г) = 2х2 + у2 + 11 z2 — 2ху-+ 4xz — Gyz — 2у + 8z, (5)
находим, что ее частные производные обращаются в нули при
х=1, У = 2, z = 0.
Второй дифференциал имеет вид '
d2F = 2 (2 dx2 — 2dxdy + dy2 + 4 dx dz — 6 dy dz + ll dz2).
В скобках — квадратичная форма относительно дифференциалов
независимых переменных dx, dy, dz. Угловые миноры ее матрицы
I 2
Д1 = 2, Д2 ~ I _ ।
;|-1, д,-
2
-1
' 2
-1
1
-3
2
-3
11
= 1
положительны. Следовательно, эта квадратичная форма положи-
тельно определенная, и функция (5) имеет в точке (1,2,0) ми-
нимум.
§ 6.« Билинейные и квадратичные формы
в евклидовом пространстве
Лемма. Пусть R — евклидово пространство и
С = [Сй] — матрица перехода от одного ортонормиро-
ванного базиса ei,e2,..., еп к другому, тоже ортонор-
мированному базису е{, е'2, ..., е'п. Тогда С — орто-
гональная матрица.
184
БИЛИНЕЙНЫЕ И КВАДРАТИЧНЫЕ ФОРМЫ
[ГЛ. VI
Доказательство. По условию,
< = сне1 + с2А + ' ••• +cnlen, 1=1, 2..п.
Рассмотрим линейное преобразование ‘ё’ с матрицей С
в базисе et, е2,..., еп. Мы имеем
+ c2ie2 + ••• = 2> •••> п.
Но преобразование переводящее хотя бы один
ортонормированный базис в ортонормированный же,
ортогонально (см. § 3 главы V). Следовательно, С —
ортогональная матрица.
Пусть теперь в евклидовом пространстве R выбран
ортонормированный базис ei,e2, ...,еп и пусть дана
билинейная функция А(х,у), которая в этом базисе
представляется билинейной формой
21 (*,!/) = 2 atkxyjk,
i, k=*l
где х — Xiei + ^2^2 + ... + хпеп, у — У\&\ + Уч^о. + ...
... + упеп- Рассмотрим линейное преобразование «я£ с
той же матрицей А в том же базисе еь е2, . .., е„.При
переходе к новому базису е,, е'2, ..., е' с матрицей
перехода С матрица А билинейной формы перейдет в
В = С'АС,
а матрица линейного преобразования &— в
С-1ЛС,
т. е., вообще говоря, эти матрицы преобразуются не
одинаково. Однако если новый базис е', е'2, е'п —
тоже ортонормированный, то матрица перехода С
ортогональна, и С= С"1. В этом случае матрица би-
линейной формы А(х,у)- и матрица линейного преоб-
разования s/ преобразуются одинаково. Таким обра-
зом, в евклидовом пространстве каждой билинейной
функции соответствует вполне определенное линейное
преобразование (имеющее ту же матрицу в любом
ортонормированном базисе).
§ 6] ФОРМЫ В ЕВКЛИДОВОМ ПРОСТРАНСТВЕ 185
Если А (х, у)—симметрическая билинейная функ-
ция, то соответствующее линейное преобразование .5/
будет самосопряженным. Но матрица самосопряжен-
ного преобразования в некотором ортонормированием
же базисе имеет диагональный вид:
"Л, 0 ... О
о х,2 ... о
_о о ... л„_
В этом же базисе билинейная форма А (х, у) при-
ведется к виду
М'Х + к2х2у'2 + ... + кпх'пу'п
(где коэффициенты X; — это собственные значения ли-
нейного преобразования <s£), а соответствующая ква-
дратичная форма А(х,х) приведется к сумме квадра-
tqb:
A/jXj + Л2х2 + .. . + Апхп •
Пример 3. Квадратичную форму
А (х, х) = 66х2 — 24хг/ + 59г/2
в евклидовом пространстве R2 с помощью ортогонального пре-
образования привести к сумме квадратов.
Решение. Характеристический многочлен матрицы этой
формы
<PW = )667? 712 | = Л2-125Л + 3750.
( "" 1Z ОУ Л |
Его корни А.) = 75, А.2 = 50.
В новом базисе (состоящем из собственных векторов, соот-
ветствующих собственным значениям М и щ)
,2 ,2
А(х, х) = 75х1 + 50/.
ГЛАВА VII
ИССЛЕДОВАНИЕ КРИВЫХ И ПОВЕРХНОСТЕЙ
ВТОРОГО ПОРЯДКА
В трех первых параграфах этой главы рассматри-
вается двумерное пространство (плоскость) с обыч-
ной, евклидовой метрикой, В последнем параграфе —
трехмерное евклидово пространство,
§ 1. Приведение общего уравнения кривой
второго порядка к каноническому виду
Установим на плоскости прямоугольную декартову
систему координат и рассмотрим общее уравнение
второй степени
f (х, у) = ацх2 + 2а12ху + а22у2 + 2«1х + 2а2у + а = 0. (1)
Как известно, при некоторых частных значениях его
коэффициентов это будет уравнение эллипса
+ = 0’ гипеРб>олы ---------1) или пар^о-
лы (у2 = 2рх). Мы докажем, что уравнение (1) всегда
'является уравнением одной из этих кривых: эллипса,
гиперболы или параболы (не считая случаев выро-
ждения— пары прямых, если левая часть уравнения
распадается в произведение двух линейных множите-
лей, точки или «пустого множества», вовсе не содер-
жащего точек).
Обозначим через е^ и е2 единичные векторы, на-
правленные, по осям выбранной (прямоугольной) си-
стемы координат. Группу старших членов
йцх2 + 2a12xz/ + а22у2 (2)
(4)
§ 1] ПРИВЕДЕНИЕ К КАНОНИЧЕСКОМУ ВИДУ 187
уравнения (1) можно рассматривать как квадратич-
ную форму от координат х, //вектора (х, у). Как было
показано в § 6 главы VI, эта квадратичная форма в
некотором (ортонормированном же) базисе е', е'
приводится к сумме квадратов
Aja/ 4* A2yz , (3)
где Л] и А2 — собственные значения матрицы
Йц 012
Vl2 а22.
а е{ и е2 — соответствующие им собственные векторы.
Пусть вектор ei получается из вектора et поворо-
том на угол ф против часовой стрелки. Так как вектор
е2 ортогонален elt а е2 ортогонален ei, то вектор е2
получается из. вектора е2 либо поворотом на угол ф,
либо поворотом на угол ф и симметрией относительно
начала координат. Во втором случае заменим его на
вектор е" = — е2, который тоже будет собственным
вектором матрицы (4) с тем же собственным значе-
нием А2: если то
з^е2 = е') = — з^е'2 ~ К2е2 — А2е".
Таким образом, можно считать, что новый базис
е[, е'2 получается из старого поворотом на некоторый
угол ф против часовой стрелкщ т. е. что
е[ — cos ф • ех + sin ф • е2,
е2 = — sin ф • в; + cos ф • е2.
Но в таком случае старые координаты х, у (вектора, а.
значит, и соответствующей точки) и новые координаты
х', у' связаны соотношениями
х = cos ф • х' — sin у • у',
у — sin ф • х' + cos ф у'. >
Подставив значения (5) в уравнение (1), мы при-
ведем это уравнение к виду '
AjV -Т К^у' + 2&1V + 2^2^ 4" b — 0, (6)
188
КРИВЫЕ И ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА [ГЛ. VII
где bi, b2, Ь — некоторые новые коэффициенты. Эта
операция называется отнесением линии к главным
осям -— из дальнейшего будет видно, что если линия
(1) представляет собой эллипс или гиперболу, то
новые оси координат параллельны главным осям
кривой.
Коэффициенты МДз— эго собственные значения
матрицы (4); их можно найти из уравнения
А/ $12
а12 а22
(7)
Они вещественны, так как матрица (4) симметриче-
ская (теорема II главы V). Произведение А.1А.2 собст-
венных значений равно свободному члену ср(О) ква-
дратного уравнения (7), т. е. равно определителю
Пи п12
П]2 #22
Рассмотрим теперь отдельно два случая: 6 ¥= 0 и
6 = 0.
1.6 = A,iA,2 ф 0.
Преобразуем уравнение (6) следующим образом:
Ап + А2 + с = 0,
г», г»!
где с = Ь — -5--г—. Сделаем подстановку
Aj Л2
Она отвечает переносу начала координат в точку
у-, — -у-) при сохранении направлений осей. При
этом уравнение (6) приведется к виду
М"* + М"2 + с = 0. (8)
Предположим сначала, что ZjZa > 0 (т. е. что
6>0). В этом случае геометрическое место точек, ко-
ординаты которых удовлетворяют уравнению (8),
нредставляет собой эллипс (рис. 13, а), если знак с
§ I]
ПРИВЕДЕНИЕ К КАНОНИЧЕСКОМУ ВИДУ
189
противоположен знаку Хг, оно сводится к одной точке,
если с = 0, и совсем не содержит точек, если знак с
совпадает со знаком V).
Пусть теперь Х[Х2 <0 (т. е. 6 < 0); тогда (8) бу-
дет уравнением гиперболы, если с ФО (рис. 13,6),
и пары пересекающихся прямых, если с = 0.
В случае I линия представляет собой центральную
кривую второго порядка (легко видеть, что для кри-
вой (8) начало координат является центром сим-
метрии).
II. б = Х1Х2 = 0, и пусть, например, Х2 Ф 0. Урав-
нение (1) приводится к виду
с^у' + 26\х' + 2Ь2у' 4-6 — 0. (9)
Если 61 Ф 0, то, выделив полный квадрат, будем иметь
/ , г>,\2 / ь ь1 \
+ Х7 +2Ц* + ~2ьГ“ ад-/= °-
С помощью переноса начала координат
, b bl 6,
= + у" — у 4--^-
*) Вместо «точки», определяемой уравнением Xtx"2 + Л2у"2=0,
говорят также о паре «мнимых прямых» у” = ± Z Т/ х", пе-
V ^2
ресекающихся в вещественной (т. е. обыкновенной, реально су-
ществующей) точке. «Пустое множество точек» Я^х"2 + Л2у"2 +
+ с = 0, где Л2, с — одного знака, называют также «мнимым
эллипсом».
190
КРИВЫЕ И ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА [ГЛ. VII
уравнение (9) приводится к виду
М"2 + = 0. (10)
Это — каноническое уравнение параболы (рис. 14).
В случае, когда bi = 0, уравне-
ние (9) приводится к виду
/ , Ь2 \2 t b*
^2\У + "Г" ) + ^ — -j— = 0,’
и после подстановки
у" = у' + х
X'
становится таким:
М"2 + с = 0.
(Н)
Это — пара параллельных прямых, если с%2 < 0,
пара совпадающих прямых, если с = 0, и «.пустое мно-
жество точек» (не содержащее ни одной точки) при
§ 2. Инварианты кривой второго порядка
Слово инвариантный значит неизменный. Ин-
вариантами кривой называются такие выражения,
составленные из коэффициентов ее уравнения, кото-
рые не меняются при переходе от одной прямоуголь-
ной декартовой системы координат к другой такой же
системе, т. е. при поворотах осей координат и при
параллельных п е р ен о с а х осей.
Теорема 1. Для кривой второго порядка (1)
сумма коэффициентов при квадратах координат
5 = йц + fl22t
определитель, составленный из коэффициентов при
старших членах
д alt fl12
V - )
_______________ Л12 а22
*) Уравнение Х2у"2 + с =• 0, где Л2с > 0, определяет, как
иногда - говорят, «пару мнимых параллельных прямых».
§2]
ИНВАРИАНТЫ КРИВОЙ ВТОРОГО ПОРЯДКА
191
и определитель третьего порядка
Д =
ап
^12
U12 И]
#22 а2
«1 а2 а
являются инвариантами.
Доказательство. Рассмотрим отдельно пере-
нос начала координат и поворот координатных осей.
Предположим прежде, что начало координат (при со-
хранении направления осей) переносится в точку с ко-
ординатами (а, р). Тогда
х = х' + а,
У = У' + ?>,
где х' и у' — новые координаты. Подставляя эти зна-
чения х и у в уравнение (1), получим
аИ (х' + а)2 + 2а12 (х' 4- а) (/ + |3) + а22 (у' + Р)2 +
4- (л/ 4- а) 4- 2й2 (у' 4- р) 4- а ~ О,
или
Оцл/ 4- 2а12х'у' 4- а22у' 4* 2 (<2ц<х 4- ^ыР 4- #1) х'
4- 2 (а;2а 4- О22Р 4- #2) У' 4-
4- (ана2 4- 2а12ссР 4- G22P2 + 4- 2а2Р +а) = 0. (12)
Мы видим, что группа старших членов вообще не
изменилась, отсюда инвариаитность s и б очевидна.
(Заметим, что коэффициент при х' равен 2(апа4-а12р4-
+ = f'x(а, р) — частной производной от левой части
уравнения (1) по х, взятой при х — а, у = р; коэффи-
циент при у' равен f'(a, Р), а свободный член равен
f(a, р), так что окончательно преобразованное уравне-
ние йринимает вцд
анх'2 4- 2ai2xfг/' 4- а22у'2 4- f' (а, р) х' 4-
4-/;(a,₽)/+/(a,₽) = 0,
где f(x,y)—многочлен, стоящий в левой части урав-
нения кривой.
192 КРИВЫЕ И ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА [ГЛ. VII
Ф(А,) =
Для уравнения (12) определитель Д равен
Oil О[2 Oi.Cl + Oi20 + Oj
О|2 О22 0,2® 4" 0220 "Ь 02 •
Оц(х + О[20 4" О[ О]2® + 0220 + Ог Оц®2 4* 2о;г®0 4" Огг02 4" 2oi® 4* 2о?0 4* о
Вычитая из последней строки этого определителя
первую, умноженную на а, и вторую, умноженную на
Р, получим
«ц П)2 «ЦО Ч" «12Р "Ь «1
«12 «22 «12° + «22^ + а2 •
at а2 «(«+ а£ + а
Проделав такие же'операции над столбцами полу-
ченного определителя, найдем, что он равен
«11 «12 «]
«12 «22 «2 >
«1 а2 а
т. е. равен старому определителю Д. Таким Образом,
инвариантность Д при переносах начала координат
тоже доказана..
• Далее, при повороте осей координат на угол ф ма-
трица перехода от старого базиса к новому
соэф — sin ф
sin ф COS ф J
ортогональна; следовательно, матрица квадратичной
формы
atix2 + 2а12ху + а22у2
преобразуется так же, как матрица соответствующего
линейного преобразования (§ 6 главы VI). Но для
линейного преобразования с матрицей
«II «12
. «12 «22.
коэффициенты его характеристического уравнения
Пц Z $12
П]2 @22 —
= Z2 - («п + а22) X + «„«22 - а22 = Z2 - sZ + 6
§2] 1 ИНВАРИАНТЫ КРИВОЙ ВТОРОГО ПОРЯДКА
193
вообще не зависят от выбора базиса (теорема 6 § 7
главы III). Этим доказана инвариантность s и 6 при
поворотах координатных осей. Аналогично, можно до-
казать и инвариантность определителя А.
В самом деле, если мы. перейдем к новому базису — такому,
что
= cos <р • gj + sin <р е2,
е2 — — sin ф • е1 + cos <р • е2,
то координаты преобразуются по формулам
х — cos <р • х' — sin <р • у',
, , , ('о)
у = sin <р • X + cos <р • у .
В трехмерном евклидовом пространстве /?3 в ортонормиро-
ванием базисе Ci, е2, рассмотрим квадратичную форму от трех
переменных:
F (х, у, z) = анх2 + 2а12хр + а22у2 + Ча^хг + Ча2уг + аг2.
F(x,y,z) при г=1 превращается в f(x,y). При ортогональном
преобразовании базиса еь <?2, е3 с матрицей
cos ф — sin <р О
sin ф cos ф О
О 0 1
координаты в R3 преобразуются по формулам
X ~ COS ф • х' — sin-ф • у',
у = sin ф • х' + cos ф • у', (14)
z = г'.
Если f(x, у) при подстановке (13) переходит в
&пх'2 + 4bI2x’y' + b22y'2 + 2bix' + ЧЬ2у’ + Ь,
то ясно, что F(x,y,z) при подстановке (14) перейдет в
бцх'2 + 2bi2x'y’ + b22y'2 + 2&]Х'г' + 4b2y'z’ + Ьг'2.
При ортогональном преобразовании базиса определитель матри-
цы квадратичной формы ие меняется; следовательно, для формы
f(x, у, г) имеет место равенство
fen fe12 bi «If «12 «1
fel2 ^22 ^2 — «12 «32 «2
bj b2 b» (2j $2 «
7 Л. И. Головина
194
КРИВЫЕ; И ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА [ГЛ. VII
Но левая часть его есть определитель Д для f(x,y) в новом
базисе et, 62, а правая часть —в старом. Следовательно, и при
поворотах координатных осей этот определитель также не ме-
няется. Теорема полностью доказана.
По значению б можно судить о типе кривой: если
б > 0, перед нцми кривая эллиптического типа
(эллипс, точка или «пустое множество» — «мнимый
эллипс»), если" б<0 — кривая гиперболиче-
ского типа (гипербола или пара пересекающихся
вещественных прямых), если 6=0 — кривая пара-
болического типа (парабола или пара парал-
лельных прямых, возможно, совпадающих или даже
не существующих — «мнимых»).
Установленная в теореме 1 инвариантность выра-
жений з, б и Д облегчает приведение уравнения кри-
вой к каноническому виду. Так, например, в случае
центральной кривой, т. е. при б =#0, если уже найдены
и Л,2, то уравнение кривой, как мы видели, приво-
дится к виду
М"2 + Ъу"* + с = 0.
Для этого уравнения
о о
М
о
о
Д =
7,2 0
0 с
откуда ЯДгГ — или 8с = Д, и с = -у. Таким образом,
«каноническое», т. е. уже упрощенное уравнение цен-
тральной кривой второго порядка будет иметь вид
XjX2 + + -у = 0.
Если
б>0 и Д=#=0,
то наша кривая —э л липе или «мнимый эллипс».
Она будет эллипсом (вещественным), если Zi и
Д , Д ^А
-у разных знаков, т. е. если 7j-y<0; но так как
б > 0, и 71 — одного знака с з, то это будет, если
зД < 0. Кривая будет «мним ы м эллипсом» в
том случае, когда эД > 0. Если же б > 0 и Д = 0, то
кривая представляет собой точку.
Ji2] ИНВАРИАНТЫ КРИВОЙ ВТОРОГО ПОРЯДКА
195
Если б <0, то кривая является гиперболой
при Д=#0 и распадается на пару пересекаю-
щихся прямых при Д = 0.
Для параболы,
к виду (10),
уравнение которой
приведено
Д=-
0
А.2
О
о
о
о
о
= — Ь\/.2,
откуда
Г '“2
и значит, Д #= 0.
пары параллельных
Здесь Ь\ =# О,
В случае
(различных, совпадающих или «мнимых»)
кривой приводится к виду
Z,2y2 + с = 0.
прямых
уравнение
В этом случае
0
О Л2
о
= 0.
Д =
О
о
0
О
с
Соберем результаты двух последних параграфов
в следующую таблицу:
б> 0 Кривая эллипти- ческого типа Д=?^0 sA < 0. Эллипс
sA > 0. «Мнимый эллипс»
Д = 0 Точка (пара пересекающихся в этой точке «мнимых пря- мых»)
б < 0 Кривая гипербо- лического типа д#=о Гипербола
А = 0 Пара пересекающихся пря- мых
6 = 0 Кривая парабо- лического типа Д¥=0 Парабола
Д = 0 Пара параллельных прямых (различных, совпадающих или «мнимых»)
7
196
КРИВЫЕ И ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА [ГЛ, VII
Из этой таблицы, в частности, видно, что опреде-
литель А равен нулю в том и только в том случае,
когда кривая распадается на пару (действительных
или «мнимых») прямых. Таким образом, о распаде-
нии или нераспадении кривой на пару прямых можно
судить по определителю А и до приведения уравне-
ния кривой к каноническому виду.
Примеры. Определить типы следующих кривых и привести
их уравнения к каноническому виду.
1. Зх2 — 2ху + Зу2 + 2х — 4у + 1 = 0;
2. Зх2 - 2ху + Зу2 + 2х - 4у + 2 = 0;
3. х2 + у2'+2х+ 1 ' =0,
4. х2 + 2ху — у2 — 6х + 4у — 3 =0;
5. х2 + Зху + 2у2 + 2х + 5у — 3 =0;
6. х2 — 2ху + у2 + 4х — бу + 1 =0;
7. х2 + 4ху + 4у2 — 2х — 4у — 3 =0;
8. х2 + 4ху + 4у2 — 2х — 4у + 1 =0;
9. х2 + 4ху + 4у2 + 2х + 4у + 2 =0.
Решение.
1. 5 = 1 J 1 | = 8>0,
I — 1 о |
Это — кривая эллиптического типа.
Д =
3
- 1
- 1
3
— 2
-2
1
-3^0;
кривая не распадается.
Далее,
IQ _ 1 __ 1 I
. „ , = Л2 - 6Х + 8 = 0, X = 3 ± 1, Х1 = 4, Х2 = 2.
— 1 о —- л I
Каноническое
уравнение кривой
2 2 3
4х' +2у' — тг = 0, или
3 8
32 ,2 , 16 ,2 ,
ГТ* +-3'4' =1
Это — эллипс-, его полуоси:
a—IL.OA
4/2
4
§ 2]
ИНВАРИАНТЫ КРИВОЙ ВТОРОГО ПОРЯДКА'
197
2-Н-?
Кривая эллиптического типа.
3
- 1
1
3
— 2
Д =
— 2 = 5=#0.
2
Кривая не распадается.
Далее, s = 6, 6 = 8 и ф (Л) = Л2 — 6Л + 8, Л] = 4, Л2 = 2. Кано*
иическое уравнение кривой
4х'2 + 2/ + = 0.
О
Это «мнимый эллипс» («пустое множество» точек).
3. б
Кривая эллиптического типа.
1
0
1
0
1
0
Д =
0
1
= 0.
Эта кривая, уравнение которой можно записать в виде
(х+ i)2 + z/2 = o,
представляет собой точку
х= - 1,
ее можно также понимать как
точке «мнимых прямых»
х + iy + 1 = 0,
. . I 1 1
4- 6 J 1 -1
Кривая гиперболического типа.
0.
пару пересекающихся в этой
х — iy + 1 = 0.
1
1
-3
-1
2
Д =
-3
2
-3
Кривая не распадается.
Далее,
s = 0, б= —2 и ф(Л) = Л2 —2; Л2=-/1
Каноническое уравнение кривой
/2х'2-/2"/ +у = 0, нли 2/2/-2/2 Xх2 =1.
198
КРИВЫЕ И ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА [ГЛ, VII
Это — гипербола, ее полуоси.: а = b 0,6.
Кривая гиперболического типа.
Кривая распадается на пару пересекающихся прямых. Следова-
тельно, левая часть уравнения кривой распадается на два лиь
нейных множителя. Чтобы найти эти множители, можно посту-
пить, например, следующим образом. Уравнение
х2 + Зху + 2у2 + 2х + 5у — 3 = х2 + (Зу + 2) х + 2у2 + 5у — 3 = 0
решим относительно х (так как уже известно, что левая часть
уравнения распадается на линейные множители, х будет рацио-
нально выражаться через у):
/3 \ /" О •
х= ~ ("г у+ 9 ± у ТУ2 + зг/+1 -2и2-5//+з=
/ Q \ / 1 \
= -(2г/+1)±(т^-2)’
Xi = -y-3, х2= —2г/+1.
Левая часть уравнения распадается, следовательно, на мно-
жители: (х + у + 3) (х + 2у — I) ~ 0, и кривая распадается на
пару прямых:
х + у + 3 = О и х + 2у — 1=0.
6.4-|_; ;|-о.
Кривая параболического типа.
Д =
- 1
1
-3
2
-3
1
1
- 1
2
— — 1 #= 0.
Кривая не распадается. Далее,
s = 2, 6=0 и <р (X) = Л2 — 2Л,
Л! = о, л2=2, у.
5'3]
ОПРЕДЕЛЕНИЕ НОВОЙ СИСТЕМЫ КООРДИНАТ
199
Каноническое уравнение кривой:
или
2у'2 ± /2х'=0,
,2= ± —L.
/2
Это — парабола.
7. 2| =
Кривая Параболического
типа.
1
2
- 1
-2
-3
= 0.
Эта кривая распадается
на пару
х + 2у + 1 = 0,
параллельных прямых*,
х + 2 у — 3 = 0.
Д =
2
4
— 2
8. б =
Кривая параболического
типй.
1
2
- 1
2
4
-2
= 0,
Д =
— 2
1
и кривая состоит из двух совпавших прямых-.
f (х, у) = (х + 2у — I)2 — 0, х + 2у — 1 = 0.
Кривая параболического типа.
и кривая представляет собой «пустое множество» точек — она
распадается иа пару параллельных «мнимых прямых»-.
f (х, у) = (х + 2у + I)2 + 1 = (х + 2у + 1 + ») (х + 2у + 1 — г) = 0.
§ 3. Определение центра и главных осей центральной
кривой. Отыскание вершины и оси параболы
В этом параграфе мы будем предполагать, что
Д=#0, т. е. что кривая не распадается на пару
прямых.
Пусть нам дано общее уравнение второго поряд-
ка (1). Найдем собственные значения Ха матри-
20'2
КРИВЫЕ И ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА (ГЛ. VII
цы (4)-и соответствующие им собственные векторы
бр е'2. Мы знаем, что в базисе, образованном этими
векторами, квадратичная форма «цх2 + 2ai2xy + а22у2
приводится к сумме квадратов М' + к2у', а урав-
нение (1) — к виду (6). Собственные векторы е' и е2
матрицы (4) находятся, как известно, из систем урав-
нений
«пМ + а{2ух = Mi,
«12Х1 + а2чУ\ = ^\У\
аих2 + апУ2 — M-v2>
«12^2 + а22у2 ~ ^2Уг>
и
каждая из которых, поскольку ее определитель
Пц П]2
«12 «22 М
i=l, 2,
равен нулю, сводится к одному уравнению:
(«и — ^1) xt + П12г/1 = 0 для первой системы,
(«и — Х2)х2 + а12у2 = 0 для второй системы.
Следовательно, для е\ — у^ имеем
У1__ ~ Ди
*1 ~ Д12 ’
а для е'2 = (х2, г/2)
У2 ^2 — Ди
х2 — а12
Таким образом, угловые коэффициенты новых осей
координат в старой системе равны
k{ =s —£11_ (для новой оси х, соответствующей М
Д12
И
k2 — ^.д^" (для новой оси у, соответствующей А,2).
В дальнейшем достаточно, как мы видели, лишь
переноса начала координат для того, чтобы уравне-
ние кривой привелось к каноническому виду; следо-
вательно, k\ и k2 определяют направления глав-
ных осей кривой (1).
§ 3] ОПРЕДЕЛЕНИЕ НОВОЙ СИСТЕМЫ КООРДИНАТ 201
Предположим, что мы рассматриваем Централь-
ную кривую второго порядка, т. е. что 6¥=0. Для
того' чтобы найти центр кривой, т. е. начало новой
системы координат, воспользуемся следующим эле-
ментарным соображением. Мы уже видели, что если,
не меняя направлений осей, перенести начало коор-
динат в точку (а, |3), т. е. если положить
х = х' + а,
У = У' + $,
то уравнение (1) приведется к виду
altx'2 + 2al2xfy' + а22у'2 + f'x (а, р) / +
₽)/ + f(a, р) = 0.
Рассмотрим систему уравнений
4 f'xU. У) = + а12у + ау = 0,
, (15)
. У) = а12х + а22г/ + а2 = 0.
Так как ее определитель 6, по предположению, не
равен нулю, то она имеет (единственное) решение
а, р. Если перенести начало координат в точку (а, р),
то в уравнении кривой исчезнут члены с первыми
степенями х', у', и значит, новое начало коордийат
будет центром кривой. Таким образом, центр цент-
ральной кривой второго порядка (эллипса и гипер-
болы) определяется из системы уравнений (15).
Рассмотрим теперь нецентральную кривую
второго порядка (при 6 = 0). Так как мы условились,
что А=#0, то это — парабола. Собственные значения
матрицы (4) пусть будут Xj = 0 и Аг; направления
новых осей определяются по-прежнему:
(дЛЯ оси оу, соответствующей ?и)
а12 а12
И
k2 = ^2~~а11' (для оси Оу', соответствующей А2).
202
КРИВЫЕ И ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА [ГЛ. VII
Новое начало координат, т. е. вершину (а, р) па-
раболы, можно найти, воспользовавшись следующим
соображением. Для параболы, заданной канониче-
ским уравнением у2 = 2рх, ось Оу служит касатель-
ной в вершине. Новая ось Оу в старых координатных
осях имеет угловой коэффициент k2 = -^2 ~ . Так
а12
как она служит касательной к параболе в ее вер-
шине (а, р), то k2 должно равняться производной ух
в этой точке. Чтобы найти у'х, продифференцируем
уравнение (1) по х, считая у функцией от х; мы по-
лучим
f'x (х, у) + f' (х, у) у'х = О,
или
, == _ f'x(x,y)
Ух f'y(x,y)’
Следовательно, в вершине (а, р)
₽)
КО >
/>.₽)
откуда
f>,₽) + ^>>₽) = 0.
Таким образом, координаты вершины (а, Р) пара-
болы можно найти, решив систему уравнений, состоя-
щую из уравнения
f'x(x,y) + k2f'y(x,y) = 0 (16)
и уравнения (1).
Выясним геометрический смысл уравне-
ния (16), в более подробной записи имеющего вид
(ацх + а12у + а,) + («12-^ + а22У + а2) = 0.
Это — прямая, принадлежащая пучку, который
определяется прямыми
ацх + а12у + й[ = 0 и а12х + а^у + а2 = 0.
Угловые коэффициенты — у1 й — ~ этих пря-
мых равны между собой, так как 6 = 0, и равны kp,
§’3]
ОПРЕДЕЛЕНИЕ НОВОЙ СИСТЕМЫ КООРДИНАТ
203
следовательно, эти прямые параллельны новой оси
Ох. Значит, и принадлежащая определяемому ими
пучку прямая (16) тбже параллельна новой оси Ох:
Но так как она проходит через вершину, то это —
ось симметрии параболы, ее главный диаметр.
Примеры. Для кривых 1, 4 и 6 предыдущего парагра-
фа найти новые системы координат и построить графики этих
кривых.
Решение.
1. Зх% •— %ху + + 2х — 4г/ +1=0, А; — 4, А-з — 2.
Направления новых осей:
ki = - = — 1 (ось Ох ),
2 — 3
k2 — —— = 1 (ось Оу').
Новое начало координат (центр кривой) находится из си-
стемы уравнений
f Зх — у + 1 = 0,
' t — х + Зу — 2 = 0,
1 5
откуда х = ——, у — -j-'. Уравнение оси Ох' (в старой системе
О о
координат):
5 ( , 1 ) , 1
Д-д-= - I x+g-l, или x + y = -^\
уравнение оси Оу':
5,1 3
#-у = х+-д, или у-х = -^.-
204
КРИВЫЕ И ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА [ГЛ. VII
График кривой изображен на рис. 15.
4. № + 2ху — у2 — 6х + 4у — 3 = 0, Л-j = /2, Х2 = — /2.
Направления новых осей:
= =/2- 1 (ось Ох');
*2=-(/2+1) (ось Оу').
Новое начало' координат находится из системы уравнений
х + у — 3 = О,
х — у + 2 = О,
5
1
откуда х = -g,
координат):
1/ = у
Уравнение оси Ох' (в старой системе
//--| = (/2-1)(х-|);
уравнение оси
Оу'-.
1/-4=-(/2+1)(х-1).
Графи» кривой изображен на рис. 16.
6. х1 — 2ху + у2 + 4х — 6г/ + 1 = 0,
Л.) = 0, Л.2 = 2.
Направления новых координатных
осей:
fei == —= 1 (ось Ох');
, 2—1 , , п
k2 = _ - = - 1 (ось Оу’).
Уравнение оси параболы
,(х-г/ + 2)-(- х + у-3),
или
5 А
х - У + у = 0.
Решая это уравнение совместно с уравнением кривой, находим
, 31 • 11
координаты вершины параболы: х—----у—--------—. Уравне-
ние новой оси Оу:
, 11 , / , 3! \ . . , ,21 .
z/ + -g-= - 1 lx+-g-l; или x + y + -j- = 0.
§4]
ПОВЕРХНОСТИ ВТОРОГО ПРРЯДКА
205
Выше мы нашли каноническое уравнение этой параболы в
виде у2 = ± Х‘ Знак в правой части определяется напра-
влением оси Ох'. Выражая у через х из уравнения кривой, по-
лучим ,
y = x + 3±V2x +8.
Следовательно, кривая расположена в области х —4, т. е.
справа от оси Оу'. Направив ось Ох' вправо, мы должны будем
в каноническом уравнении взять знак плюс ,(а направив, ось ОУ
влево — знак минус).
График кривой изображен на рис. 17.
§ 4. Исследование общего уравнения поверхности
второго порядка
В этом параграфе мы будем заниматься только приведением
общего уравнения поверхности второго порядка к каноническо-
му виду.
Пусть в прямоугольной декартовой системе координат в про-
странстве задано уравнение ’ ‘
f (х, у, г) = alxx2 + 2аХ2ху + а22у2 + 2a13xz + 2а23т/г 4- a33z2 4-
+ 2а хх + 2а2у + 2а3г 4-а = 0. (17)
Рассмотрим квадратичную форму от трех переменных:
ах хх2 + 2аХ2ху + а22у2 + 2aX3xz + 2а23«/г 4- а33г2.
В некотором, тоже ортонормированием, базисе она приводится
к сумме квадратов:
Ххх' 4- \2у' 4- •
При этом уравнение (17) приводится к виду
Ххх' + &2у' 4-Х3У 4- 2Ьхх' 4- 2&2уЛ 4- 2b3z’ + Ь = 0.
Здесь возможны три случая:
1. Все X, отличны от нуля.
2. Одно из Лг равно нулю.
3. Два из равны нулю.
Рассмотрим каждый из них отдельно.
I. Л.1Л.2Х3 =/= 0.
Точно таким же образом, как и в случае кривой второго поряд-
ка, можно избавиться от членов первой степени:
(х' 4- -у-? 4- 4- 4- h (z' 4- 4- с = 0.
\ Л1 / \ Лг / ' л-з /
20b
КРИВЫЕ И ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА [ГЛ. VII
Сделав подстановку
х" = х' +А
Г = / + -Х
*',2
г" = г' +
Аз
т. е. выполнив некоторый параллельный перенос осей координат,
мы получим уравнение
А^х"2 + A2i/"2 + A3z"2 + с= О,
Это — уравнение центральной поверхности второго порядка
(новое начало координат является ее центром).
Будем считать, что с 0 (в противном случае умножим
уравнение на —1). При с<0 возможны следующие случаи:
1. А, > О, А2 > 0, А3 > О— эллипсоид.
2. Л[ > О, А2 > О, А3 < 0 — однополостный гиперболоид.
3. At>0, А2<0, А3 < 0 — двуполостным гиперболоид.
4. Х[<0, А2<0, А3 < 0 — «пустое множество-» точек, (его на-
зывают также «мнимым эллипсоидом»).
Если с — 0 и все А; одного знака, получается точка («мни-
мый конус»), при с = 0 и А/ разных знаков — конус.
II. Один из коэффициентов А, равен нулю; пусть, например,
Аз = 0. Тогда соответствующим переносом начала координат
уравнение поверхности можно привести к виду
A1x,2 + A2i/,2 + 2&3z, + 6 = 0. (18)
Здесь возможны случаи 63 = 0 и 63 =£ 0.
При &3 — 0 уравнение приводится к виду
AjXz -Т A2r/Z Т&“0.
Это — уравнение цилиндрической поверхности, вид которой опре-
деляется её направляющей + Х2у' + Ь = 0 в плоскости
х'О'у' (Эллиптический цилиндр, гиперболический цилиндр, пара
пересекающихся плоскостей, одна прямая, или пара «мнимых
плоскостей», пересекающихся по вещественной прямой, «пустое
множество» точек, или «мнимый эллиптический цилиндр»).
При £>з#=0 уравнение (18) приводится к виду
' А^"2 + Л21/"а + 2&3z" = 0.
Если AiA2 > 0, это —- эллиптический параболоид, при
AiA2 <0 — гиперболический параболоид.
III. Среди чисел А, два равны нулю; пусть, например, Аг = 0
и Л3 = 0. Уравнение (17) приводится к виду
А]Х'2 + 2b2y’ + 2b3z' + b = 0. (19)
§ 41
ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА
207
Если 62 = 0 и 63 = О,— это пара параллельных плоскостей;
различных при Л.16 < О, совпадающих при b =0 и «мнимых»—-
при Л.16 > 0.
Наконец, если хотя бы один из коэффициентов Ь2, Ъ2 отли-
чен от нуля, в уравнении (19) положим
х' = х",
,... Ь2у"+Ь3г"
Vbl+bf ’
b3y" — b2z"
Vbl + bj '
что, как легко видеть, отвечает переходу к новому (гоже орго-
пормированному) базису с матрицей перехода
"10 О
о &3
У &2 + &з У б| + 63
О ~ Ьз
Vbl + Ц Vbl + bl
При этом уравнение (19) преобразуется в
Х|Х 4-2 У 1>2 4- б| у 4-6 = 0,
а это последнее уравнение, так как У62 4- 63=7^0, посредством
переноса начала координат преобразуется в
Я/"2 + 2 У б| 4-б| У/Л = 0.
Это — параболический цилиндр.
Заметим, без доказательства, что, как и в случае кривой
второго порядка, при преобразовании уравнения поверхности
второгд порядка можно использовать инварианты. Здесь это
будут ,-
si = аи 4" а2з 4- а2з,
all а12 I dll а13 а22 а23
а12 а22 I I а13 а33 I I а23 а33
6 =
ГГц
П12
«13
а12
Ц22
О.2з
а13
а23
а33
208 КРИВЫЕ И ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА [ГЛ. VII
(с точностью до знаков — это коэффициенты характеристиче-
ского уравнения матрицы
“11 “12 <213 \
“12 а22 “23 1
- “13 “23 а33 J / ч
и определитель
“11 “12 “13 “1
, “12 “22 “23 “2
А =
“13 “23 “33 “3
0,2 а
Уравнение центральной поверхности приводится к виду
л.,*2 + л2г2 + X3Z2 + 4 = °-
Определитель А обращается в нуль в том и только в том
случае, если поверхность является конической или цилиндриче-
ской (в частности, распадается на пару плоскостей — различных,
совпадающих или «мнимых»).
ГЛАВА VIII
ОСНОВНЫЕ ПОНЯТИЯ СПЕЦИАЛЬНОЙ ТЕОРИИ
ОТНОСИТЕЛЬНОСТИ
§ 1. Двумерные пространства со скалярным
произведением
Пусть 7? — линейное пространство, в котором опре-
делено скалярное ^произведение, т. е. каждой паре
векторов х, у из R поставлено в соответствие (веще-
ственное) число (х, у) так, что:
1) (х, У) = (У, х),
2) (ахгу) = а(х, у),
3) (х + у, г) = (х, г) + (у, г)
при всех х, у, z из R и всех вещественных а. За-
метьте, что мы не .требуем выполнения условия-4
(стр. 136).
Длиной, или модулем, вектора называется корень
квадратный из его скалярного квадрата. При этом,
вообще говоря, ненулевой вектор может иметь нуле-
вую й даже мнимую длину. (Если (х, х) = —а2 < О,
то, по определению, |х| = ai, где а > 0, a i =]/—!.)
Если в пространстве R выбран базис, то скаляр-
ное произведение представляется симметрической би-
линейной формой
U, у) = 5 gikXiyk
i, k
от координат xf и yh векторов х и у. Соответствую-
щая квадратичная форма в некотором (вообще го-
воря, другом) базисе приводится к сумме квадратов
(х, х) = х2 + х2+ ... +х2-х2+1- ... -х2+9
210
К ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
[ГЛ. VIII
(§ 3 главы VI). При этом число р положительных и
число q отрицательных квадратов являются инвариан-
тами пространства R (закон инерции квадратичных i
форм, § 4 главы VI) й определяют его тип.
Так, для двумерного пространства (плоскости) R
возможны такие значения р и q:
1. р = 2, q = 0; I
. 1'. р — 0, q — 2;
2. р.= 1, q = 0;
2'. р = 0, <?=!;
3. р = 1, </ = 1.
В случае 1 в некотором (ортонормированием) ба-
зисе скалярный квадрат произвольного вектора х =
= Х1в! + х2е2 равен x2t + х|, и это пространство евкли- .
дово.
В случае V (х, х) = — xf — х%, и пространство |
несущественно отличается от евклидова.
В случае 2 (или 2', что почти то же самое) квад-
ратичная форма (х, х) содержит только один квадрат, >
и в некотором базисе (х, х) = (соответственно — х£).
Такая плоскость называется полуевклидовой. . j
Наконец, в случае 3 квадратичная форма (х, X) |
в некотором базисе приводится к разности квадратов |
х^ —х|; такая плоскость называется псевдоевклидовой. I
§ 2. Полу-евклидова плоскость *
Пусть R— двумерное векторное пространство с
полуевклидовой метрикой и ei, е2— такой его базис,
в котором скалярный квадрат (х, х) произвольного
вектора х = x^i + х2в2 равен х|. Тогда, в частности,
(elt ej) = O, (ег, е2)=1
и
(<?< + е2, ei + е2) = 1 = (в;, <?i) + 2(et, е2) + (е2, е2) =
— 2 (в1, е2) + 1,
откуда
(ei, е2) = 0.
Такой базис условимся называть каноническим.
§ 21
ЛОЛУЕВКЛИДОВА плоскость
211
Пусть х = + х2е2 и у у у ех + у2е2 — произ-
вольные векторы из R; тогда их скалярное произве-
дение (х, у) равно
Х1У1 (eb ех) + (хху2 + x2r/i) (еь е2) + х2у2 (е2, е2) = х2у2,
а модуль вектора х равен
| X I = У xl = [ х21.
Предположим, что другой, тоже кано-
нический базис в пространстве R, и
Й11 а12
. &21 а22 .
— матрица перехода от первого базиса ко второму,
т. е. что
— @хх&х “Ь «2|«2 И в2 = «j2«j "Т «22^2*
Тогда
(е1> е1) = Й21 ~ (е1> е1) = О’
откуда «21 — 0, и
(е2’ е2) ~ а22 = (б2> ei) ~ ’
т. е. «22 = ±1. Таким образом, матрица перехода от
одного канонического базиса к другому имеет вид
G11 fl12 z<\
. О ± 1 ]• ' ш
Зафиксируем теперь какой-то канонический ба-
зис «1, е2 и угол между векторами х = ххех + х2е2 и
У = У\вх + у2е2, по определению, положим равным
Так определенный угол, вообще говоря, не инва-.
риантен относительно перехода к новому (даже ка-
ноническому) базису. Посмотрим, какие еще ограни-
чения надо наложить на матрицу перехода для того,
чтобы угол (2) не зависел от системы (канониче-
ских) координат. При переходе к новому (канониче-
скому) базису с матрицей перехода (1) координаты
212
К ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
[ГЛ. VIII
векторов х и й соответственно преобразуются в
и
Х1 = ацХг+ й12г2> х2= ± Х2>
У\ = °И^1 + ^12^2’ У2 = —^2>
причем знаки у х2 и у2 одинаковы. Тогда угол меж-
ду векторами х и у в новом базисе в силу определе-
ния (2) должен, быть равен
^1 аНУ1+а121/2 ^11^1+4^2 =
Й2 х2 — У2 ' х2
У±__^_
у2 х2
он будет иметь прежнее значение в том и только в
том случае, если .«н = ±1. Поэтому, зафиксировав
один какой-то канонический базис, мы дальше будем
допускать только такие базисы е,, е'2, матрица пере-
хода к которым от базиса вь е2 имеет вид
' ± 1 v ’
.0 ±1.
(мы ПОЛОЖИЛИ <212 = К) .
Обозначим через До матрицу
Тогда, очевидно,
И 01 Г-1 01
0 -1] °[ о 1.
Рассмотрим теперь двумерное точечно-векторное
пространство, в котором расстояние между точками
Х(хьХ2) и У(йьЙ2К считается равным модулю век-
§ 2]
ПОЛУЕВКЛИДОВА плоскость
213
тора ХУ = (г/1—Xi, г/г— х2) в полуевклидовои мет-
рике, т. е. равным
\У2~Х2\',
это — евклидова длина проекции вектора на ось ор-
динат. (В частности, длина любого параллельного ej
отрезка будет равна нулю.) Окружностью радиуса
г с центром в данной точке ЛЦа^аг) будет сово-
купность всех точек, отстоящих от точки М на одно
и то же полуевклидово расстояние г — это пара пря-
мых, параллельных оси абсцисс и отстоящих от дан-
ной точки М на (евклидово) расстояние г (рис. 18, а).
м
о-
а)
Рис.
Центром такой окружности будет также любая точка
прямой, проходящей через М и параллельной тем же
прямым. Уравнение окружности радиуса г с центром
в точке Al(ai, а2) имеет вид
(х2 - а2)2 = г2.
В частности, уравнение «единичной окружности»
(окружности радиуса единица) с центром в начале
координат имеет вид
х|= 1.
Углом между прямыми называется угол между
параллельными им векторами. Если х = (g, 1) и
г/= (т], 1) — два вектора единичной длины, то угол
между ними равен
214
К ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
• [ГЛ. VIH
он измеряется той «дугой», которую эти векторы вы-
секают на «единичной окружности» (рис. 18,6). За-
метим, что в полуевклидовой метрике смежные углы
равны между собой.
Приведем несколько примеров теорем «элементарной полу-
евклидовой геометрии».
Теорема 1. Большая сторона треугольника равна сумме
двух других его сторон.
' Действительно, так как АВ — А'В', АС = А'С', ВС = В'С'
(рис. 19, а) и А'В' — А'С' + В'С', то АВ = АС + ВС, или
с = а 4- Ь.
Теорема 2. Больший угол треугольника равен сумме двух
других его углов.
Для доказательства проведем прямую СЕ || ВА (см.
рис. 19,6)). Тогда Z.ACE = A, zLECD = В, как углы с соответ-
ственно параллельными сторонами. Но ZACE + Z. E£D =
= Z.ACD = С и, значит,
С = А + В.
Теорема 3. Стороны треугольника пропорциональны про-
тиволежащим углам.
Для доказательства проведем CD || ei (см. рис; 19, а). Тогда
CD
А — —— (где CD равно модулю разности абсцисс точек D и
S 3]
ПСЕВДОЕВКЛИДОВА ПЛОСКОСТЬ
2}5
С —евклидовой длине отрезка CD), В=——, значит, А • b = В а,
откуда
' А = А
а ~ b
Из трех последних теорем видна определенная двойствен-
ность теорем полуевклидовой плоскости, выражающаяся в равно-
правии сторон и углов треугольника. Если в формулировках этих
теорем заменить слово «сторона» словом «угол» и наоборот, то,
из теоремы 1 получится теорема 2, а из теоремы 2 — теорема 1;
они двойственны друг другу. Теорема 3 двойственна сама себе.
Такой двойственности нет на обычной, евклидовой плоско-
сти, на которой имеются параллельные прямые (угол между ко-
торыми равен нулю), но нет «параллельных точек» (расстояние
между которыми равно нулю). Эта «несправедливость» устране-
на в полуевклидовой геометрии, где наряду с параллельными
прямыми имеются и «параллельные точки» (точки, лежащие на
одной прямой, параллельной е,)'.
Читателя, интересующегося дальнейшими подробностями, от-
сылаем к упомянутой в предисловии книге И. М. Яглома.
§ 3. Псевдоевклидова плоскость
Пусть R — двумерное векторное пространство с
псевдоевклидовой метрикой, и ei, е2— тот его базис,
в котором скалярный квадрат произвольного вектора
х = х1е1 + х2е2 равен х\ — х%. Тогда, в частности,
(<?i, ei)=l, (е2, е2)=-1
и
(е1 + е2, в] + е2) = 1 - 1 = 0 = (еь £,).+ 2(еь е2) + (е2, е2) =
= 2(eh е2),
откуда
(еь е2) = 0.
Такой базис будем называть ортонор мированным.
В ортонормированном базисе скалярное произведение,
векторов
х = х^ + х2е2 и у = у1е1 + у2е2
равно
(х, у) = хгух (eb ej + (х\у2 + х2у{) (еь е2) + х2у2 (е2, е2) =
= *1У1 ~ х2у2,
216
К ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
[ГЛ. VIH
а модуль вектора х равен
|х|=
Рассмотрим теперь двумерное точечно-векторное
пространство, в котором расстояние между точками
^(хьХг) и У(г/ь у2) считается равным модулю век-
тора XY = (yi—X\,ij2 — х2) в псевдоевклидовой мет-
рике, т. е. равным
V(У1 - Xi)2 - (у2 - х2)2
Окружность радиуса г с центром в точке
M(ai, аг) — это совокупность всех точек, удаленных на
одно и то же (псевдоевклидово) расстояние г от точ-
ки М. Значит, . уравнение окружности радиуса г с
центром в точке Af(ai, аг) будет иметь вид
fa — aj2 - (х2 - а2)2 = г2
(в евклидовой метрике — это гипербола, если г =/= О,
и пара пересекающихся прямых, если г = 0; см.
рис. 2Q). Радиус такой окружности может быть поло-
§ 3]
ПСЕВД0ЕВКЛИД0ВА ПЛОСКОСТЬ
217 ’
жительным, нулевым или даже «чисто мнимым». Так,
уравнение окружности положительного радиу-
са г — а с центром в начале координат будет иметь
вид
X ' ~ Х2 а2
(гипербола с горизонтальной вещественной осью).
Окружность мнимого радиуса г — ai (с тем же
центром) имеет уравнение
х2 — xi = fl2
(гипербола с вертикальной вещественной осью). Эти
два семейства окружностей разделяются окружно-
стью нулевого радиуса
Х1 — Х2 = О
(пара прямых — общие асимптоты обоих семейств
гипербол; см. рис. 21).
Векторы х и у ортогональны (это мы по-прежнему
будем записывать как х1.у), если их скалярное
1
218
, К ТЕОРИИ ОТНОСИТЕЛЬНОСТИ '
[ГЛ. VIII
произведение равно нулю, т..е. если <
(х, ?) = ад-х* = 0.
В этом случае
Х1 1/1
Х2 t/i
— угловые коэффициенты этих векторов,
, даемых в евклидовой метрике, взаимно
значит, векторы, ортогональные в псевдоевклидовой
рассматри-
обратны и,
Рис. 22.
метрике, при изображении
на евклидовой плоскости
симметричны друг другу
относительно биссектрисы
I—III координатных углов
(см. рис. 22, на котором
ei ± ег, «1 -L а2, bi ± Ь2).
Каждый вектор, у кото-
рого |Xi | = |х21, ортогона-
лен самому себе и имеет
нулевую длину. Для векто-
ров с вещественными дли-
нами | Xi | > | х21, а для век-
торов мнимых длин |Х1| <
рис. 22, на котором векторы elt
< I-K2I (см. тот же
ci, £>i имеют вещественные длины, векторы е2, а2, Ь2—
мнимые длины, а вектор с ортогонален самому себе
и |с| = 0).
§ 4. Псевдоортогональные преобразования
Линейное преобразование псевдоевклидова
пространства называется псевдоортогональным, если J
оно сохраняет скалярное произведение, т. е. если для J
всех х, у eR
^/у) = (х, у).
Пусть — псевдоортогональное преобразование
псевдоевклидовой плоскости /?, и
^_аПа12-
L ^21 °22 J ,;
§4] ПСЕВДООРТОГОНАЛЬНЫЕ ПРЕОБРАЗОВАНИЯ 245>
—его матрица в ортонормированном базисе е{, ец.
Мы имеем
«s/ej = а11е1 + а21е2,
s$e2 = al2et + <722е2.
По определению,
(^ви ^/e1) = (eI, ei)=l, (s^e2l rte2) = (e2, e2) = -1
и (^eb ^e2) = (el, e2) = 0,
т. e. 7 и ii — СЧ C4OJ СЧ OJ «3 «3 1 1 —< OJ СЧ — СЧ —1 <3 C3 (4a)
и -
0Ц 012 021 022 = 0- (46)
Из равенств (4а) видно, что ац#=0 и а22 Ф 0.
Из равенства (46) следует, что
Д21 _ д12 /к\
«и ~ а22 1
Обозначив равные отношения (5) через р, получим
021 = ₽Я11> /g\
012 = Р022‘
Подставляя эти значения в равенства (4а), найдем, что
аи ~ ₽Mi = 1 > откуда 0ц = ——^==
± |/ 1 - р2
и
₽Ч2 - а222 = - 1, откуда = —j^==-,
а значит, матрица преобразования S& имеет вид
1_________Р
А_ */.-₽ , (7)
± ± /Гн? _
причем, .как видно из равенств (6), оба элемента пер-
вого столбца, так же как и оба элемента второго
220
к ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
[ГЛ. VIII
столбца, берутся с одним и тем же Знаком. Матрицу
такого вида мы будем называть псевдоортогон'аЛьной.
Если обозначить через До матрицу
Р '
/1 -р2
1
то, как легко видеть,
1 Р
Ki - р2 V1 - р2
Р i
/i-р2 /i-р2
О'
1
/i-р2
Р
_/1-р2
Р '
/i-Р2
1
1
/Г-уГ
р
/1-р2
р -
VI - р2 = д Г -* 1 о
1 Л° 0-1
(преобразования s&i и sh. отличаются от осевой,
a — центральной симметрией).
Определители | До | = | Д31 = 1, | Aj | = |Д2 | = — 1.
Заметим, что, поскольку то найдется такое <р, что
1 , Р <
г .. = ch <р, - -Г — - = sh ф, и тогда
/1-Р2 /1-р2
. Г ch ф sh ф 1
° L sh ф ch ф] ’
Если р непрерывно меняется от 0 до 1 (или от 0
до — 1), концы векторов и ^0е2 непрерывно
скользят по единичным окружностям xf —х2=±1,
навстречу друг другу при р-> 1, и в противополож-
ные стороны при р->—1.
§ 5] ПРИНЦИП ОТНОСИТЕЛЬНОСТИ ГАЛИЛЕЯ 221
Пусть в псевдоевклидовой плоскости R имеются
два орт о нормированных базиса, et, е2 и е', е2, и
_ «и а12
. а21 а22 J
— матрица перехода от первого ко второму. Рассмот-
рим линейное преобразование si с матрицей А в ба-
зисе elt е2 и покажем, что оно —псевдоортого-
на л ь и о е. Действительно, по условию,
siex = alle[ + а21е2 = е{
и
^2 = «12е1 + а2262 = 4
Если х = X1C1 + х2е2 и у — ytei + — произволь-
ные векторы из R, то
six = x,sie.+ x„sie„ = х,е' + х,е'
и, аналогично,
= yxsiex + y,sie2 = у^' + у2е'.
А так как оба базиса, е2 и e'i, е2, —ортонорми-
рованные, то скалярное произведение
(six, siy) = Х\у{ - х2у2 = (х, у).
Значит, преобразование si — псевдоортогональное, й
его матрица имеет вид (7).
§ 5. Пространство событий.
Принцип относительности Галилея
Предположим, что некоторая точка М движется
вдоль прямой линии I, на которой установлена си-
стема отсчета S. Это значит, что на этой прямой рас-
положена шкала с соответствующими делениями и в
каждой точке прямой имеются синхронизированные
между собой часы.
Пусть в момент времени t координата точки А1
равна х. Это обстоятельство, или, как мы будем го-
ворить, «событие», можно отметить на некоторой
222
К ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
[ГЛ. VIII
(двумерной) плоскости Р точкой с координатами
(х, I). Плоскость Р называют пространством событий.
С течением времени координаты точки в простран-
стве событий меняются, даже если точка М не ме-
няет своего положения на прямой I — за счет изме-
нения времени t. Таким образом, существование точки
в пространстве и времени будет отмечено некоторой
линией в плоскости Р. Прямой эта линия будет в том
ii только в том случае, если точка М движется по
прямой I с постоянной скоростью и\ в этом случае ее
положение в плоскости Р будет определяться урав-
нением
х = ut + b,
где b — х(0)— положение точки в момент t = 0. Если
точка М неподвижна на прямой I («движется с ну-
левой скоростью»), то соответствующая ей в плоско-
сти Р прямая параллельна оси t.
Предположим, что вдоль прямой I равномерно со
скоростью v движется другая система отсчета, S',
причем в начальный момент времени начала коор-
динат обеих систем совпадают: х = х' = 0 при t = 0.
Тогда координата х точки М в системе S и коорди-
ната ее х' в системе S' будут связаны следующим со-
отношением:
х = х' + vt.
При этом считается, что время t в системе S и вре-
мя .t' в системе S' одно и то же: для одного и того
же события t = t'.
Преобразования
<8>
или, что то же самое,
f х' = х — vt,
\t' = t
называются преобразованиями Галилея. Из них диф-
ференцированием по t получаем
§5]
ПРИНЦИП ОТНОСИТЕЛЬНОСТИ ГАЛИЛЕЯ
223
ИЛИ
и = и' + V, (9)
где и — скорость точки в системе S, а и'—скорость
ее в системе S'. Это — закон сложения скоростей в
классической механике: скорость и точки в старой .си-
стеме отсчета равна ее скорости и' в новой системе,
сложенной с «переносной» скоростью v (скоростью
движения новой системы отсчета относительно ста-
рой). Дифференцируя по t еще раз, получаем
d2x _ dW
~ dt2 •
Таким образом, ускорения точки М в системе Sue
системе S' одинаковы, откуда делается вывод, что
одинаковые силы вызывают в обеих системах одина-
ковые следствия (описываемые вторым законом Нью-
тона: вызванное силой F ускорение прямо пропор-
ционально этой силе). Другими словами это выра-
жают, говоря, что законы механики инвариантны
относительно преобразований Галилея (принцип
относительности Галилея).
Вернемся к формулам (8). Они показывают, что
при переходе от системы S к системе S' координаты
точек пространства событий подвергаются линейному
преЬбразованию с матрицей
Это обстоятельство наводит на мысль ввести в про-
странстве событий полуевклидову метрику. Тогда
расстояние между событиями Л(х1Д1) и В(х2, t2) бу-
дет иметь определенный физический смысл: оно будет
равно |^2 — —временному интервалу между собы-
тиями А и В.
Далее, так как переход от одной системы коорди-
нат к другой задается матрицей (10), то инвариант-
ным окажется и введенное в § 2 понятие угла. Чтобы
выяснить его физический смысл, рассмотрим две рав-
номерно движущиеся по прямой I точки ЛГ и М2.
Скорости их обозначим соответственно через Ui и и2.
224
К ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
(ГЛ. VHI
В плоскости Р их движения определяются прямыми
/П1 и т2. Пусть Л0(Хо,/о) — точка пересечения этих
прямых (это значит, что при t = обе точки, Af ।
и М2, находились в одном и том же месте прямой
/ — имели абсциссу х0). Предположим, что при / = Л
точка Af] имеет абсциссу хь а при t = i2 точка М2—
абсциссу х2. Тогда угол
между прямыми т.\ и т2
(в полуевклидовой метрике)
равен углу между вектора-
ми Л0А| и Л0Л2, где Д'1 (хь/1),
Д2(х2,12) (рис. 23), и зна-
чит, он равен
— относительной скорости
движения этих точек.
При такой интерпретации расстояния и угла тео-
ремы 1, 2 и 3 на стр. 214 получают определенный
физический смысл, установить который предостав-
ляется читателю.
§ 6. Принцип относительности Эйнштейна
Из закона сложения скоростей (9) естественно сде-
лать следующий вывод: если система отсчета S' рав-
номерно движется относительно S со скоростью о,
и если свет в системе S распространяется со скоро-
стью с, то в системе S' его скорость должна быть
с — ив направлении движения системы S' и с + и —
в противоположном направлении. Однако в 1881 г.
американским физиком Майкельсоном было экспе-
риментально установлено, что на движущейся Земле
солнечный свет распространяется с одинаковой
скоростью во всех направлениях.
После попыток многих ученых как-то согласовать
результаты опытов Майкельсона с теорией, в 1905 г.
была опубликована фундаментальная работа А. Эйн-
штейна, в которой излагалась новая теория простран-
ства и времени — так называемая специальная теория
§ 6J ПРИНЦИП ОТНОСИТЕЛЬНОСТИ ЭЙНШТЕЙНА 225
относительности. Мы рассмотрим здесь только самые
основные, простейшие понятия этой теории.
В основу теории Эйнйпейна был положен закон по-
стоянства скорости света во всех инерциальных*) си-
стемах отсчета.
Таким образом, принцип относительности Галилея
состоит в невозможности установить равномерное дви-
жение одной механической системы относительно дру-
гой с помощью каких-либо механических эксперимен-
тов внутри этой системы. Принцип относительности
Эйнштейна утверждает, что это невозможно сделать,
исходя не только из механических, но также и из
каких-либо оптических явлений (связанных, как из-
вестно, с электромагнетизмом).
Но приняв закон постоянства скорости света, Эйн-
штейн вынужден был отказаться от предположения о
существовании абсолютного времени, годного для из-
мерения временных интерва/юв сразу во всех систе-
мах отсчета.
То, что эта относительность времени с необходи-
мостью вытекает из закона постоянства скорости све-
та, можно видеть на следующем простом примере**).
Представим себ§ очень большой по линейным разме-
рам поезд, скорость которого сравнима со скоростью
света («п оезд Эйнштейн а»). Пусть в этом поезде
у окна находится наблюдатель, который в некоторый
момент времени зажигает фонарик, испускающий луч
света в потолок. На потолке имеется зеркало, отразив-
шись от которого луч возвращается к наблюдателю.
Путь луча света с точки зрения этого наблюдателя —
дважды проходимый отрезок А В (рис. 24, а). Для на-
блюдателя, находящегося вне поезда, путь луча света
представится в виде ломаной линии, состоящей из бо-
ковых сторон равнобедренного треугольника, высота
которого равна АВ (рис. 24,6). Следовательно, путь,
*) В физике инерциальной называют такую систему от-
счета, в которой тело без действия на него внешних сил дви-
жется равномерно и прямолинейно.
**) Этот и следующий примеры заимствованы из брошюры
Л. Д. Ландау и Ю. Б. Румера «Что такое теория относи-
тельности», М., «Советская Россия», 1963.
Л. И. Голормчй
226
К ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
[ГЛ. VIII
проходимый светом, с точки зрения наблюдателя вне
поезда, больше, чем для пассажира поезда. А так как
скорость света постоянна, то время, которое потребует-
ся свету на этот путь по часам наблюдателя вне поезда,
будет больше, чем для пассажира поезда: часы внутри
поезда отстают по сравнению с часами на станции.
Закон постоянства скорости света делает относи-
тельным и понятие одновременности, что хорошо вид-
но на другом примере. Предположим, что в центре
вагона того же поезда Эйнштейна находится наблю-
датель, который в некоторый момент времени зажи-
гает фонарик. В дверях вагона имеется механизм, бла-
годаря которому двери открываются, как только до
них доходит свет. Наблюдатель в центре вагона уви-
дит, что заднйя и передняя двери открываются одно-
временно. С тбчки же Зрения наблюдателя вне поезда
передняя дверь вагона уходит от светового луча, тогда
как задняя идет к нему навстречу. Ввиду постоянства
скорости света, С точки зрения наблюдателя вне
поезда свет достигнет задней двери вагона раньше,
чем передней, и она откроется раньше.
Больше того, даже последовательность событий мо-
жет быть разной для этих двух наблюдателей. Так,
если (например из-за неисправности механизма две-
рей) задняя дверь откроется несколько позже, чем на
йее попадет свет, то, если эта разница во времени до-
статочно мала, наблюдатель вне поезда все-таки уви-
дит заднюю дверь бткры*вак5щёйся раньше, чем перед-
няя, хотя для наблюдателя в центре вагона последо-
вательность этих событий будет обратной.
§ 71
ПРЕОБРАЗОВАНИЯ ЛОРЕНЦА
227
§ 7. Преобразования Лоренца
Итак, мы вынуждены отказаться от предположе-
ния, что время — одно и то же во всех равномерно
движущихся друг относительно друга системах отсче-
та. Мы уже не можем считать, что для одного и-того
же события t' = t. Как же связаны между собой коор-
динаты х, t точки в системе S и координаты х', t' ее в
системе S', движущейся относительно S равномерно
со скоростью у? В классической механике эта связь
линейна (преобразования Галилея). Мы сохраним это
предположение о линейной зависимости х', t' от х, t.
Пусть в некоторый момент времени (начальный
для обеих систем S и S') их начала координат сов-
падают: х = 0, х'=0 при t = 0 и t'=0. Предположим,
далее, что при t = t' = 0 из общего начала координат
обеих систем пущен световой сигнал, принятый в си-
стеме S в точке х в момент t, а в системе S' — в точ-
ке х' в момент времени t'. Ввиду постоянства ско,-
рости света с
I X I I х' I
|тг1тгс’
откуда х2— c2t2 = 0 и х'2— c2t'2 = 0. Таким образом,
если выражение
х2-сЧ2 (11)
равно нулю в одной инерциальной системе отсчета, то
оно обращается в нуль и во всех остальных. Мы сде-
лаем теперь дополнительное предположение о том,
что выражение (11) вообще является инвариан-
том, т. е. что оно одинаково во всех инерциальных
системах отсчета.
Положив х = Xi и ct = %2 (и соответственно
х'= х' и ct' = x''), мы можем наше пространство со-
бытий рассматривать как псевдоевклидову плоскость,
в которой выражение (11), равное
у2 . у 2
л2’
является квадратом расстояния точки (хц х2) от нача-
ла координат, или, что то же самое, квадратом длины
228
к ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
[ГЛ. VIII
соответствующего вектора. Но базис, в котором квад-
рат длины вектора имеет такой вид, является орто-
нормированным. Ортонормированный будет по той же
причине и соответствующий базис системы S', а зна-
чит, матрица А перехода от базиса системы S к ба-
зису S' псевдоортогональна:
1. Р
±/1-₽2 ±/1-р2
Р 1
± Ki -Р2 ± Vi -Р2 -
(причем в каждом из столбцов стоит один какой-то
знак.) '
Следовательно,
6] +
± /Гнр ’
е2
fiei + е2
Рассмотрим сначала случай, когда оба знамена-
теля положительны, и матрица А имеет вид
Р ~
И-Р2
1 •
/1-р2
р
т/ f _ Q2
А —
Тогда координаты хр х2 и х', х'2 связаны соотноше-
ниями
Xj+pX2 PX|+.V2
Xl ~ /Тнр ’ %2 ~ УТ-Р2 ’
или, в старых обозначениях,
/= сг
1'1-Р2
х’ + Pcf
х~ /Т^р5 ’
(12)
• Выражая отсюда х' и t'
мулы
, X— pct
х - /~Р2 ’
через хп I, получим фор-
/' = -4=-.
У ! -Р3
(13)
« 7]
ПРЕОБРАЗОВАНИЯ ЛОРЕНЦА
229
Каков физический смысл параметра р? Предполо-
жим, что в системе S' покоится точка М\ пусть, напри-
мер, это будет начало координат х' = 0. По первой из
формул (13) для этой точки имеем
х — §£<=0,
или
X г,
т = рс.
Но у есть скорость точки М в системе S, равная,
очевидно, скорости системы S' относительно S. Следо-
вательно,
7)
у = рс, и р = _.
Подставив это значение р в формулы (12) и (13),
получим
Мы предполагали, что в матрице перехода от ба-
зиса бг к базису e'v е'2 все знаменатели положи-
тельны. Покажем, как исключить остальные случаи.
Если бы во втором столбце матрицы перехода стояли
знаки «—» (а в первом какие угодно), то мы получи-
ли бы формулы
± х' — vt'
и увеличению t' соответствовало бы уменьшение I, что
невозможно, так как при этом последовательность
всех событий в системе S' была бы обратной после-
довательности тех же событий в системе S. Если же
230
К ТЕОРИИ’ ОТНОСИТЕЛЬНОСТИ
[ГЛ. VIII
знаки минус стоят в первом столбце матрицы пере-
хода (а во втором столбце стоят знаки плюс), то по-
лучаются формулы
— х' + vt'
X = —-
- х' +1
t =—с -
/ >-?
от которых к формулам (14) можно перейти, изменив
знак у х', т. е. изменив на противоположное направле-
ние оси Ох'.
Преобразования (14) и (15) называются преобра-
зованиями Лоренца. Заметим, что формулы (15) полу-
чаются из формул (14) простым изменением зна-
ка у о.
Формулы Лоренца имеют смысл лишь при
| -у-1 < 1, откуда следует, что | v | < с, т. е. что движе-
жение со скоростью, превышающей скорость света, не-
возможно.
Если v мало по сравнению с с, то 1 —~ 1,
а тогда
х' ~ х — vt, t' ~ t.
Таким обазом, при малом v (по сравнению с с) пре-
образования Лоренца переходят в преобразования
Галилея классической механики.
Пусть Ох и Ot— координатные оси пространства
событий системы S, Ох' и Ot' — оси системы S'
(рис. 25). Как мы знаем, оси Ох' и Ot' симметричны
друг другу относительно биссектрис ММ' и NN' коор-
динатных углов первой системы. Ось Ot' можно рас-
сматривать как график движения начала координат
системы S' относительно S: для всех ее точек х' = 0.
Наоборот, ось Ot — это график движения начала ко-
ординат системы S относительно S'. Тангенс угла на-
клона оси Ot' к Ох по абсолютной величине равен
I с/ I _ с
I X I | а I ’
§ 8] НЕКОТОРЫЕ СЛЕДСТВИЯ ИЗ ФОРМУЛ ЛОРЕНЦА '231
где у = v — скорость движения системы S' относи-
тельно S. А так как | v | < с, то тангенс этот по мо-
дулю больше единицы, и значит, все временные оси
Для прямых ММ' и NN' имеем: |~f| —1, т е.
|о| = с; во всех системах отсчета это — график дви-
жения со скоростью света.
§ 8. Некоторые следствия из формул Лоренца
1. Правило сложения скоростей.
Из равенства (15) получаем
dx' _ dx' . dt'
~dir ~ ~dt~ ' dt
v dx
c2 dt
c2 dt
u — v
-^-+1
c2
232
К ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
• [ГЛ. VIII
или
(16)
откуда
и’ + V
Это — новая формула сложения скоростей.
Если и = с, то из формулы (16) получаем
и обратно, если и' — с, то и
Если и и v малы по сравнению с с, то и' & и — и.
2. Относительность одновременности.
Предположим, что события Л и В в системе S про-
исходят в один и тот же момент времени t в точках с
абсциссами и %2- Тогда в системе S' по второй из
формул (15) эти события будут происходить в момен-
ты времени
V
z ~ ~с~2~ Хз +
откуда
, (Х1 ~ *г)
т. е. события, одновременные в одной системе отсчета,
не. будут- одновременными в другой. При этом раз-
ность t'j — ti может быть как положительной, так и
отрицательной, в зависимости от знака разности
Xi — х2. Это хорошо видно на чертеже; если события
§ 8] НЕКОТОРЫЕ СЛЕДСТВИЯ ИЗ ФОРМУЛ ЛОРЕНЦА 233
А и В одновременны в системе S, то отрезок АВ дол-
жен быть параллелен оси Ох, а если они одновремен-
ны в системе S', то он должен быть параллелен
оси Ох'.
Больше того, даже последовательность событий мо-
жет быть в системах S и S' не одинаковой. Так, на
рис. 25 события А и А' одновременны в системе S
(ЛЛ'||Ох), причем А' происходит, очевидно, позднее
О, а следовательно, и Л в системе S происходит по-
сле О. В системе S' одновременны события Л и А"
(АА" || Ох'), и значит, событие Л (вместе с А") пред-
шествует 0.
Здесь, естественно, возникает такой вопрос: не
может ли так случиться, что, например, событие О, в
системе S послужившее причиной события А, в систе-
ме S' окажется происходящим после А, что противо-
речило бы принципу причинности. Покажем, что' на
самом деле этого быть не может.
, Точки, отвечающие событиям, которые в системе S
происходят после события О — это все те и только те
точки, которые лежат выше оси Ох; точки, отвечаю-
щие событиям, которые происходят после события О
в системе S' — это точки, лежащие выше оси Ох'.
Так как все пространственные оси проходят внутри
угла MON' (см. конец § 7) и, очевидно, каждая такая
прямая служит пространственной осью некоторой си-
стемы отсчета, то пересечение всех полуплоскостей,
лежащих выше какой-либо из пространственных
осей, — это угол MON, заполненный всеми теми и
только теми событиями, которые следуют за О во
всех системах отсчета (его можно назвать «областью
будущего»). Аналогично, угол AVON' представляет
собой множество всех тех событий, которые во всех
системах отсчета происходят до события О («об-
ласть прошедшего»).
Точки же, лежащие в углах A1ON' и NOM', отве-
чают событиям, которые в одних системах отсчета
предшествуют О, в других — следуют за О. Однако ни
одно из этих событий не может иметь своей причиной
событие О. Действительно, если событие О послужило
причиной события Л (х, I) (см. тот же рис. 25), то
234
К ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
[ГЛ. VIII
какое-то возмущение должно успеть дойти от О до А.
Однако это невозможно, так как длина вектора ОА
вещественна и, значит, для него во всех системах от-
счета
х2 — с2/2>0, т. е. х2>с2/2,
откуда
X
и значит, скорость v = — такого возмущения должна
была бы быть больше скорости света, что невозможно.
Аналогично показывается, что для любых двух со-
бытий А и В закон причинности не нарушается: если
А может служить причиной В, т. е. если существует
сигнал, распространяющийся (в данной системе от-
счета S) от А к В со скоростью v < с, то А предше-
ствует В во всех инерциальных системах отсчета.
3. Сокращение длин.
Пусть в системе S покоится стержень длины /; ко-
ординаты концов его обозначим Xi и х2, где Xi < х2;
тогда
t = Х2 — Хр
Для того чтобы измерить длину Г стержня в систе-
ме S', надо отметить координаты его концов в какой-
то (один и тот же!) момент времени t'. Если эти
координаты х' и х'2, то по первой из формул (14)
откуда имеем
или, так как длина V стержня в системе S' равна
r=/y <i.
§ 8]
НЕКОТОРЫЕ СЛЕДСТВИЯ ИЗ ФОРМУЛ ЛОРЕНЦА
235
Таким образом, длина I' стержня в той системе
отсчета, относительно которой этот стержень дви-
жется, меньше, чем длина его в той системе отсчета,
относительно которой он находится в покое.
Поясним этот результат на чертеже. Пусть точ-
ка А лежит на пересечении гиперболы х2— сЧ2'= I2
с осью Ох (рис. 26); тогда в системе S ее расстояние
от начала координат равно I. Если AA!\\Ot, то точ-
ки А и А' в системе S находятся на одном и том же
расстоянии I от начала
координат. (Это — одна и
та же точка, покоящаяся
в системе S, в разные мо-
менты времени.) Но в
системе S' расстояние
точки А' от начала коор-
динат равно ОА'; оно
мейьше О В, равного I.
Наоборот, точка В,
лежащая на пересечении
гиперболы х1 — сЧ2 = I2
с осью Ох', в системе S'
находится на расстоя-
нии I от начала коорди- рИс. 26.
нат. Если BB'\\Ot', то
точка В' в системе S' находится от начала координат
на том же расстоянии I; однако в системе S расстоя-
ние точки В' от точки О равно ОВ' < ОА = I — реля-
тивистское, т. е. связанное с теорией относительности
сокращение длин взаимно.
Если v мало по сравнению со скоростью света, то
указанное сокращение длин в движущейся системе
отсчета настолько мало, что практически обнаружить
его невозможно. (Так как/' = / у 1 — Ц1 —
у2 \
2с2 } '
1 if Zf2 / I V \2
то разность I — I ~ -уу = у — ~ второго порядка
относительно -у. j Так, с космической ракеты (при
скорости 12 км] сек) диаметр Земли (12000 км) пока-
жется укороченным всего на I см.
236
К ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
[ГЛ. VIII
4. Замедление времени.
Пусть в системе S на неподвижных в ней часах
протекает время Т от до t2.
T = t2-tx.
Найдем значение t\, соответствующее t\, и t2, соот-
ветствующее t2, в одной и той же точке с абсциссой х'
в системе S'. По второй из формул (14)
откуда
где Т = t2 — t\ — отрезок времени, протекший в си-
стеме S', когда в системе S протекает время Т от
до t2; значит,
г = т У1 - - J < т.
Мы нашли, что в системе S', которая движется от-
носительно S, время течет медленнее, чем в самой
системе S. Поясним этот результат на чертеже. Рас-
смотрим гиперболу
X2 _ c2t2 = _ С2Т2
(рис. 27), и пусть точка А лежит на пересечении этой
гиперболы с осью Ot; тогда ее временное расстояние
от точки О, т. е. время, протекшее от события О до А,
в системе S равно Т. Если АА'ЦОх, то события А и
А’ одновременны в системе S. Но в системе S' время,
протекшее от О до А' равно О А' — оно меньше ОВ,
равного Т.
Наоборот, точка В в системе S' по времени уда-
лена от точки О на интервал Т. Если ВВ'\\Ох', то со-
бытия В и В' одновременны в системе S'; однако в си-
стеме S временное расстояние точки В' от О равно
О В' — оно меньше ОА, равного Т — Лоренцево замед-
ление времени взаимно.
§ 81
НЕКОТОРЫЕ СЛЕДСТВИЯ ИЗ ФОРМУЛ ЛОРЕНЦА
237
Если скорость v мала по сравнению со скоростью
света, то это замедление времени в движущейся систе-
Т (v V
ме отсчета составляет всего -j'lyl — оио второго по-
рядка относительно , и обнаружить его практиче-
ски невозможно. Так, земные сутки кажутся космо-
навту сократившимися меньше чем на -[qqqq сек.
5. Увеличение массы движущегося тела. .
Мы не будем рассматривать дальнейших выводов
теории относительности; упомянем еще только один фе-
номен— увеличение мас-
сы движущегося тела.
Если на тело действу-
ет постоянная сила, то
скорость движения его в
обычных условиях возра-
стает пропорционально
времени действия силы.
Однако ввиду существо-
вания предельной скоро-
сти эта пропорциональ-
ность не может сохра-
ниться и при больших
скоростях. При скоростях,
сравнимых со скоростью Рис- 27-
света, дальнейшее нара-
стание скорости замедляется — тело как бы оказы-
вает большее сопротивление действующей на него
силе. Можно сказать' что масса тела увеличивается^
При этом оказывается, что
m =
m0
где m— масса движущегося тела, v — скорость его
движения и т0 — масса покоя, т. е. масса тела в той
системе отсчета, относительно которой оно покоится.
Так, если в современном ускорителе электрон разго-
няется до скорости, отличающейся от скорости света
238
К ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
[ГЛ. VIII
всего на 30 км/сек, то его масса
увеличивается почти в 70 раз.
Мы рассмотрели движение точки по прямой ли-
нии. В общем случае, когда одна пространственная
система отсчета движется относительно другой равно-
мерно и прямолинейно, направление этого движения
можно принять за направление оси Ох, и тогда в
классической механике
х' = X — vt, Z/' = у, z’ — z, t' = t,
а в теории относительности
х' =
х — vt
» у' = У,
— Z,
Пространство событий в этом случае четырехмер-
но. Сокращение длин (только в направлении движе-
ния) и замедление времени в движущейся системе
-.Г\
отсчета происходят в том же отношении [/ 1 — .
ГЛАВА IX
ПОНЯТИЕ О ТЕНЗОРАХ
§ 1. Примеры тензоров
Прежде чем дать общее определение тензора, рас-
смотрим несколько примеров.
1. Линейная функция.
Пусть f(x)—линейная функция (§ 1 главы VI)
в n-мерном векторном пространстве R. Выберем в R
базис ei, е2, ..., еп, и пусть
х — xlet + х2е2 + ... + хпеп
— произвольный вектор из R. (Номера координат мы
условимся теперь писать сверху; целесообразность
такого обозначения будет видна из дальнейшего.)
Тогда
/ (х) = о^х1 + а2х2 + .., + апхп,
где а{ = 1(е{).
Перейдем к новому базису e'v е'2, ..., е', и пусть
новые базисные векторы получаются из старых по
формулам
п
e'i = e'ie1 + с2е2 + ... + = 5 c*ek. - (1)
k—l
В матрице перехода
Ч •••
240
ПОНЯТИЕ О ТЕНЗОРАХ
[ГЛ. IX
мы условимся теперь обозначать верхним индексом
номер строки, а нижним — номер столбца. Пусть в
п
новом базисе х = 2 х'1е1.-, тогда
• i = l
(3)
где
i^ciak- (4)
Таким образом, линейная функция f(x) в каждом
базисе определяется строкой из п чисел aj, а%,..., ап,
причем при переходе к новому базису эти числа пре-
образуются по формулам (4), т. е. точно так же, как
базисные векторы (1).
Примем теперь для сокращения записей следую-
щее соглашение (правило Эйнштейна): если в каком-
нибудь выражении один и тот же индекс, скажем i,
встречается дважды, один раз наверху и один раз
внизу, то имеется в виду, что по этому индексу произ-
водится суммирование (в пределах t — 1, 2, ..., п),
п
причем знак суммы У в этом случае опускается. Так,
( = 1
например, по определению,
п . п п
k Vi k VI k ,l i pq i » pq I
ctek= CiX =2jCiX , ЬГаг— z, bi4ari ит. n.
k=\ i = l i = l
В этих обозначениях равенство (1) можно переписать
так:
равенство (3)—-так:
f (х) = а\х'1,
а равенство (4)—так:
< =
Аналогично, если в одном и том же выражении
имеются по две или более пар одинаковых индексов
(каждый из которых стоит один раз наверху и один
§ 1]
ПРИМЕРЫ ТЕНЗОРОВ
41
раз внизу), то мы также всегда будем считать, что
по этим индексам производится суммирование, при-
чем все эти индексы независимо друг от друга про-
бегают значения 1,2, Так, например,
iktm VI • ilk VI m .
dmbip— 21 CtmOip, Ctipj— 21 Q-ipb И т> П.
i, m~\ i, / = 1
2. Вектор.
В заданном базисе еь е2, еп каждый вектор х
представляется строкой из п чисел (х1, х2, .... хп) —
его координат. В новом базисе е', е'г, ..., е'п тот же
вектор представляется другой строкой (х'1, х/2, . . ., х'п),
причем если (2) — матрица перехода от первого
базиса ко второму, то, как было показано в § 4
главы II,
xk = c’jx'1. (5)
Это — выражение старых координат через новые. Вы-
разим отсюда новые координаты х'1 через старые х’.
Пусть С-1 = [bl] — матрица, обратная матрице пере-
хода С. Тогда из равенства
i =
i ¥= j.
i = j,.
i ф j.
Умножив обе части равенства (5) на bk (и, естественно,
просуммировав по fe), мы получим
вытекает, что
Положим
С‘Ь^ = Ь^ = { q’
если
если
Тогда
I1’
Но,
если
если
clbt — Ь№ = б?.
blkxk = by^x'1 = 6‘х'1 = х'1
(так как д/ = 0 при i j и д/ = 1), или
х'1 = b‘.xk.
k
242
ПОНЯТИЕ О ТЕНЗОРАХ
[ГЛ. IX
Таким образом, новые координаты х'‘ вектора х
получаются из старых его координат xi с помощью
матрицы С-1, обратной матрице перехода С, причем
коэффициенты разложений xft по х* образуют стро-
ки матрицы С~1.
В двух рассмотренных примерах (линейная функ-
ция, вектор) есть нечто общее, позволяющее заклю-
чить их в рамки общего определения. И линейная
функция, и вектор в каждом базисе определяются
п числами, соответственно Я], аг, ..., ап и
х1, х2, ..., хп, причем при переходе к новому базису
эти числа преобразуются линейно — с матрицей С,
т. е. т а к ж е, как базисные векторы, в случае ли-
нейной функции, й с матрицей С-1,о б р а т н о й мат*
рице С, — в случае вектора. Коэффициенты линейной
формы (так же, как координаты вектора) представляют
собой пример тензора, если назвать тензором за-
данную в каждом базисе систему чисел, линейно
преобразующихся при переходе от одного базиса к
другому. Точное определение этого понятия будет
дано ниже; пока же мы только еще добавим, что оба
рассмотренных тензора являются одновалент-
ными, так как определяются системами чисел
щ, аг, .... ап или х1, х2, ..., хп, зависящими от од-
ного индекса. Коэффициенты линейной формы, при
переходе к новому базису преобразующиеся так же,
как базисные векторы, образуют тензор ковари-
антный, т. е. «сопреобразующийся», — преобразую-
щийся одинаково с базисными векторами. Координа-
ты вектора — пример контравариантного, т. е.
«противопреобразующегося» тензора.
Рассмотрим еще два примера.
3. Билинейная функция.
Пусть в n-мерном векторном пространстве R за-
дана билинейная функция А (х, у) (§ 2 главы VI).
Тогда, если х — х{е^ и у — yheh — произвольные век-
торы из R, то
А (х, у) —А (х1еь ykek) = xlyk A (eit ek) = aikxlyk,
&
ПРИМЕРЫ ТЕНЗОРОВ
243
§ И
где aiti = A (eit ek) ' в заданном базисе е1г е2, ..., ен
билинейная функция А (х, у) представляется билиней-
ной формой агьх1ук (по i и по k — суммирование!) от
координат векторов х и у с коэффициентами aik.
Перейдем к новому базису е{, е'2, е'п с матри-
цей перехода (2). Тогда, если х = х'1е'. и у — у'кек, то
А (х, у) = A (x'le', y'ke'k) = x'ly'kА (е', е') = a'ikx'ly'\ (6)
где
е0 = л(^е7> сК) = ^И(е/> (7)
Таким образом, билинейная функция Л(х, у) в
каждом базисе определяется системой из и2 чисел
aih, зависящих от двух индексов, причем при пере-
ходе к новому базису эти числа преобразуются по
закону (7), т. е. по каждому из этих двух индексов,
так же, как базисные векторы. Это—пример тен-
зора валентности два (зависящего от двух ин-
дексов), ковариантного по обоим индексам
(дважды ковариантного).
4. Линейное преобразование.
Каждый линейный оператор (линейное преобразо-
вание) в /г-мерном векторном пространстве Л в за-
данном базисе ei, е2, ..., еп представляется матри-
цей А = [аД] (здесь опять верхний индекс — номер
строки, нижний —номер столбца). При переходе к
новому базису е{, е'2, е'п с матрицей перехода С
эта матрица А преобразуется в
С~'АС
(§ 3 главы III)? Найдем, как выражаются элементы а'£
матрицы С~1АС через элементы аь матрицы А.
В матрице АС элемент p-Й строки и k-ro столбца
равен a’jCk. В матрице С-1ЛС элемент г-й строки и
/г-го столбца — это b{na?cL т. е.
р J f6
ak = ckbpar .
Таким образом, линейное преобразование в
каждом базисе определяется системой из п2 чисел а*к,
244
ПОНЯТИЕ О ТЕНЗОРАХ
[ГЛ. IX
занумерованных двумя индексами, нижним и верх-
ним, причем при переходе к новому базису эти числа
преобразуются по формуле (8) — по нижнему индек-
су так же как базисные векторы, а по верхнему —
с обратной матрицей, «контравариантно» базисным
векторам. Это — еще один пример тензора валент-
ности два (зависящего от двух индексов), в этом
случае один раз ковариантного и один раз
контравариантного (смешанный двухвалент-
ный тензор).
Рассмотрим смешанный двухвалентный тензор, ко-
ординаты которого в некотором фиксированном ба-
зисе ei, е2, ..., еп определяются равенствами
, ( 1, если i = /,
J ( 0, если i ф ].
В новом базисе е', е'2, ..е'п имеем
Таким образом, координаты тензора 6/ одинако-
вы во всех системах координат. Это объясняется тем,
что в первоначальном базисе ei, е2, ..., еп элементы
6/ составляют единичную матрицу, и значит, соответ-
ствующий тензор определяет тождественное преобра-
зование, матрица которого — одна и та же во всех
базисах.
§ 2. Определение и простейшие свойства тензора
Пусть в п-мерном векторном пространстве R в
каждом базисе задана система из пт+ч чисел
akk " k (занумерованных q верхними и р нижними
индексами, которые независимо друг от друга пробе-
гают значения 1, 2, ..., п), и предположим, что при
переходе к новому базису с матрицей перехода (2)
эти числа преобразуются по закону
„Л'з-Л cipbilbi2 b1^2'"^
C*PW'-' Wh-h'
(9)
§ 2] ПРОСТЕЙШИЕ СВОЙСТВА ТЕНЗОРА 245
Тогда мы говорим, что имеем (р + ^-валентный
тензор, р раз ковариантный и q раз контра-
вариантный. Числа а'^ £ £ называются коор-
динатами тензора.
Скаляр, т. е. величину, во всех системах -коор-
динат имеющую одно и то же значение, можно рас-
сматривать как тензор нулевой валентности.
Ясно, что если координаты двух тензоров одина-
кового строения (т. е. таких, у которых одинаковы
числа ко- и контравариантных индексов) совпадают
в одном каком-нибудь базисе, то они совпадают и во
всех остальных (и значит, эти тензоры равны), так,
как при переходе к новому базису координаты обоих
тензоров преобразуются одинаково. Поэтому для того,
чтобы задать тензор данного строения, достаточно
задать его координаты в какой-нибудь одной системе
координат. А это можно сделать без каких-либо огра-;
ничений: в качестве координат тензора в данном ба-
зисе можно выбрать совершенно произвольные числа.
Действительно, пусть в базисе е{, е2, ..., еп произ-
вольно заданы п^ч чисел .Тогда коорди-
наты соответствующего тензора в любом другом ба-
зисе найдутся по формуле (9), и нам остается только
проверить, что при переходе от любого базиса
е', е'2, ..., е'п к любому другому базису е", е", ...
..., е" координаты полученного тензора тоже преоб-
разуются по формуле (9).
Покажем это на примере трехвалентного тен-
зора а^. Пусть при переходе от базиса е2, •••> еп
к базису Ср е', е'п имеем
(ю)
а при переходе от базиса ех, е2, ..., е„ к. базису
е", е", ..., с"
e-=^ek. (11)
Из равенства (10) получаем
b'ke'j = b!kC™em = b™em = ek, (12)
246 ПОНЯТИЕ О ТЕНЗОРАХ [ГЛ. IX
а из равенства (11) —
б1' е" = Ь1 ске„ = е. = е . ' (13)
т i m i к т к т
Здесь матрица [б’]—обратная к матрице [с'], а ма-
трица [б'] — обратная к [с£]. Из равенств (11), (12),
(10) и (13) следует, что
e7 = ^eft = c|6/e; = d/e;
и
е’ = сте = стЬ’: е" = Не".
/ у т у mi ' / i
Таким образом, матрицей перехода от базиса е[,
е', ..., е'п к е", е".е" будет матрица
а обратной к ней — матрица
Мы имеем
a?=c"bW! (14)
И
&k — Ck&mbltth •
Из равенства (14) получаем
Ь^а'М = ММ =
• = (блс“) as* = = аГ.
Подставляя это значение а™1 в равенство (15), будем
иметь
a'k'1 = CkbmblbhCp с19аРЧ =
- аРч =
т. е. формулы преобразования координат тензора при
переходе от базиса е[, е', ..., е' к базису е", е'^, ...
е" имеют в точности такое строение, какое тре-
буется. В общем случае доказательство аналогично.
Отсюда вытекает, что если, например, х{ — произ-
ПРОСТЕЙШИЕ СВОЙСТВА ТЕНЗОРА
247
§ 2]
вольный одновалентный контравариантный тензор, то
его можно рассматривать как совокупность коорди-
нат некоторого векто-ра. Действительно, если в од-
ном каком-нибудь базисе еь е2, ..., еп взять вектор-
с координатами х’, х2, ..,, хп, то и во всех осталь-
ных базисах координаты этого вектора и заданного
тензора совпадут. Точно так же каждый дважды ко-
вариантный тензор atj можно рассматривать как со-
вокупность коэффициентов некоторой билинейной
формы, а каждый смешанный двухвалентный тен-
зор а} — как совокупность элементов матрицы неко-
торого линейного преобразования.
Тензор, координаты которого не меняют своего
значения при транспозиции любых двух индексов из
данного множества индексов i, j, ..., m (если все
эти индексы только верхние или только нижние), на-
зывается симметрическим по этим индексам.
Примером симметрического тензора может служить
совокупность коэффициентов симметрической били-
нейной формы.
Свойство тензора быть симметрическим не зависит
от выбора базиса. Рассмотрим, например, трехвалент-
ный тензор а^, и пусть в базисе вц е2, ..., еп
uji
Тогда в базисе е{, е'2> .... е'
а'н = c‘lcibrarsi
и
Заменяя здесь arst на aris, найдем, что
Но сумма не зависит от обозначения индекса, по ко-
торому производится суммирование, поэтому, заменяя
s на t, a t на s, получим
ар ~ с1с‘Ьга* ~ а'ц'
248
ПОНЯТИЕ О ТЕНЗОРАХ
[ГЛ. IX-
Кососимметрическим по данным индексам
i, j, . .. , m (только верхним или только нижним) на-
зывается тензор, координаты которого ak £ изме-
няют знак при любой транспозиции индексов из выде-
ленной группы (не меняясь при этом по абсолютной
величине). Свойство тензора быть кососимметриче-
ским по данной группе индексов тоже не зависит от
выбора базиса.
Примером кососимметрического тензора может
служить произвольная кососимметрическая билиней-
ная форма.
§ 3. Операции над тензорами
1. Сложение. Пусть даны два тензора одина-
кового строения, а^ / и • Сумма их
в каждой системе координат определяется равенством
Я ' 2 = ‘1*2 ••• ‘<7 , д‘1*2 ‘<7
akiki...kp akik2...kp^ Uklk2...kp
Легко видеть, что сумма двух тензоров будет тен-
зором такого же строения.
2. Умножение. Пусть даны два тензора
1( 2 " '<?
klk2 kp
И
_m.m„ ... mr
а Г
iJz is
какого угодно строения,
в каждом базисе определяется
np+q+s+r ЧИСел
Произведение их
как совокупность
Л/2 ... iqmim2 ...mr = i,Z2 ... i тЛ. ..mr
...is .../,*
Покажем, что произведение двух тензоров — тоже
тензор (в нашем случае валентности'/; -j- q + г + s,
р + s раз ковариантный и q + г раз контравариант-
ный). Действительно, в новом базисе
akk k = ChCk • • * Ckblbl ‘ • biatt t
B1K2 'p kl й2 “p ‘1 *2 lq tlt2‘"tp
§ 3]
ОПЕРАЦИИ НАД ТЕНЗОРАМИ
249
И
,m.m„... m_ h ft
ai I •/ Ci Ci
Ji'2 ••• ls 4 '2
h1, ml<
с, b„lb2
i S &1 ^2
.m glg2...gr
°srahlh2...hs
поэтому
г/'Л •• lqmlm2 m.
Ikxk2...kpij2... is
c ft, ft.
ckpc,c.
Rp '1 4
Л;М'
tp hlh2
— С? с.2
к\ k2
.1.1. ... i ,m m ... m
= < I i, a , , ,
klJ2 ' ’ ’ кр l^2
chsbl'bi2
iS 11 l2
ь\«ьт>ьт2
iq ^2
“Sr Z1 С fti hs
-ks~C\ ••• ЧС/1 ” C,'sl
т
S
. . Ь/'Г1
!q
^glg2'‘'gr
Ч''Л'" iphlh2-hs
Умножение тензоров некоммутативно. Рассмотрим,
например, произведение двух одновалентных кова-
риантных тензоров при п = 2. Координаты одного: Oi
и «2, координаты другого: Ь{ и Ь2. Произведение
dk = aibk — дважды ковариантный тензор, координа-
ты которого
Сц = Qj&j, С]2 = aib2, c2i~a2b[, с22 = а2Ь2.
Произведение тех же тензоров в обратном порядке —
дважды ковариантный тензор с координатами dih =
= Ьгак'.
~ = b^a^y d2[ ~ b2ai, d22 ~ b2a2.
Он, вообще говоря, отличен от первого.
Так как скаляр, т. е. величина, во всех системах
координат имеющая одно и то же значение, является
тензором нулевой валентности, то при умножении
тензора на скаляр (т. е. при умножении всех коорди-
нат тензора на этот скаляр) получается тензор того
же строения.
Вычитание тензоров одинакового строения сводит-
ся к умножению вычитаемого на —1 и сложению
(при этом получается, очевидно, тензор того же
строения).
3. Свертырание тензоров.
Эта специфическая для тензоров операция опре-
деляется следующим образом. Пусть дан, например
250
ПОНЯТИЕ О ТЕНЗОРАХ
[ГЛ. IX
тензор a% . Выделим в нем два какие-нибудь индек-
са, например, jap (один наверху, другой
внизу), отберем среди всех координат тензора те,
у которых эти индексы одинаковы, и сложим их все,
Мы получим
пИ = а11 + а12 И- ... + ain =
— свертку тензора а^ по индексам j и р.
Так, например, тензор a‘k при п — 2 имеет восемь
координат а’р а\2, а^, а’22, a2]V а212, а21, а2^. Свертывая
этот тензор по индексам i и /, получим
a\k + alk=bk’
или, подробнее: Ь^а’ц + а^, b2 = aj2 + а%2.
Свертывая тот же тензор по индексам i и k, по-
лучим а^ = с^, т. е.
С] = <4 + а22, с2 = а2у + а22.
Al =s д11 4-
и\2 и\12 ' и122»
h 1 — д 11 -L д!2
и22 и212'и222*
h2 = л^ 4~ д22
“l2 “112^u122>
= д21 -L д22
u22 u212 “ u222*
Еще пример. При свертывании тензора а1£
(при п = 2) по индексам / и I получаются восемь ве-
личин Ь1кт = а^1т или, подробнее:
А1 sss д11 -1- /7^2
“11 “ill “12Р
/)1 — Л 11 -1-
“21 “211 “22Г
ьи = 411 + 4L
ЬЪ = °^ + °%п
Покажем, что в результате свертывания тензора
получается снова тензор, имеющий на один нижний
и один верхний индекс меньше, чем исходный тензор.
Произведем, например, свертывание тензора ^а^р
по индексам / и р. Пусть В новом базисе
координаты исходного тензора имеют вид
cmcpctqb8b,ha^f
5 з]
ОПЕРАЦИИ НАД ТЕНЗОРАМИ
251
Выбрав координаты, у которых / = р, и просум-
мировав по j=l, 2, ..., п, получим
art = а'11. = cr cs,c(b{b!,aehf.
mq mjq m i q g h rst
Но с/Ьл = &ft, a blarst = afy = ajt.
Следовательно,
a'\, = cr c1 blagf.
mq m q g rt
В общем случае доказательство аналогично.
Операция свертывания может быть применена
к тензору и несколько раз. Так, Например, свертывая
тензор а1^г при п = 2 по индексам i и q и по ин-
дексам k и р, получим тензор или’ подробнее:
Ь\ = «Ш + а121 + «2X1 + fl22P ^2 = + а122 + <^2 +
А2 _ „121 J „221 । „122 i „222 1.2 _ „121 i „221 i „122 i „222
°1 а111 «121 + «211 + «221’ °2 «112 + «122 + Я212 + fl222'
При р-кратном свертывании тензора р раз ко- и
р раз контравариантного получается, очевидно, (инва-.
риантный) скаляр — величина, не зависящая от вы-
бора базиса. Это —один из способов получения чис-
ленных инвариантов. Так, при свертывании тензора
а', определяющего линейное преобразование по-
лучаем инвариант aj, называемый следом преобра-
зования (aj — это сумма элементов главной диагона-
ли матрицы А; ее инвариантность мы уже установили
в § 7 главы III: а‘ —это коэффициент при Z”"1 харак-
теристического многочлена преобразования ,$$).
Особенно часто операция свертывания применяет-
ся по отношению к произведению двух тензоров — hq.
индексам, взятым в разных сомножителях.
Если произведение тензоров а? и bhk свертывается пр
индексам / и h, мы будем говорить короче, что тен-
зоры aj и b’l свертываются по индексам j и h. Так,
например, при свертывании тензора а,- (определяю-
щего линейную функцию f(x)) с вектором х =
= (х1, х2, ..., х") получается скаляр щхг', равный,
очевидно, f(x).
252
ПОНЯТИЕ О' ТЕНЗОРАХ
[ГЛ. IX
При двукратном свертывании тензора аг;, опре-
деляющего билинейную функцию А(х, у), с парой
векторов х = (х1, х2, .... хи) и у = (у1, у2, .уп),
получается скаляр щ/СгД равный значению функции
А (х, у) для данных векторов х и у.
При свертывании тензора о', определяющего
линейное преобразование с вектором х =
= (х1, х2, ..., хп), получается контравариантный тен-
зор yi — ai.xl. Как следует из § 1 главы III, это —
заданный своими координатами у1 преобразован-
ный вектор stx (образ вектора х при преобразова-
нии st}.
Пусть даны два тензора, а} и bhk, определяющие
соответственно линейные преобразования st и <8.
Свертка их по индексам / и h — смешанный двухва-
лентный тензор dk = a!jbk, определяющий, следова-
тельно, некоторое линейное преобразование 3). Легко
видеть, что преобразование 3) равно произведению
st Я преобразований st- и $ (в смысле § 2 главы III).
Свертка тех же тензоров по индексам i и k соот-
ветствует произведению 3§st tex же преобразований
в обратном порядке.
4. Симметрирование и альтернирование тензора.
Пусть Aiii2...tk — произвольный тензор, у кото-
рого выделены какие-то k индексов й, й, . . . , й— все
только верхние или только нижние. Тогда тензор
(‘р .. lk)
где суммирование распространено по всевозможным
йерестановкам й, й, ..., й выделенных индексов,
будет, очевидно, симметрическим, а тензор
«а/-1’1''' ..
— кососимметрическим. Операции получения тензо-
ров Л(/1/2... и •••'*] из Данного тензора
§ 4] ТЕНЗОРЫ В ЕВКЛИДОВОМ ПРОСТРАНСТВЕ 253
называются соответственно симметрирова-
нием и альтернированием.
Так, на стр. 175 билинейная функция В(х, у) была
получена симметрированием, а С(х, у)—альтерниро-
ванием билинейной функции А(х,у).
§ 4. Тензоры в евклидовом пространстве
Пусть теперь 7? — «-мерное евклидово простран-
ство. Конечно, все, что говорилось о тензорах в произ-
вольном линейном пространстве, распространяется и на
этот случай. Но тензоры в евклидовом пространстве
обладают и некоторыми дополнительными свойствами.
В евклидовом пространстве 7? для любых двух век-
торов х, у определено их скалярное произведение
(х,у), являющееся симметрической билинейной функ-
цией. В заданном базисе ei, е2, .... еп оно представ-
ляется симметрической билинейной формой:
(*> У) = gikx'yk,
где gtk = (е«, еА). Взятые во всех системах координат,
величины образуют, как мы видели в § 1, два-
жды ковариантный тензор, который называется мет-
рическим тензором пространства R.
Свертка метрического тензора gth с вектором
х = (х1, х2, ..., ’хп)
Xi = gikXk (16)
является одновалентным ковариантным тензором.
Числа Xi также характеризуют вектор х, т. е. в не-
котором смысле тоже являются его координатами; их
можно назвать ковариантными координа-
тами вектора х, в отличие от его контравариантных
координат х’. Выясним геометрический смысл кова-
риантных координат. Так как
= gtkXk = (ег, eft) xk = (et, ekxk) = (eit x),
то ковариантные координаты х* — это проекции век-
тора х на базисные векторы. (Напомним, что контра-
вариантные координаты вектора х — это коэффициен-
254
ПОНЯТИЕ О ТЕНЗОРАХ
[ГЛ. IX
ты его разложения
х = xlet
по базису ei, е2, ..., еп.)
Двойная свертка gupdyb метрического тензора gn,.
с векторами х= (х1, х2, . .., хп) и у= (у', у2,..., уп) —
это скалярное произведение (х, у)-, двойная
свертка gthxixk его с вектором х •— скалярный
квадрат (х, х) векторах.
Определитель |^,й| матрицы отличен от нуля.
Действительно, при переходе к новому базису ранг
матрицы билинейной формы, в том числе и матрицы
[gift], не меняется. Но в ортонормированием базисе
матрица [£«] — единичная, и ее определитель равен 1;
следовательно, и во всех других базисах определи-
тель матрицы отличен от нуля.
Пусть будет матрица, обратная матрице
[,§«] в каком-то фиксированном базисе еь е2, ..., еп.
Тогда gikgk! = бу при всех i, /=1, 2, ..., п. Построим
дважды контравариантный тензор, коорди-
наты которого в базисе ei, е2, .,., еп равны gik', тог-
да координаты этого тензора во всех остальных
базисах определяются по формуле (9). В каждом но-
вом базисе е,, е'2, ..., е', ввиду тензорного характера
операций умножения и свертывания, будем иметь
и значит, координаты тензора gih во всех системах
координат образуют матрицу, обратную матрице
[gift]- Тензор gih называется контравариантным мет-
рическим тензором.
Переход от контравариантных координат вектора
к ковариантные его координатам по формуле (16)
можно назвать опусканием индекса. Чтобы поднять
индекс, т. е. перейти от ковариантных координат век-
тора к его контравариантным координатам, умножим
обе части равенства (16) на gn (и, конечно, просум-
мируем по i); мы получим
= g,lgi^k = 6fkxk = х>.
§ 4]
ТЕНЗОРЫ В ЕВКЛИДОВОМ ПРОСТРАНСТВЕ
255
В ортонормированием базисе
( 1, если i = k,
gik = (eh e&) = |Oj если /¥=Aj
и следовательно, х,- = х{, т. е. ко- и контравариантные
координаты вектора совпадают.
Операцию опускания или поднятия индекса в ев-
клидовом пространстве (эта операция носит вырази-
тельное название жонглирования индексами)' можно
применить к тензору любого строения. Пусть дан, на-
пример, трехвалентный тензор а^, один раз ковари-
антный и два раза контравариантный. Свертка его с
метрическим тензором
= (17)
будет дважды ковариантным и один раз контрава-
риантным тензором. Свертка
gP/a(fe = ₽pAft О8)
— трижды ковариантным, а наоборот, свертка
(19)
— трижды контравариантным тензором. Если оба
базиса ер е2, еп и ер е', ..., е'— ортонор миро-
ванные, то
fl, если i = k,
£‘k & I 0, если i^k,
и равенства (17)—(19) последовательно дают
= г»/ (1П
4Kk~^phk’ (is')
all = (19')
откуда, изменяя обозначения, получаем
В этом .случае ко- и контравариантные индексы при
переходе к новому базису ведут себя одинаково, и
закон преобразования тензора определяется исключи-
тельно его валентностью. ,
25S
ПОНЯТИЕ О ТЕНЗОРАХ
[ГЛ. IX
Последнее можно объяснить еще и следующим об-
разом. Если оба базиса, eh вг, е„ и е', е'2. ..е'п,
ортонормированные, то матрица перехода С от пер-
вого базиса ко второму ортогональна, т. е.
с~' = с'.
Но тогда = и в формуле (9) для преобразова-
.ния, например, тензора af,
a'k = с№аТ’
можно заменить одно или оба b на с, или, наобо-
рот, с заменить на Ь. Так, заменяя Ь‘ на cj, получим
= 2 c^b^af.
п
Здесь пришлось использовать знак суммы 2 >
«-1
так как индекс q, по которому происходит суммиро-
вание, стоит два раза наверху. Полагая af = arqp, по-
лучим для а!к закон преобразования в виде
а'!, = c?cq.blar = ,
lk k l г qp < В г qp’
т. е. тензор a!ik является дважды ковариантным и
один раз контравариантным. Но его координаты в
обоих базисах равны соответствующим координатам
тензора а^, один раз ковариантного и дважды кон-
травариантного.
Так, выше (§ 6 главы VI) мы уже видели, что
при переходе от одного ортонормирова иного базиса
к другому матрица билинейной формы (дважды кова-
риантный тензор) и матрица линейного преобразо-
вания (один раз ковариантный и один раз контра-
вариантный тензор) преобразуются одинаково.
й
ГЛАВА X
ОСНОВНЫЕ понятия ТЕОРИИ ГРУПП
§ 1. Примеры групп. Определение группы
Рассмотрим множество всех целых чисел. При
сложении двух целых чисел получается снова целое
число. Если одно из слагаемых равно (целому) чис-
лу 0, то сумма равна второму слагаемому: а + 0= а;
для каждого целого числа а имеется противополож-
ное к нему (целое) число —а, сумма которого с а
равна 0. Операция сложения чисел, как известно,
коммутативна (а 4- b = b + а для любых двух чисел а
и 6) и ассоциативна ((а + Ь) + с = а + (Ь + с) для
любых трех чисел а, Ь, с).
Далее, если из множества 'всех целых чисел выде-
лить подмножество чисел, делящихся на данное чис-
ло k, то и оно обладает такими же свойствами. Это
множество тоже замкнуто относительно сложения —
сумма любых двух чисел, делящихся на k, делится
на k, оно содержит 0 (нуль делится на любое число),
и если а делится на k, то и —а делится на k.
Аналогичными свойствами обладают и множество
всех рациональных чисел, множество всех веществен-
ных чисел или всех комплексных чисел — каждое из
них замкнуто относительно операции сложения; нуль
является одновременно числом рациональным, веще-
ственным и комплексным; у каждого комплексного
числа а имеется противоположное, —а, которое при
вещественном а будет вещественным, а при рацио-
нальном а — рациональным. Операция сложения в мно-
жестве комплексных чисел (а значит, и подавно в
множестве вещественных и в множестве рациональных
9 Л. И. Головина
258 . ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ГРУПП [ГЛ. X
чисел) коммутативна и ассоциативна. Все это — при-
меры «групп по сложен и ю».
Рассмотрим теперь множество всех отличных
от нуля вещественных чисел. Произведение любых
двух таких чисел — снова отличное от нуля число;
произведение любого числа а на (вещественное, от-
личное от нуля) число 1 равно а; для каждого (отлич-
ного от нуля!) вещественного числа а имеется обрат-
ное ему (и тоже отличное от нуля) вещественное чис-
ло а~1, произведение которого на а равно 1.
Аналогичными свойствами обладает и множество
всех отличных от нуля рациональных чисел, множе-
ство всех положительных вещественных чисел или
всех положительных рациональных чисел, а также
множество всех отличных от нуля комплексных пи-
ксел или множество комплексных чисел, по 'модулю
равных 1. Каждое из них замкнуто относительно опе-
рации умножения, все они содержат единицу и у ка-
ждого из их элементов имеется обратный элемент,
принадлежащий тому же множеству. Умножение ком-
плексных (а значит, и вещественных и рациональных
чисел) коммутативно (ab = Ьа для всех а и Ь) и ас-
социативно ((ah)с — а(Ьс) для всех а, Ь, с).
Это.— примеры «групп по умножению».
Можно привести и более неожиданный пример: груп-
пу по умножению образует, например, пара чисел,
1 и —1. Впрочем, множество, состоящее из одного
числа 1 (или 0) тоже образует группу по умножению
(соответственно по сложению).
Комплексные числа 1, i, —1, —i также образуют,
очевидно, группу по умножению.
Складывать можно не только числа, но, например,
векторы линейного пространства R, причем это сло-
жение подчиняется тем же законам, что и сложение
чисел: оно коммутативно и ассоциативно, в R имеет-
ся нулевой элемент 0 такой, что х + 0 = х для лю-
бого х <= R, и для всякого вектора х R имеется
противоположный ему вектор — х такой, что
х + (—х) — 0.
Складывать можно матрицы одного и того же
строения: [tn X м]-матрицы. Это сложение ассоциа-
§ 1] ПРИМЕРЫ ГРУПП. ОПРЕДЕЛЕНИЕ ГРУППЫ 259
тивно и коммутативно, имеется нулевая матрица —
матрица, состоящая из одних нулей, и у каждой мат-
рицы [яг«] имеется противоположная ей матрица
[—0;^] — такая матрица, что [я«] + [—я^] есть нуле-
вая матрица. Если складывать матрицы только с це-
лыми элементами aik, то и в сумме будут получаться
такие же матрицы, нулевая матрица имеет целые
элементы, и для каждой матрицы с целыми элемен-
тами противоположной ей будет тоже матрица с це-
лыми элементами. Все это — примеры групп по
сложению.
С другой стороны, и перемножать можно не толь-
ко числа, но, например, невырожденные квадратные
матрицы одного и того же порядка п с веществен-
ными (или только с рациональными или, наоборот,
с комплексными) элементами. Произведение двух та-
ких матриц тоже будет невырожденной матрицей
(теорема 3 главы III) с вещественными (соответствен-
но с рациональными, комплексными) элементами;
единичная матрица является невырожденной и у каж-
дой невырожденной матрицы имеется обратная
(тоже невырожденная и тоже с вещественными или
соответственно рациональными, комплексными эле-
ментами). Умножение матриц ассоциативно, однако
опо не коммутативно. Множество всех невырож-
денных матриц порядка п с вещественными (рацио-
нальными, комплексными) элементами представляет
собой пример н е-ко м м у т атив ной группы по
умножению.
Дадим теперь общее определение группы.
Определение 1. Группой называется множе-
ство G элементов а, Ь, ..., для которых определена
некоторая алгебраическая операция (обычно, назы-
ваемая умножением или сложением), ста-
вящая в соответствие каждой упорядоченной паре
а, b элементов из G третий элемент с = а°Ь, причем
так, что выполнены следующие условия-.
1. Эта операция ассоциативна-, для любых трех
элементов а, Ь, с из G:
(а ° Ь) ° с = а ° (Ь ° с);
9*
260
ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ГРУПП
[ГЛ. X
2. В G существует «нейтральный» элемент е
такой, что
а°е = е°а = а
для каждого а е G;
3. Для каждого элемента а из G существует «о б-
ратный» ему элемент а~х такой, что
а о а~} = а~' ° а = е.
Группа, в которой дополнительно выполняется
коммутативный закон:
4. Для любых двух элементов a, b s G
а ° b = Ь ° а,
называется коммутативной, или абелевой.
Группа, состоящая из конечного числа элементов,
называется конечной группой. Число элемен-
тов конечной группы называется ее порядком.
Группа, не являющаяся конечной, называется бес-
конечной.
В том случае, когда «групповая операция» а °b
называется сложением и обозначается знаком +,
группа G называется группой по сложению, или ад-
дитивной группой. В этом случае «нейтральный эле-
мент» е чаще всего обозначается символом 0 и назы-
вается нулем, а элемент обратный к а обозначается
через —а и называется противоположным к а. В том
случае, когда «групповая операция» называется ум-
ножением, а°Ь обозначается через ab, группа на-
зывается группой по умножению, или мультиплика-
тивной группой, а нейтральный элемент е иногда
обозначается просто 1 и называется единицей.
Пользуясь ассоциативным законом, можно опре-
делить произведение (сумму) трех и большего числа
элементов группы. Так как (ab)c = а(Ьс), то имеет
смысл говорить просто о произведении abc трех эле-
ментов, равном, по определению, (ab) с = а (Ь с). Так
же как для линейных пространств, можно доказать
единственность единичного (нулевого) элемента груп-
пы и единственность элемента, обратного (противо-
положного) данному.
§ 2] ГРУППЫ ПРЕОБРАЗОВАНИЯ 261
Легко видеть, что в каждой (например, мульти-
пликативной) группе однозначно разрешимы уравне-
ния
ах = b
(решением которого, очевидно, будет х = а~!&) и
уа = Ь
(для которого у = Ьа~1).
§ 2. Группы преобразований
Важный класс групп составляют так называемые
группы преобразований. Пусть М — произ-
вольное множество. Преобразованием множества М
мы теперь будем называть любое взаимно однознач-
ное отображение Р этого множества на себя. Это зна-
чит, что для каждого элемента х из М однозначно
определен его образ Рх = к' е М, причем каждый эле-
мент х' из М служит образом единственного элемен-
та х, называемого его прообразом.
Умножением преобразований называется последо-
вательное выполнение их одного за другим-, по опре-
делению,
(PQ) х = Р (Qx).
Умножение преобразований ассоциативно — это мож-
но доказать точно так же, как доказывалось выше
для линейных преобразований (§ 2 главы III), но, во-:
обще говоря, не коммутативно (не коммута-.
тивно уже умножение линейных преобразований) <
Роль единицы в этом умножении играет тождествен^
ное преобразование Е, ставящее в соответствие каж-
дому элементу х из М его самого. Для каждого пре-
образования Р множества М существует обратное
преобразование Р~\ ставящее в соответствие каждому
элементу х' из М его (единственный по условию) про-
образ х; при этом, очевидно, что
рр-1 = р-’р = £'.
Если множество М конечно и состоит из п элемен-
тов, то всевозможные взаимно однозначные ото-
бражения этого множества на себя называются
262 ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ГРУПП [ГЛ. X
подстановками, а соответствующая группа преобразо-
ваний обозначается через Sn и называется группой
подстановок из п элементов, или симметрической
группой п-й степени.
Рассмотрим подробнее симметрическую группу
третьей степени S3 — группу всех взаимно однознач-
ных отображений множества, состоящего из трех эле-
ментов а, Ь, с, на себя. Так как из трех элементов
можно составить всего шесть различных перестановок,
abc, acb, bac, bca, cab, cba,
то и число различных подстановок для них равно
шести. Обозначать их удобно следующим образом:
(й Ь с\ D —(а С\ р й Ь С\
l~\abc)' 2 \acbp 3 \cbap
D ( а b с\ р _(а b с\ р _( а b с\
4 \Ь ас/ 5 \Ь cap 6 \с abp
I а b с\
где, например, I а I ~ это такое отображение мно-
жества а, Ь, с на себя, при котором а-+Ь (а ото-
бражается в Ь), Ь-+с и с->а. Подстановки, отли-
чающиеся только порядком следования столбцов,
например,
( b а с\ /а b с\
\с b а) \Ь с а
не считаются различными,
это их последовательное
пример,
Р Р = (а b с}(а b
62 \с а Ь/\а с
Умножение подстановок —
выполнение; поэтому, на-
fl b с
с b а
з,
ибо в правом множителе а—>а, в левом а—»с, следо-
вательно, в произведении а —>с, и т. д. Единицей в
этом умножении служит тождественная под-
г, (а b с\ „ -
становкаР,= , , и для каждой подстанов-
\а b с)
ки имеется обратная ей:
РгХ = Р2, Рз1 = Рз, Pil = Pt, Р^ = Рб, Р^ = Рз.
5 2]
ГРУППЫ ПРЕОБРАЗОВАНИЙ
263
Для того чтобы получить подстановку, обратную дан-
ной, надо лишь поменять местами ее строки:
/а b с V1 _ / b с а\ (а b с\
\Ь с а) \а b с/ \с а b/
Группу Зз можно представить такой таблицей ум-
ножения:
Pl to Рэ Pi Pi Pi
Pl Pl р2 Pi Pi Pi
to сч 0, Pl Pi Pi Pi Pi
Рз Р3 «5 о. Pl Pi 1 03 Q,
р4 Pi pt Pi Pi. Pi Pi
р5 Pi Pi Pi Pi Pi Pi
(О О, р* Pz Pi Pi Pl Pi
где слева стоят левые множители -Pf, сверху — пра-
вые Pk, а на пересечении соответствующих строки и
столбца — их произведение PiPk- Таблицы такого рода
называются таблицами Кэли. Легко видеть, что
в каждой строке и в каждом, столбце таблицы Кэли
все элементы стоят по одному разу (так как из ра-
венства PiPj — PiPh умножением слева , на Р^1 полу-
чаем ' Pj = Pk, и из равенства PjPi^PkPi следует,
что Pj = Ph).
Группа З3 некоммутативна, так как, напри-
мер,
Р4Р^ = Р2, а Р5Р4 = Р3
(таблица Кэли этой группы не симметрична относи-
тельно главной диагонали).
Другим важным примером группы преобразований
может служить группа вращений правильного п-уголь-
HUiia. Пусть дан правильный многоугольник Лр42 - Ап
и пусть О — его центр. Рассмотрим совокупность
264
ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ГРУПП
[ГЛ. X
всевозможных поворотов плоскости вокруг ТОЧКИ О,
приг которых этот многоугольник совмещается сам
U с собой. Таких поворотов, очевид-
но, п:
а0 — поворот на /0 (тожде-
ственное преобразование),
/ 2л,
— поворот на Z,
а2 — поворот на Z — • 2,
ап-\ — поворот на Z — (п — I).
Умножение поворотов — это их последовательное
выполнение одного за другим:
@k ' &k+b
при этом, конечно, ап = а0 и ап+ь = a&. Поворот По яв-
ляется единичным элементом группы, и a~' = an_k.
Рассмотрим еще один пример — группу самосов-
мещений, или группу" симметрии, рбмба. Пусть
дан ромб ABCD (рис. 28). Он переходит в себя при
следующих преобразованиях:
Ь-, — тождественное преобразование,
Ь2 — симметрия относительно диагонали АС,
Ь3 — симметрия относительно диагонали BD,
Ь4 — симметрия относительно центра О.
Произведение любых двух из этих преобразова-
ний— снова одно из них. Эти преобразования обра-
зуют группу со следующей таблицей Кэли:
Ь1 Ьз Ьз bi
&1 bi bi Ьз bi
&2 bi bl bi Ьз
&3 Ьз bi bi bi
К bi Ьз Ьг bl
§ з]
ПОДГРУППА
265
§ 3. Подгруппа
Определение 2. Подгруппой группы G~
называется совокупность G\ элементов группы G, са-
ма являющаяся группой относительно заданной в
группе G операции.
Так, в аддитивной группе вещественных чисел со-
держится подгруппа целых чисел, а в ней при любом
k — подгруппа чисел, кратных k. Сама группа веще-
ственных чисел содержится в качестве подгруппы в
группе комплексных чисел.
В мультипликативной группе отличных от нуля
комплексных чисел содержится подгруппа вещесТВен-
.ных чисел, а в ней — подгруппа рациональных чисел,
подгруппа положительных вещественных чисел.
Л1ного интересных подгрупп содержит мультипли-
кативная группа невырожденных матриц порядка п
(полная линейная группа), например, с веществен-
ными элементами. Отметим, в частности, подгруппу
ортогональных матриц и подгруппу у и и м о д у-
л я р н ы х матриц (т. е. матриц с определителем,
равным 1). Подгруппами полной линейной группы
являются также группа матриц с определителем,
равным ±1? группа матриц с положитель-
н ы м определителем, группа диагональных
матриц, группа скалярных матриц, т. е. матриц
вида сЕ, где с — любое число, а Е— единичная мат-
рица, группа треугольных матриц, т. е. матриц,
у которых все элементы снизу (сверху) от главной
диагонали равны нулю, и другие.
Для того чтобы убедиться в том, что подмножеч
ство Gi группы G является ее подгруппой, надо преч
жде всего проверить, что произведение (сумма) лю-:
бых двух элементов из Gi принадлежит Gi и что если
а е Gj, то и. a~l е Gi. Но этого и достаточно, так как
ассоциативный закон, справедливый во всей группе
G, будет выполняться и для элементов из Gi, а эле-
мент е, как произведение аа~'- (как сумма а + (—а))
тоже будет принадлежать G\. Ясно, что подгруппа
коммутативной группы всегда будет коммута-
тивной.
266
ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ГРУПП
[ГЛ. X
Легко видеть, что пересечение двух подгрупп
группы G само является подгруппой в G.
Так, в аддитивной группе целых чисел пересечение :
подгруппы чисел, кратных трем, и подгруппы чисел,
кратных двум, будет подгруппой чисел, кратных
-шести.
Каждая группа имеет подгруппу, состоящую из
одной единицы (нуля), и каждая группа сама яв-
' ляется своей подгруппой. (Эти подгруппы называют-
ся несобственными.)
§ 4. Изоморфизм групп
В симметрической группе третьей степени S3
имеются три подгруппы второго порядка: {Pi, Рг},
{Pi, Рз}, {Pi, Р4} с таблицами Кэли:.
Если рассматривать их независимо от группы S3, они
отличаются друг от друга-только обозначениями эле-
ментов.
В симметрической группе S3 имеется одна под-
§ 4]
ИЗОМОРФИЗМ ГРУПП
267
Сравним ее с группой вращений правильного .тре-
угольника:
Эти группы тоже отличаются только обозначения-
ми элементов. Такие группы называются изоморф-
н ы м и.
Определение 3. Группы Gt и Gi называются
изоморфными, если между их элементами можно
установить взаимно однозначное соответствие, сохра-
няющее групповую операцию, т. е. такое, что если
xi> yi^@i> х2, y2^G2
и .
Xi х2, у{ *-+у2,
то
Xi о У1 +-+ х2 0 у2.
Можно показать, что все группы второго порядка
(а также все группы третьего порядка) между собой
изоморфны. Но для порядка четыре существуют
уже две неизоморфные между собой группы: группа
вращений квадрата и группа симметрии ромба.
Группа, изоморфная группе вращений правиль-
ного п-угольника называется циклической груп-
пой порядка п; такая группа состоит из степеней
одного из своих элементов: е, а, а2, ..., ап~}. Группа,
изоморфная аддитивной группе целых чисел, назы-
вается бесконечной циклической гру п-
п о й; эта группа тоже порождается одним из своих
элементов:
.2=1 + 1, 3=1+ 1 + 1, ит. д.
Заметим, что операции в изоморфных группах мо-
гут обозначаться по-разному. Так, мультипликативная
268
ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ГРУПП
[ГЛ. X
группа положительных чисел изоморфна аддитивной
группе вещественных чисел. Изоморфное соответствие
между ними устанавливается отображением
а In а.
§ 5. Группы преобразований плоскости
Рассмотрим еще некоторые группы преобразова-
ний (евклидовой) плоскости.
1. Движения.
Определение 4. Движением называется
такое преобразование (множества точек) евклидова
пространства (в частности, плоскости), при котором со-
храняются расстояния между точками-, если точка А
переходит в А' (мы бу-
В_______а_____ В дем писать в этом слу-
Z~ чае А —»А') и В —> В', то
/ длина отрезка А'В' равна
/ длине отрезка АВ.
---------------Такие преобразования
л а------------составляют группу, так
Рис. 29. • как если два преобразо-
вания не изменяют рас-
стояний между точками, то и их произведение обла-
дает тем же свойством; тождественное преобразова-
ние, не меняющее положения ни одной точки, яв-
ляется движением и преобразование, обратное движе-
нию, (эудет, очевидно, движением.
В группе движений выделяется подгруппа парал-
лельных переносов, которые определяются сле-
дующим образом. Пусть дан вектор а; параллельным
переносом на вектор а называется преобразование
Та, ставящее в соответствие каждой точке А плоско-
сти такую точку А', что вектор АА' равен а. Такое
преобразование является движением, так как если
А —* А' и В .-* В', то А А' = а и В В' = а, а тогда четы-
рехугольник АА'В'В — параллелограмм и, значит,
А'В' = АВ (рис, 29). Произведение ТаТь двух парал-
лельных переносов на векторы а и b тоже является
параллельным переносом Та+ъ (на вектор а + Ь),
§ 5]
ГРУППЫ ПРЕОБРАЗОВАНИЙ ПЛОСКОСТИ
269
и преобразование, обратное параллельному переносу
Та, является параллельным переносом Т_а (на век-
тор —а).
Таким образом, все параллельные переносы Т
плоскости образуют группу, являющуюся подгруппой
группы движений. Если при параллельном пере'носе
на вектор а = (ах,а2) точка А(х.у) переходит в точку
А'(х',у'), то вектор АА' = а, т. е. (х'— х, у'— у) =
= (ai, а2) и, значит,
x'-x = ai, У'-У = а2,
т. е.
х' = X + Я1,
у' = у + а2.
Рассмотрим, с другой стороны, всевозможные
движения плоскости, оставляющие на месте некото-
рую точку О; они, очевидно, тоже образуют подгруп-
пу группы движений плоскости.
Пусть В — произвольное движение с неподвижной
точкой О. Обозначим через Зв соответствующее пре-
образование векторного пространства, т. е. такое, при
котором вектор О А переходит в вектор ОА', где А'—
образ точки А при преобразовании Н. Покажем, что
Зв— линейное преобразование.
1. Пусть А—>А', В-+В'-, далее, пусть
ос = од + ов
и СС' (рис. 30, а). По условию, В'С' = ВС (так
как Н — движение), ВС = ОА (так как ОВСА — па-
раллелограмм) и ОА = ОА' (так как Н — движение).
Следовательно, В'С — ОА'. Аналогично,
А'С' = АС = ОВ = OB',
и значит, А'С' — OB'. Отсюда следует, что четырех-
угольник ОА'С'В' — параллелограмм, и значит,
ОС' =ОА' + ов\
т. е. если
ОА-^ОА7 и ОВ->ОВ',
то ___ ____ _____
О А + ОВ -> ОА' + ОВ7.
270
ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ГРУПП
(гл. к
2. Пусть Д -> Д' и В—> В', где
ОВ = аОД
(рис. 30, б). Тогда из равенств
О А' = О А, ОВ' = ОВ, А'В' = АВ
и из того, что точки О, А и В-коллинеарны, следует,
что точки О, А' и В' тоже коллинеарны и располо-
жены в том же порядке, что и точки О, А, В; а так
как
ОВ' = О В = | а | О А = | а | О А',
то ___ ______
ОВ' = аОА'.
Таким образом,
если ОЛ—>ОА', то аОА—>аОА'. .
Линейное преобразование Уб не меняет длин век-
торов, и значит, это — ортогональное преоб-
разование, т. е. либо поворот вокруг точки О
либо симметрия относительно некоторой оси, прохо-
дящей через точку О (§ 3 главы V). Такой же харак-
тер имеет и (точечное) преобразование Н\ поэтому его
тоже можно называть ортогональным.
Пусть теперь Q — произвольное движе-
ние. .Установим на плоскости прямоугольную декар-
§ 5]
ГРУППЫ ПРЕОБРАЗОВАНИЙ ПЛОСКОСТИ
тову систему координат; пусть точка О — ее начало
и О' — образ точки О при преобразовании Q. Произ-
ведение Н = Tq'oQ*) Движения Q на параллельный
перенос Тою будет движением с неподвижной точ-
кой О. Значит, //—ортогональное преобразование,
т. е. либо поворот вокруг точки О либо симметрия
относительно некоторой прямой, проходящей через
точку О. А тогда
Q = Тоо'Н.
Мы доказали, что каждое движение можно пред-
ставить в виде произведения некоторого ортогональ-
ного преобразования (т. е. поворота вокруг точки либо
осевой симметрии) и параллельного переноса**).
2. Преобразования подобия.
Определение 5. Преобразованием по-
добия с коэффициентом /г > О называется такое
преобразование евклидова пространства, в частности,
плоскости, при котором длины всех отрезков умно-
жаются на одно и то же число k: если А ~>'А' и
В-+В', то А'В' — kAB.
Всевозможные преобразования подобия на плоско-
сти образуют, очевидно, группу, содержащую в каче-
стве подгруппы группу движений.
Преобразование подобия, в некоторой системе ко-
ординат имеющее вид А(х, у)-* А'(х', у'), где
' х'= kx, y' = ky (fe=/=0), (1)
называется гомотетией с центром в начале этой
системы координат и с коэффициентом k. Каждое
преобразование подобия R с неподвижной точкой О
определяет в соответствующем, векторном простран-
стве некоторое линейное преобразование (это можно
проверить так же, как для движений). Пусть при
преобразовании подобия R (с неподвижной точкой
. *) Напоминаем, что произведение этих преобразований чи-
тается справа палево, т. е. сначала выполняется преобразование
Q, а затем параллельный перенос Т0,0 на вектор О'О.
**) Можно показать, что произведение поворота и парал-
лельного переноса является поворотом вокруг некоторой новой
точки.
272
ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ГРУПП
[ГЛ. X
О) длины всех отрезков умножаются на k. Выберем
систему координат с началом в точке О и обозначим
через К преобразование (1). Тогда преобразова-
ние Н = K~}R не меняет длин отрезков и, значит,
это — ортогональное преобразование, т. е. поворот или
симметрия. А тогда R = КН— преобразование подо-
бия с неподвижной точкой О (ц е н т р о - п о д о б и о е
преобразование) является произведением ортогональ-
ного преобразования и гомотетии с центром в точке О.
Пусть теперь U — произвольное преобра-
зование подобия, при котором начало коорди-
нат О переходит в точку О'. Тогда произведение Tq'qU
будет преобразованием подобия с неподвижной точ-
кой О, т. е. произведением ортогонального преобра-
зования и гомотетии:
T0'0U = КН,
откуда
U = ТОо'КН.
Мы доказали, что любое преобразование подобия
представляет собой либо произведение вращения во-
круг точки, гомотетии и параллельного переноса,
либо — произведение осевой симметрии, гомотетии и
параллельного переноса. В координатах
х' = k cos ф • х — k sin <р • у + аг,
у' = k sin ф • х + k cos ф • у + а2,
либо — в какой-то новой системе координат
x' = kx + at,
tf=—ky + a2.
3. Аффинные преобразования.
Пусть в аффинной плоскости установлена некото-
рая система координат. Рассмотрим преобразование
этой плоскости, при котором точка А(х, у) переходит
в такую точку А'(х', у'), что
x' = alix + a12y + a1, ,
у' = а21х + а22у + а2, W
S 51
ГРУППЫ ПРЕОБРАЗОВАНИЙ плоскости
273
где
Дц
а21
«12 -4- о
=7= 0.
Такое преобразование называется аффинным.
Из условия б ¥= 0 следует, что преобразование (2)
является взаимно однозначным, причем обратное
преобразование
= а-гг*' - а\2У' - <7iaS2 + а2а*
-а21х' +ацу'+а,а2| - а2ац
J д
с определителем
а22 _ 012
б 6 _ _1_ «22 ~ «12 _ 1 i Q
а21 <hi б2 — а21 дн 'д
d д
тоже будет аффинным.
Если наряду с преобразованием (2) задано аф-
финное преобразование
х" = Ьпх' + б12/ + 6i,
У" = Ь.21х'+ Ь22у'+ Ь2
с определителем
то. их произведен и е
х" = (&наи + Ь^а21)х+(Ьца12 + bl2a22)y + (bnat + Ь^ + Ь^,
у"=(&2ifln + ^22a2i) x^~(b2Iai2-}- b22a22)y + (&2i«i + b22a2 + Ь2)
тоже будет аффинным преобразованием, определи-
тель которого
£// _ Ьцйц + b12a2t buaI2 + bl2a221
b2ian + b22a2i b2lai2 + b22a221
равен произведению 6i62 (и значит, тоже отличен от
нуля).
Итак, перед нами снова группа — группа аффин-
ных преобразований плоскости. Аффинное преобразо-
вание (2) является, как легко видеть, произведением
274
ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ГРУПП
[ГЛ. X
(центро-аффинного) преобразования
х = + а^у,
у = а21х 4- а&у
(3)
(которому в векторном пространстве соответствует
невырожденное линейное преобразование) и парал-
лельного переноса Т;
х' = х + ait
у' = у + а2.
А так как (§ 4 главы V) невырожденное линейное
преобразование — это произведение самосопряженно-
го преобразования С (т. е. растяжения вдоль двух
взаимно перпендикулярных направлений) и ортого-
нального преобразования Н (поворота или симмет-
рии), то можно сказать, что произвольное аффинное
преобразование А имеет вид
А = ТНС = QC
(где Q — TH — движение), т. е. является произведе-
нием растяжения вдоль двух взаимно перпендикуляр-
ных осей и движения'.
§ 6.. Разложение группы по подгруппе
Рассмотрим сначала следующий пример. Пусть
G будет аддитивная группа целых чисел И А — ее
подгруппа, состоящая из чисел, кратных k. Разобьем
группу G на классы, отнеся к одному классу числа,
дающие при делении на'/г одинаковые остатки. Тогда
для того, чтобы два числа х и у попали в один и
тот же класс, необходимо и достаточно, чтобы их
разность делилась на k и, значит, принадлежала под-
группе А:
х — у = /гп А, Откуда х — у+а, где а е А.
Так мы получим, очевидно, k классов, считая од-
ним из классов и подгруппу А._
§ 6] РАЗЛОЖЕНИЕ ГРУППЫ ПО ПОДГРУППЕ ^ЯВВ|
Схематически это разложение группы целых чисел
по подгруппе чисел, кратных k при k = 5, можно
представить следующим образом:
А . . . —20, —15, -10, -5, 0, 5, ю, 15, 20, * . . .
Л + 1 ... -19, -14, -9, — 4, 1, 6, П, 16, 21, . . .
А + 2 ... -18, -13, -8, -з, 2, 7, 12, 17, 22, ...
А + 3 ... —17, -12, —7, — 2, 3, 8, 13, 18, 23, ...
А + 4 . . . -16, — И, -6, -1, 4, 9, 14, 19, 24, . . ..
ВведОхМ теперь операцию сложения в множестве
-самих классов. Пусть даны два класса В и С. Выбе-
рем в каждом из них по одному элементу (по пред-
ставителю), скажем, Ь^В и с^С, и сложим их,
а суммой, классов В + С условимся считать
класс, содержащий сумму b + с. Важно, конечно,
чтобы тот класс, в котором содержится сумма b + с,
не зависел от выбора представителей b и с в классах
В и С. Проверим, что это так. Если Ь' тоже принад-
лежит В, а с' е С, то
b — b' = kn{ и с — o' = kn2,
а тогда
(Ь + с) — (Ь' + с') = k (гц + п2)
делится на k и, значит, суммы b + с и Ь' + с' при-
надлежат одному и тому же классу.
Итак, определенная нами операция сложения
классов не зависит от выбора представителей в
них. Сложение классов ассоциативно и ком-
мутативно, так* как этими свойствами обладает
сложение в. самой группе G. Класс, совпадающий
с подгруппой А, играет роль нуля, так как в каче-
стве представителя из А можно взять нуль, и всегда
g + 0 = g; g е G. Наконец, для каждого класса В
имеется противоположный ему: если b е В, то
класс, содержащий —Ь, будет противоположным к В,
276
ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ГРУПП
[ГЛ. X
так как
Ь + (-Ь) = О^А.
Полученная группа (группа классов) называется
фактор-группой группы целых чисел по под-
группе чисел, кратных k. Она является?" очевидно,
циклической группой порядка k.
. Применим теперь аналогичную конструкцию в об-
щем случае. Пусть G — произвольная, на этот раз
мультипликативная группа, и А — некоторая ее под-
группа. Обозначим через хА совокупность всех эле-
ментов вида ха, где ае.4; хА называется левым
смежным классом группы G по подгруппе А.
Каждый элемент у, принадлежащий классу хА,
назовем эквивалентным х (будем писать //~х).
Отметим следующие свойства этого понятия:
1. Каждый элемент х эквивалентен самому себе
(х ~ х), так как х = хе е хА.
2. Если у х, то х ~ у. Действительно, если
у ~ х, т. е. у^хА, то у = ха, где аЕ=А, а тогда
х = уа~' е уА, и значит, х ~ у.
3. Если х — у и х ~ z, то х ~ z. По условию,
х ~ у, т. е. х = уа{ и у ~ г, т. е. y=za2, где а\, a2sA.
Но тогда х = za2ai е zA, и значит, х ~ z.
4. Если элементы х и у эквивалентны, то смежные
классы хА и уА совпадают. Действительно, пусть
хле хА, т. е. х' ~ х. Так как х ~ у то х' ~ у и зна-
чит, х' е уА. Аналогично, каждый элемент у' из клас-
са уА принадлежит и хА, следовательно, хА = уА.
5. Если элементы х и у не эквивалентны, то клас-
сы хА и уА не пересекаются. Действительно, если
z е хА -Г) уА, то z ~ х и z ~ у, а тогда и х ~ у.
Так вся группа G оказывается разбитой на свои
(непересекаюшиеся) левые смежные классы по под-
группе А, причем одним из этих классов является
сама подгруппа А. Если G — конечная группа, то все
смежные классы состоят из одного и того же числа
элементов (элементы смежного класса хА взаимно
однозначно соответствуют элементам подгруппы А,
так как если бы xai равнялось ха2, то щ было бы
равно а2). Отсюда вытекает важная
§ 6]
РАЗЛОЖЕНИЕ ГРУППЫ ПО ПОДГРУППЕ
277
Теорема Лагранжа. Порядок подгруп-
пы конечной группы является делителем порядка
группы.
Доказательство. Пусть G—конечная груп-
па порядка п 'и А — ее подгруппа порядка k. Разло-
жим группу G на левые смежные классы по подгруп-
пе А. Если / — число полученных классов, то, посколь-
ку каждый класс состоит из k элементов, общее чис-
ло элементов группы
п = kj,
и значит, п делится на k. Число / называется индек-
сом подгруппы А в группе G.
Каждый элемент g группы G порождает в ней
циклическую подгруппу {g}, состоящую из всех сте-
пеней этого элемента. Порядок подгруппы {g} назы-
вается порядком элемента g в группе G.
Ввиду теоремы Лагранжа порядок каждого эле-
мента конечной группы является делителем порядка
группы.
Всякая конечная группа, порядок которой — про-
стое число, является циклической, так как цикличе-
ская подгруппа, порожденная в ней любым из ее
элементов (кроме е), должна совпадать со всей
группой.
Аналогично левостороннему разложению, можно
построить правостороннее разложение группы G
по подгруппе А (на классы Ах). В коммутативном
случае оба разложения совпадают (состоят из одних
и тех же классов).
В некоммутативной группе левостороннее и право-
стороннее разложения могут оказаться различными.
Рассмотрим, например, разложение симметрической
группы S3 по ее подгруппе В={Р\,Р2}. Левосторон-
нее разложение состоит из классов
В, Р5В = Р4В = {Р4, Р5), Р3В = Р6В = {Р3, Р6],
правостороннее разложение — из классов
В, ВР6 = ВР4 — (Р,, Ps}, ВР3 = ВР3 = {Р3,-Ръ}.
278
ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ГРУПП
[ГЛ. X
В то же время левостороннее и правостороннее
разложения этой группы по ее подгруппе третьего по-
рядка А = {Pi, Р5, Р6} совпадают: каждое из них со-
стоит из двух классов
f Д=[Л, Р5,Р6] и В = {Р2, Р3, Р4}.
§ 7. Нормальный делитель
Обобщим теперь конструкцию, которая в начале
§ 6 привела нас к понятию группы классов (фактор-
группы аддитивной группы целых чисел. Пусть А —-
подгруппа произвольной группы G. Образуем всевоз-
можные левые смежные классы группы G по под-
группе А и попытаемся определить умножение этих
классов следующим образом: если даны два класса
В и С, выберем из них по представителю: Ь е В,
се С, перемножим этих представителей и в качестве
произведения ВС возьмем тот класс, в котором со-
держится Ьс. Необходимо только проверить, не зави-
сит ли это определение произведения классов от вы-
бора представителей в них?, Итак, пусть Ь' ~ Ь,
с' ~ с; будет ли произведение Ь'с' эквивалентно Ьс?
По условию, Ь' = Ьй! и с' = со2, откуда Ь'с' = baica2.
Если группа G коммутативна, то
atc = Сй[ (4)
и Ь'с' = &c(aia2), т. е. Ь'с' ~ Ьс.
В некоммутативной группе равенство (4), цообще
говоря, не имеет Места. Однако для нашей цели до-
статочно следующего, более слабого, чем коммута-
тивность, условия: достаточно, чтобы произведение
а\с можно было представить в виде са3, где а3— не-
который элемент из подгруппы А, вообще говоря, от-
личный от ai. Если это так, то Ь'с' = Ьс(а3а2), и Ь'с'
эквивалентно Ьс — произведение классов не зависит
от- выбора представителей в них.
Итак, мы будем теперь предполагать, что подгруп-
па А обладает следующим свойством: для каждого
элемента ае.4 и произвольного элемента g^G най-
дется элемент а А такой, что ag = ga. Это значит,
§ 7]
НОРМАЛЬНЫЙ ДЕЛИТЕЛЬ
279
что для любого аеЛ и произвольного gsG произ-
ведение g-'ag — а А. Обозначив через g~'Ag сово-
купность всевозможных элементов вида g-1ag, где
а^А, дадим следующее
Определение 6. Подгруппа А группы G на-
зывается ее инвариантной подгруппой, или
нормальным делителем, если для любого
элемента g G
g-'Ag^A.
Теорема 1. Пересечение двух нормальных дели-
телей группы G само является нормальным делите-
лем в G.
Доказательство. Пусть Л] и Лг —нормаль-
ные делители группы G и А = At П А2. Мы знаем, что
А — подгруппа в G (§ ’3). Далее, так как AsAi и
A s А2, то для любого элемента g е G
g-'Ag<= g~lA.g^ Л,
и
g~iAgc=g~1A2g^A2,
а значит,
g-'Ag <= AiF\A2 = А,
т. е. А — нормальный делитель.
Теорема 2. Для того чтобы подгруппа А груп-
пы G была в ней нормальным делителем, необходимо
и достаточно, чтобы для любого элемента g е G име-
ло место равенство
g~lAg = A. (5)
Доказательство. Достаточность условия (5)
следует из определения 6. Для того чтобы доказать
его необходимость, предположим, что Л — нормаль-
ный делитель группы G; тогда для любого элемента
g^G
g-'Ag^A,
а значит, и
gAg~l - (g~')~l Ag-1 <= А
С другой стороны, имеем
А = еАе = (g~lg) A (g~lg) = g~l (gAg~l) g <= g~lAg.
т. e. A ^g~lAg и, значит, g~rAg = A.
280 ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ГРУПП [ГЛ. X
Теорема 3. Для того чтобы подгруппа А была
нормальным делителем группы G, необходимо и до-
статочно, чтобы левые и правые смежные классы
группы G по подгруппе А совпадали.
Доказательство. Из равенства
§-[А§=А
вытекает, что
Ag = gA,
т. е. что для любого g е G левый и правый смежные
классы, содержащие этот элемент, совпадают.
Обратно, если для любого g е G
Ag = gA,
то
А,
и А — нормальный делитель.
Так, в симметрической группе S3 подгруппа
A = {Pi,P5, Р6} будет нормальным делителем, под-
группы же {Pi, Р2}, {Pi, Р3} и {Pj, Р4} нормальными
делителями в З3 не являются.
§ 8. Фактор-группа
Пусть G — произвольная группа, А — ее нормаль-
ный делитель и 3 — совокупность всевозможных
смежных классов группы G по подгруппе А (напоми-
наем, что левые и правые смежные классы в этом
случае совпадают). В множестве 3 введем операцию
умножения, полагая
хА уА = хуА.
Так как А — нормальный делитель, то произведе-
ние хА • уА не зависит от выбора представителей х
и у в перемножаемых классах.
Проверим, что у нас получилась группа.
1. Ассоциативность умножения классов вы-
текает из ассоциативности умножения в группе G:
(хА • у А) • zA = (ху) А • zA = (ху) zA =
= х (yz) А — хА • (yz) А = хА • (уА • zA).
ФАКТОР ГРУППА
' 281
§ 8]
2. Единичным элементом служит сама под-
группа А:
А • хА = еА хА = ехА = хА,
хА А = хА • еА = хе А = хА.
3. Обратным к классу хА будет класс х~1А,
так как
‘ хА • х~1А = хх~'А — еА = А,
х~'А • хА = х'~!хА = е/1 = А.
Пслученная^группа обозначается через G/А и на-
зывается ф а кт о р - г р у ппо й группы G по нор-
мальному делителю А.
Фактор-группа коммутативной группы коммута-
тивна, так как в этом случае для любых двух классов
хА • у А = (ху) А = (ух) А = уА - хА.
Порядок фактор-группы конечной группы равен ин-
дексу нормального делителя А в группе G (и значит,
является делителем порядка п группы G).
Фактор-группа симметрической группы S3 по ее
подгруппе А состоит из двух элементов А = {?[, Р$, Я6}
и В = {Р2, Рз, Рл} и является, следовательно, цикличе-
ской группой второго порядка (легко видеть, что
В2 = А).
Пример. Доказать, что в группе G всех невырожденных
матриц порядка п (например, с вещественными элементами) под-
группа А унимодулярных матриц (т. е. матриц с определителем,
равным 1) является нормальным делителем, и найти фактор-
группу G/A.
Решение. Унимодулярпые матрицы образуют подгруппу
в G, так как произведение двух унимодулярных матриц и ма-"
трица, обратная унимодулярной, являются унимодулярными (тео-
рема 3 главы III).
Далее, подгруппа А унимодулярных матриц является в G
нормальным делителем, так как если матрица а е А, и значит,
I а I = 1, то для любой матрицы geG
|g~‘ag| = I g~' 11 a I |g| = |g|-1 I a\ | g | = |a | = 1
и
g~l agt= A.
Найдем фактор-группу G/A. Покажем прежде всего, что для
того, чтобы две матрицы b и с принадлежали одному и тому же
/ • >
•<г >!
."/ 282 ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ГРУПП [ГЛ. X
!S
и> „
смежному классу группы о по нормальному делителю А, необ-
ходимо и достаточно, чтобы они имели равные определители.
! Действительно, если 6~с, т. е. Ь = са, где а^А и, значит,
| а | = 1, то | b | = | с 11 а | = | с |.
Обратно, если | b | = | с |, то b = с(с-'Ь), где
|с-16| = |с-Ч|&Г=|сГ'|6|=1
и, значит, с-'Ь е А, т. е. 6~с.
Таким образом, каждый смежный класс G по А вполне ха-
рактеризуется определителем входящих в него матриц. Перемно-
жению классов отвечает перемножение произвольных представи-
телей из них, и значит, произведение классов В (матриц с оп-
ределителем Р) и С (матриц с определителем у) есть класс
ВС — матриц с определителем Ру. Мы нашли; что фактор-группа
G/А изоморфна мультипликативной группе отличных от нуля
вещественных чисел.
§ 9. Нормальные делители группы преобразований
евклидовой плоскости и соответствующие
йм фактор-группы
А. Примеры нормальных делителей
1. Группа параллельных переносов является нормальным де-
лителем в группе движений плоскости.
Доказательство. Пусть Q — произвольное движение,
Т — параллельный перенос. Надо доказать, что преобразование
Q-'fQ является параллельным переносом. Пусть А и В —произ-
вольные точки плоскости; предположим, что
при преобразовании Q А А', В-> В';
при преобразовании Т А'->А", В' -> В";
при преобразовании Q~* А"-> А'", В"-> В"'.
Тогда
при преобразовании Q'lTQ А-*-А"', В В'" (рис. 31). Надо
доказать, что отрезок АА’" равен и параллелен ВВ"'.
Поскольку преобразование Q-'TQ является движением, то
А'”В"' = АВ. ' (6)
Так как при движении Q точка А->-А', и точка А'"-*-А", то
ЛЯ"' = Л'Л", (7)
а так как при этом точка В -> В' и В'" В", то
ВВ’"=В'В". (8)
Но Г — параллельный перенос, поэтому
А'А"~В'В". (9)
...о - -
§ 9]
ГРУППЫ ПРЕОБРАЗОВАНИЙ ПЛОСКОСТИ
Из равенств (7)—(9) вытекает, что
АА"' = ВВ’", (10)
а из равенств (6) и (10) следует, что четырехугольник
АА'"В'"В — параллелограмм и, значит, АА’"]]ВВ'", т. е. преоб-
разование Q-1TQ является параллельным переносом.
2. Группа параллельных переносов является нормальным^де-
лителем и во всей группе аффинных преобразований.
Доказательство. Пусть
преобразование и Т — параллельный
преобразование А~1ТА являет-
ся параллельным переносом.
В § 5 было показано, что
каждое аффинное преобразова-
ние А можно представить в виде
А = QC, где Q — движение,
а С — самосопряженное преобра-
зование. Но тогда
A-'TA^tQCT1 Т (QC) =
= С-! (Q-'TQ)C.
Произведение Q'‘TQ = Т', по до-
казанному в п. 1, является па-
раллельным переносом Рассмот-
рим С~1Т'С. Пусть система коор-
динат выбрана так, что при преобразовании С
переходит в А'^х^у) 1 при параллельном переносе Т‘
тор (пь а2) точка А' перейдет в Л"(Z.tx 4- ai, kiX + a2). А тогда
при преобразовании С"1 точка А" перейдет в А"’[х+~, у +
\ Л] Л2 /
и, значит, преобразование С-’Т'С является параллельным пере-
{ а, а2\
носом на вектор -т— .
\ Л] Л»2 /
3. Так как группа преобразований подобия является под-
группой группы аффинных преобразований, то и в ней группа
параллельных переносов будет нормальным делителем.
4. Группа движений является нормальным делителем в груп-
пе преобразований подобия. Действительно, пусть U — произ-
вольное преобразование подобия н Q — движение. Тогда U~lQU
будет преобразованием подобия, не меняющий длин отрезков
(при преобразовании U все длины умножаются на k, при пре-
образовании Q не меняются и при преобразовании U~l — умно-
жаются на k~'), следовательно, это — движение.’
Б. Ф а кто р -г р у п п ы
1. Фактор-группа группы Я аффинных преобразований по
подгруппе параллельных переносов 6.
Два аффинных преобразования и А2 эквивалентны, т. е.
принадлежат одному и тому же классу по подгруппе ® в том и
А — произвольное аффинное
перенос. Надо доказать, что
В
в
В'
Рис.
31.
л'
точка
А (х, у)'
на век-
284 ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ГРУПП [ГЛ. X
только в том случае, если Ai = ТА2, где Т — некоторый парал-
лельный перенос. Если А — произвольное аффинное преобразова-
ние, при котором начало координат О переходит в О', то пре-
образование ЕО,ОА, при котором точка О неподвижна, эквива-
лентно А: ТО,ОА ~ А. Таким образом, каждое аффинное преоб-
разование эквивалентно некоторому аффинному преобразованию
е-неподвижной точкой О. С другой стороны, если два аффинных
преобразования А) и А2 с неподвижной точкой О эквивалентны:
41 = ТА2, то произведение AtA2l = T будет параллельным пере-
носом с неподвижной точкой О, т. е. тождественным преобразо-
ванием:
Я, Л?'1 =Е,
откуда 4! = 42. Таким образом, всевозможные аффинные преоб-
разования с неподвижной точкой О (центро-аффинные преобра-
зования) .дают полную систему представителей из всех смежных
классов разложения группы SI по подгруппе S. Следовательно,
фактор-группа SX/S изоморфна группе центро-аффинных преоб-
разований с центром О; в координатах эта группа записывается
так:
х' = ОцХ + а12у,
у’= апх + а22у,
где определитель б=£0. Эта группа изоморфна, следовательно,
группе невырожденных матриц второго порядка.
2. Фактор-группа группы 2В преобразований подобия по под-
группе S параллельных переносов.
Каждое преобразование подобия эквивалентно некоторому
преобразованию подобия с неподвижной точкой О (центро-подоб-
ному преобразованию), а два таких эквивалентных преобразова-
ния одинаковы. Следовате'льно, фактор-группа SVG изоморфна
группе центро-подобных преобразований с центром О. Но каждое
такое преобразование можно представить в виде произведения
КН ортогонального преобразования Н и гомотетии К с каким-то
коэффициентом k-фО (см. стр. 272). Правда, такое представле-
ние не однозначно. Если S — симметрия с центром О, то S2 = Е и
КН = KS2H = (KS) (SH),
где SH — тоже ортогональное преобразование, a KS — гомоте-
тия с коэффициентом —k. Можно поэтому ограничиться разло-
жениями вида КН, где К—гомотетия с положительным
коэффициентом. Такое представление центро-подобного преббра-
зования будет уже однозначным, так как из равенства
KJK = K2H2 (11)
имеем
§ 9J
ГРУППЫ ПРЕОБРАЗОВАНИЙ ПЛОСКОСТИ
285
и гомотетия К2 ’/Q с коэффициентом kjk2 > 0 будет и ортого-
нальным преобразованием (не меняющим длин отрезков), а зна-
чит, kjk2 =1, и ki — k2, т. е. Ki = Кг. Отсюда и из равенства
(11) вытекает, что и Ht = Н2.
Таким образом, полную систему представителей из всех клас-
сов разложения группы 2В по нормальному делителю ® дают
всевозможные произведения вида КН, где Н— ортогональное
преобразование, а К — гомотетия с коэффициентом k > 0. "Сле-
довательно, фактор-группа изоморфна группе матриц вида
kh, где h — ортогональная матрица второго порядка, a k — по-
ложительное число.
3. Фактор-группа группы движений по подгруппе параллель-
ных переносов изоморфна группе движений с неподвижной точ-
кой, т. е. изоморфна группе ортогональных матриц второго по-
рядка.
4. Фактор-группа группы преобразований подобия ® по под-
группе движений ffi.
Для каждого преобразования подобия найдется эквивалент-
ное ему центроподобное преобразование с центром О. Каждое
такое преобразование можно представить в виде произведения
КН, где Н — ортогональное преобразование, а К — гомотетия с
коэффициентом k > 0 (п. 2). Если преобразования KiHt н К2Н2
эквивалентны, то K\H\ = K2H2Q, где Q — движение, н значит,
гомотетия К2 = Н20.Н^ 1 с коэффициентом k\/k2 > 0, будучи
движением, не изменяет длин отрезков, а потому ki/k2 = 1, от-
куда Ki = Кг- Обратно, при Ki = Кг — К преобразования KHi
и КН2 эквивалентны, потому что KZ/j ~ КН2(Н21 i ), где Н2ХН{-
движение. Таким образом, полную систему представителей для
разложения группы SB по подгруппе ffi образуют, например, все
гомотетии с центром О и положительным коэффициентом. Фак-
тор-группа 2B/ffi изоморфна поэтому мультипликативной группе
положительных чисел.
ДОПОЛНИТЕЛЬНАЯ ЛИТЕРАТУРА
1. Курош А. Г., Курс высшей алгебры, М., «Наука», 1968.
2. Гельфанд И. М., Лекции по линейной алгебре, М., «Нау-
ка», 1966.
3. Ш и л о в Г. Е., Математический анализ. Конечномерные ли-
нейные пространства, М., «Наука», 19.69.
4. К а р п е л е в и ч Ф. И., Садовский Л. Е., Элементы ли-
нейной алгебры и линейного программирования, М., Фцзмат-
гиз, 1963.
5. Ф р е з е р Р., Дункан В., Коллар А., Теория матриц и
ее приложения, М., ИЛ, 1950.
6. Бел.лман Р., Введение в теорию матриц, М, «Наука», 1969.,
7. Ефимов Н. В., Квадратичные формы и матрицы, М., Физ-
маггиз, 1964.
8. Рашевский П. К., Риманова геометрия и тензорный ана-
лиз, М., «Наука», 1967.
9. А к и в и с М. А., Гольдберг В. В., Тензорное исчисление,
М., «Наука», 1969.
10. Кильчевский Н. А., Элементы тензорного исчисления и
его приложения к механике, М., Гостехиздат, 1954.
11. Курош А. Г., Теория групп, М., «Наука», 1967.
12, Александров П. С., Введение в теорию групп, М., Уч-
педгиз, 1951.
13. Ефимов Н. В., Розен дорн Э. Р., Линейная алгебра и
многомерная геометрия, М., «Наука», 1970.
14. Проскуряков И. В., Сборник задач по линейной алгеб-
ре, М., «Наука», 1970.
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Абелева группа 260
Аддитивная группа 260
Алгебраическое дополнение 29
Альтернирование тензора 252
Аффинное преобразование 272
— пространство 83
Базис 67
Бесконечна^ группа 260
Билинейная форма 172
—- функция 172
Вектор 63
Векторное пространство 62
Выпуклое множество 92
Выпуклый многогранник 94
Вырожденное преобразование
99
Галилея принцип относитель-
ности 223
Гамильтона'-—Кэли теорема
129
Гаусса метод 54
,» Гиперплоскость 89
• Гиперсфера 149
Гомотетия 271
Группа 259 .
Движение 268
Дефект преобразования 120
Евклидово пространство 136,
147
Единичная матрица 108
Изоморфизм групп 267
— пространств 71, 143
Инвариантная подгруппа 279.
Инвариантное подпростран-
ство 122
Инварианты 190
1 Инверсия 18
Индекс подгруппы 277
Квадратичная форма 174 " '
Ковариантный тензор 242
Коммутативная группа 260
Комплексное пространство 168
Конечная группа 260
Конечномерное пространство
66
Контравариантный тензор 242
Координаты вектора 68
— тензора 245
Кососимметрическая функция
175
Кососимметрический тензор 248
Крамера формулы 11, 15г~36
Кэли таблица 263
Лагранжа теорема 277
Лежандра многочлены 142
Линейная зависимость 41, 64
— комбинация 41, 65
— оболочка 81
— функция (форма) 171
Линейное многообразие 87
— отображение 116
— преобразование 96
— пространство 62
Лоренца преобразования 230
Матрица 10, 20, 36, 115
— билинейной формы 173
— преобразования 97
Метрический тензор 253
Минор 28, 36
Мультипликативная группа
260
Невырожденное преобразова-
ние 99
Некоммутативная группа 259
Неопределенная система 44
Неравенство треугольника 138
Нечетная перестановка 19
Нормальный дей'итель 279
Нулевое преобразование' 102
Нулевой вектор 62
288
ПРЕДМЕТНЫ И УКАЗАТЕЛЬ
i
Область значений 119
Образ элемента 261
Обратная матрица 110
Обратное преобразование НО,
261
Общее решение системы 52,
54
Однородные уравнения 48
Определенная система 44
— форма 179
Определитель n-го порядка 21
Ортогональная матрица 159
Ортогональное дополнение 145
— преобразование 156
Ортогональные векторы 138
Ортогональный базис 138
Ортонормированный базис 139
Отрезок 91
Параллельный перенос 268
Пересечение подпространств
78
Плоскость ^-мерная 89
Подгруппа 265
Подобие 271
Подпространство 75
Подстановка 262
Полуевклидова плоскость 21,0
Полупространство 03
Поряден i руппы. 260
— элемента группы 277
Преобразование множества 231
Присоединенная матрица 111
Произведение матриц 107. 117
Пространство событий 222
Прямая 90
-- сумма 80 j
Псевдоевклидова плоскость
210
Псевдоортогональное преобра-
зование 218
Разложение по подгруппе. 274
Размерность просгранст 66
Paiir билинейной формы 174
— матрицы 37
— преобразованья 119
Решение системы уравнений
19, 13, 35, 1а
Самосопряженное п; еобразо-
, ванне 152
Свертка тензора 250
Свертывание тензора 2"9 .«ч«
Свободные неизвестные
Сильвестра критерий HJt) 4 -
Симметрирование тензора 252
Симметрическая группа 262
— матрица 152
— форма 174
Симметрический тензор 247 >*,
Скалярная матрица 265
Скалярное произведение 136
След матрицы 127 ejj
Сложение тензоров 248
Смежный класс 27 b
Собственное значение
Собственный вектор 123
Событие 221
Совместная система 44
Сопряженное преобразование
150
Сумма подпространств 78
- преобразований 104
— тензоров '24aL,,
Тензор 244
Точка 82
Транспозиция 12
Треугольная мат,. 265
Умножение ыа-гтиц 107, 117
— преоб"? .1 1ЧИЙ 105, 261
— тензо,- •. 242
Уп.’ыодул.- •атрица 265
Унитарная . . вица' 169
Унитарное пг-•-бразовамис 169
Фактор-груп;.." 275, 281
Фундамента,!’ чая система ре- 1(
шений 50 I,
; j
Характеристический мнсго«леи '
126
Циклическая 'pvnna 267 . ,
Эйнштейна принцип. относи- '
тельности 225
Элементарные преобразования
Ядро преобразования 119