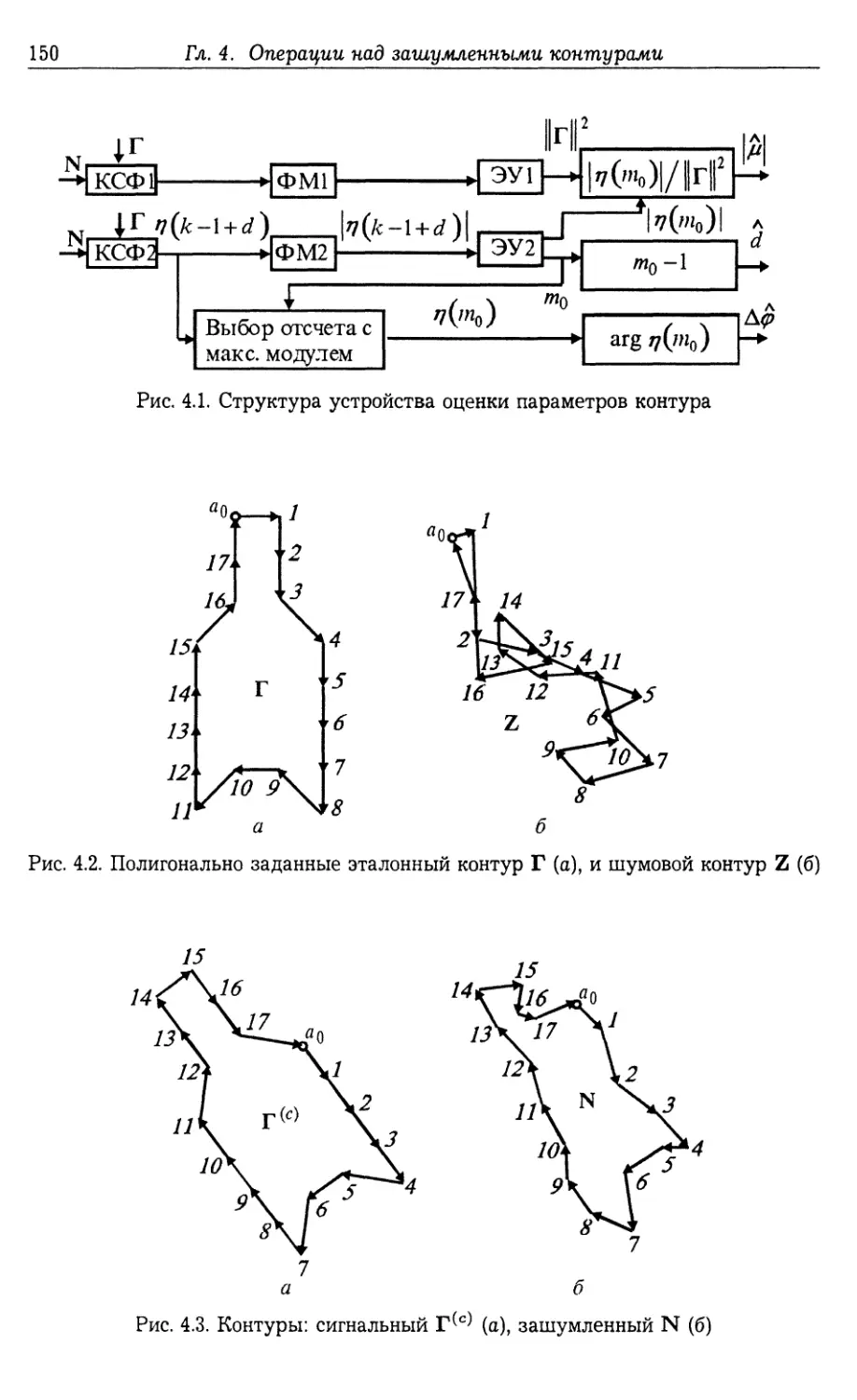
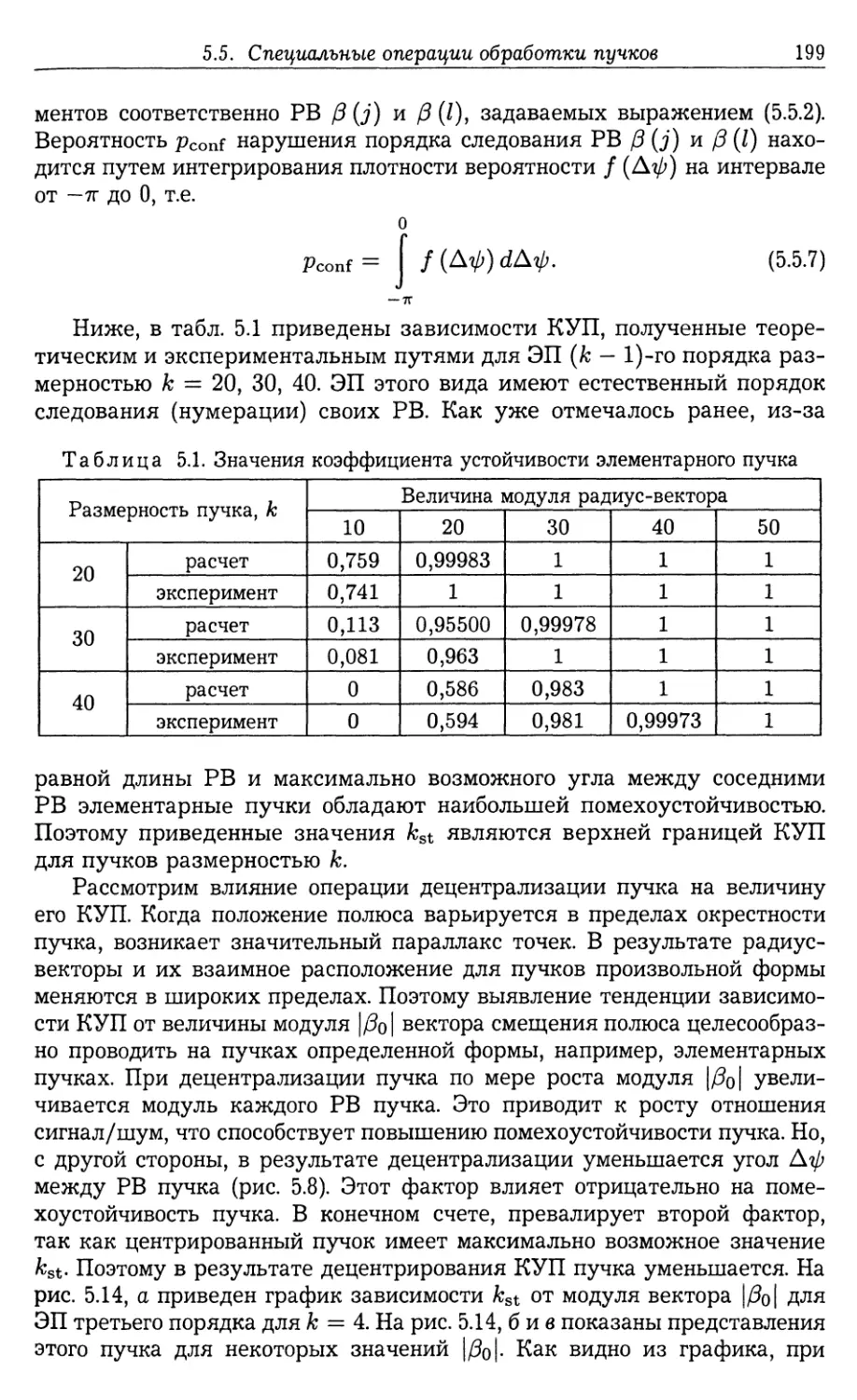
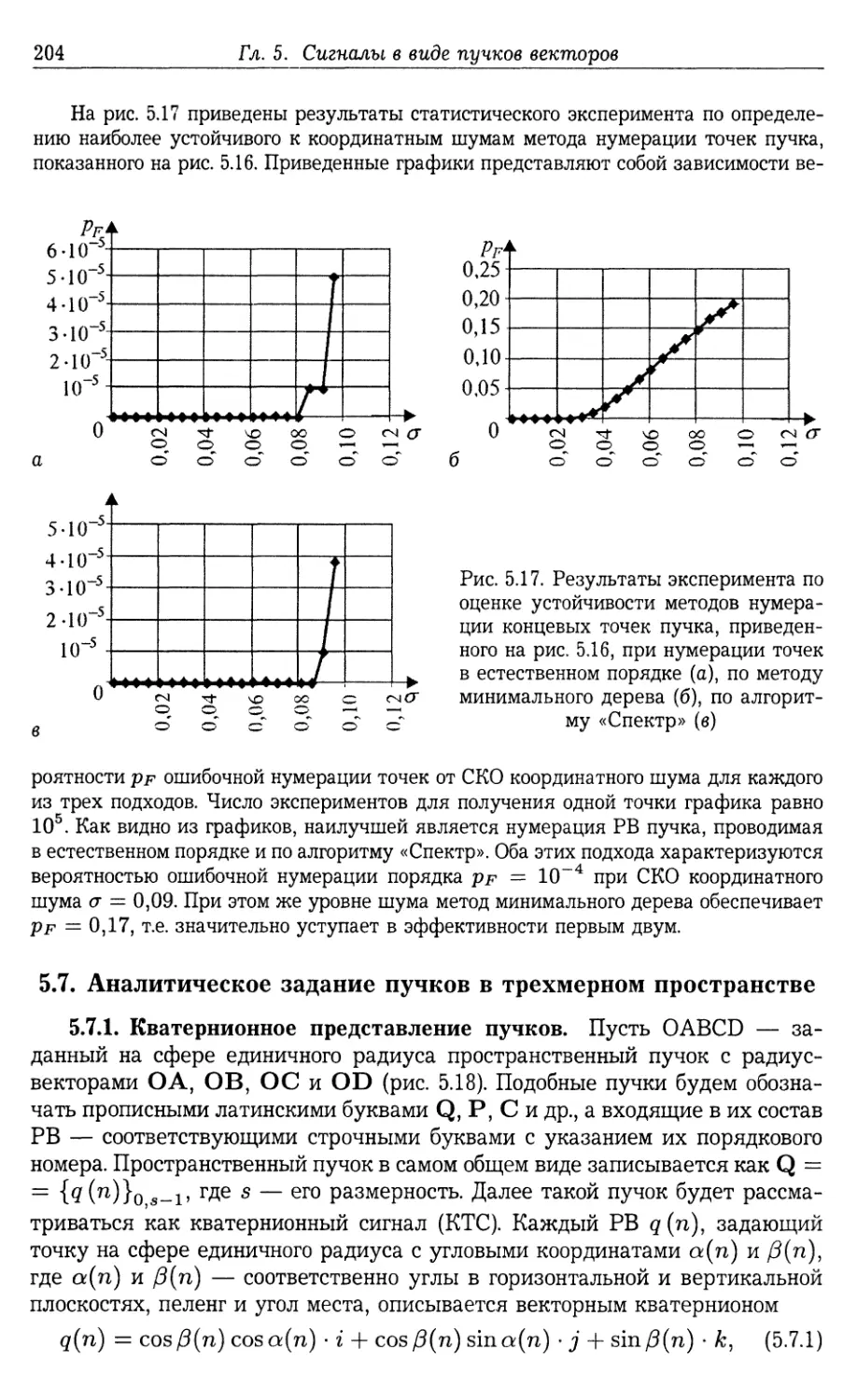
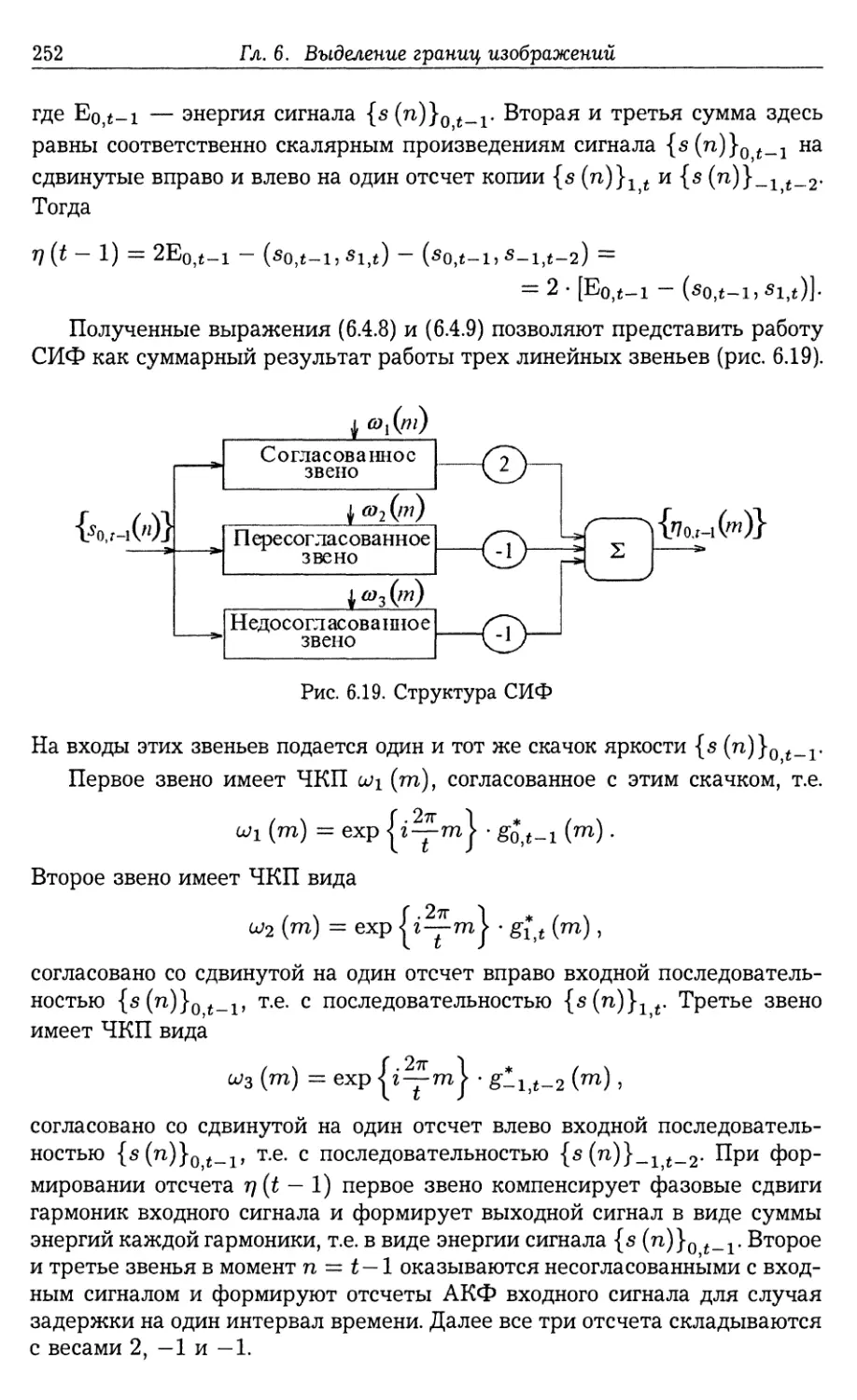
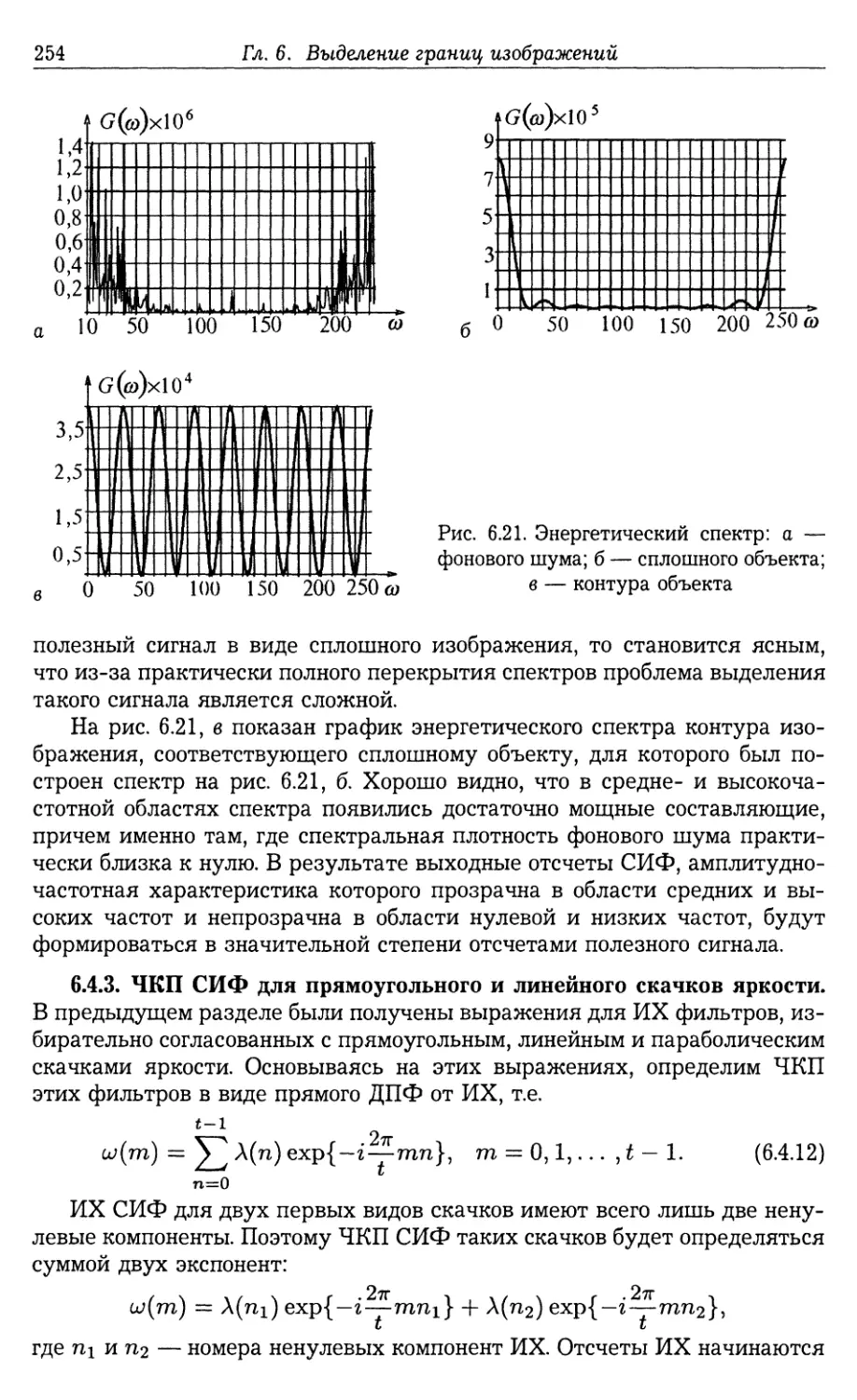
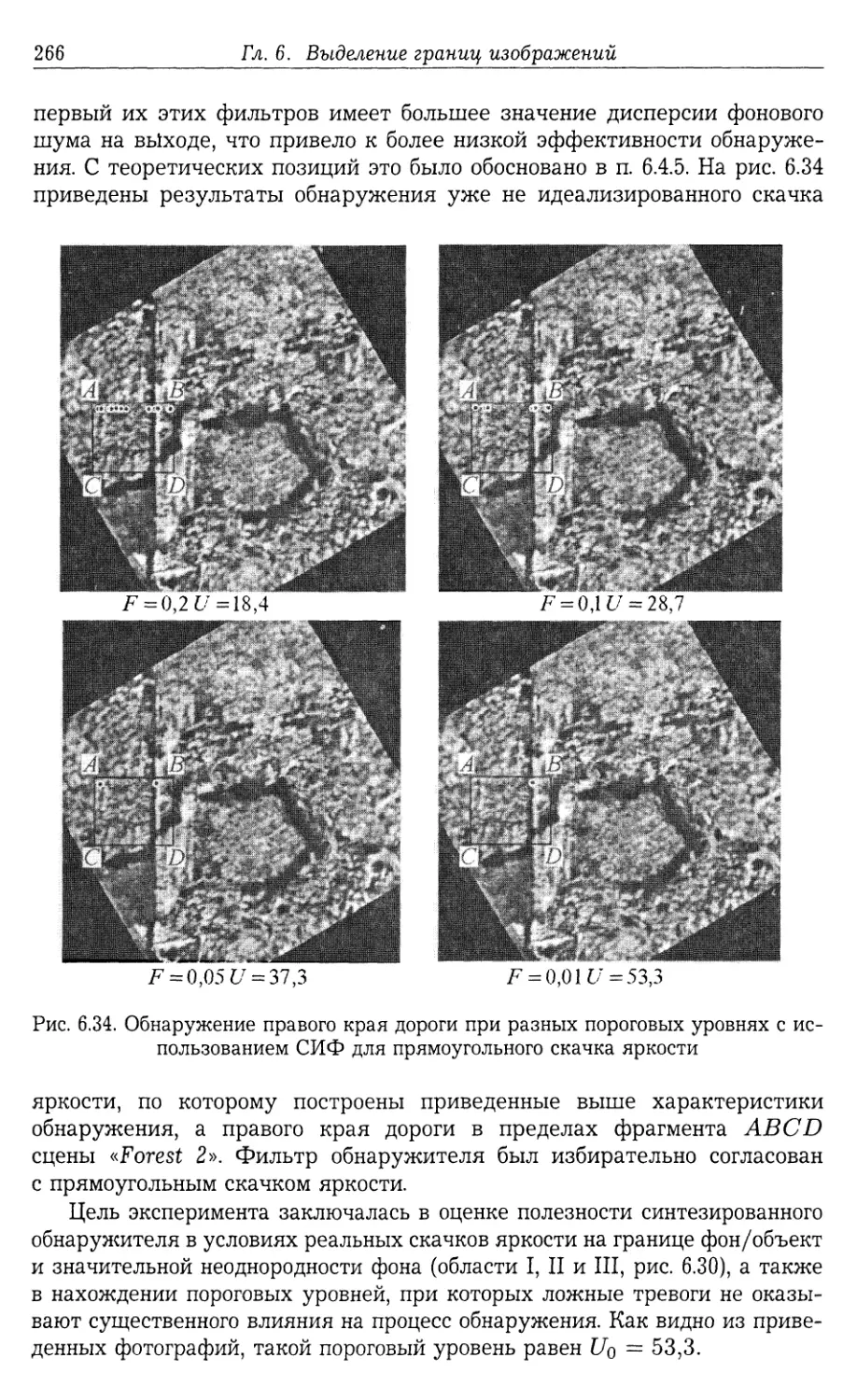
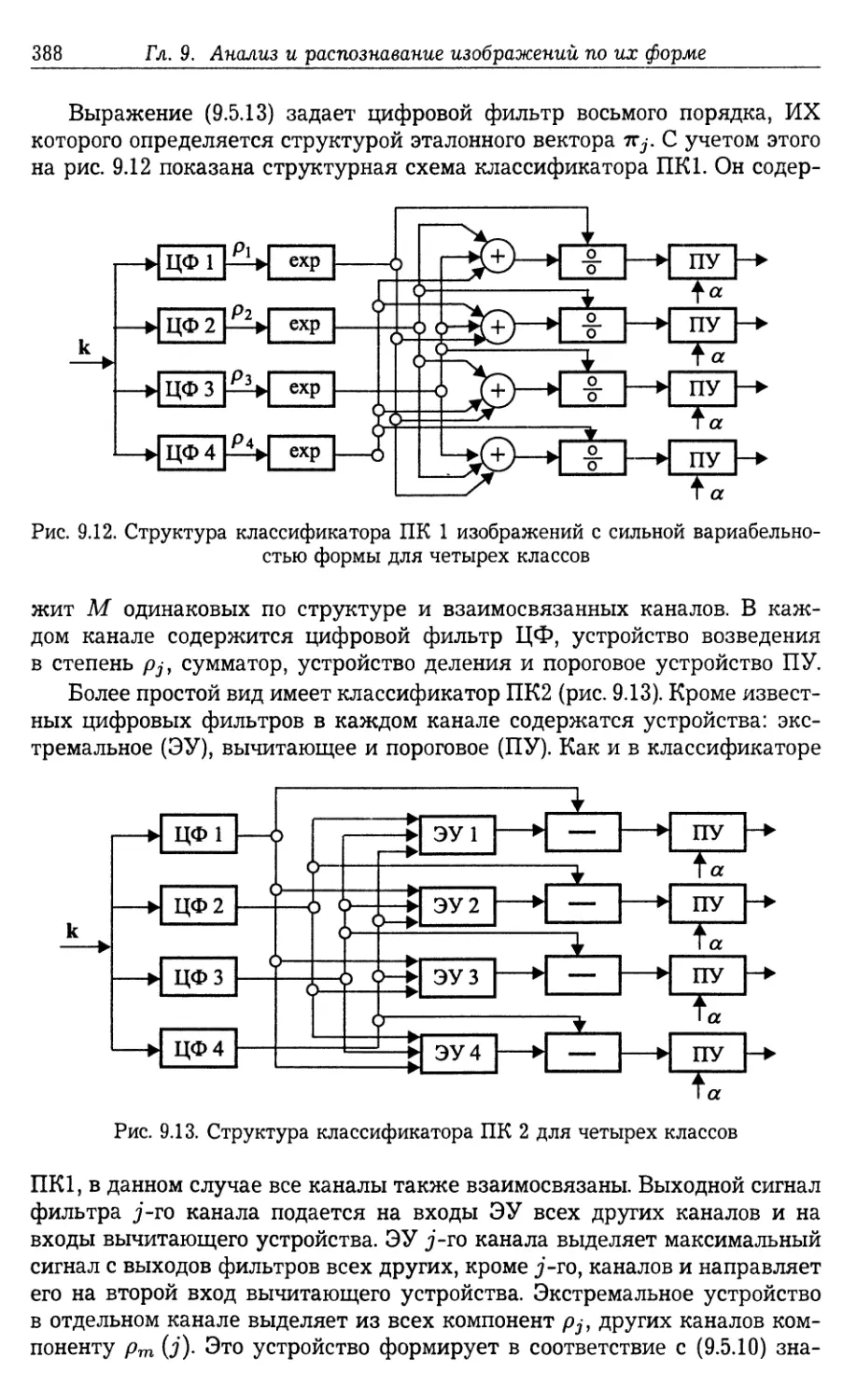
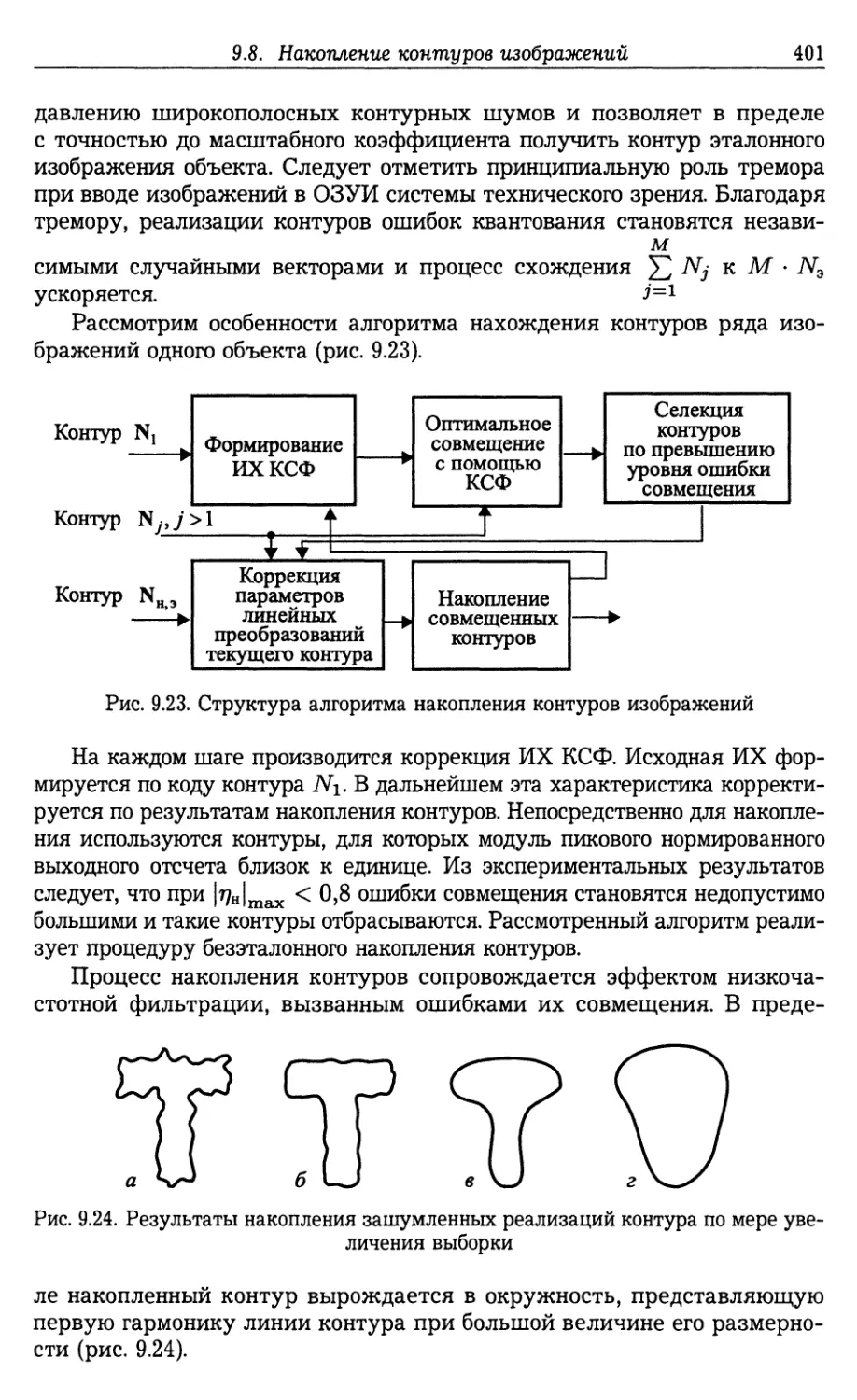
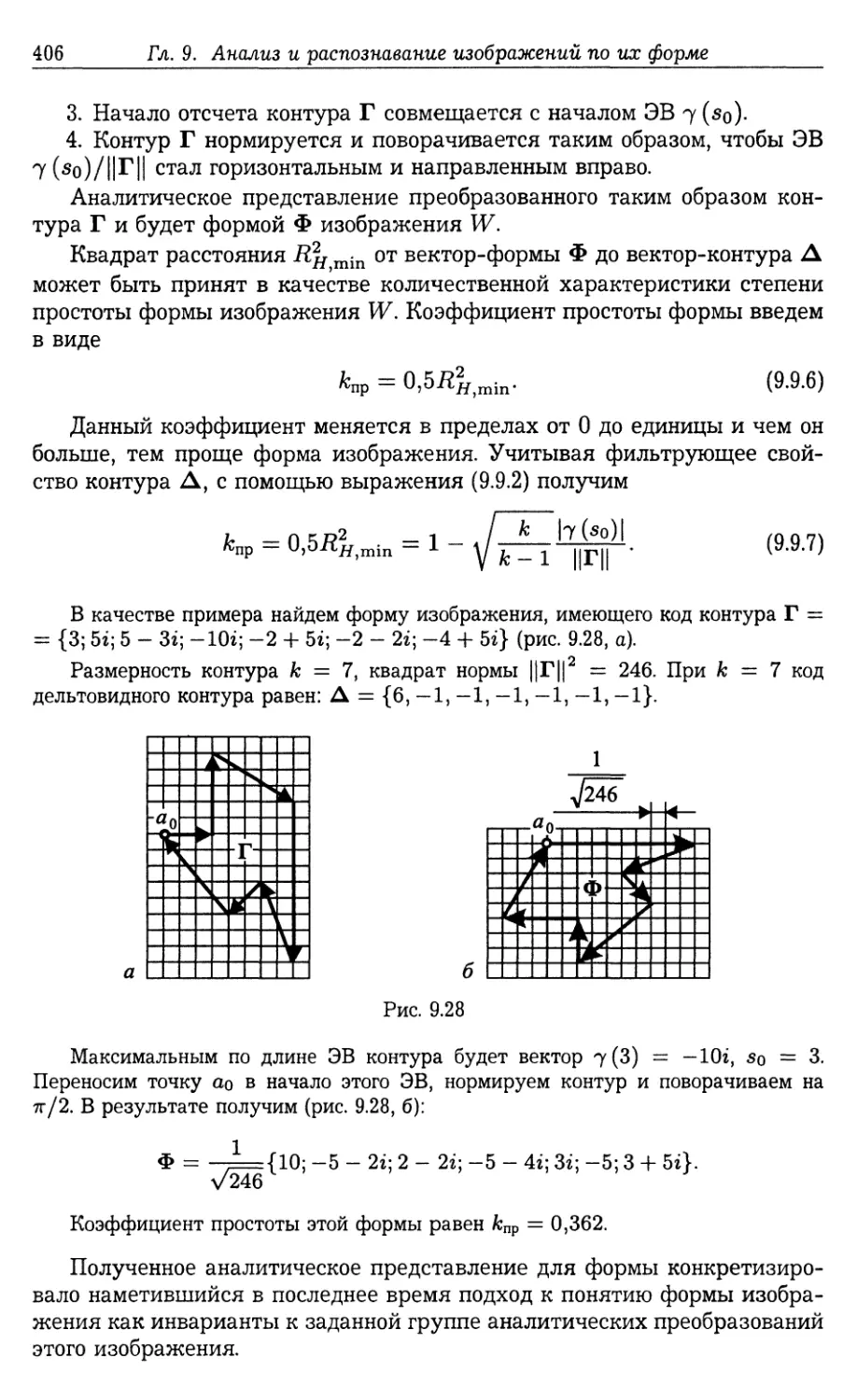
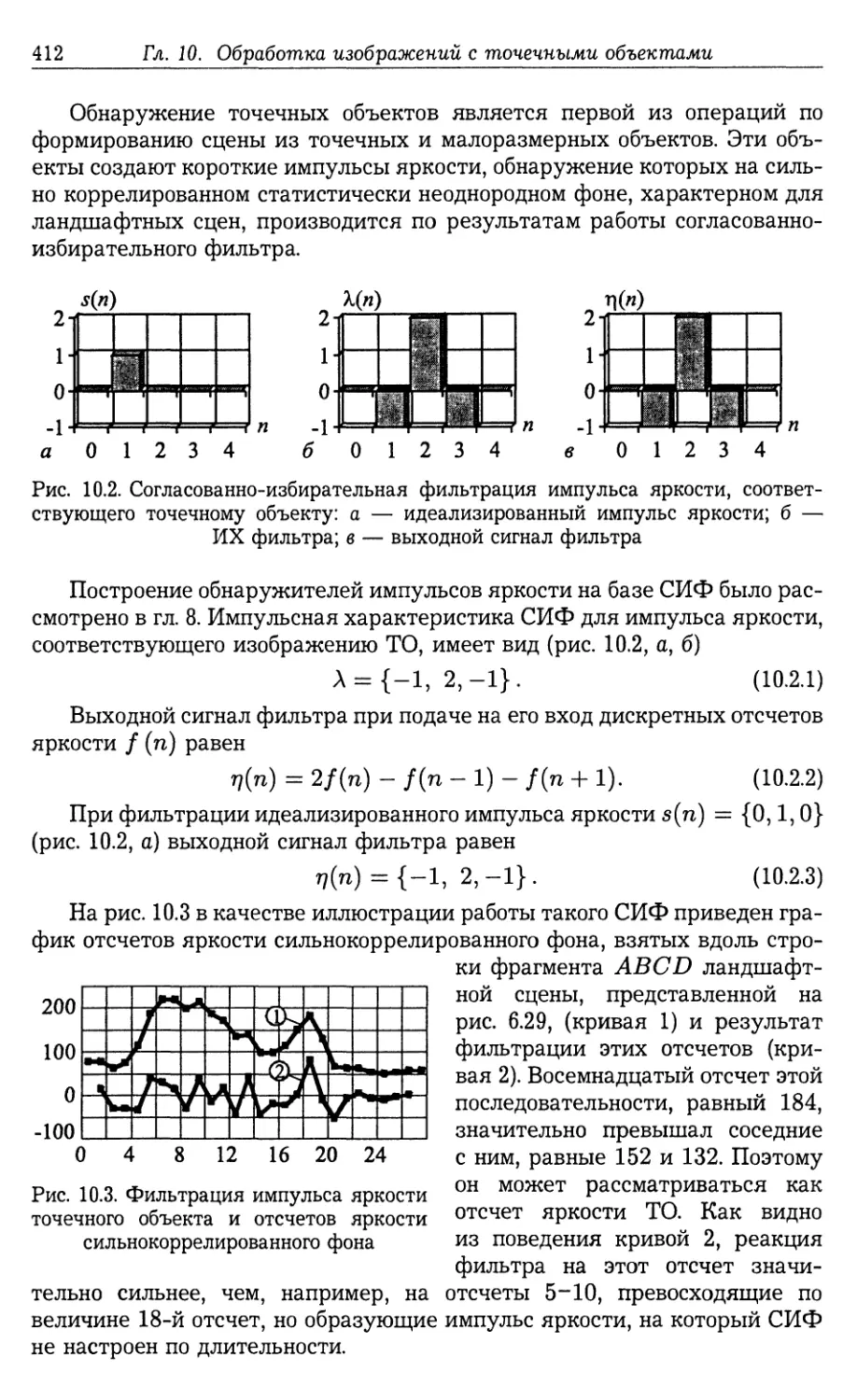
Автор: Фурман Я.А.
Теги: теория вероятностей и математическая статистика теория вероятностей математическая статистика комбинаторный анализ теория графов цифровая обработка сигналов контурный анализ
ISBN: 5-9221-0374-1
Год: 2003
Текст
ВВЕДЕНИЕ
В КОНТУРНЫЙ
АНАЛИЗ
ПРИЛОЖЕНИЯ К ОБРАБОТКЕ
ИЗОБРАЖЕНИЙ И СИГНАЛОВ
ПОД РЕДАКЦИЕЙ Я.А. ФУРМАНА
ИЗДАНИЕ ВТОРОЕ, ИСПРАВЛЕННОЕ
УДК 519.2
ББК 22.17
В24
Введение в контурный анализ; приложения к обработке изображений и
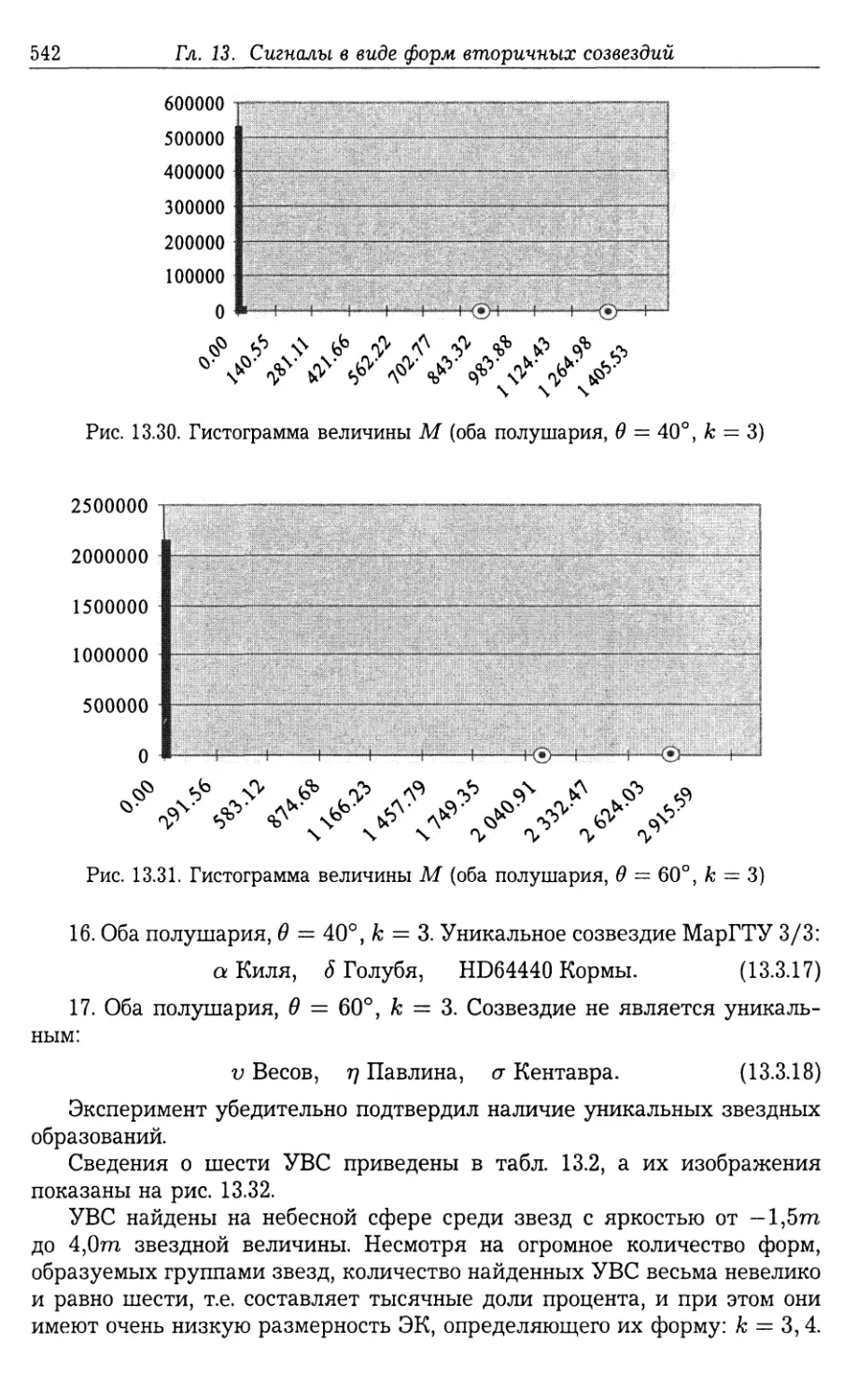
сигналов/ Я.А.Фурман, А.В Кревецкий, А.К Передреев, А.А. Роженцов, Р.Г. Ха¬
физов, И.Л Егошина, А.Н. Леухин; Под ред. Я.А. Фурмана. — 2-е изд., испр. — М.:
ФИЗМАТЛИТ, 2003. — 592 с. — ISBN 5-9221-0374-1.
Описаны дискретные комплекснозначные сигналы, представленные на плоскос¬
ти в виде полигональных контуров. Рассмотрены вопросы спектрального и корреля¬
ционного анализа контуров и их линейной фильтрации. Проведен синтез и анализ
контурных согласованных фильтров, образующих меру схожести комплекснознач¬
ных сигналов. В приложениях контурного анализа даны подходы к обнаружению
и прослеживанию границ изображений. Синтезированы устройства оценки парамет¬
ров и распознавания изображений протяженных и групповых точечных объектов
по их форме. Рассмотрены вопросы применения контурного анализа в радиотехни¬
ческих системах, в системах связи и ориентации летательных аппаратов
Для научных работников и инженеров, работающих в области обработки сиг¬
налов и изображений, а также аспирантов и студентов старших курсов соответст¬
вующих специальностей.
Первое издание — 2002 г.
Табл. 37. Ил. 387. Библиогр. 204 назв.
ISBN 5-9221-0374-1
ж А.К. Передреев,
юв, И.Л. Егошина,
ОГЛАВЛЕНИЕ
ВВЕДЕНИЕ 12
ЧАСТЬ I
ОСНОВЫ КОНТУРНОГО АНАЛИЗА
Глава 1
КОНТУРЫ КАК ДИСКРЕТНЫЕ СИГНАЛЫ
1.1. Представление изображений в системе технического зрения .... 15
1.2. Кодирование контуров бинарных изображений 17
1.3. Линейные пространства вектор-контуров 22
1.4. Особые свойства скалярного произведения в пространстве Ск ... 25
1.5. Аналитические преобразования и свойства комплекснозначных моде¬
лей контура 27
1.6. Модель контурного сигнала 29
1.7. Статистические модели контуров 31
1.8. Классификация контуров 34
1.9. Примеры 39
1.10. Основные результаты 43
1.11. Задачи и упражнения 44
Глава 2
СПЕКТРАЛЬНЫЙ И КОРРЕЛЯЦИОННЫЙ АНАЛИЗ
КОНТУРОВ
2.1. Введение 45
2.2. Ортонормированный базис из полного семейства элементарных
контуров 45
2.3. Основные свойства дискретного преобразования Фурье контурных
сигналов 49
2.4. Свойства ДПФ контуров, связанные с их замкнутостью и комплекс-
нозначностью 53
2.5. Спектры контуров специального вида 58
2.6. Разложение произвольного контура 63
2.6.1. Разложение Каппелини (63). 2.6.2. Разложение произвольного
контура в базисе из полного семейства элементарных контуров (64).
4
Оглавление
2.7. Изменения спектра при преобразованиях, связанных с вариацией
размерности контура 66
2.8. Корреляционный анализ контуров 69
2.81. Корреляционные функции комплекснозначных сигналов (69).
2.8.2. Корреляционные свойства контуров специального вида (74).
2.9. Обсуждение результатов по спектральному и корреляционному
анализу контуров 76
2.10. Вопросы и упражнения 79
Глава 3
ЛИНЕЙНАЯ ФИЛЬТРАЦИЯ КОНТУРОВ
3.1. Введение 81
3.2. Основные соотношения при линейной фильтрации контуров .... 81
3.3. Фильтрация контуров в частотной области. Простейшие фильтры . . 84
3.4. Контурный фильтр скользящего среднего 87
3.4.1. Частотный коэффициент передачи фильтра скользящего сред¬
него (87). 3.4.2. Свойства фильтра скользящего среднего (89).
3.4.3. Сравнение простейших фильтров, заданных в частотной и про¬
странственной областях (91).
3.5. Контурный фильтр скользящей разности 93
3.5.1. Задание фильтра скользящей разности (93). 3.5.2. Свойства филь¬
тра скользящей разности (95).
3.6. Контурные согласованные фильтры 97
3.6.1. Основные аналитические соотношения при контурной согла¬
сованной фильтрации (97). 3.6.2. Расчет контурного согласованного
фильтра (101). 3.6.3. Механизм работы контурного согласованного
фильтра (103). 3.6.4. Свойства контурного согласованного филь¬
тра (105).
3.7. Оценка степени сходства двух форм 111
3.8. Сопряженная согласованная фильтрация 115
3.8.1. Задание векторов в ортонормированном и косоугольном бази¬
сах (115). 3.8.2. О соотношении операций разложения и фильтрации
векторного сигнала (120). 3.8.3. Разложение сигнала в собственной
системе отсчета (123).
3.9. Фильтрация широкополосного шумового контура 126
3.9.1. Корреляционная функция и дисперсия процесса на выходе филь¬
тра (126). 3.9.2. Корреляционный момент вещественной и мнимой ча¬
стей ЭВ выходного шумового контура (127). 3.9.3. Плотности распре¬
деления вероятностей случайных величин на выходе фильтра (128).
3.10. Согласованная фильтрация зашумленного контура 130
3.10.1. Корреляционный момент вещественной и мнимой частей вы¬
ходного вектора КСФ (130). 3.10.2. Плотность распределения вероят¬
ностей зашумленного выходного вектора фильтра (131). 3.10.3. Функ¬
ции правдоподобия зашумленного и шумового контуров (133).
3.11. Сравнительная эффективность фильтров, согласованных с исходным
и сопряженным сигналами 134
3.11.1. Эффективность подавления широкополосных шумов контур¬
ным согласованным фильтром (134). 3.11.2. Коэффициент шума со¬
пряженного согласованного фильтра (137).
Оглавление
5
3.12. Обсуждение и обобщение результатов по линейной фильтрации
контурных сигналов
3.13. Задачи и упражнения
Глава 4
ОПЕРАЦИИ НАД ЗАШУМЛЕННЫМИ КОНТУРАМИ
4.1. Оценки параметров линейных преобразований контуров
4.1.1. Постановка задачи (145). 4.1.2. Оценка параметров зашумленно¬
го контура (146).
4.2. Обнаружение зашумленных контуров изображений
4.2.1. Постановка задачи (151). 4.2.2. Обнаружение полностью извест¬
ного контура (152). 4.2.3. Обнаружение контура с неизвестным углом
поворота (153). 4 2.4. Обнаружение контура с неизвестным сдвигом
начальной точки (156). 4.2.5. Обнаружение контура с неизвестным
углом поворота и сдвигом начальной точки (156). 4.2.6. Обнаружение
контура с произвольным масштабом (157). 4.2.7. Обнаружение конту¬
ра с неизвестными сдвигом начальной точки, углом поворота и про¬
извольным масштабом (158).
4.3. Разрешение контурных сигналов
4.3.1. Введение и постановка задачи (158). 4.3.2. Условия обеспече¬
ния разрешенного образа на выходе фильтра обнаружителя (161).
4.3.3. Образование отсчетов циклического фильтра для второй фазы
фильтрации по результатам первой и третьей фаз (165). 4.3.4. Полу¬
чение отсчетов циклического фильтра для второй фазы фильтрации
по результатам ациклической фильтрации (166). 4.3.5. Геометрическая
интерпретация и энергетические соотношения процесса формирова¬
ния разрешенного образа на выходе фильтра (168). 4.3.6. Формирова¬
ние разрешенного образа при произвольном расположении окна филь¬
тра (169). 4.3.7. Примеры (171).
4.4. Распознавание зашумленных контуров
4.4.1. Постановка задачи распознавания контуров (173). 4.4.2. Распоз¬
навание полностью известных контуров (174). 4.4.3. Распознавание
контуров с неизвестными углами поворотов и сдвигами начальных
точек (175). 4.4.4. Общие требования к контурам при их распознава¬
нии (176).
4.5. Обсуждение результатов
4.6. Задачи и упражнения
Глава 5
СИГНАЛЫ В ВИДЕ ПУЧКОВ ВЕКТОРОВ
5.1. Аналитическое представление заданных на плоскости пучков ....
5.2. Спектральный анализ изображений пучков
5.2.1. Связь между спектрами пучка и его контура (185). 5.2.2. Элемен¬
тарные пучки (186). 5.2.3. Разложение произвольного пучка на эле¬
ментарные (188).
5.3. Влияние преобразований пучка на вид его спектра
5.4. Согласованная фильтрация пучков
5.5. Специальные операции обработки пучков
138
143
145
151
158
173
179
181
184
185
189
192
194
6
Оглавление
5.5.1. Особенности пучка как зашумленного сигнала (194). 5.5.2. Проб¬
лема нумерации радиус-векторов зашумленного пучка (196). 5.5.3. Ко¬
эффициент устойчивости аналитического описания пучка при есте¬
ственном порядке следования радиус-векторов (198).
5.6. Некоторые подходы к решению проблемы нумерации (упорядочения)
точек ГРТО 200
5.7. Аналитическое задание пучков в трехмерном пространстве 204
5.7.1. Кватернионное представление пучков (204).
5.8. Скалярное произведение кватернионов 207
5.8.1. Умножение кватернионов, представленных в комплексной фор¬
ме (207). 5.8.2. Скалярное произведение представленных в комплекс¬
ном виде кватернионов (208). 5.8.3. Скалярное произведение кватер-
нионных сигналов (209).
5.9. Ортогональный базис для спектрального анализа кватернионных
сигналов 209
5.10. Спектральные представления кватернионного сигнала 211
5.11. Корреляционные функции кватернионных сигналов 214
5.12. Согласованная фильтрация кватернионных сигналов 216
5.13. Обсуждение результатов 219
5.14. Задачи и упражнения 220
ЧАСТЬ II
ПРИМЕНЕНИЕ КОНТУРНОГО АНАЛИЗА В ЗАДАЧАХ
ОБРАБОТКИ ИЗОБРАЖЕНИЙ
Глава 6
ВЫДЕЛЕНИЕ ГРАНИЦ ИЗОБРАЖЕНИЙ
6.1. Выделение границ как одна из задач сегментации изображений . . . 224
6.2. Согласованно-избирательная фильтрация изображений (простран¬
ственный аспект) 229
6.2.1. Принцип согласованно-избирательной фильтрации изображе¬
ний (229). 6.2.2. Сравнение свойств согласованного и согласованно¬
избирательного фильтров (231). 6.2.3. Одномерные СИФ для последо¬
вательности цифровых отсчетов яркости (234).
6.3. Согласованно-избирательная фильтрация одномерного скачка ярко¬
сти 236
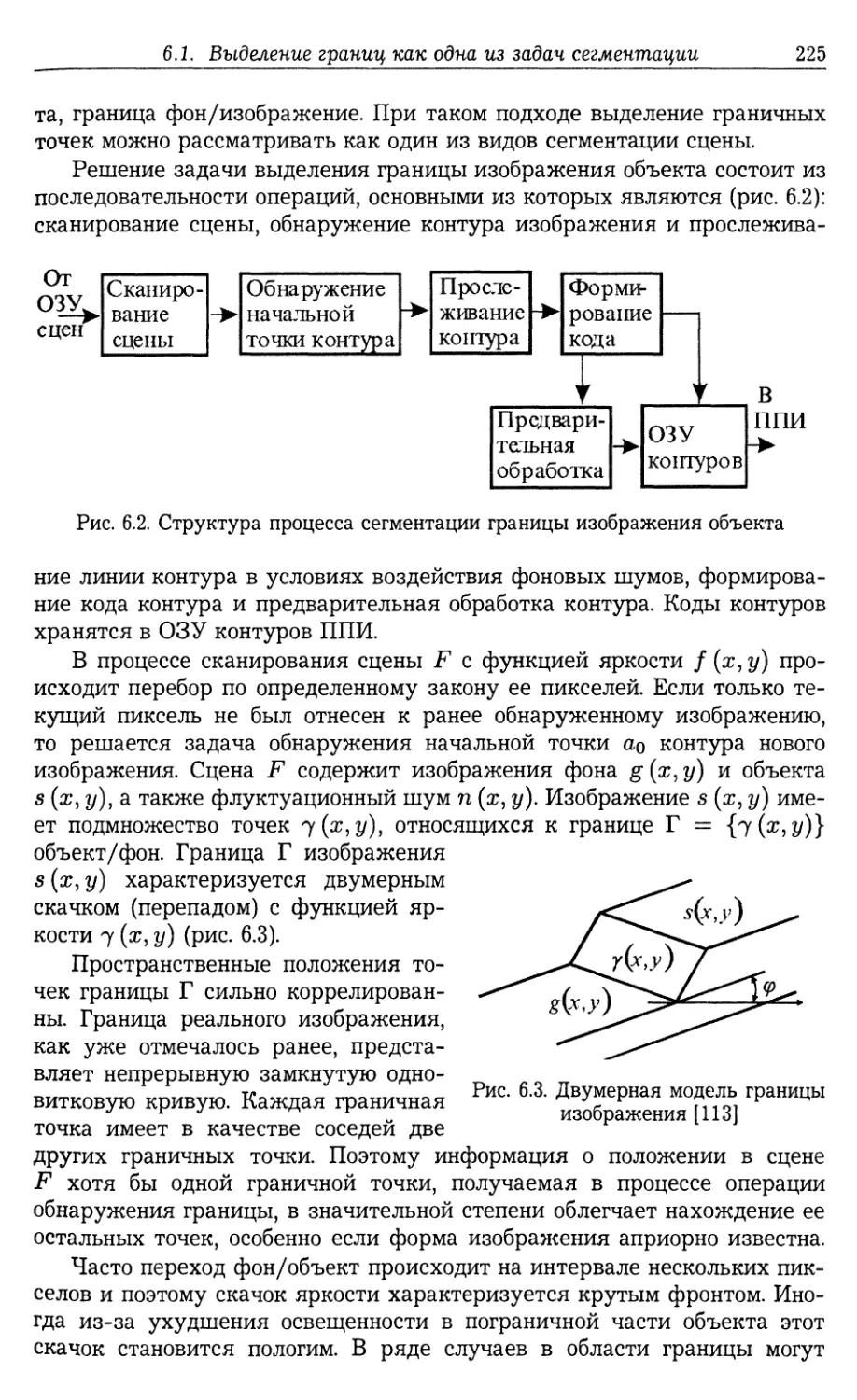
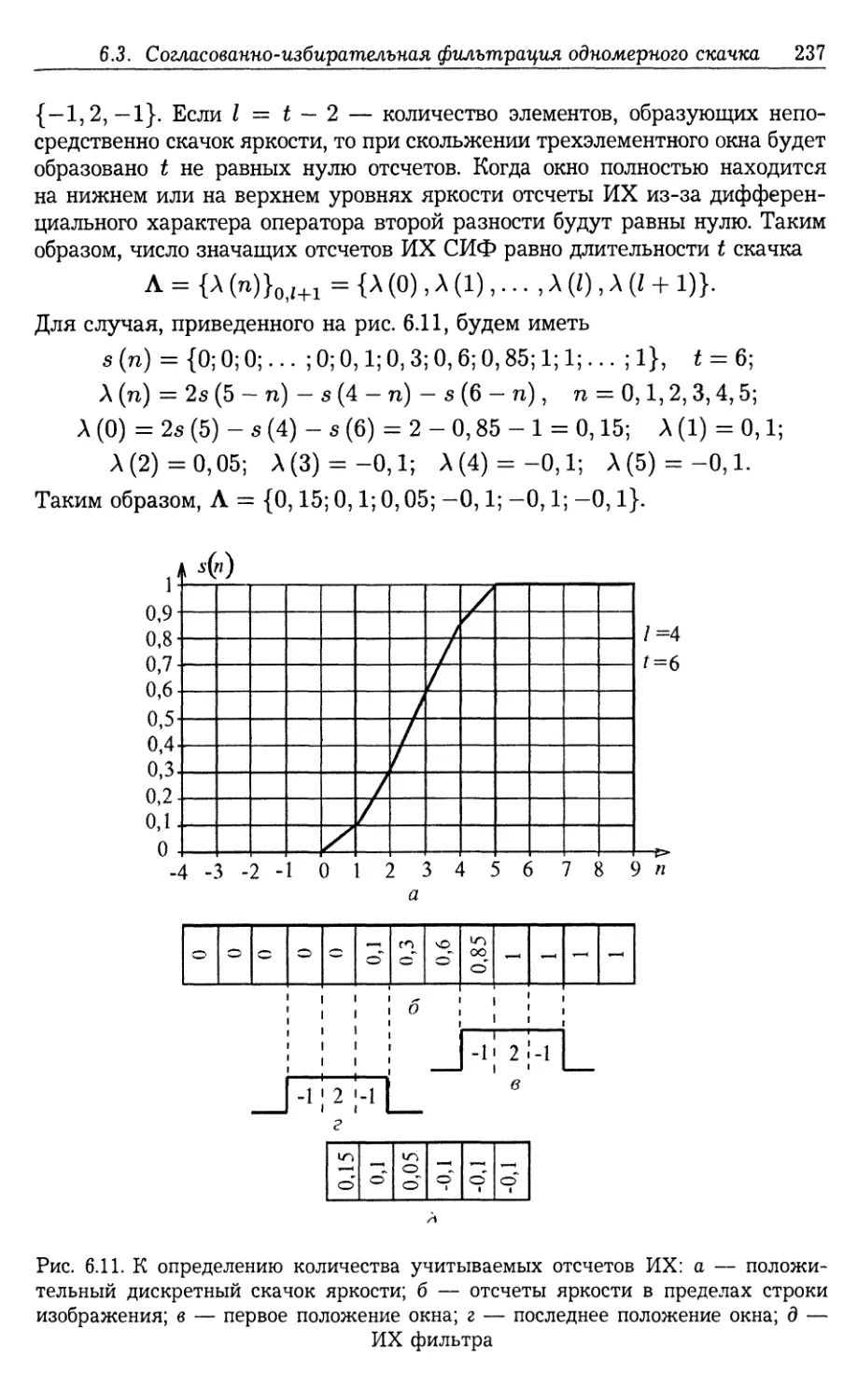
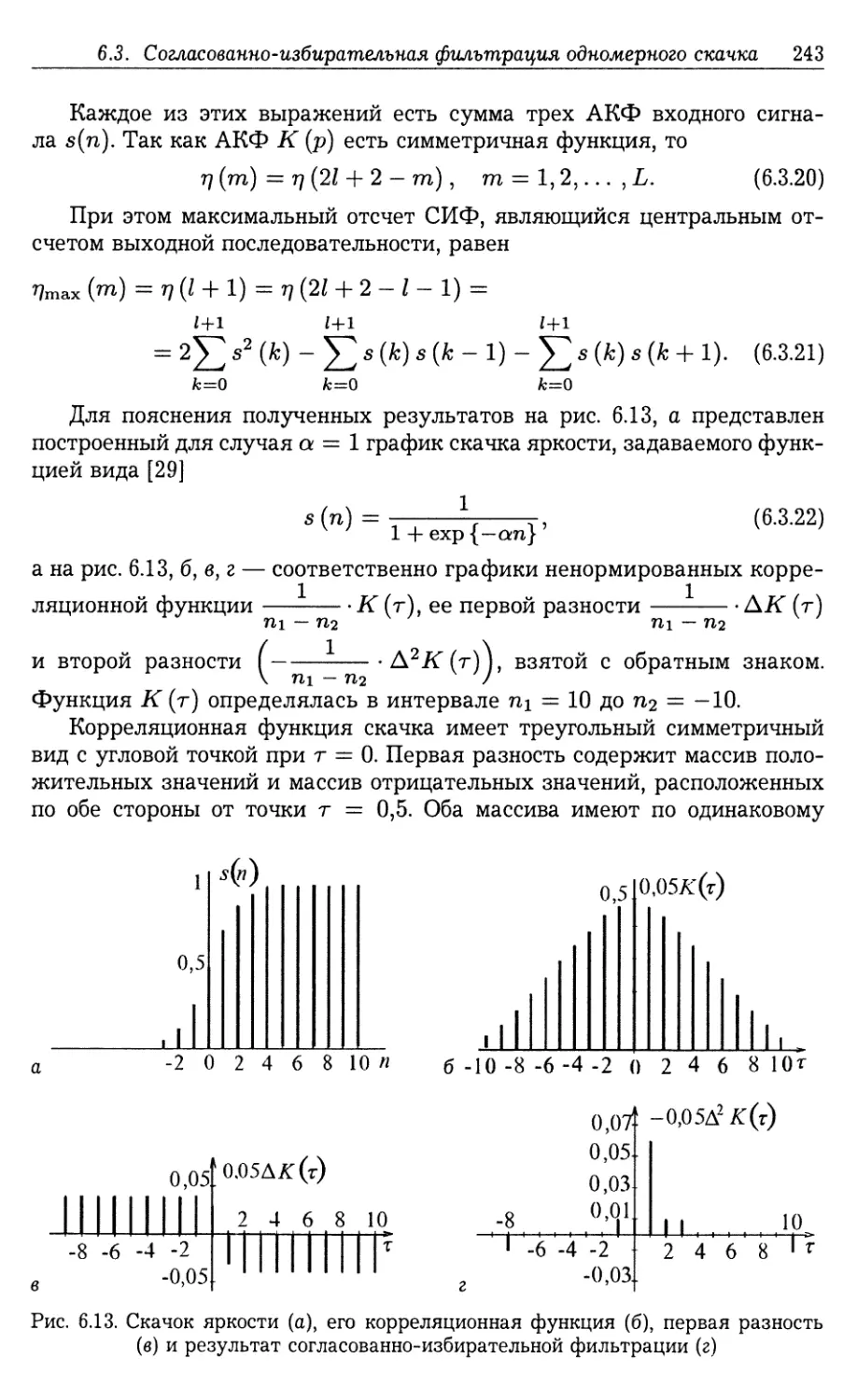
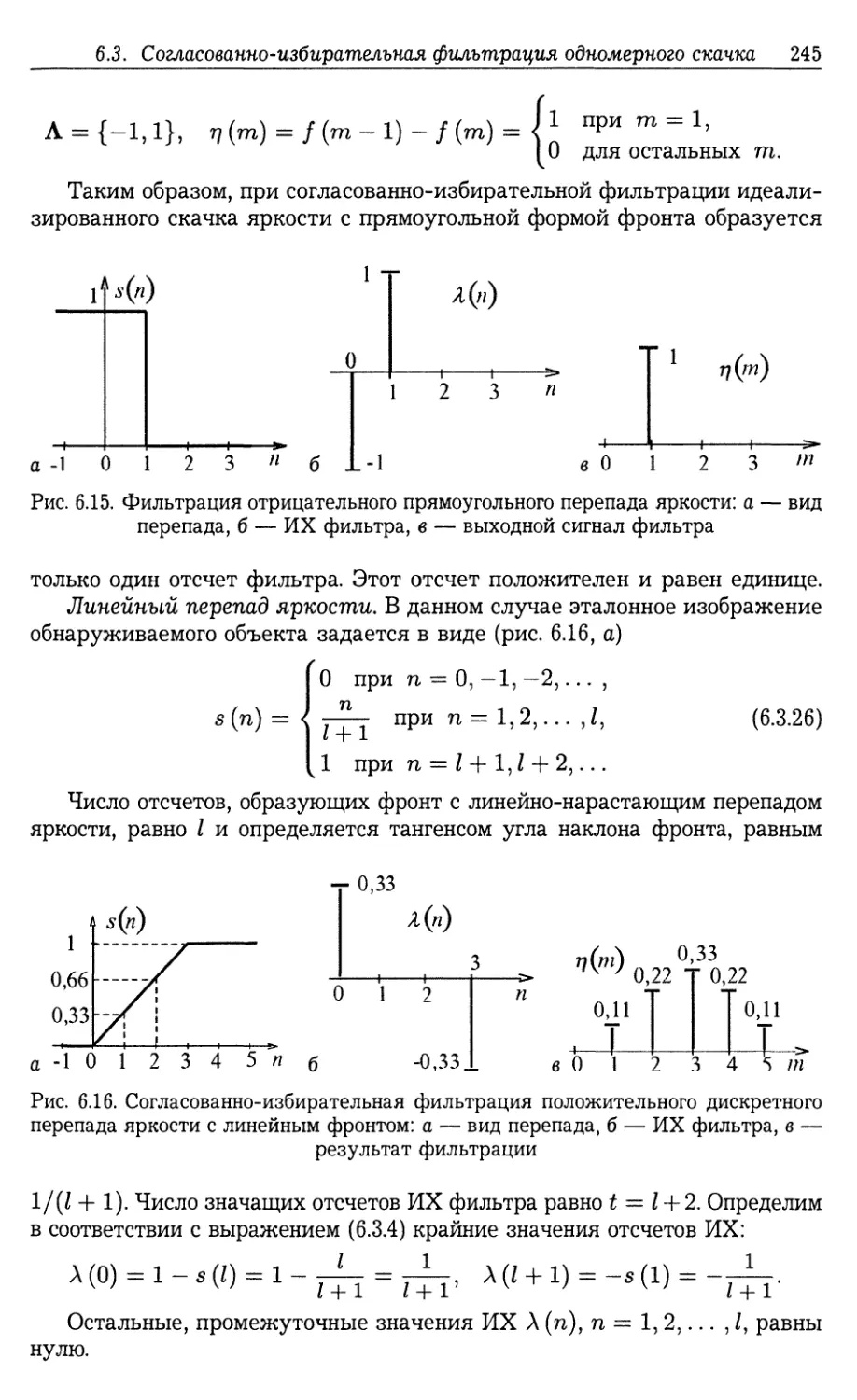
6.3.1. Идеализированные скачки яркости (236). 6.3.2. Импульсная ха¬
рактеристика СИФ (236). 6.3.3. Анализ процесса фильтрации (239).
6.3.4. Согласованно-избирательная фильтрация одномерных идеали¬
зированных перепадов яркости с простым видом фронтов (244).
6.4. Согласованно-избирательная фильтрация изображений (частотный
аспект) 248
6.4.1. Частотный коэффициент передачи фильтра (248). 6.4.2. Механизм
работы СИФ при формировании сигнального отклика (251). 6.4.3. ЧКП
СИФ для прямоугольного и линейного скачков яркости (254). 6.4.4. ЧКП
Оглавление
7
СИФ для параболического скачка яркости (256). 6.4.5. Прохождение фо¬
новых шумов через СИФ (257). 6.4.6. Энергетические соотношения при
согласованно-избирательной фильтрации зашумленных скачков ярко¬
сти (259).
6.5. Характеристики обнаружения границы изображения при использо¬
вании согласованно-избирательной фильтрации 260
6.5.1. Алгоритм работы обнаружителя (260). 6.5.2. Методика расчета
характеристик обнаружения границы (261).
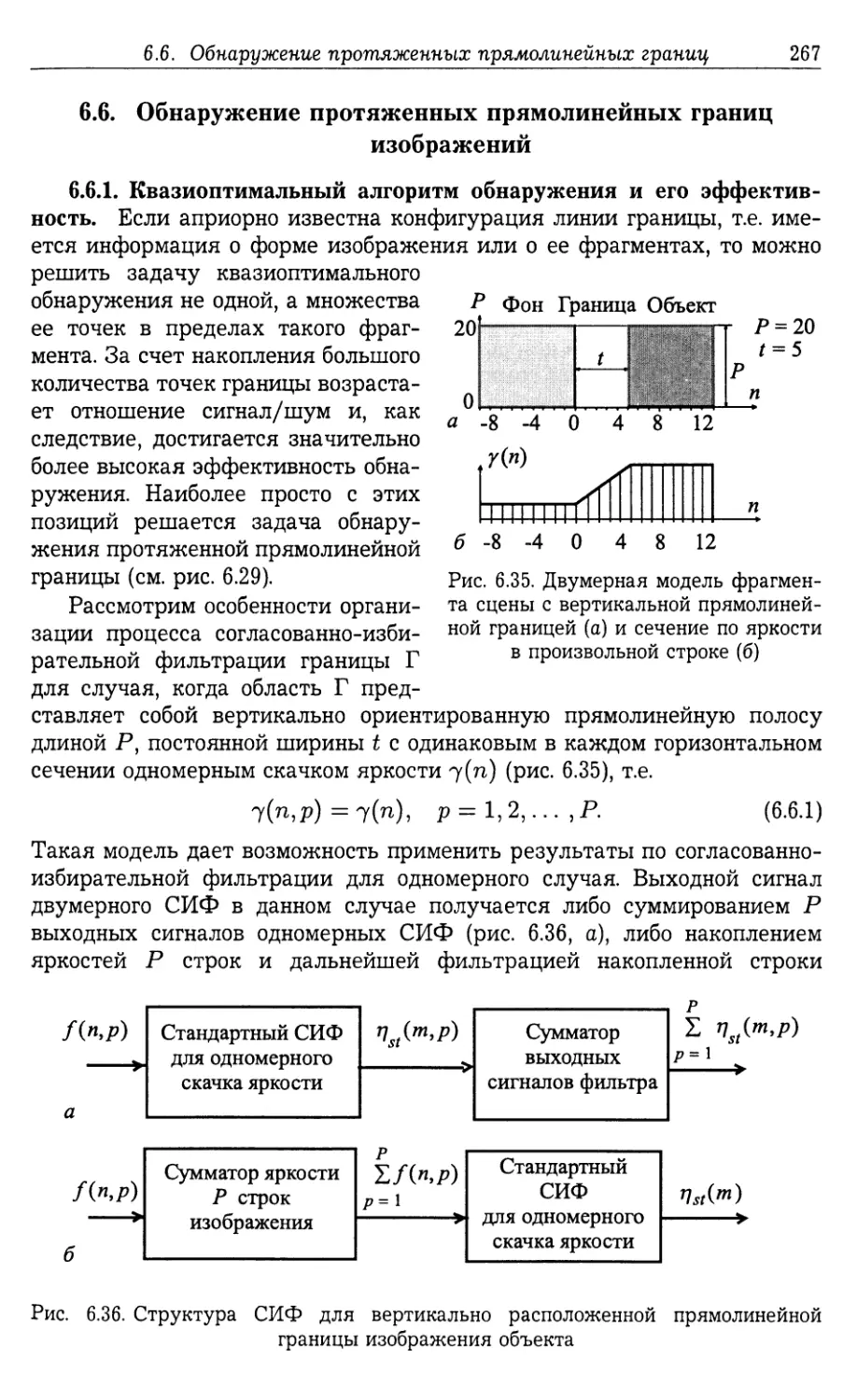
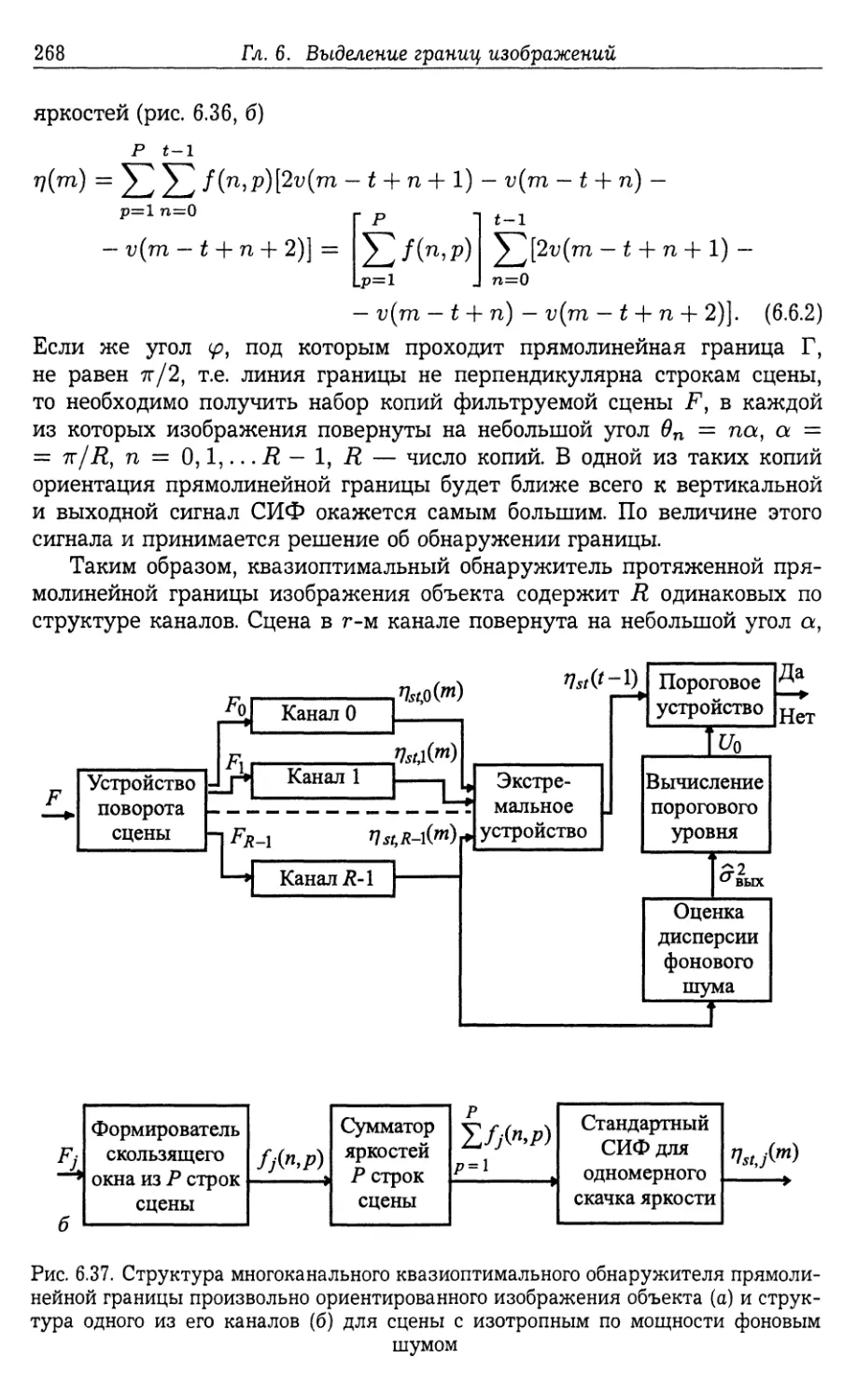
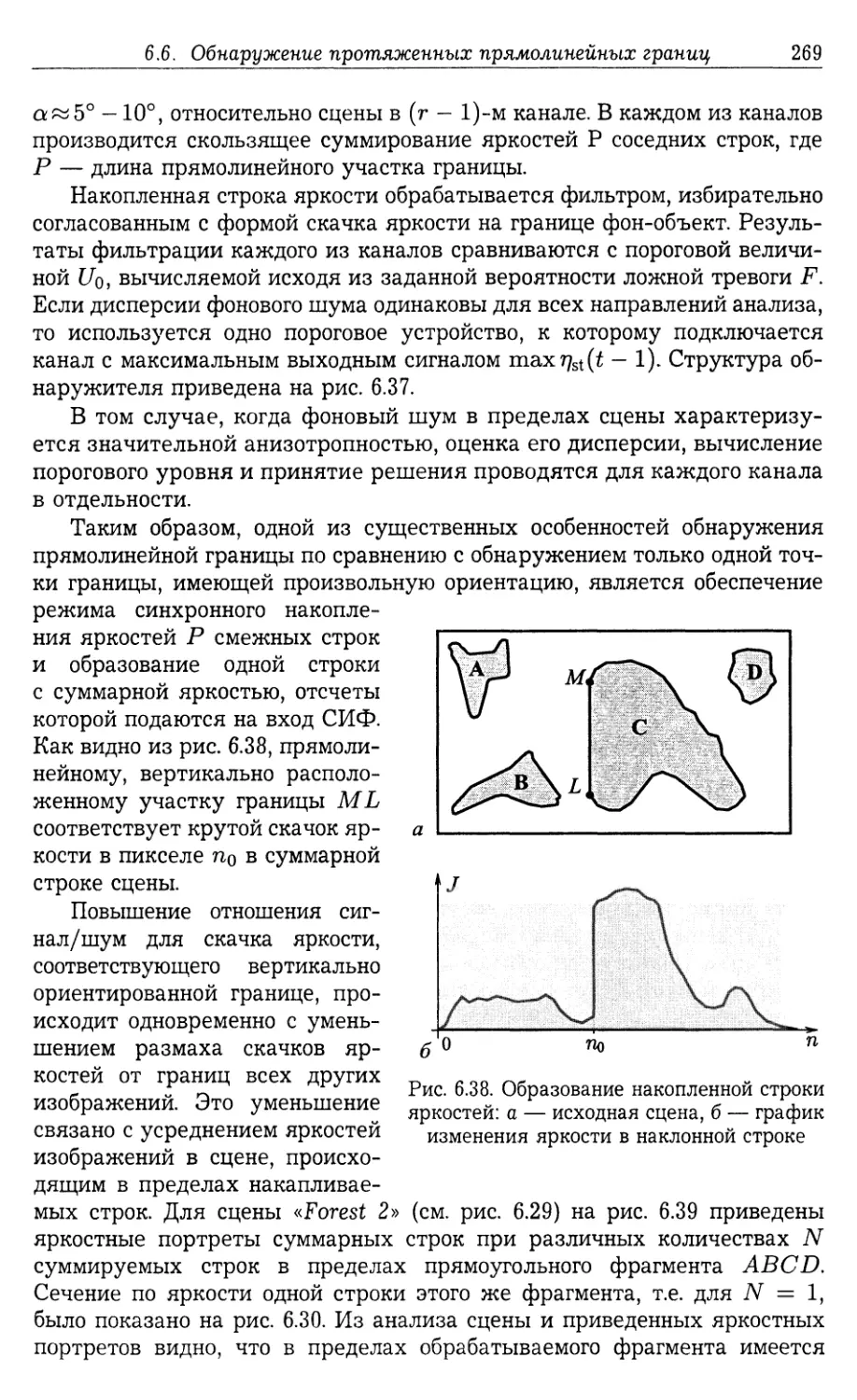
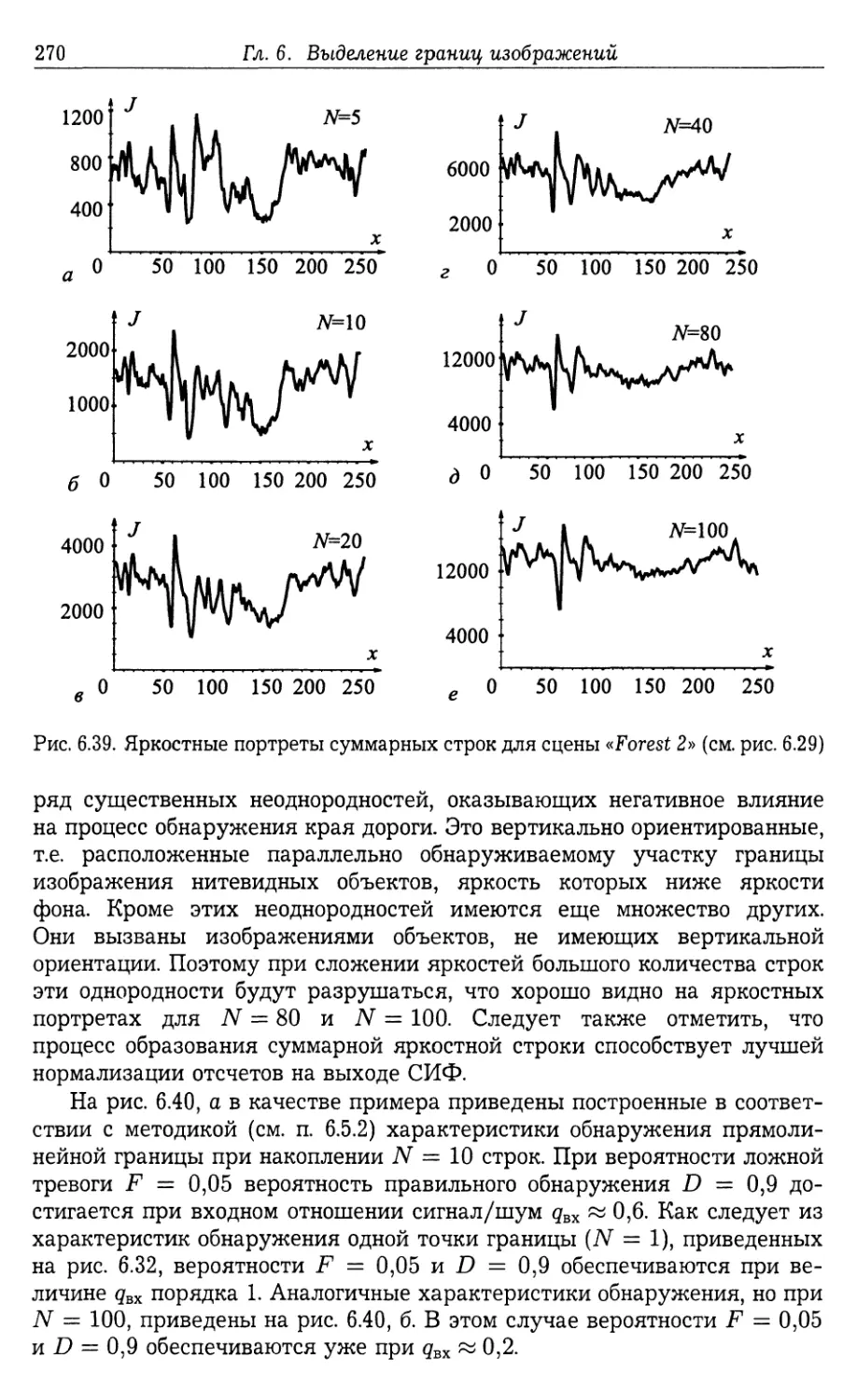
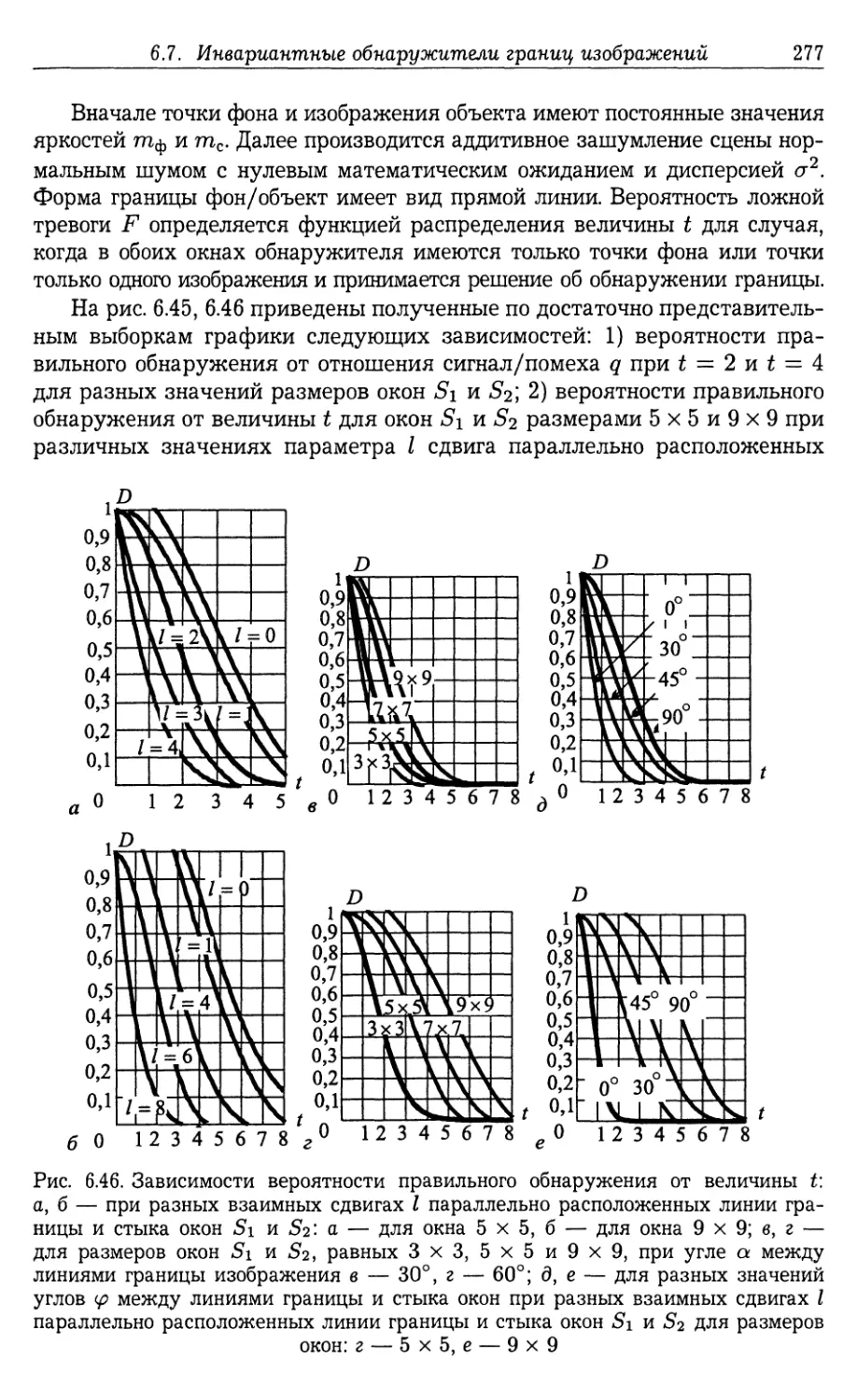
6.6. Обнаружение протяженных прямолинейных границ изображений . . 267
6.6.1. Квазиоптимальный алгоритм обнаружения и его эффектив¬
ность (267). 6.6.2. Выбор количества сдвинутых копий исходной сцены
при обнаружении прямолинейной границы с произвольной ориента¬
цией (272).
6.7. Инвариантные к характеристикам сцены обнаружители границ
изображений 273
6.7.1. Обнаружение границы на базе ί-критерия (274). 6.7.2. Характе¬
ристики ί-обнаружителя (276). 6.7.3. Инвариантный к наклону линии
границы обнаружитель (278).
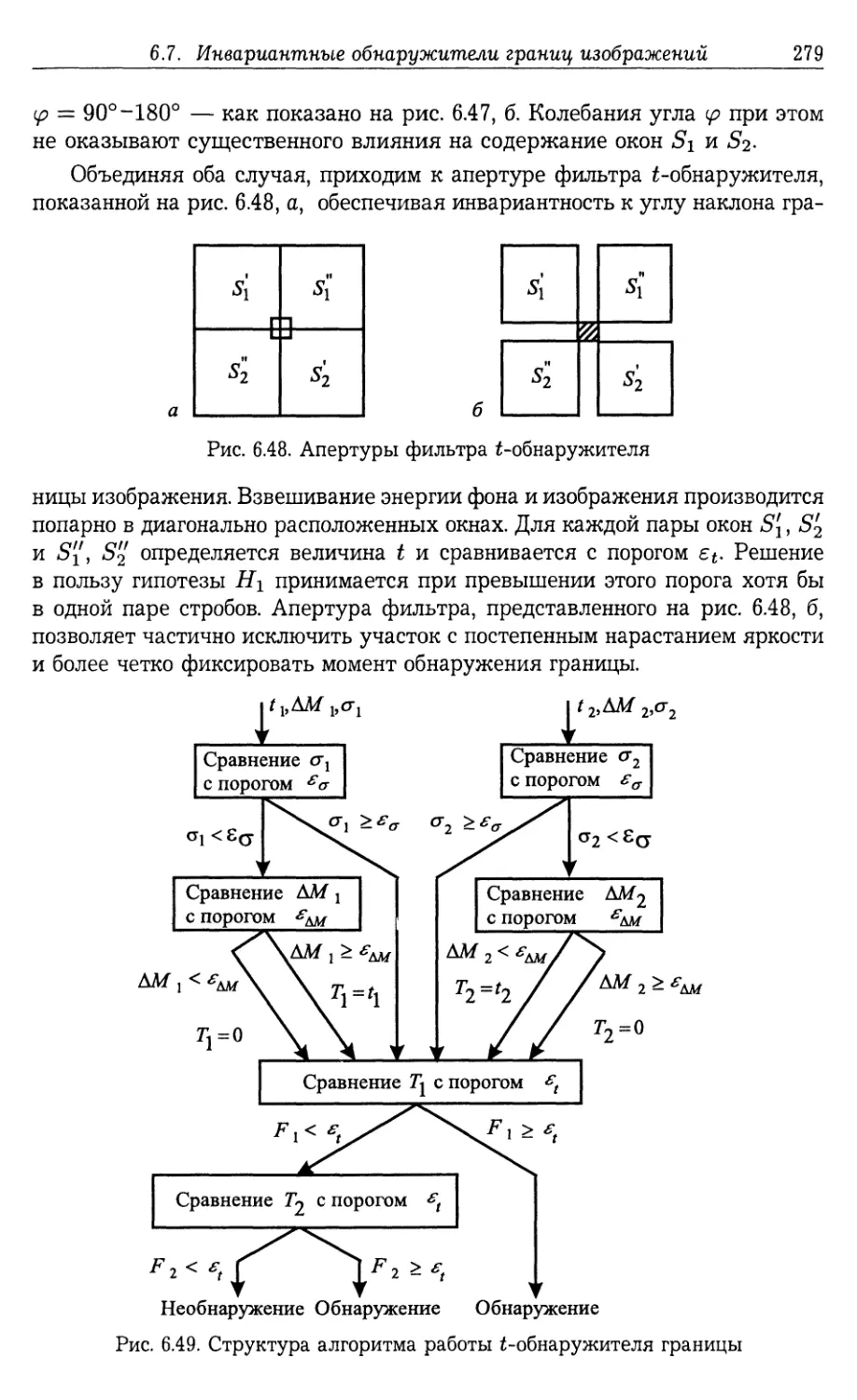
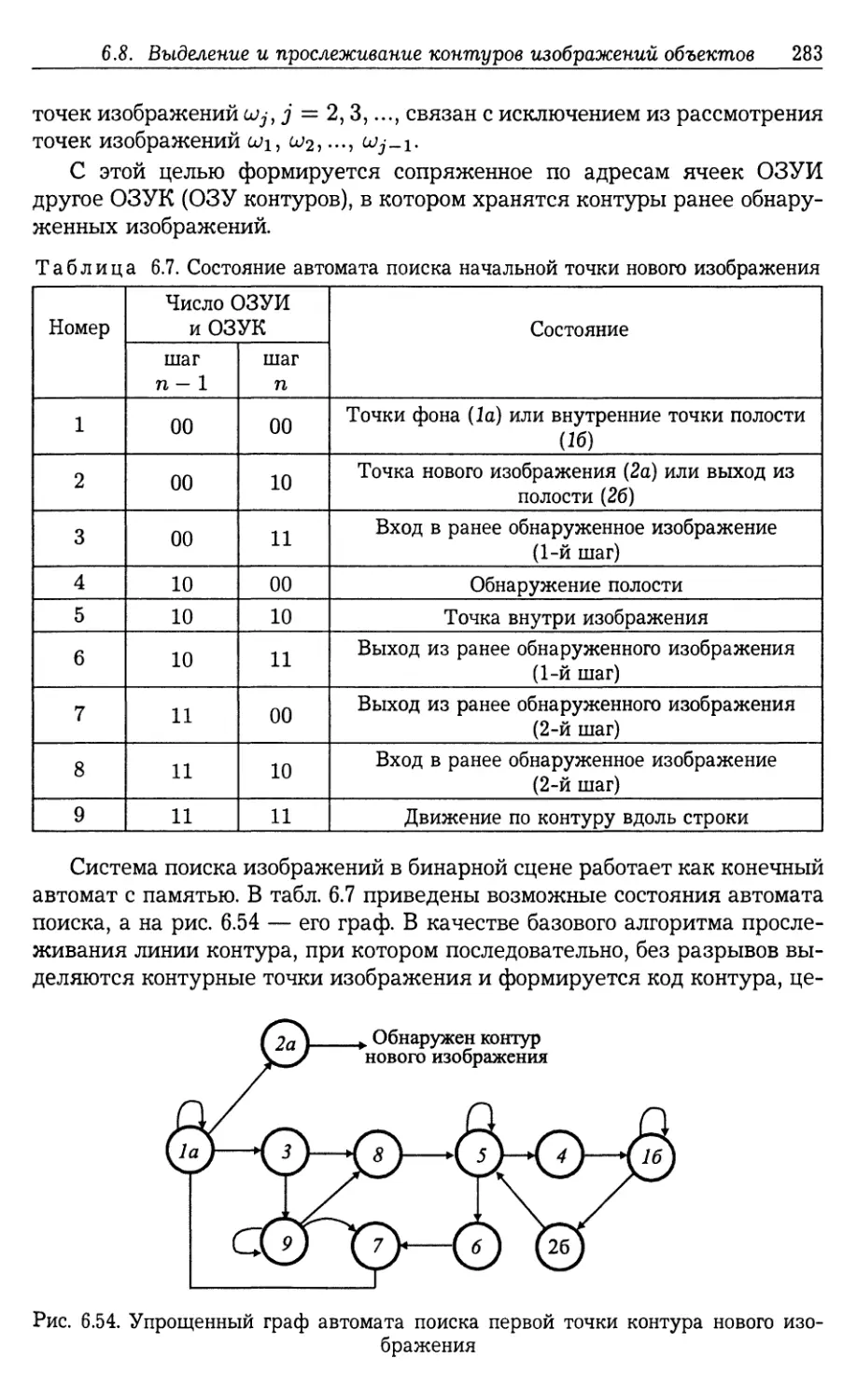
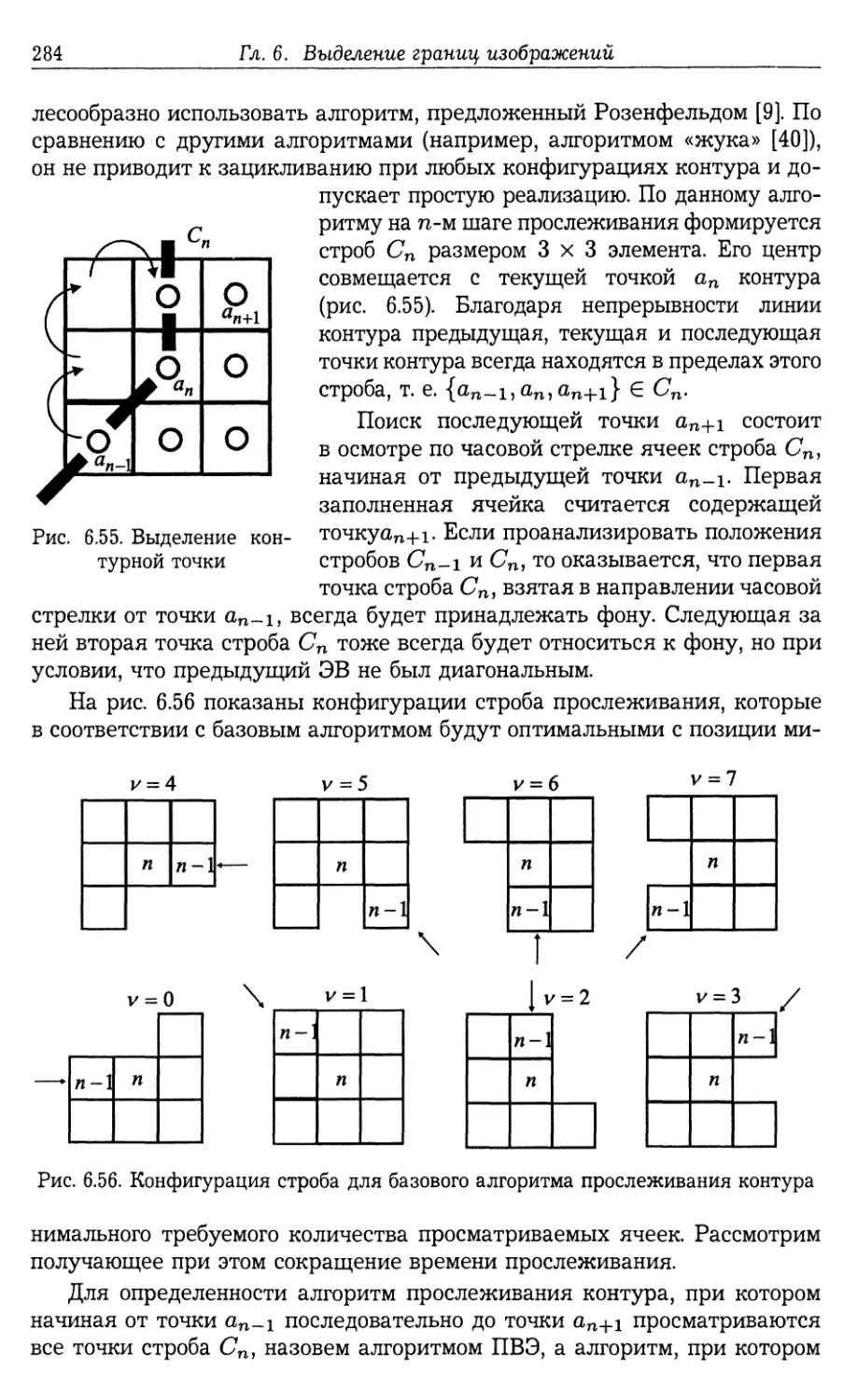
6.8. Выделение и прослеживание контуров изображений объектов . . . 282
6.8.1. Прослеживание контуров бинарных изображений (282). 6.8.2. Гло¬
бально-оптимальная процедура формирования порогового уровня для
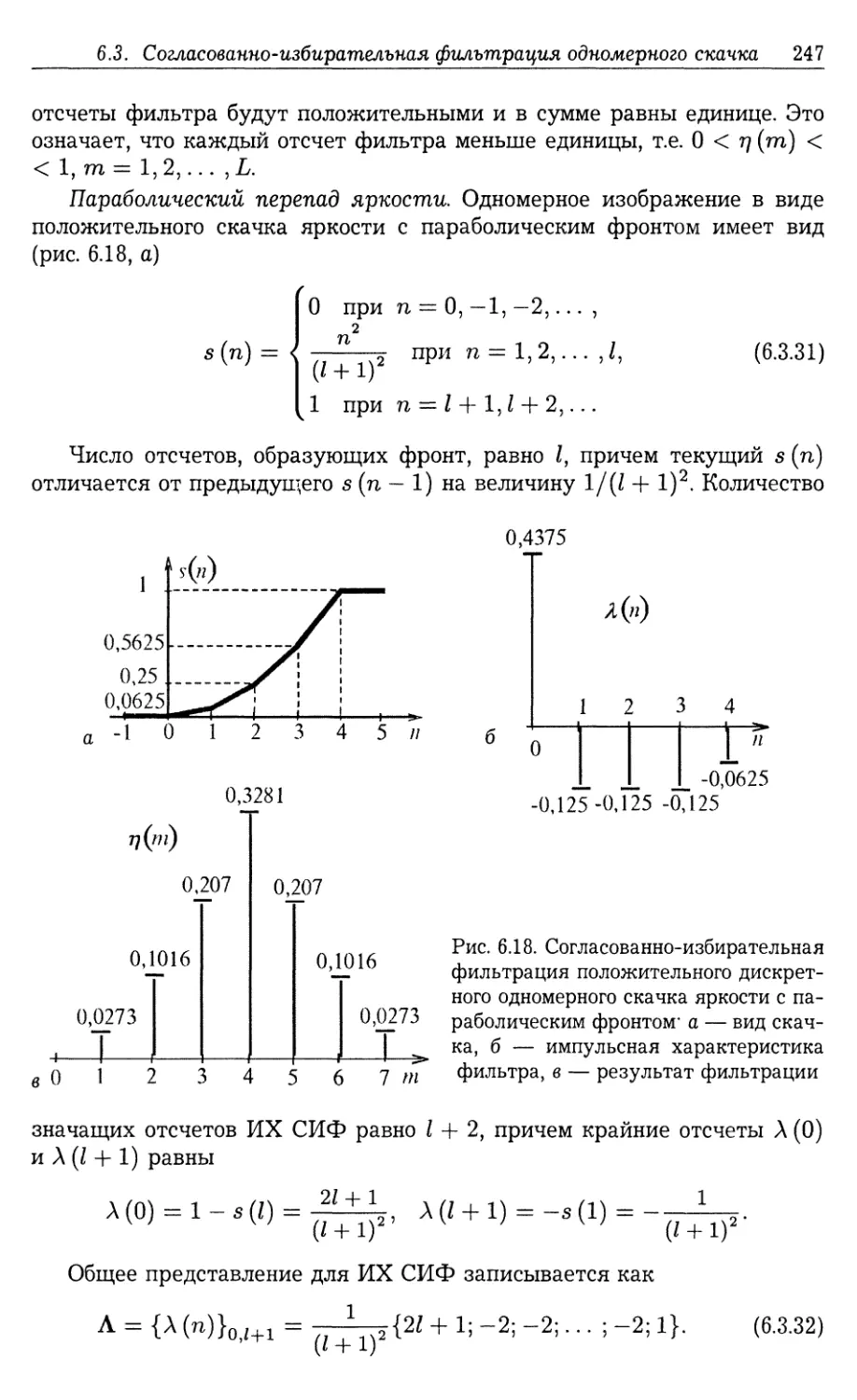
получения бинарной сцены (286). 6.8.3. Локально-опимальная проце¬
дура формирования порогового уровня для получения бинарной сце¬
ны (288). 6.8.4. Алгоритмы прослеживания контуров многоградацион¬
ных изображений, не связанные с образованием бинарных сцен (292).
6.9. Прослеживание прямолинейной границы изображения на многогра¬
дационном фоне 295
6.9.1. Марковская модель процесса прослеживания (295). 6.9.2. Анализ
процесса прослеживания прямолинейной границы изображения (297).
6.10. Обсуждение результатов 300
6.11. Задачи и упражнения 303
Глава 7
ИЗОБРАЖЕНИЯ С ПРЯМОЛИНЕЙНЫМИ ГРАНИЦАМИ
7.1. Введение и постановка задачи 305
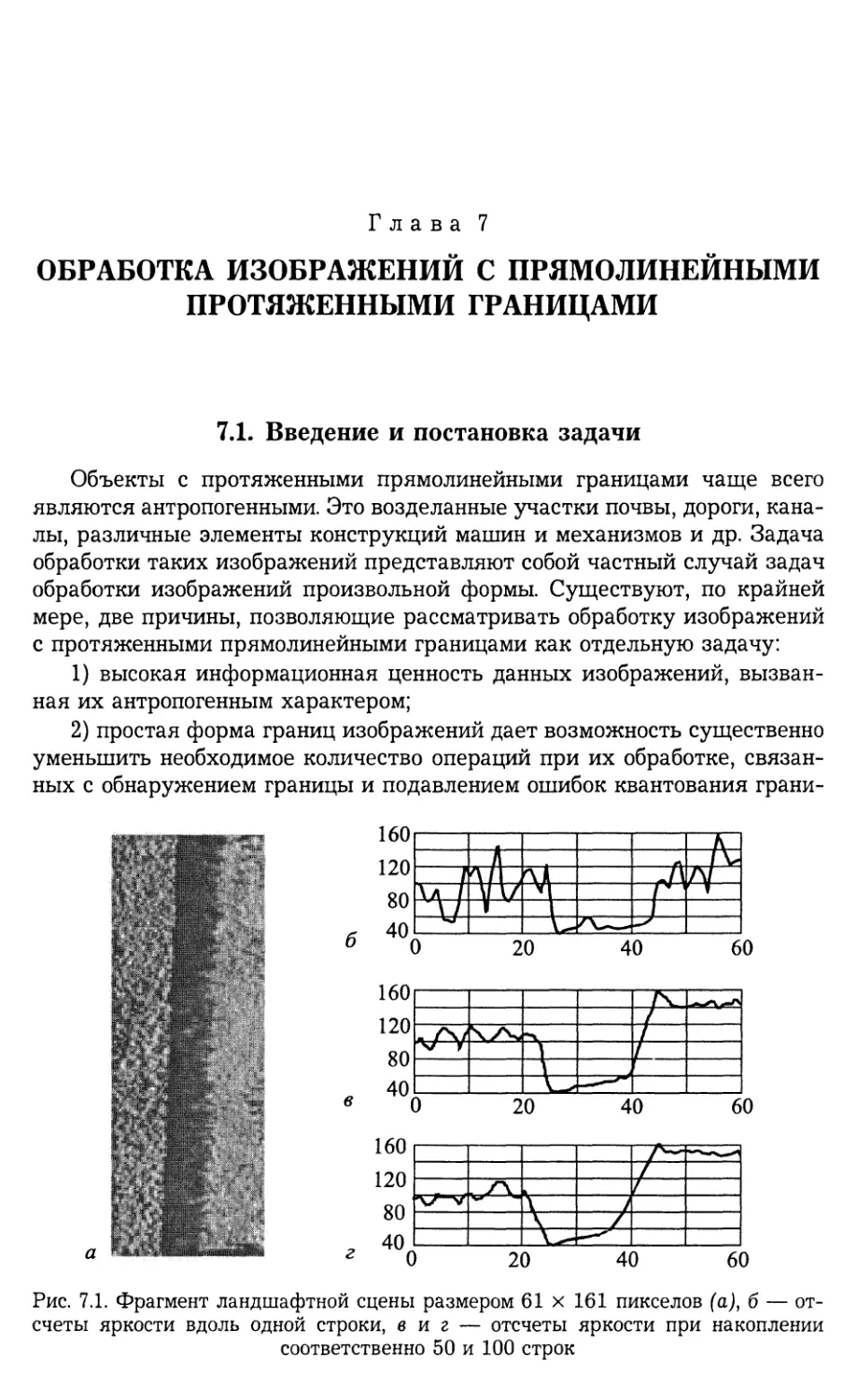
7.2. Квантование границы, проходящей через базовый сектор 308
7.3. Цепной код произвольно ориентированной прямолинейной границы . 311
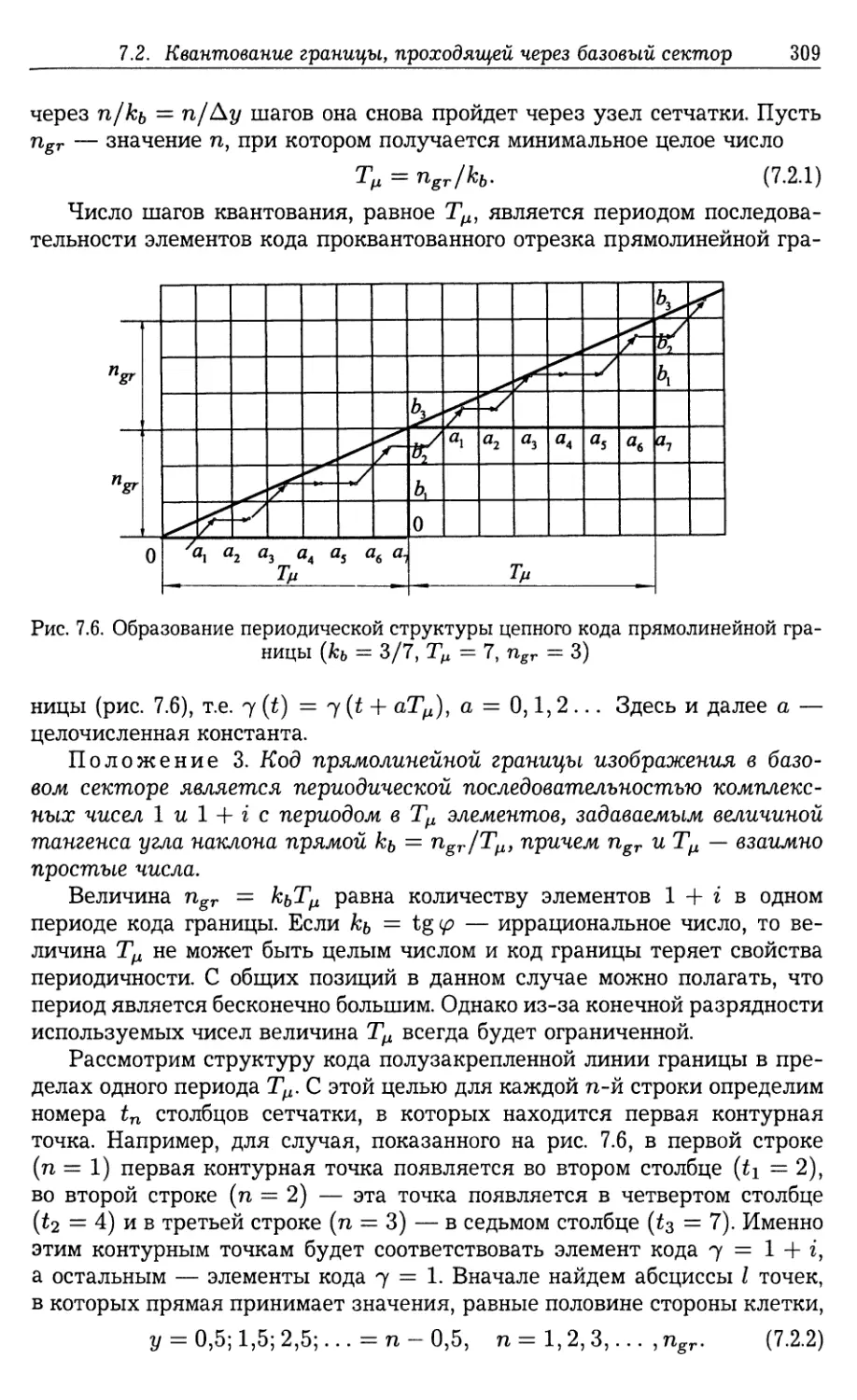
7.4. Марковская модель процесса квантования прямолинейной границы . 313
7.4.1. Синтез цепи Маркова (313). 7.4.2. Анализ марковской модели
процесса квантования (316).
7.5. АКФ цепного кода прямолинейной границы 318
7.5.1. Развернутое представление АКФ (319). 7.5.2. Компактное пред¬
ставление АКФ (322). 7.5.3. Прямое представление АКФ (324).
7.5.4. Свойства АКФ η(т) (325).
7.6. Зависимость ошибок квантования границы от преобразований мас¬
штабирования и поворота 326
7.7. Подавление ошибок квантования репрезентативного участка границы . 328
7.7.1. Энергия среднего арифметического репрезентативных векторов
ошибок квантования (328). 7.7.2. Условие полного подавления ошибок
8
Оглавление
квантования (329). 7.7.3. Расчет коэффициента подавления ошибок
квантования (330).
7.8. Идеальное восстановление прямолинейной границы 332
7.9. Оптимальное квантование прямолинейной границы изображения . . 333
7.10. Энергетические характеристики ошибок квантования для отрезков
кодов произвольной длины 334
7.11. Подавление ошибок квантования границы произвольной длины
согласованным фильтром 336
7.11.1. Основные соотношения при согласованной фильтрации грани¬
цы произвольной длины (336). 7.11.2. Анализ процесса согласованной
фильтрации прямолинейных границ изображений произвольной дли¬
ны (338).
7.12. Основные результаты 340
Глава 8
ИЗОБРАЖЕНИЯ ОБЪЕКТОВ ПРОТЯЖЕННОЙ ФОРМЫ
8.1. Введение 344
8.2. Согласованно-избирательная фильтрация импульсов яркости (про¬
странственный аспект) 345
8.2.1. Аналитическое представление одномерного импульса яркос¬
ти (345). 8.2.2. Импульсная характеристика фильтра (346). 8.2.3. Ана¬
лиз процесса фильтрации импульса яркости (347). 8.2.4. Согласованно¬
избирательная фильтрация некоторых видов импульсов яркости (349).
8.2.5. Двумерные СИФ для изображений нитевидных объектов. (351).
8.3. Согласованно-избирательная фильтрация прямоугольных импульсов
яркости (частотный аспект) 353
8.3.1. Частотный коэффициент передачи СИФ для прямоугольного
импульса яркости (353). 8.3.2. Амплитудно-частотная характеристи¬
ка (354). 8.3.3. Фазочастотная характеристика СИФ (355). 8.3.4. Спект¬
ральные характеристики выходного сигнала (355).
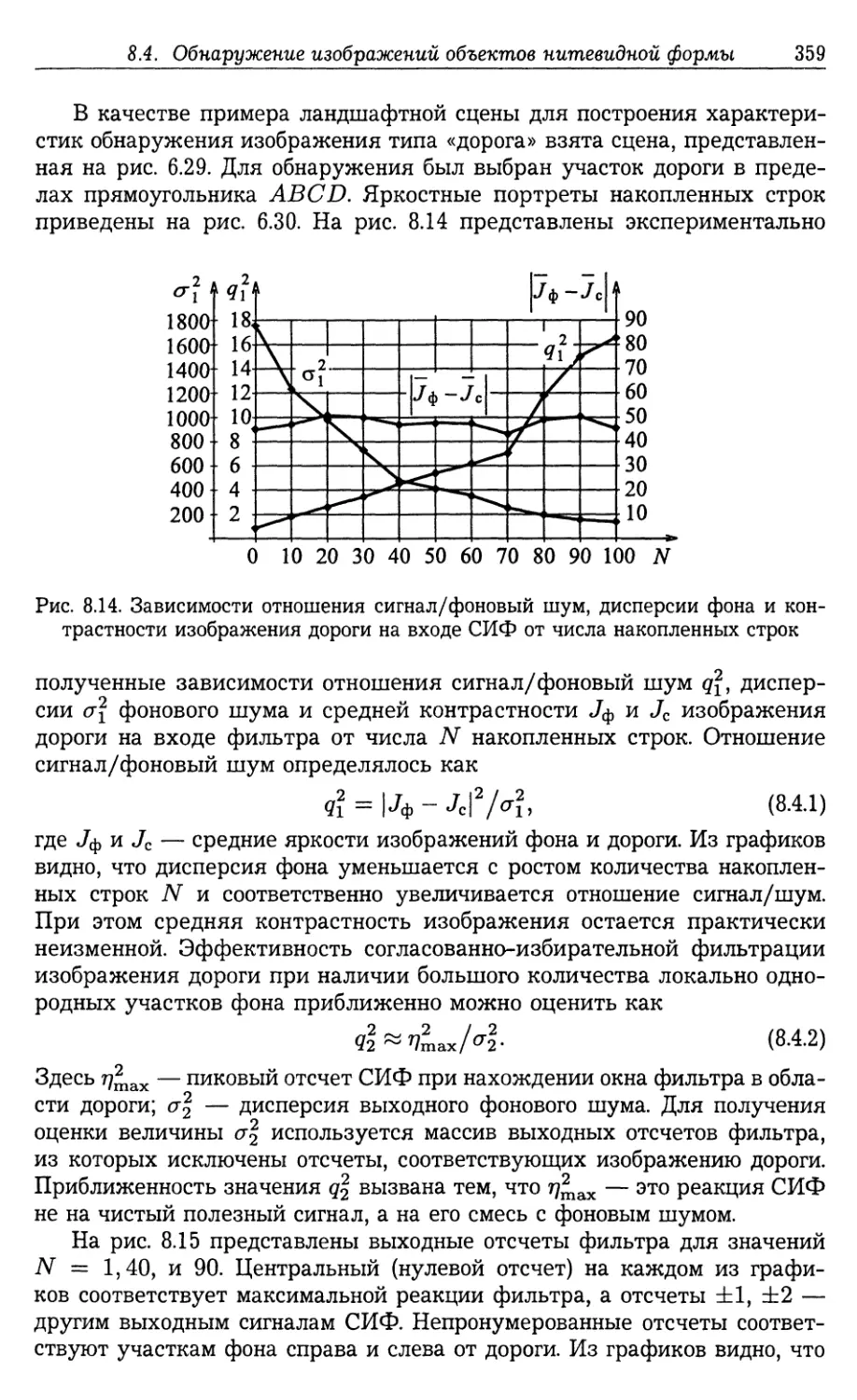
8.4. Обнаружение изображений объектов нитевидной формы 358
8.5. Прослеживание изображений объектов протяженной формы .... 364
8.6. Обсуждение результатов 366
Глава 9
АНАЛИЗ И РАСПОЗНАВАНИЕ ИЗОБРАЖЕНИЙ
ПО ИХ ФОРМЕ
9.1. Специальные операции над контурами изображений 369
9.1.1. Эквализация кода контура (369). 9.1.2. Стандартизация кода кон¬
тура (371).
9.2. Структурный анализ формы изображений фильтрами, согласоваными
с классом форм 372
9.3. Определение характеристик формы изображения 379
9.4. Информативные признаки формы, определяемые по спектру контура
381
9.5. Распознавание изображений со случайными формами 384
9.6. Распознавание близких по форме детерминированных изображений . 390
Оглавление
9
9.7. Совмещение изображений объекта 393
9.7.1. Постановка задачи и модели (393). 9.7.2. Оптимальное совмеще¬
ние контуров на основе контурной согласованной фильтрации (395).
9.7.3. Выбор формы изображения объекта для их наилучшего совме¬
щения (398).
9.8. Накопление контуров изображений 399
9.9. Аналитическое представление формы плоского изображения .... 403
9.10. Обсуждение результатов 407
9.11. Задачи и упражнения 408
Глава 10
ОБРАБОТКА ИЗОБРАЖЕНИЙ С ТОЧЕЧНЫМИ
ОБЪЕКТАМИ
10.1. Введение 410
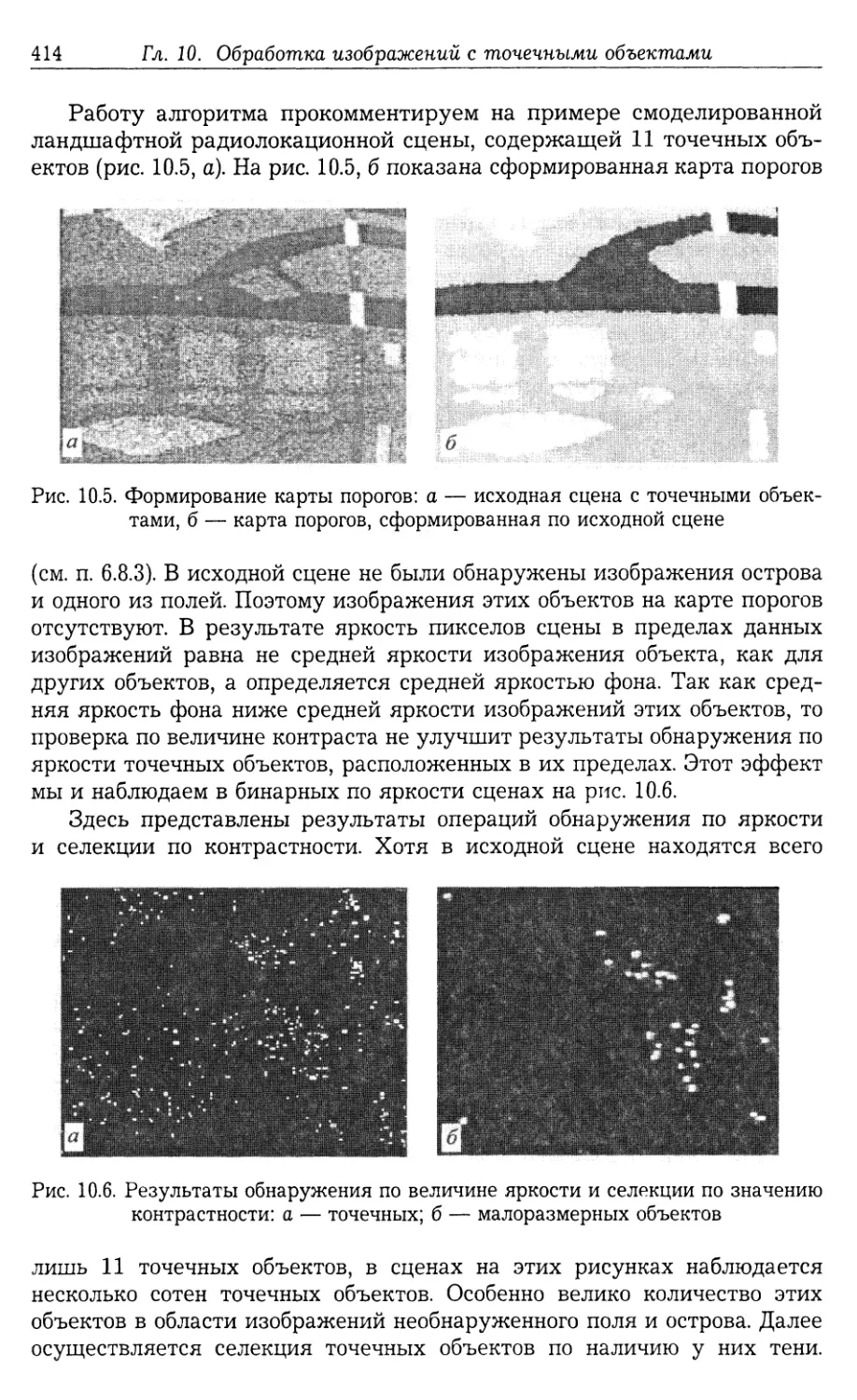
10.2. Выделение точечных и малоразмерных объектов в сценах с локально
однородным фоном 411
10.3. Прослеживание траекторий точечных отметок 416
10.3.1. Модель траектории точечной цели на квадратной сетчатке (416).
10.3.2. Алгоритм прослеживания прямолинейной траектории (417).
Глава 11
ОБРАБОТКА ГРУППОВЫХ ТОЧЕЧНЫХ ОБЪЕКТОВ
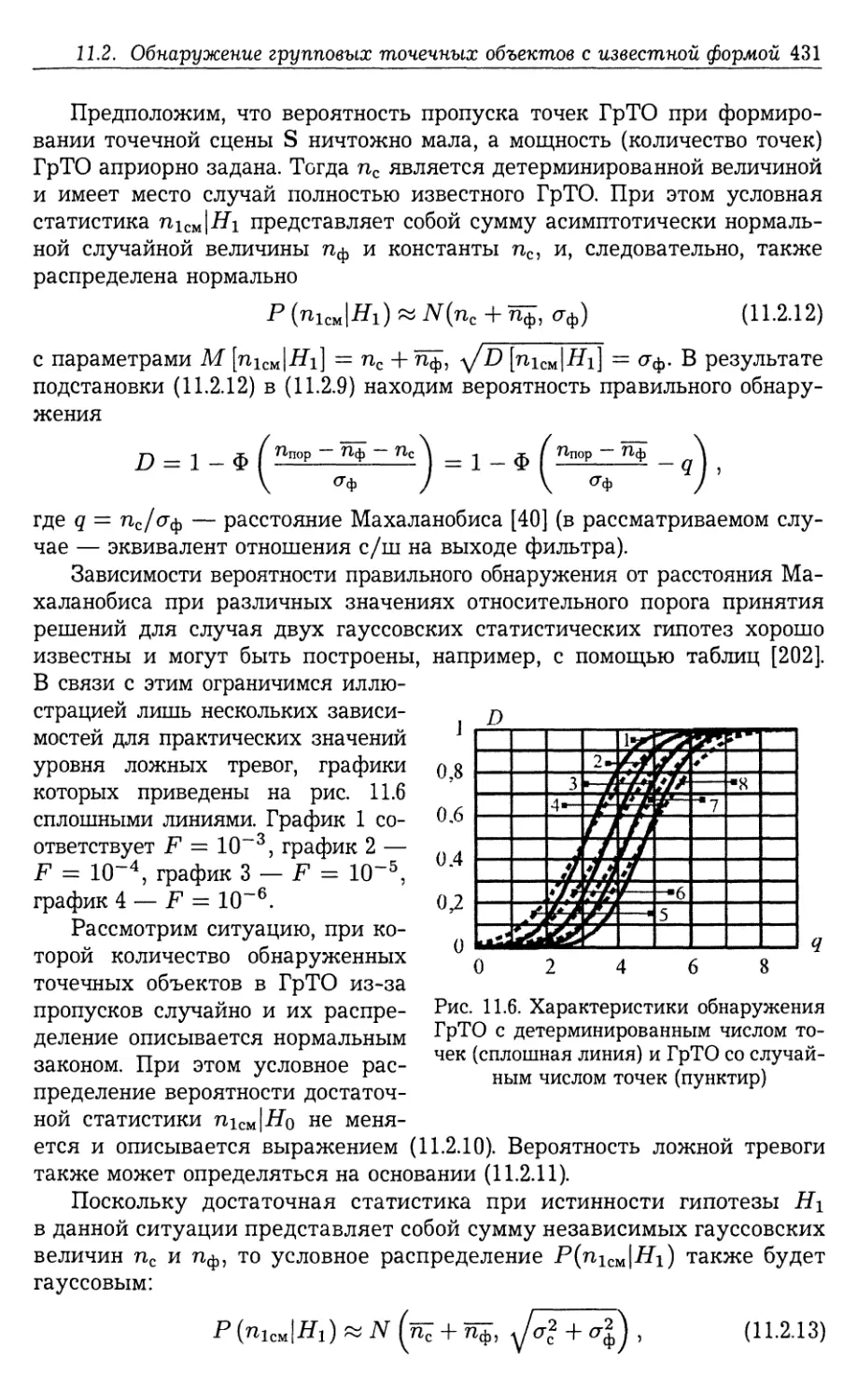
11.1. Введение 422
11.2. Обнаружение групповых точечных объектов с известной формой
ассоциированного сплошного образа 426
11.2.1. Постановка задачи и модели сигналов (426). 11.2.2. Обнаружение
ГрТО с известным положением в кадре (428). 11.2.3. Обнаружение
ГрТО с произвольным положением в кадре (432).
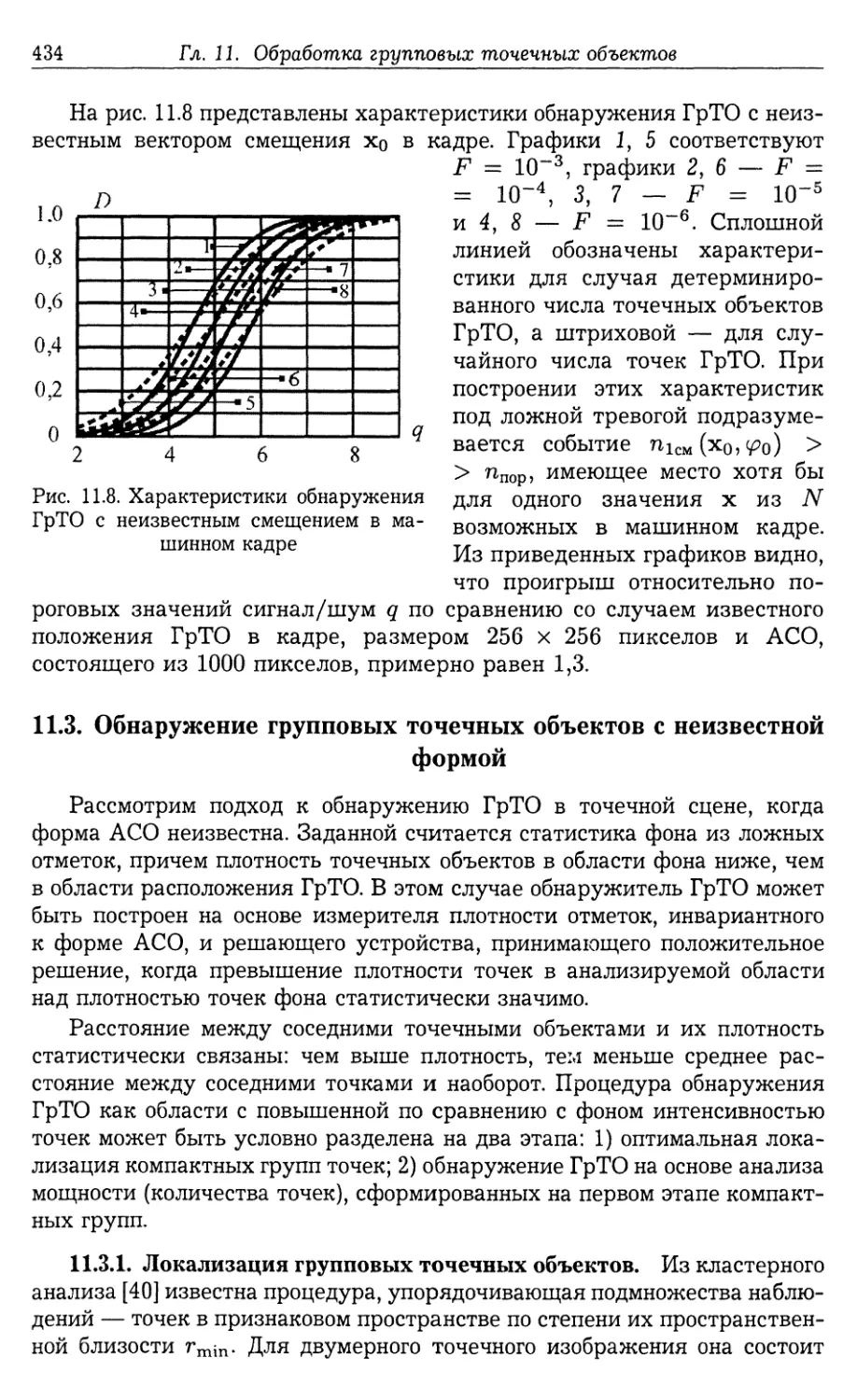
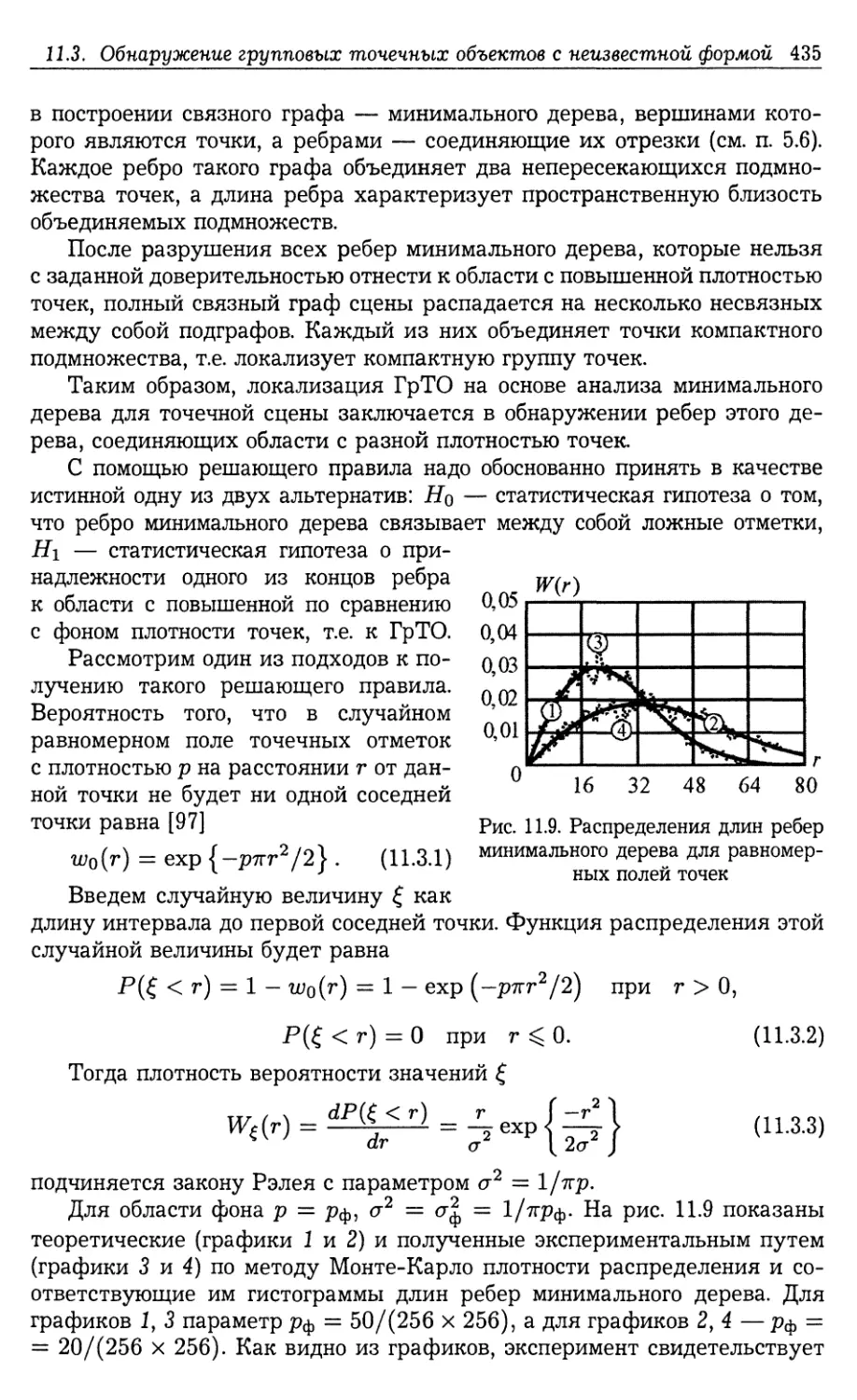
11.3. Обнаружение групповых точечных объектов с неизвестной формой . 434
11.3.1. Локализация групповых точечных объектов (434). 11.3.2. Обна¬
ружение локализованных групповых точечных объектов (437).
11.4. Распознавание групповых точечных объектов на основе анализа
первичного описания 440
11.5. Описание групповых точечных объектов вторичными признаками . . 445
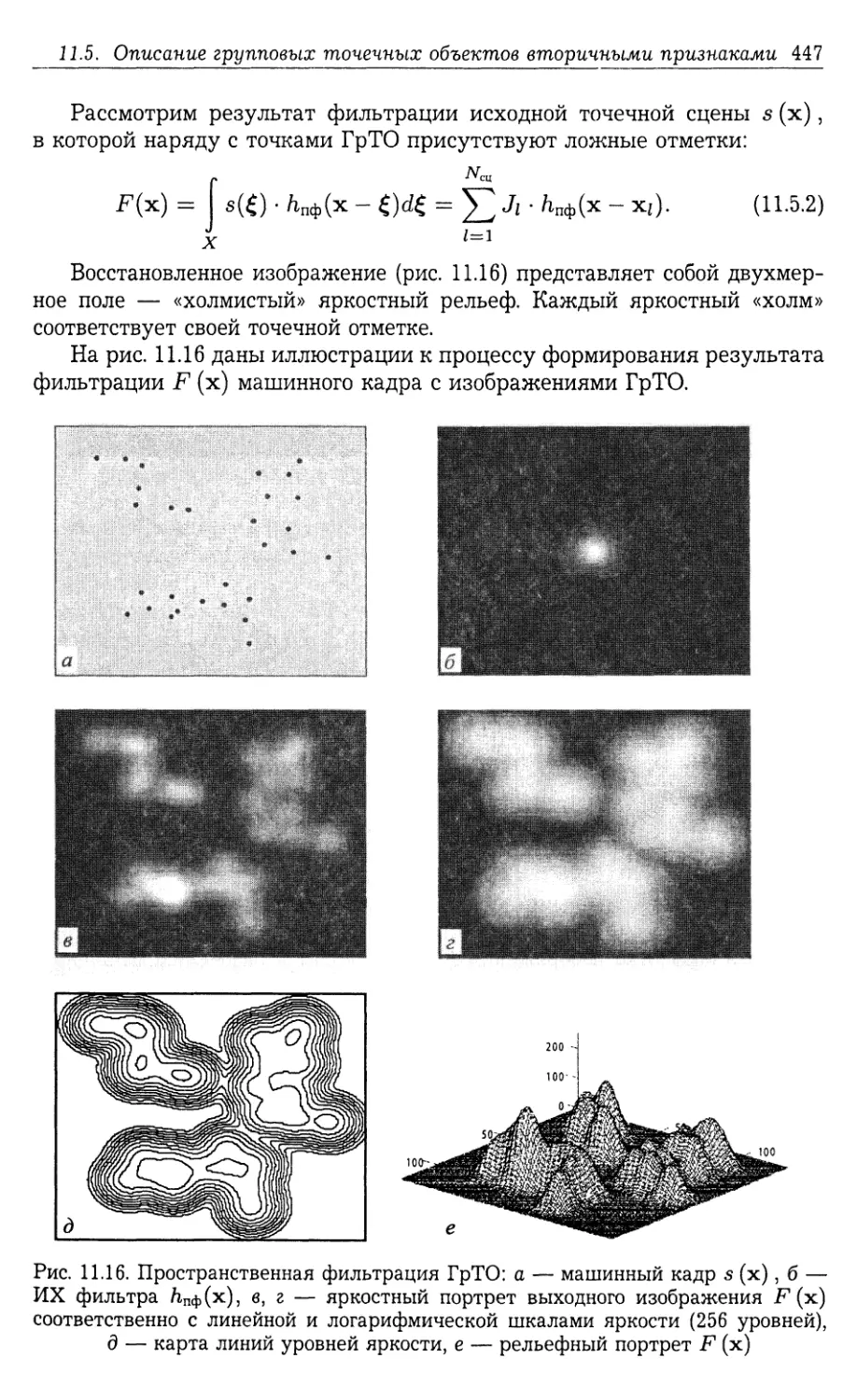
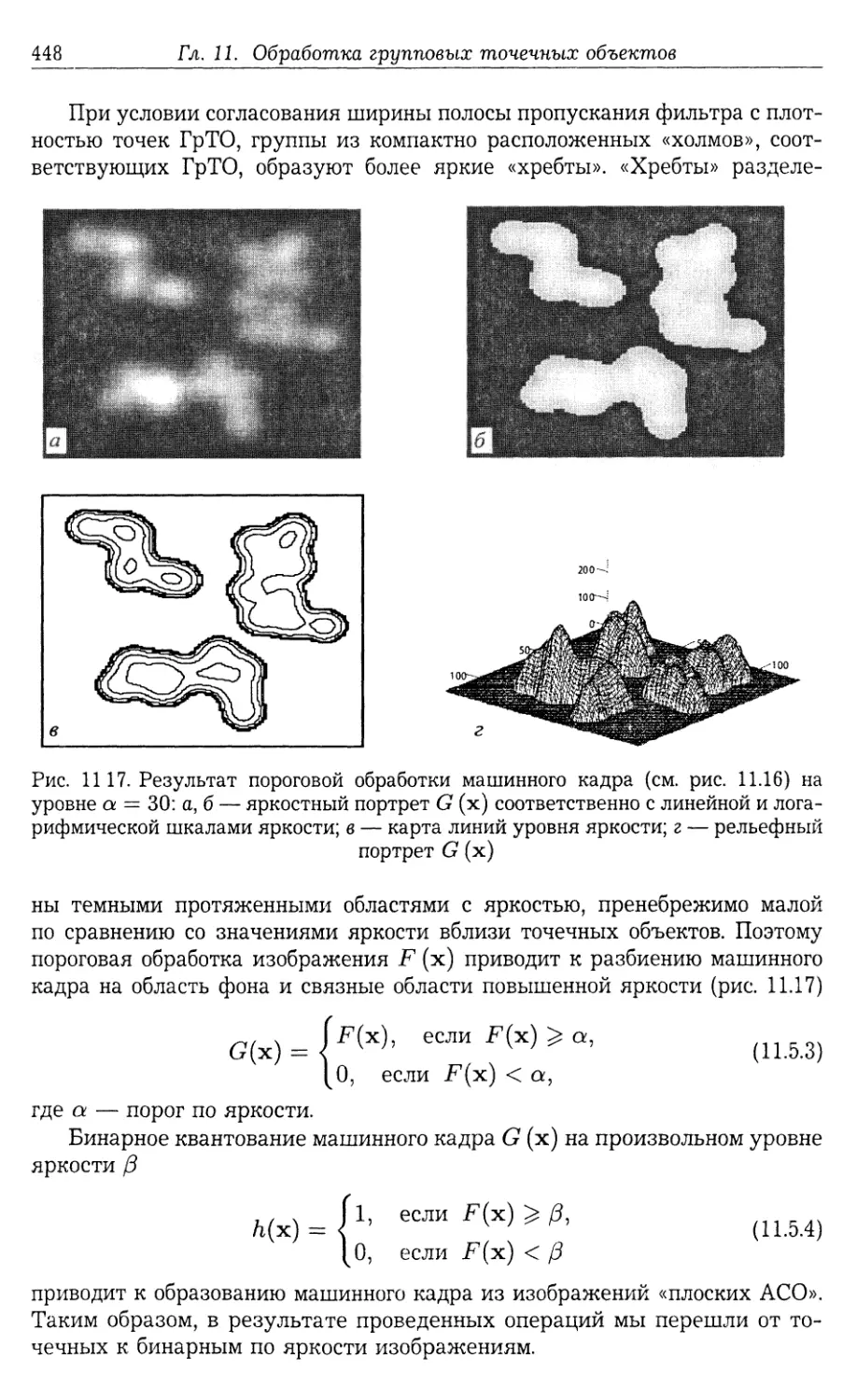
11.5.1. Введение (445). 11.5.2. Модель ассоциированного сплошного обра¬
за и локализация групповых точечных объектов (446). 11.5.3. Критерий
компактности групп точечных объектов (449). 11.5.4. Мера компактности
групп точек (451). 11.5.5. Обобщенный алгоритм локализации и обнару¬
жения компактных групповых точечных объектов с произвольной фор¬
мой АСО (453). 11.5.6. Адаптивная локализация и структурный анализ
групповых точечных объектов (454).
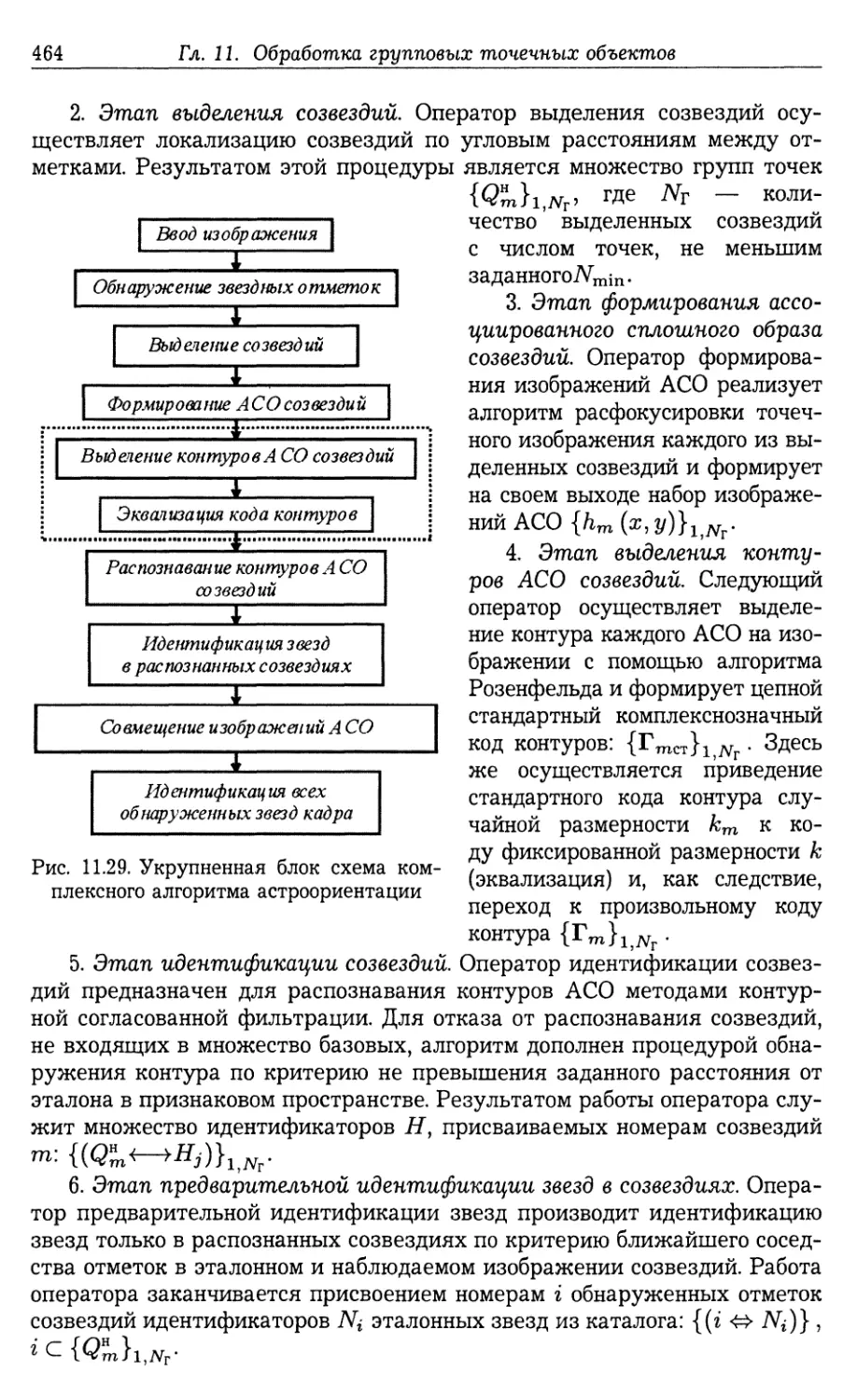
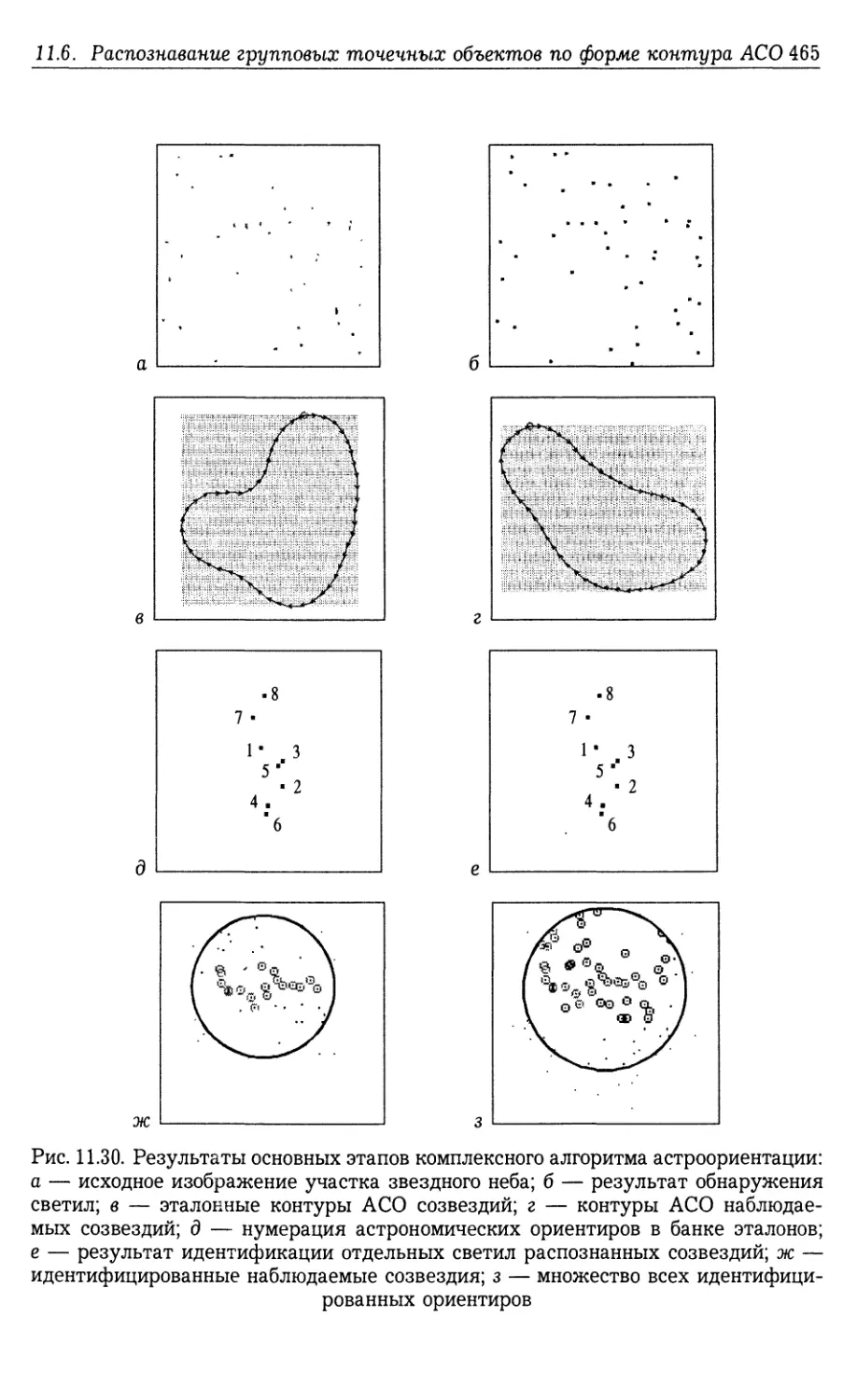
11.6. Распознавание групповых точечных объектов по форме контура
ассоциированного сплошного образа 458
11.6.1. Алгоритм распознавания (458). 11.6.2. Характеристики распо¬
знавания групповых точечных объектов по форме контуров ассоци¬
ированных сплошных образов (460). 11.6.3. Распознавание групповых
точечных объектов в виде изображений звезд (463).
10
Оглавление
11.7. Различение групповых точечных объектов с нестационарной конфи¬
гурацией 466
11.7.1. Постановка задачи и основные подходы к ее решению (466).
11.7.2. Алгоритм различения «цепочек» и «скоплений» (469). 11.7.3. Ха¬
рактеристики различителя (470).
11.8. Обсуждение результатов 472
11.9. Вопросы и упражнения 473
ЧАСТЬ III
КОНТУРНЫЙ АНАЛИЗ В ЗАДАЧАХ ОБРАБОТКИ
СИГНАЛОВ
Глава 12
КОМПОЗИЦИОННЫЕ КОНТУРЫ
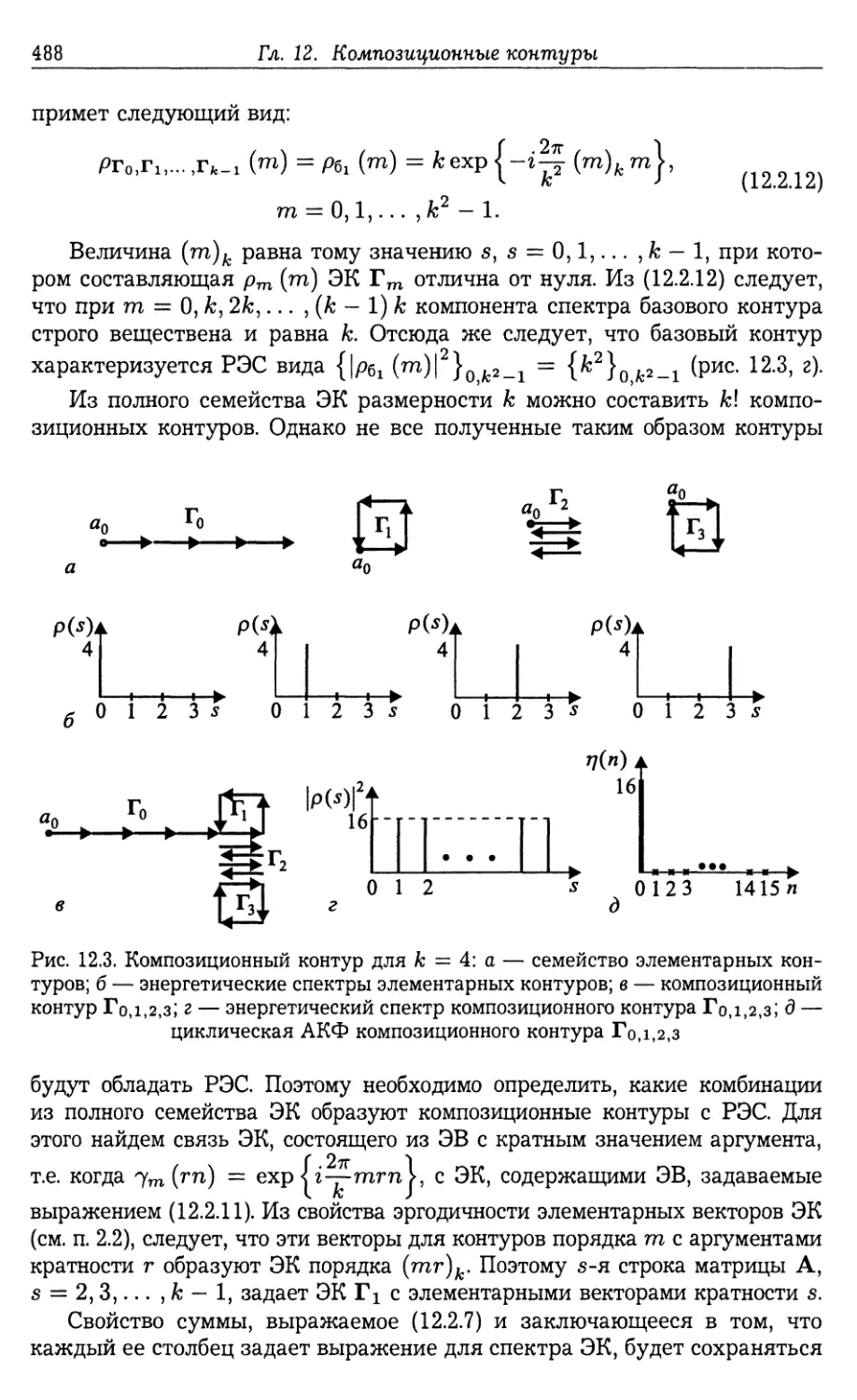
12.1. Обзор кодирующих последовательностей сложных сигналов и подхо¬
дов к их синтезу 476
12.2. Синтез последовательностей с равномерным энергетическим спек¬
тром на основе композиционных контуров 483
12.2.1. Спектрально-корреляционные свойства кодовых последователь¬
ностей с равномерным энергетическим спектром (483). 12.2.2. Вещест¬
венные сигналы с РЭС (484). 12.2.3. Алфавит кодовых последователь¬
ностей с РЭС в виде композиционных контуров из полного семейства
элементарных контуров (486). 12.2.4. Примеры синтеза кодовых по¬
следовательностей с РЭС в виде композиционных контуров из полного
семейства элементарных контуров (491).
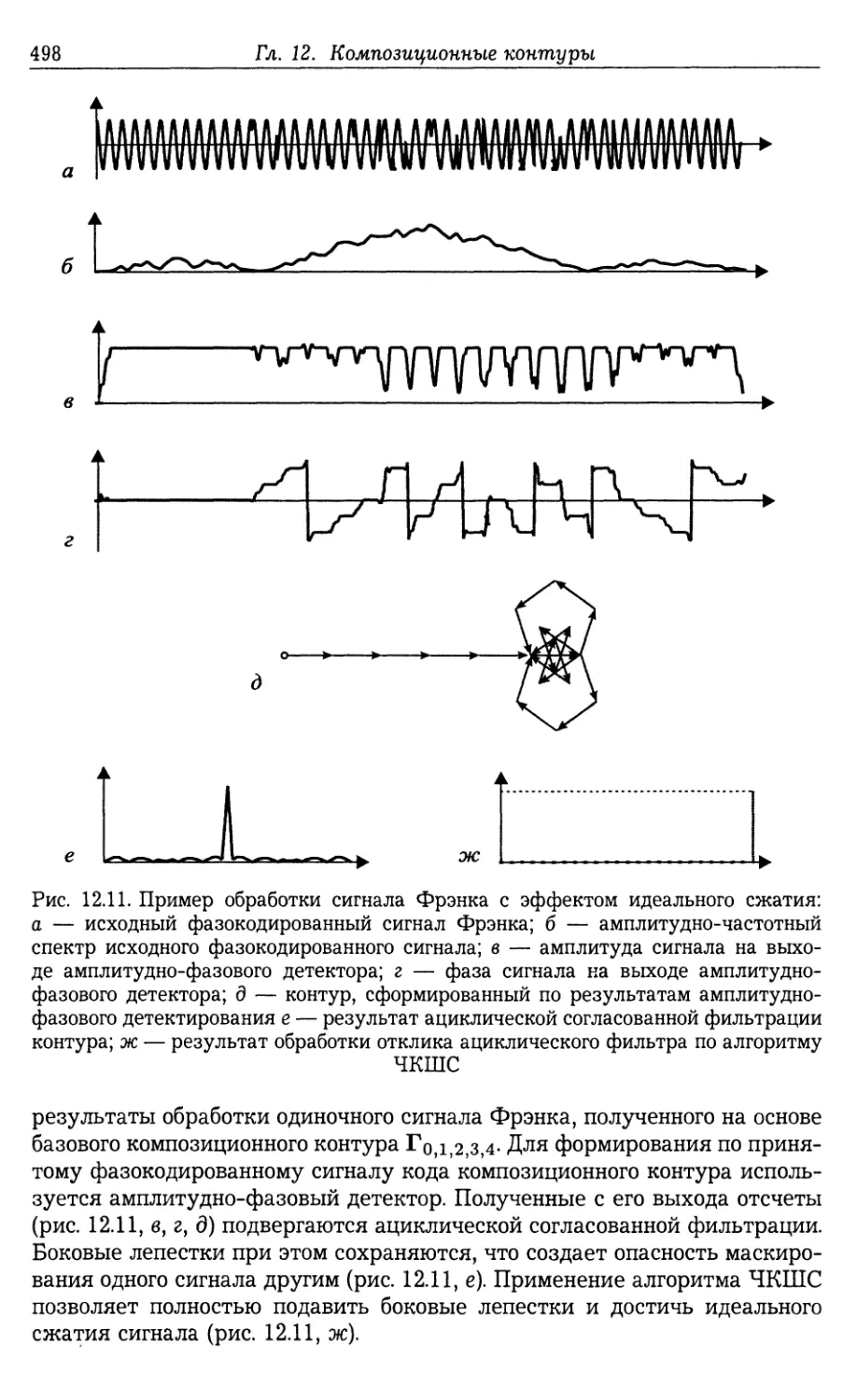
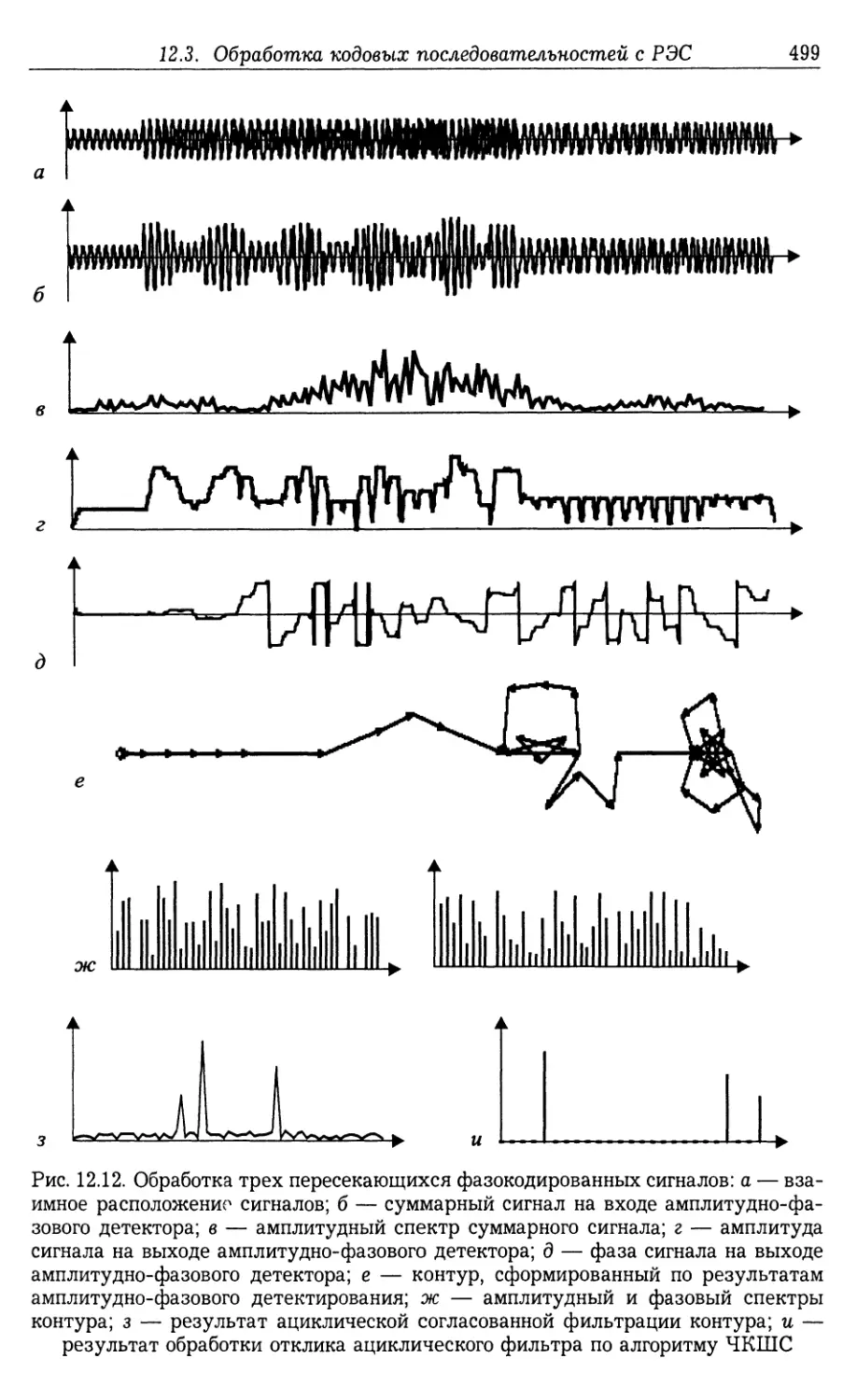
12.3. Обработка кодовых последовательностей с равномерным энергетиче¬
ским спектром 492
12.3.1. Согласованная фильтрация комплекснозначных контуров с
РЭС (493). 12.3.2. Примеры разрешения целей по дальности при ис¬
пользовании алгоритма ЧКШС и кодирующих последовательностей
в виде композиционных контуров (496).
12.4. Фильтровая версия алгоритма ЧКШС 501
12.4.1. Фильтр ЧКШС (501). 12.4.2. Аналитическое представление ал¬
горитма ЧКШС (502). 12.4.3. Частотные и временные характеристики
фильтра ЧКШС (503). 12.4.4. Механизм работы фильтра ЧКШС (505).
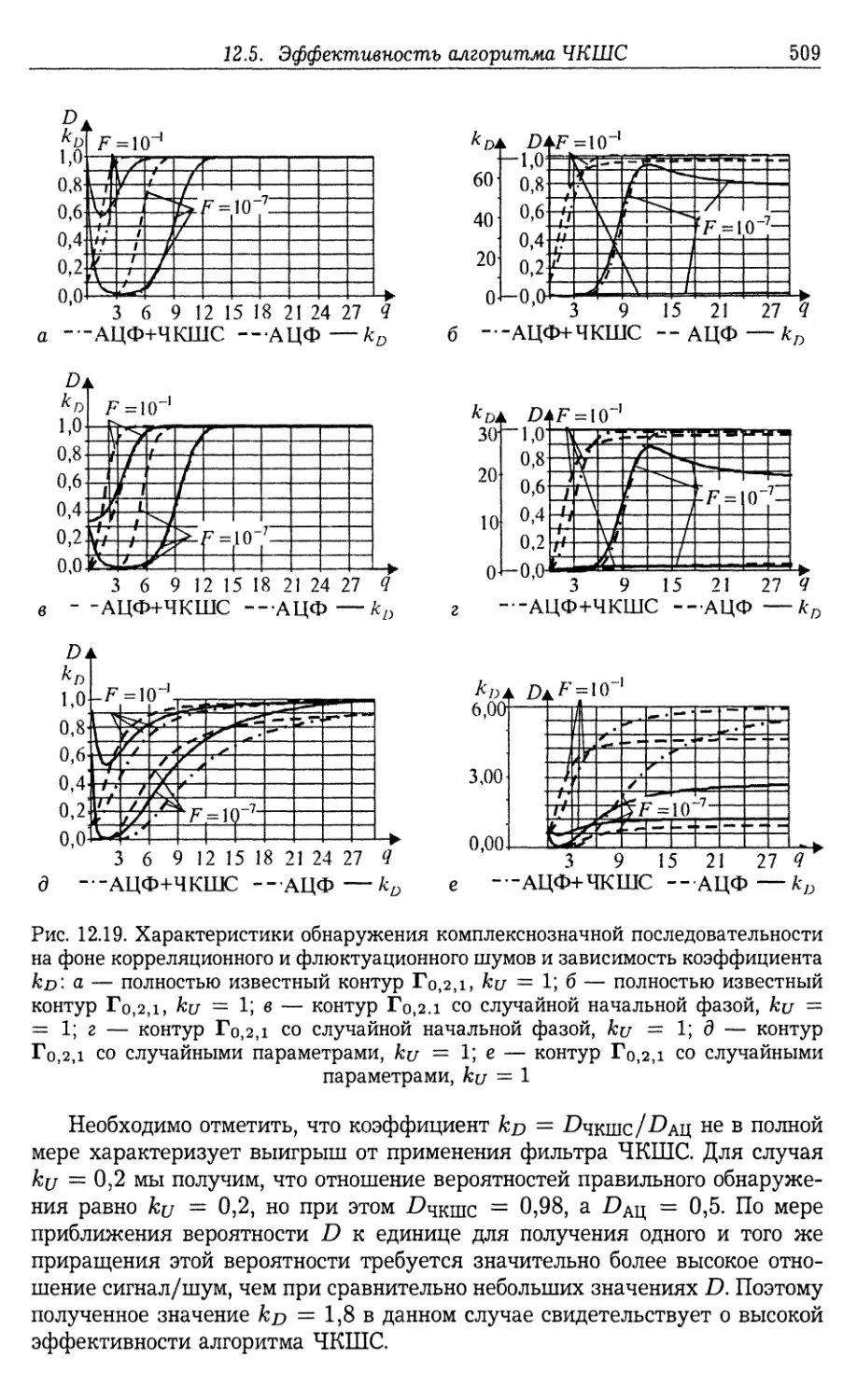
12.5. Эффективность алгоритма ЧКШС при разрешении сигналов от целей
с различными ЭПР 506
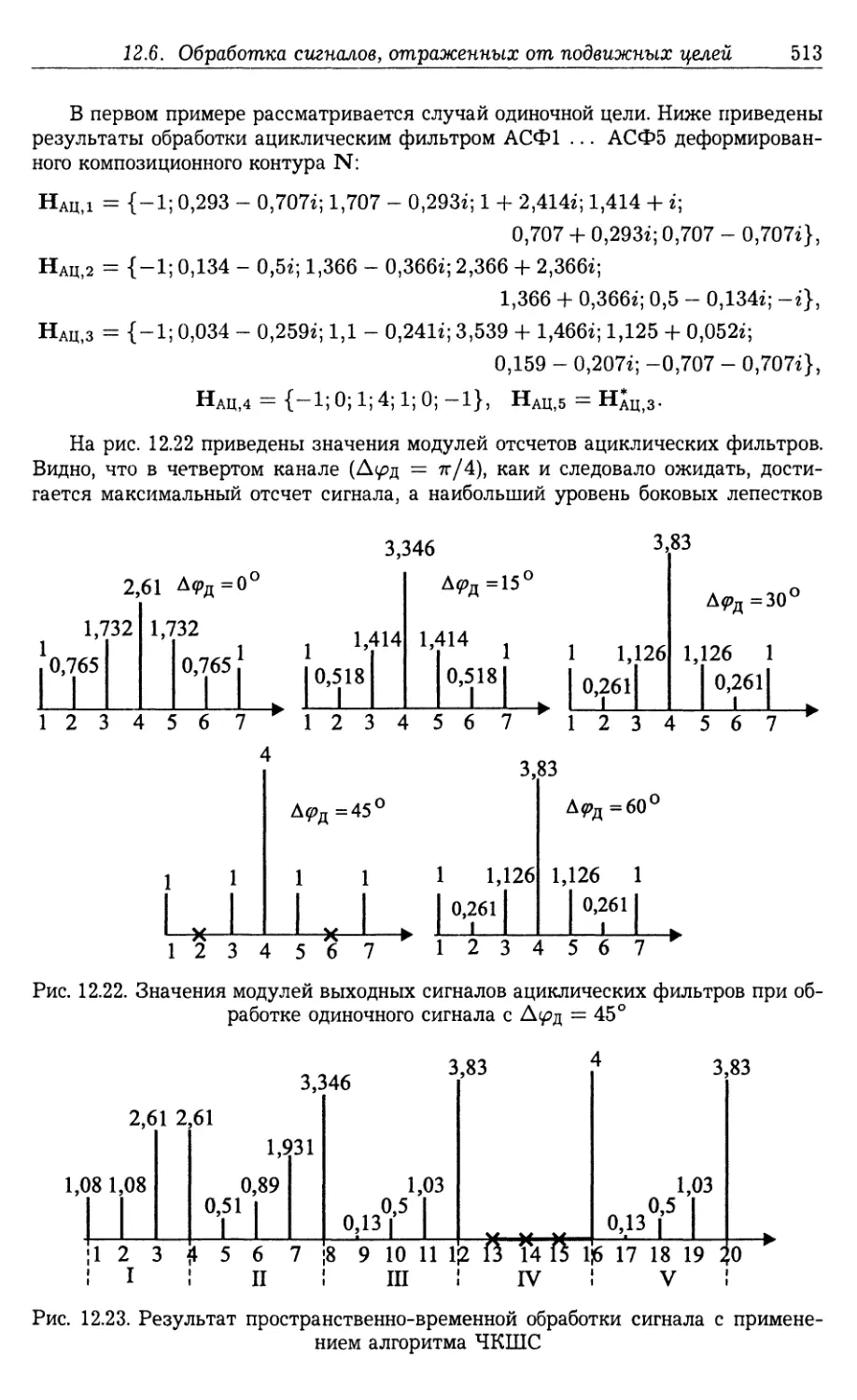
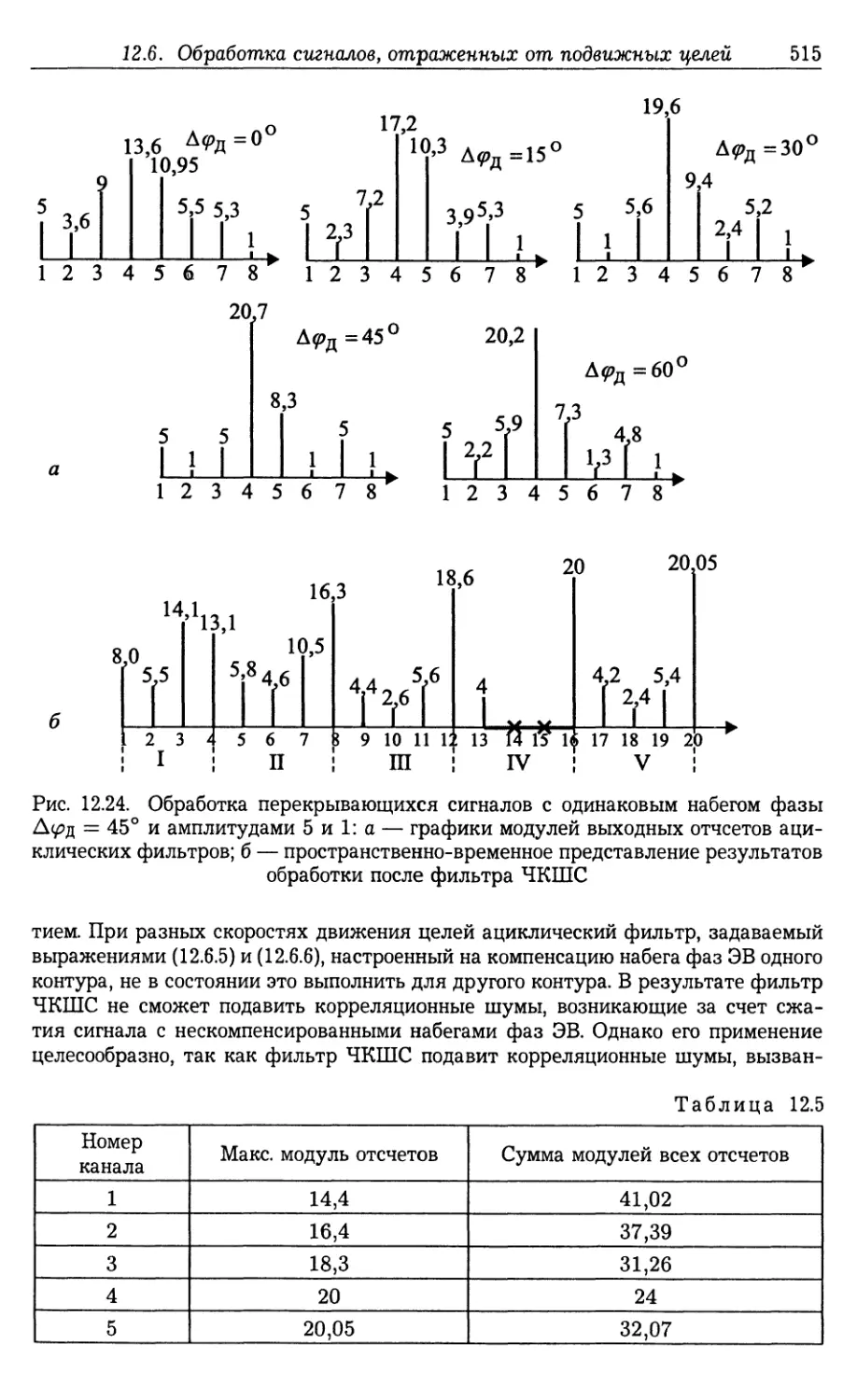
12.6. Особенности обработки сигналов на базе композиционных контуров,
отраженных от подвижных целей 510
12.6.1. Обработка сигналов на базе композиционных контуров с уче¬
том эффекта Доплера (510). 12.6.2. Режим селекции движущихся
целей (517).
12.7. Основные результаты в области анализа сложных сигналов на базе
композиционных контуров и устройств их обработки 518
12.8. Контрольные вопросы и задачи 520
Оглавление
11
Глава 13
СИГНАЛЫ В ВИДЕ ФОРМ ВТОРИЧНЫХ СОЗВЕЗДИЙ
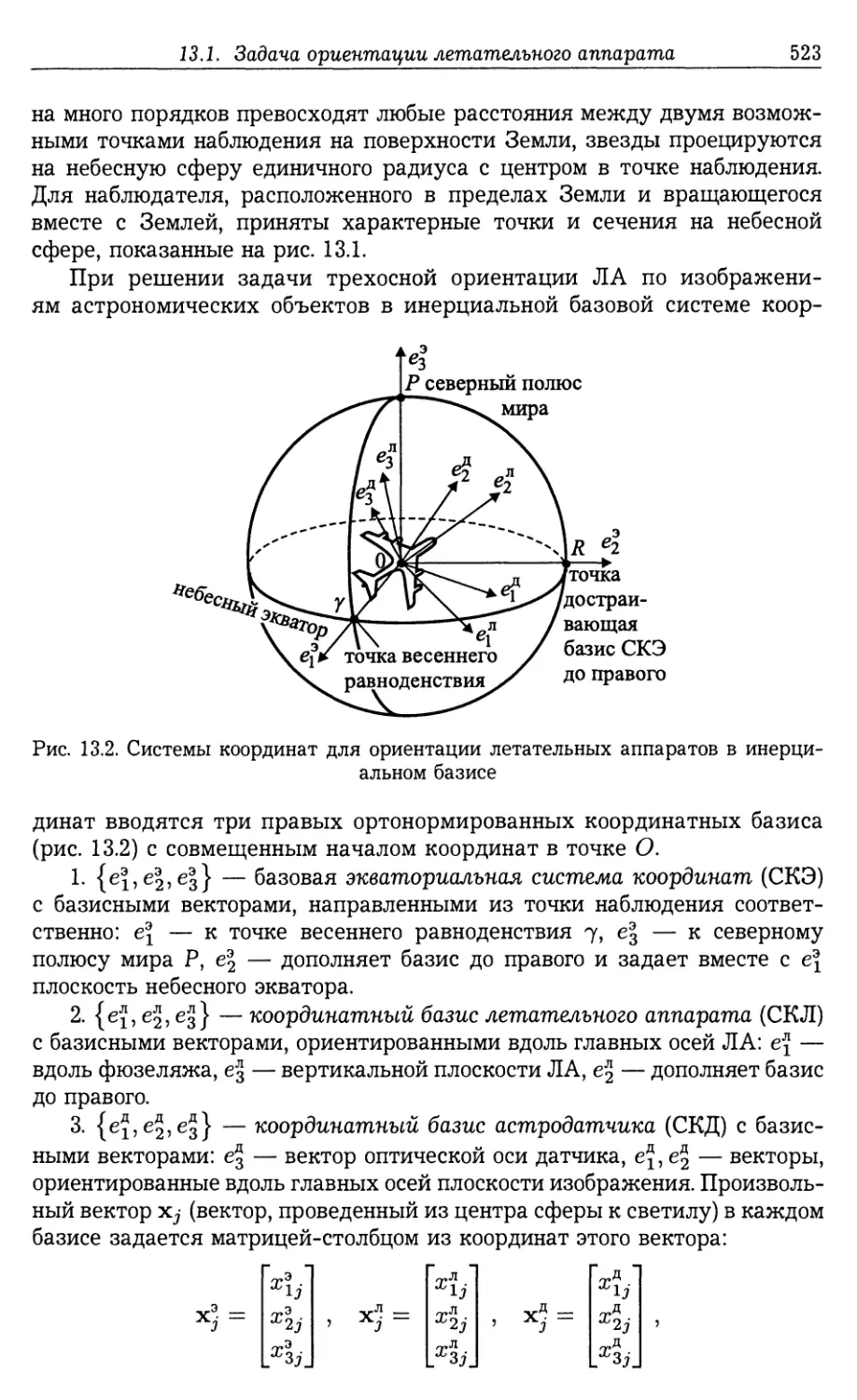
13.1. Задача ориентации летательного аппарата по изображениям созвез¬
дий 522
13.2. Формы вторичных созвездий, используемых в качестве квазиопти-
мальных ориентиров для Л А 525
13.2.1. Требования к форме вторичных созвездий для ориентации ле¬
тательных аппаратов (525). 13.2.2. Форма уникального вторичного со¬
звездия (526). 13.2.3. Коэффициент монохроматичности формы вто¬
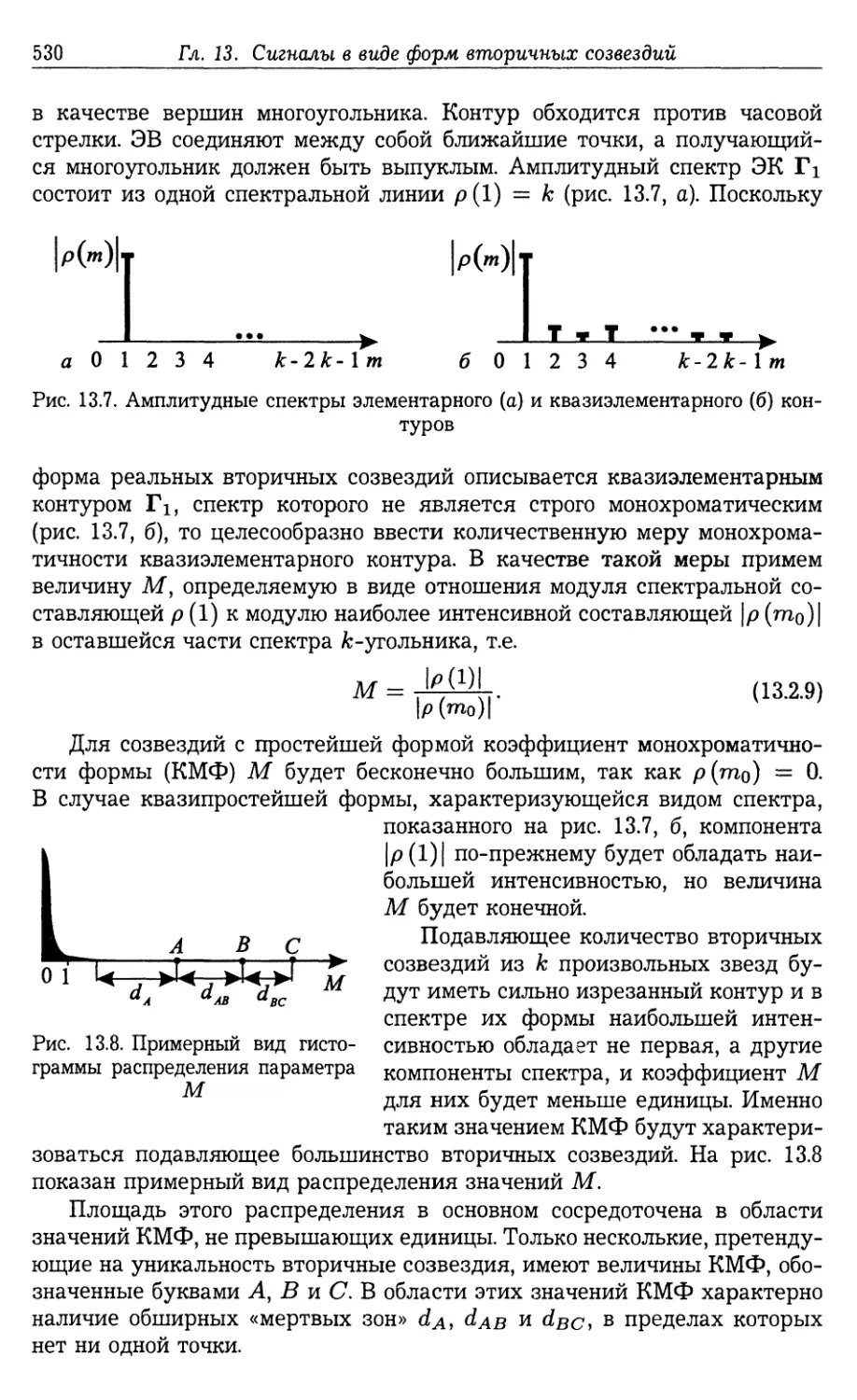
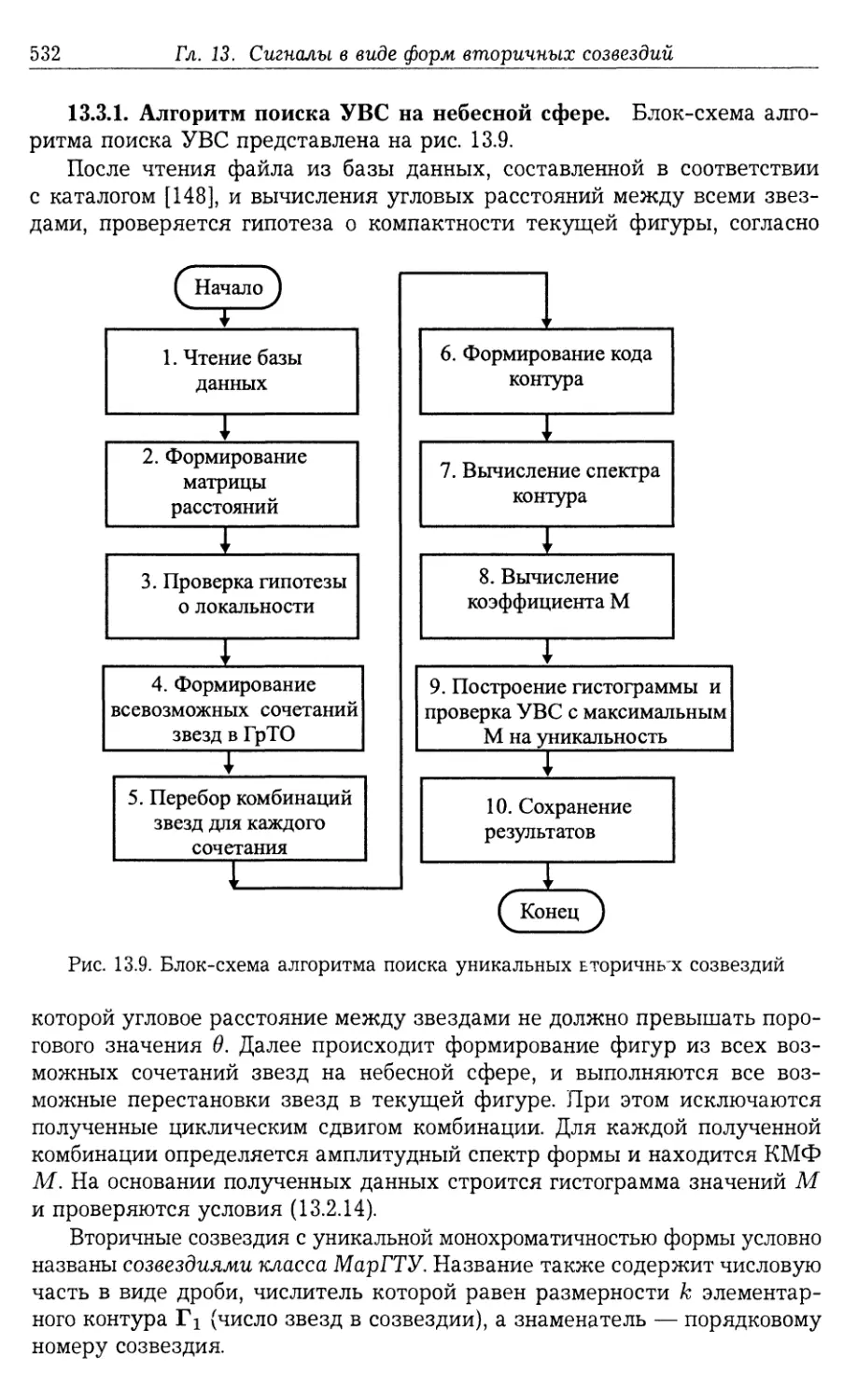
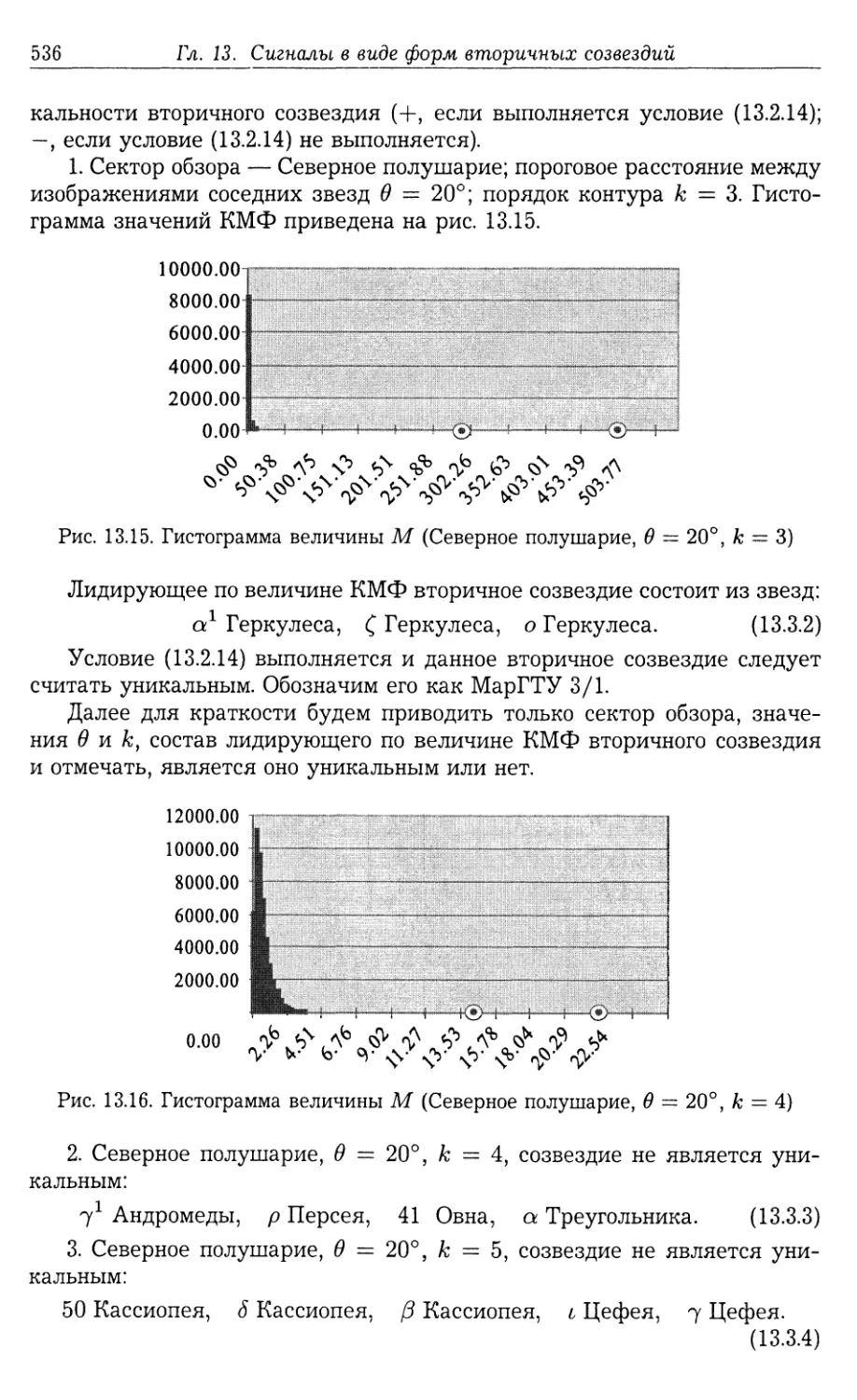
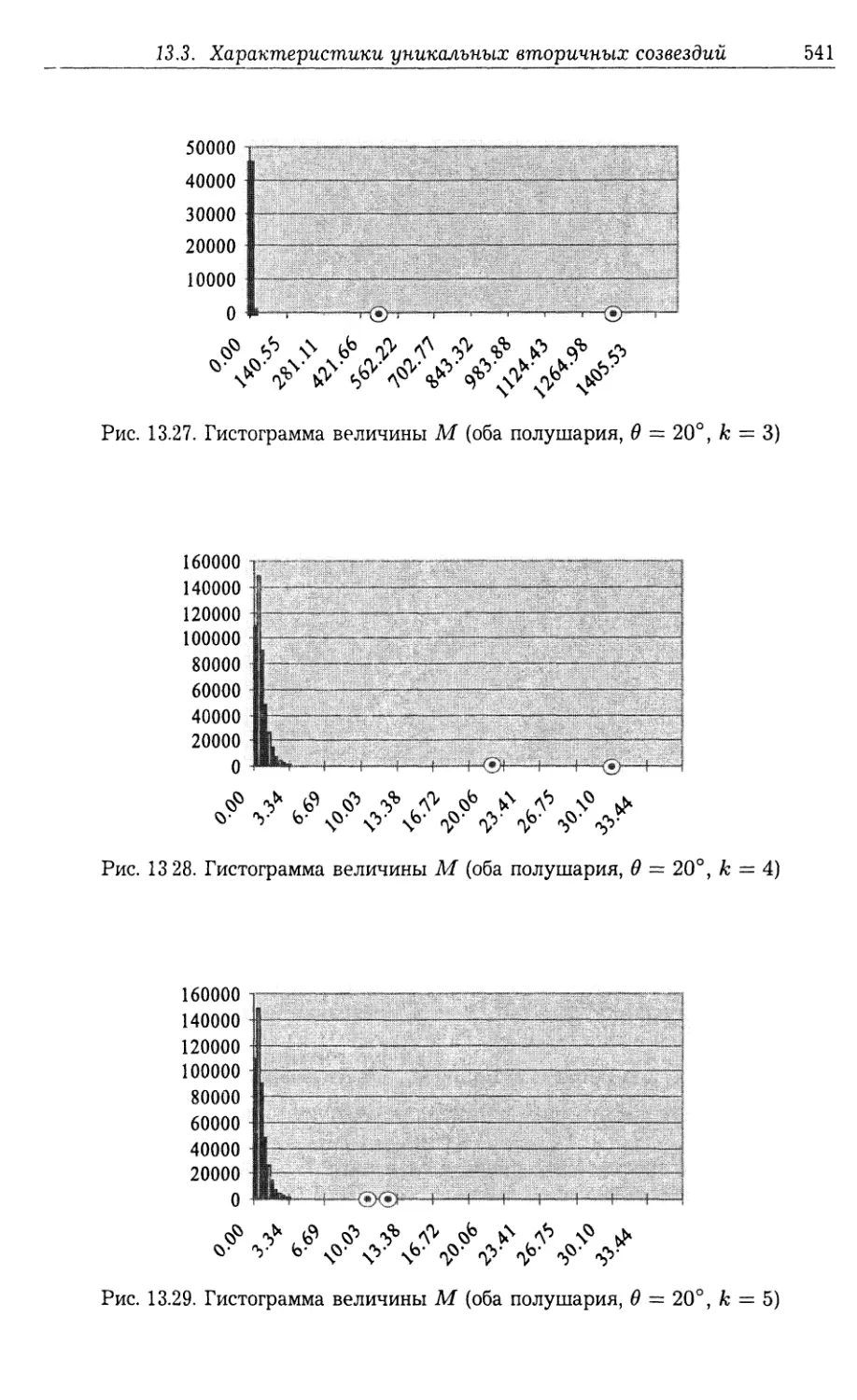
ричного созвездия (529).
13.3. Характеристики уникальных вторичных созвездий 531
13.3.1. Алгоритм поиска УВС на небесной сфере (532). 13.3.2. Результа¬
ты поиска квазиоптимальных ориентиров в виде УВС на небесной
сфере (535).
13.4. Оптимальные формы вторичных созвездий для идентификации звезд
в их составе 544
13.5. Результаты экспериментального исследования по поиску УКВС для
идентификации звезд в составе УВС 549
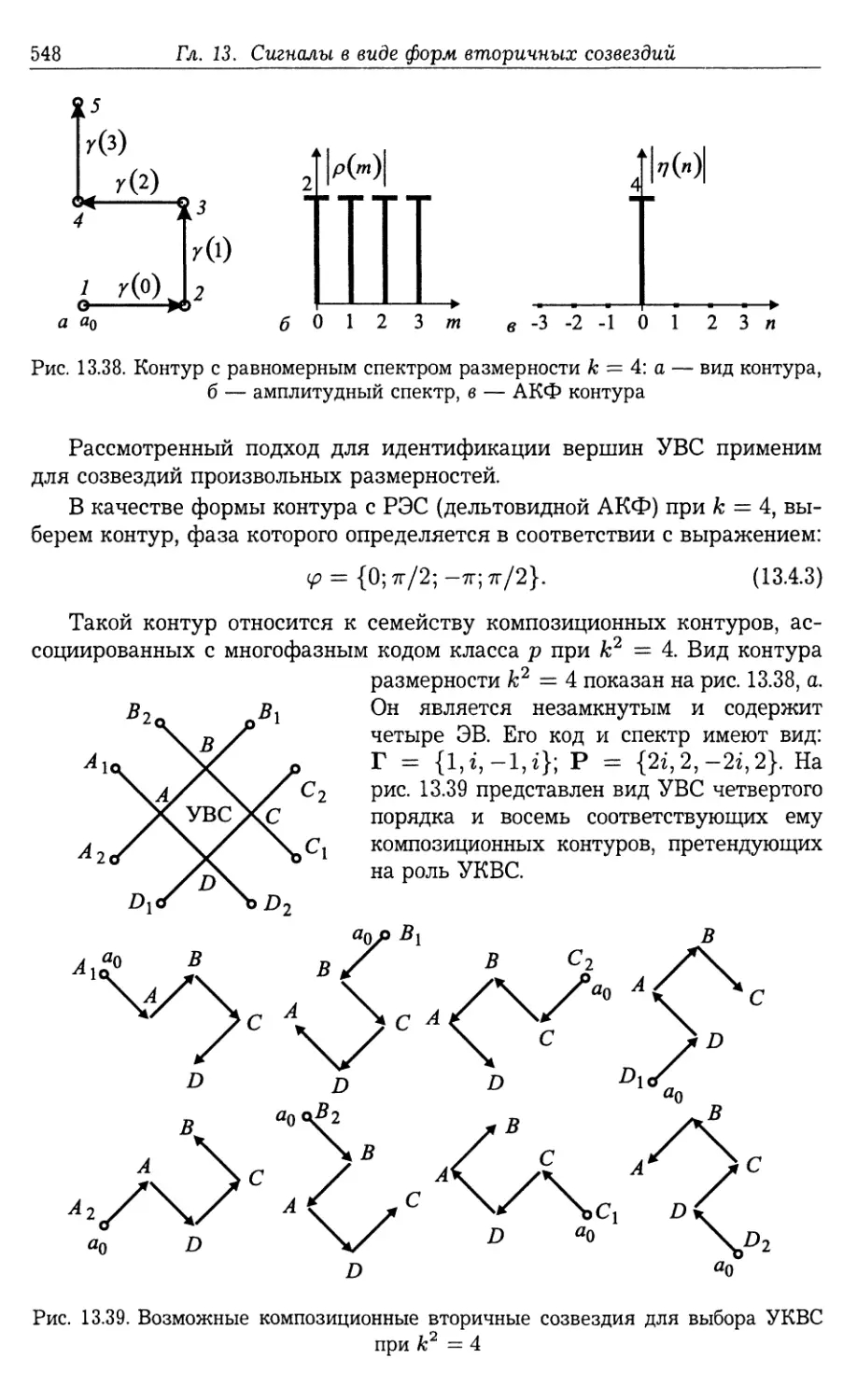
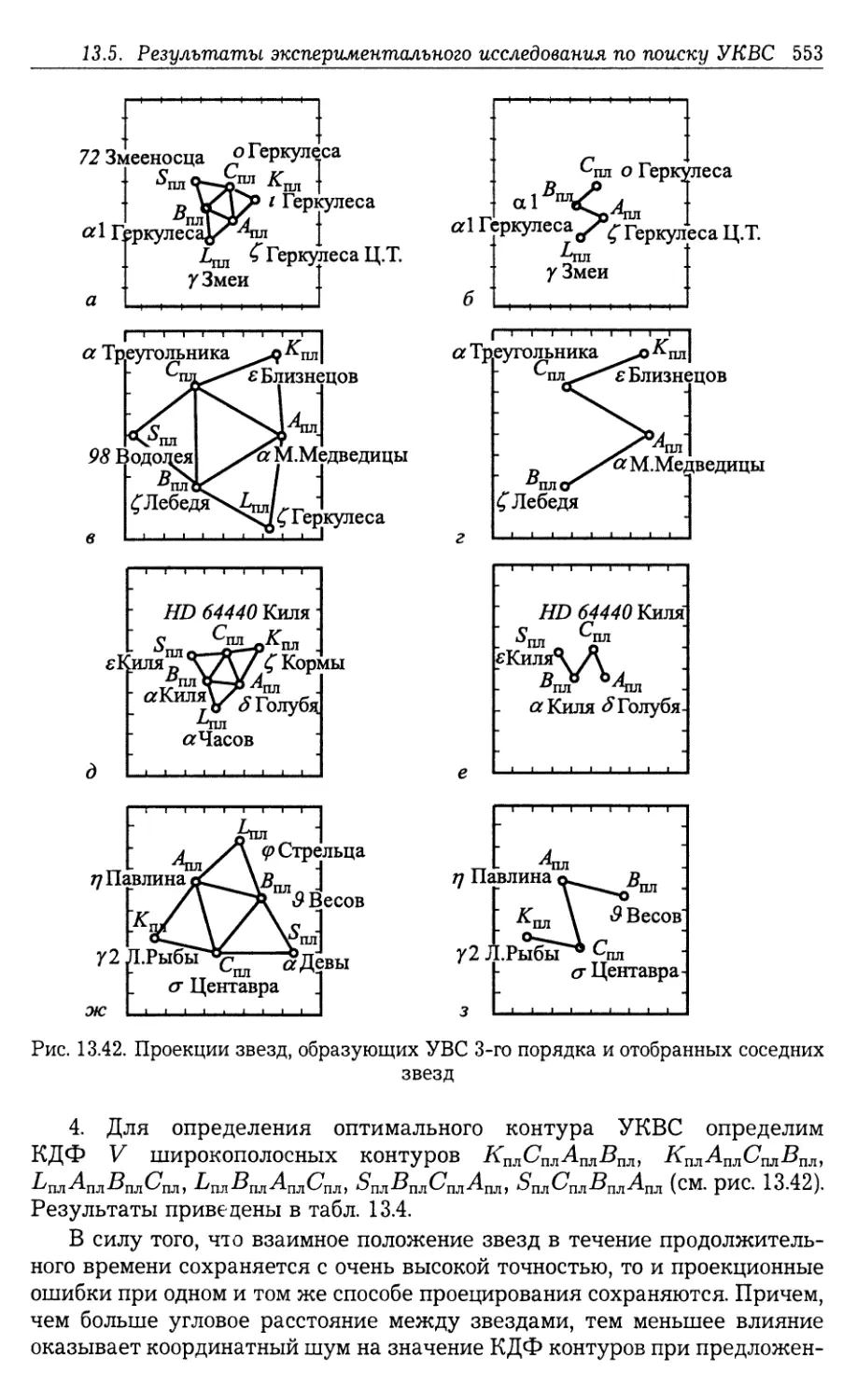
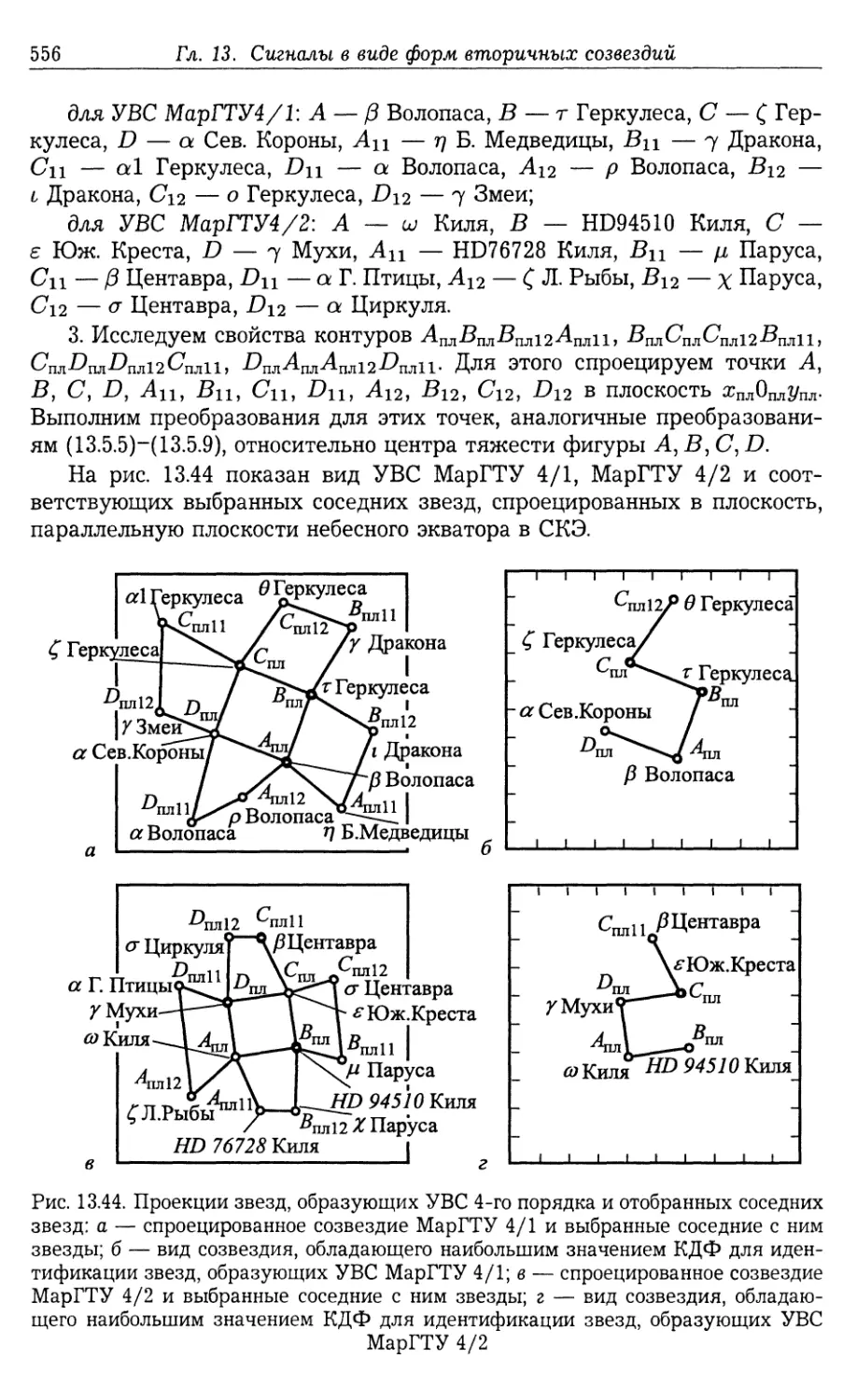
13.5.1. Алгоритм поиска УКВС третьего порядка (549). 13.5.2. Алгоритм
поиска УКВС четвертого порядка (555).
13.6. Основные результаты 558
13.7. Примеры 560
13.8. Задачи и упражнения 563
Глава 14
КОМПОЗИЦИОННЫЕ КОНТУРЫ В СИСТЕМАХ СВЯЗИ
14.1. Введение 564
14.2. Основы построения систем связи с применением комплекснозначных
сигналов 565
14.3. Применение комплекснозначных сигналов в системах связи с кодо¬
вым уплотнением каналов 566
14.3.1. Формирование и обработка группового сигнала (566). 14.3.2. Срав¬
нительный анализ потенциальной пропускной способности систем свя¬
зи с кодовым разделением каналов (570).
14.4. Сравнительный анализ помехоустойчивости систем связи с кодовым
разделением каналов 572
14.5. Обсуждение результатов 574
ЗАКЛЮЧЕНИЕ 576
СПИСОК ЛИТЕРАТУРЫ 579
Светлой памяти
Трифона Григорьевича Якутова
посвящается
ВВЕДЕНИЕ
В последнее время разработчики получили в свое распоряжение
широкий ассортимент быстродействующих элементов вычислительной
техники в микросхемном исполнении, позволяющих создать сложные
многофункциональные изделия с перестраивающимися алгоритмами.
Это открыло возможность обработки цифровыми методами многомер¬
ных сигналов, в первую очередь сцен из изображений объектов, форми¬
руемых разнообразными техническими датчиками. Такие сцены явля¬
ются результатом работы радиолокационных, телевизионных, пассив¬
ных и активных ИК систем, гидролокаторов, рентгеновских и других
установок и устройств. Чаще всего изображения содержащихся в них
объектов весьма несовершенны, обладают недостаточной по отношению
к фону контрастностью, четкостью, искажены помехами и шумами.
По этим сигналам оператору затруднительно принимать необходимые
решения в темпе поступления изображения, т.е. в реальном масштабе
времени. Особенно остро стоит эта проблема в полностью автоматизиро¬
ванных системах. Требуемая для решения поставленных задач произ¬
водительность цифрового процессора составляет 108-1014 и более эле¬
ментарных операций в секунду, что затрудняет, а в целом ряде случаев
исключает получение результатов обработки в реальном или близком
к нему масштабах времени. Ситуация усложняется несовершенством
теоретических подходов к вопросам обработки изображений. Зритель¬
ный аппарат человека и животных имеет эффективность, несравненно
более высокую, чем система технического зрения.
Данные факторы привели на современном этапе к кризису в данной
области из-за широкого применения эвристических подходов и вызванно¬
го этим большого количества слабо проверенных методов [71, 72]. Авто¬
ры данных работ отмечают заметное снижение интереса исследователей
и потенциальных пользователей к системам машинного зрения. В этой
связи представляют интерес подходы, базирующиеся на строгих теорети¬
ческих проработках, например, использующие аппарат теории сигналов,
но применяющие упрощенные модели изображений объектов, не свя¬
занные со значительной потерей информации. Один из таких подходов
заключается в отказе от обработки каждой точки изображения и переходе
к обработке лишь его контуров. Контуры являются областями с высокой
концентрацией информации, слабо зависящей от цвета и яркости. Они
устойчивы к смене типа датчика, формирующего изображение, к частот¬
Введение
13
ному диапазону, в котором он работает, не зависят от времени суток
и года. Другие характеристики изображения при этом значительно ва¬
рьируются. Исключительно важная роль анализа контуров подчеркива¬
ется в целом ряде оригинальных и обобщающих работ по> распознаванию
зрительных образов [3—16, 21-24, 32-37, 39-42].
Представляемая читателю книга посвящена теоретическим и прак¬
тическим вопросам контурного анализа, под которым будем понимать
совокупность методов описания и преобразования контуров. Контур пред¬
ставляется в виде комплекснозначного сигнала, и в этом плане к контурам
можно отнести не только функции, определяющие границы изображения,
но и различные кривые, графики, векторные диаграммы сигналов.
Контур целиком определяет форму изображения и содержит всю
необходимую информацию для распознавания изображений по их фор¬
мам. Такой подход позволяет не рассматривать внутренние точки изо¬
бражения и тем самым значительно сократить объем обрабатываемой
информации за счет перехода от анализа функции двух переменных
к функции одной переменной. Следствием этого является возможность
обеспечения работы системы обработки в масштабе времени, более близ¬
ком к реальному. Но даже в тех задачах, где нельзя пренебречь обра¬
боткой внутренних точек, методы контурного анализа дополняют другие
и поэтому безусловно полезны.
Совершенствуя датчики и увеличивая объем запоминающих устройств,
можно сформировать слабо искаженные шумами многоэлементные изо¬
бражения. При этом задача распознавания облегчается, но основные
трудности не устраняются. Они вызваны влиянием на математическое
описание изображения случайных переносов, поворотов и изменения мас¬
штаба. Методы контурного анализа в большей степени, чем простран¬
ственные методы, дают возможность использовать модели, инвариантные
к таким преобразованиям.
Контурный анализ значительно расширяет кругозор специалиста, по¬
зволяя с единых позиций подходить к обработке как известных акустиче¬
ских, радиотехнических и оптических сигналов, так и радиолокационных,
телевизионных, оптических и других видов изображений.
Монография подготовлена по результатам работ [17-21, 42, 43, 50, 56,
65-69, 74-79, 87-111 и др.]. Она состоит из трех частей. Первая часть свя¬
зана с рассмотрением вопросов теории контурного анализа, вторая и тре¬
тья — с его приложениями соотвественно к задачам обработки изобра¬
жений и сигналов. Монография составлена таким образом, что читатель
может получить первое представление о поставленных задачах, подходам
к их решению и основных результатах при ознакомлении с первыми
и заключительными разделами каждой главы.
Разработка методологии контурного анализа в значительной сте¬
пени стимулирована грантами РФФИ, Министерства образования РФ,
Министерства науки и технологий РФ. Авторы признательны руково¬
дителям фондов. Они выражают благодарность акад. РАН Ю.И. Жура¬
влеву, И.Б. Гуревичу, И.П. Цивлину, Ю.С. Лезину, П.А. Бакулеву, В.С. Кири-
14
Введение
чуку, Л.А. Школьному, А.Г. Рындыку, В.А. Сойферу, В.В. Сергееву, В.М. Чер¬
нову, Ю.А. Рябинину, Г.С. Ощепкову, В.А. Иванову, проф. Ю.В. Захарову
за поддержку работ авторов в области обработки изображений и сигналов.
Работа выполнена при финансовой поддержке по следующим грантам
и проектам:
грант РФФИ “Анализ сцен и распознавание зрительных образов”,
проект 93-012-1063, 1993-1994 гг.;
гранты Министерства общего и профессионального образования РФ:
проект ’’Интеллектуальные системы ориентации летательных аппара¬
тов на базе систем понимания изображений”, 1994-1996 гг.;
проект ’’Интеллектуальные системы ориетации летательных аппаратов
на базе систем обработки изображений оптимальной формы, расположенных
на подстилающей поверхности или небесной сфере”, 1997-1998 гг.;
грант Министерства науки и технологий РФ, проект ’’Распознавание
изображений дорог и других нитевидных объектов в сценах с аэроланд¬
шафтами”, 1998-1999 гг.;
грант РФФИ “Новые оптимальные сигналы для задач разрешения/рас-
познавания”, проект 97-01-00906, 1997-1998 гг.;
грант РФФИ “Оптимальные сигналы в виде форм точечных изобра¬
жений. Поиск уникальных звездных образований для ориентации лета¬
тельных аппаратов”, проект 99-01-00186, 1999-2000 гг.;
грант РФФИ “Новые подходы к решению класса задач обработки
изображений и сигналов, связанного с фиксацией максимума взаимно¬
корреляционной функции и подавлением корреляционных шумов”, про¬
ект 01-01-00298, 2001-2002 гг.
ЧАСТЬ I
ОСНОВЫ КОНТУРНОГО АНАЛИЗА
Глава 1
КОНТУРЫ КАК ДИСКРЕТНЫЕ СИГНАЛЫ
1.1. Представление изображений в системе технического зрения
Задачи контурного анализа возникают в системе технического зре¬
ния при обработке изображений и распознавании зрительных образов.
Структура такой системы в достаточно общем виде приведена на рис. 1.1.
Входные сцены от различных датчиков преобразуются в цифровой
вид и поступают на мультиплексор входной информации. Выбор одного
Вцдеодатчик
АЦ]
Банк
Банк
матем.
изобра¬
обеспечения
жений
Т
£
Видео датчик
АЦП-
—►
Мультиплексор
входной
информации
—►
ЦАП
А V
щ g
£ «
Он
il
1 £1
\ г >> S
Программируемый
процессор
изображений
Видеодатчик
АЦ]
Рис. 1.1. Структура системы технического зрения
из датчиков производится программируемым процессором изображе¬
ний (ППИ) или оператором. Отобранные сцены заносятся в ОЗУ сцен.
Такое и подобные ему ОЗУ изображений (ОЗУИ) имеют матричную
организацию из Μι строк и М2 колонок, причем каждая ее ячейка
содержит п разрядов. Обычно число строк равно числу колонок, кратно
степени числа 2 и варьируется от 128 до 1024 и более, а разрядность
ячейки ОЗУИ не менее 4-х. Объем ОЗУ сцен достигает большой вели¬
чины и составляет порядка 100 мегабайт и более. При работе в реаль¬
ном масштабе времени, например, с телевизионного датчика, вся сцена
16
Гл. 1. Контуры как дискретные сигналы
заносится за 20-40 мс, а время заполнения одной ячейки составляет
порядка 30-100 не.
ППИ является центральным узлом любой системы технического зре¬
ния и выполняет как вычислительные, так и управляющие функции.
Для сокращения объема быстродейству¬
ющей памяти программирование про¬
цессора производится при выполнении
каждой конкретной задачи. Хранение
обработанных изображений, а также изо¬
бражений, являющихся эталонными при
распознавании образов, осуществляется
в специальном банке изображений.
Выходная информации ППИ в циф¬
ровом или аналоговом видах поступает
для управления различными исполняю¬
щими устройствами: движением платфор¬
мы с аппаратурой, сортировкой годных
и дефектных изделий, захватом деталей
определенной формы и т.п. Обработанные
изображения передаются также на цифро¬
вой индикатор. Каждая ячейка ОЗУ инди¬
катора соответствует определенной точке
на экране дисплея. На графических иллюстрациях фрагмент страницы
ОЗУИ будем представлять в виде квадратной сетчатки.
Матричная структура ОЗУ обеспечивает одинаковую пространствен¬
ную организацию точек исходной и находящихся в ППИ плоских сцен.
Хранящееся в ячейке многоразрядное двоичное число пропорционально
усредненной в пределах некоторой окрестности δ (ζ) = δχ · Sy элемента
(пиксела) яркости исходной сцены. Поэто¬
му изображение в ППИ имеет мозаичный
характер. На рис. 1.2 для мозаики в ви¬
де квадратной сетчатки (δχ = ίτ/) показано
оцифрованное, т.е. продискретизированное
и проквантованное изображение. Подобные
сетчатки хорошо согласуются с законом
движения луча по линии светочувствитель¬
ного элемента телекамеры или по экрану
электронно-лучевой трубки. Поэтому в даль¬
нейшем для представления оцифрованных
изображений будем применять только такой
вид сетчатки.
Важную роль в контурном анализе игра¬
ют бинарные по яркости многоточечные
(распределенные) изображения. Обозначим через s (ж, г/) исходное, а через
ω (mi,m2) — оцифрованное бинарное изображения (рис. 1.3), причем
яркости I (х,у) точки (ж, у) и I (mi,m2) клетки (7711,7712) будут
0
0
0
0
1
1
0
0
0
0
0
0
0
0
1
1
1
1
1
0
0
0
0
0
1
1
1
1
1
1
1
0
0
0
1
1
1
1
1
1
1
1
1
0
0
1
1
1
1
1
1
1
1
1
0
0
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
0
0
0
0
0
0
1
1
1
1
0
0
Рис. 1.3. Пример представле¬
ния бинарного изображения на
квадратной сетчатке
1
3
2.
0
2
12
13,
1
1
о;
2
1
2
1
0
2
1
15
18
2
2
3
1
1
1
2
1
10
11
18;
20
14
13
1
2
1
0
1
12
18
22
31
30
18
12
11
1
0
0
9
15
20
3
0
2
20
25
16
10
1
1
0
8
22
28
42
44
16
14
11
0
1
1
4
1
9
21
18
32
15
1
3
2
2
2
3
2
1
1
14
И
1
0
4
1
2
1
0
4
5
0
10
12
1
3
2
3
1
0
1
3
0
2
1
1
2
1
4
0
2
Рис. 1.2. Полутоновое изображе¬
ние, занесенное в ОЗУ сцен
(цифры в клетках соответствуют
значениям яркостей, записанных
в ячейки памяти)
1.2. Кодирование контуров бинарных изображений
17
1(х,у)
{1 при (х, у) е S,
О в противном случае,
1(т1,т2)
{1 при (mi,m2) G ω,
О в противном случае.
Размер клетки (пиксела) сетчатки обычно выбирается из условия
возможности восстановления по оцифрованному о; (mi,m2) исходно¬
го изображения s (ж, у). Ошибки дискретизации вызываются наличи¬
ем граничных пикселов, в пределах которых содержатся участки как
фона, так и изображения объекта. После оцифровки каждый пиксел од¬
нозначно относится либо к фону, либо к изображению. Поэтому фор¬
мы изображений s(x, у) и о; (mi, m2) не совпадают. Величина ошибки
дискретизации зависит не только от размеров бх&у пиксела, но и от
вида критерия принятия решения о принад¬
лежности каждого из пикселов фону или
изображению. Критерий должен опреде¬
лять, какую часть клетки должно занимать
изображение объекта, чтобы в ячейку ОЗУ
сцен, соответствующую этому пикселу, была
бы занесена единица. Для определенности
примем следующее правило: если площадь
изображения не менее половины площади
δχ δ у пиксела, то в соответствующую ячей¬
ку ОЗУ заносится единица.
Граничные клетки отличаются от вну¬
тренних клеток изображения наличием в ка¬
честве соседней одной или нескольких фоно¬
вых клеток. При этом в качестве соседних к
рассмотрению берутся только горизонталь¬
ные и вертикальные соседние клетки, либо
только диагональные [9]. Границу бинарного изображения будем задавать
точками в центрах граничных клеток (рис. 1.4). Если сместить сетчатку
на величину половины длины стороны квадрата вправо и вверх, то
граничные точки изображения окажутся в узлах сетчатки. В результате
восприятие контура упрощается. В дальнейшем будем использовать оба
таких представления контура оцифрованного бинарного изображения.
0
0
0
0
•
•
0
0
0
0
0
0
0
0
•
1
1
#
•
0
0
0
0
0
•
1
1
1
1
1
•
0
0
0
•
1
1
1
1
1
1
1
#
0
0
•
1
1
1
1
1
1
1
•
0
0
•
1
1
1
1
1
1
1
1
•
•
1
1
1
1
1
1
1
1
1
♦
•
•
•
•
•
1
1
1
1
#
0
0
0
0
0
0
•
•
•
•
0
0
Рис. 1.4. Задание точками гра¬
ничных клеток бинарного изо¬
бражения при учете соседства
только по вертикали и горизон¬
тали
1.2. Кодирование контуров бинарных изображений
Кодирование контура — это этап получения дискретного сигнала, опи¬
сывающего границы оцифрованного бинарного изображения. Всякая область
D плоскости комплексного переменного содержит внутренние точки и точки
контура (граничные точки). Первые из них обладают тем свойством, что
не только они сами, но и их некоторая окрестность целиком принадлежит
области D. Точки контура не являются внутренними, но в сколь угодно ма¬
лой окрестности таких точек находятся внутренние точки области D и точ¬
18
Гл. 1. Контуры как дискретные сигналы
ки, не принадлежащие области D, — внешние (фоновые) точки. Область
D обладает свойством связности, состоящим в том, что любые ее точки
соединяются линией, целиком находя¬
щейся внутри D [28].
Линия контура Г называется вы¬
пуклой, если прямолинейный отре¬
зок, соединяющий две ее любые точ¬
ки, целиком состоит из внутренних
точек области D. Участок контура
будет вогнутым, если такой отрезок
будет включать внешние (фоновые)
точки (рис. 1.5).
Область D называется ограни¬
ченной, если все ее точки находятся
на конечном расстоянии от начала
отсчета. Число связных частей, на
которые разбивается контур ограни¬
ченной области D, называется по¬
рядком связности этой области. В пределах основного контура Г
могут находиться другие изображения sj(x, у), j — 1,2,..., со своими
замкнутыми контурами Γ(χ), Г(2), ... Такое изображение s (х,у) является
многосвязным. Если s (я, у) — бинарное изображение, то находящиеся
внутри него изображения образуют полости, в том числе и точечные.
Характерными фрагментами бинарного оцифрованного изображения
являются лучи и разрезы толщиной в один пиксел (рис. 1.6). Для каждого
Рис. 1.5. Фрагменты контура Г: 1,
2 — выпуклый; 3, 4 — неопределен¬
ный; 5, б — вогнутый
о>1 Ь2 ь Ьх со
/1
1
1
1
1
1
1
т
1
1
1
1
1
Cj с с2
lL t Li
1
]
1
1
1
1
0
1
1
1
1
1
1
1
1
1
1
1
1
(
)
1
1
1
1
1
1
1
1
0
1
1
1
1
0
1
1
1
1
1
1
1
1111 1
1
1
1
1
0
1
1
1
1
1
1
1
1
1
ω2
1
1
1
1
1
1
1
1
1
0
1
1
1
1
1
1
1
1
1
1
1
1
0
0
0
1
1
1
1
1
1
1
1
1
1
0
0
0
о"
ΊΓ
1
1
1
1
1
1
0
0
0
0
1
1
1
1
1
1
1
1
1
0
1
0
0
1
1
1
1
1
Рис. 1.6. Трехсвязное оцифрованное изображение ω с точечной полостью ω\, мно¬
готочечной полостью о>2, разрезом Ь и лучом с. Точки Ь\ и а — основания, &2
и С2 — вершины
1.2. Кодирование контуров бинарных изображений
19
контура задается начальная точка ао, отправляясь от которой обходится
весь контур. Условимся такой обход производить по часовой стрелке. Точ¬
ки лучей и разрезов при этом будут обходиться дважды. Фундаменталь¬
ными свойствами контуров реальных изображений являются замкнутость
и непрерывность их линий.
Внутренний элемент (пиксел) бинарного оцифрованного изображения
w (mi, m2) обладает свойством четырехсвязности, т.е. смежные с ним эле¬
менты — верхний, нижний, левый и правый, тоже принадлежат w (mi, тг)
(рис. 1.7, а). Для граничных элементов изображения w (mi, m2), образую¬
щих контур Г, правило четырехсвязности не выполняется [9] (рис. 1.7, б).
Для обработки контура аналитическим путем или на ЭВМ надо произ¬
вести его кодирование, т.е. поставить в соответствие каждому контурному
элементу определенное число. Последова¬
тельность таких чисел называется кодом
контура. Используем следующую тер¬
минологию при задании и кодировании
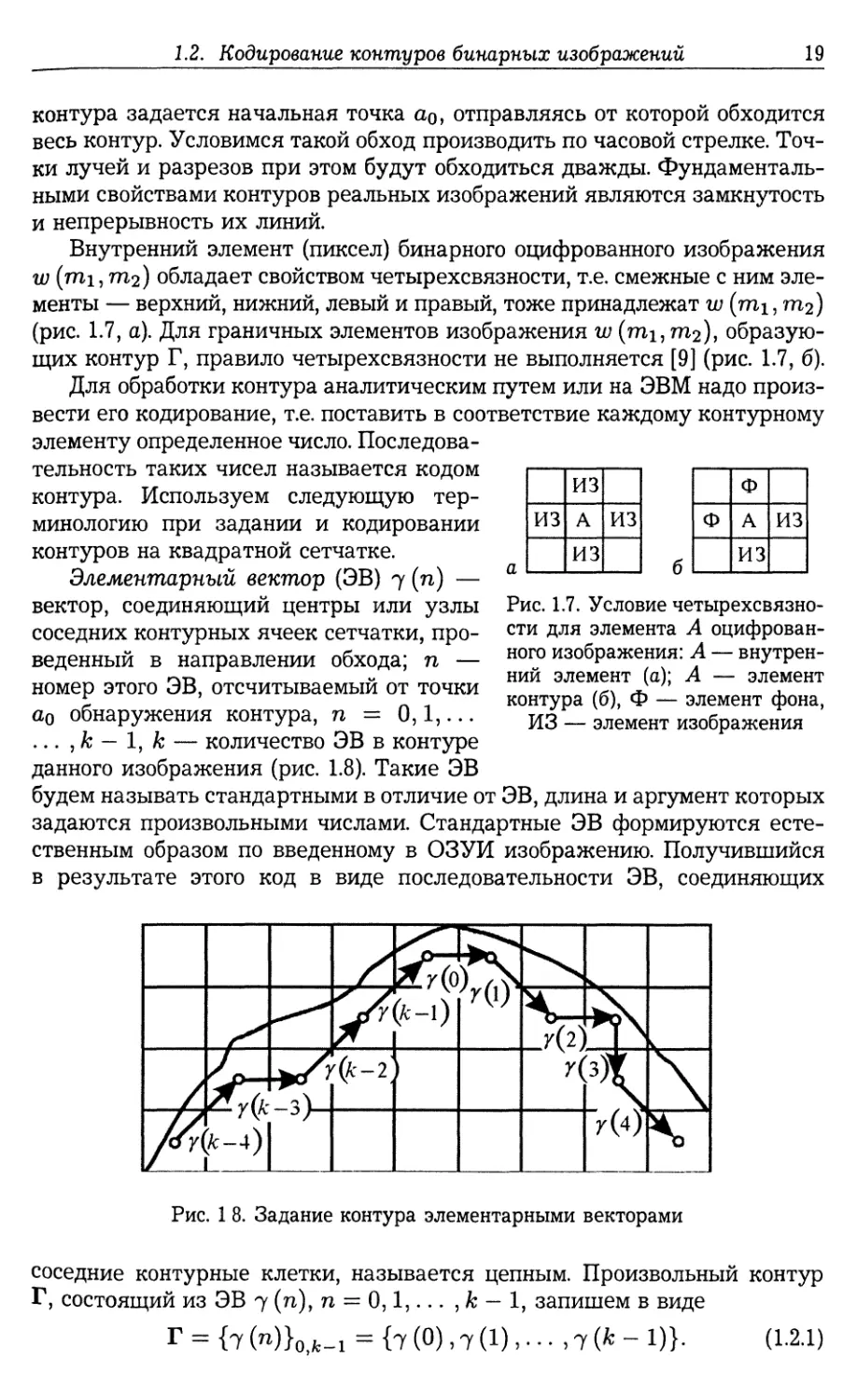
контуров на квадратной сетчатке.
Элементарный вектор (ЭВ) 7 (п) —
вектор, соединяющий центры или узлы
соседних контурных ячеек сетчатки, про¬
веденный в направлении обхода; п —
номер этого ЭВ, отсчитываемый от точки
а0 обнаружения контура, п = 0,1,...
... , к — 1, к — количество ЭВ в контуре
данного изображения (рис. 1.8). Такие ЭВ
будем называть стандартными в отличие от ЭВ, длина и аргумент которых
задаются произвольными числами. Стандартные ЭВ формируются есте¬
ственным образом по введенному в ОЗУИ изображению. Получившийся
в результате этого код в виде последовательности ЭВ, соединяющих
Рис. 1.7. Условие четырехсвязно¬
сти для элемента А оцифрован¬
ного изображения: А — внутрен¬
ний элемент (а); А — элемент
контура (б), Ф — элемент фона,
ИЗ — элемент изображения
соседние контурные клетки, называется цепным. Произвольный контур
Г, состоящий из ЭВ 7 (η), п = 0,1,... , к — 1, запишем в виде
Г = {7 (™)}0,fc-i = (7 (0), 7 (1). · · · »7 (* - 1)}·
(1.2.1)
20
Гл. 1. Контуры как дискретные сигналы
Контуры будем обозначать прописными буквами греческого алфавита
Γ,Ν,Ρ, , а их ЭВ — соответствующими строчными буквами и(п),
7(п), р(п), ... ЭВ являются первыми разностями функций, задающих
линию контура. В том случае, когда это не приводит к неоднозначному
пониманию, код контура, заданный с помощью ЭВ, перед обозначением
контура будем ставить букву Δ, например, ΔΓ.
На квадратной сетчатке возможны восемь различных стандартных
ЭВ, соединяющих соседние пикселы (рис. 1.9, а). Рассмотрим некоторые
способы кодирования контуров.
1. Кодирование по трем признакам: длине текущего ЭВ, направлению
поворота при переходе к следующему ЭВ и углу между соседними ЭВ [33].
-и
0,1
1,1
-1,0
ж
1,0
-1,-1
0,-1
1,-1
Рис. 1.9. К определению элементарных век¬
торов контуров: виды возможных элемен¬
тарных контуров на квадратной сетчат¬
ке (а), нумерация элементарных векторов по
Фримену (б)
Рис. 1.10. Координаты
элементарного векто¬
ра при двумерном ко¬
дировании
2. Кодирование текущего ЭВ трехразрядным двоичным кодом (числа
от 0 до 7) (рис. 1.9, б). Данный код был предложен Фрименом и полу¬
чил широкое распространение в задачах обработки изображений [10, 74].
3. Кодирование текущего ЭВ двумя его проекциями на оси координат
с началом отсчета, совмещенным с началом ЭВ — двумерный код (рис. 1.10).
4. Полигональное представление контура, получающееся при его ап¬
проксимации линейными сегментами (рис. 1.11). Кодирование состоит в
фиксации координат концов этих сегментов. Данный способ благодаря
компактности получаемых описаний по¬
лучил широкое распространение. При
этом возникает проблема сегментации,
сходная с проблемой дискретизации сиг¬
налов. В реальных случаях она обычно
связана с потерей информации о форме
изображений.
5. Задание ЭВ контура восемью
комплексными числами
{1,1 — г, —г, —1 — г, —1, — 1 4- г, г, 1 + г}·
(1.2.2)
Комплекснозначный код контура
Г = {7 (n)}o k-i ввеДем как обобщение
Рис. 1.11. Полигональное представ¬
ление контура как аппроксимация
контура линейными сегментами
1.2. Кодирование контуров бинарных изображений
21
цепного кода Фримена ΔΦ на плоскость дискретного комплексного
переменного с квадратной сеткой [50, 43]. Вместо номеров, кодирующих
текущие ЭВ 7 (п) контура, каждому ЭВ ставится
в соответствие координата его конечной точки
в системе отсчета, совмещенной с началом вектора
(рис. 1.12). Эти ЭВ являются стандартными. Модули
их вещественной и мнимой частей равны либо
единице, либо нулю.
Формирование стандартных ЭВ характерно для
начального этапа обработки. На этом этапе каждая
ячейка ОЗУИ ассоциируется с пикселом квадратной
сетчатки и чтобы не пропустить ни одного отно¬
сящегося к контуру пиксела, элементы кода ΔΓ
должны быть стандартными. Дальнейшая обработка
может быть оторвана от сетчатки ОЗУИ, на которой
возможны лишь восемь различных значений ЭВ. Более общий характер
имеет полигональное представление контура в виде ориентированного
/с-угольника. Выражение для элемента кода ΔΓ в полигональном
представлении имеет вид
7 (п) = 7ι (π) + ij2 (га) = |7 (га)| ехр {ίφ (п)}, (1.2.3)
где 7i (n) = Re7(n); 72 (га) = 11117(71); (7 (тг)| и ψ{η) — модуль
и аргумент ЭВ.
6. Р-представление контура основано на проведении в области изо¬
бражения ряда равноотстоящих сечений параллельно координатной оси
и определении координат точек пересечения с контуром. Контур зада¬
ется вектором, компонентами которого являются координаты граничных
точек изображения в каждом сечении. Данное представление полезно при
выводе изображения на индикатор, при определении факта пересечения
изображений, вычисления некоторых геометрических характеристик [39].
-1+/
/
1+/
-1
ж
1
-1-/
-/
1-/
Рис. 1.12. Координаты
элементарного векто¬
ра при комплексно¬
значном кодировании
Рис. 1.13. Пример задания фрагмента контура полярным кодом: В = {... ; —4;
—3 ~Ь —3 ~Ь 2ъ\ —2 -j- 4г; —1 -f- 41 -Ь 2ij... }
22
Гл. 1. Контуры как дискретные сигналы
7. Представление линии контура полярным кодом [11]. На изображе¬
нии ω(τηι,πΐ2) выбирается полюс — начало отсчета (т. Р) естественной
(собственной) системы координат, т.е. системы отсчета, связанной с этим
изображением. Центры всех граничных точек изображения соединяют¬
ся с т. Р. В результате получается последовательность радиус-векторов
β (η), однозначно задающих контур изображения (рис. 1.13). Часто полюс
совмещается с центром тяжести изображения.
8. Представление линии контура в виде функции комплексного пе¬
ременного [5, 75-78]. Контур как непрерывная замкнутая кривая в ком¬
плексной плоскости задается ее координатой ζ (Ζ), зависящей от текущей
длины I [5]. В работе [78] и ряде других используется инвариантное к
группе линейных преобразований аналитическое описание контура уг¬
ловой функции в виде зависимости θ(1) угла касательной от текущей
длины I. На основе коэффициентов Фурье для угловой функции могут
быть получены экономные и инвариантные описания контура.
Приведенные способы кодирования контуров изображений являются
только незначительной частью известных и применяемых различными
специалистами при обработке изображений. В связи с этим ниже с по¬
зиции теории сигналов, рассматриваемых как элементы линейных про¬
странств, производится выбор способа кодирования контура в качестве
базового для решения задач контурного анализа.
Для оценки эффективности того или иного метода кодирования надо
проанализировать степень адекватности кодов бинарным изображениям,
по которым они получены, а также метрические свойства пространств,
элементами которых эти коды являются.
Контуры изображений, заданные совокупностью ЭВ, в дальнейшем
будем рассматривать как к-мерные векторы, т.е. как вектор-контуры (ВК).
Пространство ВК, у которых ЭВ заданы по Фримену, обозначим через
Фк> двумерным кодом — Е2к, а комплекснозначным — Ск. Текущей
компонентой ВК в пространстве Фк будет <^(п), в пространстве Е2к —
(71 (п) ,72 (п)), в пространстве Ск — 7(72), п — 0,1,... , к — 1. Рас¬
смотрим характер линейных преобразований и представления скалярных
произведений для ВК в каждом из пространств.
Под поворотом контура Г на угол Αφ будем понимать линейное преоб¬
разование, в результате которого на этот угол поворачивается каждый ЭВ
контура. Аналогично изменение масштаба контура в |μ| раз заключается
в растяжении каждого ЭВ контура в |μ| раз.
Пространство Фк. Данное пространство является действительным
координатным пространством, в котором ВК представляется упорядочен-
4
ным набором из к чисел — φ (η), η = 0,1,... , к — 1, где φ (η) — аргумент
7Г
1.3. Линейные пространства вектор-контуров
η-го ЭВ:
1.3. Линейные пространства вектор-контуров
23
Два ВК Г = {“^r(rc)jofc и N = |~<£>Ν (η)χ равны, если
Ψτ (η) = φΝ (η), η = 0,1,... ,k — 1.
Определим линейные операции в Фк соотношениями
Р = Г + Ν = {i»jr (η) + ί*>Ν («)}0Л_,.
p = Wr = {PiwW}oji_i.
ВК Р, являющийся суммой ВК Г и N, получается поворотом компо-
4
ненты ВК Г на угол —φ(η). Нулевой ВК состоит из нулевых ЭВ и в
связи с этим не замкнут. Противоположные ВК состоят из ЭВ с противо¬
положными аргументами и одинаковыми модулями.
В Фк скалярное произведение, норма и расстояние между двумя ВК
имеют вид
71=0
ΨΓ (η) φΝ (η);
ΡΊΙ = £*
r = ^\
71=0 \
Σ [^Γ (η)-^Ν (η)]2·
71=0
Из приведенных выражений видно, что длина ЭВ при выполнении
этих операций не затрагивается. Скалярное произведение к тому же не ин¬
вариантно к повороту ВК.
Действительно, повернем контур Г на угол Δφ и найдем скалярное
произведение ВК Г и Τ^φ:
А 2 к~*
(Г,Гд^) = (-) ^ φΓ (п) [у>г (п) + Ау] =
= (π) ιιγιι2 + δ^Σ-η ·
η—О
Из последнего выражения видно, что скалярное произведение двух
ВК, соответствующее одному и тому же контуру при его повороте на угол
Δφ относительно исходного положения, является функцией угла Δφ. Это
значит, что соответствующие одному и тому же контуру ВК будут иметь
разные нормы.
Благодаря своей простоте код Фримена широко применяется целым ря¬
дом исследователей при решении задач распознавания на основе контуров
изображений. Вместе с тем, проведенный выше анализ общих свойств кода
Фримена как сигнала в линейном пространстве Фк показал, что он не от¬
ражает длины вектора. Поэтому на его основе нельзя с общих позиций
теории сигналов синтезировать оптимальные структуры устройств обра¬
ботки и осуществить обоснованное принятие решения. Для тех задач, где
24
Гл. 1. Контуры как дискретные сигналы
важно лишь знать, из каких именно стандартных ЭВ слагается контур и
какой вид имеет их конкатенация, код Фримена содержит всю необходимую
информацию. Поэтому на его основе можно получить ряд статистических
и лингвистических описаний изображения, например, матрицу вероятностей
смены ЭВ в контурах изображений определенного класса.
Пространства Е2к и Ск. Сопоставим задание ВК в пространствах
Е2к и Ск [46]. Пусть {еп}0 — ортонормированный базис в простран¬
стве Ск и Г = {71 (п) + ^72 (n)}o k-i — разложение произвольного
ВК по этому базису. Одновременно с базисом {en}0 рассмотрим
векторы 1Ш = гёт, т — 0,1,... , к — 1. Тогда произвольный ВК Г мож¬
но представить в виде Г = {71 (0) е0 + 72 (0) W, 7ι (1) ei + 72 (1) h\ · · ·
... ;71 (fc — 1) ek-i -f 72 (к — 1) h-i}· Теперь ВК можно рассматривать
как элемент действительного координатного пространства Е2к. Таким об¬
разом, мы получили два представления ВК в координатах пространства
Е2к и Ск. Тск = {Ύι (п) + {12 (п)}0 k_v ГЕ2„ = {7l (п), 72 (n)}0)fc_r
Два ВК — Г и N — равны, если 71 (η) = 17 (п) и 72 (η) = v2 (η),
η = 0,1,... , к — 1. Сумма ВК Г и N есть ВК Р, определяемый как
р с* = Гс* + N с* = {7 (га) + и (n)}0ifc_1,
PE2k = ГЕ2к + N£2fc = {71 (η) + νχ (η); 72 (η) + ^2 («)}0,fc-r
ВК Ρ, являющийся результатом умножения ВК Г на произвольный
коэффициент μ (комплексный для Ск и действительный для Е2к), имеет
вид
Рск = μΤσ„ = {μΊ 3
РЕ2к = μΤΕ2Η = {μ7ι (η),μ72 (п)}0,к-ι·
При умножении в пространстве С,А' контур растягивается в |μ| раз
и поворачивается на угол Δ<£> = arg /х, а при умножении в пространстве
Е2к только растягивается.
В качестве ортонормированного базиса в Е2к обычно выбирается ка¬
нонический базис. В пространстве Ск выбор базиса, аналогично канони¬
ческому, неоднозначен. В качестве такого базиса может служить любой
базис вида [46] е0 = (μ,Ο,... ,0); = (Ο,μ,Ο,... ,0); ... ; e^-i =
= (0,0,... , μ), где μ — комплексное число с единичным модулем.
Скалярные произведения ВК в пространствах Е2к и Ск при ортонор-
мированном базисе имеют вид
к — 1
(г>Ν) Е2к= Σ ь νι (”)+72 v2 (1·3·2)
п=0
к-1
(т,*)ск = (γ»ν)^ +ί^[72(η)ι/ι(η)-71(η)ι/2(η)].
(1.3.3)
1.4. Особые свойства скалярного произведения
25
Сравнивая эти выражения, видим, что скалярное произведение в Ск
содержит в качестве своей действительной части скалярное произведение
в Е2к [46]. Вследствие этого скалярное произведение в унитарном про¬
странстве за счет своей мнимой части более информативно, чем скалярное
произведение в пространстве Е2к. Отсюда, например, следует, что ВК,
ортогональные в Е2к, могут не быть ортогональными в Ск. Ортогональ¬
ность сохраняется лишь при 1т(Г, N)Ck = 0. В то же время нормы ВК Г
в обоих пространствах совпадают, т.е.
(к — 1 к — 1 \ /к—1 \
Σ т? ) = (Σ I7 (п)12)
п=0 п—0 / \п=0 /
Выражения для расстояния в Е2к и Ск имеют вид:
R%2k = (Т - N,T - N)&k = \\Т\\2 + \\Щ2 - 2(T,N)E,k; (1.3.4)
R2ck = (Г - Ν,Γ - N)c<= = ||Г||2 + ||N||2 - (Γ,Ν)σ* - (М,Г)С*. (1.3.5)
Так как в унитарном пространстве (Г,Ν) = (Ν,Γ)*, то RE2k = Rc
т.е. оба пространства изометричны. Отметим следующий факт: если
||Г||2 = ||N||2 = |(Г, N)Cfc|, то RCk — 0.
1.4. Особые свойства скалярного произведения
в пространстве Ск
Скалярное произведение в действительном координатном простран¬
стве Е2к позволяет ввести не только норму для вектора этого простран¬
ства, но и обобщить понятие угла между векторами:
cosy? =
(T,N)E2k
ЦГЦ ||N||
(1.4.1)
Величину, задаваемую этим выражением, будем называть нормиро¬
ванным скалярным произведением (НСП). В пространстве Ск НСП в об¬
щем случае является комплексной величиной и не может быть косинусом
какого-либо действительного угла [49]. Рассмотрим более подробно вопрос
о том, какие характеристики ВК задает их скалярное произведение в про¬
странстве Ск.
Экстремальное свойство НСП в Ск. В соответствии с неравенством
Коши-Буняковского для комплексных чисел имеем
Ы = |(Γ,Ν)σ*| < ||Г|| ||N||, (1.4.2)
причем равенство возможно лишь при Г = μΝ, где μ = |μ| exp {гАу?} —
произвольное комплексное число. На основании выражений (1.4.1) и (1.4.2)
можно заключить следующее.
Положение 1. Модуль НСП в пространстве Ск \ηοΑ = Ы/(||Г|| ||Ν||)
равен нулю, если ВК Г и N ортогональны, и принимает максимальное
значение, равное единице, если Г и N — это один и тот же контур, причем
26
Гл. 1. Контуры как дискретные сигналы
контур N может быть повернут относительно контура Г на произвольный
угол Δφ и изменен в масштабе в |μ| раз. НСП в пространстве Е2к про¬
являет близкие экстремальные свойства. Однако из-за действительного
характера множителя μ вектор-контуры Г и elAipT имеют значение НСП,
не достигающее единицы. Таким образом, НСП в Ск позволяет обнару¬
жить высокую степень близости для значительно больших значений ВК,
чем в Е2к.
Положение 2. Максимальное значение модуля НСП в Ск инвариантно
к преобразованию поворота ВК, т.е. если Г = βχρ{ίΔ<μ}Ν, то модуль
НСП сохраняет свое экстремальное значение независимо от угла поворота
Δφ: \η0Η | = / (Δφ) = const. При этом НСП в Е2к таким свойством не
обладает.
Положение 3. Значение максимума модуля НСП инвариантно к изме¬
нению масштаба контура за счет растяжения каждого его ЭВ в \μ\ раз.
Положение справедливо для НСП в пространствах Е2к и Ск.
Инвариантность максимума модуля НСП в Ск к углу поворота кон¬
тура позволяет считать повернутые относительно друг друга контуры
одними и теми же, в то время как НСП в Е2к не позволяет сделать
такой вывод. В случае, когда угол Δφ будет равен значению π/2, рас¬
стояние между этими контурами было бы максимально возможным, что
свидетельствовало бы об отсутствии схожести между контурами, а модуль
НСП в Ск показал бы, что мы имеем дело с одним и тем же контуром.
Так как цепные коды обладают инвариантностью к сдвигу контура в
плоскости рецепторного поля, то модуль НСП в Ск представляет собой
характеристику близости двух контуров, инвариантную к линейным преоб¬
разованиям сдвига, поворота и масштаба (трансляции, ротации и гомотетии).
Показательная и тригонометрическая формы скалярного произве¬
дения в пространстве Ск. Запишем выражения для скалярного произ¬
ведения в Ск в показательной и тригонометрической формах:
к-1
η = ηι+ΐη2 = Σ/ |7(n)l W («)| ехр {ΐΔφ (η)} =
η—О
k — 1
= Σ (n)l \u (n)l (cos ^ (η) + z s*n ^ (га)} > (1.4.3)
η=0
где Δφ (η) = arg 7 (га) — arg ν (ή).
Для случая, когда N = |μ| ехр {ΐΔ<^}Γ, будем иметь η = |μ|||Γ||2 х
х (cos Δφ -f г sin Δ^?). Из полученного выражения следует, что линейные
преобразования контура приводят к аналогичным преобразованиям век¬
тора скалярного произведения ВК. В этом случае tgΔφ = Im 77/Re 77;
Η=μ||Γ||2.
По результатам приведенного в этом разделе анализа можно сделать
следующие выводы.
1. Скалярное произведение в Ск является в общем случае комплекс¬
ным числом. Вследствие изометричности пространств Е2к и Ск значе-
1.5. Аналитические преобразования контура
27
ни я норм ВК в них совпадают. Реальная часть скалярного произведения
в Ск равна значению скалярного произведения в Е2к. Таким образом,
скалярное произведение в Ск включает в себя скалярное произведение
в Е2к как частный случай и поэтому обладает большой информативно¬
стью.
2. Модуль нормированного скалярного произведения ВК в простран¬
стве Ск является характеристикой близости двух контуров, инвариант¬
ной к линейным преобразованиям сдвига, поворота и масштабирования
контуров. Скалярные произведения ВК в пространствах Ф* и Е2* таким
свойством не обладают.
3. Поворот контура на угол Δφ приводит к такому же преобразова¬
нию вектора скалярного произведения ВК, соответствующих исходному и
преобразованному контурам. Поэтому аргумент вектора скалярного про¬
изведения в Ск равен углу поворота контура.
Таким образом, комплексное линейное пространство Ск является
предпочтительным для представления контуров изображений.
1.5. Аналитические преобразования и свойства
комплекснозначных моделей контура
Элементы кода Г = {l (п)}о k-i Равны первым векторным разностям
линии контура. Поэтому целесообразно данный код назвать кодом первой
разности. Аналогично можно ввести описание контура разностями более
высокого порядка, например, код вто¬
рой разности Δ2Γ = {^7(n)}ofc_1 =
= {7(η)-7(η-1)}0Λ_1·
Текущая сумма β (η) элементов кода
ΔΓ задает другой код контура, который
назовем суммарным и обозначим как В:
п
в= {Р(п)}0,к-1’ 0(п) = Хл(г)>
г=О
п = 0,1,... , к — 1,
(1.5.1)
причем β (0) = 7 (0) и β (к — 1) =
= 0. ЭВ β (п) суммарного кода задает
вектор, соединяющий начальную точку
ао контура с концом ЭВ 7 (п) (рис. 1.14).
Перечислим наиболее важные свойства комплекснозначных кодов.
1. Коды ΔΓ и В инвариантны к переносу изображений;
2. При смещении на d элементов начальной точки ао происходит сдвиг
номера ЭВ на величину d, т.е.
7(d) (η) = 7 (η + d), (1.5.2)
где 7^) (η) — ЭВ кода, полученного в результате сдвига начальной точки.
Рис. 1.14. Задание контура элемен¬
тарными векторами первой разно¬
сти и суммарным кодом
28
Гл. 1. Контуры как дискретные сигналы
При изменении начала отсчета элементы нового суммарного кода β( (п)
выражаются через элементы исходного β (п) следующим образом:
β'(η)=β(η)+β0, (1.5.3)
где β0 — комплексное число, определяющее положение начальной точки
контура относительно начала новой системы координат. Так как при этом
разностный код не изменился, то элементы нового суммарного кода зада¬
ются рекуррентным соотношением β' (η) = β' (η — 1) +7 (η)· Суммарный
код является частным случаем полярного кода при совмещении полюса
с начальной точкой
3. При многократном обходе контура элементы его кода задают пери¬
одическую последовательность с периодом fc, т.е.
7 (п) = 7 (n ± ак), β (η) = β (п± ак), а = 0,1,2,... к. (1.5.4)
4. Сумма элементов кода ΔΓ замкнутого контура равна нулю, т.е.
7(0) + 7(1) + ... + 7(k - 1) = 0. (1.5.5)
Важнейшим достоинством принятого подхода к описанию контуров
последовательностью комплексных чисел, задающих их ЭВ, является воз¬
можность преобразования этих контуров аналитическим путем. Как было
показано в п. 1.3, код Фримена таким свойством не обладает, так как
его элементы задают лишь аргументы стандартных ЭВ. Рассмотрим связь
между цепными кодами преобразованного и исходного контуров.
При умножении контура на комплексный множитель μ = \μ\ exp {ιΑφ}
происходит растяжение этого контура в |μ| раз и поворот на угол Αφ:
Γμ = μΤ — {|μ| exp {ίΔφ}η (η)}0Λ_ν (1.5.6)
Используя выражение (1.5.2), можно установить связь между кодами
контуров со сдвинутыми на d ЭВ начальными точками, т.е. между кода¬
ми {7^ (п)} и {7(п)}:
Г(<1) - {7(d) (n)}0|t_i = {7 (η + d)}0ik_r (1.5.7)
Из последних двух выражений следует, что между кодами исходного
Г и преобразованного путем поворота, растяжения и сдвига начальной
-n(d)
точки Γμ ' контуров существует связь вида
rMd) = (И ехР {ΐΔφ}Ί {п + d)}o k_v (1.5.8)
Еще одним видом линейных преобразований контура является опера¬
ция отражения контура относительно оси, составляющей угол Θ с осью
абсцисс. В отличие от рассмотренной выше тройки линейных преобразо¬
ваний отражение связано с выходом контура из плоскости и поворотом
его вокруг оси. Рассмотрим, как связаны между собой коды отраженного
и исходного контуров.
При отражении изменяется направление следования ЭВ контура. Код
и элементы контура с обходом против часовой стрелки будем отмечать
верхним индексом (+).
1.6. Модель контурного сигнала
29
Наиболее просто определяется код ΔΓ^ = {Тотр^ (гг))о fc—i 0ТРа“
женного контура при совпадении оси симметрии с осью абсцисс, т.е. при
угле наклона этой оси 0 = 0. Здесь происходит пе¬
реход к комплексно сопряженному коду (рис. 1.15)
дготр = ΔΓ* и 7отр} = 7* (п) · (1-5-9)
Если же угол 0 имеет произвольную величину,
то для нахождения кода отраженного контура
следует поступить следующим образом:
1) повернуть систему отсчета на угол 0 и задать
в нем исходный контур Г. Для этого каждый его ЭВ
необходимо повернуть на угол (—0). В результате
получим контур То = ехр{—г0}Г. Теперь ось
симметрии совпадает с осью абсцисс и можно
воспользоваться соотношениями (1.5.9);
2) перейти к комплексно сопряженному коду
ΔΓί> = {|7(га)|ехр{-г[р(п) -0]}}o,fc-i> ί1·5·10)
3) вернуться в исходную систему отсчета. Тогда
дготр = (17 (п)| ехр {-ί[ψ (η) - 26»]}}0 i._1. (1.5.11)
Отметим, что смена направления прослеживания приводит к изме¬
нению знака и порядка следования ЭВ в контуре. Если от контура Г
с ориентацией ЭВ по часовой стрелке перейти к контуру с проти¬
воположным направлением обхода, то коды этих контуров будут связаны
следующим образом:
Г(+) = {7(+) (п)}0,*-1 = {“7(* - 1 “ n)}0,k-i
И
Г = {7 (η)}0,*-ι = {-7(+) (k - 1 - n)}0 fc_r (1.5.12)
Элементы суммарного кода β^ (п) отличаются от элементов β (η)
только порядком следования, т.е.
В(+) = {/?(+) W}0,fc_1 = {β & ~ 2 - n)}0lfc_i· (1-5-13)
В последнем выражении для получения значений номеров векторов,
лежащих в пределах от 0 до к — 1, необходимо использовать свойство
периодичности суммарных векторов: β (η) = β (п ± ак).
1.6. Модель контурного сигнала
Интерпретируя обработку полигональных комплекснозначных конту¬
ров, обладающих свойствами периодичности (см. (1.5.4)) и замкнутости
(см. (1.5.5)), как дискретных сигналов, введем понятие сигнального контура.
Этот контур представляет собой исходный (эталонный) контур Г, под¬
вергнутый группе заданных преобразований. Наиболее распространен¬
Рис. 1.15. Отражение
ЭВ контура относи¬
тельно горизонталь¬
ной оси
30
Гл. 1. Контуры как дискретные сигналы
ными преобразованиями контуров является тройка преобразований F =
= (|μ|, Αφ,ά): растяжение (масштабирование), поворот (ротация) и сдвиг
начальной точки (рис. 1.16). При этих преобразованиях контур остает-
Рис. 1.16. Процесс формирования сигнального контура квадрата Г = {1; —г; —1; г}
путем растяжения в 1,5 раза, поворотом на угол π/4, сдвигом начальной точки на
два ЭВ и отражением относительно оси, проходящей под углом π/6
ся в плоскости сетчатки, а сигнальный контур Г(с) = {7^ (n)}0 k
на основании соотношений (1.2.3) и (1.5.8) связан с эталонным контуром
следующим образом:
Т(с) = |7(с) (m)}0jfc_i = {|μ|7 (η + d) exp {ΐ[φ (η + d) + Ay>]}}0)i._1.
(1.6.1)
Обобщенная структурная схема системы связи на базе контурных сиг¬
налов приведена на рис. 1.17. Полезным сигналом считается сигнальный
контур Т^с\ полученный в результате преобразований (1.6.1) эталонного
Рис. 1.17. Обобщенная схема передачи контурного сигнала по каналу связи
контура. Он передается по каналу связи, где подвергается воздействию
шумового контура Z. Суммарный сигнал N, который назовем зашумлен¬
ным контуром, образуется как аддитивная смесь сигнального и шумового
контуров, т.е.
N = Г(с) + Z. (1.6.2)
Поясним процесс формирования зашумленного контура N примени¬
тельно к системе обработки контура радиолокационного изображения во¬
доема. Эталонный контур Г в данном случае образуется береговой чер¬
той водоема и задается в памяти ППИ по предварительно полученным
данным, например, по топографической карте местности. Изображение
1.7. Статистические модели контуров
31
контура водоема по данным радиолокационной станции будет повторять
контур Г, но в зависимости от направления полета и масштаба формиро¬
вания изображения этот контур будет иметь другие параметры. Контур
водоема, выделенный по принятому изображению, вследствие действия
шумов и помех будет содержать случайную составляющую, которая учи¬
тывается вводом шумового контура.
Основными отличительными свойствами контура изображения как
сигнала являются замкнутость, определяемая выражением (1.5.5), и ком-
плекснозначность его ЭВ.
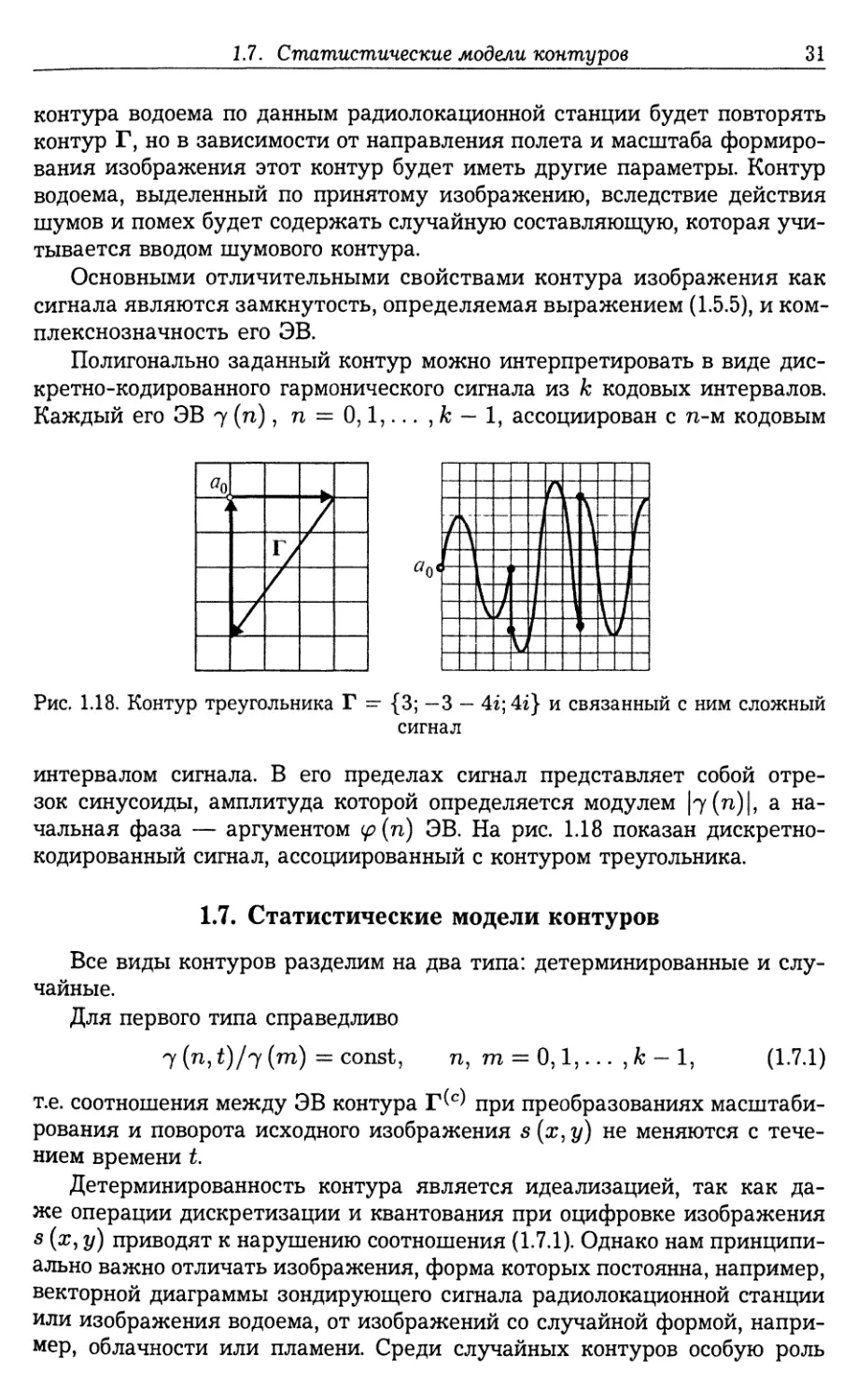
Полигонально заданный контур можно интерпретировать в виде дис¬
кретно-кодированного гармонического сигнала из к кодовых интервалов.
Каждый его ЭВ 7 (η), п = 0,1,... , к — 1, ассоциирован с п-м кодовым
Рис. 1.18. Контур треугольника Г — {3; —3 — 4г;4г} и связанный с ним сложный
сигнал
интервалом сигнала. В его пределах сигнал представляет собой отре¬
зок синусоиды, амплитуда которой определяется модулем |7(п)|, а на¬
чальная фаза — аргументом φ (п) ЭВ. На рис. 1.18 показан дискретно-
кодированный сигнал, ассоциированный с контуром треугольника.
1.7. Статистические модели контуров
Все виды контуров разделим на два типа: детерминированные и слу¬
чайные.
Для первого типа справедливо
7 (п,£)/7 (га) = const, п, т = 0,1,... , к - 1, (1.7.1)
т.е. соотношения между ЭВ контура Г(с) при преобразованиях масштаби¬
рования и поворота исходного изображения s(x,y) не меняются с тече¬
нием времени t.
Детерминированность контура является идеализацией, так как да¬
же операции дискретизации и квантования при оцифровке изображения
s (я, у) приводят к нарушению соотношения (1.7.1). Однако нам принципи¬
ально важно отличать изображения, форма которых постоянна, например,
векторной диаграммы зондирующего сигнала радиолокационной станции
или изображения водоема, от изображений со случайной формой, напри¬
мер, облачности или пламени. Среди случайных контуров особую роль
32
Гл. 1. Контуры как дискретные сигналы
играет шумовой контур Ζ, представляющий собой комплекснозначный
дискретный аналог широкополосного флуктуационного шума. Зашумлен¬
ные контуры N = + Ζ, являющиеся суммой детерминированного
сигнального контура Г(с) и шумового контура Ζ, можно рассматривать как
квазидетерминированные. К квазидетерминированным контурам относят¬
ся также контуры введенных в ППИ любых изображений постоянной
формы, случайная компонента которых вызвана шумами дискретизации
и квантования.
Модель шумового контура. Шумовой контур представим в виде
ζ = {С (")}„,*-1 = {<1 W + Кг («)>о,*-1- (1-7.2)
Составляющие £ι (n), С2 (η), η — 0, 1,... , k — 1, шумового ЭВ ζ (η) —
независимые для любого п отсчеты шума со следующими характеристи¬
ками: дисперсией
£[ίι(η)] = £>[<2(η)]=σ2, (1.7.3)
корреляционной функцией
Κ[ζι (s), <2 (η)] = Κ[ζι (s), Cl (η)] = Κ[ζ2 (s), C2 (η)] = σ2δ (s-n),
5, η = 0,1,... , k — 1,
(1.7.4)
где δ (η) — символ Кронекера:
Pf , 11 при η = s, Mr,,.
, a·7·5)
^0 при ηψ s.
Закон распределения величин ζι (п) и £2 (η) предполагается нормаль¬
ным. Случайная величина ζ (п) является комплексной, и поэтому ее ма¬
тематическое ожидание и дисперсия будут равны [25]
πίζ = 0; Ό[ζ(η)] = 2σ2. (1.7.6)
Статистическая модель зашумленного контура. В рамках принятой
аддитивной модели (1.6.2) образования зашумленного контура N и описан¬
ных выше статистических характеристик шумового контура Ζ зашумлен¬
ный ЭВ контура N равен
ν (π) = 7 (п) + С (п) I η = 0,1,... , k - I. (1.7.7)
ЭВ ν (п) является суммой постоянной величины 7 (п) со случайной
независимой величиной ζ (η), имеющей нулевое математическое ожида¬
ние, дисперсию 2σ£χ и подчиняющейся нормальному закону распреде¬
ления. Поэтому ν(η) также будет распределен по нормальному закону
с такой же дисперсией, но с математическим ожиданием, равным
ти{п) — 7 (п) ? η = 0,1,... , к - I, (1.7.8).
причем ν (s) и v (га), 5 ф га, s, т = 0,1,... , к — I, будут независимыми,
а следовательно, некоррелированными случайными величинами.
Полиномиальная и марковская модели контуров. В целом ряде случа¬
ев цепной код контура со стандартными ЭВ целесообразно рассматривать
1.7. Статистические модели контуров
33
как дискретный случайный процесс Р(Г). Случайную величину у(п),
принимающую в соответствии с (1.2.2) одно из восьми значений 7! = 1,
72 — 1 — г, 7з = —г, 74 = -1 - г, 75 = —1, 76 = -1 + г, 77 = *, 78 = 1 + *,
зададим распределением вероятностей
Ρ[7(η)] = {Ρ[7(η) = 1], Ρ[7(η) = 1-г], ..., Ρ[7(η) = 1 + г]}.
При условии стационарности процесса смены ЭВ одномерные распре¬
деления в сечении процесса перестают быть функцией от п. Если до¬
полнительно предположить независимость случайных величин на каждом
шаге, то контур изображения j-го класса описывается полиномиальным
распределением вероятностей
8 /8
Pj (ku *2, · · · , *β) = к\Ц / Π kj, (1.7.9)
v—\ / ι/=1
где k = [fci, k2,... , fcg] — вектор частот ЭВ 71 = 1; 72 = 1 — i\ 73 = —г;
74 = -1 ~ i; 75 = -1; 7б = -1 + г; 77 = г; 73 = 1 + г; π^· = Р (7^·) —
вероятность появления ЭВ в контуре изображения j-ro класса.
Дальнейшее уточнение модели контура связано с учетом зависимо¬
сти между случайными величинами ην. Предполагая, что процесс Р (Г)
обладает простым марковским свойством, получим
Ρ(Γ) = Ρ{7(0)}Π'ί’{^?1Τ)}· №0)
При условии стационарности мы приходим к простой цепи Марко¬
ва с вектором начальных вероятностей π[0] = {ячДО]}^, где π^Ο] —
вероятность того, что ην будет начальным элементом кода контура Г,
и матрицей вероятностей переходов восьмого порядка с вероятностями
переходов Ραβ, aj3 = 1,2,... ,8:
ραβ =Р{Ί (η) = ΊβΗ (η - 1) = 7α} · (1.7.11)
Масштабирование изображения приводит к изменению размерности
контура (при стандартных ЭВ) и, как следствие, к зависимости элемен¬
тов матрицы вероятностей переходов от параметра этого преобразова¬
ния. Отметим, что полиномиальная модель хотя и менее информативна,
чем марковская, однако ее вид не изменяется при масштабировании
изображения.
Наиболее полной статистической моделью контура является много¬
связанная неоднородная цепь Маркова. Однако ее применение связано со
значительным усложнением системы обработки. Например, если контур
из 100 ЭВ описывается неоднородной трехсвязной цепью Маркова, то для
хранения элементов матрицы вероятности переходов необходимо порядка
2 · 107 многоразрядных ячеек ЗУ. В то же время, как показывают экспе¬
риментальные исследования, использование многосвязных цепей Маркова
не приводит к значительному росту эффективности распознавания. Послед¬
нее обстоятельство является следствием накопления ошибок оценивания
с ростом числа признаков и характерно для задач распознавания [51].
34
Га. 1. Контуры как дискретные сигналы
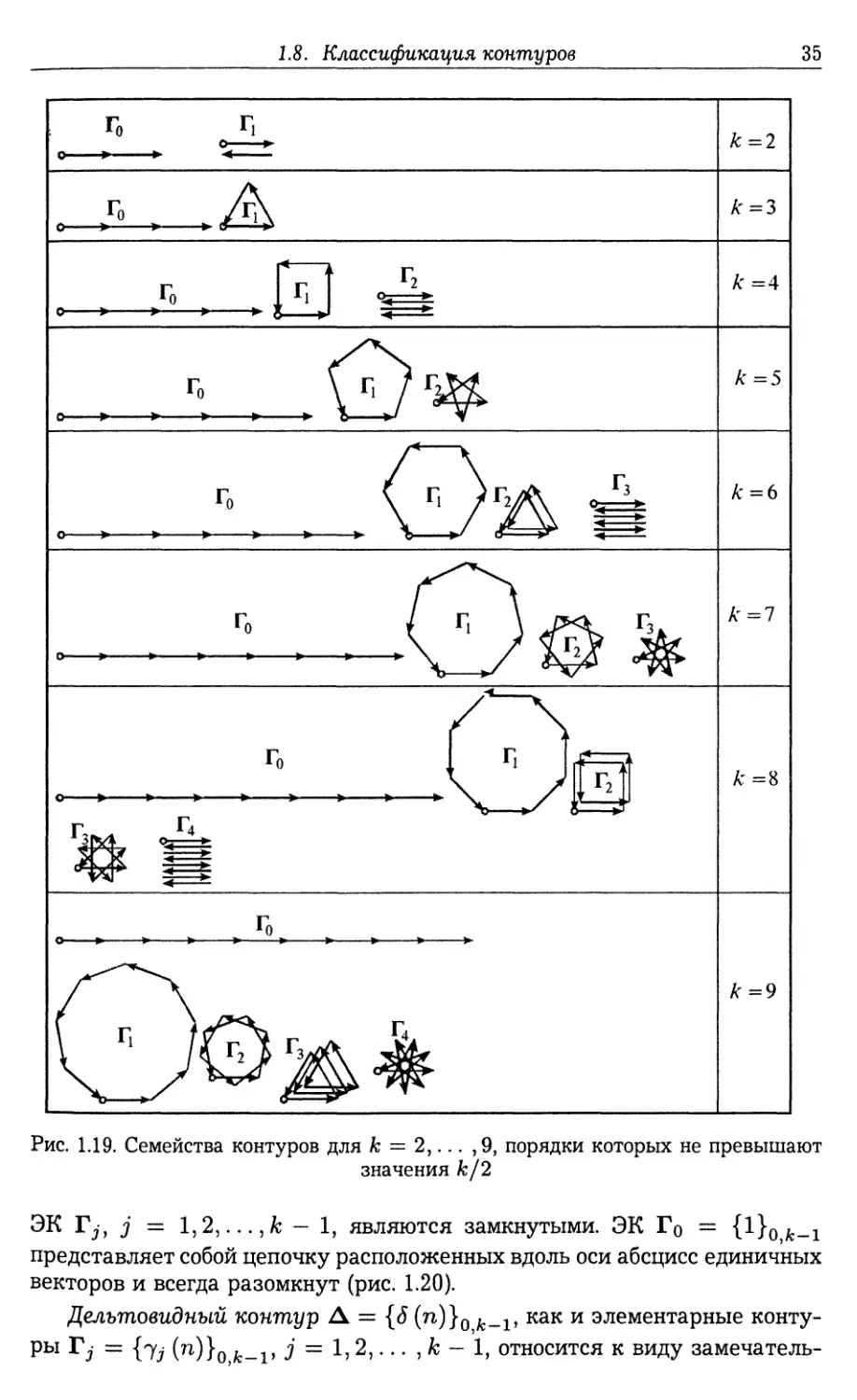
1.8. Классификация контуров
С произвольным контуром Г = {7 (п)}0 к_г связаны три следующих
вида контуров: обратный контур Гобр, комплексно сопряженный контур
и модифицированный контур Гмод.
Обратный контур Гобр получается из исходного контура Г следующим
образом:
7обР (п) = 7 (к ~ η), п = 0,1,... , к - 1, (1.8.1)
причем 7обР (0) = 7 (к) = 7 (0).
Все ЭВ комплексно сопряженного контура равны комплексно со¬
пряженным значениям ЭВ исходного контура Г:
7^ (гг) = 7* (гг), п = 0,1,... , к — 1. (1.8.2)
Контур Г модифицируется добавлением одного или нескольких рав¬
ных нулю ЭВ.
Среди большого разнообразия контуров существуют виды контуров,
пространственные или спектральные описания которых обладают особы¬
ми свойствами. Семейство контуров Г^·, j = 0,1,... , к — 1, названных
элементарными (ЭК), образуют ортогональный базис, по которому рас¬
кладывается произвольный контур. Аналогом символа Кронекера в классе
сигналов, обладающих свойством замкнутости (1.5.5), является дельтовид-
ный контур Δ = {£ (n)}0 fc_1.
Существует два вида контуров — сопряженно-симметрические (СС)
Гс/с и сопряженно-антисимметрические (СА) Гс/а, на которые раскла¬
дывается контур произвольного изображения. Рассмотрим задание этих
и некоторых других видов контуров с особыми свойствами.
Элементарные контуры. ЭК Tj = {7/ (n)}0 k_1 порядка j, j = 0,
1,... , k—1, представляет собой правильный ориентированный fc-угольник
с одинаковыми по модулю ЭВ, равными |^у| и одинаковыми по величине
углами между соседними ЭВ, равными — j :
г j ={ъ W}0,fc-1 = (ΐτΙ exp j = 0,1,... ,fc-l.
(1.8.3)
Например, при j = 1 ЭК Γι = (|7| exp является
правильным fc-угольником с обходом по часовой стрелке, а при j = 2,
к > 4 эк Г2 = {ы ехр|г^п|| будет звездчато-правильным
fc-угольником (рис. 1.19).
В дальнейшем будем полагать |^у| = 1. В табл. 1.1 приведены выраже¬
ния элементарных векторов для ЭК всех порядков для к = 2,... ,6.
В соответствии с известным тождеством
£ехр{ф»}=0,
П—О
1.8. Классификация контуров
35
Рис. 1.19. Семейства контуров для к = 2,... ,9, порядки которых не превышают
значения к/2
ЭК Tj, j = l,2,...,fc - 1, являются замкнутыми. ЭК Г0 = {1}0 k-i
представляет собой цепочку расположенных вдоль оси абсцисс единичных
векторов и всегда разомкнут (рис. 1.20).
Дельтовидный контур А = {δ (n)}0 k_v как и элементарные конту¬
ры I\j· = {7j {п)}0 k_v j — 1,2,... , k — 1, относится к виду замечатель-
36
Гл. 1. Контуры как дискретные сигналы
Таблица 1.1. Элементарные контуры размерностью fc = 2,... ,6
Порядок
контура
Аналитическое представление
к = 2
Го = {1;1};
Γι = {1,-1}
к = 3
Го = {1; 1; 1};
Γι = {1; -0,5 + 0,866г; -0,5 -0,866г};
Г2 = {1; -0,5 -0,866г; -0,5 + 0,866г}
к = 4
Го = {1;1;1;1};
Γι = {1; г; -1; -г};
Г2 = {1;-1;1;-1};
Г3 = {1; —г; —1; г}
к- 5
Г0 = {1; 1; 1; 1; 1};
Γι = {1; 0,309 + 0,951г; -0,809 + 0, 588г;
-0,809 - 0,588г; 0,309 - 0,951};
Г2 = {1; -0,809 + 0,588г; 0,309 - 0,951г;
0,309 + 0,951г; -0,809 - 0,588г};
Г3 = {1; -0,809 - 0,588г; 0,309 + 0,951г;
0,309 - 0,951г; -0,809 + 0, 588г};
Г4 = {1; 0,309 - 0.951Ϊ; -0, 809 - 0,588г;
—0,809 + 0,588г; 0,309 + 0,951г>
к = 6
Г0 = (1; 1; 1; 1; 1; 1};
Γι = {1; 0,5 + 0,866г; -0, 5 + 0,866г; -1;
—0,5 — 0, 866г; 0, 5 — 0,866г};
Г2 = {1; -0,5 + 0,866г; -0,5 -0,866г; 1;
-0,5 + 0,866г; -0, 5-0,866г>;
Г3 = {1; —1; 1; —1; 1; —1};
Г4 = {1; -0,5 -0,866г; -0,5 + 0,86бг; 1;
-0,5 - 0,866г; -0,5 + 0,866г};
Г5 = (1; 0,5 - 0,866i; -0,5 -0,866г; -1;
-0,5 + 0,866г; 0, 5 + 0,866г}
А
Г к =3 г к = 5
* V W о w ^ 1о W * k
«0
Рис. 1.20. Изображения ЭК Го нулевого порядка
1.8. Классификация контуров
37
ных контуров. Он является вырожденным fc-угольником. Нулевой ЭВ δ (0)
по модулю равен сумме модулей всех остальных ЭВ δ (1).. .δ (к — 1). Эти
ЭВ имеют одно и то же направление, которое противоположно ЭВ δ (0).
δ(θ)=9 Δ
О — ►
< 4 4—4 4 4 4—4 4—
S(9)=-l SCO—1
Рис. 1.21. Дельтовидный контур при к = 10
Если, например, ЭВ δ (0) расположен горизонтально, направлен вправо
и равен к — 1, то такой контур имеет вид (рис. 1.21)
А = {fc — 1, —1, —1,... ,-1}. (1.8.4)
В дальнейшем, если не будет особо оговорено, дельтовидный контур будет
задаваться в виде (1.8.4).
Сопряженно-симметрические и сопряженно-антисимметрические
контуры. У СС контура Гс/с элементарные векторы связаны условием
вида
7 (п) = Ί* {-п) =7* (к-п), (1.8.5)
а у СА контура Гс/а — условием вида
7 (п) = ~7* (—п) = —7* (к — п). (1.8.6)
Начальный элементарный вектор 7 (0) у СС контура является чисто
вещественным, так как равенство 7 (0) = 7* (0) возможно лишь при
Im 7 (0) = 0. Соответственно, у С А контуров 7 (0) = —7* (0), что воз¬
можно лишь при чисто мнимом характере его ЭВ 7 (0). СС контуры сим-
Г
<4-
Яо
б
Рис. 1.22. Примеры сопряженно-симметрических (а) и сопряженно-антисимметри-
ческих (б) контуров
метричны относительно вертикальной оси, а СА контуры — относительно
горизонтальной оси, проходящих через середины ЭВ 7 (0) (рис. 1.22).
Равнодольный контур. В таком контуре ЭВ связаны соотношением
вида
7 (п) = -7 (п + к/2), п = 0,1,... , к/2 - 1.
(1.8.7)
38
Гл. 1. Контуры как дискретные сигналы
Размерность равнодольного контура к всегда четное число. Ось, про¬
ходящая через концы ЭВ 7 (п) и 7 (п + к/2), делит контур на две одина¬
ковые фигуры. Простейший (при к = 4) равнодольный контур образует
параллелограмм (рис. 1.23).
Рис. 1.23. Пример равнодольного
контура
Рис. 1.24. Наложенный кон¬
тур степени 5 = 2
Наложенные контуры. Наложенным контуром степени s назовем кон¬
тур в виде k/s-угольника, повторенного s раз, причем все fc/5-угольники
совмещены друг с другом. Примером такого контура является ЭК Г2 для
к = 6 (рис. 1.24). Степень наложения для него равна s = 2. ЭВ наложенного
контура Г степени 5 обладают свойством
k / s-\-l — 1
7(η) = 7(η + ^), 7(η) = 0, * = 0,1,... ,a-l. (1.8.8)
n—l
Любая выборка из к/s ЭВ наложенного контура образует замкнутый контур.
Симметричные и антисимметричные контуры. Контур Гс, для ЭВ
которого выполняются условия
7 Μ = 7 (-гс) = 7 (к ~ гс), (1.8.9)
назовем симметричным (рис. 1.25, а), а контур Га, у которого
Рис. 1.25. а — симметричный контур Гс, б — антисимметричный контур Га =
= {0; 0, 5г; 1; —г; —1 — г; 1; —1; 1 + г; г; —1; —0, 5г}
1.9. Примеры
39
7 (η) = —7 (—η) = —7 (к — η), (1.8.10)
— антисимметричным. Поскольку для антисимметричного контура 7 (0) =
= —7 (0), то 7 (0) = 0. Поэтому контур Гс является еще и модифициро¬
ванным. При четном значении к имеем у(к/2) = —^(к/2) и поэтому
7 (&/2) тоже равно нулю. Антисимметричный контур описывает скелето¬
образную фигуру (рис. 1.25, б).
Контур с поворотной симметрией Гпс. Контур Гпс с поворотной
симметрией степени г состоит из г одинаковых фрагментов, по к/г ЭВ
в каждом. Соседние фрагменты повернуты на угол Αφ = 2π/г. Примером
такого контура с г = s является изображение звезды. При повороте кон¬
тура на угол, кратный Αφ = 2π/г, повернутое и исходное изображение
совмещаются. ЭВ контура Гпс связаны между собой соотношениями вида
7(» + «*)=7(п)ехр{— А}, (18П)
п — 0,1,... , к/г — 1, s = 0,1,... , г — 1.
Отсюда следует, что сумма соответствующих друг другу по номерам
ЭВ каждого из фрагментов равна нулю:
Σ7 (» + .£) =7(η)Σβχρ{-*^Γ«} =0·
s=0 s—0
(1.8.12)
Дельтоподобные контуры Гд. Контуры такого вида имеют один ЭВ,
значительно превалирующий по длине над всеми другими ЭВ (рис. 1.26).
Если этот ЭВ принять в качестве нулевого, то для контура Гд справедливо
следующее условие:
|7(0)|»|7(η)|, η = 1,2,... ,fc —1. (1.8.13)
1.9. Примеры
В этом разделе даны примеры, позволяющие проиллюстрировать способы
представления и преобразования контуров.
Пример 1. На квадратной сетчатке расположено бинарное изображение
S (я, у) (рис. 1.27). Определим координаты пикселей, в которых площадь, зани¬
маемая изображением, — более половины площади пикселя. В ячейки ОЗУИ,
соответствующих данным пикселам, будет записана единица:
w(mi,m2) = {1,5; 1,6; 2,2; 2,3; 2,4; 2,5; 2,6; 3,2; 3,3; 3,4; 3,6; 4,2; 4,3;
4,4; 4,5; 4,6; 4, 7; 5,2; 5,3; 5,4; 5,6; 5,7; 6,2; 6,3; 6,7}.
40
Гл. 1. Контуры как дискретные сигналы
Центры данных пикселей помечены точками. Теперь, используя понятие четы-
рехсвязанности, учитывая только горизонтальные и вертикальные связи, выделим
граничные точки полученного цифрового бинарного изображения. Эти пикселы
имеют следующие координаты:
{2, 2; 3,2; 4, 2; 5,2; 6,2; 6, 3; 5,4; 4,5; 5, 6;
6, 7; 5,7; 5,7; 4, 7; 3,6; 2,6; 1,6; 1,5; 2,4; 2,3}.
Данные пикселы относятся к контуру изображения и их центры соединены
элементарными векторами.
Пример 2. Проведем кодирование на квадратной сетчатке контура бинар¬
ного изображения, полученного в примере 1. В качестве начальной точки выбран
пиксел (2,2).
Код Фримена: {6; 6; 6; 6; 0; 1; 1; 7; 7; 2; 2; 3; 2; 2; 4; 5; 4; 4}.
Двумерный код: {0,1; 0,1; 0,1; 0,1; 1, 0; 1, -1; 1, —1; 1,1; 1,1; 0, —1; 0, —1;
-1, -1; 0, -1; 0, -1; -1,0; -1,1; -1, 0; -1,0}.
Стандартный комплекснозначный код: Г = {г, г, г, г, 1,1 — г, 1 — г, 1 + г,
1 + г, —г, —г, —1 — г, —г, —г, —1, —1 + г, —1, —1}.
Полярный код (полюс в пикселе (3,4); клетка заштрихована):
В = {-2 - г; -2; -2 + г; -2 + 2г; -2 + Зг; -1 + Зг; 2г; 1 + г; 2 + 2г; 3 + Зг;
3 + 2г; 3 4- г; 2,2 — г; 2 — 2г; 1 — 2г; —г; —1 — г}.
ПримерЗ. Для контуров N и Г, представленных на рис. 1.28 точками ABCD,
найти значения расстояния и их скалярного произведения. N и Г являются конту¬
рами одного и того же изображения, повернутого на угол (—π/2). Коды контуров
Рис. 1.28
1.9. Примеры
41
в действительном линейном пространстве и квадраты их норм равны
Νβ2* = {5,0; 0; -2; -5,0; 0,2}; ||Ν|||2* = 58;
ГВ2* = {0,5; 2,0; 0, -5; -2,0}; ||Γ|||2* = 58.
Скалярное произведение и квадрат расстояния:
(Ν, Г)Е2к = 5 · 0 + 0 · 5 + 0 · 2 + (-2) · 0 + (-5) · 0 + 0 · (-5) + 0 · (-2) + 2-0 = 0.
В.% 2fc = 58 + 58 -2-0= 116.
Коды контуров в комплексном линейном пространстве и квадраты их норм
равны:
NCk = {5; —2г; -5; 2*}; ||Ν|&* = 58;
ГСк = {5*; 2; —5*; -2}; ||Г||* * = 58.
Скалярное произведение и квадрат расстояния:
(N,r)cfc = 5 - (-5*) + (-2*) · 2 + (-5) · 5* + 2* - (-2) = -58*.
R2Ck = 58 + 58 - 2 · Re (-58*) = 116.
Равенство нулю скалярного произведения контуров в Е2к говорит об отсут-
ствии связи между формами изображений, задаваемых контурами N и Г. В то
же время модуль НСП этих контуров в простран¬
стве Ск, равный
м
1-58*1 _ 1
\/58- \/58
Ж
\Г
(+Тч
отр_\
свидетельствует о том, что эти формы абсолютно
одинаковы. При этом аргумент значения скалярно¬
го произведения позволяет принять решение о том,
что угол поворота контуров равен (—π/2).
Пример 4. Выполним аналитическим путем
поворот на угол Αφ = π/4 и растяжение в |μ| =
= 1,2 раза контура N = {ν (п)}0 3, рассмотренного
в примере 3.
N = {5; —2г; —5; 2г}.
μΝ = l,2exp{*i}N = 1,2(cos ^ +tsm^N =
= {4, 2430+4, 2430г; 1,6972-1,6972*; -4,2430-
- 4, 2430*; -1,6972 + 1,6972*}.
Вид преобразованного контура показан на
рис. 1.29.
Пример 5. Для контура с кодом ΔΓ = {1;
1 - г; -г; -1 - г; -1; -1 + г; г; 1 + г} найдем код рИс. 1.30 Отражение конту-
отраженного контура относительно оси, составляю- ра относительно оси, прове¬
щей угол Θ = 7г/4 с осью абсцисс (рис. 1.30). денной под углом π/4
Ш
/
/
\
N
7
42
Гл. 1. Контуры как дискретные сигналы
Для данного случая формула (1.5.11) принимает вид
ΔΓ^ = ||7(п)|ехр|-г^(п) - |]}}о(,·
Подставляя конкретные значения |7 (п)\ и φ (гг), получим
ΔΓ<+} = {г; -1 + г; -1; -1 - г; -г; 1 - *; 1 + г}.
Пример 6. Для контура из примера 1 (рис.1.27) построить вектор частот к =
= {fci, Л?2,... , kg} его стандартных ЭВ.
Простым подсчетом каждых из восьми возможных стандартных ЭВ получаем,
что ЭВ 7i = 1 встречается один раз, 72 — 1 — г встречается два раза, 73 = —г —
четыре раза, 74 = —1 — г — один раз, 75 = — 1 — три раза, 76 = — 1 4- г — один
раз, 77 = г — четыре раза и 73 = 1 4- г — два раза.
Таким образом: k = {1; 2; 4; 1; 3; 1; 4; 2}.
Пример 7. Поставим в соответствие контуру Г (см. пример 3, рис. 1.28)
амплитудно-фазокодированный сигнал с содержанием в пределах одного кодового
интервала двух периодов синусоиды.
Сложный сигнал будет состоять из четырех кодовых интервалов. Амплитуда
синусоиды в первом и третьем интервалах равна (7 (0) | = |7 (2) | = 2, во втором
и четвертом — I7 (1)| = I7 (3)| = 5, а начальные фазы в первом — arg7 (0) = 0,
во втором — axg7(l) = 3π/4, в третьем — arg7(2) = π/2 и в четвертом —
arg7 (3) = π/2. Вид сигнала показан на рис. 1.31.
кодовые интервалы
Рис. 1.31
Пример 8. Найдем обратный контур Г0бР для контура Г = {5; 2 — 2г; —3 — 4г;
Зг; -4 +Зг}.
ЭВ обратного контура находим по правилу: 7обР (тг) = 7 (5 — п);
Гобр = {5; —4 4* Зг; Зг; —3 — 4г; 2 — 2г}.
Для полученного контура ГобР построим комплексно сопряженный контур Г*бр:
Г0*бр = {5; —4 — Зг; —Зг; —3 4- 4г; 2 4* 2г}.
1.10. Основные результаты
43
1.10. Основные результаты
Концепция контурного анализа заключается в рассмотрении контуров
изображений как комплекснозначных сигналов, в применении к обработке
контуров изображений методов теории сигналов и в распространении этих
методов на обработку произвольных, уже не связанных с изображениями
контуров, например, контуров с самопересечением линий.
Как следует из результатов работ по вопросам восприятия изображе¬
ний и распознавания зрительных образов, контур является концентрато¬
ром информации в изображении и полностью характеризует его форму,
т.е. тот аспект воспроизводимого на экране дисплея системы технического
зрения изображения, по которому оператор чаще всего производит рас¬
познавание. Контуры объекта, в отличии от его остальных точек, устой¬
чивы на изображениях, полученных в разное время, разных ракурсах,
условиях погоды и при смене датчика. За счет того, что контурные точки
составляют незначительную часть всех точек изображения, работа с ними
позволяет резко сократить объем запоминающих устройств ППИ, по¬
высить его быстродействие, улучшить массогабаритные характеристики
и снизить энергопотребление. Контуры позволяют создать простые ана¬
литические описания изображений объектов, инвариантных к переносу,
повороту и масштабированию изображения.
Одним из основных приведенных в данной главе результатов является
обоснование выбора линейного пространства, в котором целесообразно
производить контурный анализ. Таким пространством является линейное
комплексное пространство Ск. Элементарные векторы контура адекватно
отражается в нем комплексными числами. Рассмотрены основные опе¬
рации над контурами: равенство и сложение двух контуров, умножение
контура на комплексный коэффициент, приводящее к растяжению и по¬
вороту контура, сдвиг начальной точки и отражение контура относительно
оси, проходящей под произвольным углом. Было показано, что модуль
нормированного скалярного произведения двух контуров, рассматрива¬
емых как векторы, является характеристикой близости этих контуров,
инвариантной к преобразованиям переноса, поворота и масштабирования.
При этом на основании значения самого скалярного произведения можно
оценить угол поворота и коэффициент масштабирования.
Комплексное координатное пространство контуров включает в себя
как частные случаи пространства и Е2к, в которых задаются часто
используемые для обработки контуров изображений коды Фримена и дву¬
мерный. Однако эти коды не адекватны линии контура из-за игнорирова¬
ния длины элементарного вектора (код Фримена), либо не инвариантны к
повороту изображения (двумерный код).
Одним из важных результатов данной главы является интерпретация
контура как обобщенного сложного сигнала, у которого каждый кодовый
интервал характеризуется своими, в общем случае, произвольными значе¬
ниями амплитуды и начальной фазы несущего высокочастотного колебания.
Сигнал, который ассоциируется с контуром, обладает следующими
двумя особенностями: он носит комплекснозначный характер и замкнут,
44
Гл. 1. Контуры как дискретные сигналы
т.е. сумма составляющих его элементарных векторов равна нулю. В дан¬
ном случае имеется в виду контур как фигура многоугольника. Много¬
угольник в отличие от границы бинарного изображения может характе¬
ризоваться взаимопересечением ряда своих сторон, а также повторением
(наложением) одной фигуры несколько раз. Комплекснозначные сигналы
представляют собой класс «криволинейных» сигналов, занимающий про¬
межуточное положение между одномерными и двумерными сигналами.
1.11. Задачи и упражнения
1. Найти норму контура Г = {1 4- г; 2; 5 — г; —2г; —5 — г; —2; —1 4- г; 2г}.
2. Проверить замкнутость контура Г = {3 4- 2г; 1 — г; 1 4- г; 3 — 2г; —4}.
3. Построить контур по его коду Г = {—2 — 2г; 2 — 2г; —4; 2 4- 2г; —2 — 2г; —4}.
4. Построить контур, равный сумме контуров Г = {2 -h 2г; 3; 2 — 2г; —7} и N =
= {2; —2г; —2; 2г}.
5. Контур задан кодом Фримена Г = {0,0,1,1, 2,2,3,3,4,4,5,5,6,6, 7, 7}. По¬
строить изображение этого контура и записать его комплекснозначный код.
6. Контур задан в виде Г = {2; 2 - 2г; —2г; —2 - 2г; -2; -2 4- 2г; 2г; 2 + 2г}.
Записать код этого контура в показательной и тригонометрической формах.
7. Найти комплекснозначный код полигонального контура Г = {8; 3 4- Зг; —3 — Зг;
—8; —6 — 2г; —6 4- 2г} после растяжения его ЭВ в 2 раза, поворота на угол
π/2 и сдвига начальной точки в направлении часовой стрелки на три ЭВ.
8. Найти скалярное произведение контуров Г = {2г; —3 — Зг; —2; 3 -h Зг}; N =
= {—2г; —3 -h Зг; —2г; 3 — Зг}. Объяснить полученный результат.
9. Проверить ортогональность контуров Г = {1; 1; 1; 1} и N = {1; —г; —1; г}.
10. Найти суммарный код контура, заданного разностным кодом Г = {3; 2 — 2г;
—3; 2 — Зг; —4 4- 2г; Зг}.
11. Определить длину контура Г = {3 — г; —3 — г; —Зг; — 2 4- 2г; 2 + Зг}.
12. Определить код контура, полученного отражением контура Г = {4; 1 — 2г;
—2+г;— Ц-г; — 5 — 2г; 34-4г} относительно оси, совпадающей по направлению
с ЭВ 7 (0).
13. Построить график сложного сигнала, ассоциированного с контуром Г = {3;
2 — 2г; —7; 2 4- 2г}.
14. Найти вектор частот ЭВ в контуре Г = {(1 4- г)4; (1 — г)г; (1 4- г)3; (1 — г)3;
(-1)3; (-1 - г)з; (-1 + Οι; (_1)5}·
Примечание. Нижний индекс указывает на количество одинаковых следую¬
щих друг за другом ЭВ.
15. Построить контур, обратный контуру Г из упражнения 12.
16. Вычислить коды семейства ЭК Г0, Γι, Г2 размерности к = 3.
Глава 2
СПЕКТРАЛЬНЫЙ И КОРРЕЛЯЦИОННЫЙ АНАЛИЗ
КОНТУРОВ
2.1* Введение
Метод анализа и синтеза контуров как замкнутых кривых на плоскости
с помощью фурье-описания был разработан P.JL Косгрифом [81]. Кривая
представляется параметрически как функция длины дуги или накопленное,
начиная с известной начальной точки, изменение кривизны. После нормали¬
зации эта периодическая функция разлагается в ряд Фурье и коэффициен¬
ты усеченного разложения используются в качестве признаков формы. Ко¬
эффициенты более высокого порядка описывают изменения в направлении
кривой на протяжении небольшого по длине фрагмента контура и отбра¬
сывание их эквивалентно эффекту низкочастотной фильтрации. При этом
снижается уровень зашумленности контура, а оставшиеся коэффициенты
Фурье концентрируют в себе макроскопическую информацию о форме.
За работой Р.Л. Косгрифа в этом направлении появился ряд работ, из
которых следовало, что похожие формы в пространстве фурье-описания
с эвклидовой метрикой образуют кластер. В более поздних работах [75-
78] внимание уделялось другим теоретическим и практическим аспектам
спектрального анализа контуров.
Например, в работе [78] для получения фурье-описания вводится нор¬
мализованная интегральная функция, устанавливающая связи между гео¬
метрией формы и алгебраическими описаниями свойств фурье-описания
контура. Во всех этих работах, использующих понятие спектра Фурье,
большое значение играет комплексный гармонический сигнал ехр {гит}.
Но так как контур изображения является визуальным образом, то с пози¬
ции наглядности проводимого спектрального анализа и интерпретации его
результатов целесообразно представить базисные функции также в виде
визуальных образов, т.е. в виде контуров. Кроме наглядности это по¬
зволяет оперировать при спектральном анализе и фильтрации контуров
сигналами, относящимися к одному и тому же классу.
2.2. Ортонормированный базис из полного семейства
элементарных контуров
Покажем, что любые два ЭК Г, = {7, (п)}0 к_г и Г; = {7* {п)}о к_г
из полного семейства ЭК (см. п. 1.8) являются ортогональными. В соответ¬
ствии с выражением (1.8.3) для ЭВ этих контуров
46
Гл. 2. Спектральный и корреляционный анализ контуров
7j («) = exp и 71 (и) = exp
Скалярное произведение контуров, рассматриваемых как векторы, равно
(Г,,Г,) = |ехр{^0-0п} = и (Ш)
Учитывая, что квадрат нормы ЭК не зависит от его порядка и равен
||Г,||2 = к, последнее выражение примет вид
Ч = (Г,-,Г1) = | J1
II при j - I,
при j ф I.
(2.2.2)
Отсюда видно, что если модули ЭВ взять равными 1 /\/к, то полное
семейство ЭК одной размерности к с коллинеарными начальными векто¬
рами образует в комплексном линейном пространстве ортонормированный
базис
Г 1 при j = I,
I 0 при j ф I.
(2.2.3)
Отметим, что ЭК Г, и Г; сохраняют свойство ортогональности при
повороте каждого из контуров соответственно на произвольные углы A<pj
и Αψι и растяжении каждого из контуров в \μ3\ и \μι\ раз, т.е.
η = (μ,·Γ,,
О при j ф I,
lMillwll!rl|2 при j = I,
(2.2.4)
где μ,- = |μ^ I exp {iA<pj}, μι = |μ;|βχρ {г'Д<р,}.
Благодаря свойству ортогональности энергия суммы двух ЭК разного
порядка (но одной размерности) равна сумме их энергий, т.е.
ЦГу + Гг||2 = ||Г,||2 + ||Гг||2 + 2Re (Г,·,Г,) = ||Γ,·||2 + ||Г,||2,
причем этой же величине будет равен и квадрат расстояния между кон¬
турами Tj и Гг:
Дг,.г. = ЦГу1|2 + ЦГ/ll2 - 2Re (Γ,·,Γ0 = ||Γ,·||2 + ||Гг||2,
НО
||Г,+Г,||2 = 4||Г,||2иД2.,г. =0.
При повороте одного ЭК на произвольный угол Αφ свойство ортогональ¬
ности ЭК сохраняется.
Учитывая важную роль ЭК в контурном анализе, рассмотрим другие
свойства этих контуров.
1. Радиус описанной вокруг ЭК окружности с ростом порядка j,
j = 1,2,... ,fc/2, уменьшается. Это следует из того, что длина ЭВ
контура от j не зависит, но с ростом j увеличивается центральный угол,
соответствующий этому ЭВ как хорде. После значения j = к/2 рост j
дает обратный эффект, так как этот угол становится больше π и ЭВ
2.2. Ортонормировапный базис
47
начинают соединять между собой точки, разнесенные на окружности
более, чем на 180°.
Если j < к/2, то угол поворота ЭВ ηι (1) относительно ЭВ ηι (0) мень¬
ше ж. Витки, которые делает точка, следующая за концом текущего ЭВ
по описанной вокруг ЭК окружности, происходят против часовой стрелки.
Общее количество витков / равно j, т.е. f — j при j < к/2.
Если предположить, что ЭК замыкается за время равное 1 с, то ЭК
Tj, 0 < j < к/2, можно сопоставить периодический процесс с частотой,
равной j. При j = к/2 угол поворота одного ЭВ становится равным ж
и / = к/2. Дальнейший рост порядка ЭК приводит к тому, что ЭВ jj (2)
относительно ЭВ ηj (0) делает больше одного поворота. В результате воз¬
никающего стробоскопического эффекта витки происходят уже против
часовой стрелки и их количество / до замыкания контура отстает от
величины^, достигая при j — к — 1 значения / = 1. Поэтому ЭК высоких
порядков соответствует периодиче¬
ский процесс с частотой, уменьша¬
ющейся с ростом j, а именно
/ = к — j при к/2 ^ j < к.
Таким образом, с ЭК Tj можно ас¬
социировать периодический процесс
с частотой
f _ Г j при 0 < j < к/2,
\ к — j при к/2 ^ j < к.
(2.2.5)
Зависимость частоты / от по¬
рядка j носит треугольный характер
(рис. 2.1), причем высшие частоты сосредоточены в области значений jy
близких к fc/2, т.е. в центральной части диапазона, а низшие — в его
крайних областях.
2. Сопряженность элементарных контуров. Покажем, что ЭК поряд¬
ков j и k — j являются комплексно сопряженными, т.е.
Тт = П_т. (2.2.6)
Рис. 2.1. Отношение между круговой
частотой вращения элементарных век¬
торов контура Tj и величиной его по¬
рядка
Подставим в выражение (1.8.3), задающее ЭК Г^·, т.е.
Г,- = |ехр|г^п))ок1, j = 0,1,... , к - 1, (2.2.7)
вместо j величину к — j. Тогда
г*-” =
Переходя в полученном выражении к комплексно сопряженным ве¬
личинам, получаем соотношение (2.2.6). Данное свойство свидетельствует
о том, что ЭК Tk~j получается из ЭК Tj путем отражения относительно
оси абсцисс, что связано с изменением направления обхода (рис. 2.2, а).
48
Гл. 2. Спектральный и корреляционный анализ контуров
Если размерность к является четным числом, то Тк/2 = Г^2. Для таких
ЭК угол между соседними ЭВ равен π и все ЭВ расположены горизон¬
тально, чередуясь по направлениям
Г 2(0)
у2( 2)
(рис. 2.2, б), т.е. ЭК Г*./2 четной раз¬
мерности являются вырожденными.
3. В том случае, когда сум¬
ма аргументов текущих ЭВ 7j (η),
7j (η + 1),. , 7j {n -f г — 1) стано¬
вится равной
jr
^=a,j = l,2,...,k-l,
(2.2.8)
а a — минимальное целое число,
удовлетворяющее равенству (2.2,8),
ЭК содержит s наложенных кон¬
туров. Если к — нечетное число,
то всегда г = к и 5 = 1. Поэтому
эффект наложения возникает лишь
при четном к. Отметим, что все
вырожденные ЭК одновременно яв¬
ляются наложенными, для них г =
= 2 и s = к/2. Применим, например,
выражение (2.2.8) к семейству ЭК для
к = 10. Результаты представлены
в табл. 2.1.
Из табл. 2.1 видно, что семейство содержит ЭК Г2,Г4,Гб и Г8 со сте¬
пенью наложения s = 2 и контур Г5 со степенью наложения 5 = 5. При
этом к/s-угольники для Г4 и Г6 является правильными звездчатыми пя¬
тиугольниками, а для Г2 и Г8 — простыми правильными пятиугольниками.
Гэ(2)
Рис. 2.2. Семейство замкнутых ЭК для
к = 4: a — получение ЭК Г3 пу¬
тем отражения ЭК Γι относительно
оси абсцис, б — вырожденный контур
Г 2 (для наглядности его ЭВ разнесены
друг от друга)
Таблица 2.1
3
1
2
3
4
5
6
7
8
9
г
10
5
10
5
2
5
10
5
10
а
1
1
3
2
1
3
7
4
9
S
1
2
1
2
5
2
1
2
1
4. Эргодичность элементарных векторов ЭК. Из выражения (2.2.7)
для элементарных векторов ЭК следует, что замена переменной и на
переменную j и наоборот не влияет на значение ЭВ, т.е. 7j (п) = ηη (j),
n,j = 0,l,...,fc — 1. Если дополнительно воспользоваться свойством
сопряженности, определяемым выражением (2.2.6), то получим
7,· (η) = 7η ϋ) = 7k-j (n) =7n{k- j) = jk-n (j) — lj{k — n). (2.2.9)
5. Сдвиг начальной точки ЭК на ЭВ эквивалентен умножению кон¬
тура на exp т-е· повороту на угол (^-jdТак как при повороте
ЭК свойство их ортогональности сохраняется, то это свойство сохраняется
2.3. Основные свойства дискретного преобразования Фурье
49
и при сдвиге начальных точек ЭК. Поэтому скалярное произведение двух
ЭК разных порядков с разными масштабами, углами поворота и сдвигов
начальных точек равно нулю:
(Γ,,μΓ^) = 0. (2.2.10)
Элементарным контурам Tj,j = 0,1,... , к — 1, можно поставить
в соответствие фазокодированные сигналы, у которых начальная фаза
колебаний в пределах η-го кодового интервала равна — п, а не 0 и π, как
у обычных фазоманипулированных сигналов (рис. 2.3).
Г2 ={1.-1,1,-1}
ао%=±
г, ={ι,4-ι./}
“U
Рис. 2.3. Фазокодированные сигналы, соответствующие элементарным контурам
Γ0,Γι,Γ2 иГ3 при fc = 4
ЕЕН
ШИВ
*о - и»1»1»1/
ш
Г, = {1,1,4-/}
•D И
Важным достоинством этих сложных сигналов является свойство
взаимной ортогональности, обеспечивающее их максимальную несхо¬
жесть. Данное свойство сохраняется также при разной амплитуде и
произвольном добавочном начальном сдвиге фаз каждого из сигналов
Гj, j = 1,2,... , к — 1, в отдельности.
2.3. Основные свойства дискретного преобразования Фурье
контурных сигналов
Полигональный контур Г = {7(η)}ο&-ι представляет собой пери¬
одическую последовательность ЭВ η(n), п = 0,1,... , к — 1. Его ДПФ
Р = {р (га)}0 к_± определим в виде
к-1 2
р (га) = ^2 7 (п) ехР ~
п=О
к — 1
= ^2 Ь (n)l ехР ~ ^ (п)] }’ пг = 0,1,... , /с - 1. (2.3.1)
п=0
ЭВ р(га), га = 0,1,... , к — 1, являются комплексными числами, и их
упорядоченная последовательность {р (0), р (1),... ,р(к — 1)} также об¬
разует на плоскости некоторый контур Р. ЭВ р(га) получаются сум¬
мированием всех ЭВ контура Г, каждый из которых предварительно
поворачивается на угол, равный (^—~-тп^. Обратное ДПФ для контуров
50
Гл. 2. Спектральный и корреляционный анализ контуров
записывается как
к-1
7 (n) = i ^ р(т) ехр ji^ran |, η = 0,1,... , к — 1. (2.3.2)
т=О
Рассмотрим свойства ДПФ, общие для обычных сигналов и контуров.
1. Спектр суммы контуров. Из линейности преобразования (2.3.1)
следует, что ДПФ линейной комбинации контуров Г(3) равно аналогичной
линейной комбинации контуров P(s) их спектров, 5 = 1,2,... , г , т.е.
г г
^аГ(д) 4= (2.3.3)
s=l 5=1
где μδ = \μ8\ ехр {гД</?5}, а стрелки «<£==>» означают переход к преоб¬
разованию Фурье и обратно. Из (2.3.3), в частности, следует, что сумме
исходных контуров Г(д) соответствует сумма Р(5) их спектров, а ра¬
стяжению в |μ3| раз и повороту на угол Αφδ исходного контура Г —
аналогичное преобразование его спектра.
2. Смещение начальной точки контура. Такое преобразование соот¬
ветствует смещению аргумента функции и в соответствии со свойства¬
ми ДПФ сдвиг начальной точки контура на d ЭВ (переход к контуру
Г^) приводит к умножению каждого ЭВ р(га) контура спектра Р =
= {р (wi)}0jfc_i на экспоненциальный множитель ехр т.е.
(m) ехр ^ . (2.3.4)
3. Спектр сигнального контура. Сигнальный контур предста¬
вляет собой исходный контур Г, подвергнутый заданной группе линей¬
ных преобразований (см. п. 1.6). Если эти преобразования F не связа¬
ны с выходом из плоскости, в которой расположен контур Г, т.е. F =
= {|μ|, Δ<μ, d}, то, как следует из выражений (2.3.3) и (2.3.4), контур
Р(с) = {р(с) (т)}0 к_г связан с контуром спектра исходного контура
следующим образом:
р(с) = ||μ| ехр + Δ<μ| (га) j (2.3.5)
4. Соотношение между скалярными произведениями. Для скалярных
произведений двух контуров Г = {7 (n)}0 к_г hN = {i/ (n)}0 k_v и кон¬
турами РГ = {рт (^)}0>fc_i и PN = {pN (m)}0 A._1 их спектров существу¬
ют следующие соотношения:
к-1 к-1
(Г»Ν) = Σ Τ' (η) ν* (η) = \ (рг > ρΝ) = | Σ РТ (m) Ρν М · (2.3.6)
п=0 п=О
При Г = N получаем известное равенство Парсеваля
(2.3.7)
2.3. Основные свойства дискретного преобразования Фурье
51
устанавливающее связь между энергиями контура Г и контура Р его
спектра. С помощью выражений (2.3.6) и (2.3.7) выражение для квадрата
расстояний между контурами Г и N в частотной области примет вид
Я2 = ||Г||2 + ||N||2 - 2Re (Γ,Ν) = j [||ΡΓ||2 + ||PN||2 - 2Re (Pr, PN)] ·
(2.3.8)
5. Связь между сверткой и спектрами контуров. Если
к-1
η (m) = v (n) Т (m “ n) ’т = 0’ 1’ * * * »^ ~ (2.3.9)
71=0
есть свертка Н = Г * N контуров N = {v {п)}о k-ι и Г = {7 (n)}o,fc-i>
a Pn = {pn (m)}0 k-i и рг = {рг {т)}о к-1 — соответственно контуры
их спектров, то спектр Рн = {Рн {т)}о k-i контура Н = {^(т)}0 А._1
равен
Рн (т) = pn (m) рг (m), m = 0,1,... , к - 1.
Записанное через ЭВ контуров N и Г это выражение примет вид
к-1
Σ
71=0 Ls=0
Σ v (s) 7 — s)
Г .2тг \
exp г—пт j =
7с —1
"/с — 1
^ I/ (гг) ехр г^тгг| 7 (п) ехр г^тп|
_тг=0 . _тг=0
т = 0,1,... , к — 1.
, (2.3.10)
Последнее соотношение позволяет найти через обратное ДПФ контур
свертки Н = {р{т)}0 к-1 через контуры спектров Pn и Рг. Подобный
подход к нахождению контура Н с помощью быстрого преобразования
Фурье при больших значениях размерности контура имеет значительно
меньшую трудоемкость, чем при использовании выражения (2.3.9).
6. Обратное ДПФ. Данное преобразование может быть выполнено над
контуром спектра Р по алгоритму прямого ДПФ, если предварительно
перейти к обратному контуру Р (см. п. 1.8). После преобразования резуль¬
таты необходимо разделить на к.
7. Изменение знака аргумента. Пусть п = —s. Учитывая, что 7 (—5) =
= 7 (к — s), с помощью (2.3.1) получим
/с-1 2 /с-1
р(га) = Х^7(^ ~ s) ехр j-г-^га (& - s)| = ^7 (к — s)exp
Таким образом, при изменении знака аргументов всех ЭВ контура Г
на обратный, спектр нового контура получается в результате обратного
ДПФ над обратным контуром Г0бР (см. п. 1.8).
52
Гл. 2. Спектральный и корреляционный анализ контуров
Примеры. Проиллюстрируем описанные выше свойства ДПФ на примере кон¬
туров размерности к = 5:
N = {3 — 4i\ 1 — г; 1 + 5г; —3 — г; —2 4- г};
Г = {5 + 2г; 4 - 5»; -2 - Зг; -4г; -7 + Юг}.
Спектры этих контуров, найденные по формуле (2.3.1), имеют соответственно вид:
Ρν = {0; 5,93-12,4г; -3,69 - 0, 72г; 10,07 - 4,8г; 2,68 - 2,03г};
РГ = {0; -7,99 - 0,08г; -2,96 - 12,58г; 16,58 + 4,16»; 19,37 + 18,49}.
Сумма контуров N и Г и спектр контура суммы равны
N + Г = (8 - 2г; 5 — 6г; -1 + 2г; -3 - 5г; -9 + 11»};
PN+r = {0; -2,05 - 12,52г; -6,65 - 13, Зг; 26,65 - 0,65»; 22,05 + 16,46г}.
Нетрудно убедиться в том, что спектр суммарного контура равен сумме спектров
каждого из контуров в отдельности. Сигнальный контур Г = 1,5 ехр {гтг/6}Г, по¬
лученный растяжением контура Г в 1,5 раза, поворотом на угол π/б и начальная
точка которого сдвинута на d = 2 элементарных векторов, имеет вид
Г = {-0,35 - 5,40г; 3-5,20г; -16, 59 + 7,74г; 5 + 6,35г; 8,94 - 3,49г}.
Спектр этого сигнального контура Г(с), полученный по формуле (2.3.5), предста¬
вляется как
Рг(с) = {0; 11,91 - 1,14»; -15,92 - 11, 06г; -11,26 + 23, ОЗг; 13,53 - 37,82г}.
Скалярные произведения контуров N и Г, Ρν и Рг соответственно имеют вид
(Ν, Г) = 27 - 31г; (Ρν,Ργ) = 135 - 155г.
Квадраты норм контуров Ν, Г, Ρν и Рг равны
||Ν||2 = 68; ||Г||2 = 248; ||ΡΝ||2 = 338,81; ||РГ||2 = 1240,14.
Квадраты расстояний между N и Г, найденные по формуле (2.3.8), имеют сле¬
дующие значения
R3 = ||Ν||2 + ||Г||2 - 2 Re (N, Г) = 262,
R2 = 1 [||Pn||2 + ||Рг||2 - 2 Re (PN, Рг)] = 261,79.
Свертка контуров N и Г имеет вид:
N * Г = {46 + 24г; -55 - 43г; 11 + 2г; -1 - 36г; -1 + 53г}.
Найдем поэлементное произведение контуров спектров Ρν и Рг и проверим соот¬
ношение между ним и спектром полученной свертки. Поэлементное произведение
контуров спектров
{0; -48,37 + 98,60г; 1,86 + 48,55г; 186,93 - 37,69г; 89,45 + 10,23г},
а спектр свертки
ΡΝ„Γ = {0; -48,37 + 98,90г; 1,83 + 48, 56г; 186,96 - 37,75г; 89,57 + 10,23ί}.
Сравнивая эти выражения, убеждаемся в равенстве спектра свертки двух кон¬
туров и поэлементного произведения спектров этих контуров. Найдем обратное
2 А. Свойства ДПФ контуров
53
ДПФ для контура Г. Для этого по правилу рг,обР (т) = рг (к — т) определяем
обратное представление для контура Рг:
рг,обР (ш) = {0; 19,37 + 18,49г; 16,58 + 4,16»; -2,96 - 12, 58г; -7,99 - 0,08г} .
Выполнив прямое ДПФ над массивом контура Рг,обр, найдем код контура Г.
2.4. Свойства ДПФ контуров, связанные с их замкнутостью
и комплекснозначностью
Особые свойства контуров по сравнению с обычными вещественными
сигналами обуславливают ряд характерных особенностей для их преоб¬
разований Фурье. Если сигнал X = {х (п)}0 к_г является вещественным,
то его ДПФ G = {g (m)}0 k_v определяемое выражением
к-1
g (т) — ^ х (n) ехР ш = 0,1,... , к — 1, (2.4.1)
771=0
обладает свойством сопряженной симметрии:
g (m) =g*(k-m)= g* {-τη), Ig (m)| = |g (k - m)| = |g (-m)|.
(2.4.2)
Поэтому модули коэффициентов преобразования в симметричных от¬
носительно т = 0 и т = к/2 точках одинаковы. Действительно
к — 1 ^ к—1 ^
g (к — га) = ^ ж (η) ехр j-г^ (& — га) n j = х (гг) ехр |г^гап|.
п=0 тг=0
Так как по условию х (п) — вещественное число, то изменение знака
в показателе экспоненты привело бы к тому, что комплексное чис¬
ло х (гг) ехр г-^гагг j заменилось на комплексно сопряженное х (гг) х
х ехр Поэтому g (к - т) = g* (га) и ДПФ вещественного сиг¬
нала характеризуется симметрично расположенными относительно отсче¬
та га = к/2 комплексно сопряженными парами, и при оперировании с ам¬
плитудным спектром вещественного сигнала ограничиваются половиной
отсчетов, взятых в точках га = 0,1,... , к/2.
Когда х (гг) становится комплексным, то для замены члена х (гг) х
Г . 2π 1
х ехр < —г—mnj на комплексно сопряженное значение надо изменить
знак не только в показателе экспоненты, но и в аргументе х (гг). Поэтому
комплекснозначные сигналы не обладают свойством (2.4.2) сопряженной
симметрии и в их амплитудных спектрах надо учитывать все к отсчетов
(рис. 2.4, б).
Комплекснозначный характер сигнала определяет несколько иной по
сравнению с вещественным сигналом вид АКФ и ВКФ, так как один из
сомножителей, стоящих под знаком суммы, в этих функциях является
54
Гл. 2. Спектральный и корреляционный анализ контуров
А
kK«)i
|р(«)|
15·
15"
10
'.IT, 10"
5Ϊ
_L
0
—г—* —1 —V" Г ..
1 2 3 4 m 0
ι :
г 3
а б
Рис. 2.4. Амплитудно-частотные спектры: а — вещественного сигнала {3; 5; — 3;
2; —4}, б — комплекснозначного сигнала {2 — г; 1 — г; 5 -f- 6г; —6; — Зг}
комплексно сопряженным:
к-1
η im) = X) 7 (n)l* (η + m), (2.4.3)
71=0
к —I
η (m) = ^2 ν (η)ΐ* (n + m)» m = 0,1,... , к — 1. (2.4.4)
η=0
Определим связь энергетического спектра с АКФ комплекснозначно¬
го сигнала. Энергетический спектр Wr контура Г представляет собой
распределение «мощности» каждой комплексной составляющей спектра
[62] и определяется как Wr = {|р {т)\2}0 к . Его компоненты являются
вещественными числами. Сумма этих компонент в соответствии с (2.3.7)
равна А;||Г||2. Подставим в (2.4.3) вместо ЭВ контура Г их преобразование
Фурье:
Μ = Σ
п—О
fc-1
fc-1
К s=o Lj=o
rX^(s)exp{*Ysn} fSpWexp{*yj(n + m)n} =
, s=0 ^ ' J L j=0 ^ ' m
Σρ (s)exp {*Tsn}| |Σ p* O’)exp {“‘T·7”} exp {_*T-7m}j:
= 0)ехр|-г^'т|^ехр|г^ (s-j)n|.
Последняя сумма представляет собой сумму ЭВ элементарного контура
порядка (s — j). Она будет не равна нулю лишь при s = j. Поэтому
п (го) = ^Ип)12ехр{-гтпт}·
(2.4.5)
Таким образом, АКФ контура равна прямому ДПФ его энергетиче¬
ского спектра. Аналогичный результат справедлив и для вещественного
сигнала, но его получение базируется на свойствах сопряженной сим¬
метрии спектра, которыми не обладают комплекснозначные сигналы [62].
Из (2.4.5) следует, что энергетический спектр контура может быть получен
2.4. Свойства ДПФ контуров
55
в результате обратного ДПФ:
к-1
|р (n)|2 = V (т) ехР {г^пт (2.4.6)
п=О
Обобщим полученные результаты на случай двух контуров N =
= \у (^)}о к—1 и Г = {7(n)}ofc-i* Взаимный энергетический спектр
контуров определяется как
WN,r = {рг (т) ры (m)}0)k_v (2.4.7)
Этот спектр и ВКФ также связаны между собой парой ДПФ. Проводя
выкладки, аналогичные случаю одиночного контура, получим
к-1
Т (τη) = Ρν (η) Рг (n) exp |-г γητη), (2.4.8)
η=0
к — 1
/°Ν (η) Рг (η) = τ (m) exP ~ 0’ 1» · · · ’ к — 1. (2.4.9)
71=0
Рассмотрим теперь ряд свойств ДПФ контура изображения, связан¬
ных не только с комплекснозначным характером его задания, но и с
замкнутостью.
1. Спектр контура с направлением обхода против часовой стрелки.
Пусть при сохранении положения начальной точки clq направление обхо¬
да контура изменено на противоположное, т.е. от контура Г перешли к
контуру Г(+). При этом ЭВ контуров связаны соотношением (1.5.12)
(п) = —7 (к — 1 — η), п = 0,1,... , к — 1.
Используя данное выражение и (2.3.1), запишем
К — 1 2
Рг<+> (т) = 7 (п) ехр |-i-ςτη (к - 1 - п)| =
71=О
к — 1
= — ехр 7 (гг) ехр |г^тгг |. (2.4.10)
71=0
Таким образом, для определения спектра контура Г с измененным
направлением обхода надо найти обратное ДПФ исходного контура и каж¬
дую его т-ю составляющую умножить на ехр
2. Разомкнутость контура спектра. Покажем, что контур Р спектра
контура Г всегда разомкнут. Используя выражение (2.3.2) для обратного
ДПФ при п = 0, получим
7(°) = т^р(те).
(2.4.11)
56
Гл. 2. Спектральный и корреляционный анализ контуров
Поскольку в общем случае ЭВ 7 (0) ф 0, то не равна нулю сумма всех
ЭВ контура Р, то есть он будет разомкнут. Замкнутость этого контура
достигается дополнением его ЭВ (—/ту (0)) и тогда
к-1
£p(m)-fc7(0)=0. (2.4.12)
п=0
Последнее выражение полезно для проверки правильности расчетов,
связанных с вычислением спектров контуров.
3. Равенство нулю нулевой составляющей спектра замкнутого кон¬
тура. Полагая в (2.3.1) т = 0, будем иметь
к — 1
р(°) = Хл(п)· (2.4.13)
п—О
По условию контур Г замкнут, поэтому
р (0) = 0. (2.4.14)
4. Спектр комплексно сопряженного контура. Если изменить знаки
мнимой части каждого ЭВ на противоположные, то спектр р^ (т), т =
= 0,1,... , /с — 1, комплексно сопряженного контура выраженный
через компоненты р(т), т — 0,1,... ,k—1, спектра исходного контура
Г будет равен [61]
р(т) = р* (—т) = р* (к — т). (2.4.15)
С учетом общего свойства ДПФ при изменении знака аргумента (см.
свойство 7 п. 2.3.) следует, что спектр комплексно сопряженного контура
находится как комплексно сопряженное обратное ДПФ.
5. Спектр отраженного контура. Из выражения (1.5.11) для ЭВ кон¬
тура Г, отраженного относительно оси, проходящей под углом Θ
7отр (п) = 1т (™)|ехр{—#(га) -20]} = |7 Ml exp {-iip (n)} exp {2θί},
η — 0,1,... , k — 1,
(2.4.16)
следует, что процесс отражения связан с переходом от контура Г к кон¬
туру Г* и повороту этого контура на угол (—Θ), т.е.
Г(+) =ехр{20г}Г*. (2.4.17)
С учетом линейности ДПФ и преобразования спектра при переходе
к комплексно сопряженному контуру получаем, что компонента р0тр (т)
спектра отраженного контура Готр будет равна
pW=exp{20t}p\ (2.4.18)
6. Центральный отсчет спектра. Как было показано в п. 2.2, высо¬
кочастотная часть спектра соответствует значениям т, сосредоточенным
2.4. Свойства ДПФ контуров
57
вблизи га = к/2. Найдем значения ЭВ спектра замкнутого контура р (к/2)
для четных значений размерности к. В соответствии с (2.3.1) имеем
к — 1
Р(к/2) = ^ 7 W ехр {—гтгп}.
п=0
Так как
ехр {—ιπη
1 при гг четном,
—1 при η нечетном,
то исходный ЭВ спектра будет равен разности сумм ЭВ исходного контура
Г с четными и нечетными значениями п. В связи с тем, что сумма всех
ЭВ контура равна нулю, центральный отсчет спектра замкнутого контура,
соответствующий наиболее высокочастотному колебанию, будет равен
к/2-1
р(к/2) = 2^2 7(2г),
г=О
(2.4.19)
т.е. определяется удвоенной суммой четных ЭВ контура Г. Аналогично
можно достаточно просто через элементы исходного контура выразить
отсчет спектра т = к/4.
7. Условие равенства нулю четных номеров ЭВ контура спектра.
Покажем, что для контура с четным значением его размерности (к —
четное число) при выполнении условия
7 (п) = -7 (гг + к/2), гг = 0,1,... , к/2 - 1, (2.4.20)
ЭВ контура его спектра с четными номерами равны нулю, т.е.
р(га) = 0, т = 25, s = 0,1,... , к/2 - 1. (2.4.21)
Условие (2.4.20) при нахождении спектра позволяет объединить пары
слагаемых в выражении (2.3.1) следующим образом:
^χρ(-ίγτηη) -exp(-i^m (n + f)}]> п = °> !> · · · . \ ~ 1-
(2.4.22)
Так как ехр{—i2ns} = 1 для любого целого 5, то после раскрытия
скобок в аргументе второй экспоненты получим, что последнее выражение
будет равно нулю для четных значений т.
При нечетных значениях размерности к контура Г в нем будет отсут¬
ствовать ЭВ 7 (к/2) и рассмотренное выше соотношение для его спектра
не имеет места.
Примеры. Пусть по-прежнему контуры N, Г, Pn и Рг имеют вид
N = {3 — 4г; 1 — г; 1 + 5г; —3 — г; -2 + г},
Г = {5 + 2г; 4 - 5г; -2 - Зг; —4г; -7 + Юг},
PN = {0; 5,93 - 12,4г; -3,69 - 0,72г; 10,07 - 4,8г; 2,68 - 2, ОЗг},
РГ = {0; -7,99 - 0,08г; -2,96 - 12,58г; 16,58 + 4,16г; 19,37 + 18,49}.
58
Гл. 2. Спектральный и корреляционный анализ контуров
Вычислим энергетический спектр контура Г и его АКФ:
Wr = {0; 63,85; 167,02; 292,20; 717,08},
Hr = {248; -26 + 139г; -98 + 53г; -98 - 53г; -26 - 139г},
ДПФ энергетического спектра контура Г равно
Pwr = {1240,15; -130,20 + 694,84г; -489,88 - 264,91г; -130,20 - 694,84г}.
Сравнивая выражения для Hr и Pwr, убеждаемся в справедливости форму¬
лы (2.4.6), устанавливающей связь между энергетическим спектром и АКФ конту¬
ра. Проводя обратное ДПФ для контура АКФ Нг и умножая каждый полученный
отсчет на к = 5, будем иметь {0;63,80; 166,91; 292,10; 717, 2}. Сравнивая этот
результат с выражением для Нг, видим, что АКФ контура может быть найдена
как результат обратного ДПФ от энергетического спектра.
Взаимный энергетический спектр и ВКФ контуров N и Г соответственно
равны
WN,r = {0; -46,42 + 99,82г; 20,01 - 44,28г; 146,99 - 121,56»; 14,41 - 89,00г},
Τν,γ = {27 - 31»; 16 + 54г; 23 - 29г; 8 + 5г; -74 + г}.
Выполняя прямое ДПФ над контуром взаимного энергетического спектра, получим
PWn г = {135 - 155г; 78 + 270г; 115 - 145г; 40 + 25г; -370 + 5г}.
Видно, что между контурами Ην,γ и Pwn г существует ранее установленное соот¬
ношение вида Ην,γ = ·τΡ\νΝ Г. Контур Г*, комплексно сопряженный контуру Г,
5
и его спектр соответственно равны
Г* = {5 - 2г; 4 + 5г; -2 + Зг; -7 - Юг},
Р(,) = {0; 19,37 - 18,49г; 16,58 - 4,16г; -2,96 + 12,58г; -7,99 + 0,08г}.
Сравнивая полученный контур спектра с контуром Рг, видим, что в соответствии
с выражением (2.4.15) их комплексно сопряженные ЭВ располагаются во взаимно
обратном порядке. В заключение найдем спектр контура Г, отраженного относи¬
тельно оси, составляющей угол с осью абсцисс Θ = 30°. Выражение (2.4.18) для
данного случая принимает вид: р0тр (т) = ехр{г7г/3}р* (5 — т), т = 1,2,3,4.
Вычисления по этой формуле дают следующий результат:
Ротр = {0; 25,69 + 7,52г; 11,89 + 12,28г; -12,37 + 3,37г; -4,06 - 6,88г}·
Пусть теперь ЭВ контура Г удовлетворяют условию (2.4.20), т.е. Г = {2; 1 -f г;
2 — Зг; —2; —1 — г; —2 + Зг}.
Тогда в соответствии с выражением (2.4.21) ЭВ контура его спектра с четным
значением т будут равны нулю: Р = {0; —0,46 — 1,20г; 0; 6 — 8г; 0; 6,46 — 9,20г}.
2.5. Спектры контуров специального вида
Описание контуров специального вида приведено в п. 1.8. Здесь же
будут рассмотрены особенности их спектров.
1. Сопряженно-симметрические и сопряженно-антисимметрические
контуры. При нахождении ДПФ сопряженно-симметрических контуров
2.5. Спектры контуров специального вида
59
образуется пара слагаемых вида
|7(n)|{exp{;[v?(n) - ^т.тг] } +ехр|-г^ (гг) - ^rmn]}}.
а для сопряженно-антисимметрических контуров — пары вида
|7(гг)||ехр|г^ (гг) - jmn] | -ехр|-г^ (гг) -
В первом случае получаются вещественные, а во втором — мнимые числа.
Поэтому СС контуры имеют чисто вещественное, а С А контуры — чисто
мнимое значения их спектров.
2. Равнодольный контур. Покажем, что ЭВ спектра равнодольного
контура с четными номерами равны нулю, т.е.
р(т) = 0 при т — 2s, s = 0,1,... , k/2 — 1. (2.5.1)
Соотношение (1.8.7) для ЭВ равнодольного контура дает возможность
для нахождения спектра объединить в выражении (2.3.1) пары слагаемых
следующим образом:
!l(n)l{exp{-if тп] - е*р {-i^m (n + f)}}, (i&J)
n = 0,1,... , k/2 — 1.
Так как exp {—i2ns} = 1 для любого целого s, то после раскрытия ско¬
бок в аргументе второй экспоненты, получим, что для четных т выраже¬
ние (2.5.2) равно нулю. Так как отсчет спектра получается суммированием
всех слагаемых данного вида, то результат будет нулевым.
3. Наложенные контуры. Определим особенности спектра наложенно¬
го контура (см. п. 1.8 и выражение (1.8.8)).
Очевидно, что при нахождении его спектра по формуле (2.3.1) можно
образовать цепочки из s слагаемых, которые в соответствии с (1.8.8) будут
связаны с одним и тем же ЭВ η (п) (п = 0,1,... , k/s — 1):
7 (гг) ехр г^гатг j^^exp г—гаг j. (2.5.3)
г=0
Сумма экспонент в этом выражении отлична от нуля лишь для зна¬
чений т = Is, I = 0,1,... /s — 1. Для них слагаемые (2.4.8) будут
равны S7 (гг) ехр г-^гатг |. Таким образом, спектр наложенного конту¬
ра степени 5 содержит не более (k/s - 1) не равных нулю компонент,
соответствующих значениям га, равных s,2s,... , (k/s — 1) s. Величина
р (0) = 0, так как контур Г замкнут. Если Ρ5==ι — спектр одного нало¬
женного контура Г, то ненулевые компоненты спектра контура Г будут
в s раз больше соответствующих компонент Ρ5=ι.
Отсюда следует, что если произвести прореживание спектра произ¬
вольного контура нулями, т.е. после каждой его компоненты добавить по
s — 1 нулей, то новый спектр будет соответствовать сжатому в 5 раз
исходному контуру со степенью наложения s.
60
Гл. 2. Спектральный и корреляционный анализ контуров
4. Симметричные и антисимметричные контуры. В выражении (2.3.1)
для ЭВ р (т) спектра симметричного контура с учетом (1.8.9) можно вы¬
делить пары
7 (гг) ехр | —г^гатг j
сумма которых равна
7 (к — и) ехр | —г^т (к — гг)
о / \ 2π
27 (п) cos —тп.
(2.5.4)
Аналогично, в выражении для р (к — т) можно выделить пары сла¬
гаемых
и
7 (к — п) ехр | — (к — п) (к — т)|,
сумма которых равна величине, определяемой
выражением (2.5.4). Поэтому
Рис. 2.5. Контур спек- р (т) = р (к — т), (2.5.5)
тра симметричного кон¬
тура Тс, показанного на и контур спектра симметричного контура Гс так-
рис. 1.25, а же является симметричным. На рис. 2.5 показан
спектр симметричного контура.
Проводя подобный анализ для антисиммет¬
ричного контура Га, приходим к выводу, что для него соотношение,
аналогичное (2.5.5), имеет вид
р (т) = —р(к — т), т = 0,1,... , к — 1, (2.5.6)
причем р (0) = 0.
Таким образом, контур Р спектра антисимметричного контура Га так¬
же является антисимметричной фигурой, к тому же замкнутой.
5. Контур с поворотной симметрией. В соответствии с выражени¬
ем (1.8.11) для контура Где степени г его можно разделить на г групп,
в каждой из которых ЭВ имеет один и тот же модуль:
7 (п) + 7 + · · · + 7 (и + (г — 1) =7 (п)^ехр{-г^|.
5=0
Каждой такой группе ЭВ при нахождении спектра контура Где будет
соответствовать группа слагаемых
7 (п) ехр г^тге|У^ехр (т + 1)|.
(2.5.7)
2.5. Спектры контуров специального вида
61
Сумма в выражении (2.5.7) не равна нулю при га + 1 = 0, г — 1,
2г — 1,... , к — 1. В результате спектр контура Где с поворотной сим¬
метрией степени г может иметь отличные от нуля значение лишь при
значениях (га -+-1), кратных г (рис. 2.6), т.е. при
га — st — 1, 5 = 1,2,... ук/г. (2.5.8)
6. Контур с равномерным спектром. Определим вид полигональ¬
ного замкнутого контура, все ЭВ спектра которого равны между собой
Р Р Р Р Р
-ж-*-·*-·*· 1 ■ К х-х к * »
0123456789"*
0 12 3 £-2£-1 т
Рис. 2.6. Примерный вид амплитуд¬
ного спектра для контура с поворот¬
ной симметрией при к — 10, г = 5
Рис. 2.7. Равномерный спектр
замкнутого контура
(за исключением р(0) = 0). Обозначим спектр такого контура как Р =
= {0, р, р,... , р} (рис. 2.7). В соответствии с (2.4.12) нулевой ЭВ контура
к — 1
будет равен η (0) = ——р. Покажем теперь, что все остальные ЭВ ис¬
комого контура равны между собой и равны 7 (гг) = —р/к, п = 1,2,...
... , к — 1. Предварительно отметим, что
к-1
ехр |г—гатг| = —1, η = 1,2,... , А: — 1.
771 = 1
С учетом этого равенства найдем обратное ДПФ для 7 (гг), гг = 1,2,...
... , /г — 1, искомого контура:
'r(n) = %Yl ехР{*~rmn} = -£·
m=l
Таким образом, полигональный замкнутый контур с равномерным спек¬
тром имеет вид: ^{fc — 1, — 1,— 1,... , — 1}. Сравнивая данное представле¬
ние с (1.8.4), приходим к выводу, что искомый контур является дельто¬
видным. Дельтовидный контур имеет равномерный амплитудно-частотный
спектр {p(^)}o,k-i = (p}o,fc-i и равномерный фазо-частотный спектр
{argp (т7г)}0>А._1. Но если сместить начало отсчета на d ЭВ, то фазо-ча¬
стотный спектр {^rad| ± приобретает линейную зависимость от га.
7. Дельтоподобные контуры. С учетом значительного превалирова¬
ния по длине для таких контуров ЭВ 7(0) над всеми остальными ЭВ
(см. (1.8.13)) при нахождении спектра по формуле (2.3.1) этот ЭВ вынесем
62
Гл. 2. Спектральный и корреляционный анализ контуров
за знак суммы:
К — 1 2
р (га) = 7 (0) 4- ^2 7 (п) ехР {“г^гап}, га = 1,2,... , к - 1.
Сумма в этом выражении задает вектор, замыкающий цепочку векторов
7 (гг) ехр {
1-7(0)!»
ran|, η = 1,2,.
··,*
к-1
.2π
“гТ
Ί (п) ехр (
, га = 1, 2,... , к - 1,
п=1
т.е. ЭВ спектра контура Гд задаются в основном только одной компонен¬
той, равной 7 (0), т.е.
р (га) « 7 (0), га = 1,2,... , к — 1. (2.5.9)
Следовательно, превалирование по длине одного ЭВ над остальными
ЭВ контура Гд приводит к расширению и выравниванию его амплитудного
спектра.
Пример 1. Коды СС и С А контуров, показанных на рис. 1.21, имеют соот¬
ветственно вид
Гс/с = {2; 1 + г; -2 - г; -2 + г; 1 - г},
Гс/а = {2г;4; 1 — г; —1 — г; 1 — 4},
а их спектры
РГс/с = {0; б, 58; 2,22; -3,93; 5,12},
РГс/а = {0; —5,17г; —1,41г;4,18г; 12,4г}.
Спектр контура Гс/с является чисто ве¬
щественным, спектр контура Гс/а — мнимым.
Нулевые компоненты этих спектров равны нулю,
так как контуры замкнуты.
Пример 2. Найдем спектр равнодольного
контура, показанного на рис. 2.8: Г = {2; 1 + г;
-2 - Зг; -2; -1 - г; -2 + Зг}.
Используя формулу (2.3.1), получаем? = {0; -0,46-1,20г; 0; 6-8г; 0; 6,46-
— 9,20г}.
Видно, что ЭВ спектра с четными значениями га, т.е. р (0), р (2), р (4), равны
нулю.
Пример 3. Пусть задан наложенный степени k/s контур Г, где к = 12 и s =
= 3:
Г = {4; 2 + Зг; 3 - г; -9 - 2г; 4; 2 + Зг; 3 - г; -9 - 2г; 4; 2 + Зг; 3 - г; -9 - 2г}.
Спектры контура Г и контура одного наложения Г = {4; 2 + Зг; 3 — г; —9 — 2г;}
имеют вид
I
Рис. 2.8. Равнодольный кон¬
тур Г и его доли
Р = {0; 0; 0; 18 - ЗОг; 0; 0,42 - 6г; 0; 0; -12 - 36г; 0; 0},
Р3=1 = {0; 6 - Юг; 14 - 2г; -4 + 2г}.
2.6. Разложение произвольного контура
63
Из этих выражений видно, что в спектре контура Г от нуля отличны компо¬
ненты р (3), р (6) и р (9). Кроме того, эти компоненты равны утроенным значениям
соответствующих компонент спектра Ρθ=ι.
Пример 4. Контур изображения пятиконечной звезды характеризуется по¬
воротной симметрией степени г = 5 (рис. 2.9) и имеет вид Гпс = {1 + Зг; 1 — Зг;
3,162 - 0,024г; —2, 544 - 1,878г; 0,954 - 3,015г;
-2,572 + +1,840»;-2, 572 - 1,840»; 0,954 + 3,015г;
-2,544 + 1,878г; 3,162 + 0,024г}·
При повороте контура на угол, кратный Δ<ρ = 72°,
повернутое и исходное изображения совмещаются. Спектр
контура Гпс имеет вид Р = {0; 0; 0; 0; -7,862 + 24,196г;
0; 0; 0; 0; 17,862 + 5,804г}.
Не равными нулю в спектре контура являются
компоненты
Р(т) - р(г - 1) = р(4),
р(т)-р(2г-1)=р(9).
Пример 5. Антисимметричный контур Га на рис. 1.25, б имеет код
Га = {0; 0,5г; 1; —г; —1 — г; 1; 1 + г; г; —1; —0,5г}.
Спектр этого контура равен
Р = {0; -2,95 - 0,87г; 3,45 - 2,41t; 1, 73 + 0,13г; -0,89 + 4,36г; 0,59 - 2,72г;
- 0,59 + 2,72г; 0,89 - 4,36г; -1,73 - 0,13г; -3,45 + 2,41»; 2,95 + 0,87г}·
2.6. Разложение произвольного контура
2.6.1. Разложение Каппе лини. Как следует из приведенных в [61]
соотношений для СС и СА последовательностей, произвольный контур Г
является суммой соответствующих ему контуров Гс/с и Гс/а, т.е.
Г = Гс/с + Гс/а, (2.6.1)
где
Рис. 2.10. Исходный (а) и обратный (б) комплексно сопряженный контуры
Найдем, например, разложение контура (рис. 2.10, а)
Г = {2 + 2г; 5 + г; -1 - 2г; -3; -3 - г}.
Соответствующий ему контур Г^ имеет вид (рис. 2.10, б)
☆
Рис. 2.9. Контур с по¬
воротной симметрией
степени г = 5
64
Гл. 2. Спектральный и корреляционный анализ контуров
Г$ = {2 - 2г; -3 + г; -3; -1 + 2г; 5 - г}·
Используя выражение (2.6.2), получаем (см. рис. 1.22)
Гс/с = {2; 1 + г; -2 - г; -2 + г; 1 - »}, Гс/а = {2г; 4; 1 — г; —1 — г; -4}.
В спектральной области соотношение (2.6.1) принимает вид
Pr=Prc/c+Prc/a. (2.6.3)
Учитывая данное соотношение и свойства спектров СС и СА контуров,
приходим к выводу, что реальная часть спектра контура Г равна спектру
соответствующего СС контура, а мнимая часть спектра контура Г —
спектру соответствующего СА контура, т.е.
РГс/с = Re Рг и Ргс/а = Im Рг- (2.6.4)
2.6.2. Разложение произвольного контура в базисе из полного се¬
мейства элементарных контуров. Определим вид восстановленного кон¬
тура при условии, что его спектр содержит только один не равный нулю
ЭВ р(га), ra = l,2,...,fc — 1, причем р(т) = к. Используя выраже¬
ние (2.3.2) для обратного ДПФ, получим
rm = {7т (т)}0|Яг_1 = |ехр {iymn}} , га = 1,2,... , к - 1.
(2.6.5)
Сравнивая данное выражение с выражением (1.8.3), приходим к вы¬
воду, что восстановленный контур является ЭК порядка га. В общем
случае при р (га) = sk и arg р (га) = а (га) контур Гт представляет
собой правильный fc-угольник с описанными в п. 1.8 свойствами, причем
длина каждой стороны равна s, угол поворота которого по отношению к
/г-угольнику (2.6.5) равен а (га). ^
Экспоненциальная компонента ехр | г—ran | является ЭВ ηш (п) эле¬
ментарного контура порядка га. Поэтому выражение (2.3.2) для обратного
ДПФ элементарного вектора произвольного контура можно записать как
к — 1
7 = \ Σ р (тпЬ,"г (n) > n = 0,l,... ,fc-l. (2.6.6)
771=0
Видно, что ЭВ 7 (п) является взвешенной комбинацией η-х ЭВ каждо¬
го элементарного контура Гш, га = 1,2,... , к - 1. Весами служат компо¬
ненты р (га) спектра контура Г. Если контуры Гш рассматриваются как
элементы комплексного линейного пространства Ск (см п. 1.3), то сумма
двух контуров Г^· и Г{ есть контурГ5, ЭВ которого равны сумме соответ¬
ствующих ЭВ контуров Г^· и Гг, т.е. Г5 = Г^· + Г* = (7^· (п) 4- 7,: (те)}0
С учетом этого правила сложения контуров и выражения (2.6.6) получим
к-1
Г = ^РНГт
(2.6.7)
2.6. Разложение произвольного контура
65
Данный результат имеет фундаментальное значение для контурного
анализа. В соответствии с ним произвольный контур Г равен взвешенной
сумме ЭК Гт, га = 1,2,... ,k — 1. В качестве весовых коэффициентов
служат ЭВ р (га) контура спектра разлагаемого контура. Спектральный
р(0Г1 р(2)Г2 р(з)г3 Р (Ό Г4
Рис. 2.11. Полигонально заданный контур изображения (а) и его составляющие (б)
анализ контуров, выполненный по правилам спектрального анализа обыч¬
ных сигналов, дает возможность решать задачи прохождения контурных
сигналов через различные устройства. На рис. 2.11 показаны произволь¬
ный полигональный контур Г и найденные в соответствии с выражением
(2.6.7) составляющие его ЭК р (га) Гт с весами р (га), а на рис. 2.12 про-
Рис. 2.12. Синтез контура Г (см. рис. 2.11,а) и его элементарных векторов
иллюстрирован процесс синтеза данного контура Г и его ЭВ из контуров
Гт. В том случае, когда разлагаемый контур является дельтовидным,
формула (2.6.7) предельно упрощается. Спектр этого контура имеет вид
р(га) = р, га = 1,2,... , к — 1. При условии р — к выражение (2.6.7)
бб
Гл. 2. Спектральный и корреляционный анализ контуров
Рис. 2.13. Синтез дельтовидного контура для к = 3: а — элементарные контуры Гι
и Гг и их спектры; б — формирование дельтовидного контура; в — дельтовидный
контур и его спектр
к-1
принимает вид Δ = Гш. На рис. 2.13 показан синтез контура А для
т—1
к = 3 из двух ЭК в виде треугольников. Таким образом, произвольный
контур размерности к разлагается в базисе из полного семейства ЭК
ГЬГ2,... ,Γ^_ι, причем координатами контура в пространстве Ск будут
компоненты его спектра.
2.7. Изменения спектра при преобразованиях, связанных
с вариацией размерности контура
Ранее было рассмотрено влияние на спектр контура преобразований
поворота, масштабирования, отражения и смещения начальной точки, не при¬
водящих к изменению формы изображения. При этом предполагалось,
что размерность контура к, определяемая количеством ЭВ в его составе,
является неизменной. Необходимо заметить, что представление контура
цепочкой ЭВ в определенной степени есть следствие процесса дискре¬
тизации непрерывной линии границы исходного изображения при вводе
в систему технического зрения. В зависимости от правила дискретизации
и архитектуры такой системы размерность контура, введенного в ППИ
изображений, может варьироваться при неизменной форме изображения.
Необходимость вариации размерности полигонального контура воз¬
никает при получении меры схожести форм двух изображений. Конту¬
ры этих изображений имеют векторное представление и их размерности
обычно не совпадают. В то же время для нахождения мер схожести в виде
расстояния между контурами или их скалярного произведения, размер¬
ности векторов должны быть одинаковыми.
2.1. Изменения спектра при преобразованиях
67
В этом разделе мы рассмотрим связь между спектрами исходного
контура и контура с измененной размерностью при преобразованиях мо¬
дификации и дробления ЭВ.
Модификация контура. Модифицированный контур Гмод был опреде¬
лен в п. 1.8 как контур, код которого дополнен некоторым количеством
равных нулю ЭВ. Если при этом еще и 7 (0) = 0, то из взаимного со¬
ответствия между операциями прямого и обратного ДПФ следует, что
контур Рмод спектра будет замкнутым.
Пусть модификация контура Г производится дополнением к его ЭВ
7 (0), 7 (1),... , 7 (к — 1) еще к ЭВ 7 (к), 7 (к + 1),... ,7 (2к — 1):, каж¬
дый из которых равен нулю. ДПФ ЭВ модифицированного контура равно
2к — 1 к-1
Рмод (т) = X 7 (n) exp = X 7 («) exp
п=0 п—О
т = 0,1,... , к — 1.
Примем, что т = 21 (I = 0,1,... , к — 1). Тогда
к — 1
Рмод (0 = X 7 («) ехр ln}, I = 0,1,... , к — 1.
п—О
Сравнивая данное выражение с выражением для спектральной ком¬
поненты р (т) исходного контура, приходим к выводу, что для четных
значений т рмод (т) = р (т). Компоненты рмод (т) с нечетными т,
расположенные между компонентами с четными значениями т, соответ¬
ствуют интерполированным значениям спектра.
Таким образом, дополнение кода исходного контура к нулевыми ЭВ
не приводит к нарушению формы, но и не улучшает разрешающую спо-
в г
Рис. 2.14. Изменения амплитудно-частотного спектра контура при дополнении
его кода нулями: а — для контура Г = {1,г,-1,-г}; б — для контура Г =
= {1; г; -1; -г; 0; 0; 0; 0}; в — для контура Г = {1; г; -1; -г; 0; 0; 0; 0; 0; 0; 0; 0};
г — для контура Г = {1; г; -1; -г; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0; 0}
68
Гл. 2. Спектральный и корреляционный анализ контуров
собность спектра, а лишь позволяет получить сглаженное за счет интер¬
поляции представление спектра. При этом возможно устранение неопре¬
деленностей в спектре и повышение точности оценивания его пиковых
значений [65]. На рис. 2.14 показано
изменение амплитудно-частотного
спектра ЭК Г = {1, г, —1, —г} при
последовательном наращивании его
размерности: к = 4,$, 12,16.
Дробление или повторение ЭВ
контура. Пусть размерность кон¬
тура меняется путем деления каж¬
дого его ЭВ на s одинаковых ЭВ
или же каждый его ЭВ повторяет¬
ся s раз (рис. 2.15). Естественно, что
при этом форма изображения, за¬
даваемая контуром, не нарушается.
Рассмотрим связь между спектра¬
ми исходного и преобразованного
контуров. Для конкретности будем
рассматривать контур Г5, полученный повторением s раз каждого
ЭВ контура Г. Размерность преобразованного контура Г5 становится
равной ks. При нахождении компоненты спектра контура Ts
sk—1 2
Ps (га) = 7s in) ехР г-^гап|, т = 0,1,... , sk — 1, (2.7.1)
тг=0
видим, что в выражение для нее входит составляющая
к-1 2
р (т) = 7 (п) ехр|—г^гап|, т = 0,1,... , к — 1,
п=0
являющаяся компонентой спектра исходного контура. Кроме того,
в выражение (2.7.1) входят составляющие
р (га) ехр |—г^га р (т) ехр г^2га|, ...
р (т) ехр (—(s — 1)}·
Поэтому
S —1
Ps (га) = р (га) ехр г-^rra га = 0,1,... , sk — 1. (2.7.2)
г=0
На рис. 2.16 показаны спектры контуров при повторении два и три
раза каждого ЭВ контура квадрата Γχ (см. рис. 2.15).
При преобразовании размерности контура путем дробления на s оди¬
наковых частей каждого его ЭВ спектр преобразованного контура будет
*ов
а б в
Рис. 2.15. Преобразование размерности
контура: а — исходный контур Г,
б — контур Γχ/2, полученный делением
элементарных векторов исходного кон¬
тура на два, в — контур Г2, получен¬
ный повторением два раза каждого эле¬
ментарного вектора исходного контура
2.8. Корреляционный анализ контуров
69
т
Рис. 2.16. Спектры контуров, полученных путем повторения ЭВ: а — для исходного
контура Г = {1; г; —1; —г}, б — для контура Г = {1; 1; г; г; —1; —1; —г; —г}, в —
для контура Г = {1; 1; 1; г; г; г; —1; —1; —1; —г; —г; —г}
равен
1 S~1 2
Pi/s {т) = “Р (гм) ^ exp г-^rm т = 0,1,... , sk — 1. (2.7.3)
г=0
Как следует из полученных выражений, спектры преобразованного
и исходного контуров функционально связаны, причем, если какая-то
компонента спектра исходного контура, например р(0), равна нулю, то
нулевыми окажутся компоненты ps (0), ps (0 + k), ps (0 -f 2k)... спектра
преобразованного контура. При пользовании выражениями (2.7.2) и (2.7.3)
необходимо учитывать свойство периодичности значений компонент спек¬
тра исходного контура:
р (т) = р(т-f ak), а = 0, =Ы, ±2,...
В следующих разделах будут рассмотрены процедуры эквализации
и стандартизации ЭВ контура Г, также сохраняющие при изменении
его размерности информацию о форме изображения.
2.8. Корреляционный анализ контуров
2.8.1. Корреляционные функции комплекснозначных сигналов. ВКФ
и АКФ дискретных комплекснозначных сигналов могут быть введены
на основе скалярного произведения (Ν, Г) в пространстве Ск векторов
N = {ι/(η)} и Г = (7(м)}, задающих эти сигналы. По определению
(см. п. 1.3 и [46])
к-1 к-1
(Ν,г) = ^2 ν (п) 7* (п) и (Γ,Ν) = (Ν,Γ)* = (га)* 7 (η). (2.8.1)
η=0 η—0
70
Гл. 2. Спектральный и корреляционный анализ контуров
Для получения ВКФ τ (га) сигналов N и Г полагаем, что эти сигналы
обладают свойством периодичности
ν (η) = ν (п =Ь ак) и 7 (гг) = 7 (п ± ак), п = 0,1,... , к — 1, (2.8.2)
где а — целое число, а начало одного из сигналов, например Г, меняет¬
ся скользящим образом. Тогда для каждого положения начальной точки
сигнала Г можно получить отдельные значения скалярного произведе¬
ния; к различных значений этих скалярных произведений образуют ВКФ
сигналов N и Г:
к-1
т (га) = ν (п) 7* (п + ш),
п=О
При N = Г ВКФ переходит в АКФ
к-1
т (то) = Σ 7 (п) 7* (n + m),
п=0
Из выражения (1.3.5) для квадрата расстояния между векторами N
и Г в пространстве Ск следует, что ВКФ г (га), как полный набор зна¬
чений скалярных произведений вектора N на вектор со смещенным
положением начальной компоненты 7(га), т — 0,1,... ,к — 1, является
характеристикой близости векторов N и Г(т1
Аналогично АКФ г (га) вектора Г служит характеристикой близо¬
сти этого вектора со своей копией имеющий в качестве началь¬
ной компоненты ЭВ 7 (га). Все особые свойства скалярного произведения
в пространстве Ск, рассмотренные в п. 1.4, имеют место для ВКФ и АКФ
векторов N и Г в этом же пространстве. Поэтому ВКФ в пространстве Ск
позволяет обнаружить высокую степень близости векторов N и Г инвари¬
антно к углу их взаимного поворота, сдвигу начальной точки и масштабу.
ВКФ в пространстве Е2к такими возможностями не обладает. Так как
масштаб и угол взаимного поворота двух изображений, а также поло¬
жения начальных точек их контуров не должны влиять на результаты
распознавания изображений по их форме, то ВКФ в пространстве Ск
будет в дальнейшем применяться как базовая аналитическая конструкция
при рассмотрении контуров изображений.
Отсчеты ВКФ и АКФ являются комплексными числами и могут быть
представлены последовательностью векторов на плоскости, т.е. в виде
контура Т = {т (m)}o fc_1 (рис. 2.17).
га = 0,1,... ,к-1. (2.8.3)
га = 0,1,... , к - 1. (2.8.4)
Рис. 2.17. Контуры Г и N и контур Т их взаимнокорреляционой функции
2.8. Корреляционный анализ контуров
71
Рассмотрим свойства ВКФ и АКФ, заданных выражениями (2.8.3)
и (2.8.4). Договоримся переменную га называть внешней, а переменную
п — внутренней.
1. Периодичность. Из выражения (2.8.2) следует, что
к-1
т (га ± ак) = ν (п) 7* (п + т ± ак) = г (га).
п=0
Отсюда также вытекает, что г (—ш) = τ (к — т).
2. Симметричность. Отсчет ВКФ в момент (—т) с учетом выраже¬
ния (2.8.3) равен
/с-1 /с-1
г (—т) —т(к — т) = ^ ι/ (гг) 7* (п + А; — т) = ^ г/ (гг) 7* (гг — га).
п=0 п=0
Таким образом, изменение знака внешней переменной га приводит к обрат¬
ному порядку следований отсчетов ВКФ. Если ВКФ г (га) представлена
/с-1
в виде г (га) = г/ (гг 4- га) 7* (гг), т.е. если внешняя переменная Отнесе¬
те о
на к первому, а не ко второму сомножителю, то свойство симметричности
определяется соотношением
/с-1
т {к — т) — ^ г/ (гг — га) 7* (гг).
п=0
3. Эквивалентность. Выясним связь между ВКФ, в которых внешняя
переменная относится к разным сомножителям. Покажем, что
/с — 1 k—1
г (га) = ^2 ν (п) 7* (гг 4- га) = г/ (гг — га) 7* (гг). (2.8.5)
п=0 п=0
Для этого введем новую переменную s = гг 4- га. Тогда первая сумма в
/с —1—m
выражениях (2.8.5) примет вид г (га) = v (s — га) 7* (η). Учитывая
п=0
периодичность отсчетов ν (п) и 7 (гг) и обозначая 5 через гг, получаем, что
/с-1
г (га) = г/ (гг — га) 7* (гг).
п=0
Таким образом, перенос внешней переменной в выражении для ВКФ от
одного сомножителя к другому при сохранении значения ВКФ приводит
к изменению знака этой переменной. Аналогично показывается, что
к—1 к—1
т (к — т) = ^2 v i71 4- га) 7* (гг) = г/ (гг) 7* (гг — га).
п=0 п=0
4. Комплексная сопряженность. Перенос знака комплексной сопря¬
женности в выражении (2.8.3) для ВКФ от одного сомножителя к другому
72
Гл. 2. Спектральный и корреляционный анализ контуров
приводит к комплексно сопряженному виду отсчета ВКФ, т.е. т* (га) =
к-1
= Σ ν* (п) 7 (п + га). Справедливость этого выражения основана на том,
п=О
ЧТО
I/ (гг) 7* (гг + т)
_п=О
к-1
У I/* (гг) 7 (п + ш).
п=0
к-1
Аналогично показывается, что г* (ш) = ^ ι/* (η — га) η (п).
п=О
Таким образом, основные свойства ВКФ комплекснозначных периоди¬
ческих сигналов заключаются в следующем:
1) ВКФ является периодической функцией с периодом к\
2) изменение знака внешней переменной га приводит к обратному
порядку следования отсчета функции;
3) изменение места внешней переменной га также приводит к обрат¬
ному порядку следования отсчетов функции;
4) одновременное изменение знака и места внешней переменной со¬
храняет первоначальный порядок отсчетов ВКФ:
к—1 к—1
т (га) = ν (п) 7* (гг + га) = У^ v (п — гп) 7* (гг), (2.8.6)
п=0 п=О
к — 1 к — 1
τ (к — гп) = ^ I/ (гг) 7* (гг — т) = У~^ i/(n + m) 7* (гг); (2.8.7)
п—0 п=0
5) смена положения стоящей под знаком суммы комплексно сопряжен¬
ной функции приводит к комплексной сопряженности отсчетов ВКФ
к — 1 к — 1
т* (га) — г/* (гг) 7 (гг + га) = У^ ι/* (п — га) 7 (гг),
п=0 п=0
/с — 1 к — 1
т* (к — га) = У] г/* (тг) 7 (гг — га) = У^ г/* (гг + га) 7 (тг).
Свойства АКФ сигнала Г, представленного в пространстве Ск, вы¬
текают из того, что АКФ представляет собой частный случай ВКФ при
N = Г. Однако в виду важности этой функции для целей контурного
анализа рассмотрим свойства АКФ более подробно.
к-1
1. АКФ т (га) = ^ 7 (гг) 7* (гг 4- га) контура Г = {7 (тг)}0 к_г явля-
п=0 ’
ется периодической функцией с периодом к;
2. Нулевой отсчет АКФ равен квадрату нормы (энергии) контура Г,
причем этот отсчет по модулю является максимальным, т.е. г (0) = ||Г||2
и г (0) ^ |т(га)|, га = ±1, ±2,... Действительно, при га = 0 выраже¬
2.8. Корреляционный анализ контуров
73
ние (2.8.4) принимает вид
г (°) = Σ 7 (п) 7* (η) = Σ |7 (п)|2 = ||Г|[2.
п=0 п=0
Покажем теперь, что τ (0) является максимальным по модулю от¬
счетом ВКФ. В общем случае т(га) = (Г,Г^), где — вектор Г
с начальной компонентой η (га). В соответствии с неравенством Коши-
Буняковского |(Г,Г(т))| ^ ||Г||||г(т) ||. Так как норма вектора не за¬
висит от выбора его начальной компоненты, то ||Г^т^|| = ||Г||. Поэтому
||(Γ,ΓΜ)||ζ||Γ||2=τ(0);
3. Смена знака или места внешней переменной га приводит к обрат¬
ному порядку отсчетов АКФ:
к-1 к-1
т (к — га) = ^ 7 (п) 7* (п — га) — 7 (п + га) 7* (п)\
п=0 п=О
4. Одновременная смена места и знака внешней переменной сохраняет
первоначальный порядок отсчетов АКФ:
к—1 к—1
т (ш) = 7 (п) 7* (п + ш) = 7 (гг — ш) 7* (п).
п=0 п=0
5. Отсчеты г (ш) и г (А: — ш) АКФ являются комплексно сопряжен¬
ными числами, т.е. т (ш) = т* (к — га); г (га) = т* (—га).
Отсюда следует, что смена знака аргумента АКФ приводит к ком¬
плексной сопряженности отсчета функции. Из последнего выражения
также вытекает, что |т(га)| = |т (—га)| = |т(А; — га)| и argr(ra) =
= — argr (—га) = — argr (А: — га). Если построить график модулей от¬
счетов АКФ т(га), то он будет характеризоваться центральной сим¬
метрией относительно отсчета т(0) = ||Г||2, периодичностью отсчетов
с периодом, равным к, и симметрией внутри каждого периода относи¬
тельно центрального отсчета (рис. 2.18).
Рис. 2.18. Фрагмент графика модулей отсчетов АКФ контура Г = {1 + 3г;3;
1 — 2г; 3; 2г; —2 + 2г; —6; —5г}
74
Гл. 2. Спектральный и корреляционный анализ контуров
Относительно контура АКФ отметим, что его ЭВ получаются соотноше¬
нием (1.8.5) т (га) = т* (fc — га) = т* (—га), т.е. контур Т = {т (га)}0 А._1
является сопряженно-симметрическим (см. рис. 2.19) и как показано в п. 2.5,
Рис. 2.19. Контур Г и контур Т его автокорреляционой функции
его спектр носит чисто вещественный характер. Это становится понятным,
если учесть, что роль такого спектра играет энергетический спектр исход¬
ного контура Г. При четной размерности контура т (к/2) = т* (fc/2), что
возможно лишь при Im т (к/2) =0. Поэтому величина т (к/2) будет чисто
вещественным числом, а ЭВ г (fc/2), как и ЭВ т(0), будет расположен
горизонтально.
2.8.2. Корреляционные свойства контуров специального вида. Кор¬
реляционные функции элементарных контуров. Выражение для АКФ
элементарного контура Tj, j = 1,2,... , fc — 1, понимаемое в данном случае
как набор скалярных произведений ЭК Г^· и Г^, s = 0,1,... , fc — 1, —
тот же контур Г^·, но со сдвинутой на s ЭВ начальной точкой, имеет вид
Ъ (*) = (ri> Г5Я)) = Σ ъ (п) 7# (n + s)> (2.8.9)
j = 1, 2,... , fc - 1, s = 0,1,... , fc - 1.
Прежде всего отметим, что отсчеты определенной таким образом АКФ
для произвольного замкнутого контура Г будут комплексными числа¬
ми и рассматриваются как упорядоченная последовательность ЭВ т (s),
s = 0,l,...,fc — 1. Данные отсчеты образуют замкнутый контур Т =
= (т (5)}о k-1* Действительно, суммируя компоненты АКФ, будем иметь
fc — 1 fc — 1 fc —1 fc —1 fc —1
X)T(S) = {n + s) = 5^7 7* (n + s). (2.810)
s=0 s=0 n=0 n=0 s=0
Внутренняя сумма в последнем выражении для исходного замкнутого
контура равна нулю. Поэтому нулю будет равна и сумма всех компонент
АКФ. Отсюда следует, что Т — замкнутый контур. Подставляя в (2.8.10)
выражение для ЭВ элементарного контура, получим
гз (s)= Σехр = кехр
(2.8.11)
j — 1? 2,... , к 1,
s — 0,1,... , к — 1.
2.8. Корреляционный анализ контуров
75
Из данного результата следует, что отсчеты АКФ элементарного кон¬
тура порядка j, рассматриваемые как ЭВ, образуют элементарный контур
Тj того же порядка, но растянутый в к
раз. При этом контур Tj = {tj (s)}0 к_г
прослеживается в направлении, обратном
контуру Г, и ортогонален ему (рис. 2.20).
С учетом выражения (2.8.11) и свойства
сопряженности ЭК получим, что
Tj=Tk-j = T*. (2.8.12)
Таким образом, контур АКФ Tj исходно¬
го элементарного контура Tj есть ЭК r^_j.
ВКФ элементарных контуров представляет
собой набор скалярных произведений ЭК Tj
(s)
и , где 5 — 0,1,... , & — 1, параметр сдвига начальной точки контура
Г/, причем j ф I:
к-1
Tji (s) = (г.,·, if0) = Σ 7j (η) 71* (n+ s),
а°(
1
<Г1
1
*0
1
Рис. 2.20. Исходный элемен¬
тарный контур Γι и контур
Τι его АКФ для к = 4
(2.8.13)
j, I = 1,2,... , к - 1, j ф Z, s = 0,1,... , к - 1.
На основании свойства 5 элементарных контуров (см. (2.2.10)) ВКФ
Tji (s) = 0, s = 0,1,... , к — 1. (2.8.14)
Таким образом, ВКФ элементарных контуров разных порядков, имею¬
щих произвольные масштабы, углы поворотов и сдвиги начальных точек,
везде равна нулю.
АКФ дельтовидного контура. Код дельтовидного контура Δ =
= {δ (п)}0 к_х был определен в п. 1.8 виде
А — {& - 1, -1, -1,... , -1}. (2.8.15)
Квадрат нормы такого контура равен ||A||2 = fc(A: — 1). Найдем АКФ
Т = {г (5)}o fc_1 контура А. При 5 = 0 значение г (0) = ||А||2 = к2 — к.
Для других 5 все значения АКФ г (5), определенные в соответствии с вы¬
ражением (2.8.4) и (2.8.5), будут одинаковыми и равными (—к). Поэтому
Т = {& (А: — 1), —Л, —к,... , — к}. Если данную АКФ пронормировать по
величине размерности, то Т = к А. Таким образом, АКФ дельтовидного
контура А представляет собой увеличенный в к раз контур А. Если эту
АКФ изобразить в виде графика г (5) = η (s) /к, то ее составляющая г (0)
будет по модулю в (к — 1) раз больше любой другой ее составляющей
(рис. 2.21). При больших значениях к вид АКФ Т близок к виду символа
Кронекера.
При анализе комплекснозначных сигналов, обладающих свойством за¬
мкнутости (1.5.5), контур А играет такую же роль, как и 5-функция
при анализе обычных сигналов. Ему соответствует сложный радиосигнал
из к кодовых интервалов. Амплитуда синусоиды в пределах нулевого
76
Гл. 2. Спектральный и корреляционный анализ контуров
τ(ύ
9
.9 _8 -7 -6-5 -4-3 -2 -1 0 1 2 3 4 5 6 7
1 i-IH-H И +
-1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1-1 -1 -1 -1 -1 -1
Рис. 2.21. АКФ дельтовидного контура при Л: = 10
-►
s
интервала равна k—1, а на всех других интервалах — единице. Начальная
фаза синусоиды нулевого интервала также равна нулю, а для всех других
интервалов — π (рис. 2.22).
Как и у кодов Баркера [55], АКФ дельтовидного контура имеет боко¬
вые лепестки, не превышающие единичный уровень, причем для любого
значения размерности к. Однако энергетика сигнала в виде контура А
значительно хуже, чем у сигналов
в виде кодов Баркера или псевдослу¬
чайных сигналов. Основная энергия
дельтовидного сигнала сосредоточена
в пределах нулевого кодового ин¬
тервала и в (к — 1) раз превышает
суммарную энергию во всех других
кодовых интервалах. Это объясняется
большим значением амплитуды сину¬
соиды нулевого кодового интервала,
в (к — 1) раз большей амплитуды
синусоиды в любом другом кодовом
интервале. В то же время амплитуда
синусоид в псевдослучайных сигналах и сигналах, связанных с кодами
Баркера, во всех кодовых интервалах одинакова, что, с энергетической точки
зрения, обеспечивает эффективность сжатия таких сигналов.
Сигнал в виде дельтовидного контура замечателен тем, что при данном
значении размерности к в классе замкнутых сигналов он имеет наиболее
сложную форму. Сложность формы сигнала понимается в данном случае
как практически полное отсутствие корреляционной связи между отсче¬
тами АКФ при любых значениях 5, кроме 5 = 0. Степень схожести растет
пропорционально увеличению размерности к контура А.
Рис. 2.22. Сложный сигнал, соответ¬
ствующий дельтовидному контуру при
к = 10
2.9. Обсуждение результатов по спектральному
и корреляционному анализу контуров
Вопросам спектрального анализа сигналов посвящено значительное
количество работ. Их рассмотрение традиционно в учебной литературе
по радиоэлектронике, автоматике, цифровой обработке информации и др.
отраслям знаний, связанных с обработкой сигналов.
Аппарат ДПФ широко применяется для получения спектров сиг¬
налов в частотной области и изучения их свойств. Хотя принципи-
2.9. Обсуждение рещшжттюв*
77
ально применение этого аппарата не накладывает ограничений в вид
аналитического представления сигнала, обычно расоаатрмвается лишь
случай, когда сигнал носит вещественный характер. В работе [102], по¬
священной цифровому спектральному анализу и его приложениям, под¬
черкивается это обстоятельство и указывается, что с комплекснознач¬
ными сигналами приходится встречаться, в основном; при умножении
вещественного сигнала на комплексную синусоиду exp В нашем
случае, связанным с обработкой полигональных контуров, исходный
сигнал является комплекснозначным по своей природе. Он описыва¬
ется цепочкой компланарных ЭВ, каждый из которых определяется
комплексным числом.
Контур в виде набора действительных чисел является вырожденным
и представляет сугубо частный случай. Поэтому основные результаты
спектрального анализа действительных сигналов не всегда непосредствен¬
но применимы к сигналам в виде полигональных контуров. Кроме того,
контур изображения из-за непрерывности границы реального изображе¬
ния всегда замкнут и сумма его ЭВ равна нулю. Этот фактор также влияет
на свойства контуров в частотной области.
Подводя итог проведенному в данной главе анализу, в первую оче¬
редь необходимо отметить особенности спектров полигональных контуров,
вызванных комплекснозначным характером их представления и замкну¬
тостью. При этом предполагается сравнение спектров одномерных веще¬
ственных и комплекснозначных сигналов.
Спектр вещественного сигнала из к отсчетов обладает свойством со¬
пряженной симметрии и его значения характеризуются симметрично рас¬
положенными комплексно сопряженными парами. Поэтому амплитудный
спектр вещественного сигнала симметричен относительно центрального
отсчета и при его использовании достаточно учитывать лишь одну полови¬
ну значений спектра. Спектр комплекснозначного сигнала в общем случае
свойством сопряженной симметрии не обладает, в связи с чем необходимо
рассматривать все к отсчетов.
Ряд преобразований контуров приводит к тому, что для определения
спектра нового контура используется уже не прямое, а обратное ДПФ
исходного контура. К таким преобразованиям относятся операции ком¬
плексной сопряженности, отражения и смены направления обхода.
При переходе от исходного к комплексно сопряженному контуру спектр
нового контура находится как комплексно сопряженное обратное ДПФ
исходного контура.
Спектр контура, отраженного относительно оси, проходящей под углом Θ,
определяется так же как и спектр комплексно сопряженного контура, но
дополнительно каждая его компонента поворачивается на угол 20.
Если изменяется направление обхода и контур обходится против
часовой стрелки, то для нахождения спектра нового контура также
применяется обратное ДПФ исходного контура. Кроме того, при этом
каждая его компонента поворачивается на угол 2пт/к и изменяется по
знаку.
78
Гл. 2. Спектральный и корреляционный анализ контуров
Замкнутость линии контура при многократном обходе приводит к пе¬
риодичности значений его ЭВ. Период равен числу к ЭВ, составляющих
полигональный контур. Следствием этого является периодичность значе¬
ний спектра контура с той же величиной периода. Сдвиг начальной точки
замкнутого контура на d ЭВ приводит к повороту каждой компоненты
спектра исходного контура на угол 2nmd/k.
Наиболее важным для приложений следствием замкнутости линии
контура является равенство нулю нулевой компоненты его спектра.
Отметим, что замкнутость линии исходного контура не связана с за¬
мкнутостью контура, образуемого компонентами спектра. Если нулевой
ЭВ исходного контура не равен нулю, что чаще всего имеет место, то
контур спектра всегда разомкнут.
Вторым важным результатом рассмотрения частотного представления
контуров является введение двух видов контуров, обладающих замеча¬
тельными спектральными свойствами.
Аналогом вещественного дискретного сигнала с равномерным спектром,
каким является единичный импульс, в классе комплекснозначных сигналов,
обладающих свойством замкнутости, служит дельтовидный контур.
Аналогом гармонического сигнала, спектр которого содержит только од¬
ну ненулевую компоненту, в рассматриваемом классе сигналов являются
элементарные контуры. Эти контуры задают правильные или звездчато¬
правильные fc-угольники и для каждого значения к существуют к — 1
замкнутых ЭК. Элементарный контур нулевого порядка не замкнут, так
как представляет собой цепочку из к коллинеарных контуров. С элемен¬
тарным контуром порядка т ассоциируется понятие частоты, равной т
оборотов, при 0 < т ^ к/2 и к — га, при к/2 < т < к, при враще¬
нии точки по окружности от начала до конца контура. Таким образом,
максимальная частота, соответствующая контуру, равна к/2.
Семейство ЭК с одним и тем же значением к образуют ортогональный
базис. По этому базису разлагается произвольный полигональный контур,
причем проекциями контура являются компоненты его спектра. Таким об¬
разом, подобно тому как любой вещественный сигнал представляется взве¬
шенной суммой синусоид, так и любой контур равен взвешенной сумме ЭК.
Следующий, заслуживающий внимания результат спектрального анали¬
за контуров касается соотношения между элементарными векторами конту¬
ра и шириной спектра. Под шириной спектра будем понимать частотный ин¬
тервал, в пределах которого модули компонент спектра не меньше наперед
заданного уровня. Для действительных сигналов, например, прямоугольного
видеоимпульса, имеет место хорошо известная закономерность: чем меньше
длительность импульса, тем шире его спектр и наоборот.
Для рассматриваемых видов контуров аналогичное соотношение фор¬
мулируется так: увеличение одного ЭВ контура по модулю приводит к
расширению его спектра и обратно — если одна компонента спектра
контура по модулю растет, то модули ЭВ контура уравниваются по вели¬
чине. В первом случае мы имеем широкополосный (дельтоподобный), во
втором — узкополосный (квазиэлементарный) контуры.
2.10. Вопросы и упражнения
79
Чем чаще встречаются изломы линии контура и чем резче меняется
ее направление, тем больше энергия составляющих этот контур высоко¬
частотных элементарных контуров.
Корреляционная функция Т = {т (т)}0гк_г периодических ком¬
плекснозначных дискретных сигналов вводится как упорядоченный
набор скалярных произведений вектора Г одного из сигналов на век¬
тор N(m) другого сигнала со смещенными на т элементов точками.
По сравнению с определением корреляционной функции вещественных
сигналов отличие заключается в том, что при нахождении каждого
из отсчетов один из векторов берется комплексно сопряженным. Это
позволяет модуль каждого такого отсчета рассматривать как взаимную
энергию связи векторов Г и
Контур Т = {т (т)}0 к_1 автокорреляционной функции контура Г =
= {τ(η)} является сопряженно-симметрическим. Его ЭВ подчиняются
соотношению т (т) = г* (к — т). ЭВ г (0) равен квадрату нормы ||Г||2,
расположен горизонтально и направлен вправо. Вертикаль, проходящая
через середину ЭВ т(0), является осью симметрии контура АКФ Т =
= {т (га)}0 k_v Спектр контура АКФ является чисто вещественным и яв¬
ляется энергетическим спектром контура Г.
АКФ Ту = {ту (т)}0 /е_1 элементарного контура Гу представляет
собой также элементарный контур, но сопряженный с контуром Гу и из¬
мененный в масштабе, т.е. Ту = И\_у, j = 0,1,... , к — 1. Все значения
ВКФ элементарных контуров Гу и Г/, I ф j равны нулю, т.е. ту?* (ш) = 0,
j ф1^т — 0,1,... , к - 1.
АКФ Т = {т (т)}0 к_г дельтовидного контура Δ также является дель¬
товидным контуром, т.е. Т = к А и при большом значении размерности к
она мало отличается от символа Кронекера. ВКФ дельтовидного контура
Δ и произвольного замкнутого контура Г представляет собой измененный
в масштабе комплексно сопряженный контур Г, т.е. Тд,г = кТ^*\
2.10. Вопросы и упражнения
1. Какая связь существует между скалярным произведением векторов и их
ДПФ?
2. В чем заключаются характерные особенности спектров Фурье вещественных
дискретных сигналов?
3. Почему при анализе амплитудного спектра вещественного дискретного сиг¬
нала из к отсчетов достаточно использовать половину отсчетов с р(0) по
Р(к/2)?
4. Какая характеристика полнее характеризует контур — его спектр или АКФ?
5. Дайте определение энергетическою спектра контура.
6. В чем состоят различия между спектрами Фурье вещественных и комплекс¬
нозначных сигналов?
7. Как с помощью алгоритма прямого ДПФ найти обратное ДПФ контура?
8. Во сколько раз энергия суммы ЭК Г^· и Tj при j = I больше энергии их
суммы при j ф Iе!
80
Гл. 2. Спектральный и корреляционный анализ контуров
9. Как изменяется форма ЭК при изменении его порядка от га = 1 до га = fc — 1?
10. Каким преобразованиям подвергается контур спектра, если исходный контур
поворачивается на угол Αφ = π/6 и растягивается в 2 раза?
11. Почему контур спектра исходного замкнутого контура Г при η (0) ф 0 всегда
не замкнут?
12. Каким преобразованиям подвергается контур спектра при отражении исход¬
ного контура относительно оси, проходящей под углом Θ — 45°?
13. Почему постоянная составляющая р (0) спектра замкнутого контура всегда
равна нулю?
14. Какое свойство приобретает контур спектра Р, если в исходном контуре Г
положить 7 (0) = 0?
15. Будет ли контур Г = {2г; —г; —г} дельтовидным?
16. Изобразите график спектра правильного шестиугольника.
17. Проверьте ортогональность правильных треугольников Γι = {1; —0,5 4- 0,866г;
0,5 - 0,866г}; Г2 = {1; -0,5 - 0,866г; -0,5 + 0,866г}.
18. Может ли контур спектра Р = {0;2 — г;1 + г} соответствовать контуру Г =
= {l + t;l-i;-2}?
19. Как изменится вид спектра замкнутого контура, прослеживаемого по часовой
стрелке, при изменении направления его обхода?
20. В чем отличие контура свертки двух контуров от контура взаимной корреля¬
ции этих контуров?
21. Найдите спектр квадрата Г = {1; г; —1; —г} при сдвиге его начальной точки
на d = 1 элементарный вектор.
22. Какова характерная особенность спектра контура, у которого один ЭВ по
модулю значительно превалирует над другими ЭВ?
23. Представьте контур Г = {5 -f 2г;4 — 5г; —2 - Зг; —4г; —7 + Юг} в виде
суммы сопряженно-симметрического и сопряженно-антисимметрического кон¬
туров.
24. Получите разложение контура Г = {3 — 4г; 1 - г; 1 -f 5г; — 3 — г; — 2 + г} на
ЭК.
25. Найдите обратное ДПФ контура Р = {0; —7,987 - 0,077г; -2,959 - 12, 576г;
16,577 + 4,160г; 19,369 + 18,494г}·
26. Вычислите спектр контура Δ = {5,-1,—1,-1,-1,-1}.
27. Как связаны между собой спектры контуров Г = {2; —1 + г; —1 - г} и N =
= {2; —1 — г; —1 + г}?
28. Найдите АКФ контура Г = {4г; 5 4- 2г; 2 — 6г;-7} с помощью ДПФ его
энергетического спектра.
Глава 3
ЛИНЕЙНАЯ ФИЛЬТРАЦИЯ КОНТУРОВ
3.1. Введение
В данном разделе развиваются основные положения спектрального
анализа полигональных контуров, связанные с целенаправленным изме¬
нением весовых коэффициентов при задании произвольного контура ли¬
нейной комбинацией элементарных контуров. Роль этих коэффициентов
играют элементы спектра преобразуемого контура. Уменьшение по мо¬
дулю коэффициентов при ЭК в низкочастотной области спектра контура
приводит к подчеркиванию ЭК, порядок которых близок к т = к/2, т.е.
происходит эффект высокочастотной фильтрации. В результате преобра¬
зованный контур станет более изрезанным и в нем даже могут появиться
самопересекающиеся фрагменты. Обратная процедура, т.е. уменьшение
по модулю коэффициентов при высокочастотных ЭК, приводит к эффек¬
ту низкочастотной фильтрации, и преобразованный контур приобретет
сглаженные очертания.
Таким образом, спектральное представление контуров позволяет
естественным образом перейти к их линейной фильтрации — низкоча¬
стотной, высокочастотной и полосовой. Особенности работы контурных
линейных фильтров вызваны комплекснозначным характером такого
сигнала, как контур.
К контурным линейным фильтрам в данном разделе не предъявля¬
ются требования к равномерности характеристики в заданном диапазоне
частот, крутизне среза и затуханию в полосе непрозрачности. Фильтр
рассматривается в целом как система анализа формы изображения по
его контуру [62].
Основные применения контурных линейных фильтров при обработке
изображений связаны с подавлением контурных высокочастотных шумов,
сжатием описания контуров, получением информативных признаков для
распознавания изображений, а также вычисления меры схожести двух
изображений по их форме.
3.2. Основные соотношения при линейной фильтрации контуров
Контурный линейный фильтр представим в виде линейного четырех¬
полюсника с импульсной характеристикой (ИХ) Λ = {A(n)}0?fc_1 и ча¬
стотным коэффициентом передачи Ω = W(m)}ok~v На ВХ°Д Фильтра
82
Гл. 3. Линейная фильтрация контуров
{7(n)}0fc_i, формирующий на выходе сигнал
Н = {77 (s)}o fc_1 (рис. 3.1).
Сигналы Г, Н и характеристики фильтра Л и
Ω будем рассматривать как контуры с размерно¬
стью, равной к. Отсчет выходного сигнала — ЭВ
η (s) контура Н, представленный как ЭВ свертки
контуров Л и Г, с учетом обратного ДПФ вектора
7 (η) записывается в виде
к — 1 к-1
= ιΣλ(η)Σ/>
п—0 п=0 т—О
к — 1 .„ ^
= ~ ^ р (m) exp ji^ras λ (n) exp |j,
m=0 n=0
5 = 0,1,... , к — 1.
Введем обозначение для внутренней суммы
к-1
ω (га) = ^2 λ (гс) ехр {“га = 0,1,... , к — 1. (3.2.1)
п=0
Тогда, принимая во внимание выражение (1.8.3) для ЭК, получим
к—1 к—1
н = \ Σ ω (™) р мг- = \ Σ л» (то) г”>· (3·2·2)
т=0 т=0
Величина о; (га) = рВых(га)/р (га) есть ЭВ контура частотного коэф¬
фициента передачи фильтра. Из выражения (3.2.2.) следует, что выходной
контур Н равен взвешенной сумме ЭК Гт,га = 0,1,... ,fe — 1, весами
в которой служит ЭВ рвых (га) контура спектра на выходе фильтра. Из
этого же выражения становится понятным механизм работы контурного
линейного фильтра: для получения 5-го отсчета каждый 5-й элементар¬
ный вектор ЭК порядка га, взятый с весом соответствующей спектральной
составляющей р (га), умножается на комплексное число ω (га) и получен¬
ные произведения суммируются, т.е.
(га) ехр |г-—га (5 — гг) j =
поступает сигнал Г =
Λ,β
н
Рис. 3.1. Контурный ли¬
нейный фильтр как четы¬
рехполюсник
к-1
v(s) = y^.^inh(s-n)
к — 1
v(s) = |Σ ω (m) Z5 (m) 7m (s), s = 0,l,... ,fc-l. (3.2.3)
m=0
Контурный линейный фильтр обладает всеми свойствами, характер¬
ными для цифровых линейных фильтров. Эти свойства хорошо известны
(см. например, [61-63]). Учитывая комплекснозначный характер и свой¬
ства замкнутости контура, рассмотрим, какими дополнительно особыми
свойствами обладает этот фильтр.
3.2. Основные соотношения
83
1. Условие подавления постоянной составляющей. Пусть т = 0, тогда
из (3.2.1) следует, что
к — 1
"(0) = 5>(п). (3-2.4)
п=О
Таким образом, нулевой ЭВ контура Ω частотного коэффициента пере¬
дачи равен сумме всех ЭВ контура Л импульсной характеристики фильтра.
к-1
Если контур Л замкнут, т.е. если X] А (гг) = 0, то ω (0) = 0. Покажем,
п=0
что имеет место и обратное утверждение. С учетом выражения (2.3.2) для
обратного ДПФ и представления (2.1.1) для ЭК получим
к-1
Λ = |ΣωΜΙ\η· (3.2.5)
т—О
Если to (0) = 0, то контур Л как взвешенная сумма замкнутых конту¬
ров Гт, т = 1,2,... , к - 1, будет замкнут.
2. Сумма ЭВ контура частотного коэффициента передачи. Запишем
выражение для обратного ДПФ элементарного вектора контура Л:
1 k~l 2
А (п) = - ^2 ω (т) ехР га = 0,1,... , к — 1.
771=0
Пусть п = 0. Тогда
к-1
ω (т) = кХ (0),
т=О
(3.2.6)
т.е. ЭВ кХ (0) контура Л замыкает контур Ω частотного коэффициента
передачи. Отсюда также следует, что если нулевой вектор А (0) контура Л
импульсной характеристики фильтра не равен нулю, то контур частотного
коэффициента передачи всегда разомкнут. Соотношение (3.2.6) полезно
при проверке правильности расчетов по контурным фильтрам.
3. Условие замкнутости выходного контура фильтра. Пусть филь¬
труемый контур Г замкнут. Тогда нулевая компонента его спектра рав¬
на нулю, т.е. р(0) = 0. Учитывая замкнутость ЭК Гт,т = 1,2,...
к-1
... , к — 1, из выражения (3.2.3) получим Σ η (s) = 0, т.е. замкнутость
s=0
входного контура определяет замкнутость выходного контура фильтра
при любом виде его ИХ. Отсюда следует периодичность отсчетов фильтра:
η (s) = η (s ± ak)
4. Симметричность ЭВ контура частотного коэффициента пере¬
дачи. Сравним между собой ЭВ ω (т) и ω (к — т) контура Ω частотного
коэффициента передачи фильтра. С помощью выражения (3.2.1) получим
84
Гл. 3. Линейная фильтрация контуров
Сравнивая полученное выражение с выражением (3.2Л), приходим к
выводу, что только при вещественном характере ИХ фильтра имеют ме¬
сто симметричность модулей и антисимметричность аргументов ЭВ кон¬
тура Ω частотного коэффициента передачи фильтра, т.е.
ш(тп)=ш*(к-т), \ω (ш)| = \ω (к - т)\,
/ \ /| \
arg ω (т) = — arg о; (к — т).
Таким образом, если ИХ фильтра носит вещественный характер, то ам¬
плитудно-частотная характеристика (АЧХ) фильтра, т.е. \ω(τη)\, т =
= 0,1,... ук — 1, будет симметричной, а фазочастотная характеристика —
антисимметричной.
5. Сохранение параметров линейных преобразований фильтруемого
контура. Пусть фильтруемый контур Г растягивается в \μ\ раз, пово¬
рачивается на угол Αφ, а его начальная точка сдвигается на d ЭВ, т.е.
вместо контура Г = {7 (n)}0 к_г фильтруется сигнальный контур =
= {l(c) (n)}o,fc-i = + гДе А* = 1м1 ехр {»Δ<ρ}. При этом
каждая компонента спектра исходного контура (см. разд. 2.3) умножается
на комплекснозначный, зависящий от т коэффициент μ exp
С учетом этого на основании выражения (3.2.3) для ЭВ выходного контура
получим
k-1
v(s) =/x^w(m)p(m)7m(s + «0, s - 0,1,... , к - 1. (3.2.8)
m=0
Таким образом, при фильтрации контуров параметры их линейных
преобразований сохраняются.
6. Собственные векторы контурного линейного фильтра. Каждый из
ЭК Гт, т = 0,1,... , /с — 1, при прохождении через фильтр сохраняет
свою форму и подвергается лишь линейным преобразованиям. Для до¬
казательства воспользуемся выражением (3.2.2) и учтем, что контур Ргт
спектра элементарного контура Гт содержит лишь одну, не равную нулю
составляющую, равную р{т), т.е. Ргт = {0,0,... , 0, р (т), 0,... ,0}.
Тогда Η = ω (т) р (т) Гт, т.е. выходной контур фильтра, равен конту¬
ру Гт, растянутому в \ω (т)\\р (т)\ раз и повернутому на угол Αφ =
= arg [ω (τη) ρ (τη)]. Таким образом, любой ЭК размерности к является
собственным вектором контурного линейного фильтра.
3.3. Фильтрация контуров в частотной области.
Простейшие фильтры
Аналитическое выражение для выходного сигнала контурного ли¬
нейного фильтра позволяет определить отсчет через элементы спектра
или через ЭВ фильтруемого контура. В первом случае будем говорить
о контурной фильтрации в частотной, во-втором — в пространственной
областях.
3.3. Фильтрация в частотной области
85
В первом случае основной подход базируется на выражении (3.2.2)
и состоит из следующих двух этапов.
I — спектр фильтруемого контура Г преобразуется в соответствии
с видом контура частотного коэффициента передачи.
II — с помощью обратного ДПФ определяется вид отфильтрованного
контура Н. При этом, естественно, должен быть определен или задан
спектр Р контура Г. Рассмотрим случай простейшей фильтрации в ча¬
стотной области, когда одни спектральные составляющие фильтруемого
контура отбрасываются, т.е. полагаются равными нулю, другие — про¬
ходят через фильтр без изменения. Частотный коэффициент передачи
простейшего контурного фильтра состоит из нулей и единиц. Множество
номеров ЭВ контура частотного коэффициента передачи разобьем на под¬
множества Мо и М\. Первое из них включает значения га, для которых
ω (ш) = 0, второе — значения га, для которых ω (га) = 1. Рассмотрим
ряд свойств простейших контурных фильтров.
1. Выходной сигнал фильтра в соответствии с выражением (3.2.2) имеет
вид
н = {v(r)}0,k-i = l Σ Р("Огт·
m£Mi
2. Нулевой ЭВ импульсной характеристики фильтра всегда отличен
от нуля. Это следует из выражения (3.2.6), которое в данном случае при¬
нимает вид Σ ω (ш) = (0). Так как стоящая слева сумма является
mG Μι
положительным числом, то А (0) ф 0.
3. Контур ИХ простейшего фильтра в соответствии с выражени¬
ем (3.2.5) равен Л = {А (п)}0 к_г = т J2 Гт. Отсюда следует, что
’ ^ mG Μι
А (η) = \ Σ ехр {г1Гт7г}’ п — 0,1,... , к — 1.
те Μχ
Если номер га, равный нулю, принадлежит подмножеству Мо, т.е. 0 G
€ Мо, то ω (0) = 0 и, в соответствии со свойством 1 контурных линейных
фильтров (см. п. 3.2), контур ИХ простей¬
шего фильтра будет замкнут. Справед¬
ливо и обратное: если ИХ простейшего
фильтра представляет собой замкнутый
контур, то номер m = 0 принадлежит
подмножеству М0 и ω(0) = 0. Таким
образом, простейший фильтр, у кото¬
рого контур ИХ является замкнутым,
не пропускает постоянной составляющей
сигнала.
4. Если подмножество М\ состоит из
одного элемента га = то, то выходной
сигнал фильтра Н = р (г) Гг, а его ИХ равна Л = Тг/к. Таким образом,
ωi.
2-
'L+Hb—
0 1234 m
а б в
Рис. 3.2. Узкополосная фильтра¬
ция: исходный контур (а), частот¬
ной коэффициент передачи филь¬
тра (б), результат фильтрации (в)
86
Гл, 3. Линейная фильтрация контуров
простейший фильтр с полосой пропускания шириной в один элемент
воспроизводит на своем выходе независимо от формы входного сигнала
элементарный контур Гг. Форма входного сигнала определяет лишь
масштаб и угол поворота этого контура (рис. 3.2). ИХ фильтра совпадает
сГ,
Простейший низкочастотный фильтр имеет частотный коэффициент
передачи вида Ω = {ω (0); 1,1,... , 1; 0,0,... , 0; 1,1,... , 1}, а его вы¬
ходной сигнал равен т° т°
1
к
то
ω (0) ρ(0)Γο+Σ>(т) Гт +
к-1
Р (т)
т—1
т=к—то
Простейший высокочастотный фильтр характеризуется частотным
коэффициентом передачи Ω = {0,0,... ,0,1,1,... , 1,1,0,0,... ,0}. Под¬
множество Μχ такого фильтра содержит значения от т = ш0, до т =
к—то — 1
= к — то — 1. Выходной сигнал фильтра равен Н = Σ Р (ш)Гт. Так
т—то
как га0 > 0, το ω (0) = 0 и контур ИХ замкнут.
Пример 1. Осуществим простейшую фильтрацию показанного на рис. 3.3, а
замкнутого контура Г:
Г = {—Зг; 5; -3 - 5г; -10,5 + 2г; -2 + 2г; 5 + 4г}.
Разложение контура в базисе ЭК имеет вид
Г = (1,033 + 5,843г) Γι + (-0,137 - 12,102г) Г2 + (-9,227 + 4,923г) Г3 +
+ (-12,802 - 22,762г) Г4 + (-1,539 + 12,221») Г5 + (22,672 - 9,124») Г6.
На рис. 3.3, б представлен результат низкочастотной фильтрации контура Г
с параметром то = 1. Частотный коэффициент передачи такого фильтра равен
Ω = {ω (0), 1,0,0,0,0,1}. Так как контур Г замкнут, то р(0) = 0 и поэтому
Рис. 3.3. Фильтрация контуров: исходный контур Г (а), результат НЧ-фильтрации
контура Г (б), результат ВЧ-фильтрации контура Г (в)
конкретное значение ω (0) не влияет на результат фильтрации. Спектр выходного
контура имеет вид РВых = {0; 1,033 + 5, 843г; 0; 0; 0; 0; 22,672 - 9,124г}, а кон¬
тур, найденный в результате обратного ДПФ и равный сумме контуров р (1) ГЧ +
ЗА. Контурный фильтр скользящего среднего
87
+ р (6) Гб, записывается как
Н = р (1) Γι + р (6) Г6 = {3,387 - 0,469»; 0,440 - 2,709г; - 2,812 - 2,910г;
- 3,979 - 0,919г; -2,123 + 1,764г; 1,331 + 3,118»; 3, 783 + 2,125г}.
В результате низкочастотной фильтрации (рис. 3.3, а и рис. 3.3, б) происходит
сглаживание линии контура из-за устранения резких изломов. На рис. 3.3, в пока¬
зан результат высокочастотной фильтрации контура Г. Частотный коэффициент
передачи равен Ω = {0,0,1,1,1,1,0}. Спектр и аналитическое представление
выходного контура соответственно равны
Рвых = {0; 0; -0,137 - 12,102»; -9,227 + 4,923i; -12,802 - 22,762г;
-1,539 + 12,221»; 0},
Н = Г - р (1) Γι - р (6) Г6 = {-3,386 - 2,531г; 4,560 + 2,709г; -0,162 - 2,090г;
-6,021 + 0,919г; 7,123 + 0,236г; -3,331 - 1,118»; 1,217 + 1,875»}·
После фильтрации (см. рис. 3.3, в) получился контур с самопересечением сто¬
рон, что свидетельствует о преобладании в его спектре ЭК в виде звездчато¬
правильных многоугольников.
3.4. Контурный фильтр скользящего среднего
При обработке контуров в пространственной области широко исполь¬
зуются две разновидности линейных нерекурсивных фильтров: фильтр
скользящего среднего (ФСС) и фильтр скользящей разности (ФСР). Эти
фильтры обладают свойствами соответственно фильтров низкой и высо¬
кой частот. В этом разделе мы рассмотрим свойства ФСС.
3.4.1. Частотный коэффициент передачи фильтра скользящего сред¬
него. ФСС имеет в пространственной области чрезвычайно простую ре¬
ализацию. Его выходной сигнал равен сумме ЭВ фильтруемого контура
Г = {7(n)}ofc-i в пределах фиксированного положения окна из s эле¬
ментов. При перемещении такого окна на
гг-м шаге фильтрации на одну позицию
ЭВ 7 (га) выходит за пределы окна, а ЭВ
7 (гг + s) входит в это окно (рис. 3.4).
Выходной сигнал ФСС будет равен
s-fn— 1
Va(n)= Σ j(r).
(3.4.1)
г(п +3)с\\<ч
—у(«
'(п +4)—
ШЦ7
TTВг(")
[К" +5)-
Л r(»-i) 1 1
1 1
Рис. 3.4. Расположенное на конту¬
ре скользящее окно фильтра ши¬
риной 5 = 5 элементов
Определим спектр выходного кон¬
тура Η = {η3 (n)}0>fc_1. Для этого
учтем, что при фильтрации по методу
скользящего среднего находится сумма s
контуров Г, Г^1),... со сдвину¬
тыми на один по отношению друг к другу ЭВ. Найденное через спектр
исходного контура Г дискретное преобразование Фурье контура T^d\
88
Гл. 3. Линейная фильтрация контуров
у которого начальная точка сдвинута на d элементарных векторов, равно
Pd(m) = р (га) ехр ji^radj. Поэтому спектр Ps отфильтрованного
контура Н будет
Ps = {ps (m)}o,k-i = mm)E {гТтсг}1 · (3·4·2)
I 1 J J o,fc-l
Теперь можно записать выражение для контура Ω = {ω5 (m)}0 к_1
частотного коэффициента передачи ФСС с окном шириной в 5 элементов
5 — 1
ω3 (т) — exp [i^-mdX, т — 0,1,... , к - 1. (3.4.3)
РКт) л о L к ’
а—О
На рис. 3.5 показан пример фильтрации контура по методу скользя¬
щего среднего с окном из 5 = 2 элементов. Получим более компактные
а
0-,
г
t
/
Л
V
.
2
\
J
[
<
1
**
X1
ш
1.0
0.8 +
0.6
0.4+
0.2
0
|«2("0|
#■
123456 т
б
Рис. 3.5. Фильтрация контура Г (см. рис. 3.3, а) по методу скользящего среднего
с окном s = 2: выходной контур Нг (а), нормированная АЧХ фильтра (б)
представления для частотного коэффициента передачи ФСС, не содер¬
жащие выражений в виде суммы. Запишем выражение для суммарного
вектора ЭК порядка га:
п п
Рт (га) = У 7т (г) = У ехр тг}· (3.4.4)
г=0 г—О
Сравнивая выражения (3.4.3) и (3.4.4), приходим к выводу, что ЭВ
ω3 (га) частотного коэффициента передачи ФСС равен суммарному векто¬
ру βτη (s — 1) ЭК Гт, т.е. ω3 (га) = /Зт (s — 1). Рассматривая выражение
(3.4.3) как сумму 5 членов геометрической прогрессии с начальным членом,
Г .2π Ί
равным единице, и знаменателем exp < г—т>, получим
ω3 (т) =
1 — ехр
{*Tsm}
1 — ехр
. 2π
ιν
га = 0,1,... , к — 1.
(3.4.5)
Найдем выражение для АЧХ |ωβ (га)|, га = 0,1,... , к — 1. Для этого
в последнем выражении вычислим отдельно модули числителя и знаме-
ЗА. Контурный фильтр скользящего среднего
89
нателя и учтем известное тригонометрическое соотношение 1 — cos 2а =
= 2 sin2 а. В результате получим
и
μ, (m)|
I . 7rms I
Sin —:
! k I
. 2 7Γ ms
9 sin —I—
K(™)l =—ТШГ', m = 0,l,..· ,k-l.
sin ——
k
(3.4.6)
(3.4.7)
Данные соотношения позволяют пояснить механизм работы ФСС. На
основании выражения (3.4.6) фильтр можно представить двумя последо¬
вательно соединенными звеньями. Первое из них характеризуется коэф¬
фициентом передачи ω8^ (т) = Ι/sin (ππι/k), т = 0,1,... , к — 1. Так
как в заданном диапазоне изменения т функция sin7rra/A; имеет вид
одной положительной полуволны (рис. 3.6, а), то первое звено являет-
а б в
Рис. 3.6. Графики модулей частотного коэффициента передачи ФСС и его звеньев
для к = 8, s = 2: а — первого звена, б — второго звена, в — фильтра в целом
ся фильтром низкой частоты. Второе звено с коэффициентом передачи
\ω3}2 (m)| = (sin (nms/k)\, m = 0,1,... , к — 1, является режекторным
фильтром с точками режекции, для которых величина ms/к есть целое
число (рис. 3.6, б). Совместное действие этих звеньев приводит к тому,
что амплитудно-частотная характеристика ФСС будет обладать хорошо
выраженным глобальным спадом в области высоких частот и иметь ряд
локальных минимумов во всей фильтруемой полосе частот (рис. 3.6, в).
3.4.2. Свойства фильтра скользящего среднего. 1. График АЧХ ФСС
симметричен (за исключением нулевой составляющей \ω (0)|) относитель¬
но центрального значения аргумента. Это следует из общего соотноше¬
ния (3.4.3):
s — 1 s — 1
ωδ (к - т) = ^exp ^i^-d(k — т) | = У^ехр = ω*8 (т).
d=о d=о
Таким образом, ω3 (т) = ω* (к — т) и \ω3 (т)\ = \ω3 (к — т)\.
90
Гл. 3. Линейная фильтрация контуров
Отметим также, что отсюда следует не только симметричность отсче¬
тов графика АЧХ, но и, в соответствии со свойствами линейных контур¬
ных фильтров (см. п. 3.3), — вещественный характер ИХ фильтра, т.е.
Im Л (га) = 0, га = 0,1,... , к - 1.
2. Нулевой ЭВ частотного коэффициента передачи ФСС, как следует
из выражения (3.4.3), ω3 (0) = s. Так как величина ω3 (0) есть сумма
к-1
ЭВ контура ИХ фильтра, т.е. X (га) = ω3 (0) ф 0, то контур ИХ будет
разомкнут. п=0
В соответствии с выражением (3.4.3) ЭВ ω(πι) частотного коэффи¬
циента передачи ФСС есть сумма s векторов вида exp |i~-md^d =
= 0,1,...,5-1, модули которых равны единице. При гаг = 0 эти s
векторов, имея одинаковые аргументы, складываются синфазно и обра¬
зуют максимально возможный по модулю отсчет ω (0) = 5. Если же
т — 1,2,... , /с — 1, то эти векторы из-за влияния параметра d уже
не совпадают по направлению. Поэтому \ω3 (т)\ < ω3 (0) или \us (m)| <
< 5, m = 1, 2,... , к - 1.
Таким образом, АЧХ фильтра имеет при тга = 0 максимальный отсчет,
равный 5, т.е. нулевая составляющая спектра входного сигнала проходит
через фильтр с наименьшим затуханием. При фильтрации замкнутого
контура эта составляющая всегда отсутствует и на процесс образования
выходного контура влияет лишь ЭВ ω (m), m = 1,2,... , к — 1.
3. Из п.п. 1 и 2 данного раздела следует, что импульсная характе¬
ристика ФСС задается вырожденным незамкнутым контуром, состоящим
из вещественных ЭВ. Получим теперь выражение, определяющее эти ЭВ.
Обратное ДПФ от частотного коэффициента передачи ФСС, задающее ИХ
фильтра, имеет вид
к — 1 5 — 1
λ (η) = ~ ^2 ^2ехР + п)}> 71 — 0,1, · · · j к — 1.
тп—О d=0
Изменим порядок суммирования
5-1 к-1
λ (п) = ^2 ехР + п)}’ П = 0,1,... , к - 1.
d=0 т=0
Вторая сумма в этом выражении будет равна нулю для всех значений
d + n, не равных нулю или к. Для них величина Л (гг) будет равна к/к, т.е.
единице. Таким образом, Л (гг) = 1, для гг = 0, к — 5 + 1,/г — 5 + 2,... , & — 1
и Л (тг) = 0 для тг = 1,2,... , & — 5.
4. Определим нулевые значения АЧХ ФСС. Согласно выражению (3.4.3)
ЭВ ω3 (т) частотного коэффициента передачи есть сумма векторов вида
exp j, d = 0,1,... ,5 — 1. Возможны случаи, когда эти векторы
образуют замкнутый контур. В результате формируется равное нулю
значение ω3 (m). Из выражения (3.4.6) следует, что это достигается, когда
ЗА. Контурный фильтр скользящего среднего
91
аргумент синуса будет кратен π, т.е. ω8 (га) = 0 при га = ka/s, а —
целое число, 0 < т < к.
5. Рассмотрим поведение ЭВ ω8 (га) при варьировании аргумента га,
m = 0,1,... , fc—1, для фиксированного значения ширины окна s фильтра
(рис. 3.7).
В соответствии с выражением (3.4.3) ЭВ ω8 (га) есть сумма единичных
векторов, угол между которыми равен 2кт/к. Этот угол растет с увели¬
чением га, но пока он не превышает π, т.е. пока т < к/2, суммарный век¬
тор, равный ω8 (га), будет характеризоваться уменьшающимся модулем.
В результате происходит подавление высокочастотных гармоник входного
контура, т.е. наблюдается эффект низкочастотной фильтрации контура.
При т > к/2 характер зависимости ω8 (га) меняется в силу свойства 1
на противоположный.
Г~
а
t
'J
г~
-щ
Г 1
(3)-
sj
ΰ)8
J)1-
—ωϊ
t
4
ω8(4>|
1
Ϊ ©8
L
(к
Г
ж
* 1
,)0Н
7
or
Рис. 3.7. Формирование элементарных
векторов (га), га = 0,1,... ,7, ча¬
стотного коэффициента передачи ФСС
для s = 3 и к = 8
ω
►l (l) 0 )_ I I
*1
&
/
/
*
SI
ч
ω$
id
1
ί
_L
r | | '
'®7 0)N
—►
1
г
Рис. 3.8. Формирование элементарных
векторов ω9 (га), s = 0,1,... , 7, ча¬
стотного коэффициента передачи ФСС
для га = 1 и к — 8
6. Исследуем теперь поведение ЭВ
к-1
V(m) = ^X^|p(s)|2exp|i^s(l + m)|, τη = 0,1,... , к - 1,
s=О
при варьировании ширины окна st s = 2,3,... для фиксированного зна¬
чения га (рис. 3.8).
При суммировании s единичных компланарных векторов, образую¬
щих, в конечном счете, при s = к замкнутый контур, модуль суммарного
вектора с ростом s будет все больше отличаться от величины s, равной
модулю суммарного вектора при синфазном суммировании единичных
векторов. Поэтому модуль ЭВ ω8(πι) с ростом ширины окна уменьшается
от ω8 (а) = s до единицы при s = к — 1 и нуля при s = к.
3.4.3. Сравнение простейших фильтров, заданных в частотной и про¬
странственной областях. Простейший фильтр, заданный в частотной
области, имеет частотный коэффициент передачи, значения которого рав¬
ны либо единице, либо нулю. Фильтр скользящего среднего имеет ана¬
логичные отсчеты, но только для ИХ и поэтому является простейшим
фильтром в пространственной области.
Таблица 3.1. Аналитические соотношения для простейших контурных фильтров
со
to
№
Характеристика
Задание фильтра
В частотной области
В пространственной области
1
Частотный
коэффициент
передачи
ω(πι) =
_ J 1, при т = то, · · · , то 4* s — 1;
1 0 для других т.
1 ί 2π -1
1 — exp < г—ms >
= \.2π l·’
1 — exp < г—m >
m = 0,1,... , k — 1.
2
Импульсная
характеристика
Х(п) = exp =
v ' k X k J Γ.2π Ί
1 — exp |г—ns j
1-exp {г γη}
f 1 при n — 0,1,2,... , s — 1
λ(η) = < и n — k — 1;
[ 0 для других η,
η = 0,1,... , А: — 1.
3
Выходной контур
m0+5-1
Η = Υ2 Р(т)Тт.
т—то
s-1
Η = Σ rw, d — параметр сдвига
d=0
начальной точки контура
4
Спектр выходного
контура
Рвых(т) =
Г р(т) при т = то,... , то 4* s — 1;
[ 0 для других т·
5—ί / 27г ί
Рвых(т) = р(т) Σ exp ^ i—md >;
т = 0,1,... , к — 1.
5
Симметричность
характеристик
Х(п) = A*(fc — п); |λ(η)| = |λ(Α:-η)|;
argA(n) = — argA(A; — n);
η = 0,1, · · · ! & — 1·
ω(ττι) = о;" (/с — т); |cj(m)| = |cj(/c — т)|;
arg u;(ra) — — argcj(/c — m);
m = 0,1,... , к — 1.
б
Нули графиков
характеристик
λ(η) = 0 при η = ofc/ί; α — целое число,
η = 1,2,. · · — 1·
o;(m) = 0 при m = ak/s, a — целое число,
m = 1,2,... , A; — 1.
7
Максимальное
значение отсчетов
|A(n)|max = Α(0) = η = 0,1,... , k — 1.
|w(m)|max = ω(0) = s, m = 0,1,... , к - 1.
Гл. 3. Линейная фильтрация контуров
3.5. Контурный фильтр скользящей разности
93
Поскольку частотный коэффициент передачи и ИХ контурного филь¬
тра связаны парой преобразований Фурье, то следует ожидать, что ФСС
будет обладать свойствами, аналогичными свойствам простейших филь¬
тров, но только в пространственной области (табл. 3.1). Рассмотрим соот¬
ветствие некоторых из этих свойств.
Импульсную характеристику простейшего фильтра, заданного в ча¬
стотной области, можно рассматривать как сумму s членов геометри¬
ческой прогрессии с начальным членом ехр
Г .2π
U—ηπΐο
}
и знаменателем
ехр
, где то — номер первого, равного единице отсчета, а
s —
количество равных единице отсчетов частотного коэффициента передачи
фильтра. Поэтому ИХ такого фильтра можно записать как
Л (п) = - ехр
{
. 2π
г—ηπΐο
к
}
1
1
η = 0,1,... ,k-l. (3.4.8)
Сравнивая данное выражение с выражением (3.4.3) для частотного
коэффициента передачи ФСС, видим, что они совпадают с точностью
до углового множителя ^ ехр |г^пто|. Выражение (3.4.8) справедливо
для фильтра, у которого равные единице значения частотного коэффици¬
ента передачи раполагаются одним массивом, последовательно друг за
другом. В противном случае, например, для низкочастотного фильтра,
при получении выражения для ИХ надо формировать несколько сумм
геометрической прогрессии из комплексных экспонент.
3.5. Контурный фильтр скользящей разности
3.5.1. Задание фильтра скользящей разности. Фильтр скользящей
разности (ФСР) имеет окно, содержащее четное количество элементов,
т.е. s = 2,4,... Весовые коэффициенты для элементов окна ФСР равны
{1,1,... ,1,-1,—1,... , — 1}. Выходной эффект фильтра образуется как
> v '
s/2 s/2
разность между суммами ЭВ фильтруемого контура в пределах двух
половин окна:
s/2 — 1+п s —1+п
V(n)= X 7 (г)- X 7 (г). (3.5.1)
г—п r=s/2+n
Определим связь спектра Ps = {ps (m)}0 к_г выходного контура Hs
со спектром Р = {р (т)}0 к_г фильтруемого контура Г. При этом учтем,
что при фильтрации по методу скользящей разности отдельно находятся
суммы контуров Γ,Γ^,... ,r(s/2-1) и Г^5/2), Г^/2+1\ ... ,Г^_1\ где
Г— контур Г со сдвинутой на d ЭВ начальной точкой. Далее опре¬
деляется разность этих сумм. Так как компоненты спектра р№ (т) кон¬
тура связаны с компонентами спектра р(т) исходного контура Г
94
Гл. 3. Линейная фильтрация контуров
(3.5.2)
соотношением (2.3.4), то спектр выходного контура будет равен
s/2—l s — 1
рз (га) = р (га) ^ exp |i-^radj — ^ exp ji-^radj
_ d=0 d=s/2
т = 0,1,... , к - 1.
Теперь определим частотный коэффициент передачи ФСР:
(m) = 7М = Σехр 0ттс4 ~ехр Ksm} х
^ V 9 d=О
χ Σ ехр = (* “ ехр Σ ехр
d=0 <f=0
Второй сомножитель в виде суммы экспонент в последнем выраже¬
нии есть ЭВ коэффициента передачи ФСС с окном, равным s/2, т.е.
5/2-1 г 2π )
tos/2,фсс (т) = Σ ехР Ί i-j-md >. С учетом этого получим
(m) = а;я/2>фсс (l - ехр ji^md)) .
(3.5.3)
ФСР можно представить как два последовательных звена: в виде ФСС
и звена с частотным коэффициентом передачи
1 — ехр |i^rad|.
(3.5.4)
Оба звена характеризуются окнами по s/2 элементов. Используя вы¬
ражение (3.4.5), получим следующее компактное представление для ча¬
стотного коэффициента передачи ФСР
ω8 (га) =
1 — 2ехр j + ехр — ехр
2π
1 — ехр {г ^
\ , ί.2π \
ι > 1 - ехр < г-—т >
(3.5.5)
Выражение (3.5.3) целесообразно применять при анализе работы
фильтра, а выражение (3.5.5) — при расчете его частотного коэффи¬
циента передачи. На рис. 3.9 приведен пример фильтрации контура по
методу скользящей разности. Из графика АЧХ видно, что рассматри¬
ваемый ФСР обладает свойствами фильтра высоких частот: нулевая
составляющая подавляется полностью, а наиболее высокочастотная со¬
ставляющая частотного коэффициента передачи (при га = 2) в \/2 по
модулю превышает соседние. Наличие самопересечений в отфильтро¬
ванном контуре свидетельствует об усилении высокочастотных ЭК по
сравнению с другими ЭК, составляющими контур Г.
Получим теперь выражение для импульсной характеристики ФСР.
Поступая так же, как и при определении импульсной характеристики
3.5. Контурный фильтр скользящей разности
95
Рис. 3.9. Фильтрация контура Г по методу скользящей разности (5 = 2):
а — исходный контур; б — выходной контур; в — амплитудно-частотная харак¬
теристика фильтра
ФСС, с учетом выражения (3.5.2) для частотного коэффициента передачи
ФСР запишем
A(n) = i
Σ ]>>хр{гт(п+й)}~ Σ ΣβχρΗτ(η+<ί)}
d—0 т—0 d=s/2 m=0
Внутренние суммы в этом выражении будут равны нулю для всех значе¬
ний п, кроме n + d = dk, d = 0, dtl, ±2,... Если η = fc, k — 1,... , k — s/2+
-Ы, το Λ (n) = |?7 (fc — 1) |, если же η = k — s/2, k — s/2 — 1,... , k — s + 1,
το λ (n) = -1. Таким образом,
{1 при η = 0, — 1, k - 2,... , k — s/2 + 1;
— 1 при n = k — s/2, k — s/2 — 1,... , k — s -h 1; (3.5.6)
О при n— 1,2,... , k - s.
Структура контура ИХ имеет вид
Л = { 1,0,0,... ,0,-1,-1,... ,-1,1,1,..· ,1}· (3.5.7)
k-s s/2 s/2 —1
т.е. контур импульсной характеристики ФСР является замкнутым, а его
ЭВ задаются вещественными числами.
3.5.2. Свойства фильтра скользящей разности. 1. Нулевые значения
АЧХ. Из выражения (3.5.5) следует, что нулевые значения отсчетов на
выходе фильтра достигаются при т = a2k/s, а — 0,1,2,... Сравнивая
это соотношение с аналогичным для ФСС, видим, что положение нулей
в АЧХ обоих фильтров, ФСР и ФСС, совпадает, за исключением точки
т = 0. В данной точке ФСС образует максимальный отсчет, а у ФСР по
сравнению с ФСС появляется добавочный нуль. В результате происходит
подавление постоянной составляющей фильтруемого сигнала.
2. Локальные максимумы АЧХ. Такие максимумы будут при значени¬
ях т, для которых частотный коэффициент передачи 1 — exp
второго звена ФСР будет равен максимальному значению, т.е. двум. Это
достигается при т — ak/s, а — 1,3,5,...
96
Гл. 3. Линейная фильтрация контуров
3. Особенности работы ФСР с окном из двух элементов. При s = 2
первое звено ФСР представляет собой ФСС с окном s = 1. Такой ФСС
имеет при любом значении т равный единице коэффициент передачи,
т.е. ωι(πι) = 1, т = 0,1,... , к — 1. По¬
этому работа ФСР с окном s = 2 целиком
определяется звеном с ω (т) = ω2 {т) =
= 1 — ехр|г^га|. Модуль |о;2(га)| =
= 2sin |^т}· На рис. 3.10 показано фор¬
мирование вектора ω2 (т) как разности
двух векторов: 1 и ехр |г^га |. Векторы
имеют единичные модули, а угол между
ними равен 2'кт/к. Вектор ω2 (т) нахо¬
дится как основание равнобедренного тре¬
угольника с углом при вершине 2пт/к и
единичными сторонами. Величина \ω2 (т)\
с ростом т изменяется по закону синуса от
нуля при т = 0 до двух при т = к/2 и затем падает до нуля. Отметим, что
ФСР с окном из двух элементов является в чистом виде фильтром высоких
частот, а алгоритм его работы совпадает с алгоритмом работы системы
однократной череспериодной компенсации в радиолокационной станции.
4. Механизм работы ФСР с числом элементов в окне, большим двух.
В данном случае первое звено фильтра проявляет интегрирующие свой¬
ства и ведет себя как ФСС с окном s/2 (см. п. 3.4). Второе звено имеет
частотный коэффициент передачи ω2 (т) = 1 — ехр|г^га|| и АЧХ
Рис. 3.10. К определению моду¬
ля коэффициента передачи ФСР
при s = 2
\ω2 (т) | = 2 sin ^га^|, яг = 0,1,... , к — 1. При изменении т от нуля до
к — 1 вектор exp j Делает ms/2 оборотов. Поэтому АЧХ может
иметь ms/2 нулей и столько же максимумов, значения которых равны
двум. Реальное количество экстремумов определяется в соответствии со
свойствами 1 и 2 ФСР. Например, если к = 16 и s = 6, то возможен лишь
один нуль (при т — 0) и один максимум (при т — 8) (рис. 3.11, б). Если же
& = 16и$ = 8, то будут наблюдаться четыре нуля и четыре максимума
(рис. 3.11, в).
5. При s — к частотный коэффициент передачи содержит чередую¬
щиеся ЭВ, равные нулю и единице (рис. 3.11, г). Фильтр с таким окном
формирует на своем выходе контур из нечетных гармоник исходного кон¬
тура, прошедшего через ФСС с окном s/2.
Таким образом, механизм работы ФСР состоит:
1) в подавлении постоянной составляющей входного контура,
2) в подчеркивании составляющих спектра на частотах т = ak/s,
а = 1,3,5,... ,
3) в подавлении оставляющих спектра на частотах т = 2ak/s, а =
= 0,1,2,... ,
3.6. Контурные согласованные фильтры
97
2
1.5
1
О)
*
= 16 5 =
-2
о
со(т)| к
= 16
5 =
= 6
Z
1 с
717
/ '
ч
1. J
\
/
0.5
1
/
\ /
k и.о
!
i-
\ '
О 2 4 6 8 10 12 14 т 0 2 4 6 8 10 12 14 т
Рис. 3.11. Графики амплитудно-частотных характеристик дифференциального
звена ФСР для разных значений ширины окна s, к = 16
4) в модуляции спектра входного контура дифференциальным звеном
по закону 2|sin^m||.
3.6. Контурные согласованные фильтры
3.6.1. Основные аналитические соотношения при контурной согла¬
сованной фильтрации. Формирование меры схожести двух сигналов
является основной задачей при решении вопросов, связанных, в первую
очередь, с обнаружением, распознаванием, разрешением, измерением
параметров сигналов. Образование данной меры сводится к получению
ВКФ этих сигналов (см. п.п. 1.5 и 1.6). Рассмотрим линейный фильтр,
структура которого определена формой одного из сигналов и выраба¬
тывающего сигнал в виде ВКФ при подаче на его вход другого сигнала.
Пусть необходимо получить смещенную на к отсчетов ВКФ контуров
N = Мп)}0,*-1 и г = {7(п)}0,м:
к-1
77(777) = ^2 Κη)7*(η — rn -f к — 1), (3.6.1)
n=О
с помощью линейного фильтра, заданного в виде свертки
к-1
77(771) = ^2 ν(η)λ(πι — п). (3.6.2)
п=О
Найдем ИХ Л = {λ(τι)}0Α._1 такого фильтра. Приравнивая выра¬
жения (3.6.1) и (3.6.2), получим 7*(тг — т 4- к — 1) = Х(т — п). Введем
переменную s = т — п. Тогда п = т — s и последнее выражение примет
вид
7*(fc — s — 1) = Л (s).
(3.6.3)
98
Гл. 3. Линейная фильтрация контуров
Запишем выражение (3.6.2) с учетом изменения пределов суммирова¬
ния при замене переменной п на т — s:
m — k — l
η{τη) = Σ ι/(m - s)y*(k - s - 1). (3.6.4)
s=m
В этом выражении так же, как и в (3.5.1) и (3.6.2), последовательно сум¬
мируются к произведений. Величина к является периодом сомножителей
v и 7, т.е. ι/(η) = ι/(η ± ак) и 7(η) = 7(η ± аЖ), где а — целое число.
Поэтому результат суммирования не будет зависеть от порядка сумми¬
рования элементов и сумму (3.6.3) можно записать в тех же пределах, что
и сумму (3.6.1):
к—1 к-1
77(771) = ^2 v{m ~ ft)7*(k — п — 1) = ^2 v(n)j*(n - 771 + к — 1). (3.6.5)
п=0 п=О
Выражения (3.6.1) и (3.6.5) задают в пространственной области линей¬
ный фильтр с ИХ 7*(fc—s—1), вырабатывающий значения смещенной на к
отсчетов ВКФ двух контуров. Данное устройство является согласованным
фильтром [29,55]. Особенность его работы для циклически определенных
сигналов заключается в более широком условии физической реализу¬
емости. В связи с периодичностью сигналов (гг) и 7(71), ИХ А(?г) и
входной сигнал ν (п) заданы не только для нулевого и положительного,
но и отрицательного значений тг, т.е. λ (—η) = Л (к — η) ф 0.
Отметим также, что ИХ Л (гг) фильтра, согласованного с комплекс¬
нозначным сигналом, каким является контур, повторяет этот сигнал в
обратном порядке с задержкой на число отсчетов к, составляющих про¬
должительность сигнала. Это совпадает с результатами согласованной
фильтрации вещественных сигналов. Но при согласованной фильтрации
комплекснозначного сигнала ИХ фильтра является еще и комплексно
сопряженной копией этого сигнала.
Рассмотрим теперь контурный согласованный фильтр (КСФ), за¬
данный в частотной области. Частотный коэффициент передачи Ω =
= {ω (ггг)}0 к_х связан с ИХ Л = {λ (—тг)}0 к_г дискретным преобразо¬
ванием Фурье:
к — 1
ω (т) = ^2 7* {к — 1 — п) ехр т = 0,1,... , к — 1.
71=0
Умножим обе части этого выражения на 1 = ехр
х ехр г^тп (к — 1)|. Тогда
1)}х
К— 1
г (т) = ехр |г-^7П7* (к — 1 — п) ехр г^т (к — 1 — ?г)|.
Осуществим под знаком суммы замену переменных: s = к — 1 — тг. В
результате пределы суммирования станут равными: нижний, если п = 0,
3.6. Контурные согласованные фильтры
99
то s = к — 1; верхний, если п = к — 1, то s = 0. Пределы суммирования со¬
хранились, но порядок суммирования изменился на обратный. Результат
суммирования при этом сохраняется, поэтому
к — 1
ω (т) = exp |г^т |^7* (п) ехР |г^тп
п=О
С учетом выражения (2.3.1) для ДПФ контура Г получаем
ω (т) = /?г (га) ехР га = 0,1,... , к — 1. (3.6.6)
Данный результат совпадает со случаем согласованной фильтрации ве¬
щественных сигналов: частотный коэффициент передачи КСФ с точностью
до фазового множителя повторяет комплексно сопряженный спектр конту¬
ра, с которым он согласован. Определим спектр Рвых = {рВых (m)}o fc-i
выходного контура Н = {77 (m)}o,fc-i фильтра:
Рвых (т) = ω (т) pv (т) = pv (т) pf (τη) exp
m = 0,1,... , к — 1.
Здесь {pi, (m)}0 к_г — спектр фильтруемого контура N. Если кон¬
тур N согласован с фильтром, т.е. N = Г, то
Рвых (т) = Iр (т)|2 ехр (г^т), т = 0,1,... , к - 1.
Используя обратное ДПФ, запишем выражение для выходного сигнала
фильтра:
1fc_A 2
V (т) = 1^2 Рвых (s) ехр =
s=0
к-1
= %ΣΡν (s)Pr (s)exp{iys(l +m)|. (3.6.7)
При N = Г будем иметь
к-1
η (т) = ^^2 ехР {^~jTs (* + ш)}> га = 0,1,... , к — 1. (3.6.8)
s=0
Обозначим т + 1 = п. Тогда выражение (3.6.8) примет вид
/с-1
η (п - 1) = |р (s)|2 ехр η = 0,1,... , к - 1. (3.6.9)
s=0
Отсюда видно, что смещенный на один ЭВ выходной контур может
быть найден как результат обратного ДПФ от энергетического спектра
входного контура. Процесс согласованной фильтрации контура иллюстри¬
руется рис. 3.12.
100
Гл. 3. Линейная фильтрация контуров
0 1 2 3 4 т 0 1 2 3 4 т
г д
Рис. 3.12. Согласованная фильтрация контура Г: а — фильтруемый контур, б —
контур импульсной характеристики, в — выходной контур, г — графики ампли¬
тудно-частотного спектра контура Г и АЧХ фильтра, д — амплитудно-частотный
спектр выходного контура
Смещение отсчетов ИХ КСФ на к, равное размерности контура, не
является принципиальным, так как в силу периодичности ЭВ контура при
условии хранения контура в запоминающем устройстве известны все его
ЭВ. С учетом этого выражения, например, для КСФ в пространственной
области могут быть записаны в виде
к-1 к-1
η (га) = ^2 ν (п) 7* (п — т — 1) = ^2 у (т — п) 7* (—п — 1) =
п=0 п=0
к-1
= ^2 v (m + п + 1) 7* (n), m = 0,1,... , к — 1. (3.6.10)
η=О
Определим теперь форму сигнала, для которого фильтр η (т) —
к-1
= Σ у (п) А (т — п), т = 0,1,... , к — 1, с произвольным контуром Л =
п=0
= (λ(η)}0Μ импульсной характеристики будет согласованным. Срав¬
нивая приведенное выражение с выражениями (3.6.10), приходим к выво¬
ду, что поставленное требование выполняется, если i/(n) = А* (—п — 1)
или is (т — п) = X* (п — т — 1), т = 0,1,... , к — 1. Контур согла¬
сованного с фильтром сигнала будет иметь вид: N = {v(n)}ok_1 =
= {λ* (к — 1 — гс)}0 к_г, т.е. ЭВ данного контура являются комплексно
сопряженными ЭВ контура ИХ и следуют в обратном порядке.
Например, если Л = {A(n)}0 3 = {4г; 5 4- 2г; 2 - 6г; -7}, то N =
= {ν (3 — п)}0 з = —{—7; 2 + 6г; 5 — 2г; —4г}. Последний, (к — 1)-й, отсчет та¬
кого КСФ будет равен
3.6. Контурные согласованные фильтры
101
з
»?(з) = =
П=0 = I/ (0) λ (3) + и (1) λ (2) + V (2) λ (1) + V (3) λ (0) = 134.
Приведенные выше соотношения относились к случаю, когда ши¬
рина окна s фильтра совпадала с размерностью к фильтруемого кон¬
тура. Часто встречающейся задачей является выделение с помощью
фильтра фрагмента контура заданной формы. Окно шириной s, s < к,
элементов такого фильтра скользит вдоль контура N = Mn)}o,fc-l
и на каждом m-м шаге вычисляется скалярное произведение текуще¬
го фрагмента {ν (п + т), ν (п + т + 1),... , v (п + s — 1)} фильтруемо¬
го контура и эталонного фрагмента {7 (0), 7 (1),... , 7 (s — 1)}. ЭВ 7 (п),
га = 0,1,... ,s — 1, служат весовыми коэффициентами окна и определя¬
ются формой искомого в контуре фрагмента. Предполагаем, что все ЭВ
фильтруемого контура N хранятся в ОЗУИ процессора изображений и
нет необходимости организовывать встречное движение ЭВ ν (η) и 7 (η),
как при поступлении отсчетов фильтруемого сигнала в реальном времени.
С учетом этого выходной сигнал фильтра для выделения в пределах кон¬
тура N = {1/ (п)}0 к_г фрагмента, форма которого определяется контуром
Г = {7 (ra)}0,k-i> имеет ВИД
s — 1
η (m) = ^2 v (т + п) 7* (n), т = 0,1,... , к — 1. (3.6.11)
п=0
3.6.2. Расчет контурного согласованного фильтра. Фильтрация согла¬
сованного с фильтром контура. Рассчитаем фильтр, согласованный с контуром
Г = {7; -6 Η- г; 2 + 5г; —3; —6г}. Здесь к = 5. Основные формулы (3.6.1), (3.6.10) и
(3.6.8), по которым определяется выходной вектор фильтра в пространственной и
частотной областях, принимают вид
4
η (т) — 7 (п) 7* (п — т + 4), (3.6.12)
п=о
4
ту (т) = 7 (т — п) 7* (4 — п), т = 0,1,2,3,4, (3.6.13)
п=0
1 4
η (п — 1) = ~У^ \р (s)|2 exp {0.47i\sm}, п — 0,1,2,3,4. (3.6.14)
n=0
Выходной контур, найденный по формулам (3.6.12) и (3.6.13), равен
Н = {-55 + 50г; -25 - Юг; -25 4- Юг; -55 - 50г; 160}.
Для расчета фильтра в частотной области по формуле (3.6.14) вначале опре¬
деляем комплексный, амплитудный и энергетический спектры контура Г:
Рг = {0; 15,55 - 2,82г; 10,90 + 13,87г; 12,19 - 2,69г; -3,64 - 8,36г},
{|Р (т)|}0,4 = {0; 15,8; 17,64; 12,48; 9,12},
{1рМ|2}04 = {0; 249,64; 311,7; 155,75; 83,17}.
Теперь с помощью обратного ДПФ найдем выходной контур Н;
{η (η - 1)}0 4 = {160; -55 + 50г; -25 - Юг; -25 + Юг; -55 - 50г}.
102
Гл. 3. Линейная фильтрация контуров
Учитывая смещение начала выходного контура на один ЭВ, мы получили
такой же результат, как и при расчете по формулам (3.6.1) и (3.6.10). Определим
частотный коэффициент передачи КСФ по формуле
4
ш(т) = 7* (4 — п) ехр {—0,47гтт}, т = 0,1,2,3,4. (3.6.15)
п-О
В результате получим
Π = {ω (m)}0|4 =
= {0; 212 + 15,66г; -0,67 + 17,63г; -8,28 - 9,34г; -6,82 + 6,05г}.
АЧХ фильтра: {\ω (m)|}0 4 = {0; 15,8; 17,64; 12,48; 9,11} .
Видно, что данная АЧХ, как и положено для согласованного фильтра, совпа¬
дает с амплитудно-частотным спектром {|р (т)|}0 4 контура Г.
Найдем частотный коэффициент передачи фильтра как отношение соответ¬
ствующих компонент спектров выходного и входного контуров КСФ. Спектр вы¬
ходного контура
Рн — Рвых(^)о,4 =
= {0; 77,2 + 237,58; -251,88 + 183г; -126 - 91,54г; 25,68 - 79,04г} =
= {0; 249,8 ехр {0,47гг}; 311,34 ехр {0, 8ттг};
155, 74 ехр {—0,8π«}; 83,11 ехр {—0,4πζ}}.
Спектр входного контура в показательном виде
{0; 15,81 ехр {-0,057ттг}; 17,64 ехр {0,288ттг};
12,48 ехр {0,0697гг}; 9,12 ехр {—0, бЗЪгг}}.
Тогда
("(т)1»-‘ = {тнШ0,4 = {feS =
= {0; 2,12 + 15,66г; -0,66 + 17,63г; -8, 29 - 9,35г; 6,82 + 6,04г} =
= {15,81 ехр {0,457ттг}; 17,64 ехр {0,512ттг}; 12,52 ехр {-0, 731ттг};
9,11 ехр {0,231ттг».
Видно, что результат совпадает с результатом, полученным по формуле
(3.6.15). Найдем также частотный коэффициент передачи фильтра по формуле
ω (т) = р* (га) ехр {0,47ггаг}, га = 0,1,2,3,4:
{рт (га)}0>4 = {0; 15,81 ехр {0,057ттг}; 17,64{—0,288ттг};
12,48 ехр {0,0697гг}; 9,12 ехр {0,6317гг}},
{о; (га)}0 4 = {0; 15,81 ехр {0,4577гг} ; 17,64ехр {0,512πζ} ;
12,52 ехр {-0,731ттг} ; 9,11 ехр {0,231ттг}} .
Результаты вычисления по всем трем формулам совпадают.
3.6. Контурные согласованные фильтры
103
Фильтрация несогласованного с фильтром контура. Фильтруемый контур N
и его спектр Ρν равны
N = {9г; —5; —4г; 3; 2 — 5г},
Ρν = {0; -0,95 + 19,11г; 10,1 + 13,07г; -3,39 + 10,55г; -5,76 + 2,27г}.
Определим по формулам (3.6.1) и (3.6.10) выходной контур:
4 4
η (т) = ^ ν (п) 7* (п — т + 4) = ^ и (га — п) 7* (4 — п) =
тг=0 тг=0
= {-93 + 24г; -39 - 108г; 88 + 46г; 13 - 34г; 31 + 72г}.
Найдем спектр Ρν выходного контура Н как ДПФ контура Н = {f7(m)}04
и как Рн = {ω (m) pti (m)}0 4;
Рн = {0; -301,35 + 25,66i; -237,2 + 169,31i;
126,37 - 55,64i; -53,02 - 19,32г}.
3.6.3. Механизм работы контурного согласованного фильтра. При
фильтрации согласованного контура на выходе фильтра образуется контур
k — 1
η (τη) = ^2 7 (п) 7* (n - m -f fc - 1), т = 0,1,... , к — 1. (3.6.16)
η=О
Данное выражение задает смещенную на к отсчетов АКФ фильтруе¬
мого контура Г. В момент т = к — 1 получим
к—1 к—1
V {к - 1) = 7 W 7* (п) = ^ |7 (**)|2 = ||Г||2.
п=0 п=0
Аналогичный результат получается, если воспользоваться выражени¬
ем (3.6.8) для КСФ в частотной области и учесть равенство Парсеваля.
Таким образом, при фильтрации согласованного контура в момент к — 1
образуется действительный отсчет, равный энергии фильтруемого конту¬
ра. Для выяснения механизма работы КСФ представим выражение (3.6.16)
в показательном и тригонометрическом видах:
к-1
V {т) = |7 (η)||7 (п - т + к - 1)| ехр {ΐ[φ (n)-(p(n-m + k- 1)]},
n—Q
(3.6.17)
к—1
V (т) = |у (η)||7 (п - та + к - 1)| cos [φ (η) - ψ (η - m + A; - 1)] +
η=0
к-1
+ * Σ 17 (n)ll7 (η - m + к - 1)| sin [y> (η) - φ (η - m + к - 1)], (3.6.18)
η=0
m = 0,1,... , к — 1.
104
Гл. 3. Линейная фильтрация контуров
Из выражения (3.6.18) следует, что КСФ может быть представлен
двумя параллельными звеньями: косинусным и синусным, — формирую¬
щими соответственно действительную и мнимую части выходного сигнала
η (га) = щ (га) + ίη2 (τη), га = 0,1,... , к — 1. При га = к — 1 сигнал
на выходе косинусного звена будет равен ||Г||2, а на выходе синусного —
нулю.
Выражение (3.6.16) можно также рассматривать как развернутую за¬
пись к скалярных произведений контура Г на этот же контур со
смещенной на d элементов начальной точкой, d = к-1,к — 2,... ,1,0, т.е.
η(τπ) — (Г,Г^_П_1)), то = 0,1,... ,fc —1. (3.6.19)
При т = к-1 данное выражение принимает вид η (к — 1) = (Г, Г) =
= ||Г||2. В соответствии с неравенством Коши-Буняковского имеем:
|(г,гМ)| ^ ||Г||||Г^ ||. Так как норма контура не изменяется при вырь-
ировании его начальной точки, т.е. ||Г|| = ||r(d)||, то 77 (d) = | (Г,Г^) | ^
^ ||Г||2. Равенство здесь достигается лишь при d = 0, т.е. при га = к — 1.
Применительно к КСФ это означает, что отсчет в момент га = к — 1
будет не только вещественной величиной, но и максимально возможным
по модулю для любого га, т.е. η (к — 1) ^ (77 (к — 1)|, га = 0,1,... , к — 2.
Формирование такого отсчета можно объяснить следующим образом.
Как следует из выражений (3.6.17) и (3.6.18), при т — к — 1 аргументы ЭВ
фильтруемого контура и контура ИХ становятся равными друг другу по
модулю и разными по знаку, а их сумма будет равна нулю. В результате
происходит компенсация разности фаз всех векторов вида
Ιτ (η)||7 (п - га + к - 1)1 ехр{г[<р(п) - ip(n-m + k- 1)]},
в сумме образующих отсчет η (га). При га = к — 1 этот отсчет бу¬
дет арифметической суммой квадратов модулей ЭВ 7 (п), п = 0,1,...
... , fc — 1, входного контура, т.е. происходит синфазное сложение век¬
торов (рис. 3.13). Если же фильтруется несогласованный с фильтром
контур N = {|7 (п)| ехр {гф (η)}}0^-ι* то компенсация аргументов век¬
торных слагаемых не произойдет и при образовании выходного эффек¬
та не будет синфазного сложения векторов (рис. 3.13, б).
0
/
7т
S
12
/
V]
<
к
и
\
h
<
>
10
V
9
У
0 1 2 3 4 5
7 8 9 10 1112 О
Рис. 3.13. Формирование выходного эффекта КСФ: а — контур исходного изобра¬
жения (входной сигнал); б — векторный выходной сигнал КСФ
3.6. Контурные согласованные фильтры
105
Таким образом, при поступлении на вход линейного фильтра после¬
довательности контуров с одинаковой энергией максимальный по модулю
отсчет на выходе фильтра достигается лишь для контура, согласованного с
фильтром. Этот отсчет образуется в момент т = к - 1 и равен по модулю
энергии контура. Каждый ЭВ 7 (π) = Ι7 (п)| ехр {ιφ (гг)} этого контура
поворачивается на угол [—φ (η)] и получает горизонтальную, направленную
вправо ориентацию. Затем производится квадрирование длины каждого ЭВ
и их сложение. КСФ «выпрямляет» линию контура, с которой он согласован.
3.6.4. Свойства контурного согласованного фильтра. КСФ является
линейным устройством, и поэтому он обладает всеми рассмотренными в
п. 3.2 свойствами контурных линейных фильтров. Если контур ИХ за¬
мкнут, то фильтр не пропускает постоянной составляющей, т.е. его реак¬
ция на отрезок прямой линии из к ЭВ равна нулю, а если фильтруемый
контур замкнут, то замкнутым останется и выходной контур. Любой ЭК
проходит через КСФ без искажения формы, а поворот, растяжение и
сдвиг начальной точки фильтруемого контура вызывают аналогичное пре¬
образование выходного контура. При этом поворот фильтруемого контура
по отношению к эталонному на угол Αφ приводит к умножению выход¬
ного контура на комплексный коэффициент ехр{гАу?} и отсчет КСФ в
момент т = к — 1 будет уже не вещественным, а комплексным числом
||Г||2ехр{гА<£?}. Сдвиг начальной точки фильтруемого контура на d ЭВ
обусловливает такой же сдвиг максимального по модулю отсчета КСФ.
Кроме того, отсчеты КСФ периодичны, т.е. η (т) = η(πι± ак).
Рассмотрим несколько особых свойств КСФ. Необходимо отметить, что
любой контурный линейный фильтр является согласованным с сигналом,
форма которого задается его ИХ. Поэтому эти особые свойства являют¬
ся общими для любого линейного фильтра и базируются на сравнении
процессов обработки согласованного и несогласованного сигналов.
1. Обобщенная инвариантность КСФ к линейным преобразованиям
фильтруемого контура. Пронормируем отсчет КСФ путем его деления
на произведения норм фильтруемого и эталонного контуров: ηΗ (т) =
= ν (m)/l|r||||N||.
При N = Г величина |Tj(mo)| = ||Г|| и \ηΗ(πΐο)\ = 1. Здесь то —
отсчет КСФ с максимальным значением модуля. Поскольку при повороте
контура и сдвиге его начальной точки норма контура не меняется, то дан¬
ное соотношение сохраняется при линейных преобразованиях фильтруемого
контура. Если же N ф Г, то \р(т0)\ < ||Γ||||Ν|| и \рн(то)\ < 1. Та¬
ким образом, величина \ηΗ (гао)| инвариантна к линейным преобразованиям
контура и достигает максимального значения, равного единице, лишь при
прохождении через фильтр согласованного контура. Поэтому КСФ является
устройством, вырабатывающим количественную меру схожести двух конту¬
ров, двух форм плоских изображений, инвариантную к масштабу и повороту
этих изображений, а также к сдвигу начальных точек их контуров.
2. Связь между выходным сигналом фильтра и ВКФ фильтруемого
и эталонного сигналов. Ранее было отмечено, что при обработке согла-
106
Гл. 3. Линейная фильтрация контуров
сованного с фильтром сигнала на выходе образуется смещенная на к
отсчетов АКФ этого сигнала. Принимая во внимание рассмотренные в
п. 2.8 свойства ВКФ и АКФ комплексных сигналов, уточним характер
связи между АКФ и выходным сигналом КСФ. Сравнивая между собой
выражения (2.8.4) для АКФ т (га) и (3.6.1) для
выходного сигнала η (га), га = 0,1,... , fc — 1,
согласованного фильтра:
fc-l
|Ф)|
120 ■
80 :-
40 --
0
М*)Г
120 ί
80 -
40 4-
гл
4 т
0
Т \ 5 т
т (га) = 7 (п) 7* (п + га)
η (га) = ^2 'у{п)'у*(п — т-{-к — 1),
(3.6.20)
приходим к выводу, что отношения соответ¬
ствия между ними имеют вид
η (га) = τ (к — т — 1)
т (га) = η (к — т — 1).
Отсюда следует, что выходной сигнал
КСФ, определяемый выражением (3.6.1),
представляет собой не только сдвинутую на
к отсчетов АКФ фильтруемого согласованно¬
го сигнала, но и порядки следования отсчетов
η (га) и т (га) у них противоположны (рис. 3.14).
Между контурами Т = {т(га)}0>А;_1 иН = {г; (га)}0
следующая зависимость:
Рис. 3.14. Соответствие меж¬
ду модулями отсчетов АКФ
и КСФ для контура Г =
= {4г; 5 4- 2г; 2 — 6г; —7}
существует
Т = Н
(к-1)
обр
и Н = Т
гр(1)
обр*
(3.6.21)
Здесь <ГХ)
контур, обратный к контуру Н со сдвинутой на к — 1
ЭВ начальной точкой; Т^р — контур, обрат¬
ный к контуру Т со сдвинутой на один ЭВ
начальной точкой (рис. 3.15). Соотношения
между отсчетами выходного сигнала ту (га)
фильтра и ВКФ г (т) контуров произволь¬
ного фильтруемого сигнала и ИХ также
определяются выражениями (3.6.20).
Представляет интерес рассмотрение во¬
проса о том, каким образом некоторые
свойства АКФ, приведенные в п. 2.8, пре¬
образуются в свойства КСФ.
Свойство 5 АКФ г (т) (см. п. 2.8),
обусловливающее сопряженную симметрию
контура АКФ, меняется следующим образом. С помощью формул (3.6.20)
определим, какому отсчету η (га) КСФ соответствует отсчет г (к — т)
ίι
\
Н
7
Рис. 3.15. Соотношение между
контурами Т и Н для контура
Г = {4г; 5 4- 2г; 2 — 6г; —7}
3.6. Контурные согласованные фильтры
107
АКФ. Вводя новую переменную s = к - т, найдем, что τ (к — т) =
= т7 (га — 1). Учитывая соотношение г (га) = г* (А; - га), окончательно
получаем
η (га) = η* (к - т - 2), га = 0,1,... , к - 1. (3.6.22)
Из формул (3.6.20) и рис. 3.15 видно, что контуры АКФ и КСФ про¬
слеживаются в противоположных направлениях: первый — против, а
второй — по часовой стрелке. Выражение (3.6.22) показывает, что ЭВ кон¬
тура Н расположены симметрично. Отсчет η (к — 1) = ||Г||2 представляет
собой горизонтально расположенный вектор и из (3.6.22) для него следует
равенство ?7 (Л: — 1) = η* (к — 1). Поэтому вертикальная ось симметрии
будет проходить через середину этого вектора. Если размерность контура
к является четным числом, то η (к/2 — 1) == η* (к/2 — 1), т.е. и этот ЭВ
будет задаваться чисто вещественным числом. В результате контур Н
будет содержать второй горизонтально расположенный вектор.
3. Спектральный анализ контуров. Запишем выражение для прямого
ДПФ контура Г:
k — 1
P(s) = Хл(»г)ехр{-г^вп), s = 0,1,... ,к- 1.
п=0
Величина exp |-г—sn j является элементарным вектором 7S (га) ЭК
IV Поэтому в соответствии с выражением (3.6.1) составляющая спектра
исходного контура может рассматриваться как отсчет фильтра, согласо¬
ванного с контуром Г5 в момент т = к — 1, т.е. p(s) = η8 (к — 1). Меняя
параметр s, т.е. последовательно согласовывая фильтр со всеми ЭК при
данном значении к, можно осуществить спектральный анализ контура
на базе алгоритма контурной согласованной фильтрации. Данное свойство
КСФ основано на том, что алгоритмы ДПФ и согласованной фильтрации
используют скалярное произведение векторов.
4. Выделение главного примитива произвольного контура. Как бы¬
ло показано в п. 2.4, произвольный контур Г может быть представлен
линейной комбинацией ЭК Γο,Γΐ5... ,Γ&_ι, весами в которой служат
компоненты спектра. Под главным примитивом контура Г будем понимать
контур р($)Г5 с максимальной энергией, т.е. ||ρ(β)Γβ|| > ||р(т)Гт||,
т = 0,1, — 1, т ф s. Поскольку энергии всех ЭК одинаковы,
то главный примитив будет соответствовать такому значению s, при ко¬
тором \p{s)\ > \р(т)\. Спектр контура на выходе КСФ определяется
соотношением рвых (т) = |р (т)|2 ехр {г^"т}> т — 0,1, · · · , к — 1, т.е.
происходит квадрирование модулей компонент спектра. Модуль каждой
из них увеличивается в |р (т) | раз. Отсюда вытекает достаточно простая
процедура формирования главного примитива. Для этого необходимо про¬
вести цепочку согласованных фильтраций: после фильтрации исходного
контура Г получить контур Hi, затем профильтровать контур Hi со¬
гласованным с ним фильтром и получить контур Н2 и т.д. После каждого
108
Гл. 3. Линейная фильтрация контуров
шага фильтрации возрастает степень доминирования компоненты спектра
р (s) над всеми остальными компонентами и последние перестают влиять
на процесс образования контура. Начиная с определенного r-го шага,
контуры Нг и Hr_i практически не
отличаются друг от друга и их вид
определяет главный примитив контура Г
(рис. 3.16).
5. Фильтрация отраженных конту¬
ров. Обычно входной контур задается
с точностью до параметров линейных
преобразований. Если в качестве ме¬
ры сходства фильтруемого контура N
с контуром Г, с которым фильтр со¬
гласован, принимается модуль \ηα(τη0)\
максимального нормированного отсчета
фильтра, то, как следует из свойства 1, эта величина инвариантна к
параметрам преобразований поворота, растяжения и сдвига начальной
точки контура. Теперь рассмотрим влияние преобразования отражения
контура на результат согласованной фильтрации.
Как следует из п. 1.6., записанный через ЭВ контура Г код контура,
отраженного относительно оси, проходящей под углом Θ, имеет вид
Готр = {7отр M}0,fc-1 = ехР {2Θ*} {|7 Ml ехР (~i(P (n))}o,k—1 ·
Контур Г при отражении подвергся повороту на угол 2Θ, а его ЭВ
стали комплексно сопряженными. Это позволяет записать для спектра
контура Готр следующее выражение (см. п. 2.3.2):
Ротр {т) = ехр {2θί}ρ* (к — т), т = 0,1,... , к — 1.
Таким образом, в процессе отражения спектр контура претерпева¬
ет значительные изменения из-за замены m-й компоненты спектра на
(к — т) компоненту. Так как амплитудно-частотная характеристика КСФ
повторяет модульный спектр {\р (тп)|}0 к_г контура Г, т.е. |ω(τη)| =
= |р (га)|, т = 0,1,... , к -1, то отраженный контур Готр проходит через
фильтр, согласованный с контуром Г, в общем случае, без каких-либо
преимуществ по сравнению с контурами, которые с данным фильтром
не согласованы. С учетом выражений для отраженного контура резуль¬
тат фильтрации контура Готр для т = к — 1 в экспоненциальном виде
(см. (3.6.17)) представляется как
к—1
η (k — 1) = 2е20г^Г^ |7 (п)| ехр {—%2φ (η)}. (3.6.23)
п—О
Видно, что при т = к — 1 уже не происходит компенсация аргументов
слагаемых и компоненты входного контура суммируются не арифмети¬
чески, а геометрически. Поэтому η (к — 1) < ||Г||2, причем неравенство
часто является значительным. Если предварительно известно, что филь¬
труемый контур N может быть отраженным контуром Готр, то для по-
Рис. 3.16. Результат выделения
главного примитива контура Г =
= {5г; 1 — 5г; —1}
3.6. Контурные согласованные фильтры
109
лучения с помощью КСФ меры схожести форм необходимо провести две
фильтрации: контура N и контура Ν*, а для дальнейшего* анализа взять
из полученных 2 к отсчетов отсчет с максимальным модулем
6. Полосовая фильтрация на базе КСФ. Фильтр с ширшной полосы Ат
можно получить при параллельном соединении фильтров, согласованных
с ЭК Гт, т = то,гшо -l· 1,...
ω(ηι)
7
■+-+-
Н-Ы fr-
V
wq-1 mo mo+1 mQ+Ajn-Xk-X
Рис. 3.17. Частотный коэффициент пе¬
редачи полосового фильтра на основе
набора фильтров, согласованных с эле¬
ментарными контурами
... , mo -f Ат — 1. Фильтр, согла¬
сованный с одним из ЭК Гт, про¬
пустит на выход только одну, т-ю
составляющую спектра фильтруе¬
мого контура. Набор таких фильтров
реализует полосовой фильтр с пря¬
моугольной формой АЧХ (рис. 3.17).
Определим выражение для вы¬
ходного сигнала такого полосового
фильтра. Вначале найдем значение
спектральной составляющей p(s)
фильтруемого контура Г, при ко¬
торой соответвующий ЭВ ui(s) частотного коэффициента передачи
согласованного фильтра будет равен единице. Из выражения (3.6.6) для
ЭВ ω (s) получим, что ω (s) = 1 при р (s) = exp
Применяя обратное ДПФ к последнему выражению, находим вид кон¬
тура Г5:
b.(»)W. = ϊ{βχρ{*τ*<η+1)}}ο,»-Γ
ЭВ контура импульсной характеристики Л = {A (w)}0>fc_1 будет равен
\8 (п) = 7* (к — η - 1) = ^ exp |z^sn j. Тогда согласованный с конту¬
ром Ts фильтр
Vs (г)
к-1
ϊΣτ('
п— О
п) exp г = 0,1,... , к — 1,
будет иметь частотный коэффициент передачи, везде равный нулю, кро¬
ме u;(s) = 1. Объединяя Ат таких фильтров при s = mo, получаем
требуемый фильтр:
к-1 mo+Δτη—1
η (г) = Σ ехр{*ттп}’ г = °>1>··· L
п=0 т—тпо
(3.6.24)
Из общего выражения для линейного фильтра, представленного в виде
свертки (см. п. 3.2), следует, что ИХ фильтра равна
τηο+Δτη—1
*(») = £ Σ ехр{гТтп}’
η = 0,1,... , к — 1.
(3.6.25)
по
Гл. 3. Линейная фильтрация контуров
Если АЧХ должна быть не прямоугольной, а описываться произволь¬
ной весовой функцией g (га), то
k—1 mo+Δτη—1
η (г) — (г — η) ^2 g (m) exP r =
n—0 rn—rno
(3.6.26)
Синтезируем, например, фильтр для контуров размерностью к = 7 с коэффи¬
циентом передачиω (m) = {0,1,1,0,0,0,0}, т.е. то = 1, Ат = 2. В соответствии
с выражением (3.6.24)
1 6 2 Г 2π 1
Ч (г) = у 7 (г ~ η) Σ 8 (т) ехр < г—тп |·, г = 0,1,... , 6.
п=0 т=1 ^ '
Импульсная характеристика фильтра на основании (3.6.25) равна
= explain}, « = 0.1» •••>6·
m=l ^ ^
Проверим, что коэффициент передачи имеет заданный вид. Для этого найдем
ДПФ от контура импульсной характеристики:
ω (га) = ^2 ^ (га) ехр < -г^-тп
п=0 ^
= fXexp{*Ymn}exp{-*y'mn}') =
п=0 \т=1 ^ ^ ' /
= ^Х)ехр(-гу(т-1)) + ехр j-гу (т - 2)1.
п=0 ^ ' 1 п=0 ^ '
Эти суммы не будут равны нулю лишь при т — 1 (для первой суммы) и
т — 2 (для второй суммы). В результате ω (m) = {0,1,1,0,0,0,0}.
7. Согласованная фильтрация контуров со стандартными ЭВ. Рас¬
смотрим имеющий важное значение случай согласованной фильтрации
контура со стандартными ЭВ. Такие контуры получаются при просле¬
живании границ изображения после ввода сцены в систему техническо¬
го зрения, т.е. естественным образом формируются в ОЗУ. Стандартные
ЭВ на квадратной сетчатке принимают восемь возможных значений: ±1;
±г; ± (1 ± г) (см. п. 1.2). Особенность согласованной фильтрации таких
контуров заключается в использовании таблицы из 64 комплексных чисел
для нахождения произведения ν (п) 7* (п — т -f к — 1), что значительно
сокращает время фильтрации. Эта таблица имеет вид (см. табл. 3.2).
Предположим, что ППИ оперирует с десятиразрядными двоичными
числами. Если операция умножения двух чисел в этом процессоре реа¬
лизуется программным путем, то для этого потребуется, ориентировочно,
порядка двадцати тактов для вычисления произведения и порядка пяти
тактов для организации операции. В результате для нахождения про¬
изведения двух комплексных чисел, представленных в алгебраическом
виде, необходимо порядка 130 тактов машинного времени. Выполнение
3.7. Оценка степени сходства двух форм
111
Таблица 3.2
y\v
1
1 — г
—г
-1 -г
-1
-1+г
г
1 + г
1
1
1-г
—г
— 1 — г
-1
-1 + г
г
1 + г
1-г
1 — г
2
1 1 + i
—2г
-1 + *
-2
—1 — г
—2г
—г
г
1 + г
1
1 + г
—г
-1-г
-1
-1 + г
— 1 — г
-1 + г
2г
1 + г
2
1 + г
—2г
— 1 — г
-2
-1
-1
-1 + г
г
1 + г
1
1-г
—г
— 1 — г
-1 -f г
-1 + г
-2
-1 - г
2г
1+г
2
1 — г
—2г
г
—г
-1 - г
-1
-1 + г
г
1 + г
1
1 — г
1+1
1 + г
—2г
-1 + г
-2
-1 + г
2г
1 + г
: 2
умножения двух стандартных комплексных чисел в соответствии с при¬
веденной таблицей потребует порядка 10 тактов. Таким образом, выигрыш
в трудоемкости фильтрации составляет около 10-15 раз.
При индикации обработанных контуров на экране дисплея необходимо
проведение операции стандартизации, в результате которой произвольный
ЭВ преобразуется в цепочку стандартных ЭВ [42]. Эта операция достаточ¬
но трудоемка, но в рассмотренном выше случае чрезвычайно упрощается,
так как она тоже выполняется табличным путем. Например, нестандартный
ЭВ, равный 2, представляется двумя стандартными ЭВ, равными единице.
При этом таблицы для нахождения произведения стандартных ЭВ и для
осуществления процедуры стандартизации легко объединяются в одну.
Из сказанного следует, что операция полигонализации контура, обычно
предпринимаемая для сокращения его размерности, и, следовательно, с це¬
лью упрощения расчетов, не всегда целесообразна. Если задачи обработки
связаны с согласованной фильтрацией контура, то снижение при полиго¬
нализации его размерности в пределах одного порядка не дает выигрыша
во времени выполнения операций из-за невозможности использования та¬
бличных способов умножения ЭВ и их стандартизации. Так как полигонали-
зация связана с повторной дискретизацией линии контура, то потери из-за
большей трудоемкости расчетов сопровождаются еще и неизбежными ошиб¬
ками в представлении формы изображения. Приведенные выше соображе¬
ния, связанные с целесообразностью проведения операции полигонализации,
имеют смысл лишь в том случае, когда размерности контуров ИХ фильтра
и фильтруемого контура совпадают. В противном случае для выравнивания
размерностей необходимо выполнить операцию эквализации линии контура
(см. п. 9.1.1). При этом ЭВ теряют свойство стандартности и возможность
использования табличного способа умножения исключается.
3.7. Оценка степени сходства двух форм
Контуры плоских изображений задают не только формы этих изобра¬
жений, но и содержат дополнительную информацию, связанную с мас¬
штабом, углом поворота и положением начальной точки. При установ¬
лении степени сходства формы двух изображений по их контурам эта
112
Гл. 3. Линейная фильтрация контуров
информация позволяет однозначно оценить такое сходство. В связи с этим
возникает задача «подгонки» изображений, т.е. нахождения комбинации па¬
раметров линейных преобразований изображения — масштаба |μ|, угла по¬
ворота Αφ и сдвига d начальной точки контура, при которых расстояние R
между контурами двух изображений становится минимальным [75, 76, 17,
68]. Величина Нш\п этого расстояния принимается в качестве меры сходства
изображений по их форме. Контуры изображений будем считать заданными
в полигональном комплекснозначном виде. Расстояние между двумя конту¬
рами в Ск будем определять в соответствии с выражением (1.3.5)
Я2 = ||Г||2 + ||N||2 - 2 Re (Г, N). (3.7.1)
Рассмотрим основанный на согласованной фильтрации подход к опре¬
делению меры сходства форм, задаваемых контурами Г и N, путем мак¬
симизации реальной части их скалярного произведения (Г, N).
Влияние линейных преобразований контуров на величину расстоя¬
ния между ними. Пусть Γμ^ контур Г, повернутый на угол Αφ, растяну¬
тый в |μ| раз и со сдвинутой на d ЭВ начальной точкой, т.е.
= {μΐ(η + d)}0,k-i; Μ = И ехр(г'Ду>).
Исследуем изменение расстояния между этими контурами для случая,
когда их начальные точки совпадают, т.е. d = 0, а параметры |μ| и Αφ —
произвольны. Тогда
Γμ = {vi(n)}o,k-i = {Мехр{гДу>}7(п)}0>*_1.
Норма преобразованного контура равна ||Γμ|| = |μ|||Γ||, а искомый
нормированный квадрат расстояния
Ян = Я2/||Г||2 = 1 + И2 - 2|м| cosA<p. (3.7.2)
Из данного выражения следуют частные случаи: Αφ = О, =
= (1 — |μ|)2, и Αφ = 0, |μ| = 1, R\ = 2(1 — cosA<£>).
Графики зависимости расстояния между контурами от |μ| и Αφ для
этих случаев представлены на рис. 3.18.
Вис. 3.18. Графики зависимости нормированного расстояния между подобными
контурами при d = 0 от изменения масштаба (а) и от изменения угла поворота (б)
3.7. Оценка степени сходства двух форм
ИЗ
Если Αφ = О, |μ| = 1 и происходит сдвиг начальных точек подобных
контуров, то
R2„ = 2[1 - Re т?н], (3.7.3)
где т)а = 77ЦГЦ2 — нормированные скалярные произведения контуров в
комплексном линейном пространстве Ск.
В наиболее общем случае, когда контур подвергается растяжению,
повороту и сдвигу начальной точки
#н = 1 + И2 ~ 2|μ| Re ηΗ(ά) cos Αφ. (3.7.4)
Полученные для R\ соотношения показывают, что данная величина
является функцией параметров |μ|, Αφ и d линейных преобразований
контура. Поскольку эти преобразования не меняют формы изображения,
то расстояние (3.7.4) из-за неинвариантности к указанным параметрам не
может быть принято в качестве меры сходства двух форм.
Инвариантность расстояния между нормированными контурами
к масштабу и сдвигу начальных точек контуров. Пусть Nh = N/||N||
и Гн = Г/||Г|| — два произвольных нормированных контура. Квадрат
расстояния между ними
Rl = 2 (1 - Re 77я). (3.7.5)
Отсюда видно, что единственной существенной операцией для нахо¬
ждения является получение НСП ηΗ. Рассмотрим влияние отдельных
видов линейных преобразований на величину R
Масштабирование. Пусть один из контуров растянут в |μ| раз, напри¬
мер, Г|М| = |μ|Γ. Тогда
Ян = 2[1 - \μ\ Re (TV, Γ)/|μ|||ΛΤ||||Γ||] = 2 (1 - Re ηα).
Сравнивая полученное выражение для расстояния с предыдущим, ви¬
дим, что они совпадают, т.е. масштабирование не привело к изменению
расстояния между нормированными контурами.
Поворот и сдвиг начальных точек. При повороте изображения на
произвольный угол Αφ норма его контура не меняется. С учетом этого
выражение (3.7.5) принимает вид
Ryi-2-ηα ехр {-гД^} - η* exp {ίΑφ} =
= 2 (1 — Re ηΗ cos Αφ — Im ηΗ sin Δ<μ).
Если d = 0, то Re ηΗ = 1 и Im ηΗ = 0. В этом случае
=2(1 — cos Αφ),
т.е. имеется зависимость расстояния от величины угла Αφ. Также оста¬
ется зависимость расстояния от сдвига начальной точки любого из кон¬
туров. Если считать, что угол взаимного поворота нормированных конту¬
ров Αφ = 0, то квадрат расстояния между ними будет характеризовать
различие задаваемых ими форм и параметрически зависеть от величины
взаимного сдвига d начальных точек:
rh = 2[1 - Re%(o!)]·
(3.7.6)
114
Гл. 3. Линейная фильтрация контуров
При совпадении начальных точек контуров реальная часть скалярного
произведения становится максимальной, а расстояние — минимальным.
Таким образом, если угол взаимного поворота Αφ контуров равен
нулю, то для исключения влияния на величину расстояния между ними
преобразований масштабирования необходимо перейти к нормированным
контурам и использовать значение НСП с максимально возможной реаль¬
ной частью.
Исключение влияния угла взаимного поворота между контурами на
расстояние. Пусть контуры N и Г нормированы, их начальные точки
совпадают, т.е. d = 0, а угол взаимного поворота Αφ произволен. НСП
контуров при Αφ ф 0 является комплексным числом
а величина его реальной части будет меньше реальной части при Αφ — 0.
Этим и проявляется, в конечном счете, влияние поворота на расстояние.
Для исключения этого необходимо до вычисления R% повернуть вектор
НСП ηΗ:Αφ (d) = |^η,δ<^ {d)\ exp {ίψ (m)} на угол, равный
В этом случае вектор НСП контуров становится горизонтальным и
направленным вправо, а его реальная часть совпадает с его модулем, т.е.
Не ηΗ,Αφ (d) = \ηΗ,Αφ (d)|. Тогда величина
при данном значении параметра d сдвига начальных точек будет мини¬
мальной. Максимальное значение этого расстояния равно
Лн2тт = 2[1-|%,дЛ^)|тах], «1=0,1,... ,*-1. (3.7.8)
Полученное значение #нтт может определять сходство двух плос¬
ких форм, так как влияние разных масштабов устранено выравниванием
энергий контуров до стандартного единичного уровня, угол поворота меж¬
ду ними сведен к нулю, а сдвиг начальных точек выбран таким образом,
чтобы формы оказались максимально близкими.
Если N = Γμ*\ то в этом случае модуль НСП равен единице и ве¬
личина i^Hinin Для контуров Г и N равна нулю. Чтобы в соответствии с
выражением (3.7.8) найти меру различия форм, задаваемых произволь¬
ными контурами N и Г в виде расстояния п между ними, необходимо:
1) сформировать комплекснозначные коды контуров N = Mn)}o,*-i
η«,Αφ (d) - ехР {*Δν?}?7н (d)
—ψ (т) = —arctg
Rl — 2 [1 — |τ7η,δ<^ (d)|]
(3.7.7)
иГ = {7(n)}0,M;
2) вычислить к значений их НСП
~к — 1
3.8. Сопряженная согласованная фильтрация
115
3) определить модуль каждого из этих НСП \ηΗ (d)|, d = 0,1,... , к — 1,
и выбрать максимальный из них \ηΗ (d)|max;
4) подставить найденное максимальное значение |^н(^)|тах НСП в
выражение (3.7.8) и найти квадрат расстояния между контурами.
Формирование меры сходства на базе КСФ. Выражение (3.7.8) для
оценки сходства форм плоских изображений содержит только одну пере¬
менную - максимальное значение модуля НСП контуров этих изобра¬
жений. Данная величина получается в результате работы КСФ путем
выделения максимума модуля выходной величины η(ά) и деления его
на произведение норм входного контура N и контура Г его ИХ (рис. 3.19).
Рис. 3.19. Структура устройства для оценки степени сходства двух форм
Проведенный анализ показал возможность получения количественной
оценки сходства форм плоских изображений в виде эвклидова расстояния
между комплекснозначными кодами их контуров, рассматриваемых как век¬
торы. Независимость данной оценки от угла поворота, изменения масштаба
изображения и сдвига начальной точки его контура достигается в результате
использования в выражении для расстояния между комплекснозначными
векторами максимального значения модуля НСП этих векторов.
Значение этого модуля получается при фильтрации контура одного из
изображений фильтром, согласованным с контуром другого изображения.
3.8. Сопряженная согласованная фильтрация
3.8.1. Задание векторов в ортонормированием и косоугольном ба¬
зисах Кроме контурной согласованной фильтрации мы рассмотрим еще
два линейных фильтра, параметры которых связаны с характеристи¬
ками изображения. Это инверсный фильтр, или фильтр, согласованный
с сопряженной формой сигнала (ССФ), и согласованно-избирательный
фильтр (СИФ), импульсная характеристика которого определяется кон¬
туром изображения. В данном разделе будет рассмотрена работа ССФ.
На базе такого фильтра эффективно решается задача разрешения, т.е.
разделения перекрывающихся контурных сигналов, с последующим их
обнаружением, оценкой параметров и распознаванием. Работа ССФ свя¬
зана с заданием сигнала в косоугольном базисе. Поэтому предварительно
приведем необходимые сведения из векторного анализа.
Пусть X = {xn)i k — система векторов из η-мерного векторного про¬
странства (нижний индекс при хп является номером вектора). Умножим
каждый вектор на произвольное число ап, п = 1,2и, сложив
116
Гл. 3. Линейная фильтрация контуров
полученные произведения, получим новый вектор у:
к
у = αιΧχ + α2Χ2 + · · - + a*xfc = ^ αηχ„. (3.8.1)
η—1
Вектор у называется линейной комбинацией векторов {χη)ι а чис¬
ла {an}i k — координатами вектора у. Если существует равная нулю
линейная комбинация
к
У = 53 = 0, (3.8.2)
η—1
в которой хотя бы один из коэффициентов ап не равен нулю, то система
векторов называется линейно зависимой.
Определитель линейно зависимой системы векторов равен нулю.
В противном случае система будет линейно независимой. В Аг-мерном
линейном пространстве любые к +1 векторов будут линейно зависимы¬
ми, т.е. в ^-мерном пространстве не существует более, чем к линейно
независимых векторов.
Набор из к линейно независимых векторов ^-мерного векторного про¬
странства Ек называется базисом этого пространства. Пусть {еп}1 к —
такой базис. Любой другой А:-мерный вектор х вместе с векторами базиса
образует систему к+1 векторов, которые будут уже линейно зависимыми.
Тогда
к
X ^ ^ ( Хп) = О,
п=1
где (—хп), п = 1,2,... ,&, — коэффициенты линейной комбинации век¬
торов. Отсюда следует, что
к
х = £ хпеп = χ\&ι + Х2&2 + -.. + хк&к- (3.8.3)
η—1
Числа хп, п = 1,2,... , к, являются координатами вектора х в базисе
{en)i а запись (3.8.3) — разложение этого вектора по векторам базиса.
Если векторы базиса попарно ортогональны, т.е.
= 1° ПР" ίφη' (3.8.4)
lllen|| · ||βχ·|| при j = n,
то базис называется ортогональным или прямоугольным, а при ||еп|| = 1,
η = 1,2,... ,&, — ортонормированным.
Выберем в качестве базиса в Ек векторы {un}1 к, имеющие произ¬
вольную длину и направление. В этом случае получаем косоугольную си¬
стему координат, в которой соотношение (3.8.4) не выполняется. Сравним
методы определения координат вектора в прямоугольной и косоугольной
системах координат.
(е^·, еп)
3.8. Сопряженная согласованная фильтрация
117
Используя (3.8.3), запишем выражение для скалярного произведения
векторов х и un:
(х, и„) = ([ziUi + X2U2 + .. . + ZfcUfc], u„).
Если базис {u„}ofc_1 ортонормирован, т.е.
то
[uj,Un) =
0 при j ф п,
1 при j = п,
(3.8.5)
(х,и„)=жп. (3.8.6)
В косоугольном базисе соотношение (3.8.5) не выполняется и для опре¬
деления координат вектора х вводится еще один косоугольный базис V =
= {vn)i}fc· Базисы U = {iinJ-j к и V = {vn}1 к находятся в биортогональ-
ном соотношении, т.е.
(ui.V
1 при j = п,
О при j ф п.
(3.8.7)
к
Если теперь вектор х = Σ хпип умножить скалярно на вектор vn
п=1
^1 учесть (3.8.7), то получим искомую координату вектора х в направлении
базисного вектора un
(χ,νη)=χη. (3.8.8)
Таким образом, если базисные векторы задают косоугольную систему
отсчета, то для задания в ней произвольного вектора необходимо иметь
еще одну косоугольную систему отсчета, связанную с первой соотно¬
шением биортогональности (3.8.7). Поэтому в теории обработки сигналов
косоугольная система отсчета применяется значительно реже, чем орто-
нормированная. Другим преимуществом ортонормированной системы по
сравнению с косоугольной является совпадение понятий проекций и ко¬
ординат вектора.
В соответствии с выражением (3.8.8) координатами вектора х являются
коэффициенты ап в линейной комбинации
к
χ=^αηιιη, (3.8.9)
п=1
определяемые для случая ортонормированного базиса {un}, к как
ап — (х, и„), η = 1,2,..., к, (3.8.10)
а для случая косоугольного базиса {un}, к с привлечением ортонормиро¬
ванного с ним базиса {vn}, к — как
αη = (χ,νη), η = 1,2,..., к.
(3.8.11)
118
Гл. 3. Линейная фильтрация контуров
В то же время проекция Ъп вектора х на вектор un, угол между
которыми равен φ, записывается в виде
bn = ||x||cosv?=%^, η = 1,2,..., Л. (3.8.12)
||un||
Проекция Ьп есть прилегающий к углу φ катет прямоугольного тре¬
угольника, образованного вектором х и перпендикуляром, опущенным
с конца вектора х на вектор un. Образуем новый вектор у в виде линейной
комбинации базисных векторов U = {un}1 k с весовыми коэффициента¬
ми Ъп, п = 1,2,... , к:
к к
y = £bnu„ = £^un, (3.8.13)
п=1 n=1
и выясним, в каком случае у = х. Для этого скалярно умножим обе части
последнего выражения на вектор и*:
п=1
Если базис U = {un}x к ортонормирован, то ||un|| = 1,
и
(u„,Ui)
1 при η = Z,
О при п ф I,
(y,ut) = (x,Uj).
Таким образом, в ортонормированном базисе проекция Ьп вектора х на
базисный вектор un равна координате αη, п = 1,2,... ,к, этого векто¬
ра х, т.е.
о>п = Ьп, п = 1,2,... , к - 1. (3.8.14)
Пусть теперь U = {un}1 к — косоугольный базис. Образуем сопря¬
женный с ним базис V = {vn}x fc, причем
(«η, Vi)
1 при η = ί,
О при пф1.
(3.8.15)
Умножим скалярно обе части каждого из выражений (3.8.9) и (3.8.12) на
вектор V/, ί = 1,2,... , к. В результате получим
ап = (х, ν„), Ьп
(х, u„), η = 1,2,..., к.
(3.8.16)
Отсюда видно, что при задании вектора в косоугольном базисе его
координаты не равны проекциям на соответствующие базисные векторы:
апфЪт η — 1,2,... , к. (3.8.17)
3.8. Сопряженная согласованная фильтрация
119
У1=в°]. у 2 =[°.1].
ui=[i;2l u2=E2;1].
X = [θ,75;1,25],
ау= [0,75; 1,25], Ьу=[0,75;1,25],
1 21 2 1
з;т} V2=|tt}
—, bi—[l,453;1.300l.
12 12 L J
Рис. 3.20. Представление вектора в ортонормированном и косоугольном базисах
Рассмотрим численный пример. Имеются две базисные системы векторов:
ортонормированный базис Y с ортами yi = {1,0}, уг = {0,1} и косоугольный
базис U = {ui, U2} (рис. 3.20).
Координаты векторов щ и 112 в ортонормированном базисе X равны щ =
= (1, 2) и U2 = (2,1), т.е. щ = yi + 2уг и U2 = 2yi + уг. Сигнальный вектор
х в базисе Y имеет координаты (0,75; 1,25), т.е. αχ,ν = 0,75 и а2,у = 1,25:
х = 0,75yi + 1,25у2.
Его проекции на оси yi и уг будут равны: Ь\уУ =
1|У1
(x,ui) = 0,75 · 1 +
+ 1,25 · 0 = 0,75, Ь2,у = (х, у2) = 0,75 · 0 + 1,25 · 1 = 1,25.
1|У2 [[
Таким образом, координаты вектора х в базисе Y совпадают с его проекциями
на соответствующие векторы базиса: αι,ν = 6i,y = 0,75, а2,у = 62,у = 1,25.
Найдем теперь координаты ai,fc и а2,к вектора х в косоугольном базисе U =
= {ui, U2} и проекции Ъ\ и 62 вектора х на векторы щ и 112 этого базиса. Зададим
вектор х через векторы ui и 112:
х = ai)fcui + a2,fcU2,fc = afcU,
где afc = {ai,fc,a2,fc} и U =
и и
U21
U\2
U22
1 2
2 1
Умножая обе части векторно-матричного равенства на матрицу U"
= xU-1. Обратная матрица U-1 в общем случае будет равна
, получим
и-1
1_
А
U22
-U21
-U12
till
где Δ — определитель матрицы U. В результате для координат вектора х в базисе
U = {ui,U2} найдем
^1^22—^2^21 —iClWl2 + ^2lill Л
Ql,k — д , а>2,к — д , Δ = U11U22 — U12U21-
С учетом конкретных значений координат векторов х, ιΐι, 112 в ортонормиро-
7 1
ванном базисе Y = {уьУг} получаем ai,fc = —г « 0,583; аг /ь = — ~ 0,083,
120
Га. 3. Линейная фильтрация контуров
Легко проверить, что последнее выражение в численном виде равно [0,75; 1,25] =
7 1
= — [1,2] + — [2,1] и представляет собой тождество.
Найдем теперь проекции fei,* и 62,к вектора х на векторы ui и 112 косоуголь¬
ного базиса
Ьм = 1ППГ (*iui) = ([0,75; 1,25], [1,2]) = °;75 + 2’5 « 1,453,
11иЧ1 у 22 +12 v5
Ь.ь = (XlUl) = ~aT Го (f°’75; ^ > t2> 4) = 1,5+/r1,25 « 1-300.
Ilu2|| VI2+22 v 5
Видно, что ai>fc Ф 6i>fc и a2,fc Ф 62>fc.
Из приведенных теоретических сведений и численного примера видно,
что координата ап вектора х — это мера близости векторов х и vn, где
vn — η-й вектор базиса V = {ν^ находящегося в биортогональном
отношении к базису U = {un}1 кУ в котором задан вектор х. В то же время
проекция Ьп вектора х на вектор un — это мера близости векторов х и un.
Если базис, в котором задан вектор х, обладает свойством ортонормиро-
ванности, то координата ап равна проекции ЪПу так как это базис является
самосопряженным. В общем же случае координата ап и проекция Ьпу
п = 1,2,... ,к, являются мерами близости вектора х к разным, хотя
и взаимосвязанным эталонным сигналам, задаваемым векторами {vn}
и {un}. Отсюда становится ясно, что необходимость вычисления множе¬
ства координат {an}i или множества проекций {Ьп}1 к вектора сигнала
х в выбранном базисе зависит от постановки задачи исследования. Если
определяется степень близости обрабатываемого сигнала х к каждому из
эталонных сигналов un, п = 1,2,... , к, то определяются проекции этого
вектора в базисе U = {un}lfc: bn = (х, un), п = 1,2,... , к, а если
к алфавиту сигналов V = {vn}1 fc, находящемуся в биортогональном
отношении к алфавиту сигналов U, то координаты вектора х в том же
базисе U: ап = (х, ν), п = 1,2,... , к.
Отметим, что в любом базисе — ортонормированном или косоуголь¬
ном — базовая операция обработки сигнала сохраняет свой вид и пред¬
ставляет собой скалярное произведение двух векторов, одним из которых
является вектор принятого, а другим — вектор эталонного сигналов.
3.8.2. О соотношении операций разложения и фильтрации вектор¬
ного сигнала. Ранее было отмечено, что в общем случае линейные опера¬
ции над сигналом сводятся к получению скалярного произведения обраба¬
тываемого сигнала с базисными векторами системы отсчета. Существенно
также, что эти операции не приводят к увеличению содержащейся в сиг¬
нале информации: искомый сигнал можно полностью восстановить обрат¬
ным преобразованием. Количество содержащейся в сигнале информации
инвариантно относительно преобразования координат. В связи с этим
возникают два вопроса: с какой целью необходимо переходить из одной
системы отсчета в другую и имеются ли какие-либо преимущественные
системы отсчета?
3.8. Сопряженная согласованная фильтрация
121
Вот что говорит по этому поводу известный математик К. Ланцош
[86]: «Вопрос о «наиболее адекватной системе координат» часто имеет ...
большое значение. Мы можем начать с заданной системы координат, ко¬
торая, возможно, не соответствует общим свойствам ... проблемы. Мы
можем получить лучшую основу для данного анализа, если перейдем от
первоначальной системы к более адекватной системе. Однако в принципе
все системы координат одинаково допустимы. Системы координат можно
сравнить с лесами при возведении здания. Леса не принадлежат зданию.
Они служат только для того, чтобы иметь доступ ко всем участкам зда¬
ния. И после того, как здание сооружено, леса могут быть сняты. Нельзя
смешивать свойства, принадлежащие лесам, со свойствами самого зда¬
ния. Сущность системы состоит в том, что она является вспомогатель¬
ной конструкцией, дающей только возможность некоторого определенного
описания природы, но не принадлежащей к ее подлинной сути».
Ответы на поставленные вопросы заключаются в следующем: вы¬
бор системы координат производится для выявления наилучшим обра¬
зом определенных свойств сигнала. Среди используемых при обработке
сигналов систем координат чаще всего используются два класса систем.
Первая система задается каким-либо ортонормированным базисом,
например, базисом Фурье. При этом понятия координат а = {an}0 k-i
векторного сигнала s = {s (п)}0 к_г и его проекции b = {Ьп}0к_г на
базисные векторы системы отсчета U = {un}0 к_г совпадают, т.е. а = Ь.
Определение векторов а = b в данном случае называют разложением
сигнала s в базисе U, а компоненты этих векторов — спектром сигнала
s. В результате разложения s на базе операции скалярного произведения
(s,un), п = 0,1,... ,& — 1, мы находим набор мер близости к некоторой
системе стандартных сигналов, определяемых U. Выбор этих стандарт¬
ных сигналов определяется задачей анализа сигнала s.
Чаще всего используется базис Фурье, что вызвано следующими при¬
чинами. Мы живем в мире акустических, электромагнитных и других
полей — музыки, речи, радиоволн, излучений в инфракрасном, опти¬
ческом и ультразвуковом и др. диапазонах. Внутренняя структура этих
явлений хорошо интерпретируется лежащими в их основе синусоидаль¬
ными колебаниями с разными амплитудами, частотами и фазами. На¬
ши органы чувств — слух и цветовое зрение обеспечивают восприятие
окружающего мира именно с этих позиций. Кроме того, синусоидальное
колебание относится к классу собственных функций линейного операто¬
ра: сигнал в виде синусоиды при линейных преобразованиях, например,
фильтрации, сохраняет свою форму. Преобразование Фурье позволяет
найти скрытые регулярности, обычно трудно выявляемые при временном
представлении сигнала. Оно обладает следующим замечательным свой¬
ством: если выполнить обратное преобразование с целью восстановле¬
ния исходного сигнала через его проекции (координаты), отбросив при
этом часть проекций (координат), то среднеквадратическая погрешность
восстановленного сигнала будет меньше, чем при использовании любого
другого приближения сигнала [86].
122
Гл. 3. Линейная фильтрация контуров
Вторая система векторов U, используемая для анализа векторного
сигнала s, связана не с системой стандартных функций, как первая, а с
самим сигналом s. Проведение такого анализа называется фильтрацией
сигнала. При этом система U = {un} не обязательно должна предста¬
влять ортогональный базис, и даже просто базис, т.е. к линейно независи¬
мых векторов, где к — размерность векторного пространства. Векторы un,
п = 0,1,2,..., могут быть линейно зависимыми, а угол между ними и их
количество — произвольными. Задача фильтрации связана с нахождени¬
ем мер близости векторного сигнала с каждым из векторов un системы U
в виде проекции
Ьп = (s,un)/||u„|| (3.8.18)
вектора s на вектор un. Действительно, в соответствии с п. 3.2, работа
линейного фильтра описывалась выражением свертки
к-1
η (т) = ^ s (п) λ (га — n), т = 0,1,... , к — 1. (3.8.19)
η=0
Представим это выражение в виде ВКФ двух векторных сигналов s
и un:
к-1
η (га) = ^ s (п) и(п — т). (3.8.20)
п—0
Сравнивая эти выражения, приходим к выводу, что ИХ фильтра
должна быть равна
А(г) = ti(-r), (3.8.21)
или, учитывая условие физической реализуемости фильтра,
\(г) = и(к-1-г). (3.8.22)
Тогда выражение (3.8.19) примет вид
к-1
η (га) = ^ s (п) и (п — т + к — 1), га = 0,1,...
,к- 1,
(3.8.23)
п=0
ИЛИ
η(τπ) = (s,uk-i-m), m = 0,l, ...,к
- 1.
(3.8.24)
Сравнивая (3.8.18) и (3.8.24), видим, что при ||щ_1_п|| = 1 они от¬
личаются лишь номером вектора, входящего в состав системы U. Таким
образом, линейный фильтр вырабатывает значения последовательности
проекций сигнала s на векторы системы U, или, что то же самое, отсчеты
ВКФ сигнала s с векторами этой системы.
Отметим важную особенность векторов системы U = {щ_1_ш}0
Их компоненты и порядок следования компонент одинаковы, а один вектор
отличается от другого лишь номером начальной компоненты. Выписывая эти
векторы в виде столбца, получим определяющую работу фильтра матрицу
3.8. Сопряженная согласованная фильтрация
123
\ т
0
1
2
к — 1
п\
0
" и (к — 1)
и (к - 2)
и {к — 3)
и (0) '
1
и (к)
и{к — 1)
и (к — 2)
и (1)
U= 2
и (к -f 1)
и (к)
и (к — 1)
.. и (2)
А;- 1
.и (2к — 2)
£
'ίο
?г*
1
со
и (2к — 4) ..
.. и (&-!)_
Принимая во внимание свойства периодичности компонент векторов
u(ri ак) = и (г), представим эту матрицу в виде
\^т
0
1
2
к — 1
0
*и (к — 1)
и (к — 2)
и (к —
3) ...
и(0)
1
и (к)
и (к — 1)
и (к —
2) ...
«(1)
(3.8.25)
d
II
ю
«(!)
и(0)
и (к —
1) ...
«(2)
к- 1
М (к — 2)
е
1?
1
со
и (к —
4) ...
и (к — 1).
С учетом матричного представления ИХ линейного фильтра его работа
описывается следующим векторно-матричным выражением: Н = sU, где
Н = {»7 (0), 77 (1),... ,v(k- 1)}.
Система отсчета из линейно независимых векторов U образует в об¬
щем случае косоугольный базис. Она имеет важнейшее значение в теории
обработки сигналов, так как решение основных задач — обнаружение,
разрешение, распознавание и оценка параметров, сводится к нахождению
в ней проекций сигнала s. Особенно интересным является случай, когда
векторы Uk-ι-m представляют собой смещенные копии фильтруемого
сигнала s. Такую систему отсчета назовем собственной или естественной.
Получающийся при этом фильтр является согласованным. Он формиру¬
ет количественные меры схожести (3.8.24) сигнала s с каждой из своих
смещенных копий.
3.8.3. Разложение сигнала в собственной системе отсчета. Собствен¬
ная система отсчета состоит из системы векторов, представляющих собой
сдвинутые копии вектора сигнала s = u0. Название системы подчеркивает
тесную связь между вектором сигнала ио и векторами системы отсчета.
Для обозначения базисных векторов заменим букву «и» на букву
«s», т.е. соответствующую систему отсчета будем задавать как S =
= {sk-i-m}o k-i- Матрица собственной системы отсчета примет вид
~s (к — 1)
s (к — 2)
5 (* - 3) . .
s (0)
5(0)
s (к — 1)
s (к — 2)
. 5(1)
5(1)
*(0)
s(jfc-l) ..
. 5(2)
(3.8.26)
1
со
1?
1
to
со
*5?
1
со
s (к - 4) ..
. s (к — 1).
124
Гл. 3. Линейная фильтрация контуров
Вектор последнего столбца равен самому сигналу, т.е. So = s. Все
базисные векторы имеют одинаковые наборы компонент, поэтому
|ЫЫЫ = ... = ||sfe-i|| = |MI· (3.8.27)
Определим координаты сигнального вектора s в собственной системе
отсчета, т.е. найдем вектор а = {am}0 fc_1, компоненты которого являются
весами в линейной комбинации векторов Sfc_i_m, т = 0,1,... ,к — 1,
равной s:
к-1
s = Σ amsk-l-m· (3.8.28)
т=0
Для этого введем сопряженную к S систему V = {vfc_i_m}0 к_х, где
Vfc_i_m = {ν (п — т + к — 1)}0 fc_1; S и V образуют биортогональную
систему отсчета, т.е.
= i1 nPMm = Z’ (3.8.29)
[О при тф1.
Последнее соотношение в матричном виде запишется как SV = I,
I — единичная матрица. Отсюда следует, что матрица сопряженной си¬
стемы отсчета обратна матрице, задающей собственную систему отсчета,
т.е. V = S-1. Обе части выражения (3.8.28) скалярно умножим на век¬
тор Vk-1-ι, 1 = 0,1,... - 1 :
к-1
(s, vfc_i_z) = am (sfc_i_m,vk_i_z) = а/.
т=О
Таким образом, координаты am, m = 0,1,... ,к — 1, вектора сигнала
s в собственной системе отсчета равны скалярному произведению векто¬
ров S И Vk-1-т :
ат — (s?vfc — 1—m) 5
т = 0,1,..
• ,к- 1,
(3.8.30)
или с учетом того, что So = s,
= (s0 ? Vk — 1 — τη) ·.
, т = 0,1,.
.. , к — 1.
Принимая во внимание соотношение биортогональности (3.8.29), при¬
ходим к выводу, что
&7П
{1 при т = к — 1,
0 для остальных т.
Данное выражение определяет смещенный символ Кронекера, т.е.
= {0,0,... ,0,0,1}. (3.8.31)
Таким образом, все координаты сигнального вектора s в собственной
системе отсчета, за исключением последней α^-ι, равны нулю. Данное
обстоятельство становится понятным, если учесть, что вектор сигнала s =
= so ортогонален каждому из базисных векторов v^_i_m собственной
3.8. Сопряженная согласованная фильтрация
125
системы отсчета, за исключением последнего из них Vo. В свою очередь
скалярное произведение (so, vo) = 1.
Если же фильтруется зашумленный сигнал u = s + η, то любая из его
координат
dm ~ (^, Vfc_ 1—m) — (s, V^_i_m) “h (π, Vfc_i—m) ? ^ 0,1,... , к 1,
может оказаться не равной нулю. В отличие от случая обычной согла¬
сованной фильтрации здесь лишь координата dk-i будет содержать по¬
лезную сигнальную составляющую, а все остальные — только шумовые
составляющие. В результате разница между пиковым и любым другим от¬
счетом будет больше, что в итоге увеличивает отношение сигнал/помеха.
Рассмотрим теперь фильтр, вырабатывающий отсчеты в виде коор¬
динат вектора s. Такой фильтр был назван сопряженным согласованным
фильтром (ССФ). На основании выражения (3.8.27) скалярное произве¬
дение (3.8.30), выраженное через компоненты векторов s = {s (п)}0 к_г
и Vk-1-т = {ν(η-πι +к - 1)}0>А._1, примет вид
к-1
ат = ^2 s (n) v (п — т + к — 1), т = 0,1,... , к — 1. (3.8.32)
7П=0
Определим частотный коэффициент передачи фильтра в виде отно¬
шения спектров выходного рвых (га) и входного рвх (га) сигналов
ω (т) = , m = 0,1,... ,к — 1. (3.8.33)
Рвх yd)
ДПФ выходного сигнала (3.8.31) фильтра равно
К — 1
Рвых (т) = Σ ап ехР {~*Xmn} =
п=0
= dk-ι exp г^га (к — 1)| = exp |г^га|.
Тогда
ω (т) = —-—- ехр (г'^га}, т — 0,1,... , к — 1. (3.8.34)
Рвх {dl) L Л J
Полагая
Рвх (т) - |рвх (т)| ехр {ίφ (т)},
для АЧХ и ФЧХ сопряженного согласованного фильтра получим
1 2π
l^(m)l ~ arga;(m) = т = 0,1,... ,к- 1.
(3.8.35)
Таким образом, АЧХ фильтра обратно пропорциональна амплитуд¬
но-частотному спектру сигнала, а ФЧХ повторяет с обратным знаком
и дополнительным слагаемым задержки фазочастотный спектр эталон¬
ного сигнала. Подобного типа фильтры называются инверсными [21].
126
Гл. 3. Линейная фильтрация контуров
Таким образом, при фильтрации сигнального вектора s согласованный
фильтр вырабатывает сигналы в виде проекции вектора s на базисные
векторы S = {sfc_i_m}0 k_x собственной системы отсчета, а сопряженный
согласованный фильтр — в виде координат вектора s в этой системе от¬
счета. Отметим, что система отсчета S = {sfc_i_m}0 к_г должна содержать
линейно независимые векторы. В противном случае матрица S не будет
иметь обратной и нельзя построить биортогональную систему отсчета.
3.9. Фильтрация широкополосного шумового контура
Решение таких важных задач обработки контуров как их обнаруже¬
ние, оценка параметров, разрешение и распознавание, связаны с вопросами
фильтрации шумового контура Ζ - {ζ (п)}0 к_х = {ζχ (η) + ζ2 (n)}Qtk_v
одна из моделей которого описана в п. 1.7. Для данной модели шумового
контура Z, действующего на входе контурного линейного фильтра, найдем
такие характеристики выходного контура Η = {η (га)}0 k_lf как:
1) корреляционную функцию и дисперсию;
2) корреляционный момент вещественной и мнимой частей его ЭВ;
3) распределение вероятностей модуля и аргумента ЭВ;
4) распределение вероятностей квадрата модуля ЭВ.
3.9.1. Корреляционная функция и дисперсия процесса на выходе
фильтра. Определим характеристики дискретного случайного процесса
на выходе контурного линейного фильтра. Среднее значение выходно¬
го комплекснозначного шума с учетом выражения (1.7.6) равно rj(s) =
к-1 _
= Σ λ (η) ζ (s — n) = 0. Тогда выражение для выходной АКФ
п=0
-Квых (т) = V (s) η (s + m) = Μ(f? (s) V (s + m)),
О
где V (s) = η (s) — rj(s) — центрированное значение η (s), примет вид
К-ВЫХ (jft)
{к-1
Σ
η—О
Λ (η) ζ (s — π)
У] Λ (η) ζ (s — η + 771)
Комплексно сопряженная сумма (произведение) чисел равна сумме
(произведению) комплексно сопряженных чисел. Поэтому
к-1
л
О
-Кцых (т) = м\ Σ λ (п) С (« - λ* (n) C*(s-n + m
[-
к — 1 к—1
= Σ 53 λ (η) Λ* (r)M{C (s - n) C* (s + m - r)}.
n=0 r=0
3.9. Фильтрация широкополосного шумового контура
127
Принимая во внимание выражение (1.7.4), получаем
к-1к-1
Квых (га) = 2<Т ΣΣ λ (η) Л* (г) δ (г — η — га).
п=0г=0
Данное выражение равно нулю для всех значений г, кроме г = п + га.
В результате
к-1
Къых (га) = 2σ2^ λ (η) Λ* (η + га), га = 0,1,... , к — 1. (3.9.1)
η—О
Отсюда следует, что комплекснозначный случайный процесс на вы¬
ходе линейного фильтра будет коррелированным, причем максимальное
значение АКФ, достигаемое при га = 0, равно
к-1
Квых (0) = £>вых = а2вых = 2σ2Σ |λ (η)|2 = 2σ2||Λ||2. (3.9.2)
п=0
Таким образом, мощность выходного шума пропорциональна квадрату
нормы контура ИХ фильтра. Приведем выражение для коэффициента
корреляции выходного шумового процесса
к-1
Двых (т) = = 1 Λ (η) λ* (п + ш). (3.9.3)
Вяа 11АИ п^о
3.9.2. Корреляционный момент вещественной и мнимой частей ЭВ
выходного шумового контура. Элементарный вектор шумового контура
на выходе фильтра равен
к-1 ι
Vai («) = λ С (« - n) = Vaii («) + Щш2 (s) . S = 0,1,. .. , fc - 1,
n—0
причем ζι (n) Ci (η) = & (л) С2 (л) = σ2δ (га). Определим корреляцион¬
ный момент случайных величин ηШ1 (s) и η^2 (s):
к-1
Vai (5) = [λΐ (η) + г\2 (η)][Cl (s - η) + ίζ2 (s - η)] =
п—0
к-1
= Σ){[λι (η) Cl (s - η) - λ2 (η) Сг (δ - η)] +
η=0
+ г [λι (η) Сг (s-n)- λ2 (η) Ci (s - η)]}. (3.9.4)
Отсюда получаем
к-1
Vai! (s) = Reifa (s) = Σ [Ai (n) Ci (s-n) - Λ2 (n) Сг (s - n)],
n—0
128
Гл. 3. Линейная фильтрация контуров
к-1
Пш2 («) = 1т%1 (я) = 53 [λι (η) Сг (s - ») - λ2 (η) Cl (s - η)].
η=0
В общем виде выражение для корреляционного момента величин рШ1 (s)
и Т]Ш2 (s) записывается следующим образом:
к-1
Kftoutmi8) = Чш1 00 »7ш2 (s) = 53 Κι (s “ η) λι (n) - Сг (s - η) λ2 (n)] x
n=0
fc-1
x 53 [C2 (s _ n)λι (n) — Ci (s — n) λ2 («)]· (3.9.5)
n—0
При перемножении этих сумм для одного и того же значения аргу¬
мента получаются слагаемые четырех видов, дающих при усреднении:
1) Cl (3 - п) Сг (а ~ п)А? (п) = 0;
2) Ci (а ~ п) Ci (з ~ η)Αι (η) λ2 (η) = <τ2λι (η) λ2 (η);
3) -Сг (s ~ η) Сг (s - η)Λι (η) λ2 (η) = -σ2λχ (η) λ2 (η);
4) -Ci Ο - η) ζ2 (s - η)\\ (η) = 0.
При перемножении слагаемых сумм (3.9.5) для разных значений аргу¬
ментов из независимости случайных величин (д (n), С2 (n), ζϊ (г) и ζι (г),
η ф г, га, г = 0,1,... , к — 1, получим при усреднении для каждого про¬
изведения нулевые значения. В результате искомый корреляционный мо-
мент будет равен нулю, т.е. КПш^ ,Пш2(я) = 0, s = 0,1,... , к — 1.
3.9.3. Плотности распределения вероятностей случайных величин
на выходе фильтра. Плотность распределения вероятностей веще-
ственной и мнимой частей выходного вектора фильтра. Из выражения
(3.9.4) для (s) фильтра видно, что как действительная, так и мнимая
его части получаются при суммировании большого количества нормаль¬
но распределенных случайных величин. Поэтому законы распределения
вероятностей для рШ1 и рШ2 будут также нормальными.
Рассматривая рш (s) как двумерную нормально распределенную слу¬
чайную величину с корреляционным моментом RVm ,ηαΐ2 (3.9.3), для плот¬
ности ее вероятности можно записать
Р (Пт (s)) — Р (lull (s) j Vui2 (s)) —
1
2πσ2||Λ||:
exp
2σ ||A||-
frm, («) + νί2 (*)] f- (3-9.6)
Из некоррелированности нормально распределенных действительной
и мнимой частей η следует их независимость. Таким образом, комплекс¬
нозначные шумовые векторы на выходе линейного фильтра коррелиро-
ваны, в то время как вещественные и мнимые части отдельного вектора
не только не коррелированы, но и независимы между собой.
Плотность распределения модуля и аргумента выходного вектора.
Перейдем в распределении Р(pm(s)) от переменных г/Ш1 (s) и 77Ш2 (s)
3.9. Фильтрация широкополосного шумового контура
129
к переменным Ι77 (s)| и ip(s), т.е. к модулю и аргументу вектора уш (s).
При этом учитываем, что |??ш(«)|2 = |»Ъ, (s)|2 + |»fa2 («)|2. Imi (а) =
= |т?ш (s)| cosф (s), ?7ш2 (s) = |т7ш (s)| sinф (s). Якобиан этого преобразо¬
вания
Тогда
D =
cos ф (s)
sin^> (s)
— |*7ш (s)l 5т.ф (s)
\fhn (s)l cos ip(s)
= l*ftn (e)l-
P(\Vm(s)\,1p(s)) = ^4All2 eXP(~·
2πσ ||Λ|| ( ■
^||А|Г
(s^cos2^^) 4- |т?Ш2 (s)|2 sin2 ψ (s)j | =
l»fo (a) I
2πσ2||Λ||2
ы-)Л \
2σ2||Λ||2 J
(3.9.7)
Плотность распределения вероятности модуля выходного шумового
вектора. Проинтегрируем распределение Р (\уш (s)|, ф (s)) по всем зна¬
чениям ф (s):
Р (\пш (5)1) = | Р (\Лш (в)\,ф (в)) άφ (s) exp }·
° (3.9.8)
Данное выражение показывает, что величина |77ш (s)| подчиняется рас¬
пределению Релея. При этом среднее значение модуля \уш\ = 1,253σ||Λ||,
дисперсия D{\уш\} = 0,4292σ2||Λ||2 и среднеквадратическое отклонение
σ\ηω\ = 0,655σ||Λ||.
Плотность распределения вероятности аргумента выходного шу¬
мового вектора. Для определения искомой плотности проинтегрируем вы¬
ражение (3.9.7) по всем значениям |?7Ш (s) |:
Р(ф(в))
^(|%i(s)|,^(s))d|»b(s)| =
2πσ ||Λ||
оо
■ J hm(s)|exp|-
l*fci (s)\
'2σ2||Λ||2
d\rjui (s)|·
00
Используя значение табличного интеграла J zexp{z/2}dz = 1 [26], по-
o
лучаем Р (ф (s)) = 1/(2π), т.е. величина ф (s) имеет равномерное распре¬
деление. При этом среднее значение ф (s) и дисперсия D (ф (s)) равны
соответственно ф (s) = π и D (ф (s)) = 2π/3.
Плотность распределения вероятности квадрата модуля выходного
шумового вектора. С вычислительной точки зрения |?7Ш (s)|2 является бо¬
лее удобно определяемой выходной величиной, чем сама величина |77ш (s)|.
130
Гл. 3. Линейная фильтрация контуров
В этом случае не надо вычислять квадратный корень при вычислении
норм контуров для получения результата фильтрации в нормированном
виде, т.е. в виде \ηΗ (s)|2 = (77 (s)|2/[||N||2||A||2]. Выше было показано, что
плотность распределения вероятностей модуля выходного шумового век¬
тора подчиняется закону Ре лея (3.9.8). Вводя новую случайную величину
в виде \т]ш (s)|2, по правилам нахождения преобразованных плотностей
распределения вероятностей [25] получаем, что величина |7уш (s)|2 подчи¬
няется экспоненциальному закону [26]
P(l,-w0 = i?iixpexp{-5?i^}' (3">
Это распределение характеризует мощность шума на выходе фильтра.
Числовые характеристики этого распределения равны \η^\2 = 2σ2||Λ||2,
я{Ы2}=4<74||Л||4
3.10. Согласованная фильтрация зашумленного контура
Рассмотрим один частный, но важный случай фильтрации зашум¬
ленного контура N = Г + Ζ, когда фильтр согласован с контуром Г.
Статистическая модель зашумленного контура была описана в п. 1.7. Нас
будут интересовать, как и в п. 3.9, характеристики выходного контура,
но для одного, (к — 1)-го отсчета фильтра, когда достигается пиковое
значение выходного сигнала КСФ. В соответствии с выражением (3.6.1)
для данного случая получим
к-1 А: —1
η = η (к - 1) =5^1'(η) 7* («) = Σ Wi {n) + iu2 (n)][7i (n) - ιη2 («)] =
n=0 n=0
k — 1
= Σ ft"1 (n) 71 (n) + v2 (n) 72 (n)] + i[v2 (n) 71 (η) - νλ (n) 72 (n)]}.
n—0
(3.10.1)
3.10.1. Корреляционный момент вещественной и мнимой частей вы¬
ходного вектора КСФ. Покажем, что для случая согласованной филь¬
трации в момент m = к — 1, так же как и для случая фильтрации шумо¬
вого контура Z, вещественная и мнимая части выходного вектора будут
некоррелированными. Определим вначале математические ожидания πιηι
и πιη2 величин 771 и 772*
__ __
η = rn + гЩ = Σ " 7* (η) = Σ [ύ (п) + с (П)Ь* (п) =
п=0 п=О
= Σ7 (η)7* (η) + Σ ^ (п)7* (")= иг112·
п=0 п—О
3.10. Согласованная фильтрация зашумленного контура
131
Таким образом, тт = ||Г||2 и тт = 0. Запишем выражение для кор¬
реляционного момента величин щ и 772: Ктт = Λ^{77ι,772} - тттт =
= M{?7i, 772}. С учетом (3.10.1) будем иметь
к-1 к-1
Κηιη2 — Σ iui (п) ^ (n)+1/2 (n) ^ (η)ΐΣ (η)71 (η) -1/1 (η)72 (»)]·
η—0 η=0
При перемножении сумм для одного и того же значения аргумента
получаются слагаемые следующих четырех видов:
1/1 (гг) 1/2 (η) 7ι (η), - Ι/χ (гг) I/! (η) 7ΐ (η) 72 (η),
ι/2 (η) ι/2 (η) 7ι (η) 72 (η), - 1/1 (η) ί/2 (η) 72 (η).
После перемножения величин в этих слагаемых и усреднения соот¬
ветственно получаем
7ι3(η)72(η), - 7? (η) 72 (η)-7ι (η) 72 (η) σ2,
7ι (η) 72 (и) + 7ι (λ) 72 (η) σ2, - 7ι (™) 72 («) ·
Для неравных между собой значений аргументов в суммах выражения
для Ктт также получаем четыре вида сомножителей, для которых после
усреднения можно записать
1/1 (η) 71 (п) 1/2 (s) 71 (s) = 7? (n) j2 (s) 71 (s),
-1/1 (n) 71 (n) 17 (s) 72 (s) = —7i (n) 71 (s) 72 (s),
V2 (n) 72 (ra) i/2 (s) 71 (s) = 7! (n) 71 (s) 72 (s), (3.10.3)
-^2 (n) 72 (n) z/i (s) 71 (s) = -7I (n) 71 (s) 72 (s),
n, s = 0,1,... , k — 1.
С учетом выражений (3.10.2) и (3.10.3) получи^, что КтП2 = 0.
3.10.2. Плотность распределения вероятностей зашумленного выход¬
ного вектора фильтра. Распределение вероятностей вещественной
и мнимой частей выходного вектора. Как следует из (3.10.1), действи¬
тельная 77ι и мнимая 772 части выходного вектора КСФ будут результатом
суммирования большого количества нормально распределенных величин
и поэтому также имеют нормальное распределение. При этом математи¬
ческие ожидания, дисперсии величин 771 и 772 и их корреляционный мо¬
мент в соответствии с выражением (3.10.2) и выражениями, полученными
в 3.10.1, будут равны
Пт = 11г1|2> mV2 = 0, σ2, = <т22 = σ2||Γ||2, Кщт = 0. (3.10.4)
Для плотности распределения вероятности величин (771,772) теперь
можно записать
Ρ(η) = Р (771,772) =
2πσ ||Г||
exp < -
(т-||г||2)2 + 72
2<г2||Г||2
(3.10.5)
132
Гл. 3. Линейная фильтрация контуров
Плотность распределения вероятностей модуля и аргумента вы¬
ходного вектора. Модуль вектора η и тригонометрическое представление
его частей равны |ту|2 — η\ ту|, ηι = |t7|cos<£>, 772 = \η\βιηφ. Якобиан
преобразования для определения искомой плотности распределения по-
прежнему равен \η\. Тогда
Ρ{\ν\,ψ) =
ы
27τσ2||Γ|ϊ
exp
[(|i?|cosv>- ||Г||2)2] + |?j|2 sin2 ψ 1
_ hi
2πσ2||Γ||2
exp
{
ы2 +
Ι|Γ||4 — 2|[Γ||2|τ?| cosy?
2σ2||Γ||2
Плотность распределения вероятностей модуля выходного векто¬
ра. Интегрируя распределение Ρ(\η\,φ) по всем значениям аргумента
выходного вектора, получим
р(ы)=?«
о
_ ы
^21|г|Г
ехр
ί Η’ + ΙΙΓΙΙΜ, ЛчГ\
2 2π
гдеΙ0 (\η\/σ2) = — J exp{{\η\/σ2) cos φ]άφ — модифицированная функ-
2π 0
ция Бесселя нулевого порядка от мнимого аргумента. Учитывая неотри¬
цательность величины модуля вектора η, для плотности распределения
вероятности его модуля можно записать
и
Р (|?7|) = ехр /
σ2||Γ||2
Ы2 + 1|гц4
2σ2||Γ||2
если \η\ > О,
Р (М) — 0 при |ту|<0. (3.10.6)
Данное распределение является распределением Райса. Рассмотрим слу¬
чай больших отношений сигнал/шум. При этом выходной эффект КСФ в
основном определяется контуром фильтруемого изображения, т.е. 77» ||Г||2«
&\η\ и \η\^$>σ2. При выполнении последнего условия для модифицированной
функции Бесселя существует следующее разложение в ряд [47]:
1о (У) =
ехр {!/}
л/2тгу
1 -]—1—|
% 2! (8т/)2
225
3! (8у)3
у» 1. (3.10.7)
В данном случае у = \η\/σ2, и, принимая во внимание (3.10.7), получим
3.10. Согласованная фильтрация зашумленного контура
133
Таким образом, при больших отношениях сигнал/шум модуль выходного
вектора КСФ в момент т = к — 1 имеет распределение вероятностей,
близкое к нормальному. При этом математическое ожидание модуля век¬
тора η равно |7у| = ||Г||2. Выразим распределение (3.10.6) через отноше¬
ние сигнал/шум <7ВЫХ по длине линии контура на выходе фильтра двых =
= ||Г||2/Ы|ГЦ] = 11Г11/σΒΧ. Введя переменную ν = \η\/σΒαχ = |ί?|/[σΒΧ||Γ||]
и переходя к ней в распределении (3.10.6), получим
'•М-'Ш =>'«=φ{-!4^}ΐο(^).
Плотность распределения вероятности аргумента выходного век¬
тора. Интегрируя распределение Р (|7у|, φ) по всем значениям модуля М,
получим
Ρ{ψ) = | Ρ(.\η\,<ρ)ά\η\ =
0
_ βχρ{||Γ||72σ^}||77|
2πσ
exp
M2-2||r|l2Hcos^
2σ2||Γ||2
}<*Μ·
Это выражение приводится к виду
PW = ^e»p{-1P-} +
+ Ete^l + erf(g^g^exp{-l|r|iyyl,
2 ^
где erf (х) = exp {— t2}dt — функция ошибок. При ||Г||/сг > 3, т.е.
νπ о
при достаточно большом отношении сигнал/шум, данное распределение
переходит в нормальное, а при ||Γ||/σ<^3 все значения аргумента выход¬
ного вектора становятся равновероятными [25].
3.10.3. Функции правдоподобия зашумленного и шумового конту¬
ров. При подстановке в качестве независимых переменных в выраже¬
ние fc-мерной плотности вероятностей р (и), найденной в процессе стати¬
стического эксперимента fc-мерной выборки \у (n)}0 k_v получим функ¬
цию Λ (N), называемую функцией правдоподобия. Эта функция по форме
своей записи совпадает с выражением для плотности распределения веро¬
ятностей, но зависит уже не от г/, а от параметров данного распределения,
т.е. от математического ожидания, дисперсии и др. Функция Λ (Ν) явля¬
ется мерой схожести распределения р (и) и распределения, к которому
относится выборка Mn)}o,k-l-
Найдем выражение для функции правдоподобия зашумленного кон¬
тура N = {^(™)}ο*.-ι при условии, что его модель обладает свойства¬
ми, описанными в п. 1.7. Запишем выражение для совместной плотно¬
134
Гл. 3. Линейная фильтрация контуров
сти вероятностей вещественной и мнимой частей ЭВ ν (η) = ν\ (η) +
+ ϊι/2 (η), η = 0,1,... , k — 1, зашумленного контура Ν. При этом учтем,
что математические ожидания случайных величин ν\ (п) и V2 (п) равны
1/1 (п) = 71 (я) + Cl (п) = 7ι (я), ν2 (я) = 72 (я) + Сг (я) = 72 (я), а их
корреляционный момент
къ(п)М*) = [71 (") + Ci (η)][72 (я) + С2 (я)] - 71 (я) 72 (я) =
= 7ι (п) Сг (я) + 72 (я) Ci (я) + Ci (я) <2 (я) +
+ 71 (я) 72 (я) - 71 (я) 72 (я) = 0.
С учетом полученных значений для параметров v\ (я), 1/2 (я) и
KV1 (η)ι/2(η). а также независимости случайных величин Ci (я) и Сг(я)
выражение для fc-мерной плотности распределения вероятностей веще¬
ственной и мнимой частей ЭВ зашумленного контура будет иметь вид
P[v 1 (0), vx (1), · · · , ιί (к - 1), и2 (0), v2 (1), ·.. , ι*2 (к - 1)] =
= сехр |-^2 [νι (я) - 71 (п)]2 + Ь (я) - 72 (я)]2 j =
= сехр {-^ [||N||2 + ||Г||2 - 2Re (N, Г)] }, (3.10.8)
с = 1 j (2πσ2γ.
После того как в это выражение будут подставлены конкретные зна¬
чения ЭВ ι/(η), п = 0,1,... ,fc — 1, получим функцию правдоподобия
Λ (N) зашумленного контура. Для случая чисто шумового контура N =
= Z функция правдоподобия принимает вид
A(Z) = cexp{-^||N||2}. (3.10.9)
Отметим тот факт, что выражение ||N||2 + ||Г||2 — 2Re(N,r) равно
квадрату расстояния R2 между зашумленным N и эталонным Г конту¬
рами. Поэтому
Λ (N) = Л (Г + Z) = сехр {-Я2/2σ2}. (3.10.10)
Отсюда становится ясным физический смысл функции правдоподобия
зашумленного контура: если контуры N и Г близки между собой, то R2 « О
и Λ (Ν) = Л (Г + Ζ) = с, т.е. равна максимально возможной величине.
3.11. Сравнительная эффективность фильтров, согласованных
с исходным и сопряженным сигналами
3.11.1. Эффективность подавления широкополосных шумов контур¬
ным согласованным фильтром. Пусть на вход КСФ подается зашум¬
ленный контур N = Г(с) + Ζ. Здесь Ζ — шумовой контур, а Г(с) =
= |μ| ехр{гД<р}Г — сигнальный контур, полученный масштабированием
3.11. Сравнительная эффективность фильтров
135
и поворотом эталонного контура Г. Сам фильтр согласован с контуром Г.
Аддитивное представление контура N дает возможность записать ре¬
зультат фильтрации в виде суммы реакций фильтра на сигнальный Г*(с)
и шумовой Ζ контуры, т.е. η0 (s) + 7?ш (s). Эффективность КСФ определим
как выигрыш г = Явъ1х/явх в отношении сигнал/шум по энергии на выходе
и входе фильтра.
Получим вначале величину д2х. Для этого учтем, что ЭВ сигнального
контура Гс = {7с (п)}0 к_г последовательно поступают на вход фильтра
и текущее значение энергии полезного сигнала при этом будет EBXt с (п) =
= 7с (п) 7* (п) = |7с (п)\2, п = 0,1,... , к - 1. Так как ЭВ контура
принимают произвольные значения, то целесообразно перейти к сред¬
нему значению энергии сигнала на входе фильтра Евх>с = ||Г(С)|| /к.
Аналогично можно говорить о средней энергии ЭВ ζ (η), η = 0,1,...
... , к - 1, шумового контура EBXt ш = 2σ2. Усредненное входное отноше¬
ние сигнал/шум будет равно
2 -^1
<7вх = =-
*вх Еъ
_ \К
(с)||2
2 *<7
(3.11.1)
При согласованной фильтрации после предварительного изменения
фазы и модуля компонент входного сигнала происходит их суммирова¬
ние. Далее каждая компонента задерживается таким образом, чтобы при
образовании выходного сигнала все эти компоненты существовали одно¬
временно. При фильтрации сигнального контура Г(с) фильтром, согла¬
сованным с эталонным контуром Г, пиковое значение модуля выходного
сигнала будет равно |f7(so)| = |μ| ||Г||2. Если начальные точки контуров
Г(с) и Г совпадают, то s0 = к — 1. В общем случае такого совпадения нет,
поскольку So может быть любым числом в пределах от 0 до к—1. Величина
|?7 (so)| обычно используется в качестве полезного отсчета фильтра, по¬
этому целесообразно определить выходное отношение сигнал/шум лишь
для этого значения s.
Согласованный фильтр будем рассматривать как совокупность двух
независимых звеньев — косинусного и синусного, вырабатывающих соот¬
ветственно сигналы 771 и 772:
η (s) = 771 («) + irl2 (s) =
k — 1
= ^ \v (7г)||7 (n — s 4- к — 1)| cos [ψ (n) — φ (n — s + к — 1)] -f
n=0
k-1
+■!> (n)||7 (n - s + к - 1)| sin [ψ (n) - φ (n - s + к - 1)], (3.11.2)
n=0
где ψ(η) η φ (n) — соответственно аргументы ЭВ и (п) и 7 (7г). Найдем
вначале эффективность фильтра для полностью известного контура, т.е.
когда начальные точки фильтруемого и эталонного контуров совпадают,
136
Гл. 3. Линейная фильтрация контуров
\μ\ = 1 и Αφ = 0. В этом случае Г(с) = Г, s0 = к — 1. Часть выходно¬
го сигнала, а именно η0 (к — 1), образованная только полезным входным
сигналом, равна ||Г||2, а его энергия — i£BbIX|I1I = ||Г||4. При этом энергия
шума в соответствии с (3.9.2) на выходе будет Евых>ш = 2σ2||Γ||2. Тогда
эффективность фильтрации
г
Явых
я1х
||Г||4 2 ка2
2σ2||Γ||2||Γ||2 “
(3.11.3)
Отметим, что для случая согласованной фильтрации полностью извест¬
ного контура весь полезный эффект получается на выходе косинусного
звена фильтра. На выходе синусного звена будет лишь чистый шум с
дисперсией σ2ΜΧ = σ2||Γ||2. Поэтому в качестве полезного эффекта целе¬
сообразно брать сигнал только с косинусного звена и тогда д2ых = ||Γ||2/σ2
и тcos = 2к.
Пусть теперь угол поворота сигнального контура по отношению к эта¬
лонному будет случайным, т.е. Г(с) = ехр {ίΑφ}Τ, Αφ — случайная вели¬
чина. Для получения полезного эффекта фильтрации образуется модуль
комплекснозначного сигнала на выходе КСФ, равный Ι77 (А; — 1)| = ||Г||2,
Рис. 3.21. Зависимость выигрышей в отношении сигнал/шум при согласованной
фильтрации для косинусного и синусного звеньев КСФ от угла Αφ между филь¬
труемым и эталонным контурами
и поэтому г — к. В этом случае интересен вклад каждого из звеньев КСФ.
Выходной сигнал фильтра равен η0 (к — 1) = ||Г||2 cos Αφ + г||Г||2 sin Αφ.
Выигрыши в отношениях сигнал/шум для косинусного и синусного
звеньев будут соответственно иметь вид (рис. 3.21)
т*cos = cos2 Δ<ρ, rsin = 2к sin2 Αφ. (3.11.4)
Для сигнального контура, отличающегося от эталонного не только
случайным значением угла поворота, но и масштабом, т.е. когда Г(с) =
= |μ| ехр {ζΔ<μ}Γ, выигрыши rcos и rs-in определяются также выраже¬
ниями (3.11.4). Сдвиг начальной точки сигнального контура на d ЭВ по
отношению к эталонному приводит к такому же сдвигу пикового значения
3.11. Сравнительная эффективность фильтров
137
выходного сигнала без изменения его модуля. Поэтому сдвиг начальной
точки контура при использовании в качестве полезного выходного эф¬
фекта отсчета с максимальным модулем не приводит к изменению полу¬
ченного значения г.
Таким образом, выигрыш в отношении сигнал/шум по энергии не за¬
висит от угла поворота, масштаба и сдвига начальной точки фильтруемого
контура по отношению к эталонному и равен к — размерности контура.
Если сигнальный контур известен точно, то выигрыш становится равным
2к за счет игнорирования синусного канала фильтра, на выходе которого
полезного сигнала нет. Данный фактор позволяет повысить эффектив¬
ность согласованной фильтрации следующим образом. Как показывают
графики зависимостей выигрыша г от угла Δφ, на выходе синусного и
косинусного звеньев КСФ в достаточно широком диапазоне значений угла
Δφ этот выигрыш слабо отличается от максимально возможного значения,
равного 2к, и значительно превышает выигрыш, достигаемый при форми¬
ровании выходной величины в виде модуля. Например, для косинусного
Рис. 3.22. Согласованная фильтрация контура с предварительной оценкой угла его
поворота
звена при Δφ, изменяющегося в пределах ±90°, этот диапазон составляет
±15°. Если обеспечить предварительную оценку угла Δφ зашумленного
контура в диапазоне ±15° для косинусного звена или 75° — 105° — для
синусного и воспользоваться выходом только одного соответствующего
звена, то эффективность фильтрации возрастет примерно в 2 раза. На
рис. 3.22 представлена система обработки зашумленного контура, реали¬
зующего данный подход.
3.11.2. Коэффициент шума сопряженного согласованного фильтра.
Определим коэффициенты шума г для фильтров, согласованных с исход¬
ным s и сопряженным ν сигналами. На вход фильтров поступает один и
тот же зашумленный сигнал u = s + η, где η — вектор реализации флук-
туационного шума с дисперсией σ%χ (рис. 3.23). Средняя энергия сигнала
и отношение сигнал/шум соответственно равны
Ес.
М!
kal*
(3.11.5)
В момент т = к — 1 согласованный фильтр образует пиковый сигнал,
равный энергии сигнала s, т.е. ||s||2, с энергией ||s||4 и шумовой отсчет с
энергией crgX||s||2. В результате выходное отношение <7сфвых сигнал/шум
138
Гл. 3. Линейная фильтрация контуров
(3.11.6)
£сф,вых = ||s||2/crBX2, а коэффициент шума г равен
ГСФ = *7сФ,вых/Явх
Определим аналогичные характеристики ССФ, задаваемого выраже¬
нием (3.8.32). В момент т = к — 1 на его выходе образуется сигнал
77ссф,вых {к — 1), равный скалярному
произведению сигналов s = so и v =
= vo- В соответствии с (3.8.29) это
произведение равно единице, т.е.
VcСФ,с (к-1) = (s, v) = 1. (3.11.7)
Энергия шума на выходе ССФ
равна ^вХ||у||2 (см. п. 3.9). Тогда
9ССФ,вых2 (к - 1) = 1/σΒχΙ|ν||2 И коэф-
фициент шума ССФ
Рис. 3.23. К оценке сравнительной
эффективности фильтров
_ <?ССФ,вых (к ■
гссф = 2—
Яьх
1) _
ΊΝΙ2'
(3.11.8)
Сравнивая (3.11.6) и (3.11.8), видим,
что коэффициент шума ССФ bD = ||v||2||s||2 раз хуже, чем согласованного
фильтра.
Например, пусть s = {1,1, —1} — простейший код Баркера. Сопряженный
с ним сигнал равен v = {0,5;0,5;0}. Тогда ||s||2 = 3; ||v||2 = 0,5 и D = 1,5.
Видно, что коэффициент шума ССФ для данного сигнала в D = 1,5 раза хуже,
чем у согласованного с ним фильтра. Выходные сигналы фильтров при этом равны
Нсф = {0,33; 0,33; 1}; Нсф = {0,0,1}, т.е. кроме пикового, у согласованного
фильтра имеются два других не равных нулю отсчета, являющихся помехами
при фильтрации перекрывающихся сигналов. ССФ таких помех не создает.
D — характеристика обобщенно описывает степень равномерности ам¬
плитудно-частотного спектра сигнала s. Если этот спектр равномерен, то
D = 1 и оба фильтра, согласованный и ССФ, имеют одинаковую эффек¬
тивность. Величина D тем выше, чем сильнее отличаются между собой
модули компонент спектра сигнала s. В пределе, когда одна из компонент
спектра равна нулю, то D = оо. Такая ситуация соответствует случаю, когда
определитель матрицы, задающей собственную систему отсчета, равен ну¬
лю, т.е. векторы Sk-i-m являются линейно зависимыми. В частности, такая
ситуация имеет место, когда сигнал s соответствует замкнутому контуру.
3.12. Обсуждение и обобщение результатов по линейной
фильтрации контурных сигналов
В данной главе были получены представления для контурного линей¬
ного фильтра в пространственной и частотной областях и его частотного
коэффициента передачи. Особенности работы такого фильтра связаны с
3.12. Обсуждение результатов
139
комплекснозначным характером фильтруемых контуров и контуров им¬
пульсных характеристик, их замкнутостью и структурой системы техни¬
ческого зрения.
1. Рассмотрим, к каким особенностям по сравнению со случаем филь¬
трации вещественных сигналов приводит комплекснозначный характер
сигналов. Сравним выражения (3.2.1) частотного коэффициента передачи
фильтра для двух значений внешней переменной га:
к-1 к—1
ω (га) Л (n) exp г-^ran j > ш(к — т) = ^ λ (n) exp ji^ran j.
n=0 n—0
Эти выражения будут комплексно сопряженными, если λ (η) = λ* (η),
т.е. когда ИХ фильтра задается вещественными числами. Следовательно,
ω (к — га) = ^ λ* (η) ^ехр г^гап = ω* (га),
п=0
га = 0,1,... , к — 1,
и ω (га) = ω* (к — га), \ω (га)| — \ω (к — га)|, argu; (га) = — argo; (к — га).
В этом случае для полного задания частотного коэффициента переда¬
чи фильтра необходимо знать ω(0) и еще к/2 первых значений Ω =
= {ω (га)}0 к_г Однако это еще не позволяет сократить трудоемкость
расчетов. В соответствии с выражением (3.2.3)
к — 1
η (s)= | Σ ω р (m)ехр {*Tms}’ s ~ °’■ ■ ■ ’k ~1’
m=0
для получения выходного сигнала фильтра необходимо знать поведение
компонент р(га) и ηη (s) = exp ji^rasj c изменением га. Выражения
р (га) = Σ 7 (п) ехр \—г^тп\ и р (к - га) = ^ 7 (п) ехр {г^гап}
η—η I /с J п-гП ^ к )
будут комплексно сопряженными лишь в том случае, когда 7 (п) = 7* (η),
т.е. все отсчеты входного сигнала 7 (п) должны быть не комплексными, а
вещественными числами. Тогда р (га) = р* (к — га), |р (га)| = \р (к — га)|,
argp (га) = — argp (к - га), га = 0,1,... , к - 1.
Таким образом, когда ИХ Л = {λ (π)}0 к_х фильтра и входной контур
Г = {7 (η)}0 к_х состоят только из вещественных отсчетов, для выходного
сигнала в момент к - s можно записать
к — 1
η (fc — 5) = ^ ω (m) р (га) ехр г-^ras j = 77* (5),
m=0
s = 0,1,... , к — 1.
В этом случае первая половина отсчетов фильтра целиком определяет
вторую и нет необходимости в определении всех к значений сигнала.
Так как вещественный характер ИХ фильтра встречается достаточно
140
Гл. 3. Линейная фильтрация контуров
редко, а ЭВ входного контура практически всегда комплекснозначны, то
фильтрация контуров, в отличие от фильтрации вещественных сигналов,
связана с необходимостью определения в два раза большего числа от¬
счетов. При этом высшие частоты соответствуют центральной части, а
низшие — краям частотного диапазона т = {0,1,... , к — 1}.
2. Замкнутость линии контура изображения, а также тот фактор, что
ЭВ входного контура хранятся в ОЗУИ системы технического зрения, есте¬
ственным образом обусловливает подход к фильтрации контуров на основе
периодической (циклической или круговой) свертки. В большинстве же за¬
дач, где используется свертка, имеется в виду апериодическая свертка [63].
Краевые эффекты, характерные для апериодической свертки из-за
неполного заполнения окна фильтра отсчетами сигнала в начале и в конце
фильтрации, при циклической свертке отсутствуют. Подача ЭВ входного
контура из ОЗУИ, где они все хранятся, изменяет требования к ИХ
фильтра, связанные с условием его физической реализуемости. Обычно
предполагается, что отсчеты сигнала поступают в реальном масштабе вре¬
мени и система обработки к текущему моменту времени обладает не всем,
а лишь теми значениями сигнала, которые поступили к рассматриваемому
времени. Поэтому отсчеты ИХ физически реализуемого фильтра должны
быть равны нулю до начала момента поступления сигнала. В нашем же
случае сигнал полностью известен и все его значения, «прошлые» и «бу¬
дущие», могут быть учтены. Поэтому ИХ фильтра не имеет ограничений
на свои значения до некоторого момента времени.
Замкнутость контура Λ импульсной характеристики фильтра обу¬
словливает равенство нулю нулевого отчета ω (0) частотного коэффици¬
ента передачи фильтра и наоборот. В этом случае фильтр задерживает
постоянную составляющую входного контура. Замкнутость входного кон¬
тура обеспечивает замкнутость контура на выходе фильтра независимо
от вида ИХ. Каждый элементарный контур Гт,га = 0,1,...,к — 1, при
прохождении через контурный линейный фильтр сохраняет свою форму,
т.е. является собственным контуром.
Размерность входного контура должна совпадать с контуром ИХ. На
практике это условие обычно не имеет места. Поэтому перед началом
фильтрации необходимо выравнять (эквализироватъ) порядки этих кон¬
туров (см. п. 9.11).
3. Контурный согласованный фильтр производит вычисление ВКФ эта¬
лонного и фильтруемого контуров. Он позволяет определить количествен¬
ную меру схожести двух плоских форм. ИХ фильтра воспроизводит в
обратном направлении обхода зеркально отраженный относительно го¬
ризонтальной оси эталонный контур со смещенной начальной точкой. Ча¬
стотный коэффициент передачи фильтра с точностью до фазового множи¬
теля повторяет комплексно сопряженный спектр контура, с которым он
согласован. Каждый отчет КСФ представляет собой скалярное произведе¬
ние эталонного и фильтруемого контуров с циклическим сдвигом началь¬
ной точки одного из контуров. Последний, (к — 1)-й отсчет есть скалярное
произведение эталонного контура и контура, с которым фильтр согласо¬
3.12. Обсуждение результатов
141
ван при совпадении начальных точек. В этот момент выходной сигнал
равен энергии эталонного контура. Механизм работы КСФ заключается
в компенсации углов поворота каждого ЭВ, квадрировании его модуля
с последующим арифметическим сложением всех ЭВ. В результате син¬
хронного накопления происходит «выпрямление» ломаной линии контура, с
которым фильтр согласован. Полученный при этом суммарный вектор имеет
квадрат модуля, равный квадрату нормы всего контура, т.е. максимально
возможную энергию. Если же фильтруется несогласованный с фильтром
контур, компенсация углов поворота его ЭВ отсутствует. В результате ЭВ
имеют произвольные аргументы и модуль вектора их суммы всегда меньше
суммы модулей его ЭВ. Поэтому энергия выходного сигнала фильтра в этом
случае будет меньше, чем при фильтрации согласованного контура.
Модуль нормированного выходного отсчета КСФ инвариантен к ли¬
нейным преобразованиям фильтруемого контура и достигает максималь¬
ного значения, равного единице, лишь при прохождении через фильтр
согласованного с ним контура. Свойство сопряженной симметрии АКФ
применительно к КСФ принимает вид η (га) = η* (к — га — 2). Отметим
тот факт, что любой линейный контурный фильтр может рассматриваться
как согласованный. Так, например, фильтр скользящего среднего явля¬
ется согласованным с прямолинейными фрагментами контура, а фильтр
скользящей разности — с фрагментами контура в форме «лучей».
В отличие от согласованных фильтров для вещественных сигналов, в
фильтрах для контуров используется алгоритм периодической свертки,
его ИХ представляет собой комплексно сопряженную копию эталонного
контура и выходной сигнал является ВКФ комплекснозначных сигналов.
4. Возможны два вида согласованной фильтрации контуров — ориен¬
тированная и неориентированная. В первом случае угловые положения
фильтруемого и эталонного контуров совпадают. Решение здесь принима¬
ется по выходной величине косинусного звена фильтра, т.е. по величине
реальной части выходного вектора. Во втором случае угловое положение
фильтруемого контура по отношению к эталонному считается случайным
и решение принимается по величине модуля выходного вектора фильтра.
Ориентированная фильтрация за счет использования априорной инфор¬
мации обладает большей избирательностью. Это объясняется тем, что в
данном случае отрицательные и положительные значения Re η (га) нахо¬
дятся по разные стороны горизонтальной оси и маскируют максимальное
значение Re η (га) в меньшей степени, чем в случае принятия решения
по величине |т7(га)|. Кроме того, ориентированная фильтрация за счет
одноканальной схемы формирования выходного эффекта обеспечивает
более высокое отношение сигнал/шум.
Переход от неориентированной фильтрации к ориентированной может
быть осуществлен следующим образом. Определяется выходной вектор η (то)
КСФ с максимальным значением модуля и находится аргумент φ (гао) этого
модуля. Далее контур поворачивается на угол —φ (гао), в результате чего
вектор η (то) задается чисто вещественным числом (77 (777.0)| и выходная
величина КСФ определяется выходом только косинусного звена фильтра.
142
Гл. 3. Линейная фильтрация контуров
На рис. 3.24 проиллюстрированы результаты неориентированной и
ориентированной фильтрации контура N фильтром, согласованным с кон¬
туром (рис. 3.24, а). Сплошная линия графика на рис. 3.24, б показывает
Рис. 3.24. Неориентированная и ориентированная согласованная фильтрация кон¬
туров
зависимость модуля выходного вектора фильтра от внешней переменной
га. Отсчет η (0) = 1 — 13г имеет максимальное значение модуля, равное
13,06. При этом arg η (0) = —85,6°. Поворачиваем контур N на угол Αφ =
= 85,6°. Отсчет η^φ (0), равный 13,06, по-прежнему является максималь¬
ным по модулю, но имеет чисто вещественный характер. Расстояние меж¬
ду контуром Г и повернутым контуром N стало минимально возможным,
и в качестве меры схожести берем вещественные части каждого отсчета
фильтра. Зависимость значений этих вещественных частей от га показана
на рис. 3.24, б пунктирной линией. Вид¬
но, что зависимость выходного сигнала
фильтра имеет хорошо выраженный
глобальный максимум в момент наи¬
большей схожести контуров N и Г.
/ 6. Обобщим процесс согласованной
% фильтрации контуров изображений с
учетом информативности различных
фрагментов контура. Проанализируем
траектории точек фиксации зрения при
осмотре портрета (рис. 3.25).
Большая концентрация этих точек
наблюдается в области деталей ли¬
ца, особенно в области носа и глаза.
В других частях изображения точек
фиксации зрения значительно меньше.
Этот пример свидетельствует о различной важности отдельных фраг¬
ментов изображения для принятия решения о его принадлежности к
определенному классу. Некоторые фрагменты без ущерба для принятия
решения могут меняться в значительной степени, например, форма при¬
Рис. 3.25. Фиксация точек зрения
при осмотре портрета: а — исход¬
ный портрет; б — траетория точек
фиксации зрения [70]
3.13. Задачи и упражнения
143
чески. С этих позиций целесообразно при обнаружении и распознавании
изображений по их форме использовать обобщенную (весовую) КСФ:
к — 1
η (га) = ^ β (га) и (п) 7* (п — га 4- к — 1), га = 0,1,... , к — 1,
71=0
где β (п) — вес η-го ЭВ фильтруемого контура.
Контур как сигнал занимает промежуточное положение между одно¬
мерными и двумерными сигналами, представляя класс «криволинейных»
сигналов. Рассмотренный аппарат контурной фильтрации дает возмож¬
ность решать задачи преобразования таких сигналов и определять меру
их схожести.
КСФ является основой построения устройств обнаружения и распозна¬
вания изображений по их форме, задаваемой контуром, а также устройств
оценки параметров линейных преобразований контуров изображений.
3.13. Задачи и упражнения
1. Импульсная характеристика контурного линейного фильтра имеет вид Л =
= {2;3 — г;5г; —5 — 4г}. Вычислить контур Ω частотного коэффициента пе¬
редачи фильтра.
О т в е т. ft = {0; 5 — 13г; 4 -f Юг; —1 -f 3£}.
2. Для фильтра из задачи 1 проверить, что сумма ЭВ частотного коэффициента
передачи равна кХ (0), а сумма ЭВ импульсной характеристики равна ω (0).
3. Для фильтра из задачи 1 найти результат фильтрации контура Г = {г; 2;
—3 — 2г; 1 + г}. Вычисления выполнить по формулам, задающим фильтр в
частотной и пространственной областях.
Ответ. Н = {4- 19г; 7 + ЗОг; —6 — 15г; —5 + 4г}.
4. В каком случае нулевой ЭВ ω (0) частотного коэффициента передачи контур¬
ного линейного фильтра равен нулю?
5. Какой вид имеет условие замкнутости выходного контура линейного фильтра?
6. В каком случае контурный линейный фильтр не пропускает постоянной со¬
ставляющей входного сигнала?
7. При каких условиях амплитудно-частотная характеристика фильтра будет
иметь симметричный вид?
8. Какие контуры при прохождении через линейный фильтр сохраняют свою
форму?
9. Какой вид имеет выходной контур при линейной фильтрации дельтовидного
контура?
10. Обладает ли фильтр скользящего среднего свойствами режекторного филь¬
тра?
11. На какой угол повернется выходной контур линейного фильтра при повороте
входного контура на угол π/6?
12. Для каких фрагментов контура фильтры скользящего среднего и скользящей
разности будут согласованными?
13. Вычислить результат согласованной фильтрации контура N = {4г; 5 4- 2г;
2 - 6г; -7}.
О т в е т. Н = {-8 - 124г; -118; -8 + 124г; 134}.
144
Гл. 3. Линейная фильтрация контуров
14. Найти с помощью таблицы умножения результат согласованной фильтрации
контура со стандартными значениями ЭВГ = {1 — г; — г; 1 — г;— 1;— 1; — 1 + г;
— 1; 1 + г; 1 -f- г}.
Ответ.
Н = {5 — 4г; 1 - 9г; —5 — 7г; —8 — 5г; —8 + 5г; —5 + 7г; 1 + 9г; 5 + 4г; 14}.
15. Какими способами можно проверить правильность результата фильтрации
произвольного контура согласованного с фильтром контура?
16. Синтезируйте фильтр для выделения на контурном изображении танка Г =
= {I4; —1 + г; г; 1 + г; I3; 1 — г; 17; —г; —17; —1 — г; I5; 1 - г; —гг; —1 — г; -I12;
— 1 + г; гг; 1 + г} фрагмента в виде ствола его пушки.
Примечание. При задании контура обозначение 7Г означает г следую¬
щих подряд ЭВ 7.
17. Проведите ориентированную и неориентированную фильтрации контура
N = {1з; — г; — 1; — гг; — 1; гг; — 1; г} фильтром, согласованным с контуром
Г = {1; г; —г; 12; —г; I4; г}.
18. Для какого сигнала фильтр с импульсной характеристикой Л = {3 + г; 1 — 2г;
—4 + г} будет согласованным?
19. При каких условиях результатом фильтрации контура с обходом по часовой
стрелке будет контур с обратным направлением обхода?
20. На вход контурного линейного фильтра с импульсной характеристикой Л =
= {2; —1 + г; г; —1 — 2г} подается шумовой контур, ЭВ которого соответству¬
ют требованиям п. 3.9.11 и имеют дисперсию 2σ2 = 8. Определить корреля¬
ционную функцию и дисперсию ЭВ выходного контура.
21. Для условий задачи 20 вычислить математическое ожидание, дисперсию
и среднеквадратическое отклонение модуля и аргумента выходного вектора
фильтра.
22. Определить математические ожидания ЭВ на выходе фильтра, согласованного
с контуром Г = {5 — 2г; — 6 — г; 1 + Зг}.
23. Для случая согласованной фильтрации зашумленного контура с дисперсией
на входе 2σ2 = 8 и эталонным контуром из задачи 22 записать выражение для
плотности распределения вероятностей модуля выходного вектора и определить
отношение сигнал/шум на выходе фильтра для момента т = 2.
24. Определить, на какой угол надо повернуть исходный зашумленный контур
по отношению к эталонному, чтобы уровень выходного сигнала косинусного
звена уменьшился на 5%.
25. Найти эффективность КСФ при фильтрации зашумленного контура размер¬
ностью к = 12 при условии, что в качестве выходного эффекта берутся:
1) модуль выходного вектора фильтра; 2) величина с выхода косинусного зве¬
на при отсутствии рассогласования по углу поворота с эталонным контуром;
3) величина с выхода синусного звена для случая, когда фильтруемый контур
повернут по отношению к эталонному на угол Αφ — 30°.
26. Определить выражения для функций правдоподобия зашумленного контура
N = {3 + 2г; 1 — 3,5г; —1,8 + 0,5г} и шумового контура Ζ при условии, что
эталонный контур имеет вид Г = {2 + Зг; —Зг; —2}, дисперсия шумовых ЭВ
на входе 2σ2 = 2, а модель контура N соответствует требованиям, приведен¬
ным в п. 3.9.1.
Глава 4
ОСНОВНЫЕ ОПЕРАЦИИ НАД ЗАШУМЛЕННЫМИ
КОНТУРНЫМИ СИГНАЛАМИ
4.1. Оценки параметров линейных преобразований контуров
4.1.1. Постановка задачи. Часто встречающимся на практике классом
задач является оценка параметров преобразования контура, которая форму¬
лируется следующим образом. Пусть Г — полигональный контур эталонного
(исходного) изображения объекта (сигнала), заданный в комплексной плос¬
кости, а Г(с) — сигнальный контур, полученный растяжением контура Г
в \μ\ раз, поворотом на угол Αφ и сдвигом начальной точки на d ЭВ, т.е.
Г(с) = {|μ||7 (η + d)\exp {ί[φ (η + d) + Δ<μ]}}0 Α._1. (4.1.1)
На вход устройства обработки подается зашумленный контур N = +
+ Ζ, где Ζ = {£ (п)}0 к_г — шумовой контур. Характеристики ЭВ ζ (п) =
— Cl (п) + г(2 (η), п = 0,1,... , к — 1, этого контура приведены в п. 1.7.
Устройство оценки параметров должно по контуру N определить оценки
параметров: Αφ, \μ\, d. В качестве способа нахождения этих оценок исполь¬
зуем широко применяемый на практике метод максимального правдоподо¬
бия (МП) [26], в соответствии с которым требуемая оценка параметра равна
тому значению параметра, при котором функция правдоподобия Λ достигает
максимума. Эта функция для контура N = + Ζ имеет вид (см. п. 3.10.3)
Лс (N/d, Αφ, И) = с exp {-Лг [||N||2 + ||Г<С> ||2 - 2Re(N, Г<с>)] },
(4.1.2)
где
(271
2\fc
. Ι|Ν||2 = Σ>(η)|2, ||Г(с)||2 = ^|7с
(4.1.3)
Re(N, Г(с)) — действительная компонента скалярного произведения кон¬
туров N и ГМ Принимая во внимание (4.1.1), запишем
h' — 1
Re(N, Г^) = Re^ \μ\\ν (п)\\j (η + d)\ ехр{г[в (η) — φ (η + d) - Ду?]} =
η—О
к-1
= |μ|^ \ν (η)||7(η + d)| cos [θ (тг) - φ(η + d) - Αφ}. (4.1.4)
п=0
146
Гл. 4. Операции над зашумленными контурами
Здесь Θ (п) — аргумент ЭВ и (п) зашумленного контура Ν. Мнимая ком¬
понента этого скалярного произведения равна
к-1
Im(N, Г^) = |μ|^Γ^ \ν (η)||7 (η + d)| sin [θ (η) — φ (η + d) — Δφ].
"=0 (4.1.5)
Для получения оценок чаще всего используется не сама функция Л, а ее
логарифм, имеющий более простой вид. Логарифмируя выражение (4.1.2)
и учитывая выражение для расстояния между контурами N и Г, получим
InA (N/d, Δφ, |μ|) = Inc - R2/2σ2, (4.1.6)
где
R
2 __
+ ||Г(с)|| -2Re(N,rW).
= 0,
(4.1.8)
(4.1.7)
4.1.2. Оценка параметров зашумленного контура. Получим выраже¬
ния для оценок МП параметров d, Δφ и |μ| зашумленного контура. Для этого
в общем случае необходимо составить систему из трех уравнений правдо¬
подобия. Левая часть каждого из уравнений системы представляет собой
частную производную функции правдоподобия (4.1.2) или ее натурального
логарифма (4.1.6) по оцениваемому параметру. Такая система уравнений
имеет вид
31η Λ ((Ν/d, Δ¥?,|μ|))
9(d)
ainA((N/d,Ay,H))
а (Η)
01nA((N/d, Αφ, |μ|)) л
9(Αφ)
Данная система должна быть дополнена системой неравенств, связанной
со вторыми частными производными функцией правдоподобия, позво¬
ляющими убедиться в том, что решения системы задают максимум, а
не минимум этой функции. Параметр d сдвига начальной точки конту¬
ра N принимает только дискретные значения, что исключает примене¬
ние операции дифференцирования для нахождения максимума функции
правдоподобия. Его можно найти лишь путем непосредственного перебора
значений этой функции, получаемых при варьировании d и определения
значения d, обеспечивающего минимум расстояния (4.1.7), т.е.
d — d при R -* min, d = 0,1,... , к — 1. (4.1.9)
Как следует из выражения (4.1.7) для расстояния R с учетом (4.1.1) из¬
менение величины d влияет только на значение скалярного произведения
Re(N,r(c)). Поэтому правило (4.1.9) эквивалентно следующему правилу
d — d при Re(N, Г^) —> max, d = 0,1,... , к — 1. (4.1.10)
В свою очередь, величина Re (N, Г(с)) зависит не только от d, но и от
|μ| и Δφ. Параметр |μ|, как видно из (4.1.4), в отличие от Δφ играет роль
линейного множителя и поэтому не влияет на определение оценки d. Этого
4.1. Оценки параметров линейных преобразований контуров
147
нельзя сказать о параметре Δφ, который вместе с величинами φ (п -f d)
и Θ (п) входит под знак косинуса. Поэтому предварительно необходимо
оценить угол Δφ, а затем уже станет возможным определение параметра
сдвига начальных точек d.
Параметры растяжения |μ| и угла поворота Δφ являются непрерыв¬
ными и для них существуют производные расстояния между контурами
N иГ(с), имеющие вид
2 & —1
щ = 2М1|Г||2 -2^|i/(n)||7(n + d)|cos[5(n) - <p(n + d) - Δφ},
9θ(Αφ) = (n)ll7 (" + d)\sin [θ (η) -φ(η + ά)- Αφ].
Приравнивая эти выражения к нулю, получим второе и третье урав¬
нения из системы уравнений (4.1.8) для оценки параметров |μ| и Δφ:
k-l
И11г1|2-]СИ«)1|7(п + Ф|сс«[0(п)-р(п + й)-Ду>] =0,
^0 и=и
(4U1)
W\\u (n)il7 (n + d)| sin [θ (η) — φ(η + d) — Δ^>] = 0. (4.1.12)
Δν=Δν
Остановимся на последнем уравнении, служащем для оценки Δφ. В нем
неизвестная величина Δφ влияет только на один из трех входящих в него
сомножителей, а именно, на величину синуса, который в свою очередь
зависит еще и от параметра Δφ. Поскольку величины \ν(ή)\ и \v (п -f d)\
предполагаются положительными, то решение уравнений достигается при
sin [θ (η) — φ (п -f d) — Δφ] = 0.
Для перехода к фильтровой схеме оценки параметров запишем выраже¬
ние для выходного сигнала τ\Αφ {τη + d) фильтра, согласованного с эталон¬
ным контуром Г = {7 (n)}0 k_v При подаче на его вход контура N, начало
которого смещено на d ЭВ, а сам контур повернут на угол Δφ, получим
к-1
τ]Αφ (m + d) = ^ Iv (n)||7 (n + d — m + k -l)\ x
x exp {ι[Θ (η) — φ{π-\- d — m + к — 1) — Δ<μ]}.
В момент га = к — 1 на выходе этого фильтра образуется сигнал
к-1
VAφ (к - 1 + d) = ^ \v (n)||7 (n + d)\cos{[0 (η) — φ (n + d) - Δφ]} +
n=0
к— 1
+ I17 (n)ll7 (n + «01 sin {[0 (η) - φ(η + d) - Αφ]}, (4.1.13)
n—0
d = 0,1,... , fc — 1.
148
Гл. 4. Операции над зашумленными контурами
Сравнивая приведенное выражение с уравнением правдоподобия (4.1.2)
для оценки параметра Δφ, видим, что это уравнение можно записать как
(k-1 + d) |Δν=_Δ? = 0, (4.1.14)
т.е. оценку параметра Δφ по выходному сигналу фильтра следует искать
в том случае, когда этот сигнал за счет вариации значений Δφ становится
строго вещественным. Для этого вектор η&φ (к — 1 + d) выходного сигнала
фильтра, получаемый в момент га = к — 1, надо повернуть на такой угол
a (d) , чтобы он стал горизонтальным и направленным вправо. Данный
угол равен (с обратным знаком) аргументу вектора выходного сигнала:
= = <4U5>
В результате поворота на угол а (d) получим к отсчетов фильтра
ΉΑφ,α(ά) (* - 1), d = 0,1,... , к - 1, (4.1.16)
каждый из которых задает максимум для конкретного значения d произ¬
водной натурального логарифма функции правдоподобия по Δφ.
Выражение (4.1.16) является реальной частью скалярного произведе¬
ния (Ν,Γ^). При этом на его значение исключено влияние парамет¬
ра Δφ, т.е. от функции трех переменных |μ|, Δφ и d мы переходим
к функции двух переменных . Поскольку энергетический параметр \μ\
при вычислении скалярного произведения выполняет роль масшабного
множителя, то положение максимума скалярного произведения при ва¬
рьировании d не зависит от величины |μ|. Теперь правило (4.1.10) для
оценки параметра d сдвига начальной точки конутра N принимает вид
d = d при \μ\ηΑφΜ<ί) (& - 1 + d) -* max. (4.1.17)
Отметим следующее важное обстоятельство. Для нахождения оценки
параметра d по приведенному правилу нет необходимости поворачивать
на угол a (d) вектор каждого из к отсчетов согласованного фильтра, и,
далее, в соответствии с (4.1.17) находить максимальный отсчет фильтра.
При повороте на угол а (d) каждый отсчет η&φ (к - 1 + d) становится
вещественным. Поэтому достаточно вычислить модули отсчетов филь¬
тра, \ηΑφ (к — 1 4- d)\, d — 0,1,... , к — 1, выбрать из них максимальный
\ηΑφ (к - 1 + d) |max == \ηΑφ (™о)| и взять в качестве оценки МП пара¬
метра сдвига начальной точки контура N величину d = d, при котором
достигается максимум модуля отсчета η&φ (к — 1 + d) т.е.
d = d при \ηΑφ (fc “ 1 + d)\ -» max. (4.1.18)
Обозначим через то номер к - l+d отсчета фильтра с максимальным
модулем. Тогда окончательно правило нахождения оценки МП параметра
d будет иметь вид
d = m0 + 1.
(4.1.19)
4.1. Оценки параметров линейных преобразований контуров
149
Значение оценки d, подставленное в качестве величины d в выраже¬
ние (4.1.13) для (к — 1) отсчета согласованного фильтра, максимизирует
модуль выходного вектора. Аргумент вектора при этом равен
-a(d) = arrtcImi^(fc-1+^ = areteΙπΐ[ί?Δ* (Wo)] ■
&Re^Av(k-l+d)] 8Ке[»?дДто)]
Если вектор ηΑφ{к — 1 + d) повернуть на угол a(d), то он станет гори¬
зонтальным и направленным вправо, причем его мнимая часть равняется
нулю, а реальная будет максимально возможной среди реальных частей
других выходных векторов фильтра. Таким образом, в результате пово¬
рота вектора ηΑφ^ — 1 -f d) на угол a(d) произошла максимизация его
реальной части. Теперь в соответствии с методом МП оценка параметра
Δφ будет с обратным знаком равна тому значению угла, на который был
повернут этот вектор, т.е.
(4.1.20)
Δφ = —a{d) = arctg
Im [ηΑφ (mo)]
Re [ηΑφ {то)]'
Определим теперь оценку МП параметра |μ|. Для этого в уравнение
правдоподобия (4.1.11) подставим оценки параметров d и Δφ. Так как при
Δφ = Δφ мнимая компонента выходной величины КСФ равна нулю, то
второе слагаемое в левой части уравнения, равное вещественной компо¬
ненте, есть модуль этой величины, т.е.
к — 1
|i'(n)||7(n + <i)|cos[0 (η) - <p(n + d) - Δ£>] = |r/(mo)|.
п—О
Тогда из уравнения (4.1.11) следует
|Д| = 1*7(™0)|/||гц2. (4.1.21)
Таким образом, для нахождения оценок МП параметров зашумленного
контура N = + Z необходимо:
1) вычислить к отсчетов при фильтрации контура N фильтром, согла¬
сованным с эталонным контуром Г;
2) определить номер ш0 отсчета фильтра с максимальным значением
модуля и инкрементированием значения то получить оценку параметра d]
3) найти аргумент отсчета η (mo) и принять его в качестве оценки угла
поворота Δφ;
4) вычислить оценку растяжения |μ| как отношение максимального
модуля выходной величины КСФ к квадрату нормы эталонного контура.
Структура устройства оценки параметров (рис. 4.1) содержит два
фильтра КСФ1 и КСФ2, согласованных с эталонным контуром Г. КСФ1
при подаче на его вход контура Г совместно с формирователем модуля
ФМ1 и экстремальным устройством ЭУ1 вычисляет значение ||Г||2.
КСФ2 фильтрует зашумленный контур Ν, а экстремальное устрой¬
ство ЭУ2 определяет его отсчет с максимальным значением модуля \η (m0)|
и само значение то- Далее в соответствии с выражениями (4.1.19)—-(4.1.21)
находятся оценки df Δφ и |μ|.
150
Гл. 4. Операции над зашумленными контурами
Рис. 4.1. Структура устройства оценки параметров контура
Рис. 4.2. Полигонально заданные эталонный контур Г (а), и шумовой контур Ζ (б)
Рис. 4.3. Контуры: сигнальный (а), зашумленный N (б)
4.2. Обнаружение зашумленных контуров изображений
151
Пример 1. Используя полученные результаты, оценим параметры линей¬
ных преобразований контура Ν. Эталонный контур имеет вид Г = {1; —г; —г;
1 — г; —г; —г; —г; —г; — 1 + г; —1; —1 — г; г; г; г; г; 1 + г; г; г}, ||Г||2 = 22 (рис. 4.2).
Для получения сигнального контура контур Г поворачивается на угол
Δφ = 36,87° (для этого каждый ЭВ умножается на 0,8 + 0,6г), растягивается
в |μ| = 2,5 раз и его начальная точка сдвигается на d = 4 ЭВ (рис. 4.3): =
= {0,8 + 0,6г; 0,6 - 0,8г;0,6 - 0,8г;0,6 - 0,8г; 1,4 - 0,2г;0,6 - 0,8г;0,6 - 0,8г;
0,6 - 0,8г; 0,6 - 0,8»;-1,4 + 0,2г;-0,8 - 0,6г; -0,2 - 1,4»; -0,6 + 0,8г; -0,6 +
4- 0,8г; -0,6 + 0,8г; -0,6 + 0,8г; 0,2 + 1,4»; -0,6 + 0,8г; -0,6 + 0,8г}.
Контур зашумляется контуром Z (рис. 4.2) со значением 2σ2 = 2,268:
Ζ = {0,464 - 0,137г; 0,06 - 2,526г; 1,486 - 0,354г; 1,022 - 0,472г; 1,394 - 0,55г}·
Зашумленный контур N = + Ζ имеет вид (рис. 4.3):
N = {1,964 - 1,863»; 1,560 - 4,526г;
Квадраты норм контуров и Ζ и отношение сигнал/шум соответственно
равны: ||Г<е>||2 = 137,5; ||Ζ||2 = 40,848; q = ||Γ^||/||Ζ|| = 3,366. После филь-
трации контура N фильтром, согласованным с контуром Г, получаем контур
Отсчет фильтра с максимальным модулем равен η (3) = 60,48 exp {0,707г}.
Таким образом, то = 3 и η (то) = 60,48. В соответствии с формулами (4.1.15)
и (4.1.17) получаем d — то + 1 = 4, Δφ = 0,707рад = 40,49°, |μ| = 60,48/22 =
= 2,73.
Для сравнения приведем точные значения этих параметров: d = 4, Δφ —
= 36,86°, |μ| = 2,5.
4.2. Обнаружение зашумленных контуров изображений
4.2.1. Постановка задачи. Пусть Г(с) = |μ| exp {»Ду?}Г^ — сиг¬
нальный контур, полученный путем растяжения в |μ| раз эталонного
контура Г, поворота его на угол Δφ и сдвига начальной точки на d
ЭВ. На вход обнаружителя поступают либо зашумленный контур N =
— р(с) _|_ либо шумовой контур N = Z, элементарные векторы которого
характеризуется дисперсией 2σ2 и имеют приведенные в п. 1.7 характе¬
ристики. Необходимо принять обоснованное решение, какой из контуров,
зашумленный или шумовой, находятся на входе обнаружителя. С уче¬
том выражений (3.10.7) и (3.10.8) для логарифмов функций правдоподобия
зашумленного и шумового контуров логарифм отношения правдоподобия
запишется как
2,986 - 2,354г; 2,522 - 2,472г; -2,106 - 0,055г}.
}·
In L (N) = [||Г<С>[|2 — 2Re(N,r<c>)]/2.
(4.2.1)
152
Гл. 4. Операции над зашумленными контурами
Как известно, оптимальный обнаружитель должен формировать от¬
ношение правдоподобия и сравнивать его с порогом. Класс решающих
правил, основанный на этом алгоритме, является полным. Изменение
критерия обнаружения приводит лишь к выбору соответствующего зна¬
чения порога [52].
4.2.2. Обнаружение полностью известного контура. Контур Г(с) счи¬
тается полностью известным, если контуры Г и равны между собой,
т.е. d = 0, Αφ = 0 и |μ| = 1. Принимая во внимание выражение (4.2.1) для
отношения правдоподобия, алгоритм обнаружения будет иметь вид
Re (N, Г) ^ σ21пЛ0 + 0,5||Г||2 = U0, (4.2.2)
где Ло = J?oi-P(N = Z)/jR10P(N = Г + Z) — пороговое значение, i?oi
и Rio — соответственно риски, связанные с ложной тревогой и пропуском,
Р (N = Z) и Р (N = Г + Z) — априорные вероятности отсутствия и на-
N
фспТ-
тГ
Rc (Γ,Ν)
линия сигнального контура Г^с) в контуре Ν, С/0 — порог, учитывающий
энергии эталонного и шумового контуров,
а также риски и априорные вероятности.
Обнаружитель состоит из формиро¬
вателя скалярного произведения (ФСП)
и порогового устройства (ПУ) (рис. 4.4, а).
Рассмотрим некоторые интерпре¬
тации структуры обнаружителя. Вы¬
ходной вектор фильтра, согласованного
с контуром Г, в момент т = k—1 равен
ДГксф
гТ
а
Re η (к
4 пу
Тг.
-%
да
нет*
N
ИР
гГ
б
R2
ПУ
То
да
нет*
И о
v(k-l)
= Т (п) 7* (п)
п=О
(Ν,Γ).
(4.2.3)
Отсюда видно, что в качестве ФСП
Рис. 4.4. Структуры обнаружите- можно использовать КСФ, причем ре¬
лей полностью известного контура
•УН шение принимать по выходу его ко¬
синусного звена (рис. 4.4, б). Другая
интерпретация алгоритма связана с понятием расстояния R между
контурами N и Г (рис. 4.4, в). С учетом выражения (4.1.7) для R2
алгоритм (4.2.2) можно записать в виде
R2 ^ ||Ν||2 - 2σ21ηΛ0 = VQ. (4.2.4)
Определим эффективность обнаружителя, взяв для конкретности струк¬
туру на основе КСФ. Для принятой модели шума совместная плотность
распределения вероятностей вещественной и мнимой частей выходного шу¬
мового вектора η1]1 = щш + г^ш фильтра подчиняется нормальному закону,
причем его вещественная и мнимая части независимы (см. п. 3.9). Тогда на
основании выражения (3.10.6) для вещественной части вектора в момент т =
= к — 1 получим
4.2. Обнаружение зашумленных контуров изображений
153
РЫш) ν/2πσ||Γ|
Вероятность ложной тревоги
ехр
f т щ \
1 2σ2||Γ||2 )
(4.2.5)
F = Р (?71Ш ^ U0) = | Р (щш) 0щш = 0,5[1 - erf (α0)], (4.2.6)
Uo
где erf (q0) — интеграл вероятности [26] , «о — нормированный порог,
а0 = С/0/\/2^||Г||. (4.2.7)
Совместная плотность вероятностей вещественной и мнимой частей
вектора КСФ при фильтрации зашумленного контура также подчиняется
нормальному закону (см. п. 3.10). Учитывая некоррелированность этих
частей для плотности вероятностей вещественной части вектора, на осно¬
вании выражения (3.10.4) для момента т = к — 1 можно записать
(νΐ - 1|г||2)2
Р(т) =
ί (νϊ - 11ГН2)21
\ 2σ2||Γ||2 /·
(4.2.8)
vW||n| ( 2σ2||Γ||2
Тогда вероятность правильного обнаружения контура
оо
D = Р Ы > Uo) = J Р (т) άηι = 0,5 1+ erf - ocq) . (4.2.!
Характеристики обнаружения полностью известного контура, пред¬
ставляющие семейство зависимостей вероятностей D от отношения q =
= ||Γ||/σ при фиксированных значениях вероятностей F, совпадают с ха¬
рактеристиками обнаружения полностью известного сигнала [26]. Отметим
лишь, что отношение сигнал/шум на выходе КСФ равно q = ||Γ||/\/2σ,
а не ||Γ||/σ.
4.2.3. Обнаружение контура с неизвестным углом поворота. Пусть
теперь сигнальный контур равен Г(с) = ехр{гД<^}Г, т.е. каждый его ЭВ
повернут по отношению к соответствующему ЭВ эталонного контура на
угол Αφ. Величину Αφ будем считать равномерно распределенной, т.е.
Р (Αφ) = 1/(2π) при 0 ^ Αφ ^ 2π. (4.2.10)
При повороте контура его норма не меняется, т.е. ||г(с)|| = ||Г||. По¬
этому условное отношение правдоподобия
j. /·.. л \ f 11г(с)Ц2 Re (N, Г(с)) Ί
L(N,A<P) = exp[-L^ + —^=
{||Г||2 2 \
- Vr + — У, *Ί (п) [71 (п) COS Αφ - Ί2 (п) sin Αφ] +
1(Τ σ —'
η=Ο
к-1
+ ^2 ϊ/2(«)[7ι(η)δϊηΔν7 - 72 (η) cos Δ^]) =
154
Гл. 4. Операции над зашумленными контурами
= *ф { - Щ- + 45> (п)||7 (»)| сое [Δ* + φ (η) -0(η)]1. (4.2.11)
2σ
Интегрируя по всей области изменения угла Αφ, определим безуслов¬
ное отношение правдоподобия:
2тг
Λ(Ν) = | Λ (Ν, Αφ) Р (Αφ) d (Αφ) = exp j - Д}101l?? (* ^ } ■
Благодаря монотонности функции Бесселя 1о{х} решение можно при¬
нимать при сравнении с порогом любой монотонной функции от х. Поэтому
решающее правило примет вид
|(Ν,Γ)| = \η (k — 1)\ ^ h. (4.2.12)
Таким образом, оптимальный обнаружитель зашумленного контура,
повернутого на неизвестный угол по отношению к эталонному, должен
формировать модуль скалярного произведения (N, Г) или модуль соот¬
ветствующего отсчета КСФ и сравнивать его с порогом h (рис. 4.5, а, б).
Рис. 4.5. Структуры обнаружителей контуров с неизвестным углом поворота
Рассмотрим подход к обнаружению контура, основанный не на инте¬
грировании отношения правдоподобия по параметру Αφ, а на сведении
к задаче обнаружения полностью известного контура путем определения
оценки параметра Αφ (см. п. 4.1). Если предварительно контур N повер¬
нуть на угол (—Αφ), то мы будем иметь случай полностью известного
контура, так как с точностью до погрешности оценки контуры Г(с) и Г
согласованы по углу. Тогда в соответствии с выражением (4.2.1) логарифм
безусловного отношения правдоподобия станет равным
4N-a?) = [llrLljf -2Re(N_AVirLlj]/2a2.
4.2. Обнаружение зашумленных контуров изображений
155
Так как в этом случае вектор скалярного произведения повернутых
на угол (—Δφ) контуров N иГ^ стал горизонтальным и направленным
вправо, то его реальная часть совпадает с его модулем и правило обнару¬
жения принимает вид
|(N,r(c>)| = to (Л —1)1 (4.2.13)
Из сравнения выражений (4.2.12) и (4.2.13) следует, что решающие
правила, полученные интегрированием отношения правдоподобия и пред¬
варительной оценкой параметра Δφ, совпадают. По сравнению со случа¬
ем обнаружения полностью известного контура достаточной статистикой
здесь служит модуль выходного вектора, а не его реальная часть. Как
следует из п. 3.11, при этом отношение сигнал/шум по энергии умень¬
шается вдвое. Если воспользоваться величиной расстояния, то алгоритм
обнаружения можно представить в виде
Дшш < Ι|Ν||2 - 2σ21η Λο = Vo, (4.2.14)
где — минимальное расстояние между контурами N и Г, достигае¬
мое варьированием угла их взаимного поворота. Обнаружитель (рис. 4.5, в)
содержит блок поворота эталонного контура на угол Δφ (ВПК), из¬
меритель расстояния ИР между контурами N и Гд^, экстремальное
устройство ЭУ, фиксирующее минимум этого расстояния, и пороговое
устройство ПУ.
Определим эффективность обнаружения контура. Вероятность лож-
оо
ной тревоги Рд^ = J Р (|г/ш|) d^m\, где |г/ш| — модуль выходного вектора
и0
КСФ и N = Z. Модуль этого вектора распределен по закону Релея (см.
п. 3.9). С учетом выражения (3.9.8) будем иметь
оо
и0
2σ ||Г||
= ехр { —
Up
2σ2||Γ||2
(4.2.15)
Величина нормированного порога, обеспечивающего данный уровень лож¬
ной тревоги, равна а$ = In l/F^. Вероятность правильного обнаружения
оо
определяется как D = J Ρ(\η\) ά\η\, где Р (|?j|) — плотность распределе¬
но
ния вероятностей модуля η (к - 1) = η = ηχ +ϊη2 выходного вектора КСФ
при фильтрации контура N = Г(с) + Ζ. Это распределение подчиняется
закону Райса (см. п. 3.10). Поэтому
ОО
Ы2 + 11ГЦ2
2σ2||Γ||2
156
Гл. 4. Операции над зашумленными контурами
Введем обозначения t = |τ7|/σ||Γ||, I = ||Γ||/σ. Тогда
οο
D = I t exp I —" I/о (tl) dt. (4.2.16)
осоу/2
Данное выражение является табличным интегралом для распределе¬
ния Релея-Райса. Характеристики обнаружения зашумленного контура
со случайным углом поворота аналогичны характеристикам обнаружения
сигнала со случайной фазой [26].
4.2.4. Обнаружение контура с неизвестным сдвигом начальной точ¬
ки. Пусть сигнальный контур получен сдвигом на d ЭВ на¬
чальной точки эталонного контура Г, т.е. jc (п) = j (п + d), п = 0,1,...
... , fc — 1. По остальным параметрам контуры Г(с) и Г совпадают. Алго¬
ритм обнаружения контура Г(с) получим путем перехода к обнаружителю
полностью известного контура за счет учета оценки величины d. Для этого
при использовании метода МП необходимо найти, при каком значении d
достигается максимум функции правдоподобия
L (N, d) = с exp {-^2 [l|N||2 + ||Г||2 - 2Re (Ν,Γ*)]}. (4.2.17)
В данном случае величина d будет максимальной, когда реальная часть
скалярного произведения (N,rd) достигает наибольшей величины при
варьировании d. Поэтому решение об обнаружении выносится при
Re(N,rd)max ^ 0,5||Г|| +σ21ηΛ0 = U0. (4.2.18)
Таким образом, оптимальный алгоритм обнаружения состоит в сравне¬
нии с порогом Uq максимального значения реальной части скалярного
-»|ксф
Re η(ά)
ЭУ
d = 0,1,...,*-1
Re max, ^
Н ПУ
К
да
нет
Рис. 4.6. Структура обнаружителя контура с неизвестным сдвигом начальной точки
произведения (Ν, Г^). Если в обнаружителе применен КСФ, то решение
принимается по правилу (рис. 4.6)
т (d) =
г к—1
Re^ ν (η) 7* (η — d + к —
n=0
i)
^ Uq, d = 0,1,... , к - 1.
(4.2.19)
4.2.5. Обнаружение контура с неизвестным углом поворота и сдви¬
гом начальной точки. В данном случае ЭВ сигнального контура Г(с) =
= Гд<^ имеет вид 7С (п) = I7 (п + d)\exp {ι[φ (η) + Δφ]}, а функция
4.2. Обнаружение зашумленных контуров изображений
157
Рис. 4.7. Структура обнаружителя контура с неизвестными значениями угла по¬
ворота и сдвига начальной точки
правдоподобия
Λ (Ν, Αφ, d) = с exp [||Ν||2 + ||Г||2 - 2Re (N, Гд^)]}.
После оценки методом МП параметров d и Αφ и перехода от конту¬
ра ΓΔΜ к контуру Г функция правдоподобия становится безусловной
и записывается как
Λ (Ν) = сехр {-^ [||Ν||2 + ||Г||2 - 2\η(d)|raax]}. (4.2.20)
В результате алгоритм обнаружения будет иметь вид
М™)1тах ^ 0,5||Г||2 +σ21ηΛ0 = U0. (4.2.21)
Таким образом, для оптимального обнаружения контура необходимо
осуществить контурную согласованную фильтрацию, сформировать мо¬
дуль выходного вектора, найти его максимальное значение и сравнить
с порогом Щ (рис. 4.7).
4.2.6. Обнаружение контура с произвольным масштабом. Рассмо¬
трим задачу обнаружения контура Г(с) = |μ|Γ = {|μ|7 (n)}0 k_v Отно¬
шение правдоподобия для контура N = |μ|Γ + Z равно
Λ (Ν, И) = ехр [Н2||Г||2 - 2HRe (N, Г)]}. (4.2.22)
Оценка энергетического параметра |μ| определяется выражением
(4.1.21). Подставив значение этой оценки в (4.2.22), приходим к слу¬
чаю обнаружения полностью известного контура. При этом логарифм
отношения правдоподобия lnL(N) = [Re(Ν,Γ)]2/2σ2||Γ||2, а правило
принятия решения имеет вид
[Re (N, Г)]2 > 2σ2Λ0 - ί/,2μ|. (4.2.23)
Таким образом, для обнаружения зашумленного контура с произвольным
ΝI ,*.(*-0, .
КСФI ►|Квадрирование |
гТ
ПУ
да
нет
>1
Рис. 4.8. Структура обнаружителя контура с произвольным масштабом
158
Га. 4. Операции над зашумленными контурами
масштабом необходимо сформировать квадрат вещественной части ска¬
лярного произведения контуров N и Г и сравнить его с порогом U^.
Учитывая, что Re(N,T) = щ(к — 1), структуру обнаружителя можно
представить в виде, показанном на рис. 4.8.
4.2.7. Обнаружение контура с неизвестными сдвигом начальной точ¬
ки, углом поворота и произвольным масштабом. Рассмотрим теперь
наиболее общий случай обнаружения зашумленного контура, когда сиг¬
нальный контур Г(с) определяется выражением (4.1.1) и все его парамет¬
ры неизвестны. Функция правдоподобия для контура
Λ (Ν, Αφ, d, Η) = с exp {-^ [||N||2 + |μ|2||Γ||2 - 2|/,|Re (Ν, ΓΔ^)]}.
Используя оценки МП параметров Αφ, d, определяемые выражениями
(4.1.19) и (4.1.20), получим функцию правдоподобия для контура с неиз¬
вестным масштабом:
Λ (Ν, И) = сехр {-^ [||Ν||2 + Н2||Г||2 - 2|μ||η (d)|max]}.
Учитывая теперь оценку МП параметра \μ\ (4.1.21), запишем выражение
для квадратного корня из логарифма ОП: InL (Ν) = \η (^)|тах/\/2а||Г||.
Тогда правило обнаружения зашумленного контура будет иметь вид
И<*)1юах > ν^σ||Γ||\/ϊηΛο = иы. (4.2.24)
Таким образом, оптимальный обнаружитель формирует к отсчетов
КСФ, находит их модули, выбирает максимальный по величине модуль
и сравнивает его с порогом ?7|μ|.
Пример 1. Для иллюстрации расчетов, связанных с обнаружением зашум¬
ленных контуров, рассмотрим контур из примера к п. 4.1. Зададимся отношением
рисков Roi/Rio, связанных с ложной тревогой и пропуском, равным 1000, и отно¬
шением Р (N = Z)/P(N = + Z) априорных вероятностей отсутствия и на¬
личия сигнального контура, равным 50. Тогда пороги Ло = RoiP (Ν = Z)/[Rw х
х Р(N = Г(с) + Z)] = 50000 и £7И = у/2а\\Т\\у/йГЦ = 58,098. Максимальное
значение модуля выходного вектора фильтра, согласованного с контуром Г, до¬
стигается при d = 4 и равно [77 (4)|тах = 60,48. Сравнивая это значение с порогом
£7|μ|, видим, что принимается правильное решение об обнаружении сигнального
контура при практическом отсутствии ложных тревог в условиях, когда появление
изображения объекта с контуром Г маловероятно.
4.3. Разрешение контурных сигналов
4.3.1. Введение и постановка задачи. Под разрешением понимают
операции, в результате которых из группы перекрывающихся или близ¬
ко расположенных сигналов выделяется каждый из них. Когда сигнал
характеризуется несколькими параметрами, то данная задача решается
отдельно для каждого параметра или совместно по группе параметров.
Например, в радиолокации сигналы разрешаются по дальности, скорости,
4.3. Разрешение контурных сигналов
159
угловым координатам и др. При чтении слитного рукописного текста раз¬
решение сигналов состоит в разделении непрерывной линии, соответству¬
ющей одному слову, на отрезки кривых, изображающих отдельные буквы.
Для изображения реки задача разрешения заключается в отделении изо¬
бражения главного русла от основных притоков и т.д. В данном разделе
рассмотрим задачу разрешения перекрывающихся контуров, представ¬
ленных как комплекснозначные сигналы.
Пусть Ει,Ε2,... , Е* — последовательность контурных сигналов
одинаковой размерности fc, отличающихся от эталонного сигнала Е =
— i£ (n)}o k-i масштабом |μ^| и углом поворота <pj, т.е.
= АЬ'Е, μ, = \β]\ exp Ej = {ej (η)} = (n)| exp
j = 1,2,... ,t.
Начальный ЭВ €j (0) каждого из сигналов Ej смещен в пространстве
(во времени) относительно начального ЭВ εχ (0) контура Εχ на величину
dj. Сигналы Ej, j = 1,2,... ,ί, образуют сигнал N = (ι/(η)} путем
суммирования с учетом параметра смещения dj своих ЭВ с одинаковым
номером п. Для случая к = 3 и t — 2 образование суммарного контурного
Рис. 4.9. К постановке задачи разрешения контурных сигналов: а — исходные
сигналы Εχ и Е2; б — представление отсчетов сигналов с учетом смещения начала
Е2 на с?2 ЭВ и образования суммарного сигнала N; в — векторное представление
суммарного сигнала N
сигнала N = {v (п)}0 4 поясняется на рис. 4.9. Здесь Εχ = {1, г, 1} и Е2 =
= {2г, — 2,2г} — контурные сигналы, имеющие по отношению к контур¬
ному сигналу Е = {1, г, 1} параметры μ\ = 1, di = 0 и μ2 = 2 exp {г7г/2},
d2 = 2. Суммарный сигнал равен N = {1, г, 1 + 2г, — 2,2г}.
В результате разрешения необходимо по информации об эталонном
сигнале Е и суммарном сигнале N получить информацию о параметрах
μj и dj, j = 1,2,... ,ί, каждого из сигналов Εχ, Е2,... , Е*. Нас будет
интересовать случай взаимного перекрытия сигналов. Подобная задача ха¬
рактерна для радиолокации. Сигналы Е^· представляют собой задержанные
относительно зондирующего сигнала Е отраженные от цели сигналы, отли¬
160
Гл. 4. Операции над зашумленными контурами
чающиеся масштабами и начальными фазами. С такой задачей приходится
сталкиваться также при автоматическом чтении чертежей, выборе одной из
однотипных деталей в бункере межоперационного запаса и др.
В общем случае будем представлять следующую ситуацию при реше¬
нии задачи разрешения как комплекснозначных (контурных), так и веще¬
ственных сигналов. Отсчеты суммарного сигнала N = (ι/(η)} располагаем
на горизонтальной оси, отражающей изменение времени или длины (рис. 4.10).
Положение суммарного сигнала на этой оси будем считать неизвестным.
1 0 1 о I 0 Iw(0)lЦ(1)|ы(2)| о | о | о 1
Г = 1 |5(0)|5(1)Ь(2)|
г =2 |а(0)| 5(1) |а(2)|
г =3, р= О |-т(0)М(1) Ь-(2)|
р=\ |s(0)| s(l)|s(2)]
р= 2 U0)|.t(l)|.u2)l
Фаза 1
Фаза 2
^Фаза 3
Рис. 4.10. Фазы процесса взаимодействия сигнала и с окном s согласованного
фильтра
Поэтому окно согласованного фильтра скользит вдоль оси и для каждого
фиксированного положения окна образуется выходной отсчет фильтра. Вы¬
делим следующие три фазы взаимодействия окна с сигналом.
Первая фаза характеризуется нарастанием количества элементов, об¬
щих для сигнала и окна. Во время второй фазы происходит полное сов¬
падение их положений. Для третьей фазы количество общих элементов
с течением времени уменьшается.
Все, кроме одного, отсчеты ВКФ образуются фильтром в течение пер¬
вой и третьей фаз, когда он пространственно не согласован с сигналом:
в пределах его окна находится лишь часть сигнала. Согласование во вре¬
мени имеет место лишь во время второй фазы. Тогда образуется пиковый
отсчет фильтра, содержащий в качестве полезной составляющей величи¬
ну, равную энергии незашумленного входного сигнала.
Зашумленный входной сигнал и = {и (0), и (1),... , тх (fc — 1)} =
{uU)}ok-1 представим в виде суммы полезного (эталонного) s =
= {s 0')}o,fc-l и шумового η = { n(j)}o k-i сигналов, т.е. u = s + η.
Учитывая, что пиковый выходной сигнал η согласованного фильтра
появляется с задержкой, не меньшей длительности входного сигнала и,
для первой и третьей фаз можно соответственно записать
г — 1
*7г!) = X)u(j)s(fc + 3 - r), г = 1,2,... ,к-1, (4.3.1)
з=о
к-1
»7рШ) = Σ и U) s U - Р)> V = 1,2, · · · , к - 1.
з=р
(4.3.2)
4,3. Разрешение контурных сигналов
161
Здесь г ир — соответственно номера шагов фильтрации во время первой
и третьей фаз. Если г = к или р = 0, то данные выражения определяют
выходной сигнал фильтра для второй фазы. На рис. 4.10 поясняется зна¬
чение параметров г ир для к — 3 и при отсутствии шумов. Видно, что на
каждом шаге фильтрации с фильтром взаимодействуют разные сигналы:
при г = 1 сигнал равен (0,0, гх(0)), а при р — 1 — (гх(1), гг(2), 0) и т.д.
При взаимодействии фильтра с сигналом образуется не один (как
надо с точки зрения разрешения перекрывающихся сигналов), а 2к —
- 1 ненулевых отсчетов. В общем случае 2к — 2 из них будут лишними
и играют роль коррелированной помехи. Действие такой помехи особен¬
но опасно, когда перекрывающиеся сигналы значительно различают¬
ся по масштабу. Негативный характер данной ситуации усугубляется,
естественно, из-за неизбежного воздействия флуктуационного шума
и других помех. Описанная ситуация является следствием применения
согласованного фильтра, формирующего на своем выходе ациклическую
ВКФ сигналов и и s. В условиях пространственной (временной) рассо¬
гласованности фильтра с сигналом формируемая во время фаз I и III
мера схожести не может быть везде равной нулю.
Мы рассмотрим задачу разрешения на основе сопряженного согласо¬
ванного фильтра (ССФ) (см. п. 3.8), формирующего меру схожести сигнала
и сигналом v, сопряженным с сигналом s. Как было показано в п. 3.8,
ССФ при отсутствии шумов ставит в соответствие сигналу и только один
ненулевой отсчет.
4.3.2. Условия обеспечения разрешенного образа на выходе филь¬
тра обнаружителя. Фильтр обнаружителя вырабатывает статистику, по
которой решающее устройство выносит решение о наличии сигнала на
входе. На рис. 4.11, а в качестве примера представлены поданные на вход
обнаружителя дискретные сигналы щ, U2, из и щ с амплитудами 2, 5, 1
1
η
6
. и2
J II
“4
jiM.
u3 1
111..
ЛИ 1
0
■■■■l.llll
а
Mill··, а ι·ι·ΐιιιι ' , ^
0
6
*72 °
|*74
I771
... -1
-ΐ-3 1 ν
0
в
Рис. 4.11. Сигнал на входе (а) и выходе (б, в) фильтра обнаружителя при отсут¬
ствии шумов и помех
162
Гл. 4. Операции над зашумленными контурами
и 3 длительностью к = 5. Шумы и помехи отсутствуют. Интервал между
сигналами ui и 112 равен двум, а сигналы 112 и из не только перекрыва¬
ются, но значительно, в пять раз, отличаются по амплитуде. На рис. 4.11,
б показаны выходные сигналы согласованного фильтра. Пиковый уровень
на его выходе для каждого из сигналов достигается в момент последнего
дискрета. Кроме пиковых отсчетов, фильтр образует на каждый из
входных сигналов 2Л: — 2 = 8 боковых отсчетов (лепестков) размахом
в к = 5 раз меньших пикового отсчета. Они частично перекрываются
для сигналов ub и2 и и3, причем из-за значительной разницы ампли¬
туд сигналов и2 и и3, боковые лепестки сигнала и2 по величине равны
пиковому отсчету для сигнала и3. в результате сигнал и3 не может
быть обнаружен на фоне сигнала и2 даже, как оговаривалось выше,
в отсутствие шумов и помех.
На рис. 4.11, в показана желательная картина выходных сигналов
фильтра: каждый его выходной отсчет 771, 772, Цз и щ соответствует по
времени последнему дискрету входных сигналов ub u2, и3 и и4.
Величина этого отсчета пропорциональна амплитуде входного сигна¬
ла, а боковые лепестки равны нулю. Такое распределение сигналов при
отсутствии шумов на выходе фильтра назовем разрешенным образом.
Если фильтр формирует разрешенный образ, то сохраняется информация
не только об амплитудах входных сигналов, но и о временном положении
каждого из сигналов.
Рассмотрим основные требования к процессу формирования выход¬
ного сигнала фильтра, достаточные для получения разрешенного образа
суммарного сигнала.
Первым условием является формирование выходного сигнала только
в момент временного (пространственного) согласования фильтра с сигна¬
лом, т.е. только в момент второй фазы.
Рассмотрим, в чем заключается сущность второго условия.
Пусть u = {w(j)}ofc_1n w = {w(j)}ok_ 1 — два дискретных сиг¬
нала размерности к, причем для них справедливы соотношения прямого
и обратного ДПФ
= IΣ exp
U(m)
= Σ ехр {-*Tjm}
ra=0
j=0
к-1
к-1
чл = | Σ w(m) ехр
W{m)
1 - X] w(j) εχρ
т—0 j=О
где U(т) и W(т) — соответственно спектры сигналов и и w. Из пери¬
одичности функций exp = ехР ^ а^)(т ^ где а
и β — целые числа, вытекает периодичность сигналов и и w, а также их
спектров U и W:
и (j) -u{j ± ак), w (j) = w(j± β к).
(4.3.3)
4.3. Разрешение контурных сигналов
163
Отсюда следует, что отсчеты линейного фильтра
к — 1
η (l) = ^2u(j)w(l-j), 1 = 0,1,... ,к-1, (4.3.4)
3=0
обладают свойством периодичности, т.е. η(β = η(j±.ak), а фильтр в соот¬
ветствии с выражением (4.3.4) и с учетом (4.3.3) образует отсчеты цикли¬
ческой свертки сигналов и и w. Полагая w(j) = s (к — 1 — j), из (4.3.4)
получаем
к-1
- V",
1), ук-1.
(4.3.5)
v(l) = 2^u (j) s{j -1 +к
j=о
Данное выражение представляет собой смещенную на к — 1 отсчетов
циклическую ВКФ периодических сигналов и и s. Такая ВКФ не имеет
краевых эффектов. Отсчеты сиг¬
налов и и s удобно представлять
не на прямой, а на кольце. На рис.
4.12 дана иллюстрация образова¬
ния отсчетов циклического филь¬
тра при вычислении ВКФ сигналов
и и s при I = 0. Каждому значению
Z, I = 0,1,2,... , к-1, соответству¬
ет свой угол против часовой стрел¬
ки внешнего кольца, равный 2πΐ/k.
Для образования одного выход¬
ного отсчета η(1) в пределах каждо¬
го сектора перемножаются значения
и (·) и s (·), а затем получившиеся
произведения суммируются.
Итак, второе условие обеспече¬
ния на выходе фильтра разрешен¬
ного образа состоит в применении
свободной от краевых эффектов
циклической процедуры, основанной на периодичности входных сигналов
фильтра и сигнала, определяющего его ИХ.
Отметим, что при ациклической обработке сигнала, описываемой вы¬
ражениями (4.3.1) и (4.3.2), отсчеты сигнала и ИХ фильтра считаются
непериодическими. При вычислении выходных отсчетов фильтра не про¬
исходит сдвиг отсчетов его ИХ. Каждому положению окна соответствует
не к, как при циклической фильтрации, а лишь один отсчет. Результатом
фильтрации является смещенная ациклическая ВКФ Нас, которая, как
и соответствующая циклическая ВКФ Нс, имеет отсчет, равный скаляр¬
ному произведению (u, s). Ее (к — 1)-й отсчет совпадает по величине
с (к — 1)-м отсчетом циклической ВКФ Нс и по величине является мак¬
симальным (пиковым). Остальные отсчеты циклической и ациклической
ВКФ, как правило, не совпадают.
Рис. 4.12. Образование отсчетов цикли¬
ческого фильтра при / — 0
164
Гл. 4. Операции над зашумленными контурами
Рассмотрим третье условие обеспечения разрешенного образа на
выходе фильтра обнаружителя. Спектр = {ρη {^)}0 к_г выходного
сигнала η циклического линейного фильтра (4.3.4) равен произведению
спектров Рп = {ри (m)}o fc_1 иР1/) = {pw (m)}0?fc_1 сигналов и и w, т.е.
Ρη (т) = ри (т) · pw (т), т = 0,1,1. (4.3.6)
Для обеспечения разрешенного образа фильтр должен формировать
в качестве реакции на каждый входной сигнал единичный импульс (сим¬
вол Кронекера), спектр Р^ которого равен
рч = Wo.fc-I или Ρη (0) = Ρη (1) = · · · = Ρη (к - 1) = 1. (4.3.7)
Действительно, в этом случае обратное ДПФ будет иметь вид
П (0 = | Σ Ρη (т) ехр {* γ™*} =
= 1 Vexpfi^m/U/1 ПрИ* = °’
к L к J [О ДЛЯ других 1.
(4.3.8)
Выполнение условия (4.3.7) возможно при
|Ри (т)\2 - |pw (т)|2 = 1, т = 0,1,... , к - 1,
(4.3.9)
и (или)
2 1
\Ри{т)\ = 2, т = 0,1,... ,к 1.
1р» Ml
(4.3.10)
Далее будем рассматривать следующие два соотношения спектров сиг¬
налов и и w: 1) случай равномерных энергетических спектров и 2) случай
взаимнообратных энергетических спектров.
В первом случае фильтр (4.3.4) является циклическим, согласованным
с сигналом u = s, имеющим равномерный энергетический спектр:
к-1
V (0 = s {j) s (j - I + к - 1), I = 0,1,... , к - 1.
jf=0
Во втором случае фильтруемый сигнал u = s обрабатывается сопряжен¬
ным согласованным (инверсным) фильтром
к-1
v (0 = 53 s (J)v (J ~1 + k ~ -1)’ 1 = 0> i> · · · >k -1»
j-0
где sni/ — сигналы со взаимнообратным спектром.
Условие (4.3.9) для обеспечения процесса сжатия сигнала без корре¬
ляционных шумов является достаточно жестким в том плане, что допус¬
кается только одна форма энергетического спектра.
Условие (4.3.10) включает первое условие в качестве частного случая.
Оно допускает значительное расширение класса допустимых сигналов
с нулевым уровнем корреляционных шумов. Если не принимать во вни¬
мание проблему помехоустойчивости обнаружителя, то единственным
4.3. Разрешение контурных сигналов
165
препятствием для получения нулевого корреляционного шума является
равенство нулю хотя бы одной компоненты спектра сигнала s.
Следовательно, для получения на выходе фильтра обнаружителя раз¬
решенного образа необходимо:
1) совпадение положений сигнала и окна фильтра (пространственное
или временное согласование);
2) формирование циклической ВКФ обрабатываемого и эталонного
сигналов;
3) равномерный либо взаимно обратный характер спектров обрабаты¬
ваемого и эталонного сигналов (согласование спектра сигнала и частотного
коэффициента передачи фильтра).
4.3.3. Образование отсчетов циклического фильтра для второй фазы
фильтрации по результатам первой и третьей фаз. На первый взгляд
выполнение первого условия получения разрешенного образа по срав¬
нению с двумя другими условиями кажется наиболее сложным. Окно
фильтра должно перемещаться скачками и после каждого скачка долж¬
но точно (в условиях априорной неопределенности положения сигнала)
совмещаться с ним. В действительности это условие достаточно просто
выполнить следующим образом.
Назовем комплементарными два примыкающих друг к другу положе¬
ния окна фильтра (рис. 4.13, б, в). Правая граница первого окна совпада-
Н 1 h
и(0)|«(1)|и(2)[«О)|
■4 1 К
r= 1
5(0) 5(1)
*(2)|5(3)
н—к
г =5, р =1
i 1 1 Ь
5(0)|5(1)|5(2)|5(3)|
ч—ь
+
+
Рис. 4.13. Комплементарное расположение окон фильтра для г = 1, к = 4
ет с положением левой границы второго окна, а стык окон расположен
в пределах сигнала и. Он смещен на г элементов от левого края сигнала.
Первое окно реализует первую, а второе — третью фазы фильтрации.
В течении первой фазы к-г элементов окна не пересекаются с сигна¬
лом и при отсутствии шумов первые к — г отсчетов сигнала равны нулю,
а ненулевые отсчеты сигнала смещены на величину г. Выражение (4.3.5)
для первой фазы фильтрации будет равно
к-1
vl (0 = X] u(J + r)s(j - l + k- 1),
j=k-г
I — 0,1,... , к — 1, г = 1,2,... , к — 1.
(4.3.11)
166
Га. 4. Операции над зашумленными контурами
Во время третьей фазы фильтрации окно выходит за правую границу
сигнала ир = г — &, r = fe + l,fe-f-2,... ,2k — 1, отсчетов сигнала будут
нулевыми. Ненулевые отсчеты сигнала смещены от начала сигнала и на
величину р = г - к. Выражение (4.3.5) для третьей фазы принимает вид
2к—г—1
*7гП(0= Σ u(j + r)s(j-1 + к-1),
j=о (4.3.1Z)
I = 0,1,... , к - 1, г = к + 1, к + 2,... , 2к - 1.
Образуем сумму последних двух выражений, беря все значения аргу¬
ментов по модулю к:
Vг (0 + vln (О = X)« O' + r) 8 (j - I + к - i),
j=О
1 = 0,1,... ,к-1, г = 1,2,... ,к - 1.
(4.3.13)
Данная сумма с точностью до обозначений и смещения выходного
сигнала на величину г совпадает с выражением (4.3.5) для выходного
сигнала циклического фильтра во время второй фазы:
ηΐ {I) + ηΐ11 (I) = ηΐ1 {I), 1 — 0,1,... ,к — 1, г = 1,2,... , к - 1.
(4.3.14)
Таким образом, для определения реакции циклического фильтра
при точном совпадении окна с сигналом достаточно найти сумму реак¬
ций этого фильтра для двух произвольных комплементарных положе¬
ний окна (т.е. со смещением окна на к шагов) и учесть величину сдвига
г стыка окон относительно положения фильтруемого сигнала и. Такой
способ получения необходимой серии отсчетов циклического фильтра,
соответствующих второй фазе фильтрации, назван алгоритмом ЧКШС
(«через к шагового суммирования»).
Пример 1. Для сигналов и = {1,2,3,4} и s = {2, —1, —2,4} найдем отсче¬
ты циклического фильтра для второй фазы фильтрации по результатам первой
и третьей фаз при г = 1. Применение формул (4.3.11) и (4.3.12) дает r/i =
= {-2, - 1,2,4}иг/5 = {10,16,8, - 7}.
Суммируя в соответствии с выражением (4.3.14), получим η = {8,15,10, — 3}.
Расчет по формуле (4.3.5) дает вектор η = {—3,8,15,10}. Сравнивая эти векторы,
видим, что с учетом циклического смещения на г = 1 элемент они совпадают.
4.3.4. Получение отсчетов циклического фильтра для второй фазы
фильтрации по результатам ациклической фильтрации. В п. 4.3.3 была
решена задача получения на основе алгоритма ЧКШС, примененного к
двум сериям отсчетов циклического фильтра и полученных для ком¬
плементарного положения окон, результатов второй фазы фильтрации,
т.е. когда окно точно совпадает с сигналом. Однако высокая трудоем¬
кость циклической фильтрации, в к раз большая, чем при ациклической
фильтрации, сохранилась. Учитывая, что характеристики циклического
и ациклического фильтров определяются одним и тем же эталонным
4.3. Разрешение контурных сигналов
167
сигналом s, следует ожидать определенной зависимости между резуль¬
татами их работы.
Выходные сигналы ациклического фильтра для первой и третьей фаз
фильтрации задаются выражениями (4.3.1) и (4.3.2). Сумма выходных сиг¬
налов в этих фазах равна
1—1 k — 1
ηιΓ + η™ = Y2u(j)s(k + j - г) + и (j) s (j - р),
3 =0 j—p
г = 1,2,... , к — 1; р = 1,2,... , к — 1.
Если сигналы и и s обладают свойством периодичности (4.3.3), а по¬
ложения окон фильтра комплементарны, то г = р + к или г = (р)к.
Последняя запись означает, что величина р берется по модулю к. Тогда
г—1 к—1
vl + η"1 = Σ и U) s (k + j ~ r) + X] и (j) s(k + j — r) =
j=0 j—r
k — 1
= Σ u («?) s + j “ r)’ r = 1,2,... , к - 1. (4.3.15)
Сравнивая полученное выражение с (4.3.5), приходим к выводу, что
оно определяет сдвинутый на единицу отсчет циклического фильтра при
точном совпадении окна фильтра с сигналом, т.е. для второй фазы филь¬
трации
η (г - 1) = ηΐ +η1ρ\ г = р = 1,2,... , к - 1. (4.3.16)
Данное соотношение дает возможность находить отсчеты цикличе¬
ского фильтра только для второй фазы по результатам работы зна¬
чительно менее трудоемкого ациклического фильтра. Алгоритм оста¬
ется тем же, что и при обработке выходных сигналов циклического
фильтра — это ЧКШС. Для получения по результатам работы ацикли¬
ческого фильтра (I — 1)-го отсчета циклического фильтра для второй
фазы фильтрации, необходимо просуммировать 1-й и (I + к)-й отсчеты
ациклического фильтра, Ζ = 1,2,...
Пример 2. Для сигналов и и s из примера 1 по формулам (4.3.1) и (4.3.2) при
к = 4 найдем семь значащих отсчетов ациклического фильтра:
η = {4,6,7, 10, -7,2,δ}.
^ Фаза I Фаза II Фаза III '
Применим алгоритм ЧКШС к данной последовательности. В соответствии
с (4.3.16) получаем
I = 0, η (—1) = 4 — 7 = —3; / = 2, η (1) = 7 + 8 = 15;
J = l, ry(0) = 6 + 2 = 8; I = 3, η (2) = 10 + 0 = 10.
Таким образом, η = {—3,8,15,10}. Сравнивая этот результат с результатом из
примера 1, видим, что с учетом смещения на один элемент они совпадают.
168
Гл. 4. Операции над зашумленными контурами
4.3.5. Геометрическая интерпретация и энергетические соотноше¬
ния процесса формирования разрешенного образа на выходе фильтра.
Как было показано выше, разрешенный образ на выходе фильтра об¬
наружителя может быть сформирован циклическим фильтром с по¬
следующей обработкой его отсчетов по алгоритму ЧКШС. Если сигнал
s имеет равномерный спектр, то этот фильтр будет согласованным.
Когда сигнал s характеризуется спектром произвольной формы, но без
нулевых значений — то фильтр будет согласован с сопряженным сигна¬
лом V. Сущность циклической фильтрации с позиции векторного пред¬
ставления незашумленного сигнала s = {s(™)}ofc-i была рассмотрена
в п. 3.8. Согласованная циклическая фильтрация является процедурой
вычисления проекций вектора s в собственной системе отсчета, образо¬
ванной к базисными векторами, полученными в результате циклическо¬
го сдвига вектора s. Сигнальный вектор s является одним из базисных
векторов данной системы. При этом предполагается линейная незави¬
симость этих векторов, т.е. определитель матрицы S (3.8.26) собственной
системы отсчета не равен нулю:
detS^O. (4.3.17)
Данное условие накладывает весьма слабые ограничения на вид сиг¬
нального вектора s. Поэтому угол между базисными векторами собствен¬
ной системы отсчета может быть достаточно произвольным, т.е. базис,
в общем случае является косоугольным. Для формирования разрешенного
образа путем циклической согласованной фильтрации вектора s
к-1
v(l) = Yts(j)s(j-l + k-l), 1 = 0,1,...,к-1 (4.3.18)
3 =о
необходимо обеспечить выходной сигнал в виде символа Кронекера:
77(0 = {0,0,... ,0,1}, (4.3.19)
т.е. чтобы все его отсчеты, кроме одного, были нулевыми. Применительно
к рассматриваемой задаче это означает требование равенства нулю всех,
кроме одной, проекций сигнала s в косоугольной системе отсчета. Проек¬
ция одного вектора на другой будет нулевой лишь при ортогональности
этих векторов. Отсюда становится понятным, что в собственной косоуголь¬
ной системе отсчета невозможно обеспечить попарную ортогональность
одного из базисных векторов, роль которого играет фильтруемый сигнал,
с каждым из базисных векторов. В этом и заключается причина возник¬
новения корреляционных шумов при согласованной фильтрации сигнала.
Если бы вектор s задавал собственную ортонормированную систему от¬
счета, то условие (4.3.19) обеспечивалось автоматически. Такая ситуация
имеет место при равномерном энергетическом спектре сигнала s, когда
скалярное произведение вектора s на свою сдвинутую копию равно нулю.
Когда мы переходим к согласованной обработке сигнала v, сопряжен¬
ного с сигналом s, то как показано в п. 3.8, это эквивалентно определению
координат вектора s в собственной биортогональной системе отсчета.
4.3. Разрешение контурных сигналов
169
Данный процесс реализуется фильтром
к-1
v(l) = Y,s(j)v(j-1 + к-1), 1 = 0,1,...,Л-1. (4.3.20)
j—о
Поскольку сигнальный вектор s является одним из базисных векторов
собственной системы отсчета, то одна из его координат будет строго равна
единице, а остальные — нулю. Это обуславливает следующие важные свой¬
ства процедуры нахождения координат сигнального вектора в собственной
биортогональной системе отсчета по сравнению с определением проекций
данного вектора при обычной согласованной фильтрации сигнала:
1) формирование разрешенного образа выходного сигнала фильтра, т.е.
образование только одного ненулевого отсчета на каждый входной неза-
шумленный сигнал при нулевом корреляционном шуме, что дает возмож¬
ность наилучшим образом разрешить перекрывающиеся сигналы.
2) возможность оценки параметров линейных преобразований сигналь¬
ного вектора и = μδ, где μ = |μ| ехр{гА<^}, по отношению к базисному
(эталонному) вектору s.
Данные преимущества ССФ по сравнению с обычным согласованным
фильтром достигаются, в конечном счете, за счет ухудшения отношения
сигнал/шум на выходе фильтра (4.3.20) по сравнению с фильтром (4.3.18).
Частотная характеристика ССФ будет иметь полюсы на тех частотах,
где энергетический спектр сигнала s равен нулю, что и объясняет усло¬
вие (4.3.17) реализуемости фильтра. Чем сильнее неравномерность энер¬
гетического спектра сигнала s, тем больше прозрачность ССФ для флук-
туационных шумов на частотах, слабо выраженных в спектре сигнала s.
Данное обстоятельство является решающим для применения рассма¬
триваемого алгоритма разрешения сигналов: чем более равномерен спектр
сигнала s, тем он более предпочтителен.
В п. 3.10.3 было показано, что при одинаковом входном отношении сиг¬
нал/шум, входное отношение сигнал/шум у ССФ в D раз хуже, чем у со¬
гласованного фильтра, где D = ||s||2||v||2. Если сигнал s характеризуется
равномерным спектром, то эффективность обоих фильтров одинакова.
4.3.6. Формирование разрешенного образа при произвольном распо¬
ложении окна фильтра. Процедура ЧКШС производит суммирование
отсчетов фильтра с интервалом, равным размерности к сигнала. Она осу¬
ществляется на участке ММ длиной L кодовых интервалов, L > к,
на котором расположены перекрывающиеся эхо-сигналы (рис. 4.14, а).
В результате образуется участок NN, на котором координаты отметок,
пересчитанные к началу эхо-сигнала, изменяются в пределах от 0 до к — 1
(рис. 4.14, б).
Происходит сокращение размерности пространства значений даль¬
ности, причем новая координата В! сигнала (на участке NN) связана
с исходной R (на участке ММ) соотношением
R — R,Jr хк,
(4.3.21)
170
Гл. 4. Операции над зашумленными контурами
С С
в I
}. 1.. 1
R max
А
1
oj 1 2 3 4 5 6 ■■
' \LA Ш
Г"
0 1
1
М
1
Μ
lN
а б
Рис. 4.14. Уменьшение размерности пространства отсчетов при ЧКШС для к = 4:
а — положение сигналов А, В и С до обработки; б — модифицированные отсчеты
ЧКШС сигналов А, В и С
где R' = (Е)к — остаток вычета R по модулю к, равный координате
модифицированного отсчета ЧКШС, х — порядок этого вычета.
Пусть L ^ к, т.е. начала всех перекрывающихся эхо-сигналов распо¬
ложены на интервале 0,1,... , к—1. Тогда х = 0 и R = R', т.е. координаты
сигналов до и после ЧКШС совпадают. В данной ситуации разрешаются
до /^сигналов. Для реально встречающихся ситуаций, связанных с разре¬
шением эхосигналов, величина к должна быть порядка 10... 15. в связи
с тем, что каждый шаг ЧКШС увеличивает энергию флуктуационного шу¬
ма, целесообразно искусственно ограничить интервал ММ на уровне L =
= fc, положив отсчеты эхо-сигналов за его границей равными нулю. Пред¬
варительно, по возможности, необходимо убедиться в отсутствии дру¬
гих эхо-сигналов в непосредственной близости от установленной границы.
Если же L > к, то порядок вычета неизвестен, что приводит к неод¬
нозначности определения R по значению R'. На рис. 4.14,а расстояние до
цели, задаваемой сигналом С, больше к, т.е. i? = 5,afc = 4. В результате
для этого сигнала Rf = 1, т.е. не совпадает со значением R = 5. В данной
ситуации для уточнения истинной координаты R сигнала по оси времени,
кроме отсчета R', необходима дополнительная информация. Она может быть
получена при последовательном применении сигналов разной размерности.
Пусть х\ порядок вычета R по модулю &ι, а х2 — по модулю к2, к\ ф к2.
Тогда на основании (4.3.21) можно получить следующее уравнение в целых
числах первого порядка с неизвестными х\ и х2:
xiki — х2к2 4- (Λι - А2) = 0, (4.3.22)
где А\ = (R)ki иА2 = (^)*;2 — модифицированные отсчеты ЧКШС.
Как известно [134], общее решение такого уравнения равно
XI (t) = xoi + k^t, х2 (t) = хо2 4- k\t, t — 0, ±1, ±2,... , (4.3.23)
где [ж01,ж02] — частное решение этого уравнения, причем ki и к2 —
взаимно простые числа. Для нахождения частного решения дробь к\)к2
представляется в цепном виде и отбрасывается ее последнее, η-е звено.
Получающая при этом (п — 1)-я подходящая дробь записывается в виде
PnlQ\4· Тогда частное решение уравнения (4.3.22) будет
[хоъж02] = [(—1)η-1ζ?ΐ2(^.ι — Α2)](—1)ηΡι2(Αι — А2)]. (4.3.24)
4.3. Разрешение контурных сигналов
171
Выражения (4.3.23) и (4.3.24) позволяют записать последовательность
[хх(t), x2(t)], t = О, ±1, ±2,... , общих решений уравнения (4.3.22) через
отсчеты ЧКШС Αι и А2 и поставить им в соответствие последователь¬
ность значений вычета R:
R(t) = kiXi{t) + Αχ = k2x2(t) + A2, t = 0, ±1, ±2,...
Тогда с учетом (4.3.23) получим
R(t) = (x0i + k2t)ki + Ai = xoxkx + k\k2t + Αχ. (4.3.25)
Отсюда следует, что интервал вычета для соседних значений R ра¬
вен AR = R(t) - R(t — 1) = k\k2. Данный результат означает, что
на интервале ММ существует зона шириной уже не к\ или к2, а к\к2
кодовых интервалов, в пределах которой по найденному частному решению
уравнения (4.3.22) и отсчету Αχ, полученного в результате ЧКШС, может
быть однозначно определена истинная координата (задержка) R. Можно
показать, что в общем случае, когда последовательно используются сигналы
размерностью /^, г = 1,2,... ,гг, при условии, что любые два значения к{
п
и kj — взаимно простые числа, интервал однозначности равен AR = \~[ ki.
i-1
Пусть, например, R = 10. Используются сигналы с к\ = 3, к2 = 4 и кз = 5.
Модифицированные отсчеты ЧКШС при этом соответственно равны А\ = 1, А2 —
— 2 и Аз =0. Определим по этим данным значение R. Решая соответствующие
уравнения в целых числах, получим следующую таблицу возможных значений R.
Таблица 4.1
t
-3
-2
-1
0
1
2
3
т
-110
-50
10
70
130
190
250
Поскольку к\к2кз = 60, то как видно из таблицы, возможные значения R
разделены интервалом ΔR = 60. Так как R > 0, то значения —110 и —50 мож¬
но не учитывать. Если предположить, что интервал ММ с перекрывающимися
эхосигналами не превышает 60-ти кодовых интервалов (для радиолокационных
задач этому значению при длительности кодового интервала 0,1 мкс соответствует
достаточно большой интервал дальности величиной 900 м), то величина R одно¬
значно будет равна 10.
Поскольку максимальное значение дальности ограничено конечным
значением #тах, то однозначное измерение R обеспечивается достаточно
п
просто, если выбрать ]] ki & Rmах. Результаты данного анализа сохраня-
г—1
ются на случай, когда на интервале ΜМ находится не один, а несколько
эхо-сигналов, по крайней мере, не менее kj, где kj — размерность сигнала,
имеющего минимальную размерность.
4.3.7. Примеры.
Пример 3. Пусть s = {1,2,3,4}. Сопряженный с s сигнал v = -^{—^9,
1,1,1}. График энергетического спектра сигнала s показан на рис. 4 15, а.
172
Гл. i. Операции над зашумленными контурами
tp(rn?
100
8 2 8
0 12 3 т
а
Лссф
0 Ϊ 2
б
1
1
0 12 3 /
в
Рис. 4.15. Результаты обработки одиночного сигнала: а — энергетический спектр
сигнала s = {l,2,3,4},6 — выходной сигнал циклического ССФ для второй фазы,
в — выходной сигнал циклического согласованного фильтра для второй фазы
При перемещении окна ССФ отклик фильтра в соответствии с выражени¬
ем (4.3.20) равен
ηΓ(1) = Y,sr{j)v{j-l + 3), 1 = 0,1,2,3,4,5,6, (4.3.26)
3=0
где г — номер позиции окна по отношению к положению сигнала. Взаимное
положение сигнала и окна фильтра при г = 1 имеет вид
sfT I о I о I 1 I 2 | 3 | 4 | о | 0~|
V |-0,225| 0,025 ] 0,02510,275] —►
Для значения шага г = 1 вектор сигнала s = {0,0,0,1}, для г = 2 он
равен S2 = {0,0,1,2} и т.д. Ациклическая ВКФ сигналов s и v, найденная
в соответствии с (4.3.21) и записанная в виде прямоугольной матрицы форматом
(г х 2) = (4 х 2), имеет вид
0,275 0,575 0,9 1
-0,275 -0,575 -0,9 0
Применение алгоритма ЧКШС эквивалентно суммированию элементов каж¬
дого столбца матрицы. Проводя такое суммирование, получаем результат цикли¬
ческой сопряженной согласованной фильтрации т^ссф для второй фазы, то есть при
совпадении окна ССФ с сигналом: η = {0, 0,0,1}. Таким образом, пиковый отсчет
фильтра равен единице, а корреляционный шум отсутствует (рис. 4.15, б).
Для сравнения на рис. 4.15, в приведен вид выходного сигнала η0φ циклического
согласованного фильтра для второй фазы. В данном случае уровень корреляцион¬
ных шумов очень высок. Коэффициенты шума фильтров для рассматриваемого
сигнала s = {1,2,3,4}, определенные по формулам (3.10.8) и (3.10.6), равны
NcСф = 1,05 и ЛГСф = 4. Ухудшение отношения сигнал/шум ССФ по сравнению
с согласованным фильтром в данном случае порядка б дБ. Это является платой
за разрешение перекрывающихся сигналов.
Пример 4. Рассмотрим задачу разрешения перекрывающихся по двум от¬
счетам сигналов s = {1,2,3,4} и 10s = {10, 20,30,40}, образующих суммарный
сигнал {1,2,13,24,30,40}:
10s | 10 | 20 | 30 I 40 |
суммарный | ϊ | 2 | 13 | 24 | 30 | 40 |
сигнал
4 А. Распознавание зашумленных контуров
173
Результаты фильтрации суммарного сигнала фильтром, согласованным с сиг¬
налом s = {1,2,3,4} и ν = {—0.225; 0.025; 0.025; 0.275}, показаны на рис. 4.16.
264
*сф
264250
ΙΙΙι
0 1
3 /
10
^ссф | 1
0 12 3 /
б
Рис. 4.16. Результаты обработки перекрывающихся сигналов согласованным филь¬
тром (а), сопряженным согласованным фильтром (б)
В первом случае уровень корреляционных помех настолько велик, что ста¬
вить вопрос о разрешении сигналов нецелесообразно, во втором случае эта
задача решена идеально. Отметим, что при ССФ сохраняется информация о
параметрах разрешенных сигналов, в данном случае — о их временных соот¬
ношениях и энергиях.
Пример 5. Разрешим и оценим параметры перекрывающихся контурных
сигналов Ει и Е2 (см. рис. 4.9) Ei = {l,i, 1}, Е2 = {2г, — 2,2г} по суммарному
контуру Ν = {1,ΐ,1 + 2г, — 2,2г}.
Эталонный контур равен Е = Εχ = {1, г, 1}, а сопряженный с ним контур
ν = {0.3 + 0.1г; — 0.2 - 0.4г; 0.3 + 0.1г}. В результате ациклической фильтра¬
ции суммарного контура фильтром, согласованным с сопряженным контуром,
получаем
0.3 + 0.Н; —0.3 — 0.1г; 0.8 + О.бг;
—0.1 + 0.7г; 0.3 + 2.Н; 0.2 - О.бг; -
-0.2 +О.бг; 0 0
Применяя алгоритм ЧКШС, то есть суммируя столбцы матрицы, получаем: Н =
= {0, 2г, 1}. Отсюда видно, что суммарный контур N состоит из контура Е = Ει
и контура Е2 = 2ехр {ζπ/2}Ε, смещенного на две позиции, растянутого в два
раза и повернутого на угол π/2 по отношению к контуру Е.
4.4. Распознавание зашумленных контуров
4.4.1. Постановка задачи распознавания контуров. Сформулируем
на примере двух классов задачу распознавания зашумленных контуров.
Пусть rg = {'Г(1)(п)}0>Л_1 иГ^} = {7(2) (n)}Q k_1 — эталонные конту-
ры соответсвенно классов Αχ и А2. На устройство распознавания подается
либо зашумленный контур первого класса, равный Ν(χ) = + Ζ, либо
второго класса, равный Ν(2) = + Ζ, где Ζ — шумовой контур и
Гй = |/*(1)|ехр{*Др(1)}{7(1) (n + d{1))}ok_v (4.4.1)
Г(2) = |м(2)|ехр{гД^(2)}{7(2) (n + d{2))
Параметры \μ\, Αφ и d предполагаются неизвестными.
(4.4.2)
174
Гл. 4. Операции над зашумленными контурами
Задача распознавания состоит в обоснованном отнесении зашумлен¬
ного контура N к одному из классов Αχ или А2. Для принятия решения
необходимо сформировать безусловное отношение правдоподобия и срав¬
нить его с пороговым значением. Функции правдоподобия контуров Ν(χ)
и N(2) имеют соответственно вид (см. п. 3.10.3)
Лс (N, |^(1)|,A^(1),d(1)) =
= Cexp{-^[||N||2 + ||rg||2 -2Re(N,rg)]}, (4.4.3)
Лс (Ν, |μ(2)|ιΔρ(2),<ί(2)) =
= cexp {-Λ, [||Ν||2 + ||rg - 2Re (N, rg)]}. (4.4.4)
Тогда логарифм условного отношения правдоподобия запишется как
In [L (Ν, |μ(1)|, |р(2)|.Δ<ρ(1), Δ(^(2),с?(1), tf(2))] =
= -^2{НГ(1)Ц2 - lirgll2 -2[Re(N,rg)-Re(N,rg)]}. (4.4.5)
Перейдем к рассмотрению вопроса о распознавании полностью из¬
вестных контуров. Полученные при этом результаты являются основой
построения распознающих устройств для более сложных случаев, когда
контуры содержат неизвестные параметры.
4.4.2. Распознавание полностью известных контуров. Для данного
случая Ν(χ) = Γ(ΐ) + Ζ и Ν(2) = Г(2) + Ζ логарифм безусловного
отношения правдоподобия будет иметь вид
Ini (Ν) =
= _^{llr(i)ll2_llr(2)ll2-2[Re(N,r(i))_Re(N,r(2))]}· (4·4·6)
Правило принятия решения в пользу класса Αχ запишется как
Re (Ν, Г(1)) — Re (Ν,Γ(2)) ^,2,
где U\,2 = σ21ηΛο+0,5(||Γ(χ)||2 — ||Г(2)||2). Таким образом, для принятия
решения о классе полностью известного контура надо сформировать раз¬
ность реальных частей скалярных произведений распознаваемого зашум¬
ленного контура N с каждым из эталонных контуров. Далее эта разность
сравнивается с пороговой величиной U\j2, зависящей от разностей энер¬
гий эталонных контуров, дисперсии ЭВ шумовых контуров Z, отношений
рисков и априорных вероятностей классов, учитываемых величиной Ло
(рис. 4.17, а). Оптимальное распознающее устройство можно выполнить
на базе двух КСФ, один из которых согласован с эталонным контуром
Г(1), а второй — с Г(2) (рис. 4.17, б). Если воспользоваться выражени¬
ем (4.1.7) для квадрата расстояния между зашумленным и эталонным
контурами, то логарифм ОП для полностью известных контуров (4.4.6)
можно представить как InL (N) = — [Д^,г(1) - βΝ,Γ(2)]/(2σ·2). Решение
4А. Распознавание зашумленных контуров
175
Рис. 4.17. Структуры распознающих устройств полностью известных контуров
в пользу класса Αχ в данном случае будет приниматься при условии
^ν,γ(1) ~ ^ν,γ(2) ^ 2σ21ηΛο, т.е. считается, что контур относится к
классу Αι, когда точка, задающая контур N, будет расположена ближе
(с заданным запасом) к точке, задающей эталонный контур Γ(χ), чем к
точке, задающей контур Г(2) (рис. 4.17, в).
4.4.3. Распознавание контуров с неизвестными углами поворотов
и сдвигами начальных точек. Пусть = ехр {ζΔ^>(χ)}Γ(χ) и =
= ехр {ζΔ<£>(2)}Γ(2), т.е. сигнальный контур повернут по отношению
к своему эталонному контуру Γ(χ) на угол Δ^(χ), а контур — на
угол Δ<£>(2) к контуру Г(2). Сведем задачу распознавания таких конту¬
ров к задаче распознавания полностью известных контуров, используя
оценки Δ^χ) и Δ£>(2) (см. п· 4.1)· Также учтем, что от поворота контура
его энергия не меняется, т.е. ||г|^|| = ||Γ(χ)|| и ЦГ^Ц = ||Г(2)||. Тогда
решающее правило для отнесения контура к первому классу будет
иметь вид
I (Ν, Г(1)) | - | (Ν, Г(2)) | ^ σ21ηЛо + 0,5 (||Г(1)f - ||Г(2)f) . (4.4.7)
Если потребовать, чтобы эталонные контуры обладали одинаковой
энергией, т.е. чтобы ||Γ(χ)||2 = ||Г(2)||2, то решающее правило запишет¬
ся как
| (Ν, г(1)) | - 1 (Ν,г(2)) | σ21ηΛ0.
Структура распознающего устройства для данного случая содер¬
жит два формирователя модуля скалярного произведения зашумленно-
176
Гл. 4. Операции над зашумленными контурами
Рис. 4.18. Структура распознающего устройства контуров с неизвестными углами
поворотов
го контура N с каждым из эталонных контуров, вычитающее и пороговое
устройства (рис. 4.18).
Если теперь у каждого из сигнальных контуров дополнительно про¬
изведены сдвиги начальных точек соответственно на dщ и d(2), то для
получения алгоритма распознавания находим по контуру N оценки ве¬
личин 2), Δ<^(ΐ) и Д<^(2)(см· п· 4.1) и сводим данный случай к
задаче распознавания полностью известных контуров. Решающее пра¬
вило в пользу класса А\ при одинаковых энергиях эталонных конту-
ров имеет вид |*7(1) (m)|max - \τ](2) (m)|max > σ21ηΛ0) где |r/(1) (m)|max
и |^(2) (m)|max — максимальные значения модулей отсчетов фильтров,
согласованных соответственно с эталонными контурами Г^) и Г(2). Рас-
Рис. 4.19. Распознающее устройство контуров с неизвестными сдвигами начальных
точек, углами поворотов и при ||Γ(ΐ)|| = ||Г(2)||
познающее устройство содержит два фильтра КСФ1 и КСФ2, согласован¬
ных с эталонными контурами, формирователи модулей отсчета фильтра,
экстремальные устройства для определения максимальных значений этих
модулей, вычитающее и пороговое устройства (рис. 4.19).
4.4.4. Общие требования к контурам при их распознавании. Рас¬
смотрим теперь случай распознавания контуров в составе алфавита из
М классов Αι, Л2,... , Ам· Как показано в работе [53], устройство распо¬
знавания содержит набор из М фильтров, каждый из которых согласован
с одним из эталонных сигналов алфавита. Решающее устройство опре¬
деляет номер фильтра с максимальным по модулю выходным сигналом
4 А. Распознавание зашумленных контуров
177
и при превышении порогового уровня выносится решение в пользу клас¬
са, номер которого совпадает с номером фильтра (рис. 4.20). Рассмотрим
вопрос о том, какими свойствами должны обладать контуры {Γ(η)}Ί AJf,
чтобы результаты распознавания
при использовании данного алго¬
ритма были наилучшими.
Поскольку максимальный по
модулю выходной сигнал фильтра
равен энергии контура и поэто¬
му не зависит от вида контура,
то оценивать качество алфавита
контуров, с точки зрения эффек¬
тивности их распознавания, надо
по реакции фильтра на контуры
тех классов, с которыми он не со¬
гласован. Наилучшим будет такой
алфавит, который в этом случае
обеспечит на выходе фильтра при
отсутствии шумов нулевой выход¬
ной сигнал. Так как при обра¬
ботке применяются согласованные
фильтры, то преимущество алфавита сохранится и при воздействии
на распознаваемые сигналы широкополосных шумов. КСФ (см. п. 3.6)
вырабатывает к значений скалярных произведений фильтруемого и эта¬
лонного контуров при циклическом сдвиге начальной точки одного из
них. Как известно, скалярное произведение равно нулю, если контуры
ортогональны. Отсюда следует, что контуры, входящие в состав алфавита,
должны быть взаимно ортогональны при любом сдвиге их начальных
точек, т.е. их ВКФ везде должна быть равна нулю для любой пары
эталонных контуров Г^и из рассматриваемого алфавита:
Рис. 4.20. Структура устройства распо¬
знавания образов для алфавита из М
классов
^(лДо) (т) = °>
т = 0,1,... ,к- 1, j,l = 1,2,... ,к, j ф I.
(4.4.8)
Отметим, что требование равенства нулю всех отсчетов ВКФ двух
контуров является более сильным, чем требование их ортогональности.
Пусть, например, контуры Νχ и Ν2 имеют вид: Νχ = {1,1,1, —1} и Ν2 =
= {1,—1,1,1}. Эти контуры ортогональны, т.е. (Νι,Ν2) = 0. Их ВКФ
имеет вид: Т = {0,0,4,0}, т.е. один отсчет этой функции не равен нулю.
Если сдвинуть начало одного из контуров на два ЭВ, то контуры теряют
свойство ортогональности и, более того, становятся идентичными. В ре¬
зультате ошибочное распознавание из-за неудачного выбора контуров N χ
и Ν2 в составе алфавита неизбежно.
Таким образом, алфавит контуров, наиболее эффективных для распо¬
знавания, должен составлять ортогональный базис в fc-мерном простран¬
стве. Поэтому объем алфавита равен М = к. Если же в процессе обра¬
ботки контуров допускается произвольный сдвиг начальной точки любого
178
Гл. 4. Операции над зашумленными контурами
из контуров, что практически часто имеет место, то ортогональный базис
должны составлять любые к контуров разных классов с произвольными
сдвигами начальных точек.
Лучше всего этим условиям отвечает алфавит из полного семейства
ЭК Го, Γι,... , Tk-1. Элементарные контуры попарно ортогональны, а их
ВКФ везде равны нулю (см. п. 2.2 и п. 2.8).
Таким образом, дельтовидный характер взаимно непересекающихся
спектральных составляющих контуров (рис. 4.21) обеспечивает везде рав¬
ную нулю ВКФ и является условием эффективности алфавита контуров
максимального объема с позиции их
распознавания. Отметим, что для эф¬
фективного решения задачи разреше¬
ния контурных сигналов, как было
показано в п. 4.3, их энергетический
спектр должен быть равномерным, т.е.
требования к контурам, эффективным
для задач разрешения и распозна¬
вания, взаимно противоположны. На
выбор алфавита существенное влия¬
ние оказывает лишь преобразование
сдвига начальной точки контура. Этот
сдвиг начальной точки контура может
даже в отдельных случаях, как было
видно из примера, преобразовать два
ортогональных контура в идентичные.
В то же время поворот контура на произвольный угол или его масштаби¬
рование, благодаря свойствам скалярного произведения в комплексном
линейном пространстве Ск (см. п. 1.4), не нарушают ортогональности
векторов. Поэтому, если алфавит содержит взаимно ортогональные
контуры Г0,ГЬ... , Г fc_i, то алфавит μ0Γο,μιΓι,... ,μ/^Γ^ι, где
к
01 к-1 т
Ί
0 1 к-1 т
кх
01 к-\ т
Рис. 4.21. Энергетические спектры
эталонных контуров алфавита, оп¬
тимального для распознавания
Рис. 4.22. Структура распознающего устройства для алфавита из полного семей¬
ства элементарных контуров
4.5. Обсуждение результатов
179
Vj = 1/Ъ'1 ехР {~— произвольные комплексные числа, будет
обладать такой же высокой эффективностью при распознавании.
Таким образом, если ВКФ контуров алфавита везде равны нулю, то
произвольные сдвиги начальных точек распознаваемых контуров, их мас¬
штабирование и повороты не влияют на результаты работы несогласо¬
ванных с ними контурных фильтров. Эти преобразования отражаются
лишь на выходном сигнале канала, согласованного с поданным на вход
устройства распознавания контуром. Чтобы исключить влияние данных
преобразований распознаваемого контура на работу согласованного с ним
фильтра, поступаем так же, как и в случае обнаружения контура: опре¬
деляется модуль каждого отсчета фильтра, выбирается его максимальное
значение и сравнивается с порогом 17|μ|, величина которого зависит от
оценки масштаба контура, уровня шумов, допустимых рисков и априор¬
ных вероятностей классов. Структурная схема устройства распознавания,
реализующая данный алгоритм, показана на рис. 4.22.
4.5. Обсуждение результатов
В данном разделе рассмотрены основные операции над зашумленными
контурами. Использовалась аддитивная модель зашумленного контура Ν.
Сигнальный контур Г(с) по отношению к эталонному был повернут на угол
Αφ, растянут в |μ| раз, а его начало сдвинуто на d ЭВ. Параметры Αφ,
\μ\ и d предполагались неизвестными. В процессе прохождения по кана¬
лу связи сигнальный контур Г<с> подвергался воздействию комплексного
шума. Реальная и мнимая компоненты этого шума считались независи¬
мыми нормально распределенными числами с нулевым математическим
ожиданием.
Первая задача заключалась в получении по зашумленному конту¬
ру N оценок МП параметров Αφ, \μ\ и d. Все оценки находятся по
вектору с максимальным значением модуля, формируемым фильтром,
согласованным с эталонным контуром Г. Оценка угла поворота Αφ
сигнального контура Г(с) равна аргументу вектора, оценка растяжения
|μ| — отношению модуля вектора к квадрату нормы эталонного конту¬
ра, а оценка сдвига начальной точки контура Г(с) инкрементированному
номеру вектора.
Следующей была задача обнаружения зашумленного сигнального кон¬
тура. В отличие от классической постановки задачи обнаружения сину¬
соидального сигнала на фоне белого шума [52], где неинформативными
параметрами являются его начальная фаза, распределенная по равно¬
мерному закону, и амплитуда, распределенная по закону Релея, здесь
имеются некоторые особенности. Во-первых, из-за двумерного характера
задачи в данном случае есть два неинформативных угловых параметра —
угол поворота и сдвиг начальной точки сигнального контура. Второй па¬
раметр задается не угловыми единицами измерения, а количеством ЭВ.
Во-вторых, закон распределения вероятностей значений масштаба зависит
от способа формирования изображения. При этом часто масштаб является
180
Гл. 4. Операции над зашумленными контурами
не случайной, а просто неизвестной величиной. Данные особенности не при¬
водят к значительному изменению известных решающих правил. Основ¬
ной результат заключается в следующем: для оптимального обнаружения
контура необходимо сформировать максимальное значение модуля выход¬
ного вектора фильтра, согласованного с эталонным контуром, и сравнить
его с пороговым значением, учитывающим дисперсию шума, риски ошибок
и априорные вероятности наличия и отсутствия сигнального контура.
Третья задача связана с разрешением сигналов и, в частности, контур¬
ных. При сравнительно слабых ограничениях, накладываемых на спектр
сигнала, показана возможность получения на его основе статистики для
принятия в условиях нулевых корреляционных шумов решения об его
обнаружении и разрешении в случае нескольких перекрывающихся сиг¬
налов. Задача решена путем представления вектора сигнала в биорто-
гональном базисе, задаваемом циркулянтом этого сигнала, причем сам
сигнал является одним из векторов этого базиса. Алгоритмически об¬
работка сигнала осуществляется свободным от краевых эффектов ци¬
клическим фильтром, согласованным с сопряженной формой сигнала.
Рассмотрена также возможность решения задачи по результатам бо¬
лее простой ациклической фильтрации с последующим суммированием
выходных отсчетов, взятых с интервалом, равным размерности век¬
тора сигнала (алгоритм ЧКШС). Линейность процедуры гарантирует
возможность разрешения произвольного количества перекрывающихся
сигналов с сохранением информации об их параметрах — амплитудах,
фазах, задержках и др. Платой за подавление корреляционных шумов
является увеличение уровня флуктуационных шумов.
Четвертая задача заключалась в распознавании изображений по их
форме, задаваемой контуром. Если на вход распознающего устройства по¬
дается зашумленный контур из некоторого алфавита объемом М классов,
то алгоритм распознавания предусматривает многоканальную по числу
классов процедуру. В каждом канале находится фильтр, согласованный
с эталонным контуром класса, и устройство, выбирающее из всех к его
отсчетов отсчет с максимальным модулем. Далее отмечается канал, мо¬
дуль выходного сигнала которого превышает модули выходных сигналов
остальных каналов. Если величина максмимального модуля больше по¬
рогового значения, то распознаваемый контур относится к классу, номер
которого равен номеру канала.
Были также рассмотрены свойства алфавита контуров, обеспечиваю¬
щего наибольшую эффективность распознавания. Показано, что контуры
всех классов должны быть попарно ортогональны при любом сдвиге своих
начальных точек, т.е. отсчеты ВКФ контуров любых двух классов равны
нулю. Максимальный объем алфавита равен к. Этим требованиям удовле¬
творяет алфавит из полного семейства ЭК Г0, Γι,... , Γ^_ι.
Таким образом, если мы хотим получить алфавит изображений из к
классов, которые наилучшим образом распознаются по своей форме при
наличии шумов, то эталонные контуры изображений каждого из классов
должны представлять собой один из элементарных контуров.
4.6. Задачи и упражнения
181
4.6. Задачи и упражнения
1. Проверить равенство нулю всех отсчетов ВКФ элементарных контуров Γχ =
= {Μ, -1, -г} и Гз = {1, -», —1, *}.
2. Найти расстояние между контурами а) Го = {1,1,1,1}, Гз = {1, —г, — 1, г},
б) Г = {2; г; 1 - 2г; -3 + г} и N = {1 + г; 4; -6 - 2»; 1 + »}.
3. На базе эталонного контура Г = {12 + 6г; — 9 — Зг; —3 — 6г; Зг} сформиро¬
вать сигнальный контур с параметрами |μ| = 1/3, Αφ = 30° и d = 2.
4. По методу максимального правдоподобия получить оценки параметров Αφ,
d и |μ| зашумленного контура N = {10,9 — 3, 5г; —1,8 — 9,2г; —8, 2 + 5, Зг;
—0,6 + 7,4г}. Эталонный контур равен Г = {4; — 2 - 5г; — 5 + г; 3 + 4г}.
5. Решить задачу обнаружения сигнального контура по данным задачи 4 при
условии, что отношение рисков Roi/Rio = 100, отношение априорных веро¬
ятностей P(N = Z)/P(N = Г^ + Z) = 10 и σ = 0,64.
6. Алфавит контуров состоит из двух классов с эталонными контурами Γ(χ) =
= {1; —0,5 + 0,86г; —0,5 — 0,86г} и Г(2) = {1; —0,5 — 0,86г; —0,5 + 0,86г>.
Определить класс точно известного зашумленного контура N = {1,2 — 0,4г;
—1 + 0,96г; —0,2 — 0,56г} с σ = 0,33 для случая когда величина 1пЛо = 4.
Решение. Пороговый уровень при распознавании точно известных контуров
для двух классов равен
Ui, =σ21ηΛ0+0,5(||Γ1||2 - ||Г2||2) = 0,11 · 4 + 0,5 · (3 - 3) = 0,44.
С этим пороговым уровнем надо сравнить достаточную статистику ARei7(1>2) =
= Rer7(i)(2) - Re77(2)(2), где η(ΐ)(2) и ?7(2)(2) — результаты фильтрации
контура N фильтрами, согласованными с контурами Γ(χ) и Г(2) в момент
т = к — 1 = 2. Определяем эти значения^77(1)(2) = 3,01; Rei7(2)(2) =
= 2,53 и ARe77(i?2) = 2,53. Условие ARei7(i>2) ^ и\2 (в числовом виде
2,53 ^ 0,48) выполняется и поэтому контур N относим к первому классу.
7. Алфавит контуров состоит из двух классов с эталонными контурами Γ(χ) =
= {1,4; -0,7; — 0,7г} и Г(2) = {1 — 0,5г; —0,5 + г; —0,5 — 0,5г}. Определить
классы точно известных зашумленных контуров с σ = 0,33, N = {1,6 —
-0,4»; —1,2+0,1»; -0,4+0,ЗЗг} и М = {1,1 - 0,2г; -0,2 + 0,5г; -0,9 - 0,3г}
для случая In Ло = 4.
Решение. Определяем пороговые уровни для принятия решения. Квадраты
норм эталонных контуров равны ||Γ(χ)||2 = ||Г(2)||2 = 3. Поэтому величины
пороговых уровней для обоих случаев будут одинаковыми и равными ηχ2 =
= σ2 ΙηΛο = 0,44.
Принимаем решение о классе контура Ν. Для этого определяем реальную
часть скалярных произведений (Ν, Γ(χ)) и (Ν,Γ(2)):
Re (Ν, Γ(χ)) = 3,36; Re (Ν, Γ(2)) = 2,66.
Проверяем неравенство Re (Ν,Γ(χ)) — Re (Ν,Γ(2)) ^ σ21ηΛο. Числовой
вид неравенства: 3,36 — 2,66 ^ 0,44; 0,7 ^ 0,44. Неравенство справедливо,
поэтому контур N относим к классу А2.
Принимаем решение о классе контура М.
Re (М, Г(1)) = 2,31; Re (М, Г(2)) - 2,4.
Проверяем неравенство 2,31-2,4 ^ 0,44; —0,09 ^ 0,44. Неравенство
не выполняется, поэтому контур М относим к классу А2.
182
Гл. 4. Операции над зашумленными контурами
8. Алфавит контуров состоит из трех классов Ао, А\ и А2 с эталонными кон¬
турами Г(0) = {1; 1; 1}; Γ(ΐ) = {1; -0,5 + 0,86г; -0,5 - 0,86г} и Г(2) =
= {1;—0,5 — 0,86г; —0,5-1-0,86г}· Для распознавания предъявляются три
зашумленных точно известных контура
N = {1,2-0,4г; -1 + 0,96г; -0,2-0, 56г},
Μ = {1,1 + 0, Зг; -0,2-1, Збг; -0,9+1,06г},
Π = {1,3 - 0,4г; 1,2 + 0,1г; 0,5 + 0, Зг}.
Определить классы этих контуров, выбрав для принятия решения пороговый
уровень £/0,1,2 = 1.
Решение. При распознавании одного из контуров, например, контура N,
сначала проверяем его принадлежность к одному из двух классов, Ао или
А\. Для этого находим статистику Re (Ν,Γ(0)) — Re (Ν,Γ(ΐ)) и сравниваем
ее с порогом С/0,1,2. Пусть, например, решение принято в пользу класса А0.
Далее проверяем принадлежность контура N к одному из классов Ао или А2.
Определяем статистику Re (Ν,Γ(0)) — Re (Ν,Γ(2)) и сравниваем ее с поро¬
гом. Принятое теперь решение является окончательным. Из данного подхода
к распознаванию контура N следует, что надо найти скалярное произведение
с максимальной реальной частью [Re (N, Г^·))] J = 0,1,2, и вычесть из
него реальную часть [Re (Ν,Γ^)] , I = 0,1,2, j / l. Получившуюся
разность сравниваем с порогом £/0,1,2· Если порог превышен, то контур N
относится к классу Aj, в противном случае принимается решение об отказе
от распознавания.
Распознавание контура N:
Re (Ν,Γ(ο)) = 0, Re (Ν,Γ(1)) = 3,01, Re (Ν,Γ(2)) = 0,48.
Неравенство 3,01 — 0,48 > 1 справедливо, поэтому контур N относим к
классу А\.
Распознавание контура М:
Re (М,Г(0)) = 0, Re (М,Г(1)) = -0,42, Re (М,Г(2)) = 3,72.
Неравенство 3,72 — 0,42 > 1 справедливо, поэтому контур М относим к
классу А2.
Распознавание контура П:
Re (П, Г(о)) = 3, Re (Π, Γ(ΐ)) = 0,3, Re (П, Г(2)) = 0,62.
Неравенство 3 — 0,62 > 1 справедливо, поэтому контур П относим к клас¬
су Ао.
9. Алфавит контуров из трех классов имеет эталонные контуры
Γ(ΐ) = {4 + 5г; 4 — 5г; —8г}, Г (2) = {Зг; 8; —8 — Зг},
Г(3) = {8 — 5г; —4; —4 — 5г}.
Для распознавания предъявляется зашумленный контур N = {6,5 — 14,5г;
—4, 5 — 2, 5г; —2 + 17г} с дисперсией σ2 = 2,6, случайными значениями
угла поворота, масштаба и сдвига начальной точки по отношению к эталон¬
ному контуру. Опрелить класс контура N при пороговом уровне решающего
устройства £7И = 230 и найти оценки его параметров Αφ, d и |μ|.
4.6. Задачи и упражнения
183
Решение. Квадраты норм эталонных контуров одинаковы и равны ||Г||2 =
= 146. Определим отсчеты согласованных с контурами Г(Х), Г(2), Г(3) филь¬
тров при прохождении через них контура Ν:
Н(1) = {-175,5 4-186,5г; 211,5 + 72, 5г; -36 - 253г},
Н(2) = {-32 + 285г; 146,5 - 103, 51г; -114 - 181, 5г},
Н(3) = {235,5 - 131, 5г; -114 - 85г; -121, 5 + 216, Ъг).
Находим отсчет фильтра с максимальным модулем. Это будет |?7(2) (0) | =
= 286,8, т.е. нулевой отсчет фильтра, согласованного с эталонным контуром
второго класса. Отсчет превышает пороговый уровень ϋ\μ\ = 230, контур N
относим ко второму классу. Определяем оценки параметров контура Ν:
то = 0, d = 3 — 1 = 2, \μ\ =
\V(2) (0)| _ 28М
Αφ = arctg
1Ш77(2) (0)
Re 77(2) (0)
||Г2||2 146
' 285
= arctg
-32
= 1,96,
= 96,4°.
Истинные значения параметров: d = 2, \μ\ = 2, Αφ = 90°.
10. Составить наиболее помехоустойчивый в рамках принятых в данном разделе
моделей сигналов и шумов алфавит контуров размерностью к = 5.
Глава 5
СИГНАЛЫ В ВИДЕ ПУЧКОВ ВЕКТОРОВ
5.1. Аналитическое представление заданных на плоскости
Одним из способов рассмотренного в п.1.2 представления контура было
задание его полярным кодом (см. рис. 1.13). Из произвольно расположен¬
ной на плоскости точки Р (полюса) проводятся радиус-векторы (РВ) β (п),
η = 0,1,... , к — 1, к концам ЭВ 7 (η), п = 0,1,... , к — 1, контура.
В результате формируется пучок
в виде упорядоченного набора РВ. ЭВ 7 (п) контура Г являются первыми
разностями РВ β (η), т.е.
7 (η) = β (η + 1) - β (η) = Αβ (η), η = 0,1,... , к - 1. (5.1.2)
Как было отмечено в π. 1.5, суммарный код контура Г является частным
случаем полярного кода при совмещении полюса Р с начальной точкой clq.
К пучкам в виде (5.1.1) приводит задача аналитического представления
заданного на комплексной плоскости упорядоченного множества точек
Выражение (5.1.2) представляет собой систему линейных уравнений
относительно РВ β (η), η = 0,1,... , к — 1. Для ее решения зададим на-
пучков
в = {β (n)}o,fc-i = \β (n)l exP {ΐψ WW-1 (5·1·1)
s = {£W}0,fc-i (Рис· 5·1)·
К 2)=-5
Р
Рис. 5.1. Пучок и контур, порождае¬
мые упорядоченным множеством точек
Рис. 5.2. Соотношение между поло¬
жением центра тяжести и полюсом
фигуры
а — {£ (П)}о,3
5.2. Спектральный анализ изображений пучков
185
чальные условия в виде конкретного РВ β (п), определяющего положение
полюса Р. Пусть это начальное условие дано в виде РВ β (0). Тогда
п — 1
β{η) =β(0)+ Y^7(m), (5.1.3)
m=0
или рекуррентно β (η) = β (η - 1)+7 (η - 1), η = 1,2,... , fc—1. Восполь¬
зовавшись (5.1.3), запишем выражение для суммы всех РВ пучка через
значения ЭВ кода контура и β (0):
k — 1 к — 1 п — 1 к — 1
Σ β (п) = кР (0) + Σ Σ 7 = кР (°) + Σ (fc - п) 7 (п)· (5.1.4)
п=0 п=0 гп=0 п=0
С учетом замкнутости контура получим
Величина
к-1
к — 1
Υ^β(η) = Ηβ (0) - Σ rvy (η).
у. ι
a0O = -β (0) = i Σ 7 (m) =
71 =0 771=0
i]Tn7(n)
71=0
(5.1.5)
(5.1.6)
задает вектор, соединяющий начальную точку clq контура Г с центром
тяжести О фигуры (рис. 5.2). Как следует из (5.1.6), сумма всех РВ пучка
есть вектор, равный растянутому в к раз вектору РО, соединяющему
полюс Р с центром тяжести О:
РО = £><*
(5.1.7)
5.2. Спектральный анализ изображений пучков
5.2.1. Связь между спектрами пучка и его контура. ДПФ пучка,
заданного в виде (5.1.1), имеет вид
к-1
Рв (т) = ^ β (п) exp j-z^rari т = 0,1,... , к - 1. (5.2.1)
71=0
Выясним характер связи между спектром Рв пучка В и спектром Рг
контура Г, задаваемых одним и тем же упорядоченным множеством то¬
чек Ξ. Используя выражение для ДПФ контура Г, с учетом (5.1.2) запишем
Рг (т) =
/с-1 Ас — 1
= (п)ехр|-гуттш| = ^[β (η + 1) -/3 (n)] exp {-г^ттт} =
71=0 71=0
к-1 к-1
= ^2 β(η + 1) exp ^ β (п) ехр z^ran j.
186
Га. 5. Сигналы в виде пучков векторов
Первая сумма в этом выражении определяет компоненты рв (га) спек¬
тра пучка, а вторая — спектра пучка, смещенного на один отсчет, т.е.
exp jz'^ran j · рв (гм). Поэтому
рг (га) = рв (га) j^exp jz—^ra j — lj 5 т = 0,1,... , к — 1.
Отсюда следует, что
^ , m = 0,1,... ,к — 1. (5.2.2)
т > — 1
При га = 0 знаменатель выражения становится равным нулю и ну¬
левая компонента должна быть получена другим путем, например,
из (5.2.1):
рв (га) =
ехр <
. 2π
1 к
к-1
Рв(0) = Х>(п), (5.2.3)
п—О
т.е. эта компонента спектра пучка равна сумме его РВ.
5.2.2. Элементарные пучки. Найдем аналоги ЭК в классе пучков В =
= {β in)}o k-v т*е· ПУЧКИ7 спектр которых состоит из одной нулевой
компоненты, причем скалярное произведение двух разных пучков одной
и той же размерности должно быть равно нулю. Полное семейство таких
пучков одной размерности образует ортогональный базис, по которому
может быть разложен произвольный пучок той же размерности. Восполь¬
зуемся выражениями (5.2.2) и (5.2.3). В результате получим, что спектр
пучка Pbj, соответствующего ЭК Гу, также будет состоять из нулевых
компонент, кроме рв (0) и рв (j) (рис. 5.3):
Рв (га) = 0 при га = 1,2,... , j — 1 и га = j 4-1,... , к — 1;
Ав(0) = Х>(п), рвС0 = !-
ехр
1 2π -
1 “ cos т3
(5.2.4)
Выясним условие, при котором спектр пучка В, соответствующего
контуру Гу, станет монохроматичным за счет обращения в ноль компо¬
ненты р(0). Как следует из (5.1.7) и (5.2.3), эта компонента определяется
вектором РО, соединяющим полюс пучка В с центром тяжести конту¬
ра Г. Поэтому необходимо в качестве полюса Р выбрать точку центра
тяжести О. Тогда
PBj =
0 при га = 0,1,... , j — 1 и га = j + 1,... , к — 1,
к
- при m=j, j = 1,2,... ,к - 1.
expji^j-1
(5.2.5)
5.2. Спектральный анализ изображений пучков
187
а
у(°)=1>
0(0)=
п
Ύ
= -<),4 +0,4/
СП
Г3
0(3)=
Л 2)=-1
q =—0,4—0,6/
0(0=
=0,6+ 0,4/
0(0=
= 0,6-0,6/
>("г)|
I 1 μ
\р{т\ 2,84
0,56
6 0 1 2 3 т
0 12 3 т
Рис. 5.3. Соотношения между спектрами ЭК и соответствующего ему пучка с про¬
извольным положением полюса: а — ЭК Г3, б — спектр ЭК Г3; в — пучок В, г —
спектр пучка В
Из монохроматичности спектров преобразованных таким образом пуч¬
ков следует попарная ортогональность пучков разных порядков j:
(Bj,B|) = i (Ρβ,-,Ρβ,) =
0 при зф1, j,l = 1,2,... ,k - 1,
k
Ai~cMTi)
при l = j,
(5.2.6)
т.е. семейство таких пучков задает ортогональный базис. Из полученного
выражения видно, что квадрат нормы пучка зависит от значения
его порядка j. Для исключения этой зависимости и перехода к орто-
нормированному базису надо, как следует из (5.2.5), каждый РВ пучка
В j умножить на i ^ехр|г^у| — 1^. Преобразованные таким образом
пучки назовем элементарными (ЭП) и будем обозначать как ГГ,:
П
= {*3 (»)}0,*-1 = I (ехР {*χί} - *) ifii Hlo.fc-1· (5·2·7)
Спектр ЭП порядка j равен
PUj
(5.2.8)
0 при т ф j,
1 при т = j.
Обратное ДПФ элементарного пучка ГГ, позволяет найти РВ π7· такого
пучка:
Kj (п) = ^ exp j = 1,2,... , * - 1.
(5.2.9)
188
Гл. 5. Сигналы в виде пучков векторов
Как следует из выражений (1.8.3) и (5.2.9), ЭК и ЭП одинакового поряд¬
ка и размерности при |т| = 1 имеют одинаковое (с точностью до коэффи¬
циента 1 /к) аналитическое представление. Это означает, что все свойства
ЭК, описанные в п. 2.2, распространяются на ЭП. Формально можно ввести
ЭП нулевого порядка По в виде обратного ДПФ от последовательности
отсчетов спектра, все значения которых равны нулю за исключением
рп0 (0) = 1, т.е. от рп0 (0) = {1,0,... ,0}. В результате получим П0 =
= {l/k}o,k-v ЭП П0 можно представить как к наложенных друг на друга
O.P
0—
ЯГ 0(0) = 1/4
я·,(l)=l/4/
71 o(l) = l/4
4 °’Ρ!
я0(2)=1/4
πι(2) = -1/4
0-
►
я’о(з)=1/4
nN
По *
(0 = —*/4 О,Ря'2(0) = 1/4
◄ >,
^2(3) = ~1/4
2)=1/4
π 1 (о) = 1/4
—т
я,(з) = -1/4/
тг3(з)=1/4/ \
&
.Р
ж3(2)=-1/4
яг3(0)=1/4
151з(1) = —!/4г
П 3\*/
Рис. 5.4. Семейство элементарных пучков размерности к = 4
одинаковых коллинеарных векторов, равных 1/к, выходящих из одного
полюса. На рис. 5.4 представлено семейство ЭП размерности к = 4.
Отметим, что ЭП более высоких порядков j, чем нулевой, получают¬
ся из пучков, соответствующих ЭК, путем поворота последних, как это
следует из (5.2.7), на угол
и растяжением в rj
(fj — arctg
f . 2π . '
sinTJ
,cost j~l,
2π Λ . - 0
cos— j) раз, j = 1,2,.
, к — 1.
5.2.3. Разложение произвольного пучка на элементарные. Пусть
В = {β (п)}0 к_1 — произвольный пучок, аР^ = {рв {m)}o,k-i — ег0
спектр, полученный в соответствии с (5.2.1). Обратное ДПФ от спектра Рв
дает РВ β (η), η = 0,1,... , к - 1, исходного пучка:
/С-1
β(η) = \Ύ^Ρβ (m)expjiymn),
n = 0,l,... ,fc-l. (5.2.10)
5.3. Влияние преобразований пучка на вид его спектра
189
С учетом перехода от отдельного РВ ко всему
пучку и выражения (5.2.9) получим
k-1
в - РВ (т) пт. (5.2.11)
771=0
Таким образом, произвольный пучок раскла¬
дывается в ортонормированном базисе {IIm}ofc_1,
причем координатами являются коэффициенты его
ДПФ ρβ (га), т — 0,1,... , к - 1.
Пример. Разложим по ЭП пучок, образованный со¬
единением полюса Р с вершинами фигуры, определяемой
контуром Г = {3 -Ь 4г; — 1 - 5г; — 2 + г} (рис. 5.5). По¬
люс Р совпадает с центром тяжести О фигуры контура
и поэтому РВ β (0) = - J2 ηΊ (п) —
3 п=1
Найдем остальные два ЭВ пучка:
-1 —5г + 2-(-2 + г) =
β(ί) =/9(0) + 7(0) = | +3i, β (2) = β (1) + 7(1) = | - 2i.
Пучок В и его спектр Рв равны
В = - г; | + Зг; i - 2г|, Έ>β = {0; 1,831 - 2,366г; -6,829 - 0,634г}.
рв0к0);
Рв( 0я! (О у
<
рвОкО^Л
РвОкО)/
РвОкОО/
<
Рис. 5.6. Синтез пучка В: а — пучок ρβ (1) Πι, б — пучок ρβ (2) П2, в — синте¬
зированный пучок В
В соответствии с выражением (5.2.11) данный пучок В разлагается по элемен¬
тарным следующим образом: В = ρβ (1) Πι + ρβ (2) П2 (рис. 5.6), где
ρβ (1) Πι = {0,61 - 0,79г; 0,38 + 0,922г; -0,988 - 0,136г},
ρβ (2) П2 = {-2,227 - 0,221г; 0,951 + 2,079г; 1,317 - 1,869*}·
5.3. Влияние преобразований пучка на вид его спектра
При повороте пучка на произвольный угол Αφ каждый РВ пучка В
и каждая компонента его спектра умножаются на одно и то же комплекс¬
ное число ехр {ιΑφ}, т.е.
190
Гл. 5. Сигналы в виде пучков векторов
Вду; = ехр{гД<р}В, ΡΒΔν> = ехр {гД^}Рв. (5.3.1)
При смещении начала отсчета РВ пучка В на d элементов нулевым
РВ в новом пучке будет βα{η), т.е. β<ι{η) = βα{η + d), а компонента
PBd (га) спектра пучка В<* станет равной
рвл (га) = exp |рв (га). (5.3.2)
Приведенные выше два вида преобразований пучка являлись точными
аналогами преобразований контура, описанными в п. 1.5 и п. 2.3. Ниже
рассмотрим преобразования, характерные, в основном, для пучков.
Варьирование длины произвольного РВ пучка. Пусть деформация пуч¬
ка В происходит за счет изменения длины каждого его РВ β (и) на вели¬
чину Αβ (п). Новый пучок имеет вид А = В + ΔΒ, где А = {а (п)}0 к_г,
В = {β (n)}0 k_v ΔΒ = {Αβ (n)}0 к_г. Из линейности ДПФ следует, что
спектр Ра деформированного пучка запишется как
Ра = Рв + Рдв, (5.3.3)
где Рдв — спектр деформирующего пучка ΔΒ, равный
к-1
Рав (га) = ^ Αβ (п) exp г^гапт = 0,1,... , к — 1. (5.3.4)
п=О
Изменение аргумента произвольного РВ пучка. Рассмотрим случай
малых деформаций пучка В, возникающих при изменении аргумента
произвольного РВ на величину
|Δ<^(η)| < 10°. При этом прибли¬
женно можно считать, что вектор
Αβ (η) расположен перпендикуляр¬
но к β (п) и β (η) + Αβ (η) « β (η)
(рис. 5.7).
Если а = β (η) — исходный РВ,
то b = —ίβ (п) будет перпендику¬
лярным к нему вектором. Выделим
на нем точку Е и проведем вектор
с = ОЕ, представляющий РВ β (п)
после поворота на малый угол Αφ.
Отрезок DE составляет r-ю часть
длины вектора Ь. При принятых условиях деформации Αφ « г, а вектор
DE, являющийся приращением РВ β (п) при повороте на угол Αφ, будет
равен
Αβ « rb = —Αφβ (п) г. (5.3.5)
Рассмотрим связь между спектрами исходного и деформированного
пучков. Пусть вначале деформация происходит за счет поворота на угол
-Αφ (j) только одного РВ β (j). В этом случае в соответствии с (5.3.5) РВ
Рис. 5.7. К определению спектра пучка,
деформированного поворотом РВ β (η)
на малый угол Αφ
5.3. Влияние преобразований пучка на вид его спектра
191
деформированного пучка ΔΒ = {Αβ (rc)}o,fc-i имеют вид
Αβ(η]
-t
для п ф j,
-A<p(j)P(j) для n = j,
а спектр деформирующего пучка будет равен
Рдв = i = -Δφ (j) β (j) Π*-,·.
Тогда для спектра деформированного пучка можно записать Ρβ+δβ —
= Рв — Αφ (j) β (j) Hk-j· В результате для общего случая, когда дефор¬
мируется каждый РВ пучка В, спектр результирующего пучка В + ΔΒ
представляется в виде
к-1 к-1
Ρβ+δβ = Рв ~ ^ Αφ (η) β (η) Π*_η = Рв - Αβ (η) Щ_п.
η=0 η=0
(5.3.6)
Ο Ο
Децентрализация пучка. Пучок β = {β (n)}Q k_vY которого полюс Ρ
совмещен с его центром тяжести, назовем центрированным. В противном
случае пучок является децентрированным, причем, чем больше модуль
вектора смещения полюса РО = /Зо, тем сильнее степень его децентри¬
рования. Как следует из выражений (5.1.7) и (5.2.3),
/?o = PO = ip(0), (5.3.7)
т.е. децентрирование, связанное с изменением модуля вектора РО, вли¬
яет только на значение нулевой компоненты спектра, также приводя к
изменению ее модуля. У центрированного пучка эта компонента равна
нулю, т.е. у такого пучка р (0) = 0. Произвольный РВ β (η) децентриро-
о
ванного пучка связан с соответствующим РВ β (η) центрированного пучка
соотношением
β{η)=β{η) + β о, η = 0,1,... ,fc - 1. (5.3.8)
Децентрирование приводит к увеличению нормы пучка. Квадрат нор¬
мы преобразованного пучка В связан с квадратом нормы центрированного
пучка следующим образом:
||В||2 = ||в||2 + \ Н0)|2 = ||в||2 + ьщ2. (5.з.9)
По мере удаления полюса Р от центра тяжести О, т.е. при увеличении
степени децентрирования, различие между РВ пучка уменьшается из-за
того, что \β (п)| —> |/?о| и arg/З (η) —> arg/J0, η = 0,1,... , к — 1. Отсюда
следует, что все сильно децентрированные пучки слабо отличаются друг
от друга (рис. 5.7). Если А и В — два сильно децентрированных одина¬
ковой размерности произвольных пучка, то их нормированное скалярное
произведение
|„АВ| - КА-В)1
|ί,Α-Β|Ν ||А|| · ||В||
1.
192
Гл. 5. Сигналы в виде пучков векторов
У этих пучков модуль нулевой компоненты их спектров доминирует
над модулями остальных спектральных компонент:
\ра (0)1 » \ра Ml, \рв (0)1 » \ръ (ш)|, т = 1,2,... ,к-1.
Поэтому нормы и модули скалярных произведений сильно децентри-
рованных пучков определяются лишь нулевыми компонентами спектров,
что и объясняет слабую степень их различия. Следствием данного обсто¬
ятельства является требование обеспечения высокой точности расчетов
при работе с такими пучками. Таким образом, максимальным различи-
Рис. 5.8. Влияние децентрирования на степень различия пучков: α, в — центриро-
о
ванный пучок А и модули его спектра; б, г — центрированный пучок В и модули
его спектра; д, ж — децентрированный пучок А и модули его спектра; е, з —
децентрированный пучок В и модули его спектра
ем обладают центрированные пучки, а их децентрирование приводит к
нивелированию меры схожести в виде нормированного скалярного произ¬
ведения пучков. Например, для показанных на рис 5.8 центрированных
о о
пучков А и В величина модуля НСП равна 0,8, а для децентрированных
пучков А и В — 0,98775.
5.4. Согласованная фильтрация пучков
Согласованный фильтр для заданного в комплекснозначном виде пуч¬
ка работает аналогично контурному согласованному фильтру (см. п. 3.6).
Его ИХ имеет вид Λ (η) = β* (к — η — 1), а выходной сигнал при филь-
5А. Согласованная фильтрация пучков
193
трации пучка А = {а (п)}0 к_г равен
к — 1
η (ш) = а (п) /3* (п — га + fc — 1), га = 0,1,... , fc — 1. (5.4.1)
п=0
При расчетах, связанных с линейной фильтрацией пучков, необхо¬
димо учитывать свойство периодичности РВ пучка или ЭВ его контура
(см. (1.5.4)). В этом случае номера векторов будут находиться в пределах
от 0 до /с-1. В момент т = к-1 на выходе фильтра образуется величина,
равная скалярному произведению пучков А и В:
к-1
П{к~1) = Σα{η)β* (η).
п—О
При фильтрации согласованного пучка выходная величина фильтра
к-1 2
в этот момент равна энергии сигнала: η (к — 1) = Σ β (п) β* (п) = ||В|| .
п=О
Такое значение η (к — 1) становится возможным благодаря компенсации
значений аргументов всех РВ пучка, квадрированию их модулей и сумми¬
рованию получившихся коллинеарных векторов (рис. 5.9). Данный выход-
в 2
к0(о)
0(3)
Р
0(0
0(2),
Г
|/}(o)f I/K0I2 |/3(2)f Из)|2
• * > »> ►
б »?(з)
Рис. 5.9. К образованию пикового выходного отсчета согласованного фильтра: а —
фильтруемый пучок В = {β (п)}0 3, б — выходной отсчет η (3)
ной отсчет является максимальным по модулю по отношению к остальным
отсчетам фильтра: η (к — 1) = \η (^i)|max» m = 0,1,... , к — 1.
Модуль выходного отсчета согласованного фильтра представляет со¬
бой меру схожести фильтруемого пучка А и пучка В, задающего ИХ
фильтра. В нормированном виде значение этой меры равно
Ι*?«ΜΙ = ||А||||В|Г (5А2)
Если пучки идентичны, т.е. А = В, то \ηΗ (т)\ = 1, если же |т7н (т)| =
= 0, то пучки ортогональны. Аргумент выходного сигнала в момент га =
— к —1 определяет угол поворота Αφ фильтруемого пучка А относитель¬
но эталонного пучка В, т.е.
— 1) = arctg
Ιτηη (к — 1)
Re?; (к — 1)
(5.4.3)
194
Гл. 5. Сигналы в виде пучков векторов
Результат согласованной фильтрации Н = {77 (ш)}0 к_г пучка В =
= {/3(n)}ofc_i также может рассматриваться как некоторый пучок
(рис. 5.10). При этом его РВ η (к — 1) будет расположен горизонтально
и направлен вправо. Если полюс фильтруемого пучка совмещен с центром
тяжести, то сумма всех РВ выходного пучка будет равна нулю. Отметим,
Рис. 5.10. Согласованная фильтрация пучка: а — фильтруемый пучок В =
= {г, 1, — 1 — г}, б — пучок на выходе фильтра Н = {—2 — Зг; —2 4- Зг; 4}
что ЭП является собственным сигналом любого линейного фильтра и по¬
этому он проходит через фильтр без деформации, но с измененным
масштабом и повернутым на некоторый угол. В то же время, если
фильтр согласован с ЭП Ilj, то при фильтрации пучков Пи I Ф jt
других порядков, выходной сигнал фильтра равен нулю. Это следует из
того, что ВКФ ЭП всюду равна нулю. Согласованный фильтр формирует
меру схожести эталонного и фильтруемого сигналов и в этом плане на его
основе решаются задачи обнаружения, распознавания и оценки парамет¬
ров зашумленных пучков. Алгоритмы решения этих задач не отличаются
от аналогичных алгоритмов для зашумленных контуров (см. гл. 4).
5.5. Специальные операции обработки пучков
5.5.1. Особенности пучка как зашумленного сигнала. Полярная си¬
стема отсчета, в которой задается пучок, обуславливает его некоторые
особенности как зашумленного сигнала. Рассмотрим случай, когда за¬
шумленный пучок формируется из эталонного в результате действия
ошибок измерения координат точек множества Ξ = {£(n)}ofc-i> за-
дающих пучок В.
Предполагаем, что такие ошибки для каждой из точек ξ (η) независи¬
мы, подчиняются нормальному закону распределения вероятностей с ну¬
левым математическим ожиданием и среднеквадратическим отклонением
^Re = cTim = σ, а зашумленный РВ е(п) = е\ (п) -f гв2 (п) является
суммой эталонного β (п) = βι (п) -f г/Зг (п) и шумового ς (п) = ςι (η) +
+ К2 (η), η = 0,1,... , к — 1, радиус-векторов (рис. 5.11). Выражение для
плотности распределения вероятности модуля |ε(η)| и аргумента ф (п)
5.5. Специальные операции обработки пучков
195
Рис. 5.11. Диаграмма суммы радиус-вектора эталонного пучка с шумовым радиус-
вектором
зашумленного РВ ε (п) в данном случае имеет вид
/ (|*(»)|) = ^ ехр {-^ - · /0 (JiMiM) , (5.5.1)
/ (Ψ) = СХР^ LW/2} j1 + '/zirq (п) COS [ψ (η) - φ (n)]j X
χ exp I ? (η) C(?s (зМ?)—J*(i(n) cos [ψ(η) — ψ (n)]), (5.5.2)
где 70(·) — функция Бесселя нулевого порядка от мнимого аргумента,
X
Ф (х) = (l/y/2n) J ехр{—z2/2]dz — интеграл вероятностей, q(n) =
— оо
= \β{η)\/σ.
Выражение (5.5.1) при принятых условиях представляет собой распре¬
деление Релея~Райса. Оба распределения f (\ε (п)\) и f (ψ (п)) при q^> 1
нормализуются, причем первое из них при этом характеризуется пара¬
метрами (?(η),σ2), а второе — параметрами (φ(η),σ2). При q(n)
<С 1 первое распределение переходит в распределение Релея, а второе —
в равномерное [177].
Степень различия эталонного β (η) и зашумленного ε (п) РВ зависит
при заданном значении среднеквадратического отклонения σ ошибки из¬
мерения координат точки А (рис. 5.11) от величины q (η), играющей роль
отношения сигнал/шум для зашумленного вектора ε (п). Действительно,
чем больше модуль РВ β (η), тем меньше, при фиксированной величине σ,
угол |ψ (η) — φ (п)| и разница между модулями \β (п)| и \е (га)|. Аналогич¬
ная зависимость наблюдается и при уменьшении дисперсии ошибки изме¬
рения координат точки А. Отсюда следует, что каждый РВ β (η) эталонного
пучка В определяет со своей стороны величину отношения сигнал/шум для
зашумленного РВ ε (η) пучка Е: при одинаковой для всех РВ пучка В
дисперсии ошибок σ2 измерения координат их концевых точек отношение
196
Гл. 5. Сигналы в виде пучков векторов
сигнал/шум q для каждого РВ пропорционально его модулю. Как следует из
выражения (5.5.2), при больших значениях \β (п)| уменьшается вероятность
больших значений угла |ψ (η) — φ(η) |. Это означает, что падает вероят¬
ность выполнения одного из следующих неравенств:
\Φ (η) - ψ (га)| ^ \φ (η + 1) - ψ (η)I, (5.5.3)
\Ψ (η) - ψ (η)| ^ \φ (η) -φ(η- 1)|, (5.5.4)
связанных с нарушением порядка следования РВ β (п -f 1) и β (η) или РВ
β (η) и β (η — 1). Если такое событие имеет место, то при разной длине
этих РВ существенно меняется математическое описание зашумленного
пучка по отношению к эталонному, что может привести к увеличению
ошибок распознавания пучка.
Таким образом, характерная особенность пучка состоит в том, что
его РВ могут характеризоваться различными значениями отношения сиг-
нал/шум. Достаточно иметь в составе пучка либо один РВ с небольшим
значением модуля, либо два РВ с очень близкими значениями аргумента,
как из-за ошибок измерения координат концевых точек его РВ проис¬
ходит не только изменение параметров этих векторов, но и значительно
повышается вероятность нарушения порядка следования РВ.
5.5.2. Проблема нумерации радиус-векторов зашумленного пучка.
Данное в п. 5.1 определение пучка, как совокупности РВ, соединяющих
точку полюса Р с точками Ξ = {£ (п)}0 к_г упорядоченного множества,
позволяет однозначно задать лишь эталонный пучок В. При этом номер
п текущего РВ β равен номеру текущей точки ξ (η) множества Ξ. Ко¬
гда в нашем распоряжении имеется зашумленный пучок Е = + Z,
то информация об упорядоченности концевых точек его РВ отсутствует.
Наиболее просто можно решить проблему нумерации РВ пучка Е при
условии естественного порядка следования РВ пучка В. Естественным назо¬
вем такой порядок следования РВ, при котором два РВ β (η) и β (I) имеют
соседние номера, т.е. β (η) = β (η) и β{1) = β (п -f 1), если угол Αψ (η)
между ними имеет минимально возможное для данного пучка значение:
Αψ (η) = ΑΨΗ)ι
п,1 = 0,1,.
(β(η),β(1))
\β{η)\·№)\
,. , к — 1, η = l.
(5.5.5)
В соответствии с данным определением естественного порядка при
графическом представлении пучка РВ β (η) и β (η + 1) непосредственно
следуют друг за другом в направлении часовой стрелки.
На рис. 5.12, а в качестве пучка с естественным порядком следования ЭВ
показан центрированный пучок
В = {4 + 4г; 1; 5 — г; 1 — 5г; —3 — Зг; —5 — 2 г; —2 + г; —1 + 6г}.
Номер концевой точки текущего РВ совпадает с номером этого РВ при обходе по
часовой стрелке. На рис. 5.12, б показан тот же пучок, но вектор смещения полюса
для него равен уже не нулю, а единице:
В := {5 + 4ΐ; 2; 6 — i] 2 — 5ΐ; —2 — 3i\ —4 — 2i\ —1 -b i\ 6ΐ}.
5.5. Специальные операции обработки пучков
197
Рис. 5.12. К определению естественного порядка следования РВ в пучке: а — цен¬
трированный пучок (β0 = 0); б, в — децентрированные пучки соответственно
с вектором смещения полюса βο = ΐΜ/3ο = --7ί
Здесь обход по часовой стрелке также приводит к правильной нумерации
точек множества Ξ = {£ (п)}0 у На рис. 5.12, в показан этот же пучок В, но
с другим вектором смещения βο = —7г:
В — {4 4* 11г; 1 -h 7ъ\ 5 4· 6z; 1 4* 2i; —3 4* 4i; —5 4* 5i\ —2 4* 8ΐ; —1 4· 13i}.
Если РВ этого пучка пронумеровать в естественном порядке их следования,
то код пучка будет равен
В = {4 + 11г; 1 4· 2ъ\ 5 4~ бъ\ —5 4· 5ъ\ —3 4~ 4i; —2 4* 8ij —1 4~ 13z; 1 4* 7i}.
В этом случае только подчеркнутые РВ сохранили соотвествие своих номе¬
ров номерам точек множества Ξ исходного ГРТО. В результате произошедшего
нарушения РВ мера схожести в виде НСП пучка с самим собой снизилась от
единицы до 0,87.
Из приведенных примеров видно, что естественный порядок нумера¬
ции не инвариантен к изменению положения полюса Р пучка. К такому
же эффекту перепутывания номеров РВ приводит зашумление сигнала,
например, из-за ошибок определения положения точек. Возвращаясь
к показанному на рис. 5.12, а центрированному пучку В, отметим, что
о о
в нем наиболее вероятно событие перепутывания. РВ β (1) = 1 и β (2) =
= 5 — г. В результате этого мера схожести в виде НСП пучка с самим
собой падает с единицы до 0,9. К нарушению естественного порядка
следования РВ зашумленного пучка по сравнению с эталонным пучком
приводят также такие события, как пропуск некоторых точек ГРТО
и появление ложных отметок.
Учитывая простоту естественного подхода к нумерации РВ пучка, целе¬
сообразно исследовать устойчивость аналитического описания пучка к воз¬
действию ошибок измерения координат точек, задаваемого множеством Ξ.
Кроме того, необходимо также рассмотреть и другие подходы к нумерации
точек этого множества. Если полученные при этом номера точек будут сов¬
падать с номерами точек эталонного множества, то проблема правильной
нумерации РВ пучка с произвольным порядком их следования снимается.
198
Гл. 5. Сигналы в виде пучков векторов
5.5.3. Коэффициент устойчивости аналитического описания пучка
при естественном порядке следования радиус-векторов. Как уже от¬
мечалось в п. 5.5.2, из-за ошибок измерения положения точек множества
Ξ в зашумленном пучке по отношению к эталонному может нарушаться
естественный порядок следования РВ. В результате их перепутывания
изменяется аналитическое описание пучка. Чем сильнее два соседних РВ
отличаются по величине модуля, тем больше изменяется это описание. А
чем меньше модуль РВ β (π) и угол Аф (га) = arg/З (η + 1) — arg/3 (η)
между соседними РВ, тем вероятнее это событие. Отсюда следует, что
помехоустойчивость пучка зависит от его формы. Наиболее помехоустой¬
чивой формой, а, следовательно, наиболее устойчивым к воздействиям по¬
мех аналитическим описанием обладают ЭП (см. п. 5.2.2 и рис. 5.4). В этих
пучках соседние РВ разнесены на максимально возможный угол, равный
2 π/к, а их модули одинаковы. Произвольные пучки такими свойствами
не обладают. В связи с этим для количественной характеристики устойчи¬
вости аналитического описания пучка введем коэффициент устойчивости
kst (КУП). КУП равен вероятности события, состоящего в сохранении
естественного порядка следования РВ пучка при воздействии ошибок из¬
мерения с дисперсией σ2 = 1:
где Pconf — вероятность нарушения порядка следования РВ из-за их
перепутывают.
Определим вероятность pConf нарушения порядка следования двух
произвольных РВ, например β (j) и β (I) (рис. 5.13).
Нормальным порядком следования будем считать такой порядок, при
котором Aifiji = ф (j) — ф (l) ^ 0. Для нахождения вероятности pConf
необходимо определить плотность распределения вероятности случайной
величины Αψμ. Учитывая, что закон распределения вероятностей р (Аф)
разности двух случайных величин ф (j) и ф (I) вычисляется через сверт¬
ку законов распределения этих величин, запишем
где (ф) и /^(/) (ф) — плотность распределения вероятности аргу-
kst 1 Pconf 5
π
(5.5.6)
а
Рис. 5.13. Диаграммы двух РВ пучка: а — нормальный прядок следования РВ β (j)
и β (I), б — нарушение порядка следования из-за перепутывания РВ
199
5.5. Специальные операции обработки пучков
ментов соответственно РВ β (j) и β (Ζ), задаваемых выражением (5.5.2).
Вероятность pconf нарушения порядка следования РВ β (j) и β (Ζ) нахо¬
дится путем интегрирования плотности вероятности / (Αψ) на интервале
от —π до 0, т.е.
о
Pconf= | ί{Δφ)άΔφ. (5.5.7)
—π
Ниже, в табл. 5.1 приведены зависимости КУП, полученные теоре¬
тическим и экспериментальным путями для ЭП (к — 1)-го порядка раз¬
мерностью к = 20, 30, 40. ЭП этого вида имеют естественный порядок
следования (нумерации) своих РВ. Как уже отмечалось ранее, из-за
Таблица 5.1. Значения коэффициента устойчивости элементарного пучка
Размерность пучка, к
Величина модуля радиус-вектора
10
20
30
40
50
20
расчет
0,759
0,99983
1
1
1
эксперимент
0,741
1
1
1
1
30
расчет
0,113
0,95500
0,99978
1
1
эксперимент
0,081
0,963
1
1
1
40
расчет
0
0,586
0,983
1
1
эксперимент
0
0,594
0,981
0,99973
1
равной длины РВ и максимально возможного угла между соседними
РВ элементарные пучки обладают наибольшей помехоустойчивостью.
Поэтому приведенные значения kst являются верхней границей КУП
для пучков размерностью к.
Рассмотрим влияние операции децентрализации пучка на величину
его КУП. Когда положение полюса варьируется в пределах окрестности
пучка, возникает значительный параллакс точек. В результате радиус-
векторы и их взаимное расположение для пучков произвольной формы
меняются в широких пределах. Поэтому выявление тенденции зависимо¬
сти КУП от величины модуля \βο \ вектора смещения полюса целесообраз¬
но проводить на пучках определенной формы, например, элементарных
пучках. При децентрализации пучка по мере роста модуля \βο\ увели¬
чивается модуль каждого РВ пучка. Это приводит к росту отношения
сигнал/шум, что способствует повышению помехоустойчивости пучка. Но,
с другой стороны, в результате децентрализации уменьшается угол Αψ
между РВ пучка (рис. 5.8). Этот фактор влияет отрицательно на поме¬
хоустойчивость пучка. В конечном счете, превалирует второй фактор,
так как центрированный пучок имеет максимально возможное значение
kst. Поэтому в результате децентрирования КУП пучка уменьшается. На
рис. 5.14, а приведен график зависимости kst от модуля вектора \βο\ для
ЭП третьего порядка для к = 4. На рис. 5.14, бив показаны представления
этого пучка для некоторых значений \βο\. Как видно из графика, при
200
Гл. 5. Сигналы в виде пучков векторов
βο=1 βη=2 J3ft=5
Рис. 5.14. Децентрализация пучка П = {1-Ьг,1 — г, — 1 — г, -1 4- г}: а — зависи¬
мость коэффициента устойчивости пучка от модуля вектора смещения полюса; б,
в — изображения центрированного и децентрированного пучков
\βο\ = 1 величина kst минимальна.
При данном значении \βο\ модули двух РВ пучка, а, следовательно,
и отношение сигнал/шум для них имеют наименьшие значения, равные
единице (рис. 5.14, в при \βο\ = 1) Если данный пучок сильно децентриро-
вать, например, если \βο\ = 100, величина kst = 0,24.
Один из подходов к повышению помехоустойчивости пучков состоит
в исключении из их состава РВ с низким отношением сигнал/шум. Для
этого с центром в полюсе формируется в виде окружности окрестность.
Радиус окружности определяется значением дисперсии ошибок измере¬
ния положения множества Ξ и допустимым отношением сигнал/шум в РВ
пучка. Все точки в пределах данной окружности исключаются из состава
как эталонного, так и зашумленного пучков. Например, исключение РВ
β (1) = 1 в пучке на рис. 5.12, а повышает величину КУП с kst = 0,36 до
kst — 0,82, а дополнительное исключение РВ β (6) = — 2 + г — до kst =
= 0,91. Подобная процедура целесообразна лишь при высокой дисперсии
ошибок измерений, поскольку исключаемые точки обладают высокой ин¬
формативностью.
5.6. Некоторые подходы к решению проблемы нумерации
(упорядочения) точек ГРТО
Как было отмечено в п. 5.5.2, если нумерация РВ пучка производилась
не на основе естественного подхода, обработка зашумленного пучка долж¬
на начинаться именно с этой процедуры. Затем по известному правилу
смены номеров РВ в эталонном пучке можно построить зашумленный
пучок и приступить к его обработке. Задачу нумерации точек множества
Ξ поставим следующим образом.
5.6. Некоторые подходы к решению проблемы нумерации
201
Пусть Ξ == {£(0}ofc-i — множество заданных в плоскости сцены
точек с координатами {ξι (/), £2 (0)о k-г Первичный номер Ζ, I = 0,1,...
... , к — 1, присваивается точке по какому-либо стандартному правилу,
одинаковому для всех рассматриваемых классов пучков, например, в по¬
рядке появления точки при строчном сканировании сцены (рис. 5.15, а).
Понятно, что при повороте сцены каждой точке множества Ξ будет при¬
сваиваться другой номер (рис. 5.15, б).
б
Рис. 5.15. Присваивание первичных номеров точкам множества при строчном ска¬
нировании сцены
Необходимо, используя закономерности взаимного расположения
точек множества Ξ, присвоить каждой из них номер ш, т = 0,1,...
... , к — 1, значение которого инвариантно к повороту, изменению мас¬
штаба и переносу точек, а также устойчиво при изменениях, в опреде¬
ленных пределах, положений точек, вызванных ошибками измерения
их координат (координатным шумам). Подобная процедура проводится
для эталонного и зашумленного множеств. Когда дополнительно из¬
вестно правило, по которому РВ эталонного множества присваивается
номер гг, то появляется возможность пронумеровать и РВ зашумлен¬
ного пучка. В результате номера РВ β (η), η = 0,1,... , к — 1, бу¬
дут отличаться от номера соответствующего РВ ε (п + d) зашумлен¬
ного пучка на константу d. Если, дополнительно, оговорено правило
выбора нулевого РВ β (0), то номера РВ в эталонном и зашумленном
пучках можно сделать идентичным. Из приведенного описания задачи
нумерации видно, что она представляет задачу идентификации точек
зашумленного и эталонного множеств при их принадлежности к одному
и тому же классу.
Нумерация точек в системе отсчета с началом в центре тяжести.
Это наиболее простой способ нумерации точек зашумленного пучка.
Он заключается в следующем.
1. Определяется центр тяжести О множества точек Ξ = {£ (01ο &-ι·
2. Строится пучок с полюсом, совмещенным с точкой О.
3. Выбирается РВ с минимальным (или максимальным) значением мо¬
дуля и обозначается как β (0).
4. В естественном порядке следования производится нумерация всех
остальных РВ пучка.
-©—►
—Ц)~
-©—►
—ω-
-©—►
►
-о-
Ψ
-<!>->
47^
202
Гл. 5. Сигналы в виде пучков векторов
5. Если нумерация РВ эталонного пучка была осуществлена не в
естественном порядке, а по другому правилу, то с учетом этого правила
производится перенумерация РВ зашумленного пучка.
Выбор центра тяжести в качестве полюса зашумленного пучка оправдан
тем, что дисперсия флуктуаций его положения в п раз меньше дисперсии
ошибки измерения положения любой из точек ξ (η), п = 0,1,... , к — 1. При
к > 10 случайность положения точки О по сравнению с флуктуациями
точек ξ (п) может практически не приниматься во внимание. Специфич¬
ным недостатком данного метода является высокая вероятность ошибоч¬
ной, по сравнению с эталоном, нумерации для случая, когда соседние РВ
сильно различаются по модулю. Кроме того, ошибка нумерации возникает
также при пропуске точки или появлении ложной отметки.
Алгоритм «Минимальное дерево». Рассмотрим задачу упорядочива¬
ния множества точек как задачу минимизации длины сети, связываю¬
щую заданное количество точек кабелем минимальной длины [204]. Пусть
в результате наблюдения к точек произведена их первичная нумерация
и построена матрица расстояний R. Элемент Rij, Z, j = 0,1,... , к — 1,
матрицы равен расстоянию между точками ξ (I) и ξ (j). Кроме того, по¬
лучена матрица геометрии Ω, элементы которой представляют собой
РВ, проведенные из точки ξ (Ζ), как из полюса, к точке ξ (j). Элементы
матрицы R являются модулями соответствующих элементов матрицы Ω.
Эти матрицы имеют вид
0
До1
Rq2
• · Ro,k-l
R =
Rio
0
Rl2
• ♦ Rl,k-1
-Rk-1,0
Rk-1,1
Rk-1,2 ·
0 .
0
^01
^02
• · uo,k-i
Ω =
^10
0
^12
• · ^l,k-l
&k-1,0
Uk-1,1
Mk-1,2 ·
0 _
Построение минимального дерева может быть начато с произвольной
точки, т.е. для этого может быть использована любая строка матрицы
расстояний. Выбранная начальная точка ξ (I) соединяется с ближайшей
к ней точкой ξ (j) . Элемент Rij должен быть минимальным в l-й строке
матрицы R. В этом случае ωij является первым ЭВ минимального дерева.
Точки ξ (I) и ξ (j) образуют упорядоченное подмножество N, а остальные
(к — 2) оставшиеся точки — неупорядоченное подмножество М. Дальней¬
шее упорядочение происходит за счет поочередного включения в подмно¬
жество N точек из М по правилу
υ = argmin^ mmRrnn >, т G Μ, п G N,
т I т J
где v — номер последующей точки минимального дерева, arg — оператор
взятия аргумента ξ (υ). Отметим, что для определенности в качестве на¬
5.6. Некоторые подходы к решению проблемы нумерации
203
чальной точки минимального дерева можно выбрать точку, ближайшую
к центру тяжести множеств ГРТО, либо к началу системы отсчета.
Упорядочивание точек на основе алгоритма объективной группи¬
ровки «Спектр» [132]. В соответствии с данным алгоритмом в качестве
нулевой точки может быть выбрана произвольная точка множества Ξ. Для
определенности точкой ξ (0) будем считать ближайшую к ее центру тяже¬
сти. Первой точкой, т.е. точкой ξ (1), будем считать ближайшую к точке
ξ (0). Далее находится точка ξ0 ъ являющаяся центром тяжести системы
точек ξ (0) и ξ (1). Второй точкой ξ (2) будет точка из неупорядоченного
подмножества М, ближайшая к точке £0 г. Затем находится центр тяжести
ίο,1,2 системы точек ξ (0), ξ (1), ξ (2) и ищется в качестве третьей точка
ξ (3), ближайшая к этому центру тяжести. В связи с тем, что положение
центра тяжести системы точек устойчиво к ошибкам измерения положения
точек ГРТО, следует ожидать большую помехоустойчивость рассмотрен¬
ного алгоритма по сравнению с алгоритмом минимального дерева.
Пример. На рис. 5.16 приведено изображение из семи точек. Начало си¬
стемы отсчета находится в точке Р. РВ, проведенные из полюса Р к этим
точкам, при первичной нумерации путем строчного сканирования сцены об¬
разуют пучок В = {5 + 11г; 10 -f 11г; 1 + 2г; 15 + 8г; 24 + 8г; 15 + Зг; 21 -f Зг}.
Центр тяжести точек находится в точке О, характеризующейся РВ βο = 13 -f
0 1
Рис. 5.16. Изображение ГРТО с нумерацией точек, получающейся при строчном
сканировании кадра
+ 7,57г. Ниже, в табл. 5.2, указаны номера точек, получающиеся при использо¬
вании описанных выше подходов. Из табл. 5.2 видно, что первичная нумерация
точек в результате применения этих подходов не сохранилась. Точка, первично
занумерованная в качестве третьей, стала нулевой, а номера остальных точек
полностью нигде не совпадают.
Таблица 5.2
Первичная нумерация точек
0
1
2
3
4
5
6
Номера точек в естественном
порядке
5
6
4
0
1
3
2
Номера точек минимального дерева
3
2
4
0
6
1
5
Номера точек по алгоритму
группировки
5
4
б
0
3
1
2
204
Гл. 5. Сигналы в виде пучков векторов
На рис. 5.17 приведены результаты статистического эксперимента по определе¬
нию наиболее устойчивого к координатным шумам метода нумерации точек пучка,
показанного на рис. 5.16. Приведенные графики представляют собой зависимости ве-
Pfs‘
6*10 "
5*10 ■
A 1
4 *1U
3-10 5·
2*10 *
i -
1U
/*
0 CN Ό ОО о СЧ <т
о <о © © ^
а о о" o' о о" ©~
Рис. 5.17. Результаты эксперимента по
оценке устойчивости методов нумера¬
ции концевых точек пучка, приведен¬
ного на рис. 5.16, при нумерации точек
в естественном порядке (а), по методу
минимального дерева (б), по алгорит¬
му «Спектр» (в)
роятности pf ошибочной нумерации точек от СКО координатного шума для каждого
из трех подходов. Число экспериментов для получения одной точки графика равно
105. Как видно из графиков, наилучшей является нумерация РВ пучка, проводимая
в естественном порядке и по алгоритму «Спектр». Оба этих подхода характеризуются
вероятностью ошибочной нумерации порядка pf = 10 “4 при СКО координатного
шума σ = 0,09. При этом же уровне шума метод минимального дерева обеспечивает
Pf — 0,17, т.е. значительно уступает в эффективности первым двум.
5.7. Аналитическое задание пучков в трехмерном пространстве
5.7.1. Кватернионное представление пучков. Пусть OABCD — за¬
данный на сфере единичного радиуса пространственный пучок с радиус-
векторами ОА, ОВ, ОС и OD (рис. 5.18). Подобные пучки будем обозна¬
чать прописными латинскими буквами Q, Р, С и др., а входящие в их состав
РВ — соответствующими строчными буквами с указанием их порядкового
номера. Пространственный пучок в самом общем виде записывается как Q =
= {я (n)}o,s—1’ гДе s — его размерность. Далее такой пучок будет рассма¬
триваться как кватернионный сигнал (КТС). Каждый РВ q (η), задающий
точку на сфере единичного радиуса с угловыми координатами а(п) и β(η),
где а(п) и β(η) — соответственно углы в горизонтальной и вертикальной
плоскостях, пеленг и угол места, описывается векторным кватернионом
q(n) = cos β(η) cosa(n) · г + cos β(η) sin a(n) · j + sinβ(η) · k, (5.7.1)
5.7. Аналитическое задание пучков в трехмерном пространстве 205
а сам пучок — в виде
Q = {cosβ(η) cos а(п) · г + cos β(η) siηα(η) · j + sin β (га) · &}0 s-i·
(5.7.2)
Здесь i,j,k — мнимые единицы, правила умножения которых зада¬
ются следующими таблицей и схемой [150]:
г
3
к
г
-1
к
3
j
-к
-1
г
к
3
—г
-1
J
J
(5.7.3)
В отличие от умножения комплексных чисел операция умножения
кватернионов, как следует из (5.7.3), является некоммутативной: ij = — ji,
ik = —кг, jk = —kj. Кватернион тесно связан с комплексными числами
и выражается через них [150]. Его можно представить как сумму двух
комплексных чисел, одно из которых берется с весом, равным мнимой
единице. Для кватерниона q = qo + iqi + jq2 + &<7з, qo, qi, <72 и q$ —
вещественные числа, входящего в состав эталонного (исходного) сигнала,
эти комплексные числа обозначим через t и w, а для кватерниона в со¬
ставе принятого сигнала, подвергшегося преобразованиям — через и и v.
206
Гл. 5. Сигналы в виде пучков векторов
Верхний индекс при каждом из этих чисел будет обозначать мнимую еди¬
ницу, которая используется в данном комплексном числе. В дальнейшем
будем пользоваться следующими тремя комплексными представлениями
кватерниона q\
— первая комплексная форма, или г-представление:
q = · j, где № = q0 + qi - i и = q2 4- qs · г; (5.7.4)
— вторая комплексная форма, или j-представление:
q = ίϋ) + · k, где №=qo + q2-j и = g3 4- gx · j; (5.7.5)
— третья комплексная форма, или ^-представление:
g = * г, где = go + 9з * j и = qi 4- дг · j. (5.7.6)
Целесообразность задания таких представлений кватерниона связана
с возможностями использования аппарата контурного анализа при об¬
работке КТС Q = {g(ft)}0s_i> а также в проведении коммутативного
умножения и wна х 4- гу, и — на ж 4- jy, и — на
х + ку, где ж и у — произвольные вещественные числа.
Для каждой из введенных комплексных форм можно задать пред¬
ставление кватерниона в показательном или в тригонометрическом видах.
Например, для первой комплексной формы
q = t(г) + w· j = |t« I exp {ιφ} + \w^ \ exp {г^} · j =
= |*M I (cos φ + г sin φ) + |п/г) | (cos ψ + i sin ψ) * j =
= |£WI cos φ 4- г · 1| sin φ + j · |го^ | cos ψ 4- к · | sin -0, (5.7.7)
где φ = argtfM, ψ = argil/*).
Трем формам представления кватернионов соответствуют три формы
КТС:
Q = TW 4- W(i) · j = T(i> + W(J,) · fe = T(fc) + · г, (5.7.8)
где
TW = f (n)| и WW = (w(i) (n)\ , (5.7.9)
^ J 0,5 — 1 ^ J 0,5 — 1
T°) = {<w>(n)} 1 и ww) = (ti>w)(n)} , (5.7.10)
T(fe) = (*(fc) (n)}o i и W(A:) = ju/fc) (n))o ^ (5.7.11)
— комплекснозначные сигналы, свойства и анализ которых был рассмо¬
трен выше. Выбор формы представления КТС зависит от того, вокруг
какой оси, х, у или z, возможно вращение РВ кватернионного сигнала.
Пример 1. Показанный на рис. 5.18 КТС предсталяется в следующем виде:
Q = {0,5j 4 0,86fc; 0,86г 4 0,50,86г - 0,5j; 0,5j - 0,86fc}.
5.8. Скалярное произведение кватернионов
207
Запишем три формы этого КТС в комплексном виде:
Q = Т(<) + W(i)-j = {0; 0,86г; 0,86г; 0} + {0,5 + 0,86г; 0,5г; 0,5; 0,5 — 0,86г}У;
Q = Тш + W{i)-k = {0,5j;0;0,5.?';0,5j} + {0,86; 0,5 + 0,86г;0,86г; -0,86}·*:;
Q = Tw + W(fc) -г = {0,86*:; 0,5*:; 0; -0,86*:} + {0,5*;; 0,86; 0,86 + 0,5*:; 0,5*:}-г.
Приведенные выше соотношения носят общий характер и применимы
к КТС, заданным не только на сфере. В следующих разделах данной главы
будем пользоваться только первой комплексной формой представления
кватернионов.
Таблица 5.3. Операции сопряжения для комплексных чисел и кватернионов
Комплексные числа
Кватернионы
Ή = U\ + IU2
q = go + iqi + jqi + kq3
и* = til — IU2
q* = qo ~ iqi ~ jq2 ~ kq3
(и + t)* = и* +t*
{q + pY =q* +p*
(и -t)* = и* -t*
(q ■ pY =p* -q*
и · г = г · и
u j — j u*
В табл. 5.3 даны сводки формул, связанные с операциями сопряжения
комплексных чисел и кватернионов.
5.8. Скалярное произведение кватернионов
5.8.1. Умножение кватернионов, представленных в комплексной
форме. Произведение заданных в комплексной форме двух кватерни¬
онов q = t + wj и р = и vj, полученное с учетом некоммутативности
для них этой операции, т.е. с учетом (5.7.3) и данных табл. 5.3, имеет вид
q . р = (t + wj) (и + vj) — (ut — v*w) + j (uw* + v*t*) =
= (ut — v*w) + (u*w + vt) · j. (5.8.1)
Основной базовой операцией при линейной обработке сигналов явля¬
ется скалярное произведение, служащее мерой их схожести. К образо¬
ванию скалярного произведения обрабатываемого и эталонного сигналов
сводятся такие операции как разложение и фильтрация сигналов, а также
получение их АКФ и ВКФ.
В действительном линейном пространстве Е скалярное произведение
его элементов (векторов) вводится аксиоматически и обладает следующи¬
ми свойствами [82]:
1· (х.у) = (у.х); 2. (х + y)z = (x,z) + (y,z);
3. ((Ах),у) = А(х,у); 4. (х,х) ^0.
Здесь Л — произвольное вещественное число.
В комплексном линейном пространстве С первая операция становится
некоммутативной, так как (х, у) = (у,х)*. Но если первое свойство для
208
Гл. 5. Сигналы в виде пучков векторов
пространства Е записать в виде (х, у) = (у,х)*, что не меняет его вид,
то свойства скалярного произведения в пространствах Е и С одинако¬
вы. Ниже приведены формулы для вычисления скалярных произведений
комплексных слагаемых и = щ 4- ги2 и Ь = Ь\ 4- гЬ2 кватернионов.
1. (u, Ь) = (Ь, и)* = (£*,и*) = u-t*,
2. (и, t) — и\ -f U4 · Ьч — ui · Ьч · i + U4 · £1 · г, (5.8.3)
3. (и*,t) = щ * ti — u2 · Ьч — u± · Ьч * i — ич * ti * i.
5.8.2. Скалярное произведение представленных в комплексном виде
кватернионов. Введем с учетом некоммутативности операции умноже¬
ния скалярное произведение кватернионов q = Ь + wj и р = и + vj,
обладающее свойствами (5.8.2):
(q,p) = (p,q)* = q-p*· (5.8.4)
Так как для кватернионов имеют место распределительный и сочета¬
тельный законы, то выполняются также остальные приведенные в (5.8.2)
операции:
((q + p),c) = {q,c)-r(p,c); ((A q) ,р) = \(q,p);
(q, q) фО при q0 ф 0, qi ф 0, q2 ф 0, q3 ф 0.
Здесь с = со 4- ciг 4- c2j + c$k — I 4- т · j — еще один произвольно
заданный кватернион. На основании выражений (5.8.4) и (5.8.5) скалярное
произведение кватернионов qn р записывается следующим образом:
(q,p) = {t + wj, и + vj) = (ί, и) + (t, vj) + (wj, и) + (wj, vj). (5.8.6)
В табл. 5.4 приведены найденные с помощью табл. 5.3, формул (5.8.3),
(5.8.4) и (5.8.5) выражения для слагаемых скалярного произведения (5.8.6).
Скалярное произведение (5.8.6), полученное на основании формул
табл. 5.4, имеет вид
(q,p) = (uibi 4- и2Ьч + w\Vi 4- W4V2) 4-г (-Ь\и2 4- Ь2и\ - w\v2 + w2v\) -f
-f j (—tiWi 4- b2w2 4- W1U1 - W4U4) 4- к ( b\v2 - b2vi 4- wiu2 4- w2u{).
(5.8.7)
Квадрат модуля (нормы) кватерниона получается из выражения (5.8.7)
при q = р:
(q, Я) = И2 = А + tl + w\ 4- w\ = \Ь\2 4- \w\2. (5.8.8)
Таблица 5.4
X = XI 4- 1Х2\ У = 2/1 4- гу2
1.
(x,yj) = ~(Х,У*) -3 = ~з(х*>у) = -з -X* у*
2.
(*7>у) = (х> у") ■j = j (х*,у) =j -х* - У*
3.
(х3,уз) = (зх>ЗУ)* = (х, у) = а: ■ У*
4.
(jx,y) ~j(x,y) = (y,xj) -jx-y*
5.
(xjjy) = (χι У*) = X ■ У
6.
(Зх,УЗ) = (®*!У) = Х* - у*
5.9. Ортогональный базис для кватернионных сигналов
209
На основании введенных определений для скалярного произведения
и нормы можно записать выражение для квадрата расстояния между
двумя кватернионами:
Rlp = Ы2 + |р|2 - 2R-e (q,p) ■ (5.8.9)
Данное представление удовлетворяет всем аксиомам, введенным для
такого рода мер [82]: 1) Rqq = 0. 2) Rqp = Rpq. 3) Rqp ^ Rqc + Rcp.
5.8.3. Скалярное произведение кватернионных сигналов. Скаляр¬
ное произведение двух КТС Р = U + Vj = {и (п) + v (n)j}0 3_ги Q =
= Т + Wj = {£ (η) + ω (η) j}0 s_1, выраженное через скалярные произ¬
ведения составляющих их комплексных сигналов, имеет вид
(Pi Q) = {и + V ■ j, т + w · j} =
= (U, Т) + (U, W · j) + (V · j, Т) + (V · j, w · j). (5.8.10)
Скалярное произведение двух комплекснозначных сигналов U =
= {« W}o,s-i и т = {ί (п)}0^5_1 равно
s — 1
(U,T) = 5^u(n)i*(n). (5.8.11)
п=1
Используя приведенные в табл. 5.3 формулы сопряжения, для осталь¬
ных слагаемых выражения (5.8.10) получим
(U, W · j) = -(U,W*) · j = -j · (U*,W),
(V · j, T) = (V, T) · j = j · (V*, T), (5.8.12)
(V · j, W · j) = (j ■ V,j · W) = (V, W).
Тогда скалярное произведение двух КТС можно представить через
скалярные произведения комплексных слагаемых в виде
(Р, Q) - (и, Т) + (V, W) - j · [(U*, W) - (V*, Т)]. (5.8.13)
Каждое из скалярных произведений, входящих в (5.8.13), находится
аналогично скалярному произведению (5.8.11).
5.9. Ортогональный базис для спектрального анализа
кватернионных сигналов
Метод удвоения [150] дает возможность получить на основе ортого¬
нального базиса Фурье в виде элементарных контуров (см. п. 2.2) ортого¬
нальный базис для представления кватернионных сигналов. Запишем на
основе (5.7.7) представление КТС в показательной форме:
Q = {|ί (п)| ехр {ίφ (η)}} + \w (n)| exp {гф (η)}^,. (5.9.1)
Каждый из комплексных сигналов T = {i(n)}0s_1nW = {w (п)}0 3_г
может быть разложен в базисе из элементарных контуров соответствующей
размерности. Учитывая линейность данной процедуры, получаем следующее
правило построения полного семейства элементарных КТС размерности s:
210
Гл. 5. Сигналы в виде пучков векторов
Qm — {Я.т (^0}o,s — 1 — ^т "Ь T*m ’ j — Гт (1 Н" j) 5 ТП — О, 1, . . . , S 1,
(5.9.2)
где т — порядок ЭКС, Гт — элементарный контур размерности s,
Гт = {7т (п)}0 а-1 = {exp , m = 0,1,... , s - 1.
’ ^ J J 0,s — 1
(5.9.3)
Таким образом,
Qm = {</m(n)}0,s_1 = (exp jfymnj (1 +i)}0 s l> (594)
m = 0,1,... , s — 1.
Если элементарный вектор 7m (n) ЭК Гт записать в виде 7m (η) =
— 7im (ft) + г’72т (гс), то элементарный КТС можно представить как
Qт = {7lm (jl) -f- ir)2m (^) Н“ j'Jlrn (jl) "Ь ^72га (^')}о,з —1‘ (5.9.5)
Комплексные слагаемые элементарного КТС равны
Tm=Wm=rw. (5.9.6)
Приведем для справки представления для элементарных КТС размер¬
ностей s = 2, 3, 4.
s = 2:
Qo = {1 + j] 1 + j}> Qi={l+j;-l-j}· (5.9.7)
s — Z:
Qo = {1 + j;l +j;l +j},
Qi = {1 + j; -0,5 + 0,867г - 0,5j + 0,867k;
-0,5 - 0,867г - 0,5j - 0,867fc}, (5.9.8)
Q2 = {1 + j- -0,5 - 0,867г - 0,5j - 0,867k;
-0,5 + 0,867г - 0,5j + 0,867fc}.
s = 4:
Qo = {1 + j; 1 + j; 1 + j\ 1 + j}, Qi = {1 + j;i + fc; -l - j·, -i - k},
Q2 = {1 +j; —1 — j; 1 + i; —1 — j}, Q3 = {1 +i; -i - fc; -1 - j\i + k}.
(5.9.9)
Рассмотрим некоторые свойства ЭКС.
1. Замкнутость ЭКС. Сумма кватернионов, составляющих элемен¬
тарный КТС порядка т, т = 1,2,... , s — 1, равна нулю:
s-l
У] qrn (п) = 0, т = 1,2,... , s — 1. (5.9.10)
п=О
Справедливость этого соотношения вытекает из аналогичных свойств
элементарных контуров Гт, т = 1,2,... , s — 1, и выражения (5.9.2),
связывающего ЭКС с элементарными контурами.
2. Изометричность ЭКС. Квадраты норм элементарных КТС любо¬
го порядка размерности s одинаковы и, как следует из (5.9.2), равны
||QW||2 = 2s, m = 0,1,... , s - 1.
5.10. Спектральные представления кватернионного сигнала
211
3. Попарная ортогональность элементарных КТС:
(Qm,Qz)
2s при m = Z,
О при m ф I.
(5.9.11)
Данное свойство следует из ортогональности элементарных контуров.
Пронормируем каждый из элементарных КТС. Тогда
= I' "Р" т = ‘·
\v2s у2s ) ^0 при тф1.
т, I = 0,1,... ,5 — 1.
(5.9.12)
Отсюда следует, что полное семейство элементарных КТС размерно¬
сти s задает ортонормированный базис, в котором может быть разложен
произвольный КТС Q = {q (n)}0 s_r
4. Частичная сопряженность. Из свойства сопряженности элементар¬
ных контуров (см. п. 2.2) и выражения (5.9.12) следует, что
Qs-m = Г*_т + Г*_т · j, т = 0,1,... ,s- 1. (5.9.13)
Это означает, что Qm и Qs_m будут сопряжены только по мнимым
единицам г и &, а знак мнимой единицы j у них одинаков:
Qm = Qi-m*5’ m = 0,1,... ,s-l. (5.9.14)
Верхний индекс при Q указывает по каким мнимым единицам надо
проводить сопряжение.
5. Эргодичность компонент ЭКС. Элементарные контуры Гт, т =
= 0,1,... ,5 — 1, обладают важным для обработки сигналов свойством эр¬
годичности, основанном на равноправности переменных шипв выраже¬
нии (5.9.3): 7т (п) = 7п (т), тг, т = 0,1,... ,5 — 1. Аналогичное свойство
характерно и для кватернионов, входящих в состав КТС: (η) = qn (m),
n, m = 0,1,... ,5 — 1.
Свойство частичной сопряженности позволяет расширить количество
равных между собой кватернионов, входящих в состав полного семейства
элементарных КТС фиксированной размерности. При этом набор равных
между собой кватернионов в пределах этого семейства имеет вид
Чт (п) = q{s-t ] (П) - q^'k"> (s-m)= qn (m) =
= ?*-m ] (m) = Чт’к'] (s-n). (5.9.15)
В частности, кватернионы (n) nqm(s — n) отличаются только зна¬
ками при мнимых единицах г и к.
5.10. Спектральные представления кватернионного сигнала
Спектр КТС Q =■ {q (n)}0 S-1 определим как набор его проекций (ко¬
ординат) С = {c(m)}0s_1 в ортогональной системе отсчета, задаваемой
212
Га. 5. Сигналы в виде пучков векторов
полным семейством {Qm}o s-i элементарных КТС размерности 5. При
таком подходе га-я компонента с (га) спектра равна
с(т) = (Q,Qm), m = 0,1,... ,5 - 1. (5.10.1)
Используя представление кватерниона q (п) через комплексные слага¬
емые t (ή) и w (π), выразим спектр С через спектры Pt = {pt (m)}o,s-i
и Pw = {pw (m)}0 s—l этих слагаемых. Тогда
c (m) = (Т + W j, Гш + Гт · j) =
= (T, Гте) - j (Т*,Гт) + j (W*, Гш) + (W, rm), (5.10.2)
m = 0,1,... ,5 — 1.
Учитывая, что pt (га) — (Т,Гт) и pw (га) = (W,rm), получим
с (τη) = pt (m) + pw (m) - j (m) - ptf (m)J,
где pi"1 (га) и p£^ (га), га = 0,1,... ,5-1, — компоненты спектров
и W^*), комплексно сопряженных со слагаемыми Т и W. Как следует
из (2.4.15), р(*> (га) = р* (s — га). Тогда
с (га) = pt (га) + pw (га) - [pt (5 - га) - pw (5 - га)] · j. (5.10.3)
Таким образом, спектр КТС Q = {q (тг)}0 в_г полностью определяется
через спектр составляющих КТС комплексных сигналов.
Определим спектр элементарного кватернионного сигнала Qm, га =
= 0,1,... ,5—1. Для данного случая ри (га) — р„ (га) = р (га). Тогда
с (га) —- 2р (га). (5.10.4)
Поскольку спектр элементарного контура Гт содержит только одну
ненулевую компоненту, равную р (га) = 5, то спектр элементарного КТС
в соответствии с (5.10.4) также будет состоять только из одной не равной
нулю компоненты с (га) = 2s и иметь вид
с(1) =
2s при I = га,
0 при I ф га.
(5.10.5)
Пример 1. Найдем спектр КТС вида
Q — {q (τι)}0 з = {1 4- г — j] 2г + j + к; — 2 + к] 1 — Зг — 2к}.
Комплексные слагаемые Т и W и их спектры Рт и Pw для этого сигнала
равны
Т = {1 + г; 2г; -2; 1 - Зг}, Рт = (0; 8 + 2г; -2 + 2г; -2},
W = (-1; 1 + г; г; —2г>, Pw = {0; 2 — 2г; -2 + 2г; -4}.
Так как рг (0) = pw (0) = 0, то нулевая компонента спектра КТС также
будет равна нулю, т.е. с (0) = 0. Для нахождения остальных компонент спектра
воспользуемся выражением (5.10.3)
c(l) = Pt (1) 4" Pw (1) — [pt (3) — pw (3)]j — 10 — 2j,
c (2) = pt (2) + pw (2) = -4 + 4г,
5.10. Спектральные представления кватернионного сигнала
213
с (3) = pt (3) 4- pw (3) - \pt (1) - pw (1 )]j = -6 - 6j - 4k.
Спектр KTC равен C = {c (m)}0 3 = {0; 10 — 2j\ — 4 — 4?; — 6 — 6j — 4k}.
Найдем квадрат нормы ||C||2 спектра KTC:
llcll2 = (m)=
m=0
s — 1
= Σ [Pt (m) + pw (m) - ρτ (s - m) j + pw (s - m) j) x
m=0
x [pt (m) + Pw (m) + jpx (s - m) - jp^ (s - to)] =
= 2Σ [1ptMl2 + IpwMl2] = 2 (||Pt||2 + ||Pw||2)·
m=0
Учитывая, что ||W||2 = ^||Ρ№||2, ||W||2 = 1||Ρ„,||2 и ||Q||2 = ||T||2 +
+ ||W||2, получим
IIQH2 = i|]C|S2. (5.10.6)
Данное выражение является аналогом равенства Парсеваля для КТС.
Таким образом, спектр КТС полностью определяется через компоненты
спектров его комплексных слагаемых. Определим обратное ДПФ как ска¬
лярное произведение вида
«(”) = ^(C’Q")> п — 0> 1> · · · > s - 1. (5.10.7)
Пусть U и V — комплексные слагаемые кватерниона С = (c(n)}o,s-i,
т.е. С = U + Vj. Тогда выражение (5.10.7) приводится к виду
^(c>Q») = i(u+vj'’rn-i-JTn) =
= ^[(U, г;) (1 + j) + (V, Гп) (-1 + j)]. (5.10.8)
Скалярное произведение (U,Г*) = sF"1 (U) есть обратное с весом
s ДПФ от комплексного слагаемого U, а (V, Гп) = Fn (V) — прямое
ДПФ от комплексного слагаемого V. Тогда для кватерниона, получаемого
в результате обратного ДПФ от КТС С = {с(п)}о,5-ь можно записать
q(n) - j-s(C, Qn) = sF-1 (U) (1 + j) + Fn (V) (-1 + j), (5 10 9)
n = 0,1,... , s — 1.
Пример 2. Найдем обратное ДПФ для КТС спектра из предыдущего примера
С = {0; 10 — 2j; —4-f 4г; —6 — 6j — 4А;}. Комплексные составляющие U и V
равны U = {0; 10; —4+4г; -6}, V = {0; —2; 0; —6—4г}. Обратное ДПФ сигнала U
(с весом 5) и прямое ДПФ сигнала V имеют соответственно вид
{4ц 4 + 12г; -8 4- 4г; 4 — 20г}, {-8 - 4г; 4 - 4г; 8 4- 4ц -4 - 4г}.
214
Гл. 5. Сигналы в виде пучков векторов
Воспользовавшись выражением (5.10.7), получим
ςτ(0) = 1 4-i - j, g(l) = 2t+i + fc, q(2) = -2 + k, ςτ(3) = 1 - Зг - 2k.
В заключение данного раздела рассмотрим вопрос о разложении про¬
извольного КТС Q = U 4- V · j = {(Ζ (τι)}ο β_ι в базисе из полного
семейства элементарных КТС {Qm}0,s-i = (rm (1 + j)}0 e_r Для этого
выражение (5.10.7) запишем в виде
s — 1
q^ = h = ^ Σс (m)qn (т)·
т=0
При переходе от кватернионов q (η) и qn (т) к КТС Q и Qm последнее
выражение примет вид
s-l
Q = ^X>(m)Qm. (5.10.10)
т=О
Отсюда следует, что произвольный КТС может быть представлен
взвешенной суммой элементарных КТС с весовыми коэффициентами
в виде кватернионов спектра разлагаемого сигнала.
Пример 3 Спектр КТС из примера 1 равен С = {с(п)}о,з = {0; 10 — 2j;
—4+4г; —6—6j—4k}. Представим данный сигнал в виде (5.10.10), т.е. в виде суммы
Q = 0,125-{с (0) Qo+c (1) Qi+c (2) Q24-c (3) Q3}. Используя выражение (5.9.9)
для элементарных КТС Qo» · ·., Q3, найдем слагаемые суммы
с (0) Qo = {0}0 3, с (1) · 8 · Qi = {12 + 8j; 8г + 12k; -12 - 8j; -8г - Ш},
с (2) · 8 · Q2 = {—4 -f 4г — 4j — 4к; 4 — 4i+4j — 4к;
—4 4- 4г — 4j + 4к; 4 — 4г -h 4jr — 4к},
с (3) · 8 · Q3 = {4г — 12^ — 4к] —4 + 12г + 4j; —4г + 12j> 4- 4к; 4 — 12г — 4j}.
Проверка:
|[c(l)gi(0) + c(2)ga(0) + c(3)gs(0)] = l + i-j = q( 0),
i[c(l)gi(l) + c(2)g2(l) + с(3)5з(1)] -2i + j + k = 5(1),
|[c(l)5i(2) + 0(2)52(2) + 0(3)53 (2)] =-2 + к = q{2),
i[c(l)5i(3) + c(2)52(3) + с(3)5з(3)] = 1 - 3t - 2* = 5(3).
5.11. Корреляционные функции кватернионных сигналов
Отсчет ВКФ двух комплексных сигналов U = {“(»)}ο,β-ι И Т =
= {t(n)}o,s-i равен скалярному произведению
s-l
^и,т = (U,T<d>) = ^jT^u(n)t*(n 4- d), d = 0,1,... , s — 1, (5.11.1)
5—0
5.11. Корреляционные функции кватернионных сигналов
215
где — {t(n + gO}o,s-i — комплексный сигнал со смещенным на d
элементарных векторов началом. Тогда ВКф двух кватернионных сигна¬
лов Р = U + V · j и Q = Т + W · j, представленных суммой комплексных
слагаемых, запишется как
Vp,q (d) = (P(d), Q) = (U + V ■ j, T<d> + . j) =
- (U, тМ) + (U, w«. j) + (V. J9 TW) + (V · j, W« . j).
Используя формулы из табл. 5.4, получим
m>,Q(d) = ηυ,τ(ά) + Tjv,w(d) - j · [t?u*,w(<0 “ »?v*,t(<0]. (5.11.2)
Здесь e_j
W,w{d) = (V,W^) = ]T\(n)u/*(n + d),
n=0
s—1
»7u*,w(d) = (U*,W(d>) = ^u*(n)w*(n + d), (5.11.3)
n=0
s —1
77v*,x(rf) = (V.tM) = Σ v*(n)t*(n + d).
71=0
Данные выражения позволяют найти ВКФ двух КТС, выраженных
через комплексные слагаемые. При Q = Р и, следовательно, при U = Т
и V = W, с их помощью можно вычислить АКФ кватернионного сигнала.
В этом случае выражение (5.11.2) принимает вид
ηρ(ά) = ηυ(ά) +ην{ά) - j ■ [ηυ·,ν(ά) - »7v*,и (<*)], ......
. n . . (5.11.4)
α = U, 1,... ,5 — 1.
Рассмотрим корреляционные свойства элементарного КТС Qm, т —
= 0,1,...5 — 1. Для таких кватернионных сигналов U = V = Т =
= W = Гт и выражение (5.11.2) с учетом свойств АКФ элементарных
контуров Гт (см. п. 2.8) принимает вид
Hm = ^Qm{d)}o^1 = 2sT*m = 2srs-m, m = 0,1,... s — 1. (5.11.5)
Таким образом, АКФ элементарного КТС порядка т является чисто
комплексной функцией и определяется элементарным контуром Гш та¬
кого же порядка.
Пример 1. Определим АКФ элементарных кватернионных сигналов размер¬
ности 5 = 4. Используя выражение (5.11.5) и значения элементарных контуров
размерности s — 4 (см. (5.9.9)), получим:
Но = 8Г0 - 8{1,1,1,1}, Hi = 8Г3 = 8{1, -г, -1, г},
Я2 = 8Г2 = 8{1, -1,1, -1}, Я3 = 8Γι - 8{1, г, -1, -г}.
Определим выражение для ВКФ ^Qm,Qt (d) = (Qm, Qi) элементарных
КТС, где Qm = Гт(г + j) и Qz = Г/(1+ j) В этом случае U = V = Гт,
Т = W = Г/. Тогда выражение (5.11.2) запишется как
^QmiQiM = 2?7гт,гг (d), d = 0,1,... ,5-1.
216
Гл. 5. Сигналы в виде пучков векторов
ВКФ элементарных контуров ηττη,τι (d), d — 0,1,... ,5 — 1, благода¬
ря свойству попарной ортогональности этих контуров везде равна нулю.
Поэтому
^Qm,Qj = {^Qm.QiHJo.s-i = {0}o,s-i·
Таким образом,
„ ίΛ\ — J 2sTm(d) при m = l,
VQm,QiW ~ S , (5.11.6)
(О при νηφί.
Отсюда видно, что корреляционные свойства элементарных КТС це¬
ликом совпадают с корреляционными свойствами элементарных контуров
соответствующего порядка. В частности, следует отметить, что |7m(d)| =
= 1, d, га = 0,1,... , 5 — 1, и поэтому модули всех отсчетов АКФ эле¬
ментарных КТС одинаковы, т.е. они представляет собой жестко коррели¬
рованный сигнал.
5.12. Согласованная фильтрация кватернионных сигналов
Согласованный фильтр реализует на своем выходе смещенную на s
отсчетов ВКФ двух сигналов. Один из сигналов служит эталонным и опре¬
деляет ИХ фильтра, а второй является фильтруемым и для него в про¬
цессе фильтрации вычисляется набор мер схожести (близости) к эта¬
лонному сигналу. При этом один из параметров сигналов, фильтруемого
или эталонного, варьируется в заданных пределах. Если фильтруемый
и эталонный сигналы совпадают, то существует отсчет фильтра, равный
энергии фильтруемого сигнала. Он является максимальным (пиковым) по
отношению ко всем остальным отсчетам. Так как для вычисления энергии
сигнала необходимо учесть все отсчеты входного сигнала, то пиковый
отсчет является последним выходным отсчетом фильтра и поэтому сме¬
щен на s отсчетов по отношению к начальному. В п. 3.6 рассмотрены
вопросы согласованной фильтрации дискретных комплексных сигналов.
Согласованный фильтр для сигналов U = {гх (тг)}0 3_ι и Т — {t (п)}0 8_г
вырабатывает текущий выходной отсчет 77и,т (d) следующим образом:
s — 1
m,T (d) = (и, T(s_d_1)) = ]Г и (n)t* (n-d + s- 1),
71 = 0 ' '
d = 0,1,... , s - 1,
где
T{s-d-i) = {t (n _ d + s - 1)>0>β_! (5.12.2)
— комплексный сигнал со смещенным на s — d — 1 началом.
Поскольку кватернионный сигнал представляется суммой, в состав
которой входят два комплексных сигнала, то целесообразно, учитывая
правила (5.7.3) действия с мнимыми единицами г, j и к, представить согла¬
сованный фильтр для КТС как композицию двух согласованных фильтров
для комплексных сигналов.
5.12. Согласованная фильтрация кватернионных сигналов
217
Поскольку Q = Т + W · j и Р = U -f V · то в соответствии
с (5.12.1) и (5.12.2) согласованный с КТС Q = {<7 ΜΙο,β-ι фильтр должен
выполнять операцию
Щ,р (d) = г^и,т (d) + T7v,w {d) ~ j · [Vv*,w (d) - Τ7ν*,τ (d)] —
s —1 5 — 1
= u (n) i* (n — d + 5 — 1) -f- v (n) (n — d + s — 1) —
n=0 n=0
“j *
~s-1
У] гг* (n) w* (n — d -f 5 —
_n=0
5—1
1) — ^ v* (n) t* (n — d + 5 — 1) .
n=0
(5.12.3)
Данное выражение можно записать еще и следующим образом:
?7q,p (d) = ω (η) £* (η - d Η- 5 — 1) -f ν (η) w* (η — d + s — 1) —
η=ο
s — 1
η=0
5-1
— У^ j · гг* (η) гг;* (η — d -f s — 1) Η- У^ j · ν* (гг) £* (гг — d -f s — 1),
n=0 n=0
(5.12.4)
s — 1
i?Q,p (d) = У] [u (n) + v (n) · j]t* (n - d + s - 1) +
n=0
s —1
-f У^ [г; (n) — гг (π) · j]w* (гг — d -f s — 1). (5.12.5)
n=0
Таким образом, кватернионный согласованный фильтр представля¬
ет собой совокупность двух фильтров. Один из них согласован с ком¬
плексным сигналом Т, второй — с W.
При d = s — 1 выходной отсчет фильтра равен
VQ,P (s - 1) = и (η) t* (η) + Σ V (η) w* (η)
η=0
"s — 1 5 — 1
гг* (η) w* (η) - г;* (η) £* (η)
η—О
’ J *
_n=0
(5.12.6)
В соответствии с (5.8.13) данный результат показывает, что в момент
d = s — 1 фильтр вырабатывает отсчет в виде скалярного произведе¬
ния КТС.
Если фильтруется согласованный сигнал, т.е. когда Р = Q, U = Т
и V = W, выражение (5.12.4) принимает вид
218
Гл. 5. Сигналы в виде пучков векторов
s—1 5—1
VQ (d) = ^2 и(п)и* (п - d + s - 1) -f ^2 υ (η)ν* (η - d + s — 1) -
n=0 n=0
"s—1 s—1
' i * ^2 u* (n)v* (n ~ d + s ~ 1) — ^2 v* (n)u* (n ~ d + 5 — 1)
n=0 n=0
(5.12.7)
d — 0,1,... ,5 — 1.
Нормированные выходные отсчеты кватернионного согласованного
фильтра получаются при делении выходных сигналов на ||Q|| · ||Р||:
?7q,p,h (d) = ||^|j урц} d = 0,1,... , 5 — 1. (5.12.8)
Нормы (модули) текущих нормированных отсчетов не превышают еди¬
ницы, а если фильтруется согласованный сигнал, то
„ (А\ - (d) _ (d)
Q’H ||U||2 · ||V||2 IIQII2
»?Q,h (s - 1) = 1·
(5.12.9)
(5.12.10)
Пример l.B качестве примера рассмотрим согласованную фильтрацию КТС
Q = {1 -f г — j; 2г 4- j + k\ -2 -f k; 1 — Зг — 2k}.
Комплексные компоненты этого сигнала равны
U = {1 + г; 2г; -2; 1 - Зг}, V = {-1; 1 + г; г; -2г}.
Расчетная формула (5.12.7) в данном случае принимает вид
VQ
(d) = ^2 и (п) и* (п — d 4- 3) 4- ^2 v (п) v* (п — d + 3) —
-з
У U* (η) υ* (п - d + 3) - У υ* (п) гг* (n - d + 3)
d = 0,1,2,3.
Результаты фильтрации сигналов U, U*, V и V* равны
з
(53 и (”) и* (п “ d + 3)} = (-2 + 16i; -16; -2 - 16*; 2θ),
п=0 0,3
3
v (п) v* (п — d + 3)| 2 — 2г; —4; —2 + 2г;8 j,
п—0 0,3
3
и* (п) v* (п - d + 3) j = |з + 5г;9 + г; -3 — 9г; -9 + Зг j,
п-0 0,3
3
v* (п) и* (п - d + 3)| ^ = |з - 2г;9 + г; 3 + 5г; -9 -Н3г|.
5.13. Обсуждение результатов
219
5.13. Обсуждение результатов
Точечные объекты, особенно групповые точечные объекты (ГРТО),
представляют часто встречающийся на практике класс изображений. Огра¬
ниченность разрешающей способности датчиков в зависимости от условий
наблюдения приводит к необходимости рассматривать в качестве точки изо¬
бражения любого объекта — от пылинки до звезды. Хотя отдельную точ¬
ку нельзя охарактеризовать формой, однако закономерности расположе¬
ния точек ГРТО дают возможность рассматривать его как некоторый об¬
раз и говорить о его форме как о форме некоторого сплошного изображе¬
ния, ассоциированного с ГРТО. В данной главе рассматривались вопросы
представления ГРТО в качестве сигналов и применения для их обработки
описанных ранее методов контурного анализа. Основной результат такого
рассмотрения заключается в том, что методы обработки контурных сигналов
распространены на сигналы в виде пучков радиус-векторов, соединяющих
произвольно выбранный полюс Р с каждой из точек ГРТО.
Более конкретные результаты состоят в следующем.
1. Заданное на плоскости упорядоченное множество точек представля¬
ется в виде пучка комплекснозначных векторов, направленных из одной
точки — полюса Р. Между этим пучком и замкнутым контуром из эле¬
ментарных векторов, соединяющих точки множества, существует взаимно
однозначное соответствие. Спектры контура и пучка полностью совпадают
за исключением нулевой компоненты спектра, определяемой вектором,
соединяющим центр тяжести множества точек с полюсом пучка.
2. Для заданных на плоскости пучков получен ортонормированный базис
из полного семейства элементарных пучков. В этом базисе раскладывает¬
ся произвольный пучок, причем проекциями пучка на базисные векторы
являются компоненты его спектра Фурье. Элементарные пучки обладают
свойствами, аналогичными элементарным контурам соответствующей раз¬
мерности и порядка. Отличие между ними заключается в зависимости нор¬
мы элементарного пучка не только от размерности к, но и от порядка j.
Это вызвано тем, что радиус окружности, описанной вокруг элементарного
контура, соответствующего элементарному пучку, с ростом j уменьшается.
3. Особенности пучка как зашумленного сигнала связаны с тем, что
при одной и той же дисперсии координатного шума, вызванного ошибками
измерения положения точек множества, каждый радиус-вектор харак¬
теризуется своим отношением сигнал/шум. Чем больше модуль радиус-
вектора, тем выше это отношение. Поэтому радиус-векторы с неболь¬
шим значением модуля искажаются шумом, т.е. изменяются по моду¬
лю и величине аргумента, в значительно большей степени по сравнению
с другими радиус-векторами. Специфическим результатом действия шу¬
мов является нарушение порядка следования радиус-векторов. Вероятность
этого события увеличивается в ситуациях, в которых угол между соседни¬
ми радиус-векторами имеет незначительную величину или когда соседние
радиус-векторы в большей степени отличаются величинами своих модулей.
Поскольку длина радиус-векторов зависит от положения полюса
пучка, то соответствующим выбором этого положения можно добиться
примерного равенства величин модулей радиус-векторов и уменьшения
вероятности перепутывания номеров радиус-векторов. Однако надо иметь
220
Гл. 5. Сигналы в виде пучков векторов
ввиду, что сильное децентрирование пучка при согласованной фильтра¬
ции приводит из-за увеличения нулевой компоненты коэффициента пе¬
редачи к ухудшению отношения сигнал/шум на выходе фильтра.
4. Еще одной специфической операцией обработки пучков по сравнению
с контурами является операция упорядочения (нумерации) точек подмноже¬
ства. Экспериментальные исследования различных подходов к выполнению
данной операции показали, что достаточно высокой помехоустойчивостью к
перепутыванию номеров радиус-векторов пучка при его зашумлении обла¬
дает процедура присвоения очередного гг-го номера тому радиус-вектору,
который составляет наименьший угол с (п — 1)-м радиус-вектором.
5. Для множества пространственно расположенных точек получена
модель в виде пучка векторных кватернионов. Введено с учетом некомму-
тативности операции умножения кватернионов скалярное произведение
двух кватернионов.
В связи с тем, что кватернион допускает представление в виде двух
комплексных чисел, на кватернионные сигналы были распространены по¬
нятия спектра, авто- и взаимно корреляционной функций, согласованной
фильтрации и получены попарно ортогональные элементарные кватерни¬
онные сигналы с монохроматичным спектром. Произвольный кватерни-
онный сигнал разлагается в базисе из полного семейства элементарных
кватернионных сигналов. Эти результаты позволили с единых позиций
рассматривать обработку как контуров, так и ГРТО, заданных на плоско¬
сти или в трехмерном пространстве.
5.14. Задачи и упражнения
1. Для контура Г = {1 + г; 2; 5 — г; —2г + 2; —5 — г; —2; — 1 + г; 2г} записать
полярный код, когда положение полюса совпадает с положением центра тя¬
жести и когда полюс смещен относительно центра тяжести в точку с коор¬
динатами (10,5). Найдите спектры полученных пучков и проанализируйте
влияние децентрирования пучка на вид спектра.
2. Найдите коды элементарных пучков для к = 5. Постройте полученные пучки.
Проверьте их ортогональность.
3. Найдите импульсную характеристику согласованного фильтра для пучка
В = {1 4· 5г; 3; 4 — 2г -f* 1; —i\ —5 4~ i\ —3; —2 -f- 2г; Зг}.
4. Найдите отношение сигнал/шум для элементов пучка В = {1 + 5г; 3; 4 — 2г 4-
4- 1; —г; —5 + г; —3; —2 -f 2г; Зг} при σ = 2,5.
5. Пронумеруйте точки ГРТО пучка В = {1 + 5г; 3; 4 — 2г 4- 1; —г; —5 4- г; —3;
—2 -f 2г; Зг} в естественном порядке, по алгоритму «Минимальное дерево»
и на основе алгоритма объективной группировки.
6. На примере кватернионов (l + i + ji-f-A:) и (2 — г — j — к) продемонстри¬
руйте некоммутативность операции их умножения. Найдите их скалярное
произведение.
7. Найдите г-, j-, ^-представления кватерниона Q = (2 + Зг — 4j + 5к).
8. Найдите все элементарные КТС для s = 5.
9. На примере для s = 5 покажите свойства замкнутости, ортогональности,
частичной сопряженности и эргодичности элементарных КТС.
10. Для кватернионного сигнала Q = {1 + г + j; г + j 4- к\ 1 4- j + к; 1 + г 4- &}
найдите спектр, АКФ и результат согласованной фильтрации.
ЧАСТЬ II
ПРИМЕНЕНИЕ КОНТУРНОГО АНАЛИЗА
В ЗАДАЧАХ ОБРАБОТКИ ИЗОБРАЖЕНИЙ
Введение
Достоинство методов контурного анализа в задачах обработки изобра¬
жений и распознавания зрительных образов заключается в возможности
решения этих задач с единых теоретических позиций. При этом изме¬
нение параметров положения, поворота и масштаба изображения слабо
влияет на объем вычислений.
Вместе с тем эти методы применимы лишь в том случае, когда в нашем
распоряжении имеются сами контуры, по крайней мере, локализована
область сцены, в которой сосредоточены граничные точки (края, границы)
конкретного изображения. Задача выделения контуров многоградацион¬
ного изображения на статистически сложном многоградационном фоне
эквивалентна задаче обнаружения двумерного сигнала на фоне шумов
и других сигналов, играющих роль помех. Важность решения этой задачи
не подлежит сомнению, поскольку при отсутствии линии контура нельзя
применить описанные в части I методы.
Вопросам выделения контуров посвящена обширная литература (на¬
пример, [4, 5, 9, 40, 113]). В обзорной статье известного американского
специалиста в области обработки изображений и распознавания обра¬
зов А. Розенфельда подчеркивалось, что «до сих пор нет сколько-нибудь
удовлетворительной модели краев областей цифровых изображений, хо¬
тя она была бы очень полезна при построении оптимальных операторов
обнаружения границ» [112]. Данное утверждение в значительной степени
отражает ситуацию с выделением контуров изображений на современном
этапе. Часто используемые на практике методы формирования статистик
для принятия решений, базирующихся на операторах Кирша, Собела,
Робертса, Превитта и др., являются сугубо эвристическими. Отсутствие
адекватных моделей сигналов и помех для большинства реальных сцен
приводит к тому, что в общем случае неизвестны оптимальные решающие
процедуры выделения контуров изображений. Такое положение вызвано
значительно более сложной и разнообразной по сравнению со случаями
обработки одномерных сигналов структурой сигналов и помех.
Ниже будет рассмотрен один из подходов к выделению контуров изо¬
бражений в реальной сцене, базирующийся на гипотезе экспоненциально¬
косинусной АКФ фоновых шумов и слабой информативности низкоча¬
стотной части спектра изображения. При данных допущениях, основан¬
ных на экспериментальных данных, для сцен определенного, но широко
распространенного класса, решена задача обнаружения краев изображе¬
ний с прямолинейными границами.
Инвариантность КСФ к преобразованиям переноса, поворота и изме¬
нения масштаба изображения наблюдается лишь при преобразованиях
222
Введение
уже оцифрованных изображений. Если же преобразованиям подвергается
изображение до его ввода в ППИ, то из-за нелинейного характера проце¬
дуры квантования линии в плоскости сетчатки, размерность получаемого
контура оказывается случайной величиной. Данный фактор делает невоз¬
можной процедуру контурной согласованной фильтрации, так как вектор-
контур Г, сформированный по эталонному изображению и определяющий
ИХ фильтра, и фильтруемый вектор-контур N имеют разную размер¬
ность. Поэтому предварительно должна быть проведена операция эква-
лизации (выравнивания размерностей) вектор-контуров Г и Ν. Следует
заметить, что такая операция приводит к дополнительному зашумлению
фильтруемого контура Ν, так как по своей сути является повторным
квантованием сигнала.
Флуктуации амплитуд и фаз сигналов на входе датчиков изображе¬
ний приводят, в конечном счете, к флуктуациям интенсивностей сиг¬
налов, формирующих цифровое изображение cj(mi,m2) в ОЗУИ ППИ.
В результате получающиеся силуэтные изображения становятся много¬
связными из-за образующихся полостей и разрывов, причем значительно
искажается линия края (контура) (рис. BII.1).
Рис. BII.1. Образование многосвязного бинарного цифрового изображения* а —
многоградационное изображение микросхемы, б — сформированное бинарное изо¬
бражение
Разрушение из-за указанных факторов односвязной структуры циф¬
рового изображения ω (7711,7712), а также воздействие шумов и помех
в области изображения приводят к тому, что вместо одного контура, опи¬
сывающего форму исходного изображения s(x,y), мы получаем набор
контуров пятен различной формы в пределах контура исходного изобра¬
жения. Контурный анализ этих пятен не дает необходимой информации
о классе обрабатываемого изображения. В данном случае целесообразно
переходить к пространственным методам обработки, например, к бинар¬
ной пространственной согласованной фильтрации, или к выделению по¬
дозрительных областей сцены по признаку наличия сгущений и к другим
методам, рассмотренным в [42].
Существенное влияние на возможность применения методов контур¬
ного анализа оказывает количество пикселов в составе изображения объ¬
екта. С уменьшением числа пикселов из-за искажения формы шума¬
ми дискретизации падает отношение сигнал/шум. Маскирующее влияние
шумов дискретизации приводит к потере отдельных, в первую очередь,
мелких деталей изображений, т.е. к потере информативных признаков
формы в их контурах.
Введение
223
Необходимое количество пикселов связано с шириной спектра контура
и должно выбираться исходя из теоремы Котельникова. Однако в целом ряде
случаев оно определяется возможностями ППИ и применяемых датчиков
изображений, например, шириной диаграммы направленности антенны РЛС.
В том случае, когда изображение зашумлено и (или) количество пикселов
цифрового изображения меньше необходимого для неискаженной передачи
формы объекта, эффективность распознавания становится функцией коли¬
чества распознаваемых классов. При заданном алфавите классов на качество
принятого при распознавании решения будут влиять информативные для
каждого класса признаки, т.е. такие признаки, которые хорошо выражены
в изображениях одного класса и слабо — в изображениях остальных клас¬
сов. При этом в контурах изображений рассматриваемого алфавита классов
могут присутствовать характерные фрагменты, которые сохраняются даже
при незначительном количестве пикселов, составляющих изображение. Од¬
нако они не могут улучшить результаты распознавания в том случае, когда
они являются общими для изображений всех классов.
Если информативные признаки связаны не с контуром, а с внутренней
структурой изображения, то применение методов контурного анализа ста¬
новится нецелесообразным, т.к. форма изображения при этом не несет до¬
статочной информации для принятия решения о классе изображения. Как
показывают экспериментальные исследования по распознаванию таких
изображений, при условии одинаковой информативности ЭВ, задающих
его контур и внутреннюю структуру, приемлемые для практики резуль¬
таты получаются до тех пор, пока длины контуров внутренних областей
не превышают 30-40% от длины внешнего контура.
Вредное влияние флуктуаций может быть снижено за счет процедур
предварительного накопления изображений одного и того же объекта.
Снижение одного из наиболее опасных помеховых факторов — шума зер¬
нистости в изображениях, получаемых в когерентном свете, достигается
путем усреднения нескольких независимых изображений одного и того
же участка поверхности. Рост эффективности от количества накаплива¬
емых изображений наблюдается при этом до тех пор, пока число накап¬
ливаемых кадров не превысит N & 25 [107]. Улучшение формы сильно
зашумленных контуров, в том числе и шумами квантования, может быть
достигнуто в результате накопления контуров.
Во второй части монографии будут рассмотрены вопросы выделения
границ изображений в реальных сценах со статистически сложными фо¬
нами. Обнаружители границ строятся на основе согласованно-избиратель¬
ных фильтров (СИФ), подробный анализ работы которых проводится
в гл. 6-8. Такие фильтры вырабатывают статистики для принятия ре¬
шений об обнаружении изображений и их границ. СИФ является ква-
зиоптимальным устройством и согласован с сигналом в области средних
и высоких пространственных частот. Следующими вопросами, решение
которых подробно рассматривается в девятой главе, являются структур¬
ный анализ формы изображений и распознавание изображений по их
форме, задаваемой контурами. Десятая и одиннадцатая главы посвяще¬
ны вопросам обработки точечных изображений. Здесь рассмотрены ма¬
тематические модели групповых точечных объектов (ГРТО), вопросы их
обнаружения, локализации и распознавания.
Глава 6
ВЫДЕЛЕНИЕ ГРАНИЦ ИЗОБРАЖЕНИЙ
6.1. Выделение границ как одна из задач сегментации
изображений
Сегментация является одним из способов группировки пикселов
в сцене. Она проводится с целью разбиения сцены на части со сходными
свойствами, например, на области с близкими значениями яркости. В ланд¬
шафтных сценах, характерной особенностью которых является сложный
статистический характер яркости пикселов, сегментация проводится для
разбиения сцены на статистически однородные части. Различным подходам
к сегментации изображений посвящены обстоятельные обзоры [3, 4].
Границам изображений в полутоновой продискретизированной сцене
соответствуют скачки яркости, как положительные, так и отрицательные.
Эти скачки вызваны разницей средних уровней яркости фона и объекта
(рис. 6.1).
Рис. 6.1. Гистограмма яркости (а) и скачки яркости в области границы для изобра¬
жений ярче фона (б), темнее фона (в)
Гистограмма яркости пикселов в этой области носит хорошо выражен¬
ный двугорбый характер. Фронту скачка яркости соответствует наимень¬
шее по сравнению с фоном и изображением объекта число пикселов, что
и приводит к провалу в центре графика гистограммы. Гистограммы ярко¬
стей, построенные в областях фона или в областях изображения объекта,
не имеют таких хорошо выраженных максимумов. Поэтому ориентируясь
на наличие провала в центральной части гистограммы яркостей или же на
скачок яркости в пределах небольшого участка сцены, можно все пикселы
этого участка разделить на три подмножества: фон, изображение объек-
6.1. Выделение границ как одна из задач сегментации
225
та, граница фон/изображение. При таком подходе выделение граничных
точек можно рассматривать как один из видов сегментации сцены.
Решение задачи выделения границы изображения объекта состоит из
последовательности операций, основными из которых являются (рис. 6.2):
сканирование сцены, обнаружение контура изображения и прослежива-
Рис. 6.2. Структура процесса сегментации границы изображения объекта
ние линии контура в условиях воздействия фоновых шумов, формирова¬
ние кода контура и предварительная обработка контура. Коды контуров
хранятся в ОЗУ контуров ППИ.
В процессе сканирования сцены F с функцией яркости / (ж, у) про¬
исходит перебор по определенному закону ее пикселей. Если только те¬
кущий пиксель не был отнесен к ранее обнаруженному изображению,
то решается задача обнаружения начальной точки а.о контура нового
изображения. Сцена F содержит изображения фона g(x,y) и объекта
s (ж, у), а также флуктуационный шум п (ж, у). Изображение s (ж, у) име¬
ет подмножество точек у (ж,?/), относящихся к границе Г = {7 (х,у)}
объект/фон. Граница Г изображения
s (ж, у) характеризуется двумерным
скачком (перепадом) с функцией яр¬
кости 7 (ж, у) (рис. 6.3).
Пространственные положения то¬
чек границы Г сильно коррелирован¬
ны. Граница реального изображения,
как уже отмечалось ранее, предста¬
вляет непрерывную замкнутую одно-
витковую кривую. Каждая граничная
точка имеет в качестве соседей две
других граничных точки. Поэтому информация о положении в сцене
F хотя бы одной граничной точки, получаемая в процессе операции
обнаружения границы, в значительной степени облегчает нахождение ее
остальных точек, особенно если форма изображения априорно известна.
Часто переход фон/объект происходит на интервале нескольких пик¬
селов и поэтому скачок яркости характеризуется крутым фронтом. Ино¬
гда из-за ухудшения освещенности в пограничной части объекта этот
скачок становится пологим. В ряде случаев в области границы могут
Рис. 6.3. Двумерная модель границы
изображения [ИЗ]
226
Гл. 6. Выделение границ изображений
находиться представляющие интерес отдельные точечные объекты. То¬
гда разрешение границы должно быть достаточно высоким, что приводит
к увеличению протяженности скачка.
Утверждается [114, 21], что для решения задач обнаружения изобра¬
жений функция яркости / (х, у) имеет более сложный вид, чем его задает
аддитивная модель сигнала и шума
f (х,у) = s(x,y)+п(х,у), (6.1.1)
используемая при обнаружении сигналов на фоне белого шума. В качестве
такой, более адекватной модели в работе [21] используется аддитивно¬
мультипликативная модель, имеющая с точностью до параметров смеще¬
ния изображения s (х, у) вид
/ (ж, у) = go + S (х, y)+g (х, у) п (х, у), (6.1.2)
где go — постоянная составляющая яркости, обеспечивающая неотрица¬
тельность функции / (ж, у). В ландшафтных сценах эта модель описывает
локально однородное поле случайных значений яркости. Статистическая
неоднородность вызвана медленно меняющейся детерминированной со¬
ставляющей. Поэтому при обработке таких сцен сегментация производит¬
ся с целью формирования локально однородной в статистическом плане
областей («лес», «поле», «водоем» и др.)
Функция s(x,y), х,у £ Fs, изображения объекта, как и функция
g (х, у) фона, является детерминированной функцией или реализацией
случайного поля. Эти функции всегда имеют различные первые моменты,
т.е. разные средние яркости. Поэтому переход от одной функции к другой,
т.е. от фона к объекту или от объекта к фону, всегда сопровождается
скачком яркости, расположенным в области границы фон/объект.
Несмотря на разнообразие законов распределения вероятностей зна¬
чений фонового шума, их одномерные АКФ в сценах природных аэро¬
ландшафтов, вещательного телевидения и некоторых других классов
в пределах локально однородной области хорошо аппроксимируются
экспоненциально-косинусной функцией вида [116, 118]
R (О = σΒΧ ехР {-<*/£} cos βξ, (6.1.3)
где σ%χ — дисперсия фонового шума, а — декремент затухания непери¬
одической, а β — круговая частота периодической составляющей АКФ.
В рамках аддитивной модели (6.1.1) решение об обнаружении изобра¬
жения объекта принимается путем сравнения с порогом значения стати¬
стики, формируемой оптимальным фильтром с частотным коэффициен¬
том передачи (ЧКП) [21]:
Я {ωχ,ωυ) = С_S ехр{uxXQ + ШуУо)}, (6.1.4)
|ЛГ (шх,Шу)\
где Η(ωχ,ων) — преобразование Фурье от ИХ λ (х,у) фильтра,
S* (ωχ,ων) — комплексно сопряженный спектр функции s{x,y),
\Ν (ωχ,ων)\2 — спектральная плотность мощности (энергетический
6.1. Выделение границ как одна из задач сегментации
227
спектр) шума η (ж, у), жо, уо — координаты центра тяжести изобра¬
жения, С — нормирующий множитель.
В случае белого шума |N (ωχ,ωυ)\2 = ДГ0 = const, а сам фильтр стано¬
вится согласованным с сигналом s (ж, у) и формирует на своем выходе сиг¬
нал в виде ВКФ входного и эталонного сигналов. Если же энергетический
спектр фона неравномерен, то оптимальный фильтр (6.1.4) можно пред¬
ставить последовательным соединением двух звеньев: фоноподавляющего
(обеляющего) звена с ЧКП
Ηφη(ωχ,ων) = —— (6.1.5)
\Ν (ωχ,ωυ)\
и согласованного звена с ЧКП
Нс {их,Шу) = - ехр {-г (ωχχ0 + шуу0)}. (6.1.6)
1\Q
Фоноподавляющее звено является инверсным фильтром и служит для
выравнивания спектра фона.
Рис. 6.4. Структуры оптимальных обнаружителей изображения объекта на фоне:
а — с равномерным энергетическим спектром, б — с энергетическим спектром
произвольной формы
В рамках аддитивно-мультипликативной модели (6.1.2), несмотря на ее
значительно более сложный, чем у аддитивной модели (6.1.1), вид, ЧКП
оптимального фильтра усложняется незначительно [21]:
Я (ωχ, ωυ) = ^ }ωχ,·-ν1? ехр {-г (ωχχ0 + шуу0)}, (6.1.7)
7νο|σ(ωΙ)ω,,)|
где \G (ωχ,ωυ)\2 — энергетический спектр функции фона g(x,y), х0
и уо — координаты центра изображения объекта. Согласованное звено
оптимального фильтра не изменилось, а ЧКП фоноподавляющего звена
стал равен
Дфп {ωχ 5 ) — тгтг * (6.1.8)
\G(ux,Uy)\
Задача обнаружения начальной точки контура изображения объекта
в рамках модели (6.1.2) ставится аналогично задаче обнаружения само¬
го объекта, только вместо функции яркости всего изображения s (ж, у)
обнаруживается наличие в смеси (6.1.2) функции яркости 7 (ж, у) толь¬
228
Гл. 6. Выделение границ изображений
ко границы Г. Обнаружитель, проводя анализ функции яркости / (ж, у)
сцены F, должен обоснованно выбрать одну из альтернативных гипотез:
гипотеза I —
/ (®, у) = go + 7 (х, у)+g (х, у) ■ п (х, у);
гипотеза II —
/ (я. у) = go + g (χ, у) ■ П (х, у). (6.1.9)
В начале анализа предполагается справедливость второй гипотезы,
т.е. окно фильтра обнаружителя заведомо расположено в области фона.
Фильтр обнаружителя начальной точки контура изображения должен
содержать два звена (без учета фазового звена ехр{—г (ωχχ$ + а^уо)})·
фоноподавляющее и согласованное с формой скачка яркости на границе
фон/объект (рис. 6.5).
Рис. 6.5. Структура обнаружителя начальной точки контура изображения
При анализе статистических характеристик изображений фонов из-за
высокой трудоемкости расчетов, вызванной нестационарностью этих фонов,
пользуются характеристиками, найденными на основе одномерного сигнала,
например, отсчетами яркости вдоль строки или столбца сцены. Полученные
при этом результаты целиком переносятся на изотропные двумерные поля.
Результаты ряда работ по фильтрации анизотропных фонов фильтрами,
синтезированными для изотропных фонов, показывают, что для представля¬
ющих интерес размеров окон этих фильтров наблюдается незначительное
уменьшение выходного соотношения сигнал/фоновый шум [21, 108, 117].
Поэтому качественные результаты фильтрации сцен со сложным, стати¬
стически неоднородным фоном, могут быть получены при использовании
одномерных фильтров с соответствующим образом ограниченной апертурой.
В соответствии со структурой процесса сегментации границы изобра¬
жения, представленной на рис. 6.2, после обнаружения начальной точки
контура следует операция прослеживания контура. Данная операция пред¬
назначена для определения непрерывной последовательности относящихся
к контуру изображения пикселов. Она обычно совмещается с кодировани¬
ем выделенных контурных точек. В дальнейшем код контура используется
для решения разнообразных задач, связанных с извлечением содержащейся
в нем информации о форме изображения объекта. Над сформированным
контурным сигналом проводится ряд предварительных операций, связаннык
с уменьшением контурных шумов, например, с помощью ФСС, установлени¬
ем стандартной размерности контура на основании процедуры эквализации
(см. п. 9.1.1), выделением главного контурного примитива (см. п. 3.6.4) и др.
6.2. Согласованно-избирательная фильтрация изображений
229
6.2. Согласованно-избирательная фильтрация изображений
(пространственный аспект)
6.2.1. Принцип согласованно-избирательной фильтрации изображе¬
ний, Корректно поставленная задача обнаружения сигнала в условиях
априорной неопределенности его появления требует, как следует из вы¬
ражения (6.1.4), информацию об энергетическом спектре фонового шума
|G(u;)|2, спектральной плотности N0 широкополосного флуктуационного
шума и спектре S (ω) обнаруживаемого сигнала.
Использование оптимальных фильтров для обработки реальных сцен
затруднено, главным образом, сложностью законов распределения вероят¬
ностей фоновых шумов и их нестационарностью. Удачным моментом при
обработке различных ландшафтных сцен, рентгенограмм, ряда классов те¬
левизионных изображений является одинаковый характер поведения АКФ
и, следовательно, энергетических спектров фоновых шумов. Эти АКФ с точ¬
ностью до параметров хорошо аппроксимируются экспоненциально-косинус¬
ной функцией (6.1.3), а энергетические спектры фоновых шумов в области
средних и высоких частот — квадратичной гиперболой [21, 111, 116]
К?Н|2«^· (6-2.D
ω
Пространственный энергетический спектр фонового шума представля¬
ется в виде
|G(u
a-cpttcp
2 , 2 ’
их -Ь Шу
(6.2.2)
где σ^ρ и аср — соответственно дисперсия и декремент затухания АКФ
фона, полученные усреднением по всем направлениям в локальной обла¬
сти сцены, в каждой из которых одномерная спектральная плотность
описывается выражением (6.2.1).
Как отмечается в работах [21, 30,115], низкие пространственные часто¬
ты в изображениях несут избыточную информацию и даже оказывают ме¬
шающее воздействие при распознавании. Поэтому при синтезе алгоритма
обработки надо в наибольшей степени учитывать свойства спектра в обла¬
сти средних и высоких частот. Фильтр, построенный с учетом представ¬
лений (6.2.1) или (6.2.2), учитывает эту особенность. Но при этом он теряет
свойство оптимальности и становится квазиоптимальным. Он согласован
с поведением энергетического спектра фона только в области средних
и высоких пространственных частот. Такой фильтр назван согласованно¬
избирательным (СИФ) [21]. Используя (6.1.8) и (6.2.2), запишем выражение
для ЧКП фоноподавляющего звена СИФ в виде
Ηφη(ωχ,ωυ) = (6.2.3)
tfcpttcp
Обозначим
С
230
Гл. 6. Выделение границ изображений
Тогда, подставив (6.2.2) в (6.1.8), можно записать следующее выраже¬
ние для ЧКП СИФ:
Η{ωχ,ωυ) &MS* (ωχ,ων) (ω% + ω%) exp {-г (ωχχ0 + шуу0)}. (6.2.5)
Основное отличие СИФ от оптимальных фильтров заключается в том,
что для определения его структуры нет необходимости в априорной ин¬
формации о конкретных изображениях окружающего объект фона. Физи¬
ческий смысл данного вида обработки можно пояснить при рассмотрении
ИХ Л (ж, у) фильтра, получаемой в результате обратного преобразова¬
ния Фурье от Η (ωχ,ων). Для пространственного согласованного фильтра
с ЧКП (6.1.6) результат такого обратного преобразования Фурье имеет вид
Л (ж, у) = Cs (ж0 -х,Уо~у),
т.е. ИХ повторяет форму сигнала s(x,y), но со смещением на (ж0>2/о)
и при противоположных знаках для ж и у. Как следует из (6.2.5), ЧКП
СИФ с точностью до константы отличается от ЧКП согласованного филь¬
тра наличием сомножителя + шу), зависящего от суммы квадратов
пространсвенных частот. При обратном преобразовании Фурье такой со¬
множитель приводит к результату
Л (х, у) = -MV2s (х0 - х, уо - у), (6.2.6)
где
^8{ ) = £Щу)
V ' дх2 ду2
Оператор Лапласа V2s(x,y) носит дифференциальный характер
и применительно к значениям яркости пикселов сцены будет подчер¬
кивать перепады яркости. Таким образом, ИХ СИФ представляет собой
смещенное на (яо>2/о) контурное изображение эталонного обнаруживае¬
мого объекта с обратным порядком следования отсчетов. Здесь имеются
в виду не только внешний контур, но и внутренние контуры изображения.
Рис. 6.6. Структура согласованно-избирательного фильтра
Параметры (хо,Уо) смещения результата фильтрации обеспечивают на¬
копление всех отсчетов фильтра, пока его ИХ взаимодействует со всеми
пикселами изображения. Отсчет СИФ при обработке сцены F на основа¬
нии полученного выражения для его ИХ равен
Жщах Ушах
т7(£;£) =-м2 X) f{i-x^-y)V2s{x0-x,y0-y), (6.2.7)
Ж = Жт|п У = Ут\п
6.2. Согласованно-избирательная фильтрация изображений
231
или
жтах Ушах
η{ί\β) = ~Μ 53 53 / 2/) V2S -χο + χ,β-уо + у)· (6.2.8)
Ж=Жтгп У—Ут'т
Таким образом, реализация СИФ сводится к вычислению степени схо¬
жести анализируемой сцены F с контуром обнаруживаемого объекта
(рис. б.б).
6.2.2. Сравнение свойств согласованного и согласованно-избиратель¬
ного фильтров. Наиболее часто применяемой моделью зашумленного
сигнала является аддитивная модель
/ (ж, у) = s (ж, у) + п (ж, у), f(t)=s (f) + η (ί), (6.2.9)
причем п(х,у), n(t) — нормально-распределенный белый шум. Опти¬
мальный обнаружитель сигнала при использовании данной модели со¬
держит в качестве вычислителя достаточной статистики согласованный
фильтр с ЧКП
Η (ω) = ^ — ехр {ίωίο}, (6.2.10)
No
где S (ω) — спектр сигнала s (t), No — спектральная плотность мощно¬
сти белого шума, to — момент времени, в который формируется отсчет,
равный энергии сигнала s (t). Вопросы, связанные с работой таких филь¬
тров, достаточно подробно рассмотрены в ряде работ, в частности [55].
При обработке ландшафтных сцен более адекватной является аддитивно¬
мультипликативная модель (6.1.2) зашумленного сигнала и, как следует
из п. 6.2.2, для формирования статистики, по которой принимается реше¬
ние об обнаружении изображений объекта, целесообразно использовать
не согласованный, а согласованно-избирательный фильтр. В связи с этим
рассмотрим вопрос о связи отсчетов согласованного фильтра и СИФ.
В одномерном случае фильтр при подаче на его вход согласованного
с ним сигнала s (t) формирует на своем выходе сигнал в виде смещенной
АКФ данного сигнала:
tmax
Усф(т)=С | s(t)s(t + r-t0)dt, (6.2.11)
imin
а СИФ — сигнал в виде ВКФ сигнала $ (t) со своей второй производной,
т.е.
imax
т?сиф (г) = -С | s (t) s" (t -f т - t0)dt. (6.2.12)
imin
Производные стационарной случайной функции X (ί) имеют следую¬
щие взаимно ковариационные функции [119]
Кхмхм Н = (-1)* K%+q) (г), р, q = 0,1,2,...
(6.2.13)
232
Гл. 6. Выделение границ изображений
1
1
/0 i ^
Согласованно-избирательный »
фильтр ;
Согласованный
д2
; »/0_
1
1
фильтр
д/2
1
1
1
1
1
1
1 _ .
Ь(0
1
1
Рис. 6.7. Функциональная структура согласованно-избирательного фильтра
В частности, взаимно ковариационные функции случайной функ¬
ции X (t) и ее второй производной (р = 0, q = 2) связаны соотношением
К х,х»{т) = К£{т). (6.2.14)
Отсюда следует, что выходной сигнал СИФ с точностью до констан¬
ты и знака равен второй производной выходного сигнала согласованного
фильтра (рис. 6.7):
ηαΐΦ (т) = -η'όφ (т). (6.2.15)
Учитывая, что АКФ сигнала является симметричной функцией, т.е.
К (т) = К (—т), а операция двойного дифференцирования не нарушает
эту симметрию, то отсчеты СИФ при обработке согласованного с ним сиг¬
нала будут также симметрично расположены относительно центрального
отсчета η (то):
7?СИФ (ТО + г) = 77СИФ (т0 - т). (6.2.16)
Центральный отсчет тусиФ (то) СИФ, соответствующий максимально¬
му отсчету т)сиф (то) = т?сф (^о) согласованного фильтра, для широкого
Рис. 6.8. Связь выходного сигнала СИФ с выходным сигналом согласованного
фильтра
6.2. Согласованно-избирательная фильтрация изображений
233
класса АКФ сигнала также является максимальным, т.е.
Чскф (т0) = max 7?Сф (г) . (6.2.17)
Такими АКФ являются функции вида, например, К (т) = ехр {—ат2}.
На рис. 6.8, а показан вид этой функции. После первого дифферен¬
цирования АТ' (то) = 0, но величина производной в окрестности точки т0
имеет большее значение (рис. 6.8, б). Вторая производная К (т) (рис. 6.8, в)
в точке т0 имеет отрицательный экстремум. На рис. 6.8, г показан вид
Рис. 6.9. К формированию выходного сигнала СИФ при входных сигналах s (t)
разной длительности
234
Гл. 6. Выделение границ изображений
выходного сигнала СИФ, представляющий собой симметричную относи¬
тельно точки то функцию с максимумом в этой точке.
Широкий класс сигналов характеризуется показательной АКФ вида
Кх (т) = с · ехр {—а|т|} (6.2.18)
или показательно-косинусной АКФ
Кх (т) = с · ехр {—а|т|} · cos/Зт. (6.2.19)
Эти функции имеют в начале координат угловую точку. В результате
первая производная функции в этой точке характеризуется разрывом,
а вторая — не существует. Но поскольку при цифровой обработке мы
имеем дело с дискретной последовательностью отсчетов АКФ, для кото¬
рой всегда существует вторая разность А2 К (т), то при согласованно¬
избирательной фильтрации сигналов с подобными АКФ центральный от¬
счет СИФ, соответствующий пиковому отсчету согласованного фильтра,
также остается максимальным. Отметим, что в зависимости от правила
получения конечной разности (справа или слева от точки), максимум и вся
выходная последовательность могут быть смещены на один отсчет при
сохранении ее симметричного характера.
Таким образом, выходной сигнал СИФ при обработке незашумленного
согласованного сигнала представляет собой симметричную относительно
центральной точки to функцию с максимальным значением, расположен¬
ным в этой точке. Величина пикового отсчета η (т0) СИФ зависит от
ширины спектра сигнала s (t), для которого он построен. Чем шире этот
спектр, тем уже АКФ К (т) сигнала s(t), тем круче будет проходить
в точке то линия графика первой производной К' (т), тем больше зна¬
чение второй производной К" (т) при т = т0, т.е. тем значительней
величина экстремума в этой точке (рис. 6.9).
При этом также сужается область значащих значений выходного сиг¬
нала фильтра, т.е. растет его избирательность. В пределе, когда филь¬
труемый сигнал по своему виду стремится к ^-функции, мы получаем
максимально возможный по величине центральный отсчет — К" (т)|г=То
при минимальной ширине области его выходных сигналов.
Следует также отметить, что из-за дифференциального характера
работы СИФ величина постоянной составляющей фильтруемого сигнала
не оказывает влияния на уровень его выходного сигнала.
6.2.3. Одномерные СИФ для последовательности цифровых отсче¬
тов яркости. При обработки отдельной строки сцены на вход фильтра
подается одномерная последовательность отсчетов яркости. В процессе
фильтрации непрерывные функции / (ж, у), s (ж, у) и V2s (ж, у) заменя¬
ются их конечно-разностными аналогами. Функцию яркости вдоль строки
изображения обозначим как / (п), входной сигнал — как s (η), выход¬
ной — η (η), а ИХ фильтра — через Λ (η). Оператор Лапласа V2s (ж, у)
в одномерном случае для дискретной функции яркости заменяется опе¬
ратором второй разности A2s (η) функции s (п):
A2s (η) = As (τι) — As (η — 1).
6.2. Согласованно-избирательная фильтрация изображений
235
Так как As (η) = s(n) — s(n — 1), то
Δ2δ (η) = a (η) - 2s (η - 1) + S (η - 2). (6.2.20)
Отсюда
—A2s (η) = 2s (η — 1) — s (η) — s (η — 2). (6.2.21)
С учетом (6.2.21) и (6.2.6) ИХ СИФ для случая фильтрации одномерной
дискретной последовательности отсчетов яркости будет равна
λ (η) = M[2s (щ — η -f- 1) — s (щ — η) — s (щ — η + 2)], (6.2.22)
а дискретные аналоги выражений (6.2.7) и (6.2.8) для выходных сигналов
запишутся как
к-1
η (ш) = / (т ~ rc)[2s (п0 — п + 1) — s (щ — п) — s (щ — п + 2)],
п—О
(6.2.23)
к-1
η (ш) = —М^2 / (п) [2s (т — п0 + п — 1) - s (т — щ + п) —
п=0
—$ (т — по + п — 2)], (6.2.24)
где к — число отсчетов ИХ А(п) (ширина окна СИФ), коэффициент
М определяется выражением (6.2.4). Величина смещения по результата
фильтрации равна количеству значащих отсчетов I фильтруемого сиг¬
нала. Положив для простоты, что момент возникновения фронта скачка
t± = 0, (6.2.25)
получим
По = I. (6.2.26)
Введем понятие стандартного СИФ, как фильтра описываемого выраже¬
ниями (6.2.22)—(6.2.26), но при М = — 1. Для такого фильтра
Ast (п) = 2s (/ — п -h 1) — s (I — п) — s (I — п + 2), п — 0,1,... , к — 1,
(6.2.27)
к — 1
77st {т) = ^2 f (т — n)[2s (I — п + 1) — s (I — п) — s (I — п 4- 2)],
п—О
(6.2.28)
к — 1
% {т) = / (га) [2s (т - I + п - 1) -
п—О
— s(m — l + n) — s(m — 1 + п — 2)]. (6.2.29)
В дальнейшем при отсутствии особой необходимости будем рассма¬
тривать только стандартные СИФ, причем нижний индекс «st» опустим.
Для удобства сравнения между собой фильтров, избирательно-согла¬
сованных с сигналами разной формы и длительности, введем нормировку
236
Гл. 6. Выделение границ изображений
выходных сигналов. Для этого в выражении для выходного сигнала введем
коэффициент, обратный по величине пиковому значению η8ί(ί — 1). Тогда
максимальная выходная реакция СИФ на согласованный с ним сигнал
будет равна единице, т.е.
ηΝ (t-l) = 1, (6.2.30)
где буква N в нижнем индексе указывает на нормировку выходного сигнала.
6.3. Согласованно-избирательная фильтрация одномерного
скачка яркости
6.3.1. Идеализированные скачки яркости. Введем понятие идеали¬
зированного скачка (перепада) яркости {s (rc)}0 t_v Фронт скачка описы¬
вается функцией 5ф (гг). Участок изменения яркости содержит I отсчетов.
Кроме них при задании скачка будем учитывать по одному отсчету s (η),
равных нижнему и верхнему значениям
уровня яркости, т.е. s = 0 и s = 1. Поэто¬
му общее количество t учитываемых от¬
счетов идеализированного скачка, т.е. его
длительность, равна 1 + 2, а длительность
фронта Тф будет на единицу меньше, т.е.
t = l + 2, τφ = *-1 = ί + 1. (6.3.1)
Показанный в качестве примера на
рис. 6.10 идеализированный скачок начи¬
нается при пн = 4 с последнего нулевого
значения яркости и заканчивается в мо¬
мент пв = 7, участок нарастания яркости состоит из I = 2 отсчетов,
равных 0,2 и 0,8. Для этого импульса t = 4, 7ψ = 3.
В дальнейшем при изображении скачка будем полагать, что скачок на¬
чинается не в произвольный момент, а при п = 0. Тогда в аналитическом
виде положительный и отрицательный скачки яркости запишутся как
Рис. 6.10. Идеализированный ска¬
чок яркости
S+ (п)
S- (п)
0 при п — 0, -1, -2, -3,..
< 5ф (п) при п = 1,2,... , Z,
1 при п = / + 1,1 + 2,... ;
1 при п = 0, —1, —2, —3,..
< $Ф (П) при п = 1,2,... ,/,
0 при η = I 4-1,/ + 2,...
(6.3.2)
6.3.2. Импульсная характеристика СИФ. Найдем количество нену¬
левых отсчетов ИХ при фильтрации одномерной функции яркости. Для
образования текущего отсчета ИХ фильтра вдоль строки скользит окно из
трех примыкающих друг к другу элементов с весовыми коэффициентами
6.3. Согласованно-избирательная фильтрация одномерного скачка 237
{-1,2,—1}. Если I = t — 2 — количество элементов, образующих непо¬
средственно скачок яркости, то при скольжении трехэлементного окна будет
образовано t не равных нулю отсчетов. Когда окно полностью находится
на нижнем или на верхнем уровнях яркости отсчеты ИХ из-за дифферен¬
циального характера оператора второй разности будут равны нулю. Таким
образом, число значащих отсчетов ИХ СИФ равно длительности t скачка
Л - {λ (η)}0)1+1 = {λ (0), λ (1),... , λ (0 , А (I + 1)}.
Для случая, приведенного на рис. 6.11, будем иметь
s (п) = {0; 0; 0;... ; 0; 0,1; 0,3; 0,6; 0,85; 1; 1;... ; 1}, t = 6;
λ (η) = 2s (5 — η) — s (4 — η) — s (6 — η), η = 0,1,2,3,4,5;
λ (0) = 2s (5) - s (4) - s (6) = 2 - 0,85 - 1 = 0,15; λ (1) = 0,1;
Λ (2) =0,05; λ (3) = —0,1; λ (4) = -0,1; Λ (5) = -0,1.
Таким образом, Λ = {0,15; 0,1; 0,05; —0,1; —0,1; —0,1}.
4
——■
г
4
(
7
t-
t
ο ————1^—1—————————>
-4 -3 -2 -1 0 1 2 3 4 5 6 7 8 9 η
а
О с
э о
о с
—^ г
' сГ с
■о о
= о 1
о
—
-
J
1
1
1
1
И]
1 1
1 1
■ :
1 1
1 ·
пч.
1 ох
1 J
1 ]
1 1
■l! 2 !■
1 1
в
m 1
2 о ;
0,05
-0,1
η 1
р о
λ
Рис. 6.11. К определению количества учитываемых отсчетов ИХ: а — положи¬
тельный дискретный скачок яркости; б — отсчеты яркости в пределах строки
изображения; в — первое положение окна; г — последнее положение окна; д —
ИХ фильтра
238
Гл. 6. Выделение границ изображений
Аналитическое представление для положительного s+ (п) и отрица¬
тельного s_ (п) скачков яркости связаны между собой соотношениями
(п) = S- (t — ή), (η) = (< — га).
Отсюда следует, что и ИХ Л+ = {Л+ (п)}0 /+1 и Л_ = {Л_ (п)}0 /+1
скачков яркости связаны аналогичными соотношениями
Л_|_ (га) = Л_ (t — га), Л_ (п) = Л_|_ (t — га), (6.3.3)
т.е. ИХ фильтра для одного вида скачка яркости получается изменени¬
ем порядка следования отсчетов ИХ фильтра для другого вида скачка
яркости.
Определим теперь крайние , Л (0) и А(/ + 1), отсчеты ИХ фильтра.
В соответствии с выражением (6.3.2) для положительного скачка яркости
получим
Л (0) = 25 (I + 1) - 5 (I) - 5 (I + 2), Λ(I + 1) = 2в (0) - 5(-1) -s{ 1).
Учитывая, что s (0) = 5 (-1) = 0, а 5(1 + 1) = s (I -+- 2) = 1, будем
иметь
Л (0) = 1 - в (0 , Л (/ + 1) = -5 (1). (6.3.4)
Аналогично, для отрицательного скачка яркости получим
Л_ (0) = -в (0 , λ_ (I + 1) = 1 - 5 (1). (6.3.5)
Покажем, что сумма всех отсчетов ИХ дискретного СИФ для положи¬
тельного скачка яркости равна нулю, т.е.
t-ι ι+ι
Σ>(η) = Σλ(Λ) = 0. (6.3.6)
п=0 п—О
Используя выражение (6.2.27) для ИХ стандартного СИФ:
X (п) = 2s (I — η + 1) — s (I — п) — s (I — п 2) —
= 2s (t — 1 — η) — 5 (t — га) — $ (t — 2 — га), η — 0,1,... , t — 1, (6.3.7)
запишем
ι+ι ι+ι г+i ι+ι
Σ λ (η) =2^ 3(1-η + 1)-γ^β(1-η)-^2 s (I — га ■+· 2).
71=0 η—0 77.—Ο 71=0
Поскольку значения Λ (0) и Λ (I +1) уже найдены и определяются
выражением (6.3.4), остается вычислить сумму:
II II
Л (га) =2^ s (I — η + 1) — ^ s (I — га) — ^2 s (I ~ п + 2). (6.3.8)
71= 1 71=1 η — 1 77, = 1
Отметим, что
I 1+1 I 1-1
УУ s (I - га) = ^ 5 (/ - га + 1), ^2 s(l — п + 2) = У2 s(l — п + 1).
71=1 71=2 71=1 71=0
6.3. Согласованно-избирательная фильтрация одномерного скачка 239
Тогда выражение (6.3.8) примет вид
ι ι i+i 1-1
Л (п) = 2^Р s (I — п -+ 1) — s (I — п 4-1) - У^ s (I — η + 1) =
η=1 η= 1 η=2 η—0
= s(/)-s(0) + s(l)-s(Z + l).
С учетом последнего результата и выражения (6.3.4), получим
ι+ι
У Л (n) =s (/) - s (0) 4- 5 (1) - s (I + 1) + 1 - s (I) — s (1) = 0.
n=0
Докажем теперь, что взвешенная сумма отсчетов ИХ одномерного
СИФ для положительного скачка яркости равна
1+1
53ηλ(η) = -1. (6.3.9)
п=О
Используя (6.3.7), для взвешенной суммы отсчетов ИХ можно записать
1+1 1+1 1+1 1+1
У пЛ (п) = ns (Z — п + 1) — ns (I — п) — ns(l — п + 2) =
п—0 п=0 п=0 п—О
= — (/ 4" 2) s (—1) -+ (/ + 1) s (0) + s (0) + s (—1) — s (/ + 1).
Так как s (-1) = s (0) = 0, a s (/ + 1) = 1, то последнее выражение
равно минус единице. Для отрицательного скачка яркости аналогичная
сумма равна единице.
Таким образом, текущее значение отсчета ИХ дискретного СИФ для
одномерного идеализированного скачка яркости определяется тремя от¬
счетами сигнала s (η) — текущим, предыдущим и последующим. Сумма
всех отсчетов характеристики равна нулю.
6.3.3. Анализ процесса фильтрации. Определим вначале количество
значащих отсчетов СИФ при фильтрации изображения в виде одномер¬
ного скачка яркости (рис. 6.12). ИХ фильтра в соответствии с выражением
(6.3.1) имеет ширину окна (апертуру) t = I + 2. При скольжении окна
фильтра вдоль отсчетов сигнала первый ненулевой выходной отсчет об¬
разуется, когда нулевой элемент окна фильтра совпадает с первым зна¬
чащим отсчетом скачка яркости (рис. 6.12, б,г,б), а последний ненулевой
отсчет фильтра — когда последний, /-ый значащий отсчет фронта скачка
пересечется с последним элементом окна фильтра. Поэтому количество
не равных нулю отсчетов фильтра L будет равно уменьшенной на единицу
сумме значащих отсчетов фронта скачка и окна ИХ фильтра, т.е.
L = Z + I + 2- l = 2i + l. (6.3.10)
Отметим, что независимо от I величина L всегда является нечетной.
Определим с помощью выражений (6.3.7) и (6.3.10) сумму выходных
отсчетов фильтра при обработке идеализированного скачка (6.3.2).
240
Гл. 6. Выделение границ изображений
I о I о 1 о I О I о I о,1| о,з| о,б|о,85| 11 ι I ι I ι I ι ΤΤΊ
6
l-0j|-0,l|-Q>ll0,05l0,l|(M5l
в
|o,if|o,i|o,oi|-o,i|-o,i'|-o,i|
г
о
ос
0,6 0,310,1 0 0 0 0 0 I 0 0 0
1 °
1 ° 1
1
ΓΠΊ
: |о,85|о,б|о,з| o,i| o|o|o|o|o|o|o
1 °
1 ° 1
1
Ml
1 (0,85|0,6 10,3 | 0,11 0 1 0 1 0 1 0 1 0 1 0
10
1 ° 1
1
Ml
ι | i |o,85|0,610,31 ο,ι | о | о | о | о | о
10
10 1
1
Ml
ι I i I i |o,85| о,б| о,з| o,i| о | о | о | о
10
10 1
1 I
1 1 1
i | i | i | i |o,85| о,б| о,з| o,i| о | о | о
10
1° 1
1
h 1
i | i | i | i | i |o,85| о,б| о,з| o,i| о | о
10
10 1
1
Ы
ι 1 ι 1 ι 1 ι 1 ι 1 i |o,85| 0,6| о,з| o,i| о
10
10 1
1
II
ι | ι | ι | ι | ι | ι | i |o,85| о,б| о,з| о,
ι| о
1 ° 1
ί)
10,01510,05510,125|[), 1925| Q,225|o, 192^ 0,12510,055 [ 0,0Ϊ5]
e
ж
Рис. 6.12. К определению количества значащих отсчетов СИФ: а — скачок яр¬
кости; б — отсчеты скачка яркости; в — вторая разность сигнала; г — отсчеты
ИХ; д — положения фильтруемого сигнала; е — отсчеты выходного сигнала; ж —
график выходного сигнала
6.3. Согласованно-избирательная фильтрация одномерного скачка 241
Так как для идеального положительного скачка яркости / (n) = s (п)
и s (га) = 1 при га = I + 1,1 4- 2,21 4- 1, то
2ί+1
^ ^ η (гаг) = Л (0) [/ 4- 1 4- s (1) 4- s (2) 4- ... 4- s (/)] + Λ (1) [I H- s (1) 4-
m=1
4*5 (2) 4-... 4- 5 (l)] 4* · ■ · 4- A(/ 4* 1) [s (1) 4- s (2) 4- · · · 4* s (/)] = [s (1) 4-
l-f-l
4-5 (2) 4*... 4- s (/)] ^ ^ λ (n) 4* (/ 4-1) A (0) 4- /А (1) 4-... 4* A (Z 4-1) ·
n=о
Сумма выходных отсчетов фильтра в общем случае равна
2Z-f 1 2Z-+-1 1+1 21+1
Σ V (т) = Σ Σ f (т - п) Λ (η) = λ (0) Σ / (п) +
тп=1 ш=1 п=0 п=1
21 21-1 I
+ ^ (1) ^2 / (η) + λ (2) ^2 f (п) + ... +X(l + 1) ^2 f (η)·
η=1 77=1 77 = 1
Так как сумма всех отсчетов ИХ равна нулю, а взвешенная сумма
отсчетов ИХ — минус единице, окончательно получим
21+1 1+1 1+1
Σ ‘Ч (то) = (г + 1) X λ (п) _ Σ ηλ = L (6.3.11)
777 = 1 77=0 77=0
Аналогичное соотношение справедливо и при фильтрации идеально¬
го отрицательного скачка яркости. Таким образом, сумма всех отсчетов
СИФ при фильтрации идеализированных скачков яркости равна единице.
Нетрудно также показать, что первый η (1) и последний η (L) = η (21 4* 1)
отсчеты выходного сигнала СИФ при этом равны
η (1) = η Щ = -А (0) λ (I + 1). (6.3.12)
В разделе 6.2 с общих позиций было показано, что выходной сигнал
СИФ равен (с обратным знаком) второй производной выходного сигнала
обычного согласованного фильтра. Кроме того, выходные отсчеты СИФ
образуют симметричную последовательность, а центральный отсчет этой
последовательности является максимальным отсчетом фильтра. Рассмо¬
трим какой вид эти положения принимают для дискретного варианта
СИФ, задаваемого выражением
1+1
η (гаг) = ^ 5 (тта - гг) [25 (Ζ - гг 4* 1) — s (Z — гг) - 5 (Z — га 4* 2)]
77=0
гаг = 1,2,... ,2/4*1.
(6.3.13)
Покажем, что отсчеты СИФ расположены симметрично относительно
центрального отсчета гаг = I 4* 1, т.е. что
η (I 4-1 - г) = η (I 4* 1 4* г), г = 1,2,... , / 4- 1.
242
Гл. 6. Выделение границ изображений
Полагая т = I + 1 — г, найдем r = Z + l — mnZ + l-fr = Z + l + Z-f
+ 1 — т = 21 + 2 - т. Таким образом, необходимо показать, что
η (т) = η (21 -f 2 — т) = η (L — т + 1), га = 1, 2,... , L. (6.3.14)
Выражение (6.3.13) представим в виде
1+1 1+1
η (т) = s (т — п) s (I — п + 1) — s (т — п) s (I — п) —
п=0 п=0
Z-f-1
— ^ s(m — п) s(l - п + 2). (6.3.15)
п=0
Обозначим Z -Ы — π = fc, откуда η = I +1 — А;. Если п = 0, то к = I -f1,
если η = Ζ + 1, τοΛ; = Ζ + 1 — l — 1 =0. Тогда выражение (6.3.15) запишется
как
1 + 1 ι
η (то) = 2^2 s (m -f к — I — 1) s (k) — s (m -f к — /) s (к) —
k=0 k=—1
1+2 l+l
— 5 (m + A: — l -f 2) 5 (Α;) = 2^^ s (m + A: — l — 1) s (k) —
k=1 k=0
i+1 J+l
- ^ s (ra + A; - l - 1) s (fc - 1) - ^ 5 (ra + /с - l - 1) s (k -f 1).
k=0 fc=0
(6.3.16)
Определим вид последнего выражения при т = 21 + 2 - га:
Η-ι г+ι
η (21 -f 2 - m) = 2^ 5 (Z + 1 + Λ; - ra) s (к) - ^ s (Z + 1 + A; - ra) x
k=о k=о
i+l
χ«(*-ΐ)-Σ 5 (/ -f-1 ~b A: — τη) s (& -f-1). (6.3.17)
k=0
Обозначим p = ra — Z — 1. Тогда выражения (6.3.16) и (6.3.17) примут
следующий вид:
1+1 1+1 1+1
η (га) = 2^ s(A; -f р) s(k) — ^ s(A: + р) s(A; — 1) — ^ s(A; -f р) s(A: -f 1).
/с=0 /с=0 fc=0
(6.3.18)
И-ι г+ι
η (21 + 2 - m) = 2^Р s (к — р) s (к) - ^ 5 (А: - р) s (к - 1) -
к=о fc=0
Z+1
— ^ 5 (А: — р) s (к + 1). (6.3.19)
к=О
6.3. Согласованно-избирательная фильтрация одномерного скачка 243
Каждое из этих выражений есть сумма трех АКФ входного сигна¬
ла s(n). Так как АКФ К (р) есть симметричная функция, то
η (га) = η (21 -f 2 — га), га = 1,2,... , L. (6.3.20)
При этом максимальный отсчет СИФ, являющийся центральным от¬
счетом выходной последовательности, равен
rim ах (т) = η (I + 1) = η (21 + 2 - I - 1) =
1+1 ί+1 ί+1
=2jy<*>-E s(k)s{k-l)-J2s (k) s(k + 1). (6.3.21)
k=0 k= 0 k—Q
Для пояснения полученных результатов на рис. 6.13, а представлен
построенный для случая а = 1 график скачка яркости, задаваемого функ¬
цией вида [29]
s(n)
1
1 + exp {—an}
(6.3.22)
а на рис. 6.13, б, в, г — соответственно графики ненормированных корре¬
ляционной функции — К (т), ее первой разности — АК (г)
Щ — П 2 П\ — П2
и второй разности ( —· А2К (r)V взятой с обратным знаком.
\ П\ — П2 /
Функция К (т) определялась в интервале п\ = 10 до n<i — —10.
Корреляционная функция скачка имеет треугольный симметричный
вид с угловой точкой при т = 0. Первая разность содержит массив поло¬
жительных значений и массив отрицательных значений, расположенных
по обе стороны от точки т = 0,5. Оба массива имеют по одинаковому
0,05
1 0.05ΔΑ (г)
illllllll
2 4 6 8 10
-8 -6 -4 -2
-0,05
тптлтпт
0,510-05 А'(т)
б -10 -8 -6 -4 -2 0 2 4 6 8 10τ
0,07^
1
-0.05Δ2 А (г)
0,05
0,03
,8 «У11,
I I . И)
1 -6 -4 -2
-0,03
2468 11
Рис. 6.13. Скачок яркости (а), его корреляционная функция (б), первая разность
(в) и результат согласованно-избирательной фильтрации (г)
244
Гл. 6. Выделение границ изображений
количеству отсчетов. Необходимо отметить, что значение первой разности
в угловой точке т = О незначительно отличается от соседних значений,
что объясняется дискретным способом задания функции.
График второй разности корреляционной функции (отсчеты представ¬
лены с обратным знаком) задает симметричную функцию с единственным
центральным отсчетом, имеющим максимальную величину. Процедура
взятия конечной разности привела к смещению этого отсчета на т = 1 по
сравнению с положением центрального отсчета корреляционной функции.
6.3.4. Согласованно-избирательная фильтрация одномерных идеа¬
лизированных перепадов яркости с простым видом фронтов. Прямо¬
угольный перепад яркости. Изображение s(n) в виде прямоугольного
ι .
'·*(«)
“ 1
Л (и)
1
1 ч(т)
0
1 1 ■>
2 3/1
Ч
1
а -1 <
3
1 ? 3 п б
-1 .
в 0 1
1 2
Рис. 6.14. Фильтрация положительного прямоугольного перепада яркости: а — вид
перепада; б — ИХ фильтра; в — выходной сигнал фильтра
положительного перепада яркости задается в виде (рис. 6.14, а)
β(η) = ί° при п = 0,-1, -2,...,
v ' [1 при п = 1,2,3,...
В данном случае I = 0 и количество значащих отсчетов ИХ СИФ будет
равно t = I + 2 = 2. Используя формулы (6.3.2), (6.3.4) и (6.3.23), а также
учитывая, что
s(l) = s (0) = 0, А (0) = 1 - 5 (0 = 1, А (1) = -5 (1) = -1,
получим общее выражение для ИХ Л = {A (n)}0 i+1 фильтра (рис. 6.14, б)
Λ = {λ(η)}0>1 = {1,-1}. (6.3.24)
Результат фильтрации изображения (6.3.23) фильтром с ИХ (6.3.24)
имеет вид (рис. 6.14, в)
V (™) = f (m ~ η)λ (η) = / Μ - / (m - !) = (π ПРИ т Ζ ]’
^i 1° при πιφί.
(6.3.25)
В случае отрицательного прямоугольного перепада яркости будем
иметь (рис. 6.15)
s(n) = P при » = 0,-1,-2,... ,
[О при п = 1, 2,3,... ,
6.3. Согласованно-избирательная фильтрация одномерного скачка 245
л = {-1,1},
V (т) = / (то - 1) - / (т) -
{■
при 771 = 1,
для остальных т.
Таким образом, при согласованно-избирательной фильтрации идеали¬
зированного скачка яркости с прямоугольной формой фронта образуется
■'1 иМ
в 0 1 2 3 т
Рис. 6.15. Фильтрация отрицательного прямоугольного перепада яркости: а — вид
перепада, б — ИХ фильтра, в — выходной сигнал фильтра
только один отсчет фильтра. Этот отсчет положителен и равен единице.
Линейный перепад яркости. В данном случае эталонное изображение
обнаруживаемого объекта задается в виде (рис. 6.16, а)
s(n)
О при п = 0, —1, —2,... ,
П по?
< γ^ΓΪ ПРИ = М,... ,i,
^ 1 при η = I + 1,1 + 2,...
(6.3.26)
Число отсчетов, образующих фронт с линейно-нарастающим перепадом
яркости, равно I и определяется тангенсом угла наклона фронта, равным
- 0,33
Я(п)
3
0 1 2
п
б
-о,зз.
0,33
ι\ / 0 22 -
■ 0,22
0,11
0,11
а,
0 1
3 4 5 т
Рис. 6.16. Согласованно-избирательная фильтрация положительного дискретного
перепада яркости с линейным фронтом: а — вид перепада, б — ИХ фильтра, в —
результат фильтрации
1/(1 + 1). Число значащих отсчетов ИХ фильтра равно t = I + 2. Определим
в соответствии с выражением (6.3.4) крайние значения отсчетов ИХ:
А(0) = 1-»(!) = Λ(ί + 1) = -»(1) =
Остальные, промежуточные значения ИХ Λ(η),η = 1,2,...,/, равны
нулю.
246
Га. 6. Выделение границ изображений
Таким образом, ИХ фильтра имеет вид (рис. 6.16, б)
А = {λ (η)}0ιΙ+1 = {τ^γ.ο θ’“ΓΤϊ}· (6·3·27)
Результат согласованно-избирательной фильтрации скачка яркости
с линейно-нарастающим фронтом будет равен
l-l· 1
η (т) = / (т - п) Λ (п) = λ (0) / (τη) + Λ (I + 1) / (m - l - 1) =
n=0
= ГТТ[/(т)_/(т-г_1)1’ m = 1,2,... ,L. (6.3.28)
Выходной сигнал фильтра представляет дискретную последователь¬
ность из L = 21 + 1 элементов (рис. 6.16, в). Поскольку положительный
линейный скачок яркости представляет собой монотонно-нарастающую
функцию, то / (га) > / (га — п), п = 1,2,... Поэтому из выражения
(6.3.27) следует, что все отсчеты фильтра будут положительными, т.е.
η (ш) ^ 0, т = 1,2,... , L.
1'
'А")
0,66
0,33
1 \
1_ _ \
-1 0 1 2 3 4 '
0,33'
Л(п)
0
1 2 :
5 п
..-0,33
7/(ш)
ОД 1
0,33
0,22
0,22
ОД 1
JL
в О 1 2 3 4 5 /,?
Рис. 6.17. Согласованная фильтрация отрицательного перепада яркости с линей¬
ным фронтом: а — вид перепада, б — ИХ фильтра, в — вид выходного сигнала
Фильтрация отрицательного перепада яркости с линейным фронтом
иллюстрируется рис. 6.17. ИХ фильтра и результат фильтрации для дан¬
ного перепада имеют вид
Λ = {Λ («)}0]/+1 = { —j"ijrpo> · · ■ (6-3.29)
/-f-1
η (m) = ^ / (m - π) λ (n) = Λ (0) / (m) + Λ (I -f 1) / (m - l - 1) =
n=0
= (m - 1 - !) - f (m)}’ m = l,2,... ,L. (6.3.30)
В районе фронта отрицательный линейный скачок яркости предста¬
вляет собой монотонно-убывающую функцию. Поэтому / (т) < f (т — п),
п = 1,2,..., и в соответствии с выражением (6.3.30) все L отсчетов
фильтра будут положительными, т.е. η (га) ^ 0, т = 1, 2,... , L.
Таким образом, при согласованно-избирательной фильтрации скачка
яркости с линейно-нарастающим или линейно-спадающим фронтом все
6.3. Согласованно-избирательная фильтрация одномерного скачка 247
отсчеты фильтра будут положительными и в сумме равны единице. Это
означает, что каждый отсчет фильтра меньше единицы, т.е. О < η (т) <
< 1, т = 1,2,... , L.
Параболический перепад яркости. Одномерное изображение в виде
положительного скачка яркости с параболическим фронтом имеет вид
(рис. 6.18, а)
s(n) =
0 при п = 0, —1, —2,... ,
2
—-—ό при п = 1,2,... , Ζ,
(Ζ + 1)2 Н
1 при η = Ζ + 1,ί + 2,...
(6.3.31)
Число отсчетов, образующих фронт, равно I, причем текущий s (п)
отличается от предыдущего s (п — 1) на величину 1/(1 -f I)2. Количество
0,3281
0,4375
ΊΓ
Л(п)
ι ;
> ;
3 4
0
i"
_ -0,0625
-0,125 -0,125 -0,125
Рис. 6.18. Согласованно-избирательная
фильтрация положительного дискрет¬
ного одномерного скачка яркости с па¬
раболическим фронтом· а — вид скач¬
ка, б — импульсная характеристика
фильтра, в — результат фильтрации
значащих отсчетов ИХ СИФ равно I + 2, причем крайние отсчеты Л (0)
и Λ (I + 1) равны
λ<°> = ι-!<'>=(7Τΐρι λ(ί+ !) = -*(!) = -<7^.
Общее представление для ИХ СИФ записывается как
л = {λ (n)}0il+1 - + !; -2; -2;... ; -2; 1}. (6.3.32)
248
Гл. 6. Выделение границ изображений
Выражение для выходного сигнала СИФ в данном случае равно
1~\г 1
η (т) = ^ / (т - п) λ (η) = / (m) λ (0) + / (то - 1) λ (1) + ...
η=0
... + / (га - ί) Λ (/) + / (ra - I - 1) Λ (J + 1), m = 1, 2,... , L.
С учетом представления (6.3.32) для ИХ СИФ, последнее выражение
примет вид
ι
η{τπ) =
1
(1 + 1Г
(21 + 1) s (τη) — У] s (m — n) — s (m — l — 1)
’ (6.3.33)
m = 1,2,
Отсчеты яркости в пределах фронта являются монотонно возраста¬
ющими, т.е. / (га) > /(га — η), η = 1,2,... Поэтому при фильтрации
идеального скачка яркости (6.3.28)
ι
(21 + 1) 5 (т) > 5 (га — I - 1) + ^ s (га — n), } (т — п) — s (т — п).
71 = 1
Отсюда следует, что все отсчеты фильтра будут положительными, т.е.
η (т) > 0, га — 1, 2,... , L. На рис. 6.18, б и в представлены графики ИХ
и выходного сигнала СИФ.
6.4. Согласованно-избирательная фильтрация изображений
(частотный аспект)
6.4.1. Частотный коэффициент передачи фильтра. Частотный ко¬
эффициент передачи СИФ Ω = {^(m)}ot_1 определим как результат
обратного ДПФ от ИХ фильтра. Используя в качестве представления ИХ
фильтра выражение (6.3.7), получим
г—ι ^
ι (т) = 2^ s (t — 1 - п) ехр
где
t-1 t—1 2
— s (t — n) exp {~^^Гт7г} “ 5 (£ — 2 — n) exp г^штг| =
71=0 71=0
= 2ωι (га) - ω2 (га) - cj3 (га),
t-i 2
ω\ (га) = ^2 s(t — 1 — n) exp j— г-^гатг j, (6.4.1)
n=0
t-i ^
u>2 (m) = s(t — n) exp
(6.4.2)
6.4. Согласованно-избирательная фильтрация изображений
249
£-i 2
сс?з (га) = ^ s(t — 2 — п) ехр г^тп|.
п=О
Введя переменную Л: = t — 1 — гг, для ωχ (га) получим
(6.4.3)
£-1
ωχ (т) = 5 (к) ехр z^ra (ί — 1 — &)| =
к=0
= ^ 5 (fc) ехр jz^mfcj ехр i^-mt| ехр jz^raj —
к=О
= ехр {*ym}go.t-i Μ. (6·4·4)
ГДе £o£-i(m) — комплексно сопряженный спектр эталонного сигнала
{s (fc)}0 t_i, по которому синтезировалась ИХ СИФ.
Аналогично, вводя переменную к = t — 1 — п для ω2 (га), будем иметь
t
Ш2 (τη) = ^ 5 (к) ехр i-j-m (t — fc) j =
k=1
= s (&) exP exP ^7rm}·
k=0
Пределы суммирования здесь по сравнению с (6.4.2) изменились. Что¬
бы сохранить пределы суммирования {Ο,ί — 1}, добавим и вычтем край¬
ние члены этих сумм:
t
ω2 (га) = ^2,s (&) ехР |z^mfc j + s (0) ~ s (0) + s (t) exp |z^m£ j —
1
£-1
— 5 (t) exp jz^ra£ j = ^ 5 (fc) exp |z^rafc j — 5 (0) -f s (£) =
k—0
= So,t—i (m) -s(0) + s (t). (6.4.5)
Для α>3 (m) с помощью аналогичного приема получаем
ω3 (т) = ехр (г t_x (т) + s (-1) ехр j-iymj -
— s (f — 1) ехр (—г^т). (6.4.6)
Теперь с помощью выражений (6.4.4)-(6.4.6) для ωχ (га), ω2 (га)
и о;з (т) запишем формулу для ЧКП СИФ:
ω (га) = go,t_i (т) [^2 ехр jz^m j ~ ехР {г~^2га j “ l] + s (0) - s (t) -
— exp jz^ra j[s (—1) — s(t — 1)], m = 0,1,2,... , t — 1. (6.4.7)
250
Гл. 6. Выделение границ изображений
Если СИФ предназначен для идеального скачка яркости {5(η)}0 ί_1
произвольной формы, то s (—1) = s (0) = 0 и s (t — 1) = s (t) = 1 и (6.4.7)
примет вид
ω (т) = goyt-i (т) [2ехр “ ехР “ *] +
+ ехр jz^m j ~ 1· (6.4.8)
Получим более компактное, чем (6.4.7), выражение для ЧКП СИФ.
Для этого представим входящие в состав для выражения ЧКП слагаемые
Сс?2 (ш) и сс?з (ш) в следующем виде:
t
(га) = s (к) ехр | =
к—1 £
= ехр |г^га j * 5 (Л) ехр |г^га (А: — 1)|.
к=1
Последняя сумма равна комплексно сопряженному спектру смещен¬
ного входного сигнала {s (n)}0t_v Поэтому
0J2 (га) = ехр · g£t (т), га — 0,1,... , t — 1.
Аналогично,
о;3 (т) = ехр |г^—2га| ^ 5 (А:) ехр |г^тА:| =
fc=-l
= ехр |г~^2га| ехр г^т ехР ^)}·
Последняя сумма в данном выражении равна комплексно сопря¬
женному спектру glift-2 (ш) смещенной входной последовательности
Μ*)}_μ_2· Тогда
о;3 (га) = ехр {г ^rajg* м_2 (m), m = 0,1,... , t - 1.
В результате для ЧКП СИФ получим
ω (га) = ωχ (т) + ω2 (га) -f о;3 (m) =
= exp {* [2go,t-i (TO) - gi,t (m) ~ g-\,t-2 M] · (6·4·9)
Выражение в квадратных скобках можно рассматривать как разность
второго порядка A2go,t_i (га) для комплексно сопряженного спектра эта¬
лонного сигнала {s (n)}0 t_v Тогда
ω (т) = ехр |i^m|A2gQ>i_1 (га), га = 0,1,... , t - 1. (6.4.10)
6,4. Согласованно-избирательная фильтрация изображений
251
Учитывая выражение для ЧКП обычных согласованных фильтров [26],
из (6.4.10) следует, что СИФ согласован с сигналом в виде разности второго
порядка эталонного сигнала {5 (n)}0 t_1. Известное выражение для ЧКП
согласованного фильтра с точностью до коэффициента С имеет вид
ω (га) = S* (га) ехр z'^raiо}·
Так как это выражение отличается по виду от полученного выражения
(6.4.10) для ЧКП, покажем, что они идентичны по содержанию. Подставим
в это выражение to = t — 1. Тогда
ω (га) = S* (га) ехр i-γπι (t — 1) | =
= S* (га) exp exp i~j~m (—1)| = 5* (ra) exp |г^-га|.
Полученный результат совпадает с (6.4.10).
6.4.2. Механизм работы СИФ при формировании сигнального от¬
клика. Используя (6.4.8), запишем выражение выходного сигнала СИФ
для произвольного идеализированного импульса яркости {5 (n)}0 t_x:
г-ι
V (η) = - Σ go,t-i (т) ω (то) ехр jiy топ) =
ттг=0
= ^Σ go,t-i (m)g-o.t-i (т) ■ (2ехр|гуто| - ехр |г^2то) - l) х
т=0
г-1
Х <*Р^ТтП} = 7 Σ ISo,t-i (то)|2ехр|г^то(п + 1)) -
т=О
- j Σ ISo.t-i(TO)|2exP {г^топ}- j |g0ii_i(TO)|2exp |гуто(п + 2)].
m—0 m=О
В момент п = щ = t — 1 будем иметь
г-ι г-ι
К* - !) = 7Σ Ιδο,ΐ—1 Ml2 - |go,t—1 (то)|2ехр|-гуто| -
τη—0 m=О
г-ι
- 7 Σ ISo,t-i (τη)I2 exp {ίγτη} =
m=0
1i_1
= 2E0,t-i - ^Σ go,t-i (TO) -go,t-1 (то)ехр{-гут) -
m=0
1i_1
“ 7 Σ S'0·4-1 (m)So,t-i (τη) · exp (ίγΓη), (6.4.11)
252
Гл. 6. Выделение границ изображений
где Εο,ί-ι — энергия сигнала {5 (^)}0,t-i· Вторая и третья сумма здесь
равны соответственно скалярным произведениям сигнала {s (п)}0 ь_г на
сдвинутые вправо и влево на один отсчет копии {5 (n)}x t и {s (n)}_1t_2.
Тогда
Ή (t — 1) = 2E0,t_l — ($о,г_1, «l,t) — (5o,t-l, 5_ΐ}ί_2) =
= 2 · [Eo}t_i — (^ο,ί—1 j 5i,t)]·
Полученные выражения (6.4.8) и (6.4.9) позволяют представить работу
СИФ как суммарный результат работы трех линейных звеньев (рис. 6.19).
Рис. 6.19. Структура СИФ
На входы этих звеньев подается один и тот же скачок яркости {5 (п)}0 t_v
Первое звено имеет ЧКП ωχ (m), согласованное с этим скачком, т.е.
ωι (т) = ехр то} ■ g£)t_x (то).
Второе звено имеет ЧКП вида
ω2 (то) = ехр · gi,t (т) >
согласовано со сдвинутой на один отсчет вправо входной последователь¬
ностью {5(n)}ot_1, т.е. с последовательностью {s(n)}lt. Третье звено
имеет ЧКП вида
ω3 (то) = ехр {г ^то| · glм_2 (то),
согласовано со сдвинутой на один отсчет влево входной последователь¬
ностью {s (тг)}0 т.е. с последовательностью {s(n)}_lt_2. При фор¬
мировании отсчета η (t — 1) первое звено компенсирует фазовые сдвиги
гармоник входного сигнала и формирует выходной сигнал в виде суммы
энергий каждой гармоники, т.е. в виде энергии сигнала {5 (п)}0 t_v Второе
и третье звенья в момент п = t—1 оказываются несогласованными с вход¬
ным сигналом и формируют отсчеты АКФ входного сигнала для случая
задержки на один интервал времени. Далее все три отсчета складываются
с весами 2, —1 и —1.
6А. Согласованно-избирательная фильтрация изображений
253
Рассмотрим фазовые соотношения для выходного сигнала при согла¬
сованно-избирательной фильтрации в момент п = t — 1. Все гармоники
сигнала на выходе согласованного звена в этот момент имеют одинаковый,
равный нулю, аргумент, а на выходе остальных звеньев такое положение
уже не имеет места. Однако сумма выходных сигналов этих звеньев,
равцая
£-1
γΣ (то)|2ехр{-гутп| +
m=О
£-1 £-1
+ ί Σ lsb.i-ι (то)|2ехр|г^тп| = |Σ lso,i-i (to)|2cos утоп,
m=0 m=0
является суммой действительных чисел. Таким образом, второе и третье
звенья, так же как и первое, формируют в момент времени п = t—1 сигна¬
лы, все гармоники которых имеют одинаковые аргументы, т.е. одинаковые
фазы. Такая же картина имеет место в обычном согласованном филь¬
тре. Однако при образовании результирующего отсчета из удвоенного
Рис. 6.20. Векторная диаграмма выходных сигналов звеньев СИФ в момент п =
= t- 1
выходного сигнала первого звена вычитаются выходные сигналы второго
и третьего звеньев, т.е. гармоники выходных сигналов этих звеньев имеют
в результирующем сигнале фазовый сдвиг, равный π (рис. 6.20).
Таким образом, в отличие от согласованной фильтрации, при согласо¬
ванно-избирательной фильтрации в момент образования максимального
выходного сигнала одна часть гармоник имеет фазу, противоположную
фазе другой части гармоник, что является следствием дифференциаль¬
ного характера работы СИФ.
Целесообразность согласования ЧКП фильтра со спектром изображе¬
ния именно в области средних и высоких частот поясняется на рис. 6.21.
На рис. 6.21, а и б показаны соответственно энергетические спектры
фонового шума и изображения объекта в ландшафтной сцене. Сравнивая
графики спектров, можно отметить много общих черт: значительные по
мощности нулевая и низкочастотные составляющие и очень малые по
своим значениям средне- и высокочастотные составляющие. Если учесть,
что график на рис. 6.21, а характеризует помеху, а график на рис. 6.21, б —
254
Гл. 6. Выделение границ изображений
полезный сигнал в виде сплошного изображения, то становится ясным,
что из-за практически полного перекрытия спектров проблема выделения
такого сигнала является сложной.
На рис. 6.21, в показан график энергетического спектра контура изо¬
бражения, соответствующего сплошному объекту, для которого был по¬
строен спектр на рис. 6.21, б. Хорошо видно, что в средне- и высокоча¬
стотной областях спектра появились достаточно мощные составляющие,
причем именно там, где спектральная плотность фонового шума практи¬
чески близка к нулю. В результате выходные отсчеты СИФ, амплитудно-
частотная характеристика которого прозрачна в области средних и вы¬
соких частот и непрозрачна в области нулевой и низких частот, будут
формироваться в значительной степени отсчетами полезного сигнала.
6.4.3. ЧКП СИФ для прямоугольного и линейного скачков яркости.
В предыдущем разделе были получены выражения для ИХ фильтров, из¬
бирательно согласованных с прямоугольным, линейным и параболическим
скачками яркости. Основываясь на этих выражениях, определим ЧКП
этих фильтров в виде прямого ДПФ от ИХ, т.е.
t-i
и;(га) = ^2 Мп) exp {—г—тп}, т = 0,1,... , t — 1. (6.4.12)
п=О
ИХ СИФ для двух первых видов скачков имеют всего лишь две нену¬
левые компоненты. Поэтому ЧКП СИФ таких скачков будет определяться
суммой двух экспонент:
ω(τη) = λ(ηι) exp{-i^mni} + λ(η2) ехр{-г^7?т2},
где τΐι и τΐ2 — номера ненулевых компонент ИХ. Отсчеты ИХ начинаются
6А. Согласованно-избирательная фильтрация изображений
255
с момента п = 0, а их количество равно t. Поэтому ηχ = 0, η 2 = £ — 1 = Тф.
Тогда
а;(т) = Л(0) Η-λ(£ — 1) ехр|— — 1)| = Л(0) + λ(£ — 1) ехр|г~^т|.
Отметим, что прямоугольный скачок является частным случаем линей¬
ного скачка с параметрами I = 0 и t = 2. Воспользовавшись выражени-
Таблица 6.1
\т
t\
0
1
2
3
4
5
6
7
8
2
0
2
3
0
0,866
0,866
4
0
0,471
0,666
0,471
5
0
0,294
0,476
0,476
0,294
6
0
0,2
0,346
0,4
0,346
0,2
7
0
0,145
0,261
0,325
0,325
0,261
0,145
8
0
0,109
0,202
0,264
0,286
0,264
0,202
0,109
9
0
0,086
0,161
0,217
0,246
0,246
0,217
0,161
0,086
ем (6.3.27) для отсчетов ИХ фильтра, избирательно согласованного с ли¬
нейным скачком яркости, получим
„ 2π . . 2π
^ , 2тг \ 1 — cos —т 4* г sin — т
(1 - ехр{г—m}J = t-j— 1—, (6.4.13)
m — 0,1,... ,ί — 1.
Для прямоугольного скачка t = 2 и
ω{τη) — 1 — со snm + ismnm. (6.4.14)
С учетом того, что переменная т в этом случае принимает значения
только 0 и 1, будем иметь
о/(0) = 0, о/(1) = 1 + г. (6.4.15)
Определим амплитудно-частотную
характеристику (АЧХ) СИФ как мо¬
дуль ЧКП. Тогда используя (6.4.13),
получим
M">)l = rLTsi»T'». (6.4.16)
т = 0,1,... , t — 1.
В табл. 6.1 приведены отсчеты
АЧХ СИФ для линейного скачка яр¬
кости, найденные по формуле (6.4.16).
На рис. 6.22 показан вид АЧХ СИФ для линейного скачка яркости с t — 8
(I = 6).
0,284
Рис. 6.22. Амплитудно-частотная ха¬
рактеристика СИФ для линейного
скачка яркости длительности t = 8
256
Га. 6. Выделение границ изображений
На основании полученных выражений для АЧХ фильтра можно сде¬
лать следующие выводы.
1. Фильтр не пропускает постоянной составляющей яркости.
2. Огибающая АЧХ представляет собой положительную полуволну
функции sin х.
3. АЧХ фильтра содержит t отсчетов, причем нулевой отсчет |ω(0)| =
= 0 и \ω(πι)\ = \uj(t — га)|.
4. Полоса пропускания Дгао,707 фильтра на уровне 0,707 равна
Amo,707 = 0,5£. (6.4.17)
Величина Д?по,707 прямо пропорциональна длительности скачка.
6.4.4. ЧКП СИФ для параболического скачка яркости. ЧКП филь¬
тра, избирательно согласованного с идеализированным параболическим
скачком яркости, заданного в виде (6.3.31) с учетом выражения (6.3.32)
для его ИХ, будет равен
и; (га) =
2t — 3
(t- l)2
exp
{*тта}
(t-iy
-——exP
(t- i2Z-r
v ' η—I
{-1ттп}·
Последнее слагаемое этого выражения можно представить в ви¬
де суммы (t — 2) членов геометрической прогрессии со знаменателем
ехр | — Тогда
г.2тг\ Г 2π V
ехр < г— > — exp < г—т >
ехр ' - - - ·> }-
ω(πι) =
(t-ir
2t — 3
•{‘Тт}
1 - ехр
Выполнив преобразование, получим
0 при га = 0;
ш(т) = < 2t - 1 +
ехр
\г^т\ (6-4.18)
-—- при т — 1,2,... , t — 1.
^ (*-1Г
Например, ЧКП СИФ для скачка, показанного на рис. 6.18, равен
ω(πι) =
0 при т — 0;
9-fexp|z^raj при т — 1,2,3,4,
или
Ω = {а;(т)}о,4 = {0; 0,58 + 0,06г; 0,51 + 0,04г; 0,51 - 0,04г; 0,58 - 0,06г}.
АЧХ СИФ для параболического скачка, определяемая как модуль
ω(τη), имеет вид
|ω(τη)|
0 при т — 0;
(Г-1? У^ ~ + 2^2t ~ ^cos {тто} +1
k при т — 1,2,... , t - 1.
(6.4.19)
6.4. Согласованно-избирательная фильтрация изображений
257
При значении t ^ 4 без больших потерь в точности АЧХ фильтра
можно найти как
9/ — 1
Мт)1 - -а, т = 1,2,... ,ί - 1. (6.4.20)
(t 1J
6.4.5. Прохождение фоновых шумов через СИФ. Как следует из
выражения (6.3.28), при прохождении через фильтр, избирательно-согла¬
сованный с линейным скачком яркости, происходит вычитание двух от¬
счетов входного сигнала, разнесенных на интервал 7ф = t — 1. Рассмотрим,
каким при этом преобразованиям подвергается фоновый шум.
Как следует из п. 6.1, для широкого класса реальных сцен фоно¬
вый шум представляет собой сильнокоррелированный случайный процесс
с экспоненциально-косинусной АКФ:
R(n) = σ%χ exp{-a|n|} cosβη, η = О, =Ы, ±2,... , ±(t — 1)/2, (6.4.21)
где σΒΧ — дисперсия фонового шума, а — декремент затухания АКФ и β —
частота периодической составляющей АКФ. Дисперсия разности σΒΒΙΧ двух,
разнесенных на интервал τψ = t — 1, отсчетов фонового шума равна [25]
где σ\ и σ\
aLx = σι - 2σϊσ\τχ2 + σ|, (6.4.22)
дисперсии вычитаемых фильтром отсчетов фонового шума,
разнесенных на интервал тф , а гп — коэффициент корреляции этих от¬
счетов. Так как предполагается, что фильтрация производится в пределах
локально однородного участка сцены, то σ\ = σ<ι — σΒΧ. Тогда последнее
выражение принимает вид
olJolx = 2(1 - г12). (6.4.23)
При 7*12 = 1 дисперсия фонового шума равна нулю, а при 7*12 =
= 0, т.е. в случае некоррелированного шума, а%ых = 2σΒΧ. На рис. 6.23
представлены график АКФ (6.1.3)
R(n), R(n)/R(l)
для случая σ£χ = 1, а = β =
= 0,1 и зависимость R(n)/R( 1),
тг = 1,2,... ,12.
Из последней зависимости видно
как уменьшается коэффициент кор¬
реляции отсчетов фонового шума
по мере перехода от фильтра, из¬
бирательно-согласованного с прямо¬
угольным скачком яркости (п = 1)
к фильтру, избирательно-согласо¬
ванному с линейным скачком яр¬
кости с нарастающей длительно¬
стью фронта (71 = 2,3,... 12). По
данной зависимости и с помощью
выражения (6.4.23) можно оценить
рост дисперсии фонового шума на выходе нормированного стандартного
СИФ при увеличении длительности фронта линейного скачка яркости.
Рис. 6.23. АКФ R(n) фонового шума
с параметрами σΒΧ = 1, а = β = 0,1
и зависимость R(n) /R( 1)
258
Гл. 6. Выделение границ изображений
Как видно из графика на рис. 6.24, при выбранных параметрах а —
= β = 0,1 автокорреляционной функции фонового шума минимальная
дисперсия а%ых получается в том случае, когда фильтр избирательно
согласован с прямоугольным скачком яркости.
За счет сильной декорреляции фонового шума СИФ примерно в пять
раз снижает его дисперсию. С увеличением фронта линейного скачка
дисперсия фонового шума на вы¬
ходе монотонно нарастает и при
Тф = 6 она становится равной дис¬
персии этого шума на входе филь-
тра, т.е. <т2ых « σΒ2χ.
Поясним с частотной точки
зрения эффект снижения диспер¬
сии фонового шума на выходе
нормированного стандартного СИФ
по мере уменьшения длительности
фронта скачка яркости. Фоновый
шум, как сильно коррелированный
процесс, характеризуется энергетическим спектром, сосредоточенным
в области нулевой и низших частот (рис. 6.21, а). С ростом частоты энергия
фонового шума падает. В то же время СИФ, как фильтр высоких частот,
имеет коэффициент передачи, увеличивающийся с ростом частоты, причем,
чем меньше длительность фронта τψ = t — 1 скачка яркости, тем больше
завал АЧХ в области низких частот. Поэтому СИФ для прямоугольного
скачка по сравнению с фильтром, избирательно согласованным с линейным
скачком любой длительности, подавляет большую часть энергетического
Рис. 6.24. Зависимость дисперсии вы¬
ходного фонового шума от длительности
фронта скачка яркости для нормирован¬
ного стандартного СИФ
а 0 4 8 12 16 20 24 п
σναх
Рис. 6.25. Фильтрация фонового шума нор¬
мированным стандартным фильтром, из¬
бирательно согласованным с линейным
скачком яркости: а — реализация фоново¬
го шума; б — выходные отсчеты фильтра
для скачков с длительностью фронта τψ =
= 1 и τψ = 6; в — зависимость СКО
шумовых отсчетов на выходе фильтра от
длительности фронта скачка, с которым
избирательно согласован фильтр
6.4. Согласованно-избирательная фильтрация изображений
259
спектра фонового шума. Данная закономерность работы нормированного
стандартного СИФ иллюстрируется на рис. 6.25. Реализация фонового шума
на входе СИФ приведена на рис. 6.25, а, на рис. 6.25, б представлены
отсчеты фильтра, избирательно согласованного с прямоугольным (τψ = 1)
и линейным (τψ = 6) скачком яркости. На рис. 6.25, в показана зависимость
СКО фонового шума на выходе фильтра от длительности фронта линейного
скачка, с которым он избирательно согласован.
При τψ = 1 дисперсия выходного шума в 3,4 раза ниже дисперсии
σ%χ входного шума, при 7ψ = 3 значения обеих дисперсий примерно
одинаковы, а при Тф = 6 величина более, чем в два раза превышает
значение .
6.4.6. Энергетические соотношения при согласованно-избирательной
фильтрации зашумленных скачков яркости. Отношение сигнал/фоновый
шум на входе фильтра определим как
уГЁ
& вх
_1_
0BX
1
0BX
(п)>
п—О
(6.4.24)
где ||s||2 = Σ s2 (η) — квадрат нормы вектора отсчетов яркости в фрон-
п—0
те незашумленного скачка яркости; J3 = ||s|| /(1 + τψ) — удельная энер-
Таблица 6.2
t = Тф + 1
2
3
4
5
6
7
8
9
Ve/a
0,707
0,645
0,623
0,612
0,605
0,598
0,595
0,523
гия отсчетов фронта скачка. В табл. 6.2 приведены значения у/Е для
идеализированных удельных скачков с амплитудой А.
Как и следовало ожидать, величина у/Е с ростом длительности фронта
скачка стабилизируется. Определим отношение сигнал/шум на выходе
фильтра как частное квадрата пикового выходного скачка нормированного
стандартного СИФ в момент п = t —
— 1 и дисперсии фонового шума,
т.е.
<гвых= gg·*?-·-* =4-· (6-4.25)
^вых ^вых
На рис. 6.26 приведены графики
зависимостей входного (кривая 1)
Qbx (τψ) и выходного (кривая 2)
<?вых (τψ) отношения сигнал/шум для
СИФ при условии, что дисперсия
σΒχ (тф) фонового шума на входе
равна единице, а параметры АКФ
Рис. 6.26. Энергетические характери¬
стики процесса согласованно-избира¬
тельной фильтрации идеализирован¬
ного линейного скачка яркости
260
Гл. 6. Выделение границ изображений
фонового шума выбраны равными а = β = 0,1. Значения (τψ)
соответствуют графику на рис. 6.24 при σ%χ = 1. На рис. 6.26
приведена также зависимость (кривая 3) выигрыша г (тф) в отношении
сигнал/фоновый шум при фильтрации линейного скачка яркости, как
функции длительности фронта τψ = t — 1 = 1 +1. Как видно из графика,
этот выигрыш максимален для СИФ, избирательно согласованного
с прямоугольным скачком яркости. Для данного случая он равен
г = 3,08. По мере роста длительности фронта скачка выигрыш
постепенно уменьшается и становится равным г — 1,5 при τψ = 7 и г =
= 1,27 при τψ = 12.
6.5. Характеристики обнаружения границы изображения
при использовании согласованно-избирательной фильтрации
6.5.1. Алгоритм работы обнаружителя. Оптимальный обнаружитель
границы фон/объект в пределах локально однородного участка сцены
в общем случае содержит фоноподавляющее, согласованное и пороговое
звенья (см. п. 6.1). Реальные фоны в ландшафтных сценах в области сред¬
них и высоких пространственных частот характеризуются убывающим по
закону квадратичной параболы энергетическим спектром. Поэтому стати¬
стику для работы обнаружителя целесообразно получать на основе ква-
зиоптимального фильтра, согласованного со спектром фона именно в этих
областях его энергетического спектра, или, что то же самое, с формой
скачка яркости на границе фон/объект (см. п. 6.2). Роль фильтров, вы¬
рабатывающих с учетом этих подходов статистику для обнаружения на¬
чальной точки контура изображения, играют согласованно-избирательные
фильтры, анализ работы которых был проведен в пп. 6.2—6.4.
В момент образования пикового выходного сигнала СИФ выполняет
над входным сигналом операцию (см. п. 6.2.3)
t-ι
η (t -!) = Σ f (n)λ (u) = ttC2 -% (t -1), (6-5.1)
Νοσ°*α
где
£-1
Vst = (n) [2s (n) - s (η - 1) - s (n + 1)]. (6.5.2)
n=0
Для обеспечения заданной надежности принимаемого решения в поль¬
зу гипотезы о наличии на входе СИФ скачка яркости заданной формы
величина η (t — 1) сравнивается с порогом Ло, учитывающим риски оши¬
бочных решений и априорные вероятности наличия и отсутствия этого
скачка: η (t — 1) ^ Л0, или, с учетом (6.5.2),
(t- 1) > ^ΑοΝ0σ^χα. (6.5.3)
Таким образом, обнаружитель границы фон/объект сравнивает с пози¬
ции критерия минимального среднего риска пиковое значение выход¬
6.5. Характеристики обнаружения границы изображения
261
ного сигнала стандартного СИФ с порогом, величина которого прямо
пропорциональна величине Л0, спектральной плотности мощности ши¬
рокополосного шума No, дисперсии σ2χ и декременту затухания АКФ
фонового шума.
При работе с реальными сценами априорные вероятности наличия
и отсутствия в пределах апертуры СИФ скачка яркости на грани¬
це фон/объект чаще всего неизвестны. Поэтому возникает сложность
в определении величины порога Ло и как принято, например, в ра¬
диолокации, в качестве критерия работы обнаружителя выбирается
критерий Неймана-Пирсона [55]. В соответствии с ним обнаружитель
должен обеспечивать максимум вероятности правильного обнаружения
D при заданном уровне вероятности ложной тревоги F. В рассматрива¬
емом случае обнаружения границы фон/объект близкое к максимуму
значение вероятности D достигается за счет применения СИФ и ис¬
пользования величины η (t - 1) в качестве сравниваемой с порогом Θ
статистики. Величину этого порога определяет уровень вероятности
ложной тревоги F. Таким образом, принятие решения об обнаружении
границы фон/объект происходит, если η (t - 1) ^ Θ. С учетом (6.5.2) это
правило принимает вид
?7st 1) ^ Uo,
(6.5.4)
Uo = iΘΝ0σΙχα.
(6.5.5)
Кроме априорных вероятностей обычно также неизвестны спектральная
плотность мощности No входного широкополосного шума, дисперсия σ2χ
и декремент затухания а фонового шума. Последние два параметра, σ2χ
и а, сильно варьируются при переходе из одного локально однородного
участка сцены в другой.
Таким образом, квазиоптимальное обнаружение границы фон/объект
производится по результатам сравнения с порогом Uq пикового выходного
сигнала стандартного СИФ. При этом вопрос выбора величины порога Uo,
обеспечивающего необходимую надежность принимаемого решения, оста¬
ется открытым..
6.5.2. Методика расчета характеристик обнаружения границы. Один
из подходов к определению порогового уровня обнаружения Uq основан на
гипотезе о том, что закон распределения вероятностей отсчетов фонового
шума на выходе СИФ близок к нормальному с нулевым математическим
ожиданием [94, 111].
Нормализации процесса способствует декорреляция входных отсчетов
шума при прохождении через фильтр. Величина дисперсии σ2 опреде¬
ляется значениями Nq, σ2χ и а. Если по выборочным отсчетам СИФ,
взятым в пределах локально однородного участка сцены, получить оценку
этой дисперсии, то появляется возможность определения порогового уров¬
ня U0, гарантирующего непревышение заданного уровня вероятности F
262
Гл. 6. Выделение границ изображений
(рис. 6.27), где
оо
F= Jp(77st)d%. (6.5.6)
Uq
При этом отпадает необходимость нахождения оценок Ν0,σ%χ и а,
определяющих выходной сигнал фильтра. Таким образом, обнаружитель
границы должен состоять из блока оценки дисперсии стандартных выход¬
ных отсчетов фильтра, вычислителя порогового уровня Uq по заданному
значению F и порогового устройства (рис. 6.28).
Несмещенная оценка <7gbIX дисперсии находится
по выборочным отсчетам СИФ в пределах
локально однородного участка:
^ = ^Σ·*ω, (6·5·7)
з=1
где п — число используемых выборочных от¬
счетов яркости.
Вероятность правильного обнаружения D
границы при заданных значениях порогового
уровня Uq и входного отношения сигнал/фоновый шум qBX может быть
найдена при известном законе распределения вероятностей пикового
выходного сигнала СИФ и расположении окна фильтра на этой границе.
В соответствии с принципом суперпозиции для такой линейной системы
О Ι/о η«
Рис. 6.27. К определению
порогового уровня для сиг¬
нала стандартного СИФ
м
Рис. 6.28. Структура обнаружителя границы фон/объект с вычислением текущего
значения порогового уровня
как СИФ это распределение также будет нормальным, с дисперсией σ^,
но с математическим ожиданием, равным выходному сигналу фильтра
Vst (t — 1) при подаче на его вход незашумленного скачка:
РЫ (t -1)] =
V 2πο
exp <
fort (t - 1) - Tfct (t - 1)]'
2σ„
(6.5.8)
6.5. Характеристики обнаружения границы изображения
263
Если фильтр избирательно согласован с прямоугольным скачком яркости
амплитудой А, то % (t - 1) = А и
РЫ (t - 1)] = -/=— exp {-fet(t24}
у27Г(7вых V. ^^вых J
(6.5.9)
В общем случае вероятность правильного обнаружения будет равна
Vst (t - 1) - 77st (ί - 1)]
D
= 1 f ■
\/2πσΒΜχ J
U0
exp < --
2σί
>Afa(t-l). (6.5.10)
Для экспериментального подтверждения полученного таким путем
вероятности D необходимо пиковый незашумленный выходной сигнал
77st (t — 1) располагать в различных местах строки сцены и суммировать его
с фоновыми отсчетами. После сравнения каждого такого суммарного отсчета
с порогом U0 находится доля превышающих порог отсчетов. Отношение
сигнал/фоновый шум на входе СИФ определяется отношением (6.4.23).
Для расчета характеристик обнаружения границы фон/объект можно
использовать следующую методику, основанную на приведенных выше
соображениях.
1. Подготовительный этап.
Формируем в пределах локально однородного участка сцены F строку
отсчетов яркости фоновых шумов (файл strn).
Задаемся видом идеализированного скачка яркости и синтезируем для
него СИФ.
Формируем массив отсчетов стандартного СИФ (файлы spr, spl и др.).
2. Построение зависимости вероятности ложной тревоги F от ве¬
личины порогового уровня Uq.
По формуле (6.5.7) находим оценку дисперсии а%ых отсчетов фоновых
шумов на выходе фильтра. Варьируя пороговый уровень Щ, по формуле
(6.5.6) с учетом нормального характера выходных фоновых шумов строим
зависимость / (Uq).
3. Построение зависимости D = / (qBX) при F = const (эксперимен¬
тально-теоретический подход).
Находим оценку дисперсии σ^χ отсчетов яркости в массиве strn.
Задаемся амплитудой А идеализированного скачка яркости и в соот¬
ветствии с выражением (6.4.23) находим величину отношения сигнал/фо¬
новый шум qBX на входе СИФ.
Определяем реакцию pst (t - 1) стандартного СИФ на незашумленный
скачок яркости. По графику F = f (Uq) для заданного значения F нахо¬
дим соответствующий пороговый уровень. По таблице для нормального
закона распределения вероятностей определяем искомое значение веро¬
ятности D:
п , if Г ™ _ Uo-Vst(t-l)
“"гтг· где 1=—^—
щ
(6.5.11)
264
Гл. 6. Выделение границ изображений
4. Построение зависимости D = f (qBX) при F = const (эксперимен¬
тальный подход).
Суммируем пиковый отсчет η5χ (t — 1) стандартного СИФ с каждым
входным шумовым отсчетом фильтра (массивы spr, spl и др.). Опреде¬
ляем количество w модифицированных таким образом отсчетов массива,
равных или превышающих установленный порог Щ. Находим оценку ве¬
роятности D как значение относительной частоты D* = w/Wy где W —
объем массива выходных отсчетов фильтра.
Теоретический аспект экспериментально-теоретического подхода к
построению характеристик обнаружения базируется на нормальном ха¬
рактере закона распределения вероятностей отсчетов фонового шума на
выходе СИФ, а экспериментальный аспект — на получении оценки дис¬
персии этих отсчетов по конкретной выборке. Экспериментальный подход
не требует никакой информации о законе распределения вероятностей
отсчетов и позволяет оценить степень адекватности экспериментально¬
теоретического подхода методике.
В качестве иллюстрации методики рассмотрим задачу обнаружения
границы фон/объект в области изображения дороги в типовой ландшафт¬
ной сцене «Forest 2», приведенной на рис. 6.29. Необходимо построить
характеристики обнаружения края дороги в пределах одной строки пря¬
моугольного фрагмента ABCD.
Рис. 6.29. Ландшафтная сцена Рис. 6.30. Яркостный портрет строки сцены на
с вертикально ориентирован- рис. 6.29
ным изображением дороги
На рис. 6.30 показано сечение яркости вдоль этой строки. 117 отсчетов
яркости оформлены в виде массива strnl. Используем в качестве модели
скачка яркости на границе фон/объект прямоугольный скачок и сформи¬
руем массив sprl выходных отсчетов СИФ.
По данным массива sprl в соответствии с п. 2 методики получается за¬
висимость вероятности ложной тревоги при обнаружении прямоугольного
скачка от порогового уровня Uq (рис. 6.31). Непрерывная кривая построена
на основании предположения о нормальном законе распределения вы¬
ходных отсчетов sprl значения F. Точками нанесены экспериментально
6.5. Характеристики обнаружения границы изображения
265
Рис. 6.31. Зависимости вероятности ложной тревоги F при обнаружении края до¬
роги от величины порогового уровня Uq
Рис. 6.32. Характеристики обнаружения границы при использовании фильтра, из¬
бирательно согласованного с прямоугольным скачком яркости
полученные по массиву sprl значения F. На рис. 6.32 приведены харак¬
теристики обнаружения.
Судя по ним, эффективность обнаружителя прямоугольного скачка
яркости на фоне сильнокоррелированного шума, построенного на базе
СИФ, не очень сильно отличается от эффективности обнаружителя это¬
го скачка на фоне белого шума, построенного на основе согласованного
фильтра [55]. На рис. 6.33 приведены
для случая F = 0,1 характеристики
обнаружения на базе СИФ линейного
скачка яркости {0; 0,33; 0,66; 1} (кри¬
вая 3). Здесь же для сравнения приве¬
дены графики характеристик обнару¬
жителя на базе СИФ прямоугольного
скачка (кривая 2), а также линейного
скачка яркости фильтром, избиратель¬
но согласованным с прямоугольным
скачком (кривая 1). При одинаковых
уровнях пикового выходного сигнала
фильтров и дисперсии фонового шума,
Рис. 6.33. Характеристики обнару¬
жения при F = 0,1
266
Гл. 6. Выделение границ изображений
первый их этих фильтров имеет большее значение дисперсии фонового
шума на выходе, что привело к более низкой эффективности обнаруже¬
ния. С теоретических позиций это было обосновано в п. 6.4.5. На рис. 6.34
приведены результаты обнаружения уже не идеализированного скачка
F = 0,05 U = 37,3 F = 0,01 U = 53,3
Рис. 6.34. Обнаружение правого края дороги при разных пороговых уровнях с ис¬
пользованием СИФ для прямоугольного скачка яркости
яркости, по которому построены приведенные выше характеристики
обнаружения, а правого края дороги в пределах фрагмента ABCD
сцены «Forest 2». Фильтр обнаружителя был избирательно согласован
с прямоугольным скачком яркости.
Цель эксперимента заключалась в оценке полезности синтезированного
обнаружителя в условиях реальных скачков яркости на границе фон/объект
и значительной неоднородности фона (области I, II и III, рис. 6.30), а также
в нахождении пороговых уровней, при которых ложные тревоги не оказы¬
вают существенного влияния на процесс обнаружения. Как видно из приве¬
денных фотографий, такой пороговый уровень равен Uq = 53,3.
б.б. Обнаружение протяженных прямолинейных границ
267
6.6. Обнаружение протяженных прямолинейных границ
изображений
6.6.1. Квазиоптимальный алгоритм обнаружения и его эффектив¬
ность. Если априорно известна конфигурация линии границы, т.е. име¬
ется информация о форме изображения или о ее фрагментах, то можно
решить задачу квазиоптимального
обнаружения не одной, а множества
ее точек в пределах такого фраг¬
мента. За счет накопления большого
количества точек границы возраста¬
ет отношение сигнал/шум и, как
следствие, достигается значительно
более высокая эффективность обна¬
ружения. Наиболее просто с этих
позиций решается задача обнару¬
жения протяженной прямолинейной
границы (см. рис. 6.29).
Рассмотрим особенности органи¬
зации процесса согласованно-изби¬
рательной фильтрации границы Г
для случая, когда область Г пред¬
ставляет собой вертикально ориентированную прямолинейную полосу
длиной Р, постоянной ширины t с одинаковым в каждом горизонтальном
сечении одномерным скачком яркости j(n) (рис. 6.35), т.е.
j(n,p)=j(n), р = 1,2,...,Р. (6.6.1)
Такая модель дает возможность применить результаты по согласованно¬
избирательной фильтрации для одномерного случая. Выходной сигнал
двумерного СИФ в данном случае получается либо суммированием Р
выходных сигналов одномерных СИФ (рис. 6.36, а), либо накоплением
яркостей Р строк и дальнейшей фильтрацией накопленной строки
20
Р Фон Граница Объект
Р = 20
/ = 5
а -8 -4 0 4 8 12
γ(ή)
PTOJ
А
6-8 -4 0 4 8 12
Рис. 6.35. Двумерная модель фрагмен¬
та сцены с вертикальной прямолиней¬
ной границей (а) и сечение по яркости
в произвольной строке (б)
Рис. 6.36. Структура СИФ для вертикально расположенной прямолинейной
границы изображения объекта
268
Гл. 6. Выделение границ изображений
яркостей (рис. 6.36, б)
р t-1
v(m) = Σ Σ f(n>p)[2v(m
ρ=1η=0
— v(m — t + η + 2)] =
— £ -f- η -f 1)
Σ/(η’Ρ)
-ρ=1
- v(ra — t + η) —
t-1
^[2г/(га — t + η + 1) —
n=0
— v(m — t + n)— v(m — t + n + 2)]. (6.6.2)
Если же угол ψ, под которым проходит прямолинейная граница Г,
не равен π/2, т.е. линия границы не перпендикулярна строкам сцены,
то необходимо получить набор копий фильтруемой сцены F, в каждой
из которых изображения повернуты на небольшой угол θη = па, а =
= π/Д, п = 0,1,... R — 1, R — число копий. В одной из таких копий
ориентация прямолинейной границы будет ближе всего к вертикальной
и выходной сигнал СИФ окажется самым большим. По величине этого
сигнала и принимается решение об обнаружении границы.
Таким образом, квазиоптимальный обнаружитель протяженной пря¬
молинейной границы изображения объекта содержит R одинаковых по
структуре каналов. Сцена в r-м канале повернута на небольшой угол а,
Fo
Канал О
1)
Устройство
гЧ“
Канал 1
1 ^
Экстре¬
поворота
мальное
сцены
Ί^Λ-ι
rjst,R-
устройство
Канал R-l
Пороговое
устройство
tcib
Да
Нет
Вычисление
порогового
уровня
Оценка
дисперсии
фонового
шума
=Г”
Рис. 6.37. Структура многоканального квазиоптимального обнаружителя прямоли¬
нейной границы произвольно ориентированного изображения объекта (а) и струк¬
тура одного из его каналов (б) для сцены с изотропным по мощности фоновым
шумом
б.б. Обнаружение протяженных прямолинейных границ
269
а«5° -10°, относительно сцены в (г - 1)-м канале. В каждом из каналов
производится скользящее суммирование яркостей Р соседних строк, где
Р — длина прямолинейного участка границы.
Накопленная строка яркости обрабатывается фильтром, избирательно
согласованным с формой скачка яркости на границе фон-объект. Резуль¬
таты фильтрации каждого из каналов сравниваются с пороговой величи¬
ной Uo, вычисляемой исходя из заданной вероятности ложной тревоги F.
Если дисперсии фонового шума одинаковы для всех направлений анализа,
то используется одно пороговое устройство, к которому подключается
канал с максимальным выходным сигналом max77st(i — 1). Структура об¬
наружителя приведена на рис. 6.37.
В том случае, когда фоновый шум в пределах сцены характеризу¬
ется значительной анизотропностью, оценка его дисперсии, вычисление
порогового уровня и принятие решения проводятся для каждого канала
в отдельности.
Таким образом, одной из существенных особенностей обнаружения
прямолинейной границы по сравнению с обнаружением только одной точ¬
ки границы, имеющей произвольную ориентацию, является обеспечение
режима синхронного накопле¬
ния яркостей Р смежных строк
и образование одной строки
с суммарной яркостью, отсчеты
которой подаются на вход СИФ.
Как видно из рис. 6.38, прямоли¬
нейному, вертикально располо¬
женному участку границы ML
соответствует крутой скачок яр¬
кости в пикселе по в суммарной
строке сцены.
Повышение отношения сиг-
нал/шум для скачка яркости,
соответствующего вертикально
ориентированной границе, про¬
исходит одновременно с умень¬
шением размаха скачков яр¬
костей от границ всех других
изображений. Это уменьшение
связано с усреднением яркостей
изображений в сцене, происхо¬
дящим в пределах накапливае¬
мых строк. Для сцены «Forest 2» (см. рис. 6.29) на рис. 6.39 приведены
яркостные портреты суммарных строк при различных количествах N
суммируемых строк в пределах прямоугольного фрагмента ABCD.
Сечение по яркости одной строки этого же фрагмента, т.е. для N = 1,
было показано на рис. 6.30. Из анализа сцены и приведенных яркостных
портретов видно, что в пределах обрабатываемого фрагмента имеется
Рис. 6.38. Образование накопленной строки
яркостей: а — исходная сцена, б — график
изменения яркости в наклонной строке
270
Гл. 6. Выделение границ изображений
0 50 100 150 200 250
6000
2000
J . №=40
г 0 50 100 150 200 250
1 J
j N=80
4000
д 0 50 100 150 200 250
Рис. 6.39. Яркостные портреты суммарных строк для сцены «Forest 2» (см. рис. 6.29)
ряд существенных неоднородностей, оказывающих негативное влияние
на процесс обнаружения края дороги. Это вертикально ориентированные,
т.е. расположенные параллельно обнаруживаемому участку границы
изображения нитевидных объектов, яркость которых ниже яркости
фона. Кроме этих неоднородностей имеются еще множество других.
Они вызваны изображениями объектов, не имеющих вертикальной
ориентации. Поэтому при сложении яркостей большого количества строк
эти однородности будут разрушаться, что хорошо видно на яркостных
портретах для N = 80 и N = 100. Следует также отметить, что
процесс образования суммарной яркостной строки способствует лучшей
нормализации отсчетов на выходе СИФ.
На рис. 6.40, а в качестве примера приведены построенные в соответ¬
ствии с методикой (см. п. 6.5.2) характеристики обнаружения прямоли¬
нейной границы при накоплении N = 10 строк. При вероятности ложной
тревоги F = 0,05 вероятность правильного обнаружения D = 0,9 до¬
стигается при входном отношении сигнал/шум двх ^0,6. Как следует из
характеристик обнаружения одной точки границы (N = 1), приведенных
на рис. 6.32, вероятности F = 0,05 и D = 0,9 обеспечиваются при ве¬
личине <7Вх порядка 1. Аналогичные характеристики обнаружения, но при
N = 100, приведены на рис. 6.40, б. В этом случае вероятности F = 0,05
и D = 0,9 обеспечиваются уже при qBX ^0,2.
6.6. Обнаружение протяженных прямолинейных границ
271
D
Рис. 6.40. Характеристики обнаружения прямолинейной границы: а — для N =
= 10; б — для N = 100. Фильтр обнаружителя согласован с прямоугольным
скачком яркости
у *■ ШШЯШЯШШШштсФЖжлт.. **
N = 30 Λ' = 60
Рис. 6.41. Обнаружение правого края дороги в сцене «Forest 2» при различном
количестве суммируемых строк в сцене
272
Гл. 6. Выделение границ изображений
Таким образом, выигрыш в отношении сигнал/шум при обнаружении
границы длиной 100 пикселов по сравнению с обнаружением одной точки
границы по мощности составляет порядка 15 дБ. На рис. 6.41 представ¬
лены результаты обнаружения правого края дороги в сцене «Forest 2»
в условиях различного количества N накопленных строк яркости при
фиксированном пороговом уровне Uo = 18,4, вероятности ложной тревоги
F = 0,2 и СИФ для прямоугольного скачка.
6.6.2. Выбор количества сдвинутых копий исходной сцены при обна¬
ружении прямолинейной границы с произвольной ориентацией. Бели
угол ориентации прямолинейной границы произволен, то как было отмечено
в предыдущем разделе, необходимо иметь набор из Д копий фильтруемой
сцены, каждая из которых повернута относительно соседней на угол θη —
= ηα, а = π/Д, п = 0,1,... , Д — 1. Рассмотрим на примере двумерного
скачка яркости из каких соображений следует выбирать число Д, опреде¬
ляющее количество параллельных каналов в схеме обнаружителя границы.
На рис. 6.42, а представлено произвольное положение прямолинейной
границы Г в пределах сектора с центральным углом а. Биссектриса этого
угла ориентирована вертикально по отношению к линиям строки. Граница
Г отклонена от биссектрисы на угол Αφ. Если Αφ = 0, то при накоплении
строк сцены образуется прямоугольный скачок яркости с Тф = 1.
По мере увеличения угла Αφ амплитуда скачка яркости не изменя¬
ется, но увеличивается длительность τφ его фронта (рис. 6.42, б). Из-за
Рис. 6.42. К выбору количества Д копий сцены при обнаружении прямолинейной
границы Г (Δ<^β > Αφ$ > ... > Δ<^ι)
дифференциального характера механизма работы СИФ это приводит к
уменьшению удельной энергии скачка при сохранении энергии фонового
шума, т.е. к снижению отношения сигнал/фоновый шум.
Предположим, что угол Αφ случаен и распределен равномерно. Отме¬
тим, что отклонение границы Г на углы ±Αφ от биссектрисы приводит к
одинаковому выходному эффекту. Поэтому при анализе влияния откло¬
нения линии границы от вертикали можно ограничиться вдвое меньшим
значением угла а. Отсюда следует, что среднее значение и СКО угла
между границей и биссектрисой равны Αφ = α/4, σ&φ « α/7. Если пря¬
молинейная часть границы имеет длину Р пикселов, то среднее значение
длительности фронта скачка будет равно
тф = Р tg (α/4) + 1 « 0, 25Ρα + 1.
(6.6.3)
6.7. Инвариантные обнаружители границ изображений
273
Пусть известна зависимость выходного отношения двых сигнал/фоновый
шум от длительности скачка яркости и построено семейство характери¬
стик обнаружения при фиксированном значении вероятности ложной тре¬
воги F, но для разных значений τψ (рис. 6.43, а). Если известно отношение
Рис. 6.43. К определению углового шага ао между соседними каналами обнаружи¬
теля
сигнал/фоновый шум, то варьируя значение угла а, можно построить при
данной величине F зависимость вероятности правильного обнаружения D
от а (рис. 6.43, б). Исходя из минимально допустимого значения вероят¬
ности D, заданной вероятности F и известного отношения сигнал/шум на
входе СИФ с помощью графика на рис. 6.43, б можно найти величину ао
шага углового смещения копий сцены или количество этих копий R.
6.7. Инвариантные к характеристикам сцены обнаружители
границ изображений
Рассмотрим задачу обнаружения границ изображений объектов со
случайным значением яркости в каждом из пикселов на полутоновом
случайном фоне инвариантно к наклону линии границы и слабыми огра¬
ничениями на статистические характеристики яркости изображений и
фона. В отличие от задач обнаружения границы, рассмотренных в п. 6.5
и 6.6, в данном случае обнаруживается не одна, а группа точек произ¬
вольно проходящей границы. При этом нет необходимости в информации
о форме скачка яркости на границе фон-объект, поведении корреляци¬
онных функций и энергетических спектров фоновых шумов. Основное
требование к распределениям яркостей на участке сцены, содержащем
фон и изображение объекта или изображения двух объектов, заключает¬
ся в статистически достоверной разнице математических ожиданий этих
распределений, причем конкретные значения математических ожиданий
заранее не известны. Естественно, что эффективность подобного обнару¬
жителя за счет использования минимума информации о фоне и изобра¬
жениях объектов будет ниже ранее рассмотренных обнаружителей. Она
соответствует интуитивному представлению изображений в сцене, когда
глаз реагирует на разность средних значений яркостей между различны¬
ми областями сцены и интерпретирует их как отдельные изображения.
Принцип рассматриваемого в данном разделе обнаружения границ за¬
ключается в установлении статистически достоверной разницы средних
яркостей двух смежных участков сцены.
274
Гл. 6. Выделение границ изображений
6.7.1. Обнаружение границы на базе ί-критерия. Пусть Si и 52 —
примыкающие друг к другу области изображений произвольной формы.
При неизвестной конфигурации границы знание формы областей Si и S2
не играет роли и в целях упрощения анализа примем, что Si и S2 — два
квадратных окна, содержащие по т2 = т х т пикселов. Пусть также
Si = {si (n)}ljm2 и S2 = {s2 W}1]TO2 (6.7.1)
— векторы яркостей пикселов в областях (окнах) Si и 52, причем отсчеты
яркостей в отдельных пикселях независимы.
По выборкам, состоящим из компонент векторов Si и S2, необходимо
получить оценки генеральных средних и проверить гипотезу Щ о том,
что генеральные средние Μχ и М2 статистически не отличаются друг от
друга, т.е. наблюдаемая между ними разница носит не систематический,
а случайный характер. Альтернативная гипотеза Hi предполагает, что
разница между оценками генеральных средних Μχ и М2 носит систе¬
матический характер, и, следовательно, области 5χ и 52 принадлежат
либо фону и изображению, либо двум разным изображениям. Количество
пикселов га2 в каждом из окон достаточно велико и составляет порядка
20“ 100 и более. В связи с этим создаются предпосылки для выполнения
условий центральной предельной теоремы теории вероятностей. Поэтому
можно считать, что оценка s генеральной средней М
β = ΛΣ*(η) (вд
т *—\
п=1
подчиняется нормальному закону распределения вероятностей
г _ m / m2 (5 - Μ)2 Ί . .
/(S)_ V2^aeXP { 2σ2 }’ ( ]
где σ2 — дисперсия генеральной совокупности значений яркостей пиксе¬
лов, составляющих окно 5. Разность оценок 5χ и 52 также распределена
нормально:
f(si -s2) =
φΜσϊ+σϊ)
exp
Η
1 («1 - s2 - Μι + Mi)'
2 (σϊ+σΐ)
}·
(6.7.4)
где Μχ, M2 и σ2, σ2 — генеральные средние и дисперсии для выборок
Si и 52. Поскольку нас интересует лишь абсолютное значение разности
оценок si и 52, то случайная величина |(5χ — 52)| будет подчиняться рас¬
пределению вероятностей модуля нормальной случайной величины [25]:
/(1*1 -*2|) =
*{σ\ + σΙ)
I ί т
+ exp <
ехР 1 “
т2 (|^ι — 521 — Μχ + М2)2
2(σχ -f σ2)
— 52| + Μι — М2)'
}]■
|si - s2| > 0. (6.7.5)
2(<Ji +σ2)
Если справедлива нулевая гипотеза Но, то генеральные средние Μχ
и М2 равны между собой, т.е. Μχ — М2 = М и σχ = σ2 = σ. Тогда
6.7. Инвариантные обнаружители границ изображений
275
распределение (6.7.5) принимает вид
/(|?·-*|) =У’11’}· (6·7'6»
Введем нормированную разность оценок генеральных средних с уче¬
том того, что вместо генеральной средней σ2 имеются ее оценки σ\ и σ|,
полученные по выборкам Si и S2:
t =
m\si - s2\
\βϊ
(6.7.7)
+ Щ
Тогда при t < tsi окна Si и 52 обнаружителя расположены либо
на фоне, либо в пределах внутренних точек изображения. Здесь tsX —
стандартное значение критерия, установленное в соответствии с принятой
величиной уровня значимости (доверительной вероятности). При t ^ tst
нулевая гипотеза отвергается. В том случае, когда объемы выборок в ок¬
нах Si и S2 равны соответственно т\ и га2 (mi ф т2), выражение (6.7.7)
принимает вид
t =
|$1 - S2\
уд\/mi + σΙ/πΐ2
(6.7.8)
Величина принятого уровня значимости р при определении величины t
по формуле (6.7.8) позволяет поставить каждому значению tsX вероятность
F = 1 —р ложной тревоги. В табл. 6.3 даны значения tsX и соответствующие
Таблица 6.3
^st
2
2,5
3
3,5
5
F = 1-р
0,45
0,12
0,03
0,0005
0,0000006
им вероятности F, для случая нормального закона распределения выбо¬
рок в окнах Si и S2 [121]. При небольших объемах выборок распределения
вероятностей средних значений яркостей в окнах Si и 52 отличаются от
нормального. В этой ситуации случайная величина
77117712 (ГГЦ +7712—2)
7711 + 7772
где Si и S2 — две независимые нормально распределенные выборки с объе¬
мами mi и m2, имеет распределение Стьюдента с mi + m2 — 2 степенями
свободы [121]. Этот результат сохраняется и тогда, когда выборки берутся
из распределений близких к нормальному. В табл. 6.4 для случая малых
Таблица 6.4
t
2
2,5
3
3,5
4
4,5
5
7771+7772 = 18
0,063
0,024
0,008
0,003
0,001
0,0003
14·10-5
F
7771+7772=50
0,051
0,016
0,0046
0,001
22-10-5
3·ΚΓ5
1·10~5
7771+7772=98
0,0495
0,0134
0,0036
0,0007
12 · ΙΟ-5
1·10-5
—
276
Гл. 6. Выделение границ изображений
выборок приведены значения tst и соответствующие им вероятности ложной
тревоги для случаев, когда объем обеих выборок πΐχ + га2 равен 18, 50 и 98.
Из табл. 6.3 и 6.4 видно, что для малых значений F наблюдается силь¬
ная зависимость данной вероятности от объема выборок. Таким образом,
значение t-критерия позволяет ответить на вопрос: проходит ли грани¬
ца в пределах окон Si и S2 или нет. Следовательно, t-критерий может
быть применен для решения задач обнаружения границ изображений.
В дальнейшем оператор выделения граничных точек по величине |t| будем
называть ^-обнаружителем.
6.7.2. Характеристики t-обнаружителя. В реальных случаях линия
границы между фоном и изображением или между смежными изобра¬
жениями может располагаться не только точно между окнами Si и S2,
а занимать относительно их произвольное положение. Это затрудняет
расчет характеристик обнаружителя, работающего по t-критерию.
Поэтому такие характеристики целесообразно получать в результате
статистического эксперимента. Определим зависимости вероятностей D
Рис. 6.44. Взаимное расположение линии границы и окон t-обнаружителя
и F от размеров mi и га2 окон Si и S2, взаимного расположения окон Si
и S2 и границы (рис. 6.44) от величины отношения сигнал/фон. При этом
используется следующая модель сцены.
Рис. 6.45. Зависимости вероятности правильного обнаружения от отношения сиг-
нал/помеха для размеров окон Si и S2, равных 3 х 3, 5 х 5, 7 х 7, 9 х 9: а — при
t = 2, б — при t = 4
6.7. Инвариантные обнаружители границ изображений
277
Вначале точки фона и изображения объекта имеют постоянные значения
яркостей Шф и гас. Далее производится аддитивное зашумление сцены нор¬
мальным шумом с нулевым математическим ожиданием и дисперсией σ2.
Форма границы фон/объект имеет вид прямой линии. Вероятность ложной
тревоги F определяется функцией распределения величины t для случая,
когда в обоих окнах обнаружителя имеются только точки фона или точки
только одного изображения и принимается решение об обнаружении границы.
На рис. 6.45, 6.46 приведены полученные по достаточно представитель¬
ным выборкам графики следующих зависимостей: 1) вероятности пра¬
вильного обнаружения от отношения сигнал/помеха q при t = 2 и t = 4
для разных значений размеров окон Si и S2', 2) вероятности правильного
обнаружения от величины t для окон Si и S2 размерами 5 х 5 и 9 х 9 при
различных значениях параметра I сдвига параллельно расположенных
Рис. 6.46. Зависимости вероятности правильного обнаружения от величины t\
а, б — при разных взаимных сдвигах I параллельно расположенных линии гра¬
ницы и стыка окон Si и ft: а — для окна 5 х 5, б — для окна 9 х 9; в, г —
для размеров окон Si и S2, равных 3x3, 5 х 5 и 9 х 9, при угле а между
линиями границы изображения в — 30°, г — 60°; д, е — для разных значений
углов φ между линиями границы и стыка окон при разных взаимных сдвигах I
параллельно расположенных линии границы и стыка окон Si и S2 для размеров
окон: г — 5x5, е — 9x9
278
Гл. 6. Выделение границ изображений
линий границы и стыка окон Si и 52; 3) вероятности правильного обнару¬
жения от величины t при углах φ между линиями границы и стыка окон
Si и 52, равных 30° и 60° для размеров окон Si и 52, равных 3 х 3, 7 х 7
и 9 х 9; 4) вероятности правильного обнаружения от величины t для окон
Si и 52 размером 9x9 при разных углах а наклона линии границы.
При построении графиков вероятностных характеристик обнаружите¬
ля отношение сигнал/шум q определялось как
q = Α/σ — (тф — шс)/а. (6.7.9)
Представленные на рис. 6.46 зависимости получены для отношения
сигнал/шум q — 1. Значения вероятностей ложных тревог F на приведен¬
ных графиках могут быть ориентировочно оценены с помощью табл. 6.4.
Приведенные выше аналитические соотношения и вероятностные ха¬
рактеристики могут служить основой для расчета эффективности обна¬
ружителей границ изображений в зашумленной сцене при минимальном
объеме требуемой статистической информации. Как следует из этих ха¬
рактеристик, обнаружитель достаточно эффективен. Например, при q =
— 1, 5ι = 5г = 7 х 7 и совмещении линий границ и стыка окон вероятно¬
сти D и F соответственно равны 0,96 и 0,003.
6.7.3. Инвариантный к наклону линии границы обнаружитель. Как
следует из полученных характеристик, эффективность обнаружителя, ра¬
ботающего по ^-критерию, быстро падает при смещении линии стыка окон
Si и 52 от линии границы фон/объект (при их параллельном расположении)
или при увеличении угла φ между этими линиями, Первый фактор играет
скорее положительную, чем отрицательную роль, позволяя при сколь¬
жении окон точнее зафиксировать момент точного расположения одного
из окон на фоне, а другого — на изображении. Второй фактор требует на
каждом шаге вращения линии стыка окон в пределах угла 180°, что резко
увеличивает время принятия решения и вероятность ложных решений.
Рассмотрим инвариантный к началу линии границы ^-обнаружитель.
Для достаточно протяженной границы изображения в диапазоне углов
ψ = 0~90° инвариантность к углу наклона линии границы у него дости¬
гается при расположении окон Si и 52 как показано на рис. 6.47, а, а при
Рис. 6.47. Расположение окон обнаружителя при произвольной ориентации границы
6.7. Инвариантные обнаружители границ изображений
279
φ = 90°-180° — как показано на рис. 6.47, б. Колебания угла φ при этом
не оказывают существенного влияния на содержание окон S\ и £2·
Объединяя оба случая, приходим к апертуре фильтра ^-обнаружителя,
показанной на рис. 6.48, а, обеспечивая инвариантность к углу наклона гра-
si
Si
S2
Si
г
si
Ί
L
si
J
S'i
Рис. 6.48. Апертуры фильтра ^-обнаружителя
ницы изображения. Взвешивание энергии фона и изображения производится
попарно в диагонально расположенных окнах. Для каждой пары окон S[,
и S", $2 определяется величина t и сравнивается с порогом et. Решение
в пользу гипотезы Ηχ принимается при превышении этого порога хотя бы
в одной паре стробов. Апертура фильтра, представленного на рис. 6.48, б,
позволяет частично исключить участок с постепенным нарастанием яркости
и более четко фиксировать момент обнаружения границы.
Рис. 6.49. Структура алгоритма работы ί-обнаружителя границы
280
Гл. 6. Выделение границ изображений
Критерий обнаружения границы изображения реализуется алгорит¬
мом, структура которого приведена на рис. 6.49. При реализации t-
обнаружителя необходимо иметь ввиду следующее обстоятельство. Для
малых значений дисперсий σ\ и σ\ (т.е. при работе на равномерном
детерминированном или слабо зашумленном фоне или изображении)
вычисление величины t представляет собой неустойчивый процесс. Как
следует из выражений (6.7.7) и (6.7.8), величина оценок дисперсий σ\
и σ2 определяет значение знаменателя и при указанных условиях ве¬
личина t будет иметь очень большой разброс. Для устранения этого
негативного фактора необходимо оценить степень влияния случайной
составляющей поля яркости.
Если σ\ -fa! < εσ, где εσ — пороговый уровень суммарной дисперсии,
обнаружение производится не по значению величины t, а по условию
|*1 - 1 ^
где сам — пороговый уровень для разницы оценок математических ожи¬
даний в окнах 51 и 5г. Величины t\, ΔΜχ и σχ вычисляются для пары
окон 5χ и 52, а величины £2, ΔΜ2 и σ2 — для окон 5χ и 52.
На рис. 6.50-6.52 приведены результаты работы t-обнаружителя
с окном, показанным на рис. 6.48, б, цо двум сценам. Первая сцена пред¬
ставляет собой яркостный клин в виде зашумленного прямоугольни-
Рис. 6.50. Исходные сцены для обнаружения границ объектов: а — тестовое изо¬
бражение зашумленного яркостного клина (σπι = 10); б — реальное зашумленное
изображение географического объекта
ка с плавно изменяющейся в широких пределах яркостью. Вторая сцена
содержит реальное зашумленное изображение географического объекта.
На рис. 6.51 представлены результаты обнаружения границ яркостного
клина при четырех режимах, параметры которых занесены в табл. 6.5.
Результаты работы ^-обнаружителя по зашумленной сцене с изобра¬
жением географического объекта показаны на рис. 6.52, а режимы его
работы — в табл. 6.6.
Как видно из представленных фотографий, рост апертуры фильтра
^-обнаружителя способствует снижению количества ложных контуров,
но приводит к более значительному размыванию границ изображе¬
ния объекта и исключению мелких деталей. Выбор размеров окон 5χ
6.7. Инвариантные обнаружители границ изображений
281
Рис. 6.51. Результаты обработки тестового изображения, представленного на
рис. 6.50 (комментарии даны в тексте)
Таблица 6.5
Номер рисунка
mi х Ш2
Sam
St
Рис. 6 51, а
3x3
2
3
3
Рис. 6.51, б
5x5
2
3
3
Рис. 6.51, в
9x9
2
3
3
Рис. 6.51, г
9x9
2
3
5
Рис. 6.52. Результаты обработки сцены с географическим объектом, показанным
на рис. 6.50 (комментарии даны в тексте)
Таблица 6.6
Номер рисунка
mi х гаг
Sa
Sam
St
Рис. 6.52, а
3x3
2
2
8
Рис. 6.52, б
5x5
2
2
12
Рис. 6.51, в
9x9
2
2
20
282
Гл. 6. Выделение границ изображений
и ί-обнаружителя, кроме учета его влияния на помехоустойчивость
и разрешающую способность, зависит еще и от априорной информации
о размерах самого изображения, границы которого надо обнаружить,
минимального расстояния между несколькими изображениями.
6.8. Выделение и прослеживание контуров изображений
объектов
Для формирования контура изображения в целом ряде случаев нет
необходимости решать задачу обнаружения всех его точек в соответствии
с алгоритмами, описанными в разделе 6.7, и с последующей проверкой
обнаруженных точек на связность. Учитывая сильную пространственную
корреляцию контурных точек и непрерывность линии контура, после об¬
наружения одной или небольшой группы точек, резко сужается область
пространства, где располагается последующая контурная точка. В резуль¬
тате этого операция обнаружения начальной контурной точки сменяется
операцией прослеживания контура, понимая под этим непрерывный переход
от текущей точки контура к последующей до замыкания линии контура.
Наиболее просто она осуществляется для бинарного изображения.
6.8.1. Прослеживание контуров бинарных изображений. Пусть в би¬
нарной сцене содержится совокупность {ω:7·}1 2 г оцифрованных изобра¬
жений. Начальной точкой aoj изображения uj назовем принадлежащую
ему точку с минимальным номером строки и номером столбца, минималь¬
ным в этой строке. Упорядочивание изображений выполним по правилу:
если проранжировать линейные адреса в ОЗУИ всех их начальных точек,
то номер начальной точки будет равен номеру изображения. Линейный
адрес Алин точки связан с номером пстр ее строки и номером пст ее столбца
следующим образом: Алш = Ш2Пстр -Ь П2СТ> где m2 — количество точек
в строке изображения. Наиболее просто путем строчного поиска в порядке
нарастания линейных адресов находится начальная точка изображения
ω±. Для определения ЭВ 7(0) контура необходимо найти следующую
точку а\ контура, которая определяется осмотром окружающих точку
а0 точек (рис. 6.53).
Алгоритм поиска точки ао, как первой заполненной ячейки ОЗУИ,
дает правильные результаты лишь для изображения ωχ. Поиск начальных
Рис. 6.53. Формы стробов для выделения контурных точек
6.8. Выделение и прослеживание контуров изображений объектов 283
точек изображений cuj, j = 2,3,..., связан с исключением из рассмотрения
точек изображений ωχ, и>2, Uj-ь
С этой целью формируется сопряженное по адресам ячеек ОЗУИ
другое ОЗУК (ОЗУ контуров), в котором хранятся контуры ранее обнару¬
женных изображений.
Таблица 6.7. Состояние автомата поиска начальной точки нового изображения
Номер
Число ОЗУИ
и ОЗУК
Состояние
шаг
η — 1
шаг
п
1
00
00
Точки фона (1а) или внутренние точки полости
(16)
2
00
10
Точка нового изображения (2а) или выход из
полости (26)
3
00
11
Вход в ранее обнаруженное изображение
(1-й шаг)
4
10
00
Обнаружение полости
5
10
10
Точка внутри изображения
6
10
11
Выход из ранее обнаруженного изображения
(1-й шаг)
7
11
00
Выход из ранее обнаруженного изображения
(2-й шаг)
8
11
10
Вход в ранее обнаруженное изображение
(2-й шаг)
9
11
11
Движение по контуру вдоль строки
Система поиска изображений в бинарной сцене работает как конечный
автомат с памятью. В табл. 6.7 приведены возможные состояния автомата
поиска, а на рис. 6.54 — его граф. В качестве базового алгоритма просле¬
живания линии контура, при котором последовательно, без разрывов вы¬
деляются контурные точки изображения и формируется код контура, це-
Рис. 6.54. Упрощенный граф автомата поиска первой точки контура нового изо¬
бражения
284
Гл. 6. Выделение границ изображений
лесообразно использовать алгоритм, предложенный Розенфельдом [9]. По
сравнению с другими алгоритмами (например, алгоритмом «жука» [40]),
он не приводит к зацикливанию при любых конфигурациях контура и до¬
пускает простую реализацию. По данному алго¬
ритму на га-м шаге прослеживания формируется
строб Сп размером 3x3 элемента. Его центр
совмещается с текущей точкой ап контура
(рис. 6.55). Благодаря непрерывности линии
контура предыдущая, текущая и последующая
точки контура всегда находятся в пределах этого
строба, т. е. {αη_ι,αη,α„+ι} в Сп.
Поиск последующей точки αη+χ состоит
в осмотре по часовой стрелке ячеек строба Сп,
начиная от предыдущей точки αη_χ. Первая
заполненная ячейка считается содержащей
точкуап+1. Если проанализировать положения
стробов Сп-1 и Сп, то оказывается, что первая
точка строба СП1 взятая в направлении часовой
стрелки от точки αη_χ, всегда будет принадлежать фону. Следующая за
ней вторая точка строба Сп тоже всегда будет относиться к фону, но при
условии, что предыдущий ЭВ не был диагональным.
На рис. 6.56 показаны конфигурации строба прослеживания, которые
в соответствии с базовым алгоритмом будут оптимальными с позиции ми-
Рис. 6.55. Выделение кон¬
турной точки
у = 4
П /2-1
v = 5 ν = 6
ν = 7
п
72-1
/
ν = О
72-1 «
Рис. 6.56. Конфигурация строба для базового алгоритма прослеживания контура
нимального требуемого количества просматриваемых ячеек. Рассмотрим
получающее при этом сокращение времени прослеживания.
Для определенности алгоритм прослеживания контура, при котором
начиная от точки αη-ι последовательно до точки αη+χ просматриваются
все точки строба Сп, назовем алгоритмом ПВЭ, а алгоритм, при котором
6.8. Выделение и прослеживание контуров изображений объектов 285
просматриваются только точки, в которых возможно нахождение контур¬
ной точки ап+1 — алгоритмом ПТВЭ. Для среднего времени прослежива¬
ния линии контура из к ЭВ можно записать:
м 7 7
Тк — к У ^ Pj У ^ ΊTj v У ^ βνι Pj νι,
1=0
ΣβνιΡίνΙ, (6.8.1)
j=1 ^=0
где Pj — априорная вероятность изображения j-ro класса, j = 1,2,... , Μ;
vju — безусловная вероятность ЭВ ην\ PjVi — переходная вероятность
смены вектора вектором л для изображения j-το класса. Весовые
коэффициенты /3^, равные количеству шагов, которые надо совершить
в стробе Сп от αη_ι до αη+ι, определяются алгоритмом поиска точки αη+ι
и задаются в виде матрицы В = {/3^*,}. Для алгоритмов ПТВЭ и ПВЭ эти
матрицы имеют, соответственно, вид:
0
1
2
3
4
5
6
7
0
' 2
3
4
5
б
0
0
1
1
2
3
4
5
б
7
0
1
2
0
1
2
3
4
5
б
0
Вптвэ =
3
0
1
0
2
0
3
4
5
б
7
4
б
1
2
3
4
5
5
б
7
0
1
2
3
4
5
6
4
5
б
0
0
1
2
3
7
_ 4
5
б
7
0
1
2
3
0
1
2
3
4
5
6
7
0
' 4
5
б
7
8
1
2
3 '
1
3
4
5
б
7
8
1
2
2
2
3
4
5
б
7
8
1
3
1
2
3
4
5
б
7
8
В пвэ =
4
8
1
2
3
4
5
б
7
5
7
8
1
2
3
4
5
6
6
б
7
8
1
2
3
4
5
7
_ 5
6
7
8
1
2
3
4 _
Сравним алгоритмы для двух крайних случаев,
.В
первом
есть независимый процесс, все векторы равновероятны, т. е. KjV = 0,125,
1/6 при v = 0,2,4, б,
Pul = , 7
1/7 при v = 1,3,5,7.
Во втором случае смена ЭВ представляет сильно коррелированный про¬
цесс, причем по-прежнему все векторы равновероятны, т. е. — 0,125,
1 при I = и,
^0 при I ф V.
Ри1 =
286
Гл. 6. Выделение границ изображений
Таблица 6.8. Среднее число шагов поиска в окне последующей точки контура
Алгоритм
п
эоцесс
Независимый
Сильно коррелированный
ПВЭ
5,57
4
ПТВЭ
3,75
2,5
В табл. 6.8 приведены значения среднего времени поиска контурной
точки, рассчитанные по формуле (6.8.1) для случая, когда все классы
равновероятны.
Как и следовало ожидать, наличие корреляции снижает время поиска,
так как при сильной корреляции ЭВ сохраняют свое значение, т. е. j (π) =
= 7 (η — 1), и количество элементов в стробе Сп от точки αη_χ до точки
αη+1 равно четырем для алгоритма ПВЭ и двум или трем — для ПТВЭ.
Если смена ЭВ представляет собой независимый процесс, то точка
αη+1 с одинаковой вероятностью может находиться в любом элементе
строба. Алгоритм ПТВЭ (табл. 6.8) обеспечивает по сравнению с алгорит¬
мом ПВЭ ускорение процесса прослеживания линии контура примерно
в полтора раза.
6.8.2. Глобально-оптимальная процедура формирования порогово¬
го уровня для получения бинарной сцены. Один из распространенных
подходов к выделению контуров изображений в многоградационной по
яркости сцене F базируется на получении бинарной сцены F^o, в которой
формы изображений объектов минимально искажены. При наличии сце¬
ны F6j0 контуры изображений достаточно просто выделяются на основе
базового алгоритма (см. 6.8.1).
Будем рассматривать сцену F со статистически однородным фоном,
характеризующимся гистограммой яркости /ф (J). Примем для простоты,
что яркости изображений различных объектов в ней близки между собой
и характеризуются компактной ги¬
стограммой яркости /с (J) (рис. 6.57).
При этих условиях для получе¬
ния сцены F6j0 можно сформировать
одно значение /гл0б порогового уров¬
ня ограничения сцены F по яркости.
Этот уровень назовем глобально¬
оптимальным порогом 1Тлоб опт·
Весь диапазон яркостей сцены
Рис. 6.57. Разбиение диапазона ярко- ^ от ® До -^тах^ условно разделим
стей сцены на области на пять областей. Если /глоб нахо¬
дится в первой области, то точки
бинарной сцены будут, в основном, единичными, а если в пятой — то
нулевыми. Вторая область характеризуется практическим отсутствием
точек изображения, а четвертая — точек фона. Но в четвертой области
потеряно много точек, составляющих изображение объекта (рис. 6.58).
Таким образом, нахождение величины /глоб во второй и четвертой
6.8. Выделение и прослеживание контуров изображений объектов 287
— порог; —
порог
областях приводит к недопустимо большим искажениям формы объекта
и в этих областях диапазона яркостей также нецелесообразно выбирать
порог. Как отмечается в целом ряде работ, например, в [3], единственной
областью существования такого порога является третья. Сдвиг в этой
области величины /глоб вправо приводит к тому, что линия контура будет
преимущественно проходить по внутренним точкам изображения, а сдвиг
влево дает противоположный эффект: линия контура проходит вблизи
Линия границы
допустимой ошибкой допустимой ошибкой
в области фона в области изображения
Рис. 6.59. Искажения линии границы изображения при различных подходах к вы¬
бору ВеЛИЧИНЫ 77Глоб
границы, но включает большое количество фоновых точек (рис. 6.59).
В обоих случаях длина контура увеличивается по сравнению с длиной
контура при ограничении полутоновой сцены на уровне /глоб. 0пт ·
288
Гл. 6. Выделение границ изображений
Таким образом, характер зависимости длины контура от величины по¬
рога яркости позволяет выработать подход к получению бинарной сцены
2*6,0 с минимальными искажениями формы изображений.
Пусть lj — длина контура изображения сoj (j = 1,2,..., г), в бинарной
сцене 2*б, полученной ограничением по яркости полутоновой сцены F.
Тогда величина глобально-оптимального порога обеспечивает минимум
суммы длин контуров всех изображений, т.е.
г
-^глоб — -^глоб опт. при ^ ^ lj —> min. (6.8.2)
j-1
Из практических соображений целесообразно ввести ограничение на
длину контура текущего изображения:
^min ^ lj ^ ^тах* (6.8.3)
Чаще всего контуры очень большой и очень малой длины являются по¬
меховыми. В соответствии с критерием (6.8.2) операция определения гло¬
бально-оптимального порога является адаптивной. Определенным образом
назначается величина начального порога /глоб нач = Ллоб(1) и фиксируется
сумма длин контуров при этом пороге:
г
^нач = ^2 lj,U (6.8.4)
2=1
где ljA — длина контура j-ro изображения при начальном значении порога
Далее последовательно инкрементируется величина /глоб Нач и изме¬
ряется сумма длин контуров изображений в получающихся бинарных
сценах. На всех этапах должно выполняться условие (6.8.3). При дости¬
жении условия (6.8.2) этот процесс прекращается. В качестве начального
значения порога /ГЛОб нач. можно выбрать инкрементированное значение
средней яркости Jcp полутоновой сцены 2*1, т.е. /глоб Нач = ΛР 4-1.
В реальных сценах величина Jcp не намного превышает среднюю яр¬
кость фона 7ф, а изображения объектов имеют яркость, как выше, так
и ниже средней яркости Jcp.. Поэтому целесообразно формировать из
полутоновой сцены F не бинарную, а трехградационную сцену: один уро¬
вень яркости соответствует изображениям объектов с яркостью ниже
яркости фона, третий уровень — объектам с яркостью выше яркости
фона, а второй уровень соответствует средней яркости фона 7ф.
6.8.3. Локалыю-опимальная процедура формирования порогового
уровня для получения бинарной сцены. Формирование бинарной сце¬
ны 2*б,о из исходной полутоновой сцены F при наличии только одного,
глобально-оптимального 2ГЛ0б 0пт порога по яркости является сравнительно
простой операцией. При этом контуры изображений объектов с малой
длиной границы и характеризующиеся низким отношением сигнал/фон
будут искажены значительно сильнее, чем контуры изображений объек¬
тов с большой величиной этого отношения. Более высокое качество выде¬
ленных контуров может быть достигнуто при вычислении оптимального
6.8. Выделение и прослеживание контуров изображений объектов 289
порогового уровня ограничения по яркости для каждого изображения ал,·,
j = 1,2,, г, в отдельности. Если же сцена характеризуется статистиче¬
ски неоднородным фоном, особенно неоднородностью первого начального
момента, то формирование только одного порогового уровня для получе¬
ния сцены .Рбд теряет смысл. В этом случае для каждого изображения Uj
в пределах локально однородного участка сцены F необходимо вычислять
локально-оптимальный уровень ограничения сцены по яркости. Примене¬
ние локально оптимальных порогов по яркости связано с решением двух
основных вопросов:
1) выбора меры для оценки степени зашумления контура отдельного
изображения Uj\
2) организации локальной процедуры выделения контура изображения
внутри области, ограниченной произвольной замкнутой кривой.
При автоматическом формировании величины глобально-оптимального
порога /глоб опт. в качестве меры зашумления линии контура была выбра¬
на величина его удлинения при воздействии шума. Для случая локально¬
оптимальных порогов, когда обработке подвергается только одно конкретное
изображение ов качестве такой меры целесообразно взять не только сте¬
пень удлинения контура, но и учесть размеры изображения и)j. Это позволит
отбросить ряд помеховых контуров, например, узкие протяженные контуры.
В качестве такой меры может служить значение коэффициента фор¬
мы изображения
^ф1 = л/^/^ист» (6.8.5)
где $ — площадь, a lUCT — длина незашумленного контура, периметр
изображения,
k — 1
U = Σ |7(п)|. (6.8.6)
п=0
Так как с уменьшением контурных шумов длина контура падает, то
оптимальное значение локального порога /лок опт.О') для изображения от¬
будет соответствовать максимуму коэффициента формы контура при ва¬
рьировании величины порога /лок0):
ЛюкО)—Люк опт {j) при кф\{j) —ϊ шах, j = 1,2,..., г. (6.8.7)
Кроме того, по-прежнему должно выполняться условие (6.8.3) ограни¬
чения длины контура, обеспечивающее исключение изображений с очень
большими или очень малыми длинами контуров, чаще всего являющихся
помеховыми.
Чтобы снизить влияние на величину площади изображения граничных
(контурных) точек, что важно при определении коэффициента формы
узких протяженных изображений, коэффициент формы для определения
Люк опт целесообразно вычислять в виде
кф2 = Vs - к/1Ист, (6.8.8)
где к — количество ЭВ в контуре изображения. В результате условие
290
Гл. 6. Выделение границ изображений
(6.8.7) принимает вид
I,гок (j) =1пок опт (j) при кф2 (j) -->■ max, i = 1,2,... , г. (6.8.9)
Алгоритм формирования бинарной сцены F§ на основе ограничения по
яркости полутоновой сцены F на уровне локально-оптимального порога
7Л0К опт С?) работает следующим образом.
1. Формируется начальная бинарная сцена Тб при ограничении по
яркости на уровне Ιχ = /гл0б = 7ср + 1 полутоновой сцены F.
2. Проводится строчный поиск и обнаружение начальной контурной
точки aoj текущего изображения Uj.
3. Выделяется контур j-ro бинарного изображения и если выполняется
условие (6.8.3), то вычисляется коэффициент формы. При не превышении
заданного порогового уровня считается, что обнаружен шумовой контур
и производится поиск следующего, (j 4- 1)-го изображения.
4. Для обнаруженного изображения сjj путем инкрементации преды¬
дущего порогового уровня формируется следующий пороговый уровень:
^2 j = Л\лоб "Т 1·
5. В пределах контура изображения, выделенного на уровне порога
7ι, производится поиск начальных точек всех контуров, полученных при
ограничении на уровне 72 ( процедура «контур внутри контура»).
6. Для новых контуров, расположенных внутри контура j-το бинарного
изображения, выделенного по пороговому уровню Ιχ, проводится селекция
по длине контура в соответствии с выражением (6.8.3). Для оставшихся
контуров вычисляется значение коэффициента формы и производится
селекция по величине коэффициента формы. Процедура «контур внутри
контура» необходима из-за возможного дробления контура изображения
при повышении порогового уровня ограничения полутоновой сцены F.
Благодаря проверкам по длине периметра и величине коэффициента фор¬
мы исключаются помеховые контуры. Для оставшегося контура путем
перехода к следующему пороговому уровню I^j = hj -f 1 проверяется
условие достижения максимума коэффициента формы.
Как только величина коэффициента формы при каком-то значении
порога начинает уменьшаться, считается что такой максимум достигнут
и процедура поиска локально-оптимального порога закончена. Получив¬
шийся контур считается контуром изображения Uj. Он кодируется, запо¬
минается в ОЗУК, а всем пикселям изображения иjj в пределах первого
выделенного контура на пороговом уровне Ιχ присваиваются значения
средней яркости сцены F. Это позволяет исключить изображение иjj при
поиске контура следующего изображения Uj+χ.
На рис. 6.60-6.63* приведены иллюстрации к формированию бинарных
и трехградационных сцен и выделению контуров изображений при поро¬
говой обработке исходной полутоновой сцены путем ограничения каждого
из изображений на уровне локально-оптимальных порогов. На рис. 6.60
* Авторы выражают благодарность д.т.н., проф. Л. А. Школьному за предостав¬
ленную модель радиолокационной сцены.
6.8. Выделение и прослеживание контуров изображений объектов 291
Рис. 6.61. Бинарная сцена для изображений ярче фона (а) и контуры этих изобра¬
жений (б)
Рис. 6.62. Негативное представление исходной сцены (а) и контуры изображений
темнее фона (б)
Рис. 6.63. Карта порогов (а) и трехградационная сцена (б)
292
Гл. 6. Выделение границ изображений
показана исходная сцена и результат ее низкочастотной фильтрации про¬
странственным фильтрам с окном 5x5 элементов, проводимой для умень¬
шения контурных шумов.
На рис. 6.61 представлена бинарная сцена для изображений ярче фона,
сформированная на основании локально-оптимальных порогов для каж¬
дого из изображений и контуры этих изображений.
На рис. 6.62 дано негативное представление исходной сцены и по¬
казаны контуры изображений с яркостью, ниже яркости фона. Для
данного случая также формировались локально-оптимальные пороги
для каждого из изображений. На рис. 6.63 представлена так называемая
«карта порогов» и трехградационная сцена. Карта порогов формируется
на базе сцены из выделенных контуров изображений. Пикселам внутри
каждого из контуров присваивается яркость, равная средней яркости
соответствующего изображения.
6.8.4. Алгоритмы прослеживания контуров многоградационных изо¬
бражений, не связанные с образованием бинарных сцен. Рассмотрим
несколько подходов к обобщению базового алгоритма прослеживания кон¬
туров бинарных изображений на случай многоградационных изображе¬
ний. При обнаружении и прослеживании контуров бинарных изображений
перепады яркостей на границах были идеальными. Это дает возможность
получить контуры изображений и их комплекснозначные коды, минуя
стадию формирования силуэтных изображений. При решении аналогич¬
ных задач для многоградационных изображений перепад яркости на гра¬
ницах фон/изображение или изображение/изображение становится в ре¬
альных случаях чаще всего пологим и зашумленным. В результате линия
контура в пределах ширины этого перепада, как
линия внешней границы изображения, становится
неопределенной, а действие шумов приводит к
ошибкам выделения контуров. Подавление таких
ошибок проводится методом накопления. В этом
случае строб Сп для прослеживания линии контура
будет иметь более сложную структуру: каждый
его элемент представляет собой квадратное окно из
большого количества пикселей (рис. 6.64).
При прослеживании контуров многоградацион¬
ных изображений решение на каждом шаге це¬
лесообразно выносить с учетом принятых на пре¬
дыдущих шагах. В первую очередь, в условиях
мультипликативных помех по яркости, это относится
к выбору порога cti по яркости, при превышении которого точка в стробе
прослеживания считается контурной. Величина с^, в простейшем случае
определяется как
Рис. 6.64. Строб для
прослеживания кон¬
туров изображений в
зашумленной много¬
градационной сцене
JV
α< ~ ]νΣ6·->-
3=1
6.8. Выделение и прослеживание контуров изображений объектов 293
где bi-j — яркости предыдущих контурных точек; N — число этих
точек; Δα — некоторая константа, превышающая приращение средней
яркости сцены за один шаг. Предполагается, что предыдущие контурные
точки принадлежат границе фон/объект и по значениям их яркостей
могут быть получены оценки средней яркости в окрестности последующей
контурной точки. Из-за мультипликативных помех уровень средней
яркости в пределах сцены может варьироваться в значительной степени.
Поэтому прогноз средней яркости на основании такой оценки позволяет
подстраивать порог обнаружения последующей контурной точки.
Начальная точка ао контура определяется обнаружителем на базе
СИФ или t-критерия (см. п. 6.6, 6.7). Необходимо отметить следующую
принципиальную трудность, возникающую при прослеживании контура
по алгоритму с адаптивным порогом по яркости. Так как порог опреде¬
ляется по конкретной выборке отсчетов яркости, то при приближении
к точке замыкания контура (к начальной точке ао) его прогнозируемое
значение скорее всего не совпадает со значением яркости в точке ао.
В результате точка ао окажется обойденной (см. рис. 6.65.). Для устра¬
нения замыкания линии контура на другую, кроме ао, контурную точку
можно использовать следующий подход.
Если при прослеживании контура появляется тенденция оставить точ¬
ку ао снаружи (рис. 6.65, а), то возврат к ней происходит вдоль линии уже
выделенного контура. При тенденции оставить точку ао внутри контура
Рис. 6.65. Сложные случаи замыкания контура при его прослеживании на базе
адаптивного порога по яркости
(рис. 6.65, б) область объекта ограничивалась сверху до уровня точки ао
и по показанной на рисунке пунктирной линией происходит возврат к
точке αο· Эти способы несколько искажают форму контура, но достаточно
просто реализуются.
Рассмотрим алгоритм прослеживания контуров многоградационных
изображений с классификацией точек в стробе по яркости с учетом
средних значений яркости, полученных на предыдущих шагах.
На рис. 6.66, а показаны два положения строба, формирующего ли¬
нию контура, причем Сп-\ — это строб на предшествующем шаге,
а Сп — на текущем. Буквами «Ф» здесь отмечены точки фона, «к» —
контурные точки и «О» — точки изображения объекта. Этим точкам
соответствуют полученные на предшествующих шагах средние значе-
294
Гл. 6. Выделение границ изображений
Сп-1
Г\Г\
г
Ф
Ф
Ф
ф-
Ф
2к
Зк
ф
1к
0
0
Ок
0
0
λ
Кф
ί>φ(«-ΐ) *ϋ^»—О J
Рис. б.бб. Классификация точек строба по яркостному расстоянию
ния яркостей (рис. 6.66, б): яркость объекта Ьо (η — 1), контурных точек
bk(n — 1) и точек фона 6ψ (η — 1). Центр строба Сп-\ находится в точ¬
ке 1к. На п-м шаге центр строба переместится в точку 2 к, найденную
также на (п — 1)-м шаге.
Порядок просмотра строба Сп показан стрелками (рис. 6.66, а). Анализ
базируется на допущении, что контурные точки относятся к объекту.
В процессе анализа для каждой непроклассифицированной точки строба
Сп вычисляется расстояние по яркости точки от средней яркости контур¬
ных и фоновых точек, полученных на (п — 1)-м шаге (рис. 6.66, б):
#ф = |(п) -Ьф(п- 1)|, Rk — \К (п) -Ьк(п- 1)|.
Решение о принадлежности точки к контуру выносится при выпол¬
нении условия Rф > Rk. В противном случае принимается решение о
том, что точка является внутренней для изображения. После окончания
классификации точек в стробе производится коррекция оценок яркостей
Ьф (η — 1), Ък (η — 1), Ьо (ft — 1) с учетом интенсивностей вновь получен¬
ных точек в стробе Сп.
В заключение рассмотрим один из подходов к формированию силуэт¬
ных изображений при наличии только их контуров.
До сих пор рассматривались вопросы, связанные с контуром изобра¬
жения, образованным граничными точками изображения. Пусть Ω — мно¬
жество точек изображения. Внутренняя точка этого множества обладает
свойством четырехсвязности, т.е. смежные с ней точки — правая, левая,
нижняя и верхняя — тоже принадлежат Ω. Точка этого множества будем
граничной в том случае, когда не все эти смежные точки относятся к Ω [9].
Любое изображение окаймлено границей из фоновых точек. После¬
довательность точек такой границы будем рассматривать как внешний
контур изображения. На рис. 6.67 приведен пример изображения объекта
с выделенными внешними и внутренними контурами.
Рассмотрим, каким образом наличие внешнего контура облегчает ре¬
шение задачи формирования силуэтного изображения при наличии внеш¬
него и внутреннего контуров. На рис. 6.67 показана ситуация, связанная
с наличием узкого участка толщиной в один элемент. При сканировании
изображения по строке А после первой точки внутреннего контура а^
всем последующим ячейкам строки присваивается единичная яркость до
тех пор, пока не встретится следующая точка внутреннего контура
6.9. Прослеживание прямолинейной границы изображения
295
в® Ь®
— точки внутреннего контура
(множество S)
[х|—точки внешнего контура
(множество $)
Рис. 6.67. Внешний и внутренний контуры изображений объекта
При сканировании по строке В точки а^ и Ъ^ внутреннего контура
совмещены. Поэтому значение единичной яркости будет присвоено всем
точкам фона, находящимся правее точки aS2\
Наличие внешнего контура меняет ситуацию. При сканировании по
строке заполнение точек единичной яркостью начинается после появ¬
ления первой точки внешнего контура и прекращается при появлении
второй точки внешнего контура.
6.9. Прослеживание прямолинейной границы изображения
на многоградационном фоне
6.9.1. Марковская модель процесса прослеживания. Процедура про¬
слеживания линии контура является одной из разновидностей сегментации
изображения. Получим математическую модель процесса прослеживания
границы (контура) изображения, заданного на помеховом фоне, для случая,
когда эта граница является прямолинейной и достаточно протяженной [122].
Пусть плотность распределения вероятности интенсивностей элемен¬
тов фона на локально однородном участке сцены равна /ф (J), а соот¬
ветствующая плотность для объекта — /с (J). Для определенности будем
считать, что отношения фон/шум и сигнал/шум достаточно велики. Тогда
эти распределения будут близки к нормальным. Выборки фона и объекта
подвергаются бинарному квантованию с порогом а. При этом необходимо
оптимизировать значение порога, при котором максимизируются веро¬
ятности недостижения на каждом шаге прослеживания заданной макси¬
мально допустимой ошибки £тах выделения контура.
Рассмотренная задача относится к общей задаче срыва слежения ко¬
нечного автомата и является разновидностью многошаговой процедуры
принятия решения [42].
В качестве состояния марковской цепи, описывающей процесс про¬
слеживания прямолинейной границы, возьмем значение вектора ошибки,
296
Гл. 6. Выделение границ изображений
соединяющего точку в сцене с истинной контурной точкой, и значение
выделенного ЭВ 7. Будем считать, что события превышения значения ин¬
тенсивности в каждой ячейке сетчатки порогового значения независимы
и для области фона их вероятность равна ρψ, а для области изображения
объекта — рс. Выбор состояния цепи поясняется на рис. 6.68, а, а процесс
смены состоянии — на рис. 6,68, б. На первом рисунке представлен строб
Рис. 6.68. К определению состояния и переходной вероятности марковской цепи
прослеживания. Линия истинного контура проходит через правую колон¬
ку его элементов. В качестве ЭВ контура на рассматриваемом шаге принят
вектор г, при этом получилась ошибка ε, задаваемая вектором 1, который
соединяет кратчайшим путем начало вектора ошибки с точкой истинного
контура. Данное состояние цепи обозначается как (1,г). Рис. 6.68, б фик¬
сирует момент выделения следующего ЭВ контура равного 1 + г. При
этом имеется вектор ошибки, равный 1. Таким образом, произошла смена
состояний цепи: (1, г) -+ (1,1 + г) свероятностью р (1, г/1,1 + г) = р|рс,
где рф = 1 — рф. Ниже приводится выражение для (1,*)-й строки матрицы
вероятностей переходов цепи.
1,г
1,1 -i
1,-г
-1,1-г
1,-1
1,-1 + г
1, г
1,1 + *
м
РфРсРс
—2—2
РфРсРс
—2—3
РфРс
0
0
Рф
£ф
Обобщенная структура матрицы вероятностей переходов (МВП) G для
произвольного етах приведена на рис. 6.69, а, а на рис. 6.69, б представле¬
ны положения строба прослеживания относительно линии контура для О
и ±1-го блоков матрицы.
Первый квадрат в матрице G определяет МВП для £max = 1, второй —
£тах — 2 для и т. д. Блоки в матрице G имеют размер 8x8 элементов,
причем необозначенные блоки являются нулевыми. Таким образом, при
Smax = 1 прослеживание контура описывается матрицей вероятностей
переходов 24-го порядка, при етах = 2 матрицы 40-го порядка и т.д.
Блоки В\, В2 и В% задают блуждание внутри изображения объекта,
блоки Во, В-1, В-2 — внутри фона, а блоки I — на границе фон-
объект. Все блоки с одним и тем же индексом одинаковы. В зависимости
от значения £тах некоторые состояния в крайних блоках объявляются
6.9. Прослеживание прямолинейной границы изображения
297
г
-4
-3
-2
-1
0
1
2
3
4
-
-4
Во
ш
L
-3
ш
В-2
r
-2
ш
В-
В-2
q
-1
Во
В-ι
Ώ
£
:=ι
ε =
2
= 0
loo
£з
ε4
1
ho
ίϋ
£l
2
hi
£2
B\
3
£1
Bl
4
B^
h.
h
Въ
ВЛ
_
а
Рис. 6.69. К получению марковской цепи, описывающей процесс прослеживания
прямолинейной границы: а — структура матрицы вероятностей переходов цепи,
б — положения строба прослеживания относительно границы 0-го и ± 1-го блоков
матрицы
поглощающими. Матрица G имеет блочно-ленточную структуру (не более
чем три ненулевых блока в каждой строке), что облегчает ее анализ.
Перейдем к рассмотрению задач прослеживания контуров изображе¬
ний объектов, которые можно решить с помощью данной модели. Методи¬
ка решения этих задач базируется на теории цепей Маркова с матрицами
вероятностей переходов, приведенными к нормальному виду Фробениуса
и теории срыва слежения конечного автомата [196, 43]. Особенность рас¬
сматриваемой здесь задачи в том, что переход от частной задачи срыва
слежения к общей состоит в накладывании ограничения не на время
пребывания автомата в состояниях определяющих срыв слежения, а на
сами состояния подмножеств Αβ и ΑΊ, соответствующих объекту и фону.
6.9.2. Анализ процесса прослеживания прямолинейной границы
изображения.
1. Распределение вероятностей достижения максимальной ошибки
£тах за к шагов. Объединим все состояния цепи, соответствующие значе¬
ниям ошибки, большим £тах, в одно подмножество. При любом значении
ε цепь имеет три состояния поглощения: {(ε0,1 + г), (ec, 1), (ε0,1 — г)},
соответствующие достижению максимальной ошибки прослеживания ес
в теле изображения, и три состояния поглощения {(εψ, —1 — г), (εψ, —1),
(εψ, -1 -М)}, соответствующие достижению максимальной ошибки про¬
слеживания в области фона. На рис. 6.70 приведены МВП для значений
максимальных ошибок ε0 = εψ = 1. Значения вероятности поглощения Sj,
1 + / Ο ,i 0,1 + Ϊ
298
Гл. б. Выделение границ изображений
ооооооооо
Те?
101010 о оо о ©
Ικζ Ιεχ, la, εζ
ОООООООООеЗГ^аОООО ^аО
K“ ^ ^ Ιεζ ^
I ОО© © О ©ОО© . и © © © © © О ц "и ©
-Г Ιεζ Ιεζ la,
J, ©©©©©©©©©С^©«Й©©©©СцТс^О
r-Γ ^ εζ
, т^Н
Ιεζ
, Is? к?
РГ ^ ,KJ4 и о
© © «^ Ιε£ Ιεζ © © © © © о © |с£ © ε*, а, о © ^
1а,
εζ εζ
© © Ίέζ ^ о © © |^ © © © ^ © © о о ©
с£ ^ a,
г«
wi ‘
©©^^«■©©©^©©©a, © © -^ © © a,
f^o a, a, 'εζ
Гв?
' ίβζ
i* © © Й*
e?·
k?
ί·*?
©©©^•©©©©©тГЗг^·©©©
Ιεζ
lS
°°|§ S? *? © © © ° ° ° ° ° ft Й О о
*ί
' Ti ё
^ ° ° ° ^
^ сц ε£
Те? о la, *jj-£ Τε£ «!?■<
©ΒζΟ^ΟΟΟ^ΟΟΟ^Ο^^ΟΟΙβξ
-rS «'§3 ° °ί§
к?
Ιεζ
оТко©о©'^©©©©©©©,с^©©©©©
ικ^ а, εζ
©1^©©©εζοΐίεζ©©©©©εζ©©©©©
ο © © © © Ιεζ ©©©©©©©©©©©
© /3 © © © ©
,ε^,εξ©©©©©^ο©©©©
© Ιεζ © © © 1ε^ ^ © © © © ©|ε5© © © ο ©
ε£ Βζ «$ ^
Η ίΟΝ° ° ° ΙΟ κΓ ю” ° ьсГ с<Г С<Г ° υρ ° ° кГ ьо" °
Л 7 Л 7 3 ~ X ^ X -Ϊ 3 ΐ ” ~ X ΐ
7 Л 7 Λ I ° 3 о '. о i ° 3 ~ 3 - " 3
Рис. 6.70. МВП для значений максимальных ошибок ε0 = εψ
6.9. Прослеживание прямолинейной границы изображения
299
дополняют до единицы сумму остальных элементов j-й строки. В связи
с высоким порядком матрицы G текущую вероятность W[k] достиже¬
ния подмножества поглощения Αε целесообразно вычислять с помощью
рекуррентных соотношении
п—5
W[k\ = ^2 fiW[k — г], причем W[0] = ^ [0], (6.9.1)
г=1 i£.Ae
где fc, г = 1,2,..., п — 5 — коэффициенты характеристического полинома
матрицы G, п — общее количество состояний цепи до объединения всех
поглощающих состояний в одно.
2. Средняя длина контура 1Ср до достижения ошибки £тах. Величина
1ср является математическим ожиданием в распределении W[k] и нахо¬
дится в соответствии с выражением
6
1Ср = Σ У^п W[n] = 1 - W[n], (6.9.2)
is=l
где коэффициенты yv равны
j = 1,2,... ,η — 6. (6.9.3)
Для случая, когда вероятности достижения подмножества Αε мало
изменяются за один шаг прослеживания (а именно такой случай и пред¬
ставляет практический интерес), величину /ср находят с помощью более
простого соотношения
п—6
(с ? = Ψ[0] = Σν*· (6-9.4)
ι/=1
3. Влияние результатов обнаружения линии контура на процесс
прослеживания. При определении двух первых точек контура, задающих
ЭВ 7(0), возможны ошибки, определяющие качество дальнейшего про¬
слеживания линии контура. Эти ошибки определяются начальным векто¬
ром 7?[0] цепи. Варьируя его, можно оценить влияние условий обнаруже¬
ния на процесс прослеживания контура.
4. Выбор оптимального порога квантования а. Данная задача явля¬
ется одной из наиболее важных при обработке изображений. Она может
быть решена следующим образом. Зададим критерий качества в виде
Zcp —> max или alcpψ + Ысрс max, где /срф, Zcpc — соответственно,
средние длины контура области фона и сигнала до достижения макси¬
мальных значений ошибок εψ и еСу а и 6 — весовые коэффициенты.
Определяя в соответствии с выражением (6.9.2) средние значения длин
1Ср для выбора значений порога а, выбираем то значение а = а0ПТ, при
котором выполняется данный критерий.
На рис. 6.71 и 6.72 приведены графики характеристик процесса про¬
слеживания прямолинейной границы изображения для случая, когда рас¬
пределения вероятностей интенсивностей фона и изображения являются
300
Гл. 6. Выделение границ изображений
Рис. 6.71. Зависимость средней длины Рис. 6.72. Зависимость величины оп-
выделенного контура от величины по- тимального порога квантования от
рога квантования по интенсивности разности математических ожиданий
интенсивностей сигнала и фона
нормальными с математическими ожиданиями Шф и тс и дисперсиями
σΦ = ас = 1 Для £т&х — 1 [122]. Из них видно, что величина порога,
определяемого в соответствии с критерием обеспечения максимальной
средней длины выделенного контура, приближенно равна 0,5 (тс + Шф).
6.10. Обсуждение результатов
Важнейшим условием использования описанных в части I методов
контурного анализа является наличие самих контуров и их аналитиче¬
ских представлений. Проблема выделения контуров изображений заклю¬
чается в обнаружении одной или нескольких его взаимосвязанных точек
и дальнейшим прослеживанием, т.е. последовательным, точка за точкой
без разрывов, определением всех остальных точек до момента замыкания
контура.
Наиболее просто эта проблема разрешается для бинарной сцены. При¬
менение алгоритма Розенфельда дает возможность проследить контур би¬
нарного (силуэтного) изображения сколь угодно сложной формы. Поэтому
значительная часть методов выделения контуров изображений в много¬
градационной сцене сводится к получению бинарной сцены и применению
алгоритма Розенфельда. Эта задача не проще задачи выделения контуров
изображений непосредственно по исходной многоградационной сцене, но
переход к бинарной сцене упрощает проблему с методической стороны.
Чаще всего бинарная сцена получается из многоградационной путем
сравнения яркости каждого его пиксела с заданным пороговым значением.
В том случае, когда эта яркость ниже порогового значения, в соответ¬
ствующую ячейку ОЗУИ бинарной сцены заносится нуль, а в противном
случае — единица.
Основная сложность формирования бинарной сцены связана с опре¬
делением оптимального в соответствии с принятым критерием порогового
значения яркости.
6.10. Обсуждение результатов
301
Критерии оптимальности так или иначе связаны с обеспечением мини¬
мальных искажений формы изображения объекта, задаваемой контуром
этого изображения в бинарной сцене. Если порог ниже оптимального,
то форма изображения объекта искажается за счет сильного влияния
фоновых шумов. При этом контур изображения расширяется вследствие
включения в его состав участков фона. Когда порог выше оптимального,
то форма изображения искажается из-за того, что значительная часть
точек этого изображения отнесена к фону.
Если пороговый уровень ограничения сцены по яркости одинаков
для всех пикселов сцены, т.е. носит глобальный характер, то наимень¬
шее искажение форм достигается, когда средняя яркость фона во всех
пикселах сцены одинакова и также одинаковы средние яркости рас¬
положенных в этой сцене изображений объектов. В качестве критерия
выбора порогового уровня был рассмотрен критерий минимальной дли¬
ны суммы всех контуров изображений.
Более эффективный критерий получения бинарной сцены с минималь¬
но искаженными формами объектов требует выработки индивидуального
для каждого из изображений порогового уровня ограничения по яркости.
Критерий выбирается из условия обеспечения максимума коэффициента
формы изображения. В этом случае важно не абсолютное увеличение дли¬
ны выделенного контура, вызванное действием помех (как при глобально¬
оптимальном пороге), а относительное, с учетом размера изображения.
Важной задачей при решении проблемы выделения контура изо¬
бражения является обнаружение контура в условиях сложной фоновой
обстановки, когда фоновые шумы представляют собой статистически
неоднородное случайное поле.
Если контур обнаружен, т.е. определена одна или несколько его точек,
то анализируя форму перепада яркости на границе фон/объект можно
определить локально-оптимальный пороговый уровень ограничения изо¬
бражения по яркости. При этом отпадает необходимость в трудоемкой
процедуре получения бинарных срезов изображения и их анализа при
варьировании этого уровня, начиная от уровня средней яркости сцены.
Обнаружение контура представляет собой задачу обнаружения сигна¬
ла в виде скачка яркости на фоне слабокоррелированных (широкополос¬
ных флуктуационных шумов) и сильно коррелированных статистически
неоднородных фоновых шумов.
Рассмотренный в данной главе один из видов обнаружителей исполь¬
зует для формирования статистики принцип согласованно-избирательной
фильтрации. Такой фильтр является квазиоптимальным устройством, так
как не учитывает форму низкочастотной части энегетического спектра изо¬
бражения. Но его несомненным преимуществом является инвариантность
структуры фоноподавляющего звена к виду спектра фоновых шумов. Кор¬
ректируя пороговый уровень принятия решения по результатам измерения
дисперсии фонового шума на выходе фильтра, можно учесть влияние изме¬
нений, вызванных неоднородностью постоянной составляющей и дисперсии
яркости фоновых шумов, а также декремента затухания их АКФ.
302
Гл. 6. Выделение границ изображений
Разработанная методика построения характеристик обнаружителя
дает возможность оценить его эффективность. Рассмотренный на базе
СИФ обнаружитель позволяет обосновано подходить к решению задачи
обнаружения контура, учитывая статистические характеристики фо¬
новых шумов и конфигурацию скачка яркости на границе фон/объект.
В этом плане его применение более предпочтительно по сравнению с об¬
наружением контуров на основе многочисленных масочных операторов
(Робертса, Собела и др.).
Другим рассмотренным видом обнаружителей контура является об¬
наружитель, принимающий решение на основе t-критерия. Он устанав¬
ливает статистическую достоверность разницы средних яркостей двух
смежных массивов. При обнаружении в сцене такой разницы яркостей
один из этих массивов располагается в области фона, а другой — в обла¬
сти изображения. В этом случае граница между массивами является гра¬
ницей фон/объект. t-обнаружитель инвариантен к виду распределений
вероятностей яркостей фона и объекта, а при соответствующем простран¬
ственном расположении анализируемых на статистическую достоверную
разницу средних яркостей массивов — и к углу наклона линии контура.
Один из заслуживающих внимания подходов к прослеживанию линии
контура базируется на прогнозировании положения последующей контур¬
ной точки по информации о яркости предыдущих, уже выделенных точек
контура. Благодаря такому прогнозу сужается область нахождения этой точ¬
ки, что позволяет выделить контур непосредственно по многоградационной
сцене, не прибегая к формированию на ее основе бинарных по яркости сцен.
Эффективность и трудоемкость выделения линии контура зависит от
количества априорной информации об изображении, так как аналитическое
представление контура лежит в основе ИХ СИФ обнаружителя. Но обычно
ни форма изображения, ни такие его параметры, как масштаб и угол пово¬
рота, заранее неизвестны. В результате как единственно возможная реша¬
ется задача обнаружения одной или нескольких смежных контурных точек.
Существует один важный класс объектов, для которых можно принять
решение об обнаружении контура их изображений не по одной, а по
значительно большему количеству его точек. Таким классом являются
объекты антропогенного вида, границы изображений которых содержат
протяженные прямолинейные фрагменты. Если фрагмент такой границы
расположить вертикально к направлению строк сцены и сложить яр¬
кости строк, через которые проходит этот фрагмент, то возникает ска¬
чок яркости, значительно превосходящий по величине значение яркости
остальных изображений в других точках суммарной строки. В результате
накопления энергии всех пикселов прямолинейного участка контура изо¬
бражения создаются благоприятные условия его обнаружения. Поскольку
ориентация прямолинейного фрагмента контура произвольна, описанную
выше процедуру необходимо проводить для целого ряда сцен, получаемых
последовательным поворотом исходной на небольшой угол. Решение об
обнаружении в этом случае принимается только для той сцены, в которой
эта граница расположена вертикально.
6.11. Задачи и упражнения
303
В заключение отметим, что проблема выделения контуров изображе¬
ний в реальных сценах далека от ее положительного решения. По крайней
мере, эффективность используемых обнаружителей границ по сравне¬
нию с возможностями, например, человека, несоизмерима. Но несомненно,
один из успешных путей совершенствования автоматических обнаружи¬
телей границ изображений состоит в рассмотрении его как одного из видов
квазиоптимальных обнаружителей на базе общей теории обнаружения
зашумленных сигналов [52, 55], не отказываясь при необходимости от
различных эвристических решений в качестве вспомогательных для более
глубокого понимания проблемы.
6.11. Задачи и упражнения
1. Какой вид имеют выражения ИХ СИФ для следующих видов скачков яркости:
1. s = {0, 0, 0, 1, 1, 1, 1};
2. s = {0; 0,25; 0,5; 0,75; 1};
3. s = {0; -0,2; -0,4; -0,6; -0,8; -1};
4. s = {2; 2; 4; 6; 8; 10; 10; 10}.
2. Найти выходные отсчеты СИФ при подаче на его вход одного из следующих
скачков:
1.8 = {0; 0,2; 0,4; 0,6; 0,8; 1};
2. s = {0; 0; -1; -1; -1}
3. s = {0; 0,5; 0,8; 0,6; 1; 1}
3. В чем заключаются отличия между работой согласованного и согласованно¬
избирательного фильтров? бб
Рис.
4. С какой характеристикой изображения согласован согласованно-избиратель¬
ный фильтр?
5. Почему согласованно-избирательный фильтр не пропускает постоянной со¬
ставляющей яркости сцены?
6. В чем заключается целесообразность применения огласованно-избирательных
фильтров в качестве формирователей статистики для работы обнаружителей
границ изображения?
7. Какой вид имеет частотный коэффициент передачи согласованно-избира¬
тельного фильтра?
8. Какие факторы способствуют нормализации отсчетов фонового шума на вы¬
ходе согласованно-избирательного фильтра?
9. Почему ИХ фильтра, избирательно-согласованного с идеализированным ли¬
нейным скачком яркости, имеет всего два неравных нулю отсчетов?
щ
1
i
1
1
III
i
1
i
i
1
ύ
i
1
6.73
i
111
!!#
H
m
1
44m
II
304
Гл. 6. Выделение границ изображений
10. В чем заключается разница между обычным и стандартным согласованно¬
избирательным фильтром?
11. Почему фильтр, избирательно-согласованный с прямоугольным скачком яр¬
кости, наилучшим образом подавляет сильно коррелированные шумы?
12. Из каких соображений выбирается количество параллельно работающих ка¬
налов обнаружителя прямолинейной границы?
13. Как должны быть расположены по отношению к границе изображения окна
^-обнаружителя?
14. При каком значении tst можно считать разность средних значений яркости
следующих выборок статистически достоверной:
1) {0,66; 0,16; 0,72; 0,52; 0,99; 0,78; 0,96; 0,06; 0,59; 0,54; 0,36; 0,35};
2) {0,22; 0,18; 0,20; 0,69; 0,87; 0,01; 0,10; 0,37; 0,53; 0,14; 0,23; 0,28}.
15. Сформировать по алгоритму Розенфельда контуры следующих бинарных изо¬
бражений (рис. 6.73).
Глава 7
ОБРАБОТКА ИЗОБРАЖЕНИЙ С ПРЯМОЛИНЕЙНЫМИ
ПРОТЯЖЕННЫМИ ГРАНИЦАМИ
7.1. Введение и постановка задачи
Объекты с протяженными прямолинейными границами чаще всего
являются антропогенными. Это возделанные участки почвы, дороги, кана¬
лы, различные элементы конструкций машин и механизмов и др. Задача
обработки таких изображений представляют собой частный случай задач
обработки изображений произвольной формы. Существуют, по крайней
мере, две причины, позволяющие рассматривать обработку изображений
с протяженными прямолинейными границами как отдельную задачу:
1) высокая информационная ценность данных изображений, вызван¬
ная их антропогенным характером;
2) простая форма границ изображений дает возможность существенно
уменьшить необходимое количество операций при их обработке, связан¬
ных с обнаружением границы и подавлением ошибок квантования грани-
Рис. 7.1. Фрагмент ландшафтной сцены размером 61 х 161 пикселов (а), б — от¬
счеты яркости вдоль одной строки, виг — отсчеты яркости при накоплении
соответственно 50 и 100 строк
306
Гл. 7. Изображения с прямолинейными границами
цы, вызванных оцифровкой, по сравнению с общим случаем, когда изо¬
бражение имеет произвольную форму.
На рис. 7.1, а показан фрагмент данной сцены, форматом 61x161 пик¬
селов, состоящий из части лесного массива, опушки с хорошо выраженной
прямолинейной границей, изображения тени и части примыкающей к
ней поляны. На рис. 7.1, б даны отсчеты яркости вдоль строки фраг¬
мента. В районе 26-28 пикселов виден скачок яркости при переходе от
изображения лесного массива к изображению отбрасываемой им тени.
На рис. 7.1, в и г показаны отсчеты яркости, полученные в результате
накопления яркостей 50 и 100 строк. Хорошо видно снижение дисперсии
яркости с ростом числа накапливаемых строк. Скачок яркости на границе
лес/тень становится все более пологим, что объясняется отклонением
линии границы от вертикали.
В данной главе с аналитических позиций рассматриваются вопросы,
связанные с искажениями формы таких границ при вводе изображения
объекта в одноразрядное ОЗУИ с матричной структурой и квадратной
формой пиксела со стороной Δ = 1. В ячейках такого ОЗУИ, относящихся
к внутренним точкам изображения, будут занесены единицы, а в ячей¬
ках, относящихся к фону — нули. В области границы фон/изображение
А
Г
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0,
1
0
0
0
0^
*1
1
1
1
1
\
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
Рис. 7.2. Пример квантования прямолинейных границ на квадратной сетчатке: а —
записанное в ЗУ бинарное цифровое изображение; б — исходная А и прокванто-
ванная Г прямолинейные границы
в зависимости от степени перекрытия изображения с поверхностью со¬
ответствующего пиксела в ячейку ОЗУИ будет записан либо ноль, либо
единица (рис. 7.2, а). Этот процесс назовем квантованием линий границы
(контура) изображения.
При квантовании форма изображения объекта искажается. Ошибки
квантования зададим контуром = {ψ {t)}0 z_1, определяемым из соот¬
ношения
Г = А + (7.1.1)
где А = {α(ί)}0;2_ι — контур бинарного по яркости изображения до
ввода, а Г = {/т(^)}0 ζ-ι — код К0НТУРа после ввода в ОЗУИ (рис. 7.2, б).
Если граница прямолинейная, то ЭВ а (t) контура А представляют собой
последовательность одинаковых комплексных чисел а = |а| ехр{г<^}, где
ψ — угол наклона прямолинейной границы.
7.1. Введение и постановка задачи
307
Как было условлено в п. 1.1, в ячейку ОЗУ заносится единица, ко¬
гда площадь Sim изображения в пределах пиксела квадратной формы с
единичной площадью не меньше половины площади пиксела, т.е. если
sim > 0,5 δχ Sy = 0,5Δ2 = 0,5. (7.1.2)
Процесс квантования на сетчатке является цепочкой последователь¬
ных решений об обнаружении изображения в каждой граничной клетке.
При этом часть граничных ячеек изображения будет отнесена к фону
(«пропуски»), а часть — к объекту. Как пропуски, так и правильные обна¬
ружения контурных ячеек приводят к искажению формы изображения,
что учитывается контуром Ψ. Детерми¬
нированный характер формы границы
и последующая интерполяция обуславли¬
вают сильную коррелированность ошибок
квантования и их зависимость не только
от размера пиксела, но и от угла на¬
клона ψ линии границы. В связи с этим
общепринятый подход к оценке влияния
ошибок квантования [131,133], при кото¬
ром они считаются независимыми между
собой и некоррелированными с сигналом,
в рассматриваемом случае неприемлем.
Значение угла φ разобьем на восемь
одинаковых секторов (рис. 7.3). Сектор, для
которого 0 ^ φ < π/4, назовем базовым
и присвоим ему номер и = 0. Назовем так¬
же базовыми ЭВ и элементы кода границы
в пределах этого сектора. Прямолинейный
отрезок назовем полузакрепленным, если его начальная точка совпадает
с узлом клетки. Рассмотрим несколько положений прямолинейной границы
в базовом секторе относительно клетки сетчатки (пиксела) (рис. 7.4). Из
центра нижней стороны клетки (точка F) проведем перпендикуляр до
пересечения с линией границы. Этот перпендикуляр назовем зондом и
обозначим через Ah. Для случая на рис. 7.4, а площадь изображения
в пределах квадрата равна Sim = — 0,5А; + Ъ = Ah, где Ь — АС, к =
π
2
Рис. 7.3. Номера секторов угла
наклона границы
Рис. 7.4. Взаимные положения прямолинейной границы и клетки сетчатки
308
Гл. 7. Изображения с прямолинейными границами
= tg ψ. Отсюда следует, что условие S^ 0,5Δ2 эквивалентно условию
Ah ^ 0,5. Это условие сохраняется и для случая, приведенного на рис. 7.4,
б. Таким образом, клетка сетчатки относится к изображению, если длина
зонда составляет не менее половины длины стороны клетки. В данной
главе на основе анализа вырожденной дискретной цепи Маркова, опи¬
сывающей процесс квантования незашумленной прямолинейной границы
изображения на квадратной сетчатке, решаются следующие задачи:
получение аналитическим путем кода Г = (7(2)} границы и его АКФ;
оценка влияния угла наклона φ линии границы и ошибок квантования
на искажение контура изображения; уменьшение и полное подавление
ошибок квантования; идеальное восстановление формы проквантованной
границы и выбор оптимального шага квантования.
7.2. Квантование границы, проходящей через базовый сектор
Под выполнением шага квантования в пределах базового сектора бу¬
дем понимать действие по формированию контурных клеток в пределах
одной колонки сетчатки. Приращение ординаты Ау границы за один шаг
в пределах базового сектора будет Ау = кь —
= tgip, а максимальное приращение Ауп
^ 1. Поэтому за один шаг прямая может пройти
не более чем через две соседние вертикально
расположенные клетки (рис. 7.5). Максимально
возможное значение зонда в верхней клетке,
равное 0,5, достигается лишь для полузакреп-
ленной границы при φ = π/4. Поэтому, при пе¬
ресечении границей двух соседних вертикально
расположенных клеток площадь изображения
в верхней клетке будет меньше, а в нижней —
больше 0,5. В результате нижняя клетка будет
отнесена к изображению, а верхняя — к фону.
Отсюда следует
Положение 1. За один шаг квантования
находящейся в базовом секторе прямоли¬
нейной границы возможно появление только
одной контурной клетки. Поскольку кь ^ 0,
то с ростом числа шагов квантования площадь под линией границы
не уменьшается. Поэтому в коде границы могут присутствовать только
элементы вида 1, 1 + г, г.
Элемент г приводит к появлению за один шаг двух клеток, относя¬
щихся к изображению, что в соответствии с положением 1 невозможно.
Положение 2. В базовом секторе код прямолинейной границы изо¬
бражения содержит только два элемента: 1 и 1 + г.
Рассмотрим вопрос о структуре кода проквантованной границы. При¬
ращение ординаты границы за один шаг равно Ау = кь = tg φ. Пусть
величина п/к — точно целое число. Если прямая полузакреплена, то
Рис. 7.5. Прохождение пря¬
молинейной границы через
соседние вертикально рас¬
положенные клетки
7.2. Квантование границы, проходящей через базовый сектор
309
через п/кь = п/Ау шагов она снова пройдет через узел сетчатки. Пусть
ngr — значение п, при котором получается минимальное целое число
Τμ = Tlgr/kb. (7.2.1)
Число шагов квантования, равное Τμ, является периодом последова¬
тельности элементов кода проквантованного отрезка прямолинейной гра-
Чь.
lgr
%
V
V
ьг
αι
«2
аъ
«4
*5
*6
αι
г
-У
Ь,
^7
0
с
1 \ аг а, а4 а5 а6 а,
Τμ
Τμ
Рис. 7.6. Образование периодической структуры цепного кода прямолинейной гра¬
ницы (къ = 3/7, Τμ = 7, ngr = 3)
ницы (рис. 7.6), т.е. 7 (t) = 7 (t 4- αΤμ), а = 0,1,2... Здесь и далее а —
целочисленная константа.
Положение 3. Код прямолинейной границы изображения в базо¬
вом секторе является периодической последовательностью комплекс¬
ных чисел 1 и 1 + г с периодом в Τμ элементов, задаваемым величиной
тангенса угла наклона прямой къ = η8Γ/Τμ, причем ngr и Τμ — взаимно
простые числа.
Величина ngr = &&Τμ равна количеству элементов 1 + г в одном
периоде кода границы. Если къ = tg(p — иррациональное число, то ве¬
личина Τμ не может быть целым числом и код границы теряет свойства
периодичности. С общих позиций в данном случае можно полагать, что
период является бесконечно большим. Однако из-за конечной разрядности
используемых чисел величина Τμ всегда будет ограниченной.
Рассмотрим структуру кода полузакрепленной линии границы в пре¬
делах одного периода Τμ. С этой целью для каждой п-й строки определим
номера tn столбцов сетчатки, в которых находится первая контурная
точка. Например, для случая, показанного на рис. 7.6, в первой строке
(п = 1) первая контурная точка появляется во втором столбце (ίχ =2),
во второй строке (п = 2) — эта точка появляется в четвертом столбце
(£2 =4) ив третьей строке (п = 3) — в седьмом столбце (t3 = 7). Именно
этим контурным точкам будет соответствовать элемент кода 7 = 1 + г,
а остальным — элементы кода 7 = 1. Вначале найдем абсциссы / точек,
в которых прямая принимает значения, равные половине стороны клетки,
у = 0,5; 1,5; 2,5;... = п — 0,5, п = 1,2,3,... , ngr. (7.2.2)
310
Гл. 7. Изображения с прямолинейными границами
Если такая точка прямой является еще и абсциссой центра клетки,
т.е. I = t — 0,5 = 0,5; 1,5; 2,5;..., где t — целое число, равное номеру
столбца, для которого выполняется одно из равенств (7.2.2), то значение
зонда Ah = 0,5 и данная клетка будет первой контурной клеткой в п-й
строке. При этом у = кь (t — 0,5) = η — 0,5, а величина t будет номером tn
колонки с первой контурной точкой в η-й строке. Поэтому
tn = t = п/кь - 0,5 (1/кь - 1). (7.2.3)
В общем случае значение абсциссы Z, удовлетворяющее равенству
(7.2.2), будет нецелым числом. Это значит, что равенство (7.2.2) выполняет¬
ся правее центра клетки, расположенной в ]/[ — столбце, где ]Z[ — целая
часть числа Z, и первая контурная точка в η-й строке сетчатки будет
расположена в следующем, (]/[ 4- 1)-м столбце. Пусть Е (Z) — ближайшее
целое число к числу Z, не меньшее, чем Z. Тогда номер столбца с первой
контурной точкой в η-й строке будет равен
tn = Е (п — 0,5/кь 4- 0,5) ^ Е (п/кь) > п = 1,2,... ngr. (7.2.4)
Каждый переход с нижней строки на верхнюю связан с появлением
элемента кода 7 = 1 4- г. Для η-й строки это происходит в столбце tn —
— 1, η = 1,2,... , ngr. Между этими периодами элементы кода равны
7=1. Если нумерацию элементов кода внутри периода Τμ начать не с
единицы, а с нуля, то номера элементов кода 7 = 1 4- г будут равны
tn —2,η = 1,2,... ,ngr. Таким образом, внутри периода элементы кода
можно разбить на ngr групп. Каждая группа состоит из одного элемента
7 = 1 4- г и последовательности элементов 7 = 1: {14-г,1,1,...,1}.
Приращение за один шаг точного значения tn равно
Atn = (п 4- 0,5/Аъ + 0,5) - (п - 0,5/кь 4- 0,5) = 1/кь.
Поэтому каждая группа будет содержать либо ]1 /&ь[, либо ]1 /кь[ 4-
4- 1 элементов кода. Следовательно, внутри периода Τμ код будет иметь
локальную периодическую структуру и поэтому величину Τμ целесооб¬
разно в дальнейшем называть макропериодом. Значение величины Ζ, при
котором выполняется условие (7.2.2), зависит от номера шага квантования
и количество элементов кода в текущей группе определяется предысто¬
рией процесса квантования.
Пример 1. Найдем в пределах одного макропериода код границы изображе¬
ния с къ — 3/7 (рис. 7.7). Дробь 3/7 является несокращаемой, поэтому макропери¬
од кода Τμ = 7, число групп ngr = 3, а группы будут состоять либо из двух, либо
из трех элементов кода. По формуле (7.2.4) определяем номера tn — 2,п = 1,2,3
элементов кода 7 = 1 4- г в пределах макропериода:
П = 1; *1-2 = £(^|+0,5) - 2 = Я(12/з)-2 = 0;
п = 2; *2-2 = е(^ + 0,5) -2 = £(4)-2 = 2;
η = 3; ί3 - 2 = е{^·I + Ο,δ) - 2 = Е (6 V3) - 2 = 5.
7.3. Цепной код границы
311
Таким образом, нулевой, второй и пятый элементы кода будут равны 1 -f г,
а первый, третий, четвертый и шестой — равны 1: Г = {... ;1-М;1;1-М;1;1;
1 -J- г; 1;... }.
Проведенный анализ относится к случаю, когда граница проходила
через начало координат. Однако, все полученные результаты, связан¬
ные с периодичностью элементов кода и его локальной внутрипериодной
структуры, не меняются при произвольном перемещении изображения
в плоскости сетчатки. Если угол наклона границы сохраняется, то такое
перемещение приведет лишь к изменению номера элемента кода, соот¬
ветствующего определяемому столбцу.
7.3. Цепной код произвольно ориентированной прямолинейной
границы
Определим вначале цепной код границы А В, проходящей через пер¬
вый сектор, т.е. и = 1 (рис. 7.7). В этом случае угол φ наклона границы
находится в пределах π/4 ^ φ < π/2. Ре¬
шение данной задачи проведем путем
выполнения трех следующих операций:
— перевод исходной границы в базо¬
вый сектор (и = 0);
— определение кода границы в базо¬
вом секторе;
— нахождение элементов кода исход¬
ной границы по элементам кода в базовом
секторе.
При отражении фигуры относитель¬
но оси, проходящей под углом Θ, зер¬
кальный ЭВ 7ref(£) проквантованной гра¬
ницы связан с исходным ЭВ 7 (t) =
= l7(i)|exp{t<p(i)} (ί = 0,1,2,...) coot-
ношением (1.5.11)
7ref(i) = |7(0I exp{-#(*) - 26»]}. (7.3.1)
Если θ = π/4, то находящийся в первом секторе исходный ЭВ пово¬
рачивается на угол Δφ(ί) = π/2 — 2φ{ί). Поскольку аргументы φ(ί), t =
= 0,1,2,..., стандартных ЭВ кратны π/4, то угол поворота Δφ(ί) также
будет кратен величине π/2.
Поэтому подобная операция не приведет к нарушению стандартности
ЭВ границы и переход из первого сектора в базовый целесообразно вы¬
полнять с использованием операции отражения. Прямолинейный участок
границы А'В' при отражении фигуры относительно оси, проходящей под
углом θ = π/4, будет иметь угол наклона <^ref = — φ(ί) 4- π/2, т.е. она
окажется в базовом секторе. Код проквантованной границы АВ, распо¬
ложенной в первом секторе, будет состоять из двух элементов: 7 = 1
и 7 = 1 + г. В соответствии с выражением (7.3.1) элемент 7 = г =
Рис. 7.7. К определению кода
границы, проходящей через пер¬
вый сектор
312
Гл. 7. Изображения с прямолинейными границами
= ехр{г7г/2} перейдет в е° = 1, элемент η = 1+г сохранит свое значение,
а угловой коэффициент ее станет равным кь = 1/к. Обобщим теперь
полученные результаты на произвольный номер сектора. Так как при
повороте ЭВ на угол, кратный π/2, стандартность значений элементов
кода не нарушается, то результаты, полученные для базового сектора
(и = 0), распространяются на секторы с номерами и = 2,4 и б, а для
нулевого сектора и — 1 — на секторы с номерами и — 3,5 и 7.
Если φ — угол наклона границы, то номер сектора, через который она
проходит, и = ]4φ/π[. Приведенный к базовому сектору угол наклона (рь
границы задается соотношением
π 2м + 1 — (—l)u"
*>-2 4 .·
В табл. 7.1 даны значения 1рь для произвольных углов наклона φ
прямолинейной границы, порядок смены ЭВ 71 и 72 базового сектора
элементарными векторами при переходе в другой, произвольный сектор.
Таблица 7.1
и
0
1
2
3
4
5
6
7
<рь
Ψ
7г/2 — φ
φ — π/2
π — φ
φ — π
3π/2 — φ
φ — 3π/2
2π — φ
71
1
г
г
-1
—г
—г
—г
1
72
1 + г
1 + г
-1 + г
-1 + г
— 1 — г
— 1 — г
1 — г
1 — г
<Рь = (-!)“
Поскольку код границы находится по величине кь = tg <£>&, а заданной
является величина Л: = tg <^>, то при определении характера связи между
кь и к надо иметь в виду, что величину к = tgip надо задавать в виде
натуральной дроби с сохранением знаков числителя и знаменателя, т.е.
Таблица 7.2
и
0
1
2
3
к
0 ^ к < 1,
1*1 <1
а ^ 0, b > 0
1 ^ к < оо,
|*|^1
а > 0, 6 > 0
—оо < к < —1,
1*1 >1
а > 0, 6^0
-1 ίξ к < 0,
1*1 ίξ 1
а ^ 0, 6 < 0
кь
к
1/к
-1/к
—к
и
4
5
6
7
к
0 ^ к < 1,
1*1 < 1
а ^ 0, 6 < 0
1 ^ fc < 00,
1*1 ^ 1
а < 0, 6 < 0
—оо < к < —1,
1*1 >1
а < 0, 6^0
-1 ^ к < 0,
1*1 ^ 1
а < 0, b > 0
кь
к
1/к
-1/к
-к
в виде к = tg<p = α/b. В табл. 7.2 отражена связь между величинами к,
|Л|, а, 5, номером сектора и и значением кь.
Пример 1. Пусть к = —5/4, т.е. а < 0,b > 0. Граница (см. табл. 7.2)
находится в шестом секторе (и = 6) и кь = —1/к = 4/5. Макропериод Τμ =
= 5, количество групп ngr = 4. По формуле (7.2.4) находим ίχ — 2 = 0, ti —
7.4. Марковская модель процесса квантования прямолинейной границы 313
— 2 = 1, £з — 2 = 2,£4 — 2 = 4. Таким образом, отрезок цепного кода длиной
в макропериод состоит из пяти элементов, причем первые четыре равны η =
= 1 -f- г, а пятый — η = 1: {... , 1 4- г, 1 4- г, 1 4- г, 1 4- г, 1,.. .}. По табл. 7.1
определяем, что в шестом секторе элементу 1 4- г будет соответствовать элемент
1 — г, а элементу 1 — элемент —г. В результате один макропериод искомого кода
будет иметь вид {... , 1 — г, 1 — г, 1 — г, 1 — г, —г,...}.
Учитывая связь между кодом произвольно ориентированной прямоли¬
нейной границы и ее кодом в базовом секторе, в дальнейшем остановимся
лишь на случае когда 0 ^ φ < π/4, т.е. и = 0.
7.4. Марковская модель процесса квантования прямолинейной
границы
Ранее были рассмотрены основные закономерности формирования цеп¬
ного кода прямолинейной границы изображения и выяснена его структу¬
ра. Однако они не дают возможности осуществить аналитическим путем
исследование процесса квантования. В данном разделе будет получена
математическая модель процесса, позволяющая провести такой анализ.
Выше было отмечено, что количество элементов в группе и, следова¬
тельно, значения самих элементов кода зависят от предыстории процесса
квантования. Так как данный процесс детерминирован, то следует ожи¬
дать, что он будет описан вырожденной цепью Маркова. В этой цепи
вероятности перехода будут равны либо нулю, либо единице, а матрица
вероятностей переходов (МВП) будет перестановочной. Для таких матриц
можно в общем виде получить спектральное представление для вероят¬
ностного вектора [130].
7.4.1. Синтез цепи Маркова. В качестве состояния цепи примем ве¬
личину зонда Ah, 0 ^ Ah ^ 1, граничной клетки. Если у = kb{t 4- 0,5),
t — 0,1,... )Τμ — 1, величина ординаты точки границы по центру t-го
столбца, то величина зонда представляет собой дробную часть у:
Aht = Е{у) - у- (ΤμΕ(у) - ngrt - 0,5 πετ)/Τμ = yt/Τμ. (7.4.1)
Рассмотрим, какие последовательности образуют значения зонда
в пределах одного макропериода.
Положение 4. В пределах макропериода нет двух одинаковых зна¬
чений зонда Aht· Допустим обратное. Пусть зонды Δhm и Ahj, m ф j\
m,j = 0,1,... , Τμ — 1, равны между собой, т.е.
Е[кь(т + 0,5)] - кь{т + 0,5) = E[kb{j 4- 0,5)] - kb(j 4- 0,5).
Тогда Е[кь(т 4- 0,5)] — E[kb(j 4- 0,5)]kb(m—j). Правая часть этого вы¬
ражения, как разность целых чисел, также будет целым числом. Поэтому
минимальное значение п = т — j, при котором величина кьп является
целым числом, равно Τμ, a \m — j\ ^ Τμ. Следовательно, допущение
о равенстве двух значений зонда внутри макропериода не имеет места.
Определим значения зонда Aht, соответствующие различным состояни¬
ям цепи. Число ΤμΕ(у) — ngrt в выражении (7.4.1), как разность произве¬
314
Гл. 7. Изображения с прямолинейными границами
дений целых чисел, также будет целым числом. Если ngr — четное число,
то числитель yt останется целым числом при любом t. Так как 0 ^ yt <
< Τμ, то в соответствии с Положением 4 в пределах одного макропериода он
примет значения всех целых чисел в пределах от 0 до Τμ — 1 (необязательно
в нарастающем порядке): yt = 0,1,... , Τμ — 1. Поэтому значения зонда, а,
следовательно, и состояния цепи Маркова имеют вид
Aht = 0;;
_2_
Та
Та- 1
(7.4.2)
w 7 τμ
Если ngr — нечетное число, то, рассуждая аналогично, приходим к
выводу, что yt = 0,5; 1,5;... , Τμ — 0,5 и
Л, _ 0,5 1,5. 2,5. . Τμ -0,5
rp ? ηη Ϊ rp ϊ * * * ) rp *
LL -L LL -L U iu
(7.4.3)
Таким образом, цепь имеет Τμ различных состояний, которые прону¬
меруем как 1,2,... , Τμ. Зонды, соответствующие двум соседним состоя¬
ниям, отличаются на 1/Τμ. Состояния цепи периодичны с периодом Τμ.
Рис. 7.8. Граф марковской цепи, описывающей процесс квантования прямолиней¬
ной границы при кь = 3/7
Поскольку приращение зонда за один шаг квантования равно Δу = кь =
= rigr/Τμ = то s-e состояние сменяется с вероятностью, равной
единице, состоянием s + ngr = η + &&Τμ (рис. 7.8).
При таком подходе к выбору состояний процесс квантования границы
описывается вырожденной циклической цепью Маркова [43]. МВП этой
цепи для случая кь = 3/7 имеет вид (см. рис.
7.8)
1
2
3
4
5
6
7
1
'о
0
0
1
0
0
о'
2
0
0
0
0
1
0
0
3
0
0
0
0
0
1
0
П= 4
0
0
0
0
0
0
1
5
1
0
0
0
0
0
0
6
0
1
0
0
0
0
0
7
0
0
1
0
0
0
0
(7.4.4)
7.4. Марковская модель процесса квантования прямолинейной границы 315
Матрица П служит адекватной моделью процесса квантования: она
имеет порядок Τμ, тангенс угла наклона прямой кодируется номером
кьΤμ + 1 единичного элемента первой строки; смена элементов кода
С7=1на7 = 1 + г происходит при попадании в подмножество Ωχ+i,
содержащем ngr состояний.
Пусть so — номер первоначального состояния, для которого AhSo ^
^ 0,5, а (£, п) — координаты столбца и строки клетки V(t, η), кото¬
рая в этом случае будет отнесена к изображению. Тогда предыдущая
граничная клетка V(t — 1 , η — 1) будет ее левым и нижним соседом,
а обе клетки V(t — Ι,π — 1) и V(tyn) задают элемент кода 7 = 1 4- г.
Состояние sq является начальным для подмножества Ωχ+Покажем, что
это подмножество включает подряд ngr состояний цепи, от so до so 4-
4- ngr — 1. Действительно, в следующем, (so 4- 1)-м состоянии величина
зонда в клетке Vs0+1 будет Δ/ιβ0+ι = AhSo 4-1 /Τμ ^ 0,5, а приращение
зонда за один шаг квантования при ngr > 1
ngr .
Τμ Τμ^ Τμ
Поэтому величина зонда в соседней, расположенной в данной строке
слева клетке, меньше 0,5, ив качестве граничной будет выбрана клетка,
являющаяся левым нижним соседом клетки V8o+v В результате форми¬
руется элемент кода, равный 1 4- г. Такая ситуация имеет место для всех
ngr состояний: so, «о 4-1,... , so 4- ngr — 1.
Номер начального состояния для подмножества Ωχ+ι равен
*о=ДШ + 1 + (21)П*:· (7А5)
Вектор вероятностей состояний π[ί] дискретной цепи Маркова на t-m
шаге определяется как π[ί\ = 7г[0]П*, t = 0,1,2,... Компонента π^[ί],
j — 1,2,... Τμ, этого вектора равна вероятности попадания процесса за t
шагов в состояние j при заданном векторе π[0] начальных состояний.
Пример 1. Найдем элементы цепного кода за макропериод для случая кь =
= 3/7 при начале процесса из первого состояния (Τμ = 7, ngr = 3).
В этом случае π[0] = [1000000], а МВП задается выражением (7.4.4). Опреде¬
лим семь векторов вероятностей состояний и запишем их в виде матрицы
0
1
2
#о,б = 3
4
5
6
1
2
3
4
5
6
7
1
0
0
0
0
0
0
0
0
0
1
0
0
0
0
0
0
0
0
0
1
0
0
1
0
0
0
0
0
0
0
0
0
1
0
0
1
0
0
0
0
0
0
0
0
0
1
0
0
По формуле (7.4.5) находим, что подмножество Ωι+i начинается с состоя¬
ния so = 4. Оно включает подряд три состояния: 4, 5 и 6. В этих состояниях
316
Гл. 7. Изображения с прямолинейными границами
3 5 4 5 5 5
зонд соответственно равен -у-, -у-, -у-. По матрице i?o,6 определяем элементы
цепного кода контура за макропериод, начиная с положения, соответствующего
положению первого состояния цепи: {... , 1,1 -Ь г, 1,1,1 + г, 1,1 -Ь г,...}.
7.4.2. Анализ марковской модели процесса квантования. В общем
случае матрица перестановок В записывается в виде [130]:
‘ 0 0 0 ... О 1 ’
1 0 0 ... О О
„ 0 1 0 ... О О
О 0 0 ... О О
О 0 0 ... 1 О
Характеристические числа матрицы располагаются на линии окруж¬
ности единичного радиуса: λj = £J,j = 1,2,... , Τμ, где ε = exp {i2π/Τμ}.
Семейства ортонормированных правых и левых j = 1,2,... ,Τμ,
собственных векторов матрицы В равны
л Τμ - 1 Τμ
ф. —
где е^, ν = 1,2,... , Τμ, — вектор с Τμ компонентами, причем одна, г/-я
компонента равна единице, а остальные — нулю. С учетом ортонормиро-
ванности семейства векторов е„, ν — 1,2,..., Τμ, для элементов матриц
Фт = {φμ} иФ = {Ф13} получим следующие выражения: φμ = ει^Τμ~^\
фц = eli, l,j = 1,2,... ,Τμ. Определим спектральное представление
матрицы В [43]:
V·)
где матрица Dv = ΦΤΙΙ,Ι,Φ, \vv — матричная единица. На основании
выражений для элементов матриц Фти Ф для элемента матрицы Du
можно записать diju = £ι(τ*-ι/)+ίν, ν = 1,2,... ,Τμ. При возведении
матрицы в целую положительную степень t результирующая матрица
остается перестановочной. Ее ленточная структура сохраняется, однако
единица в каждой строке циклически сдвигается на t столбцов. Поэтому,
возведя матрицу В в степень с = Τμ — ngr, получим матрицу Ф, т.е. Ф =
= Вс. Так как при возведении матрицы в степень ее собственные векторы
не изменяются, а характеристические числа возводятся в ту же степень,
то спектральное представление МВП запишется как
t
Τμ
ХУС"А
π1
7.4. Марковская модель процесса квантования прямолинейной границы 317
Умножая обе части этого равенства на начальный вектор π[0] = ер,
получим независимое представление для вектора состояний цепи на про¬
извольном 4-м шаге квантования прямолинейной границы изображения:
*(Р)М = (7-4.б)
-ίμ
где
epDv = |εΡ(τ**-ι')+·?Ι/| ,
^ > j,p
j,P= 1,2,... ,Τμ, 4 = 1,2,... ,Τμ-1.
Данное представление обладает свойствами развязки по состояниям
и шагам [43]. Поэтому на его основе с помощью (7.4.6) можно записать
следующее выражение для вероятности Ρχίμ(4) попадания на 4-м шаге
в подмножество состояний Ωχ_μ при начале процесса из состояния р:
Т
р&а)= Σ =ψ-Έε1/(ι°~ρ) Σ εί>> ρ=ι,2,-,τμ.
j=Cli+i μ ν—\ j=&i+i
(7.4.7)
В последнем выражении поменяем порядок суммирования и учтем
конкретные состояния, образующие подмножество Ωχ_μ и начинающиеся
состоянием so (см. (7.4.5)). В результате получим
1 ϊμ
ρί+Μ^^Γ Σ xy(ct+i~p)· (?·4·8)
j~s0 ν—\
Введем обозначение
Tt
f(ct + j-p) = ^-Y^e^ct+j~P^i1 nPMci + J Ρ-αΤμ, (74g)
1μν,=ι [О в противном случае.
Тогда
ρι+Μ = Σ +j - р)·
so+ngr — l
(7.4.10)
Элемент 7^(4) цепного кода проквантованной границы при начальном
состоянии цепи, равном р, через найденную вероятность Ρχ^(4) в общем
случае будет иметь вид
7(р)(<) = 1 + гЛ(+»(0· (7-4.11)
В дальнейшем нас также будет интересовать выражение для отдель¬
ной компоненты 7rj^(4), равной вероятности попадания на 4-м шаге в со¬
стояние j при начальном векторе ер:
т (
^)(<) = -Ee,'(Ct+i"/,) = i1 ПРИ ct+i~p = aT^ (7.4.12)
3 Τμ^ [О в противном случае.
318
Гл. 7. Изображения с прямолинейными границами
Пример 2. Для случая, рассмотренного в примере 1, проведем анализ цепи
Маркова, описывающей процесс квантования границы. Так как къ = 3/7, Τμ = 7,
Tlgr = 3, ТО С = Τμ — ngr, Лj = £cj = £4j , £ = β*2π^.
Матрицы правых и левых собственных векторов МВП (7.4.4) будут равны
Фт = {ε^7-·^}; Ф = = 1,2,3, 4, 5,6, 7. При начальном векторе π[0] =
= ei = [1000000] необходимые для независимого определения вектора вероятно¬
стей состояний π[ί) векторы du имеют вид: ά„ = {ε7-Ι/ -f = 1,2,... ,7.
Вероятность попадания на t-м шаге в j-e состояние цепи равна (см. (7.4.12))
j = 1,2,3,4,5,6, 7, t = 0,1,2,3,4, 5,6.
Найдем распределение вероятностей попадания процесса в первое состояние
(j = 1). Вероятность π^[ί] будет равна при любом t нулю, кроме значения t, при
котором ct + j — р = 4t = 7а, а = 0,1,2,... Выполнение этого равенства возможно
лишь при а — 0, т.е. попадание в первое состояние цепи будет лишь на первом шаге,
и искомое распределение равно {1000000}. Найдем вероятность принятия элементом
кода границы значения 7 = 1 + г. Подмножество Ωχ+i, как следует из примера 1,
включает 4, 5 и 6 состояния цепи. Тогда в соответствии с (7.4.7)
pi1) .
М+г
4ί^ε7-
Σ-
.^(4ί+3)
+ ^ει'<4ί+4)+^ε,/
(4t+5)
Подставляя значения t = 0,1,2,... 6, найдем распределение моментов попа¬
дания в подмножество Ωι+i: (0,1,0,0,1,0,1}. В соответствии с этим распределением
отрезок цепного кода длиной в макропериод при первом начальном состоянии
будет иметь вид {... ; 1; 1 + г; 1; 1; 1 + г; 1; 1 4- г;... }.
В выражениях (7.4.7), (7.4.8) и (7.4.10) для элемента цепного кода 7(t)
границы параметры j и р, характеризующие соответственно сдвиг изобра¬
жения в плоскости квадратной сетчатки и начало отсчета кода, одинаково
влияют на величину В связи с этим можно сформулировать эргоди-
ческое свойство цепного кода проквантованной прямолинейной границы
изображения
7iW=7(* + P), * = 0,1,2,... , (7.4.13)
где тj (t) — код границы после сдвига изображения, j — параметр сдвига,
р — смещение начала отсчета кода. В соответствии с этим свойством код
границы после сдвига изображения в плоскости сетчатки может быть най¬
ден путем смещения элементов кода любой проквантованной реализации.
Эргодическое свойство позволяет находить любые характеристики про¬
цесса квантования прямолинейной границы как по одной реализации кода
длиной 2Τμ элементов, так и по Τμ реализациям длиной Τμ элементов.
7.5. АКФ цепного кода прямолинейной границы
При анализе процесса квантования целесообразно дать количествен¬
ную оценку степени разрушения образа прямолинейной линии. Такую
оценку можно получить, построив кластер проквантованных прямолиней¬
ных границ. Центр кластера Л будет задаваться точкой исходной грани¬
7.5. АКФ цепного кода прямолинейной границы
319
цы, а различные реализации проквантованной границы образуют в вы¬
бранном многомерном пространстве компактную область точек, рассеян¬
ных относительно центра. Расстояния от каждой точки области до центра
служат количественной мерой степени искажения линии границы при ее
квантовании. Данный кластер представляет собой множество выходных
сигналов контурного фильтра, импульсная характеристика (ИХ) которого
согласована с линией границы.
Благодаря прямолинейности формы границы вид кластера будет ин¬
вариантен к преобразованию масштабирования изображения. Зависимость
структуры кластера от поворота изображения определяется значением к =
= tg φ, которое является параметром марковской модели процесса кванто¬
вания (см. п. 7.4) и задает порядок Τμ и значащие диагонали МВП П.
Для оценки влияния преобразования сдвига изображения на вид кла¬
стера надо найти АКФ последовательности значений вероятности Pi+i(t)
принятия элемента кода границы на t-м шаге квантования при начальном
состоянии р (см. (7.4.7), (7.4.8), (7.4.10)). Если предположить, что в результа¬
те сдвига изображения его граница может занимать по отношению к лини¬
ям сетчатки произвольные положения, то такое преобразование приводит
к произвольным смещениям элементов цепного кода, что, собственно гово¬
ря, и характеризуется АКФ. Рассмотрим несколько представлений АКФ
для проквантованной прямолинейной границы изображения, проходящей
в базовом секторе, и ее наиболее важные свойства.
7.5.1. Развернутое представление АКФ. АКФ η(τ) проквантованной
границы можно найти, принимая во внимание, что сдвиг элементов кода
происходит либо при вариациях начального вектора цепи π[0] = ер,р =
= 1,2 ,...,Τμ, либо номера шага квантования t,t = 0,1,2,... ,Τμ — 1.
Сначала определим АКФ последовательности из значений вероятности
π^ρ\ί) попадания на t-м шаге в j-e состояние цепи при начальном век¬
торе ер. Применяя выражение (7.4.12) и учитывая комплекснозначный
характер величины ε, запишем
Τμ
у^£v(ct+CT+j-p)
Σ
£-&{ct+j-p)
υ=1
Θ=1
При τ = 0 величина 77^(0) = 1. При т ф 0 выражение для АКФ
содержит две группы слагаемых — с равными и отличными друг от друга
индексами ν и Θ. Слагаемое первой группы можно записать как
ε»(α+οτ+3-ρ)£-θ(α+ί-ρ) = и = т ф 0
Количество таких слагаемых будет Τμ и при суммировании по ν в со¬
ответствии с учетом тождества
Σ«“· =
= 0
(7.5.1)
320
Гл. 7. Изображения с прямолинейными границами
они дадут ноль. Слагаемое второй группы равно e)sucretciy е).
При суммировании этих слагаемых по ί с учетом тождества (7.5.1) по¬
лучим, что r]jP\r) равно единице при г — 0, а для остальных значений
т — нулю. Данный результат становится очевидным, если учесть, что мы
находим скалярное произведение ортонормированных векторов ёр,р =
= 1,2,... ,Τμ.
Найдем теперь АКФ последовательности вероятностей pi+i (t) при¬
нятия элементом цепного кода на t-м шаге значения 7 = 1 + г как
АКФ суммы последовательностей π·(ί), j = 1,2, ...ngr. Так как АКФ
имеет интегральный характер, то она не зависит от порядка следования
образующих ее слагаемых. Поэтому АКФ η (г) будет инвариантна к но¬
меру состояния j = so при условии сохранения количества состояний
подмножества Ωχ+ί. Массив номеров состояний, образующих это подмно¬
жество, должен включать подряд ngr = кьТр номеров. С учетом данного
замечания для упрощения выкладок величины sq и р положим равными
so = 0, р = 1 и опустим в обозначениях верхний индекс. В результате
получим
Τμ — 1 Τμ Tlgr — 1
η(τ) = Σ Λ+<(ί + r)P1+i(t) =jrΣ^°Τ Σ (»*■ - \β\)εβν·
t=0 Μ"=1 /3=-(п,г-1)
Поменяем порядок суммирования в последнем выражении и исполь¬
зуем тождество (7.5.1). Так как процесс квантования прямолинейной гра¬
ницы имеет периодический характер, то зададим главные значения шага
t и задержки т в виде
О ^ M{t} < Τμ, 0 ^ М{т} < Τμ. (7.5.2)
Тогда выражение для АКФ запишется в виде
η(τ)
Σ (ngr ~ \β\) при сг ± β = αΤμ,
β=~ (ngr — 1)
О в противном случае.
(7.5.3)
Это представление АКФ η (т) назовем развернутым. Его исследование
связано с решением уравнения в целых числах:
ст ± β = αΤμ, (7.5.4)
относительно целых значений неизвестных г и а при варьировании сво¬
бодного члена β. В соответствии с данным уравнением каждое значение β,
входящее в выражение (7.5.3), связано с определенным значением г. Хотя
формально данная сумма включает 2ngr слагаемых, но отсчет АКФ для
заданного конкретного т может формироваться одним или несколькими
слагаемыми ngr — \β\. Для получения значений АКФ η (т) с помощью раз¬
вернутого представления надо решить уравнение в целых числах (7.5.4),
установить, какие значения коэффициента β соответствуют заданному
значению г и подставить их в выражение (7.5.3). Из общих свойств лю¬
бого АКФ, а также из периодичности цепного кода границы следует,
7.5. АКФ цепного кода прямолинейной границы
321
что η (т) = η (-т), η(τ) = η(τ db αΤμ). Поэтому η (г) = η(τ — Τμ) =
= η (Τμ — τ), т.е. в пределах одного макропериода каждое значение АКФ
повторяется дважды.
Найдем величину т, соответствующую в уравнении (7.5.4) /0 = 0. При
этом уравнение примет вид τΤμ( 1 — кь) = αΤμ. Откуда т = αΤμ/πξτ. По¬
скольку т — целое число, то а должно нацело делиться на величину ngr,
т.е. в данном случае принимает ряд значений: а — 0, ngr, 2ngr,... Этому
ряду ставится в соответствие ряд значений т: т = 0,Τμη^, 2TMngr,...
Но так как т должно удовлетворять еще и условию (7.5.2), то из данного
ряда подходит лишь т = 0. Поэтому а — 0 и 77(0) = ngr = кТ'μ.
Для нахождения остальных решений уравнения (7.5.4) необходимо
иметь хотя бы одно ненулевое решение. Удобнее всего найти его корень
τι, положив значение /0 = 1. Тогда остальные ненулевые решения
уравнения определяются как [134]
τβ = Μ{βπ}9 β = -1, ±2, ±3,... , ±(ngr - 1). (7.5.5)
Для получения решения т\ исходное уравнение перепишем в виде:
τχΤμ(1 — кь) + αΤμ +1 = 0, а отношение коэффициентов при неизвестных
Τμ (1 — кь)/Τμ = 1 — кь представим в виде цепной дроби [134]. Тогда
η = ϋί{(-1)<-4-ι},
где t — количество звеньев разложения величины 1 — кь в цепную дробь;
θΐ-ι — знаменатель (£ — 1)-й подходящей дроби для 1 — кь. После опре¬
деления τχ с помощью выражения (7.5.5) находим остальные решения т
уравнения (7.5.4) при β = — 1, ±2, ±3,... , ±(ngr — 1). В соответствии
с (7.5.2) при полученных значениях т АКФ будет отличаться от нуля.
Пример 1. Получим развернутое представление АКФ η (т) для прямолиней¬
ной границы изображения с кь = Ζ/Ί, Τμ = 7, ngr = 3, с = 4. Формула (7.5.4)
принимает вид
. ч ί Σ (3 ~ 101) ПРИ 4τ±β = 7α,
V{r) = < /з=о
[О, в противном случае.
При т = 0 значение АКФ равно т(0) = кьΤμ = 3. Так как знак при а
не играет роли, уравнение (7.5.4) принимает вид 4т 4* 7α ± β = 0. Представим
отношение коэффициентов при неизвестных т и а, равное 4/7, в виде цепной
дроби, отбросим последнее звено и переведем ее в натуральную. Получим 1/2.
„ .„41-8 + 7—1 „ „
Составим разность дробей - - + - = ——— = —. Приведем дроби к общему
знаменателю и отбросим его: — 4 · 2 + 7 · 2 + 1 = 0.
Сравнивая полученное выражение с уравнением 4т + 7α ± β = 0, видим, что
т = τι = — 2,/0 = 1. Главное значение т в данном случае будет М{—2} = 7 —
-2 = 5.
По формуле (7.5.3) получим η (5) = 2. На основании полученного решения
и уравнения (7.5.5) найдем, какие решения соответствуют значениям β = — 1 и ±
±2. Результаты расчетов для β и т представим в виде табл. 7.3.
322
Гл. 7. Изображения с прямолинейными гранищми
Рис. 7.9. АКФ цепного кода прямоли¬
нейной границы с кь = 3/7
Таблица 7.3
β
0
1
-1
2
-2
τ
0
5
2
3
4
Получили пять значений для т, причем
одному значению β соответствует только
одно значение т. Для двух значений т,
равных единице и шести, коэффициент β
отсутствует и поэтому η (1) = ?7 (6) =
= 0. Результаты расчетов данной АКФ по
формуле (7.5.3) показаны на рис. 7.9.
7.5.2. Компактное представление АКФ. Развернутое представление
АКФ позволяет находить значения η (т), задаваясь каждый раз упорядо¬
ченными значениями коэффициента β = -1, ±2, ±3,... , ±(ngr — 1). При
этом значения т следуют в произвольном, заранее неизвестном поряд¬
ке. Поэтому, если с помощью (7.5.3) находится значение АКФ η (т = то),
то необходимо вычислять ряд ненужных значений т до тех пор, пока
не встретим значение т = то. Найдем теперь другое, свободное от этого
недостатка представление АКФ η (т). Величина свободного члена урав¬
нения τΤμ( 1 - кь) ± β = αΤμ обладает свойством, обеспечивающим для
всех β ± αΤμ одно и тоже значение АКФ. Действительно, учитывая, что
ат\ — целое число, получим η (βτι) = η[{β ± Τμ) τχ\ = η (βτχ ± ατχΤμ) =
= ν(βτι)- Периодичность АКФ значений приводит к тому, что в пределах
макропериода имеются следующие две области ωχ и ω2 значений β по
ngr — 1 не равных нулю отсчетов η (г) (кроме 77(0) = ngr) (рис. 7.10, а):
ωχ = {1? 2, . . . , 7lgr — 1}, OJ2 = {Τμ — Tigr + 1, · . . > Τμ — 2, Τμ — 1}.
ο
Область главных
модифицированных
значений β
ωι
J 1 1
1 2 w -1
gr
я T — 7i
ω
2
T-n+l
Область главных значений β
Область главных
модифицированных
значений β
ωι
Т —и
Областылавных значений β
т>-}
β
>
г-1 Г.
Рис. 7.10. Области значений коэффициента β в пределах главного макропериода:
а — ngr < Τμ/2, б — ngr > Τμ/2
7.5. АКФ цепного кода прямолинейной границы
323
Если эти области не перекрываются, то между ними находится об¬
ласть сиз из Τμ — 2ngr — 1 отсчетов, в которых АКФ равна нулю: из =
= {ngr, ngr + 1,... , Τμ — Tigr}, Величины β = Μ{β}, удовлетворяющие
условиям 0 ^ β ^ Τμ — 1, назовем главными значениями этого коэф¬
фициента. Так как отсчеты АКФ в областях ωχ и ω2 эквивалентны, то
целесообразно ввести понятие модифицированного главного значения β:
Μ*{β}
Μ{β}, если /3 = 0 или Μ{β} G ωχ,
< Τμ - Μ{!3}, если Μ{/3} G ω2,
ngr, если Μ{/3} G (J3.
(7.5.6)
Из данного определения следует, что Μ*{β} = М*{— β}. Для по¬
лучения искомого представления АКФ выразим коэффициент β через т
и подставим результат в формулу (7.5.3). В уравнении τΤμ(1 - кь) ± β =
= αΤμ в качестве неизвестных используем а и /3, а величину τΤμ(1 -
— кь) будем рассматривать как варьируемый за счет т свободный член
уравнения. Учитывая, что с — Τμ — ngr — Τμ — &&Τμ, запишем: β +
+ αΤμ -f ст = 0. Если принять β — —ст, то при этом αΤμ = 0 и а = 0.
Данное значение а входит в область его допустимых значений. Используя
в развернутом представлении АКФ значение β = — ст и применяя его
модифицированное главное значение Μ*{β} = М*{—ст} = М*{ст},
получим следующее представление АКФ, которое назовем компактным:
ф} = lngr - м*{-г} при Μ{-τ}€ωιΛω2) (?5?)
[2ngr — Τμ при М{—т} G ωχ Л Ш2-
Выражение для η (т) в ситуации, когда часть значений М{ст} од¬
новременно принадлежат областям ωχ и ω2, получается в соответствии
с (7.5.3) путем суммирования значений АКФ для обоих случаев, т.е.
η(τ) = ngr - Μ{ί3} - Τμ + Μ{β} - ngr - Τμ.
В развернутом представлении АКФ величина β задавалась в пределах
0,1,... ,±(ngr — 1), а величина а при этом получается произвольной.
В данном же случае величина а фиксируется на уровне а = 0, а коэффи¬
циент β приобретает произвольные значения, которые за счет перехода
к модифицированному главному значению находятся в интервале от 0
до ngr. В компактном представлении АКФ можно пользоваться заданием
коэффициента β в виде β = ст, что по сравнению со случаем, когда β =
= —ст, приведет к взаимной смене областей ωχ и о>2, в которое попадает
получающееся значение β. При этом модифицированное главное значе¬
ние /3, по которому определяется отсчет АКФ, не меняется.
Пример 2. Найдем с помощью компактного представления АКФ η (г) для
границы с характеристиками кь = 5/7, ngr = 5, Τμ = 7, с = 2.
В этом случае область ω\ состоит из значений β = {1,2,3,4}, а область
CJ2 из значений β = {3,4,5,6}. Видно, что эти области перекрываются и ну¬
левых значений АКФ не будет. Выражения (7.5.6) и (7.5.7) для М*{ст} и η (т)
324
Гл. 7. Изображения с прямолинейными гранищми
принимают вид
М*{ст} = М*{2т}
Г М{2т}, если 0 ^ М{2т} ^ 4,
у 7 — М{2т}, если 3 ^ М{2т} ^ 6,
, ν _ I 5 — М*{2т} при β = -т = 0,1,2,5,6,
^ \ 3 при β = —т — 3,4.
Задаваясь последовательными значениями т, получим
77 (0) = 5 — М*{0} = 5 — 0 = 5,
77(1) = 5 — М*{2} = 5 — 2 = 3, М{2т} бел,
η (2) = 3, М{2т} G ωχ Λ α>2,
η (3) = 5 - Μ*{6} = 5-1 = 4, М{2т} € ω2>
η (4) = 5 - Μ*{8} = 5-1 = 4, Μ{2τ} в ел,
η (5) = 3, М{2т} е ωι Λ ω2,
η (6) = 5 - М*{12} = 5-2 = 3, М{2т} G ω2.
7.5.3. Прямое представление АКФ. Компактное представление по
сравнению с развернутым значительно облегчает расчеты, но не позво¬
ляет проанализировать поведение АКФ при изменении значений къ =
= tg φ. Для получения такой возможности приведем без детального вы¬
вода еще одно представление АКФ, условно названное прямым, в котором
η (т) явно зависит от къ и Τμ. Нахождение прямого представления АКФ
основано на выражении модифицированного главного значения М*{ст}
(см. (7.5.6)) и величины ngr через къ и Τμ, и подставлении найденного
значения М*{ст} в выражение (7.5.7). В результате получим
η(τ)= <
ΗΤμ - Μ*{τΤμ (1 - кь)} при Μ{τΤμ (1 - kb)} G ώχ Λω2,
Τμ (2къ - 1) при Μ{τΤμ (1 - къ)} G ωχ Λ ω2,
0 при Μ{τΤμ (1 — къ)} G ω3.
(7.5.8)
Вычисление АКФ η (т) связано с анализом взаимного расположения
областей ел, ω2 и ω3 (рис. 7.10) значений коэффициента β = М*{ст}.
С изменением къ = πξτ/Τμ их взаимное расположение также меняется,
так как их положение определяется величинами ngr и Τμ. В табл. 7.4 при¬
ведены значения АКФ, рассчитанные на основе прямого представления.
Пример 3. Запишем представление АКФ для кь = 3/7 и кь = 5/7. Для
кь = 3/7 формулы табл. 7.4 принимают вид
77(0) = 3; 77(1) = 0; 77(2) = Т^Зк - 1) = 2;
77(3) = Τμ( 1 - 2к) = 1; 77(4) = Тц(Ьк - 2) = 1.
Соответственно, для кь = 5/7 получаем
77(0) = 5; 77(1) = Τμ(2& - 1) = 3; η(2) = Т^2к - 1) = 3;
77(3) = Τμ(2 - 2к) = 4; 77(4) = Γμ(5λ: - 3) = 4.
7.5. АКФ цепного кода прямолинейной границы
325
Таблица 7.4. Прямые представления АКФ
τ
η(τ)
Интервал для
k = tg φ
0
0 ^ k ^ 0,2
Τμ (5k - 2)
0,2 < k ίξ 0,25
Τμ (1 - 3k)
0,25 < k < 1/3
0
1/3 ^ k ζ 0,4
4
Τμ (5k - 2)
0,4 <C k ^ 0,5
Τμ (2 - 3k)
0,5 < k ^ 0,6
Τμ (2k - 1)
0,6 < k < 2/3
Τμ (5k - 3)
2/3 ^ k ζ 0,75
Τμ (3 - 3k)
0,75 < k ζ 0,8
Τμ (2k - 1)
0,8 < k < 1
T
η(τ)
Интервал для
k = tgip
0
/гТ„
0 О < 1
1
0
0 ^ k ίζ 0,5
Τμ (2k - 1)
0,5 < k ^ 1
0
0 ^ k ζ 1/3
2
Τμ (3k - 1)
1/3 < k ζ. 0,5
Τμ (1 - k)
0,5 < k ζ 2/3
Τμ (2k - 1)
2/3 < k < 1
0
0 ^ k ζ 0,25
Τμ (4k - 1)
0,25 < k ζ 1/3
3
Τμ (1 - 2k)
1/3 < k ίξ 0,5
Τμ (4k - 2)
0,5 < k ^ 2/3
Τμ (2 - 2k)
2/3 < k ^ 0,75
Τμ (2k - 1)
0,75 < k < 1
По мере роста т в прямом представлении АКФ происходит сильное
дробление интервалов для η(τ). Это приводит к громоздкой записи зна¬
чений АКФ при больших значениях т. Однако отсчеты АКФ, полученные
для ограниченного количества значений аргумента на основании свойств
АКФ, приведенных ниже в п. 7.5.4, позволяют получить достаточную ин¬
формацию о всей АКФ. Отметим также, что полученные выше выражения
для АКФ относятся к последовательности Pi+i(t) вероятностей принятия
на t-м шаге квантования кода контура значения η = 1 + г. Данная АКФ
связана с АКФ К(т) цепного кода контура соотношением
К(т) = η(τ)+ Τμ, Οζτ<Τμ. (7.5.9)
Действительно, учитывая, что элемент кода границы, проходящей
в базовом секторе, в общем случае имеет вид η — l + iPi+i(t), для АКФ
границы можно записать
τμ-ι τμ-1
к{т) = Σ [1 + (*)][! - + τ)]=Τμ + ίΣ P1+i(t) +
t—0 t—Ό
Τμ-1 Τμ~ 1
+ * ^2 ^1+г(£ + 7")+ Pi+i(t)Pi+i(t + т).
t=о *=0
Так как последовательность Pi+i(t) за макропериод содержит ровно ngr
единиц, а остальные ее элементы равны нулю, то первая и вторая сум¬
мы в последнем выражении одинаковы. Учитывая, что последняя сумма
равна η(ί), получим приведенные выше выражения для К{т).
7.5.4. Свойства АКФ η(τ).
1. Максимальное значение: η(т) = η(0) = ngr = ΙζΤμ.
2. Периодичность: η(τ) = η(τ ± αΤμ).
326
Гл. 7. Изображения с прямолинейными границами
3. Внутрипериодная симметрия: η(τ) = η(—τ) = η(Τμ — τ).
4. Непрерывность значений. АКФ 77(7-) принимает за макропериод
каждое целое значение в интервале от 0 до ngr = кТ'μ. Благодаря свой¬
ству внутрипериодной симметрии каждое, не равное 0 или ngr значение,
встречается ровно два раза.
5. Сумма всех элементов АКФ. В пределах макропериода АКФ со¬
держит два одинаковых набора значений от 1 до ngr — 1 (свойства 3 и 4)
Τμ~1 о
и одно значение 77(0) = ngr (свойство 1). В результате Σ η(т) =ngr, т.е.
т=О
сумма всех значений АКФ за макропериод равна квадрату количества
групп элементов в коде проквантованной границы.
6. Взвешенная сумма элементов АКФ:
Т — 1
Σ τη=0>5Τμ(ν - !)·
т=О
7. Нули АКФ. Нули АКФ имеют место, когда существует область о>з
значений коэффициента /3, т.е. при условии Τμ > 2ngr или 0 ^ к <
< 0,5. С учетом главного значения корня уравнения τΤμ( 1 — къ) ± β =
= αΤμ следует выражение для значений т, при которых 77(7*) = 0: т =
= М{тх(пег + j)}> 3 = 0,1, · · · ,Τμ- 2ngr. В частности, η(1) = η(Τμ -
— 1) = 0. Количество нулевых значений АКФ равно Τμ — 2ngr + 1,
а значащих — 2ngr — 1.
8. Вещественность и неотрицательность значений АКФ. Из развер¬
нутого представления АКФ (7.5.3) следует, что η (τ) либо равна нулю, либо
η(τ) = ngr — /3, τ = 0,1,... , Τμ — 1. При этом значения β не превышают
положительного числа ngr = кьТ'μ. Поэтому ни одно из значений АКФ
не может быть отрицательным числом, т.е. η(τ) ^ 0.
Рассмотренные выше свойства относились к АКФ η (т) последователь¬
ности Pi+i(t) вероятностей появления на t-м шаге квантования элемента
кода 7 = 1+г. Данная АКФ отличается от АКФ К(т) комплекснозначного
кода проквантованной границы изображения на величину Τμ (см. п. 7.5.3).
Поэтому свойства АКФ К(т) просто связаны со свойствами АКФ 77(г).
Важным моментом, который необходимо при этом отметить, является
вещественность ее значений, т.е. Im К{т) = 0.
7.6. Зависимость ошибок квантования границы
от преобразований масштабирования и поворота
Участок проквантованной границы из Τμ элементов назовем репрезен¬
тативным. Такой участок, полученный при векторе начальных вероятно¬
стей π [0] = ер, обозначим как Г^ = {7^ W)o τ -v пРичем> ПРИ Р = 1
верхний индекс опустим. Модель (7.1.1) проквантованной границы запи¬
шется в виде Г^А -I- А = {c>;(t)}0 ^= {^^(£)}ог _v
р = 1,2,... ,Τμ. Для составляющих модели (7.1.1) в пределах базового
7.6. Зависимость ошибок квантования
327
сектора получим
Τμ
У]7(/,)(0 = ^(1 + М. Iir^ll =τμ( ι + h),
t=1
τ
Σ“(<) = τ#*( 1 + Μ, ||Α||2 = Γμ(ΐ + kli (7.6.1)
t=i
Τμ
5>W(f) = 0, ||фМ|| = T^kb-k2b).
t=1
Отметим, что данные выражения сохраняют свой вид при любом зна¬
чении р, т.е. не зависят от сдвига начальной точки контура. При масшта¬
бировании угол поворота рассматриваемого участка границы не меняется,
а также сохраняется положение его начальной точки. Преобразование
приводит к изменению количества стандартных ЭВ, составляющих пря¬
молинейную границу. Условие репрезентативности обеспечивает посто¬
янство значений ЭВ проквантованной границы в пределах макропе¬
риода. Отсюда следует, что код репрезентативного участка границы
не изменяется. Поэтому преобразование масштабирования изображе¬
ния не оказывает влияния на уровень ошибок квантования прямоли¬
нейного участка его границы.
Для оценки влияния на уровень ошибок квантования угла поворота
изображения и сдвига начальной точки проквантованного участка его кон¬
тура рассмотрим основные соотношения при согласованной фильтрации
прямолинейной границы.
Контурный фильтр, согласованный с линией такой границы, проходя¬
щей под углом ψ = arctg к, вырабатывает меру схожести фильтруемого
участка границы до и после квантования. Чем больше величина этой
меры, тем меньше влиияние на конфигурацию линии оказывает процесс
квантования, тем меньше уровень ошибок. Контур ИХ фильтра имеет вид
Λ = {λ(η)}1 = {α (τι)}1ιΤμ = {1 — кг}ιΤμ,
т.е. все ЭВ контура одинаковы и равны 1 — кг. Нормированный выходной
эффект фильтра с учетом (7.6.1) равен
г)м(т) =
1 — кг
1|А||||Г(р)||
Хл {р)№
1 + к2
1 + к
(7.6.2)
Из полученного выражения видно, что результат согласованной
фильтрации репрезентативного участка границы не зависит от шага
фильтрации т, положения начальной точки, определяемой параметром
р = 1,2,... ,Τμ и определяется лишь тангенсом угла наклона линии
границы.
Таким образом, мера схожести исходной и проквантованной участ¬
ков границы остается постоянной при любом положении начальной точки
328
Гл. 7. Изображения с прямолинейными гранищми
я, следовательно, уровень ошибок квантования не зависит не только от
масштаба, но и от выбора положения, с которого начинается процесс
квантования.
Влияние угла φ, под которым ориен¬
тирована прямолинейная граница, на уро¬
вень ошибок квантования можно оценить
по нормированной реакции согласованного
фильтра, задаваемой выражением (7.6.2).
При к = 0 и к = 1 величина ηπ = 1,
т.е. А и максимально схожи между
собой. Это значит, что при углах поворота
φ = 0 и φ = π/Α ошибки квантования
равны нулю. Анализ последнего выражения
в (7.6.2) показывает, что величина ηχ имеет
минимум при к = 0,414 (φ = 22,48°),
равный 0,91 (рис. 7.11).
Таким образом, уровень ошибок кван¬
тования становится максимальным, когда
Рис. 7.11. Зависимость меры
схожести прямолинейной гра¬
ницы до и после квантования
от тангенса угла ее наклона
линия границы проходит под углом φ = 22,48°
7.7. Подавление ошибок квантования репрезентативного
участка границы
7.7.1. Энергия среднего арифметического репрезентативных векто¬
ров ошибок квантования. Для оценки эффективности подавления оши¬
бок квантования при усреднении s проквантованных репрезентативных
участков границы Г^ с различными начальными точками найдем вы¬
ражение для энергии среднего арифметического s, 1 < s ^ Τμ, репре-
II1 s и2
зентативных векторов ошибок квантования, т.е. Gh(s) = -Σ ·
"sp=i Π
В соответствии с определением нормы вектора для Gh(s) запишем
Л ( έ έ = -7 ИФ(1\ Ф(1)) + 2(я - 1)(Ф<1), Ф(2)) +...
S \р=1 р— 1 / 5
... -Ь 2(Ф(1>, Ф(в))]. (7.7.1)
Скалярное произведение векторов ошибок квантования зависит лишь
от модуля разности индексов сомножителей. Определим с учетом выра¬
жений (7.6.1) скалярное произведение векторов ошибок квантования
(ф(р))ф(в))= - Α,Γ(Θ) - а) = (γ^,Γ^) -Τμ-1ί2Τμ.
Скалярное произведение (Г(р\Г^) равно отсчету АКФ АГ(т), т =
= \ρ — ε\, кода проквантованной границы. С учетом (7.5.8) окончательно
получаем
(Ф(р), Ф(0)) = η\р -θ\- к2Τμ = η(τ) - *?2Τμ.
7.7. Подавление ошибок квантования репрезентативного участка 329
С помощью этого результата выражение (7.7.1) преобразуется к виду
Gh (s) = 4 Т71 (S~T) + &Τμ (1 - ks). (7.7.2)
5 ί=ί
Найдем в качестве примера зависимость энергии ошибок квантования
при усреднении проквантованных репрезентативных участков границы
с к = 3/7(см. примеры 1 и 3 из п. 7.5). Выражение (7.7.2) для к — 3/7
принимает вид
Gh(s) = 4
2Σ tv(s - т) + 3s(l - ^s)
s = 1,2,3,4,5,6,7.
В табл. 7.5 приведены результаты расчета энергии ошибок квантова¬
ния по этой формуле. Из таблицы видно, что наибольшее уменьшение
Таблица 7.6
S
1
2
3
4
5
6
7
Gh (в)
1,71
0,214
0,158
0,089
0,034
0,048
0
энергии шума достигается при усреднении двух векторов ошибок кван¬
тования с соседними значениями индексов. Если бы ошибки квантования
носили статистический характер, то энергия этих ошибок монотонно па¬
дала бы с ростом объема накапливаемых выборок. В данном же случае
ошибки носят детерминированный характер и, в связи с этим, при уве¬
личении от 5 до 6 выборок энергия ошибок не уменьшается, а возрастает
с 0,034 до 0,048. При накоплении s = Τμ = 7 репрезентативных выборок
Gh(Τμ) — 0. Покажем, что данный результат носит общий характер. Из
соотношения (7.7.2) при s = Τμ получаем
Gh(s) = ±
2 V τη(Τμ - r)+kT2J 1 - ΙΐΤμ)
» L т=1
Используя свойства 3 и 6 АКФ η{τ) (см. п. 7.5.4), последнее выра¬
жение приводим к виду Gh(s) = -~2 (к2- кТ^ + кТ- кТ= 0.
Τμ
Таким образом, энергия ошибок квантования среднего арифметического
Τμ репрезентативных участков проквантованной прямолинейной границы
изображения равна нулю.
7.7.2. Условие полного подавления ошибок квантования. Опреде¬
лим скалярное произведение векторов А и границы до и после кван¬
тования: (А, Г^) = (А, А + ф(^) = (А, А) 4- (А, ф(^).
Векторы А и Ф^ ортогональны. Действительно, с учетом (7.6.1) полу-
'tμ
чим (А, ф(^)) = (l + ki)J2 Ψ(ί) = 0. Поэтому (А,Г(р)) = ||А|| = Τμ( 14-
t=1
4- к2). Так как работа согласованного фильтра сводится к образованию
330
Гл. 7. Изображения с прямолинейными г'ранигщми
отчетов в виде набора скалярных произведений вектора фильтруемого
сигнала с вектором ИХ, то из полученного соотношения следует, что
результаты фильтрации репрезентативного участка прямолинейной гра¬
ницы до и после квантования одинаковы. Поэтому согласованный фильтр
с ИХ Л = {о;5,'(п)}1 т = {1 — кг}г т , т.е. с окном шириной s = Τμ, при
фильтрации подобных участков производит полное подавление ошибок
квантования (см. (7.6.1)):
τμ
η(ί) = ^2^p\t)(l - кг) = Τμ( 1 + кг)( 1 - кг) = ||А||2.
t=i
Из этого выражения следует, что на каждом шаге он образует величи¬
ну, равную энергии репрезентативного участка исходной границы из Τμ
элементарных векторов а = 1 + кг.
7.7.3. Расчет коэффициента подавления ошибок квантования. За¬
дадим коэффициент подавления ошибок квантования репрезентативного
участка прямолинейной границы изображения как отношение энергии
сигнала А и ошибок квантования Ф^: r5 = Gx/Gh{s). Обработка заклю¬
чается в формировании среднего арифметического 5 участков границы
Г^, р = 1,2,... , s, либо, в соответствии со свойством эргодичности (см.
п. 7.5), в скользящем суммировании ЭВ границы в окне из s элементов на
Τμ шагах. Подставляя в выражение для коэффициента подавления г3 зна¬
чения числителя из выражений (7.6.1) и знаменателя из выражения (7.7.2),
получим
rt
32Τμ(1 + к2)
s — 1
2ΣΤ77(s ~ т) + вкТц( 1 — ks)
(7.7.3)
Ниже приведены полученные с помощью прямого представления для
АКФ (см. табл. 7.4) формулы для расчета коэффициента rs для значений
5 = 1,2,3,4:
S = 1; Гг = ;; + к2\ при 0 ^ к ^ 0,5;
(к — к )
s — 2; Г2 — + ) прИ 0 ^ к ^ 0,5;
(0,5 к-к2) F
s = 3; г3
1 + fc2
0,33к - к2
1 + fc2
fc - fc2 - 2/9
при 0 ^ к ^ 0,33,
при 0,33 < к ^ 0,5;
1 + А;2
з при 0 ^ к ^ 0,25,
0,25 к-к2 н
1 + к2
0,75 к -к2 - 1/8
5 = 4;
г 4 =
при 0,25 < к ίξ 0,5.
7.7. Подавление ошибок квантования репрезентативного участка 331
На рис. 7.12 представлены рассчитанные по этим формулам графики
зависимостей rs(k). Из них видно, что коэффициент подавления сильно
зависит от величины k = tg<p. В области малых значений к, 0 ^ к ^
^ Ι/s, выигрыш от накопления 5 реализаций приближенно равен s/k т.е.
пропорционален количеству накоплен¬
ных реализаций. Для одной прокван-
тованной реализации коэффициент г
растет с уменьшением к. Накопление
двух реализаций целесообразно при
значениях к, близких к 0,5, т.е. когда
величина г стремится к бесконечности.
Накопление трех реализаций целесо¬
образно при значениях к, близких к
0,33. В этих случаях коэффициент
подавления стремится к бесконечности.
Графики на рис. 7.12 иллюстриру¬
ют резонансный характер накопления
5 репрезентативных реализаций про-
квантованной границы или, в соответ¬
ствии с принципом эргодичности (см. п. 7.5), при фильтрации скользящего
среднего одной реализации проквантованной границы с окном шириной
5. Покажем, что резонанс, характеризующийся резким увеличением
коэффициента подавления г, наблюдается при значениях к = l/s. В
этом случае процесс квантования характеризуется параметрами ngr = 1
и Τμ = 5. В соответствии со свойствами АКФ η(т) (см. п. 7.5) количество
не равных нулю значений этой функции равно ngr = 1, т.е.
Рис. 7.12. Зависимость логарифма
коэффициента ошибок квантования
репрезентативных участков грани¬
цы от величины к
1 при т = 0,
0 при т = 1,2,... , Τμ - 1.
В результате взвешенная сумма значений АКФ, представляющая пер¬
вое слагаемое знаменателя выражения (7.7.3), будет равна нулю. Второе
слагаемое знаменателя, имеющее вид 5&Τμ(1 — ks), при к = l/s также бу¬
дет равно нулю. Таким образом, при значении к, приближающемся к 1 /5,
знаменатель выражения (7.7.3) равен нулю, а коэффициент подавления
ошибок квантования стремится к бесконечности.
Более общее условие достижения резонанса имеет вид к = a/s, где
а и 5 — положительные целые числа, не приводящие к значениям к >
> 1. В качестве доказательства отметим тот факт, что если в окне фильтра
скользящего среднего шириной s = 1/к достигается нулевой уровень оши¬
бок квантования, то этот же уровень сохранится и при фильтрации с окном
шириной а/к. В этом случае ошибки квантования в каждой α-й части окна
будут равны нулю, а выходной сигнал фильтра получается суммированием
его реакций на все области окна. Таким образом, для наиболее эффективного
подавления ошибок квантования необходимо осуществить фильтрацию кода
проквантованной границы по методу скользящего среднего в окне шириной
5 = a/к, где 5 и а — целые числа, 0 ^ к ^ 1.
332
Гл. 7. Изображения с прямолинейными гранищми
7.8. Идеальное восстановление прямолинейной границы
Рассмотрим решение задачи, обратной задаче квантования и состоя¬
щей в восстановлении формы исходной границы А по коду Т^р\
Восстановление при накоплении Τμ реализаций кода. Найдем сред¬
нее арифметическое Τμ репрезентативных реализаций кода Т^р\ р =
= 1,2,... , Τμ. Элемент усредненного кода Г = {7(t)}i т > полученный на
основании выражений (7.4.8) и (7.4.11), будет равен
Τμ so+ngr-1 τμ τμ
Ρ=1
j=s0 ρ—1
Сумма в данном выражении равна нулю при ct + j — ρ ф αΤμ. Учи¬
тывая, что индекс р последовательно принимает значения от 1 до Τμ,
при каждом значении £, t = 0,1,2,... ,Τμ — 1, существует решение
уравнения в целых числах ct + j — ρ = αΤμ. Принимая во внимание,
Γ.2πΊ
что ε = exp —j и а — произвольное целое число, получим
Σ Σ ev(ct+J-p) = Σ exp {Ϊ2πνα} =Τμ.
ρ=1 ν—1 ν=1
Тогда выражение для элемента кода 7 (t) принимает вид
sO+ngr ~1
7(0 = 1 + ^ Σ Τμ = 1 + ίψ=ί + ίΗ. (7.8.1)
Тр i=.о 1μ
Таким образом, при накоплении Τμ различных репрезентативных от¬
резков кода и соответствующем нормировании комплексный цепной код
получившегося отрезка контура будет равен Г = {...,l + ifc,l + ifc,l +
+ifc,... }, т.е. совпадает с кодом прямолинейной границы до ее квантования.
Восстановление границы при фильтрации скользящего среднего с ок¬
ном s = Τμ. Организуем скользящее суммирование Τμ элементов кода
одной реализации проквантованной границы. Независимо от начального
состояния ρ, р — 1,2,... , Τμ, отрезок цепного кода длиной Τμ элементов
содержит ngr = &Τμ элементов 7 = 1 + i и Γμ - ngr элементов 7 = 1.
Поэтому
ψ- Σ 7 (f + τ) = 1 + ik-
Τρ
Данное равенство соблюдается при любом значении t исходного шага
квантования. Поэтому снова приходим к соотношению (7.8.1). Следова¬
тельно, при фильтрации по методу скользящего среднего с окном в Τμ
элементов происходит идеальное восстановление формы границы. Необ¬
ходимо отметить, что накопление большего или меньшего, чем Τμ, чис¬
ла элементов кода всегда менее эффективно. В отличие от накопления
7.9. Оптимальное квантование
333
случайных независимых величин, в результате которого дисперсия ре¬
зультата уменьшается с ростом объема выборки [125], в данном случае
имеются фиксированные объемы выборки, кратные Τμ, когда дисперсия
результата строго равна нулю. Такое поведение дисперсии вызвано де¬
терминированным характером процесса квантования и свидетельствует
о наличии резонансных явлений. Заметим, что восстановление формы
исходной границы при фильтрации методом скользящего среднего в окне
шириной s = Τμ применимо для проквантованных реализаций произволь¬
ной длины £ при условии, что £ ^ Τμ. На рис. 7.13 показаны результаты
Рис. 7.13. Результат фильтрации скользящего среднего границы с кь = 3/7: 1 —
исходная граница и результат фильтрации с окном s = 7; 2 — проквантованная
граница; 3 — результат фильтрации с окном s = 3; 4 — результат фильтрации
с окном 5 = 10
восстановления формы прямолинейной границы для к = 3/7 при сколь¬
зящем суммировании в окнах с s = 3, 7 и 10. Видно, что с учетом краевых
эффектов при s = 7 = Τμ форма границы безошибочно восстановилась,
а при s = 3 < Τμ и s = 10 > Τμ восстановленная граница отличается от
исходной.
7.9. Оптимальное квантование прямолинейной границы
изображения
Задача формулируется следующим образом. Необходимо определить
оптимальный размер стороны Ах = Ау = Δ квадрата сетчатки, на кото¬
рой происходит квантование проходящей под углом φ — arctg к границы
длиной £, в соответствии со следующим практически важным критерием
тахД при Gh = 0, £ = const. (7.9.1)
Критерий обеспечивает наименьшее количество контурных клеток,
занимаемых прямолинейной границей на сетчатке, при условии равенства
нулю энергии Gh ошибок квантования после одного шага фильтрации
скользящего среднего. Если обеспечивается выполнение критерия (7.9.1),
то идеальное восстановление формы границы достигается при минималь¬
ном количестве шагов фильтрации и объеме ЗУ рецепторного поля. Выбор
оптимального шага квантования основывается на том, что для идеального
восстановления границы необходимо найти хотя бы один отсчет фильтра
334
Га. 7. Изображения с прямолинейными границами
скользящего среднего с окном s — Τμ. Для этого проквантованный участок
границы должен содержать ровно Τμ элементарных векторов, т.е. должно
быть выполнено ровно Τμ шагов квантования. Меньшее число шагов не
обеспечит безошибочного восста¬
новления формы границы, а боль¬
шее — является избыточным.
Для определения величины Δ
запишем следующее, вытекаю¬
щее из показанных на рис. 7.14
простых геометрических соотно¬
шений, выражение:
fc = tg Ψ = ^ = ™*.
Τμ cos φ
Поскольку угол φ считается
заданным, то известными явля¬
ются величины к = ηδΤ/Τμ = tgφ, sin^ и cos<p, а также Τμ и ngr.
Горизонтальная проекция границы равна i cos φ, а вертикальная — ί sin φ.
Поэтому размеры клетки будут равны
ίοοΈ,φ _ t $\ηφ
Рис. 7.14. К выбору размера пиксела при
оптимальном квантовании прямой
— Ау —
(7.9.2)
7.10. Энергетические характеристики ошибок квантования для
отрезков кодов произвольной длины
В реальных ситуациях квантование не является оптимальным, а от¬
резок прямолинейной границы — репрезентативным. В связи с этим це¬
лесообразно найти энергетические характеристики ошибок квантования
и коэффициент подавления этих ошибок для произвольного значения
длины ί проквантованной границы. Получим на основании (7.4.10) и (7.4.11)
общее выражение для энергии отрезка кода из i ЭВ:
«o+ngr-l 2
1 +г Σ f(ct + j-p) .
j=s0
С помощью результирующей формулы (П7.1.2) приложения 7.1 по¬
лучим
£ so+ngr-l
g\p) = t + Σ Σ f(ct + J-p)·
t—1 3=S0
Определим отношение r[p^ (i) энергий || А^||2 исходной границы А
и энергии rfy (£) ошибок ее квантования. Величина ||А^||2 равна
£
\\Ае\\2 = ^аа*=е(1 + к2).
t=l
7.10. Энергетические характеристики ошибок квантования
335
Для энергии ошибок квантования в общем случае можно записать
- (ifJ - A,, if > - А,) = ||Г,||2 + ||А*||2 - 2Re (г^, А,) .
Скалярное произведение проквантованной и исходной границ с учетом
выражений (7.4.11) и (7.4.10) будет равно
(г^А<)=а*£;7<'> (t) = (l-ki)J2
t=l
£ SQ+Tlgr-l
1 +
So+Tlgr — 1
‘ Σ
j=s0
So ~\~Tigr — 1
/ (ct +j-p)
gr — 1
k- f(ct + j-p)
=ί+Σ Σ f(ct+j-p)~i
t—1 j=s0
Обозначим
£ so+rigr-1
ρ{ρ)(£) = Σ Σ f(ct+j-p)·
t—1 j—so
Тогда для реальной части скалярного произведения можно записать
Re (if} - А*) = £ + kF(p) {£).
Принимая во внимание полученные выражения для ||Г
(р) и2
— А^), энергию ошибок квантования границы длины I запишем
. INI2
и
в виде
= Ik2 + (1 - 2k) F(f>) (£).
(7.10.1)
Тогда отношение энергии исходной границы и ошибок ее квантования
равно
ГМ (р\ _ 1|А*||2
°h,e
e(i + k2)
£k2 + (1 - 2k) F(p) (£) ‘
(7.10.2)
Проведем анализ данного выражения, учитывая, что значение функции
(ί) равно количеству ЭВ 7 = 1 + г в цепном коде границы за ί шагов.
Влияние начального состояния р (сдвига начальной точки кода). На¬
чальное состояние дискретной цепи Маркова задается вектором π[0]
и определяет момент первого появления в коде F^ элементарного век¬
тора 7 = 1 + г. До этого момента F^ (ί) = 0. Таким образом, величина р
определяет момент включения слагаемого (1 — 2к) в знаменателе (7.10.2).
Влияние начального состояния будет сказываться на интервале длитель¬
ностью 1 /&, в течении которого в силу детерминированного характера
процесса квантования обязательно появится один ЭВ 7 = 1 + г. При этом
коэффициент г[р^ (£) будет меняться в пределах от γ- до а .
1 Н~ к 2 к к
Особенно сильно сказывается влияние начального состояния при больших
значениях к, когда время до появления первого ЭВ 7 = 1 + г велико.
1 + кЛ
1 + Г
336
Гл. 7. Изображения с прямолинейными границами
Влияние величины к — tg φ (преобразование поворота изображения).
Рассмотрим случай малых значений к, 0 ^ к ^ 0,1, при фиксированном
значении р. До появления первого ЭВ η = 1 -f г коэффициент г[р^ (£) «
« 1 /к2, а после появления этого вектора происходит резкое уменьшение
этого коэффициента за счет того, что знаменатель становится близким к
единице. В результате г[р^ (£) « £. При значениях к = tgip близким к 0,5,
величина 1—2к в знаменателе (7.10.2) становится очень малой и гг (£)~5, т.е.
исчезает зависимость коэффициента гг (£) как от угла наклона <р, так и от
начального состояния р. Из-за скачкообразного поведения функции F (£)
зависимость коэффициента г\ (£) также носит скачкообразный характер.
Влияние длины отрезка кода. При £ = αΤμ величина (£) пере¬
стает зависеть от начального состояния и равна α&Τμ. Отсюда следует,
что для £ = αΤμ выражение (7.10.2) принимает вид
Γ1(αΤμ) = ^±§, а = 1,2,...
к — К
Так как значение функции F (£) равно количеству элементов кода η =
= 1 -f г, полученных при квантовании отрезка границы длиной £, а при
£ — Τμ эта функция точно равна &Τμ, то
где ]£/Τμ[ — целая часть числа £/Τμ. При больших значениях числа ]£/Τμ[
его дробной частью можно пренебречь и тогда
F (£) & £к при £^>кТ^.
Отсюда следует асимптотическое представление
Г1(*) = й?’ (7·10·3)
Таким образом, при £ > = ngrTμ отношение энергий исходной
границы и ошибок ее квантования стабилизируется и определяется его
значением М при £ = Τμ. При этом оно не зависит, как и следовало
ожидать, от начального состояния рис ростом угла наклона границы φ
сначала падает, достигая значения = 4,83 при к = 0,414 (φ = 22,48°),
и далее снова возрастает.
7.11. Подавление ошибок квантования границы произвольной
длины согласованным фильтром
7.11.1. Основные соотношения при согласованной фильтрации гра¬
ницы произвольной длины. Фильтр, согласованный с прямолинейным
отрезком границы длиной £, производит, как следует из (7.6.2), равновес¬
ное суммирование элементов кода проквантованной границы:
ι
р) (0 = (1 - кг) ^7(р) (*)·
t=1
7.11. Подавление ошибок квантования
337
В этом плане полученные в предыдущем разделе соотношения харак¬
теризуют сигнал на входе фильтра. Учитывая, что 7^ (t) — а + ф^ (£),
а также выражения (7.4.10) и (7.4.11), определим реакции фильтра 77л {£)
и (£) соответственно на сигнал в виде исходной границы А = {а}1£
и сигнал в виде ошибок ее квантования Ф^ = {ф^ (ί)}1 £. Первый сиг¬
нал равен 77а = Ga,£ = £ (l + к2). Для определения второго из сигналов
предварительно найдем сумму ί компонент вектора Ф^:
Σ>°” (о = Σ [τω (<) - о] =
-Σ
t=1
50+ngr-l
1 + г / (ct + j - р) - 1 - кг
= i\F{p){i) -ifcj. (7.11.1)
В результате реакция фильтра на вектор ошибок квантования выра¬
зится как
tk
4Р) (о =
(7.11.2)
щ {£) = (1 -ik) = J2 ·Ψ(Ρ) (<) = (* + 0 [^(Р) (*) -
t=l
Определим отношение сигнал/помеха (£) на выходе согласован¬
ного фильтра как частное квадрата реакции фильтра на сигнал в виде
векторов А = {а}1 £ и = {фМ (7п)}1 £:
г>1(£) _ £2 (l + А:2)
ЫР)(£)}2 [F^(£)-k£]2'
Функция (£) — к£ является периодической с периодом £ = Τμ. Это
следует из того, что функция F^ (£) в точке £ равна количеству элемен¬
тарных векторов 7 = 1 + г в отрезке кода проквантованной границы за £
шагов, а к£ — есть среднее число этих векторов за это же число шагов. Из
периодичности кода границы и следует периодичность функции (£) —
— к£. Следствием периодического характера данной функции является
возможность ее представления через главные значения на интервале £ =
= 1,2,... ,Γμ:
FΜ {I) -Ы = F^ (£) -Lk, (7.11.3)
где L = М{£} — числитель дробной части числа £/Τμ.
Коэффициент (£) подавления фильтром ошибок квантования опре¬
делим как отношение величин (£) и т·^ (£) (см. (7.11.2) и (7.10.3)):
tF^W-U£FM(£)+£2k2
9 ^ ’ [F(p) (£)]2 - 2UF{p) {£) + £2к2
Данное выражение дает возможность найти коэффициент подавле¬
ния ошибок квантования для прямолинейной, ориентированной под углом
338
Гл. 7. Изображения с прямолинейными границами
Рис. 7.15. Характеристики процесса согласованной фильтрации прямолинейной
границы произвольной длины для кь = 3/7
φ границы и длиной £ с учетом начального состояния р. На рис. 7.15
приведены графики для отношений сигнал/помеха на входе и выходе
согласованного фильтра и коэффициента подавления q (£) для р = 1, к —
= 3/7 в зависимости от длины £ границы.
7.11.2. Анализ процесса согласованной фильтрации прямолинейных
границ изображений произвольной длины.
Резонансные явления при согласованной фильтрации. Пусть £ = Τμ.
Тогда F^(l) = F (Τμ) = кТ'μ. В этом случае знаменатель выраже¬
ния (7.11.1) будет равным нулю, а отношение сигнал/помеха перестанет
зависеть от начального состояния р и становится бесконечно большим.
Данное свойство проявляется при любом £ — αΤμ.
Следует отметить, что для входного отношения г^ (£) при ί = αΤμ
также исчезает зависимость от начального состояния р, но резонансные
явления отсутствуют (см. рис. 7.15). Так как с ростом длины ί прокван-
тованного отрезка входное отношение стабилизируется на уровне, зада¬
ваемом выражением (7.10.3), то в асимптотике поведение коэффициента
q(£) подавление ошибок квантования при согласованной фильтрации
1 _j_ к2
повторяет поведение г2 (£) с масштабным коэффициентом ^.
к — к
Зависимость коэффициента подавления от длины границы. Выра¬
зим отношение (£) сигнал/помеха на выходе фильтра через главное
значение L длины границы £. Если величина £ меньше, чем Τμ, то L = £
и в соответствии с (7.11.2)
г{2р) (L) = L2
I + к
[F(p) (L) - kLf
Для произвольного значения £ с учетом данного выражения и равен¬
ства (7.11.2) получим
Лр)
г2
(*)
1 + к
[f(p) (е) - kef
= (|)2r^(i). (7.11.5)
7.11. Подавление ошибок квантования
339
Так как входное отношение сигнал/помеха г[р^ {£) слабо зависит от
длины границы, то аналогичное равенство имеет место и для коэффици¬
ента подавления согласованным фильтром ошибок квантования:
Я{р} {(■)=({)\(P){L). (7.11.6)
Отсюда следует, что выигрыш в подавлении ошибок квантования
при согласованной фильтрации растет пропорционально квадрату объ¬
ема входной выборки, но с учетом тонкой структуры величины q на
главном интервале значений £.
Усредненные по начальным состояниям энергетические характери¬
стики ошибок квантования на выходе фильтра. Энергия суммы компо¬
нент вектора ошибок квантования за £ шагов в соответствии (7.11.1) равна
= [>ω (*)-**]2,
а энергия среднего арифметического компонент этого вектора, т.е. средняя
энергия G^e компоненты вектора Ф ^, будет
7*0 _
ψ[ρ{ρ) (e)-tk\2.
Тогда выражение (7.10.2) можно переписать в виде
»
(£) =
1 + Г
7*)
Gaa
rip)
где Gа, 1 — энергия одного элемента кода исходной границы. Найдем теперь
выражение для выходного отношения сигнал/помеха (£), усредненное
с равным весом по всем начальным состояниям р. Для этого используем
представление для энергии Gh,e ошибок квантования прямолинейной гра¬
ницы среднего арифметического £ проквантованных репрезентативных реа¬
лизаций (см. (7.7.2)). Удельная энергия ошибок квантования при равноверо¬
ятных начальных условиях будет Gh,e = Gh.e/Τμ. Тогда
Г2(<)=__£нм1±а—
τη {£ — τ) + £¥Γμ (1 - k£)
(7.11.7)
Если £ ^ Τμ, то при использовании этого выражения надо переходить
к главным значениям аргумента АКФ (см. (7.5.2)).
Усредненный по начальным состояниям коэффициент подавления
ошибок квантования. Определим этот коэффициент как частное усред¬
ненных отношений сигнал/помеха на входе и выходе фильтра. Усреднен¬
ное по начальным состояниям отношение сигнал/помеха на входе филь¬
тра равно частному квадратов норм исходной границы А = {1 + кг}1Т^
340
Гл. 7. Изображения с прямолинейными границами
и вектора ошибок квантования Ψ = {^(0}ι,τμ» взятых для отрезков
границы длиной в макропериод Τμ. Принимая во внимание (7.6.1), получим
гг = ||А||2/||Ф||2 = (1 + к2)/[к — к2). Теперь с учетом (7.11.7) можно
записать
т =
У)
Г1 (*)
ί2Τμ (к - к2)
£-1
rri “ Т) +м (1 “ ^к)
т— 1
(7.11.8)
Получение более удобного выражения для усредненного коэффициен¬
та кода подавления q (£) базируется на свойстве периодичности суммы
компонент вектора ошибок квантования:
i L
5>(ί) = £>(*)> Ь = М{*} = 1,2,...,Т„.
t=l t—1
Данное обстоятельство приводит к тому, что зависимость энергии суммы
компонент вектора ошибок от длины £ отрезка границы также будет
носить периодический характер:
Σικο
t=1
Σ>(0
На основании данного выражения по¬
лучим
k 2
(7.11.9)
9(0 =(|) 9(i)·
Рис 7.16. Зависимость усреднен¬
ного коэффициента подавления
фильтром ошибок квантования,
кь = 3/7
На рис. 7.16 приведена зависимость
усредненного по начальным состояниям
коэффициента подавления согласован¬
ным фильтром ошибок квантования от
длины £ исходной границы при к = 3/7.
Полученные соотношения показыва¬
ют, что коэффициент подавления ошибок квантования при согласованной
фильтрации пропорционален квадрату длины отрезка границы с учетом
тонкой структуры зависимости этого коэффициента на интервале
главного макропериода. Данное свойство обеспечивает простоту опреде¬
ление коэффициента подавления q(l) согласованным фильтром ошибок
квантования при произвольном значении £.
7.12. Основные результаты
В данной главе были рассмотрены различные аспекты представления
в ЭВМ протяженных прямолинейных границ изображений. Помимо того,
что изображения с такими границами очень распространены и, в силу
своего антропогенного характера, обладают высокой информативностью,
простая форма границы позволила аналитическим путем, не привлекая
7.12. Основные результаты
341
эмпирических подходов, полностью описать процесс квантования на ква¬
дратной сетчатке, образованной рецепторным полем ОЗУ изображений.
Основное содержание главы включает описание процесса квантова¬
ния прямолинейной границы, математическую модель этого процесса
в виде вырожденной дискретной цепи Маркова, представления для
элементов кода проквантованной границы и их автокорреляционной
функции, исследование возникающих при квантовании ошибок, во¬
просы согласованной фильтрации проквантованной границы с целью
уменьшения и, в ряде случаев, полного подавления этих ошибок. Кроме
того, рассмотрены задачи, связанные с выбором размера пиксела для
оптимального квантования прямой и идеального восстановления прямой
после ее квантования.
Основные полученные результаты состоят в следующем:
1. Показано, что код проквантованной прямолинейной границы пред¬
ставляет собой последовательность не более, чем из двух разных чисел
с макропериодом, определяемым тангенсом угла наклона прямой.
2. Сформулировано свойство эргодичности процесса квантования пря¬
молинейной границы, в соответствии с которым одинаковые результаты
могут быть получены как при обработке кодов отдельных реализаций
проквантованной границы, так и по отрезку кода одной реализации в пре¬
делах скользящего окна.
3. Показано, что ошибки квантования зависят от угла наклона пря¬
молинейной границы. Они достигают максимального значения при углах
22,48°; 67,52°; 112,48°; 157,52°; 202,48°; 247,52°; 292,48°; 337,52° и ми¬
нимального значения при углах 0°, 45°, 90°, 135°, 180°, 225°, 270°, 315°.
4. Синтезирован фильтр, согласованный с линией прямолинейной гра¬
ницы до ее квантования. При ширине окна импульсной характеристики
фильтра, равной величине макропериода кода, происходит полное по¬
давление ошибок квантования. Исследованы случаи подавления ошибок
квантования при произвольных значениях ширины окна импульсной ха¬
рактеристики фильтра.
5. Решена обратная задача, связанная с восстановлением формы гра¬
ницы по ее коду, полученному в результате квантования. Идеальное вос¬
становление, без учета краевых эффектов, достигается при фильтрации
скользящего среднего кода границы с окном шириной в макропериод кода.
6. Рассмотрен вопрос оптимизации процесса квантования прямоли¬
нейной границы, состоящей в выборе максимально возможных размеров
пиксела (что обеспечивает минимальную длину кода), при которых чис¬
ло элементов кода достаточно для идеального восстановления формы
границы.
7. Получены энергетические характеристики ошибок квантования на
входе и выходе согласованного фильтра. Показано, что выигрыш в подав¬
лении ошибок квантования при согласованной фильтрации растет про¬
порционально квадрату длины границы, но с учетом тонкой структуры
процесса подавления ошибок квантования на главном интервале значений
длины, равном макропериоду.
342
Упражнения и задачи
Приложение 7.1
Произведение двух сумм вида
HfrMfr)
/.2тг\
где ε = exp ^г— j, равно
(П7.1.1)
с = I 0 при а ф О,
\т* при а = 0.
Доказательство. Произведение (П7.1.1) можно представить в виде
τμ
Σ £аи, где зе — одно из значений 1,2,..., Τμ. Так как (см. (7.5.1))
и=1
(П7.1.2)
Τμε
— a as
ТО И
при а ф О,
при а = О,
и=1
при а ф О,
при а = 0.
Из последнего выражения следует справедливость равенства (П7.1.2).
Упражнения и задачи
1. Приведите примеры квантования прямолинейных границ на квадратной сет¬
чатке, проходящих под углами 45°, 60°.
2. Запишите код прямолинейной границы, проходящей под углом 30°,40°,80°.
3. Найдите в пределах одного макропериода код границы изображения с кь =
- 2/9.
4. Найдите в пределах одного макропериода код границы изображения, нахо¬
дящейся не в базовом секторе, т.е. если кь = —2/5.
5. Определите элементы цепного кода контура границы за макропериод для
случая кь = 2/9 при начале процесса из первого состояния.
6. Для случая, рассмотренного в упражнении 5, проведите анализ цепи Марко¬
ва, описывающей процесс квантования границы.
7. Получите развернутое представление АКФ для прямолинейной границы изо¬
бражения с кь = 3/5.
8. Определите зависимость энергии ошибок квантования при усреднении s про-
квантованных репрезентативных участков границы с кь = 2/9, s = 1, 2, 3,
4, 5, 6, 7, 8, 9.
9. Приведите условие полного подавления ошибок квантования и проанализи¬
руйте его для кода прямолинейной границы с кь = 3/5.
10. Осуществите фильтрацию кода проквантованной границы с кодом в пределах
макропериода = {1 + г;1;1 + г;1,1,1 + г;1} по методу скользящего
среднего в окне шириной s = 1,2,3,4 элементов.
Упражнения и задачи
343
11. Решите задачу восстановления прямолинейной границы с кодом в пределах
макропериода = {l + i;l;l + i;l,l,l + i;l} при накоплении Τμ реали¬
заций кода.
12. Решите задачу восстановления прямолинейной границы с кодом в пределах
макропериода = {1+г; 1; 1+г; 1,1,1+г; 1} при фильтрации скользящего
среднего с окном s = Τμ.
13. Определите оптимальный размер стороны Δ квадрата сетчатки, на которой
происходит оптимальное квантование проходящей под углом φ = 30° грани¬
цы длиной I = 6.
14. Определите коэффициент подавления согласованным фильтром ошибок кван¬
тования прямолинейной границы для случая кь = 2/9 и длиной I = 7.
15. Определите коэффициент подавления ошибок квантования для прямолиней¬
ной, ориентированной под углом 50° границы при начальном состоянии р — 1
в зависимости от длины границы I = 5,10,15.
Глава 8
ОБРАБОТКА ИЗОБРАЖЕНИЙ ОБЪЕКТОВ
ПРОТЯЖЕННОЙ ФОРМЫ В ЛАНДШАФТНЫХ
СЦЕНАХ
8.1. Введение
Одной из важных задач обработки изображений в ландшафтных сце¬
нах является обнаружение, оценка параметров, прослеживание и распо¬
знавание изображений коммуникационных объектов, часто являющихся
протяженными и имеющими нитевидную структуру [14, 124-129]. Такими
объектами являются шоссейные, грунтовые и железные дороги, реки,
лесные просеки, дамбы, плотины, мосты, взлетно-посадочные полосы и т.п.
В основном они являются результатами хозяйственной деятельности че¬
ловека. Характерными особенностями, кроме большой протяженности, яв¬
ляются небольшая ширина (1-10 пикселов) и наличие значительной дли¬
ны прямолинейных участков (рис. 8.1). Часто такие изображения имеют
Рис. 8.1. Сцены с протяженными нитевидными объектами
высокую контрастность по отношению к окружающим объектам и фону.
Однако, как отмечается в работе [126], из-за относительно небольшой ши¬
рины требуется проведение обработки с целью еще большего повышения
контраста. Нередко исходные изображения коммуникационных объектов
имеют по отношению к окружающему фону низкий контраст, меняющий¬
ся случайным образом. В этом случае их обнаружение, оценка параметров
и прослеживание становятся сложной проблемой.
8.2. Согласованно-избирательная фильтрация импульсов яркости 345
В данной главе будут рассмотрены задачи обнаружения и прослежива¬
ния коммуникационных объектов нитевидной формы. Решение задачи обна¬
ружения основано на математической модели сцены, рассмотренной в п. 6.1,
и заключается в использовании в обнаружителе фильтров, избирательно¬
согласованных с обнаруживаемыми изображениями (см. п. 6.2~6.5). Обра¬
ботка изображений коммуникационных объектов базируется на том, что
они содержат участки прямолинейной формы. Как следует из п. 6.6.1,
в этом случае при условии вертикаль¬
ной ориентации этих участков путем
формирования суммарной яркостной
строки достаточно просто обеспечить
высокое отношение сигнал/шум.
На рис. 8.2 показан пример форми¬
рования суммарной яркостной строки
для стилизованной сцены в пределах
прямоугольного фрагмента ABCD.
Видно, что вертикально ориентирован¬
ный прямолинейный участок EF про¬
тяженного нитевидного объекта созда¬
ет импульс яркости, превышающий по
амплитуде значения накопленной яр¬
кости от фрагментов RN и LM. При
этом импульс яркости хорошо отража¬
ет форму фрагмента EF, в то время,
как информация о форме других фраг¬
ментов при накоплении яркости разру¬
шилась. После уверенного обнаружения
на сложном статистически неоднород¬
ном фоне, характерном для ландшафт¬
ных сцен, прямолинейного участка нитевидного фрагмента, достаточно про¬
сто организовать выделение всех остальных участков изображения ните¬
видного объекта. Поэтому использование информации о форме изображения
объекта позволяет увеличить энергию сигнала и, благодаря этому, значи¬
тельно упростить процесс его обработки. Если задача обнаружения прямо¬
линейных границ изображений сводилась к обнаружению скачка яркости на
фоне одновременно действующих слабо и сильнокоррелированных шумов,
то теперь в аналогичных условиях необходимо обнаружить импульс яркости.
8.2. Согласованно-избирательная фильтрация импульсов
яркости (пространственный аспект)
8.2.1. Аналитическое представление одномерного импульса яркости.
Узкий, шириной до 8-10 пикселов импульс отсчетов яркости (как по¬
ложительный, так и отрицательный), получаемый вдоль строки сцены,
характерен для изображений дорог и других нитевидных изображений,
ориентированных преимущественно в вертикальном направлении. Идеа-
Рис. 8 2. Стилизованная сцена с ни¬
тевидными протяженными объекта¬
ми (а) и результат накопления ярко¬
сти строк в пределах прямоугольного
фрагмента ABCD (б)
346
Гл. 8. Изображения объектов протяженной формы
Рис. 8.3. Идеализированные положительный и отрицательный импульсы яркости:
а — s+ (п) = {...; 0; 0; 0; 0,2; 0,8; 1; 1; 1; 1; 1; 0,6; 0,4; 0; 0; 0;...}; б — s_ (η) =
= {...; 1; 1; 1; 0,8; 0,2; 0; 0; 0; 0; 0; 0,4; 0,6; 1; 1; 1;...}; h = l2 = 2; τ = 5; t = 11
лизированный импульс (рис. 8.3) состоит из идеализированных положи¬
тельных и отрицательных скачков яркости, соответствующих его фрон¬
там, и плоской вершины.
Количество не равных нулю или единице отсчетов переднего фронта
обозначим через Ζχ, заднего фронта — через Ζ2, плоской вершины — через
т. Таким образом, общая длительность импульса равна
t = 1 4* Ζχ 4* τ + I2 -f· 1.
Аналитическое представление идеализированного положительного им¬
пульса яркости имеет вид
S+ (п) = <
(8.2.1)
8.2.2. Импульсная характеристика фильтра. Количество значащих
отсчетов ИХ СИФ равно t = Ζχ -f τ + Ζ2 + 2. Поэтому в общем случае для
ИХ фильтра можно записать следующее представление:
Л = {λ = {λ (0), λ (1),, λ (Ζι + т -f /2) j λ (Ζχ + т -f Z2 -f 1)}·
Выражение (6.2.22) для ИХ СИФ применительно к фильтрации одномер¬
ного импульса яркости при щ = Ζχ + τ + I2 принимает вид
λ (η) = 2s (t — 1 — η) — s (t — 2 — n) — 5 (t — n). (8.2.2)
На рис. 8.4 приведенны ИХ СИФ для показанных на рис. 8.3 импульсов
яркости. ИХ СИФ для идеализированного импульса яркости состоит из
трех частей. Одна из них соответствует переднему фронту, другая —
вершине и третья — заднему фронту. Вершина характеризуется постоян¬
ным уровнем яркости и величина второй разности равна при т > 2 нулю.
Поэтому вершине идеализированного импульса соответствуют нулевые
0
при
п =
0,-1,-2,-3,... ,
5ф1 (п)
при
72 = 1, 2, . . . , 1\,
1
при
п =
Ζι + 1, Zi -f 2,... , Ζχ -f τ,
βφ2 (п)
при
72 = Ζχ + Τ 1, Ζχ τ -J- 2, . . . , Ζχ
0
при
п =
Ζχ -Η τ -}-12 ■+■ 1, Ζχ + τ 12 Ч- 2,...
82. Согласованно-избирательная фильтрация импульсов яркости 347
λ(η) 0,4
0,2
0,4
0,2
9 10
3 4 5 6 7 8
-0,2
-0,2
-0,4
-0,4
0 А λ(η)
0,2
0,4
6 0
-0,2
7 8
4 5 6
-0,4
-0,2
-0,4
0,2
9 10 я
Рис. 8.4. Импульсные характеристики СИФ для импульсов яркости: а — для им¬
пульса на рис. 8.3, а; б — для импульса на рис. 8.3, б
значения ИХ. Переднему и заднему фронтам соответствуют отсчеты ИХ
для скачков яркости с противоположными знаками (см. п. 6.3.2).
Если т ^ 3, то ИХ фильтра вначале содержит отсчеты ИХ Л2 для
скачка яркости, относящегося к заднему фронту импульса, далее следу¬
ют г — 2 нулевых значения, вызванных плоским характером вершины,
а затем следуют отсчеты ИХ Λχ для скачка яркости, относящегося к
переднему фронту, т.е.
Л = {Л2,0,0,... ,Ο,Λχ}, г ^ 3. (8.2.3)
т-2
При т = 2 ИХ имеет вид Л = {Л2, Λχ}.
Наличие нулевой группы отсчетов в выражении (8.2.3) вызвано диф¬
ференциальным характером оператора второй разности A2s (η). Посколь¬
ку ИХ фильтра для идеализированного импульса яркости получается
в результате конкатенации ИХ фильтров для противоположных по знаку
скачков яркости и нулевой группы отсчетов, то принимая во внимание
выражения (6.3.3) и (6.3.6), приходим к выводу, что сумма отсчетов ИХ
СИФ для импульса яркости равна нулю.
8.2.3. Анализ процесса фильтрации импульса яркости. Общее ко¬
личество значащих отсчетов фильтра, соответствующее числу шагов,
в течении которых импульс взаимодействует с ИХ фильтра, равно
М = 2t — 3 = 2 (Ιι + т + l2) + 1. Процесс согласованно-избирательной
фильтрации импульса можно представить как последовательность пя¬
ти этапов фильтрации скачков яркости (рис. 8.5). На рис. 8.5, а в виде
трех блоков условно представлены ИХ Л фильтра и идеализированный
импульс яркости s. ИХ фильтра содержит блок Л2 для заднего фронта,
блок 0, для вершины и блок Λχ для переднего фронта импульса. Сигнал s
состоит из блока отсчетов Fi переднего фронта, блока единиц (или нулей)
вершины и блока F2 заднего фронта импульса.
На первом этапе фильтрации (рис. 8.5, б) перекрываются блоки Л2
и Fx, т.е. происходит обработка переднего фронта фильтром, избиратель¬
но-согласованным по отношению к заднему фронту импульса F2. Как было
показано в п. 6.5, в этом случае все отсчеты фильтра будут отрицательны-
348
Га. 8. Изображения объектов протяженной формы
, I л2 I О I "λΓΊ 1^1 1 1 *П
I л2 1 о I ~лП А
б I р2 I 1 I *П=[>
| л2 | о I Л, | А
« I Ъ I 1 I *П=[>
I ЛП 0 I ~лП А
г I Ъ I 1 1 ~*П^> *
I а2 | О | Л| 1 А
д I р2 I 1 I р\ 1=?> ί
I А2 I О I Л, 1 А
е I F2 | 1 | s
Рис. 8.5. Основные этапы фильтрации импульса яркости
ми. На пятом этапе (рис. 8.5, е) отсчеты также будут отрицательными, так
как задний фронт импульса F2, обрабатывается фильтром, избирательно¬
согласованным по отношению к переднему фронту.
На втором (рис. 8.5, в) и четвертом (рис. 8.5, д) этапах происходит
перекрытие фронтов сигнала с нулевыми зонами ИХ и выходные сигналы
будут нулевыми. Лишь на третьем этапе (рис. 8.5, г) происходит перекры¬
тие участков ИХ с согласованными участками сигнала, т.е. Λχ с F\ и Λ2 с F2.
В этом случае образуется положительный выходной сигнал. Так как при
согласованно-избирательной фильтрации идеализированных скачков ярко¬
сти сумма отсчетов равна единице, то сумма выходных отсчетов фильтра
на первом и пятом этапах равна по минус единице, на третьем — двум
(рис. 8.6). Отсюда же следует, что сумма всех выходных отсчетов СИФ равна
нулю. При обычной согласованной фильтрации образуется выходной сигнал,
I
II
III
IV
V
Σ = -1
0
Σ =
=2
0
Σ=—1
jl
1
iii
Рис. 8.6. Структура и полярность выходного сигнала СИФ
8.2. Согласованно-избирательная фильтрация импульсов яркости 349
равный энергии идеализированного входного сигнала [55]. В связи с этим
максимальный отсчет выходного сигнала такого фильтра пропорционален
длительности входного сигнала. В нашем же случае при согласованно-изби¬
рательной фильтрации идеализированного импульса, максимальный выход¬
ной отсчет не зависит от длительности импульса и не превышает величины
η (771) = 2. Данное обстоятельство является следствием дифференциального
характера процесса фильтрации, в результате которого происходит накоп¬
ление энергии лишь в пределах фронтов импульса.
Как следует из общих свойств СИФ (см. п. 6.2), его отсчеты симметрич¬
ны относительно центральной точки. Так как количество отсчетов СИФ
при обработке импульса яркости равно Μ = 2ί —3 = 2(Ζι4-τ + Ζ2)4-1,το
центральный отсчет соответствует значению то = t — 1 = Ζχ + т 4- Z2 -f 1
и свойство симметрии выходного сигнала СИФ принимает вид η (т) =
= η (2t — 2 — т) или η (т) = η[2 (Ζχ -f т + h) — т], т = 1,2,... , М.
Максимальный пиковый отсчет η (то) = η (t — 1) является централь¬
ным и равен сумме максимальных отсчетов для СИФ скачков яркости,
соответствующих фронтам импульса. Текущий отсчет СИФ при обработке
импульса яркости равен
t-1
η (т) = ^2 s(m + k - t + l)[2s (к) — s (к — 1) — s (к -f 1)], (8 2 4)
m = 1,2,... , M.
8.2.4. Согласованно-избирательная фильтрация некоторых видов
импульсов яркости.
Импульс с прямоугольными фронтами. В аналитическом виде такой
импульс задается как (рис. 8.7)
s(n) = |0 при η = 0,-1,-2,... и п = т + 1,т + 2,... , ^
\l при п = 1,2,... ,т.
Длительности фронтов равны нулю, т.е. l\ — Ζ2 = 0. Поэтому величи-
0 1 2 3 4 5 6 7
1
я(л)
0
7
1 2 3 4 5 6 8 л
а
2
η(τη)
1
13 _
0
2 3 4 5 6 '
1 8 9 10 1112
14 m
-]
■
1
Рис. 8.7. Согласованно-избирательная
фильтрация прямоугольного импульса
яркости: а — вид импульса яркости;
б — ИХ фильтра; в — выходной сигнал
350
Гл. 8. Изображения объектов протяженной формы
на t = т -f 2 и ИХ СИФ в соответствии с выражением (8.2.2) имеет вид
λ (η) = 2s (т + 1 — η) - s (τ — η) — s (τ -f 2 — η), η = 0,1,... , t — 1.
С учетом (8.2.5) получим (рис. 8.7, б)
Л = {λ (η)}^., = {-1; 1; 0; 0;... ; 0; 0;1; -1}. (8.2.6)
т-2
Выходные сигналы СИФ будут равны (рис. 8.7, в)
η (™)
— 1 ДЛЯ 771 = 1 И 771 = М = 2т + 1,
2 ДЛЯ га = т + 1,
0 для остальных значений га.
Таким образом, при обработке прямоугольного импульса яркости СИФ об¬
разует всего три ненулевых из М = 2т -f 1 возможных отсчетов. Два из
них отрицательны, равны по минус единице, и один положительный, равный
двум. Фильтрация прямоугольного импульса яркости интересна с точки зре¬
ния реализации потенциальных возможностей СИФ. Так как длительность
фронтов у такого импульса равна нулю, то его спектр имеет максимально
возможную ширину. Поэтому СИФ формирует максимально возможный по
величине выходной сигнал.
Импульс с линейными фронтами. Идеализированный положительный
импульс с линейными фронтами задается как
s (п) = <
0 при п = 0, —1, —2,...
и п = 1\ + τ 4- /2 “Ь 1» ^1 т -Ь ^2 ”l· 2,... ,
7-7-7 при п = 1,2,... ,Ζι,
ί i + l
1 при τι — 1\ + 1, l\ -f- 2,... , Ζχ т,
\ ;—L_— при 72 = 1\ + т 4* 1, l\ 4" т + 2,... , 1\ 4* т 4* I2·
h + 1
Я (я)
0,5
0,3
1 2 3 4 5 6 7
б
8 9
111 111 6
-0.16511-0,165
-0,33-0,33
83
-0,3
r?(m)
U.
0.472
°2
472
0 1 2 3 4 s ' ^
V1 151617181920
-0,5
6 7 8 91011121314
в
-0,33-0,33
Рис. 8.8. Согласованно-избира¬
тельная фильтрация импульса
яркости с линейными фронтами:
I m а — вид импульса; б — ИХ
|,165 СИФ; в — выходной сигнал
СИФ
8.2. Согласованно-избирательная фильтрация импульсов яркости 351
ИХ фильтра определяется выражением
Л (n) = 2s (t — 1 — η) — 5 (t — η) — s (t — 2 — n), Ti = 0,l,2,... , £ — 1.
Первые /2+2 отсчета данной характеристики являются ИХ СИФ для задне¬
го фронта, а последние Ζχ + 2 — ИХ СИФ для переднего фронта импульса.
Между этими отсчетами располагаются т — 2 нулевых отсчетов, соответ¬
ствующих плоской вершине импульса яркости (рис. 8.8). Выходные отсчеты
равны t_1
η (га) = ^ s(m + к — Ιι — т — Ι2 — l)[2s (к) — s (к — 1) — s (к + 1)],
к=0
тп — 1,2,... , М\ М = 21 — З5 t — l\ + т + I2 4" 2.
8.2.5. Двумерные СИФ для изображений нитевидных объектов.
В качестве модели s (η,ρ) изображения идеализированного нитевидно¬
го объекта с яркостью выше фона выберем изображение вертикально
расположенной полосы на нулевом фоне (рис. 8.9). Сечение полосы по
А Р
/| + Г+ /2
а -
1
1-
0,8.
0,6.
6-5-4-3-2-1 0
Ч")
2 3 4 5
7 8 9 1011 1213 п
II 11 п 11 II
/ Ю ОО 11 W "
1 g к> ^
0,4.
0,2.
0.
6 -6-5-
4-
3-
2-
1 (
3 1 2 3 4 5 6'
7 1
$ <
3 1
01
11
21
3 я
Рис. 8.9. Двумерная модель нитевидного изображения (а) и сечение изображения
по произвольной строке (б)
строкам одинаково и представляет собой положительный идеализи¬
рованный импульс яркости s (п), задаваемый выражением (8.2.1), т.е.
s (п,р) = s (п) при любом р. (8.2.7)
СИФ для данного изображения задается следующим образом:
р г-ι
η (га, г) = 5 (n,p)V2s (га - по + п, г - р0 - р),
р=1п=0
(8.2.8)
352
Гл. 8. Изображения объектов протяженной формы
где t = Ιχ -f т 4- h + 2; Ρ — длина изображения; V2s(ra — η0 + п,
г — ро — р) — дискретный аналог лапласиана.
Найдем дискретное приближение оператора Лапласа при выбран¬
ной модели изображения. Для первых разностей Ans (η,ρ) и Aps (η,ρ)
запишем
A„s (η,ρ) = s (η,ρ) -- s (η - 1 ,ρ), Aps (η,ρ) = a (η,ρ) - s (η,ρ - 1).
Вторые разности будут иметь вид
V^s(n,p) = Ans (η,ρ) - Ans (η — 1 ,ρ) =
= 5 (η,ρ) — 2s (η - 1 ,ρ) + s (η - 2,ρ),
VpS (η, p) = Aps (η, ρ) - Aps (η, ρ - 1) =
= s (η,ρ) — 2s (η,ρ - 1) -f s (η,ρ - 2).
Тогда
V2s (η,ρ) = Δ25 (η,ρ) + Δ25 (η,ρ) = 2s(n- 1 ,ρ) + 2s (η,ρ - 1) -
— 2s (η,ρ) — s (η — 2,ρ) — s (η,ρ — 2).
В нашем случае при задании изображения нитевидного объекта зависи¬
мость s (η,ρ) в направлении р отсутствует. Поэтому
V2s (η,ρ) = s (η) — 2s (η — 1) -f s (η — 2),
и выражение (8.2.8) для СИФ примет вид
ν(τη) = Σ
n=0 Lp= 1
Λ (m — no -f η) =
t-i
= ΡΣ s(n)[2s(m — no -l· η — 1) —5(m — no -f n) — s(m — no + n — 2)] =
n=0
t-i
= s(m — n)[2s (no — n + 1) — s (no — n) — s (no — n -f 2)],
n=0
m — 1,2,... , M\ n0 = h -f г -f Z2-
(8.2.9)
Если же фильтруется не идеальная полоса s(n,p), а произвольное
вертикально ориентированное изображение / (η,ρ) нитевидного объекта,
яркостный профиль которого может быть описан как s (п), то выходной
сигнал СИФ будет равен
п=0 Lp=l
[2 s(m —
n0 + η - 1) -
— s (т — по + η) — s (т — n0 -f η - 2)], (8.2.10)
m = 1,2,... , Μ; η0 - 1\ 4- τ Η- /2·
8.3. Согласованно-избирательная фильтрация прямоугольных импульсов 353
I /(".я)
Сумматор
Σ/(«,ρ)
г Р=1
СИФ для одномерного
импульса яркости
η(ηι)
■>М !?
9,8
9
,8
ι,δί
1,8
, } . з т1
T 11 13
“ill о”
-7-7
8 9 Μ1 m
-7-7
Рис. 8.11. Согласованно-избира¬
тельная фильтрация изображе¬
ния нитевидного объекта, пред¬
ставленного на рис. 8.9
Таким образом, фильтрация изоб¬
ражения вертикально расположенного
Рис. 8.10. Структура СИФ для нитевидного объекта сводится к на-
вертикально расположенного изо- коплению в пределах вертикального
бражения нитевидного объекта размера апертуры фильтра отсчетов
изображения и дальнейшей согласован¬
но-избирательной фильтрации накопленного одномерного импульса яр¬
кости (рис. 8.10). На рис. 8.11 представлен результат такой фильтрации
изображения, приведенного на рис. 8.9.
8.3. Согласованно-избирательная фильтрация прямоугольных
импульсов яркости (частотный аспект)
8.3.1. Частотный коэффициент передачи СИФ для прямоугольного
импульса яркости. В разделе 6.4.1 было получено следующее выраже¬
ние ЧКП СИФ:
ω (га) = go,t-i (m) [2ехР т} “ exp |г^2га| - lj + 5 (0) -
— s (t) — exp |г^га j[s (—1) — s (t — 1)], га = 0,1,2,... , t — 1.
Если СИФ предназначен для произвольного идеализированного импульса
яркости {5 (N)}0 t_lf определяемого выражением (8.2.1), то 5 (0) = 5 (t) =
= s (—1) = s(t — 1) = 0и выражение для ЧКП принимает вид
ω (m) = go,t_i М (l - exp {»'ψ™·}) =
= go)t-i (то) [(cos Щ-т — l) + * sin . (8.3.1)
ЧКП СИФ для сигнала в виде идеализированного прямоугольного им¬
пульса (8.2.5), определяемый прямым ДПФ от ИХ Λ = {Mn))ot-i =
= {-Ι,Ι,Ο,Ο,.·· ,0,0,1,-1}, будет равен
т-2
354
Гл. 8. Изображения объектов протяженной формы
t — 1
ω (т) = Л (п) exp г-^7тш| =
п—о
= 2 sin ~Ym · [ — sin ^m + г ^cos — l)], m = 0,1,2,... , t — 1.
(8.3.2)
Так как величина sin2 х всегда не отрицательна, то вещественная часть
о 2тг
ЧКП, равная — 2sin2— га, не больше нуля, т.е. Re о; (га) ^ 0. Из ве¬
щественности значений ИХ СИФ и свойств ДПФ вытекает комплексная
сопряженность значений ЧКП: ω (га) = ω* (t — га). Отсюда следует, что
вектор ω (га), τη = 0,1,2,... , t — 1, ЧКП СИФ для прямоугольного им¬
пульса всегда располагается во втором и третьем квадрантах, т.е. π/2 ^
^ argu; (га) ^ 3π/2. Нулевой отсчет ЧКП всегда равен нулю: ω (0) = 0,
т.е. СИФ не пропускает постоянной составляющей фильтруемого сигнала.
8.3.2. Амплитудно-частотная характеристика. Амплитудно-частот¬
ную характеристику (АЧХ) СИФ для прямоугольного положительного
импульса яркости определим как отсчеты модуля ЧКП (8.3.2):
I / \|2 о . 2 2π Λ 2π Л . 2 2π . 2 тг
\ω (т)\ =8 sin —mil —cos—mj = 16 sm—m · sm —m =
t V t / t t
nA · 4 π 2 ^
= 64 sm —m· cos —m.
Отсюда получим
2π
I a; (m)| = 4 · |sin -~~m * sin ^m| — 2 · jcos yra — cos y3 · ra|.
(8.3.3)
Рассмотрим некоторые свойства АЧХ СИФ, вытекающие из полученного
выражения (8.3.3).
1. Симметричность отсчетов АЧХ. Из соотношения ω (т) =
= ω* (t — m), τη = 0,1,2,... , t — 1, следует, что график АЧХ представля¬
ет симметричную относительно центрального отсчета т = t/2, функцию:
ω (т) — ω (t — т), т = 1,2,... , £ — 1.
2. Нули АЧХ:
, v 10 при т = 0 для нечетного
о; (ш) = <
[О при га = 0, £/2 для четного t.
Таким образом, график АЧХ \ω (т) |, т = 0,1,... , t — 1, представляет
собой две положительные полуволны, причем, если величина t — четное
число, эти полуволны разделены нулем.
3. Положения максимумов АЧХ. Запишем производную по т функ¬
ции (8.3.3) и приравняем ее нулю:
\ω (га)| = 2 · | — — · sm— т ± Зу · sm— m| = 0.
Отсюда следует, что sin ^ттах = ±0,816 и первое значение т, при кото¬
ром достигается максимум АЧХ, будет равно штах ι = ]0,304ί[, где ]х[ —
8.3. Согласованно-избирательная фильтрация прямоугольных импульсов 355
ближайшее целое к х. Второй максимум АЧХ с учетом симметричности
ее отсчетов достигается при mmax 2 = ]0,694t[.
4. Максимальные отсчеты АЧХ. С учетом значений mmax 1 и тптах 2
и выражения (8.3.3) для \ω (т)\ получим
Mm)lmax = |ω (^max)l = 2 · |cos 54,72° - cos 164,16°| = 3,0792.
5. Полоса пропускания СИФ. Для граничных значений АЧХ на уровне
половины значения максимального отсчета АЧХ, т.е. на уровне 1,5396,
можно записать
Jcos у777, — cos у · Зш| = 0,7698.
С учетом симметричности АЧХ
и ее структуры в виде поло¬
жительных полуволн существуют
четыре значения т, соответству¬
ющие краям полосы пропускания
СИФ, 7711, 777-2 > ТП^ И 7774 (рИС. 8.12):
7771 = 0,154£, 7772 = 0,435£,
777з = 0,564£, 7774 = 0,8451
СИФ имеет две полосы пропуска¬
ния, равные Ат1 = т,2 — ггц =
= 0,281£ и Дш2 = 7774 — 7773 = 0,2811 Общая ширина полосы пропускания
рассматриваемого СИФ равна Ат = 0,5621 Рассмотренные свойства
позволяют достаточно просто охарактеризовать АЧХ СИФ даже без ее
построения по формуле (8.3.3).
8.3.3. Фазочастотная характеристика СИФ. Фазочастотную харак¬
теристику СИФ найдем как аргумент ЧКП для прямоугольного импульса.
Из (8.3.2) получим
. 2тг / 2π Л
Sin —Ш · I COS -у—777 — 1 1
argw (m) = arctg - = ^m, (8 34)
sin —m
777 = 0, 1, . . . , t — 1.
Вектор ω (m) находится во втором или в третьем квадрантах. В последнем
случае величину argo; (777), определенную по формуле (8.3.4), необходимо
увеличить на π. Таким образом,
Рис. 8.12. Положения граничных точек по¬
лосы пропускания СИФ для прямоуголь¬
ного импульса (непрерывный случай)
7Г + 7Гm/t При 777 ^
nm/t при 777 > t/2
8.3.4. Спектральные характеристики выходного сигнала. Опреде¬
лим спектр {ρ(τ77)}0ί_ι сигнала на выходе СИФ при фильтрации иде¬
ализированного прямоугольного импульса яркости в момент образова¬
ния пикового выходного отсчета, т.е. когда входной сигнал имеет вид
φ (777) = arg ω (τη)
t/2;
(8.3.5)
356
Гл. 8. Изображения объектов протяженной формы
{s (n)}o t-1 = {0,1,1,... , 1,1,0}. Спектр этого входного сигнала равен:
t-2 ^
g (m) = ^ s (п) ехр |-г-~гапга = 1,2,... , t — 1.
п=1
Принимая во внимание, что для га = 1,2,— 1
ехр г^гап j = 1 + ^ ехр г^гап j +
п=° п=1 / о >,
+ ехр г— (£ — 1) га j = О,
получим
g (га) = - ^1 + ехр » т = 1, ·. · , t - 1.
При т = 0 значение g (0) = t—2. Таким образом, спектр входного сигнала
{0,1,1,... ,1,0}, при котором образуется пиковый выходной сигнал СИФ,
равен
1t — 2 при т — 0,
g (т) = < / 2π \ . . 2π - п
I — yl -f cos — mj — г · sm — га при га = 1,2, —1.
(8.3.6)
Действительная часть компоненты спектра входного сигнала всегда от¬
рицательна. Поэтому точки, соответствующие этим компонентам, как и
точки ЧКП, располагаются во 2-м и 3-м квадрантах.
Определим теперь амплитудно-частотный |g(m)| и фазочастотный
arg g (га), га = 0,1,...,£ — 1, спектры входного сигнала. Воспользовав¬
шись последним выражением, получим
I / ч 12 л , 2 2π . 0 2π , . 2 2π η Λ , 2?r \
Ig(m)| = 1 + cos —ra -f 2cos — ra + sm —m = 2 · f 1 -f cos —ml ,
ra — 1,... , t — 1.
Таким образом,
ls(™)l =
t — 2 при ra = 0,
I 7г I
2* cos^ra при m — 1,2, ...,£ — 1.
(8.3.7)
Найдем фазочастотный спектр входного сигнала:
arg g (га) = arctg-
. 2π
sin —га
ί . 2π
1 4- cos —га
t га*
Когда вектор компоненты спектра находится в третьем квадранте, к этому
результату надо прибавить π. Итак,
arg g(m)
^7Γ
+ ππι/ί при m<tj 2,
πτη/ί при т > tf2.
(8.3.8)
8.3. Согласованно-избирательная фильтрация прямоугольных импульсов 357
Теперь воспользовавшись выражением р (га) = ω (га) g (га), га = 0,1,...
— 1, получим спектр выходного сигнала СИФ. Определим вначале
амплитудно-частотный спектр. Используя (8.3.3) и (8.3.7), получим
|р (ш)| = \ω (га)| · |g (га)| = 4sin2 га = 0,1,... , ί - 1. (8.3.9)
Компонента фазочастотного спектра arg р(т) выходного сигнала равна
argp (га) = argg (m) + arg о; (га), m = 0,1,... , t — 1.
Воспользовавшись выражениями (8.3.5) и (8.3.8), будем иметь
О.'ТГ
arg р (га) = —m, m = 0,1,... , t — 1. (8.3.10)
Окончательно, с учетом выражений (8.3.9) и (8.3.10) для спектра выходного
сигнала СИФ при фильтрации прямоугольного импульса можно записать
р{тп) = |р(т)| · exp {i arg р(т)} = 4 sin2 γτη ■ exp jijmJ, (8311)
τη = 0,1,... , t — 1.
Теперь на основании обратного ДПФ от {p(m)}ot__λ получим простран¬
ственное представление пикового значения выходного сигнала СИФ. Для
этого найдем последнюю, (t — 1)-ю компоненту этого преобразования:
η (* ~ -1)= 7' Σр (т)ехр (гТт' ^ "1^}'
тп—О
Рис. 8.13. Спектр сигнала на выходе СИФ при
обработке прямоугольного импульса с т = 6: а —
амплитудно-частотный спектр; б — фазочастотный
спектр; в — комплекснозначный спектр
358
Гл. 8. Изображения объектов протяженной формы
Подставляя значение р (га) из (8.3.11), получим
ι(*-1) = 7·Σ
. 2 2π
sm —га.
t
Далее воспользуемся известным представлением синуса в комплексно¬
значном виде. Тогда
0,5*
t-1 t-1
ΣΓ .4π Ί Γ ·4π ϊ
ехр гтт/ ” 2^ехр ι гтт/ '
Последние две суммы в этом выражении как суммы компонент замкнутого
контура равны нулю. Поэтому η (t — 1) = 2. Этот результат совпадает
с результатом анализа СИФ, представленного в пространственной обла¬
сти.
Определим в качестве примера спектр выходного сигнала СИФ при обработке
прямоугольного импульса с т = 6. Применяя выражения (8.3.9), (8.3.10) и (8.3.11),
получим (рис. 8.13)
{р (m)}0i7 = {0; 1,414 + 1,414s; 4»; -1,414 - 1,414»; 0;
-1,414 + 1,414»; -4»; 1,414 - 1,414»};
{|р(ш)|}0,7 = {0; 2;4; 2;0; 2;4; 2};
{arg р (т)}0 7 = {0°; 45°; 90°; 135°; 180°; 225°; 270°; 315°}
8.4. Обнаружение изображений объектов нитевидной формы
Рассмотрим вопросы, связанные со структурой обнаружителя изо¬
бражений нитевидных объектов. Предполагаем, что изображение имеет
длину Р пикселей, расположено в пределах локально однородного участка
сцены. Импульс яркости в пределах поперечного сечения изображения
имеет известную форму и характеризуется длительностью г = t — 2
пикселей. Смесь / (п) фонового и широкополосного шумов с сигналом 5 (п)
описывается моделью (6.1.2). Энергетический спектр в области средних
и высоких частот подчиняется закону квадратичной гиперболы (6.2.2).
В качестве формирователя достаточной статистики используется СИФ.
Задача заключается в принятии обоснованного решения о том, что вход¬
ной сигнал / (п) представляет собой смесь шумов и импульса s (η) (гипо¬
теза Hi), либо только шумы (гипотеза Н0). В момент получения пикового
значения выходного сигнала η (t — 1) СИФ выполняет над входным сиг¬
налом одну из операций (6.2.7) или (6.2.8). При этом обеспечивается доста¬
точно большое превышение выходного сигнала η (* — 1) при истинности
гипотезы Hi над сигналом при истинности гипотезы Но.
Обнаружитель изображений нитевидных объектов имеет структуру,
аналогичную обнаружителю прямолинейных границ изображений (см.
п. 6.5.2). Отличия между ними вызваны типом используемого СИФ.
Характеристики обнаружения строятся в соответствии с методикой,
описанной в п. 6.5.2.
8.4. Обнаружение изображений объектов нитевидной формы
359
В качестве примера ландшафтной сцены для построения характери¬
стик обнаружения изображения типа «дорога» взята сцена, представлен¬
ная на рис. 6.29. Для обнаружения был выбран участок дороги в преде¬
лах прямоугольника ABCD. Яркостные портреты накопленных строк
приведены на рис. 6.30. На рис. 8.14 представлены экспериментально
Рис. 8.14. Зависимости отношения сигнал/фоновый шум, дисперсии фона и кон¬
трастности изображения дороги на входе СИФ от числа накопленных строк
полученные зависимости отношения сигнал/фоновый шум диспер¬
сии σ\ фонового шума и средней контрастности «7ф и Jc изображения
дороги на входе фильтра от числа N накопленных строк. Отношение
сигнал/фоновый шум определялось как
q\ = |J* - Jc\2/σΙ (8.4.1)
где JQ — средние яркости изображений фона и дороги. Из графиков
видно, что дисперсия фона уменьшается с ростом количества накоплен¬
ных строк N и соответственно увеличивается отношение сигнал/шум.
При этом средняя контрастность изображения остается практически
неизменной. Эффективность согласованно-избирательной фильтрации
изображения дороги при наличии большого количества локально одно¬
родных участков фона приближенно можно оценить как
(8-4.2)
Здесь 77^ах — пиковый отсчет СИФ при нахождении окна фильтра в обла¬
сти дороги; σ\ — дисперсия выходного фонового шума. Для получения
оценки величины σ\ используется массив выходных отсчетов фильтра,
из которых исключены отсчеты, соответствующих изображению дороги.
Приближенность значения вызвана тем, что ^ах — это реакция СИФ
не на чистый полезный сигнал, а на его смесь с фоновым шумом.
На рис. 8.15 представлены выходные отсчеты фильтра для значений
N — 1,40, и 90. Центральный (нулевой отсчет) на каждом из графи¬
ков соответствует максимальной реакции фильтра, а отсчеты ±1, ±2 —
другим выходным сигналам СИФ. Непронумерованные отсчеты соответ¬
ствуют участкам фона справа и слева от дороги. Из графиков видно, что
360
Гл. 8. Изображения объектов протяженной формы
100
50
0
-50
а
100
50
О
-50
п(п)
\
Τ-ί’ό 2*|J
1
1
/i?
1 η
1 п(п)
......J
Ь 4
а-ч1ЛГ2 ο"ΐ
/ ^ η
η(η)
Λ
-4\ ι
2Mrrui-rm =
•^'Ч|ет
\!
Рис. 8.15. Согласованно-избирательная
фильтрация изображения дороги с при¬
легающими участками фона при раз¬
личных количествах накопленных строк:
а — N = 1; б — N = 40; в — N = 90
пиковый отсчет 77тах, соответствующий изображению дороги, превыша¬
ет любой из фоновых отсчетов. Отметим также, что рост количества N
накопленных строк слабо сказывается на величине r;max и, в основном,
приводит снижению дисперсии фоновых отсчетов.
На рис. 8.16 приведены зависимости величины когда фильтр изби¬
рательно согласован с импульсом прямоугольной формы длительностью
т = 3,4,5,9 от длины Р изображения дороги. Видно, что наибольшее
значение q\ достигается при т = 4. При т = 9 фильтр полностью рас¬
согласован с изображением дороги и величина уменьшается примерно
в 2 раза. Если бы фильтровался идеализированный прямоугольный им¬
пульс яркости, то снижение должно было бы быть в два раза больше.
Отметим, что фильтр при обработке реальных изображений оказался
Рис. 8.16. Зависимости отношения сигнал/фоновый шум от длины изображения
дороги
8.4. Обнаружение изображений объектов нитевидной формы
361
некритичным к вариациям своей апертуры: для т = 3 и т = 5 уменьшение
#2 незначительно. Из графиков также следует, что рост отношения сиг-
нал/фоновый шум с увеличением Р замедляется. Это можно объяснить
непрямолинейностью реального изображения дороги, что сказывается на
работе фильтра при больших значениях Р.
Аналогичные зависимости были исследованы при согласовании филь¬
тра с импульсами, имеющими линейный и параболический фронты.
Характер этих зависимостей такой же, как и для случая согласования
фильтра с импульсом прямоугольной формы. При этом выигрыш в отно¬
шении сигнал/фоновый шум за счет лучшего учета яркостного профиля
дороги, очень незначителен. Отсюда следует важный для практических
целей вывод: в реальных сценах рассматриваемого вида фильтрацию изо¬
бражений нитевидных объектов целесообразно проводить фильтрами, из¬
бирательно согласованными с импульсами яркости прямоугольной формы,
как наиболее простыми.
В соответствии с методикой, описанной в п. 6.5.2, был построен ряд
семейств характеристик обнаружения изображения дороги. На рис. 8.17
Рис. 8.17. Характеристики обнаружения изображения дороги, количество накоп¬
ленных строк N = 1, длительность импульса г — 3: а — для яркостного профиля
в виде прямоугольного импульса; б — в виде импульса с линейными фронтами
представлены характеристики обнаружения дороги длиной в один пиксел
для профиля дороги в виде импульса с прямоугольными (рис. 8.17, а)
и линейными (рис. 8.17, б) фронтами длительностью т = 3.
Характеристики построены экспериментально-теоретическим (сплош¬
ная кривая) и экспериментальным (пунктир) способами. Из графиков вид¬
но, что обеспечиваемые каждым из способов результаты с достаточной
для практических целей точностью совпадают. Из сравнения соответству¬
ющих графиков также видно, что пороговые сигналы слабо зависят от
формы импульса яркостного профиля дороги.
На рис. 8.18 показаны характеристики обнаружения изображения до¬
роги шириной т = 3 пиксела и прямоугольным профилем при накоплении
яркости N = 10, 30 и 100 строк прямолинейного участка дороги. Как
следует из этих характеристик при накоплении пороговый сигнал (в при¬
веденном диапазоне изменения Ν) уменьшается примерно в y/N раз.
362
Гл. 8. Изображения объектов протяженной формы
Рис. 8.18. Характеристики обнару- Рис. 8.19. Характеристики обнаружения
жения дороги: т = 3, прямоуголь- дороги с яркостным профилем в виде пря¬
ный яркостный профиль моугольного импульса: 1) СИФ, фоновые
шумы, г — 3; 2) СИФ, фоновые шумы, т =
= 5; 3) СИФ, фоновые шумы, т — 7; 4) при
согласованной фильтрации импульса т =
= 3 на фоне белого шума
На рис. 8.19 приведены характеристики обнаружения изображения до¬
роги при N — 1с яркостным профилем в виде прямоугольных импульсов
длительностей т = 3, 5 и 7 при воздействии, как и в других ранее рассмо¬
тренных случаях, слабо и сильнокоррелированных фоновых шумов.
В отличие от случая согласованной фильтрации при согласованно¬
избирательной фильтрации из-за дифференциального характера работы
фильтра пиковый уровень выходного сигнала не зависит от длительно¬
сти импульса, с которым этот фильтр избирательно согласован. Однако
увеличение длительности импульса приводит к сужению полосы пропус¬
кания фильтра (см. п. 6.2) и, как следствие, — к уменьшению дисперсии
выходного шума. Поэтому выходное отношение сигнал/шум на выходе
СИФ с увеличением апертуры ИХ растет, хотя и не в такой степени, как
при согласованной фильтрации. Данное обстоятельство и иллюстрируется
графиками 1, 2 и 3 на рис. 8.19.
Значительный интерес при рассмотрении обнаружителей изобра¬
жений нитевидных объектов представляет сравнение эффективности
обнаружителя на базе СИФ с эффективностью обнаружителя, реали¬
зующего потенциальные возможности. В этом плане была сопоставлена
эффективность оптимального обнаружителя импульса с т = 3 на фоне
только широкополосных помех (кривая 4 на рис. 8.19) с эффективностью
обнаружителя, использующего СИФ при воздействии широкополосных
и сильнокоррелированных фоновых шумов (кривая 1 на рис. 8.19). Как
и следовало ожидать, за счет того, что фильтр согласован не со всем,
а лишь с частью спектра шумов, наблюдается проигрыш в уровне по¬
рогового сигнала. Однако проигрыш не является значительным: для
вероятности D = 0,7 входное отношение сигнал/шум при согласован¬
ной фильтрации равно q\ — 0,67, а при согласованно-избирательной
фильтрации qi = 1,23, т.е. прогрыш составляет примерно ЗдБ.
Для проверки эффективности обнаружителя исследовались ландшафт¬
ные сцены с изображениями дорог (рис. 8.20, а, рис. 8.21, а).
8А. Обнаружение изображений объектов нитевидной формы
363
На рис. 8.20 показана последовательность работы обнаружителя:
рис. 8.20, б — входной сигнал СИФ в виде строки накопленной яркости,
Рис. 8.20. Сцена с изображением земной поверхности, содержащая изображение
протяженного объекта и промежуточный результат его обнаружения (а), измене¬
ние яркости вдоль суммарной строки (б) и сигнал на выходе СИФ (в)
рис. 8.20, в — сигнал на выходе СИФ. На рис. 8.20, в хорошо виден сигнал
от изображения протяженного объекта. Результат обнаружения в каждой
строке сцены отображается на рис. 8.20, а.
На рис. 8.21, б представлен результат обнаружения изображений про¬
тяженных объектов, показанных на рис. 8.21, а. При этом согласованно-
Рис. 8.21. Сцена земной поверхности, содержащая изображение протяженного
объекта (а) и результат работы обнаружителя (б)
избирательный фильтр, формирующий достаточную статистику для при¬
нятия решения, имел следующие параметры: размер апертуры фильтра
по вертикали (количество накапливаемых строк) N = 40, фильтр изби¬
рательно согласован с отрицательным импульсом яркости прямоугольной
формы, длительность вершины импульса т — 4, количество каналов об¬
наружения — 18.
364
Гл. 8. Изображения объектов протяженной формы
8.5. Прослеживание изображений объектов протяженной
формы
После обнаружения фрагмента изображения протяженного объекта
благодаря сильной корреляции между пространственными положениями
его других фрагментов достаточно просто осуществить прослеживание
всего изображения. Под этой операцией будем понимать последовательное
определение характерных точек изображения.
При прослеживании протяженного объекта нитевидной формы на мно¬
гоградационном изображении из-за его небольшой ширины (2-10) пиксе¬
ла целесообразнее выделять не граничный контур фон/изображение или
изображение/изображение, а осевую линию объекта.
Следует отметить, что осевая линия изображений таких объектов,
как дорога, взлетно-посадочная полоса и т.п., однозначно характеризует
положение объекта в сцене. Поэтому под просле¬
живанием протяженных объектов будем понимать
процесс формирования контура их осевой линии.
Поскольку интересующий нас объект на ре¬
альном изображении представляет собой узкую
полосу, то была принята форма строба, показанная
на рис. 8.22.
Этот строб представляет собой три примыка¬
ющие друг к другу области Si, S2 и S3. Пусть
Si, S2 и S3 — три прямоугольных окна, каждое
из которых содержит п\ = d\ · Dy П2 = d>2 · D
и пз = с1з · D пикселей соответственно. Необходимо
на основании фрагментов случайных полей в пределах пар областей
Si, S2 и S3 вынести решение в пользу гипотезы Hi по отношению к
конкурирующей Но- Гипотеза Hi соответствует утверждению о том, что
точки, образующие область S2, относятся к протяженному объекту, а точки,
образующие области Si и S3 принадлежат либо более светлому фону Ωψ,
либо изображению Ω^ и фону Ωψ, либо двум разным изображениям Clj
и Ω;, смежным с изображением протяженного объекта, j = 1,2,... ,Ζ, г =
= 1,2,... ,ί, j ф г. Гипотеза Но соответствует утверждению о том, что
области Si, S2 и S3 или одна из пар областей Si, S2 и S2, S3 принадлежат
либо фону Ωψ, либо одному и тому же изображению Ctj.
Пусть ξι = (£l,l,£l,2, · · · ,£l,nl), & = (£2,1 j ^2,2) · · · >£2,n2) и £3 =
= (£з,ъ £з,2> · · · , £з,пз) — независимые выборки значений яркости в окнах
Si, S2 и S3 соответственно. Проверяемая гипотеза Но состоит в том, что все
три области сцены, либо одна из пар областей Si, S2 и S2, S3, из которых
взяты эти выборки статистически не отличаются друг от друга (т.е. распре¬
делены одинаково), и наблюдаемая между ними разница носит случайный
характер. Конкурирующая гипотеза Hi предполагает, что разница между
выборками £1 и £2 и выборками £2 и £3 носит систематический характер.
По выборкам £1, £2 и £3 получим оценки генеральных средних М\ для
области Si, М2 для области S2 и М3 для области S3. Объем выборки
*1
S2
*3
D
г d\ ,
. *3-
Рис. 8.22. Вид стро¬
ба для прослеживания
протяженных объектов
8.5. Прослеживание изображений объектов протяженной формы 365
в пределах одного окна достаточно велик и, в связи с этим, создаются
предпосылки для выполнения центральной предельной теоремы теории
вероятностей. Поэтому оценка ξ генеральной средней М:
е=
г=1
подчиняется нормальному закону распределения
/© =
{
2σ2 jη J
где σ2 — дисперсия генеральной совокупности. Разница оценок ξχ и ξ2,
как и разница оценок ξ3 и ξ2, также будет иметь нормальное распреде¬
ление вероятностей:
/ (£i - ia) = / -1 ехР
γ2ττ (σ?/ηι +σ%/η2)
(ξι-ξ2-Μι+Μ2γ\
2 · (σ\/ηι + σΙ/пг) J
(8.5.1)
/ (£з — £2) —
1 .„ί (^з-?2-Мз + М2)21
(8.5.2)
где σ2, σ2 и σ3 — дисперсии для выборок ξι, ξ2 и ξ3 соответственно.
Если справедлива гипотеза Н0, то либо генеральные средние М\ и М2,
либо М2 и М3, либо Μχ, М2 и М3 равны между собой. Тогда распреде¬
ления (8.5.1) и (8.5.2) принимают вид
/(€ i"ia) =
2π (σΐ/пг + σ|/π2)
exp
1 (ii-?2)2 1
2 σ? /πχ -f /n2 J ’
/ (€3 “ £2) = exp
у 2тг (σ|/η3 + σ|/η2)
1 (?з-?2)2 1
2 σ3/η3-f σ|/η2 J
В качестве наблюдаемой статистики используем нормированную разность
оценок генеральных средних с учетом того, что в нашем распоряжении
вместо дисперсии генеральной совокупности σ2 имеются ее оценки, полу¬
ченные по выборкам ξι, ξ2 и ξ3:
4 — ξΐ ξ2 4. _ ξβ ξ2
*1,2 — - .■= , *3,2 — -- · - - · = ·····= ·
\/σι/ηι +σ|/η2 у^з/пз +σ^/η2
Тогда при ίι?2 ^ *π и ί3)2 ^ *ш где *π — пороговое значение крите¬
рия, установленное в соответствии с принятой величиной доверительной
вероятности Р, принимается гипотеза Hi. Во всех остальных случаях
принимается нулевая гипотеза.
Збб
Гл. 8. Изображения объектов протяженной формы
Исходная точка для прослеживания определяется в результате об¬
наружения протяженного объекта. Нахождение второй и последующих
точек производится следующим образом. Центр строба устанавливается
на исходную точку. Затем происходит адаптация строба, т.е. определение
оптимального направления перемещения и ширины d2 центральной части
строба 5г. Считается, что состояние строба выбрано оптимально, если
в результате вариации направления перемещения и ширины с?2 достиг¬
нуты максимальные значения и ^3,2· Если выполняются условия
^1,2 max ^ И ^3,2 шах ^
то принимается данное направление движения и значение ширины цен¬
тральной части строба. После адаптации центр строба перемещается в вы¬
бранном направлении на один пиксел и в массив памяти заносится единич¬
ный вектор, соединяющий предыдущую точку, в которой находился центр
строба, с текущей. Набор векторов перемещения строба образует контур.
Прослеживание протяженного объекта прекращается, если значе¬
ния ti,2max и £3,2 шах оказываются ниже порога срыва слежения.
После того, как протяженный объект был прослежен в одном направ¬
лении, строб возвращается в начальное положение, т.е. центр строба вновь
устанавливается на начальную точку, и осуществляется прослеживание
в противоположном направлении.
8.6. Обсуждение результатов
В данной главе рассмотрена задача обнаружения изображений объек¬
тов протяженной формы, например, дорог, лесных просек, рек, каналов
и т.п., имеющих незначительную ширину (до 10 пикселов) в реальных
ландшафтных сценах. Изображение характеризуется отношением сиг-
нал/фоновый шум, близким к единице. Для формирования статистик, по
которым принимается решение, принят метод согласованно-избиратель¬
ной фильтрации.
Получено аналитическое представление для частотного коэффици¬
ента передачи фильтра, избирательно-согласованного с идеальным пря¬
моугольным импульсом яркости длительностью т = t — 2, образующим¬
ся в поперечном сечении изображения объекта. Амплитудно-частотная
характеристика фильтра симметрична относительно центрального от¬
счета m = t/2 и имеет вид двух полуволн с нулевыми отсчетами при
га = 0 и га = t/2. Максимумы характеристики расположены в точках
га = 0,304£ и га = 0,6941 и равны \ω (га)| — 3,0792. Общая ширина
полосы пропускания фильтра равна 0,5621
В отличие от обычных согласованных фильтров амплитудно-частотная
характеристика СИФ не повторяет амплитудно-частотный спектр сигнала.
Каждый ее отсчет отличается от соответствующего отсчета амплитудно-ча¬
стотного спектра сигнала множителем sin2 —га. Фазочастотная характери¬
стика СИФ в отличие от подобной характеристики согласованного фильтра
полностью совпадает с фазочастотным спектром сигнала.
8.6. Обсуждение результатов
367
Пиковое значение полезного сигнала на выходе фильтра не зависит от
параметров импульса яркости и равно 2C/R (0) а, где R (0) — дисперсия,
а — декремент затухания АКФ фонового шума. СИФ подавляет посто¬
янные и низкочастотные составляющие спектра фонового шума и изобра¬
жения объекта, но хорошо пропускает высокочастотные составляющие
спектра контура обнаруживаемого изображения. Отношение сигнал/шум
на выходе фильтра из-за дифференциального характера его работы слабо
зависит от длительности импульса яркости. Рост его при этом связан не
с увеличением энергии полезного сигнала, а с уменьшением дисперсии
фонового шума на выходе фильтра из-за сужения полосы пропускания.
Показано, что процедура согласованно-избирательной фильтрации
для изображения нитевидного, вертикально ориентированного объекта
постоянной ширины длиной Р пикселей состоит из накопления значе¬
ний яркости Р строк и дальнейшей фильтрации накопленного импульса.
Экспериментальным путем получена зависимость выходного отноше¬
ния сигнал/фоновый шум по мощности от длины Р изображения ните¬
видного объекта. Она имеет характер, близкий к прямолинейному.
Обнаружитель, работающий по критерию Неймана-Пирсона, содер¬
жит фильтр и пороговое устройство. Фильтр избирательно согласован
с изображением вертикально ориентированного объекта шириной т и дли¬
ной Р пикселей с известной формой импульса яркости в поперечном
сечении объекта. Чтобы исключить необходимость определения оценок
декремента затухания АКФ фонового шума и его дисперсии, обнаружи¬
тель содержит блок вычисления дисперсии σ\ фонового шума на выходе
СИФ и использует ее для формирования порогового уровня. Построе¬
ны характеристики обнаружения изображения дороги в ландшафтной
сцене для различных значений т, Р и формы фронтов импульса яркости,
образующегося в поперечном сечении изображения. Из характеристик
следует, что уровни пороговых сигналов слабо зависят от формы фронтов
импульса. Поэтому яркостный профиль поперечного сечения изображе¬
ния целесообразно аппроксимировать импульсом прямоугольной формы.
В этом случае упрощается алгоритм работы СИФ и имеется возмож¬
ность аналитическим путем рассчитать параметры фильтра. Сравнение
эффективностей обнаружителя на базе СИФ, работающего в условиях
сильнокоррелированного фонового шума, и оптимального обнаружителя
на базе согласованного фильтра при воздействии белого шума показало,
что проигрыш в пороговом сигнале у первого незначителен и имеет поря¬
док 3 дБ. Это позволяет считать рассмотренный обнаружитель изображе¬
ний нитевидных объектов, использующий для формирования достаточ¬
ной статистики согласованно-избирательный фильтр, квазиоптимальным
устройством. Поскольку изображения данных объектов в сцене имеют
произвольную ориентацию, то необходимо осуществить поворот сцены
таким образом, чтобы обнаруживаемое изображение было расположено
вертикально. Для этого можно использовать априорную информацию, на¬
пример, топографического плана. В противном случае образуется набор из
R копий фильтруемой сцены, в каждой из которых изображения повер¬
368
Гл. 8. Изображения объектов протяженной формы
нуты на угол α(π/#), а = 0,1,... , R - 1. Каждая сцена подвергается
согласованно-избирательной фильтрации и в качестве статистики для
принятия решения об обнаружении принимается максимальный по всем
копиям отсчет фильтра.
Задачи и упражнения
1. Почему при согласованно-избирательной фильтрации идеального импульса
яркости максимально возможный отсчет фильтра не зависит от длительности
импульса?
2. Чем определяется количество М не равных нулю отсчетов на выходе филь¬
тра? Постройте зависимость количества М значащих отсчетов СИФ от дли¬
тельности I фронта скачка яркости.
3. Рассчитайте импульсную характеристику и отклик фильтра, избирательно¬
согласованного с идеализированным положительным импульсом яркости: вид
переднего фронта — прямоугольный с h =0; вид заднего фронта — линей¬
ный с h = 3; длительность вершины т = 5.
4. Рассчитайте отклик фильтра, определяемого параметрами предыдущей зада¬
чи, при подачи на его вход сигнала в виде идеализированного положительного
импульса яркости: вид переднего фронта — прямоугольный с h =0; вид
заднего фронта — линейный с /г = 3; длительность вершины τ — 3. Сравните
полученные результаты с результатами предыдущей задачи.
5. Предложите структуру обнаружителя изображений объектов протяженной
формы для случая, когда ширина объекта неизвестна.
6. Рассчитайте импульсную характеристику и отклик на выходе фильтра, из¬
бирательно-согласованного с идеализированным отрицательным импульсом
яркости: вид переднего фронта — линейный eh = 2; вид заднего фронта —
линейный с h = 3; длительность вершины т = 2.
7. Рассчитайте и постройте импульсную характеристику фильтра, избирательно
согласованного с прямоугольным импульсом яркости с длительностью верши¬
ны т = 3.
8. Оцените изменение пикового выходного сигнала двумерного СИФ при нали¬
чии углового рассогласования апертуры пространственного фильтра с изобра-
женим объекта.
9. Определите спектр сигнала в виде идеализированного импульса яркости
с прямоугольными фронтами при т — 3. Рассчитайте и постройте ампли¬
тудно-частотный и фазочастотный спектры.
10. Определите спектр сигнала на выходе фильтра, избирательно-согласованного
с идеализированным импульсом яркости с прямоугольным фронтом при т =
= 3, при воздействии аналогичного сигнала.
11. В соответствии с методикой, описанной в п. 6.5.2, рассчитайте и постройте
теоретические и экспериментальные характеристики обнаружения объектов
в виде импульсов яркости с прямоугольными фронтами при т — 5.
12. В соответствии с методикой, описанной в п. 6.5.2, рассчитайте и постройте
теоретические и экспериментальные характеристики обнаружения объектов
в виде импульсов яркости с линейными фронтами при т — 4, h = 3, h = 3.
Глава 9
АНАЛИЗ И РАСПОЗНАВАНИЕ ИЗОБРАЖЕНИЙ
ПО ИХ ФОРМЕ
9.1. Специальные операции над контурами изображений
9.1.1. Эквализация кода контура. Процедуру выравнивания размер¬
ностей двух контуров назовем эквализацией контуров. Эта процедура
является вторичной дискретизацией
контура изображения. Рассмотрим
один из подходов к эквализации пу¬
тем деления контура Г = {7 (п)}0 к_г
на заданное количество р одинаковых
по длине отрезков, концы которых
соединены векторами. Эти векторы
являются ЭВ ε (г) нового эквализо-
ванного контура Е = {e(r)}ο,ρ-ι.
Каждый ЭВ ε (г) состоит из трех
частей: 1) остатка Д7<й (п) вектора
7 (п); 2) (t — 1) полных ЭВ 7(71+ 1),
7(пН-2), ..., 7(n-M — 1); 3) использованной части Δ7иСП (п + £)
элементарного вектора 7 (n -f t) контура Г (рис. 9.1). Длина отрезков,
на которые разбивается контур Г, равна
к-1
ε = ^Σΐ7(η)Ι· (9.1-1)
п=О
На каждом r-м шаге эквализации вначале проверяется условие
|Д7Й(п)|>е- (9-1-2)
При выполнении этого условия в состав ЭВ ε (г) не входят полные
ЭВ контура Г и ЭВ ε (г) выделяется из остатка Ajow (п) элементарного
вектора 7 (п) исходного контура Г. Тогда
£ (г) = |е| (та). (9.1.3)
|Δ7κτ (п)|
и остаточный вектор Д70СТ (η — 1) для следующего, (г + 1)-го шага эква-
ДГисп(л + 3)
,у(и+3)
rin+ΪΙ
Г(я +1)/
Х(я+ 4)
Ду(оЙ(")^/ (r) £(r+lK\y("+5)
Г(и)Де(г-1)
Рис. 9.1. Образование элементарно¬
го вектора эквализованного контура
370
Гл. 9. Анализ и распознавание изображений по их форме
лизации, равен
д7ост+1) (п) = (п) - е (0 · (9-1.4)
Если же условие (9.1.2) не выполняется, то проверяется значение £,
при котором начинает выполняться условие
t
|a7<S (п)| + Ц|7(и +j)l = (9.1.5)
i=l
Определив его, далее для получения ЭВ ε (г) находим модуль и само
значение части использованного ЭВ 7 (n + t) контура Г:
t-1
1д7исп (η + ί)| = |ε| - |Δ7^ (η)I - Σ |7 (« + j)I,
i=1
(9.1.6)
А7исп (гг + t) = 7 (η + t) ·
В этом случае ЭВ ε (г) для r-го шага эквализации и остаточный век¬
тор Δ7&τ+1) (n -f t) на (г + 1)-й шаг эквализации будут иметь вид
£—1
ε (г) = А<у£) (п) + Д7ИСП (n + i) + ^7(n + j), (9.1.7)
i=i
д7ост+1) (η + t) = 7 (η +1) - Д7исп (η +1) ■ (9.1.8)
Для эквализованного контура характерно: 1) концы и начало векто¬
ров ε (г) принадлежат линии исходного контура Г; 2) процесс эквализа¬
ции является сходящимся, так как
начало вектора ε (0) совпадает с кон¬
цом вектора ε (р — 1).
При
р^>к (9.1.9)
модули всех ЭВ ε (г) мало отличают¬
ся друг от друга, т.е.
к (ΟΙ =
у( о)
, 1
Ю)
r(l)
[«(Η)
ε\
АЛ
•(г:
k
Ιχ
у (6)
.εάω
i
Ηί
4,
ε
φ,
ε(4);
ι /ι г
У(:
'
Μ
9).
k
ε(
81
ε(
т
Ζγ(3)
—
Ύ(
hS
4)"
(7)
ε((
ψ
ш
X j
ζ/λ
1 ι
Г(2)
г = 0,1,... — 1.
(9.1.10)
Это значительно упрощает опера¬
ции обработки эквализованных кон-
туров, компенсируя в определенной
Ис* 9.2. Преобразование контура степени затраты на эквализацию.
^ — {т(^)}0,7 (сплошные линии)
в контур Ε = {ε (п)}0 и (штриховые
линии)
На рис. 9.2 в качестве примера
показан результат эквализации контура
из к = 7 ЭВ:
Г = {2; 2 - 2г; -г; -2 - 2г; -2 + 2г; г; -1 + г; 1 + г}.
9.1. Специальные операции над контурами изображений
371
Эквализованный контур Е содержит р = 12 ЭВ и имеет вид
Е = {1,27; 1,11 - 0,39г; 0,90 - 0,90г; 0,71 - 0,98г; -0,39 - 1,11г; -0,90 - 0,90г;
- 0,90 - 0,51г; -0,90 + 0.90г; -0,90 + 0,90г; -0,20 + 1,20г;
- 0,71 + 0,90г; 0,91 + 0,89г}.
9.1.2. Стандартизация кода контура. При различных операциях, свя¬
занных с линейными преобразованиями контуров со стандартными зна¬
чениями элементов их разностного кода, равными
1,1 — г, —г, —1 — г, —1, —1 -f г, г, 1 -f г,
элементы разностного кода теряют свойство стандартности. Например,
поворот контура, заданного стандартными ЭВ, на угол, не кратный π/2,
всегда сопровождается таким явлением. В то же время для индикации
контуров изображений, занесенных в ОЗУИ системы технического зре¬
ния, использования табличных методов умножения ЭВ, формирования
гистограммы частот ЭВ контура и ряда других случаев необходимо иметь
контур со стандартными ЭВ. В связи с этим рассмотрим одну из возмож¬
ных процедур стандартизации ЭВ произвольного полигонального контура.
На рис. 9.3 представлен фрагмент контура с двумя нестандартными
элементарными векторами О А и АВ, причем вектор О А начинается
из центра ячейки ОЗУИ. Пусть, например, проекции вектора О А на
оси х и у системы координат, совмещенной с началом вектора, больше
единицы, т.е. ОАх > 1 и ОАу > 1. Выделим из них проекции Оах и Оау,
Рис. 9.3. Формирование стандартных элементов комплексного кода
и построим стандартный элементарный вектор ОА. Если хотя бы одна из
проекций вектора аА = ОА — Оа превышает единицу, то процесс надо
продолжить. В противном случае складываем этот вектор с вектором АВ
и получаем новый вектор аВ с началом в центре ячейки. С ним посту¬
паем так же, как и с ОА. В результате получаем вектор ab, задающий
второй стандартный вектор, и разностный вектор ЬВ. Продолжая этот
процесс, получим последовательность стандартных ЭВ преобразованного
по размерности контура Г. Если полученный вектор аВ = аА + АВ
372
Гл. 9. Анализ и распознавание изображений по их форме
не имеет проекций, больших единицы, то складываем его со следующим
вектором контура до тех пор, пока не создадутся условия выделения из
просуммированных векторов стандартного вектора.
Описанный процесс стандартизации является сходящимся, т.е. по¬
следний разностный вектор исходного нестандартного кода равен нулю.
Последний шаг процесса связан с образованием вектора, конец которого
совпадает с началом нулевого вектора ОА. По принятому условию
вектор ОА начинается в центре ячейки. Поэтому полученный код так-
5 — 1
же задает замкнутый контур, т.е. Σ 7с (гс) = 0, где s — размерность
п=0
контура, состоящего из стандартных ЭВ 7С (η), η = 0,1,... , s — 1. Из
этого выражения следует равенство нулю последнего разностного век¬
тора при проведении процесса стандартизации полигонального контура
с произвольными значениями составляющими его ЭВ.
9.2. Структурный анализ формы изображений фильтрами,
согласоваными с классом форм
Согласованные фильтры, задаваемые выражениями (3.6.1) и (3.6.4), обес¬
печивают образование количественной меры схожести между фильтруе¬
мым контуром N и эталонной формой, определяемой контуром Г. Нередки
случаи, когда эталонные формы имеют ряд общих признаков, связанных
с некоторыми их общими свойствами, например: прямолинейность линии
фрагмента контура, симметричность ЭВ, степень правильности задавае¬
мой контуром фигуры и т.п. При наличии таких общих признаков можно
говорить о классе форм и появляется возможность учесть закономерности
определенного класса форм в выражении для КСФ. В результате такой
КСФ будет вырабатывать меру схожести с эталоном не для одного кон¬
кретного контура, а для целого класса контуров с общими свойствами.
Фильтрация прямолинейных фрагментов контура в сочетании с
другими фрагментами. Пусть контур N = {v{n)}ok_г, наряду с фраг¬
ментами произвольной конфигурации, содержит горизонтально ориентиро¬
ванный и направленный вправо прямолинейный фрагмент из I стандартных
ЭВ v (г), v (г -f 1), ... , v (г + / — 1), задающих с учетом дискретизации на
квадратной сетчатке данный фрагмент (рис. 9.4, а). Изображения с контура¬
ми такого вида часто встречаются при обзоре земной поверхности, например:
изображения аэродромов, дорог, участков рек и каналов, возделанных полей
и т.п. Преимущественно изображения с протяженными прямолинейными
участками внешних и внутренних границ носят антропогенный характер.
Найдем выражение для фильтра с окном С из s, s ^ /, элементов, вы¬
рабатывающего максимально возможный уровень выходного сигнала при
попадании окна в пределы прямолинейного фрагмента. Процесс фильтрации,
когда ширина окна фильтра меньше размерности контура, определяется
выражением (3.6.11). В данном случае у* (0) = 7* (1) = ... = 7* (s — 1) = 1
5 — 1
и это выражение принимает вид: η (т) = J2 v (п -f га), т = 0,1,... , k—1.
п=О
9.2. Структурный анализ формы изображений
373
Квадрат модуля выходного нормированного сигнала фильтра будет равен
ы
У] I/ (п + т)
п=0
У \и(п + т)\2
то = 0,1,... , к — 1.
(9.2.1)
° ^ 2
Здесь s — квадрат нормы эталонного фрагмента {1}0 β__1, Σ \ν (п + ш)| —
’ п=0
квадрат нормы фильтруемого фрагмента контура N в пределах окна С на
m-м шаге. Когда окно С расположено на прямолинейном фрагменте контура,
то ν (п + т)«\ν (п + т)|«1. При этом величина \ηΗ (т)\ слабо отличается
от единицы, т.е. от максимально возможной выходной величины фильтра.
Так как нормированный выходной эффект КСФ инвариантен к повороту
контура (см п. 3.6), то соотношение (9.2.1) справедливо для фильтрации
не только для горизонтально, но и произвольно ориентированных прямоли¬
нейных фрагментов контура. Отметим также, что выражение (9.2.1) задает
алгоритм фильтрации скользящего среднего (см. п. 3.4).
Если ЭВ контура не являются стандартными, то для фильтрации прямо¬
линейных отрезков контура в соответсвии с выражением (9.2.1) возможны
два следующих подхода. Первый из них состоит в проведении процедуры
стандартизации ЭВ, а второй — процедуры эквализации линии контура.
Эквализация должна быть проведена таким образом, чтобы модули эква-
лизованных ЭВ незначительно отличались друг от друга, что достигается
выбором достаточно большой размерности преобразованного контура.
Таким образом, алгоритм фильтрации скользящего среднего обеспе¬
чивает квазисогласованную фильтрацию произвольно ориентированных
374
Гл. 9. Анализ и распознавание изображений по их форме
прямолинейных фрагментов контура, состоящих из близких по модулю
ЭВ. При этом, чем меньше отношение квадрата модуля суммы ЭВ к сумме
квадратов модулей ЭВ в пределах окна фильтра отличается от величи¬
ны Ι/s, тем ближе фильтруемый фрагмент контура к прямолинейному.
На рис. 9.4 показан пример выделения прямолинейного отрезка. Окно
фильтра шириной s = 20 элементов начинает двигаться от точки а$.
Если принять пороговый уровень равным 0,8, то величина \ηΗ\ превышает
его на интервале шагов т = 10... 19. Этим шагам соответствует уча¬
сток контура в пределах от 7(10) до 7(39), который визуально близок
к прямолинейному отрезку. Если порог повысить до 0,85, то величина
|77н| превышает его на интервалах шагов га = 14,15,16 и при га =
= 18. В этом случае в качестве прямолинейных будут признаны участки
контура в пределах 7(14) до 7(34) и 7(17) до 7 (37). Эти участки по
своей конфигурации слабо отличаются от прямолинейных.
Пусть теперь необходимо выделить фрагмент контура в виде «луча»
(см. п. 1.2). Этот фрагмент содержит два прямолинейных противоположно
ориентированных отрезка. Поэтому для его выделения можно применить
два фильтра для прямолинейных отрезков, каждый с окном, равным s:
\v«(m)\2
5-1 2s — 1
У ν (η 4- m) — v (η + га)
1 η=0 n—s
2s 2s—i
Σ Ип+™)12
n=0
(9.2.2)
Пример выделения фрагмента типа «луч» фильтром (9.2.2) с окном
s = 6 показан на рис. 9.5. Отметим, что фильтр (9.2.2) для выделения
фрагментов «луч» есть ФСР. Если в общем случае необходимо выделить
фрагмент из прямолинейных отрезков, составляющих угол Αφ, то второй
прямолинейный отрезок надо повернуть на угол π — Αφ, т.е. каждый ЭВ
этого отрезка умножить на — ехр {—ιΑφ}.
Рис. 9.5. Выделение фрагмента в виде луча: а — исходный контур; б — зависи¬
мость выходного сигнала согласованного фильтра от числа шагов фильтрации
9.2. Структурный анализ формы изображений
375
фильтрации, равный сумме половинных нормированных выходных эф¬
фектов фильтров, согласованных со сторонами фигуры угла, имеет вид
М«г)|
1
2 лД
УЗ и (п + т)
п—О
-1
N
У] Ип + т)|2
п=0
2s —1
I/ (п + т)
2s— 1
N
Ип + т)12
(9.2.3)
Фильтр для выделения фрагмента контура в виде фигуры угла можно
также сделать в виде двух фильтров для выделения произвольно ори¬
ентированных и примыкающих друг к другу прямолинейных отрезков,
инвариантных к угловой ориентации этих отрезков
Ы”01 =
УЗv (п+т)
s —1
a, s53ii/(n+m)i2 211
\ п=0
I/ (п + га)
n—s
2s — 1
л «53 Ип + т)
> n=s
(9.2.4)
На рис. 9.6 показаны результаты обработки контура, содержащего
фрагмент в виде угла, равного 45°, фильтрами с окнами по s = 5, работаю-
Рис. 9.6. Выделение фрагмента контура в виде угла: а — исходный контур; б -—
зависимость выходной величины фильтра от числа шагов фильтрации
щими по формулам (9.2.3) и (9.2.4) (соответственно кривые 1 и 2). Видно,
что первый фильтр, как использующий большую, чем второй, априорную
информацию, обеспечивает большую избирательность.
Фильтры, согласованные с элементарными контурами. Такие филь¬
тры будут хорошо реагировать на правильные фигуры, задаваемые ЭК
Го, Γι,... , Г/с_1. С учетом выражения (1.8.3) для ЭК Г5 порядка s выра¬
жения (3.6.1) и (3.6.4) для КСФ примут вид
АС-1
η8 (γη) — ^2 v (n) ехР (га — n -f 1)| =
п=О
к~1
= ^2 v (т — п) ехр (п + 1)|.
376
Гл. 9. Анализ и распознавание изображений по их форме
Если через фильтр проходит согласованный с ним ЭК, то
ηs (т) = А; ехр j ехР {}»
т = 0,1,... , к — 1 и 77s (к — 1) = к.
Результатом фильтрации является тот же ЭК, но растянутый в к раз
и повернутый на угол Αφ = 2ns/к. При фильтрации несогласованного
с фильтром ЭК Г/, 1ф s, получим
к-1
Vs (ш) = ехр (lm -f exp |г^п (5 ~ 0}·
n—0
Внутренняя сумма при s ф I всегда равна нулю. Поэтому η8 (т) =
= 0, т.е. при несовпадении порядков ЭК, Г/ не проходит через фильтр,
согласованный с ЭК Г5. Если через фильтр, согласованный с ЭК Т8,
проходит произвольный контур N = {и (п)}0 к_г, то
η, (m) = pv (s) exp ji^s (m + 1)|,
s = 0,1,... , к — 1,
где pu (s) = η8 (к — 1) — s-я компонента спектра контура N (см. п. 3.6.4).
Набор фильтров, согласованных с ЭК Γ0,Γι,... ,Γ^-ι, осуществляет
полный спектральный анализ контура Ν. Так как ||Ν||2 = -||Р||2, то чем
ближе величина ^|Pi/(so)|2 к ||N||2, где So — номер доминирующей по
модулю компоненты спектра контура N, тем ближе форма фильтруемого
контура N к правильной фигуре Г5о. Отметим связь между направлением
обхода контура N и его спектром. Если энергия спектральных составляющих
в левой половине спектра больше энергии составляющих в правой половине
спектра, то в контуре N преобладают ЭК с обходом против часовой стрелки
и контур N будет прослеживаться в этом же направлении и наоборот.
На рис. 9.7 показан контур N размерностью к = 4. В спектре контура
значительно доминирует составляющая |р(3)|. Это означает, что фигура,
задаваемая контуром, близка к фигуре квадрата с обходом по часовой
Рис. 9.7. Контуры с противоположными направлениями обходов и модули их спек¬
тров
9.2. Структурный анализ формы изображений
377
стрелке. Контур отличается от контура N только направлением
обхода. Это отражается на его спектре, в котором доминирует составляю¬
щая \р (1)|, соответствующая квадрату с обходом против часовой стрелки.
Фильтры, согласованные с симметричными и антисимметричными
контурами. ЭВ симметричных контуров связаны соотношением 7 (η) =
= 7 (—η) = 7 (fc — η), η = 0,1,... , λ; — 1. Используя эту информацию,
определим выражение для фильтра, согласованного с симметричным кон¬
туром. Обозначим 5 = п — т + k — 1. Тогда —s — т — п~к-\-1и для
симметричных контуров выражения (3.6.1) и (3.6.4) принимают вид
к —1 к—1
Л (го) = Σ 7 (n)7* (m - η + 1) = 7 (ш - п) 7* (n + 1),
п=о п=о V · · ;
т = 0,1,... , А: — 1.
Аналогично, фильтр
к-1 к-1
Л (т) = -^3 7 (η)7* (τη - η + 1) = -^7 (то - п) 7* (η + 1),
п=0 п=0 у ·■ )
т = 0,1,... , А: — 1,
является согласованным для антисимметричных контуров, ЭВ которых
обладают свойством 7 (п) = -7 (—гг) = —7 (к — п).
Исследуем характер связи между аргументами перемножаемых функ¬
ций, стоящих под знаком сумм в выражениях (9.2.5) и (9.2.6). Суммируя эти
аргументы в любой из формул, получаем, что результат равен (т + 1)к,
т.е. не зависит от внутренней переменной п, а определяется лишь зна¬
чением внешней переменной т. Запись (·)*. означает, что выражение
в скобках берется по модулю к. Данный результат является следствием
разных знаков внутренней переменной п, входящей в значения аргумен¬
тов перемножаемых функций. При этом для получения отсчета η(τη)
фильтра ЭВ ν и 7 выбираются путем обхода контуров N и Г в противо¬
положных направлениях. Если аргумент первого сомножителя равен п,
то аргумент второго равен (га -Ь 1 — п)к, и наоборот. Это соотношение
приводит к тому, что под знаком суммы все сомножители разбиваются на
пары вида 7 (п) 7* (га -f 1 — п)к и 7 (ш + 1 — п)к 7* (п). При фильтрации
согласованного с фильтром контура ν (п) =7 (n), n = 0,l,...,fc — l,
и эти сомножители в сумме будут давать чисто вещественное число
7 (п) 7* (т + 1 — п)к + 7 (m + 1 — п)к 7* (п) = 2 Re [7 (п) 7 (ш — п -h 1)]
(9.2.7)
Таким образом, все отсчеты фильтра при согласованной фильтра¬
ции симметричных и антисимметричных контуров будут вещественными
числами. Данное свойство позволяет значительно снизить трудоемкость
согласованной фильтрации, уменьшив в два раза число суммируемых
слагаемых и определяя лишь их реальные части.
Аргументы п и (т — п + 1)к функций, входящих в выражение (9.2.7),
могут быть разными или одинаковыми числами. Аргументы будут одина-
378
Гл. 9. Анализ и распознавание изображений по их форме
новыми, когда п = (ш — п + l)fc или 2п = к + т +1, причем п по удловию
является целым числом. Пусть к — нечетное число. Тогда если га —
четное число, то п = (к + 1 -Ь га)/2 — целое, ап = (1 + га)/2 — нецелое
число. Если же га — нечетное число, то η = (к + 1 4- га)/2 — нецелое,
ап = (1 + ш)/2 — целое число. Таким образом, при нечетной величине
к совпадение аргументов происходит только в одном случае и для полу¬
чения одного отсчета фильтра необходимо суммировать ((к — 1)/2 4-1)
слагаемых.
Пусть теперь к — четное число. При четном га числа п = (к 4* 1 + ш)/2
и η = (1 + га)/2 будут нецелыми. Поэтому при четном значении размер¬
ности к фильтруемого контура для каждого четного значения внешней
переменной т в суммах (9.2.5) и (9.2.6) не будет ни одного слагаемого с сов¬
падающими аргументами, зато для каждого нечетного га два слагаемых
будут иметь совпадающие аргументы. В первом случае для получения
одного отсчета фильтра необходимо будет суммировать к/2 слагаемых,
а во втором случае ((к - 2)/2 + 2) = к/2 + 1 слагаемых.
Пусть, например, к = 3. Выпишем в две строки значения аргументов для
каждой величины га — 0,1,2:
га = О т — 1 т — 2
012 012 012
102 210 021
Видно, что для каждого значения га имеется по одному совпадению аргумен¬
тов первого и второго сомножителя. Пусть теперь к = 4. Выпишем аналогичным
образом значения аргументов:
га = 0 га = 1 га = 2 т = 3
0123 0123 0123 0123
1032 2103 3210 0321
Видно, что для нечетных га нет ни одного совпадения аргументов, а для
четных га имеется по два совпадения.
Если для к = 4 найти отсчеты фильтра, то
η (0) = 2 Re 7 (0) у (1) + 2 Re 7 (2) 7* (3),
η (1) = 2 Re 7 (0) 7* (2) + |7 (1)|2 + \Ί (3)|2,
η (2) = 2 Re 7 (0) 7* (3) + 2 Re 7 (1) 7* (2),
Ώ (3) = 17 (0)|2 + 2 Re 7 (1) 7* (3) + |7 (2)|2.
Результат фильтрации симметричного контура Г = {3 -|- 2г; 2 — г; —7; 2 — г},
определенный по этим формулам, равен Н = {-20; -32; -20; 72}.
Фильтры, согласованные с сопряженно-симметрическими и сопря-
женно-антисимметрическими контурами. Для элементарных векторов
СС и СА контуров соответственно имеют место следующие соотношения:
7 (п) = 7* (-п) = 7* (к - п), 7 (п) = -7* (-п) = -у* (к - п).
Вводя переменную s = п — т — 1, для фильтра, согласованного с СС
контуром, на основании выражений (3.6.1) и (3.6.4) получим
9.3. Определение характеристик формы изображения
379
к-1
к-1
η (m) = ^2 7 (п) 7 (га — п + 1) = 7 (т — п) 7 (η + 1),
га — 0,1,... , к — 1.
Аналогично для СА контура
/е—1 к-1
η (га) = —^ 7 (п) 7 (m — n -f 1) = 7 (т — η) 7 (η -f 1),
га — 0,1,... , к — 1.
Поскольку знаки внутренней переменной η в этих формулах для со¬
множителей, стоящих под знаком суммы, разные, то, как показано для
симметричных контуров, все произведения, стоящие под знаком суммы,
разбиваются на пары 7 (п) 7 (га + 1 — п) и 7 (га + 1 — п) 7 (п), либо одно
из них принимает вид η1 (га + 1 — п). В результате количество произве¬
дений уменьшается примерно вдвое и трудоемкость фильтрации падает.
В отличие от фильтрации симметричных и антисимметричных контуров
из-за отсутствия комплексной сопряженности ЭВ импульсной характери¬
стики отсчеты фильтров (9.2.8) и (9.2.9) уже не будут вещественными.
Например, результаты фильтрации СА контура Гс/а = {2г; 7; 1 — г; —1 — г; —7}
будут иметь вид
η (0) = - [27 (0) 7 (1) + 27 (2) 7 (4) -f η2 (3)] = 14 - 44г,
η (1) = - [27 (0) 7 (2) + 27 (3) 7 (4) + 72 (1)] = -67 - 18*,
П (2) = - [27 (0) 7 (3) + 27 (1) 7 (2) + J2 (4)] = -67 + 18*,
Т) (3) = — [27 (0) 7 (4) + 27 (1) 7 (3) + 72 (2)] = 14 + 44г,
η (4) = - [72 (0) + 27 (1) 7 (4) + 27 (2) 7 (3)] = 106.
9.3. Определение характеристик формы изображения
Распространенной числовой характеристикой формы фигуры явля¬
ется коэффициент формы, определяемый как отношение квадрата пе¬
риметра L к площади 5, т.е. кф = L2/S. Периметр L через элементы
разностного кода ΔΓ находится как
Получим выражение для площади полигонального контура изображе¬
ния, рассматриваемого как к-угольник. Площадь fc-угольника без самопе¬
ресечения его сторон находится как сумма площадей составляющих его
треугольников, образованных векторами суммарного кода:
к-1
(9.3.1)
п=0
(9.3.2)
380
Гл. 9. Анализ и распознавание изображений по их форме
Здесь [β (η - 1) ,/3 (п)] — векторное произведение текущих векторов
суммарного кода β (η - 1) = βι (η — 1) + г/?2 (η — 1) и β (гг) = β\ (η) +
+ г/?2 (ft). Из представления для векторного произведения векторов
\β(η-1),β(η)} =
для площади фигуры получаем
к-1
i j к
βι (η - 1) β2 (η - 1) О
βι {η) /?2 (η) 0
5 = 0,5
X) [5ι (η - 1) β2 (η) - 5ι (η) β2 (η - 1)]
(9.3.3)
При данном подходе площади одних составляющих фигуру треуголь¬
ников входят с положительным знаком, других — с отрицательным.
Применим выражение (9.3.3) для вычисления площади фигуры, контур кото¬
рой образует вогнутый многоугольник. Суммарный код этого контура равен В =
= {7,7 + 6г; 6 4- 2г; 2 4- г; 6г; 0}. Площадь фигуры, найденная с помощью сумм
векторных произведений векторов суммарного кода контура, будет равна S =
= ^ |(7 · б - 7 · 0) + (7 · 2 - 6 · 6) + (6 · 1 - 2 · 2) + (2 · 6 - 0 · 1)| = 17.
Использование выражений (9.3.1) и (9.3.2) позволяет записать представ¬
ление для коэффициента формы фигуры через ЭВ ее контура Г в виде
п 2
7с—1
Σ |7 (п)
_п=0
к-1
Σ[β(η-1),β(η)]
(9.3.4)
В ряде случаев, например при автоматическом дешифрировании изо¬
бражений, приходится сталкиваться с двумя видами задач по определе¬
нию ширины фигуры. В задачах первого вида необходимо найти длину
горизонтального отрезка с началом в текущей точке aj контура и оконча¬
нием в первой найденной контурной точке (рис. 9.8, а). Задача решается
на основе суммарного кода В. Текущая ширина h фигуры определяется
Ш
ж
ш
Ш
Ш
ш
Г
1
h
ш
щ
1
ж
<ч
1
ш
ш
У//А
щ
ш
ж
X
ш
1
Ж
1
1
Ш
1
щ
i
щ
щ
т
WA
щ
щ
S2L
Рис. 9.8. Определение текущей ширины фигуры: а — ширина фигуры в горизон¬
тальном направлении, б — ширина фигуры как минимальное расстояние между
противоположными сторонами
9.4. Информативные признаки формы
381
вектором суммарного кода контура с началом в точке aj и для которого
выполняется условие Im β{η) — Σ bn 7 (η) = 0. Тогда ширина фигуры
i=о
на уровне точки aj равна h = Re β (η).
Второй вид задач связан с определением текущей ширины h фигу¬
ры, например ширины реки, по ее оптическому или радиолокационному
изображению. Под шириной в точке aj понимается модуль вектора с на¬
чалом в этой точке, имеющий минимальную длину, и с концом в другой
контурной точке (исключая точки, соседние с точкой aj). Определение
вектора также производится с помощью суммарного кода контура реки.
Для этого с началом в точке aj строится пучок суммарных векторов и в
момент достижения модулем его радиус-вектора глобального минимума
производится отсчет значения ширины h (рис. 9.8, б).
Еще одной полезной геометрической характеристикой формы фигуры
являются ее габариты — максимальные размеры в горизонтальном Дхтах
и вертикальном Δутах направлениях. Эти размеры находятся через эле¬
менты суммарного кода контура следующим образом
Дхтах = max Re β (η) - min Re β (η);
Д^/тах — тах 1т β (гс) “ minim β (η).
9.4. Информативные признаки формы, определяемые
по спектру контура
Спектр контура, вычисленный с помощью ДПФ, содержит такое же ко¬
личество информации о форме изображения, как и сам контур, заданный
в аналитическом виде на плоскости, например, разностным или суммарным
кодами. Однако некоторые информативные признаки формы легко находят¬
ся именно по спектру контура. Кроме того, в ряде случаев имеется только
спектральное представление контура. Базируясь на сведениях, приведенных
в гл. 2, рассмотрим связь особенностей формы изображения со спектром
его контура. При этом определяемые по спектру характеристики формы
не должны зависеть от параметров линейных преобразований изображения,
таких, как масштаб, поворот и положение начальной точки контура.
1. Степень замкнутости контура. Сумма всех ЭВ контура Г равна
нулевой компоненте его спектра, т.е.
Поэтому величина модуля этой компоненты может определить степень
замкнутости контура. Если контур замкнут, то |р(0)| = 0. В противном
случае он разомкнут, причем, чем больше величина |р(0)|, тем дальше
находятся друг от друга концы линии контура. Отношение
п
к — 1
р(°) = Σι(»)·
(9.4.1)
382
Гл. 9. Анализ и распознавание изображений по их форме
где L — периметр контура, равно нулю для замкнутого контура и единице
для контура в виде прямолинейного отрезка, т.е. для контура с максимальной
степенью разомкнутости. Поэтому величину t удобно принять в качестве
количественной характеристики степени замкнутости контура. Вместо пе¬
риметра L в выражении (9.4.1) может быть использована величина нормы
контура
к-1
к ^
rn=1
\р(т) I2
определяемая через элементы спектра контура. В этом случае для за¬
мкнутого контура величина t по-прежнему равна нулю, однако контур
в виде прямолинейного отрезка уже не характеризуется значением t — 1.
2. Мера схожести двух изображений. Как показано в разделе 1.4,
в качестве меры схожести форме двух изображений может быть принят
модуль нормированного скалярного произведения контуров этих изобра¬
жений. Учитывая связь между скалярными произведениями, опреде¬
ляемыми через ЭВ контура и ЭВ его спектра, мера схожести двух форм
изображений с контурами N и Г имеет вид
\Ώ I = l(pN,Pr)|
т ΙΙΡνΙΜΙΡγΙΙ
(9.4.2)
Величина \ηΗ\ находится в пределах от нуля до единицы.
3. Особенности формы. Ряд следующих характеристик формы выте¬
кает из свойств спектров контуров специального вида (см. п. 2.5).
3.1. Если спектр контура носит чисто вещественный характер, то кон¬
тур является сопряженно-симметрическими, т.е. у (п) = у* (к — п) ,п =
= 0,1,... ,/с — 1, а если спектр является чисто мнимым - то сопряженно-
антисимметрическим, т.е. у (п) = —у* (к — п), п = 0,1,... , к — 1.
3.2. Если для контура с четным значением к ЭВ спектра равны нулю,
то контур обладает свойством равнодольности, т.е.
у (п) = -у (п + к/2).
3.3. Если контур спектра Р обладает свойством симметричности, т.е.
р (т) = р (к — т), то исходный контур Г, задающий форму изображения,
благодаря взаимному соответствию между операциями прямого и обрат¬
ного ДПФ тоже будет симметричным, т.е.
7 (п) — У {к — п).
Аналогично, если контур Р будет антисимметричным, т.е. р(т) —
= —р(к — т), то такими же свойством будет обладать исходный кон¬
тур Г, т.е.
7 Ы = -7 (к-п).
3.4. Если код контура спектра Р можно разбить на цепочки из г элемен¬
тарных векторов, г — 1 из которых подряд равны нулю, а г-й — отличен
от нуля, то исходный контур Г обладает свойством поворотной симметрии
степени г.
9А. Информативные признаки формы
383
3.5. Если спектр характеризуется ЭВ с близкими значениями их моду¬
лей, т.е. \р (1)| « \р (2)| « ... « \р (га — п)\, то в исходном контуре Г один
ЭВ будет превалировать по длине, по отноше¬
нию к другим ЭВ. Вследствие этого форма, за¬
даваемая контуром Г, будет характеризоваться
вытянутостью в направлении, задаваемом этим
превалирущим ЭВ. Эффект вытянутости про¬
является наилучшим образом при небольшом
разбросе аргументов ЭВ р (га).
Например, пусть Р = {0; 0,5 + 1,9г; 1,4 + 1,4г; 2г;
1,1 + 1,67*}. Видно, что модули ЭВ контура спектра Р
близки к двум. Обратное ДПФ для контура Р задает
исходный контур Г, который имеет следующий вид
(рис. 9.9):
Г = {0,6 + 1,394г; -0,1 - 0,28г; -0,314 - 0,704г;
- 0,032 - 0,03г; -0,154 - 0,38*}.
Превалирующий ЭВ 7 (0) имеет модуль 7 (0) =
= 1,518, а сам контур характеризуется сильной вытянутостью в направлении
этого ЭВ.
4. Контур с узкополосным спектром. Такой контур имеет одну со¬
ставляющую спектра, превалирующую по модулю над другими составля¬
ющими. Если s — номер этой составляющей, то
1И*)1 ^>|р(га)|, га ф 5, га = 0,1,... , к — 1.
Контур с подобным спектром будет близок к элементарному, т.е. мо¬
дули его ЭВ и углы между соседними ЭВ имеют малый разброс по своей
величине.
Рис. 9.9. Вытянутый в на¬
правлении элементарного
вектора 7(0) широкопо¬
лосный контур изображе¬
ния
Рис. 9.10. Узкополосный контур: а — амплитудно-частотный спектр, б — вид кон¬
тура
Например, если спектр контура равен Р == {0; 1 + 2г; 20; Зг; 2 + 2г}, (см.
рис. 9.10), то исходный контур Г имеет вид:
Г = {4,6 + 1,4*; -2,698 + 1,922*; 0,18 - 4,382г; 1,32 + 3,46г; -3,402 - 2,4г} .
Модули его ЭВ и углы между соседними ЭВ соответственно равны
{4,81; 3,31; 4,39; 3,70;4,16}; {127,6°; 127,8°; 156,8°; 146,1°; 161,7°}.
384
Гл. 9. Анализ и распознавание изображений по их форме
5. Контур нитевидной формы. Контур такой формы характеризуется
антисимметричностью своих ЭВ. Из
Рис. 9.11. Контур нитевидной формы
(а) и его спектр (б)
взаимного соответствия между пря¬
мым и обратным ДПФ и свой¬
ством спектра контура такого вида
следует, что если контур спектра
Р является антисимметричным, то
исходный контур Г будет задавать
нитевидную форму.
Например, контур Г, спектр которо¬
го равен Р = {0; 2; г; 1 + 2г; — 1 — 2г; —г;
—2}, имеет вид
Г = {0; -0,53 + 0,57г; 0,57 + 0,33г;
- 0,33 + 0,53г; 0,33 - 0,53г;
- 0,57 - 0,33г; 0,53 + 0,57г}.
Как следует из рис. 9.11, форма, задаваемая этим контуром, имеет хорошо
выраженный нитевидный характер. Отметим, что контур спектра Р также задает
форму такого вида.
9.5. Распознавание изображений со случайными формами
Примерами случайных изображений могут служить изображения об¬
лачности, листьев деревьев, пламени, профиля лица человека и т.п. Суще¬
ственная вариабельность формы изображений со случайными контурами
(см. п. 1.7) не позволяет рассматривать их как зашумленные изображения
некоторых эталонных объектов. При распознавании этих изображений
последовательность ЭВ контура представляется как случайный дискрет¬
ный процесс. В п. 1.7 описаны полиноминальная и марковская модели
случайных контуров. Первая из них предполагает независимость ЭВ η (η)
контура Г и известную вероятность Р (7 (π)) появления каждого из них.
Поскольку количество ЭВ в контуре часто встречающихся изображений
сравнительно невелико, не более к = 100... 200, то при произвольных
значениях ЭВ эти вероятности определить достаточно сложно.
В связи с этим количество разных ЭВ в контуре должно быть неболь¬
шим. Лучше всего здесь подходят стандартные ЭВ 7„, естественным обра¬
зом формирующиеся при вводе изображения в ОЗУИ. При кодировании
по Фримену
7ι = 0; 72 = 1; 7з = 2; 74 = 3; 75 = 4;
76 = 5; 7г = 6; 78 = 7,
а при комплекснозначном кодировании
7ι = 1; 72 = 1 -г; 7з =-г; 74 = -1-г;
75 =-1; 7б = -1 + г; 77 = Ц Is = 1+ г.
При сравнительно небольшом количестве разных ЭВ статистическая
достоверность частостей ки/к ЭВ 7„, v — 1,2,... , 8 в контуре изображе-
(9.5.1)
(9.5.2)
9.5. Распознавание изображений со случайными формами
385
ния j-το класса, j = 1,2,... , М будет выше. Отметим, что статистические
модели контуров удобней формировать с применением кода Фримена
(9.5.1) (см.п. 1.2).
При решении задачи распознавания изображений со случайными фор¬
мами целесообразно рассмотреть вопрос об адекватности результатов их
классификации машиной и человеком. Эксперимент по машинному агре¬
гированию выборки объемом R случайных изображений классов Αχ, А2,...
... , Ам может быть осуществлен следующим образом.
С субъективной точки зрения в этой выборке находятся Cj,j = 1,2,...
... , М, изображений каждого из классов, С = Σ с j. В качестве ана¬
литического описания контура принимается его разностный код ΔΓ =
— {7(n)}ofc-i> а в качестве признаков — частоты ки, v — 1,2,... ,8,
появления его ЭВ η (η) = 7„. Для каждого из контуров по его коду
можно составить вектор частостей Р = {Pvj}x 8, где PVj = Kj/kj, kj —
размерность контура Tj. В качестве меры близости двух контуров Aj
и Αι выбирается евклидовое расстояние между векторами Рj и Р/ их
частостей
Процедура оптимальной классификации сходна с процедурой типа
«Спектр» [132]. Случайным образом из С изображений выбирается одно
в качестве первого. Вторым служит изображение ближайшее к первому.
С помощью векторов частостей Ρχ и Р2 контуров этих изображений
находится вектор Р12, компоненты которого равны средним значениям
соответствующих компонент исходных векторов. В качестве третьего изо¬
бражения из оставшихся (С — 2)-ых выбирается то, у которого вектор
Р наиболее близок к вектору Р12 и т.д. Для уменьшения переходного
периода процедуры в дальнейшем для образования усредненного вектора
частостей берутся последние 10-20 отобранных векторов Рj.
Результаты ранжирования изображений по степени близости их друг к
другу можно охарактеризовать матрицей, номера строк и столбцов которой
равны номерам классов изображений. Элемент (jl) матрицы представляет
собой отношение числа изображений, субъективно отнесенных к классу I
и попавших в интервал класса j. При совпадении результатов субъективной
и объективной классификации матрица должна быть близка к единичной,
а при полном не совпадении все элементы — одинаковы и равны 1/М.
В первом случае создаются серьезные предпосылки для успешного решения
задачи распознавания изображений со случайными формами.
Определение статистических характеристик классов теоретическим
путем связано со значительными затруднениями и вопрос решается путем
обработки достаточно представительных выборок изображений каждого
класса. При использовании полиномиальной модели случайного контура
такой характеристикой является стохастический вектор rcj = 8·
м
8
(9.5.3)
386
Гл. 9. Анализ и распознавание изображений по их форме
Его компоненты π^· равны вероятностям появления ЭВ ην в контуре изо¬
бражения j-го класса. Оценки компонент вектора rcj всегда существуют,
причем оценкой максимального правдоподобия является частость Pvj —
— Kj/kj, v — 1,2,... ,8, соответствующего ЭВ [135]. Лишь для неболь¬
шого количества классов можно теоретическим путем решить вопрос о
виде вектора частостей Р. Таким классом являются, например, изобра¬
жения облачности. Здесь все ЭВ равновероятны и вектор вероятностей
для контуров изображений этого класса имеет вид
{0,1464; 0,1056; 0,1464; 0,1056; 0,1464; 0,1056; 0,1464; 0,1056}.
Разница в значениях компонент вектора вызвана разной длиной ЭВ
7 = 1, -г, —l,i и 7 = 1 — г, —1 — г, —1 + г, 1 + г.
Если в качестве математической модели контура используется полино¬
миальное распределение вероятностей, то целесообразно убедиться в слабой
взаимной зависимости между частостями ЭВ из построенных на основании
экспериментального материала эмпирических корреляционных матриц.
Получим алгоритм классификации случайных изображений по их кон¬
турам, используя полиномиальную модель, задаваемую выражением (1.7.8).
Для этого случая функция правдоподобия по изображениям класса Aj, j =
= 1,2,... , М, будет иметь вид
8 /8 8
L (k/Aj) = Ы Π <· / П кЛ = *, (9-5.4)
ν—\ / ι/=1 ι/=1
где к = [fcijfe,... ,fee] — вектор частот ЭВ; itj = [nUj\1 g — вектор
вероятностей этих ЭВ в контуре изображения j-το класса.
Представим логарифм этой функции как
8
In L (k/Aj) = В + ^ kv Ιηπ^·, (9.5.5)
ν—\
где В — константа, значение которой определяется вектором к.
Введем матрицу
П = {In 7Tj,j} (9.5.6)
порядка М х 8. Тогда вектор значений логарифмов функции правдопо¬
добия с точностью до постоянной составляющей, одинаковой для всех
классов, будет иметь вид
Г= Ш, 1 = [.Lj], j = 1,2,... , Μ. (9.5.7)
Матрица Π является эталонной при классификации изображений
на базе полиномиальной модели контура. Отношение правдоподобия
для класса Aj представляется как
Lj
L(k/Aj)
Σ L(k /А.)
i/=l yVifij
8 / / M 8 ч
= Π*ίϊ/( Σ Σ'*)-
Μ —Λ / 'я—-1 α-/- ή Π —1 '
(9.5.8)
9.5. Распознавание изображений со случайными формами
387
Данный классификатор реализует критерий заданного превышения
максимальной апостериорной вероятности над суммарной апостериорной
вероятностью всех остальных гипотез [136]. Подобный классификатор в
дальнейшем будем обозначать как ПК1. Применение классификатора ПК1
обосновано в тех случаях, когда принятие решения связано со значитель¬
ным риском. Более простая структура классификатора обеспечивается
при использовании критерия заданного превышения максимальной веро¬
ятности гипотезы по отношению к ближайшей к ней [12]. Такой класси¬
фикатор в дальнейшем будем обозначать как ПК2. Для классификатора
ПК2 обеспечивается соотношение
PiAj/Bt)»
^ а,
(9.5.9)
PiAv/Bi)
где P(Aj/Bi)ma>x — максимальная апостериорная вероятность; Р{Аи/В{) —
ближайшая к максимальной апостериорная вероятность; а — пороговое
значение, зависящее от требуемой надежности распознавания.
Логарифм отношения правдоподобия для ПК2 запишется в виде
8
In Lj = ^2 к» (In — In 'i
(9.5.10)
С учетом выражения (9.5.7) решающее правило для класса А,·, пред¬
ставляется как lj — 1Ш ^ а, где т — номер класса, наиболее близкий к
классу Aj.
Таким образом, классификатор ПК2 выполняет следующие операции:
1. Вектор частот к ЭВ умножается на эталонную матрицу П:
РТ,= Пкт
2. Для вынесения решения по классу Aj} j = 1,2,... , М, отбирается
компонента pj вектора ρ, а среди оставшихся Μ — 1 компонент опреде¬
ляется максимальная рш (j).
3. Формируется и сравнивается с порогом разность
Pj — Pi - Pm (j) ^ j = 1,2,... , M. (9.5.11)
Для получения конкретной структуры классификатора ПК1 выраже¬
ние (9.5.8) запишем в виде
Lj = exp
С учетом того, что
Ύ'Κ\τητνΛ У2 ехр < кд In wsv >
ν=1 ' / ν=1,νφό 4=1 '
8
Pj = У>у1п^,
(9.5.12)
(9.5.13)
получим
Lj = exp {pj} j Σ exP{M·
/ u=l ,v^j
(9.5.14)
388
Гл. 9. Анализ и распознавание изображений по их форме
Выражение (9.5.13) задает цифровой фильтр восьмого порядка, ИХ
которого определяется структурой эталонного вектора тт,. С учетом этого
на рис. 9.12 показана структурная схема классификатора ПК1. Он содер-
Рис. 9.12. Структура классификатора ПК 1 изображений с сильной вариабельно¬
стью формы для четырех классов
жит М одинаковых по структуре и взаимосвязанных каналов. В каж¬
дом канале содержится цифровой фильтр ЦФ, устройство возведения
в степень pj, сумматор, устройство деления и пороговое устройство ПУ.
Более простой вид имеет классификатор ПК2 (рис. 9.13). Кроме извест¬
ных цифровых фильтров в каждом канале содержатся устройства: экс¬
тремальное (ЭУ), вычитающее и пороговое (ПУ). Как и в классификаторе
ЦФ 1
ЦФ2
ЦФЗ
ЦФ4
ЭУ 1
О—►·—
ЭУ 2
ЭУЗ
ПУ
t а
ПУ
Ύ7
ПУ
17
ЭУ 4
ПУ
17
Рис. 9.13. Структура классификатора ПК 2 для четырех классов
ПК1, в данном случае все каналы также взаимосвязаны. Выходной сигнал
фильтра j-ro канала подается на входы ЭУ всех других каналов и на
входы вычитающего устройства. ЭУ j-го канала выделяет максимальный
сигнал с выходов фильтров всех других, кроме j-го, каналов и направляет
его на второй вход вычитающего устройства. Экстремальное устройство
в отдельном канале выделяет из всех компонент pj, других каналов ком¬
поненту рт (j). Это устройство формирует в соответствие с (9.5.10) зна¬
9.5. Распознавание изображений со случайными формами
389
чение логарифма отношения правдоподобия, которое сравнивается с по¬
роговым значением. При оценке эффективности полиномиального класси¬
фикатора непосредственное определение вероятности ошибки классифи¬
кации наталкивается на серьезные вычислительные трудности, и поэтому
эффективность оценивается на основе математического моделирования по
методу статистических испытаний. Эксперимент целесообразно проводить
в соответствии с методикой, изложенной в [136].
Для получения структуры марковского классификатора сформируем
матрицу k = [kuj], v — 1,2,... , 8, j = 1,2,... , М, двухмерных частот
ЭВ контура текущего изображения. Тогда отношение правдоподобия для
класса Ат запишется как
Lm, —
Πΐ
is,j=i
Σ
= exp {pm} / Σ exp {p„},
/ ν=\,νφτη
(9.5.15)
где
Pm
Σ
kj/j In Jpi/
(9.5.16)
Последнее выражение задает цифровой фильтр 64-го порядка. Струк¬
турная схема марковского классификатора совпадает со структурой по¬
линомиального классификатора. Она является многоканальной по числу
классов, построения всех каналов одинаковы и взаимосвязаны. В каждом
канале содержится цифровой фильтр, устройства деления, возведения
в степень и суммирования.
Для критерия заданного превышения максимальной вероятности гипо¬
тезы по отношению к ближайшей к ней отношение правдоподобия может
быть записано в виде
8
In L-m = ^ ^ kvj (In pvjrn In Pvjs), (9.5.17)
v,j=l
где s — номер класса с ближайшим к m-y классу значением функции
правдоподобия.
Вектор функций правдоподобия определяется как
рТ = П · кт, (9.5.18)
где П — эталонная матрица, строками которой являются логарифмы
вероятностей переходов каждого из классов.
Матрица П имеет размер 64 х 64, а вектор к представляет собой век¬
тор из 64 двухмерных частот ЭВ контура распознаваемого изображения.
Алгоритм принятия решения в пользу класса Ат имеет вид
= pm- Ps (m) > α, (9.5.19)
где pm — компонента вектора р для m-го класса, ps (га)— максимальная
компонента этого вектора без учета компоненты рт.
390
Гл. 9. Анализ и распознавание изображений по их форме
Пример 1. Рассмотрим классификацию изображения листьев ивы и сирени.
Обучающая выборка листьев ивы имела объем 71, а сирени — 75. Обучение
сводилось к определению оценок компонент вероятностных векторов 7Гива и 7гСИрень.
Эталонная матрица П имеет вид
V
1
2
3
4
5
6
7
8
П = сирень
7,60
3,16
0,89
2,96
5,17
3,13
0,95
2,84
ива
4,41
2,04
1,52
2,70
1,88
2,66
1,67
1,83
Элементы матрицы П равны с обратным знаком натуральному логарифму
вероятности появления соответствующего ЭВ ηUj в контуре эталонного изобра¬
жения. Учитывая сложности с получением отношения правдоподобия в аналити¬
ческом виде, ошибки распознавания были найдены косвенным путем — методом
Таблица 9.1
Класс
Среднее
значение
СКО
1 - F(x2)
Сирень
119,5
24,4
0,25
Ива
74,8
10,6
0,28
интегрирования распределения отношения
правдоподобия [11]. Для рассматриваемого
примера распределение вероятности отно¬
шения правдоподобия аппроксимируются
нормальным законом с параметрами, при¬
веденными в табл. 9.1.
Рис. 9.14. Зависимость ошибок распо¬
знавания породы деревьев по конту¬
рам их листьев от величины порога
Графики зависимостей вероятностей
ложного распознавания F и отказа от
распознавания М от величины порога а
представлены на рис. 9.14. Как видно из этих графиков, распознавание породы
деревьев по форме их листьев на основе полиномиальной модели производится
с высокой степенью надежности.
9.6. Распознавание близких по форме детерминированных
изображений
Контурный согласованный фильтр служит дискриминатором форм
плоских изображений. Выходная величина КСФ характеризует степень
схожести (различия) форм фильтруемого изображения и эталонного
изображения, по которому был синтезирован фильтр. Найдем усло¬
вие наилучшей эффективности такого дискриминатора. При отсутствии
шумов эффективность дискриминатора будем характеризовать его чув¬
ствительностью, определяемой как приращение выходной величины КСФ
при изменении формы изображения.
Ряд изображений, например озер, очертания лесных массивов, симво¬
лов и т.п. могут иметь близкие формы, что приводит к получению сла-
боразличающихся сигналов при согласованной фильтрации их контуров.
9.6. Распознавание близких по форме изображений
391
Два одномасштабных изображения с контурами
А = {a (n)}0 fc_1 = {\а (п)| ехр {ι[ψ (η) + Αφ (η) + Δρ]}},,^,
Γ = {7 (”)}0,α_ι = {|7 Ml exp {ίψ (n)}}0ifc_i,
имеющих совпадающие начальные точки этих контуров, назовем близки¬
ми по форме, если
|a(n)| w |7(η)|; \Αψ (η)| < π/10, п = 0,1,..., к - 1. (9.6.1)
При фильтрации контура Г согласованным с ним фильтром, когда угол
взаимного поворота Αφ контуров А и Г равен нулю, отсчет для т = к — 1
будет равен
к-1
η(к - 1) = щ + ίη2 & ^ |7(n)|2[cosA(^(n) + isinA^(n)] .
n=О
При выполнении условий (9.6.1) cosA<p (η) « 1 и sinA<p (η) « Αφ (η).
Тогда
к-1
η (к - 1) « ||Г||2 + 17 (η) \2Αψ (η).
η=О
Отсюда видно, что из-за малости Αφ (п) величина 771 на выходе косинус¬
ного звена части фильтра значительно превышает величину η2 на выходе
синусного звена фильтра и в то же время незначительно меняется при ва¬
риации формы. Синусное звено хорошо реагирует на небольшие изменения
формы, т.е. несет полезную информацию. В результате из-за того, что 771 <С
<С т/2, вся величина (77 (А: — 1) |, используемая в качестве меры близости
форм А и Г, слабо меняется при их вариации, т.е. происходит маскировка
полезного выходного эффекта фильтра. Выясним на качественном уровне
структуру меры близости форм, которая получается на выходе КСФ
к—1 к—1
|а(п)||7(п)|+г Σ \а (п) ||7 (7г) | sinA<£> (7г)
п—0 п—О
при нулевом сдвиге начальных точек контуров А и Г и Αφ — 0.
Первое слагаемое будет тем больше, чем меньше отличие соответству¬
ющих ЭВ контуров А и Г по модулю и аргументу. Второе же слагаемое
ведет себя противоположным образом. Поэтому косинусная часть КСФ
определяет степень схожести двух близких форм, а синусная — степень
различия. Так как интервал значений угла Αφ (п) расположен вблизи
нулевых значений, то из-за большой скорости изменения синуса в этом
интервале дискриминатор на базе синусной части КСФ будет чувстви¬
телен к слабым изменениям формы. В то же время дискриминатор на
основе косинусной части КСФ из-за слабого изменения косинуса в ну¬
левом диапазоне значений Αφ (п) будет незначительно реагировать на
степень несовпадения форм.
Проиллюстрируем эффект маскировки на примере близких по форме к кон¬
туру Г контуров Ах,Аг и А3, представленных соответственно на рис. 9.15. Коды
392
Гл. 9. Анализ и распознавание изображений по их форме
Рис. 9.15. Контуры близких по форме изображений стрелки
этих контуров имеют вид
Г = {20; г; 5 — Зг; —5 — Зг; г; —20; 4г},
Αι = {20 -f г; г; 5 — Зг; —5 — Зг; г; —20 — г; 4г},
Аг = {20 -Ь 2г; г; 5 — Зг; —5 — Зг; г; —20 — 2г; 4г},
Аз = {20 -Ь г; г; 5 — Зг; —5 — Зг; г; —20 + Ц 2г}.
Нормированные отсчеты фильтра, согласованного с контуром Г, и модули этих
отсчетов в момент т = к — 1 = 6 равны
77аьн (6) = 0,9987 - 0,04510г; |т7аьн (6) | = 0,99989,
г?А2,н (6) = 0,99552 - 0,08989г; |т7а2,н (6) | = 0,99957,
Ή Аз,и (6) = |г7а3,н (6) I = 0,99661.
Результаты показывают, что по величине \ηα (к — 1)\ трудно судить
о степени отличия контуров Αι,Α2 и А3 от контура Г, если все они близки
по форме. Поэтому в качестве результата фильтрации, определяющего меру
различия близких форм, целесообразно использовать только мнимую часть
выходного результата фильтра, образующегося на выходе его синусного
звена:
к-1
% и Σ ΗΉ I2 Δρ (п). (9.6.2)
п=0
Рассмотрим теперь вопрос о дискриминации близких по форме изо¬
бражений, фрагменты контуров которых имеют ось симметрии. Наличие
таких фрагментов приводит к тому, что аргументы симметричных ЭВ будут
отличаться только знаками. В результате синусные составляющие разных
знаков компенсируют друг друга, а косинусные накапливаются (рис. 9.16).
Поэтому выходной эффект при фильтрации симметричных участков
близких по форме изображений определяется только косинусными, слабо
меняющимися для разных изображений компонентами, и эффект кон¬
турной согласованной фильтрации изображений в плане получения су¬
щественных различий между ними будет очень низким. Действительно,
V2 » X] Ь (η) |2Ау> (η) = ]Г |7 (η) |2Δ<Ρ (η) - |7 (η) |2Δ<ρ (п),
п=0 п=0 n—s/2
9.7. Совмещение изображений
393
. sin φ А
cos φΑ
>
О
φ
φ
а
б
Рис. 9.16. К компенсации синусных и накопления косинусных составляющих на
выходе согласованного фильтра
где s — количество примыкающих друг к другу ЭВ в контуре, характе¬
ризующихся симметрией. Обе суммы в этом выражении близки между
собой и поэтому 772 « 0, т.е. результат фильтрации оказывается нулевым
для разных (но близких по форме) изображений.
Таким образом, для симметричных и близких по форме изображений
полезный эффект фильтрации не только маскируется слабоменяющейся,
но превалирующей косинусной составляющей, но и значительно компен¬
сируется за счет равных между собой по величине и разных по знаку
синусных компонент.
Демаскировка выходного эффекта КСФ может быть достигнута пу¬
тем устранения косинусной составляющей, а компенсация синусных ком¬
понент может быть устранена суммированием модулей этих компонент.
В этом случае выходной эффект фильтрации будет иметь вид
Представленный на рис. 9.15 контур А3 указательной стрелки имеет
симметричные фрагменты. При фильтрации происходит полная компен¬
сация мнимых компонент и результат оказывается чисто вещественным:
^7а3,н = 0,99661, т.е. 7723 = 0. Результат слабо отличается от единицы,
так как различие между контурами Г и А3 не только маскируется, но
и компенсируется. Если же воспользоваться выражением (9.6.3), то полу¬
чим, что 772)н = 0,045, т.е. мера различия между контурами Г и А3 такая
же, как и между контурами Г и Αχ.
9.7.1. Постановка задачи и модели. Ряд практически важных задач,
связанных с навигацией по карте местности, повышения помехоустой¬
чивости устройств распознавания визуальных образов и др., сводятся к
задаче совмещения двух изображений. Изображение W3 является эта¬
лонным и хранится в ОЗУИ системы технического зрения. Второе изо¬
бражение W оперативно формируется датчиком системы и представляет
собой искаженное шумами и помехами изображение W3, повернутое на
к-1
п=О
(9.6.3)
9.7. Совмещение изображений объекта
394
Гл. 9. Анализ и распознавание изображений по их форме
некоторый угол Αφ и измененное в масштабе в \μ\ раз. Традиционно
задача совмещения изображений W3 и W решается на основе проце¬
дуры пространственной корреляции. Этот подход неизбежно связан со
следующими недостатками: чувствительностью алгоритмов к изменению
масштаба и взаимной угловой ориентации совмещаемых изображений,
а также с обработкой большого количества (а часто и всех) точек сов¬
мещаемых изображений. Если параметры Αφ и \μ\ произвольны и неиз¬
вестны, то при совмещении изображений требуется перебор с небольшим
шагом значений каждой комбинации этих параметров, что приводит к
значительным временным затратам. Для достижения приемлемых значе¬
ний времени обработки используются различные эмпирические подходы,
в частности, метод характерных черт [138].
Рассмотрим подход к решению данной задачи на основе методов кон¬
турного анализа, в частности, с помощью контурной согласованной филь¬
трации. Этот метод использует всю информацию, имеющуюся в контурах
Ν3 и N изображений W3 и W, и инвариантен к параметрам линейных
преобразований. Из-за небольшого, по сравнению со всеми изображения¬
ми, количества контурных точек, временные затраты будут сравнительно
невысокими. Рассмотрим основные аспекты решения этой задачи.
Пусть получен ряд изображений Wj, j = 1,2,... , М, одного и того
же объекта, причем положение объекта при формировании изображения
не фиксировано: возможны линейные преобразования соответственно с па¬
раметрами h, Αφ и |μ| переноса, поворота, масштабирования. Кроме того,
каждое из изображений Wj содержит в качестве неизбежных составляющих
помехи, вызванные действием ошибок дискретизации D и широкополосного
шума п. Ансамбль полученных изображений объекта запишем как
{Wj (ft, Αφ, \μ\) + D + Μ· (ЗД
Пусть, далее, в результате применения к Wj оператора выделения
контура и последующей эквализации сформирован ансамбль контуров
этих изображений, имеющих одну и ту же размерность к. Дополнительно
осуществим нормировку этих контуров, разделив ЭВ i/j (га) каждого кон¬
тура на величину своей нормы ||Nj||. Ансамбль нормированных контуров
имеет вид
{Nj,H (h, Αφ, Η, D, η)}1Μ. (9.7.2)
Все мешающие факторы, имеющие место в представлении (9.7.1), ока¬
зывают влияние на вид комплекснозначных контуров NjiH, причем доба¬
вились шумы эквализации. Контуры, входящие в этот ансамбль, содержат
одинаковое количество ЭВ и имеют одинаковую, равную единице норму. Они
отличаются друг от друга только произвольным углом поворота и наличием
у каждого вектор-контура случайной составляющей. Процедуру совмещения
контуров одного и того же объекта определим следующим образом.
Пусть \r]ji{m)\ — модуль ВКФ контуров Nj}H и NjiH изображений
Wj и Wi, причем | ηj^ (гао)| — максимальное значение этого модуля, т.е.
\qji (гао)| = \Vji\max- Сдвинем начальную точку ао одного из изображений
9.7. Совмещение изображений
395
Рис. 9.17. Изменение модуля ВКФ двух контуров: а — при случайном положении
контуров; б — при оптимальном совмещении контуров
на то ЭВ таким образом, чтобы отсчет ВКФ \η^ (0)| стал максимальным,
т.е. чтобы |ηάι (0)| = \vji\max (рис. 9.17). Тогда контуры N^o) и Ni)H будут
оптимально совмещены по критерию максимальной схожести, задаваемой
модулем их ВКФ. Отсюда следует, что для оптимального совмещения при
неизвестном сдвиге начальной точки контуров одного и того же изобра¬
жения необходимо:
1) сформировать нормированные и эквализованные представления
этих контуров;
2) вычислить количественную меру схожести совмещенных контуров
в виде отсчета \ημ (т)\ их ВКФ при т = 0;
3) варьируя положение начальной точки одного из контуров, получить
максимальное значение меры
\Ъ1 (0)1 = Ышах· (9-7-3)
9.7.2. Оптимальное совмещение контуров на основе контурной со¬
гласованной фильтрации. Выходной сигнал КСФ представляет собой сме¬
щенную ВКФ фильтруемого контура и контура его ИХ. Поэтому если этот
фильтр согласовать с одним из совмещаемых контуров, КСФ естественным
образом позволяет оптимально решить задачу совмещения двух контуров.
В рассматриваемом случае выходной сигнал КСФ будет суммой двух со¬
ставляющих: сигнальной и помеховой, причем последняя обусловлена дей¬
ствием помех не только на фильтруемый сигнал, но и на ИХ фильтра. Если
решается задача совмещения контура NjjH с контуром N3>H эталонного изо¬
бражения, то уровень помеховой составляющей выходного сигнала фильтра
будет ниже, так как зависит лишь от фильтруемого контура.
Максимальное значение \η^\ не превышает единицы и зависит от
степени зашумления линии контура. Шумовая составляющая приводит к
размыванию максимума модуля ВКФ, что связано с появлением ошибок
совмещения контуров (рис. 9.18, а). Поэтому перед совмещением целесо¬
образно провести подавление этой составляющей фильтром, в пределах
полосы режекции которого находится значительная часть энергии шума
и сравнительно небольшая часть энергии сигнала. Для таких целей хо¬
рошо подходит ФСС, пропускающий низшие частоты спектра. Следует
заметить, что при совмещении контура NJ>H текущего изображения Wj
396
Гл. 9. Анализ и распознавание изображений по их форме
Рис. 9.18. ВКФ зашумленных контуров: а — вид ВКФ при различных отношениях
отношения сигнал/шум q\ б — определение положения точки то при деформации
шумами графика ВКФ
с контуром N3,h эталонного изображения W3 подобная фильтрация мало¬
эффективна. Это объясняется тем, что согласованный фильтр по сравнению
с другими фильтрами наилучшим образом обеспечивает подавление широ¬
кополосных шумов. В результате ФСС может воздействовать лишь на шумы
дискретизации. Если же фильтр вырабатывает меру схожести двух текущих
изображений Wj и Wi, то его ИХ формируется по зашумленному контуру
одного из изображений. Поэтому подавление шумовой составляющей этого
контура обеспечит лучшие результаты совмещения контуров.
Важным моментом является фиксация максимума модуля ВКФ. Пи¬
ковое значение модуля ВКФ \vji\max = \Vji (то)\ будет хорошо выражено
лишь для широкополосных контуров (см. п. 9.7.3) и при незначительном
уровне шумовой составляющей выходного сигнала КСФ. Шумовая соста¬
вляющая деформирует вид графика ВКФ. Особенно опасна эта деформа¬
ция в области нахождения точки то, по положению которой принимается
решение о наилучшем совмещении контуров.
Обнаружение
Эквализация
и прослеживание
контура
—►
ФСС
кода
изображения
контура
Л(т
) N
«ά—
'νη,·4Γ-
Формирование
ИХ КСФ,
вычисление
нормы
Рис. 9.19. Структура алгоритма оптимального совмещения контуров изображения
объекта W3 по результатам согласованной фильтрации
9.7. Совмещение изображений
397
На рис. 9.19 приведена структура алгоритма оптимального совмещения
зашумленных контуров одного и того же объекта. После получения ком¬
плекснозначных кодов контуров совмещаемых изображений производится
низкочастотная контурная фильтрация по методу скользящего среднего. Да¬
лее происходит эквализация кода контура с размерностью контура эталон¬
ного изображения, причем величина этой размерности для снижения влия¬
ния ошибок дискретизации линии контура должна быть достаточно большой,
порядка к « 200-500. Подобные операции проводятся над контурами всех
изображений объекта W3. Сопряженный, комплекснозначный и отсчитыва¬
емый в обратном направлении обхода код контура эталонного изображения
W3 используется в качестве ИХ КСФ, а в качестве фильтруемого сигнала —
эквализованный комплекснозначный код контура изображения Wj. Резуль¬
тат фильтрации нормируется и находятся оценки угла взаимного поворо¬
та Δφ и смещения fho начальных точек контуров WHj, WH>3 (см. п. 4.1):
Δφ — arctg
Im 7]jt3 (rap)
Re 77j,3 (mo)
(9.7.4)
По найденным оценкам осуществляется коррекция угла поворота и по¬
ложения начальной точки контура NHjj.
Величины то и Δφ являются выходными сигналами системы оп¬
тимального совмещения изображений. Они могут быть применены для
Рис. 9 20. Совмещение контуров изображений а — контур эталонного изображе¬
ния, б — зашумленное изображение на случайном поле, распределение χ2 с одной
степенью свободы, сгф = 2, σΜ = 4, в — контур зашумленного изображения; г —
результат совмещения
398
Ко]
Кот
различных целей, в том числе, для кор¬
рекции траектории летательного аппара¬
та по результатам совмещения эталон¬
ного изображения ориентира в полетной
карте с изображение этого ориентира,
сформированного в текущий момент вре¬
мени бортовыми датчиками.
Рис. 9.21. Пример совмещения
контуров [139]
Процесс оптимального совмещения
контуров стилизованного изображения
танка по результатам контурной согла¬
сованной фильтрации представлен на
рис. 9.20.
На рис. 9.21 показан результат совме¬
щения зашумленного контура с эталонным,
проведенного на основании результатов спектрального анализа контуров.
9.7.3. Выбор формы изображения объекта для их наилучшего сов¬
мещения. Задача совмещения зашумленных изображений одного и то¬
го же объекта относится к классу задач, эффективность решения кото¬
рых сильно зависят от формы объекта. К этому же классу, например,
относится рассмотренная в п. 4.3 задача разрешения контурных сиг¬
налов, а также задача накопления контуров изображения (см. п. 9.8).
Эффективность их решения лишь до определенной степени зависит от
примененного алгоритма. Есть «хорошие» и «плохие» формы изображе¬
ний для решения этой задачи.
Чтобы ответить на вопрос, какой должна быть форма «хорошего» изо¬
бражения, вернемся к рассмотренному в п. 9.7.1 алгоритму совмещения
изображений по результатам контурной согласованной фильтрации. В со¬
ответствии с ним необходимо зафиксировать момент то достижения вы¬
ходного сигнала КСФ своего пикового значения (рис. 9.17 и 9.18). Неточ¬
ность фиксации этого момента приводит, в конечном счете, к ошибке
совмещения. Очевидно, что максимум ВКФ, представляющей выходной
сигнал КСФ, должен быть хорошо выражен. Для этого остальные отсчеты
и, в первую очередь, соседние с максимальным, должны составлять (по
модулю) незначительную часть максимального отсчета, т.е.
Поскольку фильтруемый сигнал отличается от эталонного лишь сте¬
пенью своей зашумленности, то условие (9.7.5) наилучшим образом будет
выполнено для изображений, контуры которых имеют АКФ дельтовидно¬
го типа, или, что то же самое, энергетический спектр которых абсолютно
равномерен, т.е.
\η (ш0)| > \η (т0 ± г)|, г = 1,2,3,...
(9.7.5)
при т = то,
при т ф то,
(9.7.6)
\р(™)\ = И>
то = 0,1,... , к — 1.
(9.7.7)
9.8. Накопление контуров изображений
399
Таким образом, «хорошая» с точки зрения совмещения зашумленных
изображений форма объекта должна задаваться контуром с широким
и равномерным энергетическим спектром. Контуры «плохих» для сов¬
мещения изображений характеризуются узкополосным энергетическим
спектром, причем наихудшими в этом плане будут зашумленные правиль¬
ные fc-угольники, спектр которых имеет лишь одну ненулевую компонен¬
ту. Отсчеты АКФ правильных &-угольников, как элементарных контуров,
все одинаковы и определение ее максимума становится невозможным.
Одним из подходов к улучшению результатов совмещения контуров,
энергетический спектр которых не является равномерным, но и не со¬
держит составляющих, равных или близких к нулю, является использо¬
вание принципов фильтрации одного из совмещаемых контуров филь¬
тром, согласованным с сопряженным контуром другого изображения, т.е.
применение сопряженных согласованных фильтров (см. п. 3.8). ССФ выра¬
батывает координаты фильтруемого контура в биортогональной системе
отсчета, связанной с другим контуром, причем один из базисных векторов
данной системы задается этим контуром. В результате при отсутствии
шумов и помех ССФ формирует только один, не равный нулю единич¬
ный отсчет, определение положения которого не представляет никаких
сложностей. При наличии шумов кроме этого единичного отсчета появ¬
ляются соседние ненулевые отсчеты (боковые лепестки). Но в отличие от
согласованной фильтрации, при которой боковые лепестки определяются
входным сигналом и шумом, в данном случае они обусловлены только
шумом. Поэтому при ССФ эффект маскировки пикового отсчета боковыми
лепестками будет ниже, чем при использовании КСФ, и, как следствие,
возможно более точное определение параметра га0 — разницы между на¬
чальными точками совмещаемых контуров. Но применение ССФ для кон¬
туров с неравномерным энергетическим спектром приводит к худшему, по
сравнению с согласованным фильтром, выходному отношению сигнал/шум.
В связи с этим форма любого объекта, зашумленные копии которого необ¬
ходимо совместить, связана с критическим отношением сигнал/шум gi?Kp
на входе ССФ. Если совмещаемые контуры характеризуются отношением
сигнал/шум q большим критического, т.е. при q > дкр, то применение ССФ
нецелесообразно. Величина дкр связана с /^-характеристикой эталонного
контура (см. п. 3.11.2). Чем больше значение D, тем ниже критическая вели¬
чина отношения сигнал/шум на входе ССФ.
9.8. Накопление контуров изображений
При трактовке контура изображения как некоторого сигнала и при
наличии его адекватного аналитического представления естественно воз¬
никает подход к подавлению широкополосных шумов путем «синхрон¬
ного» накопления зашумленных контуров изображений одного и того же
объекта. В результате экспериментальных исследований было получено,
что зависимость между отношением сигнал/шум диз в исходном изобра¬
жении и qK0Hr в сформированном по этому изображению контуру близка
400
Гл. 9. Анализ и распознавание изображений по их форме
к логарифмической (рис. 9.22):
Qm ^ ^ #конт) (9.8.1)
где к — коэффициент пропорциональности, равный примерно 1,2. Экс¬
перимент проводился при зашумлении сцены нормально распределенным
шумом и формировании бинарной сцены, выделенной на уровне глобаль¬
но-оптимального порога по яркости
(см. п. 6.8.2). Как следует из приве¬
денной зависимости, контурные шу¬
мы резко увеличиваются при малом
значении отношения сигнал/шум ис¬
ходного изображения: при qu3 «1,2
отношение сигнал/шум в контуре
будет дКОнт « 0,6, но уже при qm и
« 4 величина qK0HT близка к 30. При
указанных условиях проведения экс¬
перимента контурные шумы имели
широкополосный характер.
Важным условием подавления
этих шумов является равенство меж¬
ду собой значений параметров линей¬
ных преобразований разных накоп¬
ленных контуров. Они должны иметь
одинаковый масштаб |μ|, нулевое значение угла Δφ взаимного поворота
и совпадающие положения начальных точек αο· Выравнивание этих па¬
раметров производится в процессе совмещения контуров накапливаемых
изображений.
Пусть Nj — текущий зашумленный контур изображения Wj, полу¬
чаемого в процессе зашумления эталонного изображения W3t имеющего
контур N3. Если согласиться с аддитивной моделью зашумленного конту¬
ра, то
N j = N3 + Zj9 j = 1,2,... , Μ, (9.8.2)
где Ζ — шумовой контур с параметрами, описанными в п. 1.7.
Выполнив процедуру оптимального совмещения контуров N j и про¬
суммировав поэлементно их комплекснозначные коды, получим
м м
J2 N ,· = MN3 + J2zi- (9.8.3)
3=1 3=1
1
Рис. 9.22. Зависимость усредненно¬
го значения логарифма отношения
сигнал/шум в контуре от величины
отношения сигнал/шум в исходном
изображении
При М —у оо сумма шумовых контуров стремится к нулевому контуру и
м
ΣΝι
= Μ·Ν3.
(9.8.4)
Таким образом, суммирование ряда реализаций оптимально совме¬
щенных контуров изображений одного и того же объекта приводит к по¬
9.8. Накопление контуров изображений
401
давлению широкополосных контурных шумов и позволяет в пределе
с точностью до масштабного коэффициента получить контур эталонного
изображения объекта. Следует отметить принципиальную роль тремора
при вводе изображений в ОЗУИ системы технического зрения. Благодаря
тремору, реализации контуров ошибок квантования становятся незави-
м
симыми случайными векторами и процесс схождения Σ Nj к Μ · N3
ускоряется. i=1
Рассмотрим особенности алгоритма нахождения контуров ряда изо¬
бражений одного объекта (рис. 9.23).
Рис. 9.23. Структура алгоритма накопления контуров изображений
На каждом шаге производится коррекция ИХ КСФ. Исходная ИХ фор¬
мируется по коду контура N\. В дальнейшем эта характеристика корректи¬
руется по результатам накопления контуров. Непосредственно для накопле¬
ния используются контуры, для которых модуль пикового нормированного
выходного отсчета близок к единице. Из экспериментальных результатов
следует, что при |ryH|max < 0,8 ошибки совмещения становятся недопустимо
большими и такие контуры отбрасываются. Рассмотренный алгоритм реали¬
зует процедуру безэталонного накопления контуров.
Процесс накопления контуров сопровождается эффектом низкоча¬
стотной фильтрации, вызванным ошибками их совмещения. В преде-
Рис. 9.24. Результаты накопления зашумленных реализаций контура по мере уве¬
личения выборки
ле накопленный контур вырождается в окружность, представляющую
первую гармонику линии контура при большой величине его размерно¬
сти (рис. 9.24).
402
Гл. 9. Анализ и распознавание изображений по их форме
Рис. 9.25 поясняет возникновение эффекта низкочастотной фильтра¬
ции. Как видно из рисунка, чем больше ошибка совмещения, тем сильнее
сглаживание фрагмента контура в виде прямого угла. Степень зашум-
Рис. 9.25. Эффект низкочастотной Рис. 9.26. Приближенное определение от-
фильтрации, вызванный ошибка- ношения сигнал/шум в контуре изобра-
ми совмещения при накоплении жения
контуров
ленности линии контура можно оценить по отношению скачка его АКФ
при т = 0 к величине примыкающего к значению η (0) отсчетов η (1)
(рис. 9.26) [13]. Данный скачок обусловлен действием только широкополос¬
ных шумов, а величина отсчета η (1) близка к значению энергии контура.
Приведенный алгоритм использует для совмещения контуров резуль¬
таты работы КСФ. На рис. 9.27 показаны результаты накопления совме¬
щенных контуров стилизованного изображения танка. На фотографиях
изображения накопленных зашумленных контуров совмещены с изобра¬
жениями их АКФ, что позволяет судить о степени уменьшения шума.
Рис. 9.27. Накопление совмещенных контуров изображений: а — исходная сцена,
б — контур зашумленного объекта, в, г — результаты накопления соответственно
двух и восьми контуров
9.9. Аналитическое представление формы плоского изображения 403
Как и в случае анализа процесса совмещения контуров, рассмотрим
вопрос о «хороших» и «плохих» формах изображений с позиции наи¬
лучшего подавления шумов при накоплении их контуров, т.е. с позиции
восстановления формы. Дать однозначный ответ, как в случае реше¬
ния задачи совмещения изображений, здесь трудно. Из-за неизбежного
негативного влияния ошибок совмещения возникающий эффект низко¬
частотной фильтрации приводит к искажению формы восстановленного
изображения за счет потери мелких деталей контура из-за подавления
высокочастотных составляющих спектра контура. Поэтому лучшие ре¬
зультаты по восстановлению формы достигаются для контуров, у кото¬
рых такие детали отсутствуют, т.е. у контуров со слабо выраженными
высокочастотными составляющими спектра.
С другой стороны, информация о параметре сдвига контуров полу¬
чается в результате выполнения операции совмещения контуров. Чем
точнее ее результаты, тем меньше получаемая ошибка совмещения и тем
выше эффект подавления контурных шумов. Но, как показано в п. 9.7.3,
для обеспечения таких результатов контуры должны иметь равномер¬
ный энергетический спектр, т.е. высокочастотные компоненты их спектра
должны иметь такую же интенсивность как и в других частях спектра.
Таким образом, требования, предъявляемые к формам контуров для их
эффективного накопления, оказываются противоречивыми и необходим
компромиссный подход к их выбору.
9.9. Аналитическое представление формы плоского
изображения
В задачах обработки изображений и распознавания визуальных об¬
разов широко используется понятие геометрической формы физического
объекта или его изображения. Представление формы должно обладать
метрическими свойствами, так как, например, решение о классе изобра¬
жения принимается по степени близости форм двух изображений (см.
п. 4.4). Общепринятое определение формы отсутствует. В большинстве
работ, где определение этого термина является важным моментом, указы¬
вается на сложность данного вопроса. Учитывая, что на понятии формы
изображения базируются важные вопросы контурного анализа, рассмо¬
трим один из подходов к его формализации.
В качестве рабочего понятия «форма изображения» примем понятие,
основанное на семантике слова «форма» и расширение трактовки этого
термина Т. Павлидисом [142] и некоторыми другими авторами примени¬
тельно к бинарным по яркости изображениям: форма Ф изображения W
представляет собой информацию, содержащуюся в контуре Г. Здесь
предполагается, что контур Г, кроме информации о контуре, содержит
дополнительную информацию, или что форма Ф является инвариантой
представленного в аналитическом виде контура Г к ряду преобразований,
которым может подвергаться изображение W, а, следовательно, и кон¬
тур Г, без искажения формы, т.е.
404
Гл. 9. Анализ и распознавание изображений по их форме
Ф = Inv WG = Inv IV, (9.9.1)
где Inv — обозначение инвариантности аналитического описания изо¬
бражения W к некоторым пока не оговоренным функциональным пре¬
образованиям G или к преобразованиям F, касающихся аналитического
описания контура Г.
Как следует из п. 3.7, минимизация расстояния между двумя кон¬
турами Г и N, задающими соответственно формы Фг и Φν, приво¬
дит к устранению влияния линейных преобразований на величину это¬
го расстояния. Минимальное значение расстояния будет мерой разности
форм, если форму определить в соответствии с выражением (9.9.1) как
аналитическое представление контура, инвариантное к определенному
классу преобразований, в данном случае к классу F = (μ, h, d), где μ =
= \μ\ ехр{гД^>}, преобразование масштабирования в |μ| раз и поворотом
на угол Αφ, d — параметр сдвига начальной точки ао на d ЭВ, a h = hi -f
+ ih2 — смещение изображения по горизонтали на hi и по вертикали
на /ΐ2· Поскольку минимальное нормированное расстояние (см. (3.78))
Дя,тin = 2[1 — |?7я,тах (то)|] (9.9.2)
характеризует различие двух форм Фг и Φν, то форму Фj произвольного
изображения Wj с контуром можно задавать следующим образом.
Пусть контур П обладает особыми свойствами по отношению к боль¬
шому количеству классов изображений. Такой контур назовем тестовым.
Примем, что форма Фп изображения с тестовым контуром задается его
контуром, т.е.
Фп = П. (9.9.3)
Совместим начало отсчета системы координат, в которой задаются
вектор-контуры Tjt j = 1,2,, с концом вектор-контура П. Тогда
форма изображения Wj есть контур Г^·, полученный в результате линей¬
ных преобразований F~xf минимизирующих его расстояние до тестового
контура П, т.е.
Ф = rj)F-i при Rh -» min, (9.9.4)
где jF-1 — линейное преобразование, не связанное с выходом из плос¬
кости и минимизирующее расстояние вектор — контура Г^· от начала
отсчета. Тогда вектор-форма Ф5 запишется в виде
Φί = |щ{|7(™-^)|ехр{г(^(М) - (9·9·5)
Таким образом, для данного подхода к заданию формы изображения
характерно следующее.
1. Понятие «форма изображения» является относительным, поскольку
форма задается относительно другого, особого, тестового изображения.
2. Форма изображения является метрической величиной, поскольку
она задается вектором и можно говорить об энергии формы и о расстоянии
между вектор-формами двух изображений.
9.9. Аналитическое представление формы плоского изображения 405
3. Форма изображения определяется его контуром, представленным
таким образом, что его расстояние до тестового контура минималь¬
но. Это необходимо для фиксации параметров линейных преобразований
контура.
4. Смена тестового изображения, а также вида линейных преобразо¬
ваний контура приводят к изменению вектор-формы изображения.
Выбор тестового изображения осуществляется на основании практи¬
чески полезных критериев. Один из подходов состоит в том, чтобы в ка¬
честве тестового выбрать изображение с наиболее сложной при фиксиро¬
ванном значении размерности к формой.
Контур такого изображения характеризуется равномерным спек¬
тром Фурье и дельтовидной АКФ. Поскольку контуры реальных изо¬
бражений всегда замкнуты, то таким изображением будет дельтовид¬
ный контур А = {δ (п)}0 к_г (см. п. 1.8). Именно такой контур, как
следует из п. 2.5, обладает в классе замкнутых контуров равномерным
спектром. Наибольшую сложность дельтовидного контура по сравнению
с другими контурами следует понимать как возможность пренебречь
взаимной энергией связи ЭВ контура, задаваемого отсчетами его АКФ
η (j), j = 1, 2,.., к — 1, по сравнению с энергией контура, равной η (0) =
= || А||2 — к2 — к. Центральный отсчет АКФ контура А значительно,
в к — 1 раз, превышает любой другой отсчет АКФ η (j) (см. п. 2.8). Это
свидетельствует о максимальной непредсказуемости, а, следовательно,
и максимальной сложности дельтовидного контура.
Конкретизируем аналитическое представление формы плоского изо¬
бражения при выборе дельтовидного контура в качестве тестового в клас¬
се преобразований F = (μ, /ц d).
Принятие контура А в качестве тестового значительно упрощает
определение формы Ф произвольного изображения W по его конту¬
ру Г в классе линейных преобразований, не связанных с выходом из
плоскости. Фильтрующее свойство дельтовидного контура позволяет
непосредственно по представлению контура Г — {7(n)}ofc-i выбрать
отсчет на выходе фильтра, согласованного с контуром А. Этот отсчет
с точностью до масштабного множителя совпадает с максимальным по
длине элементарным вектором контура Г, т.е.
\η (m0)| = |»? (m)|max = (к - 1) |7|max,
где то — номер отсчета с максимальным модулем.
Таким образом, аналитическое представление формы плоского изобра¬
жения W при выборе контура А в качестве тестового в классе линейных
преобразований, не связанных с выходом из плоскости, находится сле¬
дующим образом.
1. Определяется в полигональном виде контур Г = {l in)}o k-i и30"
бражения W.
2. Выбирается ЭВ 7 (so) этого контура, имеющий максимальную
длину.
406
Гл. 9. Анализ и распознавание изображений по их форме
3. Начало отсчета контура Г совмещается с началом ЭВ 7 ($о).
4. Контур Г нормируется и поворачивается таким образом, чтобы ЭВ
7 ($о)/||Г|| стал горизонтальным и направленным вправо.
Аналитическое представление преобразованного таким образом кон¬
тура Г и будет формой Ф изображения W.
Квадрат расстояния R2H min от вектор-формы Ф до вектор-контура Δ
может быть принят в качестве количественной характеристики степени
простоты формы изображения W. Коэффициент простоты формы введем
в виде
*пр = 0,5 R2H<min. (9.9.6)
Данный коэффициент меняется в пределах от 0 до единицы и чем он
больше, тем проще форма изображения. Учитывая фильтрующее свой¬
ство контура А, с помощью выражения (9.9.2) получим
fcnp = 0,5Д2Я)Ю1п - 1 - yCAlllM. (9.9.7)
В качестве примера найдем форму изображения, имеющего код контура Г =
= {3; 5г; 5 - Зг; - Юг; -2 + 5г; -2 - 2г; -4 + 5г} (рис. 9.28, а).
Размерность контура к = 7, квадрат нормы ||Г||2 = 246. При к = 7 код
дельтовидного контура равен: А = {6, —1,-1, -1,-1, -1,-1}.
'а0'
-
Л
“ W
-г-
V-
ш
Рис. 9.28
Максимальным по длине ЭВ контура будет вектор 7(3) = —Юг, so = 3.
Переносим точку ао в начало этого ЭВ, нормируем контур и поворачиваем на
7г/2. В результате получим (рис. 9.28, б):
Ф = —^={10; —5 — 2г; 2 — 2г; —5 — 4г; Зг; —5;3 + 5г}.
V246
Коэффициент простоты этой формы равен кпр = 0,362.
Полученное аналитическое представление для формы конкретизиро¬
вало наметившийся в последнее время подход к понятию формы изобра¬
жения как инварианты к заданной группе аналитических преобразований
этого изображения.
9.10. Обсуждение результатов
407
9.10. Обсуждение результатов
Понятие формы изображения является важнейшей предпосылкой
как для понимания восприятия человеком окружающего его визуаль¬
ного мира, так и для применения аналитических методов обработки
сформированных техническим датчиком сцен.
В экспериментальных исследованиях по психологии оператора радио¬
локационной станции обзора земной поверхности было показано, что про¬
цесс предварительного формирования у него зрительного образа состоит
из следующих этапов: грубое различение общих пропорций изображе¬
ния объекта и его положения на экране индикатора, мерцание формы,
различение резких перепадов яркости, выделение отдельных деталей,
восприятие формы и контура изображения объекта [11].
В работе [31] приводится гипотеза о формировании зрительного образа
в сознании человека. Предполагается, что при восприятии глаз осуще¬
ствляет отслеживание границы изображения объекта. В результате в со¬
знании человека отличаются характерные особенности формы объекта.
В работе [32] высказывается мнение о том, что при восприятии в сознании
человека вырабатываются два образа: образ формы и образ внутренней
части изображения объекта.
Вместе с тем, общепринятое определение формы объекта отсутству¬
ет. Например, в [120] понятие формы используется более сотни раз, но
его определение не приводится. В связи с этим становится понятным
стремление специалистов ввести аналитически определенное и отража¬
ющее воспринимаемое нами по умолчанию содержание этого термина
[142, 143]. Один из подходов к получению понятия формы, рассмотренный
в п. 9.9, основан на том, что форма изображения задается его контуром при
определенных требованиях к параметрам его линейных преобразований.
Для наделения формы метрическими свойствами введен объект тесто¬
вой формы. Формы изображений других объектов задаются относительно
формы этого тестового объекта. В качестве тестового выбрано изображе¬
ние наиболее сложной при заданной размерности пространства формы.
В результате расстояние между контурами тестового и анализируемого
изображений служит количественной мерой степени простоты формы.
Недостатком представления контура в виде вектора размерности к
является невозможность проведения операций с контурами изображений,
имеющих разную размерность. Такие изображения могут иметь близкие
формы, но сравнивать их между собой при разных значениях к нельзя.
Для устранения этого недостатка разработана специальная операция эк-
вализации, по существу являющаяся операцией повторной дискретизации
линии контура. Она позволяет привести размерность к анализируемого
контура к заданному значению размерности р. Если величина р в несколь¬
ко раз превышает значение к, то связанные с эквализацией искажения
контура будут незначительными.
Структурный анализ формы изображения, связанный с обнаружением
и выделением контуром характерных фрагментов — лучей, разрезов,
прямолинейных отрезков, углов заданной величины, оценкой степени пра¬
408
Гл. 9. Анализ и распознавание изображений по их форме
вильности формы (близости к правильным fc-угольником), симметрично¬
сти и антисимметричности, обнаружения свойств сопряженной симметрии
и антисимметрии, эффективно осуществляется контурными фильтрами,
ИХ которых согласована с фрагментами эталонных контуров, обладаю¬
щих искомыми свойствами.
Определение количественных характеристик формы изображения —
периметра, площади, коэффициента формы, ширины изображения в за¬
данном месте, габаритных размеров и др. аналитическим путем с еди¬
ных позиций проводится по разностному и суммарному кодам контура.
Спектр контура дает возможность найти еще целый ряд информативных
признаков для принятия решения о классе изображения по его форме,
задаваемой его контуром. Количество информации в коде контура и в его
спектре одинаково, но при спектральном подходе некоторые признаки
становятся более полезными и легко определяемыми, например, степень
его узкополосности или широкополосности.
Форма значительного числа окружающих нас объектов случайна. Тем
не менее мы всегда уверенно отличаем их друг от друга и успешно рас¬
познаем такие объекты: морские волны, горную гряду, лист клена, крону
дерева, язык пламени и т.п. Для машинного распознавания таких объектов
контур представляется в виде отсчетов дискретного случайного процесса.
На этапе обучения происходит оценка параметров этого процесса, а рас¬
познавание — по величине отношения правдоподобия.
Антропогенные объекты, как правило, характеризуются детермини¬
рованной формой. Распознавание таких объектов по их форме успешно
осуществляется по результатам фильтрации контурным фильтром, ИХ
которого согласована с эталонным изображением класса.
В данной главе с позиции контурного анализа рассмотрена важная
для технических изображений задача совмещения двух плоских изобра¬
жений. Эта задача интерпретируется как совмещение контуров этих изо¬
бражений и решается по результатам фильтрации контура одного из
изображений фильтром, согласованным с контуром второго изображения.
Требуемое количество операций при таком подходе значительно меньше,
чем при использовании пространственных методов, требующих обработки
каждой точки в пределах изображения. Показано, что ошибка совмещения
зашумленных контуров тем меньше, чем шире энергетический спектр
контура. Ее минимальная величина достигается при совмещении контуров
с дельтовидной АКФ.
9.11. Задачи и упражнения
1. Проведите эквализацию контура Г = {1, 2 — г, —2 — 2г, —г, —5,4 + 4г}. Раз¬
мерность эквализованного контура равна р = 10.
2. Стандартизируйте элементарные векторы следующих контуров:
Г = {3, —5г, —3,4г} и Г = {2 + Зг, -1 - Зг, 0.5 - 4г, -3 + г, 1.5 + Зг}.
3. Определите площади плоских изображений, ограниченных контурами из за¬
дачи 2.
9.11. Задачи и упражнения
409
4. Определите габаритные размеры фигуры, контур которой равен
Г = {3 4- г, —5 — 5г, Зг, —1, —1 + г, 2г, —2г, 5}.
5. Найдите вектор частот ЭВ контура, заданного кодом Фримена
Г = {0,0,0,0,0,0,0,0,0,3,3,4,4,2,2,2,2,2,2,4,4,4,4,7,
6,6,6,6,6,6,4,4,5,5}.
6. Определите степень замкнутости контура Г = {4 4- Зг, — 7г, — 6, Зг, 1}.
7. Вычислите степень схожести изображений, спектры контуров которых имеют
вид
Ρν = {4 4- 2г, —2 — Зг, —7 — 4г, —4 4- Зг},
Рг = {3, —Зг, —8 — г, —1 4- Зг}.
8. Какие общие требования предъявляются к сигналам, эффективным для ре¬
шения задач разрешения и совмещения контуров?
9. Какая характеристика контурного сигнала инвариантна к сдвигу начальной
точки и повороту контура?
10. Чем вызван эффект низкочастотной фильтрации при накоплении контуров
изображений?
11. Почему совмещение контура изображения объекта с эталонным контуром
при прочих равных условиях дает меньшую ошибку, чем при совмещении
контуров двух изображений объекта?
Глава 10
ОБРАБОТКА ИЗОБРАЖЕНИЙ С ТОЧЕЧНЫМИ
И МАЛОРАЗМЕРНЫМИ ОБЪЕКТАМИ
10.1. Введение
При локационном наблюдении в задачах ориентации и навигации ле¬
тательных аппаратов, управления воздушным движением, картографиро¬
вания местности и т.д. часто представляют интерес объекты искусственно¬
го происхождения. Например, для целей ориентации необходимо опознать
наблюдаемый ориентир с тем, чтобы по
рассогласованию его координат с коорди¬
натами эталонных объектов определить
свое положение в пространстве.
Такие объекты имеют небольшие по
сравнению с географическими объекта¬
ми размеры. Поэтому при наблюдении
с больших расстояний их изображения
близки к размерам элемента разрешения
датчика, т.е. вырождаются в отметки
в один пиксел или несколько смежных
пикселей, обладающих яркостным или
цветовым контрастом (рис. 10.1). Подоб¬
ный характер изображений позволяет
выделить соответственно классы точеч¬
ных и малоразмерных объектов. В ланд¬
шафтных сценах к такому классу относятся изображения опор ЛЭП,
отдельные строения, автомобили и т.п.
В дальнейшем, когда рассматриваемые операции для точечных и ма¬
лоразмерных объектов будут одинаковыми, для сокращения записи эти
объекты будем называть точечными.
В изображениях точечных объектов (ТО) пропадает один из самых
информативных признаков изображений — форма, а также отсутствует
возможность пространственного сглаживания яркостных шумов. Особен¬
но такая ситуация характерна для радиолокационных изображений со
спекл-шумами (шумами зернистости), где дисперсия шума достаточно
высока, что приводит к сильному маскированию полезных точечных отме¬
ток. Это усложняет обнаружение точечных объектов, а задачу их распо¬
знавания по одиночному кадру без учета контекстных признаков делает
Рис. 10.1. Наблюдаемое изобра¬
жение созвездия
10.2. Выделение точечных и малоразмерных объектов
411
практически невозможной, В то же время решение задачи определения
координат объектов упрощается до определения номеров пикселей, где
вынесено положительное решение.
Такие условия наблюдения накладывают определенную специфику
на подходы к обработке и пониманию рассматриваемых изображений.
В частности, для повышения отношения сигнал/шум на входе обна¬
ружителя используют временное накопление кадров. С целью обес¬
печения возможности пространственного усреднения (накопления) от¬
счетов, используют координатную информацию, например, при радио¬
локационном обнаружении — проверяют наличие радиолокационной
тени, ориентированной заранее известным образом по отношению к
положению наблюдателя, при наблюдении движущихся объектов —
выполняют экстраполяцию траектории отметки, и т.д.
Материалы настоящего раздела посвящены особенностям обработки
изображений точечных и малоразмерных объектов на сложном фоне из
крупноразмерных площадных объектов, а также прослеживанию их тра¬
екторий в условиях больших ошибок дискретизации изображений этих
траекторий, представленных на квадратной сетчатке.
10.2. Выделение точечных и малоразмерных объектов в сценах
с локально однородным фоном
В ландшафтных сценах, содержащих точечные отметки, все осталь¬
ные изображения играют роль фона. Поэтому при решении задач вы¬
деления этих отметок статистическая неоднородность фона усиливается
за счет включения в его состав участков с изображениями крупно- или
среднеразмерных объектов. Под решением задачи выделения точечных
объектов будем понимать операции, позволяющие из исходной много¬
градационной по яркости сцены с локально однородным фоном получить
бинарную сцену, состоящую из точечных и малоразмерных объектов. По¬
скольку решение задачи носит статистический характер, то часть из со¬
держащихся в сцене объектов будет потеряна и дополнительно появится
некоторое количество ложных объектов.
Задачу выделения точечных объектов в ландшафтной сцене целе¬
сообразно решать после распознавания находящихся в сцене крупно
и среднеразмерных объектов. Это позволяет увеличивать контекстную
информацию, на основании которой принимается решение о том, явля¬
ется точечная отметка ложной или нет. Например, если в сцене распозна¬
но изображение дороги и в пределах этого изображения выделен точеч¬
ный объект, то вероятность ошибочного решения будет намного ниже, чем
его появление на изображении пахотного поля. Даже при невозможности
решить задачу распознавания крупно-среднеразмерных объектов целе¬
сообразно выделить их контуры и определить статистические характери¬
стики полей яркости в пределах контуров. Это дает возможность в случае
расположения там точечных объектов использовать их в качестве харак¬
теристик локального фона.
412
Гл. 10. Обработка изображений с точечными объектами
Обнаружение точечных объектов является первой из операций по
формированию сцены из точечных и малоразмерных объектов. Эти объ¬
екты создают короткие импульсы яркости, обнаружение которых на силь¬
но коррелированном статистически неоднородном фоне, характерном для
ландшафтных сцен, производится по результатам работы согласованно¬
избирательного фильтра.
Рис. 10.2. Согласованно-избирательная фильтрация импульса яркости, соответ¬
ствующего точечному объекту: а — идеализированный импульс яркости; б —
ИХ фильтра; в — выходной сигнал фильтра
Построение обнаружителей импульсов яркости на базе СИФ было рас¬
смотрено в гл. 8. Импульсная характеристика СИФ для импульса яркости,
соответствующего изображению ТО, имеет вид (рис. 10.2, а, б)
А = {—1, 2,-1}. (10.2.1)
Выходной сигнал фильтра при подаче на его вход дискретных отсчетов
яркости / (п) равен
η(η) = 2f(n) - f(n - 1) - f(n + 1). (10.2.2)
При фильтрации идеализированного импульса яркости s(n) = {0,1,0}
(рис. 10.2, а) выходной сигнал фильтра равен
ч(п) = {-1, 2,-1}. (10.2.3)
На рис. 10.3 в качестве иллюстрации работы такого СИФ приведен гра¬
фик отсчетов яркости сильнокоррелированного фона, взятых вдоль стро¬
ки фрагмента ABCD ландшафт¬
ной сцены, представленной на
рис. 6.29, (кривая 1) и результат
фильтрации этих отсчетов (кри¬
вая 2). Восемнадцатый отсчет этой
последовательности, равный 184,
значительно превышал соседние
с ним, равные 152 и 132. Поэтому
он может рассматриваться как
отсчет яркости ТО. Как видно
из поведения кривой 2, реакция
фильтра на этот отсчет значи¬
тельно сильнее, чем, например, на отсчеты 5“10, превосходящие по
величине 18-й отсчет, но образующие импульс яркости, на который СИФ
не настроен по длительности.
200
8 12 16 20 24
Рис. 10.3. Фильтрация импульса яркости
точечного объекта и отсчетов яркости
сильнокоррелированного фона
10.2. Выделение точечных и малоразмерных объектов
413
Особенность обработки сцены, содержащей точечные объекты, по
сравнению, например, с задачей обнаружения зашумленного импульс¬
ного эхо-сигнала, заключается в следующем. Задача обнаружения эхо-
сигнала носит энергетический характер и ее решение оптимизируется на
основе учета статистических характеристик сигнала и шума. Выделение
точечных объектов является более сложной и далеко не в такой степени
теоретически проработанной задачей. Решение о их наличии в определен¬
ной области ландшафтной сцены принимается по результатам анализа
целого ряда признаков, а не по одному энергетическому признаку, как
в операции обнаружения. Такими признаками, например, могут быть:
— наличие оптической или радиолокационной тени;
— уровень контраста импульса яркости по отношению к прилегающе¬
му фону;
— характер подстилающей поверхности в окрестности импульса ярко¬
сти — объект естественного происхождения, антропогенный объект, фон,
граница фон/объект, граница объект/объект и т.п.;
— степень изолированности анализируемого импульса яркости по от¬
ношению к другим импульсам яркости;
— групповой или одиночный точечный объект.
Рассматриваемая с этих позиций задача выделения точечных объ¬
ектов близко смыкается с задачей распознавания образов. На рис. 10.4
представлена структура одного из возможных алгоритмов.
Анализируемая сцена
Сцена из точечных объектов
Рис. 10.4. Алгоритм выделения точечных и малоразмерных объектов в ландшафт¬
ной сцене
414
Гл. 10. Обработка изображений с точечными объектами
Работу алгоритма прокомментируем на примере смоделированной
ландшафтной радиолокационной сцены, содержащей 11 точечных объ¬
ектов (рис. 10.5, а). На рис. 10.5, б показана сформированная карта порогов
Рис. 10.5. Формирование карты порогов: а — исходная сцена с точечными объек¬
тами, б — карта порогов, сформированная по исходной сцене
(см. п. 6.8.3). В исходной сцене не были обнаружены изображения острова
и одного из полей. Поэтому изображения этих объектов на карте порогов
отсутствуют. В результате яркость пикселов сцены в пределах данных
изображений равна не средней яркости изображения объекта, как для
других объектов, а определяется средней яркостью фона. Так как сред¬
няя яркость фона ниже средней яркости изображений этих объектов, то
проверка по величине контраста не улучшит результаты обнаружения по
яркости точечных объектов, расположенных в их пределах. Этот эффект
мы и наблюдаем в бинарных по яркости сценах на рис. 10.6.
Здесь представлены результаты операций обнаружения по яркости
и селекции по контрастности. Хотя в исходной сцене находятся всего
Рис. 10.6. Результаты обнаружения по величине яркости и селекции по значению
контрастности: а — точечных; б — малоразмерных объектов
лишь 11 точечных объектов, в сценах на этих рисунках наблюдается
несколько сотен точечных объектов. Особенно велико количество этих
объектов в области изображений необнаруженного поля и острова. Далее
осуществляется селекция точечных объектов по наличию у них тени.
10.2. Выделение точечных и малоразмерных объектов
415
Предполагается, что в направлении освещения сцены за обнаруженны¬
ми в бинарной сцене точечными объектами имеется область пониженной
яркости, вызванная наличием оптической
или радиолокационной тени. Такая тень
будет отсутствовать у ложных объектов.
Изображение тени обнаруживается как изо¬
бражение отдельного объекта в исходной
сцене F путем сравнения с пороговым
значением яркости. Тень, образованная то¬
чечным объектом, считается обнаруженной,
если яркость J элемента периферийного
строба размером 3x3 элемента, в центре
которого находится объект, удовлетворяет
условию J < Jm (рис. 10.7). Для обнару¬
жения изображения тени малоразмерного
объекта производится обход по его контуру
и для каждой контурной точки в направле¬
нии тени формируется строб 3x3 элемента
и проверяется наличие тени.
Проверка на изолированность изобра¬
жений точечных и малоразмерных объ¬
ектов базируется на том, что истинные
объекты, например, опоры ЛЭП, в отличие,
от ложных располагаются друг от друг
не ближе некоторого расстояния. Для оценки
изолированности формировался строб 7 х
х 7 элементов. Точечный объект в бинар¬
ной сцене считается изолированным, если
количество содержащихся в стробе точек не превышает двух (включая
центральную точку) (рис. 10.8).
При проверки на изолированность малоразмерного объекта вокруг каж¬
дой его контурной точки образуется строб 7x7 элементов и проверяется
количество точек в его пределах. Точ¬
ки самого объекта блокируются и не
учитываются. Малоразмерный объект
считается изолированным, если для
всех положений строба обнаруженное
количество точек не превышает за¬
данного порогового уровня.
Анализ контекста сцены в окрест¬
ности обнаруженного точечного объекта
также позволяет отбросить целый ряд
ложных отметок. Область фон/объект
Рис. 10.9. Результат выделения то- или объект/объект являются участка-
чечных объектов в исходной сцене, ми с повышенным уровнем ложных от-
представленной на рис. 10.5, а меток. Такими же участками являются
Направление
освещения
Объект
W-'ll
Рис. 10.7. Проверка наличия
тени точечного объекта
Рис. 10.8. Проверка точечного
объекта на изолированность
416
Гл. 10. Обработка изображений с точечными объектами
изображения некоторых антропогенных объектов, например, моста. Как
радиолокационная цель он обладает высокой эффективной поверхно¬
стью рассеивания. Если на его поверхности и располагаются какие
либо точечные объекты, то их радиолокационная контрастность будет
очень низкой. Поэтому вероятность того, что наблюдаемые там отметки
являются ложными, очень велика и целесообразно их вообще исключить.
На рис. 10.9 приведено изображение исходной сцены (см. рис. 10.5, а) после
осуществления описанных выше операций. Все одиннадцать точечных
объектов выделены правильно, а ложные отметки практически полностью
исключены.
Дальнейшие операции с сформированной точечной бинарной сценой
связаны с анализом групповых точечных объектов.
10.3. Прослеживание траекторий точечных отметок
10.3.1. Модель траектории точечной цели на квадратной сетчатке.
В системе управления воздушным движением широко используются
цифровые индикаторы, содержащие аналого-цифровые преобразовате¬
ли, ОЗУИ, цифро-аналоговый преобразователь и дисплей. Между ОЗУИ
и ППИ происходит двухсторонний обмен информацией. Представленное
оператору на экране дисплея изображение поступает из ОЗУИ, имеющего
формат порядка 512 х 512 пикселов и выше. В ряде случаев дискретиза¬
ция изображения оказывается достаточно грубой и ошибки дискретиза¬
ции становятся сравнимыми с ошибками измерения координат цели или
даже превышают их.
На экране современной РЛС УВД ГВФ наблюдается несколько десят¬
ков и более отметок от точечных целей в условиях неизбежного присут¬
ствия помех, создаваемых соседними РЛС, отметками от птиц и т.п. Для
нормальной работы оператору необходимо отнести отметку к одной из
ранее обнаруженных траекторий, решить задачи предотвращения столк¬
новения в воздухе, идентификации целей и т.п.
Автоматизация всех процессов обработки информации, наблюдаемой
на экране дисплея, существенно повышает безопасность воздушного дви¬
жения и уменьшает психофизическую нагрузку на оператора.
Традиционно решение задач траекторной обработки проводилось для
случая, когда информация поступала с выхода детектора приемника и роль
основного мешающего фактора играли ошибки измерения координат цели,
распределенные по нормальному закону [144]. В данном же случае основны¬
ми мешающими факторами являются ошибки дискретизации. Эти ошибки,
обычно, имеют равномерный закон распределения вероятностей. Рассмотрим
алгоритмы автоматического прослеживания траектории точечной цели, на¬
блюдаемой на экране дисплея для случая значительного превышения уровня
ошибок ее дискретизации уровня ошибок измерения координат цели.
Модель прямолинейной траектории точечной цели на экране инди¬
катора можно рассматривать как частный случай контура изображения,
имеющего прямолинейные границы. В процессе квантования прямолиней-
10.3. Прослеживание траекторий точечных отметок
417
ной траектории на сетчатке происходит искажение формы. Вследствие
детерминированности формы исходной траектории и последующей ли-
нейной интерполяции ошибки квантования оказываются сильнокоррели¬
рованными и зависящими не только от размеров клетки поля, но и от угла
наклона φ прямолинейной траектории.
Математическая модель процесса квантования прямой линии, задан¬
ной на квадратной сетчатке и ее анализ рассмотрены в гл. 7. Этот процесс
описывается вырожденной цепью Маркова с матрицей вероятностей пере¬
ходов в виде матрицы перестановок. Для такой матрицы известны в общем
случае выражения ее собственных элементов — характеристических чи¬
сел и собственных векторов. Это дает возможность получить выражение
для вероятностей попадания процесса в заданное состояние на конкретном
шаге. Относительно к процессу квантования прямолинейной траектории
на квадратной сетчатке это означает, что известны вероятности значений
элементарных векторов проквантованной траектории.
10.3.2. Алгоритм прослеживания прямолинейной траектории. Будем
считать, что цель по каждой независимой координате (ж,?/,ζ) движется
с постоянной скоростью. В этом случае траекторию цели по отдельной неза¬
висимой координате можно представить как протяженную прямолинейную
границу (рис. 10.10) и обработку такого сигнала можно производить на основе
методов контурного анализа.
4
»
t
t
t
л ■
4*-
**
*
&
ί*-'
Р"
&
л*
·'/
Рис. 10.10. Траектория цели в ви- Рис. 10.11. Получение элементарных
де прямолинейной границы векторов на п-м обзоре
Процесс формирования комплекснозначного кода Г с учетом ошибок
квантования ее на квадратной сетчатке описывается рассмотренной в гл. 7.
марковской цепью. Наша задача будет состоять в распознавании точек
траектории и ставится она следующим образом: исходная, не искаженная
шумами квантования, линейная траектория задана кодом А = {а}, а =
= 1 -MV, где V — скорость движения цели по одной из независимых
координат. После квантования на сетчатке она образует траекторию Г.
Пусть к η-му обзору получен код Г = {7(m)}i,η-ъ а на η-м обзоре
поступило t новых точечных отметок. Если каждую из новых отметок
соединить с последней точкой траектории, полученной на (п—1)-м обзоре,
то будем иметь t ЭВ 7^(п)>7^2ЧП)> · · · >7^(п) (Рис· Ю.11).
Необходимо по критерию минимума расстояния в признаковом про¬
странстве между исходной траекторией А и ί полученными на сетчатке
418
Гл. 10. Обработка изображений с точечными объектами
траекториями выбрать траекторию Г, т.е. найти правило, по которому
отнести к траектории Г один из векторов 7^(тг).
Отметим, что даже при наличии в пространстве одной цели, созда¬
ющей один отраженный импульс, из-за ошибок квантования на прямо¬
угольной сетчатке может получиться несколько отметок и одну из них
надо выбрать как продолжение траектории Г.
Распознавание точек нефлуктуирующей цели. В соответствии
с рис. 10.11 сформируем на τι-м обзоре на основе траектории Γ(η_!) и по¬
лученных отметок ^-траекторий r|^ = {7(m)}i,n· Каждая из траекторий
Г (η—1) рассматривается как контур и задает в признаковом пространстве
точку. В качестве продолжения траектории на η-м обзоре выберем ЭВ
7(тг) = 7^(n), I ϊξ £, который обеспечивает в этом пространстве макси¬
мальную близость к точке истинной траектории А. Решение о близости
точек будем принимать по величине нормированного скалярного произве¬
дения (НСП) вектор-контура А = {1 + гУ} с одним из вектор-контуров
Г(п)’Г(п)’ ■ ■ · > г(п)> т-е· М°ДУЛЬ нсп будет равен
Ы
1(А,'га)|
(i-«0
7(,)(
м + Σ
т=1 J
ιιαιιιιγ{(,>
Ι|Α|| ||Γ(η)|| ιΐΛΐι ιια (η)I
Тогда для квадрата модуля НСП получим
м2
)(η) + Σ 7(т)
|7(0(п)|2 + М™)!2
(10.3.1)
(10.3.2)
Как следует из этого выражения, для случая линейной траектории
модуль НСП не зависит от конкретного значения скорости объекта и опре¬
деляется лишь значениями элементов цепного кода траектории, сфор¬
мированной на экране индикатора. Решение о принадлежности одного
из векторов 7^(гг),7^(71),... ,7^(тг) траектории Г принимается по
максимальному значению модуля полученного НСП, т.е.
7^(n) Е Г, если \η(η)\2 -* max. (10.3.3)
Распознавание точек флуктуирующей цели. Если наблюдается про¬
пуск отметки, то при принятии решения по критерию (10.3.3) в каче¬
стве продолжения траектории Г на η-м обзоре будет принята отметка,
принадлежащая другой траектории. Для исключения подобных ошибок
критерий принятия решения должен содержать пороговую процедуру,
учитывающую степень достоверности того, что вектор 7^(71) принадле¬
жит траектории Г. Для оценки степени такой достоверности, рассмотрим
влияние на величину (77(77)|2 ошибок квантования.
10.3. Прослеживание траекторий точечных отметок
419
Введем функцию F(n), равную количеству значений диагональных
ЭВ за η-шагов траектории, и далее будем рассматривать случаи, когда
|V| < 0,5. С учетом функции F(n) будем иметь
п
||г||2 - Σ |7(m)|2 =п + F(n), (10.3.4)
га=1
п
У] 7(га) = п + iF(n). (10.3.5)
т=1
Тогда выражение для квадрата модуля НСП принимает вид
I , ,,2 п2 +F2(n) 1 + [F(w)/w]
η2 + nF(n) 1 + F(n)/n
При больших значениях п функция F(n) близка к ее математическо-
(10.3.6)
му ожиданию и тогда
1 + V*
=Т+й'
(10.3.7)
Таким образом, в ассимптотике значение модуля НСП стабилизиру¬
ется на уровне г, определяемом величиной скорости движения цели по
независимой координате. Данный уровень будет определять величину по¬
рога при принятии решения о принадлежности той или иной отметки к
траектории. Так как величина скорости V при распознавании отметок
траектории неизвестна, то необходимо перейти к текущим граничным
оценкам величины V. Из того, что F(n) — Vn, следует выражение для
текущей оценки скорости цели V = F(n)/n.
Отклонение оценкиУ от истинного значения в данном случае опре¬
деляется вариациями величины F(n). Из определения функции F(n)
следует неравенство Vn-\ ^ F(n) ^ Vn+i. Тогда для текущих граничных
оценок величины V можно записать
V > ВД - Пп)п~\ (Ю.3.8)
V ^ VJn) = F(n) + 1. (10.3.9)
τι
С ростом п каждая из оценок сходится к истинному значению скорости
V. Учитывая нелинейный характер зависимости \η(η)\2 от V, с помощью
граничных оценок для скорости цели нельзя получить граничные оцен¬
ки для модуля НСП. Поэтому целесообразно разделить операции отбора
векторов 7^(п), служащих вероятными продолжениями траектории Г
(операция стробирования), и выбора только одного вектора 7^(п) 6 Г
(операция селекции).
Для стробирования рассчитываются две граничные траектории: верх¬
няя Гв и нижняя Гн, образующие в плоскости сетчатки область, вклю¬
чающую исходную траекторию цели. Граничные траектории на каждом
обзоре задаются текущими суммарными векторами βн(п) и βв(п). Для
420
Гл. 10. Обработка изображений с точечными объектами
получения вектора βн(п) используется нижняя оценка VH(n — 1) цели,
вычисленная по данным η—1 обзоров, а вектора βв(п) — соответствующая
верхняя оценка VB(n — 1):
βα(η) = n[l + iVH(n - 1)], βΒ(η) = n[l + iVB(n - 1)].
При стробировании отбираются векторы 7^) (гг), удовлетворяющие
условиям
nVH(n - 1) ^ Υπιβ^(η) ^ nVB{n - 1). (10.3.10)
С учетом выражений для VH(n - 1) и VB(n — 1) эти условия имеют вид
F(n — 1) — 1 ^ ^ Υτηβ«\η) ζ F(n - 1) +1. (10.3.11)
Векторы 7^) (n), удовлетворяющие данному условию, подвергаются
процедуре селекции. Следует отметить, что результаты операции строби¬
рования и селекции, полученные по каждой из независимых координат,
должны совпадать для отметок одной траектории. Если условию (10.3.11)
не удовлетворяет ни один вектор 7^(п), то принимается решение о про¬
пуске отметки данной траектории на п-м обзоре. В этом случае для рас¬
чета значений граничных траекторий βΗ(η 4-1) и βΒ(η 4-1) используются
оценки скорости VH и VB1 рассчитанные для η-го обзора.
Если происходит подряд ζ пропусков, то стробирование отметок на
(η = ζ)-м обзоре производится в соответствии с выражением
(п + С)[F(n) - 1] ^ ^ ΥτηβΜ(η + <)[F(n - 1) - 1]. (10.3.12)
На рис. 10.12 приведены результаты расчетов граничных траекторий
для нескольких значений скорости по данным цепного кода прокванто-
ванной траектории.
Г
ts
«*-
*=■
2L.
ν'
-
yr
ν’
Ζ9
Рис. 10.12. Стробирование исходной траектории для V = 0,1
Рассмотренные выше вопросы согласованной фильтрации относились
к случаю прямолинейной траектории V = const. Для общего случая, когда
V(п) — произвольная функция, описывающая скорость движения точки
по независимой координате, реакция согласованного фильтра в момент
наилучшего согласования проквантованной траектории с исходной запи¬
10.3. Прослеживание траекторий точечных отметок
421
сывается в виде
η
η(η) = Σ ^(то) ~ t1 + iv(n)}.
m—1
Например, если цель движется равноускоренно со скоростью V(п) =
= ап, то
п п
77(71) = ^2 7(m) + ai 7717(771).
га=1 т=1
Реакция согласованного фильтра в виде модуля НСП позволяет опре¬
делить меру близости к распознаваемой траектории полученных на тг-м
обзоре отметок и отобрать одну из них в качестве продолжения данной
траектории по критерию максимальной близости.
Глава 11
ОБРАБОТКА И ПОНИМАНИЕ ИЗОБРАЖЕНИЙ ГРУПП
МАЛОРАЗМЕРНЫХ И ТОЧЕЧНЫХ ОБЪЕКТОВ
11.1. Введение
В большом числе приложений для наблюдателя представляют интерес
не отдельные точечные объекты, а их множества (группы). В этих мно¬
жествах точечные объекты могут объединяться по различным наборам
признаков, например, по признаку пространственной близости, физиче¬
скому происхождению, яркостным или цветовым характеристикам и т.д.
После объединения каждое множество приобретает групповые признаки,
становится групповым точечным объектом (ГрТО). Групповые признаки
по сравнению с признаками отдельных малоразмерных объектов обла¬
дают большей устойчивостью к действию мешающих факторов (шумам,
помехам) и имеют большую информативность для задач понимания
изображений.
Классическими примерами ГрТО являются: изображения созвездий
на небесной сфере (рис. 11.1, а); символы матричной печати (рис. 11.1, б);
точечные коды или ключи (рис. 11.1, в); отверстия и реперные знаки
печатных плат (рис. 11.1, г); локационные изображения строев самолетов,
автомобильных потоков и скоплений (рис. 11.1, б), строений, опор ЛЭП;
изображения выборочных реализаций случайных процессов на плоскости
(рис. 11.1, е) или в трехмерном признаковом пространстве. Кроме того,
к ГрТО могут быть преобразованы изображения, состоящие из крупно¬
размерных объектов, например для описания их взаимного положения
или формы, когда объекты заменяются точками в центрах тяжести или
характерными точками перегибов (рис. 11.1, ж).
Для выделения групповых признаков таких объектов обычно необ¬
ходимо вначале обнаружить ГрТО в зашумленной сцене, провести сег¬
ментацию (пространственную локализацию) ГрТО, выполнить измерения
групповых признаков и их представление (кодирование).
В гл. 5 были рассмотрены вопросы, связанные с заданием ГрТО как
сигнала в виде пучков векторов, соединяющих произвольно выбранную
точку полюса Р с каждой точкой ГрТО. В данной главе в соответствие
ГрТО будет поставлено сплошное изображение — ассоциированный сплош¬
ной образ (АСО), форма которого отражает закономерности расположе¬
ния его точек. Данная модель позволяет непосредственно использовать
описанные в части I методы контурного анализа для обработки ГрТО.
11.1. Введение
423
g t, °C · — точки перегибов
Рис. 11.1. Примеры групповых точечных объектов
При обработке изображений ГрТО анализируется не вся сцена,
а лишь ее небольшой участок, содержащий данный объект. Этот уча¬
сток сцены в дальнейшем будем называть машинным кадром и также
обозначать s (х, у).
Пусть имеется исходный (эталонный) машинный кадр
5 (·£? У) = ^ ^ (% У ~~ Уть) (11.1.1)
η
в виде поля точечных объектов с координатами (хп,Уп) и яркостью (ин¬
тенсивностью, светимостью) J9)Tl. С учетом хаотичности изменения пара¬
метров среды распространения сигнала и ошибок измерения координат
сформированный сигнальный машинный кадр представим как
5С (^5 У) =: ^ ^ — у уп Ду) ) (11.1.2)
п
где Jc>n — яркость п-й точки, $п — случайная величина, имитирующая
пропуск полезных отметок с вероятностью рПр, причем Р ($п = 0) = рпр
и Ρ($η = 1) = 1 - рпр, (Дх,Ду) — ошибки измерения координат —
координатный шум.
424
Гл. 11. Обработка групповых точечных объектов
Кроме сигнального, ППИ формирует еще и шумовой машинный кадр
«ф у) = Σ J*'n5 ~х^У~ Уп) > (11.1.3)
п
представляющий собой случайное, равномерно распределенное поле лож¬
ных точечных отметок с вероятностью ρψ и яркостью Обработке
подвергается суммарный машинный кадр s(x, у) = sc (х, у) + 5ф (х, у).
В оцифрованном виде он дополнительно содержит шумы дискретизации
и квантования. Если яркости точечных отметок не информативны для
решения последующих задач обработки изображений ГрТО, то более ком¬
пактно машинный кадр может быть представлен в виде множества коор¬
динат содержащихся в нем точечных отметок, т.е. в виде s = {xn}o k-v
где х„ = {хп,Уп}·
Поставим в соответствие изображению ГрТО, рассматриваемому как
фрагмент машинного кадра, сплошное изображение N (х), форма кото¬
рого отражает в определенной степени закономерности взаимного распо¬
ложения и яркости всех точечных объектов. Это изображение назовем
ассоциированным сплошным образом (АСО).
Яркость и положение АСО определяется кумулятивным вкладом каж¬
дой точки ГрТО. Поэтому помехоустойчивость подобного представления
ГрТО будет более высокой, чем при его задании отдельными точками.
Кроме того, появляется возможность по контуру АСО решать ряд таких
важных задач, как оценка параметров и распознавание ГрТО.
В качестве преобразований ГрТО для получения АСО могут быть
использованы следующие линейные операции.
1. Низкочастотная пространственная фильтрация (расфокусировка)
поля точек (рис. 11.2):
N
ЛГ(х) = ^ ^ Jn · hnф (х жп, у уп |гq) , (11.1.4)
п=1
где Ииф (х \г0) — ИХ пространственного фильтра, например, колоколооб-
Рис. 11.2. Формирование ассоциированного сплошного образа ГрТО: а — исходная
точечная сцена; б — результат расфокусировки точечной сцены
11.1. Введение
425
разного вида
ЛПф(х|г0) = ехр{— (х2 +у2) До} , (11.1.5)
го — параметр, определяющий скорость затухания отклика фильтра на
дельта-импульс и согласованный с плотностью расположения точек ГрТО
в плоскости машинного кадра.
2. Построение модели потенциальных физических полей, где в каче¬
стве источников поля принимаются заряды, пропорциональные яркости
точечных отметок и размещенные в этих точечных отметках. Во вто¬
ром случае математическая запись для кумулятивного поля аналогична
(11.1.4), происходит лишь замена понятия ИХ фильтра на потенциальную
функцию.
3. Построение модели векторного поля, где помимо абсолютного зна¬
чения влияния каждого источника учитывается и направление действия
этого поля:
N
N (х) = Фвп [s(x), Кф (х |г0)] = Σ Jn ■ Кф (ж -хп,у- Уп |г 0) ехр ίφη,
п=1
(11.1.6)
где ψη — arctg ((у — уп)/(х — хп)) — направление на источник с номером
п, ^вп — оператор формирования векторного поля на множестве точек
[185, 201].
Идею последних двух методов легко представить, если предположить,
что каждая точечная отметка является источником потенциального или
векторного полей (например, аналога поля электрического заряда), убыва¬
ющего по силе с удалением от источника. Очевидно, что форма суммарного
поля в окрестности любой точечной отметки будет связана с взаимным
расположением ее ближайших соседей.
Совокупность всех значений поля в анализируемом кадре изобра¬
жения оказывается избыточной с точки зрения уникальности описания
формы классов ГрТО [88, 165]. Поэтому для повышения вычислитель¬
ной эффективности процедуры обработки изображений ГрТО целесо¬
образно использовать сечения кумулятивного поля (рис. 11.3), напри-
Рис. 11.3. Сечения яркостного рельефа ассоциированного сплошного образа в виде
линий уровня
426
Гл. 11. Обработка групповых точечных объектов
мер горизонтальные (в виде линий уровня поля) или цилиндрические
(в виде значений поля по окружности определенного радиуса с центром
в точке-источнике).
В зависимости от вида поля (потенциальное или векторное) можно
предложить два основных способа дискретного кодирования формы пере¬
численных сечений:
— цепным комплекснозначным кодом полигональных аппроксимаций
линий уровня потенциального поля, т.е. контуром областей высокой кон¬
центрации точечных объектов;
— комплексными значениями отсчетов векторного поля, взятых
с некоторым шагом по опорной окружности вокруг анализируемой точ¬
ки [185, 201].
Более высокая помехоустойчивость формы расфокусированного изобра¬
жения множества точек объясняется несколькими причинами. Во-первых,
информация о координатных шумах точек преимущественно сосредоточена
в высокочастотных составляющих спектра пространственных частот исход¬
ного изображения, а они в значительной степени отфильтровываются во
время низкочастотной фильтрации (расфокусировке). Во-вторых, как видно
из формулы (11.1.6), более яркие точки вносят наибольший вклад в форму
расфокусированного изображения, а, следовательно, более частые пропус¬
ки обнаружителем меньших по яркости отметок носят менее ощутимый
характер. В-третьих, ошибки при обнаружении отметок, расположенных
в средней части сгущения отметок, слабо влияют на положение границ АСО,
а именно границы (области наибольших перепадов яркости) концентрируют
информацию о форме АСО.
11.2. Обнаружение групповых точечных объектов с известной
формой ассоциированного сплошного образа
11.2.1. Постановка задачи и модели сигналов. Задача обнаружения
ГрТО решается после обнаружения точечных объектов в сцене и заключа¬
ется в обоснованном принятии решения о том, что некоторая совокупность
этих объектов обладает признаками, соответствующими ГрТО.
Стохастический характер формирования изображения обуславливает
случайные ошибки при обнаружении точечных объектов. Если фон по
яркости статистически однороден, то вероятность ошибки первого рода рф
одинакова для любого пиксела с изображением фона. Вероятность ошибок
второго рода рпр, связанных с пропуском точечных отметок, в общем
случае зависит от светимостей точечных объектов.
Будем для упрощения предполагать, что светимости точечных объ¬
ектов, составляющих ГрТО, мало отличаются друг от друга. Поэтому
вероятности рпр для любого точечного объекта будут одинаковыми.
В данном разделе мы рассмотрим задачу обнаружения ГрТО в точеч¬
ной сцене при условии, что известен его АСО.
Бинарное по яркости изображение АСО зададим в виде замкнутого
множества А отсчетов внутренней области АСО и опишем его двумерной
11.2. Обнаружение групповых точечных объектов с известной формой 427
функцией — огибающей поля точек ГрТО:
fl <*»■*€ Л, (И21)
χο-ο,ν>0=ο ^о в противном случае,
где хо, φο — соответственно вектор параллельного переноса и поворота
АСО в сцене. На рис. 11.4 дан пример АСО гипотетического ГрТО с ну-
ο,φο)
Рис. 11.4. Изображение группового точечного объекта и его «плоского» ассоцииро¬
ванного сплошного образа
левыми значениями параметров линейных преобразований изображения
(хо, φο =0). Например, такой АСО может быть получен объединением
элементарных площадок вокруг точечных объектов, в пределах которых
любое положение этих объектов считается равновероятным.
Примем, что в пределах АСО точечные объекты расположены равномер¬
но, т.е. ГрТО является выборкой из равномерного поля точек с усредненной
вероятностью (плотностью) р'с появления отметки в каждом пикселе.
Возможность события пропуска точечного объекта уменьшает эту плот¬
ность до величины рс < р'с, а ложные отметки, появляющиеся в пределах
АСО с вероятностью ρψ, ρψ <С 1, увеличивают ее до величины рсм =
— Рс + Рф- Таким образом, в области АСО плотность появления точечной
отметки равна рсм, а в области фона — рф.
Принятая модель машинного кадра s(x), в котором содержится ГрТО
с известной формой АСО и статистически однородный фон, является
моделью двумерного случайного поля точечных отметок с плотностями
точек в области фона, равной ρψ, а в области АСО — равной рсм:
s(x) = 5ф (х) + h (х, х0, φο) sc (х). (11.2.2)
Далее будем предполагать, что машинный кадр s(x) образован по
результатам обнаружения точечных отметок, т.е. любая точечная отметка
в нем имеет единичную яркость. Обозначим через р\ (х) и ро (х) вероят¬
ности появления отметки в η-м пикселе машинного кадра, т.е.
P(s(x-n) = 1) =Р1 (х«) И Р (s (pin) = о) = Ро (х„).
Если этот пиксел находится в пределах фона, то р\ (хп) = ρψ
и ро (хп) = 1-Рф, а если в пределах АСО, τορχ (хп) = рсм ир0 (χη) = 1-
— рсм. В этом случае распределение вероятности событий в η-м пикселе
428
Гл. 11. Обработка групповых точечных объектов
можно записать как
при s (х„) = 1, (112 3)
при S (хп) = 0.
Отсчеты в каждом пикселе считаем независимыми событиями. Поэто¬
му с учетом (11.2.3) совместное распределение вероятностей Р(S) появ¬
ления нулевых и единичных отсчетов в пикселах машинного кадра будет
равно произведению распределений Р (s (хп)), η = 1,2,... ,Ν:
N
Р (S) = П Р (s (х„)) - (1 - Рсм)ПОс“ Рф‘" (1 - Рф)П0ф · (11-2.4)
n=1
Здесь 7V — общее количество пикселов в машинном кадре S =
= {s (xi), s (X2),... , s (χαγ)} , τΐι и no — соответственно количество еди¬
ничных и нулевых отсчетов, по + п\ — N\ пiCM и посм — соответственно
количество единичных и нулевых отсчетов в области АСО, ηχψ и п0ф —
в области фона; niCM 4- ηΐφ = п\\ посм + поф = Щ-
Распределение (11.2.4) является условным, зависящим от положения
АСО в кадре, которое определяется вектором параллельного переноса хо
и углом поворота ψο, а также тем, к какому из классов A{,i = 1,2,... , М,
относится.
Не нарушая общности модели машинного кадра, выражение (11.2.4)
для распределения вероятностей отметок в нем можно распространить
и на случай отсутствия ГрТО. Введение нулевой гипотезы требует лишь
уточнения вида огибающей h (х) в выражении (11.2.2), которая равна нулю
для любого xn: ho (хп) = 0 V xn. С учетом принятой модели машин¬
ного кадра, содержащего или не содержащего ГрТО, задача обнаружения
объекта формулируется следующим образом.
Пусть по результатам обнаружения отдельных точечных объектов на
статистически однородном фоне сформирована точечная сцена s (х) и вы¬
делен машинный кадр, содержащий N пикселов. Для этого кадра возможна
одна из двух альтернативных ситуаций: 1) он представляет собой выборку
равномерного поля вф из ложных отметок с плотностью рф (гипотеза Но),
либо 2) кадр представляет собой суперпозицию поля ложных отметок $ф
и множества точек ГрТО h (х, Xq, ψο) sc(x) некоторого класса Аг·, являю¬
щегося фрагментом равномерного поля с плотностью рс (гипотеза Hi). Ре¬
зультирующая плотность отметок во втором случае равна рсм. Необходимо
принять решение в пользу одной из двух приведенных гипотез.
11.2.2. Обнаружение ГрТО с известным положением в кадре. Поло¬
жение ГрТО в машинном кадре считается известным, если задан вектор
его параллельного переноса хо и угол поворота ψο. Кроме того, заданы
закон распределения числа его точек и форма АСО. На основание выра¬
жения (11.2.4) можно получить функции правдоподобия для гипотез Н\
Р (s (Хп)) = Р (s (хп) = 1, 5 (хп) = 0) =
= Pi (*пУ(Хп) Ро (Хп)1~'(х") = \Р15Хп)
1ро W
11.2. Обнаружение групповых точечных объектов с известной формой 429
и Hq и записать следующий алгоритм обнаружения на основе отношения
правдоподобия:
Н =
если Л > Ло,
если Л < Ло,
д Р (S |Ях, хо, φο) __ р"м1с“ (1 - Рс«)П0с“ Рф1ф (1 - Рф)Поф
Р (S |Я0) ΡΪ1 (1 -Рф)"°
(11.2.5)
где Ло — пороговый уровень, определяемый принятым критерием опти¬
мальности.
После приведения подобных членов и монотонного преобразования от¬
ношения правдоподобия в виде линейной функции логарифма отношения
правдоподобия получаем эквивалентный по характеристикам алгоритм на
основе минимальной достаточной статистики
где
Я
[Но
6СЛИ Я1см ^ «пор>
вСЛИ ΤΪ-Icm ^ «пор)
_ (In Л0 - 6)
а = In
+ In
1 - РФ
1 Рем
Ь = Е · In
1 - Рем
1 - РФ
N
П1
«1см = Σ S (х„) · h (х„ - х0, φ0) = Ύ^}ι (х/ - х0, φο) ■
п=1 1=1
(11.2.6)
(11.2.7)
Отсюда следует, что решение о наличии или отсутствии ГрТО в ма¬
шинном кадре выносится при сравнении количества точечных объектов
в области АСО с пороговой величиной пП0р.
Значение порога ппор устанавливается исходя из принятого критерия
обнаружения. Например, для байесовского алгоритма
(До1 — Яро) Р (Нр) _ ,1
(Rio-Ri^PiH!)] J ’
где Я01 — стоимость ложной тревоги, Яю — стоимость пропуска ГрТО,
Яоо, Яц — стоимости правильных решений, а Я(Я0) и Р(Нг) — априор¬
ные вероятности гипотез Hq и Hi соответственно. В условиях априорной
неопределенности относительно P{Hq) и Ρ(Ηι) практически значимым
является критерий Неймана-Пирсона. В этом случае значение порога
ппор находится из граничного условия Р(пiCM > пПОр|Я0) = F, где F —
фиксированный уровень ложных тревог.
Как следует из (11.2.7), вычисление статистики niCM связано с полу¬
чением отсчета ВКФ функции, задающей машинный кадр s(x) и АСО
/i(x,x0,<pо) в точке х = х0. Устройство для получения такого отсче¬
та представляет собой пространственный согласованный фильтр с ИХ
430
Гл. 11. Обработка групповых точечных объектов
h (хо — х, φο). На рис. 11.5 приведена структура обнаружителя из согла¬
сованного фильтра СФ и порогового устройства ПУ, на которое подается
отсчет фильтра, соответствующий пикселу хо-
s(\)
[h(x0-x,<p0)
СФ
Ι£(χ-χη)
устройство п
выборки —
отсчета
Iя·»
ПУ
I: Я,
О :На
Рис. 11.5. Структурная схема обнаружителя ГрТО с известным положением в ма¬
шинном кадре
Для определения эффективности обнаружителя запишем общие выра¬
жения для вероятности ложной тревоги F и правильного обнаружения D:
оо
F — Р (tiicm > «пор|Я0) = | P(niCM|tf0)dnlcM, (11.2.8)
D = 1 - P(nicM < ηπορ|#ι) = 1 - | P(nicM|tfi)dniCM, (11.2.9)
О
где -Р(п1СМ|Яо), Ρ(ηχ0Μ|^ι) — соответствующие условные распределения
вероятностей достаточной статистики πχ0Μ.
Раскроем структуру статистики обнаружения в условиях истинности
соответствующих гипотез Яо и Яь niCM\Ho = τΐψ, niCM\Hi = Пф + пс,
где Пф — количество ложных отметок в области АСО, нс — количество
обнаруженных точек ГрТО в области АСО.
Так как события, соответствующие появлению ложных отметок в пик¬
селах машинного кадра S, считаем независимыми и наступающими
с вероятностью рф, то вероятность появления ровно и таких отметок
в пределах АСО, содержащего Е пикселов, подчиняется биномиально¬
му закону
Для практических значений Е (как правило, Е > 100) биномиальное
распределение асимптотически стремится к нормальному
Реи (п|я0) S3 —-/== ехр/_(га~^ф) | _ Я(пф,сгф), (11.2.10)
σφ\/2π L 2σΦ J
где йф = Е · рф — среднее число, а σ| = Е · ρψ(1 — Рф) — дисперсия
плотности ложных отметок. Подставив (11.2.10) в (11.2.8), получим
F = 1 — Ф ^ пеор~ Щ ^ ) (11.2.11)
где Ф(·) — функция Лапласа.
11.2. Обнаружение групповых точечных объектов с известной формой 431
Предположим, что вероятность пропуска точек ГрТО при формиро¬
вании точечной сцены S ничтожно мала, а мощность (количество точек)
ГрТО априорно задана. Тогда пс является детерминированной величиной
и имеет место случай полностью известного ГрТО. При этом условная
статистика niCM|#i представляет собой сумму асимптотически нормаль¬
ной случайной величины Пф и константы пс, и, следовательно, также
распределена нормально
р (nicu\Hi) и N(nc + Пф, <7ф) (11.2.12)
с параметрами М [niCM|#i] = пс +Щ, \JD [п!СМ|Ях] = σψ. В результате
подстановки (11.2.12) в (11.2.9) находим вероятность правильного обнару¬
жения
D = 1 — Ф ( Ппор ПФ ~ Пс ) _ 1 Ф ( Ппор ~ ПФ
V σΦ / V σΦ
где q = ηα/σφ — расстояние Махаланобиса [40] (в рассматриваемом слу¬
чае — эквивалент отношения с/ш на выходе фильтра).
Зависимости вероятности правильного обнаружения от расстояния Ма¬
халанобиса при различных значениях относительного порога принятия
решений для случая двух гауссовских статистических гипотез хорошо
известны и могут быть построены, например, с помощью таблиц [202].
В связи с этим ограничимся иллю¬
страцией лишь нескольких зависи¬
мостей для практических значений
уровня ложных тревог, графики
которых приведены на рис. 11.6
сплошными линиями. График 1 со¬
ответствует F = 10~3, график 2 —
F = 10~4, график 3 — F = 10~5,
график 4 — F = 10“6.
Рассмотрим ситуацию, при ко¬
торой количество обнаруженных
точечных объектов в ГрТО из-за
пропусков случайно и их распре¬
деление описывается нормальным
законом. При этом условное рас¬
пределение вероятности достаточ¬
ной статистики niCM\Ho не меня¬
ется и описывается выражением (11.2.10). Вероятность ложной тревоги
также может определяться на основании (11.2.11).
Поскольку достаточная статистика при истинности гипотезы Щ
в данной ситуации представляет собой сумму независимых гауссовских
величин пс и Пф, то условное распределение P{niCM\Hi) также будет
гауссовым:
Р (nlca\Hi) & N (щ+щ, + σ|) , (11.2.13)
Рис. 11.6. Характеристики обнаружения
ГрТО с детерминированным числом то¬
чек (сплошная линия) и ГрТО со случай¬
ным числом точек (пунктир)
432
Гл. 11. Обработка групповых точечных объектов
где пс и — соответственно среднее значение и дисперсия числа об¬
наруженных точек ГрТО. Тогда вероятность правильного обнаружения
ГрТО равна
Характеристики обнаружения ГрТО со случайным значением пс явля¬
ются многомерными функциями нескольких параметров. В связи с этим
выберем для иллюстрации несколько сечений многомерных характери¬
стик для частного случая равенства дисперсий числа ложных отметок
и точек ГрТО (σ€ = σψ). На рис. 11.6 пунктиром показаны графики
данных характеристик. График 5 соответствует F = 10_3, график 6 —
F = 10"4, график 7 — F = 10~5, график 8 — F = 10-6.
Из приведенных графиков видно, что проигрыш в пороговом значе¬
нии <?, вызванный отсутствием априорной информации о точном значе¬
нии мощности ГрТО, для вероятности правильного обнаружения D —
= 0,9 приблизительно равен 1,13, что составляет около 1,1 дБ. Так
например, при среднем числе ложных отметок в машинном кадре с раз¬
мерами 256 х 256 = 216 элементов разрешения, равном 50 (т.е. ρψ =
= 50/216), при F = 10“3, любой полностью известный ГрТО, содержащий
4 и более точечных отметок, на площади АСО в 1000 элементов, будет
обнаружен не хуже, чем с вероятностью 0,9. Для этих же условий, при
неизвестной мощности ГрТО минимальное среднее число точек ГрТО,
требуемое увеличивается до rQ « 4,3.
11.2.3. Обнаружение групповых точечных объектов с произвольным
положением в кадре. Воспользуемся для преодоления априорной неопре¬
деленности о положении изображения ГрТО в машинном кадре способом,
основанным на предварительном получении оценок МП параметров поло¬
жения ГрТО и подстановке этих оценок в условное отношение правдопо¬
добия. Получим алгоритм оценок МП неизвестных параметров хо и φο на
основе логарифма функции правдоподобия (11.2.4), записанного с учетом
этих параметров:
lnP(S|ffb х0, <р0) = П1СМ(х0, φο)Οι + niC2 + ЕС3 + С4, (11.2.15)
Поскольку все члены (11.2.15), кроме пгт, являются постоянными или
независящими от х0, φο величинами, и С\ ^ 0 для любых рс,Рф, то функ¬
ция (11.2.15), в свою очередь, будет монотонной функцией тгсм. Следова-
(11.2.14)
где
11.2. Обнаружение групповых точечных объектов с известной формой 433
тельно, алгоритм получения оценок МП хо и φο эквивалентен алгоритму
х0, Фо - arg max niCM(x0, φ0)· (11.2.16)
*ο, φο
Таким образом, для нахождения искомых оценок необходимо вычис¬
лить ВКФ машинного кадра s (х) и изображения АСО h (х - х0, φο) для
всех возможных положений АСО в кадре и определить значения хо = хо
и φο = φο, при которых ВКФ достигает максимума.
Отношение правдоподобия (11.2.5) монотонно зависит от пСМ) явля¬
ющейся минимальной достаточной статистикой при обнаружении ГрТО
с известными значениями Xq и Поэтому из (11.2.16) с учетом (11.2.6)
следует оптимальное решающее правило обнаружения ГрТО
Н =
Н\, еСЛИ П1см (Х(Ь ^о) ^пор?
#0, еСЛИ 77-iCM (хо, φο) ^ ^пор·
(11.2.17)
Таким образом, алгоритм обнаружения ГрТО с неизвестным поло¬
жением в сцене заключается в вычислении ВКФ машинного кадра s(x)
и изображения АСО /ι(χ — хо, φο) при всех возможных положениях АСО
в кадре и сравнении максимального отсчета этой функции с величи¬
ной τίπορ) назначаемой исходя из принятого критерия оптимальности. При
фиксированном значении φο искомая ВКФ получается в результате ра¬
боты пространственного фильтра с ИХ h{—х, <£о)‘
П1см(х, φο) = J s(£)M£ - χ>
= Х^Мхг - χ, φο),
1=1
(11.2.18)
где Ω — область определения координат пикселей машинного кадра s(x).
Структура обнаружителя ГрТО с неизвестным вектором смещения
содержит согласованный фильтр СФ, экстремальное устройство ЭУ и по¬
роговое устройство ПУ (рис. 11.7).
Рис. 11.7. Структура обнаружителя группового точечного объекта с неизвестным
смещением в кадре
В связи с неинвариантностью пространственного согласованного филь¬
тра к угловой ориентации АСО, обнаружитель ГрТО с неизвестными
значениями хо и φο должен быть многоканальным устройством. Каж¬
дый п-й канал содержит обнаружитель, показанный на рис. 11.7, для
значения φο = ηΑφ, где Αφ — шаг дискретизации по углу. Чем мед¬
леннее изменяется АКФ изображения АСО, тем меньшее число каналов
требуется для достижения заданного качества обнаружения ГрТО.
434
Гл. 11. Обработка групповых точечных объектов
На рис. 11.8 представлены характеристики обнаружения ГрТО с неиз¬
вестным вектором смещения хо в кадре. Графики 1, 5 соответствуют
F = 10“3, графики 2, 6 — F —
= 10~4, 2, 7 — F = 10~5
и 4, 8 — F = 1СГ6. Сплошной
линией обозначены характери¬
стики для случая детерминиро¬
ванного числа точечных объектов
ГрТО, а штриховой — для слу¬
чайного числа точек ГрТО. При
построении этих характеристик
под ложной тревогой подразуме¬
вается событие riiCM (х0, <£>о) >
> ппор, имеющее место хотя бы
для одного значения х из N
возможных в машинном кадре.
Из приведенных графиков видно,
что проигрыш относительно по¬
роговых значений сигнал/шум q по сравнению со случаем известного
положения ГрТО в кадре, размером 256 х 256 пикселов и АСО,
состоящего из 1000 пикселов, примерно равен 1,3.
11.3. Обнаружение групповых точечных объектов с неизвестной
формой
Рассмотрим подход к обнаружению ГрТО в точечной сцене, когда
форма АСО неизвестна. Заданной считается статистика фона из ложных
отметок, причем плотность точечных объектов в области фона ниже, чем
в области расположения ГрТО. В этом случае обнаружитель ГрТО может
быть построен на основе измерителя плотности отметок, инвариантного
к форме АСО, и решающего устройства, принимающего положительное
решение, когда превышение плотности точек в анализируемой области
над плотностью точек фона статистически значимо.
Расстояние между соседними точечными объектами и их плотность
статистически связаны: чем выше плотность, тем меньше среднее рас¬
стояние между соседними точками и наоборот. Процедура обнаружения
ГрТО как области с повышенной по сравнению с фоном интенсивностью
точек может быть условно разделена на два этапа: 1) оптимальная лока¬
лизация компактных групп точек; 2) обнаружение ГрТО на основе анализа
мощности (количества точек), сформированных на первом этапе компакт¬
ных групп.
11.3.1. Локализация групповых точечных объектов. Из кластерного
анализа [40] известна процедура, упорядочивающая подмножества наблю¬
дений — точек в признаковом пространстве по степени их пространствен¬
ной близости гтт. Для двумерного точечного изображения она состоит
1.0
0,8
0,6
0,4
0,2
0
8
Рис. 11.8. Характеристики обнаружения
ГрТО с неизвестным смещением в ма¬
шинном кадре
11.3. Обнаружение групповых точечных объектов с неизвестной формой 435
в построении связного графа — минимального дерева, вершинами кото¬
рого являются точки, а ребрами — соединяющие их отрезки (см. п. 5.6).
Каждое ребро такого графа объединяет два непересекающихся подмно¬
жества точек, а длина ребра характеризует пространственную близость
объединяемых подмножеств.
После разрушения всех ребер минимального дерева, которые нельзя
с заданной доверительностью отнести к области с повышенной плотностью
точек, полный связный граф сцены распадается на несколько несвязных
между собой подграфов. Каждый из них объединяет точки компактного
подмножества, т.е. локализует компактную группу точек.
Таким образом, локализация ГрТО на основе анализа минимального
дерева для точечной сцены заключается в обнаружении ребер этого де¬
рева, соединяющих области с разной плотностью точек.
С помощью решающего правила надо обоснованно принять в качестве
истинной одну из двух альтернатив: Но — статистическая гипотеза о том,
что ребро минимального дерева связывает между собой ложные отметки,
tfi — статистическая гипотеза о при¬
надлежности одного из концов ребра
к области с повышенной по сравнению
с фоном плотности точек, т.е. к ГрТО.
Рассмотрим один из подходов к по¬
лучению такого решающего правила.
Вероятность того, что в случайном
равномерном поле точечных отметок
с плотностью р на расстоянии г от дан¬
ной точки не будет ни одной соседней
точки равна [97]
wo{r) = exp {-ρπτ*2/2} . (11.3.1)
Введем случайную величину ξ как
длину интервала до первой соседней точки. Функция распределения этой
случайной величины будет равна
Ρ(ξ < г) = 1 — Wo (г) = 1 — ехр (—ρπτ*2/2) при г > О,
Ρ(ζ < г) = О при г ^ 0. (11.3.2)
Тогда плотность вероятности значений ξ
№ί(,) = ^!<ι! = ^Χρ{ζΐΙ} (11зд
подчиняется закону Рэлея с параметром σ2 = l/πρ.
Для области фона р = ρψ, σ2 = σ| = 1/πρψ. На рис. 11.9 показаны
теоретические (графики 1 и 2) и полученные экспериментальным путем
(графики 3 и 4) по методу Монте-Карло плотности распределения и со¬
ответствующие им гистограммы длин ребер минимального дерева. Для
графиков 1, 3 параметр ρψ = 50/(256 х 256), а для графиков 2, 4 — ρψ =
= 20/(256 х 256). Как видно из графиков, эксперимент свидетельствует
Рис. 11.9. Распределения длин ребер
минимального дерева для равномер¬
ных полей точек
436
Гл. 11. Обработка групповых точечных объектов
в том, что распределение (11.3.3) достаточно хорошо описывает реальные
значения длин ребер минимального дерева.
Примем, что длины ребер минимального дерева, построенного на мно¬
жестве точек ГрТО, также распределены по закону Релея с параметром
ас. Полагая, что Рф<^1, для области наложения ГрТО и фона приближенно
можно считать, что ас « 1/тг(рс + Рф).
Функции правдоподобия для гипотез Но и Hi будут отличаться лишь
параметром σ и равны
Wi(r\H0)^ 4-exp(-rI_}, WtirlHi) = -^ехр(-^}. (11.3.4)
(Тф ^ 2(Тф J <7С ^ 2<ТС J
Таким образом, обнаружение ребер минимального дерева, связыва¬
ющих точки ГрТО, является задачей проверки гипотез о параметре σ
распределения Релея. Решающее правило имеет вид
Н =
#ь если Лг > Лог,
Н0, если Аг < Л0г,
(11.3.5)
Л =Щг1Н1)
г W€(r|Ho)
ехр | |.
Переходя к логарифму отношения правдоподобия, получим
_ J Hi, если г2 < г§, ^2 _ 2 [in (σ\/σΙ) - 1ηΛ0
[Но, если г2 > 7*0, ° (l/^c - 1/σφ)
Η
Учитывая, что величина г всегда положительная, получим решающее
правило в окончательном виде
Я =
(11.3.6)
Hi, если г < го,
^Но, если г > Го-
Вероятность ложной тревоги, получающаяся при данном правиле при¬
нятия решении, равна
Fr = Р(г < г0\Но) = J Wt (г \Н0 )dr = 1 - exp J . (11.3.7)
о ф
Из этого выражения можно найти величину оптимального порога об¬
наружения (локализации) г0- Так, например, для критерия Неймана-
Пирсона величина порога будет равна
г0 = 2σ|1η(1 - Fr).
(11.3.8)
Вероятность правильного обнаружения ребра минимального дерева из
области расположения ГрТО определяется как
Dr = Р(г < го\Нг) = 1 — ехр
-Гр
2 σΐ
11.3. Обнаружение групповых точечных объектов с неизвестной формой 437
или, с учетом (11.3.8),
£>r = l-exp jln(l-Fr)^fj. (11.3.9)
Из полученных выражений следует, что при ас < σψ (т.е. рс > Рф) для
всех ас выполняется неравенство Dr > Fr, причем Dr монотонно возра¬
стает с уменьшением ас. Поэтому алгоритм (11.3.6) является несмещенным
равномерно наиболее мощным алгоритмом и для сложной альтернативной
гипотезы Н\ \ σ < σф.
Таким образом, оптимальный алгоритм локализации компактных групп
точек в машинном кадре заключается в построении минимального дерева
точечной сцены и разрушении всех ребер этого графа с длиной более г$.
При этом исходное множество разделяется на компактные подмножества
из связных компонент дерева.
11.3.2. Обнаружение локализованных групповых точечных объек¬
тов. На втором этапе обнаружения ГрТО с неизвестной формой АСО
необходимо проанализировать мощность каждой полученной компактной
группы и обоснованно определить какая из двух статистических гипо¬
тез, Hi или #о, является истинной. Гипотеза Щ предполагает образо¬
вание анализируемой группы точками ГрТО, а гипотеза Но — точками
только ложных отметок.
Введем случайную величину z — мощность компактной группы. Обо¬
значим через g вероятность того, что длина ребра минимального дерева
меньше порогового значения, т.е. g = Ρ(ξ < го). Из независимости собы¬
тий отнесения ребер минимального дерева к ГрТО или к фону следует,
что вероятность нахождения в компактной группе более к точек равна
Ρ(ζ > k) = gk. Тогда функция распределения вероятности величины z
равна
р^цЛ1'** ”ри к>2'
[О при к < 2,
а вероятность того, что компактная группа включает ровно к точечных
отметок будет P{z — к) — P{z ^ к) — P(z ^ к — 1) = (1 — g) · к =
= 1,2,... Поскольку для группы точек величина к ^ 2, то распределение
вероятностей должно иметь вид
Wz(k) = P{z = k) = (l-g)gk~2, к = 2,3,... (11.3.10)
Данное выражение задает геометрический закон распределения ве¬
роятностей. Если компактная группа состоит только из ложных отметок
(гипотеза Но), то соответствующая функция правдоподобия имеет вид
Wz(k\H0) = Wz(k\g = Fr) = (1 - Fr)Frk~2, (11.3.11)
где Fr — вероятность ложной тревоги (11.3.7) на этапе локализации. Функ¬
ция правдоподобия для гипотезы Hi, т.е. при предположении, что ком¬
пактная группа образована точками ГрТО, отличается лишь значением
438
Гл. 11. Обработка групповых точечных объектов
параметра q распределения (11.3.10):
Wz{k\Hi) = Wz(k\g = Dr) - (1 - Dr) Dkr~2. (11.3.12)
На рис. 11.10 приведены графики функции правдоподобия (11.3.10)
(сплошные линии) и соответствующие им гистограммы распределений
(пунктир), полученные путем моде¬
лирования на ЭВМ и использующие
данные первого этапа обнаружения
компактных групп точек — этапа
локализации. Графики изображают
многоугольники распределений дис¬
кретной случайной величины. Вер¬
шины этих многоугольников задают
отсчеты распределения вероятности.
Графики 1, 3 получены при рф =
= 20/(256 х 256), графики 2, 4 — при
Рф = 50/(256 х 256), г0 = 30.
Таким образом, алгоритм обнаружения ГрТО, как компактной группы
из области с повышенной по сравнению с фоном интенсивностью отме¬
ток, является алгоритмом проверки гипотез о параметре g распределе¬
ния (11.3.10) и заключается в следующем:
Рис. 11.10. Распределение вероятно¬
стей мощности компактных групп
Н =
Hi при А > Aofc,
Н0 при Л < Л0ь
(11.3.13)
Afc =
Wz(k\Hx) = (1 - Dr)
Wz(k\H0) (1 - Fr)
exp{(fc-2)b[|r]},
где Aofc — порог, выбираемый согласно заданному критерию оптимально¬
сти. Эквивалентное решающее правило на основе минимальной достаточ¬
ной статистики к для Dr > Fr имеет вид
fj = )Н1 при к > ко, ^ = In(Aofc) - In [(1 - Dr) / (1 - Fr)] + 2
[Но при к < ко, ln[£)r/Fr]
(11.3.14)
Отсюда следует, что алгоритм обнаружения ГрТО с неизвестной фор¬
мой АСО сводится к определению числа точек в полученных при ло¬
кализации всех компактных групп и сравнении этих чисел с порогом
/со, назначаемым согласно принятому критерию обнаружения. Основные
этапы работы этого алгоритма показаны на рис. 11.11.
При использовании алгоритма (11.3.14) вероятность ложной тревоги
и правильного обнаружения соответственно равны
Fk = P(k>ko\Ho)=F?°-\ (11.3.15)
Dk = Р(к ^ fed#,) = D^-1 = [1 — (1 — Fr)d]fc°-1) (11.3.16)
где d = σ\!σ\.
11.3. Обнаружение групповых точечных объектов с неизвестной формой 439
Рис. 11.11. Основные этапы работы алгоритма обнаружения ГрТО с произвольной
формой: а — исходное радиолокационное изображение подстилающей поверхно¬
сти с обнаруженными точечными объектами; б — связывание точечных объектов
минимальным деревом; в — локализация ГрТО разрушением длинных ребер ми¬
нимального дерева; г — представление результата локализации и обнаружения
ГрТО
Из условия Dr > Fr следует, что Dk > Fk, причем значение Dk моно¬
тонно увеличивается с ростом вероятности Dr. Поэтому правило (11.3.14)
является несмещенным равномерно наиболее мощным для сложной аль¬
тернативы Hi, где Dr > FT и, следовательно, ас < σψ, т.е. когда сведения
о ГрТО исчерпываются лишь тем, что плотность его точек выше плот¬
ности фоновых точек. Значение порога обнаружения при использовании
критерия Неймана-Пирсона определяется из (11.3.15) и равно
к°=+L (11·3·17)
Вероятность правильного обнаружения на основании (11.3.16) и (11.3.17)
будет равна
Dk
1 π d
1 _ ρ£ο-ι
k0 — 1
(11.3.18)
На рис. 11.12, а приведены характеристики обнаружения, рассчитан¬
ные согласно выражению (11.3.18) для четырех фиксированных значений
вероятности ложных тревог и к = 10, а на рис. 11.12, б — для Fk = 10-2
440
Гл. 11. Обработка групповых точечных объектов
Рис. 11.12. Характеристики обнаружения ГрТО с произвольной формой ассоции¬
рованного сплошного образа
и к = 5,7,9,11 и 13. Как видно из графиков, например, при плотности
ложных отметок ρψ = 50/(256 х 256) для обеспечения вероятности Dk >
> 0,9 при Fk = 10~2 необходимо, чтобы среднее расстояние между
соседними точками ГрТО, содержащего не менее 10 точечных объектов,
было не менее 11,4 пиксела, а для ГрТО из не менее 5 точечных объектов
это расстояние должно быть не более 8.
Для оценки величины платы за незнание конфигурации ГрТО сравним
пороговые сигналы обнаружителя, реализующего алгоритм (11.3.14) и об¬
наружителя ГрТО с известным положением в исходной сцене и заданной
формой АСО (см. п. 11.2.2). Для приведенных в п. 11.2.2 условий (площадь
АСО — 1000 элементов разрешения; интенсивность ложных отметок ρψ =
= 50/(256 х 256); уровень ложных тревог Fk = 10~2; вероятность пра¬
вильного обнаружения ГрТО — 0,9) и при заданном среднем расстоянии
между соседними точками ГрТО г = 8 пикселов для обнаружителя ГрТО
с известной формой АСО пороговое число точек равно 3.
Таким образом, платой за отсутствие априорной информацией о кон¬
фигурации ГрТО является увеличение порогового числа точек ГрТО (на
40% для перечисленных условий), или соответствующее ему увеличение
порога го-
11.4. Распознавание групповых точечных объектов на основе
анализа первичного описания
Предположим, что в машинном кадре s (х) обнаружен ГрТО. Далее
необходимо решить задачу его распознавания, т.е. обоснованно отнести к
одному из М известных классов.
Используя полученные в п. 11.2 выражения для функций правдопо¬
добия расположенного в машинном кадре ГрТО, найдем вид решающего
правила, минимизирующего полную вероятность ошибки распознавания.
Оптимальный для данного критерия алгоритм распознавания должен ре¬
ализовать стратегию максимума апостериорной вероятности:
Щ = argmax(P(#i) · jP(S|#*)) , г = 1,2,... , Μ, (11.4.1)
г
где Р (Hq) — априорная вероятность, а Р (Б\Щ) — функция правдо¬
11.4. Распознавание объектов на основе анализа первичного описания 441
подобия гипотезы Hi. Используя выражение (11.2.14) для натурального
логарифма функции правдоподобия гипотезы Hi в задаче обнаружения
ГрТО, запишем выражение для алгоритма распознавания ГрТО, относя¬
щегося к одному из М классов:
Щ = argmax {niCMiC[ + niC2 + EiC\ + С4+ 1п[Р(Я*)]} ,
г = 1,2,... ,Μ,
(11.4.2)
где
Си = In ( &с±±Рф)
[ РФ
+ In
(1 - Рф) 1
(1 — Pci - Рф) J
С2 = In
РФ
(1 - Рф)
Сзг =ln j(1 (1Р:-рф)Рф)}; С4 = N ■ 1п(1 — рф). (11.4.3)
Поскольку второе и четвертое слагаемые в (11.4.2) не зависят от но¬
мера класса г, то достаточными статистиками будут величины {ε^}, г =
= 1,2,... ,М, где
Ei = ™1смг * Сц + Е{ · Сзг + ln[P(Hi)], (11.4.4)
а алгоритм распознавания (11.4.1) преобразуется к виду
Hi = arg шах{бг}, г = 1,2,... , Μ, (11.4.5)
г
или, в другой записи,
Н = Hi, если ei — £j — Aeij > 0 при j = 1,2,... , М, г ^ j.
(11.4.6)
Так как статистики ε» зависят от параметров хо, φο, то в случае
отсутствия априорных данных число проверяемых гипотез растет про¬
порционально количеству положе¬
ний ГрТО в машинном кадре. Для
исключения этого необходимо пред¬
варительно найти оценки парамет¬
ров положения ГрТО. В результате
операция распознавания проводит¬
ся в два этапа: этап получения
оценок хои φο,ί и этап определе¬
ния класса ГрТО. Методика получе¬
ния этих оценок была рассмотрена
в п. 11.2.3. Далее, для сокращения
записи при рассмотрении вопросов,
связанных именно с определением
класса ГрТО, под обозначением ε*
будем подразумевать ε;(χ0,;, £0|<).
Как следует из выражений для
статистики распознавания (11.4.4), оптимальный алгоритм распознавания
ГрТО состоит в вычислении множества значений {ε^}, г = 1,2,... , М,
Рис. 11.13. Механизм формирования
достаточной статистики распознавания
442
Гл. 11. Обработка групповых точечных объектов
с помощью фильтров, согласованных с изображениями АСО Ы(х)
соответствующих классов ГрТО (рис. 11.13), и выборе номера фильтра
с максимальным взвешенным и скомпенсированным с учетом площади
АСО выходным эффектом.
Проанализируем эффективность полученного алгоритма распознава¬
ния. Вероятности ошибок распознавания при его использовании опреде¬
ляются как
о
P{Hj\Hi) = Р(Ae{j < 0|Hi) =
— ОС
(11.4.7)
где P(Aeij\Hi) — условное распределение вероятности статистики рас¬
познавания. Найдем вид этого распределения. Для этого раскроем струк¬
туру значения Δε^·:
Aeij — (nimiCu — niCUjCij) + (EiC^i — EjC3j) + In | р^(н\ } —
N
= C^ij + Σ s(xn){Ci* · Ы(хп) - Cij · /ij(xn)}, (11.4.8)
n=1
где = (EiC3i - EjC3j) +Ь{Р(#0/Р(Я,·)}.
Разобьем машинный кадр s (х) на области, где выполняются следую¬
щие условия: 1) hi(xn) = 1 и hj(xn) = 1; 2) /ii(xn) = 1 и hj(xn) — 0;
3) hi(xn) = 0 и hj(xn) = 1; 4) Ы(хп) = 0 и hj(xn) = 0. Тогда при
условии истинности гипотезы Щ получим
U\ и2 Us
A£ij\Hi = (C\i Clj)J2 ^см(Хп) C\j 'у ^ SCM(xn) ΟυΣ 5ф(Хп)_Ь^,3,г<7 j
η=1 η=1 η=1
(11.4.9)
ui = ]Pi[hi(xn)/ij(xn) - 1],
η= 1
N
Щ = Σ 5[Ы(хп) - hj(xn) - 1], (11.4.10)
η=1
N
η3 = Σ ί[Λί(χη) - hj(xn) + 1]
η=1
— число отсчетов, где выполняются условия 1, 2 и 3 соответственно.
Как было определено ранее (см. п. 11.2), область смеси точек ГрТО
и точек фона из ложных отметок представляет собой двумерное дискрет¬
ное случайное поле точечных отметок sCM(x) с интенсивностью pCi +ρψ,
а область фона — поле отметок с интенсивностью рф. С учетом этого
11.4. Распознавание объектов на основе анализа первичного описания 443
первые три суммы выражения (11.4.9) представляют собой биномиально
распределенные случайные величины ξι, £з соответственно. С точно-
-1/2 -1/2 -1/2
стью до малых порядка их , и2 , % их можно считать нормально
распределенными с математическими ожиданиями
Μ[ξι] = ТП\ — {Си - Cij) (Ры+Рф) ■ ии
Μ[ξ2] = т2 = Си ■ (рСг + Ρφ) · и2, (11.4.11)
М[^з] =7713 = Cij ■ Рф ■ из,
и среднеквадратическими отклонениями
0*1 = {Сц — C\j) \J(jpci "Ь Рф)(1 ~ Pci ~ Рф)^1,
<Т2 — C\i\J(Pci "Ь Рф)(1 — Pci ~ Рф)и2) (11.4.12)
0-3 = Си^Рф(1 - Рф)и3.
Последнее слагаемое выражения (11.4.9) является независящей от со¬
держания машинного кадра постоянной для каждой пары классов величи¬
ной C3)ij. Таким образом, статистика Ае^\Щ как сумма нормальных неза¬
висимых случайных величин также распределена нормально с параметрами
M[Aeij\Hi] =т1 + т2-т3 + C3tij, D[Aei0\Hi\ = {σ\ + σ\ + σ\) .
(11.4.13)
Подставляя полученное распределение вероятности в выраже¬
ние (11.4.7), находим вероятность ошибки распознавания
о
P{Hj\Hi) = | N (м[Ае„\Щ, ^D[A£ij\#<]) dA£ij =
= ф( УА£°|Я<Л , (11.4.14)
\y/D[A£ij \Hi]J
где Φ(·) — функция Лапласа.
Так как вероятность ошибки зависит от множества параметров, то
характеристики распознавания в общем случае являются многомерными.
Чтобы показать как изменяется избирательность устройства распознава¬
ния, реализующего алгоритм (11.4.5), от изменения тех или иных пара¬
метров ГрТО, приведем несколько сечений многомерных характеристик.
Графики будем строить в виде зависимостей вероятности условной ошиб¬
ки распознавания от интенсивности ложных отметок.
На рис. 11.14, а приведено семейство сечений характеристик при фик¬
сированных следующих параметрах: 1) pci = рс j = рс\ 2) Е{ = Ej = Е =
= 1000, откуда следует, что и2 = и3 = и. Значение и фиксировалось на
уровнях, взятых из ряда и = (0,2Е\ 0,3Е\ 0,4Е\ 0,522). График 1 соответ¬
ствует минимальному, а график 4 — максимальному значениям и.
444
Гл. 11. Обработка групповых точечных объектов
На рис. 11.14, б приведено семейство сечений при фиксированных
значениях: 1) pCi = pCj = 1/100; 2) U2 = щ = и = 0,4£\ Значения Ei =
= Ej = Е брались из ряда Е = (800,1000,1200). График 1 соответствует
минимальному, а график 3 — максимальному значениям Е.
На рис. 11.14, в приведено семейство сечений характеристик для усло¬
вий: 1) U2 = из = 0,4Е\ 2) Ei = Ej = 1000 3) pCi = pCj = pc. Значение pc
выбиралось из ряда рс = (1/75,1/100,1/125). График 1 соответствует
минимальному, а график 3 — максимальному значениям рс.
Рис. 11.14. Характеристики распозна¬
вания групповых точечных объектов
Рис. 11.14, а иллюстрирует зависимость дискриминационных свойств
распознающего устройства от степени непохожести форм АСО, харак¬
теризуемой узостью интервала взаимной корреляции изображений АСО
классов г и j ГрТО. Как видно из графиков, с увеличением максимальной
площади и неперекрывающихся участков АСО объектов из классов г и j
избирательность классификатора увеличивается.
Рис. 11.14, б показывает, что с увеличением площади АСО происходит
улучшение избирательности классификатора.
Рис. 11.14, в характеризует зависимость избирательности классифика¬
тора от компактности точек ГрТО. Избирательность классификатора так¬
же увеличивается с ростом плотности точек ГрТО. Повышение качества
распознавания как при увеличении площади АСО, так и при увеличении
плотности отметок рс, имеет одну и ту же природу. В обоих случаях
повышается энергия полезного сигнала за счет увеличения числа точек
ГрТО по сравнению с энергией фона из ложных отметок.
Из приведенных характеристик видно, что в условиях сложной по¬
меховой обстановки, при интенсивности ложных отметок 100/65536 даже
для ГрТО, состоящих в среднем из 10 точечных объектов, с максимальным
коэффициентом корреляции изображений АСО 0,8, вероятность ошибки
распознавания не превышает 0,1, т.е. полученный алгоритм распознава¬
ния обладает хорошей помехоустойчивостью.
11.5. Описание групповых точечных объектов вторичными признаками 445
11.5. Описание групповых точечных объектов вторичными
признаками
11.5.1. Введение. В предыдущем разделе были получены алгоритмы
распознавания ГрТО, которые следуют из принятой в п. 1.2 обобщенной
модели ГрТО и исходного двумерного описания. Данные алгоритмы обла¬
дают достаточно высокой помехоустойчивостью, однако при неопределен¬
ном положении ГрТО в кадре требуют существенного увеличения объема
вычислений по сравнению с ситуацией, когда положение ГрТО задано.
Это ограничивает область применения указанных алгоритмов системами
с низким темпом обновления информации, либо системами с производи¬
тельностью, превышающей 109 операций в секунду, способными решать
подобные задачи в реальном масштабе времени.
Преодоление вычислительных трудностей при априорной неопре¬
деленности может быть достигнуто с использованием модели ГрТО на
основе минимизированного описания вторичными признаками. В работах [5,
186] приведены базовые рекомендации, которым следует придерживаться
при выборе множества вторичных признаков минимизированного описания
наблюдений. В соответствии с ними вторичные признаки должны обладать
меньшей размерностью, быть статистически независимыми, выражать ори¬
гинальные свойства каждого из распознаваемых классов, обладать устой¬
чивостью к воздействию шумов и помех, быть инвариантными к возможно
широкому классу преобразований анализируемого изображения.
Поскольку на вход распознающего устройства подается исходное опи¬
сание наблюдения, определяемое, например, типом датчика, или форматом
представления данных на выходе устройств предварительной обработки, то
весь процесс распознавания образов на основе минимизированного описа¬
ния условно разделяется на два этапа: 1) выделение признаков (преобра¬
зование первичного описания образа в описание вторичными признаками)
и 2) формирование достаточной статистики распознавания на основе анализа
вторичного описания с принятием решения в пользу одной из гипотез.
Согласно модели ГрТО на основе ассоциированного сплошного образа,
а также с учетом полученных в п. 11.4 для данной модели алгоритмов
распознавания, информативными с точки зрения распознавания являют¬
ся всего три параметра: 1) форма АСО — инварианта к линейным гео¬
метрическим преобразованиям подобия изображения, характеризующая
отношения между элементами множества точек ГрТО; 2) количество
точек ГрТО — параметр к, также независящий от масштаба и положения
объекта в кадре; 3) степень пространственной близости точек ГрТО —
параметр г2, характеризующий плотность рс точек фрагмента поля, огра¬
ниченного АСО и связанный с масштабом изображения (рис. 11.15).
Статистически однородным по плотности ГрТО соответствует од¬
носвязный [5] АСО, множество элементов которого замыкается одним
внешним контуром. Такие объекты далее будем называть простыми
ГрТО. Существует также целый ряд сложных ГрТО, которые состоят
из нескольких пространственно разнесенных простых ГрТО (подгрупп).
Эти объекты являются статистически неоднородными по плотности и им
446
Гл. 11. Обработка групповых точечных объектов
под груша Ϊ
V
~G(x)-ACO
k=kl +k2 +k3
Vw —количество подгрупп
рк -плотность точек в подгруппах
G(x) —А СО
к-мощностъ ГрТО
рс -плотность ТО
Рис. 11.15. Примеры описания групповых точечных объектов вторичными призна¬
ками
соответствует многосвязный АСО с несколькими контурами, ограничива¬
ющими односвязные фрагменты ассоциированного сплошного образа. Для
описания сложных ГрТО введем два дополнительных признака: 4) число
подгрупп Vnr — параметр, характеризующий степень сложности ГрТО;
5) степень пространственной близости подгрупп г\.
Таким образом, в самом общем виде моделью вторичного описания
произвольного ГрТО является следующая:
где F[·] — оператор формирования вторичного описания.
Как видно из названий перечисленных признаков ГрТО, все они ха¬
рактеризуют структуру ГрТО, т.е. его элементы: к, V^r, связи между
элементами: Γχ, Г2, распределение точек ГрТО на плоскости изображения.
В связи с этим первый этап распознавания ГрТО, связанный с выделением
признаков, в дальнейшем будем называть структурным анализом ГрТО.
11.5.2. Модель ассоциированного сплошного образа и локализация
групповых точечных объектов. Рассмотрим введенные в п. 11.1 полевые
модели ассоциированных сплошных образов ГрТО в терминах теории
линейной фильтрации. Так, примем, что математической моделью «ре¬
льефного» АСО является многоградационное изображение G (х) с огра¬
ниченным спектром пространственных частот. ГрТО Q (х) будем рас¬
сматривать как результат дискретизации (выборку) изображения G (х).
Согласно теореме Котельникова, для восстановления функции G (х) по ее
дискретным отсчетам необходимо осуществить низкочастотную простран¬
ственную фильтрацию (расфокусировку) ГрТО:
Q(T,k,Vm,ri,r2) — F[s(x)],
fc
(11.5.1)
где haф (х) — ИХ низкочастотного фильтра.
11.5. Описание групповых точечных объектов вторичными признаками 447
Рассмотрим результат фильтрации исходной точечной сцены s (х),
в которой наряду с точками ГрТО присутствуют ложные отметки:
р Ncu
F(x) = s(i) · /ιπφ(χ - ξ)άζ = Ji · /ιπφ(χ - X;)· (Π.5.2)
χ ί=1
Восстановленное изображение (рис. 11.16) представляет собой двухмер¬
ное поле — «холмистый» яркостный рельеф. Каждый яркостный «холм»
соответствует своей точечной отметке.
На рис. 11.16 даны иллюстрации к процессу формирования результата
фильтрации F (х) машинного кадра с изображениями ГрТО.
Рис. 11.16. Пространственная фильтрация ГрТО: а — машинный кадр s (х), б —
ИХ фильтра /ιΠφ(χ), в, г — яркостный портрет выходного изображения F (х)
соответственно с линейной и логарифмической шкалами яркости (256 уровней),
д — карта линий уровней яркости, е — рельефный портрет F (х)
448
Гл. И. Обработка групповых точечных объектов
При условии согласования ширины полосы пропускания фильтра с плот¬
ностью точек ГрТО, группы из компактно расположенных «холмов», соот¬
ветствующих ГрТО, образуют более яркие «хребты». «Хребты» разделе-
Рис. 1117. Результат пороговой обработки машинного кадра (см. рис. 11.16) на
уровне а = 30: а, б — яркостный портрет G (х) соответственно с линейной и лога¬
рифмической шкалами яркости; в — карта линий уровня яркости; г — рельефный
портрет G (х)
ны темными протяженными областями с яркостью, пренебрежимо малой
по сравнению со значениями яркости вблизи точечных объектов. Поэтому
пороговая обработка изображения F (х) приводит к разбиению машинного
кадра на область фона и связные области повышенной яркости (рис. 11.17)
C<*)={FW’ ,„.5.3,
[0, если F(x) < а,
где а — порог по яркости.
Бинарное квантование машинного кадра G (х) на произвольном уровне
яркости β
Λ(χ) =
1, если F(x) ^ /3,
0, если .F(x) < β
(11.5.4)
приводит к образованию машинного кадра из изображений «плоских АСО».
Таким образом, в результате проведенных операций мы перешли от то¬
чечных к бинарным по яркости изображениям.
11.5. Описание групповых точечных объектов вторичными признаками 449
Свойство плоских АСО ограничивать область точечных отметок ГрТО
позволяет попутно с выделением признаков формы решать задачи ло¬
кализации и разрешения ГрТО. При этом локализация сводится к из-
Рис. 11.18. Образование плоских АСО, соответствующих ГрТО на рис. 11.16: а —
результат бинарного квантования G(x) на уровне β = 80, б — рельефный портрет
бинарного по яркости машинного кадра, в — контуры плоских АСО
вестной задаче сегментации изображений крупноразмерных объектов пу¬
тем выделения их границ (контуров) Г^·), где j — номер ГрТО в кадре
(рис. 11.18).
Приведенная модель АСО задает отображение Q (х) G (х), кото¬
рое позволяет представлять модель ГрТО моделью АСО [167] в задачах
выделения признаков формы ГрТО и распознавания формы ГрТО. Для
статистически однородных по плотности ГрТО и соответствующих им
однородных по яркости АСО вся инфор¬
мация о форме сосредоточена на границе
объекта и фона [42,5], т.е. в контурах АСО.
Это иллюстрирует рис. 11.19, на котором
линии уровня имеют максимальную плот¬
ность на границах ГрТО.
В связи с этим, для распознава¬
ния целесообразно ограничиться моделью
плоского АСО h(x) или его контура Г, ко¬
торая получается в результате пороговой
обработки расфокусированного точечного
изображения.
При этом удается отойти от много¬
численных эвристических попыток рас¬
познавания формы ГрТО и свести данную задачу к распознаванию
контуров бинарных изображений крупноразмерных распределенных
объектов.
11.5.3. Критерий компактности групп точечных объектов. Из рас¬
смотренной модели АСО следует «естественный» в данном случае кри¬
терий компактности множества точек и условие согласованности полосы
прозрачности низкочастотного фильтра ωΒ с компактностью точек ГрТО.
Два множества точек <2*и Qj, при заданном уровне ограничения по
яркости β и фиксированной ширине полосы пропускания восстанавлива¬
450
Гл. 11. Обработка групповых точечных объектов
ющего фильтра ωΒ, являются компактными, если все их элементы распо¬
лагаются во внутренней области общего АСО (т.е. их АСО пересекаются):
f «Лсомп(Фь Qj) = I? если fti(x) П hj(x) Ф О, (115 5)
1Ломп(<Эг, Qj)~ О В противном случае.
Выбор полосы пропускания 0... ωΒ восстанавливающего низкочастот¬
ного фильтра выбирается из следующих соображений.
С точки зрения обеспечения заданной разрешающей способности при
распознавании нескольких ГрТО, расположенных в плоскости машинного
кадра, значение ωΒ должно обеспечивать получение неперекрывающихся
АСО. Чем больше ωΒ, тем выше разрешающая способность алгоритма.
Верхняя граница ωΒ должна в соответствии с (11.5.5) не должна для оди¬
ночного ГрТО приводить к JK0Mп = 0· Аналогичное требование предъявля¬
ется к полосе пропускания восстанавливающего фильтра для наилучшего
соответствия между формами АСО и ГрТО.
При изменении масштаба изображения в машинном кадре необходимо
изменять значение ωΒ таким образом, чтобы сохранить заданную разре¬
шающую способность и точность описания формы ГрТО с помощью АСО.
Случайный характер изображения ГрТО приводит к тому, что значения
признака компактности JK0Mп при ωΒ = const является случайным событи¬
ем, появляющимся с вероятностью рКомп· Для обеспечения инвариантно¬
сти результатов локализации к повороту исходной сцены, дополнительно
сузим класс низкочастотных фильтров до имеющих пространственно изо¬
тропные Апф (х):
К ф(х) = Ьпф(||х||)· (11.5.6)
Форма плоского АСО, полученная путем квантования рельефного АСО
G (х) по яркости на уровне /?, зависит в определенной степени от величи¬
ны β. В связи с этим возникает задача выбора уровня /?, обеспечивающего
наилучшую устойчивость формы АСО при возможных вариациях β в за¬
данных пределах.
Для рассматриваемого случая, когда машинный кадр s (х) строит¬
ся по результатам бинарного обнаружения точечных отметок, эта зада¬
ча является задачей определения глобального порога при сегментации
непрерывных изображений. Для фильтра, согласованного с плотностью
точек ГрТО, величина β в этом случае будет соответствовать значению
функции АПф (х) в точке с максимальным градиентом [149]:
β = Апф (|Хопт|) 5
где
|х0пт| = argmax (dhu$ (|х|) /d |х|). (11.5.7)
Данное значение β будет оптимальным с позиции максимума устойчи¬
вости формы для одиночной точечной отметки при условии монотонного
характера затухания потенциальной функции. Поскольку в многоточеч¬
ных ГрТО сильное влияние на форму АСО оказывают лишь его граничные
точки, то значение порога /3, задаваемое (11.5.7), будет квазиоптимальным
11.5. Описание групповых точечных объектов вторичными признаками 451
при получении плоского АСО для ГрТО с произвольным количеством
точечных отметок.
После нахождения плоского АСО hj (х) ГрТО Qj можно получить
оценку мощности ГрТО Qf
kj = ^2 s (х) hj (х)· (11.5.8)
X
11.5.4. Мера компактности групп точек. Для решения задачи распо¬
знавания ГрТО необходимо оценивать степень компактности подмножеств
точек. Базируясь на введенном в п. 11.5.3 понятии компактности двух
подмножеств точек, введем меру этой компактности.
Иерархическая группировка. Рассмотрим процесс разделения п точек
на С групп, основанный на критерии компактности (11.5.5). Первый уровень
разделения дает С = п, т.е. получаем п групп по одной точке в каждой.
Этому разделению соответствует максимальное значение ωΒ = U7max
полосы пропускания восстанавливающего фильтра. Каждый последую¬
щий уровень разделения уменьшает уменьшает количество групп на еди¬
ницу и соответственно сужает полосу пропускания фильтра. Примем, что
находимся на Z-м уровне разделения и С = η — I -Ь 1.
Данная последовательность разделений является агломеративной ие¬
рархической группировкой, так как любые две точки, попадающие в одну
группу на уровне Z, остаются вместе на более высоких уровнях [40]. На
1 2 3 4 5
т 1й уровень
-- 2й уровень
-- Зй уровень
-- 4й уровень
-- 5й уровень
г
Рис. 11.20. Дендрограмма иерархической группировки множества точечных отметок
рис. 11.20 представлена дендрограмма группировки, в которой исходное
множество содержит к = 5 точек.
Когда возникает необходимость измерить степень компактности групп,
дендрограмма снабжается вертикальной шкалой. Деления шкалы на каж¬
дом уровне группировки дают значение ωΒ полосы пропускания восста¬
навливающего фильтра, при котором происходит объединение нескольких
подмножеств в одно.
Таким образом, данное значение ωΒ является мерой компактности. Чем
выше ωΒ> при котором происходит объединение подмножеств, тем выше
степень компактности множества из объединяемых подмножеств.
452
Гл. И. Обработка групповых точечных объектов
В ряде случаев удобней пользоваться не значением о;в, а обратной
величиной г = e/cdB, е = const, е > 0. Эта величина служит мерой уда¬
ленности подмножеств друг от друга. Можно показать, что неотрицатель¬
ная величина г является метрикой (расстоянием), так как удовлетворяет
следующим аксиомам:
r{QiiQj) = 0 при Qi = Qj, Г {QilQj) = Г (Qj, Qi) ,
riQuQmitiriQi'QA + riQj'Qm). 1 ]
Проанализируем на примере двух частных случаев характер связи
между введенной мерой компактности подмножеств точек и ИХ восста¬
навливающего фильтра. Первый случай соответствует цилиндрической ИХ.
В плоскости пространственных координат она образует круг радиусом г/2:
Л.пф —
1 при |х| ^ г/2,
0 при |х| > г/2.
(11.5.10)
Метрика г в данном случае задает не только полосу прозрачности
фильтра, но и совпадает с евклидовым расстоянием между двумя точка¬
ми, которые в результате фильтрации образуют компактное множество.
Операция иерархической группировки на основе данной метрики г =
= rmin приводит к известной процедуре построения минимального дерева
для группы точек [40]. Алгоритм локализации компактных групп при таком
виде ИХ фильтра эквивалентен к описанному в работе [189] алгоритму
перекрытия эталонных элементов. Отличие заключается только в том, что
в этой работе рассмотрен не круглый, а прямоугольный эталонный элемент.
Второй случай соответствует выбору в качестве ИХ функции, обла¬
дающей свойствами потенциальной функции [187], например:
Лпф(х|г) = ехр{-|х|2/г2}. (11.5.11)
Фильтрация точечной сцены таким фильтром соответствует проце¬
дуре построения кумулятивного потенциального поля точек сцены, кото¬
рым условно присваивается некоторый заряд, а результаты известных
процедур иерархической группировки и локализации компактных групп
точек по методу потенциальных функций соответствуют результатам для
метода на основе пространственного восстанавливающего фильтра.
Таким образом, перечисленные алгоритмы группировки и локализации
являются частными случаями рассмотренного в данном разделе алгоритма
локализации ГрТО на основе введенных критерия и меры компактности.
Следует отметить, что выбор различных видов ИХ восстанавлива¬
ющих фильтров обуславливает отличие некоторых свойств результатов
локализации. Например алгоритм группировки при ИХ вида (11.5.11) име¬
ет тенденцию объединять в первую очередь группы из большего числа
точек, в то время как при ИХ (11.5.10) мощность групп не имеет значения.
Проиллюстрируем данные свойства на примере гипотетических групп
с различным числом точек, но с совпадающим расстоянием между со¬
седними точками. При иерархической группировке на основе евклидовой
меры г = rmin (т.е. вид ИХ соответствует (11.5.10)) эти группы будут
11.5. Описание групповых точечных объектов вторичными признаками 453
получены объединением точек на одном уровне (рис. 11.21). В то же время,
при использовании метрики г, соответствующей ИХ вида (11.5.11)), за счет
ттлш
к* =
(1при х </72,
Оприх >/72
►— ■■-Ф-бКЭ-ф—
А4(«,г)=вр{-*7г1}
Рис. 11.21. Дендрограммы иерархической группировки, иллюстрирующие влияние
видов ИХ восстанавливающих фильтров на свойства меры компактности групп
точек
кумулятивности группы точек с большей мощностью будут объединены на
более низком уровне, т.е. более мощная группа является и более компактной.
Отметим еще одну особенность результатов локализации компактных
групп точек описанным в данном разделе методом. В результате более
плавного затухания функции (11.5.11) по сравнению с функцией (11.5.10)
при выборе ИХ вида (11.5.11) происходит сглаживание влияния независи¬
мых флуктуаций координат отдельных точек на форму контура АСО, что
обуславливает большую помехоустойчивость формы контуров АСО.
В связи с отличием некоторых свойств алгоритмов локализации групп
точек на основе восстанавливающего фильтра при переходе от одного
вида ИХ к другому, можно дать следующие рекомендации к выбору ИХ.
Для ситуаций, когда критическим является время принятия решений
и качество восстановления границ АСО не имеет существенного значения,
целесообразно использовать фильтр с плоской ИХ вида (11.5.10) и ев¬
клидову метрику г = rmin, поскольку для данного случая существуют
разработанные алгоритмы локализации, с невысокой трудоемкостью [40].
В противоложном случае, т.е. когда время принятия решений не критич¬
но, а определяющим является качество решений, следует использовать ИХ
в виде потенциальных функций (11.5.11) и соответствующую метрику г. При
этом восстановленные границы АСО обладают большей помехоустойчиво¬
стью, однако алгоритм локализации характеризуется существенно большим
объемом вычислений по сравнению с предыдущей ситуацией.
11.5.5. Обобщенный алгоритм локализации и обнаружения компакт¬
ных групповых точечных объектов с произвольной формой АСО. Ста¬
тистический характер фона из ложных отметок в исходном множестве
точек приводит к случайным всплескам компактности ложных отметок.
Даже если степень компактности этих локальных всплесков достигает
степени компактности точек ГрТО, то с большой вероятностью они будут
образованы меньшим, чем в ГрТО, числом точек. Это свойство полезно
для решения задачи обнаружения ГрТО с неизвестной формой АСО, т.е.
когда в исходной сцене могут присутствовать ГрТО различных классов,
отличающиеся формой АСО, или ГрТО с нестационарной формой АСО.
454
Гл. 11. Обработка групповых точечных объектов
Сформулируем задачу обнаружения ГрТО с неизвестной конфигурацией
на основе введенных в предыдущем разделе признака и меры компакт¬
ности групп точек. Предположим, что масштаб наблюдаемого изображе¬
ния известен и задана статистика фона из ложных отметок. По предъяв¬
ленной к анализу компактной группе точек Q со степенью компактности,
не превышающей г0, выдвигаются две альтернативные гипотезы: 1) Я0 —
группа образована исключительно ложными отметками; 2) Ηχ — группа
представляет собой смесь точек ГрТО и ложных отметок. Необходимо вы¬
нести обоснованное решение Н в пользу одной из данных гипотез, если
условные относительно величины г распределения вероятностей мощности
к для групп из смеси точек ГрТО и фона Р (k\Hx,r ζ го), а также групп
исключительно из точек фона Р (к\Н0, г ζ г о) заданы.
Оптимальное решающее правило на основе отношения правдоподобия
для фиксированного значения го имеет вид
где Ако — порог, назначаемый согласно принятому критерию обнаруже¬
ния. Такой алгоритм сводится к локализации групп точек с компактно¬
стью, не превышающей го, определению мощности к компактной группы
в пределах восстановленного при локализации и неизвестного заранее
ассоциированного сплошного образа, подстановке к в (11.5.12) и сравнению
найденного значения отношения правдоподобия с порогом Л^о-
Выбором соответствующих функций /ιπφ(χ)> используемых для лока¬
лизации компактных групп и определяющих свойства меры компактности
г(<2), можно получать различающиеся по трудоемкости и вероятностным
характеристикам алгоритмы обнаружения ГрТО. В частности, в п. 11.3
подробно рассмотрен алгоритм обнаружения ГрТО с неизвестной конфи¬
гурацией. Использование евклидовой метрики в этом алгоритме эквива¬
лентно применению восстанавливающего фильтра с цилиндрической ИХ
(11.5.10), а выбор данной ИХ сделан с целью минимизации трудоемко¬
сти алгоритма. При такой ИХ для группировки трудоемкую операцию
пространственной фильтрации точек можно заменить значительно более
простой процедурой построения минимального дерева.
Достоинства описанного алгоритма обнаружения ГрТО заключаются
в следующем: 1) инвариантность к параллельному переносу и повороту
исходного машинного кадра вследствие инвариантности алгоритмов ло¬
кализации ГрТО к данным преобразованиям; 2) инвариантность к форме
АСО и, следовательно, к номеру класса, поскольку в полученном алгорит¬
ме локализации происходит восстановление неизвестного априори АСО
и точки группируются естественным образом по критерию компактности.
11.5.6. Адаптивная локализация и структурный анализ групповых
точечных объектов. В предыдущих разделах были разработаны алго¬
ритм перехода от ГрТО к изображению АСО и алгоритм локализации,
позволяющий восстанавливать границы АСО и группировать компактные
11.5. Описание групповых точечных объектов вторичными признаками 455
множества точек. Также была введена мера компактности произвольных
групп точек. Рассмотрим применение этих результатов к структурному
анализу сложных ГрТО. Задача структурного анализа заключается в ло¬
кализации расположенных в пределах исходного ГрТО пространственно
разнесенных подгрупп точек, подсчете количества этих подгрупп и числа
точек в каждой из них. Результаты структурного анализа могут быть
использованы в качестве дополнительных информативных признаков для
распознавания сложного ГрТО.
Для удобства дальнейшего описания введем обобщенное понятие ре¬
бра, как синонима связи между двумя множествами связных точек Qi
и Qj (по аналогии с таким же понятием из теории графов). Договоримся,
что каждому ребру назначается определенная длина (вес), равная при¬
нятой в предыдущем разделе мере компактности г (Qi,Qj) подмножеств,
связываемых данным ребром. Тогда иерархическую группировку слож¬
ного (т.е. состоящего из нескольких компактных подгрупп) ГрТО можно
отобразить на плоскости в виде графа — минимального дерева. Пример
минимального дерева гипотетического ГрТО из двух подгрупп проиллю¬
стрирован на рис. 11.22. Каждое ребро минимального дерева показыва-
Рис. 11.22. Изображение дендрограммы иерархической группировки сложного
ГрТО в виде графа на плоскости исходной точечной сцены
ет на каком уровне компактности происходит объединение групп точек,
связанных ребрами меньшей длины. В частном случае, когда метрика
r(Qi,Qj) совпадает с евклидовой метрикой г = гтιη, ребра данного
минимального дерева становятся прямолинейными отрезками, равными
по длине евклидовому расстоянию между точками.
Разбиение ГрТО на компактные подгруппы точек при таком рассмо¬
трении осуществляется путем разрушения длинных ребер, превышающих
заданный порог г0. Для удобства последующих записей введем некоторые
обозначения: R = {гп}1 к_г — множество ребер в графе иерархической
группировки обнаруженной группы точек Q, R2 и Ri — множества ребер
внутри подгрупп и между подгруппами соответственно (R = R2 U Ri).
Предположим, что нам известны законы распределения длин ребер
внутри подгрупп ГрТО W (г\R2) и длин связей между подгруппами
W (r\Ri), а также среднее число точек в каждой из подгрупп кПТ. Тогда
456
Гл. 11. Обработка групповых точечных объектов
задачу разбиения ГрТО на подгруппы можно решать методом проверки
статистических гипотез.
После разрушения ζ обнаруженных ребер получаем оценку числа
подгрупп VnT = ζ + 1. Если распределения W (г\Ri) и W (r\R2) пере¬
крываются, то возможны ошибки первого и второго родов. В качестве
критерия оптимальности целесообразно принять критерий минимальной
погрешности оценки числа подгрупп VnT. Он приводит к ситуации, когда
ошибки обоих родов одинаково нежелательны, т.е. к различению «длин¬
ных» и «коротких» ребер графа иерархической группировки методом мак¬
симального правдоподобия.
На рис. 11.23 приведены зависимости вероятностей ошибок от отно¬
шения средних внутригрупповых и межгрупповых расстояний р = Ψϊ/r2l
Рис. 11.23. Характеристики обнаружения длинных междугрупповых связей в гра¬
фе иерархической группировки при анализе степени сложности ГрТО: а — веро¬
ятности ошибок первого рода, б — вероятности ошибок второго рода
если эти расстояния подчиняются релеевскому закону распределения ве¬
роятностей, а в качестве критерия оптимальности используется «макси¬
мальное правдоподобие».
Отметим, что повышение плотности ложных отметок увеличивает ве¬
роятность неразъединения сложного ГрТО. Этот факт иллюстрируется
семейством графиков на рис. 11.23, б. На этом рисунке приведены три
кривые зависимости 1—D = f (р), построенные для следующих значений
плотностей ложных отметок: рс = 0, рс = 40/216 и рс = 80/216. При
больших значениях р фоновые отметки оказывают слабое влияние на
вероятность объединения подмножеств ГрТО и поэтому три графика этих
зависимостей практически совпадают.
Теперь предположим, что масштаб изображения ГрТО не известен, но
задан вид законов распределения W (r\Ri)nW (r\R2) с точностью до неиз¬
вестного масштабного множителя параметров этих распределений. Анало¬
гично тому, как это было сделано в п. 11.2.3, для преодоления априорной
неопределенности такого рода предварительно оценим по результатам на¬
блюдений параметры распределений и подставим полученные значения в со¬
ответствующие плотности распределения вероятности. Далее поступаем как
при решении задачи обнаружения задачи полностью известного сигнала.
Из-за малого числа подгрупп реальных ГрТО по одной выборке —
обнаруженной группе точек — невозможно получение достоверных (с ма¬
11.5. Описание групповых точечных объектов вторичными признаками 457
лой дисперсией) оценок параметров распределения W (r\Ri). В то же
время часть выборки, составленная из внутриподгрупповых ребер мини¬
мального дерева обнаруженной группы точек, является репрезентативной
(как правило не менее 10). Следовательно становится возможным полу¬
чение достаточно достоверных оценок параметров только распределений
W (г\R,2). В связи с этим при принятии решения можно гарантировать
заданное значение вероятности ошибки только одного рода. Поэтому в ка¬
честве критерия обнаружения междуподгрупповых связей целесообразно
использовать критерий Неймана-Пирсона.
Результат адаптивной локализации и структурного анализа группо¬
вых точечных объектов по данному алгоритму приведен на рис. 11.24.
Внешний контур ассоциированных сплошных образов ГрТО получен при
Рис. 11.24. Адаптивная локализация и структурный анализ ГрТО: а — исходная
сцена, б — предварительная локализация ГрТО с глобальным значением пара¬
метров расфокусирующего фильтра, в — адаптивная локализация с локально¬
оптимальными значениями параметров расфокусирующего фильтра, г — резуль¬
тат адаптивной локализации и структурного анализа
назначении степени расфокусировки исходного изображения по моде гло¬
бальной гистограммы компактности точечной сцены с большим запасом
(рис. 11.24, б), т.е. на этапе предварительной локализации. Внутренний
458
Гл. 11. Обработка групповых точечных объектов
контур сформирован локально-оптимальным образом (рис. 11.24, в) для
каждого ГрТО, локализованного на первом этапе. Очевидно, что адаптив¬
ность такого алгоритма обеспечивает более точное соответствие формы
контура АСО и формы ГрТО. Потенциально это должно привести к по¬
вышению эффективности последующих алгоритмов распознавания ГрТО.
Анализ характеристик описанного алгоритма локализации подгрупп
показывает, что проигрыш в отношении р за счет незнания точного зна¬
чения масштаба наблюдения составляет около 1,2 дБ, т.е. невелик. В то
же время выигрыш по трудоемкости пропорционален числу классов ГрТО.
Дополнительным преимуществом алгоритма является минимальное число
параметров — в простейшем случае единственный коэффициент Сзап,
связывающий величину оценки г2 и пороговую длину ребра графа иерар¬
хической группировки: Г о = г2 · Сзап·
11.6. Распознавание групповых точечных объектов по форме
контура ассоциированного сплошного образа
11.6.1. Алгоритм распознавания. Соответствие между АСО и ГрТО
позволяет решать задачу распознавания ГрТО путем распознавания изо¬
бражений плоских АСО по форме их контуров. Основные этапы форми¬
рования дискретного контура АСО показаны на рис. 11.25.
Общие вопросы, связанные с распознаванием изображений по их фор¬
ме, задаваемой контуром, в рамках аддитивной модели зашумленного
Рис. 11.25. Этапы кодирования формы ГрТО: а — наблюдаемый ГрТО; б — ре¬
зультат восстановления АСО; в — контур АСО; г — конкатенация элементарных
векторов в контуре АСО
11.6. Распознавание групповых точечных объектов по форме контура АСО 459
сигнала (см. п. 1.6, 1.7, 3.9, 3.10), рассмотрены в п. 4.4. Поскольку изобра¬
жение АСО получается в результате пространственной НЧ фильтрации,
то линии их контуров будут плавными, без резких изломов. Поэтому
соседние ЭВ этих контуров сильно коррелированы, а спектры контуров
всех АСО являются достаточно узкими и сосредоточены в одной и той
же области низких частот. В результате контуры АСО разных классов
имеют мало индивидуальных признаков, что приводит к значительному
снижению эффективности распознавания. Поэтому целесообразно про¬
анализировать влияние корреляции контуров изображений АСО разных
классов на результаты их распознавания.
В общем случае для равновероятных возможных параметров φο =
= Αφ, \μ\ и d линейных преобразований контура АСО решающее правило
в пользу класса А;, г ф j, j = 1,2,... ,М, по методу максимальной
апостериорной вероятности имеет вид
Р (Hi) W (ν|#,·, А&, l&U ) ^ P (Hj) W (n|f,·, Aipj, ) ,
(11.6.1)
где Δ£>, I μ I и d — оценки МП параметров угла поворота, масштаба и сдви¬
га начальной точки контура для класса, номер которого указан в нижнем
индексе, М — число классов, N — контур зашумленного АСО. После ло¬
гарифмирования с учетом нормального характера закона распределения
вероятностей W для одной из частей выражения (11.6.1) получим
In {р(Я) W (ν|η, Αφ, |μ|,rf)} = InP (H) + lnC - R ;
(11.6.2)
где
R2 = ||N||2 + ||Γμ||2 - 2Re (Ν,ΓΔν,,|μΜ) (11.6.3)
— расстояние между контуром N зашумленного АСО, полученного в ма¬
шинном кадре, и контуров Г эталонного АСО с произвольными значе¬
ниями параметров линейных преобразований, С = (2п)~к^2 а~к, к —
размерность продискретизированного контура АСО.
Преобразуем выражение для реальной части скалярного произведения:
Re (N,rAv,)Wid) = Н Re {βχρ(-ΐΔ^) (N,rd)} =
= ^|[cosAy> · Re (Ν,Γ<*) + sinA^Im (Ν,Γ<*)]. (11.6.4)
Подставим в это выражение оценки сдвига d начальной точки контура
и угла поворота Αφ (см. п. 4.1):
Re (Ν’ΓΔ£,|μ|,ί) -
max
d
ы
[Re(N,rd)]2 + [Im (N,rd)]:
l(N.rd)|
l·
~ max {|μ| · |(N, Γ^)|} .
460
Гл. 11. Обработка групповых точечных объектов
Так как оценка МП масштаба контура равна |μ| = |(Ν,Γ)| / ||Г||2 , то
в* (Ν·Γ« Ιίΐ,ί) = {|<Ν· Γ')Ι! / «Γ»1 · (11.ω)
ЦГд||2 = \μ\2 ||Г||2 = |(N, rd)|2 / ||Γ||2 .
С учетом значений оценок параметров линейных преобразований контура
АСО выражения (11.6.3) и (11.6.2) соответственно примут вид
Я2 (ν,Γδ-|?μ~) = ||N||2-mjoc{i(N,rd)|2/nr||2}, (11.6.6)
In {p (Hi) W (ν|#{, A$h |£|, d) } -
I fmax|(N,rd)|2 Ϊ
= In P (H) + In C + ^2^ I — p^j2 l|N||2 >. (Π.6.7)
Теперь можно конкретизировать вид алгоритма (11.6.1) принятия ре¬
шения о классе ГрТО по контуру его АСО. После исключения слагаемых,
независящих от номера класса, запишем
Hi — arg max
з
max
d
Ι(Ν,Γ^·
2σΒ2χ1ηΡ(Ρ;) ,
j = 1,2,... ,Μ.
(11.6.8)
Номер класса г равен значению j, при котором это выражение достигает
максимума.
11.6.2. Характеристики распознавания групповых точечных объек¬
тов по форме контуров ассоциированных сплошных образов. Условные
вероятности ошибок распознавания P(Hj\Hi) соответствуют вероятности
превышения максимальным выходным эффектом j-το канала максимальный
выходной эффект г-го канала устройства распознавания, при условии, что
истина гипотеза Щ:
о
P(Hj\Hi) = | W(AVij\H,)dAVlJ, (11.6.9)
где
Atyj = max
d
Ι(Ν,Γ^)|2
ΙΙΓχΙΙ2
— max
d
l(N,rdJ)i2
Ι|Γ;||2
(11.6.10)
Теоретический расчет ошибок P(Hj\Hi) довольно сложен из-за нену¬
левой взаимно корреляционной функции эталонов. Однако для случая
сильных сигналов, т.е. когда q = ||Г|| /σΒΧ^> 1, и при равенстве априорных
вероятностей гипотез Р(Н{) = P(Hj) его можно упростить и получить
соотношения для верхних пределов значений этих ошибок. Так, вслед¬
ствие неотрицательности модулей величин, входящих в (11.6.10), условная
11.6. Распознавание групповых точечных объектов по форме контура АСО 461
вероятность ошибки равна
о
Р{Щ\Щ) = | W (AVij I Hi) dAVij,
где
л ν.. _ maxmjM _ maxl(N,rdti)|
a vtJ — max ||TV|| max .
d ЦГ.Ц d
С целью сокращения записей обозначим:
Vi = max
d
l(N,rd,oi
= max|(N,rd,i
d
Hi
Hi
Vj = max
J d
l(N,rdJ)|
Vj = maxliN,^,,·)!
d
Hi
Hi
(11.6.11)
В этих выражениях нижний индекс Hi означает, что на вход фильтра,
формирующего отсчет скалярного произведения, подан контур зашумлен¬
ного АСО класса А{. Используя правила преобразования законов распре¬
деления случайных величин, найдем условные распределения слагаемых
Vi и Vf
WVi (О = ||Γί|| · W^i (Н|Г*|||Я<),
WVj (0 = ||Γ,·|| · Wvj (ξ · ||Γ,·|||Η<). 1 " ]
Запись Wvi (ζ) , например, означает плотность вероятности случайной
величины Vi в точке £. Распределение вероятностей модулей выходного
сигнала КСФ описываются законом Райса (см. п. 3.10). Предполагая, что
на входы контурных фильтров, согласованных с сигналами классов Ai
и Aj, подается зашумленный эталонный контур АСО класса Ai, для
распределений на выходе фильтров можно записать
\νηι (ξ\Η,) = / 2- exp
<^вх 11 г II
^(№) = -т^-рехр
? + ЦГ<114'
2^Х[|Г,||2 .
?+|(Гйг,)
2<Гвх||Г,||2
(11.6.13)
ξ^ο.
(11.6.14)
Используя выражения (11.6.12), получим
Wvi (О = -V ехР
WVj (ξ) = -V ехР
2σ,
$2 + 1(г,
2σΒ2χ||Γ
€>0,
'°т
(11.6.15)
(11.6.16)
462
Гл. 11. Обработка групповых точечных объектов
Для случая сильных сигналов, т.е. когда q 1, распределение Райса
аппроксимируется нормальным законом:
WviW^NiWrilan), (11.6.17)
WVj (ξ) и N · (11.6.18)
Тогда величина Δ Vij, как линейная комбинация произвольно зависимых
гауссовских величин, подчиняется нормальному закону распределения:
W (AVij\Hi) а N (jlf [Δ^], Л1/3[ДИ,·]) , (11.6.19)
где
Μ[Δ^·] = M[Vi) - M\Vj\ = ||Γ4|| -
D[AVtJ] = D[Vi\ + D[Vj] - 2cov (И, Vj) = 2σ2ΒΧ - 2cov (VS, V·),
а условная вероятность ошибки находится как значение функции Лапласа
M[AVitj] \ ЛМ >1
D1/2[AVij)) ’ ^вх ^
(11.6.20)
Так как ковариация модулей реакций КСФ отличается для каждой
возможной пары классов, то для верхней оценки вероятностей P(Hj\Hi)
примем крайний случай: cov(V*,V}) = 0. На рис. 11.26 приведены ха¬
рактеристики распознавания по алгоритму (11.6.8) для данного крайнего
Рис. 11.26. Зависимости средней ве¬
роятности ошибочных решений при
распознавании контуров АСО от от¬
ношения сигнал/шум
Рис. И 27. Эмпирическая зависи¬
мость СКО квадратур элементарных
векторов шумового контура от СКО
координат точечных отметок
случая в виде зависимости средней вероятности ошибочных решений от
отношения сигнал/шум qBых = ||Γ||/σΒΧ для условий Р (Щ) = Р(Я),
||Tj|| = ||Г||, г = 1,2,... , М. Номера графиков последовательно соответ¬
ствуют следующим значениям модуля НСП \η^\ контуров Г* и Г7·: 0,5;
0,6; 0,7; 0,8 и 0,9.
Так как контурные шумы АСО определяются координатными шума¬
ми точечных объектов ГрТО, то целесообразно установить характер их
взаимосвязи. С этой целью на рис. 11.27 приведена в качестве примера
11.6. Распознавание групповых точечных объектов по форме контура АСО 463
эмпирическая зависимость отношения сигнал/шум qBX = \ΐ\ /σΒΧ для кон¬
тура АСО на входе фильтра к отношению q^—fjaто среднего расстояния
г междуточечными объектами к СКО σΒΧ координатного шума. Пунктиром
на графике указан доверительный интервал для Рдов = 0,9. С помощью
данного графика можно оценить
вероятность ошибки распозна¬
вания контура АСО от уровня
координатных шумов.
На рис. 11.28 приведены
эмпирические характеристики
распознавания контуров АСО,
полученные при моделировании
условий наблюдения на ЭВМ
для программных реализаций
алгоритма (11.6.8) в результате
проведения серии статистиче¬
ских испытаний. Графики ил¬
люстрируют устойчивость ал¬
горитма (11.6.8) к присутствию
в исходном изображении ложных
водились для двух классов ГрТО
Рис. 11.28. Зависимость вероятности оши¬
бок распознавания ГрТО от интенсивности
ложных отметок в машинном кадре
отметок.
С Ын «
Все эксперименты про-
0,7 при фиксированной
вероятности пропуска сигнальных отметок рпс = 0,05, СКО отклонений
точек στο = 0,2 гг, масштабе изображения, соответствующем г 2 = 5
элементов разрешения. График 1 соответствует средней вероятности
ошибочного распознавания Р0ш, график 2 условной вероятности ошибки
Р(Н,\Щ), график 3 — Р{Щ\Н0).
Как следует из приведенных характеристик, для практических ситуа¬
ций, когда ||Г|| « 100, Г2 = 5, στο ^ 0,2г2, рпс ^ 0,05, достаточно высокое
качество принимаемых решений (1 — Рош) > 0,9 обеспечивается во всем
исследованном диапазоне интенсивностей ложных отметок ρψ € [0; 80/216].
Таким образом алгоритм распознавания ГрТО по форме контуров АСО
на основе КСФ можно считать устойчивым к аномальным ошибкам в виде
ложных отметок и пропусков точек ГрТО вплоть до ρψ = 80/216 и рпс =
= 0,05 соответственно.
11.6.3. Распознавание групповых точечных объектов в виде изобра¬
жений звезд. Проиллюстрируем применение рассмотренных алгорит¬
мов к распознаванию ГрТО в виде изображений созвездий. На рис. 11.29
приведен комплексный алгоритм обработки сцены звездного неба, а на
рис. 11.30 — результаты работы основных этапов алгоритма.
1. Этап предварительной обработки. На этапе предварительной об¬
работки выполняется подавление яркостного шума путем накопления
нескольких кадров изображения, а также обнаружение звезд по призна¬
кам яркости и площади. Результатами операции обнаружения является
точечная сцена 5эт(ж, у) (для отображения на экране дисплея) и массив
координат обнаруженных изображений звезд {(ж*, Уг)}г Ν.
464
Гл. 11. Обработка групповых точечных объектов
2. Этап выделения созвездий. Оператор выделения созвездий осу¬
ществляет локализацию созвездий по угловым расстояниям между от¬
метками. Результатом этой процедуры является множество групп точек
{ЗтК.ЛГг’ ГДе Ντ ~ К0ЛИ"
чество выделенных созвездий
с числом точек, не меньшим
заданногоАГт1П.
3. Этап формирования ассо¬
циированного сплошного образа
созвездий. Оператор формирова¬
ния изображений АСО реализует
алгоритм расфокусировки точеч¬
ного изображения каждого из вы¬
деленных созвездий и формирует
на своем выходе набор изображе¬
ний АСО {hm (ж, у)} Ι,Ντ'
4. Этап выделения конту¬
ров АСО созвездий. Следующий
оператор осуществляет выделе¬
ние контура каждого АСО на изо¬
бражении с помощью алгоритма
Розенфельда и формирует цепной
стандартный комплекснозначный
код контуров: {Гтсг}1>ЛГг. Здесь
же осуществляется приведение
стандартного кода контура слу¬
чайной размерности кт к ко¬
ду фиксированной размерности к
(эквализация) и, как следствие,
переход к произвольному коду
контура {Гт}1ЛГг.
5. Этап идентификации созвездий. Оператор идентификации созвез¬
дий предназначен для распознавания контуров АСО методами контур¬
ной согласованной фильтрации. Для отказа от распознавания созвездий,
не входящих в множество базовых, алгоритм дополнен процедурой обна¬
ружения контура по критерию не превышения заданного расстояния от
эталона в признаковом пространстве. Результатом работы оператора слу¬
жит множество идентификаторов Н, присваиваемых номерам созвездий
m: {(Q»m^Hj)}1Nr.
6. Этап предварительной идентификации звезд в созвездиях. Опера¬
тор предварительной идентификации звезд производит идентификацию
звезд только в распознанных созвездиях по критерию ближайшего сосед¬
ства отметок в эталонном и наблюдаемом изображении созвездий. Работа
оператора заканчивается присвоением номерам г обнаруженных отметок
созвездий идентификаторов Ν{ эталонных звезд из каталога: {(г TV*)} ,
*c{Q£j1]iVr.
Рис. 11.29. Укрупненная блок схема ком¬
плексного алгоритма астроориентации
11.6. Распознавание групповых точечных объектов по форме контура АСО 465
Рис. 11.30. Результаты основных этапов комплексного алгоритма астроориентации:
а — исходное изображение участка звездного неба; б — результат обнаружения
светил; в — эталонные контуры АСО созвездий; г — контуры АСО наблюдае¬
мых созвездий; д — нумерация астрономических ориентиров в банке эталонов;
е — результат идентификации отдельных светил распознанных созвездий; ж —
идентифицированные наблюдаемые созвездия; з — множество всех идентифици¬
рованных ориентиров
466
Гл. 11. Обработка групповых точечных объектов
7. Этап совмещения изображений АСО. Оператор совмещения АСО
выполняет совмещение наблюдаемого кадра с опознанным АСО созвездия
и эталонного кадра с одноименным эталонным АСО. Совмещение осуще¬
ствляется путем совмещения центров тяжести контуров АСО и поворота
одного из кадров на угол, равный полученной оценке Αφ при распознавании.
8. Этап идентификации множества обнаруженных звезд. Оператор
идентификации звезд с учетом полученной предварительной оценки ори¬
ентации реализует окончательную идентификацию всех звезд кадра изо¬
бражения по критерию ближайшего соседства: {(i & Ν{)}λ Ν .
Основными достоинствами рассмотренного подхода к распознаванию
ГрТО на основе анализа вторичного описания, отличающими его от про¬
странственного подхода, описанного в предыдущей главе, являются:
1) низкая трудоемкость (в среднем до 0,8—2,5 млн операций типа
сложение/умножение при алфавите из 10 классов ГрТО) за счет малой
размерности описания (обычно не более 100), а также инвариантности
алгоритма распознавания к масштабу и угловой ориентации изображения;
2) принципиальная возможность принимать решения о классе ГрТО,
когда априорные данные о возможных значениях части признаков отсут¬
ствуют (например, неизвестна форма ГрТО).
При этом надежность принимаемых решений по совокупности при¬
знаков остается в рамках значений, представляющих практический
интерес, т.е. не хуже 0,9—0,95 в диапазоне интенсивностей ложных
отметок до 1,57· 10-3, что подтверждается расчетными и эмпирически¬
ми, полученными статистическим моделированием, характеристиками
алгоритмов.
11.7. Различение групповых точечных объектов
с нестационарной конфигурацией
11.7Л. Постановка задачи и основные подходы к ее решению. Для
различных семейств ГрТО (множеств классов с близкими свойствами)
наборы информативных признаков могут отличаться. В связи с этим для
оптимизации надежности и быстродействия распознавания необходима
предварительная классификация семейств ГрТО. Если форма ГрТО меж¬
ду сеансами наблюдения изменяется, т.е. ГрТО является нестационарным,
то детальная классификация бывает невозможной и определение его се¬
мейства имеет самостоятельное значение.
Примером семейств ГрТО, существенно отличающихся по своим свой¬
ствам, являются «цепочки» и «скопления» (рис. 11.31). Идеализированный
(в отсутствии шумов) цепочечный ГрТО представляет собой множество
точек на плоскости изображения, расположенных с некоторым (возможно
случайным) шагом вдоль гладкой линии с малой кривизной. «Скопле¬
ния» — множества точек, распределенных по площади. Очевидно, что
семейства данных объектов отличаются закономерностью расположения
точек независимо от параметров линейных геометрических преобразова¬
ний исходного изображения, т.е. отличаются формой.
11.7. Различение объектов с нестационарной конфигурацией
467
Ос
В данном разделе предлагается методика различения этих семейств
по спектрально-корреляционным характеристикам контуров ассоции¬
рованных с ГрТО сплошных образов.
Моделью контура АСО могут слу¬
жить, например, эквипотенциальная
линия поля, образованного зарядами,
размещенными в точках ГрТО, линия
одинаковой яркости расфокусирован¬
ного изображения ГрТО, а также
минимальное дерево — граф с ми¬
нимальной суммарной длинной ребер,
где точки ГрТО вершины, а ребра —
соединяющие их отрезки. Эти модели
АСО имеют близкие с точки зре¬
ния различения семейств «цепочки»
и «скопления» характеристики. С уче¬
том этого в качестве рабочего выбран
наименее трудоемкий метод описания формы ГрТО — посредством
контура минимального дерева ГрТО (рис. 11.32). Примем, что в результате
цепного комплекснозначного кодирования полигональной аппроксимации
контура Ν(χ) формируется вектор-контур N = M”)}0,fc-1 ·
ГрТО семейства
Щепочка” t .
ГрТО семейства
"Скопление"
Рис. 11.31. Изображения семейств
групповых точечных объектов «це¬
почка» и «скопление»
Рис. 11.32. Описание и кодирование формы «цепочек» и «скоплений»
Контуру N в пространстве Ск соответствуют свой спектр мощности
и нормированная АКФ
η (rf) = -ГС’ ^d)_ _ v μ* ^
ιινιι is
где ||Ν||2 — квадрат нормы (энергия) контура N, d - смещение начальной
точки контура.
Упорядоченность точек цепочечного ГрТО вдоль линии слабой кривизны
обуславливает сильную корреляцию направлений элемент ЭВ контура ми¬
нимального дерева «цепочки» Νμ, медленно убывающую с удалением одного
ЭВ от другого, и, следовательно, широкий интервал корреляции и сосредо¬
468
Гл. 11. Обработка групповых точечных объектов
Рис. 11.33. Графики нормирован¬
ных АКФ «цепочек» и «скоплений»
точенный в области низких частот спектр мощности. Для контура минималь¬
ного дерева «скопления» Nc, вследствие сильной разветвленности графика
минимального дерева, степень корреляции направлений ЭВ убывает значи¬
тельно быстрее. В результате, для контура Nc характерен узкий интервал
корреляции, и, следовательно, существенно более широкий спектр.
Таким образом, контуры минимальных деревьев ГрТО являются ре¬
ализациями либо низкочастотного узкополосного, либо широкополосного
процесса соответственно с широким и узким интервалами корреляции.
Графики модулей нормированной АКФ
контуров Гц и Гс, идеализированных
ГрТО типа «цепочка» и «скопление»
соответственно, приведены на рис. 11.33
(модуль АКФ N4 — сплошная линия,
модуль АКФ Nc — пунктир).
Следует отметить, что при наличии
ложных отметок, отнесенных на этапе
обнаружения к ГрТО, в минимальном
дереве объектов появляются допол¬
нительные, со случайной ориентацией
ложные ребра. В результате спектр
контура АСО «цепочки» расширяется,
а при значительной плотности ложных
отметок становится неотличимым от спектра «скопления». Тем не менее,
до определенного предела контур минимального дерева «цепочки»
можно считать статистически более узкополосным по сравнению со
спектром «скопления». В отличие от «цепочки», зашумление «скопления»
практически не меняет широкополосный характер спектра контура его
минимального дерева, т.е. контур Nc является шумоподобным.
В связи с тем, что лишь ширина спектра контура, а не каждый его от¬
счет в отдельности, несет информацию о принадлежности ГрТО к одному
из семейств классов, целесообразно в качестве информативного признака
выбрать именно данную характеристику ГрТО. С учетом связи шири¬
ны спектра мощности и ширины интервала корреляции сигналов для
минимизации вычислений выберем в качестве меры сосредоточенности
энергетического спектра контура в области низких частот размер его
интервала корреляции т, определяемый как ширина главного лепестка
модуля АКФ вектор-контура N: т = inf[|ry (d)\ < 7/0]·
d
Вследствие случайного характера шума размер интервала корреляции
в обоих случаях становится случайной величиной с плотностью веро¬
ятности Wn(r\q) для «цепочки» и Wc(r\q) для «скопления», где q —
параметр, характеризующий относительную мощность шума. Плотности
вероятности показаны условными, так как могут меняться с изменением
мощности шума.
Предположим, что после построения АСО обнаруженной группы и вы¬
деления его границ на вход различителя подается контур N. Необходимо
путем анализа ширины интервала корреляции т контура N принять обос¬
11.7. Различение объектов с нестационарной конфигурацией
469
нованное решение Н в пользу одной из гипотез: Н\ — контур «цепочки»,
Н-2 — контур «скопления», если статистика помех задана и, следователь¬
но, известны условные плотности вероятности W (r\Hi,q) = Wn(r\q),
W(T\H2,q) = Wc(r\q).
11.7.2. Алгоритм различения «цепочек» и «скоплений». Оптималь¬
ный в смысле критерия отношения правдоподобия различитель должен
реализовать алгоритм
Н ==
Hi при Лг ^ Л0,
#2 при Лт < Л0,
W (г \Н\,д)
r W{T\H2,q)'
(11.7.1)
W
где Ло — порог, назначаемый согласно заданному критерию оптимальности.
Степень зашумленности контура изображения минимального дерева
наблюдаемого ГрТО будем характеризовать величиной q, равной отноше¬
нию энергии эталонного контура Ег = ||Г||2 к средней энергии шумовых
составляющих Еш, отличающих наблюдаемый контур N от эталонного Г:
q = Ег/Еш [166].
Анализ результатов серии экспериментов для определения порого¬
вого уровня щ различителя с минимальной вероятностью ошибок [164]
покывает, что различимость классов улучшается с понижением уровня
?7о, а начиная со значения щ « 0,2 резко падает. Это объясняется обо¬
стрением пика главного лепестка АКФ
высокочастотными шумовыми спек¬
тральными компонентами. Спад раз¬
личимости классов на низких уровнях
щ < 0,2 обусловлен нечеткой гра¬
ницей главного лепестка с остальной
частью модуля АКФ.
Значение оптимального уровня щ
приблизительно равно 0,3. Это значе¬
ние взято в дальнейшем за фиксиро¬
ванный уровень измерения интервала
корреляции в различителе «цепоч¬
ка» — «скопление». На рис. 11.34 при¬
ведены оценки условных плотностей
вероятности W (r\Hi,q) (сплошная
линия) и W (т|#2,д) (штриховая) при q = 4,47 дБ для выбранного
уровня 770. По оси абсцисс откладывается значение т, взятое в процентах
от размерности к контура.
Анализ оценок W (r\Hi,q) и W (r|if2, q) показал, что до тех пор, пока
средняя плотность ложных отметок не превышает плотности точек ГрТО,
можно предположить, что отношение правдоподобия Лт является монотон¬
ной функцией величины т на интервале т е]0, argmax{VF(τ|ϋι, <?)}],
а на интервале т Е ] arg max {W (r\Hi,q)}, 100%] выполняется неравен¬
ство Лг » 1.
Рис. 11.34. Гистограммы распределе¬
ний ширины интервала корреляции
контуров «цепочек» и «скоплений»
470
Гл. 11. Обработка групповых точечных объектов
Тогда решающему правилу (11.7.1) эквивалентно следующее правило
Hi при г > То (q),
Н2 При Т < То(q),
(11.7.2)
где т0 (q) — функция порога различения от отношения с/ш, значение
которого определяется из равенства Лт = Л0.
Сравнение алгоритмов (11.7.1) и (11.7.2) показывает, что для реализа¬
ции второго алгоритма требуется существенно меньший объем запоми¬
нающего устройства так как достаточ¬
но хранить единственную зависимость
го (q), в отличие от алгоритма (11.7.1),
где требуется одновременно хранить
множество условных плотностей веро¬
ятностей. Кроме того, алгоритм (11.7.2)
менее трудоемок.
На рис. 11.35 приведен график за¬
висимости оценочного значения то от
отношения сигнал/шум q для крите¬
рия минимума суммы условных веро¬
ятностей ошибок различения (Л0 = 1).
Сплошной линией показано выбороч¬
ное среднее, а пунктиром — доверительный интервал истинного значения
порога т0 (q) для доверительной вероятности 90%.
11.7.3. Характеристики различителя. Разнообразие классов семейств
групповых точечных объектов затрудняет и делает нецелесообразным
построение теоретических характеристик эффективности работы полу¬
ченных алгоритмов. Для иллюстрации качества работы различителя при¬
ведем лишь результаты его статистических испытаний для конкретных
условий наблюдения. В качестве эталонов взяты идеализированные ГрТО:
1) цепочечный ГрТО из 16 точек, расположенных равномерно вдоль остов-
ной линии с кривизной, соответствующей т = 13%; 2) «скопление» из 16
точек, расположенных в виде квадратной матрицы. Масштаб изображений
обоих объектов устанавливался исходя из равенства средних расстоя¬
ний между соседними точками обоих ГрТО. При формировании исходной
сцены точки флуктуировали относительно эталонных положений по нор¬
мальному закону с нулевым математическим ожиданием и СКО, равным
10% от гс. Вероятность пропуска точки ГрТО была зафиксирована на
уровне 0,05.
График оценки характеристик оптимального различителя в виде зави¬
симости вероятности принятия ошибочного решения Р0ш = {Р{Н2 |#i) 4-
4- Ρ(Ηι \Н2)}/2 от величины д(дБ), представлен на рис. 11.36. В узлах
сплошной ломаной линии значения оценок Р0ш получены, как выбороч¬
ное среднее нескольких независимых оценок Р0ш- Причем, в каждом
случае число оценок выбиралось, исходя из равенства их доверитель¬
4,47 5,23 5,99 6,75 7,51
Рис. 11.35. График значений опти¬
мального порога различения при
различной величине шумов
11.7. Различение объектов с нестационарной конфигурацией
471
ных интервалов. Пунктиром даны границы доверительного интервала
для истинного значения Р0ш, найденные по методу Стьюдента для до¬
верительной вероятности 90%.
Результаты статистических испытаний различителя, реализующего
алгоритм (11.7.2), продемонстрировали практическое совпадение его ха¬
рактеристик с характеристиками алго¬
ритма (11.7.1). Это объясняется слабой
чувствительностью алгоритма (11.7.2)
к погрешностям в выборе порога то на
выбранном интервале д, так как значе¬
ния производных функций правдоподо¬
бия на этом интервале в окрестностях
т0 (д), заданных полученным довери¬
тельным интервалом, близки к нулю.
Для наглядной интерпретации ха¬
рактеристик рассмотренных различи¬
те л ей отметим, что указанный диа¬
пазон д(дБ) для оговоренных условий
проведения экспериментов и масштаба
изображения ГрТО, соответствующего
соседними точечными объектами гс = 5
4,47 5,23 5,99 6,75 7,51
Рис. 11.36. Характеристики разли¬
чителя «цепочек» и «скоплений»
среднему расстоянию между
элементов разрешения, пере¬
крывает диапазон интенсивностей ложных отметок от рф = 0 до рф =
= 80/216 = 1,27 · 10_3. Причем, даже для наихудшей ситуации
вероятность ошибки различения остается меньшей 10“2.
На рис. 11.37 приведены результаты работы алгоритма распознавания
ГрТО, где на первом этапе выполнено различение семейств «цепочка»
Запуск ]
3*ч
Объект N* 1
Скопление
.Я
Объект № 2
Скопление
II Выкод |
наблюдения
1) среднее число ложных отметок в сцене. 10
2) вероятность ложной тревоги 0.001
3) среднее расстояяние между соседними точками 10
4) порог обнаружения по расстоянию 28,2426406871193
5) порог обнаружения по кол-ву точек 4,95047047057715
6) вероятность правильного обнаружения ГрТО 0,992506168355629
7) порог классификации по интервалу корреляции 10
Рис 11.37. Представление результатов автоматического распознавания групповых
точечных объектов
и «скопление». На этом же рисунке даны условия наблюдения и значения
вторичных признаков по которым выполнялось распознавание.
472
Гл. 11. Обработка групповых точечных объектов
Как следует из приведенных результатов исследований, различитель,
реализующий один из рассмотренных алгоритмов, является достаточно
помехоустойчивым и обеспечивает высокую различимость ГрТО типов
«цепочка» и «скопление». Трудоемкость вычисления достаточной стати¬
стики распознавания не зависит от параметров геометрических преоб¬
разований подобия исходного изображения и составляет около 0,3 млн
операций типа сложение/умножение.
11.8. Обсуждение результатов
В данной главе рассматривались подходы к решению задач обнару¬
жения и распознавания ГрТО в зашумленных точечных сценах. Основная
идея заключается в применении методов контурного анализа для обра¬
ботки и понимания изображений групповых точечных объектов. При этом
термин «понимание изображений» в соответствии с [5] здесь предполагает
операции анализа сцены с целью обнаружения, измерения параметров,
структурного анализа и распознавания групповых точечных объектов.
Эти операции базируются на математических моделях ассоциированного
сплошного образа (АСО) и мере пространственной компактности произ¬
вольных множеств точек на плоскости.
Математической моделью АСО является изображение с ограничен¬
ным спектром пространственных частот, которое считается исходным
по отношению к результату его дискретизации в виде ГрТО. Данная
модель задает однозначное линейное отображение — расфокусировку
изображения ГрТО (построение кумулятивного потенциального поля),
которое позволяет представлять модель ГрТО моделью АСО в задачах
выделения признаков формы и распознавания формы объектов. По¬
скольку для статистически однородных по плотности точек ГрТО и со¬
ответствующих им однородных по яркости АСО вся информация о фор¬
ме сосредоточена на границе объекта и фона, то для распознавания
данных объектов использована модель контура АСО, которая получа¬
ется в результате пороговой обработки расфокусированного точечного
изображения. При этом удается отойти от многочисленных эвристи¬
ческих попыток распознавания формы ГрТО и свести данную задачу
к описанной ранее задаче распознавания контуров изображений рас¬
пределенных объектов.
Из данной модели АСО следует естественный критерий простран¬
ственной компактности или группировки произвольных множеств то¬
чек. Множество точек считается компактным, если все точки этого
множества принадлежат одному АСО. При этом естественной мерой
пространственной компактности служит ширина полосы пропускания
расфокусирующего фильтра, при которой множество точек становится
компактным.
Модель АСО и мера компактности позволили ввести количествен¬
ные характеристики плотности расположения точек ГрТО с произвольной
11.9. Вопросы и упражнения
473
(в том числе и нестационарной) формой АСО, меру схожести формы
ГрТО, и других вторичных признаков, задать правила их выделения,
получить распределения вероятностей значений этих признаков, необхо¬
димых для синтеза оптимальных решающих правил распознавания ГрТО.
Так, использование меры компактности позволяет упорядочить все
подмножества обнаруженной группы точек по степени их простран¬
ственной близости — получить граф иерархической группировки точек
или минимальное дерево, где вершины — точки, а ребра — связи между
подмножествами с длиной, равной степени их пространственной бли¬
зости. Разрушение любого ребра такого графа приводит к разбиению
группы на два непересекающихся компактных подмножества. С учетом
этого, задачи локализации компактных групп точек (группировка точек
и пространственное ограничение групп) и анализа степени сложности
ГрТО (выделения однородных компактных подгрупп неоднородных по
плотности точек ГрТО) при формировании вторичного описания объек¬
та сведены к задачам обнаружения соответственно коротких и длинных
связей между подгруппами, и решены оптимально с позиций принятых
в математической статистике и радиолокации критериев качества.
На основе данной меры синтезирован по методу отношения правдо¬
подобия обобщенный алгоритм обнаружения ГрТО с неизвестной формой
АСО и получена его конкретная реализация для случая цилиндрической
ИХ расфокусирующего фильтра. В этом случае мера компактности со¬
ответствует минимальному евклидовому расстоянию между всеми под¬
множествами заданного множества точек на плоскости. Инвариантность
алгоритма к форме АСО и положению объекта в сцене достигается за
счет восстановления АСО на этапе локализации компактных групп точек.
При этом потери в качестве принимаемых решений из-за неопределен¬
ности относительно формы АСО являются приемлимыми: снижение по¬
рогового значения плотности ложных отметок в 1,5—2 раза по сравнению
с использованием пространственного согласованного фильтра. Благодаря
инвариантности алгоритма к положению ГрТО в сцене и номеру класса
достигается существенный выигрыш в быстродействии.
11.9. Вопросы и упражнения
1. В чем заключается задача понимания изображений в точечной сцене?
2. Какими признаками характеризуются ГрТО?
3. Составьте несколько видов аналитического описания точечной сцены на
рис. 11.38, а.
4. Каковы основные мешающие факторы при обработке групповых точечных
объектов?
5. Какими способами группе точек можно поставить в соответствие сплошное
изображение?
6. Получите граф минимального дерева для группы точек на рис. 11.38, а.
7. Проведите локализацию ГрТО (рис. 11.38, б), используя алгоритм на основе
минимального дерева.
474
Гл. 11. Обработка групповых точечных объектов
и
ё
b-
Г
EV-
r
1
V..
I
IT-
i
л.
<
)
L
Г
Η
s
1>-
<
■J
?\
r
—i
D~
i
)
\
Г
1
1
Λ
1
\
ir"
Λ
J;
I
D—
_L
Рис. 11.38
I
I
-
i
/
8. Задайте необходимые параметры и постройте кумулятивное потенциальное
поле для сцены на рис. 11.38, в.
9. Выполните на уровне максимального градиента потенциальной функции би¬
нарное квантование полученного в упражнении 8 кумулятивного поля и по¬
стройте код контура плоского АСО.
10. Проведите иерархическую группировку точечных объектов в сцене на
рис. 11.38, г.
ЧАСТЬ III
КОНТУРНЫЙ АНАЛИЗ В ЗАДАЧАХ
ОБРАБОТКИ СИГНАЛОВ
Глава 12
СЛОЖНЫЕ СИГНАЛЫ
НА БАЗЕ КОМПОЗИЦИОННЫХ КОНТУРОВ
Введение
Применение методов теории сигналов к задачам обработки изобра¬
жений позволило выработать подходы к синтезу эффективных алго¬
ритмов анализа и понимания сцен. Это стало возможно за счет перехода
от поточечного анализа изображений к обработке наиболее информа¬
тивной их части — контуров. При этом контуры рассматривались как
дискретные комплекснозначные сигналы, к которым применимы все
операции, характерные для обработки сигналов: спектральный ана¬
лиз, различные виды фильтрации, обнаружение, оценка параметров,
распознавание, разрешение и др. Именно переход от действительных
сигналов к комплексным позволил увеличить информативность резуль¬
тата вычисления их скалярного произведения, являющегося базовой
операцией обработки сигналов.
«Сигнальный» подход к обработке изображений дает возможность ста¬
вить и решать задачи поиска оптимальных для различных задач форм
изображений. Полученные при этом результаты могут быть полезны и в
традиционных для обработки сигналов областях — локации и связи. Здесь,
в силу широкого применения гармонических сигналов, часто используется
их комплексное представление. Модуль вектора, заданного на комплекс¬
ной плоскости, определяет величину амплитуды гармонического сигнала,
а аргумент вектора — начальную фазу сигнала. Если сигнал состоит из
нескольких кодовых интервалов, то каждому кодовому интервалу ставит¬
ся в соответствие свой вектор. Векторная диаграмма, получаемая конка¬
тенацией векторов, образует контур, однозначно задающий описываемый
сигнал (см. п. 1.6). Поэтому ряд результатов, полученных в контурном
анализе, может быть успешно применен для синтеза и обработки радио¬
технических сигналов.
476
Гуι. 12. Композиционные контуры
В данной главе рассматриваются вопросы синтеза и анализа ко¬
дирующих последовательностей сложных сигналов и методов их об¬
работки для решения задач обнаружения, разрешения, распознавания
и оценки параметров. Требования к параметрам сигнала при решении
этих задач взаимнопротиворечивы. Ниже, в качестве кодирующих по¬
следовательностей рассматриваются особые контурные сигналы — ком¬
позиционные контуры. Их структура позволяет в определенной степени
сгладить упомянутые противоречия. Составными частями композици¬
онных контуров являются ЭК, обладающие дельтовидными спектрами
(см. п. 2.2). Они образуют алфавит сигналов, имеющих максимальную
взаимную различимость, что важно для их эффективного распознава¬
ния (см. п. 4.4). В целом композиционные контуры обладают равномер¬
ным энергетическим спектром (РЭС), дельтовидной циклической АКФ,
единичным пик-фактором, что делает их также эффективными при
обнаружении, разрешении и оценке параметров. С целью сравнения
со свойствами композиционных контуров проводится обзор некоторых
распространенных видов сложных сигналов.
12.1. Обзор кодирующих последовательностей сложных
Сигналы с линейной частотной модуляцией. Сигнал с линейной ча¬
стотной модуляцией (ЛЧМ) был одним из первых сложных сигналов, при¬
мененных в радиолокации. Аналитические представления такого сигнала
и (t) и закона частотной / (t) модуляции имеют вид [55, 57, 151]
где ти — длительность сигнала, а — параметр частотной модуляции,
φ (t) — функция, задающая закон изменения мгновенной фазы сигна¬
ла. Функция неопределенности ЛЧМ сигнала имеет ножевидную форму
с областью высокой корреляции, сосредоточенной вдоль прямой ат +
-f φ = 0. Поэтому сигналы, удовлетворяющие такому условию, являют¬
ся неразрешимыми. Одиночный ЛЧМ сигнал широко используется как
зондирующий сигнал, обладающий высокой энергией за счет большой
длительности, позволяющий при сжатии обеспечить хорошее разрешение
по дальности и высокое отношение сигнал/шум.
В качестве фильтра сжатия используются устройства с прямоуголь¬
ной АЧХ и квадратичной ФЧХ, например, дисперсионные линии задерж¬
ки. Импульс на выходе фильтра имеет огибающую вида (sin х) /ж, что
создает опасность маскировки основного лепестка сжатого радиоимпуль¬
са, отраженного от цели с малой эффективной поверхностью рассеяния,
боковыми лепестками сильного сигнала.
Дискретно-кодированные сигналы. В общем случае дискретно-коди¬
рованные сигналы (ДКС) представляют собой упорядоченные последо¬
вательности, которые воздействуют через фиксированные промежутки
времени (кодовые интервалы) на амплитуду, фазу и частоту когерентной
сигналов и подходов к их синтезу
12Л. Обзор кодирующих последовательностей
477
непрерывной несущей [57]. Общее описание этих сигналов задается в виде
( к
Σ апрп (t) exp [j{(w0 + ωη) t + Θ„}], 0 ^ t ζ ктКИ,
и (t) = < η=1
I 0 при других t,
(12.1.1)
где η = 1,2,... ,&; αη, ωη, Θη — амплитуда, частота и фаза модули¬
рующей (кодирующей) последовательности; Рп (t) — импульс единичной
амплитуды фиксированной длительности тки определяется следующим
образом
Pn{t)
P(t- [η - ljria,) = 1 при (η - 1) Тки ^ t ζ ПТки,
^0 при других t.
Функция неопределенности ДКС в общем случае записывается как [57]
к к
χΜ = ΣΣ
ип (t) «т (ί + т) ехР [—Ϊ2πφ (t)\dt,
причем
и (t) exp [—iuot\ = Σ^η(ί).
ДКС условно делятся на три основные группы, характеризуемые со¬
отношениями:
— группа I: {0„} = 0; {ω„} = 0; (α„ = (1,0)};
— группа И: {ωη} = 0;
— группа III: {о„ = (1,0)}; {0„} = 0.
ДКС группы I. Эти сигналы представляют собой последовательности
импульсов с постоянными значениями несущей частоты и начальной фа¬
зой. Аналитическое представление таких ДКС имеет вид:
/,\ I Σ) “ηΡη (β) бхр 0 ^ t ^ ктКИ,
п (t) = ч П=1
I 0 при других t.
(12.1.2)
Последовательности, описываемые (12.1.2), могут быть регулярными
и нерегулярными. Функция неопределенности |χ(τ, ψ)\ регулярной по¬
следовательности является многопиковой, поэтому возможно появление
неоднозначностей измерения дальности и скорости. Если статистическая
связь при чередовании нулей и единиц мала, то вид функции неопреде¬
ленности приближается к кнопочной. Один из способов уменьшения этой
связи состоит в варьировании интервалов между импульсами. Подобные
сигналы называют нерегулярными импульсными последовательностями.
Функция неопределенности таких сигналов имеет при |т| = тки кнопоч¬
ный вид, причем боковые лепестки ее не превышают 1/к. Преимущества
этого сигнала заключаются в возможности одновременного разрешения по
дальности и скорости при отсутствии неоднозначности по дальности.
478
Гл. 12. Композиционные контуры
ДКС группы И. Бинарные фазовые коды. Общее представление для
бинарных фазовых кодов имеет вид [57]:
( к
u(t) =
Σ Pn(i)exp[i(a;oi + 0„)], 0 ^ t ^ ктш,
η—1
О при других t,
(12.1.3)
где θη = {0, π}.
Коды Баркера. Это семейство бинарных последовательностей харак¬
теризуется соотношением
/ пч I к при п = О,
х (п, 0) = <
[±1,0 при п ф 0.
Нормированная АКФ комплексной огибающей ФМ сигнала, кодиро¬
ванного последовательностью Баркера, при временном сдвиге, кратном
длительности кодового интервала гки, равна
к — п
V (птш) = - Σ djdj+n, (12.1.4)
з=1
где dn = cos θη. Величина θη = (0, π} играет роль начальной фазы гар¬
монического колебания ν = V cos (ωοί + θη) с частотой ujq и амплитудой
V, существующего в пределах гг-го кодового интервала.
Существует всего девять последовательностей Баркера (см. табл. 12.1).
Элементы кодов Баркера с нечетным значением к связаны между собой
Таблица 12.1. Последовательности Баркера
к
{Сп}
χ(η,0), η = 0,1,... , к — 1
2
1; 1
2; 1
2
-1; 1
2; -1
3
1; 1; -1
3; 0; 1
4
1; 1; -1; ι
4; -1; 0; 1
4
1; 1; 1; -ι
4; 1; 0; -1
5
i; i; i; -ΐ; ι
5; 0; 1; 0; 1
7
1; 1; 1; -1; -1; 1; -1
7; 0; -1; 0; -1; 0; -1
11
1; 1; 1; -1; -1; -1; 1; -1; -1; 1; -1
11; 0; -1; 0; -1; 0; -1; 0; -1; 0; -1
13
1; 1; 1; 1; 1; -1; -1; 1; 1; -1; 1;
13; 0; -1; 0; -1; 0; -1; 0; -1; 0; -1;
-i; ι
0; -1
рекуррентной формулой с„ - ск-„-1 (-l)n+(fe 1)/2, где с„ = ехр{г6>„},
с„ = ±1.
М-последовательности. М-последовательности или коды максималь¬
ной длины образуются с помощью рекуррентных соотношений. Очеред¬
ной, (г + 1)-й элемент М-последовательности находится из соотноше¬
12.1. Обзор кодирующих последовательностей
479
ния a,i+i = aia,i 0 a2(ii-i 0 ... 0 ana,i-n, где коэффициенты а равны
либо 0, либо 1 и определяются на основе неприводимых полиномов [85].
М-последовательности содержат k = 2П — 1 знаков, где п — разряд¬
ность формирующего регистра. Аналитически сигналы этого вида можно
представить выражением
u{t) =
к ч -1/2 к
сп rect
п=1 ' п=1
к -Ь 1
2
)]·
где ап и ψη — амплитуда и фаза гг-го импульса. Функция неопреде¬
ленности усеченной М-последовательности приближается к кнопочной
с уровнем боковых лепестков 1 / у/к.
Для периодической корреляционной функции выполняется условие
х(М)
2П — 1, п = О mod (к),
—1, п ф О mod (к).
Это свойство аналогично результату, полученному для последовательно¬
стей Баркера.
Коды Фрэнка. Дискретным аналогом сигнала, частота которого моду¬
лирована по линейному закону, является многофазный сигнал Фрэнка
[55, 57]. Он имеет постоянные амплитуду и несущую частоту, состоит
из к = п2 элементарных радиоимпульсов длительностью τκνι. Значения
начальных фаз на кодовых интервалах определяются соотношением
ψ (п) = 2тг^7 (п) , (12.1.5)
где р — число, взаимно простое с к, 7 (п) = ] — l}>
]х[ — целая часть числа х. Закон изменения фазы аппроксимирует
квадратичный закон, характерный для ЛЧМ-сигнала. Поэтому функция
неопределенности сходна с функцией неопределенности ЛЧМ-сигнала.
Превышение максимума АКФ над наибольшим боковым выбросом воз¬
растает при увеличении числа элементарных импульсов в многофазном
сигнале и при к ^ 9 слабо отличается от 3 у/к.
Коды Хаффмана. Предыдущие примеры включали в себя только дис¬
кретные фазовые последовательности для которых {ап} = 1. Отказ от
этого ограничения позволяет получить последовательности, которые обла¬
дают свойством
X (п, 0)
г
2Е при η — 0,
< 0 при п ф 0 и |га| ф к — 1,
±1 при \п\ — к — 1,
где Е — энергия сигнала. Метод, используемый для получения таких
последовательностей, был предложен Хаффманом [57]. Общее представ-
480
Гл. 12. Композиционные контуры
ление сигналов Хаффмана имеет вид
u(t) =
Σ ьпРп
п=1
(i) exp \jw0t],
О при других £,
О < t ^ ь-ки,
где Ьп = ап ехр {г0п}. Например, одна из последовательностей Хаффмана
длиной 14, включающая только действительные коэффициенты, имеет
вид
{Ьп} = {-0,57; 0,27; -0,56; 0,55; -0,14; -0,28; -0,31;
- 1; -0,43; 0,5; 0,037; -0,34; 0,22; 0,43}.
ДКС группы III. К этой группе относятся сигналы с дискретной ча¬
стотной модуляцией. Чаще всего используется ступенчатый линейный
закон изменения частоты. Функция неопределенности при этом имеет
характерную для ЛЧМ-сигнала гребнеобразную структуру.
Корреляционные свойства сложных сигналов характеризуются коэффи¬
циентом ф — η(0) /т7б,тах, равным отношению амплитуд главного и мак¬
симального бокового лепестков АКФ кодирующей последовательности. Чем
больше значение </>, тем лучше эти свойства. В пределе сигнал с «хороши¬
ми» корреляционными свойствами не должен иметь боковых лепестков, т.е.
его АКФ являться дельтовидной, а энергетический спектр — равномерным.
Разработка импульсных сигналов с такими свойствами в течении более чем
сорока последних лет продолжает оставаться актуальной задачей.
На рис. 12.1 представлены графики энергетических спектров последо¬
вательностей Баркера [55], являющихся одними из лучших кодирующих
0 0,2 0,4 0,6 0,8
2π
Рис. 12.1. Амплитудные спектры последовательностей Баркера [55]
последовательностей сложных сигналов. Хорошо видна их зависимость
от изменения частоты, представленной в безразмерном виде. Аналогично
ведут себя и графики энергетического спектра для последовательностей
Френка [57], свойства которых еще лучше, чем у кодов Баркера. В связи
12.1. Обзор кодирующих последовательностей
481
с этим возникает вопрос, почему требование равномерности энергетиче¬
ского спектра кодирующих последовательностей не ставится при синтезе
реальных ДКС?
Для ответа на этот вопрос рассмотрим критерии, на основании ко¬
торых происходит синтез кодирующих последовательностей для таких
распространенных ДКС, как импульсные ФМ сигналы. Пример синтеза
кодов Баркера приведен в [55].
Элемент dj = cosfy, j = 1,2,... , к, находится из условия непревы-
шения боковыми лепестками АКФ η (птки) по абсолютной величине еди¬
ничного уровня. С учетом этого условия на основании (12.1.4) получается
система (к — 1) нелинейных уравнений относительно неизвестных значе¬
ний dj, j = 1,2,... , к. Принимая одно из значений d равным единице и
решая полученную систему уравнений, находим приведенные в табл. 12.1
коды Баркера.
Таким образом, синтез кодов Баркера происходит по критерию непревы-
шения боковыми лепестками АКФ кодирующей последовательности заранее
определенного уровня. Как следует из [153], оптимальные кодирующие по¬
следовательности синтезируются на основе минимаксного критерия:
найти mini/ при условии \η (птки)| < L,
η = 1,2, ...,& — 1, d~—1,1.
Этот подход связан с решением целочисленной задачи минимизации
линейной функции при нелинейных ограничениях. Для больших к она
не имеет эффективной вычислительной процедуры, позволяющей опре¬
делить глобальное экстремальное значение. Поэтому, как утверждается
в [153], отсутствует не только регулярный метод синтеза импульсных ФМ
сигналов, оптимальных по минимаксному критерию, но затруднен даже
ответ на вопрос, насколько известные сигналы с большим значением к
близки к оптимальным. Указывается, что, по крайней мере, существуют
два эффективных метода синтеза.
Первый базируется на алгоритмах итерационного типа. Их недостатки
заключаются в том, что они приводят к локальному экстремуму и при
больших значениях к резко увеличивается требуемое количество расчет¬
ных операций.
Второй метод использует связь между циклической и ациклической
АКФ кода, имеющей вид [153]
?7цикл(^) = ^7ацикл(^) “Ь ?7ацикл(^ Ttl). (12.1.6)
Для заданного значения к получаются коды с одно или двухуровне¬
выми периодическими АКФ для всех возможных параметров, при ко¬
торых |т7цикл(^)| ^ у у т ф 0. Из них отбирается код с ациклической
АКФ, у которой шах |т7ацикл(т)|, т ф 0, имеет наименьшее значение.
Значения т берутся по модулю к. Коды для известных импульсных ФМ
сигналов с хорошими свойствами ациклической АКФ — индексные коды,
М-последовательности, могут быть получены по этому методу.
Лучшими, по сравнению с ФМ сигналами, корреляционными свойства¬
ми могут обладать фазокодированные (многофазные) сигналы, кодовые
482
Га. 12. Композиционные контуры
последовательности которых имеют не два, а больше значений началь¬
ной фазы синусоиды в пределах кодового интервала. Примером может
служить код Фрэнка, характеризующийся значением ф « 3/у/к.
Рассмотренные подходы к синтезу ФМ сигналов не отвечают на во¬
прос, насколько используемый сигнал является оптимальным в смысле
наилучшего приближения его функции неопределенности к заданной. В ра¬
боте [154] синтез ФМ сигналов базируется на другом, т.е. не на минимакс¬
ном подходе, оценивающим качества сигнала по величине коэффициента
ф. Для приема эхо-сигналов от целей с малой эффективной поверхностью
рассеяния (ЭПР) на фоне целей с большой ЭПР важен критерий, учиты¬
вающий не соотношение пикового значения АКФ ФМ сигнала к уровню
максимального бокового лепестка, а средний уровень этих лепестков. Реа¬
лизация данного подхода возможна регулярными методами и заключается
в минимизации расстояния между точками, задающими идеальный и ре¬
альный сигналы. При этом неизвестно, как получить сигнал, обращающий
это расстояние в ноль, и, следовательно, как получить сигнал с нулевыми
боковыми лепестками, т.е. с минимальным корреляционным шумом.
Ответ на поставленный ранее вопрос о том, почему энергетический спектр
зондирующих сигналов с целью снижения корреляционных шумов, создава¬
емых боковыми лепестками сжатого эхо-сигнала, не является равномерным,
основан на анализе условий получения разрешенного образа (см. п. 4.3.2).
Обычно при обработке эхо-сигнала с неизвестным временем прихода
окно ациклического согласованного фильтра скользит по дальности, т.е.
его положение на дистанции плавно, с точностью до дискрета разреше¬
ния, изменяется от минимального до максимального значений измеряемо¬
го РЛС расстояния. В этих условиях, даже при наличии эхо-сигнала с РЭС
получить только по одному на каждый эхо-сигнал ненулевому отсчету
фильтра невозможно по следующим причинам.
1. Фильтр, согласованный с формой (спектром) сигнала, все время,
за исключением кратковременной второй фазы, пространственно рассо¬
гласован с ним. Окно фильтра из-за его перемещения может совпасть
с сигналом только в один из 2 к — 1 моментов времени их взаимодействия,
где к — количество кодовых интервалов (см. п. 4.3.1).
2. Реакцию фильтра в виде символа Кронекера на входной дискретно-
кодированный сигнал с РЭС можно обеспечить лишь при использовании
циклического, а не ациклического согласованного фильтра (см. п. 4.3.2).
Поскольку эти два условия, т.е. пространственное согласование фильтра
с эхо-сигналом и циклический характер работы фильтра, не выполняются,
то применение сигнала с РЭС само по себе не приводит к формированию раз¬
решенного образа. Поэтому применяемые к синтезу дискретно-кодирован¬
ных импульсных сигналов подходы лишь минимизируют, а не полностью
устраняют эффект корреляционного шума. Если же в процессе обработки
эхо-сигналов обеспечить их пространственное согласование с цикличе¬
ским согласованным фильтром, то требование РЭС остается единственным
для полного подавления корреляционных шумов при минимальном уровне
флуктуационных шумов (см. п. 4.11.2).
122. Синтез последовательностей с РЭС
483
В связи с этим возникает проблема формирования кодовых последо¬
вательностей ДКС с равномерным энергетическим спектром. Ниже будут
рассмотрены некоторые подходы к решению этой задачи.
12.2. Синтез последовательностей
с равномерным энергетическим спектром
на основе композиционных контуров
12.2.1. Спектрально-корреляционные свойства кодовых последова¬
тельностей с равномерным энергетическим спектром. Покажем, что
большинство сигналов с РЭС являются комплекснозначными. Пусть Г =
— {7 (n)}o,fc-i — цифровой комплекснозначный сигнал размерности к на
входе согласованного фильтра, состоящий из последовательности элемен¬
тарных сигналов 7 (п), т.е.
Γ = {7(0),7(1),..·,7(*-1)}, (12.2.1)
где
7 (п) = |7 (п)| ехр{гу> (η)}, п — 0,1,... , к — 1.
ДПФ такого сигнала имеет вид
к-1
р (га) = 7 (п) ехр г-^ran га = 0,1,... , к — 1,
тг=О
причем
р (га) = |р (га)| ехр {г© (га)}, га = 0,1,... , к — 1.
Пусть сигнал (12.2.1) характеризуется РЭС (рис. 12.2, а)
|р(0)|2 = |р(1)|2 = ... = |p(fc - 1)|2. (12.2.2)
Энергетический спектр и АКФ
к-1
V (п) = к Σ 7 7* (г + п)’ п = °> 1’ · · · ’к ~ 1>
г—О
этого сигнала связаны соотношением
к-1
η (п) = - ^ |р (га)|2 ехр г^гап|, п = 0,1,... , к — 1. (12.2.3)
т—О
Аналогичный результат имеет место и для вещественных сигналов, но
его получение базируется на свойстве сопряженной симметрии спектра,
|р(»«)|
а
кминимнимимхи ►
б о п
Рис. 12.2. Энергетический спектр (а) и АКФ (б) сигнала, обеспечивающего идеаль¬
ное разрешение по времени (дальности)
484
Га. 12. Композиционные контуры
не имеющего места для комплексного случая. При выполнении условия
(12.2.2) выражение (12.2.3) принимает вид
^η) = τ-Σβχρ{
||Г||2 при п = О,
О при остальных п.
(12.2.4)
Здесь ||Г||2 — квадрат нормы входного сигнала, величина равная его
энергии Е. Таким образом, если цифровой комплекснозначный сигнал
характеризуется РЭС, то его АКФ имеет только один значащий отсчет
η (0) = Е, соответствующий главному лепестку функции. Все остальные
отсчеты, образующие боковые лепестки АКФ, равны нулю (рис. 12.2, б).
Выражение для сигнала 7 (п), полученное в результате обратного
ДПФ от его спектра, равно
7 (n) = ^^P(TO)exp{^mn) = ^ Σ IP М |ехр{г [у mn + 0(m)]j,
т—0 т—0
п-0,1,... ,k- 1. (12.2.5)
Если сигнал обладает РЭС, т.е. |р (0)| = |р (1)| = ... = |р (к — 1)| = |р|,
то последнее выражение примет вид
к-1
7 (п) “ {cos [irmn ^ * s*n [^Гтп ^ (гп)] }’
т—О
п — 0,1,... , к — 1.
Отсюда следует, что такой сигнал в общем случае является комплекс¬
нозначным. Для обеспечения его вещественного характера фазочастотный
спектр {Θ (т)}0 к_г должен удовлетворять весьма специфическому усло¬
вию вида
к-1
sin + Θ (ra)j =0, n = 0,1,... , к — 1. (12.2.6)
m=0
12.2.2. Вещественные сигналы с РЭС. В предыдущем разделе бы¬
ло показано, что сигналы с РЭС являются преимущественно комплекс¬
нозначными. Однако некоторые известные действительные кодирующие
последовательности также обладают РЭС, но их количество ограничено.
Кроме того, модификация вещественных последовательностей с целью
выравнивания энергетического спектра может приводить к увеличению
пик-фактора. Это уменьшает среднюю энергию сигнала и снижает каче¬
ство решения задачи обнаружения [156].
В качестве примера рассмотрим код Баркера при к = 4: Г = {1,1,1,
—1}. Его спектр имеет вид Р = {р(т)}03 = {2г; —2г;2;2г}. Этот веще¬
ственный сигнал обладает РЭС, т.к. |р(0)| = |р (1)| = |р(2)| = |р(3)| = 2.
Из дальнейшего анализа станет понятным, почему данный код Баркера
имеет РЭС. Проверим, как для него выполняется условие (12.2.6).
12.2. Синтез последовательностей с РЭС
485
Фазочастотный спектр сигнала равен: Θ (0) = 0°; θ (1) = 270°; Θ (2) =
= 0°; Θ (3) = 90°. Тогда
з
п=0, s^n [^(m)] = sin0°-b sin 270°+ sin0°+ sin 90° = 0;
m—0
3
n = 1, ^sin[90°m -f 9(m)\ = sin0°+ sin360°+ sin 180°+ sin360° = 0;
m=0
3
n — 2, ^2 S^n [180°m + 0(m)] = sin 0° + sin 450° + sin 540° + sin 630° = 0;
m=0
3
n = 3, ^sin [270°m -f 0(ra)] = sin0°+ sin 540°+ sin 540°4- sin 180° = 0.
m=0
Таким образом условие (12.2.6) для сигнала Г = {1,1,1, -1} соблюда¬
ется. Расчеты показывают, что амплитудные, а следовательно, и энерге¬
тические спектры кодов Баркера других размерностей везде равномерны,
за исключением точки т = 0 (табл. 12.2).
Нарушение равномерности энергетических спектров может быть легко
скомпенсировано. Результаты такого преобразования кодов Баркера при-
Таблица 12.2
к
Код Баркера в цифровом виде
Амплитудный спектр
3
{1, 2, 2}
5
{1,1,1,-1,1}
{3, 2, 2, 2, 2}
7
{1, 1, 1, -1, -1, 1, -1}
{1; 2,83; 2,83; 2,83; 2,83; 2,83; 2,83}
11
{1, 1, 1, -1, -1, -1, 1, -1,
-1,1, -1}
{1; 3,46; 3,46; 3,46; 3,46; 3,46; 3,46;
3,46; 3,46; 3,46; 3,46}
13
{1, 1, 1, 1, 1, -1, -1, 1, 1, -1,
1, -1, 1}
{5; 3,46; 3,46; 3,46; 3,46; 3,46; 3,46;
3,46; 3,46; 3,46; 3,46; 3,46; 3,46}
Таблица 12.3
к
Вещественный сигнал
Амплитудный спектр
3
{1,33; 1,33; -0,67}
{2, 2, 2, 2}
5
{0,8; 0,8; 0,8; -1,2; 0,8}
{2, 2, 2, 2, 2, 2}
7
{1,26; 1,26; 1,26; -0,74; -0,74;
1,26; -0,74}
{2,83; 2,83; 2,83; 2,83; 2,83; 2,83;
2,83}
11
{1,405; 1,405; 1,405; -0,595;
-0,595; -0,595; 1,405; —0,595;
-0,595; 1,405; -0,595}
{3,46; 3,46; 3,46; 3,46; 3,46; 3,46;
3,46; 3,46; 3,46; 3,46; 3,46}
13
{0,882; 0,882; 0,882; 0,882; 0,882;
-1,118; -1,118; 0,882; 0,882;
-1,118; 0,882; -1,118; 0,882}
{3,46; 3,46; 3,46; 3,46; 3,46; 3,46;
3,46; 3,46; 3,46; 3,46; 3,46; 3,46;
3,46}
486
Гл. 12. Композиционные контуры
ведены в табл. 12.3. Все полученные таким образом вещественные сигналы
обладают РЭС.
На основе этих кодов могут быть получены ФМ сигналы. Однако
по сравнению с представляющими практический интерес сигналами,
здесь синусоиды в отдельных кодовых интервалах могут иметь разные
амплитуды. В результате пик-фактор этих сигналов будет отличаться
от единицы, что усложняет их практическое использование.
12.2.3. Алфавит кодовых последовательностей с РЭС в виде ком¬
позиционных контуров из полного семейства элементарных контуров.
Пусть А5 = {as {r)}Q fc_i, s = 0,1,... ,fc — 1, произвольные кодовые
последовательности, входящие в состав композиционной кодовой по¬
следовательности Γαο,Αι, = {A5}0)fc_i = {a(n)}0 k2_v Через
as (г), г — 0,1,... ,k - 1, обозначены ЭВ последовательностей As,
а через а (η), п = 0,1,... , к2 — 1, эти же ЭВ, но уже в составе компози¬
ционной последовательности. Спектр последовательности As обозначим
как Рд5 = {pAs (m)}o,fc-r Найдем теперь выражение для спектра
Рг = {рг (га)}0 Д;2 1 композиционной последовательности. В общем
случае ДПФ последовательности А5 = {as (г)}0 к_1У s = 0,1,... , к — 1,
имеет вид
Д2 _ 1
рг (то) = а (п)ехр {г^тп\'
п—О
т = 0,1,... ,к2 - 1,
или в развернутом виде
рг (т) =
= а0 (0) 0 m+a0 (1) е~Ф1т +... +а0 (к - 1) е-ф(*-1)”*+
+αι (0) е~^к'т +ах (1) в-Ф<*+1),т+... +аг (к - 1) (fc_1+fc) т+
+ (0) + afc_i (1) e-i$№-i)+i]-m +
... + ак-1 (к - 1) е-^к{к-1)+к~1] т.
(12.2.7)
Данная сумма состоит из к строк и к столбцов. Рассмотрим в транс¬
понированном виде только один, s-й столбец:
с*о (я) e_ixsm + ах (s) е~^(°+к)™· + ... + (e) е-<[»+*(*-1)1"*.
(12.2.8)
Для выявления закономерностей экспоненту в каждом элементе запи¬
шем в виде произведения двух экспонент. Тогда выражение (12.2.8) примет
вид к-1
exp{_*^Sm}52ar («)ехр(-г^гт|,
г—О
122. Синтез последовательностей с РЭС
487
а компонента спектра композиционной последовательности будет равна
к-1 к-1 2
Рг(т) = ^ехр{—i^sm}^ar(s)exp{-i-^rm},
s=0 r=0 '
m = 0,1,... , к2 — 1.
Пусть теперь ЭВ последовательностей As, s = 0,1,— 1, обла¬
дают свойством эргодичности, т.е. as (г) = ar (s), г, s = 0,1,... , к — 1
(см. п. 2.2). Тогда внутренняя сумма в (12.2.9) есть m-я компонента спект¬
ра Ра8 (т) последовательности А5 и это выражение примет вид
к-1
Рг {т) = Σ Ра. (т) ехр (
s=0
т
0,1,... ,к2 - 1.
(12.2.10)
Рассмотрим случай, когда последовательности А5 образуют алфавит
сигналов, эффективных для решения задачи распознавания, т.е. их спек¬
тры не пересекаются, а объем алфавита составляет к. Данному условию
отвечают комплекснозначные последовательности в виде элементарных
контуров (см. п. 2.2).
Семейство ЭК можно задать ортогональной матрицей А = {7^ (п)}
порядка к, т-я строка которой состоит из ЭВ (п) контура Г5. В со¬
ответствии со свойством эргодичности матрица А будет симметрической.
Этой матрице можно сопоставить матрицу В = {{тп)к} индексов ЭВ
полного семейства ЭК, взятых по модулю к. Матрица В также имеет
порядок к и будет симметрической.
А =
В =
’ 7о (0)
7о (1) ·
.. 7o(fc-l) '
71 (0)
71 (1) ·
.. 71 (fc - 1)
-7fc-i (0)
7fc-i (!) ·
■ · 7fc-i (k ~ !)-
1 0
0
0
1 1
2
fc- 1
1 2
4
2 (fc — 1)
(12.2.11)
.0 к — 1 2(fc — 1) ... (fc — 1) (fc — 1)_
Например, для к = 4 (см. рис. 12.3, а) эти матрицы равны
”1
1 1 1 “
Ό
0
0
O'
1
i —1 —i
; В =
0
1
2
3
1
-1 1 -1
0
2
0
2
.1
—г —1 i
.0
3
2
1.
На основании того, что спектры ЭК разных порядков не пересекаются,
последнее выражение для спектра базового композиционного контура, по¬
лученного конкатенацией ЭК с последовательным возрастанием индексов,
488
Гуt. 12. Композиционные контуры
примет следующий вид:
Рг0,г1,...,г*_1 Μ =Ρβι (т) = (12212)
т — 0,1,... , к2 - 1.
Величина (т)к равна тому значению 5, 5 = 0,l,...,fc — 1, при кото¬
ром составляющая рт (га) ЭК Гт отлична от нуля. Из (12.2.12) следует,
что при ra = 0,fc,2fc,... , (к - 1) к компонента спектра базового контура
строго веществена и равна к. Отсюда же следует, что базовый контур
характеризуется РЭС вида {\р&1 (ттг)|2}Q fc2_i = {fc2}0 fc2_1 (рис. 12.3, г).
Из полного семейства ЭК размерности к можно составить fc! компо¬
зиционных контуров. Однако не все полученные таким образом контуры
pWj
p(Oj
p(s)a
4
4
4
4
t—i 1—ь.
, , ь.
1—b>
Г0
n in),
ip. |p(*)|2'
16
ZIL
—►
©
О 1 2
0123 1415 п
Рис. 12.3. Композиционный контур для к = 4: а — семейство элементарных кон¬
туров; 6 — энергетические спектры элементарных контуров; в — композиционный
контур Г0>1,2,з; 2 — энергетический спектр композиционного контура Го,1,2,3; д —
циклическая АКФ композиционного контура Го, 1,2,3
будут обладать РЭС. Поэтому необходимо определить, какие комбинации
из полного семейства ЭК образуют композиционные контуры с РЭС. Для
этого найдем связь ЭК, состоящего из ЭВ с кратным значением аргумента,
т.е. когда 7т (гп) = ехр| г—^mrnj, с ЭК, содержащими ЭВ, задаваемые
выражением (12.2.11). Из свойства эргодичности элементарных векторов ЭК
(см. п. 2.2), следует, что эти векторы для контуров порядка т с аргументами
кратности г образуют ЭК порядка {тг)к. Поэтому 5-я строка матрицы А,
5 = 2,3,... , fc — 1, задает ЭК Γχ с элементарными векторами кратности 5.
Свойство суммы, выражаемое (12.2.7) и заключающееся в том, что
каждый ее столбец задает выражение для спектра ЭК, будет сохраняться
12.2. Синтез последовательностей с РЭС
489
только при следующих строго определенных условиях, которым должна
соответствовать матрица В.
1. Симметричность матрицы А, а значит, и матрицы В. Только в этом
случае можно воспользоваться свойством эргодичности ЭК при преобра¬
зовании суммы (12.2.7). Данное условие выполняется при умножении ма¬
трицы В на любое целое число г. При этом сумма элементов 5-го столбца
в (12.2.7) будет равна спектру контура Г5 со сдвинутой начальной точкой.
В результате суммы всех столбцов станут нулевыми за исключением
одной суммы, по модулю равной к.
2. Матрицы А и В должны содержать элементарные векторы всех ЭК.
В них не должно быть повторяющихся строк или столбцов. В противном
случае в сумме (12.2.7) одни спектральные компоненты будут повторяться
несколько раз, а другие будут отсутствовать, т.е. нарушится равномер¬
ность энергетического спектра композиционного контура. Это произойдет
в том случае, если при умножении матрицы В на г возникнут строки
с одинаковой (по модулю к) кратностью, т.е.
где si и 52 — номера строк. Тогда а = г ($2 — s\)/ky г = 1,... , к — 1,
(s2 — si) = 1,... , к — 1. Для целых а, а = 0,1,... , к — 1, данное условие
может выполняться только в случае, если числа г и (s2 — si) содержат
множители, кратные к, т.е. не являются взаимно простыми с к. Следова¬
тельно, чтобы получить последовательность ЭВ композиционных контуров
с РЭС достаточно умножить матрицу В на число, взаимно простое с к,
и взять ее элементы по модулю к. Тогда для семейства ЭК размерностью к
существует φ {к) композиционных контуров с РЭС, где φ (х) — функция
Эйлера [198].
К аналогичным результатам приводит и другой подход. В матрице В
s-я строка задает элементарные векторы ЭК порядка s. Следовательно,
первая строка задает последовательность ЭК в базовом композиционном
контуре. Умножение первой строки на целое число г, г = 1,... ,к — 1,
или переход к строке с номером г даст последовательность чисел в данной
строке, задающую порядок следования ЭК в композиционном контуре, как
и при непосредственном умножении матрицы В на число г. Следовательно,
строки матрицы В, номера которых являются взаимно простыми с к чис¬
лами, задают последовательности ЭК в базовых композиционных контурах.
Найдем выражение для спектра любого из базовых контуров поряд¬
ка г. Так как такой контур состоит из ЭК, элементарные векторы которых
имеют аргументы кратности г, то выражение (12.2.10) примет вид
(rsi)fc = (rs2)k rsi +Oik — rs2,
Здесь prs (га) — компонента спектра ЭК порядка rs, равная
О для остальных a, s.
к при s = (т)как, а, s = 0,1,... , к — 1,
490
Гл. 12. Композиционные контуры
Отсюда следует, что в сумме (12.2.7) необходимо учитывать только нену¬
левые компоненты, которые получаются при целом s = [(га)*. + ak]/r, т.е.
pr{m) = fcexp{i||™[(m)fc + a:fc]]·, (12.2.14)
а = 0,1,... , к - 1, га = 0,1,... , к2 - 1.
Полученное выражение позволяет сделать следующие выводы о свой¬
ствах спектра композиционного контура.
1. Амплитудный и энергетический спектры равномерны
\р6(т)\ = к, \рб(т)\2 = к2, т = 0,1,... , к2 - 1.
2. Фазочастотный спектр в общем случае имеет вид
arg/96 (τη) = ту — [(τη)* + ак], т = 0,1,... , к2 - 1.
к г
Новые композиционные контуры на основе базовых можно получить,
проводя преобразования, не затрагивающие форму их энергетических
спектров. Преобразуя компоненты спектра по закону
Рвых (тп) = Рб (т) ■ ехр (тргт · к ■ d), (12.2.15)
получаем контуры со сдвинутой на d ЭК начальной точкой. Величина
d может изменяться в диапазоне 1,2,... ,к — 1. Следовательно, если
существует возможность фиксации момента поступления сигнала, то та¬
кой способ позволяет получить от каждого базового контура еще к — 1
композиционных контуров с равномерным энергетическим спектром.
Таким образом, алфавит содержит φ (к) к композиционных контуров
из полного семейства элементарных контуров с РЭС.
Найдем ВКФ базового контура Гб = Год,.. ,к-1 и контура со сдвигом
на d ЭК, т.е. контура Г^ = Γ^+ι^ . ,k-i+d· Если Рб (га), га = 0,1,...
... , к2 — 1, — компонента спектра базового контура, то соответствующая
компонента спектра контура Г^ с учетом выражения (12.2.15) равна
pf> (m) = рб (га) exp {i^-md\]
6 ' I к У (12.2.16)
га = 0,1,... , fc2 — 1, d= 1,2,... ,fc- 1.
ВКФ (s), s = 0,1,... , fc2 — 1, контуров первой группы Гб и Г^ свя¬
зана со взаимным энергетическим спектром этих контуров {рб(га) р^(га)}
преобразованием Фурье, т.е.
?7(<i) (s) = j? Σ Рь {m)pt (то) exp exp =
771=0
k2-l
= р Х]|Рб (то)|2 ехр (-г^т (Ы + s)|.
771=0
122. Синтез последовательностей с РЭС
491
Так как |рб (га)| =к,т = 0,1,... , к2 - 1 (см. (12.2.14)), то
к2-1
($) = exp г^га (kd + s) (12.2.17)
m=О
Данная сумма при любом s равна нулю, кроме значения s = к2 — kd
(рис. 12.4, а). При этом значении s-й отсчет ВКФ будет равен к2. Итак,
η(ά) (s)
1Г
при s = к2 — kd,
для остальных s.
(12.2.18)
Покажем теперь, что в отличие от ВКФ η(η),η = 0,1,... , к - 1,
элементарных контуров, ВКФ различных базовых контуров с РЭС не яв¬
ляется везде нулевой. Строки матрицы В, номера которых являются с к
взаимно простыми числами, задают комбинации ЭК в композиционном
контуре. Так как первым в композиционном контуре всегда будут ЭК ну-
16"
а 0 2 4 6 8 10 12 14 п
10 12 14
Рис. 12.4. Примеры ВКФ композиционных контуров: а — для контура Го,1,2,3
и Гг,3,0,1, полученного циклическим сдвигом контура Го,1,2,3; б — для контура
Го,1,2,3 и контура Гг,1,0,3, полученного циклическим сдвигом контура Го,3,2,1
левого порядка, ВКФ которых равна к, а ВКФ последующих ЭК равна О,
то по крайней мере один отсчет ВКФ двух базовых КК не будет ра¬
вен 0. Следовательно, в отличие от составляющих их ЭК композиционные
контуры не являются ортогональными (рис. 12.4, б). Так как при обработ¬
ке композиционных контуров предполагается использование циклической
свертки, то аналогичными взаимнокорреляционными свойствами будут
обладать и контуры, полученные путем сдвига начальной точки в базовых
композиционных контурах.
Следовательно, композиционные контуры, имея дельтовидную цикли¬
ческую АКФ и являясь оптимальными для решения задачи разрешения,
не являются таковыми для задачи распознавания. Решение данной задачи
возможно, например, при использовании структурного анализа компози¬
ционных контуров, основанного на свойстве ортогональности составляю¬
щих композиционные контуры ЭК.
12.2.4. Примеры синтеза кодовых последовательностей с РЭС в виде
композиционных контуров из полного семейства элементарных конту¬
ров. Рассмотрим базовый композиционный контур Год. В соответствии
с выражением (1.8.3) для ЭК и общим представлением для композицион¬
ного контура при к = 2 получаем: Г0д = {Гт}0 г = {1,1,1, -1}.
492
Гл. 12. Композиционные контуры
Вид контура Год совпадает с видом кода Баркера при к = 4. Компо¬
зиционные контуры с другими значениями к будут комплекснозначными.
Таким образом, данный код Баркера является частным случаем комплекс¬
нозначного композиционного контура с РЭС. Другим частным случаем
композиционных контуров с РЭС являются коды Фрэнка (см. п. 12.1).
В качестве примера получения алфавита композиционных контуров
с РЭС рассмотрим случай к = 9. Существует шесть чисел, взаимно про¬
стых с числом 9. Таким образом, для к = 9 имеем шесть базовых ком¬
позиционных контуров с РЭС. Записывая последовательность взаимно
простых с числом 9 чисел от 0 до 8, умножая эти числа на s = 1,2,4,5,7,8
и переходя к значениям по модулю 9, получаем конкретные комбинации
порядков ЭК, образующих базовые контуры с РЭС:
0,1,2,3,4,5,6,7,8; 0,5,1,6,2,7,3,8,4;
0,7,5,3,1,8,6,4,2; 0,4,8,3,7,2,6,1,5;
0,2,4, б, 8,1,3,5,7;
0,8,7, б, 5,4,3,2,1.
Осуществляя циклический сдвиг порядков ЭК в каждом из шести базо¬
вых контуров, получаем, что для к = 9 алфавит сигналов имеет размерность
54. На рис. 12.5 представлен базовый компо¬
зиционный контур Год,2,3,4,5,6,7,8·
С каждым из ЭК {Гт}0 k_v составляю¬
щих композиционный контур контур, можно
связать периодический процесс с некоторой
круговой частотой Ω (см. п. 2.2). Отсюда сле¬
дует, что базовый композиционный контур
Рис. 12.5. Базовый композици- Год,... ,*_ι, у которого порядки составляю-
онный контур Год,2,з,4,5,в,7,8 щих его ЭК последовательно возрастает от
О до к - 1, является аналогом дискретного
линейного У-образного ЧМ сигнала. Базовые композиционные контуры
характеризуются сложным законом смены частоты составляющих
их ЭК. Поэтому они задают ЧМ колебания с более сложным, чем
линейный, законом девиации. Например ступенчатый ЧМ сигнал при
к = 9, у которого при смене ступеньки из к кодовых интервалов частота
меняется по закону 0, 5, 1, б, 2, 3, 8, 4 (базовый контур Г0,5д,6,2,з,8,4)
будет обладать РЭС и при соответствующем алгоритме может быть
сжат без боковых лепестков.
12.3. Обработка кодовых последовательностей с равномерным
энергетическим спектром
В предыдущих разделах было показано, что для получения идеаль¬
ной разрешающей способности по дальности кодирующая последователь¬
ность сложного зондирующего сигнала должна иметь РЭС. Обработка сигна¬
ла должна выполняться циклическим согласованным фильтром в момент
совпадения положений сигнала и окна фильтра. Невыполнение этих
условий для существующих сигналов и систем их обработки приводит
к возникновению боковых лепестков.
12.3. Обработка кодовых последовательностей с РЭС
493
В данном разделе рассматриваются методы обработки кодовых по¬
следовательностей с РЭС на базе композиционных контуров из полного
семейства ЭК, позволяющие реализовать эффект идеального разрешения.
12.3.1. Согласованная фильтрация комплекснозначных контуров
с РЭС. Устройством, формирующим смещенную АКФ сигнала, явля¬
ется согласованный фильтр. В общем случае для контура, обладающего
спектром р (га), га = 0,1,... ,k — 1, частотный коэффициент передачи
контурного согласованного фильтра равен (см. п. 3.6.1)
ω (га) = р* (га) ехр |г~^га|, га = 0,1,... , к — 1.
Если фильтр согласован с базовым композиционным контуром, то
ω (га) = А; ехр |z^ra[(ra)fc + 1]|, га = 0,1,... , к2 — 1. (12.3.1)
Отсюда видно, что АЧХ фильтра является равномерной, т.е.
\ω (га)| = fc, га = 0,1,... , fc2 — 1. (12.3.2)
Спектр выходного сигнала при согласованной фильтрации базового
композиционного контура
Рвых (rn) = ω (га) рб (га) = |рб (га)|2 exp {г^га} = ехР {^ш}>
га = 0,1,... ,к2 -1. (12.3.3)
Видно, что амплитудно-частотный спектр выходного контура остает¬
ся равномерным, а отсчеты фазочастотного спектра линейно нарастают
arg ω(τη) а
2 π
Рис. 12.6. Амлитудно-частотная и фазо-частотная характеристика фильтра, со¬
гласованного С баЗОВЫМ КОМПОЗИЦИОННЫМ КОНТУРОМ Год,... Д-1
в пределах от 0 до 2π с шагом 2π/к2 (рис. 12.6). Выходной контур, опре¬
деленный с помощью обратного ДПФ от спектра (12.3.3), равен
Ас — 1
η (п) = ^2 Σ Рвых (т) ехР т'я} =
7П=0
к2-1
= ^2 ехр ехр {j~^m ■п}=
т=0
= Σ βχρ {г5т +*)}= (?■
т=0 * I*'
О при η = 0,1,... , к2 — 2,
2 при η = /с2 — 1.
(12.3.4)
494
Гл. 12. Композиционные контуры
Таким образом, контур на выходе согласованного фильтра при об¬
работке базового композиционного контура имеет уникальный вид: все
его ЭВ равны нулю, кроме последнего, величина которого равна энергии
16
б 0123* · -1415η
Рис. 12.7. Согласованная фильтрация базового композиционного контура: а — вид
контура Го.1,2,3; б — выходной сигнал согласованного фильтра
фильтруемого контура (рис. 12.7). В отличие от кодов Баркера, псевдослу¬
чайных ФМ последовательностей и др., сигнал в виде базового компози¬
ционного контура не имеет боковых лепестков при любом значении к, т.е.
допускает идеальное сжатие и концентрирует всю энергию в пределах
одного кодового интервала.
Если через фильтр, согласованный с базовым контуром, проходит про¬
извольный контур N = {и (п)}0 k2_i, имеющий спектр {р (га)}0 к2_г, то
спектр выходного контура и сам выходной контур Hm = {qm (п)}0 к2_±
будут соответственно равны
Рвых (ш) = кр (га) exp |г^га[(га)*. + 1]|, т = 0,1,... , к2 - 1,
(12.3.5)
к2-1
v(n) = Ь Σ р ехр {*ргт[(т)л + !]} ехР (ipf™' п} =
т—О
1 fc2_1 2π
= р Σ Р (т)ехр {*|?m[(m)fc + п + !]}. П = 0,1,... , *2 - 1.
т=О
(12.3.6)
Как следует из (12.3.5), при фильтрации несогласованного сигнала
амплитудно-частотный спектр выходного сигнала, равный кр(т), т =
= 0,1,... , к2 — 1, является функцией т, т.е. в общем случае перестает
быть равномерным. Следствием этого является неравенство значений
выходного сигнала η (η) нулю при п = 0,1,... , к2 — 2, т.е. появляются
не равные нулю боковые лепестки.
Как показано в разделе 4.3, для идеального разрешения сигналов
должны выполняться условия согласования фильтра с сигналом, ци¬
клический характер обработки сигнала и равномерность спектра сигна¬
ла на выходе устройства обработки. Выполнение последнего условия
обеспечивается равномерностью энергетического спектра композицион¬
ных контуров и применением согласованных фильтров, а выполнение пер¬
вых двух условий — использованием процедур обработки, позволяющих
12.3. Обработка кодовых последовательностей с РЭС
495
получить результат эквивалентный циклической фильтрации принятого
сигнала, в частности за счет применения алгоритма ЧКШС (см. п. 4.3.4).
Структура устройства обработки сигнала в канале дальности, ре¬
ализующего алгоритм ЧКШС, показана на рис. 12.8. Сигнал с выхода
ациклического фильтра сохраняется в запоминающем устройстве ЗУ
и одновременно подается на вход решающего устройства для принятия
Рис. 12.8. Структура устройства обработки сигналов в канале дальности с исполь¬
зованием алгоритма ЧКШС
решения об обнаружении. В случае положительного решения блок управ¬
ления разрешает прохождение запомненных выходных сигналов ацикли¬
ческого фильтра на сумматор и устройство задержки на время k2lAt.
Второй вход сумматора связан с выходом этого устройства.
Обычно решение об обнаружении принимается в момент получения
пикового отсчета сигнала. Этот отсчет отстоит на к2 кодовых интервалов
от первого отсчета ациклического фильтра, с которого начинает работать
алгоритм ЧКШС. Поэтому блок управления по сигналу обнаружителя
выдает на вход линии задержки и сумматора из ЗУ необходимый массив
выходных отсчетов ациклического фильтра, который назовем локусом.
Обычно локус содержит порядка 2к2 выходных отсчетов фильтра, со¬
ответствующих одиночной цели. Если имеется априорная информация
о том, что возможно обнаружение перекрывающихся целей, то в зависи¬
мости от количества целей блок управления увеличивает размер локуса
в несколько раз.
Таким образом, дополнительная обработка сигнала по алгоритму ЧКШС
не приводит к разрушению традиционно применяемых в канале дальности
РЛС структур, а является совместимой с ними. Возрастание трудоемкости,
обусловленное применением алгоритма ЧКШС, является крайне незначи¬
тельным. На каждый отсчет выходного сигнала дополнительно требует¬
ся только одна операция комплексного сложения. Плата за получение
эффекта идеального разрешения по дальности заключается в ухудше¬
нии отношения сигнал/шум на выходе из-за необходимости суммировать
несколько зашумленных выходных отсчетов ациклического фильтра. Од¬
нако это не приводит к снижению эффективности работы обнаружителя,
так как суммирование отсчетов происходит не в канале обнаружения,
а в канале разрешения. В результате в этом канале создается допол¬
нительный шумовой фон, причем он тем выше, чем больше относите ль-
496
Гл. 12. Композиционные контуры
ная протяженность локуса, определяемая отношением его длительности
к размерности к2 сигнала. Этот фон, как и ненулевые боковые лепестки
сжатого сигнала, приводят, в конечном счете, к маскировке слабого сиг¬
нала от находящейся рядом цели с малой ЭПР. В связи с этим возникает
задача определения порогового отношения ЭПР перекрывающихся целей,
при котором целесообразно применение алгоритма ЧКШС.
12.3.2. Примеры разрешения целей по дальности при использовании
алгоритма ЧКШС и кодирующих последовательностей в виде компози¬
ционных контуров. Операции ациклической согласованной фильтрации,
а также через-А:2-шагового суммирования являются линейными. Поэтому
обработка композиционных контуров в соответствии с данными алгоритма¬
ми при отсутствии шумов обеспечивает формирование по одному ненуле¬
вому отсчету для каждого из перекрывающихся эхо-сигналов с сохране¬
нием масштабных соотношений.
При перекрытии эхо-сигналов от нескольких целей суммарный сигнал
на входе устройства обработки имеет более чем к2} а выходная функция
ациклического фильтра — более 2к2 —
- 1 отсчетов. Поэтому при использо¬
вании алгоритма ЧКШС приходится
суммировать больше двух слагаемых,
причем каждый отсчет в локусе ис¬
пользуется только один раз.
Пусть, например, три контурных
сигнала Год с масштабами один, два
и три расположены таким образом,
что три последних отсчета перво¬
го перекрываются с тремя первыми
отсчетами второго, а два последних
отсчета второго — с двумя первыми
отсчетами третьего (рис. 12.9). Сум¬
марный контурный сигнал ΝΣ и ре¬
зультат ациклической согласованной
фильтрации НАЦ имеют соответствен¬
но вид: Νς = {1,3,3,4,1,3, -3},
НАц = {-1,-2,1,3,9,5,11,1,0,-3}.
По виду дискретной последова¬
тельности Над достаточно сложно
принять правильное решение о том,
что имеются три сигнала, как они
расположены относительно друг друга
и каковы их масштабы. Применение
алгоритма ЧКШС для к2 — 4 дает следующие результаты: η (0) = 771 +
+ Т75+779 = — 1 + 9 + 0 = 8, 77 (1) = т]2 + щ + 7710 = — 2 + 5 — 3 = 0,
η (2) = 77з + η7 = 1 + 11 = 12, η (3) = щ + щ = 3 + 1 = 4.
Таким образом, Нц = {8,0,4,12} (рис. 12.9, е). Отсчеты, 77(0), 77(1)
и 77 (2) дают четкое представление о взаимном положении и масштабах
„ ГГ11111-11
л I 2 | 2 | 2 1-2 |
« I з I з 1 з |-з |
,Ji Iз 1 з 141 и31-31
11
9
5
3|
l_L
_J|
-2
121
Рис. 12.9. Разрешение трех перекры¬
вающихся сигналов Год с разными
амплитудами: а, б, в — исходные сиг¬
налы; г — суммарный сигнал (локус);
д — результат ациклической согла¬
сованной фильтрации, е — результат
обработки по алгоритму ЧКШС
12.3. Обработка кодовых последовательностей с РЭС
497
входных сигналов: сигнал с единичным масштабом отстает на один дис¬
крет от сигналов с масштабами два и три.
Рассмотрим более сложный случай, когда при перекрытии двух эхо-
сигналов процедура сжатия этих сигналов ациклическим согласованным
фильтром приводит даже при нулевых шумах к полной маскировке пико¬
вого отсчета одного сигнала боковыми лепестками другого. Пусть с пара¬
метром j — 7 перекрываются два сигнала в виде базовых композиционных
контуров Го,ι,2 с масштабами 1 и 5 (рис. 12.10). Пиковый отсчет ацикли¬
ческого фильтра, соответствующий первому сигналу, является по номеру
cn
СП
СП
тГ
»п
П
•П
in
4*
»Пл
Cjf
ιή
Г|Г
η
in
Cjf
44
4
■ 1 I - I I . 1 II I I I 1 1 1 1 I I .и _ J
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 161718 1920212223 24 25 т
45
9
г
Ϊ 23 45 6 789 т
Рис. 12.10. Обработка двух перекрывающихся разномасштабных сигналов, зада¬
ваемых контуром Го, 1,2: а — первый сигнал; 6 — второй сигнал; в — модули
выходных сигналов ациклического фильтра; г — результат применения алгоритма
ЧКШС
десятым и равен 4. Пиковый отсчет для второго сигнала имеет номер 17
и равен 44. Энергия первого сигнала равна 9, однако из-за маскировки
его боковым лепестком второго, величина пикового отсчета уменьшается
более, чем в два раза. В результате этот пиковый отсчет превышается
боковыми лепестками второго сигнала в 11 точках из 23 (рис. 12.10, б).
Поэтому обнаружить первый сигнал по данной выборке отсчетов ацикли¬
ческого фильтра непросто. В то же время алгоритм ЧКШС при к2 =
= 9, используя комплекснозначные отсчеты фильтра, дает однозначно
интерпретируемый результат (рис. 12.10, г): {9,0,0,0,0,0,0,45,0}.
На рис. 12.11 и рис. 12.12 представлены результаты комплексной обра¬
ботки зондирующих фазокодированных сигналов. Рис. 12.11 иллюстрирует
498
Гл. 12. Композиционные контуры
б
') ΓνΎνι,τγγγνΥϊνϊνν^
Рис. 12.11. Пример обработки сигнала Фрэнка с эффектом идеального сжатия:
а — исходный фазокодированный сигнал Фрэнка; б — амплитудно-частотный
спектр исходного фазокодированного сигнала; в — амплитуда сигнала на выхо¬
де амплитудно-фазового детектора; г — фаза сигнала на выходе амплитудно¬
фазового детектора; д — контур, сформированный по результатам амплитудно¬
фазового детектирования е — результат ациклической согласованной фильтрации
контура; ж — результат обработки отклика ациклического фильтра по алгоритму
ЧКШС
результаты обработки одиночного сигнала Фрэнка, полученного на основе
базового композиционного контура Год,2,з,4· Для формирования по приня¬
тому фазокодированному сигналу кода композиционного контура исполь¬
зуется амплитудно-фазовый детектор. Полученные с его выхода отсчеты
(рис. 12.11, в, г, б) подвергаются ациклической согласованной фильтрации.
Боковые лепестки при этом сохраняются, что создает опасность маскиро¬
вания одного сигнала другим (рис. 12.11, е). Применение алгоритма ЧКШС
позволяет полностью подавить боковые лепестки и достичь идеального
сжатия сигнала (рис. 12.11, ж).
Обработка кодовых последовательностей с РЭС
I—^yJ^~^rW^Vt^V^Trnmm—
lLLLL
>
Рис. 12.12. Обработка трех пересекающихся фазокодированных сигналов: а — вза¬
имное расположение сигналов; б — суммарный сигнал на входе амплитудно-фа¬
зового детектора; в — амплитудный спектр суммарного сигнала; г — амплитуда
сигнала на выходе амплитудно-фазового детектора; д — фаза сигнала на выходе
амплитудно-фазового детектора; е — контур, сформированный по результатам
амплитудно-фазового детектирования; ж — амплитудный и фазовый спектры
контура; з — результат ациклической согласованной фильтрации контура; и —
результат обработки отклика ациклического фильтра по алгоритму ЧКШС
500
Гл. 12. Композиционные контуры
На рис. 12.12 приведены диаграммы обработки трех пересекающихся во
времени фазокодированных сигналов. На вход амплитудно-фазового детек¬
тора поступает суммарный сигнал, по которому сложно непосредственно
определить количество и взаимный сдвиг сигналов (рис. 12.12, б). После
амплитудно-фазового детектирования (рис. 12.12, г, д, е) и ациклической со¬
гласованной фильтрации возникают боковые лепестки, способные замаски¬
ровать отклик от цели с малой ЭПР (рис. 12.12, з). В результате применения
алгоритма ЧКШС боковые лепестки оказываются полностью подавленными
и достигается эффект идеального разрешения сигналов (рис. 12.12, и).
До сих пор предполагалось, что кодовые интервалы эхо-сигнала сов¬
падают с положением окна фильтра (рис. 12.13, в, г). В действительно-
п
б · · · · · » · ·-►
п
е.-^ л ζ:.. 1
г « ■ 1 1 .
э. .Г. 7 J »
«» ΙΓ^-Ι»
Рис. 12.13. Взаимное положение эхо-сигнала и окна фильтра: а — тактовые им¬
пульсы в канале дальности; б — положения кодовых интервалов зондирующего
сигнала; в, г — взаимное положение эхо-сигнала и окна фильтра при совпадении
элементов окна с границами кодовых интервалов; д, е — произвольное располо¬
жение сигнала и окна фильтра
сти расположение окна относительно эхо-сигнала является произвольным
(рис. 12.13, д, е). В связи с этим рассмотрим на примере сигнала Год как
сказывается такая ситуация на результате работы алгоритма ЧКШС. Для
простоты предполагаем установку положения эхо-сигнала с точностью
периода тактового генератора.
Пусть, например, продолжительность кодового интервала равна четы¬
рем периодам At тактового генератора, т.е. I = 4. Тогда кодовая последо¬
вательность сигнала Год запишется в виде
{1,1,1,1, /1,1,1,1/1,1,1,1/ - 1, -1, -1, -1}
а результат ациклической фильтрации будет равен
Нац = {-1, -2, -3, -4, -3, -2, -1, -0,1,2,3,4,7,
10,13,16,13,10,7,4,3,2,1,0, -1, -2, -3, -4, -3, -2, -1}.
Суммирование этой последовательности с шагом Ik2 = 16 дает следую¬
щий результат (рис. 12.14): Нц = {12,8,4,0,0,0,0,0,0,0,0,0,4,8,12,16}.
>
п
п
п
п
12.4. Фильтровая версия алгоритма ЧКШС
501
Таким образом, произвольное положение эхо-сигнала по дальности
привело к размыванию главного максимума выходного сигнала (график
1 2 3 4 5 6 7 8 9 101112 1314 151617 18 1920 п
I 1-й | 2-й | 3-й | 4-й |
Кодовые интервалы
Рис. 12.14. Результат обработки сигнала Год при делении кодового интервала на
четыре части
на рис. 12.14), но в пределах одного кодового интервала. Как и следовало
ожидать, увеличение количества дискретов позволило более точно по¬
строить корреляционную функцию сигнала, состоящую из одного главного
лепестка и с нулевыми боковыми лепестками, т.е. эффект идеального
разрешения по дальности сохраняется.
12.4. Фильтровая версия алгоритма ЧКШС
12.4.1. Фильтр ЧКШС. Устройство, реализующее алгоритм через-
к2-шагового суммирования (рис. 12.15), можно рассматривать как фильтр.
На его вход поступает сигнал НАц =
= {ηη}ιυ, где ν — размерность
этого сигнала, а на выходе образу¬
ется сигнал X = {хт} 1 k2- Размер¬
ность выходного сигнала равна к2.
Для выяснения механизма рабо¬
ты фильтра ЧКШС определим виды
преобразований, которым подверга-
Рис. 12.15. Фильтр ЧКШС
ется выходная последовательность НАц = {ηn}lv и ее спектр РАц =
= {pm} 1 υ, получим выражение, связывающее сигналы НАц и X, а также
частотный коэффициент передачи фильтра.
Пусть к2 — размерность зондирующего сигнала, равная количеству
составляющих его кодовых интервалов. Последовательность h отсчетов
из нескольких перекрывающихся эхо-сигналов на входе ациклического
согласованного фильтра ранее мы определили как локус. Обозначим ее
через Е = {ε(™)}0η_ι· Если перекрываются г эхо-сигналов с парамет¬
рами juj2, ·· · Jr-'l, то
1—1
h = k2 + Y2in. (12.4.1)
n=1
Параметр jn отсчитывается по положению η-го эхо-сигнала относи¬
тельно (п — 1)-го эхо-сигнала. После циклической фильтрации локуса
502
Га. 12. Композиционные контуры
образуется последовательность из I отсчетов. При этом надо иметь ввиду,
что фильтр согласован не со всем локусом, а только с сигналом, повто¬
ряющим по форме эхо-сигнал. Когда фильтруется одиночный эхо-сигнал,
то I = 2к2 — 1. Если же локус образован г перекрывающимися сигналами
с параметрами л, J2, · · · , jr-i, то
г —1
l = 2k2+ (12.4.2)
п=1
Введем понятие окна фильтра ЧКШС, состоящего из s элементов.
Величина s равна количеству суммируемых элементов из / выходных
отсчетов фильтра, необходимых для получения одного выходного отсчета.
Так как складываются отсчеты, взятые через к2 шагов, то
s — ]1/к2 [, (12.4.3)
где )х\ — ближайшее целое число, большее чем х.
Из регулярности алгоритма ЧКШС, т.е. из того, что все время необ¬
ходимо находить сумму из s выходных отсчетов ациклического фильтра,
вытекает необходимость дополнения I выходных отсчетов последователь¬
ностью нулей (вначале или в конце), так чтобы общая длина последова¬
тельности на выходе фильтра ЧКШС была равна
V = sk2 = к2]1/к2[. (12.4.4)
Например если три эхо-сигнала в виде композиционных контуров Год
с масштабами 1, 2 и 3 перекрываются с параметрами ji = 1, j2 = 2, то
образующийся локус будет равен (см.рис. 12.9)
E = {e(n)}0te = {1,3,3,4,1,1,3,-1}.
После ациклической фильтрации этого локуса получаем следующий мас¬
сив выходных отсчетов НАц = {Vn}i ю — {—1, —2,1,3,9,5,11,1,0, —3}.
При этом
г—1
I = 2к2 - 1 + Σ jn = 2 · 4 - 1 + 1 + 2 = 10,
n= 1
а ширина окна фильтра ЧКШС будет s =]l/k2[=] 10/4[= 3.
Тогда в соответствии с (12.4.4) длина входной последовательности филь¬
тра ЧКШС будет v = sk2 = 3 · 4 = 12, а сама последовательность равна
{-1,-2,1,3,9,5,11,1,0, -3,0,0}.
12.4.2. Аналитическое представление алгоритма ЧКШС. Фильтр
ЧКШС для получения одного выходного отсчета образует массив вход¬
ных данных путем извлечения из модифицированной последовательности
отсчетов Ндцмод = {?7мод (n)}o v-i кажДОпэ к2-то отсчета, т.е. это фильтр
с расщепленной апертурой. Если длина входного массива υ = sk2, то
окно фильтра содержит s отсчетов. Выходной отсчет фильтра ЧКШС
12.4. Фильтровая версия алгоритма ЧКШС
503
образуется следующим образом:
s-l
х(т) = Х)г7мод(т + к2п), то = 0,1,... , к2 s — 1. (12.4.5)
п=0
Фильтруемый сигнал НдцМод имеет размерность v = sk2, а выходной
сигнал X — размерность к2. При таком соотношении размерностей дискрет¬
ных сигналов нельзя сравнивать их спектры. Для уравнивания размерностей
сигналов предположим, что входной сигнал периодичен, т.е. что
»7мод (η) = ηΆ0Λ (п + ask2), а — целое число. (12.4.6)
Результатом такой редукции входного массива будет равенство вход¬
ных и выходных векторов фильтра и, кроме того, периодичность значений
выходного вектора X:
X (т) = X {т + оск2), а = 1,2,... , (s - 1) к2.
С учетом выражения (12.4.5) в общем случае получаем, что выходной
сигнал X равен сумме υ — sk2 входных сигналов Ндц* о^д со смещенными
относительно друг друга начальными точками, т.е.
Y Г \ TLT | Tl(k2) I хт(2^2) I I Tj((s~l)k2)
Л — \Хт/ΐ,υ-1 — "Г ПАЦ мод + ПАЦ мод ^ ^АЦ мод “
= Σ,ΗΆ· {12·4·7)
п=О
Например, для сигнала Γ0>ι к2 = 4, s = 2, модифицированные после¬
довательности отсчетов ациклического фильтра равны
НАц мод = 1,4,1,0,-1,0},
HillMO„ = {l,0,-l,0,-l,0,l,4}.
Суммируя почленно эти последовательности, получим
х = Нац мод + H<g мод = {0,0,0,4,0,0,0,4}.
12.4.3. Частотные и временные характеристики фильтра ЧКШС.
Определим частотный коэффициент передачи ft = {ω(τη)}0υ-ι филь¬
тра ЧКШС. Для этого найдем отношение спектров выходного и входного
сигналов. Из выражения (12.4.7) следует, что выходной сигнал есть сумма
входных сигналов со сдвинутыми начальными точками. В этом случае
спектр рх (т), т — 0,1,... ,υ — 1, определяется как сумма спектров ис¬
ходных последовательностей, взятых с экспоненциальными весами, опре¬
деляемыми параметрами сдвига, т.е.
S—1 5—1
рх (ш) = ρη (т) exp i г-^тпк2 \ = ρη (т) ехр \ г—тп >,
ηΞο L sk J n=о 1 s J
m — 0,1,... , sk2 — 1.
504
Гл. 12. Композиционные контуры
Тогда выражение для частотного коэффициента передачи будет равно
s — 1
ω (т) — Рх exp \г—тп\, т = 0,1,... , sk2 — 1. (12.4.8)
РчМ ^ I а У
п=1)
Данное выражение представляет собой сумму s членов геометриче¬
ской прогрессии с равным единице начальным членом и знаменателем
ехр Поэтому
ω(τη)= m = 0,1,... , sk2 — 1.
1 — ехр < г—т >
В результате выражение для АЧХ рассматриваемого фильтра при¬
мет вид
при т = as, a = 0,1,... , к2 — 1,
для остальных га.
Отсюда видно, что фильтр ЧКШС имеет к2 линий прозрачности, от¬
стоящих друг от друга на s дискрет (рис. 12.16).
\ω (га)|
(12.4.9)
»(и)|
|t0(m)|i
, ? О
k.
A2 =4
J
t =4 J
5 = 2
S — 3
—4 b>
1 b.
Рис. 12.16. АЧХ фильтров ЧКШС для сигнала Год: s = 2 (a); s = 3 (б)
В пределах каждой линии прозрачности модуль Ω равен 5. Общая
полоса пропускания фильтра состоит из к2 линий и не зависит от ширины
окна 5, т.е. Δ/ — к2 — const.
Определим теперь ИХ Л = {A (η)}0 ν_1 фильтра. Учитывая, что ИХ
и частотный коэффициент передачи линейного четырехполюсника связа¬
ны между собой преобразованиями Фурье, получаем
^ sk2 — 1 2
λ (η) = —j ω (m) exP I ^-ran >, η = 0,1,... , s/г2 — 1.
sk _ t sk 1
m=0
В соответствии с выражением (12.4.9) А:2 значений о;(га), га = 0, s,
2s,... , (А:2 — 1)5, равны 5, а все остальные — нулю. Поэтому выражение
для А (гг) можно записать в виде
λ (гг) = ~2 [1 + ехр + ехр (z-^-2ras| -+-.··
sA: L L sk 1 t sk J 2 •• · · + exp (k2 - X) sn}] = pf Σ exP {^mn}·
12А. Фильтровая версия алгоритма ЧКШС
505
λ(η)
t ^ л Цп)\
\ к =4
к
s=2
■ > ■ ►
к2 =4
s = 3
Рис. 12.17. ИХ фильтра ЧКШС для сигнала Год: s — 2 (a); s = 3 (б)
Полученная сумма не будет равна нулю лишь в тех случаях, когда
аргумент экспоненты равен 2πα. Поэтому
\ ( \ _ (1 ПРИ п = 2&2, · · · , (« — l)fc2,
λ\η) — \ ^
^0 для остальных п.
Отсюда следует, что ИХ фильтра состоит из 5 единичных значений
на позициях п = 0, fc2,2к2,... , (s — 1) к2 (рис. 12.17).
12.4.4. Механизм работы фильтра ЧКШС. Механизм работы филь¬
тра ЧКШС с частотной точки зрения поясним на примере обработки сиг¬
нала на базе композиционного контура Год (рис. 12.18). Пространственное
Год }
1
1
1
1
3 >
а 0
1
2
.!■
4
0
X1!
h
V 6 V Ь
в 1
-1
1 2 :
\ 4
X 1 Л W
5_[ 7 п
<у(т)| 2
2
2
2
К\ 1111.
б
0
1
2
3
т
|р 1 6,9
\^АЦ 1
6,9
4
4
4
4
1,17
I
1,17
|
2 (
) 1
1 2
> 3 1
\ 5 (
1 т
00
8
8
8
ι-х-1 х 1 х X►
01234567»!
X Г-Х 1 X 1 X»
0 1 2 3 4 5 6 7»!
Рис. 12.18. Соотношения для сигналов при последовательном прохождении аци¬
клического и ЧКШС фильтров: а — входной сигнал Год; б — амплитудный спектр
сигнала Г0д; в — выходной сигнал ациклического фильтра; г — спектр сигнала
на выходе ациклического фильтра; д — АЧХ фильтра ЧКШС для s = 2 и к2 = 4;
е — спектр сигнала на выходе фильтра ЧКШС
представление этого сигнала, его спектр Рг0д и модуль спектра |Pr0)i|,
а также результат ациклической согласованной фильтрации НАц равны
(см. рис. 12.18, а, б, в)
Год = {1,1,1, -1}, РГ<М = {2; —2*; 2; 2г},
|Рг0д| = {2; 2; 2; 2}, НАЦ = {-1,0,1,4,1,0,-1,0}.
(12.4.10)
506
Гл. 12. Композиционные контуры
Спектр РнАц и модуль спектра |РнАц| выходной последовательности
ациклического фильтра равны (рис. 12.18, г)
РНац = {4; -4,828 - 4,828г; 4г; 0,828 - 0,828г;
- 4; 0,828 + 0,828г; -4г; -4,828 + 4,828г}, (12.4.ц)
|Рндц I = {4; 6,828; 4; 1,171; 4; 1,171; 4; 6,828}.
Сравнивая выражения (12.4.10) и (12.4.11), видим, что компоненты ам¬
плитудного спектра входного сигнала совпадают с квадратом значений
четных элементов амплитудного спектра выходной последовательности
фильтра. Известно, что при согласованной фильтрации именно такая за¬
висимость наблюдается между амплитудными спектрами входного и вы¬
ходного сигнала фильтра. Таким образом, в спектре выходного сигна¬
ла ациклического фильтра имеются все необходимые для согласованной
фильтрации компоненты, но результирующий эффект страдает из-за на¬
личия ненулевых нечетных компонент в спектре.
В АЧХ фильтра для данного случая линии прозрачности строго соот¬
ветствуют четным значениям т (рис. 12.18, б). На выход фильтра прохо¬
дят только четные компоненты спектра выходных отсчетов ациклического
фильтра (рис. 12.18, е). Сравнивая спектры |Рг0>1| входного сигнала Год
и |Ρλ| выходного сигнала X фильтра, видим, что получен эффект, харак¬
терный для второй фазы циклической согласованной фильтрации.
Таким образом, механизм работы фильтра ЧКШС состоит в режекции
компонент спектра выходного сигнала ациклического фильтра, искажаю¬
щих процесс согласованной фильтрации входного сигнала с РЭС.
12.5. Эффективность алгоритма ЧКШС при разрешении
сигналов от целей с различными ЭПР
Применение алгоритма ЧКШС позволяет полностью устранить влияние
корреляционного шума, но приводит к увеличению уровня флуктуационных
шумов. В связи с этим возникает задача определения порогового отношения
ЭПР перекрывающихся целей, при котором целесообразно применение ал¬
горитма. Если рассматривать задачу разрешения как задачу обнаружения
одного сигнала на фоне других, то в этом случае необходимо определить,
при каком отношении сигнал/шум алгоритм ЧКШС обеспечивает более вы¬
сокую, по сравнению с ациклическими алгоритмами обработки, вероятность
правильного обнаружения при фиксированной вероятности ложной тревоги.
Задача разрешения сигналов от целей с малой ЭПР на фоне сигна¬
лов от целей с большой ЭПР ставится следующим образом. Необходимо
принять обоснованное решение об обнаружении сигнала от цели с малой
ЭПР при наличии на входе белого гауссовского шума с нулевым матема¬
тическим ожиданием и сигнала от цели с большой ЭПР. При этом рассто¬
яние между сигналами составляет не менее одного кодового интервала.
Для решения задачи будем руководствоваться критерием оптимальности
Неймана-Пирсона, обеспечивающим максимум вероятности правильного
обнаружения D при фиксированной вероятности ложной тревоги F.
12.5. Эффективность алгоритма ЧКШС
507
В случае полностью известного сигнала на входе фильтра имеется
шум с дисперсией σΒΧ и отношение сигнал/шум на выходе фильтра при
наличии на его входе только одного сигнала составит ςψ = ||Γ||/σΒΧ.
Вероятность ложной тревоги в этом случае составит F = 1 — Ф (а),
а вероятность правильного обнаружения D = Ф (ςψ — а), где а — нор-
х
мированный порог обнаружения, Ф (х) = 1/у/2п J exp (-i2/2) dt —
интеграл вероятности. -°°
Использование алгоритма ЧКШС приводит к увеличению среднеква¬
дратического отклонения шума в yfs раз (s — количество суммируемых
отсчетов), однако влияние корреляционных шумов исключается. Выраже¬
ние для вероятности ложной тревоги останется прежним, а вероятность
правильного обнаружения составит
£> = Ф(?Ф/у/в-а). (12.5.1)
Пусть теперь в апертуре ациклического фильтра полностью находится
слабый сигнал и присутствует часть сильного сигнала, причем эти сигна¬
лы взаимно независимы. Сильный сигнал создает корреляционные шумы
с дисперсией σκ· Определим отношение сигнал/шум q на выходе фильтра
для этого случая. Энергия сигнала на выходе фильтра составляет ||Г||4,
а дисперсия флуктуационного шума на выходе σ2 = σ2χ||Γ||2. Диспер¬
сия суммы независимых случайных величин равна сумме их дисперсий.
Следовательно дисперсия случайной величины на выходе согласованного
фильтра с учетом корреляционных шумов составит
авых — СГ2 + СГк = σΒχΙ|Γ||2 + Οκ·
Тогда отношение сигнал/шум можно найти по формуле
а2 = цгц4 = 4
<^||Г||2+<г£ 1 + °к9ф/ ||г||4
Вероятность правильного обнаружения для этого случая будет равна
D = Ф (q - а). (12.5.2)
Поскольку в качестве критерия качества работы обнаружителя был
выбран критерий Неймана-Пирсона, необходимо определить условия, при
которых вероятность D, вычисляемая в соответствии с (12.5.1), будет боль¬
ше вычисляемой в соответствии с (12.5.2) при одинаковой вероятности
ложной тревоги. Поскольку функция Ф (х) является монотонной, то до¬
статочно потребовать, чтобы
2 2
^ %
S 1 + σκ4φ/ ||Г||4
Из данного неравенства можно получить величину отношения сиг¬
нал/шум для слабого сигнала при заданной величине дисперсии корреля¬
ционных шумов, начиная с которого целесообразно применение ЧКШС:
(12.5.3)
508
Гл. 12. Композиционные контуры
Данное соотношение определяет область значений отношения сиг-
нал/шум, при которых применение алгоритма ЧКШС дает выигрыш
в качестве принимаемых решений для полностью известного сигнала.
В случае сигнала со случайной начальной фазой вероятность правиль¬
ного обнаружения определяется по формуле D = 1 — Q (a, q), где а =
= -у/—2 In (F) — нормированный порог, Q (и, υ) — Q-функция Маркума
(интегральное распределение Рэлея-Райса). Для сигнала со случайными
амплитудой и начальной фазой вероятность правильного обнаружения
составляет D = \ Пороговое значение отношения сигнал/шум
определяется по аналогии со случаем полностью известного сигнала.
В качестве меры эффективности применения алгоритма ЧКШС вве¬
дем коэффициент
kD — -Очкшс/Ащ,
где 2)чкшс и Daц — вероятности правильного обнаружения более слабого сиг¬
нала на фоне флуктуационных шумов и корреляционного шума, создавае¬
мого более сильным сигналом соответственно при использовании дополни¬
тельно к ациклической согласованной фильтрации фильтра ЧКШС и без него.
На рис. 12.19 представлены примеры графиков характеристик обнару¬
жения одного сигнала на фоне другого сигнала.
Основные выводы и рекомендации по использованию алгоритма ЧКШС
состоят в следующем.
1. Эффективность применения алгоритма ЧКШС тем выше, чем выше
пороговый уровень обнаружителя, т.е. чем меньше вероятность ложной
тревоги F. Например, для полностью известного сигнала на базе компо¬
зиционного контура Г о,2,4,6,8,1,з,5,7 при отношении сигнал/шум q — 9,
отношении амплитуд kjj = ОД и F — 10-1 величина кв — 1,1, для F =
= 10“4 величина кв = 3,3, а для F = 10-7 этот коэффициент достигает
кв =80. Такая зависимость ^ от порогового уровня обнаружителя объ¬
ясняется тем, что с его ростом уменьшается степень маскировки слабого
сигнала флуктуационным шумом, а корреляционный шум не оказывает
никакого влияния, так как он полностью подавляется фильтром ЧКШС.
2. Эффективность применения фильтра ЧКШС тем выше, чем больше
отношение амплитуд кц слабого и сильного сигналов. При кц = 1 ампли¬
туды сигналов одинаковы и алгоритм ЧКШС лишь ухудшает условия об¬
наружения сигналов из-за уменьшения отношения сигнал/шум. Уровень
корреляционных шумов при этом значительно меньше уровня пикового
отсчета любого из сжатых сигналов и шумы в одинаковой степени влияют
на процесс обнаружения любого из сигналов. По мере уменьшения коэф¬
фициента kjj боковые лепестки сильного сигнала все в большей степени
маскируют пиковый отсчет слабого сигнала и эффективность обнаруже¬
ния за счет применения алгоритма ЧКШС увеличивается.
Например, для полностью известного сигнала на базе контура
Го,2,4,6,8,1,з,5,7, F = 10-7, отношения сигнал/шум q — 12 и кц = 0,2
коэффициент кв = 1,9, а при кц = 0,1 величина этого коэффициента
достигает значения кв = НО.
12.5. Эффективность алгоритма ЧКШС
509
3 6 9 12 15 18 21 24 27 Я
-АЦФ+ЧКШС -- АЦФ—kD
koi
60
40
20
0
3 9 15 21 27 Я
-•-АЦФ+ЧКШС -- АЦФ — kD
F= КГ
щ
г—1
=
=
=
=
S
1
£
—
ш!
—
н
—
—
—
—
—
—н
^НГ
7
—
—
—
rd
ь
=
=d
=
3 6 9 12 15 18 21 24 27 Я
- -АЦФ+ЧКШС —АЦФ —kL
--АЦФ+ЧКШС -- АЦФ
Рис. 12.19. Характеристики обнаружения комплекснозначной последовательности
на фоне корреляционного и флюктуационного шумов и зависимость коэффициента
кв- а — полностью известный контур Го,2,ъ ки — 1; б — полностью известный
контур Гο,2,ι, ки = 1; в — контур Го,2.1 со случайной начальной фазой, ки =
= 1; г — контур Го,2,1 со случайной начальной фазой, ки = 1; д — контур
Го,2,1 со случайными параметрами, ки = 1; е — контур Го,2,1 со случайными
параметрами, ки = 1
Необходимо отметить, что коэффициент кв — £>чкшс/£>ац не в полной
мере характеризует выигрыш от применения фильтра ЧКШС. Для случая
ки =0,2 мы получим, что отношение вероятностей правильного обнаруже¬
ния равно ки = 0,2, но при этом Г>чкшс = 0>98, a DAц = 0,5. По мере
приближения вероятности D к единице для получения одного и того же
приращения этой вероятности требуется значительно более высокое отно¬
шение сигнал/шум, чем при сравнительно небольших значениях D. Поэтому
полученное значение кв = 1,8 в данном случае свидетельствует о высокой
эффективности алгоритма ЧКШС.
510
Гл. 12. Композиционные контуры
3. По мере увеличения размерности к2 композиционного контура ра¬
стет отношение между размахом главного лепестка сжатого сигнала
и ближайшего к нему по амплитуде бокового лепестка, т.е. с ростом раз¬
мерности к2 увеличивается отношение сигнал/корреляционный шум. По¬
скольку фильтр ЧКШС полностью подавляет корреляционный шум, то
эффект от его применения будет больше для контуров с меньшей раз¬
мерностью к2. Например, для случая полностью известного сигнала, F =
= 10-7, ки — 10, s = 3 и отношения сигнал/шум q = 9 коэффициент ко
для контура Г0,2,4,6,8,1,3,57 равен 80, для контура Г0,2,4,1,з — 1400 и для
контура Г0,2,1 — 5000.
12.6. Особенности обработки сигналов на базе композиционных
контуров, отраженных от подвижных целей
Применение кодирующих последовательностей с РЭС позволяет по¬
высить качество функционирования радиотехнической системы за счет
подавления эффекта маскировки отклика от слабого сигнала боковыми
лепестками корреляционной функции от сильного сигнала, особенно в слу¬
чаях, когда на ее входе присутствуют сигналы с большим отношением
амплитуд. На практике приходится иметь дело с сигналами, отраженны¬
ми от подвижных объектов. Доплеровское смещение частоты эхо-сигнала
приводит к рассогласованию параметров сигнала и устройства обработки
и, следовательно, к возникновению корреляционных шумов.
12.6.1. Обработка сигналов на базе композиционных контуров с уче¬
том эффекта Доплера. Рассмотрим влияние эффекта Доплера на про¬
цесс сжатия сигналов в виде композиционного контура с РЭС. В качестве
физического носителя для кодирующей последовательности выберем фа¬
зокодированный сигнал. Из-за изменения частоты эхо-сигнала от подвиж¬
ной цели на каждом кодовом интервале возникает набег фазы А<рд:
Д<рд = 2 πτκ„ φΆ = 2 ωΗτκ„ ^, (12.6.1)
где ωΗ = 2π/Η — частота несущей, тки — длительность кодового интерва¬
ла, г>ц — радиальная скорость цели, /д — частота Доплера.
В результате ЭВ 7 (п) композиционного контура в принятом сигнале
будет равен
ν (п) = 7 (п) ехр {гпАрд}, п = 0,1,... , к2 — 1. (12.6.2)
Отсюда следует, что в случае движущейся цели выделенный после
амплитудно-фазового детектора контур будет деформирован из-за того,
что каждый его ЭВ 7 (η), п = 0,1,... , к2 — 1, дополнительно повернется
на угол пА<рд, не равный в общем случае углу поворота других ЭВ.
Рассмотрим вопрос о характере вызванного этим искажения спектра
контура. С учетом выражения (12.6.2) для спектральной составляющей
рд (т) контура получим:
12.6. Обработка сигналов, отраженных от подвижных целей
511
К — 1
Ра (т) = 53 7 ехр ехр {_*p'mn} =
п=О
к2-1 ,
= 53 7 (п) ехР S -*
п=0
Введем обозначение s = т — А(рдк2/2π. Тогда
Д<£д/с
2π
}■
Р (s + = 53 7 (n) ехр |-j^ns(12.6.3)
Отсюда следует, что в результате воздействия эффекта Доплера каж¬
дая составляющая исходного контура сдвинулась «по частоте» на постоян¬
ную величину Дгад = к2 Αφ%/2π. Эта величина практически всегда явля¬
ется дробным числом. Из предположения, что эффект Доплера не приво¬
дит к нарушению амплитудных соотношений в спектре композиционного
контура следует, что энергетический спектр деформированного конту¬
ра остался равномерным. Поэтому имеется принципиальная возможность
идеального сжатия деформированного сигнала, т.е. возможность полного
подавления его боковых лепестков. Проиллюстрируем это на примере по¬
следовательности Год = {1,1,1, -1} при Д</?д = π/4. Деформированная
последовательность имеет вид (рис. 12.20, б)
N = {1; 0,707 + 0,707г; г; 0,707 - 0,707г}.
Ее спектр, найденный без учета группового сдвига всех спектральных
к2
составляющих на величину Дшд = — Д</?д = 0,5, равен (рис. 12.20, в)
27Г
Рд = {2,414 + ц 2,414 - г; 0,414 + г; 0,414 - г}.
Видно, что модули спектральных составляющих не равны между со¬
бой. Поэтому ациклический и ЧКШС фильтры не обеспечивают идеаль-
Рис. 12.20. Деформация контура Γ0ι в результате движения цели с набегом по
фазе Αφ% за кодовый интервал, равным π/4: а — исходный контур; б — дефор¬
мированный контур; в — спектр деформированного контура для целых значений
т; г — спектр деформированного контура для т = —0,5; 0,5; 1,5; 2,5
ного сжатия деформированного сигнала. В то же время, спектр контура,
найденный в точках т = —0,5; 0,5; 1,5; 2,5, имеет вид Р = {2г; 2; 2г; 2}
(рис. 12.20, г), а модули этих спектральных составляющих равны {2,2,2,2},
т.е. контур характеризуется равномерным энергетическим спектром, хотя
и при дробном значении га.
512
Гл. 12. Композиционные контуры
На основании рассмотренного процесса деформации композиционного
контура получаем алгоритм работы циклического согласованного филь¬
тра, осуществляющего во время второй фазы взаимодействия сигнала
с фильтром полное подавление корреляционных шумов:
к2-1
V (т) = Σ ν (п) ехР {-*«Д^д}7* (п-т + к2 - 1), (12.6.4)
п=О
т = 0,1,... , к2 — 1.
В этой формуле произведение ν (п) ехр {—тА^д}, п = 0,1,...
... , к2 — 1, равно ЭВ 7 (п) исходного, не деформированного контура. Со¬
ответственно, выражения для выходных сигналов ациклического фильтра
для первой и третьей фаз принимают вид
j-1
rfP = Х^ (η) ехр {-тДу>д}7* (А:2 + п - j), j = 1,2,... , fc2,
n=o (12.6.5)
к2-1
77jin^ = X] z/ (n) exp {—тА</?д}7* (A;2 + η — Z), l = 0,1,... , A;2 — 1.
(12.6.6)
Фильтровая схема для рассматриваемого вида сигналов должна содер¬
жать амплитудно-фазовый детектор АФД, вырабатывающий по принято¬
му эхо-сигналу значения ЭВ композиционного контура N = {и (™)}0,fc-i>
Рис. 12.21. Структура устройства обработки эхо-сигнала на базе композиционного
контура при неизвестной частоте Доплера (а) и структура блока компенсации
доплеровского набега фазы (б)
компенсаторы доплеровских набегов фазы, каждый из которых настро¬
ен на соответствующий доплеровский диапазон с центральной часто¬
той Од^·, j = 1,2,...,/, набор ациклических согласованных фильтров
АСФ (рис. 12.21).
Рассмотрим несколько примеров обработки сигнала на базе композиционного
контура Год = {1,1,1,—1}, когда набег фазы за один кодовый интервал со¬
ставляет Αφ% = π/4. В этом случае деформированный контур принимает вид
N = {1; 0,707 + 0,707г; г; 0,707 - 0,707г}.
Система обработки имеет вид, представленный на рис. 12.21, и содержит пять
каналов, настроенных на доплеровские сдвиги частоты, приводящие к набегам фаз
за кодовый интервал, равным Αφ — {0; 7г/12; π/6; π/4; π/3}.
12.6. Обработка сигналов, отраженных от подвижных целей
513
В первом примере рассматривается случай одиночной цели. Ниже приведены
результаты обработки ациклическим фильтром АСФ1 ... АСФ5 деформирован¬
ного композиционного контура Ν:
НАЦ,1 = {-1; 0,293 - 0,707г; 1,707 - 0,293г; 1 + 2,414г; 1,414 + г;
0,707 + 0,293г; 0,707 - 0,707г},
НАЦ,2 = {-1; 0,134 - 0,5г; 1,366 - 0,366г; 2,366 + 2,366г;
1,366 + 0,366г; 0,5 - 0,134г; -г},
НАЦ,з = {-1; 0,034 - 0,259г; 1,1 - 0,241г; 3,539 4- 1,466г; 1,125 + 0,052г;
0,159 - 0,207г; -0,707 - 0,707г},
НАц,4 = {—1; 0; 1; 4; 1; 0; -1}, НАц,5 = Нац,з·
На рис. 12.22 приведены значения модулей отсчетов ациклических фильтров.
Видно, что в четвертом канале (Ау>д = π/4), как и следовало ожидать, дости¬
гается максимальный отсчет сигнала, а наибольший уровень боковых лепестков
Рис. 12.22. Значения модулей выходных сигналов ациклических фильтров при об¬
работке одиночного сигнала с А^д = 45°
Рис. 12.23. Результат пространственно-временной обработки сигнала с примене¬
нием алгоритма ЧКШС
514
Гл. 12. Композиционные контуры
минимален. На рис. 12.23 показан результат пространственно-временной обра¬
ботки сигнала с применением алгоритма ЧКШС. Вначале идут модули отсче¬
тов, соответствующих первому каналу, затем второму и т.д. В четвертом канале
произошло полное подавление корреляционных шумов с сохранением значения
максимального отсчета.
Для рассмотренной ситуации решающее устройство достаточно уверенно вы¬
берет в качестве окончательного варианта выходные сигналы четвертого канала
Таблица 12.4
Номер
канала
Макс, модуль отсчетов
Сумма модулей всех отсчетов
1
2,613
9,607
2
3,346
9,208
3
3,831
8,605
4
4
4
5
3,831
8,605
по критерию максимального модуля и минимальной суммы модулей отсчетов для
каждого из каналов. Значения этих признаков для каждого из каналов приведены
в табл. 12.4.
Во втором примере рассмотрен случай, когда перекрывается один кодовый
интервал двух сигналов с амплитудами 1 и 5 и набегом фазы за кодовый ин¬
тервал, равным А<рд = π/4. Коды Νχ и N2 этих сигналов и код суммарного
деформированного сигнала равны
Νχ = {5; 3,536 + 3,536г; 5г; 3,536 - 3,536г},
Ν2 = {1; 0,707 + 0,707г; г; 0,707 - 0,707г},
{5; 4,536 4- 3,536г; 0,707 + 5,707г; 3,536 - 2,536г; 0,707 - 0,707г}.
Модули выходных сигналов ациклических фильтров представлены в виде
графиков на рис. 12.24, а, а результат пространственной обработки сигнала ре¬
шающим устройством с применением алгоритма ЧКШС — на рис. 12.24, б. Как
и в первом примере, видно, что по результатам ациклической обработки сложно
судить о наличии двух целей с разными амплитудами, хотя на выходе филь¬
тра четвертого канала уровень корреляционного шума минимален. Применение
алгоритма ЧКШС обеспечивает, как и в случае одиночной цели, полное подавле¬
ние корреляционного шума в четвертом канале. В результате здесь проявляется
эффект идеального разрешения целей с сохранением амплитудных и временных
соотношений. Таблица значений максимальных модулей отсчетов в каждом из
каналов и сумм модулей для каждого из каналов имеет вид (табл. 12.5).
Согласно табл. 12.5, максимальные значения модулей наблюдаются на выхо¬
де четвертого и пятого каналов, но по сумме модулей всех отсчетов решающее
устройство уверенно отбирает в качестве окончательного результата отсчеты чет¬
вертого канала.
Рассмотренный случай идеального разрешения находящихся в одном импульс¬
ном объеме перекрывающихся сигналов от целей является наиболее важным, так
как перекрытие сигналов из-за одинаковости или близости скоростей целей будет
происходить в течении длительного времени. Если же скорости целей значительно
отличаются друг от друга, то перекрытие сигналов будет кратковременным собы-
12.6. Обработка сигналов, отраженных от подвижных целей
515
13,6 А^Д=0°
10,95
17,2
19,6
и
3,6
5,5 5,3
>,з 5 γ
Lu Lii
10’3 Д^>д =15°
3,95.3
о
о
ГО
II
£
<
9
4
5 5,6
5,2
ΪΊ !,
20,7
>
г
II
-ь
и»
о
8,3
5 5
1 ! 1
5
1 I 1
1 * 1 ь
5
1
12 3 4
5
6 7 8 "
1
20,2
5,9
А^д — 60
7,3
4S
Л
1 2 3 4 5 6 7 8
Рис. 12.24. Обработка перекрывающихся сигналов с одинаковым набегом фазы
Αφ% = 45° и амплитудами 5 и 1: а — графики модулей выходных отчсетов аци¬
клических фильтров; б — пространственно-временное представление результатов
обработки после фильтра ЧКШС
тием. При разных скоростях движения целей ациклический фильтр, задаваемый
выражениями (12.6.5) и (12.6.6), настроенный на компенсацию набега фаз ЭВ одного
контура, не в состоянии это выполнить для другого контура. В результате фильтр
ЧКШС не сможет подавить корреляционные шумы, возникающие за счет сжа¬
тия сигнала с нескомпенсированными набегами фаз ЭВ. Однако его применение
целесообразно, так как фильтр ЧКШС подавит корреляционные шумы, вызван-
Таблица 12.5
Номер
канала
Макс, модуль отсчетов
Сумма модулей всех отсчетов
1
14,4
41,02
2
16,4
37,39
3
18,3
31,26
4
20
24
5
20,05
32,07
516
Гл. 12. Композиционные контуры
ные сжатием одного из сигналов. Наиболее сложным является случай перекры¬
тия сигналов одинаковой амплитуды, так как при этом эффективность фильтра
ЧКШС будет наименьшей. Например, если такие сигналы задаются контуром Год,
разность набегов фаз за кодовый интервал равна Αφ% = π/4 и перекрытие
происходит с параметром j — 1, то результат ациклической фильтрации равен
(рис. 12.25, а)
Ндц = {-1; -1; 1,3 - 0,7г; 5,7 - 0,3г; 2 + 2,4г; 1,4 + *; -0,3 + 0,3г; 0,7 - 0,7г},
|Нац| = {1; 1; 1,48; 5,71; 3,14; 1,73; 0,414; 1}.
Из приведенных соотношений и диаграммы на рис. 12.25, а видно, что несмотря
на определенную маскировку корреляционными шумами второго из сигналов,
5,71
6,49
261
1,08 1,08
I ill
6 0 12 3
Рис. 12.25. Зависимость модулей отсчетов на выходе фильтра для перекрываю¬
щихся с параметром j = 1 сигналов Γοι одинаковой амплитуды для целей, движу¬
щихся с разными скоростями (Д<рд = 0° и = 45°): а — после ациклической
фильтрации; б — после ациклической фильтрации и ЧКШС
отсчеты модулей сигналов, равные соответственно 5,71 и 3,12, значительно пре¬
вышают уровень максимального бокового лепестка, равного 1,72. Это обеспечивает
достаточно уверенное разрешение сигналов, особенно после ЧКШС.
Если в первом случае отношение модуля отсчета второго сигнала к макси¬
мальному боковому лепестку было равно 3,12/1,72 = 1,82, то после фильтра
ЧКШС это отношение станет равным 2,8/1,08 = 2,6. Еще больший эффект от
применения алгоритма ЧКШС достигается, когда амплитуды эхо-сигналов разные.
Если предположить, что в рассмотренном примере амплитуда одного из сигналов
превышает амплитуду другого в пять раз, то результаты обработки таких сигна¬
лов будут иметь вид (рис. 12.26)
НАц = {-5; -1; 5,293 - 0,707г; 21,707 - 0,293г; 6 + 2,414г;
1,414 + г; -4,293 + 0,293г; 0,707 - 0,707г},
|НАц| = {5; 1; 5,34; 21,709; 6,47; 1,73; 4,3; 1},
X = {1 + 2,414г; 0,414 + г; 1 - 0,414г; 22,414 - г},
|Х| = {2,61; 1,08; 1,08; 22,44}.
Из этих данных видно, что отношение модуля сигнала, соответствующего
второму сигналу, к модулю максимального бокового лепестка после циклического
12.6. Обработка сигналов, отраженных от подвижных целей
517
22,43
2,61
1,08 1,08
11ГI,
б 0 12 3
Рис. 12.26. Результат обработки сигналов с отношением амплитуд пять к одному:
а — выход ациклического фильтра; б — выход фильтра ЧКШС
фильтра равно 6,47/5,34 = 1,21. В результате разрешение целей становится
проблематичным. После фильтра ЧКШС это отношение стало равным 2,61/1,08 =
= 2,42, т.е. увеличилось в два раза.
12.6.2. Режим селекции движущихся целей. Для подавления пас¬
сивных помех в импульсно-доплеровских РЛС применяются устройства
селекции движущихся целей, построенные на базе устройств череспе-
риодной компенсации (ЧПК). Для улучшения подавления сигналов от
неподвижных объектов часто применяют многократные системы ЧПК,
состоящие из нескольких последовательно включенных устройств че-
респериодной компенсации.
Рассмотрим работу системы однократной ЧПК в РЛС, использующей
сложные сигналы. Вследствие влияния эффекта Доплера ЭВ (п) на 5-м
периоде повторения на входе ЧПК равен
Ъ (η) = |γ| exp {ι[ψ (η) + пА<рш + δΔρπ]},
а , 4пгКИу /. - .
где Αφκ1Λ = ± /изл — доплеровский набег фазы на одном кодовом
с
интервале, /изл — частота несущей, ν — скорость цели, тки — длитель-
Λ , 4πτϊιν -
ность кодового интервала, с — скорость света, Αφп = ±—-—/изл —
доплеровский набег фазы за один период повторения сигнала тц. Пусть
амплитуда сигнала не изменяется от периода к периоду сигнала и равна
единице. Тогда ЭВ Ajs (η) на выходе ЧПК, определяемый как разность
векторов на соседних периодах повторения запишется в виде
δ7 (п) = 7s+i (п) - Ъ {п) = Ы exp {г[<р (n) + nA<pm + (s + 1) Δ<^Π]} -
- |γ| exp {ί\φ (η) + ηΑφκ„ + δΔ^π]} =
= )ύ| exp {ι[φ (η) + ηΑφκ„ + ίΔ^π]} ' (exp {ίψπ} ~ 1) ·
При рассмотрении работы системы ЧПК не имеет значения, на каком
периоде обзора анализируется ее работа, поэтому положим 5 = 0. Тогда
Aj (п) = |7| ехр {ί[φ (п) + пА<рш}} ■ (ехр {ίφη} ~ 1) ·
518
Гл. 12. Композиционные контуры
Пусть сигнал с выхода системы ЧПК поступает на вход согласованного
фильтра, т.е. ν (η) = Δ7 (п). В этом случае для момента совпадения
сигнала с окном фильтра можно записать
k2-1 к2-1
η (0, Л<рш) = Σ ν (η) Ί* = Σ ехр (п) + пА<^ки]} · Ί* (п) =
п=0 п=0
fc2-l
= (ехр {%Ψώ) ~ 1) Σ 7 (п) ехР {ΐηΔ^κ„} · 7* (п).
п=О
Пусть модуль вектора 7(71) равен единице. Тогда с учетом выражения
для суммы геометрической прогрессии получим
Если обработка сигнала происходит в канале, согласованном с сигналом по
частоте Доплера, то последнее выраже¬
ние примет вид η — к2 (ехр {г<^п} — 1), а
модуль отклика согласованного фильтра
при использовании системы ЧПК станет
равен \η\ = fc2\/2sinA</?n/2 (рис. 12.27).
Таким образом, применение системы
ЧПК при обработке контурных сигна¬
лов позволяет осуществлять режекцию
спектральных составляющих пассивных
помех.
12.7. Основные результаты в области анализа сложных
сигналов на базе композиционных контуров и устройств
их обработки
В данной главе рассмотрены кодирующие последовательности, интер¬
претированные как заданные на плоскости контуры. Показано, что для
обеспечения идеального временного разрешения сигналов их энергети¬
ческие спектры должны быть равномерными, обработка — циклической,
а сами сигналы, как правило, являются комплекснозначными.
Синтезированы комплекснозначные сигналы в виде композиционных
контуров из полного семейства элементарных контуров, представляю¬
щих собой последовательности следующих друг за другом элементар¬
ных контуров, образующих одно полное семейство. Показано, что базовый
композиционный контур Г0д,... д-ι из последовательности элементарных
контуров Γο,Γι,... ,Ffc_i, имеет равномерный энергетический спектр.
Рассмотрен метод формирования алфавита композиционных контуров
из полного семейства элементарных контуров с равномерным энергети¬
ческим спектром. Показано, что для каждого значения к имеется φ (к)
базовых контуров с равномерным энергетическим спектром, где φ (к) —
f |Δ//( «)|
2π 4π Αφπ
Рис. 12.27. Модуль отклика согла¬
сованного фильтра при использо¬
вании системы ЧПК
12.7. Основные результаты
519
функция Эйлера от числа к. Из каждого базового контура путем цикличе¬
ского сдвига составляющих его ЭК получаются еще к—1 контуров с равно¬
мерным энергетическим спектром, и общее количество композиционных
контуров с данным видом спектра равно kip {к). Конкретная структура
такого контура в виде последовательности элементарных контуров раз¬
ных порядков находится путем умножения ряда 0,1,— 1на одно
из чисел, взаимно простых с к и переходом в полученных произведениях
к значениям по модулю к.
Рассмотренный метод синтеза позволяет аналитическим путем полу¬
чить кодовую последовательность длиной к2, к = 2,3,4,..., с равномер¬
ным энергетическим спектром.
Исследованы вопросы обработки синтезированных кодовых после¬
довательностей. Показано, что амплитудно-частотная характеристика
согласованного с ней фильтра является строго равномерной, а фазо-ча¬
стотная — линейно-нарастающей в пределах от нуля до 2π. Выходной
сигнал фильтра состоит только из одной составляющей, равной энергии
входной последовательности. Такой вид сжатого сигнала, а также воз¬
можность формирования достаточно протяженных последовательностей
позволяют считать композиционные контуры с равномерным энергетиче¬
ским спектром эффективными с точки зрения решения задач обнаруже¬
ния, разрешения и оценки параметров.
Показано, что необходимым условием получения дельтовидной АКФ
при согласованной фильтрации сигнала с равномерным энергетическим
спектром является циклический характер обработки. Только в этом слу¬
чае существует взаимное положение окна фильтра и сигнала, причем
только одно, для которого при нулевом уровне шумов реализуются иде¬
альные разрешающие свойства сигналов на базе композиционных конту¬
ров, когда один отсчет сжатого сигнала равен энергии входного сигнала,
а остальные — нулю. При этом циклической согласованной фильтрации
присущи два недостатка.
1. Возрастание в к2 требуемого объема вычислений по сравнению
с традиционно применяемой для обнаружения и разрешения сигналов
ациклической фильтрацией, где к2 — размерность композиционного
контура;
2. Неопределенность выбора из (2к2 — l) получающихся при скольже¬
нии окна циклического фильтра серий отсчетов только одной, обладающей
необходимыми свойствами.
Использование алгоритма ЧКШС позволяет по результатам ацикличе¬
ской согласованной фильтрации композиционного контура с равномерным
энергетическим спектром для комплементарных положений окна фильтра
найти серию выходных отсчетов, состоящую из одного ненулевого и всех
остальных, равных нулю значений.
Показано, что применение алгоритма ЧКШС к выходным отсчетам аци¬
клического согласованного фильтра при обработке сигнала с равномерным
энергетическим спектром дает результаты, аналогичные результатам ци¬
клической согласованной фильтрации, т.е. позволяет с низкой трудоемко¬
520
Гл. 12. Композиционные контуры
стью получить сжатый сигнал без боковых лепестков. При этом происходит
удвоение энергии шума из-за расширения вдвое апертуры фильтра.
Выяснены условия, при которых целесообразно использование алгорит¬
ма ЧКШС для разрешения сигналов по дальности. Эффективность примене¬
ния алгоритма ЧКШС тем выше, чем больше различие между ЭПР близко
расположенных целей, чем ниже уровень ложных тревог на выходе обнару¬
жителя и чем меньше размерность кодирующей сигнал последовательности
элементарных векторов композиционного контура с РЭС.
Таким образом, проведенный анализ показывает, что сигнал в ви¬
де композиционного контура обладает дельтовидной автокорреляционной
функцией и равномерным энергетическим спектром, т.е. позволяет полу¬
чить идеальное разрешение по дальности. В то же время составляющие
его элементарные контуры вследствие своей взаимной ортогональности
являются оптимальными при решении задачи распознавания этого сигна¬
ла. Так как свойства композиционного контура сохраняются при любых &,
становится возможным формирование энергоемкого сигнала, а поскольку,
кроме того, амплитуда сигнала на всех кодовых интервалах одинакова
(пик фактор сигнала равен единице), то сигнал является хорошим и для
решения задачи обнаружения. Следовательно, сигнал в виде композици¬
онного контура позволяет решать ключевые задачи радиолокации: обна¬
ружение, распознавание, измерение параметров и разрешение сигналов.
12.8. Контрольные вопросы и задачи
1. Каким амплитудным спектром должен обладать сигнал с дельтовидной ци¬
клической АКФ?
2. Каким требованиям должен удовлетворять фазовый спектр действительного
сигнала с РЭС?
3. Какими свойствами обладают элементарные контуры?
4. Дайте определение композиционного контура.
5. Как формируется алфавит композиционных контуров из полного семейства
элементарных контуров с РЭС?
6. Запишите отсчеты базового композиционного контура для к = 3.
7. Вычислить отсчеты амплитудного и фазового спектров базового композици¬
онного контура для к = 3.
8. Запишите порядок следования элементарных контуров для всех базовых ком¬
позиционных контуров при к = 5.
9. Вычислить отсчеты ВКФ двух базовых композиционных контуров Γ0,ι,2
и Го,2,1.
10. Предложите алгоритм и структурную схему устройства распознавания ком¬
позиционного контура по входящим в его состав элементарным контурам.
11. Покажите, что АЧХ согласованного с базовым композиционным контуром
фильтра является равномерной, а ФЧХ — линейно-нарастающей в преде¬
лах от нуля до 2π.
12. Как определяются отсчеты на выходе циклического согласованного фильтра
для трех фаз взаимодействия сигнала и фильтра?
13. Покажите, что на первой стадии фильтрации положение максимального от¬
счета на выходе циклического согласованного фильтра соответствует моменту
начала сигнала, а на последней — моменту его окончания.
12.8. Контрольные вопросы и задачи
521
14. Каким образом формируются отсчеты циклического согласованного фильтра
для случая полного совпадения сигнала с окном фильтра по результатам
первой и третьей фаз взаимодействия циклического фильтра с сигналом?
15. Каким образом формируются отсчеты циклического согласованного фильтра
для случая полного совпадения сигнала с окном фильтра по результатам
первой и третьей фаз взаимодействия ациклического фильтра с сигналом?
16. Приведите структуру устройства обработки сигналов в канале дальности с ис¬
пользованием алгоритма ЧКШС.
17. Как зависит эффективность применения алгоритма ЧКШС от вероятности
ложной тревоги?
18. Как зависит эффективность применения алгоритма ЧКШС от отношения ам¬
плитуд разрешаемых сигналов?
19. Как зависит эффективность применения алгоритма ЧКШС от размерности
композиционного контура?
Глава 13
СИГНАЛЫ В ВИДЕ ФОРМ ВТОРИЧНЫХ СОЗВЕЗДИЙ
ДЛЯ ОРИЕНТАЦИИ ЛЕТАТЕЛЬНЫХ АППАРАТОВ
13.1. Задача ориентации летательного аппарата
по изображениям созвездий
Ориентация летательных аппаратов (ЛА) в пространстве по положе¬
нию астрономических объектов является достаточно актуальной задачей.
При ее решении выделяют следующие этапы: 1) получение изображений
участков звездного неба; 2) определение координат изображений звезд
в системе координат астродатчика; 3) идентификация изображений этих
звезд по данным бортового каталога; 4) расчет параметров ориентации.
Для астрономических ориентиров самыми общими отличительными
признаками являются их положение в пространстве в некоторый момент
времени и характер излучения. В связи с тем, что расстояния до звезд
Зенит
Рис. 13.1. Характерные точки и сечения небесной сферы
13.1. Задача ориентации летательного аппарата
523
на много порядков превосходят любые расстояния между двумя возмож¬
ными точками наблюдения на поверхности Земли, звезды проецируются
на небесную сферу единичного радиуса с центром в точке наблюдения.
Для наблюдателя, расположенного в пределах Земли и вращающегося
вместе с Землей, приняты характерные точки и сечения на небесной
сфере, показанные на рис. 13.1.
При решении задачи трехосной ориентации ЛА по изображени¬
ям астрономических объектов в инерциальной базовой системе коор-
Рис. 13.2. Системы координат для ориентации летательных аппаратов в инерци¬
альном базисе
динат вводятся три правых ортонормированных координатных базиса
(рис. 13.2) с совмещенным началом координат в точке О.
1. {е\,е\,е\) — базовая экваториальная система координат (СКЭ)
с базисными векторами, направленными из точки наблюдения соответ¬
ственно: е\ — к точке весеннего равноденствия 7, е\ — к северному
полюсу мира Р, е\ — дополняет базис до правого и задает вместе с е\
плоскость небесного экватора.
2. {ej, ез, eg} — координатный базис летательного аппарата (СКЛ)
с базисными векторами, ориентированными вдоль главных осей Л А: е* —
вдоль фюзеляжа, е% — вертикальной плоскости ЛА, е\ — дополняет базис
до правого.
3. {e^e^eij} — координатный базис астродатчика (СКД) с базис¬
ными векторами: — вектор оптической оси датчика, е\,е\ — векторы,
ориентированные вдоль главных осей плоскости изображения. Произволь¬
ный вектор Xj (вектор, проведенный из центра сферы к светилу) в каждом
базисе задается матрицей-столбцом из координат этого вектора:
Xlj
/у* Л
xlj
Xlj
X2j
II
Ί*Γ
х2 j
II
X2j
\_X3j]
_3j_
524
Гл. 13. Сигналы в виде форм вторичных созвездий
где верхний индекс обозначает соответствующий координатный базис.
Группу из п векторов {х^}1п задает матрица X, размерностью 3 х п
элементов.
Координаты вектора х^· в различных координатных базисах связаны
линейными однородными преобразованиями. Запишем переход из СКД
Каждый j-Й столбец в матрице D есть множество координат j-го ба¬
зисного вектора астродатчика в СКЭ. Поскольку оба координатных бази¬
са ортонормированны, то процедура обращения матрицы преобразования
4. — вращающая-
Рис. 13.3. Системы координат для ориен- ся относительно СКЭ с угловой
тации ЛА в неинерциальном базисе скоростью ω3 географическая си-
с началом координат в центре Земли и базисными векторами: е\ — лежит
в плоскости экватора и направлен в сторону гринвичского меридиана,
ез — ориентирован к северному полюсу мира, е\ — лежит в плоскости
экватора и дополняет координатный базис до правого. Данная система
координат является базовой для определения географического положения
воздушного ЛА.
5. {е\,еТ2, ет3} — вращающаяся вместе с СКЗ горизонтальная система
координат (СКГ) с базисными векторами: — направлен от центра
Земли к зениту наблюдателя; е\ и е\ — задают плоскость параллель¬
ную математическому горизонту, причем е\ лежит в плоскости небесного
меридиана и направлен как вектор из точки наблюдателя О' (рис. 13.3),
касательный к меридиану наблюдателя в сторону северного полюса мира;
е\ — дополняет базис до правого. Данная система координат является ба¬
зовой для определения ориентации ЛА относительно поверхности Земли.
в СКЭ:
эквивалентна процедуре транспо¬
нирования, т.е.
D-1 = DT = [dtj Г = [da).
Таким образом, каждую г-ю стро¬
ку матрицы D можно рассматри¬
вать как координаты г-ro базисного
вектора СКЭ в СКД. Аналогично
устанавливается связь и для двух
других пар систем координат.
е\ Для решения задачи ориента¬
ции ЛА в неинерциальной системе
координат вводятся два дополни¬
тельных координатных базиса.
стема координат Земли (СКЗ)
13.2. Формы вторичных созвездий
525
Наиболее удобными для описания положения светила являются сфе¬
рические координаты (Sj, aj), где Sj — угол между плоскостью (ei, б2,0)
и вектором Xj j-ro светила, olj — угол между базисным вектором е\
и проекцией вектора светила на плоскость (ei,e2,0). В СКЭ а — прямое
восхождение, δ — склонение (рис. 13.11). Склонение и прямое восхождение
каждой звезды являются известными для наблюдателя и практически
не изменяются во времени. Значения этих координат, измеренные с очень
высокой точностью, публикуются в звездных каталогах и по ним форми¬
руются бортовые электронные каталоги ЛА.
Развитие элементной базы, повышение требований к быстродействию,
надежности и точности ориентации ЛА приводят к необходимости поиска
оптимальных методов ориентации ЛА. Существующие системы ориента¬
ции ЛА по изображениям звездного неба не оптимизированны по входно¬
му сигналу. Поэтому такая система обработки сигналов имеет меньшую
эффективность, чем, например, радиолокационная, сигналы для которой
могут быть выбраны наилучшим образом с заданным критерием качества.
Целесообразность поиска оптимальных ориентиров объясняется двумя
факторами: такой ориентир обеспечивает в условиях координатных шу¬
мов наибольшую эффективность решения задач, возникающих при ори¬
ентации, и устраняет необходимость поиска других, более эффективных,
форм объектов для ориентации ЛА.
Далее проведем исследования с позиции теории сигналов изображе¬
ния объектов, расположенных на небесной сфере, используемых в целях
ориентации ЛА. Для этого определим форму вторичных созвездий, оп¬
тимальных для распознавания и идентификации составляющих их све¬
тил. Также приведем результаты экспериментов по поиску оптимальных
ориентиров на небесной сфере и идентификации светил в их составе на
фоне всевозможных созвездий в заданном диапазоне светимостей звезд
и ограниченном телесном угле наблюдения.
13.2. Формы вторичных созвездий, используемых в качестве
квазиоптимальных ориентиров для ЛА
Понятие формы плоского изображения, введенное в разделе 9.9, может
быть успешно применено для решения задач ориентации ЛА по изобра¬
жениям звездного неба. В данном разделе сформулируем требования к
формам вторичных созвездий, представляющих собой оптимальные сиг¬
налы для решения задач астроориентации ЛА.
13.2.1. Требования к форме вторичных созвездий для ориентации
летательных аппаратов. Изображения звездного неба относятся к клас¬
су точечных изображений. Форму изображения в виде группы точек
зададим контуром, получающимся при соединении по определенному
правилу этих точек векторами (рис. 13.4). Таким образом подход к опре¬
делению формы плоского изображения можно распространить на фор¬
му точечного изображения.
526
Гл. 13. Сигналы в виде форм вторичных созвездий
Сформулируем требования к вторичным созвездиям, позволяющим
использовать их для ориентации ЛА при полной априорной неопределен¬
ности углового положения оптической оси оптико-телевизионного датчика
(ОШ
1. Ограничение на величину углового диаметра Θ вторичного созвездия.
При малом значении Θ сильное мешающее воздействие будут ока¬
зывать ошибки определения координат (координатные шумы) отдельных
звезд, а при большом значении Θ резко возра¬
стает количество вторичных созвездий, которые
надо проанализировать для поиска искомого
созвездия. Величина Θ должна определяться
размерами телевизионного кадра.
2. Яркость звезд в составе вторичного созвез¬
дия должна быть выше определенной пороговой
величины.
Количество звезд, наблюдаемых в пределах
телевизионного кадра, определяется чувстви¬
тельностью ОТД. Звезды, входящие в состав
вторичного созвездия, должны уверено обна¬
руживаться на фоне собственных шумов ОТД.
Поэтому светимость отдельных звезд вторичного созвездия должна быть
достаточно высокой. В дальнейшем используемый в качестве примера для
поиска вторичных созвездий каталог звезд содержит звезды светимостью
не выше 4га звездной величины.
3. Ограничение на количество звезд к, образующих вторичное созвездие.
Чем больше величина к, тем больше комбинаций и тем больше разных
контуров можно составить из N точек. В результате резко возрастает время
анализа звездных скоплений при поиске вторичного созвездия. Кроме того,
с ростом к сильно уменьшается вероятность существования необходимого
вторичного созвездия (с учетом ограничения на яркость звезд).
4. Форма вторичного созвездия размерности к должна быть уникальной.
Данное требование предполагает отсутствие в заданной области не¬
бесной сферы других созвездий не только с такими же, но даже и с
близкими свойствами формы. Причем эти свойства должны легко распо¬
знаваться благодаря достаточно большому расстоянию в пространстве форм,
образуемых уникальными вторичными созвездиями (УВС) заданной размер¬
ности к и остальными всевозможными вторичными созвездиями.
13.2.2. Форма уникального вторичного созвездия. Как следует из
требования уникальности формы вторичного созвездия и понятия фор¬
мы плоского изображения (см. п. 9.9), форму УВС целесообразно искать
в классе форм, максимально удаленных от формы тестового изображения,
т.е. от формы, задаваемой дельтовидным контуром, в классе максимально
простых по форме изображений, для которых
Rl = ||ΔΗ - гн||2 -»· max,
Рис. 13.4. Контур вторич¬
ного созвездия, получив¬
шийся при соединении
точек 1,2,3,4,5 векторами
(13.2.1)
13.2. Формы вторичных созвездий
527
где Гн = {7Н (п)}0 fc_1, 7„ (п) = 7 (п)/||Г|| — нормированный контур
УВС, ΔΗ = {<5Н (я)}0 fc_!, δΗ (η) = δ (η)/||Δ|| — нормированный дельто-
видный контур.
С учетом этих обозначений условие (13.2.1) принимает вид
Д* = 2[1 - Re (ΔΗ) Гн)] -> max (13.2.2)
или же
Re (ΔΗ,ΓΗ) min. (13.2.3)
Для скалярного произведения контуров Гн и ΔΗ получим
*7н — (^Н5 Гн) —
у/к2 - к 11ГИ
7* (0) {к- 1) - 5^7* («)
*7* (0) - Σ 7* (и)
||r||V*(*-l)
Когда контур Г замкнут, т.е. когда Σ 7* (п) = 0, то
п=0
. (13.2.4)
ΙΙΠΙλ/* (*-1)
В результате выражение для нормированного расстояния принимает
вид
т = 2
Re 7 (0)
(13.2.5)
Полученная величина характеризует не только различие форм, зада¬
ваемых контурами Г и Δ, но еще и зависит от их взаимного поворота
и смещения начальных точек. Принимая во внимание полученное в п. 3.7
выражение для расстояния между контурами, зависящее только от сте¬
пени различия задаваемых ими форм, будем иметь
#НД,Г2 “ 2
1 _ ΐ7 mi /Ш
||Г|| Ук-1 ’
где 7 (по) — максимальный по модулю ЭВ исходного контура Г. Тогда
условие —У max становится эквивалентным условию
λ = ΐ2|^->πΰη· (13.2.6)
Таким образом, контур УВС должен характеризоваться минимальным
значением параметра Λ, равного отношению модуля максимального по
длине ЭВ 7 (по) к норме ||Г||.
Условие (13.2.6) однозначно определяет требования к модулям ЭВ конту¬
ра изображения с максимально простой формой. Квадрат величины Λ равен
528
Гл. 13. Сигналы в виде форм вторичных созвездий
\2 = |7 ЫГ = 17 (П)1тах
fc-1 fc-1
Σΐ7(«)ΐ2 Σ>(")Ι2
τι—Ο η=0
Из этого выражения видно, что в контуре изображения с наиболее
простой формой отношение квадрата модуля максимального по длине
ЭВ к сумме квадратов длин всех ЭВ должно быть минимальным. Это
возможно лишь в случае, когда все ЭВ контура одинаковы по длине, т.е.
|7(0)| = |7(l)| = ... = |7(fe-l)|. (13.2.7)
Отметим, что снижение степени доминирования по длине одного из ЭВ
над остальными ЭВ приводит к сужению спектра контура. Наиболее узким
спектром в виде одной спектральной линии обладает ЭК, стороны которо¬
го обладают свойством (13.2.7). Таким образом, наиболее простой формой
обладает изображение, контур которого будет элементарным. Следователь¬
но, форма УВС должна определяться контуром именно этого класса. Для
замкнутого ЭК Гт, га = 1,2,... , к — 1, параметр Л удовлетворяет усло¬
вию (13.2.6) и равен
, |7m (п)| _1_
1|Г|| ν'*’
а квадрат нормированного расстояния между дельтовидным и ЭК Гт,
га — 1,2,..., к — 1 равен
Rl = 2[1 - Re (Д,Гт)] = 2 ^1 - —L=) · (13-2.8)
Отсюда видно, что это расстояние увеличивается с ростом к, т.е. рост к
приводит к упрощению формы, причем порядок ЭК не играет роли. Мак¬
симальное значение нормированного расстояния, как следует из (13.2.8),
равно л/2, причем RH = 1 при к = 5. Дальнейшее увеличение размерности
ЭК слабо влияет на степень упрощения формы. Так, например, при к — 50
R'
1,2
1
0,8
0,6
0,4
0,2
0
23 45 67 8 9 10 к
Рис. 13.5. Зависимость расстояния между формами ориентира и помехового со¬
звездия от порядка элементарного контура
величина RH увеличивается всего лишь на 31% и становится равной 1,309.
Как видно из графика на рис. 13.5, ЭК минимальной размерности к = 3
уже обеспечивает большое значение RH.
13.2. Формы вторичных созвездий
529
Таким образом, с точки зрения получения простейшей формы необхо¬
димо выбирать форму УВС в виде ЭК большой размерности. Однако, чем
выше к, тем ниже вероятность наличия такого созвездия. Эта вероятность
растет с увеличением к значительно быстрее, чем #н, что приводит к
росту степени уникальности созвездия.
13.2.3. Коэффициент монохроматичности формы вторичного созвез¬
дия. Для выбора оптимальной формы вторичного созвездия были проведе¬
ны экспериментальные исследования распределения квадрата расстояний
произвольных форм полигональных замкнутых фигур, образуемых точеч¬
ными отметками в изображениях звездного неба, от тестового дельтовидного
контура (рис. 13.6), обладающего, как и широкополосная помеха, наиболее
Рис. 13.6. Экспериментальная гистограмма квадрата расстояний форм вторичных
созвездий третьего порядка от дельтовидного контура
сложной формой. Электронный каталог звезд составлен на основе астро¬
номического календаря [148]. Условия проведения эксперимента: размер¬
ность ориентира к = 3, угол зрения Θ = 60°, рассматриваемая область —
вся небесная сфера.
Как следует из рис. 13.6, количество форм с наибольшим расстоя¬
нием от помехового контура незначительно. Следовательно, в качестве
распознаваемой формы следует использовать ЭК в виде правильного
fc-угольника, задающий наиболее простую форму. Реально весьма ма¬
ловероятно, что будет найдена группа из к звезд в заданном диапазоне
их светимости и ограниченном по угловым размерам стереосекторе, точно
лежащих в вершинах правильного А;-угольника. Речь может идти лишь
о квазиправильных выпуклых многоугольниках, т.е. о поиске созвездий
с квазиправильной формой.
Вершины многоугольников, задающих ЭК любого порядка, за исклю¬
чением Го, совпадают. Поэтому, располагая лишь к точками, являющи¬
мися вершинами правильных многоугольников Γχ, Гг,... , Γ^_χ, необхо¬
димо оговорить, какой порядок га ЭК из этих к точек будет предпочти¬
тельным. Решающим фактором для такого выбора могут быть затраты
машинного времени при поиске созвездия. В этом плане предпочти¬
тельными являются ЭК Γχ или Г^_х, представляющие собой правильные
выпуклые многоугольники. Выберем, для определенности, ЭК Γχ. При
таком подходе упрощается процедура нумерации точек, принимаемых
530
Гл. 13. Сигналы в виде форм вторичных созвездий
в качестве вершин многоугольника. Контур обходится против часовой
стрелки. ЭВ соединяют между собой ближайшие точки, а получающий¬
ся многоугольник должен быть выпуклым. Амплитудный спектр ЭК Γχ
состоит из одной спектральной линии р (1) = к (рис. 13.7, а). Поскольку
|pW|i
|ρ0»)|·
0 12 3 4
к-2 к- 1 т
Т т_Т
б 0 12 3 4
к-2 к-1т
Рис. 13.7. Амплитудные спектры элементарного (а) и квазиэлементарного (б) кон¬
туров
форма реальных вторичных созвездий описывается квазиэлементарным
контуром Γχ, спектр которого не является строго монохроматическим
(рис. 13.7, б), то целесообразно ввести количественную меру монохрома¬
тичности квазиэлементарного контура. В качестве такой меры примем
величину М, определяемую в виде отношения модуля спектральной со¬
ставляющей р (1) к модулю наиболее интенсивной составляющей | р (гао)|
в оставшейся части спектра fc-угольника, т.е.
м = ^Ш.
\р(т0)\
(13.2.9)
Для созвездий с простейшей формой коэффициент монохроматично¬
сти формы (КМФ) М будет бесконечно большим, так как р(гао) = 0.
В случае квазипростейшей формы, характеризующейся видом спектра,
показанного на рис. 13.7, б, компонента
\р (1)| по-прежнему будет обладать наи¬
большей интенсивностью, но величина
М будет конечной.
Подавляющее количество вторичных
созвездий из к произвольных звезд бу¬
дут иметь сильно изрезанный контур и в
спектре их формы наибольшей интен¬
сивностью обладает не первая, а другие
компоненты спектра, и коэффициент М
для них будет меньше единицы. Именно
таким значением КМФ будут характери¬
зоваться подавляющее большинство вторичных созвездий. На рис. 13.8
показан примерный вид распределения значений М.
Площадь этого распределения в основном сосредоточена в области
значений КМФ, не превышающих единицы. Только несколькие, претенду¬
ющие на уникальность вторичные созвездия, имеют величины КМФ, обо¬
значенные буквами А, В и С. В области этих значений КМФ характерно
наличие обширных «мертвых зон» cU, йлв и (1вс, в пределах которых
нет ни одной точки.
Рис. 13.8. Примерный вид гисто¬
граммы распределения параметра
М
13.3. Характеристики уникальных вторичных созвездий
531
Введем следующие количественные условия принятия вторичного со¬
звездия в качестве уникального в пределах заданного участка Ω небесной
сферы:
Здесь к — размерность УВС, 7W (п) — ЭВ s-ro вторичного созвез¬
дия; σ — среднеквадратическое отклонение КМФ, вычисленное по всем
вторичным созвездиям в пределах области Ω, d — ширина мертвой зоны.
Первое и второе условия требуют, чтобы КМФ УВС имел максималь¬
ное значение по отношению к КМФ всех остальных вторичных созвездий
в области Ω. Третье условие задает отношение сигнал /помеха для формы
УВС не ниже величины qo, а четвертое определяет степень изолирован¬
ности КМФ УВС в пределах гистограммы значений М. Как следует из
экспериментальных данных, для уверенного распознавания УВС на фоне
остальных вторичных созвездий величины qo и ро должны удовлетворять
следующим условиям:
Увеличение размерности правильного fc-угольника снижает вероят¬
ность появления УВС. При этом рост к увеличивает степень различия
между правильным и произвольным fc-угольниками.
Таким образом, к звезд, образующие УВС размерности к, должны
находиться в вершинах правильного fc-угольника, степень правильности
которого оценивается КМФ. Величина КМФ УВС должна быть макси¬
мальной из значений КМФ всех остальных вторичных созвездий, отноше¬
ние сигнал/помеха формы УВС по отношению к формам любого другого
вторичного созвездия q = Мувс/а ^ 10, относительный размер мертвой
зоны КМФ УВС р = MyBC/d ^ 3.
Алгоритм распознавания УВС fc-го порядка заключается в следую¬
щем:
1) формируются всевозможные групповые точечные объекты (ГрТО)
в виде замкнутых fc-угольников из точечных отметок от изображений
светил, попавших в пределы зрения ОТД,
2) на основании выражений (13.2.10)—(13.2.14) выносится решение о рас¬
познавании или не распознавании УВС на звездном небе.
13.3. Характеристики уникальных вторичных созвездий
В данном разделе представлены результаты экспериментальных ис¬
следований по поиску УВС на небесной сфере и приведены количествен¬
ные характеристики их формы.
Мувс = max М при к = const, к = 3,4,5 ...;
7^ (п) е Ω, п = 0,1,... , к - 1; s = 1,2,3...;
(13.2.10)
(13.2.11)
(13.2.12)
(13.2.13)
q0 = 10, ро = 3.
(13.2.14)
532
Гл. 13. Сигналы в виде форм вторичных созвездий
13.3.1. Алгоритм поиска УВС на небесной сфере. Блок-схема алго¬
ритма поиска УВС представлена на рис. 13.9.
После чтения файла из базы данных, составленной в соответствии
с каталогом [148], и вычисления угловых расстояний между всеми звез¬
дами, проверяется гипотеза о компактности текущей фигуры, согласно
Рис. 13.9. Блок-схема алгоритма поиска уникальных ьториннь х созвездий
которой угловое расстояние между звездами не должно превышать поро¬
гового значения Θ. Далее происходит формирование фигур из всех воз¬
можных сочетаний звезд на небесной сфере, и выполняются все воз¬
можные перестановки звезд в текущей фигуре. При этом исключаются
полученные циклическим сдвигом комбинации. Для каждой полученной
комбинации определяется амплитудный спектр формы и находится КМФ
М. На основании полученных данных строится гистограмма значений М
и проверяются условия (13.2.14).
Вторичные созвездия с уникальной монохроматичностью формы условно
названы созвездиями класса МарГТУ. Название также содержит числовую
часть в виде дроби, числитель которой равен размерности к элементар¬
ного контура Γι (число звезд в созвездии), а знаменатель — порядковому
номеру созвездия.
13.3. Характеристики уникальных вторичных созвездий
533
Рис. 13.10 Изображение небесной сфе¬
ры в СКЭ
Рис. 13.11. Задание координат звезд
в СКЭ
Поиск УВС проводился на множе¬
стве из 519 звезд со светимостью от
— 1,5т до 4,0т звездной величины
(рис. 13.10), взятых из каталога [148]
в СКЭ.
Для некоторой звезды Sj ее коор¬
динаты в СКЭ задаются следующи¬
ми угловыми величинами: прямым
восхождением otj, отсчитываемым по
линии небесного экватора от точ¬
ки весеннего равноденствия 7 до
пересечения с меридианом светила,
и склонением Sj, измеряемым по ме¬
ридиану по линии небесного экватора
до пересечения с параллелью свети¬
ла (рис. 13.11). В качестве расстояния
на небесной сфере между звездными отметками S; (а;,<У и sj (oLj,Sj)
было выбрано угловое расстояние Rij, определяемое как
Rij — R (^г (^г? ^г) 5 Sj ) ^j)) —
= arccos[cos * cos Sj · cos (a* — 07) -f- sin Si · sinij]. (13.3.1)
На угловое расстояние Θ между светилами в составе вторичного созвез¬
дия должно быть наложено ограничение (см. раздел 13.2). Один из критериев
ограничения величины Θ базируется на законе распределения этих угловых
расстояний при различных способах упорядочивания светил.
При равномерном распределении светил на небесной сфере, отстоя¬
щих от данного на определенное угловое расстояние, их количество про¬
порционально площади шарового пояса некоторой толщины h, в который
попадают эти светила (рис. 1312). Площадь шарового пояса максималь¬
Рис. 13.12 Вид шаровых поясов
при различных угловых расстояни¬
ях между светилами. Αψ\ < 90°,
Αφ2 =90°, Αψ3 > 90°
534
Гл. 13. Сигналы в виде форм вторичных созвездий
на при наибольшей длине проходящей через его середину окружности.
Данная площадь пропорциональна синусу угла Αφ, поэтому и закон рас¬
пределения расстояний между светилами будет синусоидальным.
На рис. 13.13 приведена гистограмма угловых расстояний между све¬
тилами на небесной сфере, построенная на основании экспериментальных
Рис. 13.13. Гистограмма угловых расстояний между светилами на небесной сфере
данных. Проверка гипотезы о синусоидальной форме закона распределения
расстояний между светилами по критерию χ2 дает следующие результаты.
В соответствии с данным законом распределения наиболее частым
будет угловое расстояние Θ = 90°. Учитывая слабо выраженный мак¬
симум синусоидальной функции можно считать, что при 10% допус¬
ке отклонения от максимума наиболее часто встречаются значения Θ
в пределах 64° < Θ < 116°.
Упорядочивание светил по критерию максимума расстояния при
построении графа «минимального дерева» дает несколько другие ре¬
зультаты. Эксперимент в этом случае показал, что максимальное угловое
расстояние (максимальный угловой размер ребра графа минимального
дерева) не превышает 23°, причем практически угловые размеры мини¬
мального дерева не превышают 12° (рис. 13.14). Следовательно, при угле
Рис. 13.14. Гистограмма угловых расстояний между светилами на небесной сфере,
соединенными минимальным деревом
2 5ЛЛ
20
15
10
5
16
Θ порядка 20° в телевизионном кадре будут находиться либо компактные
группы, либо части этих компактных групп и становится возможным
поиск УВС, рассматриваемого как ГрТО.
13.3. Характеристики уникальных вторичных созвездий
535
При проведении эксперимента по поиску УВС пороговые значения угла
Θ были выбраны равными 20°, 40° и 60°. При Θ = 20° в пределы кадра
в среднем попадает около 40 звезд светимостью не выше четвертой звезд¬
ной величины. Данного количества достаточно, чтобы были высокими как
вероятность проявления монохроматичности формы вторичного созвездия,
так и возможность обеспечения необходимой точности определения угловых
координат звезд в кадре, хранящихся в оперативной памяти видеопроцессо¬
ра. Важным доводом для выбора стереокадра со значением Θ = 20° является
возможность обеспечения разумного значения времени поиска УВС, резко
возрастающего при увеличении количества звезд в пределах кадра.
13.3.2. Результаты поиска квазиоптимальных ориентиров в виде
УВС на небесной сфере. Результаты эксперимента в соответствии с ал¬
горитмом, описанным в п. 13.3.1, по данным каталога, составленного по
астрономическому календарю [148], приведены в табл. 13.1. Каждая стро¬
ка этой таблицы соответствует описанным ниже конкретным условиям
эксперимента. Введены следующие обозначения столбцов таблицы: N —
количество рассмотренных комбинаций; М — среднее значение коэффи¬
циента монохроматичности; σ — среднеквадратическое отклонение КМФ;
Мтах — максимальное по значению КМФ вторичное созвездие; d —
«мертвая» зона вокруг значения коэффициента М; q — значение коэффи¬
циента; р — значение коэффициента; 1* — индикатор определения уни-
Таблица 13.1. Сводная таблица результатов поиска УВС в электронном каталоге
N
М
σ
-Л4|пах
d
Я
Р
Г
1
8920
1,97
7,17
503,76
208,45
70,27
2,41
+
2
47094
0,76
0,7
22,54
4,99
32,16
4,51
-
3
244080
0,52
0,39
11,25
1,82
29,03
6,18
-
4
119374
1,88
5,05
589,1
85,34
116,6
6,9
-
5
2475792
0,77
0,71
146,27
100,75
206,4
1,45
+
6
441054
1,83
5,79
2205,9
927,57
381,3
2,37
+
7
34552
1,84
8,32
1405,6
1227,3
168,9
1,14
+
8
392328
0,76
0,67
33,41
13,883
49,99
2,41
+
9
4422384
0,53
0,39
12,22
0,3305
30,97
36,9
-
10
346342
1,77
4,99
1405,5
490,69
281,2
2,86
+
11
12333270
0,76
0,66
79,83
5,9876
120,7
13,33
-
12
12025588
1,76
5,18
2915,6
1510,1
563,2
1,93
+
13
45368
1,87
7,98
1405,5
901,78
176,2
1,56
+
14
45226
0,76
0,67
33,44
10,9
494,7
3,07
-
15
480936
0,53
0,39
12,22
0,33
31,01
36,97
-
16
529150
1,83
5,02
1405,5
901,78
280
2,86
+
17
2131714
1,84
5,43
2915,6
709,72
536,7
4,11
-
536
Гл. 13. Сигналы в виде форм вторичных созвездий
кальности вторичного созвездия (-1-, если выполняется условие (13.2.14);
—, если условие (13.2.14) не выполняется).
1. Сектор обзора — Северное полушарие; пороговое расстояние между
изображениями соседних звезд Θ = 20°; порядок контура к — 3. Гисто¬
грамма значений КМФ приведена на рис. 13.15.
10000.00
8000.00
6000.00
4000.00
2000.00
■■ ■ , ;■ ■: .7.:·;
. . 7 . . 7'
■
1
Ill 1 ® ‘ 1 1 ® ] '
& О <£>
ъ4
Рис. 13.15. Гистограмма величины М (Северное полушарие, Θ = 20°, к — 3)
Лидирующее по величине КМФ вторичное созвездие состоит из звезд:
а1 Геркулеса, С Геркулеса, о Геркулеса. (13.3.2)
Условие (13.2.14) выполняется и данное вторичное созвездие следует
считать уникальным. Обозначим его как МарГТУ 3/1.
Далее для краткости будем приводить только сектор обзора, значе¬
ния Θ и к, состав лидирующего по величине КМФ вторичного созвездия
и отмечать, является оно уникальным или нет.
Рис. 13.16. Гистограмма величины М (Северное полушарие, Θ = 20°, к — 4)
2. Северное полушарие, Θ — 20°, к — 4, созвездие не является уни¬
кальным:
71 Андромеды, р Персея, 41 Овна, а Треугольника. (13.3.3)
3. Северное полушарие, Θ = 20°, к = 5, созвездие не является уни¬
кальным:
50 Кассиопея, S Кассиопея, β Кассиопея, ι Цефея, 7 Цефея.
(13.3.4)
13.3. Характеристики уникальных вторичных созвездий
537
& л*5 л^>
ъ· V V V ν ν fe* v
с? ч5
°>· 4<δ· </
Рис 13.17. Гистограмма величины М (Северное полушарие, Θ = 20°, к = 5)
120000
100000
80000
60000
40000
20000
1 - Щ ^μμΛΜμ '
Hi
Ь-Η 1 1 1 1 —1 ■&—
+—I—®—J
ν'»
V· V V V "5
г
Рис. 13.18. Гистограмма величины М (Северное полушарие, Θ = 40°, к = 3)
2500000.00
2000000.00
1500000.00
1000000.00 —-
500000.00
0.00
& Л*?
*· Ч «?· Л4»·
Рис. 13.19. Гистограмма величины М (Северное полушарие, Θ = 40°, к = 4)
4. Северное полушарие, Θ — 40°, & = 3, созвездие не является уни¬
кальным:
7 Персея, с* Возничего, о Персея. (13.3.5)
5. Северное полушарие, Θ = 40°, /г = 4. Уникальное созвездие
МарГТУ 4/1:
β Волопаса, т Геркулеса, ζ Геркулеса, а Северной Короны. (13.3.6)
538
Га. 13. Сигналы в виде форм вторичных созвездий
Рис. 13.20. Гистограмма величины М (Северное полушарие, Θ = 60°, к — 3)
40000.00
35000.00
30000.00
25000.00
20000.00
15000.00
10000.00
5000.00
0.00
Ί—1—I—
Λ- λΛ Λ <θ> Λ (A
3V?
fr4' £>' S*' <&' Λν η&\
Рис. 13.21. Гистограмма величины Μ (Южное полушарие, Θ = 20°, к = 3)
6. Северное полушарие, Θ = 60°, к — 3. Уникальное созвездие
МарГТУ 3/2:
ζ Лебедя, а Малой Медведицы, а Треугольника. (13.3.7)
7. Южное полушарие, Θ = 20°, к = 3. Уникальное созвездие
МарГТУ 3/3:
а Киля, δ Голубя, HD64440 Кормы. (13.3.8)
8. Южное полушарие, Θ = 20°, к = 4. Уникальное созвездие
МарГТУ 4/2:
7 Мухи, ω Киля, HD 94510 Киля, ε Южного Креста. (13.3.9)
9. Южное полушарие, Θ = 20°, к = 5. Созвездие не является уникаль¬
ным:
к Скорпиона, ζ Стрельца, а Стрельца, а Телескопа. (13.3.10)
10. Южное полушарие, Θ = 40°, к = 3. Уникальное созвездие
МарГТУ 3/3:
а Киля, δ Голубя, HD 64440 Кормы.
(13.3.11)
13.3. Характеристики уникальных вторичных созвездий
539
140000.00
120000.00
100000.00
80000.00
60000.00
40000.00
20000.00
0.00
ШТТТТпГТп^/».
V л·
Рис. 13.22. Гистограмма величины М (Южное полушарие, Θ = 20°, к = 4)
-I
1 1 1 1—I 1—®K£>—I—H
$ U* Jo· 4? <> ν’ Ф ЛЪ Ч>
ν V V k* b* Λ* V <V
Рис. 13.23. Гистограмма величины M (Южное полушарие, θ = 20°, к = 5)
400000
350000
300000
250000
200000
150000
100000
50000
0
^ (о0 ψ ф Я?
Л- <Л· л\· Л* Л· Л- аУ Л*
> л? м" tP а,®1 оР ч>
Рис. 13.24. Гистограмма величины М (Южное полушарие, Θ = 40°, к = 3)
540
Га. 13. Сигналы в виде форм вторичных созвездий
4000000.00 -
3000000.00
2000000.00
1000000.00
0.00
ojb <Л oh ф о4» ф я? Л-
V ф* £· ф· ф- л>* л*
кЬ Jo оЬ
Рис. 13.25. Гистограмма величины М (Южное полушарие, Θ = 40°, А; — 4)
Рис. 13.26. Гистограмма величины М (Южное полушарие, Θ = 60°, к = 3)
11. Южное полушарие, # = 40°, к = 4. Созвездие не является уни¬
кальным:
/3 Мухи, v Киля, HD 92139 Паруса, σ Центавра. (13.3.12)
12. Южное полушарие, Θ = 60°, к = 3. Уникальное созвездие
МарГТУ 3/4:
Весов, η Павлина, σ Кентавра. (13.3.13)
13. Оба полушария, Θ = 20°, к = 3. Уникальное созвездие МарГТУ 3/3
а Киля, £ Голубя, HD64440 Кормы. (13.3.14)
14. Оба полушария, Θ = 20°, к = 4. Созвездие не является уникальным:
7 Мухи, о; Киля, HD94510 Киля, ε Южного Креста. (13.3.15)
15. Оба полушария, Θ = 20°, к — 5. Созвездие не является уникальным:
к Скорпиона, 72 Стрельца, ζ Стрельца, а Стрельца, а Телескопа.
(13.3.16)
13.3. Характеристики уникальных вторичных созвездий
541
Рис. 13.27. Гистограмма величины М (оба полушария, Θ = 20°, к = 3)
О0 ^ , fe°> * Λ'ν ef» V <\*> *
о· "5· (о· чО· ^3· Nb· rj>· rj»· ,£>· фГ
Рис. 13 28. Гистограмма величины М (оба полушария, Θ = 20°, к = 4)
160000
140000
120000
100000
80000
60000
40000
20000
0
Л Л Л /V ^<0 ^
Ь· ^^ ^
Рис. 13.29. Гистограмма величины М (оба полушария, Θ = 20°, к — 5)
542
Гл. 13. Сигналы в виде форм вторичных созвездий
Рис. 13.31. Гистограмма величины М (оба полушария, Θ = 60°, к — 3)
16. Оба полушария, Θ = 40°, к = 3. Уникальное созвездие МарГТУ 3/3:
а Киля, δ Голубя, HD64440 Кормы. (13.3.17)
17. Оба полушария, Θ = 60°, к — 3. Созвездие не является уникаль¬
ным:
ν Весов, η Павлина, σ Кентавра. (13.3.18)
Эксперимент убедительно подтвердил наличие уникальных звездных
образований.
Сведения о шести УВС приведены в табл. 13.2, а их изображения
показаны на рис. 13.32.
УВС найдены на небесной сфере среди звезд с яркостью от — 1,5т
до 4,0т звездной величины. Несмотря на огромное количество форм,
образуемых группами звезд, количество найденных УВС весьма невелико
и равно шести, т.е. составляет тысячные доли процента, и при этом они
имеют очень низкую размерность ЭК, определяющего их форму: к = 3,4.
13.3. Характеристики уникальных вторичных созвездий
543
J :
■440 Киля.
<V\ :
аКипя
Г4
6 Голубя ‘
Рис. 13.32. Изображения вторичных созвездий с уникальной монохроматичностью
формы: а — Северное полушарие МарГТУ 3/1, Θ = 20°, б — Северное полушарие
МарГТУ 3/2, ^ = 60°, в — Южное полушарие МарГТУ 3/3, Θ = 20°, г — Южное
полушарие МарГТУ 3/4, Θ = 60°, д — Южное полушарие МарГТУ 4/2, Θ = 40°,
е — Южное полушарие МарГТУ 4/2, Θ = 20°
544
Гл. 13. Сигналы в виде форм вторичных созвездий
Таблица 13.2
№
Название
Состав созвездия
к
Координаты
центра
Угл.
диам.
Коэф.
МОН.
1
МарГТУ 3/1
ζ Геркулеса Ц.Т.,
о Геркулеса,
а Геркулеса
3
17 ч 21м 16,1 с
25°11'14,4"
21,75°
503,76
2
МарГТУ 3/2
α М. Медведицы,
а Треугольника,
ζ Лебедя
3
23 ч 34 м 28 с
54°24,45,/
70,13°
2205,9
3
МарГТУ 3/3
δ Голубя, а Киля,
HD6440 Кормы
3
6 ч 53 м 34 с
—42°—43'—14,1"
22,29°
1405,5
4
МарГТУ 3/4
υ Весов, σ Кентавра,
η Павлина
3
15ч 4м 8,7с
—51°—40'—40,5"
48,7°
2915,6
5
МарГТУ 4/1
т Геркулеса,
ζ Геркулеса Ц.Т.,
а Северной Короны,
β Волопаса
4
15ч 54м 22с
36038'35"
21,81°
146,27
6
МарГТУ 4/2
HD94510 Киля,
ω Киля, 7 Мухи,
ε Южного Креста
4
11ч 29м 49,8 с
-66°-0'-0,3"
16,27°
33,441
МарГТУ 3/1
fl
О 100 200 300 400 500
А МарГТУ 3/2
X;
О 500 1000 1500 2000 2500
А МарГТУ 3/3
Н 1 1 Н 1
О 300 600 900 1200 1500
А МарГТУ 3/4
1 I I ^ 1 1 ί ►
0 500 10001500 2000 2500 3000
А МарГТУ 4/1
1 I I I 1 + · ‘ Ί ►
0 30 60 90 120 150
А МарГТУ 4/2
1 ί I I ^ 1 |-Г>
0 5 10 15 20 25 30
Рис. 13.33. Иллюстрация степени изолированности уникальных вторичных созвез¬
дий (А — область значений коэффициентов М всех вторичных созвездий, кроме
уникальных)
На рис. 13.33 приводится иллюстрация степени изолированности УВС
по значению коэффициента монохроматичности формы от всех других
вторичных созвездий.
13.4. Оптимальные формы вторичных созвездий
для идентификации звезд в их составе
Как следует из п. 13.2, УВС имеет форму правильных fc-угольников.
Правильные fc-угольники обладают поворотной симметрией, т.е. если про¬
нумеровать вершины этих фигур, а затем одну из фигур повернуть на
угол 2π/fc, то определить на какой угол была повернута фигура после
13.4. Оптимальные формы вторичных созвездий
545
окончания поворота невозможно. При этом происходит сдвиг вершин фи¬
гуры, что ведет к изменению номера вершины fc-угольника, зафиксиро¬
ванного в определенном направлении.
Поворот не влияет на положение цен¬
тра тяжести фигуры (т. 4 на рис. 13.34).
Данная ситуация является след¬
ствием того, что правильная фигура
обладает монохроматическим спектром
и является оптимальным сигналом для
решения задачи распознавания. Полез¬
ным результатом при этом может быть
визирование центра тяжести фигуры.
Задача определения номеров правиль¬
ного fc-угольника является задачей
оценки параметров сигнала и для ее оптимального решения этот сигнал
должен иметь широкий равномерный спектр. Поэтому правильный к-
угольник является наихудшим сигналом для этой задачи. В дальнейшем
задачу нумерации вершин правильного fc-угольника назовем задачей
идентификации его вершин. Компромиссным решением при выборе одного
и того же сигнала для решения задач распознавания и оценки параметров
может быть сигнал в виде композиционного контура (см. п. 12.2.3).
Энергетический спектр такого контура равномерен, а его составные
части — ЭК, имеют монохроматический спектр.
Целесообразность решения идентификации вершин fc-угольника УВС
показана на рис. 13.35. Летательный аппарат находится в т. О — начале
отсчета СКЭ. Оптическая ось его ОТД расположена в направлении ОА}
причем ее угловые координаты в данной системе отсчета неизвестны.
Рис. 13.34. Изменение нумерации
вершин правильного треугольника
относительно направления АВ при
повороте на 240°
Рис. 13 35. Ориентация ЛА по звездам уникального вторичного созвездия
546
Гл. 13. Сигналы в виде форм вторичных созвездий
Необходимо чтобы в результате ориентации эта ось совпала с направ¬
лением ОС, на котором расположена звезда 5. Пусть в процессе поиска
было найдено и распознано УВС, звезды которого являются вершинами
правильного треугольника 12 3, расположенного в пределах телевизион¬
ного кадра ТК.
Если бы было известно соответствие звезд 1, 2, 3 звездам в машинном
кадре, то с помощью векторов 1,5; 2,5 и 3,5 можно было бы найти звезду 5
и задать по лучу ОС направление ориентации Л А. Однако треугольник 123,
как правильная фигура, обладает поворотной симметрией. Угол его поворота
относительно такого же треугольника известен с точностью ±120°. Поэтому
однозначная локализация группы звезд 5 на основе распознанного УВС
невозможна. Единственная полезная информация о положении оптической
оси датчика может быть получена в результате визирования по лучу ОВ
центра тяжести фигуры УВС, т.е. точки S. Угловое положение этой точки
инвариантно к углу поворота треугольника 123.
В п. 13.2 было показано, что с ростом порядка ЭК искомого УВС резко
возрастает количество контуров, образованных к точками, и уменьшается
вероятность существования такого созвездия на небесной сфере. В то
же время ЭК при минимальной размерности к — 3 позволяет решать
задачу распознавания УВС. Поэтому, целесообразно, в первую очередь,
рассмотреть, как наиболее простую, задачу идентификации вершин УВС
такой размерности.
Из рис. 13.35 следует, что соседние с УВС звезды могут образовывать
совместно с УВС произвольные вторичные созвездия. Рассматриваемый
подход к решению задачи идентификации вершин заключается в выборе
вторичного созвездия, включающего УВС и соседние с ним звезды, наи¬
более сложной формы, т.е. с наиболее равномерным спектром, или, что
то же самое, с наиболее узкой АКФ. Для такого созвездия задача оценки
параметров может быть решена достаточно точно. Вторичное созвездие
на базе УВС и ряда соседних звезд назовем композиционным, а компози¬
ционное созвездие с дельтовидной АКФ — уникальным композиционным
вторичным созвездием (УКВС). Желательно, чтобы УКВС включало ми¬
нимальное количество соседних звезд, в идеале — только одну. В качестве
контура с РЭС, более простого, чем композиционный, выберем контур, ас¬
социированный с многофазным аналогом ЛЧМ сигнала третьего порядка,
фаза которого определяется в соответствии с выражением:
φη = ~ (гг2 + гг) , гг = 0,1,... , к - 1. (13.4.1)
Вид контура размерности к = 3 показан на рис. 13.36, а. Он является
незамкнутым и содержит три ЭВ. Его код и спектр имеют вид: Г =
= {-1; 0,5 - 0,866г; -1}; Р = {-1, 5 -0,866г; -1,5 - 0,866г; 1,732г}.
Существование УКВС обусловлено совместным действием трех сле¬
дующих факторов: 1) наличие УВС; 2) существование четвертой звезды,
образующей с заданной точностью контур со свойством (13.4.1); 3) от¬
сутствие других звезд, образующих с заданной точностью с остальными
вершинами УВС контур со свойством (13.4.1).
13.4. Оптимальные формы вторичных созвездий
547
“|рМ|
Т,732
■ 3
б О
в -2 -1 О 1 2 п
Рис. 13.36. Контур с равномерным спектром размерности к = 3: а — вид контура;
б — амплитудный спектр; в — АКФ контура
Рассмотрим требования к форме УКВС для идентификации вершин
УВС с к = 3. УВС данного порядка образует на сфере квазиправильный
сферический треугольник 1,2,3 (см. рис. 13.37). Образуем три правильных
сферических треугольника 1,2,1'; 2,3,2'; 3,1,3', каждый из которых
включает одну сторону треугольника УВС. Для каждой из вершин 1', 2', 3'
этих треугольников найдем из бортового каталога ближайшие звезды. На
рис. 13.37 они обозначены как 12 3”. Вторичные созвездия, задаваемые
Рис. 13.37. Возможные композиционные вторичные созвездия для выбора УКВС
при к = 3
контурами 2", 2,3,1 (рис. 13.37, б), 3", 3,1,2 (рис. 13.37, в) и 1", 1,2,3
(рис. 13.37, г), а также с не показанными на рис. 13.37 контурами 1,2,3,2";
2,3,1,3" и 3,1,2,1", являются кандидатами для выбора из них УКВС.
Для этого контур должен обладать квазидельтовидной АКФ и квазирав¬
номерным спектром.
Аналогично тому, как для оценки степени правильности fc-угольника
УВС был введен коэффициент монохроматичности формы М, для оценки
степени дельтовидности контура УКВС введем коэффициент V дель-
товидности формы (КДФ) контура как отношение модуля отсчета η (0)
циклической АКФ контура к модулю максимального ее бокового отсчета
1^? (о)!
max[|ij(n)|]’
п- 1,2,.
, к — 1.
(13.4.2)
Таким образом подход к выбору формы УКВС заключается в поиске
максимального КДФ по результатам вычислений нескольких циклических
АКФ, соответствующих контурам {1", 1,2,3}, (2", 2,3,1} и {3", 3,1,2}.
После выбора контура с максимальным КДФ порядок чередования вершин
однозначно идентифицирует все вершины в распознанном УВС.
548
Гл. 13. Сигналы в виде форм вторичных созвездий
и*
К3)
г®
Г V
1
о—
а До
КО
Рис. 13.38. Контур с равномерным спектром размерности к = 4: а — вид контура,
б — амплитудный спектр, в — АКФ контура
Рассмотренный подход для идентификации вершин УВС применим
для созвездий произвольных размерностей.
В качестве формы контура с РЭС (дельтовидной АКФ) при к = 4, вы¬
берем контур, фаза которого определяется в соответствии с выражением:
φ = {0;7г/2;-7г;тг/2}. (13.4.3)
Такой контур относится к семейству композиционных контуров, ас¬
социированных с многофазным кодом класса р при к2 = 4. Вид контура
размерности к2 — 4 показан на рис. 13.38, а.
Он является незамкнутым и содержит
четыре ЭВ. Его код и спектр имеют вид:
Г = {1, г, —1, г}; Р = {2г, 2,-2г, 2}. На
рис. 13.39 представлен вид УВС четвертого
порядка и восемь соответствующих ему
композиционных контуров, претендующих
на роль УКВС.
Рис. 13.39. Возможные композиционные вторичные созвездия для выбора УКВС
при к2 = 4
13.5. Результаты экспериментального исследования по поиску УКВС 549
13.5. Результаты экспериментального исследования по поиску
УКВС для идентификации звезд в составе УВС
Распознавание УВС, форма которых характеризуется монохроматич-
ным спектром, позволяет решить лишь задачу визирования ЛА точки
центра тяжести УВС, положение которой не зависит от угла поворота
и начальной точки контура УВС. Для решения задачи ориентации ЛА
этого недостаточно, так как точка визирования может служить лишь на¬
чалом отсчета новой системы координат, в которой задаются координа¬
ты ЛА и звезд. Необходимо также однозначно задать направление осей
системы, для чего следует провести идентификацию вершин распознан¬
ного УВС. Теоретически эта задача рассмотрена в разделе 13.4. Для ее
решения необходимо на базе УВС перейти к другому вторичному созвез¬
дию — к УКВС, форма которого имеет РЭС. С этой целью УВС допол¬
няется соседними звездами до образования сложных контуров. Получим
алгоритм поиска УКВС для идентификации вершин УВС: МарГТУ 3/1,
МарГТУ 3/2, МарГТУ 3/3, МарГТУ 3/4, МарГТУ 4/1 и МарГТУ 4/2.
13.5.1. Алгоритм поиска УКВС третьего порядка. Для решения за¬
дачи идентификации звезд, образующих УВС третьего порядка, восполь¬
зуемся следующим алгоритмом поиска УКВС.
1. Пусть заданы координаты звезд, образующих УВС третьего порядка
(рис. 13.40): A(xi,yi,zi), В (х2, уч, z2), C{x3,y3,z3). Необходимо найти
Рис 13.40. Пояснение к выбору соседних звезд для поиска УКВС третьего порядка
координаты точек D,E,F, одна из которых в случае обнаружения близко
от нее звезды, образует с точками А, В и С УВС требуемый широ¬
кополосный контур (см гл. 12): D (ж'15 у[, ζ[), Е (х'2,У2, z'2)> F (х'3,у'3, ζ'3).
Зафиксируем сторону АВ сферического треугольника АВС и опреде¬
лим координаты точки D. Вычисления координат точек D, Е, F удобно
550
Га. 13. Сигналы в виде форм вторичных созвездий
произвести в алгебре кватернионов. Координаты точек А, В, С образуют
соответственно векторные кватернионы:
qi = 0 4- х± · г + ух · j + z± · fc,
<72 — 0 4- Ж2 ’ * 4- У2 ■ j 4" ^2 * (13.5.1)
Яз = 0 4- ж3 · г + уз · j + z3 · к,
где i, j, к — мнимые единицы.
Для вычисления координат Df Е, F необходимо
выполнить поворот кватернионов <73 вокруг qi, qi
вокруг (72 и <72 вокруг д3 на определенные углы.
При этом будут образованы кватернионы q[, qr2 и <73.
Угол поворота а должен определяться исходя из
Рис. 13.41. Опреде- условия, что образуемые сферические треугольники
ление угла поворота ABD, ACF и ВСЕ должны быть правильными,
кватерниона Рассмотрим треугольник ABD (рис. 13.41). Требу¬
ется определить ZBQD = а при заданном угле
ZAOB = ф и при условии, что ZBAD = β = 60°.
Так как модули векторных кватернионов qf2 и <73 равны 1 (точки А,
Б, Б принадлежат поверхности сферы единичного радиуса), а Б(Э-1АО,
то имеем:
1 -Ь cos ф + 2 cos β
а = arccos
1 -f cos ф
(13.5.2)
где cos^ = ж 1Ж2 + У1У 2 4- ζχΖ2 — скалярное произведение векторов О А
тОВ.
При β = 60°: а = arccos (—CQS^—-V
^ ^ V1 + cos ф )
Чисто векторный кватернион q[ = 0 + х^г -f y[j 4* z[k определим как
Qi = Qi (<*) -Яз-Яг («)> (13.5.3)
где qi (а) = cos (а/2) 4- sin (а/2) [х\ · г 4- У\ · i 4* ^1 · ft] — вспомогатель¬
ный кватернион, a gi (а) = cos (а/2) — sin (а/2) [χχ · г 4* yi ■ j 4- 21 · к] —
кватернион, сопряженный с ним. Произведение кватернионов (13.5.3)
должно выполняться в соответствии с правилами умножения кватер¬
нионов. Пусть первый кватернион Qi = αχ 4- bii 4- c±j + d\k, второй
кватернион Q2 = a2 4- b2i 4- c2j 4- d2k} тогда их произведение Q3 =
= Qi · Q2 определится как
<2з =
(fti · а2 — b\ · Ъ2 — С\ · с2 — d\d2) 4* (ft 1 · b2 4- bi · ft2 4- Ci · <^2 — <^1^2) i 4*
+ (ai · C2 4" Ci · ft2 4- d\ · b2 — b\d2) j 4- (fti · c/2 4· c?i · ft2 4* bi · C2 — C1&2) k.
(13.5.4)
Найденные из выражения (13.5.4) значения х\, у[, z[ являются коорди¬
натами точки D. Аналогично, определяются координаты точек Е и F.
2. Определяем по данным электронного каталога ЛА, составленно¬
го в соответствии с [148], координаты звезд, являющихся ближайшими
13.5. Результаты экспериментального исследования по поиску УКВС 551
к точкам Д Е и F, т.е. координаты точек К(х”, у"\ z"), L^x'^y'^A)
и S{x'i,y4,z!l).
Для УВС МарГТУ 3/1: А — ζ Геркулеса Ц.Т., В — а1 Геркулеса,
С — о Геркулеса, К — l Геркулеса, L — 7 Змеи, S — 72 Змееносца.
Для УВС МарГТУ 3/2: А — а М.Медведицы, В — ζ Лебедя, С —
а Треугольника, К — ε Близнецов, L — ζ Геркулеса, S — 98 Водолея.
Для УВС МарГТУ 3/3: А —δ Голубя, В — а Киля, С — HD64440 Кор¬
мы, К — ξ Кормы, L — а Часов, S — ε Киля.
Для УВС МарГТУ 3/4: А — η Павлина, В — σ Центавра, С — υ Весов,
К — 72 ЛРыбы, L — а Девы, S — φ Стрельца.
3. Исследуем свойства контуров АВК, BCL и CAF. Для этого выпол¬
ним проецирование координат звезд A,B,C,K,L,S в плоскость, парал¬
лельную экваториальной плоскости Хпл^плУпл (см. рис. 13.40) следующим
способом.
Для контура УВС определим центр тяжести Ц(ггц,уц7^ц), где
_ _Х1+Х2+ХЗ .. _У1 +!&+!& _ _ Ζΐ +Ζ2 +Ζ3 покп
Хц — β ? Уц — 2 — 3 * Цо.э.э;
В сферической системе координат центр тяжести имеет координаты
Ц(а, ί), а — прямое восхождение, δ — долгота в ЭСК:
а = arctg f—V δ = arctg ( *ц ). (13.5.6)
\X«J \л/ха + Уа/
С целью нахождения проекций точек A(xi,yi,zi), В (х2,2/27^2),
C(x3,y3iz3), К (х'Ьух yZfi)t L{xfi,y4,z%), S (х%, t/3, z%) на плоскость
^плОплУпл, выполним следующие преобразования. Составим матрицу
XI
χ2
хз
х'{
х"
х'з
У1
У2
Уз
у"
Уз
(13.5.7)
*1
Ζ2
Ζ3
ζ'{
4
4\
Матрицу координат повернутых звезд определим как
X*OB = X3.Ry(-a4)R*(-f-54)
^ ^1пов
2/1пов
■ΖΙποβ
х2иов
2/2пов
ζ2ποβ
жЗпов
2/Зпов
z3noB
X 1пов
У 1пов
„гг
Ζ ΙπΟΒ
//
X 2пов
У 2пов
Ζ 2ποβ
\Х Зпов
7/"
У Зпов
А
3 пов ,
(13.5.8)
где Rz((^), Ry(<p) — матрицы вращения соответственно вокруг осей OZ
(ось OZ совпадает с осью ОР в СКЭ (см. рис. 13.40)) и OY (ось OY сов¬
падает с осью OR в СКЭ (см. рис. 13.40)) на угол φ (вращение происходит
552
Гл. 13. Сигналы в виде форм вторичных созвездий
против часовой стрелки, если смотреть с конца оси):
(cos(<p) sin(<£) 0\ / cos(<p) 0 sin(<p)\
-sin(<p) cos(<^) 0 I , Ry(<p) = [О 1 0 I
О 0 1/ \— sin (φ) 0 1 /
При повороте точки А, В, С, if, L, S будут иметь новые координаты
^4-пов (^lnoBj 2/Iiiobj ^1пов) > ^пов (^2noBj 2/2пов) 2·2ποβ) j
Спов (З'Зпов? 2/Зпов) ^Зпов) у -^пов (з> 1пов) У 1пов> Z 1пов) >
-^пов 2повз 2/ 2пов) 2 2пов) j ^пов Зпов> У Зпов*^ Зпов) ·
Следует предположить, что координаты z повернутого УВС будут
примерно одинаковыми (для идеального ЭК — одинаковые). Поэтому для
формирования кода контура в плоскости хПл®плУпл из матрицы XfI0B до¬
статочно использовать только координаты х и у, т.е. первый и второй
столбцы матрицы Хд0в. Это условие можно записать в виде
XnP = augment (χ^0Β(1\Хэпов<2>)
^•^1пов
2/1пов^
ж2пов
2/2пов
Я'Зпов
2/Зпов
г"
•^Ιποβ
2/lnoB
'г"
х2пов
^2пов
\*^Зпов
У Зпов/
(13.5.9)
Спроецированные в плоскость точки А, В, С, К, L, S будут иметь
координаты
-^■пл (^Тповэ 2/1пов) ? ВПл (®2noBi 2/2пов) ) Сил (^Зпов) 2/Зпов) ?
•^пл 1пов)2/ 1пов) ?-^пл (х 2пов чУ 2пов) у£>пл (х ЗповчУ Зпов)
На рис. 13.42 показан вид УВС МарГТУ 3/1, МарГТУ 3/2, МарГТУ 3/3,
МарГТУ 3/4 и соответствующих выбранных соседних звезд, спроециро¬
ванных в плоскость, параллельную плоскости небесного экватора в СКЭ:
а — спроецированное созвездие МарГТУ 3/1 и выбранные соседние с ним
звезды; б — вид УКВС, обладающего наибольшим значением КДФ для
идентификации звезд, образующих УВС МарГТУ 3/1; в — спроециро¬
ванное созвездие МарГТУ 3/2 и выбранные соседние с ним звезды; г —
вид УКВС, обладающего наибольшим значением КДФ для идентификации
звезд, образующих УВС МарГТУ 3/2; д — спроецированное созвездие
МарГТУ 3/3 и выбранные соседние с ним звезды; е — вид УКВС, обла¬
дающего наибольшим значением КДФ для идентификации звезд, образу¬
ющих УВС МарГТУ 3/3; ж — спроецированное созвездие МарГТУ 3/4
и выбранные соседние с ним звезды; з — вид УКВС, обладающего наи¬
большим значением КДФ для идентификации звезд, образующих УВС
МарГТУ 3/4.
Треугольники АПЛВПЛЬПЛ, ВПЛСПЛ8ПЛ и СПЛАПЛКПЛ имеют большую
асимметрию формы, что сказывается на значениях КМФ соответству¬
ющих контуров (табл. 13.3).
13.5. Результаты экспериментального исследования по поиску УКВС 553
,г к
ос 1 Геркулес;
72 Змееносца о Геркулеса
*$ГОТ O'—w>rol ^пл |
' I Геркулеса
„%л I
^ Геркулеса Ц.Т.
У Змеи I
Ош о Геркулеса
I
а\ Геркулеса^/0ς Геркулеса ц.т.
Аш
/Змеи
I I I I ' Ί " "I I Ί I' I 1
« Треугольника ^Кш\
СПТ1 -^еБлизнецов
Ат
*а М.Медведицы
98 Водоцея
' В ^ г
£Лебедячччьпл|
ί ί ί j .....i..—L.....iZa.··
^Геркулеса
■ ЯГ) Киля
с ^пл ^Кл
тг °ПЛ
еКилЯо
ох_ш
«Киля1
Am
«Часов
Кормы
пл
<5“ Голубя
1 1 1 1 »
1 I I I t I 1 1 Г—1
Ы \
4луД¥’Стре,льца
^ Весов
VAnl
У2 «Девы
' Центавра J
Рис. 13.42. Проекции звезд, образующих УВС 3-го порядка и отобранных соседних
звезд
4. Для определения оптимального контура УКВС определим
КДФ V широкополосных контуров КПЛСПЛАПЛВПЛ, ^плЛл^плА™,
^плАплВплСпл, -^плВплАилСпл, SUJlВПЛСплАилj ^пл^Ал-^пл-^пл (СМ. рИС. 13.42).
Результаты приведены в табл. 13.4.
В силу того, что взаимное положение звезд в течение продолжитель¬
ного времени сохраняется с очень высокой точностью, то и проекционные
ошибки при одном и том же способе проецирования сохраняются. Причем,
чем больше угловое расстояние между звездами, тем меньшее влияние
оказывает координатный шум на значение КДФ контуров при предложен-
554
Гл. 13. Сигналы в виде форм вторичных созвездий
Таблица 13.3. Значения КМФ контуров, прилегающих к спроецированному
в плоскость УВС третьего порядка
Наименов.
созвездия
Максимальное значение КМФ
^ПЛ-ПплСпл
AluiBjiJiLjui
-^ПлС’пл^ПЛ
-4пл Спл Кпл
МарГТУ 3/1
503,761
165,669
4,983
31,413
МарГТУ 3/2
2205,861
7,608
8,157
9,275
МарГТУ 3/3
1405,538
6,019
15,589
15,589
МарГТУ 3/4
2915,584
12,424
7,66
7,66
Таблица 13.4. Значения КДФ контуров, ассоциированных с УВС
Наименов.
созвездия
Значение КДФ
КПЛ Сил
Аил Вил
1
Кил -4.Щ1
Сил Вил
2
Вил -4пл
Вил Сил
3
Вил Вил
Апл Спл
4
♦^пл Вил
Сил Аил
5
$ПЛ Сил
Вил Аил
6
МарГТУ 3/1
33,581
29,229
162,652
143,511
33,51
5,255
МарГТУ 3/2
9,833
9,045
7,297
8,338
9,27
7,69
МарГТУ 3/3
37,178
7,393
11,548
5,109
311,757
15,66
МарГТУ 3/4
50,111
13,107
19,206
11,085
15,325
7,029
ном способе проецирования. Таким образом, можно считать, что фигуры,
представленные на рис. 13.42, образуют устойчивую форму.
Приведенные в табл. 13.4 значения КДФ могут использоваться для поис¬
ка УКВС, а в дальнейшем — в качестве входных параметров при решении
задачи идентификации звезд, образующих УВС. Приведем алгоритм иден¬
тификации звезд в УВС, использующий распределение значений КДФ.
1. Определяем максимальное значение КДФ для каждого УКВС.
2. Определяем индекс ind, соответствующий максимальному значению
КДФ. Для МарГТУ 3/1 ind = 3, для МарГТУ 3/2 ind = 1, для МарГТУ 3/3
ind = 5, для МарГТУ 3/4 ind = 1.
Определив максимальное значение КДФ для каждого созвездия, мы
тем самым идентифицируем одну из его сторон. Остальные звезды, об¬
разующие УВС, идентифицируются также в силу неизменяемости их
местоположения при определенном направлении обхода.
Для УВС МарГТУ 3/1 учтем, что два наибольших значения КДФ
при ind = 3 и ind = 4 определяют одну и ту же сторону. Поэтому
окончательно алгоритм идентификации выглядит следующим образом:
МарГТУ 3/1 = true if (ind (max (КДФ)) = 3) or (ind (max (КДФ)) = 4)
false otherwise,
(13.5.10)
МарГТУ 3/2 = true if (ind (max (КДФ)) = 1)
(13.5.11)
false otherwise,
МарГТУ 3/3 = true if (ind (max (КДФ)) = 5)
(13.5.12)
false otherwise,
13.5. Результаты экспериментального исследования по поиску УКВС 555
МарГТУ 3/4 = true if (ind(max(КДФ)) = 1) 13513
false otherwise.
13.5.2. Алгоритм поиска УКВС четвертого порядка. Получим алго¬
ритм поиска УКВС для решения задачи идентификации звезд, образую¬
щих УВС четвертого порядка.
1. Пусть заданы координаты звезд, образующих УВС четвертого по-
рядка (рис. 13.43): A(xi,yi,zi), B(x2,y2,z2), С (х3,Уз, *з), D (х4,у4, ζ4).
Рис. 13.43 Пояснение к выбору соседних звезд для поиска УКВС четвертого по¬
рядка
Необходимо найти координаты соседних звезд (см. рис. 13.43), которые
вместе с координатами УВС образуют требуемый контур:
qi = 0 + χι ■ г + у4 ■ j + zx · k, q2 = 0 + x2 ■ г + y2 ■ j + z2 ■ k,
_ _ . . . (13.5.14)
q3 = 0 + x3 · г + y3 · j + z3 · fc, g4 = 0 + x4 · г + г/4 · j + z4 · k,
где г, j, k — мнимые единицы.
Для вычисления координат Ац, Вц, Сц, £>ц определим ближайшие
координаты звезд из электронного каталога к точкам, образованным при
вращении кватернионов вокруг дх, <73 вокруг дг, <74 вокруг дз и дх во¬
круг <74 на угол
а = arccos
-14- cos ψ 4- 2 - cos (π/2)
1 4- cos ψ
— arccos
— 1 4- cos ψ
1 4- cos φ
Для вычисления координат Αχ2, Βχ2, C12, B12 определим ближайшие
координаты звезд из электронного каталога к точкам, образованным при
вращении кватернионов дх вокруг (72, <72 вокруг дз, дз вокруг д4 и д4 во¬
круг дх на угол (—а).
2. В результате имеем:
556
Гл. 13. Сигналы в виде форм вторичных созвездий
для УВС МарГТУ4/1: А — β Волопаса, В — г Геркулеса, С — ζ Гер¬
кулеса, D — а Сев. Короны, Ац — η Б. Медведицы, Вц — 7 Дракона,
Сц — а1 Геркулеса, Du — а Волопаса, А12 — р Волопаса, В\2 —
l Дракона, С12 — о Геркулеса, D12 — 7 Змеи;
для УВС МарГТУ4/2: А — ω Киля, В — HD94510 Киля, С —
ε Юж. Креста, D — 7 Мухи, Ац — HD76728 Киля, Вц — μ Паруса,
Сц — β Центавра, Бц — а Г. Птицы, А12 — ζ Л. Рыбы, В12 — χ Паруса,
Си — σ Центавра, D12 — а Циркуля.
3. Исследуем свойства контуров АплБплБПл12^пл1Ь ДшСдлСплиДип,
АлАлАл^Али, А^пИшагАтла· Для этого спроецируем точки А,
В, С, D, Ац, Вц, Сц, Аъ Ai2, В12, С12, D12 в ПЛОСКОСТЬ
Выполним преобразования для этих точек, аналогичные преобразовани¬
ям (13.5.5)—(13.5.9), относительно центра тяжести фигуры А} Б, С, D.
На рис. 13.44 показан вид УВС МарГТУ 4/1, МарГТУ 4/2 и соот¬
ветствующих выбранных соседних звезд, спроецированных в плоскость,
параллельную плоскости небесного экватора в СКЭ.
—I 1 1 1 Г"
Ат 12/
Н 1 1 1
5 Θ Геркулеса
ζ Геркулесу/
; Ол*^,
- а Сев.Короны
гГеркулеса
уРАш
А^^
Ал
β Волопаса
1 1 1 1 1—
J 1 1 1
сг Циркуля
т- гг А
а Г. Птицы
Ύ Мухи
со Киля
^пл12
ζ Л.Рыбы
АиП2 ^пл11
β Центавра
^пл12
σ Центавра
^Юж.Креста
Arnll |
μ Паруса
HD 94510 Киля
’пл12 X Паруса
HD 76728 Киля ι
“ i i i i i i i i
CnTT π Д Центавра
ЙОж.Креста
-
Впл
о Киля пиу4510 Киля_
Рис. 13.44. Проекции звезд, образующих УВС 4-го порядка и отобранных соседних
звезд: а — спроецированное созвездие МарГТУ 4/1 и выбранные соседние с ним
звезды; б — вид созвездия, обладающего наибольшим значением КДФ для иден¬
тификации звезд, образующих УВС МарГТУ 4/1; в — спроецированное созвездие
МарГТУ 4/2 и выбранные соседние с ним звезды; г — вид созвездия, обладаю¬
щего наибольшим значением КДФ для идентификации звезд, образующих УВС
МарГТУ 4/2
13.5. Результаты экспериментального исследования по поиску УКВС 557
Как и следовало ожидать, четырехугольники
АплАгы Axnl2-Auill > СПЛDUJ1 Dnjii2CUjiH И Апл АПЛАПЛ12-Апл11 ИМеЮТ большую
асимметрию формы, что сказывается на значениях КМФ соответствую¬
щих контуров (табл. 13.5).
Таблица 13.5. Значения КМФ контуров, прилегающих к спроецированному
в плоскость УВС четвертого порядка
Наименов.
созвездия
Максимальное значение КМФ
ABCD
Аил Вил
Вил12 -4-плИ
-4пл Спл
С'пл12 Bjuill
Спл Djui
Вцл12 Спл11
Вцл Алл
^4пл12 ΑμΙΙ
МарГТУ 4/1
146,2712
6,635
9,905
8,438
8,183
МарГТУ 4/2
33,441
3,999
4,393
7,07
3,849
4. Для поиска УКВС определим КДФ V широкополосных конту¬
ров. 1) AnjlUAnjlBnjlCnjlDnjl, 2) ^ПЛ12-^ПЛ^ПЛ^ПЛ^ПЛ> 2) ^плП^плСпл^плАпл,
4) ^пл12^пл Ахл-^пл^ ПЛ> 5) С?пл11^ПЛ-^ПЛ^ПЛ-^ПЛ> ^пл12 АплС7щ[-Впл.Апл,
Ч) В)плц£)плАплВплСпЛ) 8) ^пл12^пл А^^пл-Алл (СМ. риС. 13.44 И Табл. 13.6).
Таблица 13.6. Значения КДФ контуров, ассоциированных с УВС
Наименов.
созвездия
Значение КДФ
1
2
3
4
5
6
7
8
МарГТУ 4/1
27,904
29,212
67,099
117,47
14,626
7,89
10,147
5,374
МарГТУ 4/2
32,292
18,807
6,473
10,847
36,313
12,272
7,683
12,421
Значения КДФ, приведенные в табл. 13.6, могут использоваться для
поиска УКВС, а в дальнейшем в качестве входных параметров при
решении задачи идентификации звезд, образующих УВС. Приведем
следующий алгоритм идентификации звезд в УВС, используя распре¬
деление значений КДФ. Сгруппируем контуры, оканчивающиеся на од¬
ну и ту же звезду, т.е.: а) Аплц ^ПЛ-^ПЛ^ПЛ-^ПЛ И Спл^Спл^ПЛ^ПЛ-^ПЛ?
б) Япл 12 -^пл-^пл^плАлл И D^n Г)илАилВплСпл, в) Bnjl\\BUjlCUjlDnjlA1[ljl И
^пл12-^плСпл-^пл-^пл> г) СилцСпл-^пл-^-пл^пл И ^пл12^пл^пл Азл-Алл· β ЭТОМ
случае для идентификации могут применяться уже не только сами значе¬
ния КМФ, но и их линейные комбинации. Например, хорошие результаты
для идентификации представляет распределение отношений КДФ, при¬
веденных в табл. 13.7.
Таблица 13.7. Значения отношений КДФ контуров, ассоциированных с УВС
и заканчивающихся одной и той же звездой
Наименов.
созвездия
Значение отношений КДФ
КДФ1/КДФ4
КДФ2/КДФ7
КДФЗ/КДФ6
КДФ5/КДФ8
МарГТУ 4/1
0,238
2,879
8,505
2,722
МарГТУ 4/2
2,977
2,488
0,527
2,923
558
Гл. 13. Сигналы в виде форм вторичных созвездий
Согласно значениям, приведенным в табл. 13.7, алгоритм идентификации
звезд в составе УВС четвертого порядка строится следующим образом.
1. Определяем минимальное значение отношения КДФ для каждого
ассоциированного с УВС контура.
2. Определяем индекс ind, соответствующий минимальному значению
отношений КДФ. Для МарГТУ 4/1 ind = 1, для МарГТУ 4/2 ind = 3.
Определив минимальное значение отношения КДФ для каждого ассо¬
циированного с УВС контура, в котором последняя точка является общей,
мы тем самым идентифицируем эту точку, являющуюся одной из вер¬
шин УВС. При обходе в определенном направлении наименование звезд
нам известно, поэтому все звезды, образующие данное УВС становятся
проидентифицированными.
Описанный алгоритм можно представить в виде:
МарГТУ 4/1 = true if ^ind ^min () ) =
false otherwise,
МарГТУ 4/2 = true if (ind (min (fjj|^)) = з)
false otherwise,
(13.5.15)
(13.5.16)
где
ind
/КДФЗ\
\КДФ6/
— 3,
ind
/КДФ5\
\ КДФ8 /
= 4.
13.6. Основные результаты
Сформулированы требования к форме вторичных созвездий, исполь¬
зуемых для ориентации летательных аппаратов при полной априорной
неопределенности углового положения оптической оси ОТД. Они связаны
с ограничением на величину углового диаметра вторичного созвездия, на
яркость и количество составляющих его звезд, а также на уникальность
формы. Последнее предполагает отсутствие на небесной сфере других со¬
звездий не только с такими же, но даже и с близкими свойствами формы.
Эти свойства должны легко обнаруживаться благодаря очень большому
отношению сигнал/шум в пространстве форм.
Показано, что при заданной размерности к форма изображения вто¬
ричного созвездия максимально отличается от форм остальных вторич¬
ных созвездий на небесной сфере. Форма задается элементарным кон¬
туром, т.е. имеет равномерную АКФ и дельтовидный спектр. Порядок
контура не играет роли, а с позиции удобства формирования контура
по к точкам выбран элементарный контур Γχ, все компоненты спектра
которого, за исключением р( 1), равны нулю. Степень отличия формы,
задаваемая элементарным контуром, от формы контуров, образуемых
к звездами, взятых в качестве вершин многоугольника, увеличивается
с ростом к, причем наиболее резко в области небольших значений к,
а время поиска УВС при переборе всевозможных комбинаций форм,
13.6. Основные результаты
559
образуемых всеми звездами на небесной сфере в заданном диапазоне
их светимости, резко возрастает при больших значениях к. Поэтому
с позиции реализуемости данного метода ориентации целесообразно
ограничиться формой вторичного созвездия в виде элементарного кон¬
тура с размерностями к = 3,4,5.
Реальными ориентирами могут быть лишь вторичные созвездия,
задающие квазиправильные fc-угольники. Введена мера степени моно¬
хроматичности — коэффициент монохроматичности формы М — тако¬
го многоугольника в виде отношения модуля спектральной составляю¬
щей р{ 1) к модулю наиболее интенсивной составляющей в оставшейся
части спектра. КМФ характеризует степень эффективности вторичного
созвездия в качестве ориентира. Величина отношения КМФ конкретного
вторичного созвездия к среднеквадратичному отклонению КМФ, вычис¬
ленному по всем остальным вторичным созвездиям, задает отношение
сигнал/помеха q на входе системы ориентации. Для подавляющего боль¬
шинства вторичных созвездий КМФ меньше единицы.
Сформулированы в аналитическом виде условия, при которых вто¬
ричное созвездие может быть признано уникальным. В соответствии
с первым условием КМФ УВС должен превышать КМФ любого вто¬
ричного созвездия в заданной области небесной сферы, в соответствии
со вторым — величина отношения сигнал/помеха q должна при этом
превышать некоторое пороговое значение до, а третье задает степень
изолированности р КМФ УВС в пределах гистограммы значений М.
Степень изолированности р определяется в виде отношения КМФ УВС
к ширине d «мертвой зоны» вокруг значения КМФ УВС на гистограмме.
Чем меньше при этом величина р, тем шире мертвая зона и тем боль¬
ше степень изолированности. Эксперимент показал, что для уверенного
распознавания УВС должны выполняться условия: q ^ 10, р ^ 3.
При принятых ограничениях эксперимент убедительно доказал су¬
ществование на небесной сфере уникальных звездных образований на
примере шести УВС.
Задача оценки параметров местоположения летательного аппарата мо¬
жет быть успешно решена не по форме УВС, а по другому сигналу,
ассоциированному с изображением УВС. Один из подходов к получению
такого сигнала заключается в использовании отсчетов яркости звезд УВС.
Другой подход, реализованный в данной работе, основан на контексте
точечной сцены в районе УВС. На базе звезд УВС и соседних звезд
получается уникальное композиционное вторичное созвездие, контур ко¬
торого в отличие от узкополосного контура УВС является максимально
широкополосным. В качестве контура УКВС третьего порядка выбран
контур, ассоциированный с многофазным аналогом ЛЧМ сигнала третьего
порядка, а в качестве контура УКВС четвертого порядка контур, ассоци¬
ированный с кодом класса р. Оба вида этих контуров требуют минималь¬
ного количества новых звезд, имеют равномерный энергетический спектр
и дельтовидную АКФ, т.е. являются наилучшими сигналами для решения
задачи оценки параметров.
560
Гл. 13. Сигналы в виде форм вторичных созвездий
Таким образом, материал данной главы подтвердил существование
квазиоптимальных ориентиров в виде уникальных вторичных созвездий,
обладающих высокой монохроматичностью формы и сильной изолирован¬
ностью от других возможных вторичных созвездий, а также ассоцииро¬
ванных с ними уникальных композиционных созвездий с дельтовидной
АКФ формы.
13.7. Примеры
В этом разделе приведены примеры для иллюстрации наиболее важных тео¬
ретических и прикладных вопросов, связанных с обработкой сигналов, задаваемых
точечными образами.
Пример 1. Найти коэффициент монохроматичности М формы изображе¬
ния, задаваемой контуром изображения Г = {3; 5г; 5 — Зг; Юг; —2 + 5г; —2 — 2г;
-4 -f 5г} (рис. 13.45). Вычислим амплитудно-частотный спектр контура: Р =
= {0; 0,848; 1,729; 1,494; 3,731; 1,76; 3,491}.
Получим в соответствии с выражением (13.2.9) коэффициент монохроматич¬
ности формы М = 0,848/3,731 = 0,227.
Рис. 13.45
Ύ
0,5
П А
Λ Ί
Д(-0,3;0.2)
2:0.15)
Л 1
U, 1
1
-0 5 -0,3 ЮЛ 00 1 0 3 0 5 χ
α-ό.2|
-0
1)
Я(0,2;-0,35)
Рис. 13.46
Пример 2. В плоскости ОТД координаты 4-х звезд принимают следующие зна¬
чения А (0,2; 0,15); В (0,2; -0, 35); С (-0,3; -0,1) и D (-0,3; 0,2) (рис. 13.46).
Требуется найти КМФ всевозможных вторичных созвездий, состоящих из
трех звезд.
Для нахождения форм третьего порядка из четырех звезд можно образовать
четыре группы по три звезды {А, В, С}, {А, В, D}, {А, С, D} и {В, С, D}.
Каждая группа образует по шесть правильных ориентированных многоуголь¬
ников. Например, для группы звезд {А, В, С} имеем следующие ориентирован¬
ные конфигурации звезд: А, В, С; В, С, А; С, А, В; А, С, В; С, В, А; В, А, С.
Коды контуров, образуемых первыми тремя конфигурациями и последними
тремя конфигурациями, являются циклически сдвинутыми. Поэтому для ампли¬
тудно-частотных спектров контуров выполняются следующие равенства:
|Рлвс| = \Рвса\ = |Рслв| и \Расв\ = |Рсвл| = |Рвлс|·
Следовательно, рассчитаем амплитудно-частотные спектры следующих кон¬
туров:
ГАВС, Г АСВ, Г ABD-, Г ADB , Г лев, Г ADC? Г BCD, Г BDC-
13.7. Примеры
561
Разностный код каждого контура имеет вид:
Тавс = {—0,68г; -0,4 + 0,43г; 0,4 + 0,25г},
Тлев = {-0,4 - 0,25г; 0,4 - 0,43г; 0,68г},
Tabd = {—0,68г; -0,5 + 0,73г; 0,5 - 0,05г},
Г adb = {—0,5 + 0,05г; 0,5 — 0,73г; — 0,68г}
Гacd = {-0,4 - 0,25г; -0,1 + 0,3г; 0,5 - 0,05г},
Tadc = {-0,5 + 0,05г; 0,1 - 0,3г; 0,4 + 0,25г},
Tbcd = {-0,4 + 0,43г; -0,1 + 0,3г; 0,5 - 0,73г},
Tbdc = {—0,5 + 0,73г; 0,1 — 0,3г; 0,4 — 0,43г}.
Выполнив прямое ДПФ, найдем амплитудно-частотный спектр контуров:
\Равс\ = {0; |0,156 - 0,327*|; |—0,156 - 1,713г|} = {0; 0,362; 1,72},
\Расв\ = {0; |-0,52 - 0,24г|; |0,12 - 0,01г| = {0; 0,573; 0,121}},
\Pabd\ = {0; |0,675 - 0,154г|; |—0,675 - 1,886г| = {0; 0,693; 2,003}},
\Padb\ = {0; |-0,675 - 0,119г|; |0,157 + 0,169г| = {0;0,668;0,231}},
\Pacd\ = {0; |-0,297 + 0,145г|; |—0,903 - 0,895г|} = {0; 0,33; 1,271},
\Padc\ = {0; |-0,409 + 0,112г|; ( — 0,091 - 0,062г|} = {0; 0,424;0,11},
\Pbcd\ = {0; |0,292 + 1,165г|; ( — 1,492 + 0,125г|} = {0; 1,201; 1,497},
\Pbdc\ = {0; |-0,212 + 0,452г|; ( — 0,288 + 0,278г|} = {0; 0,499; 0,4}.
Рассчитаем КМФ каждого контура:
Мавс — 0,211, Масв — 4,746, Mabd = 0,346, Mabd — 2,892,
Мacd — 0,26, Madc = 3,849, Mbcd = 0,802, Mbdc — 1,247.
Пример 3. Определим КДФ незамкнутого контура Tdcab (рис. 13.46).
Разностный код контура имеет вид
Гdcab = {0,1 — 0,3г; 0,4 -f 0,25г; —0,68г}.
Циклическая АКФ контура имеет вид
|N| = {|0,785|; |-0,001 + 0,059i|; |-0,001 -0,059*|} = {0,785; 0,059; 0,059} .
Коэффициент дельтовидности формы определим в соответствии с выражени¬
ем (13.4.2): V = 0,785/0,059 = 13,301.
Пример 4. Рассмотрим УВС МарГТУ 3/1, образованное звездами: + — ζ Гер¬
кулеса Ц.Т. с координатами (αχ = 16 ч 41 мин 17,5 с; δι = 31°36/7//), В —
о Геркулеса (с*2 = 18ч 7мин 32,5 с, 62 = 28°45,45,/), С — а1 Геркулеса (аз =
= 17 ч 14 мин 38,9 с, δ3 = 14°23'25"). Вычислим КМФ УВС.
1. Преобразуем сферические координаты УВС в радианы:
* = 1,2,3,
В
Oii =
δί = -
15π / аМинг
180 (а,< + 60
15ТГ / _ ^минг
180 V Гра^ + 60
ас г_ \
3600/ ’
+
АЛ
3600 )
результате получаем
αχ = 4,3689591, δι = 0,551558,
α2 = 4,7452957, δ2 = 0,5020003,
α3 = 4,514505, δ3 = 0,2511577.
562
Гл. 13. Сигналы в виде форм вторичных созвездий
2. Перейдем из сферической системы координат в декартовую. Для этого
выполним следующие преобразования:
х = cos (δ) · cos (а), у = cos (5) · sin (α), ζ = sin ((5).
в результате получаем
X
У
Z
А
-0,2867864
-0,8019738
0,5240148
В
0,0288415
-0,8761472
0,48118
С
-0,1904269
-0,9497224
0,2485255.
3. Вычислим центр масс созвездия (Л, В, С):
1 3 1 3 1 3
»ΣΙ(' να=όΣν*· Ζ“=*Σ;
Результат: хц = —0,1494573, уц = —0,8759478, zn — 0,4179068.
Длина вектора, проведенного из центра сферы к точке, являющейся центром
масс, определится как: |ОЦ| = yj(хц)2 + (уц)2 + (zn)2 = 0,981976.
4. Найдем координаты центра тяжести У ВС в сферической системе координат.
С учетом квадранта для arctg получаем
ац — arctg
+ π = 4,5433929рад,
(5Ц = arctg (
( Zu —^
^ \/Ы2 + (уи)2'
0,439602рад.
5. Осуществим поворот вокруг осей OZ и OY фрагмента звездного неба,
включающего У ВС:
Хпов = Хэ · Ry (-С*ц) · Rz (-^
3^1 пов У 1пов
^2пов У 2пов
З'Зпов 2/Зпов
пов
•2^2 пов
-^Зпов
В результате получим
хэ
-0,2867864 -0,8019738 0,5240148
0,0288415 -0,8761472 0,48118
-0,1904269 -0,9497224 0,2485255
X
ПОВ
0,1172228
0,0699362
-0,1871589
-0,1478146
0,1757923
-0,0279777
0,9820436
0,9819399 ·
0,9819312
6. Осуществим параллельный перенос в плоскость, параллельную экватори¬
альной ПЛОСКОСТИ ЖплОплУпл-
Следует предположить, что координаты z поернутых звезд, составляющих
УВС, будут примерно одинаковыми (для ЭК — точно одинаковыми). Поэтому
для формирования кода контура в плоскости ЖплОплУпл из матрицы Хц0В До¬
статочно использовать только координаты х и у, т.е. первый и второй столбцы
матрицы Хц0В.
13.8. Задачи и упражнения
563
0,1172228 -0,1478146
Результат: Хэпр = 0,0699362 0,1757923 .
-0,1871589 -0,0279777
Отброшенная третья координата ζ, может в любое время использоваться при
обратном переходе из плоскости на сферу.
7. Сформируем код контура в плоскости хПл0плУпл'
7 (1) = (0,066993 - 0,117228) + г (0,1757923 + 0,1478146) =
= -0,0472866,-fiO,323607,
7 (2) = (-0,1871589 - 0,066993) + г (-0,0279777 - 0,1757923) =
= -0,2570951 - *0,20377,
7 (0) = (0,117228 + 0,1871589) + г (-0,1478146 + 0,0279777) =
= -0,3043817 + г0,1198369.
8. Запишем амплитудно-частотный спектр контура:
р (о) = 0, р (1) = -0,1436181 + гО,9716636,
р (2) = -0,0017582 - гО,0008427.
9. Вычислим КМФ контура УВС.
Модули соответствующих гармоник запишутся как
|р (1)| = 0,9822201, \р (2)| - 0,0019498.
Тогда
М = -Г-Ш! = 503,7608192.
|Р(2)|
13.8. Задачи и упражнения
1. Найти коэффициент монохроматичности формы контура Г = {1,1,1,—1,
-1.-1}·
2. Найти коэффициенты монохроматичности формы всевозможных вторичных
созвездий, состоящих из 4-х звезд, представленных на рис. 13.46.
3. Определить коэффициент дельтовидности формы незамкнутых контуров
Tadbc, Г вс ad, Tcdba (рис. 13.46).
4. Координаты трех звезд на небесной сфере в экваториальной системе коорди¬
нат имеют значения
oli = 16ч 40 мин 10 с; δι = 30°40'7",
Οίΐ — 15 ч 48 мин 40 с, = 25°20' 10",
с*з = 16ч 40мин Юс, δ3 = 30°15'45".
Вычислить коэффициент монохроматичности формы вторичных созвездий,
образованных этими звездами, предварительно спроецировав их относительно
центра тяжести созвездия.
5. Докажите, что КМФ циклически сдвинутых замкнутых контуров принимает
одно и то же значение, т.е.
Μ (Γι52,... ,fc—ι) = М (Г2,з,... ,fc-i,i) — ... — M (rfc_iji)...jfc_2).
6. Вычислите коэффициент дельтовидности формы замкнутого контура, пред¬
ставленного на рис. 13.45.
Глава 14
СИГНАЛЫ НА БАЗЕ КОМПОЗИЦИОННЫХ КОНТУРОВ
В СИСТЕМАХ СВЯЗИ С КОДОВЫМ УПЛОТНЕНИЕМ
КАНАЛОВ
14.1. Введение
Применяемые в системах связи сигналы и методы их обработки на¬
целены, как правило, на минимизацию взаимного влияния сигналов от
различных источников. Обычно речь о полном устранении взаимного вли¬
яния не идет. Например, в системах связи с кодовым разделением каналов
взаимное влияние сигналов из-за возникновения корреляционных шумов
при их обработке ухудшает отношение сигнал/помеха и тем самым сни¬
жает пропускную способность канала связи. При этом требования сниже¬
ния уровня боковых лепестков корреляционной функции может вступать
в противоречие с другими требованиями, предъявляемыми к сигналам,
например, максимизации расстояния между сигналами в признаковом
пространстве. В системах связи с временным разделением каналов силь¬
ное влияние могут оказывать переходные помехи.
Рассмотренные в гл. 12 комплекснозначные последовательности в виде
композиционных контуров из полного семейства ЭК обладают равномерным
энергетическим спектром и дельтовидной циклической АКФ, что позволяет
исключить при их обработке влияние корреляционных шумов. Составляю¬
щие их элементарные контуры, обладающие дельтовидными непересекаю-
щимися спектрами, образуют алфавит последовательностей, эффективных
для распознавания (см. п. 4.4). Поэтому описанные сигналы могут исполь¬
зоваться как для разрешения, так и для распознавания, т.е. для задач,
предъявляющих к спектру сигнала противоречивые требования.
Практика построения современных телекоммуникационных систем
и сетей показывает, что наиболее дорогостоящими звеньями трактов
передачи являются линии связи [195]. Поскольку экономически неце¬
лесообразно использовать дорогостоящую линию связи для передачи ин¬
формации единственной пары абонентов, то возникает задача построения
многоканальных систем передачи информации. Структурная схема про¬
стейшей многоканальной системы связи изображена на рис. 14.1. Первич¬
ные сигналы αχ (£), (£),... , аг (£), подлежащие передаче, преобразу¬
ются посредством модуляторов Μι, М2,... , Мг в электрические сигналы
Ui (t), U2 (t),... , ur (£), а затем смешиваются в аппаратуре уплотнения.
Полученный таким образом групповой сигнал и (t) передается по линии
14.2. Основы построения систем связи
565
Рис. 14.1. Структурная схема простейшей многоканальной системы связи
связи. Приемник из принятого зашумленного колебания z(t) — и (£)+п (t)
с помощью устройства разделения селектирует канальные сигналы щ (t),
преобразуемые посредством демодуляторов (детекторов) £>χ, D<i,... , Dr
в соответствующие первичные сигналы αχ (t), а>2 (t),... , ar (t).
Чтобы разделяющие устройства были в состоянии выделять каналь¬
ные сигналы из группового, должны существовать определенные призна¬
ки, присущие только сигналу данного канала. Такими признаками в общем
случае могут быть параметры переносчика, например, амплитуда, частота
или фаза в случае модуляции синусоидального переносчика, временное
положение, длительность или форма сигнала при модуляции импульсных
переносчиков. Соответственно различают и способы разделения сигналов:
частотный временной, фазовый, разделение по форме сигналов и др.
В последние годы отчетливо прослеживается тенденция роста интереса
к системам связи, использующим кодовое разделение каналов. Это объяс¬
няется рядом преимуществ, которыми обладают такие системы: эффектив¬
ным использованием частотного диапазона, высокой помехоустойчивостью,
скрытностью передачи информации и др. При кодовом разделении кана¬
лов все абоненты могут работать в общей полосе частот, а разделение
их возможно за счет различия сигналов, выделенных каждому абоненту.
Системы связи с кодовым разделением являются адресными системами,
так как сигналы абонента выполняют роль его адреса. Ниже рассматрива¬
ется возможность применения сложных сигналов на базе композиционных
контуров в системах связи с кодовым уплотнением каналов.
14.2. Основы построения систем связи с применением
комплекснозначных сигналов
Рассмотрим одноканальную систему связи, в которой в качестве ал¬
фавита сигналов используются композиционные контуры с дельтовидной
АКФ. Как было показано в гл. 12, для каждого значения размерности к
существует не менее чем φ (к) к контуров с такой АКФ, φ (к) — функция
Эйлера, к — размерность элементарного контура. Структурная схема
системы связи представлена на рис. 14.2. В таблице соответствий ТС
передатчика задаются алфавит допустимых символов и соответствующие
им номера комбинаций ЭК в композиционном контуре. Массив комбина-
566
Гл. 14. Композиционные контуры в системах связи
Передающее
устройство
гкк
“И
мэк
I
ι-ΗΚΟΦιΚΗ
I
I
4
КС
_£Ζ
1
1
ГШК
КСФ:
•^ксф,
->1 пу
ЭУ
н
тс
Приемное
устройство
И»
Рис. 14.2. Структурная схема системы связи
ций ЭК содержится в генераторе композиционных контуров ГКК, а сами
элементарные контуры — в массиве ЭК (МЭК). Поступающему на вход
системы символу в ТС ставится в соответствие композиционный контур,
который генерируется ГКК и будет передан по каналу связи КС. Шумы,
воздействующие на композиционный контур при его передаче, имитиру¬
ются генератором шумовых контуров ГШК.
Далее зашумленный сигнал поступает на вход приемника, где происхо¬
дит его распознавание. В случае полностью известного сигнала контурные
согласованные фильтры (КСФь ... , КСФм), количество которых равно
количеству эталонных контуров, вычисляют реальную часть (к2 — 1)-го
отсчета ВКФ зашумленного и соответствующего эталонного контуров:
sk2 — l
Re (N, Г,·) = Re ί ^ и (η) (η)
' η=0
где j — номер эталона. Для сигналов с неизвестными параметрами ста¬
тистикой для принятия решения является нормированное скалярное про¬
изведение (см. п. 4.4).
Экстремальное устройство ЭУ выбирает реальную часть отсчета с мак¬
симальным значением. Если она превышает порог С/о, то по таблице со¬
ответствий выбирается символ алфавита в качестве элемента сообщения.
Пороговый уровень U0 определяется допустимым значением риска ошибоч¬
ных решений, априорными вероятностями наличия и отсутствия символа,
среднеквадратическим отклонением шума σΒΧ и нормой контура ЦГ^Ц.
Эффективность системы связи характеризуется вероятностями пра¬
вильного и ошибочного распознаваний каждого символа и зависит от
объема передаваемого алфавита.
14.3. Применение комплекснозначных сигналов в системах
связи с кодовым уплотнением каналов
14.3.1. Формирование и обработка группового сигнала. Использо¬
вание комплекснозначных последовательностей с РЭС в системах связи
с кодовым разделением каналов основано на возможности идеального раз¬
14.3. Применение комплекспозпачных сигналов в системах связи 567
деления каналов при корреляционной обработке сигнала за счет нулевой
величины скалярного произведения между сигналами различных кана¬
лов, полученных путем циклического сдвига общей базовой кодирующей
последовательности. При дальнейшем изложении будем полагать, что по
каналу передается двоичная информация, т.е. для передачи сообщений
в каждом канале необходимо кодирование только двух символов (нулей
и единиц). Возможно использование двух методов кодирования. В первом
для передачи как нулей, так и единиц используются соответствующие
кодирующие последовательности. Во втором для передачи единиц исполь¬
зуется некоторая кодирующая последовательность, а нули передаются
паузами. Первый способ является более помехоустойчивым, но требует
в два раза большего количества кодирующих последовательностей. Ис¬
пользование второго способа возможно в условиях благоприятной поме¬
ховой обстановки, когда требуется увеличить количество каналов за счет
некоторого снижения помехоустойчивости.
Рассмотрим методику кодирования канальных сообщений и форми¬
рования группового сигнала. Пусть имеется базовая кодирующая по¬
следовательность Гб = {7 (n)}o k2-v При первом способе кодирования
последовательности для нуля и единицы в j-м канале получаются
циклическим сдвигом базовой последовательности соответственно на 2j
и 2j -f 1 элементов, т.е.
Г° = b°j (")}0,*»-ι = {7(« + 2Лдг}01*а_1>
Г) = W (»)}0lfci-i = (7 (η + 2j + l)jv>o,fc»-i»
где (β)^ — операция взятия по модулю к2. При втором способе кодиро¬
вания, т.е. при передаче нулей паузами, кодирующие последовательности
имеют вид
Г? = {0}0)fe=-i, Г] - {7 (п + j)w}0>fc2_r (14.3.2)
Групповой сигнал формируется путем векторного суммирования ка¬
нальных сигналов, т.е.
м-ι ,м-1 ч
!ν=ΣΓ?= Е7*Ы , (14.3.3)
j=0 4=0 Jo.fca-1
где М — количество каналов, X — символ, передаваемый в j-м канале.
На приемной стороне вычисляется скалярное произведение между эта¬
лонной кодирующей последовательностью каждого символа и принятым
групповым сигналом rgr:
к2-1
(IV, Г,·) = Vi = Σ Ъг (») 7; (п). (14.3.4)
п=0
Поскольку все используемые сигналы ортогональны, то взаимное
влияние каналов при обнаружении и распознавании сигналов исключе¬
568
Гл. 14. Композиционные контуры в системах связи
но. С учетом выражения (14.3.1) последнее соотношение можно распи¬
сать в следующем виде:
/с2 —1
т = (IV, Го) = Σ Ъг (п) 70 (п)>
п—О
k2-1 к2-1
Vi = (^gr? Γχ) = 7gr (^) 7i (n)fc2 = 7o (n »
n=0 n=0
(14.3.5)
A:2 — 1
Ή2Μ-1 — (rgr, Γχ) = 53 7ёг (П) 72M-1 (n)fc2 ~
n=0
k2-l
= Σ Tfe»· (n) Уо (n + 2M- l)fc2.
n=0
При кодировании нулей паузами необходимо вычислять не 2М, а М
скалярных произведений. Операция обработки принятой кодовой после¬
довательности сводится к вычислению ее циклической ВКФ с базовой
кодовой последовательностью:
к2-1
Vi = Σ Γ«τ7ο(η + 0*», * = 0,1,... ,2М-1. (14.3.6)
п=О
Для декодирования сигнала может использоваться устройство вычис¬
ления циклической ВКФ принятого сигнала и базового композиционного
контура.
Рассмотрим пример построения одного кадра такой многоканаль¬
ной системы связи на базе композиционного контура Го,х,2,з = {1,1,1,
1/1, г, —1, —г/1, —1,1, —1/1, —г, —1, г}. Пусть по каждому из каналов пе¬
редается двоичная информация, т.е. символы 0 и 1. Отдельному символу
в каждом канале ставится в соответствие свой композиционный контур,
получаемый последовательным сдвигом базового композиционного конту¬
ра на один элемент (см. табл. 14.1).
Количество каналов составляет при указанном методе кодирования
к2/2 = 8, где к == 4 — размерность ЭК, из которых составлен композици¬
онный контур. Допустим, что в очередном кадре передается следующая
комбинация {0,1,1,0,0,0,1,0}, т.е. в первом канале передается 0, во
втором — 1, в третьем — 1 и т.д. Групповой сигнал для этого случая будет
иметь вид rgr = {3 — г; 1 — г; 5 + г; —2; 2; 2; 2; 3 — г; Зг; 1 + г; 5 — г; 0; 0; 4;
0; 3 Ч- г}· Соответствующие ему векторная диаграмма и сигнал с ампли¬
тудно-фазовой манипуляцией приведены на рис. 14.3, а и б. На рис. 14.3, в
показан результат вычисления ВКФ между групповым сигналом и базо¬
вой кодирующей последовательностью. Видно, что положение ненулевых
элементов соответствует символам исходного сообщения, а взаимное вли¬
яние каналов при обработке отсутствует.
14.3. Применение комплекснозначных сигналов в системах связи 569
Таблица 14.1. Кодирование символов в многоканальной системе связи с кодовым
уплотнением и сигналами на базе композиционных контуров
Канал
Символ
Кодовая комбинация
1
0
1,1,1,1/1, i, —1, —*/1, —1,1, —1/1, ——1, *
1
*/1,1,1,1/1, г, -1, —г/1, -1,1, -1/1, -г, -1
2
0
-1, г/1,1,1,1/1, г, -1, —г/1, -1,1, -1/1, -г
1
-г, — 1, г/1,1,1,1/1, г, -1, —г/1, -1,1, -1/1
3
0
1, -г, -1, г/1,1,1,1/1, г, -1, -г/1, -1,1,-1
1
-1/1, -г, -1, г/1,1,1,1/1, г, -1, —г/1, -1,1
4
0
1,-1/1,-г,-1, г/1,1,1,1/1, г,-1,-г/i,-1
1
-1,1, -1/1, -г, -1, г/1,1,1,1/1, г, -1, —г/1
5
0
1, -1,1, -1/1, -г, —1, г/1,1,1,1/1, г, -1, -г
1
—г/1, -1,1, -1/1, -г, -1,г'/1,1, ], 1/1, г, -1
6
0
-1, -г/1,-1,1,-1/1, -г,-1, г/1,1,1,1/1, г
1
г, -1, —г/1, -1,1, -1/1, -г, -1, г/1,1,1,1/1
7
0
1, г, -1, —г/1, -1,1, -1/1, -г, -1, г/1,1,1,1
1
1/1,г,-1,-г/1,-1,1,-1/1, -г,-1,г/1,1,1
8
0
1,1/1, г, -1, -г/1, -1,1, -1/1, -г, -1, г/1,1
1
1,1,1/1, г,-1, -г/1,-1,1,-1/1, -г,-1, г/1
Таким образом, формирование группового сообщения сводится к сум¬
мированию отдельных кодирующих последовательностей, образуемых на
основе базовой путем циклического сдвига и выбираемых в соответствие
с передаваемым сообщением. На рис. 14.4 представлена структурная схе¬
ма системы связи с кодовым уплотнением каналов.
Символы каждого канала поступают на вход таблицы соответствий
ТС, где каждому символу ставится в соответствие номер кодовой ком¬
бинации. На основании каждого номера в генераторе композиционных
контуров ГКК формируется дискретная комплекснозначная последова-
Рис. 14.3. Векторная диаграмма суммарного сигнала (а) при использовании кодирующих
последовательностей на базе композиционных контуров, соответствующий ему фазокодиро¬
ванный сигнал (б) и результат вычисления взаимно корреляционной функции (б)
570
Га. 14. Композиционные контуры в системах связи
Рис. 14.4. Структурная схема системы связи с кодовым уплотнением каналов
с сигналами на базе композиционных контуров
тельность в виде композиционного контура. В сумматоре образуется груп¬
повой сигнал и передается в канал связи, где на него воздействуют шумы
и помехи. В приемном устройстве сигнал подвергается обработке контурным
согласованным фильтром КСФ, вычисляющем циклическую взаимно корре¬
ляционную функцию принятой и эталонной кодовых последовательностей.
Решающее устройство РУ определяет, из каких композиционных контуров
составлен групповой сигнал, и передает эти данные в таблицу соответствий,
где восстанавливаются переданные сообщения.
Рассмотренная система связи относится с синхронным адресным си¬
стема связи, в которой для нормального функционирования необходимо
обеспечение синхронизации.
14.3.2. Сравнительный анализ потенциальной пропускной способно¬
сти систем связи с кодовым разделением каналов. Предельная про¬
пускная способность системы передачи с равномерной АЧХ и линейной
ФЧХ в пределах полосы пропускания ΔF тракта передачи при наличии
стационарного гауссовского шума средней мощностью Рш и сигналов со
средней мощностью Рс определяется по формуле Шеннона [195]
С = AF log2 (1 + Рс/Рш). (14.3.7)
Как правило, при многоканальной передаче возникают специфиче¬
ские переходные помехи между каналами, обусловленные неидеально-
стью разделяющих устройств на приемной стороне и устройств формиро¬
вания сигналов на передающей, линейными и нелинейными искажениями
в групповом тракте передачи. Качество многоканальной системы с точки
зрения переходных помех можно охарактеризовать величиной затухания
Aik = lQ]g {Pi/Pik), (14.3.8)
где Pi и Pik — мощности на входе влияющего и выходе подверженно¬
го влиянию каналов. Величина затухания Aik характеризует защищен¬
ность канала от переходных помех. В соответствии с (14.3.8) для мощно¬
сти помех, наводимых г-м каналом на выходе fc-ro канала, имеем Pik =
= PilO~0,1Aik, а общая мощность переходных помех равна Рп = μΡ0, где
N
μ = Σ 10“°·Μ<* (г ф к) — коэффициент взаимных переходных помех
14.3. Применение комплекснозначных сигналов в системах связи 571
между каналами. Если формулу Шеннона (14.3.7) переписать с учетом
действия переходных помех, то
с=лг1Ц1+атЫ· (14'3'9,
Поскольку обычно Рш ^ μΡ0) то для пропускной способности системы
многоканальной связи можно записать: С = AFlog2 (1 + 1//х). Последнее
выражение позволяет учесть ограничение пропускной способности из-за
действия переходных помех.
В качестве адресных сигналов в системах связи с кодовым разде¬
лением сигналов используются линейные рекуррентные М-последова-
тельности. Для усеченной М-последовательности отношение главного
максимума к максимальному боковому лепестку автокорреляционной
функции растет приближенно как y/N, где N — число импульсов в по-
Таблица 14.2
N
М-последовательность
Aik
μ
3
1.1,-1
4,77
0,66
7
1,1,1,-1,-1,1,-1
8,45
0,857
15
-1,1,1,1, - 1, - 1, - 1, - 1,1, - 1,1, - 1, - 1,1,1
11,76
0,933
следовательности. В табл. 14.2 представлены результаты расчета коэф¬
фициента переходных помех между каналами при использовании М-
последовательностей в качестве
адресных сигналов.
На рис. 14.5 представлены за¬
висимости пропускной способности
канала С / ΔF от отношения сиг-
нал/шум в канале.
При использовании в качестве
адресных сигналов дискретных ком¬
плекснозначных последовательностей
(ДКП) на базе композиционных кон¬
туров, обладающих дельтовидной ав¬
токорреляционной функцией, вели¬
чина затухания между влияющим
г-м каналом и подверженным вли¬
янию к-м каналом в выражении
(14.3.8) стремится к бесконечности.
Коэффициент взаимных переход¬
ных помех μ при этом стремится
к нулю. Пропускная способность канала определяется при этом
выражением (14.3.7) и намного превышает пропускную способность,
обеспечиваемую усеченными М-последовательностями (см. рис. 14.4).
Рис. 14.5. Зависимость пропускной спо¬
собности канала от отношения сигнал/
шум при использовании комплексно¬
значных последовательностей с РЭС
и усеченных М-последовательностей
572
Гл. 14. Композиционные контуры в системах связи
14.4. Сравнительный анализ помехоустойчивости систем связи
с кодовым разделением каналов
Качество работы системы связи можно охарактеризовать как вероят¬
ностями ошибок при приеме символов, так и вероятностями правильного
распознавания. В симметричных каналах связи без памяти, в которых
используются ортогональные сигналы для кодирования нулей и единиц,
в отдельном канале вероятность правильного распознавания не зависит
от передаваемого сообщения и равна
= 0,5 + Φ(\/2ς),
функция Крампа, q ■
(14.4.1)
где Ф (х) = -j=J е η /2άη
ν2πο
ние сигнал-шум на выходе устройства обработки, ||Г|| — норма сигнала,
σΒχ — среднеквадратическое отклонение шума на входе устройства обра¬
ботки [197].
В системах связи, где кодирование нуля осуществляется паузой,
вероятность правильного распознавания можно определить следующим
образом. Случайная величина на выходе КСФ имеет гауссовское рас¬
пределение с математическим ожиданием либо 0, либо ||Г||2 в зависимо¬
сти от того, присутствует на входе только шум (передается ноль), либо
смесь сигнала с шумом (передается 1) и среднеквадратическим отклоне¬
нием σΒΒΙΧ = сгвх 11Г11 (см. п. 3.9.1). Поскольку функции плотности веро¬
ятности при этом симметричны и имеют одинаковую дисперсию, порог
принятия решения в пользу нуля или единицы составит Щ = ||Г||2/2.
Тогда вероятность правильного приема нуля и единицы определяется
соотношением
ОО Uq
1 Г .-(n+may/^dv= [ 6ν/2σ„
V 2π (Т вых
Uq
у/2πο
4η.
Поскольку отношение сигнал/шум на выходе согласованного фильтра q =
= 11Г11 /сгвх [42], среднеквадратическое отклонение шума будет равно ствых =
= ||Г||2/д. Окончательно имеем
ί ‘-“К**· <“">
— ОО
На рис. 14.6 приведены характеристики распознавания полностью из¬
вестного сигнала. Теоретическая характеристика построена в соответствии
с соотношениями (14.4.1) (рис. 14.6, а) и (14.4.2) (рис. 14.6, б). Эксперимен¬
тальные характеристики получены методом математического моделирования.
Для кодирующих последовательностей с РЭС на базе композиционных
контуров экспериментальные характеристики распознавания не зависят
от числа каналов, размерности кодирующей последовательности и близки
14.4. Сравнительный анализ помехоустойчивости систем связи 573
•м- экспериментальная характеристика для усеченной М-последова-
тельности (к-9,М-4)
— теоретическая характеристика
Рис. 14.6. Характеристики распознавания полностью известных сигналов в систе¬
ме связи: а — при кодировании нулей сигналами; б — при кодировании нулей
паузами
к теоретическим характеристикам, отражающим потенциальную помехо¬
устойчивость. В случае М-последовательностей вид характеристик рас¬
познавания существенно зависит от числа каналов и размерности коди¬
рующей последовательности. Для рассмотренного случая при количестве
каналов М = 4 и длине усеченной М-последовательности к — 9 помехо¬
устойчивость системы существенно ниже потенциальной и практически
не улучшается при увеличении отношения сигнал/шум.
При приеме сигнала с неизвестной начальной фазой решение выно¬
сится на основании величины модуля отсчета на выходе согласованного
фильтра. При кодировании нуля и единицы соответствующими сигнала¬
ми решение, как и в случае полностью известного сигнала, принимается
в пользу того сигнала, для которого получен максимальный отклик на
выходе фильтра. Вероятность правильного приема символа определяется
по формуле [197]
Рпр — 1 — 0,5 ехр {—0,5ς2}. (14.4.3)
При кодировании нуля паузой плотность распределения модуля вы¬
ходного отсчета фильтра описывается законом Релея-Райса, причем
параметры закона и, соответственно, форма получаемого распределе¬
ния существенно зависят от вида передаваемого сообщения и отношения
сигнал/шум. При передаче нуля закон распределения соответствует реле-
евскому, при передаче единиц и больших отношениях сигнал/шум закон
распределения приближается к гауссовскому [58]
В режиме приема сообщений порог выбирается из условия равенства
вероятностей правильных решений при передаче любого из символов. Его
величина будет зависеть от отношения сигнал/шум и определяется из
соотношения
Рпр ( ^0) ц) Рпр (^0 1 0) — 0 5
(14.4.4)
574
Га. 14. Композиционные контуры в системах связи
со
Г ( р 4- о2
-РпР(«о,д) = ί-ехр<
)lo (q-t)dt,
(14.4.5)
J 1
h
)
Uo
Г ( Р Ί
Ρηρ (ωο,Ο) =1 t · exp j
>I0 (0)dt,
(14.4.6)
о
где РПр (uo, q) — вероятность правильного приема единицы, Рпр (щ, 0) —
вероятность правильного приема нуля, 1о (х) — модифицированная функ¬
ция Бесселя нулевого порядка, щ — нормированный порог. Знание отно¬
сительного порога позволяет определить теоретическое значение веро¬
ятности правильного приема символов при данном значении отношения
Pnp4
1
L
p
2npi
1-
* W
0,8-
0,8
0,6
=ЙЙp№==
0,6-
—:
0,4-
—
0,4
0,2
0 2-
n
—► n
экспериментальная характеристика для композиционного контура
д** экспериментальная характеристика для усеченной М-последова-
тельности (k-9,M=4)
теоретическая характеристика
Рис. 14.7. Характеристики распознавания сигналов с неизвестной начальной фазой
в системе связи: а — при кодировании нулей сигналами; б — при кодировании
нулей паузами
сигнал/шум q путем непосредственной подстановки найденного значения
и0 в выражение (14.4.5) или (14.4.6). На рис. 14.7 приведены характери¬
стики распознавания сигнала с неизвестной начальной фазой. Теоретиче¬
ская характеристика построена в соответствии с соотношениями (14.4.3)
(рис. 14.7, а) и (14.4.5) (рис. 14.7, б). Как и в случае характеристик распозна¬
вания при известной начальной фазе, последовательности с РЭС обладают
значительным преимуществом в помехоустойчивости.
14.5. Обсуждение результатов
Композиционные контуры обладают равномерным энергетическим
спектром и дельтовидной циклической АКФ, что обуславливает их
эффективность при решении задачи разрешения сигналов по времени.
Элементарные контуры образуют алфавит ортогональных сигналов, эф¬
фективных для решения задачи распознавания, что позволяет распозна¬
вать составленные из них композиционные контуры. Последовательности,
14.5. Обсуждение результатов
575
полученные циклическим сдвигом композиционных контуров, при извест¬
ном времени прихода сигнала, являются эффективными и для решения
задачи распознавания и могут применяться в системах связи с кодовым
уплотнением каналов. Кодовые комбинации в подобных системах форми¬
руются путем циклического сдвига элементов базового композиционного
контура. Скалярное произведение полученных таким образом кодовых
последовательностей равно нулю, что позволяет исключить взаимное вли¬
яние каналов при их разделении. Обработка принятой кодовой последова¬
тельности сводится к вычислению ее циклической ВКФ с базовой кодовой
последовательностью. Положение ненулевых элементов на графике ВКФ
соответствует сдвигам относительно базового контура последовательно¬
стей, кодирующих переданные в этих каналах символы.
Характеристики распознавания последовательностей с РЭС в системе
связи с кодовым разделением каналов близки к потенциальным и не
зависят от количества каналов и длины кодирующей последовательности.
При использовании усеченных М-последовательностей, характеристики
распознавания зависят от числа каналов и размерности кодирующих по¬
следовательностей. Рост числа каналов приводит к росту корреляционных
шумов и, соответственно, к ухудшению характеристик. Уменьшение раз¬
мерности кодирующей последовательности приводит к увеличению отно¬
сительного уровня боковых лепестков корреляционной функции последо¬
вательности и также ухудшает характеристики распознавания. Методика
формирования сигнала с кодированием нулей и единиц в сообщениях
обладает более высокой помехоустойчивостью и дает выигрыш в отно¬
шении сигнал/шум в 2 раза. Приемник сигналов с неизвестной начальной
фазой, как и следовало ожидать, обладает меньшей помехоустойчивостью.
Проигрыш в отношении сигнал/шум составляет 2 раза.
ЗАКЛЮЧЕНИЕ
Одной из тенденций развития теории обработки сигналов является
адаптация ее методов к работе современных высокопроизводительных
средств. Примером может служить работа [200]. Следует заметить, что
большие ресурсы в производительности вычислителей и величине объ¬
ема запоминаемых данных не всегда служат основой успешного решения
поставленной задачи. В качестве примера, когда эти факторы не играют
решающей роли, можно привести ситуацию, связанную с подавлением
боковых лепестков сжатого дискретно-кодированного радиолокационного
сигнала. Как известно, лучший из таких сигналов получен Р. Френком.
После сжатия его пиковый отсчет примерно в 3 \[к раз превышает уровень
максимального бокового лепестка, где к — количество кодовых интер¬
валов в сигнале. Боковые лепестки сжатого сигнала являются помехо¬
вым фактором (“корреляционные” шумы). Они маскируют сигнал от цели
с малой эффективной площадью рассеяния на фоне сигнала от близко
расположенной цели с большой эффективной площадью рассеяния. Для
борьбы с корреляционными шумами их сглаживают, увеличивают количе¬
ство кодовых интервалов в сигнале, компенсируют шумами специального
комплементарного сигнала. Однако эти подходы не устраняют эффект
корреляционных шумов принципиально, так как направлены на борьбу
с симптомами явления, а не с его причиной. Выяснение механизма по¬
явления этих шумов показало, что для их полного подавления необходи¬
мо осуществить циклическую согласованную фильтрацию сигнала Френ¬
ка, представленного в комплекснозначном виде. Аналогичный результат
справедлив и для кода Баркера {1, 1, 1, —1}, имеющего равномерный
энергетический спектр.
Контурный анализ является основой обработки комплекснозначных
сигналов и содержит традиционные для теории сигналов разделы. При
этом не только сами сигналы, но и их спектры и корреляционные функ¬
ции, а также импульсные и частотные характеристики фильтров для их
обработки представляются в виде контуров. Также вид контуров при¬
обрели элементарные сигналы, на которые раскладывается произвольный
контур, и тестовый сигнал с равномерным в классе замкнутых контуров
спектром — дельтовидный контур.
Комплекснозначные сигналы по сравнению с вещественными обладают
важными свойствами. В первую очередь — это простота получения сиг¬
налов с заданными спектрально-корреляционными свойствами. Один из
видов комплекснозначных сигналов — композиционные контуры с равно¬
мерным энергетическим спектром, может наряду с простыми и сложны¬
ми сигналами рассматриваться как новый, третий класс сигналов: спек-
Заключение
577
трально-корреляционные свойства такого сигнала в целом противополож¬
ны аналогичным свойствам его структурных частей — элементарных кон¬
туров. Это дает возможность решения пакета задач с противоречивыми
требованиями к характеристикам сигнала. Композиционый контур имеет
равномерный энергетический спектр и дельтовидную автокорреляцион¬
ную функцию, что делает его эффективным для решения задач оценки
параметров и разрешения. Семейство элементарных контуров — струк¬
турные единицы композиционного контура, характеризуются дельтовид¬
ным спектром, причем у контуров разных порядков положения ненулевых
компонент спектра не совпадают. Данное свойство делает наборы компози¬
ционных контуров также эффективными сигналами для решения задачи
распознавания.
Подобные композиционные сигналы были применены для распозна¬
вания и идентификации звезд уникальных вторичных созвездий, фор¬
ма которых является квазиоптимальным сигналом для систем ориента¬
ции летательных аппаратов. Использование этих же сигналов в системах
с кодовым разделением каналов обеспечивает близкую к потенциальной
эффективность устройств передачи информации.
Комплекснозначные сигналы естественным образом вписываются в за¬
дачи обработки изображения. Они позволяют аналитически задать форму
плоского изображения и использовать для обработки весь аппарат теории
сигналов. Если точечные изображения рассматривать как источники по¬
тенциальных полей или как выборки некоторого сплошного изображения,
то обработка этих изображений также сводится к обработке контуров.
Комплекснозначные сигналы имеют самостоятельное математическое
значение. Они являются эффективным приложением к геометрии Аг-уголь-
ников. Новое качество, достигаемое при таком подходе, заключается
в раскрытии атомарной структуры произвольного fc-угольника: его неде¬
лимыми структурными единицами являются произвольные выпуклые
и звездчатые правильные ^-угольники — полное семейство элементарных
контуров размерности к.
Прикладной аспект контурного анализа также представляет опреде¬
ленный интерес. Мера близости двух комплекснозначных сигналов в виде
их скалярного произведения за счет наличия мнимой части является
более информативной, чем скалярное произведение вещественных сиг¬
налов. Модуль нормированного скалярного произведения в комплексном
линейном пространстве инвариантен к изменению масштаба (амплитуды)
и угла поворота (начальной фазы) сигналов. Это значительно сокращает
по сравнению с вещественными сигналами требуемый объем вычисле¬
ний при решении задач обнаружения, оценки параметров, разрешения
и распознавания. Весьма вероятны случаи, когда применение веществен¬
ных сигналов приводит к отрицательному результату при распознавании
сигналов одного и того же класса. В то же время применение комплекс¬
нозначных сигналов в подобных ситуациях дает не только правильное
решение, но и дополнительную информацию об угле взаимного поворота
сравниваемых сигналов.
578
Заключение
Таким образом, контурный анализ можно рассматривать как мате¬
матический аппарат, обеспечивающий единый подход к решению задач
обработки изображений и сигналов, включающий в качестве частного слу¬
чая применяемые подходы к обработке вещественных сигналов. В свою
очередь, контурный анализ является частным случаем кватернионного
анализа, позволяющего решать задачи обработки пространственно задан¬
ных, в частности, на сфере, изображений.
За рамками данной книги остался обширный материал, связанный
с задачами генерации комплекснозначных сигналов, их физических но¬
сителей, анализа векторных полей, порождаемых точечными изображе¬
ниями и рекурсивной фильтрации контуров. Особый интерес, на наш
взгляд, представляет также не рассмотренный здесь анализ непрерыв¬
ных комплекснозначных сигналов, позволяющий в полной мере привлечь
в качестве базы теорию комплексного переменного.
СПИСОК ЛИТЕРАТУРЫ
1. Журавлев ЮМ. Об алгебраическом подходе к решению задач распознавания
и классификации // Проблемы кибернетики. Вып. 33. — М.: Наука, 1978. —
С. 5-68.
2. Гуревич И.Б., Журавлев ЮМ., Сметанин Ю.Г. Алгебры изображений: ис¬
следовательские и прикладные задачи/ Труды IV конференции РОАИ. —
Новосибирск, 1998. — С. 74-78.
3. Бакут П.А., Колмогоров Г.С., Ворновицкий И.Э. Сегментация изображений:
Методы пороговой обработки // Зарубежная радиоэлектроника. — 1987. —
№ Ю. — С. 6-24.
4. Бакут П.А., Колмогоров Г.С. Сегментация изображений: Методы выделения
границ областей // Зарубежная радиоэлектроника. — 1987. — № 10. — С. 25-
47.
5. Прэтт У. Цифровая обработка изображений. Кн. 1, 2. — М.: Мир, 1982.
6. Анисимов Б.В., Курганов В.Ф., Злобин В.К. Распознавание и цифровая об¬
работка изображений. — М.: Высшая школа, 1983.
7. Денисов Д.А., Низовкин В.А. Сегментация изображений на ЭВМ // Зарубеж¬
ная радиоэлектроника. — 1985. — № 10. - С. 5-30.
8. Бутаков Е.А., Островский В.И., Фадеев И.Л. Обработка изображений на
ЭВМ. — М.: Радио и связь, 1987.
9. Розенфельд А. Распознавание и обработка изображений. — М.: Мир, 1972.
10. Фу К., Гонсалес Р., Ли К. Робототехника: Пер. с англ. — М.: Мир, 1989.
И. Вопросы статистической теории распознавания/ Ю.Л. Барабаш, Б.В. Бар¬
ский, В.Т. Зиновьев и др.; Под ред. Б.В. Барского. — М.: Сов. радио, 1977.
12. Селекция и распознавание на основе локационной информации/ А.Л. Горе¬
лик, Ю.Л. Барабаш, О.В. Кривошеев, С.С. Эпштейн.; Под ред. А.Л. Горелика. —
М.: Радио и связь, 1990.
13. Ярославский Л.П. Введение в цифровую обработку изображений. — М.: Сов.
радио, 1979.
14. Обработка и отображение информации в растровых графических системах/
О.И. Семенков, С.В. Абламейко, В.И. Берейщик, И.И. Старовойтов. — Минск:
Наука и техника, 1989.
15. Применение цифровой обработки сигналов/ Под ред. Э. Оппенгейма. — М.:
Мир, 1980.
16. Рабинер Л., Гоулд Б. Теория и применение цифровой обработки сигналов. —
М.: Мир, 1979.
17. Furman Ya.A., Yanshin V.V. Extraction and Linear Filtering of Closed Polygonal
Contours of Images // Pattern Recognition and Image Analysis. — 1994. — V. 4,
№2. — P. 146-166.
18. Фурман Я.А. Спектральный анализ замкнутых полигональных контуров
плоских изображений // Радиотехника. — 1994. — № 12. — С. 41-44.
19. Фурман Я.А. Согласованная фильтрация контуров изображений // Радио¬
техника. — 1995. — №6. — С. 30-33.
580
Список литературы
20. Фурман ЯЛ. Обнаружение зашумленных контуров изображений // Радио¬
техника. — 1994. — № 10. — С. 13-17.
21. Василенко Г.И. Голографическое опознавание образов. — М: Сов. радио, 1977.
22. Системы технического зрения (принципиальные основы, аппаратное и ма¬
тематическое обеспечение)/ А.Н. Писаревский, А.Ф. Чернявский, Г.К. Афа¬
насьев и др.; Под общ. ред. А.Н. Писаревского, А.Ф. Чернявского — Л..
Машиностроение, 1988.
23. Техническое зрение роботов/ Под ред. А. Пью. — М.: Машиностроение, 1987.
24. Техническое зрение роботов/ В.И Мошкин, А.А Петров, В.С. Титов,
Ю.Г. Якушенков; Под общ ред. Ю.Г. Якушенкова. — М: Машиностроение,
1990.
25. Вентцель Е.С. Теория вероятностей. — М.* Наука, 1969.
26. Лезин Ю.С. Введение в теорию и технику радиотехнических систем: Уч.
пособие для вузов. — М.: Радио и связь, 1986.
27. Ширман Я.Д., Манжос В.Н. Теория и техника обработки радиолокационной
информации на фоне помех — М.: Радио и связь, 1981.
28. Лаврентьев М.А., Шабат Б.В. Методы теории функций комплексного пере¬
менного: Учеб пособие для ун-тов. — М.: Наука, 1987.
29. Баскаков С.И. Радиотехнические цепи и сигналы. — М/ Высшая школа, 1983
30. Лебедев Д.С., Цуккерман И.И. Телевидение и теория информации — М Сов
радио, 1974.
31. Зинченко В.П., Ломов В.Ф. О функциях движения руки и глаза в процессе
восприятия изображения // Вопросы психологии. — I960. — № 1. — С 29-41
32. Распознавание образов Исследование живых и автоматических решающих
систем. — М.: Мир, 1970.
33. Грановская Р.М., Березная ИЯ. Запоминание и узнавание фигур. — Л.: ЛГУ,
1974.
34. Интегральные роботы: Сб. статей/ Пер. с англ; Под ред. ГЕ. Поздняка. —
М.: Мир, 1973.
35 Интегральные роботы Вып. 2 Сб. статей/ Пер. с англ, и яп; Под ред Г.Е Позд¬
няка. — М.: Мир, 1975
36. Фор А Восприятие и распознавание образов. — М.: Машиностроение, 1989
37. Надь Г. Цифровая обработка изображений, получаемых при дистанционном
зондировании природных ресурсов // Распознавание образов при помощи
вычислительных машин/ Под ред. Л. Хармона. — М.: Мир, 1972.
38. Шибанов Г.П. Распознавание в системах автоконтрсля. — М.: Машиностро¬
ение, 1973.
39. Чукин Ю.В. Структуры данных для представления изображений // Зару¬
бежная радиоэлектроника. — 1983 — № 1 — С. 85-107.
40. Дуда Р., Харт П. Распознавание образов и анализ сцен — М.* Мир, 1977.
41. Небабин В.Г., Сергеев Б.В. Методы и техника радиолокационного распозна¬
вания. — М.: Радио и связь, 1984.
42. Фурман ЯЛ., Юрьев А.Н., Яншин Б.В. Цифровые методы обработки и распо¬
знавания бинарных изображений. — Красноярск: Изд-во Красноярск, ун-та,
1992.
43. Фурман ЯЛ., Яншин Б.В. Многошаговые процедуры принятия решений. —
Красноярск: Изд-во Красноярского ун-та, 1989.
44. Furman Ya.A., Krevetskii A.V. Compression of Signals during Teir Representat¬
ion in a Biorthjgonal Basis // Pattern Recognition and Image Analisis. —
2001. — V. 11, № 1. — P. 159-160.
Список литературы
581
45. Курош А.Г. Курс высшей алгебры. — М.: Наука, 1968.
46. Ефимов Н.В., Розендорн Э.Р. Линейная алгебра и многомерная геометрия. —
М.: Наука, 1974.
47. Радиотехнические цепи и сигналы: Учебн пособие для вузов/ Д.В. Васильев,
МР. Витоль, Ю.Н. Горшенков, К.А. Самойло. — М.: Радио и связь, 1982.
48. Бронштейн И.Н., Семендяев К.К. Справочник по математике для инженеров
и учащихся вузов. — Лейпциг. Тойбнер, 1981; М.: Наука, 1981.
49. Колмогоров А.В., Фомин С.В. Элементы теории функции и функционального
анализа. — М/ Наука, 1972.
50. Фурман Я.А. К вопросу о распознавании изображений с сильной вариабель¬
ностью формы // Автоматизация анализа и распознавания изображений.
Вып. 2; Науч. тр. АН ЛатвССР. — Рига: Зинатне, 1979. — С131-157.
51. Ли Ц., Джадж Д., Зельнер А. Оценивание параметров марковских моделей
но агрегативным временным рядам/ Под ред. Райбмана. — М.* Статистика,
1977.
52. Сосулин Ю.Г. Теория обнаружения и оценивания стохастических сигналов. —
М: Сов радио, 1978
53. Сосулин Ю.Г. Разрешение и распознавание радиосигналов: Уч. пособие. —
М.: МАИ, 1983.
54. Фурман Я.А., Кревецкий А.В., Хафизов Р.Г. Изображения ориентиров оп¬
тимальной формы // Вестник ВВО АТН РФ. Серия “Высокие технологии
в радиоэлектронике, информатике и связи”, 2000. — С. 19-28.
55. Лезин Ю.С. Оптимальные фильтры и накопители импульсных сигналов. —
М. Сов. радио, 1969.
56. Фурман Я.А. О двух замечательных видах замкнутых контуров изображе¬
ний // Радиотехника и электроника, 1993. — Т. 38, №6. — С. 1054-1061.
57. Кук Ч., Бернфельд М. Радиолокационные сигналы/ Пер. с англ.; Под ред.
В.С. Кельзона — М· Сов. радио, 1971.
58 Радиотехнические системы: Учебн. для вузов по спец. “Радиотехника”/
Ю.П. Гришин, ВП. Инашев, Ю.М. Казаринов и др.; Под. ред. ЮМ. Каза¬
ринова. — М.: Высшая школа, 1990.
59. Кревецкий А.В. Распознавание трехмерных объектов по форме простран¬
ственных контуров // Автометрия. — 2001. — №2. — С. 21-31.
60. Леухин А.Н. Влияние пространственных искажений формы уникальных
вторичных созвездий на значение коэффициента монохроматичности //
ВВО АТН РФ. Высокие технологии в радиоэлектронике. — 1999. —
№1(6) — С. 69-73.
61. Каппелини В., Константинидис А.Дж., Эмилиани П. Цифровые фильтры
и их применение. — М.: Энергоатомиздат, 1983.
62 Введение в цифровую фильтрацию/ Под ред. Р. Богнера и А. Константини-
диса; Пер с англ. — М.: Мир, 1976.
63 Гоулд В., Рэйдер Ч. Цифровая обработка сигналов/ Пер. с англ.; Под. ред.
А.М. Трахтмана. — М.· Сов. радио, 1973.
64. Куля В.И. Ортогональные фильтры. — Киев: Техника, 1967.
65. Фурман Я.А. Оценки параметров линейных преобразований зашумленных
контуров изображений // Автометрия. — 1992. — №3. — С. 112-120.
66. Фурман Я.А. О понятии формы плоского изображения // Автометрия —
1992 — №5 — С 113-120.
67. Фурман Я.А. Помехоустойчивые символы для передачи сообщений // Авто¬
метрия. — 1996. — № 1. — С. 42-52
582
Список литературы
68. Егошина И.Л., Михайлов А.И., Фурман Я.А. Оценка степени сходства двух
плоских форм // Автометрия. — 1995. — № 4. — С. 19-26.
69. Фурман Я.А., Роженцов А.А., Хафизов Р.Г. Дискретно-кодированные сигналы
на базе композиционных контуров // Автометрия — 1996. — № 1. — С. 72-79.
70. Демидов В.Е. Как мы видим то, что видим. — М.: Знание, 1987.
71. Comment on Ignorance, Myopia and Navlete in Computer Vision Systems by
M.A. Snuder/ Ramech C. Jain, Thomas 0. Binford // CVGIP: Image Under¬
stand — 1991. — V. 53, № 1. — P. 112-117.
72. Jain R.C., Binford T.O. Revolutions and experimental computer vision/ Bowy-
er K.W., Jons J.P. // CVGIP: Image Understand. — 1991. — V. 53, № 1. —
P. 127-128.
73. Jain A.K. Advances in Mathematical Models for Image Processing // Proceedings
of the IEEE. — 1981. — V. 69, №5. — P. 9-39.
74. Freeman H. On the digital-computer classification of geometric line pattern //
Proc. Nat. Electron. Conf. — 1962. — № 18. — P. 312-324.
75. Person E., Fu K. Shape discrimination Using Fourier Descriptors // IEEE
Transactions, Man and Cybernetics. — 1977. — V. SMC-7, №3. — P. 170-179.
76. Richard C.W., Hemani H. Identification of Three-Dimention all Objects Using
Fourier Descriptions of the Boundary Curve // IEEE Transactions on Systems,
Vf Man and Cybernetics. — 1974. — V. SMC-4, №4. — P. 371-378.
77. Grandlund G.H. Fourier Preprocessing For Hand Print Character Recognition //
IEEE Transactions on Computers. — 1972. — V. C-21, №2. — P. 195-201.
78. Zahn C.T., Roskies R.Z. Fourier Descriptors For Plane Closed Curves // IEEE
Transactions on Computers. — 1972. — V. C.-21, №3. — P .269-281.
79. Furman Y.A., Janshin W.W. Spectral Analysis and Filtering of Closed Polygonal
Contours of Images/ Pattern Recognition and Image analysis. — 1992. — V. 2,
№3 — P. 306-318.
80. Пат. 4097845 США, МКИ G06 K9/00. Method and Apparatus for Automatic
Classification of Red Blood Gells. J.W. Bacus (USA), №825673. Опубл. 27.06.78.
81. Cosgriff R.L. Identification of Shape, Ohio State University Research Foundat¬
ion, Columbus, Ohio, Report 820—11, ASTIA AD-25-4792, December, 1960.
82. Харкевич A.A. Борьба с помехами. — M.: Сов. радио, 1965.
83. Бакулев Я.А., Сосновский A.A. Радиолокационные и радионавигационные
системы: Учеб, пособие для вузов. — М.: Радио и связь, 1996.
84. Компьютерная оптика/ Под общ. ред. В.А. Сойфера. — М.: Наука, 2000.
85. Варакин Л.Е. Системы связи с шумоподобными сигналами. — М.: Радио
и связь, 1985.
86. Ланцош К. Практические методы прикладного анализа. — М.: Физматгиз, 1961.
87. Фурман Я.А. Основы теории обработки контуров изображений: Учебн. посо¬
бие. — Йошкар-Ола: МарГТУ, 1997.
88. Кревецкий А.В. Обработка изображений в системах ориентации летательных
аппаратов. — Йошкар-Ола: Изд-во МарГТУ, 1998.
89. Furman Y.A. Visual structure contours with special spectrocorrelation properties //
Pattern Recognition and Image Analysis. — 1996. — №4. — P. 734-746.
90. Леухин A.H., Роженцов A.A., Фурман Я.А. Метод идентификации светил
в системах ориентации космических аппаратов на базе вторичных созвездий
с уникальной монохроматичностью спектра их формы // Космонавтика
и ракетостроение. — 2001. — № 24. — С. 47-64.
91. Фурман Я.А., Роженцов А.А., Леухин А.Н. Метод идентификации светил в си¬
стемах ориентации летательных аппаратов на базе вторичных созвездий с уни¬
Список литературы
583
кальной монохроматичностью спектра формы // 3 Международная НТК “Кос¬
монавтика, радиоэлектроника, геоинформатика”: Тез. докл. — Рязань, 2000.
92. Балухто А.Н. Нейросетевая идентификация астрообъектов на цифровых
изображениях участков звездного неба в системах астроориентации косми¬
ческих аппаратов // Сб. докл. 3-й Междунар. НТК “Цифровая обработка
сигналов и ее применение”. — Москва, 2000. — С. 4-7.
93. Furman Ya.A., Rozhentsov А.А., Leukhin A.N. Unique Point Images on Celestial
Sphere // Pattern Recognition and Image Analysis. — 2001. — V. 11, No. 2. —
P. 309-312.
94. Khafizov R.G., Furman Ya.A. Detection of Object Image in Optical Scenes //
Pattern Recognition and Image Analysis. — 1998. — №2. — P. 267-268.
95. Krevetskii AM. Improvement of the Efficiency of Recognition from Contours
by Intelligent Contour Code Equalization // Pattern Recognition and Image
Analysis. — 1998. — V. 8, №. 2. — P. 200.
96. Фурман Я.А., Кревецкий A.B. Автоматический контроль визуально различи¬
мых дефектов корпусов интегральных схем // Вестник ВВО АТН РФ. Серия:
Высокие технологии в радиотехнике. — 1995. — С. 9—14.
97. Плекин В.Я., Кревецкий А.В. Обнаружение групповых точечных объектов
с нестационарной конфигурацией // Известия вузов. Радиоэлектроника. —
1994. — Т. 37, №3. —С. 8-21.
98. Furman Y.A. The discrete coded signals processing with an ideal permission
capacity // The 1st International conference “Digital signal processing and its
Application” (June 30 — July 3, 1998). Moscow, V. 3~E, P .40-43.
99. Фурман Я.А., Кревецкий A.B., Роженцов A.A., Хафизов Р.Г., Смирнов Д.Л.
Технология распознавания номерных знаков транспортных средств для це¬
лей электронного контроля и управления дорожным движением // Вестник
ВВО АТН РФ. Серия: Высокие технологии в радиоэлектронике. — 1996. —
№1(2).— С. 19-26.
100. Furman Ya.A., Rozhentsov A.A. Visual Contour-Signal Models Efficient in the
Combined Solution of Location Problems // Pattern Recognition and Image
Analysis. — 1998. — № 3. — P. 466.
101. Леухин A.H., Роженцов А.А. Физическая реализация сигналов на базе компо¬
зиционных контуров из полного семейства элементарных контуров // Вест¬
ник ВВО АТН РФ. Серия: Высокие технологии в радиоэлектронике. —
1997. —№2(4). —С. 76-82.
102. Марпл С.Л., мл. Цифровой спектральный анализ и его приложения. — М.:
Мир, 1990.
103. Роженцов А.А. Алгоритм, реализующий восстановление отсчетов сигналов,
ассоциированных с композиционными контурами // Вестник ВВО АТН РФ.
Серия: Высокие технологии в радиоэлектронике. — 1997. — № 2(4). — С. 67-
70.
104. Егошина И.Л. Подавление ошибок квантования прямолинейных границ изо¬
бражений, заданных на квадратной сетчатке // Вестник ВВО АТН РФ. Се¬
рия: Высокие технологии в радиоэлектронике. — 1996. — С. 50-56.
105. Фурман Я.А., Егошина И.Л. Обработка изображений антропогенных объ-
енктов с протяженными прямолинейными границами // Тезисы V Всерос.
НТК “Методы и средства обработки сложной графической информации”. —
Нижний Новгород, 1998. — С. 86.
106. Фурман Я.А. Микромир форм изображений // Природа. — 1999. — №4. —
С. 64-75.
584
Список литературы
107. Elachi С., Bicknell Г., Jarden R.L., Chialin W. Spaceborne Synthetic aperture
Images Reader’s applications. Techniques and Technology // Proceedings of the
IEEE. — 1982. — V. 70, № 10. — P. 78-82.
108. Измерение радиотеплового и плазменного радиоизлучений/ А.Е. Башари-
нов Л.Т. Тучков, В.М. Поляков, Н.И. Ананов. — М.: Сов. радио, 1968.
109. Фурман Я Л, Егошина M.JI. Обработка контуров изображений с протяженны¬
ми прямолинейными границами // Автометрия. — 1999. — №6. — С. 93-104.
110. Фурман Я.А., Роженцое АЛ. Класс кодирующих последовательностей,
не приводящих к корреляционным шумам // Радиотехника. — 2000. —
№5. —С. 38-43.
111. Фурман Я.А., Хафизов Р.Г. Согласованно-избирательная фильтрация изо¬
бражений протяженной формы в реальных ландшафтных сценах // Авто¬
метрия. — 1999. — №2. — С. 12-27.
112. Розенфельд А., Дейвис Л.С. Сегментация и модели изображений // ТИИЭР. —
1979. — Т.67, №5. — С. 71-82.
113. Абду И.Э., Прэтт У.К. Количественный расчет детекторов контуров, осно¬
ванный на подчеркивании перепадов яркости с последующим пороговым
ограничением // ТИИЭР. — 1975. — Т. 67, №5. — С. 59-70.
114. Trabco Е.А., Roctleng P.G. Shape detection using incoherent illumination // J.
Opt. Soc. Am. — 1967. — V. 57, № 1
115. Глезер Б.Д. Механизмы опознавания зрительных образов. — Л.: Наука, 1966.
116. Сергеев Г.А., Янутш Д.А. Статистические методы исследования природных
объектов. — Л.: Гидрометеоиздат, 1973.
117 Левшин В.Л. Пространственная фильтрация в оптических системах навига¬
ции. — М.: Сов. радио, 1971.
118. Kretzmer E.R. Statistics of television signals // Bell. Syst. Tech. J. — 1952. —
V. 31, №7.
119. Пугачев Б.С., Синицын И.H. Стохастические дифференциальные системы.
Анализ и фильтрация. — М.: Наука, 1990.
120. Математическая энциклопедия. Т. 5. — М.: Сов. энциклопедия, 1977.
121. Крамер Г. Математические методы статистики. — М: Мир, 1975.
122. Фурман Я А., Мальгин Ю.Ю. Задача прослеживания прямолинейных гра¬
ниц изображений/ Йошкар-Ола: МарПИ, 1987. — 13 с. — Деп. в ВИНИТИ
11.08.87.— №5818 —В-87.
123. Фурман Я.А., Егошина И.Л. Выделение контуров изображений с протя¬
женными прямолинейными границами // Тез. докл. НТК РОАИ-4-98. —
Новосибирск, 1998. — 4.1. — С. 76-80.
124. Попов А А., Галкина Т.Б., Орлова Т.И. u др. Метод выделения контуров
протяженных детерминированных объектов в стохастических полях // Ра¬
диотехника и электроника. — 1991. — Т. 36, вып. И. — С. 2240-2242.
125. Поветко Б.Н., Понъкин В А. Оценка качества обнаружения пространственно¬
протяженных объектов по их изображениям // Радиотехника и электрони¬
ка. — 1993. — Т. 35, №4. — С. 685-688.
126. Information from SAR Images/ Oliver C.J. // Phys. D. — 1991. — V. 24, № 9. —
P. 1493-1514.
127. Lalltha L. A technique for road detection from high resolution satellite image //
IGARSS’89: Remote Sens.: Econ. Tool Ninetes [and] 12th Can. Symp. Remote
Sens Vancouver, July 10-14, 1989, V. 4, NY, 1990. — P. 2246-2249.
128. Grieter P. Joint STARS does its stuff // Air Force Mag. — 1991. — V. 74,
№6. — P. 38-42.
Список литературы
585
129. Furman Y.A., Khafizov R.G. Detection of Images of Extended-Shape Object
Among the Scenes of Underlying Surface // Pattern Recognition and Image
Analysis. — 1998. — V. 8, №4. — P. 612-640.
130. Маркус M.. Минк X. Обзор по теории матриц и матричных неравенств. —
М.: Наука, 1972.
131. Маркюс Ж. Дискретизация и квантование. — М.: Энергия, 1969.
132. Аркадьев А.Г., Браверман В.Н. Обучение машин классификации объектов. —
М.: Наука, 1971.
133. Лихарев Б.А. Цифровые методы и устройства в радиолокации. — М.‘ Сов.
радио, 1973.
134. Гельфонд А.О. Уравнения в целых числах. — М.: Физматгиз, 1974.
135. Кендалл М., Стюарт Д. Теория распределений: Пер. с англ. — М.: Наука,
1996
136. Горелик А. А., Скрипкин В Л. Методы распознавания. — М.: Высшая школа,
1984.
137. Михайлов AM. Обнаружитель изображений, инвариантный к ориентации
границы. — Йошкар-Ола: МарГТУ, 1996. — Деп. в ВИНИТИ №3115 — В96.
138. Принципы совмещения изображений в системах наведения управляемых ра¬
кет // Новости зарубежной науки и техники. Информационный бюллетень. —
1982. — № 18 (639). — С. 11-28.
139. Передреев А.К., Роженцов АЛ. Совмещение плоских изображений на основе
анализа спектров контурных линий/ МарГТУ, Йошкар-Ола, 1996. — 16 с. —
Деп. в ВИНИТИ 29.05.96. №1673-В96.
140. Передреев А.К., Роженцов АЛ. Накопление контуров, заданных комплексно¬
значными кодами. — МарГТУ, Йошкар-Ола, 1999. — Деп. в ВИНИТИ 9.07.99,
№ 2236-В99.
141. Фурман Я Л., Егошина И.Л. Анализ процесса квантования протяженных
прямолинейных границ на квадратной сетчатке // Тез. докл. НТК РОАИ-
3-97. — Нижний Новгород, 1997. — Ч. 2. — С. 76-80.
142. Павлидис Т. Алгоритмы машинной графики и обработки изображений: Пер.
с англ. — М.’ Радио и связь, 1986.
143. Ковязин С.А. О понятии средней формы случайного измеримого множе¬
ства // Динамика химических и биологических систем: Сб. науч. тр./ Под
ред. В.И. Быкова. — Новосибирск: Наука, 1989.
144. Кузьмин С.З. Основы теории цифровой обработки радиолокационной инфор¬
мации. — М.: Сов. радио, 1974.
145. Марр Д. Зрение. Информационный подход к изучению представления и об¬
работки зрительных образов: Пер. с англ. — М.: Радио и связь, 1987.
146. Фурман Я.А., Роженцов А.А., Леухин А.Н. Оптимальное решение задачи
ориентации летательных аппаратов по изображениям звездного неба // Ав¬
тометрия. — 2001. — № 1.
147. Furman Υα.Α., Rozentsov А.А., Leukhin A.N. The shapes of unique star forma¬
tions as efficient signals for their recognition and parameter estimation //
Pattern Recognition and Image Analysis. — 2000. — V. 10, №3.
148. Астрономический календарь на 1999 год/ Под ред. О.С. Угольникова. — М.:
Звездочет, 1998.
149. Кревецкий А.В. Распознавание образов, заданных множеством характерных
точек на плоскости изображения // Автометрия. — 1999. — № 2. — С. 28-36.
150. Кантор И.Л., Солодовников А.С. Гиперкомплексные числа. — М.: Наука,
1973.
586
Список литературы
151. Справочник по радиолокации/ Под. ред. М. Скольника. Т. 1. — М.: Сов. радио,
1976.
152. Ипатов В.П. Троичные последовательности с идеальными периодически¬
ми автокорреляционными свойствами // Радиотехника и электроника. —
1979. — № 10.
153. Свердлик М.Б. Оптимальные дискретные сигналы. — М.: Сов. радио, 1975.
154. Вакман Д.Е. Регулярный метод синтеза фазоманипулированных сигналов. —
М.: Сов. радио, 1967.
155. Сосулин Ю.Г. Теоретические основы радиолокации и радионавигации: Учеб,
пособие для вузов. — М.: Радио и связь, 1992.
156. Фурман Я.А., Рожещов А.А. Сигналы с равномерным энергетическим спек¬
тром на базе кодов Баркера. — Йошкар-Ола: МарГТУ, 1998. — 7 с. — Деп.
в ВИНИТИ 25.02.98 №556"В98.
157. Сергеев В.В., Чернов А.В. Методы восстановления изображений, основанные
на принципах теории распознавания образов* Тез. докл. РОАИ-3. — Нижний
Новгород, 1997. — Ч. 1. — С. 256-260.
158. Быков Р.Е., Гуревич С.Б. Анализ и обработка цветных и объемных изобра¬
жений. — М.: Радио и связь, 1984.
159. Фурман Я.А., Кревецкий А.В. Методика устранения боковых лепестков при
разрешении дискретных сигналов // Тез. докл. 3-й Междунар. НТК “Циф¬
ровая обработка сигналов и ее применение”. — Москва, 2000. — С. 29-31.
160. Фурман Я.А., Кревецкий А.В. Сжатие сигналов при их представлении в биор-
тогональном базисе // Труды междунар. НТК РОАИ, 2000. — 4 с.
161. Фурман Я.А., Хафизов Р.Г. Обнаружение изображений объектов протяжен¬
ной формы в оптических сценах // Тез. докл. междунар. НТК РОАИ-3. —
Нижний Новгород, 1997. — 4.1. — С. 283-285.
162. Furman Y.A., Rozentsov А.А., Leukhin A.N. Digital Processing of Signals, Effec¬
tive for Solution of the Problems of Detection, Parameters Estimation, Permis¬
sion and Recognition // The 1st International Conference “Digital Signal
Processing and its Applications”, June 30 — July 3, 1998, Moscow.
163. Фурман Я.А., Рожещов A.A. Визуальные модели контурных сигналов, эф¬
фективных при совместном решении локационных задач // Тез. докл. меж¬
дунар. НТК РОАИ. — Нижний Новгород, 1997. — Ч. 2.
164. Ильин В .А. Интеллектуальные роботы: теория и алгоритмы. — Красноярск:
САА, 1995.
165. Кревецкий А.В. Технология контурного анализа для реализации задач астро¬
ориентации летательных аппаратов // Вестник ВВО АТН РФ. — 1997. —
2(4) — С. 83-87.
166. Кревецкий А.В., Митрофанов В.И., Плекин В.Я. Различение групповых то¬
чечных объектов по форме ассоциированного сплошного образа // Известия
вузов. Радиоэлектроника. — 1997. — Т. 40, №3. — С. 44—52.
167. Корн Г., Корн Т. Справочник по математике для научных работников и ин¬
женеров. — М.: Наука, 1968.
168. Фурман Я.А., Михайлов А.И., Рожещов А.А. Оптимальные информационные
структуры в контурной среде // Тез. докл. междунар. НТК РОАИ-2. —
Ульяновск, 1996.
169. Рожещов А.А. Фазоразностное кодирование сигналов в виде композицион¬
ных контуров // 2 науч. сессия., поев. Дню радио. — М., 1997. — 1 с.
170. Leuhin A.N., Rozentsov A.A. Synthesis Method of Complex Signals by Ambiguity
Function // The 1st International Conference “Digital Signal Processing and
Список литературы
587
its Applications”.- June 30 — July 3, 1998, Moscow.
171. Кревецкий А.В. Группировка точечных объектов методом потенциальных
функций // Тезисы докладов Всесоюзной н/т конференции “Цифровые ме¬
тоды обработки сигналов и изображений”. — М.: ВВИА им. Н.Е. Жуковского,
1990. — С. 47-48.
172. Фурман Я.А., Роженцов АЛ., Jleyxun А.Н. Метод идентификации светил
в системах ориентации космических аппаратов на базе вторичных созвездий
с уникальной монохроматичностью спектра формы // Космонавтика и раке¬
тостроение. — 2000. — № 24.
173. Плекин В.Я., Кревецкий А.В. Обнаружение групповых точечных объектов
с известной формой ассоциированного сплошного образа // Известия высш.
учебн. заведений. Радиоэлектроника. — 1992. — Том 35, №4. — С. 66-73.
174. Бурый А.С., Михайлов С.Н. Методы идентификации астроориентиров в зада¬
чах ориентации и навигации космического аппарата по изображениям звезд¬
ного неба // Зарубежная радиоэлектроника. — 1994. — № 7-8. — С. 44-52.
175. Передреев А.К. Аналитическое описание группового точечного объекта,
максимизирующего меру разделимости объектов. — Йошкар-Ола: Мар-
ПИ, 1988. — Деп. в ВИНИТИ, №4210-В88.
176. Фурман Я.А., Кравцова Н.М. Задания групповых точечных объектов и ал¬
горитмы нумерации составляющих их точек // Цифровая обработка много¬
мерных сигналов: Межвуз. сб. науч. тр./ МарПИ, ЛЭТИ, МАИ, МИРЭА. —
Йошкар-Ола, 1992. — С. 25-31.
177. Левин Б.Р. Теоретические основы статистической радиотехники. — М.: Радио
и связь, 1989.
178. Плекин В.Я., Кревецкий А.В. Обнаружение групповых точечных объектов со
случайными параметрами // Известия высш. учебн. заведений. Радиоэлек¬
троника. — 1992. — Т. 35, № 12. — С. 18-27.
179. Кревецкий А.В. Устройство для вычисления двумерной свертки. — Патент
РФ № 2042209, приоритет от 30.06.92.
180. Chernov V.M., Chichyeva Μ Λ. “One step” short — length DCE algorithms with
data representation in the direct scum of associative algebras // Processing
CAIP\ 1997, Springer, LNCS 1296. — P. 590-596.
181. Смирнов Д.Л. Сравнение информативности методов вторичного описания,
основанных на модели векторного описания поля точечной сцены // Труды
3 НТК РОЛИ. — Нижний Новгород, 1997. — Ч. 1. — С. 266-270.
182. Орлов А.А., Садыков С.С., Жизнянов А.А. Применение преобразования Хо-
ха для выделения и подавления изображений ребер на флюорограммах //
Труды НТК РОАИ-5. — Самара, 2000. — С. 584-588.
183. Васильев К.К., Ташлинский А.Г. Оценка параметров деформации многомер¬
ных изображений, наблюдаемых на фоне помех // Труды НТК РОАИ-4. —
Новосибирск, 1998. — С. 261-264.
184. Завалишин Н.В., Мучник И.Б. Модели зрительного восприятия и алгоритмы
анализа изображений. — М.: Наука, 1974.
185. Смирнов Д.Л. Вторичное описание стохастической точечной сцены по методу
сечения яркостного векторного поля // Тез. докл. Всерос. НТК “Информаци¬
онные технологии в электронике и электротехнике”. — Чебоксары: ЧувГУ,
1996.
186. Автоматический анализ сложных изображений: Сборник переводов/ Под
ред. Э.М. Бравермана. — М.: Мир, 1969.
187. Ту Д., Гонсалес Р. Принципы распознавания образов. — М.: Мир, 1978.
588
Список литературы
188. Кревецкий А.В. Выделение особых точек в групповом точечном объекте //
Цифровая обработка многомерных сигналов. Межвуз. сборник, науч. трудов
МарПИ, ЛЭТИ, МАИ, МИРЭА. — Йошкар-Ола, 1992. — С.70-76.
189. Warnekar C.S., Krishna G. A heuristic clustering algorithm using union of
overlapping pattern-cells // Pattern Recognition. — 2000. — V. 11, №2. —
P. 85.
190. Айзерман M.A., Браверман Э.М., Розаноэр Л.И. Метод потенциальных функ¬
ций в теории обучения машин. — М.: Наука, 1970.
191. Репин В.Г., Тартаковский Г.П. Статистический синтез при априорной
неопределенности и адаптация информационных систем. — М.: Сов. радио,
1977.
192. Тихонов В.И. Статистическая радиотехника. — М.: Сов. радио, 1966
193. Одаюа Н. Labeled Point Pattern Matching by Fuzzy Relaxation // Pattern
Recognition. — 1984. — P. 569-573.
194. Пытьее О.Я. Морфологический анализ изображений групповых точечных
объектов // Тезисы докладов 6-й н/т конференции “Математические методы
распознавания образов”. — М.: РАН, ВЦ РАН, 1993. — С. 49-50.
195. Теория электрической связи: Учебник для вузов/ А.Г. Зюко и др.; Под ред.
Д.Д. Кловского. — М.: Радио и связь, 1998.
196. Фурман Я.А. Марковская цепь с матрицей переходов, приведенной к нор¬
мальному виду Фробениуса // Математика. Изв. вузов. — 1978. — № 4. —
С. 191-123.
197. Теория передачи сигналов/ А.Г. Зюко, Д.Д. Кловский, М.В. Назаров,
Л.М. Финк: Учебник для вузов. — М.: Связь, 1980.
198. Справочник по специальным функциям/ Под ред. М. Абрамовича и И. Сти-
ган. Пер с англ. — М.: Наука, 1979.
199. Киричук В.С., Коршевер И.И. Алгоритмы обработки последовательностей
изображений и системы реального времени для их реализации // Тез. докл.
РОАИ-3. — Нижний Новгород, 1997. — 4.1. — С. 256-260.
200. Сверхбольшие интегральные схемы и современная обработка сигналов/ Под
ред. С. Гуна, X. Уайтхауса, Т. Кайлата. — М.: Радио и связь, 1989.
201. Кревецкий А.В., Чесноков С.Е. Помехоустойчивое кодирование и иденти¬
фикация изображений подмножеств полей точечных ориентиров // Тезисы
всероссийской НК “Вавиловские чтения”, Йошкар-Ола, 2000. — 2 с.
202. Келли Т.Л. Статистические таблицы. — М.: ВЦ АН СССР, 1966. — 194 с.
203. Фурман Я.А., Роженцов А.А., Хафизов Р.Г. Комплекснозначные сигналы и их
применение в связи: Учеб, пособ. — Йошкар-Ола: МарГТУ, 2001.
204. Ермолаев Ю.М., Мельник И.Н. Экстремальные задачи на графах. — Киев:
Наукова думка, 1968.
СПИСОК ОСНОВНЫХ СОКРАЩЕНИЙ
АКФ — автокорреляционная функция
АФД — амплитудно-фазовый детектор
АЧХ — амплитудно-частотная характеристика
ВК — вектор-контур
ВКФ — взаимнокорреляционная функция
ГРТО — групповой точечный объект
ДКС — дискретно-кодированный сигнал
ДПФ — дискретное преобразование Фурье
ИХ — импульсная характеристика
КДФ — коэффициент дельтовидности формы
КМФ — коэффициент монохроматичности формы
КСФ — контурный согласованный фильтр
КТС — кватернионный сигнал
КУП — коэффициент устойчивости пучка
ЛА — летательный аппарат
МП — максимум правдоподобия
НСП — нормированное скалярное произведение
ОЗУИ — оперативное запоминающее устройство изображений
ОП — отношение правдоподобия
ПК — полиномиальный классификатор
ППИ — программируемый процессор изображений
ПУ — пороговое устройство
РЛС — радиолокационная станция
РЭС — равномерный энергетический спектр
СА — сопряженно—антисимметрический контур
СИФ — согласованно-избирательный фильтр
СКД — система координат астродатчика
СКО — среднеквадратическое отклонение
СКЭ — система координат экваториальная
СС — сопряженно-симметрический контур
ССФ — сопряженно-согласованный фильтр
УВС — уникальные вторичные созвездия
УКВС — уникальные композиционные вторичные созвездия
ФМ — фазовая манипуляция
ФСП — формирователь скалярного произведения
ФСР — фильтр скользящей разности
ФСС — фильтр скользящего среднего
ФЧХ — фазочастотная характеристика
ЧКШС — через-А:2-шаговое суммирование
ЭВ — элементарный вектор
ЭК — элементарный контур
ЭУ — экстремальное устройство
Научное издание
ФУРМАН Яков Абрамович
КРЕВЕЦКИЙ Александр Владимирович
ПЕРЕДРЕЕВ Анатолий Константинович
РОЖЕНЦОВ Алексей Аркадьевич
ХАФИЗОВ Ринат Гафиятуллович
ЕГОШИНА Ирина Лазаревна
ЛЕУХИН Анатолий Николаевич
ВВЕДЕНИЕ В КОНТУРНЫЙ АНАЛИЗ;
ПРИЛОЖЕНИЯ К ОБРАБОТКЕ
ИЗОБРАЖЕНИЙ И СИГНАЛОВ
Под редакцией Я. А. Фурмана
Редактор Е.Ю. Ходан
Оригинал-макет Е.Ю. Морозова
Оформление обложки А.Ю. Алехиной
ЛР № 071930 от 06.07.99. Подписано в печать 03.03.03.
Формат 60x90/16. Бумага офсетная. Печать офсетная.
Уел. печ. л. 37. Уч.-изд. л. 41,2. Заказ № 666.
ΥΑ.Α. FURMAN, A.V. KREVETSKY, A.K. PEREDREYEV,
A.A. ROZENTSOV, R.G. HAFIZOV, I.L. YEGOSHINA, A.N. LEUKHIN
CONTOUR ANALYSIS INTRODUCTION AND ITS IMAGE
AND SIGNAL PROCESSING APLLICATION
PHYSICS AND MATHEMATICS PUBLISHERS
International Academic Publishing Company <(Nauka})
Russian Academy of Sciences
Moscow, 2002, 592 pages
The authors of this book are the specialists in the field of signal and
image processing and recognition. Reported results were obtained on the
bases of the contour analysis methods developed by the authors of the Radio
System Department of Mari State Technical University. They received high
appraisal of Russian Association of Pattern Recognition and Image Analysis,
Russian Federation of Cosmonautics as well as a number of leading Research
institutions and higher educational establishments.
The contour analysis based on the theory of signal processing is a totality
of methods of the contour description and transformation. The contour anal¬
ysis conception was based on the works of N. Wiener, A. Rozenfeld, K. Fu,
E. Person, C.W. Richard, H. Hemani, G.H. Grandlund, C.T. Zahn, R.Z. Roskies,
R. Duda, P. Hart, W.K. Pratt, T. Paulidis, V.V. Yanshin, B.V. Varsky and the
others. The contour is represented in the form of a complex signal and so it
is possible to consider as a contour not only the lines of the image boundaries
but also different kinds of curves, graphs, vector diagrams of signals.
The complex linear space choice for the contour setting in the analytical
form is connected with the fact that the vector scalar product in this space
is more informative than in the real linear space due to the existence of the
linear part. Considering this fact it is possible to estimate more accurately the
similarity measures of signals and the standardized scalar product module
of these signals is invariant to their rotation and scalar operations.
The image contours are the high informative regions faintly dependent
on their color, brightness, observation conditions, sensor type, frequency
range in which the sensor works. The contour wholly determines the image
form and contains all necessary information for the image recognition by its
form. The above mentioned factors allow to obtain the simple and effective
data processing algorithms on the bases of the contour analysis.
The contour classification, the contour model description and the analyt¬
ical transformation techniques are given in this monograph. Special contour
types — elementary and deltoid are introduced They are analog to the si¬
nusoids of different frequencies and delta functions in the substantial signal
class. Spectral and correlation analysis problems as well as the problems
of arbitrary contour decomposition and linear filtration of complex signals
are considered Special attention is paid to the synthesis and analysis of
the contour coordinated filters forming a measure of two complex signals
similarity.
The contour analysis application to the image processing problems is
described and the methods of the boundary detection and tracing, im¬
age processing peculiarities concerning expanded rectilinear boundaries are
given. The parameter estimation algorithms and image recognition by its
form are synthesized.
The class of complex signals on the bases of the composed contour
consisting of the full family of elementary contours mastering complex code
sequence is adduced here. The cyclical coordinated signal filtration on the
bases of the composed contours with the inform energetic spectrum allows to
realize their compression without side lobes. Such a signal application in the
data transmission systems with the coded division of channels and for the
group star form finding making quasioptimal signal for the flying vehicle
orientation system is considered.
The monograph is of interest for the specialists in the field of image
processing, pattern recognition and scene analysis, digital signal processing
and scene analysis, and radar orientation and navigation of flying vehicle
and communication.