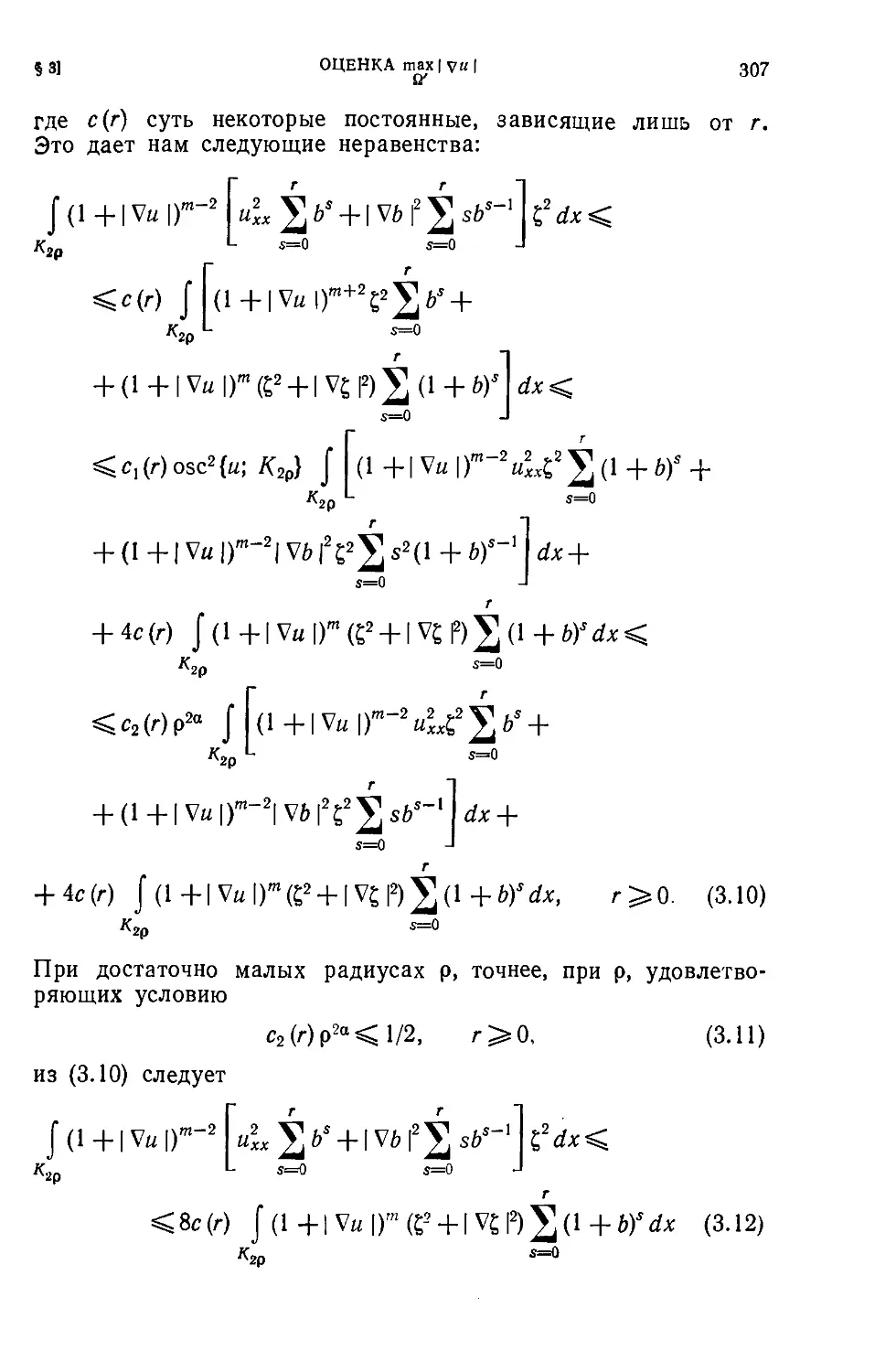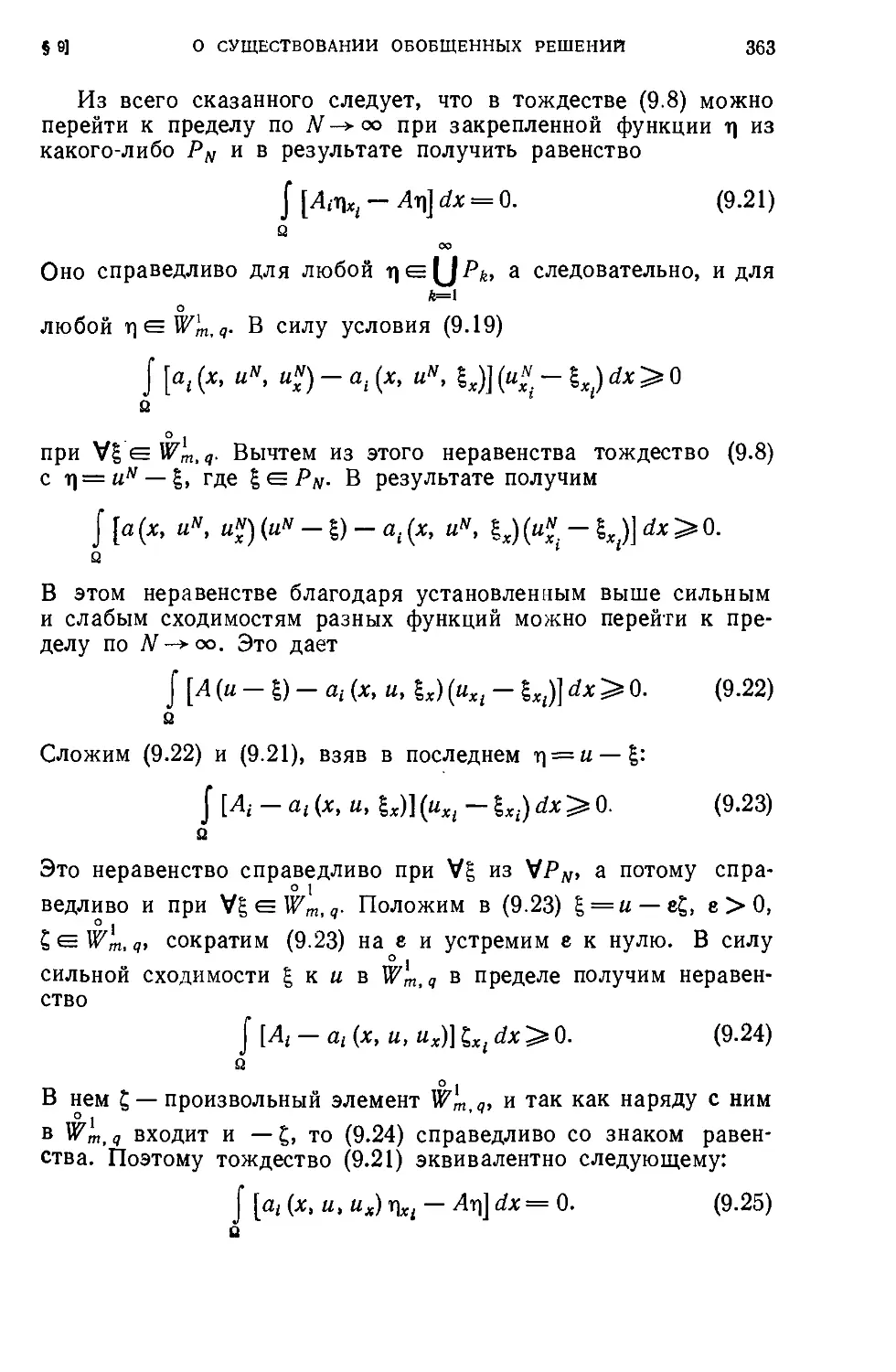О. А. ЛАДЫЖЕНСКАЯ, Н. Н. УРАЛЬЦЕВА
ЛИНЕЙНЫЕ
И КВАЗИЛИНЕЙНЫЕ
УРАВНЕНИЯ
ЭЛЛИПТИЧЕСКОГО
ТИПА
ИЗДАНИЕ ВТОРОЕ,
ПЕРЕРАБОТАННОЕ
ИЗДАТЕЛЬСТВО «НАУКА>
ГЛАВНАЯ РЕДАКЦИЯ
ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ
MOCK В А 1973

S17.2
Л. 15
УДК 517.947
Лииейиые и квазилииейиые уравнеиия эллипти-
эллиптического типа. Ладыженская О. А., Ураль-
Уральце в а Н. Н., Главная редакция физико-ма-
физико-математической литературы, изд-во «Наука», 1973.
Книга посвящена линейным и квазилинейным эл-
эллиптическим уравнениям второго порядка. В ней
проводятся качественные исследования решений этих
уравнений и на их базе устанавливается разрешимость
в целом классических краевых задач. Книга содержит
изложение основных достижений, полученных в дан-
данной области и опубликованных лишь в журнальной
литературе. В ией дается полное решение 19-й и 20-й
проблем Гильберта. Многие результаты получены
авторами книги и в развернутом виде изложены
только здесь.
Во втором издании учтены результаты, получен-
полученные после написания первого издания, улучшено
изложение ряда разделов, добавлены новые пара-
параграфы почти во все главы книги, в том числе вклю-
включены приближенные методы решения краевых задач,
наконец, исправлены замеченные недочеты первого
издания.
Библ. — 235 названий.
Q) Издательство «Наука», 1973.
Ольга Александровна Ладыженская,
Нина Николаевна Уральцева
Линейные и квазилинейные уравнения эллиптического типа
М., 1973 г., 576 стр.
Редакторы А. П. Осколков, М. М. Горячая
Техи. редактор В. Н. Кондакова
Корректоры Т. С. Плетнева, Е. В. Сидоркина
Сдано в набор 8/ХП 1972 г. Подписано к печати 5/VI 1973 г.
Бумага 60 X 907,в, тип. J* 1. Физ. печ. л. 36. Условн. печ. л. 36.
Уч.-изд. л. 35,9. Тираж 5 000 экз. Т-08163.
Цена книги 2 р. 50 к. Заказ JVt 432.
Издательство <Наука»
Главная редакция физико-математической литературы
117071, Москва, В-71, Ленинский проспект, 15
Ордена Трудового Красного Знамени
Ленинградская типография № 2 имени Евгении Соколовой
Союзполиграфпрома при Государственном комитете
Совета Министров СССР по делам издательств,
полиграфии и книжной торговли
г. Ленинград, Л-52, Измайловский проспект, 29
0232-1777
042@2)-73 U

ОГЛАВЛЕНИЕ
Предисловие ко второму изданию в
Предисловие к первому изданию 16
Глава 1. Вводная глава 25
§ 1. Основные обозначения н термины 25
§ 2. О допустимых расширениях понятия решения для линейных и
квазилинейных уравнений 34
§ 3. Основные результаты и их возможное развитие , , 54
Глава П. Вспомогательные предложения 66
§ 1. Некоторые простейшие неравенства 66
§ 2. Пространства Wlm (Q). Теоремы вложения 68
< Of
§ 3. О разных сходимостях и функциях классов Wm (О) и Wm (Q) . 80
§ 4. Некоторые другие вспомогательные предложения 88
§ 5. Об оценках max \и{к)\ и некоторых интегральных норм и (х).
Класс функций Ят„ (QR, у, I, а, г, k) 101
§ 6. Класс функций 33m (q, M, у, уь б, — \ 114
§ 7. Классы функций 58П, Ш U S,, М, у, \и 6, —) и %т (п U S,, М,
У, Yi. о, j) 121
§ 8. Классы функций «В^1 (й, Ми б„ б2, б3) Y. Yi. о, -] 125
§ 9. Класс ё% (и U.S,, v (т), М, у, уи jj 134
Глава 111, Линейные уравнения 144
§ 1. О разрешимости задачи Дирихле в пространствах С'+а (Q), /> 2.
Принцип максимума 144
§ 2. Априорная оценка Шаудера 161
§ 3. О разрешимости в С2+а (?2) других краевых задач 177
§ 4, Обобщенные решения из W2 (Q)- Первое основное неравенство 181
§ 5. Разрешимость первой краевой задачи в W\ (Q) 191
§ 6. Вторая и третья краевые задачи 200
§ 7. Внутренние оценки в L2 производных второго порядка произ-
• вольной функции через значения эллиптического оператора от нее 202
''§ 8. Второе основное неравенство для эллиптического оператора . . 208
§ 9, О разрешимости первой краевой задачи в пространстве W\ 0 (Q) 221
§ 10. О принадлежности обобщенных решений из W\ (Q) к W\ (Qj) . 227
1*
''§

4 ОГЛАВЛЕНИЕ
§ 11. О других способах доказательства второго основного нера-
неравенства 231
§ 12. О принадлежности обобщенных решений из W\ к С!+а, 1^2. 234
*.
§ 13. Об ограниченности обобщенных решений из W2 (Q) и оценке
V для них некоторых интегральных норм 236
§ 14. О принадлежности обобщенных решений из w\ (Q) к Са . . 249
§ 15. Об ограниченности max | V и | и | "*/1 ° для обобщенных ре-
решений из Wl2(Q) 251
§ 16. О методах Галеркина, Ритца и методе наименьших квадратов 253
§ 17. О разложении в ряды по собственным функциям самосопря-
самосопряженного оператора 259
§ 18. Метод конечных разностей 263
§ 19. Случай двух независимых переменных 272
§ 20. О двумерных седлообразных поверхностях 285
Глава IV. Квазилинейные уравнения с дивергентной главной частью . 291
§ 1. Ограниченные обобщенные решения. Непрерывность по Гёль-
деру 292
§ 2. Единственность в малом 300
§ 3. Оценка max I V и I 303
о-
§ 4. Оценка max | V и | во всей области ?2 310
§ 5. О существовании обобщенных производных второго порядка.
Об ограниченности градиентов обобщенных решений .... 316
§ 6. Оценка норм | и \{l+a\ I > 1 327
§ 7. Оценки интегральных норм и максимума модуля для обобщен-
обобщенных решений 333
§ 8. Оценка максимума модулей для классических решений . . . 347
§ 9. О существовании обобщенных решений 354
§ 10. Классическая разрешимость задачи Дирихле 368
Глава V. Вариационные задачи 391
§ 1. Постановка задач 391
§ 2. Нахождение функций, на которых функционал / (и) принимает
наименьшее значение 397
§ 3. Об оценке максимума модуля решений вариационных задач . . 403
§ 4. Доказательство гёльдеровости обобщенных решений 405
§ 5. Теорема единственности в малом для обобщенных решений . . 408
§ 6. Дальнейшее исследование дифференциальных свойств обобщен-
обобщенных решений 409
§ 7. Обобщенные решения квазирегулярных задач 411
Глава VI. Квазилинейные уравнения общего вида 416
§ 1. Оценка нормы |«1а+а) через норму | и |[]* 419
§ 2. Оценка \Vu\ на границе 428
§ 3. Тотальные оценки max I Vu I 433
§ 4. Локальные оценки \Vu\ 449
§ 5. Теоремы существования 456
§ 6. О двумерных задачах 461

ОГЛАВЛЕНИЕ 5
Глава VII. Линейные системы уравнений эллиптического типа .... 467
§ 1. Обобщенные решения из W\ (Q) 467
§ 2. Оценка max [ u | 470
Q
§ 3. Оценка | и |(q ] . . .' 475
§ 4. Априорные оценки | и |д/+о' и || и ||^а 477
§ 5. О разрешимости задачи A.1), A.3) в классах C{l+a) (Q) .... 480
§ 6. Дифференциальные свойства обобщенных решений 482
Глава VIII. Квазилинейные системы 485
§ 1. Априорные оценки норм | u |q+<4 '^1, через max | и, Vu I . . . 486
D
§ 2. Оценка | и &а) 488
§ 3. Энергетическое неравенство и оценка max | Vu | на границе . . 490
§ 4. Оценка max | Vu | 493
Q
§ 5. Теоремы существования 497
§ 6. Вырождающиеся системы • 498
Глава" IX. О некоторых других приемах получения оценок констант
Гёльдера для решений и их производных 504
§ 1. Случай простейшего уравнения 505
§ 2. Оценки постоянных Гёльдера для решений уравнений с дивер-
дивергентной главной частью (линейных и квазилинейных) 509
§ 3. Об оценке колебаний производных от решений уравнений с ди-
дивергентной главной частью 520
§ 4. Недивергентные уравнения • ... 521
§ 5. Способ Ю. Мозера оценки | и |^'для решений линейных урав-
уравнений. Неравенство Гарнака 523
§ 6. Оценка Ниренберга 531
§ 7. Способ Морри оценки постоянной Гёльдера для решений дву-
двумерных вариационных задач 535
Глава X. Другие краевые задачи 537
§ 1. Формулировка задач и общая схема их решения 537
§ 2. Априорные оценки норм |h|q+^ 545
§ 3. Теоремы существования 557
Литература 564

ПРЕДИСЛОВИЕ КО ВТОРОМУ ИЗДАНИЮ
С момента написания первого издания книги (дадим ему
номер [I]) прошло около десяти лет. Опишем кратко, какое
развитие получили вопросы, являющиеся предметом этой книги,
и какие в связи с этим дополнения сделаны в данном издании.
1) Большой общности добились в направлении исследования
краевых задач для линейных эллиптических уравнений и систем
с «хорошими» коэффициентами. Для них сделано то же, что
и для одного уравнения второго порядка: доказана нормаль-
нормальная разрешимость в пространствах Cl+a(Q) и Wlp(Q) при усло-
условиях, вызванных существом дела (см. работы С. Агмона, А. Даг-
лиса, Л. Ниренберга [1], В. А. Солонникова [35] и др.). Важным
моментом при этом является идея Шаудера замораживания
коэффициентов, сводящая проблему к изучению соответствую-
соответствующих задач для уравнений с постоянными коэффициентами. Это
сведение возможно, если коэффициенты в главных членах не-
непрерывны в обычном смысле для случая пространств WP(Q)
и если все коэффициенты непрерывны по Гёльдеру в случае
пространств С +a(Q). Для указанных задач построены матрицы
Грина, и для них и их производных даны предельно точные
точечные оценки. В ряде важных случаев удалось вычислить
индекс задач (см. привлекшую большое внимание работу М. Атии
и И. Зингера и ее продолжения; ей предшествовали работы по
вычислению индекса для задач на плоскости и некоторых част-
частных задач в трехмерном пространстве).
Иная ситуация возникла при попытке распространить ре-
результаты §§ 13—15 гл. III об уравнениях с разрывными
коэффициентами на эллиптические уравнения высоких поряд-
порядков и системы (о желательности таких рассмотрений сказано
в конце стр. 49 — начале стр. 50[I] или, что то же, на стр. 57
данного издания). Оказалось, что они не сохраняют свою форму.
Е. Де Джорджи [П4] и В. Г. Мазья [223] построили однород-
однородные уравнения выше второго порядка, которые имеют разрыв-
разрывные решения с конечной энергетической нормой.
2) Для квазилинейных уравнений произвольного порядка 21
с дивергентной главной частью был дан в начале 60-х годов
«прямой» метод доказательства разрешимости классических

ПРЕДИСЛОВИЕ КО ВТОРОМУ ИЗДАНИЮ 7
краевых задач в пространствах Wlm(Q). (Он применим также
и к системам таких уравнений.) Приближенные решения строятся
известным способом (по методу Галеркина), сходимость же их
к (обобщенному) решению исследуемой задачи устанавливается
своеобразно, с использованием идеи Г. Минти о слабых предель-
предельных переходах под знаком выпуклых операторов (см. в связи
с этим работы Ф. Браудера и др.). Эта идея, дополненная ори-
оригинальным рассуждением Ж- Лерэ и Ж. Лионса о предельном
переходе в младших членах, позволила доказать разрешимость
указанных краевых задач при условиях на поведение образую-
образующих уравнения функций для больших значений их аргументов,
близких к необходимым. Прототипом этого метода, с одной
стороны, является «прямой» метод разыскания функции, реализу-
реализующей абсолютный минимум функционала J(u)= [ F{x, и, ux)dx
а
при каком-либо краевом условии, а с другой — метод Галер-
Галеркина для линейных задач. Сформировался он постепенно бла-
благодаря исследованиям ряда математиков (см. в связи с этим [7,
323, 36, 18] и др.). Мы излагаем его в § 9 гл. IV применительно
к основному объекту данной книги — квазилинейным уравне-
уравнениям второго порядка, имеющим дивергентную главную часть.
В § 10 результаты § 9 сравниваются с результатами, получае-
получаемыми другими методами.
В первом издании книги (см. стр. 58 [I] или, что то же
самое, стр. 63 данной книги) мы обращали внимание на важ-
важную и сложную проблему изучения гладкости обобщенных
решений из Wlm(Q), I > 1, для квазилинейных уравнений и си-
систем произвольного порядка 21 и доказательство допустимости
такого расширения классической постановки краевых задач
для них, т. е. доказательство теоремы единственности в классе*
таких решений для малых областей (к этому направлению
относятся работы [42,, 2] Ин. Нэчаса). Решению этих вопросов
для уравнений второго порядка посвящена значительная часть
данной книги. Для уравнений высоких порядков и систем М. Ми-
Миранда, Е. Джусти и В. Г. Мазьей обнаружен новый эффект.
Эти уравнения при п > 2 (п — всюду размерность пространства
аргументов) могут иметь негладкие обобщенные решения при
гладких (и даже аналитических) функциях, образующих урав-
уравнения ([222, 223]). Более того, М. Миранда и Е. Джусти дока-
доказали, что при достаточно большом п построенное ими реше-
решение является единственным решением задачи и единственной
функцией, на которой некоторый функционал принимает свое
наименьшее значение. (Как доказывается в гл. V, это невоз-
невозможно для функционалов вида / (н)= [ F (х, и, их) с?*.) Ввиду

8 ПРЕДИСЛОВИЕ КО ВТОРОМУ ИЗДАНИЮ
этого приобретают еще большее значение результаты Ч. Морри
[397] (см. также работу [22J Е. Джусти) о гладкости обобщен-
обобщенных решений а (х) широких классов квазилинейных уравнений
высоких порядков и систем таких уравнений на открытых мно-
множествах полной меры (но не во всех точках х\).
При их доказательстве Ч. Морри использовал одну важную
идею Ф. Альмгрена, изучавшего тот же вопрос для обобщен-
обобщенных решений многомерных вариационных задач, обобщающих
задачу Плато. Вообще мысль о том, что нелинейные эллипти-
эллиптические уравнения высоких порядков и системы с гладкими
(и даже аналитическими) функциями могут иметь решения с осо-
особенностями на множествах нулевой меры, зародилась, по-види-
по-видимому, в связи с многомерной задачей Плато. Физические
эксперименты с мыльными пленками, являющимися «обобщен-
«обобщенными решениями» задачи Плато, указывали, что такие реше-
решения могут иметь особые точки и даже линии. В работах Е. Рай-
фенберга [47] и Ф. Альмгрена [4], предшествовавших упомя-
упомянутой выше работе [397] Ч. Морри, доказывалась гладкость
обобщенных решений задачи Плато и ее обобщений для почти
всех значений аргумента. Примеры, построенные итальянскими
математиками, показывают, что для всех значений аргумента
это и неверно. Иными методами изучается задача о построении
минимальной гиперповерхности в rt-мерном евклидовом про-
пространстве в работах Е. Де Джорджи [ 111.3] и М. Миранда [382].
Упомянутые здесь результаты не нашли отражения в дан-
данном издании. Их изложение потребует отдельных книг, ибо
доказаны они с использованием средств, отличных от имею-
имеющихся в данной книге. Одна книга такого плана уже появи-
появилась — это книга [14,] Г. Федерера. В ней нашли отражение
исследования самого автора, В. Флеминга и др. (в частности,
работа [142]). Методы исследования, развитые в этих работах,
весьма своеобразны, геометричны и не везде прозрачны. Они
не похожи на те, которыми работаем мы. Но нам кажется,
что с течением времени (как это много раз наблюдалось в ма-
математике) многое прояснится и будет упрощено, и в этом упро-
упрощении сыграют свою роль методы, излагаемые в данной книге
(см. в связи этим последние главы книги [396] Ч. Морри и ра-
работу [3] В. Алларда).
3) До конца 50-х годов основным объектом изучения были
п
квазилинейные эллиптические уравнения 2 ац{х, u,ux)uXiXj-\r
а(х,и,их) = 0, для которых отношение '^-~'а</ {х> и> р)Ы/ ^
i(*,H,p) не превосходит какой-либо непрерывной функ-

ПРЕДИСЛОВИЕ КО ВТОРОМУ ИЗДАНИЮ 9
ции хо(х,и) при всех p<sEn. Такие уравнения стали называть
равномерно эллиптическими. Им посвящена и данная книга.
В 60-х годах много усилий было направлено на изучение раз-
различных классов неравномерно эллиптических уравнений, т. е.
уравнений, для которых %(х, и, р) неограниченно растет при
| р j —> оо. К таким уравнениям относятся уравнения, определяю-
определяющие среднюю кривизну гиперповерхности в евклидовом и ри-
мановом пространствах, в том числе уравнение минимальных
поверхностей, уравнения Эйлера для параметрических вариа-
вариационных задач и ряд других интересных уравнений дифферен-
дифференциальной геометрии.
Основной вопрос для неравномерно эллиптических уравне-
уравнений состоит в априорной оценке max| Ун | для их решений и(х).
Если такая оценка получена, то все дальнейшие оценки для и
уже имеются, ибо х(х, и(х), их(х)) ограничена на и (х) и можно
применять результаты о равномерно эллиптических уравнениях.
Оценка | Vh | разделяется на такие задачи: а) получение оценки
max| Vh | и затем, с ее использованием, оценки max| Vh |; b) по-
лучение локальных оценок | Ун |, т. е. оценок тах|Ун| для
VO'cfi, через какие-либо характеристики известных функций,
тах|н| и расстояние от Q' до границы дп. Метод оценки
Q
max| Ун | для равномерно эллиптических уравнений восходит
да
в своей существенной части к работам С. Н. Бернштейна. Он
допускал обобщения на некоторые классы неравномерно эллип-
эллиптических уравнений (см. § 2 гл. VI). Иной метод оценки max | Ун |,
д9.
охвативший более широкие классы неравномерно эллиптических
уравнений (в том числе и уравнение средней кривизны гипер-
гиперповерхности), дан в недавнем мемуаре [51ц] Дж. Серрина. Для
таких уравнений могут играть роль геометрические характери-
характеристики граничной поверхности дп в пространстве х (например,
ее выпуклость или величина средней кривизны — см. [282]).
И. Я- Бакельманом для уравнений, определяющих среднюю
кривизну поверхности, дан иной способ оценки тах|Угг| ([323])-
dQ
Для оценки тах|Ун| при уже известной оценке тах|Ун|
обычно применяют один из двух методов, изложенных в гл. IV
и гл. VI нашей книги [I]. Метод, описанный в гл. VI, исходит
из работы [218] 1956 г., в которой было показано, что получение
такой оценки можно свести к построению решения ф (t) неко-
некоторого обыкновенного дифференциального неравенства (или,
в частности, обыкновенного дифференциального уравнения).
В самой работе [218] рассматривался еще сравнительно узкий

]0 ПРЕДИСЛОВИЕ КО ВТОРОМУ ИЗДАНИЮ
класс квазилинейных уравнений ([218] посвящена более слож-
сложному объекту — параболическим уравнениям, но то, что ка-
касается оценки \ux\s=\Vu\, одинаково для обоих типов уравне-
уравнений). Однако это было вызвано не возможностями предложен-
предложенного там способа оценки max|V«|, а неумением в то время
получать оценку постоянной Гёльдера для V«. Известные ра-
работы Е. Де Джорджи [И,] и Дж. Нэша [41] положили начало
получению оценок постоянных Гёльдера для решений и и их
производных Vh. Отправляясь от этих работ и работы [218],
оказалось возможным охватить весь класс квазилинейных рав-
равномерно эллиптических уравнений и изложить это в [I] в срав-
сравнительно доступной форме. Однако в гл. VI [I] изложение
основной идеи оценки max|V«| работы [218] сильно усложнено
Q
тем, что мы проводим ее сразу для обобщенных решений и,
не имеющих производных ихх в каждой точке х (для сравне-
сравнения напомним, что эти предположения обычно делаются даже
при получении значительно более простой оценки — оценки
тах|и| на основании принципа максимума). Такое нагромож-
дение трудностей привело к тому, что исследователям, не свя-
связанным с нами непосредственно, пришлось переоткрывать для
себя ту простую «рабочую» форму метода оценки max|V«|
Q
(см. в связи с этим вышеупомянутые работы Дж. Серрина [51И]
и И. Я- Бакельмана [32,3]), которая изложена в [218] примени-
применительно к частному случаю и которой мы пользовались сами
при изучении различных классов квазилинейных уравнений.
В данном издании книги мы учли нашу методическую ошибку
и изложили в гл. VI первый метод оценки max | Vh | в том виде,
а
в котором он более доступен, предположив, что и есть клас-
классическое решение уравнения (для неклассических же решений
см. гл. VI первого издания). Более того, мы показали
(см. [2122_24]), что он позволяет охватить наиболее широкие на
сегодня классы квазилинейных неравномерно эллиптических
уравнений второго порядка.
В гл. IV сохранена прежняя «интегральная* форма оценки
max | Vh | для обобщенных решений. Некоторое упрощение до-
достигнуто за счет дополнительного предположения, что иссле-
исследуемое решение имеет ограниченные производные Vh. Возмож-
Возможности этого метода оценки применительно к различным клас-
классам неравномерно эллиптических уравнений проанализированы
в работах [152,3t4], [24,.2i4].
В § 3 гл, VI изложена также оценка max| Vh | для решений
и
некоторого класса неравномерно эллиптических уравнений, дан-

ПРЕДИСЛОВИЕ КО ВТОРОМУ ИЗДАНИЮ ]|
ная А. В. Ивановым [143J. Упомянем еще исследования X. Джен-
кинса и Дж. Серрина по многомерному уравнению минималь-
минимальных поверхностей ([28It2]).
В гл. IV и VI проведены локальные оценки градиентов | V« |,
причем в гл. VI это сделано и для неравномерно эллиптиче-
эллиптических уравнений. Локальные оценки градиентов, данные в гл, VI,
также восходят к работе [218] 1956 г. и изложены теперь
в форме, близкой к первоначальной. Они охватывают весь
класс равномерно эллиптических уравнений и «почти» те же
классы неравномерно эллиптических уравнений, для которых
получена описанная выше оценка max | V« |. «Почти» состоит
в дополнительном ограничении: порядок роста т (х, и, р) по р
должен быть меньше 2. Это ограничение исключает упоминав-
упоминавшиеся выше уравнение средней кривизны (в том числе урав-
уравнение минимальных поверхностей) и уравнения Эйлера для
параметрических вариационных задач. Для них пришлось искать
иные методы локальных оценок, Такие оценки даны нами в ра-
работе [2124]. Ей предшествовали исследования Де Джорджи
в соавторстве с Е. Бомбиери и М. Миранда по локальным
оценкам | ?и | для гладких решений уравнения минимальных
поверхностей при любом п ^2 ([115,6]). Случай п = 2 иссле-
исследовался многими авторами (см. [162,4,5» 28J и др.). Работы [П5,
6, 2124] здесь не излагаются, ибо это вывело бы нас за пре-
пределы аналитических фактов, изложенных в гл II. В частности,
в них используется изопериметрическое неравенство Федерера —
Флеминга, доказанное ими для интегральных потоков, и ори-
оригинальное обобщение теоремы вложения C.1) из гл. II, до-
доказанное М. Миранда [38i].
Итак, гл. IV и VI и в данном издании книги посвящены
в основном равномерно эллиптическим уравнениям. Для неравно-
неравномерно эллиптических уравнений сделано лишь то, что не выхо-
выходит за рамки методов и общих аналитических предложений
гл. II первого издания. Этот объект требует дальнейшего изу-
изучения, в том числе построения примеров, очерчивающих гра-
границы, за которыми падает разрешимость «в целом» классиче-
классических краевых задач (см. в связи с этим, например, [282]). За-
Заметным продвижением в этом направлении является работа
[51ц] Дж. Серрина, в которой дан оригинальный метод оценки
max | V« | и метод оценки max | V« |, аналогичный первому ме-
меда В
тоду, излагаемому в гл. VI. Сочетание результатов работы [51ц]
по оценке max | V« | и результатов, изложенных в данной книге,
дп
приводит к наиболее общим на данное время результатам по
классической разрешимости «в целом» краевых задач для не-
неравномерно эллиптических уравнений.

12 ПРЕДИСЛОВИЕ КО ВТОРОМУ ИЗДАНИЮ
4) В первом издании книги мы не касались вырождаю-
вырождающихся уравнений, хотя методы, изложенные в [I], с успехом
используются для изучения этих объектов. В качестве иллю-
иллюстрации возможностей этих методов мы включили во второе
издание исследование вариационной задачи для функционала
|V«|mc?A: и несколько более общих квазирегулярных функ-
а
ционалов вида J F(Vu)dx. Этому посвящен § 7 гл. V. К нему
Q
примыкает § 6 гл. VIII, в котором исследуется один класс
вырождающихся квазилинейных систем. Аналитическую основу
для решения этих задач составляют результаты § 9 гл. II
о гёльдеровости элементов класса Ът, являющегося некоторым
обобщением классов 23т и 33^'. Упомянем некоторые из иссле-
исследований по вырождающимся квазилинейным уравнениям. Это
работы [13] Ю. А. Дубинского, в которых с помощью метода
Минти — Браудера, описанного в п. 2), автор доказывает су-
существование обобщенных решений задачи Дирихле для неко-
некоторых классов таких уравнений. В работе [518] Дж. Серрина
исследуются свойства обобщенных решений квазилинейных вы-
вырождающихся уравнений второго порядка. В работах [343,4]
Т. Б. Соломяк исследуется один класс таких уравнений, свя-
связанных с задачами дозвуковых течений идеальной сжимаемой
жидкости. Интересные задачи по вырождающимся уравнениям
встречаются в теории пластичности. По ним имеется немалая
специальная литература.
5) С вопросами о гладкости обобщенных решений, затрону-
затронутыми в п. 2), связана группа исследований, посвященных изу-
изучению устранимых особенностей решений квазилинейных эллип-
эллиптических уравнений. Классическим прототипом для работ этой
группы явилась общеизвестная теорема об устранимости особой
точки аналитической функции, ограниченной вблизи этой точки.
Подобными вопросами много и успешно занимался Дж.Сер-
рин ([516_,0] и др.). Некоторые из его результатов были обоб-
обобщены В. Г. Мазьей [224] на случай уравнений выше второго
порядка. Р. Финн, Дж. Серрин и др. исследовали поведение
решений разных уравнений в окрестности бесконечно удален-
удаленной точки или вблизи особых точек. Р. Финн исследовал по-
поведение решений уравнения минимальных поверхностей с пра-
правой частью ku при и = 2 в окрестности угловой особой точки
границы ([166]).
6) Ряд задач механики и в последние годы теории управ-
управления требуют решения различных условных вариационных
задач. Простейшими задачами этого типа являются задача на
определение собственных чисел и собственных значений линей-

ПРЕДИСЛОВИЕ КО ВТОРОМУ ИЗДАНИЮ 13
ного симметричного оператора (см. конец § 17 гл. III) и за-
задача на определение
inf/(«) = inf | F(x, и, ux)dx
а
среди всех функций и(х), обладающих некоторой гладкостью,
удовлетворяющих какому-либо краевому условию и подчиняю-
подчиняющихся дополнительному условию A): |«(д:)|^М (см. о ней
гл. V).
Существование обобщенных решений весьма разнообразных
условных вариационных задач, в том числе и задач, сформу-
сформулированных в последние годы, обычно доказывается сравни-
сравнительно просто на основании тех же соображений о полуогра-
полуограниченности и полунепрерывности исследуемого функционала,
которые изложены в § 2 гл. V для обычной вариационной
задачи (конечно, есть задачи, в которых и эти кардинальные
факты устанавливаются нестандартно для нашего времени, —
см. гл. IV книги [396] Ч. Морри или работы Г. Фикера [15]),
Несравнимо большие трудности наступают при исследовании
гладкости этих обобщенных решений. Так, для второй из упо-
упомянутых задач первым важным этапом было доказательство
гёльдеровой непрерывности ее обобщенного решения. Однако
при решении этого вопроса наличие ограничения A) преодоле-
преодолевалось сравнительно просто (см. конец § 4 гл. IV); при этом,
как нетрудно видеть, условие A) может быть заменено более
общим условием A'): M*)^«M^f2 x). Напротив, исследова-
исследование дальнейшей гладкости обобщенных решений таких задач
(собственно, его надо проводить лишь вблизи точек соприкос-
соприкосновения решения и(х) с ограничивающими поверхностями
н = /г(*)) потребовало специальных рассмотрений (см. ра-
работы [333]).
Весьма мало изучена гладкость обобщенных решений, воз-
возникающих при решении многомерных вариационных задач тео-
теории управления. В них и в ряде задач гидромеханики (см.,
например, [9]) мы наталкиваемся на квазилинейные уравнения,
в которых некоторый из известных функций разрывны по своим
аргументам и или их.
В работах Ж- Лионса, Г. Стампаккиа, Ф. Хартмана и др.
(см. [342,3, 24] и др.) изучались также своеобразные вариаци-
вариационные задачи, решения которых удовлетворяют не уравнению
Эйлера, а некоторым неравенствам (простейший пример тому
дает та же вторая условная вариационная задача: на ее реше-
решении первая вариация неотрицательна — это неравенство-тожде-
неравенство-тождество заменяет собою уравнение Эйлера). В исследовании не-
некоторых из таких задач полезны классы ЭД и 33, изученные в гл. II
и многократно использованные в данной книге. Насколько нам

14 ПРЕДИСЛОВИЕ КО ВТОРОМУ ИЗДАНИЮ
известно, Ж- Лионсом написана книга, в которой подробно осве-
освещаются вариационные задачи, обсуждаемые в этом пункте *).
Читатель, познакомившийся с данной книгой, будет вполне
подготовлен к чтению упомянутых работ. Исключение состав-
составляют работы по многомерной задаче Плато и ее обобщениям.
Помимо исследований, перечисленных в пп. 1) — 6), имеет-
имеется немало публикаций, непосредственно связанных с [I]. Так,
в некоторых из них тот или иной результат из [I] (чаще в ка-
какой-либо частной, но достаточно интересной ситуации) дока-
доказывается иначе, методом, более простым или более привычным
для автора. В других анализируются возможности разных ме-
методов и приемов оценок решений, данных в [I], применительно
к уравнениям, обобщающим рассмотренные в [I] в каком-либо
направлении. Так, мы упоминали выше работы, в которых
допускается рост т (х, и, р) по р, или работы, в которых сте-
степенной характер роста по р образующих уравнения функций
ai(x, и, р), а(х, и, р) (а именно такой порядок роста является
основным в [I]) заменяется каким-либо другим. Немало имеется
работ, где методы и результаты из [I] в сочетании с какими-
либо дополнительными соображениями и приемами позволяют
исследовать уравнения с вырождениями или отдельные классы
систем квазилинейных уравнений.
Наконец, отметим работы Дж. Серрина [514,s] и Н. С. Тру-
дингера [54], в которых результаты Ю. Мозера по неравенству
Гарнака распространяются на квазилинейные уравнения с дивер-
дивергентной главной частью, и работу [35] В. Литтмана, Г. Стам-
паккиа и X. Вайнбергера, в которой строится и исследуется
функция Грина для линейных уравнений с разрывными коэф-
коэффициентами из гл. III. Все эти работы имеют прямое отноше-
отношение к изучаемому здесь объекту и естественно вписываются
в рамки объектов и методов данной книги. Только недостаток
времени и места является причиной того, что они здесь не из-
излагаются.
Перечислим, чем отличается второе издание от первого. Во-
первых, мы устранили замеченные ошибки, опечатки и разные
шероховатости. Первые были найдены нами сразу по выходе
книги из печати, и их исправления были сообщены американскому
издательству, переводившему нашу книгу на английский язык.
К сожалению, эти исправления не были учтены ни в англий-
английском, ни во французском переводах, которые вышли со всеми
недочетами русского издания. Во-вторых, мы внесли ряд улуч:
шений и добавлений в изложение гл. II, в том числе выде-
выделили отдельно класс функций % в соответствии с тем, как это
*) Добавление при корректуре. См. С. Duvaut, J.-L. Lions, Les inequations
en mecanique et en physique, Paris, 1971.

ПРЕДИСЛОВИЕ КО ВТОРОМУ ИЗДАНИЮ 15
сделано в нашей книге [21ц] по параболическим уравнениям,
и добавили § 9 по классам Sm, используемым при исследова-
исследовании квазирегулярных вариационных задач (§ 7 гл. V) и неко-
некоторых классов вырождающихся квазилинейных систем (§ 6
гл. VIII). В гл. III вставлены новые параграфы: § 16 о при-
приближенных методах, § 17 о разложении произвольных функций
в ряды по собственным функциям эллиптических операторов
и § 18 о методе конечных разностей. Чтобы не увеличивать
существенно объем книги, мы выбросили § 16 о задачах диф-
дифракции, стоящий в стороне от основного направления книги.
Зато в § 13 добавлены оценки некоторых интегральных норм
обобщенных решений, о которых в первом издании есть лишь
упоминание, и принцип максимума для обобщенных решений.
То и другое легко делается на основании аппарата, разрабо-
разработанного в гл. II.
В гл. IV добавлен § 9 о разрешимости краевых задач
в пространствах Wm(Q.) Л Lq (Q.) (т. е. о существовании обобщен-
обобщенных решений таких задач). В соответствии с этим несколько
перестроен § 8 о классической разрешимости этих задач (теперь
это § 10). Выделен в отдельный параграф и расширен мате-
материал, касающийся оценки максимумов модулей классических
решений. Заново переписан параграф об оценке максимума мо-
модуля обобщенных решений, и добавлены к нему оценки инте-
интегральных норм, взятые из других параграфов гл. IV. В §5 дано
более полное доказательство существования обобщенных произ-
производных второго порядка у обобщенных решений и далеко не оче-
очевидные пояснения к одной фразе прежнего § 3, начинающейся
словами: «Нетрудно убедиться, что ... ». Вообще материал
§§ 3—5 несколько перетасован, что, мы надеемся, облегчит его
понимание. Эту перестройку мы сделали в связи с замечанием
в книге [396] Ч. Морри, где он, говоря о наших результатах по
обобщенным решениям, деликатно указывает, что не смог воспро-
воспроизвести доказательство одного факта, который мы утверждаем,
но не даем никаких пояснений. Теперь эти пояснения даны, и
они были необходимы. Итак, композиция гл. IV изменена доволь-
довольно сильно, хотя методы и результаты, изложенные в ней, те же,
что и в гл. IV 1-го издания. Исключение составляет § 9.
В гл. V заново переписаны §§ 1—3, так как прежнее изло-
изложение показалось нам неудачным, и добавлен § 7 о квазире-
квазирегулярных задачах.
Большая часть гл. VI, касающаяся оценок градиентов реше-
решений и теорем существования (т. е. §§ 2 и 3), переделана и раз-
разбита на четыре параграфа. О характере этих изменений мы
говорили выше в п. 3). Надеемся, что данное изложение мате-
материала будет восприниматься легче. Правда, при этом мы не-

16 ПРЕДИСЛОВИЕ К ПЕРВОМУ ИЗДАНИЮ
сколько огрубили результат, предположив, что и (х) есть клас-
классическое решение, тогда как в первом издании предполагалось,
что и (х) есть обобщенное решение из Wl(Q) Л Lip(Q). Для
классических решений мы смогли провести точечные оценки,
тогда как для обобщенных в [I] пришлось проводить интеграль-
интегральные оценки, которые воспринимаются при чтении труднее. Такое
огрубление результатов гл. VI первого издания не влияет на
основные ее цели: исследование классической разрешимости
задачи Дирихле. При этом исследовании все подвергаемые ана-
анализу решения заведомо принадлежат С2.
В гл. VIII добавлен § 6 об одном классе вырождающихся
квазилинейных систем, а в § 5 гл. IX приведено доказатель-
доказательство неравенства Гарнака для простейшего линейного уравне-
уравнения с разрывными коэффициентами, установленного Мозером.
Наконец, в гл. X усилен основной результат о разрешимо-
разрешимости квазилинейных уравнений при нелинейном краевом условии,
содержащем производные их от решения и (х): снято предпо-
предположение о том, что задача имеет не более одного решения.
Это потребовало некоторой перестройки в изложении всего
материала и ряда дополнительных рассмотрений.
Авторы признательны В. Г. Мазье за полезные советы,
А. П. Осколкову за прочтение рукописи и редакционные заме-
замечания и Л. С. Захаровой за помощь в оформлении книги.
Ленинград, сентябрь 1970 г. Авторы
ПРЕДИСЛОВИЕ К ПЕРВОМУ ИЗДАНИЮ
Казалось, что к 50-м годам нашего века линейные эллипти-
эллиптические уравнения второго порядка в ограниченной области
изучены если не с исчерпывающей, то с разумной полнотой и
что основные вопросы для них получили достаточно простые
решения. В работах Г. Жиро и Ю. Шаудера 30-х годов была
доказана для них разрешимость основных краевых задач при
условии достаточной гладкости коэффициентов и границы об-
области.
Затем они были осмыслены с позиций функционального
анализа. Начало этому пониманию положила работа [19,]
К. О. Фридрихса 1934 г. о полуограниченных расширениях
симметрических эллиптических операторов. Она и дальнейшие
исследования Г. Вейля, К- О. Фридрихса, С. Г. Михлина,
М. И. Вишика, О. А. Ладыженской и др. конца 40-х годов
показали, что решение основных краевых задач для эллипти-
эллиптических уравнений (мы всюду будем говорить лишь об уравне-
уравнениях второго порядка) эквивалентно решению уравнений вида

ПРЕДИСЛОВИЕ К ПЕРВОМУ ИЗДАНИЮ 17
x-\-Ax — f с вполне непрерывным линейным оператором А
в некоторых гильбертовых пространствах, построенных по ква-
квадратичной форме главной симметрической части дифференциаль-
дифференциального оператора. Такая точка зрения на краевые задачи помогла
исследованию сходимостей приближенных методов Ритца, Га-
леркина и др. Правда, такой подход давал лишь существова-
существование так называемых обобщенных (плохих по дифференциальным
свойствам) решений, про которые известно, что они имеют про-
производные лишь первого порядка. Вопросы о существовании
у них производных более высоких порядков (хотя бы второго)
и, тем самым, вопрос об удовлетворении уравнению приходилось
решать с привлечением вышеупомянутых работ Ю. Шаудера,
Г. Жиро и др., так что стройного и простого исследования
краевых задач в рамках только функционального анализа не
получалось: Как оказалось, это было непосредственно связано
с вопросом об области определения замыкания в L2 эллипти-
эллиптических операторов, который был выдвинут И. М. Гельфандом
на его известном семинаре как один из центральных вопросов
по изучению эллиптических уравнений с позиций общей теории
линейных операторов в гильбертовом пространстве.
Решение этого вопроса дано в 1950 г. одним из авторов
книги в заметке [21,] для оператора Лапласа и его итераций при
разных краевых условиях (несколько позже другое решение
этого вопроса было дано С. Г. Михлиным в [23J для оператора
Лапласа в шаре при первом краевом условии), а в 1951 г. —
Р. Каччопполи [82] для общего эллиптического оператора L вто-
второго порядка при первом краевом условии и О. А. Ладыжен-
Ладыженской [212] *) (см. также [213,5]) для таких же L и их итераций
при первом, втором и третьем краевых условиях. Ответ ока-
оказался простым и в случае первой краевой задачи не зависящим
от коэффициентов оператора; именно, в результате замыкания
приходят к функциям, имеющим обобщенные производные из
L2(Q) до второго порядка включительно. Это в определенном
отношении завершало изучение основных краевых задач для
эллиптических уравнений в ограниченной области с точки зре-
зрения функционального анализа.
В конце 40-х годов была исследована для этих задач сходи-
сходимость метода конечных разностей (см. работы Д. М. Эйдуса [37]
*) Работы [82, 212] породили большой цикл работ по получению так назы-
называемых предельно точных оценок в L2, Lp н в некоторых других функцио-
функциональных пространствах для решений уравнений высоких порядков и систем
эллиптического и параболического типов при различных краевых условиях.
Сейчас этот цикл работ близок к своему естественному завершению. В ра-
работах Л. Хермандера показано, что такие предельно точные оценки имеют
место, грубо говоря, только для операторов эллиптического и параболическо-
параболического типов.

18 ПРЕДИСЛОВИЕ К ПЕРВОМУ ИЗДАНИЮ
и О. А. Ладыженской [213,6]), что дало как простой способ до-
доказательства их разрешимости, так и реальный способ вычи-
вычисления решений.
Итак, казалось, что линейные уравнения достаточно хорошо
поняты и надо направить внимание на исследование нелиней-
нелинейных задач. Но в процессе работы над ними стало ясно, насколько
несовершенны наши знания о линейных уравнениях (в случае лю-
любого числа независимых переменных) и прежде всего об истин-
истинной зависимости дифференциальных свойств решений от диф-
дифференциальных свойств коэффициентов уравнения. Среди всех
прежних результатов для п ^2 имелся лишь один безупречный
во всех отношениях — это теорема Шаудера (дополненная Кач-
чопполи) о разрешимости задачи Дирихле в пространствах Гёль-
дера С'+а, /^2 (обозначения — см. § 1 гл. I), для уравнений
с коэффициентами и свободным членом из С1~2+а. В ней все
предположения вызваны существом дела. Она гарантирует клас-
классическую разрешимость задачи Дирихле для уравнений, коэф-
коэффициенты и свободный член которых суть непрерывные по
Гёльдеру функции. Однако один этот результат не дает воз-
возможности исследовать сколько-нибудь общие классы нелинейных
уравнений. Необходимо было изучить разрешимость краевых
задач и дифференциальные свойства решений линейных урав-
уравнений с разрывными, хотя бы ограниченными, коэффициентами.
Ранее полученные результаты и методы почти ничего не давали
в этом направлении. Анализу этих вопросов для случая двух
независимых переменных посвящены работы 40-х и 50-х годов
Ч. Морри, Л. Берса, Л. Ниренберга, И. Н. Векуа и др. Их
достаточно полное решение было получено с помощью весьма
тонких средств — теории квазиконформных преобразований и
теории обобщенных аналитических функций. К сожалению, эти
методы не допускают обобщений на случай трех и большего
числа измерений. Были основания ожидать, что и сами резуль-
результаты для многомерных задач качественно отличаются от случая
двух независимых переменных.
Новый этап в изучении многомерных линейных уравнений
начался с работы [11J Е. Де Джорджи и работы [41] Дж. Нэша
и нашел в определенном отношении свое завершение в рабо-
работах Г. Стампаккиа [52,_4], Ч. Морри [39J и авторов данной
книги [2112_21].
В работах [2118,2о, ю] построены примеры, показывающие,
что условия, при которых в этих работах установлены различ-
различные свойства обобщенных решений линейных уравнений с раз-
разрывными и, вообще говоря, неограниченными коэффициентами,
являются точными.
Изложению результатов этих работ, а также результатов
более ранних работ Ю- Шаудера, К- О- Фридрихса, С. Г. Мих-

ПРЕДИСЛОВИЕ К ПЕРВОМУ ИЗДАНИЮ 19
лина и О. А. Ладыженской по разрешимости краевых задач
в пространствах С+а, /^2, и №г, />1, посвящена третья
глава. Ей предшествует вводная глава, в которой даются исполь-
используемые в книге обозначения, излагаются примеры, достаточно
точно очерчивающие рамки желаемой и возможной теории ли-
линейных и квазилинейных уравнений (которая затем и строится
в предлагаемой книге), и излагаются основные результаты книги
и их предполагаемое развитие. Во второй главе собраны раз-
различные аналитические предложения, родившиеся главным обра-
образом в связи с изучением дифференциальных уравнений, но
формально с ними не связанные. Большая часть этой главы
посвящена изучению так называемых классов Ът — классов
функций, подчиненных некоторым интегро-дифференциальным
неравенствам. Оказалось, что именно эти классы функций тесно
связаны с эллиптическими уравнениями второго порядка.
Однако, в основном книга посвящена квазилинейным уравне-
уравнениям, которые имеют почти такую же длинную историю, как
и линейные уравнения с переменными коэффициентами. Две
гипотезы — 19-я и 20-я проблемы Гильберта — определили в на-
нашем веке основное направление их исследования. В первой
утверждалось, что все решения эллиптических уравнений суть
аналитические функции независимой переменной, если только
функции, образующие уравнения, суть аналитические функции
своих аргументов. По мере перехода от уравнений с аналити-
аналитическими функциями к уравнениям с функциями, дифференци-
дифференцируемыми то или иное число раз, эта гипотеза получила иную,
более полную формулировку: дифференциальные свойства ре-
решений эллиптических уравнений внутри области их существо-
существования определяются дифференциальными свойствами функций,
образующих эти уравнения, и не зависят ни от гладкости гра-
граничных значений, ни от того функционального пространства,
в котором эти решения первоначально найдены.
В 20-й проблеме утверждалось, что вариационная задача
на определение функции, удовлетворяющей заданному гранич-
граничному условию и дающей наименьшее значениэ данному полу-
полуограниченному выпуклому функционалу (как го зорят, регуляр-
регулярному функционалу) вида Г F(x, и, ux)dx, всегда имеет решение,
а
если его искать в достаточно широком классе функ-
функций. Эта проблема переплелась с проблемой решения и иссле-
исследования краевых задач для квазилинейных уравнений второго
порядка эллиптического типа, и применительно к этой более
общей задаче 20-я гипотеза Гильберта трансформировалась
в следующую: если имеется априорная ограниченность каких-
либо слабых норм всех возможных решений краевой задачи

20 ПРЕДИСЛОВИЕ К ПЕРВОМУ ИЗДАНИЮ
(например, их максимумов модулей), то имеется и ее разре-
разрешимость.
Обе гипотезы требовали более точных формулировок, при
этом естественным стремлением было согласование утвержде-
утверждений обеих проблем в том смысле, что класс «всех решений»
в 19-й проблеме должен был совпадать с тем «достаточно ши-
широким классом функций», в котором находилось решение вариа-
вариационной или краевой задачи. При решении этих проблем шли
в двух противоположных направлениях. В 19-й проблеме пы-
пытались снизить требуемую от исследуемого решения априорную
гладкость. Напротив, в 20-й проблеме старались доказать су-
существование решений, обладающих по возможности наиболее
хорошими дифференциальными свойствами.
Первой работой, посвященной 19-й проблеме Гильберта,
была знаменитая работа [4J С. Н. Бернштейна (см. также [42]),
в которой доказывалось, что трижды непрерывно дифференци-
дифференцируемые решения нелинейных эллиптических уравнений (мы всюду
будем говорить лишь об эллиптических уравнениях второго
порядка) являются аналитическими функциями своих аргументов.
В дальнейшем Г. Леви, Э. Хопфом и Ю. Шаудером было
показано, что это верно для всех решений нелинейных уравне-
уравнений, имеющих непрерывные по Гёльдеру производные второго
порядка, и для всех решений вариационных задач, имеющих
непрерывные по Гёльдеру производные первого порядка (для
случая двух независимых переменных Ч. Морри доказал, что
у решений вариационных задач условие непрерывности произ-
производных первого порядка можно заменить их ограниченностью).
Исследование 20-й проблемы шло главным образом по ли-
линии вариационных задач — для их решения были созданы так
называемые прямые методы. Начало этому направлению поло-
положено работами Д. Гильберта, А. Лебега и Р. Куранта ([26,
10,, 31]). Этими методами из общих и сравнительно простых
соображений доказывается существование так называемых обоб-
обобщенных решений — функций, обладающих обобщенными про-
производными первого порядка, суммируемыми с некоторой сте-
степенью т > 1 (см. в связи с этим [53, 392]). Верилось, что именно
этот класс обобщенных решений и есть тот «достаточно широ-
широкий класс функций», о котором говорится в 20-й проблеме
Гильберта. Однако этот класс, как мы видим, значительно шире
того класса «всех» решений, для которого удавалось доказать
справедливость 19-й проблемы Гильберта. Надо было или су-
сузить его и в этом суженном классе доказать разрешимость
вариационных задач, или доказать, что дифференциальные свой-
свойства обобщенных решений на самом деле лучше, чем дифферен-
дифференциальные свойства всех функций сравнения, что они опреде-
определяются лишь дифференциальными свойствами интегранта и что

ПРЕДИСЛОВИЕ К ПЕРВОМУ ИЗДАНИЮ 21
такие решения единственны хотя бы в малом, т. е. их локаль-
локальная вариация приводит к увеличению значения функционала.
Кроме прямых методов для исследования разрешимости крае-
краевых задач были созданы различные топологические методы.
Из них наиболее общим и гибким является топологический
метод Лерэ — Шаудера [324], которому предшествовали иссле-
исследования С. Н. Бернштейна (см. [42]) по разрешимости задачи
Дирихле для квазилинейных уравнений методом продолжения
по параметру. С помощью этих методов было доказано, что
разрешимость краевой задачи определяется возможностью полу-
получения априорных оценок определенного типа для всех возмож-
возможных решений исследуемой задачи. Так, для доказательства
классической разрешимости задачи Дирихле для квазилинейных
уравнений надо иметь априорную оценку нормы Гёльдера пер-
первых производных от всех ее возможных классических решений.
Таким образом, к началу 40-х годов исследование разреши-
разрешимости нелинейных задач и, в частности, 19-й и 20-й проблем
Гильберта в их расширенной постановке было сведено к полу-
получению априорных оценок для классических решений и к иссле-
исследованию дифференциальных свойств обобщенных решений ва-
вариационных задач, описанных выше. Довольно рано было по-
понято, что их положительное решение зависит не только от
гладкости входящих в задачу функций, а еще и от характера
нелинейности — их поведения при неограниченном возрастании
аргументов. Это имеет место даже при аналитичности образую-
образующих уравнение функций. Постепенно вырисовывались ограни-
ограничения на поведение этих функций, которые необходимы для
тех или иных целей, и исследователи стремились к доказатель-
доказательству их достаточности. Примерно до 1956 г. все исследования
нелинейных задач «в целом» относились к случаю двух незави-
независимых переменных, и именно для него было выработано боль-
большое количество приемов и методов исследования (большая часть
их сугубо двумерна, не обобщается на случай трех и более
независимых переменных): С. Н. Бернштейном были даны апри-
априорные оценки решений для уравнений, не содержащих явно
саму неизвестную функцию; Ж- Лерэ, Л. Ниренберг и др.
получили априорные оценки для несколько более широких
классов таких уравнений; Л. Тонелли, Э. Хопф, Ч. Морри,
А. Г. Сигалов, Л. Чезари, Л. Юнг, В. И. Плотников и др.
исследовали вопросы непрерывности и классичности обобщен-
обобщенных решений двумерных вариационных задач при различных
предположениях об интегранте. Однако даже для двумерных
задач, несмотря на большое количество первоклассных работ,
не было получено смыкания в исследовании 19-й и 20-й про-
проблем Гильберта (это было сделано при дополнительных, явно
излишних предположениях об интегранте). Исключение соста-

22 ПРЕДИСЛОВИЕ К ПЕРВОМУ ИЗДАНИЮ
вил лишь случай /п = п=2, исследованный Ч. Морри [392].
Не были получены и априорные оценки классических решений
квазилинейных уравнений только при тех предположениях о дан-
данных функциях, которые считались естественными. В отношении
исследования многомерных задач было сделано много меньше.
Первыми в направлении изучения многомерных нелинейных
задач «в целом» были работы [11,, 41, 217i 8, 9, 167] 1956—1958 гг.
(Им предшествовал ряд работ, в которых рассматривались
различные классы квазилинейных уравнений, в том или ином
смысле близких к линейным.) Из них единственным закончен-
законченным результатом о классической разрешимости нелинейной ва-
вариационной задачи был результат Е. Де Джорджи [11,] и
Дж. Нэша[41], касающийся простейшего функционала \F(ux)dx
Q
в предположении, что
где v и ц — не зависящие от р = (ри ..., рп) и ? = (?,, ..., ?„)
положительные постоянные. (Заметим, что для двух независи-
независимых переменных этот функционал был исследован С. Н. Берн-
штейном чуть ли не 60 лет тому назад.) Решение многомер-
многомерной вариационной задачи для функционалов общего вида
J F (х, и, ux)dx, причем при тех предположениях относительно
G
F(x, и, р), которые считаются «естественными», было дано авто-
авторами книги в 1959 г. (см. [2112,13]). В этих работах было полу-
получено то желаемое смыкание в изучении 19-й и 20-й проблем
Гильберта, о котором говорилось выше. Оказалось, что для
регулярных вариационных задач в качестве «всех решений» и
«достаточно широкого класса решений» в обеих проблемах надо
брать один и тот же класс функций — обобщенные решения,
даваемые прямыми методами. Их дифференциальные свойства
зависят только от F(x, и, р), и они единственны «в малом»,
т. е. их локальные вариации приводят к увеличению значения
функционала. Иным способом близкие результаты по исследо-
исследованию дифференциальных свойств обобщенных решений вариа-
вариационных задач (правда, не для всего диапазона значений пара-
параметра т, характеризующего порядок роста F (х, и, р) по р,
и при предположениях, несколько более ограничительных, чем
«естественные») получены в работах [394,5] Ч. Морри.
Одновременно с вариационной задачей авторами книги был
изучен класс квазилинейных уравнений более общих, чем урав-
уравнение Эйлера, и занимающий особое место среди всех квазили-
квазилинейных уравнений — класс уравнений с дивергентной главной
частью. Для него с той же желаемой полнотой был исследован

ПРЕДИСЛОВИЕ К ПЕРВОМУ ИЗДАНИЮ 23
вопрос об обобщенных решениях и вопрос о классической раз-
разрешимости «в целом» задачи Дирихле. Мы излагаем здесь вто-
второй способ решения обеих этих проблем, позволивший до пре-
предела снизить также и требования на гладкость известных
функций (он изложен в [2115]).
После решения этих проблем была исследована разреши-
разрешимость «в целом» задачи Дирихле для общих квазилинейных
уравнений второго порядка и определенных классов линейных
и квазилинейных систем таких уравнений [218,19, 363] и разре-
разрешимость «в целом» разных краевых задач для квазилинейных
уравнений с дивергентной главной частью [362]. С помощью
специально построенных примеров было показано [211Oi 18i20], что
те условия, при которых это сделано, вызваны существом дела.
Большая часть этих последних результатов доказана сразу для
решений параболических уравнений и изложена с доказатель-
доказательствами в [2119].
Все эти работы [2112,13,...], принадлежащие авторам дан-
данной монографии, едины по своему методу. Основная идея ме-
метода состоит, во-первых, в замене уравнения интегральным
тождеством и в переходе от него к интегро-дифференциальным
неравенствам, содержащим в себе достаточное количество чи-
числовых параметров (второй шаг достигается каждый раз за счет
специального выбора произвольной функции, входящей в инте-
интегральное тождество), и, во-вторых, в доказательстве ограни-
ограниченности или гёльдеровости функций, подчиняющихся этим
неравенствам. Оказалось, что таким неравенствам удовлетво-
удовлетворяют не только сами решения эллиптических уравнений, но и
их производные, и информация, заложенная в этих неравенствах,
вполне достаточна для получения всех необходимых априорных
оценок. Изучение функций, подчиненных этим неравенствам,
породило теоремы вложения нового типа и совместно с пер-
первым этапом (их выводом) привело к сравнительно простому и
единообразному решению перечисленных выше проблем. Первая
теорема такого типа установлена в работе [11,] Е. Де Джорджи.
Этот же метод дал возможность решить аналогичные про-
проблемы и в более трудном случае параболических уравнений
(см. [2118, 19, и]). Им пронизана почти вся книга. Исключение
составляют: 1). §§ 1 — 12 гл. III, посвященной линейным урав-
уравнениям, в которых излагаются результаты Ю. Шаудера по
разрешимости краевых задач в С1+а, /^2, результаты
К. О. Фридрихса, С, Г, Михлина и О. А. Ладыженской по
разрешимости краевых задач в Wl% (Q), /^3*1; 2) результаты
Т. Радо и Дж. фон Неймана по седлообразным поверхностям;
3) § 2 гл. V о существовании обобщенных решений вариацион-
вариационных задач (в основном результат Ч. Морри) и 4) §§ 5, 6, 7
гл. IX, в которых рписаны прием Ю. Мозера оценки нормы

24 ПРЕДИСЛОВИЕ К ПЕРВОМУ ИЗДАНИЮ
Гёльдера решений линейных уравнений, оценка Л. Ниренберга
константы Гёльдера для производных первого порядка от ре-
решений линейных уравнений при двух независимых переменных
и прием Ч. Морри оценки нормы Гёльдера обобщенных реше-
решений двумерных вариационных задач при квадратичном росте
интегранта. Результаты Л. Берса и Л. Ниренберга по линейным
уравнениям с произвольными, не обязательно непрерывными
коэффициентами при двух независимых переменных доказы-
доказываются с помощью того же общего метода, о котором сказано
выше, в § 17 гл. III, без привлечения квазиконформных пре-
преобразований и теории обобщенных аналитических функций.
Из работ С. Н. Бернштейна в книге использована, по суще-
существу, одна (зато весьма плодотворная) идея: рассматривать
наряду с решениями уравнения некоторые их функции и соот-
соотношения, которым эти функции удовлетворяют вследствие дан-
данного уравнения. В книге нет изложения методов и аппарата,
с помощью которых работают Ч. Морри, К. Миранда, Дж. Нэш,
А. Д. Александров и Г. Стампаккиа. Она имеет мало точек
соприкосновения с книгами, посвященными дифференциальным
уравнениям, в том числе и с книгой К. Миранда, подводящей
итог того, что было сделано к 1955 г. в отношении исследо-
исследования линейных и нелинейных эллиптических уравнений второго
порядка. В основном в ней подробно изложены исследования
авторов, проведенные в последние годы. Большое влияние на
них оказали работы [П^ Е. Де Джорджи по оценке постоянной
Гёльдера и работа [218] одного из авторов по оценке max \ux\
для решений и многомерных квазилинейных уравнений эллип-
эллиптического и параболического типов.
Пусть читатель не посетует на некоторое однообразие при-
приемов, с помощью которых мы решаем описанные выше про-
проблемы, и посмотрит на это как на наличие единого стиля
Добиться его было не легко.
Ленинград, 1964 г. Авторы

Глава I
ВВОДНАЯ ГЛАВА
Книга посвящена эллиптическим уравнениям и некоторым
классам эллиптических систем второго порядка. Для них изу-
изучается разрешимость краевых задач в различных функциональ-
функциональных пространствах и проводятся исследования качественного
и количественного характера, касающиеся дифференциальных
свойств произвольных решений этих уравнений. Мы начинаем
наше изложение с описания примеров, позволивших достаточно
правильно очертить контуры возможной теории этих вопро-
вопросов (§ 2), и с перечисления основных результатов данной книги
и их желаемого развития (§ 3).
Введем сначала ряд понятий, обозначений и терминов,
которые будут использованы на протяжении всей книги.
§ 1. Основные обозначения и термины
1. Сокращенные обозначения. Еп — n-мерное евклидово
пространство; * = (*,, ..., хп) — произвольная точка в нем;
всюду п ^2.
Q — ограниченная область в Еп, т. е. произвольное откры-
открытое связное множество, содержащееся в каком-нибудь шаре
достаточно большого радиуса.
S — граница Q. Иногда мы будем обозначать ее через дО..
Q — замыкание Q, так что Q = Q[JS.
Q' — произвольная строго внутренняя подобласть Q, так
что расстояние от Q' до dQ положительно.
xn = mes/Ci; ©„ — площадь поверхности шара К\.
Если и (х) — измеримая в Q функция, Кр — некоторый шар, то
и<*> (х) = max {и (*) - k; 0},
Ak = {х <= Q: и (х) > k}, Ак, р = {х е= Qp: и (х) > k).
т, ^ t , ttl /1/71
Для любого m ^ 1 положим m =—^j, tn =
т~Г '" n — m
v, ц, e, 6, bk, 0, y — положительные постоянные.

26 ВВОДНАЯ ГЛАВА [ГЛ. 1
v @ — положительная невозрастающая непрерывная функция,
определенная при t^O.
\i(t) — положительная неубывающая непрерывная функция,
определенная при /!>0.
б' —символ Кронекера, т.е. б< = 1, б' = 0 при 1ф}.
V — любой.
«L = l«x*P, a(*. и. p) — a{xu ..., *„, m, p,, ..., pn),
a(x, u, ux) = a{xu ..., xn, u, uX{, .... uXn).
Под символами тахм(дг) и тти(х) понимаем sup«(Jt)
и q а
и iniu(x) соответственно, если и(х) непрерывна в Q, и
vraisupH(Jt) и vrai inf и (х), если и(х) есть просто измеримая
a q
на й функция. Иногда, желая подчеркнуть, что непрерыв-
непрерывность и (х) не предполагается, мы пишем vrai max и (х) и
а
vrai min и (х) вместо max и (х) и min и (х) соответственно;
q a a
osc{m(*);Q} есть колебание и(х) на Q, т. е. тахи(*) — min«(Jt).
Q В
Символ Dkи(х), где k = (klt ..., kn) — мультииндекс сЛ{>О,
означает производную и (х) вида —т ^—г~> где I ^ I—
.... -\-kn— порядок производной.
ся выражения -^
В уравнениях будут встречаться выражения -^~[а(х, и(х),
"*(*))]> которые означают, что при вычислении производной -г—
axi
надо учитывать вхождение xt не только в первую группу аргу-
аргументов х, но и в две остальные, т. е. в функцию и(х) и в их(х),
так что
d . . . . . ... да . да . да ..
Здесь и всюду по парам одинаковых индексов подразумевается

$ Ц ОСНОВНЫЕ ОБОЗНАЧЕНИЯ И ТЕРМИНЫ 27
суммирование в пределах от 1 до п, в частности,
п
да VI да
Иногда, когда чэто не вызывает путаницы, знак полного диф-
дифференцирования -J— будем заменять более распространенным
д '
знаком -5—. Так, например, в линейном уравнении члены
~r^-(atl (x) их (х)) мы обычно записываем в виде -^- (а{1 (х) их (*)),
хотя и здесь при дифференцировании надо учитывать xt в обоих
аргументах: at, (x) и иХ/(х).
В тексте будут встречаться различные постоянные, опреде-
определяемые известными нам из условий величинами. Их мы
будем обозначать строчной буквой с с различными индексами.
Там, где это не может внести путаницы и где величина постоян-
постоянных несущественна, индексы у с будут опускаться, так что
в пределах даже одного доказательства буквой с с одним и тем
же индексом или просто без индекса могут обозначаться раз-
разные постоянные. В других случаях, когда желательно подчерк-
подчеркнуть зависимость постоянной от той или иной величины, эта
зависимость указывается явно.
Срезающая для Q функция ? (х) — это функция с носителем,
лежащим в Q, и со значениями между 0 и 1. Носитель ее — это
замыкание множества точек, где ?(*) отлична от нуля. Сре-
Срезающая функция считается непрерывной с ограниченными пер-
первыми производными. Там, где она обладает другими диффе-
дифференциальными свойствами, это особо оговаривается.
Финитная в Q функция — функция, имеющая компактный
носитель в Q.
Классы 3tm(Q, ...), 33m(Q, ...), ©m'(^> ¦ • •) и др. с различными
параметрами определены и исследованы в §§ 5—9 гл. II.
Если L—оператор в каком-либо гильбертовом пространстве,
то через L обозначается его замыкание. Область определения L
обозначается через D (L), "а область значений — через R (L).
n = n(Jt)—единичный вектор нормали к дп в точке х,
внешней по отношению к й; -т— означает дифференцирование
вдоль п.
2. Определения основных функциональных пространств.
Lm(?i)— банахово пространство, состоящее из всех измеримых
на Q функций, суммируемых по Q со степенью /nj>l. Норма
в нем определяется равенством || и \\т а = [ J | и \mdx\

28 ВВОДНАЯ ГЛАВА [ГЛ. I
Измеримость и суммируемость всюду берется в смысле Ле-
Лебега. Элементами Lm(Q) являются классы эквивалентных между
собою на Q функций.
Под ||иИ^ 0 понимаем vraisup| u(x)\, а под ||u||m a понимаем
и|= 1/ 2 и?.
|||u|||m в, где и = (и„ .... Мдг)
ii
Обобщенные производные понимаются так, как это исполь-
используется теперь в большинстве работ по дифференциальным урав.
нениям. Различные, но эквивалентные их определения и основ,
ные свойства читатель может найти, например, в [312] и [32],
Wlm(Qi) — банахово пространство, состоящее из всех элементов
Lm(Q), имеющих обобщенные производные всех видов до по-
порядка / включительно, суммируемые по Q со степенью т.
Норма в Wlm(Q) определяется равенством
II \\/т
11«Сп=( J 2 \Dku\mdx) , A.1)
где суммирование производится по всевозможным значениям
мультииндексов k при всех | k | от 0 до /. Для областей
с «не слишком плохой» границей Wlm(Q) совпадает с замыка-
замыканием в норме A.1) множества всех бесконечно дифференци-
дифференцируемых в Q функций. Это верно, например, для областей с гра-
границей класса С1, для выпуклых областей и даже для строго
липшицевых областей (их определение дается ниже) (см. § 4,
гл. 3 [396]). Иногда вместо Wlm(Q.) пишется Wlm, особенно если
область Q подлежит дальнейшему уточнению.
Wlm(Q) — множество элементов Wlm(Q) с носителями в Q.
Wm(En) — множество элементов Wlm(En) с компактными но-
носителями.
Wlm (Q) — подпространство пространства Wlm (Q), плотным
множеством в котором является совокупность всех бесконечно
дифференцируемых функций с носителями в Q. Известно, что
Win (Q) с Wlm (Q).
Wl. о (й) — подпространство Wl (й), плотным множеством в
котором являются все дважды непрерывно дифференцируемые
в Q функции, обращающиеся в нуль на 3Q.
Wlm. Q{Q) = Wxm{®)UL4($)-
Wm(Q) = Wlm(Q)f\Lm(Q), где т равно тпЦп — т) при
т<п, равно оо при т > п и имеет произвольное конечное
значение при /п = п. В § 2 гл. II будет доказано, что для

5 I] ОСНОВНЫЕ ОБОЗНАЧЕНИЯ И ТЕРМИНЫ 29
К 1 О |
произвольной области Q класс W2 (О) => №г (й), а для не слишком
плохих областей Q класс W\ (Q) совпадает с W2 (Q). Последнее
заведомо верно для областей Q, являющихся объединением ко-
конечного числа строго липшицевых областей (см. стр. 30).
Будем говорить, что функция и(х) удовлетворяет условию
Гёльдера (непрерывна по Гёльдеру) с показателем а, а <= @, 1),
и константой Гёльдера («)?' в области Q, если
<«}?' = sup p~a osc {и; о?) < оо, A.2)
где sup взят по всем связным компонентам Qp всех Qp с р^р0.
Если область «не очень плохая», например строго липши-
цева, то (и)^' можно определить и иначе, как
\и(х)-и (*') |
Для областей с двойным куском границы, например для
области {х <= Е2; \ хх |< 1, | х21< 1 илг#0 при | х,| ^ 1/2}, опре-
определения A.2) и A.2') не эквивалентны. В этом случае мы будем
придерживаться первого из них.
Са(п)—банахово пространство, элементами которого являются
все непрерывные в Q функции и(х), имеющие конечную вели-
величину (м>ца)- Норма в Ca(Q) определяется равенством
| и С = sup | «(*)[ +<«>?>. A.3)
Элементы C(a)(Q) можно считать доопределенными на dQ по
непрерывности изнутри, через классы эквивалентных в Q пу-
путей. Тем самым и(х) на dQ может оказаться многозначной.
Функция и(х) принадлежит Ca(Q), если она принадлежит
Ca(Q') при VQ'cQ.
Функции м(х), удовлетворяющие условию A.2) с а=1, на-
называются липшицевыми. Они -образуют банахово пространство
Lip (Q), норма в котором определяется так:
Lip(Q) есть совокупность непрерывных в Q функций, принад-
принадлежащих Lip (Q') для VQ' cz Q.
Ol(Q), 1= 1, 2, ... , — совокупность непрерывных в Q функ-
функций, у которых производные порядка /— 1 принадлежат Lip(Q)
и имеют первый дифференциал в каждой точке й.

30 ВВОДНАЯ ГЛАВА [ГЛ. I
Cl+a(Q) — банахово пространство, элементами которого
являются непрерывные в Q функции, имеющие в Q непрерыв-
непрерывные производные до порядка / включительно и конечное зна-
значение величины
Равенство A.5) определяет норму в Cl+a(Q). Элементы
Cl+a(Q) можно считать непрерывными и / раз непрерывно диф-
дифференцируемыми в Q. Для этого надо доопределить и (х) и ее
производные на dQ по непрерывности.
_C/+a(Q)—множество функций, принадлежащих C/+a(Q') при
VQ' с Q.
Аналогично определяются банахово пространство C'(Q) и
линейное множество C'(Q). Норма в C'(Q) определяется равен-
равенством
i
1«^= 2 sup|Z)*«(jc)|. A.6)
1*10 Q
C'(Q) состоит, короче говоря, из всех / раз непрерывно диффе-
дифференцируемых в Q функций.
С1 (Q) — множество функций из C'(Q) с носителем в Q.
C°(Q) и C°(Q) обозначим просто через C(Q) и C(Q) соответ-
соответственно.
Пусть Si — часть границы S области Q. Обозначим через
C/+a(QUSi) множество функций, принадлежащих C/+a(Q,), где
Q, — любая подобласть Q, отстоящая от 5 \ 5] на положитель-
положительное расстояние.
3. Об областях, границах областей и следах функций на
границах. Будем говорить, что граница S области Q (или ее
часть Si) удовлетворяет условию (А), если существуют два по-
положительный числа а0 и 0О таких, что для любого шара /Ср
с центром на S (на Si соответственно) радиуса р^а0 и любой
из связных компонент Qp пересечения Qp шара /Ср с Q имеет
место неравенство
mes Qp < A — 90) mes /CP.
( re—I
Обозначим через CRiL цилиндр \х: 2 xf<R2, —2LR<
<xn<2LR.\, а точку х = 0 назовем его центром. Область Q
называется строго липшицевой, если для V#° ^ dQ можно

§ 1] ОСНОВНЫЕ ОБОЗНАЧЕНИЯ И ТЕРМИНЫ 31
ввести координаты yk:=cki{xl—xj), (cft/)—ортогональная матрица,
так, что пересечение дп с цилиндром CRiL, соответствующим
координатам у, задается уравнением yn=<*(y'n), y'n={yv ¦¦¦> #n_i),
где ю(у'^ есть липшицева функция для |г/^|^/? с константой
Липшица, не превосходящей L, а
Числа R и L для данной области Q фиксированы. Произволь-
Произвольная выпуклая область является строго липшицевой.
Пусть х° = {х\, ..., хпп) — точка dQ, в которой поверхность dQ
имеет касательную плоскость. Назовем (у{, ..., уп) местной си-
системой координат с началом в точке х°, если у и х связаны
равенствами yt = alk(xk — х°), <=1, ..., п, где alk — ортого-
ортогональная матрица, а ось уп направлена по нормали к дп
в точке х°, внешней по отношению к Q.
Область Q называется областью класса Cl+a, I ^ 1 (или С1,
или О', /^1), если она строго липшицева, причем у, участ-
участвующие в этом определении, являются местными координатами,
а функции уп = (й(у'п), определяющие уравненне поверхности дп,
принадлежат пространству С1+а {\ у'п \ < R) (с1 или О1 соответ-
соответственно).
Мы используем также термин: Q есть область класса W^f] Lip.
Под этим понимается следующее: приграничную полосу можно
покрыть конечным числом областей Qt, <=1, ..., Л^, пересече-
пересечения Q,iE е-окрестностей которых (при каком-нибудь е > 0) с Q
гомеоморфны полушару Ке={У- \у\< 1, Уп > 0}, причем функции
xl — xl(y), осуществляющие этот гомеоморфизм, принадлежат
Wl4(Rf>)П Lip(?p), якобианы
дх
ду
и
ду_
дх
ограничены каким-либо
числом, а плоский кусок границы /Ср соответствует Qf,e П дп.
При (l—\)q>n Lip(^p)c:^(^p) (см. § 2 гл. II), и потому
в этом случае говорится об областях класса Wl4 и записы-
записывается так: Q с Wlq.
Мы часто будем говорить: распрямим кусок границы S
в окрестности какой-нибудь ее точки х°, введя новые коорди-
координаты. Это значит, что в окрестности точки *° вводятся новые
регулярные координаты (вообще говоря, не декартовы) zt = zt (*)>
i=l, ..., п, так, чтобы в них кусок границы S имел уравне-
уравнение 2, = 0 и часть области Q, примыкающая к нему, распола-
располагалась в полупространстве гп ^ 0. Регулярность новых коор-
координат z,, ..., гп означает, что между новыми и старыми

32 ВВОДНАЯ ГЛАВА (ГЛ. I
координатами существует взаимно однозначное непрерывное соот-
соответствие. Функции Zi(x), /=1, ..., п, дифференцируемы, и яко-
якобиан -j^ отличен от нуля в рассматриваемой области х. Кроме
того, функции zt(x), t=l, ..., п (а потому и обратные им
функции xt(z), /= 1, ..., п), обладают той гладкостью, которая
указывается особо. Координаты с такими свойствами для
только что определенных нами поверхностей в окрестности х°е5
можно ввести так: от х перейти к декартовым координатам у,
а от у — к новым переменным z по формулам
zi — У1> i=\, ..., п — 1,
Если часть S{ границы области Q обладает свойствами,
описанными в определении строго липшицевых областей или
областей классов С1+а, С1, О1, /^1, то будем говорить, что S,
есть строго липшицева поверхность или поверхность класса С1+а,
С1, О1 соответственно.
Пусть Si есть поверхность класса С1'+а", /, ^1,и пусть на
ней задана функция ф(з). Будем говорить, что ф(я) есть функ-
функция класса Cl+a(Si), t -\-а^.11-\-аи если она как функция ко-
координат у'п = (У\, ..., yn-i), вводимых для V^eS^ есть эле-
элемент Cl+a(D), где D есть (| у'п | ^ Щ — основание цилиндра Сд, L,
соответствующего точке х°. Наибольшую из норм|ф(г/п)
подсчитанных для всех точек x°eS,, берем за норму |ф|
Аналогично определяются функции классов_Ыр (Si), С1 (S,), O'(S,).
Если ф_(х) задана на Q и ф(х) <=C/+a(Q) (c'(Q), или O'(Q),
или Lip (Q)), то на границе S области Q, принадлежащей
классу c'1+ai (С'', О'1 или строго липшицевой) с 1^тах{1; /},
l\-\- a^l + a, ф(х) определяет функцию ф(з) = ф (х) lx=seS
класса Cl+a(S) (C'(S), O'(S) или Lip (S) соответственно). Верно
и обратное: если ф (s) e Cl+a (S) hSe Cl+a, / > 1, то ф (s) можно
продолжить на всю область Q так, ч.обы продолженная функ-
функция ф(х) принадлежала C/+a(Q). Более того, это продолжение
можно делать для всех функций ф(з) из С a(S) с помощью
одной и той же конструкции, так что нормы | ф (s) 4'+a) и | ф (х) (Q+a)
будут эквивалентны. Именно такое продолжение ф(з) на Q мы
и будем подразумевать, формулируя граничные условия с по-
помощью функции ф (х). Аналогичные факты верны и для классов
С1, О1, /> 1, и Lip (последние — в строго липшицевых областях).

$ 1] ОСНОВНЫЕ ОБОЗНАЧЕНИЯ И ТЕРМИНЫ 33
Если грайица области Q произвольная, то под | ф (^ будем
понимать следующее:
| ф 4а> = vrai max |<p(s)| + sup (р~а osc {ф (s); SP}), nj)
где sup взят по всем связным компонентам Ql0 пересечений
ЙР — К0(\& шаров /Ср с центрами на S, p<p0; S'p есть Sf|dQp.
Определим, что понимается под vrai max и (х) и vrai min и (х)
во да
для и(х) из Wlm(Q), m^l, в случае произвольной области Q.
Будем говорить, что и (х) из Wlm (Q) имеет конечный vrai max и,
dQ
если найдется функция (p(x)^Wlm(Q)(]Loa(Q), для которой
и (х) — ф (х) е Wm (Q). Обозначим класс таких функций ф через WI.
Тогда, по определению,
vrai max и = inf ('vrai max ф(д?)],
vrai min u = — vrai max (—и),
dQ dQ
vrai osc {«; dQ} = vrai max и — vrai min u.
dQ dQ
A.8)
Для строго липшицевых областей введенные нами опреде-
определения A.8) для элементов и из Wlm(Q) совпадают с обычными
определениями для следов этих функций на dQ (подробнее
об этом см. § 2 гл. II). Аналогично определяем vrai max и и
vrai min и для части Si границы Q. Именно, и(х) из Wlm(Q)
Si
имеет конечный vrai max и, если найдется функция
() oo(Q), для которой и(х) — (р(х) обращается в нуль
на S, в том смысле, что и(х) — у(х) принадлежит замыканию
в норме Wm(Q) множества элементов Wm(Q), равных нулю
в окрестности 5]. Обозначим через ЗИ, множество таких (f(x).
Тогда, по определению,
vrai max ы= inf/vrai max ф
vrai min и = — vrai max (— u),
S, Si
vrai osc {«; SJ = vrai max и — vrai min u.
s, s,
A-9)
Иногда vrai max, vrai min и vrai osc заменяются на max, min
и osc соответственно.
2 О. А. Ладыженская, Н. П. Уральцева

34 ВВОДНАЯ ГЛАВА [ГЛ. I
Если для функции и(х) из Wm(Q) конечна величина | и |^\
определяемая равенством A.7), то будем говорить, что и(х)
принадлежит Ca(S). В частности, если для некоторой ф(*)е
е Wm (Q) Л С"(Q) разность ы(*) — у(х) принадлежит Wlm(Q),
то ы (х) <= Ся (S) и норма | ы |<,а> не превосходит | ф fQa).
На протяжении всей книги у нас будут встречаться утвер-
утверждения, что такая-то постоянная определяется такими-то вели-
величинами. При этом мы в подавляющем большинстве случаев не
будем отмечать те зависимости, которые достаточно очевидны
или нам не интересны. Например, мы часто не будем явно
указывать на зависимость их от числа измерений п, хотя
во многих местах эта зависимость есть. Зависимость от области
будем отмечать лишь там, где приходится рассматривать
области сколь угодно малых размеров и где зависимость от
меры области существенна.
§ 2. О допустимых расширениях понятия решения
для линейных и квазилинейных уравнений
Основным объектом изучения данной книги являются линей-
линейные и квазилинейные уравнения второго порядка эллиптического
типа. Их целесообразно разделить на четыре группы: уравнения
вида B.1), B.2), B.3) и B.4). Относительно этих уравнений нас
интересует главным образом выявление тех закономерностей и
связей между известными функциями, образующими уравнения,
и решениями этих уравнений, которые являются общими для
всей совокупности уравнений того иного вида и которые могут
быть охарактеризованы количественно с помощью числовых
характеристик известных функций — их норм в пространствах
LS(Q), WP(Q) или Cl+a(Q). Так что эти характеристики (как реше-
решений, так и функций, известных в той или иной задаче) не
должны зависеть от конкретного уравнения и должны выра-
выражаться в терминах принадлежности к одному из только что
указанных пространств.
Будем предполагать всюду *) уравнения равномерно эллип-
эллиптическими. Что это значит, определено ниже с помощью нера-
неравенств B.5)—B.7).
Как показали последние десятилетия, нецелесообразно огра-
ограничивать себя рассмотрением лишь классических решений.
С выяснения вопроса о том, какие расширения понятия реше-
решения для линейных и квазилинейных уравнений допустимы при
тех или иных предположениях об образующих уравнения функ-
функциях, мы и начнем наши исследования.
*) Исключение составляют некоторые параграфы гл. V, VI, VII и VIII.

§ 2] О ДОПУСТИМЫХ РАСШИРЕНИЯХ ПОНЯТИЯ РЕШЕНИЯ 35
Обобщенныа решения считаем допустимыми для данного
класса уравнений, если для них сохраняются те теоремы един-
единственности краевых задач, которые имели место для класси-
классических решений. Для эллиптических уравнений второго порядка
в качестве «пробного камня» возьмем задачу Дирихле. Известно,
что для этих уравнений в классе классических решений спра-
справедлива теорема единственности задачи Дирихле «в малом»,
т. е. задача Дирихле имеет не более одного классического
решения, если область определения этих решений достаточно
мала. (В нелинейном случае накладываются иногда ограниче-
ограничения на величину отклонения сравниваемых решений и их произ-
производных). Это свойство, присущее классическим решениям,
сохраним и для вводимых обобщенных решений.
Итак, класс обобщенных решений эллиптических уравнений
второго порядка назовем допустимым, если для него
«в малом» имеет место теорема единственности задачи Дирихле.
Мы начнем поиски допустимых расширений понятия реше-
решения с линейных уравнений вида B.1), коэффициенты которых
ац, ait bit а суть разрывные функции. Для уравнений
л—(ailux,) = Q, являющихся их частным случаем, такой класс
известен — это обобщенные решения из №г(Я). Для общих же
уравнений вида B.1) мы найдем те ограничения на aiy bi и а,
которые необходимы для допустимости таких обобщенных
решений.
Далее проанализируем случай уравнений B.2) с дифферен-
дифференцируемыми коэффициентами ац(х). Затем с этой же точки
зрения исследуем квазилинейные уравнения вида B.3) и B.4).
Оказывается, для нелинейных уравнений допустимость или недо-
недопустимость тех или иных расширений понятия решения зависит не
только от гладкости образующих уравнения функций а{ (х, и, р),
а(х, и, р), ац(х, и, р) (как это имеет место в линейных урав-
уравнениях), но и от их поведения при |ы|->-оо и |/?|->-оо. Такой
предварительный анализ был нужен в нелинейных уравнениях
даже для исследования разрешимости краевых задач в рамках
классических постановок, ибо он установил и то, какие априор-
априорные оценки классических решений заведомо невозможны.
В данном параграфе мы заняты выявлением необходи-
необходимых ограничений на данные задачи, для чего строим соответ-
соответствующие примеры.
Необходимость выявляемых ниже ограничений понимается
в том смысле, что если одно из этих ограничений ослабить
(заменить, например, принадлежность к Lq принадлежностью
к Lq' с q' < q), то среди рассматриваемого класса уравнений
найдется такое, которое имеет решение, не обладающее

36 ВВОДНАЯ ГЛАВА (ГЛ. 1
обсуждаемым свойством (тем, для которого ищутся необходимые
условия). Такая необходимость не исключает возможности, что
для более узких классов уравнений, обладающих какими-либо
специфическими особенностями, эти ограничения можно осла-
ослабить или заменить другими.
Здесь же будет приведена и другая серия примеров, которая
даст условия, необходимые для того, чтобы любое допу-
допустимое обобщенное решение данного класса уравнений при-
принадлежало пространствам С", или С1+а, или W2 и т. д. и допу-
допускало оценки в нормах этих пространств.
Выявленные на этих примерах необходимые ограничения
оказались и достаточными. Доказательство их достаточ-
достаточности занимает центральное место в данной книге. Приводимые
ниже примеры дают точные контуры возможной теории крае-
краевых задач для уравнений с разрывными коэффициентами
вида B.1) и квазилинейных эллиптических уравнений -в про-
пространствах W2(Q), Wl(Q), Wl(Q)(]Ca(Q), Cl+a(Q) и др., где
Q — произвольная ограниченная область, при условии их равно-
равномерной эллиптичности.
Мы рассмотрим уравнения в следующих формах:
i, l=\ l i=\
i, /=1
d
dx
u = f{x), B.2)
2^ at, (x, u, ux) uXiXj + a (x, u, ux) = 0, B.4)
при условии их равномерной эллиптичности. Это условие для
уравнений B.1) и B.2) имеет вид
где v и ц — положительные постоянные, |], ..., |„ — здесь и
п
ниже произвольные вещественные числа, а |2=21г; Для

§21 О ДОПУСТИМЫХ РАСШИРЕНИЯХ ПОНЯТИЯ РЕШЕНИЯ 37
уравнений B.3) оно имеет вид
ГЧд^^\Г-212, B.6)
а для уравнений B.4)—вид
(х, и, рN,?/<ц(|«|)?8, B.7)
где т — число, большее 1.
Начнем с уравнения B.1). Сопоставим ему интегральное
тождество
J [(aiiUXj + atu+ft) r\Xl — (btuX( -\-au — f) r\\ dx = 0, B.8)
где г]—произвольная гладкая функция, равная нулю на гра-
границе S области Q. Если и(х) является, например, дважды
непрерывно дифференцируемой в Q функцией и все коэффи-
коэффициенты в B.1) гладкие, то легко видеть, что соотношения B.1)
и B.8) для нее эквивалентны: из B.1) следует B.8), и из B.8)
следует B.1). Однако тождество B.8) имеет смысл для функ-
функций и, обладающих производными лишь первого порядка, и для
недифференцируемых aih at fh b{, a, f. Главным членом
в нем является j ai/Uxt\x dx; соответствующая ему квадратич-
Q
ная форма Г ац1\хг\х dx определена в силу B.5) на любой
Q
функции T]S W2(Q). Поэтому естественным классом обобщен-
обобщенных решений для уравнений B.1) при условиях B.5) является
класс обобщенных решений из W\ (Q). Определим их.
Обобщенным решением уравнения B.1) из класса W2 (Q) *)
назовем любую функцию и(х) из W\(Q), удовлетворяющую
О j
тождеству B.8) при любой г\ из W2(Q).
Выясним, при каких предположениях относительно at, bh
a, ft и / тождество B.8) имеет смысл, т. е. образующие его
о 1
интегралы конечны при любых функциях и и ц из №2 (Q) (эти
предположения будем формулировать в терминах принадлеж-
принадлежности к пространствам LS(Q)). Для этого используем теорему
о ,
о вложимости пространства Wi (Q) в LP(Q) с р = 2п/(й — 2), где
Ve>0, при п = 2,
при п > 2
/ га + е,
" п
Сокращенно: об. решением.

38 ВВОДНАЯ ГЛАВА [ГЛ. 1
(см. § 2 гл. II). Показатель р в ней точен, т. е. не может быть
увеличен. Благодаря этой теореме и неравенству Гёльдера
(которое тоже точно) для конечности интегралов из B.8) при
о |
V«, t)^W2(Q) необходимо, чтобы
в<о°' q=u> B-9)
Ш12а<°°, II/IIja_ Q<°°- B.10)
fl+2 •"
Будем считать условия B.9), B.10) выполненными во всех
дальнейших рассуждениях.
Выясним теперь, не приведет ли к повышению показателя А
в условии B.9) требование допустимости обобщенных решений
из W\(й). Это требование состоит в том, чтобы задача Дирихле
для B.1) имела не более одного обобщенного решения из W^(Q)
для областей Q «малой меры», причем малость mesQ должна
определяться величинами норм || ai \ Q, || bt ||s Q, || a \ Q, а также
постоянными v и ц из условия B.5). Простым рассуждением
мы покажем, что это приведет к необходимости считать в нера-
неравенстве B,9) q большим п и при п > 2, Для этого возьмем
какой-либо оператор L вида B.1) с гладкими коэффициентами
в ограниченной области Q, звездной по отношению к началу
координат. Известно (см. гл. III), что для него спектральная
задача
Lu — ки = 0, и \gQ = 0
имеет нетривиальные (т. е. отличные от тождественного нуля)
решения. Возьмем одно из них и = и (х) и соответствующее ему
число к. Чтобы не выходить, ради простоты, из вещественного
пространства №г(&) *), предположим, что а{ = — bt. В этом
случае взятые нами и и Я будут вещественными. Рассмотрим
семейство операторов LR — -д?Е**) в областях QR, полученных
подобным сжатием в R раз области Q. Коэффициенты af. (x),
af(x), bf (x), aR(x) оператора LR определяются коэффициентами
оператора L с помощью равенств
-±-
*) В общем случае все рассуждения надо проводить в комплексном
гильбертовом пространстве W\ (&)¦
**) Е — тождественный оператор.

§ 2l 6 ДОПУСТИМЫХ РАСШИРЕНИЯХ ПОНЯТИЯ РЕШЕНИЯ 39
Легко видеть, что нормы (a?J, (b?J, aR, -5Н и постоян-
IIч ' ' v ' * Urt/2, QR
ные Vй = v и цд = ц не зависят от R, в то время как одно-
однородные задачи Дирихле
LRu-~u = Q, и1валв°
в областях QR имеют нетривиальные решения uR(x) = ы (/?" а;).
Отсюда следует, что по величинам норм la2, b2, all коэф-
коэффициентов операторов L вида B,1) и по величинам v и ц
из B,5) нельзя определить такое число т > О, что для всех
областей Q с mesQ^/n (или хотя бы для всех шаров с мерой,
не превосходящей т) задача Дирихле для L имеет не более
одного решения.
Итак, мы показали, что для допустимости обобщенных реше-
решений из №2 (Я) для уравнений вида B.1) необходимо пред-
предположить
K*?-flL»<0°' q>n- B-9°
В §§ 4—6 гл. III будет доказано, что условия B.9')» B.10)
являются не только необходимыми, но и достаточными для
фредгольмовой разрешимости основных краевых задач для
уравнений B.1) в пространстве W\ (й).
Замечание 2.1. В§2гл, I первого издания данной книги
приведен пример уравнения вида B.1), для коэффициентов кото-
которого конечны нормы B.9) cVq<n при я>3ис? = 2 при п = 2,
для которого задача Дирихле имеет неединственное обобщенное
решение из WiiKit) в шарах Kr с любым /?< 1. Это указывает
на необходимость условия B.9) и с точки зрения сохранения
теоремы единственности «в малом» для задачи Дирихле для
отдельно взятого уравнения вида B.1). В связи с этим обратим
внимание на такой факт: если уравнение B.1) фиксировано
и удовлетворяет условиям B.9) и B.10), то для него можно
указать такое малое т > 0, что в областях Q, cz Q с mes Q\ ^ m
задача Дирихле имеет не более одного решения из W2(Q\).
Обусловлено это тем, что для фиксированой функции а (х)
из LP(Q) величины ||a||pQi, Й[СЙ, стремятся к нулю при
mes Qi -> 0, точнее, по Ve > 0 можно указать такое т (е) > 0,
что при mesQ[^m(e) величина ||a|| Q^e. Однако т(е) опре-
определяется не только s и || а || Q и для бесконечного семейства
[ak(x)} с || ak (x) \\p n < С, вообще говоря, нельзя по Ve > 0 подо-
подобрать т (г) > 0 так, чтобы || ak \\р В[ < е при V& и VQ] с mes Qj <
s^m(e). В конце §§ 4, 5 гл. III будет доказано, что для

40 ВВОДНАЯ ГЛАВА (ГЛ. I
фиксированного уравнения B.1), удовлетворяющего условиям B.9),
B.10), задача Дирихле является фредгольмово-разрешимой
в Wl(Q), если я>3.
Перейдем к нахождению условий, необходимых для того,
чтобы любое об. решение уравнения B.1) было ограниченным
на VQ'czQ. Для этого рассмотрим функцию ы = 1п|1пг|,
г = \х\, в шаре Kr = Kr@), R< 1, и убедимся, что она удо-
удовлетворяется .уравнениям
Ди = / и A« =
где ^ = "^пГ7~7п^7' ft=~FWF- Легко виДеть- что эта
неограниченная функция и есть об. решение из W2(Kr) для
этих уравнений. Но f e Ln/2(KR), a f{ e Ln(KR), и потому для
того, чтобы V об. решение из W\ (Q) уравнений B.1) было огра-
ограниченной функцией, необходимо, чтобы
B<00« ИН>В<°°. Я>п. B.12)
Оказывается, что условия B.12) не только необходимы, но и
достаточны. Неравенства B.9') предполагаются выполненными
здесь и ниже. Более того, при условиях B.9'), B.12) любое
об. решение уравнения B.1) принадлежит C"(Q) с некоторым
а > 0, причем величины max| и |, | и № мажорируются постоян-
Q'
ной C(Q'), определяемой (q — п)~\ || и\\2 Q, нормами коэффи-
коэффициентов и свободных членов, выписанными в B.9') и B.12),
и расстоянием Q' до dQ.
Замечание 2.2. В связи с замечанием 2.1 встает такой
вопрос. Пусть для L выполнены условия B.9) и B.12). Будет ли V
об. решение его из tt^Q) ограниченным в Q'czQ? Оказывается,
нет. Для этого необходимо, чтобы
K-flILfl<00' q>n- ' B-9//)
Действительно, функцию ы = 1п|1пг| можно рассмотреть в Кц,
R< 1, и как об. решение уравнений
f{r)
= 0 И А"--Н1^ТЫ = 0'
коэффициенты а{ и а которых принадлежат Ln(Kfd и LnpiKit).
Следовательно, выполнение B.9) с q=*n не гарантирует нуж-
нужного нам свойства об. решений. Если же имеют место нера-
неравенства B.9), B.12), B.9"), то, как доказывается в конце § 13

§ 2] О ДОПУСТИМЫХ РАСШИРЕНИЯХ ПОНЯТИЯ РЕШЕНИЯ 41
гл. III, V об. решение принадлежит Ca(Q). Однако оценки
сверху его норм тах|ы| и | и $ зависят не только от посто-
постоянных v, ц, q и норм известных функций, входящих в условия
B.5), B.9), B.12), B.9"), но и от модулей непрерывности коэф-
коэффициентов bt в нормах Lr(Q). (Они зависят также от ||ы||2а
и расстояния Q' до Q.)
Если условия B.12) выполнены с ^ = й, то, как мы видели
выше на примере B.11), уравнения B.11) имеют неограниченные
об. решения. Однако для этих решений и(х) конечны инте-
интегралы вида J ес\и(х)Ых, с > 0. В § 13 гл. III будет доказано,
что и в общем случае для V об. решения уравнения B.1)
конечны интегралы J ес^и(х)Ых, VQ'czQ, с некоторым с > 0,
если коэффициенты L удовлетворяют B.9') nf eLrt/2(Q),f;eLrt (Q),
п^З (для и = 2 это свойство и(х) следует из принадлеж-
принадлежности и(х) к W[2(Q)).
Если f и ft суммируются со степенями <?, и q2 меньшими,
чем и/2 и п соответственно, но большими, чем степени
из B.10), то оказывается, что любое об. решение будет сумми-
суммироваться со степенью р, большей, чем показатель 2п/(п — 2)
вложения W2(Q) в Lq(Q) (и здесь считаем и^З, ибо при и = 2
все об. решения суммируются с любой конечной степенью).
Покажем, что р не может быть больше nqll(n—2ql) и nq2/(n—q2).
В § 13 гл. III будет доказано, что этот пример дает точную
зависимость р от ^, и q2, т. е. будет доказано, что любое
об. решение уравнения B.1) принадлежит LP(Q'), VQ'cQ, если
B.12')
Пример этот следующий: функция и = г-\ Я > 0, при Я < у — 1
есть об. решение из W2 (Q), Q = {x: r< 1}, уравнений
Д«= _A(-A + «-2)r-*-2sf, Ди = - 2 (l?-l"lr S (f«)*».
' i '
Отсюда ясно, что если (k-\-2)ql^n, т. е. f Ш Lqi (й), то
Я^* ——2 = — , т. е. иШЬв. Если же (Я + \)q2^n, т. е.
fi^Lq2(Q), то Я^——1= —, т. е. uesLp. Итак, если мы

42 ВВОДНАЯ ГЛАВА [ГЛ. 1
хотим, чтобы и(х) принадлежало Lp с p~>nl(n — 2), то необ-
необходимо, чтобы f и ft удовлетворяли условиям B.12').
Выясним, какими свойствами должны обладать коэффи-
коэффициенты L из B.1) для того, чтобы L были ограниченными опе-
операторами из W^2 (Q) в L2(Q). Для этого естественно записать /
в виде B.2), т. е. Lu = ailuXiXj -f AtuX{ + Аи, где At — at -f
dati да-
^b^ а ^~а^~~дх~' БУдем считать, ЧТО для А И At
выполнено условие B.9"), а для а.ц — условие B.5). Из принад-
принадлежности и к W\ (й) следует, что их. е ?2Л/(й-2) (й) (и определено
выше), а и^Ь2Пцп-4) при и > 4, суммируется с любой конечной
степенью при п = 4 и ы ограничена при и ^ 3. Ввиду этого
при всех п ^2 (ибо ^ > и и потому 2q/(q — 2) < 2п/(п — 2)) и
при п ^4. При и = 2 и 3 функция и ограничена, а Л по
условию B.9') суммируема со степенью q/2, q> n, которая
может оказаться меньшей двух. Для принадлежности Аи
к L2(Q) надо потребовать, чтобы Ле L2(й). Итак, оператор L
будет ограниченным оператором из Wl(Q) в L2(Q), если
< оо, q>n,
B.13)
при и^4, с—" v '
2, Q
при и = 2,3.
В § 10 гл. III доказывается, что при выполнении условий B.5),
B.13), действительно, каждое об. решение из 1F2(Q) урав-
дк 2/ '\ -'
нения B.1) с f + -p- s L2(Q) принадлежит U^2(,Q )» VQ czQ,
и его норма ||ы|^2J, мажорируется постоянной с(й'), опреде-
определяемой лишь (q — п)~\ v и ц из B.5), ||ы|12П, нормами из B.13),
!df, ||
f + -д— и расстоянием от Q' до дй. Первая половина этого
i , Q
утверждения сохраняется и при q = n в B.13), надо только при
п = \ считать $ > 4 (ясно, что это условие при и = 4 необхо-
необходимо для принадлежности Аи к L2(Q)). Вторая же половина
видоизменяется: постоянная с(й') в этом случае зависит также

§ 2] О ДОПУСТИМЫХ РАСШИРЕНИЯХ ПОНЯТИЯ РЕШЕНИЯ 43
от модулей непрерывности at-\-bh -~- и А в Ln (Q) и L^% a
соответственно.
Пусть условия B.5), B.13) для L из B.1) выполнены.
Выясним, при каких ограничениях на коэффициенты и сво-
свободные члены любое ограниченное решение уравнения B.1) из
Wl(Q) принадлежит С1+а(й). Пример
указывает на необходимость условия
If+ 54 <°°> Я>п. B.14)
II охг % а
причем величина q — п > 0 ответственна за величину показателя
гёльдеровости а,
да.
Если член аи + -т-5- и из Lu отнести к свободному члену
axi
и учесть, что и ограничена, то требование B.14) указывает на
необходимость еще условия
1
»,, a
Оказывается, ограничений B.13) — B.15) и достаточно.
Именно, в § 15 гл. III мы покажем, что при выполнении
условий B,13), B.14) и B.15) все обобщенные решения и урав-
уравнений B.1) из W\{u) принадлежат C1+a(Q) и для них нормы
I и ?у+а), Q'crQ, можно оценить эффективно через постоянные
v, q, ц и нормы из условий B.5), B.13) — B.15), II "if^ и рассто-
расстояние й' до Q. Этими же величинами определяется и величина
показателя a > 0.
Не лишено интереса и следующее сопоставление условий
B.9'), B.12) и B.13) —B.15), показывающее их естественную
связь. Пусть и есть обобщенное решение B.1) из tt^Q). Сово-
Совокупность функций ио = и и uk = uXk, k=l п, можно рас-
рассмотреть как обобщенное решение из W\ (Q) следующей си-
системы:
д I даЛ , df.
д I даи
Ж" \ачи* + ^7

44 ВВОДНАЯ ГЛАВА (ГЛ,
которую короче можно записать так;
-*. *-°"l »•
B.16)
Поскольку уравнения B.1) являются частным случаем си-
систем вида B.16), то условия B.9'), B.12), необходимые для
уравнений B.1), будут необходимыми (для тех же целей, ука-
указанных выше) и для всего класса систем B.16). Для B.16) они
имеют вид
!rl <oo> q>n- Bл8>
Если учесть, как А% и Bf образованы из коэффициентов урав-
уравнения B.1), то легко видеть, что условия B.17), B.18) соответ-
соответствуют условиям B.13) — B.15).
В гл. VII будет доказано, что условия B.17) достаточны
для допустимости обобщенных решений из w\ (Q), а условия
B.17) и B.18) достаточны для принадлежности всех таких ре-
решений к С" и для случая всего класса систем вида B.16).
Переходим к уравнениям вида B.2), считая aij(x) в общем
случае недифференцируемыми функциями, удовлетворяющими
лишь неравенствам B.5). Таким уравнениям невозможно сопо-
сопоставить тождество тида B.8), и потому для них нельзя рас-
рассматривать обобщенные решения и, имеющие производные
лишь первого порядка, j^x обобщенные решения должны иметь
производные второго порядка. Но этого, оказывается, мало.
Чтобы разобраться в данном вопросе, рассмотрим следующий
пример.
Функция м=г* в шаре KR = {x: I х | < R) удовлетворяет
уравнению *)
Lu = ailUx.Xj = 0, B.19)
где аи = б/ + b Ц±-, b = — 1 + -^т • Для нее «** = Ъгх-2хи
k При Ь> — 1, т. е. при А<1,
*) Факт существования у B.19) с atj = Ь[ + b (г) —1-^- решений вида
и = и (г) отмечен в работе [213].

§21 О ДОПУСТИМЫХ РАСШИРЕНИЯХ ПОНЯТИЯ РЕШЕНИЯ 45
уравнение B.19) эллиптично (неравенства B.5) выполнены).
Производные ux.Xl суммируются по Kr со степенью р < п/B—К),
а производные их. — со степенью q < и/A — Л). При к, близких,
к единице, р близко к и, a q — к бесконечности. Но такую
функцию и = г1 при X < 1 нельзя считать допустимым обоб-
обобщенным решением уравнения B.19), ибо уравнению B.19) удо-
удовлетворяет и функция у = 7? , совпадающая с гх на границе
шара Kr- Исключить этот пример можно по-разному. Мы пред-
предлагаем для любого п ^2 рассматривать-такие обобщенные реше-
решения и, которые имеют vraimaxl Vu |< оо и принадлежат W\{u).
Для и = 2 первое из этих условий можно отбросить (см. § 19
гл. III). Ниже, разбирая случай общего квазилинейного урав-
уравнения B.4), мы опишем, какими свойствами обладают такие
решения.
А. Д. Александров изучает обобщенные решения уравне-
уравнений B.2), для которых производные второго порядка сумми-
суммируемы по Q со степенью п. Для них им доказана единствен-
единственность в малом при условии, что коэффициенты а/ и а в B.2)
суммируемы по Q со степенью п, a ait удовлетворяют нера-
неравенству B.5), причем показано, что для всего рассмотренного
класса уравнений вида B.2) эти предположения о а{1, at и а
нельзя ослабить. Эти результаты опубликованы в [16,7].
Пример B.19) интересен и с точки зрения справедливости
априорной оценки
||«|fQ^[||L«||iiQ + ||«||2iQ] B.20)
для любой функции и из Wl(Q), равной нулю на S. Нера-
Неравенство B.20) при п > 2 и S еС2 установлено для оператора L
из B.2) при условии, что пц удовлетворяют неравенствам B.5)
и непрерывны, причем константа с в B.20) зависит не только
от v и [1 из B.5), но и от модуля непрерывности а{/.
Все попытки доказать это неравенство при п > 2 для любых
ограниченных ац или хотя бы показать, что для гладких пц
постоянная с зависит лишь v и ц из B.5), не увенчались
успехом. Из примера B.19) можно понять, что это и невоз-
невозможно сделать.
Действительно, пусть Q есть шар Ki-
Рассмотрим в нем семейство функций us=rK— I, A, = 2—|-+е,
ее@, 74], считая /г^З. Они удовлетворяют в Ki уравне-
уравнению B.19), для коэффициентов ae{j = Ь{ + (— 1 + i'_J
которых выполнены неравенства B.5) с v и ц, не зависящими
X;X
"

46 ВВОДНАЯ ГЛАВА [ГЛ. I
от ее@, Ч4]. С другой стороны, || и*\^]а имеет порядок е~',
в то время как нормы ||ые||2 Q равномерно ограничены для
ее@, V4]. Следовательно, неравенство B.20) не может быть
справедливым с постоянной с, не зависящей от е, для взятого
нами набора функций иЕ и Le вида B.19). (Для п = 2 этот
пример ничего не дает, ибо в этом случае А, = 2— у + е> 1,
и потому уравнение B.19) не эллиптическое. Это находится
в согласии с тем, что для п = 2 неравенство B.20) имеет место
при любых ограниченных ait, удовлетворяющих только нера-
неравенствам B.5).)
Покажем, что постоянная с в B.20) зависит не только от v
и ц из B.5), но и от каких-либо характеристик гладкости а{1,
иными словами, что она не может быть общей для всей сово-
совокупности гладких коэффициентов ац, удовлетворяющих B.5)
с одними и теми же v и ц. Действительно, усредним обе части
уравнения B.19), считая снова
«е = г^-1, Л = 2-у + е, ее@,!/4], л>3, Q = /C,,
с помощью какого-либо неотрицательного бесконечно диффе-
дифференцируемого ядра (ир(\ х— у \) (см. [312], [32]) и результат
запишем в виде
ацР(х)иех.х.(х) = Ц(х), B.21)
где oj/p(*)= J %(\x-y\)a^(y)dy,
а 1*-»1<р
/р(*) = j щ(\х-у\)аЧ,(у) \и\х. (х) - u\iyj(у)] dy.
\х-у |<р
Коэффициенты a\jP бесконечно дифференцируемы, a fl^L2(Ki)
и |/р|2 Ki->0 при р->0, когда е>0 фиксировано. Последнее
следует из неравенства
|»-jKp
]
К,
J
Xdy j ®р(\х-уЪ[u\ (x)- u\ (y)f dy <
I*-jKp
< с J j <op (I z I) [a;4 (z + y)- vfi Щ dy dz <
|г|<р|+|<1

§ 2] О ДОПУСТИМЫХ РАСШИРЕНИЯХ ПОНЯТИЯ РЕШЕНИЯ 47
правая часть которого стремится к нулю при р—>0, если е > О
фиксировано. Коэффициенты а?,р удовлетворяют неравен-
неравенствам B.5), причем положительные постоянные v и ц в них
можно выбрать общими для всех р е @, р0], е е @, '/,,]• Для а|/р
при р > 0 и е > 0 имеет место неравенство
Однако из сказанного выше ясно, что постоянные ср,е стре-
стремятся к бесконечности при е—>0 и р = р(е)->0 и, следова-
следовательно, не могут определяться только v и ц из B.5) для а*/р.
Замечание 2.3. В последнем рассуждении в доказатель-
доказательстве того, что нельзя постоянную с в неравенстве B.20) взять
общей для всех гладких коэффициентов ац(х), удовлетворяю-
удовлетворяющих неравенствам B.5) с какими-либо фиксированными v > 0
и ц > 0, мы привлекли функции и ^wl(Ki)> которые не при-
принадлежат С2 (/СО- Однако из этого уже следует, что интере-
интересующее нас неравенство B.20) не имеет места и на множестве
функций и{х) из C°°(Ki), равных нулю на дК.\- Действительно,
если бы такое неравенство было справедливым, то ввиду плот-
плотности в_ wlo(Ki) = Wl(/Ci)fl Wi(/СО множества всех функций
из C°°(Ki), равных нулю на дКи оно сохранилось бы и для
элементов ие^2,о(й). Последнее же, как показано выше, не
имеет места.
В первом издании книги мы высказали гипотезу о том, что
задача Дирихле для уравнений B.2) с разрывными коэффици-
коэффициентами aij, удовлетворяющими лишь условиям равномерной
эллиптичности B.5), «хорошо» разрешима в пространствах Wl(Q).
Такое предположение казалось нам правдоподобным ввиду
следующих трех фактов: 1) при п = 2 справедливость его дока-
доказана; 2) при и^З в рассмотренном нами примере B.19) функ-
функция и=гх (а следовательно, и функция u=rx — Rx, равная
нулю на границе шара /СЛ) не принадлежит W\{u) (для нее
и*,-«/ суммируются со степенью р < п), и, следовательно, этот
пример не противоречит нашей гипотезе; 3) результаты А. Д.
Александрова по теоремам единственности решения задачи
Дирихле для уравнений B.2) в пространстве Wl{Q), цитиро-
цитированные на стр. 45, создавали впечатление, что именно про-
пространство Wn(Q) является тем функциональным пространством,
в котором следует рассматривать краевые задачи для уравне-
уравнений B.2) с произвольными разрывными коэффициентами ац.
Однако пример, который мы сейчас приведем, показывает,
что наши прогнозы не оправдались. Именно, покажем, что

48 ВВОДНАЯ ГЛАВА [ГЛ. I
неравенство
несправедливо не только при ^ = 2, но и при любом
в том числе и при q = n, если я!>3.
Функция
есть решение уравнения L^K) = afjvxkx . = О, где
p"
v6', i > 2 или
При А. е [О, 1) величина v принадлежит интервалу @, 1], так
что оператор L^ — эллиптический. Фиксируем какое-либо зна-
значение q > 2. Семейство операторов L% с А, ^ 2/^ имеет равно-
равномерно ограниченные снизу постоянные эллиптичности v^3»
^ / +п* > О И равномерно ограниченные сверху коэф-
коэффициенты. Семейство функций v<K)(x) в шаре /(, таково, что
|| уW ||^ < оо при X<2/q и II t»W |?V,-^ °° ПРИ Л-+Щ, в то
время как max| viK\ S/vw |^const при всех к е [0, 1]. Функ-
ции у'*-' не равны нулю на <Э/Сц поэтому вместо них рассмот-
рассмотрим u^(x) = viK)(x)t,(x), где ?(х) — срезающая функция на К.и
равная единице при |дс|^'/2 и ?<=C2(/(i).
Функции и(Х)(х) равны нулю на дК\ и удовлетворяют урав-
уравнениям
где /w(л:) = 2aijv{x)it,Xj + allvw^Xlxj ограничены равномерно от-
относительно А. из [0, 1].
Таким образом, || L^«w |l?, Kl +ll"wll? Ki^ const, в то время
как || «W ^-* оо приА,-^2/^.
Обратимся теперь к квазилинейным уравнениям. Начнем
с уравнений B.4) общего вида. Уже в линейном случае была
выяснена необходимость требований ограниченности производ-
производных первого порядка для допустимых обобщенных решений,
если относительно производных второго порядка этих решений
известна, например, лишь принадлежность их к L2(Q). Мы по-
покажем, что это же необходимо требовать и от обобщенных
решений уравнений B.4) даже при сколь угодно гладких функ-
функциях a(j(x, и, р), удовлетворяющих условиям B.7).

§ 2] О ДОПУСТИМЫХ РАСШИРЕНИЯХ ПОНЯТИЯ РЕШЕНИЯ 49
Возьмем в шаре KR функцию и = гк, А. < 1. Как мы видели
выше, она удовлетворяет уравнению B.19), а потому и уравне-
уравнению
) B-23)
их
ибо | Vu р = А,2г2Я-2 и Xi=-^-r'2-x. Уравнение B.23) равномерно
эллиптично при А,<1. Однако функции а.ц(р) = ь[ + b -р-4-
недифференцируемы в точке р = 0. Поэтому вместо них возь-
возьмем другие, гладкие функции йц{р) = Ь[ + Ь .У'р , где/@
есть бесконечно дифференцируемая положительная функция
t^Q, равная t при t^to>Q и удовлетворяющая для всех
неравенству f(t)^t. функция и = гх удовлетворяет в шаре
t ч1/BЯ.-2) -.
"дт) > уравнению
Г их их ]
<^(и,)aV/ = [б{ + b n{Vu\t)\uXiXj = 0, B.24)
ибо в этом шаре для нее | Vu р = K2r2X~2 > A,2 -jj- = t0, поэтому
f(|V«p) = |V«p и уравнение B.24) совпадает с B.23). Нера-
Неравенства B.7) для йц выполняются, так что B.24) равномерно
эллиптично.
С другой стороны, уравнению B.24) удовлетворяет функция
/ t ПЯ2Я.-2) %
и = R , R = 1-р-1 , совпадающая с г на границе шара
r^.R, т. е. имеет место нарушение теоремы единственности
в малом. Этот пример показывает, что даже при бесконечно
дифференцируемых функциях йц{р) обобщенные решения для
B.4) из №г, имеющие неограниченные производные первого по-
порядка, неправомерны. (Заметим, что и = гк принадлежит Wlq
cq<nl(l— А.) и W2P с р<п/B — Х), Я, < 1.) Таким образом,
допустимые обобщенные решения из W% уравнений B.4) должны
иметь ограниченные производные первого порядка. В гл. VI
мы докажем, что такие обобщенные решения обладают всеми
нужными свойствами: они «единственны в малом», и их диффе-
дифференциальные свойства улучшаются по мере улучшения диф-
дифференциальных свойств функций ац(х, и, р) и а(х, и, р), обра-
образующих уравнение B.4). Это имеет место для всего класса B.4).
Однако если мы хотим, чтобы max | Vu |, Q, cz Q, любого
а,

50 ВВОДНАЯ ГЛАВА [ГЛ. I
допустимого решения и уравнения вида B.4) можно было оценить
через тах|ы|, какие-либо числовые характеристики функций
пц(х, и, р), а{х, и, р) и расстояние Qx до S, когда Qt — строго
внутренняя подобласть, и расстояние Q{ до 5 \ 5' и какие-либо
нормы S' а и \s,, когда Qi примыкает к части S' границы S,
то на ац, а и их частные производные необходимо наложить
некоторые ограничения, касающиеся их роста при |р|->оо.
Следующий пример покажет, что если пц удовлетворяют нера-
неравенствам B.7), то одним из необходимых условий является
\а(х, и, p)|<n(|«|)(l+|p|J, B.25)
если а(х, и, р) не имеет неограниченных особенностей при iefi
и конечных и и р. Именно, функции и6 (х) = (х{ + 6)\ 0 < 6 <! 1/2,
в кубе й = {0 ^ *ft ^'/2} удовлетворяют уравнению
A« = c|V«f(I+s), B.26)
где в = 2 A _ д.) . с = к~1~2г(к— 1). Они бесконечно дифферен-
дифференцируемы, и при 0 < X < 1 их модули не превосходят 1. Часть
границы S', принадлежащая плоскости Х\ = 0, и значения ы6
на ней имеют равномерно ограниченные нормы 1 ¦ 1(/+а) всех
порядков при любом бе@, 1/2]. Тем не менее для ыв нельзя
оценить max|V«6| для подобластей пи примыкающих к 5',
через max|«e|, числа сие, полностью характеризующие
Q
а (л:, и, p) = cp2(l+s), и расстояние пх от S \ S', ибо он неогра-
неограниченно растет при б->0. Это обусловлено тем, что а(х, и, р)
при | р | —> оо растет быстрее | р р. Следовательно, такой рост а
уже недопустим, что и выражено неравенством B.25).
Рассмотрим теперь вопрос об обобщенных решениях квази-
квазилинейных уравнений B.3) с дивергентной главной частью при
условии их равномерной эллиптичности. Пусть сначала а,- (х, и, р),
а{х, и, р) не имеют неограниченных особенностей при конечных
значениях х, и и р (в конце этого параграфа, в § 7 гл. IV
и в гл. IX рассмотрен более общий случай). Уравнение B.3)
можно заменить тождеством
J [а,- (х, и, их)г\х. — а (х, и, их) ц] dx = 0, B.27)
а
в которое входят лишь производные первого порядка от и.
Начнем с исследования ограниченных обобщенных решений,
т. е. таких, для которых vrai max| и |< оо. Основным членом
в B.27) является а{ (х, и, их)цх.. Соответствующая ему квадра-

§ 2] О ДОПУСТИМЫХ РАСШИРЕНИЯХ ПОНЯТИЯ РЕШЕНИЯ 51
да{ (х, и, р)
тичная форма, определяющая тип уравнения, ^ рср/
при |р|->оо растет, как | р \т. Ввиду этого естественно рас-
рассматривать такие ограниченные обобщенные решения и, у ко-
которых производные их принадлежат Lm (й), т. е. которые при-
принадлежат Wlm(Q), Обозначим этот класс функций через Ш. Ин-
Интеграл | а,- (х, и, их) цХ1 dx определен для любых « и т) из 1.
Q
Этот же класс является классом допустимых функций, среди
которых ищется решение вариационной задачи для функционала
/(«)=[/=' (х, и, их) dx, когда известно, что F (х, и, р) растет
я
при р->оо, как | р |т. Чтобы в B.27) интеграл J а(х, и, ux)y\dx
Q
был определен также на любых функциях и и т) из ЯК, необхо-
необходимо потребовать для любых р выполнения неравенства
\а(х, и, р)КцA«1)A +\Р\Г- B.28)
Если B.3) записать в развернутом виде, то ясно, что B.28)
есть следствие B.25). Однако B.25) требует большего; именно,
для B.3) оно приводит к условию, что порядки роста функций
За, (х, и, р) да-
а(х, и, р), ——: \Р\'<~а]Г по ' Р ' должны быть не более
чем т, т. е.
а (х, «,
да1
~дп
A+IPD
да{
~дГ:
B.29)
В гл. IV будет доказано, что условия B.6), B.29), выра-
выражающие собою равномерную эллиптичность B.3) и необходи-
необходимое согласование порядков роста по р функций at (x, и, р),
а(х, и, р) и их производных, достаточны для того, чтобы по-
получить все нужные априорные оценки норм | и |A+а) решений
уравнений B.3) и доказать на их основе классическую разре-
разрешимость «в целом» краевых задач для B.3).
Кроме того, для B.3) исследованы обобщенные решения
из Ж. В частности, доказано, что они удовлетворяют условию
Гёльдера, если выполняется неравенство B.28) и неравенства
ас(х, и, p)pi>v(\u\)\p\m-li(\u\), \
\at(x, и, />)|<ц(|и|)A+1р1Г~\ I
более слабые, чем B.6); для них справедлива теорема един-
единственности задачи Дирихле «в малом», если, кроме B.6) и B.29),

52 ВВОДНАЯ ГЛАВА (ГЛ, I
выполнены соответствующие условия на производные а(х, и, р)
по и и р, именно если
да (х, и, р)
ди
да (х, и, р)
др{
B.290
Приведенные здесь примеры и рассуждения подтверждают
необходимость ограничений типа B.29'), B.29) (при условии
выполнения B.6)), если рассматриваются обобщенные решения
из Ш. Однако если желательно изучить более широкий
класс обобщенных решений уравнений B.3) — решения из
Wm (й) П Lq (Q), q^tnn/(n — m), с, вообще говоря, неограничен-
неограниченным vraimax|«|, то надо наложить другие, более жесткие,
чем B.29), требования на поведение функций а,(л:, и, р) и
а (х, и, р) при больших и и | р \.
Для выяснения этих . требований рассмотрим следующий
пример.
Снова возьмем функцию « = гх и уравнение B.26). Если А.
взять отрицательным, то е будет меньше нуля, т. е. условие
B.28) выполняется (для B.26) т = 2). Само решение принадле-
принадлежит W[{Kr) (и даже Wlm(Kid с т < л/A — Я,)), если п > 2 и Я,
мало. И тем не менее для них нарушается теорема единствен-
единственности «в малом». Отсюда ясно, что для правомерности обоб-
обобщенных решений из Wm(Q) для B.3) при выполнении усло-
условий B.6) от функции а (л:, и, р) надо требовать большего,
чем B.28).
На примере функции и = г~к, К > 0, и уравнений
Аи = а(х, и, их) B.31)
найдем ограничения на а (х, и, р) для п > 2 в виде
\а(х, и, р)|<ф(*)A+|ыГ)A+|рИ. ф(*)е/-,@)р B.32)
необходимые для того, чтобы для уравнений B.31) были до-
допустимы обобщенные решения из WiityftLqiQ), q^2n/(n — 2)
(для B.31) m = 2, a 2n/(n — 2) есть предельный показатель вло-
жимости Wl в Lq). Определению подлежат постоянные s, а и е.
Считая функцию « = г~х, А. > 0, суммируемой со степенью
q ^ 2п/(п — 2), рассмотрим ее как решение уравнений вида
B.31) с разными а(х, и, р) = сг~&'\ и f'| p f2. Те показатели рг,
которые при этом получатся, надо исключить.
Функция и = г~х удовлетворяет уравнению
Ди = -JLj = Clr~V' | Va f', B.33)

§ 2] О ДОПУСТИМЫХ РАСШИРЕНИЯХ ПОНЯТИЯ РЕШЕНИЯ 53
где
Считаем р2 > 0; Ро> Pi ^ °- Самый большой показатель р2 полу-
чим при ро = Р! = О; он равен р2 = y+j = 1 ~г д + Г* ^ак как
м <=Lq, то А, < —, и потому р2 > 1 -| ц— . Мы исключим этот
пример, потребовав
Р2<1+^- B-34)
(Недопустимость равенства видна на примере функции ы =
= 1п|1пг|, и = 2.) Закрепим теперь fa > 0, положив Pi = 0. По-
Показатель
Нижняя граница E0 ПРИ 0 <к < nlq равна
2 — рг ПРИ Рг^Ь
Чтобы исключить функцию г~к, потребуем, чтобы
2 — Рг, Рг< 1>
Ро< о а ^«м_яч я^1 B-35)
Фиксируем теперь какие-нибудь fe > 0 и Ро^О> удовлетворяю-
удовлетворяющие неравенствам B.34) и B.35) соответственно. Тогда
„ Х + 2 - (Л+ i)p2 —Ро 2 — р2 — Ро . , -
Следовательно, к условиям B.34) и B.35) надо добавить еще
ограничение на ^:
чтобы для уравнения B.23) исключить возможность решения /•-*•
с А, из @, nlq).
Итак, этот пример показывает, что в неравенстве B.32) не-
необходимо считать
= 2-р2 >«/(« + q), B.36)

54 ВВОДНАЯ ГЛАВА [ГЛ. I
функцию ф(л:) суммируемой по Q со степенью
п/е при е^1,
s> /г . л. ,.-] , B.37)
{ л/[в + -(в— 1)J при е< 1,
а показатель а подчиняющимся требованию
o<eit*-l--f. B.38)
Оказывается, этих предположений и достаточно, причем не
только для того, чтобы обобщенные решения и (х) из W\ (й) f| Lq(Q)
уравнений вида B.31) были допустимы, но и для того, чтобы
их vraimax|«| можно было оценить через тах|м|, ||«|| Q,
||ф||5 Q и константы с, а и е, входящие в неравенство B.32).
Это будет доказано в гл. IV для общих уравнений вида B.3).
§ 3. Основные результаты и их возможное развитие
В этом параграфе мы опишем кратко основные результаты,
изложенные в данной книге. Большая часть их доказана авто-
авторами и в основном опубликована в работах, перечисленных
в списке литературы, помещенном в конце книги.
В гл. II приведены различные предложения классического
и функционального анализа, используемые в книге. Некоторые
из них хорошо известны и даны без доказательства, для дру-
других даны пояснения или доказательства. Однако в основном
гл. II посвящена исследованию классов функций 91, ЭЗт иЭЗт',
введенных и изученных авторами в работах [21,2_19]. Эта часть
гл. II является одной из наиболее важных для всего последую-
последующего материала книги, ибо оказалось, что именно к этим клас-
классам принадлежат как сами решения линейных и квазилинейных
уравнений и систем, так и их производные. Функции классов
91, 93т, 93т' удовлетворяют некоторым интегральным неравен-
неравенствам, из которых выводится, что функции класса 91 ограничены,
а функции классов 5Вт и 33^' непрерывны по Гёльдеру, и дается
оценка их норм в пространствах С и С соответственно. Эти
предложения имеют характер так называемых теорем вложения,
однако теорем вложения нового типа, неизвестных ранее. Первой
теоремой такого типа является теорема Де Джорджи [ 111]. Ей
предшествовали предложения об ограниченности или непре-
непрерывности обобщенных решений вариационных задач, установлен-
установленные в работах Ч. Морри [39,,2] и А. Г. Сигалова I28li2].
В гл. III изучается разрешимость краевых задач (в основном
первой — задачи Дирихле) для линейных уравнений в про-

§ 3] ОСНОВНЫЕ РЕЗУЛЬТАТЫ 55
странствах Гёльдера и в пространствах WL В §§ 1—3 изла-
излагаются результаты Шаудера — Каччопполи о разрешимости
в пространствах С1+а, /^2, первой краевой задачи и анало-
аналогичные результаты К- Миранда и Р. Фиоренца по другим
краевым задачам.
Они, в основном, состоят в следующем: если коэффициенты
и свободный член уравнения B.2) суть гладкие функции — эле-
элементы С1+а, /^0, то краевые задачи для них (с точностью
до спектра) разрешимы в классическом смысле, точнее, в про-
пространстве с1+2+а. Эти замечательные результаты предельны,
неулучшаемы. До последнего времени они были уникальны по
точности характеристики зависимости дифференциальных свойств
решений от дифференциальных свойств коэффициентов уравне-
уравнений. Однако они ничего не дают для уравнений, коэффициенты
или свободные члены которых не являются гладкими функ-
функциями—не принадлежат С!+а, 1^0.
Для таких уравнений падают как сами результаты, так
и методы их доказательства. Искать их решения в рамках клас-
классических постановок бесполезно: такие уравнения могут вообще
не иметь дважды непрерывно дифференцируемых решений.
Исследованию линейных уравнений с негладкими и, вообще
говоря, неограниченными коэффициентами посвящена большая
часть гл. III—§§ 4—17. В качестве характеристик свойств
коэффициентов и свободных членов уравнений мы выбрали свой-
свойства принадлежности их, а также возможных их обобщенных
производных к пространствам LP(Q). Относительно же реше-
решений таких уравнений устанавливаем их принадлежность к про-
пространствам WL /=1,2, С1 и С1+а, />0.
Как показывают примеры предыдущего параграфа, большая
часть этих результатов неулучшаема (в терминах выбранных
нами пространств). Это не исключает, разумеется, существова-
существования иных связей, выраженных в терминах иных функциональ-
функциональных пространств, между свойствами коэффициентов и свобод-
свободных членов уравнений и их решениями.
В §§ 4—6 исследуется разрешимость краевых задач для урав-
уравнений дивергентного вида в пространстве W\. Их результаты
являются усилением результатов, полученных к 1950 г. благо-
благодаря работам К. О. Фридрихса [19], Г. Вейля [56], С. Г. Мих-
лина [232], М. И. Вишика ([7J и др.) и др. Определение же
решений краевых задач с помощью интегральных тождеств
(различных по форме в зависимости от функционального про-
пространства, к которому принадлежат эти решения) и связанный
с этой формой определения решений метод их получения, изла-
излагаемый в §§ 4—6, были даны одним из авторов книги (см. [213]

56 ВВОДНАЯ ГЛАВА [ГЛ. I
и лекции О. А. Ладыженской). Центральная идея сведения
краевой задачи к функциональному уравнению в пространстве
№г(й) принадлежит К. Фридрихсу [19,], рассмотревшему B.1)
с аг = Ьг = ^ = О, а(х)^0 при первом краевом условии.
В §§ 7—11 изучается разрешимость краевых задач в про-
пространстве W\. В §§ 7—10 и 12 излагаются с небольшими уси-
усилениями результаты из работ [212,3,5] О- А. Ладыженской.
Параграфы 13 — 15 содержат результаты недавнего времени.
Они посвящены исследованию суммируемости с высокими сте-
степенями, ограниченности и непрерывности по Гёльдеру обобщен-
обобщенных решений линейных уравнений B.1) и производных этих
решений. Результаты этих параграфов являются частным слу-
случаем аналогичных фактов, установленных авторами книги для
решений уравнений параболического типа [211618] и для реше-
решений квазилинейных эллиптических уравнений (см. [2112_15]).
Они излагаются здесь самостоятельно с соответствующими
упрощениями. Предложения, близкие к теоремам §§ 13, 14,
установлены также Г. Стампаккиа [522,4, si и Ч. Морри [393].
Начало получения результатов такого типа положено работами
Е. Де Джорджи [И,] и Дж. Нэша [41].
В §§ 16 и 18 излагаются теоретические основы приближен-
приближенных методов решения краевых задач — метода Галеркина, ме-
метода Ритца, метода наименьших квадратов и метода конечных
разностей. В § 17 приводятся некоторые результаты по разло-
разложениям произвольной функции в ряды по собственным функ-
функциям симметрических эллиптических операторов.
В двух последних параграфах, 19 и 20, особо обсуждается
случай двух независимых переменных, занимающий специфиче-
специфическое место среди многомерных задач. Для него в работах ряда
авторов и прежде всего С. Н. Бернштейна, Э. Хопфа, Ч. Морри,
Л. Берса, Л. Ниренберга и И. Н. Векуа были установлены раз-
различные оценки и представления решений, позволившие к середине
50-х годов достаточно полно изучить линейные уравнения с раз-
разрывными ограниченными коэффициентами. Л. Берс и Л. Нирен-
берг сделали это с помощью аппарата обобщенных аналитических
функций и квазиконформных преобразований. Мы доказываем
их результаты, причем с некоторыми усилениями, используя, по
существу, тот же метод, который позволил разобраться и в об-
общем л-мерном случае.
Укажем некоторые из направлений в исследовании линейных
уравнений, которые нам кажутся интересными и которые непо-
непосредственно связаны с обсуждаемым здесь кругом вопросов.
Это, прежде всего, изучение уравнений вида B.2) при /г!>3
без предположений о непрерывности или какой-либо дифферен-
цируемости коэффициентов ai}. Излагаемые здесь результаты

§ 3] ОСНОВНЫЕ РЕЗУЛЬТАТЫ 57
относятся к уравнениям вида B.1), которые в случае недиффе-
ренцируемых ац неэквивалентны уравнениям вида B.2). Для
таких уравнений B.2) пока неясно, в каком функциональном
пространстве задача Дирихле разрешима в смысле Фредгольма.
Не столкнемся ли мы при этом с таким печальным обстоятель-
обстоятельством, что этот класс зависит от коэффициентов уравнения?
Было время, когда казалось, что самосопряженное расширение
по Фридрихсу зависит от старших коэффициентов аи даже в
случае их дифференцируемости. Но это опасение оказалось оши-
ошибочным (см. [212] и §§ 7—11 гл. III). Пример B.19) гл. I и по-
последующие рассуждения о невозможности оценок B.20) и B.22)
показывают, что для B.2) с разрывными ац разрешимости за-
задачи Дирихле в W2P(Q) при любом свободном члене f (x) из Lp(Q)
нет, если п > 2. Относительно таких уравнений нам известны
лишь результаты А. Д. Александрова [13.5,6,7]» касающиеся
теорем единственности и оценок max | и I их решений, принадле-
Q
жащих пространству W2n(Q), работа [3,] И. Я. Бакельмана по
оценке тах|ы| таких решений и исследования Кордеса [9], от-
носящиеся к случаю малого разброса собственных значений
формы а,-Д,-|/. Второе направление в исследовании линейных
эллиптических уравнений — это получение результатов, анало-
аналогичных результатам §§ 7—15 гл. III, для линейных эллиптиче-
эллиптических уравнений и систем высоких порядков с дивергентной
главной частью с негладкими коэффициентами. При достаточно
гладких коэффициентах метод «склейки» Шаудера (состоящий
в сведении всех трудностей к уравнениям с постоянными коэф-
коэффициентами) позволил обобщать результаты о разрешимости
краевых задач в классах Гёльдера Cl+a (Q) и Wlp(Q), p>\,
на случай произвольных эллиптических систем m-ro порядка,
т ^ /. А что будет, когда такая «склейка» недопустима ввиду не-
недостаточной гладкости коэффициентов? К каким функциональным
пространствам будут принадлежать решения тех или иных кра-
краевых задач? Для сильно эллиптических систем известны ре-
результаты, аналогичные результатам §§ 4—6 гл. III. Результаты
типа §§ 7—15 доказаны лишь для систем гл. VII.
Третье направление — это изучение краевых задач в неогра-
неограниченных областях и отыскание красивых форм постановок
краевых условий на бесконечности в случае, когда мы наталки-
наталкиваемся на непрерывный спектр. Наиболее полные результаты
в этом направлении получены пока лишь для уравнений вида
— Аы + q{x)u = f в областях, дополнением которых до всего
пространства является ограниченное замкнутое множество.
Наконец, заметим, что проведенный в данной книге анализ
уравнений второго порядка с разрывными коэффициентами

58 ЙВОДИАЯ ГЛАВА [ГЛ. 1
был направлен на выяснение тех условий на коэффициенты
и свободные члены уравнений (условий, по возможности не
только достаточных, но и необходимых!), при выполнении кото-
которых для всего класса таких уравнений имеет место разреши-
разрешимость краевых задач во вполне определенном функциональном
пространстве, не зависящем от конкретных коэффициентов или
свободных членов этих уравнений. Однако этот анализ не дает
ответа, например, на такой вопрос: пусть о функции q (х) из
Lu — — Аи ¦]- q (x)u известна лишь ее локальная суммируемость;
спрашивается, какими свойствами обладает L как оператор
в гильбертовом пространстве L2 (?„)? Из-за «плохих дифферен-
дифференциальных» свойств q (x) он не определен естественным образом
даже на гладких финитных функциях. Ясно, что как первона-
первоначальная область определения L, так и область определения его
самосопряженных расширений будут зависеть от q (x). Такие слу-
случаи мы исключили из наших рассмотрений, ставя перед собой
совершенно иную цель—выделение тех операторов L, для кото-
которых все характеристики не зависят от конкретного вида обра-
образующих их коэффициентов.
Глава IV посвящена так называемым квазилинейным
уравнениям с дивергентной главной частью. В ней проводится
полный анализ свойств их решений, начиная от обобщенных и
кончая классическими. Сначала исследования ведутся внутри
области определения решения без каких-либо предположений
0 поведении решения вблизи границы. Затем исследуется пове-
поведение решения первой краевой задачи у границы. В главе X
то же сделано и для других, более сложных краевых задач.
Класс квазилинейных уравнений с дивергентной главной частью
обладает большим своеобразием. Для него можно строить тео-
теорию обобщенных решений, имеющих лишь производные первого
порядка, чего нельзя сделать для других, не принадлежащих
к нему квазилинейных уравнений. Этот класс уравнений доста-
достаточно широк, к нему принадлежат уравнения Эйлера для ва-
вариационных задач и различные нелинейные уравнения механики.
Результаты гл. IV, IX и X обладают определенной закончен-
законченностью. Все основные предположения, как показывают примеры
предыдущего параграфа, вызваны существом дела. Результаты
"л. IV в основном доказаны авторами книги и опубликованы
з работах [2112_i5, i7]- Исключение составляет добавленный во
зтором издании книги § 9 о существовании обобщенных реше-
решений краевых задач. Результаты гл. X в развернутом виде
эыли опубликованы впервые в [I]. Их сжатое изложение дано
1 [362]. Работам [2112_ 15,17] предшествовало довольно много ра-
5от, посвященных квазилинейным уравнениям, но во всех этих
заботах для случая п > 2 предполагалось, что уравнения в том
1лн ином смысле мало отличаются от линейных. Для двух же

§ 3] ОСНОВНЫЕ РЕЗУЛЬТАТЫ 59
независимых переменных сделано было много больше (см. ра-
работы С. Н. Бернштейна [42], Э. Хопфа [27], Шаудера и Лерэ
[32Ь 2,4]. Л. Берса и Л. Ниренберга [5] и др.). Но и для этого
случая излагаемые здесь предложения новы. С тем, что было
сделано до работ, составивших основу данной книги, читатель
может познакомиться по 1-му изданию книги [37] К. Миранда,
в которой подытожен весь материал, накопившийся к 1955 г.
по эллиптическим уравнениям, и по обзорным статьям А. Г. Си-
галова, В. И. Плотникова и авторов книги [281( 262, 211012],
посвященным вариационной задаче и эллиптическим уравнениям.
Исследования гл. IV, IX и X можно продолжить в разных
направлениях. Наиболее интересным нам кажется изучение урав-
уравнений высоких порядков и систем с дивергентной главной частью
в духе гл. IV. Именно в этом направлении проводятся иссле-
исследования в гл. VII и VIII.
Другое развитие гл. III, IV, IX и X можно вести по линии
замены избранных нами пространств Lp и Wlm другими (в этом
направлении см. работы [74, 342] и др.). Эти классы естественно
связаны с уравнениями, но не являются единственно возмож-
возможными. Именно их выбором обусловлены и наши требования,
чтобы функции, образующие уравнение, росли по | Vu | степен-
степенным образом.
Третье направление — это отказ от условия равномерной
эллиптичности и согласования порядков роста (два таких слу-
случая рассмотрены в § Ютл. IV и в §§ 3, 5, 6 гл. VI). Однако, если
идти в эту сторону, то прежде всего стоит построить соответ-
соответствующий полный набор примеров, который обрисовал бы ожи-
ожидаемые при этом положения и факты, т. е. те факты, которые
на самом деле имеют место, а не только те, которые полу-
получаются из принятого исследователем метода. Исследования в этом
направлении ведутся (см. предисловие ко второму изданию).
Глава V посвящена регулярной вариационной задаче для
функционалов вида
]{и) = JF(x, и, ux)dx, C.1)
Q
с которой, собственно, и начались исследования, положенные
в основу данной книги. Регулярность гарантирует эллиптич-
эллиптичность соответствующего C.1) уравнения Эйлера
44-^ = °' C'2)
Основное направление в изучении этой задачи (так же как и
в изучении нелинейных эллиптических уравнений вообще) свя-
связано с 19-й и 20-й проблемами Гильберта (см. [26!]). В 1-9-й
проблеме утверждается, что все решения уравнения C.2)

60 ВВОДНАЯ ГЛАВА [ГЛ. I
аналитичны по х, если F (х, и, р) является аналитической функ-
функцией своих аргументов. В 20-й проблеме говорится, что вариа-
вариационная задача на определение минимума функционала C.1),
полуограниченного снизу, при условии
«ls = <P C.3)
всегда имеет решение, если его искать в достаточно ши-
широком классе функций.
Формулировки обеих проблем требовали принципиальных
уточнений: во-первых, надо было понять, что значит «все» ре-
решения уравнения C.2) в 19-й проблеме и что значит «доста-
«достаточно широкий класс функций» в 20-й проблеме; во-вторых,
надо было выяснить, не должна ли функция F(x, и, р), кроме
некоторой гладкости и выпуклости по р(последняя эквива-
эквивалентна эллиптичности уравнения C.2)), обладать какими-либо
другими свойствами для того, чтобы утверждения этих проблем
были справедливы.
С. Н. Бернштейн построил примеры (см. [42]), показавшие,
что дополнительные ограничения на F действительно необхо-
необходимы. Он сформулировал их в виде ряда условий на поведение
F(x, и, р) и ее частных производных при |р|= I/ ZjP)->оо.
Грубо говоря, они сводятся к тому, что F ведет себя при
больших | р | как полином относительно х, и, р степени т по р,
большей 1. Назовем эти требования вместе с условиями неко-
некоторой гладкости, а также полуограниченности / снизу и выпук-
выпуклости F по р естественными. К доказательству того, что
естественные условия и достаточны, стремились все после-
последующие исследователи.
К сороковому году трудами ряда математиков было уста-
установлено, что утверждение 20-й проблемы о существовании функ-
функции, реализующей минимум функционала C.1), верно, если
в качестве множества Эй допустимых функций взять все функ-
функции, удовлетворяющие условию C.3) и суммируемые вместе
со своими обобщенными производными первого порядка с та-
такими степенями, что интеграл C.1) для них конечен (наиболее
общие результаты в этом направлении были доказаны Ч. Морри).
Функции класса Щ, реализующие минимум (или, общее, экстре-
экстремум) /(и), стали называть обобщенными решениями
задачи C.1), C.3).
Однако такое расширение понятия решения задачи C.1), C.3)
требовало всестороннего анализа, выяснения того, не теряются ли
при этом основные качества любой хорошо поставленной крае-
краевой задачи и прежде всего теорема единственности решения
задачи C.1), C.3) «в целом» или хотя бы «в малом». Кроме

$ 31 ОСНОВНЫЕ РЕЗУЛЬТАТЫ 61
того, подлежало исследовать, улучшаются ли дифференциаль-
дифференциальные свойства этих решений (свойства гладкости) по мере улуч-
улучшения дифференциальных свойств функции F и, в частности,
будут ли они аналитическими функциями для аналитических F;
иначе говоря, надо было доказать (или опровергнуть), что именно
этот класс решений надо мыслить под словами «все» решения
в 19-й проблеме Гильберта.
С. Н. Бернштейном для случая двух пространственных пе-
переменных была доказана аналитичность всех трижды непрерывно
дифференцируемых решений уравнений C.2) при аналити-
аналитическом F. Трудами Э. Хопфа, Ю. Шаудера и Ч. Морри к 40-м
годам условия гладкости были ослаблены до требования огра-
ограниченности производных первого порядка в случае п = 2 и до
гёльдеровости этих производных в случае л>2. Для таких ре-
решений была установлена и теорема единственности «в малом»,
и то, что их дифференциальные свойства зависят только от
дифференциальных свойств F.
Однако теорема существования, о которой сказано выше,
для общего случая давала лишь обобщенные решения — функ-
функции со значительно худшими свойствами. Таким образом,
между теоремами существования и единственности, между клас-
классами функций, для которых удалось доказать 19-ю и 20-ю проб-
проблемы Гильберта, имелась большая брешь, заполнению которой
и посвящена большая часть работ по вариационной задаче
C.1), C.3). Это заполнение шло в основном по пути наложе-
наложения различных дополнительных ограничений на F, при которых
оказывалось возможным или доказать теорему существования
сразу в классе достаточно хороших функций (С. Н. Бернштейн,
Л. Тоннели, Э. Хопф и др.), или постепенно проследить за
улучшением дифференциальных свойств обобщенных решений
задачи (Ч. Морри, А. Г. Сигалов, В. И. Плотников и др.). Для
общего случая (при п = 2) А. Т. Сигаловым было установлено
существование непрерывных обобщенных решений. Для случая
п — т = 2 Ч. Морри провел все желаемые исследования обоб-
обобщенных решений. Все эти результаты относятся к двумерным
задачам (п = 2). Совсем медленно подвигалось изучение много-
многомерного случая, когда п > 2. Он потребовал создания новых
методов. Первым законченным результатом по классической
разрешимости задачи C.1), C.3) при п>2 явился результат
Е. Де Джорджи [Hi]; аналогичный результат мог быть полу-
получен также из работы Дж. Нэша [41] по линейным параболиче-
параболическим уравнениям. Он касался простейшего случая, когда F(x, и, р)
не зависит от х и и и имеет квадратичный рост по | р |. Для
него задача имеет единственное решение «в целом».
Вскоре авторами данной книги было дано решение задачи
C.1), C.3) в общем случае [2112-i5]. Именно было доказано, что

62 ВВОДНАЯ ГЛАВА [ГЛ. I
для любого л^2 и т> 1 только при естественных пред-
предположениях относительно функции F любое обобщенное реше-
решение и вариационной задачи из класса Эй единственно «в малом»
и его дифференциальные свойства полностью определяются диф-
дифференциальными свойствами F: если F как функция своих
аргументов принадлежит С1+а, то и решение и принадлежит С ",
в частности, при аналитической F оно аналитично. Этот резуль-
результат заполнил ту брешь, о которой сказано выше, и привел
к решению 19-й и 20-й проблем Гильберта для всего желаемого
класса функционалов вида C.1). Было дано два метода дока-
доказательства этих предложений. Первый метод, относящийся
к 1959 г., изложен в работах [2112,13], второй — в работах
[21н, is, п\- Здесь мы излагаем второй, более красивый метод до-
доказательства.
В [2112_i7] проведено исследование главным образом ограни-
ограниченных по модулю обобщенных решений. Именно для таких
решений были сформулированы естественные ограничения на F,
касающиеся поведения F при больших | р | (но не | и |1).
Если же отказаться от априорной ограниченности обобщен-
обобщенных решений, т. е. расширить их класс, то необходимо уси-
усилить ограничения на F. Последнее можно делать в разной
форме. Мы выбрали одну из них и построили примеры (см.
[21 ю, i8,2o])> показывающие, каких величин не должны превос-
превосходить константы (показатели), входящие в неравенства, ха-
характеризующие поведение F при больших \р\ и | и |. Выявлен-
Выявленные на этих примерах необходимые условия и достаточны для
допустимости уже неограниченных обобщенных решений из
Wm (Q), суммируемых с какой-либо заранее указанной степенью q.
Все это сделано нами сразу не только для уравнений Эйлера,
но и для всего класса уравнений гл. IV.
Собственно для решений задач на минимум функционала / (н)
в работе [2112] и в более ранних работах А. Г. Сигалова
[28,,2], Ч. Морри [392] и др. найдены различные случаи, когда
можно дать эффективные оценки их максимумов модулей.
Но ясно, что тут речь может идти лишь о достаточных усло-
условиях.
Отметим еще исследования Ч. Морри [394_6], в которых дан
иной способ исследования дифференциальных свойств обобщен-
обобщенных решений вариационных задач, правда, не для всего диа-
диапазона л^2, т> 1 и при ограничениях несколько более
сильных, чем естественные.
Нам представляется интересным исследование следующих
вопросов, касающихся вариационных задач:
1) исследовать разрешимость и зависимость дифферен-
дифференциальных свойств решений вариационных задач, заданных

§ 3] ОСНОВНЫЕ РЕЗУЛЬТАТЫ 63
в параметрической форме, от дифференциальных свойств инте-
гранта (несколько подробнее об этом рассказано в предисло-
предисловии к данному изданию книги);
2) сформулировать точно и доказать проблемы Гильберта
для F, зависящих от нескольких неизвестных функций и содер-
содержащих производные не только первого порядка;
3) полнее исследовать вопрос о существовании стационарных
точек функционалов вида C.1);
4) провести исследования, аналогичные исследованиям гл. V,
для случаев нестепенного порядка роста F по | р |.
Особенно интересной нам кажется первая из сформулиро-
сформулированных здесь проблем.
В гл. VI рассмотрены квазилинейные уравнения общего
вида. Для этих уравнений также строится теория классиче-
классических и обобщенных решений. Однако оказалось, что для них
класс допустимых обобщенных решений существенно уже
класса допустимых обобщенных решений для уравнений дивер-
дивергентного типа, рассмотренных в гл. IV, причем это сужение
идет не только за счет естественного требования, чтобы они
имели обобщенные производные второго порядка (ибо без этого
нельзя в общем случае придать смысл тому, что и удовлетво-
удовлетворяет уравнению), но и за счет дополнительных требований
на поведение производных первого или второго порядка. При-
Пример, построенный нами в § 2 данной главы, показывает, что
если от производных второго порядка не требовать ничего, кроме
их суммируемости со второй степенью, то при п > 2 относи-
относительно производных первого порядка необходимо предполагать
их ограниченность (в противном случае нарушится теорема
единственности даже для областей сколь угодно малых разме-
размеров). В описываемой главе мы доказываем, что эти ограниче-
ограничения на класс допустимых решений и достаточны. Для таких
обобщенных решений разумно строится вся теория: краевые
задачи имеют не более одного такого решения, если область
достаточно мала, и дифференциальные свойства этих решений
определяются лишь дифференциальными свойствами функций,
образующих уравнение.
В гл. VI мы ограничили себя рассмотрением только первой
краевой задачи. Ее основу составили работы [218> 19,363]. Для
исследования общих квазилинейных уравнений пришлось еще
больше расширить функциональные классы 23т, введенные нами
при изучении вариационной задачи и уравнений дивергентного
вида, ибо производные их решений (не говоря уже о самих
решениях), вообще говоря, де удовлетворяют неравенствам,
положенным в основу определения классов 23т. Однако оказа-
оказалось, что некоторые функции, составленные из производных,
удовлетворяют таким неравенствам. Из этих неравенств можно

64 ВВОДНАЯ ГЛАВА [ГЛ. I
вывести, что каждая из производных в отдельности удовле-
удовлетворяют условию Гёльдера.
Главы VII—VIII посвящены линейным и квазилинейным
системам второго порядка эллиптического типа. Они составляют
лишь часть всей совокупности эллиптических систем.
Этот класс систем был выделен нами по такому принципу:
для любого решения v{(x) vN(x) системы, полученной из
любой системы этого класса отбрасыванием всех членов, кроме
старших, функция z(*)=2 «?(*) (или, что то же, любая по-
ложительная возрастающая функция ф(/) от t = z{x)) удовлет-
удовлетворяют «принципу максимума», т. е. ее наибольшее значение
для любой области находится на границе этой области. Известно,
что это свойство присуще одному эллиптическому уравнению
второго порядка, и мы его положили в основу выделения опре-
определенного класса эллиптических систем. Системы этого класса
имеют ту особенность, что все образующие их уравнения имеют
одинаковые главные части. Оказалось, что для этого класса
систем справедливы все основные предложения, доказанные
нами в гл. III и IV для одного уравнения второго порядка.
Однако их доказательство базируется на более сложных анали-
аналитических фактах (о гёльдеровости функций, принадлежащих
к классам 23^'). Все ограничения, при которых они доказаны,
как показывают примеры, приведенные в § 2, вызваны суще-
существом дела.
В отношении дальнейшего исследования систем желательно
понять (построив соответствующие примеры), для каких более
широких классов эллиптических систем справедливы те или
иные априорные оценки и теоремы, доказанные в этой книге.
Довольно полно изучен вопрос о существовании обобщен-
обобщенных решений краевых задач для квазилинейных уравнений
и систем с дивергентной главной частью, обладающих обобщен-
обобщенными производными до порядка, равного половине порядка
уравнения (системы) или на единицу превышающего его. Это
сделано в последнее время в работах Т. Б. Соломяк, М. И. Ви-
шика, Ф. Браудера и др. ([34U 73,4, ТА и др.). Полученные при
этом результаты являются естественными обобщениями резуль-
результатов, изложенных в §§ 5—11, 16 гл. III и § 2 гл. V о су-
существовании обобщенных решений из Wlm№) для уравнений
второго порядка. Особенно простое доказательство существо-
существования таких решений дано в работе Браудера [72]. Вопросы
о «допустимости» таких решений, т. е. о теоремах единствен-
единственности для них «в малом», и вопросы об улучшении их диф-
дифференциальных свойств по мере улучшения дифференциаль-
дифференциальных свойств образующих их функций, и, в частности, вопрос

§ 31 ОСНОВНЫЕ РЕЗУЛЬТАТЫ 65
об их классичности еще ожидают своего решения. (В предисло-
предисловии к данному изданию мы перечисляем основные результаты
по этим вопросам, полученные со времени написания первого
издания книги.)
В гл. IX мы даем другой способ выводы оценок констант
Гёльдера для решений и их производных для всех рассмотрен-
рассмотренных ранее уравнений, при этом объединяем вместе обе трудности:
возможные особенности по х и максимальные возможные нели-
нелинейности по и и р (это объединение допустимо и в рамках
основного метода; оно не было сделано лишь из чисто мето-
методических соображений).
Соответствующие оценки, полученные в гл. III для линей-
линейных уравнений и в гл. IV—VI для квазилинейных уравнений,
являются двумя частными (крайними) случаями выводимых здесь.
Предлагаемый второй метод несколько проще и «обычнее» основ-
основного (это особенно ясно видно в случае параболических уравнений,
к которым он также применим). Все аналитические предложе-
предложения, на которых он основывается, содержатся в первом. Облег-
Облегчение достигается за счет повторного обращения к уравнению:
в первом методе мы выводим из уравнения некоторые нера-
неравенства (*) (которые входят в определение классов УЗт) 4i все
дальнейшие предложения доказываем о функциях, подчиняю-
подчиняющихся только этим неравенствам; во втором методе мы несколько
раз обращаемся к уравнению, выводя из него неравенства,
подобные неравенствам (*), как для самих решений, так и для
некоторых выпуклых функций от них.
В §§ 5—7 гл. IX излагаются некоторые другие приемы оце-
оценок констант Гёльдера для решений отдельных классов линей-
линейных и квазилинейных уравнений.
3 О, А. Ладыженская, Н. Н, Уральцева

Глава И
ВСПОМОГАТЕЛЬНЫЕ ПРЕДЛОЖЕНИЯ
В этой главе собраны предложения, касающиеся произволь-
произвольных элементов ряда функциональных пространств и играющие
для нас хотя и важную, но вспомогательную роль.
В § 1 приводятся неравенства Коши и Гёльдера и ряд
следствий из них. Второй параграф посвящен теоремам вло-
вложения и соответствующим им неравенствам, в том числе и
некоторым мультипликативным неравенствам.
В § 3 приводятся известные предложения, касающиеся раз-
различных видов сходимостеи измеримых функций, и доказывается
ряд утверждений относительно элементов пространств Lm(Q)
и Wlm(Q) и их «срезок» ы(й) (х) = max {и (х) — k; 0}. Леммы 3.6
и 3.7 и предложения § 4 используются при доказательствах
гёльдеровской непрерывности функций классов 23т и установ-
установлении свойств гладкости и суммируемости с теми или иными
степенями обобщенных решений.
Остальные параграфы (§§ 5—9) посвящены исследованию
введенных нами классов 2lm и 23т. Элементами этих классов
являются функции, удовлетворяющие некоторым системам ин-
тегро-дифференциальных неравенств. Для них доказывается,
что элементы 2lm являются ограниченными (§ 5), а элементы
классов 23т — непрерывными в смысле Гёльдера (§§ 6—9). Одно-
Одновременно с этим даются оценки max | и | для и е %т и (м)(а>
для ие8я, зависящие лишь от ||ы||р, q и от числовых пара-
параметров, входящих в определение классов %т и 23т.
Предложения, доказанные в §§ 5—9, существенно исполь-
используются в §§ 13—15 гл. III и в гл. IV—VIII, X, ибо в боль-
большинстве случаев решения и эллиптических уравнений и их
производные иХ{ принадлежат классам %т или 23т.
§ 1. Некоторые простейшие неравенства
Мы будем часто использовать несколько хорошо известных
алгебраических и функциональных неравенств. Из алгебраиче-
алгебраических неравенств нам потребуются следующие
1) неравенство Коши:

§ 1] НЕКОТОРЫЕ ПРОСТЕЙШИЕ НЕРАВЕНСТВА 67
справедливое для любой неотрицательной квадратичной формы
ctiihli с ail = ali и любых чисел \ь ..., |„ и тI( ..., Т1„;
2) неравенство Коши с е:
аЪ < 4- я2 + -тг Ь2, A.2)
^ 2 2е v '
справедливое при любом е > 0 для произвольных а и 6^0;
3) более общее, чем A.2), неравенство Юнга:
a6<-L(eia)p + -p-(-?-)P', -L + -L = l, A.3)
справедливое при любых е1 > 0 и р> 1; запишем его в более
удобной для нас форме:
'~4a/A~a)(l-a)&W-a>, A.3')
где е — произвольное положительное число, а а — любое из
(О, 1);
4) неравенства
(а + Ь)т <2т~' (ат + Ьт), A.4)
(а + бГ<A+е)ат + се,т6'", A.5)
\а-ЬГ>A-г)ат-се,тЬт, A.6)
справедливые при произвольных положительных а а Ь,
и любом е е@, 1).
Из функциональных неравенств, помимо неравенств
(*I., I (и(лс), t»(х)) К||и(х)|||| t»
первое из которых справедливо для норм любого банахова
пространства, а второе — для скалярного произведения и нормы
любого пространства Гильберта, будут использованы следую-
следующие:
5) неравенство Гёльдера:
I J и (х) v (x) dx <(\\и (х) f dx)ll4(j | v (x) f dx\l<f A.7)
при V^^l, —1—г = 1 *) и более общее неравенство:
Q
при любых %t
*) Напомним, что под ИиИ^в понимается vral m_ax | и (х) |«
3*

68 ВСПОМОГАТЕЛЬНЫЕ ПРЕДЛОЖЕНИЯ [ГЛ. II
6) неравенство Коши:
J
\а t
справедливые при произвольных измеримых функциях и(х),
v(x), щ(х), vt(x), заданных в Q и имеющих конечные нормы,
стоящие в правой части.
Из A.7) вытекают такие следствия:
с любыми q^\ и а из @, т) и
~TQ||u||flie A.11)
§ 2. Пространства Wlm№). Теоремы вложения
В § 1 гл. I были определены пространства Lm(Q) и Wlm(Q)
при m^l и целых положительных /. Эти пространства были
предметом многих специальных исследований (см. [32, 19, 312,
15, 20, 443, 8] и др.). Мы приведем здесь те из свойств этих
пространств, которые необходимы для целей данной книги.
Они касаются следов элементов пространств W'm(Q) на много-
многообразиях размерности г^п и связей сходимостей в этих про-
пространствах при разных I, т и г.
Напомним, что Lm(Q) (всюду т^\) состоит из всех изме-
измеримых на й функций и(х), для которых конечен интеграл
I и (r\ f71 r1r\ A П
определяюишй норму в Lm(Q).
В пространстве Ьт(п) плотны функции из С°°(Q). В каче-
качестве функций из С°° (Q), аппроксимирующих ы (х) е Lm (п)
в норме Lm(Q), мол<но, например, взять усреднения
ир(х) = 1сор(\ х-у \)u(y)dy, р^О, B.2)
Q
где ©р(г) = р~"©(г/р), © (т) — неотрицательная бесконечно диф-
дифференцируемая функция tj>0, равная нулю для т>1 и такая,
что ш„ \ 0(t)t"-' dx= 1 (и„ — площадь поверхности единич-
ной сферы в Еп). В Lm (Q) плотно также множество С°° (Q), в чем

§ 2] ПРОСТРАНСТВА Wlm (Я) 69
легко убедиться, взяв последовательность бесконечно дифферен-
дифференцируемых функций t,k{x) из C°°(Q), аппроксимирующих ?,(х)= 1
в норме Lm(Q), и построив для Уы(*) из Lm(Q) приближения
(u?,k)p с р, меньшими расстояния носителя t,k (x) до дп.
Пространство Wm(Q) состоит из элементов Lm(u), которые
имеют обобщенные производные Dku, \k\^.l, всех видов, при-
принадлежащие Lm(Q). Норма в Wlm(Q) чаще всего определяется
равенством
Ql \l/m
%\D>u(x)rdx) . B.3)
I ft 1=0 /
За обобщенными производными сохраняем обозначения
классических производных. Обобщенная производная —г г-
а*?'... а**»
от и(х) из Li (Q'), VQ'c:Q, определяется как функция rkl'"kn
из L, (Q'), V^' ^ Q, удовлетворяющая тождеству
-Ч^=(-1)и' Г« fe^ >-rfx B.4)
J exf' ЭХ*»
...ЭХ*»
при всех г] е С°° (Q). Хорошо известно, что Wlm (Q) есть полное
сепарабельное пространство Банаха. Любой элемент его и (х)
можно аппроксимировать функциями uk (x) из С°° (Q) в нормах
H^m(Q0, VQ'crQ. В качестве uk(x) можно взять средние ыр
о , ,
из B.2). В подпространстве Wm(Q) пространства Wm(Q), опреде-
определенном в § 1 гл. I как замыкание в норме Wlm(u) множе-
множества C°°(Q), вместо B.3) можно взять эквивалентную норму
ll«e>a=ife2/l|JDfe«llm,Q. B.6)
Эквивалентность норм B.3) и B.5) легко доказывается с по-
помощью неравенства Пуанкаре \ \ v \dx^.R \ \vXl\dx, где Q есть
Q Q
куб со стороной R, a v (х)— функция из С1 (Q), равная нулю
на одной из (п— 1)-мерных граней куба, лежащей в плоскости
хх = const. Само это неравенство элементарно получается из
формулы Ньютона — Лейбница
v(Xl,xri) = v (а, х[) + J vXl (*,, х\) йхи B.6)
а
если точку (а, х\) взять на той грани куба, где у=0,

70 ВСПОМОГАТЕЛЬНЫЕ ПРЕДЛОЖЕНИЯ [ГЛ. II
К wm (Q) принадлежат функции Wlm (Q) (т. е. элементы Wlm (Q)
с носителем в Q), ибо для и е Wlm (Q) средние ыр из B.2) схо-
сходятся к и в норме Wlm (Q) и ир е С°° (Q) при достаточно ма-
малых р.
Одной из важных формул является формула интегрирова-
интегрирования по частям
J uXiv dx= — J uvx. dx+ j uv cos (n, xt) ds, B.7)
где п — единичный вектор внешней нормали к 5. Она заве-
заведомо верна для функций и и v из Lip(Q) в строго липшицевых
областях (а следовательно, и в сумме таких областей). В конце
параграфа мы укажем, для каких более широких классов
функций и и v справедлива формула B.7).
Если ие^гР, a osf2(Q), то формула B.7) для них
имеет вид
J uX(v dx = — J uvXl dx B.8)
<> Q
при произвольной области Q. В этом легко убедиться, если
вспомнить вышесказанное о возможностях аппроксимации эле-
элементов из Wi(Q) и Wi(Q) гладкими функциями. Ниже, после
формулировки теорем вложения, будет ясно, для каких более
широких классов функций и и v верна формула B.8).
В основном нас будут интересовать пространства Wm (Q)
и Wm(Q). Для Wm(Q) верна теорема:
Теорема 2.1. Для 4ue=Wm(Q), m>l, Vr>l, справед-
справедливы следующие мультипликативные неравенства:
UaCa||«t2a, B.9)
где
а= -} , пг = , B.10)
\г р)\г ml* n — in ' v '
и
1) при т<п число р может быть любым из [r,rh], если
—-— пг\ ; при
изменении р между rum число а меняется между 0 и 1,
включая оба конца; при r = p = m в качестве а можно взять
любое число из [0, 1];

§21 ПРОСТРАНСТВА У*т{й) 7\
2) при т^п число р может быть любым из [г, оо),
а Р = тах|гс~ р; 1 -f m ~ п . При изменении р от г до оо
число а меняется от нуля до гат л. "?т _ п\ > причем правый
конец исключается. Если т > п, то B.9) справедливо и при р = оо
с некоторым р<оо, не зависящим от Q (при этом а =
гш \
ппг + г (пг — п) ) '
Напомним, что мы всюду считаем д^2. Доказательство
теоремы 2.1 можно найти, например, в книге [21,,, стр. 80—84].
о .
Из B.9) для функций и из Н7г(й) вытекают неравенства
II«1^-,, 0<с(я) II V« Co II и \f-?">, B.11)
где<7>« при д>2и <7>2при« = 2,ас(<7) = [2(д— Щп — 2)]п/ч
при д>2 и с (?) = max {q/(q — 2), 2р? при д = 2.
Далее, для V« e lFm (Q), m^l, справедливы неравенства
№Q0||V«||mia> т = -^. B.12)
с ре[1,и] при т<д и с ре[1,оо) при т^п, причем по-
постоянная с равна т при т<п и с = тах< га~" р;
2 — — | при т>«, a Q0 = {^eQ: ы(^)=^=0}. Неравенство B.12)
при т>п справедливо и для р = оо с с = р1/а, где р и а
взяты из B.9), B.10) для р = оо и г = 1.
Действительно, в силу неравенства Гёльдера и неравенства
B.9) сг=1 при р > 1 имеем
II«11Р. а < РII V« С а || и \\\2 < РII V« С, а ||« fe (mes Q0)('"a) 0 ~у) ,
и потому, учитывая — ^A j (l r-je@, оо), получаем,
B.12) с с = р1/а. Из этого же неравенства с каким-либо допу-
допустимым р>\ и неравенства Гёльдера вытекает B.12) и
для р = 1.
о
Неравенство B.12) показывает, что Vm e Wm (Q) принадле-
принадлежит Lm{Q), где здесь и ниже используем обозначение
т= "тт прит<д,
171 оо при т > п,
любое число < оо при т = п,
причем норма ||м||й,а оценивается через норму ||VM||m,a.

72 ВСПОМОГАТЕЛЬНЫЕ ПРЕДЛОЖЕНИЯ [ГЛ. II
Неравенства B.12) справедливы также для функций и(х) из
W\n{Q), равных нулю лишь на части границы Q. Мы исполь-
используем это для частного случая, когда Q есть половина шара
и и (х) равна нулю на сферической части границы. Этот слу-
случай с помощью продолжения и(х) четным образом по отно-
отношению к плоской части границы на весь шар сводится к слу-
случаю, когда функция равна нулю на всей границе.
Частными случаями B.12) являются неравенства
j _
II«11зд(„-2). о < с (Я) (mes О)» Т|| V« ||2 0, B.13)
где q^n при «> 2 и q > 2 при « = 2, с постоянной c(q),
зависящей лишь от q и п и, вообще говоря, отличной от c(q)
из B.11), и неравенство
,Qo||2iQ B.14),
с с0, не зависящей от Q. Из B.11), используя неравенство
Юнга A.3'), Для Vms W\{u) получим
II«1^,-2,. в < е || V« ||_ а + сЁ || и || а> B.15)
- q-n I n \nl{q-n) ..
где е —любое положительное число, а сг —- I — I X
X Iе {q)fqt{q~n) — постоянная, не зависящая от Q.
Переходим теперь к пространствам Wm(u), m^l. Для
произвольной области Q каждый класс функций, эквивалент-
эквивалентных на Qu (х) из Wlm (Q), имеет «хорошего» представителя ы (х),
равного limmes~'Q0(x) \ u(y)dy для *eQ (п(х) определен
для почти всех х, и и(х)— и(х) равен нулю почти всюду в Q).
Функция п(х) при почти всех значениях x'i = {xu ..., xt-x,
xi+u ..., хп) абсолютно непрерывна по х{ на всех открытых
интервалах, принадлежащих Q, и может быть по непрерывно-
непрерывности доопределена в концах этих интервалов (это так для всех
г=1,..., п). Производная -~, вычисляемая как обычная
производная от абсолютно непрерывной функции, существует
для почти всех значений xt на упомянутых интервалах и сов-
совпадает почти всюду в Q с обобщенной производной иХ{, так
что ~^- = uXi^Lm(Q). Верно и обратное утверждение: если
u(x)<=Lm(Q), если для всех /=1, .... « и(х) при почти всех
значениях x'i абсолютно непрерывна по xt (на каждом из от-

§ 2] ПРОСТРАНСТВА Wlm (Q) 73
крытых интервалов, принадлежащих Q) и если -^—, вычисляе-
ах.
мые как обычные производные от абсолютно непрерывных
функций, принадлежат Lm(Q), то u^Wlm(Q) и и(х) есть «хо-
«хороший» представитель класса функций, эквивалентных и(х)
на Q.
Пусть теперь Q — строго липшицева область. Для таких
областей Vu(x)^Wxm(Q) можно продолжить на все простран-
пространство Еп в виде функции U (x) e Wm (En) (точка наверху озна-
означает, что U (х) имеет компактный носитель), причем
l?!e, B.16)
где постоянная с(п) зависит от т и й, но не зависит от и.
Если к тому же и (*) е Lr (Q), то U^Lr(En) и
\\U\\rE <с2(О)||и||гВ. B.17)
* П *
где постоянная сх (Q) зависит от г и Q (см. стр. 74 [396], лемма
Кальдерона). Такое продолжение можно сделать и так, чтобы
все функции U(x) имели носитель, содержащийся в фиксиро-
фиксированной области Q =э Q.
Из неравенств B.16), B.17) и неравенства B.9) следует, что
для Vu<=Wln(Q)
с« (О) с'-° (Q) (|| и \^\ а)а || и ||'7?, B.18) ¦
или, короче,
II 4.Q< Р О'"ИМ""" Си' BЛ9)
где р = рс? (Q) c\~a (Q). Постоянные р, т, г, а, Р те же, что и
в B.9). Постоянная сх (Q) в B.16), а следовательно и постоян-
постоянная р в B.19), зависит от выбора норм || • |^' Q. Доказано, что
стандартной норме || и Ц^1 а эквивалентны нормы
«IIS.SV
Vse=[l,m], VY = const>0, VQ, s Q с mesQ^O,
причем эти нормы однородны: при преобразовании подобия
х->Хх они умножаются на я,("~т)/т. Более того, из B.19) с г = 1
видно, что в этих нормах в качестве s можно брать любое
•ss^m. Если в B.16) и B.19) под || • ifj,1 Q понимать одну из этих
норм, то постоянные ct (Q) и р в них, очевидно, одинаковы для

74 ВСПОМОГАТЕЛЬНЫЕ ПРЕДЛОЖЕНИЯ 1ГЛ. II
всех областей Q, получающихся друг из друга преобразованием
подобия. Для подпространства W]n{u) пространства Wxm(u), со-
состоящего из элементов Wxm(u), подчиненных условию j udx = 0,
Qj ?= Q, mes Qj > О, в качестве эквивалентной нормы можно
взять l|VM||m a. Выведем из B.19) ряд следствий.
При г е [ 1, /й] и || и |? „ = || Vu ||m в +1| и ||r_ a из B.19) следует
cVpe[r,m]. При г = т = 2 и II«Н^а = II V« ||2, а + || и ||2. а из
B.19) следует
l-i
II« КМ-2). п < Р III V« К п II« "г. а" + II«"г. о j • B-21)
где <7^« при я>2 и <7 > 2 при « = 2. Возведем обе части
B.21) в квадрат и, считая q > n, воспользуемся неравенством
Юнга в форме A.3'). Это приведет нас к неравенству
II« С-ч. Q < е II V« t. п + сг II « ft a B-22)
cVe>0, ,>« и
Рассмотрим еще B.19) при r=l, ll«C.a = ll V«||m a +||«||, a
и р = т<7/(<7 — т)> считая q > n^?tn> I. Показатель а при этом
будет меньше 1, поэтому член J5||Vm||^ о || и ||}~^ можно оценить
с помощью неравенства Юнга A.3'), отдавая произвольно малое
е>0 множителю ||Vm||ot q. Возведя B.19) в степень т и оцени-
оценивая правую часть указанным образом, придем к неравенству
II« C,-m). в < е II V« С в + се II и 1С в, B.23)
где е — любое положительное, сг зависит от Q, n, m и q,
a q > п^т> 1. Еще раз напомним, что постоянные р, се в не-
неравенствах B.19) — B.23) разные: они зависят от выбора нормы
IImICq" Посмотрим, что дают неравенства B.20) и B.22) для
ы(л:)е w\(u). Неравенство B.22) применительно к функциям их
дает
tt t' B-24)
где m = 2q/(q — 2), a q — любое, большее д. Рассмотрим сначала
^4 Для них B.20) с m = 2q/(q — 2), г = 2 и /?, равным наи-

§2] ПРОСТРАНСТВА Wlm(Q) 75
большему из возможных показателей (т. е. p=2qn/[qn—2(n-\-q)\,
причем это р больше нуля при V<7>«^4), имеет вид
II«ИР. а < Ь (II «* \\Шч-2), о + II«Н2. о)- B-25)
Из B.24) и B.25) при «>4 следует
II« С а + II V« lfc/(,-2), q < ei II««ll22. a + г., (||«H^J B.26)
с p = 2qn/[qn — 2(д + <7)]> а тем самым и с p = 2q/(q — 4) при
V<7>« и Ve, >0. Для /г = 2 или 3 из B.20) и B.22) следует
неравенство, отличающееся от B.26) только тем, что вместо
|| u\f о в нем можно поставить max и2. Объединим все эти слу-
И' а
чаи так:
I«\1 + II V« С-*,, а < е II «„ lg, а + сг (II« IQ2. B-27)
где |ы|а есть тахи2(;е) при « = 2 и « = 3 и |«1а = 11«11р>а
с р = 2qn/[qn — 2 (п + <7)] (и тем более р = 2q/(q — 4)) при п > 4.
Число <7 в B.27) любое, большее «, а е любое, большее 0.
В действительности имеет место неравенство несколько более
сильное, чем B.27), а именно:
I«\Ъ + II V« HW2)> о < е ||«,, || Q + се ||« || Q) V<7 > «. B.28)
Для и, равных нулю на 5, это непосредственно выводится
из B.27), если заметить, что из равенства
J | Vm р dx J и Аи dx
а а
следует оценка
TH>e 2srNI|e. B-29)
Для функций и(*) из 1^2 (й) неравенство B.28) легко выводится
из B.29) и из неравенств B.9) и B.15), примененных к и и их
соответственно, причем постоянная сг в B.28) в данном случае
может быть взята не зависящей от Q.
Для элементов Wm(Q) с т>п неравенство B.19) гаранти-
гарантирует их ограниченность. Однако на самом деле они будут при-

76 ВСПОМОГАТЕЛЬНЫЕ ПРЕДЛОЖЕНИЯ (ГЛ. II
надлежать пространству С т(й) и для них верно неравенство
|(')а) т>п. B.30)
Этот факт следует из леммы Морри (лемма 4.1 гл. II). Дейст-
Действительно, надо и (х) продолжить на все Еп -в виде функции
U (x) e W]n (?„), подчиняющейся неравенству B.16), и затем
к U (х) применить лемму 4.1 (с т=\), учтя, что в силу неравен-
неравенства Гёльдера J | Vu \dx^( J | У и \mdx\m(mes KpI'7"^ с$~~™ .
J | Vu \dx^( J | У и \mdx\
р Ч /
Выше было отмечено, что для строго липшицевых областей
функции класса Wm(u) допускают распространение на все
пространство Еп, причем так, что для продолженных функций
имеет место неравенство B.16). Из этого факта легко заклю-
заключить, что в Wm(Q) плотны функции C°°(Q). Действительно,
усреднения B.2) функций U (х), определенных в Еп, принадле-
принадлежат С°°(Q) и сходятся при р-»0 к и в норме Wxm(Q).
Неравенства B.30), B.19) и все неравенства B.20) — B.29),
вытекающие из B.19), справедливы и для областей Q, соста-
составленных из конечного числа строго липшицевых областей;
точнее, й есть (JQ*, ^» Л^/ = 0> *V=/> &i — строго липшицевы
области. Примером такой области может служить квадрат
с каким-либо выброшенным из него отрезком. Теоремы о про-
продолжении и аппроксимации функций из W\n (Q) бесконечно диф-
дифференцируемыми функциями для таких областей могут быть
неверны, но неравенства B.19) —B.29) для них сохраняются.
Действительно, для каждой Q* неравенства B.19) имеют
место. Возведя их в степень р и сложив по всем i от i=\
до i = N, в левой части получим ||и|Р а, а в правой части, за-
заменив в каждом члене !|m||Wq. и ||и||г 2 на большие величины
N
II«llm, о и И "II г, а соответственно, получим 2 [Р/ (II и ||W а)" || мЦ^аГ»
где §г суть постоянные из B.19) для каждой из Q/. Справед-
ливость B.30) для Q= \Jui очевидна. Неравенства B.19)—B.30)
верны и для более широких классов областей Q, например для
областей, получаемых из рассмотренных нами областей с по-
"" регулярного липшицева преобразования У = у{х) (т. е.

$2] ПРОСТРАНСТВА fl^(Q) 77
гомеомс>рфного преобразования Q на D, для которого у(х)^
~Lip(Q) и обратные функции х (у) е Lip (?»)). Известно, что
V/W из Lip(Q) имеет почти всюду в Q дифференциал и f(x)^
<= WL (Q) (теорема Радемахера; для строго липшицевых обла-
стей_верно и обратное предложение: WL(Q) cr Lip(Q), так что
Lip (Q) = Wic (Q)), Благодаря этому, если u(x)<=Wm(Q), то
в (у) = ы (х (у)) <= 1Р« (D) (и наоборот). Из B.19) - B,30) для и (х)
следуют такие же неравенства для v (у) в области D.
На основе неравенств B.19)— B,30) и теоремы Ф. Реллиха
о компактности вложения W\{Q) в L2 (Q) легко доказывается
следующая теорема С. Л. Соболева ([32]):
Теорема 2.2. Для произвольной области п *) ограничен-
ные множества функций и(х) из Wm(Q) компактны в Lp(u)
с р < ntnl(n — m) при tn^n и компактны в Са(Q) с а < 1 ——
при m > п. Для строго липшицевых областей и конечных сумм
таких областей ограниченные множества функций и (х) из Wlm (Q)
компактны в LP(Q) с р < пт/(п — т) при т^.п и компактны
eC°(Q)ca<l-i при m>n.
Переходим теперь к рассмотрению следов элементов Wlm(u),
m^sl, на поверхностях размерности п— 1. Для большей на-
наглядности пусть сначала Q есть куб: Q = {*e?'n: 0<*/<l,
/=1 «}. Обозначим через Qiik, г = 1, ..., п, & = 0, 1, его
грани: Qit0={x: х; = 0, 0 < xk < 1, k^=i) и Qtil = {x: xt=l,
0 < xk < 1, k ф i), а через Q; — (п — 1)-мерные кубы: Q( =
= [х7.; 0 < xk < 1, кфг\. Для V«eH7'Jn(Q) его представитель п. (х),
равный lim mes (/Cp(x)[\ Q) f u(y)dy для xeQ, обладает
следующими свойствами: при любом i=l, ... п, и (х) абсолютно
непрерывен по xt e[0, 1] для почти всех значений х\ из Q^ (мно-
(множество таких х\ обозначим через Q(.). Для Чх. е [0, 1] он есть
элемент Lm(Q^ и для л^ей(
xi
u(x'i, xi) = u(x'l, л^)+ J ux(x/i, x)dx
*) Напомним, что во всей книге мы рассматриваем лишь ограниченные
области Q.

78 ВСПОМОГАТЕЛЬНЫЕ ПРЕДЛОЖЕНИЯ [ГЛг II
при Vxt, x°t из [0, 1]. Отсюда следует
II
т. е. й (л^., хг) непрерывен по х. в норме Lm (Q.). Более специаль-
специальные рассмотрения показывают, что для u^Wlm{u) представи-
представители п{х\, x^Lq{u^ при Vx. е [0, 1] с q^.m{n — Щп — т)
при т<п и с V<7 < оо при т = «, причем
11"«'^Iа/<с1'"€!а B-32)
и при \х1 — х°.\->0
I xt у/т
J A 0. B.33)
Для т>п элементы Wlm(Q) принадлежат С т (Q). При q,
меньших указанных в B.32), т. е. q < т(п— \I(п — т), т^.п,
справедливы также неравенства
И«11?.а/<е11?«11т.а + се11«11г.а B-34)
с Ve > 0 и г^1. Выведены и мультипликативные неравенства
вида B.18), в частности
llfilUe^^Hul^/llufS B-35)
с а = у — , где р — любое из [2 (п — 1)/я, 2 (п — 1)/(« — 2)]
при д^З и р — любое из [1, оо) при « = 2.
о .
Если «gFb(Q), то на границе Q п{х) «принимает» нуле-
нулевые значения. При т<^.п это надо понимать как
II"(*i» xi)\ ~*° ПРИ хг->0 или xt->l, i= I, ..., п B.36)
(<7 те же, что и в B.32)). Верно и обратное: если «eHT'^(Q)
о .
.и п на S равно нулю, то KeFm(Q).
Если вместо х в Q взяты другие регулярные координаты
г/ = г/ (х)е Lip (й) (так что обратные функции х — х(у)^ Lip (Я)),

§2] ПРОСТРАНСТВА Wlm№) 79
то все сказанное справедливо и для функций и(г/) = и(х(у))
в области D, причем и(#) = п(х(у)). Ввиду этого для элемен-
элементов u(x)^Wm(Q) B строго липшицевых областях представи-
представитель п(х) однозначно доопределяется по непрерывности для
почти всех точек границы S области Q. Функция п(х) на S
принадлежит Lq(S) с тем q, что и в формуле B.32), и для нее
верны аналоги неравенств B.32) и B.34), а именно:
где q<^.m(n—\)l(n — т) при tn<n, V<7 < °° при т = п и
<7 = с» при т > п, и
с Ve > 0, r^l и q < m(n — l)/(« — т) при m e A, я]. На
основе B.38) и теоремы 2.2 нетрудно доказать следующую тео-
теорему С. Л. Соболева ([32]) (см. лекции О. А. Ладыженской):
Теорема 2.3. Для строго липшицевых областей следы на
границе функций й(х) из Wxm(Q) с \йЩ>Q^c образуют ком-
компактное в Lq(S) множество, где q те же, что и в B.38).
В строго липшицевых областях представители п(х) элемен-
тов и(х) из Wm(Q) равны нулю на границе Q, и, наоборот,
если и (х) е Wm (Q) и u(x)\s = 0, то «efj, (Q) (отсюда следует,
что такая п(х), продолженная нулем вне Q, будет элементом
Wlm(Q) в VQidQ).
Вернемся теперь к формулам B.8) и B.7). Формула B.8)
или, что то же,
[ d(uv\dxz=0 B.8')
J дх, v '
остается справедливой для произвольной области Q, если
uv e W\ (Q). Произведение же uv e W\ (Q), если «efi (Q),
v e Wlp (Q), a m и р удовлетворяют условиям: 1) — + —• ^ 1 + —,
если we(l, «), р е A, п), или 2) — + — < 1 + -^ • если ш> 1,
р ^ 1 или m ^ 1, р > 1, или 3) р = 1, m = n и не/,ю(й) или
т=1, р=« и oet^JQ). Справедливость этих утверждений
следует из теорем вложения — неравенств B.9) и B.18) и не-
неравенства Гёльдера. При этом надо учесть, что неравенства
B.18) достаточно иметь лишь для подобластей Q'crQ с хоро-
шей границей, ибо в Wm(Q) плотны финитные функции из Wm{Q),
т. е. функции из wi (Щ-

80 ВСПОМОГАТЕЛЬНЫЕ ПРЕДЛОЖЕНИЯ 1ГЛ. II
Формула B.7) остается справедливой в строго липшицевых
областях для функций «elfl(Q) и tielfp(!!)cm ир, ука-
указанными для формулы B.8'). Это следует из неравенств B.18),
B.30) и B.37) и возможности аппроксимации функций из Wlm (Q)
и Wlp_(Q) функциями из С1 (Q) (или хотя бы функциями из
Lip(Q)). Формула B.7) сохраняется и для суммы строго лип-
липшицевых областей (см. выше их определение), ибо она полу-
получается из B.7) для строго липшицевых областей простым
сложением.
§ 3. О разных сходимостях и функциях классов
Wi,(O) и &п(Щ
Сформулируем прежде всего ряд известных предложений из
теории функций вещественного переменного, которые будут
использоваться на протяжении всей книги.
Лемма 3.1. Если последовательность {ир(х)}, р = 1, 2, ...,
элементов Lm(u), m^l, сходится в норме Lm(Q) к функции и(х),
то из нее можно выбрать подпоследовательность \uPk (х)\,
k=l, 2, ..., сходящуюся к и(х) почти всюду, т. е. такую,
что на некотором множестве Q cr Q с mesQ = mesQ все ир'(х)
и и(х) принимают конечные значения и I ир (х) — и(х) I —>0 при
&-*oo. Если {ир(х)} сходятся к и(х) почти всюду, то они схо-
сходятся к и(х) и почти равномерно, т. е. по любому е > 0 можно
указать такое множество Qg cr Q с mesQe^ mesQ — e, на кото-
котором up(x) сходятся к и(х) равномерно.
Здесь, как и во всей книге, мы чаще всего не оговариваем
специально, что все функции и все множества, встречающиеся
в ней, измеримы по Лебегу. Из леммы 3.1 легко выводится
следующее предложение:
Лемма 3.2. Если последовательность {ир(х)}, р=1, 2, ...,
сходится к и(х) в норме L\(Q) и величины \\ир\\ч< а, <7>1,
р=1, 2 равномерно ограничены, то {ир(х)} сходится к и(х)
сильно в Lq(u), V<7 < Ц, и слабо в Lq(Q).
Если f(x, и) есть измеримая на Q X^i функция, непрерывная
по и для почти всех х из О,, и если для последовательности
функций {ир(х)}, сходящейся почти всюду к и(х), величины
\\f(x,up(x))\\qQ, p= 1,2,..., равномерно ограничены, Tof(x, up(x)),
р = 1, 2 сходятся к f(x,u(x)) в нормах Lq(Q), Vq<q, и
слабо в Lq(Q). Если к тому же величины \\f(x, up(x)\\ ^,
р=\, 2, ..., равномерно малы по множествам Q cr Q малой
меры, т. е. если по любому б > 0 найдется е > 0 такое, что

§3] О ФУНКЦИЯХ КЛАССОВ Wlm(Q) И Wlm(Q) 81
для произвольного множества Qs cr Q с mes QE <| в величины
|| / (х, ир (х) || fie<6,p=l,2, ..., то f(x,up(x)) сходятся к f(x,u(x))
в норме Lq (Q).
Отметим еще следующий известный факт: пространству Lq(Q),
<7 > 1, сопряжено пространство Lq' (Q), q' = q__ , так что любой
линейный функционал / в Lq (Q) представим в виде
/ (и) = J фг (х) и (х) dx, и (х) е Lq (Q),
где ф((^)е1?,(й), и между линейными функционалами в L (п)
и элементами L^ (Q) существует взаимно однозначное соответ-
соответствие.
Переходим теперь к изучению пространства Wm(Q).
Пусть и(х) есть элемент Wlm(Q), m^l. Обозначим через Ak
' О
множество точек х из Q, в которых и(х) > k, a через Ak — мно-
множество точек ней, в которых и(х) = k. Известно, что эти
множества измеримы, что Ak = (J Ak+B, Ak \}Ak= f) Ak^e и
V<! > П VE > 0
о
mes(i4%\ i4ft+g)-»0, mesMv._e \ Лй U^4)->0 при e->0.
Построим по и (х) функцию u{k) (x) = max {u (x) — k; 0} (срезку).
Имеет место
Лемма 3.3. Если u^Wxm{Q), m^l, то uik) также принад-
принадлежит Wlm(Q), причем и*(х) равна их.{х) при neij и нулю
в остальных точках.
Этот факт легко доказывается исходя из сформулированных
в § 2 свойств «хорошего» представителя п(х) элемента и(х) и
того, что таким представителем для и**1 (х) является функция
тах{й (х) — k; 0}. Из этих же свойств п(х) для и (я) е №m (Q)
следует, что если mes^ft>0, то Vu{x) = 0 на некотором под-
с о
множестве множества Ak, имеющем ту же меру, что и Ak.
Докажем теперь, что если последовательность функций ир(х),
р= 1, 2 из Wm(Q) сходится к функции и(х) в норме Wxm(Q),
то последовательность «подрезанных» функций и(^(х) также
сходится в ^„(Q) к функции u(k)(x). Для этого предварительно
убедимся в справедливости следующей леммы:
Лемма 3.4. Если ир(х), р=\, 2 сходятся в Lm(Q)
к и(х), то upk){x) сходятся в Lm(u) к uik)(x). Кроме того,
mes [Ak \ А% П Ak\ -»¦ 0 при р->&э

82 ВСПОМОГАТЕЛЬНЫЕ ПРЕДЛОЖЕНИЯ [ГЛ. II
U
mes \Al \ Al ft (Ak U Ak)] -> 0 при р->оо.
Здесь Ak есть множество точек x e Q, в которых ир (х) > k.
Из очевидного неравенства
ясно, что u(® сходятся к и<*> в ^от(й). Далее, из сходимости ир{х:
к и (л:) следует, что мера множества пр'е точек хей,в которых
| ир (х) — и (х) |^8, при любом е>0 стремится к нулю, когда
р->оо. Кроме того, в силу определения множеств Ak и Аи
имеем Ak+e Л fe \ Qp> e) cr Al, в > 0, а потому и
e л (s \ йр> е)]=лА+е л (й \ йр> е) с лг л
Представим Ak\Al{\Ak в виде
Ak \ Al (]Ak = (Ak \ Ak+e) U (Ak+г Л QP'e) U
и по произвольному числу 6>0 выберем сначала е = еF)>0
такое, чтобы mes(X \ ЛА+.)^б/2, а затем р(б) такое, чтобь
при всех р>р(б) mes й"'8'*^6/2. Тогда mes(Ak \ Al Л Ak) не
будет превосходить б при р^р(б).
Для доказательства последнего утверждения воспользуемся
тем, что Apk(]{Q\Qp's)c=Ak-e, а потому и Al(]{Q\Qpl R)a
О
cr APkf)Ak-e. Представим Al \ А\ Л (Ak (J Ak) в виде
Л?\Л?П (Ak UЛ)=U?(]{п\ Qp-e)] UИ f]Q"-s\\ [Al Л Л*-.] U
U\Al(](Ak-e\Ak\]Ak)}
и по произвольному б>0 подберем в = е(б)>0 так, чтобы
те8(ЛА_е\ ЛАиЛ°й)<б/2, а затем р(б) такое, чтобы при
mesQp-el6) <-J • Тогда mes(Л? \ Л? Л (ЛА (J Ak)) будет при
не больше б. Лемма доказана.
Лемма 3.5. Пусть функции ир(х), р=1, 2, ..., сходятс
в Wlm(Q) к функции и(х). Тогда функции и{®(х) сходятся в Wm(&
к функции и(*>.
Мы уже знаем, что ы<*> сходятся к u{k) в Lm (Q), что и™ и ы<*-
принадлежат ^(Q) и что -?- (аналогично -^-\ равна

о функциях классов wlmw и
83
соответственно
-т—
ПРИ х
(ПРИ
и нулю при
x e Q \ Ak (соответственно при x e Q \ Ak). Нам надо доказать
ди1к) duik)
лишь, что ~— сходятся в Lm(Q) к -^—. Для этого предста-
вим интеграл
I
5л;,
5л;,
в виде суммы интегралов от
того же подынтегрального выражения по множествам Ak Л Л?,
Ak \ Ak Л Al, AI \ А% Л (ЛА U Л), At Л Л, Q \ Арк U Л*. На послед-
последнем множестве подынтегральное выражение равно нулю вслед-
вследствие определения функций и^\ На первом множестве интеграл
имеет вид
I
ди
5л;^ 5л;^
dx и потому мал при больших
р в силу сходимости иРх к их. в норме Lm(Q). Интеграл по
множеству Ak\Ak[)Ak мал при больших р, ибо в силу ма-
малости меры множества Л^\ЛйЛЛь будет мал интеграл
I I **л I*™ rfje и потому равномерно малы интегралы
\ иРх Г dx (ибо иРх сходятся к иХ- в Lm (Q)V Выраже-
нйе же
J
UAk
4ft)
5л;,
5л;,
)l/m
не превосходит
( / |%г*Г+( J
\Ak\AkflAPk ) Уч^ч
l/m
и потому действительно стремится к нулю при р->оо. Интеграл
по множеству Bl = Л? \ Al Л
имеет вид
^
dx,
причем по лемме 3.4 mesB|?->0 при р->оо. Он будет мал, ибо
мал
\-=— dx и иРх_ сходятся в Lm(Q) к ин. Наконец,

84 ВСПОМОГАТЕЛЬНЫЕ ПРЕДЛОЖЕНИЕ [ГЛ, II
о
интеграл по А% Л A-k имеет вид
Г дир т Г
-т— dx =
J OX; J
дир ди
дх{
dx
и будет мал в силу сходимости иРх_ к иХ{ в Lm(Q).
Лемма 3.5 доказана.
о ,
Из леммы 3.5 и определения Wm(Q) вытекает
Следствие 3.1. Если u^Wlm(Q), то ы@) (х), равная и (х)
для х из Q, в которых и (х) > 0, и равная нулю для всех
остальных х из Еп, принадлежит Wm(Qi) для VQi э Q.
Л е м м а 3.6. Если ue=Wxm(Q) и vrai max и = М,то u(k)е= Wlm(Q)
при Vk>M.
Действительно, в силу определения vrai max и (см. § 1
s
гл. I) для Ve > 0 найдется функция фе1Гт(й) с vrai maxф^
а
о .
^ М + е такая, что у = (ф — и) е Wm (Q). Возьмем последова-
последовательность уреС°°(О) и сходящуюся к у в норме W{m{Q). Для
нее срезки и(рк) с k ^ М + е функций ир = ф — ур обращаются
в нуль в пограничных полосках и, следовательно, принадле-
принадлежат Wm(Q). В силу леммы 3.5 ир*' сходятся к ит в норме Wm(Q),
и потому uik) e IFm (Q). Это верно для V^ > М. Функция иШ)
также принадлежит ^(Q), ибо, как нетрудно видеть из самого
построения срезок, uw сходятся к иШ) в норме Wlm(Q) при
Замечание 3.1. Леммы 3.3—3.5 справедливы и для
функций й№) (х) = min {и (х); к), ибо u(ft) (х) =.и{х) — ы(А) (х).
Аналогично доказывается
Лемма 3.7. Пусть и е Wlm (Q) и vrai max u^.M для
Sp-S П Кр
какого-либо шара Кр. Тогда функция
[<*) (х) для х е Qp ?3 Кр Л Q,
I для * е /Ср \ Qp
при \fk > М принадлежит Wlm (Кр)-
Действительно, из условий леммы следует, что для V& > М
существует функция ф е Wlm (Q), с vrai max ф ^ k, такая, что
для v = u — ф имеются функции ур, р==1, 2, ..., из Wm(Q),
равные нулю в окрестности Sp и сходящиеся к у в норме Wm(Q,).

§ 3] О ФУНКЦИЯХ КЛАССОВ Wlm (П) И &^,(П) 85
Срезки и(р} для функций ир = 5р + фе?1,(?!) и обращаются
в нуль в тех же окрестностях Sp, что и функции vp. Ясно, что
функции uSk), продолженные нулем на Кр (обозначим их через й^),
принадлежат Wm(K,) и ipq^W~ Uff^ к=\й^ - uf\^;
В силу леммы 3.5 /р</ —> 0 при р, <7->°°, т. е. предельная для ?<,*>
функция й(А) принадлежит Wm(Kp)- С другой стороны, на Qp uV
сходятся к ы<*>, а на Кр \ Ор все й^ = О, следовательно, й(*> = й(*>.
Замечание 3.2 к леммам 3.6 и 3.7. Если Q — строго
липшицева область, то vrai max и для u^W{m(Q), определенный
s
в § 1 гл. I, совпадает с обычным определением vrai max п по
s
поверхности S следа представителя п элемента и из Wm (Q) на
границе S. Это следует из того, что для таких областей при-
О |
надлежность v к Wm(u) эквивалентна принадлежности v
(а потому и у) к Wlm(Q) и равенству нулю следа v на S.
Действительно, пусть u^Wlm(Q), vrai max u=M, a vrai max п = М.
s s
Тогда для V& > М найдется функция ф с vrai max ф^^ и такая,
а
о .
что [) = и-феWm(Q). Ясно, что п= v + q> и след п на S
равен следу ф на S, и потому М = vrai max ы = vrai max ф ^.k.
_ s s
Так как k —любое > M, то М^М. Верно и обратное нера-
неравенство М^М, ибо функция ф (х) = min {й (х); М) равна своему
представителю ф, имеет vrai max ф^М, след ф на S равен п
а о
(почти всюду на S), и потому ы — фе№т(й). Аналогично дока-
доказывается совпадение двух определений vrai max элементов W\n(Q)
для части Sp=^Kp(]S границы, если Q — строго липшицева
область. Надо при этом использовать лишь то, что если п
равно нулю на Sp, то существует последовательность функций
up^Wm(Q), сходящихся к ы в Wlm(Q) и равных нулю в окрест-
окрестности Sp.
Лемма 3.8. Пусть Кр — шар радиуса р. Для любой функ-
функции и (х) из Wi (Кр) и произвольного измеримого множества ЕсК.р
справедливо неравенство
[^u(x)\dx, C.1)
J
где Ео — множество точек х из Кр, в которых и (х) = 0, а р — абсо-
абсолютная постоянная, зависящая от п.

86 ВСПОМОГАТЕЛЬНЫЕ ПРЕДЛОЖЕНИЯ [ГЛ. II
Доказательство. Для почти всех х из Кр и у из Ео
верно соотношение
\х-у\
— и(х) = и(у)-и(х)= J ^ (* + »») rfr>
о
где (г, со) — сферические координаты с центром в точке х.
Проинтегрируем это равенство по у е Ео:
\х-у\
— u{x)mesE0=jdy J ur (x + rco) dr, C.2)
я„ о
и оценим сверху правую часть следующим образом:
\х-у\
Е, О
j dy J иг(л + гю)
\х-у\
2p
0 %
Отсюда и из C.2) получаем неравенство
^Р
Проинтегрируем обе его части по множеству ?:
7^]S=r. C.3)
Интеграл /= Г dx д-1 не превосходит (со„ + 1) mes1/n?, где
е 1*~ ?'
ш„ — площадь поверхности единичного «-мерного шара. Дей-
Действительно, часть интеграла, соответствующая области инте-
интегрирования Е[\{\х — ||<б}, не превосходит
IU
*?—г=ш„б.
Остальная часть интеграла, очевидно, не превосходит б~" 'mes-E.

§3] О ФУНКЦИЯХ КЛАССОВ WXm(Q) И WlmW 87
Возьмем 6 = mes1/rt Е; тогда ясно, что /<(со„+ 1)
В силу этого из C.3) следует неравенство C.1) с р = — (со„ + 1).
Лемма 3.8 доказана. Из нее легко вывести два следствия.
Первое из них является некоторой модификацией утверждения,
доказанного Де Джорджи [11], и формулируется так:
Лемма 3.9. Для любой функции и(х) из W\ (Кр) при произ-
произвольных k и I, l>k, верно неравенство
J
J \Vu(x)\dx C.4)
Ak, р \ AU р
с постоянной р из C.1).
Здесь и ниже через Аи р обозначается множество точек х
из Кр, для которых u(x)>t.
Чтобы убедиться в справедливости этого утверждения, до-
достаточно рассмотреть C.1) для функции
п(х) =
О
u(x)-k,
l-k, и (х) > /,
взяв в качестве Е множество Аи р, и учесть, что для п
J| й \dx = (l —
\Su\dx,
Другим следствием C.1) является неравенство
Ak,p
справедливое для произвольных функций и(х) из Wm(Kp) и
любых значений k. Оно получается, если применить C.1)
к функции v (х) = [max {и (х) — k, 0}]m и множеству E = Ak, p и
при m > 1 воспользоваться еще неравенством Гёльдера для

88 ВСПОМОГАТЕЛЬНЫЕ ПРЕДЛОЖЕНИЯ [ГЛ. II
оценки интеграла
J|Vo|</jc= j \V(u-k)m\dx = J m(u-k)m-{ \ V
Ak.P
W J (u-k)mdx\
Замечание 3.3. Вместо шара Кр в лемме 3.9 и ее след-
следствиях можно рассматривать области более общего вида. На-
Например, нетрудно убедиться, проследив доказательство
леммы 3.8, что в неравенствах C.1), C.4) и C.5) можно шар Кр
заменить произвольной выпуклой областью Q диаметра 2р.
Для выпуклых областей пр нам потребуется также нера-
неравенство
~*Ak Dllv"(ft) II о , C-6)
' Р
. Ak, РГ'| т = пт/{п — т),
аналогичное B.12), но отличающееся тем, что в нем функция и<*>,
о
вообще говоря, не принадлежит Wm (Qp). В C.6) р — любое из
[1, т] при т<п и любое из [1, оо) при т=-п, а постоян-
постоянная с0 определяется величинами п, т, р и областью Qp.
При pG[l, m] оценка C.6) непосредственно следует из не-
неравенства C.5) для Qp и неравенства Гёльдера. При р > т
надо воспользоваться еще неравенством B.18):
II «<*> Ир, „р < с ( || V«<*> ||m> % J р
в котором постоянная с зависит от области пр, но не меняется
при преобразовании подобия области.
§ 4. Некоторые другие вспомогательные предложения
Докажем теперь один из давно известных признаков гёль-
деровости функций, установленный Ч. Морри (см. [39]>2]).
Лемма 4.1. Пусть и(х) е Wm(Q), и пусть для любого шара
/Срсгй
J| Vufndx^cptl-m+ma, 1>а>0, 1<т<«. D.1)
^р
Тогда для любого шара КР/2, принадлежащего Q вместе с кон-
концентрическим шаром /Сзр/2,

§ 4] ДРУГИЕ ВСПОМОГАТЕЛЬНЫЕ ПРЕДЛОЖЕНИЯ 89
vraimax| и(х) |< ' | и(xf) \dx' + с,ра,
Кр,2 meSKC'24
причем С\ определяется лишь постоянными п, с, m и а.
Утверждение леммы, как нетрудно понять, достаточно дока-
доказать лишь для гладких функций. Для любой и из Wlm (Q) оно
получится с помощью предельного перехода от гладких функ-
функций к и(х). Итак, пусть и(х) — гладкая функция. Возьмем две
внутренние точки х и х'', отстоящие друг от друга на расстоя-
расстояние р и отстоящие от границы S на расстояния не меньше р.
Обозначим через
шары с центрами в точках х, х' и (х + х')/2 и радиусами р, р и
р/2. Очевидно, что при любой точке у е /С" справедливо нера-
неравенство
| и(х)~ и{хг) |<| и(х)~ и (у) | + | и(у)~и(хг) К
ди _,, , Г | ды „
Д/,
где интегрирование и дифференцирование и в правой части
проведено вдоль отрезков, соединяющих конечные точки х, у
и х', у. Проинтегрируем обе части неравенства по у е К"'-
||
К" х К"
У
У У
dy\\Su\dl+ | dy^\Su\dl^U+h. D.2)
х U'-I/|<P x'
Здесь кп — объем шара единичного радиуса.
Оба интеграла jk, k=l, 2, оценим одинаково. Именно,
вводя сферические координаты г, со с центром в точке х, инте-
интеграл ]х запишем в виде
г
;,= J J rn~xdr d<s> J* | Vm (x + /со) | dl =
= J rn~l dr J J | V« (x + /со) | Л dm.
r<p /sir I a 1=1

90 ВСПОМОГАТЕЛЬНЫЕ ПРЕДЛОЖЕНИЯ [ГЛ. II
Функция ф(л)=: J J \Wu\ln~]dld<a абсолютно непре-
рывна по г; ее производная ор' (г) почти всюду совпадает с
гп-1 Г | V« (л: + гсо) | dco, и для ф(г) верна оценка
1 1
Ф(г)= '
где c2 = jj
Ввиду этого
о
г
= |ф(/)(п-1)Гя,
о
где с3 = с2A + "~ ), и потому
- <=°
Аналогично оценивается /2, и потому из D.2) следует, что
2п+1с
и(х)-и(х')\^с1ра, где р = |дс —дс'|, а с, = Кп(п + а) • Отсюда
имеем | и(х) |<| и(х') 1 + ^р" для Ул:, л:' е /СР/2- Усредняя это
неравенство по х' s /CP/2, придем ко второму утверждению
леммы 4.1.
Нетрудно понять, что этот же метод доказательства гёльде-
ровости и (х) внутри Q может быть использован и для доказа-
доказательства гёльдеровости функции и {х) в замкнутой области,
если только граница области Q обладает некоторой регуляр-
регулярностью. Достаточные для этого свойства границы можно сфор-
сформулировать, исходя из изложенного приема оценки | и(х)—и(х') |
через \х — х'|а. Мы этого здесь описывать не будем, а приве-
приведем лишь один частный случай, который будет использован
в дальнейшем.
Лемма 4.2. Предположим, что граница S имеет плоский
кусок S,. Пусть выполнены условия леммы 4.1, и пусть, кроме
того, для шаров Кр, пересекающихся с границей в части Su
Тогда и(х) ограничена и удовлетворяет условию Гёльдера с по
казателем а в QlUSu точнее, если шар /Ср/2 с центром в QIJS

§ 4] ДРУГИЕ ВСПОМОГАТЕЛЬНЫЕ ПРЕДЛОЖЕНИЯ 91
и концентрический ему шар /Сзр/2 не имеют общих точек с S \SX,
то
osc {«(*); Ар/2|Ш<с,ра
и
f I и (xr) \ dx' + с,ра.
Постоянная ct зависит лишь от п, с, m и а.
Замечание к леммам 4.1 и 4.2. Условие относительно
интеграла от | Уы | в них можно заменить предположением, что
J \х-х°Гат\ V«r^<cpn-m, где а>0, а лс° — центр Кр.
КрпВ
Полезно следующее предложение (см. [392]):
Лемма 4.3. Если для любого шара Кр cr Q и неотрица-
неотрицательной функции v(x) имеет место неравенство
J v(x)dx<cpm+a, m>0, a>0, /п + а<«, D.3)
то для любого шара Кр, отстоящего от границы S на расстоя-
расстояние, не меньшее 2р, и любой точки у е Кр справедливо нера-
неравенство
jx-y\~m~^v(x)dx^cl9^, D.4)
«р
причем С\ определяется лишь п, с, m и а.
Заметим, что из D.4) очевидным образом следует D.3), надо
а_
лишь точку у поместить в центр шара Кр и | х — у | 2 за-
а
менить меньшей величиной р 2.
Для доказательства утверждения леммы введем сфериче-
сферические координаты \х — у\ = г, .*~у. =ю с началом в точке у
и рассмотрим функцию
р
ф(р)= J v(x)dx=\ J vrn-ld<i>dr,
абсолютно непрерывную по р. Для почти всех р
<p'(p) = p*-i J р (у + р«о) de>.
|1

92 ВСПОМОГАТЕЛЬНЫЕ ПРЕДЛОЖЕНИЯ [ГЛ. II
С другой стороны, для шара Кр = Кр {х°), указанного в лемме
4.3, и х, г/е/Ср имеем
J \x-y\
< J г т 2 v(y + ra>)d«>dr = jr m 2<p'
__а_ _
т 2 v(y + ra>)d«>dr =
0
Интегрируя справа по частям и используя оценку D.3), полу-
получим
¦ J
f (-+!)¦
а
dr
r=2p
r=0
a a
Лемма доказана. Из нее легко выводится
Следствие 4.1. Если в лемме 4.3 неравенства D.3) с Кр,
замененным на Ор = /СрПЙ, выполняются и для шаров Кр,
р^а, пересекающихся с границей S области Q, то для любой
fip и произвольной точки у из fip имеет место неравенство
а_ _а_
)\х-у\"я 2v(x)dx^clp2
с постоянной с1( зависящей лишь от п, с, т, а и а.
Действительно, продолжая v(x) нулем на более широкую
область Qj :r> Q и применяя к продолженной функции в об-
области Q] лемму 4.3, убеждаемся в справедливости высказан-
высказанного утверждения.
При доказательстве теоремы единственности «в малом» для
обобщенных решений вариационных задач и эллиптических
уравнений с дивергентной главной частью нам потребуется
следующее предложение (см. [2115]; при т = 2 оно доказано
в [392]):
Лемма 4.4. Пусть в какой-либо области Rp диаметра 2р
задана функция и (х) ^ 0, подчиняющаяся при всех у е Rp
неравенству

§ 4] ДРУГИЕ ВСПОМОГАТЕЛЬНЫЕ ПРЕДЛОЖЕНИЯ 93
о .
Тогда при любой функции | (х) из W'„. (Rp) справедливо неравенство
J и (х) |2 (х) dx < СгР2а'т J ит~2 (х) | V| p dx,
в котором постоянная сх зависит от с, п, а и m *).
о ,
Пусть п > 2. Для любой функции | (х) из Wm (RD) спра-
справедливо представление
. ' ^, т„ = (я _ 2) „Хп. D.5)
J ( t | x - у \п
Это тождество, имеющее смысл при почти всех х из Rp, легко
выводится из хорошо известного свойства ньютонова потенциала:
%а-*<*>¦ D-6)
плотность которого | (у), например, принадлежит С1 (Rp).
Пусть сначала %{у) есть непрерывно дифференцируемая,
финитная в Rp функция. Для нее представление D.6) преобра-
преобразуем в представление D.5) просто с помощью интегрирования
д' 1 д 1
по частям, если учтем, что —-^ = —s-
dxt | л; - у Г йу, | л; - у |" "*
и что при интегрировании по частям все контурные интегралы
пропадут из-за финитности |(г/). Для любой функции |(г/)
о |
из Wm(Rp) возьмем последовательность финитных в Rp функ-
функций |р(г/) из С1 (Rp), сходящихся к %(у) почти всюду и в норме
Wm(Rv), и перейдем к пределу по р-*оо в тождестве D.5),
написанном для |р(г/). В результате этого убедимся, что D.5)
ВерНО ПОЧТИ ВСЮДУ ДЛЯ ЛЮбОЙ ФУНКЦИИ 1(у) ИЗ Wm(Rp).
Из D.5) имеем
откуда
um(x)!2 (*)<**< (-2—Z.J jum(x)
p
n
*) Утверждение леммы содержательно, если интеграл \ ит 2\V%f dx<<x>.

94 ВСПОМОГАТЕЛЬНЫЕ ПРЕДЛОЖЕНИЯ [ГЛ. II
Последний множитель при 1 < т < 2 оценим, используя
неравенство Гёльдера и условие леммы, так:
и2"" (у) dy ^
Г
R I п+т-2-~
RP I X - у | 2
<1
2-т 2т-2 „
ит(у)ау \ т I { dy \ т ———
n—m+—r I i г." -
«-2
При m = 1 или т = 2 эта оценка интеграла видна непосредст-
непосредственно. Поэтому
^Jр?-т J>w Г
«-"«+-7
л; — у | 2
4 \1Гт+^
сс2A1^-J 9^ { ит~2\ V
Случай /г = 2 рассматривается аналогично.
В ряде мест мы используем следующее предложение:
Лемма 4.5. Пусть непрерывная в Q функция и(х) при-
принадлежит Wm(Q,)[]W2(Q,), m^tl, и имеет конечный интеграл
J A +1 V« |)m~2 u2xxl2 dx, где | (х) — какая-либо гладкая в Q функ-
Q
ция, и пусть произведение и (х) | (л;) обращается в нуль на гра-
границе S области Q. Тогда интеграл J A +1 v" l)m+2|2 dx конечен и
< 8 osc2 (и; Q) | {[(т + 2J + п + 2] A +1 V« I)'2 «2J2 +
Q
+ 2 A +1 V« in V| p} dx + ~ J A +1 V« |)m |2 dx. D.7)

5 41 ДРУГИЕ ВСПОМОГАТЕЛЬНЫЕ ПРЕДЛОЖЕНИЯ 95
Для доказательства рассмотрим интеграл
1Я = J [ 1 + Ь (х))т+2 иХ( [и(х)~и (*„)] A +1 Vu (x) | )12 (х) dx,
Q
ie Xq^S и выбирается так, чтобы [и(х)~ ы(*0)]| (х) \xes = 0,
(х) = min {| Vu (х) |, N}, N — положительное число, которое мы
стремим впоследствии к + °°- Преобразуем JN, перенося
роизводную -г— с и(х) — и(х0) на остальные множители.
ОХ 1
)го даст
- | [и (х) - и(*ь)] [(« + 2) A
|
- 2 A + b)m+2uXl(l +1
при этом произведение u.XlUxkUxkx\ V« Г"' в точках, где | V« | = 0,
считаем равным нулю. Правую часть оценим сверху, заменяя
\ и(х)— и(х0) I на osc{«; Q} и используя неравенство Коши A.2).
Малый множитель е отдадим членам, подобным A+6)т+2Х
XI v" |2A +1 V« |)~2!2. Кроме того, учтем, что там, где | V« |> N,
производные ЬХ{ обращаются в нуль, а при |V«|^N функ-
функции 6 (л;) и | V« (x) | совпадают. Таким образом, получим:
JN < osc {и; Q} | [(« + 2) A + 6)m+I | их х\\ Va | X
1 Va |Г2|2
+ 2A + b)m+2\ uxx II Vu |A +1 Vu I)!2 +
+ 2A +6)m+2| Vu |A +| Vu |Г2| 11| V| \]dx<
<osc {u; Q} f [4A + b)m+2\ Vu |2A +| Vu |)~2|
{«; Q} J [|
+e(l+6)m+2| V« |2A+| V« |Г2|2 + -^-A+6)т+2и2Л1 + 1 V« 1Г4
b)m+2\ V« f(l +
+ 1A + 6)m+2(l +| Vu |)-'| V|

96 ВСПОМОГАТЕЛЬНЫЕ ПРЕДЛОЖЕНИЯ [ГЛ. II
Возьмем e=[4osc{«; fi}]~'. После приведения подобных
членов будем иметь
{[A + ь)ти\х{\ +iv«ir2l2(m +
Q
|Г2| V| f\dx+~\{\+b)m+2{\+\
Q
Устремляя в этом неравенстве N к + °°. получим D.7).
Лемма доказана.
Замечание 4.1. Условие непрерывности и(х) в лемме 4.5
можно отбросить, заменив его ограниченностью и (х). В нера-
неравенстве D.7) при этом надо считать
osc {и, Q} = vrai max и (х) — vrai max и (х).
а а
В ряде параграфов при исследовании дифференциальных
свойств обобщенных решений мы будем использовать приемы,
характерные для метода конечных разностей. Так, для функций
класса Lm (Q) мы будем рассматривать разностные отношения
ии)(х, А) =[«(*, *,_,, xi+h, xi+] хп) — и(х)]А з=
?=[«(# + het) — u{x)]h~\ Они определены почти всюду в VQ',
содержащейся в Q вместе со сдвигом на А в направлении
оси xt. Имеет место
Лемма 4.6. Если и{х), uXi(x) eLm(Q), то
для любой последовательности {hk}, сходящейся к нулю, и любой
Q' с: Q. Для некоторой подпоследовательности (Аа } функции
ua){x, A* ) сходятся к иХ{ почти всюду в Q.
Если u{x)e.Lm{u) и если для некоторой последовательности
Aft->0 равномерно ограничены интегралы
x, hk)\mdx<M, Q'cQ,
то функция и(х) имеет в п' обобщенную производную ¦— и
m
dx<M.
. I ax,
or
Чтобы убедиться в сильной сходимости в Lm(Q') разностных
отношений u(i)(x, hk) к uXl(x) при hk->Q, заметим, что для

§ 4] ДРУГИЕ ВСПОМОГАТЕЛЬНЫЕ ПРЕДЛОЖЕНИЯ 97
всех достаточно малых сдвигов hk в направлении оси xt и почти
всех х е Q' верно соотношение
i
"(О (х, hk) - uXi (x) = -? J -^- (ас + т/гАег) rfr - в*, (дс) =
о
= J [и*, (дс + -chkti) - иХ{ (дс)] dx,
о
J
о
и потому
|| И{« (дс, hk)—uXl (дс) ||т „, < J | «х, (дс + тЛАе,) - «*, (дс) ||m v dx.
о
Но правая часть в этом неравенстве стремится к нулю при
ЛА->0 в силу непрерывности иХ[(х) в норме Lm(Q')> и, следо-
следовательно, u(i){x, hk) действительно сходятся к uXi(x) в норме
Lm(?i')- Отсюда следует возможность выбора подпоследова-
подпоследовательности hk., /->°°, для которой u(i)(x, hk.) сходятся к иХ[(х)
почти всюду в Q. Для доказательства последнего утверждения
леммы воспользуемся тем, что в силу равномерной ограничен-
ограниченности норм || U(d (x, hk) \\m ц, из {hk} можно выбрать подпосле-
подпоследовательность |лА/}, /->оо, для которой и{{)(х, hkj) слабо схо-
сходятся в Lm (Q0 к некоторой функции w (х), причем Г | w {"dx^.M.
В том, что w (х) есть обобщенная производная -~—, убеждаемся,
переходя к пределу по hk,-*O в тождестве
J u(x)v(i)(x, hkt)dx=*
а
= - J u(i) (д:, hk,) о (л;, х, + hk, дс„) dx, D.8)
о*
верном при любой гладкой, финитной в Q' функции v(x) и всех
достаточно малых hk,.
Итак, мы доказали существование производной -^- и ее
принадлежность к Ьт{п'). Отсюда и из первой части леммы сле-
дует, что вся последовательность щ{) (х, hk) сходится к -^—
сильно в Lm(fi"), Vfi"c:fi'. Лемма доказана.
Формула D.8) будет использована нами и в дальнейшем.
Ее естественно назвать «формулой суммирования по частям».
4 О, А. Ладыженская, Н. П. Уральцева

98 ВСПОМОГАТЕЛЬНЫЕ ПРЕДЛОЖЕНИЯ [ГЛ. II
Выделим в виде отдельной леммы следующее известное
предложение:
Лемма 4.7. Пусть последовательность yt, 1 = 0, 1, 2
неотрицательных чисел удовлетворяет рекуррентному соотно-
соотношению
У1+1<сЬ1у1+°, 1 = 0, 1 D.9)
с какими-либо положительными постоянными с, в и Ь > 1. Тогда
8 b * еУ$+г). D.10)
В частности, если уо^.в = с~11гЬ~11&', то
У1<вЬ-Ч\ D.11)
и, следовательно, *//—»-0 при 1-+оо.
Для доказательства заметим, что если D.10) выполнено для
какого-либо значения / ^ 0, то оно будет верным и для зна-
значения / + 1. так как
Уш<сЬ
Очевидно также, что D.10) выполняется при / = 0. Отсюда
заключаем, что оценка D.10) справедлива при любом / = 0,
1, 2, ...
При доказательстве непрерывности функций по Гёльдеру
весьма полезно следующее предложение:
Лемма 4.8. Пусть функция и(х) измерима и ограничена
в некотором шаре /Ср, или в его части Qp, = Kp,(]Q- Рассмотрим
концентрические с KPt шары /СР и Кьр, где b > 1 — фиксирован-
фиксированная постоянная, и пусть при любом р < Ь~ р0 для и (х) выпол-
выполняется по крайней мере одно из соотношений
osc{«; Qp}<clPe D.12)
или
osc{u; Qp}<Oosc{«; Qbp} D.13)
с некоторыми положительными постоянными си 8^1 и ф< 1.
Тогда при р < р0 справедлива оценка
osc{«; Qp}<cp-apa. D.14)
где
а — min (е, — lg6ft), с = ba max [c,p*; coo},

$ fl ДРУГИЕ ВСПОМОГАТЕЛЬНЫЕ ПРЕДЛОЖЕНИЯ 99
а
coo=:osc{h; QPo}.
Доказательство. Будем ради простоты говорить о ша-
шарах КР, а не об областях fiP (это для доказательства несуще-
несущественно). Возьмем последовательность концентрических с /Ср0
шаров /Ср , Ра = 6~*Р0> k = 0, 1, 2 и обозначим через coft
колебание и{х) в /CPft. Из условий леммы следует, что
coft < max {с,р|; ФсоА_,}, 6 = 1,2,..., D.15)
и
соо < cb~a.
Отсюда для Ук = Ькащ при 6=1, 2, ... имеем оценки
= max {ci6*(-e)pS; 6a<h/ft-,} < max {сб""; ^_t} D.16)
и, кроме того,
уо = щ^сЬ~а. D.17)
Из D.16) и D.17) заключаем, что при всех 6 = 0, 1, 2, ... верна
оценка Ук^сЬ~а> т. е.
к а(Щ D.1.8)
\Ро
Рассмотрим теперь произвольный концентрический с Кр„
шар /СР радиуса р^р0. Тогда для некоторого k^l имеем
P*<P<P*-i. и поэтому
osc [и; /Ср} < osc {«; а
т. е. утверждение леммы доказано.
При получении оценок норм Гёльдера для вектор-функций
мы будем использовать более общее предложение:
Лемма 4.9. Предположим, что в QPo задана вектор-функ-
ция и (*) = (и1 (х) uN (x)) и N} функций wl (х) wN> (х),
обладающих следующими свойствами: для любого концентри-
концентрического с /Ср, шара Кьр, Ь> 1, 6р^р0, найдется функция wr(x)
такая, кто
osc {wT; fi6p} >б, max osc{«', fi6p}, D-l9)
и имеет место хотя бы одно из неравенств
; Ор}<с,ре D.20)
или
osc К; йр} < О osc К,- Qbp). D.21)

100 ВСПОМОГАТЕЛЬНЫЕ ПРЕДЛОЖЕНИЯ [ГЛ. II
Здесь Ь, б], С], е и ¦& — фиксированные положительные посто-
постоянные, причем Ь< 1, Кр — шар, концентрический с Кр,, a fip =
л:по
/г/ш любом р^р0 верны оценки
osc {«<; Qp} < ср-ара, / = 1 N, D.22)
где
D.23)
(oo = max osc {wl;
i=\ лг,
Доказательство. Так же, как и в предыдущей лемме,
возьмем последовательность концентрических шаров /CPft, p* =
= 6~ р0, ^ = 0, 1, ... Для каждого /СР. имеется свой номер г*
г. *
такой, что для w * выполняются следующие соотношения:
oscfa/*; ОРЛ>6, max ostfu'; ОРЛ D.24)
osc {a/*; QPa+) ) <max j clPeft+I; ^osc j аЛ; QPa ) )• D.25)
Возьмем шары /СР , /CP /Cp^ , где N% — произвольное
фиксированное число, не меньшее 2NX. Среди соответствующих
им чисел r0, r, rN-i найдется не менее [AfJAf,], совпадаю-
совпадающих с каким-либо значением / из A, 2 N\). Пусть это
будут числа гР) = ... =rPm = l, /в>[-др1. Рассмотрим wk
и /CPft только с k = pj, /= 1 m. Обозначим
coy = osc {a/; Qpp/}.
В силу D.25)
со/+1 < osc [wl; пРр .+i} < max {c,f^/+1; *©,}, D.26)
/ = 1 m — 1.
Умножая обе части D.26) на baNlU+1) и обозначая yf = baNif<i>},
получим
^"+1)C+I)^ ^a%/}. D.27)
Выберем а так, чтобы Ф6аЛГ'<1 и aN} (/ + 1) — е(р, + 1)<
— е)(/ + 1)<0. Для этого возьмем a = ^-min{e; — l

5 5j об оценках max | и (х) | 101
Тогда D.27) примет вид
#/+1 <max{Cjpjj; yj\, j=\ m-1,
и, следовательно,
у, < max {с,ро; уг] < max [c^l; щЬт],
а
со,- < b~aNd max {c.pj; coo6aV'} ^ c26-aW, / = 1, . . m.
Отсюда и из D.24) получим
Так как т^\-^-}> ^-— I, то из последнего неравенства
следует
Это неравенство справедливо для всех /=1 N и любого
N2~^2NX. Если взять шар Кр с произвольным р < pQ/b2Nt, то р
будет заключено между рА+1 = 6~*~'р0 и Ра = 6~*Ро с некото-
некотоk^2N
рым k^2Nu и потому
osc W; ^ < {'
<b
Если же p^pQ/b2Ni, то
osc{«'; QpX-^-oscR Qp}<-JL<-^(-i^ ¦) <^-6 (-j .
Таким образом, при любых р^Ро будем иметь оценку D.22).
§5. Об оценках тах| и(х) \ и некоторых интегральных норм и(х).
Класс функций $&„(&#, \, I, a, e, k)
Установим несколько предложений, дающих возможность
на основании некоторых интегральных неравенств заключить
об ограниченности максимумов модулей, а также тех или иных
норм Орлича для функций из L\ (Q) и Wm(fi), I ^.m^n*).
Различные варианты предложений такого типа были доказаны
в работах [28,, 11,, 52,,4, 21,2,16,18,20 и др.] в связи с оценками
|д
*) Для т>п ограниченность vrai max и (х) и даже | и |д следует
из принадлежности и (х) к Wxm (Q) (см. те >рему 2.2). Поэтому здесь и ниже
в гл. II мы рассматриваем лишь случай

102 ВСПОМОГАТЕЛЬНЫЕ ПРЕДЛОЖЕНИЯ 1ГЛ. II
решений эллиптических и параболических уравнений и вари-
вариационных задач.
Лемма 5.1. Пусть суммируемая в Q функция и(х) при
любых k^ko^O удовлетворяет неравенствам
6Ak, E.1)
где Ak = {х: х е п, и(х) > k), a k0, у, а и б — постоянные, при-
причем 6>0, 0^а^1+6. Тогда vraimax«(;e) не превосходит
некоторой постоянной, зависящей лишь от у, а, б, k0 и mesfi.
Доказательство. Рассмотрим функцию
f(k)= j(u(x)-k)dx.
Ч
В силу определения и известных свойств интеграла Лебега
оо оо
f(k)——^(t — k)d mes At = J mes Atdt
k k
и для почти всех k верно равенство f'(k) = — mes Ak.
Поэтому E.1) можно переписать в виде
k >k0. E.2)
Интегрируя это неравенство по k от &о до &max = vrai max u(x)
и учитывая, что f(ko)^.yko mes1+6fi, получаем желаемую
оценку
шах< ^оехр { ° +б) v k6Qmes6 Q } при а=1+б.
Лемма 5.2. Пусть в условиях леммы 5.1 бе(-1,0] и
< 1 +6. Тогда для и(х) справедливы неравенства
j"dx<B с Vq<~ l +a E.3)
при б < 0 и
|еР«'-а^<5 E.4)

§б] об оценках max | и (х) | 103
/ 2а~1 (l — 2a-1) \
с Vp из (О, \ _ а)—-J при 6 = 0. Постоянные В опреде-
определяются величинами у, а, 6, k0, \\ и \\и А , а также q при б < 0
и р при 6 = 0.
Для доказательства снова проинтегрируем неравенство E.2).
При этом в случае б < 0 получим следующую оценку для
функции f(k):
. _в_ ]_ a
и, тем самым,
, , А
f(k)<ck+ e , k>2kQ, c = Y в(^Ьб) Ml-2
E.5)
а при 6 = 0 приходим к оценке
e-^-a, k>2k0, c,= T<56)
mes Ak
co. -i— YA_o)
Отсюда, используя очевидное неравенство
f (у) ~> j (« — у] dx > у mes ЛА,
выводим оценку для меры множеств ЛА:
с (уH""''*. б < 0,
_ /_*_\> — а
Of Cfe 1 Ь~1р~°' \ 2 / Д — Г)
при произвольном ^^4^0. Из нее и соотношения
Г ф (и (х)) dx= J ф' (^) mes ЛА d^,
справедливого для любой непрерывно дифференцируемой функ-
функции ф(ы), следует суммируемость функций ф(ы) = ы17 с V<? <
<(— 1 +а)/6 при 6<0 и функций ф(ы) = ер"'~а с VP < с^"
при 6 = 0, а также оценки E.3) и E.4).
Следствие 5.1. Для любой и(х) из Wn(Q) верны нера-
неравенства
E.6')
при VQ'cfl с постоянными Р>0 и В, зависящими лишь
N _
от IIи Ш'о и от расстояния Q' до дп. Если Q = 2 ^« и ^« —

104 ВСПОМОГАТЕЛЬНЫЕ ПРЕДЛОЖЕНИЯ [ГЛ. 11
строго липшицевы области, то неравенство E.6') верно и для
всей области Q. Постоянные р > 0 и В определяются || и \?>и и
областью Q.
В самом деле, умножим и(х) на срезающую для Q функ-
функцию ?(*), равную 1 в п'. Ясно, что й = |и|? и й{к) при 6^* О
принадлежат l^Jt(Q). Применяя к п(к) неравенство B.12) с р= 1,
т = /г, находим
u — k)dx^cmes ЛА|| й* |^ а <с{\\ и \$аmes Ак,
где сх зависит от расстояния Q' до дп, т. е. для и (х) выпол-
выполнены неравенства E.1) с а = 0, 6 = 0, у = с1\\и\$)а и Vk^O.
Лемма 5.2 гарантирует для й (х) оценку J ep" dx ^ с2, а тем
_ а
самым и желаемую оценку для и в Q' cr Q.
Если Q — строго липшицева область, то функцию и (х) е
eft^rt(Q) можно продолжить на более широкую область Q
с сохранением класса, причем так, что || и \\п ^^с2\\ м||„а, где с2
не зависит от и. Отсюда и из доказанного только что след-
следствия 5.1 вытекает оценка E.6) для LJ' = Q. Из этой же оценки
для строго липшицевых областей Q следует ее справедливость
и для суммы конечного числа таких областей.
Лемма 5.3. Если функция и(х) принадлежит Wlm(Q),
l^m^n, имеет ограниченный vrai max и (х) и k^k
s
^ vrai max u(x) удовлетворяет неравенствам
s
s
— Л
J | Vm Г dx < Y&a mes " Ak E.7)
Ak
с 6 > О, O^as^d + w, то vrai max и (х) оценивается постоян-
постоянной, зависящей лишь от у, а, пг, б, k0 и от mesQ.
Для доказательства заметим, что в силу леммы 3.6 функ-
О
ция и{к) {х) = max {и {х) — k\ 0} при k^k0 принадлежит Wm (Q)
и, следовательно, к ней применимо неравенство B.12). Восполь-
Воспользуемся B.12) и неравенством Гёльдера
J (и -k) dx<[ J (и -k)mdxY mes'~ Ak <
Vu\mdxV" mes ~~^+~Ak.

об оценках max | и (х) | 105
Отсюда и из E.7) следует, что для и(х) при k^k0 справедливы
неравенства
г -L JL ,+±
I (и — k) dx ^ су т k m mes m Ак
с — >0 и — ^ 1 Н , так что оценка vrai max и (х) дается
ftl fit fit о
леммой 5.1.
_ n _
Лемма 5.4. Предположим, что Q = (jQ/, причем каждую
/=i
мз Q/ можно невырожденным липшицевым преобразованием ото-
отобразить на выпуклую область Q/t Если и(х) принадлежит
Wm(Q) и при k, больших некоторого k0, удовлетворяет нера-
неравенствам E.7) с 6>0, 0<!а<;б + /я, то vrai max u{x) оцени-
Q
вается постоянной, зависящей лишь от у, а, пг, б, k0, нормы
|| и\\иА/г и от области Q.
Доказывается эта лемма так же, как предыдущая; неко-
некоторое осложнение состоит лишь в том, что функции «<ft) (x) =
= max {и (х) — k; 0} при k^k0, вообще говоря, не принадлежат
о .
Wm(Q) и поэтому нельзя непосредственно использовать нера-
неравенство B.12). Тем не менее можно доказать, что при k, боль-
больших некоторого k', зависящего от ||m||1-j4. и области Q, функции
u{k) (х) удовлетворяют неравенству B.12). Действительно, за-
мыкание области Q можно представить в виде (JQ/ и каж"
дую из Q/ невырожденным липшицевым преобразованием
z = z!(x) можно отобразить на выпуклую область Q/. Пусть
d — максимальный диаметр областей й/, / = 1 #,
а а= min mesQ/. В силу очевидного соотношения
/=1 N
kmes Alk=k mes [z^Qj1. u(z)> k}^. [ иdz^.Ci\\ и\\uA ,
J «0
4
где Ci зависит от max| z1 \UpQ , при k^k'=-j-\\u\\UAk меры Ж
не превосходят а/2, и потому mes(Q/ \ Л0>а/2, /=1 ЛЛ
Ввиду этого для каждой Q/ из C.6) следует оценка
J
Ч
(и - kf dz < cS {^-)P mes

106 ВСПОМОГАТЕЛЬНЫЕ ПРЕДЛОЖЕНИЯ [ГЛ. II
с любым р из [1, т] при т<п и с ре[1,оо) при т = «.
Переходя к старым переменным х и производя здесь сумми-
суммирование по всем /, получим неравенство
J (и - ft)" dx < с2 mes'""* Ak || Vh<*> ||^ „ , ft > ft', E.8)
с постоянной c2, зависящей только от т, N, a, d и
max| z1 (x) |Llpfl , max| Jf'B) |црд . Таким образом, функции
«<*>(*) при k^k' действительно удовлетворяют неравенству
B.12). Тем самым, лемму 5.4 можно считать доказанной. Из
леммы 5.3 выводится следующая теорема:
Теорема 5,1. Пусть функция и{х) из Wlm,q(Q) *), l^m^.n,
q^l, ограничена на S и при & ^ ? 2> vrai max м удовлетворяет
s
неравенствам
m m
J | Vm Г dx < Y ( J (и - *)' ^) ' + Y^" (mes Akf ~~+*, E.9)
где у, I, а и г — положительные постоянные, причем
I < fa =———, е > 0, m ^а < eq -f- m. E.10)
Тогда vrai max и (х) не превосходит постоянной, зависящей
а
лишь от mesQ, m, q, k, у, I, а, е, а также от нормы \\u\\ А .
k
Последнюю в случае m < а < em + m можно заменить нормой
\\и\ А , а при а = пг — величиной I J uBidx\ ' с произвольным
'k U )
в, >0.
Доказательство. Заметим прежде всего, что в нера-
неравенстве E.9) интеграл в правой части оценивается при боль-
больших k через левую часть E.9) с малым множителем. Действи-
Действительно, в силу неравенства B.12) при /<т имеем
2 i_
|| и — k ||, А ^c(meSi4ft)' m l|V«||m A . E.11)
С другой стороны,
<^II«IU, E.12)
К
*) Напомним, что Wlm . (Q) есть Wlm (Q) (] L (Q).

§51 об оценках тах|и(*)| 107
так что при
к > kr = max [k; L BYcraf'/1<*"')"""} E.13)
из E.8), E.11) и E.12) следуют неравенства
_1 \"
" Akj
{mesAk) n =\lkm{mesAk)
где 6 = e — ^-Z—> о, у,=2\1а~т, k^k'. Таким образом,
для u(x) выполнены предположения леммы 5.3 с 6 > 0, а = т,
ka=k' из E.13), и поэтому vraimax«(;t) оценивается через т,
Q
^', б, \i и mesQ.
Заметим, что в случае а = т последнее из условий E.10)
справедливо при V*? > 0, поэтому при а = т все предыдущие
оценки остаются верными, если в них положить ^ = 6!, L'=
=1 J м8- dx\Ue\ Ve, > 0.
Чтобы завершить доказательство теоремы, надо при т < а <
< em + т оценить L = || и \\^ А через || м ||lj4 для V? < т. В силу
B.23) интегральный член в правой части неравенства E.9) до-
допускает оценку
/ J (и - kY dx)"^ J | Vm Г dx + cj \ (и - k)dx)m
с любым в! > 0. Возьмем е!=у- и k = k. Тогда отсюда и из
E.9) следует
J | Vm Г dx < 2Y Гc_l || u - k \^A + ?a(mes V^"
Л? L 2v ' *
Используя еще неравенство B.12) и то, что q < tn, получаем
*• = И « II,. ЛС < ^ (II И - * IL А + & meS'/<7 Q) <
к V я
II V" II», Ak + k meS'/9 Q) < C (II « «1. Лй + !
( II»,
Теорема доказана.

108 ВСПОМОГАТЕЛЬНЫЕ ПРЕДЛОЖЕНИЯ [ГЛ. И
Замечание 5.1. Утверждение теоремы остается в силе,
если в неравенстве E.9) правую часть заменить суммой
N, j т [е
где /( < m, ег > О, т^щ < eq -f- m.
Используя вместо леммы 5.3 лемму 5.4, а вместо неравен-
неравенства B.12) неравенство E.8), можно доказать такую теорему:
Теорема 5.2. Если Q подчиняется условиям леммы 5.4 и
функция и{х) из Wm,q(Q), l^m^tt, q^l, при k^k удовле-
удовлетворяет неравенствам E.9), E.10), то vrai max u(x) оценивается
я
постоянной, зависящей от q, у, I, a, e, m, k, mesQ, нормы
|| и || А и области Q. При а < em + m норму \\ и \\ А можно за-
' k ' k
менить нормой || и ||, А .
. Переходим к получению локальных оценок vrai max и. Возь-
Возьмем шар Kr и семейство концентрических с Kr шаров Ко и
Кр-ар с -у^р — ap<p^.R. Обозначим через AkiQ множество
точек из Qp = Kp[\Q> в которых u(x)>k.
Будем говорить, что функция и(х) из Wm(Q), 1 ^л
принадлежит классу 9lm(Q#, у, I, a, e, k), если для любых
и всевозможных пар шаров Кр и Кр-ар указанного выше вида
выполняются неравенства
[am "L
E.14)
с некоторыми положительными постоянными \, е,
< ет -{- m, I < т.
Если шар Kr принадлежит Q, то класс %m(QR,y, I, a,e, k)
будем обозначать через Wm(KR, у, I, a, e, k).
Теорема 5.3. Для любой функции и{х) из класса
4Lm(KR, Y. ^> °. е> &) справедлива оценка
vrai тахм(*)^с, E.15)
KRI2
где с зависит лишь от m, \, I, a, e, k и а/ = R~nl \\u — k ||; A
Аналогичная оценка верна и для функций из 9lm (QR, у, I, а, е, k),

§ 5] об оценках max | и (к) | 109
если vrai max и(х) ^ k или QR удовлетворяет условиям леммы 5.4.
sn/Сд
При этом в E.15) надо Krp заменить на п^р. Постоянная с
зависит только от гп, у, I, ci, ft, е и at, если vrai max и (х) ^ k;
S[\K
R
в общем же случае с зависит и от QR.
Проверим справедливость первой части теоремы 5.3. Вторая
доказывается аналогично, надо только в случае, если условие
vrai max м^^ не выполнено, вместо неравенства B.12) к функ-
SUKr
циям u(k){x) применять неравенство E.8) из доказательства
леммы 5.4.
Приведем доказательство теоремы для случая m < п.
Прежде всего сделаем преобразование независимых пере-
переменных
xl — x° = Ryl, i=l п,
так что шар Kr(x°) в новых переменных перейдет в /Си а рас-
рассматриваемая функция (сохраним за ней то же обозначение
и (у)) будет удовлетворять неравенствам
J (и - k)'
k,p '
E.16)
у<р-<тр<р<1, где Yi = Ymax{2ra; 2tn).
Покажем, что можно так выбрать значение ko^k, чтобы
vraimaxM(«/)^2&0, Для этого рассмотрим последовательность
концентрических шаров /СрЛ, где рА = —Ь л+1 , h = 0, 1,2
и последовательность уровней kh = 2k0—4-, Л = 0, 1, 2
где k0 — пока произвольное число, удовлетворяющее условию
ko^k, которое будет фиксировано ниже.
Введем обозначения:
гДе SW— непрерывно дифференцируемая невозрастающая функ-
функция аргумента /е(—оо, оо), равная единице при /^1/2 и

ПО ВСПОМОГАТЕЛЬНЫЕ ПРЕДЛОЖЕНИЯ [ГЛ.11
нулю при /j>3/4. Функция ?л(г/), как легко видеть, равна еди-
единице в шаре /Срл+1 и равна нулю вне шара /СрА, Ра=у(Ра
Замечая, что
*Л+1 Л
воспользуемся для оценки /Л+1 неравенством B.12). Мы при-
применим его к функции t,hu^kfl+i\ которая принадлежит wm(Aka+1,pJ-
Это даст
*a+i' "
-.+2Л+1с'"(м - "A+l) ** ^+,.
где с' = max 11/ (t) |.
F[l/2, «>1
Далее, в силу E.16) с k = kh+l, p = pA, р —сгр = рА имеем
Отсюда и из E.17), применяя неравенство Гёльдера, выводим
_!_ 1 1
/ft+i<CYi*+3/ftmes'~* Л*а+,.Ра +
j_ ? -L+-1 JL
+ mB/)'»'i* » A +
mes
J L
В правой части E.18) оценим сверху меру множества
Akh+X,ph с помощью неравенства
1
Jh>\\u-kh\\л . >(kh+l - kh)mes* Ah+vPh =
яЛ+1 л
В результате получаем
V »/ft m +*7m /Amj. E.19)
Здесь b = 2m, а постоянная с, определяется известными вели-
величинами: п, т, I, у, а, е и константой с из неравенства B.12).

S 6J об оценках max | и (х) | 111
Величины /А при всех Л = 0, 1, 2, ... не превосходят а„ =
= \\и(у)— k\\. . , а потому из E.19) следуют неравенства
"•• л*о, Ро
/Л+1 < с2ЬнА+\ h = О, 1,2 E.20)
« em
Рассмотрим столь большие значения &0> чтобы
с2<аЛ~1/в. E.22)
Тогда для J{ будем иметь из E.20)
/, < с2аТ< Fс2)-1/вЪ~и* ^ 6, E.23)
и потому в силу леммы 4.7
/Л<е*Г(Л-1)/в-*0 при Л-*оо.
Следовательно,
vrai max и (у) ^ lim kh = 2k0,
/C Л
где ^0 определяется условиями ko^k и E.22); например, можно
положить
= max [k; {Ъс{Ь^)т~1) аА; (S
1Аал}. E.24)
Величину ал, входящую в оценку E.24), можно в свою оче-
очередь оценить через Д/^|| и(у) — k\\itA , если воспользоваться
неравенством B.12) и условием E.16) ck = k, p —ap = po = 3/4,
р= 1. Именно,
If ?. 1+i. \
flm<ciiVMiL^iPi<cY7l4fl' + ^mmesft mN' E>25)
где с—постоянная из B.12).
Справедливость оценки E.15) следует из E.23) —E.25).
Теорему 5.3 можно считать доказанной для случая т < п.
Аналогично доказывается она и в случае т = д, надо только
через Jh обозначить || и — kh \\q, Ak p с каким-либо q^l, для
которого а < е<7 + т.
Замечание 5.2. Из оценок E.23) — E.25) легко заключить,
что при а = т постоянная с = 2&0 в неравенстве E.15) линейно
зависит от величин k и at.

112 ВСПОМОГАТЕЛЬНЫЕ ПРЕДЛОЖЕНИЯ [ГЛ. II
Замечание 5.3. Правую часть в неравенстве E.14) можно
заменить членом более общего вида
-n J (u-k) hdx) h + %-hnkai mes'"-+4.P
где et > 0, tt< tn, tn^.a,i< егт + m. Кроме того, можно пред-
предположить, что в неравенствах E.14) диапазон изменения ра-
радиусов следующий: A — его) /?^Р — сгр < р<[ /?, где а0 —неко-
—некоторое число из @, 1). При этом для vraimaxH(;t) будет спра-
ведлива оценка, аналогичная E.15). Это же замечание верно
для шаров, пересекающихся с дп.
Замечание 5.4. Нетрудно видеть, что функция и(х) из
Wlm(Q) принадлежит классу 2fm(Q#, \, m, m, e, k) для любого
шара Kr, если и(х) при всех k^k удовлетворяет неравенствам
[Г !-— 1
J (и - k)m (tm +1 V? Г) dx + km mes " Ак, р , E.26)
J
[Г
J (и
Ak,P
в которых t, (x) — срезающая функция для произвольного кон-
концентрического Kr шара Кр, P^.R> У и q — фиксированные по-
постоянные, причем q > п.
Лемма 5.5. Пусть функция и (х) принадлежит Wxm (Kr)
п
и для любой пары шаров Кр и Кр~ар< "о"^Р — сгр < р^/?, кон-
концентрических с Kr, при произвольных уровнях k^k подчи-
подчиняется неравенствам E.14) со = е = 0, Km. Тогда для и(х)
справедлива оценка
J «Р« dx < BRn, E.27)
причем постоянные $ и В в E.27) зависят лишь от величин \,
k,l,mual = R-nll\\u-k\\l,4R.
Будем проводить те же рассуждения, что и при доказатель-
доказательстве теоремы 5.3, заменив последовательность уровней kh из
теоремы 5.3 другой последовательностью: &л = (Л + 1)&о> А =
= 0, 1, 2, .... а в остальном используя те же самые обозна-
обозначения, что и в теореме 5.3. Тогда неравенство (Б. 17) останется

§5] об оценках max | и (х) | 113
прежним, а справа в E.18) не будет множителя kolm. Оценивая
снизу меру Akh+Vph с помощью неравенства
h > (ftft+i - kh) mes m Auh+V Pft = k0 mes™ Akfi+v Pft, E.28)
мы получим вместо E.19) следующее неравенство:
(—^L+ — ——+ i —\
*о ' '*' + *от /Лт/ + с./г0"'/Л. Л = 0,1 E.29)
в котором постоянная с, определяется величинами т, I, у, п
и константой с из B.12). Фиксируем число k0 из условий ko~^k,
(т_ т_ \_^L HL \
ko'lal +k0 «а« + йо-'а/<1, E.30)
'1
где
; 1}.
Тогда, как нетрудно подсчитать, из неравенств E.29) и условия
/0 ^ а следует оценка
Л=1, 2, ... E.31)
В силу E.28) отсюда получаем
mesA^OrV"**, Л=1, 2, ... E.32)
Благодаря этому неравенству
в w d+ ®k mes Ki<
mes л*л-рл + em° mes
2 ер (Л+2) *«"ртл + e2Pft« mes /С,.
А=1
Поэтому при р < pm/k0 интеграл J ер"<у) dy= J ep"<JC) йл: /?~"
1
ние &о> определяемое неравенствами E.30), зависит от вели-
величины ал. Последнюю в силу E.14) можно оценить через а;- так,
как это сделано в теореме 5.3.
Лемма доказана.
не превосходит числа fi=:e2p*» -"рд-ад)' "Ь mes/Ci • Значе-
Значе53)

A4 ВСПОМОГАТЕЛЬНЫЕ ПРЕДЛОЖЕНИЯ [ГЛ. I]
Замечание 5.5. Если в неравенствах E.14) показатель а
отличен от нуля, причем а < т, то вместо E.27) будет выпол-
выполняться оценка
Г
а
Доказательство ее аналогично вышеприведенному, надо только
уровни kh выбирать иначе, чем выше, а именно:
kh = (h + l)mt{m-a).k0, А = 0, 1, ...
§ 6. Класс функций §8т(й, М, у, уи 6,-J-
Параграфы 6—8 содержат большую часть новых аналити-
аналитических средств, позволяющих установить гёльдеровость реше-
решений различных задач и их производных. Именно, в них мы
даем интегральные критерии того, когда ограниченные функции
из Wim(Q), 1 < т^п, удовлетворяют условию Гёльдера.
Первая теорема такого типа была установлена Де Джорджи
в работе [lli]. Приводимые ниже теоремы установлены в на-
наших работах, посвященных изучению эллиптических и парабо-
параболических уравнений. Способ их доказательства является раз-
развитием метода Де Джорджи. Чтобы облегчить их понимание,
начнем изложение с одного важного частного случая, который
обслуживает гл. III — V.
Будем говорить, что функция и (х) принадлежит классу
8m(Q, М, y, Yi. б, ~), если и(х) e=lP«(Q), vraimax|u|<M
\ Я I п
и функции w (х) = ± и (х) удовлетворяют неравенствам
J | Vo» Г dx <
Ak, p-ap
а-тр ^ «/max[a)(jf) —*]m + YiJmes « Ak p> F.1)
л
в которых Ак, р = {х^Кр: w (х) > k}\ /Ср-стр с а <= @, 1) и Кр —
произвольные концентрические шары, принадлежащие Я; k —
произвольное число, подчиняющееся лишь условию
k > max w (x) - 6М; F.2)
М» т, y, Yi» S, q — фиксированные положительные числа, при-
причем l<m<«, q>n, 0<б<2.

i 6] КЛАСС ФУНКЦИЙ »m(Q,M,v. Vr в. 1/*) 115
Замечание 6.1. Легко проверить, что неравенства F.1)
о Y = Y(c), yl = (Mm -{- I) cl вытекают из неравенств
Ak,p
J (w-k)m\^rdx + cl(km+l)mes~l'Akt(>, F.3)
в которых ^ (*) — произвольная срезающая функция для шара Кр-
Основной целью данного параграфа является доказательство
вложимости 33m(Q, М, у, уи б, \lq) в Са (Q) с некоторым поло-
положительным а, определяемым лишь параметрами т, у, q и б *).
Доказательство этого факта базируется на следующем важ-
важном вспомогательном предложении:
Лемма 6.1. Пусть w(x) — ограниченная функция из Wlm(Q)
и Kr, Kr/2> Kru — концентрические шары, принадлежащие Q.
Предположим, что для произвольных концентрических KR ша-
шаров Кр-ар и Кр с R/4 < р — ар < р < R функция w (x) удовлет-
удовлетворяет неравенствам
J | Vw Г dx <
^k, р—ер ^ Аи р—ар
[() ] + Y,] " Ak,p F.4)
Ak,P
при любых значениях k из фиксированного диапазона
ke=[k',k"] F.5)
и любых
/еф, 1(Л + тахю(*)I. F.6)
Kr J
причем
A<(l f)K F.7)
Здесь m, у, yit q, б0—положительные постоянные, причем ^,
ц > п. Обозначим ю = max w (x) — k''. Существует число s =
= s{m, у, q, do) > 0 такое, что если
k" > max w (x) — 2~s(a, F.8)
*) Зависимость различных величин от п в данном параграфе, как и
в большинстве других, не отмечается.

116 ВСПОМОГАТЕЛЬНЫЕ ПРЕДЛОЖЕНИЯ [ГЛ. II
ТО
(о<2smax 1 max o> — max or, (^-\т R~~\. F.9)
к*
Для доказательства леммы 6.1 предварительно установим
справедливость нижеследующих двух лемм.
Лемма 6.2. Предположим, что функция w (х) удовлетво-
удовлетворяет неравенствам F.4) при R/A ^ р — <тр < р ^ R/2, k e [k°,
k°-{-H/2], где Н = max w (х) — k°, и любых I из F.6). Сущест-
вует постоянная 6 > 0, зависящая лишь от щ, у и q из F.4),
такая, что если
mes Ak,, я/2 < QRn, F.10)
то верно по крайней мере одно из неравенств:
maxw(x)^k° +%- F.11)
хщ* 2
либо
j_ n
(^)га1~ F.12)
центрических с K.R шаров /Ср ,
h
Доказательство. Рассмотрим последовательность кон-
гл 4 2 +
и последовательность уровней
«А=« Т ~ „А+1 • Я^О, 1
и введем обозначения
^=/remesi4VPft, Z)A+1 = Л,. „. . \
Ясно, что k°^kh-^k
так что для значений k = kh, l=kh+l, р = рЛ, р —ар = рл+1
при всех Л = 0, 1, ,.., справедливы неравенства F.4). Из них
следует, что
J | Vw Г dx К У [2<Л+3) m (-f)"" ^
F.13)

5 6] КЛАСС ФУНКЦИЙ »m(Q,iW.V, Y,, б. 1/?) 117
Если неравенство F.12) неверно, т. е. если — <HmR m^ ч)t
о из F.13), применяя неравенство Гёльдера, получаем
J |Vo»|rfje</ J \^wrdxY(yhRnI~^^y^2h+eHRn-1yh~.
°h+i tan /
F.14)
Левую часть F.14) оценим снизу по неравенству C.4) с k = kh,
l = kh+u р = рл+1, предположив выполненным условие F.10)
с 6<-i-4"V
Dh+\
HR-1 у ~+J(mes Kri* ~ mes Ak>> RB)
Отсюда и из F.14) следует оценка
Ук+1<сЬ"у)Г, h = 0,1 F.15)
с постоянными
e = -jj—-i>0, b = A, с = 2п+%у11ткп\ F.16)
Если предположить, что уо^.с~11еЬ~11е, т. е. что выполнено
условие F.10) с Q^.c~1/eb~Ue\ то в силу леммы 4.7 из
неравенств F.15) можно заключить о стремлении yh к нулю
при h-* оо, а это означает, что
vrai max w (a:)< lim kh = k°-{--?r.
Таким образом, утверждение леммы 6.2 доказано, причем можно
положить
e = min{2-2n-4; c-'V'^l, F.17)
где постоянные с, Ь и е определены в F.16).
Лемма 6.3. По любым положительным постоянным 6, у, б0,
1</п<^п и q > п можно указать число s > 2 такое, что если
функция w(x) удовлетворяет условиям леммы 6.1 с
(x) — 2~s(o, где ю = таха>(л;) — Л', F.18)
и если
'~(^)"Г, F.19)

118 ВСПОМОГАТЕЛЬНЫЕ ПРЕДЛОЖЕНИЯ [ГЛ. II
то для значения
~s+1
л;) —2~s+1<d F.20)
Kr
справедливо неравенство F.10).
Доказательство. Предположим, что при некотором це-
целом 5>2 выполнены неравенства F.18) и F.19) и w{x) удо-
удовлетворяет всем условиям леммы 6.1.
Введем обозначения
kt = maxw -2Л>, Dt = Akft Rl2\ Ak Rl2, F.21)
Kr
t = 0, 1 5-1,
и рассмотрим неравенства F.4) с p = R, p — op = R/2, полагая
в них k = kt, l = kt+u t = 0, .... 5 — 2. Последнее возможно,
ибо в силу F.18) при t ё= [0, 5 — 2]
&'<&,<&", k, < kt+l = maxw - 2-('+1)(o = ±(kt + max a»).
*r z Kr
Из F.4), учитывая F.19), выводим
V» P Л <
J
f )"]«;-*«"¦ < 2"+Vrf (i)"
+ (f )]«;*«"¦ < 2"+Vrf (i)" JT". F.22)
С другой стороны, из неравенства C.4) с k = kt, l = kt+1,
р = #/2 и из условия F.7) следует, что при / ^ 5 — 2 верна
такая оценка:
mes " Aks_vRi2 ^+
6 (I?/2)rt
С
^J I Vffi) Idx
- ft,) (mes KRl2 - mes Л^,
поскольку mes Ак/, R/2 <! mes Ak\ R/2 <! A — 60) mes KR/2- Возводя
обе части неравенства F.23) в степень т, применяя неравен-
неравенство Гёльдера и учитывая затем F.22), находим
| Vw |m dx (mes Z)<)"'~1^
= 0, .... 5*- 2, F.24)

откуда
КЛАСС ФУНКЦИИ
(mesi4ft л
m(n-l)
\12) П
(U, М
1
т—\
. V. V,. 0
п—т
¦1Д?)
mes
П9
Просуммируем эти неравенства по / от 0 до s — 2, замечая,
что Ymes Z)< <! mes KRi2 = к„ гу) • В результате для mes 4^_,,я/2
получим оценку
(mes Д^. л/2)п<т-1> < *"c8_f /? т-' , F.25)
из которой следует, что для k° = ks_l выполняется неравенство
F.10): mes^_l,s/2<e/?n при
F.26)
Лемма 6.3 доказана.
Доказательство леммы 6.1. По заданным значениям т,
у и q из F.4) фиксируем число 6 > 0 в соответствии с лем-
леммой 6.2. Затем по этому значению 6 и постоянным т, у, q и б0
из условий леммы 6.1 выберем число s > 2 в соответствии
с леммой 6.3. Если окажется, что a><^.2sRl~nl4(—) "\ то
оценка F.9) доказана. Если это не так, т. е. если выполняется
неравенство F.19) и если верно F.8), то в силу леммы 6.3 для
&0 = maxa> — 2~s+i(u^k' справедливо неравенство F.10). Кроме
того, H=maxw-k° = 2-s+1<i>>Rl-n«(*-)ilm и k° + ^
Поэтому на основании леммы 6.2 заключаем, что
max w < k° + 4- = max w — 2~*+1ю + 2"sco = max w — 2~
к kr kr
т. е. снова справедлива оценка F.9).
Утверждение леммы 6.1 доказано.
Из леммы'6.1 вытекает следующее предложение:
Лемма 6.4. Для любого элемента и (х) из класса
23m(Q, M, у, уи б, 1/?) и любых концентрических шаров Kru и
KR cz Q справедливо по крайней мере одно из неравенств:
о8с{«;КЛ}<т2у-^I/га F.27)
или
osc{и; KRI4} < A - t"'2-s)osc{«; KR}, F.28)
где s = s(m, у, q, Vj) из леммы 6.1, а г = max {2; 2/6}.

120 ВСПОМОГАТЕЛЬНЫЕ ПРЕДЛОЖЕНИЯ [ГЛ. 11
Доказательство. Поскольку и (х) е 23m (Q, М,у,\и б, \/q).
то функции w (х) = ± и (х) удовлетворяют неравенствам F.4;
при любых k^maxw(x) — 6M, l>k. Положим
кр
© — T-'oscfu; KR). F.29)
Тогда
k' == max w {x) — со > max a> (*) — у osc {ы; /Сд} F.30)
k'^maxw(x)—2sc{«; KR)^maxw(x) — 6M, F.31)
и потому для w(x)= ± u(x) справедливы неравенства F.4) при
всех ki^-k', l>k. Очевидно, что имеет место по крайней мере
одно из неравенств:
mes { х <= KRi2- и (х) > max и — -g- osc {и; KR} } < у mes KRi2 F.32)
Kr
или
x s /СЛ/2: ы (л:) < mm и + j osc {ы; /СЛ} | < -^ mes /СЛ/2. F.32')
Другими словами, по крайней мере для одной из пары функ-
функций w (х) = и (х) или w {х) = — и (х) верно неравенство
mes { х <= /Сд/2: sy (д:) > max w — у osc {и; KR)} < у mes КЛ/2 F.33)
и в силу F.30) для нее
т.е. выполняется условие F.7) с 60=1/2.
Итак, та из функций w = ± и (х), для которой имеет место
F.33), удовлетворяет всем условиям леммы 6.1 с постоянными
т, у и q, входящими в определение класса ЗЗт, б^^'/г. и
k" = maxw. Поэтому в силу F.9) верно хотя бы одно из нера-
неравенств:
либо
osc {и; Kr} <! f2s (max w — max w) ^
Kr Kru
<T2s[osc{a);/Cs}-osc{uy; /Сл/4}] = t2s [osc{«; KR} — osc{u;'KR/4}],
т. е. справедлива либо оценка F.27), либо F.28), Лемма 6.4
доказана-

§7) КЛАССЫ ФУНКЦИИ 33m 121
Из этой леммы и леммы 4.8 вытекает основное утверждение
данного параграфа. Именно:
Теорема 6.1. Пусть и(х)—произвольная функция из
6m(Q, М, у, Yi, б, l/q) и /СРо — шар, принадлежащий п. Тогда
для любого шара Кр, р^Ро, концентрического с /СРо, колебание
и(х) в /Ср оценивается так;
osc{«;/Cp}<cp5-V, F-35)
где
т=тах{2; 2/6}, а число s>0 определено в лемме 6.4 и зави-
зависит лишь от параметров т, у и q. Таким образом, класс
fim(Q, М, у, уи 6, l/q) вкладывается в Ca(Q), причем а не за-
зависит от М « Yi-
Отметим одно следствие из доказанной теоремы.
Следствие 6.1. Если функция и(х) принадлежит
8m(Q, M, y» Yi» б, 1/q), то для любого шара /CpcQ верна
оценка
J | VU Г dx < С, ри-m+ma, F.37)
где постоянная.С] определяется параметрами класса 23т и рас-
расстоянием от /Ср до S, а а то же, что и в F.35).
Справедливость этого утверждения вытекает из неравенств
F.1) и F.35).
§ 7. Классы функций »m@US,, M, \, уи 6, -J-)
(i, М, V, Y., Ь, j)
Функции класса 23m(Q, М, \, уи б, 1/^) могут, вообще говоря,
портиться при приближении к границе. Мы выделим из него
более узкие классы функций, удовлетворяющих неравенствам
типа F.1) не только для внутренних шаров, но и для шаров,
пересекающих границу S области Q или часть St границы S,
и покажем, что при некоторых условиях функции этих классов
удовлетворяют условию Гёльдера и в областях, прилегающих
к границе.
Обозначим через 93m(Q|JSi, M, у, yit б, \lq) класс функций
и(х) из 2?m(Q, M, у, Yi, б, 1/?), для которых w= ± и удовле-
удовлетворяют неравенствам F.1) и для шаров К,р, пересекающих Su

122 ВСПОМОГАТЕЛЬНЫЕ ПРЕДЛОЖЕНИЯ [ГЛ. 11
но не пересекающих S\Si, при k !> max w (х) — 6М и
ср
k !> max w (x). Области интегрирования AktP для пограничных
sp
шаров (т.е. шаров, пересекающих Si) в F.1) определяются как
множества точек из /СРП^» в которых u(x)>k.
В § 1 гл. I (стр. 30) было определено «условие (Л)» для S
или ее части St. Ради несущественных сокращений наших рас-
рассуждений будем считать, что пересечения Qp области Q с ша-
шарами /Ср, р<ао> имеющими центры на S (или на Si), состоят
из одной компоненты.
Мы будем предполагать в данном параграфе, что часть S,
или вся граница S области Q удовлетворяет условию (А)
с ао^1- Покажем, что в этих случаях справедлива
Теорема 7.1. Если S удовлетворяет условию (А) и функция
и(х) из Sm(QU5, М, у, уи 6, \lq) на S удовлетворяет условию
Гёльдера, точнее, если
osc{«; Sp}<Lpe, e>0, G.1)
для шаров /Ср с центром на S радиуса р ^ ао> то и (х) удо-
удовлетворяет условию Гёльдера в Q, т. е. для любого Кр
osc{«; Qp}<cpa, G.2)
причем постоянные с и а определяются параметрами пг, у, б, l/q
класса S3m, е из G.1) и постоянной 60 из условия (А) на S, а с
зависит, кроме того, от ух, М, L и постоянной а0 из условия (А)
на S.
Если только Si удовлетворяет условию (А), а функция
и (х) е S3m (й U S], М, у, уи б, 1/^) и удовлетворяет условию
Гёльдера на Su т. е. если G.1) верно лишь для шаров /Ср, не
пересекающих S\Slt то для таких шаров
osc{«;Qp}<c(p/p0)a, G.3)
где ро — расстояние от центра /Ср до S\SU а постоянные с
и а определяются теми же величинами, что и выше.
Легко видеть, что достаточно получить оценку G.2) для
шаров /Ср с р^а0 и центрами на S, а оценку G.3) для /Ср
с p<min{p0, a0} и центрами на S,. Это вместе с теоремой 6.1
дает желаемые неравенства G.2) и G.3) для любого шара /Ср.
Рассмотрим, например, первую часть теоремы. Доказательство
ее основано на следующем аналоге леммы 6.1 для пригранич-
приграничных шаров:
Лемма 7.1. Пусть Si czS удовлетворяет условию (А). Пред-
Предположим, что в формулировке леммы 6.1 Кц — шар с центром

f 7J КЛАССЫ ФУНКЦИЙ вт 123
на Si, R^.a0, шары ЛР заменены на йр = /СрПЙ и вместо
условия F.7) выполняется неравенство
(*)> SR=*S[}KR. G.4)
( RR
sr
Для этого случая остается верным утверждение леммы 6.1
с s = s (m, y, q, 60), где 60 — постоянная из условия (А).
Чтобы убедиться в справедливости этого предложения, за-
заметим, что формулировка леммы 6.1 не изменится, если вме-
вместо w (х) рассматривать функцию max {w (x); W}. Если теперь
KR—шар с центром на Si и выполнены условия леммы 7.1,
то функция
Г max {w (x); k"}, x «= QR,
k , x e Д R \ ilR,
очевидно, принадлежит Wxm (Kr) и удовлетворяет условиям
F.4) —F.6) леммы 6.1. Кроме того, в силу условия (А)
mes Ak', л/2 = mes {* е л"л/г: & {х) > k1} < A — 60) mes /Сл/2, G.5)
т. е. для $(х) выполнено неравенство F.7) с 60 = 60. Следова-
Следовательно, для t?» (лг) справедливо заключение леммы F.1) с j =
= s(/n, y, q, 9o)> и потому, если Л" !>max sy — 2~sco, то
(о < 2s max (max w - max w; Ш
1Q V lv
С помощью леммы 7.1 доказывается следующее предложение,
аналогичное лемме 6.4:
Лемма 7.2. Если выполнены условия первой части тео-
теоремы 7.1, то для любой пары концентрических шаров /Сл/4,
KR, R^a0, с центром на Si верно по крайней мере одно из
неравенств:
osc{«; ал}<с,/?\ е, =min{l —-2.; е}, G.6)
либо
osc {и; пяц} < A - т-'2-) osc {и; QR), G.7)
где х = max {4; 2/6}, s ^ 5 (/n, y, q, 60) — постоянная из леммы 7.1, а
Так же, как и в лемме 6.4, положим и = т~1 osc {ы; Qs}.
Если osc {и; QR} ^ 4L/?B, то верно неравенство G.6). Если же
osc{«; QR) > 4L7?8, то диапазон значений «(*) на 5Л отделен

124 ВСПОМОГАТЕЛЬНЫЕ ПРЕДЛОЖЕНИЯ [ГЛ. II
от max и или от гшпы = — тах(—и) интервалом длины, не
меньшей чем -josc(«; ®r}- Другими словами, по крайней мере
для одной из функций w {х) = и (х) или w {х) = — и (х) выпол-
выполнено неравенство k' = max w — ю ^ max w — -j- osc {и; QR) ^
SR QR
!>maxa> и kf^maxw — 6M, и потому для этой функции при
s %
всех l> k^k' справедливы неравенства F.4). Лемма 7.1 га-
гарантирует для нее оценку
2~V'osc{«; QR} =
= 2-s<o < max {osc {w; QR) - osc {w; QRli); R1-"
= max {osc {«; QR} - osc {«; Qs/4};
из которой снова следует неравенство G.6) или G.7).
Вернемся к теореме 7.1. Справедливость ее вытекает из
лемм 7.2 и 4.8.
Теорема 7.1 будет использована в следующих главах для
исследования поведения решений эллиптических уравнений и
их производных вблизи границы в случае первой краевой за-
задачи, когда для исследуемой функции известна гладкость ее
на самой границе (условие G.1)).
При рассмотрении других краевых задач вместо класса
SQmiQUSi, M, у,уи 6, l/q) приходится иметь дело с другим
классом — 5Bm(QUSi, M, у, Yi, б, 1/^). Он состоит из всех функ-
функций и(х) класса23m(Q, М,у, \,,б, \lq), для которых w(x)= ± и(х)
удовлетворяют неравенствам F.1) для шаров, пересекающих не-
некоторую часть 5] границы S, но не пересекающих SxSj, при-
причем для приграничных шаров Кр> так же как и для внутрен-
внутренних, неравенства F.1) выполняются при всех k ^max w {х) — 6М.
Ясно, что этот класс функций более узкий, чем 99
М, у, уи б, I/*?). Для представителей и(х) класса ^m(Q\JSu M,
У, Yi б, 1/?) гёльдеровость вблизи Si доказывается без каких-
либо предположений о гладкости и(х) на S,. От поверхности Si
достаточно требовать выполнения лишь следующих двух условий:
1) Для Qp = /Cpr|Q, где /Ср — шар с центром в-произволь-
в-произвольной точке х0 е Sj и радиусом р ^ а, не превосходящим рас-
расстояния ро от д:0 до S\S1( и для любой функции и(х) из

§8] КЛАССЫ ФУНКЦИЙ S™1 125
Wm(Qp) должно быть справедливо утверждение леммы 3.9, т. е.
должны иметь место неравенства
/
\Vu\dx G.8)
с произвольными числами / и k, l>k. Здесь Akp — множе-
множество точек х из Qp, для которых и(х)> k. В § 3 доказано, что
эти неравенства верны для случаев, когда Qp есть шар или
выпуклая область.
2) mesQp>6mes/Cp, 6 = const > 0.
Имеет место
Теорема 7.2. Если 5, удовлетворяет условиям 1) и 2),
то функции и(х) из Sm(QU5,, M, y, y,,6, l/q) удовлетворяют
условию Гёльдера в QIJ-Si, т. е. для любого шара /Ср с рас-
расстоянием ро от центра до S\St выполняется неравенство G.3),
где постоянная а > 0 определяется только параметрами пг, 6,
у, l/q класса Sm и постоянными р и 6 из условий 1) и 2), а с
зависит, кроме того, от у, а и М.
Доказательство этой теоремы совершенно аналогично до-
доказательству теоремы 6.1, в которой получена внутренняя
оценка. Надо только под Ak. p понимать соответствующие мно-
множества не из /Ср, а из Qp = /Cpfl^. Единственными аналитиче-
аналитическими неравенствами, на которые эта замена могла бы по-
повлиять, являются неравенства C.4) леммы 3.9. Заметим, что в
теореме 6,1 они использовались лишь для таких значений k, для
которых mes/C^/2 —mes Л*, д/2 ^6omes/C^/2 (см. F.23)), и при
этом несколько огрублялись:
(/-A;)nies пЛЛр<р, J \Vu\dx, р, > 0. G.9)
Л*.рЧЛЛр
В данном случае, вследствие наших предположений об S,,
неравенства G.9) справедливы при всех k, для которых
mesQp — mes Ak>p >6mesQp, б > 0.
§ 8. Классы функций »?'(Q, Mu &,, 62, &з, V, Yi, &, Щ)
При исследовании квазилинейных уравнений общего, неди-
недивергентного вида, а так>ке при исследовании систем уравне-
уравнений мы встретимся с необходимостью дальнейшего расширения
классов 8m(Q, M, у, уи б, l/q).
Будем говорить, что вектор-функция и (я) = (ы1 (*) «^ (х)),
определенная и ограниченная в области Q, принадлежит классу

126 ВСПОМОГАТЕЛЬНЫЕ ПРЕДЛОЖЕНИЯ П"Л. II
93^>(Q, М,, 6,, б2, б3, y, y,,6, \lq), если для нее можно построитьN,
функций ф'(«'» •••> uN), ..., ф^'Сы1, ..., uN), непрерывных и
f / N
непрерывно дифференцируемых в области ||и|= 1/ 2"'2^
<vraimax| и(д:)| | и таких, что wl {х) = ф' (и1 (х) uN(x)),
Q I
1=1, ..., Nu обладают следующими тремя свойствами:
1) vraimaxl wl(x) |<M, и wl(x) e Wm(Q).
Q
2) Для любой пары концентрических шаров /СЛ/2 и KRczQ
найдется номер г, для которого
osc {wr (x); KR] > б, _max osc {«'; KR} (8.1)
и
mes {* е /Сд/2= w<r (х) > max syr — б2 osc {wr;
(8.2)
где б,-, /= 1, 2, 3 — фиксированные положительные числа.
'¦Л.--3) Для каждой из функций w (x) = wl(x), /=1 A^j, и
/Ср с й выполняются неравенства
J
Vw Г i
p-ap
< Г Ь^гг max [r« (л:) - k]m + Yi | mes" " Ak, p (8.3)
m "
L Of p
-^—^- max [w (x) - k]m + Yii mes'"
'('-т)л*.р J
при произвольных а из @,1) и при k, удовлетворяющих усло-
условию maxw(x) — k^.6Mu где б е @, 2] — фиксированное для
Р
данного класса функций число. AktP — множество точек из Кр,
в которых w {x) > k; числа т, у, yt а q фиксированы, причем
q> п, п^т > 1.
Заметим, что здесь, так же как и в § 6, нам достаточно
иметь неравенства (8.1)—(8.3) лишь для шаров, радиусы ко-
которых не превосходят какого-либо числа р. Нетрудно видеть,
что класс функций 23m(Q, M, у, ylt б, \lq) является классом
93т1 (&, Ми б,, бг, б3, у, уи б, l/q), для которого ф'(ы) = ы, ф2(«)=
= -ы, o»1(je) = «(je), o»2(je)=-«(je), ^, = 2, М1 = М, б, = 1,
б.2 = б3= 1/2, а у, уи б и l/q те же, что и для 23m(Q, Af, y, Yi>
б* Vq).

КЛАССЫ ФУНКЦИЙ
127
В приложениях к дифференциальным уравнениям нам встре-
встретятся функции <р'(и) специального вида, а именно:
-<(•'
'-«'
i=\
N
(8.4)
где Af'^vraiminH'Ot), М"^\та[тахи'(х), а число Я, > 4N.
Покажем, что функции wl±{х) = ф'±(и(д:)), 1=1, ..., N, обла-
обладают свойствами 1) и 2) при некоторых Afj, 6U б2, б3, если
ие^(С) и M'<«'(a;)<M".
Обозначим: (и' (*) — М'I{М" - М') = vl (х), 2 (о' МJ = о (д:).
Ясно, что (M"-ui(x))/(M"-M')=l-vi(x) и 0<о'(*)<1-
Свойство 1), очевидно, выполняется для Mi = X-{-N. Свой-
Свойству 2) будет удовлетворять одна из двух функций wr+ или wr_
с индексом г, взятым из условия
©г = osc {vr; KR} = max osc {vl; К
i=\ N
Проверим это. Легко видеть, что
osc {vl; KR] = osc {1 — v1-, KR),
s max со,
i=\ N
(8.5)
osc [wr±; KR} < Я,юг + 2N«>r = (A +
osc {йУг±; /Сл} > Ыг - 2Nar = (Я, -
Кроме того, верно одно из двух: или
или
гДе Ц+ ^ max vr (х), а ц!^
(8.6)
-[mes АГл/2, (8.7)
>y mes^u, (8.8)
— V(x)), ибо в каждой точке
r r
или »rW<|i'+-{fflr, или vr (x) > \ir+ - у (or; второе
же неравенство эквивалентно такому: 1 — V < 1 — Ц+ +т(°г==

128 ВСПОМОГАТЕЛЬНЫЕ ПРЕДЛОЖЕНИЯ [ГЛ. II
Пусть из двух неравенств (8.7) и (8,8) справедливо, напри-
например, первое. Покажем, что тогда условию 2) будет удовлетворять
функция wr+ (в противном случае ему удовлетворяла бы функ-
функция wrj). Неравенство (8.1) выполняется с б, = (А, — 2N)I(M" — М')
(см. (8.6)). Для проверки (8,2) заметим, что для тех точек х
из KrI2, для которых верно (8.7), имеем
'+ (*) < Я. (ц; - у со') + max v =
R
R
т. е,, иными словами,
mes {*<=/(• wr.{x) > тахйУ' ' 9ДГ osc{wr.; К») ?<
2. (8.9)
Тем самым мы проверили, что условие (8.2) выполняется
112 2N 1
для функции wr+ (или wr_) с 62= ^ + 2^'>0» бз = -2- и б1 =
= (Я, — 2N)/(M" — Л1') > 0. Сформулируем доказанное утвержде-
утверждение в виде леммы:
Лемма 8.1. Функции w'±(x) = cpl±(u(x)), где функции <р'± (и)
определены равенствами (8.4) с Mf^. vrai min и' (*), М" ^
^ vrai max и1 {х), %>AN, обладают свойствами 1), 2) из опре-
t.a
деления класса ?8m(Q, Mlt 61г бг, б3, у, Yi. S, \/q) с М, = Я + Л^,
6, = (A,—2N)I{M"-M'), 62 = (h—4N)/Bk+4N), 63=l/2, Л^,=2^.
Для функций и(лг) классов Я$ (Q, Ми б,, бг, б3, у, уи б, l/q)
справедлива следующая
Теорема 8.1. Пусть и(дг) = (ы' uN) — произвольная
функция класса fdm (О, Л!,, б„ б2, б3, у, уь б, l/q) и KPt — шар
радиуса ро< 1, принадлежащий Q. Тогда для любого шара Кр,
р < Ро. концентрического шару /СР„ колебание иЧх) в Кр оцени-
оценивается так:
osc {и1 (*); /Ср} < с (р/Ро)а, i = 1 JV, (8.10)

$ 8] КЛАССЫ ФУНКЦИЙ В^1 |29
где
причем т = max {2/6, 1/62}, a s = s(m, у, q, б3) > 0 — постоянная
из леммы 6.1.
Доказательство этой теоремы, так же как и теоремы 6.1,
опирается на лемму 6.1. Ее следует применять к функции
w(x) = wr(x), соответствующей по условию 2) шарам Krp и Kr,
считая
k'=maxwr — @ = maxwr — x~1osc{wr; Kr}-
Kr Kr
Функция wr(x) удовлетворяет неравенствам F.4) при всех k^k',
I > k; условие F.7) с бо = б3 для нее также выполнено в силу
(8.2), ибо k' ^ max wr — 62 osc {wr; KR}- Оценка F.9) для <о =
^r
= t~' osc{wr; Kr} влечет за собой справедливость следующей
леммы:
Лемма 8.2. Возьмем произвольную функцию и из
58m1 (Q, Mi» 6i> 62. 63. Y. Yi> 6. 1/<7) и соответствующие ей функции
wl {х). Для любого шара Kru, принадлежащего Q вместе с кон-
концентрическими ему шарами Krp и Kr, и функции wr (х), соот-
соответствующей паре шаров Krp и Kr no свойству 2) (т. е. wr удо-
удовлетворяет неравенствам (8.1), (8.2)), имеет место по крайней
мере одно из двух неравенств:
(^)T2y-«* (8.12)
или
osc [wr; Kru) < A - t"'2-s) osc {wr; Kr} , (8.13)
где x и s определены в теореме 8.1.
Доказательство этой леммы то же, что и леммы 6.4, надо
только вместо F.33) использовать неравенство (8.2).
Вернемся к теореме 8.1. Ее утверждение есть следствие
лемм 8.2 и 4.9. Как говорилось выше, эта теорема нужна при
изучении гладкости решений общих эллиптических уравнений
и систем внутри их области определения. Условия, которые
были наложены на функции классов ЗЗ^1 (Q, М{, б!, б2, б3, у, \\, б, 1/^),
относились лишь к внутренним шарам. Никаких ограничений
на их поведение на границе и вблизи нее не накладывалось.
Теорема 8.1, равно как и теорема 6.1, имеет локальный характер:
в качестве области Q можно взять любую ее часть, и
5 О. А. Ладыженская, II. П. Уральцсва

130 ВСПОМОГАТЕЛЬНЫЕ ПРЕДЛОЖЕНИЯ [ГЛ. 11
поведение функций и' (х) в одной части Q не влияет на их по-
поведение в другой части Q.
Если мы хотим установить гёльдеровость функций классов
23*' (Q, ...) в замкнутой области Q или в Qi = QU5,, то необ-
необходимо наложить на эти функции какие-то условия и в погра-
пограничных шарах. При исследовании решений первой краевой за-
задачи для эллиптических уравнений и систем в Q мы встретимся
с нижеследующими условиями.
Определим класс 23m (Q, Ми б,, .... б6, у, Yi> б» 1/<7) как сово-
совокупность вектор-функций и (*) = («' (я), ..., uN (х)) из класса
23^' (Q, Mi, б,, б2, б3, у. Yi» 6. !/<?)> для которых соответствующие
им функции w' (х) обладают еще следующими свойствами:
4) Для любого пограничного шара с центром на S найдется
такой номер г, что
osc {wr (*); QR) >64 max osc{«';Qd}, (8.14)
и если
osc {wr (x); QR} > 65 max osc{wl; SR}, (8.15)
TO
max wr (x) ^ max wr (x) — 66 osc {wr; UR}, (8.16)
sR QR
причем 64> 0, 65 > 1, 66<=@, 1).
5) Неравенства (8.3) с w = wl, 1=1 Nu выполняются
для всех шаров /Ср с центром на S и р ^ а0 при
k ^ max {max w (x); max w (x) — ЬМ). (8.17)
sR aR
Мы покажем, что функции этого класса удовлетворяют
условию Гёльдера в Q, если только ему удовлетворяют значе-
значения wl на S. Для этого сформулируем аналог лемм 6.2 и 7.1,
пригодный в данном случае для пограничных шаров.
Лемма 8.3. Возьмем произвольную функцию и(х) из
23m(Q, Ми б, б6, y. Yi» 6. 1/<7) « соответствующие ей функ-
функции wl(x), 1=1 N1. Пусть S удовлетворяет условию (А)
и Kr есть произвольный шар с центром на S и R^Oq, a Kr/2
и Kru — два концентрических ему шара. В силу свойства 4)
функций класса 23^' (Q l/q) шару KR соответствует функ-
функция га/(х). Для нее имеет место по крайней мере одно из не-
неравенств:
(
или
osc [wr;

§ 81 КЛАССЫ ФУНКЦИЙ 8^' J31
если только
osc{o>r; Q«}>65 max osc{a»J; SR}. (8.18)
Здесь т = max{2/6; бб}, a s = s(m, у, q, 0O) — постоянная из
леммы 7.2.
Эту лемму можно доказать так же, как и лемму 8.2, если
вместо леммы 6.1 использовать лемму 7.1 и заметить, что,
предполагая выполненным неравенство (8.18), мы будем иметь
неравенство (8.16). Последнее гарантирует возможность исполь-
использовать основные неравенства (8.3) для уровней k~^-k' =
= maxo>r — со, где <о = т~' osc {a/; QR). Для этих уровней k
QR
условие (8.17) выполнено. Так как эти уровни берутся выше
значений wr на SR, то для wr выполнены все условия леммы 7.1.
В остальном все доказательство такое же, как и для леммы 8.2.
Из лемм 4.9 и 8.3 выводится теорема 8.2 при тех же пред-
предположениях о S, что и в теореме 7.1.
Теорема 8.2. Если вектор-функция и(х) принадлежит
33m(Q, Мь 61, ..., б6, у» Yi» б» 1/?) и wl(x) на S удовлетворяют
условию Гёльдера, точнее, если
osc{^;Sp}<Lpe, /=1 Nlt (8.19)
для шаров /Ср с центром на S радиуса p^Oq, to и(х) удовле-
удовлетворяет условию Гёльдера в Q, т. е. для любого Кр с р^До
имеют место оценки
osc {«'; Qp} < ср", / = 1 N, (8.20)
причем с определяется лишь параметрами класса 53m> L и г
из (8.19) и постоянными а0 и 60 из условия (А) на S, а а за-
зависит лишь от Ni, m, у» б-2, б3, б6, б, q, 60 и е.
Если условие (8.19) выполнено не для всей S, а только для
ее части Su то вместо (8.20) выполняются неравенства
osc {«'•; Qp} < с (р/роД / = 1 N,
где р0 — расстояние от центра Кр до S\SU а с и а такие же,
как в (8.20).
Так как внутренние шары уже рассмотрены в теореме 8.1,
то для доказательства теоремы 8.2 достаточно рассмотреть
лишь шары с центром на S. Для них, так же как и для вну-
внутренних шаров, надо воспользоваться леммой 4.9, а вместо
леммы 8.2 применить лемму 8.3 и заметить, что если условие
(8.18) леммы 8.3 не выполнено, т. е. если
osc {wr; QR) < 65 max osc {w1-, SR),

132 ВСПОМОГАТЕЛЬНЫЕ ПРЕДЛОЖЕНИЯ [ГЛ. II
то это последнее неравенство сразу дает нужную оценку коле-
колебания wr. Действительно, то, что стоит справа, не превосходит
65LRe, ибо функции wl (х) удовлетворяют условию (8.19) на гра-
границе S. Итак, теорему 8.2 можно считать доказанной.
При исследовании второй и третьей краевых задач для
квазилинейных эллиптических систем мы будем иметь дело
с функциями и(лг), которые удовлетворяют всем требованиям
класса 23m (Q, М,, бь б2, б3, у, Yi> 6. 1/<7) не только для внутрен-
внутренних шаров, но и для шаров, пересекающих некоторую часть Si
границы S, при этом под Л^>р понимаются множества точек х
из Qp, где wl(x)>k. Этот класс функций обозначим через
Sm'(QLM,, М,, б,, б2, б3, Y. Yi» 6. 1/<7). Для него справедлива
Теорема 8.3. Если S, удовлетворяет требованиям 1) и 2)
теоремы 7.2, то для любой и из Sm'(Ql)Si> .. .) выполняется
оценка osc (и1; Qp} ^ с (р/ро)а, в которой с и а определяются пара-
параметрами класса 23^' и постоянными р и 0 из условий на S,,
а р0 есть расстояние от центра Кр до S\Slt причем а не за-
зависит от Yi, б, и Mi.
Это утверждение доказывается так же, как и теорема о вну-
внутренних оценках для функций класса 23т', с учетом тех заме-
замечаний, что были сделаны к теореме 7.2. Прежде чем заканчи-
заканчивать данный параграф, убедимся еще в справедливости такой
леммы:
Лемма 8.4. Функции wl± {х) = ф^. (и (я)), где функции ср1± (и)
определены равенствами (8.4) с М' ^ vrai min и1 {х), М"^
^ vrai max и' (х) и X=ION, обладают свойствами 1), 2), 4) из
i,Q _
определения класса 23^@, М,, б,, ..., б6, у, уи б, l/q) с б, =
= 8N/(M"-M'), 62= 1/4, б3=1/2, 64 = 8N/(M"-M'), 65 = 3,
66=l/24, Mi = UN, Ni = 2N.
Лемма верна при любом Я,, превосходящем некоторое число.
Мы его зафиксировали в виде \0N. При таком Я, сравнительно
красивы значения остальных параметров класса.
Справедливость свойств 1) и 2) для функций (8.4) была
проверена в лемме 8.1. Нам осталось проверить лишь свой-
свойство 4).
Введем обозначения:
= osc{t)'; QR}= м„!_м, osc{u{; QR}.

$ а] классы функций s^1 13з
Индекс г снова выберем из условия <ог = max <o'. Тогда для
v{ и w± в /(д верны те же соотношения (8.6), что и в лемме 8.1.
Поэтому неравенство (8.14) выполняется с б4 = (A,—2N)I{M"—M').
Переходим к доказательству (8.16).
Возьмем пока произвольное положительное число е<1.
Верно одно из двух: или
A — e)(or> max osc {vh SR}, (8.21)
или
A — е)(йг< max osc{v{; SR}. (8.2Г)
Второе из этих неравенств в силу (8.6) влечет за собою сле-
следующее:
osc {w'±; QR) < (Я, + 2N) ©' < \+J? max osc {v1; SR) <
Поэтому, если выполнено неравенство, обратное (8.22), т. е.
для wr=wr+ или wr=wr_, то верно неравенство, обратное
(8.210, т. е. неравенство (8.21). Итак, из (8.23) следует (8.21).
Пусть выполнено неравенство (8.23) или, что то же, неравен-
ство (8.15) с &s = -,l — B)(x — 2N) ' При этом Условии мы хотим
доказать, что для одной из функций wr+ или wr_ будет верно
неравенство (8,16) с б6 > О,
Действительно, в силу (8.21) верно по крайней мере одно
из двух: или
max vr < max vr - у <ог, (8.24)
или
r + i<o'. (8.25)
Из последнего следует:
max (I - vr) = 1 - min vr < 1 - fmin vr + ~ a1) =
SR sR \ая г )
= max(l-i>r)--5-<°r- (8.26)

134 ВСПОМОГАТЕЛЬНЫЕ ПРЕДЛОЖЕНИЯ [ГЛ. II
Если выполнено неравенство (8.24), то
maxW, <A,(maxvr — -f-юг\ + maxv =
= A,maxt/— Я--2- <ar -f- osc{i>;
<maxa,r+-^-2^)a/<maxa;;-lf+~2™ osc {a/+; Q«}, (8.27)
т. е. получаем желаемое неравенство (8.16) для wr+ с 66 =
= И 1~ол^~ (предполагается, что е > 4N/X).
Если выполнено (8.25) и, следовательно, (8.26), то анало-
аналогично только что проделанному выводу найдем, что неравен-
неравенство (8.16) выполняется для wr_ с тем же самым б6. Если е
положить равным 5N/X и в качестве Я, взять ION, то пара-
параметры 23т примут те значения, которые указаны в лемме.
Лемма доказана.
§ 9. Класс &?(QUSi, v(t), M, y, Y., j
Введем в рассмотрение еще один вариант классов 23, кото-
который будет полезен при исследовании дифференциальных свойств
решений нерегулярных вариационных задач (гл. V) и выро-
вырождающихся квазилинейных систем (гл. VII). Специфика этого
случая состоит в том, что по сравнению с §§ 6—8 в неравен-
неравенствах вида F.1), (8.3) в подынтегральном выражении будет
допускаться весовой множитель v(|u(jt)|), который может обра-
обращаться в нуль при и = 0. Именно, обозначим через Sm(QLM|,
v (т), М, у, Yi, 1/?) класс вектор-функций и (*)=(«' (х), ..., uN (*))e
^Wm(u) таких, что vraimax| u(jt) |<M и произвольные ли-
Q
n ли-
линейные комбинации вида w(x)=2, ckuk (х), 2С^!> удовлет-
воряют при любых значениях k неравенствам
J
Ak, p—ар
<maxv(|u|)[Ya-mp V я) max (о; (je) - k)m + ViJ mes 1 Akl p.
(9.1)
Здесь Kp и /Cp_Op, ue@, 1), — любые концентрические шары
с центром "в Q, не пересекающие S \ Sj; Ак. Р = UeQp: w (x) > k};

§9] КЛАССОВ U S,,v<t),.M,Y, y,.1/<?) 135
m, M, y> Yi> Я — фиксированные положительные числа, причем
1 ^ т^. п, q > п; v(t) — неотрицательная неубывающая функция
т^Х), удовлетворяющая неравенству
v(xl)<(xl/x2)lv(x2), Vt,>t2>0, (9.2)
с какой-либо постоянной к > О, причем v (т) > 0 при т > 0.
Имеет место следующая теорема *)
Теорема 9.1. Для любой и(х) из §т(й, v(t), М, у, у{, l/q)
в произвольном шаре Кр = Кр (х°) с: Q верна оценка
°SC ^{Х); *Л ^ Ср°~ара> (9-3)
>0 — расстояние х° до S, постоянная а > О определяется ве-
величиной к из условия (9.2), m, N,y и q, а с зависит, кроме того,
от М, Yi и Ро-
Если часть Si границы Q удовлетворяет условию (А) ни(х)е
sCe(S,)flSm(QUS,, v(t), М, у, yi, 1/?)» то оценка (9.3) вы- .
полняется и для шаров Кр (х°), пересекающихся с Si (но не
с S \ Si), причем в этом случае с зависит от расстояния р0 от
х° до S\SU X, m, N, у, Yi» Я> Р» I u Is,' и постоянных а0 и 0О
из условия (А), а а > О определяется величинами X, m, N, у,
Я, Р и %.
Справедливость утверждений теоремы 9.1 вытекает из
леммы 4.9 и нижеследующей леммы 9.1, доказательству кото-
которой посвящена остальная часть параграфа.
Лемма 9.1. Пусть функция и(х) принадлежит классу
$m(Q, v(t), M, у, Yi, l/<7)- Рассмотрим SN функций
и1 (х); ± 3Nul (х) + | u (je)|, / = 1 N, (9.4)
N
где | и | = 21 uk !• Для каждой пары концентрических шаров
Kr<=- Q и Kru с Q найдется по крайней мере одна функция w (x)
из семейства (9.4) такая, что
osc{w; Ki>}^bi max osc {ul; Ко) /акл
И
osc {w; /Сл/Л < ^ osc {w; KR) + c,^' ~~, (9-6)
причем постоянные 6i > 0 и •& e @, 1) определяются величи-
величинами К, пг, N, у, q, а с, зависит также от М и у1ш
Если u eC<&) (Si)nSm(QU 5,, v(t), М, у, уи l/q), S, удовлет-
удовлетворяет условию (А), центр шара KR принадлежит Si и
*) В несколько иной форме она доказана в [364].

136 ВСПОМОГАТЕЛЬНЫЕ ПРЕДЛОЖЕНИЯ [ГЛ, II
Kr(](S\S\)= 0, то по крайней мере одна из функций w из
семейства (9.4) такова, что
osc{w; Од} ^6, max osc{«'; QR} ,g j\
и
osc{w; Qr/4}<0osc{w; QdJ + c,/?8, e= min jfl, 1 — — 1, (9.8)
где 6i > 0 и ¦& e @, 1) определяются k, m, N, y, q, p и вели-
величиной 60 из условия (A), a Cj зависит, кроме того, от М, Yi»
Отметим, что часть из функций (9.4), точнее, функции
± ЗЛ^и' + |и|, /= 1, .... N, вообще говоря, не подчиняются не-
неравенствам (9.1). С другой стороны, введение именно таких
функций связано с характером весового множителя v(|u|)
в неравенствах (9.1).
Проведем сначала рассмотрения, касающиеся внутренних
оценок. Фиксируем шар /Сл cr Q. Без ограничения общности
можно предположить, что для каждой компоненты и1 (х), i =
= 1, ..., N, большая часть ее колебания в шаре Кр прихо-
приходится на область положительных значений (если для какого-
либо / это не так, то надо и1 (х) заменить на —ul(x), это не
нарушает принадлежности вектор-функции и(лг) классу Sm). Та-
Таким образом, можно считать, что для данного шара Кц при
всех i=l, ...,N выполняются неравенства
ml + ^>0, (9.9)
где
©' =а osc {и1; /Cd}; m' = min/0; min«'\<0. /a \n\
\ *R I ( '
Пусть
max <о' = ©г. /о tn
Среди функций (9.4) будем выбирать для дальнейшего рассмот-
рассмотрения либо одну из и'(х), /=1, ..., N, либо функцию
шг(л;)*=ЗЛГиг(л;) + |и(л;)| (9.12)
в зависимости от того, малы или нет величины [ ш11. Точнее,
будет указана постоянная / > 0, определяемая лишь m, N, у,
q и Я, из условий (9.1), (9.2), такая, что если
max |m'|<2~V, (9.13)
f—1, .... N v '
то справедливость "оценок (9.5), (9.6) будет доказана для ш=*
*=wr(x), а если (9.13) не выполнено, то неравенства (9.5), (9.6)

§9] КЛАСС 5?(Q US,, vdO.Af.Y.Y,, I/?) 137
будут выведены для w=ui(x) с тем номером /, для которого
|«'| = — «'> 2"V. (9.14)
Рассмотрим сначала второй случай.
Лемма 9.2. Если при некотором I выполняется неравен-
неравенство (9.14) с каким-либо t~^2, то функция w = ul(x) удовлет-
удовлетворяет неравенствам (9.5), (9.6), в которых 6, = 2~ж, постоянная
¦&^@, 1) определяется лишь m, N, q, у, Я и t, а с^ зависит
также от ух.
Доказательство. Условие (9.9) вместе с (9.11) и (9.14)
влечет оценку
<o'^2-'+V, (9.15)
т. е. оценку (9.5) с б, = 2~'+1. Обратимся к неравенствам (9.1)
для w= ± ul(x) и докажем, что при некоторых значениях k из
них следуют неравенства F.4) леммы 6.1. Имеем
max| u |^ min| u | + Мог. (9 16)
XR ^R \ • /
Кроме того, при fe>fe+s=smax и1 — ^-=т' + -j-a' > 0 в силу (9.9)
и (9.15) можно оценить |и(*)| снизу на множествах Ak,Q, соот-
соответствующих функции w = и' (х):
min| u l^-^-Zmin | u | + min| и'
АЬ.Я
«>')>i-(mln|u| + 2-'-Vy (9.17)
Вместе с (9.16) это дает при k^k'+
max|u|<2'+2^min|u|,
Ak, R Ak, R
и тем более для любых шаров /Cp_apc/CpC/Cjj» концентриче-
концентрических с Kr, и Vfe>fe+ получаем
||<2N min | u |. (9.18)
Ak, p Ak, p—ар
Аналогичные оценки |и(*)| на множествах AkiR, соответству-
соответствующих функции w=— и' (х), при k^kL = max (— и1) — 2~'~V =
= — m' - 2~'~V > 2~t~l(nr имеют вид к*
||>(ll
AKR г kr i
(|+fe)>^-(min|u| + 2-<-1(ur), (9.19)
2 kr

138 ВСПОМОГАТЕЛЬНЫЕ ПРЕДЛОЖЕНИЯ [ГЛ. II
откуда в силу (9.16) вытекает соответствующая оценка (9.18)
для k ~^k'~.
Обращаясь теперь к неравенствам (9.1) для функций до = ±ul
и учитывая (9.18) и условие (9.2), выводим, что функция w(x) =
= и1 (х) удовлетворяет при всех
fe>fe+ = max«' —-г-©', V/>fe, (9 20)
Kr 4
неравенствам F.4), в которых постоянные у и Yi заменены
на y = Bt+2N)ly и Yi = B<+2^)X Yi соответственно, а функция
w (х) = — и' (х) удовлетворяет точно таким же неравенствам при
?>?'_ = max (-и')-2~'~V, V/ > k. (9 21)
Далее, по крайней мере одна из пары функций до = ±а'(*)
удовлетворяет условию F.7) леммы 6.1 с k' = k'± соответст-
соответственно и с 60=1/2. В самом деле, верно одно из соотношений:
mes {x e Кир: a'(jc)>^+}<ymes/C/}/2
или
mes {х е КщГ. — и1 (х) > — k'+} < •_- mes Kri%
а из последнего следует, что
mes {x e Krp'. — и1 (х) > k'-} < -j mes Krp,
так как k-> — k'+.
Итак, либо для w = ul, либо для до= —и' выполнены все
предположения леммы 6.1 (с &" = тахдо), а потому верно
утверждение этой леммы — оценка F.9) с постоянной s =
= s(m, 2<<+2)Vy, q, 1/2) > 0. Для функции w = ul из F.9) сле-
следует неравенство
j
— = max «'-*+<
I I , -- - '--1
^2 max{ osc{« ; Kr) — osc{« , KruY, у mYim R qy
а для до = — и1 — неравенство
7T*~W = max (- и') - k'- < 2s max {osc {«'; KR) -
i_ _i_
— o$c{u{; Kru); у myimR

( ,Y, Y,.l/?) 139
чак что в любом случае можно утверждать справедливость
денки
"-уГ^"^' (9'22)
т. е. оценки (9.6) с #=1-2-'-*-', с, = 2t+s+ly-llmy\"".
Лемма 9.2 доказана.
Рассмотрим теперь возможность, противоположную той,
которая имела место в лемме 9.2. Именно предположим, что для
некоторого достаточно большого ^>0 оценка (9.14) неверна
ни при каком /= 1 N, т. е. выполняется неравенство (9.13).
В этом случае мы докажем справедливость утверждения
леммы 9.2 для w = а/ = ЗМмг + |и|. К сожалению, при этом
нельзя будет применять лемму 6.1 непосредственно к функциям
wr(х), потому что w = wr, равно как и ш = |и| не удовлетво-
удовлетворяют неравенствам (9.1). В связи с этим введем для данного
шара KR вспомогательную функцию
wr (x) = 3Nvr (x) + v (х), (9.23)
где
лг
vt{x) = ui{x)-mi^Q, w(x)=2 v'(x). (9.24)
Очевидно, что функции w = ± wr при любых k подчиняются
неравенствам (9.1) с постоянной Yi = 3m (Л^ + I)m вместо Yi-
Колебания u = osc{a/; Kr} и osc{wr; Kr} связаны с сог не-
неравенствами
osc {wr; KR)
J
(9>25)
Кроме того, предположение (9.13) обеспечивает справедливость
следующих соотношений:
vl (х) - Т V < |«' (х) | < v* (х) + 2~ V, (9.26)
ЛГ
N \и(х)\>^\и1 {х)\> wL7T(W\uT {х)\+Ых)\)>
> 4F № № ~ 2~ Wcor)> (9.27)
| u (x) К v (x) + 2~*N(x>r < шr (jc) + 2~гЫв>. (9_.28)
Отсюда и из (9.25) следуют неравенства

140 ' ВСПОМОГАТЕЛЬНЫЕ ПРЕДЛОЖЕНИЯ [ГЛ. П
Заметим также, что если / велико, то колебание функции wr (х)
в любом шаре Кр с: Kr мало отличается от колебания wr в /Ср,
ибо в силу (9.25), (9.26)
| osc {wr; /Ср} - osc {wr; Кр} | < 2~'u. (9.30)
В частности, при p = R это дает
©<(l— 2~0~'osc{o)r; KR). (9.31)
Имеет место
Лемма 9.3. Пусть выполнено предположение (9.13) с не-
некоторым t > 3. Тогда функция w = wr (x) удовлетворяет при
k^maxwr—~-, l>k, неравенствам F.4) с постоянными у
и Yi> замененными на 32 N у и 3m32 N y\(N -\- 1)т соответ-
соответственно, а функция w= — wr (x) удовлетворяет таким же не-
неравенствам при k<^—2~t+36>, /e\k, -s-[&+ max(— wr)\\.
L г KR J
Доказательство. Рассмотрим сначала функцию w = wr(x).
max | u (*) К max ^г + 2~'~'й ^ min wr + 25,
При k !> max wr — -§- = min wr + -f- в силу (9.29) верны оценки
min | u (x) | >^ [min wr -
так что
max|u(jc)K32Ar2minlu(Jc)|, (9.32)
Ak,R Ak,R
ft, д = {x s /Сд: й)г(>:)>^}. Отсюда, из условия (9.2) и не
равенств (9.1) для w=wr следует справедливость первого
утверждения леммы 9.3.
Обратимся теперь к неравенствам (9.1) для функции w =
s= — wr (х). Из них при V/ > k вытекают неравенства
J v(|u|)|VuTrf*<
Ak, р—op \ Al, р-ор
и |) lya"" v ~T^ max [-шг - k]m +
max v
ЛА, Р
Yil mes' ~^Akt.. (9.
+ 3m (iV + If Yil mes' ~^Akt.. (9.33)

§9] КЛАСС 5^(auSt,V(T), М, Y, Уг, Чч) 141
Здесь и ниже Ak,p — множества, соответствующие w= — wr (х),
которая в Kr неположительна. При значениях k и / из диа-
диапазонов
\ j ] (9.34)
можно вывести из (9.29) следующие оценки для величины | и(х) |
на множествах, входящих в (9.33):
max | и (х) К max w (x) + 2~'~lG> = — k + 2~'~l& < — 2k,
Ak, R Ak, R
min |и(х)|>-7^5-[ min wr (x) - 2~i+lw] =
\A Ak,R\Al,R
o-l + l-Js ' Г k O-'+
так что
max | u (x)|< 32N2 min |u(x)|. (9.35)
Ak,R Ak,R\Al,R
Отсюда, из (9.33), (9.34) и условия (9.2) вытекает справедли-
справедливость второго утверждения леммы 9.3.
Лемма 9.4. Обозначим через s число, определяемое лем-
леммой 6.1 в соответствии с постоянными пг, 32 N у, 60='/2> Я-
Если имеет место оценка (9.13) с / = s + 4, то функция
w = wr = 3Nur + I u | подчиняется неравенствам (9.5), (9.6)
с 6i=2N, лЭ- = (I — 2~s~2)(l — 2~s~4)< 1 и с постоянной с„
зависящей от пг, К, N, у, ух, q.
Заметим, что неравенство (9.5) для w = wr следует непо-
непосредственно из (9.25). Для доказательства (9.6) применим
лемму 6.1 к одной из функций w= ± wr. Это возможно в силу
леммы 9.3 и потому, что имеет место одно из двух соот-
соотношений:
a) mesl x e Kr/2'. wr (x) > max wr — -у
или
b) mes \ x s Kr/2- wr (x) ^ max wr — -^- > ^ -5- mes Kr/2-
I Kr 2 J 2
Действительно, в случае а) функция ш=й»г удовлетво-
удовлетворяет условию F.7) с б0 = '/2> а также неравенствам F.4)
с Vfe!>fe' = max wr — 4-, / > k, и с постоянными 32*W2:S> и
Kr z
3m32lN2\l(N + l)m вместо у и Yi- ПРИ этом лемма 6.1 дает

142 ВСПОМОГАТЕЛЬНЫЕ ПРЕДЛОЖЕНИЯ [ГЛ. 11
следующую оценку для ю = ю/2:
Т
< 2s max {osc {даг; Кн} — osc{wr; Kru); c2Rl~\, (9.36)
с2= у т Зу,т (N -\- 1),
откуда вытекает справедливость по крайней мере одного
из неравенств:
osc [wr; Кнц} < (I — 2~s~') osc [w; KR) (9.37)
или
n
osc {wr; KR] < 2s+lc2R ~ (9.38)
В случае b) условия леммы 6.1 выполнены для функции
о> = — wr (х) при k' = max (— w1) — -j, k" = — 2"s~'u и тех же
значениях остальных постоянных, что и выше. Поскольку
выполнена и оценка F.8): k" ^ max (— wr) — 2~%, где
со^й/2, то из неравенства F.9) леммы 6.1 снова следует
справедливость оценки (9.36), а тем самым (9.37) или (9.38).
Теперь, принимая во внимание соотношение (9.30) с р = /?/4
и (9.31), выводим из (9.37), (9.38) желаемую оценку (9.6) для
функции wr (х):
osc [wT; Kru) < osc {wr; Kru] + 2~s~4u <
< (I _ 2-5-1 + 2~s-4) & + 2s+]c2R~^ <
<(l — 2~s~2)(l — 2~s~4)-' osc [wr; KR} + 2s+lc2Rl~~. (9.39)
Лемма 9.4 доказана.
Из нее и леммы 9.2 следует справедливость утверждения
леммы 9.1, касающегося внутренних шаров /Сдс:О.
Предположим теперь, что участок S, границы Q удовле-
удовлетворяет условию (А) и «|SieCp(S,), p>0. Очевидно, что'для
wr (х) верна оценка
osc{wr; SR}^LR^, (9.40)
где SR = Sir\KR, KR— шар с центром на Su Ь = 4№\и^\
Рассуждая так же, как и выше, будем иметь дело либо с функ-
функциями wr(x) и wr(x), либо с одной из и'(х), i=l, ..., N,

§ 9J КЛАСС »? (Q U S,, V <1), М. V. V,, 1/0) 143
в зависимости от того, верно или нет неравенство (9.13), где
иг= max oscfu'iQjJ, m' = min{0; min «'(*)},
/ = s + 4. Здесь число s > 0 фиксируется так же, как и выше,
в соответствии с леммой 6.1 и постоянными т, 32AW2\, бо = 6о
и q, где 60— константа из условия (А) (см. также лемму 7.1).
Пусть, например, выполнено условие (9.13). Тогда либо
(9.41)
и, следовательно, в силу (9.25) для w=wr имеет место
оценка (9.8) с с, = 4L, либо верно одно из следующих не-
неравенств:
max wr ^ max wr — -j- (9.42)
Sr ^s 4
или
mm w ^ mm w -f- -r • (9.43)
Последнее равносильно такому:
max(—wr) ^ max (—йH — — . (9.430
<? о 4
s« "r
Неравенства (9.42) и (9.430 позволяют доказать лемму 9.3
для w = ± wT с k ^ max w —~. Из нее, используя вместо
леммы 6.1 лемму 7.1, можно, как это было сделано выше для
внутреннего шара KR, вывести оценки, аналогичные (9.37), (9.38),
в которых Kru и K.r заменены на Q#/4 и Q^ соответственно,
а затем и оценку (9.8) для -w = wr(x).
В том случае, когда предположение (9.13) c/ = s + 4 неверно,
внося аналогичные изменения в доказательство леммы 9.2,
можно убедиться в справедливости неравенств (9.7) и (9.8) для
w = «' (х) с тем номером I, для которого | т1 \ > 2~'юг.
Этим завершается доказательство леммы 9.1, а тем самым
и теоремы 9.1.

Глава III
ЛИНЕЙНЫЕ УРАВНЕНИЯ
В этой главе основным объектом исследования являются
линейные эллиптические уравнения второго порядка с неогра-
неограниченными коэффициентами, точнее, уравнения, у которых стар-
старшие коэффициенты ограничены, а остальные коэффициенты
и свободные члены суммируемы по области их задания с той
или иной степенью. Для таких уравнений будет изучен вопрос
о разрешимости основных краевых задач в пространстве W\ (й)
и будет показано, как дифференциальные свойства решений
зависят от дифференциальных свойств известных в задачах
функций. Именно, будет выяснено, когда они принадлежат
пространствам W\(Q) и C/+a(Q), 1 = 0, 1, 2, ...
Как показывают примеры, построенные в § 2 гл. I, основ-
основные результаты данной главы имеют предельный характер, не-
улучшаемы в рамках взятых здесь пространств.
Один результат такого типа известен с 30-х годов — это
знаменитая теорема Шаудера [49,] о классической разреши-
разрешимости задачи Дирихле. В ней установлена разрешимость за-
задачи Дирихле в классах C/+a(Q), /^>2, при условии, что коэффи-
коэффициенты и свободный член принадлежат Cl~2+a (Q)'. Ясно, что эти
условия вызваны существом дела: они не могут быть ослаблены,
если мы хотим, чтобы все решения всех таких уравнений принад-
принадлежали С+а. С доказательства результатов Шаудера мы и
начнем данную главу (§§ 1,2). В § 3 формулируются аналогичные
результаты К- Миранда и Р. Фиоренца по задаче с косой произ-
производной. Остальные параграфы гл. III посвящены исследованию
разрешимости краевых задач для уравнений, коэффициенты
которых уже не являются непрерывными функциями. Область Q
всюду считается ограниченной.
§ 1. О разрешимости задачи Дирихле
в пространствах Ct+a(Q), />2. Принцип максимума
Пусть коэффициенты уравнения
Lu = aif (х) и + а{ (х) и^ + а (х)и = f (x) A.1)

§ 1] ЗАДАЧА ДИРИХЛЕ В СГ+<Х (<>)./> 2 145
и свободный член / определены в_ограниченной области Q и при-
принадлежит пространству Cr~2+a(Q), /^2. На протяжении всей
книги, если не оговорено противное, будем предполагать, что
aij=^aii и уравнение строго эллиптично в Q, т. е.
aii(x)Uj^vl\ v = const >0. A.2)
Рассмотрим для уравнения A.1) задачу Дирихле в области Q,
т. е. задачу об определении функции и, удовлетворяющей в Q
уравнению A.1) и на границе S области Q условию
u\s = <f(s). A.3)
Имеет место следующая теорема Шаудера:
Теорема 1.1. Если коэффициенты оператора L принадле-
принадлежат С1~2+а(п) и uij удовлетворяют неравенству A.2), если S'
принадлежит Ct+a и если задача A.1), A.3) может иметь не
более одного решения в С+а(О), то при любых /sC!~2+a(Q)
и qpeC(+a(S) задача A.1), A.3) действительно имеет решение
из класса C/+a(Q), />2.
Эта теорема, грубо говоря, утверждает, что разрешимость
задачи A.1), A.3), так же как и в случае линейных алгебраи-
алгебраических систем, есть следствие теоремы единственности. Одним
из критериев того, что задача A.1), A.3) не может иметь более
одного решения, является следующий:
таха(х)<0. A.4)
Действительно, при выполнении условия A.4) и неравенства
aii(x)lili'^0, как хорошо известно, для любого решения урав-
уравнения A.1) из С2 (Q) Л С (Я) *) верна оценка
тах| и(х) |г^тах| тах( и |; max -Ц^г I. A.5)
а { s а а\х> IJ
Напомним ее вывод. Для доказательства достаточно рас-
рассмотреть лишь два случая: когда наибольшее значение и{х)
положительно и принимается внутри Q и когда наименьшее
значение и(х) отрицательно и принимается внутри Q. При других
возможных случаях нужная оценка очевидна.
Пусть и {х') = max и (х) > 0 и х' е Q. В этой точке все м*. = 0, а
/<0. A.6)
*) Можно предполагать о решении и (*) немного меньше, именно что оно
принадлежит О2 (?2) П С (?2),

146 ЛИНЕЙНЫЕ УРАВНЕНИЯ [ГЛ. Ill
Действительно, с помощью ортогонального преобразования
х{ — х\ = cikyk, i= 1 п, можно atjuxx в точке х' привести
к виду
A.7)
где коэффициенты %k= 2 aiyciftc/ft вследствие я*/^?/>0 неотри-
неотрицательны. Так как в точке х' uVkgk^.O, то из A.7) следует A.6).
В силу этих фактов из уравнения A.1) следует неравенство
а (хг) и (xr) ^ / (х'), и потому
max u{x) = u(xf) <-1Щ <maxЩ-.
Q w v /^ а(х') ^ Q а(х)
Если же min u{x) = u(x")<О, то в этой точке их = 0 и а,-.-«ж.г,
Отсюда и из уравнения A.1) заключаем, что
и потому
Из полученных неравенств следует оценка A.5).
Оценка A.5) показывает, что задача A,1), A.3) не может
•иметь двух разных классических решений, если выполнено
условие A.4). Действительно, разность v(x) двух таких решений
удовлетворяет однородному уравнению Lv = 0 и однородному
граничному условию w|5 = 0. Применив к ней оценку A.5),
убедимся, что v (х) =г 0.
Единственность решения задачи A.1), A.3) имеет место и при
а(х)<0, если aij{x)\i\j'^0 и один из коэффициентов аи{х) —
пусть а{i (х) — строго положителен в Q.
Это вытекает из нижеследующего неравенства A.9), которое
справедливо для любого решения и(х) уравнения A.1) из класса
C(Q)f|C2(Q). Для доказательства A.9) введем вместо и(х)
функцию v (х):
где у и Р — положительные числа. В силу A.1) она удовле-
удовлетворяет уравнению
(Y - е-»*) atiVXtX] + [а, (у - е-**') + 2р • апег**] vX{ - .
- [ре-РЧяпР- ai) - a(Y - е~^)] v = f. A.8)
Число Р выберем так, чтобы ап (х) р — а, (х) было положи-
положительно в Q. Это, очевидно, возможно ввиду предположения

§ 1] ЗАДАЧА ДИРИХЛЕ В C/+a(Q). />2 147
c) > 0. Затем выберем у так, чтобы у — ?~р*' было
а _
положительно в Q. При таком выборе у и р коэффициент при v
в A.8) отрицателен. Следовательно, для v справедливо нера-
неравенство A.5). Учитывая связь между функциями и и v, придем
к неравенству
max | и (х) К max (у — е~р*') max I max
а а [ s
Y—е
е-Р* [аи (х) Р - а, (*)] - а (х) (у - е~»*)
0'9)
Отсюда следует, что и(х) = 0 при /(д;) = 0 и и|5 = 0. Заметим,
что если для а(х) условие а{х)^.О не выполнено, но ширина
области Q в направлении оси Охх мала, то числа у и р можно
выбрать так, чтобы знаменатели в A.9) были положительны
и, следовательно, чтобы в этой области была верна теорема
единственности.
Подытожим доказанные здесь критерии единственности в виде
теоремы, причем учтем, что непрерывность коэффициентов и / (х)
при этом не использовалась. _
Теорема 1.2. Пусть и <= С2 (Q) Л С (О) и удовлетворяет в Q
уравнению A-1), коэффициенты которого в каждой точке Q
конечны и форма atf (x) g^ неотрицательна. Тогда, если а (х) < 0,
то для и справедлива оценка A.5). Если же ап(х)^йп > 0,
— а,(х)^й\ > — оо и а(х)^.й^0 или, общее, меньше неко-
некоторого положительного числа, определяемого йп, йх и шириной
Q в направлении оси хи то для и справедлива оценка A.9).
Замечание 1.1. При выполнении условий второй части
теоремы ограничение на а сводится к тому, чтобы существовали
положительные параметры р и у, при которых для i;eQ выпол-
выполнялись бы неравенства у—е~&х> > 0 и d,,p2 + йф—а (уер*'— 1) > 0.
Ясно, что им всегда можно удовлетворить, если а не пре-
превосходит достаточно малого положительного числа или если
ширина й в направлении оси хх достаточно мала (в последнем
случае osc ер*> мала и потому уе$х' — 1 может быть взята до-
достаточно малой). Меняя знак р, можно условием min #!(*)> — оо
заменить условие max ax(x) < оо. При этом мы считаем
x = 0(eeQ.
В конце параграфа мы приведем ряд других оценок тах| и\,
а
а пока вернемся к теореме 1.1.
Шаудер доказал результаты более общие, чем теорема 1.1.
Именно, он включил в уравнение A.1) член Аи (в общем случае
Я, — произвольное комплексное число, и тогда решениями урав-

148 ЛИНЕЙНЫЕ УРАВНЕНИЯ ]ГЛ. Ill
нения Lu — Xu = f являются комплекснозначные функции и (х) =
= «] (х) -f- iu2 (x) вещественного аргумента х) и доказал, что для
задачи
Lu — Xu = f, u\s=y A.10)
имеют место все теоремы Фредгольма, в частности, что спектр
ее дискретен и конечнократен. Мы не будем приводить здесь
полные формулировки этих теорем. В § 5 это сделано сразу
для более общих уравнений и произвольных областей Q в более
широком функциональном пространстве (в W\ (Q)).
Все эти предложения доказаны Шаудером на основании
следующего установленного им основного неравенства, спра-
справедливого для любой функции v из Cl+a(Q) и любого эллип-
эллиптического оператора L:
Lv |?-2+a) + max| v | + | v |<f+a>], i>2. (I.
Постоянная с (l) здесь определяется лишь /, а, величиной v
из A.2), нормами в Cl~2+a(Q) коэффициентов оператора L и гра-
границей S, которая предполагается принадлежащей классу С/+а.
Последний член в (I.II) есть норма в Cl+a(S) значений v на S
(см. ее определение в § I гл. I). Собственно, самим Шаудером
неравенство (I.II) и сформулированные только что предложения
были доказаны при несколько больших предположениях о S
и коэффициентах L (он требовал их принадлежности к С +а+в
и C/~2+a+e(Q), e > 0, соответственно), приведенные же усиления
были сделаны рядом авторов (см. [81э 372, 12J и др.).
Член тах| v \ справа в (I.II) можно отбросить в тех случаях,
когда известно, что для задачи (I.I), A.3) имеет место теорема
единственности, в частности, если выполнено неравенство A.4).
Помимо (I.II) установлены внутренние оценки, которые
не зависят от поведения v на S и от свойств самой границы S,
и оценки v в любой части Q, области Q, примыкающей к гра-
границе S. Именно
| v &+a)<c(l, Q')[l Lv (!-2+a) + max| v |], />2, A.12)
где Q' — любая строго (внутренняя подобласть области Q,
а постоянная c(l, Q') зависит от /, а, норм в С'1^) коэф-
коэффициентов L, v из A.2) и расстояния Q' до S, и
[I Lv f 2+a) + max| v | + | v g+JJ, />2, A.13)
где С (*)— произвольная функция изС/+а(О), равная нулю

§ 1] ЗАДАЧА ДИРИХЛЕ В Cl+a(Q). />2 J49
в окрестности куска S, границы S. Постоянная c(l, Q зависит
от I, а, норм коэффициентов L в С1~2+а (Q), v, функции ?, а также
от свойств части S \ S, границы S (предполагается, что S \ Si
принадлежит С1+а).
Мы изложим доказательство теоремы 1.1 и неравенств
A.11) — A.13) для 1 = 2, Для />2 они легко выводятся из этих
неравенств. Предположим сначала, что априорные оценки
A.11) — A. 13) уже имеются. Докажем тогда следующее услов-
условное предложение:
Лемма 1.1. Пусть S^C2+a, а коэффициенты L суть эле-
элементы Са (Q) и а (х) ^ 0. Пусть задача
Дм = /(х), u\s = 0 A.14)
имеет решение в классе C2+a(Q) для плотного в Ca(Q) мно-
множества f(x). Тогда задача A.1), A.3) однозначно разрешима
в C2+a(Q) для любого f(x) из Ca(Q) и <f(s) из C2+a(S).
Утверждение леммы достаточно доказать лишь для случая
Ф (s) = 0, ибо общий случай легко сводится к этому. Именно,
функция v(х) = и(х) — ф(*), где у(х) есть какая-либо функция
из C2+a(Q), равная qp(s) на S, удовлетворяет уравнению Z.w = f
с f eCa(Q) и t> [j = 0. Итак, рассмотрим задачу
Lu = f, «ls = 0. A.15)
Введем семейство операторов
?тм = Дм + т(? — Д)м, те [0,1],
и для них изучим краевую задачу
Lxu = f, u\s = 0. A.16)
В силу A.9) для всех возможных решений и (х, т) задачи A.Ш)
(мы все время будем иметь в виду разрешимость в C2+a(Q),
.так что все рассматриваемые нами решения принадлежат этому
пространству) справедлива оценка
тах|м(х, т)|<Мтах|/(л:)| A.17)
а а
с постоянной М, не зависящей от т из [0, 1]. Это так, ибо
коэффициент ах(х) при и в Lx(u) неположителен, для коэффи-
коэффициентов Lx равномерно ограничены нормы в C°(Q) и постоянная
эллиптичности v1 = min(l, v) в неравенствах
при всех т из [0, 1] строго больше нуля. Больше того, для
всех и(х, т) в силу A.11) и A.17)
\и(х, х) ?+аЧМ,| Lxu $ = Mx\f$ A.18)

150 ЛИНЕЙНЫЕ УРАВНЕНИЯ [ГЛ. Ill
с постоянной Ми общей для всех т из [0, 1]. При т = 0 за-
задача A.16) совпадает с задачей A.14), Из условий леммы и
неравенства A.18) следует, что задача A.14) имеет единствен-
единственное решение при всех f из Ca(Q). Иными словами, оператор Д
устанавливает взаимно однозначное соответствие между под-
подпространством^ Co+a(Q) пространства C2+a(Q), состоящим из эле-
элементов C2+a(Q), равных нулю на S, и Ca(Q). Обратный ему
оператор обозначим через Л. С помощью него задачу A.16)
можно записать в виде
и + тА (L - А) и = А/. A.19)
Это есть уравнение в пространстве C2+a(Q) с ограниченным
в этом пространстве оператором А~ (L — А). Ограниченность
A~'(L—А) следует из A.18) с т=0. Обозначим через | A~'(L—Д)|
норму оператора A~'(L —А) в пространстве Co+a(Q). Уравне-
Уравнение A.19) однозначно разрешимо для всех т из [0, т,), где
Ti=. _¦ -т, и, следовательно, оператор Lx при те[0, т,)
IД (^ — А) I
устанавливает взаимно однозначное соответствие между пол-
полными пространствами C0+a(Q) и C?(Q). Пусть L^1 — обратный
ему оператор. С его помощью задача A.16) может быть пре-
преобразована к эквивалентному ей уравнению
u + {x-xr)Lj{L-ts)u = L?f, A.20)
(т' —любое число из [0, т,)) в пространстве Co+a(Q). Оператор
Lx'l(L — A) ограничен в Co+a(Q), и потому уравнение A.20)
однозначно разрешимо при
0<т-т'< ' A.21)
\LX, (L — Д)|
Так устанавливается существование обратного Lxx при т, под-
подчиненных условию A.21). Этот процесс можно продолжать и
дальше. За конечное число шагов мы дойдем до т=1, ибо
нормы всех операторов \Lxl {L—А)| не превосходят одного
и того же числа, определяемого Мх из A.18) и нормами в Ca(Q)
коэффициентов L. В самом деле, для любого v из C2+a(Q)
а в силу A.18)
т. е.

§ 1] ЗАДАЧА ДИРИХЛЕ В С/+П(й), г>2 J5J
Таким образом, используя продолжение по параметру от т=0
до т= 1, мы доказали однозначную разрешимость задачи A.16)
и, в частности, задачи A.15) в пространстве C2+a(Q) при лю-
любой f из Ca(Q). Лемма 1.1 доказана.
Из этой леммы следовала бы разрешимость задачи A.1),
A.3) в случае а(х)<^.0, если бы была известна указанная
в лемме 1.1 разрешимость задачи A.14). Эта задача была
предметом многочисленных исследований, и ее решение с по-
помощью электростатических потенциалов изложено в ряде работ
и книг. Однако в наиболее известных из них ограничиваются
доказательством того, что_ решение принадлежит C(Q) f| С2 (Q)
или в лучшем случае С1 (Q) f| C2(Q). В Других же (см., напри-
например, монографию Н. М. Гюнтера [11]) принадлежность и(х) к
C2+a(Q) устанавливается при предположениях о S более жест-
жестких, чем надо, причем рассуждения, приводящие к этому,
длинны и кропотливы. Мы избежим их, применяя оценки A.12)
и A.13) и рассуждая нижеследующим образом.
Докажем сначала разрешимость задачи A.14) в простран-
пространстве С2+?(Q) при любой feC(Q) для случая, когда Q есть
шар, причем без ограничения общности будем считать, что
Q = {x: |*|< l} = .Ki. Решение этой задачи дается формулой
u(x)=JG(x, y)f(y)dy, A.22)
Q
где
(L23)
— функция Грина. Мы рассматриваем здесь случай п > 2. При
п = 2 все рассмотрения аналогичны.
Лемма 1.2. Функция и, определяемая формулой A.22),
дает решение задачи A.14) для шара п = К\ и подчиняется
неравенству
Доказательство. Если точка х находится внутри
области Q, то G(x, у) и все ее производные по х обращаются
в нуль при у е дп. Поэтому функция
Q°(x, У) = 1О(Х'У) ПРИ *eQ'
[ О при у е Еп — Q
вместе со своими производными по х непрерывна по перемен-
переменной у до всем пространстве Еп, кроме точки |/ = jc, когда х

152 ЛИНЕЙНЫЕ УРАВНЕНИЯ 1ГЛ. Ill
находится внутри Q. Запишем потенциал A.22) в виде
\, y)f(y)dy,
n
где /* — какое-либо гладкое продолжение / во все простран-
пространство Еп. Применяя формулу дифференцирования интегралов
типа потенциала (см. ниже вывод формулы B.10)), получим
"*,*,(*)= Y,/to+Hm J Qotl(x, y)f(y)dy, A.24)
гДе Уц — некоторые постоянные (у*/ = б{п~1), a G^^G^x .
Рассмотрим функции
w'ei(x)= J O^(x, y)f(y)dy.
\х-у\>е
Для любых точек х, х е Q, любого положительного доста-
достаточно малого е и любого р^2|* — х\ имеем
wlel(x) — wlj(x) =
= J [Q°u{x, y)-G°tl(x, y)]ir(y)-r\x)]dy +
\х-у\>р
+ J О°и(х, у)[Г(У)-Г(х)]с1у-
e<U-j/|<p
- J G°t,(x, у) [Г (У) -Г (x)\dy +
\х-у\<Р
\х-у\>е
+ /(*) J [G°n(x, y)-G%{x,y)]dy +
\x-yl>P
-{¦fix) J G%(x, y)dy-f(x) J G°tl(x, y)dy =
e<U-y|<p |x-j/l<p
= J [Gtl (x, y) - Gtl (jc, y)] [f (y) - f (x)] dy +
xy^p
+ J Qti(x,y)]f(y)-f(x)]dy-
s<\x-y\<p
- J G*/(*. 0)[f(iO-f (*
J G°t,(x,y)dy- J
|x-j/|
+ [f(x)-f(x)] J G°tl(x, y)dy. A.25,
l

§11
ЗАДАЧА ДИРИХЛЕ В Cl+a (Q),
153
Положим здесь р == 21л: — х |. Используя оценки
\DkxG(x, y)\<c(k, п)\х-уГп+2'к,
lkxG(x, y)-DkxG(x, f/)|<
c(k, n)\x-x\(\x-y\-n+x-k-\x-y\-n+l-k),
лтекающие из A.23) (эти оценки нужны при
A.26)
2), легко
() ( у р )
ценить первые три интеграла правой части A.25) через
/li'l \а й й
— х \а с постоянной с, зависящей лишь от и и а.
Докажем, что
J О°„(х,
A.27)
Очевидно, что при этом без ограничения общности можно счи-
считать, что р<|8~', так как в противном случае можно было
бы разбить рассматриваемый интеграл на два: по области
e^|jt— j/|^8~' и по 8~'^|л; — ?/|^р, причем оценка второго
интеграла в силу A.26) тривиальна.
Пусть сначала |л;|^2~1. Тогда
J G°ti(x,y)dy= J
e<\x-yl<p
—
х —
)dy
(первый член функции Грина дает нулевой вклад). В силу
р<4~' HUK2-1 имеем|л:-г//|{/р1 > 2-», так что оценка A.27)
очевидна.
Будем теперь считать, что 2~'^|л;|^1.
Введем следующие обозначения:
J
e<|zl<p
е<|г!<р
Число р мы будем считать сейчас произвольным, не завися-
зависящим от х. Имеем
F8,pW= J G°(x,y)dy= J
e<l*-J/l<P e<|zl
Fi\Ux)= J G°tj(x,y)dy= J G°lt(x,z + x)dz.
дх,
¦ J
8<U|<p
J •
e<lzl<p
дг,
-dz-.
= J 0°t(x, z + x) dz + J G°(x, z + x)n, (z) ds2 -
1г|=р
- J O0(x,z+x)«,(z)ds, A.28)

154 ЛИНЕЙНЫЕ УРАВНЕНИЯ [ГЛ. Ill
(в силу непрерывности G0 операция интегрирования по частям
законна) и
"Л1"Л1 |z|=p
IzM
+ J 0?(x, z + x)n, (z)dsx + J д0°(%' + х) n, (z) dsz-
|z|=p |zl=p I
- J G°l(x,z + x) m (г) ds, - J aG°(y + *> rt/ (г) dsz. A.29)
Здесь П;(г) = гг/|г|. Кроме A.26) имеет место также оценка
дО (х, у)
*!
— у\1~п.
Отсюда вытекает, что все поверхностные интегралы в правой
части A.29) ограничены при любых р и е, и дело сводится
к оценке производной
dxtdx.
Для оценки этой производной заметим, что функция Fe>p(x)
зависит только от |jt| = r. Действительно, если |дс| = |?|, то, де-
делая замену переменных интегрирования {/*=2 ацУ'> гДе A=(aii)~
i
ортогональное преобразование, переводящее I в х, легко уви-
увидеть, что Ft. р (х) = Fe, p (I).
Итак,
.Р(*) d%(>{x) xtx
tx, dFe,p /Ь[ xiXj \
7~ + ~Zr[T~~7r)
Первые производные функции F&, р в силу A.28) и A.26)
ограничены постоянной, зависящей только от п. В силу A.29)
оператор Лапласа от F&, р, а потому и ^ejp также ограничен
(при этом следует иметь в виду, что
Таким образом, оценка A.27) доказана для любого р, в том
числе и для р = 21jc — х\. Остается рассмотреть выражение
в фигурных скобках в правой части A.25). Покажем, что при
е-*0 оно стремится к нулю. Функция ГG (л:, y)dy является ре-
Q

I] ЗАДАЧА ДИРИХЛЕ В C/+<X(S).
155
шением задачи Аи(х)=1, ы|ао = 0 и потому может быть вы-
выписана в явном виде:
1'
Применяя к ней формулу A.24) с f = 1, получаем соотношение
lim f G°il(x,y)dy = 0, V*eQ. A.31)
Итак, доказана оценка
| lim [wi> (x) - wi1 (х)] | < с (я, а) | f |L°r| x - х \а-
и, следовательно,
Это неравенство составляет основу желаемой оценки. Остается
оценить максимумы модуля функции и, ее первых и вторых
производных. Оценка вторых производных вытекает из A.24) и
A.31). Действительно,
+ f(x)lim f
8>O
y) [f (y) - f (x)] dy + ±f (x)
откуда
Остальные оценки совсем элементарны.
Лемма доказана.
Рассмотрим теперь задачу A.14) в произвольной области Q
с границей S из С2+а. Хорошо известно, что она имеет един-
единственное решение и(х) из С (Q) f| C2+a (Q) для всех_^(д:) изС°°(й).
Мы хотим доказать, что оно принадлежит С2+а(п). Для этого
возьмем какой-нибудь небольшой кусок S, границы S и преоб-
преобразуем его с помощью регулярного (невырожденного) преобра-
преобразования у = у (х) в часть поверхности единичной сферы. Пусть
функции yl = yi{x), i= 1, ..., п, устанавливают взаимно одно-
однозначное соответствие между некоторой областью Qjc:Q, при-
примыкающей к Sj, и открытым шаром К.\ = {у: \у\< 1}. Обозна-

156 ЛИНЕЙНЫЕ УРАВНЕНИЯ 1ГЛ. Ill
чим через Г границу К\, а через Ту—ту ее часть, образ которой
соответствует Su Считаем, что якобиан —^ строго больше
нуля и функции yi (х) <= C2+a (Q^.
Перейдем в Q, к новым координатам у = у(х). Уравнение
п
—2- = / преобразуется при этом в эллиптическое уравнение
OX
2-
OXf
Lu=f, коэффициенты и свободный член которого f(y)=f(x(y))
суть элементы Ca(Ki). Коэффициент при неизвестной функции
и в L равен 0, и условие эллиптичности по-прежнему выпол-
выполнено. Функция « = «(*), являющаяся решением задачи A.14)
в Q, в новых координатах у дает функцию й(у) = и(х(у)), ко-
которую можно рассмотреть как решение задачи
Lv(y)=J, а|г = «|г A.32)
в шаре К\ из класса C(Ki)f\C2+a(Kl). Задача A.32) в этом
классе имеет единственное решение.
Возьмем на Г последовательность достаточно гладких функ-
функций йт> /п=1, 2, ... (например, из С2+а(Г)), равномерно схо-
сходящихся на Г к й\г и равных нулю на IV По этим функциям
найдем в К\ решения vm(y) задач
Lvm = f(y), vm\r = um\r- A.33)
В силу лемм 1.1 и 1.2 задачи A.33) однозначно разрешимы
в С2+а(К\)- При /я->оо их решения равномерно в К\ сходятся
к й(у). Это следует из того, что vm (у) — й (у) удовлетворяют
однородному уравнению
L(vm-u) = 0 A.34)
и граничному условию
(vm-u)\r = (um-u)\r A.35)
и потому в силу A.9) подчиняются неравенству
max| vm{y) — й(у)\^сmax\йт—й\, A.36)
»s/(, Г
правая часть которого стремится к нулю при т->оо. Кроме
того, для vm, как решений задач A.33), справедливы неравен-
неравенства
K(f/)S(f/)|?+a4cB, ?)[|f$+maxK|], A.37)
где ?({/) — любая бесконечно дифференцируемая в К\ функция,
равная нулю в окрестности куска границы Г \ IV Из A.36) и

5 1] ЗАДАЧА ДИРИХЛЕ В C?+a<Q), Z>2 I57
A.37) следует, что предельная для vm(y) функция й(у) принад-
принадлежит C2+a(/Ci U Fi). Переходя к старым координатам, убежда-
убеждаемся, что наше решение и(х) принадлежит C2+a(Q1[JS1). Так
как такими кусками можно покрыть всю S, то тем самым мы
доказали, что и(х) eC2+o(Q), Итак, доказано, что задача A.14)
имеет решение из C2+a(Q) для всех достаточно гладких f. Это
вместе с леммой 1.1 доказывает следующую теорему:
Теорема 1.3. Если коэффициенты L принадлежат Са(п),
удовлетворяют неравенству A.2), a(x)^.Q и S принадлежит
С2+а, то задача A.1), A.3) однозначно разрешима в C2+a(Q)
при всех f(x) из Ca(Q) и qp(s) из C2+a(S).
Если условие а(х)^0 не выполнено, то известно, что для
задачи могут не иметь места теорема единственности и теорема
существования для всех f(x). Чтобы выяснить всю картину
разрешимости задачи A.1), A.3) при любом коэффициенте при
и (х), введем в уравнение член — к и рассмотрим семейство
задач
Lu-lu = f, u\s = <p A.38)
с произвольным комплексным числовым параметром К, считая
(теперь уже без ограничения общности), что коэффициент а (х)
при и в Lu неположителен. Решение в этом случае будет комп-
лекснозначной функцией и (х) вещественной переменной х. Со-
Сохраним за пространствами, состоящими из комплекснозначных
функций v(х) = у, (х) + iv2(x) с vk(x), 6 = 1,2, из Cl+a(Q), те
же обозначения С1+а({}). Нормы в них определим так: |w|^+crt=
=| а, |<|+а> + | v2 \д+а\ Пусть коэффициенты L по-прежнему ве-
вещественны и удовлетворяют условиям теоремы 1.3; без огра-
ограничения общности считаем, что граничное условие сведено к ну-
нулевому. В силу теоремы 1.3 задача
Lu-Ku=f, u\s = 0 A.39)
сводится к задаче
u-XL~lu = L~xf, A.40)
где LT —оператор, обратный оператору L, устанавливающему
взаимно однозначное соответствие между Cl+a(Q) и Ca(Q).
Если A.40) рассматривать как уравнение в пространстве.
Ca(Q), то в этом пространстве оператор L~ вполне непреры-
непрерывен. Действительно, он любое ограниченное в Ca(Q) множество
переводит в множество, ограниченное в C2+a(Q) (это следует
из неравенства A.18)), а последнее компактно в Са(О). Но тогда
к уравнению A.40) применимы все теоремы Фредгольма (см.,

158 ЛИНЕЙНЫЕ УРАВНЕНИЯ 1ГЛ. Ill
например, [312, 48, 13]). В частности, оно разрешимо при лю-
любой правой части тогда и только тогда, когда соответствующее
однородное уравнение
u — XL~lu=0 A.41)
не имеет никаких решений, кроме м^О. Те значения X, при
которых уравнение A.41) имеет нетривиальные решения, обра-
образуют спектр задачи A.1), A.3). Теоремы Фредгольма гаранти-
гарантируют, что все такие X можно занумеровать в порядке возрас-
возрастания их модулей и каждое X имеет конечную кратность, т. е.
каждому из них соответствует конечное число линейно незави-
независимых решений. Пусть Я,, Х2, . .. есть спектр задачи A.1), A.3).
Если таких Xk бесконечное множество, то | Я* |-*¦<».
Мы не будем формулировать здесь другие утверждения те-
теорем Фредгольма, которые касаются сопряженного к L опера-
оператора. Те же, которые отмечены выше, гарантируют разрешимость
уравнений A.40) или A.41) в пространстве С* (Q). Но нетрудно
видеть, что на самом деле все их решения принадлежат С2+а(п),
если, конечно, предполагать, что /ЙЕСа(й). Действительно,
если f(x) и решение и(х) принадлежат Са(О), то V f к LT и
принадлежат^ С\+а(п), а тогда в силу самого уравнения и
и(х) е Cl+a(Q). Ввиду этого мы можем от уравнений A.40), A.41)
вернуться к задаче A.15) и задаче
Lu-Xu = 0, u\s = 0 A.42)
на определение собственных значений X и соответствующих им
собственных функций — нетривиальных решений задачи A.42).
Из сказанного ясна, в частности, справедливость утверждений
теоремы 1.1 при / = 2.
Остановимся еще на весьма важном свойстве эллиптических
уравнений второго порядка, носящем название «принципа мак-
максимума». Впервые он был обнаружен на гармонических функ-
функциях и «в чистом виде» выражается в том, что отличная от то-
тождественной постоянной гармоническая функция и(х) в любой
области Q, в которой она принадлежит С (И), принимает свое
наименьшее и наибольшее значения лишь на границе этой об-
области, так что для Vjc e Q
min и(х) <и (х) < max u(x). A-43)
да да
Это-свойство, как мы видим, дает априорную оценку для и(х)
в Q через ее значения на дп. Если функция и(х) удовлетворяет
неоднородному уравнению Лапласа: Дм = /, то для нее нера-
неравенства A.43), вообще говоря, неверны. Однако вместо них
справедливы другие неравенства, позволяющие оценить тах|ы|

§1] ЗАДАЧА ДИРИХЛЕ В C/+<X(Q). />2 159
через тах|/|, тах|ы| и те или иные характеристики области,
а аи
причем вывод их основан на тех же соображениях, что и вы-
вывод A.43). В основе доказательства этих и аналогичных им
утверждений для уравнений A.1) лежит элементарный факт:
если функция и (х) имеет в какой-либо точке *° области Q от-
относительный максимум, то для нее в этой точке H*f = 0,
^ }, i= 1,2, ..., n, и aijUx x <[0 при любой неотрицатель-
неотрицательной форме a*/(jt°) g/g/^ 0 (в точке минимума ацихх ^ 0) (см.
выше A.6)). Покажем, как с помощью указанного факта выво-
выводятся оценки типа A.43) для функций и(х), удовлетворяющих
неравенствам Lu^f или Lu^.f и принадлежащих C(Q)[\C2(Q)
(или, чуть общее, C(Q)f|O2(Q)).
Лемма 1.3. Если в п Lxu = ациХ{Х. + diUX{ > 0 и at
то и не может иметь в Q относительный максимум и для
и (х) < max и (х).
да
Действительно, в точке относительного максимума aijUxt, -
uiux. = 0, так что LiU^O, а по условию Lxu > 0 в Q. Лемма
доказана. (Заметим, что здесь и ниже функции alf, at, a, f
считаются определенными и конечными во всех точках Q и
и удовлетворяет требуемому неравенству во всех точках х е Q.)
Лемма 1.4. Пусть вй/^^о^^О, «гД^/^О и для
П
VQ' с: Q min ^ ан (х) = v (Q0 > 0. Тогда для v^efi
и (х) < max и (х). A.44)
Возьмем «барьерную» функцию а(х) = ех2, в > 0. Для нее
п
10со = 2е 2 о,ц ^ 2ev (Q0- Поэтому ац (и + <й)х{х, > 0 в Q' и
в силу леммы 1.3
и (х) + оэ (*) < max (и + со) для V* е Q'. A-45)
Устремляя в этом неравенстве е к нулю, получим и (х) ^ max и
для V* е Q', а так как Q' есть произвольная внутренняя под-
подобласть Q и u^C(Q), to верно и A.44).
Лемма 1.5. Пусть в Q Lxu = ацих.х. + а{их. ^ 0, atfefa ^ О
it t
и для yQ' e Q min an (л;) > 0 ы max I ах (х) | < оо. Гог<3а <3ля ы
справедливо неравенство A.44).
Лемма 1.5 доказывается так же, как и лемма 1.4, только
в качестве барьерной функции в Q' надо взять a = eeKXi и вы-

160 линейные уравнения [Гл. ш
брать X столь большим, чтобы L,co = (аиХ2 + а,Я) ее**'>0 в Q'
(величина X зависит от Q'). Это приведет к оценке и(х)^тахи
в Q', а ввиду произвола Q' и к A.44). дй'
Лемма 1.6. Пусть в п L2u = ai}UX{X + a{ux.-\- au^O,
ОцЫ] > 0, а < 0, ы для VQ' с Q min а,, (л;) > 0, max | a{ (х) | < оо.
Тогда для V* е Q
ы(л:)^тах{0; тахы}. A-46)
да
Рассмотрим множество Q0 = {r^eQ, u(x)>0}. Оно от-
открыто, и на нем Lxu^ — au^O. В любой его связной компо-
компоненте выполнены условия леммы 1.5, а следовательно, и ее
вывод. Но это, как легко видеть, и дает A.46).
Замечание 1.2. Если в условиях лемм 1.3—1.6 на Lt
знаки неравенств изменены на обратные, то вместо A.44) при-
придем к неравенству и(х)~^>тп\пи, а вместо A.46)—к и(х)^
^min{0; min и}. Доказывается это применением лемм 1.3—1.6
ва
к функции v (х) = — и (х). В частности, если в леммах 1.3—1.5
функция и удовлетворяет уравнению Ltu = 0, то для нее спра-
справедливы оценки
min ы^ы(л:)^ тахы. A.47)
да да
Если же ы удовлетворяет в лемме 1.6 уравнению L2u = 0, то
для нее
min{0; min ы}<ы(л;Х max{0; тахы}. A-48)
да да
Утверждения лемм 1.3—1.6 и составляют то, что принято на-
называть принципом максимума. Рассмотрим теперь случаи, когда
ы удовлетворяет какому-либо неоднородному неравенству, в ча-
частности уравнению A.1).
Лемма 1.7. Пусть и удовлетворяет в Q неравенству
в котором a^lfcj^O, в^<0, minau(x)ssuu > 0,
= й\ > — oo, min a (x) = a> — оо; тогда для V* е Q
а
и (х) <— m{e%^ + max {0; max (ы + mxeUi)}t A-49)
да
еде X — неотрицательное число, удовлетворяющее неравенству
йиХ2-\-йхХ + <3>1, /n1 = max{0; — max (fe-Xx>)}. Если же и
удовлетворяет неравенству Lu ^/, то
и (х) > гще%х" + min {0; min (ы — 1Щеи<)} A.50)
с тем же X и /?^ = niax{0; min (/?"*•*')}•

§ 2] АПРИОРНАЯ ОЦЕНКА ШАУДЕРЛ 161
Возьмем &(х) = теКх\ считая /п^О, а к таким, как ука-
указано в лемме. Для нее Leo = {ах{к2 + «i^ + a) /neUi ^ (<2цЛ2 +
+ й{к-\-й) теХх^теХх\ Число т выберем так, чтобы meXxK^—f(x)
в Q, а именноm = /n, = max{0; max(—fe~Xx>)}. ТогдаL(u + со)>0,
и, следовательно, к функции ы + со применима лемма 1.6. Это
приводит к оценке A.49). Оценка A.49) применительно к функ-
функции v(х) = — и(х) дает неравенство A.50) для и(х).
Если таха(л:) = а<0 и Lu^f, to для и имеет место более
Q
простая оценка:
и (х) <С max {0; тахы; max (/а-1)}. A.51)
да а
Она следует из непосредственного рассмотрения Lu^f в точке
jc°eQ возможного положительного максимума и(х) (см. вывод
A.5)). Аналогично проверяется, что при а з= max а (х) < 0 для
а
функции и, удовлетворяющей неравенству Lu^f, справедлива
оценка
«W>mm{0; mina; minder1)}- A.52)
оа
В начале параграфа мы показали, что тах|ы| можно оце-
Q
нить и для а (л;), принимающих положительные значения, если
только max а (л;) невелик или если ширина Q мала в напра-
направлении одной из осей xk (см. теорему 1.2). Можно оценить
max | и | и при несколько других условиях на коэффициенты L
а
и Q, выбирая иначе, чем при доказательстве теоремы 1.2, функ-
функцию со при замене и на v = u<u~K
§ 2. Априорная оценка Шаудера
Займемся теперь выводом неравенства A.11). В основе всех
его доказательств лежит идея Шаудера разбить всю область Q
на маленькие подобласти Qft, k=l, ..., N, рассмотреть
в каждой из Qk уравнение Lm = / как уравнение
- аи (х)\ uXtXj — at (x) u%i -a(x)u = F (x)
с постоянными коэффициентами и получить для решений и та-
тай ||[2+a) |F|<> б
фф у р
ких уравнений оценку нормы |M|[j2+a) через |F|<a> и более сла-
слабые нормы и (вообще говоря, по несколько более широкой
подобласти). Если коэффициенты ац(х) непрерывны, то из этих
оценок можно «склеить» желаемую оценку A.11). В соответствии
6 О. А. Ладыженская, Н. Н. Уральцеиа

160 ЛИНЕЙНЫЕ УРАВНЕНИЯ [ГЛ. III
брать К столь большим, чтобы L1<D = (a11A,2 + ax%) ге%х* > 0 в Q'
(величина К зависит от Q'). Это приведет к оценке и (х)^. max и
в Q', а ввиду произвола й'и к A-44). т'
Лемма 1.6. Пусть в п L2u = aifUx.x,+ сциХ[ + аи^О,
ОцЫ] > 0, а < 0, ы для VQ' с Q min а„ (л;) > 0, max I а, (л;) I < оо.
Тогда для V* е Q
«W<raax{0; тахы}. A-46)
да
Рассмотрим множество О0 = {л;: х е Q, ы(х)>0}. Оно от-
открыто, и на нем L\U^— аы^О. В любой его связной компо-
компоненте выполнены условия леммы 1.5, а следовательно, и ее
вывод. Но это, как легко видеть, и дает A.46).
Замечание 1.2. Если в условиях лемм 1.3—1.6 на Lt
знаки неравенств изменены на обратные, то вместо A.44) при-
придем к неравенству u(x)^minu, а вместо A-46)—к и(х)^
ва
^min{0; min и). Доказывается это применением лемм 1.3—1.6
оа
к функции v (х) = — и (х). В частности, если в леммах 1.3—1.5
функция и удовлетворяет уравнению ?/Ы = 0, то для нее спра-
справедливы оценки
min и ^ и (х) ^ max ы. A.47)
дй да
Если же ы удовлетворяет в лемме 1.6 уравнению L2u = 0, то
для нее
min{0; min и}^и(x)^max{0; тахы}. A.48)
да да
Утверждения лемм 1.3—1.6 и составляют то, что принято на-
называть принципом максимума. Рассмотрим теперь случаи, когда
ы удовлетворяет какому-либо неоднородному неравенству, в ча-
частности уравнению A.1).
Лемма 1.7. Пусть и удовлетворяет в Q неравенству Lu^f,
в котором a.ZZ.^O, a(x)^.O, minau (х) = йи > 0, min аЛлс) =
' a q
= Й! > — оо, min а (х) = й > — оо; тогда для V* е Q
а
«(*)<— m,e^' + max{0; max(ы + m{eUl)}, A.49)
д&
где Я — неотрицательное число, удовлетворяющее неравенству
dutf + dyl + <2> 1, т, = тах{0; — max (fe-Xx')}, Если же и
и
удовлетворяет неравенству Lu ^ /, то
M(jt)>/n2eUl + min{0; min (ы — m2eXx>)} A.50)
да
с тем же Л и ff?2 = max{0; m\n(fe~Kx')}.

§ 2} АПРИОРНАЯ ОЦЕНКА ШАУДЕРА 161
Возьмем &(х) = теКх\ считая /n>0, a А таким, как ука-
указано в лемме. Для нее Leo = (апХ2 + аА + а) теКх* ^ {dnk2 +
+ й{к-\-а) т^-х^теХхк Число т выберем так, чтобы X f()
в Q, а именно т = т{ = max {0; max(— fe'Xx<)}. Тогда
и, следовательно, к функции и + со применима лемма 1.6. Это
приводит к оценке A.49). Оценка A.49) применительно к функ-
функции v(x) = — и(х) дает неравенство A.50) для и(х).
Если max а(х) = а < 0 и Lu^f, то для ы имеет место более
простая оценка:
ы(л:)^тах{0; тахы; max (fa~1)}. A51)
dQ Q
Она следует из непосредственного рассмотрения Lu^f в точке
д° е Q возможного положительного максимума и(х) (см. вывод
A.5)). Аналогично проверяется, что при а =з max а (л;) < 0 для
функции и, удовлетворяющей неравенству Lu^.f, справедлива
оценка
tt(*)>min{0; min«; тт(/а-')}. A.52)
да
В начале параграфа мы показали, что max | н | можно оце-
оценить и для а(х), принимающих положительные значения, если
только max а (х) невелик или если ширина Q мала в напра-
влении одной из осей xk (см. теорему 1.2). Можно оценить
тах|и| и при несколько других условиях на коэффициенты L
и Q, выбирая иначе, чем при доказательстве теоремы 1.2, функ-
функцию со при замене и на v = ue>~K
§ 2. Априорная оценка Шаудера
Займемся теперь выводом неравенства A.11). В основе всех
его доказательств лежит идея Шаудера разбить всю область Q
на маленькие подобласти Qft, 6=1, ..., N, рассмотреть
в каждой из Qk уравнение Lu = f как уравнение
- ач(х)]ыV/ - at (x) uX{ — a(x)u = F(x)
с постоянными коэффициентами и получить для решений и та-
таких уравнений оценку нормы |ы|^2+а) через |.F|(a> и более сла-
слабые нормы и (вообще говоря, по несколько более широкой
подобласти). Если коэффициенты ац (х) непрерывны, то из этих
оценок можно «склеить» желаемую оценку A.11). В соответствии
6 О, А, Ладыженская, Н, Н, Уральцева

162 ЛИНЕЙНЫЕ УРАВНЕНИЯ [ГЛ. III
с этой идеей доказательство неравенства A.11) сводится к
доказательству соответствующих оценок (предельно точных)
для решений уравнений L°u = F с постоянными коэффициен-
коэффициентами или, что то же, уравнений Пуассона Ды = F. С получе-
получения этих оценок для решений уравнений Au = F мы и начнем
вывод неравенств A.7). Излагаемое здесь их доказательство
было дано по нашей просьбе В. А. Солонниковым.
Мы будем использовать следующие известные (см. [37J) и
сравнительно просто выводимые неравенства между различ-
различными нормами гёльдеровского типа, справедливые для произ-
произвольных функций и из C/+a(Q):
" ILZ+a)] «та[ | и
«-»> (l+o).
г—1I1—a
I и |J{> < в 2 | ?>*и |?> + ce max | и |
B.1)
Здесь с и се зависят от области Q, е — произвольно малое по-
положительное число, а се-> оо при е->0.
Заметим еще, что если и (х) равна нулю вне Q и и е С1+а (Еп),
то
Ограничимся случаем п > 2. Для п = 2 все делается прин-
принципиально так же. Некоторое качественное отличие поведения
основного сингулярного решения на бесконечности (его рост)
для нижеследующих рассуждений несущественно.
Рассмотрим в «-мерном евклидовом пространстве Еп нью-
ньютонов потенциал
w
(Х) = J g (х - у) f (у) dy = т»1 J -|7Z7p- dy, B.2)
где т„ ==«(« — 2)х„, и в полупространстве л:„^0 потенциал
двойного слоя
v(x)= J K{x-
где у' =
а у = {у', У а)-

§ 2] АПРИОРНАЯ ОЦЕНКА ШАУДЕРА
Мы будем пользоваться тем, что
163
дх,
дх,
дУ{
Ах& {х — у) = AJS (х — у) = 0 при хфу,
АхК(х—«/)^0 при хфу.
B.4)
Лемма 2.1. Пусть функция у(х'), заданная на плоскости
хп = 0, дважды непрерывно дифференцируема, величина
л-1
2 (ф„ (x'))ia) конечна и при больших | х' \ справедливы не-
*, /—г ' / Еп-\
равенства
я-1
ф
С, \Х' Г,
1=1
| ,
л-1
дх.
а-2
B.5)
где 0 < а < 1. Тогда потенциал двойного слоя v (x) также дважды
непрерывно дифференцируем в полупространстве хп > 0 и там
имеет место неравенство
л-1
с постоянной с, зависящей лишь от п и а (но не or Cj ыз B.6)).
Дока з ателье тв о. Оценим сначала величину vX{X (x')Xn)—
— Vx{x,(x', хп), где i, \фп, а хп > 0. Для этого, используя B.4),
с помощью интегрирования по частям представим vX{X (x) так:
= J
- у)
Г
Уп=°
В силу B.5) интегрирование по частям возможно, и никаких
дополнительных членов при этом не возникнет. Из полученной
формулы вытекает, что
*V/ (*'• хп) - vXiXj (x't хп) =
= J K(z', xa]

164 ЛИНЕЙНЫЕ УРАВНЕНИЯ [ГЛ. III
и так как
| \К(г', xn)\dz'=\,
то
| vx.Xj (x't xn) - vX{Xl (*', хп) |<| х' - х' Г (т,){Е]п_{ B-6)
п-\
Пользуясь уравнением Лапласа vx х = — V] vx.x. и оцен-
кой B.6), получаем
п-1
\Ухпхп {Х', Хп) ~ VXnXn (Х\ Хп) | < \Х' - X' |° 2 <Фи>?' • B-7)
Переходим к оценке величины
vXnXi (x', xn) - vXnX. (х', хп),
где 1фп.
В силу B.4) vX(Xn можно представить в виде
п-1
Пусть Км ~ шар {\У'\<М, г/„ = 0} достаточно большого
радиуса, содержащий точки х' и Jc'. Введем функцию
Для любой фиксированной точки х справедливо vX{Xn =
= lim ^ш{х). Представим разность v\T{x', хп) — Лш(х', хп)
в виде суммы трех слагаемых:
^"V, xn)~vT (х', хп) =

§ 2] АПРИОРНАЯ ОЦЕНКА ШАУДЕРА 165
Пусть Ка? (*') - шар { | у' - х' | < 2р, уп = 0}, где р = | х'-х' |.
В первых двух интегралах разобьем область интегрирования Км
на К2р(х') и tfM\tf2pС*'), причем радиус М возьмем столь
большим, что /С2р (*') ci Км- Интегралы в скобках преобразуем
в интегралы по сфере \ у' \ = М. Это даст
»!?'(*'¦ *„)-
(появляющийся при интегрировании по частям интеграл пс
сфере \х' — у' \ = 2р равен нулю). Здесь щ(у') суть компоненты
единичного вектора внешней нормали к сфере SM = { W \ = м>
#я = 0}- Теперь устремим Af->oo. При этом все интегралы по

166
ЛИНЕЙНЫЕ УРАВНЕНИЯ
[ГЛ. III
сфере SM пропадут, так как при достаточно больших М
J I x — у \n J \x — у I"" y
Sm sm
<
sM
f<9i«-*i/
\*-v\
n-1
Итак, переходя к пределу при Af->oo, получим
xixn * > п/ иХ{Хп \л > лп) —
2_
\x— x\
M
on
дх{ \х-у\
Оценим теперь каждый член правой части:
{
Л2р U )
Точно так же оценивается второй член.
Для третьего члена справедлива цепочка следующих нера-
неравенств:
д 1 д 1
дх{ | х — у
,я-2
дх{ \х — i
= (п-2)
— u I"
\x-y
\x-y\n
<(« —
=(«-5
1
<
»» |Я I v II \П\~\
x-i,|"|je-j,|" J-

§ 2] АПРИОРНАЯ ОЦЕНКА ШАУДЁРА
Из ||jc — y\ — \х — jflKp и U —*/|>2р имеем
±
- у \>\х- у |- р>\х - у | - ^^1 = ±| х- у |,
и потому
ср
2 дх, \х-у
\П-2
\х-У\
Следовательно,
При этом мы воспользовались неравенством |х' — у'
<| л:' —/l + p^yl л;'—г/'|. Таким образом,
| vX{Xa (х\ хп) - vX{Xn (х', хп) | ^^
что и требовалось доказать.
Оценим теперь разности vx.Xj {x't xn) — vXiXj (x', хп). Пусть
i ?= п, \Ф п; тогда
так как
и, следовательно,
г2

168 ЛИНЕЙНЫЕ УРАВНЕНИЯ 1ГЛ. Ш
Пусть 6 = | *„ — хп\. Представим эту разность иначе:
vx.Xj(х\ хп) - vx.Xj (х', хп) =
~ *'"' «°1dy'
i <
i J
x'-i/' i > e
x
\- !
L дхп \х — \
\х-у\п-
Первые два интеграла непосредственно оцениваются сверху
через c6a((fyty.)ia) ¦ Последний интеграл также не превосходит
с6а (Ч>У{У1){а) ¦ Это ясно, если иметь в виду, что при \х — у
¦ 1
1Л-2
сЬ
\*-У\
Мы рассмотрели случай, когда / ф п,\ ф п. Случай i = j = n
с помощью уравнения сводится к предыдущему. Пусть / Ф п,
j = п; тогда
л-1
Интеграл

§ 2] АПРИОРНАЯ ОЦЕНКА ШАУДЕРА 169
сходится и равен нулю. Поэтому
vXixn (*', ха) - vx.Xn (х', хп) =
д*« \~х~
Каждый член этой суммы оценивается аналогично тому, как
это было сделано выше при i ф п, j ф п.
Подытоживая все случаи, видим, что
л-1
ft, J=l
л-1
I vx.Xj (*', xn) - vX{Xj (x', xn) |
I vXiXj (x't xn) - vXlXj (x', xn) I
при всех i, /= 1, .... п.
Лемма 2.1 доказана.
Лемма 2.2. Пусть f (у) — финитная функция из Са (?„).
Тогда ньютонов потенциал
непрерывен, имеет непрерывные производные до второго порядка
включительно и
где постоянная с зависит лишь от п и а.
То, что потенциал w (x) непрерывен и непрерывно диффе-
дифференцируем, хорошо известно. Существование же и непрерыв-
непрерывность по Гёльдеру производных второго порядка выводятся
с помощью нижеследующих формул. Пусть сначала f(y) есть

170 ЛИНЕЙНЫЕ УРАВНЕНИЯ [ГЛ. III
финитная в Еп непрерывно дифференцируемая функция. Тогда
в силу B.4)
h (у)
WXl.
J
-ТГ1
L
Производя обратное интегрирование по частям, получим
где
Уц = (п — 2) т J cos(«, zf)
I г |=1
ар — произвольное положительное число. Из этой формулы
видно, что D\w существуют, и равенство B.10) сохраняется для
любой финитной функции f(x) из Са(Еп). Возьмем другую
точку х и представим wxx(x) иначе, разбивая область инте-
интегрирования на шар \х — у\<р и его внешность | у — х\~^р,
причем радиус шара р возьмем больше | х — х \. Центр шара,
в отличие от B.10), поместим в точку л;, а не в точку х, для
которой пишется представление на этот раз. Делая те же
преобразования, что и в первом случае, получим формулу
-'
*,*,!'-»!
I jc—

§ 2] АПРИОРНАЯ ОЦЕНКА ШАУДЕРА 171
Вычтем из B.10) равенство B.11) и результат преобразуем так:
\х-
(п-2) J ¦
!х-у |=р
|Л
Члены, стоящие в фигурной скобке, как легко понять, взаимно
сокращаются; следовательно,
Здесь р — произвольное число, большее \х — х\. С помощью
этого представления величина (ZJ^)?1 оценивается через (/)^'
так же, как это было сделано выше для vX(Xn (x't xn)—vXiXn (xr, хп).
Повторять эти рассуждения мы не будем.
Из лемм 2.1 и 2.2 следует
Лемма 2.3. Если функции f(x) и ф(*) равны нулю вне
сферы |*|^/?, то для решения и(х) задачи Дирихле
Аи = /(*), «Uo = <P(^ B-13)

172 ЛИНЕЙНЫЕ УРАВНЕНИЯ [ГЛ. III
в полупространстве хп^0, стремящегося к нулю при | л: |—> оо,
справедлива оценка
с постоянной с, зависящей лишь от п.
Представим решение и (х) в виде суммы потенциалов. Для
этого продолжим / (х) на полупространство *„<^0 четным
образом, т. е. f(x', —xn) = f(x', xn), и сохраним за так про-
продолженной функцией прежнее обозначение.
Очевидно, (/)'"' >0\ — (f)iE)' По f(x) построим ньютонов по-
потенциал w (х) = т -о dy. Функция v (х) = и (х) -f w (х)
J \х-У\
будет удовлетворять уравнению Лапласа и при хп = О обра-
обращаться в функцию ф(*') + w(x', 0). При | л: |—> оо она стре-
стремится к нулю. Поэтому
v(x) = - J К (х - у) [ф (у') + w (у', 0)] dy',
и решение и{х) есть v (x) — w(x). В силу лемм 2.1 и 2.2
для и(х) справедлива оценка B.14). Лемма 2.3 доказана.
Любую финитную функцию и(х) из С2+а(Еп) можно пред-
представить в виде ньютонова потенциала
с финитной плотностью Аи; поэтому (см. лемму 2.2) для нее
S^<c<A«>g. B.15)
Переходим теперь к выводу неравенства A.11). Пусть
н^е^'Р, S^C2+a, коэффициенты L принадлежат Са(О)
и ф (s) = и |s e С2+а (S). Возьмем конечное число бесконечно
•дифференцируемых финитных неотрицательных функций С, (х), ...
- Un (•*)> дающих в сумме при х е Q единицу, т. е.
,v
2i?*(*) = l. ^ей, B.16)
и таких, что диаметры их носителей не превосходят некоторого
малого числа 6. Величина 6 будет уточнена ниже. Она опре-

§2] АПРИОРНАЯ ОЦЕНКА ШАУДЕРА 173
деляется лишь известными нам величинами. В соответствии
с B.16) функцию и(х) представим в виде
N
2 ик(х) = и(х), где ик (х) = и (х) ?ft (x).
k=\
Обозначим Lu через f(x). Умножая равенство Lu = f на Z,k,
представим его в виде
Muk = ail(x)ukXiXj = Fk(x), B.17)
где Fk (x) = fZk + au BuxfikXl + ut,kX{Xl) — atux^k — aut,k.
Если носитель Qk функции t,k (х) принадлежит Q, то на ик (x),
продолженную нулем вне Qk, можно смотреть как на финитную
функцию из С2+а(Еп), удовлетворяющую уравнению B.17)
со свободным членом Fk {x). Если же носитель Qk лишь частично
принадлежит Q, то введем в нем новые регулярные координаты
У1 = УЛХ)> ^=1» •••> п> так, чтобы часть Sk границы 5, при-
принадлежащая Qk, имела уравнение уп = 0 и область пк П Q при-
принадлежала полупространству */„^0. Функции ук {х) должны
быть элементами С'+а{пк). В новых координатах функция
йк (у) = Uk (x (у)) будет удовлетворять уравнению того же
вида B.17), именно
Muk^ull{y)ukyiylr=Fk{y), B.18)
где йц (у\ и Fk (у) известным способом вычисляются по а{/ (х)
и Fk(x).
Доопределим йк (у) на все полупространство уп ^ 0, полагая
ик (у) = 0 для у из {уп ^ 0), не принадлежащих образу
области пк П Q. За так продолженной функцией йк (у) сохраним
то же обозначение. Она удовлетворяет в области уп > 0 урав-
уравнению B.18), а при уп = 0 — граничному условию
BЛ9)
где <p*(s) = q>(s)C*(s). а ф*(у') = Ф
Представим уравнения B.17) и B.18) в ином виде:
и
М"ыА = аи (х°) ukx.Xj = Fk (x) + [аи (*°) - аи (х)] ukX{Xj B.17')
Шк = йи (у») йкУ1У1 = Fk (у) + [йи (у°) - йи (у)] йкУ1УГ B.18')
где *° и у0 суть произвольные точки из Qk и йк соответственно.
Введем вместо х и у новые прямоугольные координаты z с на-
началом в точках *0 и у0 так, чтобы в них уравнения B.17') и B.18')
привелись соответственно к
аи @) «to|,y - Д«* = ^ W + К @) - а;.; B)] «^ B.17")

174 ЛИНЕЙНЫЕ УРАВНЕНИЯ [ГЛ. III
*'ц @) Кг.г, - ЬК = П B) + [<*'„ @) - &\, Щ ukZ{Z/, B.18")
причем полупространство {уп ^ 0} во втором случае перешло бы
в полупространство {zn ^ 0}.
К решению уравнения B.17") применим оценку B.15); тогда
^ (г) + [а'ц @) - «;, (z)] ukZ{Z^\
Вспоминая вид F'k(z), характер переходов от л; к у (х) и от у
к 2 и правила вычисления констант Гёльдера для произведения
двух функций, отсюда получим
Д <«*„>? < « max | а'ц @) - а'ц B)| ^^ ^^ +
+ c1|«Wg + c1|/L")- B.20)
Максимум I а\. @) — a' (z) | берется по всем z из носителя ы^.
Будем считать диаметр носителя настолько малым, что
с max 1^@)-^ (z) |<i-. B.21)
Это и есть единственное ограничение на выбор диаметра б вну-
внутренних областей Qk.
Для таких б из B.20) получим
2 <«*г/г/Г < 2с, | и (х) & + 2С, | / (х) ?>. B.22)
Для решений uk{z) уравнений B.18"), удовлетворяющих
граничному условию B.19) (или, точнее, условию, получаемому
из него при линейном переходе от у к z), применим лемму 2.3.
Из неравенства B.14) при условии B.21) с постоянной с, взятой
из B.14), аналогично прежнему получим
jt >?>о} < ^ [I и (х) gno +1 Ф4 Г"' +1 f I'i'no] • B-23)
Если воспользоваться неравенствами B.1), то вместо (ukZl!C)<a)
П
и (йщг^г >й\ в левых частях B.22), B.23) можно поставить
нормы | uk |^+a) и | uk f{2+>o}. Переходя затем к старым перемен-
переменным х и складывая эти неравенства по всем k, придем к не-
неравенству
| и (х) g+•> < с3 (| и g» + | f Г +1 Ф Г а)> B-24)
Из него и B.1) следует желаемое неравенство A.11).

§ 2] АПРИОРНАЯ ОЦЕНКА ШАУДЕРА 175
Нетрудно проследить, что постоянную с в A.11) можно
выбрать не зависящей от размеров области Q (для этого надо
функции t,k(x) строить так, чтобы их носители Qk имели пере-
перекрытия в числе, не превосходящем какого-либо фиксированного
числа,с(п), не зависящего от размеров Q).
Докажем, наконец, неравенства A.12), A.13). Пусть S, —часть
границы S, на которой функция qp(s) «хорошая», т. е. принадлежит
(f+a(Sl). В частности, S{ может совпадать со всей S или быть
пустым множеством. Обозначим через dx расстояние точки х
до SXSp a min(dx, dy)— через dx_ y. Введем следующие полу-
полунормы:
Mi а [и] = 2 max dlx I Dxu |,
\k\l Q
Нам понадобятся эти нормы при / = 0, 1, 2. Для них справед-
справедливы следующие соотношения:
Лемма 2.4. При любом положительном е ^ 1 для любой
функции и (х) е Cm (Q) справедливы неравенства
Ми а [и] < еМт, а [и] + се-'/<т-"М0, „ [и], I < т, B.25)
а[м], Z < т, B.26)
с постоянными с, зависящими от I, m и а, но не зависящими
от и (х) и е.
Доказательство этих фактов элементарно, но длинно (см. [37,,
12!]). Мы его приводить здесь не будем.
Введем еще одно обозначение:
2
ЛГ2+а.а[и]= 2Af,,a[«] + Af2+o,o[«].
1=0
Докажем, что для любой функции и(х) с конечной нормой
Л^2+а. а [и] справедливо неравенство
N2+a. а [и] < с [Mo, a [Lu] + Мо. о [«] +1 Ф ?+а>]. B.27)
Постоянная с в нем определяется постоянной эллиптичности v
из A.2), нормами коэффициентов L в Са (Q) и нормой куска Si
в С . Функция qp(s) есть "Wlx=seS- Неравенство B.27) пред-
представляет собою несколько уточненную форму неравенства A.13).

176 ЛИНЕЙНЫЕ УРАВНЕНИЯ [ГЛ. Ш
В силу B.26) вместо нормы N2+a. а [и] достаточно оценить
величину М2+а,а[и], которая по определению равна
М2+а, а [и] = max
I дс-г/Г
;ьмем две точки х и у из й, для которых
Могут представиться две возможности: или | х — у\~^ — d
. 0 [и]. B.28)
— dXty,
или | х — у | < -j dXt y. В первом случае
п
у М2+а, а [и] < 4а4. у 2 [ | Ux.Xj | + | Uyi4j | ] < сМ2, в [и]
t. /-1
и потому неравенство B.27) будет простым следствием B.26)
при /=т = 2. Во втором случае, при \х — y]<-^-dx>y, пусть
для определенности dx,y = dx. Возьмем шар К с центром
О
в точке х и радиусом -jdx. Введем срезающую для него функ-
функцию ^2)eC'+i1(Q), равную 1 при \х — z\^-^dx и нулю при
\ х — z\^ — dx. Функция v (z) = и (z) t,(z) удовлетворяет в КО®
следующему уравнению:
в котором F=Lu-t, + 2atIuzt,z + atjut,zz + ам1г. Продолжим
ее нулем на всю Q и за так продолженной функцией сохраним
то же обозначение и (z). К ней применимо доказанное выше
неравенство A.11). Для всех возможных вариантов расположе-
расположения К по отношению к S, (т. е. когда К пересекает Si и когда К
не пересекает 5,) его можно записать, огрубляя, так:
, .S
\х-у\а ~ \х-у\а <
< {| F р„ 0 + | ?„ g+« + Мо, в [и]}. B.30)
Функцию t,{z) считаем выбранной так, чтобы ^

§ 3] О РАЗРЕШИМОСТИ В С2+О(й) КРАЕВЫХ ЗАДАЧ 177
(?)(a) < cldax, |?гг <^.c/d2x (это, очевидно, возможно). В резуль-
результате простых подсчетов убедимся, что
п.
Л У 4т Мо> Q[uZlZj] + -~ J Мо. а [иг/] + -~ /Ио. й [и]
а ах ах
ах
1 fe* '/( П S, ^* ji+a ' *'K П S,1
Подставляя эти неравенства в B.30), умножая результат на с12х+а
и учитывая B.28), получим
у ^2+а. Q [«]< С | Ма, а [/-И] + 2j М'. Q [«] + I Ф is,
а это неравенство в силу B.26) дает B.27).
Это завершает доказательство всех утверждений, высказан-
высказанных в начале параграфа для 1 = 2. Для />2 они выводятся
элементарно из рассмотренного случая / = 2.
§ 3. О разрешимости в C2+a(iJ) других краевых задач
Разрешимость второй и третьей краевых задач и задачи
с косой производной при достаточно гладких данных иссле-
исследуется в основном так же, как это сделано в предыдущем
параграфе для первой краевой задачи. Аналитическую основу
составляют априорные оценки шаудеровского типа, т. е. нера-
неравенства типа A.11). Для второго и третьего краевых условий
такие оценки были доказаны в 1955 г. К. Миранда [372]. Усло-
Условия эти для оператора
Lu=zatl (x) иХ{Х/ + ai (x) иХ{ + а(х)и C.1)
имеют вид
Аиs=s а., (х) и cos (п, х.) + Ъ (х) и = ер (*). C.2)
При 6(л:)з==0 имеем второе краевое условие, при Ь(х)Ф0 —
третье. Однако в отличие от первого краевого условия для
существования таких априорных оценок для всего класса опера-
операторов вида C.1) и граничных условий вида C.2) на функции а,ц(х)
вблизи 5 необходимо накладывать ограничения более жесткие,
чем те, которые требуются для внутренних оценок. В самом
деле, если функция и(х) принадлежит С1+а (Q), а Lu принад-
принадлежит Са (Q), то от коэффициентов L естественно требовать

178
ЛИНЕЙНЫЕ УРАВНЕНИЯ
[ГЛ. III
принадлежности их к Са (Q). В этом случае каждый член из Lu,
а потому и все Lu, будет функцией из Са (й). В краевое же
условие C.2) входят_производные первого порядка от и (х), они
1+а
принадлежат С1+а (Q). Поэтому функция <р(х) в общем случае
должна быть элементом Cl+a(Q) (ибо, в частности, когда at/
постоянны, а &(*:) = 0, функция <р есть линейная комбинация
первых производных и). Для того чтобы все члены в C.2) были
l+a
элементами Cl+a(S), придется требовать принадлежности
к Cl+a(S). Таким образом, имеется «разнобой» в требованиях
на пц{х) внутри Q и на S. Но он неизбежен. Ввиду этого для
исследования второй и третьей краевых задач в нелинейном
случае знание относительно линейных задач лишь оценок
Миранда (он оценил | и (?+а) для произвольной функции и из
С2+а (О) через | Lu \{?\ тах| и | и | Аи |s' +а)) оказалось недоста-
недостаточным. Для исследования нелинейных задач понадобился сле-
следующий более общий результат, доказанный в 1959 г. Р. Фио-
ренца [17]:
Теорема 3.1. Пусть граница S области Q есть поверхность
класса С2+а, коэффициенты a,-/( ah а оператора L принадле-
принадлежат Са (О) и выполнено условие эллиптичности
M*)E<E/>vE2, v = const >0. C.3)
Пусть коэффициенты bt (x) и Ъ (х) граничного оператора
Ви 2= bt (х) их. + Ъ (х) и суть элементы С1+а (S) и
п
2
(х) cos (л, xt) |s
0,
Тогда для любой функции и (х) из С
венство
v0 = const > 0. C.4)
2+а (Q) справедливо нера-
нераBu fs1+a)]
+1 Lu fQa) + max | Bu \ • | bt
max| и |[max| b |-| bt fs1+a>+ (| au fsa)+l bt t^)(\ b fsM + max \a\)
b, g' + max| b\ + max | at

^ 3] О РАЗРЕШИМОСТИ В С2+О(й) КРАЕВЫХ ЗАДАЧ 179
а также
+ | Lu ?> + max\Bu\-\b, fs1+a) + I Bu g +a)] +
+ m«| и \[\b g+e) +1 a |?> + (| ft g» +max| a |)B+a)/2
h l<a) J. I A lA+a) -1- I n
b \s +1 bi\s + I a,-
(a)V
2 +a)/"+O)
постоянные с зависят только от п, констант v и v0 из усло-
условий C.3), C.4) и от границы S, которая предполагается при-
принадлежащей классу С2+а.
Второе из этих неравенств имеет следующую структуру:
| и g+e> <с, [| Lu ?>+ I Bu fs1+a) + max| и |], C.7)
где постоянная с, не зависит от и (х), а определяется лишь S
и коэффициентами операторов L и В. В C.5) и C.6) эта зави-
зависимость с, от ац, ah a, bh b и S указана явно. Знание ее
существенно при исследовании второй и третьей краевых задач
для квазилинейных уравнений (см. гл. X) и несущественно
в линейном случае.
С помощью оценки C.7) нетрудно доказать, что для задачи
Lu-\u = f(x), Бм|5 = ФE), C.8)
где Я,— комплексный параметр, имеет место следующая теорема:
Теорема 3.2. Пусть относительно S и коэффициентов L и В
выполнены условия теоремы 3.1, /(x)eC°(Q), qp (s) e C1+a(S).
Тогда задача C.8) однозначно разрешима в С2+а (О) для любых f
и ф из указанных классов при всех Я, за исключением не более
чем счетного числа значений Хи Я2, ..., составляющих спектр
задачи C.8). Для этих исключительных значений Я, = Xk9 k = 1,
2 единственной точкой накопления может быть А, = оо.
Каждое из Я^ имеет конечную кратность, т. е. соответствующая
ему однородная задача
Lu — ЯАи = 0, Bu Is = 0 C.9)

180 ЛИНЕЙНЫЕ УРАВНЕНИЯ [ГЛ. III
имеет нетривиальные решения uk (х) из С2+а (Q), причем линейно
независимых среди них будет конечное число. Эти же Xk, k = \,
2, ..., с той же кратностью образуют спектр сопряженной к
C.9) задачи. Неоднородная задача C.8) разрешима не при всех
f и ф: должно выполняться несколько условий типа условий
ортогональности к решениям однородной сопряженной к C.9)
задачи.
Доказывается эта теорема в основном так же, как и соот-
соответствующие утверждения для первой краевой задачи в § 1.
Но на этот раз надо продолжать по параметру не только опе-
оператор L, но и граничный оператор В. Схема этого следующая:
обозначим через М, оператор, сопоставляющий каждому эле-
элементу v(x) из С2+а (Q) пару функций {Lv; Bv}, которую рас-
рассмотрим как элемент пространства Са (Q) X С1 +a(S). Возьмем
семейство операторов
Mxv={Lxv\Bxv), те [0,1],
где Lxv = A - т) До + xLv, а Bxv = A - т) (~ + и) + xBv.
При каждом х из [0, 1] оператор Мх отображает простран-
пространство С2+а (Q) в пространство Са (Q) X С1+аE). Неравенство C.7),
точнее, неравенство | v f2+a) < с, (| Lxu \? + | Вхи fs'+a)), справед-
справедливое в случае, когда коэффициент а (х) при и удовлетворяет
условию a(*X0 и Ь(х)>0, гарантирует равномерную ограни-
ограниченность операторов М71 (Mi — Мо) в пространстве С2+а (Q),
коль скоро известно, что Af7* существует и определен на всем
Са (Q)XC1+aE). Это вместе с тем, что оператор А/71 при т = 0
определен на плотном в Са (Q)XC1+a(S) множестве, гарантирует
существование ограниченных операторов М^\ определенных на
всем Са (Q)XC1+a(S), при всех т из [0, 1] и, в частности, дает
однозначную разрешимость задачи
Lu = f, Bu\s = y(s) C.10)
в C2+a(Q) при любой /_из Са (Q) и ф из C1+a(S). В общем слу-
случае любого а(х) из Са (Q) и Ь(х) из Ci+a(S) имеет место альтер-
альтернатива Фредгольма, сформулированная в теореме 3.2. Существо-
Существование MqX на плотном в Ca(Q)XCl+°(S) множестве можно
доказать или непосредственно на основании теории электроста-
электростатических потенциалов, или так, как это сделано в § 1. Необхо-
Необходимые для второго пути оценки типа A.13) со срезающей функ-
функцией Z,tx) имеют место и в рассматриваемом случае граничного
условия Ви is = ф.

§ 4] ОБОБЩЕННЫЕ РЕШЕНИЯ ИЗ W^Q) I8I
§ 4. Обобщенные решения из W'2(Q).
Первое основное неравенство
Переходим теперь к изучению уравнений с неограниченными
коэффициентами. Рассмотрим уравнения вида
Lu - -?- (fl</ (x) и,. + a, (x) и) + bt (x) ux. + a (x) и = -^ + / D.1)
при услов(Ги, что их старшие коэффициенты аг/ = ац ограни-
ограничены и уравнение D.1) строго эллиптично, т. е. при условии
42<anhti<:^l2> v, ц = const >0. D.2)
В § 2 гл. I было выяснено, что если для таких уравнений
*
мы хотим рассматривать обобщенные решения из 1Иг(й), то
необходимо считать, что *)
п п ||
2 а% 2 Щ . || а \{,12ш 0 < |х, q > п. D.3)
Если хотя бы одно из этих условий не выполнено, то для
таких уравнений неправомерна теория обобщенных решений из
И?2(й), ибо в этом случае нарушается теорема единственности
«в малом» **).
*
Назовем обобщенным решением из W2(Q) (сокращенно об. р.)
уравнения D.1) функцию и (л;), принадлежащую Wi(Q) и удовле-
удовлетворяющую интегральному тождеству
L (и, т]) = J [(ациХ/ + а,-и)тц. — (М*, + аи) r)]dx =
D.4)
и
при любой функции Ti (л:) из C°°(Q) (см. § 1 гл. I).
Легко видеть, что если функции /,-, / и коэффициенты урав-
уравнения D.1) гладкие и функция и (л;) является его классическим
решением или хотя бы принадлежит wl (й) и удовлетворяет
уравнению D.1) почти всюду, то она удовлетворяет и тожде-
*) По поводу случая q = п ^ 3 см. конец параграфа.
**) Класс И^(й) определен в § 1 гл. I. При п > 3 w[(u) =
= 1^2 (-О)П L2n/{n_2) (Q), при " = 2 1^2 (й) состоит из элементов w\ (й),
суммируемых по Q с любой степенью. Для не слишком плохих п
IFj(B) = Wjlfl) (подробнее см. § 2 гл. II).

182 ЛИНЕЙНЫЕ УРАВНЕНИЯ [ГЛ. III
ству D.4). Действительно, умножая D.1) на ц, интегрируя по Q
и преобразуя ряд членов с помощью интегрирования по частям,
придем к соотношению D.4). Верно и обратное: если функция
и (л;) принадлежит Wl(Q), удовлетворяет тождеству D.4) при
любой tieC^fQ) и все остальные функции, входящие в D.4),
гладкие, то и(х) удовлетворяет уравнению D.1) почти всюду.
Оба эти обстоятельства говорят о том, что понятие обобщен-
обобщенного решения уравнения D.1) действительно является расшире-
расширением старого понятия классического решения.
о .
Чтобы тождество D.4) имело смысл при любых r\ e W2 (Q),
потребуем от ft и / следующего:
где
п при п > 2;
2 + е при п = 2; е > 0.
D.5)
Нетрудно проверить, что при выполнении условий D.2),
D.3) и D.5) интегралы от всех членов тождества D.4) конечны
при любых и и т) из Wl2(Q), и потому в этом случае в данном
выше определении обобщенного решения можно считать г\
о .
любой функцией из W2 (й).
Введенное расширение понятия решения целесообразно
с разных точек зрения. Во-первых, оно дает возможность изу-
изучать уравнения D.1) с недифференцируемыми и даже с разрыв-
разрывными и неограниченными коэффициентами, для которых левая
часть равенства D.1) может не иметь смысла. Такие уравнения
встречаются в ряде задач, например в задачах дифракции.
Во-вторых, такие решения соответствуют одному из главных
подходов функционального анализа к изучению линейных опе-
операторов. Именно, тождество D.4) задает билинейную форму
оператора L
L (и, л) = J [(<»</«*, + atu) тц - (ЬтХ1 + аи) r\] dx D.6)
Q
на подлежащих определению элементах и и любом ц из W2 (й).
Из такого задания, как будет показано в следующем параграфе,
сравнительно просто определяются и, если дополнительно из-
известны их граничные значения. В-третьих, обобщенные реше-
решения из Wl2 (Q) отвечают физической сущности задач, приводящих
к уравнениям вида D.1). Поясним это на примере задачи Ди-
Дирихле для уравнения Пуассона
Дм=/, мЬ = 0- D-7)

§4] ОБОБЩЕННЫЕ РЕШЕНИЯ ИЗ W-2(Q> 183
Известно, что к этой задаче приходят при разыскании рав-
равновесного положения и упругой однородной мембраны, закреп-
закрепленной на границе S так, что и|5 = 0, и находящейся под
действием внешних сил f. Потенциальная энергия такой мембраны
задается интегралом 1(и)= \ (\Vu f + 2uf)dx, а ее равновесное
Q
состояние, согласно принципу Гамильтона, определяется из
условия, что функционал /(и) на и достигает наименьшего воз-
° 1
можного значения по сравнению со всеми и из tt?2(Q). Отсюда
следует, что для равновесного состояния и(х)
Ы (и) а 2 { (иЛ.тц + /Л) dx = 0 D.8)
Q
для любой г] из tt?2(Q).
Таким образом, задача об отыскании равновесного положе-
положения мембраны, согласно принципу Гамильтона, сводится к на-
нахождению функции и из класса Wl(Q), удовлетворяющей ин-
интегральному тождеству D.8). Исторически сложившаяся тради-
традиция отыскания решения задачи на минимум интеграла /(и)
с помощью решения краевой задачи для соответствующего ей
уравнения Эйлера существенно усложнила задачу, привнеся
в нее дополнительное требование, не лежащее в физической
сущности задачи, — требование того, чтобы решение обладало
производными вдвое более высокого порядка, чем те, которые
входят в энергетический интеграл / (и). Такой отрыв от фи-
физики во многом обусловил трудности, лежащие на пути решения
вариационных задач и связанных с ними уравнений Эйлера.
Оказывается, задача об отыскании равновесного состояния
мембраны значительно проще задачи D.7) о разыскании клас-
классического решения соответствующего ей уравнения Эйлера.
Предложенное выше расширение понятия решения уравнений D.1)
применительно к задаче D.7) состоит в отказе от уравнения
Эйлера и в возврате к тождеству D.8), которое есть не что
иное, как интегральное тождество D.4) для уравнения
Пуассона.
Выясним теперь, что надо понимать под обобщенным реше-
решением из Wl2(Q) первой краевой задачи для уравнения D.1).
Ясно, что для существования таких решений и (х) необходимо,
чтобы функция qp(s), определяющая граничные значения и (л;),
допускала продолжение ц>(х) на всю область Q, которое при-
принадлежало бы w2(Q). Итак, пусть q»(x)^W2(Q) и граничное
условие для искомого решения есть
wls = «Pls- D-9)

184 ЛИНЕЙНЫЕ УРАВНЕНИЯ [ГЛ. III
Так как наше решение и должно принадлежать UMQ), то усло-
вие D.9) разумно записать в виде и (х) — ф (*) е Wo (Q). Из
сказанного ясна естественность следующего определения:
Обобщенным решением из W2(Q) задачи D.1), D.9) назовем
функцию и, принадлежащую Wii®) и удовлетворяющую тожде-
тождеству D.4) или, что то же, тождеству
Ни, л) = (/<> гц)-(/. Л) DЛ0)
о . о .
при любой r\^W2(Q) и условию и (х) — ф (*) е Wi (Q). Так как
обобщенных решений из других функциональных классов
в ближайших двух параграфах не будет, то условимся назы-
называть их пока просто обобщенными решениями (уравнения или
первой краевой задачи).
Краевая задача с условием D.9) легко сводится к краевой
задаче с однородным краевым условием. Именно, если вместо и
введем функцию v (x):
v(x) = u(x)-cf(x), D.11)
то для нее из D.10) получим
L(v, Л)=-Мф, л) + G„ r\Xl)-(f, л), D.12)
а из D.9) — условие
ols = 0, D.13)
которое понимаем в том смысле, что у
Вместо функции и будем искать функцию v как функцию
о .
из Wo(Q,), удовлетворяющую тождеству D.12). Найдя ее, мы
найдем и функцию и = и + ф— обобщенное решение задачи
D.1), D.9).
Пусть условия D.2), D.3), D.5) выполнены. Покажем, что при
этих условиях и ф(*) из W]2(Q) выражение
I (п) а - L (ф, л) + (ft, r]x.) - (/, л) D- И)
О j
есть линейный функционал над пространством W2 (й) и для
него верна оценка
/ (Л) К J
s с fa, Q, Ф, f, /)||Ул||2й, D.15)

ОБОБЩЕННЫЕ РЕШЕНИЯ ИЗ w\{u) [85
где f = (f, /„), II fib, o=l/ \^l]dx > а с (?, Q) - посто-
а i
a »=i
янная из неравенства
Jl4 %яКя-2), q < с (?) mes"Т О ' II Vti ||2_ о =
==с(<7, О) || VtiHj,,,, <7>Л. DЛ6)
о ,
справедливого для любой функции r\^W2(Q) (формула B.13)
гл. II).
Действительно, используя предположения D.2), D.3), D.5),
оценим |/(т])| с помощью неравенства D.16) и неравенства
Гёльдера следующим образом:
I (f, Л) КII f IIsm/<a+2). a II ^ 1Ьй/(й-2), а <
2. a II Ф IU/(G-2). a II Л IU/(G_2), Q ^ M- II V<p ||^ Q || Vt, |L a
Ф U*,/(?_2). B II Vn Ik „ + ЦII Л \\тя-2), а II Vф ||2, e +
+c(q, Q)]. D.18)
Из этих неравенств следует оценка D.15).
Переходим теперь к выводу первого основного неравенства
(иначе говоря, энергетического неравенства) для эллиптических
операторов. Для этого напомним, что для любой функции
ojjtJElf'lp справедливо неравенство
. а
[г 11| W |? fl + в-»Я«-»> A - ±) || v ||22, J , D.19)
где е — произвольное положительное число, a q > п. Оно есть
следствие неравенств B.11) и A.3) гл. II.
Представим коэффициент а (х) в виде разности: а (х) =
= а+ (х) — а~ (х), где а+ (х) = max {а (х) — а0; 0), а~ (х) = — а0 -+-

186 ЛИНЕЙНЫЕ УРАВНЕНИЯ [ГЛ. II!
+ max {— а (х) + ай\ 0}, а аа = ^g- J а (*) dx. Ясно, что flT(*)>
а
^—а0. Введем обозначение
2 +) D.20)
; Ца+1|,/2в)
(легко видеть, что М ^4ц, где ц — постоянная из условий D.3)).
Покажем, что квадратичная форма L (у, и) обладает следую-
следующим свойством:
Лемма 4.1. Пусть выполнены условия D.2) и D.3). Тогда
О |
(Зля любой функции v e U?2 (й) справедливо неравенство
D.21)
<? - /г [2Л1 Bv + 1) пс2 (?)
—— [ ^
J
Действительно, благодаря условию эллиптичности D.2) из
определения D.6) для L (у, v) имеем
(v, v) +
-\vvXt[+a+v2)dxKL(v, v) +
}> D-22)
где е — произвольное положительное число. Оценивая послед-
последние члены с помощью неравенства Гёльдера и используя обо-
обозначение D.20), получим
- И
«=i ||<?/2, a
Отсюда и из D.22) при e = v/2 получим
L(v, v} + J^l+Allvf2qKq_2)a. D.23)

§41 ОБОБЩЕННЫЕ РЕШЕНИЯ ИЗ w\{®) 187
Если последний член оценить с помощью неравенства D.19)
и взять е = 2УИ Bv + 0 с2 (о) п ' то после приведения подобных
членов придем к D.21).
Лемма 4.1 доказана.
Воспользуемся неравенством D.21) для оценки обобщенного
решения и задачи D.1), D.9). Из соотношений D.12) и D.13)
для функций у = и — ф и неравенства D.21) имеем
где /(у) определено равенством D,14). Отсюда благодаря оценке
D.15) будем иметь
J[|
ciq, Q, Ф> f, f) \\ Vv ||2, B + c, (q) \\ v \\{
||2, B + c, (q) \\ v \\{ B
Перенесем слагаемое -^|| W||2 fl из правой части налево, при-
приведем подобные члены и результат умножим на 2. Это даст
W f + ^a-v2] dx^c2(q, Q, Ф, f, /) + 2с, {q)\\v\^Q. D.24)
Особый интерес представляют те случаи, когда в неравенстве
D.24) можно «убрать» член с || v f2 a, стоящий в правой части.
Чтобы "выявить их, воспользуемся неравенством (см. B.14) гл. II)
||Vo||2iB D.25)
и тем, что а~ (х)^— а0. Отсюда видно, что если
б s [2c, (q) +1 а0] с2 mes2 Q < 1, D.26)
то из D.24) следует
J | Vy р dx <A_'%o)v2c2 (q, Q, ф, f, f), 60 = max {0; 6}. D.27)
Если ф^О, то v есть решение и уравнения D.1) и неравенства
D.24) и D.27) для него приобретают вид
J [ |V«| ^ — АаоЦ2] dx< J [|
a a
f «2. a + c (л. Q) II f Нмя/1+2). а]2 + 2ci (?) II " 'I a D-28)

188 линейные уравнения [гл. ш
и
JI V» Г dx < (,_16 [II f ||2, „ + с (Я, Q) || / ||2й;(й+2I ор D.29)
а
соответственно. В общем случае при ср Ф 0 для обобщенных
решений и=у + ф задачи D.1), D.9) неравенства D.24), D.27)
дают оценки
^С2(?)и>Ф, t,f) +
4c1(<7)lkll?.e +
^с?(<7, О, ф, f, f) + 4c1(<?)||«||22_fl D.30)
и при б<1
Q,<p,f,f). D.31)
В них постоянная c(q, ф, й, f, f) взята из D.15), а сх (q) —
из D.21). Неравенство D.30) (а также его следствие D.31)) на-
называется первым основным или энергетическим неравенством
для решений задачи D.1), D.9). При ф^О вместо него можно
пользоваться неравенством D.28) (и D.29) соответственно), ко-
которое также называется энергетическим.
Неравенство D.26) заведомо выполнено в следующих двух
случаях. Во-первых, для областей Q достаточно малой меры,
ибо | а01^ mes-^Q • || а \\ /2 а. Во-вторых, для любых областей,
если только
4 D.32)
Весьма существенно, что соотношение D.26) имеет место для
операторов Lu — ku при определенных Я, например при всех
достаточно больших положительных Я. Это следует из того,
что коэффициент при и(х) в Lu—ku равен а(х)—к и {а(х)—кH=
= а0—к. В дальнейшем вопрос о разрешимости первой краевой
задачи будет рассмотрен для всей совокупности операторов
L —кЕ при любом к на комплексной плоскости. Но начать это
изучение удобно с такого к, при котором выполнено усло-
условие D.32). Без ограничения общности можно считать, что это Я
равно нулю, т. е. что неравенство D.32) выполнено для самого
оператора L. Изучению этого случая и посвящен следующий
параграф.

§ 4] ОБОБЩЕННЫЕ РЕШЕНИЯ ИЗ Wo№) 189
Замечание 4.1. Если а(*)<^0, то разбивать а(х) на два
слагаемых указанным выше способом нецелесообразно. Вы-
Выгоднее соответствующее ему слагаемое — J av2dx оставить
в левой части соотношения D.22) и др. Если же а(х) не
удовлетворяет условию а(х)^.О, то а(х) можно разбить, на-
например, на положительную и отрицательную части, т. е. пред-
представить а (х) в виде а (х)=а+ (х)—а~ (х), где а+ (*)=тах {а (х); 0},
а а~ (х) = max {—а (х); 0}, и в неравенстве D.22) считать, что
а+ (х) и а~ (х) взяты в соответствии с этим разбиением а (х).
Но тогда при добавлении в левую часть уравнения D.1) члена
— ки соответствующее ему в D.22) слагаемое к \v2dx надо
а
оставить в левой части. Это приведет к добавлению в левые
части неравенств D.21) и D.24) слагаемых 4v-'A J v2 dx и
а
8v~lk v2 dx соответственно. При достаточно большом к эти
а
интегралы превосходят члены сх (q) || v |? а и 2ct (q) \\ v \f2 Q, стоя-
стоящие в правых частях D.21) и D.24). Ввиду этого ясно, что для
задач Lu— ки = -%-*--\-f, w|s = q> при достаточно большом к
OX t
справедлива.теорема единственности и для их решений имеют
место оценки типа D.31). Разбиение а(х), взятое на стр. 185,
имеет то преимущество перед указанным здесь, что для него
справедливо соотношение (а(х) — кH = аа — к, благодаря кото-
которому сразу видна выполнимость условия D.32) для операторов
Lu — ки при к >¦ 1.
В § 2 гл. I была показана необходимость предположения:
q > n в D.3) для справедливости предложений, доказываемых
в данной главе. Однако там же было отмечено, что при п^З
предельный случай q = n сохраняет некоторые черты, присущие
задаче Дирихле в ее классической постановке. Покажем это.
Пусть для L выполнено условие D.2) и условие
\Ъа2, %b2i, а\ <ц, п>3. D.33)
| (=i j=i |rt/2, a
Представим функции bt(x) — at (x) и а+ (х) = тах{а(х); 0} в виде
сумм:
bi(x) — ai(x)=c't(x) + c'.'(x), a+(x) = c'(x)+c"(x), D.34)
где ^(х) и с'{х) суть ограниченные функции, а с"(х) и с"(х) —
элементы Ln(Q) и LnpiQ) соответственно, имеющие малые нормы.

190 ЛИНЕЙНЫЕ УРАВНЕНИЯ ГГЛ. Ill
Пусть
maxB [<(х)]2, | с'(х) |)< Af,., 2 «'J. с"\ <е'. D.35)
Ясно, что в общем случае Мг> безгранично растет при стрем-
стремлении е' к нулю и характер этой зависимости МЕ> от е' не
определяется только величиной ц из D.33), а зависит от взя-
взятого L. Для L справедливо неравенство, аналогичное D.21).
Вывод его тот же, что и для D.21): надо взять неравенство
D.22) и оценить его правую часть, используя разбиение D.34).
Это, как легко видеть, приведет нас к неравенству
^L(v, v) +
±L М* || v \i 0 + -Ц±±- в'|| v ||22n/(rt_2)i e, D.36)
где а" (х) = тах{— а(х); 0}. Последний член правой части не
превосходит в силу D.16) величины —^1+—е'с2 (n) || Vy |^ fl. По-
Поэтому, если е' взять таким, чтобы
^l. D-37)
то из D.36) будем иметь желаемое неравенство:
D.38)
Из него, так же как D.24) из D.21), выводится первое основ-
основное неравенство для обобщенных решений у уравнения D.1) из
< v»(i-6,) [II * ll2. о + с(Л, Q) II / ll2n/(n+2), Qf + 2VJ' Af, II v |gf B,
D.39)
если заметить, что оценка D.15) имеет смысл и при q = n.
Отсюда легко следует соответствующая оценка для любого
обобщенного решения уравнения D.1) из Й?г(й), аналогичная
оценке D.30). Если между числовыми параметрами, характери-

5 5] РАЗРЕШИМОСТЬ ПЕРВОЙ КРАЕВОЙ ЗАДАЧИ В «'г (Q) 191
зующими уравнение D.1), и OicQ выполняется соотношение
б2в I [^ м*- - чг а~ {х)\ с° mes2/rtQ> < ^ • D-40)
то из D.39) следует, что для обобщенных решений v (x) урав-
о ]
нения D.1), принадлежащих W2(?li), справедливо неравенство
J I
D.41)
б3 = —5-1 — max \
Неравенство D.41), так же как и D.29), заведомо выполнено
для областей й, достаточно малой меры, так как при этом вы-
выполнено D.40). Однако в данном случае малость mes Q\ не
определяется только ц из D.5), D.33), а зависит также и от е'
и Ме> из D.35). Неравенство D.41) для Q, = Q с 63=A —б,)/2
выполняется также для операторов L\u^Lu—Ли с Л^Л0 =
2 v + 1
= —^—^е'> гЛе е' подчиняется D.37). В этом легко убе-
убедиться, замечая, что в D.38) L(v, v) = LK(v, v) — k\\vf2 a.
§ 5. Разрешимость первой краевой задачи в W2(Q)
Неравенства D.29), D.41) позволяют утверждать следующую
теорему единственности для задачи D.1), D.9):
Теорема 5.1. Задача D.1), D.9) имеет не более одного
обобщенного решения из W\(Q), если выполнены условия D.2),
D.3) и D.26). Для п~^Ъ эти условия можно заменить усло-
условиями D.2), D.33), D.37), D.40).
В самом деле, для разности и = и' — и" двух возможных
обобщенных решений из W2 (й) этой задачи справедливы нера-
неравенства D.29) или D.41), в правых частях которых стоят нули
(ибо для и свободный член и граничное условие однородны),
поэтому и{х) будет равно нулю.
Из этой теоремы, в частности, следует, что для любого
дифференциального оператора L, определенного в Q и удовлет-
удовлетворяющего условиям D.2), D.3), теорема единственности задачи
Дирихле верна в любой достаточно малой (по мере) подобласти
й4 области Q, причем величина mesQ] определяется лишь

192 ЛИНЕЙНЫЕ УРАВНЕНИЯ [ГЛ. Ш
постоянными q, v и ц *). То же верно при я^З для любого L,
коэффициенты которого удовлетворяют условиям D.2), D.33),
но в этом случае mesQi зависит от взятого L. В областях
й, с Q произвольных размеров теорема единственности задачи
Дирихле имеет место для операторов L — КЕ с А^А0, если L
удовлетворяет условиям D.2), D.3) или D.2), D.33) и Ао доста-
достаточно велико. В первом случае Ао определяется лишь q, v и ц;
во втором — числом v из D.2) и е' и Ме> из D.35), точнее,
где е' удовлетворяет неравенству D.37).
Переходим теперь к исследованию разрешимости задачи Ди-
Дирихле для D.1). Мы это сделаем для всей совокупности опе-
операторов L — КЕ, где А — произвольное число на комплексной
плоскости, без каких-либо ограничений малости на область Q.
Предположим, что для D.1) выполнены условия D.2), D.3),
D.5). Без ограничения общности можно считать, что D.26),
а потому и теорема единственности, выполнены для самого опе-
оператора L. Тогда для возможного решения и задачи D.1), D.9)
(во всем параграфе речь будет идти лишь об обобщенных ре-
решениях из W\{Q)) справедливо неравенство D.31), а для любой
функции г] (х) из U?2 (й) — неравенство
VT!M*<!-L(Tb л), E.1)
вытекающее из D.21) и D.26). Докажем теорему.
Теорема 5.2. При выполнении условий D.2), D.3), D.26)
задача D.1), D.9) имеет обобщенное решение и из Wl (Q) при
любых f{x) из L2aha+2)(Q), i(x) из L2(Q), q>(*) из W2(Q)-
Для доказательства введем в пространстве Н?2(й) новое
скалярное произведение [v, w]= J {aijVxtWx, + a~vw}dx. Соот-
a
ветствующая ему норма ] • ], в силу наших предположений
*) Это так, ибо для величины ao = nies 'qJ a(x)dx верна оценка
и
| а0 |< mes^ || a \\q/2 a, и потому условие D.26) заведомо выполняется
для й, мера которых подчинена неравенству
Г 8 --- 1
|2c1(?)mes"-'I?H v II a IIv/;. u mes•» «Qjeg<l-

§ 5] РАЗРЕШИМОСТЬ ПЕРВОЙ КРАЕВОЙ ЗАДАЧИ В w\{Q) 193
0 1
об at] и а, эквивалентна норме пространства W2(й). Действи-
Действительно, если iisrifQ), то в силу D.2), D.26)
[v, o]>-g-vJ|Vop<fc>v,(||o !?>„)*, E.2)
а
ГДе vi = -|-v(cj-mes2/n Q+ I)"'- С ДРУГ0Й стороны, из D.2) и D,3)
следует .
[v, v] < J ц | Vv p rfx +1| a" ||?/2i a || v %qM_2)< a, ¦
откуда в силу D.19) имеем
[V, v] < с, || v ||<!?. E.3)
Вместо решения и задачи D.1), D.9) достаточно найти функ-
функцию у = и — ф из условий D.12), D.13). Тождество D.12) можно
записать в виде
[v, Л] + J (а«УтЦ - btvXl4\ - a+vt\)dx = /fa), F.4)
Q
где выражение /(л) определено равенством D.14). Покажем,
что интеграл Ii(v, 1])= J (а»УПхг— Ь^х^\— a+vrfydx при любом
Q
о
фиксированном у из 1^2 (Q) определяет линейный функционал
о .
в пространстве W2 (й). В самом деле, линейность /, (у, tj) отно-
относительно г\ очевидна, а ограниченность его видна из цепочки
неравенств D.18), которая приводит к оценке
,1^ J
а потому, в силу D.19), и к неравенству
|/i(f, Л) КсзС^НоЦ^НлЩ'о E.6)
с постоянной с2 (q) = 2цс (q) -\- Me2 (q) *).
В силу теоремы Ф. Риса о линейных функционалах (см. [312],
стр. 396) функционал 1\ (у, х\) может быть представлен, и при-
притом единственным образом, в виде скалярного произведения
/,(о, л) = Иу, л] E-7)
некоторого элемента Av из Wl2 (Q) на г\. Равенство E.7) опре-
о.
деляет оператор А на любом элементе v из W2 (й). Этот опера-
оператор является ограниченным в Wi (й), ибо ввиду E.2) и E.6)
^ 1 ^
*) См. обозначение D.20).
7 О. А. Ладыженская, Н. Н. Уральцева

194 ЛИНЕЙНЫЕ УРАВНЕНИЯ [ГЛ. Ill
откуда
^ E.8)
Докажем, что оператор Л вполне непрерывен в W2(й). Пусть
{vm(x)}, m= 1, 2, ..., есть' последовательность элементов про-
странства W2(Q) с равномерно ограниченными нормами
11от1^0<с, т=1,2, ...
Тогда нормы элементов Avm, m=l, 2,..., в И?2(й) также
будут равномерно ограничены. Так как оператор вложения про-
пространства Wl(Q) в LP(Q) при р<2п/(п — 2) вполне непрерывен
(теорема 2.2 гл. II), то из {«„J и {Avm} можно выделить под-
подпоследовательности, сильно сходящиеся в пространстве LP(Q)
с p = 2q/(q — 2) (напомним, что всюду q > п.). Без ограничения
общности будем считать, что сами последовательности {vm} и
{Avm} сильно сходятся в L2q/(q-2) (й). Из равенства
[Avi — Avm, Avi — Avm] = /, (и, — vm, Avt — Avm), E.9)
равномерной ограниченности ym и Avm, m=l, 2, .... в нор-
нормах U?2(?0 и L2qi(q-2){Q) и оценки E.5) для правой части E.9)
видно, что
[Avt — Avm, Av.i — Avm] <
^ а +1| Avi - Avm \\ш^2), о).
и, следовательно, {Avm} сходятся сильно в пространстве W2(Q).
Тем самым полная непрерывность А в НРг(й) доказана.
Правая часть в E.4) при наших предположениях о ср, f, f,
как было показано в предыдущем параграфе (см. оценку D.15)),
является известным линейным функционалом в ^(й), и потому
ее также можно представить в виде скалярного произведения
о .
вполне определенного элемента F из W2(Q) на г\, а именно:
/ (tj) = [F, r\]. E.10)
Благодаря E.7) и E.10) тождество E.4) можно записать в виде
[v + Av,t\] = [F,i\], E.11)
и так как оно должно выполняться на любой ij из ^(Q), то
E.11) эквивалентно операторному уравнению в Ws(Q):
v-{-Av=-F. E.12)

§5] РАЗРЕШИМОСТЬ ПЕРВОЙ КРАЕВОЙ ЗАДАЧИ В W2№) 195
Так как А есть линейный вполне непрерывный оператор в li),
то для E.12) справедливы теоремы Фредгольма. Первая из них
утверждает, что уравнение E.12) имеет решение v при любой F
из W2 (Q), если однородное уравнение
w + Aw = 0 E.13)
имеет только тривиальное решение w = 0. Но любое решение
о .
уравнения E.13) из ^(й) есть не что иное, как обобщенное
решение из W\ (й) задачи D.1), D.9) при (p = f = f=sO, ибо
E.13) эквивалентно интегральному тождеству [w-\-Aw, ti] = 0,
а это есть не что иное, как тождество L (w, rj) = 0.
В силу теоремы 5.1 w = Q, так что уравнение E.12) дейст-
действительно имеет решение v при любой F. Это решение и есть
искомая функция у, ибо E.12) эквивалентно E.11), а E.11)
есть не что иное, как тождество D.12). Она определяет реше-
решение и задачи D.1), D.9): и (х) = v (х) + ф (х).
Теорема 5.2 доказана.
Рассмотрим теперь задачу
Lu-lu=§- + f, «Ь = Ф E.14)
при любом комплексном А. Предположения об известных вели-
величинах, входящих в E.14), оставляем прежними. Гильбертовы
пространства L2(Q), W2(Q>) и WiiQ) будем считать в данном
параграфе комплексными и сахраним за скалярными произве-
произведениями и нормами в них старые обозначения. Так, например,
(и, v) означает j u(x) v(x)dx, а [и, w]= \ [ai,uXlvx -\-a~uv)dx.
а а
В соответствии с данным в § 4 определением назовем обоб-
обобщенным решением задачи E.14) из Wl2(Q,) функцию и из Щ(&),
удовлетворяющую тождеству
L (и, fj) + Я (и, л) = (/,, тц) - (/, Л) E.15)
о о .
при любой л из U*2(Q) и такую, что u-ipG U^2(Q)- Выражение
L(u, r\) то же, что и в D.6). Для функции v = u — <р тождество
E.15) порождает тождество
L(v, r\) + X(v, Т1) = МЛ), E-16)
где
= - L (Ф, fj) + (/*, <<\xt) - (f- л) - Я (ф, л)- E-17)
7*

196 ЛИНЕЙНЫЕ УРАВНЕНИЯ [ГЛ. III
Так же, как и выше, тождество E.16) можно заменить эквива-
лентным ему операторным уравнением в пространстве tt?2(Q):
v+Av + XBv = Fk, E.18)
где оператор А определяется тождеством E.7), точнее, тожде-
ством /, (о, f\) = [Av, i\], Vw, TieW2(Q), /ч есть элемент W\{Q),
определяемый тождеством
Ш = [П, Л1, E.19)
о .
а В — вполне непрерывный оператор в Wi{u), определяемый
тождеством
[До, л] = (о, л). E-20)
Легко видеть, что В симметричен и положителен и, следова-
следовательно, имеет обратный на множестве R{B) своих значений.
Полная непрерывность В доказывается так же, как выше была
доказана полная непрерывность А. Как доказано в теореме 5.2,
о -
оператор Е-\- А имеет в №г(й) ограниченный обратный, поэтому
уравнение E.18) эквивалентно уравнению
A)-lBv = (E + A)-lFk. E.21)
Оператор (Е + Л) В вполне непрерывен, как произведение
ограниченного оператора на вполне непрерывный, и потому
для уравнения E.21) справедливы все теоремы Фредгольма.
Однородное уравнение
о + Я (Е + A)'1 Bv = 0, E.22)
соответствующее E.21), эквивалентно тождеству
L(v, й)-Що. л) = 0. E.23)
2
из W2(Q.) задачи
о
Функцию v из W2 (Q), удовлетворяющую E.23) при любой х\
из W2 (Q), естественно назвать обобщенной собственной функцией
Lv = Kv, v\s = 0, E.24)
а X — соответствующим ей собственным значением.
По второй теореме Фредгольма все нетривиальные (отлич-
(отличные от тождественного нуля) линейно независимые решения
уравнений E.22) можно занумеровать в порядке возрастания
модулей соответствующих им собственных значений Я = Я4,
k=l, 2,... Нетрудно показать, что все Kk располагаются
внутри некоторой параболы вида ReA = — с\ ImA f', где с и с1
определяются константами п, q и v из D.2), D.3), причем О 0
с, > 1.
Сформулируем установленные факты в виде теоремы.

§ 8] РАЗРЕШИМОСТЬ ПЕРВОЙ КРАЕВОЙ ЗАДАЧИ В w\w 19.
Теорема 5.3. Пусть выполнены условия теоремы 5.2. Тогда
задача E.14) имеет единственное обобщенное решение из W\ (Q(
при любых фе^г(й), fsL2(Q), / еЬ/)«/ц.2)(й) «Зля все* Я
«а комплексной плоскости, кроме не более чем счетного мно-
множества Я = Я4, & = 1, 2, ..., которое может иметь в качестве
точки накопления только точку А = оо *). Каждому k = kk соот-
о .
ветствует конечное число линейно независимых решений из W2 (Q)
уравнения E.24) или, что то же, тождества E.23). Эти исклю-
исключительные Aj, k=l, 2, ..., составляют спектр задачи E.14).
При А = А4, k= 1, 2, ..., задача E.14) ижеег решение тогда
и только тогда, когда выполнены условия
'*»«) = °» '=1 Nk, F.25)
о
где wlk суть все решения из W\{Q) уравнения
(Е + A*) w + lkBw = 0, E.26)
сопряженного уравнению E.22). Число условий E.25) совпадает
с числом линейно независимых решений уравнения E.22) при
А = А^.
Все утверждения теоремы 5.3 доказаны, кроме того, что
условия разрешимости задачи E.14) при А = А4 имеют вид E.25).
Из третьей теоремы Фредгольма следует, что эти условия для
E.21) формулируются так:
0, i=l,...,Nk, E.27)
где zlk сугь решения уравнения
z + KkB[(E + A)-1]'z = 0, E.28)
сопряженного с F.22).
Так как оператор В имеет обратный на R(B) и все Я4 ф О,
то E.27) можно преобразовать, помня E.19), к виду
0=\Fh, [(? + ЛГТ ^
Из E.28) следует, что B~^i = Wk суть все решения E.26), и
потому последнее равенство совпадает с E.25). Уравнение E.26),
как легко видеть, эквивалентно условию w e Wz (Q) и тождеству
J (
-
atjwx r\x + a.wx f\—bwf\x —awr\ + Kkwf\\ dx = 0,
Ч'Ч
*) Специальные рассмотрения показывают, что собственных значений
бесконечно много, так что | А.А | -> оо при k -> 00 (см. [31,])-

198 ЛИНЕЙНЫЕ УРАВНЕНИЯ [ГЛ. III
которое соответствует уравнению
L'w — kkw = ^- (aijWXj — biw) — a{WX{ + aw — Xkw = 0.
Если ЯШ {Я4}, то уравнение E.21) разрешимо при V/^ и |и|<:
^cj/^l. В частности, для решения задачи E.14) Сф = 0 имеем
_ _ +Н112.а). E.29)
Й+21
Заметим, что зависимость 1},(ч\) от Я вызвана неоднород-
неоднородностью граничного условия из E.14). Если ф = 0, то 4(Tl) =
= (/«» Л^) ~ (/> л)- Если к тому же /г = 0, то условие E.25)
будет означать обычную ортогональность / ко всем wlk:
Так как коэффициенты L вещественные, то спектр задачи
E.14) содержит вместе с любым Я4 число Я4, причем
если Kk соответствует собственная функция uk{x), то Kk соот-
соответствует собственная функция uk (x). Это же верно и для со-
сопряженной к E.14) задачи L'w — Xw = 0, ^^ = 0. Ввиду этого
условия разрешимости ) fwlkdx = 0 задачи E.14) при А = Я4,
fi\ = ф = 0 можно трактовать как ортогональность вида
J fvlkdx = 0, где vlk суть решения задачи L*v — Kkv = O, w|s = 0
и
при том же Я4, что и в задаче E.14).
Сформулируем еще следующее утверждение:
Теорема 5.4. Пусть для всех операторов Lm, tn = 1, 2, ...,
вида D.1) выполнены условия теоремы 5.2 с одними и теми же
постоянными. Пусть а^(х), оставаясь равномерно ограниченными,
сходятся почти всюду к ац, а функции a?, bf, am, im, fm и фт
сходятся к ah bh a, f, / и ф в нормах пространств Lq(Q), Lq(Q),
Lql2(Q), L2(Q), L2am+2)(Q) и Wl2(Q)f\L2qM-2)(Q,) соответственно.
Тогда обобщенные решения um из W-niQ) задач
7 E.30)
(Q) к обобщенному решению из W
сходятся сильно в W2(Q,) к обобщенному решению из W2(Q)
предельной задачи D.1), D.9).
Доказательство этого предложения весьма просто, и чита-
читатель проведет его сам, пользуясь следующими указаниями.

§5]
РАЗРЕШИМОСТЬ ПЕРВОЙ КРАЕВОЙ ЗАДАЧИ В w\ B)
199
Каждая из задач E.30) имеет в силу теоремы 5.2 единственное
решение и"'. Для ут = ит —ф'" справедливо тождество типа
D.12). То же верно и для о = и — ф, где и есть решение пре-
предельной задачи.
Из этих тождеств следует Lm (vm, r\) — L (v, ц) = lm (ti) — / (ti).
Полагая здесь ч\ = vm — v, мы после ряда элементарных пре-
преобразований и оценок того же типа, что и в § 4, придем к же-
желаемому заключению о стремлении к нулю \\vm — v ||<"Q.
Рассмотрим еще предельный случай, когда ^ = п^3. Пусть
для D.1) выполнены предположения D.2), D.5), D.33), и пусть
ради несущественных упрощений ф(д:)н=0, т. е. искомое реше-
решение и (х) обращается на контуре S в нуль. Представим коэф-
коэффициенты при младших членах в виде сумм:
а. (х) = а\ (х) + а'{ (х), bt (х) = Ь\ (х) + Ь'[ (х),
а+ (х) ^ max {а (*); 0} = а+' (*) + а+" (х),
в которых a", b", а+" имеют малую норму в Ln (Q), Ln (Q),
Z.n/^(Q) соответственно, a ai, b\ и а+г суть ограниченные функ-
функции, так что
max
2j (at), 2j (bi), a+
E.31)
Тождество E.15), соответствующее задаче E.14), преобразуем
так же, как и выше, к уравнению вида E.18), точнее, к урав-
уравнению
и + А'и + А" и + ХВи = Fk, E.32)
причем а~(х)^0. Здесь оператор В и элемент FK определяются
тождествами E.20) и E.19) соответственно, а операторы А'
и А"— тождеством E.7), в котором для А' надо в 1\{и, т^) под-
подставить вместо a,-, bt и а+ функции а\, h\ и а+', а для А" —
функции a", b" и а+"'. Из доказанного выше следует, что опе-
оператор В симметричен, положителен и вполне непрерывен, опе-
оператор А' вполне непрерывен, а А" ограничен и его норма стре-
стремится к нулю при стремлении к нулю е". Кроме того, опера-
операторы Е-\- А' -\-К'В в силу теоремы 5.2 обратимы для Я'>Яо =
=Bv + l)Bv)~1Me» и, что важно, нормы обратных им операторов
не превосходят некоторого числа ц,2> зависящего лишь от п и v
и не зависящего от Ме». Это последнее легко видеть из оценки
D.41) и того факта, что в ней 6{ можно взять равным нулю
(ибо для А' функции с" и с" равны нулю), а 63= 1/2.

200 ЛИНЕЙНЫЕ УРАВНЕНИЯ [ГЛ. III
Итак,
Применим оператор (? + Л' + Я'В) к обеим частям уравнения
E.32) и результат запишем в следующем виде:
и + (Е + Л' + к'ВГ1 А"и + (Я - Я') (Е + А' + \'В)~1 Ви =
= (E + A' + k'B)~~lF. E.33)
Выберем е" столь малым, чтобы норма оператора ||Л"|| была
меньше 1/ц2; тогда оператор Е + (Е + Л' + Я'?)~' Л" будет
обратим и уравнение E.33) может быть преобразовано к экви-
эквивалентному уравнению вида
и + (Я - Я') [?• + (?• + Л' + Я'В)-! Л"|"' (? + Л' + к'В)~1 Ви =
= [Е + (Е + Л' + Я'В)~' Л"]~' (? + Л' + Я'В)~! /=\ E.34)
В нем оператор, стоящий при (Я — Я'), вполне непрерывен
(ибо В вполне непрерывен, а остальные операторы ограничены),
и, следовательно, для уравнения E.34) справедливы все тео-
теоремы Фредгольма. Перефразируя их в терминах исходной за-
задачи Дирихле, приходим к заключению:
Теорема 5.5. Пусть для уравнения E,14) выполнены усло-
условия D.2), D.5), D.33), и пусть <р(х) <=&Ъ(а). Тогда для задачи
E.14) справедливы все заключения теоремы 5.3.
§ 6. Вторая и третья краевые задачи
Разрешимость второй и третьей краевых задач для урав-
уравнения
i
в пространстве Wi(Q.) для строго липшицевых областей *) иссле-
исследуется в принципе так же, как и разрешимость первой краевой
задачи в §§ 4, 5, надо только «правильно» определить, что
значит решить эти задачи в пространстве tt?2(Q). Для произ-
произвольной функции из Wi(U) не имеет смысла говорить, что она
удовлетворяет условию
= <p(s), F-2)
*) Для таких областей Wl2(Q) совпадает с Wl2(Q).

§ 6] ВТОРАЯ И ТРЕТЬЯ КРАЕВЫЕ ЗАДАЧИ 201
где 77" = a'/u*»coS(n> xi)>n ~ внешняя нормаль к S, а a(s) и
Ф (s) — заданные на S функции, ибо ее производные первого
порядка определены лишь почти всюду на n-мерной области Q
и могут быть не определены (или могут равняться <х>) на всей
(п — 1)-мерной поверхности S. Поэтому условию F.2) надо,
так же как и уравнению F.1), придать другую форму, которая
была бы пригодна для любой функции из W\ (Q). Это можно
сделать следующим образом.
Назовем обобщенным решением из W2C&) задачи F.1), F.2)
функцию и(х) из WliQ), удовлетворяющую тождеству
L (и, л) = $ [aituXi тц - (btuXt + аи)л] dx =
= - jfi\dx + j(-ou + q>)r\ds F.3)
u
при любой функции х\ из (
Если бы все входящие в F.3) функции были достаточно
гладкими, то нетрудно было бы проверить, что, проводя в F.3)
интегрирование по частям в первой группе членов, мы при-
пришли бы к тождеству
j(^ )ds = O, F.4)
из которого, в силу достаточного произвола г\, следуют и урав-
уравнение F.1), и равенство F.2). Верно и обратное: из F.1), F,2)
следует F.4), а потому и F.3). Таким образом, данное нами
определение обобщенного решения действительно является рас-
расширением классического понятия решения задачи F.1), F.2).
Разрешимость задачи F.1), F.2) в классе Wl2(Q) устанавли-
устанавливается весьма просто. Пусть относительно коэффициентов L и
функции / выполнены предположения D.2), D.3), D.5). Дока-
Докажем сначала первое основное неравенство. Для этого исполь-
используем неравенство D.23), верное при V«elF2(Q). Из него, ра-
равенства F.3) с ii= и и неравенства B.22) гл. II следует:
J (yl
Р + а-и2) dx^L (и, и) + е, || Vu |Ь\ о + св, (Ьи а+) || и &. в =
= - J fu dx + f (- a«2 + фИ) ds + e, || Vu ||* Q + cBl (bt, a+) || и ||22 0,
F-5)
где e, — произвольное малое положительное число, а cSl(bi, a+)—

202 ЛИНЕЙНЫЕ УРАВНЕНИЯ [ГЛ. III
известная нам положительная постоянная, стремящаяся к оо
при &\ -+0.
Если бы функции ст и ф равнялись тождественно нулю,
то интеграл по S отсутствовал бы и из F.5) следовало бы не-
неравенство типа D.24). В общем случае условия на ст и ф сво-
сводятся к тому, чтобы гарантировать для любой функции и из
\ неравенства
J аи2 ds < J [е | V« |2 + се (ст) и2] dx, F.6)
ds
F.7)
с произвольно малым е и с конечными се(ст) и с(ф) (постоянная
сЕ(ст) может произвольно расти при е-->-0). Если условия на ст, ф
формулировать в виде их принадлежности к пространствам Lr (S),
то, как показывают теоремы вложения (см. неравенства B.37)
и B.38) гл. II), для этого надо предположить, что функция ст
принадлежит пространству LP(S) с р > п— 1, a y^Lr(S), где
г > 2 (п — 1)/я при п > 2 и г > 1 при п = 2.
При выполнении этих условий из соотношений F.5) — F.7)
после ряда простых оценок, аналогичных проведенным в § 4,
получим
-J-1 V« |2 + а-«2) dx< 4 [с* (я, Q) || / ||22й/(й+2, 0 + с2
(о) + Cv/2o (Ь„ а+) + -?•] || и \{ 0. F.8)
Это неравенство имеет тот же характер, что и неравенство D.24).
На его основе с помощью теорем вложения § 2 гл. II доказы-
доказывается, что для задачи F.1), F.2) в пространстве WliQ) имеют
место три теоремы Фредгольма, в частности, что при всех до-
достаточно больших Я краевая задача F.2) для уравнений
Lu — ku = f однозначна разрешима при любых f, ф и ст с ука-
указанными выше свойствами. Мы не будем приводить здесь до-
доказательства этих предложений, так как они вполне аналогичны
данным в § 5 для первой краевой задачи.
§ 7. Внутренние оценки в L2 производных
второго порядка произвольной функции через значения
эллиптического оператора от нее
В этом и следующем параграфах мы хотим доказать второе
основное неравенство для эллиптических операторов, позволяю-
позволяющее оценивать нормы в L2 производных второго порядка от про-
извдльной функции и через нормы в L2 самой функции и, зна-

§ ?] ОЦЕНКИ В Li ПРОИЗВОДНЫХ 2-ГО ПОРЯДКА 203
чения эллиптического оператора от нее и нормы граничных
значений и. Это неравенство было установлено независимо
в работах [82, 21 х _3] для первого краевого условия (по поводу
двумерного случая см. § 17 данной главы) и в работах [21,_3]
для других краевых условий. (В [21,_3] установлены более общие
факты: точные оценки норм и в WfiQ), где т — любое нату-
натуральное число, через нормы итераций L(k)u в L2(Q).)
Излагаемый ниже вывод его, равно как и все дальнейшие
исследования по разрешимости краевых задач в пространстве
Wl(Q,), взят из работ [21, _3,5] одного из авторов книги. Начнем
с получения внутренних оценок, которые не зависят от значе-
значений и на границе S. На этот раз изучаемые функции будут
принадлежать пространству W\ и оператор L (см. D.1)) на
них должен вычисляться непосредственно и давать функции
из L2. Для этого потребуем, помимо ограничений D.2), D.3),
да,, да,
еще существование обобщенных производных -^—L, -5— и при-
дхк дх{
да-} dd'
надлежность -^—'- к La (Q), а -= (- а к L4l2 (Q), где q = max {q, 4}
axk 4 oxt
и q > n*). Эти условия гарантируют нам, что каждый член
выражения
Lu == ац (х) Ux{Xj + dt (х) их. + й (х) и, G.1)
дпц да, 2
где dt = -g—^ + &i + bt, a = -г (- а, при любой и из W2 (Q) дает
функцию из L2 (Q), так что L есть ограниченный оператор из
Wl(Q) в L2(Q) и
11^«1|2.в<с||и|Р0 G.2)
с постоянной с, зависящей лишь от ц из D.2), Q и норм || d,- Ц,, q ,
II й ||^/2. q (область Q считаем строго липшицевой).
Итак, запишем оператор L в виде G.1) и предположим, что
помимо условий D.2), D.3) выполнены еще условия
да
¦Ц
dxk
G.3)
/, /, k== I, ..., п, q>n, <? = max{?; 4}.
Рассмотрим сначала оператор L на функциях из W2(Q),
т. е. на финитных в Q функциях из Wl(Q). Докажем справед-
справедливость следующего предложения:
) По поводу возможности замены q на п см. конец § 8.

204 ЛИНЕЙНЫЕ УРАВНЕНИЯ [ГЛ. III
Лемма 7.1. Если относительно коэффициентов оператора L
выполнены условия D.2), D.3), G.3), то для любой функции
и eU?l(Q) справедливо неравенство
[II" Со]* < ¦?II Lu | Q + с|| и | Q G.4)
с постоянной с, зависящей лишь от величин q, v и ц из усло-
условий D.2), D.3), G.3) и не зависящей ни от и, ни от Q.
Во множестве W\ (Q) плотно (в смысле сходимости в №2 (Q))
множество С°° (Q) всех бесконечно дифференцируемых финитных
в области Q функций (действительно, обычные усреднения с бес-
бесконечно дифференцируемым ядром и достаточно малыми ра-
радиусами усреднения дают нужную аппроксимацию функции
из Wl(Q)). Поэтому неравенство G.4) достаточно доказать
лишь для функций и из C°°(Q); для любой же u^Wl(Q) оно
получится замыканием G.4) в норме Wl(Q). При этом надо
лишь помнить, что оператор L, как оператор из Wl(Q.) в L2(Q),
ограничен.
Итак, пусть и е С°° (Q). Рассмотрим интеграл
Первый член в правой части преобразуем с помощью дву-
двукратного интегрирования по частям следующим образом:
¦¦¦]dx=
u „ —-тг-(anab,)urur _ +
k xixi i ^ '' *'' xi xkxi
= \
G.5)
Покажем, что
/, (д;) = аг/ (д;) аы (x) uXtXuX{Xi > v4\x. G.6)
В самом деле, зафиксируем произвольно точку х° е Q и вве-
введем в ее окрестности новые прямоугольные координаты: yk =
= аы(х1~¦*?)• Ортогональную матрицу (aw) выберем так, чтобы
она приводила квадратичную форму в(/(дс°)|/|/ к диагональ-
диагональному виду, т. е. чтобы

§ 7] ОЦЕНКИ В L, ПРОИЗВОДНЫХ 2-ГО ПОРЯДКА 205
где ki(x),..., Кп(х) — сообственные числа формы а*/(*)!<!/.
Тогда, как легко видеть,
В силу условия эллиптичности D.2) или, что то же самое,
предположения A*(a:)^Sv, /=1, ..., п, получим
Но и2уу(х°) = и2хх (х°), так что неравенство G.6) установлено.
Ввиду этого из G.5) следует
v2 J "U ** < J (Luf dx + j[^- (auakl) и и -
q a a
4 "-*+ йи) ~
J
G.7)
Целью дальнейших рассуждений является доказательство
того, что при любом е > 0 справедливо неравенство
*)]**. G.8)
Q
причем постоянная се зависит лишь от е (при этом се->оо,
когда е-»-0) и постоянных q, v и у. из условий D.3) и G.3).
Для доказательства неравенства G.8) мы воспользуемся,
кроме неравенства Гёльдера, неравенством D.19) и неравен-
неравенством B.27) гл. II. С помощью этих неравенств оценка инте-
интеграла /2 проводится стандартным способом. Оценим для при-
примера несколько членов из /2.
Пусть /3= -^-а.,игиг _ dx, причем суммирование здесь
j axj *• *{ *kxi
не предполагается. Легко видеть, что
-2).a

206 ЛИНЕЙНЫЕ УРАВНЕНИЯ [ГЛ. 111
Воспользуемся для оценки третьего сомножителя второго
члена в правой части последнего неравенства неравенством D.19).
Тогда получим
А . dx +
xkxi
Полученная для интеграла /3 оценка есть оценка типа G.8),
ибо 8 и в| — произвольные положительные числа.
Рассмотрим для примера еще такой член:
| (х) ux.Xjau dx,
Q.
при каких-либо значениях индексов i и /. Очевидно, что
| И | <| J (
Q
J (в^ + -^ dV) dx, 82 > 0.
Q
Пусть сначала я = 2, 3. Тогда, используя неравенство B,27)
гл. II, получим
2 J
-g; max»' J йЧх <
Пусть теперь п^4. Тогда, снова используя неравенство B.27)
гл. II, будем иметь
<Ие2 J и\ dx + ^
2
Остальные члены в /2 оцениваются аналогично; при этом,
оценивая интеграл J a2u2dx, надо, как мы только что делали,
а
различать случаи п = 2, 3 и я|>4.
Итак, неравенство G.8) доказано. Из G.7) и G.8) следует
v^ J и2хх dx^\ [Luf dx + e\ u\x dx
ce (|| и

§ 7] ОЦЕНКИ В U ПРОИЗВОДНЫХ 2-ГО ПОРЯДКА 207
Отсюда, выбирая, например, e = v2/4, получим
J «'„**<4?[ (LuJdx + 4r c3V/4(II" С)'- G.9)
Соотношение G.9) вместе с неравенством B.28) гл. II и дает
нам второе основное неравенство G.4).
Сделаем ряд выводов из оценки G.4). Покажем, прежде
всего, что оператор L, определенный выше как дифферен-
дифференциальный оператор G.1) на множестве D (L) = W\(Q), допускает
замыкание в L2(Q) (см. [312]). Действительно, пусть имеется
последовательность элементов {uk}^=l из Wl(Q), сходящаяся
в L2(Q) к нулю и такая, что для нее {Luk} сходятся в L2(Q)
к некоторому элементу /. Надо доказать, что тогда f = 0.
Действительно, из неравенства G.4), примененного к функ-
функции uk — щ, k, 1= 1, 2, ... , следует, что последовательность {uk}
будет сходиться в себе в норме Wi(Q) и, следовательно, будет
сходиться к своему пределу в норме W2(Q). Но пределом {uk}
в L2(Q) является ыз=0, следовательно, {uk} будет сходиться
к нулю и в норме W\(u). Это в силу G.2) гарантирует, что {Luk}
будет иметь своим пределом 0, т. е. /==0.
Итак, оператор L допускает замыкание. Больше того, из
только что проведенного рассуждения следует, что D(L), т. е.
область определения замыкания L, совпадает с W\ (Q), т. е.
с замыканием множества Wl(Q) или, что то же, с замыка-
замыканием С°° (Q) в норме №2(Q). Полезно заметить, что на любом
гладком куске границы области Q функции из wl (Q) обра-
обращаются в нуль в среднем вместе со своими производными пер-
первого порядка (см. § 2 гл. II).
Как известно, возможность замыкания оператора L эквива-
эквивалентна тому, что сопряженный к нему оператор V определен
на плотном в L2(Q) множестве. Сопряженный к L оператор
легко определить в явном виде, если предположить дополни-
дополнительно к ранее сказанному, что коэффициенты at и Ь\ имеют
производные -—, -^- из La,2 (Q). Именно, на v We^ (Q)cD (L*)
он определяется так:
L'v = ~r{ai1vXi — b,v) — atvx. + av. G.10)
Действительно, сопряженный оператор V и его область
определения D(L*) характеризуются тем, что для любого

208 ЛИНЕЙНЫЕ УРАВНЕНИЯ [ГЛ. III
элемента и из D(L) — W\(U) должно быть верно тождество
(Lu, v) = (u, L'v). G.11)
Но тождество G.11) на самом деле верно при любой uef^Q),
если V определить равенством G.10), a v^Wl(Q). Из изла-
излагаемых ниже фактов нетрудно вывести, что при некоторой ре-
регулярности S область D(L*) совпадает с wl(Q).
§ 8. Второе основное неравенство для эллиптического
оператора
Одним из главных вопросов, связанных с эллиптическим
оператором L, является вопрос о разрешимости для него раз-
различных краевых задач. Эти задачи состоят в нахождении ре-
решений и(х) уравнения
Lu = 0p(x) (8.1)
в области Q, удовлетворяющих тому или иному краевому
условию на границе S области Q. При этом основными крае-
краевыми условиями считаются следующие:
1) первое краевое условие:
u\s = q>(s), (8.2)
2) второе краевое условие:
Ж
W
~ аЧ cos
3) третье краевое условие:
)| = фE), (8.4)
где ф(«) и o(s) суть заданные на 5 функции.
С точки зрения применяемых нами методов удобнее неодно-
неоднородные краевые условия (8.2)—(8.4) сводить предварительно
к однородным. Для этого мы вместо искомой функции вводим
новую неизвестную функцию v с помощью равенства и (х) =
= v (х) + Щ (х), где ы, (х) есть какая-либо функция из простран-
пространства W\(u), удовлетворяющая одному из условий (8.2)—(8.4).
Тогда v будет удовлетворять уравнению Lu = i|) — Luu т. е.
уравнению того же вида, что и уравнение (8.1), и соответствую-
соответствующему однородному краевому условию.
Итак, будем считать, что и удовлетворяет уравнению (8.1)
и одному из однородных краевых условий, например условию
u\s = 0. (8.2')
Задача (8.1), (8.2') с точки зрения функционального ана-
анализа состоит в нахождении оператора L~\ обратного опера-

$ Я ВТОРОЕ ОСНОВНОЕ НЕРАВЕНСТВО 209
тору L, определенному на функциях, подчиненных условию (8.2').
В предыдущем параграфе мы определили -оператор L на мно-
множестве Wl(Q)- Так как функции из #|(Q) равны нулю на гра-
границе S, то любая из них есть решение задачи (8.1), (8.2') с со-
соответствующей правой частью (именно ty = Lu). Однако такие
функции i|> (tj) из R(L), т. е. из области значений оператора (L)
и даже г|з из R(L) не заполняют всего пространства L2fli).
Действительно, если взять, например, какую-либо дважды не-
непрерывно дифференцируемую функцию v(x), равную нулю на S
и такую, что -?-\ Ф 0, и поставить задачу: найти и из условий
Lu^Lv, u\s = 0, (8.5)
то одним из решений этой задачи будет v. Если предположить,
что для оператора L выполнено условие D.26) или D.32), то
функция u = v будет единственным возможным решением за-
задачи (8.5). Но, очевидно, v Ш D (L) = W\ (Q), и потому Lv^R (L).
Тем самым R(L) не совпадает с L2(Q)«
Итак, если мы хотим решить задачу (8.1), (8.20 для всех
i|)eL2(Q) или хотя бы для плотного в L2(Q) множества, нам
необходимо заняться расширением оператора L. Известно, что
уже для простейшего эллиптического оператора — оператора
Лапласа — дефектные числа оператора Д на W\ (Q) бесконечны
и он допускает бесчисленное множество различных расширений.
Краевые задачи для оператора L порождают различные расшире-
расширения оператора L с его области определения Z) (L) = И?2 (Q) и, в
определенном смысле, наоборот (в связи с этим см. работы [72]
и [5i]). Мы рассмотрим здесь лишь одну сторону вопроса,
именно изучим те расширения оператора L с W2 (Q), которые
связаны с основными краевыми условиями (8.2)—(8.4).
Расширение оператора L желательно провести так, чтобы
область значений расширенного оператора L (или L + %Е при
каком-нибудь К) заполняла все пространство L2(Q), функции
из области определения оператора L удовлетворяли бы в каком-
либо смысле граничному условию исследуемой краевой задачи
и оператор L (или L + КЕ) имел ограниченный обратный
на L2(Q).
Ясно, что для любой из трех основных краевых задач
(8.2)—(8.4) надо присоединить к области определения D(L) опе-
оператора L прежде всего все достаточно гладкие функции, удо-
удовлетворяющие соответствующему однородному краевому усло-
условию, ибо такие функции являются решениями исследуемой
краевой задачи.

210 ЛИНЕЙНЫЕ УРАВНЕНИЯ [ГЛ. III-
Возьмем для определенности первую краевую задачу. Обо
значим через Wl, о(й) замыкание в норме №i(Q) множества всех
функций из (^(Q), равных нулю на границе S. Обозначим
через L расширение оператора L за счет дополнения D(L) до
множества Wl. o(Q). Оператор L на Wl. о(й) по-прежнему имеет
вид G.1). В дальнейшем мы покажем, что оператор L замкнут
на множестве W2,o(Q). Здесь же мы докажем, что оператор L
допускает замыкание и все функции из области определения D (L)
оператора L имеют обобщенные производные второго порядка,
квадратично суммируемые по любой строго внутренней под-
подобласти Q' области Q. Оба эти утверждения легко выводятся
из неравенства
(II "?2 С'2J < 4-1' ?Lu i а + с J  (S4 + ? + ??хх) dx> (8.6)
а
справедливого для любой и из W\ (Q). Здесь ? (х) — какая-либо
функция из C2(Q), равная нулю на S. Постоянная с в неравен-
неравенстве (8.6) зависит лишь от постоянной эллиптичности v и чи-
чисел q и |х из условий D.2), D.3), G.3).
Неравенство (8.6) доказывается так же, как и неравенство
G.4), надо только вместо ) (Lufdx рассмотреть выражение
Q
\ (LuJ?*dx и старшие члены преобразовать следующим образом:
Q
J
а
= — I \auakluXkX[XluXlt,4 + -?- (а4уа«?*) uXkXlux\dx =
= j \
(8.7)
Главный положительный член Г а.цаыиХ1Хких xg* dx, в силу
Q
доказанного в § 7 неравенства G.6), не меньше v2 J u2xxt* dx. Все
Q
остальные члены правой части (8.7) оцениваются сверху. Боль-
Большая часть цх отличается от соответствующих членов в выра-

§ 8} ВТОРОЕ ОСНОВНОЕ НЕРАВЕНСТВО 211
жении для [ {Lufdx только множителем ?4. Исключение соста-
Q
вляют члены, содержащие производные ?, именно члены
(при ?=1 они отсутствуют). Для них справедлива оценка
где е — произвольное положительное число, а постоянная с
зависит лишь от max | ati \.
Q
Проводя все дальнейшие рассуждения и оценки буквально
так же, как и выше при выводе неравенства G.9), придем
к неравенству
J
Q
+ 1 Г 9 **9 /**9 l *»9\ i 9**9 /*»9 I 5*2 I ^"9 M *-/ ** /О ОЧ
с [м?? (ь H~ ?*) "г и ъ (S т" ь* + »**)] v")
С другой стороны, для интеграла / = J ы2S2(S2 + ??) ^ спРа"
ведлива оценка
j < J [tenulg + ± «2(S2 + Q2 + 8ы2 B?2^+?i+S2?*j] ^ (8-9)
Q
с Ve > 0.
Для ее проверки надо провести в / интегрирование по
частям, перенося с одного из множителей ux.uXt производ-
д
иую -г— на все остальные, и затем воспользоваться неравен-
ством Коши A.2) из гл. II. Подставив (8.9) в (8.8), придем
к неравенству
(* ы2^4dx < 4 Г (Luf S4dx+cj(S4 + ?4 + S2SL)dx
с любым положительным 8 < Bяс)~\ Отсюда и из (8.9), как
легко подсчитать, при определенном выборе 8 следует (8.6).
Из неравенства (8.6) действительно следует, что оператор L
допускает замыкание (это доказывается так же, как в конце § 7

212 ЛИНЕЙНЫЕ УРАВНЕНИЯ [ГЛ. Ill
доказывается утверждение о том,_что оператор L допускает
замыкание) и что функции из D(L) будут иметь обобщенные
производные второго порядка, квадратично суммируемые по
любой строго внутренней подобласти Q' области Q (ибо для
любой такой подобласти Q' мы можем подобрать ?(*) так,
чтобы ?(*) = 1, когда xgQ'). Эти утверждения верны для
всех трех краевых задач (8.2) — (8.4), если D (L) определить
как замыкание в Wl(Q) множества всех функций из (^(Q),
удовлетворяющих однородному граничному условию, ибо
неравенство (8.6) верно для произвольной функции и из Wl(u).
Вернемся снова к первой краевой задаче (8.1), (8.2') и пока-
покажем, что если граница S области Q достаточно гладкая, то
Dф) = w\,о(Q), т. е. что оператор L замкнут на Wl.o(Q)- Для
этого распространим второе основное неравенство для эллипти-
эллиптических операторов на произвольные функции из Wl, о(й)-
Предположим, что область Q обладает следующими свой-
свойствами:
1) Q есть строго липшицева область.
2) Для почти всех (в смысле меры на S) точек х° ее гра-
границы S существует касательная плоскость к S, и уравнение
куска поверхности S в окрестности точки х° в местной декар-
декартовой системе координат (ось уп направлена по внешней
в точке х° нормали к S, а оси уи .... г/„_, лежат в касатель-
касательной плоскости к S в точке *°) имеет вид i/n = cu(i/i. •••> #B-i)>
причем функция со дважды дифференцируема и собственные
л-1
числа |i,(*°) nn-i(*°) квадратичной формы p
в точке х° ограничены сверху неотрицательной постоянной,
которую мы обозначим через К-
sup {М*°))</<:- (8.10)
k>S
Например, для м-мерных шаров произвольного радиуса R
^ft=—I//?, k=l, . •., п— 1, и потому в качестве К можно
взять 0 сразу для всех шаров. Другим примером таких областей
могут служить невырожденные «-мерные многогранники (в том
числе и невыпуклые) или области, полученные из них при
дважды дифференцируемом преобразовании с ограниченными
производными второго порядка и положительным якобианом.
Покажем теперь, что если область Q удовлетворяет усло-
условиям 1) и 2), то неравенство G.4) справедливо для всех функ-
функций из C2(Q), обращающихся в нуль на границе Q.

§ gj ВТОРОЕ ОСНОВНОЕ НЕРАВЕНСТВО 213
Лемма 8.1. Если область Q удовлетворяет условиям 1)
и 2), то для любой дважды непрерывно дифференцируемой в Q
функции и, равной нулю на S, справедливо неравенство
Oi"ii%J<^iiL"iil2+cii"t2' (8Л1)
причем постоянная с зависит только от постоянной эллиптич-
эллиптичности v оператора L, чисел q и \i из условий D.2), D.3), G.3)*)
и от области Q и не зависит от функции и.
Доказательство леммы состоит из двух частей. Первая часть
совпадает с доказательством леммы 7.1 и сводится к получению
неравенств G.6) и G.8). Именно, преобразуем так же, как и при
доказательстве леммы 7.1, интеграл \ (LuJdx. При этом, так
как функция и на этот раз уже не финитна в области Q, то при
двукратном интегрировании по частям выделятся граничные
интегралы и потому в правой части равенства G.5) появится
следующий интеграл:
J Is ds = J а{1ан [uXkXluXl cos (n, xt) — uXjX[uXl cos (n, xk)]ds.
s s
Повторяя рассуждения, проведенные при доказательстве
леммы 7.1, получим (см.- неравенства G.6) и G.8))
v2 [ ихх dx + | /s rfs < [ (LuJ dx+\ [zulx + ce (| Va f + u2)] dx,
Q S Q Q
(8.12)
где 8 — произвольное положительное число, се — известная
постоянная, зависящая от 8. Заметим, что равенство G.5)
с соответствующей поправкой на граничный интеграл J Isds,
s
а потому и неравенство (8.12), справедливо для любой функции
и еС2 (Q), хотя при выводе в качестве промежуточного этапа
встречались и производные третьего порядка от и. Это так,
ибо благодаря строгой липшицевости Q любая функция из С2 (Q)
может быть аппроксимирована в норме С2(п) функциями
из класса С°° (Q) (см. § 2 гл. II). Поэтому интересующие нас
соотношения верны для любой и^С2 (Q).
Переходим теперь к рассмотрению Is. Пусть х° — любая
из тех точек поверхности S, в которых существуют производные
*) По поводу возможности замены q на п см. конец § 8.

214 ЛИНЕЙНЫЕ УРАВНЕНИЯ [ГЛ. Ill
-—f—-, i, /= 1, .... п — 1. Возьмем ортогональную ма-
трицу (cki) и с ее помощью перейдем в Is от координат
{х\, .,., хп) к местной системе координат (уи ..., уп):
Ук = сы{xi - Х1)' к=1,...,п, (8.13)
где направление уп совпадает с направлением внешней нормали
в точке х°. Благодаря ортогональности матрицы (ckl) имеем
¦xl — }fil = cklyk, l=l,...,n. (8.14)
Из (8.14) следует, что
cos(n, Xt) = cnh 1=1, ..., п.
Итак, в точке *° будем иметь
= auaklcml JjL- cpkcql
ди д2и
- auaklcml — cplcql ^-^- cnk =
, , du d2u , , ди д2и
= t>mnt>P4 dym dypdyq ~ЬтрЬщ дут
где bpq = aklcpkcqh p, q=\, .... п. Воспользуемся теперь гра-
граничным условием ы|5 = 0. Вблизи точки *° с координатами
ух = ... = уп = 0 это условие имеет вид
и (у и .... уп-х, со (г/,, ..., #„_,)) = О,
причем оно выполняется тождественно по у\, ..., уп-\ вблизи *°.
Продифференцируем это тождество по yt и yt, i, j =
= 1, .... п— 1, учитывая, что в точке х°
-^=0, i=l,..., п-\.
Это дает в точке х°
д2и ди д2а> _ ди д2а> (8
~ дп dydyi ^ '
__0
dyt ~ ' dy{dyj ~~ дуп dyidyj ~ дп
С помощью соотношений (8.16) упростим выражение (8.15):
ibnnbPq - bnpbnq] -g- ^-. (8.17)
При р = д и произвольном q, при р произвольном и q = n
члены в квадратной скобке в (8.17) взаимно сокращаются, и
потому (8.17) с учетом (8.16) принимает вид
2
р, «=i

§ g] ВТОРОЕ ОСНОВНОЕ НЕРАВЕНСТВО 215
Будем считать, что координаты ух уп-\ в касательной пло-
<Э2а>
скости выбраны так, что все смешанные производные -г—-— ,
р, <7 = 1, ..., п— 1, в точке х° равны нулю (этого, очевидно,
всегда можно добиться за счет ортогонального преобразования
координат уи ..., уп_х). Тогда
Is (*°) = - S {bnnbpp ~ Ьпр) Ш ~dyf' (8-19)
и потому в силу свойства 2) поверхности S и того, что
О < bnnbpp — blp^. ц2, для Is(x°) верно неравенство
(8.20)
где ц — постоянная из условия D.2). Из этой оценки и нера-
неравенства (8.12) следует
v2 J u\x dx^ § (Luf dx+\j [eu2xx + сг (| Vu |2 + и2)] dx +
g-)V (8.21)
Так как область Q строго липшицева, то (см. неравенство B.38)
гл. II)
причем постоянная сх зависит только от области Q, а е, — произ-
произвольное положительное число. Подставляя это в (8.21), получим
v2 J и\х dx < J {Luf dx + J [(e + в, (п - 1) К»\) и\х +
q a q
J J
q a q
J
(п 1) Кц,) | уи Р + ги] dx.
Отсюда, выбирая e = ei (п — 1)/С^2С[ = v2/8, будем иметь
J и^ rfx < J [^ (^"J + с2 (| Va |2 + н2)] rfx.
а а
Это вместе с неравенством B.28) гл. II дает нам неравен-
неравенство (8.11).
Замечание 8.1. Легко видеть, что если Q — выпуклая
область, то /С = 0, /$^0, граничный интеграл J Isds в

216 ЛИНЕЙНЫЕ УРАВНЕНИЯ [ГЛ. ГН.
неравенстве (8.12) можно просто отбросить и из полученного
неравенства вывести непосредственно (8.11).
В частности, при выпуклой Q и постоянных ац, удовле-
удовлетворяющих условию dijlilj^vl2, v > 0, для любой функции
и(х)е1^2,о(й) справедливо неравенство
^\{ai!u Jdx. (8.22)
2
Итак, мы доказали второе основное неравенство для эллип-
эллиптических операторов. Это сделано для произвольной функции и
из класса С2(п), равной нулю на границе S. Но такие функции,
по определению, плотны в Wl,o(Q,), и потому, по замыканию,
неравенство (8.11) справедливо для произвольной функции и
из класса W\, o(Q). А тогда из неравенства (8.11) вытекает
следующая теорема:
Теорема 8.1. Дифференциальный оператор L замкнут
на множестве W%, о (й).
Итак, Z)(L) = D(L) = W\. o(Q). Естественно ожидать, что
L на W\, о (Q) и есть такое расширение оператора L с множе-
множества Wt(Q), которое соответствует первой краевой задаче для
оператора L.
Если К = О Ш {kk} — спектру задачи E.24), то для V«eWf,0(Q)
справедливо неравенство || и ||'>Q ^ с( || Lu ||2_ Q (ибо такое и явля-
О j
ется об. решением из W2(Q) уравнения Lu=f с f =LweL2(Q),
и для него верна оценка E.29), т. е. |и |<с2IILu||2,q), и потому
в этом (и только этом) случае неравенство (8.11) приобретает вид
||U||<2J<C||LU||2>2, (8.23)
где с = —г -\-с\. Одним из критериев того, что % = 0 е= {kk},
являе!ся выполнение неравенства D.26).
Покажем, что неравенство (8.23) справедливо для оператора
Лапласа Д, т. е. для любой функции и из класса Wl.o(Q)'-
IU|gJ<C||AU||2>2. (8.24)
Действительно, если область Q удовлетворяет условиям
леммы 8.1, то в силу неравенства (8.11)
(||ы|^<2||Д«||й + с||ы|Ц2. (8.25)

ВТОРОЕ ОСНОВНОЕ НЕРАВЕНСТВО 217
Но так как be w\ o(Q), то
{\Vu\2dx=- [ uAudx<, j\-jU2 + ~(AuJ)dx, e > 0,
О й Q
что в силу неравенства D.25) дает
и2 dx < с2 mes2/42 (~\ и2 dx + -^ J (АиJ с
Выбирая e = c;f2mes~2/nQ, отсюда и из (8.25) получим нера-
неравенство (8.24).
Из леммы 8.1 вытекает
Следствие 8.1. Пусть и е Wl(Q) и относительно области Й
и коэффициентов оператора L выполняются предположения
леммы 8.1. Тогда
(II « | аJ < 4" L" 12 + с II " II fl + ci (II Ф I№> (8-26)
где ф (*) есть любая функция, для которой и (х) — <р (*) е Wl,o(Q),
а с и С) определяются теми же величинами, что и с в (8.11).
Неравенство (8.26) легко выводится из неравенства (8.11),
примененного к функции и — <р, и неравенства G.2) для <р.
В этом и предыдущем параграфах мы дали два типа оценок
норм в W\ произвольной функции и (х): внутренние, без каких-
либо предположений о гладкости границы S и граничных зна-
значений и, и оценки во всей области, для которых такого типа
предположения делать необходимо. Полезно иметь также оценку
нормы и в Wl для области Q, у которой лишь часть границы
удовлетворяет условиям леммы 8.1. Именно, справедлива
Лемма 8.2. Пусть часть S, границы области Q есть строго
липшицева поверхность, удовлетворяющая условию 2)_леммы 8.1,
a t (x) — какая-либо функция из пространства С2 (Q), равная
нулю вблизи S \ S,. Тогда для любой функции и (х) из С2 (Q U S,),
равной нулю на Slt справедливо неравенство (8.6), в котором
постоянная с зависит лишь от величин v, \i и q из D.2), D.3),
G.3) и S,.
Доказывается эта лемма принципиально так же, как лемма 8.1
и неравенство (8.6). Именно, берется интеграл \t?(LuJdx
Q
и преобразуется так же, как при выводе неравенства (8.11).
Так как ? не равна нулю на S,, то при интегрировании по
частям выделится интеграл
J ?ЧЛ<% [«v, (cos n, x{) - uXiXj cos (n, *,)] ds,
•Si

218 ЛИНЕЙНЫЕ УРАВНЕНИЯ (ГЛ. III
Его мы оценим так же, как интеграл j Isds при доказатель-
s
стве леммы 8.1, учитывая, что ? = 0 на S \ S(. Это и дает
неравенство (8.6).
Леммы, аналогичные леммам 8.1 и 8.2 (и даже более общие
оценки для производных и любого порядка 1^2), справедливы
и для других граничных условий: для условий (8.3), (8.4)
и условий «с косой производной» (см. по этому поводу ра-
работу [213] одного из авторов). Способ, изложенный здесь,
пригоден и для этих случаев. Некоторое отличие имеется лишь
в оценке граничного интеграла Г Isds, который преобразуется
s
примерно к тому же виду, но несколько иначе, с использова-
использованием других граничных условий. Граница S при этом должна
быть из С2.
Предположим, что участок S, границы Q принадлежит
классу W2q, q > п. В этом случае для любых функций и (х)
из Wt(Q), равных нулю на S,, также выполняется неравен-
неравенство вида (8.6), точнее, неравенство, отличающееся от (8.6)
лишь тем, что коэффициент 2v~2 при ||?21ы||] а следует заменить
постоянной с0, определяемой величиной v и поверхностью S,.
То же можно сказать о неравенстве (8.11) в областях класса W2,,
q > п. Остановимся на доказательстве первого из утверждений.
Функцию ?,(х) будем предполагать равной нулю вблизи S \ Si
и такой, что пересечение Q некоторой области, содержащей
носитель ?(*), с областью Q можно отобразить невырожден-
невырожденным преобразованием у = у(х) класса W2q(Q) на полушар
К+={у-1 У К 1, г/п>°}> так что dQflSi преобразуется в плоскую
часть 2 границы К.+.
Пусть х = х(у) — обратное преобразование для у = у(х),
l(y) = Ux(y)), v(y) = u(x(y)).
Ясно, что оператор L в новых переменных перейдет в опе-
оператор L, коэффициенты которого йц, at, bt а удовлетворяют
неравенствам вида D.2), D.3), G.3) с несколько другими
постоянными v и Д. Далее, если «e^(Q) и «|Si = 0, to
v(y)^W22(K+) и у|2 = 0. Продолжим v(у) на остальную часть
шара /С = {у: \ у |< 1} нечетно относительно 2, т. е. полагая
v (г/, г/„_,, — уп) = — v (у), у е= К+- Полученная таким
образом функция v(у) принадлежит W2(K)> а ее усреднения
1>р(г/) с бесконечно дифференцируемым ядром а>р(\х — у\) при-
принадлежат С°° (К'), равны нулю на 2 П дК' и сходятся к v (у) при
р->0 в норме Wl {К), где /(' — любой концентрический с К шар

§ 8] ВТОРОЕ ОСНОВНОЕ НЕРАВЕНСТВО 219
меньшего радиуса. В силу леммы 8.2 для vp(y)l(y) с достаточно
малым р справедливо неравенство
(\\ е2п |Р \2<T9v-2\\ ?2Tv II2 -4- г Г o2f?4 4- Ё4 -J- ?2?2 \г1н
\\\ъируу\\2,к+) ^=ZV |1ё ^иР%К+ ^с J vp\$ +51/^5 Ьуу)аУ-
Устремляя здесь р к нулю и переходя к переменным х, придем
к желаемому неравенству
(II t2uxx \{ аJ < с0 II Пи t в + с [ и2 (?« + II + 1%2ХХ) dx, (8,60
Q
в котором постоянные с0 и с определяются величинами v, ^
и q из условий D.2), D.3), G.3), нормами в U^ функций у(х)
и х(у) и нижними гранями соответствующих им якобианов.
Если Q нельзя преобразовать к К+ указанным образом,
то покроем ее перекрывающимися областями Q1 QN, для
каждой из которых пт существует невырожденное преобразо-
вание_у = у™(х) класса W2q{Q.m), переводящее Qm в шар К,
если Qm cQ, или в полушар К+, если QmflSi не пусто. Пусть
функция ?,т(х) при преобразовании х = хт(у) переходит в сре-
срезающую для К функцию 1т(у)- Для каждой такой ?,т(х) не-
неравенство (8.6') доказано. Если ?(*) — произвольная гладкая
функция, равная нулю вблизи S \ S,, то можно подобрать
соответствующие ?,т(х), т=\, ..., N, так, чтобы 2?„(*) = 1>
m=l
\fx e Q. Тогда, суммируя неравенства (8.6'), написанные для
?тихх> пРиДем к (8.6') с заданной g (л:), причем постоянные с0
и с в нем будут зависеть и от JV.
В случае, если Q есть область класса W2q, q> n, u(x)^ W22(Q)
и u\s = 0, то в (8.6') можно положить ?=1, т. е. получим
неравенство вида (8.11).
Сформулируем доказанные утверждения в виде леммы:
Лемма 8.3. Если Q принадлежит W2q, q>n, то для
VueW^Q), равной нулю на S, справедливо неравенство (8.60
с ?(*)==1. Если и(х) из W22(Q) обращается в нуль лишь на
части S, границы Q mS, e W2q, то для и верно (8.60 с ? eC2(Q),
равной нулю вблизи S\S{. В обоих случаях постоянные с0 и
с в (8.60 определяются величинами v, ц и q из условий D.2),
D.3) и G.3) и областью Q.
Замечание 8.2. Неравенства (8.11), (8.60 при л>3
справедливы и при несколько меньших ограничениях на atl, й{
и d, а именно, при конечности величин j2u ~g L а = Ш№)>

220 ЛИНЕЙНЫЕ УРАВНЕНИЯ [ГЛ. III
Ц, а = ^2 (й), II й ||да Q s= Из (й)> гДе <7 = max {/г; 4} для
¦1
и q = 4-\-e, е > 0, для /г = 4. Для доказательства этого надо
покрыть Q шарами Kp(xk), &=1 N, причем для шаров,
пересекающих S, взять их центры хк на S и воспользоваться тем,
что для областей Qk = /С2р (**) (] Q hVoe №„ (Qk), равной нулю
на dQftcQ, в неравенствах B.19) гл. II постоянную р можно
выбрать не зависящей от р^р0, взяв в качестве нормы IM|^Q
( — -+— )
в B.19) величину j|| Vv \\m Qft+ mes"» » 2 Q*f|| у ||л Qft. Число р
следует взять таким, чтобы ц{(?1к), г= 1,2,3, были достаточно
малыми. После этого надо получить оценки (8.6') со срезающей
для /С2р(к*) функцией g(*), равной единице в Кр(xk), k=l, ..., N.
Делается это так же, как и для случая q > n, только оценка
младших членов через старшие проводится не с помощью не-
неравенства B.27) гл. II с произвольно малым е > 0 при старших
производных, а с помощью неравенства B.19) гл. II с предельным
показателем и с использованием того факта, что нормы всех
коэффициентов этих членов по Qk достаточно малы. Суммируя
затем .оценки (8.6'), полученные для областей Qk, получим любое
из желаемых неравенств: (8.11) или (8.6'). Внешний вид их тот же,
что и для случая q > п. Однако постоянные с, входящие в них,
на этот раз не определяются нормами коэффициентов, входящими
в условия D.2), D.3), G.3), а зависят еще от интегральных
модулей непрерывности этих коэффициентов в соответствующих
пространствах. Исключение составляет лишь случай /г = 3,
когда постоянные с от модуля непрерывности функции й(х)
в L2(Q) не зависят, ибо для оценки интеграла \ d2u2dx при
/г = 3 нужно по-прежнему использовать неравенство B.27) гл. II
с Ve > 0 и потому нет необходимости требовать малости
норм l|a||2>Qft.
Заметим, что в случае <7 = /г>3 коэффициенты а1} не обязаны
быть непрерывными и данный нами способ доказательства
неравенств (8.6), (8.11) не использует непрерывности ait, но
зато требует существования производных а.цх, из Ln(Qi). Этот
случай подробно разбирается в работе [372]. Ниже, в § 11,
будет описан другой способ вывода этих неравенств, суще-
существенно опирающийся на непрерывность коэффициентов atj,
но не использующий существования производных а^. В § 19
обсуждается случай п = 2, обладающий специфическими свой:
ствами.

§9] ПЕРВАЯ КРАЕВАЯ ЗАДАЧА В ПРОСТРАНСТВЕ w\Qi.Q) 221
Замечание 8.3. При исследовании сходимости прибли-
приближенных решений краевых задач, вычисляемых по схеме Галер-
кина, оказалось полезным неравенство
(|| и \\1 „У < с | Lu ¦ Ми dx, (8.27)
и
обобщающее неравенство (8.23) на случай двух разных эллип-
эллиптических, операторов. Это неравенство справедливо для любой
функции и из №1,0@) и любых двух эллиптических операто-
операторов, если коэффициенты этих операторов удовлетворяют усло-
условиям D.2), D.3), G.3) и если коэффициенты а(х) и а(х) в них
при функции и не превосходят достаточно больших по модулю
отрицательных чисел. В общем случае, если последнее условие
не выполнено, то вместо неравенства (8.27) имеет место не-
неравенство
(|| и |? B)s < с J Lu • Ми dx + с, || и \{ а. (8.28)
Q
Неравенство же (8.27) справедливо для операторов Lu — Ки
и Ми — ц,и при Я. и ц,, превосходящих некоторые числа Хо и ц,0,
определяемые коэффициентами L и М и областью Q. Доказы-
Доказываются эти неравенства так же, как и неравенства (8.11) и (8.23),
надо только вместо интеграла J Lu • Ludx рассмотреть интеграл
а
j Lu • Mudx, преобразовать его главные члены с помощью
Q
двукратного интегрирования по частям так же, как и выше,
и воспользоваться известным предложением о возможности
одновременного приведения двух положительно определенных
квадратичных форм к сумме квадратов (см. [219, 33]).
§ 9. О разрешимости первой краевой задачи
в пространстве W%, о (Q)
Второе основное неравенство для эллиптических операторов L
позволяет сравнительно просто исследовать разрешимость
задачи Дирихле в пространстве W\ (Q). Пусть относительно
области Q и оператора L выполнены условия, при которых
доказана лемма 8.1. Рассмотрим в Q задачу Дирихле
Lu = $ (x), u\s = 0 (9.1)
при d)(^)eL2B). Граничное условие без ограничения общности

222 ЛИНЕЙНЫЕ УРАВНЕНИЯ [ГЛ. III
считаем сведенным к однородному. Предположим сначала, что
для Vuer|o(Q)
L(v, 0)>v,||0|a, v, >0. (9.2)
В силу | L(v, v) |< ||Lv ^ оIIо 1^ о из (9.2) следует || о ^0 <
^ vp'llby ||д Q, и потому второе основное неравенство можно
записать в виде
v\\2a, (9.3)
где v — произвольная функция из Wl, о(й).
Неравенства G.2), (9.3) показывают, что дифференциальный
оператор L устанавливает взаимно однозначное соответствие
между областью своего определения W\t о(й) (такой оператор
мы условились обозначать L) и множеством своих значений
R(L) с L2(Q). Покажем, что при определенной регулярности
границы S множество R(L) совпадает со всем L2(Q).
Будем говорить, что область Q обладает свойством SR, если
задача
Ды = т|\ и|5 = 0 (9.4)
разрешима в Wl, o(Q) для какого-либо плотного в L2(Q) мно-
множества 9№ функций iK*).
Замечание 9.1. Если область Q обладает свойством 9t
и удовлетворяет условиям леммы 8.1 (так что имеет место
неравенство (8.24)), то задача (9.4) однозначно разрешима
в Wi,o(Q) Для VS|)€=L2(Q).
Имеет место следующее предложение:
Теорема 9.1. Пусть для L и Q выполнены условия
леммы 8.1 и неравенство (9.2). Пусть Q обладает свойством SR.
Тогда задача (9.1) однозначно разрешима в №2,0@) при любой
•ф(*) из L2(Q).
Доказывается эта теорема методом продолжения по пара-
параметру. Именно, вводится семейство операторов ?ги = Ди +
+ x(L — Д) и, те [0, 1], и для них устанавливается однозначная
разрешимость задач
Lxu = $, u\s = 0 (9.5)
в пространстве Wlt0(Q), начиная с т = 0 и кончая т=1.
Делается это так же, как при доказательстве леммы 1,1 гл. III,
только вместо пары пространств С +а (Q) ¦*-+¦ Са (Q) надо взять
пару пространств Wl.oi®) •*-»-^2(Q)» а вместо неравенства
Шаудера A.18) — неравенство (9.3). Для возможности продол-
продолжения до т=1 надо убедиться, что неравенства G.2) и (9.3)
справедливы для всех Lx, те [0, 1], с постоянными с и с(,

§ 9] ПЕРВАЯ КРАЕВАЯ ЗАДАЧА В ПРОСТРАНСТВЕ w\fi(O.) 223
не зависящими от т. То, что в G,2) постоянную с, можно взять
не зависящей от т, очевидно. Для доказательства же неравенства
\\v\f2\^e\\Lxv\\2Q (9.6)
с t, не зависящей от те[0, 1], учтем, что нормы коэффициен-
коэффициентов Lx, от которых зависит постоянная с в неравенстве (8.11),
взятом для Lx, мажорируются постоянной, не зависящей от т.
Нижняя граница собственных значений основной квадратичной
формы A — т)|2 + та(/|(|/, соответствующей Lx, не меньше
v1 = min{l,v}, так что обе постоянные, входящие в неравен-
неравенство (8.11) для Lx, могут быть взяты не зависящими от т.
Кроме того, в силу D.25) имеем »
(—До, о)= j\ Vv pdA:>c-2mes-2/nQ J u2rf;t = vo|| и |Q,
и потому условие (9.2) справедливо для всех операторов Lx,
те[0, 1], с одной и той же постоянной, ибо
Lx(v, v) = xL(v, о) + A-т)(-До, o)>min{v0; v,}||o|?o. (9.7)
Из (9.7) вытекает оценка || v ||.2Q<max {v-1; v~ 1}|Ltt;J2j0, а отсюда
и из (8.11) для Lx очевидным образом следует (9.6). С по-
помощью (9.6) и G.2) для Lx теорема 9.1 доказывается буквально
по той же схеме, что и лемма 1.1 данной главы, и мы ее здесь
повторять не будем. Более того, из этого же доказательства
следует справедливость и такого предложения:
Лемма 9.1. Если для L и Q выполнены условия леммы 8.1
и неравенство (9.2), то операторы Lx, те[0, 1], замкнуты
на №i,o(Q) и их области значений совпадают друг с другом.
Замечание 9.2. Легко понять, что вместо оператора Д
в условии ffi и в доказательстве теоремы 9.1 можно взять любой
из операторов с теми же свойствами, что и оператор L.
Замечание 9.3. Пространство W\0(й) было определено
нами как замыкание в норме 1^1@) множества функций и(х) из
C2(Q), равных нулю на S. Из замечания 9.1 и единственности
обобщенного решения задачи (9.4) в классе Wl2(Q) следует, что
для областей Q, удовлетворяющих условиям леммы 8.1 и обла-
обладающих свойством №, Wl0(Q) совпадает с Wi(Q) П W\(U)=W\ 0(Q).
Действительно, включение wIi0{Q)czW\.q{Q) вытекает из
определений этих пространств. Пусть и (х) есть произвольный
элемент W|.0(Q). Задача (9.4) для 1|) = Ди имеет в силу заме-
замечания 9.1 решение v (x) из Wl,0(Q). Но v (х) и и(х) суть

224 ЛИНЕЙНЫЕ УРАВНЕНИЙ [ГЛ. Ill
обобщенные решения из W2(Q) задачи (9.4) с одним и тем же
свободным членом i|) = Дм е L2(Q). В силу теоремы единствен-
единственности для задачи (9.4) в пространстве W2(Q) функции и(х)
и v(x) совпадают, и, следовательно, W\ 0 (О) = Wl, о (О).
Для областей класса С2 совпадение W2,0(Q) и W\ о (О) легко
проверить непосредственно, если учесть, что в случае полу-
полушара К+ для Чи(х) из Щ(К+), равной нулю на дК+(]К,
и любой срезающей для всего шара функции ?(*)
произведение t,(x)u(x) можно аппроксимировать в норме
дважды непрерывно дифференцируемыми в К+ функциями,
равными нулю на дК+ (см. доказательство леммы 8.3).
Для шаров и параллелепипедов условия леммы 8.1 заведомо
выполнены. Для них выполнено и условие Ш, ибо известно,
что из отличных от тождественного нуля решений задач
Д<р = А<р, <p|s = O (9.8)
можно образовать ортонормированный базис {фА}, &= I, 2, ...,
в пространстве L2(Q), причем все фй (x)^W\ 0(Q) (и даже C°°(Q)),
а соответствующие им Xk строго отрицательны. Благодаря этому
N
задача (9.4) имеет решения и(х)= 2 cklk\k (x) из W\ о(й) для
ft=i
N
любой тЬ (л:) вида 2 Сьф^ (л:), т. е. для плотного множества
функций -ф (л:) из L2(Q). Ввиду этого из теоремы 9.1 вытекает
Следствие 9.1. Если Q есть шар или параллелепипед,
a L удовлетворяет условиям теоремы 9.1, то задача (9.1) одно-
однозначно разрешима в W\, o(Q) при любой ty(x) e L2(Q).
Покажем теперь справедливость следующего факта:
Теорема 9.2. Если выполнены все условия теоремы 9.1,
кроме неравенства (9.2), то любое обобщенное решение из W2 (Q)
задачи (9.1) с i|)sL2(Q) принадлежит W\, 0(Q).
Действительно, любое об. р. и(х) из Wl2(Q) задачи (9.1)
можно рассмотреть и как об. р. из Wl2(Q) задачи
Lu — Jm = $ — Jm, u\s = 0 (9.1*)
с V/L Выберем X так, чтобы оператор L — XE удовлетворял
условию (9.2), а функцию ^ — Хи рассмотрим как свободный
член в уравнении (L — ХЕ)v = $. Очевидно, ^>^L2(Q), и по-
потому к оператору L — XE применима теорема 9.1. Она гаран-
гарантирует существование v(x) e W2, o(Q). В силу теоремы 5.1 для
L — XE m=w.

§ 9] Первая краевая задача в пространстве w|0B) 225
Из теоремы 9.2 и того, что шары и параллелепипеды удо-
удовлетворяют условию SR и условиям леммы 8.1, следует:
Следствие 9.2. Если Q есть шар или параллелепипед,
а коэффициенты L удовлетворяют условиям леммы 8.1, то лю-
любое обобщенное решение и(х) из W2(Q) задачи (9.1) с -ф е L2(Q)
принадлежит W2, о(й).
Пусть для Q и L выполнены условия теоремы 9.2. Преобра-
Преобразуем диффеоморфно область Q в область Q с помощью функ-
функций г/ = г/(*), y^Wq(Q), q>n (для у(х) производные первого
порядка ограничены в Q и 0 < с, ^ det ^ ¦ ^ с2 < <
Легко проверить, что при этом оператор L переходит в диф-
дифференциальный оператор I по переменным г/, удовлетворяю-
удовлетворяющий условиям теоремы 9.2 в области Q, и, наоборот, если L
удовлетворяет в Q условиям теоремы 9.2, то обратное преоб-
преобразование х = х (у) приведет нас к L, так же удовлетворяющему
в Q условиям теоремы 9.2.
Между пространствами L2(Q), Wl(Q), Wl,0{Q) nL2(U), W2(Q),
W2. о (О) преобразование у = у(х) устанавливает естественный
изоморфизм (он осуществляется так: и(х)->-и(х(у))=зй(у), при-
причем нормы ИиЦ^ц, 0^/^2, эквивалентны нормам Ий^'ц,
0=S^=S^2, соответственно). Задача (9.1) в новых переменных
примет вид
1й = ^>(у), у ^Q, й|д?=о. (9.1)
Из всего сказанного следует, что если коэффициенты L удо-
удовлетворяют в Q условиям теоремы 9.2, то любое об. р. м (у)
из W2(Q) задачи (9.Г) с ipeL2(Q) принадлежит W22i0(Q). Для
й(у) справедливо неравенство
*а Ci II Ш |^ -g + С II U 1^ g, @.11)
получаемое из (8.11) простым преобразованием переменных
(заметим, что условие 2), налагаемое на Q в лемме 8.1, для Q
может оказаться невыполненным). Из этого рассуждения вы-
вытекает справедливость следующей теоремы:
Теорема 9.3. Пусть область Q пространства х е Еп по-
получена из области й пространства у е Еп, удовлетворяющей
условиям леммы 8.1 и условию 9t, с помощью диффеоморфного
преобразования x = x(y)<=W2q(Q), q > п, и пусть коэффициентыL
удовлетворяют условиям D.2), D.3), G.3). Тогда любое об. р.
и(х) из W2(Q) задачи (9.1) с i|)€=L2(Q) принадлежит W22(.Q).
8 О. А, Ладыженская, Н. Н. Уральцева

226 ЛИНЕЙНЫЕ УРАВНЕНИЯ [ГЛ. III
Для и(х) справедливо неравенство вида (8.11) (т. е. в (8.11)
п и Ьй надо заменить на и и Lu, a Q на Q). В частности,
в качестве Q можно взять шар или параллелепипед.
Замечание 9.4. Все утверждения данного параграфа
остаются справедливыми и для задачи
Lu = $, и 1х = ф Is, (9.9)
если ф Is есть граничное значение функции <р (*) е №2 (Q). Дей-
Действительно, эта задача легко сводится к задаче (9.1), если
вместо и(х) искать функцию v (х) = и (х) — <р (*) и заметить,
что L<peL2(Q) (см. G.2)).
Скажем несколько слов об условии 9v. Для совпадения
R(L) с L2(Q) для всей совокупности эллиптических операто-
операторов L с хорошими коэффициентами оно, очевидно, необходи-
необходимо, а при условиях леммы 8.1 и (9.2) и достаточно (теоре-
(теорема 9.1).
Условие SH справедливо далеко не для всех областей. Его
выполнение или невыполнение, например, для областей с угло-
угловыми точками, как подметила О. В. Гусева, зависит от вели-
величин углов при этих точках. Поясним это на следующем при-
примере. В качестве Q возьмем круговой сектор {O^r^l,
O=^0=S^0O} на плоскости (х1г х2). Собственные функции опера-
оператора Лапласа для него при нулевом граничном условии имеют
особенности в точке г = 0; при 0о^я особенности таковы, что
собственные функции являются элементами 1^@), а при я<
< 0О < 2я не принадлежат Wl(Q), Следовательно, решения
задачи (9.4) в секторе с углом 0О е (я, 2я) не будут элемен-
элементами W\ 0(й) при любой -ф из L2(Q). Неравенство же (8.24)
справедливо и для такого сектора. Из всего этого следует, что
оператор Д переводит W\ о (О) в собственное подпростран-
подпространство L2(Q). Этот оператор допускает дальнейшее расширение
с сохранением симметрии, и такое расширение необходимо,
если мы хотим решить задачу (9.4) для любой -ф из L2(Q).
Нетрудно показать, что оно единственно и осуществляется до-
добавлением к множеству W\ 0(й) элементов вида с
X sin -5—, где с — произвольная постоянная, a f (r) — какая-нибудь
дважды непрерывно дифференцируемая функция, равная 1
вблизи г = 0. Если же угол 0o=S^jt, то Д (а потому и любой
другой симметрический эллиптический оператор L) самосопря-
самосопряжен уже на множестве W\ о (О). В следующих параграфах мы
покажем, что дифференциальные свойства решений эллиптиче-
эллиптических уравнений суть локальные свойства, т. е. что они зави-
зависят от соответствующих характеристик L, if и S лишь в окрест-

§ 10] О ПРИНАДЛЕЖНОСТИ РЕШЕНИИ К W^i) 22?
ности рассматриваемой точки. Используя это обстоятельство
вместе с изложенным сейчас примером и неравенствами пара-
параграфа 8, а также некоторые факты теории расширения
симметрических операторов, М. Ш. Бирман и Г. Е. Скворцов
показали [52], что дефектные числа оператора L равны числу
углов, больших я. Это дает возможность описать все самосо-
самосопряженные расширения оператора L (при п = 2),
§ 10. О принадлежности обобщенных решений
из Wl(Q) к Wliiii)
Пусть коэффициенты оператора
Lu = -^-(alt (x) uXj + at (*) в) + Ь{ (х) ux. + a(x)u
удовлетворяют условиям D,2), D.3), и пусть и есть обобщен-
ное решение из W2(Q) уравнения
Lu = -§- + f^$(x) A0,1)
для f;GL2(Q), feLsii/«+2)(Q). Никаких предположений типа
неравенств (9.2) или, общее, предположений о том, что Х = 0
не есть точка спектра для L при каком-нибудь краевом усло-
условии, не делаем. Так, в частности, и может быть собственной
функцией для L при каком-нибудь краевом условии. Целью
данного параграфа является доказательство того, что если
в какой-либо подобласти Q' области Q коэффициенты опера-
оператора L удовлетворяют еще условиям G,3) и функция *ф при-
принадлежит L2(fi'). то решение и в этой подобласти имеет обоб-
обобщенные производные второго порядка, квадратично суммируе-
суммируемые по VQ" с Q', и удовлетворяет уравнению A0,1) для почти
всех х из Q', Если же Q' примыкает к достаточно гладкому
куску S, границы Q и значения и на этом куске совпадают
со значениями какой-либо функции ф(*) е W\ (Q), то и(х) будет
иметь квадратично суммируемые производные второго порядка
и вблизи S,, В частности, если Q' совпадает со всей Q, гра-
граница S обладает определенной гладкостью и на S обобщенное
решение и уравнения A0,1) из класса W]2(Q) совпадает с функ-
функцией ф(*) е Г1 (й), то и будет принадлежать W\{Q),
Пусть сначала Q' есть внутренняя подобласть Q, Возьмем
произвольный шар Кр, принадлежащий Q' и имеющий столь
малый радиус р, что для оператора L в /Ср выполняется условие

228 ЛИНЕЙНЫЕ УРАВНЕНИЯ [ГЛ. III
D.26), а следовательно, и неравенство
С
Lp (л> л) = (аг/Пх/Пх/ "г aiW\xi — ?><т1т1х,- — аЛ ) dx^.
= c(||Tilg\ J A0,2)
о ,
с постоянной с>0 для любой tie IF2(Ар),
Построим последовательность бесконечно дифференцируемых
функций ит(х), т=\, 2, ,.., сходящихся к решению и в нор-
нормах W\(Kp) и L2qi(q-2)(KP) и рассмотрим в шаре /Ср краевые
задачи
La = ij), у (s = «m Is , m= 1, 2, ,,,, A0.3)
где Sp — граница шара /Ср. В силу результатов §§ 5 и 9 ка-
каждая такая задача имеет единственное решение vm в простран-
пространстве W\ (/Ср) (см. теоремы 5.1, 5.2 и следствие 9,2),
Для функций vm справедливо неравенство D,31), причем
правая часть его ограничена равномерно для всех /п= 1, 2, ,,.,
т. е,
ИиД'/к <с, /71=1,2, ... A0.4)
Кроме того, для vm справедливо и неравенство (8.6), причем
^го правая часть, в силу A0,4), также равномерно ограничена
для всех т=1,2 т, е,
№т?\ЦКр<с($, A0,5)
Здесь ? (*) — произвольная дважды непрерывно дифференцируе-
дифференцируемая функция, равная нулю на границе /Ср,
Вследствие A0.4) и A0.5) из последовательности {vm} можно
выделить подпоследовательность {vmk}> сходящуюся слабо в нор-
нормах WUKo) и Wl(K p\ с любым т = 2, 3, .., к некоторой
I p-TJ
функции v, также удовлетворяющей неравенствам A0.4), A0.5),
Покажем, что v совпадает с и, Для функций и и vmk при лю-
бой л из W2(/СР) справедливы соотношения Lp(u, ti) = I Щах,
Lp (umft, Л) = J ¦фл^- откуда Lp [и — vmk, л) = 0. Положим здесь
«р
Л = «тА — vmk. Тогда
Lp (umfc ^т4' Mfftfc ""

§ Ю| О ПРИНАДЛЕЖНОСТИ РЕШЕНИИ К «^(В,) 529
Второй член при k-+°° стремится к нулю, а потому ввиду A0.2)
и и Ыт —vm ||A) -*-0. Тем самым доказано, что « = и в /Ср.
II я «и2, Кр
Итак, для внутренних областей Q' утверждение, сформулиро-
сформулированное в начале параграфа, доказано. Пусть теперь под-
подобласть Qi примыкает к границе области Q. Без ограничения
общности будем считать, что Q, имеет столь малую меру, что
для оператора t в Q, выполнено неравенство D.26), а следо-
следовательно, и неравенство D.31). Кроме того, предположим,
что Q\ удовлетворяет условиям, наложенным на область в тео-
теореме 9,3, Это предположение накладывает ограничение на тот
кусок S, границы S, который является общим для границ Q
и Qp Будем считать, что m|s=0 (в противном случае мы
вычли бы из и (х) функцию ф (к), совпадающую на S] с и и
принадлежащую по условию к W\ (Qi), и все дальнейшие рас-
рассмотрения проводили бы для функции и(х) — ф (*)), Возьмем
последовательность функций ит, т=1,2, ..., равных нулю
на S[, принадлежащих Wl(Qi) и сходящихся к и в норме W]2(Qi),
и рассмотрим в области Q| задачи
Lv = $, v\s, = um\s,, m=l, 2, ..., A0.6)
где S' есть граница Q(. В силу теорем 5,2 и 9,3 задача A0.6)
имеет единственное решение vm из класса W\{u{), а в силу
неравенств D,31) и (8,6) для него справедливы оценки
II о» l^o, < с, \\vmt?\i\<c(t,) A0,7)
с постоянными, не зависящими от т. Здесь ? (*) есть произ-
произвольная дважды непрерывно дифференцируемая в области ?2
функция, равная нулю вблизи S' \ S,, т.е. той части гра-
границы S', которая не принадлежит S. ОтсюДа, так же как и
выше, заключим, что предельная для vm функция удовлетво-
удовлетворяет неравенствам A0.7) и совпадает в Q( с решением и, Так
проводится исследование дифференциальных свойств и вблизи
границы. Это вместе с результатами исследования и внутри Q
позволяет сделать выводы и о том, когда решение и принад-
принадлежит к Wl(Q). Подытожим все сказанное в виде теоремы.
Теорема 10,1. Пусть и(х) есть обобщенное решение из
W2(Q) уравнения A0.1), коэффициенты и свободные члены ко-
которого удовлетворяют условиям
1<№, v>0;
<ц, q>n;
2. Q
A0,8)

230 ЛИНЕЙНЫЕ УРАВНЕНИЯ [ГЛ. III
Если для какой-либо внутренней подобласти Q' области Q коэф-
коэффициенты оператора L, помимо A0.8), удовлетворяют еще ус-
условиям
II да,
|| дх,
где Q = max (q, 4), и
"г, а' =
дх
' Ib, a
(Ю.9)
A0.10)
то решение и {х) имеет в Q' обобщенные производные второго
порядка, удовлетворяет уравнению A0.1) при почти всех х
из Q' и
II "?2 Ца. < с (v, ц, ?> 5) [|| и ||2> й, + И 112, „,], (Ю. 11)
где ? — срезающая для Q' функция.
Если граница области ?llczQ имеет с границей S области Q
общую часть Sb причем Q{ удовлетворяет условиям, налагае-
налагаемым на область в теореме 9.3, и если граничные значения и
на Si задаются функцией у(х), принадлежащей W2(Qi), то для
решения и в подобласти Q{ справедливы только что высказан-
высказанные утверждения с тем отличием, что функция t,(x) в A0.11)
обязана равняться нулю лишь в окрестности части границы О,ь
не принадлежащей S (к выражению в квадратных скобках
в A0,11) надо прибавить в этом случае Hqpllfa,)-
Если условия A0,9), A0.10) справедливы для Q'=Q, еслиу(х),
задающая граничные значения и, принадлежит W\(Q) и если Q
может быть разбита на конечное число областей Qh /= 1, ,.., N,
таких, что каждая Qt есть строго внутренняя подобласть об-
области Qi, i= I, ..,, W, пересечение которой с Q удовлетворяет
условиям теоремы 9.3, то u^W\(Q) и для и{х) справедлива
оценка
|| и |?>в < с (v, IX, q)[\\u ||2] 0 + И ||2> 0 + || Ф |f J. A0.12)
В частности, это верно для областей Q класса W\, q > п. Все
утверждения теоремы, кроме характера зависимостей постоян-
постоянных в A0.11) и A0.12) от коэффициентов, верны и тогда, когда
Г max(n, 4) при пфЬ,
п^З, q — n, д = \ . , ^ п
ч ч I 4 + е, е > 0, при п = 4.
Доказательство этой теоремы следует из проведенных выше
рассуждений, если заметить, что области, удовлетворяющие
условиям теоремы 10.1, можно разбить на области такого же

§ 11] ДОКАЗАТЕЛЬСТВА 2-ГО ОСНОВНОГО НЕРАВЕНСТВА 231
типа, но достаточно малой меры. Такое дополнительное раз-
разбиение Q] или Q в общем случае надо сделать, ибо выше, при
доказательстве принадлежности и к W2 (Qi), мы считали меру Q]
столь малой, что для L в Q, выполнялось неравенство D.26).
Можно обойтись и без дополнительных разбиений на ма-
маленькие области, но тогда вместо уравнений Z.i> = тр в задачах
A0.3) и A0.6) надо взять уравнения Lv — kv = т|з — kv =т|>
с достаточно большим к (к, гарантирующим для Lv — kv тео-
теорему единственности в рассматриваемой области Qt). Подоб-
Подобный прием мы применили выше при доказательстве тео-
теоремы 9,2.
§ 11. О других способах доказательства
второго основного неравенства
В §§ 7, 8 мы вывели второе основное неравенство дл
эллиптических операторов вида Lu = -т—(а{1их. + atu) + biuxt +
+ аи, Для таких операторов требование дифференцируемости
коэффициентов ац и аг вызвано существом дела. Однако если
оператор, имеет вид
Mu = ai,uxtxj + aiuxt + au, A1.1)
то естественно было бы попробовать доказать второе основ-
основное неравенство
II и Со < с(|| Ми 1^+II и 11г. в) (ВД
для u^W2.o(Q) без предположений о дифференцируемости ко-
коэффициентов М. Казалось бы, что такими предположениями
должны быть, кроме условия эллиптичности, конечность
тах| ац | и конечность норм
II «г Не, ?2. II a H.j/2, а, q = max (q, A), q > п.
Но пример B.19) гл. I показывает, что для п > 2 требование
только ограниченности ац недостаточно. Покажем, что при
непрерывных аг/(л:) неравенство A1.2) уже имеет место, при-
причем постоянная с в A1.2) зависит от модуля непрерывности ац *).
Мы не будем приводить полное доказательство этого предло-
предложения. Его основная идея та же, что и идея Шаудера
*) В замечании 8.2 показано, что обсуждаемое неравенство справед-
справедливо и для L, коэффициенты которых удовлетворяют условиям D.2), D.3),
G.3) с q = п (при я>2). Непрерывность коэффициентов L из этих условий
не вытекает.

232 ЛИНЕЙНЫЕ УРАВНЕНИЯ [ГЛ. 111
доказательства неравенства- A.11), дающего оценку | и g+a> *).
Она состоит в сведении всего вопроса к соответствующим оценкам
по малым областям для эллиптических операторов, в которых
старшие коэффициенты а.ц заменены их значениями в какой-
либо точке взятой малой области, и к последующей «склейке»
этих оценок за счет непрерывности atj{x). В соответствии с этой
идеей общая схема доказательства неравенства A1.2) следую-
следующая. Пусть и е 1^2,о (Q). Обозначим значение оператора М
от « через ф (х). Покроем область Q шарами Кр (xk), k = 1, ..., N,
малого радиуса р, и пусть Qk = /?2р (хк) П &•
В силу непрерывности коэффициентов пц (х) их значения
в каждой точке области Qfe мало отличаются от их значений
в точке хк. Равенство Ми = ф запишем в виде
Мои г» аИ (**) uXtXj = ф - [а., (х) - atJ(**)] uX{Xf - a^ -au^F
и будем помнить, что коэффициент при их х справа достаточно
мал. Для операторов Мо в Qk имеют место оценки типа (8.6)
и тем более оценки
ll^lfa^-^ll^oMll^^ + c.NI^ ' A1.3)
с постоянной с1; зависящей лишь от известных нам норм коэф-
коэффициентов и тах| t,x, t,xx | (считаем, что |^|<1).
с
Правая часть в A1.3) не превосходит величины
(еЦЛ{ гаи jаA (х) - a.s (**) j) • || J uxx\ ||2. Cft + се\\ и Ig
с Ve > 0.
*) В заметке [492] эта идея описана Шаудером применительно к вы-
выводу неравенства A1.2) для случая плоских областей (« = 2) и непрерыв-
непрерывных коэффициентов a.j. При этом Шаудер знал, что такие неравенства
были доказаны ранее С. Н. Бернштейном (см. [42], а также [43]) для урав-
уравнений 2 ai I (х) их х == f (х) в круге при произвольных измеримых коэф-
фициентах a{j(x), удовлетворяющих условию v|2^ а^|;|, ^ ц|2, и для
общих уравнений Ми = f с дифференцируемыми коэффициентами пц(х),
а^х), а(х) и с a(*)<JO в выпуклых областях. Сам Шаудер видел свою
заслугу в устранении предположения Бернштейна о выпуклости области
Упоминание о всех этих результатах отсутствует в отечественной литера-
литературе до середины 50-х годов. В § 19 мы покажем, как доказать неравен-
неравенство A1.2) при « = 2 для произвольной невыпуклой области, предполагая
о пц лишь их ограниченность, а о а{ и а их принадлежность к Lg (Q), q>2,
и L2 (Q) соответственна

§ И) ДОКАЗАТЕЛЬСТВА 2-ГО ОСНОВНОГО НЕРАВЕНСТВА 233
Суммируя A1.3) по всем областям Qk, k= I, ..., N, и помня,
что для пограничных Й& функцию ? можно брать отличной от
нуля на части границы Q&, принадлежащей S (и на S считаем
равной нулю), придем к неравенству
I«1|?а < Ф + max та* I ati М — ац (**) |)' III и*х I Иг, а +
Выбирая области Qk и е столь малыми, чтобы выполнялось
соотношение
c3(e + max max | аИ{х) — au(xk) |)<-^-, A1.5)
из A1.4) получим
||y)c). A1.6)
Используя еще известное неравенство
с произвольным е > 0, из A1.6) получим A1.2).
Этих объяснений достаточно, чтобы читатель сам мог про-
провести все доказательство неравенства A1.2).
Сформулируем описанный результат в виде леммы:
Лемма 11.1. Пусть область Q удовлетворяет тем же усло-
условиям, что и в лемме 8.1 или в лемме 8.3. Если коэффициенты ац
оператора М, определяемого выражением A1.1), непрерывны в Q,
а для а{ и а конечны нормы \\at\\^a, 1|а||^/2,д» <? — max {^,4},
g> n, то для любой функции и из Wl,o (Q) справедливо нера-
неравенство A1.2) с постоянной с, зависящей от области Q, вели-
величин v и ix из неравенства v|2 ^ «t/i(-i/ <ц|2, модуля непрерыв-
непрерывности r aiS и норм || а{ ||?_ а, || а ||№ й.
Для случая « = 2, как будет показано в § 19, условие непре-
непрерывности а{}(х) можно отбросить; для п, больших двух, нельзя.
Придерживаясь изложенной здесь схемы вывода неравен-
неравенства A1.2), можно доказать, что для эллиптических операторов М
справедлив более общий факт:
Q + ||«||riC), г>1, A1.8)
где р—любое число, большее 1, а «(л:) — произвольная функ-
функция из Wp> o(Q). Относительно коэффициентов М при этом надо
предполагать, что ац(х) непрерывны и подчиняются неравен-
неравенствам D.2), а;(х) суммируемы по Q со степенью тах(р; п) при

234 ЛИНЕЙНЫЕ УРАВНЕНИЯ [ГЛ. III
рфп и п + 8, е>0, при п = р, а коэффициент а(х) сумми-
суммируем со степенью тах(/?; /г/2) при р ф п/2 и /г/2-j-e, е > О,
при р = п/2.
Постоянная ср,г определяется п, г, р, v, ц, модулем непре-
непрерывности а.ц(х), нормами at и а в указанных только что
пространствах LS(Q) и их модулями непрерывности в нормах
этих пространств. Она зависит также от области Q, которая
предполагается принадлежащей Wq, ^ = maxCp; п + е), е > 0.
Доказательства неравенства A1.8) для случая ограниченных
коэффициентов а{, а даны в работах [23, 20].
§ 12. О принадлежности обобщенных решений
из Wl к Ct+\ / > 2
Пусть функция «(л:) принадлежит ЗЯ и для почти всех х
из Q удовлетворяет уравнению
Lu = atl (x) uX{Xj + at (х) их. + а (х) u = f(x), A2.1)
коэффициенты и свободный член которого суть элементы
C'~2+a(Q), />2, и г|2<аг/^/<ц?2, v>0. Здесь Зй есть
совокупность элементов W% (Q), имеющих конечный vrai max.
Докажем, что «(л:) фактически принадлежит С1+а(п). Это до-
достаточно сделать для произвольного шара Кр малого радиуса р.
Величину радиуса р выберем по коэффициентам L следующим
образом. Во-первых, р возьмем столь малым, чтобы для опе-
операторов
x.
где х°<=Кр,
и любой функции v (х) из WzoiKp) выполнялось неравенство
|| о |f л <C||L°w||2K. A2.2)
Ар ^i Лр
Во-вторых, надо, чтобы для L0 в Кр была верна оценка A.9)
и, тем самым, теорема единственности в классе С+а(/Ср). На-
Наконец, р должно быть таким, чтобы
en max |а„М-а„(х)|<|, A2.3)
t.i:x = Kp 1
где с—постоянная из неравенства A2.2). Очевидно, всем этим
требованиям мы удовлетворим, взяв достаточно малое р.
Возьмем последовательность бесконечно дифференцируемых
и равномерно ограниченных в шаре Кр функций {ит}, т=\,2
сходящуюся в норме Wl(Kp) к функции и{х). Для каждой

§ 12] О ПРИНАДЛЕЖНОСТИ РЕШЕНИЙ К Ct+<X, />2 235
из ит рассмотрим в Кр задачу
Lvm = f, «mlSp=«mlSp, A2.4)
где Sp — граница /Ср. По доказанному выше задача A2.4) имеет
единственное решение vm из С1+а(Кр) и для него верна оценка
A.9), дающая равномерную ограниченность max |ит(л:)|. Раз-
Кр
ность wm = ит — vm удовлетворяет уравнению Lwm = Lum — f,
которое запишем в виде
L°wm = (L°-L)wm + Lum-f, A2.5)
и нулевому граничному условию Wm\s =0. Для нее неравен-
неравенство A2.2) дает
II wm ||<2)Хр < с(|| (L° - L) wm ||2 % + || Lum - f ||2> Xp). A2.6)
Но (L° — L)wm = [ait(xP) — att(x)]wmX{Xr и поэтому
|| (I» - L) wm ||2> Кр < п i mjaK I at, (л") - <ц, (х) | • || w 11^.
В силу предположения A2.3) отсюда и из A2.6) будем иметь
|| ^т 1|2>Кр< 2С || L«m-Л I2,v A2J)
Правая часть в этом неравенстве, как легко видеть, при
т-*¦ оо стремится к нулю, так что vm сходится в W\{Kp) к и.
Но для vm, m=l, 2 справедливы равномерные по т
оценки (см. A.13) и A.9))
| vM%+a)<c(t, а, ?)(| / ^+а> + max! vm I), A2.8)
где ^(х) есть какая-нибудь финитная в Кр функция из С1+а(Кр)>
постоянная с(/, a, Q зависит от нее, / и а, но не зависит от т-
Из A2.8) следует, что предельная для vm функция « будет при-
принадлежать Cl+a(Kp\Sp) и подчиняться неравенствам A2.8).
Желаемое утверждение доказано.
Аналогично, используя вместо A2.8) оценки A.11) и A.12),
устанавливаем принадлежность и (х) к Cl+a (Q) или к С'+а (Q U 5,),
если дополнительно известно, что граничные значения и на S
(соответственно на части S, границы S) принадлежат С'+а, и
если сама S (соответственно часть ее Sr) есть поверхность
класса Ct+a. Необходимые для этого небольшие дополнения
в рассуждениях описаны в конце § 10.
Сформулируем доказанные утверждения в виде теоремы:
Теорема 12.1. Пусть и(х)^Ш и почти всюду в Q удов-
удовлетворяет эллиптическому уравнению A2.1), коэффициенты и

236 ЛИНЕЙНЫЕ УРАВНЕНИЯ |1"Л. til
свободный член которого суть функции C'~2+a(Q), /^2. Тогда
и(х) есть функция из Ct+a(Q). Если к тому же граница S (или
ее часть S,) есть поверхность класса С1+а и граничные значе-
чения unaS (соответственно на S{) задаются функцией класса С1+а,
то и(х) принадлежит к Cl+a(Q) (соответственно к Cl+a(Q\jSi)).
§ 13. Об ограниченности обобщенных решений
из Wl2(Q) и оценке для них некоторых интегральных норм
Пусть «(л:) есть обобщенное решение из W2(Q) уравнения
LU = _L (aiSuXj + aiu) + Ъгих. + au = f + ¦—, A3.1)
и пусть коэффициенты L удовлетворяют условиям *)
v>0,
A3l2)
1>n.
/2.a
* I
В §§ 4,5 были установлены теоремы о разрешимости в W2 (Q)
задачи Дирихле для A3.1) при условиях, что f е /-2йдй+2)(й),
ft e L2 (Q) и граничные значения и определяются функцией
* I
ф(х)е^2(й). В этом и следующем параграфе мы покажем,
что при несколько лучших свойствах / и /, любое такое реше-
решение принадлежит классу Гёльдера Ca(Q). В § 2 гл. I на по-
построенных там примерах было выяснено, что необходимыми
для этого условиями являются следующие:
<m. я>п. A3.3)
Мы докажем, что они же и достаточны для принадлежно-
принадлежности и к Ca(Q). Более того, мы получим оценки величин тах| и \
и | и |(а) через постоянные v, ц и ц{ из условий A3.2), A3.3)
и || и ||2 Q. Оценки этих норм для всей Q будут зависеть, разу-
разумеется, еще и от соответствующих характеристик поведения
функции и на S.
Итак, пусть выполнены условия A3.2), A3.3) и и есть обоб-
щенное решение уравнения A3.1) из W2(Q), т. е. и принадле-
•) О случае q = n^'i см. замечание 13.1.

§ 13] ОБ ОГРАНИЧЕННОСТИ ОБОБЩЕННЫХ РЕШЕНИИ ИЗ W2(Q) 237
жит W2(Q) и удовлетворяет тождеству
J [(ai}uXj + atu - fi)nXi - {Ыих. + аи - f) л] dx = 0 A3.4)
при любой функции Tie^2(Q).
Возьмем здесь в качестве t] функцию ц(х) = ?,2(х)тах{и(х)—
— k; 0}, где Л—любое положительное число, а ?(*) — любая
срезающая для произвольного шара /CpciQ функция. (Опре-
(Определение срезающей функции дано на стр. 27, в частности,
0<?(х)<1.) Такая ц(х) является допустимой функцией,
так как в силу леммы 3.3 гл. II ц(х) будет принадле-
принадлежать классу w2(Q). Функция г\ отлична от нуля только на
множестве Akp точек х из Кр> где u(x)>k. Подставив эту
функцию в A3.4), после простых вычислений получим
J
»ft, p + {а.и _ /.) [Uxfi + 2SC, (и - *)] -
- F?и,, + «"-/)(«- k)?} dx = 0. A3.5)
Первый член в силу A3.2) не меньше v|V«p?2. Его мы
оставим слева и оценим снизу. Остальные члены A3.5) пере-
перенесем направо и оценим сверху, используя неравенства A.1)
и A.2) гл. II и отдавая малое е множителям, содержащим их..
Это приведет нас к неравенству
J
Ak,p
(=1
n
dx. A3.6
Возьмем здесь е = v/6, a e, = ц- Тогда
f
T f
A3.7)

238 ЛИНЕЙНЫЕ УРАВНЕНИЯ [ГЛ. lit
Отсюда следует неравенство
c0 J {u-kY\\l?dx +
Ak,P
+ c J DW + {u-kY+\\t?dx, A3.8)
где ^-i + 1)
^=SK + ^ + f?) + lflH-lfl, A3.9)
а с — постоянная, зависящая лишь от v и ц из A3.2). В силу
предположений A3.2), A3.3) величина ll^ll^ Q конечна и опре-
определяется лишь Ц\ и q.
Последний интеграл в A3.8) оценим с помощью неравенства
Гёльдера так:
J D{u2
W.P
?-2)/<7
A3.10)
где С! определяется только v, и, щ и ^ из A3.2) и A3.3).
Первое из слагаемых, стоящих справа в A3,10), в силу не-
неравенства B.13) гл. II допускает оценку
J х, A3.11)
^,р
2 2
где в] = > 0, а постоянная с2(^) зависит лишь от п и q.
Если радиус р считать таким, что
с2G)с,ср«.<72, A3-12)
то из A3.8) в силу A3.10) и A3.11) следует
{ (и- kJ\V?fdx + у' (k2 + I) mes~~Ak,p.
A3.13)

§13] ОБ ОГРАНИЧЕННОСТИ ОБОБЩЕННЫХ РЕШЕНИЙ ИЗ w\(Q) 239
Постоянная у = — + 24 (-Н +1, а у' определяется лишь величи-
величинами v, ц, щ и q. Неравенство A3.13) доказано для Лир,
удовлетворяющих условию A3.12). Будем брать ? равной еди-
единице внутри концентрического с Кр шара Кр~ар> гДе а —любое
число из @, 1), и удовлетворяющей условию |V?|<: —. Тогда
из A3.13) следуют неравенства E.14) гл. II, так что из тео-
теоремы 5.3 гл. II заключаем, что для любой Q'crQ vrai max «
Г Q'
конечен и оценивается сверху только через у, у', q, \\ и \\2 Q и
расстояние Q' до S.
Аналогичные рассмотрения для функции — и (х) приводят
к оценке снизу vrai min и. Таким образом, оценивается
vrai max| и |.
Если мы хотим иметь ограниченность обобщенных решений
и(х) вблизи какой-либо части границы, надо потребовать ко-
конечности vrai max и и vrai min и на этом куске границы (опре-
(определение vrai max и vrai min на S: см. § 1 гл. I). Пусть, на-
например, vrai max и ^ Мо. Тогда неравенства A3.13) верны для
любых шаров Кр, не пересекающих S \ SI( и любых уровней
k > Мо. Это (в соответствии с теоремой 5.3 гл. II) дает воз-
возможность мажорировать vrai max и в областях Qt, отстоящих
от S \ S, на положительное расстояние. Аналогично оцени-
оценивается снизу vrai min и, если vrai min u> — оо. В частности,
Qi S,
если vrai max| и |<M0 < оо, то будет конечен и vrai max\u\.
s a
Это последнее следует не только из теоремы 5.3 гл. II, но и из
более простой теоремы 5.1 гл. II. Именно, положим в A3.4)
¦р(л:) = max{«(*) — k; 0}, k>M0. Такая г\(х) принадлежит ^(Q).
После ряда оценок, аналогичных проведенным выше (они упро-
упрощаются, ибо в них пропадают все члены, содержащие произ-
производные функции ?, которая в данном случае всюду равна 1),
получим неравенства
V« f dx < у J (и - Щ2 dx + {k2 + 1) mes'"^" Ak
J (и -
с постоянной у> зависящей лишь от q, v, ц и \iy. Здесь k —
произвольное число, большее Мо, a Ak — множество точек х
из Q, в которых и(х) > k. Аналогичные неравенства устанавли-
раются ц для функции —и(х). Из них в силу теоремы 5.J

240 ЛИНЕЙНЫЕ УРАВНЕНИЯ [ГЛ. Ill
гл. II следует ограниченность vrai max | и(х) | и возможность
Q
оценки этой величины через v, \i, \ilf q, Af0, mesQ и \\и\ a.
Теорема 13.1. Пусть u{x) есть обобщенное решение из
W2(Q) уравнения A3.1), и пусть выполнены условия A3.2),
A3.3). Тогда для любой Q'ciQ величина vrai max| «(л:) | конечна
и оценивается сверху постоянной, зависящей лишь от v, ц, ци
q, || и ||2 Q и расстояния Q' до границы S области Q. Если
к тому же vrai maxl и(х) |<М0 для какой-нибудь части Si
границы S, то vrai max| и (х) \, где п{ — подобласть Q, отстоящая
Q,
от S\Si на положительное расстояние, конечен и оценивается
сверху постоянной, зависящей лишь от v, \i, \ilt Mo, q, ll«||2. Q и
расстояния Q{ до S\Si. Если vrai max| и (х) К Мо, то
s
vrai max| «(л:) | конечен и оценивается сверху постоянной,
Q
зависящей лишь от v, ц, ц1? q, Mo, а также от ||«||2iQ или
mesQ и \\и\\иа.
Замечание 13.1. Если при я!>3 уравнение A3.2) для bi
заменить предположением
|S6?| ,<H2<°°, A3.14)
то неравенства A3.13) будут иметь место для достаточно
малых р, точнее, для р, удовлетворяющих, помимо A3.12),
условию
>о A3Л5)
=l \\nl2, Кр
р
п
п
Это так, ибо для члена 1 = -^ I ^Ь](и — kJQ2 dx, в силу
^i1
P
неравенства Гёльдера и неравенства A3.11) с q = n, справедлива
оценка
II'=1
Однако в данном случае величина \i и выбор р- зависят и от
II п II
Д(р, х)= 2 о? . где х — центр шара Ке. Итак, если

§ 13] ОБ ОГРАНИЧЕННОСТИ ОБОБЩЕННЫХ РЕШЕНИИ ИЗ №2(Q) 241
предположение A3.2) о bt(x) заменить при я>3 предположе-
предположением A3.14), то утверждения теоремы 13.1 остаются в силе,
только величины vrai max| u(x) | будут зависеть еще и от
©(p)smaxA(p, x). Как показывают примеры §2 гл. I, эта
зависимость действительно имеет место.
Покажем, что для обобщенных решений из W\{Q) эллипти-
эллиптических уравнений и неравенств справедлив принцип максимума.
Сформулируем его в следующем виде:
Теорема 13.2. Пусть функция и(х) принадлежит Wl2(Q)
и удовлетворяет неравенству
J (
,ц - btuxtn)dx^O A3.16)
Q
о f
при любой неотрицательной ц(х) из ^г(й). причем коэффи-
коэффициенты а1} (х) подчиняются условию D.2), a bi (x) s LA (Q), где
й = п при п>2 и я = 2 + е, е>0, при я = 2. Тогда
vrai maxu(x) ^ vrai max u{x). A3.17)
я s
Предположим противное: vrai max и = М > Мо = vrai max и.
a s
Рассмотрим неравенство A3.16) с X[ = u(k){x), Af0 < k < М, за-
замечая, что при этом подынтегральное выражение обращается
в нуль при хшАк\Ам, где Ам={х<=п: и(х) = М}. При
такой т] из A3.16) следует неравенство
f biUXl(u-k)dx^
Jo*
<\ Ц bf II V« ||2, A^AJ и - k |ЦЛ_2I А^Хм. A3.18)
I ' Ы Ak\AM
Последний множитель в правой части оценим сверху по нера-
неравенству B.13) гл. II:
I " ~ * IU<*2) A\A < И « - * 112Л/(Л_2), Ah < С || VU
<*-2), Ak\AM < И « - * 112Л/(Л_2),
= c\\Vu\\2tAk^M. A3.19)
Из A3.18) и A3.19) следует, что для k<=(M0, M)
W2' Ak\AM
Но это неравенство невозможно при k, близких к М, ибо
те§ (Ан \ Ам) стремится к нулю при /?->Af, и потому

242 ЛИНЕЙНЫЕ УРАВНЕНИЯ [ГЛ, III
|2&?| ~*0 ПРИ k-*M. Следовательно, предположение
' 11й/2, Ak\AM
о том, что М>М0, неверно, т. е. справедлива оценка A3.17).
Из теоремы 13.2 вытекает
Следствие 13.1. Пусть и(х) есть обобщенное решение из
W2(Q) уравнения A3.1), коэффициенты ац (х) и а(х) которого
удовлетворяют условиям теоремы 13.1, &;(j:)et/i(Q), a)
a а;=/;=/?=0. Тогда для почти всех jteQ
min {0; vrai min u}^u (x) < max @; vrai max u). A3.20)
s s
Если а==0, то нуль из A3.20) можно отбросить.
Чтобы убедиться в справедливости этого предложения, до-
достаточно применить теорему 13.2 к функциям ±и(х) в случае
а = 0и к функциям (±ufO)(x) в случае а^.0.
Если в условиях теоремы 13.1 несколько ослабить предпо-
предположения о свободных членах fi (x) и / (х), то вместо ограничен-
ограниченности решения и из WiiQ) можно доказать или его суммируе-
суммируемость с некоторой степенью р, большей 2п/(п— 2), или даже
экспоненциальную суммируемость в зависимости от L4k(Q),
к которым принадлежат fi и /. Доказательство этих предло-
предложений содержится в двух нижеследующих теоремах.
Теорема 13.3. Пусть и(х) есть обобщенное решение из
w2{Q) уравнения A3.1), коэффициенты которого подчиняются
условиям A3.2), а свободные члены — условиям
2. й
A3.21)
где р — какое-либо число, большее 2п/(п — 2)*). Тогда и(х) при-
принадлежит Lp(Q') для любой Q'cQ u норма || и \\р Q оценивается
через постоянные v, ц, ци q и р из условий A3.2), A3.21), рас-
расстояние d от Q до S и норму || и ||2 Q. Если на некотором
участке Si поверхности S и (х) совпадает со значениями функции
ц>(х), удовлетворяющей условиям ц>^Щ(п), vraimax| и |<М0
s,
или условию (p^W]qi(Q)(]Lp(Q), то u^Lp(Qi) для VQi<=:Q,
*) Предполагается, что и>2. При и = 2 принадлежность и (х) к Lp (Q)
с любым р и даже экспоненциальная суммируемость и следует из того,
ЧТО u<=W\(Q) (см. следствие 5Л гл. П).

ОБ ОГРАНИЧЕННОСТИ ОБОБЩЕННЫХ РЕШЕНИИ ИЗ
243
отстоящей от S \ Sx на какое-либо положительное расстояние й.
Норма ||м|| fli мажорируется постоянной, определяемой v, ц,
ци q, p, d, || м||2 й, а также величиной Ма или нормами
соответственно.
'р. я
Для доказательства первой части теоремы рассмотрим то-
тождество A3.4) с
ц = и(х)^~\2, ¦фЛ1 = т1п{| и(х) |; М), A3.22)
где М — произвольное положительное число, s — целое число
^1, а ? (*) — срезающая для /^ = 0^ функция. Это дает
{(atfiXl + а,и -
t
- (b.uXi -{-аи-Г)
= 0. A3.23)
Первый член оценим снизу, используя то, что в точках, где
г|зм (х) = | и (х) \,
а где г1зм (х) Ф \ и (х) |, там а;/мХ
^ =ацихих
S-I4I2
и потому
Остальные члены в A3.23) оценим сверху, рассматривая анало-
аналогично только что проведенным рассуждениям все выражения
в точках х, где tyM (х)=\ и (х) \, и в точках, где ^м(х) = М, и
затем выбирая мажоранту, общую для всех точек х. Это, как
нетрудно подсчитать, приведет к следующим неравенствам:
f >
<2
<2
bt(u]
a^ui
/,(«¦
<2
Х-
м )ни
17') ||
| + 2|
<A
+ 1/
~I)/S?2.
_1 Bs-l)/s
^ - О
В их правых частях стоит всюду функция иг^1, которую
мы обозначим через v. Подставляя полученные неравенства

244 ЛИНЕЙНЫЕ УРАВНЕНИЯ [ГЛ, III
в A3.23) и оценивая интегралы в правой части по неравенству
Коши с произвольным е > 0, получим
\ftvXt|(s-/)s?2 + [ \atlvtitXf J + (|atv | + I h\
2 1
7 ?2+lf' iu i2 ~ s2
Возьмем e^v/Ds), тогда после приведения подобных членов
будем иметь неравенство
S2 2)x, A3.24)
2sv~l].
Члены, стоящие в правой части A3.24), оценим сверху, исполь-
используя неравенства A.3), A.7), B.15) гл. II и предположения тео-
теоремы о коэффициентах и свободных членах уравнения A3.1),
следующим образом:
dx<\\D\\ф, Q^
_2),flp<-^щIII Vt, |?|P,flp
Qp ' И ' H/,/2.0
2--?- .
p
J | f || 0 |8-'С»Аг<||/||^ J vl l
2-2)'Qp

§ 13] ОБ ОГРАНИЧЕННОСТИ ОБОБЩЕННЫХ РЕШЕНИИ ИЗ ^(й) 245
2G, /, 1 \ 2<72 /, 1 \
где Г[ = ITjfl* J)' Г2= а _ 2 \ 2s) ' а постоянная се,
зависит лишь от е,, ц, ц,, q и s. При s^ 2n p показатели rj
и г2 не превосходят 2п/(п — 2), и потому в силу неравенства
A.11) гл. II
1 л-2
Из этих оценок и неравенства A3.24) следует
1 rt-2 1п-2\
" il
[
. (mes/g " +(mes^p)r* " ill °? 1Р2п/(п_2).Яр)- A3.25)
Воспользуемся еще неравенством B.12) гл. II:
II °t in/in-2). Ор < СIIV (о?) | йр < 2с' (|| | \v | ? \\1 йр + || о
и выберем в[ в A3.25) из условия
[2 1П-2П
к
В результате получим оценку
для функции 1> = ыг1з^~' при 1 ^s ^ "~ p с постоянной с,
определяемой величинами ц, ц,, v, ^ и р из условий A3.2),
A3.21) и мерой /Ср.
Рассмотрим последовательность концентрических с Кр ша-
Р°в V P* = f + ^Г. ^ = 0 f+l, N = [lgnl(n-2)+y и
/Со .причем max max I VL |^c0— 1. В неравенстве A3.26)
*+' ft=-l. .... N Kp
пусть ^(д;) — срезающая для Кр функция, равная единице
в /Со .причем max m I |
*+' ft=-l ... N Kp
будем брать s равным (-^Гг) . S = S*W. /г = 0, 1 N — I,
так что ( i п_ ) ^ "~ у. Это, как нетрудно видеть, дает
возможность оценить последовательно нормы || и ||/ 2п \*
через ||н||2(П. В самом деле, при k = 0 из A3.26) получаем

246 ЛИНЕЙНЫЕ УРАВНЕНИЯ [ГЛ. Ш
при k= 1
откуда, устремляя М к оо, будем иметь
llttll / п 42 =||И»Л»-2)||(»-»)/П <С2,
и так далее вплоть до k~N — 1, когда будет оценена норма
ll«llAflp<<V A3-27)
Показатель р здесь равен
= Р (я —г) > где х е [0, 1), так что р <= (Р("~2 ¦ , р] • В слу-
случае, если р = р, то желаемая оценка ||u|Ls уже получена;
если же р < р, то воспользуемся еще раз неравенством A3.26),
беря в нем s = р (га — 2)/B«), ? = ?^. Это даст
II Р("-2>_ , Я / II Р(п-2)|
Показатель суммируемости р(п — 2)/п меньше р, так что правая
часть A3.28) оценивается через постоянную cN из A3.27), и
потому, переходя в A3.28) к пределу по Af->oo, будем иметь
оценку ||н||р й ^.cN+]. Ввиду произвольности шара /Cpc:Q это
дает оценку || и \\р Q, для VQ' с: Q.
Аналогично оценивается ||и|| й в областях Q,cQ, приле-
прилегающих к Si czS, надо только все рассуждения проводить для
функций max{± и (х) — (Мо + 1), 0}, если vrai max| qp |< MQ, или
s,
свести предварительно граничное условие к нулевому, если
фе 1^,@H МО)-
Замечание 13.2. Из доказательства теоремы 13.3 факти-
фактически следует более сильное утверждение о принадлежности

2j Q .
§13] ОБ ОГРАНИЧЕННОСТИ ОБОБЩЕННЫХ РЕШЕНИИ ИЗ ^2<й) 247
я-2
| и | 2п Р к W\{$). В этом легко убедиться, если заметить, что
в случае предельного показателя s = —2/Г~Р в пРав°й части
неравенства A3.25) стоит величина, оцененная нами независимо
III ( —р\1 II
от М, а предел при М -> оо левой части равен || | V \и 2п ) | ? [
Теорема 13.4. Пусть коэффициенты уравнения A3.1) /
влетворяют условиям A3.2), а свободные члены — условиям A3.21)
с р=оо. Тогда для любого его обобщенного решения и(х)
из W2 (Q) справедлива оценка
e&l «<*>!<&< В, A3.29)
где постоянные $ и В определяются величинами v, ц, ц, ы q
из условий A3.2), A3.21), нормой \\и\\2 й, а также расстоянием
Q'czQ до S.
Если на части Si границы Q vraimax|« |^Af0, то для и(х)
s,
конечны интегралы A3.29) по VQ, czQ, отстоящей от S \ S] на
какое-либо положительное расстояние d, причем $ и В опреде-
определяются d, v, ц, \iu q, ||ы||2й и Мо.
Если vrai max| и |^М0, то в качестве Q' можно взять всю
s
область Q, причем $ и В в этом случае зависят лишь от v, ц,
\iu q, Мо, mesQ и Цм||1й*).
Рассмотрим неравенство A3.7) с произвольным положитель-
положительным k. Из него следует неравенство
Ak. p Ahi p
где D' = 2 (a? + 6f)+| а ]. Второй интеграл в правой части A3.30)
i=\
оценим с помощью неравенств Гёльдера и Коши, используя
*) При доказательстве этой теоремы, так же как и теоремы 13.3, доста-
достаточно рассмотреть случай п > ?,

248 ЛИНЕЙНЫЕ УРАВНЕНИЯ [ГЛ. III
условия теоремы:
J D'[u2 + (u-k
А
к, p
_2_ _2_
mes" ч
. р +
1
J.
. 2
ч,Р' •'
Г Г
'п/2.
Ak, p
Учитывая || U" — k) ||2n/(n-2). a. < c' (IIV ((ы — /j)g) ||2, л. Vй3 этих
ft 1 p \ Й1P/
оценок и неравенства A3.30) выводим
J| V« |Ч2^<с3(те8~~ЛА.р+|) J[|V« |42+(«-/jJ|V? |2]^+
ла.р \p
+ c, J (« - /гJ1V? |2 rf* + с3/г2 mes'" Mfe p +
+ с,,!, AИ--25-) mes » Л,р> A3.31)
где с3 = с1ц1 (с2 + 2с'2). Возьмем е = -^—, а /г выберем столь
--- 1
большим, чтобы mes" ч А. „<-;—. Для этого ввиду очевид-
ной оценки /г mes'/Mfe, р^Цы ||р, а достаточно подчинить k огра-
ограничению
й>Й = 2^||и||Р,и. у=т~Т- A3l32)
Кроме того, заметим, что в силу предыдущей теоремы норма
II" Ik V Kpcz?l, при любом конечном р оценивается через из-
известные величины, а
1—i I—i 1--
k2 mes ч Ak. p < mes n Ла, p || и \\2P, Kp ^ Ci mes " Л*. p,
j^J 1_
P "" « <? "

§ 14] О ПРИНАДЛЕЖНОСТИ ОБОБЩЕННЫХ РЕШЕНИИ ИЗ w\ (fl) К С° 249
Окончательно, приходим к неравенствам
[2 -.
J (u — kJ\4?\2dx + mes~~"Ak.Q\ A3.33)
.., Ak- р J
при k~^k. Аналогичные неравенства выполняются для функ-
функции — и (х).
Из A3.33) и леммы 5.5 гл. II следует справедливость пер-
первого утверждения теоремы 13.4. Второе утверждение доказыва-
доказывается так же, надо только шары Кр брать с центрами на S\, a
уровни k считать большими max{?; MJ. Наконец, для проверки
последнего утверждения можно воспользоваться леммой 5.2
гл. II, для чего надо рассмотреть и (х) не на Ak, p, а на Ak и
воспользоваться неравенством B.12) гл. II с р = 1, т = 2. Это
позволяет вместо неравенства A3.33) получить неравенство
j (и — k) dx ^c mes Ak, входящее в условие леммы 5.2.
Замечание 13.3. Если в условиях теоремы 13.3 считать,
что неравенства A3.2) выполнены с q = n, то заключение
этой теоремы остается в силе, только зависимость посто-
•янных, оценивающих указанные в этой теореме нормы и, от
коэффициентов L сложнее: эти постоянные зависят не только от
нормы 2 а\ + 2 Ь\ + | а
11=\ i=\
(о(р) =
, но и от функции
п/2, а
Справедливость этого утверждения легко усматривается из
данного выше доказательства теорем 13.3 и 13.4. Действительно,
доетаточно все рассмотрения проводить по шарам столь малого
радиуса, чтобы обеспечить нужную малость величины со(р).
*
§ 14. О принадлежности обобщенных решений из W2(Q) к С
Покажем, что при выполнении условий A3.2), A3.3) любое
*
обобщенное решение и(х) из Wl(Q) уравнения A3.1) принадле-
принадлежит классу Са с некоторым а > 0. Для этого заметим, что из
доказательства теоремы 13.1, точнее, неравенства A3.13), сле-
следует
Лемма 14.1. Пусть выполнены условия A3.2), A3.3) и пусть
и (х) есть ограниченное обобщенное решение_из Щ (й) уравнения
A3.1). Тогда и(х) принадлежит классу 232(й, М, у, уи 2, l/q),
еде М = vrai max | и (х) |, a Yi ~~ постоянная, определяемая

250 ЛИНЕЙНЫЕ УРАВНЕНИЯ [ГЛ. III
величинами v, ц, Hi и q и величиной М, а у зависит лишь
от v-'ц из A3.2).
Из этой леммы, теоремы 13.1 и теорем 6.1 и 7.1 гл. II
о функциях классов 93 легко выводится
Теорема 14.1. Пусть и(х) есть обобщенное решение из
Wl (Q) уравнения A3.1), коэффициенты которого и свободные
члены fi и f подчиняются условиям A3.2) и A3.3). Тогда и{х)
принадлежит классу Са (й ), где й' — произвольная внутренняя
подобласть области Q. Показатель а определяется лишь v~]\i
и q из условий A3.2), A3.3). Норма \и\$ оценивается сверху
постоянной, зависящей лишь от величин v, ц, ц, и q из усло-
условий A3.2), A3.3), || и Цг, q и расстояния Q' до границы S области Q.
Если часть S{ границы S удовлетворяет условию (А) и
и Is, e С Ei), то для любой подобласти Qi области Q, отстоя-
отстоящей от S\S\ на положительное расстояние d, и (х) е Са (Q^ с а,
зависящим лишь от v'n> q, р и постоянной 0О из условия (А);
| и \$ оценивается сверху постоянной, зависящей лишь от \, jx,
Hi, q, ll«lb. a, I и \ft\ P, d и постоянных 0О и а0 из условия (А).
В частности, если вся граница S удовлетворяет условию (А) и
и \s е Се E), то и (х) е Са (Q) и норма | и \§] оценивается сверху
постоянной, зависящей лишь от v, ц, |х,, q, \\ и ||i, а, | и |(|>, р и по-
постоянных 0О и а0 из условия (А), а также от \\u\k, а или mesQ
и II и Hi, а-
Замечание 14.1. Здесь, так же как и в теореме 13.1,
условие A3.2) о bi(x) можно заменить условием A3.14), но ве-
величины норм | и |^ при этом будут зависеть и от со(р).
Замечание 14.2. Утверждения, доказанные в §§ 13 и 14,
являются следствиями того, что исследуемые функции и (х)
подчиняются неравенствам вида A3.13). В этих параграфах мы
убедились, что функции и (х), удовлетворяющие тождеству A3.4),
подчиняются таким неравенствам. Однако если для функции
«(x)elFl(Q) вместо A3.4) верно, например, неравенство
\ - ^\ + ™-fHdx>0 A4.
J [(V/ \ \
а
для всех неположительных г)(х) из ^г(й), то она также удо-
удовлетворяет неравенствам A3.13), и потому ее максимум допу-
допускает оценку сверху через величины, указанные в § 13. В гл. V
будет указан другой класс «субрешений» — функций, удовлет-
удовлетворяющих не уравнениям или заменяющим их тождествам, а
некоторой системе неравенств, и для них будет доказана их
гёльдеровость. Его небольшим обобщением является следую-
следующий класс «субрешений».

15]
ОБ ОГРАНИЧЕННОСТИ max I V« I и [ uX{ |<a> 251
Пусть u{x) e Wi(Q), vrai max| и (х) |<М и и(х) удовлетворяет
неравенствам A4.1) при всех г\(х), подчиняющихся условиям
—М<«(*) +tr)(x)^M, t e[0, 1]. Оказывается, все такие и(х)
принадлежат Са, а > 0, и их нормы | и |(а) допускают такую же
оценку, как и нормы обобщенных решений уравнений A3.1).
Доказательство этого аналогично доказательству теоремы 4.2
гл. V.
В связи с изложенным в параграфах 13 и 14, помимо ис-
исследований авторов, см. работы [393, 522] и более поздние ра-
работы [52].
§ 15. Об ограниченности max | V« | и | «ц |(а)
для обобщенных решений из
Выясним, при каких предположениях относительно коэффи-
коэффициентов и свободных членов уравнения A3.1) любое его обоб-
обобщенное решение из W\ (й) принадлежит C1+a(Q). Из результа-
результатов, сформулированных в конце § 11, следует существование
априорной оценки для НиЦ^, q > п, через ||ы||2а, постоянные
v, |х и |х, из A3.2), постоянную jx, из
дац dat dft [I
f f ^' q>n> A5Л)
xk oxi oxl II?, Q
постоянные, характеризующие область Q, и норму || ф ||^2)а
функции ф(лг), определяющей граничные значения и(х). Оценка
для IUII^q, q>n, в свою очередь дает оценку для | и |<"+а),
а=1—- (см. неравенство B.30) гл. II). Из этих априорных
оценок и доказанных выше теорем о разрешимости первой кра-
краевой задачи в пространствах С{2+а) и W\ нетрудно сделать за-
заключение о справедливости следующего предложения:
Теорема 15.1. Если коэффициенты уравнения A3.1) удо-
удовлетворяют условиям A3.2) и A5.1), Q есть область класса W2q
и ф (я) е W\ (Q), то любое обобщенное решение и {х) уравнения
A3.1) из W\(Q) принадлежит W24(Q), а следовательно, и С]+а(Q),
a = 1 — —, и величины || и if^Q, | и \?+а) оцениваются сверху по-
постоянной, зависящей лишь от п, q, v, ц, ц„ \\и\^ Q, \\y\\{2)Q и от
области Q.
Доказывается эта теорема по той же схеме, что и теорема

252 ЛИНЕЙНЫЕ УРАВНЕНИЯ [ГЛ. III
Априорную оценку для |м|A+а) можно получить иным спо-
способом, близким к тому, который был применен в §§ 13, 14 для
вывода оценок тах|и| и | и \{а). Покажем это. Продифференци-
Продифференцируем уравнение A3.1) по xk, k—\ п, и результат запи-
запишем в виде
д
l
' L v //J
-Щ uijubx,-r Zj mmum = "^T | 0/| ] -f -^r | | , A5.2)
k= 1 rt,
где ы0 = ы, Mfe = ы*., Л*m = -5*2- + 6?(am + bm), m=\ n,
k dxk
da,j \ k
+ -5—Ь a 6i — символ Кронекера. Совокупность соот-
соотношений A5.2) и A3.1) рассмотрим как систему уравнений для
Uk, k = 0, I, ..., rt. Ее характерной особенностью является то,
а 1 д
что главная часть, состоящая из членов вида -^- \aii -^j-
диагональна и одинакова во всех уравнениях системы. Такие
системы удалось исследовать столь же детально, как и одно
уравнение второго порядка. Им посвящена гл. VII. Там будет
/ п у/,
выведена, в частности, оценка максимума |«|= 2Mi < к0"
\k=o I
торая применительно к данному случаю дает желаемую оценку
для max|V«|, Q' czQ. Оценка \Su\ вблизи границы не следует
а'
непосредственно из оценки гл. VII для тах| и |, так как величина
тах|и| в гл. VII оценена через величину тах|и|, которую
a s
мы не знаем для вектора и = (и, их , ..., их ) (собственно, за-
ди
ранее неизвестна лишь величина
обходимо проводить дополнительные рассмотрения в погранич-
пограничных шарах. Из-за недостатка места мы вынуждены опустить их.
Оценки величин (иху$, й' с Q, также следуют из результа-
результатов гл. VII. Однако их можно вывести из теоремы § 14 дан-
данной главы. В самом деле, если величины M = max|«|, Mi =
а
= max|V«| уже известны, то соотношение A5.2) можно рас-
Q
смотреть как уравнение
-g-\\ )-Для ее получения не-

§ 16]
О МЕТОДАХ ГАЛЕРКИНА И РИТЦА 253
для uk, для которого выполнены все условия § 14. Следова-
тельно,' для Uk=Uxk, k=l, ...,n, будут верны и заключения
§ И —лемма 14.1 и теорема 14.1. Они дают оценку для (иХ{)$>,
Q'c:Q. Для оценки (их^){а) вблизи какого-либо куска S\ гра-
границы 5 распрямим его, вводя новые координаты. Без ограни-
ограничения общности будем считать, что S\ лежит в плоскости {*„=()}
и Q примыкает к ней сверху, со стороны хп > 0. Для произ-
производных иХх, т=1,...,п—1, граничные значения на Si из-
известны, и потому к их% можно применить вторую часть тео-
теоремы 14.1 об оценке (иХхУ§\ х= 1 п— 1, вблизи 5, (здесь
Qp — половина шара Кр с центром на 5[ принадлежащая Q).
Для оценки же (иХпУа) заметим, что из принадлежности uxv
р _
т= 1 л— 1, к 232(Ц,. •••) следует
I
n
S/»2 /TV* ^^ />f\Tl—~2-\-2? p| "^> p ^s. (I if ¦ 1 ¦» __
1=1 xxxi
а отсюда и из уравнения A3.1) —и \ и\ х dx^.Cipn~2+2a. Из
этих неравенств, как доказано в лемме 4.1 гл. II, следует при-
принадлежность их к C(a)(Qp) и возможность желаемой оценки для
(M*n)<a)> Таков второй путь вывода оценок для max | ux \ и (uXi){a)
р
для решений уравнений A3.1).
§ 16. О методах Галеркина, Ритца и методе
наименьших квадратов
Для доказательства разрешимости краевых задач в прост-
пространстве Щ(&), а также для фактического определения их ре-
решений может быть использован метод Галеркина. Опишем его
применительно к задаче
Lu = ¦%*- + [, и |s = 0. A6.1)
Предположим выполненными условия теоремы 5.2, в частности
о .
неравенство E.1). Возьмем в пространстве Wq(Q) фундаменталь-
фундаментальную систему линейно независимых функций {щ(х)}, k= 1, 2, ...,
N
так что линейные комбинации их 2 ^4<Pft (*) образуют плотное
в Wl2(Q) множество, Приближенные решения иы, N=1,2, ...,

254 ЛИНЕЙНЫЕ УРАВНЕНИЯ [ГЛ III
N
задачи A6.1) ищем в виде сумм иы'= 2С^ФАМ> коэффициенты
в которых определяются следующими равенствами:
Ми", q>*) = (f,, <P*,,)-(f, Ф*). й=1,2 N. A6.2)
Иными словами, иы определяется тем, что для него тождество
D.10), лежащее в основе определения обобщенного решения
задачи A6.1), должно выполняться при любой функции т] из
конечномерного подпространства PN пространства W2(Q), эле-
элементами которого являются суммы вида 2 ^-ьШ (*)• Само иы
также принадлежит PN. Равенства A6.2) представляют собой
систему N линейных алгебраических уравнений относительно N
неизвестных с^, с$, . . ., с$. Ее разрешимость следует из наших
предположений. Действительно, умножая каждое из уравнений
A6.2) на свое с% и складывая по всем k от 1 до N, получим
-if, uN). A6.3)
Отсюда и из неравенства E.1) следует тождественное обраще-
обращение в нуль uN, а следовательно, и всех с?\ /г=1,2, ..., N,
если правые части в A6.2) обращаются в нуль. Если же ft и /
не обращаются в нуль, то из A6.3) и E.1) вытекает априорная
оценка для uN
с постоянной с, не зависящей от номера N. Поэтому системы
A6.2) действительно однозначно разрешимы при любых f и /
из пространств L2(Q) и L2Am+2)(u) соответственно и нормы
\\uN\BuQ их решений равномерно ограничены. Покажем, что
найденная нами последовательность приближенных решений
uN, N=l, 2, ..., сходится к обобщенному решению и задачи
A6.1). Существование последнего доказано в теореме 5.1. Это
легко сделать и независимо, используя наличие приближенных
решений {u}N. Именно, из {uN} можно выбрать подпоследова-
подпоследовательность uNfn, т=\, 2, ..., сходящуюся слабо в W^(й) к не-
о .
которой функции и из W2(Q). Благодаря этому по подпоследо-
подпоследовательности Nm, m=l,2, ..., можно перейти к пределу в ра-
равенствах A6.2) и убедиться, что предельная функция и(х) удо-
удовлетворяет им или, что то же самое, тождеству D.10) при
функциях г|= q>k (x), k = 1, 2, ... Так как {<pfej образуют фунда-
О .
ментальную систему в W2(fi), то отсюда следует, что тождество

§ 16) О МЕТОДАХ ГАЛЕРКИНА И РИТЦА 255
D.10) будет выполняться для и(х) при любой функции г)(х) из
W\ (й), и, следовательно, и {х) действительно является искомым
решением задачи A6.1). Покажем, что [uNm], m=\, 2 схо-
сходится к и в норме пространства Wi (й). Для этого вычтем из
интегрального соотношения A6.3) для uNfn интегральное тожде-
тождество D.10) для и с т) =иы™ и результат L{uNm — u, «Wm) = 0
запишем так:
L (uNm - и, uN™ — u)=-L {uN™ - и, и).
Правая часть последнего равенства стремится к нулю при
т->оо в силу слабой сходимости иы>" к и в Wl2(Q), а левая
часть не меньше Ч\(\\иЫт — иЦ^цJ с v, = const>0 (см. E.1)).
Поэтому ||uNfn — иЦз'а->0 при т-><х>. Таким образом, мы до-
казали, что любая слабо сходящаяся в И^г(й) подпоследова-
подпоследовательность {uNfn} равномерно ограниченной в Щ(&) последова-
последовательности {uN} сходится сильно в норме W\(Q) к обобщенному
решению и (х) задачи A6.1). Но по предположению последнее
единственно, следовательно, вся последовательность {uN}, N =
= 1, 2 сходится к и(х) сильно в Wl2(Q). Сформулируем
доказанное предложение в виде теоремы.
Т е о р"е м а 16.1. Если выполнены предположения теоремы 5.2,
о .
то задача A6.1) однозначно разрешима в W2(Q) при любых f
из L2(Q) и f из L2fl/<n+2) (Q) и ее решение есть сильный предел
в Wi(u) галеркинских приближений uN, однозначно определяе-
определяемых алгебраическими системами A6.2).
На самом деле имеет место более общий факт: если для
задачи A6.1) справедлива теорема единственности в W'(Q) (так
что А, = 0 для нее не есть точка спектра), то приближения
Галеркина uN определяются системами A6.2) однозначно для
всех достаточно больших TV и при N-><x> сходятся в
к решению и задачи A6.1). Это утверждение для случая огра-
ограниченных bi и а и at = 0 доказано в [232]. Для неограниченных
коэффициентов оно доказывается, по существу, так же, надо
только воспользоваться неравенством B.13) гл. II так, как это
сделано в §§ 4, 5.
Утверждения теоремы 16.1 остаются справедливыми и для
других классических краевых условий — второго и третьего.
Вспоминая данные в § 6 гл. III определения обобщенных ре-
решений из пространства W\(Q) задач F.1), F.2), легко понять,
что метод Галеркина для них надо строить нижеследующим

256 . ЛИНЕЙНЫЕ УРАВНЕНИЙ [ГЛ. Ill
образом. Взять фундаментальную систему {q>k (x)} в простран-
N
стве W2(Q) и искать uN в виде суммы 2с?фА (х), коэффициенты
в которой определяются из системы
L{uN, Ф*) = -(Л фА)+ j(-ouN + q>)<pkds, k=l N.
s
Однозначная разрешимость этих систем при любом N и схо-
сходимость к решению задачи доказываются так же, как и для
первого краевого условия, надо только воспользоваться теоре-
теоремами вложения пространства Wl(Q) в Lq(S) (см. § 2 гл. II).
Метод Галеркина в описанной выше его классической форме
гарантирует сходимость приближений uN лишь в норме Wl(Q),
даже если все данные задачи A6.1) и само решение и суть
очень гладкие функции.
Однако эту форму можно изменить и добиться лучшей
сходимости, если, конечно, данные задачи достаточно хорошие
(см. [219] и др.). Связано это с наличием для эллиптических
операторов неравенств вида (8.27) и более общих неравенств
вида
j LuM^udx^vijiulf^J, v = const >0, A6.5)
Q
где Af(m)« есть т-я итерация эллиптического оператора М вто-
второго порядка. Поясним, например, как добиться схбдимости
приближений в Wl(Q) в задаче A6.1). Пусть для нее выполнены
условия теоремы 9.1. Возьмем какой-нибудь эллиптический опе-
оператор М второго порядка, обладающий теми же свойствами,
что и L (в частности, устанавливающий взаимно однозначное
соответствие между пространствами Wl,o(Q) и L2(Q)), и такой,
что для L и М справедливо неравенство (8.27) с с > 0 *).
Возьмем в пространстве Wl,o(&) фундаментальную систему
линейно независимых функций {<pfe (л:)}, k = 1, 2, ... Оператор М
переведет их в функции {Мщ}, образующие фундаментальную
систему в пространстве L2(Q). Будем приближенные решения uN
N
искать в виде суммы uN = 2c^feW> a коэффициенты ее опре-
fci
целять из системы
\[^ }dx, k=l,...,N. A6.6)
*) В качестве М можно взять, например, само L или Ми — ц« с любым
эллиптическим оператором М. коэффициенты которого удовлетворяют требо-
требованиям D.2), D.3), G.3), и достаточно большим ц.

§ 16] О МЕТОДАХ ГАЛЕРКИНА И РИТЦА 257
Умножая каждое из уравнений A6.6) на свое с% и складывая
полученные равенства по k от 1 до N, придем к соотношению
[lun- Mun dx = Г l-p- + f) MuN dx,
из которого в силу неравенства (8.27) следует равномерная
ограниченность норм || иы\\2\ и теорема единственности (а потому
и разрешимости) для системы A6.6). Рассуждая далее анало-
аналогично тому, как это было сделано выше в обычном методе
Галеркина, докажем, что uN сходятся к решению задачи A6.1)
в норме пространства Wt(Q).
Если оператор L является формально самосопряженным,
т.е. имеет вид Lu = -x—(ai.ux\-\-аи, то для него уравнение
Lu = / является уравнением Эйлера для функционала
/ (и) = J (a,,uxuXj - аи2 + 2uf) dx. A6.7)
• Поставим задачу на определение функции и (х), дающей квад-
квадратичному функционалу 1(и) наименьшее значение на Wl(Q)-
Если такая функция и существует в W2(Q) и функции ац, а
и / удовлетворяют условиям D.2), D.3), D.5), то на и {х), как
нетрудно показать, первая вариация функционала / (х) равна
нулю, т. е.
б/ (и; л) = 2 J (at}u i\ - аиц + Щ dx^O A6.8)
а
о
при любой функции ц из W2(Q). Но соотношение A6.8) есть
не что иное, как интегральное тождество, определяющее обоб-
о
щенное решение из W2(Q) задачи
Lu = f, u\s = 0. A6.9)
Таким образом, решение поставленной выше вариационной за-
О ,
дачи является обобщенным решением из W2(Q) краевой задачи
A6.9). Если а(*)<0, то, как легко проверить, задача A6.9)
может иметь не более одного обобщенного решения в №г(B) и
это решение (его существование следует из результатов § 5)
дает функционалу 1(и) наименьшее значение. Следовательно,
в случае неположительного а (х) задача на разыскание абсолют-
абсолютного минимума функционала /(«) в пространстве Wl(Q) и
9 О. А. Ладыженская, Н. Н. Уральцева

258 ЛИНЕЙНЫЕ УРАВНЕНИЯ Ц\П. Ill
задача на определение обобщенного решения из W2(fi) уравнения
Lu = f эквивалентны.
На этом основан следующий способ нахождения решения
задачи A6.9), известный под названием метода Ритца. Бе-
о
рется фундаментальная система {щ(х)} в пространстве W2(Q) и
конечномерные его подпространства PN, натянутые на N первых
элементов системы. На каждом из PN ищется наименьшее зна-
значение/(ы). Оно реализуется на некотором элементе uN подпро-
подпространства PN. Оказывается, последовательность uN является
минимизирующей для рассматриваемой вариационной задачи и
ее пределом в W\(Q) является решение задачи. Все это нетрудно
доказать непосредственно. Но мы этого делать не будем, а за-
заметим лишь, что приближенные решения иы вычисляются из
системы алгебраических уравнений (эти уравнения выражают
обращение в нуль вариации 1(и) на подпространстве PN, т. е.
6I(uN', л) = 0 при ц е PN), совпадающей с системой A6.2) урав-
уравнений Галеркина, и, следовательно, сами uN совпадают с при-
приближенными решениями, вычисленными по схемам Галеркина.
Таким образом, метод Ритца является частным случаем метода
Галеркина.
Для решения задачи A6.1) применяют еще так называемый
метод наименьших квадратов. Он состоит в нахождении
функции, реализующей наименьшее значение функционала
/ (и) = (Lu — f — -aj-] dx на множестве всех функций и из
W\ 0 (Q), по методу Ритца. Пусть {<pfe} — фундаментальная система
N
в Wl a(Q), a PN — совокупность функций вида 2 dkq>k(x). Пер-
зая вариация / (и) равна
в/(и; vt)=2J^u-f-§^)LridXt neWto(G)-
Приближение uN, реализующее inf/(«) на PN, определяется из
системы б/ (и; г\) = 0 для т^ е Pv. Но эта система совпадает
с системой A6.6) при M = L, т. е. метод наименьших квадратов
есть частный случай метода Галеркина, описанного выше.
Если L устанавливает взаимно однозначное соответствие между
Wl,o(Q) и Z.2(Q), то uN однозначно определяются для всех N и
при N->oo сходятся в норме Wl(Q) к решению задачи F.1).
Описанные здесь методы применимы и к другим краевым
задачам-.

5 17] РАЗЛОЖЕНИЕ В РЯДЫ ПО СОБСТВЕННЫМ ФУНКЦИЯМ 259
§ 17. О разложении в ряды по собственным функциям
самосопряженного оператора
Рассмотрим подробнее спектральные вопросы для симметриче-
симметрического оператора Lu = (ciiiUXj)x + аи в ограниченной области Q.
Ради несущественных упрощений будем считать а(лг)=<0. Пусть
сначала atj и а удовлетворяют условиям D.2) и D.3). Согласно
методу, изложенному в § 5, задачу
Lu = Ku, u\s = 0 A7.1)
на определение к и соответствующих им ненулевых решений и
из №г(й) можно преобразовать в спектральную задачу для
некоторого вполне непрерывного оператора в комплексном гиль-
гильбертовом пространстве Щ(й). В данном случае это удобнее
всего сделать, введя в W2(Q) скалярное произведение
[w, v]= J (auUx.vXj— auv)dx A7.2)
а
(оно несколько отличается от скалярного произведения, введен-
введенного в § 5). Так же, как и в § 5, легко проверяется, что норма
| • |, соответствующая этому скалярному произведению, эквива-
О -
лентна стандартной норме в W2(Q). Интегральное тождество
L(u, i\) = -K(u,y\), A7.3)
° 1 ° 1
в котором «ef2(Q), а г| есть произвольный элемент №г(й),
соответствующее задаче A7.1), записывается с помощью A7.2)
так:
[и, т|] Л(и, тт), A7.4)
где здесь и в A7.3) (и, т)) = J иц dx. Как показано во второй
а
части § 5, тождество
(u,ru = [Bv,t\], yv, т|е=#2(О), A7.5)
определяет (согласно теореме Рисса о форме линейного функ-
Ционала) некоторый линейный оператор В в пространстве W2(Q).
Он определен на всем Щ(&), вполне непрерывен, симметричен
(а следовательно, и самосопряжен) и положителен *).
*) Последнее проверяется так: если Bv = 0, то из A7.5) следует (о, ti) = О
0 1 ° 1
для vt) e W2(Q), а так как 1Р2(Й) плотно в L2(Q), то из (о, т)) = 0 следует,
что о = 0. Неотрицательность же [Bv, v] видна из самого определения A7.5)
оператора В.
9»

260 ЛИНЕЙНЫЕ УРАВНЕНИЯ [ГЛ. III
Благодаря A7.5) тождество A7.4) эквивалентно операторному
уравнению
A7.6)
О ]
в пространстве W2(Q). Из перечисленных свойств В и известных
из функционального анализа предложений о вполне непрерыв-
непрерывных самосопряженных операторах (см. [312, 48, 13]) следует,
что В имеет дискретный положительный спектр, который может
быть занумерован в порядке убывания спектральных значений:
ц, ^ц2^ • • •» каждое \ik имеет конечную кратность, единствен-
единственной точкой накопления для цк является ц = 0, причем ц = 0
не есть собственное значение (ввиду положительности В). Более
того, система собственных функций ф] (лг), <р2(*) соответ-
ствующих Hi, ц2 может быть выбрана ортогональной, т. е.
[фь Ф/] = 0 для кф1, A7.7)
и она образует базис в W2(Q). Как видно из A7.6), собственные
числа Ца оператора В связаны с собственными числами Xk
задачи A7.1) равенством A,fe = — ц^1, а собственные функции
у них совпадают. Из сопоставления равенств A7.5) — A7.7)
видим, что система {щ} является ортогональной и в смысле
скалярного произведения в L2(Q). Нормируем ее так:
(Ф*. <&) = «[..
Тогда
О j ° j
Как указано выше, {<pfe] есть базис в ЙР2(Й), а так как W2(Q)
плотно в L2{Q), то {q>ft} будет фундаментальной системой в L2(Q).
Более того, ввиду A7.8) {<pfe} есть базис в L2(Q). Из этих,
свойств системы {ф^} следует, что любая функция f (х) из L2(Q)
разлагается в ряд
сходящийся в L2(Q); если же /eW2(Q), то ряд A7.10) будет
сходиться в норме W2(Q), причем он может быть записан и
в виде
о .
До сих пор мы считали L2(Q) и №2(Q) комплексными гильбер-
гильбертовыми пространствами и соответствующие им скалярные про-

§ 17] РАЗЛОЖЕНИЕ В РЯДЫ ПО СОБСТВЕННЫМ ФУНКЦИЯМ 261
изведения имели вид (и, v) = J uvdx и A7.2). Но так как коэф-
а
фициенты L и kk вещественны, то систему {<pft} можно взять
вещественной (действительно, если Фй = Фй + 'Фь то и щ и фй
о . .
являются решениями из №г(?2) задачи A7.1) при К = кк), и она
будет ортогональной в смысле скалярных произведений веще-
ственных пространств L2(Q) и ^(Q), т. е.
J <fk<fldx=6lk, J (atiqikxfttx, — ащщ)<1х= — \kb[. A7.12)
В разложениях A7.10) и A7.11) по вещественной системе {фй}
надо считать (/, фй)= J fokdx, a [/, Фй]= J (a{jfXj(pkxi — afyk)dx.
а а
Будем предполагать с этого момента, что дальнейшие рассмо-
рассмотрения проводятся в вещественных пространствах и система {фй}
вещественна.
Пусть коэффициенты L и область Q удовлетворяют требо-
требованиям теоремы 9.1. Тогда все собственные функции q>k будут
принадлежать пространству Wl,o(Q) и будут удовлетворять
Q В
р рру р
уравнениям L<fk = Kk<fk почти всюду в Q. Возьмем произволь-
произвольную функцию / из Wl,o(&). Согласно вышесказанному ряд Фурье
для нее A7.10) (или, что то же самое, ряд A7.11)) сходится
к ней в норме W2(Q). Представим ее коэффициенты Фурье
в следующем виде:
W. Ф*) = (/> ^L%) = K;\Lf, <pk)^K-k1k. A7.13)
Это возможно, поскольку / и q>k принадлежат Wl,o(Q). Более
того, из этого следует также, что
2^^2,й<с(||Л|^J. A7.14)
Введем в Wl,o(&) новое скалярное произведение {и, v} = (Lu, Lv)
и соответствующую ему норму | и f2) = {и, «}1/2. В силу второго
основного неравенства, имеющего в нашем случае вид (9.2),
эта норма эквивалентна первоначальной норме №г,о(Й). По-
Поэтому достаточно доказать сходимость ряда A7.10) в норме | • |B).
Но ряд A7.10) ортогонален по отношению к скалярному про-
/I » B) \2 ю
изведению {,} н 2Ых) = 2 /|Я|. В силу A7.13) и
VI ft=i / *=i
A7.14) этот ряд сходится. Подытожим доказанное в виде тео-
теоремы.

262 ЛИНЕЙНЫЕ УРАВНЕНИЯ [ГЛ. Ш
Теорема 17.1. Если коэффициенты ait и а оператора Lu =
= (aljuxX -{-аи удовлетворяют условиям D.2), D.3) и а(х)^.О,
то спектр задачи A7.1) состоит из невозрастающей последова-
последовательности отрицательных чисел 0 > Я] ^ Я2 ^ ..., стремящейся
к — оо, а соответствующие ему собственные функции щ (х),
&=1, 2, ..., образуют ортонормированный базис в L2(Q) и
о .
базис в W2(&), ортогональный по отношению к скалярному
произведению [,]. Если а.ц и а удовлетворяют дополнительно
условиям G.3), a S — условиям теоремы 9.1, то все <pft принад-
принадлежат wl, о(Й) и образуют базис в W2i0(Q), ортогональный по
отношению к скалярному произведению { ,}.
Обратим внимание, что в этой теореме установлена воз-
возможность почленного дифференцирования рядов A7.10) один
и два раза (в зависимости от свойств L, f и Q) и сходимость
получаемых при этом неортогональных рядов в L2(Q). Такого
типа сходимости рядов Фурье по собственным функциям эллип-
эллиптического оператора L в пространствах Wf{Q) с любым целым
т~^\ и при любом из краевых условий вида м|5 = 0 или
-^г7 + ои =0 были установлены одним из авторов данной книги
G/V с
и изложены в полном виде во второй главе книги [213]. Тео-
Теорема 17.1 является одним из простейших случаев доказанных
там предложений. Эти предложения точны в следующем смы-
смысле: относительно / требуется лишь ее принадлежность к тому
пространству, к которому принадлежат собственные функции
(а следовательно, и конечные отрезки ряда G.10)) и в норме
которого доказывается сходимость.Таким образом, разложения
Фурье G.10) очень точно улавливают свойства разлагаемой
функции, если те и другие характеризовать в терминах про-
пространств W?(Q).
. Если предположение о неположительности а (х) отбросить,
то в теореме 17.1 может измениться лишь утверждение об
отрицательности спектра. При любом а(х) из Lq/2(Q), q>n,
несколько первых собственных значений могут быть положи-
положительными или равными нулю.
Система собственных функций {щ}, в соответствии со спек-
спектральной теорией вполне непрерывных положительных сим-
симметричных операторов (см. [31i,2, 232, 10,] и др.), может быть
найдена в результате решения нижеследующих вариационных
задач. Функция q>i(*) реализует минимум функционала
L (и, и) = J (atjUXiuXj — au2)dx

j 18] МЕТОД КОНЕЧНЫХ РАЗНОСТЕЙ 263
О j
на множестве всех элементов №г(Й), удовлетворяющих условию
(и, и)= \u2dx=\, A7.15)
а
причем ?(<Pi> фО =—Л]. Вторая собственная функция <р2 дает
минимум L (и, и) на множестве всех элементов W\ (Й), удовле-
удовлетворяющих, помимо A7.15), условию (и, ф[) = 0, причем
L (фг. Ф2) — — ^2- При нахождении ф3 надо функции сравнения
и(х) подчинить еще условию (и, фг) = 0 и т. д. Так последо-
последовательно находятся все фй, k=l, 2, ... Однако возможно
определить m-ю собственную функцию фот без предварительного
знания предыдущих собственных функций ф, Фт-i- Это
базируется на так называемом максимально-минимальном свой-
свойстве собственных функций, установленном Р. Курантом и из-
изложенном в [10]] применительно к разным конкретным само-
самосопряженным операторам. Это свойство состоит в том, что
-Яот= sup d{vi v^}, A7.16)
о, eW2 (Й)
где '
(«, и), A7.17)
о
причем inf находится на множестве всех функций и из №2 (Q),
удовлетворяющих условиям (и, v{) = 0, i = 1 т — 1,
(и, и)=1. Супремум в A7.16) берется по всевозможным набо-
рам v{ из №г(&). Решением этой минимаксной задачи является
функция фя.
§ 18. Метод конечных разностей
Метод конечных разностей, с одной стороны, является весьма
сильным инструментом для различных теоретических исследова-
исследований, а с другой — одним из основных способов численного
определения решений конкретных задач. Он явился первым
методом, с помощью которого удалось сравнительно просто
доказать разрешимость основных краевых задач для линейных
эллиптических уравнений с разрывными коэффициентами и
показать, что гладкость их решений* повышается с повышением
гладкости данных задачи, причем это улучшение имеет локаль-
локальный характер (см. [213]). Здесь мы дадим краткое описание
этого метода, приведем одну из простейших разностных схем
для первой краевой задачи и докажем ее устойчивость и схо-
сходимость в пространстве Wl(Q)-
В общих чертах метод конечных разностей состоит в том,
что пространство Еп разбивается на элементарные клетки и все
рассмотрения проводятся в вершинах этих клеток. Производные,

264 ЛИНЕЙНЫЕ УРАВНЕНИЯ tM. ttl
входящие в уравнения, заменяются теми или иными разно-
разностными отношениями, которые образованы из значений неиз-
неизвестных функций в вершинах клеток, и, в соответствии с этим,
сами дифференциальные уравнения заменяются линейными
алгебраическими системами. Из этих систем подлежат опреде-
определению значения искомых функций в вершинах клеток. Эти зна-
значения образуют приближенное решение, которое обозначим
через uh (индекс h символизирует взятое разбиение Еп). По uft
строятся определенным образом те или иные интерполяции;
простейшая из них — кусочно-постоянная, которую обозначим
через uh{x).
Разностная схема считается «правильной», если uh опреде-
определяются однозначно (речь идет о случае, когда исходная задача
однозначно разрешима) и если при размельчении решетки uh
стремится в каком-либо смысле к искомому решению и(х).
Так как любую производную даже при фиксированном раз-
разбиении можно аппроксимировать разными разностными отно-
отношениями, то данное только что описание метода конечных раз-
разностей заключает в себе большую неопределенность и требует
дальнейшей детализации. Оказывается, не любая правильная
аппроксимация дифференциального уравнения и граничного усло-
условия приводит к «правильной» разностной схеме, и перед ис-
исследователем прежде всего стоит задача выбрать среди множе-
множества возможных аппроксимаций те, которые в пределе (при
размельчении разбиения Еп) приведут к решению и(х) задачи.
Одним из авторов данной книги в конце 40-х годов был сфор-
сформулирован нижеследующий способ построения разностных схем.
Надо взять интегральное тождество, определяющее обобщенное
решение задачи с конечной энергетической нормой (для рас-
рассматриваемой нами задачи это тождество D.12)), и его заме-
заменить суммой Римана, соответствующей взятому разбиению Еп.
Производные, входящие в интегральное тождество, можно заме-
заменять различными разностными отношениями, но одинаковыми
для всех членов тождества (разумеется, при этом должны уча-
участвовать значения искомых функций лишь в тех точках раз-
разбиения, которые принадлежат области задания уравнения и
краевого условия). Так получаемая сумма Римана содержит
произвольные величины — значения произвольной функции т^ (х),
входящей в интегральное тождество, в вершинах разбиения.
В этой сумме надо провести перегруппировку членов, собирая
вместе все слагаемые, содержащие в качестве множителя зна-
значение Ti в одной из вершин разбиения. Так получаемые частные
суммы надо приравнять нулю, если стоящее при них т^ произ-
произвольно.
Для первой краевой задачи т^ произвольно во всех «внутрен-
«внутренних» то'чках разбиения (в «граничных» же точках оно равно нулю),

5 18] МЕТОД КОНЕЧНЫХ РАЗНОСТЕЙ 265
так что описанный рецепт дает столько уравнений, сколько вну-
внутренних точек. К этим уравнениям добавляются уравнения,
определяющие uh в «граничных» точках. Для второй и третьей
краевых задач т^ произвольно всюду, и потому из интеграль-
интегрального тождества извлекается столько уравнений, сколько «вну-
«внутренних» и «граничных» точек входит в наши рассмотрения.
Покажем, как эти общие соображения реализуются приме-
применительно к задаче D.1), D.9).
Предположим, ради экономии места, что коэффициенты урав-
уравнения D.1) суть ограниченные функции, что <р = 0 и /eL2(Q).
Общий случай, описанный в §§ 4, 5, рассматривается анало-
аналогично. Пусть, кроме того, выполнено условие
««My+(«I - ьд Uo - о* i ц, (is.о
y = const>0, a l0, li !„— произвольные вещественные
числа (его можно было бы заменить условием типа D.32) и даже
условием, что рассматриваемая задача имеет единственное ре-
решение).
Обобщенное решение задачи
о
из пространства W2(Q), как мы знаем, есть элемент
удовлетворяющий тождеству
Считаем, что
max|a(/, а{, b{, а\< оо и ||/||2, й, Ш12, а < °°> 1,}—1 п.
A8.4)
Разобьем все пространство Еп плоскостями X{ = kih, k{ = 0,
±1, ±2 i=l п, где h есть положительное число,
называемое шагом получаемого разбиения или, что то же,
шагом решетки. Кубы вида Qkr ¦¦¦, kn = {x: k{h < xi < {k{ + 1) h)
называются клетками или ячейками разбиения, а их вершины —
точками или узлами решетки. Замкнутую область, состоящую
из всех кубов Qkv •••,*„> принадлежащих Q, обозначим через Qft,
ее внутренние точки—через Qft, а границу Qft —через 5Л, так
ЧТО Q^-(-5^ = Q/}. Эти же обрзначения Щ, S^ и QA сохраним

266 ЛИНЕЙНЫЕ УРАВНЕНИЯ [ГЛ. III
и за совокупностями вершин решетки, принадлежащими об-
области Qft, ее границе 5ft или замкнутой области Qft соответ-
соответственно.
Для производной по xt в данном параграфе используем
символ -—; символ же их употребим для обозначения соот-
ОХ г *
ветствующих разностных отношений, а именно:
uXl(x) = j[u(x + htt)-u(x)] A8.5,)
и
% W = j[u(x)-u(x- htt)], A8.5a)
где в/ — орт, направленный вдоль оси xt. Перейдем к составле-
составлению разностных схем по правилу, описанному выше. Именно,
интегралы в A8.3) надо заменить суммами Римана, отвечаю-
отвечающими взятому разбиению. Так как коэффициенты и свободные
члены уравнения A8.2) не предполагаются непрерывными функ-
функциями, то в отдельных точках Q и, в частности, в узлах ре-
решетки они могут быть не определены (или «не представительны»).
Ввиду этого вместо пц, а/ и прочих известных функций сле-
следует брать не их значения в узлах решетки, а, например, их
стекловские средние по кубам
с центром в узлах решетки, т. е. а?/ = Л " j a{S(x)dx, и то же
\ К
для других коэффициентов и свободных членов уравнения A8.2).
Производные "з— и -т-L заменим разностными отношениями вида
ОХ 1 ОХ,
A8.5!) или A8.52) (можно взять и их полусуммы), но одинако-
одинаковыми для и и т) и всех /=1 п. Возьмем для определен-
определенности замену A8.5]). Эти разностные отношения и функции и
и ц рассматриваются только в вершинах решетки, и кубу
Qft,...,fc сопоставляются иХ{ и цх., вычисленные по правилу
A8.5]) в вершине x = (klh knh). Итак, интегральное то-
тождество A8.3) заменим сумматорным
U (и, ti) s= hn S {(alp + a?«)\ — *?»*.Л— анщ] =
В нем сумма распространена, на вершины Й^, однако стоящие

5 !8] МЕТОД КОНЕЧНЫХ РАЗНОСТЕЙ 267
под знаком суммы члены, как легко понять, пока не опреде-
определены для некоторых из точек 5ft. Сделаем это так: продолжим
коэффициенты и свободные члены уравнения A8.2) на все про-
пространство Еп с сохранением описанных выше свойств, а функ-
функции и и т), входящие в A8.7), положим равными нулю во всех
точках решетки, кроме точек Qh. В результате таких доопреде-
доопределений *) все члены сумм 2 теперь определены, и, более того,
%
эти суммы можно считать распространенными на все точки
бесконечной решетки Enh.
В тождестве A8.7) функция т^ произвольна в точках ре-
решетки Qft, а функция и подлежит определению в этих точках.
На 5ft (и вне Qh) та и другая равны нулю. Тождество A8.7)
эквивалентно линейной алгебраической системе, содержащей
столько уравнений, сколько точек на решетке Qh. Чтобы выпи-
выписать эти уравнения, надо собрать вместе члены, содержащие т^
в какой-либо точке Qh, и приравнять их сумму нулю. Это легко
делается с помощью формулы «суммирования по частям»
Л* S во, = - Л* S в*.о. A8.8)
Она справедлива для произвольных функций и и v, задан-
заданных на решетке, если только v равна нулю вне Qft. Применяя
эту формулу к A8.7) и меняя знак, получим
hn 2 V • Ц = hn 2 П*и + /*\ ц, A8.9)
где Lfu=(a}ljuxJrahiu\ Jrbhlux -\-ahu. Так как значения т) про-
извольны в точках Qft, то тождество A8.9) эквивалентно системе
уравнения которой соответствуют точкам QA. К ним надо при-
присоединить уравнения
«ISa = 0. A8.11)
Число уравнений в системе A8.10), A8.11) равно числу точек
решетки Qft, т. е. числу неизвестных — значений и в точках Qft.
Покажем, что при условии A8.1) эта система однозначно опре-
определяет и при любом h. Для этого необходимо и достаточно,
чтобы однородная система, соответствующая A8.10), A8.11),
*) Как будет видно из дальнейшего, в реальные вычисления войдут
только значения коэффициентов L в Q, продолжение же коэффициентов вне Q
употреблено нами лишь для удобства записи на данном этапе.

268 ЛИНЕЙНЫЕ УРАВНЕНИЯ [ГЛ. III
имела только нулевое решение. Итак, пусть правые части
в A8.10) равны нулю. Это соответствует тождеству A8.7) с пра-
правой частью, равной нулю. Положим в нем ц= и; это даст
равенство
La(b, в) = 0. A8.12)
Легко видеть, что в силу A8.1) при любом h
a)tlt\t + D - Щ) Щ - аЧ1 > v 2 I2, A8.13)
п
и потому из A8.12) следует, что vft2 2(«*,J —0. Но это оз-
начает, что и постоянно на Qft, а так как на 5ft и равно нулю,
то и = 0 всюду. Итак, теорема единственности для системы
A8.10), A8.11) доказана, а тем самым доказана и ее разреши-
разрешимость при любых fl и /л. Более того, для ее решения можно
дать априорную оценку, не зависящую от h. Действительно,
полагая в A8.7) ц=и и используя A8.13), получим
vhn 2 и\ < hn 2 (f}ux - Jhu\ A8.14)
ства B.14) гл. II
где и2х= ^j u2x . Воспользуемся разностным аналогом неравен-
неравен2х, A8.15)
справедливым для любой функции и, заданной на решетке Enh
и равной нулю вне Qft. Постоянная с в нем определяется раз-
размерами Q, но не зависит ни от и, ни от Л. Если не гнаться
за точностью зависимости с от Q, то A8.15) можно доказать
элементарно следующим образом. Пусть
— параллелепипед, содержащий Qft. Очевидно следующее пред-
представление
fc,-i
u{kh) = h 2 uXl{l\h, k2h, ..., kji).
l,=—mi
Из него в силу неравенства Коши следует
/ fc,-l \2 m,
(fi 2 в )<Bт,Л)-Л Ц u2Xi,

5 18] МЕТОД КОНЕЧНЫХ РАЗНОСТЕЙ 269
Суммируя обе части этого неравенства по точкам (kti) e П,
придем к A8.15) с с = B/п,ЛJ и м? вместо и\.
Итак, вернемся к неравенству A8.14). Оценим правую часть
его, используя неравенство Коши A.2) гл. II и A8.16), сле-
следующим образом:
л
" Е [(т + ^г)ul + i (fAJ + 2i7
где (?ЛJ= 2 (/?J- Из этого неравенства с e = cel = v/2 и A8.15)
выводим желаемую априорную оценку
Ю2 Ш A8.17)
Возьмем какую-либо последовательность hm—>-0 и соответ-
соответствующие ей решетки Qft и решения ин системы A8.10), A8.11).
Покажем, что (м/, } сходятся к решению и(х) задачи A8.2).
Для этого удобно, следуя [213], ввести различные интерпо-
интерполяции uh, определенные на всей области Q (мы считаем, что uh
равна нулю вне Qft). Одна из них, обозначаемая u'h{x), есть
непрерывная на Q функция, равная мА в точках решетки и
в пределах каждого куба Q*r ...лп линейная по каждой пере-
переменной при фиксированных остальных. Для точек шО^ kn
она определяется равенством
(xs — ksh)+ ... +«ft,
*r-V *r+l *n
причем разностные отношения ux, x, ^((ихЛ • • Л и по-
следнее слагаемое вычислены в вершине (kh). Ясно, что функ-
функция u'h{x) определена на Q, непрерывна, равна нулю на дп
и имеет в Q обобщенные производные первого порядка. Более
того, для нее верно элементарно проверяемое неравенство

270 ЛИНЕЙНЫЕ УРАВНЕНИЯ • [ГЛ. Ш
Построим по приближенным решениям uh интерполяции
и' (х). В силу A8.17) и A8.18)
fit
К Р <С1» A8Л9)
Л т 112, Q
где постоянная с, может быть взята общей для всех [uh }
(для этого надо учесть свойства усреднений, в частности то,
что правая часть A8.17) при Л->-0 стремится к "Г ¦ X
X J (f2 + cf2) dx; см. § 4 гл. IlY
Q /
Функции и' (х) равны нулю на Sh и вне области Q., так что
"т п п
и' е W2 (Q). В силу этого и оценки A8.19) существует подпо-
т
следовательность (обозначим ее по-прежнему через {hm}), для
О .
которой u'h сходятся слабо в W2(fi) к некоторой функции
°i m
и (х) е W2(Q). Докажем, что эта предельная функция и (х) и есть
искомое решение задачи A8.2). Для этого осталось показать,
что она удовлетворяет тождеству A8.3), при этом достаточно
в качестве х\(х) в A8.3) брать лишь гладкие финитные в Q
функции. Итак, пусть т^ (*) — такая функция. При всех доста-
достаточно малых h она равна нулю на dQh и потому ее значения
на точках решетки Qft допустимы для сумматорного тождества
A8.7). Запишем это тождество в виде интеграла
A8.20)
используя простейшую кусочно-постоянную интерполяцию функ-
функций, заданных на сетке. Эта интерполяция, обозначенная для
сеточной функции uh через uh(x), есть ограниченная разрывная
функция, равная в Й*,,..., kn значению м/, в вершине (kh). Сим-
Символ fj*. надо понимать как такую кусочно-постоянную интер-
интерполяцию сеточной функции цх., определенной по значениям т^
в вершинах Qft, что х\х. —(цх,)- В тождестве A8.20) у сеточных
функций и и ц надо было бы поставить внизу индекс h, ука-
указывающий, что они рассматриваются лишь на точках решетки Qft,
но мы этого не делаем, чтобы не загромождать запись. По-
Попробуем теперь перейти в тождестве A8.20) к пределу по вы-

5 18) МЕТОД КОНЕЧНЫХ РАЗНОСТЕЙ 271
бранной выше подпоследовательности /*„,-»• 0 при фиксирован-
фиксированной функции у\(х) с описанными выше свойствами. Ясно, что
f\h(x) и f\hx.(х) будет равномерно сходиться к ц(х) и ~ соот-
соответственно. Функции af;., ..., ан, оставаясь равномерно огра-
ограниченными, сходятся к а{/, ..., а почти всюду. Остается по-
понять, к чему сходятся йПт и uhXi. Оказывается, uhm сходятся
к той же функции и (х), что и u'hm, причем имеет место силь-
сильная сходимость в L2(Q). Функции же uhx. сходятся слабо в L2(Q)
к -г^-. Доказываются эти естественные факты нетрудно, надо
только учесть при этом равномерную ограниченность
hn 2 (и\ + и\^. Мы опустим эти простые рассуждения и
%
отошлем читателя к § 6 гл. I книги [213], из которой взята
вся излагаемая здесь конструкция построения и исследования
разностных схем (см. § 2 гл. IV [213] и др.).
Ввиду всего вышесказанного в A8.20) можно перейти к пре-
пределу по hm—>-0. В результате получается соотношение A8.3)
с функцией и(х), являющейся пределом как для ufhtn(x), так и
для мЛт(*). Итак, мы убедились, что предельная для u'h (x)
функция и{х) есть искомое обобщенное решение задачи A8.2).
Так как оно единственно, то нетрудно понять, что вся после-
последовательность {u'h (*)} (а не .только выбранная выше подпосле-
подпоследовательность) сходится к и{х). Больше того, имея уже в руках
решение и (х), нетрудно показать, что йА и «ft x сходятся
ди *** тл i
к и(х) и -— сильно в L2(Q).
Итак, доказана
Теорема 18.1. Пусть коэффициенты уравнения A8.2) суть
ограниченные функции, удовлетворяющие условию A8.1), а для
свободных членов выполняется условие A8.4). Тогда системы
A8.10), A8.11) однозначно разрешимы при любом h и их ре-
решения uh сходятся при Л->-0 к обобщенному решению и(х) из
Wl(Q) задачи A8.2).
Как сказано выше, предположения о данных задачах можно
ослабить до предположений §§ 4, 5 гл. III, не выходя за рамки
изложенных здесь аналитических средств. Метод конечных раз-
разностей удобен и для исследования вопросов гладкости обоб-
обобщенных решений (см. гл. IV из [213]). Ниже, в § 5 гл. IV, мы
это проиллюстрируем на значительно более сложном объекте —
квазилинейных эллиптических уравнениях.
Обоснование метода конечных разностей для решения крае-
краевых задач для эллиптических уравнений началось с работы

272 ЛИНЕЙНЫЕ УРАВНЕНИЯ [ГЛ. II]
Л. А. Люстерника «Bemerkung zur Losung des Dirichlet'schen
Problems», Матем. сб. 33, 1926, 363—366, и работы [103]
Р. Куранта, К. О. Фридрихса и Г. Леви, в которых рассмо-
рассмотрено уравнение Лапласа. Ему же посвящена и работа [252]
И. Г. Петровского. Линейные эллиптические уравнения общего
вида были рассмотрены Д. М. Эйдусом [37] и одним из авто-
авторов книги (см. [213>6] и др.). Имеется, кроме того, много работ,
посвященных разным аспектам метода конечных разностей,
связанным с вычислительной стороной дела, в том числе с оцен-
оценками скорости сходимости (в связи с последним вопросом см.
[27], [12] и др.).
§ 19. Случай двух независимых переменных
Изложенные в предыдущих параграфах результаты справед-
справедливы для любого числа независимых переменных, в том числе
и для п = 2. Однако для случая п = 2 имеют место и некото-
некоторые более тонкие факты, несправедливые при п > 2. Часть
из них приведена в § 2 гл. I. К их числу относятся следующие.
Пусть и(х) есть решение в области Q уравнения
2 2
Z.m= 2 ац(х)ихх+2>а{их4-аи = !(х), A9.1)
/, /=i ' ' /=i '
коэффициенты которого удовлетворяют условиям
ч12^аи(х)Ы{<\112, v = const >0, A9.2)
\а,\, |а|<ц,. A9.3)
Если решение и равно нулю на границе области Q, то для него
норма || и ||2)й оценивается сверху константой, зависящей лишь
от v, ц из A9.2), A9.3), H/lk й и ||м||2й. Этот факт для реше-
решений уравнений A9.1) с а, = а = 0 в круге был установлен
С. Н. Бернштейном [42,3] *)• Комбинируя прием предваритель-
предварительного преобразования уравнения A9.1), данный С. Н. Бернштей-
Бернштейном, с приемом преобразования выделяющегося при интегри-
интегрировании по частям контурного интеграла и его оценки, данным
одним из авторов [212,з.si» мы докажем здесь .сформулирован-
.сформулированное утверждение для любой области Q, подчиняющейся тем же
ограничениям, что и в § 8 для обшего случая п^2. Более
того, мы максимально возможным образом ослабим и предпо-
*) См. в связи с этим сноску на стр. 232, где указана работа Ю. Шау-
дера, посвященная снятию предположений С. Н. Бернштейна о том, что Q
диффеоморфна кругу. Ю. Шаудер добивается этого ценой предположения
р непрерывности коэффициентов Z.,

§ 19] СЛУЧАЙ ДВУХ НЕЗАВИСИМЫХ ПЕРЕМЕННЫХ 273
ложения о at и а, именно, заменим условие A9.3) предполо-
предположениями
lla4,Q' II4,q<Hi<°°> <7>2- A9.4)
Справедлива следующая
Теорема 19.1. Предположим, что п удовлетворяет усло-
условиям 1) и 2) леммы 8.1. Пусть функция и(х) принадлежит
W\о{п) и удовлетворяет почти всюду в п уравнению A9.1),
коэффициенты которого подчинены условиям A9.2), A9.4). Тогда
ll"l^a<-$-|l/ll2,a + dl«ll2>Q, A9.5)
где постоянная с определяется величинами v, \i, q и ц, из A9.2),
A9.4) и областью п.
Запишем уравнение A9.1) в виде
ai,ux.Xj = F{x), A9.6)
где F(x) = f (x) — а{их. — аи. Уравнение A9.6) умножим на
uXlXJ(h2 и результат представим так:
— и\г + —«**«** +и2хх =F^ + ul-uxxuxx. A9.7)
О22 *>*! Й22 XlX* X'Xi ' г Д22 *'*« ¦)ClJi:i ¦"•г*2
В силу A9.2) левая часть A9.7), очевидно, не меньше
(
(" "f" ulx2)' a М°ДУЛЬ первого члена правой части равенства
A9.7) не превосходит — и?., + — -т-« Поэтому из A9.7) следует
2Ц ' ' 2V 022
Рассмотрим интеграл
ад«ад-«и*|^ A9-9)
а
С. Н. Бернштейн доказал [42i 3], что этот интеграл неотрица-
неотрицателен для любой функции и из С2(й), равной нулю на S, если Q
есть круг. Покажем, что имеет место более общее предложение.
Лемма 19.1. Для любой и из Wl,0(Q) и произвольной
области Q, удовлетворяющей условиям леммы 8.1, справедливо
соотношение
If
'~ 2 J
где г/2 = ю(г/1) есть уравнение S в местной системе координат,
причем ось ух направлена по касательной к $ в точке У\ = Уг = О,

274 ЛИНЕЙНЫЕ УРАВНЕНИЯ [ГЛ. III
а у2 — по внешней по отношению к Q нормали к S в той же
точке. В частном случае, для выпуклых областей Q,
d2aiy>) >0 и потому /,>0.
dy\
Формула A9.10) есть частный случай более общего предло-
предложения (8.19), доказанного в § 8. Действительно, /, можно
представить в виде
a L i,i=i J
а этот интеграл с помощью двукратного интегрирования по ча-
частям, проведенного так, как это сделано в § 8, преобразуется
к виду
2/, = J b{bk[uXkXluXlcos(n, */) — ы^ы^ cos (n, xk)]ds, A9.11)
s
из которого ясно, что 2Ji совпадает с интегралом j /s ds из § 8,
s
вычисленным для aif = b\, и потому для него верно равенство
(8.19) или, что то же, A9.10).
По условию
A9.12)
следовательно,
Проинтегрируем обе части неравенства A9.8) по Q и исполь-
используем A9.13):
a a s
Аналогично доказывается неравенство
i- J К„ + < J* <i^r J ЯЛ + 4- J Ш' *. 09.15)
q as
Из A9.14) и A9.15) следует
/, /=
t **,<*<!?1''<* + Ч-*№ь. A9Л6)
Из этого неравенства и A9.6) неравенство A9.5) выводится так же,
Как это было сделано в общем случае в § 8,

^.,9} СЛУЧАЙ ДВУХ НЕЗАВИСИМЫХ ПЕРЕМЕННЫХ 275
Итак, мы видим, что получение оценки A9.5) для эллипти-
эллиптического оператора общего вида A9.1) при п = 2, по существу,
сводится к аналогичному вопросу для оператора Лапласа. Это
сведение сделано с помощью представления уравнения A9.1)
в виде A9.7) и перехода от A9.7) к неравенству A9.8), в кото-
котором уже нет переменных коэффициентов ац (х).
Этот прием, принадлежащий С. Н. Бернштейну, позволяет
в случае я = 2 получать желаемые оценки и(х), не дифферен-
дифференцируя коэффициенты ац(х). Ниже мы используем его для по-
получения априорных оценок max|V«(x)| и | и ?,1+а). Сейчас же
отметим один частный случай оценки A9.16).
Следствие 19.1. Если Q — выпуклая область и l
то
J
a i
где постоянные v и ц взяты из неравенства A9.2).
Если граничные значения и (х) совпадают с граничными зна-
значениями известной функции q>(x)<=Wl(Q,), то, применяя к функ-
функции v(х) = и(х) — ф(х) неравенство A9.5), для и(х) получим
оценку
II" fa < ^1 / к п + ci IIФ Со + с\\ и \Ъ а. A9.18)
Если относительно граничных значений и и границы S не
делать никаких предположений, то вместо ||«|f22)Q можно оце-
оценить норму || и |f22)Q/ для любой Q' с: Q. Для этого умножим A9.8)
на ?4 (х), где $ (х) — срезающая_функция для области Q, так что
<1, ?ls = 0 и 5еС2(Й). Интеграл
преобразуем с помощью двукратного интегрирования по частям
к виду
Л = 4 J (— uXtuXlX?ztXi + ux,uXlX?%:,) dx,
a
откуда
x, A9.19)

276 ЛИНЕЙНЫЕ УРАВНЕНИЯ [ГЛ. III
где е — произвольное положительное число. Поэтому
V dx + 2$ [в (и* + и2ххI4 + -и2Л2\ Ч pi dx.
Q Q
Складывая это неравенство с аналогичным неравенством для
производных uXlX2 и ихл и выбирая е = (8ц)~Ч, после элемен-
элементарных преобразований придем к неравенству
J
a
J
a i, l=i
Рассуждая далее так же, как при выводе неравенства (8.6),
придем к оценке вида (8.6):
(II и? CJ < ^Й ?Lu |? 0 + с J и2 (Z* +1 V? |» + Щх) dx, A9.20)
а
J
а
в которой постоянная с зависит от v, ц, q и ц, из A9.2) и
A9.4). Неравенство A9.20) верно и для ?,(х), отличной от нуля
вблизи какого-либо куска Si границы Q, если этот кусок удо-
удовлетворяет условиям леммы 8.1, a u^C2(Q) и равна нулю
на S,.
Замечание 19.1. Неравенства вида A9.5), A9.20) спра-
справедливы и для областей Q класса W\, q > 2; при этом и(х)
может быть любой из W2 (Q), равной нулю на S или S] соответ-
соответственно. В этом случае коэффициентом при ||Lm||2 q и ||?2L«|| q
соответственно будет некоторая постоянная с0, зависящая от
тех же величин, что и с. Проверяются эти факты на основе
доказанных выше утверждений точно так же, как лемма 8.3
выводилась из лемм 8.1 и 8.2.
Напомним, что через норму ||ы||2)ц оценивается норма | и ffl
с Vae@,l) и ||M|f?"o с любым конечным q.
Замечание 19.2. Неравенство A9.5) справедливо не только
при первом краевом условии и |s = 0, но и при любом другом
(
«регулярном краевом условии», т. е. условии вида (-? + ои j =0,
где -^- означает дифференцирование по какому-нибудь не каса-
касательному к S направлению, меняющемуся непрерывно диффе-
дифференцируемым образом при перемещении вдоль S, а <x(s) есть
заданная, ограниченная на 5 функция. Схема доказательства
A9.5) в этом случае та же, что и при условии и |s = 0. Основ-

g 19] СЛУЧАЙ ДВУХ НЕЗАВИСИМЫХ ПЕРЕМЕННЫХ 277
ная аналитическая часть ее состоит в доказательстве того, что
интеграл A9.9), сводящийся, как мы видели, к граничному
интегралу A9.11), и при других «регулярных краевых условиях»
преобразуется к интегралам по S, содержащим производные
от и не выше первого порядка. Такие и значительно более
общие преобразования граничных интегралов, возникающих
при исследовании производных более высоких порядков, про-
проведены в [213]. Подобные замечания о других краевых усло-
условиях справедливы и для проводимых ниже оценок норм гёль-
деровского типа.
Перейдем теперь к оценкам max|«X/| и | и (]+а) для реше-
решений уравнений A9.1).
Оценка константы Гёльдера для производных uXl, i=l, 2,
была дана Л. Ниренбергом [44J с помощью весьма простого
приема (его мы излагаем в § 6 гл. IX). Существенно сложнее,
с привлечением квазиконформных преобразований и специаль-
специальных представлений для решений двумерных эллиптических
уравнений, была получена оценка max|V«| (см. Л. Берс и
Л. Ниренберг [5li2]). Оценки | uf1+a) имеются также в книге [6]
И. Н. Векуа. Все эти способы сугубо двумерны.
Мы выведем все эти оценки с помощью нашего метода,
изложенного выше для любого «^2, причем ослабим предпо-
предположения о функции f{x) и коэффициентах оператора L макси-
максимально возможным образом. (Заметим, что возможность такого
ослабления отмечена авторами работ [5i,2].) Предположим,
что и(х) есть решение уравнения A9.1) из W\(Q), имеющее
конечный vraimax|V«|. Пусть коэффициенты ais(x) удовле-
удовлетворяют неравенствам A9.2) и
П*|. я, Л|,§а<ц,, <7>2. A9.21)
Начнем с оценки I их. |<а), считая известными числа М> тах| и |,
I » IQ q
М\ Г> vraimaxl V« |. Обозначим производную их через рх и пере-
перепишем неравенство A9.8) в виде
2<^ + c2(«^-«,iAJ, A9.22)
где с, и с2 — известные постоянные, зависящие лишь от ц и v
из A9.2). Пусть Ak<p есть множество точек х из произвольного
круга /Ср, в которых рх (х) > k; если Кр не принадлежит цели-
целиком Q, то Aki p выбирем из /Ср П й и число k берем превосхо-
превосходящим тахр,. Умножим A9.22) на %2(х), где |(х) — срезаю-
щая для К9 функция, и результат проинтегрируем по AkiP.

278 ЛИНЕЙНЫЕ УРАВНЕНИЯ [ГЛ, III
Это дает
A9.23)
4t.P
где /, = Г F2^2 dx, /2 = I (p* — р и ^
4%, р 4%, р
В силу предположений A9.21) и ограниченности |«| и | V« |
для /, верна оценка (напомним, что всюду 0^|^1)
/, <|| Т721^ Q mes'""«" Ak,p'< 00. A9.24)
Интеграл же /2 преобразуем с помощью двукратного интегри-
интегрирования по частям следующим образом:
72 = ~ f \Ри * (Pi~ k)? + Pi* (Pi- k) ¦ 2ttx +Pixuxx?\dx =
= J ["ХЛ(р, — ^Ц^ — Р1Х!(/э, — ft) • 2HJ djc. A9.25)
Хотя на первом этапе этого преобразования используется суще-
существование у и (х) производных третьего порядка, окончательное
представление для /2 справедливо, как нетрудно понять, для
любой функции и из Wl(Q). Производную иХгХг выразим из урав-
уравнения A9.1) и подставим в A9.25), после этого |/2| оценим
сверху, используя A9.21) и неравенство Гёльдера:
J "^^, A9.26)
4*.p
где с3 зависит от \\F\\ „ Q, v и ц. Подставляя A9.24) и A9.26)
в A9.23), придем к неравенствам
J (p1-^J|VifdA: + Yimes1~^.p, A9.27)
Ak, p Ak, p
в которых постоянная у определяется постоянными v и ц из
условия A9.2), a Yi зависит, кроме того, от ц, из A9.21) и

$ 19) СЛУЧАЙ ДВУХ НЕЗАВИСИМЫХ ПЕРЕМЕННЫХ 279
величины тах|ы, V«|. Аналогичные неравенства доказываются
Q
и для функции — рх = — их. Следовательно, функция рх при-
принадлежит классу 232(й, М, у, Yi, 2, l/q) и для нее верно заклю-
заключение теоремы 6.1 гл. II, иначе говоря, для нее можно оценить
нормы | рх $, fi'cfi, с некоторым а > 0, зависящим лишь
от v, ц и q, через величины, которые мы считаем известными
в данном рассуждении. Аналогично оцениваются | иХ} {?\ й' с Q,
Таким образом, доказана
Теорема 19.2. Пусть и (х) есть решение из W2 (й) с конечным
vrai max | V« | уравнения A9.1), коэффициенты которого удовлетво-
удовлетворяют условиям A9.2), A9.21). Тогда нормы | иХ{1^, /=1,2, Уй7 с: Q,
с некоторым а > 0, зависящим лишь от v, ц и q, конечны и
оцениваются сверху постоянной, определяемой M^max\u\,
М{ > vrai max | Vu |, расстоянием Q' до S и константами v, ц,
ц, и q из A9.2) и A9.21).
Если предположить некоторую регулярность границы S и зна-
значений и 1у, то можно оценить I"*,!!"' Для всей Q. Без ограни-
ограничения общности будем считать, что ы|у = 0. Пусть й e W2q,
q>2. Распрямим, вводя новые координаты yk = yk(x) ^W*,
q > 2, какой-нибудь кусок границы S{ и рассмотрим в его окрест-
окрестности сначала производную и лишь по касательному к нему
направлению. Если S, имеет уравнение #2 = 0, то возьмем uUl.
На S, функция рх&зиу обращается в нуль. Для j5, и — рх
выводим, так же как и выше, неравенства A9.27), причем
если /Ср пересекает Su то берем лишь & j>0. Из теоремы 7.1
гл. II выводим оценку | рх |<а) вблизи S,; точнее, для любого Кр,
отстоящего от S\Si на положительное расстояние и находя-
находящегося вблизи Si (там, где введены координаты уи у2),
©, (р) =з osc {/5,, /Ср П й} < с3ра. A9.28)
Для оценки ©2(p)^osc (р~2 = иу>, йр} рассмотрим неравенство
A9.27) для/5, при k — О и соответствующее неравенство для — рх
при k = 0. Складывая их и учитывая A9.28), найдем, что
J | Vj5, ||2djc<c4p2B, где p=min(a, 1—— j, а потому и
°р
J

280 ЛИНЕЙНЫЕ УРАВНЕНИЯ [ГЛ. Ill
Отсюда и из уравнения A9.1), записанного в координатах уи у2,
следует, что и
J A9.30)
Q
J
p/2
Из этих же неравенств на основании леммы 4.2 гл. II сле-
следует, что производная /?2 = ы^ также удовлетворяет условию
Гёльдера и
)Р A9.31)
где все числа с, — известные нам постоянные. Неравен-
Неравенства A9.28) и A9.31) дают оценку колебаний производ-
производных иУх, иИ2, а следовательно, и uXl, иХг вблизи куска S,. Пре-
Преобразование от хи х2 к уи у2 должно быть вблизи S, обра-
обратимым, причем производные одних координат по другим должны
быть непрерывными по Гёльдеру. В силу нашего предположе-
предположения относительно й (й е W% q > 2) такое преобразование можно
сделать в окрестности любой точки границы и получить
оценку |"xj'a) для всей области й. Мы доказали следующую
теорему:
Теорема 19.3. Пусть u(x)<=W2(Q) совпадает на S с <р(лг)
и удовлетворяет уравнению A9.1), для которого выполнены
условия A9.2) и A9.21). Если Qs^, фе^(й), q > 2, и
тах| ы|<М, vraimax |V« |<Af,, то и еСA+а)(й) с а > 0, зави-
q а
сящим лишь от v, ц и q; величина \ и |ц+а) оценивается сверху
постоянной, зависящей от v, ц, ц,, q, М, Ми \\ ф ||'2)Q и от области й.
Перейдем теперь к оценке max|V«|. Докажем теорему.
а
Теорема 19.4. Пусть и(х) еWl(й) и удовлетворяет урав-
уравнению A9.1), для которого 'выполнены условия A9.2), A9.21).
Для УЙ'сЙ величина vraimax|V«| конечна и оценивается
сверху постоянной, зависящей лишь от v, ц, \i{ и q из A9.2),
A9.21), нормы || и Ik a и расстояния й' до S. Если fielFj
и и(х) на S совпадает с <р(лг) еИ^(й), q > 2, то vraimax|V«|
Q
оценивается сверху постоянной, определяемой величинами v, ц,
ц,, q, нормами ||ы||2а, ||ф||^2)а и областью й.
Докажем сначала первое утверждение. В силу теоремы вло-
вложения B.26) гл. II из A9.20) и A9.21) следует, что для Vr>l
й Уй' ci й верна оценка

$ 19] СЛУЧАЙ ДВУХ НЕЗАВИСИМЫХ ПЕРЕМЕННЫХ 281
где с (г, Q') — постоянная, зависящая от г, нормы || и ||2 а, рас-
расстояния Q' до S и постоянных v, ц, ц,, q из условий A9.2)
и A9.21). Ввиду этого и условия A9.21) функция F = / — atux —аи
суммируется по Q' со степенью ^', сколь угодно близкой к q,
но меньшей q, и
1|/7^.а.<с1(«7/, Q0, <7'<<7> A9.33)
где Ci(q', Q')>— вообще говоря, отличная от с (г, Q') из A9.32)
известная нам постоянная, неограниченно растущая при и'-*Q
и q'-+q-
В любом шаре /(рсй при произвольном k для рх было
выведено неравенство A9.23). Для /, и /2 в силу A9.33) спра-
справедливы оценки
i-i-
/,<<:(?', QOmes *Л4.Р, </' < q, A9.34)
+ С | (p.-ftnvgpdx + c^', QOmes'^Xfcp. A9.35)
Из них и неравенства A9.23) получим
/(p.-
1 —
Vgpdx + cCflr', Q')mes' f Л,, р.
A9.36)
Так как ^' можно взять сколько угодно близким к q и q > 2,
то, считая </' в A9.36) большим 2, на основании теоремы 5.3
гл. II из A9.36) получим оценку vraimaxp^x) сверху. Проводя
аналогичные рассмотрения для — р,, получим оценку
снизу. Так же проводятся внутренние оценки для р2 = ы^. Пер-
Первая часть теоремы доказана.
Для получения оценки | V« | вблизи границы поступим так же,
как мы сделали выше при оценке колебаний uXl в окрест-
окрестности S. Именно, распрямим какой-либо кусок Sx границы S
за счет введения новых регулярных координат ух и у2 и перей-
перейдем в A9.1) к координатам ух и у2. Предполагая, что произ-
производные xt (yx, y2), i = 1, 2, по yk первого и второго порядка е Lq,
<7>2, мы получим для и(уи y2) = u(Xi(y\, y2)> ^2(г/i. г/г)) УРав"
нение, коэффициенты которого обладают теми же свойствами
A9.2), A9.21), что и коэффициенты A9.1) (легко видеть, что

282 ЛИНЕЙНЫЕ УРАВНЕНИЯ [ГЛ. Ш
dxt (у) д2Х[ (у)
ограниченность —¦- следует из принадлежности -s—Ц— к Lq,
q>2). Пусть г/2 = 0 есть уравнение куска границы Sr. Тогда
иУ1 ^ = 0. Пусть пересечение /Ср с S принадлежит S,. Обозначим
через Ak р множество точек у из /СРП^> где рх = иу > к. Оче-
Очевидно, для рх справедливо неравенство A9.23), если только
считать, что все выражено в координатах уь у2-
Для k^O интеграл
допускает представление типа A9.25), ибо выделяющийся при
двукратном интегрировании по частям контурный интеграл
J
A9-38)
будет равен нулю. Благодаря этому для /2 при k^O верна
оценка типа A9.35). Интеграл 1Х оценивается так же, как и
в A9.34) для внутренних шаров, и потому для рх при k^O
неравенства A9.36) будут справедливы и для шаров Кр, пере-
пересекающих Si (но не S \ Si). Они позволяют оценить сверху
р^иух для областей, примыкающих к Sx (см. теорему 5.3
гл. II). Аналогично, рассматривая функцию — pi, получим
оценку ы„, снизу и потому оценку тах| ы„, |для любой области Q,,
а,
примыкающей к Sx (но отстоящей от S \ S, на положительное
расстояние).
Для функции р2 = иУг неравенства A9.36) также справед-
справедливы, причем даже для всех k. Действительно, соответствую-
соответствующий ей интеграл типа /2 имеет вид
Ak. р Ак, р
и при преобразовании к виду
П - J К„, (Р. - *) 266^ - ^, (А - k) 2||J dy
выделится граничный интеграл

; 19] СЛУЧАЙ ДВУХ НЕЗАВИСИМЫХ ПЕРЕМЕННЫХ 283
который равен нулю для любых k (на S{ подынтегральное выра-
выражение обращается в нуль благодаря множителям cos (n, у^
и иУхУ). Все остальные оценки и соображения, приводящие
к оценке тах\иУ2\, те же, что и> выше для иУх. Переходя к ста-
старым переменным х, получаем оценку | V« 1= Yu% + u% вблизи S,.
Так оценивается I V« | в Q при ы|? = 0. Если "ls = <pls, q>e
e.W2q(u), то этот случай сводится к предыдущему с помощью
рассмотрения вместо и(х) функции v (х) = и (х) — <р (х). Тем
самым, закончено доказательство и второй части теоремы 19.4.
Из теорем 19.1 — 19.4 вытекает следующая теорема:
Теорема 19.5. Пусть u(x)^.W\(u) и удовлетворяет урав-
уравнению A9.1), для которого выполнены условия A9.2), A9.21).
Тогда «gC"+°'(Q) с а > 0, зависящим лишь от v, ц и q из
условий A9.2), A9.21). Норма \ и Ц+а>, VQ'crQ, оценивается
постоянной, определяемой величинами v, ц, ц, и q из A9.2),
A9.21), нормой \\и\[, а и расстоянием п' до S.
Если п е W% и \s = Ф |s и Ф €= W\ (Q) (q > 2), тои<= СA+а) (Q)
и | и Ш+а) оценивается постоянной, зависящей лишь от v, ц, ^
q, II" ll2 q > IIФ Н(?2)а " области п. Показатель а в этом случае
определяется постоянными v, ц и q.
Пусть выполнены условия второй части теоремы A9.5); тогда
уравнение A9.1) можно рассматривать как уравнение
аи (х) ux.Xj = F(x)=f (x) - atuXl - аи A9.39)
с F (x) e Lq (п), q > 2. Если предположить еще, что коэффи-
коэффициенты ац(х) непрерывны в Q, то, используя метод склейки
Шаудера, коротко описанный в § 11, и рассуждения §§_9, 10,
можно доказать, что и(х) будет принадлежать W2q{u'), fi'cfi,
при любом поведении и на S или Wl(Q), если функция <р(х),
определяющая граничные значения и(х), принадлежит W2q(Q).
Рассмотрим теперь вопрос о разрешимости первой краевой
задачи для Lu, считая а{1 (х) произвольными ограниченными
функциями, удовлетворяющими лишь неравенству A9.2), а об-
область Q такой же, как в § 9. Для этого предварительно заме-
заметим следующее: если к Lu добавить слагаемое — v0a22"
с достаточно большим v0, то для Lxu = Lu — vQa^u и произ-
произвольной функции и из Wl$(u) вместо A9.5) будем иметь нера-
неравенство
ll"l^a<dl^i"ll2>a A9.40)

284 ЛИНЕЙНЫЕ УРАВНЕНИЯ [ГЛ. III
с постоянной с, определяемой лишь постоянными v0, v, ц, q
и ц, из A9.2), A9.4) и областью Q. Действительно, рассуждая
так, как и при выводе неравенства A9.14), получим неравенство
=¦& I К*
a s
в котором F\ = L\U—aiux —аи. Из соотношения же
ихл — vou = — (Lxu — antiXiXi — 2al2uXix2 — aiUXl — аи)
имеем
J («зд " vo«J dx = \ (e^, + 2vo< + vo2«2) dx
Q Q
Из A9.41), A9.42) и наших предположений о at, а и Q уже
ясно, что число v0 можно взять настолько большим, чтобы
имело место неравенство A9.40) (величина v0 определяется
числами v, ц., Hi, q из A9.2) и A9.4) и Q).
Нас интересует первая краевая задача для оператора L.
Включим ее в однопараметрическое семейство задач
Llu — ka22u = f, u\s = 0, A9.43)
где X— произвольный параметр, а число v0 в Lx столь большое,
что для всего семейства операторов
Lxu = A — т) а2г (Аи — vou) + т (Lu — v0a22u), 0 < т < 1,
справедливо неравенство A9.40), т. е. что для любой функции и
из Wlo(Q) и т из [0,1]
. A9.44)
Как показано выше в § 9, благодаря неравенству A9.44) задачи
Lxu = f, u\s = 0, 0<т<1, A9.45)
однозначно разрешимы в W2,o(u) при любой / из L2(Q), если
только Q удовлетворяет условиям теоремы 9.1 (или теоремы 9.3);
иначе говоря, для таких Q операторы Lx, ts[0, 1], устанавли-

5 20] О ДВУМЕРНЫХ СЕДЛООБРАЗНЫХ ПОВЕРХНОСТЯХ 285
вают взаимно однозначное соответствие между полными про-
пространствами №2,0 (й) и L2(Q). Ввиду этого вопрос о разреши-
разрешимости задачи A9.43) в пространстве W\o(u) эквивалентен
вопросу о разрешимости в W\fi(u) уравнения
u-XLrl(a22u) = Lrlf, A9.46)
где 1л —оператор, обратный оператору L{ задачи A9.45)
при т=1. Оператор Лы = ?Г'(я22и) является вполне непре-
непрерывным в L2(Q), что следует из A9.44) и полной непрерывно-
непрерывности вложения №г,о(й) в L2(Q). Поэтому для уравнения A9.46)
в L2(Q) справедливы теоремы Фредгольма. В частности, урав-
уравнение A9.46) разрешимо в L2(Q) при любой правой части
из L2(Q), если только однородное уравнение
и-Я?Г'(в22и) = 0 A9.47)
имеет в L2(fi) только тривиальное решение. Отсюда и из того фак-
факта, что каждое решение из L2(fi) уравнения A9.47) и уравнения
A9.46) с / из L2(fi) является элементом Wl, о(й), следует
Теорема 19.6. Пусть для L выполнены требования A9.2),
A9.4), a Q удовлетворяет условиям теоремы 9.1 или теоремы 9.3.
Задача
Lu = f, u\s = 0 A9.48)
разрешима в Wl,o(Q) при любой правой части f из L2(fi) тогда
и только тогда, когда имеет место для A9.48) теорема един-
единственности в пространстве W\ о (Q). Если дополнительно известно,
что f(x) и а(х) принадлежат Lq(u) и U^W^, q>2,To любое
решение и задачи A9.48) из l^2io(fi) принадлежит СA+а)(й).
Последнее утверждение теоремы взято из теоремы 19.5.
Из вывода неравенства A9.40) ясно, что задача A9.43) од-
однозначно разрешима, например, при всех Я,^0.
§ 20. О двумерных седлообразных поверхностях
Рассмотрим эллиптические уравнения вида
при условии
п1,Ы,>0 B0.2)
при 111 ф 0.
Их решения обладают рядом специфических свойств. Во-пер-
Во-первых, для любой функции и, удовлетворяющей уравнению B0.1)

286 ЛИНЕЙНЫЕ УРАВНЕНИЯ [ГЛ. III
в какой-либо области Q, справедливы неравенства
B0.3)
(см. лемму 1.4 гл. III), ие=С(п) Л C2(Q).
Другой особенностью решений и уравнений B0.1) является
то, что для строго выпуклых областей Q величина max|Vu|
Q
определяется лишь граничными значениями функции и (именно
max | ф' (s), ф" (s) |, где ф (s) = и (х) \x=s s s) и не зависит от коэф-
фициентов ац.
Мы наши условия на граничные значения ф(лг) решения и(х)
сформулируем в таком виде: предположим, что нормали к пло-
плоскостям евклидова пространства (хи х% и), проходящим через
три любые точки Ри Р2, Р3 граничной кривой 1={(х, «):x = seS,
ы = ф($)}, образуют с осью и углы а, для которых |tga| не
превосходит какой-либо постоянной М{. Это же, очевидно, верно
и для плоскостей, являющихся предельными для таких пло-
плоскостей, когда какая-либо пара точек из Pt или все три точки
Р\, ^2, Рз сливаются. Область Q при этом считаем строго
выпуклой. Это условие, известное в литературе как «условие
трех точек», гарантирует для решения и уравнения A8.1),
равного ф на S, оценку
max|VuKAf,. B0.4)
Действительно, возьмем на кривой / произвольную точку х°
и касательную к ней в точке х°. Проведем через эту касатель-
касательную две плоскости П+ (*°) и П~ (*°), нормали к которым с осью и
образуют углы а*, удовлетворяющие условию Itgc^^Af,.
В силу нашего условия кривая / будет заключена между пло-
плоскостями П+ (*°) и П~ (*°), точнее, ордината и для точек (х, и)
кривой / будет заключена между ординатами и для точек П* (*°)
с теми же х. Но тогда это же будет верно и для всей поверх-
поверхности ы=ы(лг), ней. Действительно, если бы это было не так,
то существовала бы подобласть ut области Q, на границе ко-
которой решение и совпадало бы с линейной функцией u = f(x)s=a
е= Ьх (*, — д^) -f b2 {x2 — х°) + Ф (*°)> а внутри Q, было бы больше
или меньше ее. Но это невозможно, так как функция f(x) удо-
удовлетворяет уравнению B0.1); поэтому разность /(*)— и(х)
является решением того же уравнения, равным нулю на гра-
границе области Q,, а такое решение в силу отмеченного выше
свойства B0.3) должно тождественно равняться нулю в й(.

§ 20] О ДВУМЕРНЫХ СЕДЛООБРАЗНЫХ ПОВЕРХНОСТЯХ 287
Из доказанного следует, для точек х е Q верно соотношение
| и(х) — и(х°) |/| х — х° |^ЛГ,, и если функция и дифференци-
дифференцируема в Q, то |Vu| в точке х° не превосходит М{. Неравен-
Неравенство B0.4) доказано.
Покажем, что это же верно и для всей области, т. е.
max|VuKAf,. B0.5)
Q
Поверхности и = и (х), х е Q, соответствующие решениям и (х)
уравнения B0.1), являются так называемыми седлообразными
Поверхностями. Они обладают следующими свойствами:
1) Никакая плоскость не может срезать с них шапочку,
Проектирующуюся внутрь Q. Это значит, что для любой линей-
линейной функции f(x) = ЬХХ\ -f b2x3 -J- Ьъ и любого решения и {х) урав-
уравнения B0.1) замкнутые множества точек *efl, где u(x)^f(x)
или где u(x)^f(x), либо пусты, либо имеют пересечения с гра-
границей Q.
2)_Если кривая /, ограничивающая поверхность и = и(х),
*eQ, где и(х) есть решение B0.1), удовлетворяет «условию
трех точек», сформулированному выше, то любая плоскость
u = f (x) = b\X\ -f- b2x2 + Ь3 с наклоном, большим Mi (т. е. модуль
тангенса угла, образованного нормалью к ней с осью и,
больше М{), имеющая с поверхностью и = и(х), ieQ, хотя бы
одну общую точку (х°, ы°) с х° из Q, пересекает / в двух
разных точках, разбивая ее на две дуги, на одной из которых
н (*)>/(*)> а на другой u(x)<f(x). Множества точек х, где
u(x)>f(x) и где u(x)<f(x), односвязны.
Собственно, из двух описанных свойств седлообразных
поверхностей нам существенно второе (или, что то же, второе
и первое для плоскостей с наклоном, большим Мх). Докажем
его. Обозначим через Q' множество тех точек х из Q, где
u(x)^f(x). Оно содержит точку л;0. Если бы расстояние Q'
До S было положительным, то (в силу непрерывности и (х)
и f (х)) множество йе, где и(х) ^f(x) — e, при достаточно малом
положительном е также не имело бы общих точек с S. Но
функция и (х) — f (x) -f e есть решение уравнения B0.1), равное
нулю на границе области Qi, следовательно, она равна нулю
и во всей йе. Но это невозможно, так как в точке х° разность
и (х°) — f (jc°) -f e = е положительна. Полученное противоречие
доказывает, что Q' имеет по крайней мере одну общую точку с S.
При этом мыслимы следующие варианты: а) граница Q'
имеет с 5 две общие точки, которые разбивают S на две
открытые дуги: на одной из них и (х) — f (х) > 0, а на другой
и (х) — / (х) < 0; б) граница п' имеет с 5 одну общую точку х'

288 ЛИНЕЙНЫЕ УРАВНЕНИЯ 1ГЛ. Ill
(в ней ы(*0 — f(x') = O), и на 5 \ х' функция и (х) — f (х) < 0;
в) граница Q' имеет с 5 одну общую точку х', и на S\x'
u(x) — f(x)>0. Других вариантов быть не может, ибо по
«условию трех точек» плоскость ы = /(*) не может иметь с /
трех и более общих точек. Случай а) соответствует тому, что
мы хотим доказать. Случай б) невозможен. Действительно,
если бы он имел место, то функция и(х) равнялась бы f(x)
в Q' и была бы меньше / (х) в п \ пг. Повернем плоскость
u = f(x) вокруг прямой, проходящей в этой плоскости через
точку (х°, и0), где ы° = и (х°) = f (x°), параллельно касательной
к 5 в точке х\ Нетрудно понять, что если угол поворота 0
взять достаточно малым и вращение совершить в том напра-
направлении, которое соответствует увеличению ординаты и плоскости
в точке х', то для повернутой плоскости ы = /9(д;) для fe5
будем иметь /е (х) > и (х). Но это, как показано в начале
доказательства свойства 2), несовместимо с равенством /е(*°) —
- и (х°) = 0.
Случай в) также невозможен, ибо, переходя от функций и (х)
и f(x) к функциям — и (х) и —/(*), мы сведем его к случаю б).
Итак, показано, что любая плоскость u=f(x), имеющая с
поверхностью и = и(х) общую точку (х°, и0), х° <= Q, с наклоном,
большим М1; разбивает 5 на два открытых куска; на одном
из них u(x)>f(x), на другом u(x)<f(x), а в двух точках,
разделяющих эти куски, u(x) = f(x). Область Q при этом раз-
разбивается на два открытых односвязных множества: flp где
u(x)>f(x), и Q2, где u(x)<f(x), разделенных замкнутым мно-
множеством йо> где u(x) = f(x). Односвязность Q, и й2 следует
из того, что если и (x) = f(x) на границе какой-либо связной
области Q' с Q, то это равенство справедливо во всей п'.
Ниже нам потребуется следующий почти очевидный топо-
топологический факт. Возьмем какую-либо точку х° из Qi (где
и (х) > /(*)) и две точки х' и х" из й2 (где u(x)<f (x)). Соединим
точки х' и х" ломаной Р, не выходя из области й2- Вектор,
соединяющий точку ? с точкой х при движении х от х' до х"
вдоль ломаной Р, повернется на некоторый угол © (как всегда,
вращение против часовой стрелки считаем положительным,
а по часовой стрелке — отрицательным). Величина этого угла ©
(включая и его знак) не зависит от ломаной. Как нетрудно
понять, это есть следствие односвязности области Qlt
Переходим теперь к доказательству соотношения B0.5).
Предположим противное. Тогда в Q найдутся две точки х и х
такие, что
\и(х)-иСх)\ >Щ B(Ш

§ 20] О ДВУМЕРНЫХ СЕДЛООБРАЗНЫХ ПОВЕРХНОСТЯХ 289
Без ограничения общности будем считать, что точки х и х
лежат на интервале @, а) оси хи причем концы этого интервала
принадлежат границе S. Нас интересует взаимное расположение
прямой N, соединяющей точки (х, и), (х, и), где jc = (jf1; 0),
*= (*,, 0), п = и(х), и = и(х), и линии /, пересечения поверх-
поверхности и = и(х) с координатной плоскостью х2 = 0. Уравнение
линии /, такое: и = и(хи 0), 0^л:,<а. Совпадать /, с N на всем
отрезке [0, а] или даже в двух его концах не может, так как
в этих случаях, беря еще какую-либо точку на контурной
кривой /, мы провели бы через N и эту точку плоскость боль-
большого наклона (для такой плоскости модуль тангенса угла между
нормалью к ней и осью и превосходил бы Мх), что противоречит
«условию трех точек» на /. Но в таком случае или 1) на интер-
интервале Х\ < хх < *, есть точка х1}, в которой ордината кривой /,
больше ординаты прямой N, а на интервалах 0 < х1 < %х и
хх< хх< а есть точки х\ и х'{, в которых ордината кривой /,
меньше ординаты прямой N, или, наоборот, 2) в точке х\
ордината /, меньше ординаты N, а в точках х\ и х'[ ординаты /,
больше ординат N, или 3) одного из этих двух расположений
можно добиться небольшим параллельным сдвигом N или не-
небольшим поворотом (при котором удовлетворяется еще B0.6),
точнее, при котором тангенс угла наклона прямой N к оси х{
остается больше М{) и последующим параллельным сдвигом N.
Мы предоставляем читателю убедиться в справедливости этого
утверждения. Здесь же покажем, что на самом деле для наших
седлообразных поверхностей невозможны и расположения 1)
и 2). Для примера возьмем случай 1). Проведем через прямую N
какую-нибудь плоскость П: и = f (х) = bxxx -f 62*2 + b3. Она
разобьет й на три части: Q,, й2 и ®о> в ^i u(x)>f(x), в й2
u(x)<f(x), в Qo u(x) = f(x). Точка (х», 0)eQ,, точки «, 0)
и (xf{, 0) принадлежат Q2- Угол поворота © вектора, соединяю-
соединяющего точку (х\, 0) с (х^, 0\ при движении конца этого вектора
вдоль произвольного полигона, лежащего в Q2. до точки (х"{, 0)
равен -f л или — л. При непрерывном повороте плоскости П
вокруг прямой N точки (х°{, 0), (х[, 0), {х'(, 0) и полигон, соеди-
соединяющий (*ь 0) и (х'(, 0), продолжают оставаться в областях
типа Qu где и(х) >f(x), и Q2, где и(х) <f(x), и потому число ©
(а оно вообще при рассматриваемом расположении точек на
одной прямой может иметь или значение -f- я, или значе-
значение — я) остается неизменным. С другой стороны, ясно, что
плоскость П можно провести и так, чтобы со^ + я, и так,
чтобы © = — я. Полученное противоречие и доказывает не-
невозможность расположения 1). Так же устанавливается
Ю О. А. Ладыженская, Н. Н. Уральцева

290 ЛИНЕЙНЫЕ УРАВНЕНИЯ [ГЛ. И1
невозможность расположения 2), а тем самым и абсурдность
исходного предположения B0.6).
Сформулируем доказанные предложения в виде теоремы.
Теорема 20.1. Для любого решения и(х) эллиптического
уравнения B0.1), непрерывного в Q и дважды дифференцируе-
дифференцируемого в Q, справедливо соотношение B0.3). Если п — строго
выпуклая область и кривая /: {* = se.S, u = qp(s)} в простран-
пространстве (х, и), ограничивающая поверхность и = и (х), удовлетво-
удовлетворяет «условию трех точек» с постоянной Мь то и(х) удовле-
удовлетворяет в Q условию Липшица с постоянной М{; если к тому же
и(х) дифференцируема в п, то max| Vul^A^.
а
Это предложение имеется в работах [42, 43]. Данный здесь
способ его доказательства принадлежит фон Нейману 43].

Глава IV
КВАЗИЛИНЕЙНЫЕ УРАВНЕНИЯ
С ДИВЕРГЕНТНОЙ ГЛАВНОЙ ЧАСТЬЮ
Мы начинаем исследование квазилинейных эллиптических
уравнений с изучения специального класса этих уравнений—
уравнений с дивергентной главной частью. Они имеют вид
L (и) = -jj- at (х, и,их) + а (х, и, их) = 0. @.1)
Этот класс охватывает многие важные уравнения механики
и геометрии. Например, он включает все линейные эллиптиче-
эллиптические уравнения вида B.1) гл. I, квазилинейные уравнения вида
ац {х, и) ux.Xl + а (х, и, их) = 0,
уравнения Эйлера регулярных вариационных задач для функ-
функционалов Г F (х, и, их) dx.
и
Для этого класса уравнений получены наиболее полные и
законченные результаты по вопросам исследования дифферен-
дифференциальных свойств решений и разрешимости краевых задач.
Для них можно определить обобщенные решения, имеющие
производные только первого порядка. В § 2 гл. I были выяс-
выяснены те ограничения на функции at(x,u,p) и а(х,и,р), кото-
которые необходимы для того, чтобы для уравнений @.1) были
допустимы обобщенные решения и(х) из Wxm{Q) с конечным
vraimax|u| и обобщенные решения из Wlmiq=Wm(Q)(]L4(Q).
В данной главе мы докажем достаточность этих условий,
а также проследим за тем, как улучшаются дифференциальные
свойства таких обобщенных решений по мере улучшения диф-
дифференциальных свойств функций ai(x, и, р) и а(х, и, р). Начнем
мы с изучения обобщенных решений и(х), имеющих конечный
vrai max | и \.
Q
В данной главе и вообще во всех главах, посвященных не-
нелинейным задачам, кроме гл. IX, мы будем предполагать, что
функции, образующие уравнения, являются ограниченными
функциями на любом компактном множестве изменения их
аргументов. В частности, мы не будем допускать никаких осо-
особенностей этих функций по аргументу х, и потому результаты
10*

292 КВАЗИЛИНЕЙНЫЕ УРАВНЕНИЯ [ГЛ. IV
гл. III, относящиеся к линейным уравнениям с неограничен-
неограниченными коэффициентами, не будут вытекать из доказываемых
ниже теорем о нелинейных уравнениях. Однако можно было бы,
оставаясь в рамках методов, развиваемых в данной книге, рас-
рассмотреть квазилинейные уравнения с функциями а,- (л:, и, р),
а(х, и, р), имеющими особенности по л: и включающими в себя
как частный случай линейные уравнения гл. III. Мы не делаем
этого здесь, так как хотим сосредоточить все внимание читателя
на особенностях нелинейных задач и не хотим нагромождения
дополнительных трудностей, связанных с наличием возможных
особенностей функций at(x, и, р) и а(х, и, р) по х.
Такое обобщение можно сделать, используя данную здесь
методику получения априорных оценок, которая состоит в общих
чертах в том, что из интегрального тождества, заменяющего
собою уравнение, выводятся неравенства типа E.9) и F.1) гл. II,
из которых в свою очередь на основании теорем 5.1, 6.1 и 7.1
гл. II делается заключение об ограниченности и гёльдеровости
тех или иных функций.
Параграфы 1—7 отражают в основном результаты работ
[2112—15,17.2о] авторов. В § 10 с помощью теорем Шаудера и Лерэ
о неподвижных точках вполне непрерывных преобразований
и априорных оценок, установленных в §§ 1—8, доказывается
классическая разрешимость задачи Дирихле для уравнений @.1).
В § 9 исследуется разрешимость задачи Дирихле для уравне-
уравнений @.1) в классах Wm,q. Делается это с использованием ме-
метода Галеркина и ведущего свое начало от работ [361>2]
Г. Минти способа выполнения слабых предельных переходов
под знаком монотонного оператора (см. в связи с этим работы
[7], [323], [363], [18] и др.). О вкладе других математиков в иссле-
исследование уравнений @.1) см. вводную главу.
§ 1. Ограниченные обобщенные решения.
Непрерывность по Гёльдеру
Рассмотрим уравнение
L(u) = -^- at {x, и, их) + а {х, и, их) = 0. A.1)
Предположим, что функции ai{x, и, р) и а(х,и,р) определены
при ^eQ и произвольных и, р, измеримы и подчиняются
условиям
ui(x, и, p)pi>v(\ и \)\р Г- Ц(| и|), A.2)
\1/2
, и, p)J A+|р|)+|а(*,и,р)|<ц(|и1)A+|р|Г, A-3)

§ 1] ОГРАНИЧЕННЫЕ ОБОБЩЕННЫЕ РЕШЕНИЯ 293
где | р |= 1/ 2j р\, v(t) и ц(/)— известные функции, обладаю-
обладающие свойствами, перечисленными на стр. 26, а постоянная
т> 1.
Ограниченным обобщенным решением (ог. об. решением)
уравнения A.1) будем называть функцию и(х) из №,'„ (Q)
с vraimaxj и |< оо, удовлетворяющую интегральному тождеству
L(«, т])= J Га,(дс, и, их)тц—а(*. u, ux)ti]d* = 0 A.4)
Q
о .
при любой ограниченной функции г\(х) из Wm(Q).
Выше, в § 2 гл. I, мы видели, что такой класс обобщенных
решений естественным образом связан с рассматриваемым
классом уравнений A.1) —A.3). На построенных там примерах
было показано, что отказ от требования ограниченности модуля
обобщенного решения и(х) из Wxm(Q) при сохранении требова-
требований A.2), A.3) или ослабление условий A.2), A.3) при сохра-
сохранении рассматриваемого класса ог. об. решений заведомо при-
приведет к потере теоремы единственности в малом для задачи
Дирихле. Однако заранее было неясно, не надо ли помимо
условий типа A.2), A.3) накладывать какие-либо другие огра-
ограничения на характер нелинейности функций at (x, и, р), а(х, и, р)
по и и р для того, чтобы для уравнений A.1) была правомерна
в областях произвольной величины и формы теория только что
определенных ог. об. решений. В данной главе будет доказано,
что такие дополнительные ограничения не нужны. Точнее, будет
доказано, что только при выполнении условий A.2), A.3) любое
ог. об. решение будет удовлетворять условию Гёльдера, при
выполнении условий B.1), B.2) оно будет единственным в ма-
малом, при выполнении условий E.1), E.2) оно будет принадле-
принадлежать W\[\Cx+a, при дополнительной гладкости at(x, и, р),
¦а(х, и, р), именно, когда а,-, а и частные производные at по х,
и, р как функции (л:, и, р) принадлежат С1+а, оно будет эле-
элементом С2+а, и т. д. Иными словами, будет доказано, что диф-
дифференциальные свойства ог. об. решений определяются диффе-
дифференциальными свойствами функций аг{х,и,р) и а(х, и, р) (они
улучшаются по мере улучшения дифференциальных свойств
этих функций), если только порядки роста по р при |р|->оо
функций
dat да{ да{ да да да
°1< а> ~ЩГ{% ~ШГ' 1x1' ~Щ' ~д~"' ~д*к
согласованы так, как это предписывают неравенства A.2), A.3),
B.1), B.2), E.1), E.2). Такое согласование порядков для всего

294 КВАЗИЛИНЕЙНЫЕ УРАВНЕНИЯ [ГЛ. IV
. класса уравнений вида A.1), как видно из примеров § 2 гл. I,
необходимо.
Покажем прежде всего, что для ог. об. решений уравнения
A.1) можно оценить \\Vu\mdx через M^vraimax|«| и изве-
стные постоянные. Именно, докажем следующую лемму:
Лемма 1.1. Пусть и(х) есть ог. об. решение уравнения
A.1) и vrai max| и \^.М. Тогда для любого шара Кр, р^1,
расположенного в Q вместе с концентрическим ему шаром i*C2p.
интеграл \\Vu\mdx не превосходит ср"-т, где постоянная с
зависит только от М, пг и v(Af), ц(М) — из условий A-2), A.3).
Если unaS совпадает с ограниченной функцией ф (л:) из Wlm (Q)
(без ограничения общности будем считать, что уга!тах|ф|^
Q
^ vrai max| и |), то \\Slu\mdx не превосходит постоянной с,
а
зависящей лишь от М, пг, v(M) и ц(М) из A.2), A.3), ||ф|^'а
и mesQ.
Если к тому же у(х) удовлетворяет неравенствам
,р"-т, пр = Кр[]п, A-5)
йр
для любого шара Кр, Р"^* \, то и интегралы \ \ Vu Tdx не пре-
восходят ср"~т, где с определяется М, пг, v(M) и \i(M) из A.2),
A.3) и сх.
Доказательство. Рассмотрим какие-либо концентриче-
концентрические шары Кр с: К,2Р с ^> Р^1> и произвольную срезающую
для /Сгр функцию t, (x), равную единице вКр и нулю вне К^,.
В тождестве A.4) возьмем функцию х\ равной ех%т с некото-
некоторым X > 0:
f еы (Ха,иг С + а,тС~\* — аС\ dx = 0. A.6)
Из этого равенства нужную нам оценку j \4u\mdx получим
благодаря предположениям A.2), A.3), из которых следует
aiux>v\Slu\m-\x,
, где v = v(Af), ц =

§ 1] ОГРАНИЧЕННЫЕ ОБОБЩЕННЫЕ РЕШЕНИЯ 295
Здесь при оценке второго члена использовано неравенство Юнга
В силу этих неравенств из A.6) получим
v* JY"| Vu rCdx^c* J ex"[(l +| Vu
a a
где с' зависит от v, ц и т. Отсюда при A. = 2c'/v получаем
J I V« Г С dx < e4c'M/v J (?m +1 V? Г) d*.
Q Q
Выбирая t,(x) так, чтобы max |V? ^гр, выводим желаемую
Q
оценку
¦\it-m
JI Vu Г
Ф"
где с зависит только от М, m, v и ц.
Второе утверждение леммы 1.1 докажем, положив в A.4)
r\(x) = (ex\u~v\ — l)sign(u —ф). В третьем случае надо взять х\ (х),
равной (еМ"-ф| _ l)?sign(« — qp), где ? (л:) — срезающая функ-
функция для произвольного шара /С2р, р^ 1, равная единице в кон-
концентрическом с ним шаре ./Ср. После элементарных оценок,
аналогичных проведенным выше, убедимся в справедливости
второго и третьего утверждений леммы.
Докажем, что ог. об. решения непрерывны по Гёльдеру.
Очевидно, для этого нужно рассмотреть лишь случай т<^.п,
так как при т> п гёльдеровость и (х) следует из принадлеж-
принадлежности и(х) к Wlm(Q) (см. § 2 гл. II).
Пусть и(х) есть ог. об. решение уравнения A.1) с т^.п,
и пусть vrai max| и (х) |^ М. Покажем, что и(х) принадлежит
Q
некоторому классу 33m(fi, M, у, у, 5, l/q). Для этой цели положим
в интегральном тождестве A.4)
т] (х) = С (х) max {и (х) - k\ 0}, A.7)
где ? (л:) — срезающая функция для какого-либо шара Д'р,
а число k будем считать пока произвольным для внутренних
шаров д'р и не меньшим максимума и(х) на пересечении шара Кр
с границей S, если это пересечение не пусто. В силу лемм 3.3,
О .
3.7 гл. II функция A.7) принадлежит Wm(u), причем она

296 КВАЗИЛИНЕЙНЫЕ УРАВНЕНИЯ [ГЛ. IV
отлична от нуля на множестве Лй>р точек л: из йр, для которых
u(x)>k. Поэтому тождество A.4) будет иметь вид
J [а, (х, и, их) ин С + а, (и - к) тС"\ -а (и-к) Г] dx = 0.
Ak,P A.8)
Воспользуемся условиями A.2) и A.3). Тогда из A.8) по-
получим неравенство
v
*'Р k'P +(u-k)(l+\4u\)mtm\dx, A.9)
в котором постоянные v = v(M), ц = ц(М) берутся из условий
A.2) и A.3). В правой части соотношения A.9) член с | V? | оце-
оценим по неравенству Юнга (см. A.3) гл. II):
+ em-m)(u-k)m\ У?Г<е2'"-'тA +1 V« Г)gm +
+ е"A-т)(ы-А:Л V?f, A.10)
и возьмем е равным v/Bm+1p,m). Тогда при таких значениях k,
для которых
тахи(*)-*<—J—6M, A.11)
из A.9) и A.10) будет следовать неравенство
dx A.12)
: постоянной у', зависящей лишь от v, ц и т. Если теперь
срезающую функцию ?(*) брать равной единице в шаре /Ср-ар.
ое@, 1), концентрическом шару Кр, и такой, что | V?Kc/(crp),
то неравенства A.12) дадут нам одну серию неравенств:
f I V« Г rf* < Y fт^ш- max [u (x) - k\m + l] mes Лй> р,
Л * P
ЛА. p-ao *' P
определяющих класс Sm(Q, M, у, у, 5, 0) (cp, §§ 6, 7 гл. II),
Аналогичные неравенства для функции — и(х) получим, если
в A.4) положим
- ^х) = Г (х) max {- и (х) - k; 0},
где значения k таковы, что
max [- и (х)\ - k < -—^т- — 5М,

§ 1] ОГРАНИЧЕННЫЕ ОБОБЩЕННЫЕ РЕШЕНИЯ 297
а в шарах Кр, пересекающих границу S, кроме того,
Л > max [-и (*)], Sp = Kp[)S.
sp
Мы доказали, что функция и (х) принадлежит классу
S5m(Q, М, у, у, 5, 0), параметры которого у и б определяются
константами т, v(M) и ц(М) из условий A.2) и A.3). Поэтому
на основании теорем 6.1 и 7.1 гл. II о функциях класса Sm
делаем следующий вывод (при т^.п):
Теорема 1.1. Пусть выполнены условия A.2) и A.3). Тогда
любое ог. об. решение и(х) уравнения A.1) принадлежит классу
Са(й) с показателем а > 0, зависящим от М и постоянных ш,
v(М) и ц(М) из A.2), A.3), причем для любой Q'cQ норма\ и f??
оценивается через М, m, v(M), ц(М) и расстояние от й' до S.
Если граница S удовлетворяет условию (А) и если и[<;<^СР (S),
то ы(л:)еСа(й) и величина \и\?- оценивается через М, \(М),
ц (М), пг, постоянные а0 и 90 из условия (А), р и норму \ и fs,
причем а в этом случае зависит также от 0О и р (а < р).
С помощью этой теоремы докажем нижеследующие леммы.
Лемма 1.2. Пусть й' — строго внутренняя подобласть й.
Для любого ог. об. решения и(х) уравнения A.1) при tn<^n
справедливы неравенства
<Г rrin-m+am
_n+m_2»L ^L
х-у | 2 | V«rd*<cp 2 . A.14)
где шар Кр вместе с концентрическим ему шаром Л^р принад-
принадлежит й', р^1, и у — произвольная точка из Кр- Показатель а
берется из теоремы 1.1, а с определяется постоянными М, т,
v(M), \i(M) и расстоянием й' до S.
Доказательство. Неравенства A.13) и A.14) достаточно
установить лишь для малых р. Для них неравенство A.13) сле-
следует из неравенства A.12), если в последнем вместо шара /Ср
взять ДгР> функцию ?(*) взять равной 1 в шаре Кр, концент-
концентрическом с /С2р, и такой, что | V? |< 1/p, a k положить равным
наименьшему значению и(х) в К^- Такое k взять можно,
так как osc{u; Л^2р}^с1Ра для /Bр с й', и потому при с,ра^5ЛГ
требование A.11) выполнено.
Неравенства лее A.14), как показано в лемме 4.3 гл. II, сле-
следуют из A.13).

298 КВАЗИЛИНЕЙНЫЕ УРАВНЕНИЯ [ГЛ. IV
Лемма 1.3. Пусть at(x, и, р) и а(х, и, р) удовлетворяют
условиям A.2) и A.3). Тогда для любого ог. об. решения и(х)
уравнения A.1) имеет место неравенство
~т\ \) I s I > A.15)
кр кр
где ? (л:) — произвольная ограниченная функция из wm (Kp), если
только шар К2р, концентрический с шаром Кр, принадлежит
fi'cQ й радиус р не превосходит некоторого числа р0 > 0. По-
Постоянная с в A.15) и ро определяются постоянными М, m, v(M)
и ц(М) из A.2), A.3) и расстоянием от Q' до S.
Доказательство. В случае 1 < m^2 утверждение
леммы следует из неравенств A.14) и из леммы 4.4 гл. II. Рас-
Рассмотрим случай m ^ 2. Полагая в A.4) г\ (х) = [и (х) — и (х0)] |2 (л:),
где х0 — какая-либо точка Кр> и используя условия A.2), A.3),
получим
-I'
лр
(i J
+| и(х)-и(х0) |[2A+| Vu II"! 11| V| |+A+| Vu Dml2]}^<
2 + | u W-« W |[2A + | Vu |)m|2+(l+| Vu !)m-2| V| f]}dx,
«p
и так как max \и(х) — и (л:0) | ^ Сфа, то
Kp
J
Kp
. A.16)
По условию функция I принадлежит if'm (Kp), m ^ 2, поэтому
в силу B.14) гл. II для | верно неравенство Г
«р
р
Оценка A.15) при достаточно малых р следует из двух послед-
последних неравенств.
Утверждения, аналогичные леммам 1.2 и 1.3, справедливы и
для шаров Кр, пересекающих границу 5. Действительно, пусть S
удовлетворяет _ условию (А) и и |5 = <j> [j, причем <р (л:) е

§ 1] ОГРАНИЧЕННЫЕ ОБОБЩЕННЫЕ РЕШЕНИЯ 299
По теореме 1.1 для любого шара Кр, р^1.
osc{u; Qp}<c,p<\ A.17)
причем постоянная С\ не зависит от расстояния центра шара
до 5.
Рассмотрим шар Кр, пересекающий какой-либо участок
границы 5, и пусть 1(х) есть произвольная функция из Wm (Qp).
Если т ^ 2, то, проводя те же рассуждения, что и для внут-
внутренних шаров в лемме 1.3, придем к неравенству
?dx' A.18)
йр йр
в котором с зависит лишь от М, v(M), ц(М), т, aQ, 90 из
условия (А), от нормы | ф fg* и р. Радиус р в A.18) не должен
превышать при этом некоторого числа р0, определяемого теми же
величинами.
В случае иеA, 2) доказательство неравенства A.18) бази-
базируется на лемме 4.4 гл. II и следующем утверждении:.
Лемма 1.2'. Если S удовлетворяет условию (А) и функ-
функция ф (л:) принадлежит W!m (Q) f] Ce(Q) и подчиняется неравенствам
(
йр
то для любого ог. об. решения и(х) уравнения A.1), удовлетво-
удовлетворяющего условию
«ls = <Pls*). A-20)
неравенства A.13) и A.14) верны для произвольного шара Кр,
причем интегралы в A.13) и A.14) берутся по пр, а а>0 и с
зависят от М, v(M), ц(М), пг из A.2), A.3), с3, констант а0 и 80
из условия (А), нормы | Ф |д и р.
Убедимся в справедливости A.13). Для этого положим в A.4)
x](x) = [u(x)~((>(x)]t,m(x), где ? (*) — функция, срезающая для
шара Дгр. концентрического шару Кр- Главным членом в по-
получаемом равенстве будет j ai(x, и, ux)ux?m dx.
^2p
Его оставим в левой части, а все остальные члены перене-
перенесем направо и оценим сверху, используя A.17), A.19) и A.3)
*) Условие A.20) означает, что и (х) — <р (х) е= Wlm (Q).

300
КВАЗИЛИНЕЙНЫЕ УРАВНЕНИЯ
[ГЛ. IV
из гл. II. В результате этого придем к неравенству A.13). Не-
Неравенства же A.14) являются следствиями A.13).
На основании лемм 4.4 гл. II и 1.2' заключаем, что при
иеA, 2) неравенства A.18) будут выполняться, если S и <р(х)
подчинить условиям леммы 1.2'.
В §§ 2—6 мы устанавливаем еще ряд свойств ог. об. реше-
решений уравнений @.1). Так как условия, налагаемые на функции
at(x, и, р), а(х, и, р) в этих параграфах, заведомо включают
в себя условия A.2), A.3), то согласно теоремам § 1 любое
ог. об. решение непрерывно в смысле Гёльдера. Это исполь-
используется в дальнейшем, часто без специальных указаний.
§ 2. Единственность в малом
Предположим, что функции at (x, и, р) и а(х, и, р) при j;eQ
и произвольных и, р дифференцируемы по переменным и, р,
причем выполнено условие равномерной эллиптичности урав-
уравнения A.1)
\)m~2f < '
др.
1H+1 р
B-1)
и неравенство
B-2)
Заметим, что из этих предположений следуют неравенства
A.2) и A.3), ибо
а{ (х, и, р)
1
Г
= р^, J
x, и, р)
dpj
и,
p=xp
+ I Р 1Г- l]l Р 1-1* (I и 1I Р l>v, (| и 1I р Г-
(г, (| и
При этих условиях справедлива следующая теорема о един-
единственности в малом ог. об. решений уравнения A.1):
Теорема 2.1. Два ог. об. решения, и'(х) и и"(х), равные
друг другу на поверхности шара ^pcQ'c Q, совпадают в Кр,
если только радиус р меньше некоторого числа р0, определяе-
определяемого величинами M^maxlu', u"\, v(M), ц(М) и m из уело-
Q
вий B.1), B.2) и расстоянием от Q' до S.

§ 2] ЕДИНСТВЕННОСТЬ В МАЛОМ 301
Доказательство. Для любой ограниченной функции
т}(л:)е Wlm(Kp) имеем
0 = L (и', x\)~L (и", x\)^^L (и1, х]) dt,
о
где и = A — /) и" -\- tu'. Отсюда
О — J I J iK \ ' x) dt (u' - u")Xj + J —rdt(u'-u")\4Xidx-
г 1 1 -i
_ Г Г _*?_Л (и' _ ы") + f ^Ldt(u' - ы") л rf*. B.3)
J I J 5и ' «^ ди
К L о */ 0 J
В силу предположений B.1), B.2) для at,= — / dt
J ди
0 xf
верно неравенство
" I) I ^йг/?,-!/<^
•2 A +1 Vu' | +1 Vu" \)m-\\ cuc2> 0, B.4)
l l
Г да, С да С да
a{=\'dt, bl=\—T-dt, a=\—rdt
1 J ди' l J ди* J ди'
о о -"г о
— неравенства
п
M)<c3(l+|Vu'|+|Vu'|) ' i B.5)
а для
l
Все они легко выводятся из неравенств B.1), B.2). Положив
в B.3) х\ = и' — и" и использовав приведенные здесь оценки,
получим
а следовательно, и неравенство
1 +| Vu' | +1 Vu") |Г| Vti |V*
J A +1 Vu' | +1 Vu" |)m tf dx B.6)

302 КВАЗИЛИНЕЙНЫЕ УРАВНЕНИЯ [ГЛ. IV
с постоянной сА, не зависящей от р. Рассмотрим отдельно слу-
случай иеA, 2) и случай т^2. Поскольку \Vu'\ и \Vu" \ под-
подчиняются неравенствам A.14), то при т из A, 2) в силу
леммы 4.4 гл. II справедливо неравенство
«р
f (l+\Vuf\ + \Vu"\)
< ср2* J A +1 Vu'! +1 Vu" I)"-2! Vt| f dx. B 7)
Если р столь мало, что с4ср2а < 1, то из B.6) и B.7) следует
равенство нулю ц, т. е. совпадение и' с и".
При т^2 это же заключение будет верно для р, удовлет-
удовлетворяющих неравенству 2тс4сра < 1, где постоянная с взята из
неравенств A.15) для и' и и". Действительно, в этом случае
из неравенств A.15), справедливых для и' и и", следует не-
неравенство, получаемое из B.7) заменой р2а на 2тра. А из такого
неравенства и неравенства B.6) вытекает совпадение и' с и"
при малых р.
Мы доказали свойство единственности в малом ог. об. ре-
решений уравнений A.1) для любой строго внутренней под-
подобласти Q' cz п. Предположим, что два решения ы' и и" на
границе 5 совпадают с функциями q/ и qp" соответственно,
причем для 5 и граничных значений ы' и и" на S выполнены
предположения леммы 1.2'. Тогда в силу леммы 1.2' и тео-
теоремы 1.1 постоянные в неравенствах A.12) — A.14), A.17) и A.18)
равномерно ограничены, где бы ни был расположен шар Кр
с р<р0.
Пусть ы' и и" совпадают на границе области Ор = А^рПЙ,
р^р0. Для них так же, как и выше, выводятся неравенства B.6)
и B.7), причем интегралы в B.6), B.7) берутся по Qp, а по-
постоянные с4 и с уже не зависят от расположения шара Кр,
а определяются лишь величинами M^maxl u'(x), и"(х)\, по-
постоянными т v(M), ц(М) из условий B.1), B.2), а также нор-
нормами | ф', ф" fg1, константами с3 и р из A.19) для ф' и ф" и
константами а0 и 90 из условия (А) на 5. Поэтому можно утвер-
утверждать, что если р не превосходит некоторого числа, зависящего
от указанных постоянных, именно, если р^р0 и 2тс4сра < 1.
то и' и и" совпадают в Qp.
Сформулируем это утверждение в виде теоремы.
Теорема 2.2. Пусть ог. об. решения и' и и" уравнения A.1)
удовлетворяют граничному условию A.20) с ф = ф' и ф = ф"

§ 3] ОЦЕНКА max|v«| 303
соответственно, причем граница S и функции q/ и ф" подчи-
подчиняются требованиям леммы 1.2'. Тогда существует число ро>О,
зависящее только от M^max\ и'(х), и"(х)\, постоянных пг,
а
\{М) и ц(М) из условий B.1), B.2) и постоянных из условий
на ф', ф" и S, такое, что если и' и и" совпадают на границе
области Qp и р^ро, то и' = и" в Qp.
§ 3. Оценка max| V« |
В этом параграфе мы покажем, как для решений и (х)
эллиптических уравнений с дивергентной главной частью @.1)
можно оценить максимумы модулей первых производных по
любой внутренней подобласти п' через постоянные, характе-
характеризующие функции п[ (х, и, р) и а(х, и, р), тах| и \ и расстояние
Q
от п' до 5. Оценка vrai max| Vu \ во всей Q дается ниже, в § 4.
В обоих случаях существенно будет использовано то, что
оценки | и (^ нам уже известны (см. теорему 1.1) и и (х), тем
самым, есть непрерывная функция.
Эти же вопросы исследуются в §§ 2—4 гл. VI для общих
квазилинейных уравнений. Результаты гл. VI применимы, разу-
разумеется, и к уравнениям @.1). Это надо иметь в виду, ибо
в гл. VI рассмотрены также и случаи неравномерно эллипти-
эллиптических уравнений, которые, здесь вне нашего поля зрения *).
При этом выгоднее не формально применять окончательные
результаты §§ 3, 4 гл. VI, а повторить их доказательства,
учитывая дивергентную структуру уравнения @.1) (см. в связи
с этим также § 3 гл. IX). Это позволяет избежать требования
двукратной дифференцируемости функций а, (я, и, р). Метод,
применяемый в данном параграфе, имеет перед методом §§ 3, 4
гл. VI то преимущество, что он позволяет непосредственно
рассматривать обобщенные решения, а при получении априор-
априорной оценки max|V«| в предположении принадлежности и (х)
к W\ (Q) Г) Lip (Q) не предполагать функцию а(х, и, р) диф-
дифференцируемой.
Относительно функций аг (х, и, р) на (х, и, р), входящих
в уравнение @.1), будем предполагать выполненными следую-
следующие условия: при х е Q и произвольных и и р функция а (х, и, р)
измерима, функции а,- (л:, и, р) дифференцируемы по х, и и р,
*) Возможности данного здесь метода применительно к неравномерно
эллиптическим уравнениям проанализированы в работах [15г-4. 24j,2] и др.

304 КВАЗИЛИНЕЙНЫЕ УРАВНЕНИЯ
и все они подчиняются неравенствам
[ГЛ. IV
1/2
C.2)
с т > 1.
Из C.1) и C.2), в частности, следует A.2):
at(x, u,p)pt>vl(\u\)\pr-\ii(\u\), v, >0,
так что неравенства A.2) и A.3) имеют место. Нас интересуют
ограниченные обобщенные решения из Wm(Q). Однако сначала
будем предполагать решение и (х) более хорошим, именно, в этом
и следующем параграфах будем считать, что ые№1(й') Г) Lip(q')
для VQ' cz Q. Для таких решений оценим vraimax|V«| через
а'
постоянные т, v(M) и ц (М) из условий C.1),
C.2) и расстояние Q' до 5. Далее, в § 5, это будет сделано
для произвольного ог. об. решения из Wxm (Q).
Итак, пусть и (х) есть ог. об. решение уравнения @.1),
удовлетворяющее указанным условиям. Оценим сначала инте-
интегралы Г \Vu\ldx, / > 0. При 1^.т такая оценка дается лем-
леммой 1.1. При 1>т оценим их для произвольных шаров Кр
достаточно малого радиуса р, величина которого будет фикси-
фиксирована ниже в зависимости от т, v(M) и \и(М) из C.1), C.2)
и нормы | и f?\ В данном параграфе мы рассматриваем инте-
интегралы Г \Wu\ldx по внутренним шарам, точнее, по шарам,
которые принадлежат области Q вместе с концентрическими
им шарами К2р. отстоящими от 5 на-положительное расстояние.
Положим в тождестве A.4) функцию i](x) равной \Хг{х),
где | (л:) — произвольная, достаточно гладкая, финитная в Q
функция, а г=1, ..., п, и в первом члене проинтегрируем
по частям. В результате получим тождество
и,
г=1 П. C.3)

§ 3] ОЦЕНКА max | v« I 305
Нетрудно убедиться, что при наших предположениях отно-
относительно и (х) в качестве | (я) в C.3) можно взять функцию
| = Ь*их?2, s ^ 0, где ? (л:) — срезающая для шара Дгр функция, а
b(x) = \Vu(x)\2.
В результате подстановки этой функции в C.3) будем иметь
x = 0. C.4)
Проведем суммирование по г от 1 до п. В результирующем
равенстве оставим слева два основных положительных члена,
а остальные перенесем в правую часть и оценим сверху, исполь-
используя условия C.1), C.2). Это приведет нас к неравенству
*2р
Vu |)m+4l Vg | + 26JA +| Vu |)m-'| Ujeje |?| Vg |1^. C.5)
Для оценки снизу положительных членов, стоящих в левой
части, воспользуемся условием C.1), члены же правой части
оценим сверху по неравенству A.2) гл. II, отдавая малое е>0
тем множителям, которые подобны членам левой части. В ре-
результате придем к неравенству
, C.6;
, в котором c(s) зависит лишь от s, m, v(M), \i(M). Здесь и ниже
I при s = 0 и 6^0 величина bs считается равной единице, а
! величина sbs~^ — нулю. Применим теперь к функциям и (х) и

306 КВАЗИЛИНЕЙНЫЕ УРАВНЕНИЯ [ГЛ. IV
|(А:) = A _[- 6)s/2g неравенство D.7) леммы 4.5 гл. II;
< с, osc2 {и; К2р) J! A +1 Vu |)m A + 6)s «
+ 2
<c,osc2{«; K2p]
J
| Vu|)m A+6)Ч2^, s>0. C.7)
При малых р величина osc{«; А^2р} мала, ибо по доказан-
доказанному в § 1
osc{«; Л:2р}<с2ра. C.8)
В силу этого и установленной в лемме 1.1 оценки || Vu \\m K
из неравенств C.6) и C.7) можно заключить о том, что инте-
интегралы
{ Vu Г+2+2s + A +1 Va lV"-2+2s «L] dx C.9)
не превосходят постоянной с (s), определяемой лишь величи-
величинами s, т, М, v (M), ц (М) и расстоянием i*C2p До границы 5.
В самом деле, просуммируем C.6) и C.7) в пределах ots = 0
до s = r, после чего правую часть первого из полученных
неравенств оценим сверху с помощью второго из полученных
неравенств и учтем, что
S A + b)s < с (г) S Ь\ S s2 A + ЬУ'1 < с (г) 2 sbs~l,
S=0 «=0 S=0 «=0

$ 3] ОЦЕНКА max | v« I 307
где с (г) суть некоторые постоянные, зависящие лишь от г.
Это дает нам следующие неравенства:
к2р
{«; /C2p} J
к2р L
<Cl(r)osc2{
+ О +1
+ 4c(r) J A +| Va \)
2р L s=o
s=0
r
m «2
r
C.10)
При достаточно малых радиусах р, точнее, при р, удовлетво-
удовлетворяющих условию
с2(г)р2а<1/2, г>0, C.11)
из C.10) следует
J О +1 Vu |)m [iiL 2 bs +1 Wb
s=o
<8c(r) /(l+IVuir^ + IVCR^O+ft)*^ C.12)

308 КВАЗИЛИНЕЙНЫЕ УРАВНЕНИЯ [ГЛ. IV
И
*2p
<c3(r) |(l+|V«r(?2 + |VgpM](l+^^. *->0. C.13)
*2P
Обозначим через К1, /= 1, 2, ..., последовательность шаров,
концентрических с /Сгр и имеющих радиусы р + ~т. J= 1» 2, ...
Полагая в C.13) и C.12) г = 0, получим желаемую оценку для
(l+|Vu|) ~?,2dxn (l+|Vu|) ~ uxxt, dx, а следовательно,
и для j(l+\Wu\)m+2dx и j(l+\Wu\)m-2u2xxdx. Из нера-
венства C.13) при г=1 и срезающей функции ?, равной нулю
вне шара К1, выведем оценку для интеграла j A +1 V« |)m~2X
XA+^)S2^> что в свою очередь гарантирует оценку для
J (I +| Vu \)m+A dx. Продолжая это рассуждение, убедимся
к?
в возможности оценить интегралы C.9) через известные нам
величины. Для наших дальнейших целей число s в C.9) доста-
()
точно взять равным so= Г . т] в случае т^2 и равным
при т<2
Так как шар Кр в C.9) был выбран при одном лишь усло-
условии, что концентрический с ним тар А^2р принадлежит Q и i*C2p
отстоит от 5 на положительное расстояние, то мы вправе
считать установленной оценку
$ \\Vu\m+2+2s + (I +\Vu\)m-2+2s u2xx]dx^c(s, QO C.14)
Q'
для любой внутренней подобласти Q' области Q с постоянной
c(s, Q')> зависящей лишь от s, M, v(M), \i(M), m и расстояния
от Q' до 5.
Переходим к оценке vrai max | V« |. Пусть t, (x) — срезающая
для п функция, равная единице в Q' (напомним, что 0<^?^ 1).
Будем считать сначала, что т^>2, и положим в C.3)
| (х) = uXr (x) t2 (х) max {| Vu (x) f g2 (x) - /; 0},

8 3] ОЦЕНКА max | v«| 309
где /^0. Суммируя полученные равенства по г от 1 до п,
придем к соотношению
J {[-и" "v/ + -Ж" в*г + 1г] [««л? < I v« P С - 0 +
F ?\. ?uXf + (I Vu p g2 -
Производя здесь оценки с помощью неравенств C.1), C.2) и
неравенства Коши с е > 0, получим
{ A + I Vu \)т~2 \и2хх(\ УиП2-0? + 2 [(I V« 1% I2?4 ^<
<с J (l+|V«|)m+4(l+|VgP)^. C.15)
Будем теперь рассматривать неотрицательную функцию
w(x) = \Vu(x)pi,2(x) и через Ak обозначим множество точек
области Q, для которых w(x)>k. Для нее
| V» Р< 2 S [(| V« р)^]2^4 + 81 Vu Г ?\ Ч ?¦
Отсюда и из C.15) для любого k > 0 следует оценка (при т^2)
l + \Vu\)m+idx C.16)
с постоянной с, зависящей от max| Wt,\ и постоянных т, v(M)
и ц(Л!) из C.1) и C.2).
Правую часть C.16) оценим по неравенству Гёльдера,
используя оценку C.14). Это даст
I Vw f dx ^ с I (I + | Vu | Y dx I (mes.
Ak W I
(s0, Q") (mes Л,)'-(т+4)/г, C.17)
где г = m -f- 2 + 2s0, a Q" — внутренняя подобласть Q, вне
которой ^(л:) равна нулю.
Поскольку so>{m + 4\n~2m -1, то ^т^<-|. и потому
в силу леммы 5.3 гл. II из C.17) следует оценка vrai max | Vu \
через известные нам величины.

310 КВАЗИЛИНЕЙНЫЕ УРАВНЕНИЯ [ГЛ. IV
В случае, когда 1 < т < 2, нужно в тождестве C.3) взять
| (х) = [ 1 + | Vu (x) pf-m)/2 uXf (x) ? (х) max {| Vu (*) |2 ?2 (*) - /; 0}.
Тогда получим
X [uXrxt (I Vu I21? - I) Z? + (I Vu I2 ?)x.? uXf +
4^ A +1 Vu РГ1 (| Vu PL (I Vu PS2- 0?V
+ (| Vu I212 - I) %lx.ux\ + a \uXrXf (I Vu f S2 - 1) Z,2 +
+ (I Vu K2)Xrl2uXr + ^ A+1 Vu РГ1 (I Vu PS2-0S2u,r0 Vu
По сравнению со случаем m^2 мы имеем здесь дополнитель-
дополнительные члены, содержащие производные от A +| Vu p)B""m)/2. Однако
самый сильный из этих членов оказывается неотрицательным,
а остальные оцениваются по неравенству Коши.
В результате вместо неравенства C.15) будем иметь сле-
следующее:
J
Iv«I4'>'
- 0A +1 Vu РГ1 ?22 [(I
J
4'
[
1=1
u|)e(l+|VSp)rfx. C.18)
Дальше оценки проводятся точно так же, как выше при
Из этих рассуждений, леммы 1.1 и^теоремы 1.1 следует
Теорема 3.1. Пусть выполнены условия C.1), C.2) и
и(х) есть ог. об. решение уравнения @.1), принадлежащее
Wi(Q')fl Lip(Q') для VQ'cQ. Тогда величина vraimax|V«|
оценивается сверху постоянной, зависящей лишь от М^ max | и |,
m, v(M), ц(М) из условий C.1), C.2) и от расстояния Q' до S.
§ 4. Оценка max|V«| во всей области Q
Выше была дана оценка max|V«| по любой внутренней по
отношению к Q области Q'. При этом никаких предположений
относительно границы S и значений и на S не делалось.

§41 ОЦЕНКА max|V«l ВО ВСЕЙ ОБЛАСТИ Q 311
В этом параграфе мы установим оценку тах|Уы|для решений
первой краевой задачи для уравнения @.1) в предположении,
что u(x)^.Wl(u) П Lip(Q), оценка vrai max| Vu КМ, на S (или
части S) известна, a S (или ее часть) является достаточно
гладкой. Оценка vrai max | V« | будет дана позже, в § 2 гл. VI,
s
сразу для решений квазилинейных уравнений общего вида
аи(х, и, ux)ux.Xt + a(x, и, их) = 0, D.1)
удовлетворяющих условию «|s = <pls, где ф(л)еО!(Й). При-
Применительно к уравнениям @.1) из теоремы 2.2 гл. VI вытекает
следующее утверждение:
Лемма 4.1. Пусть и (х) е O2(Q) |~l C(Q), удовлетворяет
в Q уравнению @.1), а на SiCzS краевому условию A.20)
с <р (л:) е O2(Q,), где Q, есть подобласть области Q и
dQ1f\dQ = S1. Пусть, далее, S^O2 и max| и(х) |<М. Отно-
а
л. - / \ a dai (*' "' р)
сительно функции а{(х, и, р), их производных ^
да{ (х, и, р) да{ (х, и, р)
> —и а(х, и, р) предположим, что при х
z
I u I <! M и произвольных р они подчиняются неравенствам
} * <—w,—|г|/^
да. (х, и, р) да1 (х, и, р)
v A +1 Р I Г-Ч2 < дп* %"' Р) 1,-1/ < IX A +1 p \Г~212, D.2)
а (х, и, р) -\
ди Ht ' дх{
D-3)
с какими-либо положительными постоянными v, \i и tn.
Тогда max " , ~..х'* для S2, принадлежащей Si и
Jtes,. лея, \х — х\
отстоящей от Q \ Q, на положительное расстояние d, оценивается
сверху постоянной Мь зависящей лишь от v, \i, М, \ ф |^>, d
и нормы Si в О2. Если Q, = Q и Su тем самым, есть dQ,
то max .1 и(*)~^(х>\ мажорируется постоянной, определяе-
J5<=S. xesQ \X — X \
мой v, ц, М, | ф g)' и нормой dQ в О2.
Перейдем теперь к оценке max|V«|. Величины max|V«|
ар ^Р
для шаров Кр, отстоящих от S на положительное расстояние,
оценены в § 3. Поэтому достаточно оценить лишь max | V« | для
шаров Кр с центрами на S. Все рассмотрения будут носить
локальный характер и будут использовать некоторые сведения
о и(х) лишь вблизи исследуемого куска Sj поверхности 5.

312 КВАЗИЛИНЕЙНЫЕ УРАВНЕНИЯ [ГЛ. IV
Итак, пусть в некоторой подобласти Q, с Q, примыкающей
к гладкому куску Sl границы S, решение и(х) имеет конечные
нормы max|V«| и ||«|2)Q, причем мажоранта М для maxlul
и мажоранта для | и |^' считаются известными. Кроме того,
предположим, что u|Si = 0 (случай неоднородного условия
« lSi = Ф |Si сводится к этому заменой и (х) на v (х) = и (х) — ф (х),
если ф(л:) предположить, например, принадлежащей O2(Q) или
даже Wq (Q), q > n). Начнем с получения оценки
v«ir~ «L + (l+|V«|)m
D-4)
для Q2p=:/C2pn ^ с: Q,, считая, что центр шара /С2р лежит
на Si, a t, (x) — срезающая для К2р функция.
Введем в окрестности S, такие координаты у = у (х), в кото-
д2ц
рых уравнение Si имеет вид уп = 0, а функции -г—|— огра-
ОХ•OXt
ничены. Возьмем тождество A.4), положим в нем ti= ^ у ,
где 1а (у) — пока гладкая финитная в Q функция, отличная
от нуля лишь вблизи Si, перейдем к интегрированию по пере-
переменным у и в первом члене проинтегрируем по частям, пере-
перенося -t— на первый множитель. Это даст
dya
где / = Detf f, " "" Л. Нетрудно проверить, что тожде-
\ о Oft Уп) I
ство D.5) остается справедливым, если в. нем |а положить
равной UyJ,2, а ф п. Подставив эту функцию в D.5) н про-
просуммировав полученные равенства по а в пределах от 1 до
п—1, мы получим равенство, в котором главным членом
бУДеТ Ж^ <Va"«a^2/ ИЛИ' Т0ЧНее' -д^-иУах{иУах?Ч (последний
*) Чтобы не вводить новых обозначений, мы указываем области инте-
интегрирования для переменных х, а не у. Индекс а в D.5) произвольно фикси-
фиксирован, суммирования по нему иет.

g fl ОЦЕНКА max|V«l ВО ВСЕЙ ОБЛАСТИ й 313
от первого отличается «несущественным» слагаемым, возни-
возникающим из-за того, что дифференцирования -^— и -г— не-
неперестановочны). Этот главный член оставим в левой части,
а все остальные перенесем направо и оценим сверху, используя
предположения C.1), C.2). В результате этого получим
га—1 п
Оценивая члены правой части с помощью неравенства Коши
вида A.2) гл. II и приводя затем подобные члены, мы из D.6)
выведем неравенство
+ (l+|V«n|Vg|2]/^. D.7)
2Р
п—1 п п—1 п
В левой части D.7) вместо 2 S «?, , поставлено 2 2 «;, „ •
a=i ,-=i yaxi a=l (=1 ^f
Это возможно, так как обе величины равносильны. В левой
части D.7) недостает члена с Чупуп- Покажем, что его туда
можно «вставить». Для этого возьмем уравнение @.1), запишем
его в координатах у и выразим из него Щпуп через остальные
члены. Из этого выражения в силу предположений C.1), C.2),
как легко проверить, следует неравенство
<c[(l +| V«|)m-22' 2 I uyu. I +A+| V« If] , D.8)
L o=i (=i' a f' J
из которого, в свою очередь, вытекает другое:
п—Х га "I
+ [V«(r-22 Ли* +(l+\Vu\)m+3\. D.9)
a=l <=1 yayl J

314 КВАЗИЛИНЕЙНЫЕ УРАВНЕНИЯ [ГЛ. IV
Умножим D.9) на ?2/, проинтегрируем по Q2p и сложим с D.7).
В результате получим
п
Jd+ivai)-»^ ^
dy. D.10)
Это неравенство вместе с неравенством D.7) гл. II гарантирует
оценку D.4) для всех достаточно малых р^р0. Постоянная с
в нем и р0 определяются М, v (М) и ц (М) из C.1), C.2), т, | и f^
и нормой Si в О2.
Получим теперь оценки вида C.14) с любым s^l для
Qp = Kpf\&, где Кр — шар, концентрический рассмотренному
выше шару /С2р с центром на S,. По-прежнему будем считать,
что и |S[ = 0, и, кроме того, предположим, что vrai max | V« | ^ Ми
Возьмем в тождестве C.3) функцию l(x) = bs (х)их (х)?2(х),
1, г= 1, ..., п, где
0 при |Vu(Jt)KM1(
\Vu (х)\2 — М2 при \Уи(х)\^Ми
а ?(^1 —гладкая срезающая для шара /С2р функция.
Легко видеть, что при s^l функция bsux?,2 обращается
в нуль на границе О, и в силу предположений о и (х) является
допустимой для тождества C.3). Эта функция мало отличается
от функции I/иХ/?,2, которую мы брали при выводе внутренних
оценок, и получаемые с нею соотношения в существенном
такие же, как и выше. Именно, в результате подстановки bsuX/t,2
в C.3) и оценок, аналогичных вышеприведенным, получим
неравенства типа C.6), в которых b (x) заменено на b (x), а /С2р
на Q2p. Единственное важное отличие состоит в том, что эти
неравенства (обозначим их через C.6)) выведены нами не для
s^O, как C.6), а для s^l. Для s = 0 присоединим к ним
неравенство D.4).
Справедливы также аналоги неравенств C.7), именно нера-
неравенства C.7), получаемые из C.7) заменой функции b (х) на Ь(х)
и шара /С2р на область Q2p. To, что в данном случае ?(*) обра-
обращается в нуль не на всей границе Q2p, несущественно, ибо там>
где ?(х) ф 0 (на пересечении /Сгр с Si), обращается в нуль
функция и, и этого, как видно из леммы 4.5 гл. II, вполне
достаточно.

§41 ОЦЕНКА max|V«l ВО ВСЕЙ ОБЛАСТИ Й 315
Итак, в нашем распоряжении неравенство C.6) для s^l,
неравенство D.4) и неравенство C.7) для s^O. Из них так же,
как и выше, выводится оценка интегралов
J [ | Vii |m+2+2s + A + | Vii If-2+2s a2,] dx<c (s). D.11)
С помощью неравенств D.11) величина max|V«| в области
йр/2 = /(р/2Л й, где Кр/2— шар, концентрический с Кр, оценивается
таким же образом, как для внутренних подобластей. Надо лишь
при подстановке в C.3) функций
l(x) = uXr{x)t>2(x)max{\Vu(x)\2t>2(x)-l;0} при т^2
или
6 (х) = иХг (х) I2 (х) A + | Vn (х) I2I2" X
V« (л:) |2 ?2 (л:) — /; 0} при 1 < т < 2
брать значения l^M2 (здесь ? (л:) — срезающая для Кр функция).
Для таких / функции g (х) обращаются в нуль на S и, следова-
следовательно, являются допустимыми для C.3).-Соответственно этому
неравенства C.17) будут выполняться не для всех положитель-
положительных уровней k, а для k, больших некоторого k > 0, зависящего
от М,. Этого, как видно из леммы 5.3 гл. II, достаточно, чтобы
оценить max|V«|2?2. Итак, доказана следующая лемма:
аР
Лемма 4.2. Пусть относительно а{ (х, и, р) и а (х, и, р)
выполнены условия C.1) и C.2), а и{х) есть ог. об. решение
задачи @.1), A.20), принадлежащее W\{Q) Л Lip(Q). Если ф(х)е
еО2(Й), vrai max| V« |<! M1 и S^O2, то vraimax|V«| оцени-
s a
вается постоянной, зависящей лишь от m, M, v (M) и [i (M)
из C.1) и C.2), М» |Ф|® и S.
Если только часть St границы S принадлежит О2,
vrai max | V« К А!, и cpeO^Q,),
s,
где Qj — подобласть Q, граница которой имеет с S общую часть,
принадлежащую Sb то для любой подобласти Q2 области Qu
отстоящей от части границы Qu принадлежащей Q, на какое-либо
положительное расстояние d, величина vrai max | V« | не превос-
а,
ходит постоянной, зависящей лишь от m, M, v (М) и ц (М)
из C.1), C.2), М\, |?g, d и поверхности S,.
Из лемм 4.1 и 4.2 следует

316
квазилинейные уравнения
[ГЛ. IV
Теорема 4.1. Пусть функции at(x,u,p) и а(х,и,р) при
x^il, | и К М и произвольных р удовлетворяют неравенствам
C.1), C.2), a S е= О2. Пусть и(х) обладает свойствами, nepenw
сленными в лемме 4.1 и лемме 4.2, и удовлетворяет уравне-
нию @.1), а на S удовлетворяет условию u|s = (p(s), где ф(л:)е=
gO2(Q). Тогда vrai max | V« | оценивается постоянной Мь зави-
B)
сящей лишь от М, m, v(M) и ц(М) из C.1), C.2), |<р|а
от поверхности S.
а также
§ 5. О существовании обобщенных производных
второго порядка. Об ограниченности градиентов
обобщенных решений
В §§ 3 и 4 были получены априорные оценки для max I V« |
Й'
и max| V« | в предположении ограниченности \Vu\ и существова-
а
ния у решения и производных второго порядка. Здесь мы вер-
вернемся к рассмотрению ог. об. решений и из Wlm (Q). В § 1 было
доказано, что любое ог. об. решение и принадлежит Ca(Q),
если только а,- и а удовлетворяют условиям A.2) и A.3).
Покажем, что при несколько более сильных ограничениях на
функции а{ и а каждое такое и обладает обобщенными произ-
производными второго порядка и для него справедливы оценки, про-
проведенные в § 3, в частности vrai max |V« |^С(У) < се. Пусть
при jefi и произвольных и и р функции а{ (х, и, р), а(х, и, р)
дифференцируемы по х, и и р и удовлетворяют неравенствам
\m-2,
<
даг (х, и, р)
, E.1)
- E-2)
Легко видеть, что неравенства A.2) и A.3) следуют из этих
предположений, и, следовательно, мы вправе считать, что

% Ь] ОБ ОБОБЩЕННЫХ ПРОИЗВОДНЫХ ВТОРОГО ПОРЯДКА 317
о решении и(х), помимо конечности норм ||и|^ й и тах| и |<М,
известно: «еСа(й')и|« № < М (Q') < °° Для V^' <= Q-
Возьмем произвольный шар Кр, принадлежащий Q вместе
с концентрическим ему шаром /С2р, и функцию г\ (х) =
= [f («(ft) (*)) ?2 Wl(ft). где ? (*) — гладкая срезающая для /Ср функ-
функция, a H(fe) и [ ]_—правое и левое разностные отношения,
определенные в § 1 гл. I, именно: н(й)(л:) —Л [и (x + hek) — и (х)],
u(j){x) = h~1[ti(x) — и{х — Лей)]. Функция/(/) равна / для т>2
(/ е (— оо, оо)). При (иеA,2) / (/) есть нечетная функция, рав-
равная при />0 интегралу f f'(x)dx, где /'(т) есть 1 для ts[0, yv]
о
и JV2~mTm~2 при x^N. Функция / зависит от параметра N >0,
и потому ее лучше было бы обозначить, например, так: /#(/).
Однако для упрощения записи индекс N в выкладках будем
опускать. Функция /(/) имеет производные f и /" (последняя
при т < 2 разрывна в точке t = N), причем /'(/)>0. Элемен-
Элементарно проверяется, что 0^.tf(t)^.cmt2ff(t) для всех t, причем
постоянная ст = 1 при /и>2 и cm = (m—1) при шеA,2).
Кроме того, (^-//f7^)J </'(/)•
При Л<!р взятая нами функция г\(х) допустима для тож-
тождества A.4). Подставим ее в A.4) и в обоих членах проведем
«суммирование по частям» в соответствии с формулой D.8)
гп. II:
0= J {а, (х, и, их)[/(«(ft,)%2]ф)Х{-а(х, и, их)[f (u(k))t,2]^} dx =
Q
- - J {[af (x, u, ux)]w (f'uw xp + ШХ{) ~ [a (*, u, ux)\k) f?) dx.
Q E.3^
Ho
о *
*'.«'. 4) Л _L f ^,(^>^4) dt _
,4

3)8
КВАЗИЛИНЕЙНЫЕ УРАВНЕНИЯ
[ГЛ. IV
где
x' =
Поэтому из E.3) следует
-t)x + t (x
Из этого соотношения, учитывая предположения E.1) —E.2) и
неравенства B.4), B.5), получим неравенство
. E-4)
где Pk = 1 + | V« (л:) | + | V« (л: + Aefe) |, а с, определяется постоян-
постоянными из условий E.1), E.2). Каждый член правой части E.4),
содержащий I V«(fe) |, оценим по неравенству A.2) гл. II так,
чтобы первое слагаемое было равно е, умноженному на подын-
подынтегральное выражение, стоящее в левой части E.4). Собирая
затем эти первые слагаемые вместе и перенося их сумму налево,,
получим после приведения подобных членов половину интеграла,
стоящего в левой части E.4), если е возьмем равным (Sci)~ .
Слагаемые, оставшиеся после оценки членов с | V«(fe) |, имеют
вид с2 [рГ (!21П ivg|2 + nfulg + nit + К if 1П t] - cjv
Остальные четыре члена подынтегрального выражения, стоящего
в правой части E.4), можно оценить с помощью неравенства A.2)
гл. II с е= 1 так, чтобы они не превосходили слагаемых, входя,
щих в выражение /,. Наконец, заменим в /, дробь/2(«(fe))/(f'(«(ft))
величиной, не меньшей cmu^k)f («(fe))- Все сказанное показывает,
что из E.4) следует неравенство
u2(k)\ V? f
J [
с постоянной с3, определяемой Cj из E.4) и т.
E.5)

§6] ОБ ОБОБЩЕННЫХ ПРОИЗВОДНЫХ ВТОРОГО ПОРЯДКА 319
Для оценки интеграла /2= | P^fu^tdx при т^2 исполь-
зуем лемму 1.3. А именно, запишем неравенство A.15), во-пер-
во-первых, для решения и(х) уравнения A.1) и i = ?V7'«ffe) и, во-
вторых, для функции v (х) = и (х + hek), являющейся решением
уравнения
¦gj- а{ (x + hek, v(x), vx (x)) + a (x + Ae*. v(x), vx(x)) = 0,
t
имеющего те же свойства, что и уравнение A.1), и той же
функции | = ? V/'u(*)- Сложим эти неравенства и восполь-
воспользуемся элементарными неравенствами A -\-а + b)m < 2 X
справедливыми при Va, 6^0, т ^2. Это даст
;2= fp^/'«L?2^<2m Г [A +| V«|)m + A +1 Vo
РГ2| v|frfx<2m+1,paJРГ2 [(-^/?T@Jl(=u(ft X
XI v«,*) I2 ?2 + Л& I v? f ] rfx < 2m+1cpa J p?-2/' («(ft)) x
J
«p
jc. E.6,)
При me(l, 2) оценим интеграл/2 так, как указано в лемме 4.4
гл. II, взяв в ней в качестве и(х) функцию Pk(x), в качестве |
функцию ? Vf'ufky a B качестве а показатель am. Условия этой
леммы выполнены, ибо Рк(х)^0 и в силу леммы 1.2 данной
главы, примененной к решениям и (х) и v (x),
*р
-п+т-^-
>т \\x-y
г am
+ Р
am am
"t s— . —2~

320 Квазилинейные уравнения [ГЛ. iv
при р^1. Оценка, даваемая леммой 4.4 гл. II для /2, имеет
тот же вид, что и последнее из неравенств (б-б^, так что для
любого т > 1 приходим к неравенству
f)dx, р<1, E.62)
с известной нам постоянной с5. Для р, удовлетворяющих усло-
условию с3с5ра<72, из E.5) и E.62) следует
Г pm-2r' .у ,2 2 , ^
J
< с6 J (РГ2/'и(% | V? |2 + Pkf't,2) dx e= c6j3 (h), E.7)
a отсюда и из E.62) и
J Pk I U(k)t, dx ^ c7]3 (h) E.8)
Интеграл /3(А) при Л^-0 стремится к
Действительно, согласно лемме 4.6 гл. II щк) сходится к иХк
в норме Lm(Kp) и почти всюду, а по теореме Д. Ф. Егорова и
почти равномерно (т. е. равномерно на Кр, за исключением не-
некоторых множеств сколь угодно малой меры). Кроме того, инте-
интегралы вида /4, взятые по множествам малой меры, малы. Рав-
Равномерно малы и интегралы вида /3(Л), взятые по тем же мно-
множествам малой меры. Это так в силу сильной сходимости щк)
к uXk в Lm(Kp) и выбора функции f(t) (напомним, что для
m>2 f (/) = /, а для те A,2) 0< t2f'(t) <N2~m\t Г при
| /1 > N). Из всего сказанного следует, что /3(Л)->-/4 при h ->0,
и, тем самым, /3(Л) не превосходит некоторой постоянной.
Перейдем в E.8) к пределу по Л—>0, используя для левой
части известную лемму Фату о том, что для неотрицательных
функций F (х, К), сходящихся при Л->-0 почти всюду к F(x) и
имеющих равномерно ограниченные интегралы j F(x, h) dx,
*p
справедливо неравенство J F(x)dx^\im \ F (x, h) dx. В

§ 6] ОБ ОБОБЩЕННЫХ ПРОИЗВОДНЫХ ВТОРОГО ПОРЯДКА 321
результате получим неравенство
J A + 2 | V« | Г Г (ич) u\g dx < с7/4, E.9)
«о
из которого для Ш ^2 следует конечность интеграла
11 Vm Г м^ ?2 dx. Для иеA,2) перейдем в E.9) к пределу по
«р
N-^-oo. Интеграл /4 при этом будет иметь своим пределом
интеграл
*р
Неравенство E.9) приведет к неравенству
. E.10)
Суммируя E.10) по k, получим
при любом т > 1.
Из E.7) при т ^2 заключаем о равномерной ограниченности
интегралов Г | VM(fe) ft?dx, что в силу леммы 4.6 гл. II гаран-
«р
тирует существование производных V«Xft и сходимость почти
всюду и почти равномерную V«(ft) к V«Xft в /Ср- Благодаря
этому переход к пределу по Л->0 в E.7) и суммирование по k
дает неравенство
6/6> где P=1+2|V«|. E.12)
Чтобы доказать справедливость E.12) для теA, 2), воспользуем-
воспользуемся уже доказанной суммируемостью |V«|m+2? по Кр (см. E.11)).
Она гарантирует сходимость u(k) к uX/t в нормах L2+m (Kp-e)>
Ve > 0 (см. лемму 4.6 гл. II). В неравенстве E.7), как нетрудно
видеть, в качестве функции / (/) можно теперь взять /(/) = / и
для случая теA,2). Ввиду этого положим в E.7) }'= 1 и
11 О, А, Ладыженская, Н, Н, Уральцева

322 КВАЗИЛИНЕЙНЫЕ УРАВНЕНИЯ [ГЛ. IV
перейдем к пределу по h-*-0, считая ? равной нулю в погра-
пограничной полоске. Правая часть E.7) при этом имеет своим преде-
пределом с6/5, а левая часть E.7), тем самым, не будет превосхо-
превосходить некоторой постоянной с8. Это и неравенство Гёльдера
Г |
«P
m)l21 J РГ2\ Щк f ?2 dx\ml2
РГ2\ Щк) f ?2 dx\
гарантируют равномерную (по h) ограниченность интегралов
\m?2dx, из которой в силу леммы 4.6 гл. II следует
р
существование производных V«<ft и сходимость почти всюду и
почти равномерно в Кр V«(ft) к УиХк. Благодаря этому переход
к пределу по Л->0 в E.7) с /'s 1 и суммирование по k от 1
до п приводят к неравенству E.12). В нем мы должны счи-
считать ? равной нулю вблизи <Э/СР- Но так как в остальном
функция ? произвольна, то легко понять, что E.12), так же как
и E.11), остается справедливым и при любой гладкой ?, рав-
равной нулю на (Э/Ср.
Так как шар Кр выбран с одним лишь условием, что кон-
концентрический ему шар /С2р принадлежит й, то из проведенных
рассуждений следует существование у и(х) обобщенных произ-
производных второго порядка в Q и оценок E.11) и E.12) не только
для шаров /Ср, но и для любой Q'_cz Q с ?, равной нулю на дп'.
Кроме того, для всех т > 1 и VQ' с Q доказана равномерная
ограниченность интегралов
/(т, Q0,
kml
E.13)
Of)
при всех достаточно малых h.
Перейдем к доказательству ограниченности Vm и получению
оценок vraimax| Vm |. Для этого мы покажем ниже, что в C.3)
в качестве функции | можно взять произведение b%(x) uXr(x) t, (л:),
s>0, где ? (л:) —срезающая для шара К2р функция, а
Ы*) —min{|V«(*)p; N), N > 0.
Относительно Кчр предполагаем, что концентрический ему шар Ка9
принадлежит Q. Если в C.3) положим | равной функции

§ 5] ОБ ОБОБЩЕННЫХ ПРОИЗВОДНЫХ ВТОРОГО ПОРЯДКА 323
%ы = Ь%их{? (заметим, что lN имеет обобщенные производные
¦?—lti) и раскроем выражение для -%— \N, то придем к соот-
ОХ J ОХ ^
О[ J ОХ ^
ношению C.4), в котором Ь заменено на Ъы. Все полученные
при этом члены будут суммируемы по /С2р- Более того, все
неравенства, начиная от C.5) и кончая C.14), выведенные в § 3
из C.3), сохраняются при замене Ъ на bN, причем постоянные с,
входящие в эти неравенства, не зависят от N.
При проверке этих утверждений надо иметь в виду, что Vbff
отличен от нуля только на том множестве, где | Vm |2 < N, т. е.
там, где bN = \Vuf. Это, в частности, дает равенство
r\Vu\)mVbt
которое надо использовать для перехода от C.5) к C.6) при
b = bN. Так как постоянные в неравенствах C.5)—C.13) не
зависят от N, то из C.12) и C.13), последовательно увели-
увеличивая г, начиная от г = 0, выведем желаемую конечность
интегралов, входящих в C.14), и саму оценку C.14).
Для законности всех этих рассуждений надо доказать, что
в C.3) в качестве | можно взять |# = Ьыих t при Vs^ О, N > О
и любой гладкой ?, равной нулю вне /С2р. Введем функции
In, а = Флг (I va« Р) "(/-)?2. гДе 4>n @ — неотрицательная, дважды
непрерывно дифференцируемая функция /^0, равная const
п
при t~^N, | VftM |2= 2 и?*)) а ? — дважды непрерывно диффе-
ренцируемая функция х, равна нулю вне /С2р> и функцию FNl(t),
равную 1 при t^Ni, нулю при t^2Nx и Л^Г1 B^1 — /) при
t^[Nu 2Ni\. Исследуемое решение м(х) удовлетворяет почти
всюду уравнению A.1). Умножим это уравнение на (lN,f)XrX
1 + 21 V+u\2 , где | Vm*(x) | = | Vm (x + hek) \ при k > 0,
fe=0 /
+0
a | Vm(x) | = | Vm(x) |, и результат проинтегрируем по Q:
i l/ 1
м, их)](Ь, h)XrX
. E.14)
Благодаря уже известным свойствам м (х) и предположе-
предположениям E.1), E.2) интеграл, входящий в E.14), конечен. Более
11»

324 КВАЗИЛИНЕЙНЫЕ УРАВНЕНИЯ [ГЛ. IV
того, в E.14) можно провести двукратное интегрирование по
частям в следующем порядке: (
О = J [" a, (lN, h)XrXi FKi - at (|„, ^ ^ + a (|„ ^ ^ j dx
= J [dbt ($N. h)X{ FN, + ai FjV. ft)*, ~d^7 ""
Интегралы, входящие в E.14) и E.15), сходятся благодаря
функции FN[ 1/ 1 + 2l ^и | ], «срезающей» те множества, на
\ " ь=о /
» +k
которых 1 + 2j I Vm(x) pX2yV;J. Действительно, там, где 1 +
+ Е!Уы%)р<B^J, функции ихх(х) и «„(* + Ае*). * =
fe=0
= 1, ...,«, а потому и функции щк)хх(х) = -j[ихх{х + htk) —
— иХх(х)] квадратично суммируемы в силу E.12), а функции
Щк) xt = -? [иХ{ (х + hek) — Ux{{x)] ограничены (заметим, что пока h
фиксировано). В равенстве
J dxr w, hi r^-r at [Sn, h)x dxr
= 0
функция lNih дифференцируется один раз. Ввиду этого не-
нетрудно понять, что E.16) справедливо не только при дважды
непрерывно дифференцируемых функциях q>N(t), входящих в %NtU
но и при ф,у (/), равной ts, s^O, при t ^. N и рав-
равной № при t~^N. Будем в дальнейшем считать, что ф^(/) = Г
при ts^N и Ф^@ = Л^5 при t^N. Покажем, что в E.16) можно
перейти к пределу по /г-»0 и в результате получить равенство
=o' El7)
где lN = b'Nux S2, bN=min{\ Vm f; N}. Действительно, подынте-
подынтегральное выражение E.16) сходится почти всюду к подынте-

$5]
ОБ ОБОБЩЕННЫХ ПРОИЗВОДНЫХ ВТОРОГО ПОРЯДКА
325
тральному выражению E.17). Ввиду этого достаточно убе-
убедиться, что интегралы E.16), взятые по множествам Q8cQ'
малой меры, равномерно (по h) малы. Действительно,
da,
—2,
dxT
= |<P"(IVI>
V|2)«(^;
\+Рт), P=
I2)
x, I s2
NS\ щг) |2?|
поэтому
Рт)[\
|]?X
^c(N, N,) J (\ux
где Qe (Ni) = I x <= Qe: 1 + 2j I Vm \^.BN1J \. Оценивая правую
часть по неравенству Коши, убедимся, что
\h\^c(N, Nt)( J (\uxx\+lL>
x
п
В силу E.12) первый из интегралов правой части мал, если
мала mes Qe, причем интеграл не зависит от h. Второй же рав-
равномерно (по К) ограничен в силу E.13). Аналогичные оценки
показывают, что и все остальные интегралы E.16), взятые
по Qe, равномерно (по h) малы при малой mesQe. Тем самым
показано, что E.16) при Л-»0 переходит в E.17). Устремим
теперь в E-17) N\ к се и покажем, что в пределе получим
соотношение
j{^ )x = 0, E.18)
с теми же функциями %N, что и в E-17).

326 КВАЗИЛИНЕЙНЫЕ УРАВНЕНИЯ [ГЛ. IV
Подынтегральные выражения в E.17) и E.18) различны лишь
на множествах Qjv, = {х е Q: 1 + (п + 1)| Vm (х) f > N2}, поэтому
для справедливости E.18) достаточно убедиться в том, что инте-
интегралы E.17), E.18), взятые по Qjv,, стремятся к нулю при
Для ЦЫ, tf,)-
имеем
J (
Рт-2\ ихх | + Рт){\ их
Так как mesQjv, ->0 при Л^-х», то это вместе с E.11), E.12)
гарантирует нужную малость ](N, NJ при достаточно боль-
больших Ni. Далее,
dx<
Из этого соотношения, как показано на стр. 323, следует
конечность интегралов, входящих в неравенство C.14). Бла-
Благодаря этому сохраняют силу все рассуждения и выводы § 3,
проведенные после C.14). Действительно, функции |, использо-
использованные при выводе неравенства C.16) для и^2 и неравенства
C.18) для те A,2), принадлежат Wl(Q"), где Q" с: Q. Такие
же | являются допустимыми для тождества C.3), ибо в силу
предположений тах| и |< се, C.1) и C.2) и оценки C.14) функции
и
л /у\ ddjix, и(х), их(х)) л/ \_ / / ч / ^
йи \Х) = -j-K и а(х) = а(х, и (х), их (Х))
квадратично суммируемы по VQ" с Q.
Итак, доказана
Теорема 5.1. Пусть выполнены условия E.1), E.2) и и есть
ог. об. решение уравнения @.1). Тогда и имеет в Q обобщенные
производные второго порядка, принадлежащие L2(Qr), VQ'czQ,
а его производные первого порядка ограничены в любой Q' с Q.
Величины || и ||12V,, и vraimax|V«| не превосходят постоянных,

5 в] оценка норм | и |(Z+a). /> i 327
определяемых tn, М>тах|м|, v(M) и ц(М) из C.1), C.2) и рас-
расстоянием от Q' до S. _
Заметим, что в силу теорем § 1 и есть элемент Ca(Q') и его
нормы (и^ и || и 1^q, определяются М, постоянными из A.2),
A.3) (и тем более из C.1), C.2)) и расстоянием от Q' до S. Эти
факты были использованы при доказательстве теоремы 5,1 и
учтены в ее формулировке.
§ 6. Оценка норм |«|<z+a), l>\
Предположим, что и{х) есть решение уравнения @.1), при-
принадлежащее классу и^г(й) и имеющее ограниченные первые
производные. Покажем, что они непрерывны по Гёльдеру при
условии, что уравнение @.1) эллиптично на и(х), т. е,
v>0. F.D
Относительно функций а{(х, и, р) и а(х, и, р) достаточно
предположить, что а{ (х, и, р) дифференцируемы по аргументам
х, и, р, функция а(х, и, р) измерима и
max
да{(х, и(х), их(х)) да{
ди ' дх,
i, 1=1 я. F.2)
В интегральном тождестве A.4) положим r\ = %Xl, где %(х) —
достаточно гладкая функция, финитная в Q, а / — одно из чи-
чисел 1, ..,, п. В результате интегрирования по частям получим
равенство
Как легко видеть, оно будет справедливо в силу наших пред-
о .
положений при любой | (х) из W2 (Q). Запишем его в виде
х dx =* °' F'4)
где
dai{x, u(x), их(х))
7
ачМ Шх

328 КВАЗИЛИНЕЙНЫЕ УРАВНЕНИЯ [ГЛ. IV
да{ (х, и (дс), и (х))
ft М = —~ ди % W +
dat (х, и (*), и (х)) ,
-\ ~ Yx + 6i п (*' " М' "* W)'
В силу условия F.2) и ограниченности vrai max | Vm | ^ M2
функции 1\{х) ограничены по модулю некоторой постоянной
с(М2, Hi). Поэтому каждую из производных ы„, /=1, ..,, п,
i
можно рассматривать как решение линейного уравнения вида
D.1) гл. III с ограниченными измеримыми коэффициентами ait
и flr Отсюда на основании теоремы 14.1 гл. III заключаем, что и
принадлежат Ca(Q) и их нормы ы„ (а> для любой Q'cQ можно
оценить через М2, v, ц, и ц{ из F.1), F.2) и расстояние Q' до S,
Показатель а зависит лишь от ц/v.
Чтобы получить такие же оценки для всей области Q, пред-
предположим, что граница S принадлежит классу О2, vrai max | Vm |^
2
=^М2 и и(х) на S удовлетворяет условию A-20) с ф(х) из W2q(Q)
с q > п. Рассмотрим произвольный кусок S,cS и введем, как
обычно, координаты уи ..., уп, в которых уравнение S, есть
д2Уь
^/„ = 0 и функции -^—^—ограничены. В новых переменных
OX t OX t
уравнение @.1) будет иметь вид
F.5)
Как мы видели выше, для и справедливо тождество D.5) или,
что то же, тождество
причем, в качестве | здесь можно взять произвольную функ-
О |
цию из UMQ), отличную от нуля лишь вблизи S]. Тождеству
можно придать вид

58) ОЦЕНКА НОРМ I «|('+a), Z>1 329
где
да,(х,и(х),их(х))
и
da- (лс, и (лс). и (*)) da,
суть ограниченные в Q функции х, и рассмотреть иУ[ как обобщен-
обобщенное решение из Wii®) линейного уравнения — (a'/°* +/') = 0-
Пусть Q, — часть области Q, примыкающая к S, и отстоя-
отстоящая от S \ S] на положительное расстояние d.
Из теоремы 14.1 гл. III о линейных уравнениях следует,
что иУ[ е Ca (Qi), /= 1, ..., п — 1, и их нормы J иУ{ j(a) можно
оценить через известные нам постоянные. Условие упомянутой
теоремы о том, чтобы граничные значения и =ф„ ПРИ"
Si
Si
надлежали С6 {Si), тоже выполнено, ибо из принадлежности <р
к W2g (Q), q > п, следует по теоремам вложения принадлеж-
принадлежность ф к C1+a(Q) с 6=1--.
В случае / = п нельзя непосредственно использовать тео-
теорему о линейных уравнениях, так как нам ничего не известно
о гладкости иу на S\. Поэтому поступим иначе — докажем,
что для любого шара Кр с центром в Q] и радиусом р ^ d/4
верно неравенство
P>0. F-7)
гд,е Qp = Kp(]Q\- Тогда из леммы 4-2 гл. II будет следовать,
что \иу Р оценивается через у, d и тах\иу I.
Разрешая уравнение F.5) относительно иУпуп, получим Щпуп =
= 2 2 buUy у + Ь с ограниченными Ъц и Ь. Отсюда видно, что
I 1Фп ' '
для того, чтобы доказать F.7), достаточно установить анало-
аналогичные неравенства для иу с / Ф п, т. е.
/=1, .... я-1. F.8)
аР

330 КВАЗИЛИНЕЙНЫЕ УРАВНЕНИЯ [ГЛ. IV
Итак, докажем справедливость оценок F.8). Для этого
в тождестве F.6) для иу с каким-нибудь 1Ф п положим
\ = (и— ф)^ ?2, где ? — срезающая для /Сгр функция, равная еди-
нице в /Ср. Очевидно, что |е и^2,(Й2р). В результате будем иметь
J {щЩ^Щ,*}? - atjUypflgpfc* + aijUy[Xj (utl - щ) 2??ж< +
\x=о.
Оценивая первый интеграл снизу по неравенству F.1),
а остальные члены по модулю с помощью неравенства Коши
с 8] s @, 1], будем иметь
^pdx + b J
JP «-1 Q2p '-1
т J ("»' ~ W2'vsfdx + imesQ2p> F-9)
где постоянная с определяется max I a,,, fi I. Заметим, что
Q* _
ф^ e С (Q) и по доказанному выше иУ[ е С" (Q2p)« «^ 6. так что
max | ип — щх |2 < ср«".
а2р
Кроме того, max|Vg|^c/p и
I
I, *—1
<t>|f aJmes'
Поэтому, полагая в F.9) e, = v/2, получим желаемое неравен-
неравенство F.8) с p = min{a, {q—n)/q} и постоянной v'> зависящей
лишь от ||ф||^2)а, тах|а;/, f{| и константы v из F.1).
Сформулируем доказанные в этом параграфе предложения
в виде теоремы.
Теорема 6.1. Пусть и(х) принадлежит №г(й), имеет огра-
ограниченные ha Q первые производные и удовлетворяет почти
всюду в Q уравнению @.1), причем для а{ и а выполнены усло-
условия F.1) и F.2). Тогда производные иХ[, /=1, ..., п, принад-
принадлежат классу Са (Q) с показателем а > 0, определяемым лишь цу'1
из условия F.1). Нормы | и (j,+a) (Эля VQ'cQ мажорируются

§ 6] ОЦЕНКА НОРМ | и \Н+а). Z> 1 331
постоянной, зависящей лишь от v, ц, ц, из условий F.1), F.2),
М, ^ vrai max \Vu\ и расстояния от Q' до границы Q.
2
?слм /с тому же и (х) удовлетворяет граничному условию A.20)
с ф (х) <= U^? (й), <7 > «. и 5 принадлежит классу О2, то произ-
производные их (х), /= 1. • • •. «. непрерывны по Гёльдеру в замкну-
замкнутой области Q с показателем р > 0, определяемым v~lp. и q.
Норма | ы ^+Р) мажорируется постоянной, зависящей лишь от v,
ц, ji,, M2, <?, lf
Замечание 6.1. Как легко видеть из доказательства тео-
теоремы 6-1, в ней можно ослабить требование F.2) на at и а,
\да,(х, и(х), их(х)) да{
именно, можно считать, что ^ ' F'а ^
II / Ид. Q
И! < се, q>n, i, /=1, ..., п (см. по этому поводу гл. IX).
Из теорем 6.1 и 51 и замечания 6.2 вытекает справедли-
справедливость такого предложения:
• Теорема 6.2. Пусть и (х) есть ог. об. решение у равнения @.1),
и функции at(x,u,p) и а(х, и, р) удовлетворяют условиям.
(б. 1), E.2). Тогда и (х) принадлежит С1+а' (q') f) Wl (qO для Vq' с: Q
U нормы и(х) в С1+а(й') и Wl(?i') оцениваются постоянными,
определяемыми m, M>max|«|, v(M) и ц(М) из C.1), C.2) и
расстоянием от Q' до S. Показатель а определяется m и
()'(M)
)()
Рассмотрим уравнение @.1) и какое-либо его решение
из WUti) с тах|м|^М и vrai max| Vm |^M,, для которого
а а
верно F.1). Предположим, что а{(х, и, р) и а(х, и, р) принад-
принадлежат классам С1+р и & соответственно в области
= {xeQ, |«|<M, IpKM,}, Запишем уравнение @,1) в виде
ац (х) uX{Xf + А (х) = 0,
где
да{ (х, и (х), и (х))
дих
да{ (х, и (х), и (х)) да{
А(х)= ди иХ{(х)+-^ + а.
В силу теоремы 6.1 ы(х) еС|+а(й), и потому ац(х) и Л(х)
непрерывны по Гёльдеру в Q с показателем ар. Результаты
§ 12 гл. III о линейных уравнениях (теорема 12.1 гл. III) дают
возможность утверждать, что ы(х) eC2+ap(Q). Отсюда следует,
что alt(x) и А(х) принадлежат Ср(й), поэтому, применяя еще раз
теорему 12.1 гл. III, убеждаемся, что «(x)eC2+p(Q) и его

332 КВАЗИЛИНЕЙНЫЕ УРАВНЕНИЯ [ГЛ. IV
норма | и ^,+р) для любой Q'cQ оценивается через М, Ми
I я* С+^ . I a С > константу v из неравенства F.1) и расстоя-
ние Q' до S, Если, кроме того, S<=C2+Si и ы |s <= С2+р (S), то
точно так же с помощью теоремы 6,1 гл. IV и теоремы 12,1
гл. III можно оценить норму | и (^+р\ Аналогично устанавли-
устанавливается принадлежность м(х) к С1+а и Cz+a(Q) при любом / > 2.
Резюмируя только что сказанное, можно утверждать спра-
справедливость такой теоремы:
Теорема 6.3. Пусть м(х) есть решение уравнения @.1)
из W\{u) с max |ы(х)|^М, vrai max| V«(x) \^М{. Если урав-
нение @.1) «а и(х) эллиптично {т. е. выполнено неравенство F.1))
и если
<ц (х, и, р) е= С'-'+Р (9Ям, м), а (х, ы, />) <= С'+Р (Шм, м), I > 2,
то и (х) принадлежит Cz+P (Q) и для любой Q'cQ норма \ и |^,+р)
оценивается постоянной, зависящей лишь от М, Ми \ at |™~1+M,
il—24-fti ^
| aL , константы v ыз F.1) ы от расстояния Q' (Эо S. Если,
кроме того, S е Cz+P и и \s e Cz+p (S), то норма \ и |[|+р) оцени-
оценивается постоянной, зависящей лишь от М, Ми \ а{ |^
Замечание 6.2. То, что в теореме 6.2 показатель Гёльдера
для иХ{ можно выбрать не зависящим от расстояния Q' до S,
вытекает из следующего рассуждения. Мы доказали, что для
V^p,(x°)cQ osc{m^z; Кр (х0)} <с'ра', Vp<pb где с' и а' зависят
от расстояния /Ср,(х°) до S. В силу этого в /СР(х°) с с' |/йра'^
<min{j. p,lотношение max A+| V«(x) D^/mind+l V«(x) Г<
^2 '. Отсюда и из E.1) следует, что в этом шаре нера-
неравенство F.1) выполняется с у = И*Л' = 2'т~2|ц,(М)Д>(М). Но
тогда теорема 6.1 гарантирует для иХ[ показатель Гёльдера at
зависящий лишь от m и n(M)/v{M).
Подытожим основные факты, установленные нами в §§ 1—6
для ог. об. решений уравнения @.1).
В § 1 доказано, что ог. об. решения и (х) из Wlm (Q) непре-
непрерывны по Гёльдеру, и даны_оценки гёльдеровских норм ы(х)
для внутренних подобластей Q'cQh для всей Q. В § 5 выяс-
выяснено, при каких условиях такие решения обладают обобщенными
производными второго порядка и имеют ограниченный тах| Ум |.

§ 7] ОЦЕНКИ ДЛЯ ОБОБЩЕННЫХ РЕШЕНИИ 333
Теорема 6.4. Предположим, что в областях вида 2№лш,
с произвольными М и М\ > 0 функции а{ (х, и, р) принадлежат
классу С'-1+E, /^2, а а{х, и, р) — классу С'+Р при / > 2 и С1
npU l = 2 соответственно и at (x, и, р) и а (х, и, р) удовлетво-
удовлетворяют неравенствам E.1), E.2). Тогда любое ог. об. решение и(х)
из Wm{Q) уравнения @.1) в любой Q'cQ принадлежит Cz+p(Q')-
Кроме теорем 6.2—6.4 из предложений, доказанных ⧧ 1—6,
вытекает следующая теорема об априорных оценках для реше-
решений уравнения @.1):
Теорема 6.5. Пусть решение и{х) уравнения @.1) при-
принадлежит tt^l(й)ПLip(Q) и тах| и(х) \^М. Пусть, далее, функ-
ции at(x, и, р) и а(х, и, р) удовлетворяют условиям C,1),_C.2).
Тогда и(х) е С1+а(й') и нормы \и&+а) и || ыЦ^, для VQ'cQ
мажорируются постоянными, зависящими лишь от m, M, v(M)
и ц(М) из C.1), C.2) и расстояния от Q' до границы S обла-
области Q. Показатель а определяется m и \i(M)v~l (M). Если
•к тому же_ и (х) е О2 (Q) f) Wl(Q) f) Lip (Q), S<=02 и u\s = y\s,
Ф (x) e O2(Q), то и (x) e C1+a (Q) и нормы \ и fj+a) и || и |f22)Q мажо-
мажорируются постоянными, зависящими лишь от m, M, v (М) и ц (М)
из C.1), C.2), |Ф?? и S.
Если, кроме того, а^(х, и, р) и а(х, и, р) на множестве
ЯЯм, м, = {х е Q; |м|<М, | р |< MJ, где М, > max | Vm (х) |, при-
надлежат классам С1~1+а(Шмм) и С'-2+а(а№мм,). />2, соответ-
соответственно и S<= Cl+a, ф (х) <= С'+а (Q), го ы (х) <= С'+а (Q) ы | и ?+а)
оценивается постоянной, определяемой m, M, v (M) ы ц (М) из
C.1), C.2), нормами at(x, и, р) и а(х, и, р) в С'-1+а(Щмм) и
С1-2+а(Жмм) соответственно, нормой ф(х)_в Cz+a(Q) и S.
Как отмечено в гл. I, условие ф(х) е Cz+a(Q), l^s 1, и ф(х) е
еО2(й) здесь и во всех других местах можно заменить усло-
условием <р Ь <= Cl+a (S) и ф|5е02E), если S<=Cl+a или О2 соот-
соответственно.
§ 7. Оценки интегральных норм и максимума модуля
для обобщенных решений
До сих пор мы рассматривали ограниченные обобщенные
решения из W1m(Q), m > 1 *), и предполагали известной оценку
для vrai max | и (х) | решений и (х). В этом параграфе мы выде-
Q
*) Утверждения данного параграфа распространяются и на случай m = 1,
но поскольку во всех остальных параграфах m > 1, то и здесь мы будем
считать m > 1.

334 КВАЗИЛИНЕЙНЫЕ УРАВНЕНИЯ [ГЛ. IV
лим ряд случаев, когда для таких решений, а также для обоб-
обобщенных решений более широких классов — решений из Wm (Q)
или из Wm.q(&) = Wm(Q)(]Lq(Q) — можно оценить vraimax| u(x) \
a
или какую-либо интегральную норму. В большинстве случаев
мы будем предполагать, что решение имеет ограниченный
vraimax|«| на границе области Q. Для таких функций при-
принадлежность их к пространству Wm(Q) влечет за собой вло-
вложение и (л) е is (Q) с т = т= п™ при т < п, Vm < то при
т = п и т = то при m > п (см. теорему 2.2 гл. II и лемму 3.6
гл. II). Исключение составляет теорема 7.4, в которой и (х) на
границе Q совпадает с, вообще говоря, неограниченной функ-
функцией ф(л:). В ней мы предполагаем, что ф е Wm (Q) f) Ьт (Q).
В связи с этим естественно изучить следующие классы ре-
решений:
1) решения из Wm<q(Q) при т < п и каком-либо конечном
;
2) решения из Wm(Q), m = n, принадлежащие Lm(Q) с лю-
любым /й < то;
3) ограниченные обобщенные решения из Wm(Q) при т > 1.
. Обобщенные решения и(х) уравнения @.1) из Wm, ч(п) (Wm(Q))
определяются как элементы Wm,q(Q) (Wm(Q)), удовлетворяющие
интегральному тождеству A.4), т. е.
L (и, ц) = J [а. (х, и, их) тц — а (х, и, их)т]] dx = 0 G.1)
Q
при ^^Wm,q^Wm(Q)[]Lq(Q) (Wm(Q)).
Напомним, что ограниченные обобщенные решения уравне-
уравнения @.1) определены в § 1.
Для того чтобы эти определения имели смысл, надо на
функции а{(х, и, р), а(х, и, р) наложить такие ограничения, при
которых интегралы, входящие в G.1), были бы сходящимися
при любых допустимых и и т). Эти ограничения для случая
т < п и q < то имеют вид *)
| at (х, и, р)|< с\ р Г + с | и \ч1т' + ф1 (л:), Ф, <= Lm< (Q), G.2)
|а(лг,«,р)|<с|рГ/9Чс|«ГЧф2М, <p2^Lq<(Q), G.3)
где q'=ql{q— 1), т' = т/(т — 1).
•) В этом параграфе и § 9 мы допускаем особенности у функций
at (x, и, р) и а {х, и, р) по х.

j 7] ОЦЕНКИ ДЛЯ ОБОБЩЕННЫХ РЕШЕНИИ 335
В случае m = n неравенство G.2) надо заменить на
|а,(*,и,р)|<с|рГ + с|и|* + ф1(*), ф,6^(О), G.2)
а неравенство G.3) на неравенство
1 ftstJQ), G.3)
и считать в них k < то, е > 0, q{ > 1.
Наконец, в случае ограниченных обобщенных решений из
Wm(&) с т>1 ограничения на at(x, и, р) и а(х,и,р) сле-
следующие:
G.1)
G.3)
где Hi (и) — непрерывные функции ы. Докажем следующую тео-
теорему:
Теорема 7.1. Пусть функции ai(x,u,p), a(x, и, р) удо-
удовлетворяют условиям G.2), G.3) при m < n или условиям G.2),
G.3) при т = п. Пусть, далее, при JceQ, \u\^k0 и ре?п
для них справедливы неравенства
а, (х, и, p)pt>v\Pr - jiil «|e-| и Р Фз (х). G.4)
п (v ti п\ и ^* ¦! | п Iй _1_ it I it I® _1_ \ it № п\ /*А П К\
(Л \ЛУ Ну р) И ^^ JLLq | у | ~Т" |Lli | И | "т" I " I фз \**/> \* *^/
в которых 0<n0<v, ф3 e L?| (Q), q{>nlm, и tn<a<tn +
+ q — при m < п, а > m при m = п. Гог<Эа любое обобщенное
решение и из Wm, ч (Q) (при пг<п) или из Wlm (Q) [при т = п)
с vrai max | и |^ Мо < то является ограниченной функцией и
да
vrai max| ы | оценивается сверху постоянной с, определяемой лишь
нормой || и ||г 0 и величинами m, r, (v — цо)~1, ци а, \\ ф3 ||?i Q, qu k0,
Mo и mes Q. Здесь в качестве г можно брать Vr ^ 1, удовле-
удовлетворяющее условию (а — т) — < г < <7 при m < п и а — m<r
при т = п.
Замечание 7.1. Мы ограничились здесь тотальной
оценкой vrai max | м |, при получении которой требуется знать,
Q
что vrai max I и К Мп. Если это последнее не имеет места, то
ая
при выполнении остальных условий теоремы 7.1 можно оценить

336 КВАЗИЛИНЕЙНЫЕ УРАВНЕНИЯ [ГЛ. IV
vraimax|«| для VQ'cQ. Как это сделать, читатель поймет,
просмотрев доказательства теоремы 7.1 и теоремы 13.1 гл. III.
Пример B.31) гл. I показывает, что показатели а и q~l не
могут быть увеличены.
Для доказательства теоремы 7.1 рассмотрим тождество G.1),
предполагая для определенности, что т < п. Функцию т| (л:)
в нем можно взять равной и^Цх) = тах{и(х) — k; 0}, где k~^
о .
^max{Мо; k0}, ибо она принадлежит Wm, q(Q). При этом из
G.1) в силу предположений G.4), G.5) будут следовать нера-
неравенства
G.6)
где Ak = {x gQ; u(x)>k}. Так как по условию ц0 < v, то из
G.6) выводим:
Ak °
Оценим интегралы }{= Г | и |аdx и j2 = | I « ГФзdx, исполь-
зуя соотношение ll"a~mllr/(a_m) = ll"lf~m и условия qx > — ,
а — m m
/l < II «a"m Ида-.), Л Jl «m ИдгЧа-.),, Л, <
| и - k ||^ Ak + km mesm/Zl Лй), G.8,)
?'nmes'n/Z2
h < II Фз II, , A II «m II,'. л < 2m-'|| Фз II,,. л,(|| и - k If, л +/?'nmes'n/Z2 Л,).
G.82)
Здесь показатели /, = mr/[r — (a — m)] и /2 = ™.Ц\1{Я\ — 1) в СИЛУ
наших предположений принадлежат промежутку (m, /й). От-
Отсюда и из G.7) получаем неравенство
2
J | V« Г dx < ^ с, (|| и - k \§ш ч + km mesm/z' Л,), G.9)
t=i

§ 7] ОЦЕНКИ ДЛЯ ОБОБЩЕННЫХ РЕШЕНИИ 337
в котором с, = 2т (v - ЦоГ1 ц, || и ||г%"\ с2 = 2т (v - щ) || Фз 1^ Q.
Как легко видеть, для и(х) выполнены все условия теоремы 5.1
гл. II (точнее, замечания 5.1 к ней), и потому для и(х) имеет
место желаемая оценка сверху. Аналогично, рассматривая функ-
функцию v(x) = — u(x), оценим и(х) снизу. Все приведенные рас-
рассуждения остаются в силе и для случая т = п.
Теорема 7.1 доказана. Она выделяет класс уравнений вида
@.1), для которого любое обобщенное решение и(х) из W1^q(Q)
с конечным vraimax|«| оказывается ограниченным. Проблема
дп
оценки vraimax|«| для таких решений свелась к получению
я
оценки ||ы||г п. Оценить ||ы||г Q только через известные в задаче
Дирихле величины в общем случае нельзя. Примером тому
могут служить линейные уравнения Lu-\-Xu = f, u|s = 0; при
собственных значениях I задача имеет нетривиальные решения
для f = 0, так что никакую их норму нельзя оценить через
какую-либо норму f. Можно дать некоторые достаточные усло-
условия, когда это возможно.
Пусть, например, at и а при х е Q и \и\> k0 удовлетво-
удовлетворяют неравенствам
а1(х,и,р)р1^\р\т-ЬЛи\т-щ(х), 1
I ( }
в которых O^Ho<vi 6b 62^0, ф4е1, (Q), т > 1. Тогда, ана
логично G.7), получим для /г1 = тах(/г0, Мо) (Мо ^ vrai max | и |)
dQ
11 V« Г dx < (v - но)"' { [Fi + 6i)l и Г + 2ф4] dx <
Ah, Akl
< cm 6'+6гA + e) mes»^ ЛЙ1 f | VU Г йл: +
+ (v-Ho)"' f [Fi + 62) се, т/гГ + 2ф4] dx, Ve>0. G.11)
Постоянная с взята из неравенства B.12) гл. II (она зависит
только от п и т), а се, m из A.5) гл. II. Если 61+62 настоль-
настолько мало, что
h+h ln Q>0> G.12)
V
то из G.11) следует оценка для ||V«||m A . Аналогично, проводя
рассуждения с функцией —и(х), получим оценку ||V«||m Bft no
множеству Bkl={x: и(х)<— /г,}, й, = тах{/г0; Мо}. Это и тео-

338 КВАЗИЛИНЕЙНЫЕ УРАВНЕНИЯ (ГЛ. IV
рема вложения 2.1 гл. II гарантируют оценку ц и \\т Q с т = т =
= пт/(п — т) при т< п, с любым конечным m при т = /г и
с m = то при т> п.
Если в неравенствах G.10) вместо | и Г стоит \и( с г < т,
то 6; и б2 могут быть любыми. Действительно, если воспользо-
воспользоваться неравенством A.3) гл. II: | и Г < -~ Ьт'г \ и \т + —¦ 6-m/(m-r)
с V6 > 0, то из данных условий будут следовать неравенства
G.10) с коэффициентами при \и\т, равными б, — 6m/r и б2 — 6m/r
соответственно. Ввиду свободы выбора б > 0 мы удовлетворим
условию типа G.12), взяв б достаточно малым.
Рассмотренные случаи относятся к обобщенным решениям и
из U^m(Q). Если u^Wm, q(Q), то можно привести еще такие
достаточные условия:
at(x, и, p)pl>v\p\m-6l\u\m + 63\u\r-<p4(x),
а (х, и, р) и < цо1 р Г + 621 и Г + б4| и Г + ф4 (х), G.13)
Пусть здесь ц0 < v, а 6] и б2 удовлетворяют условию G.12).
Тогда так же, как и выше, оценивается норма || и \\л Q, если
г>т и 63^64 или если Km, a 63 и 64 произвольны.
Если же в условии G.13) б3 > б4, то можно получить оценку
нормы || и \[. Q, предполагая лишь, что ц0 ^ v, а постоянные 6]
и б2 равны нулю при г < т и могут быть произвольными ^0
при г > т. Наконец, если б3 > б4, г > т, ц0 < v, то легко
видеть, что вместе с нормой ||ы||г Q мы оценим и норму ||«||л Q.
Доказываются все эти утверждения аналогично предыду-
предыдущему, надо только в случае необходимости использовать нера-
неравенство | U Г<8| ыГ + се.г,т При Г < ГП ИЛИ | «Г<8| U Г + Се,т,г
при г > т, подбирая е > 0 достаточно малым. Ясно, что число
таких «удачных» случаев можно приумножить. Итак, справедлива
Теорема 7.2. Пусть функции at{x, ы, р) и а(х, и, р) удо-
удовлетворяют неравенствам G.2), G.3) с m< n, q^m и при xeQ,
\u\^k0 подчиняются условию G.13) с каким-либо r^.q и
(p4eL,(Q). Пусть и (х) — обобщенное решение из Wxm, ч(п)
с vrai max| и \^М0. Верны следующие утверждения:
дй
1) Если ц0 < v, 6] и б2 подчиняются неравенству G.12), г > m
ы 63 ^ б4, то норма || и \\м Q оценивается сверху постоянной, опре-
определяемой лишь m, n, jh, Mo, k0, v, ц0> (ц, б2> ||ф4||, Q и mesQ.
2) Если ц0 < v, выполнено неравенство G.12) и г < т, то норма
|| и j|ft Q оценивается сверху постоянной, зависящей от тех же
величин, что и в пункте 1), а также от г, б3 и б4.

§ 7] ОЦЕНКИ ДЛЯ ОБОБЩЕННЫХ РЕШЕНИИ 339
3) Если no^v и б3 > б4, то норма \\u\\r Q в случае г < m
и б] = б2 = 0 оценивается сверху постоянной, зависящей только
от пг, п, Мо, k0, б3, 64, НфД q и mesQ, а в случае r>m и
произвольных б] и б2 постоянная, мажорирующая норму \\u\\r Q,
зависит также от г, Ь\ и б2.
4) При ц0 < v, б3 > б4, г > пг и произвольных б1? б2 ^0 нормы
\\и\[. Q и || и ||й Q оцениваются сверху через те же величины, что
и в пункте 2).
Теорема 7.3. Утверждения 1) —4) теоремы 7.2 остаются
справедливыми для решений и(х) из Wlm(u) с m = n и для
ограниченных обобщенных решений из Wm(Q)_c пг> 1, если
условия G.2), G.3) заменить на G.2), G.3) и G.2), G.3) соответ-
соответственно, а в G.13) допускать Vr^l.
Напомним, что в теоремах 7.2 и 7.3 пг = m = ппг/(п — пг)
при пг < п, пг — V положительное число при пг = п и пг = оо
при пг> п.
Рассмотрим еще случай, когда и(х) неограничена на дп.
Пусть и есть обобщенное решение уравнения @.1) из класса
W\n>q(u) с пг<п или из класса Wm(Q) с пг = п и и совпадает
на дп с фе^,,(й) или Wln(Q)(]LM(Q), Vm < то; соответ-
соответственно. Рассмотрим интегральное тождество G.1) с г\ = и — (р:
J [а. (х, и, их) (uXi - Ф^) - а (х, и, их)(и - Ф)] dx = 0. G.14)
Пусть для at, а при х е Q и произвольных ы и р выполнены
неравенства G.13), а также при пг<п неравенства
I а, (х, и, р) |<с| р Г' + с| и Г/МЧ ФбМ. Ф5 sLrf(Q), 1
I «(*, и, р) |< с| р Г7' + с| и f + ф6 W, Фб е L,- (Q), J
где s = max{m, r}. При m = n вместо G.15) предполагаем
I а* (х, и, р)|< с| р Г + с| и |s/m' + ф5 М, ф5 s Lm' (Q),
\а(х, и, )|<||т-е + |Ге + М ^ЬДЙI
с какими-либо е > 0, qx > 1 и тем же s. Исходя из G.14), можно
оценить || и ||д Q или || и ||r Q при тех же условиях на входящие
в G.13) параметры, что и в пунктах 2), 4) теорем 7.2 и 7.3.
Для этого надо воспользоваться известными алгебраическими
неравенствами A.5), A,6) гл. II.

340 КВАЗИЛИНЕЙНЫЕ УРАВНЕНИЯ [ГЛ. IV
Именно, из G.14) в силу G.13) следует
(v - Но) J I V« Г dx + F3 - б4) J I и Г dx <
Q Q
J [Fi + fi2) I " Г + 2% + a,<fx ~ аф] <Ц G-17)
Благодаря G.15) при т < n имеем
J (afl - оф) Ac < (c || V11 ||^ + с II u ft' + || Ф51, Q) IIV9 ||m_ Q +
Q
+ (CII V" Iff О + CII " If О + II Фб II,', о) II Ф II,. Q <
<e1||V«|diO + e1||«lC>o + cei, V8,>0. G.18)
Постоянная се, определяется 8] (cei->oo при 8] ->0) и известными
величинами: с, m, q, ||Уф||та, ||ф||?а, 11ф5|Ца и
Точно так же при т=п выводим из G.16)
J (а(Ф - аФ) dx< (с|| V« |Д + с|| и |f ^ + IIФ51Ц 0)IIV9 ||m,
Q
C. + eill«lC>o + Cel, Ve,>0. G.19)
Подставим G.18), G.19) в G.17) и приведем подобные члены:
(v - цо - 8,) || V« С_ 0 + (бз - б4) || и \(г< 0 <
< (б. + б2) II и ?, 0 + 8, || и \\sSt 0 + Се, + 21| Ф4II,, 0. G.20)
В силу неравенств A.5), A.6) гл. II при Ve2 > 0
| V« Г >{\ - е2)I V« - УФ Г - сгъ т\ УФ Г, G.21)
I и Г <A + е2)| и - Ф Г + си,т\ Ф Г. G.22)
Кроме того, примем во внимание оценку ||ы — ф11т Q через
||Уы —Уф||тй (см. неравенство B.12) гл. II). Эта теорема вло-
вложения вместе с G.20), G.21) и G.22) позволяет заключить
о справедливости следующей теоремы:
Теорема 7.4. Пусть функции at(x, и, р), а(х, и, р) удо-
удовлетворяют неравенствам G.13) и, кроме того, неравенствам G.15)
при tn< п или неравенствам G.16) при пг = п. Предположим,
что функция у(х) принадлежит Wlm,q(&) с 1 < m < n, q^m
или Wln (Q) П Lm (Q) с Vm < 00. Тогда для обобщенных решений и {х)
из класса Wlmi я (Q) при m <п и из Wlm (й) при т = п соответ-

§ 7] ОЦЕНКИ ДЛЯ ОБОБЩЕННЫХ РЕШЕНИЙ 341
ственно, совпадающих на dQ с указанной функцией ф, остаются
справедливыми утверждения 2) и 4) теорем 7.2 и 7.3 об оценках
норм \\и\\ма и ||и||га. При этом вместо Мо в оценки войдут
величины с, НфвН^.а» НфбН^.а из условий G.15) и нормы ||ф||? Q,
HV(Pllm.Q в слУчае гп<п и величины с, е, IIФ5Н^о, 11фб11?1,а из
условий G,16) и нормы ||ф||т/е>0, IMIs/e,Q> IIФII,;, 0. 11^фНт>0 в слу-
случае т = п.
Во всех теоремах 7.1 — 7.4 имеется ограничение v > ц0
(в некоторых случаях оно заменено на условие v ^ ц0). В § 9
будут доказаны теоремы существования обобщенных решений
из Wm, а задачи Дирихле для уравнений @.1). Одно из главных
условий состоит в том, что для V« e Wm, q (Q) справедливо
неравенство
L (и, и) >f (|| V« ||m Q +1| и \\ч< Q) - с, G.23)
где / (т) > 0 — непрерывная функция т ^ О, стремящаяся к беско-
бесконечности при т->оо. Если предположения на а{ и а формули-
формулировать в виде неравенств типа G.4), G.5), то для справедли-
справедливости G.23) необходимо предположить, что v > ц0.
Другие предположения теорем § 9 таковы, что они также
приводят к неравенствам типа G.4), G.5) и G.13) с v > ц0.
Поясним это на случае т < п, q = m теоремы 7.1. На функ-
функции а( и а в § 9 накладываются условия G.2), G.3) с заменой q
на какое-либо q < т. Тогда произведение \а(х, и, р)и\ можно
оценить сверху суммой вида е | р Г + се | и f -f | и \ ф2 (я) с Ve > О,
причем q<tn = n"^1 =тп , т. е. q удовлетворяет усло-
условию теоремы 7.1, наложенному на показатель а. Условие же
эллиптичности и условие G.2) с q вместо q на а{ гаранти-
гарантируют G.4) с некоторым v>0 и a=q. Выбирая е < v, мы удо-
удовлетворим обсуждаемому условию: v>no = e.
Итак, предположение v > ц0 с точки зрения условий тео-
теорем § 9 не есть, по существу, дополнительное ограничение.
Однако если мы уже знаем, что и есть ограниченное обобщен-
обобщенное решение уравнения @.1) и нас интересует оценка для него
какой-либо интегральной нормы или тах|ы(;с)|, причем
Q
функции фг (х), входящие в наши условия, суммируются с до-
достаточно высокими степенями, то условие v > ц0 можно снять.
Предположения G.2), G.3) и G.2), G.3) заменяются более сла-
слабыми: G.2) и G.3) при любых т > 1. Пусть и есть ограниченное
обобщенное решение из Wm (Q), т > \, причем vrai max| и КМо,
дй

342 КВАЗИЛИНЕЙНЫЕ УРАВНЕНИЯ [ГЛ. IV
и пусть щ и а удовлетворяют при \u\^ko^Mo неравен-
неравенствам G.10), в которых v > 0, цо^О, 6A>0, а ф4 суммируется
с достаточно высокой степенью, величина которой будет уточнена
ниже. Рассмотрим тождество G.1) при r\ (х) = us~{ (x) (us (х) — k)
для ^е4 = (^ л:ей, u(x)>klls} и т)(л:) = 0 для хшАк\
число k считаем ^ks0\ число s в дальнейшем будет выбрано
достаточно большим. Обозначим через v (x) функцию, рав-
равную и"(х) для ^еА, и нулю для хША0. Подставим взятое ti
в G.1):
J [salU2s-2ux. + (s-1) сци*-2(v-k) ux-au*-1 (v-k)] dx=0. G.24)
Ak
В силу G.10) отсюда следует
J [su2s~2 + (s - 1) us~2 (v - k)] [v | Vu Г - б,ыт - ф4] dx <
< J «s (o - Л) (m, I V« Г + 62«m + Ф4) rfJf,
откуда, учтя 0 < v — k < ы*, получим
2*-21 V« Г + (s-'b'-^ „s-2 (y _ k) | Vu |m] dx
:. G.25)
&-2-+1
Введем обозначение: w (х) = и т для х е Ло. Ясно, что
ш)г = ( h 11 ut'2s~2^mUr и I Vw \m =
Возьмем в G.25) s = 1 + HoV *) и перепишем его в виде
J | Vay Г dx < J (схтт + c2O)Bs-2> /B«-2+т)ф4) ^д.> G.26)
^ft Ак
W2s — 2i.\m/2s— 1»_|б2\ 2 / 2s - 2 , - \т
2s-2 1
k= k ms s n Ak = {x: x ^Q, w(x) > ft}. Последнее слагае-
слагаемое правой части оценим по неравенству Юнга так:
*) В качестве s можно брать любое число ^ 1 +
..-1

ОЦЕНКИ ДЛЯ ОБОБЩЕННЫХ РЕШЕНИИ 343
.c2a>Bs-2)m/Bs~2+m)(p4 г^ео>т + ст s еф^-2+т)/т и в соответствии
с этим G.26) заменим неравенством
J | V» Г dx < J [(С, + 8) W" + Cm_ e> еф^-2
Из этого неравенства можно оценить J | Voj |m dx, если с{ + е
или теэЛ^ достаточно малы. Именно, как и выше в G.11),
заменим wm на A + е,) (w — ft)m + cm, e,ftm и используем теорему
вложения B.12) из гл. П. Это приведет к неравенству
[1 - (с, + е) A + е,) ст mes/" Ak] J | V» Г dx <
+ 8) e«..F + «-, , Е<рГ2+т)/1 ^ G.28)
где е и 8] — произвольные положительные числа, a
— ft?-2+MVM. Если
1 — схст mesm/n Q > б0 > 0, G.29)
то положим 8] = е, где е — наибольшее из чисел, удовлетво-
удовлетворяющих неравенствам
(8 + c,8 + 82)c"Imes"I'nQ<60/2, е<1. G.30)
Тогда коэффициент в левой части G.28) будет не меньше бо/2,
и потому
J | V. rdx <ytf-me. А
к
б"'
где у, = 2б0"' (с, + 1) ст> „ Y2 = 260~Vm, s,,.
Итак, если <p4eLBs_2+m),m(Q), то G.31) дает оценку
lVtofd.*: через известные нам величины. Отсюда, в свою
очередь, следует оценка для ||о>||л>л . а тем самым и для
II « IUBa-2+m) л С /Й = "" При /И < П, V/Й > 1 При /И = П И
.А. «"ОТ
/й = оо при т>п. Аналогично оценивается || и \\дBs-2+m> {B<0)-
Заметим, что при уменьшении mesQ e не уменьшается, и, сле-
следовательно, Yi и Y2 не возрастают. Таким образом, мы

344 КВАЗИЛИНЕЙНЫЕ УРАВНЕНИЯ [ГЛ. IV
получили оценку || «IUBs-2+m> Q ^ М, где М есть возрастаю-
т '
щая функция mes Q.
Предположим теперь, что т^.п и по-прежнему выполнено
условие G.29). Если функция ф4(*) суммируется со степенью
г •> ЦЦ—.—™Lt T0 неравенства G.31) позволяют оценить
сверху vrai ma* w. Действительно, в силу неравенства Гёльдера
п
имеем
J
dx
а отсюда и из G.31) следует неравенство
J | V» Г dx < Vlftm mes A-k + y3 (mes Л4I-|В"|+в, б > 0, G.33)
где Y3 ^ Y2IIФ4 Il^2s^+m)/m. Воспользуемся теперь леммами 5.1 и
5.3 гл. II, принимая во внимание зависимость постоянных Yi
и уз от mes Q. Из них следует, что w (x) не превосходит по-
постоянной ftmax, определяемой ^0, с, Yi. Y2. 6. wi. IIФ4 Пг, о и mesQ,
причем kmax есть возрастающая функция mes Q и /г0- Из
оценки же таха>(л:) вытекает соответствующая оценка тахы(л:).
Q Q
Аналогично оценивается снизу тти(х).
Q
Итак, доказана следующая
Теорема 7.5. Пусть и(х) есть ограниченное обобщенное
решение из W1m(Q), m>\, уравнения @.1). Пусть для функций
at(x, и, р), а(х, и, р) справедливы при \ и |^/?0^vrai max| и \
неравенства G.10) с некоторыми постоянными v > 0, ц0, бь 62^0,
удовлетворяющими условию G.29), в котором С] та же, что
в G.26), s= I -f H0V1, а с взята из неравенства B.12) гл. II
с р=т. Тогда, если <P4eLBs_2+m)/m(Q), товеличина\и\2$_2+т)тт<а
оценивается сверху постоянной М, определяемой m, v, k0, ц0,
бьб2. IIФ4llBs-2+m)/m, о " mesQ. Если (f4<=Lr(u)cr>n{2s—2+m)lm\
m^n, то величина vrai max| и \ оценивается сверху постоянной М,
Q
определяемой m, v, ц0, бь б2, Нф4 11г,я. г, k0 и mesQ. В обоих
случаях М есть возрастающая функция mes Q и k0.
Теорема 7.5 примечательна тем, что она дает оценку той
или иной нормы и по областям Q достаточно малой меры при

5 71 ОЦЕНКИ ДЛЯ ОБОБЩЕННЫХ РЕШЕНИИ 345
выполнении лишь неравенств G.10) с какими-либо входящими
в них постоянными. Величина mesQ определяется только по-
постоянными т, v, Но. 6i и ^2 (условие G.29)). В § 9 она будет
использована для доказательства теоремы о разрешимости за-
задачи Дирихле.
Если считать известной величину I|«II?(Q с каким-либо <7^1,
то условие G.29) в теореме 7.5 можно отбросить и оценить
vrai max| и | через перечисленные в теореме 7.5 величины и норму
Q
|| и || _. Более того, в этом случае неравенство G.10) можно
заменить менее ограничительными неравенствами G.4), G.5)
с произвольными v>0, Но. Hi. m<a<mn nq и <p3GL,,(Q),
<7i > max {n/m; 1}. При т^п эти утверждения доказываются,
исходя из G.24), так же, как в теореме 7.1. Именно, в силу
условий G.4), G.5) мы получим из G.24) неравенство, отли-
отличающееся от G.25) лишь тем, что в правой части u2s-2+m за-
заменено на u2s~2+a, u2s-2(fi на u2s-2+m(p3 и 61 = 62 = Hi- В соответ-
соответствии с этим вместо G.26) будем иметь неравенство
J | Voj Г dx < J (с,о>тыа-т + с2а)тфз) dx G.34)
Ч Аа
с теми же с, и с2, что и в G.26), k ^ kQ = kf
Интеграл в правой части G.34) можно оценить так же, как
это делалось в теореме 7.1 при выводе G.9) из G.7). Это при-
приводит к неравенству типа G.9) для w (x):
2
k>k0, G.35)
с Cl = 2mcl\\u\\^, ^ = 2мс2|фз|?11О, l{ = mql[q-{a-m)) и
h=mq\l(9i—1)- Отсюда в силу теоремы 5.1 гл. II (точнее,
замечания 5.1 к ней) следует оценка vrai max w через постоян-
Q
ные с'и Сь U, U, m, ko и величину L = ( \ wEldx\ ' при каком-
\As )
либо 8] > 0. В частности, можно взять 8] = mq/Bs — 2 + т),
так что L<||«fQ-2+m)/m.
Пусть т> п. В этом случае для оценки таха> достаточно
оценить J | Vw f1 dx при каком-либо k^O. Так же, как и выше,
н

346 КВАЗИЛИНЕЙНЫЕ УРАВНЕНИЯ [ГЛ. IV
выводим неравенство G.34) и оцениваем интеграл }2= \ wm(p3 dx.
Ak
Интеграл /, — j wmua~mdx оцениваем иначе, именно:
AR
. m?q I mBs-2+g)\
J (w - k) nB^-2+m) dx + ce{ 1 + k 2s~2+m )mes Ak, G.36)
—'¦
где е — произвольное положительное число, и к интегралу
в правой части применяем неравенство B.9) гл. II:
J (» - kf
тд \mjn
J | V» Г dxl j (w — k) 2s~2+m dx j
\m/n
Далее, || w — k ||™ A надо оценить сверху через J | Voj f" dx,
" * Ak
пользуясь неравенством B.12) гл. II, а затем полученные
оценки /, и /2 подставить в G.34) и взять е и k~l столь малыми,
чтобы коэффициенты при \ \Vw\m dx в правой части в сумме
не превосходили '/г (при этом малость mes Ag следует из нера-
неравенства mesll4Ak^:\\u\\(j ak~ml{2s~2+my). Тогда после приведения
подобных членов придем к оценке ||Va»||^ Ак через k, mesAg
и НфзН<л, л,- Так как т>п и тахщ>^?0. Т0 отсюда следует,
что max w не превосходит некоторого числа, определяемого
Q
известными нам числами. Это дает оценку и (х) сверху. Анало-
Аналогично оценивается и(х) снизу.
Сформулируем доказанное утверждение в виде теоремы.
Теорема 7.6. Пусть функции at(x, и, р), а(х, и, р) удо-
удовлетворяют условиям G.2), G.3) с m > 1 и при JteQ, | ы|^й0,
ре?„ для них справедливы неравенства G.4), G.5) с какими-
либо постоянными v > 0, ц0, Hi, a>m и ф3 (х) е L?, (Q),
qi > max {n/tn; 1}. Тогда для любого ограниченного обобщенного

5 g] ОЦЕНКА КЛАССИЧЕСКИХ РЕШЕНИЙ 347
решения и{х) из Wm(Q) уравнения @.1) величина vraimax|«|
оценивается сверху постоянной, определяемой величинами v, цо>
ц,, а, пг, <7ь Нфз1!?„а из условий G.4), G.5), а также k0,
vraimaxl и |, mesQ и нормой \\u\\ Q с каким-нибудь q>n\ — — 1).
§ 8. Оценка максимума модулей для классических решений
В этом параграфе мы приведем ряд достаточных условий,
когда можно оценить тах|ы(х)| для классических решений и
Q
квазилинейных уравнений общего вида. Во второй половине
параграфа этот же вопрос рассматривается для решений из
С1 (Q)[)C(Q) уравнений @.1), т. е. квазилинейных уравнений
с дивергентной главной частью. То, что решения для @.1)
берутся неклассические, для дальнейших наших приложений
в § 10 несущественно. Рассмотрения второй части продиктованы
главным образом желанием освободиться от предположений
о двукратной дифференцируемости аг (х, и, р) и дифференци-
руемости а (х, и, р) по р, которую надо потребовать при непо-
непосредственном применении теоремы 8.1 или ее следствий 8.1—8.4
к уравнениям @.1). Желанием снизить предположения о глад-
гладкости функций, образующих уравнения, обусловлено и наличие
теорем 8.1' и 8.2.
В основе получения оценок тах|ы(х)| лежит принцип мак-
Q
симума. В его классической форме он применялся для той же
цели, начиная с работ Пикара и С. Н. Бернштейна и кончая
работами (см. [51ц] и др.) самого последнего времени. Одно
из главных мест среди них занимают результаты Э. Хопфа [27].
Утверждения первой половины данного параграфа имеют много
общего с результатами, полученными ранее разными авторами,
в том числе Э. Хопфом, Дж. Серрином [51,,], Редхеффером [46]
и нами, и было бы затруднительно выяснять их связи. Ма-
Материал второй части параграфа при всей его близости к пред-
предшествующему имеет и своеобразные особенности. Он получен
на основе принципа максимума для обобщенных решений, ко-
который изложен в § 13 гл. III.
Рассмотрим семейство эллиптических операторов
Lo (и) = аИ (х, v, ux) uXiXj + A (x, v, ux) (8.1)
и соответствующее ему уравнение
L,,(u)^L(u) = Q. (8.2)
Будем предполагать во всем параграфе форму аи(х, и, р)Ы,

348 КВАЗИЛИНЕЙНЫЕ УРАВНЕНИЯ [ГЛ. IV
положительно-определенной, хотя многие утверждения остаются
справедливыми и для случая аг/|г^/^0. Кроме того, функции
att(x, и, р), А(х, и, р), а также те их частные производные,
существование которых будет оговариваться, считаем ограни-
ограниченными на любом компакте вида Шм, м, = {(*» и, р): х gQ,
| и \^М, | pl^Af,}. Эти свойства alt и А ниже не указываются,
но подразумеваются выполненными. Докажем теорему:
Теоре_ма 8.1. Пусть функции и(х) и а>(х) принадлежат
С2 (Q) Л С (Q). Если они удовлетворяют в Q неравенству
}{и, ©) = Lu(«)-?u(<o)^O (8.3)
во всех точках, где и(х) — со (лг) > 6,, то
и(х)<со(х) -f max{b\\ max (и — ю)}<
3Q
<max{co(jc)+ 6]; osc {со; Q} + max и). (8.4)
dQ
Если & (x) e= С2 (Q) f) С (Q) u
i(«, 4)<0 (8.5)
во всех точках, где и (х) — & (x) < 62. ^o
u(x)~^& (x) -f min{62; min(u — &)}^
dQ
> min {& (jc) + b2; — osc {&; Q} + min ы}. (8.6)
dQ
Функции ait(x, и, р) и А(х, и, р) считаем при этом дифферен
цируемыми по р.
Замечание 8.1. Утверждения теоремы 8.1 остаются в силе,
если в правую часть (8.3) подставить члены вида Bt(x, и, ю, их, coJX
Х(«х,— «>*,) с какими-либо функциями Bt(x, и, ю, р, q), огра-
ограниченными на любом компакте. Это же усиление допустимо и
в (8.5).
Представим /(ы, ю), следуя § 2, в виде
/да,, дА
/ (и, ©) = а„ (х, и, их) vXiXj + \J +
где v (х) = и(х) —(й(х), и рассмотрим это неравенство в области
Q6i = {ji:: JteQ, у (х) > 6J. Согласно лемме 1.5 гл. Ill ^
а это и доказывает (8.4). Аналогично проверяется
справедливость (8.6).
*»*.

$ g] ОЦЕНКА КЛАССИЧЕСКИХ РЕШЕНИЙ 349
Выведем из теоремы 8.1 ряд следствий.
Следствие 8.1. Пусть и(х), att и А обладают гладкостью,
указанной в теореме 8.1, и есть решение уравнения (8.2) и
signu- A(x, и, 0)<0 при |ы|>М. (8.7)
Тогда
max| ы|<тах{М; тах| и |} = max(Af; m). (8.8)
Q д<2
Возьмем со(х) = М. Так как Lu(ю) = А(х, и, 0)<0 при и > М,
то условие (8.3) выполнено с 6, = 0, а это гарантирует оценку
ы (х) < М + max {0; max (и — М)} = max (Af; m). В качестве ю (х)
надо взять — М. Это дает оценку и(х) снизу.
Следствие 8.2. Пусть Q содержится в некотором шаре K.R,
причем центр Кц не принадлежит Q, и пусть
для \и\^М и |р|>/ (/>0). (8.9)
Тогда для классических решений ы уравнения (8.2) с тах| и\ = т
верна оценка аа
max | и К max {M; т} + 2//?. (8.10)
Q
Функции аг/ (х, и, р) м А (х, и, р) должны быть дифференци-
дифференцируемы по р.
Пусть центр шара KR находится в начале координат. Он
лежит вне Q. Рассмотрим функцию
<s>{x) = M + lR{e-e\x\i*). (8.11)
Легко видеть, что | а>х | = /е'*1'л:>/, (o(jc)^Af и при и(х)>М
Следовательно, для ы и ю выполнено условие (8.3) при
и (х)—© (*) > 6, = 0 и потому и (х) ^ © (х) + max {0; max (ы—со)}
^ max (M, m) -\- 21R. Аналогично получается оценка и (х) снизу.
Следствие 8.3. Пусть и(х), ait и А обладают гладкостью,
указанной в теореме 8.1. Пусть, далее, для некоторого фикси-
фиксированного направления v и всех и и р > 0 справедливо
\Л^Ж p = pv, (8.12)

350 КВАЗИЛИНЕЙНЫЕ УРАВНЕНИЯ [ГЛ. IV
где &'(х, и, р) = аи(х, и, р) ptpj, Ф(р) — положительная неубы-
неубывающая непрерывная при р > 0 функция, такая что
/
Ш =
Тогда тах|ы| для классического решения и(х) уравнения (8.2)
Q
не превосходит некоторой постоянной, определяемой лишь
т = тах|ы|, Ф и диаметром d области Q.
ва
Без ограничения общности будем считать, что v совпадает
с направлением оси хп и Q лежит в полосе 0^.xn^.d. Рас-
Рассмотрим дважды дифференцируемую функцию со = со (хп) с а/ > 0.
Для нее
г/
Lu (ю) = & (х, и, р) -j^y +A(x,u,p), p = co'v.
Выберем положительные числа а и р (а < р) так, чтобы
3
гфр( ¦. ~d, и возьмем в качестве (л(хп) функцию, имеющую
а
параметрическое задание: со= . .р, , -f m, хп =
р р
р е [а, р]. Легко подсчитать, что со' з= -^- = — р, а со" =
= —2 ((о'JФ (р). Отсюда и из (8.12) следует, что Lu (ю) < 0 при V«
(иначе, при и — ю > 6, = — оо). Но тогда по теореме 8.1
з
ц(х)<ю(х)<т+ j рфРр) в Q.
а
Аналогично получаем оценку и(х) снизу.
Замечание 8.2. Условие (8.13) было использовано лишь
для того, чтобы существовали положительные числа аир, для
з
которых р =d. Оно может оказаться выполненным как
а
за счет поведения Ф(р) при р->оо, так и за счет поведения
Ф(р) при р->0.
Следствие 8.4. Пусть и есть классическое решение урав-
уравнения (8.2) с ац(х, и, р), не зависящими явно от и, и
— д'ц" ^0. и пусть aij и А дифференцируемы по р. Тогда,
если есть функция со (х) е С2 (Q) Л С (Q), удовлетворяющая нера-

§ g) ОЦЕНКА КЛАССИЧЕСКИХ РЕШЕНИЙ 351
венству L(ffl)<0, то_ для и верна оценка (8.4) с &, = 0. Если
же &(х) eC2(Q)DC(Q) и L(&)>0, то для и верна оценка (8.6)
с Ь2 = 0. Если А(х, и, р) также не зависит от и, то оценки
(8.4) и (8.6) верны с bl = — oo, Ь2 = + °о.
Для вывода следствия 8.4 из теоремы 8.1 достаточно заме-
заметить, что в силу наших условий Lu (ю) ^ Ьф (со) s L (ю) при
ы>ю и Lu (&) > Lu (ю) при ы<&, а отсюда и из Lu(u) = Q
следуют посылки (8.3) и (8.5) теоремы 8.1 с bt = b2 = Q.
В теореме 8.1 и ее следствиях предполагалось, что ац(х,и,р)
и А(х, и, р) дифференцируемы по р. От этого ограничения
можно избавиться, заменив знаки !> и ^ в условиях этих пред-
предложений на знаки > и < соответственно. Именно, справедлива
Теорема 8.1'. Теорема 8.1 остается в силе, если условие
дифференцируемости ait и А отбросить, а в (8.3) и (8.5) поста-
поставить строгие неравенства.
Для доказательства (8.4) достаточно убедиться, что v (x) =
= и(х) — а>(х) не может внутри Q достигать максимума, боль-
большего Ь\. Действительно, в такой точке х0 было бы иХ{ = ®х ,
ait(x, и, их)(и — а>)хх <0, а благодаря этим соотношениям и
(8.3) и
О <ХВ («)-?„(<->) =
= аи (х, и, их) (и — а>)Х{Х + А (х, и, их) — А (х, и, ыж)< О,
т. е. противоречивое неравенство. Аналогично доказывается (8.6).
Из теоремы 8. Г вытекают следствия:
Следствие 8.5. Утверждения следствий 8.1—8.4 и заме-
замечания 8.2 остаются справедливыми, если в них отбросить усло-
условие дифференцируемости ait и А по р, но (8.7) заменить усло-
условием
sign и ¦ А (х, и, 0)< 0 для | и \ > М, (8.70
(8.9) — условием
для \и\>М и \р\>1 (/>0), (8.9')
а (8.12), (8.13) оставить в прежней форме.
Условия же следствия 8.4 надо заменить или условием стро-
строгого монотонного убывания А (х, и, р) по и, или условием не-
невозрастания по и плюс предположениями /^(со) < 0 и L& (&) > О
соответственно.
Усиление (8.7') по сравнению с (8.7) кажется незначитель-
незначительным. Однако оно исключает, например, класс уравнений (8.2),
в которых А (х, и, их) = At (х, и, их) их. -\- а (х) u2m+l, где

352 КВАЗИЛИНЕЙНЫЕ УРАВНЕНИЯ [ГЛ. IV
(, a m — целое число. Ввиду этого наряду с (8.7')
может оказаться полезным такой критерий (в нем а.ц и А также
не обязаны быть дифференцируемыми):
Следствие 8.6. Пусть и есть классическое решение урав-
уравнения (8.2), в котором функция А (х, и, р) удовлетворяет
условиям:
— А (х, и, р) > At (х, и, р) рь и^т^О,
и
— А (х, и, р) < А{ (х, и, р) рь и < т2 < О,
в которых функции At(x, и, р) и Ai(x, и, р) ограничены на
любом компактном множестве изменения их аргументов. Тогда
min{m2; min«}^«(jc) ^ max {mi,* тахы}. (8.14)
dSi dQ
Правое из неравенств (8.14) есть следствие леммы 1.5 гл. III
применительно к функции и, как к функции, удовлетворяющей
неравенству
аИ{х, и, ux)uX{Xj — Ai(x, и, Ых)*ц>0
в области Q, = {x: x e Q, и (х) > mj. To же верно и для левого
неравенства из (8.14).
Ясно, что функции А (х, и, их) = At (х, и, их) иХ[ + а (х) и2т +1
при a(jc)^O и целом т удовлетворяют условиям следст-
следствия 8.6.
Остановимся еще на случае эллиптических операторов
L(u)es-^ at (x, и, их) + а (х, и, их). (8.15)
Если at(x, и, р) — дифференцируемые функции (х, и, р), то (8.15)
приводятся к виду (8.1) с
ait(x,
A(x,
и,
и,
p) =
dp,
dat (x, и, р
du
') da{
i
(8.16)
и к (8.15) применимы доказанные выше предложения. Однако,
в теореме 8.1 и ее следствиях 8.1 — 8.4 требуется дифферен- •
цируемость ац и А по р, что приводит для (8.15) к условию
существования у at производных второго порядка. Это весьма
нежелательное предположение можно снять с помощью прин-
принципа максимума для обобщенных решений линейных уравнений

§ g) ОЦЕНКА КЛАССИЧЕСКИХ РЕШЕНИЙ 353
(см. теорему 13.2 гл. III). Покажем, как это делается. Введем
обозначения
^- at(x, и, а>х) + а(х, и,
Lu (со, ц, п) = J [— а{ (х, и, а>х) тц + а (х, и, а>х) r\] dx.
(8.17)
Следуя § 2 данной главы, представим Lu (и, г], Q) — Lu(co, r\, Q)
в виде
Lu (и, ц, Q) — Lu (со, г), Q) =
да. да
Далее,
/ ^ ga/ (*¦ »¦ mJ | dat (*' и>
хV/ ^i
+ а (х, и, со,) » Мц (со) + дп< {Х'дии'
где Ми{а>) = аи{х, и, coje>XiXj + Л(х, и, сох), причем аг/(д;, и, р)
и Л(х, ы, р) взяты из (8.16) (заметим, что Ми (и) = Lu (и) =
= L(«)).
Справедлива
Теорема 8.2. Пусть и(х) еС1 (Q)ПС(Q), a со(*) еС2(Q)Л
Л С (Q). ?слы /гры каком-либо 6, ^ — оо ы Vt] e W^ (Qft) справед-
справедливо неравенство
h{u, ц, Qbl)^Lu(u, T], Qb)- jAfB(®)Tirfx>O, (8.20)
где Q6l = {jc: jteQ, и (х) — со (х) > 6]}, то вермо (8.4). Если & (jc)e
s С2 (Q) Л С (Q) ы при тех же ц (х) и каком-либо Ь2^ + оо спра-
справедливо неравенство
j, (8.21)
где йб2 = {x: jcsQ, ы(a;) — со(x) < uj, то eepwo (8.6). Функции
o.i (x, и, р) предполагаются дифференцируемыми no x, u, p,
a a (x, u, p) — дифференцируемой по p.
12 О. А. Ладыженская, Н, Н, Уральцева

354 КВАЗИЛИНЕЙНЫЕ УРАВНЕНИЯ [ГЛ. IV
Для доказательства (8.4) представим j{ (и, х\, Q6l), исполь-
используя (8.18) и (8.19), в виде
дй , даЛх> "• ш*
^+1 + .
(8.22)
Отсюда и из условия (8.20) следует, в силу теоремы 13.2
гл. III, неравенство (8.4). Аналогично доказывается (8.6).
Замечание 8.3. В правую часть неравенств (8.20) и (8.21)
вместо нуля можно подставить J Bt (х, и, ю, их, а>х) X
X («хг — «>*.) т] dx с произвольными B-t (х, и, (о, р, q), ограни-
ограниченными на каждом компакте.
Из теоремы 8.2 вытекает
Следствие 8.7. Пусть и(х) и at(x, и, р), а(х, и, р) обла-
обладают гладкостью, указанной в теореме 8.2, и и (х) есть обоб-
обобщенное решение уравнения L(u) = 0 с L(u) из (8.15). Тогда,
если для А (х, и, р) из (8.16) выполнено одно из условий: (8.7),
или (8.9), или (8.12) — (8.13), то для и(х) справедливы оценки,
указанные в следствиях 8.1 — 8.3 соответственно. Если а{ (х, и, р)
не зависят от к и —а "' ^ 0 и если есть функция (o(jc)e
eC2(Q)f)C(Q), удовлетворяющая неравенству L (ю) ^ 0, то
для и(х) справедлива оценка (8.4) с 6, = 0; если же есть функ-
функция & (х) е С2 (Q)f) С (Q), для которой L(co)>O, то для и(х)
справедлива оценка (8.6) с Ь2 = 0. Наконец, если а(х, и, р)
также не зависит от ы, то оценка (8.4) верна с 6, = — оо,
а оценка (8.6) — с 62 = -|-оо.
Выводятся эти утверждения из теоремы 8.2 так же, как
следствия 8.1 — 8.4 из теоремы 8.1.
§ 9. О существовании обобщенных решений
Существование обобщенных решений из Wlm< q = Wm (Q) f)
) 1 1 Д й A)
р < q (
? tn> 1, 1^<7< oo, задачи Дирихле для уравнений @.1)
можно доказать сравнительно просто, используя метод Галер-
кина. Правда, при этом будет наложено помимо «естествен-
«естественных» требований одно ограничение (неравенство (9.2)), которое
для случая линейного оператора L означает, что весь спектр L
(отвечающий данной области и первому краевому условию)
находится в левой полуплоскости. (В § 16 гл. III это условие
также предполагается выполненным— см. неравенство E.1),
но там оно может быть снято с помощью результатов § 5
о фредгольмовой разрешимости задачи Дирихле в простран-

§ 91 О СУЩЕСТВОВАНИИ ОБОБЩЕННЫХ РЕШЕНИЙ 355
стве №2 (Q).) Для случая т>п есть еще одно ограничение, не
вызванное существом дела: рост а(х,и,р) по р предполагается
меньшим т.
В следующем параграфе, где дается другой метод доказа-
доказательства разрешимости задачи Дирихле, эти условия заме-
заменяются менее ограничительными. Схема метода Галеркина для
квазилинейных уравнений та же, что и для линейных. Но при
проведении предельного перехода в интегральном тождестве,
которому удовлетворяют приближенные решения uN(x) задачи,
имеется одна специфическая трудность: нелинейность его чле-
членов по и^{х). Первоначально она была преодолена тем, что
на функции а{ (х, и, р), а(х, и, р) накладывались дополнитель-
дополнительные ограничения, позволяющие дать априорную оценку для и%х,
из которой следует сходимость и^ (точнее, некоторой подпосле-
подпоследовательности) для почти всех х из Q (см. [34Ь 2, 7з,4]). Чуть
позже в теорию дифференциальных уравнений пришла новая
простая, но ценная идея выполнения слабых предельных пере-
переходов под знаком так называемых монотонных операторов, ве-
ведущая свое начало от работы [36J Минти (см. также [362,3. 72]).
Применительно к квазилинейным эллиптическим операторам
она развивалась в ряде работ последнего десятилетия [323, 13ь
18, 396]. Для уравнений @.1) она позволяет доказать разре-
разрешимость в Wlm>q, имея в руках априорную оценку лишь нормы
IIи" Urn, q, q э IIv"" \\n. q + IIuN \. q- Рассмотрим ради несуществен-
ных упрощений случай однородного краевого условия, т. е.
задачу
L(u) = -^-ai(x, и, их) + а(х, и, их) = 0, (9.1,)
Относительно at(x, и, р), а(х, и, р) прежде всего потребуем,
чтобы
1) они удовлетворяли неравенствам G.2), G.3) при т< п,
неравенствам G.2), G.3) при т = п и неравенствам G.2), G.3)
при т > п. Это необходимо для сходимости интегралов, вхо-
входящих в интегральное тождество G.1), лежащее в основе опре-
определения обобщенных решений.
Далее наложим ограничение, о котором говорилось в начале
параграфа и которое гарантирует априорную оценку как для
решений задачи (9.1г). так и для приближений uN. Именно,
*) Другие классические краевые условия рассматриваются аналогично
(см. соответствующие указания в § 6 гл. III).
12*

356 КВАЗИЛИНЕЙНЫЕ УРАВНЕНИЯ [ГЛ. IV
2) для VueWL,,s^(Q)f]L,(Q) должно иметь место не-
неравенство
где С] > 0, a f (т) — непрерывная положительная функция,- стре-
стремящаяся к бесконечности при т-*¦<». Это условие принято
сейчас называть условием коэрцитивности. Напомним, что
L(u, 11) в* J [а, (х, и, их) тц — а (х, и, их) r\\ dx. (9.3)
Q
Из условия (9.2) следует, что для всех возможных решений и
задачи (9.1г). i=U 2, будет справедлива оценка
где постоянная с2 есть наибольший из корней уравнения
f(%) = Cl.
Наконец, будем считать, что at(x, и, р) и а(х, и, р) изме-
измеримы по (х, и, р) е Q X Е\ X Еп и непрерывны по (и, р).
Покажем, что при выполнении перечисленных условий си-
системы, определяющие галеркинские приближения uN, разре-
разрешимы при любом N. Пусть {%(*)} есть фундаментальная
о
система линейно независимых функций в пространстве Wm>q.
Приближенное решение uN по методу Галеркина ищется в виде
лг
uN = 2 c^k (x) из уравнений
k=i
L(u",$k) = Q, /e= 1, 2 ЛГ, (9.5)
которые представляют собою систему N нелинейных уравне-
уравнений относительно Af неизвестных с%. Для доказательства раз-
разрешимости этой системы перепишем ее в виде одного функ-
функционального уравнения в банаховом пространстве PN, элемен-
лг
тами которого являются суммы х\ = 2 dk$k (х) с произволь-
*1
*1
ными числами dk, а норма определяется равенством ||т)||р==
= 11 illlm,q,Q' Рассмотрим PN как линейное Л/'-мерное простран-
пространство EN векторов d = (rfi, ..., dN) с нормой ||d||w = \\х\||Рдг.
Легко проверить, что || • ||w действительно есть норма в EN.
Введем в EN гильбертову структуру со скалярным произведе-
произведением
(с, d)JV=

§91 О СУЩЕСТВОВАНИИ ОБОБЩЕННЫХ РЕШЕНИЙ 357
га—
и соответствующей нормой | с \N = 1/ 2 с\ • Как известно,
в конечномерных линейных пространствах все нормы эквива-
эквивалентны, в частности, и
vff|d|ff<||d||ff<nff|d|ff, vw>0. (9.7)
Не будем в дальнейшем различать эти две реализации про-
лг
странства PN: как совокупности функций г\= 2i dki!pk(x) и как
совокупности векторов d — и вместо (с, d)N будем писать (|, ti).v,
лг лг
где | = 2 ck^k (х), г] = 2 dktyk (х), а вместо | с \N — число 11 \N.
fc=i *=i
Умножим каждое из уравнений (9.5) на свое число dh и все
уравнения сложим в пределах от k = 1 ro k = N. Это даст
тождество
L{uN, ti) = 0, (9.8)
справедливое при всех элементах х\ из PN. Левая часть его
является линейным функционалом в PN над ц при любом
фиксированном uN из PN, ибо, как нетрудно проверить, в силу
предположений 1) и теорем вложения 2.1 гл. II
\L(uN, T|)KMI«"|ff)|T||ff, (9.9)
rAefi(x) есть некоторая непрерывная функция т^О. Ввиду
этого по теореме Рисса L (uN, ti) можно представить в виде
скалярного произведения некоторого элемента A{uN) гильбер-
гильбертова пространства PN на элемент х\ (точнее, d) этого же про-
пространства, т. е.
L(uN, r]) = (A(uN), r])N. (9.10)
Элемент A (uN) определяется uN однозначно. Благодаря нашим
предположениям о функциях at (x, и, р), а (х, и, р) и, в част-
частности, их непрерывности по (и, р) оператор А, определенный
на всем пространстве PN, непрерывен. Действительно, пусть
vr, r= 1, 2, ..., и v принадлежат PN и vr сходятся к у в PN.
Возьмем Ve > 0 и соответствующее ему множество Qe с: Q
с mes QE ^ mes Q — е, на котором | tyk (х) I и | Vi|>ft (x) |,
k=l, ..., N, не превосходят какого-либо числа сг. На Qe
функции vr и Vvr равномерно сходятся к v и Vv соответ-
соответственно и
max(| vr (x) — v(x)\ + \ Vor (x) - Vv (х) |) < бг, бг -^0

358 КВАЗИЛИНЕЙНЫЕ УРАВНЕНИЯ [ГЛ. IV
при г->оо. При Vt] e Р№
(A (vr) — A (v), r\)N = L (vn r\) — L (v, r\) =
= J {[a, (x, vn vrx) - at (x, v, vx)] r\X{ — [a (x, vn vrx) -
- a (x, v, vx)] r)}dx+ J {...} dx s /<',>, + /e«r.
Интеграл IIW-+Q при r-+oo, a /lfr в силу предположений 1)
и равномерной ограниченности || vr \\m q Q +1| v ||m ? Q имеет оценку
/12)г ^ с || т] ||m q Q\B с постоянной с, общей для всех ог и v.
Так как ||Ti||m Q. Q -^-0 при е-^-0, то сумма Д!г+42)г может
8
быть сделана при уменьшении е и увеличении г меньше лю-
любого наперед заданного числа. В силу конечномерности про-
пространства PN слабая и сильная сходимость в нем равносильны,
так что из доказанного следует, что A (vr) —> A (v) в норме PN.
Тем самым непрерывность оператора А доказана.
Так как х\ в (9.8) и (9.10) — произвольный элемент PN, то
тождество (9.8) эквивалентно в силу (9.10) операторному урав-
уравнению
A(uN) = 0 (9.11)
в гильбертовом пространстве PN. Рассмотрим однопараметри-
ческое семейство операторов
Для них из (9.2) и (9.10) следует, что для Vt] e PN
а потому для х\ с | r\ \N, равной достаточно большому числу RN
(оно определяется лишь N, с, и f(t)), величины (Ax(r\), r\)N,
O^t^l, будут положительны. При т = 0 оператор А0(г\)
определяет тождественное преобразование в PN, так что урав-
уравнение Л0(т1) = 0 имеет в шаре KRN^{f\' \^\n^Rn} единствен-
единственное решение ti = 0. Это вместе с доказанным выше неравен-
неравенством (Ах(л), ti)^ > 0, 0<т<1, для I л Iw = ^/v гарантирует
существование у уравнения Л1(|п) = 0 или, что то же, у урав-
уравнения (9.11) по крайней мере одного решения в Krn (cm. тео-
теорему Брауэра, например, в [13], ч. I). Итак, доказана
Лемма 9.1. При выполнении условий 1) и 2) и непрерывно-
непрерывности функций а-, (х, и, р), а (х, и, р) по (и, р) система уравнений
Галеркина (9.5) имеет по крайней мере одно решение uN из PN.

§ 9] О СУЩЕСТВОВАНИИ ОБОБЩЕННЫХ РЕШЕНИЙ 359
Займемся теперь предельным переходом по N-+oo. Пока-
Покажем, что при дополнительных предположениях, основное из
которых гарантирует монотонность оператора А(и) (или неко-
некоторых связанных с ним операторов) по и, каждая из предель-
предельных в смысле слабой топологии в Wm, q точек и для {uN},
#=1,2, ..., является обобщенным решением из Wln,q за-
задачи (9.1).
Монотонность оператора А(и) означает выполнение нера-
неравенства
(Л (и)-Л (о), и-о)>0 (9.12)
для любых элементов и и v пространства Р, в котором рас-
рассматривается А. Скобки (w, v) в общем случае дают значение
линейного функционала w на элементе v пространства Р. При-
Применительно к нашим операторам А, возникающим во всех про-
пространствах PN, N=\, 2, ..., это условие имеет вид
J {[а{ (х, и, их) — at (х, v, vx)\ (иХ( — vXi) —
Q
— [а (х, и, их) — а (х, v, vx)] (и — v)}dx^0 (9.13)
при V«, v e PN.
Мы считаем это неравенство выполненным для всех эле-
элементов и и v из пространств PN, N=l, 2, ... Но так как
°° °
сумма (J Рк плотна в Wm,q, то (9.13) фактически будет иметь
о .
место для любых элементов и и о из Wm, q-
Покажем сначала, как выполнить предельный переход по
N-+oo в том простейшем случае, когда условию монотонности
удовлетворяет весь оператор А(и), т. е. когда справедливо не-
неравенство (9.13). Благодаря (9.2) для uN справедлива оценка
(9.4)
(9.14)
Поэтому последовательность {uN} имеет по крайней мере одну
предельную точку и в смысле слабой топологии в wm,q- Без
ограничения общности будем считать, что вся последователь-
о -
ность {uN}, N=l, 2, ..., сходится слабо в Wm,q к некоторой
функции и из Win,,,-
При такой сходимости uN к и нельзя, вообще говоря, утвер-
утверждать, что предельным соотношением для (9.8) будетЦы, т|)—О,

360 КВАЗИЛИНЕЙНЫЕ УРАВНЕНИЯ [ГЛ. IV
ибо их входят в (9.8) нелинейно. Тем не менее это верно бла-
благодаря предположению (9.13). Действительно, в силу (9.13)
J {К (*. ""• "Л - ai (*> I. г,)] К - Ц) -
- [а(х, и", и»х) - а(х, |, 1Х)]К- ?)}dx^O (9.15)
о .
при любой функции | из Wm,q. Вычитая из (9.15) тождество
(9.8) с x] = uN — |, где | — произвольно фиксированный элемент
PN, получим неравенство
- J К (х> 1.1Я) К - Ц) - «(*. I. У (»" - 6)] ^ > о,
в котором можно перейти к пределу по N-+°° при закреплен-
оо
ном I из \JPk- Это даст неравенство
- J[ai (Jc, I, Ы (и*, - Ц) - а {х, |, 1J (и - D] Лс > 0,
Q
оо
которое справедливо при любом | из [_JPft, а потому и при
о .
любом | из Wm, q. Положим в нем | = гг\ + и, е > 0, где х\ —
О |
произвольный элемент Wm>q, затем сократим на е и перейдем
к пределу по е->0. Так как функции at(x, u-\-er\, их-\-ех]х),
а(х, и + ег), их -\- гцх) в силу наших предположений о а{(х, и, р)
и а(х, и, р) и леммы 3.2 гл. II сходятся слабо в Lm'(Q) и
Lq>(Q) к аг (jc, и, их) и а (л;, ы, их) соответственно*), то в резуль-
результате этого предельного перехода получим
J [щ (х, и, их) r\Xi — а (х, и, их) Т[] dx > 0. (9.16)
Q
о .
Это неравенство справедливо при любой функции х\ из Wm-q>
° i ° i
а так как наряду с любой х\ из Wm,q в Wm,q входит и функция
— г\, то в (9.16) имеет место знак равенства, т. е, тождество
L(u, n) = 0.
Тем самым доказана
Теорема 9.1. При выполнении условий леммы 9.1 и усло-
условия (9.13) задача (9.1г) имеет по крайней мере одно решение из
l
¦) На самом деле имеет место сильная сходимость

j 91 О СУЩЕСТВОВАНИИ ОБОБЩЕННЫХ РЕШЕНИЙ 361
Условие (9.13) для произвольной Q не следует из усло-
условия эллиптичности уравнения @.1) даже при «хороших» функ-
функциях at{x, и, р), а(х, и, р) и гладких функциях и (х) и v(x).
Как видно из рассмотрений § 2, оно имеет место, вообще го-
говоря, лишь для малых областей Q. Покажем, что оно может
быть заменено условием эллиптичности, но при этом предпо-
предположения 1) при т< п и т> п должны быть несколько усилены.
Рассмотрим случай т < п (остальные изучаются аналогично).
Предположим, что вместо G,2), G.3) выполнены неравенства
I 11 г*' I _. ( y\ rr\ ¦ J (C\\ /Q 1 7\
| a (x, u, p) | < с | p f/9' + с | u Г' + ф2 (jc), ф2 е Lr (Q), (9.18)
с q < q = max(m, q), q' = ql{q—\), m'=^ml{m—\). Условие
же (9.13) заменим на следующее: при jheQ, |ы|^М,, |^|^М
и любых р
[а,- (х, и, р) — at (х, и, q)] (pt — qd>h{\p — q \, Af,, Af2, jc), (9.19)
где f2(r, Af,, Af2, ^ — непрерывная функция своих аргументов,
не убывающая по г и положительная при г > 0, Если функции
at{x, и, р) дифференцируемы по р, то (9.19) есть следствие ус-
условия эллиптичности C.1), точнее, неравенства
^11Ы1>ч(х,и)A+1рГ-Ч>, (9.20)
где v (я, и) есть непрерывная положительная функция (я, и).
Действительно, представим левую часть (9.19), следуя § 2,
в виде
/е= [cii (х, и, р) — at (х, и, q)] (р,- — qt) =
5а(- (х, и, q + t(p — q))
dt ipt - qt) {p, - q,)
и оценим ее снизу с помощью (9,20). При т~^2 ясно, что (9.19)
будет выполняться с функцией f2(r, Mu M2, x) = r2 minv (а;, и).
, и) J
При те A,2)
+\q + t(p - q)\r-> dt\ p - q
i
> v (jc, u) I p - q ? J A + \q | + 11 p - q |)m~2 dt =
о
= v (jc, u) -li^i [A + \q | +1 p - q I) - A + \q I)]

362 КВАЗИЛИНЕЙНЫЕ УРАВНЕНИЯ [ГЛ. IV
и, следовательно, (9.19) выполняется с функцией
f2(r, Мь М2, х) =
= min v (jc, и) —Г—г [A + \q I + г)—1 - A + \q I)™"'].
inia от—i
Докажем, что при выполнении предположений (9.17)—(9.19) и
(9.2) задача (9.1г) имеет по крайней мере одно обобщенное ре-
шение из Wm, q. Для этого используем ту же, что и выше,
схему метода Галеркина. Лемма 9.1 гарантирует существова-
существование приближенных решений uN. Для них верна оценка (9.14).
Она и теоремы вложения (см. §§ 2, 3 гл. II) гарантируют сла-
слабую компактность и% в Lm(Q), a uN в L-(Q), а также сильную
компактность uN в любом Lq (Q) с q < q. Будем ради простоты
написания считать, что вся последовательность uN, ;V=1,2
сходится к некоторой функции и указанным образом и почти
всюду в Q. Ясно, что функция и есть элемент Wm, q *). Дока-
Докажем, что она есть обобщенное решение задачи (9.1,). Функции
ai (х, uN (х), u% (x)) s A. v (а;), как сложные функции х, равно-
равномерно ограничены в норме Lm' (Q). В этом легко убедиться,
используя (9.17) и (9.14). Ввиду этого они слабо компактны в
Lm'(Q), и потому Ai, n(x) сходятся слабо в Lm'(Q) к некоторым
функциям At (x) соответственно. Далее, функции а{(х, uN (х),
vx(x))s=ui<N<v(x) при произвольно фиксированной функции
v(x) из Wlm(Q) сходятся почти всюду к di(x, u(x), vx(x)) и рав-
равномерно ограничены в Lm(Q); более того, величины \\di,n, oIU'.q'
равномерно малы для Q' с малой mesQ'. Ввиду этого Ui.n, v(x)
сходятся к cii(x, u(x), vx(x)) в Lm'(Q) (см. лемму 3.2 гл. II).
Равномерная малость || d,-, лг, v llm\ & при малой mesQ' есть след-
следствие (9.14) и того, что показатель q/mf у \и\ в (9.17) строго
меньше предельного показателя q/m', так что при оценке со-
соответствующего члена мажоранты (9.17) мы можем воспользо-
воспользоваться неравенством Гёльдера и «заработать» в качестве мно-
множителя mes Q' в некоторой положительной степени. Из (9.18).
и (9.14) следует равномерная ограниченность норм в Ly функ-
функций Ац (х) = а (х, uN (х), и^(х)). Это дает слабую сходимость
AN{x) в L?'(Q) к некоторой функции А(х) gL,-'(Q).
*) Здесь и далее каждый раз из компактной последовательности надо
выбирать сходящуюся подпоследовательность. Но мы вместо этого, экономя
место, будем считать, что все встречаемые ниже компактные последователь-
последовательности являются сходящимися. Читатель легко поймет, как сделать последу-
последующие рассуждения вполне строгими-

§ 9] О СУЩЕСТВОВАНИИ ОБОБЩЕННЫХ РЕШЕНИЙ 363
Из всего сказанного следует, что в тождестве (9.8) можно
перейти к пределу по N-+оо при закрепленной функции ц из
какого-либо PN и в результате получить равенство
x = 0. (9.21)
Q
oo
Оно справедливо для любой i\^{JPk, а следовательно, и для
о
любой x]^Wlm,q. В силу условия (9.19)
J [в, (*. и", и») - а, (х, и", I,)] (и* - 1 ) dx > О
Q
о .
при V| e Wm, q. Вычтем из этого неравенства тождество (9.8)
с ц= uN — |, где | е PN. В результате получим
J [а (х, и», и?) (а* -1) - а. (х, и", %х)« - | )] dx > 0.
В этом неравенстве благодаря установленным выше сильным
и слабым сходимостям разных функций можно перейти к пре-
пределу по N-+oo. Это дает
J [А (и - |) - at (х, и, %х) (uXi - Ц)] dx > 0. (9.22)
Q
Сложим (9.22) и (9.21), взяв в последнем г\ = и — |:
J [At - а, (х, и, %х)] (uXi - tx.) dx > 0. (9.23)
Q
Это неравенство справедливо при V| из VPW, а потому спра-
справедливо и при V|elFm,,. Положим в (9.23) 1 = и — е?, е > О,
S e Wm, q, сократим (9.23) на е и устремим е к нулю. В силу
сильной сходимости I к и в Wm, q в пределе получим неравен-
ство
J [At - at (х, и, их)] $Xi dx > 0. (9.24)
В нем t, — произвольный элемент Wlm,q, и так как наряду с ним
в Wm, q входит и — ?, то (9.24) справедливо со знаком равен-
равенства. Поэтому тождество (9.21) эквивалентно следующему:
J [a, (jc, и, и,) ^ - Ах]] dx = 0. (9.25)

334 КВАЗИЛИНЕЙНЫЕ УРАВНЕНИЯ [ГЛ. IV
До сих пор наши рассуждения были близки к доказательству
теоремы 9.1. Докажем теперь, что
А(х) = а(х,и(х),их(х)). (9.26)
Для этого используем предположение (9.19) во всей его пол-
полноте. Возьмем последовательность ич, N=1, 2, ..., сильно
о
сходящуюся к и в норме Wm, q и такую, что каждое uN e PN.
Это возможно ввиду наших предположений о системе {^(д;)}
координатных функций. Вычтем из (9.25) тождество (9.8), счи-
считая г] = uN — uN = (и — uN) + (uN — и), и результат запишем так:
J К (х> uN> "*) - ai (x>«v. О] К - <)dx+
Q
к- (х>"'",)- fl, (*. "w. "*)] (% - <)dx=
= J [A - a (x, uN, и*)] (uN - uN) dx +
x. (9.27)
J
Q
+ J \ai (x' "' «*) " «, (*. «">
Q
Все интегралы, кроме первого, при N—>oo стремятся к нулю,
ибо в каждом из них один из множителей стремится к нулю
сильно в некотором Lr (Q), а другой равномерно ограничен
в Lr'(Q). Поэтому и первый интеграл
j B J [flj (*, и", <) - а, (х, и", их)} (< - и ) ^ - 0 (9.28)
Q
при N-+oo. Это вместе с условием (9.19) и сходимостью uN
почти всюду kkgL, (Q) позволяет заключить, что и% сходятся
почти всюду к их. Из сходимости же почти всюду uN к и
и и% к их и из непрерывности а(д;, ы, р) по (ы, р) следует, что
а(х, uN(x), u^(x)) почти всюду сходятся к а(х, и(х), их(х)), т. е.
равенство (9.26) действительно имеет место.
Итак, доказана
Теорема 9.2. Пусть функции at{x, и, р), а(х, и, р) непре-
непрерывны по (и, р) и удовлетворяют условиям (9.2) и (9.17)—(9.19),
причем me(U), Тогда задача (9.1/) имеет по крайней мере
о
одно'обобщенное решение из Wm,q.
Идея доказательства даваемого теоремой 9.2 обобщения
теоремы 9.1 принадлежит Ж- Лерэ и Ж- Лионсу (см. ее изло-
изложение в книге [396] Ч. Морри, гл. V, § 12). Аналогично рас-
рассматриваются случаи т=п и т > п. При т = п условия (9.17),

§9] О СУЩЕСТВОВАНИИ ОБОБЩЕННЫХ РЕШЕНИЙ 365
~ ~ о ¦
(9.18) надо заменить на G.2), G.3), причем пространство Wn, q
о . о о
совпадает с Wn(Q). При т> п Wmt.q также совпадает с Wm(Q),
причем элементы Wm(Q) суть непрерывные по Гёльдеру функ-
функции х в Q. Ввиду этого uN будут сходиться к и равномерно.
Условия (9.17), (9.18) в этом случае надо заменить предполо-
предположениями
\at(x,u, р)КМ«)AрГ~' + Ф1(*)), Ф.е^№), (9.29)
I а (х, ы, р)|< 1*2 («) (I Р Г"е + Ф2 (*)), е > 0, ф2 е= L,, (Q), ?, > 1,
(9.30)
где цг (ы) — непрерывные функции и. Если выполнены при этом
остальные условия теоремы 9.2, то ее заключение справедливо
и при гп^-п.
Замечание 9.1. В случае неоднородного граничного
условия
«Ь-фЬ. (9-31)
где ф (*) е Wlm_ q, предположение (9.2) надо заменить на сле-
следующее:
L(u, u-<v)^f(\\u\\m<qtQ)-F(\\<?\\m>q a), (9.32)
где ^(т) — какая-либо непрерывная функция т^О, а прибли-
приближенное решение uN искать в виде ылг = ф + у?, где у? =
= Zj ^^M» a {"tftWl — фундаментальная система в Wlm .
Л—— 1
Коэффициенты с^ определяются из системы уравнений
Доказательство разрешимости этой системы и предельный пере-
переход проводятся так же, как и выше для однородного краевого
условия.
Остановимся еще на вопросе о единственности решения
задачи (9.1,), (9.31) в классе Wlm q. В общем случае (см. гл. III)
единственности нет даже для линейных уравнений в классах
сколь угодно гладких решений. Поэтому речь может идти лишь
об указании ряда достаточных условий, когда она имеет место.
Для области Q любого размера таким условием является вы-
выполнение неравенства
J [[at (х, и, их) - аг (х, v, vx)] (uX{ - vX{) —
Q
— [а (х, и, их) — а(х, v, vx)] (и - v)} dx>0 (9.33)

Збб КВАЗИЛИНЕЙНЫЕ УРАВНЕНИЯ [ГЛ. IV
для любых двух не равных тождественно друг другу элемен-
элементов и и v из IFffl,,, имеющих одинаковые значения на S. Ясно,
что оно гарантирует теорему единственности. Его естественно
назвать условием строгой монотонности (см. (9.12) и (9.13)).
Выражение, стоящее в фигурной скобке в (9.33) (обозначим
его через J (и, v)), можно преобразовать, следуя § 2, к виду
да
где uf = tu-\-{\—t)v> если функции at и а дифференцируемы
по и и р. Если предположить, что при jugOh произвольных и,
р, | справедливо неравенство
да^х, и, р) ^ f fdat За \ да
> v, (jc, и, р) 2 1J + v2 (jc, «, р) feg, (9.34)
где V; (а;, и, р) суть непрерывные неотрицательные функции,
причем V! (*, и, р) > 0 при х е Q, с: Q, a v2 (x, и, р) > 0 при
jee(Q — Q,), то нетрудно понять, что неравенство (9.33) будет
иметь место при u(x)^v{x) и и \s = v \s. Так что условие (9.34)
гарантирует теорему единственности.
Теоремы 9.1 и 9.2 утверждают при определенных условиях
разрешимость задачи (9.1/) (и аналогично (9.1,), (9.31)) в классе
Wm<q(Q) = Wlm(Q)(}Lq(Q). Теорема 7.1 гарантирует ограничен-
ограниченность любого из таких решений, причем условия теоремы 7.1
не могут быть в общем случае ослаблены. Теоремы §§ 1, 5, б
данной главы и теоремы §§ 2 и 3 гл. IX дают достаточные
условия того, когда каждое такое решение обладает той или
иной гладкостью, в частности, когда оно будет элементом С2+а (Q).
В следующем параграфе будет исследован вопрос о классиче-
классической разрешимости задачи (9.1i), (9.31) без использования ре-
результатов данного параграфа. Условие (9.2) будет заменено
менее ограничительным требованием ограниченности тах|ы(д;)|
Q
или || и \\q a всех возможных решений некоторого однопараметри-
ческого семейства задач типа (9.1i), (9.31) (точнее см. § 10).
Кроме того, обратим внимание на следующее различие усло-
условий, налагаемых на функции at (x, и, р) и а {х, и, р) в данном
параграфе и в § 10. В § 10 рассматриваются классические

§9] О СУЩЕСТВОВАНИИ ОБОБЩЕННЫХ РЕШЕНИЙ 367
решения и(х), о которых в большинстве случаев заранее из-
известно, что тах|ы(л:)| не превосходит некоторого числа М.
а
Ввиду этого поведение функций at (x, и, р), а {х, и, р) при
\и\^М не имеет значения. В данном же параграфе, напротив,
все наши условия содержали те или иные требования на по-
поведение ai и а при больших \и\. Правда, от части этих тре-
требований можно нередко избавиться, если известно, что все воз-
возможные обобщенные решения задачи из Wlmiq ограничены.
Поясним это на примере задачи
L (и) = Аи — ые?" + f (х) = 0, u|s = 0,
f^Lqi(Q), Qi>-^=Y' n>2> Y = const >0.
Для нее
(9.35)
= р2, аи = — и2е^и + fu < fu, (9.36)
а
L (и, и) = J (| Vu f + u2ev" - fu) dx> J (| Vu p- fu) dx>
Q Q
Q. (9.37)
Неравенство (9.37) есть неравенство типа (9.2). Оно гара'нти-
рует априорную ограниченность IIuII^q. Из соотношений (9.36)
видно, что для L выполнены условия G.4), G.5) теоремы 7.1,
в которой дается оценка тах|ы| через ||ы||„ о. Ясно, что и
Q
условие монотонности (9.19) для L имеет место. Однако функ-
функция а(х, и, р) = — ueyu-\-f(x) растет с ростом и так, как не
допускается уже условиями G.2), G.3), и потому теоремы 7.1
и 9.2 непосредственно к уравнению (9.35) неприменимы. Рас-
Рассмотрим тогда вспомогательную задачу
Г (и) = Да + 3 (и)+ /(*) = 0, u|s = 0, (9.38)
где а (и) = — ие^и при | и \ ^ М, а (и) = — Ме^м при и ^ М и
а (и) = Ме~т при и < — М. В качестве М возьмем постоянную с
из теоремы 7.1. Она определяется Q и llfll^Q и мажорирует
vraimax| u(x) |. К задаче (9.38) применимы теорема 9.2, гаран-
гарантирующая существование по крайней мере одного решения и(х)
о .
из W2(Q), и теорема 7.1, утверждающая, что для любого такого
решения vrai max| u(x) |<Л4. Но при |«|<М уравнения (9.35)
Q
и (9.38) совпадают, следовательно, решения и(х) задачи (9.38)
являются решениями и задачи (9.35). При конструировании

368 КВАЗИЛИНЕЙНЫЕ УРАВНЕНИЯ [ГЛ. IV
уравнения L (и) = 0 мы следили за тем, чтобы постоянные, вхо-
входящие в условия (9.2) и G.4), G.5) для L и L, были бы оди-
одинаковыми. Эти постоянные определяют мажоранты для || и ||^ а
и vraimax|«|, т. е. число М, которое входит в определение
а
функции а (и).
Аналогичные рассуждения позволяют иногда ослабить тре-
требования §§ 7 и 9 на рост функции а(х, и, р) по р (заменить
их предположением A.3)).
§ 10. Классическая разрешимость задачи Дирихле
В этом параграфе будут даны достаточные условия разре-
разрешимости задачи Дирихле
LW^-r—aiix, и, их) + а(х, и, ыл) = 0, A0.1,)
в пространстве C2+a(Q)*). Результаты данного параграфа пред-
предшествовали тем, которые изложены в § 9, и не могут быть
в полной мере выведены из последних даже с использованием
всего арсенала априорных оценок, изложенных в §§ 1—8.
В конце § 9 было объяснено, как из разрешимости задачи A0.1;)
в Wlm< , и результатов §§ 1—8 можно выводить заключения
о том, что каждое решение и этого класса обладает той или
иной гладкостью, в частности, принадлежит C2+a(Q). Однако
возникающие при этом ограничения на at (x, и, р) и а(х, и, р)
в общем случае несколько сильнее тех, при которых в данном
параграфе будет доказана разрешимость в C2+a(Q). Помимо
этого в § 9 есть еще одно условие —неравенство (9.2), которое
в данном параграфе будет заменено менее ограничительным
предположением 1): тах|ы(д;, т)| не превосходит какой-либо
а
постоянной для всех возможных решений и(х, т) из C2+a(Q)
некоторого однопараметрического семейства задач вида A0.1;)
L» = 0, u\s=4f(x,s)ls, tg[0,1]. A0.2)
Относительно этого семейства задач предполагаем, что оно
гладко зависит от т (это будет уточнено ниже), при т=1 за-
задача A0.2) есть задача A0.1;), а при т=0 задача A0.2) имеет
*) Заметим, что результаты гл. III о линейных уравнениях гарантируют
принадлежность любого решения и нз С2+^ (Q) н даже из C1+^(Q) задачи
A0.1,), A0.12) к классам C/+a(Q) н C/+a(Q), />2, если а{, a, S н <р обла-
обладают соответствующей гладкостью (см. § 12 гл. III и § 6 данной главы).

§ Ю] КЛАССИЧЕСКАЯ РАЗРЕШИМОСТЬ ЗАДАЧИ ДИРИХЛЕ 369
конечное число решений и их суммарный индекс отличен от
нуля (см. [324]).
Сравним условия (9.2) и 1) на примере линейной задачи
M(u)s(atjUXl)Xt + au = ku + f(x), «|s = 0. A0.3)
Неравенство (9.2) для нее эквивалентно тому, что число X
должно быть больше всех собственных значений оператора М,
соответствующего задаче A0.3) (напомним, что собственные
значения М образуют последовательность, стремящуюся к — оо).
С другой стороны, рассмотрим следующее семейство задач:
«|s = 0, те [0,1]. (Ю.4)
Если X не есть точка спектра М, то, как следует из резуль-
результатов гл. III, задачи A0.4) однозначно разрешимы для любой f
и максимумы модулей их решений и(х, т) не превосходят не-
некоторой постоянной, определяемой ац, а, X и f. При т = 0 за-
задача A0.4) имеет единственное решение ы = 0 и его индекс
равен ±1. Таким образом, условие 1) для A0.3) выполнено,
если X не есть точка спектра М. Как видим, это условие суще-
существенно слабее условия (9.2). Более того, для линейных задач
оно и необходимо, ибо, как доказано в § 5 гл. III, задача A0.3)
разрешима при любой f тогда и только тогда, когда X не есть
точка спектра М.
Мы покажем, что условие 1) (вместе с C.1) и C.2) и неко-
некоторой гладкостью известных в задаче функций) достаточно для
разрешимости задачи Дирихле и в общем случае нелинейных
задач A0.1;), только решений при этом может быть не одно,
а несколько. В условии 1) имеется большой произвол в выборе
семейства Lx (и), причем младшие члены Lx (и) можно брать
комплексными. В этом параграфе, как и в большей части книги,
мы ограничиваемся уравнениями с вещественными функциями,
хотя.основные результаты книги справедливы и для уравнений
с комплексными функциями, образующими младшие члены
уравнения.
Для исследования разрешимости задачи A0.1г) можно вос-
воспользоваться, следуя Шаудеру и Лерэ, различными принципами
неподвижной точки для вполне непрерывных преобразований.
Мы рассмотрим два из них: принцип Лерэ — Шаудера и прин-
принцип Шаудера. Первый, будучи более общим, охватывает большее
число случаев. Второй же (при несколько меньших возможно-
возможностях) привлекает своей относительной простотой. Мы его изло-
изложим в конце параграфа (см. равенства A0.27) и далее).
Опишем сначала формальную схему сведения задачи A0.1^)
к задаче о разыскании неподвижных точек некоторых «хороших»

370 КВАЗИЛИНЕЙНЫЕ УРАВНЕНИЯ [ГЛ. IV
преобразований. Возьмем семейство дифференциальных опера-
операторов вида A0.10:
Lx (и) = -j^- {at (х, и, их, т)) + а (х, и, их, т),
где функции at(x, и, р, т) и а(х, и, р, т) гладко зависят от т
из [0, 1] и при т=1 совпадают с функциями щ{х, и, р) и
а(х, и, р) соответственно. Характер зависимости этих функций
от т уточним ниже, а пока предположим, что они обладают
при те[0, 1] теми же свойствами, что и при т=1. Нелиней-
Нелинейным задачам
L» = 0, « |s = тФ |s, те=[0, 1] A0.5)
сопоставим линейные задачи
да- (х, v, о„, т)
^ о>V/ + А (х, v, vx, т) = 0, w |s = тФ Is, A0.6)
Х1
где
.да, (х, v, v , т) да, (х, V, о , т)
состоящие в определении функции w (x) в Q по известной функ-
функции v(x). Линейная задача A0.6) однозначно разрешима, если
только входящие в нее известные функции обладают некоторой
гладкостью. Она определяет нелинейный оператор
ш(*) = Ф(о,т), A0.7)
сопоставляющий любому т из [0, 1] и v(x) из некоторого про-
пространства решения задачи A0.6). Неподвижные точки преобра-
преобразования Ф(и, т), как нетрудно видеть, являются решениями
задачи A0.5), и наоборот. Таким образом, задача A0.5) свелась
к задаче на определение неподвижных точек преобразования
Ф(и, т) или, что то же, на определение решений уравнения
и = Ф(и,х). A0.8)
Сформулируем теорему Лерэ — Шаудера о существовании ре-
решений функциональных уравнений вида A0.8).
Теорема 10.1. Пусть Н есть полное банахово простран-
пространство, а Ш — замыкание какого-либо связного ограниченного от-
открытого множества Ш в Н. Пусть <8 есть топологическое произ-
произведение Н на отрезок [0^т^1] (гак что элементами <§ =
= Н X [0, 1] являются пары (v, т), где сеЯ, ате[0, 1]),
a S'tj = !Ji X [0, 1]. Уравнение A0.8) имеет по крайней мере одно
решение в Ш при всех т е [0, 1], если
1) преобразование Ф(ы, т) определено и вполне непрерывно
из Шх в Н;

§ 10] КЛАССИЧЕСКАЯ РАЗРЕШИМОСТЬ ЗАДАЧИ ДИРИХЛЕ 371
2) граница области ЭТ не содержит решений уравнения A0.8)
ни при каком те[0, 1];
3) при т = 0 уравнение A0.8) имеет в %1 конечное число ре-
решений и суммарный индекс их отличен от нуля.
Условие полной непрерывности Ф (и, т) на Ш{ означает, что
ф(ы, т) непдерывно в каждой точке ?Я, и множество значений
Ф(ы, т) на 9^ компактно в Я. Оно заведомо будет выполняться,
если Ф(ы, т) удовлетворяет условиям: а) непрерывно по (и, т)
на 91у, Ь) при каждом фиксированном т из [0, 1] преобразует Ш
в компактное множество и с) непрерывно по те [0, 1] равно-
равномерно относительно «еЯ,
Индекс решения и0 уравнения A0.8) при т = т0 равен сте-
степени отображения в(ы, то)^ы — Ф(ы, т0), рассмотренного в ма-
малой окрестности точки ы0 пространства Я. Если, например,
ф(ы, то) = О, то в есть тождественное преобразование и его
степень отображения равна +1. Эта ситуация имеет место,
например, для Ф(ы, т) = тФ(ы) при т = 0.
Наиболее трудно проверяемым условием этой теоремы приме-
применительно к дифференциальным уравнениям является пункт 2). Ап-
Априорные оценки, которым посвящена большая часть книги, и по-
получены нами прежде всего для того, чтобы проверить это услозие.
Вернемся к задачам A0.5). Обозначим через Шм, мГ> как и
выше, совокупность точек (*, и, р) евклидова пространства
E2n+i cJteQ, | и | ^ М, | р | ^ М{. Предположим, что при VM, М,
и Vtg=[0, 1] функции ui(x, и, р, т) и а(х, и, р, т) суть эле-
элементы С1+а(Шм, м) и Са(Шм, м) соответственно, равномерно не-
непрерывно зависящие от т в нормах этих пространств. Пусть,
кроме того, феС2+аE) и S^C2+a. В качестве пространства Я
возьмем C1+P(Q) с каким-либо ре@, 1), а в качестве ^ — ка-
какой-либо шар в Я с центром в нулевом элементе Я. Если
взять любую функцию v (х) из C1+P(Q) и подставить в уравне-
уравнение A0.6), то его коэффициенты будут функциями из Caf> (Q).
Мы потребуем, чтобы уравнение A0.6) было равномерно эл-
эллиптическим. Тогда по теореме Шаудера (см. § 1 гл. III) реше-
решение w(x, т) задачи A0.6) существует, единственно и принадле-
принадлежит С2+сф(О), так_что Ф(и, т) при каждом т преобразует функ-
функции v(x) из C1+P(Q) в функции w (x, т) из C2+af5(Q). Более того,
Для решений w(x, т) имеет место оценка
I w
i.I
а потому и
w la
,B+aP)

372 КВАЗИЛИНЕЙНЫЕ УРАВНЕНИЯ [ГЛ. IV
где F(%, ^ — некоторая вполне определенная, непрерывная,
монотонно возрастающая функция |, т^О. Так как множество
функций, ограниченное в норме C2+a|3(Q), компактно в про-
пространстве C1+e(Q), то из сказанного ясно, что преобразование
Ф(и, т) переводит любое ограниченное в !f = C1+P(Q) X [O^
множество пар (v, т) в множество, компактное в CI+|3(Q).
Покажем, что преобразование Ф(и, т) непрерывно по (v, т).
Пусть функции о' и числу т соответствует решение w'(x, т),
а (и", т) — решение w" (х, т). Нормы | о>', до" f2+aW не превосхо-
превосходят, в силу A0.10), некоторого числа с. Для их разности w =
= w' — w" из уравнения A0.6) выводим соотношение
dat (х, у, ух, х) _ Г dui (х, у", v", х) dat (х, у', у'х, х) П
+ А (х, v", v';, т) -А(х, v', v'x, т), ш к = 0. A0.11)
Так как его можно рассматривать как линейное уравнение
относительно функции w, то для w справедлива оценка типа
A0.9). Если в ней ар заменить на у < а8, то правая часть в этом
неравенстве стремится к нулю равномерно относительно т,
когда | v'— v" |q+|3)->0. Это доказывает непрерывность Ф(и, т)
по v на Ш, равномерную относительно те[0, 1]. Аналогично
устанавливается непрерывность Ф(и, т) по т, равномерная от-
относительно v из Ш. Это гарантирует непрерывность Ф(и, т)
по (v, т).
Переходим к условиям 2) и 3) теоремы Лерэ — Шаудера.
Из них мы считаем выполненными условие 3) и условие
max|u(jc, т)|<М A0.12)
Q
для всех возможных решений и(х, т) задачи A0.5) из класса
C2+a(Q). Все такие решения и(х, т), очевидно, являются реше-
решениями уравнения A0.8). Верно и обратное: если и(х, т) есть
решение уравнения A0.8) из пространства C1+P(Q), то оно будет
и решением уравнения A0.5) из C2+a(Q).
Действительно, в силу определения преобразования Ф(ы, т)
функция Ф(ы, т) есть решение задачи A0.6), когда в коэффи-
коэффициенты уравнения A0.6) вместо v (x) подставлено и. Так как
получаемые при такой подстановке коэффициенты как функции х
будут из Cap (Q), то решение задачи A0.6) будет принадлежать
C2+a|3(Q). Но Ф(ы, т) совпадает с и, так что ыеС2+а|3(О), и по-
потому коэффициенты в уравнении A0.6), когда в них вместо_и
подставляется и, фактически принадлежат не только С (Q),

s 10] КЛАССИЧЕСКАЯ РАЗРЕШИМОСТЬ ЗАДАЧИ ДИРИХЛЕ 373
но и Ca(Q), и, следовательно, решение и = Ф(и, т) будет при-
принадлежать C2+a(Q). Итак, решения уравнений A0.8) фактически
являются более гладкими функциями х, чем функции из C1+P(Q),
именно, они принадлежат C2+a(Q) и, кроме того, удовлетво-
удовлетворяют уравнению A0.5).
Возвратимся к условию 2) теоремы Лерэ— Шаудера. Чтобы
решения и(х, т) уравнения A0.8) (или, что то же, задачи A0.5))
при изменении т в пределах от 0 до 1 не вышли на границу
области Ш, достаточно доказать, что для них нормы | и (х, т) |gI+|3)
не превосходят какого-либо числа Мо. Тогда, беря VI так, чтобы
оно содержало шар радиуса Мо, мы будем знать, что решения
и(х, т) не выходят на границу Ш. Таким образом, проверка
условия 2) сводится к получению априорных оценок всех воз-
возможных решений задачи A0.5) в норме C1+P(Q).
Теоремы 4.1, 6.1 показывают, что для такой априорной
оценки и (х, т) надо потребовать, чтобы функции at (x, и, р, т)
и а (х, и, р, т) при х е Q, | и \ ^ М, те[0, 1] и произвольных р
удовлетворяли неравенствам
\а(х. и, р,
где ц и v — положительные константы, а т> 1. При выполне-
выполнении этих условий из теорем 4.1, 6.1 следует
max\Vu(x, t)|<M,, S (их ,)'р) < М2, A0.14)
Q
где постоянные Ми М2 и р определяются лишь величинами п,
М, т, v и ц из A0.13) (зависимость от Q и ф нас здесь не
интересует). Индекс р, определяющий основное пространство
# = C+|3(Q), мы возьмем равным показателю р, входящему
в оценку A0.14). Постоянные М, М{ и М2 нам известны, по-
поэтому нет надобности считать преобразование Ф(и, т) опреде-
определенным на всем пространстве C1+P(Q), достаточно его рас-
рассмотреть лишь на множестве 1R функций v (x), подчиненных

374 КВАЗИЛИНЕЙНЫЕ УРАВНЕНИЯ [ГЛ. IV
неравенствам
max| v{x) |<M + e, max| S/v(x)\ <M, +е,
a q
где е—произвольное положительное число. Сформулируем те-
теперь первую теорему существования.
Теорема 10.2. Предположим следующее:
a) При xeQ, | и |^М, хе [0, 1] и произвольных р функции
at(x, и, р, х), а (л;, и, р, х) измеримы, at{x, и, р, х) дифферен-
дифференцируемы по х, и, р и удовлетворяют неравенствам A0.13).
b) ai{x, и, р, х) и а(х, и, р, х) при Vt e [0, 1] суть элементы
С1+а(Шм,м,) и Са(Шм,м) соответственно, равномерно непрерыв-
непрерывные по х на [0, 1] (М{ — постоянная из A0.14), определяемая
теоремой 4.1).
c) S^C2+a, (peC2+a(Q).
Тогда, если модули всех возможных решений и (х, х) задач
A0.5) из пространства C2+a(Q) при те[0, 1] не превосходят
числа М и задача A0.5) при т = 0 имеет конечное число реше-
решений, суммарный индекс которых отличен от нуля, то задача
A0.5) имеет по крайней мере одно решение и(х, х) из C2+a(Q)
для всех х из [0, 1].
Поясним условие Ь) на примере функции а(х, и, р, х): при
Vre[0, 1] функция а(х, и, р, х)^Са(ШМм) и для Чх,х-\-
+ Лте=[0, 1]
| а(х, и, р, т + Ат)— а(х, и, р, х) |^ ^<е(| Ат|),
где в (| Ат |) —V 0 при Дт->0. Из этого условия, в частности,
следует, что а(х, и, р, х) есть непрерывная на Шм.м, X [0, 1]
функция (а;, и, р, х).
Для доказательства теоремы применим теорему Лерэ —
Шаудера так, как мы только что описывали. В качестве про-
пространства Я возьмем C1+P(Q) с показателем р из неравенства
A0.14), гарантированного теоремой 6.1. Преобразование Ф(и, т),
а следовательно, и уравнение A0.8) рассмотрим на множестве
гК1==?ЯХ[0<т<1] пространства & = Н X [0<т< 1], где Ш
состоит из функций v (х), удовлетворяющих неравенствам
е, тах| S/v(x) |<M, + е,
xe=Q
A0.16)

§ Ю] КЛАССИЧЕСКАЯ РАЗРЕШИМОСТЬ ЗАДАЧИ ДИРИХЛЕ 375
где е — какое-нибудь положительное число. Нам желательно,
чтобы функции at (х, и, р, т), а (х, и, р, т) удовлетворяли усло-
условию Ь) нашей теоремы на этом множестве %. В силу Ь) мы
можем добиться этого, изменяя, если надо, функции at (x, и, р, т),
а {х, и, р, т) на множествах, где М < | и | =< М + е или М, < | р | ^
<!Mi + e. За так измененными функциями at и а сохраним
прежние обозначения. То, что они, может быть, не совпадают
с первоначальными at и а вне множества Шм,м„ не повлияет
на наш основной результат — определение решений и (х, т) урав-
уравнения A0.8), ибо последние, если существуют, то удовлетво-
удовлетворяют неравенствам | и \^М, | Vm |^M1; т. е. принадлежат тому
множеству значений аргументов функций аг и а, на котором
старые и измененные функции at и а совпадают.
Итак, преобразование Ф(и, т) рассматриваем на 3^. Из при-
приведенных выше рассуждений видно, что все требования тео-
теоремы Лерэ — Шаудера выполнены в силу условий теоремы:
требование 1) следует из предположений а) — с), требование 3)
есть следствие последнего предположения теоремы 10.2 (ибо
решения уравнения A0.8) и задачи A0.5), как выяснено выше,
совпадают), а требование 2) выполняется в силу предположения
max тах|м(лг, т)|^М и условия а) (см. теоремы 4.1 и 6.1).
те [0, 1] Q
Поэтому теорема 10.1 гарантирует существование при любом т
из [0, 1] по крайней мере одного решения и(х, т) уравнения
A0.8) из C1+P(Q). Как показано выше, любое такое решение
и{х, т) фактически принадлежит С2+а(О) и удовлетворяет усло-
условиям A0.5), т. е. является искомым решением задачи Дирихле
для уравнений A0.5). Теорема 10.2 доказана.
Можно указать разные случаи, когда все условия теоремы
10.2 выполнены. Начнем со следующего.
Пусть функции at дифференцируемы. Перепишем уравне-
уравнение A0.1,) так:
L(u)t=au(x, и, ux)ux.Xj + A{x, и, их) = 0,
где
даг (х, и, р)
ач(х, и, р) = ^ ,
а
, , ч / . , да, (х, и, р) да. (х, и, р)
А (х, и, р) = а (х, и, р) Н l—^ pi H ~
Рассмотрим следующее семейство операторов:
-ц [A
те [0,1], A0.17)

376 КВАЗИЛИНЕЙНЫЕ УРАВНЕНИЯ [ГЛ. IV
где ji = const > 0, ц = const !> О, и соответствующие им задачи
Lx(u) = 0, и Ь = тФ |s. A0.18)
Предположим, что для А(х, и, р) выполнено или условие
(8.7), или (8.9), или (8.12) + (8.13) и, как всюду, неравенство
аи(х, и, p)%i%i= ' д'р —hli > 0 ПРИ lil=1- Тогда, если
функция а(х, и, р) дифференцируема по р и ц = 0, то для всех
возможных решений и(х, т) задач A0.18) следствие 8.7 гаран-
гарантирует равномерную оценку тах|м(л:, т)|^М с известной нам
Q
постоянной М. Для справедливости этого достаточно убедиться,
что квадратичная форма йц(х, и, р, т)|f|/, соответствующая
Lx {и), положительно-определенна. Но это так, ибо
йц(х, и, р,
-f)(l +P2)(m-4)/2[(l +P2)I2 + (m-2)plp,Ul]>
; т- \}12>
>min{v; jimin(l; m- 1)}A+p2)(m)/2|2. A0.19)
Далее, легко проверить, что если функции at {x, и-, р) и
а(х, и, р), образующие уравнение A0.1,), удовлетворяют усло-
условиям а) — Ь) теоремы 10.2, то этим же условиям удовлетво-
удовлетворяют и функции
щ (х, и,р,х) = xai (х, и, р) + A - т) ji A +1 V« |2)(m)/2 йХ{,
а{х, и, р, х) = ха(х, и, р),
образующие уравнение A0.18). Если число ji взять, напри-
например, так:
где v и ц взяты из A0.13), то для функций щ{х, и, р, х) и
а(х, и, р, х) неравенства A0.13) будут выполняться с постоян-
постоянными v(t)= v и ц (т) <:2ц + р, ¦ тах{т— 1; 1}. Ввиду сказанно-
сказанного из теоремы 10.2 вытекает
Теорема 10.3. Предположим следующее:
а) При хе2 и произвольных и и р функции at {x, и, р)
дифференцируемы по х, и, р, a (x, и, р) дифференцируема по р,
даг (х и, р) > Q ||=1 u для A{XtUtf)) из (Ю.10 вы-
полнено одно из условий: (8.7), или (8.9), или (8.12) + (8.13).

4 101 КЛАССИЧЕСКАЯ РАЗРЕШИМОСТЬ ЗАДАЧИ ДИРИХЛЕ 3?7
Ь) При х е Q, | и \^М (где М—верхняя граница тах| и (х, т) |
п
для всех возможных решений задачи A0.18) с ц = 0, гаранти-
гарантированная следствием 8.7) и произвольных р функции аг и а
удовлетворяют неравенствам A0.13).
с) На множестве Шм.м, {где М{ — постоянная из A0.14),
.да, да, да,
определяемая теоремой 4.1) функции at, ~-> ~ir~' !Г~ ' а не~
прерывны по Гёльдеру с показателем а > 0 относительно х, и
и р.
а) оес , фе с (о).
При выполнении этих условий задача A0.1г) имеет по край-
крайней мере одно решение из С2+а(й).
Для доказательства этого предложения включим параметр т
так, как указано в A0.17), A0.18), с ц = 0. Тогда, как легко
проверить, условия а) — с) теоремы 10.2 и условие равномер-
равномерной ограниченности тах|м(лг, т) | для A0.18) следуют из усло-
а
вий а) — d) теоремы 10.3. Обратимся к последнему условию
теоремы 10.2 — неравенству нулю суммарного индекса всех
решений задачи A0.5) при т = 0. При т = 0 задача A0.18)
¦имеет единственное решение: и (х, 0) == 0. Кроме того, w =
= Ф(и, 0) = 0 при VueC1+p(Q), ибо при т = 0 соответствую-
соответствующая задача A0.6) имеет вид
+ Mm-2)(l+\S/v?)(m-4)'2vX[vXlwXlXl=0, 0^ = 0, A0.21)
и так как ? > 0 и справедливо A0.19), то ее решение w дей-
действительно при любом v равно тождественно нулю. Поэтому
преобразование v — Ф(и, 0) функции v является тождественным
и его степень равна 1.
Итак, при т = 0 задача A0.18) имеет единственное решение
и(х, 0)s0 и его индекс равен 1. Таким образом, выполнены
все условия теоремы 10.2, а потому утверждение теоремы 10.3
о существовании хотя бы одного решения задачи A0.1^) дока-
доказано.
В теореме 10.3 можно отбросить условие дифференцируе-
дифференцируемое™ а (х, и, р) по р, но при этом в пункте а) надо видоизме-
видоизменить ограничения на А{х, и, р) в соответствии со следствием 8.5.
Именно, справедлива такая
Теорема 10.4. Утверждение теоремы 10.3 остается в силе,
если в ее условии а) отбросить предположение о дифференци-
руемости atx, и, р), но считать, что А(х, и, р) из A0.Ц)

378 КВАЗИЛИНЕЙНЫЕ УРАВНЕНИЯ [ГЛ. IV
подчиняется одному из следующих условий: (8.7'), или (8.9'),
или (8.12)-J-(8.13), или условиям следствия 8.6.
В случае, когда выполнено для А (х, и, р) условие (8.7') или
signM ¦ А(х, и, 0) <0, число |Г в A0.17), A0.18) надо взять
положительным.
Условие а) теорем 10.3 и 10.4 гарантирует оценку
rnax| u(x, т) |. Для получения этой оценки можно привлечь
Q
также теорему 8.2. Но для этого параметр т надо включить
так:
Lx(u)zss-jj-ai (хх' та> "*) + ха (хх' ™, м*) = 0, и Is = тф Is
или, что то же,
Lx(u) за ац (хх, те, их) uX[Xl + хА (хх, те, их) = 0, и \s = xq> \s.
A0.22)
Функции at(x, и, р), а(х, и, р) (а тем самым ац и А) считаем
определенными для хей,, где Qi состоит из точек х вида
л; = тг/, г/eQ, те [0,1], причем пусть точка л=0ей.
Предположим,_ что существуют две функции со (л:) и & (х)
из С2(Й!)ПС(Й,) с со @) = &@) = 0, удовлетворяющие в Q,_
неравенствам
Ма (со) = аи (х, и, со*) coV/ + А (х, и, со*) < 0 A0.23)
при Vm > 0 и
Ма(&)>0 A0.24)
при Vm < 0. Легко видеть, что тогда для решения и (х) урав-
уравнения A0.1,) выполняются условия (8.20) и (8.21) теоремы 8.2
с 61 = &2 = 0. Так как и(х, 0) = 0, то оценку max| u(x, x) \ для
Q
решений задач A0.22) достаточно получить для те@, 1]. Рас-
Рассмотрим функции Q{x, х) = — о (та;), tg@, 1]. Они определены
для xgQ и по модулю не превосходят некоторой постоян-
постоянной с. Подсчитаем для них величину
Ml (Q) si ац (хх, те, Qx) QXfXj + хА (хх, те, Qx). A0.25)
Для этого обозначим хх через у. Тогда
QXk (х, х) = -f^g- = щк (у), Qx.Xj (х, х) = хщ1У1 (у),
и потому
Ml (Q) = х [аи (у, те, %) Щр! + А (у, те, со^)], у s Q(.

§ 10] КЛАССИЧЕСКАЯ РАЗРЕШИМОСТЬ ЗАДАЧИ ДИРИХЛЕ 379
В силу A0.23) Mj(Q)<0 при V« > 0, те@, 1], xeQ, При-
Применим теорему 8.2 к функциям и(х, х), Q(x, т) и опера-
оператору Lx. Функция и(х, х) удовлетворяет уравнению A0.22), т. е.
Lt(k)sM«t(i() = 0, функция Q — неравенству A?J(Q)<0 при
Vm > 0, а тем самым и при и (х, т)—Q (*, т) > b{ == — min Q (a;, t).
а
Следовательно, условие (8.20) для них выполнено с Ь{ =
= — min Q (а;, т), и потому справедлива оценка (8.4), т. е.
Q
и (х, х) <; О (х, х) + max {— min Q (a;, t); max (и — Q)}^.
Q dQ
<osc{Q(a;, t); Q} + max| m (a:, t) |< max osc{(o(a:'t) ;
aQ те [0,1] I T
max|
dQ
Аналогично с использованием условия A0.24) устанавливается
равномерная оценка снизу для и (х, т). В частности, если
at {х, и, р) и а {х, и, р) не зависят от и, то для оценки
тах|м(АГ, т) | можно привлечь последнее утверждение след-
Q
ствия 8.7. Именно, пусть существует классическое решение со (а;)
уравнения A0.1,). Тогда функции Q (х, т) = со (а;, т)/т, те@, 1]
удовлетворяют уравнению М\ (Q) = Lx (Q) = -j— at (xx, Qx) +
+ ха {xx, Qx) = 0, и потому для пары и (х, х), Q (х, х) спра-
справедливы оценки (8.4) и (8.6) с Ь{ — — оо и Ь2—-\- °° соответ-
соответственно, т. е. для те@, 1]
Q (х, х) + min [и (х, x) — Q (х, т)] < и (х, х) <
да
<Q {х, х) + max [и (х, х) - Q (х, х)],
причем max max| Q(x, х) |< оо. Прит = 0 решение и(х, 0)^0.
те @,1) Q
Проверка для уравнений A0.22) других условий, при кото-
которых можно оценить нормы | и (х, х) ^+а), не вызывает затрудне-
затруднений. Именно, из неравенств A0.13) для L (и) следует спра-
справедливость этих неравенств для всех L% (и), а из условия с)
теоремы 10.3 для ai(x,u,p), a(x,u,p) следует его выполнение
и для функций, образующих операторы Lx. Наконец, послед-
последнее условие теоремы 10.2 о разрешимости задачи A0.22) при
т = 0 тоже выполнено. Действительно, при т = 0 задача A0.22)
имеет вид
аи@, 0, ux)uXlXj = 0, w|s = 0. A0.26)

380 КВАЗИЛИНЕЙНЫЕ УРАВНЕНИЯ [ГЛ. IV
Ее единственным классическим решением является и (х, 0) = 0.
Более того, единственным классическим решением задачи
ait @, 0, vx) wXiXj = 0, ay Is = 0
при VoeC1+e(Q) является ву = О, т. е. Ф(и, 0) = 0, и потому
индекс решения и (х, 0) задачи A0.26) равен 1. Таким образом,
доказана
Теорема 10.5. Утверждение теоремы 10.3 остается в силе,
если в ее условии а) заменить предположения относительно
функции А (х, и, р) предположением о существовании функций
со (а;) и со (а;) класса C2(Qi)f|C(Qi), удовлетворяющих неравен-
неравенствам A0.23) и A0.24). Кроме того, все условия теоремы 10.3
надо считать выполненными в области Qi = {#: у=тх, xeQ,
те=[0, 1]}.
Если функцию а (х, и, р) не предполагать дифференцируе-
дифференцируемой, то A0.23) и A0.24) надо считать выполненными со знаком
строгих неравенств.
Если at {x, и, р) и а (х, и, р) не зависят от и, то условия
A0.23), A0.24) можно заменить предположением о существо-
существовании хотя бы одного классического решения со (л:) уравне-
уравнения A0.li). В этом случае задача A0.1*) имеет единственное
решение из C2+a(Q).
Замечание 10.1. В пунктах а) и Ь) теоремы 10.3 и соот-
соответствующих требованиях теорем 10.4 и 10.5 мы предполагали
ту или иную гладкость функций at(x, и, р) и а(х, и, р) при
всех значениях (и, р) или р. Однако на самом деле нам доста-
достаточно ее иметь лишь при |м|^М и Ipl^M,, где М и М, —
мажоранты для тах|м| и тах| Vu |, вычисляемые по известным
а а
нам величинам.
Рассмотрим еще одно включение параметра т в задачу A0.1*),
а именно:
Lx {и)=-^- at {х, и, их) + а (х, и, и„ х) = 0, и \s = тф |s, A0.27)
где а(х,и, их, т) = (т — 1) "' д"' " + ™ (х> "> «*)¦ ПРИ т = !
задача A0.27) совпадает с задачей A0.1*). Задачам A0.27) сопо-
сопоставим линейные задачи
A0.28)

§ ю] КЛАССИЧЕСКАЯ РАЗРЕШИМОСТЬ ЗАДАЧИ ДИРИХЛЕ 381
определяющие по v (х) и т функцию w {х, х). Примечательной
особенностью преобразования (v, х) в w является его линей-
линейность по х: w = xO(v). Легко проверить, что неподвижные точки
этого преобразования, т. е. решения уравнения и = хФ(и),
являются решениями задачи A0.27). Для обнаружения же
неподвижных точек у преобразования тФ(и) можно воспользо-
воспользоваться следующей теоремой Шаудера (см., например, [13]):
Теорема 10.6. Пусть A(v) есть вполне непрерывное (т. е.
непрерывное и компактное) преобразование в банаховом про-
пространству Н, переводящее какое-либо ограниченное, замкнутое,
выпуклое множество Ш в себя (т. е. А (Ш) с Ш). Тогда в Ш
для А имеется хотя бы одна неподвижная точка v0 (т. е.
A(vo) = vo^W).
Из этой теоремы легко выводится следующее известное
Следствие 10.1. Если A(v) есть вполне непрерывное
преобразование в банаховом пространстве Я и если все воз-
возможные решения уравнений v = xA(v), те[0, 1), лежат внутри
шара Kr={v: \v\h<^R} пространства Я, то A (v) имеет в Kr
по крайней мере одну неподвижную точку.
Для доказательства построим по A(v) новое преобразова-
преобразование A (v) в Kr, сопоставляющее точке v^Kr элемент A(v),
если | A (v) \н < R, и элемент R\ A (v) |~' A (v), если | A (v) \н > R.
Ясно, что A (v) вполне непрерывно и переводит Kr в себя.
По теореме 10.6 найдется по крайней мере одна точка vo^Kr,
для которой Л(ио)=ио. Покажем, что для нее A(vo) = vo.
Действительно, если | A (v0) |н <! R, то A (vo) = A (v0), и потому
A {v0) = v0. Если же | A (v0) \н > R, то v0 есть решение уравне-
уравнения vo = A(vo) = R\ A(v0) \~l A(v0), т.е. уравнения vo=xA(vo)
с т< 1. Но последнее не допускается одним из условий след-
следствия, и потому v0 действительно есть решение уравнения
A()
o (o)
Замечание 10.2. Если о вполне непрерывном преобра-
преобразовании А известно, что для всех возможных решений уравне-
уравнений v = хА (v), х е [0, 1], нормы | v \н < R, то уравнение v = A (v)
имеет по крайней мере одно решение с | о |я <1 /?.
Действительно, для А и шара KR+E = {v. \ v \H < R + е}
с произвольно малым е > 0 следствие 10.1 гарантирует по край-
крайней мере одно решение v уравнения у = Л(и) в шаре KR+t.
Но в силу нашего предположения для него | v \н <: R, т. е.
фактически оно лежит в Kr-
Замечание 10.3. В теореме 10.6 и следствии 10.1 пре-
преобразование А может быть заданным только на Ш и Kr соот-
соответственно, а в замечании 10,2 — в шаре KR+i с каким-либо

382 КВАЗИЛИНЕЙНЫЕ УРАВНЕНИЯ [ГЛ. IV
Вернемся теперь к задаче A0.27). В силу замечания 10.2
для разрешимости ее при т=1 достаточно установить, что все
возможные ее решения и (х, х), т е [0, 1], имеют норму | и {х, х) \н\
не превосходящую какого-либо числа R. В качестве простран-
пространства Я, как и выше, будем брать пространство C1+P(Q) с не-
некоторым р > 0- Полная непрерывность преобразования Ф(и),
определяемого задачей A0.28), устанавливается так же, как и
выше, с помощью результатов §§ 1,2 гл. III о линейных урав-
уравнениях. Для получения же априорных оценок всех возможных
решений и(х, т) задач A0.27) надо привлечь результаты §§ 1—8
данной главы. Если оценка тах| и(х, т) |^ М для Vt e [0, 1]
Q
уже имеется (или предполагается), то оценки более сильных
норм max| Vu(л;, т) |, \и{х, х) |q+P), | и{х, х) (?+а) выводятся для
для решений и (х, х) при тех же предположениях относительно
щ{х, и, р), а(х, и, р), ф и S, что и для и(х,1), т. е. для решений
задачи A0-27) при т= 1. Для возможности же получения эффек-
эффективной оценки тах| и(х, х) | надо налагать дополнительные усло-
Q
вия, позволяющие применить то или иное утверждение §§ 7
или 8. Например, следствие 8.7 гарантирует оценку
max | и (х, х) | ^ max {M; max | ф |}
о s
для всех возможных решений и(х, х) задач A0.27), если при
всех | и | > М выполнено неравенство
дх{
и функция -= Ь а {х, и, р) дифференцируема по р, Мы
axi
axi
не будем перечислять здесь все ситуации, при которых можно
оценить max | и (х, х) |, пользуясь утверждениями §§ 7 и 8, ибо
а
это нетрудно сделать самостоятельно.
Мы привели здесь ряд случаев, когда можно дать эффек-
эффективную оценку тах| и \ для возможных решений и задачи (ЮЛ;).
Q
Число их можно приумножить, но ясно, что описать все по-
подобные случаи невозможно.
Обратимся снова к общей теореме 10.2. Результаты § 7 по-
показывают, что условие равномерной ограниченности max| u(x,x) \
Q
можно заменить условием равномерной ограниченности
|| и (х, х) \\ц а с каким-либо <7^1, но для этого необходимо нера-
неравенство A0,13) дополнить неравенствами G.4), G,5) (см. тео-

I Ю] КЛАССИЧЕСКАЯ РАЗРЕШИМОСТЬ ЗАДАЧИ ДИРИХЛЕ 383
рему 7.6). Далее, теоремы 7.3—7,5 дают достаточные условия
того, когда норму || и \\^ а можно оценить через данные задачи.
Различные сочетания теорем § 7 с изложенными здесь дают
еще одну серию условных и безусловных теорем о разреши-
разрешимости задачи A0.lt). Мы не будем приводить формулировки
этих теорем, надеясь, что при необходимости читатель это смо-
сможет сделать самостоятельно.
В предыдущих теоремах 10.2—10.5 было гарантировано су-
существование классических решений задачи A0. Ь), точнее, ре-
решений из C2+a(Q). Для существования таких хороших решений
наши предположения о гладкости функций аг, а, ф и границы S
были минимально возможными. Ослабление тех или иных пред-
предположений о гладкости S, ф или ah а приведет к ухудшению
соответствующих дифференциальных свойств решений и(х, т),
Так, например, если снять условие гладкости с S и ф, то это
приведет к потере гладкости и на S, Если отбросить условие
да, да, да,
непрерывности функций -=-*-, -^-, -^-, а по Гельдеру, оставив
Ор г ОН ОХ 1
вместо этого лишь условие их ограниченности (неравенства
A0.13)), то решения и не будут принадлежать С2+а. Они будут
иметь ограниченные производные первого порядка и обобщен-
обобщенные производные из L2(Q) второго порядка и будут удовлетво-
удовлетворять уравнению A0.1^ для почти всех х из Q-
Все эти и подобные им теоремы о судествовании решений
более плохих, чем решения из C2+a(Q), можно получить из тео-
теорем 10.2—10.5 путем аппроксимации ait a, S, ф гладкими функ-
функциями ar{, ar, Sr, фг, удовлетворяющими условиям теорем
10.2—10.5, и последующего предельного перехода в последова-
последовательности решений иг, г=\, 2 этих «сглаженных» задач
A0.1г) с использованием соответствующих теорем §§ 1—8
об априорных оценках решений иг.
Покажем, как осуществить эту идею на примере некоторых
из перечисленных случаев. Для большей ясности и простоты
сделаем это при одном из тех условий, когда можно дать явную
оценку тах|ы|. Пусть, например, для уравнения (Ю.^) выпол-
выполнены неравенства (8.70. Теорема 10.4 гарантирует для него раз-
разрешимость задачи Дирихле в классе C2+a(Q) npnS, ф(л:)еС2+а,
аге=С1+а, а<=Са. Предположим, что условия S, ф(л:)е=С2+а
теоремы 10.4 заменены более слабыми, именно: S удовлетво-
удовлетворяет условию (А), а ф(лг) <=Ca(Q)(\C2+a(Q). Покажем, что при
сохранении всех остальных условий теоремы 10.4 имеет место
теорема существования по крайней мере одного решения задачи
A0.1,) из Cv(Q)nC2+a(Q) с некоторым у > 0.

384 Квазилинейные уравнения tivi. iv
Действительно, возьмем последовательность расширяющихся
областей Qr, r =1,2, ..., с границами Sr из С2+а, сходящихся
к Q и удовлетворяющих условию (А) с одними и теми же по-
постоянными а0 и 0О. В каждой из Qr имеем ф(х)еС2+а(Ог).
В силу теоремы 10.4 задача A0.1г) для каждой из обла-
областей Qr имеет по крайней мере одно решение иг(х) из C2+a(Qr).
Для всей совокупности этих решений следствие 8.5 и теоре-
теоремы §§ 1—6 дают оценку | иг $ ^с и для любой й'сг Q при
всех достаточно больших г оценку | ur §,+а)^с(й')> гДе постоян-
постоянные с, ciQ^ не зависят от г, а постоянная c(Q') зависит от
расстояния ?У до S.
Отсюда легко видеть, что для последовательности {иг} су-
существует по крайней мере одна предельная функция и(х), при-
принадлежащая Су(Q)()C2+a(Q) и удовлетворяющая A0.U). Осла-
Ослабим теперь требования на at и а, именно, отбросим требование
да, да. да,
непрерывности по Гёльдеру функций -=-*-, ~^-, —^, а, но
ОР г ОН @^1
оставим все остальные предположения об at и а и предполо-
предположение о-непрерывности а(х, и, р\ по (х, и, р)- Мы не можем
использовать теперь оценки Шаудера для нормы Гёльдера
производных и (х) второго порядка, но все остальные оценки норм
решений в Сх+У vlW\— в нашем распоряжении. Аппроксимируем
функции at {x, и, р), а {х, и, р) функциями а\ (х, и, р), аг (х, и, р),
удовлетворяющими всем условиям теоремы 10.4. Кроме того,
функции а^х, и, р), аг(х, и, р) выберем так, чтобы они удовле-
удовлетворяли неравенствам, указанным в теореме 10.4, с постоян-
постоянными, не зависящими от г. В качестве сглаженных функций а\
и аг, как нетрудно видеть, можно взять усреднения исходных
функций at, а по всем переменным с бесконечно дифференци-
дифференцируемым неотрицательным ядром, зависящим от разностей аргу-
аргументов. Правда, так усредненные функции будут определены
не для всех х из Q. (Что касается аргументов мир, то мы
считаем функции at а а определенными или доопределенными
для всех и из ?, и р из Еп так, что выполняются условия а)
и Ь) теоремы 10.4.) Это обстоятельство можно исправить двумя
разными способами: или ¦ предварительно доопределить функ-
функции at, а на более широкую область Q=> Q с сохранением всех
их свойств, указанных в условиях теоремы, или рассматривать
а\, аг при каждом г на своей области Qr cr Q с гладкой гра-
границей, отстоящей от S на расстояние, не меньшее радиуса усред-
усреднения по х.

§ 10] КЛАССИЧЕСКАЯ РАЗРЕШИМОСТЬ ЗАДАЧИ ДИРИХЛЕ 385
Выберем второй способ. Задача A0.1г) в области Qr для
усредненных а\ и аг имеет по крайней мере одно решение иг.
Для всей совокупности этих решений будем иметь оценки
\ и fy)<~r \ и Р+у)<~ г (О'\ II и Н<2) <Г г (О'\
I ит b ** ' I иг Ь' ^* \и '» II иг  Q' ^ \" /
с постоянными с, с(й') и y'. не зависящими от г. Постоянные
с (Q0 и Y' зависят от расстояния Q' cr Q до S. Эти неравенства
также позволяют выбрать из {иг}, г=1,2, ..., подпоследова-
подпоследовательность, равномерно сходящуюся к функции и (х), принадле-
принадлежащей Cv(Q)nC1+v'(Q0n^2(Q0 при любой Q'crQ и удовлетво-
удовлетворяющей почти всюду уравнению A0.1,) и граничному условию
A0.12).
Если в обоих только что рассмотренных случаях ослабле-
ослабления условий теорем 10.2—10.5 считать S^O2, a ipeO2(Q),
то для определяемых решений можно с помощью оценок §§ 4
и 6 доказать, что они суть элементы C1+?(Q)f| ^(Q) с некото-
некоторым y > 0-
Так с использованием теорем 10.2—10.5 и априорных оценок
из разных параграфов данной главы доказываются различные
теоремы о существовании решений более плохих, чем решения
из C2+a(Q).
Мы доказали из них следующие предложения:
Теорема 10.7. Пусть выполнены все условия теоремы 10.3
{или 10.4), кроме пункта d), который заменен условием dO S е О2,
(реО2(й)млм условием д.") S удовлетворяет условию (A), (peCp(Q).
Тогда задача A0.1,-) имеет по крайней мере одно решение, и
которое в первом случае есть элемент Cl+y (u)()C2+a(Q)(\ Wl{Q),
а во втором — элемент Cy(Q)(]C2+a(Qi) с некоторыми у и \,
бблыиими нуля.
Пусть, кроме того, вместо условия с) теоремы 10.3 (или тео-
теоремы 10.4) предполагается лишь непрерывность а(х,и,р) по
(х, и, р). Тогда задача A0.1/) имеет по крайней мере одно ре-
решение из_ C1+i*(Q) П Wt(Q), если условие d) заменено условием d'),
и из Су (Q) П C1+v' (Q0 П ^1 (Q0, где Q' — любая строго внутренняя
подобласть области Q, а у' — некоторый зависящий от О/ поло-
положительный показатель, если условие d) заменено на А").
Такие же ослабления с такими же следствиями (относи-
(относительно свойств решений задачи A0.1г)) допускают и другие
теоремы данного параграфа.
Условие а) теорем 10.3, 10.4 и 10.7, гарантирующее оценку
тах| и(х, г) |, можно заменить, например, условиями
2 ai(x,u,p)pi>v\p\m-6l\u\m-63,v>0
13 О, А. Ладыженская, Ht Ht Уральцева

386 КВАЗИЛИНЕЙНЫЕ УРАВНЕНИЯ [ГЛ. IV
с произвольными постоянными, если только mesQ достаточно
мала. В теореме 7.5 указано явно ограничение на mes Q, при
выполнении которого для всех возможных решений и (х, т) задач
A0.18) можно дать оценку max max| u(x, т) |. Величина допу-
те[0, 1] Q
стимой mesQ определяется постоянными т, v, ц0, 6, и 62, вхо-
входящими в неравенства A0.29). Итак, справедлива
Теорема 10.8. Утверждения теорем 10.3 и 10.7 сохраняют^
ся, если условие а) в них заменить следующим: а') при xeQ
и произвольных и и р функции ai{x,u,p), a{x,u,p) удов-
удовлетворяют неравенствам A0.29), a mesQ достаточно мала
(ее величина определяется постоянными m, v, ц0, 6, и 62 из
A0.29)).
Теоремы 10.1 — 10.8 вместе с оценками §§ 1—8 позволяют
исследовать и те случаи, когда задача A0.1г) имеет лишь обоб-
обобщенные решения с производными первого порядка, причем по-
получаемые на этом пути результаты не покрываются теоре-
теоремами § 9. Однако мы не будем здесь этого делать ввиду
громоздкости рассуждений.
Остановимся на вопросе о теореме единственности для задачи
A0.1г). Разность и двух возможных решений и' и и" задачи
A0.\i) удовлетворяет однородному граничному условию m|s = 0
и соотношению
(auUXj + aiu)x + btux. + аи = 0, A0.30)
в котором функции йц, й{, Si, а те же самые, что и в тожде-
тождестве B.3) данной главы, и которое может быть рассмотрено
как линейное уравнение относительно и. Ввиду этого для дока-
доказательства тождественного равенства нулю функции и могут
быть привлечены теоремы гл. III о линейных уравнениях. Пусть
относительно функций ai(x,u,p) и а(х,и,р) известна ограни-
ограниченность их и их частных производных по и и р на любом
компактном множестве значений их аргументов. Тогда, если
решения задачи A0.1/) имеют конечный тах| и', и", Vu', Уи" |,
а
то коэффициенты уравнения A0.30) суть известные ограничен-
ограниченные функции и к A0.30) применимы теоремы §§ 4, 5 гл. III,
в том числе и те, в которых гарантируется обращение и в нуль
(теорема единственности). Если о решениях задачи известна
ограниченность лишь их самих, но не их градиентов, то никакая
гладкость известных функций а,- (л;, и, р), а [х, и, р) не гаранти-
гарантирует, вообще говоря, нужных нам свойств коэффициентов A0.30),
и, чтобы доказать теорему единственности в классе таких ре-
решений, надо накладывать еще ограничения на поведение а{ (х, и, р)
и а(х, и, р) при |jo|->oo. Такого типа рассмотрения были про-
проведены выше, в § 2 данной главы.

$ 10] КЛАССИЧЕСКАЯ РАЗРЕШИМОСТЬ ЗАДАЧИ ДИРИХЛЕ 387
Если о решениях задачи A0.1,-) известна, например, их при-
принадлежность к С2 (Q) П С (Q) и если у функций а,- (л;, и, р) суще-
существуют производные второго порядка, ограниченные на каждом
компактном множестве значений их аргументов, то разность
двух возможных решений удовлетворяет также уравнению вида
uuUXlXj + dtuXl + uu*=0 A0.31)
с ограниченными на VQ' cr Q коэффициентами, и потому она
равна тождественно нулю, если й^.0 (см. § 1 гл. III).
Таковы способы доказательства теорем единственности для
задачи A0.1,-). Мы не будем перечислять все те ситуации, когда
тот или иной из них приводит к нужной цели. Отметим лишь,
что единственность заведомо имеет место в вышеописанных
случаях, если область Q достаточно мала. Она будет иметь
место также в первом и третьем случаях, если в левую часть
уравнения A0.li) добавить слагаемое —Ям и считать Я доста-
достаточно большим числом (действительно, член —Ям добавится
тогда в левые части уравнений A0.30) и A0.31), а это, как
известно, гарантирует нужную нам единственность).
Рассмотрим один случай неравномерно эллиптических урав-
уравнений, именно, уравнения вида
-^а,(их) = 0 A0.32)
с дифференцируемыми функциям:! а{(р), удовлетворяющими
условию
^-Ui>0 (Ю.ЗЗ)
при 151=1 и произвольных р. Примером таких уравнений
является уравнение минимальных поверхностей
= 0.
Для него неравенство A0.33) имеет место, тогда как усло-
условие B.1) не выполнено. Известно, что для классической раз-
разрешимости задачи Дирихле для этого уравнения необходимо, по-
помимо гладкости ф=м |s и dQ, накладывать дополнительные усло-
условия на форму области Q ([51]). Ввиду этого предположим, что Q
выпукла и функция (p(s) и S удовлетворяют я-мерному аналогу
«условия трех точек». Последнее означает следующее: (p(s) не-
непрерывна, и потому max | q> (s) | = М< оо и существует положи-
s
тельное число R, обладающее тем свойством, что если взять
в пространстве (*, м) любую точку вида (s, q>(s)), где
s gS, провести через нее (п— 1)-мерную плоскость, касающуюся
13*

388 КВАЗИЛИНЕЙНЫЕ УРАВНЕНИЯ [ГЛ. IV
(«— 1)-мерного многообразия 3 = {ssS, м = ф(«)}, и через эту
плоскость провести две я-мерные плоскости П±, наклон кото-
которых к плоскости и = 0 не меньше R, точнее, их уравнения
имеют вид
и-фИ=±/2сл(хй-4). *0==s> }/%c\>R, A0.34)
то все многообразие 3 будет заключено в том двугранном угле
между П+ и П_, в котором содержится множество {j;eQ,
и = ф(;с0)}. Это условие будем называть «условием « + 1 точки».
Можно показать, что оно заведомо выполняется для строго
выпуклых областей Q, если граница S и функция (p(s) доста-
достаточно гладкие.
Из § 1 гл. III следует, что для классических решений и(х)
задачи A0.32), A0.12) справедлива оценка
тах| и[х) |<М. A0.35)
Q
Покажем, что для них
max|Vu|</?. A0.36)
Q
Поверхность и = и(х), хей, заключена в любом из двугранных
углов, описанных в «условии п + 1 точки», ибо если бы это
было не так, то по крайней мере одна из функций
V±(X) = U (X) Т 2 Ck (Xk - 4) - ф (jfi)
имела бы положительный максимум или отрицательный минимум
внутри области Q+ с= Q, на границе которой она обращается
в нуль. Но это невозможно, ибо v± удовлетворяет уравнению
да. (и ) —
¦¦ g x v ±x.xj — 0. Если предположить, что aGC'(Q), то
отсюда следует, что тах|Ум|^/?. Далее, каждая производ-
s _
ная ul^ux может быть рассмотрена в Й'с2 как обобщенное
решение из С1 (Q') линейного невырожденного эллиптического
уравнения
¦sr(«wM%) = o A0-37)
с ограниченными в п' коэффициентами а.ц {х) = —'-^—-
U*I
(уравнение A0.37) есть результат дифференцирования A0.32)
по xt). В силу теоремы 13.2 гл. Ill max | щ \х) \^ max | щ {х) |,
_ Q' ас
и так как Ui(x) непрерывна в Q и это неравенство справедливо

§ 10] КЛАССИЧЕСКАЯ РАЗРЕШИМОСТЬ ЗАДАЧИ ДИРИХЛЕ 389
при VQ'crQ, то оно сохранится и для Q. Тем самым нера-
неравенство A0.36) доказано*). После этого при оценке более силь-
сильных норм реа1ений и(х) неравномерность эллиптичности урав-
уравнения A0.32) роли, очевидно, не играет, и теоремы § 6 гаран-
гарантируют эти оценки, если а,- (р), и(х), ф(лг) и S обладают
соответствующей гладкостью.
Для доказательства разрешимости задачи A0.32), A0.12)
параметр т включим только в граничное условие и (х, т) |s =
= тф(лг) |s. Ясно, что для и(х, т), те[0, 1], справедливы оценки
A0.35), A0.36) и те же оценки норм | и(х, т) |Q+a>, что и для и(х, 1).
При т = 0 имеется только одно решение и(х, 0) = 0, и его
индекс равен 1 (кстати, единственность имеет место при всех
те[0,1]). Разрешимость задачи A0.32), A0.12) (равно как и
ряда случаев, рассмотренных выше) можно доказать, и не при-
прибегая к теореме Лерэ — Шаудера, а используя лишь теорему
Шаудера 10.6 о существовании неподвижной точки вполне
непрерывного преобразования замкнутого выпуклого множества
в себя. При различных предположениях о гладкости данных
исследуемой задачи получим разрешимость ее в том или ином
классе. Приведем один из результатов.
Теорема 10.9. Пусть Q — выпуклая облает ьи для ф (s) = и |s
и S выполнено «условие «+ 1 точки» с числом R. Пусть функ-
функции ai (р) принадлежат С1+а({р: | р К /?}), / > 1, и для | р |< R
удовлетворяют условию A0.33). Тогда задача A0.32), A0.1_2)
имеет единственное решение и из Cl+l+a (Q), если ф е Cl+l+a (Q)
Результаты §§ 2—4 гл. VI позволяют доказать разреши-
разрешимость задачи Дирихле для более широкого класса неравномерно
эллиптических уравнений. Более того, за период между первым
и вторым изданиями данной книги появилось довольно много
работ и других авторов, в которых исследованы различные
Классы неравномерно эллиптических уравнений (собственно, для
них надо получить лишь априорную оценку тах| Vu |, а оценки
Q
более сильных норм даются теоремами § 6). Однако этот объект
мы здесь специально не рассматриваем.
Вернемся еще раз к вопросу о гладкости обобщенных реше-
решений и(х) из Wlm,q(Q) уравнения @.1). В §§ 1— 7 дан прямой
путь его исследования. Это же можно сделать, используя тео-
теорему 10.8 и теоремы § 2. Именно, пусть и(х) есть произвольное
обобщенное решение из Ср (Q) f"| ^i, (Q) уравнения @.1) (вопрос
о принадлежности решений и(х) из Wlm<q к & исследован
*) Этот факт легко доказывается и без использования теоремы 13.2 гл- III.
Так он и был установлен первоначально в заметке [217].

390 КВАЗИЛИНЕЙНЫЕ УРАВНЕНИЯ [ГЛ. IV
в §§ 1 и 7). Рассмотрим его в шаре Кр с= Q достаточно малого
радиуса р (величину р определим ниже по известным нам
характеристикам уравнения и М^тах\ и(х) |).
Относительно а,- (а;, и, р) и а (х, и, р) предположим, что для
них выполнены условия B.1), B.2), а тем самым и A,2), A.3).
Изменим, если ^адо, а;(х, и, р), а(х, и, р) при \и\^М-\- 1 так,
чтобы при х е LI и произвольных и, р
at{x,u, P)pi>v1\p\m-»i,
с какими-либо положительными (X;, V(. Кроме того, для изменен-
измененных а,-, а (мы их обозначили через а,, а) должны оставаться
справедливыми предположения B.1), B.2) (может быть, с не-
несколько измененными функциями v(|m|) и ц(\и\)).
Исследуемую функцию и (х) можно рассмотреть как обобщен-
обобщенное решение из Ср (КР) П ^т (КР) задачи
--?- а{ (х, v, vx) + а (х, v, vx) = 0, v\aK=u \дК . A0.39)
С другой стороны, согласно теореме 10.8 задача A0.39) имеет
хорошее решение v, если только радиус р достаточно мал.
Величина р определяется постоянными т, vt, jx0, (Xj из A0.38).
Далее, в силу теоремы 7.5 постоянные т, v,, jx0, ц{ из A0.38)
и М определяют и мажоранту М, для тах|а(л:)|, где v есть
кр
любое из решений задачи A0.39), причем эта мажоранта не
возрастает с уменьшением р. Согласно теоремам § 2 по вели-
величине Mi можно определить р такое, что в шарах Кр с р ^ р будет
иметь место теорема единственности для задачи A0,39) в классе
ог. об. решений из Wlm(KP), не превосходящих по модулю Мх.
Беря в задаче A0.39) р = р, получим, что исследуемое реше-
решение и совпадает в Кр с решением v, гарантированным теоре-
теоремой 10.8. Гладкость v в Кр определяется гладкостью функций
ui{x,u,p), а(х,и,р). В теореме 10.8 прослежена гладкость
вплоть до принадлежности v к С2+а(Кр)- Дальнейшее увеличе-
увеличение гладкости гарантировано теоремами § 6.

Глава V
ВАРИАЦИОННЫЕ ЗАДАЧИ
§ 1. Постановка задач
Данная глава посвящена исследованию вариационных задач
для функционалов вида
I(u)=JFbc,u,ux)dx A.1)
Q
в ограниченной области Q при граничном условии
«ls = «P(s). A-2)
(Другие граничные условия классического типа рассматриваются
аналогично.) Нас будут интересовать функции и(х), на которых
первая вариация 6/ (и; г\) функционала I (и) обращается в нуль
при всех допустимых вариациях ц(х), т. е. для которых
6/ (и; т]) = J \FUx (x, и, их) r\S{ + Fu (х, и, их) п] dx = 0. A.3)
Такие функции и(х) называются стационарными точками функ-
функционала /(«). Для них, в основном, рассматривается вопрос
о их гладкости. Если функция и(х) дает наименьшее значение
функционалу /(«) на множестве Зй, состоящем из всех функций,
на которых I (и) конечен и которые удовлетворяют условию A.2),
то при некоторых естественных предположениях относительно
F(x,u,p) первая вариация 1{и) на и(х) будет равна нулю.
В § 2 будет исследован вопрос о нахождении функций, реали-
реализующих Ы1(и).
ш
Как известно, эти задачи тесно связаны с решением уравне-
уравнения Эйлера
L{u) = -j^FuXt-Fu = 0 A.4)
при краевом условии A.2). Любое не слишком плохое реше-
решение и(х) уравнения A.4) удовлетворяет тождеству A.3), и,
наоборот, любая достаточно хорошая функция и(х), удовлетво-
удовлетворяющая тождеству A.3), является решением уравнения A.4).

392 ВАРИАЦИОННЫЕ ЗАДАЧИ [ГЛ. V
Соотношение A.3) является не чем иным, как интегральным
тождеством, определяющим обобщенные решения уравнения A.4).
Одно из основных условий, при котором изучаются все эти
вопросы, — это выпуклость функции F(x, и, р) по переменным р.
Оно может быть записано или в виде
Е {х, и, р, p) = F {х, и, p) — F (x, и, р) —
-Fp{(x,u,p)(pi-pi)>0, рФр, A.5)
где р и р — произвольные вектора из области задания функ-
функции F(x, и, р), или в виде
FPiPj(x,u,p)lilj>0, A.6)
где |, 1п — произвольные вещественные параметры, не
равные одновременно нулю, если функция F дважды дифферен-
дифференцируема по р.
Если F удовлетворяет неравенству A.5) или A.6), то говорят,
что вариационные задачи регулярны. Неравенство A.6) есть
не что иное, как условие эллиптичности уравнения A.4) или,
что то же, уравнения
L (и) = FUxux. (х, и, их) uXiXj + Fux.uUXt + FUxiX. -Fu = 0. A.4')
Более жестким, чем условие A.6), являгтся неравенство
(х, и, р) ltlt + 2FpiUU0 + FUUH > 0, A.7)
где |о. li In такие же, как и в A.6), называемое усилен-
усиленным условием регулярности.
Опишем несколько подробнее связи, которые имеют место
между вариационными задачами для A.1) при условии A.2) и
краевой задачей A.4), A.2). Легко подсчитать, что
/(ы + л) = /(«) + б/(";л) + б2/(« + ел;л). es[0, i], A.8)
где б2/ есть вторая вариация функционала /, вычисленная на
некотором «промежуточном» значении ее первого аргумента.
Она имеет вид
64 (и; Л) - у J \Кх.их. (х> и. их) лхгтц + 2FUx ицХ(Ц + Fuurf\ dx.
В простейшем случае, когда функция F достаточно гладкая и
выполнено условие A.7), вариационная задача на определение
стационарных точек функционала A.1) при условии A.2) и
краевая задача A.4), A.2) имеют единственное общее реше-
решение и (х) и это решение реализует абсолютный минимум функ-

$ 1] ПОСТАНОВКА ЗАДАЧ 393
ционала, Действительно, для любого решения и(х) этих задач и
любой допустимой вариации г\ Ф О первая .вариация 61 (и; tj) = 0,
а 62/(м; ti) > 0, и потому в силу A.8)
1(и + л) >/(«)• A.9)
Но это нерав&нство и означает, что и(х) реализует абсолютный
минимум / (и) и единственно. Ввиду этого все обсуждаемые здесь
задачи эквивалентны друг другу, если выполнено условие A.7)
и если F — достаточно гладкая функция. Если F(x,u,p) не
зависит от и, то условие A.7) совпадает с условием A.6). Именно
этот случай был предметом исследований С. Н. Бернштейна
(см. [42]) по двумерной вариационной задаче, которую он иссле-
исследовал как краевую задачу для уравнения A.4) с очень глад-
гладкой функцией F. К нему же относятся и .исследования
Де Джорджи [Hi] по многомерной вариационной задаче.
Де Джорджи доказал классическую разрешимость вариацион-
вариационных задач A.1), A.2) или, что то же, задачи A.4), A.2) для
функционалов A.1) с достаточно гладкой F, зависящей только
от р, причем такой, что
v?2 <FPiPj (p) lilj < jx?2, (х, v = const > 0.
В общем случае, когда выполнено лишь соотношение A.6) или
A.5), нельзя утверждать, что вариационная задача на опреде-
определение infl(u) и задача A.4), A.2) эквивалентны. Связь между
задачей A.4), A.2) и задачей на определение стационарных
точек для / нами уже понята: решения второй задачи суть
обобщенные решения первой из того класса Tt, которому при-
принадлежат функции сравнения, и наоборот. К задаче же на
минимум они имеют следующее отношение: если и(х) есть
обобщенное решение задачи A.4), A.2) с max| u(x), Vu{x) [< оо
а
и F(x, и, р) дважды непрерывно дифференцируема по и и р, то для
локальных вариаций г\(х) с такими же, как у и, свойствами спра-
справедливо A.9). Действительно, если ц (х) отлична от нуля лишь
в области Qi c= Q достаточно малой меры, то, имея в виду
неравенство B.14) гл. II, получим
62/(« + 9Л; Л)>4 J
- -J| Vr, I2 - 4
^22

394 ВАРИАЦИОННЫЕ ЗАДАЧИ [ГЛ. V
а потому и 1(и + т)) > 1{и). Из последнего неравенства следует,
что задача A.4), A.2) в области Qj имеет не более одного ре-
решения указанного класса. (Для нелокальных вариаций нера-
неравенство 1(и + ц) > /(«) может не иметь места даже для гладких
решений задачи A.4), A.2).) Однако .если относительно обоб-
обобщенного решения и(х) задачи A.4), A.2) нам известна, напри-
например, лишь принадлежность его к Wlm(Q) и неизвестна конеч-
конечность тах| и, Vu\, to вышеприведенное рассуждение о поло-
Q
жительности 621 (и-{-Qr\; т\) падает, и вопрос о том, дает ли
и(х) «локальный» минимум/(м), требует специального изучения
даже для аналитических F(x, и, р). С ним непосредственно
связан вопрос о единственности обобщенного решения задачи
A.4), A.2) и вариационной задачи на минимум для A.1) в обла-
областях достаточно малой меры. Прежде всего, положительное ре-
решение его упиралось в доказательство правильности замены
классической постановки вариационных задач обобщенной. Для
случая п = 2 и второго порядка роста F(x, и, р) по р он был
решен Ч. Морри в конце 30-х годов (см. [39К2])> для общего
случая — авторами книги в конце 50-х годов ([2112> i3], см. также
[2115] и [394,5,6]). В §§ 3—5 показывается, что для обобщенных
решений из Wlm(Q) вариационных задач действительно сохра-
сохраняются свойства их классических решений: единственность
«в малом» и неравенство A.9) для малых локальных вариаций г\.
Уравнение A.4) является частным случаем уравнений с ди-
дивергентной главной частью, рассмотренных нами в гл. IV. Если
функция F(x, и, р) удовлетворяет лишь некоторым естественным
условиям, то для уравнений A.4) справедливы все утверждения,
доказанные в гл. IV. Эти условия, грубо говоря, выражают
выпуклость F(x, u,p) пор, ограниченность снизу функционала 1(и)
и полиномиальное поведение F и ее частных производных при
больших | и | и | р |, в том числе наличие мажоранты *)
<1Л0)
где \|)(а;) — какая-либо функция из L,(Q), ц{ = const, jx (т) —какая-
либо неубывающая непрерывная функция т^О, a m = m =
s=nm/(n — т) при tn < п и т — произвольно г число при т = п.
Ниже они будут сформулированы более детально и дифферен-
*) Ради несущественных упрощений изложения будем предполагать
в данной главе, что для области Q имеет место совпадение W'm(Q) с №m(Q)
(см. стр. 28). В противном случае надо предполагать, что для ср (s) есть
продолжение ср(л:)е ^^ (Q^ и от всех функций сравнения и(х) требовать:
и - qss W'm (С),

$ 1] ПОСТАНОВКА ЗАДАЧ 395
цированно в соответствии с тем, какие будут устанавливаться
свойства обобщенных решений. Благодаря мажоранте A.10)
функционал A.1) имеет конечное значение на любой функции и
из Wlm(Q) и для него наиболее естественным и широким клас-
классом 3R функций сравнения в вариационной задаче A.1), A.2)
является множество всех элементов Wm(Q), равных на S функ-
функции (p(s) из A.2).
Теоремы § 10 гл. IV дают достаточные условия разреши-
разрешимости задачи A.4), A.2) в классах гладких функций. Теоремы
§ 9 гл. IV дают для нее существование обобщенных решений
из Wxm< q = Wxm(u)[\Lq (Q). Исследованиям, изложенным в §9
гл. IV и выполненным в 60-е годы, предшествовали (и в суще-
существенном способствовали их получению) так называемые прямые
методы вариационного исчисления. Эти методы позволяют найти
решение задачи на абсолютный минимум функционала A.1),
минуя уравнение A.4). Свое начало они ведут от знаменитой
работы Д. Гильберта 1900 г., в которой впервые дается строго
математическое обоснование идеи Римана находить решение за-
задачи Дм = 0, M|s = (p(s) как функцию, на которой интеграл
Дирихле I(u)= j | Vm fdx принимает наименьшее значение
а
(в качестве функций сравнения выбирались гладкие функции,
равные ф(лг) на S). Эта работа Гильберта явилась отправной
точкой для многих исследований нашего века и способствовала
как успешному решению ряда важнейших задач вариационного
исчисления и теории краевых задач, так и возникновению и
изучению таких кардинальных понятий и предложений класси-
классического и функционального анализа, как обобщенные производ-
производные, пространства Wlm(Q), сильные и слабые предельные пере-
переходы, критерии слабой и сильной компактности в Wlm(Q) и пр.
Мы не будем излагать здесь историю создания и развития
прямых методов вариационного исчисления. (Некоторое пред-
представление об этом дает введение; более подробное освещение
дано в [392,6], [28,], [262] и др.) Более того, эта небольшая
глава не претендует и на полноту изложения этого обширного
материала, который накопился по вариационным задачам для
функционалов A.1) примерно за 70 лет. Наша цель — пэказать,
во-первых, как при наличии теории пространств Wxm(Q) срав-
сравнительно просто, «в лоб», решается задача на определение
функции и(х), реализующей inf/ (и), и как устанавливается
аи
затем, что гладкость этой функции определяется не гладкостью
всех допустимых функций сравнения (они суть любые функции
из Wm(Q), удовлетворяющие условию A.2)), а функцией F (х, и,р).

396 ВАРИАЦИОННЫЕ ЗАДАЧИ [ГЛ. V
Попутно устанавливается, что локальное варьирование 1(и)
приводит к увеличению значения /. Зависимость гладкости и(х)
только от свойств функции F доказывается для всех стацио-
стационарных точек функционала /. Эти освещаемые в данной главе
результаты являются положительным ответом на предполо-
предположения, высказанные Д. Гильбертом в 19-й и 20-й проблемах.
Результаты о существовании по крайней мере одного обоб-
обобщенного решения задачи на минимум для функционалов A.1)
при любых т и п в своей основной части были получены
к концу 30-х годов Ч. Морри. Им предшествовали исследования
других авторов, из которых отметим работы А. Лебега [31],
Р. Куранта [102] и Л. Тонелли [53]. Мы излагаем эти резуль-
результаты в § 2, следуя при доказательстве теоремы 2.1 рассужде-
рассуждениям автора заметки [17], выполненной по идеям руководителя
А. Г. Сигалова. В остальных параграфах излагаются результаты,
полученные нами в конце 50-х годов. Они касаются гладкости
обобщенных решений. Этому же вопросу посвящены работы [394,5]
Ч. Морри.
Сделаем ряд замечаний в связи с излагаемым в этой главе
материалом. В качестве допустимого множества ffl при опре-
определении inf/(M) мы взяли в § 2 совокупность всех элементов
из Wlm{Q), удовлетворяющих граничному условию A.2). Из
этого же класса рассматриваются и стационарные точки функ-
функционала I (и).
Можно было бы элементы Ш подчинить каким-либо допол-
дополнительным ограничениям, например считать их элементами Wm< q
с q > tn при т < п. Все доказанное ниже в гл. V справедливо,
разумеется, и для такого ЗЯ. Более того, при этом можно не-
несколько ослабить предположения типа A.10) на рост F(x, и, р)
по и аналогично тому, как это было описано в §§ 7 и 9 гл. IV.
На элементы Ш можно наложить ограничения иного типа,
а именно:
/,(*)<«(*), Ar<=QlC=Q; м(*ХЫ*)> *e=Q2c=Q, A.11)
где f{ (x) — заданные функции. Доказательство существования
функции и(х), реализующей inll(u), данное в § 2, сохраняется
и для этого случая. Справедливы также утверждения §§ 3 и 4
об ограниченности и гёльдеровости и(х) (для последнего тре-
требуется небольшая гладкость ft (x)), несмотря на то, что первая
вариация 6/(м; г\) при таком выборе Зй, вообще говоря, не равна
нулю, а удовлетворяет лишь неравенству 61 (и; г\)^0. Однако
этого достаточно, чтобы доказать ограниченность и гёльдеро-
вость и(х), используя методы и аппарат, содержащиеся в данной
книге. Мы иллюстрируем это на типичном случае условной ва-
вариационной задачи, в которой ft (x) = const. В связи с условной
задачей общего вида A.11) укажем на интересную работу [333],

5 2] НАИМЕНЬШЕЕ ЗНАЧЕНИЕ ФУНКЦИОНАЛА /(ц) 397
в которой проводится дальнейший анализ гладкости ее обоб-
обобщенных решений.
Заметим, наконец, что многое из излагаемого в данной главе
применимо к другим краевым условиям (например, естественным)
и к другим вариационным задачам (например, изопериметри-
ческим).
§ 2. Нахождение функций, на которых функционал /(а)
принимает наименьшее значение
Пусть функция F(x, и, р) непрерывна вместе со своими
частными производными Fu и FPi на множестве {(а;, и, р): JteU,
ие(- оо, оо), р g ?„), и пусть для нее выполнено более сла-
слабое, чем A.5), условие квазирегулярности вариационной задачи:
Е(х,и,р,р)>0 B.1)
при xeQ и любых и, р, р. Кроме того, предположим, что
F(x,u,p)>0 B.2)
и
/(«)= \F{x, и, ux)dx^f (|| и|?а)-ц, т>1, B.3)
а
где f (т) — непрерывная функция т, стремящаяся к оо при т—> оо.
Неравенство B.3) должно выполняться для любой функции и(х),
принадлежащей классу Ш, состоящему из всех элементов Wm(Q),
принимающих на S значения q>(s). Предположим, наконец, что
существует по крайней мере одна функция q>(x)^Tt, на кото-
которой /(ф)<оо. Тогда справедлива
Теорема 2.1. При выполнении только что сформулированных
условий существует по крайней мере одна функция и (х) из Wm (Q),
равная (p(s) на S, дающая функционалу I (и) значение, не пре-
превосходящее значения I на любой другой функции класса Ш.
Заметим, что если функция F(x, и, р) вместо B.2) удовлет-
удовлетворяет условию F(x, и, р)^Ч>(*)> ty^Li(Q), то этот случай
просто сводится к предыдущему. А именно, вместо / (и) надо
рассмотреть функционал 7 (и) = J [F (х, и, их) — г|) (*)] dx, который
Q
имеет те же экстремали, что и I (и).
Для доказательства теоремы 2.1 рассмотрим I (и) на тех
функциях из ЗЯ, на которых он конечен. В силу условий тео-
теоремы множество это не пусто и нижняя грань d значений I (и)
на этом множестве конечна и неотрицательна.

398 ВАРИАЦИОННЫЕ ЗАДАЧИ [ГЛ. V
Возьмем какую-нибудь минимизирующую последовательность
щ, «2 т. е. последовательность функций из Ш, для которой
/(iik) = dk-*d при k—>oo. Для них в силу B.3) равномерно
ограничены нормы в Wm(Q):
II "*l?a< const. B-4)
Выберем из {uk} подпоследовательность, которая сходится почти
всюду в Q, сильно в Lm (Q), а также слабо в Wm (Q) к некоторой
функции и {х). Это возможно ввиду B.4). Предельная функция и {х)
также будет принадлежать классу Ш. Сохраним за подпосле-
подпоследовательностью то же обозначение {uk}. Докажем, что / (и) =
= inf / (у) = d. По теореме Д. Ф. Егорова по любому е > 0 можно
39!
выбрать множество Qe cr Q, мера которого отличается от меры
всего Q не более чем на е и такое, что на нем последователь-
последовательность {uk} сходится к функции и равномерно. Далее, обозначим
через Qjy множество точек области Q, на котором | и | +1 Vu |< N.
Так как и е Wlm (й), то mes (Q \ QN) -> 0 при N ~>оо. Обозначим:
% П йдг = Qe, N. Из сказанного ясно, что
mes (Q \ Qe, N)
В силу условия выпуклости B.1) будем иметь
Rk= J [F(x, uk, ukx) — F(x, и, ux)]dx^
J FuXj (x, uk, ux) (uk - u)Xj dx +
J [F(x, uk, ux) - F(x, u, ux)] dx. B.5)
"8, N
Qe, N
Оба интеграла, стоящих справа, стремятся к нулю при &->-оо,
ибо функции Fux (x, uk, ux) и F (x, uk, ux) сходятся равномерно
на Qe, n K FUx (x, и, их) и F(x, и, их) соответственно, а функ-
функции щх. сходятся слабо в Lm (Q) к их . Поэтому
lim J F(x, uk, ukx)dx^ J F(x, u, ux)dx.
Интеграл, стоящий слева, ввиду неотрицательности F не пре-
превосходит dk, так что j F(x, и, ux)dx^d. Так как е и N

§ 2] НАИМЕНЬШЕЕ ЗНАЧЕНИЕ ФУНКЦИОНАЛА /(« ) 399
произвольны, то и I (u)^d. Но d= inf /(и), поэтому /(«) = d.
Теорема доказана. асн!И
Условие B.2) можно заменить другим условием, а именно:
пусть при т^п
\F{x, и, рЖц,[|рГ + |иГ1 + Ф,(х), B.6)
| Fp. (х, «, р) j < (х2 [| р Г1 +1 « Г/т'] + ^2 (*), B.7)
где Ht = const, m < т, т' = т/(т — 1), ip, <=L,(Q), \|J etm'(Q),
а при -т> п
\F(x, и, p)|<n(|«|)[|pr + *iW], B.8)
|/>.(*, «, р)| <ц (|и|) Ь Р Г~' + Фя (Jc)J. B-9)
где (х (т), — как всюду, неубывающая непрерывная положитель-
положительная функция т>0, ^(jc) gL,(Q), a \|JeLm>(Q). Покажем, что
при такой замене условия B.2) утверждение теоремы 2.1
остается в силе. Начало доказательства то же. Однако из
оценки B.4) извлечем большие следствия о {uk}, чем раньше.
А именно, uk сходятся к и сильно в L^ (Q) при т^п и равно-
равномерно при пг> п (здесь и ниже, имея компактную последова-
последовательность, надо выбирать из нее сходящуюся; будем считать,
что такой выбор каждый раз подразумевается, но явно не
указывается). В силу условий B.6) или B.8) соответственно
интеграл /(«) на предельной функции и(х) существует и конечен.
Неравенство вида B.5) справедливо и для интегралов, распро-
распространенных на всю область Q. Обозначим такое неравенство
номером B.5'). Функции FUx (x, uk, их) сходятся сильно в Lm'(Q)
к FUx (x, и, их) (действительно, сходимость почти всюду имеет
место; кроме того, интегралы от FUr {x, uk, их) т' по множест-
/
вам малой меры равномерно малы; это легко выводится из
предположений B.7) и B.9) соответственно). Производные же ukx
сходятся к их слабо в Lm(Q). Ввиду этого первый интеграл
правой части B.5') стремится к нулю. Сходимость F(x,uk,ux)
к F(x, и, их) почти всюду и равномерная малость интегралов
от \F(x, uk, ux)\ и \F(x, и, их)\ по множествам малой меры,
гарантируемая условиями B.6) и B.8) соответственно, обеспечи-
обеспечивают сходимость к нулю и второго интеграла правой части B.5').
Ну, а тогда из неравенства B.5') будет следовать, что /(«)^
< lim^I (uk) = d, и потому I(u) = d. Итак, доказана
Теорема 2.2. Утверждение теоремы 2.1 остается в силе,
если ее условие B.2) заменить условиями B.6), B.7) при ^
И условиями B.8), B.9) при m > п.

400 ВАРИАЦИОННЫЕ ЗАДАЧИ [ГЛ. V
Заметим, что условия теоремы 2.2 гарантируют конечность
I (и) на любой функции и(х) класса Ш.
Аналогично теоремам 2.1 и 2.2 доказывается следующая
теорема для условной вариационной задачи:
Теорема 2.3. Пусть N —какое-либо фиксированное число,
и пусть при \u\^N выполнены все условия теоремы 2.1 или
неравенства B.8), B.9) теоремы 2.2. Тогда существует по край-
крайней мере одна фунщия и (х) е Ш, непргвосходящая по модулю N,
на которой I (и) принимает свое наименьшее значение по сра-
сравнению со всеми остальными функциями v (x) из Ti
с vrai max| v \^.N.
a
Функции, существование которых гарантировано теоремами
2.1—2.3, назовем обобщенными решениями из класса Wlm (Q)
или, короче, просто обобщенными решениями соответствующих
вариационных задач (на минимум).
Будем теперь предполагать, что функционал /(«) ограничен
на любой функции и из Зй, точнее, будем считать, что для
F(x, и, р) справедливы неравенства
\F(x и р)\<1 vkpF+luf + Voix)], 1<т<л, B.10,)
{' 'Р ^1 A1)[1Г + Ы*)]> ш>п, B.10а)
где \|)oeLi(Q), tn = th для т < n и m—какое-либо число (как
и всюду, не меньшее т) при т = я.
Покажем, что при некоторых ограничениях на F первая
вариация функционала обращается в нуль на обобщенных ре-
решениях задачи на минимум для / (и). Ограничения эти следую-
следующие: при 1 < т ^ п
I Fu (х, и, р) |< (х [ч>, (х) +1 и Г +1 p Г/Л'].
| ^ (*, «, Р) | < (х [i|>2 (*) +1 и f!m' +1 р Г];
при т> п
\FPl(x, и, р)\^ц(\
Здесь функции а|), (х), ф2 (х) и ^з (*) принадлежат пространствам
Lm>(Q), Lm'(Q) и Li(Q) соответственно, a m то же, что в B.10t).
О
Пусть г\(х) есть произвольная функция из Wm(Q), а и (х)
есть одна из тех функций класса 9W, на которых I(u) = d =

§ 2]
НАИМЕНЬШЕЕ ЗНАЧЕНИЕ ФУНКЦИОНАЛА /(и)
401
= inf I(v). Тогда / (и + tr\) > / («) при всех /. Формально вы-
численная производная ——г-—— имеет вид
—г-
и
U
B.13)
В силу предположений B.11), B.12) каждое слагаемое под
знаком интеграла существует и оценивается сверху равномерно
по /е[— 1, 1] через функции, суммируемые по Q. В самом
деле, при 1 <
т — 1
<с[\ ф2 Г'.+ | и Г + 1 Л Г + 1 Vu Г + 1 Vt, Г],
а при т> п
/til) (|г|J Г' +1 V« Г + | Vt, |т
ц |(х (тах| и + h\\)(\$31 + | V« Г + 1
' (тах|«
| Vt, |m
Г).
Из этих неравенств следуйт соответствующие оценки для раз-
разностных отношений -?j-[F(x, и-\-{t-{-&t)r\, ux-{-(t-{-ht)r\x)—
— F(x, и + tr\, ux -\-tr\x)], которые для почти всех х сходятся
при At—>0 к подынтегральным выражениям в B.13). Поэтому
производная -г-1 (и + tr\) действительно существует и равна
интегралу B.13). Так как при / = 0 функция I(u-\-tr\) прини-
принимает свое наименьшее значение, то в этой точке ее производ-
производная по / равна нулю, т. е.
6/
(и; л) = J [FUxi (х, и, их) цХ1 + Fa (х, и, их) i\] dx = 0. B.14)
Итак, доказана
Теорема 2.4. Пусть функция и (х) доставляет функционалу
I (и) минимум в классе ЗЯ. Тогда для нее выполняется тожде-
тождество B.14) при любой ц(х) из Wlm(Q), если функция F удовле-
удовлетворяет условиям B.10,) и B.11) для случая 1 </п</г« B.102),
B.12) для случая т> п.

402 ВАРИАЦИОННЫЕ ЗАДАЧИ [ГЛ. V
В соответствии с определениями гл. III и IV назовем функ-
функцию и (х) из Wm (Q) обобщенным решением уравнения Эйлера
A.4), если она удовлетворяет тождеству B.14) при любой
О |
функции г\ (х) из Wm (Q).
Замечание 2.1. Утверждения теоремы 2.4 остаются спра-
справедливыми, если относительно и (х) известно, что она дает мини-
минимум /(«) лишь при гладких малых локальных вариациях г\(х).
В самом деле, для таких г\(х) B.14) будет справедливо. Но
о
тогда оно будет справедливо и для любой r\ (x) e Wm (Q), ибо
О
б/(«; г\) линейна по г\(х) и любой элемент Wm(Q) можно при-
о N
близить в норме wm (Q) суммами вида 2 с*% (х)> гДе % (*) —
гладкие функции с малым носителем и малым max|% (x), Vr\k (x) |.
а
Замечание 2.2. Если при т <п вместо B.3) выполняется
условие
"fclLo; ll«IU)-n, B,3')
где f(t, |) — непрерывная функция, стремящаяся к + оо при
т2 +12—>оо, a q>m, то естественно от класса ffi. функций
сравнения потребовать дополнительно, чтобы они принадлежали
Lq(Q). Теоремы 2.1—2.4 остаются справедливыми и при таком
выборе Ш. Больше того, условия B.6), B.7) и B.10,), B.11) при
этом могут быть ослаблены: показатель th в них можно заме-
заменить на V$ < q, a in на q.
Теоремы § 9 гл. IV дают достаточные условия существова-
существования обобщенных решений из Wxm<q задачи A.2), A.4). Мы не
будем приводить здесь результаты, вытекающие из этих теорем,
применительно к уравнению A.4), ибо никаких существенных
упрощений в формулировке их условий при этом не получается.
Большая часть доказываемых ниже утверждений будет от-
относиться к обобщенным решениям уравнений Эйлера, а не
только к обобщенным решениям вариационной задачи на ми-
минимум, и основным соотношением, из которого мы извлечем все
последующие свойства этих решений, будет соотношение B.14).
Только в § 3 две теоремы об оценках максимума модуля и(х)
будут относиться лишь к обобщенным решениям вариационной
задачи на минимум.
Выясним, чем следует заменить соотношение B.14) в случае
условной вариационной задачи. Пусть и (х) есть решение услов-
условной вариационной задачи. Возьмем лишь такие вариации г\(х),
которые допустимы вместе с tr\(x), /e[0, 1]. Для них

j 3] ОБ ОЦЕНКЕ МАКСИМУМА МОДУЛЯ 403
Предполагав, что F при т> 1 удовлетворяет условиям B.102)
и B.12), из последнего неравенства находим, что
б/ (и; Л) = J \Рих. (х, и, их) тц + Fu (x, и, их) r\] dx ^ 0. B.15)
Сформулируем это предложение в виде отдельной теоремы.
Теорема 2.5. Пусть функция и(х) есть обобщенное реше-
решение условной вариационной задачи. Тогда для нее выполняется
неравенство B.15) при любой ч\{х) из Wxm(Q), удовлетворяющей
неравенствам — N ^ и (х) + tr\ (x) ^ N, t е [0, 1], если только для
F(x, и, р) при jcsQ, ImI^A/1 и произвольном р справедливы
неравенства B.102) и B.12).
§ 3. Об оценке максимума модуля решений
вариационных задач*)
В § 7 гл. IV доказаны теоремы, гарантирующие ограничен-
ограниченность обобщенных решений из Wm<q задачи Дирихле для урав-
уравнений, включающих в себя уравнения A.4). Они, очевидно,
применимы к решениям вариационных задач, рассмотренных
в § 2. Мы не будем их здесь повторять, а приведем две теоремы
о решениях вариационной задачи на минимум. Близкие предло-
предложения доказывались А. Г. Сигаловым для решений двумерных
вариационных задач ([28li2])-
Теорема 3.1. Предположим, что и (х) реализует абсолютный
минимум функционала I (и) в классе ЗЛ и vraimax| ф |^М0.
s
Пусть функция F(x,u,p) при \u\~^MQ удовлетворяет нера-
неравенствам
F(x, и, 0)<|Г + 1П() I
где tn^n, v > 0, (x ^ 0, as (m, m = nm/{n — m)), i|) e L?, (Q),
qi>n/tn. Тогда vrai max | и (х) \ ограничен и оценивается посто-
Q
янной, определяемой п, m, v, jx, a, Mo, qh II ¦ф II,If q, IIVu||m>fl
и mesQ.
Обозначим через Ak подмножество точек Q, на котором
u(x)>k, а через uk(x) — функцию, равную и(х) на Q \ Ak и k
*) В данном параграфе, так же как и в § 2, Ш есть совокупность всех
элементов v (х) из Wlm (й), совпадающих на S с q, (x).

404 ВАРИАЦИОННЫЕ ЗАДАЧИ [ГЛ. V
на Ak. При k^M0 она входит в класс 5й допустимых к срав-
сравнению функций, и так как и(х) дает inf/(«), то
J F (х, и, их) dx < J F (x, k, 0) dx.
Ak Ak
В силу C.1) отсюда следует неравенство
v j\Vu\mdx- j(ii\u\a + \u\m^)dx^ j (yka + km$) dx, C.2)
совпадающее, по существу, с неравенством G.7) § 7 гл. IV,
из которого была получена там оценка сверху vraimax«(jc).
Q
Действительно, в данном случае u^Wlm{Q), тогда как в тео-
теореме 7.1 гл. IV рассматривается более общая ситуация, когда
u^.Wmq. Если в теореме 7.1 считать q = m (где т — показа-
показатель вложения Wlm (Q) в Lft (Q)) и заметить, что т п при
q = tn равно т, то станет ясно, что условия на а доказываемой
теоремы и теоремы 7.1 при q = m совпадают и неравенство C.2)
того же типа, что и G.7).
Благодаря этому выводы, сделанные в § 7 гл. IV из G.7),
справедливы и для C.2). Они приводят к желаемой оценке
сверху vraimaxu (x), если учесть, что в данном случае считается
Q
известной оценка l|V«||mQ (а тем самым и ||u||fiiQ).
Оценка и (х) снизу выводится точно так же, надо только
вместо Ak брать множества' Ак точек jcsQ, для которых
— и(х)> k.
Теорема 3.2. Пусть функция F(х, и, р) обладает следую-
следующим свойством: существует число k > 0 такое, что при всех
jcsQ, u>k справедливы неравенства
F(x, u,0)>F(x, k, 0),
F(x, и, р) > F(x, k, 0), если \ р \ > 0,
а при jcsQ, и < — k — неравенства
F(x,u, 0)>F{x, -k,0),
F(x, u, p)>F(x, -k, 0), если | р \ > 0.
Тогда, если vrai max| qp(s) \^k и и(х) реализует минимум
s
функционала A.1) на мноокестве Ш, то max|«(jc)| не превос-
превосходит k.

§ 4] ДОКАЗАТЕЛЬСТВО ГЁЛЬДЕРОВОСТИ ОБОБЩЕННЫХ РЕШЕНИИ 405
Действительно, в данном случае для каждой допустимой
функции v(x) с vraimaxl и |>& имеется допустимая функция
v(x) =
k, v (х) > k,
v(x), \v(x)\^k,
— k, v(x)< — k,
на которой
| F(x, v, vx)dx = J F(x, v, vx)dx,
J F(x, v, vx)dx =
\v\>k
= J F(x, k, 0)dx + J F(x, —k, 0)dx< J F(x,v,vx)dx,
v>k v<-k |a|>ft
и, следовательно, I(v)<I(v). Ввиду этого vrai max| и |^ k.
a
Заметим, что условиям этой теоремы удовлетворяют, на-
например, функции F вида
F (х, и, р) = Fx (x, р) + ф, (х) | и Iе,
где \\ р \ms^.Fi(x, pX(x| p\m, v, ц > 0, ф, (х) — неотрицательная
функция, а = const ^0.
§ 4. Доказательство гёльдеровости обобщенных решений
Начиная с этого параграфа, мы будем исследовать лишь
обобщенные решения и (х) уравнений Эйлера (и тем самым ва-
вариационной задачи A.1), A.2)) с vraimaxl и |< оо и будем со-
Q
кращенно обозначать их «ог. об. р.». Допустимые вариации ti(*)
тоже будем брать лишь с vraimaxl ц(х) |< оо. Ввиду этого
Q
при 1</п</г условия B.IOj), B.11) можно заменить на
условия вида B.102), B.12) соответственно. Ради простоты из-
изложения будем считать, что функции г|)/ (х), г = 2, 3, в B.12)
ограничены, т. е.
Ii\FPi(x, и, p)\(l +\ p\) +\ Fu(x, и, р)\^ц(\ и\)A +\ р\)т. D.1)
В данном параграфе, кроме неравенств D.1), мы будем
предполагать выполненным неравенство
FP.(x,u,p)Pi^v(\u\)\p\m-\i(\u\), m>\, D.2)
где v (/) — как всегда, положительная невозрастающая функция
^0. Это неравенство накладывает ограничение на поведение/7

406 ВАРИАЦИОННЫЕ ЗАДАЧИ [ГЛ. V
лишь при больших \р\. Если бы функция F(x, и, р) была пред-
ставима при больших | р | в виде суммы
F (х, и, р) = Fm (x, и, р) + F' (х, и, р), D.3)
где Fm(x, и, р) есть положительно-однородная функция р сте-
степени т>\, a \p\-m\F'(x, и, р) | + | рГт+1 \F'p.(x, и, р) |-> 0
при |р|->оо, то D.2) было бы следствием условия F(x, и, р)^
^ v, (| и |) | р \т, где v, (т) > 0 при т ^ 0. Из этих предположений
следует, что при больших | р |
Fm(x,u,p)>-^v,(\u\)\p\m,
Fpi (х, и, р) р, = FmpiPi + F'PiPi = mFm + Fppl% D.4)
и потому D.2) имеет место.
Из представления D.3) можно видеть, почему существенно
условие т> 1. Предположим, что Fm и F' можно дифферен-
дифференцировать дважды и что
К/| при \р\ ->оо.
Тогда
^р.Р/ (Jf. «. Р) Р.-Р, = т (т - ^/
и так как первый член имеет больший порядок роста по \р\,
чем второй, то коэффициент т(т— 1) при нем должен быть
положительным, если мы хотим заниматься равномерно эллип-
эллиптическими задачами.
Кроме того, заметим, что неравенство D.2) есть следствие
D.1) и условия эллиптичности уравнения Эйлера в форме
Fp.Pl (х, и, р) Ы, > v (| и |) A+ I P I Г12 D.5)
при т > 1 (см. по этому поводу начало § 2 гл. IV). Такова
связь условия D.2) с условием регулярности задачи и полу-
полуограниченностью F (точнее, с предположением F(x,u,p)~t^
>v,(|«|)|pr, v, (т) > 0 при т>0), указывающая на его
естественность.
В данном параграфе мы будем предполагать выполненными
относительно F лишь неравенства D.1) и D.2).
В этом и следующих двух параграфах мы хотим доказать,
что для F, удовлетворяющих этим «естественным» условиям,
обобщенные решения уравнений Эйлера (и, следовательно,
обобщенные решения вариационных задач) на самом деле лучше
По своим дифференциальным свойствам, чем произвольные
функции сравнения, т. е. функции из Wxm{u). Первой теоремой
такого типа является следующая:

§ 4] ДОКАЗАТЕЛЬСТВО ГЁЛЬДЕРОВОСТИ ОБОБЩЕННЫХ РЕШЕНИИ 407
Теорема 4.1. Пусть функция F удовлетворяет неравен-
неравенствам D.1) и D.2). Тогда любое ог. об. р. и{х) уравнений
Эйлера A.4) принадлежит классу Са (Q) с некоторым а > 0,
определяемым лишь константами пг, М = vraimax| и |, а также
_ Q
v(M) и ц{М) из D.1), D.2). Норма \ и f?\ Q'czQ, зависит от
тех же величин и расстояния от Q' до границы S. Если гра-
граница S удовлетворяет условию (А), а граничная функция q>(s)
удовлетворяет условию Гёльдера | ф f® < оо, то u^Ca(Q) и
норма \и(^ определяется величинами m, M, v(M) и ц(М) из
D.1), D.2), р, | ф (У и константами 80 и aQ из условия (А). По-
Показатель а, помимо прежних величин, зависит еще от р и 0О.
Эта теорема является частным случаем теоремы 1.1 из
гл. IV.
Аналогичное утверждение имеет место для условной вариа-
вариационной задачи. Точнее:
Теорема 4.2. Пусть выполнены условия теоремы 4.1, и
пусть и(х) есть функция из Ш с vraimax|« \^N, для которой
б/(«;л)>0 D.6)
о .
при любой функции г\(х) из Wm(Q), удовлетворяющей нера-
неравенствам
^N D.7)
при всех t из [0, 1J. Тогда для нее верны все утверждения
теоремы 4.1.
Напомним, что обобщенные решения и(х) условной вариа-
вариационной задачи удовлетворяют всем требованиям этой теоремы
и потому для них верны ее утверждения.
Доказательство теоремы 4.2 почти такое же, как доказа-
доказательство теоремы 4.1 или, точнее, теоремы 1.1 гл. IV. Надо
только при выборе вариации ti (х) следить за выполнением
условия D.7). Утверждения теоремы будут доказаны, если мы
установим, что u(jc)e93m(Q,iV, у, уи б, 0). В качестве ц (х) возьмем
функцию ц(х) = — t,m (x) max {и (х) — k; 0}, где Z, (х) — срезающая
функция для шара Кр, a k — произвольное число из промежутка
[— N, N], если /CpCzQ, и k принадлежит [-N, N] и удовле-
удовлетворяет неравенству k 2& max и (х), если Кр пересекает границу 6'
Kpns
Это возможно, ибо значения
О-О«(*)+#"* при
и (х) + /ti (х) = { , .
v ^ 'w I u{x) при и < k

408 ВАРИАЦИОННЫЕ ЗАДАЧИ [ГЛ. V
при любом х заключены между k и и(х), т. е. между — N
и N. Подставляя эту функцию в неравенство D.6), получим
нужную нам оценку интеграла j IVuft^dx. Это делается
так же, как и в случае безусловной вариационной задачи-
Аналогичные оценки для функции — и (х) получим, беря в ка-
качестве т|(л-) функции ii(jt)=?m(jc)max{— u(x) — k; 0} с &s[—N, N]
и k > max (— и (х)).
Таким образом доказывается, что и(х) принадлежит 23m(Q, N,
Y, Yi. б. 0)- Отсюда на основании теорем 6.1 и 7.1 гл. II сле-
следует справедливость всех утверждений теоремы 4.2.
§ 5. Теорема единственности в малом
для обобщенных решений
Для рассматриваемых нами обобщенных решений вариа-
вариационных задач справедлива теорема единственности, причем
такого же типа, как и для классических решений, именно:
Теорема 5.1. Пусть F(x, и, р) удовлетворяет неравенствам
v(l«|)(l+lpl)mi2</?P/P/(A;, и, р)Ы,<
+ 1р1Г~2!2, E.1)
«1)О+1Р1Г,
и пусть и' и и" являются ог. об. р. уравнения Эйлера A.4).
Тогда, если они равны друг другу на поверхности шара К9 с: Q,
радиус которого достаточно мал (его величина определяется
только числами М = тах|«', и" \, пг, v(M) и ц(М) из E.1) и
Q
расстоянием от Кр до S), то они совпадают во всем шаре Кр.
Если функции а:(х, и, p) = FPi(x, и, р) и а(х, и, р) =
= — Fu(x,u,p), образующие уравнение Эйлера A.4), удовле-
удовлетворяют дополнительно условиям теоремы 7.1 гл. We q = m,
то теорема единственности в малом имеет место в классе про-
произвольных обобщенных решений и из W{m(Q) уравнения A.4)
с ограниченным vraimax|«|. Радиус шара при этом зависит
s
от норм решений в Wlm(Q), их максимумов модулей на S и
расстояния Кр до S. Аналогичное утверждение верно для обоб-
обобщенных решений из Wlm (Q), реализующих абсолютный мини-
минимум /(«), если для F выполнены помимо E.1) условия тео-
теорем 3.1 или 3.2.

$ 6] ДИФФЕРЕНЦИАЛЬНЫЕ СВОЙСТВА ОБОБЩЕННЫХ РЕШЕНИЙ 409
Эта теорема является частным случаем теоремы 2.1 гл. IV
для ог. об. решений и следствием этой теоремы и теорем 7.1
гл. IV и 3.1 — 3.2 данной главы для произвольных обобщенных
решений из Wlm(Q,). Из теоремы 2.2 гл. IV, теоремы 7.1 гл. IV
и теорем §§ 3, 4 данной главы следует совпадение возможных
решений и в областях, прилегающих к 5.
Заметим, что теорема 5.1, равно как и большая часть других
теорем гл. IV и V, сформулирована не во всей возможной
общности. Именно, в этих главах, желая сосредоточить вни-
внимание читателя на новом обстоятельстве — нелинейности задачи
по и, мы предположили ради чисто формальных упрощений
функции ai(x, и, р), а(х, и, р), F(x, и, р) и частные произ-
производные F ограниченными функциями х. Вместо этого можно
было бы считать их суммируемыми по Q с достаточно высо-
высокими степенями и работать с ними так же, как это сделано
в гл. III. Это привело бы к доказательству того, что
ог. об. решения и(х) принадлежат не Sm(Q, M, у, уи 6, 0), а
23m(Q, М, у, Yi, б, l/q) с q > п. Но непрерывность по Гёль-
деру имеет место в обоих случаях, меняются только постоян-
постоянные, что несущественно.
Указанные усиления нетрудно сделать с помощью изложен-
изложенного здесь метода. Несколько иначе это сделано в гл. IX.
§ 6. Дальнейшее исследование дифференциальных
свойств обобщенных решений
Поскольку обобщенные решения вариационной задачи A.1),
A.2) являются обобщенными решениями уравнений Эйлера,
а уравнения Эйлера являются частным случаем эллиптических
уравнений с дивергентной главной частью, то для них спра-
справедливы все результаты гл. IV. Поэтому мы не будем форму-
формулировать применительно к вариационной задаче все эти резуль-
результаты, а ограничимся формулировкой лишь одного из них,
гарантирующего классичность ог. об. решений или, точнее,
принадлежность их к классу С1+а, 1^2. Результат этот пре-
предельно точен в отношении требований гладкости F (х, и, р).
Именно, мы доказываем, что и принадлежат С1+а, 1^2, если
F(x,u,p) как функция своих аргументов принадлежат тоже С1+а.
Из вида уравнения Эйлера FUx ux их.Х/ +FUUxuXt -f FXju —Fu = 0
ясно, что наши предположения о гладкости F минимальны.
Кроме условий гладкости, на F накладываются еще пред-
предположения о росте F и ее частных производных при | р |—> оо.
Как показывают примеры § 2 гл. I, эти ограничения также

410 ВАРИАЦИОННЫЕ ЗАДАЧИ [ГЛ. V
вызваны существом дела. Они имеют вид
v(\u\)(l-\-\p\)m-2t2<FPlPl(x, и, р)Ы,^
<М1«1)A + 1р1Г-212, F.1)
[\FPt (x, u,p)\ + \ FPlU (х, и, р) |] A+1 Р I) + | FPtx, (x, и, р)\ +
+ \Fu(x, и, p)\ + \Fm(x,u,p)\ +
+ \Fuxt(x, и,р)|A+|р|Г'<М1«1)A+1р1Г. F.2)
причем т > 1.
Если бы функция F(x, и, р) была, напр ivie;, пр i б «гьших | р \
полиномом по всем своим аргументам, га-однородным по р,
то все неравенства F.1), F.2) вытекали бы лишь из двух
требований: положительности F(x, и, р) и ее выпуклости по Pk-
Неравенство F.1) выражает собою условие «равномерной эллип-
эллиптичности» уравнения Эйлера, Ограничения F.1), F.2) назы-
называются «естественными».
Одним из следствий теоремы 6.4 гл. IV является следующее:
Теорема 6.1. Пусть F(x, и, р) принадлежит классу Г'ёль-
дера Cl+a (xe=Q, |«|<M, |pKAf,), />2, а > 0, при любом
Mi < °° и удовлетворяет неравенствам F.1), F.2) с v = v(M),
(х = (х (М). Тогда любое обобщенное решение и (х) уравнения
Эйлера с vraimaxi и \^.М будет принадлежать классу Cl+a(Q).
Q
Из этой теоремы и теоремы об аналитичности любого доста-
достаточно гладкого решения уравнения Эйлера A.4) для функции
F(x, и, р), аналитически зависящей от своих аргументов (по
поводу этого последнего предложения см. работы [4,,2, 25,,
33,,2, 39J), следует
Теорема 6.2. Если F(х, и, р) есть аналитическая функция
своих аргументов, удовлетворяющая неравенствам F.1), F.2),
то любое ог. об. решение и(х) уравнения Эйлера A.4) для нее
аналитически зависит от х.
Если не предполагать заранее ограниченности vraimaxi u\
для об. решения и (х) уравнения A.4), то для справедливости
утверждения теоремы 6.2 на F(x, и, р) необходимо наложить
дополнительные ограничения. Эти ограничения сформулированы
в теоремах § 7 гл. IV и § 3 данной главы.
На этом мы заканчиваем исследование вариационной за-
задачи A.1), A.2) для функций F(x, и, р) общего вида. Доказан-
Доказанные здесь теоремы дают точную формулировку и решение 19-й
и 20-й проблем Гильберта для достаточно широкого класса
функций F (см. § 3 гл. I). Из них видно, грубо говоря, что
вариационная задача на разыскание минимума / («) «всегда
разрешима», если ее ставить в пространстве Wlm{Q), ее решения

§7] ОБОБЩЕННЫЕ РЕШЕНИЯ КВАЗИРЕГУЛЯРНЫХ ЗАДАЧ 411
обладают, вообще говоря, лучшими дифференциальными свой
ствами, чем произвольные функции из Wxm{Q), и эти свойства
полностью определяются функцией F. Условия на функцию
F(x, и, р), при которых эти утверждения доказаны, нельзя
ослабить, если их формулировать в принятой нами форме
и не ограничиваться какими-либо специальными классами
функций F, областей Q и граничных функций ф.
§ 7. Обобщенные решения квазирегулярных задач
Выше при исследовании проблемы существования, ограни-
ограниченности и непрерывности по Гёльдеру обобщенных решений
вариационной задачи A.1), A.2) мы не требовали, чтобы задача
была регулярной. Напротив, для доказательства единственности
в малом, ограниченности max| V« | и оценок более сильных норм
обобщенных решений существенно было условие F.1) регуляр-
регулярности задачи или, что то же, равномерной эллиптичности
соответствующего уравнения Эйлера. Покажем, что для не-
некоторых классов нерегулярных функционалов обобщенные реше-
решения обладают непрерывными по Гёльдеру первыми произ-
производными.
Для простоты изложения мы ограничимся рассмотрением
функционалов вида
I(u)=JF(ux)dx G.1)
Q
с F (р) еС2+р(?„), удовлетворяющей при Vp e Еп неравенствам
l*i(l+lp|)m, m>2, цо, |*,>0. G.2)
Вместо условия регулярности F.1) наложим следующее тре-
требование:
th^pr'V, IV ^з>0' G-3)
из которого следует, что функционал / (и) квазирегулярен (см.
условие B.1)) и при |и*| = 0 происходит вырождение эллип-
эллиптичности соответствующего уравнения Эйлера. Простейший
пример такого рода дает функция F = |p|m, m > 2; для него
, так что неравенство G.3) вы-
выполняется с ц2= 1, ц3='" —1. Заметим, что, разделив урав-
уравнение Эйлера на | их \т~2, можно получить равномерно эллип-
эллиптическое уравнение, но оно теряет при этом дивергентную
форму и коэффициенты его становятся разрывными по их
при \их |=0,

412 ВАРИАЦИОННЫЕ ЗАДАЧИ [ГЛ. V
Пусть и(х) есть ограниченное решение из Wm(Q) уравнения
Эйлера для G.1), т. е. и(х) удовлетворяет интегральному
тождеству
б/
(и, т,) - J FUx (ux) т, dx = О, Vt, s #,1, (Q). G.4)
В силу результатов §4 и^С6 (Q). Если было бы уже известно,
что и (х) имеет квадратично суммируемые по Q производные
второго порядка и vrai max| V«|<oo, то, беря в G.4) у\ = ?>х,
/=1, ..., п, с произвольной, гладкой, финитной в Q функ-
функцией 1(х) и производя интегрирование по частям, мы приш-
пришли бы к тождествам
«' Ч)=- J v, ("J V/6*«rfx=°' '=!'••""¦G>5)
Ы
Очевидно, здесь допустима Vg (х) е 1^2 (й).
Таким образом, в этом случае вектор-функцию их =
= («*, ..., их\ можно было бы рассматривать как ограничен-
ограниченное обобщенное решение из W\{u) квазилинейной системы
^•(fliiWib^O G.6)
с коэффициентами ац{р) = РР1р (р), удовлетворяющими усло-
условию G.3). Такие и более общие вырождающиеся системы
изучаются ниже, в § 6 гл. VIII. В частности, из теоремы 6.1
гл. VIII вытекает, что для VQ' с: Q норма | мх |q"' оценивается
постоянной, зависящей от т, ц2, Из> max|u^ | и расстояния Q'
а
до дп, причем величина а > 0 определяется лишь постоян-
постоянными т и Из/н^- Чтобы исследовать произвольные ограниченные
решения из Wm (Q), докажем следующую лемму:
Лемма 7.1. Обобщенное решение задачи G.1), A.2) един-
единственно в классе Wlm(Q).
Доказательство. Пусть U\ и ы2 — Два возможных ре-
шения, и = их — и2. В силу G.4) при Vr]ett7m(Q) имеем
0 = ol (и„ n) - ol (u2, n) = J ut/ (х) и тц dx, G.7)
1
где функции йц (х) = J FUjc ux {tulx + A — /) и2х) dl подчиняются

$ 7] ОБОБЩЕННЫЕ РЕШЕНИЯ КВАЗИРЕГУЛЯРНЫХ ЗАДАЧ 413
неравенствам
тт~х,1,A v«, г2 +1 v«2 Г) 1я<йи(х)Ui<
< 2т~\3 (I V«, Г2 +1 V«2 Г) ?2, Vg <= ?„. G.8)
Полагая в G.7) т):=и и учитывая G.8), приходим к неравенству
f (l V«, f ~2 +1 V«2 Г)I v« I2 d* < 0, из которого следует совпа-
дение «1 (*) с ы2 (*) почти всюду в Q. Лемма доказана.
Фиксируем какой-либо шар ^crQ и в нем рассмотрим
вспомогательные вариационные задачи на отыскание абсолют-
абсолютного минимума функционалов
YI2 G.9)
г ° i i
в классе 3Ru={v(x): v — и ^Wm(KR)\. В силу результатов
§§1—6 при каждом е е @, м-ol существует единственное реше-
решение ие{х) такой задачи, причем ие{х) принадлежит C2+^(KR)f\
Л Сй(Кц) и удовлетворяет тождеству
6Р (ые, л) = J ^ К) r\x. dx = 0 G.10)
о
при Vi](л:) е l^m (ЛГ«). Для иг(х) справедливы равномерные
относительно е е @, ц0] оценки
f I V«« Г d* < М, |ив|!?'<Л<1, G.11)
i p
|u-|(*><M2, G.12)
Лр
где АГР — произвольный концентрический с KR шар радиуса
р < R, причем постоянная М, зависит от | и |^}, М равна
а зависит лишь от ц-з/н^ я т, а М2 определяется величинами
M-Vfe /и, { I V« Г dx и (У? — р)~'. Оценка || V«s ||m< Kr следует не-
посредственно из того, что ие дает минимум интегралу G.9)
в классе Ши, с учетом условия G.2).
Для доказательства G.12) обратимся к тождествам
J Пи К) «^Ц dx-0, I = 1, • • •, п, G,13)
KR

414 ВАРИАЦИОННЫЕ ЗАДАЧИ [ГЛ. V
в которых 1(х)— произвольная функция из wI(Kr). Они вы-
выводятся из G.10) точно так же, как G.5) из G.4). Из G.13)
видно, что вектор-функция иех = (иех , .. ., ы* \ может быть рас-
смотрена как ограниченное обобщенное решение из С1+^(К#),
системы вида G.6) с коэффициентами
atl (Р) = П?, (р) = тг A + р2)(т-2)/2[б{ + (т - 2) ^] + />,0/ (р).
В силу предположения G.3) они удовлетворяют неравенствам
v(lp|)i2<ai;(pH<?/<rnax{-g-; m — I }v(|p |)|2, G,14)
где функция v (| р |) = ц21 Р Г~2 + е A+ р2)(т~2)/2, очевидно, под-
подчиняется условию
()m~2v(/,), V/2>/,>0. G.15)
Неравенства G.14), G.15) и теоремы 6.1, 6.2 гл. VIII гаранти-
гарантируют справедливость оценки G.12).
Из оценок G.11), G.12) можно заключить, что для неко-
некоторой последовательности е->0 последовательность функ-
функций ы8 сходится к мое3йц равномерно в KR, u\ слабо сходятся
в Lm(K^ к их , i= 1, ..., п, а в каждом внутреннем шаре /Ср,
р < R, производные иех сходятся к и°х равномерно. Ясно, чтоы°(л:)
есть обобщенное решение уравнения Эйлера для G.1), u°(x)<s
еС1+°(^) и для и°(х) верны оценки G.11), G.12).
В силу леммы 7.1 и°(х) совпадает в KR с исследуемым
решением и(х).
Итак, мы доказали следующую теорему:
Теорема 7.1. ПустьF(p) принадлежитС2+$(Еп)и при Vpe?n
подчиняется условиям G.2), G.3). Тогда ограниченное обобщен-
обобщенное решение и (х) из Wlm (Q) уравнения Эйлера, соответствующего
интегралу G.1), принадлежит классу Cl+a(Q) с а > 0, опреде-
определяемым лишь величинами m и Цз/н^ из условия G.3). Для VQ'crQ
норма | и |^+<х) оценивается сверху постоянной, зависящей только
от m, H3/V2. Hi/W f I V« \mdx и расстояния Q' до границы Q.
а
Замечание 7.1. Утверждение, аналогичное теореме 7.1,
можно доказать и для более общих функционалов A.1), если
предположить, что функция F(x,u, p), помимо условий G.2), G.3),

$ 71 ОБОБЩЕННЫЕ РЕШЕНИЯ КВАЗИРЕГУЛЯРНЫХ ЗАДАЧ 415
подчиняется следующим ограничениям:
Например, в качестве такой F можно взять F = F0 (р) я|з (л:, и),
где о|) (л:, и) — положительная дважды непрерывно дифференци-
дифференцируемая функция, a F°(p) удовлетворяет условиям вида G.2), G.3).
Рассмотрение этого общего случая требует небольших уточне-
уточнений результатов §§ 1, 2 гл. IV и § 6 гл. VIII, и мы ради эко-
экономии места не будем на этом останавливаться.

Глава VI
КВАЗИЛИНЕЙНЫЕ УРАВНЕНИЯ ОБЩЕГО ВИДА
Квазилинейные уравнения с дивергентной главной частью,
рассмотренные нами в гл. IV, не охватывают всего класса
квазилинейных уравнений второго порядка, ибо не каждое квази-
квазилинейное уравнение
аи (х, и, их) uXlXj + а (х, и, их) = 0 @.1)
может быть преобразовано к виду A.1) гл. IV. Они занимают
особое положение среди всех уравнений @.1). Для них имеет
смысл говорить об обобщенных решениях, обладающих лишь
производными первого порядка, и начинать исследование именно
с таких решений. Это и было сделано в гл. IV. Для уравне-
уравнений @.1) в общем случае решение и(х) обязано иметь произ-
производные не только первого, но и второго порядка, ибо без этого
непонятно, что значит, что и(х) удовлетворяет уравнению @.1).
Более того, как показывает построенный в § 2 гл. I пример,
на производные и необходимо наложить еще дополнительные
требования; в противном случае потеряется теорема единствен-
единственности для задачи Дирихле в шарах сколь угодно малого
радиуса. Мы эти необходимые требования взяли в таком виде:
производные второго порядка квадратично суммируемы, а произ-
производные первого порядка ограничены; заменить последнее условие
принадлежностью их к Lq(Q) с каким-либо q<oo, не усиливая
требования на вторые производные, нельзя. В данной главе
будет доказано, что эти требования на обобщенные решения
и достаточны для того, чтобы строить всю теорию. Точнее,
мы покажем, что дифференциальные свойства любого такого
решения зависят лишь от дифференциальных свойств функций
ац{х, и, р) и а(х, и, р) и это верно для всех уравнений
вида @.1), лишь бы они были эллиптическими на и(х). В част-
частности, будет доказано, что любое такое обобщенное реше-
решение и{х) уравнения @.1) принадлежит пространству C2+a(Q),
если функции ац {х, и, р) и а(х, и, р) на компакте Зй =
= {{х, и, р): xeQ, | и |^тах| и{х) \, \ р |^ тах| Vu(x) \] суть
элементы О1 и Са соответственно, и иеС|+а(й), /^3, если

КВАЗИЛИНЕЙНЫЕ УРАВНЕНИЯ ОБЩЕГО ВИДА 417
at! и а принадлежат С1~2+а{Ш). Отсюда и из доказанных
в гл. III фактов о линейных уравнениях следует, что для опи-
описанных здесь обобщенных решений уравнений @.1) справедлива
теорема единственности для задачи Дирихле в достаточно малых
областях, если только функции ац и а суть элементы О1 (Эй). Эти
предложения достаточно точно описывают границы справедли-
справедливости 19-й гипотезы Гильберта применительно к квазилинейным
эллиптическим уравнениям второго порядка. С доказательства
этих предложений мы и начнем данную главу. Они относятся
ко всему классу эллиптических квазилинейных уравнений @.1).
Условие эллиптичности для @.1) имеет вид
v (х, и, р) ?2< аи (х, и, р) lili < |i (х, и, р) ?2, @.2)
где \(х, и, р) и ц {х, и, р)— положительные непрерывные функ-
функции своих аргументов. Деление обеих частей уравнения на
v{x, и, р) приводит к неравенству @.2) с v=l. Однако мы не
будем считать, что такое деление (такая нормировка @.1)) раз
и навсегда выполнено, ибо для разных целей нам полезна
разная «нормировка» уравнения @.1).
До 60-х годов нашего века в основном изучались так назы-
называемые равномерно эллиптические уравнения, т. е. уравне-
уравнения @.1), для которых отношение т (х, и, р) = ^-Л' ^ р} ^ Hi =
= const для хей и произвольных и и р. Эти уравнения
являются основным объектом изучения и для данной книги.
Однако методы, развитые при их изучении, оказались приме-
применимыми и для довольно широких классов неравномерно эллипти-
эллиптических уравнений, т. е. уравнений, для которых отношениет (х, и,р)
неограниченно растет при | и | +1 р \-> оо. Во всех изучаемых нами
случаях тах|ы(л:) |для решений и(х) не превосходит некоторого
Q
конечного числа (оно или находится явно через данные задачи,
или предполагается существующим по условию). Ввиду этого
все функции аргумента (х, и, р) (если не оговорено противное)
рассматриваются лишь при х ей и | и \^М, в частности, и не-
неограниченность х(х, и, р) для неравномерно эллиптических урав-
уравнений интересует нас лишь в связи с неограниченностью \р\.
Если х(х, и, р) при | р |—> оо растет, какс|рР, то говорят,
что порядок неравномерности эллиптичности уравнения @.1)
равен пг. Поведение х{х, и, р) при | р |—> оо существенно в во-
вопросе получения априорной оценки тах|Ум(л:)| для всех воз-
можных решений и(х) уравнений @.1). Там же, где считается
известной оценка сверху для max| Vu(x) |, случаи равномерно и
Q
неравномерно эллиптических уравнений, очевидно, неразличимы
14 О, А. Ладыженская, Н. Н. Уральцева

418 К6АЗИЛИНЕЙНЫЕ УРАВНЕНИЯ ОБЩЕГО ВИДА [ГЛ. VI
(так обстоит дело в § 1 при исследовании гладкости их и
более старших производных и).
В § 2 мы рассматриваем вопрос о получении априорной
оценки max|V«| на границе 5. Излагаемый метод восходит
к работам С. Н. Бернштейна и дает нужный результат для
всего класса равномерно эллиптических уравнений. Данная
нами модификация его позволила охватить и некоторые классы
неравномерно эллиптических уравнений. Другой способ оценки
max|V«| дан в работе [51М] Дж. Серрина. Он позволил охва-
s
тить новые классы неравномерно эллиптических уравнений.
Параграф 3 посвящен получению так называемой тотальной
оценки |V«|, т. е. оценки max|V«| для всей области Q, когда
известны границы М^тах\и(х) \ и Mi ^max| Vu(x) |. В § 4
q s _
даются локальные оценки max | V« (x) | для любой Q' с: Q, при
которых считается известной лишь мажоранта М цля тах| и (х) |.
Q
Метод получения этих оценок идет от работы [218] 1956 г.
одного из авторов книги. В нем использована важная идея
С. Н. Бернштейна: вместо max| V« (x) | оценивать max| Vy (x) | для
специально подобранной функции и, связанной с и равенством
ы = Ф(а). В работе [218] дается способ определения таких функ-
функций Ф(а), тогда как в работах С. Н. Бернштейна и в работах
других авторов, использовавших эту идею С. Н. Бернштейна,
берется та или иная конкретная функция Ф(у) без указания
способа ее подбора и устанавливаются лишь тотальные оценки.
Более того, до работы [218] исследовался лишь случай п = 2
и данные для него методы оценки | Уи | существенно использо-
использовали особенности двумерной евклидовой плоскости. Подход
к получению тотальных и локальных оценок | V« |, данный
в работе [218], позволил охватить наиболее широкие классы
равномерно эллиптических уравнений, а в отношении тотальных
оценок наиболее широкие классы неравномерно эллиптических
уравнений. В первом издании данной книги мы придали ему
«интегральную форму», позволившую исследовать обобщенные
решения уравнений @.1). Это значительно усложнило его. Здесь
мы решили вернуться к его первоначальной форме, более про-
простой для восприятия и работы. Небольшое дополнительное
рассуждение позволило от решений и из С3 перейти к реше-
решениям из С2 (в работе [218] и во всех других работах, исполь-
использовавших метод работы [218], в том числе и в работе Дж. Сер-
Серрина [51М], предполагается, что и^Сг).
В конце § 3 изложена оценка тах| Уи |, данная в работе [143]
Q
А. В. Иванова. Она относится к одному классу неравномерно

g 1] ОЦЕНКА НОРМЫ | в \%+а) ЧЕРЕЗ НОРМУ | и \$> 419
эллиптических уравнений, выходящему за пределы классов,
охватываемых теоремами 3.1—3.3.
В § 5 доказываются теоремы существования классических
решений задачи Дирихле для уравнений @.1). Делается это
на основе теоремы Лерэ — Шаудера о неподвижных точках
вполне непрерывных преобразований и полученных в преды-
предыдущих параграфах априорных оценок норм | и (?+а) всех возмож-
возможных решений задачи Дирихле для уравнений вида @.1). Резуль-
Результаты §§ 1—5 справедливы при любом п^2. Параграф 6
содержит ряд дополнительных результатов для случая п = 2.
Именно, в нем дан другой способ оценки max|V«|, исполь-
зующий несколько иные, чем в § 3, предположения о поведении
функций att(x, и, р) и а{х, и, р) при | р |—*¦ оо. В соответствии
с этим условия теорем существования, доказанных в § 6,
несколько отличаются от условий § 5.
§ 1. Оценка нормы |и|д1+<1) через норму | «|q *
В этом параграфе будет доказано, что для всего класса
квазилинейных эллиптических уравнений
Lu = at,(x, и, ux)uXlXj + a(x, и, их) = 0 A.1)
имеет место следующее утверждение:
Теорема 1.1. Пусть и(х) есть обобщенное решение уравне-
уравнения A.1) из класса Wl(Q) с vrai max| и \^М и vrai max| V« |=S^M|.
Q Q
Если уравнение A.1) эллиптично на нем, т. е.
at, (х, и (х), их (х)) Ы, > vg2, v = const > 0, A.2)
и если на множестве Шм, м{ = {(х, и, р): хей, | и | ^ М, | р | <^ Mi}
функции ац{х, и, р) дифференцируемы по всем своим аргумен-
аргументам, а а{х, и, р), ац(х, и, р) и частные производные atl{x, и, р)
по xi, и, pk ограничены какой-нибудь постоянной М2, то и (х)
принадлежит классу С1+а (Q) с некоторым а > 0, причем а за-
зависит лишь от v, М[ и М2, а нормы | uXl |(а) для VQ' cr Q зависят
от тех же постоянных и расстояния Q' до границы S. Если
к тому же 5е02 и и (х) |5=q> (x) \s, где q> (x)<=W2q (Q), q>n, то и (х) е
s Cl+a (Q), причем а и | иХ{ |(а) определяются постоянными v, M,
Mu M2, ПфН^о, q и границей S.
Докажем сначала первую часть теоремы. Без ограничения
общности функции их, г=1, 2, ..., п, будем считать норми-
нормированными в том смысле, что их значения не выходят из
14*

420 КВАЗИЛИНЕЙНЫЕ УРАВНЕНИЯ ОБЩЕГО ВИДА [ГЛ. VI
отрезка [0, 1]: ()<«*,< 1, 1= 1, 2, ..., п. В противном слу-
случае мы в уравнении A.1) сделали бы замену исследуемой
функции и(х) на v(х) = [и(х) + М, Д} xt lBMi) и все рассуждения
проводили бы с функцией v. Очевидно, что v (x) есть решение
квазилинейного уравнения того же вида A.1) с аналогичными
свойствами функций atj, a.
Пусть U есть вектор с составляющими их , ..., их . Дока-
Докажем, что он принадлежит классу 23|" (й, М3, 6i, 62, 63, у, у, б, 1Д?)
с некоторыми М3, 6;,уА q, определяемыми постоянными v.Af,, M2.
В качестве функций ф'(С/) возьмем
-2j«b /=1, 2, .... п. A.3)
Для них vrai max <pl±(U (x))\ ^ lln, поэтому за Мг можно
взять lln. В силу леммы 8.1 гл. II нам достаточно доказать,
что функции wl± (х) = у1± (U (х)), 1 = 1, 2, ..., п, удовлетворяют
неравенствам (8.3) гл. II, входящим в определение класса
23г"(й, Мз, 6\, б2, б3, у. Y. 6» !/?)• Покажем, что эти неравенства
справедливы для них с ? = оо, Для этого составим тождество
J [а1{ (х, и, их) uX[Xf + а (х, и, их)\ y\Xl {x) dx = 0, A.4)
Q
о,
где г)(х) — произвольная ограниченная функция из W2(Q), и
с помощью двукратного интегрирования по частям главных
членов преобразуем его к виду
дач .. .. i
= I "I *!/«*,*,.
П
даИ да{, \ Л
T Uu + -? U) л + Щ] dx
дац да1
ди*т
иХтХ[иХ1Х/ $1- uXluX[Xi - -— uX[Xjj ц + aruj dx. A.5)

$ n ОЦЕНКА НОРМЫ | и |jj1+a) ЧЕРЕЗ НОРМУ | и \$ 421
Введем обозначения:
~ "' ди ' dx '
ди*1 ~ "' ди ' dxi
да и
ди "xi
Тождество A.5) перепишется так:
+ a'uXlXj
+ атц] dx = 0. A.6)
Все коэффициенты в нем в силу предположений теоремы суть
ограниченные функции. В него, равно как и в исходное то-
тождество A.4), входят производные от и не выше второго по-
порядка, причем производные второго порядка входят в степени
не выше второй и с ограниченными коэффициентами.
Ввиду этого тождества A.4) и A.6) справедливы для любого
решения и(х) из ^(Q) с конечным vraimax|V«|, несмотря
о
на то что при выводе A.6) было использовано существование
у и(х) производных третьего порядка. Действительно, возьмем
последовательность трижды непрерывно дифференцируемых
функций и(Р) (х), р=1,2, ..., с равномерно ограниченными
vraimax| V«<p> (х) |, сходящихся к и(х) в норме Wl(Q). В каче-
Q
стве такой последовательности можно взять, например, усред-
усреднения функции и (х) с бесконечно дифференцируемым ядром.
Правда, усреднения ир{х) определены не во всей области Q,
а лишь для областей Q' с: Q, расстояние которых до 5 не
меньше р. Однако для первой части теоремы это не имеет
значения, ибо решение и(х) исследуется лишь внутри Q, и
поэтому функцию т] в A.4) и A.6) можно брать равной нулю
в целой пограничной полоске около 5. Итак, возьмем функ-
функции ы<р). Для них невязка
att (*' ". "*) uTtx} + а (х, и, их) э= ер (х) A.7)
стремится к нулю в L2(Q). Отсюда, а точнее, из аналога то-
тождества A.4)
{ (а */«?*, + а) тц dx = J грг\Х[ dx
а а
получим тождество типа A.6), в котором, как легко видеть,
можно перейти к пределу по р-»оо и получить A.6). Итак,

422 КВАЗИЛИНЕЙНЫЕ УРАВНЕНИЯ ОБЩЕГО ВИДА [ГЛ. VI
тождество A.6) доказано для ограниченных финитных ц из Wi (Q),
о
а потому и для всех ограниченных ц из W2 (Q).
Возьмем в A.6) тг\ = иХ1{х)Ф(х), где Ф\х) — ограниченная
финитная функция из ^(Q), и полученные тождества просум-
просуммируем по / от 1 до п. Это даст
Q
+ (a?jUxmxlUxlxj + a'uXlXj
+ а Аи Ф + аиХ1ФХ1]dx = °-
Введем еще следующие обозначения:
fc=l
Тогда последнее тождество перепишется в виде
* , 1
J [auux^ux^
о
+ — aijUx хРх,Ф-\- Ьцих.х.Ф + агФх d* = 0. A.8)
Это тождество сложим с тождеством A.6), в котором функ-
функцию ц возьмем равной 5пФ. Результат запишем как некоторое
тождество для функции wl+ = \0nuXl + v, именно:
f[a..B „ ф + ±а„т1+хФх +
i
dx = 0, A.9)
c\ = Ь + 5na'b\ + ЪпЬ1ц, c\ = ai-\- bnab\.
где c\{ = ц ц
Из A.9) нужное нам соотношение выводится так же, как
это делалось выше, в §§ 14, 15 гл. III и §§ 1,6 гл. IV.
Именно, положим в A.9) Ф (х) = 2?2 (х) max lwl+ (x) — k, 0]. Здесь
? (х) — срезающая для шара Кр с: Q функция (как всегда,
O=S^?s^l). Обозначим через Ak,р множество точек шара Кр,
в которых w'+(x)> k. Результат подстановки такой Ф(я) в A.9)
после простых преобразований дает следующие тождества:
/ [2aiiuXrXluXfXj (w+ - k) t + aijW+x^+x^ +
+ 2a..w\Xj« - k)?Ц + ^w\xuXmXiК - k) ? +
К
A.10)

$ Ij ОЦЕНКА НОРМЫ | и |?+0) ЧЕРЕЗ НОРМУ | и |Ц> 423
Положительными членами здесь являются первые два. Их мы
оставляем слева и оцениваем снизу. Остальные члены перене-
перенесем направо и оценим сверху по неравенству Коши, помня, что
?, до' и все коэффициенты в A.10) ограничены известными нам
константами. В результате этого получим
J
Г S2] dx
+ <x« - *) ?2+т I Vtw+ Г К - *) ?2 +1 И*-
Здесь е-произвольное положительное число, а у' —известная
постоянная. Если е взять равным, например, v/2y', to отсюда
будем иметь более простое неравенство;
где у" — тоже известная нам постоянная.
Будем брать теперь только такие k, которые близки
к тахдо+, именно, такие, для которых
Ак, р
max до' — k = max до' — k < 6 vrai max I до' |
»*.р + *p + a ' +l W
Для таких k из последнего неравенства выводим одну из основ-
основных для нас серий неравенств:
J|V<|sg»<te<V[
k,P
и тем более-
[L],p. A.12)
J
J |hpY[1r«
Ak. p-ap *•p
Аналогичные неравенства получаем для функций wl_ =
n
*= ЮпA — uXl{x)} + 2 «I ix)' Это завершает доказательство

424 Квазилинейные уравнения общего вида [гл. vi
того, что вектор U = (ux, ..., «*J принадлежит к классу
ЯЗ^" (Q, М3 0). Отсюда в силу теоремы 8.1 гл. II следует, что
и%1 е Са (Q). Первая часть теоремы доказана.
Переходим к изучению производных их. (х) вблизи границы S.
Пусть S^O2, a (p(*)eW*(Q), q > п. Распрямим какую-либо
часть границы так, чтобы в новых координатах мы имели те же
свойства для и и уравнения, что и в старых (для этого надо,
чтобы переход от одних координат к другим и обратно совер-
совершался дважды дифференцируемыми функциями с равномерно
ограниченными производными первого и второго порядков), и
рассмотрим и(х) вблизи этой части S,. Пусть хх хп —
уже новые координаты и уравнение куска S{ в них хп = 0.
Рассмотрим и(х) в какой-либо подобласти Q, области Q, при-
прилегающей к Si, причем функции их также считаем нормиро-
нормированными на «0—1», т. е. 0 ^ их ^ 1, /=1,2, ..., п.
Возьмем вектор-функцию ?/ = (ы*](л:) "'„-i^)' Также,
как и выше, проверяется, что она принадлежит классу
23^"(Qi, ...), причем функции yl±(U) для нее берем в виде
л-1
1=1, 2, ..., п — 1, и поэтому до'± (х) = ф'± (и,, (х), ..., uXfi_i (x)).
Надо только при выводе неравенств A.12) для wl±(x) в членах,
содержащих производную «*„*„. заменить ее из уравнения A.1)
на апп(Х\,их) I ~а <*• "• «*> ~ ^ a""V ~ ^ ^ ulnUx^ I (ЭТО
п-\ п-\ П
-а(х,и,их)~ 2 ачих^ - 2 ? a,««V|i
необходимо потому, что среди «главных» положительных чле-
членов, содержащих иХ{Х], не будет члена с «*„*„)• Таким образом,
для шаров /Ср сг Q, и функций до = до^, 1= 1, 2, ..., п— 1,
неравенства A.12) выполняются для всех уровней &, близких
к их максимуму в /Ср: max до — k «^ б max до. Кроме того, функ-
функции wl±, 1=1, 2 /i—l, удовлетворяют неравенствам A.12)
и для шаров /Ср, пересекающих границу dQ области Qi, если
только уровни k при этом, помимо условия k ^ max w — б max до,
удовлетворяют еще и условию k ^ max до. Вывод этих нера*

$ ,j ОЦЕНКА НОРМЫ \и\?+а) ЧЕРЕЗ НОРМУ \и$ 425
венств для пограничных шаров ничем не отличается от данного
выше вывода для внутренних шаров. Из сказанного здесь,
того, что функции иХ[, /=1, 2 п— 1, удовлетворяют на S,
условию Гёльдера, и теоремы 8.3 гл. II следует, что
osc{«^, /Ср Л ^} <Cpa. a>0. /=1,2 п— 1, для шаров Кр,
которые могут пересекать S,, но отстоят от dQ \ S] на положи-
положительное расстояние.
Осталось оценить колебание иХп в таких шарах /Ср. Для
этого достаточно (см. лемму 4.2 гл. II) доказать, что
+е, е>0. A.13)
В силу уравнения A.1) эти оценки достаточно установить лишь
для uX[Xj, 1= 1, 2 п, j= 1 п— 1, т. е.
га га—1
•2+8, е>0. A.14)
Для их получения выведем неравенства, близкие к A.11). Са-
Самих неравенств A.11) недостаточно, потому что они для при-
приграничных шаров выведены не при всех k^O, а лишь при
ft> тахш. По условию функция ср (х), задающая граничные
Kpnsi
значения и на S, принадлежит W2q(Q), q>n. В силу теоремы
2.1 гл. II ф (х) е= С'+а(Q) с а=1 — -. Обозначим: v(x) =
= и (х) — ф (х). Эта функция удовлетворяет уравнению того же
типа, что и функция и, только младший член в нем будет не
ограниченной функцией, а функцией из Lq (Q). Составим из ее
производных функции
п— 1
$+ = |*оЖ/ + 2 о^, ц = const > 1,
tl + Zvl, 1=1,2,
A.15)
Они равны нулю на Sj и по доказанному выше удовлетворяют
условию Гёльдера вблизи Su Для них верны неравенства типа
A.11), точнее, неравенства A.11), в которых вместо 1 стоит
mes~2/<?i4fe,р. Это дает при любых *>0 и достаточно малых р
оценки
| \Vw?dx^y'pn-2+2a, w = wl±, 1=1,2 n—1,
Ak,p/2
Q некоторым положительным a< a= 1 —^-.

426 КВАЗИЛИНЕЙНЫЕ УРАВНЕНИЯ ОБЩЕГО ВИДА [ГЛ. VI
При k = 0 они дают
\Vw?dx^y'f>n-2+2a, w = til±, 1=1,2 п-\, A.16)
А0, Р/2
где Ло,р/2 означает множество точек из KppftQi, в которых
w (х) > 0. В каждой точке х е /СР/2 П Qi Для любого /= 1, . .., п—\
по крайней мере одна из функций wl± (x) неотрицательна. Всю
подобласть Kpft{]ui можно покрыть конечным числом замкну-
замкнутых областей Q QL таких, что каждой Q, i^L, сопо-
сопоставляется набор из п — 1 неотрицательных на Q' функций гё>,
причем в их число из каждой пары wl± входит лишь одна
функция.
Берем одну из й' и соответствующие ей функции w (кото-
(которые на ней неотрицательны); пусть, например, это будут функ-
функции &+, 1=1, 2 п— 1. Для них в силу A16) имеем
оценку
/=1, 2 п-\, A.17)
а в силу A.15) систему равенств
Д1 , "^' /=1, 2 п-\,
^s=№^ + 2 2V?s, s==li2 n
Эту систему равенств рассмотрим при закрепленном s как ли-
линейную систему (п — 1)-го порядка относительно vXsX[ с опре-
определителем D = \ цб| +2vx ,|. При ц > 2n max max I vx I опреде-
I /I / Q '
литель D отличен от нуля и величины vXjc . /= li 2 n— 1,
однозначно определяются через ш+* и vx, 1=1, 2 п— 1.
Все это верно при любом s E=1, 2 п). Отсюда и из
A.17) следует, что
V2+2 s = 1, 2 п.
Эти неравенства имеют место для всех п1, i=\, 2 L,
Поэтому
j

j 1] ОЦЕНКА НОРМЫ | U|^1+a) ЧЕРЕЗ НОРМУ | ul^" 427
Отсюда уже следуют соотношения A.14) и A.13) с е = 2а, ибо
для ф(*) верно такое же неравенство с a = (q — n)lq. Из них,
как сказано выше, получаем оценку колебания для иХп в /Ср(] Qi:
osc{«*n, /CPD^i}<cPa вблизи куска границы Si. Вв"иду доста-
достаточного произвола в выборе S\ фактически оценены колебания
всех производных иХ[, /=1, 2, ..., п, в любой области Ко(]п
с р^Ро- Теорема доказана.
Эта теорема примечательна тем, что она относится ко всему
классу квазилинейных эллиптических уравнений. Для случая
л = 2 теорема была доказана сравнительно давно и просто
(см. [44,, 52], а также § 19 гл. III и § 6 гл. IX), для произ-
произвольного же п упорно не поддавалась доказательству.
Итак, мы доказали, что любое решение и(х) уравнения A.1),
принадлежащее №г(й) и имеющее конечный vraimaxl V« |, при-
Q
надлежит классу C1+a(Q) с некоторым a > 0, если для функций
ац(х, и, р) и а выполнены условия теоремы 1.1. Если относи-
относительно а (х, и, р) предположить больше, именно, что а (х, и, р)
на множестве ЗЯм, м, принадлежит пространству Се (ЗЯм, м,), то
решение и(х) будет принадлежать классу C2+B(Q). Действи-
Действительно, и(х) можно рассмотреть как решение линейного
уравнения
ai/(*)«V/ + a(x) = 0 A.18)
с коэффициентами utj(x)=*atl(x, u(x), их(х)), а(х) — а(х, и(х),
их(х)) из Cap(Q). По теореме 12.1 гл. III и(х) будет принад-
принадлежать C2+aB(Q). Это в свою очередь гарантирует принадлеж-
принадлежность а.ц{х) и й(х) к Св (Q), и из той же теоремы 12.1 гл. III
следует, что и (х) е С2+р (Q).
Такими же рассуждениями из теоремы 1.1 данного пара-
параграфа и теоремы 12.1 гл. III выводится дальнейшее увеличе-
увеличение гладкости и(х) в Q и в Q по мере увеличения гладкости
функций ац, a, u\s и S. Сформулируем результат в виде
теоремы.
Теорема 1.2. Пусть относительно и (х) и функций ац (х, и, р),
а(х, и, р) выполнены условия теоремы 1.1. Тогда, если дополни-
дополнительно а е Се (Шм, м), то и(х) будет элементом C2+B(Q) при
произвольных S и <р = и |s и и(х)^ С2+в (Q) при <р и S <= С2+в.
Далее, если at, и а е= С'~2+в(Эйм,м.). ^>3. то и (х) s= Cl+& (Q)
при произвольных S и <р и ы (*) е Cl+& (Q) при ф и S е С/+р.

428 КВАЗИЛИНЕЙНЫЕ УРАВНЕНИЯ ОБЩЕГО ВИДА [ГЛ. VI
§ 2. Оценка |V«| на границе
Пусть функции ctijix, и, р), а(х, и, р) из @.1) ограничены
на любом компактном множестве изменения их аргументов.
Точнее, они интересуют нас лишь при х е Q и и е [и{1), и{2)],
где «A)<;min« (х), а и{2)^тахи(х), причем числа ыA) и ыB)
а а
в общем случае предполагаются уже известными (они не нужны
тогда, когда можно обойтись без введения вспомогательной
функции Ф; см. ниже). Мы получим локальные оценки макси-
максимума | Vu | на S, т. е. мажоранты для max|V«|, где Sp есть
sp
пересечение S с шарами Кр(х), центры которых х лежат на S.
используя информацию о решении и(х) и уравнении @.1) лишь
в Q2p = Qn К2р(х)- Пусть х есть какая-либо точка S. Примем ее
за начало координат и оси повернем так, чтобы ось хп была
направлена по внутренней нормали к S в точке Jc = (O). Пусть
уравнение @.1) пронормировано так, что
2аи(х, и, р)=\. B.1)
Форму {A{p)l,l) = {Al,l) = ali{x,u,p)lllj будем считать
неотрицательной. В силу этого и B.1) \ai{(x, ы, р)|^1, i, / —
= 1, ..., п. На функцию а(х, и, р) наложим условие
\а(х,и,р)\^с^(р) + с2, B.2)
где &{р) = {А(р)р, р) = аи(х, и, p)piph Пример B.26) гл. I
показывает, что в общем случае нельзя в B.2) вместо &(р)
подставить \ pfS'(p) с е > 0.
Пусть функция и (х) принадлежит в Qp = Q Л Кр @) классу
С(Qp) Л С1 (Qp), ее производные первого порядка дифференци-
дифференцируемы в Qp и в каждой точке нейр функция и(х) удовлетво-
удовлетворяет уравнению @.1). Пусть, кроме того, и(х) на Sp совпадает
с ф(*)еО2(Йр).
Рассмотрим сначала случай строго выпуклой области. Точ-
Точнее, предположим, что Qp расположена в шаре Kd(xf) радиуса d
с центром на полуоси хп > 0, касающемся плоскости хп = 0
в точке х= 0.
Рассмотрим в Qp функцию п(х) = и (х) — ср (х). Для нее из @.1)
получаем уравнение
аИ (х, и, их) uXlXj = — a(x, и, их) — аи (х, и, их) q>XlXj, B.3)
причем
ttL = 0. B.4)

12) ОЦЕНКА | V | НА ГРАНИЦЕ ' 429
Введем вместо п новую функцию v с помощью равенства п =
= Ф(у), где Ф(у) есть дважды непрерывно дифференцируемая
функция с Ф/(о)>0, Ф"(у)<0 и ф@) = 0, которая будет кон-
конкретизирована ниже. Очевидно, йд^Ф'о*,, й*(«/ = Ф/оЯ(«/ +
4-Ф"Охгол.. Подставим это выражение для ы*^ в B.3) и ре-
результат запишем в виде
®'auvX{Xj WattvXlvXt -a- atffXlXj. B.5)
В силу неотрицательности формы {А\, |) справедливы нера-
неравенства
(А (их) vx, vx) = -jpy (Aux - А<рх, их — цх) =
^4" и)
~ 2 ^Ивх. «*) У'Мф*. Фх) + Иф*. Фх)]
Благодаря им, а также | аи |< 1 и B.2), из B.5) следует
lV/l WF^- BJ)
Возьмем в качестве Ф(у) одно из решений уравнения
—$?¦ = &.. B-8)
именно
Ф(о) = -2^-1пA + о), B.9)
считая С] > 0 (случай сх = 0 можно было бы разобрать от-
отдельно, но мы этого делать не будем). Оно удовлетворяет по-
поставленным выше условиям: Ф' > О, Ф"<0, Ф@) = 0. Так как
Ф (у) = п = и — ф, то
2с, max | и (*)-Ч> (*) I
max(l + d) = max е2с'<"(*>-('> <*»<<? qp =c3,
qp qp
и потому тах(Ф') ^2c]C3. Благодаря такому выбору Ф из
Q
B.7) следует неравенство
ailVX!XI> — Ci, B.10)
где с.—2с,с3 Гс2+2с, max m^+max S IФ-, ll- Кроме того, у k=0.
L % QP '^' ' 'Li p

430 КВАЗИЛИНЕЙНЫЕ УРАВНЕНИЯ ОБЩЕГО ВИДА [ГЛ. VI
Возьмем в качестве «барьерной» функции
до(*)=^[(л:-*'2)-<*]-с5л:„, B.11)
в которой постоянная с5 ^ 0 столь велика, что (о + до)
Q s ^
В силу max v ^ с3 — 1 и того, что хп для точек dQp \ Sp не
меньше p2/Bd), мы удовлетворим требованию (о + до) \dQ ч s ^ 0,
положив c5 = 2d(c3— 1)/р2. При таком с5 функция v (х) + до (х)
неположительна на всей границе <?Qp, причем в точке * = 0
равна нулю. Кроме того, для нее atj{v -\-w)XiX ^0 в Qp. В силу
принципа максимума о (х) + до (х) достигает своего максималь-
максимального в Qp значения в точке * = 0. Поэтому разностное отноше-
отношение А(у+до)/А/ в точке * = 0 неположительно по любому
направлению I, выходящему из точки * = 0 в Q. Отсюда, вспо-
вспоминая выражение v через и и <р, получим оценку
lim
I АЛ
Аналогичные рассуждения с функцией #(*)= — и(х) как реше-
решением уравнения аИ{х, — й, — ux)uX{Xj — а(х, — й, — их) = 0
приводят к оценке
lim
Аи
1Д/1
B.13)
Таким образом, доказана
Теорема 2.1. Пусть в Qp= Q(]l(p(x), JceS, выполнены
следующие предположения:
a) и{х)^С (Qp) Л С1 (Qp), ее производные первого порядка диф-
дифференцируемы в Qp, и (х) удовлетворяет уравнению @Л) во все*
точках Qp ы «a Sp = S П Кр (х) совпадает с <р (х) е О2 (Qp).
b) Функции ац (х, и, р), а (х, и, р), образующие уравнение
@,1), при яеОр, произвольных р и u g [«•'•, «И], где ыA><
<min«D ыB)^тахы (х), удовлетворяют условиям B.1), B.2)
и аи(х, и, p)ltl,^
с) Область Qp принадлежит шару Kd{x'), граница которого
содержит точку xgS (точнее см. стр. 428).

§2] ОЦЕНКА |Vu| НА ГРАНИЦЕ 431
Тогда для любого направления I, выходящего из точки х
в Qp,
dl
2с, max | и (*)-Ф (*) |
где с3 = е qp
Условия теоремы 2.1 вызваны существом дела для всех рав-
равномерно эллиптических уравнений @.1). Более того, форме
ац(х, и, p)lilj разрешена неравномерность любого порядка и
даже вырождение, лишь бы не обращались в нуль одновре-
одновременно все ее собственные значения (условие B.1)). Правда,
падение роста ац(х, и, р)^Е/ в направлении Е = р влечет за
собою соответствующие ограничения на рост а(х, и, р) (усло-
(условие B.2)). Это последнее не выполняется, например, для случая
уравнения
[A + us)b{ - uXiuXj] uXlXj =пЖ{\ + ulf12, B.14)
определяющего среднюю кривизну Ж поверхности и = и (х),
если Ж Ф 0. Действительно, для B.14) аг/Е(Е/ = Е2A + и^) —
— (их, If, т. е. &(их) = и2х, тогда как а имеет третий порядок
роста по \их\. Для уравнения B.14) мы сталкиваемся как раз
с самым неблагоприятным для теоремы 2.1 случаем, когда
порядок роста формы а,-/^Е/ в направлении 1 = их меньше,
чем в любом другом направлении |. Напротив, для уравнения
вида
(в{ + uXluXj) uXlXj + a(x,u,ux) = 0 B.15)
направление | = их дает максимальный порядок роста формы
aifc&r Для него &(их) = и1A +"х) и' следовательно, условия
теоремы 2.1 допускают четвертый порядок роста а по | их \.
Заметим, что форма аг/1г1/ при (|, их) = 0 равна g2, т. е. урав-
уравнение B.15) не является равномерно эллиптическим.
Заменим теперь условие с) теоремы 2.1 следующим:
с') Существует шар КА{х") {как всюду, к Kd(x") не причи-
причисляется его граница), не имеющий общих точек с Qp и содер-
содержащий точку jc e S на своей границе.
Относительно функций ац, а, кроме условий теоремы 2.1,
предположим .
Сб. B.16)

432 КВАЗИЛИНЕЙНЫЕ УРАВНЕНИЯ ОБЩЕГО ВИДА [ГЛ. VI
Перейдем от л; к новым координатным функциям у = у (х),
соответствующим преобразованию инверсии относительно сферы
dKj(x"). Область Qp при этом перейдет в область Qp измене-
изменения у. Она расположится внутри сферы дКа(х"), причем точка
х=^у останется неподвижной. Функции у = у(х), xgQp, и
обратные им функции * = *(#), у е Qp, будут, очевидно, огра-
ограничены вместе со своими производными первого и второго
порядков некоторой постоянной с7, определяемой лишь й и
диаметром пр. Преобразуем уравнение @.1) к новым коорди-
координатам:
b = 0, B.17)
, dyk dyt d2yk
где hi = au gf-g^-, b = a + bkUyk, a bk = a4 дх *х . Здесь и
fg^ yk 4 дх х
ниже мы сохраним за и (и другими функциями х) их прежние
обозначения, хотя теперь они рассматриваются как сложные
функции у (например, и = и (х (у))). Дальнейшие рассуждения
аналогичны доказательству теоремы 2.1, только вместо урав-
уравнения @.1) мы имеем уравнение B.17). Форма (fig, l)=bkilklt
обладает, по существу, теми же свойствами, что и Я;Д/Е/-
Меняется лишь нормировка: вместо B.1) 2 bkk^vu = const > 0—
fei
и границы: | Ъм |^Цо = const < <х>. функция же b отличается
от а слагаемым bkUyk. Чтобы иметь для Ъ такого же типа оценку,
что и в теореме 2.1 для а, мы и потребовали выполнения
условия B.16). Именно, в силу B.2), B.16) и указанных выше
свойств координатных функций у = у(х) для b справедлива
оценка
+ с,) % (их) + с2 + с6с8 = с9 (Виу, иу) + с10, B.18)
где C9 = c8c5 + Ci, cl0 = c2-\-c6c8, а с8 определяется постоянной с7.
Это неравенство отличается от B.2) лишь заменой постоянных
С] на с9, а с2 на с10. Итак, для уравнения B.17), его решения и
и области Qp изменения аргументов у выполнены, по существу,
все условия, благодаря которым выше были получены оценки
B.12) и B.13) для верхнего и нижнего пределов отношения
(и (у) — и (х))/\ у — х | при у-+х в точке х е OS. Возвращаясь
к переменным х, получим оценки для пределов отношения
(и(х)-и(х))/\х-х\.
Теорема 2.2. Пусть выполнены условия а) и Ь) теоремы 2.1,
а вместо условия с) — условие

§ 3] ТОТАЛЬНЫЕ ОЦЕНКИ max! v«! - 433
с') существует шар К^{х"), не имеющий с йр общих точек
и содержащий точку х gS на своей границе.
Пусть, кроме того, выполнено неравенство B.16). Тогда
Аи
Аи
где постоянные Сц и С\2 определяются постоянными си с2, с5, с6,
Заметим, что условие с') выполняется для всех точек гра-
границы S с некоторой постоянной d > О, если S е О2. Теорема 2.2
охватывает весь класс равномерно эллиптических уравнений,
а также класс неравномерно эллиптических уравнений, у ко-
которых порядок неравномерности формы ait (x, и, р) ifa не
выше 1 (т. е. более узкий класс, нежели теорема 2.1). Огра-
Ограничения же на член а в обеих теоремах одинаковы.
Укажем на работу Дж. Серрина [51ц], в которой дан иной
метод оценки max| V«|, охватывающий другие классы неравно-
s
мерно эллиптических уравнений. В частности, он позволил дать
оценку max| Vu | для уравнений B.14), причем не только в вы-
s
пуклых областях. Другой метод оценки max|V«| для уравне-
s
ний B.14) имеется в работах И. Я. Бакельмана [32,3]-
§ 3. Тотальные оценки max|V«|
В данном параграфе будет получена оценка сверху max| V« |
а
для решений и(х) уравнений @.1) в предположении, что числа
ыA) ^ min и (х), иB) ;> max и (х) и М{ ^max| V« | нам известны.
a a s
Для этого придется наложить ограничения на поведение функ-
функций ац(х, и, р), а(х, и, р) при |р|-><х>. Будем предполагать
функции аи(х, и, р), а(х, и, р) дифференцируемыми на множе-
множестве Ш{={{х, и, р): л: ей, и е [««'>, и&\, \р\>М2}, где М2-
какая-либо постоянная, не меньшая М,. Кроме того, сами функ-
функции ац, а и их частные производные по х, и и р считаем огра-
ограниченными на любой компактной части 3№,. Уравнение @.1)
должно быть эллиптическим на Т1и т. е. для него на ЗЯ[ вы-
выполнены неравенства @.2) с положительными непрерывными
фуркц'иями v(x, и, р) и ц(х, и, р). Для целей данного параграфа
и^ 4 нам выгодно не нормировать уравнение @.1) каким-либо
одним способом, а сохранить возможность умножать уравне-
уравнение @,1) на произвольную гладкую положительную функцию

434 КВАЗИЛИНЕЙНЫЕ УРАВНЕНИЯ ОБЩЕГО ВИДА [ГЛ. VI
f(x, и, их). Ввиду этого мы и предполагаем условие эллиптич-
эллиптичности выполненным в форме @.2).
Используем в данном параграфе и далее сокращенные обо-
обозначения и{ = иХ{, иц = иЖ{Х .
Рассмотрим сначала частную ситуацию, когда функции а{/
и а зависят только от их. Пусть а{! (р) и а (р) дифференцируемы
при всех р и ограничены вместе со своими производными пер-
первого порядка на любом компактном множестве р *). В этом
случае для каждой из производных uk справедлив принцип
максимума в его простейшей форме. Действительно, продиф-
продифференцируем уравнение @.1) по хк и результат запишем в виде
дац да
aijUkii + AiUkt = O, где uki; = uXkX.Xj, а Л/ = -^-и{1 + ^~- Если
и(х) gC3(Q)A С1 (Q), то пц и At ограничены в любой области
Q'cQ, a ai)(ux)li%)^VQ\2 с v0 = const>0 в Q, и, следова-
следовательно, max| uk |^max| uk | (см. § 1 гл. III). Это же заключе-
а да
ние справедливо и для и(х) е C2(Q)QCl(Q). Действительно,
как показано в § 1 данной главы, и(х) удовлетворяет тожде-
тождеству A.6), которое для нашего случая будет иметь вид
I (a//ufe/% + AjUkjX^) dx = О,
а
где
%ц да1т \ да
о .
с любой r\ (x) e W2 (Q'). й'сй. Это тождество показывает,
что uk может быть рассмотрено как обобщенное решение
из W\{u') (и даже из С(й')) соответствующего линейного урав-
уравнения, и потому для него max| uk |<Imax| uk \ (см. теорему 13.2
Q' дй'
гл. III). Устремляя п' к Q и пользуясь непрерывностью ик
в Q, убедимся, что тах| ик |^тах| ик |.
Q дй
Итак, доказана _
Теорема 3.1. Пусть и(х) еС2(Q)(]С1 (Q) и удовлетворяет
в Q уравнению (ОЛ) с a{j = a{t(p) и а = а(р). Пусть функции
ац(р), а(р) дифференцируемы no p при всех р и ограничены
вместе со своими производными первого порядка на любом ком-
*) Эти условия можно считать выполненными только для | р \ > М2.
В этом случае рассуждения, следующие ниже, надо проводить не во
Области Q, а в Qj ={ж: «sQ, j Vu (х) | > М?),

^8] ТОТАЛЬНЫЕ ОЦЕНКИ max I vu I . 435
пактом множестве изменения р *). Тогда при выполнении усло-
условия эллиптичности @.2) для каждой из производных uXk верна
оценка max|«*A| <max|«xfe |.
Утверждение теоремы 3.1, давно известное для случая и (х) е
eC3(Q) Л C(Q)f несправедливо для более общих уравнений @.1),
Для них приходится оценивать не отдельные производные uk,
a |V«|. Покажем, как это можно сделать в предположениях,
описанных в_начале параграфа. Пусть пока решение и (х) е
sC3(Q)flc'(Q)' Введем вместо и(х) новую функцию v (x), свя-
связанную с нею равенством ы = Ф(у), где Ф(у)—монотонно воз-
возрастающая функция, для определения которой будет получено
сравнительно простое дифференциальное неравенство. Подставим
в @.1) вместо иц их выражения через гз{ и уG:
Щ = ФЧ-. Щ{ = Ф'О</ + WViVj,
и, поделив на Ф', запишем полученное равенство в виде
ац(х, и, ux)vij = - ^г(а + -^р-^), C.1)
где
Ш = S (их), а <§Г (р) ^ ау (х, и, р) piPi = % (х, и, р). C.2)
Вычислим от обеих частей C.1) оператор
d I д , д , д
Ф' dv2x д . Ф"
2 дх{
где через б обозначен оператор
2 дх{ ди1 ^
8=А^ + |«,|^. C.3)
Обозначим v\ через w и учтем, что ЪьРкц = -^Шц — vklvki,
Тогда результат применения оператора Vb-j— к C.1) после
k
ряда элементарных преобразований можно представить в виде
\ C.40
*) Если предположить, что эти условия выполнены лишь при | р \ ^ М2,
то все рассуждения надо проводить не в Q, а в Q, = {х: «sQ, | V« (д:) |>М2}.
В результате докажем, что max \u I < max Ш2, max I ux 11.

436 КВАЗИЛИНЕЙНЫЕ УРАВНЕНИЯ ОБЩЕГО ВИДА 1ГЛ. VI
где
Ф' доц 1 да Ф" д8
А1 — ~ 2 ~bTfVit~Y'dT;"~ 2(Ф'J 57" ( ^
Здесь и ниже будет использовано обозначение:
P% = Pkj^-. если г|з = гр (х, и, р),
и
Р^р = uk4jr< если г|з = ф (х, и, их).
k
Мы подберем функцию Ф так, чтобы в тех точках области
Q] = {x: хей, | их (х) \ > М2), в которых ш(л:) имеет максимум,
величина /[ была положительной. При такой Ф(у) из соотно-
соотношения C.4[) следует, что w не может иметь в пх точек макси-
максимума, и, следовательно, max w (x) = max w (x). Но
а, аа,
aa, aa, (Ф'(v)J ~~~* тшФ' [Ф (и (х))] '
\ a /
и потому
/тахФ'[Ф~1{и{х))] \2
a * "^ 21 тшФ'[Ф"'(«(*)I /
\ a /
Функция Ф(у) будет выбрана так, что Ф'(у)>0 и при изме-
изменении « = ф(у) в диапазоне от uSl) до ы<2> функция у(х) =
= Ф~' (и (х)) меняется в конечных пределах от уA> до уB). Бла-
Благодаря этому правая часть C.5) окажется ограниченной сверху
известной нам постоянной.
Итак, вопрос получения оценки max|V«(x)| сведен к по-
построению функции Ф (у) с указанными выше свойствами. Однако,
прежде чем заняться разысканием функции Ф(у), покажем, как
предположение о принадлежности и{х) к C3(Q) заменить на
принадлежность и(х) к C2(Q). Для этого запишем соотношение

5 31 ТОТАЛЬНЫЕ ОЦЕНКИ max | Vu | - 437
C.4,) в виде
4^(<w)-<w=/i, (з.б)
1 da4 i л
Пусть M2>max|V«|. Тогда из принадлежности и(х)
к С2(Й)ПС'(^) следует, что S^cQ и af/, a* H_/If рассмотрен-
рассмотренные как сложные функции х, непрерывны в Q,, а шеС^Й,).
Благодаря этому ш (х) можно рассматривать как обобщенное
решение из W\(&i) (и даже из С1 (Q{)) линейного уравнения C.6),
т. е. считать, что оно вместо C.6) удовлетворяет тождеству
dx = 0 C.7)
1
при VrieU^Qi) (проверяется это так же, как аналогичный
факт в § 1 данной главы). Пусть функция Ф(у) выбрана такой,
как описано выше при выводе оценки C.5). Покажем, что
тогда max w = max w. Действительно, предположим, что это не
а, «за,
так, т. е. maxw = k > max да. Пусть ^ = {x:^gQ,, w(x) = k).
Si, <3Q,
&k — замкнуто в /Яи причем /[(*:)> О при lel'j, В силу не-
непрерывности /[ (х) оно положительно и в некоторой окрестно-
окрестности множества ё"к, и потому существует область Q[ с гладкой
границей такая, что Шь с: Qi с: Qu max w (x) < k и /[ (х) > 0 при
xgQi. Благодаря этому из C.7) следует неравенство
4- at,w,r\t + atwfl\) dx < 0 C.8)
ai
для любой неотрицательной х\ (х) s Щ (Qi)« Но C.8) невозможно
в силу принципа максимума для обобщенных решений из W[2{q[)
(см. теорему 13.2 гл. III). Итак, доказано, что тахш(л:) =
о.
= max w (x), откуда, как выяснено выше, следует оценка C.5).
да,
Итак, получение оценки max|V«(x)| сведено к нахождению
а
функции ф(у). Как было сказано выше, она должна быть
Дважды непрерывно дифференцируемой на некотором конечном
.отрезке [vw, v{2)] и должна на нем удовлетворять условиям
„B)
Ф' (о) > О, J Ф' (v) dv = (?> (у<2>) - Ф (у('>) = и® - и») = ©. C.9)

438 КВАЗИЛИНЕЙНЫЕ УРАВНЕНИЯ ОБЩЕГО ВИДА [ГЛ8 VI
Кроме того, в точках Qh где w(x) имеет максимум, величина /2
должна быть положительной. Пусть
min ац (х, и, р) |,|, > v, (x, и, р), C.10)
5: 151=1
(?, Р)=0
где V[ (х, и, р) — непрерывная положительная функция.
Пусть Xй есть произвольная точка максимума w (x) в Ql
их°е Q,. В ней
Wt = 2vkvk{ = -QrUkvk{ = 0, i=\, .... п.
Поэтому в точке х°
а (
и
ц (х< "- их) vkivki > vi (*. ". их) v2xx C-11)
'¦ Pat-In
vu —
Из проведенных выше рассуждений можно сделать пока
следующее заключение:
Теорема 3.2. Пусть и (х) е С2 (Q) П С1 (Q), удовлетворяет в Q
уравнению @.1) и u{1)^.minu(x), u{2) ^ max и (х), М{^тах\Уи\.
а а да
Пусть на множестве 3Rl = {(x, и, р): jcsQ, и е [ыA>, иB)], |р|^
^M2>MJ функции ац(х,и,р), а(х, и, р) дифференцируемы
и на любой его компактной части ограничены вместе со своими
частными производными первого порядка. Кроме того, предпо-
предположим, что ац удовлетворяют C.10) на Ш{ с некоторой поло-
положительной непрерывной функцией Vi (х, и, р), и а{! (х, и, р) \i\j > 0
для | ? I = 1 • Тогда, если существует дважды непрерывно диф-
дифференцируемая функция Ф(у), удовлетворяющая условиям C.9)
и такая, что при (х, и, р) е Ши v e [уA), уB)] и произвольных vtl,
, *) Напомним, что 1\ и /2 определены в равенстве C.42). Зависимость /3
от аргументов v^, Ф' и Ф" — это та, которая выписана явно, зависимость
же /3 от аргументов х, и, их сложнее: она определяется функциями а =
= а(х, и, «х), % = % (д;, и, uj =a{j (ж, и, их) их.их и др., причем и и
их рассматриваются как независимые аргументы.

§ 31 ТОТАЛЬНЫЕ ОЦЕНКИ max I vu I . 439
связанных с х, и, р и Ф (v) лишь равенствами
а„ [х, u,p)vt, = - -щ^у [а (х, и, р) + (^,ffJ S (х, и, р)], C.13,)
Р*о« = 0, / = 1 л, C.13а)
выполняется неравенство
13(х, и, р, о,„ Ф'(о), Ф"(о)) > 0, C.14)
то для max\Vu(x)\ справедлива оценка C.5).
а
Легко проверить, что 1з(х, и, р, х>ц, Ф'(о)> Ф"(о)) не меняется
при переходе от функций ац (х, и, р), а (х, и, р), 8 (х, и, р) к falh
fa, f& при любой гладкой f =f (х, и, р) > 0, если v;t считать
связанными с другими аргументами равенством C.13!). Иначегово-
ря, условия теоремы 3.2 инвариантны по отношению к нормировке
уравнения @.1). К сожалению, это свойство нарушается в фор-
формулировках даваемых ниже достаточных условий на ац и а, га-
гарантирующих существование функции Ф(у). Предположим, что
при (х, и, р) (= 3№i функции ait (х, и, р), а (х, и, р), помимо C.10),
удовлетворяют условиям
EpL C.15)
Г2, C.16)
C.17)
рр1. (ЗЛ8)
-Ьа^съ8\р\, C.19)
где с2 и с3, очевидно, неотрицательны, а остальные постоян-
постоянные с{ произвольны. В них 8 = &{p) = ai{{x, и, p)plpj> a vj =
= vl(x, и, р) взято из C.10). Подчиним искомую функцию Ф(у)
дополнительному условию: Ф"(у)^0. Тогда для /3 в силу
предположений C.15)—C.19) получим следующую оценку снизу:
- Ф'Ф"

440 КВАЗИЛИНЕЙНЫЕ УРАВНЕНИЯ ОБЩЕГО ВИДА [ГЛ. VI
Здесь 8! — произвольное положительное число. Возьмем 8! = v,/2
и вместо /3 > 0 удовлетворим более сильному неравенству:
- (-??)' + с' [%гJ - с"Ф" - с'" (Ф'J > 0, C.20)
в котором с' = с{ — Ц-, с" = с4, с'" = — с5 + -у + е, а е- про-
произвольно малое положительное число. Из C.20) следует /3 > 0,
ибо Ф'(у)>0. Если с"'^0, то функция Ф(у) = у удовлетво-
удовлетворяет всем требуемым условиям. Рассмотрим теперь случай,
когда с'" > 0, помня, что, помимо требований C.9), производ-
производная Ф" должна быть неположительна. Если с'> 1, то вместо
C.20) мы удовлетворим более сильному требованию: неравен-
неравенству C.20), в котором с' заменена на 1. В этом случае, как
будет видно из последующих рассмотрений, нужная нам функ-
функция Ф(у) существует при любых значениях остальных по-
постоянных.
Итак, пусть в C.20) с'^1. Будем искать Ф(у) как решение
уравнения
+ с' [w-J ~ С"Ф" ~ с"'(ф/J = 0. C.21)
Введем для этого функцию r\(v) с помощью равенства Ф'(у) =
= ет)(о)_ для нее из C.21) следует уравнение
- г\" + с' {х\'У - с"е\' — с'"е^ = 0. C.22)
Рассмотрим г\ как аргумент, a g = Ti' = -J- как новую неиз-
неизвестную функцию. Тогда для ? из C.22) выведем уравнение
~s "if + с'?2 -с"^ - с'"е^=0> C-23)
а для a= — tfi~^ уравнение
а -р- = — A - с') а2 + с"а - с'". C.24)
Так как Ф"(у) = ё*(°>-^- = —ае2т>, то ввиду требования Ф"(у)<О
надо брать а^0. Проинтегрируем C.24) в пределах от а = а0
до а > а0, взяв т^ —0 при а=:а0:
F(a, а0) s J A _ е,)а2а^аеДа + с<» = - Л- C-25)
а,
В качестве а0 возьмем 0, если полином p(a)s(l — с') а2 —
— с"а + с'" не имеет неотрицательных корней. Если же р (а)
обращается в нуль при каком-либо а ^ 0, то за а0 возьмем
число, чуть большее наибольшего из корней р (а), который мы

§ 3) ТОТАЛЬНЫЕ ОЦЕНКИ max I vu I . 441
обозначим через сц (так что р(а]) = 0 и а^О). При измене-
изменении а от а0 до оо переменная \\ меняется от 0 до оо, если
с' = 1 и с" > 0, и х\ меняется от 0 до — оо во всех остальных
случаях. Исключим пока случай с'=\, с" > 0. Соотношение
C.25) однозначно определяет a = a(Ti)^a0. По функции а(т])
из уравнения ?—~t^~ = — а{х^ёц определим одно из его ре-
решений:
а(т))е'
При изменении т] от — оо до 0 переменная v меняется от
у2 = Ч;(—оо) до оA) = 0, причем v2 может оказаться как ко-
конечным положительным числом, так и оо. Соотношение C.26)
однозначно определяет х\ как функцию v на интервале [0, v2)-
В силу Ф/(у) = еТ)(:') функцию Ф(у) по т](а) определим равен-
равенством
ы = ф (у) = «<•>+ Jei<i»d0> os[0, Oj). C.27)
о
Она удовлетворяет уравнению C.21) и требованиям: Ф'(у) > 0,
Ф"(у)^0. Однако есть еще одно требование — C.9), которое,
как мы увидим, наложит ограничение на постоянные с', с", с'"
и ©. Для этого, учитывая связи между Ф, г\ и а, подсчитаем
интеграл
= \ *•-?*, = - J ^j- =
0 0
оо оо
J a da J (l-c')a2-c"a+c'" "
a,
Чтобы удовлетворить условию C.9) с t/B> < оо (в качестве
берем 0), надо потребовать:
J
da ->co. C.28)
(l-c')a2-c"a
Ес.ли с'= 1, то интеграл расходится и условие C.28) удовлет-
удовлетворяется при любом ©<оо. Рассмотрим еще отброшенный
случай, когда с'= 1, а с" > 0. Как сказано выше, для таких С
и с" переменная т] при изменении а от а0 до оо меняется от о
До оо. В силу этого v, определяемая равенством C.26), при

442 КВАЗИЛИНЕЙНЫЕ УРАВНЕНИЯ ОБЩЕГО ВИДА [ГЛ. VI
изменении г\ от 0 до оо будет меняться от 0 до — оо. Опреде-
Определим по t](v) функцию ы = Ф(у), вместо C.27), равенством
V V
и = ф(о) = и»+ J Ф'(а)^ = ы<2) + j e^Mdv, oe (—00, 0].
о о
C.29)
— оо оо
Интеграл J Ф'(у)^у= J _с„д" с„, расходится, и потому
О а,
ф(у) = ы<1) при некотором конечном v = v{1), каково бы ни было
и*1» > — оо. Итак, в этом случае функцию Ф(у) рассматриваем
на отрезке [уA), уB) = 0], причем уA) > — оо.
Итак, мы показали, что при с'=1 (и тем более с' > 1)
задача C.20), C.9) имеет решение Ф(у) с Ф"(а)<0. Если же с'< 1,
то для существования решения Ф(у) задачи C.21), C.9) с Ф"(о)^0
не'обходимо и достаточно, чтобы выполнялось неравенство C.28).
Если знаменатель р(а) не имеет корней на [0, оо), то а0 берем
равным нулю. Если же ,о(а) = 0 при каком-либо a = aj^O, то
условие C.28) удовлетворяется (ибо а0 можно брать как угодно
близким к cii). Обратим, наконец, внимание на то, что в с'"
входит е, которое мы можем выбрать сколь угодно малым
положительным числом. Установленные нами критерии разре-
разрешимости задачи для Ф таковы, что в них, как нетрудно видеть, е
можно положить равным нулю. Итак, доказана
Теорема 3.3. Пусть и(х) и a{j, а удовлетворяют условиям
теоремы 3.2, а предположение о существовании функции Ф(у)
заменено условиями C.15) — C.19). Пусть, далее, постоянные
Cj, ..., с5 удовлетворяют или 1) неравенству с'" = — с5 + -?- ^ О,
или 2) неравенству c'=Ci — -у-> 1, или 3) при с'" > 0 и с' < 1
полином р(а)Е==A — с') а2 — с"а + с"', где c" = cit имеет не-
неотрицательный корень, или, наконец, 4) при с'" > 0, с' < 1 и
р (а) > 0 для а ^ 0 выполняется неравенство
да
I
da _ > a a „B) _ „A), C 30)
A-е')а2-с"а + с'" ^ •
о
Тогда существует функция Ф(у) с Ф'(а)^0, удовлетворяю-
удовлетворяющая C.9) ы C.14), и для max\Vu(x)\ справедлива оценка C.5).
Q
Условие C.30) можно рассматривать и как ограничение на
колебание © решения и(х) в Q при фиксированных постоян-
постоянных сь ..., с5.
Замечание 3.1. Нетрудно проверить, что если постоян-
постоянные с', с", с'" и © удовлетворяют одному из четырех условий

5 3] ТОТАЛЬНЫЕ ОЦЕНКИ max | v« | 443
теоремы 3.3, то и достаточно близкие к ним постоянные будут
удовлетворять одному из них (может быть, другому). Иначе
говоря, условия 1) —4) теоремы 3.3 таковы, что они выделяют
в пространстве (с', с", с"', ©) е ?4 открытое множество.
Замечание 3.2. Постоянные Cj c5, а потому и постоян-
постоянные с' —с'" не меняются при умножении уравнения @.1) на
постоянную. Однако при замене aijt а на fal{, fa и, соответ-
соответственно, & на f&, a Vi на fvu где f = f (x, и, их) — какая-либо
гладкая положительная функция, постоянные сх с5, вообще
говоря, изменятся. Этим обстоятельством надо пользоваться
при проверке критериев 1) —4) теоремы 3.3: может оказаться,
что при удачном выборе f один из них удовлетворится, а при
другом выборе f ни один из них не будет выполнен. Проил-
Проиллюстрируем это на примере уравнения B.14), считая Ж = Ж(х, и).
Для него а.. = A + р2) Ц — ptpr а= — пЖA-\- р2K/2, следова-
тельно, & = р2, a Vi = 1 +р2. Легко проверить, что 2 — = 0,
п
т. е. Cj = 0, а 2 (p<*i inJ = 4р2 (п — 1), так что с2 можно взять
равным 4(п— 1). Далее, 6|Г = 0; а при больших \р\ имеет вид
и, следовательно, рар — а = — 2пШ\ р р 1 + См—А . Если не
предполагать, что сЗ^^О, то неравенство C.18) не выполняется
ни при каких с4 и условия теоремы 3.3 тем самым не удовлет-
удовлетворены. Тем не менее, если уравнение B.14) поделить предва-
предварительно на | их р, то для полученного уравнения Ш =\,
а а равно — пШ \ р \{\ -\—А , и, следовательно, рар—а =
== ЪпШ\ р Г1 [l + О f-^-Y]. Если предположить, что | Ж |< Hi, то
условие C.18) выполняется. Постоянная с3, очевидно, равна нулю.
п
Сумма 2 (раИрJ = 4п/р\ a Vi =A+р2)/р2, поэтому с2 можно
взять сколь угодно малой, взяв М2 достаточно большим (напом-
(напомним, что все рассмотрения проводятся лишь для |p|^Af2).
Постоянная ^ = 2, и потому с' = с{—Ц- будет ^1 при с2^2.
Ввиду этого значения других постоянных с3 — с5 несущественны,
лишь бы | с51< оо. Для конечности с5 достаточно предположить,
что | <3#x |<const, a ^„^0. Если Ж зависит и от р, то, как
нетрудно подсчитать, для справедливости C.18) достаточно
предположить, что | р9$р |< const| p Г1. Итак, мы убедились

444 КВАЗИЛИНЕЙНЫЕ УРАВНЕНИЯ ОБЩЕГО ВИДА [ГЛ. VI
в возможности применить теорему 3.3 для получения оценки
max|Vtt(jc)|, если относительно !№ = Ж{х,и,р) выполнены
условия:
I С№ I <г"""* л| я I I С№ I <г"""* /> *}№ *"*"^ Г\ I м /Jifi I *<""* />1 *л1~1 /О О1\
I &*Э ^^> С | U к | ^0? v ^^> С* ( &\й м ^^^ \) ¦ I Ij&v) гч ^^^ СТО 1О»О1)
для (jc, в, р) е SR,.
Замечание 3.3. Так как нас интересует вопрос о разыска-
разыскании хотя бы одной функции Ф(у), удовлетворяющей усло-
условиям C.9), C.20) и Ф"<10, а не вопрос об интегрировании
уравнения C.21) при дополнительных условиях C.9) и ф"<!0,
то при некотором огрублении условий на сх с5 можно дать
явное выражение для Ф(у) (это и делалось в наших прежних
публикациях и работах других авторов, следовавших описан-
описанному здесь пути получения оценки maxl Va |, —см., напри-
например, [I], гл. VI, [51ц, 32,3])- Так, например, если с' и с" произ-
произвольно фиксированы, а с"' и ©2 достаточно малы, то всем усло-
условиям удовлетворяет функция
Ь 3©<? J e~s ds C.32)
о
с некоторым большим q (см. [I], стр. 405). Действительно, при
изменении и от ыA) до ыB) интеграл Г e~s ds меняется в интер-
о
вале Up, -x-\ , так что
При любом q^-Х значения функции e~s<l заключены между е~1
1 O^^l 0 1 ^
р q фу
и 1 на интервале O^s^l и между 0 и 1 для всех
поэтому при всех q ^s I
0
и
1,B) 1/2 1,B) „B)
1-=^ e-sqds = \ e-*"ds+ J e-*ds>-y+ J e^"ds,
0 0 1/2 1/2 •
т. e. yB) < 1/2. Итак, при всех

... ТОТАЛЬНЫЕ ОЦЕНКИ max I vo I • 445
Далее,
ф' = Зше1-"', Ф" = —
Для взятой Ф(и) неравенство C.20) имеет вид
q2vq-2 [l _ 1 + c'V + с© ^-е1-^ -
- 9c"V Л и2-^-2а?] > 0. C.33)
При q-+oo второй, третий и четвертый члены квадратной скобки
стремятся к нулю. Возьмем q^2 и такими, чтобы их сумма
по модулю не превосходила, например, 1/2. Тогда, если
c"'(i?<^2q2(<oe)-4, то неравенство C.33) будет выполняться.
Подсчитаем, какой рост по | р \ функций ац(х, и, р), а(х, и, р)
и их частных производных допускается требованиями C.10).
C.15) —C.19). Сделаем это для нашего основного объекта изуче-
изучения — равномерно эллиптических уравнений. Для них справед-
справедливы неравенства @.2), причем х(х, и, р)<!const < оо. Иными
словами, функции aif(x, и, р) при | р|-*оо ведут себя как функ-
функция v(jc, и, р). Функцию V[(x, и, р) из C.10) можно считать, оче-
очевидно, заключенной в пределах v(x, и, p)^v1(x, и, p)^ii(x, и, р).
Функция &(р) растет при | р |-* оо, как v(x, и, р)\ р р. Как показы-
показывает пример B.26) гл. I, для возможности оценки max|Vu(x)l
Q
через известные в задаче Дирихле величины необходимо, чтобы
порядок роста функции а(х, и, р) не превосходил порядка
роста IT, т. е. чтобы
)а(х, и, jo)|<Hiv(a;, u,p)\pf, ц, = const. C.34)
Если функции ац(х,и,р), а(х, и, р) при дифференцировании
по р ведут себя как полиномы, т. е. дифференцирование по pk
понижает их порядок роста (по крайней мере) на единицу, то
неравенства C.15) и C.16) являются следствием @.2). Вспоминая
рьд д
определение оператора б ==т-п- -з Ь I P hj^-. легко подсчитать,
что остальные неравенства C.17) — C.19) также будут следст-
следствиями @.2) и C.34), если при дифференцировании alh a no и
порядок роста по | р \ не возрастает, а при дифференцировании
по х может даже возрастать, но не более чем на 1. Запишем

446
КВАЗИЛИНЕЙНЫЕ УРАВНЕНИЯ ОБЩЕГО ВИДА
[ГЛ. VI
эти условия на частные производные пц и а в виде неравенств
да
дР
Pk да
рР +
да
¦и
ди
да,,
дх
. да
C.35)
C.36)
C.37)
= const. C.38)
Если ац и а удовлетворяют неравенствам @.2), C.34) — C.38),
то тем более они удовлетворяют неравенствам C.10) и C.15) —
C.19) с Ci, вычисленными по [г*. Теорема 3.3 гарантирует воз-
возможность оценки max|Vu(jt)|, например, в случае 1) когда
а
постоянные [i3, щ и | [i51 при произвольно фиксированных
других постоянных и © достаточно малы, или 2) когда ц5 есть
достаточно большое положительное число, или 3) когда © доста-
достаточно мало (более точно см. теорему 3.3). Нам неясно, выз-
вызваны ли ограничения теоремы 3.3 на величины постоянных,
входящих во все эти неравенства, существом дела или избран-
избранным нами методом оценки max[Vu|.
а
В работе [143] А. В. Иванова дана оценка max| V« | для
а
решений и (х) из С3 (Q)(]C1 (Q) неравномерно эллиптических
уравнений @.1), обладающих следующими специфическими осо-
особенностями. Квадратичная форма (At,, 1) = ац (х, и, р) hli = Al(p)
для них положительно определенна и удовлетворяет условиям
datj (x, и, р)
: = 1, .... л, C.39)
daif (x, «, р)
ди
<МЧрIр
.-I
дап (х, и, р)
дх.
n,
C.40)
C.41)
при |?|=1 и (х, и, р) е 3Ri, причем постоянная ц2 достаточно
мала. Эти условия допускают неравномерный рост формы А1 (р)
по разным направлениям |, но требуют, грубо говоря, чтобы
эта неравномерность по ? была одинаковой для всех форм А (р),
A\k (p), А\ (р) и A\k (p). Относительно а (х, и, р) предполагается,

j 3) ТОТАЛЬНЫЕ ОЦЕНКИ max I vu I ' 447
что на Wli
4 (x, u, p) + aa (x, u, p) +
+1 P Г1 l/ ? < (*. «. P) < (i3 Sp Л (p) C.42)
с достаточно малой постоянной [i3- Здесь А (р), как и выше, —
матрица с элементами ац(х, и, р).
Для оценки max|Vu| вычислим от обеих частеД @.1) опе-
d
ратор uk-j— и результат запишем в виде
Y auvu = auukiuk/ — -j (aP[ — ацР[иц) vt —
-У^[Ьа + {ЬаИ)щ,1 C.43)
где v = u2x (в связи с этим см. начало параграфа; C.43) есть
частный случай C.4,-) при Ф (у) = у). Рассмотрим C.43) в точке
xgQ, где |Vu(jc)|>M2. Сумма аииыиы = Sp {D2uAD2u}, где
i4 = ||a</||, D2u = || ulf ||, D2uAD2u — произведение этих матриц,
а символ Sp В здесь и выше означает след матрицы В.
Представим матрицу D2u в виде D2u = TD2uT*, где D2u
fin 0
О ппп
— диагональная матрица, а Г — ортогональная
матрица \\тц\\, преобразующая матрицу D2u в D2u. Ввиду этого
и инвариантности следа матрицы при ортогональных преобра-
преобразованиях
аииы4, = SP {S^ADhi} = аий2н, C.44)
где А = Т'АТ. Аналогично этому представим сумму
{aU)
й„ C.45)
(при этом мы использовали то, что элементы Т определяются
величинами иA, которые рассматриваются как независимые
от аргументов х, и и р). Такое же представление справедливо,
очевидно, и для
C.46)

448 КВАЗИЛИНЕЙНЫЕ УРАВНЕНИЯ ОБЩЕГО ВИДА [ГЛ. VI
Коэффициент ait = (Т*АТ)Н = аыхыхи = (Ах\ т'), где т' =
= (т». Тгь ¦¦¦> тп(-) —/-столбец Г. В силу условия C.39)
|a,7P,|<M««l", Г'- v C.47)
Отсюда и из C.45) следует 'г
<7S'^' + C'Sp^44 C-48)
Из C.46) и C.40), C.41), вспоминая определение C.3) опера-
оператора б, получим
| (да.,) и., | VT <тйийи + WP SP ^' C-49)
а благодаря C.42)
— Fа) Vv~> — \i3v Sp A. C.50)
В силу Sp Л = Sp A, C.44) и C.48) - C.50) из C.43) следует
неравенство
+ ^ "~ ViT SP Л "~ C2l*20 Sp Л - (i3y Sp Л >
Т U4Vn + Т ар,°
о2
>-еи SpA-c^-^-SpA, C.51)
в котором е — достаточно малое число.
Представим v в виде v = zv = (а — | х Р) v, где а — достаточно
большое число. (Начало координат считаем принадлежащим Q
и область Q, как всюду, ограниченной.) Подставим выражения
для vt и V[f через у, у; и vif в C.51). После элементарных
оценок получим
Т 2а//б// + [aazi + Т
— - о[8с,ц? ~р- Sp Л + е(а-х2) Sp Л- Sp A + аР/х/]. C.52)
Принимая во внимание условие C.42) для ар , видим, что при
достаточно большом а и достаточно малых е и [i3 правая
часть C.52) неотрицательна. Это верно для всех точек JceQ,

§ 4| ЛОКАЛЬНЫЕ ОЦЕНКИ | v« I " 449
где М2^\Уи(х)\= \^zv. Но тогда в силу принципа максимума
Mi
; maxv(x)].
Отсюда следует желаемая оценка max|Vu(jt)|. Итак, доказана
Q _
Теорема 3.4. Пусть и(х)еС3(О.)|"|С1 (Q), удовлетворяет эл-
эллиптическому уравнению @.1) м ыA)< и(лг)<ыB), max| Vu(x) К Afj.
dQ
Предположим, что функции ац(х, и, р), а(х, и, р) обладают
той же гладкостью, что и в предыдущих теоремах, и на ЗЯ{
удовлетворяют неравенствам C.39) — C.42) с достаточно малыми
постоянными [х2 и ц3. Тогда max|Vu(jt)| оценивается сверху
Q
постоянной, определяемой постоянными, входящими в условия
теоремы, и диаметром области Q.
Замечание 3.4. Из доказательства предыдущих теорем
видно, что относительно и (х) достаточно предположить и (х) е
В работе [143] с помощью изложенного способа оценки
max| Vu(x)| рассмотрен ряд других классов неравномерно элли-
Q
птических уравнений @.1).
§ 4. Локальные оценки |V«|
В этом параграфе мы покажем, что при несколько более
жестких условиях на функции a(j{x, и, р), а(х, и, р) можно
оценить сверху max| Vu (x) | для любой внутренней подобласти Q'
области Q через границы ыA), ыB) изменения и (х), постоянные,
характеризующие поведение ац и а при больших | р |, и рас-
расстояние от О.' до S (при стремлении этого расстояния к нулю
оценка max|Vu| неограниченно растет). От свойств S и значе-
значений Vu на S эти оценки не зависят.
Относительно ац и а предполагаем ту же ограниченность
и дифференцируемость на множестве Ши что и в § 3. Условие
эллиптичности @.2) должно выполняться на Шь причем так же,
как и в § 3, функции v(jc, и, р) и ц (х, и, р) из @.2) ни в какие
оценки не входят: из @.2) мы используем лишь факт поло-
положительной определенности формы ati(x, и, р)^|/ и положи-
положительность min min ац(х, и, p)h^,i Ha любой компактной
(х, и, ) 5|1
15 О. А. Ладыженская, Н. Н. Уральцева

450 КВАЗИЛИНЕЙНЫЕ УРАВНЕНИЯ ОБЩЕГО ВИДА [ГЛ. VI
части Ш[ множества Ши Условие C.10) заменим несколько
более сильным:
(X, U, р) Ы; > К (X, U, р) - Щ (X, U, р) (у^у, у|у)] 1\ D.
где V[ и [1, — непрерывные положительные функции, причем
И! (х, и, p)/V[ (х, и, р) ^ [i2 = const. Кроме того, потребуем, чтобы
Ж(р) = пц (х, и, р)pip,> v0(x, и, p)\pf, k>0, D.2)
a v0 (х, и, p)/v, (х, и, р) ^ v2 = const > 0. Пусть сначала
и (х) е С3 (й). Введем функцию v с помощью равенства
ы = ф(о). Для нее верны соотношения C.1) и C.4,-). Рассмо-
Рассмотрим теперь функцию y = v2xt,=^wt,, где ?(х) — неотрицательная
функция из C2(Q) с компактным носителем в Q. Для нее
Hi^WiZ+w^, уЦ = и)цЪ+ w&j + wfi,t + wt,t,. Выразим из этих
равенств w, wjt, и w!ft, через у и ее производные:
S/ -' i
= У// — У1 -у — У/ -у + У
и подставим эти выражения в равенство C.4[), умноженное
на ?. После элементарных преобразований получим уравнение
для у:
'¦au-f-]yi =
tt i f- \
•s/4, D.3)
в котором /2 и Л; те же, что и в C.42), C.43). Функция y = wt,
неотрицательна и обращается в нуль в пограничной полоске
у дп, следовательно, она принимает свое наибольшее значение
(которое будем считать большим нуля) лишь во внутренних
точках области О,.
Мы покажем, что при определенных условиях на функции <Хц
и а можно так подобрать функцию Ф(и), что /4 будет больше
нуля в любой точке х° е й, где у достигает своего максимума,
если этот максимум больше М\, где Мз — некоторое достаточно
большое число. Если этот факт установлен, то из равенства D.3)
следует, что таких точек максимума, как х°, быть не может
и, следовательно, всюду y(x)^Ml.
Это непосредственно ясно для и(х) ^C3(Q) (для них
у (х) е С2 (Q)). Если же u(x)eC2(Q), то у принадлежит только
C(Q) и не удовлетворяет D.3) в обычном смысле. Однако

§4]
ЛОКАЛЬНЫЕ ОЦЕНКИ | Vu I - 451
u(x) может быть рассмотрено как обобщенное решение урав-
уравнения D.3) из класса Wl2(Q) (и даже из класса С1 (О,)) и для
него справедливо то же заключение: г/(х)<М2, что и для
случая (/еС2(й). Доказывается это так же, как аналогичный
факт в § 3.
Будем считать ?(xXJl. Тогда из неравенства г/(х°) =
= w (х°) • ? (х°) > Ml следует w (x°) > М\, а отсюда
| \и (х°) | > М3Ф' (и (х°)) > М3 min Ф' (у (*)) = М^.
Величина б[ нам будет известна, и она положительна. Постоян-
Постоянную М3 возьмем большей или равной М26~1, тогда | Vu (х°) | > М2,
и, следовательно, в точке х = х°, и = и (х°), р = их(х°) и в не-
некоторой ее окрестности функции ati{x, и, р), а(х, и, р) обла-
обладают свойствами, указанными в начале § 3, а также подчи-
подчиняются неравенствам D.1), D.2) и другим условиям, которые
мы будем накладывать на них ниже (напомним, что все огра-
ограничения на ац(х,и,р), а(х, и, р) должны выполняться лишь
для (х, и, р) е Шь причем аргумент и нигде не выходит за
пределы отрезка [ыA), ыB)]). В силу этого и под окрестностью
точки (х°, и(х°), их(х0)) мы понимаем пересечение настоящей
б-окрестности ее в пространстве (х, и, р) со слоем ыA) <| и <| ыB).
Итак, получение оценки
у (х) - v\ (х) I (х) = фщ~ < Ml D.4)
сведено к вопросу разыскания функции Ф(и), для которой
в любой точке х° (х° е О.) максимума у (х) с у (х°) > М\ вели-
величина /4 > 0. В этой точке yk = 2u(.uife? + v2xZk = 0. k=l, ..., n,
и потому
u_x_ Vkx \ ( vx vkx \ tk \vx\
"x\' \°kx\) \\Vx\' \vkx\) 2? \°kx\'
где vkx = (vkU ..., Vkn)- Благодаря этому и D.1)
vivlx --W
vxx\\Zk\\vx\>
vxx\\Zk\\vx
'lvxx 2g I *x\ ф' =='
 Er
йттгтги2, D-5)
с произвольным в] > 0. Это неравенство заменяет собою не-
неравенство C.11) и приводит вместо C.12) к следующей оценке:
V^ »2 («О U .. я,
И?—^-Т^Т- D'6)
16*

452
КВАЗИЛИНЕЙНЫЕ УРАВНЕНИЯ ОБЩЕГО ВИДА
[ГЛ. VI
Функцию Ф (v) будем искать такой, чтобы
/з^/3(*. и,р, о,/, Ф'(о), Ф"(о))>
(ф'J + |Ф''| + (Ф'L-1^- D.7)
с каким-либо е>0 (/3 определено в C.12)).
Так как е находится в нашем распоряжении, то задача
определения Ф(и), -по существу, такая же, как задача § 3 на
определение Ф(о), для которой /3 > 0. Ниже мы покажем, что
условия теоремы 3.3, гарантировавшие существование такой
функции Ф(и), при которой /3 > 0, достаточны и для существо-
существования функции Ф(и), для которой выполняется неравенство D.7)
с некоторым малым е. Предположим пока, что нужная нам
функция Ф(о) уже найдена, т. е. для нее имеют место нера-
неравенство D.7) с некоторым е>0 и соотношения C.9).
Подчиним функции ац(х,и,р) и а{х, и, р) следующим
ограничениям:
1/2
и, p)j <CeVl(x, и, р),
SI dS
I dPi
t
1/2
D.8)
D.9)
D.10)
D.11)
где с6 — какая-либо постоянная. Мы обозначили ее через с6,
ибо с,- с номерами /= 1, ..., 5 уже использованы в неравен-
неравенствах C.15) — C.19) и эти неравенства в дальнейшем будут
предполагаться выполненными. Благодаря D.7) —D.11) спра-
справедливы следующие оценки:

ЛОКАЛЬНЫЕ ОЦЕНКИ |vu|
453
и аналогично
Б/
Б/
2?
да
ди{
д$
ди1
!6е2
2
C6V1
где е2 — произвольное положительное число. Далее,
5*5,
C6vi
D.13)
D.14)
D.15)
D.16)
Из этих неравенств следует
!
2
1/2
v'xi
и.
«
(О/J 32е2
D.17)
Используем D.6), D.7) и D.17) для оценки снизу правой
части уравнения D.3), именно:
\>8 Г
(фО2 I
е(Ф'J + е|Ф"|+(е-е,)(ФТ
- * (ф')г - *'ф'' -
Возьмем е[ = 82 = е/2. Тогда
где Bl = C6 + _L
D.18)
= f. число е и
функция Ф(у) уже выбраны, причем 0 < б] <Ф'(и)<о2 < оо.
Поэтому В, и В2 не превосходят некоторой постоянной, которую

454 КВАЗИЛИНЕЙНЫЕ УРАВНЕНИЯ ОБЩЕГО ВИДА [ГЛ. \ ¦
мы обозначим через с7. Используем теперь предположения D.2):
v2v, | их ? = v2v, (Ф')Й1 vx \k = v2v,
и y{x°)>Mt Благодаря им из D.18) следует
Возьмем ?(х) = ц^к (х), где ц(х) — произвольная неотрицательная
функция из C2(Q) с компактным носителем вОи т](х)^1 *).
Элементарный подсчет показывает, что для такой Z,
с постоянной ся, зависящей лишь от k, и Сц=:Сйтах(т12 + ri|ri IV
о Q V х | хх\)
Подставим D.20) в D.19):
4 ^ У<Э ? . D.Z 1 )
Из этой оценки ясно, что если М3 взять равной
то U^-jy$ > 0, что и требовалось.
Итак, мы пришли к желаемому заключению, допустив, что
функция Ф(у) удовлетворяет требованиям C.9) и D.7). Срав-
Сравнивая эту задачу с задачей C.9), C.14), видим, что она такая же,
лишь на е изменились коэффициенты при членах (Ф'J, IФ" I
2
Vi V
и (Ф04 - 2 хх-. В силу произвольной малости е достаточные
условия теоремы 3.3 будут достаточными и для разрешимости
задачи C.9), D.7) (см. в связи с этим замечание 3.1 к тео-
теореме 3.3).
Наши рассуждения сохраняют силу и для случая, когда
носитель ?(х) пересекает границу О, по какой-либо части 5Ь
если только известно, что ыеС2(й)ПС (О, [}S{) и max| Vu |^M2.
s,
Действительно, так как в анализируемой точке х° возможного
максимума у = v2xt, величина | их (х°) | > М2, то х° принадлежит Q,
*) Из сопоставления условий D.2) и D.8) ясно, что k <1 2, причем k =
соответствует случаю равномерно эллиптических уравнений,

^ 4| ЛОКАЛЬНЫЕ ОЦЕНКИ | vu I ¦ 455
а не Si, и потому в ней сохраняются все проведенные выше
оценки вплоть до оценки у(х)^.М3. Это завершает доказа-
доказательство следующей теоремы:
Теорема 4.1. Пусть «еС2(й) и удовлетворяет в п урав-
уравнению @.1), причем uil)^.m'mu(x), a uB) > max и (х). Пусть на
множестве Т1{ функции аи(х, и, р), а(х, и, р) дифференцируемы
и на любой его компактной части ограничены вместе со своими
частными производными первого порядка. Кроме того, предпо-
предположим, что аг, и а удовлетворяют на Ш{ условиям D.1), D.2)j
D.8)—D.11) и aijlilj>Q при |||=1. Тогда, если существует
дважды непрерывно дифференцируемая функция Ф(и), удовле-
удовлетворяющая условиям C.9) и такая, что при (х, и, р)<^.Щ{,
ое[!)(|>, уB)] и произвольных vif, связанных с х, и, р и Ф(у)
лишь равенствами C.13i) и C.132), выполняется неравенство D.7)
с каким-либо е > 0, то для Vu справедлива оценка
| Vu (*) | if'* (х) ^ Mit D.22)
в которой постоянная М4 определяется е, Ф(и), постоянными k,
ц2, v2 и с6 из условий D.1), D.2), D.8) —D.11) и max (т? +1 цхх | т|),
12
а г\ (х)— произвольная неотрицательная функция из С2(п)
с компактным носителем в Q и ц(х)^. 1.
Если функции ац и а, помимо условий D.1), D.2), D.8)—D. И),
удовлетворяют еще на Шх условиям C.15) —C.19), в которых
функция vt(x, и, р) взята из неравенства D.1), а постоянные
сь ..., с6 удовлетворяют критериям теоремы 3.3, то нужная нам
функция Ф(у) существует при некотором е > 0 и, следовательно,
для | Vu | справедлива оценка D.22).
Оценка D.22) сохраняется и для случая, когда носитель ч\{х)
пересекает границу Q по какой-либо части 5Ь если относи-
относительно и(х) известно дополнительно, что ueC2(Q)f|C (Q \}Si) и
max| Vu I^Afo.
s,
Условия теоремы 4.1 отличаются от условий теорем 3.2
и 3.3 лишь одним существенным усилением: наличием мно-
множителя | р \k, k > 0, в правой части неравенства D.2). Из усло-
условий D.2) и D.8) следует, что порядок неравномерности урав-
уравнения @.1) должен быть меньше 2. Это неприятное ограничение
приводит к тому, что для уравнений B.14) не выполняются
условия теоремы 4.1. Для них пришлось искать другие методы
локальных оценок Vu (о них см. [6, 115, 2124]2.
Следствие 4.1. Пусть ueC2(Q)nC'(Q), max|u|<M,
Q
u|<M2 и maxosc{u(*); Qp}<co(p), причем са(р)->-0 при
к р

456 КВАЗИЛИНЕЙНЫЕ УРАВНЕНИЯ ОБЩЕГО ВИДА [ГЛ. VI
р-*0. Пусть на множестве Tti функции ац(х, и, р), а(х, и, р)
дифференцируемы, а на любой его компактной части ограничены
вместе со своими частными производными первого порядка.
Тогда, если atl и а на 9№, удовлетворяют неравенствам D.1),
D.2), D.8)—D.11), C.15) —C.19) с какими-либо постоянными
с,, ..., с6и atjlilj > 0 при |||= 1,тотах| V« | оценивается сверху
постоянной, зависящей лишь от М, М2, © (р), ц2> V2_H Ci» • • •, с6.
Для доказательства утверждения надо покрыть Q конечным
числом открытых шаров Kp(xt), t=l. .... N, радиуса р, при-
причем р надо взять столь малым, чтобы со (р) удовлетворяло
условию C.30). Тогда в каждом из шаров Kp-e(xi), е > 0,
max| Vu | будет оцениваться некоторой известной нам постоянной
ti (е), и так как при достаточно малом е Q cz \J Kp-t {xt), то
max| Su К max ct (e).
Q ,=1, .... ДГ
§ 5. Теоремы существования
В § 10 гл. IV мы показали, как умение получать априорные
оценки всех возможных решений задачи Дирихле позволяет
сделать вывод о ее разрешимости. Имеет при этом исследуемое
уравнение дивергентную главную часть или нет, не существенно.
Рассуждения, проведенные в § 10 гл. IV для уравнений с ди-
дивергентной главной частью, сохраняют свою силу и для общих
квазилинейных уравнений
L(u) = atl(x, и, ux)ux.Xj + a(x, и, их) = 0, E.1)
« Is = Ф U- E-2)
Отличие состоит лишь в условиях, при которых установлены
априорные оценки решений тех и других уравнений. Ввиду
этого мы не будем повторять здесь всех рассуждений § 10
гл. IV, а сформулируем лишь окончательные результаты (причем
только основные из них), используя априорные оценки, полу-
полученные в данной главе для решений задачи E.1), E.2), и дадим
к ним необходимые пояснения.
Во всех теоремах будет предполагаться, что функции
аи(х, и, р), а(х, и, р) на любой компактной части множества
ЗЯ = {(х, и, р): xeQ, «e?[, ре?я) ограничены и удовлетворяют
неравенству
at,(x,u,p)hbi>0 при 111=1. E.3)
Эти условия в дальнейшем не всегда будут формулироваться
явно.

§51
ТЕОРЕМЫ СУЩЕСТВОВАНИЯ 457
Так же, как в § 10 гл. IV, задачу E.1), E.2) рассмотрим
не изолированно, а вместе с однопараметрическим семейством
задач того же типа:
L% (и) = пц (х, и, их, т) uXlXj + а (х, и, их,т) = 0, J
Пусть наша задача E.1), E.2) получается из E.4) при т=1.
Рассмотрим вопрос о разрешимости задач E.4) в пространстве
C2+a(Q).
Теорема 5.1. Предположим, что выполнены следующие
условия:
S^C + , ф(х)еСт (Q). ^ _
b) Для всех возможных решений и(х, т) из C*+a(Q) задач E.4)
справедливы оценки
тах| и(х, т) \^М E.5)
а
и
ш(р, т) = max osc {ы (л;, т); Qp} < М (р) -> 0 при р->0; E.6)
max в E.6) взяг по всел шарам Кр радиуса р.
c) При те[0, 1], л;ей, | и \^М и произвольных р функции
aij(x, и, р, т), а(л:, и, р, т) подчиняются неравенствам
(х, и, р, т) Ы, > 0 пры |g|=l E.7)
и
| р | +1 а (х, и, р, т) | Г < схШ (р) Г'1 + с2, E.8)
п
где в"(р) = а4/ (л:, и, р, т) ptp,, Т = 2 а«< (л;, и, р, т).
Предположения а) — с) гарантируют априорную оценку
max| V«(jc, т) |<М, (см. теорему 2.2).
d) Яа множестве Эй, X [0, 1]^{(л;, и, р, т): xefi, | м |<М,
\Р\>М2, те[0, 1]}, Af2>Af,, функции а,,(х, и, р, т), а(л;, и, р,т)
дифференцируемы по х, и, р, на любой его компактной части
ограничены вместе с частными производными первого порядка и
удовлетворяют неравенствам D.1), D.2), D.8)—D.11), C.15) —
C.19) с какими-либо постоянными си ..., с6.
Предположения a) — d) гарантируют априорную оценку
тах| Чи(х, т)| <М3 (см. следствие 4.1).

458 КВАЗИЛИНЕЙНЫЕ УРАВНЕНИЯ ОБЩЕГО ВИДА [ГЛ. VI
е) Функции ац(х, и, р, т), а (л;, и, р, т) равномерно непре-
непрерывны по те[0, 1], как элементы Са(Ш2), где
Т12 = {(х, и, р): хей, \и\^М, |р|^М3},
и частные производные а(; по х, и и р ограничены на ЭК2Х[0, 1].
Тогда задачи E.4) имеют по крайней мере одно решение и(х,х)
из С'+а(п) при Vt е [0, 1], если при т = 0 имеется конечное
число решений и их суммарный индекс отличен от нуля.
Как указано в самой теореме, условия а) — с) гарантируют
равномерную оценку max|Vu(jc, т) | (см. теорему 2.2); они и
s
условие d) гарантируют оценку max|Vw(jc, т)|^М3 (следст-
Q
вие 4.1). Из оценки тах| ?и(х, т) | и условий а) и е) выводится
а
оценка \и(х, т)^+а)^^И4 (см. теоремы 1.1, 1.2 данной главы и
теоремы §§ 1, 2 гл. III).
Эта равномерная оценка | и \^+а) для всех возможных реше-
решений задач E.4) и теорема Лерэ — Шаудера (теорема 10.1 гл. IV)
позволяют заключить о разрешимости задачи E.1), E.2) (более
подробно см. § 10 гл. IV).
Теорема 5.2. Теорема 5.1 остается справедливой, если в ней
в условии с) заменить неравенство E.8) более слабым неравенством
\а(х, и, р, т)|Г<с,1Г(р)Г-1+с2, E.9)
но предположить, что Q есть строго выпуклая область.
Доказательство этой теоремы отличается от доказательства
предыдущей только в одном пункте: для оценки max|Vu(jc, т) |
s
вместо теоремы 2.2 надо привлечь теорему 2.1.
В теоремах 5.1 и 5.2 есть одно неприятное условие: нера-
неравенство E.6). Для уравнений общего вида E.1) (в отличие от
уравнений гл. IV) неизвестны способы получения априорной
оценки osc{w; йр}. Ввиду этого исключим это требование. Но
тогда для оценки max| Vu | нам придется привлечь теоремы § 3.
о
Так, с использованием теорем § 3 вместо следствия 4.1 до-
доказывается
Теорема 5.3. Теоремы 5.1 и 5.2 остаются справедливыми,
если в них отбросить условие E.6), а в условии d) все неравен-
неравенства заменить на неравенство C.10), и на требование существ
вования функции Ф(и) для уравнений E.4) с описанными в тео-
теореме 3.2 свойствами, или на условия теоремы 3.3 (или 3.4) для
функций а,,(х, и, р, т), а(х, и, р, т). Функция Ф(у) и постоян-
постоянные Cj, ..., с5 не должны зависеть от f.

> 5] ТЕОРЕМЫ СУЩЕСТ ВОВАИНЯ 459
Рассмотрим два конкретных включения параметра т. Одно
з них имеет вид
Lx(u) = au(x, и, ux)uXiXj + xa{x, и, их) = 0, 1
иЬ = тфк, те [0, 1]. J
Соответствующее ему преобразование ау = Ф(и, т) определяется
шнейной задачей
ац(x, v, vx) wx.x. + та (*, v, vx) = 0, w \s = щ\ s. E.11)
Ясно, что w от т зависит линейно, т. е. а;(т) = Ф(у, т)=т0(у).
Для нахождения неподвижных точек преобразования Ф(у, т) —
= т©(и)> т. е. решений уравнения
и = т8(и), те [0, 1], E.12)
можно воспользоваться следствием 10.1 гл. IV из теоремы
Шаудера (теорема 10.6 гл. IV). Для ее применимости доста-
достаточно убедиться, что нормы всех возможных решений задачи
E.12) в пространстве Н не превосходят некоторой полчэяшой с.
В качестве Н возьмем банахово пространство С + (О) с неко-
некоторым р > 0. Функции ац(х, и, р), а(х, и, р), у(х) и граница 5
предполагаются столь же гладкими, как и в теореме 5.1. Ввиду
этого решения уравнений E.12) будут принадлежать не только
С (О), но и С2+а(О) и будут решениями задач E.10). Таким
образом, вопрос о разрешимости задач E.10) сведен к вопросу
получения априорной оценки величины max | и (х, т) A+В) для
_te[0. 1J
всех их возможных решений из С2+а(п). Относительно j{ =
= max max|u(jc, т) | надо или предполагать, что его ограни-
• т<=|0, 1| Q
ченность нам дана по условию, или считать выполненными
условия одного из тех предложений, в которых даны достаточные
условия для его оценки. Например, если для Ll(u) выполнены
условия одного из следствий 8.1—8.3, 8.5, 8.6 гл. IV, то они,
очевидно, будут выполненными для всех L%(u), те[0, 1], и
для j{ будет желаемая оценка. Итак, пусть мы получили, что
Ji^M. Для оценки /2 = max max|Vu(jc, т) | привлечем тео-
т е= [0,1] S
ремы § 2. Их условия таковы, что они выполняются для
всех Lx(u), те[0, 1], если только они верны для /,'(")• Обо-
Обозначим через М1 получаемую с помощью этих теорем оценку /2.
Переходим к оценке
h= max max| Vu(х, т) | E ,о\
те|0, 1] Q [O.IO)
с помощью теорем § 3. Для применимости теоремы 3.1 надо
считать функции аи, а не зависящими явно от х и и. В этом

460 КВАЗИЛИНЕЙНЫЕ УРАВНЕНИЯ ОБЩЕГО ВИДА [ГЛ. VI
случае она гарантирует, что /з^М,. Условия теоремы 3.2 при-
применительно к оператору LT(u) уже будут зависеть от т. Пара-
Параметр т войдет в выражение /3 для Lx(u). Однако вхождение т
в /3 сравнительно простое: т станет множителем при членах
рпр — и Ьи
— Ф" ¦%¦— и — (Ф'J-1—г= . Все остальные составляющие /3
сохранят свой прежний вид, соответствующий V (и). Параметр т
войдет и в равенство C.13) в качестве множителя при — а/Ф'.
Для применимости теоремы 3.2 надо потребовать существо-
существования функции Ф(и), не зависящей от т и такой, чтобы для
нее min /3(т) был больше 0. Кроме того, она должна удовлетво-
т<=[0, 1]
рять требованиям C.9), в которых ыA) = — М, uB)= M. Посмо-
Посмотрим, что дает теорема 3.3 для оценки /3. Почти все ее условия
не зависят от т. Исключение составляют неравенства C.18) и
C.19). Они должны быть заменены на следующие:
\>с?\р\, E.14)
Г|р|*). E.15)
Итак, теорема 3.3 обеспечивает оценку /3, если постоянные
си с2, с3 и с4 = с4, с5 = с5 удовлетворяют ее требованиям с © = 2М.
Условия же теоремы 3.4 таковы, что из выполнения их для L1 (и)
следует их справедливость для всех L1(и).
Наконец, теорема 1.L дает оценку j.= max \u(x, т) RJ+W
т е= [0, 1]
с некоторым р > 0 без каких-либо дополнительных ограничений
на ац и а. Подытожим сказанное в форме теоремы.
Теорема 5.4. Пусть функции аи(х, и, р), а(х, и, р) не-
непрерывны на Ш и ац удовлетворяют условию E.3). Кроме того,
предположим выполненными следующие условия:
a)Se С2+а и ф(х) е= С2+°(Й),
b) atj и а удовлетворяют условиям одного из следствий
8.1—8.3, 8.5, 8.6 гл. IV. (Это дает мажоранту М для \ и(х, т) |.)
c) Если Q — произвольная область, то ац и а удовлетворяют
неравенству E.8); если п — строго выпуклая область, то только
неравенству E.9). (Это дает мажоранту Mi для | уи (х, т) 115.)
d) На множестве Ш\, определенном в теореме 5.1, функции
ац (х, и, р), а (х, и, р) дифференцируемы по х, и, р и на любой
компактной части его ограничены вместе с частными производ-
производными первого порядка. Функции а,-у (jc, и, р) удовлетворяют
неравенству C.10) с некоторой положительной непрерывной функ-
функцией v, (jc, и, р), и для всего семейства операторов Lx(u), те [0, 1],
*) Напомним, что с4 и съ, а также и с4, ёъ не предполагаются непре-
непременно неотрицательными.

H] О ДВУМЕРНЫХ ЗАДАЧАХ 461
существует функция Ф(у) с описанными в теореме 3.2 свойствами.
В качестве ыA) и ыB) надо взять числа —М и М, где М — ма-
мажоранта /ц получаемая благодаря условию Ь), а в качестве
М\ — мажоранту /2, получаемую благодаря условию с). Суще-
Существование такой функции Ф(у) гарантируется выполнением
условий теоремы 3.3 для функций ац {х, и, р), а (х, и, р), если
только в них постоянные с4 и с5 заменены на постоянные с4 и с5
из E.14) и E.15) соответственно. Вместо условий теоремы 3.3
можно предположить выполненными для ац, а условия тео-
теоремы 3.4.
Тогда задачи E.10) разрешимы в классе С2+а (Q) при всех
те[0,1]. Нормы | и (х, т) ^+а) их решений ограничены некоторой
постоянной, определяемой лишь известными из условий a) — d)
величинами.
Рассмотрим еще один способ включения параметра т,
а именно:
U (ы) ?а aij {хх, ты, их) u4Xj + ха (т*, ты, их) = 0, ы | s = Тф | s.
E.16)
Он полезен для получения оценки max| u(x, т) | с помощью тео-
Q
ремы 8.1 или следствия 8.4 гл. IV. В этом случае надо пред-
предполагать, что оператор Ll(u) определен для всех ^принадлежа-
^принадлежащих области Q,, содержащей наряду с точками Q и все точки
вида хх, xefi, те[0, 1] (начало координат считаем лежащим
в О). В § 10 гл. IV мы показали, как получается в этом случае
оценка j{. Нетрудно понять, как к этому, семейству /,т(ы) при-
применяются теоремы 2.1, 2.2, 3.2, 3.3 и 1.1, позволяющие оценить j2,
j3 и /4, а тем самым и доказать разрешимость задач E.16).
В теоремах 5.1—5.4 установлена разрешимость задачи E.1),
E.2) в пространстве C2+a(Q). Теоремы §§1,4 позволяют исследо-
исследовать разрешимость этой задачи в пространстве C2+a(Q) П С (Q) при
меньших предположениях относительно S и <р. Мы не будем
излагать здесь этот вопрос, а отошлем читателя к § 3 гл. VI
первого издания этой книги (см. теорему 3.3). По поводу тео-
теоремы единственности для задачи E.1), E.2) см. конец § 10 гл. IV.
§ 6. О двумерных задачах
Теоремы, доказанные в предыдущих параграфах, справед-
справедливы для любого п 1>2. Однако для л = 2 можно указать
ряд дополнительных случаев разрешимости задачи Дирихле.
Приведем два из них: один для равномерно, а другой для

462 КВАЗИЛИНЕЙНЫЕ УРАВНЕНИЯ ОБЩЕГО ВИДА [ГЛ. VI
неравномерно эллиптических уравнений. Итак, рассмотрим сна-
сначала задачу
2
2 ац(х,и,их)ихх+а(х,и,их) = О, «15 = 0*), F.1)
считая выполненным условие равномерной эллиптичности
где v(t) и ц(т) обладают свойствами, описанными на стр. 26.
Для доказательства разрешимости задачи F.1) используем тео-
теорему Шаудера, точнее, ее следствие 10.1 и замечание 10.2 из
гл. IV. Для этого включим задачу F.1) в семейство задач
аи (х, и, их) uHXj + та (*, и,их) = 0, и \g = 0, т е= [0,1]. F.3)
Согласно тому, что изложено в конце § 10 гл. IV (уравнение
A0.27) и далее), для разрешимости задачи F.1) в пространстве
С2+а (й) достаточно знать, что все возможные решения и(х, т)
задач F.3) из С2+а (Q) имеют равномерно ограниченные нормы
| и |[]+Р) с каким-нибудь р > 0. Допустим, что для всех и (х, т)
верна оценка
тах|и(х, т)|<М, F.4)
Q
и пусть при xeQ, | «|^Af и любых р функция а(х, и, р) под-
подчиняется неравенству
|а(*. и, рI<б(М)|рр + ц,(А1)[1+|рГЧ F-5)
где б! — какое-либо положительное число, а МЬ(М) — достаточно
малое число (его величина определяется значениями \(М)
иц(М) из F.2) и 5-см. F.10)).
Из неравенства A9.5) теоремы 19.1 гл. III в силу условий
F.4) и F.5) следует
II и (*. т) |g>0 < с || а (х, и, их) ||2_ Q + ctM mes Q <
с = 2ц(М) \~2(М), F.6)
где постоянная сх определяется \(М), \i(M) и границей S.
*) Однородность краевого условия несущественна. Можно работать или
непосредственно с неоднородным условием, или свести его предварительно
к однородному.

§ 6] О ДВУМЕРНЫХ ЗАДАЧАХ 463
Для оценки первого слагаемого правой части F.6) воспользу-
воспользуемся неравенством
j\Wu МлА1/2<B + / 2)тах| и \( j u\xdx\'2, F.7)
Q \q
которое выводится так (напомним, что u|s = 0):
J | Vm I4 dx = J ux.uXjuXkuXk dx =
a a
= — J и [Auux.ux. + 2uXjuXjuXkXj\ dx
М* \f \ u
Ldx.
a
Для оценки второго слагаемого используем неравенство ab^~
^ iHL. -f -г (—j , — + -г = 1, справедливое при любом е > 0.
Оно дает
/ { [ ^ |(f>. F.8)
q a
Подставляя F.7) и F.8) в F.6), получим
|| и(х, х) |g>a < [ев (М) + сц, (Af)]/1 - ^ в'Л2-в.>] у J | vm I4 d
сц, (М)^ 1 - T" e1/B-Sl)]B + /2) Al || и |f'0 + ee, F.9)
где c, =
Пусть
B + /2~)сА1в(А1)< 1, c = 2n,(M)v-2(M). F.10)
Возьмем в F.9) е таким, чтобы B+^2) Мсц, (М) -|/" 1 —| е'/<2-б'> <
< 1 — B + /2~)МсЬ(М) = б2, б2 > 0. Тогда F.9) даст следующую
оценку:
|| и (х т)||а
и (х, т)||<2)а<се/62. ¦ F.11)
Эта оценка получена при условии F.10), которое выше было
сформулировано как условие «достаточной малости вели-
величины МЬ(М)»,

464 КВАЗИЛИНЕЙНЫЕ УРАВНЕНИЯ ОБЩЕГО ВИДА [ГЛ. VI
Из неравенства F.11) и теоремы об ограниченности вложе-
вложения W22(Q) в Wlr(Q) с Vr<oo (неравенство B.28) гл. II) сле-
следуют оценки
1|и(*. т)|ро<с(г) F.12)
с постоянными с(г), зависящими только от г, М, себГ' из F.11)
и области Q. Из F.12) и F.5) в свою очередь следует оценка
|| а (х, и (х, т), их (х, т)) ||д 0 < с, (?) F.13)
при V? < оо. Фиксируем какое-либо д>2 и рассмотрим урав-
уравнения F.3) как линейные уравнения относительно ц(х, х) с
коэффициентами йц(х, х) = аи(х, и(х,х), их(х, х)) и свобод-
свободными членами f (х, т) = та(л;, и(х, х), их(х, х)) из Lq(Q). В силу
F.2), F.4) и F.13) для решений этих уравнений справедлива
теорема 19.5 гл. III, гарантирующая оценку
\и(х, т)Е+ю<Л*1 F.14)
с некоторым р > 0. Итак, желаемая оценка получена. На ее
основе, как показано в § 10 гл. IV, доказывается
Теорема 6.1. Пусть для всех возможных решений и(х, х)
задач F.3) из C2+a(Q) справедлива оценка F.4) и S<=C2+a.
Пусть, далее, при xeQ, |и|^Л1 и Vp функции atl(x, и, р)
и а(х, и, р) удовлетворяют условиям F.2), F.5), постоянные
в которых подчинены требованию F.10), и на компакте Мм, м,=
= {(л:, ы, р): xgQ, | и |<М, | р |<М,} принадлежат Са(Шм,м)
(Mi — постоянная из F.14), определяемая постоянными из усло-
условий F.2), F.5)). Тогда задача F.1) имеет по крайней мере одно
решение из C2+a(Q).
Рассмотрим теперь случай неравномерно эллиптических
уравнений вида
ац(х, и, ux)uXlXj = 0.
Для них справедлива следующая теорема:
Теорема 6.2. Задача
2
2 ац(х, и, их)ихх =0, u\s — q>\s F.15)
имеет по крайней мере одно решение_ и из С2+а (Q), если
Q — строго выпуклая область, <р е С2+а(п), S е С2+а,
а{,(х,и,р)Ы1>0*) F.16)
*) Достаточно требовать, чтобы это неравенство выполнялось лишь на
множестве 9ЛЛ{| щ

5 6) ° двумерных задачах 465
и atl(x, и, р) на множестве Шм,м, = {(*> ", р): х(=п, \ и |<Af,
| р К Л1,}, где Л1 = max | <р |, a Af, — некоторая постоянная, опре-
деляемая лишь у и S, удовлетворяют условию Гёльдера по
(х, и, р) с показателем а > 0.
Для доказательства этого утверждения можно воспользо-
воспользоваться теоремой Шаудера (теоремой 10,6 гл. IV). Действительно,
рассмотрим преобразование w = 8(и), определяемое задачей
ац (х, v, vx) wXlXj = 0, йу|5 = ф|5. F.17)
Для VogCi+A(Q) существует единственное решение w за-
задачи F.17) из пространства C2+a(Q) (см. теорему 1.1. гл. III).
Более того, для w в силу леммы 1.4 гл. III справедлива оценка
тах| до |^т»х| <р \ = М, F,18)
q s
а в силу теоремы 20.1 гл. III—оценка
maxIV» |< Af,, F.19)
Q
где All определяется только <р и S.
Далее, теорема 19.3 гл. III гарантирует оценку
F.20)
в которой р > 0 и М2 определяются М, Л1,, ф, S и нижней
и верхней границами квадратичной формы а{1(х, v(x), vx (x)) l&i
при |2=1*). Будем рассматривать 8 (и) только на v, удовле-
удовлетворяющих условиям
max I v (x) \^LM, max| S/v(x) I^Ali. F.21)
Q Q
Для таких v (x) постоянная Л12 может быть взята не зависящей
от v(x), ибо таковыми могут быть выбраны нижняя и верхняя
границы формы atj(x, v(x), vx{x))?,?/ при ?2=1. Итак, при
условиях F.21) постоянная Л12 в F.20) определяется Л1, Ми ф и S.
Рассмотрим преобразование 8 (и) на множестве
2Я = lv: max| v |<M, max| Vv |< Alj, \v fo+P><M2)
Q Q
*) В теореме 19.3 рассмотрен случай однородного граничного условия.
Но наш случай F.17) легко сводится к рассмотренному в теореме 19.3,
если вместо w ввести новую функцию ш>(х)= w (х)—<р(х),гдеф(х)еС2+а(й)
и совпадает с ф (s) на S. Получаемое для гй уравнение имеет свободный
член — ац (х, о, vx) <fx x , ограниченный по модулю известным нам числом.

466 КВАЗИЛИНЕЙНЫЕ УРАВНЕНИЯ ОБЩЕГО ВИДА [ГЛ. VI
пространства C1+|5(Q). Это множество ограничено, замкнуто
и выпукло в Cl+p(Q). Функция 8 (и) преобразует его в себя
(что видно из неравенств F.18) — F.20)). Преобразование 8 (и)
компактно, ибо оно переводит 9R в множество, компактное
в C1+P(Q). Действительно, для решений задач F.17), помимо
оценок F.18) — F.20), справедлива оценка
lH2+a)<M3, F-22)
гарантированная теоремами §§ 1, 2 гл. III. Постоянная М3
определяется, помимо М и Mlt числом а, нормой | ф |^2+а), S,
нормами -\ац(х, и, р) $ и нижней гранью ац(х, и, p)hlj
при |2= 1 на Шм,м,- Множество же функций w(x), удовле-
удовлетворяющих неравенству F.22), компактно в пространстве Cl+p(Q).
Непрерывность 6(и) на Ш выводится на основании теорем §§1,2
гл. III так же, как это было сделано в § 10 гл. IV (см. A0.9)
и далее). Мы этот вывод повторять здесь не будем.
Итак, проверено, что 6 (v) есть вполне непрерывное пре-
преобразование Ш в себя. Но тогда теорема 10.6 гл. IV гарантирует
существование по крайней мере одного решения задачи F.15).
Теорема 6.2 доказана. При несколько более сильных ограниче-
ограничениях на гладкость ац и ф (а именно: ац е С2+а и ф е С3+а)
она была установлена в работе [324] Ж.. Лерэ и Ю. Шаудера,
при сформулированных здесь условиях — в работе [44,] Л. Ни-
ренберга.

Глава VII
ЛИНЕЙНЫЕ СИСТЕМЫ УРАВНЕНИИ
ЭЛЛИПТИЧЕСКОГО ТИПА
В этой главе мы рассмотрим классы линейных систем эллип-
эллиптического типа, для которых имеет место векторный аналог
принципа максимума. Для них будут установлены те же резуль-
результаты, что и выше для одного уравнения второго порядка
(см. [2119]).
То, что специфично для систем, будет излагаться подробно,
то, что близко к случаю одного уравнения, — более схематично.
Из краевых задач мы выбрали первую. Необходимые видо-
видоизменения в рассуждениях при изучении второй и третьей
краевых задач для систем читатель сделает сам, прочтя соот-
соответствующие параграфы для одного уравнения второго порядка.
Число независимых переменных п всюду больше либо равно 2.
§ 1. Обобщенные решения из
Рассмотрим в ограниченной области Q системы вида
Lu - -^[а„ (х) их. + А, (х) и] + В, (х) Uje< + В(х) и = §- + f. A.1)
Здесь u, ft и f суть вектор-функции с N компонентами:
и = (м1 (х), ...,и»(х)), f,. = (/'(*),..., ff(х)),
f = (V(x) fN(x)),
a Ai(x), Bt(x) и В(х) — квадратные матрицы с jV2 элементами,
зависящими от х, ац(х) — скалярные функции.
Здесь и ниже используем следующие обозначения скаляр-
скалярных произведений и норм векторов и вектор-функций:
Г N 1/2
i= 2(t>*J ,
U=i J
(v,w)=j\(x)w(x)dx1 || v |
N Г N 11/2 N п
vw = 2 vkwk, | v
= 111 V I ",, Q-
(v, wjj'o =

468 ЛИНЕЙНЫЕ СИСТЕМЫ УРАВНЕНИИ ЭЛЛИПТИЧЕСКОГО ТИПА |ГЛ. VII
Принадлежность вектор-функции v(a;) какому-либо функциональ-
функциональному пространству Z,2(Q), Wi(Q), С1+а(п) и пр. означает, что
каждая компонента вектора принадлежит этому пространству.
Будем предполагать, что коэффициенты ац системы A.1)
удовлетворяют неравенствам
^12<аи(х)Ы1^ц1\ v, n = const>0, A.2)
при любых вещественных %и ..., |„, так что система A.1) —
эллиптического типа. Для нее рассмотрим задачу Дирихле
и Is = «Pis. A-3)
считая ф (s) = <р (х) |s, ф (л:) е W\ (Q). Ради небольших упроще-
упрощений в изложении будем предполагать, что для области Q
имеют место теоремы вложения § 2 гл. II.
Мы начнем исследование задачи A.1), A.3) с изучения ее
разрешимости в пространстве Wl(Q). Как выяснено на приме-
примерах в § 2 гл. I, для разумности таких рассмотрений необхо-
необходимо, чтобы элементы al!"(x), b\m{x) и blm(x), I, m=l, -.., N,
матриц Ait Bt и В суммировались по Q со степенями q, q и q/2,
где q > п, соответственно *). Если эти условия не выполнены,
то в классе обобщенных решений из W\ (Q) нарушается теорема
единственности для задачи Дирихле в любой сколь угодно
маленькой области Q, т. е. теряется свойство, которое присуще
этой задаче в ее классической постановке.
Итак, будем предполагать, что
К"'*!Ч.О' H&/4,2.Q<Hb Я>П. A.4)
Относительно f*(*), f(x) и ф(д;) будем считать, что
II'ilk. о» 'HIWm^.q. НЧ>С<«>, A-5)
где А = п для л>2 и й = 2 + е, е>0, для п = 2. Эти пред-
предположения относительно th f и ф также необходимы для суще-
существования обобщенного решения из И^г(й) задачи A.1), A-3)
(если, конечно, эти условия формулировать в терминах при-
принадлежности данных функций к пространствам LP(Q)).
Обобщенным решением из W^iQ) системы A.1) называем век-
вектор-функцию и(д:) из WliQ), удовлетворяющую интегральному
*) Граничный случай д = л для систем A.1) имеет те же особенности,
что и для одного эллиптического уравнения, и исследуется аналогично.
Ввиду этого в данной главе мы его рассматривать не будем.

§ 1) ОБОБЩЕННЫЕ РЕШЕНИЯ ИЗ tt^(Q) 469
тождеству
Q
при любой ц (д;) е №2 (Q).
Обобщенным решением из №г(О) задачи A.1), A.3) назовем
то обобщенное решение системы A.1) из этого класса, для ко-
которого и (я) — ф (х) е= W\ (Q).
Так же, как и для случая одного уравнения, доказывается
теорема:
Теорема 1.1. Пусть выполнены предположения A.2), A.4),
A.5) и Q — ограниченная область. Тогда относительно разреши-
разрешимости задачи A.1), A.3) в пространстве ^(Q) выполнены все
теоремы Фредгольма.
Мы не будем приводить доказательство этой теоремы и ее
подробную формулировку. Она базируется на первом основном
неравенстве для решений системы A.1), которое имеет вид
|| Vu || 0 < с, (q) || и \\{ 0 + с (^ S || Ь |? а + с, (Л, Q) || f 4/(rt+2)> Qj +
+ ct(q, Q)(HlQ2. A.7)
Постоянная с в нем зависит лишь от п и v из A.2), с, (q)— от
л, N, v, ц, ц,, ^ из A.2), A.4), а с, (9, Q) — еще и от п (зависи-
(зависимость от Q обусловлена лишь использованием неравенства B.21)
гл. II для оценки || qp \\lq/{q_2)i a). В ряде случаев член с, (q) || u Ц^ а
можно исключить из правой части. Это возможно, например,
когда mesQ^6, где б — достаточно малое число, или когда
матрица В такова, что
Ви-и<-ц,|ир, A.8)
где ц, — достаточно большое число (величина б определяется
лишь лис, (q)).
Доказательство всех этих предложений принципиально не
отличается от доказательства аналогичных фактов для одного
уравнения второго порядка. В частности, для вывода A.7) надо
положить в A.6) u = v + qp» a ti = v и воспользоваться предпо-
предположениями A.3) —A.5).
Во всех случаях, когда в A.7) можно исключить ||u||2Q из
правой части, имеет место теорема единственности для обоб-
обобщенных решений из W^iO). Действительно, для разности двух
возможных обобщенных решений задачи A.1), A.3) мы имеем
неравенство A.7) с нулями в правой части (ибо для нее !*=з
s=f = qp==O), что и указывает на совпадение решений.

470 ЛИНЕЙНЫЕ СИСТЕМЫ УРАВНЕНИЙ ЭЛЛИПТИЧЕСКОГО ТИПА [ГЛ. VII
§ 2. Оценка max|u|
В этом параграфе мы займемся оценкой максимумов модулей
решений и (л:) системы A.1). Как следует из примеров § 2 гл. I,
для конечности vraimaxl u |, кроме условий A.2), A.4), необхо-
необходимо, чтобы а
IIf/ И,. о- IIf \р, о < Hi ПРИ Я>п. B.1)
Будем считать эти условия выполненными.
Мы покажем, что если и (л:) есть обобщенное решение A.1)
из №г(О) и если для него конечны интегралы
f I u \4dx f I и I21 Ун \2dr О 9\
I I U I WvV) I I U II V U I WA) \?i*?i)
J j x
Q <J
то vraimaxl u | для любой внутренней подобласти Q' области Q
Q'
оценивается через п, N, q, v и ц из условий A.2), A.4), [2.1),
Г | u I4 ofд: и расстояние от Q' до 5. От величины интеграла
Q
I | u р| Vu fdx величина vrai max| u | не зависит. Для оценки
J О'
Q
vraimaxl u| по всей области Q надо сделать дополнительные
й
предположения о граничной функции ф(д:). Мы проведем эту
оценку ради экономии места для случая ф(д:) = 0, т.е. для
u|s = 0. B.3)
Более того, в этом случае предварительно докажем, что если
и (х) есть обобщенное решение задачи A.1), B.3), то интегралы
B.2) для него будут конечны.
Начнем с доказательства конечности интегралов B.2). Для
этого положим в A.6) т!(л:) = и(л:)Ф(л:), где Ф(л:) — произволь-
о .
ная.функция, обладающая тем свойством, что и(д;)Ф(д:) е №г(О).
Это даст тождество
1
aiiux.ux.(?> + irCtnVjc ФХ) + {AiU — h)(иж,Ф + иФ^ ) —
Q
— (В(их. + Bu — f) иФ] dx = 0, B.4)
где v (х) = | и (х) р.
Возьмем в качестве Ф функцию
ф (х) = ф(г) (х) = min {v (х), г), г > 0.
(Легко видеть, что и(х)Ф(г)(х) ^Wl(Q).) Первые два члена
из B.4) оставим в левой части и оценим их снизу, а остальные

I 21 ОЦЕНКА max|u|
перенесем в правую часть и будем оценивать сверху:
г
+
471
t У l.m
к I+i/S W? iu i+1f i) iu i ф(г>1dx <
У l.m j J
+ |f IVо &r)\dx. B.5)
При этих оценках мы использовали то, что
I U | Ф*. | Фд;(. .
Возьмем е = v/2 и приведем подобные члены. Остальные
члены оценим по неравенству Гёльдера следующим образом:
тJ иФ(г) dx 5
VqП {Vv&r)yqlD~2) dx\
\« /
l
2) \(q-2)/2q
¦ J
G-2)/7
3 ?-2
\Q I \a
Для оценки правых частей воспользуемся неравенством B.9)
гл. II, точнее, его следствием B.15)
ur{4Adx) <е И Vu fdx + cJ |u|d*| , Vе > О»
I I la У
о
справедливым для любой функции ueUT2(Q), и неравенством

472 ЛИНЕЙНЫЕ СИСТЕМЫ УРАВНЕНИИ ЭЛЛИПТИЧЕСКОГО ТИПА [ГЛ. VII
Из них следует
'>| Vu f d* + Ce/J v dx\\
Подставляя все эти оценки в B.5) с достаточно малым е, при-
приводя затем подобные члены и учитывая предположения о ко-
коэффициентах и свободных членах системы, будем иметь
а потому и
*-i
причем постоянная с, не зависит от г. Устремляя в последнем
неравенстве г к оо, убедимся, что
B.6)
т. е. интегралы B.2) для обобщенного решения u^Wi(Q) за-
задачи A.1), B.3) конечны. При этом относительно коэффициентов
системы мы использовали те же предположения A.2), A.4),
что и в § 1,-*а относительно ff и f ограниченность норм
х | II и It 0 + S №| lC+2, g + II f li;,(,+6), 0] .
. Я>П- B.7)
Переходим теперь к оценке vraimax|u|, не предполагая
решение и непременно равным нулю на 5, но считая известной
ограниченность интегралов B.2). В силу этой ограниченности
в качестве Ф в B.4) можно взять функцию
Ф (х) = max {2 [v (x) - k] ?2 (x), 0},
где k — какое-либо неотрицательное число, a t,(x) — гладкая
неотрицательная функция со значениями между 0 и 1, равная
нулю вне шара KccQ. В результате элементарных оценок по

§. 2] ОЦЕНКА max | u I 473
неравенству A.2) гл. II получаем
J
+ ce J [(v -kJ\%f + (D2 + E)(v2 + 1)?2] dx. B.8)
Здесь AkrP есть множество точек х из /Cp, для которых
v (x) > k, a
В силу условий A.4), B.1) нормы \\D\\q Q, \\E\\ql2 a ограничены.
Поэтому последний член допускает оценку
[ (D2 + Е) {v2 + 1) ?2 dx < с Г [ (?1>J*/A?-2) с
;Г [\Uv-k)fqM-2)dx\q-
UL J
. р < 2с
Учитывая ее и полагая в B.8) e = v/2, из B,8) будем иметь
при k~^ \
J {v-kJ\Slfdx +
ft.p
+ K(v-k)iqM_,hAkp + k2 mes' Л,.p] B.9)
с известной нам постоянной с,.
Неравенство B.13) гл. II применительно к функции и =
= (v — k)Z, дает
¦ <°-*> 5 UM. ,.».„<
^) J [| Vup?2f {v-kf\ Vt,f]dx. B.10)

4?4 ЛИНЕЙНЫЕ СИСТЕМЫ УРАВНЕНИЙ ЭЛЛИПТИЧЕСКОГО ТИПА [ГЛ. VII
Для р, удовлетворяющих неравенству
неравенство B.9) порождает более простое:
1
,-i
B.12)
P
В этом неравенстве k.^l, p удовлетворяет B.11) и KpczQ.
Постоянная у определяется лишь п, N, q (q>n), v, ц из A.2),
A.4) и B.1). Следовательно, v(x) принадлежит классу
2 2 \
312 (Кр,у, 2, 2, , 11 (см. замечание 54 гл. II), и потому
на основании теоремы 5.3 гл. II vraimaxu в концентрическом
Круг
шаре Kpi2 оценивается через у, q н р~я/2||о||, к =P~n/2l|u||f „ .
Ввиду произвольности шара Кр cr Q отсюда вытекает оценка
max v = max | u |2 для y/U'czil (она, разумеется, зависит от рас-
расстояния Q' до S). Если u |s = 0, то неравенства B.12) при тех же
k^ 1 верны и для шаров Кр> пересекающих S, т. е. ие
е 212(ЙР, y. • •., 1)' Доказывается это так же, как и для внутрен-
внутренних шаров. Из всех этих неравенств на основании теоремы 5.3
гл. II следует
Теорема 2.1. Пусть для системы (IЛ) выполнены условия
A.2), A.4), B.1). Тогда для обобщенного решения и(х) си-
системы A.1) из Wl2(Q) с конечными интегралами B.2) величина
vraimaxl и(д;) | оценивается через п, N, q, v, ц, ц, из A.2), A.4),
B.1), ||u||4 Q и расстояние Q' до S. Если же и(х) есть обобщен-
обобщенное решение задачи A.1), B.3) из WiiQ), то vraimaxl и(д;) | оце-
нивается через п, N, q, v, ц м. ц, из A.2), A.4), B.1) и l|u||2Q.
Заметим, что vraimaxl u | при выполнении условий второй
о
части теоремы проще оценить сразу для всей области Q, не
разбивая Q на шары Кр малого радиуса. Для этого надо в то-
тождестве B.4) взять Ф (х) = max {2 [v (x) — k], 0}, v = | u f, считая
k > 0. Срезающая функция ? при этом не нужна. Производя
оценки того же типа, что и выше, придем к неравенствам
p dx < y J (о - W dx + k! mes' " * A J B.13)
Ь J
J (о - W d

§ 3] ОЦЕНКА | и \g> 475
для k, превосходящих 1. Здесь Ak есть множество точек jteQ,
в которых v(x)>k. На основании теоремы 5.1 гл. II из B.13)
следует желаемая оценка vrai max v.
а
§ 3. Оценка \\х^
Покажем, что при выполнении неравенств A.2), A.4), B.1)
можно оценить не только max|u|, но и нормы Гёльдера для
каждой компоненты и с некоторым положительным показателем
а > 0. Для этого достаточно доказать, что ограниченные обоб-
обобщенные решения и (х) системы A.1) из W\ (Q) принадлежат классу
Пусть и (х) е W\ (Q) и vrai max |u|<M. Ради удобства будем
считать, что 0^м*(х)^ 1, /= 1, ..., N. Этого всегда можно
добиться, вводя в A.1) вместо ul(x) функции й1 = {и1 + М)/BМ).
Предположим, что это уже сделано.
В качестве функций фг+(и) для и(д:) (см. определение клас-
классов ЗЗ2^ в § 8 гл. II) возьмем функции
Л'
ф'! (u)= 10jVm' + 2 («О2.
N
ф*_ (и) = 1 ON A — «') + 2 (M02> / = 1 > ...» Л^.
г—\
В силу леммы 8.4 гл. II достаточно проверить, что функции
м»± (*) = Ф± (и (*)) удовлетворяют условиям 3) и 5), входящим
в определение классов Ъ\ы. Для этого сложим тождества A.6)
ci) = 5Л^Ф (лс) ez и тождество A.6) с г\ = иФ (д;), где Ф (д;) — огр а-
О |
ниченная функция из W2(Q), а е* — единичный вектор, у кото-
которого компонента, стоящая на 1-й месте, равна 1, а остальные
N — 1 равны нулю. Это даст интегральное тождество для w = wl+:
o-ijUx и«.Ф Н— ciiiWjc Фх. -\- {А{\х — f^) (и*,Ф -\- иФл, -\- 5jVe Флг.)—
и
- (BiUx. + Bu-f) (иФ + 5ЛГФеО] dx = 0. C.1)
Это тождество того же типа, что и B.4). Положим в нем
>(о>-*К2,0}, C.2)
где k — произвольное число, ? (х) — срезающая функция для
произвольно взятого шара Кр, лежащего внутри Q. Главными

476 ЛИНЕЙНЫЕ СИСТЕМЫ УРАВНЕНИИ ЭЛЛИПТИЧЕСКОГО ТИПА [ГЛ. VII
членами в нем будут J 2aij\xXjaXl (да — k) ?2 dx и J aijWx^xjt? dx,
Ak,P Ak.P
где AkiP есть множество точек х из Кр, в которых w(x) > k. Все
остальные оцениваются через них и члены вида j (w — kJ\ V? fdx
и mes q AkiP с помощью неравенств A.1) и A.2) гл. II так же,
как это сделано в § 14 гл. III для одного уравнения. При этом
надо учесть, что vrai max| u \^M.
а
В результате из C.1) выводим неравенства
1-1
= ^-, C.3)
для да = да'+, /=1, ..., ^V, произвольных k и /CpcrQ. Постоян-
Постоянная Yi определяется N, v и ц, из A.2), A.4), B.1) и М.
Аналогично устанавливаются неравенства C.3) для w = wl_,
/=1, ..., N. Как легко видеть, из C.3) следуют неравенства
(8.3) гл. II. Это гарантирует принадлежность и (л:) к классу
Щ"(п, Ми б,, б2, б3, Y> Yi> 2> Чя), а следовательно (см. теорему 8.1
гл. II), и оценку | и ^ для любой Q'crQ. Для получения оце-
оценок норм Гёльдера и во всей Q надо получить неравенства C.3)
для шаров Кпу пересекающих границу, с &^ max до. Но такие
s
sp
неравенства действительно имеют место, и их вывод тот же,
что и для /CpCrQ, ибо функции Ф, определяемые равенствами
C.2), принадлежат W2 (Q) при k ^ max w, несмотря на то что ?2,
sp
вообще говоря, не обращается в нуль на Sp.
Таким образом, доказана
Теорема 3.1 Пусть для системы A.1) выполнены условия
A.2), A.4), B.1). Тогда любое ее ограниченное обобщенное ре-
решение и (х) из Wl2 (Q) с vrai max | u | ^ М принадлежит Сп (Q)
Q
с некоторым а > 0, причем \ и l^ оценивается сверху постоянной,
зависящей лишь от N, q, v, ц и ц, из A.2), A.4), B.1), М и
расстояния Q' до S. Показатель а определяется N, q и ц/v из
A.2). Если к тому же S удовлетворяет условию (А) и и |s e C^(S),

« 4] АПРИОРНЫЕ ОЦЕНКИ |u |[],+а) И ||u||^)Q 477
то ugC"(Q) и | и |^ оценивается сверху постоянной, зависящей
лишь от N, q, v, ц и ц, мз A.2), A.4), B.1), М, | u f|}, 0 м по-
стоянных а0 и 80, входящих в условие (А). Сал<о а в эгои случае
определяется значениями N, q, ц/v, 0 м 80.
§ 4. Априорные оценки | и ?,+а) и ЦиЦ^
Оценим | Vu |ц,+а) для любой внутренней подобласти Q'crQ
в предположении, что обобщенное решение и из W\{u) системы
A.1) имеет обобщенные производные второго порядка и конеч-
конечный интеграл
Коэффициенты аИ, af1 и f\ считаем дифференцируемыми и
такими, что
\%!-,^,Щ <ц„ ,>я. D,)
II °X 6X 0X II
Кроме того, предполагаем выполненными условие эллиптич-
эллиптичности A.2) и условие
\\а1Г,Ь\т,Ь1т,!\,!\а<щ, q>n. D.2)
Оценка величины vrai max| u | = M уже известна.
Q
Продифференцируем формально систему A.1) по хк и ре-
результат запишем в виде
4" \ач w u% + <¦""""" + Щ = °- D'3)
Здесь
flk _ xife ( ti
ulk _ ul
Kk
д{\ да\т
х,
k
Соотношения D.3) при /= 1, ..., #, k=l, ..., п предста-
представляют собою систему вида A.1) относительно функций и1к,
1=1, ..., N, k=l, ..., п. Ее коэффициенты atj(x), alf:ml{x)
и свободные члены fltk(x), как легко видеть, удовлетворяют
предположениям теорем 2.1 и 3.1. Поэтому для их решений и1к,
которые также обладают требуемыми в теоремах 2.1, 3.1

478
ЛИНЕЙНЫЕ СИСТЕМЫ УРАВНЕНИИ ЭЛЛИПТИЧЕСКОГО ТИПА [ГЛ. VII
свойствами, справедливы заключения теорем 2.1 и 3.1. Сфор-
Сформулируем это в виде теоремы.
Теорема 4.1. Пусть выполнены условия A.2), D.1) и D.2),
п
и пусть и есть обобщенное решение из Wi(Q) системы A.1)
с конечным интегралом
Тогда норма | u f^+a) с некоторым a > 0 для любой Q' cz Q оце-
оценивается сверху постоянной, зависящей лишь от п, N, M, q,
v, ц, [i, из A.2), D.1), D.2), j\Vu?dx и расстояния Q' до S.
Q
Число а определяется N, q и \а\~х из условия A.2).
Оценим теперь || u||2)n и ||Vu||4 Q, предполагая о системе A.1),
что для нее выполнено условие A.2) и
q>n,
q.Q
blm.
daf
дх,
7, 4).
D.4)
Граничное условие ради простоты возьмем однородным:
u|s = 0. D.5)
Ограничения на S те же, что и в случае одного уравнения (§ 8
гл. III).
Рассмотрим систему A.1) как набор отдельных уравнений
вида
{l^ Fl(x), 1=1, ..., N, D.6)
где
= --?-(Aiu-fl)-BiuXi-Bu
= (f, ..., F").
В силу леммы 8.1 гл. III для и1, 1=1, ..., N, верно неравен-
неравенство (8.11) гл. III. Суммируя по всем /, получим
D.7)
с постоянной с, зависящей от S, v и ц из A.2) и —
да.

§ 41 АПРИОРНЫЕ ОЦЕНКИ | u |[],+a) и |!u||!,2)Q 479
q > п. Величину || F1^ Q нетрудно оценить сверху с помощью
неравенства Гёльдера, используя предположения D.4), следую-
следующим образом:
||5;^ +||f|yia, D.8)
2, 9.
где |ul есть ||и||2?/(^4). а ПРИ п^4 И "iax|u| при /г = 2, 3,
а постоянная с определяется величинами ц2 и q из D.4). Но
для любой функции и из Wl, о (Й) верно неравенство
II V" ll2,/(,-2). i, + I U | < в || U |f 0 + Cg || U ||2| 0 D.9)
с произвольно малым е и с постоянной се, зависящей от е и Q
(см. B.28) гл. II). Поэтому из D.7) —D.9), как легко видеть,
следует оценка
с постоянной с, зависящей лишь от N, q, v, ц и \i2 из A.2),
D.4) и S. Ее мы и хотели доказать. Она аналогична оценке (8.11)
гл. III, выведенной для одного уравнения, причем предполо-
предположения о коэффициентах и свободных членах те же. Она верна
и для случая общих эллиптических систем (см. работу [10]
О. В. Гусевой и последующие работы Ф. Е. Браудера,
Л. Н. Слободецкого, Л. Ниренберга, С. Агмона, А. Дуглиса
и др.).
Для оценки Г | Vu |4 о?дг умножим D.6) на — m'|Vu|2, про-
а
суммируем по / от 1 до N и результат проинтегрируем по Q.
В левой части полученного равенства проведем одно интегри-
интегрирование по частям. Это даст следующее равенство:
J [a4nXlnXj | Vu р + atl (uX/u) 2 (u,ftu^.)] dx =
a
ju|Vuprfx D.11)
В силу A.2) из D.11) вытекает
v J | Vu fdx< J [e| Vu Г + -J-I u |X* + el Vu f + -?-| u |2| F p] dx
с произвольным е > 0. Выбирая е = v/4 и учитывая уже най-
найденные оценки max|u| = M, f u2 dx и F, из этого неравенства

480 ЛИНЕЙНЫЕ СИСТЕМЫ УРАВНЕНИИ ЭЛЛИПТИЧЕСКОГО ТИПА [ГЛ, VII
ВЫВОДИМ
где постоянная с зависит лишь от п, N, постоянных v, ц, ци q
из неравенств A.2), D.4) и S.
Мы оценили || u |f22)Q и Г | Vu |4 dx в предположении, что
а
u[s = 0. Можно было бы дать и внутренние оценки, точнее,
оценки этих норм по Q' cz Q, не делая никаких предположений
о поведении и вблизи S (см. начало § 7 гл. III).
§ 5. О разрешимости задачи A.1), A.3) в классах С'+а(Щ
Разрешимость задачи Дирихле в классах Гёльдера Cl+a(Q),
1^2, для системы A.1) доказывается так же, как и для одного
уравнения в § 1 гл. III. Центральное место при этом принад-
принадлежит неравенствам
^+a) ] , E.1)
', b,, Ь
km
E.2)
в которых постоянные сA) определяются значениями /, v
из A.2), коэффициентами системы A.1), точнее, величиной щ
из неравенства
а также границей S класса С1+а.
Покажем, что неравенство E.1) для системы A.1) можно
получить как следствие аналогичного неравенства A.11) гл. III
для одного уравнения того же вида. Для этого запишем си-
систему A.1) в виде
= f*. k=\ N, E.3)
отнеся в правую часть все члены, кроме первых (старших).
Неравенство A.11) гл. III для каждого из уравнений E.3) дает
lPfj-2+a)+max|Mft| + |«ft|(i+a)]- E-4>
Q

§ S) О РАЗРЕШИМОСТИ ЗАДАЧИ A.1), A.3) fi КЛАССАХ c'+Ct(O) 481
Раскрывая в E.4) выражение | f* |(Q~2+a) с учетом известных
(кольцевых) свойств нормы С1+а
и предположений E.2), получим
E.6)
Используем еще одно свойство норм С1+а (см. B.1) гл. III):
?1+а)?+а)
е, /)max|u|, E.7)
а
где е — произвольное положительное число, а с (е, /) — постоян-
постоянные, растущие безгранично при е-*0. Неравенства E.7) верны
для произвольной функции и из Cl+a(Q). Подставим оценку
E.7) в E.6), затем E.6) просуммируем по всем k в пределах
от 1 до N и выберем е достаточно малым. После приведения
подобных членов это приведет к неравенству E.1) с указан-
указанными выше свойствами постоянной с (/). Ясно, что неравен-
неравенства E.1) предельно точны (в общем случае все условия, при
которых они доказаны, необходимы). Благодаря им, используя
метод продолжения по параметру, так же, как и для одного
уравнения, доказывается справедливость теорем Фредгольма
для задачи A.1), A.3). Сформулируем две из них.
•Теорема 5.1. Пусть S^Cl+a, 1^2, и выполняются усло-
условия A.2), E.2). Если при f = О, f,sO, / = 1 п, фаО един-
единственным решением задачи A.1), A.3) в классе Cl+a(Q) является
ц==0, то задача A.1), A.3) имеет решение из Cl+a(Q) при
. любых f e= c'-2+a (Q), ft е= Cl~l+a (Q), <p e= Cl+a (Q). Существует
не более чем счетное множество значений Я = Я(, Я2, ... на
комплексной плоскости Я, для которых задача
, + М) + В{иХ{ + Ва = Ы, и к — 0 F.8)
имеет в С+а(п) отличные от тождественного нуля решения.
Это множество значений {кк} образует спектр задачи A.1), A.3).
Каждое из кк имеет конечную кратность. Все Я6 расположены
18 О. А. Ладыженская, Н. Н. Уральцев»

482 ЛИНЕЙНЫЕ СИСТЕМЫ УРАВНЕНИЙ ЭЛЛИПТИЧЕСКОГО ТИПА [ГЛ. VII
внутри некоторой параболы с осью, направленной по вещест-
вещественной оси и расширяющейся в сторону отрицательной вещест-
вещественной полуоси.
Так же как и для скалярного случая, специальные рассмо-
рассмотрения показывают, что спектральных значений {Kk} бесконечно
много и ReA*->— <х> при k-*<x>.
Легко указать ряд случаев, когда задача A.1), A.3) может
иметь не более одного решения. Два из них даны в конце § 1
для обобщенных (и тем более гладких) решений.
§ 6. Дифференциальные свойства обобщенных решений
Теоремы § 1 и § 5, а также априорные оценки §§ 2—4
данной главы позволяют показать, что дифференциальные свой-
свойства обобщенных решений из W\ (Q) системы A.1) улучша-
улучшаются по мере улучшения дифференциальных свойств данных
задачи.
Свойство это, так же как и для одного уравнения второго
порядка, локальное. Однако мы рассмотрим лишь случай, когда
дифференциальные свойства данных задачи улучшаются сразу
во всей области Q. Более того, ограничим себя предположе-
предположениями, что граничное условие однородно и выполнено нера-
неравенство A.8) с достаточно большой постоянной |хt (такой, что
оценка A.7) справедлива без ||u||2 Q в правой части, и, следо-
следовательно, для задачи A-1), A.3) заведомо имеет место теорема
единственности в W2(Q)). Покажем, что из установленных в пре-
предыдущих параграфах предложений следует
Теорема 6.1. Пусть и(х) есть единственно возможное обоб-
обобщенное решение задачи
Lu = -t--§-, u|s = 0 F.1)
из пространства W\{Q), и пусть коэффициенты L удовлетво-
удовлетворяют условиям
v>0, F.2)
(x2, Я>п, F.3)
и неравенству A.8) с достаточно большим Ць Тогда, если S
удовлетворяет условию (А) и
Я>п, F.4)

а1Г, 1
дац
dxk
Пт, blm,
da1/71
' dxk
fl fl
ti> 1
11G, Q ^*
\<
Из,
[i3, q
>n,
§ 61 ДИФФЕРЕНЦИАЛЬНЫЕ СВОЙСТВА ОБОБЩЕННЫХ РЕШЕНИИ 483
то u принадлежит пространству Са (Q) с некоторым а > О и
норма | и |^ оценивается постоянной, зависящей лишь от N, по-
постоянных v, ц, ц(, ц2, <7> mesQ и постоянных а0 и 80 из усло-
условия (А). Показатель а определяется \iv~~l, q и 80.
Если коэффициенты L и свободный член системы удовле-
удовлетворяют более сильным условиям: F.2) и
F.6)
a S^O2, то решение и принадлежит Wl(Q,)(]Cl+?l (Q). Норма
| u l[y , где Q' — любая строго внутренняя подобласть Q, оце-
оценивается постоянной, зависящей лишь от N, v, ц, ц1( ц3, q,
mes Q и расстояния Q' до S. Норма || u |f22)n мажорируется по-
постоянной, определяемой N, v, \i, ц,, ц3, q, mesQ и «нормой» S
в пространстве О2.
Доказательство этой теоремы близко к доказательству тео-
теорем 10.1 и 15.1 гл. III, в которых аналогичные факты устано-
установлены для одного уравнения второго порядка. Ввиду этого
мы только наметим общий план доказательства. Коэффициенты L
и функции f,, f аппроксимируем гладкими функциями, удовле-
удовлетворяющими условиям теоремы 5.1 при / = 2.<и сходящимися
к своим пределам в нормах, соответствующих предположениям
F.2) - F.4) или F.2), F.5).
Область Q также аппроксимируем монотонно расширяющи-
расширяющимися областями Qx cr Q2 cr ..., границы которых принадле-
принадлежат C2+v и удовлетворяют условию (А) с одними и теми же
постоянными а0 и Эо. (Для доказательства второй части тео-
теоремы 6.1 надо, чтобы «нормы» границ dQk, 6=1,2,...,
в пространстве О2 были равномерно ограничены.) В каждой
из О, рассмотрим краевую задачу
di(r)
LOu = -fO_-_L-, ul^-0. F.6)
Нетрудно показать, что, начиная с достаточно большого номера
аппроксимации г0, все они однозначно разрешимы в C+y(Qr),
r^r0. Для их решений и(Г), г^г0, теоремы §§ 1—4 дают рав-
равномерные оценки норм в ФгЩ, Ca(Qr), C1+P(Q'). W\{ur). Из
этих оценок следует, что для и( > существует предельная функ-
функция, эта функция есть обобщенное решение задачи F.1) и
16*

484 ЛИНЕЙНЫЕ СИСТЕМЫ УРАВНЕНИЙ ЭЛЛИПТИЧЕСКОГО ТИПА [ГЛ. VII
она принадлежит W\ (Q) П Са (Q) или W} (Q) П Са (Q) f] C1+p (Q') f]
П Wl (й) соответственно. В силу предположения о единственности
обобщенного решения задачи F.1) эта функция совпадает
с исследуемым обобщенным решением и(д;).
Такова схема доказательства теоремы 6.1.
Заканчивая данную главу, отметим, что для системы A.1)
можно было бы провести исследование краевых задач столь же
полное, как это сделано в других главах для одного уравнения
второго порядка. Но нам кажется, что изложенного здесь
вполне достаточно для того, чтобы читатель сам смог воспроиз-
воспроизвести все необходимые рассуждения.

Глава VIII
КВАЗИЛИНЕЙНЫЕ СИСТЕМЫ
В данной главе мы рассмотрим эллиптические системы вида
а„(лс, и)и? +а'(*,и,и,) = 0, 1=1, ...,N, @.1)
в которых неизвестна вектор-функция и(х) = (и1, ..., uN). При-
Пример системы (см. Хайнц [25])
<Риг
dx2
—[(¦?)'+(¦?)"]*
@.2)
которой удовлетворяют функции ul(x) = cos рх, и2 (х) = sin px,
указывает на невозможность получения априорной оценки
и даже нормы Гёльдера (и1, и2) через
max
0<х<2я
dx ' dx
max | и1, и21 для всех эллиптических систем вида @.1) при
0<х<2я
квадратичном росте функций
а'(*,и,р) по |р |=
2
Это является отличительной чертой систем, ибо в случае одного
уравнения вида @.1) такие оценки возможны и сделаны нами
выше при квадратичном росте а(х, и, р) по | р |. (Более высокий
рост по | р | недопустим уже и для одного уравнения второго
порядка.)
Однако если в системах @.1) члены из а1, растущие по | р |,
как | р р, имеют специальный вид, именно bt{x, u, р)р\, а остав-
оставшиеся растут медленнее | р р, то max|Vu| можно оценить
через max|u| и известные характеристики системы.
Иными словами, для систем вида
а{] (х, u) uXiXj + bt (х, и, их) uXi + Ь1 (х, и, их) = 0, @.3)
/=1, ..., N,
возможно оценить max|Vu| через max| u | при условии, что
коэффициенты bt(x,,u, р) растут при |р|-*-оо не быстрее | р |,

486 КВАЗИЛИНЕЙНЫЕ СИСТЕМЫ [ГЛ. VIII
а Ьг(х, и, р) — медленнее | р |2. Более же сильные нормы решений:
| и |(|+а>, | и |B+а) и пр. — оцениваются через max (| u |, | Vu |) для
а
всего класса систем @.1) без каких-либо предположений о функ-
функциях alt, а1, кроме условий соответствующей гладкости коэф-
коэффициентов и эллиптичности системы.
На основе этих априорных оценок будет исследована раз-
разрешимость в целом первой краевой задачи для системы @.3).
Лишь ради экономии места будем проводить все результаты
для случая однородного граничного условия
u|s = 0. @.4)
§ 1. Априорные оценки норм |u|Q'+a), 1^1,
через max | u, Vu |
а
Пусть и (а;) есть классическое решение системы @.1), т. е. и (л:)
принадлежит C2(Q) и удовлетворяет @.1). Предположим, что
нам известны величины М^тах\и\ и Af,]>max|Vu| и что
а а
функции пц {х, и) дифференцируемы по Xk и и . Тогда систему @.1)
можно записать в виде
-?г(аИ{х, u)uX]) + al(x,u,ux) = 0, 1=1,..., N, A.1)
где
dx{ xi duk xl xl dxi xl'
и функции а1 рассмотреть как свободные члены, для которых
известны оценки тах| а'(х, и(х), их(х))\^с (М, МЛ. Для каждой
функции и1, 1=1, ..., N, будем иметь свое уравнение дивер-
дивергентного вида с ограниченным свободным членом. Из результа-
результатов § 15 гл. III следует, что для каждой из и1 можно оценить
нормы \и%+а), Q'cQ, через
да-, dui
Мьс(М,МЛ, vrai max - '¦ ~' " 1
Q, |u|<M
дхк ' дик
и константу эллиптичности v(M) из неравенства
\)V!. A.2)
После этого от A.1) вернемся к системе @.1) и рассмотрим ее
как набор отдельных уравнений, для старших коэффициентов

§ 1] АПРИОРНЫЕ ОЦЕНКИ НОРМ | u ||j+a), l>\ 487
ац (х, и (л;)) и свободных членов а1 (х, и (*), их (х)) которых известны
оценки норм в Ca(Q). Теоремы §§ 12 и 1 гл. III гарантируют
принадлежность и к C2+a(Q) и дают оценку | и1 ^,+а) через
известные нам величины. Рассуждая таким образом и далее,
получим оценки | и1 |^+а) для любых k^z2. В указанных пара-
параграфах гл. III исследовано поведение решений и получены соот-
соответствующие оценки и для замкнутой области Q. Из результа-
результатов этих параграфов вытекают следующие предложения:
Теорема 1.1. Пусть и(х) есть решение системы @.1), при-
принадлежащее С2(Q) с тах| и(л:) \^М, тах| Vu |^Af,, и система@Л)
Q Q
Q
эллиптична на нем, т. е.
ч?^аИ(х,и(х))Ы,^1112. A.3)
Пусть в М = {л:, и, р: *e=Q, | u |<M, I p |<Mi} функции аи{х, и)
дифференцируемы по хк и и1 и они, их частные производные
по хк и и1 и функции al(x, и, р) измеримы и ограничены какой-
либо постоянной М.2. Тогда нормы | и*г|(а), /= 1, ..., п, VQ'cQ,
при некотором а > 0 можно оценить только через величины N,
М, М\, М2, v и расстояние ?У до S.
Если к тому же ц g С2 (Q), и |s = 0 и S е С2, то нормы ] uX[ |(a)>
1 = 1, ..., п, оцениваются постоянной, зависящей от N, М, М\, М2,
v и S. Показатель а в обоих случаях определяется отношением ц/v
из A.3).
Теорема 1.2. Пусть и(х) есть решение системы @.1), при-
принадлежащее классу ck+2+® (Q), k ^0, и система @.1) эллиптична
на нем, т. е. выполнено неравенство A.3). Пусть функции aCj(x, и),
al(x, и, р) принадлежат классу Ck+^(Tt), где Ж определено
в теореме 1.1.
Тогда нормы \ и |^,+2+Р), V&' с ^. можно оценить только через v,
W, М, М\, | и $~а\ Q' с п" с Q, расстояние от Q' до границы
подобласти п" и нормы ац(х,и) и а'(х, и, р) в пространстве
С*+Р(ЭЯ)
Если к тому же и (х) «= Cft+2+e (Q), и |s = 0 и Sg Ck+2+ p, то
норма | и |^+2+w He превосходит постоянной, зависящей от v, N,
М, Мх, | и ^+а), норм ац(х, и), а1 (х, и, р) в пространстве Ch+9 (Ш)
и от S.

488 КВАЗИЛИНЕЙНЫЕ СИСТЕМЫ [ГЛ. VIII
§ 2. Оценка |u|{,e)
Все дальнейшие оценки и рассуждения будем проводить для
систем вида @.3), предполагая, что при л;е Q, | u \^М и произ-
произвольных р выполнены неравенства
v (М) |2 < аи (х, u) Ui ^ И Ш) I2, B.1)
IM*,u,p)|<|i(Af)(l + |p|), B-2)
I Ь (х, и, р)К [е (М) + P(p,M)]{l+\p P), B.3)
B.4)
Здесь b (л;, и, р) = (Ь1 (х, и, р), ..., bN {х, и, р)); е (М) — достаточно
малая величина, определяемая лишь N, М и v(Af), a P(p, Af)->-0
при [ р |—> оо. Из сказанного выше ясно, что ограничения B.1) —
B.4) вызваны существом дела.
Пусть и(л:) есть решение системы @.3), принадлежащее
классу C2(Q), и max|u|^M. Покажем, что и принадлежит
классу 58^ (Q, Mv б,, б2, б3, y. Y(. б, 1/^), параметры которого
определяются известными нам величинами. Учитывая лемму
8.4 гл. II, введем 2N функций
<tl+(u)=l0Nvl+v, <fl_(u)
где vl = BM)-l(ul + M), v = (o', ..., vN), o=|v|2, и покажем,
что функции wl± (x) = ф'± (и (а;)), /=1, ..., N, удовлетворяют
неравенствам, входящим в определение класса ЭЗ^1 с JV(=2iV.
Умножим систему @.3) скалярно на вектор — ч (а;) е W2 (й)
и проинтегрируем по Q. После интегрирования по частям
в первом члене получим
J [
(х, и) ихрХ] + (-^— b) ихр - Ьч] dx = 0. B.5)
1озьм*м т) — Bи + lOiVe*) Ф (х), где Ф(х) т W\ (Q), а е1 — IV-
мврный вектор вида вг = @, ..., 0, 1, 0, ..., 0) с 1-я компо-
компонентой, отличной от нуля. Подставив этот вектор tj в B.5),
запишш результат в виде
J [М-1а{1(х, и) их их ф + 2Matjwl+x Фх + 2Mctwl+x Ф + с'+Ф] dx «= 0,
B.6)

J21 ОЦЕНКА | ui'q' 489
Положим в B.6) Ф(х) = ?2(х) max [w\ (x) — k,0], где ?(*) —
срезающая для шара Кр с Q функция. Тогда
Maltuxux (wl+ — k)?,2-
• p
Здесь Лй р — множество точек х из шара /Ср, где wl+ (x) > k.
Левую часть оценим снизу, используя условие эллиптичности
B.1), а правую часть оценим сверху, используя предположения
B.1) —B.4). Малость величины е (М) + Р (р, М) в B.3) при
больших | р | используем для того, чтобы оценить сверху пра-
правую часть в неравенстве
1 Af)] A +! иж р)
через М'Ч (М) \их |2+ с, с какой-нибудь постоянной с,. Ясно,
что для этого достаточно, чтобы
A + 11ЛГ) в (М) < Af-'v (Af). B.8)
Постоянная с( при этом будет зависеть от Р(р, Af).
В результате всех этих оценок, аналогичных тем, которые
мы проводили неоднократно выше (см., например, § 1 гл. VI),
придем к неравенствам
^ft,p
B.9)
для всех уровней k, удовлетворяющих условию max (wl+—
kp
где б — достаточно малое, но фиксируемое по известным нам
величинам положительное число, М^ llN^max\wl.\.
Q
Такие же неравенства B.9) выводятся и для wl_, 1=1', . •., N.
Из этих неравенств вытекают неравенства (8.3) гл. II, входящие
в определение классов ЭЗг^1 с Ni=2N. Таким образом, мы
доказали, что и принадлежит ftf (Q, Ми ..., 6,0) и его пара-
параметры определяются известными нам величинами.
Для оценки | и |(а) во всей области Q надо доказать, что
и е Ъ22М (Q, М и ..., 6,0). Возьмем произвольный шар КР, пере-
пересекающий границу S. В нем для ад = ад/± верно B.7), а потому

490 КВАЗИЛИНЕЙНЫЕ СИСТЕМЫ [ГЛ, VIII
и B.9), если только уровень k подчинить условию k^2smax.w(x)>
3>ns
k ^max w {x) — ЬМХ. Это и показывает, что и е $дТ (Q, ..., 0).
крпа
3^
Отсюда и из свойств функций классов 23^@, ...), ^iN (Q, ...)
следует
Теорема 2.1. Пусть u(jc)eC2(Q), max| u(а;) |<!М и и(х)
удовлетворяет системе @.3), для коэффициентов которой выпол-
выполнены неравенства B.1) —B.4) пои x^Q, | и \^М = тах| и (а;) |
и произвольных р, причем постоянная г{М) в B.3) подчиняется
неравенству B.8). Тогда для любой внутренней подобласти Q'cQ
норму | и |[°* можно мажорировать постоянной, определяемой
величинами N, М, v(M), \i(M), &{M), P(p,M) из B.1) —B.4) и
расстоянием Q до S. Показатель а определяется этими же
величинами, кроме расстояния ?У до S. Если и к тому же при-
принадлежит Lip(Q) и S удовлетворяет условию (А), то для и
можно оценить \ и (^ через N, М, \(М), ц(М), е(М), Р(р,М)
из B.1) — B.4), норму |и?, Р и постоянные а0 и 0О, входящие
в условие (А). Показатель а определяется N, M, v(M), \i(M),
е(М), Р(р,М), р и е„.
Заметим, что утверждения теоремы, так же как и в случае
одного уравнения из гл. IV, верны и для обобщенных решений
системы @.3) из пространства W2 (й). Однако мы во всей этой
главе ограничим себя рассмотрением лишь классических реше-
решений. Теория обобщенных решений системы @.3) строится анало-
аналогично тому, как это сделано в гл. IV для одного уравнения
с дивергентной главной частью.
§ 3. Энергетическое неравенство и оценка max|Vu|
на границе
о .
Пусть ugIFHQ) удовлетворяет тождеству B.5) с ограничен-
ными т)(л:)из Щф) и vrai max | u К М. Пусть относительно
и
системы @.3) выполнены те же условия B.1)—B.4), что и в § 2.
Тогда для любого шара Кр имеет место оценка
Vuprfx<c, C.1)
J
крпа
где с определяется лишь известными постоянными из B.1) —
B.4), Nap. Действительно, возьмем в B.5) т) = 2u (tlv — 1 К2,

§31
ЭНЕРГЕТИЧЕСКОЕ НЕРАВЕНСТВО
491
где v = | и |2, X > 0 — большой числовой параметр, а ? (л:) — сре-
срезающая для К2р функция. Это дает
л
- I)?2
2Р
+
[ ^7 - b' } v*t
- 1) S2 - 2 bu (**» - 1) ф* = 0. C.2)
Учитывая наши предположения B.1)—B.4), в том числе до-
достаточную малость г{М) в B.3), и выбирая X достаточно боль-
большим, из этого равенства получим оценку C.1).
Итак, доказана
Лемма 3.1. Пусть ueliH(Q) удовлетворяет тождеству B.5)
о .
с T)<=1F2(Q), vrai max | т) | < с» и vrai max | и | ^ М. Пусть отно-
и а
сительно системы @.3) выполнены те же предположения, что и
в теореме 2.1. Тогда для и и любого шара Кр справедлива
оценка C.1) с постоянной с, зависящей лишь от N, М, р и
мажорант из B.1) —B.4).
Займемся теперь оценкой | Vu | на S. Докажем, что имеет
место
Лемма 3.2. Пусть и есть решение системы @.3) из С2(Q)П
П C'(Q) с max|u|sSCAf, равное нулю на S, а для @.3) спра-
ведливы неравенства B.1)—B.3), C,5). Тогда max| Vu | оценивается
s
постоянной, зависящей лишь от N, М, величин v(M), \i(M),
е(М), Р(р, М) из B.1) —B.3) и S, которая предполагается
принадлежащей О2.
ди 11
По условию u |s = 0, следовательно, | Wul \ \s = -^- , где
-rj- есть производная по внешней к S нормали. Возьмем точку xQ
на S и номер г из 1 JV такие, что
дп
= max max
*• 1=1, .... N S
ди1
дп
диг
Пусть для определенности -^— < 0. Тогда возьмем функцию
СП Yn
wr = ur + v s ur +1 u р. IВ случае
функцию — ит + v.) Для нее -J^-
> 0 надо рассмотреть
диг
дп
. Из @.3) следует,
что Z/(u) + 2 2 ulLl(u) = 0, где Lr(u) есть левая часть г-го

492 КВАЗИЛИНЕЙНЫЕ СИСТЕМЫ [ГЛ. VIII
уравнения системы @.3). Это равенство можно записать в виде
аа (*> «) Ktxj ~ 2ац\иХ] + btKt + сг = 0. C.3)
где ст = 2Ь (х, и, их) u-\-br (x, и, их). Введем вместо дог функцию vr
с помощью равенства дог = ф@г). Функцию ф(г/) выберем ниже,
но так, что ф'(г/)>0. Подставим в C.3) вместо wrx величину
ФV , а вместо до' „ величину т'& + ф"оС. о' и полученное
равенство поделим на ф'. Это дает
Отсюда в силу предположений B.2), B,3) будем иметь
- aiPxixi ~$ Wx/x, + jratJuxuXj <
^ ). C.4)
Если е (М) таково, что
BAf+l)e'(A0<v(Af), (З.б)
то из C.4) легко выводится неравенство
с известной нам постоянной с.
Подберем функцию ф(г/) так, чтобы
v(M)<*p0, Ф@) = 0,
где v(M) взято из B.1), а с —из C.6). Этим условиям удо-
удовлетворяет функция
При такой ф(г/) неравенство C.6) дает
Функция vr, так же как и дог, равна нулю на S, и -^-
' — с достигает своего минимума на S
an
в той же точке х0, что и -—-. Построим какую-либо барьерную

* 4) ОЦЕНКА max | vu I 493
функцию яр(я), т. е. функцию, удовлетворяющую соотношениям
— a.j(х, и) tyx х < — с, max op (х) = яр (л:0).
* I S
В качестве такой функции можно взять, например, функцию
¦ф (х) = те~ш w с достаточно большими X и m и с дважды
непрерывно дифференцируемой функцией Ф(л:), обладающей
следующими свойствами:
1) Ф(л:)>0 в Q;
2) |VO|>const>0 в Q;
3) поверхность Ф(л:) = 0 содержит точку хо.
Если область Q расположена вся по одну сторону от пло-
плоскости, касающейся S в точке х0, — пусть это будет плоскость
хп = х°п—и Q лежит в полупространстве {хп^х°Л, то в каче-
качестве Ф(л:) можно взять Ф (*) = *„ — х°п. В противном случае
надо с самого начала преобразовать область Q так, чтобы она
располагалась по отношению к точке х0 указанным образом.
Для функции vr (х) + яр (а;) — atj (vr + ip)^ x < 0. Следова-
Следовательно, ее максимум достигается на S. Но max (vr + яр) = max яр =
s s
= г|>(л:о), и потому
d(vr+ty)
Это в силу соотношений -~ =
дп
¦vg >— *_»
ди'
dv ' — ' ~~ и max max
диТ I
д— дает нужную
on \Y
max max
i=\ N S
дЛ_
дп
диг
дп
an
Хо
S i=] N S
да
v(Af)
дп
Xl
Лемма 3.2 доказана.
§ 4. Оценка max| Vu ,
а
Пусть и(х) есть решение системы @.3). В §§ 2—3 для него
были получены априорные оценки | и I!?', || и ll'^, max|Vu| через
s
max|u| и известные величины. Общая схема их получения та
а
же, что и для одного уравнения второго порядка с дивергент-
дивергентной главной частью, но аналитические факты, лежащие в основе
оценки | u |ja) (свойства классов 23№), более сложные. Дальней-
Дальнейшие оценки для и, именно оценки max | Vu | и max | Vu |, можно
а' а

494 КВАЗИЛИНЕЙНЫЕ СИСТЕМЫ [ГЛ, VIII
провести почти так же, как и для одного уравнения в §§ 3, 4
гл. IV. Поэтому мы дадим лишь основные указания, не про-
проводя подробного вычисления всех постоянных. Итак, докажем
теорему:
Теорема 4.1. Пусть выполнены все условия первой части
теоремы 2.1. Тогда max|Vu| для любой 2'с2 оценивается
через те же величины, что и | u fg) в теореме 2.1, и mesQ. Если
к тому же ugC2(Q), S^O2, u|s = 0 и верно C.5), то можно
оценить max| Vu | постоянной, зависящей лишь от N, Af^maxl и |,
q а
постоянных из условий B.1) —B.4), mesQ и S.
Положим в B.5) л = — ("**?) - гДе К*) —Дважды непре-
рывно дифференцируемая в Q функция, равная нулю на S
вместе со своими производными первого порядка, и получен-
полученные равенства просуммируем по k в пределах от 1 до п. После
очевидных интегрирований по частям придем к тождеству
fL u
J I 'У *
О L
т\- ь>\ ~ь) (Au| +u* A)]dx=°'
D.1)
где K = |Vu|2.
Положим в D.1) | = 2KS?2, где t,{x) — срезающая функция
для шара Кр с Q, а Vs есть s-я степень V hs = 0, 1, ... Пер-
Первые два члена подынтегрального выражения дадут основные
положительные члены. Их мы оставим слева и оценим снизу,
а все остальные перенесем в правую часть и оценим сверху,
используя предположения B.1) — B.4). Это приведет нас к не-
неравенству
< с E) J (Vs+l | V? f + Vs+\2 + S2I 4 I2) dx D.2)
с некоторой постоянной c(s), зависящей от известных нам
констант и числа s (при s->oo c(s)->oo).

§ 4) ОЦЕНКА max | vu I 495
С другой стороны,
КР
Kp
= - J (u - uo) [Vs+\2 Au + (s + 1) K^2uXft2 (u*puvj +
v f ["„.+2,2 ,
C2 + V*+l I VC П rf*. D.3)
ft=l J
Если в качестве и0 взять значение и в центре шара Кр, то
в силу теоремы 2.1
max | и — u01 ^ сра, а > 0. D.4)
Выбирая р достаточно малым (так, чтобы cci(s)pa<l),
из D.3) получим
j Vs+\2 dx < ClPa j \vs J] | Vu,ft f S2 + K^+11 V? |21 dx. D.5)
Kp Kp L *-l J
Это неравенство вместе с D.2) дает при всех малых р
2 SIVu**Г ^C2 + Vs+\2] dx^ c2(s) J (K5+11 V? P +
+ |VS|2 + S2)d*. D.6)
Неравенства D.5), D.6) справедливы для s = 0, 1, ... Они
вместе с исходным неравенством C.1) позволяют последова-
последовательно по s дать оценки
\VS+Idx^c(s, Q0 D.7)
для любой подобласти Q'cQ и любого s = 0, 1, ...
Дальнейшие рассуждения также близки к соответствующим
рассуждениям § 3 гл. IV. Именно, возьмем функцию
w(x)=V(x)Z,2 = \Vu\42,
где ? (я) — срезающая функция для какой-либо &' с Q, и рас-
рассмотрим равенство

496 КВАЗИЛИНЕЙНЫЕ СИСТЕМЫ [ГЛ, VIII
где L (и) — левая часть системы @,3), а ЛА — множество точек
xczQ', в которых до(*)>А,^0. После ряда преобразований и
оценок, аналогичных сделанным в § 3 гл, IV, и учета неравенств
D.7) получим
J|Vw|2rfje<c,mes1-ei4x D.8)
Ак
со сколь угодно малым е (но с се->-оо при е->¦()), Для оценки
max до достаточно, чтобы е в D.8) был меньше 2/п, а для этого
Q' Г Зп 1
надо использовать D,7) с s^ -=- + 1- При таком е из
леммы 5,3 гл, II следует, что до ограничена в Q' сверху кон-
константой, зависящей лишь от е, се, ||до||, Q, и mes Q'.
Из всего сказанного следует справедливость первой части
теоремы 4.1, Осталось провести аналогичную оценку в окре-
окрестности границы. Величина max|Vu| = M2 нам уже известа из
s
леммы 3.2, Оценка II и ||^>а дана для всей области Q. Надо до-
доказать D.7) для шаров ^р, пересекающихся с границей S, точ-
точнее, для пересечений Кр с Q. Для чисел s>l мы получим
неравенства D,2) — D,6) так же, как и выше, если только в D.1)
вместо ? = 2К*?2 подставим
(*). V(x)>Ml
0, V(x
Это допустимо, ибо такое | равно нулю на всей границе
области интегрирования Кр П й. В случае же s = 0 возьмем в D.1)
l
V (х) < Ml
Это после ряда преобразований и оценок, аналогичных сделан-
сделанным в § 4 гл. IV для случая одного уравнения, приводит
К оценке D.7) по /Ср f) Q, а следовательно, и к оценкам
s+ldx^c(s), s = 0, I max|Vu|<const.
й
Теорема доказана.
Замечание 4,1. Если в теореме 4,1 предположить изве-
известной оценку |и|(ц\ то в неравенстве B,3) е(М) можно считать
произвольным числом, так что max|Vu| можно оценить для
любой системы вида @.1) с квадратичным ростом функций
а1 (х, и, р) по | р |.

J 5] ТЕОРЕМЫ СУЩЕСТВОВАНИЯ 497
§ 5. Теоремы существования
Полученные в §§ 1—4 для решений систем @.3)
L (u) s ач (х, и) uXiX] + bi (x, и, их) uXl + b (х, и, их) = 0
априорные оценки позволяют исследовать разрешимость в целом
первой краевой задачи для @.3) (по поводу других краевых
задач см. гл. X и [I]). Мы не будем приводить здесь
формулировки результатов в той общности, которая дана в § 10
гл. IV (они такие ж*, как и для одного уравнения), а огра-
ограничимся одним из конкретных включений параметра т в си-
систему @.3) и одним из тех случаев, когда можно дать эффек-
эффективную оценку max|u|. Именно, рассмотрим семейство систем
а
E.1)
зависящее от параметра те[0, 1], где
L0(u) = Au — u.
Предположим, что для E.1) выполнены условия
ац(х,
0 | и |>#х s Q VP « EnN.
Ь (х, и, р) u = bl (х, и, р)и' < 0, | и |>#, х s Q, VP « En ) { ' '
Тогда, как нетрудно видеть, для любого классического реше-
решения и(х, т) системы E.1) верна оценка
max|u(*, т)|<М = тах(тах| u|, r\ . E.3)
a is)
Действительно, умножим E.1) скалярно на 2u и результат
запишем в виде уравнения для о = |и(л:, т)р:
[A - т) б/ + та,, (х, а)] [^ - 2иЯ|Ия/] +
+ т6,-^-2[A-т)о-тЬи] = 0. E.4)
Если v(x) достигает своего максимума в какой-нибудь внутрен-
внутренней точке JCoeQ и v(х0) > Я2, то в этой точке vx. = 0, первый
член из E.4) неположителен, а последний—отрицателен в силу
условия E.2). Полученное противоречие доказывает E.3).
После того, как оценен max | u (х, т) |, мы можем получить
Q
все дальнейшие оценки для и(х, т) при условиях, сформули-
сформулированных в §§ 1—4, если заметим, что эти условия (неравен-
(неравенства B.1)—B.4)) будут справедливы и для всего семейства Lx(u),
t«[О, 1], с положительными постоянными, не зависящими от т..

498 КВАЗИЛИНЕЙНЫЕ СИСТЕМЫ [ГЛ, VIII
В частности, эти постоянные определяют оценку сверху max| Vu |
Q
для всех возможных решений и(х, т) системы E.4), равных
нулю на S:
max| Wu(x, т)|<М,, те [0,1]. E.5)
Q
Все это дает возможность утверждать справедливость следую-
следующей теоремы:
Теорема 5.1. Пусть при х е Q, \ и |> R и \/p^EnN выполне-
выполнены неравенства E.2). Пусть при xgQ, | u |^М, где М взято из
E.3), и произвольных р выполнены неравенства B.1)—B.4) с
е(М), подчиняющимся условиям B.8), C,5). Пусть на множестве
Ш = {х <= Q, | и | ^ М, | р | <; MJ, где Mi взято из E.5), функции
bi(x, u, р), Ь(х, и, р) непрерывны по Гёльдеру с показателем {5
«Sg C2+p. Тогда система @,3) при условии u]s = if <= C2+\S)
имеет по крайней мере одно решение u<=C2+p(Q). Если к тому
же atj, bt и Ъ на 3R принадлежат классам Ck+$CR), k^l,
& и S s Cft+2+&, го решения и будут принадлежать
§ 6. Вырождающиеся системы
Остановимся на изучении одного класса квазилинейных систем
6,и, u)^. + 6'(^. u) = 0, / = 1 ^V, F.1)
допускающих вырождение эллиптичности при|и| = 0. Именно,
предположим, что здесь аи{х, u), bt{x, и), bl(x, и) —скалярные
функции х <= Q, це?„, непрерывные относительно и и удовле-
удовлетворяющие условиям
v(\u\n2^au(x, u)hti<»v(\ix\n2, Vl^^n, F-2)
п IN \ 1/2
[v (I u I)] S | 6, (*, u) |2 + (^ I &f (л:, u) |2J < v (| u |) ф (x), F,3)
<f{x)eLq/2(Q), q>n, F.4)
где ц — постоянная, a v(/) — непрерывная неотрицательная воз-
возрастающая функция t e [0, оо) такая, что при некотором X > 0
(*,), V^2>^.>0, F,5)
и v(/) >0 при ^>0.
Для решений системы F,1) установим сначала априорные
оценки норм |и^ в любой подобласти Q'cQ и в Q'=Q,
а затем с помощью этих оценок исследуем разрешимость задачи

$ 6] ВЫРОЖДАЮЩИЕСЯ СИСТЕМЫ 499
Дирихле для F,1) в классе непрерывных по Гёльдеру функ-
функций. В нижеследующих двух теоремах мы предполагаем, что и(х)
есть ограниченное обобщенное решение системы F,1) из
класса W\>(Q), т. е. что для любых х\(х) из WliQ) выполняется
интегральное тождество
J \ач(х, u) ux4\Xt - bi (х, и) ихч\ - Ы(х, и)tj] dx = О, F.6)
/=1 N.
Теорема 6,1. Пусть при х е= Q и \и\^.М выполняются
F.2)—F.5) и и(х) есть решение из ^(Q) системы F.1)
с vrai max| и |^М, Тогда и(х) принадлежит Ca(Q) с некото-
Q
рым а > 0, определяемым величинами N, К, ц и q. Для любой
Q' с: Q норма | и |^ оценивается сверху постоянной, зависящей
лишь от N, К, ц, q, M, || ф \\ф Q и от расстояния Q' до S.
Если к тому же S удовлетворяет условию (А) и ueff (S),
то ueC°(Q) с а, зависящим от N, к, ц, q, р и постоянной 60,
входящей в условие (А), и норму | и |д можно оценить через эти же
постоянные и величины М, \\ ф || /2 Q, | и |s и а0.
Для доказательства проверим, что и(х) принадлежит
классу f&m, введенному и изученному в § 9 гл. И. Линейные ком-
бинации вида w(x)= 2 clul{x) с 2(с'J<[1 в силу F.6) удо-
удовлетворяют тождеству
Jul
fliy (х, и) wXj4Xl - bt (х, и) wx.r\ - clbl(x, и) i\]dx = 0 F.7)
а
при Vti<= \v2(Q). Подставим сюда ц = wik)(x)t(*)> где t,{x) —
произвольная срезающая функция для шара Кр, k — любое
число в случае /Со с: Q и k ^ vrai max w {x) в общем случае.
p
Производя в полученном равенстве оценки с помощью условий
F,2)—F.5), придем к неравенствам
I
maxv (| u |)[y f (w - kf\ V? f dx + y, mes'-2/Mft, p] F.8)
с у =
, Yi = DM2+1)||ф||2/2 Q, из которых следует, что
, v(^), M, y> Yi. l/<7)- Учитывая условие F.5), на

500 КВАЗИЛИНЕЙНЫЕ СИСТЕМЫ (ГЛ, VIII
основании теоремы 9.1 гл. II заключаем о справедливости
утверждений теоремы 6.1. __
Теорема 6.2. Предположим, что при х <= Q и \fu e EN функ-
функции ац(х, u), bi(x, и), b'(x, и) подчиняются условиям F.2)—F.5).
Тогда для любого ограниченногЬ обобщенного решения и(х)
из W\(Q) системы F.1) и VQ'cQ величина vraimax|u| оцени-
оценивается сверху постоянной, зависящей только от v A), А, ц, q,
|| Ф 11^2 Q, Г | и |2v(| и \)dx и от расстояния Q' до границы Q,
Q
a vraimax|u| оценивается через v A), %, ц, q, ||ф|1в/2и,
Г | и рv(| и \)dx и vraimax|u|.
Q S
Доказательство. Пусть сначала Кц с:Q — произволь-
произвольный шар, такой, что концентрический ему шар Kjr/2 лежит
в Q', ? (*) — срезающая функция для KR, Полагая в F.6)
г\ =-рт1 и |(*Ч2. k > 1, и производя суммирование по / от 1 до N,
придем к соотношению
а'u •"'u
Отсюда с помощью условий F,2)—F.5) выводим
<2 | v(|u|)[4{x|VSp(|uM:J +
+ 2(| u \-kf<t(x)$2+ф(х)mdx.
Рассмотрим функцию о(*) = Ф(| и(*) |), где Ф(/) = / Vv (t).
Легко видеть, что условие F.5) гарантирует оценки
\)\\u
\X(\
о
I
u(x)\-k) J /v(t| u(x) I) dt>2~il+2)l2(\ u(x) I—jfe)/v(l u (x) D;
1/2

f 9| ВЫРОЖДАЮЩИЕСЯ СИСТЕМЫ 601
поэтому из неравенств F.9) следуют аналогичные неравенства
для функции v (х):
[
Ак, R Ак, R
+ II (v - к) I \f2q/{q_2)i Ak R + k2 mes'-2/Mft, R], Vk > У^Щ, F.10)
где с, - 2^{Х + 2J ({х +1| Ф ^ д Q), Л, ,= {хе^ч (а:) > k). Если
шар Кц пересекает границу Q, то при выводе F.9) надо счи-
считать &^vraimax|u| и соответственно неравенства F.10) будут
Kns
выполняться при 6^тах{уЧA); vrai max v]. Воспользуемся оче-
KRns
видной оценкой ^2mes Л4#/г^ Г v2dx и неравенством B.13) гл. II:
Q
II (v-kKh,M-2>. AktR<c mes^"TAk,R|| V[(v - k)?]|^ ^ R.
Ясно, что отсюда и из F.10) при /djcQ и
6 > А:о = max |DС2С,Г/4('-п) ( J | и р v (| и |)
следуют неравенства
''ft, R Ak, R
( — -— \
с y = 2ci\1 +2c2mesn i KrJ- В общем случае эти же неравен-
неравенства справедливы для V& > max{^0; vraimaxo}.
snK
Итак, доказано, что функция v (x) принадлежит классу
Ц*. Y. 2, 2,-|—-|,^), где ^ = ^0. если Кк <= Q. и ? =
= max {^0; vrai max о} в случае произвольного шара Кк. При-
меняя к v(x) теорему 5.3 гл. II, приходим к оценке vraimaxo
UR/2
сверху через постоянную, зависящую лишь от у, q, it и
#~n|| v II2, Q = R~n Г | u ? v(| u |) dx. Отсюда следуют и желаемые
Ч
¦ оценки для vrai max| u | и vrai max| u |.
Q' Q
Рассмотрим вопрос о разрешимости задачи Дирихле для
системы F.1), считая, что функции aij(x, u), bi(x, и) и bl{x, и)

502 КВАЗИЛИНЕЙНЫЕ СИСТЕМЫ [ГЛ. VIII
подчиняются условиям E.2), F.2), F.3) с ipeL^fQ) и v@)=0.
Пусть граничное условие имеет вид
u|s = *(s). F.11)
Функцию и (х) будем называть обобщенным решением за-
задачи F.1), F.11), если: 1) и(х) принадлежит Ср (Q) с каким-ли-
каким-либо р > 0 и удовлетворяет условию F.11); 2) на множестве Ао =
= {*<= Q: |u(jf)| > 0} и(х) обладает обобщенными производными
первого порядка и f v (| и |) | их f dx < °о; 3) при Vti е= #2 (Q) u (*)
A,
удовлетворяет интегральному тождеству F.6), в котором вы-
выражения v(| и(х) |) и*, (х) считаются равными нулю при |u(*)| =0.
Теорема 6.3. Пусть выполнено условие E.2), S удовлетво-
удовлетворяет условию (A), ij> <= Ca (S). Предположим, что на множестве
Ш = {х, u: «gQ, ue?lV; |и|<М}, где М — постоянная из
оценки E.3), функции ац(х, и), bi (x, и) и bl(x, и) принадлежат
классам С1+а (Ж), Са (Щ) и Са (Ш) соответственно и подчиняются
неравенствам F.2), F.3), в которых фе!м (Q), a v (t) — не-
непрерывная возрастающая функция t е= [0, оо), равная нулю
при t = 0 и удовлетворяющая условию F.5) с X > 1 + а. Тогда
существует обобщенное решение задачи F.1), F.11).
2 2+
Предположим сначала,
смотрим невырожденные
Ly = (atfux) +b\*ux +
что S e
системы
¦ 6<Т)'= 0
С2
+a и
/ =
г|зб
1, •
... Л^
E),
и
(О
F
рас-
>0),
.12)
где atf = х6{ + а.. (х, u),b^ = bl(x, u), b{x)' = bl(x, и). Они удо-
удовлетворяют всем условиям теоремы 5,1, и потому при Vt > 0
существует решение uT (x) e= C"+a (Q) задачи F.1), F,11), причем
для ит в силу E.3) и теоремы 6.1 верны равномерные относи-
относительно tg@, 1] оценки
max|uT(*)KM, \щ(х)№*?С1, F.13)
Q
JT + v(|ut|)]|ut,F<fo<c2. F.14)
Отсюда следует, что т Г и[хц1х dx^>0 при т->-0 и существует
Q
подпоследовательность хт (сохраним за ней то же обозначение)
такая, что функции Yv (| их \) и\х сходятся слабо в L2(Q) к неко-
некоторым (x>lt(x)eL2(Q), причем на множествах Ak={x^Q; \u(x)\ >k},

§ 6] ВЫРОЖДАЮЩИЕСЯ СИСТЕМЫ 503
\fk > 0, а следовательно, и на Ао со'= У%(| и \)и'х_. Переходя
к пределу по тт-»-0 в интегральном тождестве, соответствую-
соответствующем F.12), F.11), получаем
/Г ац{х, u) bt(x, и) 
, -co'/if ¦\--7==®Ы + bl(x, и)r\l\dx=Q, 1=1,,..,N.
L Kv(|u|) ' xi Kv(|u|) J
Q F.15)
Здесь подынтегральное выражение в силу F.2), F.3) равно нулю
при х (= Ао, и, следовательно, F.15) равносильно интегральному
тождеству F.6), если в последнем область интегрирования Q
заменить на Ао. Легко видеть, что и (я) удовлетворяет всем
требованиям, накладываемым на обобщенное решение задачи
F.1), F.11).
Мы доказали теорему 6.3 при дополнительном предположе-
предположении о гладкости S и i|)(S). Эти ограничения нетрудно снять,
рассуждая так же, как при доказательстве теоремы 10.7 гл. IV.
Предположение X > 1 + а в теореме 6.3 связано с условием
ац{х, и)е С1+а(ЗК), которое использовалось для доказательства
разрешимости задачи F.12), F.11). Если в условии F.5) считать
А,<!1, то, очевидно, функции ац(х, и) не будут обладать не-
непрерывными по Гельдеру производными при и = 0. В связи
с этим представляет интерес следующее предложение:
Теорема 6.4. Предположим, что alt(x, u) = alt{x, | u |),
bt (x, u) = bt (x, | u |), bl (x, u) = b(x, | u |) и1, причем b (x, t) > 0
при t> R. Пусть выполнены условия F.2), F.3), F.5) cipeL^(Q),
VA, > 0 и непрерывной возрастающей функцией v (t), равной нулю
при t = Q. Тогда, если S удовлетворяет условию (A), iteCa(S)
и если функции ait{x, t), bt(x, t) u b(x, t) принадлежат классам
C1+a, Ca и Са соответственно на множестве Q X @. М\ (М—по-
(М—постоянная из E.3)), то существует обобщенное решение задачи
F.1), F.11).
Для доказательства этой теоремы параметр т > 0, снимаю-
снимающий вырождение системы, включается в F.12) следующим обра-
образом: a(if (x, u) = aij {x, |/|ир + т), и аналогично определяются
Ь\х\ Ых). Предварительно функции atj{x, t), bt{x, t) и b(x, t) надо
доопределить на множестве п X Ш, М + е), е > 0 так, чтобы
сохранялись свойства их гладкости, а Ь было бы на нем поло-
положительным. Тогда для т из @, е] существуют решения их(х)
задач F.12), F.11), для них верны равномерные по т оценки
F.13) и равномерно ограничены интегралы J v (| uT |) | ихХ |2 dx.
и
Отсюда так же, как в теореме 6.3, выводится сходимость ит
к обобщенному решению задачи F.1), F.11),

Глава IX
О НЕКОТОРЫХ ДРУГИХ ПРИЕМАХ ПОЛУЧЕНИЯ
ОЦЕНОК КОНСТАНТ ГЁЛЬДЕРА ДЛЯ РЕШЕНИИ
И ИХ ПРОИЗВОДНЫХ
В этой главе мы прежде всего дадим другой способ полу-
получения оценок констант Гёльдера для решений (и их производ-
производных) линейных и квазилинейных уравнений с дивергентной
главной частью и для производных от решений общих квази-
квазилинейных уравнений при тех же минимальных предположениях
об образующих уравнения функциях, при которых это было
сделано в предыдущих главах.
Более того, мы объединим вместе обе трудности: неограни-
неограниченные особенности по х коэффициентов в случае линейных
уравнений и нелинейности (по и и р) в случае квазилинейных
уравнений с дивергентной главной частью, рассмотрев уравне-
уравнения вида .
-к- (а, (х, и, их)) + а (х, и, их) = О @.1)
с функциями at (х, и, р), а (х, и, р), имеющими особенности не
только при и и р, равных °о, но и при х е Q. Для того чтобы
были возможны обсуждаемые здесь априорные оценки, эти
особенности функций а( и а по х, и и р должны быть согла-
согласованы друг с другом. Общая тенденция такова: чем сильнее
нелинейности, тем слабее должны быть особенности по х. Рас-
Рассмотренные в гл. III и IV уравнения представляют собой два
крайних случая: 1) когда at (x, и, р) и а(х, и, р) линейны по
и и р и имеют по х максимальные возможные особенности и
2) когда a-i (х, и, р) и а (х, и, р) ограничены по х и имеют мак-
максимальный рост по и и р.
Из результатов по оценкам констант Гёльдера, которые бу-
будут доказаны здесь, соответствующие результаты гл. III и IV
получаются как два частных (крайних) случая. Такого же типа
обобщение дадим и для квазилинейных уравнений общего вида.
Все эти обобщения, как указывалось выше, возможны и в рам-
рамках основного метода, изложенного в предыдущих главах и
опирающегося на свойства функций классов ЗЗт. Предлагаемый
в данной главе метод оценки констант Гёльдера несколько
проще и обычнее основного. Все аналитические факты, соста-
составляющие его, содержатся в §§ 1—5 гл. II. Упрощение же до-
достигается за счет повторного обращения к уравнению. В ос-
основном методе мы используем уравнение лишь один раз, выводя

§ 1] СЛУЧАЙ ПРОСТЕЙШЕГО УРАВНЕНИЯ 505
из него неравенства F,1) гл. II, лежащие в основе определения
классов 23т. После этого дальнейшее изучение относится уже
к произвольным функциям, удовлетворяющим этим неравенст-
неравенствам, а не только к решениям эллиптических уравнений, и по-
потому получаемые при этом результаты имеют более общую
значимость, чем вывод априорных оценок для решений эллип-
эллиптических уравнений. В данном же методе из уравнения извле-
извлекаются две серии неравенств: одна для самого решения и(х)
(или его производной), другая, аналогичная неравенствам F.1)
гл. II, для некоторых специально подобранных выпуклых функ-
функций о = ф(м) от и(х), из ограниченности которых можно за-
заключить о гёльдеровской непрерывности и(х) (идея введения
таких функций принадлежит Ю. Мозеру [40i]). Вывод этих не-
неравенств несколько сложнее вывода неравенств F.1) гл. II.
Зато получение необходимых из них следствий (об ограничен-
ограниченности функций, входящих в эти неравенства), несомненно, проще,
чем доказательство гёльдеровости функций классов 23т.
Мы проиллюстрируем этот метод сначала на примере про-
простейшего уравнения эллиптического типа -г—(ац {х) их ) = О,
а затем применим его и к общему случаю. При этом ограни-
ограничимся внутренними оценками. Оценки вблизи границы читатель
может сделать сам. Все необходимые для этого аналитические
. предложения даны в гл. II.
Кроме того, мы изложим некоторые другие красивые приемы
оценок констант Гёльдера для решений отдельных классов
эллиптических уравнений, а именно: способ Ч. Морри [392]
для двумерных задач вариационного исчисления, способ Л. Ни-
ренберга [44J оценки постоянной Гёльдера для производных «^
от решений двумерных квазилинейных уравнений общего вида
и способ Ю. Мозера [40J оценки нормы Гёльдера | и |??, Q'cQ,
для решений уравнений A.1) и доказательства неравенства
Гарнака.
§ 1. Случай простейшего уравнения
Пусть и{х) удовлетворяет тождеству
Q '
при Vti (x) e V?2 (Q). Считаем, что
vl2<ail(x)lll]^nl2; v, ц = const >0, A.2)
а и (х) е W\ (Q) и vrai max | и | ¦« М < <х>. Известно (см. лемму 4.8
Q _
гл. II), что для получения оценки (и)д?, Q'crQ, достаточно,

506 ОЦЕНКА КОНСТАНТ ГЕЛЬДЕРА [ГЛ, IX
например, показать, что для любых двух концентрических
шаров Kr с: /С2« с: Q имеет место соотношение
osc {и; KR] < ft osc {и; K2R} A.3)
с постоянной Ф, меньшей 1 и не зависящей ни от и (х), ни от R.
Без ограничения общности будем считать, что колебание и (х)
в /<2д равно 1 и 0^.и(х)^1. Для и{х) в Кц выполнено по
крайней мере одно из двух: или mes< x e Kr, и {к) ^-j [^
^-jmes/C^, или mesj.x: е/Сл, 1 — и^Ху j Byrnes /Сл. Пусть
выполнено, например, первое. Тогда все дальнейшие рассужде-
рассуждения будем проводить с функцией и{х) и использовать лишь то,
что она удовлетворяет неравенству
о .
с любой неотрицательной ц (х) е W2 (/Сг«)- В противном случае
мы рассмотрели бы функцию w (х) = 1 — и (х) и для нее исполь-
использовали бы то же неравенство A.4) с ц(х)^0.
Возьмем функцию v {х)= Ф(«(*)), где ф(и)=—In 2A—и + е),
а е — положительное число, которое в дальнейшем устремим
к нулю. Если мы покажем, что v(x) в Kr ограничена сверху
некоторой постоянной М{, не зависящей от е, то в Кц будем
иметь 2A — и + е)^е~м\ а следовательно, ии(х)^1 —2'е~М'<
т. е. A.3) будет справедливо с ¦&— 1 —-^е~мк Для доказатель-
доказательства ограниченности v(x) положим в A.4) т|(л:) = ¦ф/(и)§ =
= %{хI\\ — и(х)-\-г], где 1(х) — финитная в /Сг« неотрицатель-
неотрицательная функция. Это даст
или, что то же,
Возьмем здесь в качестве | функцию ?2(| х — х01//?), где ?)
равна 1 при те[0, 3/2] и линейно спадает до нуля к т = 2.
В силу предположений A.2) отсюда заключим, что
I
A.6)

$ 1] СЛУЧАЙ ПРОСТЕЙШЕГО УРАВНЕНИЯ 507
С другой стороны, нам известно, что v(x) ограничена снизу
числом — In 2A + в) и неположительна на множестве, мера
которого не меньше ymes/C^. Это вместе с A.6) гарантирует
оценку (см. C.5) гл. II с k = 0)
J v2dx^clRn, A.7)
где с{ — постоянная, определяемая лишь v, ц и п.
Положим теперь в A.5) | (х) = ?2 (х) max {v (х) — k; 0}, где
k — произвольное число, а % {х) — срезающая функция для
шара /Ср с р е /?, -^Щ' и отбросим первый неотрицательный
член. Это даст
где ЛА,р—множество точек х из /Ср, в которых v{x)>k.
Из A.8), используя A.2), получим
Ak, р ЛА, р
j (о —
A.9)
А отсюда и из A.7), как известно (см. теорему 5.3 гл. II),
следует, что
vrai max v (л
где М, определяется лишь v, ц и п. Итак, желаемое утвержде-
утверждение доказано.
Можно видоизменить конец данного доказательства так,
чтобы вместо теоремы 5.3 гл. II об ограниченности функций у,
удовлетворяющих неравенствам A.9), можно было воспользо-
воспользоваться более простой леммой 5.3 гл. II. Но при этом придется
привлечь изящную, но довольно трудно доказываемую лемму
Иона — Ниренберга [29] о том, что из неравенств типа A.6),
A.7) для произвольных шаров следует суммируемость v(x)
по Ks/iR с любой степенью и оценка:
Пусть A.10) известно. Покажем, как из A.10) и A.5) при
1^0 можно оценить верхнюю границу v(x) в KR, используя
лемму 5.3 гл. II. Без ограничения общности это рассуждение

Б08 ОЦЕНКА КОНСТАНТ ГВЛЬДЕРА [ГЛ. IX
достаточно провести лишь для /?=1. Положим в A.5) ?(*) =
= t,2(x)max{w(x) — k; 0}, где w(x) = v {хI2{х), a g(jc) —срезаю-
—срезающая функция для шара К'/,- Это дает
J[ai/V*,?2(ro~
где Ak есть множество точек шара /С»/2, в которых ш(лс) > ^
Член aijvxwxja2 представим в виде atjwx fwx —2vt,t,x\ и A.11)
запишем так:
h = J
< /[Ч^^-Ч/^Ц^-*)]^. A.12)
Ак
Отсюда, используя неравенство Коши A.1) гл. II, получим
а после приведения подобных членов и
A.13)
Возьмем в качестве ?(лс) функцию, равную 1 в /С,, c|V?|<;2.
Для такой ?(jc) из A.13) в силу условия A.2) следует
J
v
Ак Ак
а это и A.10), справедливое при любом s > 0, гарантируют
справедливость неравенств
J | Vny pdx<с( J (I + Vs) dx?1'mes1-2^ Ак <
Ак \Ак )
^csmesl-2'sAk при Jfe>l, A.14)
с любым s > 0. Нам достаточно знать, что в A.14) можно
взять s>n. При таком s, как утверждается в лемме 5.3 гл. И,
из A.14) следует ограниченность w(x) сверху в шаре К»/,, а тем
самым и ограниченность v (х) в Кх.

% 2] УРАВНЕНИЯ С ДИВЕРГЕНТНОЙ ГЛАВНОЙ ЧАСТЬЮ 509
Обе из изложенных только что схем применимы и для
общего случая. Как это сделать, читатель увидит в следующих
параграфах, где мы приводим первую из них, как несколько
более простую и короткую.
§ 2. Оценки постоянных Гёльдера для решений уравнений
с дивергентной главной частью (линейных и квазилинейных)
Рассмотрим эллиптические уравнения вида
d
dx
— (at (х, и, их)) + а (х, и, их) = 0 B.1)
при таких предположениях относительно функций at{x, и, р)
и а(х, и, р), которые охватывают сразу и случай линейных
уравнений с неограниченными коэффициентами, и случай квази-
квазилинейных уравнений с максимально возможным ростом функ-
функций at и а по р, т. е. оба крайних случая, изученных нами
в гл. III, IV. Величину М = тах|и| считаем уже известной.
Q
Предположения об at (x, и, р) и а (х, и, р) следующие: они
измеримы при JteQ, |ы|^М, р^Еп и удовлетворяют не-
неравенствам
at (x, и, р) pt > v | р Г - Фо (*), v = const > 0, B.2)
[S (at (х, и, р)J]1/2 < ц | р Г + Ф| (*), I* = const, B.3)
\а(х, и, р)|<ц|рГ + Ф2(*). B.4)
где иеA, п], а фЛ*) неотрицательны и
11фо> ф211?/т,а> II Ф| 1Цт_„, а < I*. Я>п. B.6)
В случае линейных уравнений
) иХ/ + at (x) u + ft (х)) + bt (х) иХ{ + а (х) и + f(x) = 0
условия B.2) — B.5) могут быть выражены в виде
(*)?i?/<nga, v>0,
Будем заниматься, в основном, внутренними оценками. Для
того чтобы оценить сверху величину (м)^"', Q' с: Q, достаточно,
согласно лемме 4.8 гл. II, показать, что для любого шара Кц>
лежащего в Q вместе с концентрическим ему шаром К2ц> спра-
справедливо неравенство
osc {и; /С*} < « osc {и; К2ц} + #" B.6)

БЮ ОЦЕНКА КОНСТАНТ ГЕЛЬДЕРА [ГЛ. IX
с постоянными г > 0, ft < 1. Здесь и ниже все постоянные
будут определяться лишь п, М = тах| и | и v, ц, т и q из усло-
условий B.2) —B.5). Радиусы R будем считать < 1.
Относительно функции и{х) предположим, что она есть
ограниченное обобщенное решение из Wlm(Q) уравнения B.1),
т. е. что она принадлежит Wlm(Q), имеет max| u | = М < оо и
удовлетворяет тождеству
J [а( (х, и, их) цХ{ — а (х, и, их) ц] dx = 0 B.7)
Q
о .
при любой ограниченной функции ц (х) из Wm (Q). Мы рассма-
рассматриваем здесь лишь случай т^.п, ибо для т>п гёльдеро-
вость и(х) и оценка (и)^' следуют непосредственно из теорем
вложения (см. B.30) гл. II).
Из B.7) в силу B.2) —B.5) при указанных только что г\(х)
имеем
\at{x, и, uxLX{dx^ J[|i|V« Г + Ф2]1 Л 0dx. B.8)
Докажем, что из B.8) с г\(х)^0 при условиях B.2) —B.5)
следует
K2R
^lie^ v ' mes/C2R[2 max| V? |m + (l +-^"+ m)<
*2R B.9)
где 5 W —срезающая для /е2дс:й функция.
Для этого положим в B.8) ц(х) = еХи{хI,т(х), где Я —доста-
—достаточно большое число, которое будет выбрано ниже:
K2R К2Д
Отсюда в силу B.2) — B.4) следует
r^< J /"[fxiv«rr+<p2
/C2R
+ т (ц | Vu Г"' + Ф|) Г"' I V? |]
max e^ f [ЯФоГ + Ф2^т + отф1Г"' I V? I ] d*. B.
K U

§ 2] УРАВНЕНИЯ С ДИВЕРГЕНТНОЙ ГЛАВНОЙ ЧАСТЬЮ 511
Последний интеграл, стоящий справа, оценим с помощью
неравенства Гёльдера следующим образом:
/о= J ФоГ^^ЦфоЦ^^тез'-^/С^, B.12)
h = J ФаГ dx^W Ф2 |(,/т> Кад mes1-»/» *2Й, B.13)
= J Ф|Г"'1
< max | V? | • II Ф, \\ql(m^ - mes'-fm-o/* *ад. B.14)
%2R H
Для оценки интеграла J3= \ eKu\Vu\m~l?>m~l\V?,\dx восполь-
воспользуемся неравенством Юнга в следующей форме:
/3 < Г (JZLzl | v« Г ^e^e1""-0 + -1 V? Г e""e-m) rfx, B.15)
где e — произвольное положительное число, которое для вы-
вывода B.9) можно положить равным 1. Подставляя эти оценки
в B.11), получим после приведения подобных членов
\kv - цот) J еы | V« Г lm dx
+ ц/п max I V? Imes1-"»-')" /C2«l • B.16)
^2« J
Последнее слагаемое справа оценим по неравенству Юнга так:
maxl
-I max| V? Г + ^- mes-»"/C2 J mes /Сад. B.17)
Возьмем Я таким, чтобы коэффициент при интеграле, стоя-
стоящем слева в B.16), был положительным, например равным v
(при этом X = 1 + V-mfo)\ тогда из B.16) и B.17) будем иметь
v J elu\
K2R
< ехм mes K2R [^ max I V? Г + I* (A + «) mes-m/^2«]> B.18)

512 ОЦЕНКА КОНСТАНТ ГЁЛЬДЕРА (ГЛ. IX
откуда ясна справедливость B.9). Для дальнейшего нам доста-
достаточно несколько более грубое неравенство (при R <; 1)
f I Vtt Г С dx < cRn (R~m + max | V? |m), B.19)
k2r K>*
которое, как видно из приведенного вывода B.9), справедливо
прн q^n. Постоянная с определяется лишь т, М, v и ц из
B.2) —B.5). Итак, доказана
Лемма 2.1. Если функция u(x)^Wlm(K2R) A<т^.п),
vraimaxl и \ = М и для и(х) справедливы неравенства B.8) при
любой ограниченной неотрицательной функции ц(х) из Wm(K2n)
и если имеют место неравенства B.2) — B.5) с q^n, причем
нормы ф/ в B.5) вычислены по шару K2r> то для и(х) справед-
справедливы оценки B.9) и B.19), где ?,(х) — произвольная срезающая
для K2r функция, a R^l.
Переходим теперь к доказательству B.6). Покажем, что
справедлива следующая
Лемма 2.2. Если и(х) удовлетворяет условиям леммы, 2.1 и
mes {x s KR, и (х) < max и (х) — б2 osc (и; /С2Л)} > б3 mes Kr, B.20)
где б2 и б3 — два каких-нибудь положительных числа, и если
выполнены предположения леммы 2.1 при q > n, то
osc {и; KR} < A - б,) osc {и; K2R) + Rr, B.21)
где r=\— —, с некоторым б| > 0, определяемым лишь б2, б3,
от, М, v, (i, <7 из B.2) - B.5).
Доказательство. Пусть osc {и; /С2Л} = со. Без ограниче-
ограничения общности будем считать, что 0 <! и (лс) ^ со в K2r (ибо фор-
формулировка леммы 2.2 инвариантна относительно замены и на
и-\-с). Тогда osc{«; /(,>}< max и (лс), и потому достаточно оце-
нить max и через правую часть B.21), считая ©!>/?. Рас-
Kr
смотрим в К2ц функцию v (jc)=i1> (и (х)), где -ф (ы) = — lnm~^e—.
Для нее верна оценка а(лс)> — 1п-т—• Если мы покажем, что
при любом x^Kr функция v (х) ограничена сверху каким-либо
числом М{, не зависящим от R, т. е. если — 1п -—^^ ¦ < М,
в KR, то отсюда получим и_и6B^ + /?г<ем', т. е. оценку B.21)
с б, = Ьф~мк

§ 2] УРАВНЕНИЯ С ДИВЕРГЕНТНОЙ ГЛАВНОЙ ЧАСТЬЮ 613
Итак, наша цель — найти оценку сверху для v (х) в /Сд. Мы
сделаем это с помощью теоремы 5.3 гл. II. Но для того, чтобы
ею воспользоваться, надо знать оценку нормы || v \\m К) . По-
Покажем сначала, что для v(x) справедливо неравенство
f I Vo Г lm dx < cR" (max | V? Г + %"")> B.22)
аналогичное неравенству B.19) для и(х), причем постоянная с
зависит лишь от т, М, q, v и ц. Вывод его несколько отли-
отличается от вывода B.19), ибо на этот раз мы считаем оценку
сверху max | v | неизвестной. Зато известна оценка B.19), кото-
рую мы используем ниже.
Положим в B.8) л(*) = (иц(Ц%-,^
срезающая для /С2« функция. Это возможно, ибо такое
обладает всеми требуемыми свойствами (в частности, (
Это дает
а{(х, и, их)[(т-
.Отсюда в силу неравенств B.2) — B.4) и определения v имеем
| (m
K2R
J [(/п-
\
+ CBl-m(ix\Vur + cp2)]dx, B.23)
Интегралы, стоящие справа, оценим примерно так же, как ин-
интегралы /( выше (см. B.12) —B.15)). Именно, благодаря нера-
неравенству Гёльдера
/о= J
Л- J
B.24)
< R~r (m-"ll Ф2 \\qlm_ 4r mes'-m/%« < сР?-т+г, B.25)
17 О. А. Ладыженская, Н. Н. Уральцева

514 ОЦЕНКА КОНСТАНТ ГЕЛЬДЕРА [ГЛ. IX
П= J q>1Em~l|V?|B|-mrf*<
< max| VC | /?-"(m-1) || Ф| ||,/(m_0 к тез1"*-1»" /С2Л <
< с max | V? | /?"-m+1 < ctf" (^- R~m + J- max | V? h, B.26)
/3=
откуда в силу неравенства Юнга при любом е > О
j'z ^ Г (Л=± | Vy Г j'V/e»-') _[_ _L | vg Г e-m) djc. B.27)
С помощью этого же неравенства Юнга с е > 0 оценим
/J= J |УиГВ1~т?т<**= J I Va lm-4m~'l VulgrfA;,
&2R K-2R
именно:
/j ^ J (ilLziL 1 Vy Г ?»e»/<«-') + _L| уи Г ?me-m) dx. B.28)
Полученные оценки B.24) — B.28) подставим в B.23) и при-
приведем подобные члены, считая е^1 и
[(m-l)v- (/n-~)em/(m-VJ J
%\ms~'") + — e~m \VuFCdx. B.29)
m 4
Выбирая е так, чтобы коэффициент слева был равен, например,
•^—v, и используя уже установленную выше оценку B.19),
из B.29) получим B.22).
Из неравенства B.22), ограниченности v(x) снизу (v(x)>
>—ln-T-J и того, что в силу предположения B.20) v(x) непо-
ложительна на множестве, мера которого не меньше
следует
J | о Г <**<<?!#• B.30)

§2] УРАВНЕНИЯ С ДИВЕРГЕНТНОЙ ГЛАВНОЙ ЧАСТЬЮ 5'5
с постоянной с{, определяемой лишь т, М, v, ц, б2 и б3 (см.
неравенство C.5) гл. II).
Покажем, что v (x) удовлетворяет следующей серии нера-
неравенств:
J | Vo Г lm dx <
А"- ° г 1
J V / Э "Г В, р V • /
U.p
при всех k, превосходящих некоторое число k0, и р ^ р0.
Здесь Ak, p есть множество точек х из шара Кр, в которых
v(x)> k, a % (х) — срезающая для Кр функция. Постоянная у
определяется лишь т, М, р0) v и ц, а &0 — постоянными б2) М
и v. Для проверки B.21) неравенство B.31) достаточно уста-
установить лишь для шаров Кр, концентрических /С2д. с р из
\R, -х-Щ и ^^1- Для доказательства B.31) возьмем в B.8)
Ц (х) = С (х) В1' max {v (x) - k, 0},
где В (х) = со — и (х) + Rr, а ? (х) — срезающая для Кр функция.
Такая т| (л:) допустима. Результат представим в виде
j [aiB]-mvXiC + (m - 1) a.-B-X (a - ^) ?m| dx <
^ J * i
dx. B.32)
Отсюда, принимая во внимание B.2) —B.4), получим
n(v-k)C +
dx. B.33)
Интегралы, стоящие справа, оценим, в основном, так же, как
выше интегралы // и /;. Некоторое отличие вносит множитель
17*

516 ОЦЕНКА КОНСТАНТ ГЁЛЬДЕРА [ГЛ. IX
(v — k). Именно, применяя неравенство Гёльдера, будем иметь
Г [1 + (от - 1) (о - k)] dx <
Множитель || (о —Л) SL оценим с помощью неравенства B.12)
гл. II:
<i?mesl'M/kfP(||| Va m ^ p ? m ^
а затем содержащий его член оценим по неравенству Юнга
с е>0:
/о < II Фо \\qlm Wrm mes' ~Т ЛА, р + (от - 1) с (|| | Vo | ? ||m +
+ II (о - *) I VS I ID /?-rm mes' +
' "T~+T A/k< J
ii()i sic
. ..2 / m \ rm2 m I m L4._L
p-fe)i vsic
m2 m
-' mes™
B.34)
Для оценки интеграла J" = [ ф25'~т(у — k)Z,mdx используем
неравенства, только что выведенные. По сравнению с J" инте-
интеграл У{ имеет лишь «лишний» множитель В = со — и + Rr, ко-
который мы, ввиду его ограниченности, вынесем за скобки, так
что из B.34) следует
/" < (ш + Rr) [ctR-rm mes' ~f Ak, p + c{em || | Vo | ? С +
+ 1||()?fl B.35)
Почти так же оценивается и J'(
J ?,(o-
• m-l I

j 2] УРАВНЕНИЯ С ДИВЕРГЕНТНОЙ ГЛАВНОЙ ЧАСТЬЮ 617
откуда, применяя неравенство Юнга, получим
/! ^^l-Uv - k)\Vl\? + ^- R~rm mes'T Ak<0]. B-36)
Интеграл
/;'= J |V«r~' B'~m{v
Ak.
J \Vv\m-l(v-k)t,m~l\4\dx
оценим так же, как выше /з, присоединяя (v — k) к | V? |,
именно:
/^ Г Ji!LZ±|Var^mem/(m-|) + -^-(a-^)m|V^re~m)dA:. B.37)
Осталось оценить еще один интеграл:
/?= J \Mur{v-k)lmBx-mdx= J {\Vv\l)m{v-k)Bdx.
Ak, p Ak,
Функция Ф (x, k, со) = [v (x) — k]B (x) = [v (x) — k] 62coe-° <x) для
всех со ^ 2М и х е ЛА, р не превосходит функции Ф (^) =
= 2Мб2е~|~*, стремящейся к нулю при &-><х>. Поэтому
Vy|m^mdA:. B.38)
Подставляя неравенства B.34) — B.38) в B.33) и приводя по-
подобные члены, получим (помня, что /?^1, а ^О)
(v - BAf + 2) схът - ц (от - 1) em/C"- » - цФ (k)) J | Vo Г ?m dx +
+ [BAf + 2) с, + ц (от - 1)] /?~rm mes1"" Л*. p. B.39)
Выберем е, например, так, чтобы BМ + 2)c1em + ц(от — 1)Х
Xem/(m~l) = v/4, а числа /fe будем считать превосходящими
число &0, которое выберем из условия
B.40)

618 ОЦЕНКА КОНСТАНТ ГЕЛЬДЕРА [ГЛ. !Х
Как легко видеть, для k^kQ и R^p^3/2R<J3/г из B.39) сле-
следуют B.31).
Итак, для функции v установлены неравенства B.30) и B.31)
в предположении, что г=1—-!>0 (т.е. что q^ri) и что
& > &о» R<^p^3/2R^:3/2- Входящие в них постоянные не за-
зависят ни от R, ни от р, ни от со. Они определяются лишь т,
М, v, ц, Ь> и 6j.
На основании теоремы 5.3 гл. II (точнее, замечаний 5.3,
5.4 к ней) из B.30), B.31) следует, что при q>n таху(лс) огра-
к«
ничен сверху постоянной Ми определяемой лишь сх из B.30),
Y из B.31), а также kQ, п, т и q, т. е., в конечном счете, п,
т, М, q, v, (i, б2 и 6j. Лемма 2.2 доказана.
Из этой леммы следует, что если и(х) удовлетворяет нера-
о .
венствам B.8) при любой ограниченной ц(х) из Wm{K,2R) и
тах|и| = Л1, то для нее верно соотношение B.6).
Действительно, рассмотрим две функции: ш, (х) = и {х) и
щ(х)= — и(х). По крайней мере для одной из них
mes \x s KR: wt (x) < max w{ (x) — т osc {wt; K2r)\ > 4- mes KR- B.41)
1 K2R Z J Z
Если B.41) справедливо при i = \, то лемма 2,2 гарантирует
справедливость неравенства B.6) с ¦&= 1 — б, при 62 = 63= 1/2.
Если B.41) справедливо при 1 = 2, то лемму 2.2 можно
применить к функции w2. Действительно, условие B.20) для
нее выполнено с 62 = 6.;= 1/2. Из других предположений леммы
надо убедиться лишь в том, что w2(x) удовлетворяет неравен-
неравенствам B.8) с ц(х)^0. Но это так, ибо из справедливости не-
неравенств B.8) для и(х) при ц(х) любого знака следует, что
для w2(x) имеют место неравенства
J а.(х, w2, wix) цХ; dx < j [ц j \w21"' + Фя]| т| |dx, B.42)
в которых функции й{(х, w, p)= — cii(x, — w, — p) удовлетво-
удовлетворяют, как легко видеть, тем же условиям B.2) — B.5), что и
at (x, а, р).
Итак, лемма 2.2 применима к — и(х), а это приводит, как
и выше в первом случае, к неравенству B.6) с тем же 0 =
= 1—6,. Сформулируем доказанное утверждение в виде леммы.
Лемма 2.3. Если и(х) е Wlm(K2R)(l < m^.n). vrai max| и | =
*<2R
= М и для функции и(х) справедливы неравенства B.8) при
о .
любой ограниченной функции r\(x) e Wm(K2R), причем для

§ 2] УРАВНЕНИЯ С ДИВЕРГЕНТНОП ГЛАВНОЙ ЧАСТЬЮ 519
cti (х, и, р) и ф2 выполнены условия B.2), B.3), B.5) с q > п и
нормы ф/ в B.5) вычислены по шару K2R, то при некотором
б, >0
osc{«; /С*}<A - 6,)osc{«; K2R} + Rr, r= 1 - n/q.
Постоянная б! здесь определяется лишь п, m, M, q, v и ц
из B.2), B.3) и B.5). Вместо указанного требования о справед-
справедливости B.8) для и(х) при любых знакопеременных г\(х) можно
предположить, что для каждой из двух функций w(x)= ± и(х)
справедливо свое неравенство вида
J af {x, w, wx) тц dx < J [ц | Va> \m + Ф2] Ц dxy B.43)
в которых функции af(x,w,p) и ф2 удовлетворяют условиям
B.2), B.3), B.5), а г\(х) — неотрицательные ограниченные эле-
элементы W]m(K2R).
Из этой леммы и леммы 4.8 гл. II следует
Теорема 2.1. Пусть u(x)<=Wlm(Q), I < /n<«, vraimax| и \ =
а
= М и для функций до (#) = ± и (х) справедливы неравенства
B.43), в которых функции af{x,w,p) удовлетворяют условиям
B.2), B.3), B.5), а г\(х) — произвольная неотрицательная огра-
ничейная функция из Wm (Q). Тогда для любого шара /Ср с: Q
osc{«;/y<cPo-V. B.44)
Здесь с и а — положительные постоянные, определяемые лишь М,
п, m, q, v и \i, а р0 — расстояние от центра Кр до границы
области Q.
В частности, утверждение теоремы справедливо для огра-
ограниченных обобщенных решений уравнения B.1) из Wlm(Q), т. е.
для и(х) е Wxm(Q), имеющих vrai max\и\ = М< оо и удо-
Q
влетворяющих тождеству B.7) при всех ограниченных г\(х)
о
из Wm(Q), если для ai(x,u,p) и а(х, и, р) выполнены условия
B.2)-B.5).
Оценка (ы)^' для всей области Q гарантируется следующей
теоремой:
Теорема 2.2. Пусть выполнены условия теоремы 2.1, и
пусть S удовлетворяет условию (А), а и \s = ф (s) — условию
Гёльдера с показателем р > 0. Тогда существуют такие а > 0
(а^Р) и с > 0, зависящие только от М, п, m, q, v, ц и р,

520 ОЦЕНКА КОНСТАНТ ГЕЛЬДЕРА 1ГЛ, IX
постоянных а0 и Эо из условия (А) и | и Щ\ что
<«>?><*• B.45)
Доказывается эта теорема так же, как и теорема 2.1. Необ-
Необходимые видоизменения рассуждений читатель может найти
в § 14 гл. III и в § 1 гл. IV.
§ 3. Об оценке колебаний производных от решений
уравнений с дивергентной главной частью
Если и(х) удовлетворяет уравнению B.1), то каждую из его
производных Uk(x) = uXk(x) можно рассматривать как решение
уравнения того же типа. В самом деле, продифференцируем
B.1) по xk и получаемый при этом результат запишем в виде
?Н- (ЗЛ)
Соотношение C.1) есть линейное относительно щ уравнение
вида B.1) с
a, (x, v, р) = аи (х) pi + 5, (x) v + // (х), а (х, о, р) = О,
где
_ dat (х, и (х), их (х)) _ dat (x, и (х), их (х))
dat{x,u(x),u(x)) k
U (х) = — J7—'—L + а(х,и (х), их (х)) б?.
C.2)
Ввиду этого из теоремы 2.1 следует
Теорема 3.1. Пусть ы(х) <= №l(Q), vrai max| Vu |=M,<oo
Q
и и{х) почти всюду удовлетворяет уравнению B.1). Пусть для
него функции, определенные в C.2), подчиняются неравенствам
v, ц>0, 1
Тогда для любого /Ср с Q
еде р0 есть расстояние от центра /Ср до границы S, а с и
а — положительные постоянные, определяемые лишь Mlt n, q,
v и ц из C.3).

I 4] НЕДИВЕРГЕНТНЫЕ УРАВНЕНИЯ 521
§ 4. Недивергентные уравнения
В данном параграфе рассмотрим в области Q квазилиней-
квазилинейные уравнения второго порядка общего вида
L (и) нз at/ (х, и, их) uXlxt + а (х, и, их) = О D.1)
и для них дадим оценку постоянных Гёльдера («хг)(а), /= 1, ...
..., п, через тах|ы| = М, тах\Чи\ = Ми константы, характе-
q я
ризующие функции аг1{х,и,р) и а(х,и,р), и расстояние Q' до
границы S. Единственное предположение относительно D.1) (не
считая условий некоторой регулярности at/ и а) — это его
эллиптичность на исследуемом решении и{х). Этот результат
доказан нами в § 1 гл. VI. Из § 1 гл. VI мы возьмем общий
план получения оценок для («x,)(a,'> H0 изменим его конец, за-
заменив доказательство гёльдеровости вектор-функций классов ЗЗт'
несколько более обычными и короткими рассуждениями, по-
подобными тем, какие даны ранее. Итак, докажем теорему, являю-
являющуюся небольшим усилением теоремы 1.1 гл. VI.
Теорема 4.1. Пусть и{х) есть решение уравнения D.1),
принадлежащее Wl(Q), причем vrai max| V« |^ М{. Пусть функ-
а
ции аи(х,и,р) дифференцируемы по х, и, р в окрестности
многообразия {jceQ, и = и(х), р = их{х)} и
«(я), «,(*))^/<и?2> v, ц = const > 0. D.2)
4>п. D.3)
Пусть, кроме того,-при и = и{х), р = их(х)
да,
да,, да,
ХИ
ди
Тогда и(х) принадлежит Cl+a(Q) с некоторым а>0 и для лю-
любой подобласти Q' cr Q нормы \их,I', i= I, ..., п, оцениваются
через п, Mit q, v и \i и расстояние Q' до границы Q. Постоян-
Постоянная а определяется лишь п, М{, q, v и ц.
Без ограничения общности будем считать функции uXl(x),
/=1, ..., п, «нормированными на 0 и 1», т. е. такими, что
1, /=1, ..., п, JceQ. Покажем, что для функций
%ul (x),
wl (x)=l0n(l-ux,(x))+2lul(x), /=1 п,
vl (x)=Wn(l-uXl(x))+2uli(x)

522
ОЦЕНКА КОНСТАНТ ГЁЛЬДЕРА
[ГЛ. IX
при любой неотрицательной функции г\(х) из W%(Q) справед-
справедливы неравенства
J [йц W К. + 2с\ (*)] \ dx < Y J [ I Va>' |2 + Ф (*)] л Лс, D.5)
в которых all(x) = att(x, и(х), их{х)\ а |с[|7 Q и ||ф||?/2?2 ограни-
ограничены сверху постоянными, определяемыми, как и у, числами М{
и ц из D.3). Неравенства D.5) суть следствия тождества A.9),
установленного нами в § 1 гл. VI, именно, тождества
J К
D.6)
где г\(х) — произвольная ограниченная функция из
аТ,-
да
Ч
да
1т
<?«„
с\ =
5паЬ[,
cla = ab) + a1 (ux. + 5nbli) + Ькц (ич + 5пб?) ,
да,, да,, , да,, д
ди
дх,
D.7)
В силу предположений теоремы коэффициенты с1ц и cj сум-
суммируемы по Q со степенью q, a аг/ и а^ ограничены. Оценим
члены, стоящие под интегралом в правой части D.6), так
(суммирование по повторяющимся индексам не предполагается):
^ ""'-А4 + Ъ
+ - Ф W л.
D.8)
где функция ф(х) имеет конечную норму ИФИ^о» не превосхо-
превосходящую известной нам величины. Подставляя эти оценки в D.6),
выбирая е достаточно малым и приводя подобные члены, по-
получим для неотрицательных ч\(х) неравенства D.5). Эти нера-
неравенства являются частным случаем неравенств B.8). Они сов-
совпадают с B.8), взятыми для и = 2 и аг(х, и, р) =йц(х, и(х),
ux(x))pj + 2c'.(х, и(х), их{х)). Остальные предположения о функ-
функциях фг и at также соответствуют друг другу. Однако имеется
одно принципиальное отличие: неравенства B.8) справедливы
^разу для пары функций и(х) и — и(х), неравенства же D.5)

§ 5] СПОСОБ Ю. МОЗЕРА ОЦЕНКИ I и \[f) 523
имеют место лишь для wl(x) (но не для — да' (x)). Однако D.5)
верны как для wl+(x), так и для wl_(x) и роль пары ± и(х)
на этот раз будут играть функции wl±(x). Как видно из рас-
рассуждений § 2, выполнение неравенств для обеих функций ± и(х)
было использовано лишь в одном месте: там, где делался вы-
выбор ме-кду этими двумя функциями в зависимости от того,
какое из двух неравенств mesjxe/(s: ы(х)^у|^у mes/(s
или mes|jce/Cs: и(х)^-у>^уmesKR заведомо выполняется.
Если, например, выполнялось первое неравенство, то все даль-
дальнейшие рассуждения проводились с функцией +«(*), и это
неравенство использовалось лишь для того, чтобы заключить,
что из неравенства B.22) следует неравенство B.30).
В данном случае будем поступать так. Возьмем два произ-
произвольных концентрических шара KR cr /С2д cr Q. Среди функций
uXi(x), /=1 п, выберем ту, которая в /(ад имеет наиболь-
наибольшую осцилляцию; пусть osc \ux ; K2r) = о/ = max со'. Согласно
1 г ; г=| п
лемме 8.1 гл. II osc [wr±; K2R] ^60wr и хотя бы для одной из
функций wr± выполняются неравенства
mes {x e KR: wr (x) ^ max wr — б2 osc {wr; K2r}} ^ 6j mes KR, D.9)
где 60, б2 и 6j — некоторые вполне определенные положитель-
положительные числа. Пусть это верно, например, для хюг+. Тогда для W+
выполнены все условия леммы 2.2, и поэтому
osc
;; KR} <A - б,) osc {да;; /Сад) + Rr, г = I - n/q,
с некоторым б! > 0. А отсюда на основании леммы 4.9 гл. II
заключаем о гёльдеровости их. и возможности получить оценку
сверху для («^)<а), Q'cr Q. Теорема 4.1 доказана.
§ 5. Способ Ю. Мозера оценки | и (^ для решений
линейных уравнений. Неравенство Гарнака
Ю. Мозер в работе [40)] предложил для уравнений вида
JL(att(x)uXj) = 0 E.1)
способ оценки | и $, Q'cr Q, их обобщенных решений из W2(Q)
через ||ы||2 п, числа v и ц из неравенства
&2 E.2)

624 ОЦЕНКА КОНСТАНТ ГЁЛЬДЕРА [ГЛ. IX
и расстояние от Q' до границы S, отличный от данных ранее
способов Е. Де Джорджи и Дж. Нэша.
Изложим этот способ оценки | и f?\ предполагая ради про-
простоты, что о решении и заранее известна его ограниченность,
и считая п > 2. Итак, пусть и(х) принадлежит Wl2(Q), удовле-
удовлетворяет тождеству
J atl(x)uXj4Xidx=Q E.3)
о .
при любой r\ (x) e Wi (Q) и тах|ы|<оо. Положим в E.3)
Q
, E.4)
о .
где l(x)&W2(Q), тах|?|<оо, а ф@ — дважды непрерывно
Q
дифференцируемая функция t с (f"(t)^Q. Это дает
где v (х) = ф (и(х)). Отсюда при ?(х) ^0 следует
tl(x)vXilXt4x^0. E.6)
Назовем функции v(x), удовлетворяющие неравенству E.6) при
любой неотрицательной функции 1(х) из Wz(u), субреше-
субрешениями E.1).
Легко проверить, что для решений и{х) и неотрицательных
субрешений v{x) уравнения E.1) справедливо неравенство
\ J о»| Vg p dx, E.7)
где /Ср — произвольный шар, принадлежащий Q, l, (x) — срезаю-
срезающая для /Ср функция. Чтобы убедиться в этом, надо положить
в E.3) (соответственно в E.6)) х\(х) = и (х) Z? (х) & (х) = v (x) Z? (х))
и провести элементарные оценки с помощью неравенств
Коши A.1), A.9) гл. И.
Оценим сначала тах|ы(х)|, ^cQ. Для этого учтем, что
функции o(jc) = | и(х) |!+Е при е > 0 являются неотрицательными
субрешениями E.1). Действительно, функции ов = (ы2 + 6)A+е)/2
являются субрешениями при любой 6 > 0. Устремляя 6 к нулю

§ 5) СПОСОБ Ю. МОЗЕРА ОЦЕНКИ | и |$' 525
в E.6) для ов, убедимся, что E.6) справедливы и для v. Ввиду
этого для v(x) верна оценка E.7), т. е. при любом е >0
E.8)
Кроме того, нам понадобится теорема вложения B.12) гл. II
в следующей форме:
w2kdx\"k < рр2 ?| \'w |2dx,
E.9)
где k = -n _ 2 , a ywdx = (mesKp)~ J ^d*. Она справедлива
О |
для любой функции w(x) из W2(/Cp).
Возьмем последовательность концентрических шаров /еА=/СдЛ,
Rh = R(l -\—г), Л = 0, 1, 2, ..., /C2pcQ, и соответствующие
\ 2" /
им последовательности функций оА = |ы|*, /г = 0, 1, 2, ...,
и срезающих функций ?A(x) таких, что ih(x) равна 1 в /CA+i,
нулю вне К/1 и max| V?A |^2fl+l/?~l. Обозначим:
В силу определения vh и неравенства E.9) имеем
?2 f I V (V&h) fdx <
. E.10)
4
Правую часть E.10) оценим с помощью E.8), взятого для
1 + в = kh и p = Rh- Это даст
-?+ l) f Ол|У?Л|2^<22*+5р(^+ l)
яЛ
т. е. рекуррентное соотношение
: = 0, 1, 2, ..., E.11)

526 ОЦЕНКА КОНСТЛ11Т ГЕЛЬДЕРЛ [ГЛ. IX
где с = |25р (-?¦ +1I. Отсюда следует (см. лемму 4.7гл. II), что
**-!
h
*-!Ф*\
а потому и
vrai max\ и(х)\= \\т { \\ и
«2R I
E.12)
где с, = тах{1; с}.
Итак, доказана
Теорема 5.1. Для ограниченных обобщенных решений и(х)
уравнений E.1) из W2(Q) верна оценка E.12), где постоянная с,
зависит лишь от v, \i и п.
Замечание 5.1. Предположение об априорной ограничен-
ограниченности и можно отбросить.
Замечание 5.2. Нетрудно убедиться, проследив данный
только что вывод неравенства E.12), что если v(x) есть неотри-
неотрицательное субрешение уравнения E.1), то для него верна оценка
1/2
vrai max 0(jeXBnc,r '"ч I \ v2 dx \ E.13)
с той же постоянной си что и в E.12).
Оценим теперь для решения и{х) уравнения E.1) постоянную
Гёльдера. Возьмем три концентрических шара Kr cr /C2S cr /C3S,
принадлежащих Q. Пусть ш2 = vrai max и (х), аю, = vrai min и (х)
на шаре /C3S. Всегда справедливо по крайней мере одно из не-
неравенств:
или
e/<-2S: Ю1 + ю2- и(х)< Ю| + Ю2 |>-1 mes/C2R- E.142)
Если мы покажем, что из E.140 и E-3) для и(х) следует
max и (х) ^ о>2 — бш, б > 0, ш = ш2 — ш1( E.15)
то этот результат, примененный к функции v (х) = о^ + ш2 — ы (*)
в тех же шарах, гарантирует, что из E.142) и E.3) будет сле-
следовать max [а>! + ш2 — и (х)] ^ ш2—бш, и тем самым будет дока-
зано, что из E.3) следует
osc {и; /С*} < A - 6) osc {u; K3Rl E.16)
Это же в силу леммы 4.8 гл. II позволяет получить оценку («)^.

§ 5] СПОСОБ Ю. МОЗЕРА ОЦЕНКИ | и |$> 527
Итак, пусть для и(х) справедливо E.14!). Рассмотрим функ-
функцию до(*) = ф(ы(*)) = In——^Г77ГГ7Г> гДе 6i — положительное
число, которое в дальнейшем будет устремлено к нулю. Она
является положительным субрешением уравнения E.1), ибо
ф" (и) = 1/(ш2 — и + М2 > 0- Поэтому в силу замечания 5.2 к тео-
теореме 5.1 для нее справедливо неравенство E.13):
(i' \1/2
\w2dx\ . E.17)
Для оценки интеграла, стоящего справа, выпишем тожде-
тождество E.5), которому удовлетворяет w (x). Оно имеет вид
1 (ап
Возьмем здесь ?(*) = ?2(|х — х° |), где ?,(t) равна 1 при
нулю при />3/? и CR — t)/R при 2R^t^3R, а х° — центр
шара /C3/f- Тогда из E.18) в силу E.2) легко выводится, что
С другой стороны, в тех точках К2ц, где и (х) < ю' ^ г. функ-
функция до^^Ь-^^—- = In 2, а так как мера таких точек,
по
1
предположению E.14i), не меньше -r-mes/Cj^, то неравенство C.5)
гл. II дает
J [w(x) — \n2]2dx^$'R2 J \Vw\2dx, E.20)
где р' — некоторая постоянная, зависящая лишь от п. Здесь
А\П2,2« есть множество точек х из K2r, где до (я) > In 2. В силу
E.19) и E.20)
E.21)
а отсюда и из E.17) получаем
vrai max до (х) <; с4, E.22)

528 ОЦЕНКА КОНСТАНТ ГЁЛЬДЕРА [ГЛ. IX
причем постоянная с4, равно как и все остальные постоянные,
вошедшие в наши оценки, определяется лишь п, v и ц и не
зависит от R, и(х) и 6, > 0. Устремляя б[ к нулю, убедимся, что
т. е. (б. 16) имеет место с 6 = e~Ct.
Это заканчивает доказательство соотношения E.16).
Метод Ю. Мозера отличается от метода, изложенного в § 1,
доказательством ограниченности вспомогательной выпуклой
функции о = ф(и). Ю. Мозер получает для этого рекуррентное
соотношение E.11) для интегралов Фй= т| v |2* dx, из которого
4 н
делает заключение о равномерной ограниченности Ф]/2* ,
А=1, 2, ..., а следовательно, и vraimax|t»|. Мы же получаем
для v неравенства A.9), содержащие произвольный параметр k,
и из них выводим ограниченность vraimax|t»|. Исследование
к*
уравнений общего вида @.1) можно проводить двумя путями,
используя основную идею одного или второго метода. Как это
сделать на первом пути, показано в §§ 2—4. Второй путь
можно взять совпадающим с первым во всех частях, кроме
доказательства ограниченности у. Для нахождения же границ I о I
можно получить рекуррентное соотношение Фл+1^сл(Фл+ О*,
близкое к E.11) (в нем с—постоянная, определяемая извест-
известными параметрами), из которого легко заключить об ограни-
ограниченности | v |. Сделать это нетрудно, используя соотношения
и неравенства, выведенные в §§ 2—4. Однако вся совокупность
преобразований и оценок оказывается более громоздкой, чем
на первом пути, подробно изложенном в §§ 2—4.
Развивая далее свой метод, Ю. Мозер доказал, что для поло-
положительных в Q решений из Wl2(Q) уравнений E.1), коэффи-
коэффициенты atl которых подчиняются лишь условиям E.2), справе-
справедливо неравенство Гарнака
min u(x) ^стахи(х), E.23)
Q' Q'
где положительная постоянная с зависит только от п, v, ц
и расстояния Q' до границы Q (см. [402]). Основу доказатель-
доказательства неравенства Гарнака составляют два момента: во-первых,
применение неравенства E.12) или, что то же самое, неравен-
неравенства E.13) к неотрицательным субрешениям уравнения E.1) и,
во-вторых, использование следующей леммы Иона — Ниренбер-
га [29], которую мы сформулируем в удобной для нас форме:

f 61 СПОСОБ Ю. МОЗЕРА ОЦЕНКИ | и \$ 629
Лемма 5.1. Пусть функция v(x) суммируема в кубе K.2R
с длиной ребра 2R и для любого куба /Ср сг K2R удовлетворяет
неравенствам
J (о — t>p) dx^c mes /Cp E.24)
с некоторой постоянной с, где t>p = mes~'/Cp \v(x)dx. Тогда
существуют положительные постоянные б0 и В, зависящие лишь
от с и п, такие, что
ев»° М dx | e-e»° W djc < В mes2 /С2л- E.25)
Нетрудно проверить, что если и(х)—положительное реше-
решение E.1), то v = us будет субрешением уравнения E.1) при
любом s > 1 и s < 0. В частности, беря w = «~e, где 6 >0
сколь угодно мало, получим из E.13)
1/2в
. E.26)
J
Докажем, что для достаточно малых б
<c2/ ^u-26dx\ . E.27)
\K2R J
Для этого положим в E.5) о = ф(ы) = 1пы, а в качестве I возь-
возьмем срезающую функцию для произвольного куба /Сгр cz Q,
р^2#, равную единице в концентрическом с /Сгр кубе /Cpcz/C2S,
такую, что | V?|^p~'. Это даст оценку
Отсюда и из неравенства Пуанкаре следует, что
J | v — wp p dx < с3 mes /Cp.
Тем самым доказано, что функция у = 1пи удовлетворяет усло-
условиям леммы 5.1, и потому при некотором б0 > 0, определяемом
постоянной с3,
ee0 in и (х) dx f е-б„ in и (х) dx^B mes2 /C2p •

530 ОЦЕНКА КОНСТАНТ ГЁЛЬДЕРА [ГЛ. IX
Тем самым неравенство E.27) установлено при б = ба/2 в пред-
предположении, что концентрический с /C2S куб KiR cr Q. Применяя
неравенство Гёльдера, нетрудно заключить, что тогда оно спра-
справедливо и при любом б ^ б()/2.
Покажем, что для наибольшего б, удовлетворяющего усло-
условиям: б < ~- и lgft -2g- = \\gk -rftj + -j • справедливо неравенство
/ (' \1/2в
max«(jc)<c4 \u-6(x)dx\ , E.28)
Ui )
в котором с4 зависит лишь от v, ц и п. Для этого заметим,
что при выводе оценки E.12) для и фактически использовалась
лишь следующая информация относительно vh: сама функция и
и все ее степени вида v,t = uk , k = n/(n — 2), /г = 0, 1
будучи субрешениями уравнения E.1), подчиняются неравен-
неравенствам E.7). Рассмотрим функцию уй = (и6)*'- Для нее соотно-
соотношение E.5) при | = 1>й?2, где ? — срезающая для V/Cp cr /C2S
функция, принимает вид
J x = 0.
Если 2б/гл — 1 ^= 0, то отсюда и из E.2) следуют неравенства,
аналогичные E.7):
«Р
где с5(б) = 4 min [1 — B6>feA)~1]2- Ясно, что при б, указанном
й=0. I, ...
выше,с3(б) = 4 min \1 — k~h+1+^Sk^V > 0. Ввиду сказанного
л=о, 1,...
выше при таком б будет справедлива оценка вида E.12):
т u26dx I с постоянной с6, зависящей лишь от v, ^i
*L j
и п. Тем самым неравенство E.28) установлено, и постоянная с4
в нем равна с^5. Из него, E.26) и E.27) следует справедливость
неравенства Гарнака E.23) с постоянной, зависящей лишь от п,
v и [I в любом кубе KR, принадлежащем области Q вместе
с концентрическим ему кубом KiR. Но тогда, как нетрудно убе-
убедиться^ неравенство E.23) будет верно для произвольной об-
области Q' cz Q, причем постоянная с в нем будет определяться
величинами п, v, ц из E.2) и расстоянием Q' до границы Q.

§6] ОЦЕНКА НИРЕНБЕРГА 53!
Из неравенства Гарнака легко вывести оценку постоянной
Гёльдера для решений и(х) уравнения E.1). В самом деле, для
произвольного куба /С4д cz Q рассмотрим положительное реше-
решение v (х) = и (х)— Wi+e уравнения E.1), где w1 = min«, e > 0.
В силу E.23) для концентрического /С4Л куба KR имеем нера-
неравенства
osc {v; К в) < A — с) max v < A — с) max v =
Kr Km
= A- с) (osc {»; /С4й} + е)
с постоянной cg@, 1), зависящей лишь от n, v и ц. Отсюда
в силу произвольности е>0 следует оценка osc {и; Kr}^
^A—с) osc {и; /С4Д}, которая в силу леммы 4.8 гл. II дает
оценку («Уц,1 с а = — 1п4 A — с).
§ 6. Оценка Ниренберга
Изложим здесь простой и красивый способ оценки постоян-
постоянной Гёльдера первых производных от решений квазилинейных
эллиптических уравнений
2
/.(«)= .2_а</(*. и, ux)uXlXl + a(x, и, их) = 0, F.1)
данный Л. Ниренбергом в работе [44J. Он сугубо двумерный
и не переносится на случай уравнений с тремя и большим
числом независимых переменных. Пусть на исследуемом реше-
решении и (х), которое ради простоты предположим дважды непре-
непрерывно дифференцируемым,
vl2^au(x, u(x), иЛх))^^^, v>0, F.2)
\а(х, и(х), Mjr(je))K|i. F.3)
Функции аИ(х, и(х), их(х)) и а(х, и(х), их(х)) переменной х
будем записывать просто atj и а. Возьмем выражение
/ \
и
/ и их х \
= aiiur.x.\ ' ' И —) и представим его в виде
V 1 \ #22 1 '
В силу F.1) и F.2) и этого представления / получим
- а (^ + J
F.4)

532
ОЦЕНКА КОНСТАНТ ГЁЛЬДЕРА
[ГЛ. IX
Возьмем круг /Ср cr Q и будем считать, что начало коорди-
координат находится в его центре, так что /Ср = {г = | х | < р}. Пусть
g (jc) = g (г) есть какая-нибудь срезающая функция для круга Кр
с |-V?|^cp~'. Умножим обе части неравенства F.4) на г~а?2(г),
затем проинтегрируем по Кр и правую часть оценим сверху
следующим образом:
V
J r~V Kx, - uxlX,Ux2x) dx + -ЩГ 7l + ¦? J r"^2 djC- F'5)
Во втором члене интеграла
/2 = J r~a^2 (и2^ — uxxuXiX^ dx
проведем интегрирование по частям один раз по хх, а дру-
другой — по х2. После приведения подобных членов получим
h = J [ir~%2)Xl Чх^хл — ('¦~a?2)X; uXlXluXl] dx =
J v ь ~r
|^f "*¦
где -gQ^ = r[-gj-ux*x2 — -^7«зд] есть частное дифференцирова-
дифференцирование по углу 0 в полярной системе координат г, 0. Второй член
интеграла F.6) оценим так:
J 2г-«й' [-f- «Х!х2 - ^
<
где е — любое, большее нуля, а первый член F.6) предвари-
предварительно представим в виде
р 2л
j J
о о
р
= -a J
р 2л
J
[«*, (г, 9)-и,, (г,
о и

ОЦЕНКА НИРЕНБЕРГА
533
2я
Г
I
о
дих
что возможно, ибо I -^-^0 = 0, и используем оценку
о
2л 2л / G ч 2
kC, в) —Mxi(r,
2л / G
= J J
о \о
Это даст
р 2л
о о
дих (г, ф)
^
~2[uXl(r, Q)-uXl(r, O
2л 2л
<
J
r-aZ2u2xxdx.
Подставляя полученные для | /31 и | /41 оценки в F.6), получим
|/2|< J [(е
где Л1! = тах|Уи|. Эту оценку, в свою очередь, подставим
в F.5) и выберем е и а столь малыми, чтобы
Л__2
При таких е и а будем иметь
F.8)
т. е. для любого /СР/2 и концентрических ему кругов Кр,
J r-au2xx dx < | /-a?2w

534 ОЦЕНКА КОНСТАНТ ГЕЛЬДЕРА [ГЛ. IX
при p^d. Это же неравенство (см. замечание к леммам 4.1,
4.2 гл. II) дает возможность оценить константы Гёльдера
(Ux{)q'2)> *"=!. 2, для любой Q'crQ (в F.9) ?=1 в КРр).
Для кругов Кр, пересекающих границу, общая схема дока-
доказательства та же: оценивается интеграл I\ no KQf\Q- При этом
предполагается, что известны верхние границы модуля первой
и второй производных и по дуге s границы 5.
При интегрировании по частям в /2 выделяются члены по
пересечению круга Кр с границей 5. Для их оценки удобнее
с самого начала распрямить кусок границы, в окрестности
которого исследуется и, и все рассуждения проводить в новой
системе координат. Пусть такое преобразование уже сделано
и интересующий нас кусок 5Р границы 5 лежит на оси х2.
После интегрирования по частям выделится интеграл
/B= J r-VuXiux^dx2.
Но он не превосходит известной нам величины
,2р'-а
sp
Встретится еще одно отличие при оценке интеграла /4.
в2 (г)
Оно вызвано тем, что на этот раз интеграл
<39
в, и
будет браться, вообще говоря, по разомкнутому контуру и
потому не обязан обращаться в нуль. Однако концы этого
контура принадлежат Sp и удалены друг от друга не больше
чем на 2г, поэтому
в» (г)
Г duXi (r, G)
J д9
Mr)
и* (г, 6, (г)) - иХ1 (г, 92 (г)) | < 2r max | uXv
Этой информации -достаточно, чтобы вывести по вышеуказан-
вышеуказанному плану желаемую оценку для /[. _
Итак, получена оценка для («хг)(а/2), V Q' с Q, /=1,2, через
max| V« |, v и A из F.2), F.3) и расстояние от п' до 5 и оценка
(Uxi)al2) чеРез max|V«|, v и yi из F.2), F.3) и норму в С2
граничных значений и в предположении, что 5 сг С2.

§ Г\ СПОСОБ МОРРИ ОЦЕНКИ ПОСТОЯННОЙ ГЕЛЬДЕРА 535
§ 7. Способ Морри оценки постоянной Гёльдера
для решений двумерных вариационных задач
Пусть интегрант функционала
I(u)=JF(x,u,ux)dx G.1)
а
удовлетворяет при x^Q и произвольных и и р неравенствам
v\pf^F(x,u,p)^ii\pf, G.2)
где v и ц — положительные числа. Пусть и(х) есть обобщенное
решение из Wi(Q) вариационной задачи на минимум для /(и)
при каком-нибудь граничном условии, так что и(х) дает наи-
наименьшее значение функционалу G.1) среди всех функций W\ (й),
удовлетворяющих этому граничному условию (которое, в част-
частности, может и отсутствовать). Докажем, что при этом и(х)
будет непрерывна по Гёльдеру. Ограничимся внутренними
оценками. Возьмем произвольный круг /(s cr Q и концентри-
концентрические ему круги /Ср с p^i?. Функция ир(х), равная вне Кр
функции и(х), а в круге Кр совпадающая с гармонической
функцией vp(x), принимающей на границе Кр те же значения,
что и и(х), будет допустимой функцией сравнения (это есть
следствие известных предложений о свойствах элементов про-
пространства W\ (&))• Поэтому
Ци)^1(иР). G.3)
Отсюда, из G.2) и определения функции ир следует, что
F(x, и, ux)dx^^ F{x, xfi, o;)dx<|i J|
Kp /Cp Kp Kp
или, короче,
J |
dx < p 11 VVp |2dx, 0<p^R, G.4)
где р = M./v. Введем в Kr полярные координаты г, 0 с началом
координат в центре KR- Разложим и и ор в ряды Фурье по 0:
оо
и (г, 0) = ^Р- + V [а, (г) cos kQ + Ък (г) sin Щ, г < R,

536 ОЦЕНКА КОНСТАНТ ГЁЛЬДЕРА [ГЛ. IX
Легко видеть, что
p
f I VwP f dx = n V. k \a\ (p) + Ъ\ (p)l.
Kp ft=l
Из этих равенств и G.4) следует
р), р<Я. G.5)
4=1
Проинтегрируем это неравенство, точнее, представим его в вице
-^— (р~1/ргКр))^О и проинтегрируем в пределах от г до #:
/?~1/рг|з (/?) — г~1/рг|з (г) ^ 0. Это неравенство дает желаемую
оценку
Ч> (/•)<(-?-)'%(*), G.6)
из которой в силу леммы 4.1 гл. II следует неравенство
osc{«; /Ср/2} ^ ср'^р и возможность оценить \и$, Q'cQ,
с а=1/2р через ||м||^1)а, Р и расстояние от Q' до границы 5.
Изложенный здесь способ оценки | и ?? принадлежит
Ч. Морри [392]. Он прост и красив, но применим лишь к слу-
случаю т = п = 2.

Глава X
ДРУГИЕ КРАЕВЫЕ ЗАДАЧИ
§ 1. Формулировка задач и общая схема их решения
В предыдущих главах в основном рассматривалась первая
краевая задача. Другим краевым задачам посвящены лишь §§ 3
и 6 гл. III для линейных уравнений. Однако большая часть
данных выше различных априорных оценок решений линейных
и квазилинейных уравнений не зависит от граничных условий
(это так называемые внутренние оценки) и потому относится
в равной мере ко всем краевым задачам. Ввиду этого для
исследования других краевых задач достаточно изучить пове-
поведение их возможных решений лишь в- окрестности границы.
В линейном случае и даже в нелинейном случае, когда произ-
производные от решения и входят в гранич-ное условие линейно, все
исследование можно провести в основном по той же схеме,
что и для первой краевой задачи. Как это можно сделать,
читатель увидит ниже. Сложнее обстоит дело со случаем общего
нелинейного краевого условия: Для его изучения пришлось при-
прибегнуть, кроме теоремы Лерэ — Шаудера, к другой топологи-
топологической теореме о существовании решений абстрактных уравне-
уравнений определенного класса.
Понимая, что уже пора заканчивать данную книгу, мы огра-
ограничиваемся изложением лишь наиболее трудного и специфиче-
специфического случая, когда краевое условие зависит от их нелинейно.
Для случая же линейной зависимости граничного условия от их
даем необходимые указания, которые позволят читателю самому
провести все рассуждения, используя априорные оценки, при-
приводимые ниже.
Начнем с предварительного анализа интересующих нас
краевых задач и с описания основного плана их решения.
В ограниченной области Q рассмотрим задачи следующего вида:
Ь(и) = ац(х, и, ux)uXiXj + a(x, и, их) = 0, A.1)
,?Ю(и)мш[Ь(х, и, ux) + bi(x, u)uXt + bo(x,u)]\s = O, A.2)
в предположении, что уравнение A.1) равномерно эллиптично
и при произвольно фиксированных и и р в каждой точке jcsS
вектор 1(х, и, р) с составляющими ЬР.(х, и, p)-\-bi(x, и) не

538 ДРУГИЕ КРАЕВЫЕ ЗАДАЧИ [ГЛ. X
лежит в касательной к 5 плоскости. Точнее, будем считать, что
[Ьр.(х, и, p) + bt{x, «)jcos(n, *,)>v,(| и |, \р\), Vj > 0. A.3)
Так же, как и в случае первой краевой задачи, вопрос о разре-
разрешимости задач A.1), A.2) постараемся свести к вопросу о суще-
существовании неподвижных точек у некоторых преобразований,
обладающих рядом хороших свойств. Для этого запишем гра-
граничное условие A.2) в виде
s
= {-b(x, u,O)~bo(x,u) + u}\s A.4)
и рассмотрим следующие задачи:
&ц (х) их.х. + й (х) = 0, hi (х) иХ{ + и Is = ф (х) Is, A.5)
где
&И (х) = аи (х, v (x), vx (х)), й(х) = а (х, v (x), vx (x)),
Ь ( ) — f db(x' v(x)' p) dtA-b( ( ))
ф (л;) = - b (х, v (х), 0) - Ьо (х, v (х)) + v (x),
a v (х) — произвольная функция из C1+a(Q). Задача A.5) линейна
в отношении неизвестной функции и(х). Известно, что для
нее справедлива теорема единственности и что и(х) однозначно
определяется по v(x). Обозначим это, вообще говоря, нели-
нелинейное соответствие (преобразование) так:
и = Ф(о). A.6)
Неподвижные точки этого преобразования будут решениями
задачи A.1), A.2). Посмотрим, какими свойствами обладает
преобразование Ф. Если v(x)^Ci+a(Q), а все известные функ-
функции ац{х,и,р), а(х,и,р), Ь(х,и,р), Ь{(х, и), Ь0(х, и) и ф(л:)
достаточно гладкие, то функции йц(х) и й(х) принадлежат Ca(Q)
и, следовательно, есть основания ожидать, что задача A.5)
будет иметь решение и(х) из C2+a(Q). Однако функции bt(x)
в общем случае принадлежат лишь Са (ибо они образованы
из vx^, и потому относительно решения задачи A.5) нельзя
утверждать, что оно будет элементом пространства С +a(Q)
или хотя бы C1+a+E(Q), е >0 (см. §3 гл. 111). Тем самым
нельзя утверждать, что преобразование Ф вполне непрерывно

) I] ФОРМУЛИРОВКА ЗАДАЧ 539
(существенноулучшает v(x)), и, следовательно, нельзя применить
к нему, например, критерий Лерэ — Шаудера о существовании
неподвижных точек. Есть один случай, когда это сделать воз-
возможно, — это случай Ь(х, и, их) = 0. Для него hi (х) = bt (x, v (x))
и ф(;к) являются элементами С1+а и к задаче A.5) применимы
теоремы из § 3 гл. III, гарантирующие принадлежность реше-
решения и(х) к C2+a(Q). Для этого случая все рассуждения можно
строить так же, как и для первой краевой задачи. Основной
аналитической частью является получение априорных оценок
решений этой задачи в норме C1+a(Q). Такие оценки будут
установлены сразу для решений общей задачи A.1), A.2).
Для исследования общей задачи A.1), A.2) мы будем исполь-
использовать следующую теорему о разрешимости абстрактных урав-
уравнений в банаховых пространствах (см. [37!, § 41]):
Теорема 1.1. Пусть Хи Y — два банаховых простран-
пространства, I — отрезок [0,1], а х, у и т — элементы X, Y и I соответ-
соответственно. Предположим, что Ф — непрерывное отображение пря-
прямого произведения XX/ в Y, имеющее производную Фх (х, т),
непрерывную по (х, т) в операторной топологии /, {X —»¦ Y), и
удовлетворяющее следующим условиям:
1) Для любого решения х уравнения
Ф{х,%) = 0, A.7)
отвечающего произвольному т аз I, оператор Фх(х, т) имеет
ограниченный обратный Ф^1 (х, т): Y-^-X.
2) Множество всех решений уравнения A.7), отвечающих
всем те/, компактно в X.
3) При некотором фиксированном г из I существует един-
единственное решение х уравнения A.7).
Тогда при каждом те/ уравнение A.7) однозначно раз-
разрешимо в X.
Для доказательства теоремы убедимся, что множество /0 сг /,
состоящее из точек т, для которых уравнение A.7) однозначно
разрешимо, открыто и замкнуто, — тогда в силу условия 3)
/0 совпадает со всем промежутком /. Пусть т„ е /0 и хп стремятся
к т0 при д->оо, а хп— решения уравнения Ф(хп, т„) = 0. Усло-
Условие 2) позволяет выделить из {хп} сходящуюся подпоследова-
подпоследовательность: xnk^>-x при nk~^-oo. Переходя к пределу в равенстве
Ф(хПк, т„А) = 0, получим Ф(л:, то) = О, т. е. уравнение A.7) раз-
разрешимо и при т = т0. Легко видеть, что других решений у него
нет. В самом деле, если бы для некоторого х' ф х выполня-
выполнялось равенство Ф(х', то) = О, то в силу условия 1) по теореме
о неявной функции (см. [13]) существовали бы сколь угодно
близкие к х' решения уравнения A.7) при всех т, достаточно

640 ДРУГИЕ КРАЕВЫЕ ЗАДАЧИ [ГЛ. X
близких к т0, а это невозможно, ибо при т = т„А решение хПк
единственно и т„й-»-То, хПк^>х при дА-»-оо. Итак, доказано,
что т0 е /0, т. е. множество /0 замкнуто.
Проверим теперь, что оно открыто. Пусть тое/оиФ (х0, т0) = 0.
Прежде всего заметим, что по теореме о неявной функции урав-
уравнение A.7) разрешимо при т, близких к т0. Надо доказать, что
решение уравнения A.7) единственно при всяком т из неко-
некоторой окрестности т0. Предположим противное, что существует
последовательность т„—»-т0 при п-> оо такая, что для каждого т„
есть по крайней мере два различных решения х'п и х% уравне-
уравнения A.7). Без ограничения общности можно считать, что каж-
каждая из этих последовательностей имеет предел. Этот предел
равен х0—единственному решению уравнения A.7) при т = т0.
Обозначим через Ап линейный оператор А,— [Ф.*{*о> ^о) —
о
— Фж(^'+ A — t)x'n, T:n)]dt, действующий из X в Y. Легко
видеть, что норма Ап стремится к нулю при я^ю и
К « - О - ф, К g « - О - ф «• О + ф ft. **)=
Отсюда в силу условия 1) вытекает равенство
которое при достаточно больших п невозможно, ибо
|Ф*(*01 т0)i4n|-»-0 при п^уоо. Полученное противоречие пока-
показывает, что существует окрестность т0, в которой уравне-
уравнение A.7) однозначно разрешимо, т. е. множество /0 открыто.
Теорема 1.1 доказана.
Близкое утверждение в книге К. Миранда [37!] использо-
использовалось для доказательства теоремы существования и единствен-
единственности задачи Дирихле для нелинейных эллиптических уравне-
уравнений. (Подчеркнем, что, в отличие от принципа Лерэ — Шаудера,
теорема 1.1 неприменима к задачам, в которых имеет место
неединственность решения.) К исследованию краевых задач
других видов оно применялось Р. Фиоренца [17].
Чтобы свести решение задачи A.1), A.2) к теореме 1.1, введем
два банаховых пространства: в качестве X возьмем С +a(Q) (его
элементы будем здесь обозначать через и (х)), а в качестве Y— про-
пространство пар элементов «/ = {/, <р}, где f(x)^Ca(u), <p(s)
sC1+a(S), с нормой /La> k1+a>

; И формулировка задач 541
Исследуемую задачу A.1), A.2) включим в семейство задач,
зависящих от параметра te[0, 1]. Для простоты ограничимся
случаем линейной зависимости от т:
L» = tL(u) + A-t)L0(u) = 0, ^Q, I
Lf (и) s tL(s> (и) + A - т) Lf («) = 0, x e= S, I ( '
где Lo и L(oS> — дифференциальные операторы такого же вида,
как L и L(S) соответственно, причем при т = 0 задача A.8) одно-
однозначно разрешима в C2+a(Q).
Преобразование Ф определим следующим образом: V(«, т) е
gZX/сопоставим элемент г/ = {LT(u), L(f](и)} еУи потребуем
такую гладкость известных функций, чтобы Ф было непрерывно
дифференцируемо по и. Условие 3) теоремы 1.1 выполнено.
Чтобы удовлетворить условию 1), предположим, что на любом
решении и(х, t)eC2+a(Q) задачи A.8) соответствующая задача
в вариациях неограниченно разрешима, т. е. при V/eCa(Q),
feCl+o(S) существует единственное решение w(x) из C2+a(Q)
задачи
да], дах
A.9)
dbx dbl
где
aI/ = Tai/+(l-T)a?/, ат = та+A-т)а°, &J = тЫ-A-т)&?, A.10)
/ = 0 л, 6т = т6 + A+тN°.
Левые части в A.9) определяют значение оператора Ф„(и, т)
на элементе w. A.9) представляет собой линейную относи-
относительно w задачу вида C.8) гл. III. Если коэффициенты в гра-
граничном условии A.9) и их частные производные по х, и, р и
коэффициенты уравнения A.9) как функции (х, и, р) непре-
непрерывны по Гёльдеру с показателем а по переменным л: и с по-
показателем а' > а по переменным и, р, то оператор Ф„ (и, т)
непрерывен относительно (и, т). В силу теоремы 3.2 гл. III опе-
оператор Фа(«,т) при « = «(*, т) имеет ограниченный обратный

542 ДРУГИЕ КРАЕВЫЕ ЗАДАЧИ [ГЛ. X
в том и только том случае, если однородная задача A.9)
имеет лишь тривиальное решение w = 0.
Итак, исследование разрешимости задачи A.1), A.2) сведено
к выяснению условий, при которых выполняется предположе-
предположение 2) теоремы 1.1, т. е. множество всех решений и (х, т) из C2+a(Q)
задачи A.8), отвечающих всем т из [0, 1], компактно в про-
пространстве С +a(Q). Это предположение можно ослабить. Именно,
следуя К. Миранда [37J и используя установленные Р. Фио-
ренца [17] оценки для решений линейных задач (см. § 3 гл. III),
можно заменить требование компактности решений в C2+a(Q)
компактностью в C'(Q). Сформулируем это в виде теоремы.
Теорема 1.2. Предположим, что выполнены следующие
условия:
a) На множествах ЭЯдш, = {х, и, р: jceQ, | ы |< Af, \р КМ{)
с произвольными М > 0 и М{ > О функции а{! (х, и, р) и а (х, и, р)
и их частные производные первого порядка по и и р,{, функции
Ь(х, и, р), ——, и их частные производные первого порядка
аи gpi
по xk, и, рк, а также функции bi{x, и) и — *^ и , / = 0, .... п,
и их частные производные по xk, и удовлетворяют условию
Гёльдера по х с показателем а и условию Гёльдера по (и, р)
с показателем а' > а.
b) 5 есть поверхность класса С2+а.
c) Уравнение A.1) эллиптично, т. е. на V« e ЗИ.м.и,
ац(х, и, p)hli>v(M, МО!2, v>0.
d) Функции b(x, и, р) и bt(x, и) удовлетворяют условию A.3)
Пусть, кроме того, имеются дифференциальные операторы Lo
и LqS) такого же вида, как L и L(S) в A.1), A.2), для которых
соответствующие им функции а\,, a0, b, b°{, г = 0, ..., п, под-
подчиняются условиям а), с), d), причем при т = 0 задача A.8)
имеет единственное решение в C"+a(Q). _
Если на любом решении и(х, т) eC2+a(Q) задачи A.8)
соответствующая задача в вариациях A.9) неограниченно раз-
разрешима и если для всех возможных решений и(х, т) задачи A.8),
отвечающих всем те [0, 1], величины тах| и{х, т) \и тах| Vu(x, т) |
а а
равномерно ограничены и производные иХ{(х, х), /=1, ..., п,
равностепенно непрерывны по х в Q, то задача A.8) имеет при
каждом % из [0, 1] единственное решение и(х, t)eC2+°(Q).
Из сказанного выше и предположений теоремы 1.2 следует,
что преобразование Ф, определяемое задачей A.8), удовлетво-

§ 1] ФОРМУЛИРОВКА ЗАДАЧ 543
ряет требованиям пунктов 1) и 3) теоремы 1.1. Займемся про-
проверкой пункта 2), т. е. докажем, что множество решений
задачи A.8), соответствующих всем те[0, 1], компактно
в C2+a(Q). Из условий теоремы 1.2 следует, что из любой после-
последовательности решений задачи A.8) можно выделить подпосле-
подпоследовательность ик(х, хк), k = \,2, ..., сходящуюся в норме C'(Q).
Надо доказать, что ик(х, %к) образуют сходящуюся последова-
последовательность в C2+a(Q). Без ограничения общности можно считать,
ЧТО Tfc—>Т0 ПрИ &—»-ОО.
Обратимся к неравенствам B.1) гл. III. Первое из них
п ри / = 2 дает
[ГТ[Г A.11)
а второе при 1 = 2
[t*}6[W}l-\ ве @,1). A.12)
Таким образом, для рассматриваемой последовательности ик
справедливы оценки
с постоянной си зависящей лишь от области Q и от | ик ($
(последние по предположению равномерно ограничены для всей
последовательности {ик}).
Рассмотрим разность и = и'—и" двух произвольных функ-
функций из последовательности {ик}, соответствующих значениям
х' и х". Она удовлетворяет линейному уравнению
Lu = Lt(u')—LX"(u") = aij(x)ux.Xl + ui(x)uX{ + а(х)и = f (x) A.14)
и граничному условию
Ds)u -= Lf>) W)- L[SJ(и") = bi (x) ux. + J"W« = $(x), A.15)
где
ati{x) = a«(x,u'(x),u'x(x)),
С dgjk(x,u',u'x) Гда*(х,и',их)
\x> J -t "' + -t dt,
- / ч
ai W =
a(x)=w;{Xi(x) J - >\ut ш + J
(*• «'. 4)
^t *> dt,

544
ДРУГИЕ КРАЕВЫЕ ЗАДАЧИ
[ГЛ. X
f (*) - (т* - т') [в|/ (х, «", и>>) - а°, (х, и", и"х)] u'Vt +
+ {%" - %') \а (х, и", и"х) - а0 (х, и", и»)],
ф (х) = (т" - т') [Ь (х, и", и"х) - Ь° (х, и", и?) +
+ Ь{ (х, и") u"Xi - Щ (х, и") u"Xi + b0 (х, и") - Ь°о (х, и")],
причем
Используя A.13) и условие а) теоремы 1.2, нетрудно подсчи-
подсчитать, что для коэффициентов L и Z(S> и свободных членов f
и ф задачи A.14), A.15) верны оценки
max| uij, b{, b
\*и.
max |
Ф fi»
Ф fi» + max | f
с | r' - r" | [ 1 + (| u"
A.16)
Здесь й ниже постоянная с не зависит от k. Задача A.14),
A.15) есть линейная относительно и(х) задача вида C.1), C.2)
гл. III, и потому, принимая во внимание условия b)— d), к и(х)
можно применить оценку C.5) гл. III и в результате, учиты-
учитывая A.16), получить неравенство
^ + |t'-T"|]. A.17)
Из A.17) прежде всего можно заключить, что равномерно
ограничены нормы | uk |^+a>. Действительно, так как последова-
последовательность {uk} сходится в норме С (Q) и | хк — т01 —>¦ 0 при k -»• °о,
то для k, больших некоторого k0 > 0, имеем

$aj априорные оценки норм | и |^1+Р) 545
и потому в силу A.17)
, К2+а) ^. ,B+а) . ^2+а) ^
I «A Iq ^sl «А — «fee Iq "Г I «ft» Iq ^
откуда следует оценка
l«*k2+a><l + 3|rUa2+a>. Vfe>fe0. A.18)
Из ограниченности же норм | ик i^+a) и неравенства A.17) немед-
немедленно вытекает, что \ик — и/|д+а>—>0 при к, I—>оо, что и тре-
требовалось доказать.
Теорема 1.2 доказана.
Эта теорема сводит исследование разрешимости краевых
задач A.1), A.2) к получению априорных оценок норм | и |[j+w
с каким-нибудь р > 0 или хотя бы оценок | и $ и модуля непре-
непрерывности первых производных решений и(х).
В следующих параграфах мы покажем, что для уравнений
с дивергентной главной частью и нелинейных граничных усло-
условий, обобщающих второе и третье краевые условия для линей-
линейных задач (см. (8.3), (8.4) гл. III), такие оценки удалось уста-
установить [Зб2]. Более того, в этом случае оказалось возможным
избавиться от весьма жесткого требования неограниченной раз-
разрешимости задачи в вариациях, соответствующей A.8), и тем
самым установить существование решения и в тех случаях, когда
решение не обязательно единственно.
§ 2. Априорные оценки норм | a |q+p>
Рассмотрим квазилинейное уравнение с дивергентной главной
частью
М«)=-^ (а, (*,«,«,))+a (*,«,«,)=/(*) B.1)
при граничном условии
[cti {x, и, их) cos (n, х{) + ф (*, и)] Is = ф0 (*) *), B.2)
где функции ф(л;, и) и <fo(x) считаются определенными при всех
Представляет интерес доказать теоремы существования для
задачи B.1), B.2) при естественных ограничениях на а{ и а
того же типа, что и в случае задачи Дирихле (см. гл. IV). Для
этой цели, как выяснено выше, требуется получить априорные
*) Выделение «свободных членов» в уравнении и граничном условии
удобно для формулировки ограничений на входящие в них функции.
18 О. А. Ладыженская, Н. Н. Уральцева

546
ДРУГИЕ КРАЕВЫЕ ЗАДАЧИ
[ГЛ. X
оценки решений в норме Cl+ot(Q) при естественных ограниче-
ограничениях на at и а. Для любой внутренней подобласти Q' cr Q такие
оценки уже установлены в §§ 1—б гл. IV, так что здесь мы
займемся оценками вблизи границы 5, предполагая, что на S
выполняется условие B.2).
Оставив пока в стороне вопрос об оценке максимума модуля
самого решения и(х), получим последовательно оценки (u)q ,
max|V«| и («xA)(Qa>, считая, что max | и (л:)КМ и u(x)^C2(Q).
Предположим, что функции at(x, и, р) и а(х, и, р) при jceQ,
|и|<М и произвольных р дифференцируемы по своим аргу-
аргументам и подчиняются естественным ограничениям
да,(х,и,р) ^ ,. .W1 ,|я|чт-2.о
др,
да,
~др~}
да,
~ди
да-
дх,
да
да_
ди
да
дх,
т>\, B.3)
B.4)
Кроме того, считаем, что
О2 ({х, и: х е= Q, | и | < Щ, f
2, функция q>(;t, и) принадлежит
(Q), Фо е О1 (Q).
Фиксируем произвольно какой-нибудь участок S! границы S
и требуемые оценки установим в небольшой области Q], при-
примыкающей к S]. Для этого предварительно «распрямим» St,
делая преобразование независимых переменных tji = tji (x),
i=l, ..., п. Пусть в новых координатах S{ задается уравне-
уравнением уп = 0. Уравнение B.1) и условие B.2) примут вид
da, (х, и, их) dyt ) = f( )
dyt dX[-Ta(x'u'ux) — rW,
= 0.
[а,(х, и, их) ¦%*¦ + *(«/,«)}
B.1')
B.2')
где
* (у.«) = у
[ф {х'и) -фо {х)]-
Из B.1') и B.2') выводим, что и(х) удовлетворяет интеграль-
интегральному тождеству
J" [«!(*• в'в-)^-^
= O B.5)
•s.

J2J АПРИОРНЫЕ ОЦЕНКИ НОРМ I и |[j+P) 547
при любой г] из Wl (Q), равной нулю вне Q2 =э Qp Тогда, пре-
преобразовывая в B.5) граничный интеграл к объемному, приходим
к интегральному тождеству
^ ]-0.B.6)
Положим в B.6) r) = gmmax{« — k, 0}, где k — любое число,
а ? (у) — срезающая функция для V шара Кр с центром на Su
лежащего в Qj, где введены координаты у. Тогда в силу B.3),
B.4) так же, как и в§ 1 гл. IV, при k^maxu — dM получаем
неравенство
(и- fc)m| V? Г<ty +mesAk.pl. B-7)
Ak, p L"A, p
Здесь AkiQ — множество из пересечения Кр с Q, на котором
и(у) > k, а б > 0 — некоторое число, определяемое М и постоян-
постоянными из неравенств B.3), B.4) и условий на ф, ф0 и 5.
Аналогично, полагая в B.6) r) = ?mmax{— и — k, 0}, придем
при &^тах(— и) — 6М к неравенствам B.7) для функции — ti(y).
Заметим, что в случае первой краевой задачи неравенства B.7)
для и и — и были доказаны при дополнительных ограничениях
на k: k^maxu и k^max(-u) соответственно. Здесь этих
Kpns Kpns
ограничений нет. Из B.7) на основании теоремы 7.2 гл. II выво-
выводится оценка нормы | и fa) вблизи S{.
Предположим, что мы уже оценили max| V« |. Получим тогда
оценку (tix^Q, Qi cr QU^p Для этого положим в тождестве B.6)
г\ = 1у , г ф п, где | — произвольная достаточно гладкая функ-
функция, равная нулю вне Q2, и результат преобразуем так:
J [ dyf 4 dxt ^ ai dxt дуг Ч
Это тождество, очевидно, будет оставаться верным при любой
\(у) из W\{Q), равной нулю вне Q2.
Фиксируем одну из касательных, к 5! координат уТ (г Ф п),
и пусть AkiQ — множества, отвечающие функции иУг. Беря в B.8)
сначала 1 = ?2тах[иУг — k, 0], а затем 1 = ?2тах {— uUf — k, 0j
18*

548 ДРУГИЕ КРАЕВЫЕ ЗАДАЧИ [ГЛ. X
с любым k и учитывая ограниченность max| Vu | и условия B.3)
Q
и B.4), выводим неравенства
J
B.9)
Ak, p Ak.
r=l п— 1,
и аналогичные неравенства для — иу . Они справедливы при
любых k. Отсюда и из теоремы 7.2 гл. II получаем оценку
(«j/r)(p> ^ с, г ф п, с некоторыми с и р > О, зависящими от
max|V«|. После этого оценка в СрШЛ для производной по
а
нормали к S{ устанавливается с помощью уравнения B.1') и
неравенств B.9). Действительно, из B.9) при k = min uy сле-
/cpna r
дует, что для шаров KQ, лежащих в области Q2> верна оценка
J |V«J/rj2d«/<YPn-2+23. гфп. B.10)
крпа
С другой стороны, разрешая уравнение B.1') относительно и.упуп,
находим, что Щпуп= 2 ЬсгиУгу{-\-Ь с ограниченными Ыг и Ь.
гфп
Отсюда видно, что неравенства B.10) верны и при г = п, и,
следовательно, в силу леммы 4.2 гл. II величина (иуп)(^>
i, оценивается через известные нам постоянные и
расстояние Q, до S \ S,.
Обратимся к оценке тах|Уи|в примыкающей к Si части Q[
области Q. Оценке max|Vu|, так же как и в случае первой
а,
краевой задачи, будет предшествовать, во-первых, оценка ин-
интегралов
j\Vu\ldy B.11)
а,
с достаточно большим (но конечным) / и, во-вторых, оценка
максимума модуля градиента и(х) на S. Последняя в первой
краевой задаче основывалась на том, что из граничного усло-
условия были известны на S первые производные и по касатель-
касательным направлениям.
В данном случае, если бы удалось оценить максимум на S[
производных и по касательным направлениям, то производную
по нормали, а тем самым и max|V«| можно было бы сразу

5 2J АПРИОРНЫЕ ОЦЕНКИ НОРМ | и |jj+P» 549
оценить, исходя из граничного условия. Действительно, B.2')
дает
= 0,
откуда с помощью условий B.3) и B.4) легко выводится оценка
-^— через тах|«| и max max I и» I.
°Vn S, S, гфп Si ' rl
Итак, требуется оценить интегралы B.11) и максимум моду-
модулей касательных производных uVf, г фа, на S\. Начнем с оценок
интегралов B.11).
Прежде всего, рассматривая B.7) с k= min u(x) и учитывая
О|ПКР
установленную выше оценку (и)^, находим, что
B.13)
J
при р^р, где рис определяются лишь М и известными нам
постоянными.
Для получения оценок B.11) с 1>т приходится использо-
использовать, кроме B.6), еще тождество B.8), причем в последнем
надо предварительно провести интегрирование по частям:
дх, Л|> дх. \ d (a — фии„ Y1
+^l^-L^rsl\''!'=0- B14)
г = 1 п.— 1.
Здесь gj = — {atykXitlk + f + ^J6^ + a{ дх 1&у растет не быстрее
(m — 1)-й степени | V« | при больших | V« |.
Введем следующие обозначения:
*=.i ** fc=i **
В тождестве B.6) положим
Ц = [и(у)-и(г/о)] v*+*w%2, s,
ГДе ? (#) — срезающая функция для шара Кр с центром yQ^Sl
и радиусом р<р, меньшим расстояния у0 до S\Sj. Тогда

550 ДРУГИЕ КРАЕВЫЕ ЗАДАЧИ [ГЛ. X
B.6) будет иметь вид
J {aiux.vs+]W>? + (и - и (г/о)) [at (s + 1) vsvx.w%2 +
+ aivs+]aw4~]wr ?2+ alvs+]wq2ttr + bvs+]w%2 +
2} dy = 0, B.15)
d2y,
где b = ai dx gy —a + f+ г|)цы^ + г|)^. Из наших предположе-
предположений следует, что
\Ъ(х, и, р)|<ЦоAи|)A+|р1Г. B.16)
Произведем в B.15) оценки с помощью условий B.3), B.4) и
B.16), замечая, что в силу B.3)
а,(я, и, р)л>уо(|и|)|рГ-Щ»(|и|). vo>0. B.17)
В результате получим неравенство
т
J vs+]w" ~g2d«/<
< с, тах| и - и(у0) \ f \[(s + 1) as^l V» |?2
J.-2L
2?
J »5
в котором С\ определяется постоянными ц(М), НоШ) и "
из B.4), B.16) и B.17), а также max 1|>B, гр^ и грани-
цей S. К членам в правой части применим неравенство Коши
A.2) гл. И с е=1 и воспользуемся тем, что max| и — и(у0) К
ар
^с2ра. Тогда при р < Cclc2)~lla будем иметь
. т г т—2
2 g2d«/<cpa J L(s+ IJ1-1©
г т2
a J L(s+ IJ»1-1© 2 | V» p?2 +
(p) B.18)
с известной нам постоянной с(р), конечной при р > 0.

§2]
АПРИОРНЫЕ ОЦЕНКИ НОРМ
551
Рассмотрим теперь тождество B.14), считая в нем | рав-
равными и„ vswqt? с г Ф=п:
да.
да,
it
да,
dx, d
да
да
да
i/ = 0> r=l n~L
Произведем суммирование по г от 1 до п — 1 и выделим два
положительных члена:
да,
да,
да,
= -щ- (uX/yr - uyiyiXjyr) UyrX{
s да.
Их оценим с помощью неравенства B.3), а остальные перенесем
в правую часть и оценим по модулю, замечая, что в силу
условий на S, f(x), ф0 (лг) и <f(x, и) и B.4)
диг yrxj k
и
dUx U«l dXj
ди
Это даст
Г
Я
V» рg2l dy <
J
\гфп
-l\ Vw

652 ДРУГИЕ КРАЕВЫЕ ЗАДАЧИ [ГЛ. X
Применяя теперь неравенство A.2) гл. II, получим при
<7 = s = 0 неравенство
J ш(т-2)/2 2 Ц2 ?2 rf^ <- с J („шт/2?2 + „ш(т-2)/21 yg р) dy B.19)
р гфп т ар
ар гфп т ар
и при произвольных s > 0, ?2>0 неравенства
J
ш(т-2)/2 Г ^ Ы2^„.Ш^2 _|_ ?.
Из B.19) и неравенства B.18) с <7 = s = 0 следует, что для
достаточно малых р, не превосходящих некоторого числа р0,
определяемого а и константами из B.18) и B.19), справедлива
оценка
f dy + с(p),
Qp
и поскольку vwml2~] f^.wml2, то отсюда на основании B.13)
можно заключить, что
!d«/<c,(p). B.21)
Пусть теперь s > 0. Нетрудно видеть, что
| Vw |2 < cw 2 и2уут + cw3. B.22)
Действительно, wy = 2 2 иуМу,уА поэтому | Уш г^*4дом^, и
производную % у можно выразить из уравнения через осталь-
остальные и убедиться, что в силу B.3) и B.4)
I uWn I ^ с' ^ | путу | + c'w- B-23)
Используя B.22), легко заключить из B.18) и B.20), что
при достаточно малых р (меньших некоторого р0 > 0) и при
таких q, для которых отношение q2/s много меньше единицы,

§ 2] АПРИОРНЫЕ ОЦЕНКИ НОРМ | и |[]+Р> Б53
будут верны неравенства
^| X) t№ (т " Т* X) XS) / tttt Jt*4 I CltJ ^?»
I Ш^Л I I
О
^C(s,q)jvs+lwq+im-2)l2\4?dy + c(s,q), O<p<pOl B.24)
причем постоянные с (s, q) и р0 в них зависят от s, q и S.
Рассмотрим последовательность областей Й„ , р = —Н—^п,
ps s 2 2i+1
s=l, 2, ..., и пусть ?s — срезающая функция для шара Кр ,
равная единице в Kps+i- Считая сначала q равным нулю, вы-
выводим из B.24) и B.21), что
J s
при любых s > 0. После этого, проводя в B.24) индукцию по
<7 = 0, 1 убеждаемся в ограниченности интегралов
pЦ dy < с (S, ,), B.25)
ар/2\ r+n J
причем постоянная c(s, q)—>oo при s, ^—>oo. Принимая во
внимание B.23), окончательно можно написать
J A +1 Va I)' A Н- a^rfy <c @. ' B-26)
Яр/2
Займемся теперь оценкой max|«j, I, гфп, вблизи S{. Для
этого будем оценивать максимум функции z = v?>2, где ?(«/) —
срезающая функция для шара /СР/2, рассмотренного выше.
В случае т^2 это можно сделать таким же способом,
каким в § 3 гл. IV оценивался | Vm | внутри Q. Именно, по-
положим в тождестве B.8)
I = Uyt? max {z (y)-k,O), гфп, k^ О,
и обозначим через Ак множество точек i/gQ, для которых
z(y) > k. После суммирования по г от 1 до п — 1 получим
J (?**+&-,+&W-*>?+
]y = O, B.27)

554 ДРУГИЕ КРАЕВЫЕ ЗАДАЧИ [ГЛ. X
и так как UyrXjuyl? = у vXjt? = у (zX/ — 2»?Ц), то из B.27) на
основании условий B.3), B.4) можно заключить, что при
4
Постоянная ct зависит от v(M) и ц(М) из условий B.3), B.4),
а также от радиуса р/2 шара Крр. Однако последнее в данном
случае несущественно, поскольку шар Др/2 считается фиксиро-
фиксированным.
Применяя затем к интегралу j (I +| V« \)m+idy неравенство
Гёльдера с показателями р = //(т + 4) и р' = 1/A— т — 4), где
/ > (т + 4) п/2, и учитывая доказанное выше неравенство B.26),
приходим к неравенствам
из которых в силу леммы 5.4 гл. II следует оценка max2 =
t2 при m^2.
а
В случае 1<т<2 для того, чтобы оценить maxz, поло-
а
жим в B.8)
| = Uyfvswt,2 max {z (у) — k, 0}.
Основными членами в полученном подынтегральном выражении
будут
да, 1 йа(
= а?- 4yrx,UyrvswXi (z - k) g2 = у —i- оЯ/а»я<о* B -
из которых первые два положительны, а последний имеет ту же
структуру, что и соответствующее выражение в B.27). Член /э,

§2] АПРИОРНЫЕ ОЦЕНКИ НОРМ | u41+P> 555
содержащий wX{, оценим по неравенствам Коши A.1), A.2)
гл. II, используя при этом B.22) и условия B.3), B.4):
1 ;з I < т ж~ v*tv*ivS~lw B ~k) &2 +
Здесь v = v(Af), ц = ц(М) — постоянные из условий B.3), B.4).
Если s взять достаточно большим, так чтобы c(xn2/Dsv) < 1,
то теперь уже довольно просто вывести неравенства
а следовательно, и неравенства
J | Vz I2 dy < с, J A +1VM |)m+6+2s dy. B.28)
Ak Ак
Они, так же как и выше, в силу B.26) с / > ——^—~ п °^е"
/п-\ \
спечивают оценку maxz = max 2 *4 + ! )?•
a a \r=i r /
Итак, доказано, что max|% I^Af, при тфп, тем самым,
а, ' г|
как было выяснено выше, оценен max| V« |. Кроме того, имеются
s,
неравенства B.26). Все это дает возможность провести оценку
max| V« | вблизи Sx так, как это было сделано в первой краевой
задаче (см. § 4 гл. IV).
Сформулируем доказанные здесь утверждения об оценках
и(х) в виде теоремы.
Теорема 2.1. Предположим, что функции at(x, и, р),
а(х, и, р) при xgQ, |ы|^М и произвольных р дифференци-
дифференцируемы по своим аргументам и удовлетворяют неравенствам B.3)
и B.4); f(x)e ?,„(?); Ф(х, ы)е=О2(Й Х[-М> М]); Фо^О'(?2) и
тах|Ф, ф^ц, ф„ц, ух., Фц, ф0) Фо^| <ц(| и |). B.29)
Пусть граница S области Q принадлежит О2.
Тогда для любого дважды непрерывно дифференцируемого
решения и(х) задачи B.1), B.2), для которого тах|и|<Л1,
норма | и fQ оценивается при некотором Р > 0 постоянной,

556 ДРУГИЕ КРАЕВЫЕ ЗАДАЧИ [ГЛ. X
зависящей лишь от М, постоянных пг, v(M) и ц (М) из B.3), B.4)
и B.29) и границы S. Этими величинами определяется и пока-
показатель р.
Оценить максимумы модулей решений и(х) задачи B.1),
B.2) через данные задачи в общем случае, как известно, не-
невозможно. Приведем два случая, когда такие оценки имеют
место.
Теорема 2.2. Пусть при достаточно больших |м|^>/? вы-
выполняются неравенства
при xe=S, |p|<oo и xe=Q, p = 0, B.30)
sign и ¦ \dat{Xd'x"'0) + а (*' "• °) - f (*)] < °- * s Q' B-31)
sign и • [а{ (х, и, 0) cos (n, xt) + ф (х, и) — <р0 (х)] > 0, xgS. B.32)
Тогда для любого решения и (х) <= С2 (Q) f| Cl (Q) задачи B.1),
B.2) тах|ы|^#. Предполагается, что S принадлежит О2,
а
¦ да, да, да{
существуют производные -^-=-, ~Г=-, -г-1 и они ограничены при
орл он ®%1
конечных значениях и и р = 0.
Доказательство этой теоремы несложно. Оно опирается на
принцип максимума для эллиптических уравнений. Сначала
с помощью B.31) и B.30) проверяется, что внутри Q решение
не может иметь максимумов, больших R, и минимумов, мень-
меньших — R. После этого оценивается тах| и \. Поясним последний
s
этап.
Пусть максимум функции и(х) больше R и достигается
в точке Ао границы S. Преобразуем, вводя координаты ух,..., уп,
кусок S, границы в окрестности Ао в плоскость г/„ = 0 так,
чтобы внешняя нормаль в точке Ао совпадала с осью уп. Тогда
граничное условие B.2) примет вид
\ait(x, ы, ux)-~-uykcos{n, Xt)-\-ai{x, ы, O)cos(n, xt) +
+ Ф (х, и) - ф0 (*)] | = О,
где
1-1/2
f dat(x, «, tux)
aii=\ к*-,) ' С08(п^)|*
В точке Ао обращаются в нуль производные вида иИг с г ф п,

3) ТЕОРЕМЫ СУЩЕСТВОВАНИЯ 557
а иу ^>0. Поэтому в силу условия B.30) имеем в точке Ао
at (х, и, 0) cos (n, Xi) + ф (х, и) — ф0 (х) < 0,
но это противоречит B.32).
Аналогичные рассуждения в точке минимума и (х) приводят
к оценке и снизу.
Теорема 2.3. Если at(x, м, р) и а(х, и, р) удовлетворяют
условиям теоремы 7.6 гл. IV, f <= L4l (Q), ф0 е Wlqi (Q) с qx>
> max{n/m; 1} и если при xgS и \u\^R выполняется нера-
неравенство U(f(x, u) ^>0, то для любого ограниченного обобщенного
решения и(х) из Wlm(Q) задачи B.1), B.2) vraimax|«| оцени-
Q
вается постоянной, зависящей лишь от /?, mes Q, || f \\4i, a, \\ ф0 Щ, а,
qx, нормы ||u\\4tq с каким-либо q>n(—— 1), а также от ве-
величин v, Цо- Цк a. tn, k0, || ф3 ll<rt. a из условий G.4), G.5) гл. IV.
Доказательство этой теоремы аналогично доказательству те-
теоремы 7.6 гл. IV. Можно привести различные критерии типа
теоремы 7.5 гл. IV, гарантирующие оценку нормы \\и\\я, а. Мы
здесь на этом останавливаться не будем.
§ 3. Теоремы существования
Оценок, установленных в § 2, достаточно, чтобы на осно-
основании теоремы 1.2 доказать существование решения задачи B.1),
да., да, да,
B.2). Будем предполагать, что аг/= —, -^ р, + -^- + а,
Ь0(х, и) = <р(х, и) — ф0 a S удовлетворяют условиям а)-с) теоре-
теоремы 1.2, f(x)<=Ca(Q) и, кроме того, at(x, и, p)cos(n, xt) подчи-
подчиняются ограничениям, наложенным в пункте а) теоремы 1.2 на
функцию Ь(х, и, р). Предположим, далее, что при х е Q, | и \*?^М
с произвольным М > 0 функции at(x, и, р), а(х, и, р) и <f(x, и)
удовлетворяют условиям теоремы 2.1. Для доказательства раз-
разрешимости задачи B.1), B.2) рассмотрим семейство задач, за-
зависящих от параметра т е [0, 1]:
= rf (x), xgS,
<» (и) = [ха{(х, и, их) + A - т) а°(их)] cos(n, xt) +
+ тф(лг, «) + A — т)ы = тфо(л:), xeS,
C.1)
где а] (их) = A + ы 2ут-2)/2 и^

558 ДРУГИЕ КРАЕВЫЕ ЗАДАЧИ [ГЛ. X
При т = 0 задача C.1) удовлетворяет условиям теоремы 2.2
с V7? > 0, и потому и s 0 является ее единственным решением
в классе С2 (Q) Л С1 (Q).
Предположим, что для всех решений и(х, т) задачи C.1),
те [0,1], можно дать равномерную относительно те [0,1]
оценку тах|м(л:, т)|=^Л4. Тогда в силу теоремы 2.1 справед-
справедлива оценка | и (х, т) |(^+р) ^ с с некоторыми р > 0 и с, завися-
зависящими от М и общими для всех те[0, 1]. Ввиду этого теорема
1.2 гарантирует существование единственного решения и(х, т)е
eC2+"(Q) задачи C.1) при Уте [0,1] при условии, что соот-
соответствующие задачи в вариациях неограниченно разрешимы в
классе C2+a(Q). Сформулируем это утверждение в виде теоремы.
Теорема 3.1. Предположим следующее:
а) На множествах ЗИлш, = {х, и, р: х е Q, \и\^М, | р |^ Мх)
с произвольными положительными М и Мх функции at (x, и, р),
да, (х, и, р) да, (х, и, р)
l и их частные производные по х^, и
j
, , ч да да dm d2qp бф
и рк, а также функции а(х, и, р), -^, ^-, ф, -^, j^, ^,
-j— удовлетворяют условию Гельдера с показателем а по
переменным х и условию Гельдера с показателем а' >а по
переменным и, р.
b) Выполнены неравенства B.3), B.4), B.29).
c) Se=C2+a, f(x)e=Ca(Q), q>0(x) e CI+a(Q).
d) Для всех решений и(х, т) класса C2(Q) задачи C.1) верна
оценка тах| и(х, т) \^М с постоянной М, не зависящей от т из
[0, 1]. а
e) На любом решении и(х, т) задачи C.1) соответствующие
задачи в вариациях неограниченно разрешимы.
Тогда при каждом т е [0, 1] существует единственное реше-
решение задачи C.1) и, в частности, задачи B.1), B.2), принадле-
принадлежащее C2+a(Q).
Покажем, что от условия е) можно освободиться, если дока-
доказывать только существование решения.
Предварительно установим следующее вспомогательноэ пред-
предложение, касающееся разрешимости нелинейных краевых задач
более простого вида:
dx-t dxt
A] (x, ux) cos(n, xt) + и = тФ (х), x<=S.
C.2)

SI
ТЕОРЕМЫ СУЩЕСТВОВАНИЯ
559
Лемма 3.1. Пусть на множествах 3RMt = {x, р: j;eQ, | р |<
L
с произвольным М, > 0 функции At(x, р),
д%А1 д%А1
Я г а
удовлетворяют условию Гельдера с показателем у
dPjdxh dPjdpk
по х и условию Гельдера с показателем у' > у по р, причем
v>0.
C.3)
Тогда, если S е= C2+v. то при любых F e= CY(Q), Ф е= C1+Y(Q) и
те [0, 1] существует единственное решение и(х, T)eCHv(S) за-
(Зачы C.2).
Заметим, что C.2) есть упрощенный вариант задачи C.1) с
а=—ф=—и и ui, не зависящими явно от и. Теорема 2.2 га-
гарантирует для решений и(х, т) задачи C.2) оценку тах| и (х, т) |<
где постоянная /?=maxj
max
а
dAt(x, 0)
дх,
-F(x)
; тах|Лг(д;, 0)Х
Xcos(n, Xi)— Ф(х) |} не зависит от те [0,1]. Поэтому в силу
теоремы 3.1 для доказательства леммы 3.1 остается убедиться
в том, что соответствующие C.2) задачи в вариациях неограни-
неограниченно разрешимы или, что то же, однородные задачи в вари-
вариациях имеют лишь тривиальное решение. Последние имеют вид
дА-Ах, их)
_
да%их)\ 1
S 14
рщ 8(П| Xt)+w=Ot
C.4)
Тождественное равенство нулю решений w(x, т) этой задачи
вытекает из соответствующего ей интегрального тождества
I Г
справедливого при V-q
условие C.3) на
|
= 0> C-5)
(Q). Полагая в нем т) = ш и учитывая
и аналогичное свойство
<?«, дих
что до з=0.
\\т&к, лемму 3.1 можно считать доказанной,
заключаем.

560 ДРУГИЕ КРАЕВЫЕ ЗАДАЧИ [ГЛ. X
Вернемся к общей задаче C.1). Предполагаются выполнен-
выполненными лишь условия a)— d) теоремы 3.1.
Из теоремы 2.1 следует, что при некотором р >0 для всех
возможных решений задачи C.1) справедлива оценка | и |[]+р>^
s^M2. Пусть v (х) — произвольная функция из CI+P(Q). Сопо-
Сопоставим задаче C.1) задачу C.2) с
А[(х, ux)=at(x, v(x), ux),
F(x) = f (x) -a(x,v (x), vx (х)) - v (x),
Ф (х) = Фо (х) - ф [х, v (х)) + v (х).
C.6)
Легко проверить, что в силу предположения а) функции At (x, р),
F (х) и Ф (х) удовлетворяют условиям леммы 3.1 с v = niin{a, p},
и потому лемма 3.1 гарантирует при любой фиксированной
ogCi+p(Q) существование единственного решения м(лг,т)е
<= C2+Y (Q) задачи C.2), C.6) при каждом т из [0, 1]. Таким обра-
образом, задача C.2), C.6) определяет в пространстве CI+e(Q) пре-
преобразование
u = W(v, т), C.7)
зависящее от параметра те [0,1]. Неподвижные точки этого
преобразования и будут искомыми решениями задачи C.1).
Для доказательства существования у Чг(о, т) неподвижных
точек обратимся к теореме Лерэ-Шаудера 8.1 гл. IV. В ка-
качестве множества %1 в ней следует взять шар | v |J1+P)^Af2+e,
е > 0, в пространстве C1+0(Q), так что неподвижные точки Ч?
не попадают на границу шара.
Чтобы проверить выполнение условий теоремы Лерэ-Шау-
Лерэ-Шаудера, установим оценку разности двух решений задачи C.2),
C.6), отвечающих двум различным функциям v из CI+B(Q) и
различным значениям параметра т. Это сделаем, как и при до-
доказательстве теоремы 1.2, с помощью оценок § 3 гл. III для
линейных задач.
Лемма 3.2. Для разности
u = u'-u" = W (vf, т') - ЧГ (о", т")
при Vy^ap справедливо неравенство
I « IL2+Y> <C\V'-V" {J+V> + С A +1 U' g+Y) +
* - u" fl> -f-11 - r" | +1 V' - v" Ц>], C-8)

ТЕОРЕМЫ СУЩЕСТВОВАНИЯ 561
где постоянная с определяется только нормами \ v' ||J+P\ | v" ?
| и' f$ и | ы" 1У* *) и не зависит от х из [О, 1].
Рассмотрим функцию и = и' — и" как решение линейной за-
задачи типа A.14), A.15):
dat. (х) _
ац(х)ихх-\ т—их-и f(x), xsQ,
' dxi ' C.9)
an (x) cos (n, xt) uXj + и =— ф (a:), x&S, J
где
(д) _ j
Г Г
f (X) = (v'X{ - v'^ Г Г*«Г(*' p*' 4) + т Да (х,^,уЩ dt
f ff ff\
г,(х, v , ux)
7 /M
7xt
a(x, v",v"x)\,
о L " dv J
x — x")\at (x, v", u^')cos(n, л:,)— а\(х, u^')cos(n, x() —
— Фо (x) + Ф (x, v") — v],
u<(x) = tu' (x) + (l-t) u" (x), v* (x) = Ы (x) + A - /) v" (x). C.10)
Принимая во внимание условие а) теоремы 3.1 и используя,
как в доказательстве теоремы 1.2, неравенства A.11), A.12),
можно вывести для коэффициентов и свободных членов в
уравнении и граничном условии C.9) следующие оценки,
*) Мы не отмечаем здесь и ниже в доказательстве децмц зависимость
g от характеристик известных функций-

ДРУГИЕ КРАЕВЫЕ ЗАДАЧИ
[ГЛ. X
аналогичные A.16):
max
(х)
dx,
iL2+v)
max | ф |< с [max | v' - v" \ + \ x' - x" \ ],
a a
maxlf | + max|Vqj|<c(max|»'-»"
q q a
X
c\v'-v"t\
id)
C.11)
c\v'-v"?+y).
Здесь постоянная с зависит лишь от | и' Q\ | ы" <?\ | v'
I Г
Для решения ы(а:) линейной задачи C.9) справедливо нера-
неравенство C.5) гл. III. Из него в силу C.11) следует желаемое
неравенство C.8).
Обратимся к доказательству непрерывности преобразова-
преобразования Ч? по (о, т). Для этого предположим, что при &->°о по-
последовательность [vk(x)} сходится к функции vo(x) в норме
CI+P(Q), ат4->т0. Через ик(х) и ио(х) будем обозначать соответ-
соответствующие решения задачи C.2), C.6). Из условий Ь) — с) тео-
теоремы 3.1 и из теорем 2.1^ 2.2 следует, что последовательность
[ик(х)} компактна в C'(Q). Пусть {ы^(х)} — какая-либо подпо-
подпоследовательность {Uk}. Из нее в свою очередь можно выбрать
подпоследовательность {м^'Ь сходящуюся в норме С1 (Q). При-
Применим теперь неравенство C.8) к двум каким-либо функциям
и" = ит», u' = Uk" этой подпоследовательности. В результате
получим неравенство
Г - Тя,- | + I Vh» - Vm" {j+Y)J. C.12)

i 3] ТЕОРЕМЫ СУЩЕСТВОВАНИЯ 563
Отсюда так же, как в конце § 1 из A.16), выводим, что
|«*»-«m»fa2+Y)-*0 при k", т"-*оо.
Предельный переход по данной подпоследовательности в задаче
C.2), C.6) показывает, что единственной предельной функцией
для Ukr может быть лишь иа(х,х), т. е. | Uk« — Mo f?+y)->0 при
&"—><». Так как подпоследовательность {м^} выбиралась из {uk}
произвольно, то, очевидно, и вся последовательность \uk}
сходится к ы0(л:, т) в норме C2+Y(Q). Таким образом, непрерыв-
непрерывность преобразования Чг(о, т) по (v,x) установлена.
Докажем, что Ч* преобразует Э?Х[О, 1] в компактное в C'+P(Q)
множество. Для этого рассмотрим произвольную последова-
последовательность uk = W(vk, xk), где »?<=Ш, тА_е=[0, 1], k = l, 2, ...
Так как ^ — шар в пространстве C'+P(Q), то {vk} компактна
в CI+P'(Q) с Vp'< Р, и потому из доказанного выше следует,
что последовательность {ик}, k = 1, 2, ..., компактна в C2+Y'(Q),
у'=аР, и тем более компактна в C1+P(Q). Итак, дока-
доказано, что преобразование 4?(v, x) в пространстве C1+p(Q) непре-
непрерывно и компактно, т. е. вполне непрерывно. Из всех условий
теоремы Лерэ — Щаудера осталось убедиться, что при т = О
суммарный индекс неподвижных точек отличен от нуля.
Мы уже видели выше, что при т = 0 единственным реше-
решением задачи C.1) или, что то же, единственной неподвижной
точкой преобразования ~*?(v, 0) является функция м = 0. Заме-
Замечая, что при т = 0 задача C.2), C.6), определяющая преобра-
преобразование W(v, 0), совпадает с_ задачей C.1) с т = 0, выводим,
что 4f(v, 0)s0 при V»<=CI+P(Q), и, следовательно, v — W(v, 0) —
тождественное преобразование. Это означает, что индекс не-
неподвижной точки м=0 преобразования W(v, 0) равен единице.
Таким образом, выполнены все условия теоремы 10.1 гл. IV,
и потому при каждом те[0, 1] существует неподвижная точка
и(х, х) преобразования Ч^о, т)._Из доказанного выше следует,
что и(х, х) принадлежит C2+Y(Q) и является решением задачи
C.1).
Итак, доказана следующая
Теорема 3.2. При выполнении условий а) — d) теоремы 3.1
при каждом х из [0, 1J_существует решение и(х, х) задачи C.1),
принадлежащее C2+Y (Q) с некоторым у > 0, зависящим от по-
постоянной М из d).

ЛИТЕРАТУРА
I. Ладыженская О. А., У р а л ь ц е в а Н. Н., Линейные и квазилинейные
уравнения эллиптического типа, «Наука», 1964.
1. Александров А. Д.
1) Внутренняя геометрия выпуклых поверхностей, Гостехиздат, М., 1948.
2) Некоторые теоремы об уравнениях в частных производных второго
порядка, Вестиик ЛГУ, № 8 A954), 3—17.
3) Теоремы единственности для поверхностей «в целом>, I—VII, Вест-
Вестник ЛГУ, № 19 A956), 5—17; № 7, серия матем., мех., астр., вып. 2
A957), 15—44; № 7, серия матем., мех., астр., вып. 2 A958), 14—26;
№ 13, серия матем., мех., астр., вып. 3 A958), 27—34; № 19, серия
матем., мех., астр., вып. 4 A958), 5—8; № 1, серия матем., мех.,
астр., вып. 1 A959), 5—13; № 7, серия матем., мех., астр., вып. 2
A960), 5—13.
4) Задача Дирихле для уравнений Det\\Zij\\ = q)(Zl Zn, Xh ..., Х„),
Вестник ЛГУ, № 1, серия матем., мех., астр., вып. 1 A958), 5—24.
Б) Исследования о принципе максимума, I—VI, Изв. вузов, Матем.,
№ 5 A958), 126—157; № 3 A959), 3—12; № 5 A959), 16—32; № 3
A960), 3—15; № 5 A960), 16—26; № 1 A961), 3—20.
6) Некоторые оценки, касающиеся задачи Дирихле, ДАН СССР 134,
№ 5 A960), 1001—1004.
7) Условия единственности и оценки решения задачи Дирихле, Вестник
ЛГУ, № 13, серия матем., мех., астр., вып. 3 A963), 5—29.
8) Общий метод оценки решения дифференциального уравнения, Сиб.
матем. журн. 7 {1966), 486—498.
9) Мажорирование решений линейных уравнений второго порядка,
Вестник ЛГУ, № 1, серия матем., мех., астр., вып. 1 A966), 5—25.
10) О мажорантах решений и условиях единственности для решений
эллиптических уравнений, Вестник ЛГУ, № 7, серия матем., мех.,
астр., вып. 2 A966), 1—20.
11) Принцип максимума, ДАН СССР 173, № 2 A967), 247—250.
2. Б а б и ч В. М.
1) К вопросу о распространении функций, УМН 8, вып. 2 E4) A953),
111—113.
Бабич В. М. и СлободецкийЛ. Н.
2) Об ограниченности интеграла Дирихле, ДАН СССР 106, № 4 A956),
604—606.
3. Бакельман И. Я.
1) К теории квазилинейных эллиптических уравнений, Сиб. матем. жури.
2, №2 A961), 179—186.
2) Гиперповерхности с данной средней кривизной и квазилинейные
эллиптические уравнения с сильными нелинейностями, Матем. сб. 75
A17), №4 A968), 604—638.
3) Средняя кривизна и квазилинейные эллиптические уравнения, Сиб.
матем. журн. 9, № 5 A968), 1014—1040.
4. Бернштейн С. Н.
1) Sur la nature analytique des solutions de certaines equations aux deii-
vees partielles du second ordre, Math. Ann. 59 A904), 20—76.

ЛИТЕРАТУРА 565
2) Собрание сочинений, т. III, Изд. АН СССР, Москва, 1960.
3) О некоторых априорных оценках в обобщенной задаче Дирихле, ДАН
СССР 122 A959), 735—738.
5. Б и р м а н М. Ш.
1) К теории самосопряженных расширений положительно определенных
операторов, Матем. сб. 38 (80) A956), 431—450.
Бирман М. Ш. и Скворцов Г. Е.
2) О квадратичной суммируемости старших производных решения за-
задачи Дирихле в области с кусочно-гладкой границей, Изв. вузов,
Матем., № 5 C0) A962), 12—21.
6. В е к у а И. Н.
Обобщенные аналитические функции, Физматгиз, Москва, 1959.
7. В и ш и к М. И.
1) Метод ортогональных и прямых разложений в теории эллиптических
дифференциальных уравнений, Матем. сб. 25 F7) A949), 189—234.
2) Об общих краевых задачах для эллиптических дифференциальных
уравнений. Труды Моск. матем. об-ва 1 A952), 187—246.
3) • Квазилинейные сильно эллиптические системы дифференциальных
уравнений, имеющих дивергентную форму, Труды Моск. матем. об-ва
12 A963), 125—184.
4) О первой краевой задаче для квазилинейных эллиптических уравне-
уравнений и систем высших порядков. Материалы к совместному советско-
американскому симпозиуму по уравнениям с частными производными.
Август 1963 г., Новосибирск.
8. Головкин К- К.
К теоремам вложения, ДАН СССР 134, № 1 (I960), 19—22.
9. ГольдштикМ. А.
Математическая модель отрывных течений несжимаемой жидкости, ДАН
СССР 147, № 6 A962), 1310—1313.
10. Гусева О. В.
О краевых задачах для сильно эллиптических систем, ДАН СССР 102
A955), 1069—1072.
11. Гюитер Н.М.
Теория потенциала и ее применения к основным задачам математиче-
математической физики, Гостехиздат, 1953.
12. Демьянович Ю. К.
Метод сеток для некоторых задач математической физики, ДАН СССР
159, №2 A964), 250-253.
13. Дубинский Ю. А.
1) Первая краевая задача для вырождающихся квазилинейных эллип-
эллиптических систем дифференциальных уравнений, ДАН СССР 156, № 5
A964), 1018—1021.
2) Некоторые интегральные неравенства и разрешимость для вырожден-
вырожденных эллиптических систем дифференциальных уравнений, Матем. сб.
64 A964), 458—480.
14. Иванов А. В.
1) Локальные оценки максимума модуля первых производных решений
квазилинейных неравномерно эллиптических уравнений дивергентного
вида, Записки иауч. семинаров ЛОМИ 7 A968), 87—125.
2) Локальные оценки максимума модуля первых производных решений
квазилинейных неравномерно эллиптических и неравномерно парабо-
параболических уравнений и систем общего вида, Труды МИАН им.
В. А. Стеклова ПО A970), 45—64.
3) О задаче Дирихле для квазилинейных неравномерно эллиптических
уравнений 2-го порядка, Труды МИАН им. В. А. Стеклова 116
A971), 34—54.

566 ЛИТЕРАТУРА
15. И в оч кин а Н. М.
1) Задача Дирихле для квазилинейных двумерных эллиптических урав-
уравнений 2-го порядка, Проблемы матем. анализа, ЛГУ, вып. 2 A969),
140—153.
Ивочкина Н. М. и Осколков А. П.
2) Нелокальные оценки первых производных решений задачи Дирихле
для неравномерно эллиптических квазилинейных уравнений, Записки
науч. семинаров ЛОМИ 5 A967), 37—109.
3) Нелокальные оценки первых производных решений первой краевой
задачи для неравномерно эллиптических и неравномерно параболиче-
параболических педивергентных уравнений, Записки науч. семинаров ЛОМИ 11
A968), 6—72.
4) Нелокальные оценки первых производных решений первой краевой
задачи для некоторых классов неравномерно эллиптических и нерав-
неравномерно параболических уравнений и систем, Труды МИАН им.
В. А. Стеклова ПО A970), 65—101.
16. Ильин В. П.
1) О теореме вложения для предельного показателя, ДАН СССР 96,
№ 5 A954), 905—908.
2) Некоторые неравенства в функциональных пространствах и их при-
применение к исследованию сходимости вариационных методов, Труды
МИАН им. В. А. Стеклова 53 A959), 64—127.
17. Казимиров В. И,
О полунепрерывности интегралов вариационного исчисления, УМН 11,
вып. 3 F9) A955), 125—129.
18. К а ч у р о в с к и й Р. И.
Нелинейные монотонные операторы в банаховых пространствах, УМН
23, вып. 2 A40) A968), 121—168.
19. Кондратов В. И.
О некоторых оценках семейств функций, подчиненных интегральным не-
неравенствам, ДАН СССР 18 A938), 235—240.
20. К о ш е л е в А. И.
Об ограниченности в Lp производных решений эллиптических диффе-
дифференциальных уравнений, Матем. сб. 38 (80), № 3 A956), 278—312.
21. Ладыженская О. А.
1) О методе Фурье для волнового уравнения, ДАН СССР 75 A950),
765—768.
2) О замыкании эллиптического оператора, ДАН СССР 79 A951),
723—725.
3) Смешанная задача для гиперболического уравнения, М., Гостехиз-
дат, 1953.
4) О решении общей задачи дифракции, ДАН СССР 96, № 3 A954),
433—436.
Б) Простое доказательство разрешимости основных краевых задач и
задачи о собственных значениях для линейных эллиптических урав-
уравнений, Вестник ЛГУ, № 11 A955), 23—29.
6) Метод конечных разностей в теории уравнений с частными производ-
производными, УМН 12, вып. 5 G7) A957), 123—148.
7) О дифференциальных свойствах обобщенных решений некоторых
многомерных вариационных задач, ДАН СССР 120, № 5 A958),
956—959.
8) Решение первой краевой задачи в целом для квазилинейных пара-
параболических уравнении, ДАН СССР 107 A9S6), 636—639; Труды Моск.
матем. об-ва 7 A958), 149—177.
9) Об интегральных оценках, сходимости приближенных методов и ре-
решениях в функционалах для линейных эллиптических операторов,
Вестник ЛГУ, № 7, серия матем., мех., астр., вып. 2 A958), 60—69.

ЛИТЕРАТУРА 567
10) О разрешимости «в целом» краевых задач для линейных и квазили-
квазилинейных параболических уравнений и уравнений Навье — Стокса, Тру-
Труды IV Всесоюзного математического съезда 1961 г., т. I, 1963, 134—157.
Ладыженская О. А., Солонников В. А. и Уральцева Н. Н.
11) Линейные и квазилинейные уравнения параболического типа, «Нау-
«Наука», М., 1967.
Ладыженская О. А. и Уральцева Н. Н.
12) Квазилинейные эллиптические уравнения и вариационные задачи со
многими независимыми переменными, УМН 16, вып. 1 (97) A961),
19—90 (доклад, прочитанный в Ленингр. матем. об-ве 24.9.1959 г.).
13) О вариационной задаче и квазилинейных эллиптических уравнениях
со многими независимыми переменными, ДАН СССР 135, № 6 A960),
1330—1334.
14) О дифференциальных свойствах ограниченных обобщенных решений
многомерных квазилинейных эллиптических уравнений и вариацион-
вариационных задач, ДАН СССР 138, № 1 A961), 29—32.
15) On the smoothness of weak solutions of quasilinear equations in seve-
several variables and of variational problems, Comm. Pure and Appl.
Math. 14, № 3 A961), 481—495.
16) Краевая задача для линейных и квазилинейных параболических
уравнений, ДАН СССР 139, № 3 A961), 544—547.
17) О регулярности обобщенных решений квазилинейных эллиптических
уравнений, ДАН СССР 140, № 1 A961), 45—47.
18) Краевая задача для линейных и квазилинейных параболических
уравнений, ч. I, Изв. АН СССР, сер. матем. 26 A962), 5—52; ч. И,
там же, 753—780.
19) Краевая задача для линейных и квазилинейных уравнений и систем
параболического типа, ч. 111, Изв. АН СССР, сер. матем. 27 A963),
161—240.
20) О допустимых расширениях понятия решения для линейных и ква-
квазилинейных эллиптических уравнений второго порядка, Вестник ЛГУ,
сер. матем., мех. и астр., № 1 A963), 10—25.
21) О непрерывности по Гёльдеру решений и их производных для ли-
линейных и квазилинейных уравнений эллиптического и параболиче-
параболического типов, ДАН СССР 155, № 6 A964), 1258—1261.
22) О некоторых классах неравномерно эллиптических уравнений, За-
Записки науч. семинаров ЛОМИ 11 A968), 129—149.
23) О тотальных оценках первых производных по х решений квазили-
квазилинейных эллиптических и параболических уравнений, Записки науч.
семинаров ЛОМИ 14 A969), 127—155.
24) Local estimates for gradients of solutions of non-uniformly elliptic
and parabolic equations, Comm. Pure and Appl. Math. 23, № 4 A970),
677—703.
22. M а з ь я В. Г.
1) Некоторые оценки для решений эллиптических уравнений второго
порядка, ДАН СССР 137, № 5 A965), 1057—1059.
2) О слабых решениях задач Дирихле и Неймана, Труды Моск. ма-
матем. об-ва 20 A969), 137—172.
3) Примеры нерегулярных решений квазилинейных эллиптических урав-
уравнений с аналитическими коэффициентами, Функц. анализ и его при-
приложения 2, вып. 3 A968), 53—57.
4) Классы множеств и мер, связанные с теоремами вложения. Теоремы
вложения и их приложения, Труды симп. по теоремам вложения
1966 г., Баку A970), 142—159.
23. Михлин С. Г.
1) О некоторых оценках, связанных с функцией Грина, ДАН СССР 78»
№ 3 A951), 443—446,

668 ЛИТЕРАТУРА
2) Проблема минимума квадратичного функционала, Гостехиздат, М. —
Л., 1952.
24. Осколков А. П.
1) О некоторых оценках для неравномерно эллиптических уравнений и
систем, Труды МИАН им. В. А. Стеклова 92 A966), 203—232.
2) Априорные оценки первых производных решений задачи Дирихле
для неравномерно эллиптических квазилинейных уравнений, Труды
МИАН им. В. А. Стеклова 102 A967), 105—127.
3) Замечание об оценке постоянной Гёльдера для некоторых неравно-
неравномерно эллиптических квазилинейных уравнений, Записки науч. се-
семинаров ЛОМИ 7 A968), 178—183.
4) О некоторых классах неравномерно эллиптических квазилинейных
уравнений, Записки науч. семинаров ЛОМИ 14 A969), 156—172.
Осколков А. П. и Ивочкина Н. М. см. Ивочкина Н. М.
25. Петровский И. Г.
1) Об аналитичности решений уравнений с частными производными, Ма-
тем. сб. 5, № 1 A939), 3—68.
2) Новое доказательство существования решения задачи Дирихле мето-
методом конечных разностей, УМН 8 A941), 161—170.
26. Плотников В. И.
1) О дифференцируемое™ решений регулярных вариационных задач в
непараметрической форме, Матем. сб. 47 (89): 3 A959), 355—396.
Плотников В. И., Сигалов А. Г. и Уральцева Н. Н.
2) Квазилинейные эллиптические уравнения и вариационные задачи,
Труды IV Всесоюзного математического съезда т. 1 A963), 199—213.
27. Ривкин д В. Я
1) Об оценках скорости сходимости решений разностных уравнений
к решению эллиптического уравнения с разрывными коэффициентами и
об одном методе решения задачи Дирихле, ДАН СССР 149, № 6 A963).
2) Приближенный метод решения задачи Дирихле и об оценках скоро-
скорости сходимости решений разностных уравнений к решениям эллипти-
эллиптических уравнений с разрывными коэффициентами, Вестник ЛГУ, № 13,
серия матем., мех., астр., вып. 3 A964), 37—52.
28. С и г а л о в А. Г.
1) Двумерные задачи вариационного исчисления, УМН 6, 2 A951), 16—101.
2) Двумерные задачи вариационного исчисламя в параметрической
форме, Труды Моск. матем. об-ва 2 A953), 201—233.
3) Двумерные задачи вариационного исчисления в непараметрической
форме, преобразованные в параметрическую форму, Матем. сб. 38
(80), A956), 183—202.
Сигалов А. Г., Плотников В. И. и Уральцева Н. Н. см. Плот-
Плотников В. И.
29. Скворцов Г. Е. и Бирман М. Ш. см. Бирман М. Ш.
30. С л о б о д е ц к и й Л. Н. и Б а б и ч В. М. см. Бабич В. М.
31. Смирнов В. И.
1) Курс высшей математики, т. IV, Физматгиз, 1951.
2) Курс высшей математики, т. V, Физматгиз, 1960.
32. Соболев С. Л.
Некоторые применения функционального анализа в математической фи-
физике, Изд. ЛГУ, 1950.
33. Соболевский П. Е.
Об уравнениях с операторами, образующими острый угол, ДАН СССР 116,
№5 A957), 754—757.
34. С о л о м я к Т. Б.
1) Краевые задачи для одного класса квазилинейных уравнений и си-
систем эллиптического типа, Изв. вузов, серия матем., Я? 5 A2) A959),
184-196, '

ЛИТЕРАТУРА 569
2) О разрешимости краевых задач для одного класса квазилинейных
эллиптических уравнений с сильными нелинейностями, ДАН СССР
146, № 6 A962), 1282—1285.
3) Задача Дирихле для одного класса вырождающихся квазилинейных
эллиптических уравнений, Изв. вузов, серия Матем., № 2 A970),
76—85.
4) Приложение теории вырождающихся уравнений к обратным задачам
дозвуковых течений сжимаемых жидкостей. Сб. докладов Всесоюз-
Всесоюзной науч. конференции «Краевые задачи и их приложения в меха-
механике жидкостей и газов>, Казань, 1970.
35. С о л о н н и к о в В. А.
1) Об общих краевых задачах для систем, эллиптических в смысле
Даглиса — Ниренберга, Изв. АН СССР 28, № 3 A964), 665—706.
2) Об общих краевых задачах для систем, эллиптических в смысле
Даглиса—Ниренберга, Труды МИАН им. В. А. Стеклова 92 A966),
233—297.
3) Об оценках в Lp решений эллиптических и параболических систем,
Труды МИАН им. В. А. Стеклова 102 A967), 137—160.
4) О матрицах Грина для эллиптических краевых задач, I, Труды МИАН
им. В. А. Стеклова ПО A970); II, Труды МИАН им. В. А. Стеклова
116 A971), 181—216.
Солонников В. А., Ладыженская О. А. и Уральцева Н. Н.
см. Ладыженская О. А.
36. Уральцева Н. Н.
1) О регулярности решений многомерных эллиптических уравнений и ва-
вариационных задач, ДАН СССР 130, № 6 A960), 1206—1209.
2) Краевые задачи для квазилинейных эллиптических уравнений и си-
систем с дивергентной главной частью, ДАН СССР 147, № 2 A962),
313—316.
3) Общие квазилинейные уравнения второго порядка и некоторые клас-
классы систем уравнений эллиптического типа, ДАН СССР 146, № 4 A962),
778—781.
4) Вырождающиеся квазилинейные эллиптические системы, Записки
науч. семинаров ЛОМИ 7 A968), 184—222.
Уральцева Н. Н. и Ладыженская О. А. см. Ладыженская О. А.
Уральцева Н. Н., Плотников В. И. и Сигалов А. Г. см. Плот-
Плотников В. И.
37. Э й д у с Д. М.
О решении краевых задач методом конечных разностей, ДАН СССР 83,
№2 A952), 191—194.
1. A g m о п S., D о u g I i s A. and Nirenberg L.
Estimates near the boundary for the solutions of elliptic differential equa-
equations satisfying general boundary values, 1, Comm. Pure and Appl.
Math. 12 A959), 623—727; II, Comm. Pure and Appl. Math. 17 A964),
35—92.
2. AronszajnN.
Boundary values of fonctions with finite Dirichlet integral. Conference on
partial differential equations, Studies on eigenvalue problems, № 14 (Univ.
of Kansas, 1955).
3. A 11 a r d W. K.
On boundary regularity for Plateau's problem, Bull. Amer. Math. Soc. 75,
№ 3 A969), 522—523.
4. A1 m g r e n F. J.
Existence and regularity almost everywhere of solutions of elliptic vafia-
tional problems among surfaces of varying topological type and singula-
singularity structure, Ann. of Math. 87, 2 A968), 321—391.

570 ЛИТЕРАТУРА
5. В е г s L. and NirenbergL
1) On a representation theorem for linear elliptic systems with disconti-
discontinuous coefficients and its applications, Convegno intern, sulle equazioni
lineari alle derivate parziali, Trieste, 1954, 111—140.
2) On linear and nonlinear elliptic boundary value problems in the plane,
Convegno intern, sulle equazioni lineari alle derivate parziali, Trieste,
1954, 141—167.
6. В о m b i e r i E., D e G i о r g i E. and Miranda M.
Una maggiorazione a priori relative alle ipersuperfici minimali поп para-
metriche, Arch. Rat. Mech. Anal. 32, 4 A969), 255—267.
7. Browder F. E.
1) Functional analysis and partial differential equations, 1., Math. Ann.
138 A959), 55—79.
2) Variational boundary value problems for quasilinear elliptic equations,
Proc. Nat. Acad. Sci. USA 50, № 1 A963), 31—36; № 4 A963), 592—
598; № 5 A963), 794—798.
8. С а с с i о р р о 11 i R.
1) Sulle equazioni ellittiche a derivate parziali con n variabili indipendenti.
Rend. Ace. Lincei 19 A934), 83—89.
2) Limitazioni integrali per le soluzioni di un'equazioni lineare ellit-
tica a derivate parziali, Giorn. Mat. Battaglini 80 A950/51),
186—212.
9. Cordes H. O.
Cber die erste Randwertaufgabe bei quasilinearen Differentialgleichungen
zweiter Ordnung in mehr als zwei Variablen, Math. Ann. 130 A956),
278—312.
10. Couran t R.
Courant R. and H i 1 b e r t D.
1) Methods of Mathematical Physics, vol. 1 A933); vol. 2 A937, 1962).
2) Dirichlet's principle, conformal mappings and minimal surfaces, New
York, 1950.
Courant R., FriedrichsK. O. and Levy H.
3) Cber die partiellen Differentialgleichungen der Physik, Math. Ann. 100
A928/29), 32—74.
11. De Giorgi E.
1) Sulla differenziabilita e l'analiticita delle estremali degH integrali
multipli regolari, Mem. Ace. Sci. Torino 3 A957), 1—19.
2) Un'estensione del teorema di Bernstein, Ann. Sc. Norm. Super. Pisa 19
A965), 79-S5.
3) Frontiere orientate die misura minima, Seminario Mat. Scuola Norm.
Pisa, 1960/61.
4) Un esempio di estremali discontinue per un problema variazionale di
tipo ellittico, Boll. Unione mat. ital. I A968), 135—137.
5) Una maggiorazione a priori relative alle ipersuperfici minimali, Atti
del Convegno di Analisi Funzionale, Roma, 1968.
6) See Bombiery E.
12. Douglis A.
D о u g 1 i s A. and Nirenberg L.
1) Interior estimates for elliptic systems of partial differential equations,
Comm. Pure and Appl. Math. 8 A955), 503—538.
Douglis A., Agmon S. and Nirenberg L
2) See Agmon S.
13. D u n f о г d N. and Schwartz J.
Linear operators, part I: General Theory, 1958; part II: Spectral Theory.
Self Adjoint operators in Hilbert space, 1963.
14. Federer H.
1) Geometric measure theory, 1969.

ЛИТЕРАТУРА 571
Federer H. and Fleming W. H.
2) Normal and integral currents, Ann. of Math. 72 A960), 458—520.
15. Fichera G.
1) Problemi elastostatici con vincoli unilaterali: problema di Signorini con
ambigue condizioni al contorno, Mem. Ace. Lincei 7 A964), 91—140.
2) Elastostatics problems with unilateral constraints: The Signorini pro-
problem with ambiguous boundary conditions, Sem. 1962/63, 1st. Naz.
Alta Mat. Roma 2 A965), 613—679.
16. Finn R.
1) Isolated singularities of solutions of non linear partial diff. equations,
Trans. Amer. Math. Soc. 75 A953), 385—404.
2) On equations of minimal surface type, Ann. of Math. 60 A954), 397—
416.
3) Growth properties of solutions of non linear elliptic equations, Comm.
Pure and Appl. Math. 9 A956), 415—423.
4) New estimates for equations of minimal surface type, Arch. Rat. Mech.
Anal. 14 A963), 337—375.
5) Remarks relevant to minimal surfaces and to surfaces of prescribed
mean curvature, J. Anal. Math. 14 A965), 135—160.
Finn R. and С о n с u s P.
6) On a class of capillary surfaces, J. Anal. Math., 23 A970), 65—70.
Finn R. and G i 1 b a r g D.
7) Three-dimensional subsonic flows and asymptotic estimates for elliptic
partial differential equations, Acta Math. 98 A957), 265—296.
17. Fiorenza R.
Sui problemi di derivata oblique per le equazioni ellitiche, Ricerche di
Mat. Napoli 8 A959), 83—110.
18. F1 e m i n g W. H. and F e d e r e r H.
See Federer И.
19. Fried rich s K. O.
1) Spektraltheorie halbbeschrankter Operatoren und Anwendung auf die
Spektralzerlegung von Differentialoperatoren, Math. Ann. 109, Hf. 4—5
A934), 465—487, 685—713.
2) The identity of weak and strong extensions of differential operators,
Trans. Amer. Math. Soc. 55 A944), 132—151.
FriedrichsK- O., CourantR. and Levy H.
3) See Courant R.
20. G a g 1 i a r d о Е.
1) Proprieta di alcune classi di funzioni in piu variabili, Ricerche Mat. 7,
№ 1 A958), 102—137.
2) Ulteriori proprieta di alcune classi di funzioni in piu variabili, Ricerche
Mat. 8, № 1 A959), 24—51.
3) Caratterizzazione delle trace sulla frontiera relative ad alcune classi
di funzioni in piu variabili, Rendiconti del Sem. Mat. Univ. Radova 27
A957), 284—305.
21. Gilba rg D.
1) Boundary value problems for non linear elliptic equations in n variab-
variables, Symp. Non-Linear Problems, Univ. Wisconsin Press, 1962, 151—159.
Gi lbarg D. and Finn R.
2) See Finn R.
G i 1 b a r g D. and S e r r i n J.
3) On isolated singularities of solutions of second order elliptic differen-
differential equations, J. Anal. Math. 4 A954/56), 309—340.
22. G i u s t i E.
1) Sulla regolarita parziale delle soluzioni di sistemi ellittici quasi-lineari
di ordine arbitrario, Ann. Sc. Norm. Super. Pisa 23, № 1 A969), 115—
141.

572 ЛИТЕРАТУРА
G i u s t i E. and M1 r a n d a M.
2) Un esempio di soluzioni discontinue per un problema di minimo rela-
tivo ad un integrate regolare del calcolo delle variazloni, Boll. Unione
mat. ital. II (}968).
3) Sulla regolarita delle soluzioni deboli dei sistemi ellitici, 1st. Mat.
L. Tonelli, Univ. Pisa, 1968, 1—13.
4) Sulla regolarita delle soluzioni di una classe di sistemi ellittici quasi-
linear, Archive Rat. Mech. and Anal. 31, № 3 A968), 173—184.
23. G г е с о D.
Nuove formale integrali di maggiorazione per le soluzioni di un'equazione
lineare di tipo ellittico ed applicazioni alia teoria del potenziale, Ricerche
Mat. 5 A956), 126—149.
24. Hart man Ph. and StampacchiaG.
On some non-linear elliptic differential-functional equations, Acta Math.
115 A966), 271—310.
25. HeinzE.
On certain non-linear elliptic differential equations and univalent mapp-
mappings, J. Anal. Math. 5 A956/57), 197—272.
26. H i 1 b e r t D.
1) Mathematische Probleme, Ges. Abh. Ill, 1935.
2) Cber das Dirichletshe prinzip, Jahresber. D. Math, verein 8 A900),
184—188; Math. Ann. 59 A904), 161—186.
27. H о р f E.
Elementare Bemerkungen flber die L5sungen partieller Differentialgleichun-
gen zweiter Ordnung von Elliptischen Typus, Sber. Preuss. Acad. Wiss. 19
A927), 147-152. ч
28. J e n к i n s H. and S e r r i n J. \
1) Variational problems of minimal surface type, I, Archive Rat. Mech.
Anal. 12 A963), 185—212.
2) The Dirichlet problem for the minimal surface equation in higher di-
dimensions, J. reine und angew. Math. 229 A968), 170—187.
29. J о h n F. and N i r e n b e r g L.
On functions of bounded mean oscillation, Comm. Pure and Appl. Math.
17, № 3 A961), 415—426.
30. К a d 1 e с J.
1) On the maximum principle for second order elliptic equations and the
method of Wiener, Czech. Math. J. 14 A964), 154—155.
К a d 1 e с J. and N e б a s J.
2) Sulla regolarita delle soluzioni di equazioni ellittische negli spazi #*'*",
Ann. Sc. Norm, super. Pisa, 21 A967), 527—545.
31. Lebesgu e H.
1) Integrale, longueur, aire (thesis), Ann. mat. pura ed appl. 7 A902),
231—359.
2) Sur le probleme de Dirichlet, Rend. Circ. Mat. Palermo 24 A907), 371 —
402.
32. L e г а у J.
1) Majoration des derivees secondes des solutions d'un probleme de Di-
Dirichlet, J. Math. Pures et Appl. 17 A938), 89—104.
2) Discussion d'un probleme de Dirichlet, J. Math. Pures et Appl. 18
A939), 249—284.
L e г а у J. and L i о n s J. L.
3) Quelques resultats de Visik sur les problemes elliptiques non lineaires
par les methodes de Minty — Browder, Bull. Soc. Math. France 93
A965), 97—107.
L e г а у J. and Schauder J.
4) Topologie et equations fonctionnelles, Ann. Ec. norm. Super. 51 A934),
45—78.

ЛИТЕРАТУРА Б73
33. L e w у Н. "
1) Ober den analytischen Charakter der Losungen elliptischen Differential-
gleichungen, G5ttingen. Nachr., 1927, 178—186.
2) Neuer Beweis des analytischen Charakters der Losungen elliptischer
Differentialgleichungen, Math. Ann. 101 A929), 609—619; 107 A934),
804.
Lewу Н. and Stampacchia G.
3) On the regularity of the solutions of a varlational inequality, Comm.
Pure and Appl. Math. 22 A969), 153—188.
34. L i о п s J. L.
Lions J. L. and Ler ay J.
1) See Leray J.
L i о п s J. L. and Stampacchia G.
2) Inequations variationelles non coercives, C. R. Acad. Sci. Paris 261
A965), 25—27.
3) Variational inequalities, Comm. Pure and Appl. Math. 20 A967), 453—
519.
35. Li tt man W., Stampacchia G. and Weinberger H. F.
Regular points for elliptic equations with discontinuous coefficients, Ann.
Sc. Norm. Super. Pisa 17 A963), 43—77.
36. M i n t у G.
1) Monotone nonlinear operators in Hilbert space, Duke Math. J. 29
A962), 341—346.
2) Two theorems on nonlinear functional equations in Hilbert space, Bull.
Amer. Math. Soc. 69 A963), 691—692.
3) On a «monotonicity> method for the solution of nonlinear equations in
Banach spaces, Proc. Nat. Acad. Sci. USA 50 A963), 1038—1041.
37. Miranda C.
1) Equazioni alle derivate parziali di tlpo ellittico, Springer, Berlin, 1955;
Second revised edition Springer, Berlin, 1970.
2) Sur problema misto per le equazioni lineari ellittiche, Ann. Mat. Рига
ed Appl. 39 A955), 279—303.
38. M i r a n d a M.
1) Disuguaglianze di Sobolev sulle ipersuperficl minimall, Rend. Sem.
Mat. Univ. Padova 38 A967), 69—91.
2) Sul minimo dell' integrale del gradiente di una funzione, Ann. Sc.
Norm. Super. Pisa 19, 4 A965), 627—665.
Miranda M., В о m b 1 e r i E. and De G i о r g 1 E.
See Bombieri E.
Miranda M. and G1 и s t i E.
See Ciusti E.
39. Morrey С. В.
1) On the solutions of quasilinear elliptic partial differential equations,
Trans. Amer. Math. Soc. 43 A938), 126—166.
2) Multiple integral problems In the calculus of variations and related
topics, Univ. of California Publ. 1 A943), 1—130.
3) Second order elliptic equations in several variables and Holder conti-
continuity, Math. Z. 72 A959), 146—164.
4) Existence and differentiability theorems for variational problems for
multiple integrals, Univ. of Wisconsin Press, Madison Wis. 1961, 241—
270.
5) Quelques resultats recents du calcul des variations, Colloques Inter-
nationeaux du Centre National de la Recherche Scientifique, 117, Paris,
Juln 1962, 25—30.
Multiple integrals In the calculus of variations, Springer-Verlag, 1966.
Partial regularity results for non-linear elliptic systems, Univ. of Cali-
California, June 1967, 1—34.
6)
7)

574 ЛИТЕРАТУРА
40. М о s е г J.
1) A new proof of De Giorgi's theorem concerning the regularity problem
for elliptic differential equations, Comm. Pure and Appl. Math. 13, 3
A960), 457—468.
2) On Harnack's theorem for elliptic differential equations, Comm. Pure
and Appl. Math. 14 A961), 577—591.
41. Nash J.
Continuity of solutions of parabolic and elliptic equations, Amer. J. Math.
80,4 A958), 931—954.
42. N e с a s J.
1) Sur l'existence de la solution reguliere pour le probleme de Dirichlet de
l'equation elliptique non-lineare d'ordre 2ft, Rend. Ac. Lincei 42 A967),
347—354.
2) Sur la regularite des solutions variationnelles des equations elliptique
non-lineaires d'ordre 2k en deux variables, Ann. Sc. Norm. Super. Pisa
21 A967), 427—457.
N e с a s J. and К a d 1 e с J.
3) See Kadlec J.
43. Von Neumann J.
Uber einen Hilfsatz der Variationsrechnung, Abhandl. Math. Seminar
Hamburg 8 A931), 28—31.
44. NirenbergL.
1) On nonlinear elliptic partial differential equations and Holder conti-
continuity, Comm. Pure and Appl. Math. 6 A953), 103—156. ч
2) Remarks on strongly elliptic partial differential equations, Gomm. Pure
and Appl. Math. 8 A955), 648—674.
3) On elliptic partial differential equations, Ann. Sc. Norm. Super. Pisa,
13 A959), 115—162.
Nirenberg L., Agmon S. and D о u g 1 i s A.
4) See Agmon S.
Nirenberg L. and В егs L.
Ng
5) See Bers L.
Nirenberg
6) See Douglis A.
Nib L
e .
irenberg L. and D о u g 11 s A
S Dli A
) g
Nirenberg L. and John F.
7) See John F.
45. R a d о Т.
On the problem of Plateau, Ergeb. Math. 2, Berlin, Springer-Verlag, 1933.
46. R e n d h e f f e r R.
An extension of certain maximum principles, J. reine und angew. Math
211 A962), 70-77.
47. R e i f e n b e r g E. R.
1) Solution of the Plateau problem for m-dimensional surfaces of varying
topological type, Acta Math. 104 A960), 1—92.
2) An epiperimetric inequality related to the analyticity of minimal sur-
surfaces, Ann. of Math. 80 A964), 1—14.
3) On the analyticity of minimal surfaces, Ann. of Math. 80 A964),
15—21.
48. R i e s z F. and Sz.-N a g у В.
Lemons d'analyse functionnele, Budapest, Akad. kiadd, 1955.
49. SchauderJ.
1) Cber lineare elliptische Differentialgleichungen zweiter Ordnung, Math.
Z. 38 A934), 257—282.
2) Sur les equations lineaires du type elliptique a coefficientes continue,
С R. Acad. Scl. Paris 199 A934), 1366—1368.
3) Sur les equations quasilineaires du type elliptique a coefficients con-
tlnus, С R. Acad. Scl. Paris 199 A934), 1666—1568-

ЛИТЕРАТУРА 575
4) Numerische Abschatzungen in elliptischen linearen Differentialgleichun-
gen, Studia Math. 5 A934), 34—42.
5) Equations du type elliptique, problemes lineaires, Enseign. Math. 35
A936), 126—139.
SchauderJ. and L e г а у J.
6) See Leray J.
50. S с h w а г t z J. and D u n f о г d N.
See Dunford N.
51. Serrin J.
1) On the Harnack inequality for linear elliptic equations, J. Anal. Math.
4 A955/56), 297—308.
2) On a fundamental theorem of the calculus of variations etc., Acta
Math. 102 A959), 1—32.
3) On the definition and properties of certain variational integrals, Trans.
Amer. Math. Soc. 101 A961), 139—167.
4) A Harnack inequality for non linear equations, Bull. Amer. Math. Soc.
69 A963), 481—486.
5) A priori estimates for solutions of the minimal surface equations,
Arch. Rat. Mech. Anal. 14 A963), 376—383.
6) Pathological solutions of elliptic differential equations, Ann. Sc. Norm.
Super. Pisa 18 A964), 385—387.
7) Removable singularities of solutions of elliptic equations, I, II, Arch.
Rat. Mech. Anal. 17 A964), 67—78; 20 A965), 163—169.
8) Local behavior of solutions of quasi-linear elliptic equations, Acta
Math. Ill A964), 247—302.
9) Singularities of solutions of quasilinear equations, Proc. Symp. Appl.
Math. Amer. Math. Soc. 17 A965), 68—88.
10) Isolated singularities of solutions of quasilinear equations, Acta Math.
113 A965), 219—240.
11) The problem of Dirichlet for quasilinear elliptic differential equations
with many independent variables, Philos. Trans. Roy. Soc. London
264 A969), 413—496.
S e r r i n J. and G i 1 b a r g D.
12) See Gilbarg D.
S e r r i n J. and Jenkins H.
See Jenkins H.
52. StampacchiaG.
1) Contributi alia regolarizzazione della soluzioni dei problemi al contorno
per le equazioni del secondo ordine ellittiche, Ann. Sc. Norm. Super.
Pisa 12 A958), 223—245.
2) Problemi al contorno ellittici, con dati discontini, dotat di soluzioni
holderiane, Ann. Mat. Рига ed Appl. 51 A960), 1—38.
3) On some regular multiple integral problems in the calculus of varia-
variations, Comm. Pure and Appl. Math. 16 A963), 383—421.
4) Some limit cases of Lv estimates for solutions of second order elliptic
equations, Comm. Pure and Appl. Math. 16 A963), 505—510.
5) Le probleme de Dirichlet pour les equations elliptique du second ordre
a coefficientes discontinues, Ann. Inst. Fourier Grenoble 15 A965).
189—258.
Stampacchia G. and H a r t m a n Ph.
See Hartman Ph.
Stampacchia G. and L e w у Н.
See Lewy H.
StampacchiaG. and Lions J. L.
See Lions J. L.
Stampacchia G., Littman W. and Weinberger H. F.
See Littman W.

576 ЛИТЕРАТУРА
53. Т о n e 11 i L.
1) Fondamenti del calcolo delle variazioni, vols. 1—3, Zanichelli, Bologna,
1923.
2) Sulla quadrature delle superficie, Atti Reale Acad. Lincei, Ser. 6, 3
A926), 633—638.
3) Sur la semi-continuite des integrales double de calcul des variations,
Acta Math. 53 A929), 325—346.
4) L'estremo assoluto degli integrali doppi, Ann. Sc. Norm. Super. Pisa,
S. 2, 3 A933), 89—130.
54. T r u d i n g e r N. S.
On Harnack type inequalities and their application to quasilinear elliptic
equations, Comm. Pure and Appl. Math. 20 A967), 721—748.
55. W e i n b e r g e r H. F., L i 11 m a n W. and Stampacchia G.
See Littman W.
56. W e у 1 H.
The method of orthogoonal projection in potential theory, Duke Math. J. 7
A940), 411—444.