Министерство образования Российской Федерации
Южно-Уральский государственный университет
Кафедра прикладной математики
519.1@7)
Э157
А.Ю. Эвнин
ЗАДАЧНИК
ПО ДИСКРЕТНОЙ МАТЕМАТИКЕ
Издание второе, переработанное и дополненное
Челябинск
Издательство ЮУрГУ
2002

УДК 519.1@76.1)+511.2@76.1)+510.6@76.1)
Эвнин А.Ю. Задачник по дискретной математике. 2-е изд., пе-
рераб. и доп. - Челябинск: Издательство ЮУрГУ, 2002. - 164 с.
Сборник задач соответствует курсу дискретной математики для сту-
студентов специальностей "Прикладная математика", "Прикладная матема-
математика и информатика" и "Программное обеспечение вычислительной тех-
техники и автоматизированных систем". Задачник может быть использован
также для проведения практикумов по решению олимпиадных задач.
Первое издание вышло в 1998 г.
Ил. 27, табл. 9, список лит. — 63 назв.
Одобрено научно-методическим советом по математике.
Рецензенты:
д. ф.-м. н. М.М. Кипнис, ЧГПУ,
к. ф.-м. н. СМ. Воронин, ЧелГУ
©А.Ю. Эвнин, 2002.
ISBN 5-696-02145-Х ©Издательство ЮУрГУ, 2002.

Оглавление
Предисловие 5
1 Предварительные сведения 6
1.1. Множества и операции над ними 6
1.2. Высказывания и предикаты 7
1.3. Метод математической индукции 8
1.4. Правило произведения 10
2 Элементы теории чисел 13
2.1. Наибольший общий делитель. Простые числа 13
2.2. Сравнения по модулю 15
2.3. Китайская теорема об остатках 16
2.4. Теоремы Эйлера, Ферма, Вильсона 17
2.5. Квадратичные вычеты и невычеты 19
2.6. Уравнения в целых числах 20
2.7. Мультипликативные функции 22
3 Начальные понятия общей алгебры 24
4 Элементы математической логики 27
4.1. Формулы и их преобразования. Двойственность 27
4.2. Полные системы связок 29
4.3. Теорема Поста 30
4.4. Нормальные формы 31
4.5. Контактные схемы 32
4.6. Булева алгебра 34
4.7. Аксиоматические теории 35
4.8. Исчисление высказываний 35
4.9. Исчисление предикатов 38

4 Оглавление
4.10. Рекурсивные функции 42
4.11. Машина Тьюринга 46
5 Комбинаторика 50
5.1. Сочетания 50
5.2. Полиномиальная формула. Комбинаторные тождества .... 52
5.3. Формула включения-исключения 53
5.4. Задача о беспорядках и встречах 54
5.5. Числа Фибоначчи 55
5.6. Производящие функции 58
5.7. Рекуррентные соотношения 60
6 Теория Пойа 64
7 Введение в теорию графов 67
7.1. Определения и примеры 67
7.2. Гамильтоновы и эйлеровы графы 70
7.3. Деревья 72
7.4. Укладки графов 75
7.5. Ориентированные графы. Алгоритмы 77
7.6. Турниры 79
7.7. Доминирование, независимость, покрытия, паросочетания . . 81
8 Дополнительные задачи 86
8.1. Инвариант и полуинвариант 86
8.2. Задачи с целыми числами 89
8.3. Числа Кармайкла 92
8.4. Формула обращения Мёбиуса 93
8.5. Бинарные операции и отношения 96
8.6. Разные комбинаторные задачи 97
8.7. Тождества 100
8.8. Две классические задачи 103
8.9. Теорема Рамсея 103
8.10. Ожерелья 106
8.11. Графы 107
Ответы. Указания. Решения 109
Литература 160

ПРЕДИСЛОВИЕ
По темам задач и по структуре, а также по терминологии и обозначениям
данная книга соответствует учебному пособию [9].
Необходимость составления задачника объясняется тем, что в насто-
настоящее время практически отсутствуют сборники задач, в которых были
бы представлены все темы, составляющие современный курс дискретной
математики (в первую очередь, математическая логика, комбинаторный
анализ и теория графов). Наиболее полно отвечающий учебной програм-
программе указанной дисциплины задачник [20] издан тиражом менее 5 тыс. экз. и
малодоступен. Кроме того, в нем отсутствует материал, соответствующий
первым трем главам, §7.2, §7.7 и большей части последней главы (в т.ч.
§8.4, §8.9) настоящего издания.
Названия первых семи глав сборника совпадают, в основном, с соответ-
соответствующими заголовками из [9]. Весьма обширная последняя глава, содер-
содержащая задачи повышенной трудности и дополнительный теоретический
материал, может быть использована для кружковой работы.
Во втором издании наибольшей переработке подверглась четвертая
глава, при этом существенным образом использованы материалы лекций
по математической логике Ю.П. Нестеренко.
Основными источниками задач послужили книги [1], [2], [4], [5], [6], [8],
[23], [24], [27]. Результаты, сформулированные в задачах 327 и 385, принад-
принадлежат моему учителю и коллеге М.М. Гольденбергу. Некоторые задачи, в
том числе 77, 123.6, 126, 140, 290, 315, 325.2, 369, 370, 374, 502, 540, 553, 556,
609, 612, 647, 660, 669, 671, 677, 678, 696, придуманы (или "переоткрыты")
составителем сборника. Формулировки ряда задач возникли как (обрат-
(обратный) перевод с языка олимпиад на язык научный. В частности, широ-
широко использованы материалы Всероссийской, Соросовской и Путнамовской
олимпиад последних лет, а также задачных разделов журналов "Квант"
и "Математика в школе". Указать (и даже установить) авторство всех за-
задач сборника не представляется возможным, но все-таки назову авторов
нескольких красивых задач, придуманных совсем недавно и вошедших во
второе издание сборника: С.Л. Берлов (задача 731), А.С. Голованов A35),
В.М. Гуровиц E14), Д.В. Карпов A2), СИ. Токарев G33).
Электронный адрес автора: evnin@prima.susu.ac.ru. Буду благодарен за
замечания и советы.
А.Ю. Эвнин, 10 апреля 2002 г.

Глава 1
Предварительные сведения
1.1. Множества и операции над ними
1. Какие из следующих утверждений верные?
1)феф; 2) ф с ф;
3) а е {а, Ь}; А) а С {а,Ъ};
5) {а} е {а,Ь}; 6){а}с{а,Ь};
7) {а, Ь} е {а, Ь, {а, Ь}}; 8) {а, Ь} С {а, Ь, {а, Ь}}.
2. Пусть А = [0,1] х R, В = Rx [0,1]. Найти множества
АПВ, A U В, А\В, В \ А, изобразить их на координатной плоскости.
3. Пусть An = [—n;n] (отрезок числовой прямой). Найти:
А" оо А" оо
1) U Ап (к е N); 2) U Ап; 3) П Ап (к е N); 4) П Ап.
п=1 п=1 п=1 п=1
4. Пусть Ап = @; ^) (интервал числовой прямой). Найти:
А" оо А" оо
1) U Ап (к е N); 2) U Ап; 3) П Ап (к е N); 4) П Ап.
п=1 п=1 п=1 п=1
5. Доказать: А С В «=> А П Б = А <(=^ A U Б = Б.
6. Доказать дистрибутивные законы:
(А п В) U С = (A U С) П (Б U С); (A U Б) П С = (А П С) U (Б П С).
7. ( Законы двойственности де Моргана). Рассматривается се-
семейство подмножеств некоторого множества U: для г = 1,...,п Д С U.
Пусть для любого множества Б С U запись Б означает дополнение к В:
В = U\B. Доказать, что
1) (П"=1 Ai) = Uf=1Ai (дополнение к пересечению есть объединение допол-
дополнений) ;
2) (U"=1 Ai) = C\f=1Ai (дополнение к объединению есть пересечение допол-
дополнений) .

1.2. Высказывания и предикаты
8. Определить местность предикатов.
1) х2 - 2х - 15 = 0; 2) Vx х2 - 2х - 15 = 0; 3) Зх х2 - 2х - у = 0.
9. Связать свободную переменную квантором так, чтобы получить ис-
истинное высказывание (предметная область — множество действительных
чисел).
1)\х\ = -х; 2) х2 > 0; 3)sinx^2; 4) Зх х2 - 2х - у = 0.
10. Пусть Р(х,у) — двухместный предикат
"Окружность х вписана в треугольник у".
Прочитать следующие высказывания, определить значения их истинности,
построить отрицания данных высказываний.
l)VxVy Р{х,у); 2Kх\1у Р{х,у); 3) Ух Зу Р(х,у).
11. Сформулировать отрицания следующих высказываний в утверди-
утвердительной форме (т.е. так, чтобы отрицание не начиналось со слов "не" или
"неверно, что").
1) В любом городе есть район, в каждой школе которого есть класс,
все ученики которого учатся без троек.
2) Существует город, в каждом районе которого есть футбольная ко-
команда, все игроки которой не старше 18 лет.
3) В каждом городе есть улица, на которой по крайней мере в одном
доме все окна выходят на юг.
4) Существует книга, на каждой странице которой есть не менее чем
одна строка, в которой буква "ы" встречается по меньшей мере два раза.
5) В каждом городе хотя бы одна улица застроена только такими до-
домами, в которых есть однокомнатные квартиры.
12. Бизнесмен Вася вывесил в своем супермаркете четыре рекламных
лозунга:
A) Всё дешёвое невкусно! B) Всё невкусное дёшево!
C) Всё вкусное недёшево! D) Не всё вкусное дёшево!
Борющийся за экономию коммерческий директор заметил, что два ло-
лозунга утверждают одно и то же. Какие?
Задачи о рыцарях и лжецах
Рыцари всегда говорят правду, а лжецы всегда лгут.

8 Глава 1. Предварительные сведения
13. Жители некоторого государства делятся на рыцарей и лжецов.
Как-то в комнате собралось 10 жителей этого государства, и каждый из
них сказал, обращаясь к остальным: "Все вы — лжецы". Сколько среди
этих людей было рыцарей и сколько лжецов?
14. В другой комнате собралось четверо жителей того же государства
(А, В, С, D), и между ними произошел такой разговор:
А: Все мы рыцари.
В: А лжёт.
С: По крайней мере двое из нас — лжецы.
D: По крайней мере трое из нас — лжецы.
Кто лжец, а кто рыцарь?
15. В думе государства рыцарей и лжецов 101 депутат. Каждый из
них заявил, что если его выведут из думы, то среди оставшихся лжецы
составят большинство. Сколько рыцарей в думе?
16. По кругу сидят рыцари и лжецы. Каждый из них сказал: "Все, кро-
кроме, быть может, меня и тех, кто сидит рядом со мной, — лжецы". Сколько
рыцарей сидит за столом?
17. Вокруг стола расселись рыцари и лжецы. Каждый из них сказал
о своем соседе справа, правдив тот или лжив. Известно, что на основании
этих заявлений можно однозначно определить, какую долю от присутству-
присутствующих составляют рыцари. Чему она равна?
1.3. Метод математической индукции
Простейший вариант метода математической индукции состоит в следую-
следующем.
Рассматривается некоторый предикат А(п), где п — натуральное
число. Пусть известно, что
1) [база индукции] высказывание А{1) истинно;
2) [индукционный шаг] для любого k e N из истинности А{к) следует
истинность А{к + 1).
Тогда для любого п е N высказывание А{п) истинно.
Действительно, поскольку А{1) истинно, a A{1) влечет АB), выска-
высказывание А{2) также истинно. ^4B), в свою очередь, влечет ^4C). Значит,
и высказывание АB>) истинно. Продолжая эти рассуждения, можно "до-
"добраться" за конечное число шагов до высказывания А{п), где п — любое

наперед заданное натуральное число, и это высказывание оказывается ис-
истинным.
18. Доказать тождества:
1I *)
2)
) 6;
3) I3 + 23 + ... + п3 = A + 2 + ... + пJ;
V 1-2 ~ 2-3 ~ - - - ~ п-(п+1)
19. Методом математической индукции доказать, что п-элементное
множество имеет 2™ подмножеств.
20. Плоскость поделена на части несколькими а) прямыми; б) окруж-
окружностями. Доказать, что эти части можно раскрасить в два цвета так, что
любые две смежные (то есть имеющие общий участок границы) части бы-
были разного цвета.
21. Доказать, что при п > 3 существует п различных натуральных
чисел таких, что их сумма делится на каждое из этих чисел.
22. Выпуклый 2п-угольник с равными сторонами можно разрезать на
ромбы. Доказать.
23. Пусть по = 2000, an = ^/2000 + yJan-\. Доказать, что при п > 1
целая часть числа an есть величина постоянная.
В следующих задачах используются более сложные схемы индукции
(где другой вид имеют индукционный шаг и база индукции).
24. Пусть х + ^ — целое число. Доказать, что для любого натурального
п число хп + -\ также целое.
25. Доказать, что для любого п > 5 квадрат можно разрезать на п
квадратов.
26. Доказать, что для любого п > 70 куб можно разрезать на п кубов.
27. Доказать, что многочлен fn(x) = 1 + х + |f + ... + ^ при нечётном
п имеет один действительный корень, а при чётном п не имеет действи-
действительных корней.
28. Доказать, что многочлен, принимающий только неотрицательные
значения, представим в виде суммы квадратов многочленов.

10 Глава 1. Предварительные сведения
1.4. Правило произведения
29. Из города А в город Б ведут 5 дорог, а из города Б в город В 7
дорог. Сколько есть различных маршрутов из города А в В через Б?
30. В меню столовой 3 первых, 5 вторых и 3 третьих блюда. Сколькими
способами можно выбрать обед из трёх блюд (первое, второе и третье)?
31. Сколько есть двузначных чисел, не содержащих цифр 0, 2, 5?
32. Сколько есть двузначных чисел, не содержащих цифр 1, 3, 6?
33. Номер автомашины состоит из трёх букв латинского алфавита (со-
(содержащего 26 букв) и трёх цифр. Сколько можно составить различных
номеров автомашин?
34. У рояля 88 клавиш. Сколькими способами можно извлечь после-
последовательно 6 звуков?
35. Сколько натуральных делителей имеет число 23 • З4 • 56?
36. Сколько натуральных делителей имеет число 23 • З4 • 45?
37. Сколько есть пятизначных чисел,
1) оканчивающихся двумя семёрками?
2) начинающихся с двух одинаковых цифр?
3) в каждом из которых нет одинаковых цифр?
4) в каждом из которых соседние цифры различны?
5) делящихся на 4 и не содержащих цифр 0, 4, 6, 8?
6) в записи которых есть одинаковые цифры?
7) в записи которых есть хотя бы одна чётная цифра?
38. Сколько есть перестановок цифр 0, 1, 2, ..., 9, в которых
1) цифра 3 занимает третье место, а цифра 5 — пятое?
2) цифра 1 следует непосредственно за цифрой 0?
3) цифра 0 занимает одно из первых трёх мест, а цифра 1 — одно из
последних четырёх мест?
4) цифра 0 занимает одно из первых пяти мест, а цифра 1 — одно из
первых трёх мест?
5) между цифрами 0 и 1 стоят ровно три цифры?
6) цифра 0 расположена левее цифры 1?

11
7) цифра 1 расположена между цифрами 0 и 2?
8) хотя бы одна из первых трёх цифр делится на 3?
39. Сколькими способами можно рассадить за десятью партами 10
мальчиков и 10 девочек так, чтобы за каждой партой сидели а) мальчик
слева, а девочка справа? б) мальчик и девочка?
40. Сколькими способами можно прочитать слово ПАРУС, двигаясь
вправо или вниз по каждой из следующих таблиц?
П
У
С
А
С
У
С
С
П
П
А
п
А
Р
П
А
Р
У
П
А
Р
У
С
41. Сколькими способами можно расставить на шахматной доске 8
одинаковых ладей так, чтобы никакие две из них не били друг друга?
42. Сколькими способами можно расставить на шахматной доске 8
одинаковых ладей так, чтобы они били все поля?
43. На координатной плоскости рисуются всевозможные несамопере-
секающиеся ломаные, все вершины которых имеют целые координаты, а
звенья параллельны координатным осям; Ln — число таких ломаных, вы-
выходящих из начала кординат и имеющих длину п. Доказать, что
4 • Т'1 < Ln < 4 • З".
44. Ключом шифра, называемого "решётка", является трафарет, сде-
сделанный из квадратного листа клетчатой бумаги размером пхп {п — чётное
число). Некоторые из клеток вырезаются с тем, чтобы в получившиеся
отверстия на чистый лист бумаги того же размера можно было вписы-
вписывать буквы шифруемого текста. Одна из сторон трафарета помечается;
при наложении трафарета на чистый лист бумаги четырьмя возможны-
возможными способами (помеченной стороной вверх, вправо, вниз, влево) его выре-
вырезы полностью покрывают всю площадь квадрата, причем каждая клетка
оказывается под вырезом ровно один раз. Буквы сообщения, имеющего
длину п2, последовательно вписываются в вырезы трафарета при каждом
из четырёх его возможных положений. После снятия трафарета на листе
бумаги оказывается зашифрованное сообщение. Найти число различных
ключей шифра для произвольного чётного числа п.

12 Глава 1. Предварительные сведения
45. При каком наибольшем m с помощью п гирь на чашечных весах
можно взвешивать грузы в1,2,3, ...,тг? Какими дожны быть при этом
массы гирь? Рассмотреть два случая:
а) гири могут быть только на одной чашке весов;
б) гири могут быть на разных чашках.
46. Каково наибольшее число подмножеств n-элементного множества,
любые два из которых имеют непустое пересечение?

Глава 2
Элементы теории чисел
Математика — царица наук, арифметика — царица математики.
К. Гаусс
Господь Бог создал целые числа, все остальное — дело рук человеческих.
Л. Кронекер
Целые числа составляют костяк дискретной математики.
Д. Кнут
2.1. Наибольший общий делитель.
Простые числа
47. Является ли число 57599 простым?
48. Доказать, что нечётное число п > 1 является составным тогда и
только тогда, когда оно представимо не менее чем двумя способами в виде
разности двух квадратов неотрицательных целых чисел.
49. Два соседних натуральных числа взаимно просты. Доказать.
50. Числа тип взаимно просты. Доказать, что числа тп и т + п
также взаимно просты.
51. Числа тип взаимно просты. Какие общие делители могут иметь
числа т + п и т — п?
52. Числа тип взаимно просты. Доказать, что числа тп и т2 + п2
также взаимно просты.
53. Числа тип взаимно просты. Какие общие делители могут иметь
числа т + п и т2 + п2?
54. Найти наибольший общий делитель чисел
1) 321 и 843; 2) 2166 и 6099; 3) 6787 и 7194; 4) 23521 и 75217.
55. Любые два соседние числа Фибоначчи (определение см. §5.5) вза-
взаимно просты. Доказать.

14 Глава 2. Элементы теории чисел
56. Пусть гп — n-значное число 11... 1. Доказать: (rn,rm) = r^my
57. Последовательность (ага) задается соотношениями по = О, ап =
P(ara_i), где Р(х) — многочлен с целыми коэффициентами. Доказать, что
{a-mO-m) = a-(n,m)-
58. Показать, что простое число р является делителем п\ с кратностью
59. Записать 20! в виде произведения степеней простых чисел.
60. Доказать, что кратность простого числа р в каноническом разло-
разложении п\ не превосходит а) -^; б) п^-.
61. Доказать, что л/йГ < Прп^^ (произведение берется по всем про-
простым делителям п).
62. Доказать неравенство П^пР^ — ?• Показать, что из него следует
бесконечность множества простых чисел.
63. Пусть (т, п) — наибольший общий делитель чисел тип, [гп, п]
— их наименьшее общее кратное. Аналогичный смысл имеют обозначения
(то, 71,/г) и [то, п, к]. Доказать, что имеет место тождество (то, п)[то, п] =
ran. Верно ли, что(то, п, /г) [то, п, к] = mnk?
64. Пусть р — простое число. Доказать, что для п = 1,2,.. .,р — 1 числа
п и р — п взаимно просты.
65. Доказать, что для любого п найдётся п последовательных нату-
натуральных чисел, каждое из которых — составное.
66. Доказать, что для любого п > 3 между п и п\ найдётся по крайней
мере одно простое число.
67. Доказать, что для любого п > 1 между п и 2п найдётся по крайней
мере одно простое число.
68. Доказать, что если 2га > A + п)к, то среди чисел 1, 2, 3,..., 2га суще-
существует по крайней мере к + 1 простое число. Показать, что отсюда следует
бесконечность множества простых чисел.
69. Доказать, что среди чисел {1, 2,..., п} не менее четверти свободны
от квадратов. Получить из этого утверждения доказательство бесконеч-
бесконечности множества простых чисел.

15
2.2. Сравнения по модулю
70. Найти остаток от деления
1) б100 на 7;
2) б100 на 35;
3) 1010 + 10100 + 101000 + ... + 10101° на 7.
71. Доказать, что
1) 30" + 61100 делится на 31;
2) 43101 + 23101 делится на 66;
3) II10 - 1 делится на 100;
4) 7120 - 1 делится на 143.
72. Пусть кип — натуральные числа. Доказать, что кп+2 + (к + 1Jга+1
делится на к2 + к + 1.
73. Доказать, что если сумма квадратов двух целых чисел делится на
3, то и каждое из них делится на 3.
74. Доказать, что если сумма квадратов двух целых чисел делится на
7, то и каждое из них делится на 7.
75. Двузначные числа от 19 до 80 выписаны подряд. Доказать, что
полученное число 192021... 7980 делится на 1980.
76. Можно ли все двузначные числа от 32 до 86 выписать в некотором
порядке одно за другим так, чтобы получилось простое число?
77. Можно ли числа 145, 146, ..., 151 выписать в некотором порядке
одно за другим так, чтобы получилось простое число?
78. Пусть п = 2(mod3), n = 3(mod5). Найти остаток от деления п на
15.
79. Существует ли в сутках момент, когда расположенные на общей
оси часовая, минутная и секундная стрелки правильно идущих часов об-
образуют попарно углы в 120°?
80. Выяснить, при каких к < 11 сумма квадратов к последовательных
натуральных чисел может быть квадратом натурального числа.
81. Число 1144664411 представить в виде суммы наименьшего возмож-
возможного числа четвёртых степеней натуральных чисел.

16 Глава 2. Элементы теории чисел
82. Можно ли множество натуральных чисел разбить на три подмно-
подмножества так, чтобы для любого п G N числа п, 2п, Зп принадлежали разным
подмножествам?
2.3. Китайская теорема об остатках
Теорема, которой посвящен параграф, открыта в Китае в первом (по дру-
другим сведениям, в четвертом) веке нашей эры. Она имеет много приложе-
приложений. Например, она используется в разработанном в 60-х годах двадцатого
века алгоритме быстрого преобразования Фурье. См. об этом в статье
М. Кельберт. Что такое преобразование Фурье? //Математическое про-
просвещение. - 2000. Сер. 3, вып. 4. - С.188-202.
Мы рассмотрим два доказательства этой теоремы — комбинаторное
и конструктивное. См. также лабораторную работу №6 в рамках
практикума, разработанного под руководством известного специалиста по
теории чисел X. Монтгомери (программы, составляющие Computational
Laboratories In Number Theory (CLINT) имеются на кафедре прикладной
математики ЮУрГУ).
83. [Китайская теорема об остатках.] Пусть q\,q2,... ,qn попарно
взаимно простые натуральные числа; целые числа Т\,г2,...,гп таковы,
что Vi 0 < Гг < qi. Тогда существует такое целое число х, которое для
любого г имеет остаток Г{ от деления на $¦ Доказать.
Доказательство. Обозначим через N произведение чисел qf.
N = qi ¦ q2 •... • qn. Заметим сначала, что если два числа имеют одинаковые
наборы остатков при делении на qi, q2,... ,qn, то их разность кратна N.
Действительно, если Vi а = b(modqi), т.е. Vi а — Ь : qi, то в силу того,
что числа qi,q2,... ,qn попарно взаимно просты, а — Ь делится и на их
произведение N.
Рассмотрим множество чисел А = {0,1,... ,N — 1}. Разность любых
двух (различных) чисел из этого множества по абсолютной величине мень-
меньше N, поэтому она не кратна N, и, следовательно, любые два числа из А
имеют разные наборы остатков при делении на qi, q2,..., qn. Подсчитаем
теперь, сколько всего может быть различных наборов остатков при деле-
делении числа на qi, q2,..., qn. При делении на qi остаток принимает одно из
qi значений:
0,1,... ,qi — 2 или qi — 1.
Согласно правилу произведения всего наборов будет qi ¦ q2 ¦ ... ¦ qn, т.е.

17
как раз N. Таким образом, для любого набора остатков от деления на
qi, q2, ¦ ¦ ¦, qn в множестве А найдётся (и при том ровно одно) число, обла-
обладающее им.
84. Пусть qi,q2,... ,qn попарно взаимно простые натуральные числа.
Для каждого % найти число ti, удовлетворяющее следующим условиям:
1) yj ^i U = 0(modqj);
2) ti = l(modqj.
85. На основе предыдущей задачи получить конструктивное доказа-
доказательство китайской теоремы об остатках.
86. Найти наименьшее натуральное число, которое даёт при делении
на 3 остаток 2, на 4 — остаток 1, на 5 — остаток 2.
87. Пусть qi,q2,... ,qn попарно взаимно простые натуральные числа;
целые числа ri,r2,... ,гп таковы, что Vi 0 < г* < %¦ Доказать, что суще-
существует такое целое число ж, что
х = ri(modgi), х + 1 = r2(modg2), ...,x + n—l = rn(modqn).
88. Доказать, что для любого п найдётся п последовательных нату-
натуральных чисел, каждое из которых делится на квадрат простого числа.
2.4. Теоремы Эйлера, Ферма, Вильсона
89. Найти остаток от деления
1) 2100 на 101;
2) З102 на 101;
3) 8900 на 29;
4) 7120 на 143.
90. Доказать, что для любого натурального п число п73 — п37 делится
на 10.
91. Доказать, что если п не делится на 17, то либо п8 — 1, либо п8 + 1
делится на 17.
92. Пусть р — нечётное простое число. Доказать, что п~^~ при делении
на р дает остаток 0, 1 или р — 1.
93. Доказать, что если сумма квадратов двух целых чисел делится на
простое число р = Ак + 3, то и каждое из них делится на р.

18 Глава 2. Элементы теории чисел
94. Пусть а и Ь — взаимно простые числа, р — нечётный простой дели-
делитель числа а2 + Ь2. Доказать, что для некоторого натурального п выпол-
выполняется равенство р = An + 1.
95. Пусть а — целое число, р — нечётный простой делитель числа а4 + 1.
Доказать, что р имеет вид р = 8п + 1.
96. Пусть а — целое число, р > 3 — простой делитель числа а2 + а + 1.
Доказать, что р имеет вид р = 6п + 1.
97. Пусть а и Ь — взаимно простые числа. Доказать, что
98. Пусть а > 1 — произвольное натуральное число,
р > 2 — простое число, взаимно простое с а2 — 1. Положим п = а 2Р~1.
Доказать, что 1) п — составное число; 2) ап~1 = l(modn).
Пусть f{x) = аохп + a\xn~l + ... + ап — многочлен с целыми коэффи-
коэффициентами. Решить сравнение
f(x) = O(modm) A)
означает найти все целые значения переменной х, ему удовлетворяющие.
Как известно, если х = хо (mod m), то и f(x) = f(xo)(modm). Поэтому
в качестве решений уравнения A) можно рассматривать классы вычетов
по модулю т. Будем говорить, что сравнение A) имеет столько решений,
сколько классов вычетов по модулю m ему удовлетворяют. Степень мно-
многочлена f(x) называют степенью сравнения A).
99. Пусть р — простое число. Тогда сравнение
f(x) = aoxn + aixn~l + ... + an = O(modp) B)
равносильно сравнению степени не выше р — 1.
100. Если сравнение n-й степени B) по простому модулю р имеет более
п решений, то все коэффициенты многочлена f(x) кратны р.
101. Пусть п — составное число. Доказать, что (п — 1)! + 1 не делится
на п.
102. Пусть п > 4 — составное число. Доказать, что {п — 1)! делится на
п.
103. Если р — простое число, то (р — 1)! + 1 делится на р.
Замечание. Задачи 101 и 103 показывают, что имеет место следующий

19
критерий простоты числа.
Теорема Вильсона. Для того, чтобы число р было простым, необходи-
необходимо и достаточно, чтобы (р — 1)! + 1 делилось на р.
Другое доказательство этой теоремы (не использующее малую теорему
Ферма) можно найти в [60] (с. 23).
104. [Теорема Лейбница.] Число р > 2 является простым тогда и
только тогда, когда (р — 2)! — 1 делится на р. Доказать.
105. Если р = Ак + 1 — простое число, то (^у^1)!2 + 1 делится на р.
Доказать.
106. Доказать, что если р > 2 — простое число, то
1) I2 • З2 • 52 • ... • (р - 2J ее (-l)^(modp),
2) 22 • 42 • б2 • ... • (р - IJ ее (-l)^(modp).
2.5. Квадратичные вычеты и невычеты
Пусть р — простое число. Число а, не делящееся на р, называется ква-
квадратичным вычетом по модулю р, если разрешимо (относительно х)
сравнение х2 = a(modp), и квадратичным невычетом в противном
случае.
107. Пусть р — нечётное простое число. Доказать, что среди чисел
1, 2,... ,р — 1 квадратичных вычетов ровно половина.
Для простого числа р символ Лежандра ( - 1 определяется так:
(ч ( О, если а делится на р,
— ] = < 1, если a — квадратичный вычет,
Т) I I
F' I — 1, если a — квадратичный невычет.
108. [Лемма Лежандра.] Если р — нечётное простое число, то
(
109. Доказать, что (^) = (j) (j) .
110. Найти все простые р > 2, для которых число —1 является ква-
квадратичным вычетом.

20 Глава 2. Элементы теории чисел
111. Решить сравнение х2 = 5 (mod 19).
112. [Лемма Гаусса.] Пусть р — нечётное простое число, q = (р —
1)/2, Р = {1, 2,... , д} и для каждого k G Р число s^ G { — 1,1} выбрано
так, что число aksk сравнимо по модулю р с каким-нибудь числом из Р.
Тогда
= I I ?к-
L\
113. Найти все простые р > 2, для которых число 5 является квадра-
квадратичным вычетом.
2.6. Уравнения в целых числах
114. Решить в целых числах уравнения:
1) 16х + Ау = 1830; 2I3ж + 7у = 1;
3) 21ж + 19у = 5; 4) 1994ж - 171у = 1.
115. Пусть а и Ь — взаимно простые натуральные числа. Найти наи-
наименьшее натуральное п такое, что при любом натуральном т, большем п,
разрешимо в натуральных числах уравнение ах + by = т.
116. Пусть а и Ь — взаимно простые натуральные числа. Сколько су-
существует натуральных чисел, не представимых в виде п = ах + by, где х
и у — неотрицательные целые числа?
117. Один фермер потратил 1000 долларов на покупку 100 различных
домашних животных. Каждая корова обошлась ему в 100 долларов, сви-
свинья в 30 долларов, а овца — в 5 долларов. Сколько голов скота каждого
вида он купил?
118. Другой фермер потратил 1800 долларов на покупку 100 различ-
различных домашних животных. Каждая корова стоила 72 доллара, свинья — 36
долларов, овца — 6 долларов. Известно, что коров было куплено больше,
чем свиней. Сколько голов скота каждого вида купил фермер?
119. Три мужа — Андрей, Иван и Степан пошли со своими жёнами —
Анной, Екатериной и Ольгой за покупками. Каждый платил за каждую
вещь по стольку рублей, сколько он купил вещей. Андрей купил больше
Анны на 23 вещи, Иван — больше Екатерины на 11 вещей. Определить, кто

21
на ком женат, если каждый из мужей израсходовал на 63 рубля больше
своей жены. (Задача экзамена Кишиневской гимназии за 1879 г.).
120. Пусть pi,P2, ¦ ¦ ¦ iPn — различные нечётные простые числа. Дока-
Доказать, что их произведение можно представить в виде разности квадратов
2й способами.
121. Доказать, что следующие уравнения не имеют решений в целых
числах, выбрав подходящим образом модуль для сравнения.
1)у2 = 5х2 + 6; 2) x2 + y2 = 4z-l;
3) 15ж2 - 7у2 = 9; 4) х2 - 7у = 10;
5) х3 + 21у2 + 5 = 0; 6) х2 + у2 + z2 = 8t - 1.
122. Решить в целых числах уравнения
1) х + у = х2 — ху + у2; 2) у2х = 9999?/ + х; 3) 2ху — Ъх + у = 55.
123. Решить в натуральных числах уравнения:
1) х2 - у2 = 1988; 2) Зт + 7 = 2й;
3) 3 • 2т + 1 = п2; 4) 19я + 94^ = 19932;
5) 2я+ 3 = 11»; 6) 2х + ЗУ = 52;
7) хУ+1 - (х + 1)» = 2001; 8) 1 + 3х = 3^ + 52.
124. Решить в натуральных числах уравнение
1 1 1 тг
arctg —Ь arctg —Ь arctg - = —,
х у z 4
считая, что х > у > z.
125. Найти натуральные числа х < у < z, для которых
1 1 1 _ 19
х ху xyz 97
126. Решить в целых числах уравнение х2 + у2 = 31 (z2 + t2).
127. Найти все пары целых чисел таких что сумма их суммы, разности,
произведения и частного равна 150.
128. Даша гадает на ромашке: "Любит — не любит — плюнет — поце-
поцелует — к сердцу прижмёт — к черту пошлёт". Глаша при гадании к этим
шести вариантам добавляет ещё один: "своей назовёт". На ромашках с п
и 2п лепестками у Даши хорошее предсказание, а у Глаши плохое. Чему
равно п, если считать, что на ромашке не может быть более 100 лепестков?

22 Глава 2. Элементы теории чисел
129. На плоскости проведено п прямых. Каждая прямая пересекается
ровно с 1999 другими. Найти все возможные значения п.
130. На клетчатой бумаге нарисован прямоугольник. Количество его
клеток, примыкающих к границе прямоугольника, равно количеству
остальных его клеток. Найти размеры прямоугольника.
131. Первоначально во всех клетках таблицы 100 х 100 записаны плю-
плюсы. Допускается операция одновременного изменения знака во всех клет-
клетках одной строки или одного столбца. Можно ли получить таблицу, в ко-
которой а) 2001; б) 1990; в) 2002 минусов?
132. Найти все натуральные п, при которых уравнение
nXl + ... + nXwo = 1997 разрешимо в целых числах х\,..., жюо-
133. Пусть Ьо, bi, 62, ¦ ¦ ¦ — геометрическая прогрессия, к < m — взаимно
простые числа, bo, bk и bm — натуральные числа. Доказать, что при любом
г < m число bi также натуральное. Верно ли, что все члены прогрессии
натуральные числа?
134. Пусть р и г, q и s — две пары взаимно простых чисел. Доказать,
что любое положительное рациональное число представимо в виде аГ>Ль1,
где a, b,c,d — натуральные числа.
135. Если бесконечная возрастающая арифметическая прогрессия со-
содержит точный квадрат и точный куб, то она содержит и 6-ю степень
некоторого целого числа. Доказать.
Большое количество задач по элементарной теории чисел собрано в [60].
См. также §§8.2, 8.3 настоящего сборника. Ряд задач из других разделов
также тесно связаны с теорией чисел.
2.7. Мультипликативные функции
136. Пусть ш{п) — число различных простых делителей п. Доказать,
что функция f{n) = сш(и) — мультипликативная.
137. Доказать, что произведение мультипликативных функций муль-
мультипликативно.
138. Найти количество чисел, не превосходящих m и взаимно простых
с m для m = 25, 60, 250, 1 000 000.
139. Сколько существует правильных несократимых дробей со знаме-
знаменателем 288?

23
140. Пусть число а оканчивается на 1, 3, 7 или 9. Доказать, что о400000
оканчивается на 000001.
141. Доказать тождество ip(m)ip(n) = ip((m,n))ip([m,n]).
142. При п > 2 число <р(п) четно. Доказать.
143. Доказать, что сумма всех натуральных чисел, не превосходящих
п и взаимно простых с п, равна п<р(п)/2.
144. Из равенства <p(piP2 ¦ ¦ -Ps) = (Pi - 1)(Р2 - 1) • • • (Ps - 1)
(pi,P2, ¦ ¦ ¦ iPs — различные простые числа) вывести бесконечность множе-
множества простых чисел.
т(п) есть число (натуральных) делителей числа п, s(n) — их сумма.
145. Доказать: т{п) нечётно •<=>¦ п — квадрат.
146. Доказать: s(n) нечётно <^=> п — квадрат или удвоенный ква-
квадрат.
147. Доказать, что произведение всех делителей числа п равно пт^п''2.
148. Каким количеством нулей может оканчиваться произведение всех
делителей числа?
п
149. Исходя из соотношения Y2 \ = 1пгг + 0A), докажите, что
?>(*;) =n(lnn +0A)).
к=1
Таким образом, на долю каждого их первых п натуральных чисел при-
приходится в среднем примерно In n делителей.
150. Доказать неравенство s(n) + <p(n) > In.
151. Доказать, что при п > 1 справедливо неравенство
s(n) < n(lnn + 1).
Существует ли такая константа С, что для всех п справедливо s(n) < Cnt
Продолжение темы мультипликативных функций — в §8.4.

Глава 3
Начальные понятия общей алгебры
152. Какими свойствами (рефлексивность, антирефлексивность, сим-
симметричность, антисимметричность, транзитивность) обладают следующие
бинарные отношения на множестве действительных чисел?
1) хду •<=>¦ х2 = у2; 5) хду •<=>¦ х2 + х = у2 + у;
2) хду •<=>¦ х2 + у2 = 1; 6) хду •<=>¦ х3 + х = у3 + у;
3) хду <(=> ху > 1; 7) хду <(=> х - у G Z;
4) хду <(=> у = \х\; 8) хду <(=> х - у G N.
153. Какие из отношений предыдущей задачи являются отношениями
эквивалентности? Для каждого из таких отношений выяснить, что пред-
представляют собой классы эквивалентности и сколько элементов они содер-
содержат.
154. На множестве учеников класса введем отношение "учится лучше".
Будем говорить "Ученик А учится лучше ученика В", если по большин-
большинству контрольных работ А имел оценки выше, чем В. Обладает ли данное
отношение свойством транзитивности?
155. На множестве А введено симметричное и транзитивное отношение
д такое, что
Va ЗЬ адЬ.
Доказать, что отношение д рефлексивно.
Соглашение. В задачах данного раздела е обозначает нейтральный
элемент группы.
Пусть А = {ai, 02,..., а„} — конечное множество, на котором опреде-
определена бинарная операция *. Таблица из п строк и п столбцов, в которой на
пересечении i-й строки и j-ro столбца стоит элемент множества А, равный
щ * Oj, называется таблицей умножения, или квадратом Кэли.
156. На множестве {1, 2, 3, 4, 6,12} определим две бинарные операции:
1) a * Ъ = (а, Ъ) (наибольший общий делитель);
2) a*b = [a,b] (наименьшее общее кратное).
Составить для этих операций квадраты Кэли.

25
157. Составим матрицу коэффициентов дробно-линейной функции
Аг=(а*
г
Какая матрица будет соответствовать сложной функции /Д/Дж))?
158. На множестве функций {х, ±, |=i, |^, ±=§, ±^§, -±, -ж} выберем
в качестве бинарной операции композицию функций (будем считать, что
областью определения всех функций является множество R\{ —1,0,1}).
Составить квадрат Кэли для данной операции. Доказать, что рассматри-
рассматриваемая алгебраическая структура является группой.
159. На множестве (Q \ 0) х Q введена операция
(а, Ь) (с, d) = [ас, bc + d).
Доказать, что данная алгебраическая структура является группой.
160. Доказать, что в квадрате Кэли конечной группы каждый элемент
группы встречается в каждой строке (и каждом столбце) ровно один раз.
161. Составить квадрат Кэли для следующих групп:
1) вращений правильного треугольника;
2) вращений квадрата;
3) вращений правильного пятиугольника;
4) симметрии ромба, не являющегося квадратом;
5) симметрии правильного треугольника;
6) симметрии прямоугольника, не являющегося квадратом;
7) симметрии квадрата.
162. Доказать, что группа из задачи 158 изоморфна группе симметрии
квадрата.
163. Какие из следующих числовых множеств образуют аддитивные
группы?
Z, 2Z, N, 2Z + 1, Q+, Q, R \ Q, {-1,0,1}.
164. Какие из следующих числовых множеств образуют мультиплика-
мультипликативные группы?
R, R \ {0}, R+, Z, 2Z + 1, Q, Q \ {0}, {1, -1}, {1, 2, §}, R \ Q, {2« | n G Z}.
165. Доказать, что если в группе каждый элемент себе обратен
(Уа а * а = е), то группа — абелева.

26 Глава 3. Начальные понятия общей алгебры
166. Найти с точностью до изоморфизма все группы, состоящие не
более, чем из 4 элементов.
167. Пусть ip : G —>¦ Н — сюръективное гомоморфное отображение
абелевой группы G на группу Н. Доказать, что Н — абелева группа.
168. Пусть < С, • > группа, д G G. Доказать, что отображение
(fg : G —>¦ G, заданное правилом <рд(х) = д~ххд, является изоморфизмом.
169. Пусть < G, • > — конечная группа. Доказать, что
VgeG 3neN gn = е.
Наменьшее п > О, при котором дп = е, называют порядком элемента д.
170. Доказать, что конечная группа четного порядка обязательно со-
содержит элемент второго порядка.
171. Пусть группа обладает единственным элементом второго порядка.
Доказать, что этот элемент перестановочен с каждым элементом группы.
172. Пусть х и у — элементы (мультипликативной) группы с указан-
указанными ниже свойствами. Доказать, что ys = e.
1) х2 = е, хух~1 = у3; s = 8;
2) х2 = е, xyx~l = yn; s = п2 — 1;
3) х3 = е, хух~1 = у4; s = 63;
4) xm = e, xyx~l =yk) s = km — 1.
173. Пусть G — группа с единичным элементом е; ф : G —» G —
функция такая, что Ф(д\)ф(д2)ф{дъ) = ^(^1)^(^2)^(^3M всякий раз, когда
#1#2#з = е = /ii/i2^3- Доказать, что существует такой элемент oGG, что
функция ip(x) = аф(х) есть гомоморфизм (т.е. Ух, у ф(ху) = ip(x)ip(y)).
174. Элемент х ф 0 кольца < К,+,- > называется нилыютентным,
если хп = 0 для некоторого n G N. Доказать, что нильпотентность эле-
элемента х влечет обратимость элемента 1 — х в любом кольце с единицей.
175. Пусть для элементов а, Ь, с кольца с единицей выполняются ра-
равенства A — аЪ)с = 1 = сA — аЪ). Показать, что если d = 1 + Ьса, то
A — ba)d = 1 = d{l — Ьа). Таким образом, из обратимости элемента 1 — аЪ
следует обратимость элемента 1 — Ьа.
176. Доказать, что кольцо идемпотентов < К, +, • > (Va G К а2 = а)
коммутативно.
177. Найти все гомоморфизмы поля действительных чисел в себя.

Глава 4
Элементы математической логики
4.1. Формулы и их преобразования.
Двойственность
178. По мишени произведено три выстрела. Пусть А^ есть высказы-
высказывание: "Мишень поражена при г-м выстреле". Что означают следующие
высказывания: 1) Ах V А2 V А3; 2) А1кА2кАъ\ 3) (Аг V Л2)&А3?
179. По обвинению в ограблении перед судом предстали А, В и С.
Установлено следующее:
1) если А не виновен или В виновен, то С виновен;
2) если А не виновен, то и С не виновен.
Виновен ли А!
180. Определить, кто из четырёх подозреваемых участвовал в ограб-
ограблении банка, если известно:
1) если А участвовал, тоиВ участвовал;
2) если В участвовал, то или С участвовал, или А не участвовал;
3) если D не участвовал, то А участвовал, а С не участвовал;
4) если D участвовал, то и Л участвовал.
181. В санатории на берегу моря отдыхают отец, мать, сын и две до-
дочери. До завтрака члены семьи часто купаются в море. Известно, что
1) если купается отец, то обязательно купаются мать и сын;
2) если купается сын, то обязательно купается старшая дочь;
3) мать и младшая дочь порознь не купаются;
4) кто-то из мужчин обязательно купается.
Однажды утром из дочерей купалась только одна. Кто купался в это утро?
182. Выяснить, является ли следующее рассуждение логически пра-
правильным; для этого представить каждое предложение пропозициональ-

28 Глава 4. Элементы математической логики
ной формой и проверить, является ли заключение логическим следствием
конъюнкции посылок.
Если инвестиции останутся постоянными, то возрастут
правительственные расходы или увеличится безработица. Если
правительственные расходы не возрастут, то налоги будут снижены.
Если налоги будут снижены и инвестиции останутся постоянными,
то безработица не увеличится. Следовательно, правительственные
расходы возрастут.
183. В городе А живут люди, всегда говорящие правду. Жители города
В, напротив, всегда лгут. У развилки двух дорог, ведущих в Л и Б, путе-
путешественник встречает местного жителя. Какой вопрос, требующий ответа
"да" или "нет", должен задать путешественник, чтобы узнать, какая дорога
ведёт в А!
184. Является ли тождественно истинной формула
(х ^ у) ^ ((х V z) ^ (у V z))?
185. Равносильны ли формулы / и gl
1) / = (xVyVz) -»¦ ((xVy)(xVz)), g = x~z;
2) / = (x -» у) -» z, g = x^ (y^z);
3) / = (x->y) V ((x->z)y), g = xy(y -»¦ xz).
186. Проверить, имеют ли место следующие равносильности:
1) х V (у ~ z) = (х V у) ~ (х V z);
2) х ->¦ (у ~ z) = (х ->¦ у) ~ (х ->¦ z);
3) х(у ~ z) = ху ~ жг;
5) ж ->¦ yz = (х ->¦ г/)(ж ->¦ г);
6) ж ->¦ (у ->¦ г) = (ж ->¦ г/) ->¦ (ж ->¦ z);
7) ж ->¦ (жг/ ->¦ ((ж ->¦ г/) ->¦ y)z) = у ->¦ (ж ->¦ г).
Говорят, что логическая функция / сохраняет ноль (единицу), если
/(О,..., 0) =0 (соответственно /A,..., 1) = 1).
187. Подсчитать число логических функций от п переменных, сохра-
сохраняющих ноль.
Назовем логическую функцию самодвойственной, если она является
двойственной к самой себе, т.е. f(xi,..., хп) — самодвойственная функция,
если f(xi,...,xn) =J(xi,...,x?).
188. Найти число самодвойственных логических функций от п пере-
переменных (допуская и фиктивное вхождение переменных).

29
189. Найти все самодвойственные логические функции от двух и трёх
переменных.
190. Пусть f(xu...,xm), gi(xi,...,xn),...,gm(xi,...,xn) -
самодвойственные функции. Доказать самодвойственность сложной
функции h(xi,...,xn) = f(gi,...,gm)(xi,...,xn).
4.2. Полные системы связок
191. Доказать, что система связок {&, V, —>} не является полной.
192. Выразить через стрелку Пирса I (А I В = А V В) операцию
отрицания, конъюнкцию и дизъюнкцию.
Многочлены Жегалкина
Введем операцию сложения по модулю 2:
х + у = х ~ у.
193. Докажите, что {+,&, I}1 — полная система связок.
Назовем одночленом конъюнкцию любого числа попарно различных
переменных или константу 1 (пустую конъюнкцию), а многочленом Же-
Жегалкина сумму по модулю 2 попарно различных одночленов
/ j xhxi2 ¦ ¦ ¦ xik,
где суммирование ведётся по наборам (h,... ,ik), среди которых может
быть и пустой. Пустую сумму (число одночленов равно нулю), как обычно,
полагаем равной нулю.
194. Выписать все одночлены от двух переменных (х и у) и подсчитать
число многочленов от двух переменных.
195. Представить многочленом Жегалкина следующие логические
функции:
1) х V у V Z) 2) ху V xz V yz; 3) xyz V xyz V xyz V x у ~z.
196. Доказать, что любая логическая функция однозначно представи-
ма многочленом Жегалкина.
1 Константу 1 можно считать О-арной связкой, задающей функцию, которая не имеет
аргументов.

30 Глава 4. Элементы математической логики
4.3. Теорема Поста
Всякое множество Т логических функций, замкнутое относительно супер-
суперпозиции (т.е. такое, что любая суперпозиция функций из Т входит в Т),
называется функционально замкнутым классом.
197. Выяснить, какие из указанных ниже множеств являются функ-
функционально замкнутыми классами:
1) множество функций от одной переменной;
2) множество функций от двух переменных;
3) множество L линейных функций (линейная функция — это многочлен
Жегалкина степени 1);
4) множество S самодвойственных функций;
5) множество Ро функций, сохраняющих ноль;
6) множество Pi функций, сохраняющих единицу;
7)Р0ПРТ;
8) множество А всех логических функций.
198. Доказать, что если функционально замкнутый класс не пуст и не
совпадает с А, то дополнение к нему не обладает свойством функциональ-
функциональной замкнутости.
Пусть Е = {0,1}. Упорядочим это множество, полагая 0 < 0,0 <
1,1 < 1. На единичном n-мерном кубе Еп введем частичный порядок
следующим образом: (xi,..., хп) < (г/i,..., уп), если для любого i име-
имеем Х{ < yi. Логическая функция / называется монотонной, если условие
(х1,...,хп) < (г/i,..., уп) влечет /(жь ...,хп) < /(г/i,..., г/„).
199. Выяснить, какие из указанных ниже функций монотонные.
l)xVy; 2) ху\ 3)х^у; 4) х -»¦ (х -»¦ у);
5) х у ~ (х V у); 6) ху V yz V zx; 7) х + у + ху.
200. Множество М монотонных функций функционально замкнуто.
Доказать.
Множество логических функций Т называется полным, если любая
логическая функция представима суперпозицией функций из Т. Мини-
Минимальное полное множество логических функций (т.е. такое полное множе-
множество, что если из него удалить любую функцию, то оно перестанет быть
полным), называется базисом.
201. Привести примеры базисов из одной, двух и трёх функций.

31
Функционально замкнутый класс, отличный от ф и А называется
предполным, если он не содержится ни в каком функционально
замкнутом классе, отличном от себя самого и от А. Известно ([24]), что
существует ровно пять предполных классов: Po,Pi,L,M,S. Имеет место
следующая теорема:
Теорема Поста. Множество логических функций Т полно тогда и
только тогда, когда для каждого из классов Po,Pi, L, M, S в Т есть
функция, ему не принадлежащая.
202. С помощью теоремы Поста показать, что множество функций
{0,1, х + у + z, ху} является базисом.
203. Из множества логических функций {ху V ху, ху + z,(x + у) ~
z, xy V yz V zx} выделить всевозможные базисы.
204. С помощью теоремы Поста доказать, что базис не может содер-
содержать более а) пяти; б) четырёх функций.
Вопросы, затронутые в настоящем параграфе, обстоятельно изучаются
в монографии [24].
4.4. Нормальные формы
205. С помощью равносильных преобразований привести к ДНФ сле-
следующие формулы:
1) (xi V x2x3)(x1 Vx3);
2) (xi V ?2X3X4)((х2 ^ ха) —>¦ ?1X3X4) V х2х3 V Х\ V Х4-
206. Привести к СДНФ, КНФ и СКНФ следующие формулы:
1)хх\/Х2Хз; 2)xix2 V Х1Х3; 3)xi V Х1Х2 V ?2X3-
207. С помощью метода Блейка построить сокращённую ДНФ по за-
заданной ДНФ:
1) Х\Х2 V Х1Х3Х4 V ?2X3^4;
2) xix2x3 V X1X2X4 V ?3^4;
3) XiX2 V Х1Х3 V XiX2X3X4 V XiX2X3X4-
208. Построить сокращённую ДНФ по заданной КНФ:
1) (xi V х2 V х3)(х1 V х2 V х3)(х2 V х3);
2) (xi V X4)(x2 V х3 V X4)(x"i V x2 V х3);
3) (xi V X2 V Хз)(х V Х4)(Х2 V Х3 V Х4).

32
Глава 4. Элементы математической логики
209. Построить СДНФ, СКНФ и минимальную ДНФ для функции
со следующей таблицей истинности.
Xi
0
0
0
0
1
1
1
1
0
0
1
1
0
0
1
1
?з
0
1
0
1
0
1
0
1
/(хьх2,х3)
1
1
1
0
0
1
0
1
210. Построить сокращённую ДНФ и все тупиковые ДНФ для функции
/ = х у z V х yzV xyz V xyz V xyz V xy~z.
211. Привести пример логической функции от п переменных, у кото-
которых любая ДНФ и любая КНФ являются совершенными.
212. Пятеро друзей решили записаться в кружок любителей логиче-
логических задач: Андрей (А), Виктор (В), Семен (С), Дмитрий (D), Евгений
(Е). Но староста кружка предложил им выдержать вступительный экза-
экзамен. "Вы должны приходить к нам по возможности больше вечеров, однако
в разных сочетаниях, соблюдая следующие условия:
1) Если А приходит вместе с Е, то В должен присутствовать.
2) Если Е отсутствует, то В должен быть, а С пусть не приходит.
3) Л и С не могут одновременно ни присутствовать, ни отсутствовать.
4) Если придёт Е, то D пусть не приходит.
5) Если В отсутствует, то Е должен присутствовать, но это в том слу-
случае, если не присутствует С. Если же С присутствует при отсутствии В,
то Е приходить не должен, a D должен прийти".
Сколько вечеров и в каком составе друзья должны приходить, чтобы
выдержать экзамен?
4.5. Контактные схемы
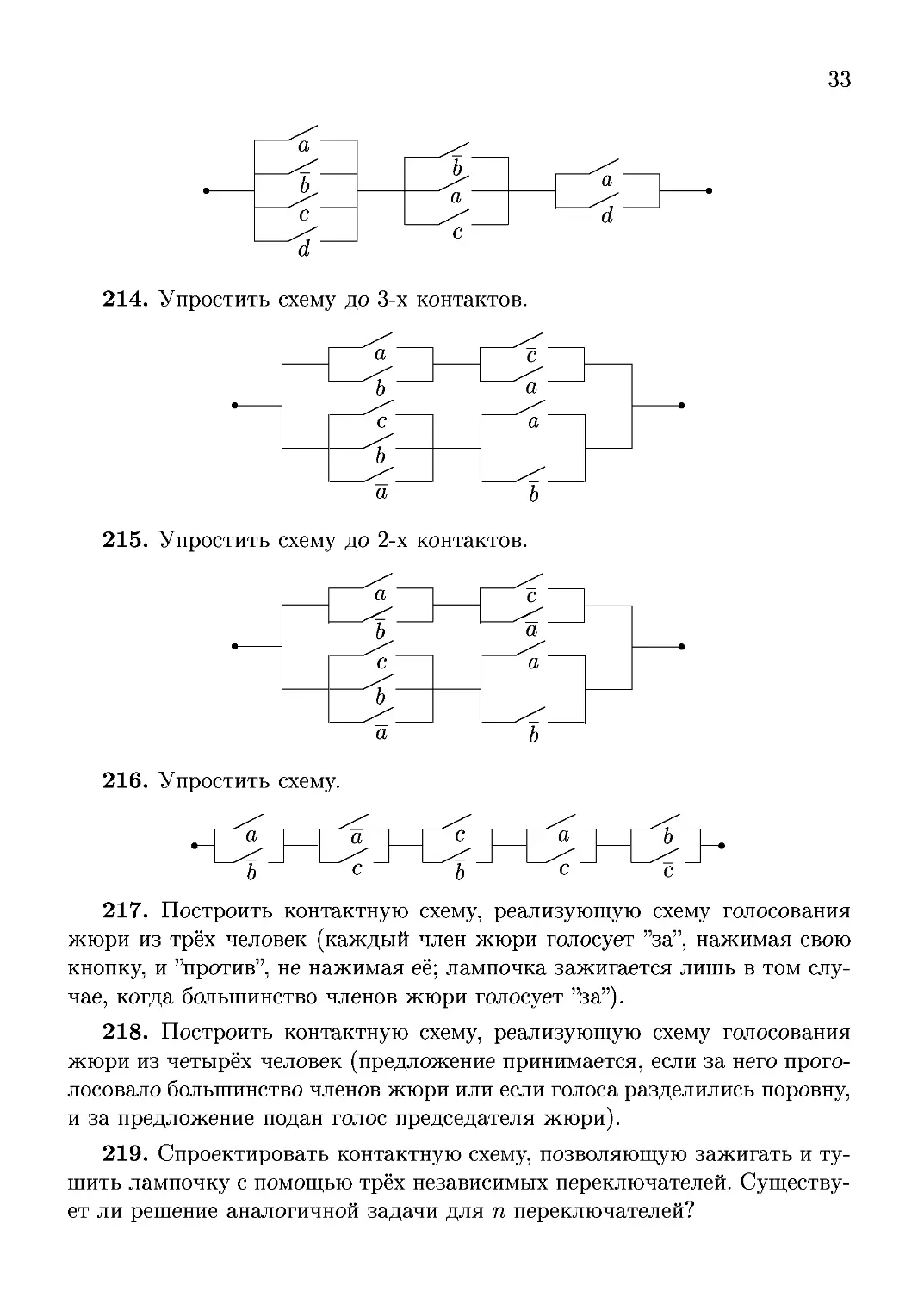
213. Упростить схему до 4-х контактов.

33
b
a
с
a
d
214. Упростить схему до 3-х контактов.
215. Упростить схему до 2-х контактов.
216. Упростить схему.
а
с
b a
с
b
а
а
h
а
b
с
b
а
с
а
а
h
а
с
с
Ъ
а
с
217. Построить контактную схему, реализующую схему голосования
жюри из трёх человек (каждый член жюри голосует "за", нажимая свою
кнопку, и "против", не нажимая её; лампочка зажигается лишь в том слу-
случае, когда большинство членов жюри голосует "за").
218. Построить контактную схему, реализующую схему голосования
жюри из четырёх человек (предложение принимается, если за него прого-
проголосовало большинство членов жюри или если голоса разделились поровну,
и за предложение подан голос председателя жюри).
219. Спроектировать контактную схему, позволяющую зажигать и ту-
тушить лампочку с помощью трёх независимых переключателей. Существу-
Существует ли решение аналогичной задачи для п переключателей?

34 Глава 4. Элементы математической логики
4.6. Булева алгебра
Пусть на множестве S = {A,B,C,...} определены две бинарные операции,
обозначаемые + и -2, так, что при этом выполняются следующие свойства
(аксиомы булевой алгебры):
1. Множество S замкнуто относительно операций + и •.
Для любых А, В, С е S
2. А + В = В + А, А • В = В • А (коммутативность операций + и •);
3. А + (В + С) = (А + В) + С, А(ВС) = (АВ)С (ассоциативность);
4. А + А = А, А- А = А (идемпотентность);
5. А(В + С) = АВ + АС, А + ВС = (А + В)(А + С) (дистрибутивность).
6. Существует элемент О е S, называемый нулем, такой, что
S A + O = A.
7. Существует элемент I G S, называемый единицей, такой, что
VAeS A-I = A.
8. У А е S ЗА е S A + А = I, A- A = О (существование обратного
элемента ).
Тогда алгебраическая структура < S;+,- > называется булевой алге-
алгеброй.
Данная система аксиом не является независимой: некоторые аксиомы
являются следствиями других.
220. Вывести аксиому 4 из аксиом 5-8.
221. Используя только аксиомы 5, 7, 8, доказать, что УА А + I = I.
222. Вывести аксиому 6 из аксиом 5, 7, 8.
223. Доказать закон двойственности: если в любом тождестве бу-
булевой алгебры заменить + на •, • на +, I на О, О на I, то вновь полу-
получится тождество.
224. Вывести аксиому 3 из аксиом 4-8.
2Этот знак иногда будет опускаться.

35
4.7. Аксиоматические теории
Формальная аксиоматическая теория определена, если
1) задан алфавит (множество символов);
2) из множества слов (конечных последовательностей символов алфавита)
выделено множество формул;
3) из множества формул выделены аксиомы;
4) заданы правила вывода (отношения между формулами).
Если g — отношение на множестве формул и (А\, А2, • • •, Ak-, А) €
g, то говорят, что формула А есть непосредственное следствие фор-
формул Ai, Aii ¦ ¦ ¦ 1 Ак, или: формула А непосредственно выводима из гипотез
А\, Ai-, ¦ ¦ ¦ 1 Ак- При этом используют такую запись:
Ai, A2, ¦ ¦ ¦, At
А '
Выводом формальной теории называют последовательность формул,
в которой каждая формула — либо аксиома, либо непосредственное след-
следствие каких-либо предыдущих формул. Последнюю формулу вывода на-
называют теоремой.
Говорят, что формула А выводима из множества формул Г (запись:
V \- А), если существует последовательность формул, в которой каждая
формула — либо аксиома, либо принадлежит Г, либо непосредственное
следствие каких-либо предыдущих формул, и при этом последняя фор-
формула последовательности есть А. Если Г = {А\, Ач-, ¦ ¦ ¦, Ак}-, записывают
также
Ai,A2,-. .,Ak\~ A.
В случае Г = ф получаем, что А — теорема (запись: Ь А).
lib. Доказать следующие свойства выводимости:
I. Т,А\-А.
П. Если Г Ь А, то Г, В Ь А.
III. Если Г Ь А, Г Ь В и А, В Ь С, то Г Ь С.
IV. Если Г Ь А и Г, А Ь В, то Г Ь В.
4.8. Исчисление высказываний
Алфавит включает в себя
логические символы ~ и —>¦, скобки ( и );
пропозициональные переменные х, у,..., х\, yi,...

36 Глава 4. Элементы математической логики
Формулы определяются следующим образом:
• любая пропозициональная переменная является формулой;
• если А — формула, то А — формула;
• если А и В формулы, то (А —>¦ В) — формула.
Для сокращения записей внешние пары скобок будем иногда опускать.
Аксиомы. Для любых формул А, В и С следующие формулы являются
аксиомами:
А1. А^(В^А);
А2. (А ->¦ (В ->• С))_-+ {{А ->¦ В) ->• {А ->¦ С));
A3. (В^А)^ ((В -> Д) ->¦ В).
Правило вывода — modus ponens (m. р.): из формул А и А —>¦ В
непосредственным следствием является формула В:
А, (А^В)
В
226. Доказать, что если Г Ь (Д ->¦ #) и Г Ь Д, то Г Ь В.
227. Доказать, что Д Ь (В ->¦ Д).
228. Доказать, что Ь (Д ->¦ Д).
229. [Теорема дедукции.] Доказать, что
Т,А\- В тогда и только тогда, когда Г Ь (Д —>¦#).
230. Получить следующие следствия из теоремы дедукции:
1) если Д Ь В, то Ь Д ->¦ В;
2) [правило транзитивности] Д —>¦ Б, В —>¦ С h (Д —>¦ С);
3) [правило сечения] Д —>¦ (В -^ С), 5 h (Д -^ С).
231. Доказать, что
2) Ь Д -^ Л;
3) h (В ->• Д) -^ (Д -^ В);
4) Ь(Д^В)^(В^Д);
5) ЬД^(Д^В);
6)\-А^(В^А
7)\-(А^В)-

37
232. Доказать, что если Г, А Ь В и Г, А Ь В, то Г Ь В.
233. Доказать, что если формула Л выводима в исчислении высказы-
высказываний, то она является тождественно истинной в алгебре высказываний.
Пусть А = Л(х1, Х2, ¦ ¦ ¦, хп) — формула исчисления высказываний, со-
содержащая пропозициональные переменные xi,x2,... ,xn, a a принимает
значения 0 и 1. Введём обозначение
Л, если о" = 1;
Л, если G = 0.
В частности, для пропозициональной переменной х имеем
х, если G = 1;
х, если G = 0.
234. Пусть в алгебре высказываний (<7i, 02,..., сгга) — произвольный
набор значений переменных (х\, X2,... ,хп) формулы А{х\,Х2, ¦ ¦ ¦, xn), a
a = Л(G1, G2,..., <7П). Доказать, что в исчислении высказываний
235. Доказать, что если формула Л, содержащая из логических свя-
связок лишь ~~ и ^-,3 тождественно истинна в алгебре высказываний, то она
выводима в исчислении высказываний.
Задачи 233 и 235 говорят о полноте исчисления высказываний:
множество выводимых формул исчисления высказывании совпадает с
множеством тождественно истинных формул алгебры высказывании.
Пусть в формальной аксиоматической теории вместе с каждой форму-
формулой А определена формула А. Теорию называют противоречивой, если
найдётся такая формула А, что одновременно выводимыми являются фор-
формулы Л и Л. В противном случае теория — непротиворечивая.
236. Доказать, что исчисление высказываний — непротиворечивая те-
теория.
Формальную аксиоматическую теорию называют полной в узком
смысле, если добавление к списку аксиом любой невыводимой формулы
делает теорию противоречивой.
3Напомним, что всякую логическую функцию можно представить в таком виде.

38 Глава 4. Элементы математической логики
237. Доказать, что исчисление высказываний полно в узком смысле.
238. Доказать, что ни одна из аксиом Al, A2 и A3 не выводима из двух
других.
4.9. Исчисление предикатов
Алфавит включает в себя
предметные переменные х, у,..., х\, у\,...;
предикатные символы P^n\ Q^n\ ..., p[n), Q^,..., п = О,1,2,.. .;
логические символы ~ и —>¦;
квантор общности V и квантор существования 3;
служебные символы: скобки (и) и запятую.
Формулы (а также их свободные и связанные переменные) опре-
определяются индуктивно следующим образом:
1. Если Р(п) — предикатный символ, а х^, Xj2,..., Xin — предметные
переменные, то P^n\xi1,Xi2,..., Xin) — атомарная формула; пред-
предметные переменные атомарных формул называются свободными.
2. Если Л — формула, то Л — формула; свободные и связанные пере-
переменные формулы Л остаются такими же для формулы А.
3. Пусть Л и В — формулы, и при этом ни одна свободная переменная
любой из формул не является связанной переменной другой форму-
формулы. Тогда (Л —>¦ В) — формула, в которой свободные переменные
формул Л и В остаются свободными, а связанные переменные оста-
остаются связанными.
4. Пусть А — формула, для которой х — свободная переменная. То-
Тогда Ух Л и Зх Л — формулы, в которых х — связанная переменная
(остальные свободные (связанные) переменные формулы А остают-
остаются свободными (связанными)). Формулу Л называют областью дей-
действия соответствующего квантора.
Для упрощения записей верхние индексы у предикатных символов, а так-
также некоторые пары скобок будем иногда опускать. Кроме того, определим
и другие логические символы: записи Л У В, A&zB, A ~ В будут обо-
обозначать соответственно Л —>¦ В, Л —>¦ В, (В —>¦ Л) —>¦ Л —>¦ В (именно так

39
выражаются дизъюнкция, конъюнкция и эквиваленция через отрицание
и импликацию в алгебре высказываний).
239. Определить, какие из переменных следующей формулы являются
свободными, а какие связанными.
(УхЗу P^(x,y,z))^(VxQB\x,t)).
Аксиомы. Для любых формул А,ВиС следующие формулы являются
аксиомами:
A2. (A ->¦ (В ->¦ C))_^ ((A ->¦ В) ->¦ (A ->¦ С));
A3. (B^A)^ {{В -> Д) ->¦ В);
A4. (Vx A(x)) —>¦ A(y) (здесь формула А(х) не содержит переменной у);
А5. А(у) —>¦ (Зх А(х)) (здесь формула А(у) не содержит переменной х).
Правила вывода.
1. Правило modus ponens (m. p.): ' ^~*" .
2. Правило связывания квантором общности: в_^ j) \\, где формула
В не содержит переменной х.
3. Правило связывания квантором существования: Cх ^)t в, где фор-
формула В не содержит переменной х.
4. Правило переименования связанной переменной: связанную перемен-
переменную формулы А можно всюду в этой формуле заменить другой пе-
переменной, не являющейся свободной в А.
240. Доказать, что
1) Vx Д(х) Ь Зх Л(х);
Интерпретация формулы. Равносильные формулы. Интерпре-
Интерпретация формулы исчисления предикатов состоит в указании множества М
(области интерпретации) и соответствия между предикатными символами
и предикатами соответствующей местности. При заданной интерпретации
считают, что предметные переменные принимают значения из множества
М, а логические символы и кванторы имеют обычный смысл. При этом
всякая формула становится предикатом от своих свободных переменных
(если таковые отсутствуют, то — высказыванием).

40 Глава 4. Элементы математической логики
241. Пусть область интерпретации — множество неотрицательных це-
целых чисел, а предикаты S(x, у, z) и Р{х, у, z) означают соответственно
x + y = z~Kxy = z. Записать формулу с использованием данных пре-
предикатов, истинную тогда и только тогда, когда
1) х = 0; 2) х = 1; 3) х — чётное число; 4) х — нечётное число;
5) х < у; 6) х = у; 7) х < у; 8) у делится на х;
9) z — наибольший общий делитель х и у; 10) х — простое число.
242. Пусть область интерпретации — множество /3(А) всех подмно-
подмножеств множества А, а предикат Р(Х, Y) есть X С Y. Записать с исполь-
использованием данного предиката формулу, означающую, что
1) X U Y = Z; 2) X П Y = Z; 3) X = ф; 4) X = А;
5) Y — дополнение к X.
243. Ввести соответствующие предикаты, и с их помощью записать
следующие высказывания:
1) Всякое натуральное число, делящееся на 12, делится на 2, 4 и 6.
2) Жители Швейцарии обязательно владеют французским, или итальян-
итальянским, или немецким языком.
3) Каждый студент группы выполнил по крайней мере одну лабораторную
работу.
4) Через любые две различные точки проходит единственная прямая.
5) Если a — корень многочлена с действительными коэффициентами, то
сопряженное число a — также корень этого многочлена.
6) Функция, непрерывная на отрезке [0,1], сохраняет на нем знак или при-
принимает нулевое значение.
7) Функция / непрерывна, но не является равномерно непрерывной, на
интервале @,1).
Пусть формулы А и В имеют одинаковые множества свободных пере-
переменных и фиксирована некоторая общая для них интерпретация. Форму-
Формулы А и В называются равносильными в данной интерпретации, если
они принимают одинаковые значения истинности на любом наборе значе-
значений предметных переменных. Формулы А и В называются равносиль-
равносильными на множестве М, если они равносильны в любой интерпретации,
для которой множество М является областью интерпретации. Формулы
А и В равносильны, если они равносильны в любой интерпретации.
244. Привести пример интерпретации формулы Р{х, у), в которой рав-
равносильны формулы P(x,y)&zP(y,z) и P{x,y)k.P{x,z).

41
245. Привести пример множества М, на котором равносильны форму-
формулы Уж Р(х) и Зх Р(х).
246. Равносильны ли следующие формулы:
1)
2)
3)
4)
5)
6)
7)
8)
9)
Ух
Зх
Ух
Зх
Ух
Зх
Ух
Зх
Ух
(P(x)kQ(x))
(Р(х) V Q(x))
(Р(х) V Q(x))
(P(x)kQ(x))
(Р(х) V Q)
(P(x)kQ)
(Р(х) -». Q)
{-ТУХ) f Kal)
(Q -»Р(х))
10) Зж (Q -»¦ Р(ж))
11) Зж (Р(х) -). Q)
и
и
и
и
и
и
и
и
и
и
и
(Уж Р(ж))&(Уг/ Q(y))-
(Зх
(Ух
P(x))yCyQ(y));
P(x))\Z(yyQ(y));
(Зх Р(х))кCу Q(y))-
(Ух
Р(х)) V Q;
(Зх P(x))kQ-
(Ух
(Зх
Q-
Q-
(Зх
Р(х)) -». Q;
Р(х)) -)> Q;
л. fV/T- Pfr^V
7 1 VX J. \Jj 1 1 j
T I \Jb J. \*jb 1 1 у
P(x)) -». Q?
Формула называется выполнимой в данной интерпретации, если
существует набор значений переменных, на котором она становится истин-
истинным высказыванием. Формула называется истинной в данной интер-
интерпретации, если при любом наборе значений переменных она принимает
значение ИСТИНА. Формула называется общезначимой, если она ис-
истинна в любой интерпретации.
247. Привести пример интерпретации, в которой истинной является
формула Р(х) V Р(у).
248. Выполнимы ли в какой-либо интерпретации следующие формулы:
1) Зх У у Р(х, х)кР(х,у);
2) Зх Р(х) -). Р(у);
3)Ух Зу Р(х) ~ Р(у);
4) Зу Ух Р(х) ~ Р(у)?
Теорема о полноте исчисления предикатов ([35]). Множество вы-
выводимых формул исчисления предикатов совпадает с множеством об-
общезначимых формул.
249. Доказать, что исчисление предикатов — непротиворечивая тео-
теория.
250. Является ли исчисление предикатов полным в узком смысле?

42 Глава 4. Элементы математической логики
4.10. Рекурсивные функции
В этом разделе под множеством натуральных чисел будем понимать мно-
множество N = {0,1,2,...}. Функцию / : Nra —> N, где n e N, называют
п-местной арифметической функцией.
Простейшие функции:
1) О(х) = 0 (нулевая функция);
2) S(x) = х + 1 (прибавление единицы);
3) I^(xi,... ,xn) = xm (функция проектирования, или выбора аргумента).
Операторы.
1. Пусть f — m-местная, a gi, ¦ ¦ ¦, gm — n-местные арифметические
функции, а функция h : Nra —у N задаётся следующим образом:
h(xi, ...,xn) = f{g\{xi,..., хп),..., gm(x1,..., хп)).
Тогда говорят, что функция h получена из функций f и </1;..., gm с помо-
помощью оператора суперпозиции.
2. Пусть / и g — соответственно {п + 2)- и n-местная арифметические
функции, а функция h : Nra+1 —>• N задаётся следующим образом:
h(xi,...,xn,0) =g(xi,...,xn);
h(xi, ...,xn,y+l) = f(xi, ...,xn,y, h(xb ...,xn, y)).
Тогда говорят, что функция h получена из функций / и g с помощью
оператора примитивной рекурсии.
3. Пусть f — (п + 1)-местная арифметическая функция, а функция
g : Nra+1 —у N задаётся следующим образом:
g(xi,...,xn) = у, если при любом t < у f(xi,... ,xn,t) > 0, и
f(xi,..., хп, у) = 0. Тогда говорят, что функция g получена из функции
/ с помощью оператора минимизации. При этом используют
обозначение
д(хъ ...,xn) = fiy[f(xi, ...,xn,y) = 0].
Арифметическая функция называется примитивно рекурсивной,
если она может быть получена из простейших функций с помощью ко-
конечного числа применений операторов суперпозиции и примитивной ре-
рекурсии.
251. Доказать примитивную рекурсивность следующих функций:
1) О(х1,...,хп) = 0;

43
2) f(x) = x + n, где п = const e N;
3) +(x,y) =x + y;
,s Г О, если х = 0; / ч
4)sga;=|1'j еслиж>0' (сигнум);
сч Г1, если ж = 0; / ч
5) sgx = [ о'; если х > 0' (антисигнум).
252. Показать, что из примитивно рекурсивных функций с помощью
операторов суперпозиции и примитивной рекурсии вновь получаются при-
примитивно рекурсивные функции.
253. Доказать примитивную рекурсивность следующих функций:
1 \ • Гх — У, если х > у; , ч
1) х-у = | о, если х<у (Усеченное вычитание);
2) \х -2/|;
3) -(х,у) =х-у;
4) хУ;
5)х\;
6) тт(х,у);
7) тах(х,у).
Пусть f — (п + 1)-местная арифметическая функция, а функция д :
Nra+1 —у N задаётся следующим образом:
д{хъ ...,хп,у) = ^2 /(жь • • •, хп, г).
г=0
Тоща говорят, что функция д получена из функции f с помощью опера-
оператора ограниченного суммирования.
254. Доказать, что оператор ограниченного суммирования не выводит
из класса примитивно рекурсивных функций.
255. Доказать примитивную рекурсивность следующих функций:
1) [х/у] (положить, что [х/0] = х;);
2) rest (ж, у) — остаток от деления х на у (положить, что rest (ж, 0) = х);
о\ d;v(T „ч _ / 1, если rest(x,y) = 0;
6) <hv(x, 2/J - | о, если restfo у) ф 0;
л\ р ( "\ _ / 1> если х — простое число;
' ^r\x) ~ \0 в противном случае;
5) тг(х) — количество простых чисел, не превосходящих х;
6) q(x) =

44 Глава 4. Элементы математической логики
256. Пусть / — (п+1)-местная, д\ и д2 — n-местные примитивно рекур-
рекурсивные функции, а функция h : Nra —> N задаётся следующим образом:
д2{х1,...,хп)
h(xu...,xn) =
Доказать, что функция h — примитивно рекурсивна.
Пусть f — (п + 1)-местная арифметическая функция, а функция д
Nra+1 —> N задаётся следующим образом:
gyx\,..., d,m У) —
г=0
Тогда говорят, что функция g получена из функции f с помощью опера-
оператора ограниченного перемножения.
257. Доказать, что оператор ограниченного перемножения не выводит
из класса примитивно рекурсивных функций.
Арифметическая функция называется частично рекурсивной, если
она может быть получена из простейших функций с помощью конечно-
конечного числа применений операторов суперпозиции, примитивной рекурсии и
минимизации. Частично рекурсивная функция называется общерекур-
общерекурсивной, если она всюду определена.
Тезис Чёрча. Всякая эффективно вычислимая функция является ча-
частично рекурсивной.
Тезис Чёрча не является математической теоремой, которую можно
доказать (или опровергнуть), поскольку понятие эффективной вычисли-
вычислимости носит интуитивный характер. Частичная рекурсивность — одна из
возможных формализации эффективной вычислимости.
258. Доказать частичную рекурсивность функции
_ Г х - у, если х > у;
\ не определена, если х < у.
259. Доказать, что общерекурсивная функция, ограниченная сверху
примитивно рекурсивной функцией, является примитивно рекурсивной.
260. Пусть р(п) — n-е простое число (р@) = 2,^A) = 3,^B) = 5,...).
Доказать, что р(п) — примитивно рекурсивная функция.

45
Функция Аккермана
Пусть
п раз
Определим следующую последовательность функций:
/*\i_ I nf 1 nr* L_ I • /*v . I nr* 1 /"V I T* 1
Ccy I ^ / ^ П^ -L j *-Л^ \ / 2 1 V / *
261. Найти явные выражения для qji(x) и qj2(^).
262. Доказать следующие свойства функций аДж):
2) Vi ««(ж) — возрастающая функция от ж;
3) Уж cti(x) — возрастающая функция от ц
л\ ( \ ^> ( ( w
263. Пусть / — примитивно рекурсивная n-местная функция, которая
может быть получена из простейших функций применением (в совокуп-
совокупности) менее, чем к операторов суперпозиции и примитивной рекурсии.
Доказать, что при всех xi,... ,хп выполняется неравенство
f(xi, ...,xn)< ak(m&x(xi,..., хп)).
264. Доказать, что функция Аккермана A(n) = an(n) не является
примитивно рекурсивной.
Рекурсивные и рекурсивно перечислимые множества
Характеристической функцией множества А называется функция
. . Г 1, если х е А;
ЫХ)= \0, если х^ А.
Множество А называется примитивно рекурсивным (рекурсивным^,
если примитивно рекурсивна (общерекурсивна) его характеристическая
функция.
265. Доказать, что конечное множество примитивно рекурсивно.
266. Пусть А и В — примитивно рекурсивные множества. Доказать,
что множества АГ\ В, Аи В, А\ В — также примитивно рекурсивны.

46 Глава 4. Элементы математической логики
267. Пусть / — примитивно рекурсивная функция. Доказать, что мно-
множество прообразов любого из её значений А = {х \ f(x) = а} примитивно
рекурсивно.
Множество называется рекурсивно перечислимым, если оно пусто
или является множеством значений некоторой примитивно рекурсивной
функции.
268. Доказать, что всякое примитивно рекурсивное множество рекур-
рекурсивно перечислимо.
Рекурсивность множества означает существование алгоритма, разре-
разрешающего проблему вхождения произвольного наперед заданного элемента
х е N в данное множество. В связи с этим рекурсивные множества также
называют разрешимыми.
В свою очередь, рекурсивная перечислимость множества говорит о том,
что существует алгоритм, в результате работы которого формируется дан-
данное множество.
Подробно изучает данные понятия теория вычислимых функций[17].
4.11. Машина Тьюринга
Многовековая практика человечества
от Евклида до Кнута не встретилась с примером
алгоритма, который нельзя было бы записать как
программу машины Тьюринга.
Н.К. Верещагин, А. Шень [17]
Английский математик Алан Тьюринг в 1936 г. с целью формализации по-
понятия алгоритма придумал абстрактное вычислительное устройство, на-
названное позже в его честь машиной Тьюринга.
Пусть имеется лента, разбитая на ячейки, в каждой из которых за-
записан один из символов 0 или 1. Имеется также управляющая головка,
которая в каждый момент времени находится в одной из ячеек. В каждый
момент времени головка находится в одном из внутренних состояний
qo, qi,..., qm. Считают, что q\ — начальное состояние, а qo — конечное.
В зависимости от символа, расположенного в данной ячейке, и вну-
внутреннего состояния головка записывает в ячейку некоторый символ и ли-
либо передвигается в одну из двух соседних ячеек, либо остается в прежней,

47
переходя при этом в новое состояние (возможно, прежнее). В результа-
результате работы машина меняется конфигурация ленты (совокупность запи-
записанных в её ячейках символов) от начальной к конечной, тем самым по
некоторому алгоритму осуществляется переработка исходных данных.
Дадим теперь формальное описание. Пусть
S = {О,1} внешний алфавит;
Q = {?о, Qi, ¦ ¦ ¦, Qm} внутренний алфавит, или множество состоя-
состояний головки;
D = {L,R,C}.
Командой называют 6-буквенное слово вида qiSj —> spdqa, где
qi,qa e Q, s^sp e S, de D.
Машиной Тьюринга называют упорядоченную пару < Q, К >, где
Q — внутренний алфавит, а К программа — множество команд, удо-
удовлетворяющее следующим условиям:
1) оно не содержит команд, начинающихся с символа qo;
2) оно не содержит двух шестерок, начинающихся с двух одинаковых сим-
символов.
Конфигурацией ленты, или словом Поста называют слово вида
W = AqiSjB, где А и В — слова в алфавите S (возможно, пустые). На-
Начальное слово Поста имеет вид AqiSjB. Заключительное слово Поста
имеет вид Aq0SjB.
Работа машины Тьюринга состоит в поэтапной переработке слов По-
Поста (от начального к заключительному) в соответствии с её программой:
W(i) ^ WB) ^ . при этом W{n+i) = (уу(п)у ^ где w, из w получается
по следующему правилу.
Пусть W = AqiSjB. Тогда
1) если г = 0, машина останавливается и W — заключительное слово
Поста — результат работы машины Тьюринга;
2) если i > 0, но в К нет команды, начинающейся с символов qiSj, то
машина сломалась (W не определено);
3) если i > 0 и в К есть команда qiSj —> spdqa, то при
а) d = R
al) W = AspqaB в случае В ф ф,
а2) W = Aspqa0 в случае В = ф,
6)d = L
61) W = AiqaSkSpB в случае А =
62) W = qa0spB в случае А = ф,

48 Глава 4. Элементы математической логики
W = AqaspB.
Программу, моделирующую работу машины Тьюринга (автор — Максим
Абушаев), можно найти в локальной сети кафедры прикладной математики
ЮУрГУ
Н:/students/Учебные материалы/EVNIN/TIURING.
Через ап обозначим п-буквенное слово в алфавите S, все символы ко-
которого есть а; при п = О будем иметь пустое слово.
Пусть f — арифметическая n-местная функция. Говорят, что машина
Тьюринга вычисляет функцию f(xi,...,xn), если любое начальное слово
Поста вида
gi01iBl01iB2...01iBn0
она переводит в заключительное слово
Если при этом не приписывались нули слева, то будем говорить, что
машина Тьюринга правильно вычисляет функцию f(xi,...,xn), или:
функция / правильно вычисляется (машиной Тьюринга).
269. Какую функцию f(x) вычисляет машина Тьюринга со следующей
программой?
giO -
fel -
9з1 -
g4l -
¦> 0Дд2;
-> 1#9з;
¦> 0Rq5;
g30 -
961 -
g2O -
¦> 0Rq2;
¦> 0Lg6;
¦> i^9o;
¦> 0Cg0-
270. Построить машины Тьюринга, правильно вычисляющие следую-
следующие функции:
1)О(х) = 0; 2)S(x)=x + l; 3) h{x,y) = х-
4)f(x)=2x; 5) f(x, у) = х + у; 6)f(x)=x-l.
Если машина Тьюринга перерабатывает слово W в слово W, не припи-
приписывая нули при этом на ленте ни справа, ни слева (т.е. в процессе работы
не возникают ситуации а2 и 62), будем использовать запись W\^- W.
271. Построить машины Тьюринга, следующим образом перерабаты-
перерабатывающие слова Поста:

49
1) [перенос нуля] Z : giOOFO^ g001x00;
2) [сдвиг вправо] S+ : giOOFO^ OFgoO;
3) [сдвиг влево] S~ : OFgiO|=^ goOFO;
4) [транспозиция] Т : OFgiOFOfi
5) [удвоение] D : ^OFO^3^
Машиной Тьюринга a(M)p называется программа (множество
команд), полученная из программы машины М следующим образом:
1) при i ф О во всех командах qi заменяется на qi+a;
2) q0 заменяется на qp.
На множестве машин Тьюринга введем функцию I: если М — машина
Тьюринга с множеством состояний Q = {q0, qi,..., qm}, то l(M) = m.
Композитом MN машин М и N называется машина Тьюринга с мно-
множеством состояний {q0, qi,..., qi(M)+i(N)} и программой
o(M),(M)+i Uj(M) (Юо-
Введем обозначение Мп следующим образом: М1 = М, а для любого
натурального % Мг+1 = МгМ.
272. Пусть машины М и N следующим образом перерабатывают слова
Поста. М : А =*> B'qosaB"; N : B'qisaB" =*> С.
Убедитесь в том, что композит MN переводит слово Поста А в слово С.
273. Машина Тьюринга Cn = (E+T)n-1JD(T5-)n-2T)n действует так:
Cn : giOl^Ol*2... Ol^O2^ Ol^Ol*2... Ol^goOl^Ol*2... 01^00,
где z = xi + x2 + ¦ ¦ ¦ + xn + n + 2. Проверьте это.
274. Постройте машину Тьюринга, правильно вычисляющую функцию
275. Пусть функции /(жь ..., хт), gi(xu ..., хп),..., дт(х1, ...,хп) пра-
правильно вычисляются машинами Тьюринга. Тогда и суперпозиция этих
функций f(gi,..., gm)(xi,... хп) обладает тем же свойством. Доказать.
276. Пусть функция д(х) получена из функции f(x,y) с помощью опе-
оператора минимизации д(х) = ^y[f(x, у) = 0]. Доказать, что если функция /
правильно вычислима, то и функция д правильно вычисляется машиной
Тьюринга.
Имеет место следующая теорема[35].
Теорема. Множество частично рекурсивных функций совпадает с
множеством функций, которые правильно вычисляются машиной Тью-
Тьюринга.

Глава 5
Комбинаторика
5.1. С очетания
277. Вычислить: С?, С2°о, С\„ СЦ С84, СЦ
278. Найти число подмножеств X множества {0,1,2,3,4,5,6,7,8,9},
обладающих следующими свойствами:
1)|Х|=3;
2) |Х|=5, 1еХ;
3) |Х|=6, 2<?Х;
4) |Х|=7, {О,1}СХ, 2^Х;
5) множество X состоит из трёх чётных и двух нечётных чисел;
6) |Х| <5.
279. На окружности последовательно отмечены точки А\,..., Аи-
Сколько существует
1) хорд с концами в отмеченных точках;
2) треугольников с вершинами в отмеченных точках;
3) выпуклых четырёхугольников с вершинами в отмеченных точках;
4) треугольников с вершинами в отмеченных точках, не имеющих общих
точек с прямой А2А%;
5) треугольников с вершинами в отмеченных точках, имеющих общие
точки с прямой А\А5?
280. На окружности отмечено п точек. Точки соединяются всевозмож-
всевозможными хордами; известно, что никакие три из них не пересекаются в одной
точке внутри круга. Найти:
1) число точек пересечения хорд внутри круга;
2) количество частей, на которые хорды делят круг.
281. На прямой I отмечено 8 точек, а на параллельной ей прямой т
(/ ф т) — 11 точек. Сколько существует
1) треугольников с вершинами в отмеченных точках;
2) выпуклых четырёхугольников с вершинами в отмеченных точках?

51
282. п человек в совокупности выписывают к журналов, причем каж-
каждый выписывает два журнала, каждый журнал выписывают четверо, а
каждая пара журналов выписывается только одним человеком. Найти п
и к.
283. Две команды играют в волейбол до 4 побед. Сколько существует
разных вариантов изменения счёта в игре по партиям?
284. Сколькими способами можно разложить 4 белых и 3 чёрных шара
по 6 различным ящикам?
285. Решить предыдущую задачу при дополнительном условии: ни
один ящик не должен быть пустым.
286. Сколькими способами можно разложить 20 одинаковых шаров по
5 различным ящикам так, чтобы
1) в каждом ящике оказалось не менее двух шаров;
2) в каждом ящике оказалось не более 5 шаров;
3) оказалось не более двух пустых ящиков?
287. Найти коэффициент при ж100 в разложении многочлена
288. Доказать, что
т
Е-¦
289. Пусть п — произвольное натуральное число, большее 1. Доказать,
что существует бесконечно много натуральных чисел, не представимых в
виде суммы
1) щ 2) не более, чем п
слагаемых, каждое из которых есть п-я степень натурального числа.
290. Дан квадрат. Каждая его сторона разбита на п равных частей. Че-
Через точки деления проведены прямые, параллельные сторонам. Сколько
существует 1) прямоугольников, 2) квадратов, ограниченных проведённы-
проведёнными линиями?
291. В правлении банка 7 человек. Каково должно быть минимальное
число замков от сейфа и как следует распределить ключи между членами
правления (каждый член правления может получить ключи от нескольких

52
Глава 5. Комбинаторика
замков), чтобы любое большинство сейф могло открыть, а любое меньшин-
меньшинство — не могло?
292. Каким числом способов можно прочитать слово "абракадабра",
двигаясь вправо или вниз по таблице?
А
Б
Р
А
К
А
Б
Р
А
К
А
Д
Р
А
К
А
Д
А
А
К
А
Д
А
Б
К
А
Д
А
Б
Р
А
Д
А
Б
Р
А
293. На клетчатой бумаге нарисован прямоугольник ABCD, стороны
которого лежат на линиях сетки, причём длина отрезка AD в к раз больше
длины отрезка АВ (к — натуральное число). Рассматриваются всевозмож-
всевозможные пути, проходящие по линиям сетки и кратчайшим образом ведущие
из А в С. Доказать, что среди этих путей в к раз больше тех, у которых
первое звено лежит на AD, чем тех, у которых первое звено лежит на АВ.
294. Изучите поведение последовательности (а^), где а& = С% (при
фиксированном п), с точки зрения возрастания-убывания.
295. Имеется 12 точек, никакие четыре из которых не лежат в одной
плоскости. Доказать, что существует разносторонний треугольник с вер-
вершинами в этих точках.
296. Имеется карточная колода из 52 карт. Каким числом способов
можно раздать по 13 карт четырём игрокам?
5.2. Полиномиальная формула.
Комбинаторные тождества
297. Найти коэффициент при хк в разложении многочленов:
1) (х + 2I0, к = 3;
2) A - 2хO, к = 4;
4) Cv^-xv^)9, A; = 11;
5) (х2-х + 2)8, к = 7;
6) {y^+^c + ^cf, к = 2.

53
298. С помощью формулы бинома Ньютона
A+ *)"
fe=0
доказать следующие тождества:
1)
з)
7)
V QkCk
fe=O
X) kCn -
fe=O
n .
¦^ fe+1
fe=O
2ra
E(-i)fe
fe=O
= 10";
= n2n;
^fe \2 _ / i\n
2)
4)
^2ni °)
^(_1)«-*2*C* =
fe=O
fe=O
feib fe+1
2n-l
E(-i)
fe=O
= i;
0;
299. С помощью комбинаторных рассуждений доказать:
п п—г+т
l)J2kC* = n2*-1; 2) Е C?C:-J = С:+\.
к=0 к=т
Пусть Е = {0,1}. Назовём n-мерным кубом п-ю декартову степень
этого множества Еп (множество всех двоичных последовательностей дли-
длины п). Элементы Еп — вершины куба. Множество вершин с фиксиро-
фиксированными значениями n — k координат называют гранью размерности
к.
300. Пусть ik — число граней размерности к у n-мерного куба. Вычис-
Вычислить ik для всех допустимых значений к и доказать, что
io-h + i2-... + (-1Г-Ч-1 = 1 - (-1)". (*)
301. Доказать, что формула (*) имеет место и для n-мерной пирамиды
(её задают п+1 вершин, а любые к+1 вершин определяют /с-мерную грань,
к = 0,1,... ,п).
5.3. Формула включения-исключения
302. На кафедре лингвистики работают 13 человек, причем каждый из
них знает хотя бы один иностранный язык. Десять человек знают англий-
английский язык, семеро — немецкий, шестеро — французский. Пятеро знают

54 Глава 5. Комбинаторика
английский и немецкий, четверо — английский и французский, трое —
немецкий и французский. Сколько человек знают 1) все три языка; 2)
ровно два языка; 3) только английский язык?
303. В сборнике [53] предлагается для решения следующая задача.
В группе из 25 студентов 12 изучают латынь, 10 — греческий и 9 —
санскрит. Для каждых из двух языков найдётся ровно пять студентов,
изучающих оба эти языка. Сколько студентов изучают все три языка?
Корректна ли эта задача?
304. 1) Показать, что количество натуральных чисел, делящихся на п
и не превосходящих положительного числа х, равно [х/п].
2) Сколько есть чисел, не превосходящих 10000 и не делящихся ни на 3,
ни на 5, ни на 7?
3) Сколько есть четырёхзначных чисел, не делящихся ни на 3, ни на 5, ни
на 7?
4) Сколько есть чисел, не превосходящих 10000 и не делящихся ни на одно
из чисел 6,10 и 15?
5) Показать, что если п = 30т, то количество натуральных чисел, не
превосходящих п и не делящихся ни на одно из чисел 6,10 и 15, равно
22т.
305. Пусть п > 5. Показать, что простых чисел в множестве
{п + 1, п + 2,..., п + 30} не больше восьми.
306. На каждой стороне треугольника ABC отмечено по п точек, раз-
разбивающих её на п + 1 равных частей. Рассмотрим всевозможные треуголь-
треугольники с вершинами в отмеченных точках (по одной на каждой стороне).
Сколько среди этих треугольников таких, у которых ни одна из сторон не
параллельна стороне треугольника ABC?
307. Сколько существует 6-значных номеров (первые цифры могут
быть и нулями) с суммой цифр 27?
308. В кошельке лежит по 20 монет достоинством в 1, 2 и 5 рублей.
Сколькими способами можно из этих 60 монет выбрать к монет?
5.4. Задача о беспорядках и встречах
309. С помощью рекуррентных соотношений найти число беспорядков
Dn для п = 1,..., 8.
310. Доказать, что Dn = [^ + \].

55
311. Сколькими способами можно расставить на шахматной доске 8
одинаковых ладей так, чтобы никакие две из них не били друг друга и
чтобы ни одна ладья не стояла на главной диагонали?
312. Сколькими способами можно раскрасить клетки шахматной дос-
доски 8 х 8 в 8 цветов так, чтобы клетки, имеющие общую сторону, были бы
окрашены в разные цвета и чтобы в каждом горизонтальном ряду встре-
встречались все 8 цветов?
313. Две колоды карт, содержащие по 52 карты, тщательно тасуются,
после чего сравниваются карта за картой. Какова вероятность того, что
не будет ни одной пары совпадающих карт?
314. Для числа перестановок п элементов с к встречами Dn<k доказать
тождества:
1) Е А,,* = п\; 2) Dn>k = ? A,-i>fc_i (к = 1,..., п);
к=0
3) Е kDnjk = п\; 4) Е CknDk = п\;
к=1 к=0
5) Е c?Dn,k = 5; 6) Е (к - iJDn,k = п\.
к=т к=0
315. Случайным образом выбирается перестановка чисел 1,2..., п.
Пусть ? — количество элементов, остающихся на своих местах. Найти ма-
математическое ожидание и дисперсию случайной величины ?.
316. Секретарше нужно отправить п различных писем по п различным
адресам. Она подписывает конверты и случайным образом вкладывает
письма в конверты. Сколько в среднем писем дойдет до своего адресата?
5.5. Числа Фибоначчи
Последовательность чисел Фибоначчи (/„) задается соотношениями:
/о = 0, Л = 1, Vn G No fn+2 = /n+i + /n-
317. Прыгун перемещается слева направо вдоль клетчатой ленты, со-
совершая прыжки на одну или две клетки. Каким числом способов он может
переместиться из 1-й клетки в п-ю?
318. Доказать следующие утверждения:
1) /l + /з + • • • + /2п+1 =
2) l + /2 + /4 + ... + /2n

56
Глава 5. Комбинаторика
3)/i + /2+ ... + /„ = /„+2-1;
4) fkfk+1 — fk-lfk = fk'i
°) i 1-2 + 2-3 3-5 + • • • T I -U /n_l/n - /„ ,
•) Jn+m = Jn—ljm ~r Jnjm+l'i
8) /2и = /„+i — fn-l'i
9) /n +/n+l = /2n+lJ
10) /n+1 + fn~ fn-l = /зп!
11) если n делится на m, то /„ делится на /то;
12) для наибольшего общего делителя двух чисел Фибоначчи справед-
справедливо соотношение (/„, /то) = /(И)ТО);
13) если m > 2 и /„ делится на /то, то п делится на тп.
319. Найти все п, для которых /„ = п2.
320. Доказать тождество Ylk=o ^n-k = fn+i-
321. Вычислить трехдиагональный определитель размера п х п
1
1
0
0
0
-1
1
1
0
0
0
-1
1
0
0
0
0
-1
0
0
... 0
... 0
... 0
... 1
... 0
0
0
0
1
1
0
0
0
-1
1
322. Доказать, что
/„
о; v fn fn-
323. Доказать тождество [Кассини, 1680 г.] fn+ifn-i — fn = (~1)"-
324. Продолжив последовательность чисел Фибоначчи влево (сохраняя
рекуррентное соотношение), докажите, что /_„ = (—]
325. Доказать тождества
*-) Jn+k ' Jm—k Jn ' Jm — (^ *-) ' Jm—n—k ' Jkj
2) 2/„ = fn-2 ¦ fn+2 + fn-l • fn+U
3) fn+lfn+2 — fnfn+3 = (~1)"-

57
326. Доказать для чётного п
arctg ( — ) = arctg ( -— ) + arctg ( -—
\JnJ \Jn+l/ \Jn+2
Вывести отсюда равенство
1 7Г
327. Доказать для нечётного п
A+2-1
Вывести отсюда равенство
п
= 3.
328. Найти число двоичных последовательностей длины п, не содер-
содержащих единиц ни в каких двух соседних позициях.
329. Доказать, что из р нулей и q единиц можно составить С1+1 различ-
различных последовательностей, в каждой из которых нигде не окажется рядом
две единицы.
330. С помощью двух предыдущих задач дать комбинаторное доказа-
доказательство тождества задачи 320.
331. Найти число различных покрытий прямоугольника 2 х п прямо-
прямоугольниками 1x2.
332. Требуется составить набор из 10 гирек (каждая гирька весит целое
число граммов), с помощью которых можно взвесить любой вес, выража-
выражающийся целым числом от 1 до 55, даже если любая из гирек может быть
потеряна. Предполагается, что гирьки кладутся на одну чашку весов, а
взвешиваемый груз — на другую.
333. Имеется а) 76, б) 199 карточек, на которых написаны различные
числа. Карточки разложены на столе по окружности числом вниз. Требу-
Требуется найти какие-нибудь три идущие подряд карточки такие, что число,
написанное на средней из этих трех карточек, больше, чем на каждой из

58 Глава 5. Комбинаторика
двух соседних. Перевернуть одну за другой можно не более а) 10, б) 12
карточек. Как надо действовать, чтобы наверняка добиться успеха?
334. Доказать, что X)nLi т" < 4.
J п
335. Доказать, что 2nfn = 2 EUo1 C^TO+15m.
336. Пусть р — простое число, большее 5. Доказать, что
1) 5V = fp(modp);
2) fl = l(modp).
337. Доказать, что если р — простое число, большее 5, то ровно одно
из чисел /р_1 или /р+1 делится на р.
338. Можно ли из последовательности чисел, обратных натуральным,
выбрать а) сколь угодно длинную; б) бесконечную подпоследовательность,
в которой каждое число равно разности двух предшествующих?
339. Найти все функции f(x), непрерывные на R и для которых имеет
место тождество f(f(x)) = f(x) + х.
340. Назовем множество эгоцентричным (или э-множеством), если
оно содержит свою мощность (число элементов). (Например, {2,3},
{3,5,8} — э-множества, а {3,5}, {2,5,8} не являются таковыми). Найти
число подмножеств множества {1, 2,..., п}, являющихся минимальными
э-множествами (или мэ-множествами), т.е. такими эгоцентричными
множествами, чьи собственные подмножества — не э-множества.
(Пример. {2,3} — мэ-множество в отличие от {1,2}).
С числами Фибоначчи тесно связаны числа Лукаса, о которых см. конец
§5.7.
5.6. Производящие функции
Производящая функция является устройством, отчасти напоминаю-
напоминающим мешок. Вместо того, чтобы нести отдельно много предметов,
что могло бы оказаться затруднительным, мы собираем их вместе, и
тогда нам нужно нести лишь один предмет — мешок.
Д. Пойа
Найти производящие функции следующих последовательностей:
341. ап = \ ' П~ л\ ''"' '
1 0, п > N.

59
342. an =
344. аи = аи, п = 0,1,2,...
345. an =n2, n = 0,1,2,...
Пусть (an), (bn) — последовательности, А(х) и В(х) — соответствующие
производящие функции. Выразить А(х) через В(х) при следующих соот-
соотношениях между последовательностями:
346. а0 = 0, ап = &„_1, п = 1, 2,...
347. ап =bn+l.
348. ап = bn+k,k G N.
349. ап = апЪп.
350. а0 = 0, ап = Ъп — bn_i, n = 1, 2,...
351. аи = &и+1 - Ь„.
352. аи = ЕГ=о&-
353. аи = Y^=
354. аи = пЪп.
355. аи = ELo Го
356. аи = ЕГ=ПС*6*- Доказать, что Ьп =
357. Пусть ап = Y,"=QC%+j, n G No;
&о = 0, Ъп = Е"=о С'й1' n e N. Доказать, что
= ап + Ьп;
2) А(х) - 1 = хА(х) + В(х), В(х) = х(А(х) + В(х)).
3) Найти А(х) и В(х).
4) Получить явные формулы для ап и Ьп.
358. Показать, что функция A — 4х)~1//2 является производящей для
последовательности ап = С%п.
359. Доказать тождество Y2=oC2kC2n-2k = 4"-

60 Глава 5. Комбинаторика
5.7. Рекуррентные соотношения
360. Последовательность (а„) удовлетворяет соотношению
an+2 = aan+i + f3an;
уравнение х2 — ах — /3 = 0 имеет два различных ненулевых корня х\ иг2.
Доказать, что имеет место тождество
ап = \
для некоторых с\ и с2, однозначно определяемых а,\ и а2-
361. Найти формулу общего члена последовательности:
1)аи_1_2 = 4аи_|_1 — Зап; а\ = 10, а2 = 16;
2)аи+2 = 2coscran_|_i — ап\ а,\ = cos a, a<i = cos 2a.
362. Найти количество n-значных чисел, состоящих из цифр 1, 2, 3, в
которых первая и последняя, а также любые две соседние цифры различ-
различны.
363. Сколько существует раскрасок вершин n-угольника, если соседние
вершины должны быть разного цвета, а всего имеется к цветов?
364. Пусть п-й член последовательности задается формулой
ап =
, где
х2.
Доказать, что для последовательности имеет место рекуррентное соотно-
соотношение
ап+2 = aan+i + f3an, где а = х\ + х2, /3 = —Х\Х2.
365. Найти ах4 + by4, если
1)
a -
ax -
x2-
x3-
Yb
Yby
У by2
Yby3
= 1,
= 2,
= 3;
a -
ax -
ax2 -
ax3 -
Yb
Yby
Yby2
Yby3
= 1,
= 2,
= 5,
= 14;
a -
ax -
ax2 -
ax3 -
Yb
Yby
Yby2
Yby3
= 23,
= 79,
= 217,
= 691.
366. Решить задачу 24 с помощью задачи 364.
367. Доказать, что для любого натурального п число

61
является целым и нечётным.
368. Найти первые 100 знаков после запятой у числа E + \/26I01.
369. Доказать, что числа
^ (A + л/2)" - A - л/2)99) и ±= (A
являются целыми и взаимно простыми числами.
370. Доказать, что целая часть числа —Wl+ \/2I000 является чётным
числом.
371. Доказать, что число [C + \/5)га] + 1 делится на 2п.
372. Пусть Ъ\ =4, Ъ2 = 14, Ъп+2 = 4&га+1 — Ъп. Обозначим через Sn
площадь треугольника со сторонами Ъп — 1, Ьп, Ъп + 1, а через гп радиус
вписанной в него окружности. Получить рекуррентные формулы для Sn
и гп.
373. Доказать, что для любого чётного п число tgra 15° + ctgra 15° пред-
ставимо в виде суммы квадратов трех последовательных целых чисел.
374. Пусть к ? N, к > 1. Доказать периодичность функции, для кото-
которой при любом х
/(x + l) + /(x-l) = 2cos— f(x).
375. Найти число двоичных последовательностей длины 11, не содер-
содержащих единиц ни в каких трех соседних позициях.
376. Найти общие решения рекуррентных соотношений:
1) ап+2 + 2an+i + ап = 0;
2) ап+3 + Шп+2 + 32ап+1 + 32ап = 0;
3) ап+3 + 3an+2 + 3an+i + ап = 0.
377. Найти ап по рекуррентным соотношениям и начальным условиям:
1) ап+3 - Зап+2 + ап+х - Зап = 0, ах = 3, а2 = 7, а3 = 27;
2) ап+3 — Зага+1 + 2ап = 0, ах = а, а2 = Ь, а3 = с.
378. Пусть Pi(x) = A + х + х2 + ... + х9у = ^?=0 <Ь,кХк'¦
1) Доказать, что а^к = Щ,9г-к, гДе 0 < к < 9г.
2) Доказать, что a2i^ = Y?k=ua\k-
3) С помощью тождества Рг+\{х) = A + х + х2 + ... + ж9) • Рг(х) выразить
ai+itk через aifi, щл,..., aiyk.
4) Вычислить аб,27-

62 Глава 5. Комбинаторика
379. Найти коэффициент при х2 в многочлене
Рп(х) = (... ((ж — 2J — 2J — ... — 2J (здесь п пар скобок).
380. Последовательность (ап) задана соотношениями по = О, ai = 1 и
VneN an+1 = an_
Доказать, что все члены этой последовательности — целые числа.
381. Пусть р ф О,1/2,1, g = 1 — р. Доказать, что
i=0 ^ У
382. Чёрт предложил карточному шулеру: "Каждый раз, как ты пе-
перейдешь мост и вернешься обратно, твои деньги в кармане удвоятся, но за
это ты мне заплатишь в первый раз 50 руб, во второй — 100 руб, в третий
— 150 руб и т.д." Шулер прошел по мосту 17 раз вперед и назад. Сна-
Сначала он значительно обогащался, однако затем не только спустил то, что
приобрел, но даже остался должен чёрту 360 руб 72 коп. Сколько денег
у шулера было изначально? Как бы изменилась ситуация, если бы этих
денег было на копейку больше?
(Журнал "Математический вестник", 1914 г.)
383. Бесконечная последовательность нулей и единиц
01101001100101... строится так: первая цифра — нуль; следующий
шаг повторяется бесконечное число раз: к уже построенному куску
последовательности приписывается новый кусок той же длины,
получаемый из него заменой нулей на единицы, а единиц на нули.
Является ли эта последовательность, начиная с некоторого места,
периодической?
Числа Лукаса
Последовательность чисел Лукаса Aп) задается соотношениями:
10 = 2, li = 1, Vn G No ln+2 = ln+\ + In-
384. Пусть a = 1+2^5; j3 = l~^ ¦ Показать, что числа Фибоначчи и
Лукаса задаются формулами

63
385. Доказать тождества
1) J2n = in ' In',
2)Рп = 12п + 2-(-1Г;
3) fk • fn = sih+n — (—l)ra4-n)-
В статье А.Н. Рудакова [43] приведено доказательство следующего ре-
результата.
Теорема (Э. Лукас, 1876 г.). Пусть q = Ak + 3 — простое число.
Число М = 2я — 1 является простым тогда и только тогда, когда число
Лукаса 12я-1 делится на М.
С помощью этой теоремы Э. Лукас установил простоту числа М =
2127 — 1, которое с 1877 г. по 1951 г. являлось самым большим извест-
известным простым числом. Как сообщается в [43], доказательство простоты
указанного 38-значного числа М потребовало около 100 часов вычислений
(напомним, дело происходило 125 лет назад).
386. Пусть ri = l2i. Показать, что Г\ = 3, и имеет место рекуррентное
соотношение Гг+\ = г\ — 2.
387. Написать программу, определяющую, является ли число 2я — 1
простым, если известно, что q = Ak + 3 — простое число.

Глава 6
Теория Пойа
388. Пусть S = {a,b,c,d} и G = {7Г1,7Г2,7Гз,7Г4} — группа подстановок,
действующая на множестве S:
а Ъ с d\ (а Ъ с d\
a b с d J ' 2 у b а с d
a b с d \ f a b с d \
a b d с J \ b a d с J
1) Убедиться в том, что G — группа, составив для неё квадрат Кэли.
2) Отношение эквивалентности на S порождается группой G. С помощью
леммы Бернсайда найти число классов эквивалентности.
3) Выписать классы эквивалентности в явном виде.
389. Составляются трехбуквенные слова из букв а и Ъ. Два различных
слова считаются эквивалентными, если они получаются друг из друга при
перемене местами крайних букв; например, abb ~ ЪЪа. Определить число
классов эквивалентности, пользуясь леммой Бернсайда. Выписать классы
эквивалентности в явном виде.
390. Вокруг стола рассаживаются п человек. Сколько существует раз-
различных расположений, если отождествлять такие, которые получаются
одно из другого сдвигом всех людей по часовой стрелке на произвольное,
но одинаковое для всех число мест?
391. На листках бумаги пишут числа от 00000 до 99999 (числа, меньшие
10000, дополняют слева нулями). Будем считать, что при переворачивании
цифры 0, 1, 8 не меняются, а цифры 6 и 9 переходят друг в друга. На-
Например, для чисел 06981 и 18690 можно приготовить только один листок.
Сколько всего листков понадобится?
392. Составляются ожерелья из бусин трех цветов. Каждое ожерелье
состоит из 1) 5; 2) 6 бусин. Не будем различать ожерелья, получающиеся
друг из друга поворотом в плоскости. Пользуясь леммой Бернсайда, найти
число различных ожерелий.

65
393. Решить предыдущую задачу в предположении, что не различа-
различаются ожерелья, получающиеся друг из друга поворотом в пространстве.
394. Решить задачи 392, 393 с помощью следствия из теоремы Пойа.
395. Сколько ожерелий можно составить из двух красных, двух зелё-
зелёных и двух синих бусин в предположениях задач 392 и 393?
396. Завод выпускает погремушки в виде кольца с надетыми на него
р красными и q синими шариками. Сколько различных погремушек мо-
может быть выпущено? Две погремушки считаются одинаковыми, если мо-
могут быть получены друг из друга передвижением шариков по кольцу или
переворачиванием.
Еще один подход к задаче о числе ожерелий продемонстрирован в §8.4.
Некоторые общие результаты по подсчету числа ожерелий содержатся
в §8.10.
397. Сколькими способами можно раскрасить в к цветов 1) рёбра;
2) грани тетраэдра, который может свободно вращаться в пространстве?
398. Сколькими способами можно раскрасить в к цветов 1) вершины;
2) рёбра; 3) грани куба, который может свободно вращаться в простран-
пространстве?
399. Сколькими геометрически различными способами можно раскра-
раскрасить вершины куба в два цвета так, чтобы вершин каждого цвета было
поровну?
400. Сколькими способами можно раскрасить 5 рёбер куба в синий
цвет, а остальные рёбра в красный цвет?
401. Найти число существенно различных способов размещения вось-
восьми одинаковых пометок на шахматной доске размера 8x8. Два способа
разметки считаются существенно различными, если их нельзя преобразо-
преобразовать друг в друга вращением доски или отражением относительно любой
из четырёх осей симметрии.
402. Конструктор интегральных схем строит чипы с 16 элементами,
расположенными в виде матрицы 4x4. Чтобы реализовать различные схе-
схемы, эти элементы нужно соединять; непосредственно соединяются только
элементы, соседние по горизонтали или по вертикали, например

66
Глава 6. Теория Пойа
Чтобы напылить межкомпонентные соединения, необходим фотошаблон
рисунка соединений. Для двух рисунков, показанных выше, используется
один и тот же фотошаблон (схемы симметричны относительно диагонали).
Сколько требуется фотошаблонов для того, чтобы на этих чипах реализо-
реализовать все возможные рисунки соединений?
403. Следующие две картинки называются соответственно "Звезда Да-
Давида" и "Мечи Магомета":
Л
V
Представим себе, что эти фигуры составлены из кусков проволоки, спаян-
спаянных в точках пересечений. Сколько существует различных звёзд и мечей
с точки зрения вида пересечений? Две фигуры отождествляем, если одну
из них можно переместить в пространстве так, что они становятся нераз-
неразличимыми по виду пересечений. Например,
Ф
См. также задачи 445, 485 и §8.10.

Глава 7
Введение в теорию графов
7.1. Определения и примеры
Напомним некоторые стандартные обозначения.
Nn — пустой граф с п вершинами;
Кп — полный граф с п вершинами;
Kn,m — полный двудольный граф, в долях которого пит вершин;
Сп — циклический граф с п вершинами;
Wn = Ni + Cn-\ — колесо;
Еп — граф, соответствующий п-мерному кубу.
Простой граф — граф без петель и кратных рёбер.
404. Пусть Gn — простой граф с множеством вершин {v\,... ,vn}, в
котором вершины Vi и Vj смежны тогда и только тогда, когда числа % и j
взаимно просты. Изобразить графы G± и G6 и найти их матрицы смежно-
смежности. Показать, что если m < n, то Gm С Gn.
405. Для графов из каждой пары графов, изображенных на рисунке,
выяснить, изоморфны ли они.
а) б) в) г) д)
406. Найти все (с точностью до изоморфизма) простые графы, в ко-
которых не более пяти вершин.
407. Сколько существует попарно неизоморфных простых графов с 10
вершинами и 1) 44; 2) 43 рёбрами?

68 Глава 7. Введение в теорию графов
408. Сколько существует помеченных простых графов с п вершинами?
Сколько из них имеет m рёбер?
409. Доказать, что в простом графе с не менее чем двумя вершинами
найдутся две вершины одинаковой степени.
410. Если в простом графе G с п > 2 вершинами в точности две имеют
одинаковую степень, то либо в G, либо в G имеется ровно одна изолиро-
изолированная вершина. Доказать.
411. Пусть в простом графе никакие две вершины одинаковой степени
не соединены цепью длины 2. Доказать, что в графе есть висячая вершина.
412. Для любого конечного множества неотрицательных целых чисел,
в котором количество нечётных чисел четно, существует граф, для кото-
которого это множество является множеством степеней его вершин. Доказать.
413. Показать, что рёберные графы L(Kn) и L(Kn^m) являются регу-
регулярными.
414. Доказать, что при п > 2 звёздный граф Ki^n не является рёберным
графом.
415. Пусть pi, р2,..., рп — степени вершин графа G. Сколько вершин
и рёбер содержит рёберный граф L(G)?
416. Доказать, что простой граф изоморфен своему рёберному гра-
графу тогда и только тогда, когда он является дизъюнктным объединением
циклических графов.
417. Привести примеры (когда это возможно)
1) двудольного графа, являющегося регулярным;
2) кубического графа с 9 вершинами;
3) (для каждого п) простого графа с п вершинами и (П~1КП~2) рёбрами;
4) (для каждого п) простого графа с п вершинами, изоморфного своему
рёберному графу;
5) связных графов, являющихся регулярными графами степени 4.
418. Какие из Платоновых графов являются двудольными?
419. [Теорема Кёнига.] Граф является двудольным тогда и только
тогда, когда все его циклы имеют чётную длину. Доказать.
420. Доказать, что в Еп нет циклов нечётной длины.
421. Доказать, что в непустом двудольном регулярном графе доли со-
содержат равное число вершин.

69
422. Может ли регулярный степени выше 1 двудольный граф иметь
мосты?
423. В связном графе степени четырёх вершин равны 3, а степени
остальных вершин равны 4. Доказать, что нельзя удалить ребро так, чтобы
граф распался на две изоморфные компоненты связности.
424. Пусть в графе среди любых четырёх вершин найдётся вершина,
смежная с тремя остальными. Доказать, что радиус графа равен единице.
425. Найти дополнения к графам, соответствующим тетраэдру, кубу и
октаэдру.
426. Вычислить
1) С4 + N2; 2) Кп + Кт; 3) Кп>т\ 4) G + Я (G и Я простые графы).
427. Пусть G, Я и К — простые графы; доказать или опровергнуть
следующие равенства:
1) G U (Я + К) = (G U Я) + (G U К);
2)G+(HUK) = (G + H)U(G + К).
428. Найти матрицы смежности графов Kn,Nn и Сп.
429. Чем характерна матрица смежности двудольного графа?
430. Какова связь между матрицами смежности простого графа и его
дополнения?
431. Пусть А — матрица смежности регулярного графа степени к. До-
Доказать, что к есть собственное значение матрицы А. Найти отвечающий
ему собственный вектор.
432. В графе Петерсена найти циклы длины 5, 6, 8 и 9.
433. В графе Петерсена найти разрезы из 3, 4 и 5 рёбер.
434. Доказать, что дополнение к (простому) несвязному графу есть
связный граф.
435. Доказать, что рёберный граф связного графа связен.
436. Пусть G — граф с множеством вершин {vi,...,vn} и матрицей
смежности А. Доказать, что число маршрутов длины к из Vi в Vj равно
(i,j)-My элементу матрицы Ак. Показать также, что если G — простой
граф, то число треугольников (циклов длины 3) в G равно tr A3/6 (где
tr А = Х)Г=1 °" — след матрицы А). Верно ли, что число циклов длины 4
равно trA4/8?

70 Глава 7. Введение в теорию графов
437. Основываясь на результате предыдущей задачи, предложите ал-
алгоритм определения диаметра графа по его матрице смежности.
438. Пусть в простом графе G степень каждой вершины не меньше г,
где г > 2. Доказать, что в G существует цикл длины > г + 1.
439. Доказать, что при п > 10 верно утверждение: если в простом
графе 2п вершин и степень каждой вершины не меньше п, то в графе
имеется подграф К3<3.
440. [Экстремальная теорема Турана.] Пусть G — простой граф с
2п вершинами, не содержащий треугольников. Доказать, что в G не более
п2 рёбер и привести пример, когда эта верхняя граница достигается.
441. Найти максимальное число рёбер в простом графе с 2п + 1 вер-
вершинами, не содержащем треугольников.
442. Найти радиус и диаметр графа Петерсена.
443. Графом Клебша называют граф, образованный вершинами, рё-
рёбрами и главными диагоналями четырёхмерного куба. Другими словами,
в качестве вершин графа Клебша можно рассматривать упорядоченные
двоичные наборы 0000, 0001,..., 1111; и вершины являются смежными то-
тогда и только тогда, когда их двоичные представления различаются либо
в одном, либо во всех разрядах. Найти радиус и диаметр графа Клебша.
444. Для каждого п построить пример графа, центр которого состоит
из п вершин и не совпадает с множеством всех вершин.
445. Пусть а) п = 4; б) п = 5.
1) Найти цикловой индекс группы подстановок на множестве рёбер
полного графа с п вершинами, порождённых перестановками вершин.
2) С помощью теоремы Пойа найти число попарно неизоморфных про-
простых графов с п вершинами и m рёбрами.
7.2. Гамильтоновы и эйлеровы графы
446. Для каких чисел тип следующие графы являются а) эйлеровы-
эйлеровыми; б) гамильтоновыми: 1) Кп; 2) Кт<п\ 3) Wn; 4) Еп?
447. Привести пример эйлерова графа, не являющегося гамильтоно-
вым, и гамильтонова графа, не являющегося эйлеровым.

71
448. Пусть G — двудольный граф, доли которого содержат тип вер-
вершин соответственно. Доказать, что
1) если G — гамильтонов граф, то т = щ
2) если G — полугамильтонов граф, то \т — п\ < 1.
449. Может ли а) конь; б) король; в) ладья побывать на каждой клет-
клетке шахматной доски размером 8x8 ровно один раз и последним ходом
возвратиться в исходную позицию? Решить такую же задачу для доски
7x7.
450. Можно ли прогуляться по парку и его окрестностям (см. рис.)
так, чтобы при этом перелезть через каждый забор ровно один раз?
451. При каких п можно пометить вершины выпуклого ^^—--
угольника так, чтобы для каждой пары различных натуральных чисел,
не превосходящих п, нашлась сторона, концы которой помечены этими
числами?
452. Доказать, что если граф G связен и имеет к > 0 вершин нечётной
степени, то минимальное число не имеющих общих рёбер цепей, объеди-
объединение которых содержит каждое ребро графа G, равно к/2.
453. Дан кусок проволоки длиной 120 см. Какое наименьшее число раз
придется ломать проволоку, чтобы изготовить каркас куба с ребром 10 см?
454. Можно ли сетку, составленную из единичных квадратов,
представить в виде объединения 1) восьми ломаных длины 5; 2) пяти ло-
ломаных длины 8?
455. С помощью алгоритма Флёри найти эйлеров цикл в графе на
рисунке.

72 Глава 7. Введение в теорию графов
456. Любой разрез эйлерова графа состоит из чётного числа рёбер.
Доказать.
457. Доказать, что рёберный граф простого эйлерова графа является
одновременно эйлеровым и гамильтоновым.
458. Доказать, что рёберный граф простого гамильтонова графа яв-
является гамильтоновым.
459. Пусть G — простой негамильтонов граф, содержащий п > 3 вер-
вершин. Доказать, что если несмежные вершины и и v соединяет гамильто-
гамильтонова цепь, то
1) число вершин, не смежных с и, не меньше числа вершин, смежных
с г> (и наоборот);
2)p(u) + p(v)<n-l.
460. С помощью предыдущей задачи доказать теорему О.Оре.
Если в простом графе с п вершинами (п > 3) для любой пары несмежных
вершин и и v выполняется неравенство
р{и) + p{v) > п,
то граф является гамильтоновым.
461. При каком наименьшем числе рёбер в простом графе с 10 верши-
вершинами этот граф заведомо гамильтонов?
462. [Теорема Л. Поша.] Пусть в графе G имеется п > 3 вершин и
для любого натурального к < Гк^- число вершин со степенью, не превос-
превосходящей к, меньше к. Тогда G — гамильтонов граф. Доказать.
7.3. Деревья
463. Найти все (с точностью до изоморфизма) деревья, в которых не
более семи вершин.
464. Волейбольная сетка имеет вид прямоугольника 50 х 600 клеток.
Какое наибольшее количество верёвочек можно перерезать так, чтобы сет-
сетка не распалась на куски?

73
465. Доказать, что каждое дерево является двудольным графом. Ка-
Какие деревья являются полными двудольными графами?
466. Если в дереве не менее двух рёбер, то его радиус меньше диаметра.
Доказать.
467. Доказать, что центр дерева состоит из одной вершины, если диа-
диаметр дерева есть чётное число, и двух вершин в противном случае.
468. Верно ли, что в дереве с нечётным диаметром любые две простые
цепи наибольшей длины имеют хотя бы одно общее ребро?
469. Выразите радиус дерева через его диаметр.
470. Пусть п — количество вершин дерева, г — его радиус. Доказать,
что п > 2г.
471. Верно ли, что если диаметр графа равен к > 2, то граф имеет
стягивающее дерево диаметра к?
472. Для каждого из указанных ниже графов найти какое-нибудь стя-
стягивающее дерево и фундаментальную систему циклов относительно него.
1) К5; 2) #3,з; 3) W5; 4) С6; 5) граф Петерсена.
473. Пусть Т\ и T<i — стягивающие деревья связного графа G. Пока-
Показать, что для любого ребра е из Т\ существует ребро / из Т2 такое, что по-
после "замены" в Т\ ребра е на ребро / вновь получится стягивающее дерево.
(С помощью подобной процедуры можно построить последовательность
стягивающих деревьев Ti,... ,Т2, в которой каждое дерево получается из
предыдущего заменой одного ребра).
474. Показать, что если р\,..., рп — заданные натуральные числа, то
дерево сп > 1 вершинами, в котором степень Vk равна р& (для каждого
к), существует в том и только в том случае, если Y^k=i Рк = ^(п ~ -О-
475. Доказать, что число рёберно-помеченных деревьев с п > 3 вер-
вершинами (в которых помечены не вершины, а рёбра) равно пп~3.
476. Показать, что при больших п вероятность того, что случайным
образом выбранная вершина дерева с п вершинами является висячей, при-
приближенно равна 1/е.
477. Найти стягивающее дерево минимального веса для каждого графа
на рис.

74
V\ 3 V2 1
2\2
3V
Глава 7. Введение в теорию графов
vi 2 v2 4 V3 1 г>4
4
3\3
2M
Корневые деревья
Дерево с выделенной вершиной (корнем,) называют корневым дере-
деревом.
478. Найти число помеченных корневых деревьев с п вершинами.
В книгах, посвященных исследованию структур данных (например,
[30], [42]), корневое дерево определяют рекурсивно следующим образом.
Корневое дерево Т — это непустое конечное множество Т с элемен-
элементами, называемыми вершинами, такими, что
1) имеется выделенная вершина, называемая корнем данного дерева;
2) если множество остальных вершин непусто, то оно разбивается на m
множеств Т\,... ,Тт, каждое из которых в свою очередь является
корневым деревом.
Деревья Т\,..., Тт называются поддеревьями данного корня. Из опре-
определения следует, что каждая вершина дерева является корнем некоторого
своего дерева. Число поддеревьев дерева с корнем г — порядок вершины
г. Вершины нулевого порядка называют листьями; остальные вершины
называют внутренними.
479. Сколько листьев имеет дерево с к внутренними вершинами, по-
порядок каждой из которых равен двум?
480. В турнире по олимпийской системе ("проигравший выбывает")
участвует п человек. Сколько встреч будет проведено?
481. Некто купил курицу. После того, как она снесла два яйца, её
съели. Из яиц вывелись цыплята. Петухов съедали сразу, а куриц — после
того, как они сносили по два яйца. И т.д. В какой-то момент вывелись одни
петухи, и процесс закончился. Сколько куриц было съедено, если съели 97
петухов?
482. Сколько листьев имеет дерево, в котором (кроме листьев) содер-
содержится п\ вершин порядка 1, П2 вершин порядка 2,..., ns вершин порядка s?
Бинарное дерево Т определяется рекурсивно следующим образом:
Т = ф ('пустое дерево) илиТ =< L,c,R> упорядоченная тройка, где с —

75
корень дерева (элемент некоторого множества), L и R — бинарные деревья;
L и R называют соответственно левым и правым поддеревом дерева Т.
Вершинами дерева называют его корень, корни его поддеревьев, корни
поддеревьев его поддеревьев и т.д.
483. Найти число различных бинарных деревьев с п вершинами.
Высота бинарного дерева — наибольшая длина цепи от корня до
какой-либо другой вершины. Дерево называют сбалансированным,
если для любой его вершины высоты левого и правого поддеревьев
различаются не более чем на 1 (например, если одно поддерево пусто, то
второе должно состоять только из своего корня).
484. Пусть высота сбалансированного бинарного дерева равна п. Найти
наибольшее и наименьшее число вершин в этом дереве.
Бинарное дерево назовем полным, если расстояния от всех листьев до
корня равны между собой.
485. Будем раскрашивать вершины полного бинарного дерева в два
цвета, отождествляя при этом раскраски, которые могут быть получены
друг из друга перестановками левого и правого поддеревьев некоторых
вершин. Подсчитать число различных раскрасок в два цвета полного би-
бинарного дерева высоты 2 с помощью а) леммы Бернсайда; б) следствия из
теоремы Пойа.
7.4. Укладки графов
486. При каком к можно так расположить 6 точек на плоскости и
соединить их попарно непересекающимися отрезками, чтобы каждая точка
была соединена ровно с к другими?
487. При каких п графы Gn (определение см. в задаче 404) планарны?
488. Проверить формулу Эйлера, связывающую число вершин, рёбер
и граней плоского графа, для следующих графов: 1) Wn; 2) К2>п', 3) графа,
соответствующего клетчатому полю s x t.
489. Пусть Д — число fc-угольных граней выпуклого многогранника.
Доказать, что 3/3 + 2/4 + /5 > 12 + /7 + 2/8 + 3/9 + 4/10 + ....
490. Пусть в связном плоском графе каждая грань ограничена s рё-
рёбрами, а степень каждой вершины равна р. Доказать, что ^ + - = | + ^,
где m — количество рёбер графа.

76 Глава 7. Введение в теорию графов
491. С точностью до изоморфизма найти все регулярные связные плос-
плоские графы, в которых каждая грань ограничена одним и тем же числом
рёбер.
492. Всегда ли планарен рёберный граф планарного графа?
493. Пусть в простом графе G не менее 11 вершин. Доказать, что граф
G и его дополнение G не могут быть одновременно планарными.
494. Используя тот факт, что в простом плоском графе есть вершина
степени не больше 5, доказать, что его вершины можно раскрасить не
более чем в 6 цветов так, чтобы смежные вершины были разного цвета.
495. Планарен ли простой регулярный граф степени 5, в котором 10
вершин?
496. Доказать, что не существует плоского графа с пятью гранями
такого, что любые две его грани имеют общее ребро.
497. [Теорема Эрдёша.] Пусть R u r — максимальное и минималь-
минимальное расстояния, определяемые п точками на плоскости. Тогда R встре-
встречается не более п раз, а г — не более 2>п — 6 раз. Доказать.
498. В любом плоском графе найдутся две грани с одинаковым числом
сторон. Доказать.
Назовем картой связный плоский граф без мостов.
499. Грани карты G можно раскрасить в два цвета так, чтобы любые
две смежные грани были разного цвета, тогда и только тогда, когда G —
эйлеров граф. Доказать.
Числом скрещиваний cr(G) графа G называется наименьшее чис-
число попарных пересечений рёбер, получаемых при изображении графа на
плоскости. В этом определении пересечение понимается так: жордановые
кривые, соответствующие двум рёбрам, пересекаются в точке, которая ли-
либо не соответствует никакой вершине графа, либо соответствует вершине,
не инцидентной хотя бы одному из данных двух рёбер.
Ясно, что cr(G) = 0 тогда и только тогда, когда G — планарный граф.
500. Пусть граф G образован вершинами, сторонами и главными диа-
диагоналями правильного 2п-угольника. Доказать, что cr(G) = 1.
501. Найти ст(К5) и сг(^3,з)-
502. Доказать, что
а) при п > 5 cv{Kn) > С*/5;
б) при m, n > 3 ст{Кт>п) > С2тСЦЪ.

77
503. Найти число скрещиваний графов К6, К3>4: и
504. Доказать, что cr(Km,n) < [f ] • [*ti] . [|] Г«-
2
Подробно вопрос о числе скрещиваний полного графа и полного дву-
двудольного графа изучается в книге [44].
505. Доказать, что в любом графе G порядка п найдётся такая верши-
вершина, что после её удаления (вместе с инцидентными ей рёбрами) возникнет
граф G', удовлетворяющий условию
cr(G) -
То
506. Пусть Р — граф Петерсена. Доказать, что сг(Р) = 2.
7.5. Ориентированные графы. Алгоритмы
507. Пусть А — матрица смежности орграфа с множеством вершин
{wi,..., vn}. Какой смысл имеют суммы строк и суммы столбцов матрицы
А? Доказать, что (г, j)-ft элемент матрицы Ак равен числу путей длины к
ИЗ Vi В Vj.
508. В дереве с п вершинами рёбра ориентируются случайным обра-
образом. Какова вероятность того, что найдётся вершина, из которой ведут
пути ко всем остальным вершинам?
509. Пусть G — связный граф. Зафиксируем некоторую его вершину v.
Доказать, что можно так ориентировать рёбра графа, что в получившемся
орграфе существует путь от v до любой другой вершины.
Ориентированный граф называют сильно связным, если для любых
его вершин и и v существует путь из и в v.
510. В связном графе степени всех вершин четны. Доказать, что можно
так ориентировать рёбра графа, чтобы
1) получившийся орграф был сильно связным;
2) для каждой вершины полустепень исхода была равна полустепени
захода.
511. В ориентированном графе со связным основанием для каждой
вершины полустепень исхода равна полустепени захода. Доказать, что ор-
орграф эйлеров.

78
Глава 7. Введение в теорию графов
512. Доказать, что существует циклическая последовательность длины
кп, составленная из к различных символов, в которой встречаются все
возможные строки из этих символов длины п.
513. Доказать, что существует последовательность длины кп + к — 1,
составленная из к различных символов, в которой встречаются все воз-
возможные строки из этих символов длины п.
514. По кругу расставлены вазы с конфетами. Ход состоит в том, что
из какой-то вазы берутся все конфеты и раскладываются по одной в каж-
каждую вазу, начиная со следующей вазы (движение происходит по часовой
стрелке). Доказать, что за несколько ходов из любого первоначального
распределения конфет по вазам можно получить любое другое.
515. В связном графе чётное число рёбер. Доказать, что можно так
ориентировать его рёбра, что в получившемся орграфе полустепени исхода
всех вершин будут чётными.
516. В орграфе, основанием которого служит колесо Wn, нет источни-
источников и стоков. Доказать, что орграф сильно связный.
Связный граф называют ориентируемым, если ориентацией его рё-
рёбер можно получить сильно связный орграф.
517. [Теорема Роббинса.] Связный граф является ориентируемым
тогда и только тогда, когда в нем нет мостов. Доказать.
518. Найти кратчайший путь от 1-й вершины до всех остальных (см.
рис. 1, а, б).
Рис. 1
519. Пусть проекты описываются взвешенными графами (см. рис. 2,
а, б), где дуги соответствуют операциям (этапам) проекта, а вес дуги обо-
обозначает время выполнения соответствующей операции. Найти наименьшее
время выполнения проектов, критические пути и резервы времени для вы-
выполнения каждой операции.

79
Рис. 2
520. Найти максимальные потоки и минимальные разрезы в транс-
транспортных сетях (см. рис. 3, а, б). Число рядом с дугой есть её пропускная
способность.
A5)
G)
Рис. 3
521. Пусть имеется т неженатых мужчин, п незамужних женщин и к
свах. У каждой свахи есть список своих клиентов; между любыми муж-
мужчиной и женщиной из этого списка сваха может устроить брак. Для г-й
свахи число устроенных ею за год браков не превосходит числа &j. Переве-
Перевести задачу нахождения наибольшего числа браков, которые могут устро-
устроить свахи за год, в задачу нахождения максимального потока в некоторой
сети.
7.6. Турниры
Орграф, в котором каждые две (различные) вершины соединены ровно
одной дугой, называют турниром. Таким образом, турнир получается из
полного графа ориентацией рёбер.
522. Доказать, что сумма квадратов полустепеней исхода всех вершин
турнира равна сумме квадратов полустепеней захода.
523. Доказать следующие утверждения.
1) Существует турнир, в котором нет ни одного замкнутого пути.

80 Глава 7. Введение в теорию графов
2) При этом орграф обязательно содержит ровно по одному источнику
и стоку.
3) Существует ровно п\ турниров, имеющих по п вершин и обладающих
свойством из п. 1).
524. Доказать, что при любом п, не равном 2 и 4, существует турнир
с п вершинами, в котором для любой упорядоченной пары вершин (г*, v)
найдётся путь из и в v, состоящий из одной или двух дуг.
Числом очков вершины турнира называют её полустепень исхода.
525. В турнире все вершины имеют одно и то же число очков. Дока-
Доказать, что для произвольных вершин и и v найдётся путь из и в v из одной
или двух дуг.
526. Пусть и — вершина турнира с наибольшим числом очков. Дока-
Доказать, что для любой вершины v есть путь из и в v, состоящий из одной
или двух дуг.
527. Будем говорить, что вершины и и v орграфа являются взаимно
достижимыми, если существуют пути из и в v и из v в и. Показать, что
это отношение является отношением эквивалентности. Показать также,
что в случае турнира соответствующие классы эквивалентности можно
пронумеровать таким образом, что из вершины, принадлежащей классу
с меньшим номером, идут дуги во все вершины из классов с большими
номерами.
528. Показать, что если турнир не является сильно связным графом, то
в нём существует дуга, изменение ориентации которой приводит к сильной
связности графа.
529. Доказать, что любой турнир полугамильтонов.
530. Если турнир с п вершинами сильно связен, то в нём есть циклы
длины 3, 4,..., п (в частности, он гамильтонов). Доказать.
Треугольники
Назовём треугольником замкнутый путь из трёх дуг.
531. У двух вершин турнира одинаковое число очков. Доказать, что в
турнире есть треугольник.
532. Доказать, что если турнир — сильно связный граф, то любая его
вершина входит в некоторый треугольник.

81
533. Доказать, что число треугольников в турнире с п вершинами рав-
равно
г=1
где для каждого г через Si обозначено число очков г-й вершины.
534. Доказать, что число треугольников в турнире с п вершинами не
3 3 л
больше п ~п при нечётном п и п ~ при чётном п.
7.7. Доминирование, независимость,
покрытия, паросочетания
"Во многих прикладных задачах требуется найти в конечном множестве
объектов максимальную систему объектов, попарно не связанных друг с
другом, или же выбрать минимальную систему объектов, связанных со
всеми другими. Формулировки подобных задач на языке теории графов
приводят к понятиям независимости и покрытия." ([7])
Подмножество V С V вершин графа G =< V,E > называется доми-
доминирующим (или внешне устойчивым), если каждая вершина из V \ V
смежна с некоторой вершиной из V.
Наименьшую мощность доминирующего множества графа называют
числом доминирования графа (или числом внешней устойчивости^)
и обозначают 8(G).
535. Найти число доминирования для следующих графов:
Kn;Wn; Kn<m; Сп; графа Петерсена; графа Клебша (определение см. в за-
задаче 443).
536. Пусть в графе нет изолированных вершин. Доказать, что в нем
можно указать такое доминирующее множество, дополнение к которому
также является доминирующим множеством.
537. Показать, что для регулярного графа G степени ken верши-
вершинами справедливо неравенство 8(G) > у^. Привести пример графа, для
которого в указанном соотношении имеет место равенство.
538. Найти число доминирования (i-мерного куба при d = 1, 2,3,4, 7.
539. Показать, что 2m\

82 Глава 7. Введение в теорию графов
540. Пусть граф G порядка п имеет диаметр 2. Доказать, что
8(G) < л/п\пп+ 1.
Множество попарно несмежных вершин (рёбер) графа называется
независимым. Независимое множество — максимальное, если оно не
является подмножеством некоторого другого независимого множества.
Независимое множество с наибольшим числом элементов называется
наибольшим.
541. Доказать, что наибольшее независимое множество является мак-
максимальным.
542. Доказать, что независимое множество вершин является макси-
максимальным тогда и только тогда, когда оно доминирующее.
543. Показать на примерах, что доминирующее множество вершин
наименьшей мощности может быть независимым, а может и не быть та-
таковым.
Используется также следующая терминология. Независимое множе-
множество вершин называют внутренне устойчивым. Независимое множество
рёбер называют паросочетанием.
Мощность наибольшего независимого множества вершин (рёбер) графа
G обозначают ао(G) (соответственно a\{G)).
544. Доказать, что ao(En) = 2n~l.
Говорят, что вершина и ребро графа покрывают друг друга, если
они друг другу инцидентны. Подмножество V' С V вершин графа G =<
V, Е > называется покрытием графа, если вершины из V покрывают (в
совокупности) все рёбра графа (т.е. каждое ребро из Е инцидентно хотя
бы одной вершине из V).
545. Доказать, что подмножество вершин графа является его покры-
покрытием тогда и только тогда, когда дополнение к нему — независимое мно-
множество.
Подмножество Е' с Е рёбер графа G =< V, Е > называется рёбер-
рёберным покрытием графа, если рёбра из Е' покрывают (в совокупности)
все вершины графа (т.е. каждая вершина из V инцидентна хотя бы одно-
одному ребру из Е'). Таким образом, нет рёберных покрытий лишь у графов,
имеющих изолированные вершины. Наименьшую мощность покрытия (рё-
(рёберного покрытия) графа G обозначают /3o(G) (соответственно /3i(G)).
546. Найти ao(G),/3o(G),ai(G),/3i(G) для следующих графов:
Cn; Kn; Wn; Кп<т; графа Петерсена.

83
547. Пусть граф G содержит п вершин. Доказать, что
ao(G) + /30(G) = п.
548. Доказать, что для любого графа G справедливо неравенство
/3o(G)>a,(G).
549. Пусть граф G порядка п не содержит изолированных вершин.
Тогда «1 (G) + /5i (G) = п. Доказать.
550. Для любого двудольного графа G справедливо, что
/30(G) = ai(G). Доказать.
Паросочетание называется совершенным, если оно одновременно яв-
является рёберным покрытием, ^-фактором графа называется его остов-
ный регулярный подграф степени к. Таким образом, совершенное паросо-
паросочетание и 1-фактор есть совпадающие понятия.
551. Доказать, что если в графе 8 вершин, и степень каждой вершины
равна 4, то в графе есть совершенное паросочетание.
552. В графе 2п вершин (п > 2). Какие три вершины ни взять, среди
них найдётся смежная с двумя другими. Доказать, что в графе существует
совершенное паросочетание.
553. Доказать, что кубический граф, являющийся гамильтоновым,
распадается на совершенные паросочетания.
554. Доказать, что граф Петерсена не распадается на совершенные
паросочетания. Получить отсюда негамильтоновость графа Петерсена.
555. Привести пример кубического графа, в котором нет совершенного
паросочетания.
556. Если граф, все вершины которого имеют нечётную степень, рас-
распадается на совершенные паросочетания, то в нем либо все рёбра — мосты,
либо нет мостов. Доказать.
557. Показать, что граф К2п распадается на 2п — 1 совершенное паро-
паросочетание.
558. Можно ли раскрасить рёбра графа Кп в п — 1 цветов так, чтобы
все рёбра, исходящие из произвольной вершины, были разного цвета?
559. Показать, что число различных совершенных паросочетаний в
(помеченном) графе К2п равно ^^ = Bп — 1)!!.
560. Показать, что число различных наибольших паросочетаний в (по-
(помеченном) графе K2n+i равно Bп+ 1)!!.

84 Глава 7. Введение в теорию графов
561. Показать, что число различных совершенных паросочетаний в
(помеченном) графе Кп>п равно п\(п — 1)!... 2!.
Задача о свадьбах
Пусть G — двудольный граф с долями V\ и Vi. Совершенным паро-
сочетанием из V\ в Vi называется паросочетание в G, покрывающее V\
(т.е. для всякой вершины из V\ в паросочетаний найдётся инцидентное ей
ребро).
Пусть А С V — подмножество вершин графа G =< V, Е >. Окруже-
Окружением множества А называют множество
Т(А) = U Г» \ А,
veA
где T(v) — множество вершин, смежных с v.
Имеет место следующая теорема (см., например, [7] или [8]):
Теорема [Ф. Холл, 1935 г.] Совершенное паросочетание из V\ в V?, в
двудольном графе G существует тогда и только тогда, когда
VAc Vi |Г(Л)| > \А\.
562. В любом непустом регулярном двудольном графе существует со-
совершенное паросочетание. Доказать.
563. Любой непустой регулярный двудольный граф распадается на
совершенные паросочетания. Доказать.
564. Задача о свадьбах. Имеется множество юношей, каждый из
которых знаком с некоторыми девушками. При каких условиях можно
одновременно женить всех юношей так, чтобы каждый из них женился на
знакомой ему девушке?
565. В некотором районе, состоящем из нескольких деревень, число
женихов равно числу невест. В каждой деревне общее число женихов и
невест не больше половины общего их числа. Доказать: можно всех пере-
переженить так, что в каждой паре жених и невеста будут из разных деревень.
566. На танцевальном вечере каждый юноша знаком с к девушками,
а каждая девушка знакома с к юношами. Доказать, что можно провести
к (медленных) танцев так, чтобы каждый участник вечера станцевал со
всеми своими знакомыми (противоположного пола).
567. На шахматной доске пометили 16 из 64 клеток так, что на каждой
вертикали и горизонтали оказалось по две помеченные клетки. Доказать,

85
что на помеченных клетках можно расставить 8 чёрных и 8 белых фигур
так, чтобы на каждой вертикали и каждой горизонтали стояло по одной
белой и одной чёрной фигуре.
568. Вуз посылает 8 юношей и 8 девушек на стажировку по восьми спе-
специальностям в 8 зарубежных университетов, причем каждый университет
принимает по два человека и учит их двум разным специальностям, и
каждой из восьми специальностей учат два университета. Всегда ли мож-
можно так распределить студентов, чтобы в каждом университете стажирова-
стажировались юноша и девушка, и при этом как юноши, так и девушки обучались
(в совокупности) по всем восьми специальностям?

Глава 8
Дополнительные задачи
Ultra posse nemo obligatur. 1
8.1. Инвариант и полуинвариант
Ниже предлагаются задачи, в каждой из которых задан некоторый объект
и описаны преобразования, которые разрешено производить над этим объ-
объектом. Каждый раз задается вопрос, можно ли объект из одного состояния
перевести в другое.
Предположим, что существует некоторая характеристика объекта, ко-
которая не меняется при указанных преобразованиях (это и есть инвариант
задачи). Если для двух состояний объекта значения инварианта различ-
различны, то ответ на заданный вопрос будет, очевидно, отрицательным.
569. Дан куб ABCDAiBiCiDi. В вершинах A,B,D и середине М ре-
ребра АА\ сидели четыре мухи. В некоторый момент одна из мух взлетела и,
пролетев параллельно прямой, соединяющей некоторых двух из оставших-
оставшихся мух, села на поверхность куба. Затем снова какая-то муха совершила
аналогичный маневр. И т.д. Могут ли мухи после нескольких перелетов
оказаться в вершинах А, В, D, А{!
570. На острове Серобуромалин обитают 13 серых, 15 бурых и 17 ма-
малиновых хамелеонов. Если встречаются два хамелеона разного цвета, то
они одновременно меняют свой цвет на третий. Может ли случиться так,
что через некоторое время все хамелеоны будут одного цвета?
571. Имея числа а и Ь, можно получить число a + Ъ + ab. Можно ли,
имея первоначально числа 1 и 4, с помощью (многократного) применения
указанной операции, получить а) 1999; б) 2000?
572. Числа а и Ь можно заменить числами д^=- и д^=. Можно ли, имея
первоначально числа 2, у/2 и 1/л/2, с помощью (многократного) примене-
применения указанной операции, получить числа 1, у/2 и 1 + \/2Р.
1 Никого нельзя обязать сверх его возможностей (лат.).

87
573. На льду лежат три шайбы. Хоккеист бьет по одной из них так,
что она пролетает между двумя другими. Так он делает 25 раз. Могут ли
после этого шайбы оказаться на исходных местах?
574. Допускаются следующие преобразования квадратного трехчлена
f(x) = ах2 + Ьх + с: 1) можно менять местами а и с; 2) многочлен f(x)
можно заменить на многочлен f(x — к), где к — произвольная константа.
Можно ли из х2 — Зх — 4 получить х2 — х — 1?
575. По кругу растут п деревьев. Первоначально на каждом дереве
сидит один чиж. Иногда какие-нибудь два чижа перелетают в противопо-
противоположных направлениях, причем каждый чиж садится на дерево, соседнее
с тем, с которого он взлетел. Могут ли чижи собраться на одном дереве?
576. По кругу расположены 12 лампочек, каждая из которых может
находиться в двух состояниях (гореть или не гореть). Допускается
(многократное) выполнение следующей операции: изменить состояния
любых трех рядом расположенных лампочек. Вначале горит одна
лампочка. Можно ли зажечь все лампочки?
577. В вершине А\ 12-угольника стоит минус, в остальных — плюс.
Можно одновременно менять знак в любых а) 6; б) 4; в) 3 последователь-
последовательных вершинах. Доказать, что нельзя добиться того, чтобы минус стоял в
вершине, соседней с А\, а в остальных вершинах были плюсы.
Полуинвариант — (числовая) характеристика объекта, которая меня-
меняется монотонно (например, увеличивается) при каждом преобразовании.
578. По кругу выписаны п чисел. Если последовательно против часо-
часовой стрелки стоят числа а, Ь, с, d и (а — d) (b — с) < 0, то числа бис можно
поменять местами. Доказать, что эту операцию можно проделать лишь
конечное число раз.
579. Числа а и Ь можно заменить числами a + | и Ь — |. Можно ли,
имея первоначально два ненулевых числа, с помощью (многократного)
применения указанной операции, прийти к исходному набору чисел?
580. Каждый член парламента имеет не более 2k + 1 врагов. Доказать,
что парламент можно разбить на две палаты так, что каждый депутат
будет иметь в своей палате не более к врагов.
При решении двух следующих задач используется понятие чётности
перестановки.

88
Глава 8. Дополнительные задачи
581. Имеются катушечный магнитофон, пять катушек с магнитной
лентой и одна пустая катушка. Можно ли добиться того, чтобы каждая
лента оказалась на той же катушке, но перемотанная?
582. В плоской квадратной коробке размещены 15 одинаковых фишек
квадратной формы, одно место остается свободным. Можно ли, не выни-
вынимая фишек из коробки, а лишь передвигая их друг за другом на свободное
место, перейти от одной конфигурации к другой?
1
5
9
13
2
6
10
14
3
7
11
15
4
8
12
2
5
9
13
1
6
10
14
3
7
11
15
12
583. Двое по очереди пишут цифры 2/с-значного числа, употребляя
только цифры 1, 2, 3, 4, 5. Может ли второй игрок добиться того, чтобы
полученное число делилось на 9, если первый стремится ему помешать?
1) к = 15; 2) к = 10.
584. Пусть вершины правильного 2п-угольника занумерованы по по-
порядку числами от 1 до In. Доказать, что нельзя занумеровать вершины
другого правильного 2п-угольника так, чтобы при любом совмещении мно-
многоугольников (в плоскости) для некоторой вершины совпадали оба номера.
585. При каких п в таблице n x n
1
п
п- 1
2
2
1
п
3
3
2
1
;
4
п
п- 1
71-2
;
1
можно выбрать п чисел от 1 до п так, чтобы любые два из них стояли в
разных строках и разных столбцах?
586. Окружность разбита 2п точками на равные дуги. Доказать, что у
любой замкнутой ломаной с вершинами во всех точках есть параллельные
звенья.
587. Имеется бесконечная клетчатая доска. Фигура "волк" за один ход
перемещается на п клеток в одном направлении (по горизонтали или вер-
вертикали) и на п+1 клетку в перпендикулярном направлении. За какое наи-
наименьшее число ходов "волк" сможет переместиться из какой-нибудь клетки
в соседнюю (т.е. имеющую с исходной общую сторону)?

89
588. В n-мерном кубе покрашено более половины вершин. Доказать,
что имеется не менее п ребер, у которых оба конца покрашены.
8.2. Задачи с целыми числами
Теория чисел немало служит к изощрению разума начинающих и боль-
большое проворство в исчислении приносит.
Л. Эйлер
589. Пусть п — совершенное число (т.е. равное сумме всех своих
натуральных делителей, отличных от самого числа). Найти сумму
Y--
590. Доказать, что число 11... 1, в десятичной записи которого Зга еди-
единиц, делится на Зга и не делится на Зга+1.
591. Верно ли, что если сумма цифр числа делится на 81, то и число
делится на 81?
592. Найти все п, при которых число ап = 1010... 01 (в его записи п
единиц и п — 1 нулей) является простым.
593. В ряду 60 точек, двое поочерёдно заменяют любую точку на циф-
цифру. Доказать, что второй может сделать так, чтобы полученное число де-
делилось на 13.
594. Если число с суммой цифр 2 делится на 19, то оно делится и на
13. Доказать.
595. Для каких натуральных тип число 2п + 1 делится на 2т — 1?
596. Доказать, что 2т — 1 делится на 2п + 1 тогда и только тогда, когда
т делится на 2гг.
597. Доказать, что при любом натуральном п
1) 2903п - 803п - 464П + 261П делится на 1897;
2) 1492П - 1770п - 1863П + 2141П делится на 1946.
598. Доказать, что при любом нечётном п
1) 46П + 296 • 13П делится на 1947;
2) 2269П + 1779П + 1730п - 1776П делится на 2001.

90 Глава 8. Дополнительные задачи
599. Доказать, что если п — нечётное число, кратное 5, то
12n + 9n + gn + 6n делится на 1991.
600. Доказать, что натуральное число не представимо в виде суммы
последовательных натуральных чисел тогда и только тогда, когда оно яв-
является степенью двойки.
601. Доказать, что
A + 2)A + 22)A + 222)A + 223)... A + 22П~1) = 22П - 1.
602. Доказать, что число 22™ — 1 имеет не менее п различных простых
делителей.
603. Доказать, что любые два числа последовательности
3,5,17,...,1 + 22Г\...
взаимно просты.
604. Используя утверждение предыдущей задачи, доказать бесконеч-
бесконечность множества простых чисел.
605. Доказать, что число 22" + 22П +1 имеет не менее п различных
простых делителей.
Л. Эйлер предложил следующий способ разложения на множители
нечётного числа, для которого известны два представления в виде сум-
суммы двух квадратов ([48]).
Пусть п = х2 + у2 = u2 + v2, причем х и и — чётные числа, а у и v —
нечётные. Тогда х2 — u2 = v2 — у2 и
х — u v + у a
v — у х + и 6'
где a/b — несократимая дробь. Для некоторых целых t\ и ?2 имеем равен-
равенства
х — u = ati, v + у = at2,
v — у = bt\, х + и = bt2-
Поскольку числа х ± и и v ± у четны, а одно из чисел а или b нечётно,
заключаем, что числа t\ и ?2 четны. Разрешив написанные выше уравнения
относительно х и у, получим
aty + bti at2 — bt\
x ; у

91
откуда п = х2 + у2 = \ ((atx + bt2f + (at2 - btif) = \(a2t\ + b2t\ + a2t2 +
ЪН2) = \(a2 + b2)(t2 + t2) = (a2 + b2)((ti/2J + (t2/2J).
606. С помощью метода Л. Эйлера разложите на множители следую-
следующие числа: 1000001 = 1992 + 9802; 1000009 = 2352 + 9722;
1000049 = 6322 + 7752; 1000169 = 1552 + 9882; 1000361 = 6562 + 7552;
1000441 = 2402 + 9712; 1000529 = 6732 + 7402.
607. Обобщите метод Л. Эйлера для нахождения разложения на мно-
множители нечётного числа п, для которого известны два представления вида
п = х2 + dy2 = и2 + dv2.
608. Разложите на множители число
13 717421 = 7612 + 7 • 13702 = 4392 + 7 • 13902.
609. Пусть ai,a,2,... ,ап и &1; Ь2,..., Ьп — полные системы вычетов по
модулю п. Доказать, что если п > 2, числа aibi, а2, Ь2,..., anbn не образуют
полной системы вычетов по модулю п.
610. Докажите, что для п > 2
п цифр п — 1 цифр
22 = 22 (modn).
611. Доказать, что если а — 1 : km, то ак — 1 : km+l (где a,k,m G N).
612. Пусть а — произвольное натуральное число, (ип) — последова-
последовательность, задаваемая рекуррентно
щ = a, un+i = aUn, n E N.
Доказать, что при п > 3 разность двух соседних чисел последовательно-
последовательности (un+i — ип) делится на 10га~2.
Замечание. Из результата данной задачи следует свойство стабилизи-
руемости цифр "сверхстепеней": какой бы разряд ни взять, начиная с
некоторого числа в последовательности
a,aa,aaa ,aaa ,...
цифра в этом разряде не меняется.
613. Пусть р — простое число, п > 1, (р — 1)п + 1 : п. Доказать, что п
делится на р.

92 Глава 8. Дополнительные задачи
614. Пусть р — простое число, р > 3, к = [2р/3]. Доказать, что сумма
биномиальных коэффициентов Ср + С? + ... + С? делится на р2.
615. Для каждого натурального п запишем сумму $^m=i l/m B виДе
«га/^п, где а„ и /Зга — взаимно простые числа. Найти все п, при которых
/Зп не делится на 5.
616. Для 71 = 10 определить, четно или нечётно число упорядоченных
n-элементных наборов натуральных чисел (х\, х2,..., хп) таких, что
11 1
— + — + ... + — = 1.
Х\ Х2 Хп
8.3. Числа Кармайкла
Составное число то такое, что для любого числа а, взаимно простого с
то, выполняется соотношение am~l = l(modm), называется числом Кар-
Кармайкла.
617. Доказать, что любое число Кармайкла нечётно.
618. Доказать, что числа 561, 46657 = б6 + 1,101101 являются числами
Кармайкла.
619. Пусть m — свободное от квадратов составное число, обладающее
тем свойством, что m — 1 : р — 1 для произвольного простого числа р,
делящего т. Доказать, что т — число Кармайкла.
Справедливо и обратное утверждение, что доказывает следующая се-
серия задач.
620. Пусть число m делится на квадрат простого числа р и
am-\ = l(modm). Доказать, что oP~l = l(modp2).
621. Верно ли, что (р + l)p~l = l(modp2) (где р — простое число)?
622. Доказать, что число Кармайкла свободно от квадратов.
623. Пусть m — число Кармайкла, р — простой делитель т. Доказать,
что т — 1 :р — 1.
Утверждения задач 619, 622, 623 показывают, что справедлива
Теорема. Число m является числом Кармайкла тогда и только тогда,
когда т — свободное от квадратов составное число, обладающее тем
свойством, что то — 1 делится нар — 1 для произвольного простого числа
р, делящего то.

93
624. Составьте алгоритм и напишите программу нахождения чисел
Кармайкла.
8.4. Формула обращения Мёбиуса
В этом параграфе будем считать, что мультипликативная функция
определяется соотношениями: /A) = 1; (n, m) = 1 =$¦ f(nm) = f(n)f(m).
625. Мультипликативная функция однозначно определяется своими
значениями на степенях простых чисел. Доказать.
Функция Мёбиуса /i(n) вводится следующим образом.
Mi) = 1;
если п делится на квадрат простого числа, то ji{n) = 0;
если п свободно от квадратов и представимо в виде произведения s раз-
различных простых чисел, то /i(n) = (—l)s.
626. Вычислить 1л(п) для п = 1, 2,..., 12.
Определим функции E(n), I{n), J(n):
E[n) = 1 Vn; I[n) = n Vn; J[n) = { J'
1, если п = 1,
если п > 1.
Мультипликативность этих функций очевидна.
Произведением Дирихле функций f(n) и g(n) называется функция
d\n
627. Доказать коммутативность и ассоциативность операции о.
628. Доказать, что из мультипликативности функций f(n) и g(n) сле-
следует мультипликативность fog (n).
629. 1) Проверить, что J о / = / для любой функции f(n).
2) Пусть f(n) — мультипликативная функция. Доказать, что существу-
существует такая мультипликативная функция f'(n), что / о /' = J.
Замечание. Последние три задачи показывают, что мультиплика-
мультипликативные функции образуют коммутативную группу с единичным элемен-
элементом J и произведением Дирихле в качестве групповой операции.
630. Доказать, что из мультипликативности функций f(n) и / о д(п)
следует мультипликативность д(п).

94 Глава 8. Дополнительные задачи
Функция F = f о Е называется сумматорной функцией для f(n).
Таким образом, F(n) = Yld\nf(d), где суммирование ведется по всем де-
делителям числа п (включая 1 и п).
631. Доказать, что f(n) — мультипликативная функция тогда и только
тогда, когда мультипликативна её сумматорная функция F(n).
т(п) — число (натуральных) делителей числа n, s(n) — их сумма.
632. Проверить, что Е о Е = т;1 о Е = s.
633. Доказать, что // о Е = J.
634. Найти II о т и II о s.
635. Доказать, что ipoE = I, т.е. что сумматорная функция для функ-
функции Эйлера имеет вид:
d\n
636. С помощью задач 635 и 631 доказать мультипликативность функ-
функции Эйлера.
637. [Формула обращения Мёбиуса.] Доказать, что
F = / о Е ^^ f = Fofi.
Таким образом, найдено выражение функции f(n) через её сумматорную
функцию:
638. С помощью задач 635 и 637 доказать:
d\n p\n
639. Убедившись в справедливости равенства
d\n
найти сумматорную функцию для натурального логарифма.

95
640. Пусть Л(п) = { 1Г?' 6СЛИ П = /; ГД6 Р ПР°СТОе ' к G ^
4 7 (^ О в противном случае.
Доказать: 1) Л о Е = In; 2) Л = In о//.
На множестве (линейных) последовательностей длины п, элементы ко-
которых принимают значения из некоторого конечного множества, зададим
отношение эквивалентности
(аь ..., an) ~ (а*, ai+i,... ,an,au ..., Щ-i) (г = 1,..., n).
Класс эквивалентности назовем циклической последовательностью.
Подсчитать число различных циклических последовательностей не так
просто, поскольку в разных классах эквивалентности может быть разное
число (линейных) последовательностей; например, постоянная цикличе-
циклическая последовательность порождается одной линейной последовательно-
последовательностью, а циклической последовательности из п попарно различных элемен-
элементов соответствует п линейных последовательностей.
Период циклической последовательности {а\,... ,ап) — наименьшее
число d такое, что di+d = a% для всех i, где сложение ведется по модулю п
(т.е. если i + d > п, то i + d заменяется на i + d — n).
641. Пусть M(d) — количество циклических последовательностей дли-
длины и периода d, элементы которых могут принимать к различных значе-
значений. Доказать, что kn = Yld\
642. С помощью задач 641 и 637 найти количество циклических после-
последовательностей длины и периода п.
643. Доказать, что общее количество циклических последовательно-
последовательностей длины п равно
- Х Y^
П d\n
644. Составляются ожерелья из бусин трех цветов. Каждое ожерелье
состоит из 1) 5; 2) 6; 3) 7; 4) 8 бусин. Не будем различать ожерелья, полу-
получающиеся друг из друга поворотом в плоскости. Пользуясь результатом
предыдущей задачи, найти число различных ожерелий.

96 Глава 8. Дополнительные задачи
8.5. Бинарные операции и отношения
645. Пусть на множестве S определена коммутативная и ассоциатив-
ассоциативная операция *. Имеется разбиение S на множества Т и U (т.е. Т U U =
S; Т П U = ф), обладающее свойством:
Vtut2,t3eT ti*t2*t3eT;
Vmi, щ, щ G U щ * щ * щ ? U.
Доказать, что по крайней мере одно из множеств Т или U замкнуто отно-
относительно операции *.
646. На множестве X задана бинарная операция * такая, что для лю-
любых x,y,z G X выполнено равенство х * (у * z) = у * (z * x), а из равенства
х * у = х * z следует у = z. Доказать, что операция * является коммута-
коммутативной и ассоциативной.
647. На множестве действительных чисел определена бинарная опера-
операция *, обладающая свойствами: для любых x,y,z x* (х*х) = х; х* (у*z) =
(х * у) + z. Найти все такие бинарные операции.
648. На множестве действительных чисел определена бинарная опера-
операция *, обладающая свойством: для любых х, у, z, t (x*y)z + y(z*t) = (xz)*
(y*t). Доказать, что для найдётся такая постоянная С, что х*у = С(х — у).
649. На множестве X задана бинарная операция * такая, что для лю-
любых х, у G X выполнено равенство (х*у)*х = у. Доказать, что имеет место
и равенство х * (у * х) = у. Разрешить относительно х уравнения х * a = Ъ
и a * х = Ъ. Пусть к тому же X — конечное множество, и его мощность
не кратна трем. Доказать, что в X найдётся идемпотентный элемент, т.е
Эх G X х * х = х.
650. Бинарная операция на множестве целых чисел п * m = —n — m
коммутативна и не ассоциативна. При этом имеют место тождества
(п * т) * т = п, т * (т * п) = п.
Пусть в произвольной алгебраической структуре < X, * >
Vx, у G X (х * у) * у = х, у * (у * х) = х.
Доказать, что операция * является коммутативной.
651. Пусть S — множество упорядоченных троек (a,b,c) различных
элементов конечного множества А. Выполняются следующие условия:

97
1. (a, b, с) G S ¦<=?¦ (b, c, a) G S;
2. (a,b,c) e5^ (c,b,a) $ S;
3. (a, b, c), (c, d, a) G S ¦<=?¦ (b,c,d),(d,a,b) G 5.
Доказать, что существует такая функция g : Л —> R, что из двойного
неравенства д(а) < д(Ь) < д(с) следует: (а, Ь, с) G S.
8.6. Разные комбинаторные задачи
652. Предположим, что сейчас в России имеется 110 млн телефонов.
Можно ли ввести 10-значные номера таким образом, чтобы ошибка в на-
наборе одной цифры обнаруживалась и исправлялась? (Например, если име-
имеется номер 240-877-2082, а по ошибке набрано 240-872-2082, то все суще-
существующие номера, кроме первого указанного, должны отличаться от на-
набранного номера не менее, чем двумя цифрами).
653. В квадрате отметили 10 точек и соединили их непересекающи-
непересекающимися отрезками друг с другом и с вершинами квадрата так, что квадрат
разбился на треугольники. Сколько получилось треугольников?
654. Выпуклый п-угольник разбит на треугольники диагоналями, не
пересекающимися внутри n-угольника. Сколько получится треугольников
и сколько диагоналей?
655. На какое количество частей делят плоскость п прямых общего
положения (т.е. среди них нет параллельных и никакие три прямые не
пересекаются в одной точке)?
656. На какое наибольшее количество частей могут разделить про-
пространство п плоскостей?
657. На какое наибольшее количество частей могут разделить плос-
плоскость п окружностей?
658. На какое наибольшее количество частей могут разделить про-
пространство п сфер?
659. Сколькими способами можно из цифр 2, 7, 9 составить три таких
п-значных числа, что их сумма равна 2A0" — 1)?
660. Сколько существует квадратов с вершинами в узлах квадратной
сетки {п — 1) х {п — 1) клеток?

98 Глава 8. Дополнительные задачи
661. Сколькими способами можно расположить в ряд к\ единиц, к2
двоек, ..., кп чисел п так, чтобы любому числу (к + 1) предшествовало по
крайней мере одно число к?
662. Сколько существует перестановок (с повторениями) In чисел
1,1, 2, 2,..., п, п таких, что для любого г все числа, расположенные в
перестановке между двумя вхождениями числа г, больше г?
663. Сколько существует перестановок чисел 1, 2,..., п, в которых для
любого числа г, стоящего не на первом месте, хотя бы одно из чисел г — 1
или г + 1 стоит левее г?
664. На правой чашке весов лежит груз массой 11111 г. Весовщик
последовательно раскладывает по чашкам гири в 1, 2, 4, 8,... г. В какой-то
момент весы оказались в равновесии. На какую чашу весов попала гиря в
16 г?
665. Некоторые из подмножеств n-элементного множества М — "осо-
"особые". Найти наименьшее возможное число особых подмножеств, если из-
известно, что любое подмножество М представимо в виде пересечения осо-
особых.
666. Доказать, что среди п + 2 подмножеств n-элементного множества
найдутся два, не сравнимых по отношению включения (т.е. ни одно из
этих двух множеств не является подмножеством другого).
667. Какое наибольшее число подмножеств n-элементного множества
можно указать таких, что любые два из них не сравнимы по отношению
включения?
668. Среди 250 сотрудников международной фирмы в любой паре со-
сотрудников каждый знает язык, который не знает другой сотрудник из этой
пары. Какое наименьшее возможное число языков знают (в совокупности)
сотрудники фирмы?
669. При фиксированном чётном числе к > 4 найти наименьшее п, при
котором в п-элементном множестве можно выделить такие к подмножеств,
среди которых нет одинаковых и взаимно дополнительных, что каждый
элемент исходного множества входит ровно в половину этих подмножеств.
670. Какое наибольшее число тупоугольных треугольников можно со-
составить из 16 различных отрезков, если отношение длин самого длинного
отрезка и самого короткого не больше 2?

99
671. Найти число умножений при вычислении определителя п-го по-
порядка с помощью рекурсивной процедуры разложения по элементам столб-
столбца.
672. Найти формулу общего члена последовательности, определяемой
соотношениями
хп = (п- l)(xn_i + хп-2), п>3; х\ = О, х2 = 1.
673. Пусть {х\, Х2, ¦ ¦ ¦, хп} = {1,2,... ,п}. Найти как функцию от п
{п > 2) наибольшее значение выражения
Sn = Х\Х2 + Х2Х3 + ... + Xn-iXn + ХпХ\.
674. Пусть а\, а2,..., ап — различные действительные числа. Доказать,
п
что величина Y1 ?гаг, где ?г = ±1, принимает не менее (п2 + п + 2)/2 раз-
г=1
личных значений. Показать, что эта оценка точная.
675. Пусть N — наибольшее число пар различных натуральных чисел
таких, что суммы чисел в парах различны между собой и меньше нату-
натурального числа п. Доказать, что N < Bп — 3)/5.
676. Для строки S, состоящей из единиц и нулей, обозначим через
A(S') разность числа единиц и нулей. Например, АA001001) = —1. На-
Назовем строку S сбалансированной, если для любой подстроки Т (последо-
(последовательных символов) S —2 < А(Т) < 2. Так, строка 1001001 не является
сбалансированной, так как содержит подстроку 00100. Найти число сба-
сбалансированных строк длины п.
677. Дан правильный треугольник с длиной стороны п > 2. Каждая
его сторона разбита на п равных частей. Через точки деления проведены
прямые, параллельные сторонам.
1) На сколько маленьких треугольников (со стороной 1) разбит исход-
исходный треугольник?
2) Сколько получилось треугольников со стороной 2?
3) Сколько всего есть треугольников, ограниченных проведенными ли-
линиями?
678. п мальчиков имеют по некоторому количеству яблок. Первый
мальчик взял из своих яблок половину и ещё одно яблоко и разделил эти
яблоки поровну между остальными мальчиками. Затем так же последо-
последовательно поступают и остальные мальчики (каждый берет половину всех

100 Глава 8. Дополнительные задачи
накопившихся у него яблок и ещё одно яблоко и и делит эти яблоки по-
поровну между остальными мальчиками). В результате у всех оказалось по
а яблок. Известно, что все яблоки остались целыми. Каким наименьшим
может быть а и сколько при этом яблок было у каждого мальчика перво-
первоначально?
679. [Задача Иосифа2.] По кругу стоит 300 человек, пронумерован-
пронумерованных последовательно по часовой стрелке числами от 1 до 300. Удаляют,
начиная считать с первого человека, каждого третьего по ходу часовой
стрелки до тех пор, пока не останется один человек. Каков его номер?
680. Пусть по кругу стоят m человек, а удаляется каждый k-й. Напи-
Напишите программу на любом известном вам языке программирования, нахо-
находящую номер последнего оставшегося человека.
681. Некто, имея п монет одинаковой массы, хочет при помощи ча-
чашечных весов без гирь доказать окружающим, что все эти монеты весят
одинаково. Какое наменынее число взвешиваний ему придется сделать?
682. За круглым столом сидят п игроков. Каждый из них первоначаль-
первоначально имеет по одному рублю. Первый игрок передает рубль второму, после
чего второй передает два рубля третьему. Затем третий игрок передает
рубль четвертому, а четвертый два рубля пятому и т.д. Игроки пооче-
поочередно передают рубль или два рубля следующему игроку, у которого ещё
есть деньги; игрок, лишившийся денег, выбывает из игры и покидает стол.
Найти бесконечное множество таких п, при которых игра заканчивается
тем, что у некоторого игрока оказываются все п рублей.
683. В школе работает 6 кружков. Каждый из 20 учеников класса
может посещать любое количество кружков — от 0 до 6. Верно ли, что
обязательно найдутся такие 5 учеников и такие 2 кружка, что все пяте-
пятеро либо посещают оба кружка, либо не посещают ни один из этих двух
кружков?
8.7. Тождества
684. Доказать тождество ?Li *'
685. Пусть 1 < m < п. Доказать тождество $^?=1(—1)кктС^ = 0.
2О происхождении названия задачи см. [25].

101
686. Комбинаторными рассуждениями доказать тождество
k = 0.
687. Доказать формулу для матрицы, обратной нижнетреугольной ма-
матрице биномиальных коэффициентов:
\
-1
о
с? с\
2 2
Со°
-с?
\
-С\
V
688. Пусть an = Y%=QC%- Доказать, что &n = Y,k=o(-l)n~kCfrk-
689. Известно (см. [9]) следующее соотношение между числами Стир-
линга I и II рода:
1, если п = к;
0, если п ф к.
j=o
Пусть ап = YH=o ^(n: к)Ьк. Доказать, что Ьп = YH=o s(n>
690. Доказать, что число хп = (у/2 + у/3 + \/bJn+l имеет вид
хп = CLnV^ + Ьп\/2> + спл/5 + dny/30, где ап, bn, cn, dn — целые числа. Найти
\iman/dn.
691. Числа от 1 до Am2 — 1 разбиты на две группы: в первую собраны
числа, для каждого из которых ближайшим к нему квадратом является
квадрат нечётного числа, а во вторую — все остальные. Доказать, что
суммы чисел в группах совпадают.
692. Пусть п — чётное натуральное число. Запишем числа 1, 2,..., п2
в клетки квадрата п х п так, что к-я строка есть
(к - 1)п + 1,(к-1)п + 2,...,(к- 1)п + п.
Раскрасим клетки в чёрный и белый цвет таким образом, чтобы в каждой
строке и каждом столбце чёрных и белых клеток было поровну. Доказать,
что для любой такой раскраски суммы чисел на чёрных и белых клетках
равны.
693. Доказать тождество $^ь=2[\/^] = Sfe=2^0SA;n] (ПРИ п > 2).

102 Глава 8. Дополнительные задачи
694. Пусть тип — взаимно простые числа, большие 1. Доказать, что
^ \кп~\ (т — 1)(п — 1)
\\
\т
k=i l
695. Пусть N — натуральное число. Вычислить для каждого N > 2
Е -•
*-^ тп
\<m<n<N, m+n>N, (m,ra)=l
696. Доказать:
№ Pog2n] pog4n]
697. Пусть s(x) есть расстояние между числом х и ближайшим к нему
целым числом. Для произвольного натурального п вычислить
• ( (т\ (т\\
т=1
698. Пусть атуП есть коэффициент при хп в разложении многочлена
A + х + х2)т. Докажите, что для всех целых к > О
Г—1
I- з J
г=0
699. Пусть п — натуральное число, с — действительное число. После-
Последовательность (ж*;) определяется соотношениями хо = 0, х\ = 1 и
- (п -
Пусть при фиксированном п число с принимает наибольшее значение, при
котором xn+i = 0. Выразить xfc через пик, где 1 < А; < п.

103
8.8. Две классические задачи
В данном разделе на основе формулы включения-исключения решаются
две классические комбинаторные задачи — задача мажордома и задача
о супружеских парах. В [2] приводится три решения первой из этих
задач. Вторая задача была сформулирована в 1891 г., но окончательно
решена была лишь в 1934 г.
700. Задача мажордома. К обеду за круглым столом приглашены
п пар враждующих рыцарей (п > 2). Требуется рассадить их так, чтобы
никакие два врага не сидели рядом. Каким числом способов это можно
сделать?
701. 1-я лемма Капланского. Число способов выбрать из п точек,
расположенных на одной прямой, к точек так, чтобы никакие две из них
не были соседними, равно
f(n,k)=CZ_k+1, k<^.
702. 2-я лемма Капланского. Число способов выбрать из п точек,
расположенных на одной окружности, к точек так, чтобы никакие две из
них не были соседними, равно
П „и П
703. Задача о супружеских парах. К обеду за круглым столом
приглашены п супружеских пар. Требуется рассадить их так, чтобы муж-
мужчины и женщины чередовались и никакие двое супругов не сидели рядом.
Каким числом способов это можно сделать?
8.9. Теорема Рамсея
704. По двум ящикам размещаются п предметов. Каким должно быть
число п,чтобы обеспечить попадание р предметов в первый ящик или q
предметов во второй ящик?
705. Доказать, что в любой компании из шести человек найдётся трое
попарно знакомых или трое попарно незнакомых.

104 Глава 8. Дополнительные задачи
706. В графе К6 каждое ребро покрашено в красный или синий цвет.
Доказать, что существует по крайней мере два одноцветных треугольника.
707. В графе К$ каждое ребро покрашено в красный или синий цвет.
Доказать, что в графе есть два одноцветных треугольника без общих вер-
вершин.
708. В графе Кп каждое ребро покрашено в красный или синий цвет.
Доказать, что в графе есть одноцветный треугольник.
709. Во всякой группе из 9 человек, в которой нет трёх попарно незна-
незнакомых, найдутся четверо попарно знакомых. Доказать.
710. В простом графе G 18 вершин. Доказать, что К^ С G или К\ С G.
711. Пусть а\ = 2, an = n-ara_i + l. Доказать, что в графе порядка а„+1,
рёбра которого окрашены в п цветов, найдётся одноцветный треугольник.
Показать, что an = [п\е].
712. [Теорема Рамсея.] Пусть p,q,r G N, причем р > г, q > г.
Существует число N(p, q, r) со следующим свойством.
Для произвольного множества S из п элементов рассмотрим произ-
произвольное разбиение множества всех его г-элементных подмножеств Т на
две части: Т = о; U /3, а Г) /3 = ф. При п > N(p, g, r)
• найдётся р-элементное подмножество А С S, все г-элементные
подмножества которого принадлежат а, или
• найдётся q-элементное подмножество В С S, все г-элементные
подмножества которого принадлежат C.
Доказательство. В силу задачи 704 можно положить N(p, q,l) = p +
q — 1. Покажем, что в качестве N(r,q,r) подходит q. Действительно, если
а не пусто, то любое r-элементное подмножество из а годится для роли А.
Если же а = ф, то все r-элементные подмножества содержатся в /3 и В =
S. Аналогично N(p, г, г) = г. Три найденных соотношения служат базой
индукции. Теперь, предположив существование N(p— I, q, r), N(p, q — l,r)
и N(p', q', r — 1) для любых р' и q', докажем, что существует N(p, q, r) (это
и будет индукционный шаг).
Считая, что г>1, р > г и q > г, положим
Pi = N(p - 1, q, r), Ql = N(p, q-l,r), N(p, q, r) = N{puqur - 1) + 1.
Достаточно доказать теорему для случая п = N{p, g, r).

105
Пусть x(zShS' = S\ {х}. По произвольному разбиению Г = aU /3 по-
построим следующее разбиение множества Т' = a' U /3' всех г — 1-элементных
подмножеств множества S':
а' = {X | X U {х} С а], $ = {X | X U {х} С /3}.
По предположению индукции
• найдётся pi-элементное подмножество А' С S", все (г —1)-элементные
подмножества которого принадлежат а', или
• найдётся qi -элементное подмножество В С S, все (г — 1)-элементные
подмножества которого принадлежат /3'.
Рассмотрим подробно первый случай (для второго рассуждения аналогич-
аналогичные). Поскольку pi = N(p — l,q,r),
• существует [р — 1)-элементное подмножество А" С S', все
r-элементные подмножества которого принадлежат а (тогда
множество А = A" U {х} — искомое); либо
• найдётся g-элементное подмножество В С S', все r-элементные под-
подмножества которого принадлежат /3 (в этом случае В и есть искомое
множество).
Теорема доказана.
Наименьшее число N[p,q,r) из формулировки теоремы Рамсея назы-
называют числом Рамсея и обозначают R(p, q, r).
713. Доказать, что R(p, q, 1) = р + q — 1.
714. Доказать, что R(r, q, г) = q, R(p, г, г) = р.
715. Доказать, что ДC, 3, 2) = 6.
716. Доказать, что R(p, q, 2) < Срр~]_2, где p,q>2.
Ниже рассматриваются геометрические задачи, последняя из которых
решается с помощью теоремы Рамсея, а первые две имеют характер вспо-
вспомогательных лемм.
Всюду будет предполагаться, что точки лежат в одной плоскости.
Пусть рассматривается некоторое множество точек. Будем говорить,
что это точки общего положения, если никакие три из них не лежат на
одной прямой.

106 Глава 8. Дополнительные задачи
717. Из любых пяти точек общего положения можно выбрать четыре,
являющиеся вершинами выпуклого четырёхугольника. Доказать.
718. Даны п точек общего положения, причем любые четыре из них
являются вершинами выпуклого четырёхугольника. Доказать, что эти п
точек — вершины выпуклого п-угольника.
719. [Теорема Эрдёша-Секереша.] Для любого натурального
п можно указать такое натуральное число к = к(п), что из любых
к точек общего положения можно выделить п точек, являющихся
вершинами выпуклого п-угольника.
Доказать теорему, положив к = Д(п, 5,4).
8.10. Ожерелья
Данный параграф служит продолжением темы последнего примера §6.5
учебного пособия [9].
720. Доказать, что цикловой индекс группы подстановок на множе-
множестве вершин правильного п-угольника, порождённых его вращениями в
плоскости, есть
n
d\n
721. Составляются ожерелья из щ бусинок 1-го вида, п2 бусинок 2-
го вида, ..., пт бусинок m-го вида. Не считаются различными ожерелья,
которые могут быть получены друг из друга вращением в плоскости. До-
Доказать, что число различных ожерелий равно
(n/d)\
(nl/d)\(n2/d)\...(nm/d)V
где суммирование ведется по всем числам d, одновременно являющимся
делителями чисел щ, п2,..., nm.
722. Найти цикловой индекс группы подстановок на множестве вершин
правильного п-угольника, порождённых группой его симметрии.

107
8.11. Графы
723. Простой граф, изоморфный своему дополнению, называется са-
самодополнительным. Доказать, что число вершин самодополнительного
графа при делении на 4 дает остаток 0 или 1. Найти все самодополнитель-
самодополнительные графы с числом вершин меньше 6.
724. Доказать, что самодополнительный граф связен и его диаметр
равен 2 или 3.
725. Диаметр графа равен 2, степень каждой вершины не больше 3.
Каково максимальное число вершин графа?
726. Какие из Платоновых графов являются а) эйлеровыми; б) гамиль-
тоновыми? Указать в каждом случае эйлеров или гамильтонов цикл.
727. Реберный граф L(G) гамильтонов тогда и только тогда, когда в
графе G есть цикл, содержащий хотя бы по одной вершине из каждого
ребра G. Доказать.
728. Доказать, что граф К2п распадается на п гамильтоновых цепей.
729. Доказать, что граф K2n+i распадается на п гамильтоновых ци-
циклов.
730. На плоскости проведено 100 прямых общего положения. Докажи-
Докажите, что части, на которые они делят плоскость, нельзя обойти, переходя
каждый раз в соседнюю (по стороне), побывав в каждой части ровно один
раз и вернуться после этого в исходную часть.
731. В простом графе порядка 2п + 1 у любых п вершин есть общая
смежная вершина. Доказать, что радиус графа равен единице.
732. Пусть в графе G для любых двух вершин число общих смежных
вершин нечётно. Доказать, что
1) G — эйлеров граф;
2) число вершин G нечётно.
733. При каких п и к > 1 существует простой граф с п вершинами, в
котором любые к вершин имеют ровно одну общую смежную вершину?
734. Найти порядок регулярного степени 6 простого графа, в котором
у любых двух вершин ровно две общих смежных вершины.
735. Пусть в графе G любые две смежные вершины не имеют общих
смежных вершин, а любые две несмежные вершины имеют две общие
смежные вершины.

108 Глава 8. Дополнительные задачи
1) Доказать, что G — регулярный граф.
2) Пусть п — порядок графа G, а к — степень каждой его вершины.
Доказать, что п = 1 + к + С\.
3) Пусть А — матрица смежности графа G. Доказать, что если Л —
собственное значение Д отличное от к, то Л2 + 2Л — к + 2 = 0.
4) Найти кратности собственных значений матрицы А.
5) Доказать, что число к представимо в виде к = 1 + т2, где m — целое
число.
6) Найти графы, удовлетворяющие условию задачи при m = 1, 2, 3.

Ответы. Указания. Решения
15. 50. 16. 2 рыцаря. 17. 1/2.
28. Пусть Р(х) — многочлен из условия задачи. Очевидно, что он чёт-
чётной степени. Пусть с — его наименьшее значение. Все действительные
корни многочлена Q(x) = Р(х) — с имеют чётную кратность. Поэтому
для некоторого всюду положительного многочлена R(x) имеем Q(x) =
T2[x)R(x), где Т2(х) — произведение всех множителей многочлена вида
{х — а) (каждый множитель берется столько раз, какова кратность соот-
соответствующего корня). Поскольку R(x) имеет степень меньше, чем Р(х),
можно воспользоваться предположением индукции. Осталось заметить,
что Р{х) = Q{x) + (v^J.
35. 140. 36. 70. 39. а) 10!2; б) 10!2 • 210. 41. 8! 42. 2 • 88 - 8! 44. 4/4.
45. аJп-1; 1, 2, 22,..., 2"; б) (Зп - 1)/2; 1, 3, З2,..., З".
46. 2п~\
47. 57599 = 2402 - 1 = 239 • 241. 51. 1 и 2.
52. Пусть d — общий делитель чисел van и то2 + п2. Тогда d делит и
(т±пJ. Если (т + п,т — п) = 1, то ((то + пJ, (то — пJ) = 1, откуда
d = 1. Если (то + п,т — п) = 2, то то и п нечётные числа (чётными они
быть не могут, так как взаимно просты) и ((то + пJ, (то — пJ) = 4. Таким
образом, d — нечётный делитель четырёх, то есть d = 1.
53. 1 и 2. Используйте тождества 2то2 = (то2 + п2) + (то + п)(т — п) и
2п2 = (то2 + п2) — (то + п) (то — п).
54. 1) 3; 2) 57; 3) 11; 4) 1.
57. Положим Pi(x) = х, Рп+\{х) = Р(Рп(х)). Тогда ап = Рп@), ап =
Рп-т(ат) (при п > то). В силу теоремы Везу Рп(х) = Pn@) + xQn(x) = ап +
xQn{x), где Qn{x) — некоторый многочлен с целыми коэффициентами. По-
Поскольку ап = Рп_т(ат) = an_m+amQn_m(am), имеем (ап, ат) = (an_m, am).
Из последнего соотношения следует, что {ап,ат) =

110 Ответы. Указания. Решения
59. 218 • З8 ¦ 54 • 72 • 11 - 13- 17-19.
67. См. доказательство бесконечности множества простых чисел в [9].
68. Пусть среди чисел 1, 2, 3,..., 2п содержится г < к простых чисел
Pi,P2, ¦ ¦ ¦ iVr- Тогда каждое число, не превосходящее 2га, представимо в ви-
виде pSiPs22 • • -Prri гДе' очевидно, каждый показатель степени S{ не больше п.
Однако чисел такого вида (по правилу произведения) A + п)г, что меньше
2п. Полученное противоречие доказывает утверждение задачи. Поскольку,
как известно из анализа, показательная функция "растет быстрее" степен-
степенной, и для любого (сколь угодно большого) к при достаточно больших п
неравенство 2п > A + п)к имеет место, получено доказательство бесконеч-
бесконечности множества простых чисел.
69. Среди чисел {1, 2,..., п} имеем не более п/р2 чисел, делящихся на
р2. Поэтому количество чисел, делящихся на квадрат простого числа, не
больше
р^< 4 +^к(к + 1) = 4+П^к~к + Г = Т'
^ +Пкк + Г Т
к=2
Утверждение задачи позволяет получить не только доказательство беско-
бесконечности множества простых чисел, но и оценку сверху для к-го простого
числа Pk- Первые (по возрастанию) к — 1 простых чисел порождают 2к~1
чисел, свободных от квадратов. Поэтому среди чисел от 1 до A-2k~l = 2k+l
содержится по меньшей мере к простых чисел (в противном случае доля
чисел, свободных от квадратов, была бы менее четверти), т.е. Рк < 2к+1.
70. 1) 1; 2) 1; 3) 5. В последнем примере имеем:
1Ою = з10 = 95 = 25 = 4(mod7); 10100 = A010I0 = 410 = (-3I0 = З10 = 4.
Далее по индукции легко доказать, что V/c 1010 = 4(mod7).
75. Поскольку 1980 = 20-99, достаточно доказать делимость на 20 и на
99. Первое очевидно. Для доказательства второго утверждения заметим,
что 100т = 1 (mod99). Поэтому 1920 ... 80 = 19 + 20 +.. . + 80 = 0(mod99).
76. Нет. Получившееся число обязательно делится на 11.
77. Нет. Получившееся число обязательно делится на 37.
78. 8. 80. При к = 2 и 11.
81. 11 • 1014. Четвёртая степень целого числа при делении на 16 даёт
остаток 0 или 1.

Ill
82. Да. Представив число п в виде п = т • 2г • З-7, где т не делится на 2
и на 3, будет относить его к одному из трёх подмножеств в соответствии
с остатком от деления на 3 числа г — j.
84. Пусть N = qi •... • qn, щ = N/qi. Из условий задачи следует, что tj
кратно щ. Положив tj = щх^, из второго свойства числа tj имеем, что для
некоторого целого yi выполняется равенство щхг = 1 + ^г/*. Получили ли-
линейное диофантово уравнение, в котором коэффициенты при неизвестных
взаимно просты.
85. х = 5>jtj(modiV). 86. 37.
87. По китайской теореме об остатках найдётся такое число х, что
х = ri(modgi), х = г 2 — I(modg2)> ¦ ¦ ¦ ,х = гп — п + l(modqn).
89. 1) 1; 2) З102 = З100 • З2 = 9(mod 101);
3) 8900 = 82832 • 84 = 84 = б2 = 7(mod29); 4) 1.
92. {п2^- - \){п^ + 1) \р.
2) п - 1 = ^5^f = (аР~1 ~ 1)a2(^-'i+1)- B СИЛУ малой теоремы Ферма из
последнего соотношения получаем: п — 1 : р. Покажите, что п — нечётное
число. Отсюда п — 1: 2р и ап~1 — 1: а2р — 1. В то же время из определения
числа п следует: а2р — 1 : п. Таким образом, ап~1 — 1 делится на п. Это и
требовалось доказать.
99. Поделим многочлен f(x) на многочлен хр — х:
f(x) = (хр - x)q(x) + г(х),
где степень остатка г{х) не превосходит р — 1. Из малой теоремы Ферма
следует, что f(x) = r(x)(modp).
100. Доказательство можно найти в [3].
101. Пусть q — простое число, являющееся делителем числа п. Так
как 2 < q < п — 1, число q является делителем (п — 1)!. В силу задачи 49
(п — 1)! + 1 не делится на q, а, значит, и на п.
102. Пусть п — составное число. Может представиться два случая.
а) п не является квадратом простого числа. Тогда п представимо в виде
произведения двух различных целых чисел: п = щ ¦ п2, каждое из
которых больше 1. Заметим, что при этом п — 1 > щ ип-1 >n2.

112 Ответы. Указания. Решения
Значит, (п — 1)! содержит в качестве множителей и пь и П2, в силу
чего (п — 1)! : щ • п2 = п.
б) п является квадратом простого числа: п = р2. При п > 4 выполняется
неравенство п — 1 = р2 — 1 > 2р и, следовательно, (п — 1)! в числе
своих множителей содержит как р, так и 2р. Таким образом, вновь
(п-1)\\п(=р2).
103. Если р = 2, то доказываемое утверждение проверяется непосред-
непосредственно. Будем считать, что р > 2. Введем в рассмотрение многочлен
f(x) = xp~l - 1 - (х - 1)(х - 2)...(х - (р - 1)).
Легко видеть, что степень f(x) не превосходит р — 2. По малой теореме
Ферма хр~1 — 1 делится на р при ж = 1,2, ...,р — 1. Тем же свойством
обладает и многочлен /(х). Итак, сравнение
х
р~1 -1-(х-1)(х- 2)...{х - (р - 1)) = O(modp)
имеет степень не выше р — 2, в то время как число его решений не меньше
р — 1. В силу задачи 100 все коэффициенты многочлена /(ж) кратны р,
в частности, его свободный член, равный — A + (р — 1)!). Таким образом,
(р — 1)! + 1 делится на р.
106. По теореме Вильсона 1 • 2 • 3 • ... • (р — 1) = —l(modp).
1) В левой части сравнения каждый чётный множитель 2к следует заме-
заменить на нечётное число — (р — 2к).
2) В левой части сравнения каждый нечётный множитель 2к — 1 следует
заменить на чётное число — (р — 2к + 1).
107. Сначала заметим, что х2 = y2(modp) тогда и только тогда, когда
хотя бы одно из чисел х + у и. х — у делится на р (поскольку р — простое
число). Если не равные друг другу числа х и у берутся из множества
А = {1,2,.. .,р— 1}, то 0 < \х — у\ < р и.
x2=y2(modp) <S=^ x + у : р.
Поскольку А — приведенная система вычетов, квадрат любого числа из А
сравним по модулю р с некоторым числом из того же множества А. Разо-
Разобьем множество А на пары вида {к,р — к}. Квадраты любых двух чисел
из разных пар не сравнимы по модулю р, а квадраты двух чисел из одной

113
пары сравнимы по модулю р. Таким образом, каждой паре соответству-
соответствует свой "индивидуальный" квадратичный вычет, а квадратичных вычетов
столько же, сколько и указанных пар, то есть (р — 1)/2.
108. Рассмотрим три возможных случая.
• а кратно р. Здесь утверждение тривиально.
• а — квадратичный вычет. Для некоторого числа Ь, не кратного р,
имеем а = 62(modp). Тогда, используя малую теорему Ферма, полу-
получим
а^г = ь2^) = if-1 = l(modp).
• а — квадратичный невычет. Поскольку (a*V J = aP~l = l(modp),
число а~2~ сравнимо по модулю pel или —1. Мы уже выяснили, что
сравнению ж~г~ = l(modp) удовлетворяет ^^ квадратичных выче-
вычетов. В силу задачи 100 других решений у данного сравнения нет.
Значит, для квадратичного невычета остается лишь возможность
а~2~ = —l(modp).
110. p = 4fc + l.
111. Сначала убедимся в том, что 5 — квадратичный вычет по модулю
19:
(^Л = 59 = б4 • 5 = (-2J • 5 = I(modl9).
Итак, 59 = 1 (mod 19). Отсюда 510 = 5(modl9) и х = ±55 = ±9(modl9).
Аналогично решаются сравнения вида х2 = a(modp), где р — простое
число вида р = Ак + 3.
112. Убедитесь в том, что когда число к пробегает по Р, то и число
д
k пробегает по Р. Пусть К = YI к. Тогда
я я / \ я
К = Д акек ее а?КЦек ее f - 1 КЦek(modp).
к=1 к=1 W' к=\
/ \ я
Сократив на К, получим A1 YI ?к = l(modp), откуда и вытекает требу-
v ' к=\
емое.

114 Ответы. Указания. Решения
113. р = ±l(mod5). Примените лемму Гаусса, перебирая возможные
остатки от деления р на 10.
114. 1) Решений нет; 2) х = -1 + 7*, у = 2- 13t, t e Z;
3) х = -7 + 19*, у = 8 - 21*; 4) х = 56 + 171*, у = 653 + 1994*.
115. аЬ. Решение. Если т = ab, то х : Ь, у : а и ах + by > 2ab. Пусть
теперь m > ab. Общее решение уравнения ax + by = m в целых числах:
х = хо — Ы, у = уо + at, где ах0 + &2/о = тп. Покажем, что найдётся
такое целое число *, что х > 0 и у > 0, то есть Ь* < х0, at > —г/0) или
—уо/а < t < xo/b. Выразив у0 через х0, имеем ^ — ^ < t < ^. Осталось
заметить, что интервал (у — f|,^f) имеет длину, большую 1, и значит,
содержит целую точку.
116. (а — 1)(Ь — 1)/2. Решение. Все натуральные числа > ab,
представимы указанным образом. Проверьте, что для каждого из
чисел 0,1,...,аЬ — 1 указанное представление единственно (если оно
существует). Рассмотрим на координатной плоскости прямоугольник с
вершинами 0@,0), А(Ь, 0), С(Ъ,а), В@,а). Пусть ах + by < pq. Тогда
точка (х, у) лежит в прямоугольнике О ABC ниже диагонали АВ.
Несложный подсчет: всего прямоугольник содержит (а+ 1)(Ь+ 1) точек с
целыми координатами, на диагонали АВ точек, отличных от Л и В, нет (в
силу взаимной простоты а и Ь), стало быть, ниже диагонали расположено
2 точек. Каждой точке соответствует число ах + by < ab (и
разным точкам — разные числа). Значит, чисел, не представимых в виде
ах + by с неотрицательными х и у, будет ab — ab+a+b~1 = (д-1)^-1) _
117. 5 коров, 1 свинью, 94 овцы. 118. 15 коров, 7 свиней, 78 овец.
119. Андрей женат на Ольге, Иван — на Анне, Степан — на Екатерине.
122. 1) @,0), B, 2), A,2), B,1), A,0), @,1);
2) @, 0), (±1010, ±10), (±100, ±100), (±6666, ±2).
123. 1) D98, 496), G8, 64); 2) m = 2, п = 4; 3) (т,п) = C,5), D, 7);
4) решений нет; 5) C,1);6) A,1,1), D, 2, 2); 7) A3,2); 8) C,1,2). Подроб-
Подробное решение шестого уравнения приведено в первом издании настоящего
сборника. См. также журналы "Квант", 1998, №4, С.50 и "Математика в
школе", 1999, №3, С.60.
124. G, 3, 3), (8, 5, 2), A3,4, 2). 125. 5, 49, 97.
126. Воспользуйтесь результатом задачи 93.
127. (-300,-2), (-36,-6), B4, 4). 128. 17. 129. 2000 и 3998.

115
130. 12 x 5 или 8x6.
131. а) нет; б) да; в) нет. Указание. Пусть х (у) — количество строк
(столбцов), в которых знак менялся нечётное число раз. Тогда количество
минусов в таблице равно жA00 — у) + 2/A00 — х).
132. 2, 8, 272, 1898.
133. Докажите, что знаменатель прогрессии — рациональное число.
Контрпример: Ь{ = 2т~г.
134. Для представления числа т/п указанной дробью ищите а,Ь,с и d
в виде произведения степеней тип.
135. Если квадрат а2 и куб Ь3 совпадают, то утверждение задачи триви-
тривиально. Рассмотрим различные случаи взаимного расположения квадрата
и куба в прогрессии.
I. Пусть а2 <Ь3.
1) Рассмотрим случай, когда b делится на а. Положив b = ка, будем
искать натуральное х, для которого
а2 + х(Ь3 - а2) =а2 + х(к3а3 - а2) = у\
Удобно положить, что у = at. Тогда х = ak3all ¦ Видно, что если t = к2, то
х G N.
Итак, при b = ка прогрессия содержит член (aft2N.
Например, если прогрессия содержит 22 и б3, то в ней будет и член,
равный 186.
2) Пусть а и b — взаимно простые числа. Сведем этот случай к преды-
предыдущему, найдя в прогрессии число z3 такое, что z кратно а. Имеем
а2 + х(Ь3 - а2) = z3, x = Z- °-= 1 + ^-
№ — а2 № — а2
Пусть z = b + t(b3 — а2). Тогда z3 — b3 : z — b: b3 — a2 ax G N. Подберем t так,
чтобы z = b + tb3 — ta2 делилось на a. Для этого необходимо и достаточно,
чтобы для некоторого у выполнялось равенство b + tb3 = ya, или
ау - ЪЧ = Ь. A)
Поскольку а и Ъ3 взаимно простые числа, уравнение A) разрешимо в на-
натуральных числах.
Пример. Если a = 2, b = 5, из уравнения 2у — 125t = 5 найдём t =
1,у = 65, z = 5 + 1 • E3 - 22) = 126. Таким образом, вместе с 22 и 53

116 Ответы. Указания. Решения
прогрессия содержит и 1263. Используя далее результаты предыдущего
пункта, обнаруживаем в прогрессии член F32 • 2N (хотя можно найти в
этом конкретном примере и меньшую шестую степень: 486).
3) Рассмотрим, наконец, общий случай. Пусть Р\,Р2, ¦ ¦ ¦ — все простые
делители чисел а и Ь,
= (Ъ3,а2) = ()
Заметим, что если 3ftj = 2rrii = Sj, то Sj : 6 и все числа вида а2 + х(Ъ3 — а2)
делятся на (р* N. Поэтому вместо чисел а и Ь можно рассматривать числа
а/р™* и Ь/р**. Таким образом, без ограничения общности можно считать,
что для любого % ровно одно из чисел Ь3 Id и a2 Id делится на р^, отсюда
h3-n2 h3-n2
d не делится на Pi и число с = d взаимно просто с а.
Пусть д = Y[Pi' ~ наименьшее натуральное число, куб которого де-
делится на d. Легко убедиться, что для любого г выполняется неравенство
ki > S{. Значит, Ь кратно д. Положим Ь = дЬ\. Найдём член прогрессии z3
с z, делящимся на а. Исходя из равенств
z3 Ь3
Ь3 + х(Ь3 а2) = z3
Ь3 + х(Ь3 - а2) = z3, х =
будем искать z в виде z = gz\. Тогда
о3 — а2
3/ Q -ш О ч О О
и \Z] — t/i ) и z-i —
x= У K 1 l> - У l
d(b3/d-a2/d) d с '
Поскольку д3 : d, для того, чтобы x G N, число zi можно определить как
z\ = Ь\ + ct. Если положить zi = ay, то будем иметь уравнение
ау — ct = Ъ\. B)
Как уже было отмечено, коэффициенты а и с взаимно просты (и положи-
положительны), поэтому уравнение B) разрешимо в натуральных числах. По у
находим z = gay: а такое, что z3 — член прогрессии. Вновь задача сведена
к случаю 1).
Пример. При а = 480, Ь = 72 имеем d = (b3, a2) = 29-32, д = 23-3, Ьг = 3,
О/|3 ,~3 оЗ ,~3 оЗ
29-32 34-50 31 '

117
zi = 3 + 31* = 480?/, 480?/ - 31* = 3.
Одно из решений последнего уравнения у = 25, t = 387. Отсюда
z = 24 • 480 • 25 = 600 • 480, и прогрессия содержит член D80 • 360000N.
П. Пусть Ь3 < а2.
Будем искать в прогрессии куб, больший, чем а2 :
Достаточно положить z = b+t(a2—b3), где * нужно выбрать столь большим,
чтобы z3 было больше а2. Таким образом, задача сведена к случаю I.
138. 20, 16, 100, 400000. 139. 96.
143. Числа, взаимно простые с п, разбейте на пары вида < к,п — к > .
144. Если бы числами px,...,ps исчерпывался весь список простых
чисел, то ни одно число, кроме 1, не было бы взаимно просто с их произ-
произведением Р = pi • ... • ра, откуда <р(Р) = 1, что противоречит формуле из
условия задачи.
150. Пусть l = di<...<dk=n — все делители числа п. Количе-
Количество чисел из множества {1, 2,... , п}, которые делятся на rfj, равно n/di.
Поэтому количество чисел, не превосходящих п и не являющихся взаимно
простыми с п, не больше f- + f-... + j- = d^-x + <4-2 + ... + rfi = s(n) — n.
Таким образом, п — ip(n) < s(n) — n, что и требовалось доказать.
151. Используя обозначения из решения предыдущей задачи, имеем
s(n) = ^di = ^у < n^2- < n(l + / —) =n(lnn + 1).
i=i i=\ di i=i г Jl x
С другой стороны, s(n\) > n\ X)iLi 1 А- Множитель при п! может быть
сколь угодно большим при достаточно большом п (как частичная сумма
гармонического ряда). Поэтому ответ на вопрос задачи отрицательный.
154. Нет. 157. Произведение матриц A{Aj.
173. Решение можно найти в [63].
174. A - х)A + х + х2 + ... + Xя-1) = 1.
177. Нулевой гомоморфизм и тождественное отображение.
179. Да. 180. Все участвовали. 181. Мать и младшая дочь. 182. Нет.

118
Ответы. Указания. Решения
183. Эта дорога ведёт в ваш родной город? Положительный (отрица-
(отрицательный) ответ означает, что указанная дорога ведёт в А (соответственно
в Б).
Решение. Пусть х означает высказывание "встреченный путешествен-
путешественником житель правдив", а у означает высказывание "некоторая фиксиро-
фиксированная (конкретная) дорога ведёт в А". Для того, чтобы составить вопрос,
положительный (отрицательный) ответ /(ж, у) на который означает, что
указанная дорога ведёт в А (соответственно в В), составим таблицу истин-
истинности.
X
1
1
0
0
У
1
0
1
0
Ожидаемый ответ
Да
Нет
Нет
Да
f(x,y)
1
0
0
1
Из таблицы видно, что f(x, у) = х ~ у. Таким образом, нужно выяснить
соответствие направления дороги и места жительства "аборигена".
187. 22П~\ 188. 22".
189. х, х, у, у, z, ~z, xyVyzV zx, xy\/y~z\/~zx.
191. Если все переменные принимают значение ИСТИНА, то любая
их комбинация, содержащая из связок лишь &, V или —>¦, истинна. Таким
образом, отрицание не выражается через указанные логические операции.
193. х = х +jj
х V у = х ¦ у = (х + 1) (у + 1) = (х + 1) (у + 1) + 1 = ху + х + у;
х^-у = х\/у = (х + 1)\/у = х + 1 + у+(х + 1)у = х + ху + 1.
194. 1, х, у, ху; 16 многочленов @,1,..., 1 + х + у + ху) соответствуют
всевозможным подмножествам 4-элементного множества одночленов.
195. 1) х + у + z + ху + xz + yz + xyz; 2) ху + xz + yz; 3) х + у + z.
196. Существование вытекает из 193. Приведем также явную конструк-
конструкцию, позволяющую получить многочлен от п переменных, если известно
представление в виде многочлена любой функции от п — 1 переменных:
f(xu ...,хп) = /@, х2,..., хп) + xi (/@, х2, ¦ ¦ ¦, хп) + /A, х2,..., хп)).
Проверьте!
Единственность докажем двумя способами.

119
Комбинаторное доказательство. Из 2п одночленов от п перемен-
переменных можно составить 22™ многочленов. Столько же имеется и различных
логических функций от п переменных (поскольку таково число различ-
различных таблиц истинности функции от п переменных). Так как любая функ-
функция представима многочленом и число функций равно числу многочленов,
каждая функция представима ровно одним многочленом.
Доказательство по индукции. Индукция проводится по числу пе-
переменных. База индукции (число переменных равно нулю) очевидна. Ин-
Индукционный шаг. Пусть для функций от п — 1 переменных единствен-
единственность представления многочленом установлена. Предположим, что неко-
некоторая логическая функция от п переменных представима двумя много-
многочленами: /i(xi,..., хп) и /2(xi,..., хп). Пусть / = /i + /2. Из предположе-
предположения следует, что / — многочлен, при всех значениях переменных равный
нулю. Нужно доказать, что / — пустой многочлен (не содержит непу-
непустых одночленов), поскольку это равносильно совпадению многочленов fx
и /2. Сгруппировав слагаемые, содержащие х±, получим f(xi,... ,хп) =
Xig(x2,..., хп) + h(x2,..., хп). Подставив х\ = О, имеем h = 0. Подставив
теперь х\ = 1, имеем g + h = 0, откуда g = 0. Таким образом, задача
сведена к многочленам от п — 1 переменных.
197. 1), 3), 4), 5), 6), 8). Указание. 2) х VyVz = (х У у) V z; 7) функция
х + у входит в указанное множество, а функция х + у + z не входит.
198. Все дело в штрихе Шеффера.
199. 1), 2), 6).
204. б) Покажите, что P^cMuS.
212. Пусть высказывание а(Ь, с, d, е) означает: "А (соответственно
В, С, D, Е) присутствует". Тогда заданным условиям отвечают следующие
сложные высказывания:
1) s\ = а&е —>¦ Ь = aVeVЬ\
2) s2 = ё ->¦ Ь&с = е V be;
3) s3 = ak,c V alkc = (a\/c)(a\/ с) = dcV ас;
4) s4 = e->cl = eV(l;
5) s5 = (c -»¦ F -)¦ e))k(bkc -»¦ ekd) = (c V b V e)F V с V ed) =
= 6 V (c V e) (c&ed) =bV cedV ec.
Каждый вечер (с точки зрения присутствия на нем А, В, С, D, Е) мож-
можно описать совершенной элементарной конъюнкцией aaiba2ca3da4ea5, где О{
— логические переменные, не обращающиеся одновременно в 0. Таким об-

120
Ответы. Указания. Решения
разом, задача сводится к нахождению СДНФ для формулы
/ = S1&S2&S3&S4&S5.
Исходя из высказывания s3, рассмотрим два возможных случая.
• Пусть a = 1. Тогда с = 0, Si = ё V b, s2 = е V b, s5 = Ъ V е и
/= (eVb)(eVb)(eVd)(bVe) = 6(eVd).
• Пусть а = 0. Тогда с = 1, Si = 1, s2 = e, s5 = Ь V e<i и
/ = е(ё V d) F V ed) = edF V ed) = ebcl.
Значит, / = acb(e V d) V acebd = abcde V abode V abcde V abode.
Ответ. 4 вечера: Л, Б, Е; А, В, D; А, В; В, С, Е.
213. См. рис. 4, а). 214. См. рис. 4, б). 215. См. рис. 4, в).
216. См. рис. 4, г).
a
Ь
в)
а~ Ъ с —
г)
Рис.4. Схемы с минимальным числом контактов
220. АА = АА + О = АА +
А + А = (А + А) ¦ I = (А + А)(А
221. A + I= (A
222. Л + О = Л
( А)^ А-1 = А;
= А + АА = А + О = А.
= А
А = А + А =
224. Обозначим X = (А + В) + С, Y = А + (В + С). Нужно доказать,
что X = Y. Имеем:
АХ = А((А + В)+С)= А(А + В) + АС = А + АС = А;
АУ = А_(А+(В + С))=А_ + А(В_+С)=А; _ _ _
АХ = А((А + В)+С) = {АА +_АВ) + АС =^АВ + АС = А(В + С);
AY = А(А +(В + С))_= АА_ + А(В + С)= А(В + С).
Итак, АХ = AY, AX = AY. Поэтому
X = (А + А)Х = АХ + АХ = AY + AY = (А + A)Y = Y.
Доказана ассоциативность сложения. Из закона двойственности теперь
следует ассоциативность умножения.

121
238. Независимость аксиомы А от В и С будем доказывать указанием
интерперетации, при которой аксиомы В и С и все выводимые из них
формулы принимают одно значение, а формула А не всегда имеет это
значение.
Независимость А1 от А2 и A3. Будем считать, что каждая формула
имеет одно из значений 0, 1 или 2, и при этом логические связки —>¦ и ~~
задаются следующими таблицами.
В
А
0
1
2
0
А
1
0
0
1
->¦
1
1
1
2
В
1
0
1
А
0
1
2
А
1
0
1
Проверьте, что при любых значениях переменных формулы А2 и A3 при-
принимают значение 1, а из формул, принимающих значение 1, по правилу
modus ponens выводится формула, имеющая также значение 1. В то же
время при А = 2 и В = 1 формула А1 имеет значение 0.
Независимость А2 от А1 и A3. Будем считать, что каждая формула
имеет одно из значений 0, 1 или 2, и при этом логические связки —>¦ и ~~
задаются следующими таблицами.
В
А
0
1
2
0
А
1
0
2
1
->¦
1
1
1
2
В
1
1
1
А
0
1
2
А
1
0
0
Проверьте, что при любых значениях переменных формулы А1 и A3 при-
принимают значение 1, а из формул, принимающих значение 1, по правилу
modus ponens выводится формула, имеющая также значение 1. В то же
время при А= 1, В = 2, С = 0 формула А2 имеет значение 0.
Независимость A3 от А1 и А2. Будем считать, что каждая формула
имеет одно из значений 0 или 1, и при этом логические связки —>¦ и ~~
задаются следующими таблицами.
в
А
0
1
0 1
А^В
1 1
0 1
А
0
1
А
0
0

122 Ответы. Указания. Решения
Проверьте, что при любых значениях переменных формулы А1 и А2 при-
принимают значение 1, а из формул, принимающих значение 1, по правилу
modus ponens выводится формула, имеющая также значение 1. В то же
время при А = 1 и В = О формула A3 имеет значение 0.
250. Нет. К аксиомам исчисления предикатов можно добавить без про-
противоречия невыводимую в нем формулу
(Зх А{х)) ->¦ (Vx A{x)).
253. 6) min(x,2/) = х— (х—у); 7) тах(х, у) = у + (х—у).
255. 1) [x/y] = irSg(x-iy)-l;
2) rest(x, у) = х-[х/у] ¦ у; 3) div(x, у) = sgrest(x, у);
4) Pr(x) = sg(x-l) • sg (? div(x, i)-2)) ; 6) q(x) = ? sg(x + 1-г2)-1.
\г=0 / г=0
259. Пусть д(хь...,хп) = /J,y[f(x1,...,xn,y) = 0] < h(xu ..., хп),
где h — примитивно рекурсивная функция.Тогда
д(хъ...,хп) =
260. р(п) = /л[\тг(у) — п\ = 0]. Ограниченность сверху примитивно ре-
рекурсивной функцией р(п) < 2га+2 установлена в решении задачи 69.
261. ах{х) = 2(х + 1); а2(х) = 2Х+2 ¦ х + 2Х+3 - 2.
268. Пусть А — непустое примитивно рекурсивное множество, а —
некоторый его элемент. Положим
д(х) = х ¦ fA(x) + a ¦ sgfA(x).
Покажите, что множество значений функции д совпадает с А.
278. 6) B10 + С150)/2.
280. 1) С^. Каждая точка пересечения хорд однозначно задается
(неупорядоченной) четверкой точек — концов этих хорд.
2) 1 + С^ + С^. Будем последовательно проводить хорды. Каждая новая
хорда увеличивает количество частей на величину, равную количеству от-
отрезков, на которые хорда разбивается ранее проведёнными хордами, т.е.
на единицу больше, чем число её точек пересечения с ранее проведёнными

123
хордами. Поскольку при этом каждая точка пересечения считается ровно
один раз, количество частей, первоначально равное единице, после про-
проведения всех хорд увеличится на сумму числа точек пересечения и числа
хорд. Интересен ответ к задаче при п = 1,2,..., 6. Он таков: 1, 2, 4, 8,
16, 31. Физик из известного анекдота на основании первых пяти результа-
результатов заявил бы, что общий ответ — 2я, а число 31 возникло в результате
погрешности эксперимента.
282. п = 10, к = 5. 283. 2С? = 70.
286. l)Cj°; 2)Cf=126; 3)Cf° - Cfcf - 5 = 10431.
287. 5151.
288. Левая часть тождества — это число наборов г0, г1; ... ,in, удо-
удовлетворяющих неравенствам т > гп > in_\ > ц > i0 > 1. Пусть х0 =
г0 — 1, xi = ii — ц,..., хп = in — in-i, xn+\ = m — in. Тогда xo,xi,... ,xn+\
— неотрицательные целые числа, чья сумма равна т — 1. Число наборов
(хо, Х\,..., хп+\) равно Сп+2 = Сп+т = Сп+т.
289. Пусть Ак = {1, 2, 3,..., кп - 1}. Если а = ??=1 хп{ < кп, где х{ -
неотрицательные целые числа, то Vi Х{ < к — 1.
1) Из п натуральных чисел, каждое из которых не превосходит (к — 1),
можно составить (к — 1)п упорядоченных выборок. Поэтому в множестве
Ак по крайней мере кп — 1 — (к — 1)п чисел не представимо в виде Y^=i x?-
Число кп — 1 — (к — 1)п может быть сколь угодно большим за счет выбора
числа к.
2) Можно считать, что речь идет о представлении числа в виде суммы
ровно п слагаемых ~^^л=\х1^ если допустить, что некоторые из них могут
быть равны нулю. В указанной сумме каждое из п слагаемых принимает
одно из к значений: 0,1, 2га, Зга,..., (к — 1)п. Поэтому можно образовать не
более С% = С^+га_1 таких сумм. Заметим, что
L 2 3 ""¦ га 2 '
откуда
„_i, & + 1ч „_, jfc-l
/ll ^1, I m 1 IV \ IV I IV •
L L
Значит, не менее kn~l ¦ ^- чисел не представимы в указанном виде.
290. 1) (С2+1J; 2) га(га + 1)Bга + 1)/6. 292. Cf0.
294. Составьте отношение ак+\/ак-

124 Ответы. Указания. Решения
295. Покажите, что число равнобедренных треугольников с фиксиро-
фиксированным основанием не больше 3. Поэтому число треугольников, не явля-
являющихся разносторонними, не превосходит С22 • 3 = 198.
296. 52!/A3!L.
299. 1) Подсчитайте двумя способами сумму мощностей всех подмно-
подмножеств n-элементного множества.
306. (п — IK при нечётном п; (п — IK + 1 при чётном п.
307. С%7 — 6 • С\7 + Cl ¦ С\. Решение. Пусть U — множество последова-
последовательностей (аь п2, ¦ ¦ ¦, Об), составленных из шести неотрицательных целых
чисел с суммой 27; а для каждого г множество А{ С U состоит из таких
последовательностей, в которых щ > 10. Для решения задачи нужно вы-
вычислить | П Aj\. Заметим, что |С7| = Cf, \А{\ = С$7, \AiC\Aj\ =С\{%ф j),
а пересечение двух и большего числа множеств А{ пусто.
Замечание. Как отмечно в [9], ответ к данной задаче даёт число
счастливых 6-значных билетов (в которых сумма первых трёх цифр равна
сумме последних трёх цифр).
310. Используйте оценку остаточного члена ряда из признака Лейбни-
Лейбница.
311. 14833. 314. 6) (к - IJ = 2!С| - 1\С1к + 1. 315. М? = D? = 1.
317. fn.
318. 7) Можно доказать индукцией по т (или п). Существует также
комбинаторная трактовка этого тождества, связанная с "задачей о пры-
прыгуне".
319. О, 1, 12.
320. Примените индукцию.
325. 1) С помощью соотношения fn+k = fn-\fk + /n/fe+i проверьте ма-
матричное тождество
Теперь вычисление соответствующих определителей даёт желаемый ре-
результат. 2) Сложите тождества из п. 1) при т = п, к = 1и.т = п,к = 2.
335. 2nV5fn = A + V5)n - A - Vb)n.
336. 1) Используйте результат предыдущей задачи, а также следующие
соотношения:

125
2p~l = l(modp); Ckp : p при 1 < к < р.
2) Следствие 1).
337. Используйте задачу 323.
338. а) Да. Если условие задачи выполняется для последовательности
^-, ^-,..., ^-, то это же будет верно и для последовательности
711712 ' 7llGll+7!.2) ;
б) Нет. Покажите, что если бесконечная последовательность ^-, ^-,...
удовлетворяет условию задачи, то
n ^±a < ^ <
^ < < %.
/2ra+l Щ Нп
Переходя к пределу в двойном неравенстве по п, отсюда получаем,что
П2 у /п+1 1 + V5 ,
— = Inn —^ = —-— ^ Q.
339. f(x) = кх, где к = ^fi.
340. fn — п-е число Фибоначчи. Решение. Обозначим число искомых
подмножеств fn. Выпишем минимальные э-множества при п < 6:
{1}, {2, 3}, {2,4}, {2, 5}, {2, 6}, {3, 4, 5}, {3,4, 6}, {3, 5,6}.
Прямой подсчет показывает: /i = /2 = 1,/з = 2,/4 = 3,/5 = 5, /б = 8.
Возникает предположение, что для для любого натурального п
fn+2 = /n+i + fn- Убедимся в этом.
Разобьем все мэ-подмножества множества {1,2,...,п + 2} на два клас-
класса: множеств, содержащих число п + 2, и множеств, не содержащих это
число. Всякое множество из второго класса является мэ-подмножеством
множества {1,2,...,п + 1}, поэтому во втором классе fn+\ множеств.
Заметим, что в минимальном э-множестве, содержащем к элементов,
не могут присутствовать числа меньше к (из-за минимальности), и так как
множество — эгоцентрично, то число к — его элемент. Легко проверить, что
верно и обратное: произвольное ^-элементное множество с минимальным
элементом к будет мэ-множеством.
Возьмем теперь произвольное множество из первого класса (пусть к
— число его элементов; ясно, что к > 2), удалим в нем элемент п + 2, а
все остальные элементы уменьшим на единицу. Получим к — 1-элементное

126 Ответы. Указания. Решения
множество с минимальным элементом к — 1 — это мэ-множество, при-
причем максимальный элемент его не превосходит п. Установлено взаимно
однозначное соответствие между множествами из первого класса и мэ-
подмножествами множества {1,2,... ,п}. Таким образом, первый класс со-
содержит fn множеств. Соотношение fn+2 = /ra+i + fn доказано.
Замечание. Из чисел 1,2,... ,п можно составить C*zl ^-элементных ми-
минимальных э-множеств (к числу к нужно добавить ещё к — 1 больших к
чисел). Поэтому
2 -I
к
f — Г° 4-Г1 -А- Г2 -А- —
Jn — °п-1 "Г °п-2 "Г °n-3 "I"---—
fe=0
Другие доказательства данного тождества см. в задачах 320 и 330.
356. А(х) =В(х + 1).
357. 3) А(х) = ^4=^,
4)^ = Фе (A + л/5)
362. 2- (-1)п + 2п.
372. Sn+2 = 145га - Sn-i; rn+2 = ^rn+i - гп.
375. 927. Указание. Обозначим через ап число двоичных последова-
последовательностей длины п, удовлетворяющих условию задачи. Найдите началь-
начальные условия и рекуррентное соотношение для последовательности (ап).
378. 4) 55252.
379. A6П - 4п)/12. Решение можно найти в [58].
380. Сделайте замену уп = 2ап + 1 и докажите, что уп+\ = Ауп — уп-\.
381. Обозначив левую часть доказываемого тождества через Sn, дока-
докажите, что Sn+i = Sn — pqSn_\.
382. 99 руб 99 коп. Если бы у шулера было 100 руб, то он был бы
всегда в выигрыше.
383. Нет. Решение. Каждый шаг удваивает длину последовательно-
последовательности. После очередного шага она имеет вид (для некоторого п)

127
1°. Докажем индукцией по к, что У к а2к = 1 — огк-ъ или a2k + &2к-\ = 1-
База индукции очевидна. Пусть доказываемое утверждение верно
для к < 2п. Докажем его справедливость для к, удовлетворяющего
двойному неравенству 2п < к < 2га+1. Действительно,
«2"+2г = 1 - «2г, «2"+2г-1 = 1 ~ «2г-1 (гДв 1 < 21 - 1, 21 < 2п), Откуда
«2"+2г + «2«+2г-1 = 2 — (fl^i + O2i-l) =2—1 = 1.
2°. Вновь по индукции докажем, что \lk a2k-i = ctk- Для к = 1 это утвер-
утверждение тривиально. Пусть оно выполняется для к < 2п. Тогда при
г < 2п имеем а, = а2г-ь °2™+г = 1 ~ аи a2n+2i-\ = 1 — агг-ь откуда
а2«+1+2г-1 = а2п+г, т.е. доказываемое соотношение выполняется и при
А; < 2п+\
3°. Пусть ага — периодическая с некоторого места последовательность и Т
— период. Докажем, что число Т — четно.
Если Т нечётно, найдётся период, первый элемент которого имеет
нечётный индекс. Рассмотрим этот период и следующий за ним:
O.2J-1, U2j, ¦ ¦ ¦ , U2J+T-2] fyy+T-b • • • j «2J+2T-2-
В силу 1° этот отрезок последовательности содержит поровну нулей
и единиц, этот "паритет" должен иметь место и для каждого периода,
что, однако, невозможно из-за нечётности Т.
4°. Пусть Т = 2s — наименьший период. Тогда 3&о V& > ко cife+т = Q-к- В
силу 2° Ук >к0 ак = a2fe-i = а-2к-\+т = a2(k+s)-i = ^k+s, то есть s —
также период последовательности, что противоречит минимальности
Т.
Доказано, что последовательность не является периодической.
390. (п - 1)! 391. 98475. 395. 16 и 11 соответственно.
401. l(Cl4 + 2C2m + ЗС|2 + 2(С|8 + CfCf8 + CfCf8 + CfC^ + CD) =
= 553 332 533.
402. |B24 + 2 • 26 + 3 • 212 + 2 • 24 • 210) = 2 102 800.
403. 13 звёзд и 88 мечей.
406. Существует 11 простых графов с 4 вершинами и 34 — с 5 верши-
вершинами.
407. 1) 1; 2) 2.

128 Ответы. Указания. Решения
411. Пусть v — вершина максимальной степени; k = p(v). Если ни одна
из к вершин, смежных с v, не является висячей, то степени этих вершин
принимают значения от 2 до к; поэтому по крайней мере две из них имеют
одинаковую степень, хотя соединены цепью длины 2.
415- \ E"=i Pi вершин и \ YTi=i{p1 ~ Pi) Рёбер.
Решение. Вершина рёберного графа L(G), отвечающая ребру V{Vj в G,
имеет степень (pi + pj — 2). В сумме А = ^{pi + Pj — 2), где суммирование
ведётся по всем рёбрам G, степень каждой вершины pi встречается ровно
Pi раз. Поэтому удвоенное число рёбер L(G) равно А = ^2р2 — 2m, где
2m = ^2 Pi — удвоенное число рёбер исходного графа G.
Другое решение. Ребра, инцидентные г-й вершине в графе G, образу-
образуют Ср. пар смежных рёбер, каждой паре соответствует ребро в рёберном
графе. Суммируя CPi по всем г, вновь найдём общее число рёбер L(G).
416. Достаточность очевидна. Необходимость. Из предыдущей за-
задачи следует: Ya=\ Pi = 2n5 YH=\p\ = 4n> откуда Y!i=i(pi ~ 2J = °> T-e-
Vi pi = 2. Связный регулярный граф степени 2 есть циклический граф.
441. п2 + п.
445. 1) а) Р^(хих2, ¦ ¦ ¦) = 2^0? + 9х2х22 + 8х23 + Ьх\х\);
2) Положив вес ребра равным х, а вес неребра равным 1, получим следую-
следующие производящие функции J^amxm, где т — число графов с т рёбрами:
а) ?amzm = ? W(F) = Р4A+х, 1+х2,...) = 1+х+2х2+Зх3 + 2х4+х5+х6;
б) Y,amXm = Y,wiF) =Р5A + х,1 + х2,...) = 1 + х + 2х2 + 4х3 + 6х4 +
6х5 + 6х6 + 4х7 + 2х8 + х9 + хю.
451. При нечётных п.
453. 3 раза. См. задачу 452.
454. 1) Да; 2) нет.
459. В гамильтоновой цепи и —>¦ ... —>¦ v, где вершины и и v не смежны,
произвольная вершина, смежная с и (обозначим её и'), не может следовать
за вершиной (например, г/), смежной с v. Действительно, гамильтонова
цепь u—>...—>v'—>u'—>...—>v легко преобразуется в гамильтонов цикл
и —>¦ ... —>¦ v' —>¦ v —>¦ ... —>¦ и' —>¦ и. Поэтому число вершин, не смежных с
и, не меньше числа вершин, смежных с v, то есть п — 1 — p(u) > /o(w), или
yo(u) + p(v) < п — 1.
460. Предположив, что граф не является гамильтоновым, будем после-
последовательно добавлять к нему рёбра до тех пор, пока он не станет гамильто-

129
новым. Удалив последнее добавленное ребро uv, получим полугамильтонов
граф G', не являющийся гамильтоновым. В нем существует гамильтонова
цепь и —>...—> v, причем вершины ииине смежны. Применение резуль-
результата предыдущей задачи даёт: p'(u)+p'(v) < п—1, где р'(и), p'(v) — степени
вершин и hvb графе G'. Осталось заметить, что р'(и) > р(и), p'{v) > p(v),
откуда р{и) + p(v) < р'(и) + p'(v) < п — 1 < п. Получено противоречие с
условием.
461. 38.
462. Упорядочим степени вершин графа по неубыванию:
Pi < /02 < ¦ ¦ ¦ < /0га. Условие теоремы теперь можно сформулировать так:
V&<^-^ pk>k. (*)
Предположив, что граф негамильтонов, будем, пока это возможно, доба-
добавлять к нему рёбра так, чтобы не получить гамильтонова графа. В резуль-
результате получим граф, в котором любые две несмежные вершины соединены
гамильтоновой цепью, и, как показывает задача 459, сумма их степеней
не больше п—1. Для степеней вершин полученного графа G' условие (*)
сохраняется. Выберем в G' пару несмежных вершин и hv, сумма степеней
которых принимает наибольшее значение. Пусть к = р(и) < p(v). Тогда
(поскольку р(и) + p(v) < п — 1) выполняется неравенство к < ^^-. Кроме
того, степень любой вершины, не смежной с v, не превосходит р{и) = к.
Вершин, не смежных с v, не меньше, чем вершин, смежных с и (см. задачу
459), т.е. не меньше к. Таким образом, не менее, чем к вершин, имеют сте-
степень не больше к. Поэтому pk < к. Полученное противоречие доказывает
теорему.
466. Рассмотрите вершину, смежную с концом самой длинной цепи.
469. г = [^] . 471. Нет. 478. п11'1. 479. к + 1.
482. 1 + YH=i кщ — X)fe=infe- Из общего количества вершин нужно
вычесть количество внутренних вершин.
483. C2V(n + l).
484. Наибольшее число вершин равно 2n+l — 1, а наименьшее /га+3 — 1.
Указание. Пусть ап — наименьшее число вершин в сбалансированном
дереве высоты п. Тогда а0 = 1, а,\ = 2, ап+2 = 1 + ап + ап+\. Отсюда для
разности ип = ап — ап_\ имеем щ = 1, и2 = 2, ип+2 = ип+\ + ип, то есть
ип = /ra+i — n+1-e число Фибоначчи. Значит, ап = ura+ura_i + .. .+щ + а0 =
/ra+i + /n + ¦ ¦ ¦ + /2 + /i- Осталось использовать тождество 3) задачи 318.

130
Ответы. Указания. Решения
485. 42. 486. к < 4.
490. 2m = sf = p{m - / + 2).
491. Пять Платоновых графов, циклические графы и графы с двумя
вершинами без петель. Указание. Если в графе из условия задачи более
двух вершин, то степень каждой вершины не превосходит 5. Используйте
далее тождество предыдущей задачи.
492. Нет.
493. Если у планарного графа п вершин и m рёбер, то выполняется
неравенство m < Зп — 6.
494. Индукция по числу вершин.
495. Нет. Указание. Докажите связность графа. Применяя лемму о
рукопожатиях, легко найти число рёбер графа: m = 25. Если бы граф был
плоским, то (по формуле Эйлера) он имел бы 17 граней. Так как каждая
грань ограничена не менее, чем 3 рёбрами, для m имеем неравенство 2т >
3-17, а оно не выполняется.
497. Доказательство можно найти в [44], с. 100.
498. Возьмём грань с наибольшим числом сторон. Сколько сторон мо-
может быть у смежных граней?
500. См. рис.
502. 1) В Кп имеем С\ полных подграфов с 5 вершинами. Каждый
из них даёт хотя бы одно скрещивание, а каждая пара скрещивающихся
рёбер входит в п — 4 таких подграфов. Отсюда
l_ = n(n-l)(n-2)(n-3)(n-4) = С^_
п — А 5! • п — 4 5
2) В Кт!П имеем С^ • С\ подграфов вида -Кз,з- Каждый из них даёт хотя
бы одно скрещивание, а каждая пара скрещивающихся рёбер входит в
(т — 2)(п — 2) таких подграфов. Отсюда
>
ст(Кт:П) >
СЗ
т '
¦ Сп
(m-2)(n-2)

131
503. cr(X6) = 3; cr(X3,4) = 2; сг(#4,4) = 2.
505. Acv{G)/n — это среднее число скрещиваний, приходящихся на
рёбра, инцидентные вершине графа.
506. На рис. приведено изображение графа Петерсена с двумя пересе-
пересечениями.
Для доказательства того, что одним пересечением при изображении графа
обойтись нельзя, используйте утверждение задачи 505.
508. и/Т1'1.
510. В исходном графе существует эйлеров цикл.
511. Перенеся доказательство теоремы Эйлера на случай графа из
условия задачи, можно построить замкнутый путь, содержащий все ду-
дуги орграфа.
515. Произвольно ориентируем рёбра графа. Поскольку сумма полу-
полустепеней исхода {пси) всех вершин равна числу рёбер и, значит, есть число
чётное, число вершин с нечётной пси четно. Возьмём произвольную цепь,
соединяющую две такие вершины, и поменяем ориентацию всех входящих
в нее дуг. Теперь пси этих вершин станут чётными, в то время как пси
остальных вершин не изменятся. Повторяя эту процедуру, пока она воз-
возможна, получим в конце концов требуемую ориентацию дуг.
522. Пусть в турнире п вершин. Исходя из соотношений J^ V(w) =
и *P(V) + ~t(v) = п - 1 (Vw), получим: ? У2(^) - Ys~f?2{v) =
) - t(v))(*p(v) + t(v)) = (n - 1) U*P(v) ~ -f(v)) = 0.
524. Постройте соответствующие примеры при п = 3игг = 6и приду-
придумайте, как от турнира с п вершинами перейти к турниру с п+2 вершинами.
529. Примените индукцию по числу вершин.
530. Примените индукцию по длине цикла.
532. Из сильной связности следует, что всякая вершина входит в неко-
некоторый цикл; например, V\ входит в цикл V\ —> v^ —>...—> vn —»¦ v\ длины
п. Если п > 3, то можно указать цикл меньшей длины. Действительно,

132 Ответы. Указания. Решения
если в графе есть дуга v3v\, то это цикл v\ —> v<i —> v3 —> г>1; в противном
случае — цикл v\ —>¦ г>3 —>•...—>¦ vn —>¦ г>1.
536. Рассмотрите остовный лес графа. Он является двудольным гра-
графом.
538. 1, 2, 2, 4, 16. Пример минимального доминирующего множества
при d = 7:
0000000, 0000111, 0011001, 1100001, 0101010, 1010010, 0110100, 1001100,
1111111, 1111000, 1100110, 0011110, 1010101, 0101101, 1001011, 0110011.
540. Так как диаметр графа равен 2, доминирующим множеством бу-
будет Г(г>) — множество вершин, смежных с v, где v — произвольная вершина
графа. Поэтому S(G) < mmveV p(v).
При S(G) = 1 доказывемое утверждение очевидно. Считая, что S(G) >
2, положим т = S(G) — 1. Тогда Vw p(v) > т. В силу того, что ника-
никакое множество из т вершин не является доминирующим, для любых т
вершин графа G найдётся вершина, не смежная с этими т вершинами.
Поскольку всего существует С™ множеств из т вершин, найдётся такая
вершина и в графе G, для которой существует не менее С™/п неупо-
неупорядоченных наборов из т вершин, ни с одной из которых эта вершина
не смежна. Действительно, обозначив через fcj число т-элементных мно-
множеств вершин, не пересекающихся с T(vi), получим Y^a=\ &i — С™, откуда
max ki > С™/п. С другой стороны, так как р(и) > S(G) = т + 1, для дан-
данной вершины и найдётся п — 1 — р(и) < п — т — 2 вершин, не смежных
с ней. Из указанных вершин можно составить не более С™_т_2 наборов
по т вершин. Таким образом, выполняется неравенство С™_т_2 > С™/п,
или C^lto_2/C™ > 1/п. Последнее неравенство запишем в виде
(п — т — 2)(п — т — 3)... (п — 2т — 1) _
п(п — 1)... (п — т + 1)
т+2
)>.
п — т + 1/ п
В полученном произведении первый множитель больше всех последующих
и поэтому больше среднего геометрического всех т множителей, которое,
в свою очередь, не меньше, чем 1/ у/п. Получено неравенство
т + 2 1
п \/п

133
Прологарифмируем его: ln(l — m^L) > —^f • Применив (справедливое для
О < х < 1) неравенство 1пA — х) < —х, получим теперь — m^L > — ^, или
т2 + 2т < п\пп, откуда т < — 1 + л/п\пп + 1.
Таким образом, S(G) = т+1 < л/п In п + 1, что и требовалось доказать.
546.
граф Сг
ao(G)
A) (G)
ai{G)
Pi(G)
сп
[Я
[fl
1
n-1
wn
[?]
[?]
max(n, m)
min(n, m)
min(n, m)
max(n, m)
граф Петерсена
4
6
5
5
549, 550. Доказательство можно найти в [7].
551. Используйте теорему О. Оре (задача 460).
552. Доказательство ведётся индукцией по п.
553. Число вершин в кубическом графе четно. Гамильтонов цикл рас-
распадается на два совершенных паросочетания. Оставшиеся рёбра составля-
составляют ещё одно совершенное паросочетание.
555. См. рис.
556. Если совершенное паросочетание одно, то "структура" графа оче-
очевидна. Пусть теперь число совершенных паросочетаний, на которые рас-
распадается граф, не менее двух и в графе есть мост — ребро uv. Рассмотрим
ту компоненту, которой принадлежит вершина и после удаления ребра uv.
В этой компоненте имеется одна вершина чётной степени, а остальные вер-
вершины нечётной степени. Из леммы о рукопожатиях получаем, что в этой
компоненте связности нечётное число вершин. Значит, после удаления ре-
ребра uv граф не содержит совершенного паросочетания. По условию ребро
uv входит в одно из совершенных паросочетаний; других, стало быть, нет.
Полученное противоречие доказывает утверждение задачи.

134
Ответы. Указания. Решения
557. Данную задачу решают организаторы спортивных турниров, про-
проходящих по круговой системе (когда каждый играет с каждым).
Если вершинам графа K<in сопоставить участников турнира, а рёбрам
— встречи между ними, то каждому туру состязания соответствует неко-
некоторое совершенное паросочетание (участники образуют п пар).
Шахматисты поступают следующим образом. Если участник турнира
получил при жеребьевке номер i < 2п, то он последовательно встречает-
встречается с игроками, имеющими такие номера: 2гг. + 1 — г, 2п + 2 — г,..., 2п —
1,1,2,... ,г — 1, 2п, % + 1,..., 2п — %. Для иллюстрации приведем расписа-
расписание встреч для турнира с 8 участниками. В каждой клетке следующей
таблицы проставлен номер тура, в котором встречаются соответствующие
участники.
N участника
1
2
3
4
5
6
7
8
1
¦
2
3
4
5
6
7
1
2
2
¦
4
5
6
7
1
3
3
3
4
¦
6
7
1
2
5
4
4
5
6
¦
1
2
3
7
5
5
6
7
1
¦
3
4
2
6
6
7
1
2
3
¦
5
4
7
7
1
2
3
4
5
¦
6
8
1
3
5
7
2
4
6
¦
В турнирах по настольному теннису принят иной алгоритм распределения
встреч по турам. В качестве примера приведем расписание встреч для 8
участников (каждая колонка отвечает очередному туру).
1-8
2-7
3- 6
4-5
1-7
8-6
2- 5
3-4
1-6
7- 5
8- 4
2-3
1-5
6-4
7-3
8-2
1 - 4
5-3
6-2
7- 8
1-3
4- 2
5- 8
6- 7
1 - 2
3-8
4-7
5- 6
При переходе к очередному туру 1 стоит на месте, а любое другое число
сдвигается против часовой стрелки на одну позицию либо (после "встречи"
с единицей) на две позиции.
Читателю предлагается самостоятельно доказать корректность описан-
описанных алгоритмов.
В книге [39] (гл. 8, §3) приводится ещё один способ составления распи-
расписания встреч кругового турнира.

135
558. Ребра одного цвета должны составлять совершенное паросочета-
ние. При нечётном п ответ отрицательный, при чётном п — положитель-
положительный (см. предыдущую задачу).
564. Решение задачи о свадьбах существует тогда и только тогда, когда
любые к юношей из данного множества знакомы в совокупности не менее,
чем с к девушками.
569. Нет. Инвариант — объём тетраэдра, в вершинах которого сидят
мухи.
570. Нет. Разность числа хамелеонов разного цвета каждый раз либо
не меняется, либо меняется на 3.
571. а) да; б) нет. Изучите остатки от деления на 3.
573. Нет. После каждого броска меняется ориентация треугольника.
574. Нет. Инвариант — дискриминант квадратного трёхчлена.
575. Только при нечётном п. Инвариант — сумма номеров деревьев,
занимаемых чижами, по модулю п.
576. Пронумеруем лампочки, начиная с зажённой, числами от 1 до
12. Подсчитайте, как может измениться за каждый ход число горящих
лампочек в множестве {1, 2, 4, 5, 7, 8,10,11}.
578. Сумма попарных произведений соседних чисел увеличивается с
каждой операцией.
579. Полуинвариант — сумма квадратов чисел.
580. Разделим сначала парламент на две палаты произвольным обра-
образом. Если перевести в другую палату того, у кого в данной палате более
к врагов, то общее число пар врагов в парламенте уменьшится.
581. Нет. 582. Нет. 583. 1) Да; 2) нет.
584. Пусть а = тг/п. Для приведения к противоречию предположим,
что при повороте второго многоугольника на угол к а его вершина с номе-
номером Cfe совпадает с вершиной первого многоугольника, имеющей тот же но-
номер (к = 1,..., 2п). Тогда первоначально эта вершина занимала позицию,
чей "номер" сравним по модулю 2п с числом с^ — к. Заметим, что числа с^
принимают все значения от 1 до 2п; числа с^ — к образуют полную систему
вычетов по модулю 2гг. С одной стороны, ^^(с* — к) = ^ с& — ^ к = 0.
С другой стороны, J22kLiick — к) = Bп + 1)п ф 0(mod2n). Противоречие
получено.

136 Ответы. Указания. Решения
585. Число п должно быть нечётно.
Если п = 2к-\-1, то на диагонали, идущей с верхней правой клетки к ниж-
нижней левой клетке, стоят неповторяющиеся числа
2к + 1, 2к - 1, 2к - 3,..., 1, 2к, 2к - 2,..., 2.
Пусть п = 2к. Обозначим через ац элемент таблицы, стоящий в г-й стро-
строке и j'-m столбце. Имеет место соотношение ац = j — % + l(modn). Если
{ii,..., in) = {ju ..., jn} = {1,..., n) (т.е. aiujl,..., aindn — числа, взятые
по одному из каждой строки и каждого столбца таблицы), то ^Щк^к =
^2(jk — Ч + 1) = п = O(modn). Если бы все числа а^^,..., (iinjn были бы
разными, то выполнялось бы сравнение Yl aik,jk = ^Г ' п = A + %к)к =
к (mod 2 к), противоречащее ранее найденному.
586. Занумеруем вершины по ходу часовой стрелки числами от 1 до
2гг. Звенья ломаной г — j и к — I параллельны тогда и только тогда, когда
г + j = к + /(mod2n). Пусть идущие по порядку вершины ломаной име-
имеют номера ai,a,2, ¦¦¦ ,an,a,i. Рассмотрим остатки от деления на 2п чисел
щ + aj+i. Если все они различны (что равносильно отсутствию в ломаной
параллельных звеньев), то они принимают все значения от 0 до 2п — 1
и их сумма равна пBп — 1), что сравнимо с п по модулю 2гг. С другой
стороны, J2f=\(ai + ai+i) = 2 J2f=\ i = 2ггBгг + 1) = 0(mod2n). Полученное
противоречие доказывает утверждение задачи.
587. За 2гг + 1 ход. Решение. Пусть
к (т) — разность числа ходов волка вправо и влево с горизонтальной
составляющей п (соответственно п+ 1);
г (s) — разность числа ходов вверх и вниз с вертикальной составляющей
п (соответственно п + 1).
Если волк передвинулся в соседнюю сверху клетку, то
кп + т(п + 1) = 0; A)
rn + s(n+ 1) = 1. B)
Из A) следует, что к : п + 1, т : п. Если к = 0, то т = 0, а s четно;
равенство т = 0 влечет чётность г; но тогда левая часть B) четна, что
невозможно. Поскольку к ф 0 и та ф 0, имеем: \к\ > п+1 и \т\ > п. Значит,
общее число ходов не меньше 2гг + 1. Покажем, как за 2гг + 1 ход попасть
в нужную клетку. Для этого можно сделать п ходов типа (п, — (п + 1)),
один ход (гг, п+1) и п ходов типа (—(гг + 1), гг), где (a, b) означает ход на а
клеток по горизонтали и Ь клеток по вертикали, а знак минус соответствует
движениям влево или вниз.

137
588. Докажите, что любые две противоположные (п— 1)-мерные грани
соединяет ребро с покрашенными концами.
589. 2. 591. Нет.
592. При чётном п число ап делится на 101; при нечётном п имеем
разложение
/102fe+i_1
{
9
595. m = l,neN; m = 2, n = 3.
605. Используйте метод математической индукции. В тождестве ж4 +
х2 + 1 = (х2 + 1 - х)(х2 + 1 + х) положите х = 22". Числа 22" - 22" + 1 и
22П+22" +1 взаимно просты, так как если бы у них был общий (нечётный)
множитель q, то их разность 22" +1 делилась бы на q, что неверно.
606. 1 000 001 = 101 • 9901; 1 000 009 = 293 • 3413;
1000 049 = 353-2833; 1000169=197-5077; 1000 361 = 97-10 313;
1 000 441 = 13 • 41 • 1877; 1 000 529 = 29-34 501.
608. 13 717421 = A02 + 7 • 232) • F02 + 7 • I2) = 3803 • 3607.
609. Доказательство будем вести методом от противного. Предполо-
Предположим, что ai&i, 0262, ¦ ¦ ¦, ctnbn — полная система вычетов. Если при % ф
j ai = 0(modn) и bj = 0(modn), то аф^ = ajbj = 0(modn) и числа
ai&i, a,2, 62, ¦ ¦ ¦, ctnbn не образуют полной системы вычетов по модулю п. По-
Поэтому без ограничения общности можно считать, что an = bn = 0(modn).
Можно также положить, что Vi щ = г. Рассмотрим два возможных слу-
случая.
• Число п свободно от квадратов.
Пусть п = рт, где р — наибольший простой делитель п. Тогда р > 2
и т не делится на р. Если j : т, то ajbj = jbj : m и остаток от деления
ajbj на п кратен т. Для полной системы вычетов ai&i, a^-, &2, • • •, CLnbn
остатков такого вида должно быть ровно р (включая нулевой). По-
Поэтому для любого j, делящегося на т, число bj также кратно т.
Вычислив произведение чисел ajbj для j = т, 2т,... ,(р — 1)т, по-
получим
р-1
TTafcmfrfcm = т • 2т • ... • (р — 1)т = (р — l)!mp~1(modn).
fc=i

138 Ответы. Указания. Решения
С другой стороны,
р—1 р—1 р—1
fc=l fc=l fc=l
Таким образом, (р — l)\mp~l = ((р — l)!mp~1J(modn), или
(р— l)\mp~l((p— l)!mp~1 — 1) :рт, откуда в силу простоты р следует,
что (р — 1)!тр~1 — 1 : р. По теореме Вильсона (р — 1)! = — l(modp).
Стало быть, тр~1 + 1\р. В силу малой теоремы Ферма
mp~l = l(modp), и, значит, 2 : р, что невозможно, так как р > 2.
Получено противоречие.
• Число п делится на квадрат некоторого простого числа.
Пусть п = p2s, где р — простое число. Тогда
aj = 3 :Р ^=^ bj : р <^=^ ujbj : р
(в противном случае среди чисел a\b\,a2,b2, ¦ ¦ ¦, anbn будет "больше,
чем нужно" (для полноты системы вычетов) таких чисел, которые
при делении на п дают остаток, кратный р). Таким образом, если
cijbj : р, то cijbj : р2, и среди чисел a\b\, а2, Ь2, ¦ ¦ ¦, anbn нет, например,
имеющего остаток р от деления на п = p2s. Вновь пришли к проти-
противоречию.
Замечание. В [41] рассмотрен частный случай этой задачи, когда п —
простое число.
п цифр
2
610. Обозначим ап = 22 и Ьп = ап — ara_i. Докажем сначала,
что в последовательности (Ьп) каждый член (начиная с Ь3) делится на
предыдущий (значит, и на все предыдущие). Действительно, Ь2 = 22 — 2 =
2; Ь3 = аз — а2 '¦ 2 = Ь2. Предположим, что bk+\ : bk- Тогда
bk+2 = ak+2 - ak+l = 2a*+' - 2ak = 2a» Bak+1~ak - 1) = 2akBbk+1 - 1).
Поскольку последовательность (ak) возрастающая, 2ak : 2ak~1. Так как (по
предположению индукции) bk+\ ¦ bk, имеем также 2bk+1 — 1 : 2bk — 1. Таким
образом, bk+2 : 2ak~lBbk - 1) = bk+l.

139
Перейдем к непосредственному доказательству утверждения задачи.
Оно также проводится методом математической индукции. База индукции
очевидна (&2 = 2). Пусть теперь для любого к < п выполняется Ьк : к.
Представим число п в виде п = 2st, где t — нечётное число. Легко
проверить, что при п > 3 имеет место неравенство ага_2 > п. Отсюда
Ьп : 2пп-2 : 2п : 2s. Теперь осталось доказать, что 2Ьп~1 — 1 : t.
Применим теорему Эйлера. Заметим, что <р(п) = <pBs) -<p(t) = 2s~l(p{t).
Поэтому ip(t) < (р(п) < п — 1. Для любого к < п — 1 имеем bn-i : bk : к.
В частности, bn-\ : tp(t). Отсюда следует, что 2Ьп~1 — 1 : 2V^ — 1. В силу
теоремы Эйлера 2^1' — 1 : t. Из последних двух соотношений и вытекает,
что 2Ьп~1 — 1 : t. Таким образом, Ьп : п.
611. ак - 1 = (а - 1)(ак~1 + ак~2 + ... + 1).
Так как а = l(modA;), то а-7 = l(modA;) и 5Z,-Zq a? '¦ к.
612. Доказательство проведём в несколько этапов.
1°. Применив п раз утверждение задачи 611, получим следующий резуль-
результат:
Если а - 1 : кт, то акп - 1 : кт+п.
2°. Докажем, что Vn ип+\ — ип : 2п.
При чётном а число ип = aUn~l делится на 2п (так как ura_i > п).
Пусть теперь а нечётно. Доказательство будем вести по индукции.
База индукции очевидна: г*2 — и\: 2. Пусть щ+\ — щ = s ¦ 2к (s e N).
Тогда щ+2 — Щ+1 = Uk+i(aUk+1~Uk — 1) : as'2 — 1. Осталось заметить,
что as — 1:2 и поэтому (в силу 1°) (asJ — 1: 2k+l. Индукционный шаг
доказан.
3°. Докажем, что Vn > 2 ип+\ — ип : 5га~2.
Если а кратно 5, то Vn ип = а""-1 : Ъп (так как ura_i > n). Отсюда
следует, что Vn ип+\ — ип\Ъп. Если а не делится на 5, то по малой
теореме Ферма а4 — 1 : 5. Вновь применяя индукцию, предположим,
что Ufe+i — Ufc = s ¦ 2k • 5k~2. Тогда (при к > 2)
uk+l = uk+Mk+1~Uk " 1) = uk+l(aAt-5k~2 - 1),

140 Ответы. Указания. Решения
где t = s-2k~2. Так как а4 —1:5, au —1:5 и в силу 1° имеем: (а4*M 2 —
1 : б*1. Индукционный шаг доказан, а база индукции очевидна.
4°. Из 2° и 3° вытекает утверждение задачи.
Замечание 1. Аналогично можно доказать,что
Vm 3/ Уп > I un+i — un : mn~l.
Замечание 2. Развитие темы двух последних задач см. в [56].
614. Отметим сначала, что каждое слагаемое делится на р
(Ср = п,р'_1у— целое число; числитель дроби кратен р, а знаменатель
— нет (так как р — простое число)). Доказываемое утверждение
равносильно делимости на р суммы Yli=i^-~E- Проведем сравнение по
модулю р:
Щ fc!(p-l)(p-2)...(p-» + l) = (-1)*-^! d
i
=
pi (i — 1)!
Итак, задача сводится к проверке того, что
По условию р не делится на 3. Рассмотрим два возможных случая.
1) р = Зт + 1. Здесь т — чётное число (иначе р делилось бы на 2). Тогда
к = [^] = 2т. Имеем:
Bт)! Л -! + ...- -Ц=Bт)! fl + 1
\ 2 2т/ V 2
-1-1-...-
2
... + 1...
2т 2 т
m + 1 m + 2 2m) f-Л—'- \m
m/2 B V
= Cm+l)V--—^— -!3m+l=p.
2) р = Зт + 2. Здесь т —нечётное число (иначе р делилось бы на 2). Тогда
к = [^f^] =2m + l. Имеем:

141
m+l
m
—- ^ = VBm+1)! (—^
2m + 2 -
m+l
2
= Cm + 2)V
Bm + 1)!
: 3m + 2 = p.
615. /Зп не делится на 5 при только при
п = 1,..., 4, 20,..., 24,100,..., 104,120,..., 124. Подробное решение см. в
[63].
616. Нечётно. Решение приведено в [63].
620. ат = a(modm) => aP~l = aTO^~^(modm). Так как к тому же т\р2,
отсюда следует, что ap~l = aTO^~^(modp2). Наконец,
т \ р => ат^-^ - 1 ! ар(р-^ - 1 = а?^ -lip2.
621. Нет.
623. Достаточно доказать, что наибольший общий делитель
г = (т — 1,р — 1) равен (р — 1). Поскольку
Уа, (а, т) = 1 а -1\т:р, а?'1 -1\р,
имеем: {ат~1 — 1, аР~1 — 1) = а^то~1>р~^ — 1 = аг — 1 \р. Таким образом, при
г < р—1 сравнение хг — 1 = 0(modp) имеет р—1 > г решений A, 2,... ,р—1).
Осталось применить результат задачи 100 и получить противоречие.
624. В таблице приведены числа Кармайкла < 2 117 000.
561
1105
1729
2465
2821
6601
8911
10585
15841
29341
41041
46657
52633
62745
63973
75361
101101
115921
126217
162401
172081
188461
252601
278545
294409
314821
334153
340561
399001
410041
449065
488881
512461
530881
552721
656601
658801
670033
748657
825265
838201
852841
997633
1024651
1033669
1050985
1082809
1152271
1193221
1461241
1569457
1615681
1773289
1857241
1909001
2100901
Студент Алексей Гуйдо составил программу, которая нашла первые 336
чисел Кармайкла. Самое большое из них — 146 843 929. Пусть с(п) — коли-
количество чисел Кармайкла, не превосходящих п. Известны ([49]) следующие
значения с(п).

142
Ответы. Указания. Решения
к
cA0fe)
3
1
4
7
5
16
6
43
7
105
8
255
9
646
10
1547
Интересные сведения о числах Кармайкла можно найти в Интернете по
адресу
www.utm.edu/research/primes/glossary/CarmichaelNumber.html.
627. (fog) о h(n) = fo(goh)(n)= ? f{dl)g{d2)h{dz).
628.
= ?
di\n,d2\m
di\n
(fog(m)).
d2\m
629. Определим функцию f'(n) следующими соотношениями. /'A) =
1. (Тогда /о/'A) = / • /'A) = 1.) Для каждого простого числа р пусть
f'(p) = —f(p)- (Отсюда следует, что / о f'(p) = 0.) Положив
/V) = -(/(Я + f(pn-lf(p) + ¦¦¦ + /OO/V)).
мы добьемся того, что Vn /о f'(pn) = 0. Пусть теперь /' — мульти-
мультипликативная функция. Поскольку значения /' определены на всех степе-
степенях простых чисел, свойством мультипликативности функция полностью
определена. В силу задачи 628 функция Ф = / о /' мультипликативна. По-
Поскольку ФA) = 1 и для любого простого числа р и любого натурального п
справедливо Ф(рп) =0,
Доказано, что / о /' = J.
630. Пусть /' — мультипликативная функция со свойством / о /' = J.
Тогда функция д = Jog = (f'of)og = /'о(/од) также мультипликативна.
633. Пусть п = р\1рГ2 ¦ ¦ -ргкк, где к > 1. Поскольку /j,(d) ф 0 только
если число d свободно от квадратов, имеем: ~Yld\nn{d) = цA) + J^l^{Pi) +
l-k + C2k-C3k-... + (-1)к = A - l)fe = 0.

143
634. /jLOT = E, /jLO S = I.
635. Пусть d — делитель п и Ad — множество чисел к < n таких, что
(к,п) = d. Элемент Ad представим в виде к = dk\, где число к\ взаимно
просто с числом n/d и не больше его. Поэтому \Ad\ = ip(n/d). Осталось
заметить, что п = У^ \Ad\.
637. Следствие задачи 633.
639. ЪюЕ(п) = ^
642. {) ^
643.
d\n c\d d\n
^Щ = ly П = ly ._
с ^ е ^ с n/c n c n
c\n e\^ c\n c\n d\n
644. 1) 51; 2) 130; 3) 315; 4) 834.
645. Предположите противное.
647. Последовательно докажите: ж*ж = 0, ж*0 = ж, х * у = х — у.
648. Определим С = 1*0. Из тождества задачи при х = 1, у = 0 имеем
Cz = z * 0, а при z = 1, ? = 0 соответственно х * у + Су = ж * 0 = Сх,
откуда х * у = С(х — у).
649. a*x = b=>x = b*a; x*a = b=>a = b*x=>x = a*b.
Если в X нет идемпотентных элементов, то число клеток в квадрате Кэли
должно быть кратно трем ввиду соотношения
x*y = z=$>z*x = y, у * z = х.
650. х * (у * х) = (у * (у * х)) * (у * х) = у; у * х = у * ((х * у) * у) = х * у.
651. Пусть в множестве А п элементов. Из 2) следует, что ровно полови-
половина всех упорядоченных троек (различных) элементов А входит в S. Зафик-
Зафиксируем некоторый элемент w е А и на множестве А\{ги} введем отношение
р: хру <^=^ (w,x,y) e S. Легко видеть, что оно антисимметрично: ес-
если хру, то неверно, что урх.Докажем, что данное отношение транзитивно.
Пусть хру и ypz. Тогда (w, х, у) е S и (w, у, z) e S. В силу 1) и (у, г, ги) е 5.
В силу 2) 5 принадлежат и тройки (x,y,z), (z,w,x). Опять применяя 1),
получим, что (w, х, z) e 5, т.е. xpz, что и требовалось доказать. Обозначим

144 Ответы. Указания. Решения
через ki количество элементов х из множества А \ {w} = {a,\, 0,2, ¦ ¦ ¦, an-\]
таких, что щрх. Если щра^, то из-за транзитивности и антисимметрич-
антисимметричности ki > kj. (Действительно, с одной стороны, щра^а^рх =>¦ щрх —
этим обеспечивается нестрогое неравенство; с другой стороны неверно, что
ujpai). Нетрудно видеть, что верно и обратное: если ki > kj, то щра^ (по
закону контрапозиции). Положим д(щ) = п — 1 — k{, g(w) = п. Покажем,
что функция д обладает требуемыми свойствами. Если д(а) < д{Ь), то арЬ,
или (w, a, b) G S. Если с = w, то из того, что(с, a, b) G S в силу 2) следу-
следует: (a,b,c) e S. Если же с ф w, то из д(Ъ) < д{с) получаем: (w,b,c) E S,
стало быть, (Ь, с, w) E S. Поскольку при этом и (w, a, b) G S, то в силу 3)
(а, Ь, с) Е S.
652. Нет. 655. ^fil + L
656. " +g"+6. Решение этой и предыдущей задачи можно найти в [26],
с. 46-47.
657. п2 - п + 2. 658. п(п2 - Зп + 8)/3.
659. 6й.
660. Назовем любой квадрат со сторонами, параллельными линиям
сетки, основным. Каждый квадрат вписан в некоторый основной квадрат,
а в основной квадрат с длиной стороны к можно вписать к различных
квадратов (с вершинами в узлах сетки). Несложно подсчитать, что имеется
(п — кJ основных квадратов со стороной к. Далее вычисляем:
-. га—1 га—1 л о
Iv^w n П V^ , / ,ч П - П
X Ic I 'Yl iC I 'Yl » iC I 'Ю к* I
z fc=l l fc=l iz
661- nr=ic'fe*+fei+i+...+fen-i-
Все возможные расположения чисел, удовлетворяющие условию задачи,
можно получить в результате выполнения следующих действий.
1) Поместить 1 на первое место, а остальные единицы на любые к\ — 1 из
ki + k<i + ... + кп — 1 оставшихся мест.
2) Поместить 2 на первое свободное место, а остальные двойки на любые
&2 — 1 из &2 + ¦ ¦ ¦ + кп — 1 оставшихся мест. И т.д.

145
662. Bn — 1)!! О связи данной задачи с задачей 559, а также с за-
задачей о монотонных плоских деревьях см. статью [14], в которой также
приводятся новые результаты, связанные с числами Стирлинга.
663. 2"-1.
664. На левую. Решение. Пусть последняя гиря имела вес 2п г, а
на левую чашку весов был выставлен вес в х г. Тогда имеем равенство
х = 2n+l - 1 -х +11111, или х = 2п + 5555. Заметим, что 2п + 5555 > 11111,
откуда 2п > 5556 (и даже 2п > 8192). Теперь имеем х = 2п + 4096 + 1024 +
256 + 128 + 32 + 16 + 2 + 1.
665. п + 1. Решение. Ясно, что М — особое множество. Пусть М =
{х\,..., хп}. Обозначим М^ = М \ {xi}. Если выбрать в качестве особых
множеств М, М\,..., Мп (всего п + 1 множеств), то условие задачи выпол-
выполняется, поскольку произвольное множество А С М представимо в виде
А = П Mj.
Xi<?A
Докажем теперь, что менее чем п + 1 особых множеств быть не может.
Пусть их не больше п. Тогда отличных от самого множества М особых
множеств имеем не более п — 1, а число пересечений, которые можно со-
составить из особых множеств не превосходит 2й, что меньше 2п — общего
числа подмножеств множества М.
667. Сп ¦ Решение Будем рассматривать подмножества множества
U = {1,2,...,п}. Пусть А С U и \А\ = к. Будем говорить, что переста-
перестановка чисел от 1 до п порождена множеством А, если первые к элемен-
элементов перестановки принадлежат А. Очевидно, что А порождает к\(п — к)\
различных перестановок. Если А\ В ф ф и В \ А ф ф, то множества пе-
перестановок, порожденных А и В соответственно, не пересекаются. Пусть
теперь Ai, А^,..., Ат — семейство подмножеств, удовлетворяющих усло-
условию задачи; для каждого % положим к{ = \А^\. Тогда
fc*!(n- ki)\ < n!
г=1
Учтя, что к\{п — к)\ > ([п/2])!(п — [п/2])!, имеем
откуда т < Сп ¦ С другой стороны, если рассмотреть все Сп подмно-
подмножеств мощности [п/2], то они удовлетворяют условию задачи.

146 Ответы. Указания. Решения
Замечание. Этот результат впервые получил Шпернер в 1928 г. Дру-
Другое решение (основанное на понятиях цепи и антицепи) см. в [34], с. 172—
173. С содержанием задачи тесно связана теорема Дилворта A950 г.), её
формулировку и доказательство можно найти также в книге [34], на с.
177-178.
668. 10.
669. Если к = 21, то наименьшее значение п равно 1 + 1, а если к = 21 — 2
или 21 < к < 2l+l — 2, то наименьшее значение п равно 1 + 2.
Решение (В. Белокобыльский). Пронумеруем элементы множества
числами от 1 до п, и сопоставим каждому подмножеству двоичную
последовательность длины п, в которой i-я цифра равна 1 @), если
г-й элемент исходного множества входит (соответственно, не входит)
в данное подмножество. Для краткости двоичную последовательность
будем называть маркером, а маркер длины п — n-маркером. Введём
также следующие определения. Маркеры одинаковой длины —
противоположные, если они различаются в каждом разряде. Набор
маркеров одинаковой длины — уравновешенный, если по каждому
разряду данных маркеров число единиц совпадает с числом нулей.
Очевидно, что уравновешенный набор всегда состоит из чётного
числа маркеров. Уравновешенный набор — правильный, если в нём
нет совпадающих или противоположных маркеров. Очевидно, что в
правильном наборе не менее четырёх маркеров. В новых терминах
исходная задача формулируется так:
При каком наименьшем п существует правильный набор из к маркеров
длины п ?
Пусть А — правильный набор n-маркеров. Обозначим через а маркер,
противоположный к а. Пусть также А = {а \ a е А}. Поскольку А и А
не пересекаются, правильный набор содержит не более 2й маркеров, то
есть к < 2п~1, или
п > \og2k + 1. (*)
1°. Покажем, что при к = 21, где / > 2, оценка (*), является точной.
Действительно, с одной стороны, из (*) имеем п > 1 + 1. С другой стороны,
рассмотрим всевозможные (/ + 1)-маркеры, среди последних трёх разрядов
которых чётное число единиц. Легко проверить, что эти маркеры образуют
правильный набор, и их ровно к = 21.
2°. Пусть 21 < к < 2l+1 - 4, где I > 2. Из (*) имеем п>1 + 2. Покажем,
как построить правильный набор (/ + 2)-маркеров мощности к. Для этого
сначала из 2l+l маркеров длины / + 1 выделим к — 4 маркера таких, что в

147
каждом из них не все первые / — 1 разрядов совпадают, и каждый маркер
выделен вместе со противоположным себе (поскольку к — 4 < 2l+1 — 8, а
(/ + 1)-маркеров, у которых первые 1 — 1 разрядов одинаковые, как раз во-
восемь, и маркер, противоположный "запрещённому", тоже "запрещённый",
то это всегда возможно). Получен набор, состоящий из пар взаимно про-
противоположных маркеров. Пронумеруем эти пары числами от 1 до ^=^. К
маркерам, входящим в пары с нечётными номерами, припишем справа
единицу, а к остальным — ноль. При этом противоположных маркеров не
станет (совпадающих, конечно, тоже не возникнет).
Если к кратно четырем, то число указанных пар четно, и полученный
набор правильный. Дополним его такими (/ + 2)-маркерами:
0...0000,0...0110,1...1011,1...1101.
Если же к при делении на 4 даёт остаток 2, то число пар нечётно, и в по-
последнем разряде единиц на две больше, чем нулей. В этом случае дополним
набор такими маркерами длины 1 + 2:
0... 0000,0... 0110,1... 1010,1... 1101.
В обоих случаях возникает правильный набор маркеров.
3°. Пусть к = 21 — 2. Из (*) следует, что п > 1 + 1. Покажем, что
равенство здесь невозможно.
Назовем два маркера одинаковой длины почти равными (п.р.), если
они различаются только в последнем разряде, и почти противоположны-
противоположными (п.п.), если у них совпадает только последний разряд. Для маркера а
обозначим через а' п.р. маркер, а через а п.п. маркер. Очевидно, что мар-
маркеры а' и а — противоположны (значит, вместе с а в правильный набор
одновременно они входить не могут), а множество всех маркеров разби-
разбивается на четвёрки вида {а, а, а', а}. Пусть теперь А — правильный на-
набор к = 21 — 2 маркеров длины 1 + 1. Тогда множество A U А содержит
2l+1 — 4 (различных) маркеров. Заметим, что если не менее трёх маркеров
(а, Ъ, с,...) из А не имеют в Л ни п.р., ни п.п. маркера, то за предела-
пределами Л U Л остается не менее 6 различных маркеров (а!, а, У, Ь, с', с,...), что
невозможно, поскольку всего имеется 2l+l маркеров длины 1 + 1. Таким
образом, А состоит из пар п.р. и п.п. маркеров и ещё не более двух непар-
непарных маркеров (точнее, нуля или двух, поскольку общее число маркеров в
правильном наборе четно).
Докажем, что на самом деле непарных маркеров нет. Действительно, в
каждом из первых I разрядов пары почти равных маркеров число единиц

148 Ответы. Указания. Решения
равно 0 или 2, а по всем таким парам оно четно. А для любой пары по-
почти противоположных маркеров в каждом из указанных разрядов имеем
в совокупности ровно одну единицу. Для уравновешенности набора об-
общее число единиц в каждом разряде должно быть равно k/2 = 2' — 1,
то есть нечётно. Значит, в каждом из I разрядов общее число единиц по
двум непарным маркерам должно иметь фиксированную чётность. В слу-
случае четного числа единиц имеем совпадающие или почти равные маркеры,
а в случае нечётного числа единиц — противоположные или почти проти-
противоположные маркеры. В любом случае приходим к противоречию.
Итак, непарных маркеров нет. Рассуждение, изложенное в предыдущем
абзаце, говорит о том, что число пар почти противоположных маркеров
нечетно. Рассмотрим последний разряд. По парам почти равных марке-
маркеров число единиц в этом разряде совпадает с числом нулей. Значит, этот
паритет должен иметь место и по парам почти противоположных мар-
маркеров — количество таких пар, оканчивающихся единицей, должно быть
равно количеству пар, оканчивающихся нулем. Но тогда количество пар
п.п. маркеров четно — противоречие!
Мы показали, что в случае к = 21 — 2 выполняется строгое неравенство
п > I + 1. Используя конструкцию из 2°, можно построить правильный
набор (/ + 2)-маркеров.
670. 360. Указание. Положим, что длина наименьшего отрезка рав-
равна 1. Пусть имеется m отрезков длины меньше \/2, п отрезков длины из
промежутка [л/2, л/3). Тогда 16 —m—n отрезков имеют длину из промежут-
промежутка [уЗ, 2]. Итак мы имеем три класса отрезков, квадраты длин которых
принимают значения соответственно от 1 до 2 A-й класс), от 2 до 3 B-й
класс) и от 3 до 4 C-й класс). Тупоугольный треугольник характеризуется
тем, что в нем квадрат большей стороны больше суммы квадратов двух
других сторон. В условиях задачи тупоугольный треугольник не может
иметь более одного отрезка из 3-го класса; поэтому число тупоугольных
треугольников не уменьшится, если считать, что все отрезки из 3-го клас-
класса имеют длину 2. Аналогично можно положить, что все отрезки из 1-го
класса имеют длину 1,1, а из 2-го — 1,6. Тогда треугольник будет тупо-
тупоугольным в двух случаях:
• он содержит по одному отрезку из каждого класса (таких треуголь-
треугольников mnA6 — m — n));
• ровно две его стороны из 1-го класса (количество таких треугольни-
треугольников С?,A6 - т)).

149
Осталось максимизировать функцию F(m7 п) = тп(\6—т—п)+С2чA6—т)
при условии 0 < т, п, т + п < 16.
671. Пусть уп — число умножений при вычислении определителя п-го
порядка. Тогда yi = О, уп = пуп-Л + п, откуда ^ = ^jy + (^tjt- Для
последовательности с общим членом ап = ^ справедливы соотношения:
а\ = 0, ап — ап-\ + , ' , = а>п-2 4- / ^21! + / \у — ... — Y^kZi ту- Таким
образом, уп = п\ Ea = i Ь.- Полезно заметить, что lim ^у = е — 1.
672. хп = Dn = п\ /2к=2 —j число беспорядков.
Рекуррентное соотношение можно переписать так: хп —пхп-\ — —(хп-\ —
(п — 1)а:п_2). Пусть уп — хп — пхп_\. Тогда уп — —уп-\- Из начальных
условий у2 = 1; поэтому предыдущее соотношение даст равенство
уп = ( —1)". Итак, хп = nxn-i + ( — 1)™. Далее можно действовать, как при
решении предыдущей задачи.
R74 Q — 2я3+Зя2-Пя + 18
U ( О. Jn — g
Решение. Можно считать, что числа х\,х2,... ,хп расположены по кругу
и Sn — сумма попарных произведений соседних чисел.
Докажем по индукции следующее утверждение: если Sn максимально,
то число п стоит между числами п — 1 и п — 2. База индукции (п = 3)
очевидна. Индукционный шаг. Пусть утверждение справедливо при п — к.
Если число к + 1 вставляется между числами а и Ъ, то сумма попарных
произведений изменяется так:
При фиксированном а Ак = (к + \)а+Ь(к + 1 — а) тем больше, чем больше Ь.
Аналогично при фиксированном Ь Ад. увеличивается с ростом а. Поэтому
Д, <~ Aс 4- \\Aс 4- (к \W hih ]\ — k2 4- 9h 1
fa _^ \гь n^ ± i \гь ~r~ l *^ // V / — "г ^-*ь ^-*
По предположению индукции если Sk максимально, то числа к и к — 1
стоят рядом. Если к +1 вставить между этими числами, то получим мак-
максимальное значение Afe = к2 + 2к — 1, а заодно и Sk+-\ = Sk + Ак, что и
требовалось доказать.
Теперь легко найти Sn. S2 = 1-2 + 2-1 = А. При п > 2
п—\ п п п

150 Ответы. Указания. Решения
676. 2BШ+2^1-1).
677. 1) n2; 2) п2 -3n + 3;
3) j(j + l)Dj + l)/2 при n = 2j, j(Aj2 -j- l)/2 при n = 2j - 1.
"Указания. 1) Сравните площади треугольников. 2) Каждый треугольник
со стороной 1, не лежащий "на границе" исходного треугольника, взаимно
однозначно определяет треугольник со стороной 2. 3) Подробное решение
содержится в первом издании настоящего сборника.
678. Подробное решение — в первом издании настоящего сборника.
См. также журнал "Математика в школе", 2001, №5, С.74.
679. 191. Решение. Пусть по кругу стоят п человек и ап — "счастли-
"счастливый" номер. Получим рекуррентное соотношение для последовательности
(ап). При увеличении числа человек на единицу задача сводится к пре-
предыдущей после удаления первого человека (имеющего номер 3), при этом
отсчет начинается не с 1-го, а с 4-го человека. Поэтому новый счастливый
номер на 3 больше предыдущего (по модулю п + 1). Отсюда
ai = 1;а2 = 1 + 3(mod2) => а2 = 2;а3 = 2 + 3(mod3) => а3 = 2:
а.4 = 2 + 3(mod4) => а^ = 1; а5 = 4; а6 = 1; а? = 4: а8 = 7:
а9 = 1:а10 = 4:... ;а13 = 13:...
Легко видеть: если ап = п, то ап+\ = 2; если ап = п — 1, то ап+\ = 1.
Пусть as = 1, тогда равенство as+k = as+k-\ +3 будет выполняться,
пока 1 + ЗА; < s + к, или 2А; < 5 — 1. Поэтому положив при нечётном 5
А = ^г", имеем а8+д = 2. Если же 5 четно, то для А = s/2 выполняется
равенство а5+д = 1.
Пусть теперь as = 2, тогда равенство а3+ь = а3+^_1 + 3 будет выпол-
выполняться, пока 2-\-Зк < s + к, или 2к < s — 2. Отсюда при четном 5 положив
А = s/2, имеем а8+д = 2. Если же 5 нечётно, то для А = ^ выполняется
равенство а8+д = 1.
Последовательно применяя найденные соотношения, получаем:
а6 = 1, Д = 3,а9 = 1, А = 5,аы = 2, А = 7, g2i = 2, А = 10,
а31 = 1, А = 16, а47 = 2, Д = 23, а70 = 1, Д = 35,
а105 = 1, А = 53, а158 = 2, А = 79, а237 = 2, а300 = 2 + 3 • 63 = 191.
680. Повторим решение предыдущей задачи в общем виде. Пусть o,i
— счастливый номер для круга из г человек (если удаляется каждый к-й
человек). Тогда щ+\ = щ + к(то(И + 1). Заметим, что если щ +к < г + 1, то

151
выполняется простое соотношение щ+\ = оц-\-к. Более того, при оц-\-кА <
i + А (т.е. когда Д < ^zf) выполняется равенство щ+а — Щ + к А. Если же
в качестве Д взять наименьшее целое, большее j^f, то для вычисления
Q-i+A нужно вычислять остаток от деления а, 4- кА на i 4- Д.
При составлении программы будет излишним организовывать массив
для значений щ, поскольку переход (г, щ) —> (г + Д, а«+д) не требует знания
других элементов рассматриваемой последовательности.
Ниже приведен текст соответствующей программы на языке Си.
/* Решение задачи Иосифа */
/* По кругу стоят ш человек, выбывает каждый k-й */
/* happy(ш,к) - номер последнего оставшегося */
int happydnt m,int к)
{
int i; /* число человек в круге */
int h; /* номер последнего оставшегося */
int delta; /* приращение к i */
if(k==l)return(m);
for(i=h=l; Km; ) {
delta=l+(i-h)/(k-l);
if(delta>m-i){h+-(m-i)*k; i-m;}
else {i+=delta; h+=k*delta;
h=h°/,i; if(h==0)h=i;
return(h);
681. n- 1.
682. Решение можно найти в [63].
683. Нет. Решение. Заметим, что С| = 20. Пусть каждый ученик
посещает ровно три кружка, причем у каждого набор кружков отличен
от других. (В силу сделанного замечания это возможно.) Тогда и наборы
непосещаемых кружков также будут разными у разных учеников. Если
бы некоторые 5 человек посещали одновременно какие-нибудь два круж-
кружка, тогда из оставшихся четырёх кружков по крайней мере один пришлось
бы посещать одновременно двум (принцип Дирихле), что приводит к про-

152 Ответы. Указания. Решения
тиворсчию. Последняя фраза останется справедливой, если в ней перед
словами "посещали", "посещать" поставить частицу "не".
685. Левая часть тождества легко выражается через числа Стирлинга
II рода ([9], §5.11): ?Li(-1)*c'n/;m = n!(-l)nS(m, n). Известно, что при
п > тп справедливо равенство S(m, n) = 0.
Замечание. Тождеству данной задачи посвящена статья |13|3, в кото-
которой приводится ещё 4 способа доказательства данного тождества. Прочи-
Прочитать указанную статью весьма полезно начинающим математикам.
690. s/lb. Указание. Примените полиномиальную формулу. Покажи-
Покажите, что если (\/2 + \/3 + \/5Jn+1 = an\/2 + bny/3 4- спу/Е + dn\/36, то
(л/2 + л/3 — л/5Jп+1 = Яп\/2 4- Ьп\/3 — сп\[Ъ — б^л/ЗО. Данные соотношения
и еще два аналогичных составляют систему линейных уравнений относи-
относительно an,bn,cn,dn.
693. Обе части тождества выражают собой число решений в натураль-
натуральных числах неравенства ху < п.
694. [к ¦ ^] — это количество точек вида (к, у), где 0 < у < к ¦ ^.
Подсчитайте количество точек с целыми координатами, лежащих внутри
прямоугольника [0,m] x [0, и], лежащих под диагональю.
Другое решение (А. Бадзян). [к-^\ — к-^-{к'^}. Числа п, 2п,..., (т —
Х)п образуют приведенную систему вычетов по модулю т.
695. 1/2.
696. Тождество возникает в результате решения различными способа-
способами следующей задачи:
Сколько нужно взять различных натуральных чисел, не превосходящих
п, чтобы среди них наверняка одно было вдвое больше другого? Подроб-
Подробности — в первом издании настоящего сборника.
697. 698. Решения можно найти в [63|.
699. Запишем рекуррентное соотношение в виде
(n - k)xk + (к + 1)хк+2 = cxk+uk = 0,
3Эта статья помещена также в сборнике |27], JV95.

153
С учетом условий X(i = хп = О, Х\ = 1 получим матричное уравнение
Ах — сх, где А — трёхдиагональная матрица, х — вектор-столбец:
\
А =
0
n —
1
n
1
0
2
2
0
О
2
\
п-2
0 п-\
1 О
: x =
\
X\
ПХп
\
j
Теперь задача сводится к нахождению наибольшего (вещественного) соб-
собственного значения матрицы А и к определению отвечающего ему соб-
собственного вектора (с условием х\ =1)- Для локализации спектра матри-
матрицы используем круги Гершгорина. Поскольку главная диагональ матри-
матрицы состоит из нулей, а сумма модулей всех внедиагональных элементов
каждого столбца равна (п — 1), заключаем, что собственные значения ма-
матрицы А расположены в круге (комплексной плоскости) радиуса (п — 1)
и с центром в нуле. Легко проверить, что число (п — 1) является соб-
собственным значением матрицы А и, значит, является искомым. Переходим
к нахождению собственного вектора. Имеем: х\ = 1, xi = п — 1; х% =
(n-i)s2-(n-i)si = (п-Щп-2) =C2_v далсс индукцией по к легко доказать,
что для к = 1, 2,..., п выполняется равенство ж*. = C*l].
700. Bn)! + ELit-1)^2*^1^ -к-1)\. Решение. Пусть А - мно-
множество всевозможных расположений рыцарей за круглым столом, а А{ —
множество расположений рыцарей за круглым столом, при которых ры-
рыцари из г-й пары врагов сидят рядом {% = 1,..., п). Тогда требуемое число
есть мощность множества А\ П ... П Лп, где, как обычно, Л, = А \ Ai \/i.
Найдём \Ail П ... П Aik\ — число расположений рыцарей, при которых
рыцари из к фиксированных пар сидят рядом враг с врагом. Каждое такое
расположение можно получить с помощью следующих действий.
• Разместить первую пару. Это можно сделать An способами (пару со-
соседних мест из In мест за круглым столом можно выбрать In спо-
способами, после чего два рыцаря могут разместиться на этих местах
двумя способами).
• Разместить всех остальных рыцарей, рассматривая каждую из к — 1
пар как один объект. Имеем к — 1 пар врагов и ещё 2п — 2к рыцарей —

154 Ответы. Указания. Решения
всего Bп — к — 1) объектов, которые можно переставить Bп — к — 1)!
способами.
• Определить для каждой из к — 1 пар, кто из двух рыцарей сидит
слева от своего врага. Данное действие выполняется 2fc~1 способами.
Применяя правило произведения, получаем:
.Aj, П...П-AjJ = Ап{2п — к — 1)!2*. Данная формула годится и для случая
к = 1. Учитывая теперь, что & пар из п можно выбрать С^ способами,
получаем ответ.
701. Поставим в ряд п — к нулей. Теперь для расстановки к единиц
имеется п — к + 1 возможных позиций.
702. Справедливость доказываемого утверждения для п = 2, 3 легко
проверяется. Зафиксируем некоторую точку и разобьем наборы точек, сре-
среди которых нет соседних, на два класса в зависимости от того, попадает
в набор данная точка или нет. Очевидно, что классы содержат соответ-
соответственно f(n — 3, к — 1) и f(n — 1, к) наборов. Поэтому
д(п, к) = f(n - 3,к - 1) + f(n - 1,к) = Скп_\_х + Скп_к.
По известному комбинаторному тождеству С\_к = VLYLChn~Jk_^ откуда име-
ем: CknlU = ^-кСкп-к- Стало быть, д(п, к) = Ск_к{^~к + 1) = ^^*-*-
Решение. Разместим сначала жён. Это можно сделать 2п! способами (сна-
(сначала определяем, на четных или нечётных местах будут сидеть жёны, а
затем размещаем п жён по п предназначенным им местам).
Идя по часовой стрелке, пронумеруем жён числами от 1 до п; каждому
мужу присвоим такой же номер, как у его жены. Идя по часовой стрел-
стрелке, начиная с 1-й жены, пронумеруем свободные места числами от 1 до п.
Теперь нам предстоит разместить мужей по свободным местам так, что-
чтобы 1-й муж не занимал n-го или 1-го места, 2-й муж — 1-го или 2-го,...,
п-п муж — п — 1-го или n-го. Обозначим через Р, событие: 1-й муж, си-
сидит на %-м месте; через Р[ — событие: %-й муж сидит на i — 1-м месте
(г = 2,..., п), через Р[ -событие: 1-й муж: сидит на п-м месте. В цикли-
циклической последовательности Р[, Р1: Р^, Р-}, ¦ ¦ ¦, Р^, РП1 Р{ любые два соседних
события не могут осуществляться одновременно, а любые два нссоседних
— могут.
Пусть А — множество всевозможных расположений мужей, а Л, — мно-
множество расположений мужей, при которых i-й муж сидит рядом со своей

155
женой, Ai = А \ Ai (i = 1,..., п). Тогда число расположений мужей (при
фиксированном расположении жён) есть мощность множества А\ П ... П
Ап. Для того, чтобы иметь возможность применить формулу включения-
исключения, найдем ^2 \Aij П ... П А(к | A < %\ < i2 < ... < %к < fi).
Мужья из некоторых к пар могут сидеть одновременно рядом со своими
жёнами, если события, отвечающие этим мужьям, не противоречат друг
другу. Число способов разместить к мужей есть число способов выбрать
из циклической последовательности Р[, Р\, Р^, Рг,..., Р^, Рп, Р[ к попарно
нссоссдних элементов, т.е. дBп, к) — -^ц,С\п_к (согласно 2-й лемме Кап-
ланского). Оставшиеся п — к мужей на свободных местах размещаются
(п - к)\ способами. Таким образом, ^ \Aix П ... П ДJ — ^k^n-ki71 ~ ^У
Применяя формулу включения-исключения, получим:
\А, п... п Ап\ = Yrk^{-\)k^-kck,n_k{n - к)\
704. п > p + q - 1.
711. Индукция по п. При п = 1 утверждение очевидно. Пусть п = к-\-\.
Зафиксируем некоторую вершину и. Среди (к + 1)а^ 4-1 рёбер, инцидент-
инцидентных и, найдётся а& + 1 рёбер одного цвета (скажем, синего). Если из а& + 1
концов этих рёбер, отличных от и, по крайней мере две (например, v и w)
соединены синим ребром, то получаем синий треугольник uvw. В против-
противном случае в подграфе, порожденном а^ + 1 вершинами, синий цвет отсут-
отсутствует, то есть рёбра покрашены в к цветов. По предположению индукции
в этом подграфе найдётся одноцветный треугольник. Положив Ьп = ^у,
п п
получим Ь-[ = 1 4- YT и Ьп = 6п_т + ^у, откуда Ьп = J2 Ь. и пп = п!' ^ ?. ¦ Для
к=0 ' к=0
доказательства того, что ап — [п\е\, с помощью оценки остаточного члена
формулы Маклорена для функции ех при х = 1 проверьте выполнение
неравенства
717. Если выпуклая оболочка точек А, В, С, D, Е представляет собой
пяти- или четырёхугольник, то утверждение очевидно. Пусть выпуклой
оболочкой является треугольник ABC. Тогда точки D и Е находятся вну-
внутри него. Прямая DE не может пересекать все стороны треугольника. Ес-
Если она не пересекает, например, отрезок АВ^ то точки A, D, Е: В будут
вершинами искомого выпуклого четырёхугольника.

156 Ответы. Указания. Решения
А
718. Выпуклая оболочка п точек представляет собой многоугольник.
Если число его вершин меньше п, то какая-то из заданных точек (скажем,
D) лежит внутри указанного многоугольника. Всевозможные диагонали
многоугольника, проведенные из некоторой его вершины, делят выпуклую
оболочку на треугольники, одному из них (например, ABC) принадлежит
точка D.
.С
А
Точки Л, В, С, D не удовлетворяют условию задачи. Полученное противо-
противоречие доказывает утверждение задачи.
719. Пусть к = R(n, 5, 4); множество а составляют четвёрки точек, вы-
выпуклые оболочки которых — четырёхугольники, множество /3 тогда состо-
состоит из четвёрок точек, чьи выпуклые оболочки — треугольники. Согласно
теореме Рамсея
1) существует п точек (из заданных к) таких, что любые четыре из них
являются вершинами выпуклого четырёхугольника, либо
2) найдутся такие пять точек, что никакие четыре из них не могут быть
вершинами выпуклого четырехугольника.
Задача 717 показывает, что второй случай осуществиться не может,
значит, имеет место первая ситуация. Осталось воспользоваться результа-
результатом задачи 718.
720. В |9| выведена формула PG{xi, х2,...) = \ YT3 = 1 ^/{ljT B полу'
ченной сумме нижний индекс при х принимает значения всех делителей
числа п. В качестве упомянутого индекса число d встретится столько раз,
сколько есть чисел j от 1 до п, для которых (n,j) = n/d. Такие числа
имеют вид j = kn/d, где число к взаимно просто с of и не превосходит d.
Значит, d будет в качестве нижнего индекса ровно (f(d) раз.
721. Применив теорему Пойа, выражение для циклового индекса из
предыдущей задачи и полиномиальную формулу, получим:

157
Нас интересует коэффициент при w™1 ... w^1. Указанное произведение
возникает лишь при d, делящем одновременно пу,... ,пт. Дальнейшее
просто.
*..-,.-, р .. п 1 /V~* nld i i\ , rt 9 га/2-1 , 71 п/2\ г^
722. Если п четно, то Pq = 2n\z^d\nxd ifiid) + %х{х2 +f^2 )• ^сли
nld "-'
п нечётно, то Pg = ^~(z2d\nxd tfiW + пх-\Х22 )¦
724. Пусть G" — граф, дополнительный к G. Расстояния в G и G" будем
обозначать соответственно d и о!'. Докажем, что если диаметр G не меньше
3, то диаметр G' не больше 3.
Пусть d(u, v) > 3. Тогда ни одна вершина х графа G не может быть
одновременно смежна с и и v, так как в этом случае d(u, v) < d(u, x) +
d(x,v) — 2. Если вершины х и у не смежны с одной и той же вершиной
(скажем, и), то d'(x, у) < d'(x, и) + d'{u1 у) = 2. Если же ж и у не смежны с
разными вершинами (например, х с и, а у с vI то, поскольку и и v также
несмежны, имеем d'(x,y) < d'(x,u)+d'(u,v)+d'(v,y) = 3. Итак, расстояние
между двумя произвольными вершинами графа G" не превосходит 3.
Для самодополнитсльного графа G справедливо: d(G) = d(G'). Пре-
Предыдущее рассуждение показывает, что d(G) < 3. С другой стороны, если
d[G) = 1, то G — полный граф и не может быть изоморфен своему до-
дополнению (пустому графу). Поэтому 2 < d(G) < 3. Осталось придумать
примеры самодополнительных графов диаметров 2 и 3.
725. 10.
728. Обозначим вершины графа числами 1,2,..., 2п. Рассмотрим цепи
(к = 1,..., п), (к каждому неположительному числу добавляем 2п). Каж-
Каждая такая цепь является гамильтоновой, поскольку числа к — п + 1,к — п +
2,...,к + п — 1,к + п образуют полную систему вычетов по модулю 2п. Так
как в к-й цепи сумма номеров соседних вершин сравнима с 2к или 2к + 1
по модулю 2п, данные цепи не имеют общих рёбер. Осталось заметить, что
общее количество рёбер в указанных цепях равно пBп — 1) и совпадает с
количеством рёбер графа К2п.
729. Гамильтонову цепь к —> ... —» к + п из решения предыдущей
задачи дополним до гамильтонова цикла добавлением цепи
к + п —> 2п + 1 —> к.
730. Используйте результаты задач 655, 20 и 448.
731. Докажите, что в графе есть полный подграф порядка п + 1.

158 Ответы. Указания. Решения
732. 1) Связность графа очевидна. Осталось доказать, что степень
каждой вершины четна. Для произвольной вершины v рассмотрим (мак-
(максимальный по количеству рёбер) подграф G, образованный вершинами,
смежными с v. Степень каждой вершины этого подграфа нечетна, поэто-
поэтому число его вершин (суть степень v) четно.
2) Пусть V — множество вершин графа; п — число вершин; Г(г>) — мно-
множество вершин, смежных с г>; fi[u,v) — число общих вершин, смежных с
и и v. Тогда при вычислении суммы S — ^2u€V\{v] №(uiv) каждая вершина
го, смежная с г>, учитывается р(ю) — 1 раз. В силу предыдущего пункта за-
задачи \Г(у)\ — чётное число, a (p(w) — 1) — нечётное для любого w. Сумма
чётного числа нечётных слагаемых S = YlW?rtv)(p(w) ~ 1) чстна- С другой
стороны, S есть сумма [п — 1) нечётных слагаемых /j,(u:v). Стало быть,
число п нечетно.
733. Если к = 2, то п — нечётное число > 3; если к > 3, то п = к + I.
Указание. В случае к = 2, как следует из результата предыдущей задачи,
п — нечётно (ясно, что п > 1). Примером графа с 2t + 1 вершинами, удо-
удовлетворяющего условиям задачи, является объединение t треугольников с
общей вершиной.
Докажите, что 1°) у любых двух вершин ровно к — \ общих смежных
вершин; 2°) в графе найдётся полный подграф К^+у.
Пусть к > 3 и Y = {?/], у2,..., Ук + \] — множество вершин полного под-
подграфа, a v (? Y. У вершин у-\ и у2 в силу 1° все общие смежные вершины
входят в У, поэтому общая смежная вершина уиУ2 и v принадлежит У.
Значит, v имеет смежную вершину из У. Если у v есть две смежные верши-
вершины из У, то у этих двух вершин будет не менее к общих смежных вершин
(это оставшиеся к — 1 вершин из У и вершина г>), что противоречит 1°. Та-
Таким образом, у v ровно одна смежная вершина из У — пусть это вершина
х. Возьмем вершину у из У, отличную от х. У вершин v,x и у есть общая
смежная вершина, и она принадлежит У (так как все общие смежные вер-
вершины х и у из У). Но тогда у v сеть две общие смежные вершины из У.
Полученное противоречие говорит о том, что множество У совпадает с
множеством вершин графа, то есть граф — полный, при этом п = к + 1.
734. 16.
735. 1), 2) Возьмем произвольную вершину v. Пусть п — число вершин
графа, к = p{v). Для любых двух вершин Vi и Vj, смежных с v, найдет-
найдется общая смежная вершина Wij, не смежная с v. Причем все вершины
wiji hJ' — !>¦¦¦! &i i Ф 3 разные (иначе некоторая вершина, не смеж-

159
ная с v, имела бы с ней более двух общих смежных вершин). Вершинами
v, v\,..., Vk, ЭД12,..., w\?, • • •, Wk-i,k исчерпывается все множество вершин
графа. Значит, п = l + fe+ 2 • ^т0 УРавнснис имеет (при фиксированном
п) единственное положительное решение относительно к. Таким образом,
степень каждой вершины определяется однозначно порядком графа. По-
Поэтому граф является регулярным.
3) Из условия задачи вытекает матричное равенство
A2+2A + B-k)I = 2J, A)
где / — единичная матрица размера п х п, J — матрица того же разме-
размера, состоящая из одних единиц. Пусть х — собственный вектор матрицы
А, х' = (х[,..., хп). Умножив обе части матричного равенства A) на х,
получим
xd, B),
где j — вектор, все координаты которого единицы. Поскольку Л ф к, век-
вектор х не коллинсарсн вектору j (который как раз отвечает собственному
значению к). Значит, равенство B) возможно лишь при
\2 _i_ од _i_ (о АЛ = 2 > х- = О
4) Матрица А как матрица смежности связного графа удовлетворяет
условиям теоремы Псррона-Фробениуса, согласно которой наибольшее по
модулю собственное значение матрицы А положительно и имеет алгебра-
алгебраическую кратность 1 (см. |33|). Таким образом, собственное значение к
имеет алгебраическую кратность 1. Для определения кратностей г\^ соб-
собственных значений Л1;2 = —1 ± \/к — 1 нужно решить систему линейных
уравнений
I- Л2г2 4- к - 0.
(Последнее соотношение есть следствие того факта, что сумма собствен-
собственных значений матрицы, взятых с учетом их алгебраической кратности,
равна сумме сё диагональных элементов).
5) вытекает из 4).
6) Сч, граф Клебша (определение в задаче 443) и граф Гевиртца ([29|).
Замечание. Рассмотренные в данной задаче графы относятся к так на-
называемым сильно регулярным графам (см. [29|, [611, [52|).

Литература
|lj Башмаков М.И., Беккер Б.М., Гольховой В.М. Задачи по математи-
математике. Алгебра и анализ. — М.: Наука, 1982. - 192 с.
|2| Виленкин Н.Я. Комбинаторика. — М.: Наука, 1969. - 328 с.
|3| Виноградов И.М. Основы теории чисел. — М.: Наука, 1981. - 176 с.
|4| Гаврилов Г.П., Сапоженко А.А. Сборник задач по дискретной мате-
математике. — М.: Наука, 1977. - 368 с.
|5| Комбинаторный анализ. Задачи и упражнения /Под ред. К.А. Рыб-
Рыбникова. — М.: Наука, 1982. - 365 с.
|6| Куликов Л.Я., Москаленко А.И., Фомин А.А. Сборник задач по алге-
и теории чисел. — М.: Просвещение, 1993. — 288 с.
|7| Лекции по теории графов /В.А. Емеличев, О.И. Мельников, В.И.
Сарванов и др. — М.: Наука, 1990. - 384 с.
|8| Уилсон Р. Введение в теорию графов. — М.: Мир, 1977. — 208 с.
|9| Эвнин А.Ю. Дискретная математика: Конспект лекций. — Челя-
Челябинск: ЮУрГУ, 1998. - 176 с.
ДОПОЛНИТЕЛЬНАЯ
[10| Айерлэнд К., Роузен М. Классическое введение в современную тео-
теорию чисел. — М.: Мир, 1987. - 415 с.
[11] Басакер Р., Саати Т. Теория графов и сетей. — М.: Наука, 1974. - 366
с.

161
|12] Березина Л.Ю. Графы и их применение. — М.: Просвещение, 1979. -
144 с.
113] Вагутен В.Н. Числа С^, многочлены, последовательности //Квант.
- 1973. -т. - С.27-34.
|14| Васильев Н., Коганов Л. Разбиения, ГС-перестановки и деревья
//Квант. - 1997. - №6.
|15] Венгерские математические олимпиады. — М.: Мир, 1976. - 543 с.
|1б| Верещагин Н.В., Шень А. Логические формулы и схемы //Математи-
//Математическое просвещение. - 2000. - Сер. 3. - Вып. 4. - С.53-80.
|17] Верещагин Н.К., Шснь А. Вычислимые функции. — М.: МЦНМО,
1999, - 176 с. Интернет:
ftp://ftp.mccme.ru/users/shen/logic/comput.
|18] Вилснкин Н.Я. Популярная комбинаторика. — М.: Наука, 1975. - 208
с.
|19| Воробьев Н.Н. Числа Фибоначчи. — М.: Наука, 1992. - 190 с.
|20] Гаврилов Г.П., Сапоженко А.А. Задачи и упражнения по курсу дис-
дискретной математики. — М.: Наука, 1992. - 405 с.
|21] Галочкин А.И., Нестсренко Ю.В., Шидловский А.Б. Введение в тео-
теорию чисел. — М.: Изд-во МГУ, 1995. - 160 с.
|22| Гашков С.Б, Чубариков В.Н. Арифметика. Алгоритмы. Сложность
вычислений. — М.: Высшая школа, 2000. - 320 с.
|23] Генкин С.А., Итенберг И.В., Фомин Д.В. Ленинградские математи-
математические кружки. — Киров: АСА, 1994. - 272 с.
|24] Гиндикин С.Г. Алгебра логики в задачах. — М.: Наука, 1972. — 288 с.
|25| Грэхем Р., Кнут Д., Паташник О. Конкретная математика. — М.:
Мир, 1998. - 703 с.
|2б] Олимпиады ЮУрГУ для абитуриентов. Математика. Задачи и ре-
решения /В.Л. Дильман, В.И. Заляпин В.И., Ю.Г. Малиновский и др.
и др. — Челябинск: Изд. дом Обухова, 2000. - 100 с.

162 Ли тера тура
[27] Задачник "Кванта": Математика. — В трех частях/ Под ред. Н.Б.
Васильева. — М.: Бюро Квантум, 1997 (Прил. к журналу ':Квант': №1,
№3, №5).
|28] Избранные задачи из журнала "American Mathematical Monthly". —
М.: Мир, 1977. - 598 с.
[29] Камерон П., ван Линт Дж. Теория графов, теория кодирования и
блок-схемы. — М.: Наука, 1980. - 139 с.
[30] Кнут Д. Искусство программирования для ЭВМ. Т.1. Основные ал-
алгоритмы. - М.: Мир, 1976. - 736 с.
[31] Кострикин А.И. Введение в алгебру. Основы алгебры. — М.: Наука,
1994. -318 с.
[32] Кофман А. Введение в прикладную комбинаторику. — М.: Наука,
1975. - 480 с.
[33] Ланкастер П. Теория матриц. — М.: Наука, 1978. - 269 с.
[34] Липский В. Комбинаторика для программистов, — М.: Мир, 1988. -
213 с.
[35] Нефедов В.Н., Осипова В.А. Курс дискретной математики. — М.:
Изд-во МАИ, 1992. - 264 с.
|3б] Новиков П.С. Элементы математической логики. — М.: Наука, 1973.
- 400 с.
[37] Новиков Ф.А. Дискретная математика для программистов. — СПб.:
Питер, 2000. - 304 с.
[38] Мендельсон Э. Введение в математическую логику.— М.: Наука,
1976. - 320 с.
[39] Оре О. Приглашение в теорию чисел. — М.: Наука, 1980. - 128 с.
[40] Оре О. Теория графов. - М.: Наука, 1980. - 392 с.
|41] Полиа Г., Сеге Г. Задачи и теоремы из анализа. — М.: Наука, 1978.
- Т.2. - 432 с.

163
|42] Рейнгольд Э., Нивсргсльт Ю., Дсо Н. Комбинаторные алгоритмы.
Теория и практика. — М.: Мир, 1980. - 478 с.
|43] Рудаков А.Н. Числа Фибоначчи и простота числа 2т — 1 //Матема-
//Математическое просвещение. - 2000. Сер. 3. - Вып. 4. - С.127-139.
|44] Саати Т. Целочисленные методы оптимизации и связанные с ними
экстремальные проблемы. — М.: Мир, 1973. - 304 с.
[45] Ссндсров В., Спивак А. Малая теорема Ферма //Квант. - 2000. - №1.
— С.9-16, 37; №3. - С. 11-17; №4. - С. 15-18.
|46] Сборник задач по алгебре /Под ред. А.И. Кострикина. — М.: Факто-
Факториал, 1995. - 452 с.
|47] Тараканов В.Е. Комбинаторные задачи и @,1)-матрицы. — М.: На-
Наука, 1985. - 192 с.
|48| Трост Э. Простые числа. - М.: ГИФМЛ, 1959. - 136 с.
|49] Уильяме X. Проверка чисел на простоту с помощью вычислитель-
вычислительных машин //Кибернетический сборник. - Вып. 23. — М.: Мир, 1986.
[50] Харари Ф. Теория графов. - М.: Мир, 1973. - 302 с.
[51] Холл М. Комбинаторика. — М.: Мир, 1970. - 424 с.
|52| Цветкович Д., Дуб М., Закс X. Спектры графов. Теория и применение.
— Киев: Наукова думка, 1984. - 383 с.
[53] Школа в "Кванте": Арифметика и алгебра /Под ред. А.А. Егорова.
— М.: Бюро Квантум, 1994 (Прил. к журналу "Квант"). - 128 с.
[54] Эвнин А.Ю. Девятнадцать доказательств теоремы Евклида
//Квант. - 2001. - №1. - С.35-38. Интернет:
http://www.vivovoco.rsl.ru/quantum/2001.01/matkr_l_01.pdf.
[55] Эвнин А.Ю. Две заметки по комбинаторике //Математическое об-
образование. - 2000. - №3A4). - С.27-34.
|5б| Эвнин А.Ю. Сверхстепени и их разности //Математическое образо-
образование. - 2001. - №1A6). - С.68-73.

164 Литература
|57] Эвнин А.Ю. Букет окрестностей одной задачи, или О методах сум-
суммирования //Математика в школе. - 2000. - №8. - С.64-67.
[58] Эвнин А.Ю. Решение задач на возвратные последовательности
//Математика в школе. - 2001. - №7. - С.69-70.
[59] Эвнин А.Ю. Возвратные последовательности в олимпиадных зада-
задачах //Математика (прил. к газете "Первое сентября"). - 1999. - №36.
-С.15-16.
[60] Эвнин А.Ю. Элементарная теория чисел: Сборник олимпиадных за-
задач. - Челябинск: ЧГТУ, 1996. - 76 с.
[61] Юбо К. Сильно регулярные графы //Кибернетический сборник. — М.:
Мир, 1987. - Вып. 24.
|62] Яглом И.М. Булева структура и ее модели. — М.: Сов. радио, 1980.
- 193 с.
|63] http://uuu.zaba.ru/cgi-bin/tasks.cgi?tour=national.putnam.