РОССИЙСКАЯ АКДЕМИЯ НАУК
01-14
204-1
1ИЯ им. В.А. ТРАПЕЗНИКОВА
А. В. БАБИЧЕВ А.Г.БУТКОВСКИЙ СЕППО ПОХЬОЛАЙНЕН
к
ЕДИНОЙ
ГЕОМЕТРИЧЕСКОЙ
ТЕОРИИ
УПРАВЛЕНИЯ
1Й
МОСКВА «НАУКА» 2001
УДК 007 ББК 65.050.2
Б 12
О гветствснныи редактор академик Л.Б. Куржанский
Рецензенты: член-корреспондент РАН Ю.Н. Павловский, доктор физико-математических наук Н.А. Бобылев
Бабичев А.В., Бутковский А.Г., Похьолайнен Сеппо
К единой геометрической теории управления. - М.: Наука. - 2001.-352 с.
ISBN 5-02-002557-7
В книге рассматриваются теоретические и практические проблемы управления структурами, существенно отличающиеся от проблем управления состояниями. Вводятся основные понятия теории управления: система, система с управлением, управление, синтез, обратная связь, блочно-структурная схема и др. Выясняется связь понятия управление с понятиями современной теоретической физики, где фундаментальные поля рассматриваются как порождения принципа локальной калибровочной инвариантности и нарушения симметрии и являются связностями в геометрическом представлении расслоенных пространств. Излагается ряд новых конкретных результатов по исследованию структур управления.
Для читателей, интересующихся ролью управления в природе и обществе и перспективами развития науки об управлении.
ТП 2001-I-236B
Babichev A.V., Butkovskiy A.G., Pohjolainen Seppo
Towards Unified Geometrical Theory of Control. M.: Nauka. — 2001. — 352 p.
ISBN 5-02-002557-7
Theoretical and practical problems of structure control unlike state control are considered. The key concepts of system, system with control, control, synthesis, feedback and others are introduced. It is realized deep connections between control and fundamental concepts of local gauge invariance and spontaneous violation symmetry in the modern physical theory, where fields are considered as connections in fiber bundle. The series of new results on control are given on the base of the methods mentioned above. The book can be useful for the wide circle of readers interesting in developments of control science.
ISBN 5-02-002557-7
© Издательство "Наука", 2001
2008114995
ISBN 5-02-002557-7
9785020 025578
ОГЛАВЛЕНИЕ
Предисловие..................................................... 7
Введение .............................................. 10
1.	Философские, идейные, общеметодологические, логические и математические принципы Программы создания
“Единой геометрической теории управления — Теории структур управления”
1.1.	Философия ................................................ 15
1.2.	Логика.................................................... 22
1.3.	Анализ и синтез. Элемент и множество. Натуральное число ..	24
1.4.	Абстракция, или идеализация. Сложность.................... 26
1.5.	О языках ................................................. 31
1.6.	Цивилизация и культура ................................... 36
1.7.	Постиндустриальная эпоха и глобализация................... 42
1.8.	Воспитание и образование.................................. 44
1.9.	Наука. “Закон 100%-эффективности математики”.............. 48
1.10.	Математика .............................................. 53
1.11.	Кибернетика. “Управленческая парадигма мира”............. 60
1.12.	Предикаты ............................................... 62
1.13.	Симметрия (общее понятие)................................ 64
1.14.	Калибровочная симметрия.................................. 73
1.15.	Сохранение структур...................................... 78
1.16.	Вакуум и творчество ..................................... 84
1.17.	Точка зрения на “Законы Природы” ........................ 87
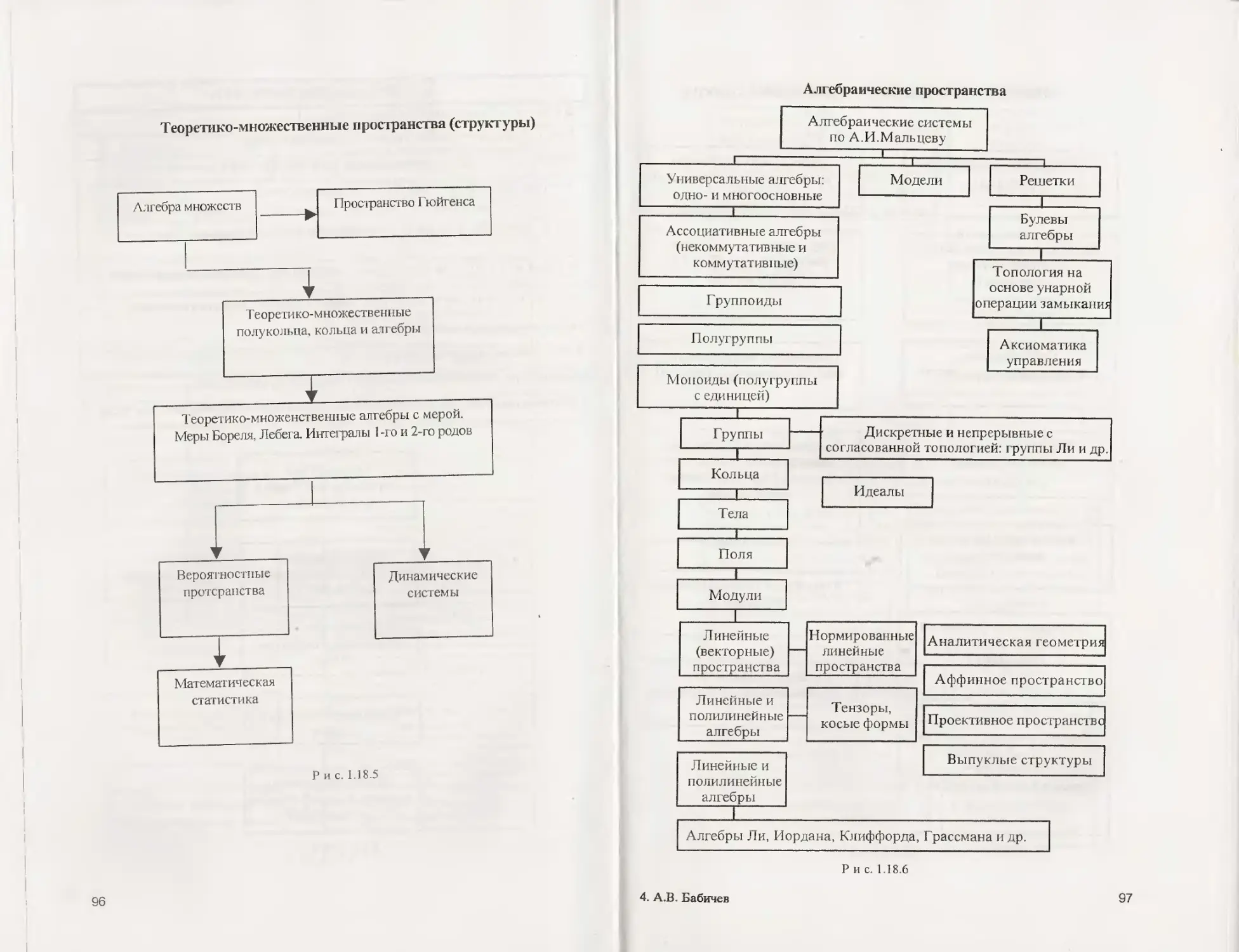
1.18	Структурированная энциклопедия............................ 90
1.19.	Структуры и обучающие среды ............................ 103
2.	Отношения
2.1.	Множество как отношение ................................. 108
2.2.	Общее понятие отношения .......................... 113
2.3.	Бинарное отношение как граф. Дискретные системы с управлением .......................................................... 115
3
2.4.	Операции над отношениями. Пространства отношений....	117
2.5.	Отношение отображения ................................... 119
2.6.	Отношение эквивалентности ............................... 127
2.7.	Отношение порядка........................................ 133
2.8.	Отношение толерантности (близости).................. 137
2.9.	Размытые множества....................................... 139
3.	Основные структуры математической логики
3.1.	Пространство высказываний .......................... 143
3.2.	О предикатах ............................................ 158
3.3.	Язык узкого исчисления предикатов ....................... 162
3.4.	Теории и доказательства.................................. 165
3.5.	Метаязык и субязык ...................................... 169
3.6.	Шкалы Бурбаки, структуры, симметрии...................... 171
3.7.	Расслоение............................................... 173
3.8.	О симметрии множества ................................... 177
3.9.	Системы с управлением и симметрия........................ 179
3.10.	Системы с управлением и марковские процессы ............ 188
3.11.	Управление с точки зрения аксиомы выбора Цермело...	190
4.	Структуры собственно математики
4.1.	Теоретико-множественные пространства .................... 195
4.2.	Мера — пространство с мерой ........................ 198
4.3.	Пространство Гюйгенса ................................... 200
4.4.	Метрика. Метрическое пространство ....................... 202
4.5.	Алгебраические пространства — алгебраические системы ....	203
4.6.	Простейшие алгебраические пространства................... 207
4.7.	Более сложные алгебраические пространства ............... 210
4.8.	Линейные топологические пространства .................... 215
4.9.	Элементарное многообразие и многообразие................. 217
4.10.	О понятии категория .................................... 224
4.11.	Пример алгебраической структуры, порожденной блочноструктурными схемами систем ..................................... 231
4.12.	Применение идеи компенсации для решения новых краевых задач, реализованное блочно-схемным методом.................. 235
5.	О понятии структуры оптимального управления
5.1.	Предварительные замечания ............................... 242
5.2.	Описание структуры пространства систем управления на ос-
нове отношения порядка .......................................... 244
4
5.3.	Разбиения в пространстве допустимых ................. 247
5.4.	Постановка задачи оптимального управления............ 249
5.5.	Метрический подход к задаче оптимального управления . 251
5	6. Управление в топологических пространствах ......... 259
5.7.	Управление в метрических пространствах............... 261
6.	Фазовые портреты дифференциальных включений (дифференциальных систем с управлением)
6.1.	Дифференциальное включение как система с управлением ...	268
6.2.	Геометрические построения, связанные с дифференциальными включениями ............................................ 271
6.3.	Фазовый портрет ДВ УДС на двумерном многообразии...	273
6.4.	Общий случай фазового портрета дифференциального включения ....................................................... 276
6.5.	Лагранжиан УДС. Собственная метрика УДС.............. 278
6.6.	Декомпозиция ФП УДС для многомерного случая.......... 281
7.	Многомерные управляемые дифференциальные системы
7.1.	Описание (т, н)-УДС ................................. 285
7.2.	Геометрическое представление решения ................ 287
7.3.	Понятие /«-вектора .................................. 289
7.4.	УДС как w-векторное включение ....................... 290
7.5.	Операция однороднизации ............................. 292
7.6.	Представление (ш, и)-УДС в виде системы уравнений
Пфаффа (СУП) ................................................ 293
7.7.	Представление (т, «)-УДС в виде (1, т + «)-УДС....... 295
7.8.	Собственная /«-метрика (/и-мера) для (т, «)-УДС...... 297
7.9.	Задачи управляемости, финитного управления и собственно-
го оптимального управления для (т, п)-УДС.................... 298
7.10.	Потоковое представление для 1-УДС и принцип экстремальных токов ............................................... 300
7.11.	Потоковое представление для (т, «)-УДС ............. 303
7.12.	Описание допустимых линий тока в сплошных средах, их
связь с ФП 1-УДС ............................................ 305
7.13.	Принцип максимума объема (меры) области достижимости.
Многомерный принцип оптимальности (МПО)...................... 308
7.14.	Физический принцип максимума объема области освещенности 	 311
7.15.	Пример сведения уравнения с частными производными общего вида к нормальной системе с управлением............... 314
5
7.16.	Один специальный вид индикатрис............... 317
7.17.	Калибровочно-компенсационный подход к выводу условий оптимальности.......................................... 317
7.18.	Многомерный принцип максимума................. 320
Приложения:
1.	Калибровочные поля в физике фундаментальных взаимодействий ........................................... 324
2.	Законы сохранения в теории поля.............. 329
3.	Интеграл Фейнмана ........................... 331
Литература ......................................... 333
Предисловие
Название книги “К единой геометрической теории управления” может показаться претенциозным и озадачивающим . Если слово геометрическая, возможно, стало привычным в связи с интенсивным развитием геометрических методов в механике и физике, то слово единая, безусловно, интригует и озадачивает. Сразу же возникает вопрос: “Возможна ли вообще единая теория чего-либо, а тем более такого категорийного, т.е. очень общего, понятия, как управление?”. Во избежание недоразумений и отрицательных эмоций, связанных со словом единая з заголовке, авторы хотят сразу оговориться и подчеркнуть тот факт, что это слово здесь не несет абсолютного характера как чего-то вечного, незыблемого и окончательного на все времена. Скорее его нужно понимать как заимствование из современной теоретической физики, где идет интенсивная захватывающая работа по созданию “Единой геометрической теории всех физических полей”, о которой, безусловно полусерьезно (кто как), говорят, что это — Теория Всего. Однако еще на рубеже XIX и XX вв. господствовало убеждение, что в физике уже все сделано, т.е. открыты все или почти все закономерности, которые могут объяснить все или почти все, “за исключением” лишь небольшого числа незначительных явлений, которые, как тогда уверенно считали, вскоре будут объяснены с помощью тех же, уже известных, фундаментальных закономерностей.
Как “гром среди ясного неба” было воспринято появление теории относительности и квантовой механики. Эти новые идеи и явления буквально перевернули и фундаментально изменили философию и методологию науки и жизни вообще.
На наш взгляд, человеку, и даже всему человечеству, свойственно периодически делать мелкие и крупные ошибки, впадать в эйфорию и наивность, проявлять чрезмерную гордыню (не путать с гордостью).
Рецепт против этой хронической до сих пор болезни, по-видимому, только один — не надо забывать или, лучше сказать, надо всегда помнить, что все по-настоящему глубокие и вечные истины выглядят банальными. Сейчас, как это было и сто лет назад, нельзя говорить и даже надеяться, что мы сможем что-то понять до конца, а тем более соз-
7
ми Icopiiio Всего. Для этого достаточно, па наш ни ляд, осознать и iipiiioiи. in тину, которую можно высказать следующим обраюм: “Всяким ре.ни.носи. непостижимо сложна”.
И так, общие философские соображения о “невообразимой сложно-III любой сущности” и практический “жестокий опыт” развития есте-1 гневных наук говорят нам о том, что, по-видимому, создание самой единой и самой общей окончательной теории не только “всего”, но и какой-то “части всего” невозможно в принципе. Един и всеобщ может быть только Бог. Поэтому слово единая и в физике, и в других науках надо понимать, как попытку осознать, осмыслить накопившиеся к данному моменту времени знания и опыт. Времена “разбрасывания камней” и “собирания камней” чередуются. XX век стал веком бурного развития не только механики и физики, но и кибернетики, которая стала очень разветвленной, в ней появились много направлений, подходов, методов, дисциплин, которые проникли почти во все поры повседневной жизни человеческого общества. Язык кибернетики стал сложным и разнообразным, появились много субязыков многих отдельных дисциплин, поэтому специалисты даже соседних отраслей стали плохо понимать друг друга. Поэтому естественно ставятся вопросы о преодолении разобщенности, в связи с чем необходимо начать поиск и выработку подходов и средств к тому, чтобы вновь создать нечто единое и стройное, которое бы органическим (интегрированным) образом охватило собой наибольший объем всего того, что проявило себя за последние годы. Такая работа трудна, подчас неблагодарна и, конечно, не под силу одному Человеку и даже небольшой -группе лиц, ибо она необычайно многогранна. Наметка лишь программы создания такой теории — дело очень непростое.
Авторы надеются, что книга внесет свой вклад в решение нелегкой задачи построения обобщающих теорий управления, а главное — укрепит серьезный интерес и поможет глубже понять фундаментальную актуальность подобного рода задач.
Авторы заранее просят извинить их за те огрехи, которые они допустили невольно, с признательностью выслушают критику и учтут ее в дальнейшем. Мы уверены, что дело не в том, чтобы не ошибаться — мы это делаем на каждом шагу, и жизнь состоит из непрерывной цепи ошибок, ибо она непостижимо сложна, — а в том, чтобы у нас всегда работал внутренний регулятор, сознательно нами доведенный до автоматизма постоянным воспитанием, учебой и работой над собой (в основном головой), который бы чувствовал эти ошибки и стремился их устранить, скомпенсировать оптимальным образом, хотя, что такое оптимальный образ и мера никто не знает, но их надо искать всегда, часто с переменным успехом, с надеждой на то, что в поиске меры и “золотой середины”, компромисса и терпимости состоит один из главных смыслов жизни, направленных на ее поддержание и развитие.
8
За обсуждение, поддержку и критику авторы выражают глубокую благодарность чл.-корр. РАН Ю.Н. Павловскому, проф. Н.А. Бобылеву и проф. В.Г. Лабунцу.
За большую помощь в работе авторы выражают благодарность канд. техн, наук В.И. Финягиной, а также проф. Р. Пише и доктору О. Нюк-конену за помощь и обсуждение ряда вопросов.
За поддержку работы в целом авторы благодарны академику РАН А.Б. Куржанскому.
Авторы выражают признательность РФФИ за поддержку исследований грантом № 98-01-00038.
Пастушонку Пете трудно жить на свете. Тонкой хворост иной управлять скотиной. Если бы корова понимала слово, То жилось бы Пете — лучше всех на свете.
Но коровы в спуске, за рекой у леса, Говоря по-русски, смыслят ни бельмеса. Им бы лишь мычалось, да трава качалась. Трудно жить на свете пастушонку Пете!
Сергей Есенин.
“Сказка о пастушонке Пете, его комиссарстве и коровьем царстве”
ВВЕДЕНИЕ
Цель данной работы — в компактной, конспективной форме изложить программу и некоторые результаты построения “Единой геометрической теории управления” (ЕГТУ), или “Теории структур управления” (ТСУ). В работе с единых философских, методологических, логических и точных математических позиций излагается взгляд авторов на кибернетику как науку об управлении. Даются точные определения ряда исходных понятий предлагаемой теории, таких как управление, структура, система, пространство и др. При этом предполагается, что методом изучения этих понятий в кибернетике и математике служит универсальный метод, в основе которого лежит понятие симметрии.
На вопрос, почему единая теория управления должна быть геометрической, можно ответить словами Н. Бурбаки: “Таким образом классическая геометрия переросла себя и из живой самостоятельной науки превратилась в универсальный язык всей современной математики, обладающий исключительной гибкостью и удобством” [36, с. 137]. Известный физик Дайсон, ссылаясь на сподвижника Ньютона Генри Пембертона, отмечал: “Ньютон всегда выражал огромное восхищение геометрами древней Греции и осуждал себя за то, что в своих трудах не следует им в той мере, как это следовало бы” [232, с. 10]. Более того, Ньютон считал, что геометрическое истолкование или представление любого утверждения и есть доказательство его истинности.
10
В ЕГТУ—-ТСУ выяснилось, что на сегодня наиболее адекватным математическим аппаратом, отвечающим теоретической кибернетике, является аппарат теории расслоений, куда понятия управление и симметрия входят наиболее естественным образом. Надо отметить, что понятия главного и ассоциированного расслоений уже использовались в теории управления гладкими дифференциальными системами, которые описывались конечным набором обыкновенных дифференциальных уравнений (см., например, [15, 185, 237, 309, 370, 547]. Нам представляется, что понятие расслоения надо рассматривать в более широком смысле, не ограничиваясь, например, предположением об эквивалентности всех слоев одному стандартному слою. Целесообразно принять, что слои могут быть неизоморфны между собой. Такой подход более естественным образом позволяет учитывать разнообразные ограничения, присущие широким классам систем с управлением. Использование методов теории расслоений привело к выявлению связи между кибернетикой и калибровочными принципами современной теоретической физики. Важно подчеркнуть, что понятие геометричность ни в коем случае не противопоставляется понятиям алгебраичности, аналитичности, алгоритмичности и не исключает их. Все эти понятия скорее сращиваются и переплетаются, появляются дисциплины и теории с названиями алгебраическая геометрия и геометрическая алгебра, аналитическая геометрия и др.
Есть несколько смыслов, вкладываемых в понятия геометрия и геометричность. Назовем некоторые из них.
1.	Первоначальный исторический смысл: геометрия — наука об измерениях на земной поверхности (гео — земля, метрия — измерения).
2.	Более широкий смысл по сравнению с первым: геомертия — это количественные соотношения между фигурами (плоскими, объемными, «-мерными).
3.	Выделение топологии, понятий метрики и меры',
4.	Понятие геометрия как независимость от систем координат, как инвариант всевозможных преобразований координат, как симметрия.
5.	Еще более широкое понятие: геометрия как независимость от видов представления и вообще языка описания.
Однако то, что не удается увидеть, понять, сделать на одном языке, в одном описании и представлении, то удается сделать в другом, если этот язык оказывается более понятным и близким индивиду, изучающему проблему.
Понятие геометричности как независимости от систем координат, выбираемых субъективно, вовсе не отказывается от идей координат и понятия числа. В современной математике эти идеи получили далеко идущие расширения, обозначенные Г. Вейлем термином координация,
11
о чем пишет в своей книге И.Р. Шафаревич [349], объясняя, что такое алгебра. Близким по смыслу к этому я вляется термин индивидуализация.
Идею координации, или индивидуализации, можно понимать как стремление ко все большей различимости и повышению точности измерений и наблюдений. “Измерить все, что измеримо, и сделать измеримым все, что таковым еще не является”.
Перефразируя это высказывание, можно сказать, что геометрия, включая топологию в современном ее понимании, направлена в том числе и на то, чтобы “проинтегрировать все, что интегрируемо, и сделать интегрируемым все, что таковым еще не является”. Например, есть актуальная необходимость понять, что такое “шероховатая” поверхность как альтернатива гладким дифференцируемым поверхностям, и как она может получиться как результат некоторого интегрирования, в частности, дифференциальных включений, описывающих системы с управлением. Нетривиальные соображения о негладкости пространств высказывал еще Клиффорд, говоря, что на самом деле, в действительности нет гладких и даже непрерывных пространств [221].
Необходимость создания ЕГТУ—ТСУ родилась не только из присущего науке стремления создать наиболее общую теорию, но из стремления помочь разрешить самые актуальные технические и технологические проблемы: например, создание стабилизирующих систем управления для процессов в горячей и холодной плазме; создание теории и методов конструирования современных композитных материалов; создание теории и методов управления когерентными полями на квантовом уровне, например, для лазеров; создание интеллектуальных сред, например, типа нейронных и компьютерных сетей и систем; наконец, создание научно обоснованных методов для различных организационных и социальных перестроек и реформ и управления развитием такого рода структур.
В ЕГТУ—ТСУ основной проблемой является проблема управления системами как структурами. В этой теории речь идет об управлении структурами и их симметриями, что поднимает задачи управления на качественно новый уровень, существенно отличный от уровня классических задач управления состояниями систем при фиксированной (неизменной) их структуре.
Как показано в ЕГТУ—ТСУ, структуры часто описываются отображениями (или функциями). Поэтому ЕГТУ—-ТСУ явилась развитием теории управления системами с распределенными параметрами, где речь идет о задачах управления функциями, распределениями.
Геометрический подход, в частности разработка понятия фазового портрета дифференциального включения и соответствующего метода фазового портрета, позволил с единых геометрических позиций взгля-
12
путь на традиционные объекты, такие, как сплошные среды, поля и уравнения с частными производными [50, 409].
Задачи по управлению структурами и симметриями, выдвинутые в ЕГТУ-—ТСУ, породили новую философскую концепцию — “Управленческую парадигму Мира”, которая дает новый взгляд на такое фундаментальное понятие, как “Законы Природы”. Она дает новую возможность посмотреть на “Законы Природы” не как на нечто постоянное и неизменное, а как на объект управления и искусственного конструирования, на возможность искусственно менять и устанавливать новые “Законы Природы”. Однако в отличие от непродуманных лозунгов типа “Не ждать милости от природы, но взять их — наша задача” такие вещи, хотя они и принципиально возможны, надо делать крайне (!) осторожно и продуманно в части их согласования с другими структурами, представляющими непреходящую ценность. Сама эта возможность должна широко и глубоко обсуждаться и многократно продумываться со всех сторон, ибо есть большая опасность упустить ч го-то очень существенное.
Отметим важную, на наш взгляд, методологическую роль ЕГТУ— ТСУ как основы создания нового общего и гибкого языка кибернетики, который позволяет, в частности, в определенной мере упорядочить (например, в виде графов) основные математические структуры и пространства, создать структурированную энциклопедию математики с использованием мультимедийных, гипертекстовых компьютерных систем, что будет полезным в трудном процессе обучения студентов самых разных специальностей.
Опыт показывает, что переход на новый язык в науке занимает по меньшей мере время одного поколения, т.е. 20—30 лет. Начинать этот переход нужно и можно уже сегодня.
Авторы вполне осознают возможность больших или меньших пробелов в обосновании сделанных утверждений, неоправданных упрощений и популяризации выдвинутых в ЕГТУ—ТСУ положений, высказываний и утверждений. В этом случае их автоматически нужно воспринимать как соответствующие гипотезы, подлежащие дальнейшей разработке, уточнению, развитию и обоснованию или, возможно, отвержению как неисправимо несостоятельных. Поэтому содержание этой работы имеет смысл воспринимать как определенную программу создания ЕГТУ—ТСУ, требующую больших усилий по ее разработке, обоснованию, проверке и внедрению. Награда за большие усилия — это те достоинства, которые имеются в работе.
Первое, с чего начинается изучение какой-нибудь реальности (которая невообразимо сложна и допускает сколь угодно глубокое изучение), — это ее обозначение, или присвоение ей имени (слова, сочетания
13
слов, термина), за которым вначале пока что еще ничего не стоит, за ним почти нет содержания, смысла и формы.
Для людей это слово-имя-термин сначала остается совсем не ясным, не раскрытым. По сути, кроме термина, еще почти ничего нет. Далее у пытливых людей возникает стандартный вопрос: “А что это такое?” Такие вопросы чаще слышим от детей и, к сожалению, реже — от взрослых. После этого начинается более глубокое изучение реальности, ее структуры и симметрий и связи с другими структурами.
Энциклопедии и словари различных отраслей знаний посвящены первому описанию терминов: описанию их содержания, структур, симметрий и связей. Там даются ссылки на источники с более глубоким изучением данного термина и понятия, которое за ним находится.
Представляется, что на основе ЕГТУ—ТСУ можно будет создавать структурные энциклопедии с указанием перекрестных связей между ними, которые представляют собой “живую” систему в том смысле, что допускают неограниченное развитие по мере учета новых знаний, почти не разрушая ранее созданных структур и связей. При этом возможно создание нескольких уровней подробности и популярности таких энциклопедий с тем, чтобы они были доступны всем — начиная от школьников и кончая профессиональными исследователями. Современная техника, в том числе вычислительная, в частности интерактивные среды, позволяет автоматизировать процесс пользования такими уникальными и универсальными источниками знаний и обучения, что дает огромный (качественно новый) выигрыш в скорости, производительности, широте и глубине охвата вопроса или предмета и позволяет экономить денежно-материальные затраты на обучение, консультации ит.д.
Заключая введение, подчеркнем, что в книге поставлено больше вопросов, чем получено ответов. Оправданием этому является только то, что в Программе создания ЕГТУ—ТСУ поставлены слишком обширные и сложные вопросы и задачи, разрешение которых, как уже отмечалось, не под силу коллективу в несколько человек; по-видимому, на это способно по меньшей мере только целое поколение.
По содержанию книгу можно разделить на три части. В первой (разд. 1) излагаются философские, идейные и методологические взгляды авторов (не профессионалов в этих областях), составляющие исходные позиции развития Программы. Вторая часть (разд. 2—4) посвящена краткому описанию известных структур. Наконец, третья часть (разд. 5—8) посвящена некоторым результатам, связанным с развитием Программы создания РЗГТУ—ТСУ.
1. ФИЛОСОФСКИЕ, ИДЕЙНЫЕ, ОБЩЕМЕТОДОЛОГИЧЕСКИЕ, ЛОГИЧЕСКИЕ И МАТЕМАТИЧЕСКИЕ ПРИНЦИПЫ ПРОГРАММЫ СОЗДАНИЯ "ЕДИНОЙ ГЕОМЕТРИЧЕСКОЙ ТЕОРИИ УПРАВЛЕНИЯ — ТЕОРИИ СТРУКТУР УПРАВЛЕНИЯ"
1.1.	ФИЛОСОФИЯ
Философия — это наука о смысле всего сущего. В переводе с греческого философия означает любомудрие, любовь к мудрости. Близко к этому любознательность — любовь к знаниям (не путать с праздным любопытством). Все сущее, всякую сущность будем называть реальностью.
Понятию реальности трудно, скорее даже невозможно, дать нетавтологическое определение, ибо это, по-видимому, самое основное понятие. Мы можем только отметить ее важнейшие, на наш взгляд, свойства.
Всякая реальность — бесконечно, невообразимо, непостижимо сложна и обладает невообразимым разнообразием в любой своей части и в целом. Последнее утверждение очень важно для всего нашего последующего изложения, и мы будем часто ссылаться на него.
Другое принципиальное, как мы думаем, свойство реальности состоит в том, что любая реальность неповторима и не воспроизводима со 100%-й точностью. В мире нет двух, не говоря уже более, абсолютно одинаковых реальностей. Если мы захотим воспроизвести какую-нибудь реальность абсолютно точно, то это нам в принципе никогда не удастся; у новой реальности всегда существует и, вообще говоря, может быть найден признак, отличающий ее от исходной. Таким образом, всякая реальность, по-видимому, абсолютно индивидуальна. Разных реальностей “бесконечное, необозримое количество”; “множество” всех реальностей также необозримо велико и сложно устроено.
Ответы на глубочайшие вопросы познания и осмысления реальности надо искать на путях разработки все новых и новых расширяющихся способов мышления, последовательно разрешающих возникающие парадоксы. Диалектика, впервые сформулированная Гегелем, является па сегодня одним из главных способов продвижения по этому пути. В
15
науке XX в. диалектический способ мышления ярко проявился в Принципе (или Теории) дополнительности Нильса Бора, открытом им для осмысления парадоксов, доставленных теорией относительности А. Эйнштейна и квантовой механикой Бора, Шредингера, Гайзенберга, де-Бройля, Дирака, Паули, Борна, Гильберта, Вейля и др.
Реальность можно отождествить с понятием Бога, тем самым вложив в это понятие всю глубину понятия реальности.
Бог — вездесущ и един.
Человек обладает способностью, данной ему от Бога, порождать, творить смысл путем мышления, рассуждения и размышления. Обладание этой способностью называется Разумом. Homo Sapiens — человек мыслящий. Понятие Разум — также некая реальность, это — способность понимать, осмысливать.
Мы исходим из того, что любая реальность может быть в той или иной мере осмыслена, и ее смыслу может быть придана точная логикоматематическая форма в виде соответствующей математической структуры, описывающая эту реальность с наперед заданной точностью, что означает теорию данной реальности. По сути это утверждается в первом (прямом) утверждении формулировки “Принципа 100%-эффективности математики”, в этом первый смысл термина “100%-эффективность” (см. подразд. 1.10). Важнейший вопрос о единственности структуры, описывающей данную реальность, здесь обсуждаться не будет (отсылаем читателя к книге Е. Вигнера “Этюды о симметрии” [73, с. 193]).
В любую реальность можно вложить определенный смысл. Отсюда, в частности, следует, что любая “бессмыслица” может быть осмыслена. Бессмыслица — это еще неосмысленная реальность.
Последний тезис также очень важен, ибо он провозглашает веру и надежду на познаваемость реальности как возможность осмысления любой реальности. Одно из выражений этого принципа содержится в “Принципе 100%-эффективности математики”.
Итак, центральным и основополагающим понятием для нас является понятие смысла. Так как наряду с понятием реальность это самое основное понятие, то дать ему определение, т.е. выразить через другие понятия, невозможно. Это первое неопределяемое понятие, которое может быть понято только интуитивно. Оно должно быть как бы вложено в нас изначально, от Бога. Стремление, любовь к смыслу (философия) — это, по-видимому, то, что выделяет человека среди остальных реалий.
Смысл имеет то, что понятно. Понять что-то новое — это значит установить связь этого нового с тем, что уже понято ранее, уже осмыслено. Связь можно рассматривать как установление отношения между
16
реальностями. Отношения в логике выражаются предикатами с соответствующей “местностью” по числу объектов, между которыми устанавливаются отношение, связь, смысл. В дальнейшем мы увидим, что понятие связи и связности можно ассоциировать с понятием управление. Тем самым управление становится одним из самых фундаментальных понятий, основой для попытки предложить “Управленческую парадигму Мира”.
Нас будут интересовать общие основополагающие термины-слова и стоящие за ними понятия; отношение, структура, пространство, система, взаимодействие, движение, управление, сложность, информация и, наконец, симметрия. Они составляют основу теоретической кибернетики. Мы попытаемся придать им максимально точный логикоматематический смысл, соответствующий современному уровню развития философии, логики и математики.
Сейчас, когда наблюдается лавинообразный рост данных и знаний, очень важно иметь максимально точный общий язык, понятный широкому кругу специалистов самых разных специальностей, включая гуманитарные.
Мы возьмем на себя смелость отождествить понятие смысл с другими понятиями, которые для целей ЕГТУ—ТСУ будем считать равнозначными — это понятия отношение и структура. Осмыслить реальность — это увидеть, распознать в ней некоторое отношение или структуру: выделить в реальности какие-то “предметные” части и установить их свойства, или общее, установить отношения между ними. Часто это можно делать на языке логики предикатов.
Это положение будет для нас центральным и ляжет в основу самих определений понятий структура, пространство, система и др. Например, под мышлением можно понимать способность осмысливать реальность. Эта способность, несомненно, присуща человеку.
“Пища”, или материал, для осмысления поступает человеку в виде сигналов той или иной физической природы, на том или ином материальном носителе и воспринимается посредством его органов чувств-. зрения, слуха, обоняния, осязания, вкуса.
Проблема распознания механизма осмысливания (превращения сигналов, воздействий в смысл и обратно) является, пожалуй, самой фундаментальной научной проблемой человечества.
Эта способность состоит в том, что той или иной реальности, которая воздействует на человека, каким-то образом ставится в соответствие смысл, т.е. та или иная конкретная реальность “отображается” в смысл. Более того, и обратно, каким-то образом сформированному смыслу может ставиться в соответствие определенная реальность так, что между реальностями и их смыслами устанавливается, по крайней
17
мере приближенно, с какой-то точностью (статистической или детерминированной), взаимно однозначное соответствие.
Возможно, целесообразно все реальности разделить на две части: материальные и идеальные, мир материи и мир структур', по-видимому, это то, что Платон назвал миром идей. Для каждой материальной реальности существует “много” структур, которые с той или иной точностью отображают, представляют, описывают ту или иную сторону, свойство материальной реальности, осмысливают ее в виде форм, образов, знаков, языков, структур и т.д. Этих форм достаточно, чтобы данную реальность описывать сколь угодно хорошо, отвечать на любые вопросы к этой реальности, предсказывать поведение этой реальности. Все это происходит в мыслящих системах, которыми прежде всего являются люди. Они способны наблюдать, порождать идеи и использовать их для описания и овладения всякой реальностью, как материальной, так и своей собственной идеальной реальностью, так сказать, своим самосознанием. Это и называется деятельностью интеллектуальных систем. Описание, осмысление и использование интеллектуальных систем — это предмет теории интеллектуальных систем, куда входят философия, логика и математика.
Об этом факте будем говорить как о явлении (тоже реальности) согласованности, или понимании (взаимопонимании), установления взаимной связи двух самых общих понятий: реальности и смысла.
Смысл каким-то образом хранится, вкладывается, находится и извлекается из памяти, передается, обрабатывается, воспроизводится. Став на кибернетическую точку зрения, заманчиво рассмотреть явление осмысливания человеком реальности с более общей точки зрения, а именно, как явление согласования, понимания и взаимопонимания, связи и взаимосвязи вообще между двумя (или более) отдельными системами. Эти системы можно рассмотреть как подсистемы, входящие в одну “общую” систему.
Под согласованностью (понимаем связью) между двумя системами (подсистемами одной системы) можно понимать возможность или действительность их совместного существования (без повреждений или разрушений участников взаимодействия). Это совместное существование в наиболее общих терминах, по-видимому, должно выражаться в существовании движений в каждой подсистеме и выдаче воздействий на другую систему, получении воздействий от другой системы. Движения и воздействия с научной точки зрения могут носить как материально-физический характер так и сигнально-информационный.
Уже в этом подходе явным и прямым образом используется первейшая способность человека — различать, разделять, отделять, дифференцировать. Например, мы говорим об отдельных системах и под
18
системах. Это начало аналитических способностей человека, т.е. способности к анализу. После чего проявляется способность к синтезу — рассматривать взаимодействие выделенных частей (подсистем), тем самым объединяя и интегрируя их в целое, целую систему.
Часто понятие смысл связывается (осознается) через понятие цель (назначение, предназначение). Более того, понятие смысл определяется через понятие цель и, таким образом, первичным понятием становится цель, а смысл — вторичным.
Существование или предположение (гипотеза) о существовании этих основных первичных понятий целей и смыслов, как показывает опыт развития человечества, является плодотворным и эффективным средством выживания и развития как отдельных индивидов, так и общества в целом.
Отсюда уже рукой подать до самого фундаментального, но и самого сложного понятия — понятия Бога — носителя всех смыслов и всех целей. Он щедро делится этим своим непреходящим богатством с теми людьми, которые хотят приобщиться к нему.
Антиподом понятия Бог в указанном смысле является понятие дьявол (падший ангел), который мешает людям приобщиться к божественным мудростям, который сбивает людей со “здравого Божеского смысла”, путает их мысли и цели, делает их сумасшедшими, обессмысливает всякую реальность, включая самого человека, отнимает веру и надежду па счастливую жизнь. Недаром говорят, что “Если Господь желает наказать, то он лишает разума”.
Итак, смысл — это осознанное отношение между реальностями. Это важно и удобно для нас, так как отношение — это важнейший термин для дальнейших наших рассмотрений логики, математики, кибернетики и науки вообще.
Философия — очень сложная наука, ею занимались и занимаются лучшие умы человечества. Содержание этого подраздела — лишь некоторые немногие принципиальные замечания, касающиеся философии (сделанные не специалистами в этой области), попытка придать философско-методологическую и идейно-логическую стройность ЕГТУ— ТСУ.
Сделаем еще несколько принципиальных, на наш взгляд, замечаний. Еще раз подчеркнем важность философии как науки. Изучая разнообразные конкретные науки, нельзя забывать об истории и сути самих наук, которые произошли от главной науки — философии. Можно сказать, что “Философия — это царь наук”. Недаром не так давно была лишь одна (!) ученая степень — доктор философии.
Если “Философия — это царь наук”, то математика — это тоже наука особой важности, что выражается пословицей “Математика —
19
царица наук”. Мы надеемся, что наши дальнейшие рассмотрения помогут точно понять смысл этик поговорок (см. подразд. 1.10).
Отсюда следует, что всякая наука должна иметь философские и математические основания. К этому вопросу мы будем возвращаться в дальнейшем.
Так как человек сам является реальностью, то философия обязана осмысливать и самого человека, и его способность осмысливать реальность. В проблеме осмысления реальности человека мы ясно различаем два аспекта, две подпроблемы, одна из которых — проблема познания реальности, другая — проблема морали, этики и эстетики. Очень коротко обсудим их в подразд. 1.6.
Говоря о смысле реальности, нельзя не сказать о методологии — науке о методах, т.е. способах, путях, образах, алгоритмах осмысления реальности. ЕГТУ—ТСУ утверждает, что существует универсальный, наиболее общий философский метод, метод осмысления реальности — это метод симметрии. В переводе с ] реческого симметрия дословно означает соразмерность. По смыслу надо добавить сюда согласованность, гармоничность. Симметрия — это очень сложное и глубокое понятие, которое имеет большое количество проявлений и выражений, описываемых такими терминами, как сохранение, инвариантность, баланс, равновесие, постоянство, независимость, устойчивость и др. Фундаментальная важность этого понятия была замечена нашими предками, о чем свидетельствует известное латинское изречение: "‘Бог сохраняет все”.
Как и сам Бог, симметрия едина во многих лицах.
Эти высказывания можно также поставить эпиграфом ко всей Программе создания ЕГТУ—ТСУ, ибо мы пытаемся утвердить и осмыслить факт, провозглашаемый этой поговоркой, а также попытаться объяснить, как Бог это делает, как ему удается сохранять все. В этом объяснении и будет состоять принцип, выдвигаемый в ЕГТУ—ТСУ — “Принцип управленческой парадигмы Мира”. Если очень кратко, то суть “Принципа управленческой парадигмы Мира” состоит в том, что все в Мире сохраняется и поддерживается путем управления, а точнее, путем создания, образования систем управления, в том числе основанных на принципе обратной связи, которая реализована регуляторами. Таким образом, утверждается, что осмысление реальности (например, как говорят, познание “законов, управляющих Миром”) может быть выражено в виде утверждений “Мир стоит на регуляторах”, “Мир — это многосвязная система управления и регулирования”; всякую осмысленную сущность (реальность) можно представить себе как некоторую систему управления (регулятор), который как раз и призван сохранять и поддерживать эту осмысленную сущность.
20
Отсюда следует порочность известного требования “наведения порядка”. В человеческом бытии должен господствовать принцип: “Порядок надо не наводить, а постоянно поддерживать и сохранять”.
Проблемами управления занимается кибернетика — наука об управлении (в переводе с греческого означает — кормчий, рулевой). На наш взгляд, это хороший термин, созвучный другим важным терминам: логика, математика, физика, механика. Поэтому не надо стесняться в широком и частом его применении. В более широком смысле кибернетику можно понимать как триаду — управление, система, информация. Эти три понятия представляют собой три тесно связанных и взаимодействующих аспекта одной очень глубокой реальности, которой можно дать единое имя кибернетика.
Таким образом, в ЕГТУ—ТСУ, помимо основных терминов — отношение, симметрия — должен быть включен термин управление, а также тесно с ним связанные термины система, информация.
В дальнейшем мы отождествим термин отношение с другим фундаментальным термином — структура. Далее важный термин система будет отождествлен с термином пространство, понимаемым в широком смысле. Фундаментальный термин система с управлением, может быть отождествлен с термином открытая система, что на языке кибернетики означает “система, имеющая вход и выход”, а на физическом языке — “система, взаимодействующая с окружающей средой, другими системами”.
В ЕГТУ—ТСУ мы попытаемся придать этим понятиям и терминам соответствующий точный логико-математический смысл, дать им точные логико-математические определения.
Перефразируя один из эпиграфов в замечательной книге Поля Самуэльсона “Экономика” [278, 533], можно в шуточной форме выразить следующую мысль: “Даже из попугая можно сделать образованного математика и кибернетика: все, что должен он усвоить, — это три слова: структура, симметрия, управление”.
Сделаем еще одно важное замечание, связанное с понятием оптимальности или экстремума — максимума или минимума. Этот термин можно включить в ряд упомянутых выше фундаментальных терминов, что фактически сделал Леонард Эйлер, который говорил, что Бог так устроил природу, что в ней нет ничего такого, в чем бы ни был виден смысл какого-нибудь максимума или минимума.
Действительно, можно взять на себя смелость и сказать, что проблема оптимальности как математическая проблема так или иначе содержит в себе почти все проблемы современной математики.
Для решения проблем оптимальности, включая вариационное исчисление, составляющих фундамент современных естественных наук,
21
были развиты вариационные методы (методы вариаций), которые однозначно допускают четкое управленческое толкование и тесную связь с принципами симметрии. Среди последних находится “принцип локальной калибровочной инвариантности (симметрии)”, который вместе с “принципом спонтанного (самопроизвольного) нарушения симметрии' рассматривается как самое большое достижение в современной науке, так как он описывает все известные на сегодня силы и взаимодействия. Трудно найти классика естественных наук, который не занимался бы этой проблемой.
Во избежание недоразумений заметим, что термин нарушение симметрии вовсе не означает разрушение или деградацию структур (отношений и смысла), а скорее наоборот: означает развитие, усложнение смысла, отношений, структур. Для этого мы хотим предложить еще один термин — детривиализация.
В ЕГТУ—ТСУ, в отличие от Природы, ставится задача более общая — изменять симметрии, а следовательно, отношения и структуры, целенаправленным способом, т.е. управлять с целью получения желаемых, заданных структур, отношений, симметрий.
В этом смысле ставится, на первый взгляд, абсурдная задача; научиться изменять и конструировать новые заданные законы Природы, ранее в Природе не наблюдавшиеся. Оказывается, что ничего абсурдного в этом нет, такая задача вполне осмыслена и ее можно ставить, изучать и реализовывать практически: нужно только построить соответствующие регуляторы и управления.
Здесь реализуется известная банальная поговорка: “Ничто невечно под Луной”. Даже то, что мы называем законами Природы, в классическом понимании смысла этих слов также подвержено изменениям. Например, сейчас в физике предсказывается возможность процесса распада протона, что повлечет радикальное изменение наблюдаемых структур, законов Природы.
1.2.	ЛОГИКА
Если философия — наука о смысле всего сущего, то логика — это наука о формах, или структурах, смысла, о преобразованиях (рассуждениях, умозаключениях, передаче и запоминании смысла), сохраняющих смысл, т.е. не допускающих его искажение или подмену. Всякий язык определяет формы смысла и является носителем смысла.
Впервые формализовывать и преобразовывать смысл предложил Аристотель, создав учение о правилах рассуждений и умозаключений в виде теории силлогизмов. В логике выделилась форма смысла в виде понятий истинности и лжи, правды и неправды. В настоящее время —
22
это главная форма смысла во всей науке, включая саму логику и математику. Основы этой формы смысла изучаются в таких разделах логики, как теория высказываний и теория предикатов. На этих разделах логики основаны вся математика и другие науки.
Логика как наука занимает промежуточное место между философией и математикой, она тесно связано с обеими. Поэтому логику рассматривают и изучают или вместе с философией, или вместе и с точки зрения математики, и тогда ее называют математической, или теоретической, логикой. В этом случае в самой логике строят и изучают математические структуры, например, математические структуры типа функций и алгебр Буля. Буль был родоначальником математической логики, он начал реализовывать идеи Лейбница о создании точного математического логического исчисления смысла с последующей автоматизацией этого исчисления с помощью вычислительных устройств. Можно сказать, что логика осуществляет связь, или отношение, между философией и математикой.
Отметим еще один очень важный, по нашему мнению, аспект, особенно ярко и плодотворно проявившийся с возникновением в логике двузначности в связи с понятием истины и лжи. Мы имеем в виду возможность постановки вопросов о форме вопросительных предложений и двузначных взаимоисключающих ответов типа “да”, “нет”, причем третьего не дано: “Tertum non datur”. Это знаменитый основополагающий логический закон или, лучше сказать, принцип, который называется “Принцип (закон) исключенного третьего”. Примененный к математике, он на долгие годы стал в ней основным принципом “работы со смыслом”. И лишь относительно недавно стал вопрос об ограниченности этого принципа, т.е. стал обсуждаться вопрос о возможности все-таки существования чего-то третьего. Эта критика закона исключенного третьего идет со стороны так называемого конструктивистского подхода к математике, родоначальником которого был Брауэр, отстаивавший свои взгляды в очень горячих дискуссиях с самим патриархом математики первой трети прошлого века Давидом Гильбертом.
Ясно, что вопрос о существовании той или иной реальности — это центральный вопрос философии, ибо речь идет о существовании смысла, трансформированный в существование какого-то конкретного объекта. Для ЕГТУ—ТСУ и управленческой парадигмы Мира — это тоже важнейший вопрос, так как, другими словами, речь идет о творчестве, о том, что такое творчество, что значит что-то создать, т.е. сделать существующим нечто, что ранее не существовало. Таким образом, речь идет о том, что такое возможность, и о превращении возможности в действительность. Но так как управление — это также определенный выбор или реализация возможностей, то становится ясным, что понятие творчество очень близко к понятию управление.
23
Был сделан ряд попыток обобщить закон исключенного третьего, заменить его другими, более широкими и гибкими принципами [488]. В ЕГТУ—ТСУ эта попытка реализуется в понятиях тривиализации (деградации, утраты части смысла) и детривиализации (развития, появления нового смысла). Нам представляется, что теория расслоения на сегодня наиболее подходящий математический аппарат для представления и изучения этой проблемы.
Существуют и другие попытки выйти из ограничений, наложенных законом исключенного третьего. Например, введение закона (принципа, аксиомы) детерминированности [143, с.35].
Логика имеет большую практическую ценность. Всегда существует опасность потери, искажения и подмены смысла при изложении или обсуждении каких-либо тем. Но логика призвана для того, чтобы строго сохранять смысл, т.е. логика — это способ “борьбы” с бессмыслицей и глупостью, которая, как известно, беспредельна. Китайская пословица гласит: “Ум человеческий — ограничен, глупость человеческая — беспредельна”.
1.3.	АНАЛИЗ И СИНТЕЗ. ЭЛЕМЕНТ И МНОЖЕСТВО. НАТУРАЛЬНОЕ ЧИСЛО
Первая, врожденная способность человека — это способность различать, выделять нечто или что-то. Эта способность проявляется буквально с первых минут рождения, появляется самая первая ‘‘двоичная ” структура: “да—нет”, “есть—нет”, первый бит информации. В дальнейшем эта способность стала важнейшей способностью и способом познания мира и получила название анализ. Она включает в себя способность различать, разделять, выделять, дифференцировать и т.д.
Способность к анализу породила понятие элемента с двумя его характеристиками: 1) все элементы попарно различны, 2) элементы — неделимы, т.е. “бесструктурны” по определению. Отсюда простейшие конечные множества могли дать толчок к порождению натуральных чисел 1, 2, 3,... На первых порах эти понятия стали характеристиками множества, а затем развились в понятие мощности множества — одной из важнейших структур всей математики.
Вместе с этим, по-видимому, стала развиваться противоположная способность человека — способность синтезировать. Это способность более высокого уровня: синтезировать труднее и сложнее, чем анализировать. Грубо говоря, разделять легче, чем объединять; в математике, например, дифференцирование легче интегрирования. Эти две способности — анализа и синтеза — несимметричны. Аналогично несимметричны понятия Бога и дьявола, добра и зла, созидания и разрушения.
24
Итак, под синтезом понимается способность, обратная анализу. Это — способность объединять, группировать, классифицировать, соединять, конструировать, интегрировать и т.д.
Если способность анализа, в частности, породила понятие элемент, то способность к синтезу породила понятие множество как объединение элементов или общее — породила понятие отношение. Первую теорию множеств в математике создал Грегор Кантор только лишь в конце XIX в. Понятие множества — это основная математическая структура, основное математическое отношение — бинарное отношение между двумя понятиями или предметными областями “элемент” и “множество”, называемое отношением принадлежности, или членства.
Современная математика имеет теоретико-множественное основание. Дело в том, что всякая математическая проблема так или иначе может быть сведена к проблеме теории множеств. Поэтому сейчас обоснования математики сводится к обоснованию теории множеств.
Упомянем еще один важный прием синтеза как целенаправленной деятельности, это — прием повторений, итераций и рекурсий, причем часто многократный. В частности, он часто используется в обучении и вообще для передачи какого-либо смысла. Есть пословицы “Повторение — мать учения”, “Делай, как я” и др. Теория рекурсий играет важную роль в современной математике, она органически входит в математическую логику и конструктивную математику, где изучается важное понятие алгоритма, его практическая реализация и теория вычислений.
Создав теорию множеств, Грегор Кантор, по словам некоторых ученых (одним из них был Д. Гильберт), создал “настоящий рай для математиков”. Канторовская теория множеств с самого начала своего зарождения получила впечатляющие, неожиданные результаты. Однако уже в начале XX в. Б. Расселом был открыт парадокс, который ясно показал, что “наивное” определение понятия множества как собрания (коллекции, объединения и т.д.) некоторых элементов приводит к логическим парадоксам. Сложность реальности, вернее ее свойств, обозначенных именем множества, таким образом, проявилась достаточно быстро, как только реальность начали изучать. Парадокс Рассела получил много различных форм и реализаций, но все они свелись к одному простому вопросу: “Может ли множество быть элементом самого себя?”
Была доказана теорема, смысл которой выглядел абсолютно противоречиво: “Для того чтобы множество было элементом самого себя, необходимо и достаточно, чтобы оно не было элементом самого себя”.
Выход из этого положения стали искать в логике и в построении непротиворечивой аксиоматики теории множеств. Теория множеств поэтому стала тесно переплетаться с логикой. До построения “оконча
25
тельной” теории множеств, по-видимому, еще далеко, и есть сомнение, что оно в принципе возможно. В этой связи нужно иметь в виду взгляд А. Пуанкаре на смысл понятия существование’, существует все то, что непротиворечиво.
1.4.	АБСТРАКЦИЯ, ИЛИ ИДЕАЛИЗАЦИЯ. СЛОЖНОСТЬ
Абстракция, или идеализация, — это другая важнейшая способность человека, данная ему от природы и свыше. Она очень тесно связана со способностью анализа и синтеза. Абстракцию можно рассматривать как способ “борьбы ” со сложностью, ибо любая реальность невообразимо сложна. Как же этот способ действует? Дело в том, что в результате использования нашей способности к абстракции порождаю гея понятия Понятие по своей природе, по определению, есть абстракция. В подразд. 1.3 мы заметили, что способность к анализу и синтезу породили два замечательных понятия — элемента и множества. Очевидно, что, например, понятие элемента в “природе” не существует, так как элемент мы наделили свойством неделимости, которого не существует в реальности: любой элемент как объект реальности имеет невообразимо сложную структуру.
Таким образом, элемент — это абстрактное идеальное понятие, в природе не наблюдаемое, это продукт нашей способности абстрагироваться, создавать идеальные объекты. Вместо невообразимо сложного объекта, чем является любая реальность, мы породили простой, обозримый объект конечной (!) сложности, характеризуемый одним битом информации (да-нет, элемент-не элемент), в отношении принадлежности, принадлежности к множеству. Таким образом, вместо необозримо сложного набора реальностей мы получили одно понятие элемента, а вместо набора элементов получили возможность рассматривать опять лишь одно (!) понятие — понятие множества. Итак, элемент и множество — это пример абстрактных понятий, на которых стоит вся совре-меннная математика.
За счет абстракции и введения абстрактных понятий мы получаем огромное упрощение: вместо необходимости оставаться один на один с невообразимо трудными реалиями имеем лишь конечное множество понятий. В этом и состоит способ “борьбы” с “проклятием” сложности. Возможно, что Р. Беллман имел это в виду, когда говорил о “проклятии размерности”.
Конечно, нас всегда могут совершенно справедливо упрекнуть в том, что нельзя использовать “такое” упрощение везде и всегда без осторожности, без оглядки, не отдавая себе отчет в том, как и за счет чего получено это благо упрощения. А цена упрощения состоит в том, что
26
полученное нами понятие на “самом деле” хотя и является одним-единственным, но зато остается очень сложным. Вся сложность реальности оказалась собранной в одном единственном (!) объекте — понятии.
Абстракция, идеализация, модель реальности — это ограничение или "гомоморфизм” реальности в “множество” конечных отношений или структур [70].
Эти категории позволяют невообразимо и непостижимо сложную реальность заменить одним (!) целым и неделимым термином, словом или словами, моделью, теорией.
Они доставляют нам универсальный способ борьбы с “проклятием” или скорее с “чудом” бесконечности — бесконечной сложностью реальности: понятие вбирает в себя и скрывает в себе “бездну” реальности. Этот факт надо помнить всегда, и всегда отдавать себе отчет в этом. Никогда не должно быть иллюзий, — которые, к сожалению, нередко имеют место, — что знание термина, обозначения, слова — это и есть знание соответствующей реальности. Именно в этом смысле надо понимать изречение “Слово или суждение, произнесенное, высказанное, есть ложь”, ибо никогда понятие, обозначенное термином, не может раскрыть всю глубину реальности, которую оно обозначает (идеализирует, моделирует, абстрагирует). Понятие имеет “определение”, которое может в лучшем случае лишь развиваться, т.е. расширяться, углубляться, уточняться, однако в принципе не может достигать 100% точности и 100% исчерпания любой реальности. Забвение этого положения часто является источником многих человеческих конфликтов, недоразумений, недопонимания и т.д. В каждой конкретной реальной ситуации требуется истолкование понятий (политика, юриспруденция — наиболее типичные места для таких недоразумений). Дело доходит до того, что понятия истолковываются искаженно, иногда вплоть до неузнаваемости и полной своей противоположности: “Война — это мир”, “Свобода — это рабство”, “Правда — это ложь” и т.д.
Даже простые, казалось бы, понятия стол и дом могут иметь очень широкое толкование-определение: “И под каждым ей кустом был готов и стол и дом” (И.А. Крылов. Басня “Стрекоза и муравей”). Поэтому бытует практика издания “Комментарий” ко всякого рода “Сводам Законов”, где разъясняются понятия, их смысл.
Приведем другой пример. Много тысяч лет человечество наблюдало механическое движение — движение массивных тел. И только относительно недавно, порядка 400 лет назад, гений Ньютона написал исчерпывающую и очень простую (!) формулу этого движения: F=ma.
Формула выглядит изумительно простой (!) и связывает всего три буквы: F, т, а. Неискушенный человек подумает, чего тут особенного, найти правильную комбинацию всего из трех букв? Да, это просто, но
27
совсем не просто, и в этом состоит гений Ньютона, образовать понятия, которые стоят за каждой из этих букв: F— сила, т — масса на — ускорение. Для выделения этих понятий и потребовалось человечеству несколько тысяч лет наблюдать и накапливать опыт, чтобы, наконец, гений Ньютона смог эти понятия окончательно выработать. Достаточно сказать, что всего за одним (!) понятием ускорения, обозначаемого одной буквой а, стоит целое дифференциальное и интегральное исчисление, специально созданное Ньютоном и Лейбницем. Таким образом, понятие ускорения, хотя и обозначается всего одной буквой а, является довольно сложным понятием.
Итак, за очень простой формулой, являющей собой огромное научное достижение, стоит огромный прогресс цивилизации, стоят очень сложные понятия, абстрактные понятия. В этом весь (!) смысл научного прогресса — вырабатывать простые формулы, законы, принципы, формулировки, теоремы, доказательства и т.д. Однако эта простота (лишь кажущаяся) достигается, покупается, оплачивается за счет постоянного усложнения научных понятий, за счет постоянного роста уровня абстракции. “Экономия мысли” как известный философский принцип растущего знания, таким образом, оплачивается необходимостью вырабатывать, рассматривать, изучать и понимать непростые абстрактные понятия, все более и более высокого уровня и, следовательно, все более и более емкие и сложные. Одно из проявлений культуры человечества можно толковать как осознание необходимости вырабатывать точные абстрактные понятия, осмысленно ими владеть и учиться им.
Так что в этом смысле “чудес в природе не бывает”, “за все надо платить”. По-видимому, это единственный (!) способ познавать невообразимо сложную реальность. Таким образом, на самом деле никакого упрощения не происходит, так, по-видимому, имеют место закон и “Принцип сохранения сложности, в том числе и бесконечной сложности всякой реальности”.
Па самом деле происходит лишь перекачка сложности: от формул (формулировок) к понятиям, и обратно. Если формула (формулировка) простая, то понятия (термины этой формулировки) — сложные, и обратно, если понятия примитивные, то формулировки длинные и сложные. Именно в этом смысле нужно понимать поговорки “Краткость — сестра таланта” и “гениальная простота”.
Одним из проявлений “проклятия” или “чуда” бесконечности и невообразимой сложности любой реальности является факт плохого понимания систем, имеющих конечное, но огромное число состояний (или структур с огромным числом параметров). Проще говоря, мы плохо понимаем большие числа. Числа, с которыми нам приходится иметь дело, можно разделить на три группы:
28
1)	"обычные”, с которыми человеку приходится иметь дело в повседневной жизни. Это числа приблизительно до 1О10;
2)	физические, включая астрономические. Это числа приблизительно от 1О20 до 1О50;
3)	наконец, комбинаторные — порядка, скажем, 1О100 и более. Этим числам пока что нет естественных аналогов ни среди обычных, ни среди физических чисел, ибо, например, они существенно превышают число всех элементарных частиц (в современном понимании этого термина) во всей наблюдаемой сегодня Вселенной!
Однако эти огромные, плохо вообразимые комбинаторные числа совершенно естественно появляются, казалось бы, в безобидных и элементарных задачах типа известной легенды о вознаграждении изобретателю игры в шахматы.
Более существенно то, что невообразимо большие, хотя в принципе конечные, числа появляются и господствуют в кибернетике и важных технических устройствах, например, таких как компьютеры и компьютерные системы (сети), включая интеллектуальные системы, скажем, типа "нейронных сетей”.
Такие системы имеют дискретное и конечное число состояний, так как они основаны на взаимодействии “триггеров” — элементарных систем, имеющих всего два состояния. Состояния систем, собранных в принципе только из триггеров, описываются уже комбинаторными числами. Здесь, по-видимому, также нужны новые понятия, смысл которых, как всякого понятия, состоит в редукции сложности: перекачке сложности из количества (больших комбинаторных чисел) в сложность качества понятия, с которым, однако, легче оперировать, а в их терминах проще формулировать научные утверждения.
Напомним, что комбинаторика— это раздел математики, в котором решаются задачи выбора элементов из определенных совокупностей в соответствии с точно определенными правилами и подсчета числа способов такого выбора. Как увидим в дальнейшем, управление — это тоже некоторый выбор. Поэтому указанная “проблема очень больших чисел” имеет самое непосредственное отношение к теории управления.
Следствия, вытекающие из изложенного в этом подразделе, довольно серьезные. О них весной 1998 г. говорил известный физик-теоретик Hawking (Хоукинг) в своей специальной лекции представителям американской элиты во главе с президентом США. Смысл обращения Хоукинга, на наш взгляд, состоял в том, что если какое-нибудь сообщество или страна хочет оставаться во главе развития, то совершенно необходимо постоянно повышать уровень науки и образования, который не может идти иначе, как только по пути неизбежного повышения уров
29
ня абстракций и выработки новых, все более общих, мощных, емких, гибких абстрактных и точно определенных научных понятий.
Но как раз этим и занимаются философия, логика и математика. К сожалению, сейчас имеется большой разрыв между уровнем достижений в науках и средним уровнем подготовки по этим дисциплинам всех специалистов. Такой разрыв может привести и уже приводит к большим издержкам в обществе, и не исключены более тяжкие последствия.
Эта ситуация ставит важные, но трудные проблемы ликвидации упомянутого разрыва путем выработки новых методологий, например, в таких дисциплинах, как математика и кибернетика. Одна из таких методологий, на наш взгляд, заключена в ЕГТУ—ТСУ, где вырабатываются точные математические абстрактные понятия высокого уровня и соответствующий гибкий язык, позволяющие унифицировано ликвидировать указанные разрывы и непонимание между специалистами разного профиля.
В ЕГТУ—ТСУ такими понятиями являются следующие — отношение, структура, симметрия, пространство, управление, система с управлением, обратная связь, регулятор, расслоение, движение, управляемость-достижимость, связность, оптимальность и др.
На основе этой методологии уже можно вырабатывать конкретные методики представления материала для обучения и самого процесса обучения с широким использованием возможностей современных компьютерных технологий.
В заключение рассмотрим еще одну иллюстрацию принципа перераспределения (редукции в прямом смысле наподобие редуктора — коробки передач в автомобиле) сложности — понятия спроса и предложения в экономике.
Это центральные понятия, о чем свидетельствует эпиграф к главе ‘‘Спрос и предложение” знаменитой книги “Экономика”, написанной Нобелевским лауреатом Полем Самуэльсоном: “Даже из попугая можно сделать образованного политэконома — все, что он должен усвоить, — это два слова: спрос и предложение” [278, 533].
Ясно, что понятия спроса и предложения — очень сложные понятия, отражающие многие характерные черты такой реальности, как человек или сообщество людей. Понятия спроса и предложения выражают желания, интересы, страсти, многие сложнейшие психологические переживания, а также физиологические и культурные потребности и многое другое.
Спрос и предложение выражают взаимодействие экономических подсистем. При этом вся сложность и неоднозначность этих понятий возникает в самых, казалось бы, простейших ситуациях. Рассмотрите, например, ситуацию, когда в пустыне взаимодействуют два человека,
30
причем один имеет только хлеб, а другой — только воду. Чтобы им выжить, совершенно необходимо произвести “товарообмен”: у каждого есть свои спрос и предложение на данные товары. К чему приведет такая ситуация, однозначно сказать невозможно, это зависит от многих факторов, некоторые из которых упомянуты выше.
Но если эти абстрактные понятия спроса и предложения уже выработаны, и выработаны соответствующие понятия “кривой спроса” и “кривой предложения”, то, например, основной закон экономики — закон спроса и предложения — формулируется очень просто: “Экономическое равновесие (в экономической системе) имеет место в точке пересечения кривых спроса и предложения”. Ясно, что всю нагрузку от сложности данной реальности принимают на себя именно абстрактные понятия: спроса и предложения — это и есть немалая цена Простых Законов Природы. Это еще один пример “Принципа экономии мысли”. Мы видим, что “экономия мысли” достигается за счет огромного труда и опыта по выработке емких, гибких и общих понятий. Поэтому самое главное и трудное в обучении — это научить понятиям, их пониманию и применению, а запомнить “формулы законов” очень легко, ведь они, как правило, простые и краткие.
1.5. О ЯЗЫКАХ
Жизнь современного человечества на всех его уровнях — от семьи до человечества в целом — основана на общении — связи — между членами общества, которое осуществляется с помощью языков. Как отмечалось выше, осмысление реальности человеком (или другой “нервной системой”) прежде всего основано на его врожденной способности различать, отличать, выделять какую-то одну реальность от всех остальных реальностей, на “фоне” других реальностей.
Заметим, что другая важнейшая врожденная особенность человека — любознательность, стремление к порядку (упорядочению), что, помимо эстетического удовлетворения, приносит ему и пользу.
Эти способности как бы стимулируют его деятельность по различению реальностей. Различение —это первый шаг осмысления.
Врожденная способность человека к абстрагированию, идеализации начинается с того, что выделенной, различенной, реальности присваивается обозначение, имя, метка г. В результате прежде всего появляется набор имен: гь г2,..., г„. Все эти имена попарно разные — по смыслу, по определению. За этими именами пока что не скрывается ничего более детального, чем одна различенная реальность как целое, неделимое целое, “штука”. Другими словами, каждое i = 1, ..., п — элемент, а их объединение — это множество г; в канторовском “наивном” понимании г - {г,-, i - 1,..., п} = {Г],..., г„}.
31
На первых порах для человека реальности с именами г, никак между собой ле связаны — это набор или множество в полном смысле этого слова (всякие связи напрочь отсутствуют). Однако мы знаем, вернее, это наш первый философский принцип — все реальности так или иначе связаны друг с другом, и эти связи сами есть определенная реальность. Процесс изучения человеком реальности после образования множества поименованных реальностей г продолжается в направлении установления других реальностей, описывающих связи между поименованными реальностями г. Начинается процесс синтеза. Он состоит в установлении связей (тоже реальностей) между элементами множества г.
Итак, получается следующая “диалектическая” картина. Некая невообразимо сложная реальность получает однозначным образом имя г, е г, т.е. нечто элементарно простое неделимое. Этот результат можно рассматривать как первый шаг в “борьбе” человека с “проклятием” невообразимой сложности реальности: за простым именем стоит бесконечно сложная реальность. Это первый шаг детривиализации — набор г имен г,- уже различенных и тем самым получивших “первую” определенность оо-сложных реальностей. За словом-термином простое стоит оо-сложное понятие. После этого начинается процесс более высокого уровня — различение другого сорта реальностей, описывающих связи между г,-. Так начинает развиваться понятие отношения между rh или системы, и множество г уже получает смысл множества состояний системы.
Все это —- основополагающие процессы становления научного подхода человека к реальности, основанного на его способности строить язык, способности давать обозначения, имена различенным им реальностям и выявлять отношения между ними, т.е. структурировать. Человек начинает познавать реальность с помощью языка. Более глубокое познание соответствует более развитому, более богатому языку, имеющему больший запас слов и грамматических конструкций. Создание языка дает новые возможности человеку, например, он может передавать, сообщать свои знания другим людям. Важно, что полученные знания имеют ту же силу, что и знания у передающего. Опыт передающего согласован (идентичен!) с опытом принимающего!
Приведенную схему можно толковать как усилитель знаний в том смысле, что знания, ранее известные одному человеку, становятся известными другим людям, однако при одном существенном условии (это — цена усиления): люди должны иметь общий язык и грамотно им пользоваться. Как известно, обучение языку — это тяжелый труд. Таким образом, уже на самых первых стадиях развития человечества возникает важнейшая основополагающая реальность — понятие обучения'.
32
Итак, язык и обучение — это два самых важных и неразрывно связанных понятия для отдельного человека и человечества в целом. В их развитии и обучении, в обеспечении передачи новым поколениям состоит важнейшая задача для отдельного человека и человечества в целом. Деградация языка и обучения — это деградация и гибель человека и человечества.
Язык — это форма выражения отношений, связей между так или иначе осознанными сущностями, объектами реальности. Вопрос о связях между сущностями и языках как способе реализации связей очень глубокий и сложный. Немецкий философ Хейдекер дал замечательную метафору: “Язык — дом бытия”.
В соответствии с разными способами обозначения имен и связей языков существует много. Среди множества всех языков выделим группу естественных, которые повседневно используются людьми на нашей планете, — это, например, русский, английский, китайский, финский, грузинский, армянский и другие языки. Их в мире насчитываются тысячи и тысячи. Кроме естественных языков, существуют языки жестов, танца, музыки, изображений, интонаций и др.
Известно, что существует фундаментальнейшая проблема перевода с одного языка на другой: выражение одного и того же смысла на разных языках. Это проблема симметрии как проблема сохранения смысла при преобразовании объекта. Интерфейс — это широкое понятие перевода как взаимопонимание систем разной природы.
В каждом естественном языке существует словарь слов-понятий-терминов; существуют правила их точного изображения — грамматика', существуют правила образования из этих слов предложений — синтаксис. Основная единица естественного языка — предложение. Важно, что предложение выражает законченную мысль, оно имеет смысл\ Смыслом в языке занимается семантика.
Человечество давно мечтает о том, чтобы осмыслить свое бытие и зафиксировать его смысл, причем сделать это с наибольшей точностью, чтобы максимально укрепить понимание смысла и сделать его универсальным, единым для наибольшего количества людей. В результате такого стремления и сформировалось фундаментальное понятие (категория) науки. Как отмечалось выше, исторически первой наукой, по-видимому, является философия. Это — наука о смысле всего сущего. Связь и язык нужны для понимания, хранения (запоминания) и передачи смысла той или иной сущности (возможной или актуальной).
Помимо упомянутых естественных языков, существуют ряд формальных языков и особо важные языки, как, например, язык математики и науки вообще. Формальные языки, к которым относятся алгоритмические языки, играют основополагающую роль в развитии цивилизации и культуры. Они являются основой компьютеризации общества.
2. А.В. Бабичев
33
Язык имеет фундаментальное значение для развития самого общества. Он развивается по пути постоянного подъема своего уровня, богатства и гибкости, однако при соблюдении вырабатываемых стандартов, ибо в противном случае язык потеряет свое значение как средство осмысления реальности, запоминания и общения. Язык в данном сообществе является индикатором уровня развития и состояния самого сообщества. Признаками деградации, например, являются плохой стиль естественного языка, употребление большого количества заимствованных из других языков слов и терминов без понимания тонного их смысла (наукообразие), широкое использование жаргонов (слэнгов) — специальных языков, понятных только узкому кругу людей.
Математический язык осуществляет жесткий контроль над естественными языками, которые обладают гибкостью и свободой, что подчас оплачивается недостаточно высокой точностью, большой вероятностью недоразумений и разночтений, как, например, язык поэзии, допускающий метафоры, аллегории и другие фантастические связи.
Мы живем в мире отношений и хотим понять, как разные объекты, выделенные в результате анализа, относятся друг к другу после стадии различения, анализа. Отношения реализуют важную задачу — задачу установления смысла путем установления отношений между различными объектами. В этом заключается синтез.
Язык -— это средство, предназначенное для фиксации форм, представлений, отношений и выражений смысла, их переформулировок (преобразований симметрии и инвариантности), это средство согласования, понимания и взаимопонимания, это связность. Что-то понять — эго значит установить связь (отношение) с чем-то уже ранее установленным и понятым. В дальнейшем покажем, что связь и связность нужно отождествить с понятием управление.
Естественный язык используется учеными для приближенного описания постепенно оформляющихся в мозге научных идей, часто изначально возникающих в виде образов, а не словесных текстов. Однако, как показывает весь исторический опыт, решающее влияние на цивилизацию и культуру оказали именно словесные тексты естественных языков. Вначале было Слово!
Тексты естественных языков доставляют “пищу (информацию) к размышлению”. В конечном счете осмысливание фиксируется на формальных языках конкретных наук. На этих языках смысл уже записывается (можно даже сказать кодируется) в виде конкретных теорий, высказываний, алгоритмов и компьютерных программ, решающих определенные задачи.
Интересно отметить, что в принципе обычный естественный язык обладает возможностями высокоточных описаний любых реальностей,
34
однако для этого как раз и нужно хорошо владеть родным языком. В этом смысле К. Паустовский в одном из своих произведений дал такое художественное описание падения капель дождя на поверхность озера, что его точностью восхищались профессиональные гидродинамики.
Подчеркнем очень важный принципиальный аспект способов осмысливания реальности и его описание на каком-то языке. Этот аспект есть принцип противоположной двойственности. Имеются в виду пары крайних характеристик и описаний в естественных и научных языках. Например, да—нет, плохо—хорошо, белое—черное, добро—зло, любовь—ненависть, война—мир и т.д. Аналогично в точных науках имеем: истина—ложь, сосредоточенность—распределенность, случайность—детерминированность, хаос—порядок, обратимость—необратимость, дискретность—непрерывность, волна—частица, поле—материя, замкнутость—открытость, управляемость—неуправляемость, устойчивость—неустойчивость и т.д.
Принцип состоит в том, что каждый из этих терминов и стоящих за ним понятий является идеализацией, приближением, математической абстракцией, которые на определенном уровне понятия реальности не описывают ее с нужной точностью. Это примеры “чистых”, крайне идеализированных понятий. На самом деле смесь, вернее, система чистых понятий лучше, точнее описывает реальность. Используя смеси чистых понятий, можно добиться существенно большей точности описания реальностей. Примером такой ситуации является понятие смешанного ансамбля в квантовой механике.
Лучшее, что здесь достигнуто, на наш взгляд, это известный “Принцип дополнительности Нильса Бора”, который гласит, что глубокая истина состоит в том, что существуют два взаимоисключающих утверждения (из двух разных теорий), которые оба истинны. Классическим примером такой глубокой истины является “квантово-механический дуализм” де Бройля “волна—частица”: “электрон — это частица, электрон — это волна”. Каждое из этих утверждений в отдельности является неверным в смысле их неполноты. Но новая синтетическая теория, пользующаяся “принципом дополнительности”, уже верна, она точнее описывает реальность в более широких условиях.
Глубокая и трудная проблема состоит в том, что просто и наглядно дуализм противоположных понятий представить себе очень трудно, ибо нет никаких простых наглядных образов. Выход состоит в исполь-ювании абстракции-, надо понять абстрактные математические структуры, которые описывают такую наглядно не представимую реальность.
Цель ЕГТУ—ТСУ — сформулировать и разъяснить эти общие принципы абстрактного научного мышления, в частности в кибернети
2*
35
ке и математике, которые основаны на понятиях структуры, симметрии и управления.
Таким образом, основным, первоначальным, исходным для нас будет всегда и везде понятие смысл. Оно формально неопределимо, ибо нет понятий, не зависимых от понятия смысла, и в то же время через которые понятие смысла может быть определено. В этом трудность этого понятия. Нет универсального понятия смысла конкретной реальности, кроме ее самой, ибо реальность бесконечно сложна и индивидуальна. Поэтому одной и той же реальности можно придать много смыслов, осмыслить ее по-разному. Понять смысл реальности точно и во всей глубине невозможно. Смысл данной реальности вырабатывается в процессе конкретной деятельности, связанной с данной реальностью, одного или многих людей па конкретных примерах. Чем больше этих примеров, тем лучше для уточнения понятия смысла данной реальности. Смысл вырабатывается в замкнутой системе с обратной связью: во взаимодействии опыта и теории.
Научить осмыслению реальности невозможно, этому можно только учиться на конкретных примерах, никогда не научившись этому окончательно на 100% за всю жизнь и за все время существования человечества. Можно только неограниченно совершенствоваться в этом, постоянно добавляя новые примеры нового опыта и постоянно переосмысливая старые смыслы старых опытов.
Но всякий смысл выражается на том или ином языке. Текст, написанный на языке, — это реальная форма смысла. С помощью языка смысл фиксируется, хранится, передается, обрабатывается. Важнейшее требование: при хранении, передаче, обработке смысл должен сохраняться, не разрушаться, быть инвариантным к указанным действиям — преобразованиям смысла.
1.6. ЦИВИЛИЗАЦИЯ И КУЛЬТУРА
В этом подразделе будет подчеркнуто различие между понятиями цивилизация и культура. Это важно сделать, ибо цивилизация и культура — это важнейшие характеристики любого человеческого сообщества, причем разные, хотя и тесно взаимосвязанные. В.Ю. Ключевский в своей книге “Курс русской истории” [149, ч. 1, с. 15] говорил: “Накопление опытов, знаний, потребностей, привычек, житейских удобств, улучшающих, с одной стороны, частную, личную жизнь отдельного человека, а с другой — устанавливающих и совершенствующих общественные отношения между людьми, — словом, выработка человека и человеческого общежития — таков один предмет исторического изучения. Степень этой выработки, достигнутую тем или другим народом,
36
обыкновенно называют его культурой или цивилизацией', признаки, по которым историческое изучение определяет эту степень, составляют содержание особой отрасли исторического ведения, истории культуры или цивилизации'’.
Однако понятия цивилизации и культуры имеет смысл разделить. Разделение поможет, на наш взгляд, понять природу современных общественных кризисов.
На наш взгляд, под цивилизацией нужно понимать сумму знаний и навыков, в том числе научных знаний, технологий производств, включая произведения искусств, ремесел.
Под культурой нужно понимать способы, методы и цели использования и применения цивилизации. Поэтому, например, цивилизация может быть высокой, а культура — низкой, но может иметь место и обратная ситуация.
Гармонически развитое общество предполагает высокий уровень и цивилизации, и культуры, в нем нет коллизий и противоречий между ними. Можно сказать и так: цивилизация доставляет нам возможности выбора, а культура осуществляет этот выбор. Цивилизация отражает материально-информационный уровень развития общества, а культура — духовный, включающий этический, эстетический.
Этика — это набор правил, законов поведения человека или общества. Часто эти правила носят запретительный характер: не гордись, не убей, не укради, не обманывай и др.
Эстетика — это принятые нормы красоты, гармонии, счастья. Сюда входят и понятия долга, ответственности, справедливости.
Одна из важнейших задач науки, в частности психологии и теологии, — найти соответствующие точные математические структуры, описывающие категории культуры. Сейчас мы еще далеки не только от научно обоснованных решений этой проблемы, но отсутствуют даже более-менее точные их формулировки. Многие из этих понятий находятся лишь в стадии осмысления, не имея достаточно точного выражения на естественных языках, а тем более, в терминах математических структур.
Недаром философия тесно переплетается с теологией — наукой о Боге. Различные религии — это различные “теории” или учения о Боге. Они отражают самые различные представления о самом сложном понятии. Важнейшим аспектом этого понятия всегда были мораль, этика, эстетика как учения о душе и духе, о законах и правилах поведения в обществе и отношениях между людьми и сообществами, как представления о красоте, гармонии, согласии.
Понятие Бога, которое человечество осознало за последние тысячелетия, является выражением интуитивного, врожденного стремления
37
человека к точному научному осмыслению реальности и видению в ней красоты, симметрии. Нам оно представляется как интуитивно открытые человеком операции замыкания и пополнения, т.е. операции симметризации в глобальном масштабе. Сейчас мы видим, что эти операции занимают центральное место и в математике, являясь выражением главнейших симметрий многих математических структур. Грубой аналогией может служить операция присоединения к пространству состояний “несобственных”, “абстрактных” элементов, описывающих “особые” точки, например, удаленные на бесконечные расстояния, но которые существенным образом характеризуют свойства системы, как, например, несобственная прямая в проективной геометрии. Великий Д. Гильберт восхищался идеей “идеальных” элементов.
Трудности осмысления понятия Бога такие же, как в осмыслении любой реальности. Поэтому говорят: “Бог — везде и во всем”, “God is omniwhere”. Бог — это предельно сложное понятие и единственный абсолют, а все остальное условно и относительно. Поэтому для осмысленного принятия этого понятия или даже интуитивной догадки о нем нужны прежде всего очень большая интеллектуальная подготовка и большие знания. Поэтому все выдающиеся ученые мира, как правило, так или иначе приходили к понятию Бога, что называлось Верою в Бога. Для этого понадобилась большая способность к абстракции, что свойственно научному способу мышления. С этой точки зрения язычество опирается в основном лишь на конкретно осязаемые и наблюдаемые предметы и явления. Принимается лишь то, что можно конкретно наблюдать, например, дерево, Солнце, икону, вождя и т.д.
Ясно, что самым коренным вопросом смысла является вопрос о смысле существования самого человека.
Несмотря на значительное количество разных религий и религиозных учений, между ними есть много общего; по крайней мере теоретические представления об идеале, о том, что такое хорошо и что такое плохо. Все лучшее ассоциируется с Богом, с любовью, с верой и доверием, созиданием, развитием, жизнью. Все худшее ассоциируется с дьяволом, с ненавистью, разрушением, деградацией, смертью, неверием, обманом. Понятия Бога и дьявола часто трактуют как дополнительные противоположные понятия.
Однако нужно подчеркнуть, что симметрии между Богом и дьяволом, добром и злом нет. Божеское и хорошее должно превалировать над дьявольским и плохим — это существенная и глубочайшая асимметрия.
Э. Шредингер характеризовал жизнь как “апериодический кристалл”. Это “противоречивое” высказывание глубоко характеризует предмет в стиле “Принципа дополнительности” Н. Бора. В противопо
38
ложность этому смерть можно характеризовать как “абсолютную или максимальную симметрию”, описывающую нулевой уровень организации.
Опыт показывает, что как только устраняется или игнорируется понятие Бога в том смысле, о котором мы говорили выше, на его место (ибо “Свято место пусто не бывает”) так или иначе воцаряется нечто, очень часто в виде мертвого или живого идола, вождя, культа, кумира и прочее. Недаром говорят: “Не сотвори себе кумира” — ибо последствия замены Бога идолом или кумиром, как показывает опыт, ведет к ограничению культуры, ограничению свободы, возникновению и росту разрыва, “ножниц” между культурой и цивилизацией (даже в случае высокого уровня последней) и к дальнейшим неприятностям в виде войн, разрушений, деградации и гибели. Это и есть наказание за неосознанные и нераскаянные грехи.
Поэтому переход от язычества и идолопоклонства к развитым религиям, возникновение понятия Бога как абсолюта невообразимой сложности, индивидуальности и разнообразия всего сущего является громадным шагом в развитии всего человечества, которое стало лучше понимать смысл всего сущего, включая самого себя.
Выражением этого факта является изречение “Бог — везде”, “God is omniwhere”, он — ив нас, и в любом предмете, он — в любой ничтожной соринке, пылинке и песчинке, во Вселенной и любой “элементарной” частице, он — во всех делах и мыслях. Например, исследование “ничтожной пылинки” может бы гь вознаграждено Нобелевской премией, если исследователю удастся открыть в этой пылинке новый лик Бога в виде необычных свойств этой самой — на вид ничтожной — пылинки. Вспомните роль мушки Дрозофилы.
Таким образом, идея Бога является, пожалуй, самой плодотворной и самой мощной идеей, открытой человечеством.
Опыт показывает, что даже в самых богатых природными и человеческими ресурсами странах, где вместо Бога господствуют идолы, цивилизация и культура обречены на неизбежную деградацию. Наблюдаемый в действительности рост цивилизации и культуры в таких странах происходит ровно настолько, насколько хватает ресурсов, накопленных до эпохи идолов. Когда эти ресурсы кончаются, крах неминуем. Если человек, страна или народ попали в такую ситуацию, то выход из нее только один (не считая гибельного). Они немедленно должны вернуться к идее Бога и не на словах, а на деле. И дело это прежде всего состоит в признании своих грехов и немедленном и искреннем раскаянии в них, в осознании и осмыслении того и другого. Причем самый первый и страшный грех — это грех гордыни.
39
Человеку свойственно грешить (т.е. ошибаться сознательно или нет), ошибки и грехи сопровождают его всю жизнь. Но дело не в том, чтобы не грешить и не ошибаться, это в принципе невозможно, а в том, чтобы минимизировать свои грехи и ошибки. Но это можно сделать при одном и только при одном условии: если относиться критически прежде всего к себе самому, а не искать причины ошибок и бед где-то, в чем-то, в ком-то другом. В этом и состоит суть раскаяния. Оно непременно должно сопровождаться просьбой о прощении не только у Бога, но и у тех людей, которым твой грех, твоя ошибка принесли какое-то, хоть малое, несчастье или обиду, и искупить свой грех не только словами, но и делом, прежде всего перед людьми, а тем самым и перед Богом.
Таким образом, мы опять приходим к банальной истине “Надо учиться”. И учебу надо понимать как способ минимизации своих ошибок, а не как способы познания, как месть обидчикам. Опыт показывает, что, с одной стороны, самые глубокие истины банальны, а с другой — именно их труднее всего уяснить и сделать руководством к действию. В этом глубокое “диалектическое” противоречие между цивилизацией и культурой в самом широком понимании смысла этих терминов.
Если поставить на открытое (!) голосование или открыто задать вопрос любому: “Хорошо ли быть вором, лжецом, убийцей, аферистом, гордецом, хвальбой и т.д.”, то подавляющее большинство однозначно ответит: “Нет, не хорошо и даже очень плохо”.
Так ответят в том числе и воры, и лжецы, и убийцы. Но ответят они лицемерно, не выдавая своей истинной натуры. Преступники не боятся ничего, кроме открытости (гласности), ибо открытость чревата наказанием, которое, конечно, их страшит. Там, где нет открытости, прозрачности, гласности — там наверняка “дело не чистое”. Это показывает исторический и жизненный опыт.
Здесь хочется отметить один типовой прием, применяемый нечистоплотными людьми для достижения своих неправедных целей. Это — демагогия, под которой можно понимать: 1) подмену главных вопросов для обсуждения второстепенными; 2) широкое использование “софизмов”, т.е. в прямом смысле “цирковых фокусов”, использующих “обман зрения”; 3) способ гипнотизирования своих жертв с целью дальнейшего их принуждения делать бессмысленные, нелепые и вредные вещи и поступки, выгодные гипнотизеру.
Демагогии могут противостоять только истинные научные знания (интеллект цивилизации) и культура (воспитанность воли и внимания в Божеском духе). Все, что не обладает этими свойствами, становится легкой добычей демагогов.
40
Итак, мы хотим подчеркнуть, что цивилизация отражает материальную сторону бытия данного сообщества, воплощенность научных знаний и искусств Культура в отличие от цивилизации отражает качественную сторону бытия, духовную, идеальную, оценочную, целевую и методологическую ее стороны. Она показывает, как используются и применяются достижения цивилизации. Цивилизация и культура постоянно находятся, с одной стороны, под действием неуправляемых возмущающих факторов, часто негативных, а с другой — эти структура и распределение должны находиться (!) под действием управляющих. факторов, противостоящих действию разрушительных возмущений. Управляющие возмущения должны использовать все достижения цивилизации и культуры для стабилизации и поддержания Божеской души и духа общества. На языке теоретической кибернетики это означает необходимость создания системы постоянно действующих регуляторов обратной связи, системы “автоматического” управления для поддержания “божеских” структур и недопущения их разрушения. Еще раз подчеркнем, что порядок надо не наводить, а постоянно поддерживать.
Если заниматься только наведением (а не поддержанием) порядка, то беспорядок будет всегда (!), за исключением, возможно, только очень коротких мгновений, когда наведение порядка оканчивается. Важно еще понимать, что наведение порядка стоит намного дороже его постоянного поддержания.
Душу и дух можно понимать очень конкретно — это внутренняя система наблюдения человека за состоянием своего собственного тела и духа. Эта способность человека наблюдать за самим собой и управлять самим собой требует как минимум разделения нервной системы на две части: наблюдающую и управляющую. Такая способность к “анализу и синтезу” самого себя безусловно имеется у человека, ее только нужно обнаружить в себе, обучиться ею владеть. Такая же система должна быть и у общества в целом.
Происходит постоянное взаимодействие бытия и сознания в замкнутой системе со взаимно обратными связями. Очень наивно и недальновидно идеализм и абстракционизм противопоставлять материализму и реализму. Без идеализма и абстракционизма разумное существование homo sapiens просто невозможно. Без этого определенно, как показывает опыт, наблюдаются деградация и разрушение как отдельного человека, так и его сообществ. Идеализм и материализм — это типичные дополнительные понятия по Н. Бору.
Бессмертие души поэтому можно трактовать как постоянное самоощущение своего “Я”. Реально оно может происходить лишь в каком-то материальном воплощении (человека или системы любой матери-
41
альной природы). Конечно, существуют “провалы” этого самоощущения своей “личности”, своего “Я”. Их нет до создания и после разрушения материальной системы, реализующей “Я”. Для лучшего понимания этого можно привести только одну аналогию. Наше “Я” мы ощущаем только во время бодрствования. Где было наше самоощущение нашего “Я”, когда мы крепко спали некоторое время? Нередко после такого сна мы просыпаемся “другим человеком”. Однако за счет памяти мы четко осознаем связь между нашим старым и новым “Я”. Возможно, нечто аналогичное происходит с нашим “Я” и в более широком смысле: после смерти, т.е. после разрушения материального носителя “Я”. Это “Я” неожиданно, без связи с предыдущим “Я” начинает ощущаться в другой материальной системе, в другом “существе”. Это называется другой жизнью нашего “Я”, “нашего самосознания”.
К сожалению, на сегодня нет никаких научных указаний на существование какой-либо определенной связи между старым и новым “Я”. Эта связь пока что известна только Богу. Возможно, он ее использует, чтобы наказывать грешников и награждать праведников. Это толкование “Суда”, “Рая”, “Ада”. Таким образом, понятие Бога можно определить и так: “Бог — это невообразимо сложная система управления”.
В этих рассуждениях и взглядах нет ничего мистического, ибо, по-видимому, нет логических препятствий принять их как возможности, а следовательно, и как реальности в соответствии с философским принципом: “Все, что может произойти, реально происходит”, возникают только вопросы: “Когда?”, “Где?” и “Как?”.
1.7. ПОСТИНДУСТРИАЛЬНАЯ ЭПОХА И ГЛОБАЛИЗАЦИЯ
Проблема согласованности как гармонии цивилизации и культуры встает особенно остро сейчас, когда мы вступили в так называемую эпоху постиндустриализма, постиндустриального общества и глобализации. Нам представляется также правомерным назвать это эпохой кибернетического общества, где на первое место выходят проблемы управления, информации и систем, системной организации общества.
Что это означает, как это можно понять, осмыслить? С определенной степенью правдоподобия можно сказать, что проблема производства и соответствующих технологий как проблема реализации хорошо описанных и понятых структур в значительной мере решена. Грубо говоря, сейчас нет принципиальных проблем что-то произвести и в заданных количествах. В обществе накоплены знания и возможности создавать нужные технологии, причем в очень сжатые сроки. Создана мощная “материальная” основа материальной жизни и выживания. Неимоверно возросла производительность труда. Для производства дос
42
татка не надо много работать, “рабочее” время сильно сократилось и продолжает сокращаться.
Однако решение материальных проблем породило сильнейшее обострение культурных проблем, связанных с осмыслением самого человеческого существования, целей и способов его жизни. Возникает вопрос, что же делать, чем и как заниматься человеку, если у него практически нет материальных проблем, имеется достаток в еде, одежде, жилье, медицинском обслуживании, транспорте, связи, есть время для отдыха, развлечений, чтения, слушания музыки, хобби и т.д.? Возникает острейшая проблема невостребованности не только “простой” рабочей силы, но рабочей силы с высшим университетским образованием. И дело не в том, что безработные будут нуждаться в чем-то материальном. Но что им делать, когда все время — свободное?
С другой стороны, постиндустриальное общество характеризуется быстрым количественным и качественным ростом, улучшением характеристик средств связи и передвижения и всевозможной информации о событиях, знаниях, идеях, учениях, суждениях и т.д., причем в глобальном, всемирном масштабе.
На языке теории систем это означает, что появились усилители с огромными коэффициентами усиления по мощности с большими “радиусами” действия, распределенные по всей планете, например, высокоэффективное, мощное и сверхмощное оружие физического и психологического действия, массовое вещание, Internet.
Из той же теории систем известно, что большие коэффициенты усиления являются факторами, способствующими потере устойчивости системы, что ведет к нарушению работоспособности системы в целом и ее частей или даже к полному ее разрушению, причем с очень большой скоростью (экспоненциальное нарастание).
Таким образом, создаются эффективные, относительно недорогие и легкодоступные, а вместе с тем очень мощные средства управления, которые могут быть использованы как во зло, так и во благо. Если при этом больше ничего не предпринимать, то с уверенностью можно прогнозировать рост преступности и терроризма во всем мире, возобладание в массовом порядке “дурных” привычек (пьянство, курение, наркомания, всяческие извращения и крайности проявления чувств, агрессивность от избытка неизрасходованных сил при низкой культуре воспитания, психические расстройства и т.д.). Неутешительные тенденции роста всех этих негативных и опасных явлений уже сейчас явно наблюдаются во всем мире.
Все это ставит перед человечеством очень трудные и качественно новые проблемы. На наш взгляд, только наука и ее фундаментальные разделы и только вместе с добрыми, т.е. Божескими, намерениями в
43
сердцах и умах ученых смогут повлиять на остальную часть человечества с тем, чтобы правильно осмыслить постиндустриальную эпоху и глобализацию и найти способ поддержать Божеское развитие человечества.
1.8. ВОСПИТАНИЕ И ОБРАЗОВАНИЕ
Понятия воспитания и образования в точности соответствуют понятиям культуры и цивилизации. Так же, как не надо путать культуру с цивилизацией, не надо путать воспитание с образованием. Путаница этих понятий нередко наблюдается в действительности. Человек может быть образованным, но не воспитанным, и обратно. Возможны и два других сочетания этих двух понятий. Поэтому интеллигент — это воспитанный, т.е. культурный человек. Слово интеллигент нередко путают со словом интеллектуал. Понятие интеллигент надо ассоциировать со словом разум, а интеллектуал. — со словом рассудок, что больше связано с эрудицией и образованностью, но вовсе не всегда напрямую с воспитанием и культурой. Воспитание, как правило, должно идти вместе с образованием или опережая его.
Образование — это познание человеком достижений цивилизации, воспитание — это познание человеком достижений культуры и человеческого духа. Образование без воспитания, как и цивилизация без культуры, как правило, несет вред и отдельному человеку, и обществу в целом и в конечном счете ведет к деградации и гибели.
Поэтому воспитание человека должно начинаться с самого раннего детства, а еще лучше — с воспитания родителей ребенка. Немецкая поговорка гласит: “То, что Гансик не выучил, то Ганс не выучит”. Образование должно идти также вместе с воспитанием, чтобы не потерять конечный смысл и назначение образования — способствовать развитию культуры.
В силу сказанного в подразд. 1.6, по-видимому, первым предметным элементом воспитания должен стать “Закон Божий”, т.е. на приемлемом для ребенка уровне сложности он должен начать усваивать абсолют Бога и связанные с этим элементы культуры, или культурные заповеди. Воспитание и самовоспитание, образование и самообразование должны проходить непрерывно, перманентно на протяжении всей жизни человека, с детства и до глубокой старости, пока есть силы для этого.
Можно выделить четыре ступени образования и обучения в любой науке.
Ступень 1. Заучивание и зазубривание наизусть всех основных положений и формулировок. Это формальное знание, еще неуясненное и неосознанное. Однако нужные слова, термины, предложения и т.д., т.е. точный язык, закладываются на этой ступени.
44
Ступень 2. Уяснение, понимание, осмысление всех положений, заученных на ступени 1, умение выполнять стандартные упражнения и задачи. Эту ступень назовем пониманием.
Отметим, что ступени 1 и 2 для обучения в университетах примерно соответствует уровню бакалавра наук, т.е. первой ученой степени, а обучение этому длится в среднем порядка 4 лет.
Ступень 3. Умение применять знания, полученные на ступенях 1 и 2, к решению нестандартных, оригинальных задач. Эту ступень назовем ступенью применения. Она соответствует уровню дипломированного специалиста того или иного профиля после университета и второй ученой степени “Master of Science”.
В рамках этой ступени можно выделить еще один, более высокий, уровень, соответствующий обучению в аспирантуре. Это уровень “кандидата наук” (в России), “Doctor of Phylosofy”, доцента, “Associate Professor”. Здесь есть еще одна промежуточная ступень — лицензиат, что соответствует сдаче экзаменов по серьезно продвинутым спецкурсам и спецпредметам.
Ступень 4. Умение развивать теорию и методы. Это — высшая ступень образования, способность к высокому уровню творчества.
В России и некоторых других странах это соответствует ученой степени “Доктор наук”, “Doctor of Science” и званию “Профессор”, “Full Professor”.
Итак, образование и соответствующее обучение проходят четыре этапа (ступени, уровня): знание, понимание, применение, развитие. Нужно знать, понимать, применять, развивать.
В России традиционно предъявлялись высокие требования к учености, поэтому существовало много градаций ее степени. Достаточно сказать, что лица, преодолевшие только три из всех четырех уровней образования, упомянутых выше, формально не рассматривались как ученые в полном смысле этого термина, и соответствующая высшая для третьей ступени степень учености называлась кандидат наук. Ученый в полном смысле этого слова должен обладать ученой степенью доктора наук. Доказательством этого факта являлось признание научной общественностью, состоящей из докторов наук в данной области, значительного вклада данного лица в развитие непосредственно и собственно самой науки, а не чего-то около нее или как-то косвенно связанного с ней. Например, ученая степень не должна присуждаться только за ту или иную помощь кому-то, за руководство без получения конкретного личного результата. Появились “примазывания” и “приписывания” таких помощников и руководителей к собственно авторам научных результатов. К сожалению, в последние десятилетия все эти требования, позволявшие держать очень высокий уровень российской
45
науки, практически девальвировались до неузнаваемости: развалились и исчезли многие научные школы, возглавлявшиеся докторами наук со всемирным признанием, исчезли кандидаты наук, способные в этих школах вырасти до уровня докторов. Появилось много отдельных “самоучек” без научных школ, которые даже своим большим количеством не способны “компенсировать” утраты.
Таким образом, образование без воспитания может разрушить само образование.
Обратим внимание еще на два важнейших понятия — волю и внимание — и на их воспитание, доведение их до автоматизма, безусловного рефлекса.
С точки зрения теории управления под волей нужно понимать регулятор обратной связи, который выдает управляющие воздействия на исполнительные органы организма с целью устранения “ошибки”, т.е. рассогласования между действительным и желаемым состояниями. Именно такая замкнутая система автоматического управления, где воля играет роль регулятора, противостоит всем помехам (пытается их отфильтровать) и в то же время достигает желаемой цели (отслеживает цель).
Во время сеансов гипноза гипнотизер “разрезает” цепь обратной связи в нервной системе (блокирует ее). Такая система, полностью лишенная воли, уже не может противостоять внешним воздействиям, идущим от гипнотизера, и полностью выполняет все его команды (даже самые нелепые, часто на виду большого скопления публики), которые при других обстоятельствах испытуемый не стал бы выполнять ни при каких условиях. Интересно отметить, что “датчики” наблюдения подопытного при этом функционируют вполне исправно, испытуемый прекрасно видит и понимает, что он находится на сцене в зале, что нет никаких прекрасных цветов, растущих у него под ногами, и, несмотря на это, он приказами гипнотизера понуждается к “сбору” этих мнимых цветов. Каков механизм “перерезания” обратных связей, ответственных за волю индивида, остается загадкой.
Воля и внимание, способность ими управлять и “концентрировать” их — это важнейшие элементы культуры человека, имеющие большое значение для его последующего успеха в жизни.
В заключение сделаем еще ряд замечаний.
В силу центральной роли математики в развитии наук имеет смысл организовать перманентное математическое образование специалистов не только во время обучения в университете, но и после его окончания в рамках постоянного повышения квалификации, чтобы не отстать от жизни и быть на уровне бурно растущей цивилизации.
46
Для математического образования в соответствии с желанием и подготовкой слушателей надо иметь не менее двух—трех концентров как по уровню сложности и доступности — простой, средний, высокий, так и по степени общности (абстрактности) — узкоконкретный, средней общности и наиболее общий, достигнутый на данный момент в науке. Такие курсы, включающие порядка двадцати часов занятий повышения математической подготовки, должны проходить большинство специалистов примерно один раз в год.
Хорошее знание математики и ее применение на практике придает специалисту универсализм, делает его подготовленным к быстрым переменам специальностей и технологий, дает быстрое понимание сути новых проблем. Кроме того, математика способствует поддержанию высокого общего культурного уровня.
Именно глубокой фундаментальной подготовкой специалистов в области математики, физики, химии, биологии, родного и иностранных языков славилось профессиональное образование в Царской России. Специалисты из России, особенно инженеры, очень высоко ценились и оплачивались в Европе и во всем мире. Нередко российским инженерам платили существенно больше, нежели местным. Предпринимателю было выгоднее нанять одного русского вместо двух, а то и более, местных, ибо русский инженер мог и сталь сварить, и мост построить. Они быстро осваивали “секреты” новых технологий, так как за счет глубокой, фундаментальной подготовки российский специалист за ограниченное время легко мог понять любую специальную литературу. В то время как специалист без углубленной фундаментальной подготовки этого сделать не может в принципе.
В проблеме воспитания и образования очень важно развивать “чувство юмора”. Это чувство поистине одно из самых замечательных свойств человека. Однако всегда нужно помнить замечательное стихотворное высказывание А.С. Грибоедова:
“Когда в делах — я от веселья прячусь, Когда дурачится — дурачусь.
А смешивать два эти ремесла Есть тьма искусников!
Я — не из их числа.”
Юмор — это прекрасная вещь, но его надо четко отделять от серьезных вопросов.
Важнейшей целью воспитания подрастающего поколения является воспитание самокритичности как своего рода регулятора обратной связи для поддержания адекватности (соответствия) индивида и реальности. Это означает быть честным, прежде всего перед самим собой, не бояться правды, какой бы ужасной она ни была, воспитывать глу
47
бокое уважение и стремление к правде и истине. Это важнейшее и необходимое условие устойчивости как отдельной личности, так и общества в целом.
1 9. НАУКА. "ЗАКОН 100%-ЭФФЕКТИВНОСГИ МАТЕМАТИКИ"
“Через науку Бог сообщает нам, как он устроил мир” — это высказывание очень хорошо отражает смысл науки, ее предназначение.
Обсудим содержательно смысл понятия наука, основные требования, предъявляемые к тому, что называется наукой. Эти требования довольно жесткие.
Основные признаки науки, ее характеристические свойства, на наш взгляд, состоят в следующем.
1.	Объективность как независимость от индивидуальных особенностей и восприятия ни исследователей и разработчиков, ни пользователей.
2.	Неограниченные воспроизводимость и повторяемость опытов. При этом опыт (все его атрибуты) должны быть описаны достаточно точно, исчерпывающим образом, гарантирующим объявленную точность.
3.	Достоверность предсказаний, их высокая точность.
, 4. Алгоритмичностъ.
5.	Всеобщность.
6.	Использование точного (без возможности двусмысленности) языка, наличие теории.
7.	Доказательность, обоснованность утверждений — как эмпирических, так и теоретических (т.е. математических) — как страховка от произвола в обращении с наукой и ее ценностями.
Дорогостоящие и многократные эксперименты заменяются вычислениями на основе знания структур, моделей и алгоритмов, полученными из предыдущих наблюдений и опыта. Это дает огромную экономию средств и ускорение цивилизации. Ценность науки состоит в ее предсказательных возможностях, дорогостоящие эксперименты заменяются вычислениями по правилам, вытекающим из теории. “Учись, мой сын. Науки сокращают нам опыты быстротекущей жизни” (М.В. Ломоносов).
Наука фиксирует осознанный смысл той или иной реальности, вырабатывая понятия и отношения между ними и придавая им универсальную общедоступную форму.
Любая наука на основе своих опытных данных должна развивать свою теорию. Всякая теория, по определению, должна быть математической. Образцами развития теории являются точные науки. Всякая
48
наука, включая так называемые гуманитарные науки, должна быть точной, наподобие физики (механика, электродинамика, квантовая механика и др.).
Только в силу очень большой сложности явлений, изучаемых, скажем, медициной, историей и другими науками, уровень познания реальностей и построения точных структур в этих науках еще не столь высок, как в точных. Именно в этом смысле можно понимать высказывания о том, что, скажем, “медицина или история — это не науки”. Это, конечно, очень строгое, очень придирчивое понимание науки. Однако с развитием цивилизации и культуры уровень гуманитарных наук неуклонно растет, приближаясь к уровню точных наук.
Идет бурное развитие представлений по созданию точных математических моделей (структур, систем) отдельных, фрагментов той же медицины, истории и других туманитарных наук. Объединение и согласование моделей отдельных фрагментов ведет к построению все более общих теорий в точном математическом смысле.
Одна из важнейших задач науки состоит в том, чтобы определять все новые и новые свойства, по которым можно отличать реальности.
Например, состояние физики таково, что свойство, по которому можно отличить два электрона друг от друга, еще не найдено. Поэтому электроны на сегодня (!) считаются неразличимыми и идентичными. Однако последние исследования в области “элементарных” частиц, в частности электронов, дают указания на существование “внутренней” структуры электрона и, следовательно, набора “внутренних” состояний, по которым можно отличить один электрон от другого. Но сегодня изучение этих тончайших свойств только начинается.
Задача любой науки — уловить смысл наблюдаемой и интересующей ее реальности, сформулировать его и дать ему имя. Это делается с помощью опыта и теории.
Экспериментальная часть состоит в наблюдении реальности (явлений и (или) процессов), организации пассивных и (или) активных опытов, исчерпывающем описании условий и результатов опытов.
Важнейшая черта научного эксперимента — получение количественных данных путем наблюдения и измерения. Осмысление (философия) эксперимента составляет теорию данной науки. Наиболее точная форма осмысления должна быть математической.
К теоретической части относится выработка языка данной науки, т.е. выработка ее понятий и обозначающих их терминов, аксиом (постулатов, научных принципов) и утверждений (теорем). Основная задача любой науки — разработка широких, но непротиворечивых теорий, способных объяснять и предсказывать явления. Для развития теории важны открываемые ею противоречия, парадоксы, несовместимо
49
сти как сигналы того, что мы плохо понимаем данную реальность, которую изучает эта наука, а следовательно, необходимо расширение и обобщение наших понятий, языка и введение более сложных структур.
Всякая новая теория должна удовлетворять следующим условиям:
1)	соблюдать принцип соответствия (принцип Н. Бора), т.е. переходить в “старую” теорию в некотором предельном переходе (когда, например, некоторые параметры обращаются в ноль или стремятся к нулю. исчезают);
2)	должен быть указан соответствующий ей новый, более общий содержательный принцип или принципы, из которых вытекают ее положения;
3)	обладать более мощной предсказательной силой, т.е. предсказывать новые свойства и явления, ранее неизвестные, которые могут наблюдаться в опыте;
4)	как правило, ей должны соответствовать новые отношения, новые пространства, новые структуры и новые симметрии, которые отсутствовали в “старой” теории.
Теория любой науки должна быть математической, так как математика доставляет наиболее точный и универсальный язык и алгоритмы вычислений и моделирования реальности. Можно высказать даже такую “крайнюю” точку зрения: идеальная теория должна состоять лишь из определений, а теоремы и их доказательства нужны для уверенности в согласованности этих определений между собой.
Любая наука должна стремиться к созданию своей теории — теории того круга явлений реальности, который она изучает. Образцом такой науки является теоретическая физика, в частности механика.
Мы исходим из принципа познаваемости наукой любой реальности, однако лишь с конечной точностью на каждом данном этапе развития науки, которая отражает относительность и условность устанавливаемых истин.
Довольно четко была понята роль математики как способа описания и познания в физике: “Чистая математика и физика становятся связанными все теснее, хотя их методы и остаются различными. Можно сказать, что математик играет в игру, в которой сам изобретает правила, в то время как физик играет в игру, правила которой предлагает Природа. Однако с течением времени становится все более очевидным, что правила, которые математик находит интересными, совпадают с теми, которые избрала Природа. Трудно предсказать, каков будет результат всего этого. Возможно, оба предмета в конце концов сольются и каждая область чистой математики будет иметь физические приложения, причем их важность в физике станет пропорциональна их интересности в математике”. [120, с. 245—254, 433, с. 122—129]. Созда
50
ется впечатление, что это пророчество Дирака начинает сбываться, по крайней мере в том, что касается дифференциальной геометрии и калибровочных теорий поля. Так сказано в предисловии к книге [87].
Эти принципы научной познаваемости реальности можно сформулировать в виде “Принципа 100%-эффективности математики”, который коротко звучит следующим образом: “Для любой реальности (естественной или искусственной) существуют условия ее наблюдения и точно определенная математическая структура, которая описывает эту реальность с любой наперед заданной конечной точностью. Обратно, для любой точно определенной математической структуры существует реальность (естественная или искусственная) вместе с условиями ее наблюдения, которая описывается этой структурой”.
Принцип 100%-эффективности математики содержит принцип познаваемости любой реальности с помощью соответствующих математических структур.
Первая, или прямая, часть Принципа 100%-эффективности математики высказывалась еще в 20-е годы XX столетия после открытия квантовой механики. Многие выдающиеся физики были поражены и восхищены “непостижимой эффективностью” математики. Несмотря на то что никто никогда ранее не подозревал о существовании квантовой реальности, проявившейся при изучении атомов, в математике уже существовали, т.е. были открыты и в значительной степени изучены структуры, которые с большой степенью точности описывали неожиданно открытую “квантовую” реальность.
Обратное утверждение Принципа 100%-эффективности математики провозглашает обратимость прямого утверждения: какие бы математические структуры в математике не были бы найдены, описаны, открыты, в Природе найдется реальность (явление, процесс и т.д.), которая как раз и описывается данной математической структурой.
Сделаем критические замечания относительно приведенной формулировки Принципа 100%-эффективности математики. В этом законе существенную роль играет слово-термин-понятие точность. Это далеко не тривиальное понятие, которое, в частности, связано с фундаментальной дисциплиной “Теория и методы измерений”. В нем заключается вся суть понятия прикладная математика, с этим связана фундаментальная проблема перевода или “интерфейса” между языком природы и языком математики.
На языке “морфизмов”, т.е. понятий, расширяющих понятие отображение, можно сказать, что математика — это результат “гомоморфизма” реальности, который можно сделать сколь угодно близким к изоморфизму.
Математика — это наука о структурах и их симметриях.
51
Это означает, что роль предметов, изучаемых в математике, играют структуры, а метод их изучения — метод симметрии. Если вы хотите решить какую-нибудь задачу, разобраться в какой-нибудь сложной структуре, то “ищите симметрию”. В дальнейшем мы попытаемся точнее определить два этих фундаментальных понятия: структура и симметрия.
Сделаем еще несколько замечаний о смысле науки.
“В науке нет царской тропы”. Это известное высказывание означает, что никому, даже самым высокопоставленным лицам, не дано овладеть наукой, ее методами и ее эффективным использованием без систематического (длящегося практически всю жизнь) и упорного труда по ее изучению и овладению ею. Недаром наука сравнивается с гранитом — одной из твердейших пород, — который должны “грызть” ученики и ученые. Все знают, как трудно выучить какой-нибудь иностранный язык, овладеть им и более-менее свободно им пользоваться, даже специалисты учатся ему всю жизнь. Аналогично обстоит дело и при изучении языков наук и овладении ими.
Нет необходимости “царю” быть ученым, хотя он должен быть образованным и культурным, чтобы понимать советы разных ученых. Но принимать решения он должен сам.
Это особенно важно понять крупным деятелям, оказывающим политическое влияние на общество. В определенном смысле даже опасно, когда недалекий ученый, увлекшийся какой-то теорией, становясь начальником, начинает ее “внедрять” во что бы то ни стало, чтобы удовлетворить свои амбиции. О такой ситуации говорят, что “путь в ад устлан благими намерениями”.
Теоретики, которые хоть когда-нибудь занимались внедрением в практику своих теорий, должны хорошо понимать существенную ограниченность любой теории. Для того чтобы данная теория оказала положительное влияние на практику, т.е. принесла реальный прогресс вместо регресса, необходимо очень внимательно рассмотреть и учесть много других структур, не учтенных внедряемой теорией, и опытным путем скурпулезно пытаться их согласовать между собой. В этом смысле “всепобеждающих и единственно правильных” теорий в принципе существовать не может.
Обсудим один важный и принципиальный вопрос — вопрос о связи и различии между изобретательством и наукой. Подчеркнем здесь принципиальное различие чистых видов этих понятий. Изобретательство и наука — это принципиально разные реальности. Отсюда следует, что не надо путать, смешивать, а тем более, приравнивать друг другу изобретателя и ученого. Хотя нередко бывают люди, которых можно одновременно считать и тем, и другим. Но не надо, например, пу
52
тать музыканта с музыковедом. Отсюда также следует, что нельзя присуждать ученые степени и звания изобретателям только за то, что они сделали какие-то очень важные и полезные изобретения и даже открытия. Например, Эдисон был гениальным изобретателем, давшим целый ряд выдающихся изобретений, оказавших огромное влияние на жизнь всего человечества. Однако никому не пришло в голову присудить ему ученую степень доктора наук, да он и сам никогда не выдвигал таких претензий, отлично понимая разницу между изобретательской и научной деятельностью. Более того, есть примеры, когда изобретения и открытия делали совершенно неграмотные люди.
К сожалению, не во всех обществах эту принципиальную разницу хорошо понимают. Надо отличать технические изобретения от технических или естественных наук. Это — разные вещи!
В качестве альтернативы Эдисону как самому яркому примеру гения технических изобретений можно вспомнить гений Фарадея. Он тоже своего рода (!) изобретатель, но он изобретал (творил!) свои “механические” опыты и делал открытия с научными (!) целями, т.е. с целью установить законы (!), структуры открытых им реальностей вследствие изобретений (!) на основе поставленных им технических опытов. При этом он дал настолько точные описания (!) открытых им реальностей, что позже Максвелл, написавший дифференциальные уравнения электромагнетизма, высказывал ту мысль, что все сделал Фарадей, а ему осталось только записать это в виде математических уравнений.
Можно сказать, что всякое изобретательское творчество настолько близко к науке, насколько изобретатель сумел точно описать структуру своего изобретения или открытия, допускающую точное и общее математическое представление. Конечно, вопрос о степени близости изобретательства (от полностью нулевой до близкой к 100%) в общем случае может оказаться не простым. Однако нужно понимать, что такой вопрос существует и его надо грамотно решать. Между наукой и изобретательством стоят подчас весьма тонкие прямые и обратные связи.
1.10.	МАТЕМАТИКА
Теперь постараемся охарактеризовать саму математику и понять ее дух и значение по отношению к другим наукам, обосновать ее роль как “царицы наук”, как уникальной и универсальной науки, имеющей прямое отношение ко всем наукам.
Математика — это сложное понятие, поэтому, как и для всякого сложного понятия, для нее трудно подобрать одно короткое и вместе с тем исчерпывающее определение. Существуют много определений математики, каждое из которых характеризует, выделяет какой-то один аспект этого необычайно богатого предмета.
53
Мы приведем несколько разных высказываний о математике, сделанных выдающимися учеными разных времен и народов.
Известный ученый Фридман предварил одно из своих сочинений замечательной цитатой из Библии: “Вся мерою и числом сотворил еси” [216, с. 248, прим. 12]. Интересно следующее высказывание о человеческих корнях происхождения математики: “Любой мыслящий человек — это коллекционер чего-либо, это его стремление к порядку, полноте, законченности; тут есть элемент патологии, но открытой и гордой; это дает пребывание в радости души, сердца и ума”.
Рене Декарт дал одно из замечательнейших определений математики, которое разделял позже и Леонард Эйлер:
I “Математика — это наука о порядке и мере”.
Такой взгляд Эйлера на математику почти автоматически приводит к тому, что множество всех натуральных чисел многими учеными рассматривается как основной источник и инструмент для построения многих математических структур.
Действительно, как учат уже в школе при изучении грамматики родного и иностранных языков, числительные имеют два назначения: 1) они могут быть порядковыми и 2) они могут быть количественными, т.е. характеризовать меру каких-то вещей.
В связи с этим существует убежденность, что “все имеет свою меру”.
Надо сказать, что определение Эйлера очень созвучно с современным кибернетическим представлением: понятие порядка и упорядоченности — основное свойство управления, а мера — понятие оптимального управления.
Сюда же можно отнести:
| “Математика — это наука о количестве и пространстве”.
Выражение Гельмгольца:
| “Математика — это наиболее точный язык”.
Приведем еще несколько определений математики, отражающих ее связь с логикой.
(“Математика — наука о выводе необходимых заключений, т.е. дедуктивный метод о выводе следствий (заключений) из посылок” (Пирс).
I “Математика может быть наукой о чем угодно, что имеет образ (структуру) предложений вывода (дедукции) и заключения”.
1 “Абстракция, формализация, аксиоматизация, дедукция — все это ингредиенты доказательства”.
I “Расследование уголовного преступления может быть рассмотрено как математическая дисциплина”.
54
I “Математика — это искусство называть разные вещи одним и тем же именем”.
Здесь можно добавить:
|“и обратно, в одной и той же вещи видеть много разных вещей и назвать их разными именами”.
“Математика — это одновременно благороднейшая и чистейшая форма мысли, которая выводится из чистого сознания с небольшой помощью или вовсе без помощи со стороны внешнего мира”.
(“Математика — это абстракция, и обратно, абстракция есть математика”.
| “Бог есть математик”.
“Так как здание всего мира совершенно и возведено Творцом, то в мире не происходит ничего, в чем не был бы виден смысл какого-нибудь максимума или минимума” (Эйлер)1.
| “Бог движет Мир по геометрическим линиям” (Платон).
Совершенно поразительное по своей глубине высказывание сделал Римский Папа Сельвестр Второй:
| “Физика не есть отдельная наука, а отрасль математики”.
В этом же духе высказывался и Вернер Гейзенберг:
I “Последней основой атомной структуры является математический закон, математическая симметрия”.
Из самых последних работ о сути и значении математики отметим работу Н.Н. Непейвода [226]. В новейшей истории математики XX в. титаническую работу по выявлению форм сути математики провели Бурбаки. Эта работа подвела определенный итог всего предыдущего развития математики.
Действительно, многотомный труд выдающихся французских математиков под псевдонимом Никола Бурбаки можно рассматривать как взаимосвязанное системное описание главных известных на сегодня математических структур. Отсюда можно сказать:
| “Математика — это науки о структурах”.
1 Характерно, что последняя приведенная здесь цитата Эйлера, вследствие цензуры или самоцензуры, использовалась, как правило, в усеченном виде: полностью отбрасывалась начальная часть фразы и приводилась лишь ее часть после слова “то”.
55
Ту же самую мысль, на наш взгляд, можно выразить следующим образом:
| “Математика — это наука об уравнениях и тождествах”.
При этом фундаментальная и общая проблема математики состоит в нахождении (описании) множества всех решений. Каждая математическая дисциплина или ее раздел имеет свой — характерный для нее — класс уравнений и соответствующих тождеств, изучение которых, по сути, и составляет предмет данной дисциплины. Именно они — уравнения и тождества — определяют структуры данной математической дисциплины.
Таким образом, в ЕГТУ—ТСУ мы исходим из определения математики, включающего в себя не только объект, но и метод его изучения.
(“Логика и математика — это науки о формах выражения смысла, т.е. о языках и их эквивалентности при преобразованиях, сохраняющих смысл или о симметрии”.
Совсем коротко можно сказать;
| “Математика— это наука о сгруктурах и их симметриях”.
В ЕГТУ—ТСУ подчеркивается, что объектом изучения в математике являются структуры, а метод их изучения — это метод симметрии. Таким образом, симметрия наряду со структурой является центральным понятием, с помощью которого человек познает природу и которое пронизывает все его творчество.
Интересно отметить, что симметрия, выступающая как метод исследования структур, сама может стать объектом или структурой, которая в свою очередь должна изучаться методами симметрии. Таким образом, имеется рефлексия — симметрия изучает саму себя.
Известно, какое огромное значение симметрия имеет в искусстве, архитектуре, дизайне и т.д. Симметрия есть выражение красоты, и “красота спасет мир”, потому что добро и есть красота, по определению, в самом глубоком Божественном смысле этой категории.
Однако здесь необходимо сделать очень существенное замечание, предостерегающее от возможных недоразумений и наивного, в смысле общежитейского или упрощенного, понимания симметрии. Дело в том, что симметрия, как и структура, вообще говоря, очень сложные понятия. Симметрии, как и структуры, могут иметь любую сколь угодно большую наперед заданную сложность.
Отсюда следует, что красоту не так просто обнаружить и понять. Подчас распознать даже один элемент симметрии какой-то сложной структуры, увы, далеко не тривиальная задача. Это не то, чтобы указать очевидные элементы симметрии в таких “простых” структурах, как круг, шар, квадрат, прямоугольник, простой кристалл и т.д.
56
Но уже задача описания и классификации всех возможных симметрий такой упрощенной физической абстракции, как кристаллическая решетка или узоры на ковре, как известно, является нетривиальной задачей.
Поэтому высокий художественный вкус в искусстве и науке, да и во всех областях человеческого бытия, можно охарактеризовать как высокую способность различать, находить, выделять элементы сложной, нетривиальной симметрии в том или ином объекте, будь то музыка или техническое устройство или вообще любая реальность. Симметрия в точном математическом смысле может стать основой для разработок количественных мер оценки произведений искусств, литературы и поэзии. Конечно, такой талант может проявиться не у всякого, но воспитание и образование как раз и призваны к тому и направлены на то, чтобы вызвать и развить этот талант распознавания всевозможных симметрий, т.е. красоты.
Таким образом, математика имеет не только образовательное, но и огромное воспитательное значение. Поэтому математическая грамотность желательна для любого человека.
Математика уже с детства воспитывает важнейшие элементы вкуса, характера и духа будущего взрослого человека. Она приучает четко, логично, недвусмысленно мыслить и точно выражать свои мысли на бумаге и при живом общении, приучает к аккуратности и самокритичности, она учит отличать добро от зла и красоту от уродства, суть дела от демагогии. Она учит точно формулировать отличия (разногласия) и обсуждать их в дискуссиях, спорах и даже конфликтах, учит находить разумные, Божеские компромиссы, тем самым устанавливая согласие, согласованность и мир в обществе. Математика — это важный рациональный, осознанный, осмысленный инструмент, данный нам свыше для подъема не только материального, но и духовного благосостояния.
I “Математика —- это инструмент, специально созданный для того, чтобы иметь дело с абстрактными понятиями любого сорта. Нет предела действенности этого инструмента” (Дирак).
К сожалению, красота и эстетическая важность математики, столь полезные для воспитания молодых людей, очень часто не доносятся до них в школе, на решающем этапе формирования личности (“Двадцать лет — ума нет, и не будет”). Но это зависит от учителей, а это — другая важная проблема.
Упомянем высказывание великого Д.И. Менделеева, приведенное в книге А. Меня [216, с. 251|. Там говорится о “Троице самобытных величин: веществе (материи), силе (энергии) и духе”.
В связи с этим замечательным высказыванием Менделеева просто невозможно не обратить внимания на корреляцию с подходом ЕГТУ— ТСУ к математическому осмыслению общего понятия сплошная среда и поле и перенесение его на кибернетику.
57
Троица Менделеева принимает следующий вид.
Вещество (материя) — это субстанция как физические величины, характерные для данной сплошной среды или поля; сила (энергия) — это мера, выраженная понятием и мера, и действие', наконец, дух — это симметрия, проявляющаяся в многочисленных законах сохранения субстанции.
Аристотель в своей “Метафизике” писал:
I “Математические науки, в частности, выражают порядок, симметрию и ограничение, и все это — величайшие формы прекрасного”.
Таким образом, математика, несмотря на наши всегда ограниченные возможности, дает нам мощный и вместе с тем универсальный способ конечными возможностями постигать невообразимо, бесконечно сложную реальность.
“Величие математики я усматриваю именно в том, что почти во всех ее теоремах в силу самой ее сущности всякий вопрос о бесконечном решается на уровне конечного...” (Герман Вейль [70, с. 127]).
Сделаем теперь несколько замечаний о прикладной математике.
Прежде всего подчеркнем, что прикладная математика не есть какая-то другая математика, отличная от того, что мы и называли здесь математикой. Математика едина и не существует никаких иных математик, например “чистой” математики. Прикладная математика — это способы применения, приложения, использования математики для наиболее точного описания и представления той или иной реальности. Прикладная математика изучает гомоморфизмы (морфизмы) между реальностью и математикой [96]. Она разрабатывает способы “борьбы” с невообразимой сложностью любой реальности, когда бесконечное “тривиализуется” в конечное или “квази-конечное” в виде понятий, структур и отношений. При этом допускается и обратный “процесс” детривиализации, т.е. усложнение этого конечного с целью более глубокого и более точного приближения к данной реальности. Говоря на “компьютерном” языке, прикладная математика — это интерфейс математики и реальности.
Отсюда следует, что специалист по прикладной математике, а таким должен быть теоретик любой науки, должен нести двойную нагрузку — быть хорошим математиком и хорошим специалистом в данной конкретной науке.
Таким образом, прикладная математика занимается построением математических (в отличие от физических) моделей реальности, а точ
58
нее — использованием готовых или построением новых математических структур.
Принцип 100%-эффективности математики можно истолковать так же, как выражение сути прикладной математики, ее 100%-эффективности в деле изучения и познания реальности.
“Законы Природы должны выражаться языком математики” — так, по словам Е. Вигнера [73, с. 189], утверждал Галилей. Е. Вигнер, по-видимому, впервые употребил оборот о “сверхъестественной” и “непостижимой” эффективности математики [73, с. 183].
"Я бы мог определить математику как науку о хитроумных операциях, производимых по специально разработанным правилам над специально придуманными понятиями. Особенно важная роль отводится придумыванию новых понятий” [73, с. 184].
Там же [73, с. 190] приводятся слова Эйнштейна:
|“Мы с готовностью воспринимаем лишь те теории, которые обладают изяществом”.
Под “изяществом” можно точно понимать наличие оригинальной симметрии.
Наконец, выскажем самое широкое, на наш взгляд, определение математики и логики.
Математика и логика — это все то, что дает возможность правильно мыслить, т.е. оперировать со смыслом, не теряя его, добывать знания, с помощью которых происходит понимание и уточнение тех или иных сторон и свойств той или иной невообразимо сложной реальности и овладение ими.
Существуют люди, обладающие от природы даром математика и логика, даже не имеющие какого-то специального образования в этих областях. О таких людях говорят, чго у них есть “здравый смысл” и что они — мудрые.
Приведем высказывание Максима Исповедника, сделанное много сотен лет назад: “Человеческая мудрость собирает доказательства из показаний чувств, и всякая нужда в силлогизмах заставляет использовать геометрию”.
В то же время духовные качества ответственны за цели и способы применения интеллекта — это то, что называется культурой.
В индустриальную и постиндустриальную эпохи качество сообществ определяется высоким уровнем как интеллекта, так и духовных качеств всех его членов. Высокий уровень интеллекта при низких духовных качествах означает дискомфорт и кризисное состояние общества, чреватое его потрясениями вплоть до одичания и гибели.
59
1.11.	КИБЕРНЕТИКА. "УПРАВЛЕНЧЕСКАЯ ПАРАДИГМА МИРА"
Кибернетика — это наука об управлении, системах и информации. Современный мир характеризуется бурным развитием кибернетики. На наших глазах происходит глубочайшая кибернетическая революция цивилизации и культуры, которая меняет их до неузнаваемости.
Понятие информация отражает наши знания, понятие управление — наши действия (актуально и потенциально). Реализация знаний и действий происходит в системе. Таким образом, управление, система, информация — это три аспекта одной и той же науки.
Кибернетика — слово греческого происхождения (означает кормчий, рулевой). Оно созвучно названиям других наук также греческого происхождения: математика, механика, физика. Основоположник кибернетики Норберт Винер дал такое определение: “Кибернетика — это наука о связи и управлении в машинах и живых организмах”.
Мы хотим показать, что такие основные математические понятия, как структура и симметрия, с одной стороны, и такие основные кибернетические понятия, как система, управление, информация, движение, с другой стороны, являются тесно связанными и определяются друг через друга.
Однако надо принять во внимание, что кибернетика — это относительно молодая наука с историей развития на протяжении около полувека, в то время как математика и теоретическая физика имеют многовековую историю, а их последний период наиболее интенсивного развития составляет около 400 лет — со времен Галилея, Кеплера, Ньютона, Лейбница, Гюйгенса, Ферма, Декарта.
Широкий взгляд на кибернетику позволяет выдвинуть новую философскую концепцию устройства мира — это “управленческая или кибернетическая парадигма мира”. Величайшим, ключевым открытием новейшей цивилизации является открытие, или изобретение, Дж. Уаттом в прошлом веке автоматического регулятора, или обратной связи, для регулирования, поддержания скорости хода паровой машины независимо от нагрузки (возмущений) и в соответствии с уставкой (заданием).
Управленческая (кибернетическая) парадигма мира означает, что все, что сохраняется в мире, происходит за счет работы систем управления с обратной связью, регуляторов, естественно присутствующих в природе и обществе, а наблюдаемые в природе флуктуации (любая величина в реальности имеет флуктуацию, принципиально отличную от тождественного нуля) — это ничто иное как наблюдаемая ошибка, или погрешность работы этих регуляторов.
При этом реально могут быть наблюдены только те системы управления и соответствующие им законы природы, которые “достаточно”
60
устойчивы, т.е. в течение “достаточно” большого интервала времени система управления обеспечивает “достаточно” малые значения абсолютной ошибки регулирования, в пределах которой находятся флуктуации регулируемой величины.
Именно в смысле управленческой парадигмы мира можно понять известное латинское изречение “Бог сохраняет все” и добавить “с помощью обратных связей, регулирования, создания систем автоматического регулирования (управления)”.
Понятие кибернетики можно определить компактнее: кибернетика — это наука об управлении. Здесь слова система и информация опущены, так как можно показать, что они в определенном смысле сводятся к понятию управление. В винеровское определение они также не входят.
Именно понятие управление может быть рассмотрено как основополагающее. В частности, с философской точки зрения понятие управление, выражающее свободу выбора, является одним из наиболее фундаментальных понятий и проблем: “Существует ли в мире свобода выбора и если да, то в какой мере, или, вообще, в каком смысле?’
На первый взгляд кажется, что понятие управление не может существовать (не имеет смысла) без понятий система и информация. Однако последние исследования показывают, что можно создавать аксиоматику понятия управления без априорного использования того, что мы называем системой и информацией (см. разд. 5).
После определения понятия управление можно говорить о системе и информации: система — это пространство управлений, а информация — это сложность управлений.
Таким образом, в таком подходе наиболее фундаментально понятие управления, а понятия системы и информации — вторичные понятия.
Во избежание недоразумений еще раз подчеркнем, что подход, в котором за основу берется понятие управления, ни в коей мере не исключает возможности, где за основу берется понятие информации или системы.
Однако сейчас более понятным и естественным с развиваемой точки зрения нам представляется подходящим именно такое представление, где первичным является понятие управления. Не надо думать, что хотя бы в какой-то мере отвергаются альтернативы, которые очень популярны сейчас, например, “системный подход” или “системноинформационный”.
Н. Винер, как видно из его книги [76], всегда понимал широкую значимость кибернетики как науки, методы которой имеют общий, если не всеобщий, характер, включая физиологию, психологию, экономику, социологию, политику, юриспруденцию, медицину и т.д., не говоря уже о производственно-технологических дисциплинах.
61
1.12.	ПРЕДИКАТЫ
Понятие предиката является центральным в математической логике. Он является важной формой смысла. Язык современной математики, а следовательно, любой науки (поскольку теория любой науки должна быть математической) — это язык предикатов.
Предикат можно понимать как функцию от высказываний, принимающую одно из двух возможных значений. Эти два возможных значения часто обозначают “0” и “1”, а также условно называют ложь и истина. Предикат имеет определенную структуру: имеется субъект (предмет) высказывания, т.е. то, о чем происходит высказывание, и предикат высказывания, т.е. то, что высказывается о субъекте.
Понятие предиката формализуется математически на основе понятия множества, и эта формализация называется отношением.
Отношение — это подмножество прямого произведения А} х Л2 х А„ множеств Ai, ... А,„ где натуральное число п называется местностью отношения (число мест в отношении).
Указанное подмножество обозначим В. Множество i = 1, ... п, описывает субъекты предиката z-ro “сорта”; конкретный субъект z-ro сорта — это какой-то элемент а, множества Л,-, <2/ g Л,-. Множество Ai называют предметной областью z-ro сорта предиката или отношения.
Таким образом, вся совокупность А1 х ... х А„ субъектов (яь ..., ап) делится на два непересекающихся подмножества, составляющие в объединении все множество А\ х ... х Ап.
Итак, если (аь ..., а„) g В, то последовательность (а},..., а„) обладает данным (обобщенным) свойством, т.е. среди at, ..., ап имеет место данное отношение; если (а\, ..., а„) g В, то среди at, ..., а„ данного отношения не существует.
Одноместный предикат (отношение) называется свойством. Заметим, что иногда произвольное высказывание рассматривается как нуль-местный предикат.
Таким образом, изучение предикатов — языка всей науки — сводится к изучению множеств — основного объекта в математике. Вот почему важно в самой математике иметь хорошо развитую, эффективную и непротиворечивую теорию множеств.
Описать подмножество какого-то множества можно с помощью характеристической функции (отображения) этого подмножества.
Характеристическая функция Р(х) подмножества В а А ] х ... х Ап — это функция вида
62
1,	если х g В
Р(х) = \	_ •
[О, если х е В
Таким образом, предикат (отношение) однозначно описывается функцией Р(х), с которой он и отождествляется, т.е. Р(х) и будет называться предикатом, или отношением.
Итак, имеет место отождествление: предикат = отношение з Р(х).
Необходимо подчеркнуть, что термин отождествление здесь понимается в смысле эквивалентности, или равносильности'. задать предикат — это значит задать отношение, или Р(х); задать отношение — значит задать предикат, или Р(х)', задать Р(х) — значит задать предикат, или отношение.
Представляется целесообразным в рамках задач ЕГТУ—ТСУ расширить эти отождествления, чтобы придать точный смысл таким основным словам-терминам, как структура, пространство и система. Итак, произведем отождествление: предикат = отношение = структура = пространство = система.
Но почти все понятия в математике описываются предикатами, поэтому для того чтобы сделать эти понятия более содержательными, необходимо в каждом конкретном случае применения этих отождествлений производить их уточнения. Они останутся отношениями, т.е. предикатами, но возможно более специального вида. Например, с термином и понятием пространство часто, ио не всегда связан термин и понятие размерность, размерность пространства, что, несомненно, характеризует еще одну структуру, присущую понятию пространства. Аналогично с понятием система неразрывно связаны понятия состояние и движение, которые в свою очередь описываются соответствующими предикатами и отношениями.
Сделаем еще терминологическое замечание.
Если в предикате все множества A,, i = 1,..., п, одинаковые, т.е. = А, V/, то предикат Р(х) называется п-арным и х е А х ... х А = А" — нулъ-арным, унарным, бинарным, тернарным и т.д. Унарный предикат описывает просто свойство одного предмета а е А. Нуль-арный предикат можно отождествить просто с высказыванием. Это аналогично тому, как “постоянную” функцию можно отождествить с ее постоянным значением.
Если, как мы сказали, унарный, или одноместный, предикат описывает свойство одного предмета, то можно сказать, что /7-арный, или п-местный, предикат описывает свойство упорядоченной совокупности п предметов.
63
1.13.	СИММЕТРИЯ (ОБЩЕЕ ПОНЯТИЕ)
Математика — это наука о структурах и симметриях. Причем симметрия — это наиболее общий метод изучения структур. Конечно, сама симметрия может стать объектом изучения, поскольку, как мы увидим, имеет свою собственную структуру. Но что же такое симметрия?
Дословно в переводе с греческого симметрия — это соразмерность. Дадим сначала содержательное описание симметрии, т.е. попытаемся понять ее смысл, а затем придадим этому смыслу форму в виде некоторого точного математического понятия.
Итак, пусть дан любой объект совершенно произвольной природы, т.е. имеется некоторая произвольная реальность. Зададим вопрос: “Когда можно сказать, что данный объект имеет симметрию, обладает симметрией?” Ответ на этот вопрос следующий.
Объект обладает симметрией, если существует одно или более его преобразований таких, что полученный в результате этих преобразований новый объект совпадает с исходным объектом, а лучше сказать, неотличим от исходного. При этом каждое из таких преобразований называется преобразованием симметрии, преобразованием инвариантности, элементом симметрии или просто симметрией.
Хотя данное выше определение симметрии лишь содержательное (еще не формализованное), но из него можно вывести ряд важных следствий и сделать ряд принципиальных замечаний о сути понятия симметрии.
1.	Прежде всего подчеркнем относительность понятия симметрии для любого данного объекта. Из определения сразу следует, что симметрия данного объекта существенно зависит от способности различать или отличать один объект от другого.
Важно сразу обратить внимание на условность слова неотличим в определении симметрии. Действительно, то, что различимо в одних условиях (например, в условиях дневного освещения), может стать неразличимым в других условиях (например, в условиях темноты, ночью). В этом и состоит условность, или относительность, понятия симметрии. Это замечание — принципиально, ибо характеризует, возможно, всю суть математики и ее отношение к реальности. Дело в том, что, как говорилось выше, двух одинаковых реальностей не бывает, каждая реальность невообразимо сложна, самобытна, неповторима, не похожа ни на что другое. Если это так, то отсюда следует, что ни для какой реальности никакой симметрии не существует, ибо всякое преобразование, за исключением тривиального, когда преобразование состоит в том, что никаких преобразований не делается, в принципе меняет объ-
64
екг, подверженный какому-то преобразованию. Поэтому в определении симметрии вместо “совпадения” (чего никогда не бывает) мы говорим о “неразличимости”, что сразу делает понятие симметрии относительным, т.е. зависящим от средств наблюдения.
Таким образом, в реальности симметрии не существует. Тогда о чем идет речь? Это означает, что из бесконечной и невообразимо сложной совокупности свойств реальности мы выбираем и фиксируем лишь конечное число ее свойств, а всю остальную необозримую массу свойств игнорируем. В результате вместо реального объекта возникает его абстрактное, идеальное представление, которое описывает реальность. Предикат и отношение призваны осуществлять такое приближенное описание объекта. Это в корне меняет ситуацию. Идеальный объект, в отличие от реального, уже имеет нетривиальные симметрии.
Ясно, что если мы возьмем реальный объект и преобразуем его так, чтобы нарушились только его несущественные, отброшенные при идеализации свойства, а свойства, учтенные идеализацией, не изменились, то идеальные объекты до и после преобразования будут неотличимы, т.е. одинаковы (с этой упрощенной, приближенной, идеальной точки зрения).
Итак, мы видим, что симметрия условна, относительна, зависит от принятых условий, схем идеализации и используемых условий наблюдения.
Развитие любой науки в том и состоит, что происходит постоянное улучшение качества наблюдений за изучаемым объектом, например, за счет усовершенствования старых и изобретения новых приборов и вообще средств наблюдения, которые позволяют различать все более и более тонкие черты и свойства наблюдаемого объекта. Термин неразличимость в определении симметрии характеризует уровень и мощь наших возможностей наблюдения, средств и приборов наблюдения, измерения. Неразличимость часто напрямую связана с точностью измерений. Например, когда-то элементом считался атом, но внутри атома мы еще ничего не могли различить. Поэтому его и назвали атомом, т.е. неделимым. Все атомы казались как бы на одно лицо и были неразличимы. С развитием средств наблюдений и теоретических представлений атомы научились различать. В результате выяснилась их внутренняя структура: атом состоит из ядра и электронов. На этом уровне атомы стали различимы. Но появился новый уровень — уровень электронов и атомных ядер. С развитием средств наблюдения (ускорители, счетчики и камеры) и ядра атомов стали различимыми — у них разное число протонов и нейтронов. Но электроны остались неразличимыми. Однако последние достижения физики дают указание на то, что и электроны неодинаковы.
3. А.В. Бабичев
65
Таким образом, уровень неразличимости в симметрии характеризует глубину развития любой науки. Интересен эффект прибытия европейца, скажем, в Китай. В первое время все китайцы выглядят на одно лицо, но со временем уровень различимости увеличивается; аналогичное явление имеет место и для китайцев, прибывших в Европу.
2.	Из первого замечания вытекает следующее. Если в идеальном объекте учесть еще какое-нибудь новое свойство, то симметрия может нарушиться, т.е. симметрия строго идеального объекта может не быть симметрией нового идеального объекта. Таким образом, множество всех симметрий S2 нового идеального объекта будет, как правило, “меньше” множества Si всех симметрий старого объекта, т.е. S2 с Sj.
Интуитивно ясно, что из Si будут выкинуты более “простые” симметрии, а останутся и войдут в S2 более “сложные”, ибо новый идеальный объект стал “сложнее” старого за счет более тонкого и более широкого учета, присоединения его новых, ранее не известных свойств. В этом и состоит принцип нарушения симметрии.
Усложнение изучаемого объекта происходит в виде нарушения его ранее известных симметрий: их становится меньше, зато они становятся сложнее. В этом и состоит “более глубокое изучение” реальностей в терминах нарушения симметрии. В пределе реальный объект имеет всего один элемент симметрии — это тривиальная симметрия, которую симметрией в полном смысле и назвать нельзя. Скорее это следует назвать асимметрией. Таким образом, всякая реальность характеризуется асимметрией.
Отсюда становится понятным, почему Эрвин Шредингер сравнивал жизнь с “апериодическим кристаллом”. Это понятие, выглядящее внутренне противоречивым, надо понимать как предельное, когда элементы симметрии неограниченно усложняются, а их общее число уменьшается. В результате остается лишь один тривиальный элемент симметрии.
3.	Отметим другое важное свойство симметрии, которое можно назвать критичностью симметрии, неустойчивостью симметрии, не-грубостъю симметрии или хрупкостью симметрии (как всякой истинной красоты).
В определенном смысле симметрия легко нарушается. Мы не будем вдаваться глубоко в обсуждение этого нетривиального вопроса, но поясним суть дела простым примером. Рассмотрим идеальную окружность. Ясно, что она имеет бесчисленное множество симметрий — поворотов вокруг центра на любой угол. Однако, стоит как угодно мало (!) деформировать окружность, например, сколь угодно малый кусочек окружности заменить хордой, “число” элементов симметрии резко сократится: теперь симметриями будут лишь повороты на углы, кратные
66
2л. Поэтому с симметрией нужно обращаться очень бережно и внимательно.
4.	Другая важная особенность понятия симметрии, характеризующая его необычайную мощность и общность, состоит в том, что оно обладает широким спектром разновидностей, а именно: сохранение, баланс, инвариантность, неизменность, постоянство, независимость, устойчивость, согласованность, соразмерность, декомпозиция, равенство, тождество, уравнение и др.
Таким образом, симметрия — многоликое и вездесущее понятие.
5.	Можно с уверенностью сказать, что для того чтобы решить частично или полностью какую-либо задачу, необходимо и достаточно найти и описать ее симметрии.
6.	Интуитивно ясно, что если Si и S2 два преобразования симметрии объекта, то выполненные подряд эти две симметрии, причем в любом порядке, также будут симметрией. Это важное полугрупповое свойство самого множества всех симметрий данного объекта.
Перейдем к более формальным определениям.
Пусть изучаемая реальность, т.е. объект В, приближенно описывается предикатом Р(х), х е А, А = Аг х ... х А„. Это означает, что объект2? отождествляется с непустым подмножеством, которое обозначим снова В. множества А = А\ х ... х А„. Иными словами, предикат, или отношение, Р(х) описывается характеристической функцией.
Итак, если х е В, то говорят, что упорядоченная совокупность х = = (хь ...,х„) £ А обладает свойством, заданным предикатом (отношением) Р(х). В этом случае также говорят, что среди предметов х; е И,-имеет место отношение, заданное предикатом Р(х). В противном случае, т.е. когда х ~ (хь ..., хи) £ В, говорят, что упорядоченная совокупность х = (хь ..., х„) не обладает данным свойством или среди предметов Xi е А, данное отношение места не имеет. Теперь можно дать точное определение понятия преобразование S объекта В.
(Определение 1. Преобразование 5’ объекта В — это всякое сюръективное отображение вида S •. А —> А, иными словами, это отображение множества А на себя.
Для преобразования S объекта В будем использовать также и ’функциональные” обозначения вида х' = Т(х), х е А, х' е А.
Множество {S’} всех преобразований 5* объекта В никогда не пусто, ибо оно всегда содержит по крайней мере один элемент — единичное, или тождественное, преобразование.
3*
67
Отсюда уже можно дать точное определение того, что будем называть преобразованием симметрии объекта В, описываемого предикатом, или отношением, Р(л), х е Далее это преобразование симметрии будем обозначать S’, чтобы отличить его от произвольного преобразования объекта В. Множество всех S обозначим {5}. Для краткости преобразование симметрии S иногда будем называть просто симметрией S (данного объекта В).
I Определение 2. Симметрия 5 объекта В — это любое преобразование объекта В такое, что выполняется тождество P(S(x)) = = Р(х) для Vjc € А.
Ясно, что множество {S’} всех симметрий объекта В никогда не пусто, ибо оно всегда содержит по крайней мере один элемент — единичное (тождественное) преобразование.
Далее, если S) и S2 две любые симметрии из {S’}, то композиция этих отображений, выполненная в любом порядке, также будет симметрией, правда, необязательно той же самой.
Таким образом, в {5} всегда определена бинарная операция, по отношению к которой множество {S} замкнуто, т.е. оно сохраняется в том смысле, что результат всякой такой бинарной операции снова принадлежит множеству {S}: из S) е {S’} и S2 е {S'} следует, что существуют элементы, обозначаемые S’iS2 и S2S], такие, что S’i52 е {S} и S^S) е {£}.
Таким образом, множество всех симметрий {S1} данного объекта В как минимум обладает структурой моноида, т.е. полугруппы с единицей So.
Нередко в множество всех симметрий {S’} вместе со всяким S входит в обратное преобразование S"1, т.е. всякое отображение симметрии S’ имеет обратное. Тогда {S’} имеет более сложную (чем моноид) структуру, которая называется группой. В этом случае {S} называют группой симметрий (данного объекта В, описываемого предикатом, или отношением, Р(х)).
Отсюда становится ясной важнейшая роль во всей математике таких структур, как группы и моноиды, ибо они описывают симметрии структур, которые в силу закона 100%-эффективности математики описывают и реальности. Эта мысль имеет геометрическое толкование.
Симметрия — это та часть всевозможных преобразований S’ множества А на себя, которая сохраняет (оставляет теми же самыми)
68
подмножества равного уровня, которых у предиката всего два: со значениями 0 и 1. Таким образом, S’ должно сохранять подмножество В, описывающее предикат Р(х).
Преобразования симметрии 5 еще называются автоморфизмами (самосохранения ми). Чтобы изучить объект, структуру, надо изучить множество всех его автоморфизмов.
Автоморфизмы можно еще назвать движениями (данной системы или пространства). Ф. Клейн в своей Эрлангенской программе (программе изучения разных геометрий с помощью идей сохранения, т.е. симметрии) движениями называл такие преобразования пространств, которые сохраняют метрику, метрическую структуру, присущую геометрии данного вида. Например, движениями евклидовой плоскости называются все те ее точечные преобразования на себя, которые сохраняют евклидово расстояние между любыми парами точек до и после преобразования. Это все те и только те преобразования, которые сдвигают и поворачивают любые фигуры на плоскости, но не деформируют сами формы этих фигур, их формы остаются неизменными, независимыми, инвариантными от действия допустимых (по определению) преобразований. Такие преобразования, или движения, называются еще изометрическими (сохраняющими метрические размеры).
Если р(х;, х2), X] g X, х2 g X — метрика, то изометрическое движение — это преобразование S’ такое, что выполняется тождество
p(Sx], Sxfi) = р(%1, х2) для Vjq е X, \/х2 g X.
Это — структурное тождество данной симметрии.
Рассмотрим еще один важный пример общего характера. Пусть структура описывается просто функцией (отображением) f: X -> У, У = Дх), X G Х,у G У.
Что такое симметрия такой структуры?
I Определение 3. Симметрией функции у - fix), х е X, у е У, называется функция^: Ал—> X, х' = g(x), х е Х,х' е X, такая, что выполняется тождество (структурное тождество)fig(x)) = fix) для Vx е X.
Совокупность {g} всех таких функций g (для фиксированного/) как минимум образует моноид, ибо:
69
1) единственный элемент g(x) = х, очевидно, есть элемент симметрии, так как Дх) =/{х);
2) последовательное применение преобразований, заданных разными симметриями gi е {g} и g2 е {g}, т.е. суперпозиция g] -g2 - gi(g2(x)) или g2-gi= g2(g\(x')), также есть симметрия g3 - gi -g2 или g4 = g2-gb так KaK/(g3(x)) =/(gi(g2(x))) =/(g2W) = Ж n/(g4(x)) = f (g2(gi(x))) = =/(gi.W) =ЛХ\
Если к тому же всякая функция g е {g} имеет обратную g-1(x), то последняя обязана также принадлежать {g}, и совокупность {g} является уже группой автоморфизмов функции f
Например, для функции комплексного переменного у = |х|2, х е С, у g V, где С и V — множества комплексных и действительных чисел соответственно, группой ее ав томорфизмов будет множество {е'“}, а е V, Введем еще два полезных понятия, связанных с вышеизложенным.
I Определение 4. Действием преобразования 51 на элемент х е X называется элемента' е X, равный х1 = S(x).
Определение 5. Орбитой элемента (точки) х е X называется совокупность всех действий 5 на точку х, когда 5 пробегает все множество {S'} (обозначается 0(х)).
Для указанного выше примера функции у = |х|2 действием преобразования S = е'“ на элемент х g X будет поворот точки х на угол а около точки ноль, 0 е С. Орбитой точки х будет окружность радиуса |х| с центром в точке ноль.
Орбиты обладают следующим свойством.
(Теорема 1. Если {£'} — группа, a 0(xi) и 0(х2) орбиты двух точек
X] g X их2 е Xсоответственно, то они или совпадают, т.е. 0(х[) = = 0(х2), или не пересекаются, т.е. О^) п 0(х2) = 0.
Отсюда следует, что {£} порождает разбиение X на множество не-пересекающихся орбит.
Здесь уместно процитировать Г. Вейля: “... вывод, ставший руководящим принципом современной математики, состоит в следующем: всякий раз, когда нам приходится иметь дело с некоторым объектом, наделенным структурой, попытайтесь определить группу его автоморфизмов, т.е. группу, элементами которой являются преобразования, оставляющие без изменения все структурные соотношения. Вы можете рассчитывать на то, что на этом пути вам удастся глубоко проникнуть во внутреннее строение обьекта” [66, с. 159].
Более того, сама симметрия может рассматриваться как математический объект, который можно изучать с помощью симметрии. Таким
70
образом, речь идет о “симметрии симметрии”. Изучению симметрии с помощью самой же симметрии соответствует изучение групп (которые всегда сами по себе описывают и представляют симметрию какого-либо математического обьекта: пространства, системы и т.д.) с помощью ее собственных групп автоморфизмов. Это и есть “симметрия симметрии”.
Идею нарушения симметрии как источник новых структур проиллюстрируем на примере понятия информации, которую можно рассматривать как результат нарушения некоторой симметрии.
Пусть мы имеем лишь один фон, т.е. бесструктурное множество 30 или пространство с 0-структурой Со, которое задается постоянным отображением Со: So с0 = const g Y. Знание такой структуры, т.е. наблюдение за значением Со, не дает возможность хоть как-то различить элементы множества So. В таком случае естественно считать, что Со не несет никакой “информации”. Но такое бесструктурное множество Sb допускает, выдерживает любое преобразование симметрии, сохраняющее 0-структуру, т.е. структуру принадлежности элементов множеству 30- Интуитивно ясно, что если на 30 была бы еще какая-то структура С, отличная от Q. и оно стало пространством Sc, то уже не любое преобразование Sc на себя сохранило бы эту структуру. Иными словами, “количество”, или “объем”, группы автоморфизмов в этом случае стал бы меньше.
Посмотрим на этот факт с точки зрения информации, содержащейся в данном пространстве. В силу вышесказанного естественно принять, что бесструктурное множество не несет никакой информации, но появление какой-то структуры должно соответствовать ее увеличению. Поясним эту ситуацию на примере конечного множества So, состоящего из N элементов. Ясно, что множеством всех автоморфизмов такого бесструктурного множества является симметрическая группа всех перестановок (или подстановок) элементов из 30. Число всех таких преобразований симметрии равно N\
Предположим теперь, что 30 снабжено некоторой структурой С так, что оно превратилось в пространство Sc. Например, какое-то число ZV], 0 < N\ < N, элементов So, образующих подмножество 3] с 30, получило какую-то “метку”, одну и ту же для всех элементов, и тем самым стало отличаться от оставшихся немеченными элементов подмножества S2 в числе = N - элементов 30. Можно сказать, что на 30 возникла новая структура С, превратившая 30 в пространство Зс.
Структурное отображение С здесь задается “характеристической” функцией ср(х) множества Sj меченных элементов:
Cj если х g St, ct g Y
c2 если x g S2 = So - Sj, c2 g Y, Cj ф c2 .
<p(x) =
71
Структура С фактически описывает разбиение множества So на два подмножества — S( и S2. Пространству Sc с такой структурой естест-д/| венно приписать информацию /(Sr) в количестве I(SC) = lg2----.
Nx! N 2!
Здесь информация берется в логарифмическом по основанию два масштабе, чтобы в согласии с классической теорией в качестве единицы измерения иметь бит.
Легко видеть, что при таком определении информации, фоновой структуре Со (т.е. 0-структуре) соответствует нулевая информация /(So) = 0, ибо N\ - О, TV2 = N. Ясно, что это минимально возможное значение информации. Наибольшее ее значение, как известно, достигается при TV, = N2 = N/2, если TV четно, или при TVi® N2, если TV нечетно.
В более общем случае, когда имеется разбиение So на к попарно не-пересекающихся подмножеств Sb ..., S* с числом элементов N\, Nk, где TV] + ... + М- = N, информация определяется выражением №
/(Sr) = Ig2-------.
‘'Характеристическая” функция ф(х) такого Л-разбиения, играющего здесь роль структурного отображения, имеет вид <р(л)={с(-, если х g S*}, где все с,- е X, z = 1,..., к, попарно различны.
С помощью таких “характеристических” функций можно аппроксимировать и другие, более сложные, структуры, задаваемые отображениями, определенными на So-
Эффект увеличения информации или сложности за счет образования новых структур можно истолковывать как эффект нарушения симметрии (в физике - - это эффект “спонтанного нарушения симметрии”). Действительно, первоначально, когда мы имели лишь 0-структуру So, симметрия имела наибольший “объем”, оцениваемый величиной 7V! Введение дополнительной структуры уменьшило “объем” преобразований симметрии до величины ?Д! ... АД и тем самым нарушило исходную симметрию, хотя и увеличило информацию.
Такой подход к рассмотрению информации является предметом развивающейся в настоящее время алгебраической теории информации [109], имеющей большое количество приложений в кибернетике (распознавание образов, реляционные базы данных, хранение и обработка данных в компьютерах, кодирование и др.).
Более непосредственный, а не аппроксимационный подход к введению понятия информации, содержащейся в данном пространстве или структуре, в случае, когда So содержит неограниченное число элементов, в частности континуум, и преобразования симметрии непрерывны, должен быть связан с понятием меры множества бесконечных и непре
72
рывных преобразований симметрии, т.е. сохраняющих данные структурные отображения. Эти вопросы, по-видимому, связаны с колмогоровским подходом к определению понятия информации, сложности и энтропии функций и динамических систем как некоторых их инвариантов [154].
1.14.	КАЛИБРОВОЧНАЯ СИММЕТРИЯ
Калибровочной симметрией, или калибровочной инвариантностью, называется симметрия уравнения или системы уравнений под действием преобразований масштабов (калибров) величин, входящих в данные уравнения.
Эта симметрия изучалась еще в XIX веке. Ее считали естественно присущей всякому “закону природы”, так как выбор масштаба — дело субъективное, а “законы природы” — вещь объективная, т.е. не зависимая от любых действий и желаний исследователя. Иными словами, “законы природы” и уравнения, которые им соответствуют, должны сохраняться (не нарушаться), если изменить масштабы измерений любой совокупности величин, входящих в уравнения для какого-то закона.
Это означает, что уравнения (т.е. равенства) должны сохраниться, если, скажем, величину х в уравнениях заменить величиной ах, или даже сделать “афинное” ее преобразование х -» ах + р, где а характеризует изменение масштаба (например, единиц измерения) величин, а Р — изменение “начала отсчета” (“выбор нуля”). Например, еслиДх) = = 0 — некоторое уравнение, то должно иметь место тождество/(ах + Р) = =/(х) для Х/х.
Позже такая калибровочная симметрия стала называться глобальной калибровочной симметрией. Термин глобальная означает, что параметры изменения масштабов (или “систем отсчета”), т.е. аир, должны быть постоянными, т.е. не зависящими от того, в каком месте и в какое время производится измерение данной величины х.
Этот естественный принцип, несмотря на свою простоту, оказался очень эффективным и широко используется в науке и технике около двух веков. Он был хорошо разработан в теории “физического” моделирования, когда инженеры, прежде чем строить реальные сооружения, например, трубопроводы, плотины, летательные аппараты, нагревательные устройства (печи) и многое другое, сначала создавали небольшие по размерам и существенно более дешевые “модели” реальных объектов и, экспериментируя на них, делали предсказания о пове-юнии реальных объектов. Наука об этом получила название теория подобия.
73
Например, пусть мы хотим исследовать процесс теплообмена через толстую стену какого-либо реального здания. Мы знаем, что “закон теплообмена” описывается уравнением теплопроводности
dQ/dt = cTQ/dx2,	(1.14.1)
где Q(t, х) — распределение температуры по толщине стены х, 0 < х < 5, в момент времени /, 0 < t < Т. Изменим величины, входящих в уравнение: Q -> 6 Q + Pi; аг —> fyc + р2; t -> it + р3.
Подстановка новых значений в (1.14.1) дает новое уравнение: dQldt = (т/^2)^/дх\	(1.14.2)
где тД2 — постоянная, вообще говоря, не равная единице.
Следовательно, уравнения (1.14.1) и (1.14.2) в общем случае окажутся разными. Но в силу принципа глобальной калибровочной инвариантности уравнение (1.14.1) не должно меняться (оно должно сохраниться), т.е. (1.14.1) и (1.14.2) должны быть идентичными! Отсюда следует, что постоянная т/f,2 не может оказаться произвольной, но должно выполняться условие
т/^2 = 1 или т = %.	(1.14.3)
Условие (1.14.3) и есть условие “подобия”, а лучше сказать, идентичности процессов в реальности с процессами в ее модели. Если мы, например, хотим уменьшить время моделирования в 100 раз, то толщина стенки модели должна уменьшиться всего в 10 раз: 10 = V100 , ибо 5, = д/т .
Выражение в левой части (1.14.3), т.е. функция от т и £,, называется критерием подобия. Критерии и “уравнения подобия” типа (1.14.3) можно пытаться получить для любых “законов природы” и уравнений.
Из этого примера видно, что критерии подобия получаются особенно просто, если уравнения однородны, т.е. их левые и правые части являются однородными функциями переменных процесса.
Калибровочную инвариантность еще называют компенсационной инвариантностью или компенсационной симметрией, а условие (1.14.3) — компенсационным условием или компенсационным уравнением. Действительно, можно сказать, что (1.14.3) показывает, как нужно изменять одну часть параметров (скажем, £,), чтобы скомпенсировать изменение другой части параметров (скажем, т), т.е. сохранить условие (1.14.3). Из (1.14.3) это условие компенсации получается легко: = л/т или т = £2.
Термин компенсация подсказывает нам, что соблюдение калибровочной инвариантности можно толковать на языке теории регулирова
74
ния (управления)! Например, если параметр т по каким-то причинам ’“плывет”, то его можно рассматривать как “возмущение”, поступающее в систему, которое должно быть “скомпенсировано” посредством “управляющего воздействия” £ так, чтобы ошибка (погрешность) регулирования Дх, определяемая как Vr = Дх, стала нулевой: Дх = 0. Таким образом, в системе должен работать регулятор, т.е. некоторая замкнутая система с обратной связью, “цель” которой поддерживать “‘ошибку в системе” Дх = 0!
В примере с теплопроводностью интересно отметить другой глубокий и замечательный факт: условия, или уравнения, компенсации (1.14.3) вообще могут получиться только из уравнения вида (1.14.1). Таким образом, и обратно: условия или уравнения компенсации однозначно определяют фундаментальное уравнение! Фундаментальное уравнение, описывающее “закон природы”, из них следует! Правда, для однозначности нужно еще добавить условия “наибольшей простоты” уравнения: условие минимума порядка производных.
Идея глобальной калибровочной инвариантности получила свое развитие в виде ее обобщения до идеи локальной калибровочной инвариантности. Это сделал в 1918 г. Герман Вейль.
Действительно, нет никаких логических препятствий считать, что законы природы и соответствующие им уравнения не должны меняться (т.е. должны сохраняться), если масштабы величин, входящих в эти уравнения, меняются, причем меняются как угодно и, самое главное (что отличает его от глобального принципа), независимо в каждой точке пространства и времени, в котором эти законы (уравнения) действуют.
Несмотря на логическую безукоризненность такого принципа, его приняли не сразу даже выдающиеся ученые. Например, Эддингтон в своих возражениях Вейлю использовал даже высказывания из Библии [70, с. 204.].
Но идея Вейля оказалась очень плодотворной. Принцип локальной калибровочной инвариантности сейчас рассматривается как самое крупное достижение теоретической физики XX в.
Этот принцип можно расширить до так называемого принципа всеобщей ковариантности законов природы, который утверждает, что законы природы и соответствующие уравнения не зависят от выбора систем отсчета (координат), ибо этот выбор делается человеком, а законы природы от него пока еще не зависят.
С помощью этого принципа, правда с учетом “квантовомеханических соображений”, удалось вновь вывести уравнения Максвелла и закон сохранения электрического заряда. При этом максвел-
75
донское электромагнитное поле оказалось тем самым компенсирующим полем (которое на языке ЕГТУ—ТСУ получает смысл управления, или управляющего поля), которое и реализует (!) поддержание условий инвариантности (симметрии!), т.е. сохранения заряда.
Другие естественные принципы симметрии, или сохранения, позволили вывести более общие уравнения (законы природы), например уравнения Янга-—Милса, которые описывают компенсационные (т.е. регулирующие, управленческие!) поля самой разнообразной природы.
Эти замечательные открытия и факты при разработке ЕГТУ—ТСУ натолкнули на мысль, что всякое управление с обратной связью в замкнутой системе, а не только в физических системах, является компенсационным, или калибровочным, полем, реализующим сведение к нулю ошибки регулирования Ах, где уравнение Дх = 0 выражает условия локальной качибровочной инвариантности, или симметрии, и сохранения некоторой субстанции, например, тепла, заряда, импульса, количества движения, энергии и т.д.
Эту мысль можно представить в виде “Принципа управленческой парадигмы Мира”, который сформулирован в подразд. 1.11 и будет еще обсуждаться.
Интересно, что идея, или принцип, локальной калибровочной инвариантности фактически была использована по сути еще Лагранжем, в классической задаче о выводе решения неоднородного линейного обыкновенного дифференциального уравнения под названием метод вариации постоянных. К идее локальной калибровочной инвариантности близки и другие методы, например, метод возмущений, метод малого параметра, в которых так или иначе, явно или неявно используется симметрия. Более общо эту идею можно выразить как общую рекомендацию: “Если имеются некоторые постоянные параметры задачи, то варьируй их, а условия симметрии (инвариантности, компенсации, сохранения, устойчивости, непрерывности и т.д.) приведут к новым, возможно, нетривиальным и неочевидным результатам: уравнениям, формулам, законам и т.д.”. Примерно та же идея составляет суть наиболее общих и вместе с тем наиболее мощных и эффективных “вариационных принципов механики” и “вариационного исчисления”.
Напомним суть метода вариации постоянных Лагранжа.
Уравнение х = Ах имеет решение х = x(Z) = СехрА t для любой константы С. Проварьируем С, т.е. положим С = С(Г), и подставим у(0 = = C(t)expAt в исходное уравнение. Получим новое уравнение С (Z) еА‘ + + AC(t)eA/=AC(t)eAt.
Отсюда следует у (/) = Ay(t) - С (Z) еАГ.
76
Последнее уравнение показывает, что y(t) не удовлетворяет исходному уравнению. Чтобы все-таки уравнение сохранилось, должен появиться компенсирующий член, восстанавливающий инвариантность. Он равен Д/) = -С(/)ел'.
Последнее уравнение и есть условие компенсации. Его можно рассматривать как уравнение компенсирующего воздействия (“поля”), или как калибровочное поле. В данном случае оно легко решается:
С(0 = - je-A/(T)d^ + C0, О
где Со — новая произвольная константа.
Отсюда, как легко видеть,
y(t)=C(t) еЛ= (Со- |е-А/(т)*)еЛ О
есть решение неоднородного уравнения у = Ay + ft), что и требовалось получить.
Приложение идей симметрии к задачам устойчивости и управления линейных нестационарных систем рассмотрено в [92].
С точки зрения компенсационной, или управленческой, симметрии и инвариантности могут быть рассмотрены многие фундаментальные математические понятия, например, непрерывность или устойчивость.
Вспомним, что функция fx), х g (a, b) cz R,fx) g R, называется непрерывной в точке х = с g (а, Ь), если и только если для Ve > 0 35 > О такое, что | х - с | < 8 => | fx) -fc) | < е.
Это означает, что для непрерывности функции Дх) необходимо и достаточно существование функции (по крайней мере одной)
8 = ф(е), е > 0, 8>0,	(1.14.4)
связывающей параметры в и 8, которые фигурируют в определении непрерывности. Если ввести “ошибку” Д = ф(е) - 8, то условие (1.14.4) можно трактовать как условие компенсации. Другими словами, условие
Д = Ф(е)-3 = 0	(1.14.5)
можно рассматривать как задание регулятору в системе с обратной связью, призванной поддерживать условие (1.14.5). Этот регулятор на возмущение параметра е отвечает регулирующим (управляющим) воздействием 8 так, чтобы сделать ошибку Д равной нулю, т.е. поддерживать и сохранять уравнение (1.14.5), которое можно рассматривать как условие, выражающее “сохранение понятия” непрерывности. С такой же точки зрения можно рассмотреть устойчивость и другие понятия.
77
Итак, мы видим, что здесь компенсационный (калибровочный) регулятор является средством поддержания или сохранения целого п о -и я т и я! Таким образом, сами понятия как концентрированное выражение симметрии существуют лишь постольку, поскольку существуют соответствующие регуляторы и системы автоматического управления и компенсации. По сути, они сохраняют наш язык, с помощью которого мы выражаем смысл всего сущего.
Точно так же дело обстоит и в самой реальности (в природе и обществе). Все, что мы в ней наблюдаем, т.е. все определенные структуры (дома, деревья, людей, моря, парламенты и т.д.) только потому и наблюдаемы, что они поддерживаются, предохраняются от разрушения (по крайней мере на каком-то интервале времени) посредством регуляторов, парирующих возмущения и отслеживающих цель.
В подразд. 1.15 будет рассмотрена общая схема такого подхода.
Для лучшего понимания связи калибровочных симметрий физики и управления полезно сделать следующее замечание. То, что в физике называют внутренними степенями свободы системы, с точки зрения теории управления — это внешние воздействия на систему, к которым, в частности, относятся и управления. И наоборот, то, что в кибернетике считается внешним воздействием (включая и управления) на систему, в физике можно естественно толковать как внутренние степени свободы системы. Таким образом, во избежание недоразумений надо иметь в виду, что здесь существует в определенном смысле “обратная” терминология между соответствующими понятиями физики и кибернетики.
1.15.	СОХРАНЕНИЕ СТРУКТУР
Одна из основных идей ЕГТУ—ТСУ состоит в том, что в ней рассматриваются идеальные математические структуры, которые по “закону 100%-эффективности математики” только приближенно описывают реальность. Но так как “ничто не вечно под Луной”, то даже если эти структуры существуют в реальности, то они подвергаются внешним воздействиям, которые сознательно или бессознательно пытаются их разрушить, дезорганизовать их правильную, идеальную работу. Значит, если мы наблюдаем эти структуры в реальности (описываем их, например, системами математических уравнений, тождеств, неравенств, включений) на каком-то заметном интервале времени, то они — эги структуры— должны как-то сохраняться (сохраняя определенную точность описания этой реальности). Калибровочный, или компенсирующий, принцип современной теоретической физики подсказывает, что средство, или метод, поддержания структур состоит в использовании обратной связи, т.е. должен работать регулятор, или система авто
78
матического регулирования (управления), по принципу обратной связи. Ганой регулятор должен “’наблюдать” рассогласования между реально наблюдаемыми (измеряемыми) величинами и требуемыми величинами. Далее регулятор должен сформировать “ошибки” регулирования, если говорить в терминах теории управления. Поскольку ошибки вызываются внешними возмущающими (разрушающими) воздействиями (или помехами), то желательно наблюдать помехи, ибо лучше нейтрализовать причину ошибок, чем ждать их заметного проявления, т.е. ждать, пока ошибка не достигнет значительной величины. В криминалистике это называется профилактика правонарушений. Здесь подходящее место сделать важное замечание, из которого следуют два принципа построения регуляторов. Первый и наиболее очевидный из них состоит в следующем.
Если мы наблюдаем (измеряем) возмущения (помехи), действующие на структуру, то регулирующие и поддерживающие структуру воздействия могут быть “быстро” вычислены, например, в силу знания уравнений, описывающих поддерживающую структуру. Таким образом, компенсирующее управляющее воздействие на структуру тем самым обеспечит компенсацию “помех”, и структура будет сохраняться, что и требуется. Это — обратная связь, но только по помехам. В теории управления такой способ называется регулирование по возмущению. Недостатки этого идеального способа регулирования, т.е. поддержания требуемой структуры, очевидны: надо довольно “много” знать, измерять и вычислять.
Но был найден принципиально другой способ компенсации помех. Он открыт в XIX в. Уаттом, который изобрел регулятор хода паровой машины. На наш взгляд, это — величайшее, эпохальное изобретение, обогатившее человечество не только мощнейшим практическим ускорителем цивилизации, но обогатившее и наши теоретические, философские воззрения. Глубина принципа обратной связи еще далеко не исчерпана. Суть этого принципа состоит в формировании обратной связи, или регулятора, по ошибке, по рассогласованию между требуемой и истинной структурами. Самое трудное здесь — это: 1) описать меру рассогласования в “пространстве структур” и 2) описать способ управления, минимизирующий меру рассогласования. Эта задача, пожалуй, самая фундаментальная задача кибернетики.
Очевидно, что могут быть комбинированные способы поддержания структуры и по наблюдению за помехами, и по наблюдению за ошибками. Таким образом, третий способ сохранения структур — это просто совместное и согласованное использование первого и второго способов (и по помехам, и по ошибкам вместе).
79
В связи со вторым способом регулирования (обратная связь по ошибке) сделаем, на наш взгляд, очень важное и принципиальное замечание. Оно связано с проблемой построения эффективных высококачественных регуляторов и систем автоматического регулирования почти для всех областей.
Непонимание, с нашей точки зрения, именно теоретической, т.е. математической, сути дела привело к нагромождению серьезных недоразумений, имевших драматические последствия. Здесь имеются в виду события, начавшиеся в 1939 г. и связанные с именем выдающегося инженера и ученого Г.В. Щипанова, который выдвинул принцип идеального регулирования и идеального регулятора обратной связи, использующего ошибку, т.е. расхождение между действительным и желаемым (заданным) значениями регулируемой величины. Дискуссия вокруг этого принципа длилась с переменной интенсивностью на протяжении нескольких десятилетий. Этому посвящено много литературы. Мы укажем только на [186, 187], где можно найти много других ссылок. Конечно, теперь, “задним числом”, можно сказать, что в конце 1930-х гг. теория управления только начала зарождаться. Теория “скользящих режимов” и “систем с переменной структурой” начала развиваться лишь в 1960-х гг.
Как выяснилось, идеи •систем с переменной структурой, скользящие режимы и большие коэффициенты усиления начали проливать свет на те принципы, которые предлагал Г.В. Щипанов. Этим можно объяснить и тот факт, что в конце 30-х гг. даже выдающиеся ученые и математики не смогли понять гениальную для того времени догадку Г.В. Щипанова [294, с. 90—96].
Тогда идея Г В. Щипанова представлялась парадоксальной и непонятной. Действительно, парадоксальность и непонятность состояли в том, что, по Щипанову, как это понимали и толковали тогда его критики, ошибка регулирования (обозначим ее Д) равнялась нулю тождественно! Иными словами, Д = 0, и саму ошибку Д понимали как классическую непрерывную функцию от непрерывного аргумента, роль которого играло время t, т.е. Л(Т) = 0, t > t0.
Именно “сигнал” Д = 0 воспринимал “наблюдатель” в виде регулятора (обратной связи), и на “его основе” (по этой “информации”) он должен был выработать свое управление, которое бы компенсировало произвольные, вовсе заранее не известные помехи, т.е. поддерживать “все время” Д(Т) = 0.
Возник совершенно законный вопрос: “Что же это за чудо (в прямом смысле)?” Действительно, регулятор независимо от вида помех поддерживает одну и ту же ошибку Д = 0. Раз ошибка одна и та же, т.е.
80
Л = 0, то регулятор, по крайней мере его вход, на который поступает ошибка Д, может быть вообще отключен от объекта. Таким образом, регулятор, не получая никакой (!) информации от объекта, вместе с тем идеально справляется со своей работой — идеально компенсирует любые помехи, которые пытаются расстроить работу объекта. Отсюда делался вывод: никаких идеальных регуляторов Щипанова существовать не может, они противоречат элементарному “здравому смыслу” — это идеализм, мистицизм и лженаука.
Все эти тривиальные соображения против идей Щипанова, для которых не было нужно даже никаких теорий и математики, были верны лишь при одном предположении, т.е. лишь при условии, что ошибка Д(/) — непрерывна и Д(0 = 0 при всех t > tQ.
Однако в то время никому не пришло в голову, что в принципе — или по крайней мере для широкого класса “случаев” — тождество Д(/) = О может пониматься лишь как некоторый предел, возможно, и не достижимый абсолютно точно, но достижимый приближенно и со сколь угодно высокой, но не 100%-й точностью.
Принцип Г.В. Щипанова можно коротко сформулировать так:
“Для любого е > О, любого момента времени /0 и любой структуры, т.е. объекта регулирования, говоря на языке теории управления, и при любых помехах, действующих на этот объект, существует (!) регулятор (обратная связь), наблюдающий ошибку Д(/), и такой, что |Д(/)| < е для любых t > 10".
Теперь можно сформулировать “образный” ответ критикам Щипанова тех времен и сказать им через несколько десятилетий: “Вы не правы, ибо на самом деле вместо идеального нуля ошибки Д, который вы имели в виду, критикуя Щипанова, на самом деле имеет место “шероховатый нуль” ошибки Д, который в действительности есть предел и в этом смысле'идеальный, абстрактный математический объект, который образно можно себе представить как “пилу”, которая на каждом сколь угодно малом участке своей длины имеет бесконечное число зубцов, каждый из которых имеет бесконечно малую высоту”.
Таким образом, ненулевая ошибка регулирования почти всегда есть, но она “очень” маленькая, исчезающе маленькая. Именно она несет информацию, столь необходимую для работы всей системы поддержания структуры в целом. Последнее обстоятельство — малость ошибки — влечет за собой необходимость иметь в регуляторе усилители с очень большими коэффициентами усиления, в пределе бесконечно большие.
Реальный усилитель всегда имеет ограничение. В теории эти ограничения стали моделировать с помощью идеального релейного эле
81
мента, который имеет бесконечно большой коэффициент усиления, но в бесконечно малой окрестности точки переключения. “Шероховатый нуль” заставляет это реле очень часто срабатывать, в пределе частота его переключений, оно работает в “вибрационном режиме” (“chattering regime”), а регулятор работает в “скользящем режиме” (“sliding regime”).
Наличие большого коэффициента усиления порождает другую фундаментальную проблему — проблему устойчивости.
Из теории линейных конечномерных и сосредоточенных систем известно, что при достаточно больших коэффициентах усиления система, как правило, теряет устойчивость, становится неработоспособной, и, как следствие этого, соответствующая структура разрушается. Синтезировать систему на “скользящем” режиме дело не простое и требует большого искусства в смысле нахождения компромисса между противоречивыми требованиями высокой точности и высокой степени устойчивости. Кроме того, структура может содержать “малые параметры”, учесть которые очень трудно. Для систем с распределенными параметрами, включая поля и сплошные среды, эта проблема представляет собой очень трудную математическую и инженерную проблему.
До сих пор теория таких режимов достигла заметных успехов только для тех объектов, которые достаточно точно аппроксимируются линейными сосредоточенными объектами невысокого порядка.
Однако многие важные процессы технологии (плазма, композиты и др.) требуют создания распределенных регуляторов, которые поддерживают, сохраняют не одну или несколько скалярных величин, а распределения, т.е. функции (отображения), которые в большинстве случаев и описывают достаточно точно структуры, нуждающиеся в сохранении.
По аналогии со сосредоточенными системами здесь прежде всего нужно понять, что такое “шероховатая поверхность” или вообще “шероховатая фигура” размерности п > 1, и лишь затем приступать к синтезу “пространственно многомерного распределенного скользящего режима”, обеспечивающего достаточно высокую точность. При этом регулятор, обеспечивающий “пространственно распределенный скользящий режим” должен еще обеспечивать и устойчивость всей системы в целом.
На сегодня нет такой теории систем с распределенными параметрами, которая бы имела достаточно хорошо разработанные методы построения таких регуляторов, — это крайне трудные математические задачи, которые подчас даже трудно поставить, не говоря об их решении.
Для сосредоточенных систем эти принципы декомпозиции реализуются, например, в задачах каскадного регулирования, когда в слож
82
ном объекте “локальные” регуляторы поддерживают некоторые “локальные” (внутренние, промежуточные) величины, тем самым существенно уменьшая их вредное, разрушающее воздействие на главные регулируемые величины, что облегчает работу главного регулятора. Для этого все такие “локальные регуляторы” должны работать очень быстро, их время регулирования должно быть на порядки меньше времен, допустимых для регуляторов более “глобального” уровня. “Большая” система регулирования должна как бы “расслаиваться” на локальные системы регулирования Поэтому для современной теории управления столь важен математический аппарат современной геометрии — аппарат теории расслоений. Локальные регуляторы можно толковать как регуляторы, служащие для обеспечения “локальной калибровочной инвариантности”, или “локальной компенсации” возмущений. Роль такого реализатора расслоений (декомпозиции) может играть подвижное управление как в системах со сосредоточенными, так и распределенными параметрами. Другими словами, подвижное управление именно за счет своей подвижности может оказывать регулирующие воздействия локально, независимо от других точек.
В теории управления “многосвязными” системами [214] такой прием назывался развязыванием сложной многосвязной системы и состоял в “фиксации” некоторой части или даже всех переменных, от которых зависят ошибки регулирования. Это обозначалось х, = const = inv. Их фиксация должна достигаться за счет работы локальных регуляторов.
Здесь уместно снова напомнить в несколько более развернутом виде об “Управленческой парадигме Мира”.
Она состоит в том, что всякая, без исключений, наблюдаемая в Мире (природе или обществе) структура существует, проявляется и функционирует (в виде закона природы или общества) лишь пока и поскольку она устойчиво поддерживается на определенном интервале времени посредством одного или нескольких регуляторов, сосредоточенных или распределенных. При этом наблюдаемые в Мире (живой, неживой, искусственной природе или обществе) флуктуации всех без исключения наблюдаемых величин (например, необязательно физических) есть ничто иное, как ошибки регулирования этих систем управления, которые используются регулятором обратной связи для выработки управляющих воздействий, поддерживающих структуры объекта регулирования.
Таким образом, возникает нетрадиционная, “управленческая” точка зрения на устройство Мира, которая прежде всего поражает нас своей определенностью (например, существованием “Законов Природы”) и устойчивостью этих определенностей, хотя всегда имеются некоторые
83
флуктуации. Во истину, порядок надо не наводить, а поддерживать так, как это делается в Природе.
За определенность в Природе побеспокоилась сама Природа, она сама создала регуляторы, обеспечивающие поддержание ее Законов.
За определенность в человеческом обществе должны беспокоиться сами люди. Если люди сочли нужным создать те или иные структуры своего общества, то они должны побеспокоиться и о создании надежных регуляторов, работающих на принципах регулирования по возмущению и по “ошибке” регулирования, которые будут поддерживать нужные людям структуры.
Опыт показывает, например, что силовые структуры, действующие по принципу наказания или штрафа за нарушение законов общества, работают ненадежно. Более эффективный способ состоит в воспитании с раннего детства членов общества в духе следования Заповедям Божьим, которых не так много и которые, по сути, разделяются всеми религиями.
1.16.	ВАКУУМ И ТВОРЧЕСТВО
Традиционно под понятием вакуум понималась абсолютная пустота.
Если убрать все известные и даже неизвестные нам частицы и поля (электромагнитное, гравитацию), тогда останется то, что и есть абсолютный вакуум, абсолютная пустота. Однако недавно в физике были выдвинуты очень неожиданные теории, по которым из того, что мы классически называли вакуумом, или абсолютным ничто, может рождаться нечто, и весьма ощутимое, реальное и наблюдаемое, дальнейшее развитие которого ведет к образованию элементарных частиц вплоть до всей нашей Вселенной со звездами, планетами и всеми нами. Возникла языковая дилемма’. 1) нечто материальное может рождаться из пустоты или 2) вакуум на самом деле не пуст, хотя там нет того, что мы до сих пор явно наблюдали (частицы, поля). Но вместо явно ощущаемого там есть что-то другое, чего мы никогда прежде не ощущали. Однако стоит только подобрать какие-то “воздействия” и условия наблюдения, как прежде не ощущаемое проявит себя вполне ощутимо. Вакуум начнет порождать субстанции, которые уже были ранее нам знакомы: частицы и поля. Мы не знали об этом замечательном свойстве “пустоты”: она ассоциировалась с бесплотным духом. Но с ростом энергий воздействия и развитием средств наблюдения выяснилось, что этот “дух” может материализоваться! Когда же был превзойден некоторый порог по энергиям и средствам наблюдения, то открытия посыпались как из рога изобилия.
Вакуум — это вместилище всех возможностей (потенциальностей). (ср.: душа — это вместилище духа.) Явление превращения воз
84
можности (потенциальности) в действительность (актуальность) назовем явлением детривиализсщии, а обратное превращение — тривиали-зацией. Детривиализацию можно назвать взрывом вакуума. В физике сейчас обсуждается и разрабатывается взрывная теория рождения нашей Вселенной “Big Bang”.
Трудно переоценить идею Дирака, работавшего над созданием общей теории поля, который смело истолковал математические уравнения (тождества), выглядевшие парадоксально, как заполнение вакуума возможными частицами (электронами и позитронами). Эта возможность — детривиализация вакуума— вскоре блестяще реализовалась в виде электронно-позитронных пар, что дало указание на то, что вакуум имеет свою нетривиальную структуру.
Чтобы описать эту опытно наблюдаемую реальность, теоретики придумали новые, ранее не виданные в теории и практике поля, которые не соответствуют никаким ранее знакомым элементарным частицам, электромагнетизму, гравитации. Эти поля, которые назвали вакуумными, описывают вакуум с его удивительными свойствами. Возникает вопрос: “Считать ли эти поля придуманными (т.е. нереальными) или считать, что они и есть сама реальность, т.е. “то, что описывает реальность, и есть сама реальность”, т.е. сделать такое отождествление?” Об этом можно спорить, но практически этот спор чисто риторический, толковательный, имеющий скорее философское, чем практическое значение. Вакуум — это вместилище и источник всех возможностей, это потенциал всех идей, структур, отношений.
Творчество — это выбор из вакуума, из множества всех возможностей, т.е. актуализация потенциала, превращение возможностей в действительность путем управления. Дело в том, что понятие управление мы будем отождествлять с понятием выбора.
Таким образом, теперь можно не говорить, что “нечто появилось из ничего”, так как это будет только порождать недоразумения, например, типа “я добыл деньги из ничего”, такого действительно, по-видимому, не бывает. Так что имеет смысл утверждать, что “из ничего — ничего не получится”. Для того чтобы что-то получилось, все-таки всегда надо иметь нечто\ Этим нечто для вакуума, пустоты и являются реальности, описанные нетривиальными вакуумными полями, которые показывают, что вакуум хотя и пуст от частиц и тех полей, которые нам привычны, все-таки имеет доселе нам неведомую и своеобразную (и в этом смысле реальную!) структуру, т.е. симметрию. А рождение из вакуума знакомых или незнакомых нам вещей в виде частиц и полей есть следствие нарушения этой симметрии под действием подходящих управляющих воздействий.
Такой подход к понятию вакуума привел к его новому, более содержательному определению, которое точнее соответствует той реальности. которую мы действительно наблюдаем на опыте.
Теперь вместо одного абсолютного вакуума, в котором отсутствует абсолютно все, говорят об относительном вакууме, в смысле отсутствия чего-то конкретного. Например, нет денег в кармане, нет совести у некоторых людей и т.д. Однако нет никаких логических препятствий предположить, что если отсутствует что-то нам знакомое, возможно, там присутствует то, что нам было незнакомо до сих пор. Действительно, нередко это нечто, ранее нам совершенно незнакомое и которое мы считали совсем не существующим, оказывается, существует и даже начинает поставлять очень реальные и привычные для нас вещи (в том числе и деньги, и совесть, и многое другое).
Итак, вакуум — конкретен, это полное абсолютное отсутствие, но чего-то конкретного.
Вакуум — это пространство еще не открытых структур (симметрий), имеющих, возможно, в качестве величин, их характеризующих, совсем другие величины, непохожие на наши привычные, скажем, такие, как масса и заряд, пространство—время и др. Не исключено, что существуют физические реальности, другие Вселенные, физика которых совсем не похожа на физику нашего мира и о которых мы даже не подозреваем. Невольно вспоминается Шекспир:
На свете много есть такого, друг Гораций, О чем не помышляют наши мудрецы.
Неотъемлемым атрибутом постиндустриальной эпохи является компьютер. Его можно рассматривать как конструктора абстрактных структур и виртуальных пространств со своими собственными симметриями (движениями). Типичным примером необычных пространств со своими законами, часто совершенно не похожими на законы нашего физического или социального мира, являются компьютерные игры и различного рода анимации.
Чтобы избежать несколько шокирующих высказываний типа “нечто возникает из ничего, из пустоты”, что по недоразумению может быть истолковано как мистика, мистификация, чудо в самом худшем смысле этого слова, можно стать на другую точку зрения, более материалистическую. А именно, будем считать, что никакой пустоты, вакуума на самом деле нет. То, что мы понимаем под вакуумом и неправильно назвали пустотой, на самом деле как раз наоборот: это склад, набитый необозримым и невообразимым количеством самых разнообразных реальностей, которые, однако, нами не наблюдаются из-за отсутствия соответствующих условий. Однако если создать “соответствующие” ус
86
ловия, например, физическими средствами и трудом мозга, то ранее неощутимые фантомы получают совершенно ощутимые материальные воплощения в виде очень конкретных вещей, явлений, процессов. Все дело в создании надлежащих условий научного наблюдения.
В заключение сделаем о вакууме одно замечание, касающееся следующей аналогии. Дело в том, что детривиапизацию физического вакуума, пустоты, из которого рождаются, скажем, элементарные частицы под действием сильных энергетических воздействий или спонтанно, можно сравнить с возникновением идей в головном мозге человека под действием или в результате некоторой и часто очень напряженной работы головного мозга; при этом суть творческого процесса, на наш взгляд, можно представить себе как некоторую последовательность вопросов и ответов: ?! ?! ... ?! ... ! Аналогом подходящего воздействия на физический вакуум в мыслительном процессе является поиск подходящего вопроса. Недаром говорят, что хорошо поставленный вопрос или задача содержит 50% правильного ответа или решения.
Точно так же, как наша Вселенная родилась в результате “Большого взрыва” вакуума, возможно, порождаются идеи и мысли. Они возникают в результате детривиализации, в результате некоторого “взрыва” в мозгу человека. Суть “Большого взрыва” — это детривиализаг^ия вакуума материи и идей (мыслей), это — нарушение симметрии, в результате чего структуры становятся наблюдаемыми.
Всякая правильно поставленная задача имеет две структуры: условий задачи и возможных ответов к этой задаче. Решение состоит в том, чтобы выяснить, согласованы (совместны) ли эти структуры друг с другом. Если структуры несовместны, то мы говорим, что задача не имеет решения или даже не имеет смысла.
В противном случае, т.е. когда эти структуры согласованы (совместимы), мы говорим, что решение задачи существует. В последнем случае имеет смысл говорить о поиске этих решений. Решением задачи будет то и только то движение, которое является движением для обеих структур вместе, т.е. их общее движение. Исчерпывающее описание пространства общих движений и будет полным решением задачи.
1.17.	ТОЧКА ЗРЕНИЯ НА "ЗАКОНЫ ПРИРОДЫ"
Здесь речь пойдет о законах в самом широком смысле, т.е. о любых законах всего сущего, включая и законы природы (живой и неживой), и о всякого рода социальных законах (юридических, моральных, этических, экономических и т.д.) человеческих сообществ (скажем, от семьи до государства).
87
Законом называется всякое равенство (называемое уравнением закона), для которого значение каждой входящей в него величины (понятия) может быть измерено (определено) совместно и независимо, каким-нибудь способом или способами, причем подстановка этих значений в уравнение закона превращает это уравнение в верное равенство; иными словами, уравнение закона есть не что иное, как тождество, определенное и верное для любой совокупности всех совместно и независимо измеренных (определенных) значений, входящих в уравнение величин (понятий), например, таковым является закон Ньютона: F = та.
Здесь слово совместно выражает совокупность условий, зафиксированных в каком-нибудь тексте описания условий наблюдения данного явления и измерения (определения) полного набора величин (понятий), входящих в уравнение закона (т.е. в том числе описание способов и принципов измерения теми или иными реальными средствами).
Важность и практичность законов состоят в том, что знание этих законов, т.е. их уравнений, позволяет уменьшить число измеряемых величин, которые мы вынуждены измерять (непосредственно на опыте, в реальности, приборами); при этом остальные величины вычисляются с помощью уравнений закона (“по формулам”). Таким образом, законы позволяют измерения заменить вычислениями (по определенным правилам, алгоритмам, программам), которые можно автоматизировать.
В каком смысле можно управлять законами? Управлять законом — эго значит устанавливать закон произвольно, возможно из какого-то определенного класса законов.
Для реального установления закона необходимо создать (или уже иметь, как мы наблюдаем в природе, а иногда и в обществе) системы управления или регуляторы, обеспечивающие поддержание этого закона. При этом назначение регулятора состоит в отслеживании этой уставки. Роль таких регуляторов в природе играют силовые поля (гравитация, электромагнетизм, слабое и сильное взаимодействие). В обще-, стве эту роль играют так называемые силовые структуры разного у ровня (в государстве — это полиция, армия, разведка, в семье — это носители и хранители традиций, скажем, представители старшего поколения: бабушки, дедушки, отцы, матери, другие родственники и члены семейства или общины).
Конечно, установить “по своей воле” какой-то новый закон в природе или обществе — дело не простое, так как, во-первых, надо разработать принциП-регулятора, обеспечивающего сохранение этого закона (его устойчивость, быстродействие, качество регулирования, адаптацию и т.д.), а во-вторых, надо реально его построить и наладить в реальных условиях (например, в обстановке “тяжелых окружающих условий”, активных помех, противодействия и т.д.).
88
Таким образом, для преодоления вышеуказанных трудностей реализации “установление новых законов” требует от сообщества больших научных знаний, творческих способностей, экономических и технических, организационных (властных) возможностей и политической воли.
Итак, в принципе можно установить любой закон в любой реальности, а метод, с помощью которого это можно сделать, — это метод управления, создания регуляторов обратной связи, работающих на принципе компенсации, создания компенсационных полей, обеспечивающих требуемую инвариантность (симметрию).
С этой точки зрения, например, летящий самолет — это распределенный регулятор, одно из предназначений которого состоит в том, чтобы компенсировать поле силы тяжести, не считая компенсации других возмущений. Именно в этом смысле мы понимаем слово устраняет, когда говорим, что летящий самолет, т.е. соответствующий распределенный регулятор, устраняет поле тяжести и тем самым делает эффективной работу полей управления, в результате чего самолет может двигаться по любому (из определенного класса) требуемому закону. Например, его центр тяжести движется вдоль желаемой траектории, которая является “уставкой”, или “заданием”, для “летящей” системы управления. Проблему создания такого сорта распределенных регуляторов можно назвать проблемой построения активных сплошных сред с заданными характеристиками.
Конечно, когда в Природе или обществе создается новая структура, а вместе с ней и регулятор обратной связи, поддерживающий эту структуру, то нужно очень серьезно позаботиться о совместимости этой новой структуры с другими существующими структурами. Дело в том, что работа систем регулирования, поддерживающих другие структуры, будет создавать возмущения, помехи для работы системы, поддерживающей вновь созданную структуру. Поэтому новая система управления должна обладать достаточной степенью устойчивости, чтобы успевать отфильтровывать “вредные” возмущения на ее входе, идущие от других структур, и вместе с этим отслеживать задания с заданной степенью точности, т.е. чтобы флуктуация ошибки была достаточно мала.
Эти процессы управления и есть “борьба за существование” вновь образованной структуры.
С другой стороны, вновь созданная структура, находясь в борьбе за свое существование, создает для других существующих структур опасные для них помехи и возмущения. Может оказаться, что помехи и возмущения от новой структуры могут частично или полностью разрушать старые структуры. Такое явление особенно опасно в человече
89
ском обществе, ибо структуры, подвергшиеся деградации в результате действия новых структур, могут оказаться жизненно важными для человека. Вывод отсюда состоит в том, что при создании любых новых структур надо быть очень осторожным, тщательно, а главное, всесторонне продумывать и предсказывать все негативные, как в медицине говорят, побочные действия вновь создаваемых структур.
1.18.	СТРУКТУРИРОВАННАЯ ЭНЦИКЛОПЕДИЯ
Идею и методологию структурированной энциклопедии (СЭ) попытаемся описать на примере математики. По-видимому, математика единственная из всех наук представляет собой наиболее структурированную науку. Да и сама математика определяется нами как наука о структурах и их симметриях. Конечно, СЭ могут и должны создаваться и для других отраслей.
Перечислим ее основные характерные черты.
1.	Наибольшая эффективность СЭ должна достигаться при высоком уровне автоматизации при ее использовании для широкого круга пользователей. Сегодня высокий уровень этой автоматизации может быть достигнут на базе интерактивных гипертекстовых компьютерных средств и сред, в которые СЭ должна быть помещена.
2.	СЭ может иметь несколько концентров, уровней и объемов того или иного раздела. Она может быть ориентирована на разные группы пользователей. Можно выделить три их большие группы: 1) школьники, студенты, любители; 2) аспиранты, преподаватели, специалисты различных отраслей знаний; 3) профессионалы.
3.	СЭ может быть использована для различных целей: 1) как справочник; 2) как учебник, задачник, учебное пособие; 3) как источник получения детальных или беглых представлений о тех или иных, больших или меньших разделах и понятиях.
4.	СЭ должна обладать способностью быть легко перестраиваемой ' и корректируемой, представлять собой живой и развивающийся организм. Эта способность может обеспечиваться самим принципом построения СЭ, а именно, блочно-структурным принципом (БСП), который дает возможность корректировать вплоть до полной смены содержание любого блока СЭ и связи между разными блоками СЭ.
5.	Поскольку, например, математика изучает структуры, то в основе СЭ математики лежат блоки, соответствующие тем или иным математическим структурам (отношениям, пространствам, системам, моделям). Среди них должны быть выделены блоки, соответствующие “элементарным” математическим структурам (простейшим, основным, исходным, например полугруппа, метрическое пространство, отноше
90
ние порядка, отношение эквивалентности и др.). Другие блоки соответствуют “сложным” математическим структурам, получающимся “комбинациями” элементарных структур, сначала бинарным, потом тернарным и другим с указаниями способа их согласования (взаимодействия). При этом под элементарным блоком можно понимать не только простейший (далее неделимый), но и любой другой блок, структура которого достаточно хорошо изучена.
6.	При изучении каждого блока, соответствующего некоторой простой или сложной структуре, большое внимание должно уделяться симметриям данной структуры, т.е. ее преобразованиям и отображениям, которые что-то в этой структуре сохраняют. Другими словами, внимание уделяется проблеме инвариантности данной структуры под действием тех или иных возмущений.
7.	В СЭ математики может быть полезен аксиоматический метод построения и изложения математических теорий и дисциплин с определенным (возможно, разным для разных групп пользователей) уровнем строгости формулировок и доказательств в соответствии с уровнем требований той или иной категории пользователей — от школьников и любителей до профессионалов.
8.	В СЭ математики при изложении той или иной дисциплины или описании математической структуры используются “неделимые единицы знаний” или, по-другому, атомы, гранулы знаний, информации, данных.
Их небольшое количество. Это аксиомы, определения, теоремы и их доказательства. Из этого набора “атомов”, логически между собой взаимосвязанных, например, в виде графа логических связей, создается канонический остов, или скелет, любой дисциплины или теории. Он составляет “суть дела”, но не может служить привлекательной базой для широкого круга пользователей из-за его “сухости”.
“Канонический скелет” дисциплины или теории должен сопровождаться целым набором атрибутов для его оживления. Перечислим некоторые. Прежде всего, это:
конкретные примеры различного уровня, что составляет “душу” того или иного вопроса и результата;
контрпримеры — экзотические, неожиданные, неочевидные, показывающие особенности и “подводные камни”, предупреждающие о возможных недоразумениях и ошибках;
упражнения, позволяющие уяснить суть общих формулировок;
задачи (разного уровня сложности), позволяющие понять суть дела и овладеть результатами теории, чтобы далее их применять;
проблемные задачи, решение которых позволяет развивать данную теорию;
91
формальные замечания',
мотивация, неформальные комментарии к тому или иному “атому” информации, в частности, с указанием связей с другими математическими дисциплинами, а также возможностей и примеров применения данного результата в других разделах данной науки или других науках;
перспективные и исторические обзоры, справки, методологические замечания и другие приложения, например, графические, вычислительные, алгоритмические и программно-компьютерные средства, библиография;
литературные ссылки с комментариями, именные и предметные
указатели простых и сложных терминов.
Рис. 1.18.1
Все это может и должно в любой мере сопровождать каждый формальный элемент, например аксиому, определение, теорему, доказательство.
Этим обеспечивается оптимальное сочетание формальной строгости и точности с неформальным содержанием, включая “популярные” объяснения.
Подчеркнем, что смысл СЭ состоит именно в четкой структуризации знаний, представляемых отдельными структурами (блоками). Структуры (блоки) могут быть простыми и сложными. При описании сложного блока надо: 1) четко перечислить все более простые структуры, составляющие его описание и 2) четко описать способы взаимодействия всех простых составляющих.
Что касается программно-компьютерного обеспечения, реализующего создание СЭ, то здесь можно использовать большие достижения в построении реляционных баз данных. На рис. 1.18.1—1.18.12 приведены блок-схемы, довольно укрупненно показывающие основные структуры, включая арифметику, логику, алгебру, геометрию, анализ и математическую (теоретическую) физику.
92
Р и с. 1.18.2
93
Р и с. 1.18.3
94
Основные числовые множества
В = {0, 1} — Булево числовое множество
N = {1,2, 3,. . .} — множество всех натуральных чисел
N = {0, 1,2, 3,. ..} — множество всех натуральных чисел с нулем
Z = {о,± 1,± 2,± 3,...} — множество всех целых чисел
<Q = < — : т g Z, п g Z, п * ОУ — множество всех рациональных чисел Iп	J
[R = {lim q : <7 g q} — множество всех действительных (вещественных) чисел
С = {а + ib : a g R, b g [R, Z2 = -1} — множество всех комплексных чисел, i — число, называемое мнимой единицей (НС — гиперкомплексные числа
Просгранства.нрямоугольных матриц с числовыми элементами
Пространства Бэра — множество всех последовательностей натуральных чисел
Аксиоматики арифметики (Пеано и фон Неймана)
Арифметические структуры (пространства)
Теория чисел
Комбинаторная теория чисел
Аналитическая теория чисел
Теория диофантовых уравнений и диофантовых приближений
Рис. 1.18.4
95
Теоретико-множественные пространства (структуры)
Рис. 1.18.5
96
Алгебраические пространства
4. А.В. Бабичев
97
Р и с. 1.18.6
Некоторые разновидности топологических структур
Топологические пространства (топологии)
Т3-пространства (топология с третьей аксиомой отдельности)
Топология со счетной базой (со второй аксиомой счетности)
Регулярные топологические пространства, т.е. (Ti + Т3)-пространства
Сепарабельные топологические пространства
Т4-пространства (нормальные топологические пространства)
Топология с первой аксиомой счетности
Tp-пространства (вполне регулярные топологические пространства или Тихоновские пространства)
Связные топологические пространства
Компактные (топологические) пространства
Ti-пространства (топология с первой аксиомой отдельности
Счетно-компактные (топологические) пространства
Т2-пространства (топология со второй аксиомой отдельности —-Хаусдорфовы пространства)
Рис. 1.18.7
98
Пространства с геометрическими структурами
Алгебраическая топология
Теория гомологий
Теория гомотопий
Теория узлов
Теория кос
Теория размерности
Комбинаторная топология
Функциональные пространства ("элементы" основного множества-функции)
Теория отображений К" в Кп Предел, последовательности, ряды, дифференциальное и интегральное исчисления
Теория неявных функций и принцип сжимающих отображений. Функциональные уравнения
Теория отображений С"1 в Сп Предел, последовательности ряды, дифференциальное и интегральное исчисления.
Теория аналитических функций и конформных отображений
Гильбертовы пространства
Банаховы пространства
Другие функциональные пространства
Теория Фредгольма-—Гильберта интегральных уравнений
Теория обобщенных функций
Теория функциональных операторов. Линейные операторы, их спектральная теория
Теория интегрирования в функциональных пространствах.
Интеграл Фейнмана
Рис. 1.18.8
4*
99
Дифференциальные пространства
Многообразия с метрикой (Римана, Финслера, Рашевского)
Стра гифицированные многообразия
Дифференциальные уравнения (обыкновенные и с частными производными),
Пфаффовы уравнения
Дифференциальные уравнения с отклоняющимися аргументами (запаздывание, опережение, смешанные)
Тензорные поля.
Теория интегрирования и интегрируемости дифференциальных форм, уравнений и включений
Теория фазового портрета дифференциальных включений (управляемых дифференциальных систем (УДС))
Теория малого параметра и ассимптотические методы
Вариационное исчисление, оптимальное управление, теория игр
Метод разделения переменных, метод характеристик
Интегральные преобразования и передаточные функции
Метод блочно-структурных схем для представления систем инте! ро-дифференциальиых уравнений
Компенсационный метод решения краевых задач
Рис. 1.18.9
100
Некоторые основные математические структуры физических и других наук
КЛАССИЧЕСКАЯ МЕХАНИКА И ФИЗИКА
Механика Ньютона		Механика Лагранжа
		
Механика специальной		
теории относительности		
Механика Гамильтона (симплекгаческие структуры)
Геометрическая оптика Гюйгенса и Ферма
Термодинамика; равновесная, неравновесная, открытых систем
ПОЛЯ И СПЛОШНЫЕ СРЕДЫ
Электродинамика Максвелла
Диффузия тепла и массы
Гидро-, газодинамика, акустика
Упругость и пластичность тел, оболочек и конструкций
Реология
Сплошные среды	Теория волн и колебаний		Теория кристаллических решеток и дислокаций
Теория композитных сред
Теория плазмы (горячей и холодной)		Теория гравитации, общая теория относительности		Теория потенциала
Теория подобия и физического моделирования
ВАРИАЦИОННЫЕ ПРИНЦИПЫ
Принцип наименьшего действия
Энтропийные экстремальные принципы
Общее вариационное уравнение Эйлера—Лагранжа. Уравнение Янга—Миллса.Теория расслоений
Принципы сохранения
Теорема Л иувилля
Теорема Нетер
Общая теория тензорных и спинорных субстанций (нел инейных, неодпороди ых, неизотропных полей и сред пассивных и активных)
Аппроксимирующие структуры, в том числе для вычислений.
Прямые вариационные методы, метод конечных разностей, метод конечных элементов
Метод блочно-структурных схем (диаграмм) на основе операций композиции
Р и с. 1.18.10
101
I
Максвелла
Статистическая физика
КВАНТОВЫЕ СИСТЕМЫ
.......1______
Ферми—Дирака
Уравнения Шредингера
Уравнения Гейзенберга
Квантовые уравнения Лиувилля
Фейнмановский интеграл для амплитуд перехода
Теория
У-матрицы
Уравнения смешанных состояний
Теория соответствия Я(х,р)оЯ(х,^) ох . 5 р <=> i— дх
Фейнмановские диаграммы для описания взаимодействий
Теория четырех фундаментальных взаимодействий (сил)
Электромагнитное
Гравитационное
Сильное Слабое
Объединяющие теории
Теория электрослабого взаимодействия
Теория сильного взаимодействия
Теория великого объединения: электро-слабо-сильное
Теория супервеликого объединения всех взаимодействий: __________________теория суперструн__________________
Проблема объединения: Единая теория = квантовая теория поля + + общая теория относительности, единая квантовая статистика
Руководящие принципы: локальная калибровочная симметрия и спонтанное нарушение симметрии (группы Ли)
Перспективы отказа от причинности и непрерывности
"Симметрия перестает быть лишь эстетическим достоинством конкретной модели и становится ее наиболее великой чертой" (М. Каку. "Введение в теорию суперструн". М., Мир. 1999. С. 17 )
Рис. 1.18.11
102
Некоторые структуры управления
Рис. 1.18.12
1.19. СТРУКТУРЫ И ОБУЧАЮЩИЕ СРЕДЫ
Всякое теоретическое исследование связано с построением набора наиболее простых абстрактных структур, в терминах которых можно детально изучить рассматриваемое явление или вопрос. Эти структуры должны обеспечивать значительную “экономию мышления” и позволять тем самым наиболее просто исследовать рассматриваемый вопрос. Как правило, формирование таких структур в сознании отдельного человека или, скажем, научного сообщества связано с длительным рациональным анализом, часто требующим отказа от привычных представлений и понятий. Ситуация выглядит несколько парадоксально — наиболее простые для наблюдения и запоминания явления, например привычные события повседневной жизни, имеют очень сложную структуру, а простейшие абстрактные структуры, например математические, оказываются практически ненаблюдаемыми, и для их уяснения и запоминания требуется специально организованный процесс обучения. С учетом того выросшего количества информации и знаний, которыми должен владеть современный человек, становится актуальной задача разработки специальных систем обучения [513, 515, 517, 528, 530]. Эти системы должны быть основаны на современных педагогических методах, обеспечивающих глубокое и быстрое освоение фундаментальных принципов науки и различных аспектов применения их на практике, поддерживать методическими и техническими средствами обмен огромными массивами информации между различными пользователями системы, обеспечивать возможность как технической, так и
юз
информационной модернизации. Более того, весьма желательным свойством систем такого рода является возможность обучения на различных квалификационных уровнях людей разных возрастов и находящихся территориально в различных местах, т.е. фактически обучать человека на протяжении всей его жизни.
Интенсивное развитие информационных технологий, в первую очередь телекоммуникационных, увеличение мощности персональных компьютеров, повсеместное распространение сети “Интернет” и “Мировой Паутины” указывают на определенные тенденции в разработке обучающих систем. Важнейшей из них является согласование всех возможностей сетевого обмена информацией с современными педагогическими принципами построения процесса обучения. Эта тенденция естественным образом выражается в использовании гиперпространства и конструировании мультимедийных обучающих сред, обладающих специально разработанной архитектурой, которая позволяет использовать предварительно структурированные базовые знания для создания на их основе и проведения различных по тематике, новизне и сложности учебных курсов. Она открывает доступ к курсам и возможность интерактивного взаимодействия с различными пользователями в сети, позволяет модернизировать как базу знаний, так и прикладную ориентацию курсов в соответствии с новыми задачами мирового уровня.
Из сказанного следует, что проблемы разработки структурной теории по фундаментальным направлениям научного знания, в том числе математики, кибернетики, теории управления, имеют непосредственное практическое значение с точки зрения построения эффективных обучающих систем. Ряд таких примеров демонстрируют работы по созданию гипермедийных обучающих систем в области общезначимых студенческих курсов по математике [515, 516, 529]. Хотя здесь и имеются определенные успехи, однако развитие структурных методов представления даже “студенческой” математики еще весьма далеко от завершения. Например, в такой области, как теория управления системами с распределенными параметрами, несмотря на большой научный, педагогический и практический опыт авторов [38, 44, 48, 51, 402, 406, 411, 417, 508—512, 514], можно говорить только о первых шагах, сделанных в направлении структуризации информации и разработки баз знаний [367].
Остановимся подробнее на основных моментах, характеризующих гипермедийную систему открытого обучения. С точки зрения педагогических принципов, реализуемых в этой системе, важнейшими из них являются принципы, представленные в [477], а именно:
104
конструктивность — учащиеся конструируют новое знание на основе ранее полученных знаний совместно с другими участниками процесса обучения;
ответственность — учащиеся должны быть включены в интеллектуальную обработку информации и должны разделять ответственность за конечный результат;
сотрудничество — учащиеся должны быть способны работать совместно над созданием новых знаний и уметь использовать знания и навыки друг друга;
целеустремленность — учащиеся должны быть обеспечены таким материалом, который помог бы им охотно и активно достигать целей, ставящихся в процессе обучения, грамотно осуществлять поиск на правильно поставленные вопросы, уметь ставить такие вопросы, ибо это важнейший элемент любого творчества;
конкретность — изучаемые вопросы должны быть обусловлены значимыми проблемами реального мира теоретического или практического характера и вводиться на основе примеров из реальной жизни, чтобы облегчить их понимание и поддержать осмысленное изучение;
переносимость — учащиеся должны быть способны переносить знания из ситуаций и контекстов, в которых происходило обучение, в другие ситуации и уметь использовать свои знания;
рефлексивность — учащиеся должны уметь внятно излагать то, что они уже изучили, и размышлять над изучаемыми процессами и теми решениями, которые они должны принимать, владеть предметными языками науки.
В системе открытого обучения эти принципы реализуются как интерактивные, взаимосвязанные и согласованные подсистемы всей системы в целом, что обеспечивается архитектурой системы.
Для обеспечения конструктивности система открытого обучения содержит когнитивный инструментарий, который студенты могут использовать в процессе обучения. Этот инструментарий зависит от изучаемого курса и представляет собой, например, калькуляторы, средства для решения задач, связи с приложениями Matlab и Maple, имитационные программные средства или средства навигации. Материал курса имеет структуру топиков, так что учащиеся могут видеть, как соотносятся между собой различные понятия. Студенты сами могут решать, где им следует начинать и как далее продвигаться в процессе их обучения. Они также могут составлять записи, чтобы видеть, каким путем продвигались в процессе обучения. Помимо когнитивного инструментария, система открытого обучение включает инструменты авторинга. Сетевые инструменты разработаны для всех участников создания учебных курсов — от профессоров до ассистентов, чтобы помочь им в подготовке учебных материалов и, таким образом, в построении знания.
105
Инструменты авторинга и навигации в системе открытого обучения поддерживают не только конструктивность, но и активность обучения. В этой системе учащимся отведена активная роль в построении новых знаний на основе ранее полученных. Учащиеся отвечают как за процесс своего обучения в целом, так и за его конечный результат. Студенты строят свои знания во взаимодействии со всеми остальными участниками данного курса. При этом материалы курса могут содержать, например, вопросы, задаваемые и проверяемые компьютером с целью перманентной проверки правильности и результативности обучения.
Учащийся посредством коммуникационной системы может связываться с другими участниками курса и заинтересованными лицами, в том числе преподавателями, экспертами, студентами, администрацией и техническим персоналом. Эта система обеспечивает сотрудничество между студентами в процессе обучения, так как они работают совместно и используют навыки и уменье. друг друга. Инструменты связи включают внутреннюю электронную почту, файлы новостей, “чат”. В некоторых курсах для поддержки обучения используются такие средства обмена информацией, как видеоконференции, классные доски, странички с набросками, средства типа NetMeeting.
Поддержке целеустремленности студентов в обучении способствуют средства навигации, с помощью которых они могут ставить свои собственные цели занятий, издавать свои индивидуальные учебные программы, основанные на общей программе курса и структуре изучаемых тем. Все ситуации в процессе обучения могут быть спланированы с учетом индивидуальных особенностей студента, например возраста, пола, предыдущей подготовки, целей и интересов. Целеустремленность студентов может также поддерживаться посредством соответствующего содержания курса. Учебные задания составляются на основе проблем, возникающих в реальной жизни, причем учитываются те моменты, которые могли бы быть интересными и стимулирующими для студентов. Этим обеспечивается свойство конкретности обучения. Данное свойство поддерживается также инструментами авторинга и навигации. Наличие инструментов навигации в системе дает уверенность в том, что студент может получить контекстуально связанное и осмысленное руководство по определению направления дальнейшего продвижения в течение всего его обучения. Другие участники учебного процесса могут помогать студенту в плане такого руководства через коммуникационную систему.
К этому примыкает свойство переносимости усваиваемых знаний, которое может поддерживаться несколькими способами. Инструменты авторинга позволяют включать в процесс обучения различные кон
106
кретные средства, имитацию и другое, показывая, как приобретенные знания и навыки их применения могут использоваться на практике в конкретных областях деятельности.
Свойство рефлексивности в значительной степени обеспечивается посредством коммуникационной системы. Студенту приходится осознать свой процесс обучения прежде, чем он сможет обсуждать его с другими участниками курса, причем такое обсуждение используется для определения дальнейшего хода процесса обучения. В течение всего курса студент может как давать отзывы, так и получать их от других лиц, участвующих в учебном процессе. Кроме того, имеются средства, позволяющие оценивать этапы процесса обучения данного студента^ включая конечный результат. Это поддерживается системой таким образом, что студент всегда может прочесть свой персональный файл с указанием ошибок. Кроме того, в системе сохраняются промежуточные состояния этого файла, по которым преподаватели могут оценивать динамику работы студента. Обратная связь в процессе обучения обеспечивается также элементами диагностики, которыми снабжены некоторые из разделов курса, и портфелем работ данного студента, который используется для самооценки и для оценки другими студентами и преподавателями.
С точки зрения вопросов управления гипермедийная система открытого обучения, развиваемая в Технологическом Университете г. Тампере (Финляндия), представляет собой распределенную систему управления, которая реализуется по схеме клиент—сервер на основе всемирной паутины. Система включает в себя серию баз данных по учебным, курсовым и администрационным материалам, инструментарий системы Maple и многое другое. Они расположены на сервере и включают гипермедийную среду, организующую процессы коммуникации, навигации и поиска информации, имитацию учебных классов и семинаров, библиотеки, комнаты экспертов, комнаты преподавателей, находящиеся под управлением системного администратора. Сервер работает на мощной рабочей станции Unix, в то время как пользователи имеют дело с клиентской частью системы, работающей на обычных веб-браузерах. Благодаря этому достигается эффективное и удобное для пользователей взаимодействие с системой. При этом важным достоинством системы является то, что включение относительно небольших порций новой информации в ассоциативную структуру, над которой строится гипермедиа, позволяет расширять возможности интеллектуальной навигации в системе и добавлять новые педагогические возможности ценой малых усилий, не нарушая работоспособность уже имеющихся структур.
2.	ОТНОШЕНИЯ
2.1.	МНОЖЕСТВО КАК ОТНОШЕНИЕ
В этом подразделе понятия множество и элемент рассмотрим как некоторое бинарное отношение. Конечно, этим самым мы не хотим создать ‘‘порочный круг”, ибо, как было сказано в разд. 1, всякое отношение уже есть некоторое множество. Однако представляется целесообразным посмотреть на понятие множество с этой точки зрения. Итак, “определим” понятие множество следующим образом.
Множество — это двухместное отношение Р(х, у), т.е. отношение между двумя реальностями х и у, названными элементами х и множествами у. Назовем это отношение отношением принадлежности.
В специальном обозначении Р(х, у) = х е у это означает, что если взять две произвольные реальности х и у и составить из них Р(х, у), то, если Р(х, у), ставшее уже просто некоторым высказыванием, верно, имеет место факт “х е у” — элемент х принадлежит множеству у. В противном случае, т.е. если Р(х, у) неверно, то имеет место факт “х g у” — элемент х не принадлежит множеству у.
Так как двухместных предикатов много, то, чтобы выделить предикаты, ответственные за понятия множество и элемент, необходимо наложить дополнительные ограничения. Отметим лишь некоторые из них.
1.	Существует единственная реальность у такая, что Р(х, у) неверно при любом х; ее мы обозначим 0 и назовем пустым множеством, т.е. х е 0 при Vx g R, где х — любая реальность R.
2.	Р(у, Т) неверно при Vy g R, т.е. у е у при Vy g R, т.е. никакое множество не есть элемент самого себя; аналогично Р(х, х) неверно при любом х g R, т.е. элемент х не принадлежит самому себе. Однако имеет место следующая аксиома (п. 3).
3.	х е {х}, т.е. Р(х, {х}) верно при любом х g R. Это аксиома существования одноэлементного множества. Таким образом, допускается двойственное толкование любой данной реальности х:
1) как элемента х, принадлежащего какому-то множеству X,
2) как одноэлементного множества {х}, их 6 {х}. Но запись х g х не имеет смысла, т.е. отношение включения нерефелексивно.
108
4. Отношение принадлежности несимметрично всегда, т.е. если х е у, то у е х для Ух е R и У у g R; или из х е у => у е х.
Следующее требование к отношению принадлежности (порождающему понятие элемента и множества) — это аксиома различимости, или отличимости, элементов между собой, если их больше одного.
5. Из X] е у и х2 G у всегда следует, что х, х2. Это означает, что любые два элемента Х] и х2 из у неодинаковы в данной идеализации, различимы, отличимы друг от друга.
Отметим еще раз, что понятие различимости сильно зависит от “способов наблюдения реальности”. Например, изделия какого-то массового производства (шарики для подшипников данной марки, таблетки данного лекарства, автомобили и т.д. и т.п.) могут быть неразличимы для данного способа наблюдения, в частности, ничем не вооруженного глаза человека. Однако мы можем (и так действительно делают) ставить номера (метки) на каждое изделие даже массового производства (например, все автомобили имеют персональные номера кузова, двигателя и машины в целом) и тем самым различать их.
В природе до недавнего времени электроны считались неразличимыми, на них нельзя даже повесить метки-числа. Однако сейчас в связи с развитием средств наблюдения появились указания на существование внутренней структуры электрона, а следовательно, различных наблюдаемых его состояний. Это дает возможность различать электроны по их разным внутренним состояниям.
Математика изучает отношения (свойства и обобщенные свойства) идеальных или идеализированных абстрактных объектов или реальностей. Они существенно проще “настоящих” реальностей и допускают в определенном смысле описание конечной сложности.
Однако имеется и цена, которую приходится платить за эти достоинства, т.е. имеются и недостатки. Дело в том, что нет гарантии, что та или иная принятая идеализация (абстракция) рано или поздно не приведет к противоречиям, недоразумениям, непониманию, бессмыслице. Более того, по мере роста нашего опыта, накопления опытных фактов, развития культуры и цивилизации всегда при любой конечной (хоть и сколь угодно “сложной”) идеализации и абстракции рано или поздно найдутся наблюдения и опыты, которые будут несовместимы, противоречивы с данной абстракцией, сколь угодно развитой и сложной она бы ни была. И тогда снова возникает проблема развития, углубления, перестройки и реформации имеющейся на сегодня абстракции + идеализации. Новое описание должно лучше согласовываться с новым открытием, новым опытом и наблюдениями; конечно, при этом не должны разрушаться старые согласованности. В этом состоит научный принцип соответствия Н. Бора — новая теория должна включать в
109
себя старую целиком. Классическим примером такой ситуации является квантовая физика, включающая в себя классическую.
Теперь можно определить отношение равенства любой пары множеств, скажем, yi и у2.
Определение 1. Два множества yt и у2 называются равными (обозначается у1 = у2), если из х G у1 следует х g у2 (т.е. если верно х с у,, то верно и х g у2), и обратно: из х g у2 => х g у(. Короче, два множества равны, если они состоят из тех же самых элементов. В противном случае у] ^у2, т.е. множества не равны.
Можно показать, в частности, что все пустые множества равны, и в этом смысле существует единственное пустое множество.
Теперь определим следующее отношение — отношение включения. Это тоже двухместное отношение, скажем У2), определенное на любой паре множеств yt и у2. Оно обозначается специально yi с у2 и читается у! есть подмножество множествау2-
Обратим здесь внимание на одно очень важное и совершенно типовое обстоятельство, пронизывающее всю математику. Сейчас для определения нового отношения (или понятия) включения нам нужно будет проверять, является ли истинным значение предиката Pj(yi, у2), аргументами которого являются множестваyi, у2. Типовое обстоятельство, упомянутое выше, здесь состоит в том, что для указанной проверки, т.е. действий с предикатом Pi(yi, у2), мы обязаны использовать и делать проверки для других предикатов, которые описывают “внутренние” и ранее определенные отношения для объектов у. Таким образом, отношение включения — это отношение более высокого уровня, чем отношение принадлежности, в том смысле, что для проверки существования включения необходимо использовать отношение принадлежности, но не наоборот.
Выше отмечалось, что в качестве элементов множества можно брать любую реальность. Поэтому в принципе нам ничто не мешает брать в качестве элементов и множества, рассматривая их как элементы уже другого множества, т.е, рассматривать “множество множеств”. Однако “множество множеств” часто лучше называть классами множеств или семействами множеств, чтобы отличить их от множеств, у которых элементы действительно рассматриваются нами как элементы в прямом смысле, т.е. как уже далее неделимые, не имеющие никакой внутренней структуры. Например, будем рассматривать классы множеств, имеющих определенную структуру класса, а не множества. Без такого подхода почти невозможно рассматривать такие многие важные математические структуры, как, например, меры или структуры управления.
110
Такая же ситуация имеется, например, в функциональном анализе, где в качестве элементов (бесструктурных точек) рассматриваются функции, имеющие априори нетривиальную внутреннюю структуру, которая существенно используется, например, для понятия сложения и умножения “элементов” функционального пространства (т.е. “сложения точек”).
Ясно, что можно строить следующую “ступень иерархии классов”. Все это будут множества принципиально новой природы, если учитывать, что элементы таких множеств на самом деле не элементы как неделимые, а за ними скрываются целые множества. Но если забыть внутреннюю структуру элемента, абстрагироваться от нее и рассматривать элемент как элемент в прямом смысле, то множество любого уровня (любой класс) ничем не будет отличаться от “обычного” множества. Но, например, операции с множествами более высокого класса “реализуются” на основании знания структуры элементов этих множеств, т.е. на основе знаний строения множеств низшего класса иерархии.
Таким образом, надо всегда четко понимать, когда и где элемент рассматривается как истинный (бесструктурная точка), а когда мы пользуемся тем, что на самом деле за “бесструктурным элементом” скрывается его нетривиальная внутренняя структура. В этом состоит противоречивость понятия элемент', на него можно смотреть двояко. Но надо четко понимать и разделять эти две стороны одного и того же понятия элемент.
Например, человек, едущий в автобусе, — это пассажир — простой элемент с точки зрения автобусной компании. Но это далеко не простой элемент, если его, допустим, рассматривать как сотрудника, способного выполнить ту или иную работу. Однако для транспортной компании такая “детривиализация” элемента (пассажира) вовсе ни к чему. У компании другие задачи.
Таким образом, вопрос о “детривиализации” элементов множеств нужно ставить в зависимости от задач. Уровень детривиализации должен быть согласован (адекватен) с теми вопросами, которые ставятся в задаче.
Например, в механике, когда мы хотим рассчитать движение маховика на оси вращения, вовсе не требуется исследовать распределение его параметров во всех точках тела маховика, в том числе не надо знать распределение плотности массы маховика. Достаточно знать лишь момент инерции относительно оси вращения. Этого вполне достаточно, чтобы рассчитать движение маховика по закону Ньютона.
Однако если мы ставим другую и более сложную задачу, например, рассчитать прочность маховика, то детривиализация должна идти глубже (здесь недостаточно знать только один параметр — момент
111
инерции). Необходимо знать распределение напряжений по всему телу маховика, и простым уравнением Ньютона здесь уже не обойдешься.
Отметим другой принципиальный момент общего характера, касающийся фундаментальной проблемы — проблемы образования понятий как основного носителя и формы смысла любой сущности, любой реальности, основной составляющей любого языка. Рассмотрим, например, два понятия — множество и элемент, точнее, элемент множества и множество элементов. Этим мы хотим подчеркнуть тот факт, что множество и элемент определяются вместе и только вместе. По отдельности множество и элемент в математике не имеют смысла.
Полезно пользоваться системной терминологией. В этом случае можно сказать, что понятия множество и элемент приобретают смысл только как “замкнутая” система понятий с “обратной связью”: множество определяется через элемент и одновременно элемент определяется через множество. В этом смысле это два равноправных и неразделимо связанных понятия, образующих замкнутую систему.
Пользуясь “кибернетическим” языком в применении к математике, можно сказать, что множество элементов и элементы множества взаимодействуют друг с другом (действуют друг на друга). Именно это взаимодействие порождает математическое понятие отношение принадлежности (элементов к множеству).
Идея взаимодействия, порождающая новые понятия, может быть использована для определения новых понятий (новых отношений, структур, систем, пространств) путем приведения во взаимодействие ранее известных отношений (понятий). Это способ образования сложного понятия из относительно простых понятий. Развитие современной науки как раз идет в основном по этому пути: образование новых более сложных понятий путем ”организации” взаимодействия между простыми или, лучше сказать, ранее известными понятиями. Например, в математике наиболее простыми примерами такой организации сложного понятия (путем приведения во взаимодействие простых понятий) через простые являются примеры кольца, поля, модуля, линейного пространства и др. В приведенных примерах взаимодействие простых “систем” реализуется через свойство (аксиому) дистрибутивности. Именно она связывает два простых понятия — группа по сложению и группа по умножению — в одно сложное понятие — кольцо или поле.
Отметим, что проверка истинности предикатов в математике или проверка выполнения отношений идет на основании логики, проверка истинности утверждений в самой логике идет на основании философии, т.е. на основании смысла, который мы можем вложить в наблюдения за реальностью, в наш опыт, пассивный или активный.
112
Рассмотрим пример из области теории блочно-структурных схем с линейными блоками. Блок 1/(1 + у?2) — элементарен, хотя он является блоком 2-го порядка, а не 1-го, как \/ р и 1/(1 кр), или нулевого порядка, как блок усиления с коэффициентом к. Но его можно представить через взаимодействие “неопределенных” блоков 1-го порядка. Т ем самым он находит свое точное определение лишь во взаимодействии и причем двух разных типов (последовательное или параллельное соединения):
1	= 1 1
1 + у?2	\ + ip	\-ip
или
1__ = 0,5 + _0,5_
1 + р2 1 ip 1 - ip
Вне этой схемы отдельно блоки 1/(1 + ip) и 1/(1 - ip) не определены (бессмысленны). Конечно, в “более широкой схеме” с использованием комплексного анализа и чисел они могут быть осмыслены, т.е. определены и независимо друг от друга.
2.2. ОБЩЕЕ ПОНЯТИЕ ОТНОШЕНИЯ
В разд. 1 было сказано, что понятия предиката и отношения отождествляются. Предикат — это понятие логики, т.е. в соответствии с определением логики как науки о формах смысла предикат — это одна из важнейших форм смысла, которой мы пользуемся в науке. Иными словами, “язык” предикатов — это основной язык всякой науки, основной способ выражения смысла всякой реальности, заключенного в тех или иных свойствах реальности.
В этом подразделе будут даны основные понятия теории отношений и рассмотрены некоторые главные из них.
Напомним формальное математическое определение отношения.
I Определение 1. /г-местное отношение на конечной последовательности множеств А\, А„ — это непустое подмножество R прямого произведения множеств Л,..А,;.
Rc Aj х А2 х ...х Ап - ] [А,: .
i=i
Прямое произведение А} х ... х А„ — это множество, элементами которого служат все последовательности вида (cris ..., ап), где а, — произвольный элемент множества А, для любого i = 1, ..., п, т.е.
(«I, ..., а„) е R, а, е A,, i = 1, ... , п.
113
Отношение R между элементами обозначается R(ax, ..., п„) или (аь cin)R. Для 2-местного отношения axG Ah А2 часто используется обозначение a\Ra2. Подмножество R ст Ах х ...х Ап называют графиком отношения R.
Последовательность — это расположение предметов в таком строгом порядке, когда можно сказать, какой элемент 1-й, какой — 2-й и т.д. и, наконец, какой элемент есть последний. Таким образом, порядок — это тоже некоторое отношение, о котором подробно будет сказано в подразд. 2.7.
Подчеркнем, что отношение, как и предикат, задает или устанавливает связь между элементами, вообще говоря, различных множеств Аь ..., Ап, 'которые в теории предикатов называются предметными областями. Иными словами, предикат, или отношение, устанавливает “структуру связи” среди элементов различных предметных областей Ait i = 1, ..., п.
Иногда говорят, что //-местный предикат, или «-местное отношение, R задает обобщенное свойство последовательности (аь ..., а,,') элементов множества Л1 х ...х А„.
Рассмотрим некоторые частные случаи общего понятия отношения при различных п и различных условиях на множества/!/, i = 1,
При // = 1, очевидно, отношение — это просто подмножество одного единственного множества А. Это отношение задает еще какое-то “дополнительное” свойство для элементов а 6 А, которые среди всех элементов А выделяют те и только те элементы, которые обладают свойством, заданным отношением R,RcA, .
Другой очень важный частный случай /г-местного отношения R состоит в том, что множества Л/, i = 1, ..., п, попарно равны: А = А» / = 1,... , п. Это просто п “экземпляров” одного и того же множества А, которые различаются только “несущественной” нумерацией Аь А„, но “на самом деле” все они совпадают между собой: “ един во многих лицах”.
В этом случае //-местное отношение называют п-арным отношением, в частности, Парное называют унарным, 2-арное — бинарным, 3-арное — тернарным и т.д. В этом случае прямое произведение п одинаковых множеств А обозначают Ап. Про /7-ариые отношения иногда просто говорят, что они задают отношения на одном множестве Л.
В свою очередь среди н-арных отношений выдающуюся роль во всей математике играют бинарные отношения, т.е. подмножества R ст А1. В частности, бинарными отношениями являются главнейшие математические отношения на множестве А — эквивалентность и порядок, а также некоторые другие, например, толерантности или равенства.
114
Унарное отношение (при п = 1), которое мы назвали просто свойством, можно еще по смыслу назвать отношением включения подмножества R в множество А. Это отношение обозначается R а А.
Имеет смысл подчеркнуть, что отношение принадлежности “е” и отношение включения “с” — это разные отношения между разными предметными областями: одно — между элементами и множествами, второе — между множествами и тоже множествами.
Правда, нередко имеет место смешение этих понятий и терминов в том смысле, что отношение принадлежности, скажем а е А, также называют включением, т.е. говорят, что элемент а “включен” в множество А, хотя надо иметь в виду, что лучше, точнее говорить, что элемент а принадлежит множеству А. Так, для выражения х е 1(х) говорят, что это дифференциальное включение (вместо дифференциальная принадлежность).
Отметим, что если R = Aj х ...х Ап, то отношение R называется полным отношением наА1, ...,Ап.
2.3. БИНАРНОЕ ОТНОШЕНИЕ КАК ГРАФ. ДИСКРЕТНЫЕ СИСТЕМЫ С УПРАВЛЕНИЕМ
Наиболее наглядно толкование отношения как связи между элементами предметной области можно показать на примере бинарного отношения R (п ~ 2) на произвольном множестве А. Для простоты произвол в выборе А ограничен тем, что будем считать А конечным множеством из п элементов: щ, ..., ап.
В таком случае бинарное отношение на множестве А однозначно определяется квадратной таблицей, или квадратной матрицей, которую обозначим В = (bj), i =1, ..., п, j = 1, ..., л, размерности N х Nс элементами by. Эти элементы определим так:
10, если (а,, а7) с 2?с Л
[ 1, если (at:, aj) g R cz A
Такая матрица, выражающая данное бинарное отношение R, равносильно задается графом, который строится следующим способом: его вершины находятся во взаимно-однозначном соответствии с элементами а,- множества/!. В противном случае, т.е. еслиR(cn, aj) = 1 (упорядоченная пара находится в бинарном отношении R), рисуется ребро, идущее от а, к а^ на что указывает стрелка на этом ребре. Если 2?(я/, aj) = = 0, т е. упорядоченная пара (a,. aj) не находится в отношении R, ребро со стрелкой, идущее от а, к О/, не изображается на графе.
115
Таким образом, каждому бинарному отношению R ставится в соответствие ориентированный граф. Очевидно, что существует и обратное соответствие.
Теперь несложно показать, что если дано бинарное отношение R, то ему можно поставить в однозначное соответствие дискретную систему с управлением (ДСУ). Более того, если такая ДСУ построена, то ей можно однозначно сопоставить отношение R, которое и будет совпадать с тем же самым исходным бинарным отношением R.
Действительно, по определению, ДСУ есть включение
я„+|е/(п„), олеА, п = 0,1,2,3,...,	(2.3.1)
где А — множество состояний ДСУ; всякое а е А называется локальным состоянием или просто состоянием ДСУ, 1(a) — заданное подмножество А, зависящее от а е А. Управление ДСУ, вернее, допустимое управление (многократный выбор), по определению, есть конечная (длины к) последовательность (п0, ah а2, а3,	а£) и такая, что для
\/п0 G А и для всех ап, п = 1, 2, 3, ..., к, к е N, выполняется включение (2.3.1). Число к назовем длиной управления.
Для ДСУ можно естественным образом поставить три основные задачи: 1) управляемости-достижимости, 2) финитного управления и 3) оптимального управления по быстродействию, или собственного оптимального управления.
Задача управляемости-достижимости состоит в выяснении, существует ли по крайней мере одно допустимое управление при к е У для данных (70 и Ok.
Задача финитного управ чения состоит в описании множества всех допустимых управлений, решающих задачу управляемости-достижимости.
Задача собственного оптимального управления состоит в построении функции ф(ао, я„), (^0, ап) G 2(2, п е N, значение которой есть наименьшая длина допустимого управления с начальной точкой aG и конечной точкой а„.
Для того чтобы данному бинарному отношению Л поставить в соответствие ДСУ (2.3.1), надо задать множества 1(a) для \/а е А. Это нетрудно сделать следующим образом:
1(a) = {аоа А: (а, а,,) е R се А для Va,EA}, а е А. (2.3.2) Обратно, если дано ДСУ с помощью (2 3.2) при фиксированном отношении R, то R можно однозначно восстановить по формуле
R = {(а,а{) е А2 : п,- е 1(a), а е А},	(2.3.3)
г.е. пары (а, а;) “пробегают” все подмножество А, когда а в (2.3.3) “пробегает” все множество А.
116
Можно убедиться, что подстановка (2.3.3) выражения для R в равенство (2.3.2) вместо R дает тождество по а е А.
Не будем выписывать это тождество из-за его некоторой громоздкости, но укажем, что это важное нетривиальное (хотя и не очень сложное) тождество, которое характеризует ДСУ в его связи с бинарным отношением R. Вследствие этого такое тождество можно назвать структурным тождеством ДСУ.
В заключение сделаем принципиальное замечание, проливающее свет на возможный вопрос: “Почему мы хотим понятие управления отождествить с понятием связности?” Если обратиться к топологии, то там понятие связности (линейной) ассоциируется с существованием пути (непрерывной в данной топологии “линии”), связывающем две произвольные точки топологического пространства. В ДСУ роль пути играет допустимое управление, определенное упорядоченной парой (д0,«Д.
Таким образом, в отличие от топологии, в ДСУ имеются две связности, которые соответствуют двум задачам — управляемости и достижимости — и которые в определенном смысле являются обратными друг к другу.
В подразд. 3.9 будет показано, что введенное здесь понятие ДСУ можно обобщить, используя более сильное, чем бинарное отношение на одном множестве А, понятие — понятие расслоения.
2.4.	ОПЕРАЦИИ НАД ОТНОШЕНИЯМИ. ПРОСТРАНСТВА ОТНОШЕНИЙ
Существуют по крайней мере два способа сопоставить одному или нескольким данным отношениям другие отношения, которые связаны с исходными или, как говорят, которые ими порождаются.
Один из этих способов основан на том, что всякое отношение как математическое понятие есть некоторое множество, вернее, подмножество некоторого “хорошо” определенного множества (прямого произведения). Следовательно, как и для множеств, для отношений в принципе можно попытаться определить операции сложения (объединения, дизъюнкции) отношений, перемножения (пересечения, конъюнкции) отношений и взятия дополнения (отрицания) как соответствующие теоретико-множественные операции: если а = (дь ..., ап) е А\ х ... х Ап, то
№ и R2 ) (а) <=> A, (a) U R2 (а) <=> или R} (а) или R2 (а),
(Ai n R2) (а) <-> Ri (а) n R2 (а) <=> и Rr (а) и R2 (а),
А(а)<=> At х...х А„ /R(a) <^> не R(a).
Например, отношение равенства “=”, определенное на множестве А, — это подмножество А2, совпадающее с диагональю квадрата А2, т.е. подмножество всех пар вида {а, а), где а е А.
117
Дополнение этого отношения есть отношение неравенства Отношение “меньше—равно” (<) есть объединение отношений равенства с отношением неравенства: (=) и (<).
Пересечение (=) п (<), очевидно, пусто и представляет собой ложное отношение. Это означает, что между данными объектами никаких отношений вообще не существует.
Таким образом, можно сказать, что совокупность всех отношений R на х ... х Ап при каждом фиксированном п вместе р тремя операциями — сложения, умножения и дополнения — образует алгебру Буля, т.е. один из видов теоретико-множественного пространства (структуры).
При этом тождественно выполняются свойства (аксиомы)-
1)	xvjx- х — идемпотентность;
2)	хи у = у и х — коммутативность;
3)	(xuy)uz = хи(у uz) — ассоциативность;
4)	х п (у lj z) - (х п у) u (х n z) — дистрибутивность;
5)	(х') = х;
6)	(хиу) =х'гту';
7)	хи(упу') = х.
Из этих тождеств можно получить двойственные тождества на основе тождеств двойственности Моргана', дополнение суммы равно произведению дополнений и дополнение произведения равно сумме дополнений.
Другой способ образования новых отношений из старых порождает две операции — обращения отношения и свертки двух отношений. Эти операции более специфические.
Определение 1. Если дано отношение R, то обращением (или инверсией) отношения 2? на Л] х ... х А„ называется такое отношение (обозначается У?-1), что
..., ап) <=> Мап,..., <?,) для Va g х...х Ап.
Иными словами, инверсное отношение между элементами (ai, ап) равносильно исходному отношению между теми же элементами, но расположенными в обратном порядке по отношению к исходному.
Операция свертки определяется так.
Определение 2. Пусть заданы два двухместных отношения: на
А х В и R2 на В х С. Тогда свертка R[ ° Rz двух отношений — это такое двухместное отношение на А х С, которое справедливо тогда и только тогда, когда для Ца, с) g А х С в В существует такой элемент b g В, для которого справедливы и R фа, Ь), и R2(b, с), т.е выполняются эти два отношения между указанными парами.
118
Заметим, что свертка считается неопределенной для двух произвольных двухместных отношений, скажем, А3 на А х В и Л4 на С х D, если В # С.
Рассмотрим совокупность всех бинарных отношений на одном множестве А и совокупность из пяти определенных выше операций на множестве А. Множество А будет замкнуто относительно всех этих операций в том смысле, что результат этих операций над бинарными отношениями на множестве А снова будет бинарным отношением на множестве А.
2.5.	ОТНОШЕНИЕ ОТОБРАЖЕНИЯ
Отношение отображения — это двухместное отношение между элементами двух произвольных непустых множеств, скажем Л и В.
Отношение отображения часто называется функциональным отношением, или просто функцией.
Понятия множества и отображения (функции) — это два, пожалуй, самых основных понятий всей математики, без которых, как правило, не обходится ни одно рассмотрение в ней.
Отображение обозначается несколькими равносильными способа-f
ми: f : А -> В', А->В\ y = f (х), х е А, у&В.
В самом общем случае отображение f: А —> В называется отображением из А в В, в отличие от частного случая (см. далее) отображения из А на В. Короче говоря, отображением/из А в В, обозначаемым, скажем /: А В, называется правило, которое любому х g А ставит в однозначное соответствие некоторый элемент у g В. Элементы множества А называются аргументами функции/ а элементы/я) g В иногда называются значениями функции/
В отличие от всех остальных двухместных отношений отображение характеризуется двумя свойствами (аксиомами):
1)	аксиома определенности, или соответствия’, для любого х G А существует у g В такой, что (х,у) g G, где G — график отображения;
2)	аксиома единственности, или однозначности соответствия'. элементу g В в аксиоме определенности — единственный.
Отображение можно определить как график, который, по определению, есть совокупность (множество) всех значений/х) g В во всех соответствующих точках х g X. Это множество, представляющее отображение / можно записать в виде
/ = {(х, /(х)): Vx g А, f(x) g В}.
119
Отметим и такую терминологию, которая используется в приложениях.
Отображение можно рассматривать как распределение на А значений у величины В. Отображение также записывается в виде тройки (f, А, В).
Множество А называется множеством (“областью”) определения отображения f Множество В называется множеством (“областью”) значений отображения f Иногда А называют областью отправления, а В — областью прибытия при отображении f Отображение f: А —> В еще называют отношением однозначного соответствия. Есть обозначения Dom f - А\ Vai f = 1ш/ = В . Говорят также, что элементы а е А отображением f переводятся в элементы J[d) = b & В.
Множество//!) называется полным образом отображения. Он находится в В, т.е. с В.
Частичным образом f[A\) отображения (в В) называется совокупность всех точекДа) е В, когда а е А], где И, есть подмножество Л: А\ а А:
f(Ai)={f(a):aEAi}.
Частичный образ fiA^ отображения можно назвать просто образом А] в В при отображении/
Можно поставить “обратный” вопрос: “Какие элементы из Л в качестве образа имеют элементы данного подмножества В^ с J9?” Совокупность всех таких элементов из А естественно обозначить /-1 (В}) . Это подмножество множества Л, которое, по определению, есть
f-^B^iaEAifta)^}.
Р\В{) называется прообразом множества Вх с В. Из определения отображения следует, что f~] (В) — полный прообраз В — совпадает с А: f~] (В) = А . В то время как — полный образ А — не обязан совпадать с В, а только есть непустое подмножество В.
Интересно, что имеет место некоторое “исчисление” образов и прообразов отображений, которое характеризуется рядом доказуемых теоретико-множественных тождеств:
/(4 v4) = /(4)^/(4);
Г'(В, ^В2) = Г'(В1)^Г\В2у,
Однако, например, неверно, вообще говоря, что/Л1 п А2) =/Л1) п п/Л2) [155].
120
С понятием отображения f : А-> В связан еще целый ряд важнейших понятий, в том числе специальных, важных разновидностей общего понятия отображения, естественно являющихся частными случаями этого общего понятия. Перечислим их.
Тождественное отображение, или единичн ое отображение, — это частный случай, когда, во-первых, В = А и, во-вторых, каждому а е А ставится в однозначное соответствие само это а. Тождественное отображение обозначается id : А -> А или 1: А -> Л, у = 1(х), х е А, у е А. Иногда пишут 1А. Очевидно, 1Л — единственное тождественное отображение на Л.
Композиция двух отображений f : Л -> В и	при В сзВ} —
это отображение h : Л —> С такое, что
h{x) = g(/(*)), х е A, h(x) е С.
Композиция обозначается g° f, т.е. /? = go f .
По смыслу композиция двух функций, если она существует, единственна, т.е. строится однозначно.
Важно обратить внимание на то, что композиция двух отображений определена далеко не для всякой (произвольной) пары отображений f: Л —> В и / : Л] -> В}, ибо для ее существования необходимо и достаточно, как видно из определения композиции, чтобы В cz Ль т.е. область прибытия первого отображения должна содержаться в области отправления для другого. В противном случае композиция просто не существует или не определена.
На композицию отображений можно смотреть как на бинарную операцию, определенную на отображениях, которая каждой паре отображений, скажем/и g, ставит в соответствие результат этой операции, называемый композицией, go f. Если go f существует (в смысле определено), то, как мы видели, вовсе необязательно, что существует и f о g. Поэтому, вообще говоря, операция композиции некоммутативна:
g°f * f°g,
даже если обе композиции существуют (определены), но каждая из них есть функция, определенная на своем множестве, не совпадающем с другим.
Однако, в частности, для тождественного (единичного) отображения, если определено f о 1 и 1 ° f, имеет место тождество
/01=10/ =/
121
Но операция композиции ассоциативна, т.е.
° (/ ° g) = ° У) ° g = h ° f ° g,
и скобки можно опускать, конечно, если все композиции определены (существуют).
Очень важным понятием является понятие обратной функции {обратного отображения) по отношению к данному (прямому) отображен ию f:'А > В .
Из нижеприведенного определения будет ясно, что далеко не для всякого данного отображения f: А —> В определено, т.е. существует, его обратное отображение, обозначаемое , вида у-1 : В -> А.
Определение 1. Отображение	>А называется обрат-
ным отображением для отображения f :В-> Л, если и только если:
1)	определены две композиции
УУ* И
2)	они соответственно есть тождественные (единичные) отображения
/о/"' И /-’о/ = 1л.
Существование обратной функции для данной, как видно из определения, есть довольно сильное (жесткое) требование. Отметим, что в силу однозначности композиции единственно, если оно существует.
Второе требование можно записать и как две функции:
У ЧУС*)) ~х Для VxgA, f(f~' (я)) = У для Vy е В.
Операция получения	из данной f— унарная операция на ото-
бражениях, называемая обращением отображения. В этом случае говорят, что отображение f допускает обращение у-1. Здесь уместно обратить внимание на необходимость различения символов У"1 в двух выражениях — /-1 (А) и у-1, где символ f~x имеет совершенно разный смысл — в (А) не надо понимать у-1 как обратное отображение по отношению к f
Ясно, что нетрудно придумать отображения f: А-> В , для которых не определены (не существуют) ни f о у-1, ни f~x о f вместе или в отдельности (одно существует, а другое нет). В частности, для данно
122
го f может существовать f 1 такое, что f о f 1 и, более того,
В этом случае говорят, что отображение f: А-> В допускает (для него существует) правое обращение . Аналогично, если существует такое, что	° f = 1А , то говорят, что f : А-> В допускает (для
него существует) левое обращение .
Таким образом, сравнивая с общим определением обращения, видим, что обращение существует, если и только если f допускает вместе и левое//“’, и правое f~x обращения.
Понятия обращений играют фундаментальную роль в математике, ибо они из необозримого “моря” разнообразных отображений выделяют специальные классы функций.
Определение 2. Отображение f : А -> В называется сюръективным отображением, сюръекцией, наложением, отображением “на”, если и только если f (А) = В, т.е. полный образ ДЛ) совпадает с В, или для любого b & В существует его прообразДЛ) в А, т.е. b =fla).
На рис. 2.5.1 изображена сюръекция.
Оказывается (и это нетрудно доказать), что отображение f: А -» В есть сюръекция, если и только если существует правое обращение . Это равносильно тому, что из равенства gi о f = g2 ° f следует
gi = g2 для любых двух функций gb g2, область определения которых есть В, т.е. допускается сокращение на f справа.
Определение 3. Отображение f: А -» В называется инъективным отображением, инъекцией, вложением, если и только если из/(а1) = следует ах- а2, т.е. разные элементы ах и а2 из А переводятся в разные элементы Ьх = Дщ) и b2 = flph)-, из ах * а2 следует/щ) ^Ж).
Очевидно, что сюръекция, вообще говоря, отлична от инъекции, и наоборот. Оказывается, и это также нетрудно доказать, что f: А -> В
123
есть инъекция, если и только если существует левое обращение fi 1. Эго равносильно тому, что равенство f о g{ = f °g2 можно сокращать на т.е. из него следует, что gi = g2 для любых двух функций g] и g2, области значений которых содержатся в А. Инъекция изображена на рис. 2.5.2.
Заметим, что образ инъекции ф(А) необязательно совпадает с В, r.e.fiA) цля инъекции может быть собственным подмножеством В, fiA) е В.
Определение 4. Отображение f: А В называется биективным отображением, биекцией, взаимно-однозначным соответствием, если и только если оно вместе есть сюръекция и инъекция.
Отсюда сразу следует, что f есть биекция, если вместе существуют //* и //*, или, что равносильно,/обратимо, т.е. существует обратное отображение /'* (рис. 2.5.3).
Р и с. 2.5.2	Рис. 2.5.3
Нетрудно проверить, что композиция биекций (если она существует) тоже биекция.
Понятие биекции или взаимно-однозначного соответствия между двумя множествами А и В играет фундаментальную роль во всей современной математике, ибо на нем основано понятие изоморфизма, а следовательно, принципы классификации всех математических структур, пространств, систем, отношений и предикатов. Понятие биекции входит как необходимое в определение всех изоморфизмов и классификаций. Математическое понятие изоморфизма отражает интуитивное понятие полного (в рамках рассматриваемых свойств) подобия двух реальностей.
На рис. 2.5.4, 2.5.5, 2.5.6 условно изображены в виде графиков соответственно примеры трех разновидностей отображений: сюръекции, инъекции и биекции.
Заметим еще одно полезное свойство: инъекции f :А—> В можно однозначно поставить в соответствие биекцию / : А -> /(А), где ДА) с В.
Выяснение свойств операции обращения (данного отображения) — фундаментальная задача всей математики, ибо она является основной для многих ее разделов.
124
Это объясняется тем, что, как мы уже говорили, математика может также рассматриваться как наука об уравнениях и методах их исследования, в частности, нахождения решений данного уравнения. Но всякое уравнение можно записать в виде f(x) = b, где f— отображение f \ А —> В, b е В — некоторый известный элемент, х — неизвестный элемент из А, х е А.
Рис. 2.5.4
Отсюда, например, видно, что для того, чтобы для этого уравнения существовало решение и притом единственное, необходимо и достаточно, чтобы f было обратимо. Тогда общее решение имеет вид
x-f~\(b) для Х/ЬеВ.
Этому решению соответствует тождество
ЛГЧь^ь, Х/ЬеВ.
Таким образом, обращение отображения служит одним из источников разнообразных тождеств.
Отметим еще, что понятие биекции играет важнейшую роль в “наивной'’ канторовской теории множеств. Г. Кантору не удалось создать законченную теорию множеств, свободную от парадоксов, но ему удалось открыть важнейшее понятие всякой теории множеств, а следова
125
тельно, и всей математики. Это —- понятие мощность множества. Мощность множества — естественная структура, которая в рамках канторовской теории множеств присуща любому множеству: всякое множество обладает структурой мощности (“мощностной структурой”). Понятие мощности множества уточняет интуитивное определение размера множества в смысле “количества” элементов, которые в нем содержатся.
Здесь имеет смысл сказать, что существует еще одно важнейшее математическое понятие, которое непосредственно (при некоторых довольно общих условиях) связано с множеством и которое также уточняет интуитивное понятие размер, объем или емкость данного множества. Это — понятие мера множества. Мера — это другая структура, которая может быть определена на данном множестве. Существуют “теории меры”, по которым всякое множество обладает структурой меры (“мерной” структурой), т.е. не существует неизмеримых в этом смысле множеств.
Сравнительное изучение этих двух естественных структур на данном множестве — мощности и меры — представляет фундаментальную проблему математики, тесно связанную с логикой и философией.
Отметим, что вместе с вышеопределенным понятием отображения существуют и иногда используются еще по крайней мере два близких понятия: 1) многозначное отображение и 2) частичное отображение. Подчеркнем, что эти понятия не являются отображениями в определенном выше смысле этого термина.
Многозначное отображение — это отображение без требования аксиомы единственности, иными словами, в многозначном отображении допускается, чтобы значению а е А соответствовал не один единственный элемент, а некоторое непустое подмножество множества В, что исключено для понятия отображение. Таким образом, многозначное отображение не есть отображение в точном смысле.
Частичное отображение — это отображение, в котором нарушена первая аксиома (требование) к понятию отображения, а именно, существуют такие элементы а е А, для которых не определены соответствующие элементы Ъ е В. Таким образом, и частичное отображение не есть отображение. Например, \/х на 7? есть частичная функция на R, ибо она не определена при х = 0. На Я - {0} выражение 1/х определяет отображение.
Отметим, что многозначному отображению можно поставить в соответствие истинное отображение, если в нем область значений В заменить на область значений {В}, где {В} — множество всех подмно
126
жеств множества В, т.е. вместо f-.A-yB рассмотреть F\A->[B}, где F уже “настоящее” отображение.
Что касается понятия частичного отображения, то оно также далеко не бесполезно и используется, например, в математической логике и теории алгоритмов. Его также можно преобразовать в “обычное” отображение, если поставить ему в однозначное соответствие отображение Ф: А{ -> В, где А} с Л, и такое, что для Va е J41 существует элемент b е В, который ставится в однозначное соответствие а g Ау
Отметим еще один широко используемый класс отображений, называемых характеристическими функциями.
Определение 5. Характеристической функцией множества X, которое есть подмножество множества У, X с У, называется отображение (у), у е Y, вида
[ 1, если у е X
Хх(у)= n	-v-
[О, если у е X
Если известна характеристическая функция xeY множества X, то множество Xописывается равенством
X = {Y^y) = \}.
Таким образом, характеристические функции дают альтернативное описание множеств, это — способ представления того или иного множества в терминах отображений.
Отметим еще некоторые полезные общие понятия, связанные с понятием отображение.
Определение 6. Расширение отображения F— это отображение, график которого включает в себя график расширяемого отображения F.
Определение 7. Сужение отображения F\ — это отображение, график которого включается в график сужаемого отображения F\.
2.6.	ОТНОШЕНИЕ ЭКВИВАЛЕНТНОСТИ
Отношение эквивалентности — это бинарное отношение на множестве А. Другими словами, это некоторое подмножество^ прямого произведения А х А или X2, Е е А2. Чтобы отличить именно бинарное отношение эквивалентности от всех других бинарных отношений на множестве А, формулируется ряд свойств этого отношения в виде аксиом (постулатов) данного отношения.
127
Определение 1. Отношение эквивалентности Е на множестве А — это бинарное отношение на множестве Л, для которого выполнены следующие аксиомы.
1.	(а, а) е Е, для Va е А. Это аксиома рефлексии. Графически она означает, что диагональ квадрата А2 всегда входит в Е, если Е отношение эквивалентности.
2.	Если (а,, а2) е Е, то (я2, щ) е Е. Это аксиома симметрии. Ее графический смысл состоит в том, что подмножество Е с А2, если оно описывает эквивалентность, должно быть симметрично относительно диагонали квадрата Л2.
3.	Если (аь а2) е Е и (п2, щ) е Е, то (а,, а3) е Е. Это аксиома транзитивности. Она накладывает новые ограничения на график отношения эквивалентности. Как легко видеть, из нее следует, что подмножество Е, описывающее эквивалентность, должно состоять из непересекакпцихся квадратов в А2 с диагоналями, лежащими на общей диагонали “большого” квадрата Л2 (рис. 2.6.1).
Отсюда видно, что отношение эквивалентности однозначно определяет разбиение множества А. Напомним, что разбиением множества А называется совокупность множеств {Л,} таких, что:
1) они попарно не пересекаются, т.е. Л/ пД =0, если Л, е {Л} и Л7е {Л};
2) объединение всех множеств из {Л,} есть само множество Л, т.е. л = ил-
Обратно, если дано какое-то разбиение {Л(} множества Л, то оно однозначно определяет на множестве А отношение эквивалентности.
Нетрудно доказать теорему о том, что между всеми отношениями
эквивалентности на множестве Л
и всеми разбиениями множества Л существует взаимно однозначное соответствие.
Каждое множество Л,- е {А,} из разбиения {А;} множества Л называется классом эквивалентности.
Частным случаем отношения эквивалентности на множестве Л является отношение равенства на Л, когда график Е отношения эквивалентности совпадает с диаго-' налью квадрата Л". В этом случае все непересекающиеся “квадратики”, из которых складывается любое отношение эквивалентности,
128
вырождаются в точки диагонали (а, а) е А2. Каждая точка а е А, вернее, одноэлементное множество {о} е А есть один из классов эквивалентности. Здесь А как бы разбивается на множество своих точек (элементов).
Обратно, если исходить из отношения равенства, то можно сказать, что отношение эквивалентности, или просто эквивалентность, есть обобщение понятия равенства.
Понятие эквивалентности на множестве порождает важное понятие классов эквивалентности, т.е. совокупности подмножеств, на которые разбивается множество Л.
Совокупность всех классов эквивалентности множества называется фактор-множеством множества Л по эквивалентности Е (обозначается Л/£).
Тот факт, что два элемента — а\ и а2 — из множества А находятся в отношении эквивалентности, обозначается ах ~ а2. В противном случае, если <71 и я2 неэквивалентны, то пишут Е а2.
Таким образом, а} ~ а2, если и только если а\ е К и «2 е К, где К — класс эквивалентности, Кс А!Е.
Если какой-то элемент а е А принадлежит данному классу К эквивалентности, т.е. а е К, то сам этот класс эквивалентности К удобно обозначать а = К .
Для каждой эквивалентности Е существует отображение л: а=л(а), a G А, аеА/Е,
которое каждому а е А ставит в соответствие тот класс эквивалентности а , которому он и принадлежит, а е а .
Очевидно, что отображение л — ты АА!Е — это сюръекция.
Отображение л называется естественным отображением, каноническим отображением, естественной проекцией или, наконец, канонической проекцией в данном отношении эквивалентности Е.
Теперь отметим следующие важные положения.
Теорема 1. Любое отображение f . А ж В порождает одно определенное разбиение области определения А этого отображения.
Доказательство. Действительно, рассмотрим подмножество К(Ь) а А, определяемое формулой
K(b) = {a:f(a)=b}, bef(A)c:B.
Пусть b играет роль параметра, “пробегающего” множество ДЛ)с:В.
Ясно, что К(Ьб не пересекается с К(Ь2), если Ь} и Ь2 — два разных значения параметра Ь, т.е. Ь} Ф Ь2, ибо в противном случаеf про-
s. А.В. Бабичев
129
сто не было бы отображением, где требуется, чтобы каждому значению а 6 А соответствовало одно единственное значение b е В
(взяв а е К(Ь\) п К(Ьг) ^ О, мы получим, что а соответствуют два разных значения — Ь\ и Z?2)- -Ясно также, что объединение всех K(b) nob е flA) даст в “сумме” в точности множество А:
А= U К(Ь).
В силу доказанной теоремы можно также сказать, что любое отображение f порождает единственную эквивалентность на А, соответствующую разбиению А на классы K(b), b с
Смысл классов К(Ь), b е flA\ также совершенно ясен — это подмножества уровня отображения f в области его определения А или функции b =ДА), а е А,Ь е В.
Таким образом, произвольному отображению f\A->B соответствует эквивалентность Е на множестве А, порожденная этим отображением, т.е. Е - E(f).
Рассмотрим теперь отображение / — f-.A/E—>B, построенное по очень простому правилу: если К(Ъ) е А/Е, то f (К(by) - b .
Ясно, что / —это, вообще говоря, инъекция: f(A/Е) а В. Конечно, не исключено, что / будет и биекцией. Но в любом случае — это инъекция.
Ясно также, что определена композиция отображения л. (естественной проекции) и только что рассмотренного инъективного, вообще говоря, отображения / : / о л.
Легко видеть, что композиция / ° л в точности совпадает с исходным отображением /: А —> В , i.o.f— f о л .
Таким образом, получена важная общая теорема о разложении (факторизации) произвольного отображения.
Теорема 2. Для любого отображения / : А В существует единственное его представление (разложение, факторизация) / = = / о л в виде композиции его естественного отображения л (сюръекции) и некоторой инъекции /.
Единственность такого представления следует из однозначности естественного отображения л, соответствующего данному/ Теорема допускает графическое толкование в виде коммутативной диаграммы (рис. 2.6.2).
130
Отношение эквивалентности, как увидим	f
в разд. 5, вместе с другими структурами иг- д --------------> g
рает важную роль в построении аксиоматики X.
понятия управления, в гом числе оптималь- 71	д
кого управления.	А/Е
Особую роль среди этих структур будет играть отношение порядка, с помощью которого, например, можно пытаться упорядочивать множество классов эквивалентности, полученных из какого-то отношения эквивалентности.
В заключение этого подраздела покажем, как отношение эквивалентности, примененное к некоторой совокупности множеств, порождает плодотворное и фундаментальное понятие, важное для почти всей математики, — понятие мощность множества. В математике выясняется, что понятие мощности помогает ввести некоторую структуру упорядочения множеств по мощности, которая представляет собой обобщение структуры порядка для обычных чисел, порождая теорию трансфинитных чисел. С началами этой теории можно познакомиться в [ 155].
Итак, определим понятие эквивалентности для множеств.
Определение 2. Два множества А и В называются эквивалентными (обозначается А — В), если существует биекция f :А—> В, т.е. между элементами множеств А и В можно установить взаимнооднозначное соответствие.
Легко видеть, что все три аксиомы эквивалентности: 1) рефлексивности (А ~ А), 2) симметричности (если А ~ В, то и В ~ А), 3) транзитивности (если А ~ В, В ~ С, то А ~ С) следуют из биективности композиции двух биекций.
Из определения немедленно следует, что если А и В — оба конечные множества, то они эквивалентны, если и только если содержат одинаковое число элементов, т.е. |Л| = |В|.
Но понятие эквивалентности множеств позволяет сравнивать между собой и бесконечные множества. Этот факт был, по сути, первым фундаментальным шагом в науке, точно сформулированным математически в отношении изучения оэ-сложной реальности. Этот шаг был предпринят Г. Кантором в его теории множеств.
Понятие эквивалентности двух множеств сразу же порождает понятие мощность множества. Мощность — это класс эквивалентности множеств.
Обозначим мощность множества А через т(А). Если А конечное множество, то т(А) естественно рассматривать как обычное натуральное число т(А) = |Л|. Но если А бесконечное множество, то символ
5*
131
т(А) уже никак не может считаться обычным числом, ибо тогда \А\ = = со, и это все, что мы можем сказать о бесконечном множестве, т.е. это довольно бессодержательно.
Простейшим бесконечным множеством является множество N = = {1, 2, 3, ...} всех натуральных чисел. Всем множествам А, ему эквивалентным, припишем один и тот же символ /и(Л)= Ко, где Ко (читается “алеф-нуль”) — стандартное обозначение “наименьшей” возможной мощности, отличной от мощности конечных множеств. Здесь как бы уже считается, что Ко строго больше любого натурального числа. Поэтому Ко тоже называется числом, но, чтобы подчеркнуть его необычность, называется первым трансфинитным числом.
При сравнении двух бесконечных множеств, т.е. при выяснении вопроса об их эквивалентности или неэквивалентности, возникают утверждения, к смыслу которых надо специально привыкать, вырабатывая для этого соответствующую интуицию, которую надо подкреплять строгими доказательствами, ибо уж слишком она необычна. Действительно, если множество конечно, то его собственное подмножество никак ему не эквивалентно. Это очевидно из нашей “обычной” интуиции. Однако для бесконечных множеств это, вообще говоря, не так, что показывают простые примеры. Так, множество N эквивалентно (!) своему собственному подмножеству всех четных чисел, ибо, очевидно, существует биекция
fп2п, п е 7V, которая устанавливает между N и всеми четными числами взаимнооднозначное соответствие. Поэтому им обоим следует приписать одну и ту же мощность алеф-нуль Ко.
В этом и состоит основная идея — приписывать разным, но эквивалентным множествам, т.е. множествам из одного класса эквивалентности, скажем Ап В, один и тот же символ т = т(А) = т(В) или одно и то же трансфинитное число т и называть их равномощными.
Теперь естественно спросить: когда можно разумно и наиболее естественно считать, что мощность т(В\ скажем, строго больше мощности т(Аф т.е. когда т(А) <'т(ВУ? По-видимому, наиболее разумный ответ на этот вопрос состоит в следующем: т(А) < т(В), если и только если В имеет подмножество, эквивалентное Л, но в Л не существует подмножества, эквивалентного В.
Аналогично, если и только если А имеет подмножество, эквивалентное В, но в В нет подмножества, эквивалентного А, то естественно принять, по определению, что т(А) > т(В).
Такой подход в сравнении мощностей основан на одной из важнейших теорем теории множеств, дающей критерий эквивалентности двух множеств.
132
Теорема 3 (Кантора—Бернштейна). Эквивалентность двух множеств А и В, а следовательно, их равномощность т(А) = т(В) равносильна тому, что вместе выполняются два условия: 1)А эквивалентно подмножеству В и 2) В эквивалентно некоторому подмножеству А.
Наконец, логически мыслим случай, когда ни в А, ни в В нет подмножеств, эквивалентных (равномощных) другому. В этом случае естественно считать, что мощности т(А) и т(В) несравнимы друг с другом, т.е. неверно, что т(А) = т(В), неверно, что т(А) < т(В) и неверно, что т(А) > т(В).
Можно показать, что этот случай не реализуется. Иными словами, получается важный вывод, что несравнимых (по мощности) множеств не существует, т.е. для любых двух множеств А и В имеет место альтернатива' 1) или т(А) = т(В), или 2) т(А") > т(В), или 3) т(А) < т(В).
Естественно возникает вопрос: “Существует ли множество X с наибольшей мощностью m(JV)?” Нетрудно показать, что предположение о существовании множества X с наибольшей мощностью т(Х) никак не может подтвердиться.
1 Теорема 4. Если Р(А) — множество всех подмножеств множества
А, то т(А~) < т(Р(А)).
Доказательство этой теоремы можно найти, например, в [155, с. 29].
Принято, что если ц = т(А), то мощность В(А) обозначают 2Р, т.е. всегда р < 2м. Такое обозначение определено свойством конечных множеств: если конечное множество содержит р элементов, где р е 7V, то множество всех его подмножеств тоже содержит конечное число элементов, равное 2Ц, и всегда р < 2м для “обычных” чисел р.
Классическим примером такой ситуации является сравнение мощности множества натуральных чисел, обозначенной “алеф-нуль” Ко, и мощности множества всех подмножеств N, обозначаемой теперь 2Л/ = Й, где К читается как алеф. Мощность множества N имеет также специальное название мощность континуума.
2.7.	ОТНОШЕНИЕ ПОРЯДКА
Отношение порядка — это еще одно важнейшее отношение в математике. Важную роль это отношение играет при попытке определить понятие управление.
Существуют несколько разновидностей порядка: частичный, линейный (просто порядок), совершенный и др.
I Определение 1. Частичный порядок на множестве А — это бинарное отношение Е на Л, подчиненное следующим трем аксиомам:
133
1)	{a, d) e E для Va e A — аксиома рефлексивности. Графически она означает, что диагональ квадрата А2 всегда входит в подмножество Е из А2, описывающее отношение частичного порядка;
2)	если (ab а^) е Е, то (a2,af) «= £ для V(ab а2~) е А — ак-: сиома антисимметрии-,
3)	если (ан а2) е Е и (а2, ^з) е Е, то (аь а3) е Е для \/а} е А, \/а2 & А и Va3 е А — аксиома транзитивности.
Отношение частичного порядка часто обозначают знаком “<”, т.е. запись а < b означает, что пара (a, b) е Е. Говорят еще, что элемент а не превосходит элемент Ъ, и обратно, элемент b не меньше элемента а, или говорят, что а подчинен Ъ или Ъ подчиняет а.
Множество А, на котором определен частичный порядок, называют частично упорядоченным множеством, а иногда — просто упорядоченным множеством.
Два элемента а е А и Ъ & А называются сравнимыми, если (a, b) е Е, в противном случае, т.е. если (а, ЬУ'Ё Е, элементы а и Ъ называются несравнимыми:
Подчеркнем, что на частично упорядоченном множестве А не любая пара (a, b) е А2 сравнима. Заметим еще, что частичный порядок отличается от эквивалентности только одной аксиомой, причем для эквивалентности нужна симметрия, а для частичного порядка — антисимметрия
Определение 2. Порядок на множестве А — это частичный порядок на А, но при котором любые два элемента (a, b) е А2 сравнимы. Порядок еще называется линейным порядком, совершенным порядком или цепью.
Таким образом, порядок на Л — это частный случай частичного порядка Л.
Если на А существует порядок, то А называется упорядоченным множеством, совершенно упорядоченным множеством или ъ^епъю.
Хотя в частично упорядоченном множестве А существуют, вообще говоря, несравнимые элементы, в нем могут существовать цепи, т.е. подмножества В cz А, совершенно упорядоченные.
Введем следующие важные понятия: наибольшего и наименьшего элементов и максимального и минимального элементов частично упорядоченного множества Л.
Определение 3. Наибольший (наименьший) элемент частично упорядоченного множества А — это элемент а е А такой, что х < а для Vx е А (соответственно а < х).
134
Наибольший (наименьший) элемент, если он существует, единственный (для данного А).
Определение 4. Максимальный (минимальный) элемент частично упорядоченного множества — это элемент а е А такой, что из а < х следует а = х (соответственно из х < а следует а — х).
Максимальный (минимальный) элемент, вообще говоря, не единственный: в данном А может оказаться несколько максимальных и несколько минимальных элементов.
В частности, наибольший (наименьший) элемент, если он существует, является и максимальным (минимальным) элементом, но не обратно. На рис. 2.7.1 показана диаграмма, иллюстрирующая некоторый частичный порядок на множестве всех подмножеств конечного множества, состоящего из трех элементов {а, Ь, с}. При этом частичное упорядочение подмножеств происходит в соответствии с включением, например {и, Ь} < {а, Ь, с}, ибо {a, b} cz {а, Ь, с}. Стрелки указывают подчиненность пары элементов. Не все пары здесь, очевидно, сравнимы. Например, {а} и {£?, с} несравнимы.
Отметим один “типовой” факт, пронизывающий всю математику: для того чтобы “проверить” один предикат (в данном случае предикат порядка для установления его истинности {а, Ь} < {а, Ь, с}), надо проверить и другой предикат (в данном случае предикат включения {а, Ь} а с: {а, Ь^с}).
Из диаграммы видно, что на множестве всех подмножеств есть наибольший элемент {а, Ъ, с}, и он же единственный (в данном примере) максимальный элемент. Аналогично пустое множество 0 есть наименьший элемент и единственный минимальный.
На рис. 2.7.2 показана диаграмма частично упорядоченного множества, где наибольший элемент не существует, хотя имеются три раз
135
личных максимальных элемента. Минимальный элемент (самый нижний) единственный, и он же является наименьшим.
Иногда наименьший (наибольший) элемент называют первым (последним) элементом. Первый элемент подчинен всем остальным, последний элемент подчиняет себе все остальные элементы частично упорядоченного множества/.
Введем еще более узкое понятие, чем понятие упорядоченного множества.
Определение 5. Вполне упорядоченное множество — это упорядоченное множество такое, что всякое его непустое подмножество имеет наименьший, т.е. первый, элемент.
Ясно, что всякое конечное упорядоченное множество есть вполне упорядоченное множество, вернее, на этом множестве вполне можно ввести (или на нем существует) упорядоченность. Очевидно также, что всякое непустое подмножество вполне упорядоченного множества тоже вполне упорядочено. Примером невполне упорядоченного множества служит отрезок [0, 1]. Хотя это множество имеет наименьший (первый) элемент — число ноль, но у него есть подмножества, у которых нет первого элемента. Например, таким подмножеством является совокупность всех строго положительных чисел на отрезке [0, 1].
Введем еще несколько полезных понятий.
Определение 6. Верхняя грань подмножества В частично упорядоченного множества А (В с. А) — это элемент а е А, которому подчинены все элементы В.
Ясно, что подмножество В может иметь много верхних граней. Но если среди всевозможных таких верхних граней существует наименьшая, то она называется точной верхней гранью подмножества В. Аналогично можно ввести понятия нижняя грань подмножества В и точная нижняя грань подмножества В. Нетрудно показать, что точные верхняя и нижняя грани, если они существуют вместе или в отдельности для данного В, единственны.
Определение 7. Решетка — это частично упорядоченное множество, у которого любое его конечное непустое подмножество имеет точную верхнюю и точную нижнюю грани.
Заметим, что вместо термина решетка употребляется иногда термин структура. В этом смысле термин структура мы не будем употреблять, ибо он зарезервирован для более общего понятия. Фундаментальное значение для математики и теории управления играют следующие равносильные утверждения.
136
| Теорема 5 (Цермело). Всякое множество можно вполне упорядочить.
Теорема 6 (Куратовского — Цорна; лемма Цорна). Если всякая цепь частично упорядоченного множества обладает верхней гранью, то всякий элемент этого частично упорядоченного множества подчинен некоторому максимальному элементу этого множества.
А1 = А х А
А
Р и с. 2 7 3
Эти теоремы не только равносильны, но и эквивалентны аксиоме Цермело.
Наконец, заметим, что графически отношение частичного порядка легко получить из отношения эквивалентности, и обратно, ибо они отличаются лишь одной аксиомой. Для отношения эквивалентности — это аксиома симметрии: если {а, Ъ) е Е, то и (b, а) е Е, а для отношения порядка — это аксиома антисимметрии: если (a, b) е Е, то (b, а) "е Е. Графически отношение порядка представлено на рис. 2.7.3. Заштрихованное множество соответствует отношению частичного порядка. Пунктирное добавление описывает множество, соответствующее эквива
лентности. Здесь {Л,} — непересекающиеся классы сравнимых элементов из А, на которые разбивается А.
2.8.	ОТНОШЕНИЕ ТОЛЕРАНТНОСТИ (БЛИЗОСТИ)
Это отношение имеет много приложений, в частности в теории выбора, что очень тесно связано с теорией управления. Толерантность — это общность, сходство, близость, похожесть. Два объекта толерантны, если имеют какие-то общие признаки, делающие их похожими, близкими в каком-то смысле.
Определение 1. Отношение толерантности — это бинарное отноше-
ние Е, т.е. подмножество Е с/, удовлетворяющее двум аксиомам:
1)	(а, а) е Е для Vn е Е — аксиома рефлексивности, т.е. диагональ квадрата А2 принадлежит Е;
2)	если (a, b) е Е, то (b, a) е Е — аксиома симметричности.
Из определения видно, что отношение эквивалентности есть частный случай отношения толерантности, ибо здесь отсутствует требование .аксиомы транзитивности. Эквивалентность — более жесткое отношение, так как оно производит разбиение на классы эквивалентно
137
сти. Толерантность также описывает некоторые классы близости, но в отличие от классов эквивалентности они не образуют разбиение исходного множества.
Примеры толерантности:
1)	два автомобиля одной и той же марки, но разных модификаций;
2)	два брата-близнеца;
3)	две точки (xi и х2) на интервале [а, Ь\, если и только если |%i -х2|
4)	отношение парного знакомства;
5)	две точки (а и &) в пространстве, если и только если расстояние между ними р(а, Ь) < е;
6)	совпадение некоторых внешних признаков двух людей (цвет волос и глаз, наличие общих родственников и т.д.);
7)	субъективные мнения различных экспертов или наблюдателей (свидетелей), например, разные мнения о том, что такое “молодой человек”.
Интересно сравнить отношение толерантности с понятием размытого множества (см. подразд. 2.9). Графически отношение толерантности в множестве А описывается произвольным подмножеством квадрата А2 = А х А, но таким, что: 1) ему обязательно принадлежит диагональ квадрата А2, т.е. все элементы А2 вида (а, а) для Va е А, и 2) это подмножество должно быть симметричным относительно диагонали квадрата А2.
Отметим, что отношение толерантности “несет ответственность” за такое явление, когда накопление небольших, подчас очень маленьких, незаметных, неощутимых изменений дает совершенно неожиданные результаты, например, приводящие к полному перерождению исходного объекта вплоть до превращения его в свою противоположность, часто имеющую негативный характер. Такой эффект можно назвать эффектом интегратора, или ползучего переворота. Изменения могут быть незаметными, что “усыпляет бдительность”, а когда “интеграл” изменений стал заметным, то “принимать меры” к стабилизации уже поздно.
Например, в последовательности слов fish—bish—bist—birt—bird два соседних слова отличаются “мало”, всего на одну букву. Однако накопление этих малых изменений довольно быстро, всего за четыре шага изменяет смысл до неузнаваемости: “рыба” превратилась в “птицу”. В политике, например, так происходит “ползучая” агрессия, полная переориентация политического или социального курса и многое другое.
Если в отношении эквивалентности границы между классами эквивалентности очень резкие (происходит скачок в свойствах различимости элементов исследуемого множества объектов), то в отношении то
138
лерантности резкую границу между разными классами провести трудно. В искусстве проявление отношения толерантности можно увидеть на известной гравюре М.К. Эшера “Небо и вода”.
Нетрудно проверить, что следующее утверждение равносильно характеризует отношение толерантности, данное выше.
Рассмотрим абстрактное множество X и множество всех его подмножеств {X}, а из {X} — два его элемента а и b — два подмножества из множества X. Тогда элементы а и b находятся в отношении толерантности, если их пересечение (как подмножеств множества X) не пусто, т.е. ar\b^ 0.
Нетрудно проверить, что обе аксиомы толерантности здесь выполнены.
Классы толерантности даются следующим определением.
Определение 2. Отношение толерантности Т на данном множестве Л — это покрытие множества А, т.е. семейство {т} непустых подмножеств т множества А, т g А, таких, что (Jт = А . те{т)
Класс т толерантности Т на множестве А — это любое подмножество т g {т}, где {т} покрытие А. Два элемента ах g А и а2 & А находятся в отношении толерантности, если и только если <71 е Т| иа2 е т2, где т, ит2 пересекающиеся классы толерантности, т.е. Т] п т2 * 0.
На рис. 2.8.1 изображено только четыре класса толерантности Т на А из всего множества классов {т} толерантности, покрывающих А. Здесь О] и а2, а2 и а2 находятся в отноше-нии толерантности, но ах и а2 уже не на- 0х ходится в отношении толерантности, ибо /	•	\
отношение толерантности, вообще гово- I v£lz-	\
ря, не транзитивно, хотя, в частности, \	/
может оказаться транзитивным, но тогда	viz z^
оно станет не просто толерантностью, а	--------
гораздо более жестким отношением —	р и с 2 8 1
отношением эквивалентности. Элемент
аА не толерантен ни одному из ах, а2, а2.
2.9.	РАЗМЫТЫЕ МНОЖЕСТВА
Отношение толерантности конкурирует с понятием размытого множества, когда нет однозначной границы между классами сходных (похожих) элементов, которые не образуют разбиения множества А. 11оэтому имеет смысл дать краткое описание некоторой математической структуры, которая называется размытым множеством.
139
На самом деле, как мы здесь увидим, размытое множество — это вовсе не множество в точном смысле этого понятия, а именно некоторая структура, характеризующаяся определенного вида отображением. Эта структура была введена Л. Заде в 1965 г. в одной из статей журнала “Information and Control”. Дело в том, что в понятии множество, обозначим его А, факт принадлежности элемента а с А —- очень “резкий” факт: или а е А, или а А, причем третьего не дано, как и должно быть в классической логике, где всякий факт, “облаченный” в высказывание, имеет двоичное и только двоичное значение истинности: “верно” и “неверно”. При этом никаких промежуточных “степеней” этого факта не рассматривается.
Однако сплошь и рядом имеют место высказывания, истинность которых не может быть установлена так резко однозначно: “да” или “нет”. Для них истина относительна и зависит от мнения того, кто оценивает этот факт, т.е. от эксперта. Например, высказывание “Иванов — молодой человек” будет истинным или ложным в зависимости от возраста эксперта: для одних — это верно, а для других — это неверно.
Здесь есть соблазн использовать хорошо установленное понятие вероятность. Однако высказыванию “Иванов — молодой человек” с вероятностью 28% трудно придать однозначный смысл.
Аналогичная ситуация возникает очень часто, когда мы пользуемся плохо определенными дополнительными понятиями типа “большой— маленький”, “холодный—горячий”, “сильный—слабый”, “много—-мало”, “волна—частица” и др.
Таким образом, надо предложить другое понятие: что-то вроде “взвешенного членства”, но отличное от понятия вероятность членства, которое часто трудно корректно описать или оценить. Предлагается следующее понятие.
Определение 1. Размытое множество А в множестве 5 — это отображение а вида а : S -> [0, 1 ], где [0, 1] — отрезок действительных чисел.
Здесь “размытое множество А” надо понимать как один нерасчле-няемый термин, ибо “размытое множество” — это вовсе никакое не множество, а указанное отображение (функция) а.
Функция ос называется характеристической функцией членства элементов s е S. Элементы 5 принадлежат множеству >5 в обычном смысле отношения принадлежности (членства). Однако, кроме этого, вводится функция а, которая показывает степень этого членства (принадлежности). Таким образом, здесь все происходит, как по Орвилу: “Все животные равны между собой, но некоторые из них — равнее”.
140
Функция сс определяет на S' некоторое отношение порядка, разбивая S на классы порядка (порядковые классы), вводя, так сказать, “классовое общество” на множестве S' элементов s g S'. При этом в один класс попадают те и только те элементы 5 е 5, которые лежат на одном и том же множестве уровня {х g 5 : ot(x) = const}. Естественно считать, что элемент 5] “более низкого класса”, чем з2, если a(5i) < а(52)-
Итак, “размытое множество” — это не более того, чем просто еще одна структура, или пространство, задаваемое парой {S', ot}, где S' — основное множество; ot — структурное отображение.
Важность структуры “размытых множеств” как важность всякой точно построенной структуры в математике определяется эффективностью ее приложений как внутри самой математики, так и для решения “реальных” задач. В конце этого подраздела мы приведем один простой пример такого приложения [29, с. 29].
Очевидно, что На одном и том же фиксированном основном множестве S можно ввести различные размытые множества, каждое из которых задается своей характеристической функцией членства. Выясняется, что на совокупности размытых множеств можно ввести “исчисление”, т.е. операции с размытыми множествами, наподобие исчисления обычных множеств с операциями их сложения (объединения), умножения (пересечения) и т.д. [29]-.
Рассмотрим ряд операций с размытыми множествами на фиксированной основном множестве S’.
Определение 2. Пусть на множестве S даны два размытых множе-
ства сс(х) и р(х), Vx е S. Тогда:
1)	их суммой (объединением') называется размытое множество, обозначаемое сори задаваемое равенством
ос up = max (сс(х), р(х)), Vx g S;
2)	аналогично произведение (пересечение)
а. гф = min (ot(x), Р(х)), Vx g S;
3)	дополнение ct(x) = 1 - a(x), Vx g S';
4)	можно ввести бинарное отношение включения: размытое включение а с р, если а(х) < Р(х) для Vx g S.
Проверьте, какие стандартные свойства введенных операций “1”, “2”, “3” — коммутативности, ассоциативности, дистрибутивности — выполняются? К какому типу отношений можно отнести отношение, определяемое указанным выше включением отношений ot ст р?
Как покажет пример, приведенный ниже, полезно ввести следующее понятие.
141
Определение 3. Е-размытое множество на .S' — это функция
11, если р(х,Е,ос) =
10, если
а(х) - е ос(х) < Е
Таким образом, е-размытое множество на .8 ставится в однозначное соответствие каждому размытому множеству а на S по указанной в определении формуле. В свою очередь е-размытое множество на «S’, порожденное данным размытым множеством а, однозначно определяет подмножество A с .S’по формуле А = {х е S : а(х) < е}.
При этом |т(л, 8, а) играет роль обычной характеристической функции множества/!. Эти определения проиллюстрированы на рис. 2.9.1.
3.	ОСНОВНЫЕ СТРУКТУРЫ МАТЕМАТИЧЕСКОЙ ЛОГИКИ
3.1.	ПРОСТРАНСТВО ВЫСКАЗЫВАНИЙ
Напомним, что логика изучает формы смысла. У человека важнейшим средством выражения смысла служат естественные языки. Большинство естественных языков состоят из набора слов и предложений. Предложение естественного языка — это набор слов естественного языка, удовлетворяющих определенным правилам. Предложение выражает законченную мысль, которая должна быть понятна определенному кругу лиц. Из множества предложений естественного языка можно выделить три их разновидности: утвердительные, повелительные и вопросительные. Есть и другие разновидности.
В теории высказываний изучают утвердительные предложения, которые называются высказываниями, утверждениями или предложениями. В теории алгоритмов используются повелительные предложения — команды: сложи, умножь, подставь, перейди к следующему действию и т.д. Отметим, что в творческом процессе, как говорилось в разд. 1, часто используются вопросительные предложения.
Итак, в классической логике высказывания — это любые утвердительные предложения, необязательно простые, которые обладают следующими свойствами.
1.	Из них можно образовать новые высказывания путем следующих операций:
а)	отрицание данного высказывания А с помощью частиц типа “не” с обозначением А\
б)	конъюнкция двух и более высказываний А, В с помощью союза “и”, с обозначением А л В ;
в)	дизъюнкция двух и более высказываний с помощью союза “или” с обозначением Av В;
г)	импликация двух высказываний с помощью союза “если..., то...” с обозначением А -> В\
д)	эквиваленция двух высказываний с помощью союза “..., если и только если...” с обозначением А <-> В .
143
2.	Единственный смысл каждого высказывания сосюит в том, что ему приписывается одно и только одно значение истинности из двух возможных {верно, неверно}, что иногда обозначается {истина, ложь}, {И, Л}, {да, нет}, {1,0}, {+, -} (возможны и другие обозначения).
Возникает вопрос, по каким правилам приписывать одно из двух значений истинности данному составному высказыванию в зависимости от одного из двух значений истинности для его составляющих высказываний? Нетрудно понять, что естественно принять правила, сведенные в таблицу (рис. 3.1.1).
Высказывания, полученные с помощью приведенных выше пяти операций (Л , А/\В , Av В, А —> В, А<ч> В) будем называть элементарными составными высказываниями. Путем повторного применения операций можно получить новые, более сложные высказывания. Ясно, что сложное высказывание, в силу того, что оно тоже высказывание, имеет определенное значение истинности, которое может быть “вычислено” (рис. 3.1.1) в зависимости (как функция) от значений истинности ее “аргументов” Л, В и т.д.
А	А	в	А лВ	Av В	А^>В	Av» В	а\в
Л	И	И	И	И	И	И	л
Л	И	л	Л	И	Л	Л	И
И	Л	И	л	И	И	Л	И
И	л	л	л	Л	л	И	И
Р и с. 3.1.1
Иными словами, можно рассматривать следующее огображение: f'.En-+E, е = f{ex,...,e„),
где е, е Е, i = 1, ...-, н; е g Е; Е — “множество” высказываний. От функции/надо “потребовать”, чтобы выполнялось условие
t{f(ei,...,e„}') = B(t{el},...,t{e„)}, Че, &Е,
где t - t{e), е g E,t g {И, Л} — функция истинности высказываний, и должна существовать функция В = B(tx, ..., tn):
в-.{и,л}п ->{и,л}.
Функцию/(ёч, ..., е„) называют логическим выражением {формой или формулой). Функцию В называют булевой функцией.
Отметим важное понятие тождественно истинной формулы, или тавтологии, как формулы, принимающей только истинное значение при любых значениях истинности ее аргументов. Например, A v А — тождественно истинное высказывание (тавтология).
144
Понятие тавтология может быть выражено через понятие равносильность. Однако изначально равносильность — это понятие не теории высказываний, а теории отношений. Равносильность — это бинарное отношение эквивалентности (равенства) на множестве высказываний.
Говорят, что две формулы/ nf2 логики высказываний равносильны, что обозначается/ =/, если эквиваленция как формула высказывания “/ о Л” есть тавтология, и обратно. Подчеркнем еще раз, что выражение / = f2, т.е. равенство, не есть выражение теории высказываний, а является выражением метаязыка, в данном случае языка теории отношений (предикатов).
В логике часто используются следующие “стандартные” равносильности: А = А (закон тождества), т.е. формула логики высказываний “А <-> Л” — тавтология. Аналогично имеем: АлА =Л — равносильность (закон); A v А = И — закон исключенного третьего; A v А - А, А л А = А — закон идемпотентности; А л В - В л A, Av В = Bv А — законы коммутативности; (А л В) л С = А л (В л С), (A v В) v С = = Av(BvC) — законы ассоциативности; Ал(ВуС) = (АлВ^(АлС), Av (В л С) = (Av В) л (Av С) — законы дистрибутивности; наконец, законы двойственности де-Моргана А л В = A v В, Av В = А л В . Комбинируя эти законы, можно получать неограниченное количество все более сложных тождеств (тавтологий), и обратно, добиваться упрощения сложных тождеств (тавтологий).
Одно из важнейших применений понятий тождественно истинной эквиваленции, т.е. тавтологии и равносильности, — это образование с их помощью новых понятий по определению, которые пополняют специальный язык (субязык) новыми словами — терминами, делая выражения на этом языке короче. Например, если А — “квадрат” (“квадрат есть квадрат”, очевидно, истинно по закону тождества), а В — “прямоугольник с равными сторонами”, то указанные выражения есть определение квадрата, делающее слово квадрат равноправным термином математики и более коротким, чем В.
Таким образом, здесь идет речь о специальной структуризации сложного высказывания, определения его в виде “Л о В”. Как только мы имеем “А <-> В”, всегда можно одно из А и В принять за определение другого, введя короткий термин для обозначения одного из них. Естественно, то же самое можно делать на языке отношений (предикатов), используя отношение равносильности (эквивалентности или равенства).
Введем еще естественное понятие логического следования.
145
(Определение 1. Формула В(хь %„) есть логическое следствие формулы Л(хь х„), что обозначается А => В, если В имеет значение истинно на всех х}, .<.,х„, для которых А истинно.
Можно показать, что А => В, если и только если формула А —> В тавтология, т.е. тождественно истинная формула, иными словами, А => В и А -> В — тавтологии, имеющие один и тот же смысл, но выраженный на разных языках: языке отношений и языке высказываний.
Также нетрудно показать, что А В или А ~ В, если и только если вместе А В и В А, что означает тождественную истинность (тавтологию) формулы логики высказываний: (А -> В) л {В —> А).
Сформулируем теперь понятие высказываний в сжатой форме.
Пространство высказываний — это пара (Е, С), где Е — произвольное непустое множество, состоящее как минимум из двух элементов, которые называются высказываниями, С — это совокупность структурных отображений', С = (С), С2, С3, С4, С5), где:
1)	С| '.Е—> Е — нульарное отображение (операция), дающее константу И, называемую истинной',
2)	С2 : Е —> Е — нульарное отображение (операция), дающее константу Л, называемую ложной',
3)	С3 : Е —> Е — унарное отображение (операция), называемая отрицанием и обозначаемая и(б) или ё со свойством ё = е для Ve е Е (закон двойного отрицания);
4)	С4 : Ег —> Е — бинарное отображение (операция), называемая дизъюнкцией, или логическим умножением, обозначаемая е} л е2, со свойствами: е} ле2 = б2 л б! — коммутативности для Vei е Е и Уб2 G Е\ (е\ л е2) л е3 = в] л (е2 л е3) — ассоциативности; et л е{ = et — идемпотентности;
5)	С5 : £2 —> Е — бинарное отображение (операция), обозначаемая 6i v е2 и называемая конъюнкцией, или логическим сложением, со свойствами (аналогичными дизъюнкции): в] V62 = e2 V6j — коммутативности; (б1 v б2) v б3 = 6i v (б2 v в3) — ассоциативности; et v et = 6t — идемпотентности. Для этих операций должны выполняться аксиомы, которые можно толковать как свойства согласованности разных операций (структурных отображений):
дистрибутивность —
(61 V б2 ) Л б3 = (б1 А 63 ) V (б2 А б3 ),
(б! а б2) V бз = (61 V е3) а (е2 V б3);
146
поглощение —
6] v (ei ле2) = е,, е1 л (<?! v е2) = в];
двойственность (законы де-Моргана) —
б! л е2 = ej v ё2,
е( v е2 = ё] л ё2;
е л И = е, е v Л = е, е л Л — Л, е v И = И.
В математике пространство высказываний, рассматриваемое абстрактно, т.е. безотносительно к смыслу элементов основного множества Е (т.е. е — это необязательно высказывание), называется пространством Буля, или алгеброй Буля. Таким образом, алгебра Буля рассматривается как представитель большого класса пространств (категорий), называемых алгебраическими пространствами, или алгебраическими системами.
Из определения пространства высказываний следует, что Е состоит не менее чем из двух элементов, так как в него входят И и Л, а если Е — конечное множество, то оно должно состоять из четного числа элементов 2N и допускать разбиение на два равномощных подмножества высказываний, одно из которых составляет класс И всех истинных высказываний, а другое — класс Л всех ложных высказываний.
Пространство высказываний, а следовательно, всякое булево пространство допускает по крайней мере две реализации (представления, модели): одна — теоретико-числовая, другая — теоретикомножественная. При этом обе реализации могут быть минимальными в том смысле, что Е состоит всего из двух элементов: {И, Л}.
Минимальная теоретико-числовая реализация осуществляется, если положить Е = {0, 1}, где 0 и 1 — обычные числа. Операция логического сложения осуществляется как обычное сложение, но по модулю “2”, т.е. 0v0 = 0 + 0 = 0, Ovl = 0 + 1 = 1, l+l=lvl=0; логического умножения — как обычное числовое умножение; операция отрицан ия определяется так: 0 = 1, 1=0. Тогда легко проверить, что такое пространство есть действительно булева алгебра, а в частности может служить моделью, реализацией или представлением соответствующего пространства высказываний.
Для любого булевого пространства существует гомоморфизм в минимальное булево пространство, т.е. отображение Е —> {0, 1}, сохраняющее все операции со всеми их свойствами. Такой гомоморфизм осуществляет, например, функция истинности t(e), е& E,t е {0, 1}.
147
Теоретико-множественную реализацию булева пространства можно установить посредством отображения биекции Е Т, где, Т — совокупность подмножеств некоторого множества X (например, совокупность {X} всех подмножеств множества X). При этом операциям отрицания, логического умножения и сложения соответствуют теоретикомножественные операции дополнения, умножения и сложения множеств. В этом случае говорят об изоморфизме пространства высказываний и теоретико-множественного пространства. Изоморфизм — это частный случай гомоморфизма, когда отображение Е -> Т есть биекция.
Заметим, что формула импликации А -> В будет тавтологией, если и только если подмножество, соответствующее А, будет подмножеством подмножества, соответствующего В
Операция “Л «-> 5” будет тождественно истинной, т.е. высказывания А и В равносильны, А <=х> В или А = В, когда подмножества, соответствующие А и В, совпадают, т.е. равны в теоретико-множественном смысле термина равны.
Для “логической замкнутости” описания пространства высказываний, его терминов и понятий нужно еще коснуться понятия представления формул в пространстве высказываний. Это нужно для того, чтобы в конце рассмотреть и решить центральную проблему для любого пространства высказываний — проблему распознания тождественной истинности любой предъявленной формулы (функции). Дело в том, что для открытия и описания все более сложных и глубоких свойств какой-нибудь конкретной реальности, нам приходится строить подчас очень сложные высказывания, записываемые (представляемые) сложнейшими формулами. Собственно говоря, такая сложная формула и представляет собой описание и выражение истинности наших знаний о той или иной реальности, в частности законов природы.
Формально дело обстоит так. Все наши утверждения, например в математике, могут в конечном счете быть представлены в единой форме: в виде высказываний “А —> В” или “ А <-> В ”.
Знания заключены в том, что формулы А —> В и А <-> В тождественно истинны, или тавтологии. В этом смысле, в частности, можно говорить, что вся математика основана на тождествах. В каждой ее дисциплине существуют характерные для нее тождества, определяющие эту дисциплину и отличающую ее от других дисциплин. Такие тождества можно назвать предметно-определенными тождествами. Предметно-определенным тождеством является, например, с этой точки зрения закон Ньютона F = та в механике движения массивных тел. С этой же точки зрения, в частности, пространство высказываний тоже
148
есть конкретная предметная область, описывающая некоторые свойства реальности, называемой естественным языком — средством выражения смысла (свойства) всяких других реальностей.
Поскольку вся наша цивилизация и культура основана прежде всего на естественных языках, служащих для выражения смысла окружающих нас реали й, то пространство высказываний должно б ыть “оболочкой”, или “скрепляющим цементом”, для всех остальных конкретных пространств, описывающих другие свойства других реалий. Само пространство высказываний, являясь особым и в определенном смысле главным среди других пространств (структур и систем), все же подвергается дальнейшему изучению или, как мы говорим, детривиализации, результатом которой будет более сложное пространство — пространство предикатов. Появление пространства предикатов аналогично появлению функциональных пространств.
Рассмотрим один важный конкретный вопрос, связанный с пространством высказываний. Дело в том, что в вышеприведенной формулировке определения пространства высказываний использовано только пять операций: истина, ложь, А л В, A v В и А . В то же время, как мы видели, в конечном счете важны лишь две операции и соответствующие им формулы, построенные только в терминах этих операций: А —> В и А <-> В.
Замечательным фактом теории высказываний является то, чго имеют место равносильности (эквивалентности):
А-^> В - A v В = А а В\
А ++ В = (А В) л (В А) = (A v В) л (Av В).
Более того, выясняется, что любую операцию можно выразить (в виде равносильности) всего лишь через две операции, например: 1) отрицание и логическое умножение или 2) отрицание и логическое сложение. Пример:
AaB = AvB, AvB = AaB.
Оказывается, что существует одна единственная бинарная операция — штрих Шеффера, обозначаемая х\у (см. рис. 3.1.1), через которую можно выразить все операции:
Ла£ = 7|£, AvB = A\B, А^В = А\В, Л^5 = (Л|5)|(В|Л).
Штрих Шеффера А\В формализует смысл сложного союза — “или не Л, или не 5”, где “или” — неразделительный союз.
149
Теперь нетрудно установить, что любую формулуХ^ь •••, хп), х е Еп можно равносильно представить в виде так называемой нормальной формы, имеющей “канонический” вид:
/(*!,...,)=/(1,1,..., 1,1) A Aj А...АХ„ V

1,0)	А... АЛ„ V
V /(1,1,...,0,1) Л Xt A...AX„_y АХ„ V
v /(0,0,...,0,0)лТ] л...лх„.	(3.1.1)
Правая часть этой формулы есть конъюнкция дизъюнктивных членов (поэтому формула еще называется дизъюнкт иеной нормальной формулой) или, другими словами, это логическая сумма логических произведений.
Эту формулу можно записать еще короче, используя обозначения и правила “суммирования”, навеянные правилами тензорного исчисления. А именно, предыдущая формула коротко записывается так:
/W = {U/(51,...,5„) ах,5' а...ахй8" :S,. g {0,1} = {И,Я},
г = 1,...,«},	(3-1-2)
где 5, при каждом i = 1, ..., п принимает значения из двухэлементного множества {И,Л}, обозначаемого еще {1, 0}:
если
если
5,- = Я1	(xi}
5,- = Л J	(xf,
В (3.1.3) мы “заодно” определили еще бится в (3.1.4).
если е, = Л если 8(- = И символ Е/, который понадо-
(3-1.3)
Каждый член логической суммы в (3.1.1) и (3.1.2) соответствует
значению упорядоченного набора (конечной последовательности) 5Ь ..., 5„. Таких наборов всего 2". Столько же, 2", различных логических функций (формул), зависящих от п логических переменных хь ..., хп,
каждая из которых принимает только два значения.
Здесь величины/51, ..., 5Л) могут быть найдены, если / задана своей таблицей истинности, т.е. обычным заданием значений функции в виде таблицы, когда аргументы х1} ..., хп “пробегают” все свои значения. Ясно, что в нашем случае эта таблица будет конечной. Это существенно, так как далеко не всякую функцию можно задать конечной таблицей. Это существенное положительное свойство логических функций (формул) — конечность их таблиц. Однако это положительное свойство омрачается тем, что конечная величина 2" очень быстро
150
растет с ростом числа переменных п и даже при небольшом п становится очень большой: 2Л» 1 и 2"» п.
Отметим еще, что “двойственным образом”, используя законы логической двойственности (де Моргана), формулу (3.1.1) можно равносильно записать в виде нормальной конъюнктивной формы, т.е. в виде логического произведения логических сумм:
/(*) = {ГШ1> >	v...vxn6" :efi=^...,n}.	(3.1.4)
Здесь в,- — знак, как указано в (3.1.3), двойственный 5,-, т.е.
5< = е,, е, = 5, для Vi = 1, ..., п. Такое представление может оказаться проще дизъюнктивного.
По аналогии с обозначениями тензорного исчисления формулу (3.1.4) можно записать еще короче, опуская знаки общего суммирования (общего произведения):
/W = A...5n xf' =/Е1...Еп *Г ...4",
где суммирование (перемножение) происходит по всем парам индексов, один — наверху, другой — внизу, а символы е и 5 различают суммирование и умножение.
Формулы (3.1.1)—(3.1.4) показывают, что тождественную истинность любой данной логической формулы можно проверить, просто составив таблицу истинности для этой формулы.
Хотя в принципе, в силу конечности таблицы, это всегда можно сделать, однако, с другой стороны, практическое составление этой таблицы, что требует около 2” операций, может оказаться не осуществимым из-за огромной величины 2". В этом смысле нормальные формы в принципе могут сократить “тупой табличный перебор”, если некоторые члены нормальной формы просто будут отсутствовать. Как было показано выше, независимость есть проявление симметрии. Таким образом, приведение или запись данной формулы в ее нормальном виде с этой точки зрения означает способ выявления симметрий данной формы.
Дизъюнктивная нормальная форма выявляет независимость f от “нулевых” слагаемых в сумме, тогда как конъюнктивная нормальная форма выявляет “единичные” сомножители.
Иными словами, здесь для выявления симметрии f используется “двойственность”. В частности, переход от проверки (доказательства) тождественной истинности к проверке тождественной ложности может оказаться существенно проще.
Понятие (категория) пространства высказываний дает возможность построить еще одно понятие или структуру — структуру логического вывода.
151
Логический вывод обосновывает (доказывает) наши умозаключения, которые априори неочевидны, точно так же, как априори неочевидна тождественная истинность той или иной предъявленной формулы или, что то же самое, но на другом языке, как неочевидна равносильность двух предъявленных формул.
Конечно, например, выяснить равносильность двух предъявленных формул, т.е. доказать равенство (тождество)
/1(Х1, ..., x„) = /2(xi,	х„), хе Еп,
в принципе всегда можно с помощью таблиц истинности для / и/2. Однако такое доказательство, как говорилось выше, может оказаться практически неосуществимым из-за огромной величины 2" числа операций по составлению этих таблиц. Поэтому и стали искать альтернативный табличному способ задания логической функции, способствующий явному выявлению их симметрий. Конечно, симметрии можно распознать, “глядя” на уже готовую таблицу, но, во-первых, это будет уже априори, а, во-вторых, это пример пока еще плохо формализованной общей фундаментальной проблемы распознавания образов.
Точно такая же ситуация имеет место и в проблеме обоснования (доказательства или вывода) данной формулы с помощью других данных формул или равносильностей. Задачи такого рода в логике совершенно аналогичны задачам вывода формул и тождеств, скажем, в обычной “школьной” алгебре.
Только в логике высказываний делается предельное обобщение “операции” вывода, пригодное для любых выводов, доказательств и обобщений, что отражает общую способность (свойство) разума что-то доказывать, обосновывать, выводить с помощью формул, не прибегая к часто дорогостоящему эксперименту. Этот факт отражает важнейшую суть и смысл любой науки — опыт заменять рассуждениями, сделанными по точно определенным правилам или, по крайней мере, без нарушения этих правил. Поэтому структура высказываний — это важнейшая структура, открытая человечеством и осмыслявшаяся на протяжении более 2000 лет, начиная от Аристотеля.
Итак, укажем, как в логике высказываний делается обоснование, доказательство или вывод данной тождественно истинной формулы (тавтологии). Удобнее (короче) говорить именно об обосновании тавтологии, т.е. говорить на языке самой теории высказываний, а не пользоваться эквивалентной терминологией “равенства (равносильности) формул”, вообще говоря, относящейся к теории предикатов (отношений). Тавтологию еще называют теоремой.
Отсюда видно, что вся математика основывается на тождествах, которые характеризуют ту или иную математическую структуру. Этим
152
обосновывается взгляд на математику как науку о тождествах и уравнениях. В каждой математической дисциплине имеются свои основополагающие нетривиальные тождества, называемые структурными тождествами. Верно и обратное: всякое нетривиальное тождество, полученное детривиализацией какого-либо тривиального тождества, например, 0 = 0, дает начало соответствующей структуре.
Вывод (доказательство) в теории высказываний определяется как некоторые правила преобразования одной тавтологии в другую. Иными словами, речь идет о преобразованиях симметрии, сохраняющих тавтологию, т.е. о структуре формулы, обеспечивающей ее тождественную истинность.
Оказывается, что такие преобразования действительно существуют, правда, как аксиоматические правила преобразования формул, справедливость которых предсказывает наш опыт. Таких правил всего два:
1) правило подстановки, которое гласит, что если вместо любой переменной х,- в тавтологии fixx, ..., Х[, ..., х„) подставить тавтологию ср(лг], ..., Хп), то в результате такой композиции получится новая тавто-логияДль ..., <р(х1, ...,Хп), ...,Хп);
2) правило “modus ponens”, которое гласит, что если формулы /и /-> <р обе вместе есть тавтологии, то и формула <р — тавтология.
Имея какой-то набор тавтологий /,/, -^fn, вообще говоря, бесконечный, и используя в произвольном линейном порядке всего два указанных выше правила, можно получить какие-то новые тавтологические формулы, в том числе, возможно, и не входящие в исходный набор {/}. Иными словами, таким способом можно получать “цепочки”-последовательности различных тавтологий ср0, <р15 ..., <ри, ... различной длины — как конечной, так и бесконечной, вообще говоря. Назовем такую цепочку допустимой для набора {/}.
Теперь ясно, что естественно считать данную тавтологию/обоснованной (доказанной, выводимой), если существуют: 1) набор данных тавтологий {/} и 2) допустимая цепочка вида (р0, <Pi, •••, <pn-i, /, где/— последний член этой последовательности, причем естественно предъявить существенное требование: п — конечное число, п е N. Такую цепочку назовем допустимой для f в данном исходном наборе {/}.
В теории высказываний имеет место следующий замечательный и нетривиальный факт, впервые доказанный Э. Постом в 1921 г. Его смысл состоит в том, что существует конечное (!) множество тавтологий {/1,	такое, что любая (!) тавтология/имеет свою допустимую
цепочку, построенную из данного набора. Замечательно то, что для любой тавтологии существуют конечный набор и конечная цепочка, которая и называется доказательством или выводом
153
Факт, установленный этой теоремой, что можно доказать любую тавтологию, называется полнотой “исчисления” высказываний. Другими словами, в этой “теории” недоказуемых формул быть не может.
Естественно возникает вопрос: как велико универсальное множество {fi}, из которого можно вывести все тождественно истинные формулы? Оказывается, что его мощность невелика. Например, существует набор, предложенный Гильбертом и Бернсайдом, состоящий всего из 15 несложных тавтологий, включая, например, х —> х, (xj ах2) —> Xi, Xi —> (х2 —> ху) и др. Этот набор {//} не единственный, можно указать и меньшие наборы, достаточные для любого вывода. Можно указать набор {fi} из значительно меньшего числа тавтологий, который также достаточен для вывода любой тавтологии [197, с. 49].
Тавтологии f из {f} называются аксиомами исчисления высказываний.
Кроме проблемы полноты набора аксиом, которая решается теоремой Поста и указанием конкретных наборов аксиом, ее обеспечивающих, существуют и другие проблемы, связанные с набором аксиом.
Проблема независимости аксиом состоит в указании такого полного набора аксиом, что никакая аксиома не выводима из остальных.
Проблема непротиворечивости набора аксиом состоит в том, чтобы из него не получились бы допустимые цепочки, для которых тавтологиями оказались вместе и А, и А .
Проблема разрешимости состоит в указании “массового алгоритма”, т.е. недвусмысленного правила построения допустимой цепочки для любой тавтологии.
Оказывается, что такой алгоритм всегда существует. Иными словами, проблема разрешимости исчисления высказываний всегда разрешима. Другое дело, как найти такой алгоритм явно, да к тому же еще “минимальной” сложности. Последняя задача своего полного разрешения еще не получила. Эта проблема имеет важное практическое значение для построения релейно-контактных и вообще технических вычислительных схем (hardware), реализующих наперед заданные тавтологии. С этой точки зрения, например, всякая цифровая вычислительная машина — это релейно-контактная схема.
Отметим, что в силу того, что предикат при фиксированном значении предметной переменной является высказыванием, то для него можно определить понятие, аналогичное понятию тавтологии, которое называется общезначимостью.
Однако в отличие от исчисления высказываний проверить общезначимость предикатной формулы так, как это, по сути, делается для вы-сказывательных форм, не представляется возможным в силу возмож
154
ной бесконечности предметных областей определения предикатов. Осу ществить перебор всех элементов бесконечного множества, осуществляя проверку какого-то свойства, даже в принципе невозможно. Этот факт еще раз показывает “пропасть” между “конечным” и “бесконечным”. В 1936 г. А. Черч доказал теорему о том, что проблема разрешимости предикатов (в отличие от разрешимости высказываний) алгоритмически неразрешима, т.е. не существует универсального алгоритма вывода общезначимых предикатных формул.
Конечно, это не означает отсутствие таких алгоритмов в частных случаях. Например, нетрудно установить разрешимость предикатных формул в случае, когда их предметная область конечна. Тогда квантор-ные операции в формулах можно заменить конечным числом операций дизъюнкций и конъюнкций для высказываний. Тем самым логика предикатов просто сводится к логике высказываний, где проблема тавтологий алгоритмически разрешима. Есть и другие частные случаи, когда проблема разрешимости для предикатов разрешима [197, с. 104].
Упомянутая теорема А. Черча об алгоритмической неразрешимости дала отрицательный ответ на вопрос Д. Гильберта о том, чтобы найти универсальный алгоритм, проверяющий или доказывающий общезначимость предикатных формул, т.е. проверяющих истинность или доказывающих все или почти все теоремы математики.
Сделаем еще такое важное замечание. Фактически в математической логике высказываний мы рассмотрели две, строго говоря, различные структуры: 1) пространство алгебры высказываний и 2) пространство исчисления высказываний. Однако, по сути дела, это два разных языка с разными словами, описывающие одну и ту же суть — логику высказываний. В одном мы говорим об “алгебре”, в другом — об “исчислении” высказываний. Но даже и слова в них тоже почти одинаковые: в обоих пространствах говорят о “формулах” и “формах”. Связь между этими пространствами настолько тесная, что можно сказать: каждое из них служит “моделью” другого.
Алгебра и исчисление высказываний моделируют друг друга в том смысле, что каждая формула алгебры высказываний толкуется как формула исчисления высказываний, и обратно. Между ними есть изоморфизм. В нашем тексте во многих местах мы просто отождествляли (не различали) эти два понятия.
Однако для большей обоснованности такого толкования желательно строго доказать соответствующие теоремы, например, следующего типа [197, с. 99]: формула, доказуемая в исчислении есть тождественно истинная в алгебре, и обратно. Нужны соответствующие теоремы об осмыслении (установлении) связи между выводимостями в алгебре и исчислении. Объединяя эти две структуры — алгебру и исчисление — в одну, можно говорить о единой математической теории высказываний.
155
Упомянем здесь важное понятие системы логических уравнений, которую всегда можно записать в виде одного логического уравнения f(a, х) = И,
где а — высказывание или их совокупность, играющее роль параметра, х — неизвестное высказывание или их совокупность,/(о, х) — формула или функция от а и х; И— истинное высказывание.
Решить это уравнение — значит найти формулу х(о) как функцию от а так, чтобы
f(a, х(а)) = И при Va е А, где А — область высказываний. Иными словами,/(о, х(о)) — тавтология. Нахождение решений таких уравнений даже относительно простого вида — задача далеко нетривиальная.
Итак, основой всей математики можно считать формулы теории высказываний. Идея формального языка состоит в том, что всякую формулу можно рассматривать как слово, состоящее из букв какого-то алфавита. Разные формулы — разные слова, и обратно, точно так же, как обычные слова обычного естественного языка. При этом, естественно, все слова делятся на правильные (имеющие какой-то смысл) и неправильные (не имеющие смысла). Под смыслом здесь понимаются слова, удовлетворяющие синтаксическим правилам, которые, на наш взгляд, лучше было бы назвать грамматическими правилами (грамматикой), так как обычно в учебниках языка грамматика — это правило написания слов, а синтаксис — это правило написания предложений.
Заметим, что формальный язык можно понимать несколько иначе, что иногда бывает удобней. Именно, всякую формулу можно рассматривать как предложение (а не как слово), составленное из слов (а не букв), взятых из какого-то словаря (а не алфавита).
При этом имеются правила, отделяющие правильные предложения от неправильных, которые, на наш взгляд, в этом контексте правильнее назвать правилами синтаксиса (синтаксисом). Упомянем, что, кроме или вместо правил грамматики и синтаксиса, есть еще правила семантики, или осмысления. Это правила более общего характера, а потому более сложные, так как они имеют уже прямое отношение к философии как науке о смысле всего сущего, любой реальности. Дело в том, что нередко можно увидеть и услышать грамматически правильно написанные слова и синтаксически правильно построенные фразы, однако не имеющие смысла, по крайней мере для достаточно широкого круга людей. Правда, иногда бессмыслица, непонятная широкому кругу лиц, на самом деле является вполне однозначным “сигналом” или, лучше сказать, кодом (шифром), который может быть осмыслен, т.е. расшифрован осведомленными в нем лицами.
156
Остановимся на толковании формулы как слова, а не предложения в формальном языке. Смысл и действенность идеи формального языка состоят в том, что, кроме того, что формула представляется словом (грамматически, синтаксически правильным), сам вывод одной формулы из других может быть представлен как последовательность (цепочка, цепь) допустимых преобразований слов, т.е. получения новых слов из старых. При этом допустимое преобразование слова состоит в том, что в преобразуемом слове выделяются подслова (тоже правильные), вместо которых подставляются другие слова в соответствии с заданным правилом (отображением), например, просто списком или таблицей допустимых подстановок слов. В этих терминах, или на этом языке, задача построения дедуктивной цепочки вывода или доказательства факта А В состоит в том, чтобы найти последовательность (цепочку) допустимых подстановок, начиная от исходного слова (соответствующего А) и кончая требуемым словом (соответствующим В).
Интересно отметить, что такую процедуру вывода можно рассматривать как управление в дискретной системе управления (ДСУ) вида хк+1=/(хк,ик),	(3.1.5)
гдех*, к = 0, 1,2, ...; хк е А"для W = 0, 1, 2, ..., где А"— множество состояний ДСУ, отождествляемое с множеством допустимых слов формального языка; ик е U, к = 0, 1,2, ..., где ик — управление, т.е. допустимая подстановка слов, U— множество всех допустимых подстановок, которое, вообще говоря, зависит от состояния х, т.е. от данного слова: х & X, U = U(x).
Отсюда доказуемость логического следствия А=> В (или тавтологии Л —> I?) можно рассматривать как существование управляемости из начальной точки (начального состояния ДСУ) х0 = А в конечное состояние хп = В, где N — некоторое конечное число “шагов” цепочки дедукции к = 0, 1,2,
Задача определения доказательства (вывода) теперь осмысливается как задача определения допустимого финитного управления д(0), и(1), ..., w(7V) и соответствующей этому управлению траектории:
х0 = х(0) = А, хь х2, ..., x/v+i = В.
Далее можно формулировать в терминах ДСУ различные задачи управления, например оптимального управления. В частности, задача кратчайшего вывода логического следствия А => В становится задачей быстродействия, т.е. минимума времени или минимума числа шагов N, при котором хдг+1 = В. Более того, задача определения алгоритма вывода дедукции А => В (например, для “массовой” задачи вывода, когда А и В заранее не фиксированы, но про них известно, что они при
157
надлежит некоторым подмножествам XQ и X пространства X) может рассматриваться как задача синтеза ДСУ. Она состоит в том, чтобы, во-первых, выяснить существование функции и(х, х0, •**), где х — переменное состояние, х е X, х0 е Хо, х, е X, во-вторых, ее конструктивно определить, в-третьих, определить все функции и(х, х0, л*), причем такие, чтобы рекуррентное уравнение
хм = f(xk,u(xk, х0\ xPf), к-О, 1, 2,...,	(3.1.6)
имело решение х0 = A, xh х2, ...,х^1 = хл = В, где N е N.
Среди всех функций синтеза (синтезирующих функций для данной ДСУ) можно искать оптимальные в указанном выше смысле.
Ясно, что можно формулировать и многие другие задачи управления в пространстве X, если осмыслены соответствующие понятия управления: например, устойчивости, наблюдаемости, чувствительности, идентификации и др.
Для более строгого обоснования такого “изоморфизма” между задачами логики и теории управления можно, например, показать, что каждая конкретно запрограммированная машина Тьюринга может быть представлена как синтезированная система с управлением указанного выше вида (3.1.6), и обратно. Но здесь это доказательство не рассматривается. Сама машина Тьюринга может рассматривагься как система с управлением вида (3.1.5), как разновидность автомата.
Таким образом, можно в определенном смысле сказать, что помимо трех парадигм алгоритма — 1) рекурсии, машины Тьюринга, 3) нормального алгоритма Маркова — существует четвертая парадигма алгоритма — синтез системы с управлением (синтез автомата, реализующего алгоритм). С этой точки зрения классический автомат — это “частный” случай системы с управлением, когда имеется дискретный параметр “шагов”. Система с управлением может иметь и “непрерывный” параметр, в качестве которого выступает, например, время.
3.2.	О ПРЕДИКАТАХ
Формально предикат Р(х) можно отождествить с подмножеством В е Ах х ... х Ап, где A,-, i = 1, ..., п, — предметные области. Для данного п > 1 предикат можно назвать «-местным предикатом, или «-местным отношением, или обобщенным свойством (упорядоченной совокупности предметов из Ль ..., Ап). При п = 1 предикат Р(х) называется свойством предмета из А. Кроме того 0-местный (нульместный) предикат есть просто высказывание. Множество В иногда называется множеством истинности данного предиката. Несмотря на отождествление на
158
ми понятий “предикат” = “отношение”, надо иметь в виду, что отношение — это термин языка математики, ибо отношение — это некоторое множество, а множество есть математический термин.
Через отождествление “предикат” = “отношение” происходит перевод с одного языка на другой. Предикат, или отношение, можно описывать другим математическим понятием — характеристической функцией множества В как подмножества Л! х ... х А„.
Предикат можно рассматривать как “переменное высказывание”, т.е. как функцию, но от независимых параметров, роль которых играют элементы х, g A,, i - 1, ..., п, упорядоченных предметных областей А;.
Так как значения предиката можно рассматривать как высказывания, то на предикатах определены все те операции, которые определены для высказываний с теми же аксиомами пространства высказываний Е. Определено также понятие равносильности предикатов.
Например, уравнения и неравенства — это разновидности предикатов. Упрощение уравнений и неравенств происходит на основе понятия равносильности предикатов.
Для предиката Р, соответствующего отношению (подмножеству) В, естественно определяется операция отрицания Р, при этом Р соответствует отношение (подмножество) В, дополнительное к В в А\ х ...хЛ„.
Если предикаты Р\(х) и Р2{х) имеют одну и ту же предметную область А\ х ...х А,„ то для них естественно определяются операции Р](х) л л Рг(х) и Р|(х) v Р2(х), при этом результирующее отношение для конъюнкции равно пересечению отношений В{ и В2, а для дизъюнкции — объединению отношений В} и В2 в теоретико-множественном случае.
Поскольку предикаты отождествляются с отношениями, то для них могут иметь место и другие операции (см подразд. 2.4), например, операция взятия обратного предиката к данному или свертки двух предикатов (при определенных условиях на их предметные области).
Кроме операций логического отрицания, сложения и умножения, еще есть кванторные операции К, которых два вида:
1)	кванторная операция всеобщности по переменной хк предиката Р(х{, ...,Хп), обозначаемая 'Х/хкР(х\, ..., х„);
2)	кванторная операция существования по переменной хк предиката Р(х\, ..., х„), обозначаемая 3xkP(Xi, ..., х„). При этом переменные хк называются связанными переменными. Остальные переменные называются свободными.
В результате применения кванторной операции к /7-местному предикату Р(х) ему ставится в соответствие единственный (и - 1)-местный предикат Р[{хх,...,хк,...,хп'), где хк означает, что от параметрической
159
переменной хк он не зависит. Ясно, что эти операции можно повторять до полного исчезновения всех свободных переменных. Если все переменные в предикате связанные, то он становится просто высказыванием.
Кванторные операции ассоциативны, но, вообще говоря, некоммутативны и недистрибутивны. Иногда кванторную операцию называют сверткой предиката Р по переменной х с помощью квантора. Такую переменную называют сверточной, или немой, переменной — наподо-1
бие переменной х в интеграле J f (x)dx.
о
Выражение \/xkP(xif...,xk,...,xn) читается и осмысливается так: “Для любого (каждого, всякого, всех) хк е Ак имеет место свойство Р(хъ	х„)”. Кванторное выражение ЭхкР(хх,...,хк,...,хп) чита-
ется и осмысливается так: “Существует такое хк е Ак, что имеет место свойствоP(xi, ...,хк ...,х„)”.
По определению, можно записать:
\/xkP(xl,...,xJ = п Р(х1,...,хк,...,хп) = Р}(х},...,хк,...,хп), хкеАк
ЭхкР(х},...,хп) = и Р(хг,...,хк,...,хп) = Р^хх,...,хк,...,х„У хкеАк
Отсюда видно, что, используя закон двойственности де Моргана, один квантор можно сводить к другому, а также ввести понятие отрицания квантора К . Например,
Х/хР(х) = ЗхР(х), Я хР(х) = V хР(х).
Применяя отрицание к обеим частям этих формул, получим новые равносильности:
VxP(x) = 3 хР(х\ Я х Р(х) = V х Р(х).
Заметим еще, что в математике нередко используют тот факт, что тождественно истинную формулу Дх) можно записать равносильным образом, добавляя к ней квантор общности Vx/(x), чтобы подчеркнуть явно тождественную истинность Дх).
Любое выражение логики предикатов, где используются те или иные кванторы Кх, ..., К,п, с помощью выписывания последовательности равносильных формул можно привести к канонической форме, характерной тем, что все кванторы вынесены вперед, т.е. в виде
^?lXj, P2X2, ’-чК-т^тР •ч^-л)-
160
Такая форма называется предваренной нормальной формой. Кроме указанных выше равносильностей, имеют место равносильности:
Vx Р(х) л Vx g(x) = Vx(P(x) л б(х)), Я х Р(х) v 3 х g(x) = 3 х(Р(х) v Q(xJ).
Эти равносильности нетрудно доказать, используя такие довольно очевидные равносильности:
Vx Р(х) v С = Vx(P(x) v С),
3 х Р(х) л С = 3 х(Р(х) л С),
где С не зависит от х.
Предикат можно рассматривать как детривиализацию высказывания. В пространстве высказываний каждое высказывание как элемент этого пространства имеет одно и только одно единственное значение истинности: или И, или Л, но не оба вместе. Однако полезно детривиа-лизовать каждый такой элемент в зависимости от значений каких-то “внутренних” переменных (“внутренних степеней свободы”). Таким образом, вместо одного значения, которое имело каждое высказывание, мы будем рассматривать целую функцию, принимающую значение И или Л в зависимости от значений “внутренних” аргументов. Это означает, что пространство высказываний Е превратилось в “функциональное” пространство.
Это похоже на алгебраизацию арифметики, когда вместо числа рассматривается буква, которая теперь может принимать различные числовые значения и даже зависеть от чего-то еще, т.е. быть функцией. Можно сказать, что теория высказываний так относится к теории предикатов, как арифметика чисел -— к алгебре чисел.
Предикат — это высказывание, но как функция от других переменных. Переменные хь ..., х„ называются предметными переменными, а Ji, ..., Ап — предметными множествами. Предикат Р(хх, ..., х,г) показывает, существует ли какое-либо отношение между этими п предметами или нет. Отношение между хь ..., х„ существует, если значение этой функции (предиката) на данном наборе (хь ..., х„) есть И, и не существует в противном случае.
Значение предиката можно еще рассматривать как одно из двух высказываний: И или Л. Предикат можно рассматривать как отображение Ai х ...х А„Е, где Е — некоторое пространство высказываний.
Сделаем несколько замечаний.
Аристотель — это Евклид в логике. Структура логики Аристотеля и структура геометрии Евклида — это первые гениальные образцы точной научной мысли, результат осмысления невообразимо сложной ре
6. А.В. Бабичев
161
I
альности и первое математическое описание важнейших свойств этой реальности.
Аристотель и Евклид дали нам парадигму (образец, пример для подражания) науки как средства осмысления реальности через логику и математику, которая не утратила своего выдающегося значения до сих пор и, более того, по-видимому, будет продолжать служить еще долго. Наша задача — глубже осмыслить эту парадигму, дать ей точное описание и по возможности развивать далее.
Аристотель и Евклид, а позже Буль дали примеры математических структур. Бурбаки положили понятие структура в основу всей математики. К этому надо добавить понятие симметрия как наиболее общий метод изучения структур.
Следующим шагом в решении фундаментальнейшей проблемы понимания того, как человек мыслит и осмысливает реальность, делает умозаключения и выражает их, был шаг, сделанный еще по сути Аристотелем, дальнейшей детривиализации понятия высказывание, в результате которого сейчас мы имеем мощное понятие предиката и отношения, в терминах которых можно описать почти всю математику.
3.3.	ЯЗЫК УЗКОГО ИСЧИСЛЕНИЯ ПРЕДИКАТОВ
Язык узкого исчисления предикатов (ЯУИП) — это “осторожный”, заведомо “ограниченный” язык в том смысле, что принимается во внимание парадокс Рассела в теории множеств. На ЯУИП просто автоматически не могут формулироваться противоречивые предложения (слова) и формулы в качестве априори допустимых слов. Оказалось, что почти всю математику можно изложить на ЯУИП. Более того, ту часть, которая естественно на нем не формулируется, а требует языка “более высокого порядка”, можно так или иначе (более пространно и длинно), но выразить в конце концов на ЯУИП. Это мнение сейчас принято, ибо пока неудач в таких попытках не наблюдается до сих пор [290]. Опишем кратко , суть ЯУИП и основанное на нем исчисление предикатов 1-го порядка [244].
Как всякий формальный язык он состоит из алфавита — набора допустимых символов (букв) и слов — набора допустимых выражений (формул), составленных из букв этого алфавита. Алфавит ЯУИП состоит из символов нескольких сортов:
1)	символы а, Ь, с, ..., alf а2, ..., обозначающие индивидуальные (конкретные) предметы какого-то основного множества, например, это числа 1, 2, 3, ..., л, е, ..., -5, 41. Этих символов допускается даже трансфинитное число;
162
2)	символы х, у, z, ..., хь х2, обозначающие переменные предметы (предметные переменные), которые имеют своими значениями индивидуальные предметы. Их допускается не более счетного числа;
3)	символы Р, Q, R, Р\, Р2, обозначающие индивидуальные (конкретные) предикаты той или иной местности или арности (включая нуль-арные предикаты, т.е. высказывания), описывающие конкретные отношения между предметными переменными. Их может быть трансфинитное число;
4)	логические символы (буквы) — отрицание, конъюнкция, дизъюнкция, импликация, кванторы V и 3 и вспомогательные символы (скобки, запятые).
Один ЯУИП отличается от другого фиксацией символов сорта (пп. 1 и 3) и обозначается той или иной буквой, например L. Далее в ЯУИП надо определить все допустимые формулы (слова). Они исчерпываются следующими правилами алгоритмически индуктивного типа.
1.	Выражение вида Р(хх, ...,хп,а\, ...ап) есть формула (простая, элементарная, атомарная). Если переменная х, входит в эту формулу вместе с квантором Зх(- или Vx,, то х/ называется связанной переменной, если X, входит в эту формулу без кванторов, то она называется свободной.
2.	Если F уже есть формула, в которую х входит свободно, то ЗхР и VxP тоже формулы.
3.	Если/7, — формула, то отрицание F тоже формула.
4.	Если Fi и F2 — две формулы, то Fi \/ F2, Fr лР2, Fi —> F2 тоже формулы, однако при одном существенном условии (ограничении): одна и та же предметная переменная, скажем X], не встречается свободной в F] и связанной в F2, или наоборот.
Формула называется замкнутой, если в ней нет ни одной свободной переменной х. Всякая формула ЯУИП имеет вид
F(ai,..., ат; хь..., х«; РЬ...,РА).	(3.3.1)
Опишем применение ЯУИП, состоящее в том, что любая модель (в смысле алгебраической системы по Мальцеву) может быть описана на ЯУИП или представлена в нем. Такое представление делается по правилам математической логики.
Пусть М — модель, описываемая своим “основным” множеством предикатов {Р}, a L — ЯУИП. Говорят, что L задан на Л/, если существует (указано) произвольное отображение, обозначаемое знаком следующего вида:
1)	нуль-арному предикатному символу из L по соответствует значение истинности: Л или И',
2)	не нуль-арному предикатному символу из/, по соответствует предикат той же арности из {Р};
6*
163
3)	каждому предметному символу из L по соответствует эле- , мент основного множества М.
Отображение называется истолкованием (содержательным) языка L на модели М. Если М есть истолкование L, то каждая атомарная формула языка L может рассматриваться как предикат модели М. Другими словами, можно просто отождествить предикатные символы L с предикатами М и предметные символы L с элементами основного множества модели М. Содержательному толкованию L на модели М способствуют следующие естественные правила.
1. Если	хт) и F2(xm+t, ..., х„) —две формулы ЯУИП, где
все xi, ..., хп — свободные, то значения истинности формул F\ л F2, F\ v F2, F[ —> F2, Fi, рассматриваемых как предикаты на M, вычисляются просто по правилам теории высказываний, причем ах,ап — какие-то фиксированные элементы из М.	•
2. Кванторы 3 и V сопоставляют //-местному предикату (л - 1)-местный предикат так же, как это делается в исчислении предикатов.
Указанные правила позволяют любую формулу вида (3.3.1) рассматривать просто как соответствующий предикат на М. В частности, если F замкнута, то предикат на М— это просто высказывание о модели М в целом. Если это высказывание истинно, то говорят, что формула F выполняется на модели М. Если конечный или бесконечный набор замкнутых формул выполняется на М, то М служит моделью этого набора. Такой набор называется совместным, если существует хотя бы одна его модель.
Всякий совместный набор замкнутых формул языка L определяет, вообще говоря, много моделей, или класс моделей. Очевидно, что они являются абстрактными классами моделей в смысле и в силу изоморфизмов, существующих между любыми парами моделей из этого класса. В то же время о “замкнутости” относительно гомоморфизмов моделей с необходимостью сказать нельзя, но есть условия, когда это сказать можно [244, с. 67].
Наконец, отметим важное обстоятельство: ЯУИП можно расширить за счет добавления в его алфавит символов, обозначающих алгебраические операции, и добавить соответствующие правила для допустимых формул в этом расширении. Тогда моделью языка L может служить и любая алгебраическая система по Мальцеву [206, 244]. Именно это обстоятельство дало нам возможность (см. подразд. 1.12) произвести отождествление предиката со структурой.
Заметим еще, что все те “аргументы”, которые стоят в скобках (о,-, Xj, Pk) в формуле (3.3.1), называются термами. Таким образом, термы и
164
формулы — это два класса (естественно не пересекающиеся, как и положено быть классам) допустимых слов данного ЯУИП, которые следует четко различать и не смешивать, ибо в этом и есть суть ЯУИП, помогающая избежать парадоксов и двусмысленностей.
Такой эффект достигается (ничего даром не дается) за счет ограничений, которые фактически (из правил) диктуются для образования формул ЯУИП. А именно, как видно, в нем не допускаются предикаты, которые в качестве значений своих аргументов имеют другие предикаты или функции (например, операции алгебраических систем) и, кроме этого, нет кванторных операций по предикатам или функциям.
3.4.	ТЕОРИИ И ДОКАЗАТЕЛЬСТВА
Последнее замечание в подразд. 3.3 позволяет четко определить такие важные понятия во всей науке, и в частности математике, как понятия теории, аксиомы, теоремы и ее доказательства. Теории, основанные ца ЯУИП, называются соответственно формальными аксиоматическими теориями 1-го порядка. В их основе лежат аксиомы. Но аксиомы лежат в основе и других теорий, которые по тем или иным причинам являются еще не полностью формализованными. Они называются аксиоматическими неформализованными теориями. В них понятие доказательства и вывода остается неформализованным предельно строго и в этом смысле расплывчатым и не определенным до конца. В них все основывается в конце концов на понятии множества, а избежание противоречий контролируется “здравым смыслом”.
Всякая формальная аксиоматическая теория 1-го порядка — далее просто теория — это прежде всего множество высказываний. Она определяет “предметную область” теории и как множество высказываний имеет собственное подмножество высказываний, называемых теоремами, для которых существует их чисто логический вывод из высказываний, образующих еще меньшее подмножество и называемых аксиомами. Обычно фиксируют множество аксиом, а затем пытаются сформулировать новые высказывания, выводимые и, возможно, не выводимые из заданного множества аксиом.
Доказательством (длины п) теоремы называется конечная последовательность высказываний е^, ..., е„, где еп — доказываемая теорема, а все остальные высказывания —	..., e„_i — это или аксиомы, или ра-
нее доказанные теоремы. Аксиому можно считать доказанной теоремой длины 1. В доказательстве (еь ..., ея) каждое “звено” этой последовательности, т.е. переход от е, к ег+1, i = 1, ..., п - 1, должен осуществляться путем логического вывода, о котором мы говорили в теории высказываний (правило “modus pones” — если А и А В, то В — правило
165
подстановки одной формулы теории высказываний в другую). Помимо этих правил, в теории 1-го порядка входит еще “правило связывания квантором всеобщности”, или “правило обобщения”, — если В, то для \/хВ.
Все аксиомы теории делятся на два класса: 1) логические аксиомы и 2) специальные (нелогические, собственные “предметные”) аксиомы теории. Логические аксиомы — это аксиомы теории высказываний. Они являются атрибутом любой теории (по крайней мере теорий 1-го порядка, о которых здесь только и говорится).
Класс специальных аксиом может для некоторых теорий оказаться пустым. Такая теория может называться чисто логической теорией. В частности, теория (см. подразд. 3.3), как легко видеть, именно чисто логическая теория, называемая исчислением предикатов 1-го порядка, или узким исчислением предикатов (УИП). Теории, содержащие специальные аксиомы, называются специальными теориями. Многие теории используют понятие равенства — специальный случай эквивалентности. Такие теории называют эгалитарными.
Аксиомы, о которых здесь говорится, называют еще схемами аксиом, так как они абсолютно абстрактны и не наполнены конкретным предметным содержанием, которое дает всякая модель данной теории. Здесь модель понимается в смысле, изложенном в подразд. 3.3.
Нетрудно привести многие примеры аксиоматической теории 1-го порядка. Из них состоит подавляющая часть современной математики. Например, это отношение эквивалентности, отношение упорядоченности, евклидова геометрия (классическая первая полностью аксиоматизированная теория, которая уточнялась от Евклида до наших дней), аффинная геометрия, аксиоматическая теория натуральных и других чисел, алгебраические системы. Более подробно об этом можно узнать, например, из [197].
Интересно отметить саму теорию высказываний. Она играет роль “интерфейса” между логикой и математикой и, как отмечалось, пронизывает почти всю математику, являясь необходимой составляющей основ любых теорий, даже необязательно полностью или частично формализованных и аксиоматизированных. Теорию высказываний, рассмотренную в подразд. 3.1, можно назвать написанной на субязыке, который мы пытались “чисто” логически описать и объяснить с помш цью метаязыка самой логики. Это похоже на изложение, например, теории русского языка в учебнике, написанном на том самом русском языке.
Отметим важное принципиальное положение. В современных аксиоматических теориях не обсуждают истинность тех или иных ее аксиом и не интересуются ею. Но интересуются лишь теоремами, которые могу г быть выведены (доказаны) или не могут быть выведены (не
166
доказуемые) из данных аксиом, а также построением доказательств, выводов и их алгоритмизуемостью.
Такая точка зрения (на истинность теорий и их аксиом) появилась после шокирующего открытия неевклидовой геометрии, а сейчас она укрепилась. Шок был на чисто логической почве. Оказалось, что не имеет большого смысла с самого начала построения абстрактной (формальной, аксиоматической) теории предполагать истинность или ложность той или иной аксиомы. Иногда это даже вредно. Ведь если бы эта, возможно, простая, но нетривиальная идея была осознана и осмыслена, скажем, не в XIX веке, а раньше, то геометрия Лобачевского—Бояи была бы открыта задолго до них, например гением Гаусса, который уже, как говорят историки, о чем-то подобном догадывался. Самое главное для всякой теории — это выяснить ее непротиворечивость, т.е. невозможность вывести вместе две формулы —А и не Л — из одного и того же набора аксиом.
Для проверки на непротиворечивость в математической логике предложен метод моделей. Если можно построить “предметную” модель формальной аксиоматической теории, то этим и доказывается ее “право на жизнь” и на эффективное применение, и больше ничего! Вот уж где верно, что “практика (жизнь) есть критерий истины”.
Интересно, что одна и та же формальная теория может иметь совершенно непохожие модели (реализации и представления) так, что сразу и не очевидно, что они есть модели одной и той же аксиоматической теории. Такой интересный и неожиданный пример модели евклидовой геометрии как аксиоматической теории приведен в [350]. Более естественная модель евклидовой геометрии — аналитическая геометрия.
Осознание того факта, что кроме непротиворечивости от теории не надо требовать истинности (а тем более очевидной), значительно облегчил, как нам представляется, и работу Эйнштейна по созданию теории относительности и аксиоматики СТО и ОТО. Но, несмотря на урок неевклидовой геометрии, открытие Эйнштейна еще долго не понимали и не принимали многие ученые, включая и некоторых выдающихся. Тот же самый урок позже был преподнесен появлением квантовой механики, принципы (аксиомы) которой, выработанные уже задним числом, оказались совершенно загадочными и остаются таковыми по настоящее время. Так что требовать от аксиом и принципов априорной очевидности, наглядности и “привычной” простоты неразумно и вредно, ибо это может сильно тормозить развитие науки.
Именно эту мысль в том числе отражает сформулированный в подразд. 1.9 “Принцип (Закон) 100%-эффективности математики”, особенно в его второй части, утверждающей, что любая (!) математическая
167
структура (естественно, с непротиворечивой аксиоматикой) описывает некоторую существующую в природе или обществе реальность.
Заметим, что непротиворечивость евклидовой геометрии и теории действительных чисел до сих пор не доказана. В то же время неполнота некоторых известных теорий уже установлена. Она означает, что в теории существуют высказывания, которые не могут быть выведены из аксиоматики данной теории, причем никакое расширение этой аксиоматики не гарантирует отсутствие такого рода невыводимых утверждений. Однако можно доказать непротиворечивость исчисления предикатов 1-го порядка, не содержащих специальных аксиом.
Отметим, что существует другое, более узкое понятие полноты. Аксиоматическая теория называется полной в узком смысле, если добавление к набору ее аксиом любого недоказуемого в ней утверждения (при сохранении в ней всех правил вывода) превращает эту теорию в противоречивую. Нетрудно показать, что любая полная теория будет полной в узком смысле (см., например, [197]).
Наконец, отметим важные проблемы алгоритмической разрешимости, естественно возникающие в той или иной теории. Здесь требуется установить алгоритм построения вывода (доказательства) одного класса формул из другого класса формул или доказать его отсутствие.
Эти фундаментальные результаты математической логики имеют большое значение в теории управления. Например, они показывают, что проблема синтеза системы с управлением, т.е. нахождение подходящей обратной связи, алгоритмически разрешима, по-видимому, далеко не всегда, а поэтому всегда будет оставаться искусством конструктора. Первым отрицательным результатом был результат Черча в 1936 г.: “Проблема распознавания выводимости (невыводимости) алгоритмически не разрешима”.
Проблема эквивалентности в ассоциативном исчислении была сформулирована норвежским математиком Туэ еще в 1914 г. В 1946 и 1947 гг. А.А. Марков и Э. Пост независимо друг от друга построили примеры ассоциативных исчислений, где проблема эквивалентности слов, которую можно толковать как проблему “финитного управления”, алгоритмически неразрешима. В 1955 г. П.С. Новиков установил алгоритмическую неразрешимость довольно общей аналогичной проблемы для теории групп, что очень важно для всей математики, ибо исследование структур и их симметрий теснейшим образом связано с группами.
Цейтин рассмотрел очень простое ассоциативное исчисление всего из пяти букв {a, b, с, d, е} и семи допустимых подстановок (управлений) — ас-са, ad-da, bc-cb, bd-db, abac-abacc, eca-ae, edb-be — и доказал, что написать алгоритм, который бы “автоматически” по любым
168
двум заданным словам (например, abode и cadedb} выдавал бы ответ “да”, если они “соединимы” выводом, и ответ “нет” в противном случае, построить нельзя: такой вычислимой функции управляемости и(с\, сф) для любых С\ и с2 со значением 1 или 0 не существует.
3.5.	МЕТАЯЗЫК И СУБЯЗЫК
Формализацию смысла можно рассматривать как перевод с естественного языка на специальный язык логики. Основная задача всякого перевода — сохранить смысл того аспекта или свойства реальности, которые хотим описать, и при этом сделать это как можно точнее. Например, в логике высказываний сохраняется одно и только одно свойство предложения, высказанного на естественном языке, — это свойство “быть истинным” или “быть ложным”. Все остальные свойства первоначального предложения игнорируются, от них абстрагируются, и тем самым происходит упрощение.
Таким образом, специальный, формальный или искусственный язык нужен там, где требуется предельное упрощение (абстракция, идеализация), т.е. там, где надо освободиться, порой от неопределенности и многозначности естественного языка. При этом описание специального языка происходит на естественном языке, который понятен широкому кругу людей. После того как какая-то группа людей обучилась и поняла суть нового языка, между собой они могут общаться на этом языке, причем непосвященные их уже понимать не будут.
Когда о каком-то языке Lx говорят на другом языке L, то язык L (по отношению к L\) называют метаязыком (надязыком, или языком верхнего уровня), а язык L\ называют субязыком (или языком низшего уровня). Символически это можно изобразить включением L\ cz L.
Более того, язык может использоваться для описания самого себя. Это наиболее важное и удивительное свойство, например, естественных языков. Примером такого применения языка может служить “Учебник русского языка”, написанный на русском языке. В нем русский язык является вместе и мета- и субязыком. В тексте иногда слова одного языка, понимаемого в смысле другого языка, выделяются кавычками. Другим примером могут служить учебники одного иностранного языка, но с объяснениями на другом иностранном языке, который является “родным” языком для какой-то группы лиц.
Важным примером субязыка является язык какой-нибудь конкретной научной дисциплины: математики, механики, физики, химии, биологии, медицины, юриспруденции, экономики и т.д. Всякий научный текст, как правило, пишется как минимум ria двух языках: естественном, играющем роль метаязыка, и на языке данной научной дисцип
169
лины, играющем роль субязыка. Однако не исключено, что в данном научном тексте используются сразу несколько субдзыков. Например, в статьях по техническим дисциплинам часто используется язык математики и физики.
Основой всякого языка являются слова и их правильное построение, придающее им точный смысл в рамках контекста одной научной дисциплины. Такие слова называются терминами данного научного языка. При использовании сразу нескольких языков очень важно согласование смыслов одного и того же слова-термина, но разных языков. Проблема состоит в том, что, если попытаться установить соответствия слово (форма) —> смысл и обратно, смысл -> слово, то эти отображения будут многозначными и, следовательно, точность выражения смысла может оказаться недостаточной.
Как мы уже говорили, несоблюдение этого непременного условия согласования часто наблюдается в плохо написанных научных статьях и ведет к бессмыслице и парадоксам. На смешении смыслов, несогласованных употреблениях одних и тех же слов в разных смыслах основано много шуток и анекдотов. Это называется игрой слов. Например, слово дом в одном контексте означает помещение для жилья, а в другом, например в грамматике, это просто слово из трех букв. Чтобы различать слова в разных смыслах, часто их выделяют тем или иным способом: подчеркивают, ставят в кавычки, пишут другим шрифтом, цветом и т.д.
Вопрос о “двусмысленности”, т.е. о том; как различать разные смыслы одного й того же слова, часто является далеко не тривиальным. Так, например, фундаментальный парадокс теории множеств основан на том, что одному и тому же объекту можно приписать два смысла: рассматривать его как элемент множества и как множество элементов. Следовательно, из одного и того же текста при наличии .двусмысленности можно сделать разные выводы (умозаключения), нередко имеющие противоположный смысл, и их использование как “руководство к действию” нередко приводит к совершенно различным результатам, вплоть до прямо противоположных.
Вопросом толкования слов или предложений одного языка в терминах другого языка занимается наука о переводах, продукцией которой являются словари самых различных типов и машинные программы автоматического перевода. Обобщенно эти проблемы называются проблемами толкования, интерпретации, моделирования и даже идентификации.
Особенно трудны эти проблемы при переводе литературных произведений, скажем, поэтических. Переводчик в этой области должен быть особенно высококультурным, образованным и в совершенстве
170
владеть обоими языками, чтобы понять смысл произведения, часто очень сложный (разносторонний), и сохранить его в переводе на другой язык, в другой форме. Недаром лучшие переводы классических произведений были сделаны выдающимися поэтами и писателями.
Аналогично мы рассматривали прикладную математику как науку о переводе с “языка реальности” на язык математики. Общая проблема смысл—форма состоит в том, что один смысл может иметь много форм своего выражения и одна форма может иметь много смыслов (много толкований, интерпретаций). Вопрос о правильном (адекватном) толковании слов и текстов очень важен во всех областях деятельности как отдельного человека, так и сообществ. Особенно это важно в таких областях, как политика, военное дело, медицина, ибо часто это связано с жизненно важными реалиями.
Примерами субязыков являются различные формальные языки, например, язык логики высказываний, язык логики предикатов, язык модальной логики. Среди формальных языков важное место занимают языки программирования, которые понятны и людям, и компьютерам и которые “заставляют” компьютер работать так, как требуют программисты. Иногда такие проблемы называют проблемами интерфейса — проблемами общения и взаимопонимания между человеком и машиной. Здесь важно сделать наиболее естественный, “дружественный человеку” интерфейс.
Языки программирования образуют иерархию языков от субязыков самого низшего уровня до метаязыков высокого уровня: язык кодов компьютера, алгоритмический язык (например, ФОРТРАН, Бейсик). Сейчас бурно идет создание метаязыка предикатного уровня (логический язык программирования) [218]. Наконец, важнейшей задачей является создание автоматического переводчика естественного языка на язык программирования.
3.6.	ШКАЛЫ БУРБАКИ, СТРУКТУРЫ, СИММЕТРИИ
Н. Бурбаки ввели важное понятие, получившее название шкала Бурбаки, на основе которого ими было введено понятие структуры [146].
Определение 1. Шкала Бурбаки — это семейство множеств, получаемых последовательно по определенному правилу из фиксированного конечного набора множеств Д, ...,Ап, называемых базисными начального уровня. При этом первый уровень шкалы Бурбаки определяется набором всевозможных множеств, получаемых из базисных множеств путем образования из них множества всех подмножеств и множества всех декартовых произведений. Полученные таким способом множества называются базисными множествами 1-го уровня. На следующем шаге этот набор принимается за базисный набор начального уровня, и повторяется процедура образования из него новых множеств 2-го уровня и т.д.
171
По Бурбаки, задать структуру наДь Ап, т.е. на базисных множествах начального уровня, означает фиксацию определенных элементов, т.е. множеств из совокупности базисных множеств тех или иных уровней.
Например, фиксирование определенного подмножества декартова произведения А\ х ...х Ап равносильно заданию «-местного предиката. Обратно, задание какого-либо «-местного предиката Р(х) равносильно фиксации подмножества в некотором декартовом произведении «-множеств, взятых из подходящих уровней шкалы Бурбаки.
Рассмотрим коротко, что означает симметрия (инвариантность) структур. Иными словами, рассмотрим преобразования, сохраняющие структуру.
Для простоты возьмем случай л-арного предиката F(x), где х е А" = = А х ...х А, и Л/ — отвечающее ему подмножество в А". Пусть G — группа всех подстановок множества А, т.е. группа симметрий множества Д или группа, действующая наД.
Тогда предикат Р(х) инвариантен относительно элемента g е G, если и только если М — допустимое подмножество в Ап, т.е. при любом g g Н, где Я— некоторая подгруппа G, выполняется М ° g = М.
В частности, рассмотрим пример управления отображениями. Пусть F(A, В) — множество всех отображений множества А в множество В, а G — группа, действующая на А и В. Каждому элементу f g F(A, В) однозначно соответствует подмножество М с: А х В, называемое графиком отображения/. Группа G действует и в множестве всех подмножеств А х В, и, следовательно, для любого g g G множество М ° g также определяет некоторый элемент Д в F(A, В). Поэтому можно говорить о действии группы G в F(A, В), полагая f ° g = f\-
В частности, группа G на В действует тождественно, т.е. значения отображений остаются неизменными, а происходит только преобразование a(f о о) = (а о о-1)/ множеств уровня отображения. Такое представление группы G на F(A, В) часто используется в различных задачах по решению уравнений и классификации, например, функций по их симметриям.
Дело в том, что фиксированное в шкале Бурбаки множество, названное структурой, может “включать” в свой состав другие структуры, т.е. зависеть еще от некоторых множеств или пространств, играющих роль параметров. Например, структура “линейное пространство” называется векторным пространством, если параметр — это поле, и называется модулем, если этот параметр — кольцо.
172
3.7.	РАССЛОЕНИЕ
Расслоение — важное геометрическое понятие, так как слово расслоение естественно ассоциируется с некоторым геометрическим образом. Именно понятию расслоение обязано прилагательное геометрическая в названии ЕГТУ. Как выяснилось, все калибровочные физические теории, являющиеся основой единой теории всех фундаментальных взаимодействий (полей) в природе, математически могут быть основаны на понятии расслоения. В ЕГТУ мы предлагаем в качестве ее математической основы также взягь понятие расслоения, которое, на наш взгляд, на сегодня наиболее точно описывает основное понятие кибернетики — систему с управлением.
В этом подразделе коротко приведем необходимые формальные определения, характеризующие понятие расслоения в его наиболее общем смысле, т.е. оставив только минимальное количество необходимых конструкций. Например, попытаемся не использовать даже понятие непрерывности, относящееся к топологии (топологической структуре), которое традиционно включается в определение расслоения.
Определение 1. Расслоение — это тройка (X, В, п), где X — произвольное непустое множество, В — произвольное непустое множество, л — произвольное отображение, однако подчиненное следующим условиям (аксиомам расслоения):
I) л — это отображение вида л: X—> В\
2) л — сюръекция.
J
В связи с этим возникает серия понятий и терминов, т.е. язык теории расслоений. А именно, X называется пространством расслоения, или расслоенным пространством, или просто расслоением (как результат “процесса расслоения”). Дело в том, что первоначально в множестве X могут находиться какие-то структуры и X действительно будет пространством, а не только “голым” множеством. Поэтому в дальнейшем — в связи с рассмотрением X как расслоения — могут возникать вопросы согласования изначальных структур на У со структурой X как расслоения.
Множество В называется базой расслоения, отображение л — проекцией расслоения (на базу В'), л-1(Д), b е В называется слоем расслоения над точкой b базы В — это прообраз в X образа Ъ при отображении л-проекции X на В. Отсюда получается множество слоев л“’(/>), когда b “пробегает” базу В. Каждый слой л“’(Д) служит элементом множества {л \b}}, b е В всех слоев. Это множество параметризировано, или индексировано, элементами Ъ базы В.
173
Поэтому можно сказать, что расслоение порождает совокупность слоев, т.е. совокупность некоторых множеств, обозначенных л"1 (6) и параметризованных базой (множеством) В.
Подчеркнем следующее обстоятельство, которое полезно всегда иметь в виду: если взять, скажем, элемент Xi из произвольного слоя и элементу из произвольного слоя л-1 (Ь2), то они всегда будут разными, т.е. хх Ф х2. Это следует из того, что Л"— множество.
Из смысла построения расслоения также следует, что тотальное пространство расслоения, т.е. X, можно представить как теоретикомножественную сумму слоев:
Х = {Хп~\Ь):ЬеВ}.
Поскольку слои не пересекаются между собой при разных b g В, то можно сказать, что расслоение порождает разбиение тотального пространства % на слои. Очевидно и обратное: если дано разбиение некоторого непустого множества X на некоторую совокупность его непустых подмножеств {X,}, которую можно параметризовать некоторым индексом i g I, то данному разбиению можно однозначно поставить в соответствие расслоение с тотальным пространством в виде самого X, базой в виде множества I индексов i и слоями Х[ = л-1 (?), где проекция л : X -» I работает по правилу: каждому х е XjCZ X ставится в однозначное соответствие i е I.
Поскольку между разбиениями и классами эквивалентности любого отношения эквивалентности на каком-то множестве X существует взаимно однозначное соответствие, то классы эквивалентности, индексированные некоторым параметром b е В, можно рассматривать как расслоение с тотальным пространством Xи базой В с очевидной проекцией л.
Введем следующие важные понятия.
Определение 2. Сечение расслоения — это отображение s \ В X такое, что свертка (композиция) л °5 = zJ = b,T.e. сечение, — это правое обратное отображение сюръекции (проекции) л. Нередко под сечением расслоения понимают образ s(B~) в X.
Определение 3. Ограничение расслоения (X, В, л) на подмножество А с В — это расслоение (X, А', л') такое, что X' - л-1 (А) и л' = л | X' — сужение л на X'. таким образом, ограничение расслоения — это некоторое индуцирование нового расслоения.
Приведем несколько примеров объектов, которые можно представить как расслоение.
174
Прямое произведение А х В можно рассмотреть как расслоение, если положить X = А х В, в качестве базы взять В, а в качестве л — отображение, которое (а, Ь)А х В ставит в соответствие b g В. Возникает вопрос: что является слоями этого расслоения? Ответ вроде бы таков: здесь все слои “одинаковы” и “равны” множеству А. Но выше мы подчеркивали, что у расслоения все слои разные. Чтобы избежать этой коллизии, каждый слой индексируют элементами b множества В и говорят, что каждый слой Аь изоморфен (а не равен) одному и тому же множеству А и, следовательно, все слои Аь при b g В изоморфны друг другу и вместе изоморфны А. При этом А называют иногда типичным слоем, а расслоение А х В — тривиальным расслоением. Так поступают, когда хотят различить плохо различимые объекты, например изделия, сходящие с конвейера для различения их снабжают маркерами (номерами, паспортами и пр.). Можно сказать, что слои Аь получены тиражированием, или копированием, множества Л.
Ясно, что в качестве базы вместо В можно с таким же успехом взять А, и тогда В будет типичным слоем.
Другой пример расслоения — это расслоение, называемое расслоение-база, которое можно записать в виде (В, В, idB). Здесь базой является некоторое непустое множество В, слой над точкой b е В состоит всего из одной точки, которой является сама точка Ъ, а проекция п — тождественное отображение idB: В -» В.
Расслоение, называемое расслоением над точкой, или расслоением-слоем — это расслоение, состоящее всего лишь из единственного слоя X = л-1 (fe), где Ъ — единственный элемент одноэлементного множества В = {Ь} базы расслоения.
Богатым источником для всевозможных расслоений какого-либо множества являются системы координат, если их можно ввести на данном множестве. Например, если множество снабжается структурой некоторого многообразия, то на нем, по определению, существуют некоторые системы координат.
Тогда за базу расслоения можно и удобно взять некоторое координатное многообразие (“поверхность”), а слои можно составлять из многообразий, составленных из оставшихся координат, не задействованных на базе.
Этот прием часто используется при геометрическом представлении дифференциальных уравнений, когда за базу (или слой) удобно взять те или иные интегральные многообразия этих уравнений. Такой прием часто значительно упрощает исследование и представление решений (его иногда называют спрямлением).
Система с управлением может быть рассмотрена как расслоение {Ь g В, п~1(Ь)}, где база В этого расслоения рассматривается как про
175
странство состояний данной системы с управлением, а каждый слой л-|(£>), “висящий” над изображающей точкой b (локальным состоянием системы с управлением), рассматривается как множество допустимых управляющих параметров, причем каждый элемент этого множества может оказывать действие на состояние Ъ, в результате чего осуществляется управляемое движение в системе с управлением. Сечение расслоения можно рассматривать как фиксацию одного единственного управляющего параметра, который оказывает управляющее воздействие на состояние, над которым “висит” это фиксированное значение параметра. Таким образом, сечение фиксирует синтез системы с управлением, превращая ее просто в систему.
Такой взгляд на систему с управлением, очевидно, еще не завершен, ибо остался неопределенным “закон действия управляющего параметра на соответствующее ему состояние, т.е. закон управления". Мы называем это связностью в расслоении, отождествляя ее с каким-то законом управления, выбранным в данной системе с управлением.
Обычно связность содержится в топологии. Как будет показано в подразд. 5.4 и 5.5, топология уже по сути достаточно полно определяет систему с управлением.
С точки зрения расслоений под связностью в самом широком смысле, по-видимому, надо понимать правило или закон однозначного перехода от слоя к слою. На языке систем с управлением это означает фиксацию финитного управления как функции от упорядоченной нары локальных состояний. В этом смысле фазовый портрет дифференциальной системы с управлением описывает все множество финитных управлений, т.е. все множество допустимых синтезов или, другими словами, все множество связностей.
Можно поставить обратную задачу, исходя из первичности связности. а не топологии: какую топологию определяет данная система с управлением или какая топология совместима с данным множеством связностей, т.е. “связующих” финитных управлений, определенных данной системой с управлением?
Отметим еще одну важную разновидность расслоения.
Определение 4. Локально-тривиальное расслоение - - это расслое-
ние (X, В, л), для которого существует множество У7 такое, что:
1) для любой точки х & В существует “подмножество” 0(х) с. В, (х е 0(х)), прообраз которого л“’(0(х)) изоморфен прямому произведению 0(х) х F;
2) изоморфизм 0(х) х F -> л~’ (0(х)) согласован с отображением проекции л, т.е. диаграмма (рис. 3.7.1) коммутативна.
176
Роль изоморфизма играет coot-	g
ветствующая биекция.	О(х) х F <‘(О(х))
Мы имеем дело с локально-	\	У
тривиальным расслоением в том	п
частном случае, когда множество (пространство) U управляющих параметров не зависит от локаль-	Рис.3.7.1
ного состояния системы с управлением.
Понятие расслоения нам представляется очень гибким хотя бы с той точки зрения, что оно может описывать понятие детривиализации, или развития, когда над каждым элементом b е В некоторого множества В возникает (“вырастает”) новое множество в виде слоя л-1 (6), реализующее детривиализацию ранее тривиального элемента Ъ е В, как бы снабжая его “новыми степенями свободы”, “внутренними параметрами”, превращая элемент в целое множество (пространство).
При этом нарушается изначальная симметрия множества В, она становится более сложной.
Рассуждая с другой стороны, можно сказать, что расслоение снабжает структурой множество X, разбивая его на отдельные слои. Такая “операция” расслоения множества X также нарушает его изначальную симметрию.
3.8. О СИММЕТРИИ МНОЖЕСТВА
Поскольку объектами математики являются различные структуры, го симметрия в математике — это симметрия структур. В свою очередь всякая структура может быть представлена так или иначе некоторым определенным множеством. В этом, по сути, и состоит идея теоретико-множественного обоснования всей математики, которая, как известно, является очень сложной проблемой. В свою очередь она изучается средствами логики и философии и во многом связана с проблемой языка и языков, перевода с одного языка на другой как формализованным средством выражения всякого смысла, в том числе и осмысления такого центрального математического понятия, как множество.
Поэтому, говоря о симметрии как основном математическом методе изучения любых математических структур, надо прежде всего уяснить понятие симметрии применительно к понятию множества. Другими словами, надо вначале понять, что такое симметрия данного множества. Как уже говорилось, симметрия — это прежде всего некоторое преобразование, т.е. в данном случае мы должны говорить о преобразовании данного множества, под которым надо понимать любое отображе
177
ние f множества А (необязательно симметрии) в любое другое множество В. т.е./: А-+ В. где А дано и фиксировано, &BvJпроизвольны. В результате преобразования / множества А мы всегда получаем множество f{A), и такое, что/Л) с: В.
Множество//!) можно также назвать преобразованием множества/! под действием отображения/
Таким образом, имеем два множества: A M-fiA"). Спрашивается: “При каких условиях можно естественным образом считать, что А обладает симметрией, а отображение / является преобразованием симметрии, T.e.f(A) — результат преобразования симметрии?”
Естественный ответ на этот сакраментальный вопрос, по-видимому, должен звучать так: “Это будет тогда, когда А и ДА} будут неразличимы (неотличимы) в каком-то смысле”.
Таким образом, вопрос о симметрии множества сводится к осмыслению и формализации понятия два произвольных множества X и Y неразличимы.
Первое и “наиболее” естественное, что приходит в голову, — это считать, что X м Y неразличимы, если X = Y, в теоретикомножественном смысле. Иными словами, считать, что данное А обладает симметрией, если существует такое его преобразование / что /(Л) = А, т.е. существует сюръекция/: А ->А.
Таким образом, трудно возразить против того, чтобы всякую сюръекцию /: А -> А считать преобразованием симметрии данного множества А. Однако только такое понимание симметрии данного множества А, по-видимому, будет узким и стеснять наше воображение. Но в математике появилась очень мощная идея, которая позволяет раздвинуть эти узкие рамки понимания симметрии, т.е. неразличимости, как абсолютно тождественного совпадения объектов до и после преобразования. Эта идея подобна идее теории относительности в физике, когда отказались от понятия абсолютности событий и перешли к способам их сравнения с той или иной точки зрения, т.е. в том или ином смысле.
В математике такой революционной идеей относительности стала идея эквивалентности, которая оформилась как отношение эквивалентности, т.е. бинарное отношение, подчиненное трем аксиомам: рефлексивности, симметричности и транзитивности. Это понятие дало много новых степеней свободы для творческого осмысления и формализации понятия неразличимости.
Итак, в расширенном смысле два множества — А и f(A) ст В, где В произвольно, — считаются, по определению, неразличимыми, если они находятся в отношении эквивалентности, а/: А А есть преобразование симметрии множества А. Отношение эквивалентности будем обозначать “я”, т.е. вместо жесткого требования равенства/Ц) = А введем требование послабее: //) « А. А эквивалентно /Л), что дает больше
178
возможностей для творческой фантазии придумывать те или иные, подходящие для решения или постановки той или иной проблемы, отношения эквивалентности “®” и отображения f вместо жесткого равенства ‘ ” только в одном смысле — теоретико-множественном.
В математике часто в качестве такой эквивалентности используется 1 - 1 соответствие или взаимно однозначное соответствие между двумя множествами А и У, которое описывается отображением биекции:
0:А->У, Р(А) = У, р-’(У) = Х.
Такое отображение, по определению, сохраняет не само множество X, а только его мощность N(X), т.е. имеем N(X) = N(Y) = 7V(P(A)) = = 7V(p-1(T)). Но этого оказывается достаточно, чтобы считать А и У неразличимыми с этой новой, более широкой точки зрения. Отсюда, в частности, расширенное понимание симметрии множества А — сохранение не самого А, а лишь его мощности, т.е. А обладает симметрией/ если N(A) = WVO).
Легко проверить, что такое понимание эквивалентности действительно есть отношение эквивалентности, удовлетворяющее всем трем аксиомам эквивалентности.
Итак, наше первое узкое понимание симметрии множества А как преобразования, сюръекции на себя s : А А, s(A) = A, f = s можно теперь расширить до преобразования сюръекции о множества на любое множество В:
о :А-> В, но при условии, что существует биекция
Р : сг(Л) -> В.
Объединяя эти условия, можно сказать, что преобразованием симметрии множества А в расширенном смысле, по определению, является всякое преобразование множества , Л на множество В:
Р°су:Л -» В,
где р о с — композиция сюръекции и биекции, что тоже является сюръекцией : А —> В. Короче говоря, симметрией А в широком смысле можно снова назвать любую сюръекцию s} А —> В, сохраняющую мощность множества Л, т.е. N(A) = N(B) = N(sx(A)).
3.9. СИСТЕМЫ С УПРАВЛЕНИЕМ И СИММЕТРИЯ
В соответствии с понятием структуры, определенной в терминах шкал Бурбаки или в терминах предиката Р(х), х е А и соответствующих ему отношений, в конце концов всякую структуру, систему или пространство можно представить как некоторое множество, т.е. только
179
как некоторое отношение принадлежности (попарно различимых элементов). Такое множество скорее всего будет подмножеством какого-то другого множества. Но сейчас нас будет интересовать само это множество безотносительно к тому, во что оно “вложено”. Например, структура может определяться каким-нибудь отображением/: А —> В, а поэтому она задается графиком Г, т.е. некоторым подмножеством в А х В. Нас будет интересовать лишь само множество Г, и не будет иметь значения, что оно в то же время есть подмножество какого-то другого множества.
Итак, в этом подразделе под системой будем понимать любое непустое множество, называемое множеством состояний этой системы. Такой крайне упрощенный пример системы как “голого” множества (без всяких дополнительных структур, с ним связанных) сделан для того, чтобы было легче уяснить суть основных математических положений ЕГТУ.
Прежде всего покажем, что такое симметрия системы и как с ее помощью естественным образом поставить ей в соответствие систему с управлением (ССУ).
Итак, пусть имеется непустое множество X с элементами х, которые будем называть точками, или изображающими точками, системы с множеством (пространством) состояний X. Общее понятие преобразования множества и его преобразования симметрии было дано в подразд. 3.8.
Заметим, что если бы мы имели дело с общим понятием системы как пары (X, С), где С — структурное отображение данной системы, описывающее ее структуру, то ее симметрией назвали такие преобразования 5 множества X, которые, кроме сохранения самого X, сохраняли бы еще и структурное отображение. Таким образом, все нижеследующие рассмотрения остаются в силе и для произвольной системы, а не только для систем в виде непустого абстрактного множества X, не снабженного никакой дополнительной “надстройкой” над ним, т.е. структурой.
Напомним следующее.
IОпределение 1. Преобразование симметрии множества X — это любое сюръективное отображение s : X —> X.
Преобразование у будем называть просто симметрией множества X. Множество всех таких симметрий обозначим £ и будем называть множеством В'симметрий множества X. Очевидно, что S с {/}, т.е. 5’ есть некоторое собственное подмножество множества {/} всех преобразований множества %.
180
Отметим, что иногда симметрией X называют само множество 5, а его элемент s е S— элементом симметрии.
Обратим внимание на фундаментальный факт — множество £ всех симметрий обладает своей собственной структурой, что описывается следующими свойствами.
1.	Множество £ обладает свойством мультипликативности', для любых двух элементов Si g S и s2 е S существует, т.е. определена, операция их перемножения, которая имеет смысл композиции s2 ° sx двух сюръективных отображений.
2.	В силу того, что композиция сюръекций снова сюръекция, имеем s2 о g S, т.е. результат операции перемножения снова принадлежит исходному множеству S. Таким образом, множество симметрий S любого множества X замкнуто относительно бинарной алгебраической операции в этом множестве.
3.	В силу сюръективности s2, s3 из £ операция перемножения, т.е. в данном случае операция композиции трех симметрий, ассоциативна'.
(*i °£2)о*з = si °02 °5з)-
Из этих трех свойств можно заключить, что множество симметрий S имеет структуру полугруппы.
4.	Более того, в силу того, что тождественное (единичное) преобразование s0 • X X, очевидно, есть сюръекция, то она тоже принадлежит S, т.е. so g S. Поэтому множество всех симметрий S любого множества X есть моноид (полугруппа с единицей). В частности, моноид симметрий может оказаться группой симметрий.
Заметим, что:
1) операция композиции не обязана быть коммутативной, т.е., вообще говоря, S] о s2 Ф s2 О Sj;
2) отображение s1, обратное s, не обязано существовать для любого s е S.
В частном случае, когда множество X конечно, т.е. состоит из конечного числа элементов, сюръекция s : X —> X обязана быть биекцией, т.е. устанавливать взаимно однозначное соответствие между разными элементами множества X. В этом частном случае для каждой симметрии s существует другая симметрия s-1 множества X, причем такая, что sos"1 = s-1 о s = s0 есть тождественное преобразование множества X и тоже его симметрия, принадлежащая {£}. В этом случае говорят не о моноиде симметрий, а о группе симметрий. Если X конечно, то его группа симметрий — это группа всех перестановок элементов из X.
Теперь покажем, как из одной данной системы X с моноидом 5 всех ее симметрий естественным образом можно получить различные системы с управлением. Для этого исходную систему представим как
181
прямое произведение X х S’, которое будем называть расслоением с базой X и слоями S, которые все попарно идентичны. Каждый слой S будем считать “висящим” i [ад точкой х базы X и обозначать его Sx, х е X, при этом Sx = S для Vx g X.
Для того чтобы данной системе поставить в соответствие ССУ, зададим ограничения, которые состоят в том, что в каждой точке х зафиксируем некоторое непустое подмножество Vx слоя Sx, т.е. Vx cz Sx. Таким образом, в каждой точке х е X существуют только допустимые симметрии vx е Кх, которые осуществляют допустимые действия на данную точку х g X(рис. 3.9.1). Заметим, что единичный элемент моноида симметрий может не входить в Vx.
На рис. 3.9.1 изображено еще сечение S' расслоения, задаваемое отображением ср, которое каждому х g X ставит в соответствие элемент vx g Vx, т.е.
vx = ср(х), х е X, vx g Vx.	(3.9.1)
 Это понятие описывает синтез системы с управлением.
Зафиксируем точку х и подей-ствуем на нее один раз каждой \\V\^	симметрией vx из Vx. В результате
Л\V \\W\VД^\ \\ \ V получим подмножество Дх) с X х \\ vx\\V\ \\\	всех точек вида х' = vx • х, когда vx
“пробегает” Vx. Множество Дх), х g X, назовем индикатрисой х х	управляемости точки х. Совокуп-
л п п ,	ность всех Дх) на % назовем полем
индикатрис управляемости на множестве X. Определим заодно понятие дуальной (двойственной, сопряженной) индикатрисы 7(х), х с Д к индикатрисе Дх).
Дуальная индикатриса /(х) к индикатрисе Дх) — это множество вида
7(х) = {х' g X: х е Z(x')}, хеХ.	(3.9.2)
Таким образом, имеем теперь два поля на Х\ индикатрис и дуальных индикатрис.
По понятным причинам дуальную индикатрису 7(х) можно было бы также назвать индикатрисой наблюдаемости, или индикатрисой достижимости, если Дх) называть индикатрисой управляемости. Индикатрису 7(х) можно также было бы назвать индикатрисой обратного времени, или индикатрисой попятного движения, если пользоваться
182
терминологией, введенной А.А. Фельдбаумом. Не надо путать введенное здесь понятие индикатрисы с понятием индикатрисы, введенной в разд. 6, где она имеет другой смысл, а именно, индикатрисы скоростей дифференциальной системы.
Понятие поля индикатрис будет исходным для дальнейших рассмотрений, ведущих к понятию ССУ. Конечно, можно было бы сразу задать поле индикатрис I(x), х е X. Однако использованный нами способ показывает возможный генезис (происхождение) поля индикатрис, существенно связанный с понятием симметрии исходной системы X
Расслоение с базой X и слоями Vx, х е X, или поле индикатрис 1(х), х е X, назовем системой с управлением. В этом смысле наша исходная система, множество X, или пространство (X, С), тоже система с управлением. Таким образом, всякую систему или пространство можно рассматривать как ССУ. В этом смысле систем без управления не бывает.
Подчеркнем, что ССУ определяется одним из двух полей индикатрис: или Z(x), х 6 X, или 7(х), х е X, которые однозначно определяют друг друга по формуле (3.9.2). Таким образом, ССУ на А— это пара (X; Дх), х g X), состоящая из двух объектов: множества А и поля индикатрис 7(х), х е X.
Аналогично, но дуальным образом ССУ может задаваться парой (X; 1(х), х е А) = (A, 7(х)) = (A, Z). В частности, если Дх) = 1(х), то индикатриса Дх) называется самодуалъной (самосопряженной). Если это условие выполняется для всех точек множества А, то ССУ также называется самодуальной (самосопряженной). Для этого еще можно использовать термин автодуальная.
Введенное понятие ССУ порождает ряд основных понятий, органически с ней связанных, в число которых по самому смыслу должно войти центральное понятие управление в данной ССУ, которое будет также называться допустимая.
Перейдем к последовательному введению и рассмотрению этих понятий. Прежде всего порождаются понятия множеств управляемости из точки х е X.
Определение 2. Множество управляемости из точки х е Аза i шагов, обозначаемое Dj(x), I = 1, 2, 3, ..., — это множество, определяемое рекуррентной формулой
ВД = {ДИ>НМ). 1 = 1,2,...,
где D] (х) = 1(х), х g А.
Множество
1=1
называется множеством управляемости точки х.
183
Аналогично определим множество достижимости в точку х е Х\ Dy (х) = Z(x), Д. (х), D (х) = (х), х е X . Точку х назовем порождающей точкой этих множеств.
Эти множества обладают целым рядом очевидных свойств:
Z(x) = Д (х) с... с	(х) с:... <z £>(х);
Z(x) = Dy (х) с... с Д (х) с... с £>(х).
Это свойство моно^понности последовательностей множеств:
(Д (х),..., Д (х),..., £>(х)) и (Д (х),..., Д (х),..., D (х)),
где х — любое фиксированное состояние ССУ.
Далее, если xj е D(x), то
Д (х1) сZ>(x), Vf = l, 2,
Аналогично, еслиX] е £>(х),то
ВДсДх), Vz = l,2,...,oo.
Эти свойства в свою очередь порождают понятие частичного транзитивного порядка на X, ибо его можно рассматривать как классический частичный порядок, но ослабленный удалением из него требований выполнения двух аксиом: рефлексивности и антисимметричности. Таким образом, получаем следующее определение транзитивного частичного порядка.
Определение 3. Транзитивный частичный порядок на %— это бинарное отношение на X, обозначаемое Х| < х2, для которого выполнена аксиома транзитивности: из х, < х2, х2 < х3 следует Х] < х3.
Точки Xi и х2 называются сравнимыми по этому порядку, если или Xi < х2, или х2 < X]. В противном случае они называются несравнимыми.
ССУ порождает на X, вообще говоря, два различных частичных транзитивных порядка, один из которых соответствует полю Z(x), а другой — полю Z(x).
Транзитивный частичный порядок на X, порожденный ССУ (X, Г), задается условием: точки Xj е X и х2 g X сравнимы друг с другом, т.е. между ними существует отношение частичного транзитивного порядка, если и только если выполняются или оба вместе, или только одно из двух следующих условий:
x2^D{x{\	(3.9.3)
и тогда Xi < х2;
xj е D (х2), (х2 е D (xj)),	(3.9.4)
и тогда х2<хь
184
Порядок, соответствующий (3.9.3) назовем прямым порядком, а (3.9.4) — обратным. Здесь нетрудно проверить выполнение аксиомы транзитивности.
Таким образом, в силу отсутствия аксиомы антисимметричности для этого порядка, могут оказаться истинными вместе оба “противоположные” утверждения: и xj < х2, и x2<xj.
Это важная особенность транзитивного порядка, расширяющая класс рассматриваемых ССУ, так как такой порядок может оказаться естественным для некоторых ССУ. Заметим, что могут существовать ССУ, для которых снова требуется выполнение аксиом антисимметричности и рефлексивности (вместе или по отдельности).
Определение 4. Подмножество Y с X называется слабой цепью, если и только если любые X] е У и х2 е У сравнимы по крайней мере только по одному из порядков — прямому или обратному.
Конечно, не исключено, что У является слабой цепью по обоим порядкам вместе (но целиком по каждому, а не вперемежку). В дальнейшем вместо слабая цепь для краткости будем писать цепь, если это не приводит к недоразумениям.
Здесь не будем заниматься интересным, но нетривиальным обратным вопросом: как по данному транзитивному частичному порядку построить согласованное с ним поле индикатрис (ССУ), т.е. такое поле, чтобы оно порождало заданный транзитивный частичный порядок.
Теперь можно дать важное определение допустимого управления, или просто допустимой, в ССУ. Сначала определим линейную, или цепную, допустимую ССУ.
(Определение 5. Линейная (цепная) допустимая ССУ — это слабая цепь в X.
Цепные допустимые будем обозначать у.
I Определение 6. Кусок у[а, д] цепной допустимой у — это подмножество у[а, Ц cz у такое, что а < х < b для любого х е у[а, Ь].
Очевидно, всякий кусок у[а, 6] цепной допустимой — тоже цепная допустимая. Вместо неравенств а < х < b в определении куска могут иметь место следующие: а< х, а < х; х < Ь; х < Ъ, а < х < Ь, а < х < Ь. Точка а называется начальной точкой куска, точка Ъ — конечной. Вообще говоря, начальная и конечная точки могут не принадлежать куску.
Понятие цепной допустимой вводит на множестве X данной ССУ понятие линейной связности.
I Определение 7. Множество X (или какое-нибудь его подмножество У) называется линейно связным вперед, если для любой упорядоченной пары точек а и b из X(из У) существует хотя бы одна допустимая цепь у[я, &] или у[£>, а].
185
Просто линейная связность означает существование и у[а, Ъ], и у|7>, а], которые как множества (без указания порядка) могут или совпадать, или не совпадать друг с другом.
Говорят, что упорядоченная пара точек (а, Ь) управляема (достижима), если существует у [а, (соответственно у[6, я]). Одна и та же упорядоченная пара (а, Ь~) может быть и управляема, и достижима вместе, если точки аиЬ линейно связны.
Таким образом, во всякой ССУ имеется структура управляемости— достижимости, которая есть по существу бинарное отношение связности на X. Естественно, что существует структура финитного управления, по которой каждой упорядоченной паре (а, Ъ) точек X ставится в соответствие совокупность всех допустимых между а и Ь.
Наконец, можно говорить и о третьей — естественной, или собственной, — структуре, связанной с данной ССУ, а именно, о структуре собственного оптимального управления. Эта структура задается на связных (а, Ъ) g А3 отображением в допустимые цепи у (д, Ъ) минимальной “длины”, где “длина” у(д, Ъ} — целое число i такое, что b g Д(о), но b g' Di+l (а).
Скажем несколько слов о синтезе цепных допустимых. Предположим, что задано сечение (3.9.1) для данной ССУ. Тогда с каждым локальным состоянием х g X однозначно связан допустимый оператор управления vv = ср(х), vY g Под действием данного оператора vx точка х “сместится” в “следующую” точку х' - vx -х = ср(х) • х. Из х' под действием оператора произойдет “смещение” в новую точку х" = yv- • х' и т.д. Этот процесс можно начать из произвольной точки a g X. В результате однозначно получим некоторую допустимую цепь уа, зависящую от a g X. При этом могут иметь место два взаимно исключающих случая:
1) цепь уа заполнит все множество X, последовательно “пройдя” все его точки (наподобие кривой Пеано, сплошь заполняющей квадрат);
2) множество X будет разбито на некоторую совокупность попарно непересекающихся допустимых цепей уа, параметризованных некоторым множеством {а} параметров a g X.
Заметим, что каждая /акая цепь уа реализует некоторое нарушение симметрии множества X, которое характеризуется моноидом М своих сюръекций. Действительно, каждая цепь уа задает некоторое подмножество G cz М. Множество G состоит из симметрий 5 g G, и это множество “замкнуто” в том смысле, что из g G и s2 g G следует, что произведение (композиция) s} °s2 &G. Таким образом, G представляет
186
собой некоторую полугруппу, вложенную в моноид М всех симметрий множествах. Такая полугруппа может оказаться довольно сложной.
Если множество X конечно или счетно, то все вышесказанное допускает наглядное толкование в виде графа, вершины которого изображают состояния Xj е X, i - 1,2, ..., N, а ребра со стрелками между х, и Xj изображают индикатрисы.
Рассмотрим еще одно порождение данной ССУ, которое можно назвать надсистемой ССУ (сокращенно НССУ). НССУ характеризуется множеством 2Л = {X}, т.е. множеством всех подмножеств множествах Множество {X} назовем множеством состояний НССУ, а его элементы X] g {X}, т.е. Xi cz X, локальными состояниями, или просто состояниями, НССУ. Подмножества множества {X}, за исключением пустого множества, назовем глобальными состояниями НССУ.
Рассмотрение НССУ, скорее, вызвано не стремлением ко все более широким обобщениям, а насущной необходимостью искать подходящие точные математические описания для сложных систем с управлением, например, систем с распределенными параметрами (СРП), в частности, сплошных сред и полей.
Дело в том, что в СРП приходится иметь дело с управлением не отдельными точками л в X, а с управлением целыми множествами Хь являющимися подмножествами множества X, X]. cz X. Более того, если при этом основное множество X снабжено еще некоторой дополнительной структурой С, то требуется сохранить и эту структуру С над X. Например, если X снабжено дифференциально'й структурой, то часто требуется сохранить еще достаточную гладкость управляемых подмножеств.
Здесь мы ограничимся рассмотрением НССУ, пороченных только множеством X с полем индикатрис I(x), х е X. Рассмотрим какое-либо непустое подмножество X] cz X как элемент Х\ е {X} и введем понятие индикатрисы J(X]):
J(Xi)?{EZ(^):xgXj}, VX1C={X}, VX, g {X}.
Эта индикатриса есть просто подмножество /(Xj) в множестве X, но в прост ранстве состояний НССУ — это одна единственная точка J(Xi), J(Xj) е {X}. Так как X] g {X} — тоже точка в {X}, то индикатриса /(XJ, связанная с этой точкой, показывает, куда переходит точка Х{ за один шаг. Проделав эту процедуру для VT cz X или, что то же самое, для VF g {X}, получим поле индикатрис J(Y), Y g {X}.
В отличие от поля индикатрис I(X), х е X, где каждая 1(х) — это, вообще говоря, многоэлементное множество, поле J(Y), Y е {X} состоит из индикатрис J(Y), которые представляют собой лишь одноточечное подмножество в {X} для любого Y е {X}.
187
Это похоже на поле векторов, которое задает обыкновенное дифференциальное уравнение, в котором дальнейшее движение выбранной изображающей точки определяется однозначно (никакого выбора разных движений в этой точке нет).
Таким образом, в НССУ, построенной над данной ССУ и в которой есть довольно широкий выбор в управлении, весь выбор управления сводится к выбору “начальной” точки Ко е {У} (начального подмножества Yq cz X, если говорить в терминах ССУ и X). Выбор и фиксация Yo g {X} при к = 0 однозначно предопределяет всю “траекторию” в {X} при дальнейших шагах к = 1, 2, 3, Уо, 1ь  > X,  > где Yk = /(Zt-i).
Примером такой траектории может служить последовательность
х0 ,/(х0), Y2(xo), Y3(x0), ..., Yk(xo), ..., Y<Xx),
где начальное множество {х0} = Yo, т.е. одноэлементное множество, состоящее из одной точки х0. Эта последовательность (подмножеств в X) представляет собой последовательность точек в {X}.
Задача управления в НССУ может, например, состоять в том, чтобы выяснить следующее: пусть дано К. е {Y}, т.е. подмножество YcX, ограниченное каким-то допустимым классом Ко; спрашивается, существует ли Уо 6 Ку cz {X}, где Ку — тоже класс допустимых, такое, что в “траектории”, т.е. в последовательности Уо, Уь ..., Yk, ..., найдется Y„, п < оо, для которого выполняется условие К. cz Yn (условие накрытия данного К множеством У„). Если такое Уо е Ку существует, то требуется найти его и наименьшее п.
Это задачи управляемости, финитного управления и оптимального управления, но не для локальных состояний ССУ, а для ее глобальных состояний (подмножеств из X). Теория таких задач для НССУ почти не разработана.
3.10. СИСТЕМЫ С УПРАВЛЕНИЕМ И МАРКОВСКИЕ ПРОЦЕССЫ
Система с управлением может порождать марковский процесс со специфическим распределением вероятности. Напомним очень кратко суть марковского процесса. Пусть имеется множество состояний X ССУ. Введем параметр t е Т, где Т — некоторое линейно упорядоченное множество. Параметр t назовем временем. Будем рассматривать точки (Г, х) е Т х X, где х е X — изображающая точка ССУ. Предположим, что на Т х Xможно ввести плотность вероятностиp(t0, х0; ty, хЦ, где точки (fo, х0) и (6, Xj) — элементы (Г х X). Смысл этой функции состоит в том, что ее значения показывают плотность вероятности случайного события, состоящего в том, что изображающая точка ССУ в
188
момент времени t\ > tG окажется в точке хь если в момент Zo она находится в точке х0. Таким образом, плотность вероятности по существу есть условная плотность вероятности, которую надо было бы, как принято в теории вероятностей, обозначатьp(t\,xx/tG, х0), где случайное событие (Zb х\) происходит при условии, что событие (Го, х0) достоверно. Но мы оставим прежнее обозначение. Для марковского процесса на X его структурное тождество (уравнение) имеет вид
p(tx,xp, tQ,xQ) = J р(Ь,ху, t,x)p(t,x; r0,x0)d(f,x),	(3.10.1)
где [Zo, Zj — множество всех t таких, что tQ < t < t}. Это тождество есть не что иное как широко известная формула полных вероятностей.
В частности, если множество Xнаделено еще структурой «-мерного евклидова пространства R", a t g 7?', то при некоторых естественных аналитических условиях функция p(t, х; 10, х0), и это не трудно показать, удовлетворяет уравнению Колмогорова
^ + aaP(Z,x)-^- + fea(Z,x)-^- = 0,	(3.10.2)
dt	дх^дх*	дха	V 7
где х = (х1, ..., х”) =(х“), сс = 1, ..., п; Р — 1, ..., п, и идет суммирование по парно входящим индексам а и Р, а функции яаР(Г, х) и Ьа(Г, х) вычисляются некоторым “инфинитезимальным” йнтегрированием около каждой точки (Г, х) через неизвестную функцию плотности р. Таким образом (3.10.2) довольно сложное интегро-дифференциальное уравнение [250]. Марковский процесс состоит в случайном блуждании изображающей точки х в множестве X. Плотность р полностью описывает это блуждание.
Но вернемся к ССУ, описанной в подразд. 3.9. В этом случае время t будет принимать дискретные значения 0, 1, 2, ..., к, t0 = 0. Если изображающая точка х ССУ в момент /0 = 0 находится в точке х0, то в следующий момент (Zj = 1) она может принадлежать только множеству Z(x0), т.е. индикатрисе около точки х0. Таким образом, если ввести плотность вероятности p(t\, xytG, х0), то р>(1, ху, 0, х0) будет финитной функцией аргумента Xi при любом х0 е X с носителем в виде индикатрисы Z(x0), т.е. везде вне индикатрисы Z(x0) вероятность будет тождественным нулем.
В качестве такой функции р(1, х^ 0, х0) можно взять положительную. функцию при Xi е Z(x0) и любом х0 е X, которая тождественно равна нулю при Xj ё Z(x0) и Vx0 е X. Например, можно положить /^(l, х^ 0, х0) = const = С > 0, где С можно найти из условия нормировки вероятности.
189
Чтобы найти плотность на втором шаге, т.е. при к - 2, очевидно, нужно применить формулу полных вероятностей (3.10.1), считая время t дискретным 0, 1, 2, ... и упорядоченным. Имеем:
д, (2,х2;0,хо) = \рх (1,х2;0,л)
Ц-<о)
где, конечно, требуется измеримость множества 7(х0). Отсюда видно, что функция р2 также финитна с носителем D2(x0) (см. подразд. 3.9), на котором она положительна, а при х2 еЛ2(х0) плотность р2 = 0 при любом х0 е X.
Вычисление плотности рз(3, х3; 0, х0) при к ~ 3 можно произвести рекуррентно:
/?3(3,х3; О,хо) - [р3(1,х3;0,х) р2(2,х; O,xo)dx.
Р2(-<о)
Продолжая этот процесс, можно шаг за шагом вычислить и далее Рк(к, х; 0, х0), к = 2, 3, 4, ..., оо, где рк также будет ненулевой положительной функцией только лишь на множестве Z)fc(x0), а вне его рк = 0 при Vx0 е X.
Эту картину можно описать так: точка х0 является постоянно действующим точечным источником некоторой субстанции ненулевой плотности некоторой величины (в данном случае такой субстанцией является вероятность или мера). Эта субстанция постепенно (в данном случае по шагам к = 0, 1,2, ..., оо) “заливает” множество X. Точки, которые оказались наводненными в момент t = к имеют смысл точек управляемости из точки х0, где действует источник. Эта картина вполне согласована с принципом Гюйгенса (см. подразд. 4.3), где роль субстанции играет некое возбуждение (например, освещенность), которое распространяется в множестве X.
Однако описанная выше вероятностная картина дает существенно большую информацию: кроме ответа типа “да, точка х возбуждена в момент t = Л” или “нет”, значение р(х, к; 0, х0) показывает интенсивность возбуждения в точке х.
3.11. УПРАВЛЕНИЕ С ТОЧКИ ЗРЕНИЯ АКСИОМЫ ВЫБОРА ЦЕРМЕЛО
В этом подразделе будет показана связь таких фундаментальных понятий кибернетики, как управление и система с управлением, с известной в математике аксиомой выбора Э. Цермело. Мы попытаемся ответить на вопрос: “С каким математическим понятием следует отождествлять понятие управление?” По-другому вопрос можно поставить так: “Какая математическая структура несет ответственность за понятие управление?”
190
Как уже неоднократно подчеркивалось, по существу и содержательно управление — это всегда выбор', есть выбор из некоторого непустого множества возможностей — есть и управление, нет выбора — нет и управления. При этом выбор может производиться многократно и каждый раз, вообще говоря, из разных множеств.
С другой стороны, понятие выбор играет фундаментальную роль в математике. В начале XX в. Эрнесто Цермело сформулировал аксиому выбора, без которой нельзя осмыслить и доказать существенную часть основополагающих математических утверждений.
По общему мнению, вопросы, связанные со смыслом и правомерностью применения аксиомы выбора в математике, являются самыми глубокими и спорными, самыми принципиальными и трудными, несмотря на “очевидную” истинность утверждения этой аксиомы (см., например, 1183, с. И, 26]). Кроме того, доказательства утверждений в математике и, следовательно, сами утверждения разбиваются на два класса в зависимости от того, используются или не используются в них утверждения, эквивалентные аксиоме выбора. По-видимому, глубина, спорность и трудность вопросов, связанных с аксиомой выбора, являются отражением фундаментальной философской проблемы о свободе воли, извечных проблем судьбы (фатальности) и о том, в какой мере мы ей распоряжаемся и управляем ходом истории, общественной или своей собственной. Ведь в нашей жизни выбор или управление мы осуществляем все время. Даже “ничего неделание” — это тоже выбор между активной деятельностью и пассивным бездельем.
В кибернетике понятие управление, как правило, неразрывно связано с понятием система. При этом говорят, что управление “воздействует на систему”, “управление происходит в системе” и т.д. Результатом этого является изменение состояния системы, или движение в системе.
Поэтому принят термин система с управлением. Этот термин мы предпочли “расхожему” термину система управления, ибо последний используется в очень широком классе контекстов с плохо определенным своим значением.
Попытка описать аксиоматику понятий управление и оптимальное управление без связи с понятием система предпринята в разд. 5.
Связь управления с аксиомой выбора Цермело состоит в том, что синтезирующая функция системы с управлением, отождествленная с сечением расслоения, оказывается однозначно связанной с функцией выбора, фигурирующей в формулировке аксиомы, приведенной ниже.
Всякая ССУ имеет следующие атрибуты, для которых сделаем соответствующие отождествления с атрибутами расслоения (см. подразд. 3.7). Пространство состояний ССУ отождествляется с базой расслое-
191
ния, обозначенной через X, элементы (точки) х е X будем называть локальными состояниями, или изображающими точками; с каждой точкой х g X свя жем слой Ux расслоения, который отождествим с пространством допустимых значений и управлений, т.е. и э Ux. Здесь точку х можно рассматривать как индекс, параметризующий совокупность {64} всех слоев Ux, когда х “пробегает” все пространство X. Пусть эта параметризация задается функцией, которую назовем параметризующей'.
Ux = a(x), хеХ, Uxg{Ux}.
Расслоение, отождествленное с ССУ, конструируется с помощью совокупности S?
S={Ux} = {Ux'.x^X}.
В частности, когда все слои идентичны, т.е. Ux = U для любого х с X, функция ос(х) является постоянной функцией наХ
Естественно принять, что любое Ux является непустым множеством и совокупность S тоже не пуста.
В этих терминах управление как многократный выбор, о котором говорилось выше, состоит в том, что выбирается по одному элементу и из каждого множества Ux, когда х “пробегает” X.
Выбор значения и управления из Ux в состоянии системы х е X должен каким-то способом определить другое состояние х’ е X. В состоянии х’ снова происходит выбор и' е Ux>, который определяет другое состояние х", и т.д. Это и есть “схема многократного выбора”, которая должна определить управление.
Но на языке теории расслоений такой многократный выбор, т.е. управление, можно задать связностью на расслоении. Таким образом, управление естественно отождествить с понятием связность в расслоении. Дело в том, что слои Ux априори никак между собой не связаны, — это просто совокупность слоев. Именно связность вносит в S определенное взаимодействие и согласование.
Связность — это просто правило перехода от слоя к слою, из которого следует соответствующее правило перехода от состояния к состоянию, т.е. правило изменения состояния, или правило движения изображающих точек пространства состояний X ССУ. Естественно, что это правило должно сохранять структуру ССУ. Иными словами, связность, или структура связности, должна быть согласована с заданной (фиксированной) структурой ССУ. Связность как раз и призвана для того, чтобы что-то сохранять. Например, одна из первых классических связностей — это аффинная связность. Она служит для сохранения “аффинной структуры” пространства, т.е. сохранения параллельностей при движениях в этом пространстве. Метрическая связность должна
сохранять метрическую структуру. Связность в математике была открыта лишь в начале XX в.
Отсюда вытекает, что понятие сечение расслоения, естественно отождествляется с понятием синтез ССУ и описывается функцией (р:
и = (р(х), х g X, и е Ux , которая в теории управления для данной системы с управлением называется синтезирующей функцией. Она может еще называться обратной связью, регулятором или просто синтезом.
Введенные выше определения (отождествления) подсказаны геометрическим подходом, господствующим сейчас в теоретической физике, по которому все классические физические поля (гравитационные, электромагнитные и др.) представляются как сечения некоторых (дифференцируемых) расслоений.
На этом подходе основана успешно выполняющаяся в физике Программа создания “Единой геометрической теории поля”.
Теперь есть все основания, чтобы явно найти связь теории управления с аксиомой выбора Цермело. Для этих целей удобна следующая формулировка аксиомы выбора.
“Если определена любая непустая совокупность {А}, состоящая из любых непустых множеств А, то существует функция, называемая функцией выбора, вида
а = Т(Д), А е {А}, аеА".
Таким образом, аксиома выбора утверждает лишь существование функции выбора Т Однако никаких соображений и тем более алгоритмов относительно эффективного ее построения в общем случае до сих пор не предложено и не ожидается в перспективе. Конечно, такие соображения и алгоритмы не исключены в частных “конкретных” случаях задания совокупности {А}.
В этом состоит парадоксальность аксиомы выбора: функция существует, но, по-видимому, никаких указаний по поводу ее строения, вообще говоря, не существует.
Такая парадоксальность аксиомы выбора у математиков конструктивистского направления вызывает большие сомнения в правомерности и обоснованности ее ничем не ограниченного применения.
Теперь для установления искомой связи достаточно положить (отождествить)
A = UX, {А} = {Ux}, хеХ.
С учетом этих отождествлений видно, что любая синтезирующая функция ср для фиксированной системы с управлением с пространством состояний X и пространствами Ux допустимых значений управлений
192
7. А.В. Бабичев
193
является суперпозицией функции выбора Т и параметризующей функции сс, т.е.
t/ = T(a(x)), хеХ, ueUx.
В этих терминах аксиома выбора Цермело формулируется следующим образом:
| “В любом расслоении существует его сечение”,
и аналогично:
| “Для любой системы с управлением существует ее синтез”.
  J1- СТРУКТУРЫ СОБСТВЕННО МАТЕМАТИКИ
4.1. ТЕОРЕТИКО-МНОЖЕСТВЕННЫЕ ПРОСТРАНСТВА
В этом подразделе рассматриваются некоторые основные теоретико-множественные пространства (структуры), ТМП (ТМС). Они характеризуются тем, что их элементами являются абстракт] [ые множества. Таким образом, предполагается, что элементы ТМП подвержены дет-ривиализации — с каждым элементом ТМП связано некоторое абстрактное множество.
Такой подход позволяет определить операции с элементами ТМП, в точности соответствующие всем теоретико-множественным операциям над абстрактными множествами: сложение (объединение), произведение (пересечение), дополнение, разность, симметрическая разность. Более того, например, понятие подмножества какого-то множества позволяет вводить на ТМП отношение частичного порядка и другие отношения.
Часто в качестве элементов ТМП рассматриваются множества, принадлежащие семейству всех подмножеств какого-нибудь одного фиксированного множества А".
ТМП обладают мощным потенциалом для своего собственного развития, позволяющим вводить на них новые структуры, которые часто задаются просто некоторыми отображениями на ТМП. Например, так вводится структура меры множеств.
ТМП по примеру многих пространств характеризуется симметрией, которая выражается свойством замкнутости определенных операций — результат операций над элементами ТМП снова есть элемент ТМП.
Мы рассмотрим наиболее известные и важные ТМП.
Поскольку “нехорошо” говорить о “множестве множеств” (вспомните о парадоксах, связанных с этим понятием), то в математике вместо этого часто предпочитают говорить о классе множеств. В этом смысле ТМП — просто некоторый класс множеств, который обозначим К.
Кольцо множеств — это один из примеров ТМП.
(Определение 1.Кольцо множеств — это класс К множеств, обладающий следующими свойствами замкнутости операций:
1) если А g К и В е К, то (А п В) g К, т.е. пересечение элементов К снова элемент К\
7*
195
2) если А е К и В е К, то (Л А В) о К, т.е. симметрическая разность А Л В = (А - В) + (В - А) как множество снова принад- * лежит К.
Из этого определения непосредственно вытекают новые важные утверждения о кольце множеств.
I Теорема 1. Кольцо множеств К замкнуто по отношению к операции теоретико-множественной разности.
Это утверждение непосредственно следует из теоретикомножественного тождества А-В = А А (АпВ), которое нетрудно доказать. Отсюда, в частности, следует, что пустое множество 0 е К. Также довольно очевидно, что пересечение любого множества колец тоже есть кольцо. Имеет место теорема существования и единственности наименьшего кольца.
Теорема 2. Каждому произвольному классу К множеств однозначно соответствует минимальное кольцо KQ такое, что: 1) К с KG и 2) Ко cz К', где К'— любое кольцо, содержащее К.
Примером кольца является класс К всех конечных подмножеств произвольного множества, а также класс всех ограниченных подмножеств множества всех действительных чисел.
I Определение 2. о-кольцо — это кольцо множеств, если оно вместе с любой последовательностью своих элементов содержит и их сумму.
I Определение 3.6-кольцо — это кольцо множеств, если оно вместе с любой последовательностью своих элементов содержит и их пересечение.
IОпределение 4. Полукольцо — это класс К множеств таких, что:
1)	он содержит пустое множество;
2)	он замкнут по отношению операции пересечения;
И
3)	если А е К, то имеет место конечное разложение А = (J Ак, k=i
где Ak с К и Ак попарно не пересекаются.
Из определения следует, что всякое кольцо есть и полукольцо. Примером полукольца, не являющегося кольцом, служит совокупность всех интервалов, полуинтервалов и отрезков на числовой прямой.
(Определение 5. Алгебра множеств — это кольцо множеств с единицей, а о-алгебра — о-кольцо с единицей.
Единица Е класса К — это элемент этого класса такой, что пересечение Е п А = А для Х/А е К.
196
Важную роль в анализе и теории меры играет борелевское множество — минимальная алгебра на совокупности всех отрезков числовой прямой.
(Определение б.Поле множеств — это класс К множеств таких, что:
1)	все его элементы — это подмножества одного множества А;
2)	он замкнут по отношению к операциям сложения, умножения и дополнения элементов.
Отсюда следует, что поле множеств в то же время есть алгебра множеств.
I Определение 7. Борелевское поле множеств — это поле множеств, которое еще дополнительно замкнуто относительно операции суммирования любого бесконечного множества своих элементов.
Топологическое пространство также можно рассматривать как некоторое ТМП.
Определение 8.Топология — это класс К множеств таких, что:
I) все его множества — это подмножества одного множества/!;
2)0 е К;
3)	объединение любого числа любых множеств из К снова есть множество класса К;
4)	пересечение конечного числа любых множеств из К снова есть множество класса К.
Пара (А, К) называется топологическим пространством. Каждое множество из К называется открытым множеством данного топологического пространства. Множество, дополнительное к открытому в А, называется замкнутым. Отсюда следует, что не исключено, что один и тот же элемент из К, т.е. одно и то же подмножество из К, может оказаться вместе и открытым, и замкнутым.
Фильтр и ультрафильтр — это ТМП, играющие важную роль в топологии и алгебре, в частности, в теории моделей.
'Определение 9. Фильтр на множестве А — это множество F подмножеств множества А такое, что:
1)еслиу4,зэ5и5 е F,to/1] g Fдля всякого подмножеств? А} <аА',
2)	пересечение любого конечного числа множеств из F — это тоже множество из F;
3)	пустое множество не принадлежит F.
fОпределение Ю.Ультрафильтр на множестве А — это фильтр F на множестве А такой, что для любого В с А либо В g F, либо
В g F, где В = А- В — дополнение В относительно А.
197
Определение И.Центрированное ТМП на множестве А — это любая совокупность подмножеств множества Л такая, что пересечение любой конечной совокупности подмножеств из нее непусто.
Значение последнего понятия состоит в том, что всякое такое пространство порождает на А некоторый фильтр [244, с. 69]: “Пусть D — некоторое центрированное пространство на А, и D' — система подмножеств из D, являющаяся пересечением всех конечных подмножеств из D. Тогда система D" подмножеств А, содержащая некоторое подмножество D', будет фильтром на Л”.
4.2.	МЕРА — ПРОСТРАНСТВО С МЕРОЙ
Мера — это далеко идущее обобщение таких понятий, как длина линии, площадь двумерной фигуры, объем трехмерной фигуры, интеграл от функции и др. Таким образом, речь идет о разумном приписывании числа некоторому множеству, т.е. мера — это функция множеств. На понятии меры основаны все естественные науки. Теория меры есть научная основа понятия измерения в опытах и наблюдениях, как активных, так и пассивных,
Понятие меры мож] ю точно определить, имея как минимум понятие кольца множеств, а следовател ьно, распространить это понятие на совокупности множеств типа полукольца, алгебры и поля множеств.
Определение 1. Мера на кольце К (или о-кольце) — это отображение
д : К -» R, д = д(Л), А е К, д е Л, где R — расширенное пространство действительных чисел (т.е. включающее элемент “со”), причем д удовлетворяет следующим условиям (аксиомам меры):
1)д(Л)>0 для VA е К —неотрицательность;
2)	д(0) = О;
( п Л W
3)д ХЛ	-чля любых непересекающихся А,- е К,
v=i ) i=I
i = 1, п — конечная аддитивность.
Для о-колец К требуется аддитивность для любой бесконечной, но счетной совокупности непересекающихся множеств Л, е К, i = 1, 2, ..., т.е.:
у»=1 j /=1
Это называется аксиомой счетной аддитивности меры ц.
198
Таким образом, в самом общем случае мера — это структура или пространство, задаваемое парой (К, ц), где К играет роль основного множества (множества состояний), ар, — структурное отображение.
Существуют много разновидностей пространств с мерой, которые получаются из указанного выше путем конкретизации и наложения дальнейших условий (аксиом) на К" и ц, но не противоречащих аксиомам из приведенного определения меры. Они являются частным случаем указанной меры. Например, мера Лебега, которая для своего построения, т.е. определения функции р, существенно использует дополнительные структуры евклидова пространства. На этой мере покоится весь классический анализ.
Другим важным частным случаем общей меры является понятие вероятностная мера, или попросту — вероятность данного случайного события. Для нее о-кольцо сужается до понятия су-поле. Элементы супоня называются случайное событие, 0 — невозможное событие, единица о-поля — достоверное событие, пара взаимно дополнительных элементов о-поля — противоположные события.
Тогда вероятность (вероятностная мера) — это просто мера на и-поле с одной дополнительной аксиомой — аксиомой нормируемости, гласящей, что Р(А) = 1, где А — единица о-поля. Простым примером меры является любая действительно-значная (включая “бесконечное” значение) и неотрицательная функция/(Д х е А.
Если кольцо определить как совокупность всех конечных подмножеств множества Л, то
ц({д1,...,д„}) = £/(д/), р(0) = О.
/=1
Классическая вероятность есть частный случай этой меры, когда А есть конечное множество из Nэлементов дь ..., Дд/, а событие — какое-то его подмножество, причем наложено дополнительное условие Hop-д'
мировки X /(ai) ~ 1-
i=\
Менее тривиальный и важный пример классической меры имеет место в случае кольца, состоящего из всех ограниченных множеств (полуинтервалов) на числовой прямой: {х е R: -со <а<х <Ь Тогда мера р определяется равенством
|1([д,6]) = Ъ - а
для любого а на числовой прямой. На этой мере основывается определение классического интеграла Римана.
199
4.3.	ПРОСТРАНСТВО ГЮЙГЕНСА
В этом подразделе рассмотрим понятие пространство Гюйгенса как важный пример ТМП. Эта структура была предложена Гюйгенсом около 300 лет тому назад и послужила ему и Ферма основой для построения фактически первой математической теории, объясняющей или описывающей такую давно наблюдаемую реальность, как свет и его движение (распространение). Было естественно объяснено явление отражения и преломления света (этим занимался Ньютон). Эта структура породила такие важные понятия, как фронт освещенности и луч света. На основе этой структуры довольно естественным образом возникли новые вариационные задачи и задачи на максимум и минимум, ставшие прародителями современной общей теории оптимального управления и других задач на экстремум. Более 300 лет тому назад Ферма на основе идей Гюйгенса сформулировал свой знаменитый принцип, или закон природы, о кратчайшем пути распространения лучей света. Правда, Ферма неявно использовал и другие структуры, в частности метрические.
Более того, примерно через 150 лет после открытий Гюйгенса и Ферма Гамильтоном было сделано потрясающее открытие: пространство (структура, или принцип) Гюйгенса может быть положено в основу механики и фактически почти всей физики. Конечно, значение этого факта мы понимаем более отчетливо только сейчас, после открытия теории относительности и квантовой физики.
С современных позиций, грубо говоря, открытие или гениальная догадка Гамильтона состояла в том, что “волновые” фронты в принципе Гюйгенса можно отождествить с множествами уровня функции действия механической, а по сути физической системы. Вместе с этим произошло другое смелое отождествление: физическое пространство, где распространяется свет, было отождествлено с абстрактным пространством состояний механической (физической) системы! Так как пространство механической системы, вообще говоря, многомерно, то, обращая это отождествление, совершенно естественно можно придти к революционной идее о том, что и физическое пространство также на самом деле многомерно. Трехмерность — лишь та его сторона, которая нам открывается с очевидностью в силу устройства человеческих органов чувств. На самом деле — в силу ограниченности возможностей наших органов чувств — многие “размерности” физического пространства остаются ненаблюдаемыми для естественных органов чувств. Для их наблюдения нужны приборы, расширяющие диапазон возможностей естественных органов чувств. Нам представляется, что идеи пространства Гюйгенса не исчерпаны до сих пор.
200
Формально пространство Гюйгенса можно описать следующим образом.
Рассмотрим прямое произведение R х X, где R — множество всех неотрицательных действительных чисел t (переменная t обычно имеет физический смысл времени).
Каждой паре (/, х0) е R х X поставим в соответствие единственное непустое подмножество Н множества X. Таким образом, получаем семейство Н = H(t, xq), t е R, х0 е X, подмножеств НсХ, или Н е {X}, зависящее от t и xG как параметров. Такое параметрическое семейство подмножеств H(t, х0) назовем семейством Гюйгенса, если для него выполняются следующие условия (аксиомы Гюйгенса):
1)	Я(0, х0) = {х0} — однозначное подмножество X, состоящее из единственного элемента х0 &X, {х0} cz {X};
2)	Н(й + 12, х0)= H(t2, х): х е Я(^, х0)} для Уц и Vz2 из R и Vx0 е X.
Из второй аксиомы следует, что х) cz H(t2, х), если б < t2 при Vx е X. Если мы рассмотрим подсемейство	t g R, которое получается
из семейства {H(t, х)} путем фиксации точки xg X, то получим, что указанное подсемейство {Hx(t)} представляет собой цепь с первым элементом {х} = Дх(0), т.е. представляет собой вполне упорядоченное множество. Упорядочение НХ(Г) < ЯЛ(^) при < t2 порождается указанным выше включением, вытекающим из второй аксиомы.
“Физический” смысл множества H(t, х0) состоит в следующем. Точка х0 является источником некоторого возбуждения (например, света или какой-нибудь другой субстанции), который начинает работать в нулевой момент времени t = 0, а результатом этой работы является то, что в момент t > 0 оказываются возбужденными все точки множества H(t, х0) и только они. В момент t = 0 множество 77(0, х0) состоит всего из одной точки х0, о чем говорит первая аксиома.
Более того, если какая-то точка х е X оказалась возбужденной в какой-то момент б > 0, то она сама становится с этого момента источником возбуждения и порождает “свое собственное” множество возбуждений 77(0 + t, х), зависящее от t. Это явление формализуется второй аксиомой Гюйгенса.
Вторую аксиому Гюйгенса полезно несколько обобщить на тот случай, когда в момент t = 0 в X начинает действовать не один точечный источник, расположенный в точке х0, а целое множество Х\ cz X источников и H(t, х) есть множество возбуждения в момент t.
Этот случай формализуется следующими аксиомами:
3)	Я(О,А-,) = Х;
4)	Я(/,Х)={ЕЖх0):х(,еЛ-,}, где H(t, Х{) можно рассматривать как образ при отображении прямого произведения R х {X} в {А}.
201
Здесь также можно рассмотреть подсемейство {НН/)} = {Н(/, У)}, Y с X, которое при фиксированном Y образует вполне упорядоченное множество с первым элементом Н(0, ХС) - Х}.
Простейшим примером пространства Гюйгенса является евклидово пространство Rn, в котором множество Гюйгенса H(t, х0) представляет собой шар радиуса t с центром в точке х0. Такое пространство Гюйгенса описывает распространение возбуждения, например света, в однородной и изотропной среде.
В подразд. 4.4 мы увидим, как пространство Гюйгенса связано с метрикой. В подразд. 6.16 и 6.17 мы вернемся к принципу Гюйгенса и его связи с понятием управления.
4.4.	МЕТРИКА. МЕТРИЧЕСКОЕ ПРОСТРАНСТВО
Метрическая структура является одной из важнейших математических структур. Достаточно сказать, что такие основополагающие математические структуры и понятия, как топология и оптимальное управление, теснейшим образом связаны с понятием метрики.
Определение 1. Метрическое пространство (структура) — это пара (X, г), где X — произвольное непустое множество, а г — структурное отображение, называемое метрикой (на данном X), следующего вида:
r:X2-^R, r = r(xl,x2), (х},х2)еХ2, где R — множество, за которое обычно принимают пространство действительных чисел и при этом должны выполняться следующие условия (аксиомы):
1)	г(хь х2) > О — неотрицательность метрики;
2)	г(х, х) = 0 для Vx е X:
3)	если г(хь х2) = 0, то х, = х2;
,	4) г(хь х2) = г(х2, %1) для V(xb х2) е X2 — симметричность
метрики;
5)	г(хь х3) < г(хъ х2) + г(х2, х3) для Vxj, х2, х3 из X— аксиома “неравенства треугольника”.
Приведенное определение задает классическую метрику, которой, например, является евклидова метрика. Однако, как стало выясняться в последнее время, важны неклассические метрики, отличающиеся от классическим тем, что в них отказываются от соблюдения третьей и четвертой аксиом (вместе или в отдельности). Как показано в разд. 5, такие метрики находят применение в теории оптимального управления.
Из нетрадиционных метрик здесь рассмотрим только одну. Мы покажем, как можно естественным образом (не привлекая никаких дополнительных множеств и структур) снабдить метрикой пространство
202
Гюйгенса, о котором речь шла в подразд. 4.4. Метрика Гюйгенса дается следующим определением.
Определение!. Метрика Гюйгенса на пространстве Гюйгенса элементов (точек) х е X — это отображение г вида г: X1 -> R, задаваемое функцией г = г(х0, хО, (х0, jq) g R2, г g R, определяемой равенством
r(x0,Xj) - {inf t: t g R; xteH(t,x0)}.
Метрика Гюйгенса, вообще говоря, неклассическая, ибо по крайней мере для нее может не выполняться четвертая аксиома симметрии, требуемая для классической метрики. Однако первая, вторая и пятая аксиомы для метрики Гюйгенса выполняются, как это нетрудно проверить.
По сути, говоря с позиции сегодняшнего дня, идея Гамильтона состояла в том, чтобы функцию действия S(x0, xj механической или вообще физической системы отождествить с введенной выше метрикой Гюйгенса r(x0, Xj).
Обратно, всякая метрическая структура r(x0, Х]) на произвольном непустом множествеX задает на нем и структуру Гюйгенса:
H(t, х0) = {хб %:г(х0,х) </}, Хо<=Х, t>0.
Выполнение аксиом Гюйгенса (подразд. 4.3) нетрудно проверить.
4.5.	АЛГЕБРАИЧЕСКИЕ ПРОСТРАНСТВА — АЛГЕБРАИЧЕСКИЕ СИСТЕМЫ
Здесь будет рассмотрен один из основных классов структур, называемый классом алгебраических структур (пространств, систем). В настоящее время этот класс, следуя А.И. Мальцеву, чаще называется классом алгебраических систем [206].
Алгебраической системой называется произвольное непустое множество X, на котором определены одна или несколько алгебраических операций и предикатов, удовлетворяющих некоторому набору условий (аксиом).
Отметим, что можно рассматривать и многоосновные алгебраические системы с несколькими основными множествами Л], ..., Хп вместо одного основного множества X, на каждом из которых или на некоторых их прямых произведениях определены алгебраические операции и предикаты, возможно, сопровождаемые набором условий согласования и их свойств, выраженных в виде соответствующих аксиом. В основном мы рассмотрим одноосновные алгебры.
203
Напомним, что w-арной алгебраической операцией А на X называется отображение
А: Хп -+ X,
а и-арным предикатом на X называется отображение
Р -.Хп —> {О,1}.
Таким образом, общая алгебраическая система — это совокупность {Ху, Аа, Рр} (где а, р, у — индексы операций и предикатов), дополненная, как правило, соответствующими аксиомами согласования. При у > 1 алгебраическая система называется многоосновной, а при у = 1 — одноосновной
Ясно, что такая алгебраическая система является реализацией широкого класса структур, под которой мы понимаем некоторый (возможно, достаточно сложный) предикат. Иными словами, алгебраическая система {Ху, Аа, Рр} может быть представлена одним сложным предикатом, если учесть, что и-арная алгебраическая операция эквивалентна некоторому (п + 1)-арному предикату.
В алгебраической системе происходит конкретизация некоторых предикатов в виде алгебраических операций на множестве.
Если алгебраическая система задается только алгебраическими операциями, а предикаты отсутствуют, то алгебраическая система в этом частном случае называется универсальной алгеброй, или просто алгеброй. Напротив, если алгебраическая система задается только предикатами, а алгебраические операции отсутствуют, то она называется моделью, или реляционной системой (системой отношений).
Мы ограничимся рассмотрением универсальных алгебр, которые широко используются в самой математике. Коротко они называются просто алгебрами. Модели, или реляционные соотношения, также используются, но, пожалуй, чаще в математической логике и программировании вычислительных машин.
Существуют несколько способов фиксации конкретных алгебр, которые основаны на том, что фиксируется общее количество алгебраических операций в данной алгебре и их арность. Дальнейшая конкретизация состоит в том, что накладываются ограничения на свойства операций, которые часто состоят в требовании выполнения некоторых тождеств, которые называются структурными.
Большой класс алгебр составляют алгебры с одним основным множеством Xи конечным числом операций f,	расположенных в по-
рядке убывания их арностей. Алгебру тогда можно обозначить как (X, Последовательно выписывая их арности (тъ ..., /и„), получаем тип алгебры. Если две такие последовательности от двух алгебр совпадают, то они называются однотипными. Две однотипные алгебры
204
А} = (А,ф,. . . ,ftn) и Л2 = {В, gb . . . , gm) называются изоморфными, если существует их изоморфизм, т.е. биекция <р: А -> В, и такой, что операции между соответствующими элементами сохраняются, т.е.
Изоморфные алгебры с абстрактной точки зрения не различаются между собой и в этом смысле могут быть отождествлены, несмотря на то, что по другим своим конкретным деталям и воплощениям они могут выглядеть не похожими.
Рассмотрим, например, две на вид, казалось бы, различные алгебры. Первая (7?+, •, _|, 1) —множество всех положительных действительных чисел с операцией умножения (бинарной), операцией взятия обратного числа (унарной) и фиксированной единицей (0-арная операция — фиксация элемента) имеет тип (2, 1, 0). Такой же тип имеет и другая алгебра (R, +, -, 0), где R — множество всех действительных чисел со сложением, вычитанием и фиксированным числом ноль, хотя, на первый взгляд, эти две алгебры не похожи друг на друга. Но легко видеть, что они изоморфны, ибо существует изоморфизм:
ф(х) = logх, хе R+, <р(х)gR.
С точки зрения ЕГТУ алгебра представляет собой пространство вида (X Q, где X — произвольное множество, а С — структура, или структурное отображение, которое в случае алгебры вида (Х,ф, ...,frn) задается набором отображенийф, ...,фт.
Отметим, что изоморфизм двух однотипных алгебр есть частный случай более общего понятия — их гомоморфизма.
Если в вышеприведенном определении изоморфизма отказаться от требования, чтобы <р было биекцией, то <р следует назвать гомоморфизмом алгебры Ai в алгебру А2, а алгебру А2 следует назвать гомоморфной алгебре Аг. Напомним, что гомоморфизм дословно означает подобие, или подобие форм, а изоморфизм — совпадение форм. Таким образом, гомоморфизм — это ослабление более сильного требования изоморфизм. Сейчас имеется тенденция вместо термина гомоморфизм употреблять более короткий термин морфизм с различными приставками, отличающими один вид морфизма от другого (рис. 4.5.1).
Отметим, что множество всех изоморфизмов двух однотипных алгебр обладает структурой эквивалентности, ибо выполняются все требования (аксиомы) отношения эквивалентности:
1)	рефлексивность — изоморфизм алгебры на себя посредством тождественного отображения (р;
2)	симметричность — изоморфность ср и ср ;
3)	транзитивность — свертка изоморфизмов есть снова изоморфизм.
205
Поэтому все множество изоморфизмов однотипных алгебр разбивается на классы таких алгебр. При этом достаточно изучить лишь по одному представителю из каждого класса, чтобы изучить все множество. Этим занимается универсальная алгебра как раздел математики.
Другим примером изоморфизма алгебр может служить изоморфизм пространства высказываний и булевой алгебры множеств. Более общее высказывание содержится в известной теореме Стоуна.
(Теорема 1. В сякая булева алгебра изоморфна некоторой булевой алгебре множеств.
Отсюда, в частности, вытекает следующая теорема.
J Теорема 2. Любые две конечные булевы алгебры с одинаковым числом элементов изоморфны.
Тип булевой алгебры есть (2, 2, 1,0, 0), так как она содержит две бинарные операции (а и v), одну унарную операцию (отрицание) и две 0-арные операции — константы (“ложь”, “истина”).
В подразд. 4.6 рассмотрим примеры простейших алгебр, которые, однако, играют фундаментальную роль во всей математике. Это так называемые ассоциативные алгебры, где максимальная арность операций равна двум и эти операции подчиняются условию (аксиоме) ассоциативности. Такие универсальные алгебры называются группоидами. Простейшими из них являются полугруппы и полугруппы с единицей (моноиды). Если в моноиде есть еще унарная операция взятия обратного элемента, то получается группа-алгебра типа (2, 1, 0). Роль моноидов и групп в математике трудно переоценить, ибо достаточно сказать, что в терминах этих структур описывается любая симметрия любой структуры, пространства или системы.
В заключение составим полезную, на наш взгляд, таблицу (рис. 4.5.1), которая упорядочивает различного вида гомоморфизмы (морфизмы). Итак, пусть имеются две однотипные алгебраические структуры (пространства)
4=(^Ё>-,А) и А2 = (B,gl,...,gm),
где А и В — основные их множества, а операции^, g,-, z = 1, ..., т, описывают их структурные отображения. Пусть далее существует отображение ср:
(р: А В,
такое, что
Ф(Л («I >	)) = £, (<P(A ), •••> <р(%))
для Vz — 1, ..., т.
206
В зависимости or типа отображения ср, т.е. является ли оно сюръекцией, инъекцией, биекцией или оно совершенно произвольно, различают соответственно и виды морфизмов (гомоморфизмов), которые задают это отображение (рис. 4.5.1).
Вид морфизма	<р — произвольно: (р: А —> В	Ф — сюръективно: <р(Л) = В	ср — инъективно: ф(х) = = <р(у)=> х=у	Ф — биективно: 1 -1 соответствие А++В
1. Гомоморфизм (морфизм)	ABM			
2. Эндоморфизм	А = В			
3. Эпиморфизм				
4. Мономорфизм			Г 		
5. Изоморфизм				
6. Аиюмор-физм				А = В
Рис. 4.5.1
Отметим, например, простой изоморфизм
<-> а + ib между
а -Ь b а матрицами и комплексными числами. Проверьте этот факт. Аналогичный изоморфизм имеет место между телом кватернионов и квадратных матриц определенного вида.
Отметим еще раз фундаментальность понятия автоморфизм как основы для введения понятия симметрии того или иного пространства: преобразование пространства в себя с полным сохранением его структуры.
4.6.	ПРОСТЕЙШИЕ АЛГЕБРАИЧЕСКИЕ ПРОСТРАНСТВА
Здесь кратко рассмотрим примеры некоторых простейших, но важных алгебраических пространств.
Начнем с полугруппы — своего рода “минимальной” алгебры с точки зрения условий, ее определяющих.
Определение 1. Полугруппа — это пространство (X, С), где X — произвольное непустое множество; С — структурное отображение — бинарная операция на X:
С: Х‘ -> Х\ х3 = С(л'1,х2) = ххх2, (хх,х2)еХ2, х3 е X, с единственной аксиомой ассоциативности (тождеством)
(тс1,х2)л3 = X, (x2,JC3) для любых х2, х3 из %.
207
Примером полугруппы является множество всех четных натуральных чисел с операцией обычного перемножения (сложения) чисел.
(Определение 2. Моноид — это полугруппа с единицей, т.е. таким элементом 1 s X, что х1 = 1л = х для любого х е X.
Примером моноида является совокупность всех квадратных матриц с числовыми элементами произвольной фиксированной размерности с обычной операцией перемножения (сложения) матриц и с единичной матрицей в качестве единицы моноида.
Моноид — это очень важная алгебраическая структура, ибо совокупность всех преобразований симметрии любой структуры сама обладает структурой моноида, где бинарной операцией является свертка двух преобразований симметрии, а роль единицы играет тождественное (единичное) преобразование, которое, очевидно, является преобра-зованием симметрии для любой структуры.
Полугруппа и моноид, в частности, могут оказаться не только ассоциативными, но и коммутативными, если бинарная операция удовлетворяет аксиоме коммутативности (тождеству) %ix2 = для любых X, и Х2 из X.
Коммутативные полугруппы еще называются абелевыми полугруппами.
Заметим, что при рассмотрении моноида, который образовался из полугруппы, если в ней есть элемент “1”, моноид можно рассматривать как универсальную (одноосновную) алгебру с. двумя алгебраическими операциями — вторую операцию, кроме основной бинарной, составляет 0-арная операция фиксации элемента со свойством “единицы” и обозначенного “1”. Поэтому “аксиому единицы” можно рассматривать как аксиому согласования двух структурных отображений: бинарной операции перемножения и унарной операции единицы.
Если моноид дополнить еще одной операцией — унарной операцией обращения (взятия обратного элемента по отношению к данному элементу7), то приходим к такому определению.
Определение3.Группа — это моноиде операцией обращения
С, : X -> X х2 = C,(x,) = 1/х, = xf1 для Vx, е X.
При этом выполняется следующая аксиома (тождество): для
Vx g X существует х-1 е Xтакой, что
-I -1	,
хх = х х = 1.
Обратим внимание на то, что все указанные выше аксиомы есть не что иное, как определенные тождества, характеризующие данную структуру, “отделяя” ее от структур другого типа. Такие тождества-аксиомы назовем структурными тождествами.
208
Уже на примере трех структур — полугруппа, моноид, группа — видно, что они образуют некоторую иерархию. В данном случае она получается за счет добавления новых условий (ограничений) в виде требования выполнения новых аксиом (тождеств). Естественно, что при наложении дополнительных условий в каком-то описании мы получаем все более специальные и более сложные структуры (рис. 4.6.1).
Здесь имеет смысл отметить одно общее и важное понятие (структуру), играющее большую роль во многих разделах математики и имеющее приложения, например, в проблеме решения некоторых классов уравнений.
I Определение 4. Левый идеал полугруппы — это подмножество I\ а X, где X— основное множество полугруппы 5 такое, что, ес-ли t е 7] и х е X, то tx <= /]. Аналогично, правый идеал полугруппы — это подмножество I2 а X, где X — то же самое, что и выше, такое, что, если t g /2 и х е X, то xt е 12. Наконец, идеал полугруппы (двусторонний идеал) — это такое подмножество / с X, что имеет место совпадение = I2 = I.
Идеалы в полугруппе задают некоторые инвариантные множества в том смысле, что они сохраняются (проявляют “устойчивость”) под действием любых возмущений в виде умножения на любой элемент из
полугруппы.
Отметим важную разновидность более широкого понятия согласованности — понятие вложение одной структуры (пространства) в дру-
гую структуру (пространство), как правило, того же рода или того же алгебраического типа. Есть много типов вложений, индексируемых разными типами гомоморфизмов. Например, говорят, что группоид G гомоморфно вкладывается в группоид если существует гомомор-
физм (в частности, изоморфизм) группоида G на некоторый подгруппоид группоида Gi.
Отметим еще один существенный факт, игнорирование которого может привести к недоразумениям при осуществлении гомоморфизмов универсальных алгебр [183, с. 157]. Дело в том, что одна и та же универсальная алгебра может быть эквивалентно задана
Рис. 4.6.1
209
разными наборами операций, которые естественно также назвать эквивалентными наборами операций этой универсальной алгебры А. Такие два набора определяются тем, что каждая операция одного набора есть производная от операций другого набора.
Чтобы понять, что такое производная операция, возьмем произвольное слово w = ivfxj, ..., хл;) в этих операциях относительно свободных элементов хц, ...,х„, п > 1. Заменим к из этих элементов, 0 < к < п, например последние к, некоторыми фиксированными Ь\, ..., Ьк из алгебры А. Тогда w(xi, ... , хп_к, by, ... , bk) определяет в А (п - А)-арную операцию, при которой последовательности элементов (сц, ..., ап к) из А однозначно соответствует элемент из А вида w(ab ... , а„.к, Ь\, ... , Ьк).
Всякая операция, полученная таким способом, называется производной операцией алгебры А.
Производная операция называется главной, если к = 0. В частности, все исходные операции в А есть главные.
Нужно помнить, что понятие гомоморфизм двух алгебр относится только к данному фиксированному набору операций в алгебре и может потерять смысл при переходе к другому, даже эквивалентному набору операций. Однако, если всякая операция из двух наборов операций в А является главной производной операцией от другого набора операций, то потери смысла не происходит, и рассмотрения бу руг равносильными.
4.7.	БОЛЕЕ СЛОЖНЫЕ АЛГЕБРАИЧЕСКИЕ ПРОСТРАНСТВА
Рассмотрим — также предельно кратко — еще несколько важных, но более сложных алгебраических пространств (структур). Они усложнены за счет увеличения до двух числа бинарных операций. К такого рода пространствам можно подойти как к пространствам, получающимся в результате “согласованного взаимодействия” двух “простейших” пространств из числа рассмотренных в подразд. 4.6, т.е. полугруппы, моноида и группы с разными свойствами коммутативности (некоммутативные и коммутативные).
Организовывая “согласованное взаимодействие” этих простейших пространств в разных парных их комбинациях, можно получать различные виды более сложных пространств с двумя бинарными операциями. Забегая вперед, отметим, что роль “согласованного взаимодействия”, в частности, часто играют аксиомы дистрибутивности и отвечающие им тождества дистрибутивности. Отметим, что уже в простейших алгебраических пространствах мы видели аксиомы “согласованности взаимодействия” операций разных арностей, например, хх~х = х~хх = 1 — аксиома согласованности между тремя разными операциями: бинарной (перемножение), унарной (обратный элемент) и
210
0-арной (единица). В этом, на наш взгляд, и есть черты системнокибернетического подхода к математическим структурам, или взгляда на них. Здесь сложное пространство рассматривается как “согласованное взаимодействие” более простых подпространств, являющихся “элементарными блоками” некоторой струкгурной схемы, представляющей более сложную систему.
Например, в этом смысле важное алгебраическое пространство, называемое кольцом, можно рассмотреть как одноосновную алгебру и представить как “согласованное взаимодействие” двух разных “простых” пространств, определенных на одном и том же основном множестве X. При этом для кольца одно из этих пространств должно быть коммутативной (абелевой) группой, где ее бинарную операцию естественно назвать сложением и обозначить знаком “+”. В то же время другое “простое” пространство (система) предполагается полугруппой, а ее бинарная операция называется умножением.
“Согласованность взаимодействия” этих двух “подсистем” (с одной и той же основой X), т.е. фактически “согласованность взаимодействия” их разных бинарных операций на одном и том же X, обуславливается аксиомами дистрибутивности — требованием соблюдения следующих двух тождеств, входящих в состав структурных тождеств кольца: 1)л(у + z)=xy + хг, и 2) (у + z)x = ух + zx для любых х, у, z из X.
Если, например, в полугруппе, входящей в данное кольцо, потребовать еще выполнение аксиомы существования обратного элемента для любого элемента X, за исключением нуля абелевой группы (ее “единицы”), то получим существенно новое пространство, называемое телом. Иногда тело называют алгеброй с делением, ибо существование обратного элемента означает возможность операции “деления” одного элемента Xна другой (кроме нуля). Это также равносильно требованию разрешимости уравнения ах = b относительно х = a~'b, если а #0.
Отметим здесь еще одно очень важное в математике пространство.
I Определение I. Поле — это коммутативное кольцо с единицей
1	0, в котором каждый элемент, отличный от нуля, обратим.
Таким образом, поле получается из кольца или тела, если от входящей в них полугруппы потребовать, чтобы она была коммутативной группой. Эта группа так и называется: коммутативная мультипликативная группа поля. Примерами поля являются множества всех действительных или комплексных чисел R и С.
В [159, с. 185] есть замечательное высказывание: “Поле представляет собой гибрид двух абелевых групп — аддитивной и мультипликативной, связанных законом дистрибутивности” (курсив здесь наш). В этих словах просматривается идея “гибридизации” различных про
211
странств, которые мы называем организацией “согласованного взаимодействия” или согласованной связи, или даже “связности” между пространствами, рассматриваемыми как “элементарные блоки структурной схемы”, описывающей сложную систему в целом.
Заметим, что такая структурная блок-схема может строиться на использовании понятия эквивалентности разных наборов операций одной и той же алгебры, где можно пользоваться независимыми (от этих наборов) гомоморфизмами, например, на разного рода подалгебры. Например, кольцо, с одной стороны, — это одна универса пьная алгебра, но она эквивалентна двум взаимодействующим подалгебрам. Таким образом, слово гибрид получает смысл “соединения” структур на основе “двойственного” подхода: 1) как целого и 2) как составного, что должно быть эквивалентно так же, как два параллельно соединенные блока с двумя передаточными функциями (И7, и W2} эквивалентны одному блоку с одной передаточной функцией (ИбБ7?).
Аналогичным способом можно рассмотреть более сложные пространства, например модули, линейные пространства и еще такие более сложные пространства, как алгебры над линейными (векторными) пространствами (алгебры Ли, Банаха, Иордана и др.). Такого рода алгебры получаются путем добавления к линейному пространству еще одной бинарной операции, в частности, некоммутативной и даже неассоциативной .
Новые операции также должны удовлетворять ряду условий (аксиом) согласования. В результате этих согласованных комбинаций простых пространств получаются уже довольно сложные пространства (структуры), которые подчас хорошо описывают многие важные реальности, изучаемые в других науках — механике, физике, теории управления, экономике и т.д.
Таким образом, в математике структуры синтезируются путем “согласованной организации” взаимодействия и “надстроек” одних структур над другими. Примером пространства, получаемого путем “надстройки”, может служить линейное нормированное пространство, где структуру нормы можно считать “надстроенной” над исходным (основным) пространством — линейным (векторным). “Сама по себе” структура нормы существовать не может в силу ее специфики. Она, например, бессмысленна, если ее “надстраивать” над произвольным абстрактным (бесструктурным) множеством, она органически по своему смыслу требует не простой “почвы” линейного пространства. В отличие от нормы метрика как структура гораздо менее “прихотлива”, она может быть осмыслена на “голом” множестве.
Другая важная “ветвь гибридизации” развивается при “согласованном взаимодействии” рассмотренных в этом разделе алгебраических
212
пространств с отношениями (структурами) эквивалентности и особенно упорядоченности. Здесь прежде всего мы имеем в виду понятие решетки. Это пространство, как показано в разд. 6, разделяет ответственность за фундаментальное понятие кибернетики —управление.
На наш взгляд, особенно перспективной для кибернетики, где изучаются понятия управление, система, информация, алгоритм, программа, интеллектуальная система и другие, в самом широком смысле является теория булевых решеток. Это довольно сложная структура, являющаяся гибридом нескольких также не простых, но все же “более элементарных” структур математической логики: упорядоченности, алгебраических структур (полугрупп, моноидов, групп, колец, полей) и топологии [84]. Но в силу ограниченности объема данной книги мы, к сожалению, не можем детально проанализировать этот важнейший аспект связи математики и кибернетики, хотя это предполагается быть включенным в программу ближайших исследований по ЕГТУ—ТСУ.
Отметим важную задачу анализа данной сложной структуры, которая часто называется проблемой декомпозиции систем. Здесь, на наш взгляд, очень перспективными являются многолетние исследования, выполненные Ю.Н. Павловским и группой его учеников и последователей [238, 239]. Ясно, что задачи анализа и синтеза неразделимы, и поэтому эти работы можно рассматривать с таким же успехом, как вклад и в проблему синтеза сложных систем из более простых или условно “элементарных” блоков.
В заключение подчеркнем один важный аспект теории “абстрактных” структур, в частности, рассматриваемых здесь алгебраических. Речь идет об идее, или методе, реализаций этих абстрактных структур с помощью более конкретных и привычных, т.е. “менее абстрактных”, тех же математических структур и пространств. В логике эта идея преломляется в понятии модели для данной абстрактной, чисто аксиоматической теории, отождествленной с некоторой абстрактной структурой, например, структурой группы. В логике понятие модели играет, в частности, вполне специальную роль как средство доказательства “реальности”, или “существования”, данной абстрактной “схемы аксиом”, описывающей ту или иную абстрактную структуру. Другими словами, модель — это средство доказательства непротиворечивости схемы аксиом для данной абстрактной структуры, например евклидовой геометрии.
Вне логики понятие модели приобретает слегка иной нюанс — как регулярное, рабочее средство для изучения данной, возможно, сложной структуры, что заменяется терминами реализация и представление данной алгебраической структуры. Реализация и представление в свою
213
очередь формализуются, или описываются, морфизмами. Здесь модель реализуется или представляется в виде конкретных и привычных множеств и операций на них. Например, широко используются множества действительных, комплексных и гиперкомплексных чисел, некоторые функциональные множества (например, многочлены), а также матрицы с числовыми или функциональными (операторными) элементами.
Аналогично тому, как в логике предметные области предикатов наполняют содержанием формальную алгебру и исчисление высказываний, так указанные числовые, функциональные и матричные, включая векторные, множества и пространства наполняют содержанием абстрактные пространства (структуры и схемы), делая их необычайно богатыми в смысле широты и эффективности приложений. Возможно, этот прием моделирования (представления, реализации) абстрактного с помощью одной или нескольких разновидностей “конкретных” (т.е. более привычных, наглядных и лучше изученных) объектов и делает математику “непостижимо эффективной”, тем самым демонстрируя некоторое “чудо или Бога из машины”.
В математике, в частности, всегда подчеркивалась особая и “загадочная” роль чисел и числовых множеств, особенно множества N всех натуральных чисел как первоосновы всего. Известно изречение: “Натуральные числа — это от Бога!” На наш взгляд, от Бога, от Природы человек обладает своей первейшей способностью — способностью различать и идентифицировать. Эта способность проявляется у ребенка, находящегося еше в утробе матери, и, несомненно, с первых минут и часов после рождения. С нашей точки зрения натуральные числа N есть прямой продукт этой способности.
В Программе ЕГТУ—ТСУ нам представляется перспективной идея композиции (свертки, подстановки, нелинейной суперпозиции) как способ осмысления идеи моделирования, реализации и представления. Важность такого осмысления видится весьма практичной, если попытаться сделать своего рода исчисление моделей, реализаций, представлений, рассматривая их как нелинейные суперпозиции или подстановки в “формулы пространств”: вместо “более абстрактных” символов и понятий — “менее абстрактные” (“более конкретные”), или “более предметные”, переменные и константы.
Иными словами, речь идет о создании блок-схем из элементарных и более конкретных блоков для получения новых, более сложных структур и пространств. Это уже можно толковать как шаг в направлении создания теории управления структурами (пространствами и системами как таковыми, а не только их состояниями).
Надо сказать, что пока еще интуитивно такие процессы в направлении решения именно такого аспекта в математике начались в конце
214
первой половины XX века. Это выразилось, например, в появлении теории категорий с попыткой ее применения в теории систем [133]. В последнее время эта попытка получила более концентрированное “системно-кибернетическое” осмысление в упоминавшихся выше работах группы Ю.Н. Павловского, в частности, по исчислению “родов структур” (в смысле Бурбаки) и их связи с теорией категорий.
Подчеркнем еще раз, что над всем этим господствует идея симметрии, наиболее ярко проявляющаяся прежде всего в виде замкнутости пространств. Например, именно по этому требованию симметрии из множества N последовательно родились числовые пространства (множества) Z, Q, R и С. Таким образом, возникает задача: построить непротиворечивую и замкнутую теорию блочно-структурных схем исчисления пространств (структур). Такое логическое исчисление про странств (структур) можно было бы назвать логико-структурным исчислением блок-схем. В частности, отсюда могло бы следовать логическое программирование [218].
Очень важным аспектом “замкнутости” как симметрии должно служить понятие замыкание обратной связью аналогично тому, как это делается в классической блочно-структурной теории управления и других технических дисциплинах [48, 411]. Осмысление обратной связи в исчислении структур равносильно идее составления уравнений в этом исчислении, где в качестве неизвестной может служить желаемая заданная структура, или пространство, которую мы хотим найти, т.е. синтезировать. Отсюда естественно возникнут проблемы разработки методов, алгоритмов, языков программирования и самих программ (для вычислительных машин) для решения такого рода необычных уравнений.
4.8.	ЛИНЕЙНЫЕ ТОПОЛОГИЧЕСКИЕ ПРОСТРАНСТВА
Продолжим рассмотрение примеров важных основных “неалгебраических” пространств математики, которое уже не являются “элементарными”, а построены путем комбинации более простых пространств (структур).
Линейное топологическое пространство (ЛТП), или топологическое линейное пространство (ТЛП), как говорит его название, является согласованной комбинацией двух более простых пространств — линейного и топологического [155, с. 167].
Определение 1. ЛТП, или ТЛП, — это топологическое пространство (X, т), где X — основное множество, т — структура топологии на нем, причем такое, что на X как основном множестве также определена структура линейного пространства (X, Ху где А. —
215
линейная структура на X и структуры т и X согласованы в том смысле, что все операции линейного пространства непрерывны в топологии т.
Примерами ЛТП являются все нормированные линейные пространства. Условия согласованности накладывают жесткие требования на топологию т. Не всякая топология может оказаться согласованной с линейностью. Например, для согласованности необходимо, чтобы топология т, например, была регулярной [155, с. 167].
Теория ЛТП оказалась плодотворной для развития теории обобщенных функций. Оказалось, что в этом случае полезно рассматривать линейные пространства с топологией, задаваемой способом, отличным от задания ее с помощью нормы векторов.
Замечательным свойством ЛТП является то, что топология во всем пространстве однозначно определяется заданием системы окрестностей нуля линейного пространства, т.е. заданием топологии всего лишь около одной точки. Действительно, если х — произвольная точка ЛТП, то “сдвиг” окрестности нуля нал: дает окрестность точки, сохраняя всю топологию окрестности нуля.
Если в ЛТП 0] и 02 — два открытых множества, то их линейная комбинация + Х202 также открытое множество, если X] и Х2 не равны нулю вместе. Если А замкнутое множество, то АЛ тоже замкнутое при любом X.
Линейное топологическое пространство является примером элементарного многообразия (см. подразд. 4.9).
Задание топологии в ЛТП посредством нормы векторов ||v|| или расстояния p(viv2) = ||v2 - Vi|| сообщает ему “жесткость”. Если норма и расстояние евклидовы, то мы имеем дело с евклидовым пространством. Трехмерное ЛТП хорошо “моделировало” наше реальное физическое пространство до начала XX в. Но после открытия Эйнштейном СТО (специальной теории относительности) выяснилось, что имеет смысл говорить не о трехмерном ЛТП с тремя только пространственными координатами (хь х2, х3), а четырехмерном ЛТП с координатами (t, хь х2, х3), где t — время. При этом вместо евклидовой нормы X(t, A0) = ^lX(t,a0) надо взять норму, вычисляемую по формуле Минковского д/с2/2-х2-xf-х32 , где с — скорость света в пустоте. Эта формула качественно отличается от формулы для евклидовой нормы (расстояния). Из нее сразу видно, что существуют вектора, для которых нет естественного понятия их нормы, ибо по приведенной формуле Минковского норма таких векторов становится мнимым числом типа /X, где i — мнимая единица, X — действительное положительное число. Понятие нормы как бы теряет
216
свой привычный смысл. Из формулы Минковского легко видеть, что обычную норму имеют те и только те четырехмерные вектора v(t, х}, х2, Х3), ДЛЯ которых C2t2 -х2 -х2 -х3 > 0.
Но эта формула в четырехмерном линейном пространстве описывает конус Л" (рис. 4.8.1). Причем вектора, лежащие на поверхности этого конуса, имеют норму | |v|| = 0. Вектор Vi измерйм, если лежит внутри конуса, и тогда он называется времяподобным вектором; вектор у2 — вне конуса К — называется пространственно подобным вектором, он неизмерим в норме Минковского в том смысле, что имеет необычное мнимое значение своей нормы. Сам конус К называется световым конусом. Физический смысл пространства Минковского стал существенно отличным от физического смысла трехмерного евклидова пространства (для трех измерений только пространственных координат). Этот новый смысл стал носить информационный характер. Мнимое значение нормы 11и| | стало означать, что две точки , х,, х2, х3) и (t2, х{, х2, х3) не имеют никакой связи между собой и никак не могут влиять друг на друга, если точка v = (t2 - tx, х[ - х,, х2 - х2, х3 - х3) ей К . Связь между ними с помощью световых сигналов возможна только в случае, если у е К. Ясно, что это обусловлено тем, что свет имеет хотя и большую, но конечную скорость с < со. И эта скорость не зависит от движения самих точек (она постоянна), которые увлекают в своем движении пространства Минковского. В этом состоит суть аксиом Эйнштейна для СТО. Относительно недавно выяснилось, что понятие фазового портрета для дифференциальных систем с управлением может служить моделью не только СТО, но и ОТО (см. разд. 6).
4.9.	ЭЛЕМЕНТАРНОЕ МНОГООБРАЗИЕ И МНОГООБРАЗИЕ
К общему понятию многообразия мы подойдем постепенно, стараясь показать, как происходит последовательное усложнение математических структур и пытаясь разложить этот процесс усложнения структур на элементарные “составляющие”, показывая при этом, как происходит согласование (взаимодействие) “пристраиваемых” новых струк
217
тур со “старыми” структурами, обычно за счет новых условий (аксиом). Дело в том, что многообразие в определенном смысле “соткано” или “склеено” из элементарных многообразий.
Определение 1. Элементарное многообразие М размерности п и гладкости 5 — это топологическое пространство (X, т), где X — множество, т — топология на нем, с дополнительными аксиомами:
1)	множество X гомеоморфно любой связной и односвязной области D в Рп, т.е. существует биекция f
f: XD, f~x\D-*X, где fvif] непрерывны в топологии т и 7?л;
2)	если D\ и Z?2 — Две такие области с гомеоморфизмами Д и Д соответственно, то существует гомеоморфизм ср этих областей такой, что
(p:Di-*D2; ср"1 : Г>2 -> Dx,
и диаграмма (рис. 4.9.1) коммутативна.
При этом гладкость элементарного многообразия 5 равна максимальной возможной гладкости функции ср, начиная от непрерывности, конечной или бесконечной дифференцируемости, и кончая аналитичностью ср.
Рис. 4.9.1
Из определения сразу следует, что множество X должно иметь в точности мощность континуума.
Функции Д и Д можно назвать координатными, ибо если в D\ и Z)2 существуют какие-то координаты (координатные “сетки”), а они всегда существуют, то посредством функцииД или
Д они переносятся на многообразие. С помощью функции (р осуществляется, в конце концов, преобразование координат и на М. Система координат на М называется картой. Итак, элементарное многообразие — это топологическое пространство X, наделенное картой.
Элементарное многообразие М будет отличаться от общего понятия многообразия М тем, что на М существует одна система координат, пригодная для всего М. В то же время для произвольного многообразия М одной “глобальной” системы координат не существует, но его
можно покрыть конечным множеством карт, которое называется атла
сом на М. На перекрытии карт должно существовать достаточно гладкое преобразование перехода от одной карты к другой.
Таким образом, грубо говоря, многообразие — это такое множество, которое можно покрыть картами, т.е. на нем существуют координа
218
ты его элементов х :х <-> (л1,хп), причем близким точкам соответствуют близкие координаты, и обратно.
Многообразие замечательно еще и тем, что на нем можно определять вектора, например, как скорости точек, движущихся на М. Но на многообразии априори нет метрики, и в этом оно не жестко и похоже на топологическое пространство, но оно гладко и телесно, в том смысле, что имеет размерность. Многообразие оказалось, по сути, первой фундаментальной моделью нашего физического пространства — трехмерным евклидовым пространством с евклидовой квадратичной метрикой и, возможно, не фиксированным началом (т.е. аффинное пространство). Это многообразие — элементарное, ибо можно ввести одну глобальную систему координат и в ней, например, вычислять евклидово расстояние между двумя любыми точками. Более того, это линейное многообразие проявляется как линейное топологическое пространство. Однако уже окружность, сфера или тор не есть элементарное многообразие, ибо не существует одной системы координат, чтобы вместе выполнялись и взаимная однозначность между точками окружности и координатами, и непрерывность, а тем более гладкость.
Надо отметить, что все элементарные многообразия, по крайней мере одной и той же размерности п, неотличимы друг от друга. Они не имеют жесткой формы. Например, круг и эллипс (без границ) — это одно и то же двумерное многообразие. Иными словами, они имеют только один класс эквивалентности, так как все изоморфны друг другу. Про такие многообразия говорят, что они диффеоморфны. Диффеоморфизм — это дифференциальный изоморфизм, гомеоморфизм — это топологический, или непрерывный, изоморфизм. Диффеоморфизм отличается от гомеоморфизма только степенью гладкости отображения. Структуры топологии и многообразия позволяют точно определить само понятие гладкости биекции, без которого непрерывность и гладкость (дифференцируемость, аналитичность) вообще лишены смысла (не определены).
Определение 2. /7-мерное многообразие — это пара (Л, Л/), где для множества X существует его покрытие, состоящее из конечного г числа /7-мерных элементарных многообразий (Xh Мд, т.е.
X = 22 X,, причем в каждой области перекрытия, т.е на XXj 0, 7=1
существует преобразование \|/ координат на Л} в координаты на Xj', преобразование должно быть биекцией, т.е. иметь обратное преобразование Наибольшая и единая для всех перекрытий степень гладкости преобразований и у-’ будет гладкостью всего многообразия (X, М).
219
В отличие от элементарных многообразий многообразия даже одной и той же размерности не все диффеоморфны между собой. Например, сфера и поверхность тора не диффеоморфны, ибо они даже не го-меоморфны, так как нельзя одно непрерывными деформациями преобразовать в другое.
Из определения многообразия следует важнейшее его свойство: для каждой точки xQ е М многообразия существует ее окрестность 0(хо) с М, в смысле топологии на М, и такая, что в окрестности О(хо) существует линия, проходящая через х0, такой же гладкости, как и М. Иными словами, эту линию можно задать уравнениями
x = x(t), t eQ(10) c:R, x = (xl,...,xn), x(/)eO(xo), где Ao = х(/0) и все функции х = x\t) имеют гладкость s многообразия М.
Теперь можно определить касательное пространство ТХ(М к М в точке Xq как классы эквивалентности всех кривых х = л(/), t е О(/о), х0 = = х(4,), причем в один класс попадают те кривые, для которых все х(?) коллинеарны между собой.
Короче говоря, в каждой точке х0 g М можно определить вектор v = %(Z0), а совокупность этих векторов образует линейное пространство, связанное с точкой х0- Это пространство и называется касательным пространством к М в точке л0 и обозначается 1 М.
Замечательно то, что такое пространство можно построить в каждой точке многообразия М, ТХ^М, х0 е М, и рассматривать его как слой, ‘‘висящий” над точкой х0, а само многообразие М можно принять за базу некоторого расслоения М, Т М, х0 е М. Все эти слои пока никак между собой не связаны. Чтобы их связать, надо задать связность, т.е. правило перехода от слоя к слою. Поскольку элементами этого слоя являются векторы у, то надо определить правило переноса вектора v из одного слоя, свя занного с точкой х0, в другой слой, связанный с точкой л']. Наиболее естественным должно быть правило, по которому вектор в одном слое “считается” параллельным вектору в другом слое. Такая связность называется аффинной.
Поскольку с каждым линейным пространством векторов v связано линейное пространство ковекторов w, то с касательным линейным пространством Т М связано касательное линейное пространство TXqM ковекторов w. Напомним, что каждое такое w задает линейный функционал, определенный на v е Т М. Таким образом, в каждой точке М имеем два линейных пространства (Т^М и соответственно век
220
торов v и ковекторов w. Отсюда в каждой точке х0 е М можно задавать и тензоры типа (т, г). Это означает, что на многообразии можно задавать тензорные поля, т.е. тензоры как функции от точки многообразия. В частности, это могут быть скалярные (т.е. на М задается численнозначная функция), векторные и ковекторные поля.
Пусть на многообразии М задана скалярная функция fix), х g М, а все наши рассмотрения будут локальными. Это означает, что функцию fix) мы будем рассматривать не на всем М, а только в окрестности точки xG & М такой, где окрестность представляет собой элементарное многообразие 2И0 как часть М. Поэтому существует одна система координат х = (х1, ..., х") точек х для всего MQ. При этом без ограничения общности эту систему можно выбрать так, что, например, х0 = = (0, ...,0).
Теперь функцию fix) можно рассматривать просто как отображение R. Это верно всегда, по крайней мере локально, т.е. в окрестности Мо точки х0, которая теперь представляется областью D cz Rn, а х0 е D.
Здесь была использована важнейшая структурная особенность всякого многообразия, которую можно выразить так: всякое многообразие, по крайней мере локально, неотличимо от области R'1. Но за глобальное поведение М отвечает уже не Л", а топологическая составляющая его структуры. Хотя сфера, тор, лист Мёбиуса локально действительно изоморфны области в R!1, глобально — как топологические пространства — они совершенно разные, так как, очевидно, путем непрерывной (топологической) деформации (без разрывов и склеек, сохраняя непрерывность — близкие точки должны оставаться близкими и после деформации) их нельзя перевести друг в друга.
Рассмотрим теперь дифференциал функции fix) в точке х0, помня, что у нас есть координаты х = (х , ..., х ):
d/'(x) = ^-dx“.
дха
Таким образом, мы предполагаем, чтоДх) по крайней мере один раз непрерывно дифференцируема.
Сейчас сделаем одно из решающих замечаний, которое аналитическое рассмотрение функций и их дифференциалов переводит на геометрический язык векторов, ковекторов, форм и вообще тензоров.
Дифференциал d/(x) будем рассматривать как значение 1-формы, заданной ковектором
„эк...
^Эх1 дхп ) \дха )
221
на векторе v = (dr1, dx") = (dx“). При этом считаем, что v g Т М и
w g ТХМ. Таким образом, в таком подходе grad /(х) = |	| есть
\дха )
1-форма, или ковектор из ТХ^М, а не вектор, как думали раньше, ибо не всякий набор п чисел можно толковать как координаты вектора, и в данном случае видим, что это лучше толковать как ковектор, т.е. как 1-форму. Далее, дифференциал dx = (dx1, ..., dx") независимых переменных (х1,	х") можно толковать как вектор из Т М с координатами,
т.е. числами, (dx“), сс = 1, ..., п. Вектор (0, ..., О, dx\ 0, ..., 0) при этом есть не что иное как касательный вектор к А-й координатной линии в точке х0, которая и проходит через х0 на М.
Совокупность таких векторов, когда к “пробегает” 1, ..., п, дает п векторов из Т М, которые образуют так называемый координатный базис: ek = (0, ..., 0, dx\ 0, ..., 0), k = 1, ..., п. Этот базис непрерывно меняется от точки к точке на М. Конечно, в ТХ^М можно выбрать и другие — некоординатные — базисы, не обладающие свойством быть координатным базисом по отношению к данной системе координат (х1, ..., х") наМ
Таким образом, на М можно рассматривать и поля базисов касательных пространств Т М как всюду координатных, так и некоординатных. Считают, что эти поля по крайней мере непрерывны. Но для классической теории интегрирования, например, дифференциальных уравнений на М, этого бывает мало, и требуется еще существование непрерывных производных более высокого порядка, иногда вплоть до аналитичности соответствующих функций.
Выше говорилось, что в Т М, как во всяком векторном пространстве, можно задавать и тензоры различных типов. Для примера рассмотрим один такой тензор типа (2, 0), который играет важную роль и для самой математики, и для теоретической физики. Речь идет о метрическом тензоре. Это полилинейная функция, определенная на двух векторах V] и v2 из У М. В частности, метрический тензор можно задать просто формулой (в какой-то фиксированной системе координат):
g(Vi,v2) = g = gapv“v2₽,	(4.9.1)
т.е. это некоторая квадратичная форма от переменных v“ и , ос, Р = = 1, ...,«, gap — координаты тензораg.
222
Из геометрического и физического смысла того, для чего этот тензор будет использован, на него накладывают еще дополнительные ограничения. Если с его помощью надо что-то измерять (далее покажем это на примере измерения длины линии, лежащей в М), то часто требуют, чтобы (4.9.1) была положительно определенной, что достаточно для того, чтобы с помощью g задать норму ||v|| по формуле
H = V^V)=7'gaPV<Xv₽’
которая удовлетворяет всем требованиям нормы вектора.
Метрика (4.9.1) называется римановой метрикой наМ Многообразие М с определенным на М тензором (4.9.1) и положительно определенной квадратичной формой называется римановым многообразием. Подчеркнем, что риманово многообразие — это больше, чем просто многообразие, ибо исходное многообразие М снабжено дополнительной (метрической) структурой, “надстроенной” над исходным М.
Отметим, что введенные таким образом метрики называются дифференциальными, локальными в отличие от глобальных, интегральных метрик, которые на многообразии сразу не так просто задать, как, например, евклидову глобальную метрику в R" по формуле
Р(х,У) = д/Oi-*1)2+- + (Л ~*п)2-
Чтобы все-таки определить глобальную метрику на многообразии, идут по другому, из-за необходимости более сложному пути, связанному с интегрированием и минимизацией. Например, длина I линии у(я, Ь) на многообразии М, соединяющей точку а с точкой Ъ, определяется интегрированием:
Z[T(a.*)] = fH)||dr,	(4.9.2)
О
где х = х(0, 0 < t < Т, х g М, х(0) = а, х(7) = Ъ — параметрическое уравнение этой линии и v(z') = %(/).
Формулу (4.9.2) можно представить в беспараметрической форме
Z[y(a,Z>)] = f||dx||.
у(«Л)
Исходя из (4.9.2) можно поставить вариационную задачу: найти г(а,Ъ') = inf Z[y(a,Z>)], а&М, Ь&М
в некотором “допустимом” классе линий у(я, Ъ). Можно показать (см. разд. 5), что г(а, Ъ) есть уже глобальная метрика на многообразии.
223
В разд. 7 будет рассмотрена более общая задача, где введено понятие w-метрики, с помощью которой через т-кратный интеграл можно определить понятие площади куска m-мерной поверхности в М, которую также можно задать соответствующими параметрическими уравнениями.
4.10.	О ПОНЯТИИ КАТЕГОРИЯ
С точки зрения ЕГТУ—ТСУ цели теории категорий представляются привлекательными, так как понятие категории (морфизма, функтора, объектов) наиболее органично “интегрирует” в себе понимание математики как науки о структурах и симметриях; они находятся в таком отношении друг к другу, что можно говорить о цепочке “структура— симметрия—структура	(симметрии)—симетрия	(структуры
симметрии) и т.д.” и, следовательно, обратной связи.
В теории категорий произведена попытка “возвыситься” над противоречивым понятием множества, а следовательно, и отображения и выработать и узаконить как математические новые “надпонятия” объекты и морфизмы, заменяющие соответственно старые понятия множество и отображение.
Можно сказать, что теория категорий, наряду с теорией расслоений, является теорией детривиализаци (развития), которая призвана учесть возможности и варианты “неожиданной” детривиализации объектов, которые ранее считались бесструктурными (элементарными). Таким образом, речь идет об интеграции в одну теорию не только связки “структура—симметрия”, но и понятия нарушение симметрии, или общее — изменение симметрии и структуры вместе, т.е. то, на что и направлено “в большом” идея создания ЕГТУ—ТСУ.
Первые опыты относительно молодой теории категорий уже дают некоторые обнадеживающие практические результаты. Например, в [379] делается попытка в терминах теории категорий осмыслить такое сложнейшее понятие современной теоретической физики, как квантовая теория поля, причем в самом глобальном (топологическом) смысле. До сих пор в теоретической физике не хватало мощности ее собственного языка, имевшегося до настоящего времени, чтобы компактно и обще описать это понятие в целом и “единым” образом.
Можно сказать, что теория категорий как бы не очень обращает внимание на понятие множество, а скорее подчеркивает “отношения”, т.е. свойства и связи между объектами. Но понятие связи уже можно ассоциировать с понятием управления. Здесь структура (отношение) и управление становятся почти не различимыми понятиями. Родство здесь понимается не как “принадлежность”, а более “демократично” —
как связь или все же как принадлежность, но в очень широком смысле категории (например, принадлежность “человечеству”, а, например, не узкому кругу “аристократов”).
Теорию категорий, ее смысл можно понимать как попытку провести некоторую экспансию собственно математики в область метаматематики (“надматематики”), которая является пограничной между собственно математикой и собственно логикой и даже философией. При эгом наблюдается “благородная” цель преодолеть узость строго аксиоматического понятия множества, которое родилось с целью преодоления известных парадоксов и противоречий внутри самого понятия множество, например, в связи с понятием множество множеств, которое говорит о “незамкнутости” широкого понимания, что такое множество. Это попытка реабилитировать “неудачу” Кантора, придав его идее новый смысл.
Далее возникают еще более трудные вопросы при изучении совокупностей пространств (структур, систем, предикатов), когда множество снабжено еще к тому же какой-то структурой. Так, выражение “множество всех групп” точно так же противоречиво, как и “множество всех множеств”. Эту трудность можно понять и с кибернетической точки зрения — это трудность в понимании того, “что такое обратная связь в системе?”
Дело в том, что, как мы знаем из опыта, именно операция обратной связи (замыкания), когда “выход” системы подается на ее “вход”, ведет к получению новых, “чудесных”, свойств устойчивости, гомеостазиса, адаптации, поддержания каких-то величин и т.д. Но именно здесь возникают вопросы, связанные с удовлетворением основного требования — согласованности сигналов выхода предыдущего блока с входом последующего.
Подчеркнем, что с аппаратной точки зрения в теории категорий очень привлекательна идея морфизма вместе с основной ее аксиомой замкнутости бинарной операции композиции морфизмов (в частности, отображений), которая к тому же еще должна быть ассоциативной (т.е. аналогом класса ассоциативных алгебраических систем), содержать единицу (т.е. быть аналогом моноида — полугруппы с единицей). Такая операция уже точно отражает симметрию в смысле замкнутости (по принадлежности фиксированной категории или “множеству” объектов).
Эти понятия уже лет тридцать в кибернетике пытаются использовать, чтобы примирить и согласовать, т.е. описать, отношение (связь) между двумя альтернативными способами описания систем: 1) через пространство (множество) состояний и 2) через входо-выходные соответствия, где “элементарным” является понятие блока. Из них можно
224
8. А.В. Бабичев
225
строить блочно-структурные схемы. Это очень популярный и среди инженеров эффективный способ описания сложных систем, которым они пользуются интуитивно и творчески, не очень заботясь подчас об их точном математическом осмыслении.
Идея блочно-структурных схем ярко выражает свойства такой фундаментальной аналитической проблемы, как декомпозиция сложных систем, и аналитической проблемы композиции (интеграции). В ЕГТУ—ТСУ ставится вопрос о точном определении понятия управление акими блочно-структурными схемами с целью получения “нужной” блок-схемы.
Много примеров из математики категорного подхода к изучению структур приведены в [350].
В заключение приведем некоторые исходные формулировки понятия категорий.
Говорят, что задана категория, если имеют место следующие условия:
1)	задано множество ОЬ(2?) объектов В, где элементы b называются объектами (данной категории);
2)	для любых двух таких объектов — В\ и В2 — задано еще одно множество, обозначаемое Н(ВХ, В2) или Hom(£i, В2), элементы которого называются морфизмами ВгвВ2н обозначаются/ /, f2, ...;
3)	для любых трех объектов — 2?ь В2, В3 (В{ g Ob(Z?), i = 1, 2, 3) — и любых двух морфизмов — / е Н(В\, B2),f2 е Н(В2, В3) — существует третий морфизм f3 е H(Bit В3), называемый произведением (или композицией) морфизмов / и f2, что обозначается “равенством” /з =/2 АЛ-
ИНЫМИ словами, имеется двухместная (и, вообще говоря, некоммутативная) “операция” Н(В2,В3)хН(В2,В})-> Н(Вг,В3), от которой, однако, требуется ассоциативность;
4)	требуется существование единичного морфизма, обозначаемого вА е Н(А, А) с аксиомами f °еА= еА° f = f для любого морфизма f^H{A,B).
Таким образом, терминами множество и отображение пользуются “диалектически”: иногда вместо “множество множеств” можно использовать понятие класс множеств, следуя Б. Расселу и веруя, что это избавляет от опасности противоречий (парадоксов).
Исходя из понятия категории, можно определить еще несколько важных понятий, прежде всего выделить два класса объектов данной категории.
Универсальный отталкивающий, или инициальный, объект данной категории — это такой объект, для которого существует единственный морфизм, “отображающий” или “переводящий” этот объект А в любой
226
другой объект В этой категории, т.е. этот морфизм однозначно определятся только объектом В при фиксированном Л.
“Сопряженное”, или своего рода “обратное” к этому, понятие следующее.
Универсальный притягивающий, или терминальный, объект данной категории — это такой объект А, для которого существует единственный морфизм, “отображающий” или “переводящий” в этот объект А любой другой объект В, т.е. этот морфизм однозначно определяется только объектом В при фиксированном Л.
Эти понятия являются обобщающими аналогами известных понятий управляемости—достижимости, пригодными для построения такой же теории или по крайней мере языка, но уже в пространстве структур, в частности, в пространстве блок-схем.
Содержательность понятия категории во многом обусловлена существованием такого важного понятия, как функтор. Оно описывает гомоморфизмы или морфизмы более высокого уровня, когда роль объектов категории играют сами категории. При этом различают два сорта функторов — ковариантный и контравариантный.
Эта терминология заимствована из тензорного исчисления не без оснований. Указанные два функтора в определенном смысле “дополнительны” или “обратны” друг другу точно так же, как ковариантные и контравариантные тензоры, при этом можно сохранить подобие “сверток” при исчислении соответствующих функторов.
Определение 1. Ковариантный функтор F — это “отображение” од-
ной категории Кх в другую К2, т.е. F: К{ -+ К2, причем, такое что:
1)	каждому объекту А из Кх однозначно ставится в соответствие объект В из Кг, что обозначается В = F(A);
2)	каждому морфизму f е МогА^ однозначно сопоставляется морфизм из MorF2, обозначаемый F(/); при этом должны выполняться следующие аксиомы:
а)	если f е Mor(J,F), то F(f) е Мог(Л(Л), F(2?));
б)	для любой пары морфизмов из Кх соблюдается условие
в)	F(eA) = eF(A} для любого объекта А из Кх, где, напоминаем, еА — единичный морфизм
Определение 2. Контравариантный функтор F — это дословно то же самое, что ковариантный функтор F, за исключением того, что аксиомы согласованности “а” и “б” для F заменяются на аксиомы “а”’ и “б”’ для F путем перемены некоторых порядков в них, а именно:
а*) если f е Мог(Л, В), то F(f) е Mor(F(F), F(A)); ^F^A^F^Fifd.
8*
227
Иными словами, если F — это гомоморфизм (морфизм) двух категорий — Кх и Кг, то F — это своего рода антигомоморфизм (анти-морфизм) двух категорий — Ку и К2, где порядок умножения меняется на противоположный.
Понятия категории и функтора для двух категорий могут оказаться очень похожими. Понятие категории позволяет изучать объекты одной и той же категории, сравнивать их, оперировать ими, например, категорией множеств, топологических пространств (их гомео- и гомоморфизма), линейных пространств (морфизмы — это линейные операторы, если множество объектов состоит всего из одного объекта, и линейные преобразования, если имеется несколько линейных пространств как объектов этой категории линейных пространств).
Таким образом, категории позволяют сравнивать и менять структуры пространств, но в пределах одной категории (“однотипных” структур). В то же время функтор расширяет возможности категорного подхода, олицетворяя связи и отношения между разнотипными сообществами (категориями) структур (пространств, систем).
На языке функторов уже можно в определенном смысле говорить об управлении структурами, об их существенной модификации, вплоть “до неузнаваемости”, ибо могут происходить преобразования структур одного “рода” в структуры совсем другого “рода”, отличающиеся качественно от исходного, а не только количественными значениями параметров (например, изменениями размерности в категории линейных пространств) в пределах одной категории К.
Нам представляется в виде догадки, что то, что сделал Атья (Atiyah) в [379, с.18 и далее], определив общую (нелинейную) топологическую квантовую теорию поля как некоторый функтор, должно иметь под собой очень глубокую причину в самых исходных принципах квантовой механики. В [121] Дирак в качестве такого принципа выдвигал принцип линейной суперпозиции и затем довольно систематично, насколько это позволила именно квантовая механика (но не теория поля), описал квантовую механику, исходя, по сути, из этого единственного принципа. Однако теория категорий, включая функторы, возможно, позволит сделать больше для нелинейной квантовой теории, если попытаться принцип линейной суперпозиции расширить до принципа нелинейной суперпозиции, понимая под нелинейной суперпозицией и более общее понятие нелинейная свертка, или вообще композиция произвольных морфизмов, в частности отображений. Такая попытка по сути уже была осуществлена в фейнмановской трактовке квантовых процессов, где широко используются диаграммы. Нужно только строго и четко определить функтор (или функторы) между категорией фейнмановских диаграмм и некоторой категорией “категорных диаграмм”, которыми
228
широко пользуются в самой теории категорий и ее приложениях к другим математическим дисциплинам. Отметим, что робкая попытка найти такой “примитивный” функтор была предпринята в [48, 411], где по сути проводилось сопоставление категории блочно-структурных схем для описания систем с распределенными параметрами и категории фейнмановских диаграмм, описывающих взаимодействие элементарных частии.
Отметим здесь другой — “нефизический” — аспект возможных перспектив приложения категорно-функциональных методов, а именно, их приложение к теории программирования работы вычислительных машин (ВМ). В частности, имеется в виду создание языков программирования очень высокого уровня, близкого к естественным языкам. Это очень широкая проблема изучения и создания интеллектуальных систем. (Включить бы еще сюда проблему создания культурных, гуманистических, высокодуховных, добрых систем?)
Коротко говоря, здесь также речь может идти о точном описании категорий и соответствующих функторов между, с одной стороны, современными средствами программирования ВМ — искусственными языками и блок-схемами программ, на них написанными, диаграммной техникой самой теории категорий — с другой, блочно-структурными схемами (графами) систем, описанными на языке вход—блок—выход, и, наконец, категорией логических структур — высказываний и предикатов — с третьей. Надо отметить, что такая зачаточная тенденция уже появилась со стороны теории программирования ВМ [218]. Конечно, это огромная программа перспективных и трудных работ, которая в определенном смысле “изоморфна” программе создания ЕГТУ—ТСУ.
Отметим важный аспект этих проблем, связанный с концепциями теории кодирования, в том числе при наличии случайных факторов, учитываемых с помощью статистики и математической статистики в широком смысле (вероятность, байесовский и минимаксные подходы для описаний неопределенностей, размытые множества, распознавание образов и даже фракталы).
Очень коротко говоря, теория кодирования изучает различные структуры, задаваемые отображениями произвольного множества в множество каких-то конечных последовательностей, скажем, слов, составленных из букв какого-то алфавита, в частности, это “двоичные” последовательности из нулей и единиц. Кодирование — это прямые отображения, а декодирование — это обратные отображения. При этом рассматриваются большие семейства (категории) таких отображений, которые пытаются как-то параметризовать. При этом параметр играет роль конкретного шифра или ключа. В более широком смысле речь идет о кодировании целых пространств (структур и систем). Есть такая
229
философская точка зрения на реальность: законы Природы (свойства и отношения между реальностями) закодированы в математических структурах, а научная работа рассматривается как работа по декодированию (расшифровке) и осмыслению этих “текстов”.
На категории полезно посмотреть с общей “структурной” точки зрения, т.е. как на отношение. Категорию можно рассматривать как функциональное, бинарное отношение на абстрактном множестве ОЬ, называемом множеством объектов, смысл которых состоит в том, что их детривиализация часто представляет собой в свою очередь очень сложную структуру — целое пространство или систему весьма конкретного вида, например конкретное линейное пространство, конкретный автомат, конкретное многообразие и т.д. Само это отношение задается символом Мог (Л, В), где А и В принадлежат множеству, а лучше сказать, классу (имея в виду их возможную детривиализацию). Смысл этого символа и есть бинарное функциональное отношение f: АВ на множестве ОЬ.
Также полезно посмотреть на категорию с алгебраической точки зрения, рассматривая f :А—.> В как алгебраическую унарную операцию в ОЬ. Тогда в силу требований определения категорий, предъявляемых к морфизмам — множеству Мог (Л, В), в Мог (Л, В) можно выделить подмножества, например Мог (Л, А), которые являются моноидами, т.е. подгруппами с единицей. Но такая структура является непременным атрибутом любой симметрии.
В заключение отметим следующее. Понятие категории соответствует современной тенденции понимать теорию аксиоматически, т.е. не обращать внимание на предметы, абстрагироваться от них, а обращать внимание только на отношения между предметами, а аксиомы — это и есть отношения, вернее, свойства отношений.
Категории изучают отношения (разные симметрии) между крупными образованиями — пространствами, в частности, одного и того же рода (множества или топологии, или линейные пространства). Здесь, например, в категории линейных пространств могут быть пространства разного вида (конечномерные, бесконечномерные и др.).
Категории можно изображать графами или диаграммами (разновидностью блочно-структурных схем), где объекты категории — точки (вершины графа), а отображения — направленные ребра (со стрелками).
“Умножать”, т.е. осуществлять суперпозицию (композицию, свертку) можно не всегда, а тогда и только тогда, когда первый сомножитель выходит из той точки, куда входит второй сомножитель. Умножение ассоциативно, и существует единица умножения (тождественное отображение), рис. 4.10.1. Как заметил один математик, “графами можно изобразить почти все”.
230
Нам представляется, что было бы очень полезно для теории систем и управления расширить понятие категории в том смысле, чтобы помимо одной, хотя и широкой, операции композиции отображений, которая очень естественно описывает последовательное соединение блоков (систем, пространств), а также до
полнить еще сравнимость (некоторую однотипность) блоков как обобщение понятия параллельного соединения блоков.
Конечно, еще более общее пожелание — алгебраизировать (достаточно содержательно для нужд кибернетики) теорию категорий в мальцев-ском смысле алгебраических систем со всеми вытекающими отсюда по
следствиями, включая создание исчисления, языка исчисления, алгоритмов и машинных языков программирования высокого уровня, т.е. интеллектуальных, могущих оперировать с глубоко детривиализованными понятиями. Такие работы, как мы отмечали, фактически уже начаты.
Здесь, как обычно, есть два рода задач — синтеза и анализа. Синтетические задачи — это задачи “сборки” структурных схем из блоков с учетом допустимых их сочетаний в композиции, аналитические задачи — это задачи декомпозиции (в частности факторизации) блоков.
4.11.	ПРИМЕР АЛГЕБРАИЧЕСКОЙ СТРУКТУРЫ, ПОРОЖДЕННОЙ БЛОЧНО-СТРУКТУРНЫМИ СХЕМАМИ СИСТЕМ
Блочно-структурные схемы (БСС) получили очень широкое распространение как способ представления, анализа и синтеза систем в науке и технике [48, 411]. Благодаря наглядности и гибкости их можно наращивать, прибавляя новые блоки, их можно сворачивать, объединяя несколько блоков в один, в соответствии с определенными правилами. Таким образом, с блоками можно оперировать. В силу замкнутости этих операций получаются некоторые алгебраические пространства (структуры, системы).
В основе БСС лежит понятие блока (рис. 4.11.1), где х называется входным сигналом, или входом, у — выходным сигналом, или выходом, G — оператором блока. Выход у получается как результат действия оператора G на вход х по формуле
y = Gx.	(4.11.1)
231
Мы будем предполагать, что сигналы х и у являются элементами соответствующих линейных пространств X и Y. Оператор G принадлежит некоторому определенному классу К линейных операторов. Другими словами, G можно рассматривать как произвольное линейное отображение G : X Y одного линейного пространства на другое.
Оказывается, что для так определенных блоков можно определить операцию их последовательного и параллельного включения. Этим двум возможностям соответствуют две формальные операции с отображениями G: перемножения двух элементов G е К (свертки отображений) и суммирования двух элементов GeK (рис. 4.11.2, 4.11.3).
р и с. 4.11.1
Р и с. 4 11 2
Для выполнимости операции перемножения двух блоков надо только следить за тем, чтобы пространство Yr выходов первого блока было бы не шире пространства Х2 входов последующего блока. Для выполнимости операции суммирования двух блоков надо потребовать, чтобы Х\ — Х2 и Y] = У2.
Ясно, что для БСС (рис. 4.11.2) существует одно отображение С264 в силу равенству2 = G2x2 =	= G2(GiXi) = (G2Gi)xj.
Для БСС (рис.4.11.3) имеем у] + у2 = G{X} + G2x2 = (Gi + C2)xi.
Далее будем считать, что для блока (рис. 4.11.1) пространства входных и выходных сигналов совпадают (X = Y).
Таким образом, БСС (рис. 4.11.2) можно заменить одним блоком с отображением G2Gi, а БСС (рис. 4.11.3) можно заменить также одним блоком с отображением Gi + G2. Иными словами, на классе отображений К определены две операции: 1) перемножения C2Ci и 2) сложения Gj + G2.
Если для любых Gi е Ки G2 е К снова имеем С2С] е К и (Gx+G^ е К, то эти операции замкнуты и налицо алгебраическая структура неком
232
мутативного кольца, ибо, вообще говоря, G2Gi Ф G\G2, хотя вторая операция по смыслу коммутативна. Очевидно, что каждая из этих операций ассоциативна. Вместе они и дистрибутивны (справа и слева):
Gj(G2 + G3) — G\Gi + G\Gj и (Gj + G-^Gt, + G\Gy + G2G2.
В кольце К всегда есть единица как тождественное отображение
Однако нетрудно видеть, что помимо указанных двух операции, делающих кольцо К, вообще говоря, некоммутативным, на нем можно определить еще одну специфичную бинарную операцию, которая называется операцией обратной связи, или операцией замыкания (обратной связью). В тер-М1шах БСС ей соответствует схема (рис. 4.11.4).
Легко видеть, что результат G бинарной операции Gl®G2~>G получается, если потребовать разрешимость следующего линейного функционального уравнения относительно G при заданных 6] и G2:
С?! + (GG2)G = G.
Это уравнение можно разрешить в символическом виде:
G = [1-G1G2]_,G1 ^G = G,oG2, что дает в “явном виде” результат G от бинарной операции обратной связи для двух блоков — Gt и G2‘. G = Gl°G2. Операция обратной связи, вообще говоря, некоммутативна, ибо
[l-G.GJ-’G, *[1-G2G,]-'G2;
и неассоциативна, ибо, как легко проверить,
(Gi о G2) ° G3 * G] ° (G2 ° G3).
Описанная алгебраическая структура реализуется, в частности, в системах с распределенными параметрами, если в качестве сигналов рассматривать функции
Q —fix), х е D c:Rn, Q g. R, где D — некоторая область в Rn.
233
Для простоты будем считать, что все сигналы определены на одной и той же области D. Тогда блок, описывающий линейную систему с распределенными параметрами, СРП-блок, представляется в виде
D
где «(£,), е D, u(Q е R, — входной сигнал СРП-блока; Q(x), х е D, <2(х) е R, — выходной сигнал СРП-блока; G(x, Q, х е D, е D, G е R, — функция Грина СРП-блока, которая имеет еще ряд названий: импульсная переходная функция, функция источника, функция влияния. Она описывает оператор G блока. Эти названия оправдываются тем, что если в качестве входа взять сигнал 6(х - х0), то очевидно, что выход будет иметь вид G(x, xq).
Очевидно также, что выходной сигнал Q(x) последовательного соединения п блоков с соответствующими функциями Грина Gfa, £), i = 1,..., п, имеет вид
D D
n
Следовательно,
ew=jG(x,5)«©d5,
D
где u(x) — входной сигнал последовательности из п блоков; G(x, £,) — функция Грина этой последовательности:
G(x© = f..J G„(x,5,’I...G,©_„5)d4,
D D ,
п
В символическом виде последнее равенство можно записать так:
G = G„ ® Gn_t ®..® (?!.
Очевидно, что функция Грина параллельного соединения блоков равна просто сумме:
G(x,^) = £g,.(x,5), хе£>, ce/j.
i=l
Передаточная функция G(x, £,) обратной связи является решением интегрального уравнения Фредгольма 2-го рода:
G, (х, Q + JG12 (х,Г)) G(n, £) dr| = G(x,Q,
D
где С12 (х, т|) = G2 ® G{ = f G2 (х, £,) G} (£, r|)	— ядро этого интеграль-
ного уравнения.
234
Если G2 в обратной связи имеет вид “вырожденного” ядра, то, как известно, решение этого интегрального уравнения можно найти в явной и конечной форме. В частности, если
G2 = r&(x - Z>)5(^ - а), то искомое
G(x, 5) = G, (х, О + rGi^>Z>)gi(a^).
5	1	l-rG,(a,fc)
Если операторы структурной схемы описываются в терминах передаточных функций W(x, %, р) СРП, где р — параметр интегрального преобразования, порождающий передаточную функцию, то передаточная функция системы с обратной связью имеет вид
W(x, р) = W, (х, р) +
1 - г (а, Ь, р)
Здесь параметр г также может зависеть от параметра р.
4.12. ПРИМЕНЕНИЕ ИДЕИ КОМПЕНСАЦИИ ДЛЯ РЕШЕНИЯ НОВЫХ КРАЕВЫХ ЗАДАЧ, РЕАЛИЗОВАННОЕ БЛОЧНО-СХЕМНЫМ МЕТОДОМ
Здесь дается простой пример применения блочно-схемного метода к получению решений новых краевых задач для уравнений математической физики. Этот пример можно рассматривать как иллюстрацию получения новых структур (нарушения симметрии) за счет “управленческой парадигмы”.
Пусть имеется передаточная функция WQ(x, £>,р),х g D,^ g D,p g С (или, что то же самое, преобразование Лапласа от функции Грина Gq(x, /)), соответствующая некоторой краевой задаче, и мы хотим решить новую краевую задачу, состоящую в том, что в “старой” задаче добавляется новое краевое условие, например,
Q(a,t) = 0, X/t,	(4.12.1)
где а — фиксированная точка области D.
Для решения этой задачи применим принцип компенсации, т.е. организации обратной связи. Иными словами, попытаемся сделать такую систему автоматического регулирования (т.е. систему с регулятором в обратной связи), которая путем подачи входного воздействия в точку х = а области D определения объекта будет автоматически поддерживать величину Q(x, а) как регулируемую, равной заданному значению, которое в данном случае — в соответствии с новым требованием (4.12.1) — равно нулю.
235
Для решения этой задачи с новым условием (4.12.1) воспользуемся формулой, выведенной (см. подразд. 4.11) для передаточной функции W(x, ^р) системы автоматического регулирования (рис. 4.12.1). Структурная схема этой системы показана на рис. 4.12.2.
Р и с. 4.12.2
Передаточная функция этой системы (см. подразд. 4.11) от входа w(x,p) к выходу Q(x, р) дается конечной алгебраической формулой
W(x, ^,p) = WQ (х, р) + Wl W° Ъ- W° ,	(4.12.2)
где W\(p) — передаточная функция регулятора в цепи обратной связи.
Теперь положим в (4.12.2) b = a, W\(p) = к > 0, где к — действительный числовой параметр. Тогда (4.12.2) примет вид
Wk(х,5,р) = wo(x,t,,p) + —°,	.	(4.12.3)
1 - kW0 {а, а, р)
236
Такую систему автоматического регулирования можно рассматривать как систему, служащую для поддержания заданного значения величины Q(a, t). Регулятор, несмотря на все возмущения, стремится поддержать величину Q(a, t) равной нулю. Чтобы в таком пропорциональном регуляторе с коэффициентом усиления избежать динамических и статических ошибок регулирования, при которых Q(a, t) О, устремим коэффициент усиления к в (4.12.3) к бесконечности. Тогда из (4.12.3) получим:
И'(хЛ./,)= lim Wt (х, Ъ р) = W„ (х, р) -	(х’"’ Р) (а’ Р'!. (4.12.4)
(Л,Д>Р)
Формула (4.12.4), как легко проверить, действительно дает решение новой краевой задачи (4.12.1) в терминах передаточной функции, т.е. преобразования Лапласа по времени от искомой функции Грина новой краевой задачи. Формула (4.12.4) получилась как “Бог из машины”.
Формулу (4.12.4), как легко видеть, можно переписать в терминах детерминанта:
1	f^0(x,a,p)
Wfia,a,p) W0(a,^,p) W0(a,a,p)
Для примера рассмотрим задачу о теплопроводности в стержне, неограниченно протяженном в оба своих конца:
—-Р2-^-^ = /(х, Z), -оо<х<оо, t > 0,	(4.12.5)
dt Н дх2 J	k 7
где Q = Q(x, f) — распределение температуры; Р > 0 — коэффициент температуропроводности; fix, t) — плотность теплоисточников. Функция Грина для этой задачи имеет вид [51, с. 294, 406]:
= -Л— ехр ЗРд/тг t
4Р2/
а соответствующая передаточная функция
- GG
(4.12.6)
где х е (-со, сю), £ е (-со, оо), t > 0, р е С — комплексный параметр, причем
W(x,^p) = je-^G(x,^t)dt —
о
преобразование Лапласа G(x, £,, /) по переменной t.
237
Физический смысл функции Грина (в терминах тепла и температуры) состоит в следующем: значение функции G(x, %, t) равно температуре в точке х в момент времени t, если до момента времени t = 0 распределение температуры на оси х было тождественно равно нулю, а в начальный момент t = 0 в точке оси х мгновенно выделилось единичное количество тепла. Последнее означает, что распределение плотности источников тепла, т.е. функция Дх, t) в (4.12.5), имеет вид
Ж О = 5(Г) 8(х-^).
Покажем, что, используя передаточную функцию (4.12.6) этой зада-чи, можно найти решение другой задачи для уравнения (4.12.5), в которой задаются краевые условия в конечной части оси х. Например, пусть нужно найти решение (4.12.5) при новом дополнительном краевом условии
0(6, 0 = 0,	(4.12.7)
где b — фиксированная точка оси х, т.е. надо найти решение на полупрямых х> Ьпх < b с границей х - Ь.
В данном конкретном случае уравнения теплопроводности (4.12.5) и условия (4.12.7) легко вычислить Ж2(х, £, р), используя (4.12.6). Учитывая, что без ограничения общности можно считать Ъ = 0 и что нас интересует та часть стержня, где х > b и £ > Ь, после подстановки (4.12.6) в (4.12.4) вместо И4) получим:
хехр
exP -y-IM =
1 ----7= exp
exp —p l-'-Sl -exP
exp —“2PVp-
1
2PVp
exp -~-|x-£| -exp	-.(4.12.8)
P	P
1
2pV7

Р
Р
р
X
Формула (4.12.8) для W2 дает искомую передаточную функцию для новой краевой задачи уравнения (4.12.5) с условием (4.12.7).
Имея передаточную функцию (4.12.8), можно поставить еще одно новое краевое условие типа (4.12.7). Для решения этой новой задачи можно снова воспользоваться формулой (4.12.4). Для этого надо в (4.12.4) вместо Wo поставить W2, определенную формулой (4.12.8).
Таким итеративным способом можно найти в явном виде передаточную функпию для (4.12.5) с любым количеством новых краевых условий типа (4.12.7).
Отметим еще, что изложенный здесь принцип компенсации можно считать результатом осмысления идей Г.В. Щипанова, которые полу
238
чили не только теоретическое развитие, ставшее поистине жемчужиной теории управления, но и значительное практическое применение, одним из которых является изобретение решающего усилителя, получившего сейчас широкое распространение во многих технических устройствах, а первоначально в ЭМУ — электронных моделирующих устройствах (аналоговых вычислительных машинах).
Суть решающего усилителя состоит в следующем. Пусть имеется
электрическая цепь в виде последовательного соединения двух резисторов с сопротивлениями и г2 (рис. 4.12.3), где Ц — входное напряжение, С;2 — выходное напряжение, 1\ и 12 — токи в цепях с сопротивлениями rt и г2 соответственно. Здесь по закону Кирхгофа (закон природы) мы имеем = /2, а при Ц # и2 (скажем, U2 = kUi, где к > 1)
потенциал U в точке А не равен нулю (U 0), что также есть следст-
вие закона Ома, т.е. законов природы.
Может ли быть U = 0 при U2 = kU\, к Ф 1? Конечно, нет, ибо это было бы нарушением законов природы, что считается невозможным. Однако, если использовать идею регулирования (компенсации) и построить систему управления (регулирования), заданием для которой служит потенциал U в точке А, равный нулю (U =
Рис. 4.12.3
= 0), то ошибка регулирования А = |[7- С7*| = |С7|, а регулятор своими
управляющими воздействиями на систему должен ее сводить к нулю!
Роль такого регулятора может выполнить некоторый вспомогательный усилитель напряжения с коэффициентом усиления а. К схеме (рис. 4.12.3) его надо подсоединить так, как показано на рис. 4.12.4. Отсюда имеем равенства:
I2=(&-U2)/r2; Ц-12=Г, U2=aU.
Теперь усиление напряжения нашей цепи с наперед заданным коэффициентом
k = U2/Ux=r2/rx,
который легко менять выбором сопротивлений гх и г2, можно осуществить! Такую цепь и назначают “решающим усилителем”. Чтобы его реализовать, надо только выполнить следующие “технические” условия для нашего регулятора, т.е. просто для усилителя с коэффициентом усиления а:
239
1) усилитель должен быть настолько большой мощности, чтобы ток 1, им потребляемый, был бы пренебрежимо мал, что в “идеале” означает 7=0;
2) коэффициент усиления усилителя должен быть таким, чтобы |а| » 1.
Тогда из приведенных выше соотношений получаем (в силу того, что Ц = 12, так как I = 0):
(Ux-U)/ri = (U-U2)/r2.
Подставляя сюда U = —U2, получим: а
(1/,--С/2)/г,=(-С/2-Я)/г2.
ОС	ОС
Отсюда видно, что, если |а| настолько велик, что величиной — U2 а
можно пренебречь, т.е. положить — U2 =0, то получается требуемый а
решающий усилитель, что и требовалось вначале:
U2IUx=r2lrx=k.
Здесь возникают практические трудности, как и во всякой системе регулирования с большими коэффициентами (|а| » 1): система может оказаться неустойчивой, могут возникать генерации. Те, кто работал практически с такими усилителями, знают эту проблему. Несмотря на это, решающие усилители в ЭМУ сыграли огромную роль в деле ускорения технического прогресса в начале второй половины XX в.
Отметим следующий принципиальный момент. Если бы наша система регулирования была скрыта от наблюдения, то эффект усиления (к = U2! UX,UX = rxI, U2 - г2Г) мог бы показаться “чудом”, ибо потенциал U в точке А казался бы нулевым. Только очень чувствительные приборы, которыми мы могли в принципе не обладать, обнаружили бы, что U # 0, да и то могли принять это за флуктуации! С другой стороны, это “чудо” можно воспринять как новый закон природы, который, однако, обеспечивается скрытым от нас регулятором. Создавая такие регуляторы искусственно, как в приведенном примере, мы как
240
бы продолжаем дело природы. При этом создаются новые структуры, не встречавшиеся ранее в природе.
Но законы Ома и Кирхгофа, которые мы рассматривали как законы природы, на самом деле тоже не выполняются, если использовать приборы измерения повышенной точности. При этом наблюдаются флуктуации, которые выглядят совершенно хаотически.
“Управленческая парадигма мира” утверждает, в частности, что и законы Ома и Кирхгофа соблюдаются постольку, поскольку “достаточно хорошо” работает регулятор, обеспечивающий их. “Достаточно хорошо” означает, что ошибка (погрешность) регулирования очень мала, а воспринимается нами при измерениях повышенной точности как хаотическая флуктуация.
Поэтому, не дай Бог, если природные регуляторы по каким-то причинам перестанут работать достаточно точно и устойчиво. Тогда наш физический мир, который мы наблюдаем сейчас и благодаря которому поддерживается наше физическое существование, начнет разваливаться и превращаться в хаос из-за роста флуктуаций. То, что мы, к счастью, еще не наблюдали в физическом мире, однако, наблюдаем в человеческих обществах, где нередко- имеет место развал (скажем, психики) не только отдельных личностей, семей, организаций, но и развал больших человеческих сообществ.
5.	О ПОНЯТИИ СТРУКТУРЫ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ
5.1.	ПРЕДВАРИТЕЛЬНЫЕ ЗАМЕЧАНИЯ
В этом разделе будет описана довольно общая структура управления, охватывающая широкие классы систем.
По сути речь идет о проблеме создания аксиоматики теории управления. Безусловно, авторы отдают себе отчет в том, насколько трудной и глубокой является эта задача. Создание аксиоматики является одной из главнейших проблем любой науки. Достаточно вспомнить многовековую историю создания аксиоматики евклидовой геометрии, над которой трудились многие выдающиеся ученые.
К нас гоящему времени теория управления получила большое развитие: управляют непрерывными и дискретными, сосредоточенными и распределенными, дифференциальными и интегральными, детерминированными и стохастическими системами, а также системами разнообразных “смешанных” типов. Более того, современное состояние общества требует развития теории управления для решения качественно новых задач — задач об управлении структурами систем (достаточно вспомнить проблемы проведения реформ и структурных перестроек). На каждую из этих тем написано много статей и книг. Однако приходит время компактифицировать наши знания в целом, чтобы не распалась связь между отдельными научными дисциплинами, чтобы наши знания были более универсальными и эффективными и чтобы легче было учить студентов нового поколения. Неизбежная цена этому — повышение уровня абстракции, более полное использование новых достижений в математике и логике.
Современные геометрия и алгебра доставляют нам новый мощный язык — язык теории структур (в смысле Н. Бурбаки), теории расслоений и категорий. Опыт показывает, что переход на новый язык — это процесс, занимающий по меньшей мере период одного поколения, т.е. 20—30 лет. Примерно столько времени занял переход современной теории управления на язык функционального анализа. Поэтому актуальной задачей является скорейшая разработка идей и понятий теории управления в терминах нового универсального языка.
242
В основу подхода положены идеи и принципы порядка и меры, которые еще Эйлер рассматривал как суть всей математики. В такой же степени это относится и к теории управления. Идея упорядоченности в той или иной форме присутствует во всех задачах управления и, возможно, является одной из наиболее общих и абстрактных, но математически хорошо формализуемых идей, вокруг которой, на наш взгляд, можно в явном виде сконцентрировать основные положения теории управления. Идея измеримости (меры и метрики) в свою очередь охватывает не только понятие оптимального управления, но и многие другие понятия, например управляемости и допустимости. В данной работе идеи упорядоченности и измеримости применяются для построения точного формального описания структур управления, соответствующего содержательным задачам.
С помощью предложенной аксиоматики для широкого класса систем управления ставится некоторая общая задача оптимального управления, проводится ее исследование, выводится ряд необходимых, достаточных и одновременно необходимых и достаточных условий оптимальности. Центральную роль здесь играет введенное ниже понятие обобщенной метрики (первичной и Личной), универсальное в смысле ее применимости к широкому классу систем управления. Имеется своеобразная иерархия, или цепочка, связанных друг с другом метрик, характеризующих “топологические препятствия” в пространстве движений системы, которые отражают ограничения на управление в задаче оптимального управления. При этом важно, что допустимость управления (движения) отождествляется с его измеримостью. Таким образом, все многообразие различных ограничений, имеющих место в реальных задачах, сводится к одному понятию измеримости в некоторой метрике (мере). В дальнейшем, кроме специально оговоренных случаев, вместо терминов допустимое управление, допустимое движение, допустимая траектория будет использоваться один общий термин допустимая. Подразумевается, что множество всех допустимых, наделенное соответствующими структурами порядка и меры, как раз и будет образовывать пространство системы управления, т.е. пространство допустимых.
Смысл постановки и анализа этой задачи оптимального управления заключается в возможности описать и исследовать таким путем именно структуру пространства системы управления и отличить, например, общую задачу оптимального управления от общей задачи оптимизации. По-видимому, этот подход является альтернативным к “целостному (интегральному)” подходу, широко использующему идеи и методы функционального анализа, что ближе к задаче оптимизации. Отличие излагаемого ниже подхода от “целостного” состоит в применении
243
идеологии разбиения, которая лучше соответствует именно задачам управления и оптимального управления как некоторого упорядоченного выбора [53].
В соответствии с принятым подходом сначала обсуждается абстрактный математический объект — решетка, подходящий для описания пространств допустимых в широком классе систем управления и дается его формальное описание, связывающее естественное отношение упорядоченности допустимых с алгебраическими свойствами решетки. Надо заметить, что в математической литературе вместо термина решетка иногда встречается термин структура [183, 289]. Однако в ЕГТУ—ТСУ термин структура зарезервирован для гораздо более широкого понятия, чем решетка [41, 45]. В качестве основного источника ссылок на теорию решеток будет использоваться работа выдающегося математика и механика Г. Биркгофа [26]. Затем определяется понятие разбиений для допустимых и доказываются их свойства. Наконец, на основе введенного отношения эквивалентности (обобщенной границы) и понятия разбиения строится метрическая теория задачи оптимального управления, доказываются необходимые и достаточные условия оптимальности, и анализируется свойство минимальности относительно иерархии метрик.
5.2.	ОПИСАНИЕ СТРУКТУРЫ ПРОСТРАНСТВА СИСТЕМ УПРАВЛЕНИЯ НА ОСНОВЕ ОТНОШЕНИЯ ПОРЯДКА
На интуитивном и содержательном уровне можно выделить ряд общих черт, присущих соответствующим пространствам состояний систем управления. Ниже будет предпринята попытка в некотором смысле обратного построения, а именно: сначала сформулировать математически абстрактное описание этих “общих черт", а затем формально определить структуру, соответствующую системам и задачам управления.
Предположим, что всевозможные допустимые движения, или траектории, некоторой системы управления, соответствующие различным управлениям, различным начальным и граничным условиям и т.д., образуют абстрактное множество А = {а} допустимых а этой системы. В качестве основного постулата примем существование отношения частичной упорядоченности [26, 183, 289] на этом множестве. На содержательном уровне отношение а < b для элементов а и b множества А будет означать, что допустимая а является частью допустимой b (например, в теоретико-множественном смысле в фазовом пространстве системы). Если же элементы а и b не сравнимы между собой, то ни одна из этих допустимых не является частью другой, хотя они могут
244
иметь некоторый общий участок. Чтобы иметь возможность выделять такие участки, введем формальную операцию пересечения для элементов множества Л.
Положим, что для любых а е Л, b е А определено пересечение с -= а л b так, что
с < а, с < Ь,	(5.2.1)
и, если существует с'еА такое, что с' < а, с' <Ь, то с' < с.
Имеет смысл ввести также операцию объединения элементов множества А и рассматривать объединение двух допустимых как новую допустимую. Для сосредоточенных систем это легко представить, когда конец одной допустимой траектории является началом другой. Если же эти траектории не имеют общих точек в фазовом пространстве, то их теоретико-множественное объединение можно рассматривать как допустимую, являющуюся решением составной задачи финитного управления, образованной совокупностью двух исходных задач финитного управления, соответствующих этим траекториям.
Положим, что для любых а е А и b е А определено объединение d -= a v b, d е Л так, что
d> a,d > Ь,	(5.2.2)
и, если существует d’ е А такое, что d' > a,d'> b, то d' > d.
[Определение 1. Частично упорядоченное множество Л, в котором заданы операции пересечения (5.2.1) и объединения (5.2.2), называется решеткой.
Предположим также, что множество Л содержит единственный универсальный элемент О такой, что О < а, Ча е А. Тогда, если допустимые а и b не имеют общих участков, то выполняется условие а/\Ь = О.
В дальнейших рассуждениях важную роль будут играть алгебраические свойства решетки как пространства допустим ых. Они понадобятся. чтобы ввести формальное понятие обобщенной границы допустимой (в частности, начальной и конечной точки траектории сосредоточенной системы) и понятие разбиения допустимой, на основе которого будет развит метрический подход к задачам оптимального управления. Поэтому приведем важную теорему [183, с.179; 26, с. 21].
Теорема 1. Любая алгебраическая система А с двумя бинарными
* операциями а и v, удовлет воряющими четырем законам:
Л1 ала= а, а ч а = а (идемпотентность);
Л2 а лЪ = Ъ л a, a v b = b v а (коммутативность);
ЛЗ а а (Ь л с) = (а л b) л с, a v (Z? v с) = (a v b) v с (ассоциативность);
Л4 а а (я v b) = a, a v (а л Ь) - а (поглощение), является решеткой, и обратно.
245
Кроме того, неравенство а < b равносильно каждому из условий а л b = а и a v b -Ъ (совместимость).
Заметим, что операции пересечения и объединения в решетке определены непосредственно для элементов множества Л, что сильно отличает их от стандартных теоретико-множественных операций, определенных для множеств. Поэтому в решетке не определена операция вычитания. В то же время возможна ситуация, когда известны допустимая с е А и некоторая ее часть а < с (например, некоторая начальная часть заданной допустимой траектории сосредоточенной системы), а нас интересует вопрос об оставшейся (конечной) части а' допустимой с.
Введем необходимые алгебраические понятия, описывающие этот случай. Под замкнутым интервалом [Ь, с] будем подразумевать множество всех элементов х е А таких, что b < х < с.
Определение 2. Элемент х' из некоторого замкнутого интервала [Z?, с] называется относительным дополнением элемента х е [Ъ, с] в этом интервале, если х л х' = Ъ и х v х' — с.
Вопрос об “оставшейся” части тогда имеет смысл для решеток следующего вида [26].
I Определение 3. Решетка А называется решеткой с относительными дополнениями, если во всяком ее замкнутом интервале любой элемент имеет относительное дополнение.
В качестве “оставшейся” части допустимой с примем дополнение а' допустимой а в интервале [О, с], т.е. а л а' = О, a v а' - с.
Заметим, что данное определение, вообще говоря, не гарантирует единственность дополнения. Однако вместо того, чтобы просто потребовать эту единственность, предпочтем получить ее как следствие естественного требования дистрибутивности решетки, необходимого для последующего построения разбиений.
Легко видеть, что условия А1—Л 4 (теорема 1) не содержат дистрибутивного закона; из них следуют лишь неравенства:
a v (b л с) < {a v Ь) a (a v с), а л(Ь v с) > (а л й) v (а л с).
В то же время, рассматривая в точечном фазовом пространстве теоретико-множественные пересечения и объединения допустимых траекторий некоторой системы как конкретное представление абстрактной решетки, мы сталкиваемся с операциями, которые должны удовлетворять закону дистрибутивности. Поэтому в формальное определение пространства допустимых целесообразно включить условие (аксиому) дистрибутивности:
А5 a v (b а с) = {a v b) a (a v с),
246
эквивалентное двойственному к нему условию
а л(Ь v с) - (а л b) v (ал с).
Решетка со свойством А5 называется дистрибутивной.
Теперь при фиксированной начальной части допустимой оставшаяся ее часть существует и единственна в силу следующей теоремы [26, с. 31 ].
(Теорема 2 В любом замкнутом интервале \Ь, с] дистрибутивной решетки с относительными дополнениями элемент х е [Ъ, с] имеет единственное дополнение х' такое, что х л х' = b, х v х' = с.
Суммируя сделанные предположения, дадим формальное определение пространства допустимых для рассматриваемого класса систем управления.
Определение 4. В качестве пространства допустимых для системы управления, по определению, примем произвольную заданную дистрибутивную решетку с универсальным наименьшим элементом О и относительными дополнениями.
Здесь следует упомянуть, что такая решетка становится булевой алгеброй, как только в ней доопределено общее дополнение [26]. Однако возможность и целесообразность этого доопределения представляются отдельным важным вопросом и в данной работе не рассматривается.
5.3.	РАЗБИЕНИЯ В ПРОСТРАНСТВЕ ДОПУСТИМЫХ
Основную роль при построении метрического подхода к задачам оптимального управления играет понятие разбиения допустимой. Интуитивно предполагается, что разбиение должно удовлетворять целому ряду условий, обеспечивающих возможность суммирования по разбиению, доказательству аддитивности некоторой меры, согласованности представлений о “более крупном” и “более мелком” разбиении и т.д. Приведем формальное определение понятия конечного разбиения и установим его свойства, необходимые для дальнейших рассуждений. Все выводы будут целиком построены на введенной выше алгебраической структуре пространства допустимых.
Определение 1. Разбиением Р(а) допустимой а называется конечная совокупность попарно непересекающихся допустимых ah объединение которых равно а, что будет обозначаться Р(а) = = {а,} с требованием а, л ц — О, i v а, = а.
i
Разбиение называется тривиальным, если оно состоит из самой допустимой а.
247
Отметим, что не исключается случай, когда допустимая а может не иметь никаких нетривиальных разбиений.
Во множестве {Р(а)} всех разбиений допустимой а имеется естественное отношение частичной упорядоченности. Действительно, пусть фиксированы допустимая а и два ее разбиения Р\(а) = {«*}, Р2(а) = = {aна совокупности, вообще говоря, различных элементов aj и aj . Будем говорить, что разбиение Р2(«) содержит разбиение Р\(а), и писать Р1(л) < Р2(а), если всякая допустимая а} из Р\(а) представима как объединение некоторых aj из Р2(а). Иными словами, Р\(а) < Р2(а) означает, что разбиение Р2(«) является измельчением разбиения Р\(а). Установим простое, но важное свойство множества разбиений.
I Лемма 1. Множество {Р(а}} всех разбиений произвольной фиксированной допустимой а направлено, т.е. для любых двух разбиений Р\(а) и Р2(я) существует их общее измельчение Р3(а): Р\(а) < Р3(а) и Р2(а) < Р3(а).
Доказательство. Обозначим через а?, пересечения элементов первых двух разбиений а?- = aj л aj. Очевидно, а?-л а^ = О как только пары индексов (z,j) и (Д Z) не совпадают. Действительно, пусть, например, i *к. Тогда в силу законов А2 и АЗ (теорема 1) имеем: бД л ац = а] л aj л а{л aj =(a-Aaj)A aj л aj = = О л aj л aj = О. В то же время объединение возможных допустимых aj дает исходную допустимую а:
x/aj = v (aj л aj ) = v (v (aj л aj)) = v (aj ла) = va — a, ij	ij	i j	i	i
где второе, третье и четвертое равенства выполняются в силу законов ассоциативности АЗ, дистрибутивности А5 и поглощения А4 соответственно. Таким образом, совокупность {а?} = Р3(а) является разбиением допустимой а. Согласно определению элементов ajj, имеем: Р^(а) < Р3(а) и Р2(а) < Р3(а).
Несмотря на простоту понятия разбиения, имеются тонкости, требующие аккуратного обращения с разбиением как с формальным объектом. Пусть, например, Р(а) = {а{} и P(b) = {bj} — разбиения допустимых а и b соответственно. Согласно определениям I и 3 (подразд. 5.2), объединение с = a v b также является допустимой. Однако, теоретико-множественное объединение {«J u {bj} может не быть разбиением допустимой с, так как условия а,- л bj = О, вообще говоря, могут не выполняться. Поэтому важна следующая лемма.
248
Лемма 2. Пусть допустимая а является частью допустимой с(а < с). Тогда существует единственная допустимая b такая, что совокупность любых двух разбиений Р(а) и Р(Ь) дает некоторое разбиение Р(с).
Доказательство. В силу определений 2 и 3 (подразд. 5.2) допустимая а имеет единственное относительное дополнение в интервале [<9, с], которое обозначим через Ь. Тогда элементы а, и bj любых двух разбиений Р(а) и Р(Ь) не пересекаются между собой: а, л bj=O. В то же время, в силу законам ассоциативности АЗ, коммутативное объединение v a, v v bj = (v a,) v (v bj) = a v b = c i j ‘	j
совпадает с допустимой с. Таким образом, совокупность элементов {tzj о {bj} образует разбиение Р(с) допустимой с.
Приведем без доказательства простые следствия из этой леммы,
I Следствие 1. Всякая часть а < с допустимой с является элементом некоторого разбиения Р(с) допустимой с, и наоборот, всякий элемент с, разбиения Р(с) является частью допустимой с, т.е. с, < с.
I Следствие 2. Пусть Р{а) = {а,} — некоторое произвольное разбиение допустимой а. Для каждого элемента определим в свою очередь некоторое разбиение = {а^}, где i фиксировано. Тогда, совокупность элементов atj для всевозможных значений i и j образует новое разбиение Р\(а), являющееся измельчением разбиения Р(а) < Р\(а).
Дальнейший анализ свойств разбиений допустимых будет проводиться по мере определения необходимых дополнительных понятий, например, понятия обобщенной границы допустимой.
5.4.	ПОСТАНОВКА ЗАДАЧИ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ
Предположим, что на множестве А допустимых задан вещественнозначный неотрицательный функционал F, F(a) > 0, Va е А. Кроме того, примем, что этот функционал аддитивен относительно объединения непересекающихся допустимых в смысле операций в решетке А:
F(a v b) = F(a) + F(b), алЬ = О.	(5.4.1)
Прокомментируем это предположение. В конкретных описаниях большинства систем управления, как правило, минимизируемые функционалы удается определить только на достаточно “хороших” подмножествах некоторого пространства — измеримых кривых, поверхностях и т.д. Здесь же, согласно принятым определениям 1 и 3 (подразд. 5.2), в класс допустимых могут попасть теоретикомножественные объединения и пересечения этих “хороших” подмно
249
жеств, устроенные весьма сложно, С этой точки зрения сделаем предположение, что для функционала F существует его продолжение на все элементы в решетке А с сохранением аддитивности функционала F. При этом оказывается справедливой оценка значений функционала на объединениях и пересечениях допустимых, которая вытекает из следующей леммы [26, с. 302].
Лемма 1. Для действительнозначного функционала F на решетке
[ с универсальным наименьшим элементом О и относительными дополнениями, удовлетворяющими условию (5.4.1), справедливо равенство
Д(<з) + F(Z>) = F(a v b) + F(a л b), Х/а, Vb. (5.4.2)
Отсюда, учитывая, что F(a v b) > 0, получаем важное неравенство
F(a v b) <F(a) + F(b), Х/а, X/b.	(5.4.3)
В тех же случаях, когда допустимая а имеет разбиение Р(а) = {«,}, функционал F, очевидно, аддитивен на множестве {а,}:
F(a) = Р(а) = |о;}.	(5.4.4)
В этом и последующих соотношениях, содержащих символ X, под-разумевается суммирование по всем индексам из выражения, стоящего после этого символа.
Для постановки задачи оптимального управления, например задачи быстродействия сосредоточенной системы, следует ввести понятие обобщенной границы а е А допустимой. Предположим, что на решетке А задано отношение эквивалентности (рефлексивное, симметричное и транзитивное) д (обозначим через адЬ эквивалентность допустимых а и Ь). Потребуем также, чтобы это отношение удовлетворяло свойству подстановки в операцию v , т.е. чтобы из эквивалентности допустимых а и b следовала эквивалентность объединений (« v с) и (Ь v с) при любой допустимой с:
adb -> (a v с) д(Ъ v с), Х/а, Х/b, Х/с.	(5.4.5)
Рассмотрим фактор-множество А/д множества допустимых а е А по отношению эквивалентности д на А.
I Определение 1. Обобщенной границей допустимой а назовем элемент да фактор-множества А/д решетки А по отношению эквивалентности д, подстановочному в операцию v .
Заметим, что при исследовании как вариационных задач, так и решеток в отдельности, часто используется понятие конгруэнции [26]. В данных терминах это соответствует отношению эквивалентности, подстановочному как в операцию v, так и операцию а. Однако для наших
250
целей достаточно лишь введенной выше подстановочное™ д в одну только операцию v. В случае непрерывных сосредоточенных систем управления этому требованию можно удовлетворить, например, с помощью подходящих параметризаций допустимых движений системы. Эквивалентными будут, например, все движения, имеющие одно и то же начальное и конечное состояния.
Задачей оптимального управления при заданном элементе g множества А/д, т.е. при заданной обобщенной границе допустимой, назовем следующую задачу.
1.	Требуется найти величину F, определяемую равенством
F = {infF(c) : а g А, да = g & А/д}.	(5.4.6)
2.	Требуется найти допустимую a g А такую, что
F(a} - F,da=g,	(5.4.7)
которую назовем минималью а с заданной границей g, если а существует Эта задача будет рассматриваться ниже.
5.5.	МЕТРИЧЕСКИЙ ПОДХОД К ЗАДАЧЕ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ
Определим на множестве А/д обобщенных границ допустимых a g А неотрицательную функцию р, положив при каждом фиксированном g g А/д, что p(g) = F. Тогда, по условию (5.4.7), допустимая а является минималью с некоторой заданной границей да, если и только если
li(da)=F(a).	(5.5.1)
Установим важное свойство функции р, которое по аналогии естественно назвать неравенством треугольника.
Теорема 1. (Неравенство треугольника.) Для любой пары допустимых ах, а7 и их объединения а = ах v а2 справедливо неравенство:
у/да) < |4дщ) + р(да2).	(5.5.2)
Доказательство. Рассмотрим пару произвольных представителей классов эквивалентности дах и да2 (допустимые Ь{ и Ь2 соответственно); дЬх = дах, дЬ2 = да2. Тогда, в силу свойства подстановки (5.4.5) отношения д, имеем (b\ v b/)8(b} v а2) и (bx v а2) х х 5(щ v а2)- Так как отношение д транзитивно, получаем (bx v b/) х X д(щ V а2).
Обозначив Z?i v b2 = b и учтя, что аг v а2 = а, имеем Ьда. При этом значение функционала F на допустимой b в силу соотношения (5.4.3) удовлетворяет неравенству F(b) - F(b\ v b2} < F(bi) + F(b2). Таким об
251
разом, для любых двух представителей Ьх и Ь2 классов эквивалентности дал и да2 имеется представитель b класса да, значение функционала F на котором не превосходит сумму значений F на представителях Ьх и Ь2. Согласно определению функции ц и понятию инфинума inf в формуле (5.4.6) это означает справедливость неравенства (5.5.2).
Обозначим через {Р(а)} множество всех возможных разбиений допустимой а. Тогда из “неравенства треугольника” (5.5.2) легко получить следующее следствие.
Следствие 1. (Неравенство многоугольника.) Для любой допустимой а и любого разбиения Р(а) е {F(a)}, Р(а) = {а,}, справедливо “неравенство многоугольника”:
M(da)<ElW.	(5.5.3)
Учитывая, что функция ц определена как функция обобщенной границы допустимой и удовлетворяет неравенству (5.5.2), дадим следующее определение.
(Определение 1. Функцию ц, заданную (5.5.1), назовем обобщенной метрикой в множестве А.
Установим важное свойство минималей задачи оптимального управления.
Теорема 2. Всякая часть at произвольной заданной минимали
а е А, ах< а, является минималью.
Доказательство. В силу леммы 2 (подразд. 5.3) существует единственная допустимая а2 такая, что и а2 образуют разбиение допустимой а .
Применяя последовательно соотношения (5.5.1) и (5.4.4) к этому разбиению, получаем равенство
ц(3а) = F(a) = F(a.) + F(a2).	(5.5.4)
Пусть а} — не минималь. Тогда ц(3ах) < F(at) и, следовательно, существует допустимая а с обобщенной границей да = = дах такая, что F{a ) < F(ax). Рассмотрим объединение a v а2. Согласно свойству подстановки (5.4.5), имеем д( я v а2~) = = д(а}у а2) = да , а согласно свойству (5.4.3) функционала/7, | получаем F( a v а2) < F( а ) + F(a2) < F(a}) + F(a2). Таким образом, приходим к противоречию ц(Э а) > F( a v а2), д( a v а2) =
] = да. Теорема доказана.
I Следствие 2. Для любого разбиения Р(а) е {F(a)|, Р(а) =
= {д'} минимали а е А выполнено равенство ц(дя)=Хц(5я,.).	(5.5.5)
252
Это следствие вытекает по индукции из равенства (5.5.4), если учесть, что в силу теоремы 2 выполняются равенства F(a^ = и F(a2) = ц(да2).
Утверждение, обратное следствию 2, вообще говоря, не имеет места, т.е. если любая часть ах заданной допустимой а & А, строго меньшая а, ах< а, является минималью, то это еще не означает, что а — ми-нималь. Иными словами, если всевозможные элементы всех нетривиальных разбиений допустимой а минимали, то эго не означает, что сама а — минималь.
Пример такой ситуации легко построить, если в качестве функционала F(a) взять длину плоской кривой, а в качестве метрики ц(да) — евклидово расстояние на плоскости. Тогда, например, три стороны (ах, а2 и а3) произвольного треугольника будут минималями при граничных условиях, определяемых соответствующими парами вершин треугольника. В то же время ломаная v д2, составленная из минимален а\ и а2, имеет ту же границу, что и а3, д(а{ v «2) = да3, но не является минималью, так как по неравенству треугольника (5.5.2) длина стороны а3 будет меньше длины этой ломаной. Если теперь предположить, что пространство допустимых некоторой системы управления по определению состоит только из элементов а2, а3 и их объединений, то единственным нетривиальным разбиением допустимой v а2 окажется разбиение на части ах и а2, т.е. Р(а\ v tz2)={«i, а2}. Таким образом, то, что все части ах и а2 всех нетривиальных разбиений (в данном случае — единственного) допустимой (а} v а2) минимальны, не означает, что допустимая («i v д2) — минималь. Однако имеет место следующая теорема.
 Теорема 3. (Достаточное условие для минимали.) Если для произвольно заданной допустимой а е А существует разбиение Р(а) = {а,}, каждый элемент а, которого есть минималь, и, кроме того, выполнено равенство
ц(5а) = ХдДдя,),	(5.5.6)
|то а является минималью.
Доказательство. Согласно свойству аддитивности функционала F на разбиениях (5.4.4) и условию минимальности (5.5.1) получаем/ДД = F(v а()= ^F(a,} = Хд(о<2,-) = |1(Эя), что и i
требовалось доказать.
Равенство (5.5.6) необходимо для минимальности допустимой а, но недостаточно без дополнительных условий, например, условия минимальности а, в теореме 3. Действительно, рассмотрим на евклидовой
253
плоскости треугольник с произвольными заданными сторонами а2, а3. Положим, что пространство допустимых А некоторой системы управления порождено двумя элементами — стороной а3 и ломаной а, образованной сторонами а2, т.е. А = {а, а3, a v а3}. Единственным разбиением допустимой а является тривиальное разбиение Р(а):=а, и равенство (5.5.6) для а выполняется автоматически: ц(<Э<я) = р(дя). Однако в классе допустимых с заданной границей да = да3 минималью (кратчайшей) будет сторона треугольника а3, но не допустимая а.
Почти очевидно еще одно достаточное условие для минимали.
Теорема 4. Пусть:
1)	существует минималь а е А с заданной границей да;
2)	существует и единственна допустимая а е А с заданной границей да = да;
3)	а удовлетворяет равенству (5.5.6) при всевозможных своих разбиениях Р(а) е {/’(2')}. Тогда допустимая а совпадает с минималыо а, причем а — единственна.
Доказательство. Так как а — минималь, то, согласно следствию 2, она удовлетворяет равенствам (5.5.5) и (5.5.6) при любых своих разбиениях. Но по условию теоремы такая допустимая единственна и ей является а , т.е. а = а.
Ясно, что в этой теореме требование существования некоторой минимали а в заданном классе допустимых с границей да является необходимым. Если же отказаться от этого требования, то даже существование и единственность допустимой а, удовлетворяющей равенству (5.5.6) при всехР(я) е {Р(а )} не гарантируют того, что а будет минималью. Например, не исключен случай, когда имеется указанное а, но в классе допустимых с границей да вообще нет минимали. Такой пример легко построить, если в качестве множества, порождающего пространство допустимых, рассмотреть бесконечную последовательность {ак}, к = 0, 1, ..., непересекающихся между собой допустимых, имеющих общую фиксированную границу да, причем каждое а, имеет лишь тривиальное разбиение. Пусть функционал F(a) не достигает минимума на элементах этой последовательности (например, F(a) — монотонная убывающая функция на {</}). Тогда в заданном классе допустимых с границей да вообще нет минимали, хотя равенство (5.5.6) выполняется тождественно для всех ак: ц(дак) = ц(<Э«А) = ц(5я) в силу тривиальности разбиений Р(ак).
Введем теперь новую обобщенную метрику v, определенную на множестве обобщенных границ А/д. Для этого зададим дополнительно на множестве А функционал L(a, ц). который будем интерпретировать
254
как “длину” или “меру” допустимой а в метрике р. Традиционным образом этот функционал будет определяться как верхняя грань множества “частичных длин”, соответствующих различным разбиениям допустимой а.
Определение 2. Частичной длиной допустимой а в метрике р называется функционал
1(а, р, Р(а)) = Sp(d я,), Va е А,	(5.5.7)
зависящий от разбиения Р(д) = {а,} е {Р(я)} и метрики р.
Определение 3. Длиной (мерой) допустимой а в метрике р называется функционал
L (а, р) = {sup 1(а, р, Р(а)) : Р(а) е {Р(«)}}.	(5.5.8)
Очевидно, что этот функционал неотрицателен и в силу свойств разбиений, выраженных леммами 1 и 2 (подразд. 5.3), аддитивен на не-пересекающихся допустимых относительно операции объединения v в решетке А. Поэтому для него так же, как и для функционала F(a), справедливо утверждение леммы I (подразд. 5.4) и выполняются неравенства (5.4.2), (5.4.3) и (5.4.4).
I Определение 4. Обобщенной вторичной метрикой v по отноше-
I нию к метрике р называется функция на множестве А/д обоб-| щенных границ допустимых, заданная формулой
v(c'a) = {inf L( а, р) : а еА,да =да}.	(5.5.9)
В силу указанных выше свойств функционала Ца, р) на метрику v распространяется утверждение теоремы 1 (подразд. 5.5), т.е. верна следующая теорема.
(Теорема 5. Для вторичной метрики v справедливо неравенство треугольника
v(da) < v(da]) + v(da2), VO], \fa2, а = щ v а2.	(5.5.10)
Следствие 3. Для любой допустимой а и любого разбиения Р(а) е {Р(а)}, Р(а) = {а} справедливо “неравенство многоугольника”
v(3a) < SvOa,-).	(5.5.11)
Сравним первичную метрику ц со вторичной метрикой v.
Теорема 6 Для всякой обобщенной границы да е А/д и произвольного неотрицательного функционала р, удовлетворяющего неравенству треугольника (5.5.2), справедливо неравенство
р(бя) < v(da), \/да е А/д.	(5.5.12)
255
Доказательство. Рассмотрим произвольную допустимую а из класса допустимых с фиксированной границей g е А/д, да = g. Пусть P(a)-{aj} — произвольное разбиение этой допустимой. Тогда в силу определения 3 (подразд. 5.5) и следствия 1 (подразд. 5.5) имеем:
I L(a, ц) >1{а, ц, Р(а)) = XiAdaJ >р(Эа), Х/Р(а) е {Р(а)}. (5.5.13)
Используя формулу (5.5.9) и учитывая, что значение р(5я) не зависит от допустимой а, да = да, из неравенства (5.5.13) получаем неравенство (5.5.12).
Целесообразно выделить важный частный случай, когда соотношение (5.5.12) становится тождественным равенством.
I Определение 5. Если для всякой обобщенной границы да е А/д выполнено равенство ц(<3я) = v(da), то метрика ц называется са-мовторичной.
Важно заметить, что полученные выше неравенства для метрик ц и v не зависят от происхождения метрики ц, которая была определена через функционал F(a) в задаче (5.5.1), а обусловлены лишь справедливостью неравенства треугольника (5.5.2) для метрики ц.
Рассмотрим вторую задачу оптимального управления:
1) найти
{inf L(a, ц) : а е А, да = g е А/д} = v(da);	(5.5.14)
2) найти допустимую а е А,да= g (если она существует) такую, что
Ца, p) = v(da).	(5.5.15)
Эту допустимую а назовем минималъю ьторои задачи оптимального управления.
Докажем следующую теорему.
Теорема 7. (Необходимое и достаточное условие для минимали второй задачи оптимального управления.) Допустимая а е А является минималью второй задачи оптимального управления (5.5.14), (5.5.15), если и только если для любого разбиения Р{а} =
= {о,.}, Р(а} е {Р(я)} выполняется равенство
v(3a) =Ev(5a,.), V Р(а) е {Р(а)}.	(5.5.16)
Доказательство. Необходимость вытекает из цепочки равенств, справедливых для произвольного разбиения Р(а) заданной минимали а :
v(d а} = L( а, ц) (at, ц) = Sv (6 а,), где второе равенство отражает аддитивность функционала L относительно операции объединения непересекающихся элементов at решетки Л.
256
Достаточность. Пусть существует допустимая а, удовлетворяющая условию (5.5.16). Тогда в силу соотношений (5.5.8), (5.5.7) и (5.5.12) имеем:
р) = {supEp(da,-) : Р(а) = {а,-}, Р(а) е {Р(я)}} <
< {supSv(aaJ : Р(а) = {а,}, Р(а) g (Р(а)}} =
= {supv(d а) : Р(а) = {а,.}, Р(а) g {Р(а)}} = v (да), где предпоследнее равенство выполняется в силу предположения (5.5.16). Напротив, из определения 4 следует: L(a, р) > v(da).
Таким образом, получаем: L( а, р) = \(да), т.е. допустимая а является минималью второй задачи оптимального управления (5.5.14).
Из этой теоремы вытекает важное следствие.
Следствие 4. Пусть задан некоторый неотрицательный функционал pi(atz) на множестве А/д, удовлетворяющий неравенству треугольника (5.5.2), который будем называть первичной метрикой. Пусть также функционал F первой задачи оптимального управления (5.4.6), (5.4.7) порожден этой метрикой рр
F(a) = L(a, gj), Va g A,	(5.5.17)
причем в определениях 2 и 3 вместо метрики р подставлена метрика р. Тогда равенство (5.5.5) в следствии 2 становится не только необходимым, но и достаточным условием существования минимали а первой задачи оптимального управления.
Рассмотрим теперь первую задачу оптимального управления с функционалом F(a) = L(a, pi). Метрику р, определенную в (5.5 1), можно тогда считать вторичной по отношению к метрике рь поэтому обозначим ее р2 = р; в свою очередь метрика v, определенная в (5.5.9), будет вторичной по отношению к метрике р = р2 и “третичной” по отношению к метрике рь поэтому обозначим ее р3 = v. Таким образом, можно построить иерархию Личных метрик по отношению к некоторой первичной метрике (учитывая, что неравенства (5.5.10), (5.5.11) будут выполняться по индукции), соответствующих первой, второй и т.д. задачам оптимального управления. Отметим важное свойство этих метрик, являющееся следствием теоремы 6.
Следствие 5. Для всякой обобщенной границы да g А/д и последовательности А-ичных метрик рь р2, р?, ... справедливы неравенства:
ц,(Э<2) < Рг(д<2) Цз(Эя) Уда g А/д.
9. А.В. Бабичев
257
Покажем, что эти неравенства превращаются в равенства для произвольной фиксированной границы g е А/д, как только для нее существует минималь а, да = g, в первичной метрике щ, т.е. минималь первой задачи оптимального управления с функционалом F(a), заданным формулой (5.5.17).
I Теорема 8 Пусть допустимая а е А, да — g является минималью первой задачи оптимального управления (5.4.6), (5.4.7) с функционалом (5.5.17). Тогда она является также минималью второй задачи оптимального управления (5.5.14), (5.5.15) с функционалом L(a, р2)-Доказательство. По определению 3 имеем:
Ца, ц2) - {sup X Д2 (5а,-): Р(а) g {Р(а)}} = {sup ц2 (5а): Р(а) g {Р(а)}} = ц2 (да), где второе равенство выполнено в силу необходимого условия (5.5.6) для минимали a, 5(a) = g, задачи оптимального управления (5.4.6), (5.4.7). Поэтому из неравенства (5.5.12) вытекает Т(я,ц2) = ц,(5а) < ц3(5а), откуда по определению 4 получаем £(я,ц2) = ц3 (5a), т.е. а является минималью второй задачи оптимального управления, что и требовалось доказать.
По индукции получаем, что множество всех минималей Личной метрики включается в множество всех минималей (к + т)-ичной метрики, \/т = 0, 1,..., и значения минимумов на них совпадают с соответствующими значениями метрик на границах этих минималей.
Возникает обратный вопрос: “Являются ли минимали вторичной метрики ц2 минималями первичной метрики щ?” При существенном дополнительном предположении положительный ответ на этот вопрос дает следующая теорема.
I Теорема 9. Пусть допустимая b е A, db = g g А/д является минималью второй задачи оптимального управления (5.5.14), (5.5.15) с функционалом L(a, ц2). Обозначим 5/г обобщенную границу элемента разбиения Р(Ь) = {£,}. Пусть далее для границы db- каждого элемента bt любого разбиения P(b) g е {Р(Ь)} найдется минималь а,-, 5а,- = 55,- первой задачи оптимального управления (5.4.6), (5.4.7) с функционалом F(a) = L(a, p.j). Тогда допустимая b является минималью первой задачи оптимального управления.
258
(Доказательство. Учитывая совпадение границ dbi = д ai, из теоремы 8 получаем равенство значений метрик ц2 и ц3 на ' этих границах:
Р2(^) = ц2(Эа,.) =	ц2) = ц3(аа;) = ц3(^.).	(5.5.18)
Отметим, что полученные соотношения справедливы и на тривиальном разбиении. Поэтому для всех разбиений P(b) е {Р(Ь)} имеем:
L(b, ц2) = {supXР2 (^.): Р(Ь) е {Р(Ь)}} =
{sup£ц3(db,): Р(Ь) е {Р(Ь)}} =	(5.5.19)
= {sup Из (<^): Р(Ь) е {Р(Ь)}} = ц3 (db),
I где первое равенство является определением функционала ’ L(b, ц2), второе — следствием соотношений (5.5.18), а третье — । необходимым условием (5.5.16) для минимали Ь. Учитывая ра-| венство (5.5.18) на тривиальном разбиении, получаем из (5.5.19): {sup£p2(dZ0 : P(F) е {P(F)}| = ц2(эь).
В силу “неравенства многоугольника” (5.5.3) следует:
Хц2(з^) = кг(а),/>(?) £{/>(&)).
Согласно следствию 4, это равенство означает, что b являет-|ся минималыо первой задачи оптимального управления, что и требовалось доказать.
Обозначим через М(щ) множество минималей задач оптимального управления с метрикой к = 1, 2,... В силу теорем 8 и 9 получаем последовательность вложений:
7И(р1) с М(ц2) с 7И(р3) с ...
Заметим, что если /с-я метрика является самовторичной, то начиная с М(щ) эта последовательность представляет собой цепочку равенств 7И(ц^)= М(ц^+1) = ... В этом смысле полученную иерархию метрик ц15 ц2, Цз... можно рассматривать как глобальную характеристику структуры оптимального управления для заданной системы А.
5.6. УПРАВЛЕНИЕ В ТОПОЛОГИЧЕСКИХ ПРОСТРАНСТВАХ
Пусть пара (X, т) есть топологическое пространство, т.е. X — произвольное непустое множество, т — топология на нем [33]. (Далее точки пространства X будут считаться локальными состояниями системы с управлением (изображающими точками), а не целыми допустимыми, как в подразд. 5.1—5.5.)
9*
259
Определение 1. Допустимое управлениеу(а, Ь) в (X т) есть, если таковое существует, линейно упорядоченный образ, обладающий наименьшим а е X и наибольшим b е X элементами гомеоморфного (в смысле топологии т) отображения <р : [0, 7] -> X с “естественной” топологией отрезка [0, 7], которое можно записать в виде
л = <р(Д, 0 < t < Т, Т> 0, л е X, а = <р(0), b = <р(7),	(5.6.1)
где упорядочение задается естественным (арифметическим) порядком на [0, 7], точка а — начальная точка, b — конечная точка управления у(а, Ь).
Далее для краткости допустимое управление будем называть управлением.
Возможно, что требование гомеоморфности ср можно ослабить до непрерывности, но этот вопрос выяснять не будем.
Управление у(а, Ь) назовем 1-мерной цепью в X, которую ниже будем называть коротко — цепью. Итак, управление — это линейно связное и линейно упорядоченное множество в X, где точки а и Ъ соответственно наименьший и наибольший элементы множества у(а, Ь), рассматриваемого как линейно упорядоченное множество. Отображение (5.6.1) — это способ параметризации управления у (а, Ь) с помощью действительного параметра t G [О, Т\, линейно упорядоченного на [О, Т\ естественным образом. Если игнорировать линейную упорядоченность, задающую ориентацию на у(а, Ь), то у(а, Ь) называется путем, связывающим пару (а, Ь) без указания их порядка. Имеет смысл вместо термина управление в определении 1 использовать термин траектория.
Смысл определения 1 для теории управления (кибернетики) состоит в том, что оно дает возможность ставить по крайней мере задачи управляемости и финитного управления. Более того, в топологических пространствах, допускающих метризацию, можно поставить и задачу оптимального управления, которую, как обосновано ниже, естественно назвать задачей собственного оптимального управления.
Здесь не рассматривается более широкий, на наш взгляд, очень важный и принципиальный вопрос о том, какой набор (желательно минимальный) структур, необязательно включающий метрическую структуру, необходим или достаточен для постановки задач управляемости, финитного управления и оптимального управления. Ниже показывается, что наличие только одной метрической структуры на произвольном множестве X достаточно для постановки задачи оптимального управления.
260
5.7. УПРАВЛЕНИЕ В МЕТРИЧЕСКИХ ПРОСТРАНСТВАХ
Понятие метрики и метрического пространства вводится следующим определением.
Определение 1. Метрическим пространством (X, г) называется пара (X, г), где X— произвольное непустое множество, г — метрическая структура (метрика) на Л, задаваемая действительнозначной функцией г = г(х, у), х е X, у е X (или (х, у) е Хх X = = Х~), г е R, или отображение
r:X2^R,	(5.7.1)
где R — пространство всех действительных чисел; при этом имеют место аксиомы метрики:
г(а, Ь)>0) для V(a, 6) е X2, г(а, а) = О для Х/а е X, г(а, Ь) < г(а, с) + г(с, Ь) для Х/а е X, X/b еХ, Х/с е X, (5.7.2)
Аксиома (5.7.2) называется аксиомой неравенства треугольника или проще — аксиомой треугольника.
Функция г называется метрикой, а также метрической функцией, функцией расстояния или просто расстоянием, а иногда имеет смысл называть ее глобальной или интегральной метрикой на X, чтобы четко отличать от дифференциальных или локальных метрик на гладких многообразиях типа метрики Римана, Финслера и им подобных.
В определении I отсутствует аксиома симметрии г(а, Ъ) = г(Ъ, а), \/а G X, \/b G X, присущая “классической” метрике; она часто оказывается неадекватной реальной ситуации, когда расстояние в одну сторону не равно расстоянию в обратную сторону (например, время наискорейшего восхождения на вершину горы, играющее роль расстояния, может отличаться от времени наискорейшего спуска в исходный пункт). В определении 1 отсутствует также аксиома, по которой из г = 0 следует а = Ь.
Отметим также, что метрика (5.7.1) из-за ее несимметричности порождает две топологии на X, одна из которых (ti) порождается семейством окрестностей, принадлежащих^в теоретико-множественном смысле,
01 (xG, е) = {(ло, х) е J2 : r(x0, х) < е, в > 0}.	(5.7.3)
Подмножество О1(то, е) с X содержит все те и только те точки х g X, расстояние которых до фиксированной точки xQ g X меньше фиксированного числа в > 0. Вторая топология (т2) порождается семейством окрестностей
О2(хо, е) = {(%о, х) G А3 : г(х, х0) < е, е > 0}.
261
Подмножество O2(xo, е) cz X содержит все те и только те точки х G X, расстояние которых от фиксированной точки G X меньше фиксированного числа е > 0.
Топологии Т] и т2 совпадают только тогда, когда метрика г удовлетворяет аксиоме симметрии, что не является необходимым по определению 1.
Ниже управления у(щ Ъ) будем рассматривать в топологии (5.7.3). Метрика г может измерять управление у(а, Ъ) в том смысле, что с ее помощью каждому управлению, если оно определено (существует), можно поставить в однозначное соответствие действительное число, называемое длиной управления у (а, Ь). Для этого в определении 3 (подразд. 5.5) в качестве допустимой рассмотрим цепь у(а, Ь), а в качестве метрики р — введенную выше метрику г.
Если цепь у(а, Ь) имеет длину, то она называется спрямляемой (в метрике г), а управление у(а, Ь) — измеримым (в данной метрике г) или допустимым в метрике. Таким образом, допустимость управления мы отождествляем с его измеримостью, что означает универсализацию довольно разнообразных условий допустимости, встречающихся в конкретных задачах управления, которая сводится к единой проблеме измеримости управления у(а, Ь).
Воспользуемся определением 4 (подразд. 5.5) и введем вторичную метрику 1(а,Ъ) в пространстве X, полагая, что точки а и b являются граничными для семейства допустимых у(а, Ъ}, на котором ищется ин-финум функционала L.
(Определение 2. Расстояние, или метрика, 1(а,Ъ) называется вторичной метрикой на X по отношению к исходной, или пер-
; вичной, метрике г(а, Ь) на X, задающей метрическое пространство (X, г) и соответствующую топологию наХ. Пространство (X, I) называется вторичным метрическим пространством по отношению к исходному (первичному) пространству (X, г). Метрическое пространство без препятствий (X, г) — это метрическое пространство (X, г) со свойством
r(a, b) = 1(а,Ь) для Х/(а, Ь) е X2,	(5.6.4)
I т.е. первичная и вторичная метрики совпадают. Такое простран-
I ство и метрику г(а, Ъ) назовем также самовторичными.
Подчеркнем, что, вообще говоря, (X, г) и (X, Z) — это разные метрические пространства, а управление в (X, г) не есть управление в (X, I).
262
Ясно также, что существуют и такие метрические пространства (X, /), что для метрики г выполняется строгое неравенство
r(a, b) < I(а, Ь)	(5.7.5)
по крайней мере для некоторых (а, Ь) G X2.
Примером такой ситуации (5.7.5) может служить метрическое пространство (X, г), где г — сужение евклидовой метрики, первоначально заданной на Rn (т.е. роль X играет Rn\ на подмножество Rn - S множества Rn, где S — шар конечного радиуса г > 0. Проще говоря, (X, г) — это евклидово пространство с вынутым из него шаром.
В этом примере вынутый из R'1 шар S создает своего рода препятствие, каверну, в ранее “беспрепятственном” Rn.
Таким образом, имеет смысл ввести такое определение.
Определение 3. Метрическое пространство (X, г) с препятствиями — это метрическое пространство (X, г) с таким свойством: существует по крайней мере одна такая пара (a, b) е X2, что выполняется строгое неравенство r(a, b) < I (а, Ь~), т.е. вторичная метрика не совпадает с первичной тождественно на всем X. Мет • рику г с таким свойством естественно назвать несамовторичной, а соответствующее пространство (X г) можно назвать еще неса-мовторичным метрическим пространством.
Интересно сравнить топологию несамовторичного пространства (X, I) с топологией исходного пространства (X, г).
(Теорема 1. Топология пространства (X, г) слабее (грубее), чем топология несамовторичного пространства (X, /).
Детальное доказательство проводить не будем, ибо оно довольно длинное, хотя и не сложное. Оно базируется на определении понятия окрестность точки х е X (см. [122, с. 64], определение 4) и свойствах совокупностей всех окрестностей (см. [122, с. 64—65]), а также на определении топологического пространства в терминах окрестностей точек х е X(см. [122, с. 65, определение 6]).
В свою очередь окрестности точки х G X, точнее основная, “исходная” часть всего множества окрестностей, определяющих топологии т и ть задаются окрестностями специального вида, где явно фигурируют метрики г и I соответственно:
О(хо, б) = {,т G Х\ г(хо, х) < б} и О(хо, 8) = {х G X: 1(х0, х) < б}, которые непусты, ибо х0 с О(хо, б) и х0 g O(xo,s) в силу аксиомы г(хо, хо) = 0 и Z(x0, х0) = 0.
263
Но в силу (5.5.12), г < I, имеет место включение
б(х0,Е) с: О(хо, е),
а это означает, что, если О(хо, е) есть окрестность х0, то и О(хо, б) есть окрестность х0. Отсюда уже можно показать, что если множество принадлежит топологии Т], то оно принадлежит и топологии т. Но это в точности означает, что Ti сильнее т (tj z> т, см. [122, с. 62, определение 1]).
Перейдем теперь к некоторым примерам. Рассмотрим линейное пространство R!' с евклидовой метрикой г = |Z? - а\, Va g Rn, \/l g Rn, т.е. рассмотрим метрическое пространство — пару (Rn, г), где
г = r(a,b) = \b -а| = СЕ (6, ~ ai)2)1/2 и а = (а;) = (аь ..., ап), b = (bi) = f=i
= (Z?i,..., bn) — две произвольные “точки” Rn.
Покажем, что (Rn, г) — беспрепятственное пространство. По определению 2 это означает, что метрика г самовторична, т.е. вторичная метрика I тождественно совпадает с исходной (первичной) метрикой г:
I (а,Ь) = г(а, Ь) для Х/(д, b) G Rn х Rn.
Действительно, в соответствии с (5.5.9) имеем:
I(а,Ъ) = {inf 1(у(а, 6)] : у(а, b) G Г(<я, Ь)} = \Ь - а\,
т.е. метрика / тождественно совпадает с метрикой г, и, более того, нижняя грань достигается, т.е. существует управление у(а,Ъ), описываемое уравнением
х = ср(О = а + t(b - а), 0 < t < 1 (Т = 1),
т.е. имеется отрезок прямой, соединяющий начальную точку а с конечной точкой Ъ (ср(О) = а, ср(1) = Ъ), на котором выполняются тождества (5.5.16). Тогда имеем следующее тождество по t\
\b-a{ = \а-(а +.t(b-d))\ + |(а -I- t(b-a))-b\ = t\b-a\+ (1 -?)|^-д| для Vz G [0,1].
Аналогичные тождества имеют место для любого куска y(c,d) управления у(а,Ь).
В силу теоремы 7 (подразд. 5.5) это и означает, что данное управление есть минималь.
Рассмотрим другой пример. Возьмем на??2 метрику следующего вида: г(хьх2) = {max|%2 z = 1, 2},
где Xj = (х1? xj) g Я2, x2 = (x2, x2) g 7?2; х,1, x2, x2, x2 — действительные числа.
264
Легко видеть, что эта метрика г самовторична и, следовательно, данное метрическое пространство (Я2, г) без препятствий, т.е. метрики г и / в данном примере полностью совпадают:
I (a, b) = r(a, b), \f(a, b) е R2.
Будем искать в этом (R2, г), т.е. X = R2, минималь у(х15х2), где для определенности фиксируем точки (рис. 5.7.1):
а - X! = (0, 0), Ъ = х2 = (2, 1).	(5.7.6)
На рис. 5.7.1 последовательность (хь х2), представляющую точку х векторного пространства R2, для удобства описания будем толковать как координаты точки (вектора) х на плоскости (назовем ее тоже Л2) в некоторой прямоугольной (в смысле евклидовой метрики наТ?2) и прямолинейной системе координат. На рис. 5.7.1 изображен прямоугольник aCbD, сторона аС которого есть отрезок биссектрисы того координатного квадранта, в котором лежит точка Ь, т.е. это 1-й квадрант на рисунке, поскольку в данном примере точка b = (2, 1) лежит в 1-м квадранте.
Можно указать необходимое и одновременно достаточное условие, т.е. критерий того, что цепь у (а, Ь), где (а, Ъ) фиксировано условием (5.7.6), будет минималью в терминах фазового портрета [50, 60, 409,
Рис. 5.7.1
6(2,1)
265
420]. Для данной задачи фазовый портрет определяется в пределах прямоугольника aCbD как совокупность всевозможных прямых углов с вершинами в его точках и с двумя сторонами, параллельными его сторонам, идущими до пересечения с отрезками СЪ и Db соответственно. На рис. 5.7.1 показан один из таких углов — угол 123 со штрихованными внешностями его сторон. Такой штрихованный угол назовем воронкой фазового портрета с вершиной в точке 2. Другая воронка с вершиной 5 изображается углом 456, подобным углу 123. Каждую точку прямоугольника aCbD можно принять за вершину воронки, а все воронки подобны между собой. Совокупность всех таких воронок и есть фазовый портрет данной задачи.
Тогда цепь у(а, Ъ), т.е. любая непрерывная ориентированная кривая с началом а и концом Ъ, будет минималъю, если и только если она согласована с фазовым портретом задачи. Термин согласована означает, что если взять любую точку р G у(д, Ь) (за исключением точки Ь), то на у(а, Ь) найдется следующая за точкой р точка q такая, что отрезок прямой pq целиком принадлежит воронке с вершиной в точке р и, более того, этой же воронке принадлежит любой отрезок pqb где точка qx е у (а, Ь) и расположена между точками р и q. Другими словами, ориентированная непрерывная кривая, идущая из а в Ь, будет минималью тогда и только тогда, когда она заштрихованную границу каждой воронки пересекает со стороны штриховки (но не наоборот — в сторону штриховки), как, например, диагональ ab прямоугольника aCbD или ломаная a52db, которые есть минимали.
Действительно, для любой точки цепи у(л, Ъ), согласованной с фазовым портретом, легко подсчитать, что ее длина Z[y(«, fr)] = r(a, b) = 2, что в силу (5.7.4) означает: у(а, Ь) — минималь, т.е. у(а, Ь) = у(а,Ь). Ясно, что для данной задачи существует бесконечное множество ми-нималей у (а, Ь), так как точка b = (2, 1) не лежит на биссектрисе никакого квадранта координатной системы, и точку а без ограничения общности всегда можно принять за начало координат, т.е. а = (0, 0).
В противном случае (т.е. когда b лежит на какой-то биссектрисе координатного угла) существует единственная минималь y(a,Z?) — направленный отрезок ab, лежащий на этой биссектрисе. При этом прямоугольник aCbD вырождается в отрезок ab.
Ломаная а789Ь (рис. 5.7.1) не является минималью в силу того, что ее кусок — отрезок 78 — не согласован с фазовым портретом. Но легко видеть, что для этой ломаной тождественно выполняется равенство
г(а, Ь) = г(а, х) + г(х, Ь) для Х/х е (а789Ъ),	(5.7.7)
266
которое является необходимым условием собственной оптимальности теоремы 7 (подразд. 5.5). Однако нарушается по крайней мере условие (5.5.16), если в качестве с взять точку 7, в качестве d взять точку 9, а в качестве х взять точку 8, то видно, что
г(7, 9) < г(7, 5) + г(8, 9)	(5.7.8)
и тем самым необходимое равенство (5.5.16) нарушено, что и означает неминимальность ломаной а789Ь. В (5.7.7) и (5.6.8) уже существенно использован тот факт, что метрика г самовторична.
Отметим еще, что функция г(а, х) + г(х, 6), х е R2 при фиксированных а = (0,0) и Ъ = (2, 1) достигает минимума в точках х, заполняющих весь замкнутый прямоугольник aCbD.
Аналогичные результаты можно получить для такой же задачи в к" при п > 2. Интересно было бы решить аналогичную задачу в Rn с известной метрикой 1Р для произвольного р > 1.
В соответствии с целью данного раздела — построением общей структуры задачи оптимального управления — автоматически возникла необходимость глобального описания пространства допустимых системы. Принятый аксиоматический подход позволил дать такое описание и обосновать справедливость метрического анализа как глобального анализа структуры задачи оптимального управления. Представляется интересным в дальнейшем применить этот анализ к пространству допустимых, снабженному дополнительной дифференциальной структурой, и получить конкретные выводы глобального типа о структуре оптимального управления в терминах собственных лагранжианов систем управления.
6.	ФАЗОВЫЕ ПОРТРЕТЫ ДИФФЕРЕНЦИАЛЬНЫХ ВКЛЮЧЕНИЙ (ДИФФЕРЕНЦИАЛЬНЫХ СИСТЕМ С УПРАВЛЕНИЕМ)
6.1.	ДИФФЕРЕНЦИАЛЬНОЕ ВКЛЮЧЕНИЕ КАК СИСТЕМА С УПРАВЛЕНИЕМ
В этом разделе будет дан очень краткий обзор относительно нового понятия, связанного с геометрической теорией управляемых систем, которое позволило по-другому посмотреть на многие старые задачи, поставить ряд новых и открыть неожиданные связи между ними.
Понятие фазового портрета (ФП) дифференциального включения (ДВ), или дифференциальной системы с управлением (УДС), является нетривиальным обобщением широко известного понятия фазового портрета обыкновенного дифференциального уравнения (ОДУ). Можно сказать, что ФП ДВ — это детривиализация ФП ОДУ.
Рассмотрим ОДУ
—	хеХ, х&ТхХ,	со), (6.1.1)
dz
где X — некоторое «-мерное многообразие; ДАТ — касательное пространство к А" в точке х, которое можно отождествить с Rn-, t — скалярный параметр, имеющий физический смысл времени; f— некоторое отображение (функция) из X в ДАТ.
Для простоты будем считать (если это не оговорено), что X — это пространство 7?”. Это почти не меняет сути дела, по крайней мере для рассмотрений “локальных” вопросов.
Можно считать, что ОДУ (6.1.1) определяется сечением расслоения (X Т^Х) = R" х Rn = R2n, смысл которого состоит в том, что оно в каждой точке х е X задает вектор х е Т,Х. Точку х е X будем называть изображающей точкой ОДУ, а вектор х = v е Т^Х— скоростью изображающей точки. В этой терминологии ОДУ (6.1.1) задает на Xполе скоростей изображающей точки, или локального состояния х. Локальное состояние там, где это не ведет к недоразумениям, будем для краткости иногда называть просто состоянием х.
268
С ОДУ связано понятие решение ОДУ, которым называется функция
X = x(t), t е Т,х g X,	(6.1.2)
для которой на Т существует производная x(Z) и которая после подстановки в (6.1.1) обращает ее в тождество по t\
x(t)=fix(fi),^t е Т.
Хорошо известно, что при некоторых предположениях гладкости для функцийу(-х) и Д7) гарантируются существование и единственность (локальная или глобальная) решения х(Д, t > t0, при фиксированном начальном условии
x(to)=x0,x0 G X.	(6.1.3)
Задача нахождения (6.1.2) при условии (6.1.3) для (6.1.1), как известно, называется задачей Коши для ОДУ.
Если для определенности положить Т = [0, оо]з t0 = 0, то геометрически решение (6.1.2) с условием (6.1.3) означает определенной степени гладкости некоторую линию в X, называемую траекторией, начинающейся в точке х0. Дело существенно меняется, когда вместо ОДУ (6.1.1) рассматривается равенство
х =fix, и),х е X, х е ДХ, и е U(x),	(6.1.4)
где и (= U(x); U(x) — некоторое фиксированное множество, возможно, зависящее от х е X и называемое множеством допустимых управляющих параметров; и — управляющий параметр. Равенство (6.1.4) будем называть дифференциальной системой с управлением, или сокращенно уде.
Равенство (6.1.4), говоря точно, уже не есть просто ОДУ — это ОДУ с параметром. Более того, в задачах управления параметр и, как правило, считается нефиксированным в смысле его независимости от переменной t, t е Т или х g X. Иными словами, как правило, управляющий параметр и рассматривается как функция от I:
u = u(f),t G Т, и G U(x)	(6.1.5)
или как функция от х:
и = и(х),х g X, и е U(x).	(6.1.6)
Функция (6.1.5) называется управлением, функция (6.1.6) — синтезом УДС. Только при подстановке (6.1.5) или (6.1.6) равенство (6.1.1) снова становится ОДУ: х = fix, и(Д) и, соответственно, х = =fix, и(х\). При этом существенно, что решение этих уравнений х =
269
= x(t) будет считаться и называться допустимым, если и только если будет выполняться условие допустимости управления fit) или синтеза fix), т.е. будут выполняться условия fit) е J7(%(7)) для \/t G Т И fifif)) G t/(x(/)) для V/ G Т.
Траектория, соответствующая допустимому решению x(t), будет называться допустимой траекторией или просто допустимой.
Таким образом, в отличие от ОДУ (6.1.1) для УДС (6.1.4) при фиксированном начальном условии х0 е X, но разных управлениях, или синтезах, существует, вообще говоря, целый “пучок” допустимых -траекторий, исходящих из точки х0, каждая из которых соответствует своему допустимому управлению w(f), или допустимому синтезу г/(х).
Рассмотрим УДС (6.1.4) с геометрической точки зрения. В отличие от ОДУ (6.1.1) в каждой фиксированной точке х е X имеем, вообще говоря, не одну, а много скоростей х - v, т.е. имеем целое множество векторов в пространстве 1\Х. Обозначим это множество 7(х) и назовем индикатрисой УДС в точке х. Таким образом, вместо векторного поля скоростей для ОДУ (6.1.1) для УДС (6.1.4) имеем поле множеств, или поле индикатрис. Вектор х = v е fix) назовем допустимой скоростью УДС (6.1.4) в точке х. Тогда очевидно, что траектория x(t), t е Т, будет допустимой, если и только если fit) е Z(x(0) Для V/ е Z (или почти любого t g Т, если речь идет об измеримых функциях х(/)).
Ясно, что множество fix) при каждом фиксированном х е X получается как образ fix, U(x)) множества допустимых параметров U(x) при отображении f{x, u):U(x)-> ТхХ. Иными словами, когда и “пробегает” U(x), вектор х = v “пробегает” множество fix, U(x)) = fix) при любом фиксированном х е X.
Таким образом, УДС (6.1.4) в отличие от ОДУ (6.1.1) описывается не уравнением (дифференциальным), а включением (дифференциальным) вида
x&fix) или xg f(x,U(x)), хеХ.	(6.1.7)
Кратко его будем обозначать ДВ УДС, где ДВ означает дифференциальное включение. Более полно его можно было бы назвать обыкновенным дифференциальным включением (ОДВ) или включением для векторов v е fix), чтобы отличить от аналогичных включений для частных производных, поливекторов, градиентов и т.д.
Заметим, что fix) имеет смысл и для ОДУ (6.1.1), но тогда fix) состоит всего из единственного вектораДх).
270
6.2.	ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ, СВЯЗАННЫЕ С ДИФФЕРЕНЦИАЛЬНЫМИ ВКЛЮЧЕНИЯМИ
Изобразим ДВ (6.1.7) геометрически, как показано на рис. 6.2.1, где скорость v отождествлена с х, т.е. v = х. Здесь 0(х) означает начало (нулевой вектор) линейного пространства 7ДГ = Rn, связанное с точкой х е X, где Т^Х = А" — слой, “висящий” над точкой х касательного расслоения {ЬД :хе X} с базойX.
С каждой индикатрисой 1(х) свяжем конус К(х), который назовем конусом допустимых направлений (скоростей у ДВ (6.1.7) в точке х):
К{х) = {осу :а > 0, у е7(х)}, \/хеХ.
Таким образом, К(х), х е X, — это поле конусов, связанное с данным ДВ (6.1.7), рис. 6.2.2. Каждый конус К(х) снабдим штриховкой. Вместе с полем конусов полезно рассмотреть поле сопряженных конусов А?(х), х g X:
К(х) - {ос/?:а > 0, реТхХ, рх <0},
где р g ТхX — элемент сопряженного с ТхХ линейного пространства
ТхХ\ рх — линейный функционал на ТхХ.
Сделаем одно существенное замечание. Дело в том, что по сути, не ограничивая общности, вместо произвольного и по смыслу непустого множества 7(х) при Vx g X будем рассматривать его овыпукливание, т.е. наименьшее выпуклое множество, содержащее в себе данное 7(х) при Vx g X.
Чтобы избежать усложнения в обозначениях, указанное выпуклое множество будем обозначать по-старому: 7(х). Иными словами, далее везде индикатриса 7(х), х е X, — это некоторое выпуклое множество.
271
Не будем здесь обосновывать допустимость такой операции овы-пукливания: оно связано с рассмотрением так называемых скользящих режимов управления.
Границы (“поверхности”) индикатрис 1(х) и конусов К(х) обозначим д1(х) и дК(х) соответственно. Индикатрисы I(x), х g X, будем считать замкнутыми множествами.
Итак, 1(х, х е X) — это поле замкнутых выпуклых множеств, а соответствующее поле К(х, х g X) будем считать полем замкнутых выпуклых конусов.
Здесь надо обратить внимание на то, что если 1(х) — выпуклое множество, то соответствующий конус К(х) с необходимостью тоже выпуклый. Однако, если 1(х) — замкнутое множество, то соответствующее множество — конус К(х) — может оказаться и не замкнутым. Например, если 1(х) — шар в R”, а начало 0(х) лежит на сфере д1(х), то К(х) будет не замкнутым — это открытое полупространство, определяемое плоскостью, касательной к д1(х) в точке 0(х); сама эта плоскость не принадлежит К(х).
Конусы К в Rn будем классифицировать по типам. Тип (т, г) конуса А? — это пара натуральных чисел (т, ri), т g N, г g N, где г — наименьшая размерность того линейного подпространства U в Rn, которое целиком вмещает в себя конус К, отсюда 0 < г < п и, если г = п, то К называется телесным конусом; т — максимальное число “линейно независимых” и отделяющих плоскостей в U для конуса К, отсюда 0 < т < г < п. Общее число различных типов (т, г) равно 0,5 п(п +1).
В различных прикладных задачах конусы К(х) (и соответствующие индикатрисы 1(х)), как правило, не телесны и, более того, число г > 2, но значительно меньше п. Это означает, что число существенных “скалярных” управляющих параметров, как правило, бывает невелико и намного меньше числа п управляемых параметров.
Более того, в практических задачах поле К(х) таково, что тип (т, г) зависит от точки х g Rn, т.е. т - т(х) и г = г(х). Этот факт делает теорию ФП УДС по трудности намного превосходящей соответствующую теорию ОДУ, как локальную, так и глобальную.
Понятие типа (т, г) конуса К разбивает X на подмножества постоянного типа, где т(х) и г(х) не зависят от х. “Границы” между множествами постоянного типа составляют особые множества данной УДС (аналог особых точек УДС) Как правило, особое множество состоит из нескольких подмногообразий различных размерностей, меньших п.
272
Условие для выделения подмножеств в X постоянного типа (т, г) в терминах гамильтониана УДС будут даны ниже. Множество постоянного типа в X будем обозначать
6.3.	ФАЗОВЫЙ ПОРТРЕТ ДВ УДС НА ДВУМЕРНОМ МНОГООБРАЗИИ
Смысл фазового портрета ДВ УДС состоит в том, что позволяет описывать все допустимые траектории этого включения точно так же, как фазовый портрет ОДУ позволяет описывать все его траектории, где (в отличие от УДС) через каждую точку х g X, если она неособая, проходит только одна траектория.
Поэтому, зная ФП УДС, можно гораздо легче решать многие задачи управления, такие, например, как управляемости—достижимости, финитного управления, оптимального управления и др.
Легче всего ФП УДС строится на двумерном многообразии, например на плоскости R2. Итак, пусть дана УДС
х =flx, и), х g R2, t> 0, и. е U.	(6.3.1)
Построим для нее поле индикатрис и конусов (рис. 6.3.1). На этом рисунке ясно видно, что в каждой точке х е R2 однозначно выделяются два векторных поля, назовем их — левое и правое:
гг=Д(х), Vx g R2,	(6.3.2)
=f2(x), Vx g R2.	(6.3.3)
Отметим, и это нам пригодится в общем многомерном случае, что vr и V/ формально определяются принципом максимума (при каждом фиксированном х g X):
ргуг = {sup : v е 1} = О,
p2vr ~ {SUP Piv: v g /} = О,
гдерх и р2 — векторы (ненулевые) из дК, как показано на рис. 6.3.2. Зафиксируем какую-нибудь точку х0 g X. Решая ОДУ (6.3.1) и (6.3.2) по отдельности на каком-то интервале времени, приняв х0 за начальные условия, получим у/ и уг — две траектории с общим началом в х0, соответствующие ОДУ (6.3.1) и (6.3.2), рис. 6.3.3. Эти траектории образуют “боковую поверхность” (“боковую границу”), которую обозначим К(х0), где И(х0) называется воронкой У(х0, т) включения (6.3.1) или областью управляемости из точки х0 за время т (иногда будем опускать аргумент т и писать х0).
273

Рис. 6.3.2
Воронка Г(х0) замечательна тем, что всякая (!) допустимая траектория у(х0) УДС (6.3.1) принадлежит целиком У(х0) по крайней мере для достаточно малого интервала времени х, если t0 = 0 и х(10) = л(0) = х0.
Отметим здесь связь ФП УДС с пространством Гюйгенса (см. подразд. 4.3). Воронку Г(т, х0) можно рассматривать как
элементы X(t, х0) пространства Гюйгенса, т.е. отождествить t = т и Г(т, Xq) = X(t, х0).
Штриховка границы ЭГ(х0) воронки У(х0) показывает, что никакая
допустимая траектория у(х0) УДС (6.3.1) не может пересечь границу ЭГ(х0) изнутри этой воронки наружу. Конечно, как правило, существует много допустимых траекторий УДС (6.3.1), которые пересекают границу ЭК(х0) снаружи и “втекают внутрь” воронки Г(х0). Но любые такие у начинаются вне воронки Г(х0). Таким образом, штриховка границы ЭГ(х0) воронки Г(х0) имеет физический смысл полупрозрачного зеркала (или стенки), которое пропускает лучи (или субстанцию) извне
воронки, но не пропускает их изнутри ее.
Фазовым портретом дифференциального включения (дифференциальной системы с управлением) называется семейство штрихованных воронок У(х0), когда вершина х0 достаточно плотно заполняет многообразие X, т.е. в данном случае плоскость R2.
Практически, чтобы построить ФП на двумерном многообразии, достаточно просто построить два обычных фазовых портрета для двух ОДУ (6.3.2) и (6.3.3), и затем вдоль траекторий нанести нужные штриховки. Более того, в двумерном случае можно вообще не наносить никаких штриховок! Достаточно расцветить двумя разными цветами тра
274
ектории ОДУ (6.3.2) и ОДУ (6.3.3) и нанести стрелки на траектории, указывающие направления допустимых скоростей на них. Эта информация эквивалентна ФП УДС (6.3.1).
Осталось обсудить один существенный элемент ФП УДС, который называется многообразием (а на плоскости просто линией) перемены штриховки (МПШ). МПШ — это такой же существенный элемент ФП УДС, как особые точки для ОДУ, которые определяют глобальные (топологические) свойства ОДУ. Каждый ФП УДС характеризуется в топологическом смысле (управляемости—достижимости в большом на конечных расстояниях) именно видом МПШ. В отличие от ОДУ, где особые многообразия это, как правило, точки, МПШ — это уже, как правило, линии (в плоскости R2) или поверхности разных размерностей для общего случая X. Этот факт делает качественную теорию дифференциальных включений намного сложней соответствующей теории для ОДУ.
Итак, МПШ на двумерном многообразии (в частности, на Л2) — это геометрическое место точек на X, удовлетворяющих условию коллинеарности векторов vz и vr:
vz = Kvr, (или vr = Kv,),
где К — действительное число.
Отметим один частный случай: на произвольном многообразии X существует замкнутая область D такая, что точка 0 — начало векторного пространства Т^Х — принадлежит внутренности индикатрисы 1(х) для любого х е D. Такая область D cz X называется областью нестесненных движений Это название оправдано тем, что любая траектория, целиком лежащая в D, будет, очевидно, допустимой для УДС х g 1(х), X G X.
На рис. 6.3.4 приведен только один пример ФП УДС для классической, но простейшей системы на плоскости:
х} =х2, х2 =и,
|w|<l, (Xj,X2) G R2.
Физический смысл этой системы с управлением, вытекающий из 2-го закона Ньютона, довольно очевиден. Отметим только, что ось %] является многообразием перемены штриховки.
Рис. 6.3.4
275
6.4.	ОБЩИЙ СЛУЧАЙ ФАЗОВОГО ПОРТРЕТА ДИФФЕРЕНЦИАЛЬНОГО ВКЛЮЧЕНИЯ
Определение ФП УДС, данное в подразд. 6.3, является общим. Но как построить штрихованную воронку К(х0) в данной точке х0 е X для данного ДВ
хеДх), хеХ?	(6.4.1)
Оказывается, что искомая штрихованная воронка есть ничто иное как знаменитый коноид Монжа для одного дифференциального уравнения с частными производными первого порядка для одной неизвестной скалярной функции Q(x), х g X. Это уравнение имеет вид
Я(х,у?) = 0, Р = ^-.	(6.4.2)
дх
Так как рассмотрение локально, то без потери общности можно сказать, что X = Rn, х = (хь ..., хп). Как найти F(x, р), соответствующее данному включению (6.4.1)? Нетрудно понять, что искомое F(x,p) однозначно определяется условием максимума
F(x,p) = {sup pv : v g I(x)}, xeX, peTxX.
Эта функция, очевидно, положительно однородна первой степени по р при Vx е X. Поэтому ниже вместо F(x, р) будем использовать обозначение Я0(х, р), т.е. F(x, р) = Н0(х, р), и функцию Н0(х, р) называть гамильтонианом данного дифференциального включения, или системы с управлением. В этих терминах соответствующая УДС вновь описывается дифференциальным уравнением с управляющим параметром
х=дН^х’Р\	(643)
Ф
где р играет роль управляющего параметра, р g Т^Х, и не стеснено никакими дополнительными ограничениями. Поле дК(х) при этом описывается уравнением
Яо(х,р) = 0,	(6.4.4)
а само К (х) условием Яо (х, р) <0.
Рассмотрим второе уравнение
р = -®^Р),	(6.4.5)
дх
которое, как хорошо известно, вместе с (6.4.3) образует каноническую систему уравнений Гамильтона, соответствующую уравнению (6.4.2)
276
или (6.4.4). Теперь искомую штрихованную воронку У(х0) — основной элемент нашего ФП УДС — описать уже можно. Для этого зафиксируем точку х0 о У и вектор р0 = АДх0). Другими словами, возьмем (х0, р0) так, чтобы
Но(х0,ро) = О.	(6.4.6)
Для этих начальных условий, решив систему Гамильтона (6.4.3), (6.4.5), получим:
х = x(t; хо,ро), t > 0, х(0; *о, Ро) = х0
и соответственно допустимую траекторию у(х0, /?()) в X с началом в х0 g X, а также
р =р (*; хо,ро), t > о,хо; *0, а) =Ро-
Вектор р = р(Г, ро) как функция от t, отложенный от соответствующих точек траектории у(х0, р0) будет все время находиться на dK{x(t\ х0, р0)) в силу сохранения условия (6.4.6) не только для начальных, но и любых моментов времени t > 0, т.е. имеем тождество по
*0,РоУ-
H(x{t\ x0,p(t; х0,/?о))) = 0.
Таким образом, траектория у(х0,р0) все время, по крайней мере достаточно малое, при t > 0 будет лежать на границе 5Г(х0) искомого коноида— воронки для включения (6.4.1) или УДС (6.4.3).
Взяв другое p’q g ЛДх0) при фиксированном х0, получим новую траекторию у(л'о>Го) ’ которая также целиком лежит на Г(х0), и т.д. Когда pQ “обежит” всю границу гЖ(х0), получим всю границу ЭГ(л-0) искомой воронки V(xq). Граница dV(x0) будет как бы соткана из всех допустимых траекторий у(х0,р0) как криволинейных образующих (рис. 6.4.1).
При этом направление векторов p(t; х0, ро) показывает ту сторону воронки 'К(х0), которая должна быть заштрихована.
Таким образом, мы разобрали случай “общего положения” вещей в вопросе о построении штрихованной воронки К(х0) ФП УДС. Не будем здесь касаться инте
277
ресного, важного и трудного вопроса о построении такой воронки в особых и вырожденных случаях, например, когда воронка Е(х0) не имеет полной размерности, т.е. dimV(x0) < п. Такой случай, как известно, если говорить в терминах УДС, связан с наличием инвариантных многообразий УДС, т.е. таких “поверхностей” в 26-размерности, меньшей п, с которых никакая допустимая траектория сойти не может и целиком ей принадлежит, хотя бы в какой-то своей части (локально).
Здесь мы только коснемся вопроса об условиях существования МПШ — многообразий перемены штриховки в X — и скажем, что МПШ -— это подмножество множества 5 особых точек УДС, о которых говорилось в подразд. 6.2. Укажем только для фиксированной УДС в X, dinrV = п, необходимые и достаточные условия того, чтобы точка х g X принадлежала множеству D” cz X постоянного типа (т, г), 0 <т < г < п.
В фиксированной точке х g X искомое число г = и - где г, — число всех линейно независимых векторов р, удовлетворяющих системе из двух уравнений:
Я0(х, р) = 0,	Н0(х, -р) = 0.
Если через тх обозначить число всех линейно независимых решений р одного уравнения Рф(х,р) = 0, (rt < тх), то искомое число т = п-тх.
6.5.	ЛАГРАНЖИАН УДС. СОБСТВЕННАЯ МЕТРИКА УДС
Пусть УДС определяется включением
xgZ(x), хеХ,	(6.5.1)
где 1(х) — произвольное непустое множество в ТхХ. Дадим следующее определение.
Определение 1. Лагранжиан УДС (6.5.1) — это действительнозначная неотрицательная функция L0(x, v), х е X, v g Т\Х, определяемая равенством
£0(x,v) = {inf — : X > О, Xvg/(x)}.
X
Легко видеть, что эта функция выпукла и положительно однородна 1-й степени по у при Vx g X. Функция £0(х, у) впервые была введена Г. Минковским и называется еще калибровочной функцией (при фиксированном х). Аргумент х в ней играет роль параметра, задающего поле таких функций в X. Уравнение
Z0(x, v) = 1	(6.5.2)
278
при каждом фиксированном х можно рассматривать как уравнение “переднего фронта” овыпукленной индикатрисы 1(х). При каждом фиксированном х е X лагранжиан LQ(x, у), как легко проверить, можно рассматривать как норму ||v|| вектора v: ||v|| = Z0(x, v).
В отношении многообразия X лагранжиан играет роль метрики, точнее дифференциальной (локальной, инфинитезимальной) метрики:
||dx|| = Lq (х, dx).	(6,5.3)
Не всякий вектор v измерим в этой метрике. Он измерим, если принадлежит R(x), х g X. Такая метрика называется собственной метрикой УДС (6.5.1). С помощью этой метрики можно измерить длины Z[y(x0,Xj)] допустимых траекторий у(х0, xj УДС (6.5.1), связывающих начальную и конечную точки в X:
1[у(х0,хх)] = JZ0(x,dx).	(6.5.4)
yUo.-O
Формула (6.5.4) дала повод назвать функцию Lo лагранжианом, так как, имея (6.5.4), можно поставить задачу на экстремум: в множестве Г(х0, хх) = {у(х0, X])} всех допустимых траекторий у(х0, х,), где (х0, xj g X2 фиксированы, найти у(х0, х,) так, что
г(х0, Х|) = {inf Z[y (х0, х,)]: у(х0, х,) е Г(х0, х,)} = Z[y(x0, х,)]. (6.5.5)
Если у(х0,Х]) в (6.5.5) существует, то она называется собственной оптимальной траекторией (собственная минималь данной УДС) в смысле ее длины в собственной метрике УДС. Функция r(xQ,xx}, как нетрудно проверить, есть глобальная метрика в X, порожденная локальной метрикой (6.5.3).
Заметим, что в силу положительной однородности Lo по v при Vx g X из (6.5.4) следует:
Т	т
Z - Z[y(x0, х,)] = Jzo(x, v = х) dx = Jdx = Т, о	о
где параметр т выбран так, что выполняется (6.5.2) при движении изображающей точки вдоль траектории у(х0, х,). При этом скорость dx
v = х = — в каждый момент времени максимальная по норме в силу dr
(6.5.2). Очевидно, что такой параметр х играет роль времени, которое имеет смысл собственного времени в точном смысле, как в физической теории относительности Эйнштейна. Поэтому его можно назвать
279
собственным временем данной УДС (6.5.1), а траекторию у(х0,х1) назвать оптимальной по быстродействию траекторией УДС (6.5.1) в ее собственном времени.
Между собственным лагранжианом и гамильтонианом Н0(х, р\ введенным в подразд. 6.4, имеется тесная связь, аналогичная связи, осуществляемой преобразованием Лежандра в классической механике. Однако вместо тождеств Лежандра в теории УДС (6.5.1) используются тождества Эйлера, так как Lo и Но положительно однородные 1-й степени по v функции при любом хеХ.
Имеем равенства х = ————; рх = р —- 	= Но (х, р).
др	др
.	dL0(x,v) dL0(x,v) т , .
Аналогично при x = v имеем р - ——---; pv - —-	z у = Lo(х, у).
dv	dv
Отсюда получаем L0(x, у) = H0(x, p). По аналогии с (6.5.2) можно рассмотреть уравнение Н0(х, р) = 1, которое описывает некоторую поверхность в пространстве ТхХ при каждом х е X. Эта поверхность есть “передний фронт” некоторого выпуклого множества в ТхХ. Это множество назовем фигуратрисой УДС (6.5.1) и обозначим Ф(х). Уравнение (6.5.1) описывает “передний фронт” фигуратрисы, “сопряженный” переднему фронту индикатрисы Дх).
В выпуклом анализе функция Нфх, р) имеет смысл опорной функции множества (индикатрисы) Z(x). Уравнение Н0(х, р) = 0 описывает дК(х) — поверхность, сопряженную с дК(х), если конус К(х) не пуст, a Z0(x, р) = 0 описывает дК(х) — поверхность, сопряженную с дК (х).
Вдоль минимали у(х0,Xj),	описываемой х = х(Г), 0 < t < Т,
х(0) = х0, х(7) = х,, все время выдерживается условие
Яо (x(Z), Д(0) = Lo (x(Z), х(0) = 1,
что вытекает из известного принципа максимума Понтрягина [250]. При этом, если у(х0, X!) — минималь, то существует ненулевая функция p(t), 0 < Г <Т, удовлетворяющая системе Гамильтона
•	^0 ( х •	^0 7 X
х = —-^-(x5jp); р =——^-{х,р}. др	дх
В терминах Lo минималь x(t) удовлетворяет уравнению Эйлера
d d/
dL0 (х, х) дх
dL0(x,x) дх
280
Существуют и другие связи между собственными лагранжианом и гамильтонианом данной УДС, имеющие интересный геометрический, механический и физический смысл [50, 409].
6.6. ДЕКОМПОЗИЦИЯ ФП УДС ДЛЯ МНОГОМЕРНОГО СЛУЧАЯ
Как отмечалось выше, построение ФП УДС для размерности dim А" = и>3 может оказаться довольно сложной задачей. В общем случае эта задача на порядки сложнее задачи построения и исследования ФП ОДУ в пространстве размерности три и выше.
Здесь рассматривается один вид УДС, который допускает некоторую декомпозицию своего ФП в том смысле, что вся информация о ФП УДС высокой размерности может редуцироваться в ФП меньшей размерности. Рассмотрим, например, УДС вида
х = Д(х) + ug(x), xeR3, -со <«<+оо.	(6.6.1)
Примем, что все точки траектории уравнения х = g(x) взаимно достижимы для УДС (6.6.1) за произвольно малое время вследствие отсутствия ограничений на управление. Поэтому будем считать такие точки эквивалентными между собой и перейдем от пространства Д к новому фактор-пространству, каждая точка которого соответствует целой траектории поля g(x) в R3. Предположим, что эти траектории расслаивают исходное фазовое пространство, образуя совокупность слоев расслоения, а указанное фактор-пространство является двумерным гладким многообразием — базой расслоения [122, 258]. На базе можно построить ФП УДС, полученной в результате проектирования исходной системы из R3 в касательное расслоение к базе, и по нему исследовать задачу достижимости исходной УДС в R3. ФП исходной УДС в R3 будет подъемом вдоль слоев расслоения ФП с базы.
Пусть о — некоторая область на базе или целиком вся база, вложенная в R3. Тогда в соответствии с конструкцией гладкого расслоения всякая траектория поля g(x), проходящая через с, пересекает о трансверсально и лишь в одной точке. Обозначим у(т,х) — решение уравнения x = g(x) с начальной точкой xeR3. Спроецируем УДС (6.6.1) на базу вдоль слоев расслоения. Под действием дифференциала проекции бл векторы f из точек у(т,х), -оо<т<+оо, отобразятся в касательное пространство До к базе о в точке х. Пусть До cz R3 описыва-
281
ется уравнением (х,£) = 0, хео, £ е Тхс с: R3. Тогда du : /(у(т,х)) £(т,х), где
^(T,x) = /(T,x)-g(x)
(7(т,х),х) (£(*), *)
7/ х ду(-т,х) г. .	..	“ (- 1)л jk .. ч к
/(^*) =------L f(y^,x))=X~^-adkf(x)Tk,—
ох {т }	к=0 , kl *
результат параллельного переноса вектора /(х) вдоль слоя из точки у(т,х) в точку х.
Таким образом, на базе оказывается определена двумерная УДС, соответствующая УДС (6.6.1):
х = £,(т,х), хе с, -оо<т<+со,	(6.6.2)
где т — теперь кусочно-гладкое управление.
Для УДС (6.6.2) траекторная воронка на базе описывается канонической системой уравнений (6.4.3), (6.4.5), где вместо Н(р,х~) берется гамильтониан на базе
Яа(Р,*) = sup {^(т,х)}, хе о,	^(т,х)еДс>.
— со£ Т <+оо
Множество точек особого управления этой системы имеет, вообще говоря, меру нуль, поэтому каноническая система уравнений
дЯо(р,х)
Ф
Р = -дН^Р-,Х^ , хе о, реТ*ха, дх
с начальными условиями pQ,xQ\ На(ро,хо) = О позволяет построить фазовый портрет на базе о.
Определим конус допустимых направлений системы (6.6.2) в точке х на двумерной базе о. Граничные векторы этого конуса могут быть либо предельными для семейства векторов ^(т,х), т —> ±оо, либо собственно векторами £(та,х) для некоторых фиксированных та. Границы траекторных воронок УДС (6.6.2) на базе образуются интегральными кривыми векторных полей, порождаемых крайне “левыми” и “правыми” граничными векторами конуса допустимых направлений.
Доказаны теоремы 1 и 2, помогающие отыскать граничные векторы конуса допустимых скоростей на базе в произвольной точке.
282
Теорема 1. Пусть Е,(та,х)^0 (рис. 6.6.1) является граничным вектором конуса в точке х е о , т. е.
Этй : £(та,х) = f/7i(/(y(Ta, х))) * О, 3А> * 0е 7;*<у:	х0) = 0 л р0£(та,х) = 0.
Тогда в точке у(та, х) справедливо равенство
I adgf, /, g | y(ra, х) = 0,
где ad f = g— - f— — коммутатор векторных полейДх) и g(x). дх дх
Для случая аналитических полей справедлива следующая теорема, г
Теорема 2. Пусть / (х), g(x) £ Сю и выполнены условия теоремы 1.
Тогда либо существует целое четное и > 1 такое, что в точке у(та, х) выполнены соотношения
I adgf^ f, g I УОа» X) = °’ Vk< П’
I ad'gf, f, g | у(та, x) Ф 0, либо
\adksf,f, g|T(T„ x)*0, Wt = l,2,...
Из теорем 1 и 2 вытекает правило поиска граничных векторов конуса допустимых направлений на базе. Аналогично процедуре поиска глобального экстремума функции необходимо выделить с помощью этих теорем локальные граничные векторы, а также изучить поведение векторов £>(т,х), т -> ±оо, и затем выделить сравнением глобальные граничные векторы.
Теорема 3. Пусть траектории поля g(x) замкнуты и для V? существует целое нечетное и > 1 (возможно, зависящее от х) такое, что:
\adkgf, f, g|y(Ta, х) = 0, Vk<n,
\adgf, f, g\y(ra, х)*0, Vr.
Тогда у УДС (6.6.1) существует область полной управляемости, содержащая некоторую 8-трубку траектории у(т,х).
Геометрический смысл этой теоремы заключается в том, что при выполнении ее условий конус допустимых направлений УДС (6.6.2) в точке х совпадает со всем касательным пространством к базе. Поэтому локально достижима некоторая окрестность точки х на базе с. Отсюда следует существование s-трубки траектории у(т,х), принадлежащей области полной управляемости.
283
В силу компактности траекторий поля g(x) конус допустимых направлений в некоторой точке х может либо совпадать со всем До, либо быть замкнутым, поэтому альтернативой теореме 3 для замкнутых траекторий поля является теорема 4.
Теорема 4. Пусть траектории поля g(x) замкнуты и пусть конус допустимых направлений в точке х не совпадает с касательным пространством к базе. Тогда конус замкнут, т.е. существуют моменты времени такие, что векторы £(та, х) - dTt( f(y(xa, х))) являются граничными векторами конуса допустимых направлений УДС (6.6.2) на базе, причем выполнено равенство
I adsf, f, g | у(та, x) = 0.
В терминах гамильтониана УДС (6.6.2) теорема 3 формулируется следующим образом.
Теорема 5. Пусть выполнены условия теоремы 3. Тогда на базе существует окрестность точки х0, являющаяся областью нестесненных движений, т.е. Яа(/?0,х0) > О, Х/р с.
В заключение отметим, что случаи, когда УДС допускает построение достаточно хорошего расслоения фазового пространства, весьма редки. Тем не менее дифференциально-геометрический анализ такого рода может быть полезен для декомпозиции систем специальных классов, например, билинейных, когда фазовое пространство удается разбить на хорошо расслаиваемые области, указав затем правила перехода между ними.
Рис. 6.6.1
7.	МНОГОМЕРНЫЕ УПРАВЛЯЕМЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ СИСТЕМЫ
7.1	ОПИСАНИЕ (/77, /7)-УДС
Широкий класс систем с распределенными параметрами (СРП) описывается системой п уравнений с частными производными первого порядка относительно п неизвестных действительнозначных функций от т независимых действительных переменных следующего вида, которую будем называть системой в нормальной форме и обозначать (т, л)-УДС:
= P(x,Q,u), а = 1.....т; ₽ = л, (7.1.1)
дх
где независимая переменная х = (х1 ,...,хт) g Dm (х) с /?"'(х); Dm (х) — rn-мерная область изменения независимой переменной х в m-мерном евклидовом пространстве Rm(x) (здесь и далее в скобках иногда будем ставить символ той переменной, для которой эта область или пространство служит областью значений. Например, Rn(Q) означает обычное и-мерное линейное евклидово пространство Rn, в котором величина Q принимает свои значения); зависимая переменная Q - (Q1, ..., Qn g Rfl (g), Q = Q(x), — неизвестная вектор-функция; и — параметр, принимающий свои значения из данного непустого множества U cz R’(u), которое, возможно, зависит от пары (х, Q); f$(x,Q,u), — заданные действительнозначные функции своих аргументов (x,Q,u) g Dm(x)xRn(<2)xU; Rm(х), R"(Q); Rr (и) — евклидовы пространства соответственно размерностей т, п, г.
Параметр и будем называть допустимым управляющим параметром, или допустимым параметром управления. Этот параметр в (7.1.1) можно рассматривать как функцию от независимой переменной х:
и = и(х), х € Dw(x), и g и.	(7.1.2)
Наряду с (7.1.2) можно рассматривать и более общую зависимость
и = и(х, Q), х е Dm, Q G А", и g U.	(7.1.3)
Функции (7.1.2) и (7.1.3) назовем допустимым управлением. Для т = 1(1, л)-УДС будем называть проще: 1-УДС; она описывается ОДУ.
285
Ясно, что при каждом конкретном выборе допустимого управления — (7.1.2) или (7.1.3) — система (7.1.1) превращается в определенную систему уравнений с частными производными, записанную в нормальной форме, относительно п неизвестных действительнозначных функций <2Р =	— > *m), Р = 1, и, от п независимых переменных х1, ..., У"
или просто точки х е D,n. Пусть заданы какое-то допустимое управление, скажем, типа (7.1.3)
U = и(х, <200), х g Dm(x), Q(x) е Rn; и g U(x, Q(x))
и функция Q = Q(x), которые при подстановке в уравнение (7.1.1) превращают его в тождество по х g Dm. Такую пару (Q(x), u(xj) назовем допустимым решением (т, «)-УДС вида (7.1.1). Решением (7.1.1) также будем называть просто функцию (вектор-функцию) Q = Q(x), конечно, при каком-то допустимом управлении и = и(х), если пара (Q(x), и(х)) допустима.
В тексте, иногда без оговорок или ссылок на соответствующие теоремы, будет предполагаться существование или единственность соответствующих решений (7.1.1).
Систему (7.1.1) коротко запишем в векторно-матричной форме Q' = Л-*, <2, и), где
<2 =	f = /(х,е,«) = (Д (x,Q,U)) = (Д).
СХЛ> \ С/Л у
Решение Q = Q(x) как функцию, определенную на Dm, будем называть глобальным состоянием (тп, п)-УДС. С другой стороны, значение функции Q = Q(x) в данной точке х е Dm будем называть локальным состоянием (т, ч)-УДС в данной точке х. Таким образом, глобальное состояние (т, и)-УДС — это совокупность (объединение) всех ее локальных состояний (по всем х е Dm(x)).
На первый взгляд, кажется странным такое разделение понятия состояние данной системы. Однако стоит подчеркнуть, что понятие состояния является одним из самых фундаментальных понятий почти всей науки вообще и, возможно, наиболее сложным и тонким. Как показывает опыт, даже специалисты мало задумывались над вопросом, как “правильнее”, например, говорить — поле температуры или поле температур (т. е. нужно ли употреблять в этом термине единственное или множественное число). Конечно, тот и другой термины правильные, однако они соответствуют разным подходам, разным способам описания СРП, в частности сплошных сред. Термин, где употребляется единственное число, соответствует эйлеровскому подходу, а термин во
286
множественном числе — лагранжеву способу описания состояний в сплошной среде. Можно также сказать, что эйлеров подход сродни использованию методов функционального анализа и представлению состояний в бесконечномерных пространствах. Собственно теория управления СРП почти с самого начала и до наших дней в основном использовала подход и аппарат функционального анализа, где если и используется, то геометрия бесконечномерных пространств. В развиваемом в данной книге подходе мы встаем скорее на ту точку зрения, где используется геометрия существенно конечномерного пространства размерностей порядков т, п, т + п.
7.2.	ГЕОМЕТРИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ РЕШЕНИЯ
Будем рассматривать (т + и)-мерное евклидово пространство Rm(x) х х Rn(Q) = Rm+n(x, Q) = Rm+n(y), где у = (х, Q). В Rm+"(y) введем область У(х) х Rn(Q) = 27”+"(х, Q) = ZZ,+n(y) е R”"n(y) и декартову прямолинейную и прямоугольную систему координат — ортонорм ированный базис так, что точки х, Q и у будут иметь соответствующие координаты:
х = (х',...,хт) = (ха), а = 1,..., т\
е=(е',-.ел)=(е1'). у=(/.-, г*0)=
= (х1,..., хт ,Ql,..., Q") = (уу), У = 1>—, т + п> уу=ху
при у =	уу = Qr~m, у = т + 1,..., т + п.
Тогда очевидно, что локальное состояние (т, и)-УДС характеризуется точкой у е Dm"r;(y), где у = (х, Q), которую можно назвать изображающей точкой. Глобальное состояние (т, и)-УДС будем характеризовать m-мерной (ориентированной) поверхностью У в D”+"(y), которая в выбранной системе координат описывается уравнениями
или в векторной форме Q = Q(x).
Чтобы сохранить преемственность терминологии со случаем т = 1, будем также глобальное состояние называть т-траекторией, или просто траекторией (т, л)-УДС.
Пусть У — некоторая m-траектория. В каждой точке у е У (т.е. в каждом локальном состоянии) будем рассматривать касательное пространство к поверхности У (обозначим ДУ), представляющее собой просто касательную w-мерную плоскость к поверхности У в ее точке у. Касательное пространство ДУ, очевидно, является m-мерным линейным подпространством касательного пространства ДО'^'Д’). Введем помимо матрицы Дх, Q, и) матрицу F, dimF = (т + п) х т\
287
1	0...	о
О	1...	о
где Е — единичная матрица, у = 1, ..., т + л; сс = 1, ..., т. Обозначим уа, а = 1, ..., т, соответствующие вектор-столбцы матрицы F. Эти векторы в силу (7.2.1) всегда линейно независимы и каждый из них будет касательным вектором к поверхности У в точке у = (х, Q(x)), т.е. va е Т^У, а = q, т.
В терминах новой переменной у, рассматриваемой как функция от х е EF(x), уравнения (7.1.1) с учетом (7.2.1) принимают вид:
^ = Fj(y,M), дха
сс = 1,..., т; у = 1,..., т + гг,
(7.2.2)
или в векторно-матричном виде:
У' = — =	и).
ох.
(7.2.3)
Отсюда, в частности, va
Г 6yY > дха J
т.е. va — (т + л)-мерный вектор
с компонентами ду11 дха, у = 1,..., т + п, при каждом фиксированном a = 1,
Запишем условия интегрируемости системы (7.1.1) при допустимом
управлении:
д ( dQ* дх' < дха )
д Г ggH дха ч дх1 J
a < i = 1,..., т\ Р = 1,..., п.
(7.2.4)
Теперь, с учетом (7.1.1)'вычислим левую часть в (7.2.4):
^Д(х,е,и(л,е))=^.+<	=
=	f)+^L f>
dx* 8Qj Ji du dx* du ' dQj ’
a,i = 1,..., m; P = 1,..., n,	(7.2.5)
где суммирование проведено noj: = 1, ..., п .. Здесь и далее принято соглашение о суммировании по парно входящим индексам (один —
288
верхний, другой — нижний), как в тензорном исчислении. Аналогично вычислим правую часть в (7.2.4). Для этого надо в (7.2.5) поменять местами индексы i и а.
^-Д(х,е.М(х,е))=<+< f>+SL ™ дха J‘ *	*	QQJ J“ Su Sxa
rJ
ч--— /У --cc, i = 1,..., т;
ди Ja dOJ
и.
(7.2.6)
Для интегрируемости (7.1.1) нужно, чтобы последнее выражение в (7.2.5) было тождественно (по х и Q) равно правой части в (7.2.6) при данном допустимом и(х, Q) и при каждом значении £ = 1, ..., п, i,j = = 1, ..., т. Итак, получаем условия интегрируемости (7.1.1):
ад , ЗД < /, ад , ад f l ди _ дх' dQJ ' ди дх1 ди ' dQj
гр	гр ,, ад ди ад ди
дха dQj а	ди дха	ди а dQj
Предположим теперь, что допустимое управление и(х, Q), удовлетворяющее (7.2.7), неизвестно. Тогда (7.2.7) можно рассматривать как систему квазилинейных уравнений с частными производными первого порядка для неизвестной функции и(х, Q). Итак, мы вывели уравнение, которое может служить для отыскания допустимого управления, удовлетворяющего условиям интегрируемости.
7.3.	ПОНЯТИЕ /77-ВЕКТОРА
Назовем ти-вектором величину, которую обозначим Ут (причем индекс т будем иногда опускать); она, по определению, представляет собой упорядоченный набор т обычных (?л+н)-мерных векторов ..., vm из Rm+n. Эти векторы назовем составляющими w-вектора. Поэтому т-вектор будем еще обозначать в более явном виде: v, a...avot. Таким образом, имеем
И = V. A...AV.	(7.3.1)
Заметим, что при т = 1 вектор V{ — обычный вектор. Определим понятие равенства двух /«-векторов.
Два /л-вектора называются равными, если одновременно выполнены следующие три условия: объемы параллелепипедов, натянутых на соответственно составляющие их векторы, равны между собой; линейные оболочки составляющих их векторов совпадают; составляющие их
10. А.В. Бабичев
289
векторы имеют одинаковую ориентацию [356, 358]. Координатной формой представления ///-вектора V (7.3.1) назовем прямоугольную матрицу размера (т + /г) х т вида (у^ ), ос = 1,..., т\ у = 1,..., т + п, где
— координаты вектора та, а = 1, ..., т, в некотором базисе. Евклидовой нормой \Vm\ вектора Vm назовем абсолютное значение объема параллелепипеда, натянутого на его составляющие. Причем можно показать, что в орзоиормированном базисе
1/2
l^l=7det(vi’v/Vi,.,«

(7.3.2)
где подкоренное выражение — определитель Грама составляющих векторов; М с индексами — соответствующий минор матрицы (v*).
Определим произведение ХЕ, где X — действительное число. По определению, если V = v} л...лги, то XE = (X1v1) л... a(Xwvw),
X = X1...Xm.	(7.3.3)
В этом определении есть неоднозначность в задании чисел Xj... \п, которые подчинены лишь ограничению (7.3.3). Но эта неоднозначность имеет свою положительную сторону, так как доставляет соответствующую свободу в выборе X! ... Х^. Эта свобода будет нами использована.
Приведем понятие скалярного произведения т-векторов V =v1a...avz„ и W = w, л... a wm, которое, по определению, есть число VW = det(vz, иу), i,J = 1, ..., т, где (v„ иу) — обычное скалярное произведение 1-векторов. Отсюда, в частности, |Г| = 7Ё^, где Г2 — скалярный квадрат /71-вектора К
7.4.	УДС КАК /ттВЕКТОРНОЕ ВКЛЮЧЕНИЕ
Понятие /^-вектора дает возможность толковать основное уравне-
ние (7.2.3), эквивалентное (7.1.1), для (т, и)-УДС как равенство двух
тя-векторов в левой и правой частях этого уравнения. Действительно, в
этом случае уравнение (/и, л)-УДС принимает вид V = F(x, Q, и) или
Г = F(y, и), где V и F—это m-векторы, причем
т, у = 1,..., т + и,
(7-4.1)
F = F{ л...лРт.
(7 4.2)
290
Такое толкование (хи, «)-УДС сохраняет преемственность с 1-УДС, которые описываются ОДУ в нормальной форме и представляются обычными векторами (т = 1).
Когда управляющий параметр и “пробегает” все множество U своих допустимых значений при каждом фиксированном у = (х, Q) е Dw+n(y), то в силу (7.2.3) у' = ду/дх “пробегает” некоторое подмножество 7(х, Q) = Ку) множества всех матриц размера (т + п) х т, которое обозначим {ду/дх}, т.е. 1(у) а {<?у/6х}. Множество Ку) назовем индикаторным множеством (т, «)-УДС или просто индикатрисой. Оно может быть записано в виде Ку) = F(y, U(y)),y е D(m+n\y).
В терминах индикаторного множества Ку) (т, я)-УДС может бы гь представлена в виде дифференциального включения с частными производными вида
yeD^fj).	(7.4.3)
дх
Заметим, что обратный переход от включения (7.4.3) к (7.1.1) или (7.2.3), вообще говоря, неоднозначен. Однако эта неоднозначность, как правило, несущественна для многих задач управления. Аналогично истолковывая левую и правую части (7.2.3) как w-вектора, (7.2.3) и, следовательно, (7.1.1) можно представить как //(-векторное включение V е /(у), у е 1Уп+п(у), где 1(у) также будем называть индикаторным множеством (т, л)-УДС, но теперь это множество всех допустимых т-векторов, т.е. некоторое подмножество в множестве {К} всех т-векторов V. Таким образом, (т, и)-УДС также задается полем индикаторных множес гв Ку) для m-векторов в дУ^Ку)- Оставим одинаковые обозначения Ку) для индикаторных множеств обоих типов, так как из контекста будет ясно, о матричном или /и-векторном индикаторном множестве идет речь.
С полем индикаторных множеств Ку) свяжем другое поле, которое играет важную роль в геометрическом подходе к (т, и)-УДС. Поле конусов допустимых направлений m-векторов, которое обозначим К(у), у е 1Уп+п(у), по определению, задается равенством
K(y) = {XV:X>0, Vel(y)}, y&D,n+n(y).
Отсюда следует вывод: m-вектор V будет допустимым (в данной точке у) тогда и только тогда, когда найдутся число Л, > 0 и другой rn-вектор W е К(у) такие, что вектор V + X.W допустим.
10*
291
Как видно из определения /и-вектора с составляющими в виде обычных (ли-1-л)-мерных векторов, он определяется (т + п)т числами, элементами матрицы (7.4.1) или (7.4.2), которые будем называть координатами т-вектора. Предположим, чго индикаторное множество /(у) непусто, телесно при каждом у е Dm+n(y) и описывается неравенством
L(y,V)<0,	(7.4.4)
а его граница описывается равенством
Z(y,F) = 0,	(7.4.5)
где L(y, V) — некоторая вещественная функция от всех своих числовых аргументов, т.е. координат точки у и m-вектора К
7.5.	ОПЕРАЦИЯ ОДНОРОДНИЗАЦИИ
Рассмотрим операцию однороднизации функции в (7.4.5), смысл которой состоит в том, чтобы преобразовать уравнение (7.4.5) в эквивалентное уравнение вида
ZoCv, У) = 1,	(7-5.1)
где L0(y, V) — положительно однородная первой степени функция по аргументу V при каждом фиксированном у. Итак, будем рассматривать у как параметр, а (7.4.5) запишем в эквивалентном виде:
Z(b|4^/|p) = 0,	(7.5.2)
где | И] — положительное число, равное норме | К] тя-вектора V.
Пусть уравнение (7.5 2) допускает выражение величины |Р] через у и Р7]К], т.е. существует функция Z0(y, V/\ К]), положительно однородная нулевой степени по аргументу К, и такая, что
И = /„(гЛ/И)-	(7-5.3)
Конечно, такое разрешение относительно |Р], вообще говоря, может быть неоднозначным. Но мы выберем ту ветвь Zo, которая дает наибольшее |Р]. Из (7.5.3) получаем нужное нам представление вида (7.5.1): Zo(>-, V) = \V\H0(y,V/\V\).
Будем предполагать, что Lo обладает теми же условиями гладкости, что и L, а внутренность 1(g) удовлетворяет условию L0(y, F) < 1. Функцию Lq будем называть однородным лагранжианом (т, «)-УДС. Смысл этого термина будет объяснен в подразд. 7.8.
292
7.6.	ПРЕДСТАВЛЕНИЕ (/77, /?)-УДС В ВИДЕ СИСТЕМЫ УРАВНЕНИЙ ПФАФФА (СУП)
Напомним [93, 270], что пфаффова система (ПС) имеет вид
со₽ (dy) = <рР (у) dy7 = 0,	(7.6.1)
где у = (у1, ...,угп+п') е 7?га+и; co₽(dy) — линейная дифференциальная 1-форма; фР(у) — коэффициенты линейной формы, заданные функции от аргумента у, у = 1, ..., т + п, fl = 1, п. Предполагается, что в некоторой окрестности точки у е Rn+n имеем
гапкфО) = п,	(7.6.2)
где ф(у) — матрица, сНтф(у) = п х (т + п), с элементами срР (у).
Условие (7.6.2) позволяет разрешить систему (7.6.1), рассматриваемую как система п линейных алгебраических уравнений относительно величин dQ^ = dym+₽, Р = 1, ..., п, если представить у = (х, Q), где х = = (л1, ...,хт) - (л“), а = 1, ..., т, Q = (Q1, ..., Qn) = (g₽), р = 1, ..., п. Тогда получим
dg|i-./a(1(x,e)d*a=0,	(7.6.3)
где	— известные функции. Легко видеть, что (т, и)-УДС
(7.1.1)	имеет эквивалентное представление в виде (7.6.3):
= о.	(7.6.4)
Конечно, («?, л)-УДС с самого начала можно было бы задать в виде, аналогичном (7.5.1):
фР(у,г/)Фт=0,	(7.6.5)
где коэффициенты линейной формы зависят от управляющего параметра и е U.
Чтобы очень кратко объяснить, что нужно понимать под решением ПС (7.6.1), лучше всего обратиться к геометрическому рассмотрению. Для этого в каждом Р-м из п уравнений (7.6.1) коэффициенты (pf ,...,срР+п =фР, Р = 1, ..., п, будем толковать как (т + «)-мерный вектор (с началом в точке у е Rm+n) в Rm+n. В силу (7.6.2) все эти п векторов линейно независимы и, следовательно, определяют «-мерное линейное (векторное) подпространство Rn в Rm+n. Поэтому никакой поверхности размерности выше т в Rm+n через точку у не может проходить так, чтобы m-мерная касательная плоскость к этой поверхности в
293
точке у была бы ортогональна всем п линейно независимым векторам Ф₽(у), Р = 1, •> w- Таким образом, самое большое, что может удовлетворять условию ортогональности, — это поверхность размерности т. Конечно, могут существовать и поверхности размерности меньшей, чем т. Поверхность размерности т = 1, т.е. некоторая линия, всегда может удовлетворять условию ортогональности. Однако для целей управления (т, п")-УДС нас будет интересовать существование поверхностей максимально возможной размерности, в точности равной т. Если такая /«-мерная поверхность существует, хотя бы в окрестности точки у е то (7.6.1) называется вполне интегрируемой. Такая /«-мерная поверхность будет описываться уравнениями Qp = = £?р(*)> Р =	а функции Qp(x), Р = 1, ..., 72, будут решением
исходной системы (7.1.1).
Как упоминалось выше, (т, «)-УДС можно с самого начала задать в виде ПС (7.6.5). При фиксированном допустимом управлении и = и(х) система (7.6.5) примет вид
Ф?(Ь«(Т))4УТ =0-	(7.6.6)
Заметим, что полезно еще рассматривать квадратную матрицу
размерностью (т + п) х (т + п) вида
Ет
0
-Еп
где Ет и Еп —
единичные квадратные матрицы размерностей т и п. Поэтому, чтобы существовала соответствующая допустимая m-траектория Q = = Q(x), необходимо и достаточно потребовать, чтобы (7.6.6) было вполне интегрируемой ПС. Это, конечно, не означает, что каждое отдельное [3-уравнение из (7.6.6) вполне интегрируемо. Более того, среди уравнений (7.6.6) может не оказаться ни одного отдельно взятого вполне интегрируемого уравнения. Однако если (7.6.6) вполне ин
тегрируемо, то это означает, что существует интегрирующая матрица Цр',(у), которая является невырожденной квадратной матрицей размерности п х п, [3, Р' = 1, ..., я, и такая, что ПС вида
Ф? (У)	= Цр-, 0>)ф?' (У, и{х)) dyY =0, Р = 1,...,72,	(7.6.7)
является ПС, эквивалентной (7.6.6). Более того, теперь каждое отдельное из 72 уравнений (7.6.7) вполне интегрируемо. Последнее означает, что существуют 72 вещественнозначных функционально независимых функций/^(у), Р = 1, ..., 72, таких, что фР(у) dyy ^tZFp(y).
294
Отсюда получаем п функционально независимых интегралов ПС (7.6.6):
Е*(у) = СР,	(7.6.8)
где Ср, Р = 1,— произвольные постоянные. Вспомним, что у = = (х, Q). Тогда (7.6.8) можно разрешить относительно п переменных Q&. В результате получим п функций = Qp(x, С),С = (с1, ..., с”), описывающих искомую /^-траекторию.
Отметим, что представление (/и, /г)-УДС в виде ПС обладает достоинством: это симметричное представление УДС в том смысле, что все переменные, зависимые и независимые, равноправны. Действительно, самый симметричный способ представления (т, п)-УДС — это задание и дифференциальных 1-форм от (т + п) переменных у = (у*) = (у1, ..., у'”4’"), Y ~ L •••> т + п‘
ttJ (у) dyy = О, 0 = 1, где управляющими параметрами служат непосредственно коэффициенты тгР
Таким образом, можно говорить о матрице л = (л^) параметров управления и матрице л(у) = (л^(у)) управлений. На элементы этой матрицы могут быть наложены ограничения л е 1(у).
7.7.	ПРЕДСТАВЛЕНИЕ (т, /7)-УДС В ВИДЕ (1, т + /7)-УДС
Если обе части (7.6.4) поделить на величину dr, где т — некоторый числовой параметр, то легко видеть, что система (7.6.4) эквивалентна следующей системе (т + п) ОДУ первого порядка:
/а (х, б, w)wa, ос = 1,..., /п; 0 = 1,и<= U, (7-7.1)
dx
где и,и можно рассматривать как новые, дополнительные управления, входящие линейным образом. Очевидно, что (7.7.1) можно рассматривать как (1, т + /г)-УДС. Более того, зная (7.7.1), можно легко построить соответствующее ему уравнение вида (7.1.1) и тем самым получить (т, «)-УДС.
Ясно также, что наименьшая размерность инвариантной поверхности Sm в D”,+n для (7.7.1), если она существует, равна т. Напомним, что инвариантной называется поверхность, с которой изображающая точ
295
ка у = (х, Q) не может сойти при любых управлениях и & U и w = (w1,..., и/") , где штрих означает транспонирование матрицы. Отсюда видно, что допустимые траектории Sm для (7.1.1) есть не что иное, как инвариантные многообразия (1, т + я)-УДС наименьшей размерности, равной т.
С уравнениями (7.7.1) естественно связывается следующая система квазилинейных уравнений с частными производными первого порядка относительно одной неизвестной числовой функции <7(х, 0:
|^ + т||уЛР(*>е^(х,0), oc = l,...,m,	(7.7.2)
оха cQv
где и(х, Q) е U — некоторое допустимое управление.
Из теории уравнений (7.7.2) известно [297, 300] что для того чтобы это уравнение определяло искомое m-мерное многообразие (поверхность Sm) для (1, т + «)-УДС (7.7.1) или, что то же самое, допустимую ///-траекторию (т, и)-УДС (7.1.1), необходимо и достаточно, чтобы система (7.7.2) была полной. В этом случае система (7.7.2) имеет ровно п функционально независимых решений (интегралов):
G\x, Q) = с®, р = 1,... , и,	(7.7.3)
где ср — произвольные постоянные, из которых путем разрешения алгебраической системы (7.7.3) относительно п переменных Qp, £ = 1, ..., п, находим п функций Qp = Qp(x, с), £ = 1, ..., п, где с = (с1, ..., с") — про
извольные постоянные, которые и задают п параметрических уравнений искомой /л-траектории ///-мерной инвариантной поверхности У", соответствующей данному допустимому управлению.
Таким образом, (7.7.2) можно рассматривать как еще одно представление (га, и)-УДС, равносильное (7.1.1).
Отметим еще, что в терминах представления (7.2.2) уравнение
QG
(7.7.2) принимает вид (у, и(у\)-- 0,
ос = 1,..., т.
Тогда условие полноты можно выразить в терминах ///-векторных полей Fa = (FJ), ос = 1, ..., т (у = 1, ..., т + п), а именно: совокупность {Уй} векторных полей должна составлять подалгебру алгебры всех векторных полей в Dm+n(y), т.е. быть замкнутой по отношению к операции коммутирования. Иными словами, операция коммутирования любых двух полей из т полей Fa должна давать поле, принадлежащее той же подалгебре {Fa}.
296
7.8.	СОБСТВЕННАЯ М-МЕТРИКА (л^МЕРА) ДЛЯ (/77, /7)-УДС
Собственной m-метрикой (т, я)-УДС (7.4.3) называется действительнозначная Функция L0(y, Гт),у е Dm+n(y), Vm е {ДД, определяемая равенством
=	Л.Г„е/(Д	(7.8.1)
[A	J
Функция L0(y, Vm) — положительно однородная первой степени функция от m-вектора Vm при каждом у. В случае т = 1 функция Lo совпадает с известной калибровочной функцией Минковского [273]. Ее смысл сос гоит в том, что она калибр} ет (измеряет) вектор И] с помощью множества /(у). Поэтому функцию Lo в (7.8.1) в общем случае можно назвать т-калибровочной функцией. Отсюда, в частности, вытекает, что функцию L0(y, Vm) можно также назвать нормой т-вектора Vm, которую будем еще обозначать ЦДЛ:
W^W-L^V^.	(7.8.2)
Очевидно, что (7.8.2) определяется 1(у) и зависит от точки у е D”' '"(у)-
Величину Д можно рассматривать как меру (около точки у), так как это объем элементарной площадки, натянутой на m-вектор Д„, построенный в точке у. Так как эта мера зависит от индикатрисы (т, я)-УДС, то Lo можно назвать собственной m-метрикой или m-мерой данной (т, и)-УДС. При т = 1 это просто известная метрика Финслера—Рашевского [270, 274]; Lo можно рассматривать как интегрант классического многомерного интегрального функционала, подлежащего минимизации. Другими словами, Lo — интегрант классической многомерной вариационной задачи, т.е. лагранжиан. Поэтому имеет смысл назвать Lo еще и лагранжианом или однородным лагранжианом (т, «)-УДС.
Заметим, что интересно рассмотреть функцию Lo как функцию от Vm или как функцию от упорядоченной совокупности т векторов Va, а = 1, ..., т, в Rm+n с точки зрения дифференциальных форм. Например, если определить норму или, вернее, псевдонорму ||Дп|| не как абсолютное значение объем параллелепипеда, натянутого на т векторов Fa, а взять этот объем со знаком, который меняется при перестановке любой пары векторов из совокупности Иа (т.е. знак меняется при перемене ориентации совокупности Ea, a = 1, ..., т), то получим кососимметрическую полиоднородную функцию от т векторов Va. Такие функции в [231] названы нелинейными т-формами. По сравнению с обычными (т.е. кососимметрическими и полилинейными) формами
297
они теряют свойство линейности, а точнее, аддитивности, сохраняя лишь однородность.
С точки зрения предлагаемой нами концепции структур, связанных с (т, «)-УДС и соответствующими задачами для них, введенная выше функция Lq определяет метрическую структуру, порожденную данной (т, «)-УДС. Это позволило называть эту структуру собственной метрической структурой (т, «)-УДС, а соответствующую /«-метрику (rn-меру) — собственной ///-метрикой (т-мерой) для (т, «)-УДС. Как увидим в подразд. 7.9, эта структура органически связана с данной (т, п)-УДС, и, более того, отождествляется с задачей, которая названа нами задачей собственного оптимального управления для данной (т, п)-УДС. Задание функции L0(y, V) полностью описывает (т, «)-УДС.
7.9.	ЗАДАЧИ УПРАВЛЯЕМОСТИ, ФИНИТНОГО УПРАВЛЕНИЯ
И СОБСТВЕННОГО ОПТИМАЛЬНОГО УПРАВЛЕНИЯ ДЛЯ (/77, /7)-УДС
Пусть Г — некоторое множество в Rm+n(x, Q). Назовем его множеством управляемости—достижимости, или просто множеством управляемости для (т, «)-УДС (7.1.1), если существует допустимая т-траектория Sm для (7.1.1) такая, что Г cz Sm. Задача управляемости (т, «)-УДС относительно данного множества Г состоит в том, чтобы ответить на вопрос, является ли оно множеством управляемости для этой (т, «)-УДС или нет.
Возникает задача, которая называется задачей финитного управления и которая состоит в том, чтобы для любого данного Г описать все допустимые /«-траектории данной (т, «)-УДС, для которых Г — множество управляемости. Роль множества Г может играть контур в Rm+n размерности (х, Q), меньшей т. Например, для т = 1 т.е. для (1, «)-УДС, роль контура Г часто играют две точки: начальная и конечная точки 1-траектории. Задачу финитного управления для этого случая (т = 1) решает ФП УДС.
Перейдем к задаче собственного оптимального управления для (т, «)-УДС. Пусть теперь Г — какой-нибудь замкнутый (простой, без самопересечений) контур размерности (т - 1) в Dm+n(y). Пусть Г — множество управляемости (т, «)-УДС, заданной своей локальной т-метрикой (/«-мерой) L0(y, V). Это означает следующее. Во-первых, существует (по крайней мере одна) допустимая «/-мерная поверхность S™ данной (т, «)-УДС, содержащая контур Г, т.е. Г cz Sm с D’n+n(y). Во-вторых, если У" задана своим параметрическим уравнением у = у(£), | е D "'(£,), у е Dm+n(y), где D"'(O cz Rm+n(Q — область изменения неза
298
висимого параметра £, то в каждой точке у е Sm определен /«-вектор V = V] л...лут, где va =ду7(S,)/S£,a, a = 1, т. Следовательно, определен интеграл
А(5"”,Г) = J L0(y(£)> И©)^.	(7.9.1)
D"' (4)
Отсюда видно, что сама по себе («?, и)-УДС порождает задачу оптимального управления для нее самой. Эту задачу назовем задачей собственного оптимального управления, для данной (ти, «)-УДС. Эта задача относительно данного контура Г состоит в том, чтобы найти
г(Г) = {inf l(Sm, Г) : dSm = Г и Sm — допустимая}. (7.9.2)
Более того, требуется выяснить существование допустимой Sq , на которой достигается нижняя грань в (7.9.2), т.е. сообщается минимум функционалу (7.9.1), и найти ее. Величину г(Г) можно назвать емкостью контура Г. В частности, если положить Lo в соответствии с формулой (7.3.2), то функционал (7.9.1) имеет смысл обычной «/-мерной площади поверхности S”, натянутой на контур Г. При этом задача (7.9.2) становится задачей о поиске поверхности S™, dS™ = Г, наименьшей площади. Ясно, что при т = 2, п=1 (7.9.2) означает классическую задачу Плато о нахождении двумерной поверхности минимальной площади, натянутой на одномерный замкнутый контур, расположенный в А3. Такие поверхности коротко называются минимальными поверхностями [118]. Отметим, что, в частности, при т - 1 величина г(Г) — расстояние в Rl+n(y) между начальной и конечной точками. Величину ДГ) можно также назвать глобальной ///-метрикой или глобальной т-мерой контура Г для данной (т, «)-УДС. В отличие от нее /«-метрика (т-мера), введенная в подразд. 7.8 и определяемая функцией То, может быть названа локальной (или инфинитезимальной) ///-метрикой или «/-мерой, а также плотностью ///-метрики или плотностью /«-меры.
Заметим еще, что в силу положительной однородности Lo в (7.9.1) можно положить LQ(y, V) = 1, т.е. V должен принадлежать “сфере” единичного радиуса в пространстве ///-векторов {V} при каждом у. Тогда функционал (7.9.1) есть не что иное, как ///-мерная площадь /«-мерной области Т)т(^), расположенной в параметрическом пространстве параметра £ е Rm(Q-
Имеет смысл площадь области /У'(О назвать собственной площадью (т, «)-УДС, так как при т = 1 эта площадь превращается в собственное время в точном соответствии со значением этого понятия в физической теории относительности [24]. Таким образом, задача собст
299
венного оптимального управления для (т, и)-УДС геометрически трактуется как задача нахождения наименьшей собственной площади. Для т = 1 это просто задача быстродействия для 1-УДС или задача о кратчайшем пути между двумя заданными точками в собственной метрике данной УДС.
7.10.	ПОТОКОВОЕ ПРЕДСТАВЛЕНИЕ ДЛЯ 1-УДС И ПРИНЦИП ЭКСТРЕМАЛЬНЫХ ТОКОВ
Если дано векторное поле Р е Rk и вычисляется интеграл fFdzz,	(7.10.1)
где S— (к- 1)-мерная поверхность в Rk, ап — нормаль к этой поверхности, то вектор Р будем называть потоком (некоторой скалярной субстанции, например, тепла или массы), а сам интеграл (7.10.1) — током (данной субстанции) через поверхность 5. В этом смысле поток (субстанции) становится плотностью тока (данной субстанции).
Рассмотрим сначала следующую классическую вариационную задачу, которую будем трактовать как принцип наименьшего действия (ПНД) для механической системы с одной степенью свободы, заданной своим лагранжианом L(t,q,q'\q' - dq/dt,q е Rl,q' e Rl,t g Rl. Пусть движение этой системы описывается функцией
= t0 <t<t*, qM = q0, q(t*) = q*.	(7.10.2)
Это движение будем представлять кривой в плоскости (/, q) g R2, соединяющей точку (/0, #0) с (t*,q*). Эту кривую обозначим у(Г0, q0; t„, q*) или короче — просто у. В соответствии с принципом наименьшего действия на истинном движении функци онал действия
А- \L(t, q, q')dt	(7.10.3)
?0 достигает экстремального значения среди всех гладких кривых (7.10.2), где точки (r0, qo) и (/*,<?*) фиксированы (не варьируются). Пусть далее существует гамильтониан Н как преобразование Лежандра функции L по аргументу q' при каждом фиксированном (t, q):
H(t, q, p) = max q, q') + pq').	(7.10.4)
(i
dH
Максимум в (7.10.4) достигается при q' =--(t,q,p).
др
300
В этих терминах (7.10.3) примет вид
A = j \pq'-H(t,q,p)]dt = j(pdq-Hdl). (7.10.5) г0	Y
Представим (7.10.5) в виде
А = J (p,FF)(dq, -dz) = f Р dn.	(7.10.6)
Y	Y
Выражение (7.10.6) можно толковать как ток векторного поля потока Р = (Н, р) g R2 через линию у е R2, где п — нормаль к у в точке (Z, q) е у; dn = (dq, -dz).
Таким образом, ПНД (7.10.3) для механической системы с одной степенью свободы можно истолковать как принцип экстремального тока Р через кривую у е R2, представляющую собой движение или 1-траекзорию данной системы.
Обозначим Р = (рь р2), P\ = р, р2 = Н. Тогда (7.10.6) примет вид А = f (Pi Pi) d/7, где вектор (pt, р2) = (р, р2~) = Р подчинен условию
Y
p2=H(t,q,p).	(7.10.7)
В [285] условие (7.10.7) называется уравнением энергии, но в свете используемой здесь терминологии это условие можно назвать уравнением потоков. Условие (7.10.7) можно толковать геометрически: конец радиус-вектора Р = (р\,Рг) в “потоковом” пространстве Ре А2 при каждой фиксированной точке (Z, q) пространства состояний системы R2 должен принадлежать кривой, описываемой уравнением (7.10.7). Эту кривую можно назвать фигуратрисой [274]. На самом деле (7.10.7) описывает целое поле фигуратрис на пространстве состояний, (Z, q) е R2.
Итак, принцип наименьшего действия получает следующее “потоковое” толкование: истинное движение данной системы будет представляться той кривой в пространстве состояний (с фиксированными концами), через которую проходит экстремальный ток векторного поля потока, подчиненного уравнению потока (7.10.7). Такое толкование принципа наименьшего действия назовем принципом экстремального тока.
Варьируя кривую у при фиксированных ее концах и поток Р при условии (7.10.7), получаем известную гамильтонову систему
?' = ^ (Л Я, Р),	(7-Ю.8)
p' = -—(t,q,p).	(7.10.9)
301
Обратим внимание на то, что уравнение (7.10.9) можно теперь, в рамках данного потокового представления, истолковать как уравнение сохранения некоторой скалярной субстанции, ибо (7.10.9) можно представить в виде
div Р = div (/?], р2) = div (р>,Н) = — +	= 0.	(7.10.10)
dt dq
Вместе с этим уравнение (7.10.8) можно истолковать как условие интегрируемости.
Итак, уравнения Гамильтона (7.10.8), (7.10.9) истолковываются как система двух уравнений: первое — условие интегрируемости, второе — условие сохраняемости. Аналогичное рассуждение можно провести и для системы с любым конечным числом к степеней свободы и дать аналогичное “потоковое толкование”. Действительно, пусть
^=(^ь ...,^) G Rk,p = (pi, ...,Рк) е Rk,pk+l = H(t,q,p), (/, q^ е R\i = 1, ... , Pf = (ph H) = (phpk+l) e R2.
Кривую у, изображающую траекторию механической системы в пространстве состояний у е (/, q) е Rk+l, спроектируем на двумерное подпространство (z, qt) е R2, i = 1, ..., к. Поток Pt = (ph Н). соответствующий (Z, qt) е R2, назовем i-м парциальным потоком. Таким образом, система 2Л-го порядка уравнений Гамильтона может быть представлена в виде системы
?'= —(Л<ЬА,<7>Р)>	(7.10.11)
Ф
Р\ = ~~ (t,qt, pifq,p), i = l,...,k,	(7.10.12)
Ф
где	Р =	состоящей
из к пар уравнений (7.10.11), (7.10.12). Каждое z-e уравнение (7.10.12) можег истолковываться как уравнение сохранения, ибо оно может представляться в виде, аналогичном (7.10.10). Соответственно (7 10.11) также истолковываются как условия интегрируемости, т.е. условия существования гладкой кривой в каждой z-й плоскости (Z, q) & R2.
Важно то, что эти довольно простые соображения “потокового представления”, приводящие к истолкованию условий оптимальности, т.е. уравнений Гамильтона как совокупности уравнений сохранения и интегрируемости, могут быть обобщены, как увидим в подразд. 7.15, на класс СРП (систем с бесконечным числом степеней свободы, сплошных сред и полей), которые представляются как (т, я)-УДС.
302
7.11.	ПОТОКОВОЕ ПРЕДСТАВЛЕНИЕ ДЛЯ (т,
Распространим рассмотренное в подразд. 7.10 потоковое представление на (ти, «)-УДС, исходя из принципа наименьшего действия для процесса движения некоторой скалярной субстанции в некоторой сплошной среде: требуется найти вектор-функцию Q = Qq(x), х е ЕР'{х), Q е Rn, возможно, принимающую заданное значение на границе dDm(x), и такую, что функционал
А = J L\х, Q, |dx, dx = dx'... dx"1	(7.11.1)
D'"(x) \ dx J
на этой функции принимает экстремальное значение. Обозначим Sm поверхность в Rm+l, описываемую уравнением Q = Q(x), х е Dm(x).
Введем матрицу, которую назовем потоком данной многокомпонентной субстанции, в соответствии с формулой
\ дх
дх J
Определим функцию Н как преобразование Лежандра функции L:
Н(х, Q, Р) = max ~ll х, Q,-| + Р—
[L \ йх) дх ( д.Х J
(7.11.2)
dQ дН .	„
причем максимум в (7.11.2) достигается при — =----(х, Q, Р), где Р =
дх дР
= (Р‘, ...,Рт) е R.
В этих переменных (7.11.1) примет вид
А = f P^--H(x,Q,P) dx.
£>"<(Л)[_ SX
Перепишем последнее равенство в виде
А =
f (ЛЯ),
9Q дх
-1 dx= JF dw, 7	S'"
где «-нормаль к поверхности Sm, Р = (Р,Н}- Тогда величина А приобретает смысл тока векторного поля потока через Sm. Таким образом, исходная вариационная задача (7.11.1) при п = 1 сводится к задаче о минимизации тока:
303
A=:fPdn	(7.11.3)
S’"
при условии
Ртлх = H(x,Q,P).	(7.11.4)
Уравнение (7.11.4) назовем уравнением потока. Это аналог уравнения энергии [285]. Его геометрический смысл состоит в том, что конец (т + 1)-мерного радиус-вектора потока Р должен лежать нат-мерной поверхности в Rm+X, описываемой уравнением (7.11.4). Эту поверхность назовем фигуратрисой.
Итак, принцип экстремального действия (7.11.1) для СРП при п = 1 эквивалентен принципу экстремального тока (7.11.3) при условии (7.11.4).
Варьируя поверхность Sm (при фиксированном SS’'") и поток Р при условии (7.11.4), приходим к замкнутой системе уравнений:
(7.11.5) ох дР
divue)P=0 или divxP + ^(x,Q,P) = 0, Р=(Р,Н)- (7.11.6)
Уравнение (7.11.5) — условие интегрируемости, т.е. условие существовав ия функции Q = Q(x), а уравнение (7.11.6) — условие сохранения (субстанции). При этом первое равенство (7.11.6) говорит о том, что в (т + 1)-мерной области Z)"’(x) х Rl(Q), в которой определено поле потока Р и в которой расположена поверхность Sm, не имеется “внешних” источников. Второе уравнение в (7.11.6) равносильное первому в (7.11.6), говорит о том, что в m-мерной области Dm(x), в которой определен поток Р скалярной субстанции, имеется источник этой дН субстанции с плотностью Q->
При т = 3, п = 1 из (7.11.5) и (7.11.6) следует:
rot^(x,e,/’) = 0,	(7.11.7)
&nxP = -—Ax,Q,P\	(7.11.8)
3Q
Таким образом, для решения уравнений (7.11.5), (7.11.6) с заданной функцией Н требуется найти векторное поле Р(х) и скалярную функ
304
цию Q(x), совместно удовлетворяющие системе (7.11.7), (7.11.8). Эта задача близка к классической задаче об определении векторного поля Р по заданному вихрю и расходимости.
7.12.	ОПИСАНИЕ ДОПУСТИМЫХ ЛИНИЙ ТОКА В СПЛОШНЫХ СРЕДАХ, ИХ СВЯЗЬ С ФП 1-УДС
Введенный в подразд. 7.11 потоковый формализм позволяет дать описание допустимых линий тока, которые являются интегральными кривыми векторного поля потока. Описание основано на идее отождествления физического пространства той сплошной среды (СРП), в которой имеют место потоки субстанции с пространством состояний некоторой 1-УДС (ССП).
Рассмотрим процесс распространения (теплопроводности или диффузии) некоторой скалярной субстанции (тепла или массы) в некоторой сплошной среде. Предположим, что этот процесс подчиняется следующему вариационному принципу наименьшего действия. Пусть сплошная среда занимает область Dm(x) е Р'"(х), а распределение плотности скалярной субстанции описывается функцией Q = Q(x), х е Z)"’(x), Q е R1, причем, возможно, фиксированы (не варьируются) некоторые граничные условия (например, значения функции Q(x) на границе dDm(x) области D"'(x)). Вариационный принцип состоит в том, что истинное распределение Q(x) доставляет наименьшее значение интегральному функционалу
A- \L х,dx, dx = dx'...dx"1.
(7.12.1)
QQ дх
(7.12.2)
Векторное поле потока Р(х) этой субстанции определяется формулой
V йх
Интегральные кривые векторного поля называются линиями тока этой субстанции (в теории поля аналог — силовые линии). Соотношение (7.12.2) назовем материальным соотношением данной сплошной среды, оно связывает градиенты dQI дх потенциалов Q субстанции с потоками Р этой субстанции. Будем рассматриватьр = dQIдх как управление, определенное при х е £У"(х). Когда р пробегает все свои допустимые значения, которые совпадают с Rm, поток Р соответственно пробегает множество
7(х) = —(x,Pm), хейга.
Ф
(7.12.3)
305
Это означает, что допустимые потоки описываются включением Р е 1(х), х е D”1.
Индикатрису 1(х) можно отождествить с индикатрисой некоторой 1-УДС, имеющей пространство состояний Dm(x). Таким образом, мы производим отождествление “физического” пространства ^(х), занимаемого сплошной средой, с абстрактным пространством состояний некоторой 1-УДС с индикатрисой (7.12.3). Назовем ФП этой 1-УДС фазовым портретом пиний тока (ФП ЛТ) данной СРП. ФП ЛТ несет полезную информацию о состоянии СРП. Эта информация нетривиальна для нелинейных, неоднородных и неизотропных СРП естественного или искусственного происхождения.
Таким образом, возникает мысль провести следующее отождествление:
L(x,p)^Hx(x,p),	(7.12.4)
где Нх(х,р) — гамильтониан соответствующий 1-УДС. Однако без потери информации о ФП ЛТ данной СРП, но с приобретением существенной степени свободы имеет смысл вместо (7.12.4) провести следующее отождествление:
Н(х,р) = -Рцх,р),	(7.12.5)
р(х)
где р(х) >0 — некоторая функция.
Если Н(х,р) — гамильтониан 1-УДС, то скорость 1-УДС
дН,	.	1 дЦх,р)
у = — (х,р) =	(7.12.6)
др	р(х) др
Отсюда и в силу (7.12.2) •
Р = pv	(7.12.7)
и, следовательно, р = р(х) > 0 получает смысл объемной плотности субстанции в потоке Р, а скорость v — смысл скорости субстанции в потоке Р. Но скорость v в (7.12.6) имеет также смысл скорости изображающей точки 1-УДС в ее пространстве состояний Р)т(х). Таким образом, произошло отождествление скорости субстанции в СРП и скорости изображающей точки 1-УДС.
Задание лагранжиана L и граничных условий (если они фиксированы) однозначно определяет некоторое конкретное распределение потенциала Q(x).
306
Обозначим р(х) = Z(x, р(х)), р(х) =	, Н(х, /?(х)) =	— х
дх	р (х)
х£(х, р(х)) = 1, Vx е D™.
Из (7.12.2) и (7.12.7) имеем:
v(*) = ~;,	(7.12.8)
р(х)
— .	1 dL . _.
где Р(х) = —- — (х,/?(х)).
р(х) др
Выражение (7.12.8) для v(x) можно истолковать как поле скоростей в области Dm(x) механической систем ы с гамильтонианом Н(х, р) и с уравнением энергии Н(х, р) = 1, где Q (х) — некоторое решение уравнения Гамильтона—Якоби
И х.Я-1.	(7.12.9)
I дх )
Аналогично у(х) можно истолковать как поле оптимальных скоростей 1-УДС с гамильтонианом (7.12.5). Конечно, обратное неверно: не всякое решение Q(x) уравнения (7.12.9) будет решение исходной вариационной задачи (7.12.1) для СРП (или соответствующего уравнения Эйлера—Лагранжа). Однако пусть нам известно поле скоростей v(x) механической системы с гамильтонианом (7.12.5). Тогда соответствующая плотность р(х) будет определяться только из уравнения сохранения субстанции div (p(x)v(x)) = 0. Это уже уравнение с частными производными первого порядка (а не второго, как уравнения Эйлера— Лагранжа для (7.12.1). Его решение определит в СРП некоторый поток Р(х) = p(x)v(x).
Из материальных соотношений (7.12.2) можно найти площадь
(7.12.10) дх
Интегрируя (7.12.10), определим и распределение потенциала Q(x). Отметим, что таким способом, например, можно искать фундаментальные решения в линейных задачах СРП.
В заключение еще раз подчеркнем, что индикатриса 7(х) потока Р (7.12.3) для СРП и индикатриса Ц(х) соответствующей 1-УДС, имеющая тот же фазовый портрет, могут отличаться лишь некоторым ка
307
либровочным множителем р(х) > 0, имеющим физический смысл объемной плотности субстанции I(x) = р^У^х).
7.13.	ПРИНЦИП МАКСИМУМА ОБЪЕМА (МЕРЫ) ОБЛАСТИ ДОСТИЖИМОСТИ. МНОГОМЕРНЫЙ ПРИНЦИП ОПТИМАЛЬНОСТИ (МПО)
Рассмотрим автономную 1-УДС, описываемую включением v = х g I(x),xeR11, и задачу быстродействия на отрезке [О, Т\, Т > О для нее. Пусть ее изображающая точка при t = 0 стартует с какой-нибудь начальной точки х0 пространства состояний этой 1-УДС. Рассмотрим множество достижимости D(t, х0), которое обозначим проще: D(t), t е [О, Т], в произвольный момент времени t > 0. Будем предполагать, что через каждую точку D(t) проходит одна и только одна экстремаль, а следовательно, одна и только одна оптималь. Предположим для простоты, что область D(t) имеет ту же размерность, что и размерность пространства состояний данной 1-УДС.
Тогда можно утверждать, что область D(t) имеет наибольший объем (или меру), которую обозначим p[Z)(r)], по сравнению с мерами любого другого множества М(Т) тех точек пространства состояний, в которых может побывать изображающая точка УДС на отрезке времени [0, Д при своем допустимом движении с началом х0. Действительно, для множества M(f) таких точек выполняется включение M(t) с. D(t), ибо в противном случае D(f) не была бы областью достижимости, так как существовали бы точки пространства состояний, принадлежащие M(f), но не принадлежащие D(t). Отсюда ц[7И(/)] < p[Z)(f)], что и требовалось показать.
К этому результату можно прийти и по-другому — через принцип максимума для оптимальности по быстродействию. Действительно, возьмем какую-нибудь точку x(t) оптимальной траектории. Она должна принадлежать границе dD(f) области достижимости D(f) (под границей 8D(t) понимаем совокупность тех точек пространства состояний, в которые можно попасть в оптимальном процессе в точности за время г). Предположим, что в точке x(f) е D(t), где x(t) — оптималь, существует внешняя нормаль к dD(f), которую обозначим p(t). Тогда выполняется “принцип максимума”:
max p(f) х - р(х) x(t) = 1.	(7.13.1)
xel
Последнее равенство в (7.13.1) означает, что проекция скорости x(t) на направление нормали p(t) максимальна по сравнению с про
308
екциями всех допустимых скоростей л е I данной 1 -УДС в данной точке x(Z). Таким образом, точка x(Z) как точка границы d[D(Z)] имеет максимальную скорость в направлении нормали к этой границе.
В механике [9] величина 1 p(f) | называется нормальной медлительностью фронта распространения возбуждения, а величина, ей обратная — у, будет иметь смысл нормальной скорости фронта распространения возбуждения. Аналогично можно сказать, что любая точка границы области достижимости S[7)(Z)] имеет максимальную допустимую скорость в направлении нормали к границе в этой точке. Отсюда следует, что величина vv(z) = —ji [z?(Z)] имеет максимально возможное
dZ значение, т.е.
40 = т н к (0] *	[й(о] = 40	(7-13.2)
dZ	dZ
и максимум величины в левой части неравенства (7.13.2) достигается при M(t) = Z)(Z). Этот факт будем называть принципом максимума скорости изменения объема (меры) области достижимости. Так как
p[D(Z)] = fw(Z)^>	(7.13.3)
о
то и pi[Z)(Z)] также принимает максимально возможное значение при любом Z е [0, 7]. Другими словами, (7.13.3) означает, что справедлив принцип максимума объема (меры) области достижимости. Итак, объем и скорость изменения объема области достижимости в каждый момент времени принимают наибольшие значения.
В то же время равенство (7.13.3) выражает следующий принцип: для того чтобы значение интеграла (7.13.3) в момент Z > 0 было наибольшим, необходимо и достаточно, чтобы подынтегральное выражение в каждый момент времени т, 0 < т < Z, принимало наибольшее значение. В одномерном случае этот очевидный, но важный принцип был известен [140]. Однако в многомерном случае его формулировка нам не известна, а желательно ее иметь. Действительно, возьмем тождество, которое выражает тот факт, что при определенных условиях многомерный интеграл можно представить как повторный:
\f{x,u)dx=\dy \f{y,z,u)dz,	(7.13.4)
D	D D(z)
где D — некоторая ^-мерная область в 7^, которая допускает слоение на слои Dy, с базой Dy, где Dy — область изменения переменной z при фиксированном у. Этот факт запишем так: D = D х Dy, где х = (у, z)', при
309
этом к = dimD(x) = dimD(y) + drniD^z). Кроме того, f(x, и) — некоторая функция от переменной х е D и параметра и <= U, где U— область значений этого параметра (область U может сама зависеть от х).
Считая и управляющим параметром, рассмотрим задачу оптимального управления: найти и = й(х), х е D(x), и g U, такую, что
max J/(x, w(x))dx = J f(x, и(x)) dx.	(7.13.5)
"W D	D
В силу тождества (7.13.4) очевидны равенства (которые, однако, доказывать строго не будем):
max f /(х, м(х)) dx = J dy max J/(y, z, и (z))dz "(x) £>(.r)	D(y) иУ& Dy(z)
= J max/(x,ux) dx, D(x) L wW
(7.13.6)
Заметим, что знак “max” здесь можно везде заменить на знак “min”.
Равенства (7.13.6) выражают многомерный принцип оптимальности. Первое равенство в (7.13.6) означает, что определение максимума многомерного (A-мерного) интегрального функционала сводится (с необходимостью и достаточностью) к определению максимума интегрального функционала любой фиксированной промежуточной размерности А,: 0 < кх < к. Однако этот, последний, максимум (хотя он и проще из-за меньшей размерности интеграла) мы должны искать многократно — при каждом значении переменной у g Л(у), которая выступает в этом случае как параметр. В частности, последнее равенство соответствует кх = 0 и означает, что задача максимизации многомерного интеграла (7.13.5) сводится просто к задаче “статической” оптимизации: найти и = й(х), х g D,u g U так, что
{max /(х, и\.и g U} = /(х, w(x)). ueU
(7.13.7)
Однако задача (7.13.7) предполагает многократную максимизацию, т.е. надо находить максимум/х, и) по и g U для каждого фиксированного значения х g D.
По-видимому, наиболее общая формулировка принципа оптимальности существенно связана с аддитивностью функционала критерия оптимальности. Тогда наиболее общая формулировка принципа оптимальности будет состоять в следующем: всякий кусок (часть) оптимальной траектории (оптимали) есть снова оптималь. При этом граничные условия для куска оптимали должны быть согласованы с оставшейся частью исходной оптимали.
310
Это — общий принцип, из которого фактически выводится, например, принцип динамического программирования Р. Веллмана. Обычно оптималь — это многообразие определенной размерности т. До сих пор, когда мы применяли этот принцип, в качестве куска оптимали брали кусок той же пространственной размерности тп, какую имеет вся оптималь. Но кто сказал, что можно (допустимо) и нужно брать куски только той же размерности ml Почему не брать куски, скажем, меньшей размерности: к = т, т - 1, ..., 1, 0. Или даже куски размерности, большей т, скажем, к = т + 1, т + 2, ...
Таким образом, предлагается построить теорию, допускающую расширение класса кусков, где в качестве кусков допускается брать куски пространственной размерности к, отличной от размерности т исходной оптимали.
Такой подход дал бы возможность не ограничиваться априори многообразиями одной фиксированной размерности т, а допускать в качестве искомой оптимали конструкции, состоящие из многообразий разных размерностей.
Принцип оптимальности выражает некоторые свойства симметрии (сохранения оптимальности) под действием определенных преобразований или операций типа “взятия куска оптимали”. Отметим, что, по-видимому, принцип взятия кусков разных размерностей, в частности, взятие кусков меньших размерностей, аналогичен принципу “спонтанного нарушения симметрии” в единой теории поля.
7.14.	ФИЗИЧЕСКИЙ ПРИНЦИП МАКСИМУМА ОБЪЕМА ОБЛАСТИ ОСВЕЩЕННОСТИ
Рассмотренное в подразд. 7.13 наводит на мысль сформулировать физический (в рамках геометрической оптики) принцип распространения света, который является альтернативным по отношению к известному принципу Ферма, но не противоречащим ему. Он состоит в следующем:
“Свет в природе распространяется так, что, начав испускаться своим источником в определенный начальный момент времени, в каждый последующий момент времени он (свет) занимает область пространства, называемую областью освещенности, наибольшего возможного объема (меры) по сравнению с объемом (мерой) того множества точек пространства, куда он мог бы попасть виртуально, т.е. без нарушения ограничений на скорость его распространения в любой точке пространства и в любом направлении”. К этому можно добавить следую
311
щее: скорость приращения объема (меры) области освещенности также максимальна в каждый момент времени.
Речь идет о распространении света, вообще говоря, в любой неоднородной и неизотропной сплошной среде, но прозрачной для света. Под областью освещенности в данный момент времени можно понимать область, ограниченную поверхностью, называемой в геометрической оптике волновым фронтом Гюйгенса, построенным для этого момента времени.
В свете изложенного в подразд. 7.13 справедливость высказанного принципа не вызывает сомнений, ибо область освещенности можно толковать как область достижимости в соответствующей задаче быстродействия для некоторой 1-УДС. При этом лучи света играют роль оптималей быстродействия для 1-УДС. Заметим, что, вообще говоря, любой физический принцип (закон) не может быть доказан никаким способом в точном логическом смысле. Его можно только опровергнуть, предложив условия опыта, в котором данный принцип будет неверен, в том смысле, что результаты опыта в рамках фиксированной точности (например, измерений) будут отличаться (не согласовываться) с предсказаниями, вытекающими из формулировки данного физического принципа. Классическим примером точной ситуации является второй закон Ньютона, который “опровергается” в экспериментах с околосветовыми скоростями. Однако хорошо, конечно, иметь теорию (а всякая достаточно развитая теория является и должна быть математической), которая дедуктивным методом выводила бы новые физические принципы (законы), которые были бы всегда верны в рамках теории, а на практике получили бы многочисленные подтверждения до тех пор, пока не будут созданы такие реальные условия, не учтенные в теории, что данный закон оказался бы неверным. И тогда нужно создавать новую, уточненную теорию, где уточненный закон уже будет снова обоснован и подтверждаться в многочисленных опытах.
Отметим еще, что указанный физический принцип “максимума области освещенности” с таким же успехом может быть переформулирован в принцип “максимума области возбуждения”, ибо вместо распространения света можно рассматривать распространение любого возбуждения, аналогичного распространению света [98]. Более того, сплошную среду можно заменить на дискретную, состоящую из отдельных точек, между которыми может передаваться процесс возбуждения по закону включения xk+l е f(xk), который в дискретный момент времени к + 1 показывает множество точек, возбуждавшихся под действием точки хк, возбужденной в момент времени к, к = 0, 1, 2, ... Например, такой
312
дискретной сплошной средой может быть нейронная сеть. В этом случае мерой объема служит просто число возбужденных нейронов.
Принцип “максимума области освещенности” может быть использован также и в новых физических опытах как альтернатива тем физическим опытам, в которых использовались лучевые представления и принцип Ферма. Например, в опытах по проверке общей теории относительности, где вместо экспериментов по измерению отклонений лучей в поле силы тяжести можно проводить опыты по изучению формы областей освещенности. Такие опыты дали бы возможность строить и оценивать форму и размеры индикатрис скоростей той реальной сплошной среды (поля), в которой проводится опыт, по крайней мере в приближении геометрической оптики. Зная индикатрисы (поле индикатрис), можно построить (оценить) лагранжиан в принципе наименьшего действия, тем самым идентифицируя данную сплошную среду, поле или вообще СРП.
В связи с рассмотренным в подразд. 7.13 интересно сделать следующее замечание: задачу построения области достижимости D(t) можно рассматривать как своего рода изопериметрическую задачу о построении плоской фигуры наибольшей площади с заданным периметром. Такие задачи можно назвать неевклидовыми, или дифференциальными, изопериметрическими задачами. В задаче о построении области достижимости D(f) роль периметра или линейного размера, пропорционального ему, будет играть время t, а роль фигуры наибольшей площади — сама область достижимости D(f).
Область достижимости можно также рассматривать как шар “радиуса” t, расположенный в искривленном пространстве с 1-метрикой, определяемой полем индикатрис I.
Таким образом, в природе проблема о соотношении мер и метрик различной размерности должна решаться автоматически. Действительно, пусть, например, свет, испускаемый из какой-то точки пространства в момент t0, осветил к моменту некоторую область D фиксированного объема W, принятого за единицу объема. Тогда единицей длины будет длина луча света от источника до некоторой точки Р на 3D, куда попадает этот луч. Конечно, как и положено, в искривленном пространстве эта длина будет зависеть от точки Р g 3D. Ясно, что в таком опыте область D и ее объем надо стремиться сделать как можно меньшими. В инфинитиземальном пределе при W —> 0 область D должна совпасть с индикатрисой световых скоростей в той точке, где расположен источник света. Тем самым можно идентифицировать индикатрисы скоростей света и найти метрику данного пространства.
313
(7.15.1)
а2е
(7.15.2)
7.15.	ПРИМЕР СВЕДЕНИЯ УРАВНЕНИЯ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ ОБЩЕГО ВИДА К НОРМАЛЬНОЙ СИСТЕМЕ С УПРАВЛЕНИЕМ
Пусть дано общее уравнение с частными производными второго порядка относительно одной скалярной неизвестной функции Q = Q(x, у), Q g R1, от двух независимых переменных (х, у) g D2cR2:
PLV„ SQ 6Q d2Q &>Q d2Q } dx dy dx2 dxdy dy2 J
где и — управляющий параметр, и g Uy, Fx — известная функция от всех своих аргументов. Естественно предположить, что это уравнение разрешимо относительно какой-либо из самих старших производных
второго порядка, например — dxdy
Таким образом, (7.15.1) можно представить, например, в виде
d2Q	п dQ dQ d2Q d2Q
dy2	dx dy dx2 dxdy J
Производные, входящие в правую часть (7.15.2), последовательно обозначим через дополнительные неизвестные функции, считая
е=е. ад=ез, *?е=е<; ^e=es, dx	ду dx1 dxdy
х = х1, у = х2, u = ui^Ul.
Тогда с учетом этих обозначений и (7.15.2) получаем следующую систему в нормальной форме:
dx2
дх2 *
^- = F(xl,x2,Q',Q2,Q3,Q\Qs,u). (7.15.3) dx1
Из (7.15.3) видно, что переменные Q4 и Q5 входят только в правые части системы (7.15.3), т.е. их первые производные в левых частях (7.15.3) отсутствуют и вовсе не входят в (7.15.3). Такие переменные имеют смысл “свободных” переменных, которые наподобие управляющих параметров могут принимать независимые значения (Т4 g 7?1 и Q5 е R{. Поэтому и отождествим их с дополнительными независимыми управляющими параметрами:
Q4 = и2 е Rl; Q5 = и3 е R1.
dx[ * ^ = Q\ дх1
дх1
(7.15.4)
314
С учетом (7.15.4) система (7.15.3) принимает вид, в точности соответствующий нормальной системе (7.1.1) при т = 2; п = 3:
^=е2. дхх дх]	^=в2, дх2 v дх2 ^~ = F{xl,x2,Ql,Q2,Qi,u2,u1,ui), (7.15.5)
где управляющие параметры (и1, и2, и3) е U = Ux х Rl х R2.
Таким образом, видим, что УДС (7.15.1) есть (2, 3)-УДС. Интересно отметить, что вообще система, описываемая уравнением (7.15.1), даже
когда ее левая часть явно не зависит от параметра управления и, на самом деле является управляемой дифференциальной системой, как показывает его нормальная форма в виде (2, 3)-УДС (7.15.5), ибо в (7.15.5) помимо управляющего параметра и = их в нем с необходимостью появляются два новых параметра управления: и2 и и3. Этот факт показывает, что уравнения и системы уравнений с частными производными, как правило, содержат большой произвол и далеко неоднозначно определяют свои решения. Как мы знаем, установление условий однозначности (начальных, краевых или каких-либо других) — часто сложная проблема.
Из приведенного примера ясно, что к нормальному виду (7.1.1) можно свести произвольную систему уравнений с частными производными любых порядков относительно любого числа неизвестных функций произвольного числа независимых переменных (меняющихся, правда, в одной и той же области). Например, нетрудно видеть, что для уравнения теплопроводности
dQ d2Q	Т7 / ч тч
------= u&U, (x,y)^D, дхду2
гл? V может зависеть от х, у, Q и производных, нормальная форма (2, 3)-УДС имеет вид
&.=и,'
ох	дх	ох
=	г ^ = п2-и'
_	И а	_	И а	_	И	а
дх2	дхх	дх2
где их е U, и2 е R\ и3 е R1.
315
Аналогично для волнового уравнения
d2Q д2О	гт ,
= ueU, (x,y)eD
ох оу
соответствующая (2, 3)-УДС имеет следующую нормальную форму:
^=е>, ^=ез, йх1	дх2	дх1
где и1 е U, и2 е R\ и2 е Rx.
Для уравнения Пуассона
d2Q 82Q ТТ ( А
—~ +—^ = «, ueU, (х,у)е£), йх2 ду2	2
соответствующая (2, 3)-УЦС имеет вид
		QQ2 2
йх1	йх2	йх1
sq2	QQ3 .3	SQ3
		Г" — « 5		 - и —и
йх2	йх1	дх2
где z/' е U, и2 е R1, и3 е R'.
Отсюда уже легко представить полученные системы уравнений в других формах, например Пфаффовой, в виде (1, m + я)-УДС и др.
Отметим, что если написать условия вполне интегрируемости для нормальной формы (7.15.3), то они окажутся эквивалентными исходному условию, выраженному уравнением (7.15.1), что и следовало ожидать. Интересно отметить, что традиционная классификация уравнений с частными производными второго порядка (7.15.1) на эллиптический, параболический и гиперболический типы теперь — после их представления в виде (т, п)-УДС (7.15.3) — может быть произведена в терминах конусов К(х, Q) допустимых направлений /эт-вектора, т.е. действительно в геометрических терминах, а не только в терминах соответствующих алгебраических форм. Такого рода замечания показывают, что существуют определенные нетрадиционные возможности рассматривать математические объекты с точки зрения теории управления, в частности, существует возможность рассматривать уравнения с частными производными, в том числе уравнения математической физики, как (т, и)-УДС. По-видимому, многие разделы й задачи уравнений с частными производными могут получить истолкование в терминах теории управления, и обратно.
316
7.16.	ОДИН СПЕЦИАЛЬНЫЙ ВИД ИНДИКАТРИС
Сначала рассмотрим специальный вид индикатрис для 1-УДС:
I(x) = {ve TxRn :||v-£z||<г}, xeRn(x),	(7.16.1)
где v = x — скорость изображающей точки в пространстве состояний Rn(x) (конечно, R\x) можно заменить и другим множеством, а также некоторым гладким многообразием); величина а = а(х) — вектор (поле) сноса; числовая величина г = г(х) — радиус сферы нормированного векторного пространства; вектор а — радиус-вектор смещения центра этой сферы.
Выражение (7.16.1) описывает телесную, или полномерную, индикатрису размерности п. Однако нередко индикатриса бывает нетелесной, неполномерной. Такая индикатриса характеризуется тем линейным подпространством в TJRn минимальной размерности к < п, куда она целиком помещается. Ясно, что такое подпространство характеризуется набором из п - к линейных однородных уравнений:
лг = 0,	(7.16.2)
где тг = (тг< (х)) — матрица размерности (п - к х к).
Индикатриса (7.16.1) целиком лежит в линейном подпространстве, описываемом уравнением (7.16.2).
Ясно, что (7.16.2) эквивалентна соответствующей пфаффовой системе, и если она вполне интегрируема, то интегральная поверхность будет играть роль инвариантного многообразия для исходной 1-УДС. Это инвариантное многообразие (/с-мерная поверхность в Rn) становится новым пространством состояний размерности к.
Для (т, и)-УДС рассмотрение специального случая аналогично: вместо вектора v будет фигурировать w-вектор V, а вместо пфаффовых систем (7.16.2) получим соответственно систему квазилинейных однородных или неоднородных уравнений с частными производными.
7.17.	КАЛИБРОВОЧНО-КОМПЕНСАЦИОННЫЙ ПОДХОД
К ВЫВОДУ УСЛОВИЙ ОПТИМАЛЬНОСТИ
Этот подход проиллюстрируем на задаче оптимального по быстродействию управления для 1-УДС, описываемого включением
v = xel(x), xeRk, I(x)&TxRk = Rk,	(7.17.1)
где I(x) — непустое замкнутое выпуклое и телесное (содержащее внутренние точки) множество для \/х е Rk.
317
Задача быстродействия эквивалентна задаче минимизации длины траектории х = x(f) в метрике (7.17.1), т.е. в своей собственной 1-метрике, определяемой (7.17.1).
Дадим, например, схему вывода условий типа принципа максимума в этой задаче как необходимых условий оптимальности. Введем необходимые для этого понятия.
Определим функцию Н0(х,р) — гамильтониан 1-УДС [50, 409] HG(x, р) - {шах рх: х е I(x)}, х & Rk,p & Rk.
Предположим, что Н0(х, р) — непрерывная и достаточно гладкая функция своих аргументов х, р. Тогда 1-УДС (7.17.1) представляется в гамильтоновой форме [50, 409] так:
л ту
х = —(х,р\	(7.17.2)
Ф
гдер g Rk играет роль управления.
Важно, что в силу однородности имеем тождества
Н0(х,Хр) = ХН0(х,р), “к>0, ^^(х,кр) = ^^-(х,р), Х>0. др	др
Заметим, что X может быть произвольной функцией X = Х(х, р) > 0.
Подход состоит в следующем. Будем исходить из невозмущенной задачи, а именно: сначала предположим, что индикатриса Дх) не зависит от л, т.е. 7(л) = 7 для VxERk. Таким образом, рассмотрим 1-УДС вида х е I и предположим, что искомая оптималь существует (в данном случае это просто прямая). Ясно, что оптимальная скорость v вдоль оптимали будет лежать на границе 5(conv 7) множества conv I и будет постоянной (v = const). Здесь <?(conv7) — граница выпуклой оболочки conv I множества I (не будем уточнять, что такое граница <9(conv7)). По сути в этом и состоит один из смыслов принципа максимума JI.С. Понтрягина: если путь уже есть, то для быстрейшего его прохождения надо вдоль него включить максимальную скорость в любом случае.
Сформулируем это условие по-другому: для того чтобы у g 5(conv 7), необходимо и достаточно, чтобы существовал такой ненулевой и постоянный вектор р cRk, для которого выполняется условие максимума для почти всех t е [0, 7]:
{max pv: у е I} = pv- Н(р) = 1.	(7.17.3)
318
Обратим внимание на тот факт, что равенство (7.17.3) — это просто задача оптимизации (статической) или нелинейного программирования: найти максимум линейного функционала^ на множестве I,v е I. При этом оптимальное значение v не зависит от “длины” вектора р, т.е. вместо р можно взять Хр, где X — любое положительное число (скаляр), и тем самым имеет место глобальная инвариантность значения v от величины числа X > 0. Поэтому для любого ненулевого р} всегда можно найти такое X > 0, что для р = 'крх будет выполняться последнее равенство в (7.17.3), т.е. Н(р) =	= 1.
Таким образом, на (7.17.3) можно смотреть как на некоторый достоверный принцип, закон сохранения (в данном случае “энергии”) или, если угодно, как “закон природы”. Следуя теперь принципу локальной калибровочной инвариантности, скажем, что закон (7.17.3) не должен нарушаться под действием возмущений.
Рассмотрим вытекающие отсюда следствия. Пусть оптимальная траектория в возмущенном случае существует. Обозначим ее x(f). Если индикатриса I и скорость v = х(Г) становятся функцией отх, а вдоль оптимальной траектории х = х(?) становится функцией от t, то и вектор р = p(f) становится функцией от t, причем такой, чтобы сохранить соотношение (7.17.3) (“закон природы”), т.е. компенсировать изменение индикатрисы 1(х) в зависимости отл = x(f).
Таким образом, вдоль оптимальной траектории x(f) должен существовать вектор p(f) такой, что тождественно почти для всех t е [0, 73 выполняется условие максимума (принцип максимума):
H(x(t), p(t)) = 1 для почти всех г е [о,T’J	(7.17.4)
В силу тождественности (7.17.4) по t путем дифференцирования (7.17.4) по t находим:
^(х(Г), p(t))x(f) + p(t)^-(x(t), p(l)) = 0.	(7.17.5)
дх	др
С учетом (7.17.2) получаем:
x(t) = 0.
Из (7.17.5) видно, что если p(t) в какой-то момент времени t удовлетворяет (7.17.4) и дифференциальному уравнению
(ад,Ж) + Ж дх
319
дН
Р = —^~(х>Р)	(7.17.6)
дх
вдоль оптимальной траектории х= x(f), то принцип максимума (7.17.4) будет справедлив и в возмущенном случае. Подчеркнем, что мы исходили фактически из “статической” задачи нелинейной оптимизации, определили ее калибровочную инвариантность под действием преобразования р —> Хр, X > О, которая при индикатрисе I, не зависящей от х, является глобальной калибровочной инвариантностью. Затем включили “принцип локальной калибровочной инвариантности” и использовали его так, чтобы скомпенсировать возмущение индикатрисы I -> 7(х) как функции от х (вдоль данной оптимальной траектории х = х(0).
С другой стороны, если принять принцип (7.17.4), т.е. закон сохранения энергии, и принцип сохранения импульса (7.17.6), то (7.17.5) будет выполняться, если выполнено (7.17.2), т.е. уравнения УДС или условия интегрируемости.
В результате если до возмущения управление р было постоянным полем (можно сказать ненаблюдаемым), то после возмущения и управление р стало переменным полем: оно как бы материализовалось и стало наблюдаемым, так как траектории стали кривыми под действием “сил управления”. В этом смысле управляющее поле р - p(t) — это калибровочное, или компенсационное, поле (вдоль точек х е Rk траектории х(/)). Можно еще добавить, что уравнение (7.17.6) можно рассматривать как уравнение параллельного переноса вектора управления р(0 в искривленном пространстве вдоль оптимальной траектории x(Z), которая получает смысл геодезической. Точно так же и скорость v(r) = x(?) “параллельно” переносится вдоль оптимальной траектории. С точки зрения структур, присутствующих здесь, можно сказать, что такой параллельный перенос определяет афинную связность, которая в данном случае и сохраняет требуемый здесь “закон природы” (принцип максимума, оптимальное управление, метрическую структуру).
7.18.	МНОГОМЕРНЫЙ ПРИНЦИП МАКСИМУМА
Рассмотрим л)-УДС
(х Q и) u&U, хеDm, а - 1, ..., т\ Р = 1, ..., п, (7.18.1) дха
320
и функционал вида
f f\x,Q,u)Ax,	(7.18.2)
D
где/°(х, Q, и) и /ар(х, Q, и) — заданные функции указанных аргументов.
Задача оптимального управления состоит в том, чтобы для (т, п)-УДС (7.18.1) найти такую допустимую пару
(Q (х), и(х)), xeD, й eU, Q&R”,	(7.18.3)
где Q(x) возможно, но необязательно удовлетворяет еще некоторым граничным условиям на dDm(x), чтобы интеграл (7.18.2) достиг минимума. Такую пару (7.18.3) назовем оптимальной парой.
Сформулируем в виде гипотезы многомерный принцип максимума (МПМ), который для данной задачи оптимального управления дает, вообще говоря, только необходимые условия оптимальности управления. Название МПМ обусловлено тем, что для т = 1 МПМ представляет собой известный принцип максимума в оптимальном управлении для 1-УДС [140, 250]. Итак, МПМ формулируется следующим образом. Введем функцию
П(х, Q, и, Р) = -X Г U, Q, + Р£  fS (х, Q, и)
и функцию Н по формуле
Н(х, Q, Р) = шах П(х, Q, и, Р), ueU
где Р - (Рра (х)) — матрица с (х) g R1 и Л. > 0. В терминах функции Я“овыпукленные” уравнения (7.18.1) записываются в виде
agp ая(х,е,р) , о
=’ oc-l,...,m; Р-1,...,и, (7.18.4) ОХа сРу’-
где матрица Р И1 рает роль управляющего параметра, причем без каких бы то ни было дополнительных ограничений. Это представление будем называть потоковым представлением (т, и)-УДС. Заметим, что представление (т, и)-УДС (7.4.4), (7.4.5), (7.5.1) можно назвать лагранжевым представлением, а представление (7.1.1) — представлением, аналогичным представлению Фельдбаума—Понтрягина в случае т = 1 [250]. В рамках рассмотренного в данной работе потокового представления можно сказать, что компоненты управления Р в представлении (7.18.4) имеют физический смысл парциальных потоков некоторых субстанций, распределенных в пространстве-времени.
11. А.В. Бабичев
321
Вернемся к формулировке МПМ. Предположим, что оптимальная пара (Q(x\u(xy) существует. Тогда МПМ утверждает, что с необходимостью существует матричнозначная функция Р(х), х е Drn, которая играет роль управления в (т, и)-УДС (7.18.4), и такая, что:
1) она удовлетворяет уравнениям
р=1 й> (71
дха	<Qr
где предполагается суммирование по а' = 1,..., т;
2) выполняется условие, которое названо МПМ:
Я(х, Q (х), Р(х)) = max П(х, Q (х), и, Р(х))	(7.18.6)
ueU
для почти всех х е Dm.
Уравнения (7 18.5) имеют дивергентный вид. Следовательно, уравнения (7.18.5) выражают законы сохранения соответствующих субстанций. Уравнения (7.18.4) могут быть истолкованы как условия интегрируемости, обеспечивающие существование g(x). Таким образом, условия оптимальности могут истолковываться как совокупность двух условий — интегрируемости и сохраняемости, для обеспечения которых необходимо выполнение условий МПМ.
Система уравнений оптимального управления принимает следующий гамипьтонов вид:
^JH(X,Q,P} g^_a^(X,g,P)^ = v
дха дР£ дха dQ?
где по ос идет суммирование от 1 до т, а по р — от 1 до п.
Конечно, в системе (7.18.6) название гамильтоновым условно, ибо здесь нет обычной симплектической структуры. По-видимому, строго доказать МПМ в широких условиях, накладываемых на входящие в задачу функции, включая граничные условия, является далеко не тривиальной задачей.
Сформулируем МПМ в инвариантном виде, используя понятие дифференциальной формы. Для этого задачу оптимального управления, заданную формулами (7.18.2), (7.18.3), запишем в инвариантном виде в терминах m-вектора И: найти V так, чтобы выполнялось включение Ve I(y), I(y)eAmTvRm+n, и К доставлял минимум функционалу f L0(y, Р), где L0(y, Р) — “нелинейная” m-форма от К в каждой точ-D
322
кеу е R'"'n, aS— /«-мерная поверхность в Rm+n, причем для простоты ограничимся случаем, когда класс варьируемых поверхностей задается “достаточно” гладким отображением 5 области D с R'n в Р"!+”.
Аналог функции Понтрягина будет выглядеть так:
П(у, И) = -ХР0(у,И) + Р(у,П),
где Р(у, У) — некоторая ///-форма на Г в точке у е Pm+n и число Л > 0. Тогда П(у, И) — тоже некоторая «/-форма на Г в той же точке у.
Теорема 1(МПМ в инвариантной форме). Если искомая минималь существует (обозначим ее 5), то существует замкнутая дифференциальная форма Р(у, I7) такая, что (X, Р(у, У)) не равна нулю тождественно, и выполняется условие
{max П(у, Г): V 6 1(у)} = П(у, Е(у)) = 0,
I где Е(у) е Л"ТГ5 для почти всех у е S.
Трудность доказательства этого утверждения состоит в доказательстве существования замкнутой дифференциальной формы Р, соответствующей существованию вектора Р(х) в формулировке МПМ (7.18.6).
11*
ПРИЛОЖЕНИЯ
1. КАЛИБРОВОЧНЫЕ ПОЛЯ В ФИЗИКЕ ФУНДАМЕНТАЛЬНЫХ ВЗАИМОДЕЙСТВИЙ
В настоящее время имеется определенная уверенность, что все четыре известные на сегодня самые фундаментальные физические взаимодействия — электромагнитное, слабое, сильное и гравитационное — могут быть представлены соответствующими калибровочными полями.
Электромагнитное взаимодействие, или квантовая электродинамика (КЭД), наиболее изученное из всех. Оно описывает взаимодействие между “калибровочными” частицами — фотонами и электрически заряженными частицами, например электронами. Переносчиками взаимодействия здесь являются фотоны. С помощью КЭД создан мощный расчетный аппарат, позволяющий вычислять физические величины, например магнитный момент электронов, с недостижимой доселе точностью — девять значащих цифр.
Слабое взаимодействие описывает взаимодействие между так называемыми промежуточными бозонами и нейтрино как переносчиками взаимодействия. Была создана калибровочная теория этого взаимодействия, причем единая с КЭД. Она предсказала существование ранее не известных частиц, например “очарованных”, которые впоследствии наблюдались экспериментально.
Сильное взаимодействие описывает очень большие силы взаимодействия частиц внутри атомного ядра, в которое, как известно, входят адроны, прогоны и нейтроны. Нейтроны в ядре плотно упакованы и из-за одноименности своих отрицательных зарядов должны испытывать сильное отталкивание. Однако из-за наличия больших сил сцепления ядро остается устойчивым. Переносчиком этого удерживающего взаимодействия являются частицы, называемые кварками. Именно они, как и аналогичные частицы в упомянутых выше взаимодействиях, обеспечивают калибровочное, или компенсационное, регулирующее воздействие на адроны, препятствуя развалу структуры. Сейчас в основном создана единая калибровочная теория трех упомянутых выше взаимодействий, названная Великим объединением.
324
Гравитационное взаимодействие, известное с незапамятных времен, остается наименее изученным и понятым. Хотя существует общепринятое мнение, что и она должна быть калибровочной, т.е. компенсационной, теорией. Более того, есть надежда на основе калибровочного принципа создать теорию супергравитации, описывающую вообще все четыре взаимодействия единым образом на основе подходящей калибровочной группы локальных симметрий.
С математической точки зрения выяснилось, что аппарат, адекватный калибровочным принципам, это тополого-геометрический аппарат теории расслоений, или расслоенных пространств. Особенно интересным оказалось то, что топологическая структура расслоений оказалась очень важной физической характеристикой. Это стало понятно после теоретического открытия магнитного монопля и инстантона как решений спеиифических калибровочных уравнений, которые мы попытаемся здесь объяснить, естественно, в крайне сжатой форме.
Все рассмотрения в теории физических полей, как правило, ведутся в 4-мерном многообразии времени-пространства А" “мировых” точек х с координатами хц, ц = 1, 2, 3, 4, где четвертая координата соответствует времени. Калибровочные теории, описывающие поля, задаются математическими объектами двух видов — потенциалами и напряженностями.
1. Калибровочные потенциалы А"(х) представляют собой поля 1-форм на многообразии X, х g X, в количестве Nштук, <7=1,2,..., N, которые можно представить как матрично-значную 1-форму вида
A^gTaA-,
где g — калибровочная постоянная; Та — представление алгебры Ли соответствующей группы.
Представление Т алгебры Ли — это множество из N антиэрмитовых бесследовых матриц Та, удовлетворяющих следующему структурному тождеству, характерному для данной алгебры Ли, записанному через коммутаторы матриц:
[гй, Tb\=fabcT, ayb,c = \,...,N,
где fabc — действительные структурные постоянные соответствующей (компактной) группы Ли. Представление Т всегда можно выбрать так, что след Tr(TaTb) = kbab, где ЬаЬ — символ Кронекера; к — константа, вообще говоря, зависящая от представления Т. Калибровочный потенциал называется калибровочным полем.
325
2. Напряженность Fgv калибровочного поля — это дифференциал поля А^, который в конце концов получает вид (в матричной форме):
+ [4. 4 ]=[-4 + 4,idv + Av ], где I— единичная матрица. Заметим, что иЛр и F^v — это антиэрми-товы бесследовые матрицы.
В координатной форме получим выражение
Отметим статические калибровочные поля Афх), т.е. не зависящие от координаты времени х4. Отсюда сМДх) = 0 для Vx е А”. Это соответствует тому, что, как и в теории автоматического регулирования, имеется статический режим постоянной, или нулевой, ошибки регулирования по времени.
Искомые уравнения для неизвестных потенциалов и напряженностей можно получить как классические уравнения Эйлера—Лагранжа для вариационной задачи с функционалом действия:
s=A^v’Fpv^4=i^“v/;“lfa4a0’ (П,1Л)
где выражение в скобках (..— скалярное произведение Картана, которое определяется формулой
(Та,Ть} = ЪаЬ,	(И. 1.2)
и, следовательно, пропорционально следу tr(IaIb').
Некоторые другие математические факты, нужные здесь, мы очень кратко приведем в конце этого приложения.
Для статических калибровочных полей (не зависящих от х4) функционал действия (П.1.1) естественно заменить функционалом энергии:
s0-	(П.1.3)
По определению, или, если угодно, по условию локальной калибровочной инвариантности, функционалы (П.1.2) и (П.1.3) инвариантны относительно калибровочных преобразований:
4 4 U-{A^U + и~1дци,	(П. 1.4)
F^U^U,	(П.1.5)
где U = ехр (Xя(х)Та); Xя(х) — Nпроизвольных функций, которые как бы играют роль вариаций в стандартной процедуре варьирования
326
функционалов в вариационном принципе. Если все F^v обращаются в нуль, т.е. отсутствует напряженность поля, то описывает “чистую” калибровку А = U~ld^U для некоторого U(x). “Чистая” калибровка важна, когда поле предполагают нулевым вне какой-то области.
При действии калибровочного преобразования (П.1.4), (П.1.5) величина daF^v+ [Аа, ДД преобразуется естественно просто и получает вид П-1 (Д Дх,+[Д, ДУ])С/. Чтобы так же просто преобразовалась величина ДД^ определяется ковариантная производная	+ А^, что
заставляет коммутатор [Д, Ду] вести себя при калибровочных преобразованиях так же просто (сравните это с методом вариации постоянных Лагранжа, толкуемого в подразд. 1.14 как калибровочное преобразование).
Стационарные значения функционалов (П.1.1) и (П.1.3), необязательно минимумы, находятся стандартным приемом вариационного исчисления и приводят к уравнениям Эйлера—Лагранжа:
+ [А„ F,v] = [Д, ДД = О	(П.1.6)
или в координатном виде:
Уравнения (П.1.6) и (П.1.7) называют уравнениями Янга—Милса. Они являются системой нелинейных дифференциальных уравнений с частными производными для калибровочного потенциала
Заметим, что если какое-то их решение найдено, то нужно еще проверить, доставляет ли оно функционалу локальный минимум, ибо важные физические реалии определяются именно локальными минимумами.
Для казавшейся безнадежной задачи решения уравнений Янга— Милса и исследования этих решений на локальный минимум были найдены некоторые его решения, которые были истолкованы как монополи и инстантоны. Коротко воспроизведем ход мысли, приведшей к этому решению.
Используем тождество Якоби (в калибровочной теории оно называется тождеством Бьянки) для	+ А:
[Д, [ Д, Д ]] + круговая перестановка индексов = О,	(П. 1.8)
а поле Ду запишем в виде Ду = [Д, Д].
Тогда, умножая (П.1.8) на £цуаР, получим:
[Д,*ДУ] = О,	(П.1.9)
где *Д v = | еgvap Fap — тензор, дуальный к Д v.
327
Если
p.V 1 |AV J
(П.1.10)
то такое поле называется автодуальным.
Сравнивая (П. 1.9) с уравнением Янга-—Милса, получаем, что любое автодуальное поле автоматически удовлетворяет уравнению Янга— Милса. Таким образом, задача свелась к уравнению (П.1.10), которое проще уравнений Янга—Милса, хотя и является нелинейным дифференциальным уравнением первого порядка для А°. Инстантоны и моно-пли и есть решения уравнения (П.1.10).
Теперь предельно сжато рассмотрим математические факты, которые составляют аналитический аппарат калибровочной теории.
Рассмотрим TV-мерное компактное многообразие точек х = (хь ..., хл) = (хД р = 1,	7V, с метрикой gaP = 8аР, где 5ар — символ Кронеке-
ра. Поэтому можно не различать контрвариантные и ковариантные координаты ха = ха, а скалярное произведение имеет вид:
р
% ...аг
~ 6^a^av = a\b\ + ... + а^Ъ^.
Полностью антисимметричный тензор задается формулой
1, если (а,,..., ос N)—четная перестановка, е =1-1, если она нечетная,
О в остальных случаях.
Этот тензор удовлетворяет тождеству

п ' Ео □ — det cq ... адг Pj ... Рдг

Отсюда
det Лер ДА! е“1 ’ ’'' ’ Е₽1 " ' £Pw ^а1₽1 '' ’ ^«wPw'
Отметим еще простые, но важные тождества и определения ТгЯаР = - Ааа, где идет суммирование по парно входящим греческим индексам /г(ЯВ) = tr(BA), det (АВ) = det А  det В, [А, В] = АВ - ВА.
Для любой матрицы имеем:
1)	Я+— эрмитово сопряженная к Я;
2)	Я”1 — обратная к Я;
3)	А — эрмитова, если Я ' = Я;
4)	Я — антиэрмитова, если А + - -А;
5)	А — унитарна, если Я + = А 1.
328
д д
dxt ’	’ dxN
Для дифференцирования имеем д =---
Для матрицы А, зависящей от х, имеем тождество
tr (А ‘а А) = —- a (det А) = д (In det А), det А
а также тождество [7, ац, А] = д^А, которое следует из равенств
[г ац, А] в = ац (АВ) -Ад^в = (дцА)в.
Важную роль для понимания топологии калибровочных полей играет формула Гаусса—Остроградского о дивергенции, которая утверждает, что полный поток поля через замкнутую поверхность dD равен интегралу дивергенции этого поля по области D, ограниченной этой поверхностью Обобщением этой теоремы служит формула, называемая формулой Стокса, которая выражена в терминах дифференциальных (косых) форм.
2.	ЗАКОНЫ СОХРАНЕНИЯ В ТЕОРИИ ПОЛЯ
Законы сохранения в теории поля можно получить с помощью важных теорем Нётер. Существуют четыре утверждения Нётер, которые группируются в две теоремы, каждая из которых содержит прямое и обратное утверждения. Эти теоремы можно сформулировать в рамках лагранжева вариационного подхода к теории по’ля и сплошной среды, и они имеют ясную физическую интерпретацию.
Пусть в соответствии с принципом наименьшего действия система описывается интегралом действия
S = \L(x,Q,dQ,d2Q)dx,	(П.2.1)
D
где Q(x) — функции, описывающие поле; х — пространственно-временные переменные; L — лагранжиан (или “плотность” лагранжиана). Тогда первая теорема формулируется так.
Теорема 1. Если интеграл действия 5" инвариантен относительно некоторой конечно-параметрической группы Ли Gr, где г — число конечных параметров этой группы, то существует г линейно независимых комбинаций лагранжевых производных (т.е. левых частей уравнения Эйлера, решение которых есть экстремали принципа наименьшего действия), которые имеют вид дивергенций, и обратно, из этого условия следует, что действие 5 инвариантно к некоторой конечно-параметрической группе Ли Gr.
329
Заметим, что выражения, стоящие под знаком дивергенции в теореме Нётер, имеют смысл токов субстанции поля, или потоков субстанции в нашей терминологии. Поэтому, если выполняются уравнения Эйлера, т.е. лагранжевы производные интеграла (П.2.1) равны нулю, то получаются дифференциальные (локальные) законы (уравнения) сохранения субстанции.
Путем интегрирования обеих частей уравнений сохранения (по специально выбранным пространственным гиперповерхностям с определенными граничными условиями) получаются глобальные (интегральные) законы сохранения субстанции, например, закон сохранения энергии-импульса, сохранения заряда и др.
Однако локальные калибровочные группы, группы “общековариантных” преобразований координат, относятся, вообще говоря, к бесконечным группам (квазигруппам Ли), ибо они зависят от функций, а не от конечного числа г числовых параметров. Отметим, что в силу “надкоординатности” калибровочных групп в каждой точке х пространства-времени сохраняется алгебра конечной группы Ли, из которой (группы Ли) произошли локальные группы (путем замены конечного числа параметров функциями). В случае функциональнопараметрической группы этот факт, вообще говоря, места не имеет.
Вторая теорема Нётер звучит так.
Теорема 2. Если интеграл действия 5 инвариантен относительно группы, зависящей от г функций (функциональных, а не числовых параметров) и их производных до порядка к включительно, то существует г тождеств, левые части которых представляют собой тождественно нулевое соотношение, зависящее только от лагранжевых производных вариационной задачи и производных от них до к-ro порядка, а правые части равны нулю. Верно и обратное.
Из этих теорем Нётер, в частности, следует, что если и только если конечно-параметрическая группа инвариантности Gr есть подгруппа бесконечно (функционально)-параметрической группы, то потоки становятся линейными комбинациями лагранжевых производных задачи и, следовательно, на экстремалях обращаются в ноль. Такие потоки Нётер назвала несобственными. Более того, такие потоки можно представить как дивергенцию от некоторого антисимметричного тензора (т.е. формы) и, следовательно, ток соответствует некоторому потенциалу. Более подробное обсуждение и доказательства можно найти в [98, 157].
330
3.	ИНТЕГРАЛ ФЕЙНМАНА
Интеграл Фейнмана — это удивительное по простоте, общности, красоте, эффективности и глубине понятие. В силу своей глубины ‘‘явление” фейнмановского интеграла еще не осмыслено до конца ни философски, ни математически. Оно является плодом изобретения глубокой интуиции Р. Фейнмана, которое он подарил миру без строго математического обоснования, но с довольно определенной физической идеей.
Первоначально Фейнман придумал свой интеграл как альтернативу двум классическим подходам к квантовой механике, идущим соответственно от Шредингера и Гейзенберга. Суть этих двух подходов состоит в составлении и решении уравнений для функций СР-функция Шредингера, или амплитуды вероятностей состояний квантовой системы) и операторов (операторы физических величин Гейзенберга). В отличие от этого Фейнман предложил не уравнение, а интеграл, выражающий амплитуду A[to, х0; h, -И) перехода системы из начального состояния (/0, х0) в конечное (Zb Xi). Поэтому, по Фейнману, проблема сводится не к решению обычных дифференциальных уравнений, т.е. интегрированию дифференциальных уравнений, а к вычислению интеграла. Можно сказать, что Фейнман фактически догадался, как записать решение дифференциальных уравнений, которое также можно рассматривать как решение некоторой вариационной задачи принципа наименьшего действия в виде “одной квадратуры”.
Интеграл А называется в квантовой теории поля пропагатором. Он похож на классическую функцию Грина, функцию источника, находящегося в точке (/0, х0), функцию влияния или переходную функцию в терминологии теории управления Это тоже настоящий “Бог из машины”. При этом Фейнман исходил из представлений классической аналитической механики, где центральным понятием является понятие действия S физической системы как функционала Sfyfyo, Г1)] на классической траектории у(у0, j/J системы в ее пространстве состояний Y, соединяющей начальную у0 и конечную yi точки локальных состояний у е У.
Таким образом, в этом подходе автоматически соблюдается требование — принцип соответствия Н. Бора, или “стыковки” в пределе, с ранее известными, но менее глубокими теориями. С другой стороны, Фейнман естественным образом учел “принцип усреднения” для фаз волн квантовых амплитуд, что фактически отражает главный принцип классической квантовой механики — принцип линейной суперпозиции волн вероятностей, или амплитуд вероятностей, которыми собственно и описываются системы в квантовой механике.
331
Фейнмановский интеграл можно записать в виде
А(Уо > У1) = f ехр [г 4т(Уо > У1)]] cWo = У1), у(уо,У\)
где А(у0, yi) — амплитуда вероятности перехода квантовой системы из состояния уо е У в состояние уг е Y; 5'[у(у0, У1)] — классическое действие — функционал от классической траектории у(у0, соответствующей классической системы; i — мнимая единица; dy(y0, yi) — некоторая мера в пространстве всех допустимых классических траекторий УОо, У1).
Вся “загвоздка” в обосновании этого интеграла как хорошо определенного математического объекта состоит в определении указанной меры. Фейнман дал ряд эвристических “рецептов” для вычисления своего интеграла и показал на ряде примеров, как его нужно составлять и вычислять [313].
Подчеркнем, что фейнмановский интеграл, по-видимому, имеет существенно большую область применения, чем те условия, в которых он рассматривается сейчас.
Дело в том, что в приведенном выше интеграле Фейнмана надо знать только одну характеристику, или один параметр, исследуемой системы — это действие S как функционала на допустимых траекториях у(уо> Л) в каком-то пространстве состояний Y. Поэтому в принципе не нужно даже знать, например, лагранжиана и гамильтониана системы, которые существенно предполагают гладкость дифференциальных структур, поскольку для них, например, требуется понятие скорости изображающей точки системы в пространстве состояний Y.
Но, как показано в разд. 5, действие 5[у(у0, У1)] может приобретать смысл длины (или другого аддитивного функционала) на допустимых траекториях у(у0, уу), часто стесненных очень “нетрадиционными” ограничениями, присущими классической механике и физике. Экстремальное значение ^(yo^'i) действия 5[у(у0, Ji)] приобретает ясный геометрический смысл вполне определенной метрики, т.е. функции на (уо, yi) е У2, которая нами названа вторичной метрикой.
Подчеркнем еще один интересный аспект фейнмановского интеграла, который в рамках теории возмущений может быть представлен фейнмановскими диаграммами для изучения систем элементарных частиц: такие диаграммы можно рассматривать как реализации общей блочно-структурной схемы для систем с распределенными параметрами (см. подразд. 4.11).
Литература
1.	Айзерман М.А., Каянелло Э.Р. Исследования по теории структур: Сб. науч, трудов. М., 1988.
2,	Аккардо К., Смолакова А.М. Преобразование гаусовских мер, лапласиан и обобщенные следы // ДАН. Т. 350. № 1. 1996. Сентябрь.
3.	Александров А.Д., Нецветаев Н.Ю. Геометрия. М., 1990.
4.	Алексеева ТА. Современные политические теории / Моск. гос. ин-т между -нар. отношений (ун-т). М., 2000.
5.	Аминов Ю.А. Минимальные поверхности. Харьков, 1978.
6.	Андреев Д.Л. Роза Мира. М., 1991.
7.	Андреев Ю.Н. Дифференциально-геометрические методы в теории управления // Автоматика и телемеханика. 1982. № 10. С. 5—46.
8.	Ансельм А.А. В поисках единой теории фундаментальных взаимодействий // Современная теория элементарных частиц: Сборник. М., 1984.
9.	Арнольд В.И. Математические методы классической механики. М., 1989.
10.	Арнольд В.И, Варченко А.И., Гусейн-Заде С.М. Особенности дифференцируемых отображений. М., 1982. Т. I.
11.	Арнольд В.И., Варченко А.Н., Гусейн-Заде С.М. Особенности дифференцируемых отображений. М., 1984. Т. И.
12.	Артин Э. Геометрическая алгебра. М., 1979.
13.	Бабак С.Ф., Ильясов Б.Г., Кабельное Ю.С. Об одном подходе к построению структурной теории систем // Известия РАН. Теория и системы управления. 1995. №2. С. 15—21.
14.	Бабичев А.В., Бутковский А.Г. К общему понятию структуры оптимального управления. // Известия РАН. Теория и системы управления. 1999. № 6.
15.	Бабичев А.В., Бутковский А.Г, Лепе Н.Л. Декомпозиция фазового портрета динамической системы с управлением с помощью аппарата расслоений // Автоматика и телемеханика. 1989. № 5.
16.	Барвайс Дж. Справочная книга по математической логике: В 4 т. Т. 1. Теория моделей. М., 1982.
17.	Барвайс Дж. Справочная книга по математической логике: В 4 т. Т. 2. Теория множеств. М., 1982.
18.	Барвайс Дж. Справочная книга по математической логике: В 4 т. Т. 3. Теория рекурсий. М., 1982.
19.	Барвайс Дж. Справочная книга по математической логике: В 4 т. Т. 4. Теория доказательств и конструктивная математика. М., 1983.
20.	Беллман Р. Введение в теорию матриц. М., 1969.
21.	Беллман Р. Динамическое программирование. М., 1960.
22.	Берг А.И. Кибернетика — наука об оптимальном управлении. М., 1964.
333
23.	Бердичевский В.Л. Вариационные принципы механики сплошной среды. М., 1983.
24.	Беркс У. Пространство — время, геометрия, космология. М., 1985.
25.	Библия. СПб, 1902.
26.	Биркгоф Г Теория решеток. М., 1984.
27.	Биркгоф Д.Д. Динамические системы. М., 1941.
28.	Бобылев НА., Емельянов С.В., Коровин С.К. Функциональный анализ. М., 1999.
29.	Бобылев НА., Коровин С.К Топологические методы в вариационных задачах. М., 1997.
30.	Боголюбов Н.Н., Логунов А.А., Тодоров И.Т Основы аксиоматического подхода к квантовой теории поля. М., 1969.
31.	Боголюбов Н.Н., Медведев Б.Н., Поливанов М.К. Вопросы теории дисперсионных соотношений. М., 1958.
32.	Борецкий И.Ф., Павлов В.Г. О некоторых свойствах динамических систем, связанных с их симметрией // Кибернетика и вычислительная техника. Киев, 1980. Вып. 47. С. 25—34.
33.	Борисович Ю.Г. и др. Введение в топологию. М., 1995.
34.	Бочаров А. В. и др. Симметрии и законы сохранения уравнений математической физики. М., 1997.
35.	Бурбаки Н. Модули, кольца, формы. М., 1966.
36.	Бурбаки И. Очерки истории математики. М., 1963.
37.	Бурбаки Н. Теория множеств. М., 1965.
38.	Бутковский А.Г Теория оптимального управления системами с распределенными параметрами. М., 1965.
39.	Бутковский А.Г. Что такое оптимальное управление? М., 1966.
40.	Бутковский А.Г. Геометрический подход к управлению системами с распределенными параметрами // Новые концепции общей теории управления: Сб. науч. трудов / Под ред. А.А. Красовского. (Материалы сессии Отделения машиностроения, механики и процессов управления РАН, 24—25 сентября 1994 г.). Таганрог, 1995. С. 58—64.
41.	Бутковский А.Г. К геометрической теории управления системами с распределенными параметрами // Известия РАН. Теория и системы управления. 1995. № 4. С. 137—179.
42.	Бутковский А.Г. К общей теории систем и управления И Международная научно-практическая конференция “Анализ систем на рубеже тысячелетий: теория и практика— 1998” (Москва, 15—17 декабря 1998 г.): Тезисы. М., 1998. С. 245—246.
43.	Бутковский А.Г. Кибернетика и структуры // Национальная АН Украины, Проблемы управления и информатики: Юбилейный выпуск журнала. 1996. № 1—-2. С. 8—20.
44.	Бутковский А.Г. Методы управления распределенными системами. М., 1975.
45.	Бутковский А.Г. На пути к геометризации управления // Известия РАН. Теория и системы управления. 1997. № 1. С. 1—12.
46.	Бутковский А.Г. Обобщение закона Ома с помощью вольт-амперных операторов И Электричество. 1997. № 4. С. 69—71.
47.	Бутковский А.Г. Системы с распределенными параметрами и единая геометрическая теория управления // Приборы и системы управления. 1994. № 11. С. 24—27.
48.	Бутковский А.Г. Структурная теория распределенных систем. М., 1977.
334
49.	Бутковский А.Г. Управление в метрических пространствах // Автоматика и телемеханика. 1999. № 7. С. 11—24.
50.	Бутковский А.Г. Фазовые портреты управляемых динамических систем. М., 1985.
51.	Бутковский А.Г. Характеристики систем с распределенными параметрами. М.. 1979.
52.	Бутковский А.Г. Частотные критерии робастной устойчивости // Известия РАН. Техническая кибернетика. 1993. № 3.
53.	Бутковский А.Г. Что такое управление с точки зрения аксиомы выбора Цермело И Автоматика и телемеханика. 2000. № 7. С. 182—185.
54.	Бутковский А.Г, Бабичев А.В. К геометрической теории управления дифференциальными системами // Российская научно-техническая конференция "Надежность механических систем" (Самара, 21—24 ноября 1995 г.): Тезисы докладов. Самара, 1995. С. 40—41.
55.	Бутковский А.Г, Бабичев А.В. Результаты и перспективы выполнения программы создания единой геометрической теории управления // Приборы и системы управления. 1996. № 12. С. 31—33.
56.	Бутковский А.Г. и др. Математические структуры в теории управления // Труды Института проблем управления РАН. М., 1999. Т. V. С. 63—80.
57.	Бутковский А.Г, Малый С. А., Андреев Ю.Н. Оптимальное управление нагревом металла. М., 1972.
58.	Бутковский А.Г, Малый С.А., Андреев Ю.Н. Управление нагревом металла. М., 1981.
59.	Бутковский А.Г, Пустыльников Л.М. Теория подвижного управления системами с распределенными параметрами. М., 1980.
60.	Бутковский А.Г, Самойленко Ю.Н. Управление квантово-механическими процессами. М., 1984.
61.	Вайскопф В. Физика в двадцатом столетии. М., 1977.
62.	Ван дер Варден Б.Л. Алгебра. М., 1976.
63.	Ван Хао,Мак-Нотон Р. Аксиоматические системы теории множеств. М., 1963.
64.	Вапник В.Н. Восстановление зависимостей по эмпирическим данным. М., 1979.
65.	Вапник В.Н. Алгоритмы и программы восстановления зависимостей. М., 1984.
66.	Вапник В.Н., Лернер А.Я., Червоненкис А.Я. Системы обучения распознаванию образов // Техничекая кибернетика. 1965. № 1.
67.	Вапник В.Н., Червоненкис А.Я. Теория распознавания образов. М., 1974.
68.	Вариационные принципы механики: Сб. статей. М., 1959.
69.	Варшамов Р.Р. Введение в новую нетрадиционную математику. М., 1999.
70.	Вейль Г. Математическое мышление. М„ 1989.
71.	Вейль Г. Симметрия. М., 1968.
72.	Беличенко В.В. О вариационном подходе в проблеме инвариантности управляемых систем И Автоматика и телемеханика. 1972. № 4. С. 22—35.
73.	Вигнер Е. Этюды о симметрии. М., 1971.
74.	Визгин В.П. Развитие взаимосвязи принципов инвариантности с законами сохранения в классической физике. М., 1972.
75.	Виленкин НЯ. Специальные функции и теория представления групп. М., 1965.
76.	Винер Н. Кибернетика или управление и связь в животном и машине. М., 1958.
77.	Виноградов А.М., Красильщик ИС. Симметрии и законы сохранения. М., 1997.
78.	Виноградов А.М., Красильщик И.С., Лычагин В.В. Введение в геометрию нелинейных дифференциальных уравнений. М., 1986.
79.	Виноградов А.М., Купершмидт Б.А. Структура гамильтоновой механики // УМН РАН. 1977. Т. 32. Вып. 4. С. 175—236.
335
80.	Винтген П. Дифференциальная геометрия и расслоения. М., 1960.
81.	Владимиров В.С. Методы теории функций многих комплексных переменных. М., 1964.
82.	Владимиров В.С. Уравнения математической физики. М., 1971.
83.	Владимиров В.С. , Волович И.В., Зеленое Е.И. p-adic Numbers in Mathematical Physics. Singapore, 1994.
84.	Владимиров Д. А. Булевы алгебры. M., 1969.
85.	Владимиров Ю.С. Реляционная теория пространства-времени и взаимодействия. Ч. 1. Теория систем отношений. М., 1996.
86.	Волков О. Погружение во тьму. Послесловие М.Кириллова "К свету" // Роман-газета. 1990. № 6 (1/32). С. 123—128.
'	87. Волобуев И.П., Кубышин Ю.А. Дифференциальная геометрия и алгебры Ли и их приложения в теории поля. М., 1998.
88.	Вулих В.З. Введение в теорию полуупорядоченных пространств. М., 1961.
89.	Габасов Р., Кириллова Ф.М. Качественная теория оптимальных процессов. М., 1971.
90.	Габасов Р., Кириллова Ф.М. Особые оптимальные управления. М., 1973.
91.	Лабасов Р. и др. Конструктивные методы оптимизации. Минск, 1998.
92.	Гайшун И. В. Введение в теорию линейных нестационарных систем. Минск, 1999.
93.	Гайшун И.В. Вполне разрешимые многомерные дифференциальные уравнения. Минск, 1983.
94.	Галиуллин А. С. Обратные задачи динамики. М., 1981.
95.	Гантмахер Ф.Р. Теория матриц. 4-е изд. М., 1988.
96.	Гастев Ю.А. Гомоморфизмы и модели. М., 1975.
97.	Гелбаум Б., Олмстед Дж. Контрпримеры в анализе. М., 1967.
98.	Гельфанд И.М., Фомин С.В. Вариационное исчисление. М., 1961.
99.	Гельфер Я.М., Любошиц В.Л., Подгорецкий М.М. Парадокс Гиббса и тождественность частиц в квантовой механике. М., 1975.
100.	Гильберт Д., Аккерман В. Основы теоретической логики. М., 1947.
101.	Гильберт Д., Бернайс П. Основания математики. Логические основания и формализация арифметики. М., 1982.
102.	/ йрко В.Л. Теория случайных детерминантов. Киев, 1980.
103.	Гладкий А. Б. Математическая логика. М., 1998.
104.	Глушков В.М. Теория алгоритмов. Киев, 1961.
105.	Глушков В.М. Энциклопедия кибернетики. Киев, 1974. Т. 1,2.
106.	Гнеденко Б.В. Курс теории вероятностей. М., 1954.
107.	Голдблатт Р. Топосы и категорный анализ логики. М., 1983.
108.	Голубев В. В. Лекции по интегрированию уравнений движения тяжелого твердого тела около неподвижной точки. М., 1953.
109.	Гоппа В.Д Введение в алгебраическую теорию информации. М., 1995.
110.	Горшков А.Г., Рабинский Л.Н., Тарляковский Д.В. Основы тензорного анализа и механика сплошной среды / Под ред. Д.М. Климова. М., 2000.
111.	Гротендик А. Урожаи и посевы (размышления о прошлом математика). Ижевск, 1999.
112.	Губарев В.Ф., Ладиков Ю.П., Паславский Ю.С. Удержание жидкого металла в двухчастотном индукторе // Кибернетика и вычислительная техника: Сборник. Киев, 1974. №23.
113.	Гюнтер Н.М. Интегрирование уравнений первого порядка с частными производными. М., 1934.
336
114.	Дайсон Ф. Математика и физика // Успехи физических наук. 1965. Т. 85. №2. С. 351—364.
115.	Данилов Н.Ю. и др. Геометрические и алгебраические методы в теории управления. М., 1999.
116.	Де Рам Н. Дифференцируемые многообразия. М., 1956.
117.	Джекобсом И. Алгебра Ли. М., 1964.
118.	Дзо Чонг Тхи, Фоменко А.Т. Минимальные поверхности и проблема Плато. М„ 1987.
119.	Дидук ГА., Золотов О.И., Пустылъников Л.М. Специальные разделы теории автоматического регулирования и управления. Теория систем с распределенными параметрами. СПб, 1999. Т. I, И.
120.	Дирак П.А.М. Отношение между математикой и физикой // К созданию квантовой теории поля: Сборник. М., 1990. С. 245-—254.
121.	Дирак П.А.М. Основы квантовой механики. М.; Л., 1937.
122.	Дубровин Б.А., Новиков С.П., Фоменко А.Т. Современная геомегрия. М., 1979.
123.	Дьедонне Ж. Основы современного анализа. М., 1964.
124.	Евстигнеев В.А., Касьянов В.Н. Сводимые графы. Новосибирск, 1999. С. 288.
125.	Егоров Ю.В. Лекции по уравнениям с частными производными. М., 1985.
126.	Егоров Ю.Л., Мищенко С.Н. Диалектика структуры и функции в системах управления. М., 2000.
127.	Елкин В.И. Редукция нелинейных управляемых систем. М., 1997.
128.	Емельянов С. В. и др. Полугрупповой подход к задачам описания класса допустимых возмущений // Доклады АН СССР. 1990. Т. 312. № 5. С. 1057—1061.
129.	Емельянов С.В., Коровин С.К. Новые принципы обратной связи. М.. 1997.
130.	Ефимов Н.Е. Введение в теорию внешних форм. М., 1977.
131.	Жуков В.П. Полевые методы в исследовании нелинейных динамических систем. М., 1992.
132.	Журавлев В. Ф., Климов ДМ. Прикладные методы в теории колебаний. М., 1988.
133.	Журавлев Ю.И. Математические методы в теории систем: Сб. статей. М., 1979.
134.	Затуливетер Ю.С. Информация и эволюционное моделирование // Труды Международной конференции “Идентификация систем и задачи управления SICPRO’2000” (Москва, 26—28 сентября 2000 г.). М., 2000.
135.	Захаров В.Е., Кузнецов Е.А. Гамильтоновский формализм для нелинейных волн// Успехи физических наук. 1977. Т. 167. № 11. С. 1137—1167.
136.	Зорич В.А. Математический анализ. М., 1984. Т. 2.
137.	Ибрагимов Н.Х. Групповой анализ обыкновенных дифференциальных уравнений и принцип инвариантности в математической физике // УМН РАН. 1992. Т. 47. Вып. 4(286). С. 83—144.
138.	Ибрагимов Н.Х. Группы преобразований в математической физике. М., 1983.
139.	Ильин Е.П. Психология воли. СПб, 2000.
140.	Иоффе А.Д., Тихомиров В.М. Теория экстремальных задач. М., 1974.
141.	Каку М. Введение в теорию суперструн / Пер. с англ. М., 1999. Пер. изд.: Michio Каки. Introductoin to Superstrings. Springer-Verlag, 1988.
142.	Канатников А.И, Крищенко А.П. Симметрии и декомпозиция нелинейных систем //Дифференциальные уравнения. 1994. Т. 30. № 1 Г С. 1880—1891.
143.	Кановей В.Г. Аксиома выбора и аксиома детерминированности. М., 1984.
144.	Кац М., Улам С. Математика и логика. М., 1971.
145.	Келли Дж.Л. Общая топология. М., Наука. 1968.
146.	Кириллов А.А. Элементы теории представлений. М., 1978.
337
147.	Клаассен КБ. Основы измерений. М., 2000.
148.	Клини С.К. Введение в метаметомику. М., 1957.
149.	Ключевский В.О. Курс русской истории. Пг., 1918. Ч. 1. С. 48—49, 50—66. (Перепечатка со 2-го изд. М., 1915).
150.	Кобаяси Ш. Группы преобразований в дифференциальной геометрии. М., 1986.
151.	Кобаяси Ш., Нимидзу К Основы дифференциальной геометрии. М., 1981.
152.	Козлов В.В. Симметрии, топология и резонансы в гамильтоновой механике. Ижевск, 1995.
153.	Кокс Д., Литтл Дж., О’Ши Д. Идеалы, многообразия и алгебры. Введение в вычислительные аспекты алгебраической геометрии и коммутативной алгебры / Пер. с англ. М., 2000. Пер. изд.: Сох D., Little J., O'Shea D. Ideals, varieties, and algorithms. In Introduction to Computational Algebraic Geometry and Commutative Algebra. Second Edition. Corrected printing, 1998. Springer-Verlag, N.-Y.
154.	Колмогоров A.H. Теория информации и теория алгоритмов. М., 1987.
155.	Колмогоров А.Н., Фомин С.В. Элементы теории функций и функционального анализа. М., 1968.
156.	Кон 77., Коен П. Универсальная алгебра. М., 1968.
157.	Коноплева. Н.П., Попов В.Н. Калибровочные поля. М., 1980.
158.	Корнфельд И.П., Синай Я.Г., Фомин С.В. Эргодическая теория. М., 1980.
159.	Кострикин А.И. Введение в алгебру. М., 1977.
160.	Коэн П. Теория множеств и континуум гипотеза. М., 1969.
161.	Краснощеков П.С. , Петров А. А. Принцип построения моделей. М., 2000.
162.	Красовский А.А. Проблемы физической теории управления // Автоматика и телемеханика. 1990. № 11.
163.	Красовский А.А. Системы автоматического управления полетом. М., 1973.
164.	Красовский А.А. Статистическая теория переходных процессов в системах управления. М., 1968.
165.	Красовский Н.Н. Теория управления движением. М., 1968.
166.	Красовский НН, Субботин А.И. Позиционные дифференциальные игры. М„ 1974.
167.	Крейдлина Г. Е. Язык и интеллект. М., 1995.
168.	Крищенко А.П. Синтез алгоритмов терминального управления для нелинейных систем // Известия АН. Техническая кибернетика. 1994. № 1. С. 48—57.
169.	Крон Г. Тензорный анализ сетей. М., 1978.
170.	Кротов В.Ф., Гурман В. И. Методы и задачи оптимального управления. М„ 1973.
171.	Крутько П.Д. Обратные задачи динамики управляемых систем. Линейные модели. М., 1987.
172.	Крутько П.Д. Обратные задачи динамики управляемых систем. Нелинейные модели. М., 1988.
173.	Ктитарев Д.В. Формула Фейнмана для систем псевдодифференциальных уравнений в бесконечномерных пространствах // Вестник МГУ. Сер. Математика. 1988. №2. С. 76—78.
174.	Кубышкин В.А. О максимальном значении определителя, вектор-столбцы которого принимают значения в заданных множествах // Известия РАН. Теория и системы управления. 1997. № 4.
175.	Кубышкин В.А., Финягина В.И. Метод расчета программных граничных управлений для многомерных систем с распределенными параметрами // Известия АН СССР. Техническая кибернетика. 1994. № 1. С. 141—155.
338
176.	Кулаков Ю.И., Владимиров IOC., Карнаухов А. В. Введение в теорию физических структур и бинарную геомсцюфпзику. М., 1992.
177.	Кулик Б.А. Логические основы «драного смысла. М., 1997.
178.	Куликовский В. Оптимальные и адаптивные процессы в системах автоматического регулирования. М., 1967.
179.	Куликовский Ф., Мотов В. В. Теоретические основы информационных процессов. М., 1987.
180.	Куратовский К., Мостовский А. Теория множеств. М., 1970.
181.	Куратовский К.К. Топология. М., 1966. Т. I.
182.	Куржанский А.Б. Управление и наблюдение в условиях неопределенности. М., 1977.
183.	Курош А.Г. Лекции по общей алгебре. М., 1973.
184.	Кутепов С.А., Яковенко ГН. О структуре множества достижимости: Тезисы // Механика твердого тела. 1981. № 6. С. 165.
185.	Кухтенко А. И. Абстрактная теория систем и прикладные исследования // Кибернетика и вычислительная техника. 1982. Вып. 54. С. 3-—9.
186.	Кухтенко АН. Основные этапы формирования теории инвариантности. Ч. I // Автоматика и телемеханика. 1984. № 2. С. 3—13.
187.	Кухтенко А.И. Основные этапы формирования теории инвариантности. Ч. II // Автоматика и телемеханика. 1985. № 2, С. 3—14.
188.	Кухтенко А.И. Проблема инвариантности в автоматике. Киев, 1963.
189.	Кушнер Б.А. Лекции по конструктивному математическому анализу. М., 1973.
190.	Ладиков Ю.П. Стабилизация процессов в сплошных средах. М.„ 1978.
191.	Ландау Л.Д., Лифшитц Е.М. Теория поля. М., 1962.
192.	Ланкастер П. Теория матриц. М., 1978.
193.	Лернер А.Я. Введение в теорию автоматического регулирования. М., 1958.
194.	Лернер А.Я. Метод изохрон для оптимального управления И Автоматика и телемеханика. 1954. №6.
195.	Ли Э.Б., Маркус Л. Основы теории оптимального управления / Пер. с англ. М., 1972.
196.	Лионе Ж.Л. Оптимальное управление системами, описываемыми дифференциальными уравнениями с частными производными. М., 1972.
197.	Лихнерович А. Теория связностей в целом и группа голономий. М., 1966.
198.	Логические исследования. Вып. 7 И Труды 2-й Международной конференции “Смирновские чтения” (Москва, май 1999 г.). М., 2000.
199.	Лурье КА. Оптимальное управление в задачах математической физики. М., 1975.
200.	Лурье К.А., Черкаев А.В. Эффективные характеристики композиционных материалов и оптимальное проектирование конструкций // Успехи механики. 1986. Т. 9. Вып. 2. С. 3—81.
201.	Люстерник Л.А., Соболев В.И. Элементы функционального анализа. М.; Л., 1951.
202.	Ляпин Е.С. Полугруппы. М., 1960.
203.	Магарил-Ильяев Г.Г., Тихомиров В.М. Выпуклый анализ и его приложение. М., 2000. С. 174.
204.	Малинецкий Г.Г. Хаос. Структуры. Вычислительный эксперимент. Введение в нелинейную динамику. Сер. Кибернетика: неограниченные возможности и возможные ограничения. М., 1997.
205.	Малкин И.А., Манъко В.И. Динамические симметрии и когерентные состояния квантовых систем. М., 1979.
206.	Мальцев А.И. Алгебраические системы. М., 1970.
339
207.	Мальцев А.И. Алгоритмы и рекурсивные функции. М., 1986.
208.	Манин ДЛ. Калибровочные поля и комплексная геометрия. М., 1984.
209.	Маслов В.П. Комплексные марковские цепи и континуальный интеграл Фейнмана. М., 1976.
210.	Маслов В.П., Колоколъников В.Н. Идемпотентный анализ и его применение в оптимальном управлении. М., 1994.
211.	Математическая энциклопедия: В 5 т. М., 1984.
212.	Мах Э. Механика // Регулярная и хаотическая динамика. М., 2000. С. 387.
213.	Мацуо Комацу. Многообразие геометрии. М., 1981.
214.	Мееров М.В. Системы многосвязпого регулирования. М., 1965.
215.	Менский М.Б. Группа путей, измерения, поля, частицы. М., 1983.
216.	Мень 4. История религии. М., 1991. Т. 1.
217.	Месарович М., Такахара Я. Общая теория систем: математические основы. М„ 1978.
218.	Метакидес Г., Нероуд Л. Принципы логики и логического программирования. М., 1998.
219.	Мизес П. Вероятность, статистика, истина. М., 1933.
220.	Мизнер Ч., Торн К., Уилер Дж. Гравитация: В 3 т. М., 1977.
221.	Монастырский М.И. Риман. Топология. Физика. М., 1999.
222.	Монастырский М.И. Топология калибровочных полей и конденсированных сред. М., 1995.
223.	Налимов В.В. Разбрасываю мысли. М., 2000.
224.	Нарасихман Р. Анализ на действительных и комплексных многообразиях. Волгоград, 1998.
22-5. Неймарк М.А. Теория представления групп. М., 1977.
226.	Непейвода Н.Н. Математика. Ижевск, 1999.
227.	Нетер Э. Инварианты любых дифференциальных выражений. Инвариантные вариационные задачи // Вариационные принципы механики / Под ред. Л.С. Полака М., 1959. С. 604—630.
228.	Нетушил А.В. и др. Теория автоматического регулирования. М., 1983.
229.	Никольская И.Л. Знакомство с математической логикой. М., 1998.
230.	Новиков П.С. Элементы математической логики. М., 1973.
231.	Новиков С.П., Фоменко А.Т. Элементы дифференциальной геометрии и топологии. М., 1987.
232.	Новые проблемы физики: Сб. статей. М., 1965.
233.	Овсянников Л.В. Групповой анализ дифференциальных уравнений. М., 1978.
234.	Овсянников Л.В. Лекции по основам газовой динамики. М., 1981.
235.	Олвер П. Приложение групп Ли к дифференциальным уравнениям. М., 1989.
236.	Павленко В.Н. Об одном классе задач управления распределенными системами параболического типа с разрывными нелинейностями: Доклад на Международном семинаре "Негладкие и разрывные задачи управления и оптимизация" (Москва, 1994 г.) // Известия АН СССР. Техническая кибернетика. 1994. № 4. С. 204—209.
237.	Павловский Ю.Н. Теория факторизации и декомпозиции управляемых динамических систем и её приложения // Известия АН СССР. Техническая кибернетика. 1970. №5. С. 25—32.
238.	Павловский Ю.Н., Смирнова Т.Г. Проблема декомпозиции в математическом моделировании. М., 1998.
239.	Павловский Ю.Н., Яковенко ГН. Группы, допускаемые динамическими системами//Методы оптимизации и их приложения. Новосибирск, 1982. С. 155—189.
340
240.	Пенроуз Р. Структура пространства-времени. М., 1995.
241.	Петров Б.Н и др. Информационно-семантические проблемы в процессах управления и организации. М., 1977.
242.	Петровский И.Г. Лекции об уравнениях с частными производными. М., 1961.
243.	Петухов С.В. Биосолитоны. М., 1999.
244.	Плоткин Б. И. Группы автоморфизмов алгебраических систем // Математическая энциклопедия. М., 1966. Т. 4. С. 585. Термин "Представление бесконечных групп".
245.	Плоткин Б.И., Гринглаз Л.Я., Гварамия А.А. Элементы алгебраической теории автоматов. М., 1994.
246.	Поваров Г.П О групповой инвариантности булевых функций // Применение логики в науке и технике: Сборник. М., 1960. С. 263—341.
247.	Полак Л.С. Вариационные принципы механики. М., 1960.
248.	Поляк Б.Т., Цыпкин Я.З. Робастная устойчивость линейных систем И Итоги науки и техники. Сер. Техническая кибернетика. М., 1992. Т. 32.
249.	Понтрягин Л. С. Непрерывные группы. М., 1954.
250.	Понтрягин Л.С. и др. Математическая теория оптимальных процессов. М., 1961.
251.	Попов В.Н. Континуальные интегралы в квантовой теории поля и статистической физике. М., 1976.
252.	Постников М.М. Лекции по алгебраической топологии. Основы теории гомотопий. М., 1984.
253.	Постников М.М. Лекции по алгебраической топологии. Теория гомотопий клеточных пространств. М., 1985.
254.	Постников М.М. Лекции по геометрии. Семестр I. Аналитическая геометрия. М., 1986.
255.	Постников М.М. Лекции по геометрии. Семестр II. Линейная алгебра и дифференциальная геометрия. М., 1979.
256.	Постников М.М. Лекции по геометрии. Семестр II. Линейная алгебра. М., 1986.
257.	Постников М.М. Лекции по геометрии. Семестр III. Гладкие многообразия. М., 1987.
258.	Постников М.М. Лекции по геометрии. Семестр IV. Дифференциальная геометрия. М.. 1988.
259.	Постников М.М. Лекции по геометрии. Семестр V. Группы и алгебра Ли. М., 1982.
260.	Прангишвили И.В. Системный подход и общесистемные закономерности. М„ 2000.
261.	Прасад М.К. Инстантоны и монополи в теориях калибровочных полей Янга—Миллса // Геометрические идеи в физике: Сб. статей / Под ред. Ю.И. Манина; М„ 1983. С. 66—96.
262.	Прасолов В. В. Многочлены. М„ 2000.
263.	Пригожин И. Конец определенности. Время, Хаос и Новые Законы Природы. Ижевск, 1999.
264.	Проблемы социальной истории науки и техники: Сб. статей. М., 1996.
265.	Пугачев В.С., Синицын И.Н. Теория стохастических систем. М., 2000.
266.	Пугачев В.С., Синицын И.Н. Стохастические дифференциальные системы. М., 1985.
267.	Разумихин Б.С. Физические модели и методы теории равновесия в программировании и экономике. М., 1975.
268.	Райдер Л. Квантовая теория поля. М., 1987.
269.	Рапопорт Э.Я. Оптимизация процессов индукционного нагрева металла. М„ 1993.
341
270.	Рашевский П.К. Геометрическая теория уравнений с частными производными. М., 1947.
271.	Рождественский Б.Л., Яненко Н.Н. Системы квазилинейных уравнений. М., 1978.
272.	Розенвассер ЕЛ., Юсупов Р.М. Чувствительность систем управления. М., 1981.
273.	Рокафеллер А.Ф>. Выпуклый анализ. М., 1973.
274.	Рунд X. Дифференциальная геометрия финслеровых пространств. М., 1981.
275.	Садовничий В.А. Квантовый компьютер и квантовые вычисления. Регулярная и хаотическая динамика: Сб. статей. Ижевск, 1999.
276.	Самойленко Ю.И. Некоторые задачи управления электромагнитным полем // Кибернетика. 1970. № 3.
277.	Самойленко Ю.И., Губарев В.Ф., Кривонос Ю.Г. Управление быстропро-текающими процессами в термоядерных установках. Киев, 1988.
278.	Самуэльсон П. Экономика. М., 1964.
279.	Сарданашвили ГА. Современные методы теории поля. М., 1996. Т. 1.
280.	Сарданашвили Г.А. Современные методы теории поля. М., 1998. Т. 2.
281.	Сарданашвили ГА. Современные методы теории поля. М., 1999. Т. 3.
282.	Седов Л. И. Механика сплошной среды. М., 1970. Т. 1.
283.	Секей Г. Парадоксы в теории вероятностей и математической статистике. М., 1990.
284.	Сикорский Р. Булевы алгебры. М., 1969.
285.	Синг Дж.Л. Классическая динамика. М., 1963.
286.	Сингер А. Дифференциальная геометрия, расслоение пространства и физические теории И Физика за рубежом: Сборник. М., 1983.
287.	Сиразетдинов Т.К. Оптимизация систем с распределенными параметрами. М., 1977.
288.	Сиразетдинов Т.К. Устойчивость систем с распределенными параметрами. Новосибирск, 1987.
289.	Скорняков Л.А. Элементы теории структур. М., 1970.
290.	Слупецкий К, Борковский Л. Элементы математической логики и теория множеств. М., 1965.
291.	Смирнов В.М. Курс высшей математики. М., 1958. Т. 1.
292.	Смоляное О.Г, Фомин СВ. Меры на топологических линейных пространствах И У МН. 1976. Т. 31. С. 3—56.
293.	Соар Р.И. Вычислимо перечислимые множества и степени. Казань, 2000. Пер. изд.: Soare R. I. Recursively Enumerable Sets and Degrees. Springer-Verlag. Berlin etc., Cop., 1987.
294.	Соболев С. и др. Лженаучные работы Института автоматики и телемеханики Академии наук СССР (Раздел "Критика и библиография") // Большевик. 1941. № 9. Май. С. 90—-96.
295.	Спенсер Л. Гегель для начинающих. Ростов н/Д, 1998.
296.	Справочная книга по математической логике. М., 1982. Ч. I, II.
297.	Степанов В.В. Курс дифференциальных уравнений. М., 1953.
298.	Стоянов Й. Контрпримеры в теории вероятностей. М., 1999.
299.	Трее Ф. Введение в теорию псевдодифференциальных и интегральных операторов Фурье. М., 1984. 1'. 1, 2.
300.	Трикоми Ф. Лекции по уравнениям в частных производных. М., 1957.
301.	Трофимов В.В., Фоменко А.Т. Алгебра и геометрия интегрируемых гамильтоновых дифференциальных уравнений. М., 1995.
302.	Трусделл К. Первоначальный курс рациональной механики сплошных сред. М., 1975.
342
303.	Тьюринг А.М. Может ли машина мыслить? Саратов, 1999.
304.	Улам С. Нерешенные математические задачи. М., 1964.
305.	Успенский В.А., Семенов А.Л. Теория алгоритмов: основные открытия и приложения. М.„ 1987.
306.	Уткин В.И., Орлов Ю.В. Теория бесконечномерных систем управления на скользящих режимах. М., 1990.
307.	Фаддеев Л.Д. Энциклопедия математической физики. М., 1998.
308.	Федерер Г Геометрическая теория меры. М., 1987.
309.	Фёдоров А.Ю. Условия управляемости нелинейных динамических систем // Автоматика и телемеханика. 1984. № 4.
310.	Фейнман Р Квантовая электродинамика. М., 1997.
311.	Фейнман Р. Статистическая механика. М., 1978.
312.	Фейнман Р.Ф., Мориниго Ф.Б., Вагнер У.Г. Фейнмановские лекции по гравитации. М., 2000. Пер. изд.: Feynman R.P., Morinigo F.B., Wagner W.G. Feynman Lectures on Gravitation. Addison-Wesley Publishing Company (Advanced Book Program).
313.	Фейнман P., Хиббс А. Квантовая механика и интегралы по траекториям. М.. 1968.
314.	Фейс К. Алгебра: кольца, модули и категории. М., 1977. Т. 1.
315.	Фельдбаум А. А. Вычислительные устройства в автоматических системах. М., 1959.
316.	Фельдбаум А.А. Основы теории оптимальных автоматических систем. М., 1966.
317.	Фельдбаум А. А. Основы теории оптимальных систем. М., 1963.
318.	Фельдбаум А. А., Бутковский А.Г. Методы теории автоматического управления. М., 1971.
319.	Фельдбаум А.А. и др. Теоретические основы связи и управления. М., 1963.
320.	Филиппов А.Т. Многоликий солитон. М., 1990.
321.	Филиппов А.Ф. Дифференциальные уравнения с разрывной правой частью. М., 1985.
322.	Филиппов А.Ф. О некоторых вопросах теории оптимального регулирования // Вестник МГУ. Сер. Математика. 1959. № 2. С. 25—32.
323.	Философия, логика и методология пауки И Труды Международной конференции "Смирновские чтения". М., 1997.
324.	Финягина В.И. Моделирование подвижного управления в двумерных СРП // Известия АН СССР. Техническая кибернетика. 1989. № 6. С. 68—77.
325.	Финягина В.И. Реализация подвижного граничного управления в многомерных системах с распределенными параметрами // Конференция ученых России и стран Европы "Надежность механических систем" (Самара, 28—30 ноября 1995 г.): Тезисы докладов. Секция "Проблемы управления сложными системами". Самара, 1995.
326.	Флоренский П.А. Столп и утверждение истины. Сер. Из истории отечественной философской мысли. М„ 1990. Т. 1, 1а.
327.	Фоменко А.Т. Вариационные методы в топологии. М., 1983.
328.	Фон Нейман Дж. Общая и логическая теория автоматов // Тыоринг А.М. Может ли машина мыслить? Саратов, 1999.
329.	Фрейд 3. Неудобство культуры И Художник и фантазирование: Сборник. М„ 1985. С. 299—336.
330.	Фрейд 3. Эрос и смерть // Создание и разрушение: Сборник. М., 1998.
331.	Френкель А., Бар-Хиллел И. Основания теории множеств. М., 1966.
332.	Френкель Я.И. Статистическая физика. М.; Л., 1948.
343
333.	Фушич В.И., Никитин А.Г. Симметрии уравнений квантовой механики. М„ 1990.
334.	Хант Э., Мартин Д, Стоун Ф. Моделирование процессов формирования понятий на ВМ. М., 1970.
335.	Харди Г. Апология математики. Ижевск, 2000.
336.	Харитонов ВЛ. Полиномиальная устойчивость семейства систем линейных дифференциальных уравнений// Дифференциальные уравнения. 1978. Т. XIV. № 11.
337.	Хачатурян А.Г. Теория фазовых превращений и структур их твердых растворов. М., 1974.
338.	Хирш М. Дифференциальная топология. Новокузнецк, 1999.
339.	Хованский А.Г. Малочлепы. Сер. Библиотека математика. Вып. 2. М., 1997.
340.	Хозмюллер Д. Расслоенные пространства. М., 1970.
341.	Хыоитт Э., Росс К. Абстрактный гармонический анализ. М., 1978.
342.	Цирлин А.М. Оптимальные циклы и циклические режимы. М., 1985.
343.	Цыганков В.Д. Вселенная Хоукинга и нейрокомпьютер. М., 2000.
344.	Цыпкин Я.З. Адаптация и обучение в автоматических системах. М., 1968
345.	Цыпкин Я.З. Основы информационной теории идентификации. М., 1984.
346.	Чеботарев Н.Г Теория групп Ли. М.; Л., 1940.
347.	Черноусько Ф.Л. Декомпозиция и синтез управления в динамических системах И Известия АН СССР. Техническая кибернетика. 1990. № 6. С. 64—82.
348.	Черч А. Введение в математическую логику. М., 1960.
349.	Шафаревич И.Р. Основные понятия алгебры. Ижевск, 1999.
350.	Шафаревич И.Р. Основы алгебраической геометрии. М., 1972.
351.	Шварц А. С. Квантовая теория поля и топология. М., 1989.
352.	Шварц Л. Анализ. М., 1972.
353.	Шеннон К. Машины для игры в шахматы // Работы по кибернетике и теории информации: Сборник. М., 1963.
354.	Шенфилд Дж. Математическая логика. М., 1975.
355.	Шеффер X. Топологические векторные пространства. М., 1971.
356.	Шилов ГЕ. Введение в теорию линейных пространств. М., 1956.
357.	Шилов ГЕ. Математический анализ. Функции нескольких действительных переменных. М., 1972.
358.	Шилов ГЕ. Математический анализ. Конечномерные линейные пространства. М., 1969.
359.	Шилов ГЕ. Математический анализ. Функции нескольких вещественных переменных. М., 1972.
360.	Шипов ГИ. Теория физического вакуума. М., 1993.
361.	Шиханович Ю.А. Введение в современную математику. М., 1971.
362.	Шубин М.А. Псевдо дифференциальные операторы и спектральная теория. М„ 1978.
363.	Шубников А.В., Копцик В.А. Симметрия в науке и искусстве. М., 1972.
364.	Шульц Д., Шульц С.Э. История современной психологии. СПб, 1998.
365.	Шутц Б. Геометрические методы математической физики. М., 1984.
366.	ЭйзенхартЛ.П. Непрерывные группы. М., 1947.
367.	Эпштейн В.Л. Гипертекст и гипертекстовые системы. М., 1998.
368.	Яковенко ГН. Групповые свойства динамических систем. Конечномерный случай. М., 1994.
369.	Янг Л. Лекции по вариационному исчислению и теории оптимального управления. М., 1974.
344
370.	Яценко В.А. Инвариантное описание одного класса нелинейных управляемых систем // Сб. материалов совещания “Теория и практика использования методов агрегирования в планировании и управлении”. Ереван, 1986. С. 251—258.
371.	Aaltonen М., Tanttu J., Pohjolainen S. A Distributed Parameter System Simulator//Simulation. 1986. № 47:4. P. 145—151.
372.	Ahmavaara Y. The Cybernetic Theory of Development. (Mathematical Model for Re-Evaluation of the Is-Ought Problem). Helsinki: Tammi, 1974.
373.	Ahmed N.U., Teo K.L. Optimal Control of Distributed Parameter Systems. North-Holland Publ. Co. Amsterdam, N.-Y., Oxford, 1981.
374.	Aktas G. etc. Strings and Symmetries. Springer, 1995.
375.	Aldrovandi R., Pereira J.G. An Introduction to Geometrical Physics. World Scientific, 1999.
376.	Amari S., Kurata K., Nagaoka H. Information Geometry of Boltzmann Machine // IEEE Transactions on Neural Networks. 1992. March. Vol. 3. № 2.
377.	Ashby W.R. An Introduction to Cybernetics. Chapman and Hall Ltd and University Paperback, 1971.
378.	Ashby W.R. Design for a Brain. N.-Y.: John Willey and Sons, Inc., 1952.
379.	Atiyah M. Geometric and Physics of Knots. Cambridge University Press. Cambridge; N.-Y.; Sydney, 1990.'
380.	Aziz A.K. Control Theory of Systems Governed by Partial Differential Equations. Academic Press, N.-Y., 1977.
381.	Bachman G. Elements of Abstract Harmonic Analysis. N.-Y.: Academic Press, 1966.
382.	Baggett Laurence W. Functional Analysis. Marcel Dekker Inc., 1992.
383.	Baldomir D., Hammond P. Geometry of Electromagnetic Systems. Clarendon Press, Oxford, 1996.
384.	Barmish B.R., Fu M., Salesh S. Stability of a polytope of matrices: counterexamples// IEEE Trans. Autom. Control. 1988. Vol. ЛСЗЗ. № 6. P 569—572.
385.	Barnett S., Storey C. Matrix Methods in Stability.Theory. Great Britain: Nelson and Sons, 1970.
386.	Baumann G. Symmetry Analysis of Differential Equation with Mathematics. Springer, 1999.
387.	Bellman R. Introduction to Matrix Analysis. N.-Y.: McGrow-Hill Book Company, 1960.
388.	Benaserraf P., Putman H. Philosophy of Mathematics. Cambridge: Cambridge Univ. Press, 1985.
389.	Bernstein D.L. Existence Theorem in Partial Differential Equations. Princeton Univ. Press, 1950.
390.	Blaquiere A. Systems Theory: A New Approach to Wave Mechanics // Journal of Optimization Theory and Applications. 1980. № 4. P. 463—478.
391.	Blauberg I.V., Sadovsky V.N., Yudin E.G. Systems Theory (Philosophical and Methodological Problems). Moscow: Progress Publishers, 1977.
392.	Boothby W.M. An Introduction to Differential Manifolds and Riemannian Geometry. Academic Press, 1975.
393.	Borden Robert S. A Course in Advaced Calculus. Dover Publications, 1998.
394.	Brockett R. Characteristic Phenomena and Model Problems in Nonlinear Control // Proceedings of 13th Triennial World Congress. San Francisco, USA, 1996.
395.	Brown James Ward, Churchhill Ruel V. Complex Variables and Applications. McGrow Hill Book Co. International Edition, 1996.
396.	Budach I. etc. Algebraic and Topological Properties of Posets. Teubner; Leipzig, 1988.
345
397.	Burke W.L. Applied Differential Geometry. Cambridge University Press, 1981.
398.	Burkill J.C. The Lebesgue Integral. Cambridge University Press, 1961.
399.	Burton T.A. Stability and Periodic Solutions of Ordinary and Functional Differential Equations. Academic Press, 1985.
400.	Butkovskiy A.G. A Geometric Theory of Control for Systems with Distributed Parameters // Journal of Computer and Systems Sciences International. Scripta Technica, Inc., 1996. №34(5). P. 1—40.
401.	Butkovskiy A.G. Contribution to the Programme of “Unified Geometric Theoiy of Control (UGTC)” // Proceedings of the 1 -st International Conference ‘Control of Oscillations and Chaos (COC’97)’. (St. Peterburg, Russia, August 27—29, 1997). St. Peter-burg. 1997. Vol. 2 of 3. P. 287—290.
402.	Butkovskiy A.G. Distributed Control Systems. American Elsevier Publ. Co. N.-Y., USA, 1969.
403.	Butkovskiy A.G. Geometrical Approach to the Controlled Differential Systems (CDS) И Systems Science. 1996. Vol. 2. № 2. P. 5—11.
404.	Butkovskiy A.G. Geometrical Approach to the Controlled Differential Systems // Proceeding of the 12th International Conference on Systems Sciences. (September 12—15, Wroclaw, Poland). Oficyna Wydawnicza Politechniki Wroclawskiej, Wroclaw, 1995. Vol. II. Systems Engineering Control Engineering Flexible Manufacturing Systems. P. 29—34.
405.	Butkovskiy A.G. Geometrical Structures in Control Theory // Proceedings of the 13th International Conference on Systems Science (15—18 September 1998, Wroclaw, Poland). Oficyna Wydawnicza Politechniki Wroclawskiej, Wroclaw, 1998. Vol. 1. p. 44—49.
406.	Butkovskiy A.G. Green's Functions and Transfer Functions. Ellis Horwood Publ., England, 1982.
407.	Butkovskiy A.G. Mathematical Structures in the Theory of Control and Systems // Proceedings of the International Congress “Nonlinear Analysis and its Applications” (Moscow, Russia, September 1—5, 1998). Moscow, Mechanical Engineering Research Institute (MERI), Russian Academy of Sciences (RAS), 1998. P. 81.
408.	Butkovskiy A.G. Nature and Human World from Control Point of View // Proceedings of "Einstein Meets Magritte" Conference (Brussels, Belgium, May 29—June 03, 1995).
409.	Butkovskiy A.G. Phase Portraits of Control Dynamical Systems (Differential Inclusions). Kluwer Academic Publishers. Dordrecht; Boston; London. 1991.
410.	Butkovskiy A.G. Some Principal Features of “Unified Geometric Theory of Control (UGTC)” or “Theory of Control Structures (TCS)” // Problems of Nonlinear Analysis in Engineering Systems. International Journal. Kazan. International Federation of Nonlinear Analysis. Nonlinear Sciences Academy. KS7U of A.N. Tupolev’s name. 1998. P. 9—15.
411.	Butkovskiy A.G. Structural Theory of Distributed Systems. Ellis Horwood Publ., England, 1983.
412.	Butkovskiy A.G. To the Theory of Control Structures // Труды V Международного семинара “Устойчивость и колебания нелинейных систем управления” (Москва, Россия, июнь 1998 г.): Тезисы докладов. М., 1998. С. 68.
413.	Butkovskiy A.G. Towards Axiomatic Theory of Control // Proceedings of the International Conference on Control Problems “60th Anniversary of the Institute of Control Sciences” (June 27—July 3, 1999, Moscow). Moscow, Institute of Control Sciences, 1999
346
414.	Butkovskiy .4 G'. Towards the Unified Geometric Theory of Differential Systems with Control // XI llcrbstsehule "Variationsrechnung, Optimale Prozesse und An-wendungen". Plenary Session (13—18 September, 1993, Stralsund Germany 'Variationsrechnung, Optimale Pro/esse und Anwendungen'). Preprint-Reihe Mathematik Greifswald, Germany. 1994. № 1. P. 5-—-8.
415.	Butkovskiy A.G. Towards Geometrization of Control // Journal of Computer and System Sciences International. Scripta Technica, Inc. 1997. Vol. 36. № 1.
416.	Butkovskiy A.G., Babichev A.V., Finyagina V.I. Symmetries and Structures, Systems and Control // Proceedings of International Scientific-Practice Conference “Control for Large Systems” (Russia Academy of Sciences, Institute of Control Sciences, National Committee of IFAC) (Moscow, Russia, September 22—26, 1997). Moscow, 1997. P. 306—307.
417.	Butkovskiy A.G., Pohjolainen S. Structural Method for Modelling and Simulations of Distributed Parameter Systems // AIRO'91 Conference "Operations Research and Knowledge—Based Models and Systems" (Riva del Garda, Italy, 18—20.09, 1991). Riva del Garda, 1991.
418.	Butkovskiy A.G., Pustilnikov L.M. The Mobile Control of Distributed Parameter Systems. Ellis Horwood Ltd. Publ., England, 1987.
419.	Butkovskiy A.G., Pustilnikov L.M. Characteristics of Distributed-Parameter Systems. Handbook of Equations of Mathematical Physics and Distributed Parameter Systems. Kluwer Academic Publishers. Dordrecht; Boston; London, 1993.
420.	Butkovskiy A.G., Samoilenko Yu.I. Control of Quantum-Mechanical Processes and Systems. Kluwer Academic Publishers. Dordrecht; Boston; London, 1990.
421.	Choquet-Bruhat K, De Witt-Morette C., Dillard-Bleick H. Analysis, Manifolds and Physics. North Holland, 1982.
422.	Chung K.L., Zhao Z. From Brourn Motion to Schrodinger's Equations. Springer, 1995.
423.	Cohn P Algebra. John Willey and Son, 1989. V. 1, II.
424.	Cannes A. Noncommutative Geometry. N.-Y.: Academic Press, 1994.
425.	CotlarM., Cignoli R. An Introduction to Functional Analysis. North Holland, 1965.
426.	Curtain R.F., Pritchard A.J. Infinite Dimensional Linear Systems Theory. Berlin: Springer Verlag, 1978.
427.	Dairs P C., Brown J. Superstring: A Theory of Everything? N.-Y.: Cambridge Univ. Press, 1988.
428.	Davis P.J., Hersh R. The Mathematics Experience. Penguin Books, 1981.
429.	Demetrios G.Magiros. Selected Papers / Ed. by S.G. Tzafestas. Dordrecht: Reidel Publishing Co, 1985.
430.	Di S., Poliquin R. Contingent Cone to a Set Difmcd by Equality and Inequality Constraints at a Frechet Differentiable Point// J. Optimiz. Theory and Appl. 1994. V. 81. № 3. P. 469—478.
431.	Dubrovin B.A., Fomenko A.T., Novikov S.P. Modem Geometry. N.-Y.: Springer Verlag, 1985. № 1,2.
432.	Differential Geometry and Control. AMS Conference. 1999. Vol. 64. www.ams.org/bookstore/. Order code: PSPU M/64SN95.
433.	Dirac P.A.M. The Relation between Mathematics and Physics // Proc, of the Royal Soc. Edinburg. 1938. Vol. 59. P. 122—129.
434.	Dyson F. Mathematics in Physical Sciences // Scientific American. 1964. Vol. 211.№3.P. 128—146.
435.	Eisenhart L.P. Continous Groups of Transformations. N.-Y., 1933.
436.	Encarta 98 CD Electronic Encyclopaedia.
347
437.	Encyclopedic Dictionary of Mathematics, 2nd ed. MIT Press, 1993. (EDM2).
438.	Escultura E.E. Set-Valued Differential Equations and Applications to Quantum Gravity // The Third International Conference "Differential Equations and Applications" (June 12—17, 2000, Saint Petersburg). Book of abstracts, 2000. P. 39.
439.	Existance and Uniqueness of Integral Curves (Frobeniqus Theorem). Encyclopaedic Dictionary of Mathematics (EDM2) (Second Edition. Vol. 1 (A-N), vol. 2 (O-Z)). MIT Press, 1993. Vol. 1. P. 1075.
440.	Falb P. Methods of Algebraic Geometry in Control Theory. MIT, Cambridge MA, 1999. Part II.
441.	Felsager B. Geometry, Particles and Fields. Springer, 1998.
442.	Feynman R.P. Quantum Electrodynamic. N.-Y.: W.A. Benjamin, Inc., 1961.
443.	Feynman R.P. Statistical Mechanics. W.A.Benjamin, Inc. Massachusetts, 1972.
444.	Feynman R.P., Hibbs A.R. Quantum Mechanics and Path Integral. N.-Y.: McGrow-Hill Book Company, 1965.
445.	Finyagina V.I., Kubishkin V.A. A Method for Designing Program Boundary Controls for Multidimentional Distributed Parameter Systems // Soviet Journal of Computer and Systems Sciences International. Scripta Technica, Inc. 1994. Nov.-Dec. Vol. 33. №6.
446.	Finyagina VI., Kubishkin V.A. Research Methods for Control Systems with Mobile Action Sources // Proceedings of International Congress “Non-Linear Analysis and its Applications”. Section “Non-Linear Control Theory” (Moscow, 1998). Moscow, 1998.
447.	Fraisse R. Theory of Relations. North-Holland, 1986.
448.	Fraleigh J.B. Abstract Algebra. Addison-Wesley Publishing Company, 1999.
449.	Frankel T. The Geometry of Physics: an Introduction. Cambridge University Press, 1997.
450.	Friedman A. Foundations of Modem Analysis. N.-Y.: Dover Publications Inc., 1982.
451.	Fuhrmann P.A. Linear Systems and Operators in Hilbert Space. McGrow Hill Book Co, 1981.
452.	Gelbaum B.R., Olmsted J.M.H. Counterexamples in Analysis. San Francisco: Holden-Day, Inc., 1964.
453.	Gersting J.L. Mathematical Structures for Computer Science (4th edition). N.-Y.: Freeman and Co, 1999.
454.	Giles J.R. Introduction to the Analysis of Metric Spaces. Cambridge University Press, 1987.
455.	Goldberg S.I. Curvature and Homology. N.Y.: Dover Publications Inc., 1982.
456.	Goldstain H. Classical Mechanics. Addison-Wesley Press. Inc. Cambridge 42. Mass, 1982.
457.	Goldstein L.G. Abstract Algebra: A First Course. Prentice Hall. Inc., Englewood Cliffs, New Jersey, 1973.
458.	Grassman IV. K, Tremblay J.P. Logic and Discrete Mathematics. Prentice Hall, 1999.
459.	Griffiths P.A. Extorior Differential Systems and the Calculus of Variations. Birkhausen; Boston; Basel; Stuttgart, 1983.
460.	Grossman S.I. Multivariable Calculus, Linear Algebra and Differential Equations. 3-th Edition. International Edition, Sundess College Publishing, Harcout Brace College Publishing. 1995. Library of Congress Catalogue Cod № 94-21766.
461.	Hagelin J.S. Restructuring Physics from its Foundation in Light of Maharishi's Vedic Science. Maharishi International University, Fairfield, Iowa. September, 1989. (MIU-THP-89/48).
462.	Halmos P.R. Naive Set Theory. Princeton, N.J., 1967.
463.	Hamalainen T, Pohjolainen S. A Finite-Dimensional Robust Controller for Systems in the CD-Algebra// IEEE Tr. Aut. Control. 2000. Vol. 42. № 3. March. P. 421^131.
348
464.	Hamalainen Г, Poltjolamcn 8 Multivariable Tuning Regulate» loi Di itib uted Parameter Systems (invited (taper) // International Journal of Robust tind Nonina u Control, Special Issue. 1996. Vol 6. I’. 479—500.
465.	Hamalainen /', Polijolainen S. The Design of Linear Controllers with Symboli. Algebra//Computers & Mathematics with Applications. 1996. Vol. 32. № 7. P. 105—116.
466.	Hamming R. IV Ihc Unreasonable Effectiveness of Mathematics // American Mathematical Monthly. 1980. February. Vol. 87. № 2.
467.	Hao Wang, McNaughton R. Les Systemes Axiomatiques De La Theorie Des Ensembles. Paris: Gathier-Villars, 1953.
468.	Hilbert I)., Ackermann IT. Grundzuge der theoretischen Logik. N.-Y., 1946.
469.	Holtzman J.M. Nonlinear System Theory. Prentice Hall, Englwood, Cliffs, NcwJersy, 1970.
470.	Hopcroft J., Ullman J. Introduction to Automata Theory, Languages and Computation. Addison-Wesley Press. Inc. Cambridge 42. Mass, 1979.
471.	Horn Roger A., Johnson Charles R. Matrix Analysis. Cambridge University Press, 1985.
472.	Horn Roger A., Johnson Charles R. Topics in Matrix Analysis. Cambridge University Press, 1991.
473.	Hutchinson A. Algorithmic Learning. Oxford, Clarendon Press, 1994.
474.	Hutson V., Pym J.S. Applications of Functional Analysis and Operator Theory. Academic Press, 1980.
475.	Irwin M.C. Smoth Dynamical Systems. Academic Press. N.-Y.; London, 1980.
476.	Jacobson N. Lie Algebras. N.-Y.; London: John Wiley and Son, 1977.
477.	Jonassen DJI. Supporting Communities of Learners with Technology: A Vision for Integrating Technology with Learning in Schools // Educational Technology. N.-Y. 1995. P. 60—63.
478.	Jones Neil D. Computerbility Theory (an Introduction). Academic Press. N.-Y.; London. 1973. P. 1—154.
479.	Jurdjevic V., Sussmann H.J. Control Systems on Lie Groups // Journal of Differential Equations. 1972. № 12. P. 313—329.
480.	Kass R E. The Geometry of Asymptotic Inference // Statistical Science. 1989. Vol. 4. № 3. P. 188—234.
481.	Keister M.J. Mathematical Logic and Computability. N.-Y.: McGrow Hill Book Co, 1999.
482.	Klaassen K.B. Electronic Measurement and Instrumentation. Cambridge Univ. Press, 1996.
483.	Kline M. Mathematics: The Loss of Certainty. N.-Y.: Oxford Univ. Press, 1980.
484.	Kolman B., Busby R.C. Discrete Mathematical Structures for Computer Science. Prentice Hall International Editions, 1987.
485.	Kolmogorov A.N., Fomin S. И Introducting Real Analysis. Dover Publications. Inc., N.-Y., 1975.
486.	Kron G. Tensor Analysis of Networks. N.-Y.: John Willey and Sons, Inc., 1965.
487.	Kuratovski K., Mostovski A. Set Theory. North Holland Publishing Company, Amsterdam, Polish Scientific Publishers, Warszawa, 1967.
488.	Lakotos I. Proofs and Refutations. Cambridge: Cambridge Univ. Press, 1976.
489.	Lang S. Introduction to Differentiable Manifold. N.-Y.: Columbia University, 1962.
490.	Lankaster P. Theory of Matrices. N.-Y.: Academic Press, 1969.
491.	Leinonen T, Ruokamo H. KUOMA — Learning Environment -— An Implementation and Evaluation of Collaborative Project Learning in the World Wide Web // In Gil-Mendieta, M.H. Hamza (eds.). Computers and Advanced Technology in Education (CATE'98). Proceedings of the IASTED International Conference. A Publication of the
349
International Association of Science and Technology for Development—LASTED. LASTED/ACTA Press. Anaheim, Calgary, Zurich. CATE’98 Conference. May 27—30, 1998. Cancun. Mexico, 1998. P. 134—137.
492.	Liao X.X, Мао X. Razumikhin Type Theorem (in the paper 'Exponential Stability' of Stochastic Delay Interval Systems') // Systems and Control Letters. 2000. № 40. P. 171—181.
493.	Mangiarotti L., Sardanashvily G. Connections in Classical and Quantum Field Theory. National Academic Press USA, 2000.
494.	Marsden J.E. Lectures on Mechanics. LMS Lecture Note Series. Cambridge University Press, 1991.
495.	Mesarovich M.D. Views on General Systems Theory. Proceedings of the Second Systems Symposium at Case Institute of Technology. N.-Y.: John Willy & Sons, 1964.
496.	Mesarovich M.D., Takahara Ya. General Systems Theory: Mathematical Foundations. Academic Press. N.-Y., 1975.
497.	Metakides G., Nerode A. Principles of Logic and Logic Programming. Amsterdam: Elsevier, 1996.
498.	Misner C.W., Thorne K.S., Wheeler J.A. Gravitation. San Francisco: V.H. Freeman and Company, 1973. Vol. I, II, III.
499.	Multisilta J., Pohjolainen S. Hypermedia and Animation in CACSD Education // Int. J. Math.Educ. Sci. Tcchnol. 1995. Vol. 26. № 4. P. 599—618.
500.	Murray F.J., Mullar K.S. Existence Theorem for Ordinary Differential Equations. N.-Y.: Univ. Press, 1954.
501.	Misner C.W., Thorne K.S., Wheeler J.A. Towards Geometrization of Control // Journal of Computer and System Sciences International. 1997. Vol. 36. № 1. January— February.
502.	Nakahara M. Geometry, Topology and Physics. Adam Hilger, 1990.
503.	Neetman E. Science, Religion and Reality. Eddington, 1925.
504.	Ochionero F. Birth of the Universe and Fundamental Physics. Springer, 1995.
505.	Olver P. Applications of Lie Groups to Differential Equations. Springer Verlag. N.-Y.; Berlin; Heidelberg; Tokyo, 1986.
506.	Parathasarathy K.R. Probability Measures on Metric Spaces. Academic Press, N.-Y., 1967.
507.	Patterson E.M. Topology. Oliver and Boyd, Edinburg and London; N.-Y.: In-tcrsciencc Publishing, Inc., 1963.
508.	Pohjolainen S. A Feedforward Controller for Distributed Parameter Systems // Int. J. Control. 1981. Vol. 34. № 1. P. 173—184.
509.	Pohjolainen S. Computation of Transmission Zeros for Distributed Parameter Systems//Int. J. Control. 1981. Vol. 33. P. 199—212.
510.	Pohjolainen S. On the Optimal Tuning of a Robust Controller for Parabolic Distributed Parameter Systems // Automatica. 1987. Vol. 23. P. 719—728.
511.	Pohjolainen S. Robust Controller for Systems with Exponentially Stable Strongly Continuous Semigroups // J. Math., Anal. & Appl. 1985. Vol. 111. November. P. 622—636.
512.	Pohjolainen S. Robust Multivariable Pl-Controller for Infinite-Dimensional Systems 11 IEEE Tr. Aut. Control. 1982. Vol. 27. № I. P. 17—31.
513.	Pohjolainen S. etc. On the Design and Evaluation of an Open Learning Environment (invited paper) // Special Issue, Virtual Laboratories: Simulations, Models, Microworlds. International Journal of Continuing Engineering Education and Life-Long Learning. 1999. Vol. 9. № 2. P. 249—261.
350
514.	Pohjolainen .S', / atti / Robust (out roller for Boundaiy < 'onliol Sy n nm // Ini J. Control. 1983 Vol 18 о 1» 1189 1197.
515.	Pohjolainen .S', Multisilta J., Antenev K. A Hypermedia Learning Environment for the Mathematical Sciences // Human Interaction in Symbolic Computation. Texts and Monographs in Symbolic Computation. Springer, 1998.
516.	Pohjolainen Л'., Multisilta J., Antchev K. Matrix Algebra with Hypermedia (invited paper) // Education & Information Technologies. 1996. Vol 1. № 2. P. 123—141.
517.	Pohjolainen V, Ruokamo H Distance Learning in the Multimedia Networks Project: Current State of the Art and Perspectives for Future // In Gil-Mendieta, M.H.Hamza (cds.). Computers and Advanced Technology in Education (CATE'98). Proceedings of the IASTED International Conference. A Publication of the International Association of Science and Technology for Development — LASTED. LASTED/ACTA Press. Anaheim, Calgary, Zurich. CATE'98 Conference. May 27—30, 1998. Cancun. Mexico, 1998. P. 91—95.
518.	Post E.J. Formal Structure of Electromagnetics. North-Holland Publ. Co. Amsterdam, 1962.
519.	Prigogine I. The End of Certainty. Time, Chaos and New Lows of Nature. Free Press, 1997.
520.	Quality in Optimization (article Non-linear Programming). Encyclopaedic Dictionary of Mathematics (EDM2). (Second Edition. Vol. 1 (A-N), vol. 2 (O-Z)). MIT Press, 1993. Vol. 1. P. 1097.
521.	ReiglerHJ. Mathematical Logic and Computability. McGrow Hill Book Co, 1996.
522.	Richtmyer R.D. Principles of Advanced Mathematical Physics. Springer Verlag. N.-Y.; Heidelberg; Berlin, 1981. Vol. 2.
523.	Rivasseav Ж Constructive Physics. Springer, 1995.
524.	Rockafellar R.T. Convex Analysis. Princeton, N.J.: Princeton University Press, 1970.
525.	Rosen J. Symmetry in Science. Springer, 1995.
526.	Rubinfeld R. On the Robustness of Functional Equations // SIAM Journal on Computing. Paper published electronically. 1999. June, August. Vol. 28. № 6. P. 1972—1997.
527.	RundH. The Differential Geometry of Finsler Spaces. Berlin: Springer-Verlag, 1959.
528.	Ruokamo H., Pohjolainen S. Distance Learning in a Multimedia Networks Project: Main Results (invited paper) // British Journal of Educational Technology. 2000. Vol. 31. №2. P. 117—125.
529.	Ruokamo H., Pohjolainen S. Pedagogical Principles for Evaluation of Hypermedia Based Learning Environments in Mathematics // Journal for Universal Computer Science (invited paper). 1988. № 4 (3). P. 292—307, http://www.iicm.edu/jucs.
530.	Ruokamo-Saari H., Pohjolainen S. Pedagogical Issues for the Design of a Hypermedia-Based Learning Environment (HBLE) // In D. Dicheva, I. Stanchev (eds.). Proceedings of the IFIP WG 3.3 Working Conference, Human Computer Interaction and Educational Tools (HCI-ET) (Sozopol, Bulgaria. May 27—28, 1997). Sozopol, 1997. P. 82—91.
531.	Russel B. The Analysis of Matter. London: Georg Allen and Unwin Ltd, 1959.
532.	Ryder L.H. Quantum Field Theory. Cambridge University Press, 1984.
533.	Samuelson P.A. Economics. Fifth Edition. N.-Y.: McGrow Hill Book Co, 1961. Chapter 4.
534.	Schikhov W. (Шихов В.). An Introduction to p-adic Analysis. Cambridge. Cambridge Studies in Adv. Math. 4, 1984.
535.	Schutz B.F. Geometrical Methods of Mathematical Physics. Cambridge University Press, 1982.
536.	Sikorski R. Boolean Algebras. Berlin; Gottingen; Heidelberg, 1964.
351
537.	Simmons G.F. Introduction to Topology and Modem Analysis. McGrow Hill Book Co, 1963.
538.	Singer I.M. Physics Today. 1982. March. P. 41.
539.	Slupecki J., Borkowski L. Elementy logiki matematycznej i teorii mnogosci. Warszawa, 1963.
540.	Song Jian, Yu Jingyuan. Population System Control. Berlin: Springer Verlag; Beijing: China Academic Publishers, 1988.
541.	Spivak M. Calkulus on Manifolds. W.A. Benjamin Inc., 1965.
542.	Steen L.A., Seebach J.A. Counterexamples in Topology. Holt, Rinehart and Winston, Inc., N.-Y. at al, 1970.
543.	Synge J.L. Classical Dynamics. Handbuck der Physik. Encyclopedia of Physics / Ed. by S.FL GGE/Marburg. Vol. III/1. Springer Verlag/ Berlin; Guttingen; Heidelberg, 1960.
544.	Szekely G.J. Paradoxes in Probability Theory and Mathematical Statistics. Budapest: Akademiai Kiado, 1986.
545.	Truesdell C. A First Course in Rational Continuum Mechanics. Baltimore: The John Hopkins University, 1972.
546.	Turunen E. Mathematics Behind Fuzzy Logic. Physica-Verlag, Aspringer-Verlag Co, 1999.
547.	Van der Schaft A.T. Observability and Controllability for Smooth Nonlinear Systems // SIAM J. Contr. and Optim. 1982. V. 20. № 3. P. 338—354.
548.	Van der Warden B.L Algebra. Springer, 1967.
549.	Vidyasagar M. Nonlinear Systems Analysis. Prentice Hall, New Jersy, 1993.
550.	Von Westenholz C. Differential Forms in Mathematical Physics. Amsterdam: North Holland, 1981.
551.	Wang P.K.C. On the Feedback Control of Distributed Parameter Systems // International Journal of Control. 1966. № 3. P. 255—273.
552.	Weisskopf Victor F. Physics in the Twentieth Century. MIT Press, 1972.
553.	Young L.C. Lectures on the Calculus of Variations and Optimal Control Theory. W.B: Sounders Company, 1969.
Научное издание
Бабичев Александр Владимирович
Бутковский Анатолий Григорьевич, Похьолайнен Сеппо К ЕДИНОЙ ГЕОМЕТРИЧЕСКОЙ ТЕОРИИ УПРАВЛЕНИЯ
Утверждено к печати Ученым советом
Института проблем управления им. В. А. Трапезникова РАН
Зав. редакцией Р.С. Головина. Редактор И.С.Лицов
Художник ТВ. Болотина. Художественный редактор В.Ю. Яковлев Набор и верстка выполнены в издательстве на компьютерной технике
ЛР № 020297 от 23.06.1997
Налоговая льгота -
общероссийский классификатор продукции ОК-005-93, том 2; 953000 - книги, брошюры
Подписано к печати 26.07.2001. Формат 60х 90*/1б. Гарнитура Таймс. Печать офсетная
Усл.печ.л. 22,0. Усл.кр.-отт. 22,0. Уч.-изд.л. 23,0. Тип. зак. 4170
Издательство "Наука", 117997 ГСП-7, Москва В-485, Профсоюзная ул., 90 Санкт-Петербургская типография "Наука", 199034, Санкт-Петербург В-34, 9-я линия, 12