»f

Яков Дымдрский Ирина 3abipah
Эм CTATU О ТОПОЛОГИИ- ИАУК1, ИЗУЧАЮЩЕЙ САИЫ1 ГЛОЫЛкЩ	Па •ИГУ», II ИХ С1ОЙСТ1А, КОТОРЫ1 HI
ИЗН1Н1ЮТС1 ПРИ РАЗЛИЧНЫХ Д1ФОРМАЦН1Х ФИГУР: НЗГИ1ДНИ1Д	3 ГАСТ1Ж1НИ1Х... ОДНИМ И] ТАКИХ ТОПОЛОГИ-
Ч1СКНХ HHIAPHAHTO1IMIITCI (ОЛНЧ1СТ1О ТОЧ1К П1Р1С1Ч1НН1 Д1УХ ЗАМКНУТЫХ КРИ1ЫХ НА ПОМРХНОСТН, 1СЛИ, ПРА1ДА, СО0ТНТСТ1УЮЩИМ OIPA3OM УСЛО1ИТкС11ЫЧНСЛШ 1ТО КОЛНЧ1СТ1О. Но - ICI ПО ПОР1ДКУ.
Тор
Бублик— толстая баранка. СИ. Ожегов. Словарь Русского языка
Проще всего сказать, что тор — это поверхность бублика. Определение, конечно, наглядное, но для решения математических задач не очень удобное. Геометрически тор Т получается при вращении окружности S2 вокруг оси I (рис. 1). Во время вращения точка О движется по окружности Sy На каждой точке С окружности S, «навешена» окружность, равная S2 и полученная поворотом S2 вокруг оси I на угол ОМС.
Исследовать тор удобно с помощью его развертки. Разрезав Т по S2 и разогнув его, получим боковую поверхность цилиндра
(рис. 2). Точки окружности S2 при этом, если так можно выразиться, раздвоились, а окружность S, превратилась в отрезок. Теперь режем по этому отрезку и разворачиваем, — получаем прямоугольник (рис. 3). Пользоваться прямоугольником проще, нежели тором. Необходимо только помнить, что одна и та же точка тора может изображаться двумя или даже четырьмя точками прямоугольника.
Упражнения
1. Где должна находиться точка тора, чтобы иметь: а) одно; 6) два; в) четыре изображения на прямоугольнике?
2. Назовите полуостров, принадлежащий России, который на политической карте мира обычно имеет два изображения.
Разрезав тор  по  S2 и  S,, мы  автома-
Рнсунок 2
О
о
I
Рисунок 1
ОС	О
Рисунок 3

18
ЯКОВ ДЫМАРСКИ^,  ИРИНА ЗАВСРАЧ
У
—*
Уо
4
а
Ф
А
•
Рисунок 4
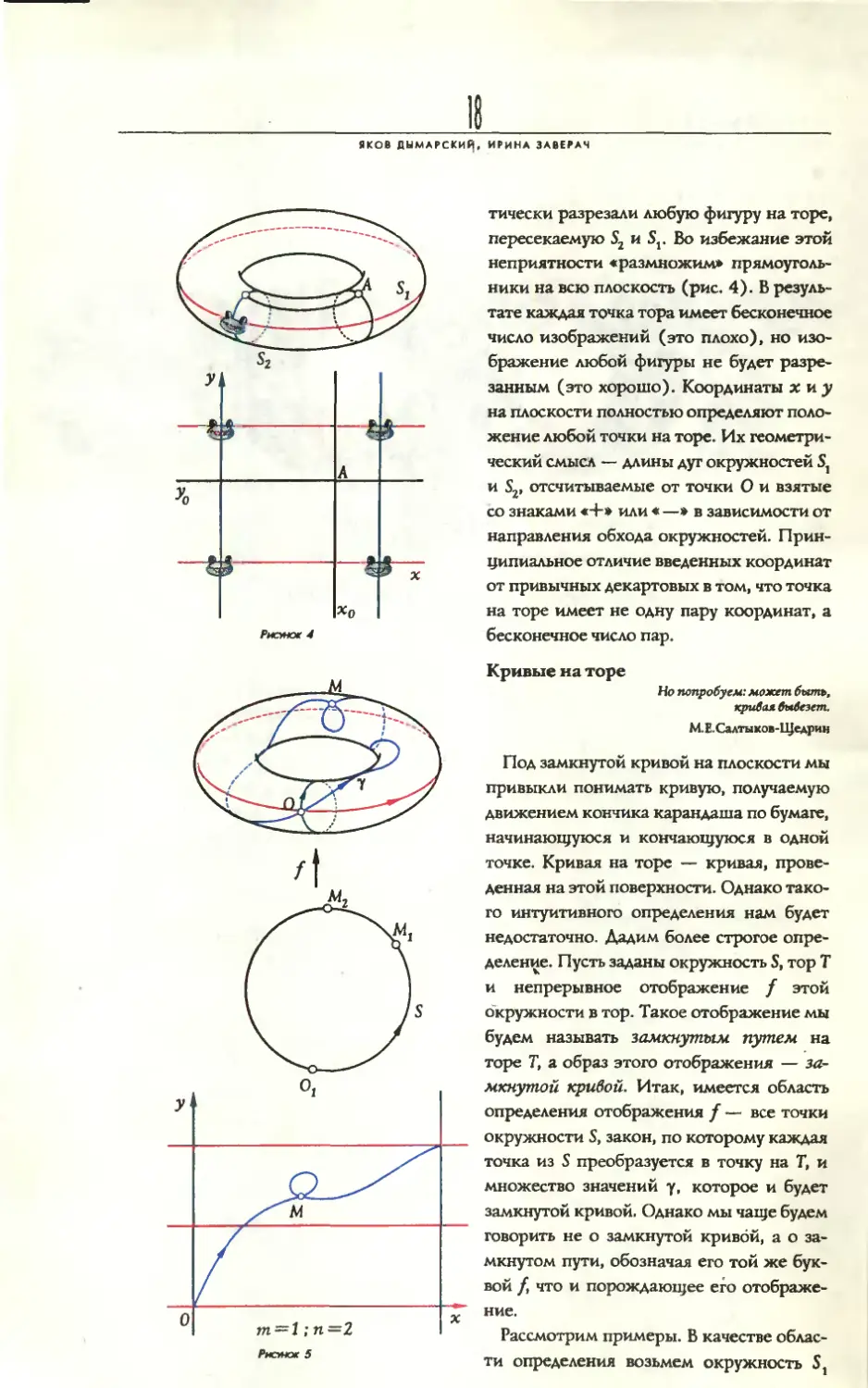
тически разрезали любую фигуру на торе, пересекаемую S2 и Sr Во избежание этой неприятности «размножим* прямоугольники на всю плоскость (рис. 4). Б результате каждая точка тора имеет бесконечное число изображений (это плохо), но изображение любой фигуры не будет разрезанным (это хорошо). Координаты х и у ня плоскости полностью определяют положение любой точки на торе. Их геометрический смысл — длины дуг окружностей S, и Sv отсчитываемые от точки О и взятые со знаками «+» или « —» в зависимости от направления обхода окружностей. Принципиальное отличие введенных координат от привычных декартовых в том, что точка на торе имеет не одну пару координат, а бесконечное число пар.
Кривые на торе
Но попробуем: может быть, крива* вывезет.
M.F Салтыков-Щедрин
Под замкнутой кривой на плоскости мы привыкли понимать кривую, получаемую движением кончика карандаша по бумаге, начинающуюся и кончающуюся в одной точке. Кривая на торе — кривая, проведенная на этой поверхности. Однако такого интуитивного определения нам будет недостаточно. Дадим более строгое определение. Пусть заданы окружность S, тор Т и непрерывное отображение / этой окружности в тор. Такое отображение мы будем называть замкнутым путем на торе Т, а образ этого отображения — замкнутой кривой. Итак, имеется область определения отображения / — все точки окружности S, закон, по которому каждая точка из S преобразуется в точку на Т, и множество значений у, которое и будет замкнутой кривой. Однако мы чаще будем говорить не о замкнутой кривой, а о замкнутом пути, обозначая его той же буквой /, что и порождающее его отображение.
Рассмотрим примеры. В качестве области определения возьмем окружность S,

I?
ПЕРЕСЕЧЕНИЕ ДВУХ  КРИВЫХ  НА ТОРЕ
ft непрерывно изменяется с изменением t
Рисунок 6
(рис. 1) — определение не запрещает этого. Рассмотрим отображение <р,, которое каждой точке St ставит в соответствие ее же, т.е. тождественное отображение. Очевидно, множество значений у совпадает в данном случае с областью определения S,. Аналогично определим путь <р2 с областью определения Sr
Мы не исключаем возможности замкнутым путям иметь точки самопересечения. Так будет в том случае, если найдутся точки Мл и Мг на S, которые отображаются в одну и ту же точку тора:
Деформация кривых на торе
Надо только начать и потом не отставать^нуть свою линию, несмотр* ни на что.
АП.Чехов
Любые два замкнутых пути на плоскости можно продеформировать один в другой. Что это значит? Представим себе, что отображение / непрерывно меняется во времени. В момент t=\ оно совпадает с отображением fv а в момент t =2 — с отображением fv В промежуточные моменты t оно есть отображение ft. Такое семейство отображений^ называется деформацией замкнутого пути /j в путь fr Пример подобной деформации можно увидеть на рисунке 6. Если рассмотреть плоскость с дырой, то тут уже не всякие два замкнутых пути можно продеформировать один в другой. Например, на рисунке 7 путь fx нельзя продеформировать ни в путь fv ни в путъ/ъ — мешает дырка.
Аналогично обстоит дело с замкнутыми путями на торе. Так, путь <р, нельзя продеформировать в <р2> оставаясь на торе, — мешают «дырки» тора: одна внутренняя, другая внешняя. Какие же пути можно продеформировать друг в друга? Образный ответ на этот вопрос таков: друг в друга деформируются те замкнутые пути, которые одинаково намотаны вокруг внутренней и внешней дырок тора. Чтобы придать    этому    утверждению    четкий
Рисунок 7

ЯКОВ ДЫМЛРСКИЙ,   ИРИНА ЭАВЕРАЧ
смысл, введем следующие характеристики путей: «число витков вокруг S,» и «число витков вокруг S2».
Зададим на окружности S стрелкой направление обхода — ориентируем S (рис. 5). Можно считать, что путь / проходит через точку.О =/(0,). В противном случае перенесем начало координат О в точку /(О,). Пусть точка N движется по S в выбранном направлении, начиная от точки О,, тогда точка/(N) обойдет кривую у, выйдя из О и вернувшись в нее же. В результате обхода по замкнутому маршруту у мы совершим несколько полных оборотов вокруг внешней дырки тора. Каждому обороту припишем знак «+», если он совершен в том же направлении, что и единственный поворот пути <р,. Это направление совпадает с направлением оси абсцисс. Знак « —» приписывается обороту в противоположную сторону. Алгебраическую сумму всех оборотов назовем «числом витков вокруг Sj». Аналогично, подсчитывая обороты вокруг внутренней дырки, определяем «число витков вокруг S2». Запись /(т, и) будет обозначать, что у пути /число витков вокруг S, равно т, а вокруг S2 равно и. Числа тип легко увидеть на плоскости Оху (рис. 5).
Теорема 1. Д&г пути fx(mv nt) uf2(m2, п2) деформируются один в другой тогда и только тогда, когда тл= тг, и,= п2.
Идея доказательства состоит в том, что деформация осуществляется непрерывным образом, и поэтому все характеристики кривой меняются непрерывно. Но числа тип могут принимать только целые значения- Переход от одного целого числа к другому может произойти только скачком. Следовательно, тип не меняются.
Пусть на плоскости Оху пути изображаются дугами У] и у2, соединяющими изображения О, и 02 точки О (рис 8), т.е. обе кривые проходят через точки О, (0; 0) и O2(2nKjmj,27iR2ni)- Продеформируем на плоскости Yi в у2. Эта деформация порождает искомую деформацию пути fx в
\
\
\
"О,
т=2      п=-3
Рисунок В
путь f2 на торе.
Среди кривых с данным набором витков (т, и) выделим ту, которая на плоскости изображается отрезком, соединяющим точки ОДО, 0) и O2(27iR,m,27iR2n) (рис. 8). Если числа тип взаимно просты, то отрезок 0,02 не проходит через другие узлы решетки на плоскости. А если числа тип имеют общие делители, то отрезок 0,02 разобьется узлами решетки на ?=НОД(т, и) частей. Это означает, что кривая на торе будет проходиться при движении по соответствующему пути ровно к раз.
Взаимное расположение двух кривых
В общем случае ставить вопрос о количестве общих точек двух кривых проблематично. Так, кривые на рисунке 9, а имеют бесконечное множество общих точек, а на рисунках 9, б и 9, в — одну общую точку, но при сколь угодно малой деформации эта точка либо исчезает, либо их становится две. Такие ситуации назовем нетипичными и будем их по возможности избегать.
Общую точку А двух кривых назовем типичной, если кривые в этой точке имеют касательные, причем различные (рис. 10). Можно показать, что типичная точка устойчива, т.е. не теряет типичности при достаточно малой деформации, а нетипичная общая точка неустойчива, т.е. может быть устранена сколь угодно малой дефор-

ПЕРЕСЕЧЕНИЕ ДВУХ  КРИВЫХ  НА ТОРЕ
Риансж 9а
Рисунок 9б
Рисумсж 9а
мацией (еще раз взгляните на рисунок 9). Будем говорить, что две кривые находятся в типичном положении, если они имеют только типичные общие точки или же совсем не имеют общих точек. Справедлива следующая
Риансж 10
Теорема 2. Количество общих точек двух замкнутых кривых, находящихся в типичном положении, конечно.
Заметим, что незамкнутые кривые могут иметь бесконечное число типичных общих точек. Например, точки пересечения синусоиды с осью Ох.
Итак, мы можем подсчитать количество общих точек двух замкнутых кривых, находящихся в типичном положении. Если же кривые находятся в нетипичном положении, то с помощью малой деформации их можно привести в типичное положение и... И ничего не получится, так как разные деформации приводят к разным результатам (опять рисунок 9). Что же отсюда следует? Следует, что либо задача о количестве общих точек некорректна. либо мы еще не научились правильно подсчитывать это количество.
Учимся считать количество общих точек
Ты, пожалуйста, их перечти, — сказал
Чичиков, — и сделай подробный
реестрик всех поименно.
Н. В. Гоголь
Вспомним, что при подсчете числа витков пути вокруг Sj и S2 существенным был учет направления обхода, т.е. ориентация витка. Попробуем ориентировать общие точки путей, после чего подсчитаем их количество с учетом ориентации.
Пусть ftuf2 — рассматриваемые пути, находящиеся   в   типичном   положении

ЯКОВ ЯЫМАРСКИЙ,   ИГИНА ЗАВЕРАЧ
(рис 11). Окружность S уже ориентирована. Отображения fx и /г переносят ориентацию на дуй. В точке пересечения ориентация с дуг переходит на касательные Z, и 1г — на них возникают направления, отмеченные стрелками. Припишем общей точке знак «+», если минимальный угол от положительного направления 1Л к положительному направлению 1% направлен против часовой стрелки. Знак «—» приписываем точке, если названный угол направлен по часовой стрелке. Алгебраическую сумму всех общих точек назовем индексом пересечения путей /J и ^. Обозначим его N(fv /г~). Вычисление индекса — это правильный способ подсчитывать количество точек пересечения. Подтверждением служит
Теорема 3. Индекс пересечения не меняется при деформации, т.е. является топологическим инвариантом.
Действительно, в результате деформации индекс может поменяться только при переходе через нетипичную точку. Но на самом деле этого не происходит. Ситуации, изображенной на рисунке 9, а можно вообще избежать при деформации. Что же касается рисунков 9 б, в, то здесь индекс не меняется при малой деформации. Посмотрите на рисунок 9, б. В результате деформации 1 общая точка исчезла, т.е. вклад в индекс нулевой. В результате деформации 2 она распалась на две точки А и Б, имеющие разную ориентацию и в сумме дающие тоже нуль (сравните с рисунком 11).
Упражнения
3. Рассмотрите самостоятельно случай на рисунке 9, в
4. Докажите свойство индекса: N(JV f^)= —
5. Докажите, что количество общих точек двух путей /j и f2 без учета ориентации не меньше, чем N(/j, f2y, т.е. модуль индекса оценивает количество общих точек снизу.
а>0
знак А "+
знак В "-"
Рисунок II
Мы обнаружили две топологических характеристики замкнутых кривых на торе: число витков (га,, п,) и (т2, п2) каждой кривой и индекс пересечения этих кривых N(ft, f2). Оказывается, вторая характеристика выражается через первую: Ж/,. /2)=m,n2— тгпу
Это утверждение, которое можно рассматривать как основную теорему о числе точек пересечения кривых на торе, вы можете доказать самостоятельно, воспользовавшись топологической инвариантностью чисел, о которых идет речь в этой теореме. Для этого достаточно рассматривать те замкнутые пути, которые на развертке изображаются прямыми линиями. Рассмотрите несколько примеров, а потом исследуйте, как меняется число N(/,, /г), если одно из чисел т,, пу,тг,п2 увеличить на единицу.
Надеемся, что вы благополучно добрались до этих заключительных строк и чтение позволило вам хотя бы немного почувствовать дух топологических идей и методов, которые сейчас проникают во все области математики.